Курс физики. Том 1. Механика. Кинетическая теория материи - Астахов А.В.

Автор: Астахов А.В.

Теги: физика механика кинетика

Год: 1977

Похожие

Механика сплошной среды. Том 1

Курс теоретической физики Т.2. Статистические законы

Абстракция в математике и физике

Теория и приложения уравнения Больцмана

Текст

КУРС ФИЗИКИ
Под общей редакцией
Ю. М. ШИРОКОВА
ТОМ I
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛЦТЕРАТУРЦ
Москва 1977

А. В. АСТАХОВ
МЕХАНИКА
КИНЕТИЧЕСКАЯ
ТЕОРИЯ МАТЕРИИ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия для студентов
высших технических учебных заведении
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1 977

530
А 91
УДК 530
Александр Валентинович Астахов
КУРС ФИЗИКИ, ТОМ 1
Механика
Кинетическая теория материи
М » 1977 г , 331 стр. с илл.
Редактор В. Л. Григорова
Техн. редактор И. Ш. Аксельрод
Корректор Л Н. Бороеина
Сдано в набор 31 01 77. Подписано к печати 28,06 77 Бумага 60X90'/ie
тип. № 1. Физ. печ. л. 24. Условн. печ. л 24. Уч -изд. л. 23,03.
Тираж 47 500 экз. Цена книги 90 к Заказ № 490.
Издательство «Наука>
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфпрома при Государственном
комитете Совета Министров СССР по делам издательств, полиграфии
и книжной торговли. 198052, Ленинград, Л-52, Измайловский проспект, 29.
А 20401 — 104 rq qQ о- ~- © Главная редакция
A- rt. .. -, БЗ-33-33— (I физико-математической литературы
053 @2J-77 издательства «Наука», 1977

ОГЛАВЛЕНИЕ
Предисловие 7
Введение 9
ЧАСТЬ I
МЕХАНИКА
Глава 1. Кинематические представления механики , 20
§ 1.1. Пространство, время, движение , % 20
§ 1.2. Кинематика материальной точки 27
§ 1.3. Преобразования Галилея .36
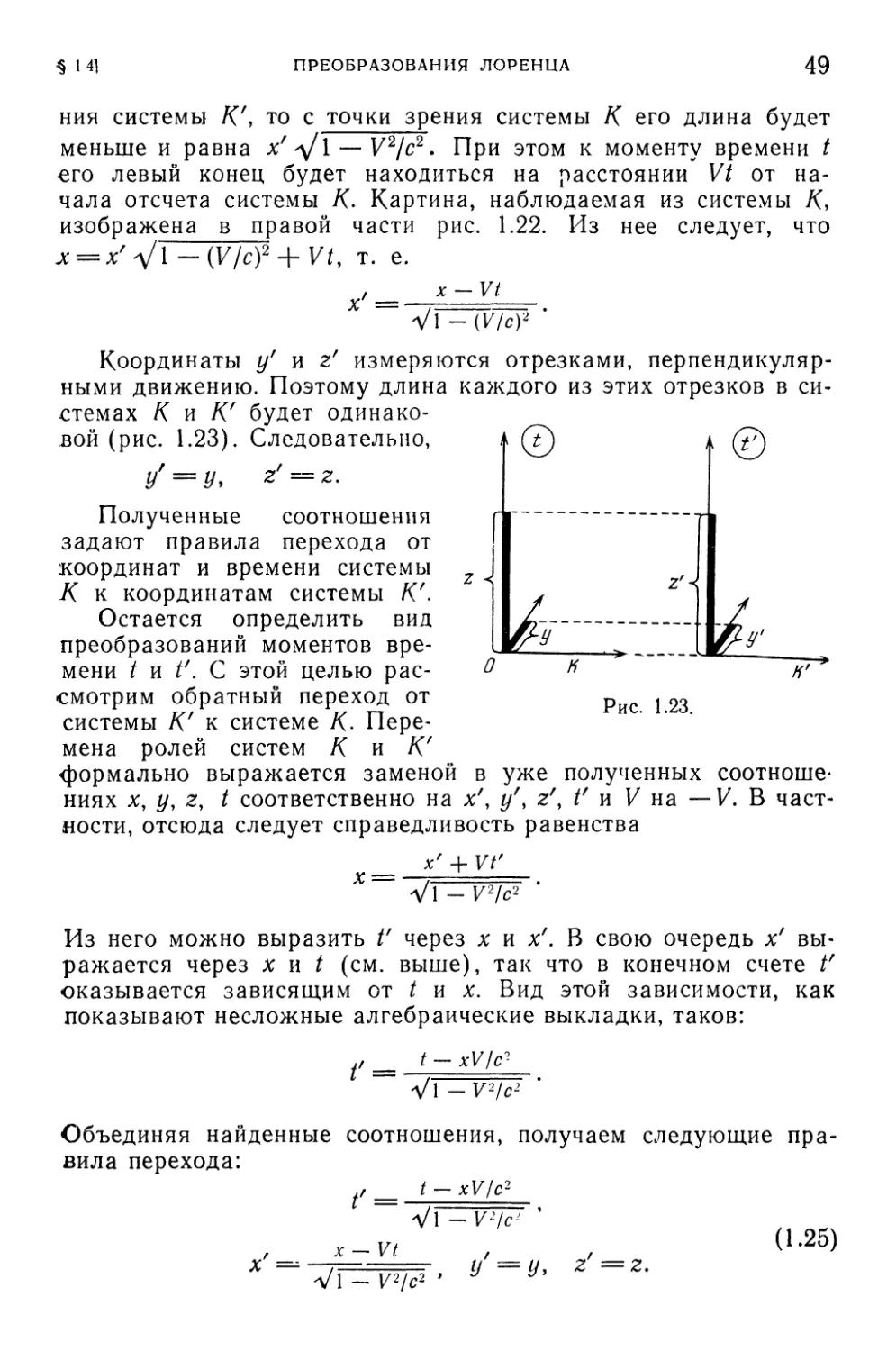
§ 1.4. Преобразования Лоренца 41
Глава 2. Динамические принципы механики 54
§ 2.1. Состояния 54
§ 2.2. Уравнения движения 56
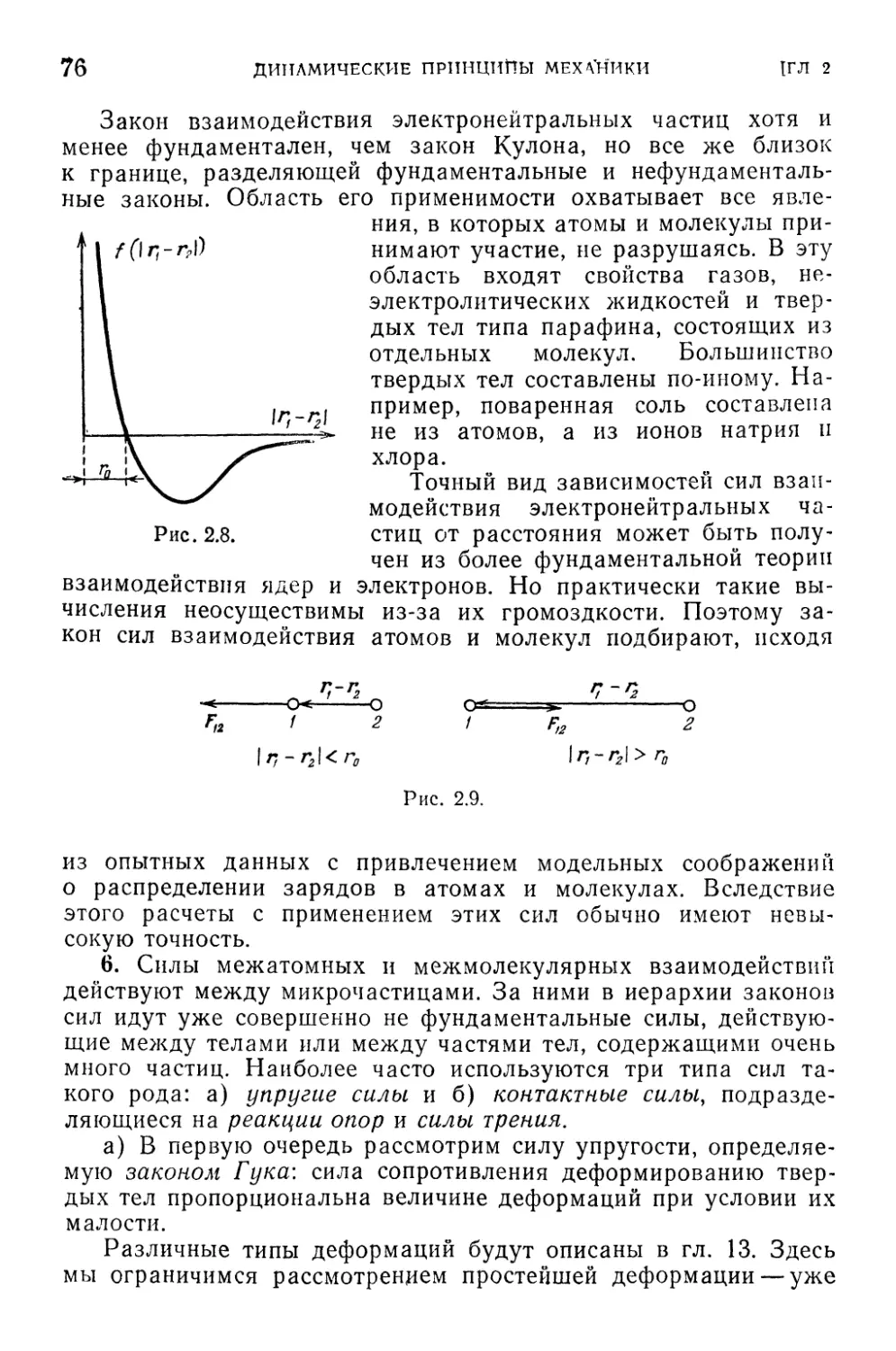
§ 2.3. Виды взаимодействий и силы , , , 67
§ 2.4. Потенциальная энергия 81
Глава 3. Законы сохранения 90
§ 3.1. Происхождение законов сохранения 90
§ 3.2. Закон сохранения импульса в классической механике .... 94
§ 3.3. Закон сохранения энергии в классической механике 97
§ 3.4. Закон сохранения момента импульса в классической механике . 108
Глава 4. Движение частицы в различных силовых полях 114
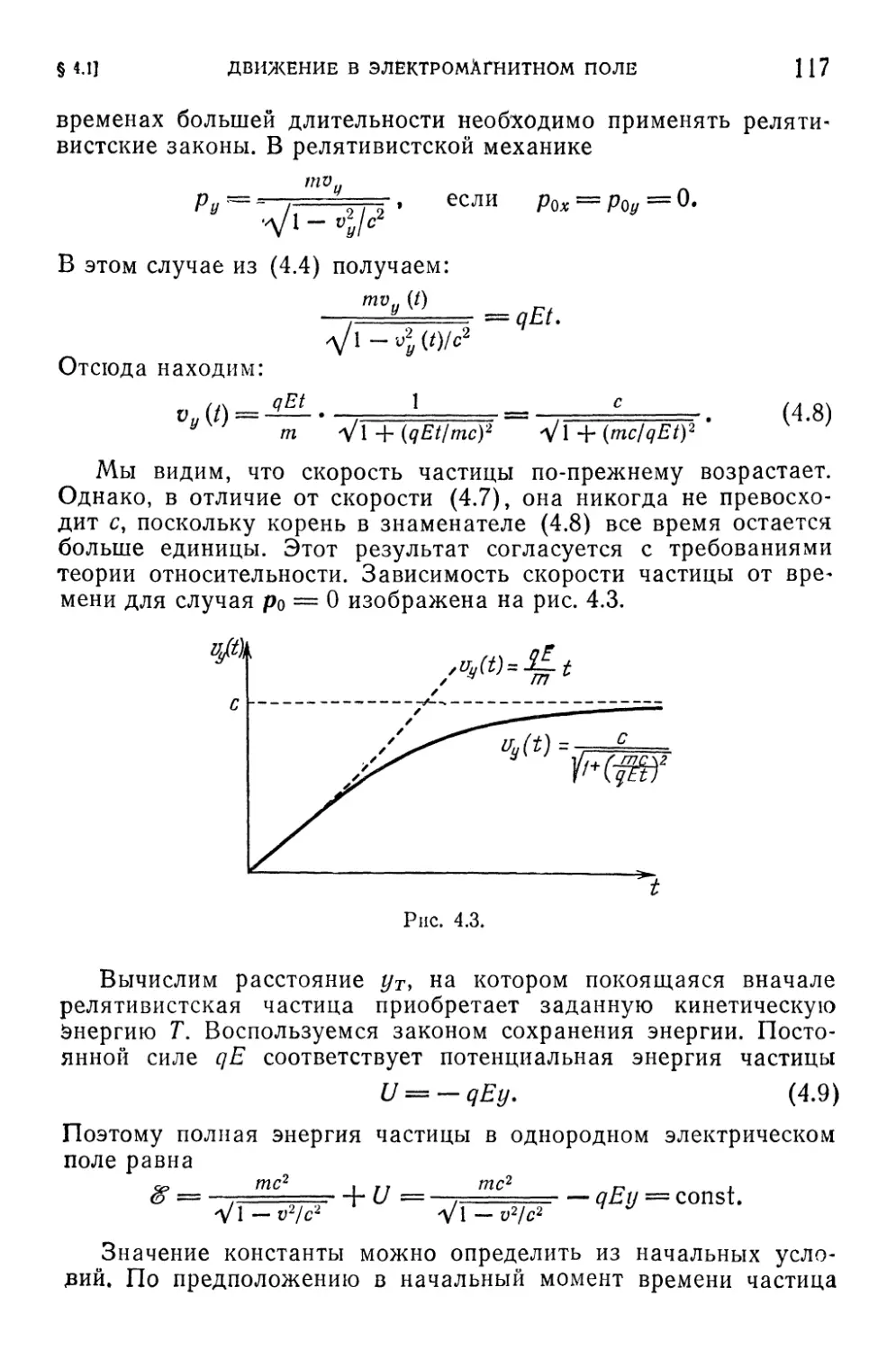
§ 4.1. Движение заряженной частицы в электромагнитном поле . . .114
§ 4.2. Нерелятивистское движение частицы в центральном поле . . .124
§ 4.3. Движение в кулоновском поле 131
Глава 5. Столкновения , # ........ 141
§ 5.1. Упругие и неупругие столкновения , , 141
§ 5.2. Сечение рассеяния 148
Глава 6. Движение абсолютно твердого тела 158
§ 6.1. Кинематика движения твердого тела 158
§ 6.2. Уравнения движения твердого тела 161
§ 6.3. Кинетическая энергия твердого тела 168
Глава 7. Колебания и волны . , 172
§ 7.1. Одномерный гармонический осциллятор 172
§ 7.2. Одномерный осциллятор с трением. Затухающие и вынужден-
вынужденные колебания , . , 180

6 ОГЛАВЛЕНИЕ
§ 7 3. Колебания в системах с несколькими степенями свободы . . . 189
§ 7.4. Эффекты сложения волн 201
ЧАСТЬ II
КИНЕТИЧЕСКАЯ ТЕОРИЯ МАТЕРИИ
Глава 8. Макроскопические состояния 209
§ 8 1. Тепловое движение 209
§ 8.2. Макроскопические параметры 214
§ 8.3. Уравнение состояния , ¦ 222
§ 8.4. Внутренняя энергия * ¦ 227
Глава 9. Статистические распределения 235
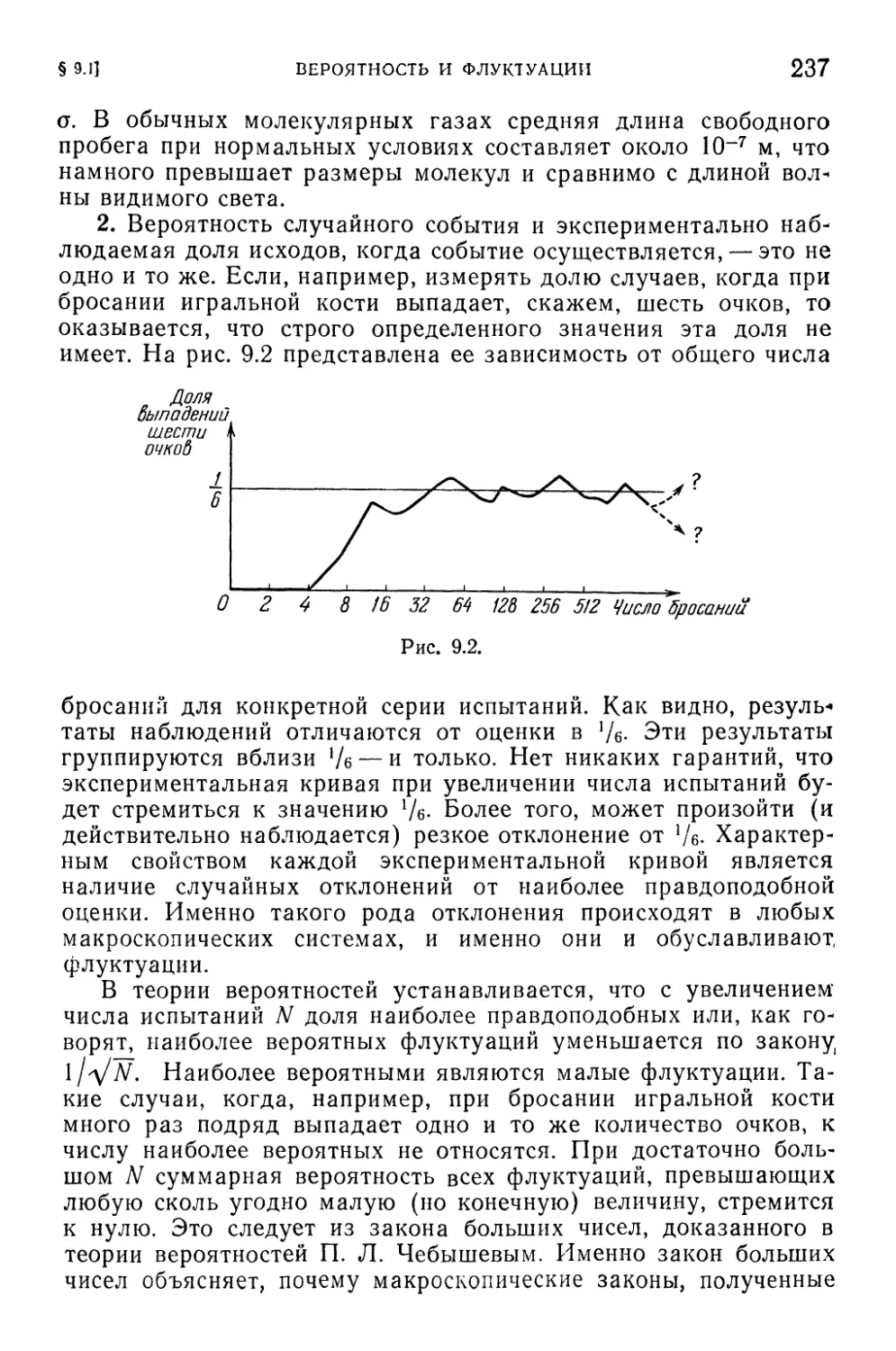
§ 9.1. Вероятность и флуктуации . 235
§ 9.2. Распределение Больцмана .......... 239
§ 9.3. Распределение Максвелла , . 245
§ 9.4. Распределение Гиббса 251
Глава 10. Основы- термодинамики , 258
§ 10.1. Тепловые процессы * 258
§ 10.2. Первое начало термодинамики 260
§ 10.3. Энтропия ; : 267
§ 10 4. Второе начало термодинамики 275
Глава И. Явления переноса , . . * 285
§ 11.1. Общая характеристика явлений переноса 285
§ 11.2. Диффузия и теплопроводность ............. 293
§ 11.3. Вязкость 300
Глава 12. Фазовые превращения 306
§ 12.1. Фазовые диаграммы 306
§ 12.2. Критическая точка- .... 313
§ 12.3. Метастабильные состояния . 319
§ 12.4. Тройная точка 323
Глава 13. Кристаллическое состояние 326
§ 13.1. Строение кристаллов .... ... 326
§ 13 2» Дефекты кристаллов ... 333
§ 13.& Механические свойства твердых тел . 342
§ 13.4* Тепловое движение в* твердых телах 354
Глава 14. Звук . * , 361
§ 14.1. Скорость звука . 361
§ 14 2. Физические характеристики звука 369
§ 14 3. Ударные волны » 374
Предметный указатель . s , 382

ПРЕДИСЛОВИЕ
Настоящая книга является Первым томом курса физики для втузов, рас-
рассчитанного на стандартную продолжительность обучения в три учебных се-
семестра. Отправной точкой к его созданию послужила экспериментальная про-
программа, разработанная десять лет назад на кафедре физики Московского
Горного института (МГИ). На основе этфй программы в МГИ осуществлялся
поиск путей дальнейшего улучшения преподавания физики. Данный курс яв-
является обобщением накопленного опыта.
В первом томе изложены основы классической механики и кинетиче-
кинетической теории материи. Содержанием второго тома будет классическая физика
электрических и магнитных явлений. Вопросам квантовой физики отводится
третий том курса. Автором первого тома является А. В. Астахов. Авторами
последующих томов будут А. В. Астахов и Ю. М. Широков.
Основная цель курса заключается в изложении физики как единой науки,
опирающейся на небольшое число фундаментальных законов, обобщающих
колоссальное множество опытных фактов»
В современных условиях быстрого и все возрастающего темпа развития
науки и техники инженеру все чаще приходится сталкиваться с качественно
новыми для него областями физических явлений. Поэтому мы убеждены в
том, что для будущего инженера важно не столько описательное ознакомле-
ознакомление с обширным кругом различных физических явлений, сколько усвоение
иерархии физических законов и понятий, позволяющее эффективно использо-
использовать их в конкретных ситуациях.
Стремление подчеркнуть единство и внутреннюю логику физики повлияло
на отбор материала, а также на порядок и методику его изложения. В част-
частности, в первый том включен ряд вопросов, обычно рассматриваемых в по-
последующих частях курса (основы теории относительности, движение заряжен-
заряженных частиц в электромагнитных полях, понятие о спине, некоторые экспери-
экспериментальные методы исследования строения вещества и свойств элементарных
частиц и др.).
В отношении методики особое внимание уделялось точности и конкретно-
конкретности определений, систематическому указанию пределов применимости зако-
законов и понятий, подчеркиванию значимости фундаментальных понятий, в част-
частности таких, как состояние физической системы и ее уравнения движения.
Уже опыт первого тома показал, что последовательное выполнение отме-
отмеченных методических установок ведет не только к изменению частных форму-
формулировок, но и к коренной перестройке изложения. Наиболее существенной и

8 ПРЕДИСЛОВИЕ
особенно мучительной для автора и редактора перестройке подвергнуты важ-
важнейшие разделы об основах механики. Традиционные способы изложения в
значительной мере базируются на законах Ньютона в их первоначальной фор-
форме. В этих способах изложения механика получается оторванной от остальных
разделов физики. С развитием теории электромагнитного поля и квантовой
теории выяснилось, что законы Ньютона имеют сложную структуру и состав-
составлены из совокупности самостоятельных законов, имеющих различные области
применимости. Попытка выделения такой системы элементарных (в смысле не
составных) законов и сделана в настоящем томе.
Мы сознаем, что принятая система изложения имеет свои недостатки й
трудности. Но у нее есть и свои преимущества. Во-первых, все понятия и за-
законы, выходящие за рамки классической механики (например, законы сохра-
нения), излагаются сразу в должной степени общности, позволяющей избе-
избежать дублирования в следующих томах. Во-вторых, наличие общих законов
дает возможность выявить общие черты, связывающие в единую науку меха-
механику, электромагнетизм и квантовую физику.
Во всех томах курса большое внимание будет уделяться оценкам поряд-
порядков физических величин. Умение быстро и уверенно производить такие оценки
особенно важно для активного использования физических знаний при решении
новых технических проблем. Действительно, если физик старается выделить
интересующий его процесс в «чистом» виде, то инженер, как правило, имеет
дело со сложными системами, в которых протекает множество разных физиче-
физических процессов, играющих различную роль по значимости и полезности.
Книга написана с учетом изменения школьных программ по физике и ма-
математике. И, конечно, мы рассчитываем, что читатель освоил простейшие фи-
физические понятия. Например, ему хорошо известно, какое движение тела яв-
является поступательным. Петит применяется для изложения относительно гро-
громоздких расчетов и вопросов повышенной трудности.
На различных этапах работы, завершением которой является данный
курс, нам оказали большую помощь О. И. Завьялов, Н. А. Розанов, А. Д. Су-
Суханов, М. Л. Харахан, а также другие сотрудники кафедры физики МГИ. От-
Оттачиванию методических установок курса во многом способствовали неодно-
неоднократные обсуждения на пленумах научно-методического Совета Минвуза
СССР, на различных конференциях и совещаниях. Особенно ценными для нас
были критические замечания рецензентов книги Я. М Гельфера, А. И. Ель-
кина, В. Ф. Киселева и А. А. Склянкина, а также обсуждения на семинарах
и совещаниях у А. С, Ахматова, И. В Савельева, Б М Яворского. Мы при-
приносим глубокую благодарность всем отмеченным лицам и коллективам.
А В. Астахов
/О, М. Широков

ВВЕДЕНИЕ
Что такое физика
1. Развитие техники базируется на достижениях физики. По-
Поэтому четкое понимание логики постановки и решения физиче-
физических вопросов необходимо для плодотворной деятельности
современного инженера. Современная физика — обширная и
разветвленная наука, но ее разделы имеют много общих черт.
Знание характерных черт физики как науки облегчает ее
освоение и помогает эффективно использовать ее методы и кон-
концепции.
2. Физика — наука опытная. Современные физические теории
(например, квантовая механика) выглядят как сложные аб-
абстрактные математические конструкции. Однако все эти теории
опираются на опыт, и только опыт является критерием их
правильности. Следует подчеркнуть, что далеко не всякое
измерение является физическим опытом.
Физическим опытом, или физическим экспериментом, яв-
является только такое измерение, в котором все воздействия но
исследуемую систему поддаются учету.
Важнейшим свойством физического эксперимента является
его воспроизводимость. Повторение физического эксперимента
в другой лаборатории с измерительными приборами других
конструкций должно дать те же результаты, что и в первом
опыте. Для пояснения проанализируем смысл привычной фра-1
зы: «Сегодня в тени двадцать градусов, а на солнце — три-
тридцать два». Очевидно, что здесь говорится о двух измерениях-
Но только первое из них является физическим экспериментом,
в котором измерена определенная физическая величина — тем-
температура окружающего воздуха. Измеряя температуру в раз-
разных местах затененного пространства термометрами разных
конструкций, мы будем получать одно и то же значение. Во
втором измерении термометр не находится в тепловом равно-
равновесии с окружающим воздухом. Материал термометра погло-
Щает энергию солнечного излучения и постепенно передает ее
окружающему воздуху. Температура термометра зависит от

10 ВВЕДЕНИЕ
множества причин, таких как прозрачность атмосферы, цвет
шкалы, конструктивные особенности термометра, скорость
ветра и т. д. Учет всех этих влияний крайне сложен. По-
Поэтому понятие «температуры на солнце» не является физиче-
ской величиной, а ее измерение не есть физический экспери-
эксперимент.
Далеко не все физические явления воспроизводимы в лабо-
лабораторных условиях. Так, в лаборатории нельзя воссоздать
условия, в которых вещество находится на поверхности Солнца,
не удается получить искусственную шаровую молнию. Для изу-
изучения таких явлений приходится пользоваться не контролируе-
контролируемыми экспериментами, а природными наблюдениями.
Прогресс науки и техники непрерывно расширяет области
физики, доступные исследованию с помощью контролируемых
опытов.
3. Все физические измерения производятся с ограниченной
точностью. Ограничение точности ставит предел степени под-
подробности информации, получаемой из опыта. Поэтому при
каждом физическом измерении указывается не только его ре-
результат, но и точность, с которой этот результат получен.
Только в пределах точности измерений можно сравнивать
результаты разных опытов друг с другом и с соответствующими
предсказаниями теории.
Разные величины доступны измерению с различной точ-
точностью. Одним из самых точных опытов является измерение
смещения энергии гамма-кванта на долю в 10~17 под действием
силы тяжести при подъеме на три метра.
Повышение точности измерений расширяет возможности
познания окружающего мира и поэтому является важнейшей
научной и технической проблемой.
4. На основе результатов физических экспериментов форму-
формулируются физические законы. Каждый из них в конечном счете
является обобщением некоторой совокупности опытных фактов.
Физический закон формулируется так, чтобы он был в согласии
с имеющимися опытными данными и давал возможность пред-
предсказывать результаты новых опытов и даже существование
новых физических явлений.
Опытные факты, использованные для получения определен-
определенного физического закона, всегда ограничены как по точности
проведенных измерений, так и по области измерения физиче-
физических величин (ограниченные интервалы температур, давлений,
размеров и т. д.). Поэтому каждый физический закон имеет
определенную область применимости. Область применимости
физического закона задается: а) указанием допустимых преде-
пределов изменения физических величин, входящих в формулировку
закона; б) наивысшей допустимой точностью измерения этих

ВВЕДЕНИЕ 11
величин; в) обширностью круга физических явлений, для кото-
которых закон имеет смысл. Внутри своей области применимости
закон выполняется для любых физических явлений.
Области применимости разных законов сильно отличаются
•друг от друга. Например, закон сохранения импульса на сегод-
сегодняшний день является универсальным, т. е. выполняется для
всех известных физических явлений при измерениях с наивыс-
наивысшей доступной точностью. Закон Кулона для электростатиче-
электростатического взаимодействия двух зарядов имеет огромную, но все же
ограниченную область применимости. Он выполняется от сколь
(угодно больших расстояний до внутриядерных. На расстояни-
расстояниях, превышающих межатомные, закон выполняется практиче-
практически абсолютно точно (т. е. отклонения не обнаружимы сущест-
существующими методами), на расстояниях порядка межатомных
|A0~10 м) возникает отклонение на 10~~4%, которое доходит до
|1О-~2О/о на расстоянии К)-13 м и меньше.
Наконец, область применимости законов сухого трения
крайне ограничена. Эти законы выполняются в узком (для
физики в целом) интервале температур и скоростей, при опре-
определенной обработке трущихся поверхностей и с точностью, не
превышающей нескольких процентов. Кроме того, законы сухо-
сухого трения имеют смысл для узкого круга явлений. Действи-
Действительно, закон Кулона действует во всех веществах, поскольку
все вещества составлены из заряженных частиц — атомных
ядер и электронов. Законы же сухого трения имеют смысл
только при скольжении одного твердого тела по поверхности
другого. Для газов, жидкостей, потоков элементарных частиц
законы сухого трения теряют какой бы то ни было смысл.
Физические законы, имеющие наиболее обширные области
применимости, называются фундаментальными. Например, фун-
фундаментальными являются закон сохранений энергии, законы
Ньютона, закон Кулона. Одно из величайших достижений фи*
зики состоит в том, что небольшого количества наиболее фун-
фундаментальных законов в принципе достаточно для получения
почти всех остальных законов и вообще для объяснения и
предсказания хода почти любых физических процессов. Исклю-
Исключением являются те новые разделы физики, для которых фун^
даментальные законы еще не установлены. Главным из этих
исключений является физика элементарных частиц сверхвысо-
сверхвысоких энергий. С этими исключительными ситуациями, не охваты-
йасмыми фундаментальными законами, не только инженеры, но
Ж большинство физиков не сталкиваются.
Многие законы частного (в масштабах физики в делом)'
характера действительно прямо выводятся из фундаменталь-
фундаментальных. Так, излагаемые в главе 4 части I законы Кеплера
Для движения планет вокруг Солнца можно вывести из

12 ВВЕДЕНИЕ
фундаментального закона всемирного тяготения. Законы, непо-
непосредственно выводимые из фундаментальных, называются за*
конами фундаментального происхождения.
Однако большинство физических законов, используемых
физиками и инженерами, не могут быть выведены из одних1
только фундаментальных законов без использования дополни-
дополнительных частных предположений. Например, фундаментальные
законы, определяющие взаимодействие электронов со всеми
частицами, из которых составлен металл, хорошо известны. Но,
пользуясь только фундаментальными законами, не удается
получить закон Ома. Такая задача может быть математически
сформулирована и несомненно имеет решение. Но это решение
невероятно громоздко и недоступно даже всем существующим
ЭВМ, вместе взятым.
В таких случаях широко используются различные модели.
Моделью называется абстрактная система, являющаяся
упрощенной копией исследуемой реальной физической системы.
При этом модельная система должна: а) иметь область при-
применимости, в которой свойства модели с заданной точностью
совпадают со свойствами реальной системы; б) допускать до-
достаточно простое математическое описание.
Модель тем лучше, чем шире ее область применимости и
чем проще ее описание. Например, замечательной моделью
является концепция абсолютно твердого тела, используемая в
механике. В этой модели реальное тело, имеющее сложнейшую
атомную структуру и обладающее многочисленными свойства-
свойствами, — механическими (пластичность, прочность, ...), тепловы-
тепловыми (теплоемкость, тепловое расширение, ...), электрическими
и другими (горючесть, цвет, ...), — заменяется на абсолютно
твердый монолит вещества, не имеющий никакой внутренней
структуры и никаких свойств, кроме плотности и абсолютной
твердости. И такая сверхупрощенная модель имеет обширней-
обширнейшую область применимости. Можно сказать, что почти вся тео-
теоретическая механика основана на двух моделях: материальной
точки и абсолютно твердого тела.
Во многих задачах механики, однако, приходится учитывать
упругие деформации тел. В этих случаях модель твердого тела
заменяется на более сложную, но и имеющую большую область
применимости модель абсолютно упругой среды. Область при-
применимости этой модели исключительно обширна, хотя, конечно,
тоже ограничена: деформации должны быть достаточно малы-
малыми, чтобы соблюдался закон пропорциональности между силой
и деформацией.
Здесь полезно подчеркнуть два обстоятельства, общие для
всех моделей. Во-первых, общим свойством всех моделей яв-
является наличие эмпирических констант. Например, модель

ВВЕДЕНИЕ 13
упругой среды содержит неизвестный параметр — множитель
пропорциональности между силой и деформацией. Величина
этого параметра определяется из опыта. Для таких подгоноч-
подгоночных модельных параметров используется несколько терминов:
эмпирические коэффициенты, опытные константы и др. Смысл
этих терминов одинаков. Во-вторых, из самой модели нельзя
получить пределы ее применимости. Эти пределы могут быть
установлены либо опытным путем, либо с помощью более
общей модели (или точной теории). Так, пределы применимо-
применимости модели абсолютно твердого тела определяются через коэф-
коэффициент пропорциональности в законе Гука для модели абсо-
абсолютно упругого тела. Пределы применимости закона Гука
определяются опытным путем по измерению отклонений от
этого закона.
Кроме моделей, в физике, особенно прикладной, часто ис-
используются эмпирические или, как их часто называют, феноме-
феноменологические закономерности. Эмпирической закономерностью
называется любая систематизация опытных данных, обычно в
виде формул или графиков, не претендующая на объяснение
механизма исследуемого физического процесса, структуры ис-
исследуемых физических объектов и т. д. Типичной эмпирической
закономерностью являются законы сухого трения.
Часто эмпирическая закономерность выражается некоторой
формулой с неизвестными коэффициентами, значения которых
подбираются по опытным данным. Так, например, эмпирически
найдено, что сила лобового сопротивления воздуха для до-
дозвуковых самолетов пропорциональна квадрату скорости.
Коэффициент пропорциональности определяется опытным
путем.
Подавляющее большинство эмпирических закономерностей
(особенно устанавливаемых в прикладных исследованиях)
имеют крайне узкую область применимости и тем самым крайне
ограниченную предсказательную силу.
Наибольшей предсказательной мощью обладают фундамент
тальные законы, которые поэтому занимают главенствующее
положение в физике. Для прикладных отраслей физики, одна^
ко, ценность закона определяется не только степенью фунда-»
нентальности, но и тем, как часто этот закон фактически ис^
пользуется. Так, для электротехники самым важным является
закон Ома, который далеко не фундаментален.
5. Для количественного описания физических явлений ис-
пользуются различные физические величины. Используемая фи-
физическая величина должна иметь четкое определение. Каждое
такое определение должно содержать либо количественный
метод (хотя бы принципиальный) измерения этой величины,
либо ее выражение через другие величины, считающиеся

14 ВВЕДЕНИЕ
известными. Словосочетания типа: «температура есть степень
нагретости тела» или «сила является мерой механического воз-
воздействия материальных тел» являются качественными пояснен
ниями, но не количественными определениями физических
величин. В определении необходимо также указывать, что
именно характеризует определяемая величина: процесс, состоя-
состояние и т. д.
Следует помнить, что само понятие физической величины,
как правило, имеет ограниченную область применимости. Так,
килограмм воды имеет определенную температуру, но темпе-
температуры трех молекул воды не существует.
Физические величины, подобно физическим законам, раз-
различаются по степени фундаментальности, т. е. по области
применимости. Наиболее важны для физики фундаментальные
константы, входящие в формулировки фундаментальных физи-
физических законов. Этих констант восемь: скорость света в пустоте;
постоянная Планка; заряд электрона; массы электрона, прото-
протона, нейтрона; гравитационная постоянная и постоянная слабого
взаимодействия. Решая фундаментальные уравнения, в прин-
принципе можно выразить через эти восемь констант любую другую
физическую величину — электропроводность диода данной мар-
марки, плотность такого-то раствора, интенсивность химической
реакции, период радиоактивного распада и т. д. Практически
в физике и особенно в технике приходится использовать огром-
огромное число нефундаментальных, эмпирических величин, имеющих
узкую область применимости.
6. Для выражения количественных закономерностей в физи-
физике широко применяется математический аппарат. При этом
использование того или иного раздела математики в конечном
счете диктуется опытными фактами. Так, опытный факт непре-
непрерывности пространства и времени привел к необходимости
использования дифференциального исчисления: большинство
физических законов выражаются дифференциальными уравне-
уравнениями. Точно так же опытный факт эвклидовости пространства
привел к использованию векторной алгебры, и т. д.
Каждая формула, встречающаяся в физике (даже в проме-
промежуточной выкладке), имеет четкий физический смысл. Чаще
всего формула имеет смысл либо как закономерность, либо
как определение физической величины. Нередки и комбиниро-
комбинированные ситуации. Например, формула закона Ома U =a RI
выражает и закон, и определение. Закон Ома состоит в том,
что в определенных условиях ток линейно зависит от разности
потенциалов. В области применимости этого закона та же форму-
формула служит определением новой физической величины — сопро-
сопротивление R. При таком комбинированном толковании формул
надо следить за тем, чтобы не возникал «порочный круг».

ВВЕДЕНИЕ 15
Общие физические понятия
1. Первой и часто главной трудностью, встающей при ре-
решении конкретной физической задачи (возникшей в реальной
обстановке, а не взятой из задачника), является вопрос о том,
какие из многочисленных явлений и свойств необходимо учи*
тывать и какими явлениями и свойствами можно пренебречь,
чтобы сделать формулировку задачи решаемой и вместе с тем
достаточно точно описывающей реальную ситуацию. Тем самым
возникает вопрос о том, какие физические величины малы или
велики.
Надо отчетливо понимать, что в физике не бывает величин
просто больших или просто малых. Каждая конкретная вели-
величина мала или велика лишь по отношению к другой, характер-
характерной для данной задачи величине (конечно, той же размерно-
размерности). Например, длина волны красного света ничтожно мала
по сравнению с размерами человека. Именно поэтому в свето-
светотехнике пренебрегают волновыми свойствами света, считая, что
он распространяется по прямолинейным лучам. Напротив, по
сравнению с отдельным атомом длина волны красного света
огромна. Поэтому при рассмотрении взаимодействия света с ато-
атомом часто принимают, что амплитуда световой волны в каждый
момент одинакова во всех точках атома.
Другой пример. Температура 20000°С почти во всех обла-
стях техники является высокой. Но в термоядерных исследова-
исследованиях плазма этой температуры считается низкотемпературной.
Подчеркнем, что понятия бесконечно большого и бесконечно
малого в физике иные, чем в математике. Бесконечно большой
является величина, достаточно большая по сравнению с вели-
величиной, характерной для данной задачи, а бесконечно ма-
малой— величина, достаточно малая по сравнению с харак-
терной.
Более того, нередки случаи, когда бесконечно малая физи-
физическая величина оказывается ограниченной не только сверху,
но и снизу. Например, при выводе уравнения, описывающего
звуковые волны в среде, рассматривают состояние бесконечно
малого объема, размеры которого малы по сравнению с
длиной звуковой волны, но велики по сравнению с межатом-
межатомными расстояниями. Тем самым полученное уравнение приме-
применимо лишь тогда, когда можно удовлетворить обоим нера-
неравенствам.
2. Характер физических явлений существенно зависит от
размеров изучаемых объектов и вообще от размера области
пространства, в которой происходит явление. В табл. 1 дана
шкала масштабов различных величин, исследуемых современ-
современной наукой»

16
ВВЕДЕНИЕ
Таблица I
1
1
1
Метры
102д Размер видимой тети Вселенной
Расстояние междц галактиками
10
10 Размеры галантин
infB
/и
15 Межзвездные расстояния
Размер Солнечной системы
106 Размер Земли
10 3 Высота больших гор на Земле
1 Размер человека
10'3 Размер песчинка
10 Предел разрешения обычного
микроскопа
Размер вируса
ю-9
_,? Размер атома
10 П
!0~15 Размеры атомных ядер
W~iB Исследуемая структура
элементарных частиц
Самой главной для физики характеристической величиной
этой шкалы является размер атома, имеющий порядок 10~10 м.
Этим масштабным размером все физические явления разде-
разделяются на макроскопические и микроскопические.
Макроскопическими называются явления, происходящие с
очень большим количеством атомов или молекул в областях,
превышающих размеры атомов и молекул на несколько и бо-
более порядков, т. е. примерно от 10~8—10~7 м. Микроскопически-
Микроскопическими называются явления, происходящие в областях, сравнимых
с атомными размерами и меньших.
Каждое макроскопическое явление имеет микроскопический
механизм. Например, макроскопическое давление пара на пор-
поршень обусловлено микроскопическими явлениями ударов от-
отдельных молекул воды по поверхности поршня. Понимание
микроскопического механизма макроявлений является, пожа-
пожалуй, главным направлением современной прикладной физики.

ВВЕДЕНИЕ 17
Именно на этом пути лежат возможности получения новых
материалов с заданным комплексом свойств. Например! полу-
полупроводниковый диод нельзя было получить методом проб. Воз-
Возможность создания таких диодов сначала была предсказана
теоретически на основе понимания микроструктуры полупровод-
полупроводниковых материалов.
3. Все окружающие нас физические тела состоят из элемен-
элементарных частиц трех сортов — протонов, нейтронов и электронов.
Тем не менее мы говорим, что газ состоит из молекул, дом —¦
из кирпичей и т. д. Понятие «состоит из ...» в физике является
Относительным.
Общее правило тут таково. Элементарной составной частью
тела можно считать такую его структурную единицу, которая
в рассматриваемом круге явлений не разрушается и не деформи-
деформируется заметным образом.
Например, нейтроны и протоны в атомных ядрах настолько
прочно «сцементированы» друг с другом, что никакие химиче-
химические реакции, электрические разряды и другие макроскопиче-
макроскопические воздействия практически не влияют на ядра. Поэтому *
атомной и макроскопической физике ядра считают бесструк-
бесструктурными заряженными материальными точками.
Для прикладной физики важен вопрос о микроскопическом
составе макроскопических тел. Газы состоят из атомов или
молекул. Вопрос о составе жидкостей и твердых тел более
сложен.
Обычно он решается так. Электроны в каждом атоме рас-
расположены по слоям, называемым оболочками. Предельно воз
можное число электронов в каждой оболочке строго фиксиро-
фиксировано. Оболочка, целиком заполненная электронами, называется
замкнутой. Замкнутая оболочка отличается высокой прочностью
Она не только не разрушается, но даже не деформируется
заметным образом при соединении атомов в молекулы, в жид-
жидкость или в твердое тело и при макроскопических процессах
(механических, химических, тепловых, электрических). Элек-
Электроны наружной оболочки связаны с атомом менее прочно.
При соединении атомов в молекулу или твердое тело такие
электроны могут отодвигаться и даже уходить от атома. По-
Поэтому электроны внешних оболочек обычно рассматриваются
как отдельные частицы^ а ядро вместе с электронами замкну-
замкнутых оболочек рассматривается как единое целое, называемое
|юнным остовом или просто ионом.
Таким образом, молекулы, жидкости и твердые тела в боль-
большинстве случаев следует считать состоящими из ионных остовов
vt электронов наружных оболочек. Например, кристалл пова-
поваренной соли состоит из ионов (не атомов!) натрия и хлора.

18 ВВЕДЕНИЕ
Жидкий натрий состоит из ионов натрия и свободных элек*
тронов.
4. Типичной задачей физики является ответ на вопрос о том*
как будет вести себя исследуемая физическая система в дан*
ных условиях. Для того чтобы сформулировать и решить такую
задачу, необходимо задать для исследуемой системы ее состоя-»
ние и уравнения движения.
Состояние физической системы определяется набором неза*
висимых друг от друга физических величин. Например, состоя-
состояние макроскопической материальной точки определяется ее
положением и скоростью. Состояние составной системы опре-
деляется через состояния ее составных частей. Уже здесь вид-
видно, что задание состояния часто само является непростой зада-*
чей: если считать тело состоящим из очень многих составных
частей, то состояние будет описано очень точно, но математиче-
математические уравнения окажутся непреодолимо громоздкими. Если же
ограничиться «крупноблочным» описанием состояния, то можно
«упустить» исследуемый эффект.
Например, если считать металлическую медь состоящей из
атомов меди, то ее электропроводность получится, в противо-
речии с опытом, ничтожно малой, как бы точно ни вести
дальнейший расчет. Более того, даже приняв, что металличе-
металлическая медь состоит из ионов меди и электронов внешних оболо-
оболочек, мы не получим нужного значения электропроводности,
если будем считать, что состояние каждого электрона опре-
определяется его положением и скоростью. Здесь нас подстерегает
один из самых трудных моментов современной физики: в микро-
микромире описание состояния изменяется коренным образом в
соответствии с законами квантовой механики. И только на
основе квантового метода описания состояния электронов
удастся получить удовлетворительное теоретическое описание
электропроводности меди.
5. Уравнения движения описывают изменение состояния
во времени. Если состояние системы задано, то выписы-
выписывание уравнений движения сводится к применению известных
физических законов той или иной степени фундаменталь-
фундаментальности.
Распространено мнение, что после выписывания уравнений
решение задачи — дело вычислительной математики, которое
при наличии достаточно мощной электронной вычислительной
машины ни с какими трудностями не связано. На практике это
мнение редко оказывается верным. В подавляющем большин-
большинстве случаев машинное решение сколько-нибудь нетривиаль-
нетривиальной физической задачи требует глубокого физического осмыс-
осмысливания для выбора разумных приближений и эффективной
методики решения,,

ВВЕДЕНИЕ 19
б. В книге в основном используется Международная система
единиц, называемая сокращенно СИ. Эта система утверждена
в 1960 г. XI Генеральной конференцией по мерам и весам и
рекомендована согласно ГОСТ 9867-61 для предпочтительного
применения в СССР во всех областях науки, техники, народного
[хозяйства, а также при преподавании. Как исключение, будут
использоваться некоторые традиционные для физики внесистем-
внесистемные единицы, такие как, например, ангстрем. Для чтения физи-
физической литературы инженер должен знать и гауссову систему
СГС, которая широко используется в физике, как более удоб-
удобная и естественная.
Ю. М, Широков

ЧАСТЬ I
МЕХАНИКА
ГЛАВА 1
КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ
§ 1.1. Пространство, время, движение
1. Мир изученных к настоящему времени материальных яв-
явлений характеризуется очень широким диапазоном расстояний,
промежутков времени и скоростей движения. Так, размер части
Вселенной, доступной для наблюдений с помощью современных
приборов, составляет величину порядка 1026 м. Время существо-
существования Вселенной оценивается в 10—12 миллиардов лет, т. е.
примерно в 1018 сек. Эти цифры дают представление о том, что
физики сейчас называют самыми большими расстояниями и
временами.
Очень малые расстояния и времена характеризуются такими
цифрами. Размеры атомных ядер по порядку величины равны
10~15 м. В опытах на крупнейших ускорителях структура эле-
элементарных частиц исследуется до расстояний 5-10~18 м. Ком-
Комбинированными радиотехническими методами удается измерять
времена жизни нестабильных элементарных частиц до 10~и сек.
Естественным масштабом скоростей в природе является ско-
скорость распространения света в вакууме
с = 2,998- 108 м/сек^З- 108 м/сек. A.1)
Ее фундаментальное значение определяется тем, что
скорость 2,998-108 м/сек является предельно высокой ско-
скоростью движения любого материального объекта. Поэтому ее
называют универсальной или мировой постоянной. Если ско-
скорость движения v пренебрежимо мала по сравнению со ско-
скоростью с, так что (v/cJ <C 1, то движение является нереляти-
нерелятивистским. В противном случае движение носит релятивистский
характер.
Опыт свидетельствует о том, что законы нерелятивистских
и релятивистских движений отличаются качественно. Так, за-
законы кругового движения протона, завершающего цикл уско-
ускорения в дубненском синхрофазотроне и обладающего на этом
этапе скоростью около 0,99 с, совсем иные, чем законы обра-

§1.1]. ПРОСТРАНСТВО. ВРЕМЯ ДВИЖЕНИЕ 21
щения спутника вокруг Земли (при скорости спутника v «
« 8-Ю3 м/сек отношение (v/cJ « 7.100< 1).
Характер законов движения качественно различен также для
движений в малых и больших пространственно-временных мас-
масштабах (микромир и макромир). Так, движения электронов во-
вокруг ядер в атомах и планет вокруг Солнца имеют совершенно
различный характер. Напомним (см. Введение), что к макро-
макроскопическим относятся тела, размеры которых намного пре-
превышают атомные. Порядок линейных размеров атомов со-
составляет 10~10м. Линейный размер в 10~10м, как характери-
характеристический, принят в качестве специальной единицы измерения
длины. Эта единица называется ангстремом и обозначается
символом А. Все макроскопические тела состоят из микроско-
микроскопических. К последним относятся, например, атомы и атомные
частицы (электроны, протоны, нейтроны), а также другие
микроскопические частицы, со свойствами которых мы позна-
познакомимся в томе III.
Движения макроскопических тел подчиняются классический
(неквантовым) законам. Движения микрочастиц подчиняются
законам, качественно отличным от классических, если хотя бы
одна из характерных для движения величин размерности
кг-м2/сек оказывается сравнимой с постоянной Планка ft*):
ft = 1,054- 10~34 кг-м2/сек. A.2)
Такие движения называются квантовыми. Наряду со скоростью
света, постоянная Планка также является универсальной кон-
константой, с которой связано разграничение законов физики на
квантовые и классические.
Поясним, почему квантовые закономерности, как правило,
проявляются на малых расстояниях. Произведение mvr массы
частицы на ее среднюю скорость и на размер области, в кото-
которой происходит движение, имеет размерность постоянной План-
Планка. Согласно только что приведенному критерию движение ча-
частицы будет иметь классический характер, если mur>ft, и
квантовый, если mvr порядка ft. Отсюда видно, что при задан-
заданной массе частицы и при фиксированной средней скорости
квантовые закономерности проявятся лишь при достаточно ма-
малых г. При т= 10~30кг и v =0,01 с (электрон в атоме водо-
водорода) движение будет квантовым при г« 10~10 м (размер
атома водорода).
Многочисленные геодезические и астрономические измере-
измерения, а также экспериментальные данные о явлениях микромира
Позволяют утверждать, что вплоть до очень больших масштабов,
за исключением лишь сравнимых с масштабом наблюдаемой
*) Читается: «аш» пере 1еркнуroe.

22
КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ
1ГЛ. 1
части Вселенной, геометрия мирового пространства с высокой'
точностью является эвклидовой. Однако на расстояниях, срав-
нимых с величиной 1026 м, эвклидовость пространства нару*
шается. На таких расстояниях оно оказывается искривленным*
Рис. 1.К
Рис. 1.2. a+P + Y=180°; <*' + Р' +
+ Y' Ф 180°; (ЛВJ + (АСУ = (ВСJ;
(Л'^В'J + (^C7J ^ E'C'J.
что, как оказалось, является результатом действия сил грави-
тационного притяжения между телами, заполняющими области
пространства столь больших размеров.
Нарушение авклидовости мирового пространства на больших
расстояниях подобно изменениям в геометрических свойствах,
которые наблюдаются при переходе от плоскости к поверхности
сферы. Эти изменения выражаются, например, в том, что на
сфере кратчайшее расстояние между двумя точками измеряется
дугой большого круга, проведенного через данные точки. На
плоскости расстояние измеряется отрезком прямой (рис. 1.1)*
В сферическом треугольнике, в отличие от плоского, сумма
углов не равна 180°, и для сферических прямоугольных тре-
треугольников не выполняется теорема Пифагора (рис. 1.2). Эвкли-»
довость мирового пространства в не слишком больших масшта-
масштабах подобна геометрическим
свойствам малых участков
сферической поверхности, кото-
которые С ВЫСОКОЙ ТОЧНОСТЬЮ МОЖ-:
но считать плоскими (рис. 1.3).
Подобно радиусу сферы,
характеризующему степень ее
искривленности, искривлен-
1.3. ность мирового пространства
характеризуется радиусом кри-j
визны Вселенной. В настоящее время считается, что он не мо-.
жет быть меньше 1026 м.
Вблизи очень больших масс искривление пространства на-
наблюдается и на меньших расстояниях. Так, луч света, проход

§ T.U ПРОСТРАНСТВО, ВРЕМЯ, ДВИЖЕНИЙ 23
дящий от звезды к Земле около края Солнца, отклоняется
на 1,75*.
По современным представлениям механика, цель которой
заключается в изучении законов перемещения тел в простран-
пространстве, подразделяется на классическую и квантовую, и в преде-
пределах каждой из них на релятивистскую и нерелятивистскую. Ре-
Релятивистские и к&антовые представления носят более общий
характер по сравнению с нерелятивистскими и классическими
(неквантовыми) законами. Законы нерелятивистской механики
вытекают из релятивистских (но не наоборот!) в пределе малых
скоростей, т. е. при (и/сJ<1. Этот переход осуществляется,
если в релятивистских уравнениях с~>оо. Законы классических
/движений являются предельным случаем квантовых при ft—>О.
Свойства пространства и времени с учетом существования
предельной скорости с рассматриваются в теории относительно-
относительности, которая подразделяется на специальную и общую. Общая
теория отличается от специальной учетом эффекта искривления
мирового пространства, обусловленного силами тяготения.
Нерелятивистская механика значительно проще релятивист-
релятивистской, а неквантовая несравненно проще квантовой. Поэтому
всюду, где это допустимо, стараются пользоваться нерелятивист-
нерелятивистской классической механикой, которую, следуя традиции, мы
часто будем называть просто механикой.
В части I будут рассмотрены основы классической меха-
механики, включая главные положения специальной теории отно-
относительности. Знакомство с общей теорией относительности будет
ограничено разъяснением содержания ее главного исходного по-
положения — принципа эквивалентности.
Законы классической механики являются теоретической
основой многих технических наук (сопротивления материалов,
технической механики, гидравлики и технической гидродинами-
гидродинамики и т. д.) и небесной механики, изучающей движение разно-
разнообразных небесных тел, включая звезды, их скопления и меж-
межзвездный газ. Законы квантовой механики составляют базу
разнообразных наук, изучающих свойства вещества и разра-
разрабатывающих методы целенаправленного их изменения и исполь-
использования. К их числу относятся атомная и ядерная физика,
химия, материаловедение и т. д. Основы квантовой механики
будут изложены в третьем томе курса.
2. Понятие перемещения в пространстве или движения имеет
строго определенное содержание только при указании, относи-
относительно каких именно тел перемещается рассматриваемый
объект. В этом заключается фундаментальное свойство при-
природы, состоящее в том, что всякое движение относительно. По-
Поэтому описание движения возможно только при наличии си-
системы отсчета.

24 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ ггл. 1
Системой отсчета называется совокупность прибора для от-
отсчета времени (часов) и некоторого набора тел, по отношению
к которым движение рассматривается. При этом тела и часы
считаются неподвижными.
Подчеркнем, что в этом определении понятие «часы» имеет
более широкий смысл, чем тот, который ему придают в житей-
житейских условиях. Именно, для отсчета времени можно использо-
использовать любой периодический процесс, период которого задает
единицу измерения времени. Необходимость в таком широком
понимании очевидна. Например, процессы, протекающие на
Солнце, естественно рассматривать из системы отсчета, жестко
связанной с Солнцем. Но часов в обиходном смысле на Солнце,
конечно, нет. Отсчет же времени можно осуществлять и там,
используя в качестве единицы измерения, например, период
вращения Солнца вокруг своей оси.
Системы отсчета необходимы для фиксации точки зрения
на движение. Поэтому в системах отсчета как физических те-
телах абстрагируются от всего, что связано с их конкретным
строением и внутренними свойствами. Важным является только
то, как выглядит по отношению к ним пространство и как те-
течет время. Опытным фактом является трехмерность мирового
пространства и его эвклидовость на расстояниях, малых по
сравнению с радиусом кривизны Вселенной. Поэтому систему
отсчета изображают трехмерной прямоугольной системой ко-
координат, оси которой жестко связаны с набором тел, образую-
образующих совместно с неподвижными относительно них часами си-
систему отсчета. Сами тела при этом не изображаются. Точка
пересечения координатных осей х9 у, z называется началом
системы отсчета. В тех случаях, когда необходимо будет под-
подчеркнуть, что системой отсчета является не
Q) только набор неподвижных тел, но и покоя-
покоящиеся относительно них часы, производящие
отсчет времени t, в изображение системы от-
отсчета мы будем вводить элемент, указываю-
указывающий на это обстоятельство, в виде кружка
*~х с буквой t внутри, так, как это показано на
рис. 1.4.
Рис< **4* Подчеркнем, наконец, что поскольку про*
странство и время всегда рассматриваются
с точки зрения какой-либо системы отсчета, то пространство
и время относительны, так же как относительно движение.
3. Системы отсчета можно связывать с различными телами.
Особо важный класс тел составляют свободные, тела.
Свободным называется тело, настолько удаленное от всех
остальных, что их воздействие на движение данного тела пре-
пренебрежимо мало.

§ 1.Ц ПРОСТРАНСТВО, ВРВМЯ, ДВИЖЕНИЕ 2&
Представление о свободном теле связано с общим свойством
всех наблюдаемых взаимодействий. Оно заключается в том, что
по мере увеличения расстояния между телами их взаимодей-
взаимодействие ослабевает, стремясь к нулю. Не существует ни одного
опытного факта, противоречащего этому положению. Поэтому
достаточно удаленные друг от друга тела движутся практиче-
практически независимо.
Для свободных тел справедлив принцип инерции Галилея,
называемый также первым законом Ньютона. Он является
обобщением известных в настоящее время опытных фактов и
утверждает, что
существуют системы отсчета, в каждой из которых свобод-
свободные тела могут двигаться равномерно и прямолинейно. Такие
системы называются инерциальными.
В области явлений классической физики под равномерным
и прямолинейным подразумевается только поступательное дви-
движение свободного тела. При переходе к микромиру квантовых
явлений конкретизация принципа инерции изменяется.
Частным случаем равномерного и прямолинейного движения
является состояние покоя. Поэтому любая инерциальная си-
система связана с некоторой совокупностью покоящихся друг от-
относительно друга свободных тел. Вследствие принципа инерции
Галилея различные инерциальные системы движутся друг от-
относительно друга равномерно и прямолинейно и в частном слу-
случае могут покоиться.
Принцип инерции фундаментален. Его область применимости
охватывает всю физику.
Естественной для земного наблюдателя инерциальной си^
стемой отсчета является система, связанная со звездами. Со-
Современные приборы не в состоянии зафиксировать ускорение
звезд даже при наблюдениях, непрерывно производимых в те-
течение нескольких сотен лет. Поэтому с точностью, определяемой
существующими средствами наблюдений, можно считать, что
одиночные звезды являются свободными телами. Инерциальную
систему образуют три взаимно перпендикулярные оси, пере-
пересекающиеся в центре Солнца, совместно с неподвижными от-»
носительно этого центра часами. При этом координатные оси
должны быть ориентированы по трем одиночным звездам. Из-за
крайней медленности перемещения звезд друг относительней
друга можно даже не добавлять, что все четыре звезды (Солнце
и три остальных) должны находиться в состоянии относитель-
относительного покоя. Даже если его и нет, то разориентация осей будет
столь медленной, что этим эффектом вполне можно пренебречь.
Такая система, однако, не очень удобна для рассмотрения
Движений в околоземном пространстве, составляющих подав-
подавляющую часть всех видов движения, с которыми приходится

26 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ 1ГЛ.
сталкиваться в различных практических задачах. В этих
чаях более естественной является система отсчета с началом
в центре Земли и с осями, направленными на три одиночные
звезды. Еще более удобной была бы система с координатными
осями, жестко связанными с Землей. Однако в этих системах
отклонения от инерциальности уже поддаются обнаружению.
Эти отклонения обусловлены двумя причинами. Во-первых,
центр Земли обращается (а не движется прямолинейно) вокруг
Солнца. Во-вторых, Земля вращается вокруг своей оси. Цен-
Центростремительное ускорение при вращении Земли вокруг Солн-
Солнца составляет около 6 -10~3 м/сек2. Центростремительное уско-
ускорение Земли при вращении вокруг собственной оси равно при-
приблизительно 3-10-2 м/сек2. Первое из них на четыре, а второе
на три порядка меньше ускорения свободного падения, близкого
у поверхности Земли к величине 9,8 м/сек2. Поэтому влияние
центростремительных ускорений обращения Земли вокруг Солн-
Солнца и ее вращения вокруг собственной оси проявляется в малых
изменениях силы тяжести. В тех ситуациях, когда этими ма-
малыми поправками тможно пренебречь, системы отсчета, связан-
связанные с Землей, можно считать инерциальными.
4. Инерциальные системы отсчета являются выделенными по
сравнению с другими., неинерциальными системами. Это обстоя-
обстоятельство связано с одним из самых фундаментальных свойств
природы, которое выражается принципом относительности. Так
же как и принцип инерции Галилея, принцип относительности
является обобщением всех известных экспериментальных фак-
факсов и гласит, что
все законы физики имеют одинаковый вид во всех инер-
циальных системах отсчета. Другими словами, все инерциаль-
инерциальные системы физически эквивалентны друг другу и понятия
абсолютного покоя и абсолютного равномерного прямолиней-
прямолинейного движения лишены смысла. Областью применимости прин-
принципа относительности является вся физика в целом, включая
квантовую физику и теорию относительности.
Этот фундаментальный закон выражает тот опытный факт,
что два любых опыта, поставленных одинаковым образом в
двух разных инерциальных системах, дают одни и те же ре-
результаты.
Физические законы формулируются одинаковым образом
только в инерциальных системах. В различных неинерциальных
системах отсчета они выглядят по-разному. Поэтому физиче-
физические явления естественно изучать с точки зрения инерциальных
систем отсчета. В дальнейшем везде, где это не оговорено
особо, мы будем использовать именно инерциальные системы.
Физические законы формулируются как количественные со-
соотношения между различными физическими величинами, т. е.

4 Т.2] КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧШ 27
записываются в виде математических уравнений. Поэтому прин-»
цип относительности выражается в неизменности вида этих
уравнений при переходе из одной инерциальной системы отсчета
в другую. Неизменность вида уравнений при каких-либо пре-
образованиях в математике называется инвариантностью урав-
нений относительно этих преобразований. В этих терминах прин-
цип относительности формулируется следующим образом:
Физические законы инвариантны относительно перехода из
одной инерциальной системы отсчета в другую.
Принцип относительности в его общей формулировке вклю-
включает в себя не один, а несколько различных законов. Для их
получения перечислим сначала возможные инерциальные си*
стемы.
Если какая-то система отсчета инерциальна, то инерциаль*
ными будут системы, у которых относительно исходной: а) на-
чало координат сдвинуто на любое расстояние в любом на-
направлении; б) начало времени сдвинуто на любой промежуток;
в) тройка координатных осей повернута на любой угол вокруг
оси, ориентированной в любом направлении; г) начало отсчета
движется равномерно с любой скоростью (меньшей скорости
света в вакууме!).
Принцип относительности утверждает, что любое физическое
явление выглядит одинаково в каждой системе отсчета, полу-
полученной из исходной одним из перечисленных выше преобразо-
преобразований (а) — (г). Образно говоря, один и тот же опыт (прове-
(проведенный с такой точностью, что систему отсчета, связанную с
Землей, можно считать инерциальной) даст тот же результат,
будучи воспроизведен в другом городе, в другой день, в по-
повернутой установке или в установке, смонтированной в поезде
(едущем достаточно плавно и равномерно),
§ 1.2. Кинематика материальной точки
1. Для описания структуры физических объектов в меха-
механике используются различные модельные представления. Наи-
Наиболее простыми из них являются понятия материальной точки
или частицы и абсолютно твердого тела.
Материальной точкой или, что то же, частицей называют
тело в тех случаях, когда изучается только поступательное дви^
жение тела как целого, при условии, что размеры, форма и
другие его структурные свойства, а также протекающие в нем
процессы в пределах точности измерений*) не влияют на два*
жение тела.
*) Поскольку любое физическое утверждение имеет смысл только в пре*
Делах какой-то точности измерений, мы в дальнейшем не будем оговаривать
Vro обстоятельство, считая, что читатель постоянно помнит об этом.

S8 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. 1
Например, траекторию будильника, выпавшего из окна пя-
пятого этажа, можно рассчитать в модели материальной точки
с точностью порядка г/Л — 0,1 %, где г — размер будильника,
h — высота окна над грунтом. Для оценки же изменения хода
будильника в период падения модель материальной точки не
пригодна. Здесь уже необходимо учесть возможное вращение
будильника и его конструктивные особенности.
Абсолютно твердым называется физическое тело в тех слу-
случаях, когда его отдельные части остаются неподвижными друг
относительно друга.
Раздел механики, в котором нерелятивистские классиче-
классические движения рассматриваются в рамках моделей материаль-
материальной точки и абсолютно твердого тела, выделился в самостоя-
самостоятельную науку, называемую теоретической механикой. В теоре-
теоретической механике используются также модели идеальных
нитей, идеальных шарниров и др. Соответствующие определения
читатель может дать сам в качестве упражнения.
Сплошное тело (причем не только абсолютно твердое) в
рамках механики можно мысленно разбить на достаточно мел-
мелкие части, каждую из которых можно трактовать как частицу.
Тем самым задача о движении любого тела может быть сведена
к задаче о движении системы частиц.
Если известно, каким образом изменяется со временем по-
положение каждой частицы тела, то говорят, что определен закон
движения тела.
Необходимо иметь в виду, что в классической механике
частицы должны быть классическими телами. Это означает, что
хотя их размер как реальных физических объектов и может
считаться малым, тем не менее их движение в условиях, в ко-
которых они находятся, должно быть классическим, а не кван-
квантовым. Например, в состав любого тела входят электроны, яв-
являющиеся составными частями атомов, образующих тело. Од-
Однако эти очень маленькие по своим размерам частицы нельзя
считать материальными точками классической механики, по-
поскольку движение электронов в атомах носит квантовый ха-
характер.
Отметим, что материальными точками могут считаться тела
весьма внушительных размеров. Так, при описании движения
Луны вокруг Земли Луну можно считать материальной точкой.
В самом деле, по условию задачи интерес представляет изме-
изменение взаимного расположения Луны и Земли, расстояние
между которыми равно примерно 3,8-108 м. Диаметр же Луны
составляет около 3,5-106 м, т. е. менее процента рас-
расстояния между Землей и Луной. Очевидно, что при этом
пространственной протяженностью Луны вполне можно прене-
пренебречь. Это, конечно, не означает, что так можно поступать

§1-2]
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
У
Рис. 1.5.
всегда. Например, в задаче о распределении массы вещества
Луны в объеме этого небесного тела считать Луну материаль-
материальной точкой было бы абсурдным.
2. Описать движение физической системы значит в каждый
момент времени указать положение всех ее частей в простран-
пространстве по отношению к выбранной системе отсчета. Для этого
необходимо задать какое-то число па-
параметров, характеризующих положе-
положение тела в пространстве в каждый мо-
момент времени.
Минимальное число параметров,
задание которых полностью опреде-
определяет положение физической системы в
пространстве, называется числом ее
степеней свободы.
Положение материальной точки в
пространстве однозначно определяет-
определяется тремя ее координатами х, у, z по
отношению к системе отсчета
(рис. 1.5). Поэтому положение части-
частицы описывается радиус-вектором. Ра-
Радиус-вектором г называется вектор, проекции которого на оси
системы отсчета равны координатам частицы х, у, г:
г = {х,у,г}. A.3)
Согласно этому определению число степеней свободы частицы
равно трем. Если тело состоит из N частиц и все они могут
перемещаться друг относительно
друга во всех направлениях, то оно
обладает 3N степенями свободы.
Если на взаимные перемещения
частиц наложены ограничения, на«
зываемые связями, то число степе-
степеней свободы будет меньше. Его кон-
конкретное значение зависит от числа
наложенных связей. Так, для зада-
задания положения абсолютно твердого
тела в пространстве необходимо
указать положения трех его частиц,
не лежащих на одной прямой.
В этом случае положения всех
остальных частиц, жестко связанных с этими тремя, будут
определены автоматически. Это иллюстрирует рис. 1.6, на ко-
котором изображено абсолютно твердое тело и указаны три вы-
выделенные точки А, В и С. Если их положения известны, то тем
самым однозначно определено положение любой точки D*
Рис. 1.6.

30 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ {ГЛ. I
Положения точек Л, В и С определяются девятью координатами
#а> Уа> 2а, .,., хс, ус, zc. Однако из этих девяти величин не-
независимыми являются только шесть, поскольку существуют три
ограничения, обусловленные требованием сохранения трех рас-
расстояний АВ, АС и ВС. Поэтому число степеней свободы абсо-
абсолютно твердого тела равно шести.
При движении радиус-вектор частицы изменяется. Он мо-
может удлиняться и укорачиваться, может изменять свою ориен-
ориентацию в пространстве. Это означает, что он является функцией
времени t:
r = r(t) = {x(t),y(t),z(t)}.
Эта функция определяет закон движения классической частицы*
При движении частицы конец радиус-вектора описывает в про-
пространстве линию — траекторию частицы.
Подчеркнем, что траектория является исключительно клас-
классическим понятием. Квантовые частицы движутся не по траек-
траекториям.
Для важного частного случая вращательного движения су-
существует еще и другой способ описания. Любой поворот пол-
полностью определяется указанием оси
вращения и угла поворота Аф относи-
относительно этой оси. Если поворот осу-
осуществляется на малый угол Дф (та-
(такой, что Аф<С2я), то можно ввести
понятие вектора угла поворота Дф
(рис. 1.7). Он определяется так. Век-
Вектор Дф направлен вдоль оси враще-
вращения, т. е. перпендикулярен плоскости,
в которой вращение происходит.
Ориентация этого вектора определяет-
определяется правилом буравчика. При враще-
Рис* **7' нии буравчика, ориентированного пер-
перпендикулярно плоскости вращения, в
направлении движения перемещение его оси указывает направ-
направление Дф. Абсолютное значение вектора Дф равно углу пово-
поворота Дф.
Для того, чтобы величина была вектором, она должна не
только иметь направление и абсолютное значение, но и удов-
удовлетворять правилу сложения векторов. Мы оставляем читателю
в качестве самостоятельного упражнения доказать, что для ве-
величин Дф векторный закон сложения соблюдается лишь с точ-
точностью Дф/2я и, следовательно, только с этой точностью Дф
можно считать вектором.
Так же как и радиус-вектор, вектор угла поворота является
функцией времени: Дф = Дф@,- Изменение его направления ха-

§ Т 2]
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
31
рактеризует изменения как ориентации плоскости вращения в
пространстве, так и направления вращения частицы вокруг ка-
какого-либо центра. Изменение его абсолютного значения опре-
определяет угловое смещение частицы.
3. Величиной, характеризующей изменение положения ча-
частицы, является скорость (рис. 1.8). Скоростью v называется
вектор, равный производной радиус- f
вектора по времени, т. е.
/
Очевидно, что в каждый момент вре~ /
мени скорость ориентирована по каса- '
тельной к траектории.
Через vXi vy, vz будем обозначать
компоненты скорости, определяющие
проекции вектора v на координатные Рис. 1.8.
оси системы отсчета: v = {vXy vyy vz}.
В компонентах, определяющих проекции скорости на коор*
динатные оси, векторное равенство A.4) эквивалентно трем со-
соотношениям:
Наряду со скоростью v для характеристики вращательного
движения вводится понятие угловой скорости, которую обычно
обозначают символом ю. Угловой скоростью называется век-
вектор ш, направление которого определяет ориентацию плоскости
вращения и, по правилу буравчика, направление вращения. Аб-
Абсолютное значение вектора <о равно производной от угла по-
поворота по времени, так что
Угловая скорость, в отличие от угла поворота, является
точным вектором. Действительно, предел
конечен, а отклонение от векторного закона
lim
—0.
Поэтому можно складывать векторно не только малые, но и
большие угловые скорости,

32
КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ
(ГЛ. 1
Ф
Выбрав начало координат на оси вращения, скорость v дви-
движения частицы можно выразить через угловую скорость вра-
вращения со и радиус-вектор частицы г. Обратимся к рис. 1.9.
Пусть за бесконечно малое время dt частица смещается на
бесконечно малый вектор dr. Очевид-
Очевидно, что он лежит в плоскости враще-
вращения, т. е. перпендикулярен вектору dip.
Вектор dr вследствие его малости
можно считать перпендикулярным
вектору р = г — /?, где R — радиус-
вектор центра окружности вращения.
Величина вектора dr равна p-dcp, где
dtp — угловое смещение частицы за
время dt, a p — радиус окружности
вращения, равный абсолютному зна-
значению вектора р. Эти свойства векто-
вектора dr выражаются формулой
Но векторы R и dq> параллельны (рис. 1.9). Поэтому векторное
произведение [dy-R] = 0. Следовательно,
dr = [dip ¦ г] - [Ар • R] = [dq> • г]. A.6)
Разделив A.6) на dt и учитывая A.5), находим:
4. Помимо скорости очень важной величиной в классической
механике является ускорение. Ускорением а называется вектор,
равный производной от скорости по времени:
dv
d2r
dt2
A.8)
Через аХу ау, аг обозначим компоненты ускорения, опреде-
определяющие проекции вектора а на координатные оси системы от-
отсчета: а = {ax,ay,az}.
Между компонентами ускорения, скорости и радиус-вектора
существуют следующие соотношения:
(t)
dt2
ay(t) =
dvy (t) d2y (t)
dt
dt2
d2z(t)
dt2
В отличие от скорости, ускорение может иметь любую
ориентацию по отношению к направлению движения частицы.

2]
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
г".
Приведем пример. Тело, брошенное на Луне под углом к
горизонту, будет двигаться по параболе (если высота подъема
пренебрежима по сравнению с радиусом Луны). Из-за отсут-
отсутствия на Луне атмосферы ускорение тела в течение всего вре-
времени движения будет одним и тем
же — ускорением свободного паде-
падения на Луне ?л, ориентированным
к центру Луны (рис. 1.10), хотя
направление движения тела все
время изменяется.
Так как в общем случае ускоре-
ускорение имеет проекции как в направле-
направлении движения, так и перпендику-
перпендикулярно ему, то различают тангенци-
тангенциальное at и нормальное ап ускоре-
ускорения. Тангенциальным ускорением
называется проекция ускорения на
направление скорости. Нормаль-
НормальРис. 1.10.
ным называется проекция ускорения на плоскость,
кулярную скорости. Согласно этому определению
перпенди-
перпендиA.9)
где пит — ортогональные друг другу векторы единичной
длины: |л| = |т|= 1. Первый из них направлен вдоль и, а вто-
второй лежит в плоскости, перпен-
перпендикулярной скорости (рис. 1.11).
Смысл разделения ускорения
на тангенциальную и нормаль-
нормальную части таков: тангенциальное
ускорение характеризует измене-
ние абсолютного значения скоро-
сти, а нормальное — изменение
направления скорости.
Действительно, за малый про-
промежуток времени А/ приращение
скорости частицы Аи равно
Дг> = а • Д^ = at Ы • п + ап А/ • т.
Допустим, что ап = 0. Тогда
Av = atAt-n, т. е. Av направлено
вдоль скорости v. Поэтому при ап = 0 будет изменяться только
величина скорости. Ее направление будет неизменным.
Если же at = 0, то Аи = anSt-m. Найдем в этом случае
квадрат абсолютного значения скорости по истечении време-
времени Д*. Сама скорость будет равна v + Дг> = v + апА1-т =
= on -f- апМт. Мы представили скорость v в виде v = vns
Рис. 1.11
2 А. В. Астахов

34 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ 1
где v — ее абсолютное значение. Интересующая нас величина
будет равна скалярному произведению:
({v + Дг>) • (v + Дг>)) = ((vn + anM -m)- (vn + anbt- т)) =
= v2 (п • л) + а\ Ы2 (т-т) + 2van Д/ (п • т) = v2 + а\ Д/2.
При этом мы учли, что по определению (я-л)= п2 = (тт) =
= т2 = 1 и (n-m)=0. Так как Д/ предполагалось малой
величиной, то с точностью до величины второго порядка мало-
малости абсолютные значения скоростей v и v -j- Дг> равны. Следо-
Следовательно, при at = 0 скорость изменяется только по направле-
направлению.
Найдем выражения для нормального и тангенциального
ускорений. Записав скорость v в виде v = vn, имеем:
Обратим внимание, что вектор dn/dt ортогонален вектору л, так
как их скалярное произведение равно нулю:
Поэтому
/ ч dv , \ \ ( dn\ dv
(na) (nn) + v(n)
Из A.9) следует, что (па) = at. Таким образом,
С учетом A.11) из A.9) и A.10) вытекает, что апт = v —-.
Разделив это равенство на v2, получим:
±4 4^
v dt dr
AЛ2)
где dr = v dt — абсолютное значение смещения частицы за
время dt. Умножим соотношение A.12) скалярно на вектор т.
Так как он имеет единичную длину, то
Вспомним, что величина вектора п также постоянна. По-
Поэтому dn/dr характеризует лишь изменение направления скоро-
скорости. Следовательно, вектор dn/dr направлен по вектору т. Это

§ 1.2] КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ 35
означает, что произведение (т • -?rj равно абсолютному зна-
значению вектора dn/dr. Найдем его.
Обратимся к рис. 1.12. На нем изображена траектория ча-
частицы и два положения частицы, одно из которых получается
из другого при смещении
вдоль траектории на рас-
расстояние dr. При этом на-
направление скорости изме-
няется на dn и скорость по-
поворачивается на угол dQ.
Ввиду малости dQ абсолют-
абсолютную величину вектора dn
можно принять равной дли-
длине дуги окружности единич- ^
ного радиуса, на которую ^ -"*
опирается центральный угол Рис j 12
dQ, т. е. \dn\ = dQ. Следова-
Следовательно, длина вектора dn/dr
равна dd/dr. Последняя производная определяет кривизну тра-
траектории, т. е. насколько траектория искривляется при смещении
на единичное расстояние. Так как dQ/dr имеет размерность
обратной длины, то ее представляют в виде
R имеет размерность длины и называется радиусом кривизны
траектории в данной точке. Он имеет смысл предела радиуса
окружности, проведенной через три точки кривой при неогра-
неограниченном приближении этих точек к данной. Для произвольной
кривой радиус кривизны различен в разных участках кривой.
Он имеет постоянное значение лишь для окружности.
Суммируя изложенное, находим, что ajv2 = l/Ry т. е.
«»=4' AЛ4>
Наконец, для характеристики вращательных движений су-
существует понятие углового ускорения. Угловым ускорением на-
называется вектор е, равный производной по времени от угловой
скорости со:
??33
5. С чисто кинематической точки зрения круг величин, ха-
характеризующих движение, можно было бы расширять неогра-
неограниченно. Помимо скорости и ускорения (угловой скорости и
углового ускорения) можно было бы рассматривать более
2*

36 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ (ГЛ. I
высокие производные радиус-вектора (угла поворота). Однако
оказывается, что в этом нет необходимости. Как будет выяснено
в следующей главе, для систем классических материальных
точек ускорения выражаются через координаты и скорости, т. е.
не являются независимыми величинами.
§ 1.3. Преобразования Галилея
1. Равноправие инерциальных систем отсчета дает возмож-
возможность в каждом конкретном случае подбирать систему коорди-
координат, наиболее удобную для решения рассматриваемой задачи.
Проследим, как производится выбор нужной системы отсчета
и какие задачи приходится при этом решать.
Сначала необходимо установить инерциальность какой-то
одной системы отсчета. После этого можно выбирать наиболее
удобную систему путем изменения а) начала отсчета времени,
б) начала координат, в) ориентации координатных осей, а
также г) путем перехода к системе координат, движущейся
поступательно с некоторой постоянной скоростью.
При переходе от одной системы отсчета к другой координа-
координаты частиц, компоненты их скоростей и другие величины изме-
изменяются. Поэтому возникает задача о переходе от одной системы
отсчета к другой, т. е. о выражении величин, заданных в одной
системе отсчета, через те же величины в другой системе. В слу-
случаях (а), (б), (в) такие преобразования очевидны и одно-
однозначны.
При смещении отсчета времени на промежуток t0 и начала
координат на вектор г0 время t и радиус-вектор г в исходной
системе отсчета связаны с временем V и радиус-вектором г'
в новой системе соотношениями (рис. 1.13)
t = t' + io, r = r' + rQ. A.16)
При повороте координатных осей, например, на угол ср в
плоскости ху исходные координаты выражаются через новые по
формулам, известным из аналитической геометрии (рис. 1.14):
л; = #'cos qp — у' sinqp, у ¦==xr s\n^> + г/cos ср. A.17)
Переход к движущейся системе координат более сложен и
даже неоднозначен, если не принять дополнительных физиче-
физических допущений о связях между пространством и временем. Эти
допущения, конечно, должны базироваться на опытных фактах.
Ниже будет видно, что одно из таких допущений ведет к нере-
нерелятивистской теории, а другое —к релятивистской.
Прежде чем переходить к получению преобразований пере-
перехода к движущимся системам отсчета, следует отметить, что
эти преобразования достаточно получить для простейшего слу-

1.3]
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
37
чая, когда исходная система (назовем ее системой К) с коорди-
координатными осями х, уу z и временем t считается покоящейся, а но-
новая система К' с координатами х\ г/', zr и временем V движется
Рис. 1.13.
со скоростью V, направленной вдоль оси х (рис. 1.15). Любое
другое преобразование перехода к движущейся системе отсчета
сводится к комбинации только что указанного с преобразова-
преобразованиями смещений и поворотов.
Рис. 1.15.
2. Из опытных фактов следует, что с точностью до (V/cJ,
где с — скорость света, ход часов не меняется при переходе
к движущейся системе координат. Для всех тел, размеры кото-
которых намного превышают атомные, (V/cJ<^ 1. И действительно,
Часы, покоящиеся на Земле, идут так же, как и часы в летящем
Самолете или спутнике. Произведем оценку. Скорость искус-
искусственного спутника Земли, — одна из самых больших, которой
*ш можем воспользоваться в целях непосредственной проверки
влияния движения на ход времени, — равна 8-Ю3 м/сек (первая

33 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. I
космическая скорость). Отсюда следует, что относительное из-
изменение хода часов, установленных на спутнике, составляет
(8.103/3.108J«7-10-10.
Поэтому для нерелятивистской скорости V можно, ссылаясь
на опыт, утверждать, что в системах /С и /С7 время течет одина-
одинаково. В частности, если ход часов в этих системах был синхро-
синхронизирован в тот момент, когда координатные оси систем К и К'
совместились, то и в дальнейшем показания часов будут совпа-
совпадать. Это означает, что
течение времени носит абсолютный характер во всех инерци-
альных системах отсчета, движущихся друг относительно друга
с нерелятивистскими скоростями:
Теперь выясним вид преобразований, связывающих про-
пространственные координаты систем К и К', предполагая синхро-
синхронизацию хода часов осуществленной в момент совмещения си-
систем К и /('.
Пусть в момент времени t, определенный по часам системы
/С, произошло некоторое событие в точке с координатами х, у, г,
например, в этой точке была зафиксирована какая-то частица
(рис. 1.15). Наблюдатель, связанный с системой /С', при приня-
принятом способе синхронизации часов систем К и К' зафиксирует то
же самое событие по своим часам в момент V = t. Штрихован-
Штрихованные координаты этого события будут следующими: у' = у;
zr = 2, а координата хг будет меньше х на величину пути, кото-
который к моменту времени i = V будет пройден началом О' си-
системы отсчета К' по отношению к началу О системы /С. Этот
путь равен Vt (рис. 1.15). Таким образом, связь между систе-
системами К и К' оказывается такой:
x/ = x-Vti A.18)
Эти соотношения называются преобразованиями Галилея.
Преобразования Галилея выражают нерелятивистские пред-
представления о пространстве и времени. Требование инвариантно-
инвариантности физических законов относительно преобразований Галилея
называется принципом относительности Галилея или требова-
требованием галилеевой инвариантности. Оно распространяется только
на нерелятивистские (в том числе и квантовые) движения.
Помимо абсолютного течения времени, к важным след-
следствиям преобразований Галилея относятся также следующие.

<§ 1.3] ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ 39
а) Преобразования Галилея оставляют неизменным расстоя-
расстояние между двумя точками. Это свойство выражает тот опытный
факт, что в нерелятивистской области размеры тел не зависят
от их движения.
В самом деле, пусть в одно и то же время t в системе от-
отсчета К зафиксированы два события в точках с координатами
хи уи z\ и *2, У2у %2- Вследствие абсолютного характера течения
времени эти же два события произойдут одновременно и с точ-
точки зрения наблюдателя системы К' в момент времени V = t.
При этом по отношению к системе К' координаты точек, в кото-
которых эти события будут наблюдаться, согласно преобразованиям
A.18) будут равны
и
Х2 = Х2 V ty У2=== У2> ^2 === ^2*
По отношению к системе К расстояние между точками, в кото-
которых наблюдаются события, будет равно
/l2 = У (*2 — *lJ + (#2 — У if + Bi — Zl?-
Расстояние, измеренное в системе К', составит величину
= У(*2 -Vt-xx + Vtf -t- (y2 - yxf + (z2 - z{f = /12.
б) Если скорость движения в одной системе отсчета равна
v, а в другой v\ то
v = v' + V, A.19)
если вторая система отсчета движется относительно первой со
скоростью V.
В этом заключается содержание классического закона сло-
сложения скоростей. Его можно применять только к нерелятивист-
нерелятивистским движениям и в этой области он подтверждается многочис-
многочисленными фактами. Так, скорость движения парохода относи-
относительно берегов реки (одна система отсчета) складывается из
скорости парохода относительно воды (другая система) и из
скорости течения воды (скорости относительного движения си-
систем отсчета). Скорость любой подвижной части двигателя
автомобиля относительно земли складывается из ее скорости
относительно корпуса автомобиля и из скорости движения авто-
автомобиля относительно земли. Число подобных примеров неогра-
неограниченно велико, однако все они относятся к медленным, нере-
нерелятивистским движениям.

40 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. Г
Последовательный вывод нерелятивистского правила сложе-
сложения скоростей из преобразований Галилея достаточно провеет»
для частного случая двух инерциальных систем отсчета, изо-
изображенных на рис. 1.15.
Предположим, что наблюдается перемещение частицы в х~
направлении. Это означает, что скорость частицы имеет отличной
от нуля только одну х-компоненту. Пусть положения частицы-
no отношению к системе К определяются координатами x(t), a
по отношению к системе К' — координатами x'(t). Следователь-
* dx (t) v
но, скорость частицы будет равна vx = ¦ ,, в системе К и*
vx = —,,, в системе д . Если воспользоваться преобразова-
преобразованиями Галилея A.18), то
x A.20)
Как видно, этот результат является частным случаем закона
A.19).
в) Все тела по отношению к различным инерциальным си-
системам отсчета движутся с одинаковыми ускорениями.
Действительно, дифференцируя по времени равенство A.19)
с учетом первого из преобразований A.18) и постоянства V, по-
получаем:
dv dv' _ dv'
dt dt dt' '
что и требовалось доказать.
3. Исторически именно закон сложения скоростей явился1
пробным камнем, на котором были установлены пределы при-
применимости представлений о времени и пространстве, вытекаю-
вытекающих из опытных данных о свойствах медленных движений.
Ограниченность галилеевых представлений о свойствах про-
пространства и времени вытекает из следующего опытного факта:
Скорость света в различных инерциальных системах отсчета
имеет одно и то же значение.
Очевидно, этот факт находится в резком противоречии с за-
законом сложения скоростей A.19). Согласно этому закону по
отношению к системе отсчета, догоняющей свет, скорость света
должна быть меньше, чем по отношению к покоящейся системе.
На самом деле этого не наблюдается.
Впервые постоянство скорости света было обнаружено в
опытах А. Майкельсона и Е. Морли, поставленных в период с
1880 по 1887 г. В этих опытах в качестве движущейся системы
отсчета использовалась Земля, которая движется по околосол-
околосолнечной орбите со скоростью 3-Ю4 м/сек. Скорость света вдоль

-§ 14] ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 41
направления движения Земли сравнивалась со скоростью света
поперек этого направления. Измерения велись в разное время
года, так что направление вектора скорости Земли менялось от
•опыта к опыту. Было обнаружено, что в пределах ошибок экс-
эксперимента (составляющих приблизительно 7б орбитальной ско-
скорости Земли) «поперечная» и «продольная» скорости света все-
всегда равны друг другу. Это означает, что движение Земли не
оказывает влияния на скорость распространения световых сиг-
сигналов.
Другим фактом, указывающим на ограниченность нереляти-
нерелятивистских представлений о свойствах пространства и времени,
-явилась неинвариантность относительно преобразований Галилея
-законов, описывающих электромагнитные явления. Эти законы
выражаются уравнениями Максвелла, которые будут рассмот-
рассмотрены в томе II. Из них также вытекает постоянство скорости
•света. Делались попытки видоизменить уравнения Максвелла
так, чтобы законы электромагнетизма стали галилеево инвари-
инвариантными. Однако следствия, вытекающие из «подправленных»
уравнений Максвелла, противоречили опыту.
«§ 1.4. Преобразования Лоренца
1. В 1905 г. А. Эйнштейн предложил отказаться от поиска
объяснений, почему скорость света во всех инерциальных систе-
системах отсчета оказывается одинаковой. Им была высказана смелая
мысль о том, что постоянство скорости света является фундамен-
фундаментальным свойством природы, которое нужно констатировать как
•опытный факт.
Требование постоянства скорости света во всех инерциаль-
инерциальных системах отсчета известно под названием постулата Эйн-
Эйнштейна. Этот постулат входит в число наиболее фундаменталь-
фундаментальных законов природы. Его область применимости до настоящего
-времени является всеобъемлющей.
Постулат Эйнштейна требовал коренного пересмотра сло-
сложившихся представлений. Новые, согласующиеся с этим посту-
постулатом представления о свойствах пространства, времени и дви-
движения составили содержание специальной теории относительно-
относительности Эйнштейна.
Чтобы глубже осознать последствия, к которым приводит
Постулат Эйнштейна, рассмотрим следующий наглядный при-
пример. Представим себе, что движущейся системой отсчета яв-
является поезд. Пусть в момент, когда хвостовой вагон поезда
поравнялся с телеграфным столбом, из этого вагона послан
¦световой сигнал машинисту; через время At' машинист его реги-
регистрирует. Обозначим длину поезда через А/'. Тогда скорость
света с = Д/'/Д^'. Предположим, что за тем же самым процессом-

42
КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ
[ГЛ. t
наблюдает стрелочник, стоящий на насыпи. Чтобы определить
скорость света, стрелочник также должен разделить путь, прой-
пройденный светом, на время прохождения. Обозначим время,
отсчитываемое стрелочником, через At. Что же касается пути,
пройденного светом, то с точки зрения стрелочника он состоит
из длины поезда А/ и расстояния, на которое за время At хво-
хвостовой вагон успеет отъехать от телеграфного столба. Если
скорость поезда V, то это расстояние равно V At. Кажется
очевидным, что при этом должны выполняться «естественные»
равенства А/ = А/' и At = At'. Однако не будем торопиться
с выводами.
Итак, для скорости света с точки зрения стрелочника мы
получим выражение —
= __|-i/% Согласно же постулату
Эйнштейна оно также должно быть равно ?=="тр-- Очевидно,
д/' М , тг
что равенство ттг = -тг + ^ несовместимо с «естественными»
условиями Al' = A/; At' = At. Нужно либо считать, что Д/ < А/',
т. е. с точки зрения стрелочника поезд стал «короче», либо до-
допустить, что время в движущейся системе отсчета идет медлен-
медленнее, чем в неподвижной. Как мы увидим ниже, имеет место и то,
и другое одновременно.
2. Оказывается, что постулат Эйнштейна не вносит измене-
изменений в нерелятивистские представления о пространственных со-
соотношениях в направлении, перпендикулярном движению.
Размеры тела в направлении, поперечном движению, совпа-
совпадают с соответствующими размерами покоящегося тела.
Прежде всего заметим, что в любом направлении, перпен-
перпендикулярном скорости, изменение размеров (если оно есть) со
скоростью должно быть одина-
одинаковым, так как ни одно из
этих направлений не выделено
перед другими. Так, покоящее-
покоящееся круговое кольцо при пере-
переходе к системе отсчета, движу-
движущейся перпендикулярно пло-
плоскости кольца, в принципе мо-
может только сжаться или рас-
расшириться, но сохранит круго-
круговую форму и останется пер-
перпендикулярным скорости. Рас-
Рассмотрим теперь два одинаковых соосно расположенных кольца
A и 2 на рис. 1.16). Пусть теперь первое кольцо покоится,
а второе кольцо стало двигаться вдоль оси навстречу первому.
Если размер движущегося кольца стал меньше покоящегося, то
Рис. 1.16.

1.4]
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
43
второе кольцо пройдет внутри первого. Но тогда в системе по-
покоя второго кольца, наоборот, первое кольцо пройдет внутри
второго. Согласно же принципу относительности факт нахожде-
нахождения одного кольца внутри другого не может зависеть от выбора
системы координат (кольца, например, могут поцарапать друг
друга). Возникшее противоречие разрешается единственным об-
образом: поперечный размер колец не может изменяться в зави-
зависимости от того, движутся кольца или покоятся.
3. Постулат Эйнштейна сказывается только на представле-
представлениях о временных соотношениях и о пространственных соотно-
соотношениях в направлении движения.
Движущиеся часы идут медленнее покоящихся. Если проме-
промежуток времени между какими-либо двумя последовательными
событиями по покоящимся часам равен At, то по движущимся
часам он будет меньше и равен
At' = At^/l — (V/cJ<M, A.21)
где V — скорость относительного движения часов, с — скорость
света. Этот эффект называется лоренцевым сокращением про-
межутков времени и свидетельствует о том, что течение времени
не является абсолютным и зависит от движения.
Для доказательства рассмотрим две инерциальные системы
отсчета К и К''. Систему К будем считать покоящейся, а систему
К' — движущейся со скоростью V. Предположим, что в системе
К' находятся часы специальной конструкции. Они состоят из
неподвижных относительно системы К' источника света и си-
системы двух параллельных зеркал, расположенных так, как
показано на рис. 1.17. Свет включается на короткое время и
///77//////////
И Л
Рис. 1.17.
производится инжекция света в пространство между зеркалами.
После этого свет движется вверх и вниз, попеременно отра-
отражаясь от верхнего и нижнего зеркал. В таких часах качаю-
качающимся маятником является луч света.
Рассмотрим один из полупериодов, когда свет движется
сверху вниз. Пусть с точки зрения наблюдателя системы К!

44 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ t
свет от верхнего зеркала до нижнего движется в течение вре-
времени At'. Тогда расстояние между зеркалами равно с At\ при-
причем оно является поперечным по отношению к движению си-
системы К'. Поэтому и по мнению наблюдателя системы К рас-
стояние между зеркалами также будет равно с At'. Однако, а
отличие от наблюдателя системы /С, он будет видеть наклонное-
распространение света (рис. 1.18). При этом скорость света
согласно постулату Эйнштейна также будет равна с. Предполо-
Предположим, что время прохождения света от источника до оси х, кото-
которое измеряет наблюдатель системы К (естественно, по часам-
этой системы), равно At. Тогда с его точки зрения-
свет пройдет наклонный путь с At (рис. 1.18), при-
cAt'\\cAt чем расстояние, на которое свет будет снесен за
это время вследствие движения системы К', со-
составит величину V At. Применяя теорему Пифаго-
Пифагора к треугольнику, изображенному на рис. 1.18,
получаем:
~VA t (с At'J + (V At? = (с AtJ.
Рис. 1.18 Аналогичное соотношение будет выполняться и.
для другого полупериода, когда свет идет снизу
вверх. Из полученного равенства следует связь промежутков
времени в двух системах отсчета. Легко видеть, что она имеет
вид A.21).
Свойства пространственных соотношений в направлении дви-
движения формулируются следующим образом:
Размеры тел в направлении движения сокращаются. Если'
размер покоящегося тела в некотором направлении равен /, то
при движении тела в этом направлении со скоростью V он
уменьшается до величины
Y = / л/l-iV/cf < U A.22>
где с — скорость света. Этот эффект называется лоренцевым-
сокращением длины и свидетельствует о зависимости простран-
пространственных соотношений от движения.
Для доказательства рассмотрим две инерциальные системы
отсчета К и К'. Однако теперь в систему отсчета К' поместим
стержень, ориентированный в направлении оси х\ т. е. в на-
направлении относительного движения систем отсчета К' и К
(рис. 1.19). Предположим, что относительно системы К' стер-
стержень покоится. Обозначим его длину в этой системе через /.
В качестве процедуры ее измерения выберем следующую. На
левом конце стержня поместим источник света, посылающий
узкий пучок параллельных лучей в направлении к правому
концу. Там же поместим приемник света. На правом конце по-
поместим зеркало. Посылая световой сигнал, зафиксируем по ча-

§ 1.4]
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
45
сам системы отсчета К' время А/', за которое свет пройдет рас-
расстояние от левого конца стержня до правого и вернется назад.
Его возвращение будет фиксироваться приемником света
(рис. 1.19). Тогда
1 = (с-Ы')/2. A.23)
Посмотрим теперь, как воспринимается эта процедура изме-
измерения наблюдателем системы К. Предположим, что с его точки
зрения за время At\ свет идет от левого конца к правому, а за
z i
г л
/У//////////////'
Рис. 1.19.
время At2 возвращается обратно, так что полное время измере-
измерения составляет интервал At = At\ + At2 (он отсчитывается по
часам системы /С). Время прямого и обратного распространения
света в системе К будет разным (см. рис. 1.20). На первом
этапе свет догоняет уходящий от него правый конец стержня.
с At,
с Л L
VAt,
L'
Рис. 1.20.
На втором он движется навстречу левому концу. В первом слу-
случае ему приходится пройти путь, на V Ati больший по сравне-
сравнению с длиной стержня (V At\ определяет смещение отражаю-
отражающего зеркала за время At\ относительно системы отсчета /С).
Во втором случае свет пройдет путь на V At2 меньший по
сравнению с длиной стержня (VAh равно смещению левого
конца стержня навстречу свету за время Д^) (рис. 1.20). Обо-
Обозначим длину стержня относительно системы отсчета К через 1\
Тогда
cAtx = l' + V Atu с Д/2 = /' - V Д/2,
ибо и в системе К согласно постулату Эйнштейна свет распро-
распространяется со скоростью с. Определяя из этих равенств Д^ и

46 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. I
At2i найдем:
м = д*! + д/2 = 2Г
т. е.
v2 \ *
1--?¦)•
2
Принимая во внимание A.21), выразим At через Д*'. Тогда
A.24)
С учетом A.23) формула A.24) эквивалентна A.22), что и тре-
требовалось доказать.
Необходимо иметь в виду следующее важное пояснение. Эф-
Эффекты лоренцева сокращения были установлены с помощью
специальных мысленных устройств, в которых важную роль
играло распространение света. Тем не менее эти эффекты не
являются специфическими только для оптических явлений.
Лоренцево сокращение промежутков времени и длин яв-
является проявлением всеобщих свойств пространства и времени.
Этот вывод следует из принципа относительности. Действи-
Действительно, рассмотрим, например, двое покоящихся друг относи-
относительно друга часов. Одни из них являются световыми, а дру-
другие— обычными, употребляемыми в быту. Пусть в системе от-
отсчета, в которой часы покоятся, они идут одинаково. Допустим
теперь, что ход обычных часов от движения не зависит. Тогда
по отношению к системе отсчета, движущейся относительно пер-
первой, обычные и световые часы будут идти по-разному, что про-
противоречит принципу относительности.
Формулы A.21) и A.22) подтверждают высказанное в § 1.1
положение о том, что скоростей движения, превышающих ско-
скорость света с, не существует. Действительно, при V > с входя-
входящие в эти формулы корни являются мнимыми числами и соот-
соотношения A.21) и A.22) становятся физически абсурдными. Для
медленных движений, т. е. при (V/cJ <С 1, эти корни отличаются
от 1 на хмалую величину порядка (V/cJ. Если она недоступна
измерению, то эффекты лоренцева сокращения не проявляются
и мы приходим к галилеевым представлениям о пространстве и
времени. В этом заключается одно из подтверждений более об-
общего характера релятивистских представлений, которые содер-
содержат нерелятивистские в качестве предельного случая, о чем уже
упоминалось в § 1.1.
Время, отсчитываемое покоящимися часами, называется соб-
собственным. Собственными называются также размеры тела в си-
системе отсчета, в которой тело покоится. Вследствие эффектов

§ 1.4]
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
47
Рис. 1.21.

48
КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ
[ГЛ I
лоренцева сокращения течение собственного времени является
наиболее медленным, а собственные размеры являются макси-
максимальными.
Релятивистское замедление времени не только наблюдается
на опыте, но и используется в ускорительной технике для полу-
получения пучков нестабильных элементарных частиц, таких как
заряженные пионы и каоны. Эти частицы имеют время жизни
порядка т=10~8 сек. За такой промежуток времени частица
успевает пройти расстояние, не превышающее сх = 3 м. Но т —
собственное время, отсчитываемое часами, движущимися вместе
с частицей. Поэтому, если пионы и каоны образуются со скоро-
скоростями, скажем, порядка 0,995с (для Серпуховского синхрофазо-
синхрофазотрона эта величина — далеко не предел!), то лабораторное
время жизни частицы окажется порядка , , =-^10~ сек.
VI — {У 1сJ
За это время частица успевает-пройти уже 30 м. Такое расстоя-
расстояние уже достаточно для того, чтобы отделить пучок нужных
частиц от множества других, образующихся в мишени, и рас-
расположить громоздкую измерительную аппаратуру (рис. 1.21).
4. Установим вид преобразований координат и времени при
переходе из покоящейся инерциальной системы отсчета в дви-
движущуюся, принимая при этом во внимание постулат Эйнштейна.
Их вывод проделаем для частного случая тех же самых систем
отсчета К и К\ которые были рассмотрены ранее.
Рис. 1.22.
Предположим, что наблюдатель системы К' в момент вре-
времени f фиксирует некоторое событие в точке с координатами
х\ у', z'. Пусть то же самое событие наблюдатель системы К
видит в точке с координатами х, у, z в момент времени t. Рас-
Рассмотрим координату х'. Она измеряется длиной отрезка, кото-
который изображен жирной линией в левой части рис. 1.22. По-
Поскольку этот отрезок ориентирован вдоль направления движе-

14]
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
49
ния системы /С', то с точки зрения системы К его длина будет
меньше и равна х' д/l — V2/c2. При этом к моменту времени t
его левый конец будет находиться на расстоянии Vt от на-
начала отсчета системы К. Картина, наблюдаемая из системы /(,
изображена в правой части рис. 1.22. Из нее следует, что
х = х'а/\ -{V/cJ + Vt, т. е.
х, = х- Vt_
Vl - (V/cJ *
Координаты yf и zr измеряются отрезками, перпендикуляр-
перпендикулярными движению. Поэтому длина каждого из этих отрезков в си-
стемах К и К' будет одинако-
одинакой ( 123) С (Т) (р)
с К К уд д
вой (рис. 1.23). Следовательно,
у' =
= z.
Полученные соотношения
задают правила перехода от
координат и времени системы
К к координатам системы К'.
Остается определить вид
преобразований моментов вре-
времени / и V. С этой целью рас-
рассмотрим обратный переход от
системы К' к системе /С. Пере-
Перемена ролей систем К и К'
формально выражается заменой в уже полученных соотноше-
соотношениях jc, у, г, / соответственно на х\ у\ z\ V и V на —V. В част-
частности, отсюда следует справедливость равенства
х' + Vt'
Рис. 1.23.
X —
Vl -
Из него можно выразить V через х и хг. В свою очередь х' вы-
выражается через х и t (см. выше), так что в конечном счете /'
оказывается зависящим от t и х. Вид этой зависимости, как
показывают несложные алгебраические выкладки, таков:
/ - xV/с*-
Vl — V2/c2
Объединяя найденные соотношения, получаем следующие пра-
правила перехода:
,, t - xV/c2
v~
A.25)
X =
Vl - V2/c2

50 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. 1
Они называются преобразованиями Лоренца. Эти преобра-
преобразования существенно отличаются от преобразований Галилея
только в релятивистской области. При {VIсJ «С 1 A.25) пере-
переходят в A.18).
Преобразования Лоренца выражают релятивистские пред-
представления о пространстве и времени, в основе которых лежит
постулат Эйнштейна. Требование инвариантности физических
законов относительно преобразований Лоренца называется
принципом относительности Эйнштейна. Он является более об-
общим по сравнению с принципом относительности Галилея, но
существенно отличается от последнего только для релятивист-
релятивистских движений и только в этой области приводит к качественно
иным следствиям.
Перечислим некоторые из них.
а) Течение времени зависит от движения и абсолютным не
является.
Этот эффект непосредственно вытекает из вида преобразо-
преобразований A.25), в которых f ф t. Одним из его проявлений яв-
является лоренцево сокращение времени. Кроме того, оказы-
оказывается, что
понятие одновременности является относительным. Оно
имеет смысл только при указании системы отсчета.
В самом деле, предположим, что по отношению к одной из
рассмотренных выше систем отсчета, например, по отношению
к системе /С, в одно и то же время t\ = t2 = t произошли два
события в точках с координатами Х\, у\, z\ и л?2, */2> ^2 соответ-
соответственно. Воспользуемся преобразованиями Лоренца и перейдем
в систему /С'. Тогда первое событие (то, которое в системе К
произошло в точке с координатами хи У\, Z\) по часам системы
К' произойдет в момент времени
Yi - (v/cv f
а второе — в момент
, _ t2 - x2V/c2 _ t — x2V/e2
2~~ Yi - (VicJ ~ Yi - (vieJ '
Как следует из этих формул,
if s (x\ — х2) Vic2 , Л
если Х\ Ф х2, т. е. по отношению к системе отсчета К' события
произойдут в разные моменты времени.
б) Пространственные расстояния при преобразованиях Ло-
Лоренца изменяются.

'$ 1.4] ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 51
Это проявляется, например, в эффекте лоренцева сокраще-
сокращения длины. Формальную проверку несовпадения
/12 = V(*I ~ Ъ? + (#1 - У*?
II
где штрихованные и нештрихованные координаты связаны пре-
преобразованиями A.25), мы оставляем читателю в виде упражне-
упражнения. Проделав его, он сможет убедиться также в неизменности
(инвариантности) при преобразованиях Лоренца величины
Она называется интервалом между двумя событиями, простран-
пространственное расстояние между которыми равно 1\2 и которые про-
происходят в моменты времени t\ и t2.
В релятивистской механике интервал играет ту же роль,
какую в нерелятивистской теории играет расстояние между
двумя точками в трехмерном пространстве. Последнее сохра-
сохраняется при преобразованиях Галилея. Интервал же сохраняется
при преобразованиях Лоренца. Он даже по внешнему виду не-
несколько схож с обычным расстоянием. Тот же квадратный ко-
корень, который извлекается из комбинации квадратов некоторых
величин. Правда, в этой комбинации есть члены с отрицатель-
отрицательными знаками и, кроме того, она содержит моменты времени.
Это и не удивительно, поскольку преобразования Лоренца «сме-
«смешивают» пространство и время. Так, в формулу, определяющую
преобразование моментов времени, входят пространственные
координаты. По этой причине было введено представление о че-
четырехмерном множестве пространственных координат и момен-
моментов времени. Оно называется четырехмерным пространством —
временем или пространством Минковского в честь математика,
впервые предложившего это понятие. В этом пространстве
время является дополнительным измерением, равноправным
с обычными пространственными измерениями, а расстояние
между двумя четырехмерными точками определяется интер-
интервалом.
в) Для релятивистских движений закон сложения скоростей
отличается от классического. В частном случае, когда движение
рассматривается из двух систем отсчета с параллельной ориен-
ориентацией одноименных осей, релятивистский закон сложения ско-
скоростей формулируется так:
Пусть в одной системе отсчета скорость частицы равна
v = {vXi vyt vz}. Тогда по отношению к другой системе отсчета

52 КИНЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ МЕХАНИКИ [ГЛ. Г
компоненты скорости частицы v' равны
, ._ vx-v , / У2 уУ
vx~ \- wx/c2 ' Vy—V[ с2 1 - Vvx/c2 ' (
V2
1 - Vvjc2 '
если вторая система отсчета движется относительно первой &
х-направлении со скоростью V, сравнимой со скоростью света с.
Для доказательства рассмотрим уже известные нам системы
К и /('. Предположим, что в системе К' за время dtr частица
смещается на вектор drf = {dx', dy\ dz'}. Следовательно, в этой
системе скорость частицы равна
x' duf dz
г иг ч
Согласно преобразованиям Лоренца A.25) и с учетом постоян-
постоянства V
dt'=* , "\ r=dt , °~ a^=dt- ]
— V2/c2
dx-Vdt dtl~dr~V) vx
i = —=— = at —.
Vi
dy' = dy, dzf = dz.
Здесь dx, dy, dz — компоненты перемещения dr частицы за вре-
время dt, каким оно представляется наблюдателю системы К. С его
точки зрения скорость частицы равна
( dx dy dz \
— \-dr> ЧГ> ГГ
n dx' dy' dz' -
Составляя отношения -jp-, -^p"* ITF' ПРИХ°ДИМ к преобразо-
ваниям A.26).
В нерелятивистской области закон A.26) совпадает с класси-
классическим. В самом деле, в пределе (V/cJ~~*0 соотношения A.26)
совпадают с равенствами v'x — Vx — V; v'y = vy\ v'z = v2. С уче-
учетом направленности переноса системы К' последние формулы
эквивалентны векторному равенству v = vr + V.
Замечательным свойством преобразований A.26) является
то, что они никогда не приводят к скоростям, превышающим
скорость света с, и не меняют величины скорости, если она
равна скорости света с. Тем самым они, в отличие от классиче-

§.141 ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 53:
ского правила сложения скоростей, не противоречат постулату
Эйнштейна и еще раз подчеркивают тот факт, что скорость-
света является максимально возможной.
Действительно, допустим, что по отношению к системе от-
отсчета К свет распространяется вдоль х-направления. Следова-
Следовательно, v = {vXi vv, vz} = {с, О, 0}. Подставляя эти значения
компонент скорости движения света в A.26), найдем, что
Мы видим, что скорость в новой системе отсчета К' остается
равной с при любом значении и любом знаке скорости 1/, в пол-
полном соответствии с постулатом Эйнштейна.
г) Ускорения тел по отношению к различным движущимся
друг по отношению к другу инерциальным системам отсчета не
одинаковы.
Убедиться в этом мы предоставляем читателю в качестве
самостоятельного упражнения.

ГЛАВА 2
ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ
§ 2.1. Состояния
1. Общей целью механики (а с небольшими оговорками — и
всей физики) является создание методов решения задач типа:
дана определенная физическая система в определенных внеш-
внешних условиях; найти, что произойдет с этой системой через ка-
какой-то промежуток времени. Решение этой задачи распадается
на а) установление величин, описывающих состояние физиче-
физической системы, б) составление уравнений движения, описываю-
описывающих изменение состояния во времени, и в) нахождение физиче-
физических величин, опытное измерение которых дает возможность
судить о том, что происходит реально с исследуемой системой.
Начнем с установления понятия состояния простейшего объ-
объекта механики — частицы. Из опыта следует, что
в классической физике состояние частицы полностью опреде-
определяется ее координатами х, у, z и компонентами ее скорости vXJ
vy, vz в заданный момент времени, т. е. радиус-вектором частицы
г и ее скоростью v.
Это определение состояния частицы является фундаменталь-
фундаментальным законом классической физики. Он действителен во всех
случаях, если
mvr » ft,
где m — масса частицы, v — средняя скорость ее движения, г
характеризует линейный размер области движения, a ft — по-
постоянная Планка A.2).
При нерелятивистских скоростях состояние любой системы
частиц полностью определяется совокупностью состояний всех
частиц системы и имеет поэтому чисто механическую природу.
Состояние системы N нерелятивистских классических частиц
описывается радиус-векторами Г\, ..., rN[ и скоростями
Vu •. •, Vn всех частиц в заданный момент времени.
Для такой системы полное число величин, определяющих
состояние, равно 6ЛЛ Заметим, что число степеней свободы здесь
равно 3N, т. е. в два раза меньше.

§ 2.1J СОСТОЯНИЯ 55
Классическое понятие механического состояния кажется про-
простым и очевидным. Между тем эта проблема фактически была
поставлена и решена только Ньютоном. Аристотель удивлялся,,
почему топор, опущенный с размаха, легко раскалывает по-
полено, а приставленный к полену даже не оставляет зарубки.
Сейчас ответ прост: в момент соприкосновения с деревом в
обоих случаях положения топора одинаковы, однако значение
его скорости разные. Поэтому неудивительно, что разные со-
состояния топора в начальный момент ведут к разным результа-
результатам.
Из определения механического состояния следует, что все-
величины, характеризующие свойства любой системы классиче-
классических нерелятивистских частиц, являются функциями положений
и скоростей этих частиц.
2. В релятивистской области определенное выше понятие
состояния применимо без дополнительных ограничений толька
для свободных классических частиц. При наличии взаимодей-
взаимодействия возникают довольно жесткие ограничения, из-за которых
область применимости классической релятивистской механики
исчерпывается движениями заряженных частиц в не очень силь-
сильных электромагнитных полях. В самом деле, в настоящее время
известен единственный способ разгонять частицы до реляти-
релятивистских скоростей — это воздействовать на них электромагнит-
электромагнитными полями. Нарушение механического характера движения
заряженной релятивистской частицы проявляется в том, что
частица начинает излучать электромагнитные волны. Они в
свою очередь влияют на движение частицы, и это влияние назы-
называется реакцией излучения. Интенсивность излучения зависит
от ускорения частицы, которое определяется силой внешнего
поля. Следовательно, только при достаточно слабом внешнем
поле можно пренебречь излучением и его реакцией. Подробнее-
этот вопрос будет рассмотрен в следующем томе курса.
В системе из двух и более заряженных релятивистских час-
частиц механическое понятие состояния теряет смысл из-за эф-
эффекта запаздывания взаимодействия. Он связан с тем, что
частицы взаимодействуют друг с другом через электромагнит-
электромагнитное поле. Каждая частица создает вокруг себя поле, а это поле
уже действует на другую частицу. Со времен Фарадея известно^
что процесс создания поля частицей протекает путем близко-
действия. При перемещении в новое место частица сначала
создает поле в ближайшей к заряду области пространства. Из-
Изменение поля в этой области порождает изменение поля в со-
соседней области, и так далее. Это изменение поля распростра-
распространяется в пустое пространство со скоростью света с (согласно
постулату Эйнштейна быстрее оно распространяться не может).
Поэтому в момент t на вторую частицу будет действовать поле».

*56 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 2
г>
созданное первой частицей в более ранний момент t , где
R — расстояние между частицами, взятыми в разные моменты
времени (рис. 2.1). Говорят, что воздействие первой частицы на
вторую запаздывает на время R/c.
Следовательно, зная положения и скорости обеих частиц
в момент /, мы еще не можем определить, как действуют эти
частицы друг на друга. Для этого необходимо еще знать поло-
положения и скорости в более ранние моменты времени. Это и озна-
, чает, что в этом случае приведен-
Чистица! Частица 2
6 момент t ^3 момент t ное выше понятие механического
состояния теряет смысл. Лишь при
условии ?//с<1, где v — скорость
л R
частицы, ее смещение Ar = v— за
с
время запаздывания будет ничтож-
ничтожно малым по сравнению с /?,
Аг v 1
Частица 1 р ~~дГ — r ^ *¦ •
о момент i
с В этом случае взаимодействие мож-
Рис 2.1. но считать мгновенным. Только при
этом условии можно говорить о со-
состояниях так, как это было определено выше. В противном
случае необходимо учитывать как динамический объект поле,
переносящее взаимодействие.
Вопрос о состоянии электромагнитного поля будет рассмот-
рассмотрен в следующем томе курса.
§ 2.2. Уравнения движения
1. Согласно изложенному в предыдущем параграфе, для
полного описания механического состояния ускорения частиц
задавать не надо. Это означает, что для системы любого числа
N частиц ускорение каждой частицы является функцией радиус-
векторов и скоростей частиц системы:
d2r.
а = -?г = at(ги ..., rN; vu >.., vN) =
= <Цгь ..., rN\ -^-t ..., -^f-)\ '=1, 2, ..., N. B.1)
Вид функций в правой части системы B.1) должен опреде-
определяться свойствами частиц, а также внешними условиями, в ко-
которых они движутся. Если эти условия меняются со временем,
то в правых частях B.1) добавится явная зависимость от вре-
времени t.

§ 2 21 УРАВНЕНИЯ ДВИЖЕНИЯ 57"
Соотношения B.1) называются уравнениями движения клас-
классической механики.
Разъясним это название. Рассмотрим, например, одну ча-
частицу. Соотношение
является дифференциальным уравнением второго порядка отно-
относительно неизвестной векторной функции r(t). Она находится4
путем двух интегрирований выписанного уравнения и опреде-
определяет закон движения частицы. При каждом интегрировании
возникает неопределенная постоянная — постоянный вектор.
Поэтому для однозначного выделения закона движения следует
уравнение движения дополнить двумя условиями, определяю-
определяющими эти постоянные. Эти условия фиксируют, задавая со-
состояние частицы в какой-то (обычно в начальный) хмомент вре-
времени, т. е. указывая значения радиус-вектора и скорости при
/ = 0:
r@) = r0, v(O) = vo.
Этот пример отражает характерные черты процедуры отыска-
отыскания решений любых задач механики:
Общее решение может быть найдено, если, во-первых, изве-
известны уравнения движения и, во-вторых, если задано состояние
в начальный момент времени или, что одно и то же, определены
начальные условия.
Здесь следует подчеркнуть, что для физики более важной
является задача отыскания вида функций в правой части си-
систем типа B.1) для конкретных физических ситуаций. Решение
же составленных уравнений в большей степени дело матема-
математиков, чем физиков.
Для составления механических уравнений движения в фи-
физике разработаны достаточно простые и общие методы. Для их
изложения нам понадобится ввести несколько дополнительных
понятий и придать уравнениям движения иную, более удобную
форму.
Одним из важных является представление об изолирован-
изолированной, или замкнутой, системе. Это представление есть обобщение
понятия свободного тела. Когда говорят о теле, то обычна
имеют в виду нераспадающийся на отдельные части объект.
В системе же отдельные части могут расходиться друг от друга
на сколь угодно большие расстояния.
Система частиц называется изолированной, если каждая из
частиц системы не взаимодействует ни с какими внешними те-
телами.

58 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 2
Например, с высокой точностью изолированной является
Солнечная система, включающая в себя Солнце, планеты, их
естественные и искусственные спутники, астероиды.
2. В этом и последующем пунктах будет рассматриваться
только нерелятивистская механика.
Рассмотрим некоторую изолированную систему. Допустим,
что она состоит из N частиц, скорости которых обозначим через
vь ..., vN. Опытным путем установлено, что для такой системы
выполняется следующий закон. Частицы системы характери-
характеризуются определенными константами ти ..., mN такими, что
N
2 ™>iVi = const. B.2)
Каждая из констант т называется массой частицы. Масса
Бе зависит от взаимодействий, в которых частица участвует.
Лектор
p = mv B.3)
называется импульсом частицы, а сумма
Р=Ер* = 2> < B.4)
определяет полный импульс системы.
Постоянство полного импульса изолированной системы яв-
является фундаментальным свойством природы. Закон, его выра-
выражающий, называется законом сохранения импульса.
На будущее отметим, что под сохранением мы будем всегда
^понимать независимость физических величин от времени.
Кроме того, вспомним (об этом уже говорилось во Введе-
Введении), что в физике формула нередко играет двойную роль — и
закона, и определения новой физической величины. Сейчас это
уместно в связи с соотношением B.2). Оно несет двойную «на-
«нагрузку» и содержит не только закон сохранения импульса, но и
определение массы. Проверим последнее, т. е. покажем, что
соотношение B.2) дает возможность определять массы частиц,
если массу одной из частиц принять за эталонную.
Припишем частице-эталону массу т0, что будет соответство-
соответствовать выбору системы единиц. Для нахождения массы m другой
частицы рассмотрим процесс столкновения этой частицы с эта-
эталоном. Детальным ходом процесса столкновения можно не ин-
интересоваться. Будем только считать, что массы частиц при столк-
столкновении не изменились и что в начальном и конечном состоя-
состояниях частицы находятся достаточно далеко друг от друга, чтобы
каждую из них можно было считать свободной. Пусть t/0Hti —
скорости эталонной и исследуемой частиц до столкновения, a Vq

§ 2.2] УРАВНЕНИЯ ДВИЖЕНИЯ
= mQv'o + mv'.
и v'— их скорости после столкновения. Согласно B.2)
movo + mv = mQv'o
Перегруппировав слагаемые, получим
Отсюда
I vo - vo I
Таким образом, измерив скорости, мы можем получить зна-
значение т массы исследуемой частицы.
Импульсы можно использовать для описания состояния ча-
частиц. Действительно, при заданной массе импульс однозначно-
связан со скоростью, поэтому состояние частицы полностью*
определено, если задать ее радиус-вектор г и импульс р. Такое-
модифицированное определение состояния на первый взгляд ка-
кажется тривиальной заменой переменных. В дальнейшем мы
постепенно убедимся, что переход от скоростей к импульсам
имеет глубокий физический смысл.
3. Рассмотрим одну частицу. Предположим, что она не изо-
изолирована. Тогда ее импульс будет зависеть от времени. Произ-
Производная импульса частицы по времени называется силой, дей-
действующей на частицу со стороны ее окружения. Обозначив силу
через F, приведенное определение выразим формулой
Очевидно, что именно сила характеризует воздействие окру-
окружающих тел на движение частицы, которое и проявляется в
изменении импульса частицы. Из определения следует, что сила
полностью охарактеризована, если заданы ее величина и на-
направление, а также указано, на что и со стороны чего сила дей-
действует.
Соотношение B.5) выражает один из фундаментальных за-
законов классической физики, названный вторым законом Нью-
Ньютона. Разъясним, почему казалось бы простое определение B.5)
оказывается фундаментальным физическим законом. Причина
заключается в том, что из B.5) следует очень важный вывода
Сила является функцией состояния системы.
Действительно, подставив B.3) в B.5), получим:
dp d (mv) dv „ /Г4 ~v
-JL = -±rL = m-ir = ma = F, B.6>
т. е. с точностью до постоянного множителя m уравнение типа
B.1). Отсюда прямо следует, что сила является функцией меха-
механического состояния.
Подчеркнем, что этот вывод базируется на двух положениях^
каждое из которых имеет очень широкую область применимости^

fH ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 2
Во-первых, в его основе лежит определение механического
состояния, применимое во всех случаях, в которых пренебрежимо
малы квантовые эффекты и релятивистские эффекты реакции
излучения и запаздывания взаимодействия. Во-вторых, мы исхо-
исходили из закона сохранения импульса. В следующей главе мы
увидим, что этот закон имеет область применимости, превы-
превышающую область применимости классического понятия механи-
механического состояния.
Свойство силы быть функцией состояния превращает второй
закон Ньютона в мощный инструмент исследования классиче-
классических механических движений. Почему это так, будет разъяснено
в следующем параграфе. А сейчас мы продолжим рассмотрение
тех свойств сил, которые всегда используются при составлении
уравнений движения. Одно из них определяется третьим зако-
законом Ньютона. Рассмотрим изолированную систему двух частиц.
Дифференцируя по времени полный импульс системы Р=р{-\-р2
и учитывая закон сохранения импульса, получим:
dp\ , dpi _ q /о уч
Согласно B.5)
dt I2f dt lu
где F\2 — сила, с которой вторая частица действует на первую,
a F2\— сила действия первой частицы на вторую. Силы F\2 и
F2[ называют силами действия и противодействия. Таким обра-
образом, из равенства B.7) следует третий закон Ньютона:
F12 = —F2I. B.8)
Отметим, наконец, что для изолированной частицы первый
закон Ньютона, т. е. принцип инерции Галилея, является просто
законом сохранения ее импульса.
Еще одно важное свойство сил является фундаментальным
законом, независимым от изложенных выше:
Сила, с которой одна частица действует на другую, зависит
только от радиус-векторов и скоростей только этих двух частиц.
Присутствие других частиц на эту силу не влияет. Это свойство
называется законом независимости действия сил или законом
парности взаимодействия. Область применимости этого закона
охватывает всю классическую механику.
В квантовой области закон парности взаимодействия*) вы-
выполняется с ограниченной точностью. Например, при движении
электронов в атоме он справедлив с точностью около 0,01%.
*) Здесь не случайно слово «сила» не упоминается и использован более
общий термин — взаимодействие Движение частиц, составляющих атомы и
молекулы, подчиняется квантовым законам. А в квантовой физике понятие
силы отсутствует из-за иного, чем в классике, описания состояний.

2.2]
УРАВНЕНИЯ ДВИЖЕНИЯ
61
Из закона независимости действия сил следует, что в слож-
сложной системе сила, действующая на данную частицу, равна век-
векторной сумме сил, действующих со стороны каждой из осталь-
остальных частиц:
dt
¦ = г12
dp
dt
L = F2\ + F2\ + ..
И Т. Д.
Рис. 2.2.
Для сил между протяженными телами закон парности взаи-
взаимодействия может нарушаться. Приведем пример. Рассмотрим
силу, действующую на незаряженный
шарик со стороны отрицательно заря-
заряженного (рис. 2.2). Механизм возник- О~
новения этой силы известен из курса 2
•средней школы. Электрическое поле
заряженного шара поляризует незаря-
незаряженный шар, в котором раздвигаются
положительные и отрицательные заряды. При этом положитель-
положительные заряды концентрируются на поверхности, обращенной к за-
заряженному шару. Так как абсолютная величина действия одного
заряда на другой падает с расстоянием, то сила притяжения
изображенных на рис. 2.2 положитель-
положительных зарядов превысит силу отталки-
отталкивания отрицательных зарядов. В ре-
результате возникает суммарная сила
притяжения Fi2. Если же рядом с от-
отрицательно заряженным шаром 2 по-
поместить такой же шар 3 (рис. 2.3), то
сила, действующая на нейтральный
шар, увеличится более чем в два раза. Действительно, заряд
шара 3 увеличит поляризацию нейтрального шара, так что ка-
каждая из сил F'm, F'z по величине станет больше силы F{2.
4. Из закона сохранения импульса в форме B.4) можно вы-
вывести два важных следствия, которые называются законом со-
сохранения центра инерции и законом аддитивности массы.
Центром инерции системы частиц с радиус-векторами
гь Г2, ... называется точка с радиус-вектором
Рис. 2.3.
? mirt
B.9)
где суммирование производится по всем частицам системы.
Закон сохранения центра инерции формулируется так:
Центр инерции изолированной системы частиц движется
равномерно и прямолинейно.

62 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 2
Для доказательства вычислим производную V вектора R по
времени:
Zdr.
dRd__ J. _ _J j. 2L
at ?m - %mi - %„
i
i
где m—Х^ь a P = ]C Pt = 2 m^/ — полный импульс систе-
i i /
мы. Так как для изолированной системы Р = const, то V =
= const. Это и есть закон сохранения центра инерции.
Так как скорость центра инерции определяется полным им-
импульсом физической системы, то движение центра инерции на-
называют движением этой системы как единого целого. Очевидно,
что это движение тождественно с поступательным движением
системы.
Данное определение согласуется с принципом инерции Га-
Галилея в применении его к изолированному (т. е. свободному)
протяженному телу. Действительно, между частицами тела мо-
могут действовать любые силы, тело может вращаться, но соглас-
согласно закону сохранения центра инерции при отсутствии внешних
воздействий центр инерции тела будет двигаться равномерно и
прямолинейно.
Законом сохранения центра инерции удобно пользоваться
при решении многих задач механики. Например, в задаче о
движении двух частиц, взаимодействующих только друг с дру-
другом, уравнения движения пишутся для радиус-векторов Г\ и г2.
Если же перейти к новым векторным переменным R и г,
t*- '@-г,-г„ B.10)
то при любом виде взаимодействия имеем R(t)= Vot ¦+¦ Ro, где
Ro, Vo — радиус-вектор и скорость центра инерции частиц в на-
начальный момент. Тем самым исходная система из шести диф-
дифференциальных уравнений для компонент r\(t) и r2(t) сводится
к системе трех уравнений для компонент r(t), характеризующих
относительное положение частиц.
Обратим внимание на то, что импульс центра инерции свя-
связан со скоростью центра инерции так же, как импульс и ско-
скорость одной частицы. При этом коэффициент пропорционально-
пропорциональности т между импульсом и скоростью центра инерции равен
сумме масс отдельных частиц и, очевидно, имеет смысл массы
всей системы. В этом выражается закон аддитивности массы.
Аддитивностью вообще называется свойство, состоящее в
том, что величина, характеризующая систему в целом, склады-

$ 2.2] УРАВНЕНИЯ ДВИЖЕНИЯ 63
вается из величин того же рода, характеризующих каждую
часть системы.
Если система не изолирована, то
Здесь Р — полный импульс системы, a F — сумма всех сил, дей-
действующих на систему извне. Эти силы называются внешними.
Уравнение B.11) по виду совпадает со вторым законом Нью-
Ньютона для одной частицы B.5) и называется уравнением посту-
поступательного движения системы как единого целого.
Убедимся в справедливости B.11). Имеем:
dP ^ dpt
dt '
i
где pi — импульсы частиц системы. Согласно второму закону
Ньютона сумма, стоящая справа, равна сумме всех сил, дей-
действующих на каждую частицу, в которой по третьему закону
Ньютона силы взаимодействия частиц друг с другом взаимно
компенсируются и остается только сумма внешних сил.
5. Перейдем к релятивистским движениям. Напомним, что в
рамках классической механики могут быть рассмотрены только
свободные движения и движения одной частицы в электромаг-
электромагнитном поле. Закон сохранения импульса действует и в реля-
релятивистской механике. Поэтому релятивистское уравнение дви-
движения частицы также имеет вид B.5). Однако релятивист-
релятивистский импульс зависит от скорости не по формуле B.3), а
иначе.
Импульс релятивистской частицы массы m равен
'-таг- B12>
Обратим внимание, что в нерелятивистском пределе и2/с2<с1
B.12) переходит в B.3). При этом содержание закона B.12)
является более богатым, что подчеркивает большую общность
релятивистских представлений. Так, из B.12) следует возмож-
возможность существования безмассовых частиц. Действительно, при
m = 0 импульс конечен, если скорость v = с. При этом условии
в B.12) возникает неопределенность типа 0/0, которая может
быть любой конечной величиной. Частицы с m = 0 действи-
действительно обнаружены. Ими являются кванты света (фотоны).
Чтобы убедиться в справедливости B.12), рассмотрим процесс лобового
упругого столкновения двух частиц в системе отсчета с нулевым суммарный
импульсом и с осью х, направленной по линии движения частиц. Закон

64 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 2
сохранения импульса вдоль оси х в такой системе (рис. 2.4) имеет вид
Pi + р2 = — Р\ — р2 = 0
Частицы в результате столкновения изменяют направление движения на об-
обратное, сохраняя при этом абсолютные значения импульсов. В нерелятивист-
нерелятивистском случае, переходя к скоростям, получим
nil vl Ч- m2v2 = - ni\V{ — m2v2 = 0. B.13)
В системе отсчета, движущейся вдоль оси * со скоростью —V, это соотноше-
соотношение согласно закону сложения скоростей A.19) перейдет в равенство
тх (у, + V) + т2 (v2 + V) = m, (- Vl + V) + m2 (- v2 + V) = (m, + m2) V.
Именно этого и надо было ожидать: импульсы до и после столкновения
остались равными, а суммарный импульс стал равным произведению массы
-v,< 0} -/?, < 0 -иг> 0гр2>0
Рис. 2.4.
системы в целом на ее скорость. Но если подставить в B.13) скорости, пре-
преобразованные по релятивистскому закону A.26), то равенство импульсов до
и после столкновения нарушится. Тем самым мы придем в противоречие с
принципом относительности. Этого не произойдет, если, переходя к скоростям,
мы воспользуемся формулой B.12). Действительно, в этом случае вместо
B.13) будем иметь
Перейдем теперь в систему отсчета, которая движется со скоростью —I/,
но уже с помощью релятивистских преобразований A.26), согласно которым
При этом учтем тождество
V-
с2 A ±viV/c2f I ±v.V/c'

^ 2 21 УРАВНЕНИЯ ДВИЖЕНИЯ 65
С этой вспомогательной формулой подстановка B.15) в первое из равенств
B.14) дает:
m, (о, + V) , т2 (v2 + V)
v2jc2 Vl - V2/c2 V1 - vtl°2 Vl - V2/
2/c2
_v, + V) + m2 (- v2 + V)
Ic2
Ш|
-^2 J
Vl
где введено обозначение
у i -yi/
B.17)
Разберемся в трех знаках равенства в цепочке B.16). Первый знак ра-
равенства является утверждением, сделанным на основании принципов относи-
относительности: закон сохранения импульса должен соблюдаться во всех инер-
циальных системах отсчета. С помощью B.14) легко убедиться, что этот знак
равенства действительно соблюден. Это означает, что выражение B.12) для
релятивистского импульса написано правильно. Второй знак равенства полу-
получен использованием равенства нулю выражений B.14). Наконец, третий знак
равенства равносилен определению B.17). Оно интересно вот в каком отно-
mV
шении: стоящее в конце цепочки B.16) выражение Р = —. — являет-
Vi - v2/c
ся импульсом системы в целом и вместе с тем имеет форму B.12). Что ка-
касается скорости I/, то она, конечно, есть скорость системы в целом, поскольку
в исходной системе отсчета суммарный импульс равнялся нулю, так что си-
система в целом покоилась. Поэтому мы вынуждены принять т за массу си-
системы двух частиц. Согласно этой формуле в теории относительности закон
аддитивности массы нарушается*).
Отметим также, что закон сохранения центра инерции для релятивистских
частиц соблюдается, но определение центра инерции видоизменяется.
6. Величины, входящие в физические законы, измеряются
в определенных единицах. Измерить физическую величину озна-
означает сравнить ее с величиной того же рода, условно принятой
*) В литературе можно встретить понятие массы движущегося тела, рав-
равной — —, т. е. зависящей от скорости. Теоретически это понятие
V 1 — v2/c2
было введено для сохранения закона аддитивности массы в теории относи-
относительности. Сейчас в физике высоких энергий, в которой в сущности только и
Ьриходится сталкиваться с релятивистскими частицами, употребляется исклю-
исключительно понятие постоянной (инвариантной) массы. Поэтому и в настоя-
настоящем курсе понятие «массы движущегося тела» не используется.
3 А, В, Астахов

66 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ [ТЛ. 2
за единицу. Физические законы определяют условия, наклады-
накладываемые на размерности входящих в них величин. Поэтому су-
существует ограниченное число единиц измерения, которые можно
выбирать произвольно. Единицы измерения, устанавливаемые
произвольно, называются основными. Зависимые от них еди-
единицы измерения называются производными.
В системе СИ в качестве основных единиц выбраны единицы
длины, времени, массы, силы электрического тока, температуры
и силы света. Поскольку единица массы является основной, то
вопрос о размерностях и единицах измерения физических вели-
величин мы рассматриваем в этом параграфе, тем более, что после
формулировки уравнений движения необходимо установить раз-
размерности и единицы измерения таких важных характеристик,
как импульс и сила.
В СИ длина измеряется в метрах (м), время в секундах
(сек), масса в килограммах (кг), сила электрического тока в
амперах (А). Мы упоминаем о единице измерения силы тока
уже теперь, поскольку в следующем параграфе среди прочих
будем обсуждать силы электромагнитной природы и говорить
об электрических зарядах. Для этого нужно знать, в частности,
единицы измерения электрического заряда. В СИ единица изме-
измерения электрического заряда в число основных не входит и яв-
является производной. В этой системе размерность электрического
заряда определяется как А/сек и 1 А/сек называется кулоном
(Кл). Соотношение единиц измерения заряда в СГС и СИ та-
таково;
1 ед. СГС = ~- 1(Г9Кл.
В СИ компоненты радиус-вектора частицы измеряются в
метрах, скорость в м/сек, ускорение в м/сек2. Единицей измере-
измерения импульса является 1 кг-м/сек. Единица измерения силы
равна 1 кг-м/сек2 и называется ньютоном (Н). В СГС те же
величины измеряются: компоненты радиус-вектора — в санти-
сантиметрах, скорость в см/сек, ускорение в см/сек2, импульс в
г-см/сек. Единица измерения силы 1 г -см/сек2 называется ди-
ной (дин). При этом
1 дин==10 Н.
Помимо ньютона и дины часто, особенно в технических рас-
расчетах, применяется специальная внесистемная единица 1 кило-
грамм-сила (кгс). Сила в 1 кгс определяется как сила притя-
притяжения к Земле массы в 1 кг на уровне моря на широте в 45°з
1 кгс = 980 665 дин = 9,80665 Н ^ 9,8 Н.

§ 2.3) ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ 67
§ 2.3. Виды взаимодействий и силы
1. Главный результат предыдущего параграфа состоит в том,
что уравнения классической механики всегда представимы в
виде
^L = Ft{ru ..., rN\ vu ..., vN), B.18)
где ru . .*, rN —- радиус-векторы, ри ..., ря, vu ...» vN — им-
импульсы и скорости частиц изучаемой системы (предполагается»
что число частиц в системе равно N). Функция состояния
Fi(rh ..., rN; v\y ..., vN) определяет силу, приложенную к-ча-
к-частице с номером i, и описывает закон действия этой силы. Та-
Таким образом, для составления уравнений движения необходимо
знать законы действия сил. В основе этого знания всегда ле-
лежит опыт.
Схематически это можно пояснить следующим образом.
Предположим, что экспериментальное изучение позволило уста-
установить законы действия сил в некоторой системе. Но область
применимости найденных законов никогда не исчерпывается
только одной физической системой. Эта область всегда значи-
значительно шире и включает в себя множество других систем. Таким
образом, оказывается, что для каждой такой системы имеется
возможность составить уравнения типа B.18) с уже известными
правыми частями. А это означает, что в нашем распоряжении
оказывается некоторая система уравнений, решив которую мы
можем проанализировать все свойства данной системы. Именно
это имелось в виду, когда в предыдущем параграфе мы гово-
говорили о том, что второй закон Ньютона является мощным ин-
инструментом исследования классических механических движений.
Поясним сказанное примером. Исторически закон всемир-
всемирного тяготения был установлен Ньютоном путем изучения
движения Луны и планет Солнечной системы. Однако силы
тяготения действуют во многих других случаях. Например, они
действуют внутри звезд, в звездных скоплениях и больших
скоплениях газа в мировом пространстве, между искусственным
спутником и Землей и т. д. Поэтому закон всемирного тяготения
позволяет объяснить свойство многих систем, подчас совсем
внешне не похожих на Солнечную систему.
2. Одну и ту же силу часто можно описывать законами,
имеющими разные степени фундаментальности, т. е. разные об-
области применимости. Рассмотрим, например, поведение куска
парафина под действием силы сжатия (рис. 2.5). Со всех сто*
рон, за исключением одной, с которой давит поршень, парафин
находится в абсолютно твердой оболочке. В первом приближе-
приближении изменение линейного размера А/ парафина в направлении
з*

68 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ П"Л 2
сжатия будет пропорционально сжимающей силе. Измерив ко-
коэффициент пропорциональности k, мы получим закон действия
в виде
F = -*.A/. B.19)
Им можно пользоваться для определения силы при не слишком
больших деформациях. Коэффициент k называется коэффициен-
коэффициентом упругости тела (в данном случае парафина).
Закон B.19) прост, но зато имеет весьма узкую область при-
применимости. Он пригоден для определения силы по степени сжа-
сжатия (или наоборот) при небольших А/. Этот
I I I I I j j | частный закон можно вывести из значительно
¦ ¦ f | ¦ ¦ т | более фундаментального закона сил межмо-
межмолекулярных взаимодействий (см. ниже), дей-
действующих между двумя молекулами парафи-
парафина. Зная этот закон (т. е. зависимость сил от
расстояния между молекулами), можно полу-
получить не только соотношение B.19), но и рас-
рассчитать значение постоянной k, а также опре-
Рис. 2.5. делить область применимости соотношения
B.19). Более того, по закону действия сил
между молекулами в принципе можно рассчитать все констан-
константы, характеризующие механические и тепловые свойства па-
парафина.
Но закон действия сил между молекулами парафина еще не
самый фундаментальный. Область его действия ограничена мо-
молекулами, имеющими не слишком большие скорости. Закон дей-
действия сил между молекулами парафина также не позволит
ничего сказать о силах между молекулой парафина и молеку-
молекулой иного вида, о процессах возбуждения и разрушения моле-
молекул при их столкновениях с большими импульсами и т. д. Это
связано с тем, что закон межмолекулярных сил очень грубо
учитывает структуру молекул и составляющих их атомов. Ответ
на все эти вопросы, по крайней мере в принципе, может быть
получен на основе квантовой теории взаимодействия атомных
ядер и электронов друг с другом. Эта теория фундаментальна.
С ее помощью в принципе возможен расчет почти любого свой-
свойства или явления, связанного со структурой атомов, молекул
и тел в различных агрегатных состояниях. Однако практически
такой расчет удается осуществить далеко не всегда. Поэтому;
на практике используются законы разной степени общности.
В настоящее время установлены фундаментальные взаимо-
взаимодействия, к которым в конечном счете сводятся силы любой при-
роды, и получены законы сил, которые не являются фундамент
тальными, но имеют достаточно большую область применимо-*
сти и эффективно используются в физике и технике.

i 2.9 виды взаимодействий и силы 69
По современным представлениям все многообразие явлений,
наблюдаемых во Вселенной, обусловлено четырьмя видами фун-
фундаментальных взаимодействий: гравитационными, слабыми,
электромагнитными и сильными или, что то же самое, ядер-
ядерными взаимодействиями.
Самым слабым является гравитационное взаимодействие.
Оно осуществляется между любыми массами и проявляется
в форме сил тяготения. Роль сил тяготения возрастает при пе-
переходе к большим массам. В микромире силы тяготения прак-
практически никакой роли не играют. Их роль является определяю-
определяющей только в крупномасштабных явлениях. (Сила притяжения
тел Землей играет определяющую роль в геофизических и дру-
других явлениях на поверхности Земли, таких как горообразова^
ние, течение рек, ходьба человека и т. д. Силы тяготения под-
поддерживают существование Солнечной системы и различных
звездных скоплений.)
Слабые взаимодействия, в отличие от гравитационных, не
способны создавать устойчивые состояния вещества, наподобие,
например, Солнечной системы. Они обусловливают нестабиль-
нестабильность многих микроскопических частиц, приводя к их распадам,
и характерны только для определенного круга микроскопиче-
микроскопических квантовых процессов.
Электромагнитные взаимодействия осуществляются между
телами, в состав которых входят электрически заряженные ча-
частицы. Эти взаимодействия обусловливают существование ста^
бильных атомов, связывают атомы в молекулы, являются при*
чиной действия сил между частицами газов, жидкостей, твердых
тел, плазмы и играют основную роль во всех физико-химиче-
физико-химических и биологических процессах. Именно к электрическим взаи-
взаимодействиям сводятся практически все силы нефундаменталь-
нефундаментального характера.
Сильные взаимодействия являются наиболее мощными. Они
осуществляются между частицами из групп так называемых
мезонов (за исключением мюона) и барионов — микрочастиц,
обусловливающих процессы ядерной физики высоких энергий.
Именно эти взаимодействия связывают протоны и нейтроны в
атомных ядрах. Характерной особенностью сильных взаимодей-
взаимодействий является их малый радиус действия. Они проявляются
только в том случае, если расстояние между сильно взаимо*
действующими частицами по порядку величины не превышает
Ю-15 м.
В классической механике все силы имеют гравитационную
и электромагнитную природу. Слабые взаимодействия играют
роль в специфических микроскопических явлениях существенно
квантовой природы. Сильные взаимодействия также не могут
быть включены в схему классической механики, так как

70
ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ
\ГЛ 2
действуют только на очень коротких расстояниях, т. е. опять-
таки существенны для микроскопических квантовых явлений.
Ниже мы опишем наиболее важные силы классической механики.
3. Гравитационные взаимодействия подчиняются закону все-
всемирного тяготения. Его нерелятивистская формулировка: лю-
любые две частицы притягиваются друг к другу с силой, на-
направленной вдоль линии, соединяющей частицы; величина силы
пропорциональна произведению масс частиц и обратно пропор-
пропорциональна квадрату расстояния между
ними. Коэффициент пропорциональности
Y называется гравитационной постоян-
-П ной. В СИ
п~
Рис. 2.6.
у = 6,672- 10~и Н-м2/кг2.
Пусть одна из частиц с массой Ш\ на-
находится в точке с радиус-вектором ги
а положение другой частицы с массой /п2
характеризуется радиус-вектором г2.
Обозначим силу, которая действует на массу Ш\ со стороны
массы т2, через F\2. Тогда закон всемирного тяготения выра-
выражается формулой
n, B.20)
где \г2 — Г\\ обозначает длину вектора г2 — гь а
1*2 -~"" 1*1
I г2 — Гх |
'—единичный вектор в направлении вектора г2 — гь характери-
характеризующий направление действия силы F{2 (рис. 2.6). По опреде-
определению п2 = 1.
Силы тяготения между телами, с которыми человеку при-
приходится иметь дело в повседневной жизни, очень малы. Так,
два тела с массами по 104 кг (масса железнодорожного вагона)
на расстоянии в 1 м притягиваются с силой порядка 10~2 Н. Эта
сила находится на пределе возможностей современной измери-
измерительной техники. С другой стороны, спадание силы тяготения
с расстоянием сравнительно медленное. Поэтому при достав
точно больших массах силы тяготения могут проявляться и
действительно проявляются на очень больших расстояниях,
вплоть до астрономических.
Замечательным свойством силы B.20) является ее пропори
циональность массам взаимодействующих частиц. Поэтому за^
кон всемирного тяготения дает возможность принципиально
иного, гравитационного измерения масс, Определенные именно

2.3]
ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ
71
таким образом коэффициенты тх и т2 в законе B.20), которые
можно назвать гравитационными массами, могли бы и не сов-
совпадать с массами частиц, измеренными по методу, описанному
в предыдущем параграфе. Так измеренные массы называют
инертными. Однако инертные и гравитационные массы удиви-
удивительным образом совпадают. Это является экспериментальным
фактом, установленным Р. Этвешем в 1894 г.
Суть опытов Этвеша заключается в следующем. Любое тело
на Земле участвует в движении Земли. Поэтому ускорение тела
всегда имеет составляющую ап, имеющую смысл нормального
ускорения, обусловленного вращением Земли. Таким образом,
ускорение тела в любых условиях на Земле должно записы-
записываться в виде а + ап, где а — ускорение, вызванное действием
на тело какой-либо силы. В условиях опыта тело является не-
нерелятивистской частицей. Тогда, если она испытывает действие
только силы тяготения, то уравнение ,
ее движения будет иметь вид
где m — инертная масса частицы, а
F— сила тяготения. Из этого урав-
уравнения видно, что ускорение а мож-
можно рассматривать как результат
действия двух сил: силы тяготения
F и фиктивной силы —man. Сила F
направлена к центру Земли, а сила
—man направлена от оси вращения
Земли (рис. 2.7). Эти силы совпа-
совпадают по направлению только на
экваторе. На всех остальных широтах эти силы не параллель*
-ны. Поэтому направление суммы сил F и —man зависит от от-
отношения инертной массы m к гравитационной массе частицы,
входящей в выражение для F. Если бы это отношение менялось
от тела к телу, то направления ускорений а различных тел
слегка отличались бы друг от друга. Однако проведенные
Этвешем измерения с точностью до 10~9 не обнаружили такого
отклонения. Недавно В. Б. Брагинский довел точность этого
опыта до К)-11.
Следовательно, гравитационная и инертная массы пропори
циональны друг другу, При соответствующем выборе коэффи^
циента в законе всемирного тяготения (гравитационной постоян-*
ной у) они будут одинаковыми.
Из равенства гравитационной и инертной масс следует, в
частности, что одна и та же сила тяготения сообщает одинако-
одинаковое ускорение всем телам, независимо от того, какова их масса*
Это связано с тем, что в уравнении движения каждой частицы
Рис. 2.7.

72 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ 1ГЛ. 3
произвольной системы (произвольного тела), испытывающей
действие только сил тяготения, масса частицы никакой роли не
играет. Она входит коэффициентом и в левую (через импульс),
и в правую (через силу) части уравнения движения и таким
образом может быть сокращена.
Отмеченная особенность гравитационных сил позволяет про*
вести следующую аналогию. Рассмотрим систему свободных тел
с точки зрения какой-либо неинерциальной системы отсчета,
т. е. системы отсчета, движущейся с некоторым ускорением от-
относительно инерциальной системы. Очевидно, что относительно
неинерциальной системы все тела также будут обладать оди-
одинаковыми ускорениями, т. е. будут вести себя так, как если бы
появились силы тяготения. С другой стороны, возможно и об-
обратное рассуждение. Связав с телом, находящимся под дей-
действием гравитационных сил, движущуюся вместе с ним неинер-
циальную систему отсчета («лифт Эйнштейна»), мы получаем
возможность «избавиться» от тяготения, поскольку в этой си-
системе тело будет вести себя как свободное. Следовательно, из
равенства инертной и гравитационной масс вытекает всеобщий
фундаментальный закон, называемый принципом эквивалент-
эквивалентности:
Переход к неинерциальной системе отсчета эквивалентен по-
появлению гравитационных сил, и, наоборот, гравитационные
силы в любой достаточно малой области пространства «выклю-
«выключаются» переходом к подходящей неинерциальной системе от-
отсчета.
Принцип эквивалентности является законом, положенным
А. Эйнштейном в основу теории тяготения, известной под на-
названием общей теории относительности.
4. Основным фундаментальным законом сил, создаваемых
электромагнитными взаимодействиями, является закон Кулона.
Он определяет силу взаимодействия двух неподвижных или
медленно движущихся друг относительно друга*) заряженных
частиц. Кулоновская сила направлена вдоль линии, соединяю-»
щей частицы. Величина силы пропорциональна произведению
зарядов частиц и обратно пропорциональна квадрату расстоя*
ния между ними. В СИ коэффициент пропорциональности ра-
вен &=:9-109 Н-м2/Кл. В СГС он равен 1. Заряд частицы яв-
является физической величиной, зависящей только от вида ча-
стицы и не меняющейся в присутствии внешних сил.
Если частица с зарядом q\ находится в точке с радиус-век-
радиус-вектором ги а частица с зарядом q2 находится в точке с радиус-
вектором г2, то сила F\2 действия второй частицы на первую
*) То есть со скоростями, ничтожными в сравнении со скоростью света
в вакууме с»

§ 2.3] ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ 73
согласно закону Кулона записывается так:
п обозначает единичный вектор, который теперь определен как
Г\ — Г2
I г, - г21 •
Сила тяготения всегда является силой притяжения. Куло-
новская сила может быть и силой отталкивания. Это озна-
означает, что заряд может быть как положительным, так и отрица-
отрицательным, а также равным нулю. В последнем случае частица
называется нейтральной. Как видно из B.21), притяжение осу-
осуществляется только для разноименных зарядов, т. е. при усло-
условии <7i<72 < 0. Одноименно заряженные частицы, для которых
Я\Ч2 > 0, отталкиваются.
Закон Кулона дает возможность измерять заряды частиц,
т. е. содержит определение заряда. Напомним, что единица из-
измерения заряда в СГС как раз и устанавливается с помощью
закона Кулона.
Область применимости закона Кулона превосходит область
применимости самой классической механики и простирается от
самых больших расстояний до 10~13 м. На еще меньших рас-
расстояниях он также применим, но уже с точностью 10~4. В обла-
области квантовых явлений (например, для электронов в атомах)
закон Кулона формулируется в ином виде.
Интенсивность кулоновских сил чудовищно велика. Для ил-
иллюстрации сравним гравитационные и кулоновские силы между
двумя протонами. Масса протона равна 1,7-10~27 кг, так что
величина их гравитационного притяжения на расстоянии г со-
составляет A,9-106)/г2 ньютонов. Электрический заряд протона
равен 1,6-109 Кл. Следовательно, сила электрического оттал-
отталкивания протонов на том же расстоянии г составит B,3- 10~30)/г2
ньютонов. Как видно, кулоновская сила превосходит гравита-
гравитационную в 1036 раз!
Подобно гравитационным, кулоновские силы имеют прак-
практически неограниченный радиус действия. Грамм протонов, на-
находящихся на Солнце, притягивает грамм протонов, находя-
находящихся на Земле, с силой в 50 ньютонов.
Во многих случаях приходится сталкиваться с системами
электрически заряженных частиц, движущихся в электромаг-
электромагнитных полях, созданных сторонними источниками. Так, в уско-
ускорителях ускорение заряженных частиц и стабилизация их
траекторий движения осуществляется с помощью электриче-
электрического и магнитного полей. Режим движения электронов в элек-
электронно-лучевой трубке телевизора и осциллографа также
определяется электрическим полем. Движение зарядов, т. е.

74 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ (ГЛ 2
электрический ток в проводнике, к которому приложено напря-
напряжение, вызывается электрическим полем. Список подобных при-
примеров, указывающих на практическую значимость и важность
взаимодействия заряженных частиц с внешним электромагнит-
электромагнитным полем, очень велик. Несмотря на различие в конструкции,
форме и габаритах систем, в которых это взаимодействие играет
основную роль, общим для всех них является фундаментальный
закон действия силы со стороны электромагнитного поля на
заряженную частицу. В СИ этот закон имеет следующий вид:
F = qE + q[vB], B.22а)
где q — заряд частицы, a v — ее скорость. В B.22а) Е и В обо-
обозначают электрическое и магнитное поле*) соответственно,
a [vB] — это векторное произведение v и В. Силу B.22а) на-
называют силой Лоренца, При этом ее составляющую qE назы-
называют электрической, а составляющую q[vB] — магнитной силой
Лоренца. Легко видеть, что последняя действует только на дви-
движущуюся частицу. При v = О частица испытывает лишь дей-
действие электрического поля.
В СГС сила Лоренца имеет несколько иной вид, а именно:
F=qE + ±[vB], B.226)
где с — скорость света в вакууме.
Свойства электрического и магнитного полей будут рассмот-
рассмотрены в следующем томе курса. В настоящем же томе там, где
нам придется встретиться с полями ? и В, мы будем считать
их заданными, т. е. известными величинами.
Напомним единицы, в которых поля Е и В измеряются.
В СИ электрическое поле измеряется в вольтах, отнесенных
к метру (В/м), а магнитное поле — в теслах (Тл). Из закона
B.22а) следует, что
1 В/м = 1 Н/Кл, 1 Тл = 1 Н • секДКл • м).
В СГС единицей измерения поля Е является дина, отнесенная
к единице измерения электрического заряда в этой системе:
1 дин _ Ю Н _р ^ Ю4 —
ед. СГСЭ 7з-Ю~9 Кл * м *
Поле В измеряется в гауссах (Гс): 1 Гс = 10~4Тл,
*) В некоторых книгах этч же величины именуют, соответственно, напря-
напряженностью электрического поля и индукцией магнитного поля. Однако в со-
современной физической литературе эти термины не используются, Они не бу-
будут применяться и в настоящем курсе

§ 2 31 ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ 75
Отметим, наконец, что законы B.22) применимы всюду, где
справедливо классическое понятие механического состояния, и
более того, они: обобщены на квантовые частицы.
5. Помимо заряженных частиц очень широко распростра^
нены в целом электронейтральные системы заряженных частиц.
Таковы, например, атомы и молекулы, в которых суммарные
заряды ядер и электронов равны по абсолютной величине. Такие
системы взаимодействуют друг с другом посредством электро-
электромагнитных полей, создаваемых электрически заряженными ком-
компонентами систем.
Так, законы сил, действующих между атомами и молекул
лами, совсем не похожи на кулоновский, хотя силы эти в конеч-
конечном счете имеют электрическое происхождение. Точный вид
закона взаимодействия частиц такого рода очень сложный.
В частности, сила их взаимодействия оказывается зависящей
не только от расстояния между взаимодействующими части-
частицами, но и от их взаимной ориентации. Однако в подавляющем
большинстве случаев достаточно знать силу взаимодействия,
усредненную по всем их возможным ориентациям. Закон дей-
действия усредненной таким образом силы оказывается сравни*
тельно простым. Его характерными свойствами являются сле^
дующие.
Сила направлена по линии, соединяющей частицы, и зависит
от расстояния между ними. На малых расстояниях действует
сила отталкивания, величина которой очень быстро возрастает
по мере уменьшения расстояния между частицами. В этом вы-
выражается сопротивление частиц взаимопроникновению. На
больших расстояниях действует сила притяжения. С увеличе-
увеличением расстояния сила притяжения сравнительно медленно убы-
убывает (но значительно быстрее кулоновской, примерно как г~7),
стремясь асимптотически к нулю. При некотором расстоянии
сила обращается в нуль. Это расстояние называется равновес-
равновесным и составляет величину порядка нескольких ангстрем.
Если, например, два нейтральных атома находятся в точках
с радиус-векторами Г\ и г2, то сила Fi2 действия второго атома
на первый имеет вид:
F12 = /(|r1 —г2|).л, B.23)
где f(\ri—r2\)—функция расстояния между атомами, харак*
тер которой изображен на рис. 2.8; п = Г[ ~ Г2 ,¦ , п2 = 1. На
рисунке равновесное расстояние обозначено через го. При г < г0
функция / характеризует силу отталкивания (левая часть
рис. 2.9). При г > го функция f характеризует силу притяжения
(правая часть рис. 2.9) %

76 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ 1ГЛ 2
Закон взаимодействия электронейтральных частиц хотя и
менее фундаментален, чем закон Кулона, но все же близок
к границе, разделяющей фундаментальные и нефундаменталь-
нефундаментальные законы. Область его применимости охватывает все явле-
явления, в которых атомы и молекулы при-
f(\rrrP\) нимают участие, не разрушаясь. В эту
область входят свойства газов, не-
неэлектролитических жидкостей и твер-
твердых тел типа парафина, состоящих из
отдельных молекул. Большинство
твердых тел составлены по-иному. На-
Например, поваренная соль составлена
не из атомов, а из ионов натрия и
хлора.
Точный вид зависимостей сил взаи-
взаимодействия электронейтральных ча-
Рис. 2.8. стиц от расстояния может быть полу-
получен из более фундаментальной теории
взаимодействия ядер и электронов. Но практически такие вы-
вычисления неосуществимы из-за их громоздкости. Поэтому за-
закон сил взаимодействия атомов и молекул подбирают, исходя
\rf-r2\<r0 \rf-r2\>r0
Рис. 2.9.
из опытных данных с привлечением модельных соображений
о распределении зарядов в атомах и молекулах. Вследствие
этого расчеты с применением этих сил обычно имеют невы-
невысокую точность.
6. Силы межатомных и межмолекулярных взаимодействии
действуют между микрочастицами. За ними в иерархии законов
сил идут уже совершенно не фундаментальные силы, действую-
действующие между телами или между частями тел, содержащими очень
много частиц. Наиболее часто используются три типа сил та-
такого рода: а) упругие силы и б) контактные силы, подразде-
подразделяющиеся на реакции опор и силы трения.
а) В первую очередь рассмотрим силу упругости, определяе-
определяемую законом Гука: сила сопротивления деформированию твер-
твердых тел пропорциональна величине деформаций при условии их
малости.
Различные типы деформаций будут описаны в гл. 13. Здесь
мы ограничимся рассмотрендем простейшей деформации —уже

§ 2.3]
ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ
Т7
знакомого нам одностороннего сжатия (рис. 2.5, стр. 68). Для
такой деформации закон силы имеет вид B.19).
Как известно, твердые тела имеют кристаллическое строе-
строение. Частицы, составляющие кристалл, стремятся занять так
называемые равновесные положения, в которых сила, действую-
действующая на каждую частицу, равна нулю. Предположим, что ча*
стицы кристалла являются нейтральными атомами. Тогда, по*
скольку они взаимодействуют друг с другом по закону B.23),
они стремятся расположиться
друг от друга на равновесных
расстояниях г0. Если тело де-
деформируется, то расстояния
между частицами становятся
либо больше, либо меньше го.
Однако если смещения частиц,
которые мы обозначим через
Аг, малы по сравнению с г0
(это и означает, что деформа-
деформации являются малыми), то в
малой области около точки г0
поведение функции f(r), где
г = \г{— г2|, можно аппрокси-
аппроксимировать прямой линией
—k-Ar, изображенной на
рис. 2.10 пунктиром. Если в Рис 2.10.
направлении деформирования
тело содержит N частиц, то каждая из них в этом направле-
направлении будет оказывать сопротивление, измеряемое силой —k-Ar.
Следовательно, сила сопротивления деформированию со сторо-
стороны всего тела будет равна —kN-Ar. Очевидно, что Al = N-Ar
определяет полное изменение размеров тела в направлении
деформирования. Тогда сила сопротивления будет равна —k-AL
Так как А/ характеризует величину деформации, то тем самым
мы убеждаемся в справедливости сформулированного выше за-
закона Гука в форме B.19).
Мы видим, что закон Гука может быть выведен из более
фундаментального закона B.23) и, таким образом, может быть
установлена область его применимости (разумеется, для тел.
состоящих из нейтральных молекул).
Можно поставить и обратную задачу: по постоянной закона
Гука — коэффициенту упругости k — получить информацию о
силах между молекулами. При этом оказывается, что для до-
достаточно твердых тел, таких, например, как алмаз и даже по^
варенная соль NaCl, силы между микрочастицами, составляю-
составляющими кристалл, на порядок и даже более превосходят силы
B.23). Это свидетельствует о наличии иных, более сильных

ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ
[ГЛ 2
типах свпзей в к . -сталлах. На этом вопросе мы остановимся
позднее, в ::уе Hi курса.
В дальнейшем нам не раз придется встречаться с дефор-
деформациями типа изображенной на рис. 2.11. Пусть пружина ориен*
тирована в ^-направлении и обладает коэффициентом упруго-
упругости k. Если она, например, сжата так, что ее конец сместился
на расстояние g относи-
относительно того положения,
которое он занимав до
деформирования, то в
этом случае закон Гука
можно записать в форме
X
Рис. 2.11.
= {-ft?, 0,0}. B.24)
б) Контактными называются силы, возникающие при со-
соприкосновении двух тел и действующие со стороны одного тела
на другое. Эти силы важны для расчета прочности подшипни-
подшипников, зубчатых передач и др. Мы ограничимся рассмотрением
этих сил, предполагая твердые тела абсолютно твердыми.
В этом случае контактные силы сводятся к силам реакции опор
и трения.
Сила реакции опоры, которую испытывает тело, приведенное
в контакт с другим, направлена по нормали к поверхности кон-
контакта в сторону от тела, являющегося источником реакции опо-
опоры. Для пояснения мы приводим рис. 2.12, на котором изобра-
изображены два контактирующих тела 1 я 2.
Вектор /?i2 изображает силу реакции
опоры, которую испытывает тело / со
стороны тела 2. При этом, согласно
третьему закону Ньютона, сила /?2i, дей-
действующая со стороны тела 1 на тело 2,
по абсолютной величине равна R\2 и про-
противоположно направлена: /?2i = —R\2-
Сила реакции опоры является пре-
предельным частным случаем упругой силы.
Область применимости силы реакции
ограничена ситуациями, в которых можно пренебречь дефор-
деформациями тел.
Механизм трения заключается в следующем. Если одно тело
приведено в движение относительно другого и при этом нахо«
дится с ним в контакте вдоль некоторой поверхности, то ча«
стицы тел, расположенные вблизи этой поверхности, начинают
друг за друга цепляться. В этом и заключается природа тор-»
мозящего действия. Такие силы пока не поддаются точному
расчету на основе микроскопических представлений о строении
Рис. 2.12.

§ 2.3] ВИДЫ ВЗАИМОДЕЙСТВИЙ И СИЛЫ 79
тел. Поэтому законы их действия устанавливаются опытным
путем. Основными из них являются следующие.
Сила сухого трения между двумя контактирующими твер<
дыми телами направлена в сторону, противоположную движе-
движению тела, на которое она действует. Ее абсолютное значение
не зависит от скорости относительного движения тел и пропор-
пропорционально силе реакции опоры. Коэффициент пропорциональ*
ности называется коэффициентом трения. Он определяется экс^
периментально.
Рис. 2.13 поясняет этот закон. На нем изображены два тела
1 я 2У причем первое движется относительно второго со ско-
скоростью v. Вектор Fi2 изобра-
изображает силу трения, действие ко-
которой испытывает тело 1, век-
вектор /?i2 — сила реакции опоры
со стороны тела 2;
v /л лг-ч ^
12=^12-»-. B.25)
V
л л. Рис 2.13.
где |и — коэффициент трения.
Значение коэффициента \х за-
зависит не только от соприкасающихся материалов, но и от мно-
многих свойств поверхностей соприкосновения: их обработки, за-
загрязненности и т. д.
Подчеркнем, что, во-первых, от скорости не зависит только
абсолютная величина силы трения. Если скорость относитель-
относительного движения тел изменяет направление, то меняет свое на*
правление и вектор силы трения. Во-вторых, постоянство абсо-
абсолютного значения силы трения между твердыми телами не-
несколько нарушается при малых скоростях, где наблюдается
Рис. 2.14.
некоторое увеличение силы трения. И то, и другое замечание
иллюстрирует рис. 2.14. На нем представлено, как меняется
х-компонента силы трения от скорости для движения, изобра-
изображенного на рис. 2.13. При стремлении скорости к нулю значение
силы трения по абсолютной величине несколько возрастает.

80
ДИНАМИЧЕСКИЕ ПРИНЦЙПЬ! МЕХАНИКИ
ТгЛ. г
Однако при v = 0 сила трения — она называется силой трения
покоя — однозначно не определена. Ее значение может быть лю-
любым в пределах отрезка, выделенного на графике (рис. 2.14)
вертикальной жирной линией.
На тело, движущееся в жидкости или газе, действует сила
сопротивления окружающей тело среды. Так же как и сила
трения, сила сопротивления ориентирована противоположно
Рис. 2.15.
скорости тела. Абсолютное значение силы зависит от того, ка-
каким образом вещество среды обтекает тело, что в свою очередь
определяется величиной его скорости. Если скорость тела не-
невелика (критерий малости будет установлен в § 11.3), то воз-
возникающие в среде течения носят ламинарный характер
(рис. 2.15). При ламинарном течении сопротивление опреде-
определяется законом Стокса: сила сопротивления пропорциональна
скорости движения тела,
F = -av. B.26)
Коэффициент пропорциональности а является постоянной, зна-
значение которой зависит от размеров тела и от вязких свойств
среды.
Рис. 2.16.
При больших скоростях закон сопротивления имеет другой
вид. С возрастанием скорости течение среды из ламинарного
превращается в турбулентное (рис. 2.16). При турбулентном те^
чении и скоростях движения, не превосходящих скорости звука
в среде, сопротивление определяется законом Ньютона\ сила
сопротивления пропорциональна квадрату скорости движения!

§2.4]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
81
тела,
B.27)
Коэффициент |3 является постоянной, значение которой зависит
от размеров и формы тела, а также от плотности среды.
Законы Стокса и Ньютона будут подробно обсуждаться
в § 11.3, где будет приведено их микроскопическое обоснование.
Мы перечислили, конечно, не все феноменологические, не-
нефундаментальные силы. Например, остались нерассмотренными
силы поверхностного натяжения. Можно, однако, сказать, что
перечисленных сил достаточно для решения многих практиче-
практических задач о движении, которое не сопровождается полным или
частичным разрушением тел.
§ 2.4. Потенциальная энергия
1. Очень важной величиной, характеризующей свойства дви-
движения частицы под действием силы, является работа, которую
сила производит. Остановимся на определении этой -величины.
Из курса физики средней школы известно, что если на частицу,
движущуюся по прямой линии, действует постоянная сила F>
направленная под углом а к движению, то работа силы при
перемещении частицы на вектор Дг
равна z'
ДЛ = F Дгсоэа.
В векторных обозначениях эта форму-
формула записывается так:
ДЛ = 0Р- Дг). B.28а)
Здесь (F-Дг) обозначает скалярное
произведение векторов F и Дг.
Напомним, что в СИ работа изме-
измеряется в джоулях A Дж = 1 Н-1 м),
а в СГС — в эргах A эрг = 1 дин-1 см). При этом 1 эрг =,
= Ю-7 Дж.
Формула B.28а) справедлива только в случае постоянной
силы и прямолинейного движения частицы. Если эти условия
не соблюдаются, то правило вычисления работы определяется
следующим образом. Рассмотрим бесконечно малый участок
траектории произвольного вида, заключенный между бесконечно
Олизкими точками с радиус-векторами т' и rf + dr' (рис. 2.17).
Предположим, что в точке г' на частицу действует сила F.
Вследствие малости участка мы можем пренебречь изменением
силы, считая ее постоянной во всех точках участка и равной F.
Рис. 2.17.

82 динамические Принципы механики \тл 2
Кроме того, сам участок можно считать практически не отли-
отличающимся от вектора dr', полагая тем самым, что частица дви-
движется прямолинейно вдоль вектора dr'. К такому бесконечно
малому перемещению уже можно применить формулу B.28а):
dA = {F-dr'). B.286)
Здесь dA называется элементарной работой силы, производи^
мой при перемещении частицы из точки г' в положение с ра-
радиус-вектором г' -\-dr' (рис. 2.17).
Работа, производимая в единицу времени, называется мощ-
мощностью. Если перемещение dr' осуществляется за время dt, то
мощность равна
где v = dr'jdt — скорость частицы.
В СИ мощность измеряется в Дж/сек. Единица 1 Дж/сек
называется ваттом (Вт):
1 Вт = 1 Дж/сек.
В СГС мощность измеряется в эрг/сек,
1 эрг/сек = 10~7 Вт.
Работа на любом конечном участке траектории, заключен-
заключенном между точками г0 и г, определяется суммой всех элемент
тарных работ, производимых при данном перемещении. Эта
сумма равна
и называется интегралом от силы вдоль данного участка траек-»
тории.
2. Поскольку работа получается суммированием по многим
точкам, т. е. по многим состояниям, то в общем случае работа
зависит от того, как меняется состояние.
Любое изменение состояния называется процессом.
Таким образом, в общем случае работа является функцией
процесса. Иными словами, работа, совершаемая при перемещен
нии частицы, зависит от формы ее траектории.
Существуют, однако, силы, работа которых определяется
только начальным и конечным состояниями частицы и форма
траектории на величину работы не влияет. Такие силы назы-
ваются потенциальными или консервативными. Все остальные
относятся к силам непотенциальным или неконсервативным.
Поясним сказанное на рис. 2.18. На нем изображены участ*
ки АСВ и ADB двух траекторий, соединяющих одни и те же

§ 2.4] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 83
точки А и В. Если интеграл от силы вдоль участка АС В сов-
совпадает с интегралом от силы вдоль участка ADB, то сила по-
потенциальна. Если это не так, то сила относится к числу непо-
непотенциальных. Примеры как тех, так и других будут приведены
ниже.
Согласно определению интеграл от потенциальной силы за-
зависит только от пределов интегрирования. Если они опреде-
определяются радиус-векторами г0 и г, то для потенциальной силы
работа является функцией только г0 и г:
Эта функция обладает двумя очевидными свойствами. Во-
первых,
НтФ(г0, г) = 0,
ибо при отсутствии перемещения работа не совершается. Во-вто-
Во-вторых,
ф(г0, г) = Ф(г0, г') + Ф(г', г),
где г' — радиус-вектор любой промежуточной точки на данном
участке траектории. Действительно, сумма работ на двух по-
последовательных участках траектории
определяет работу при перемещении
от начала первого участка до конца
второго. При любом законе действия
потенциальной силы функция Ф(г0, г)
будет обладать указанными свойства-
свойствами только в одном случае, а именно
тогда, когда она имеет вид разности
значений в точках г0 и г одной и той
же функции U положения частицы в Рис- 2-18#
пространстве: Ф(г0, r)= U(г0) — U(г).
Таким образом, работа потенциальной силы может быть пред-
представлена в виде
АА
= J dA = J (F . dr) = U (r0) - U (г). B.30)
Функция U положения частицы в пространстве называется
потенциальной энергией частицы. Она всегда имеет смысл энер-
энергии взаимодействия с объектами, создающими данное силовое
воздействие на частицу. Работа потенциальной силы всегда
равна со знаком минус изменению потенциальной энергии ча-
частицы при ее перемещении из одного положения в другое. Если
же начальное положение частицы фиксировано, то работа по-
потенциальной силы зависит только от конечного состояния ча-
частицы.

Г X
Р
1 Ч "
т?
Г z
dU(r)
dx
dU(r)
dy
dU(r)
dz
dU (x, у,
дх
dU {ху i/,
ду
dU (х, у,
dz
z)
2)
z)
84 ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ 1ГЛ. S
Потенциальная энергия измеряется в тех же единицах, что
и работа.
Потенциальная энергия частицы как функция радиус-век-
радиус-вектора точки пространства зависит от трех переменных х, у, z—
координат радиус-вектора. Оказывается, что если эта функция
U(r)= U(x,y,z) задана, то компоненты силы, действующей на
частицу в точке с радиус-вектором г, определяются формулами
B.31)
В правых частях равенств B.31) фигурируют частные произ-
производные U{x,y,z) по переменным х, у, z. В математике вектор
с компонентами |-^г> -y-i ~^г < называется градиентом функ-
функции U и обозначается либо символом grad ?/, либо симво-
символом VU. В этом томе мы будем пользоваться первым обозна-
обозначением. Таким образом, в векторной форме равенства B.31)
записываются так:
F = - grad U. B.32)
Докажем справедливость B 31). Для этого предположим, что начальное
п конечное положения частицы отличаются на бесконечно малый вектор dr—
= {dx, dy, dz} Тогда с одной стороны работа равна (F • dr) = Fxdx + Fydy-\-
+ Fzdz, а с другой стороны она же может быть определена в виде
U {r)-U (г Л- dr) = U (х, у, z)-U {x + dx, у + dyy z + dz) =
dU . dU . dU ,
= r— dx r— dy r— dz.
dx dy v dz
Сравнение этих выражений и доказывает справедливость B.31).
Обратим внимание на следующую важную особенность. Если
к потенциальной энергии добавить постоянную величину, то
сила от этого не изменится, поскольку ее вычисление связано
с дифференцированием потенциальной энергии. Следовательно,
потенциальная энергия определяется не однозначно, а с точ-
точностью до произвольной постоянной, и прибавление этой по-
постоянной не меняет картины силового взаимодействия. Обычно
произвольную постоянную выбирают таким образом, чтобы зна-
значение потенциальной энергии частицы, далеко удаленной от
источника силы и потому не испытывающей действия силы,
было равно нулю.

§2 4] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 85
3. Из B.31) следует, что действующая на частицу потен-
потенциальная сила и потенциальная энергия частицы могут зави-
зависеть только от координат точки пространства, в которой нахо-
находится частица. Поскольку каждой точке пространства отвечает
определенный вектор силы, то значения силы во всех точках
характеризуют силовые свойства окружающего частицу про-
пространства. В этом случае говорят, что задано потенциальное
силовое поле, в котором движется частица.
Заметим, что рассмотренные в предыдущем параграфе силы
тяготения, взаимодействия зарядов, взаимодействия нейтраль-
нейтральных атомов и молекул, сила упругости зависят только от ко-
координат частиц. Рассмотрим сначала три первые силы. Для них
можно ввести единое обозначение, а именно:
-Fl2 = Ф ( I '"l — Г2 |) • Л.
Здесь Г\ — радиус-вектор частицы, испытывающей действие силы
со стороны другой частицы, являющейся источником силы и
занимающей точку с радиус-вектором г2. Для силы тяготения
фA Г1 —г2|) = —|ГУ^2.2 » Для кулоновской силыф(| rl—r2\) =
== ^ 1—_—pi a Для силы межатомного или межмолекуляр-
межмолекулярного взаимодействия <р (| г\ — г2 |) = / (| Г\ — г21).
Отметим, что силовое поле тяготения и электрического дей-
действия зарядов принято называть кулоновским. Своим проис-
происхождением это название обязано тому, что, с точностью до
постоянных коэффициентов, законы действия сил тяготения и
Кулона одинаковы.
Зафиксируем положение источника силы Fi2, т. е. радиус-
вектор г2. Выберем такую систему отсчета, в которой источник
силы находится в начале координат. В этой системе г2 = 0.
Поскольку эта переменная теперь будет отсутствовать, то в це-
целях упрощения записи радиус-вектор Г\ переобозначим на г.
Тогда
Fi2 = F12 (г) = Ф (| г I)^ = Ф (г) f . B.33)
Индексы у силы мы сохранили, чтобы подчеркнуть, что она
действует со стороны одной частицы на другую.
Существует специальная терминология, применяемая к силам
вида B.33) и к соответствующим полям. Сила, закон действия
которой имеет вид B.33), называется центральной. Соответ-
Соответствующее силовое поле называется центрально-симметричным,
а место расположения источника силы — силовым центром.
Центральная сила направлена по прямой линии, соединяю-
щей частицу с силовым центром, а абсолютное значение силы
зависит только от расстояния до силового центра.

86
ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХЛИИКИ
ГГЛ 2
Именно этими свойствами и обладает выражение B.33).
Вектор F\2 направлен вдоль (или против, если ф < 0) радиус-
вектора г. Абсолютное значение силы равно ф(г). Во всех точ-
точках сферы радиуса г оно одинаково (рис. 2.19).
Проверим непосредственно, что работа сил вида B.33) не
зависит от формы траектории частицы. Интеграл от силы Fl2
вдоль участка любой траектории,
соединяющего точки г0 и г, равен
Рис. 2.19.
Воспользуемся тождеством (г' • dr') =
= -~d (г' • г') = ^ dr'2=r' dr\ где г'
обозначает абсолютное значение
вектора г'. Согласно этому тожде-
тождеству
Здесь уже фигурирует обычный одномерный интеграл по пере-
переменной г'. Пределы интегрирования, очевидно, определяются
абсолютными значениями векторов г0 и г, т. е. равны г0 и г.,
Следовательно,
где —U(r)—первообразная функции ф(г). Тем самым установ-
установлено, что силы тяготения, взаимодействия между заряженными
частицами, взаимодействия между нейтральными атомами и
молекулами являются потенциальными.
Функция U (г) определяет потенциальную энергию частицы
в поле действия силы вида B.33). Мы получили, что эта энер-
энергия зависит только от модуля радиус-вектора точки простран^
ства и не зависит от его направления. Именно так и должно
быть, поскольку в центрально-симметричном поле все точки на
любой сфере, центр которой совмещен с источником силы, фи^
зически эквивалентны.
Потенциальная энергия частицы в кулоновском поле, удов^
летворяющая требованию обращения в нуль при бесконечно
большом удалении частицы от силового центра, равна
?/(г) = у, B.34)
Если же силовой центр занимает точку с радиус-вектором г2,
а частица, потенциальная энергия которой рассматривается,
находится в точке с радиус-вектором Т\% то потенциальная

§2 4] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 87
энергия определяется формулой
В B.34) и B.35) в случае тяготения а = —ут\т2, а в слу-
случае кулоновского взаимодействия а = kq\q2. Мы остановимся
только на до1?а§&тельстве B.34). Формула B.35) является три-
тривиальным обобщением B.34). Справедливость B.34) устанав-
устанавливается непосредственным вычислением. Рассмотрим, напри-
0U
мер, - —:
ди _ d (\\_ JL(X\EL—1L EL
~~ dx ~~~~a~dx~\r )~~-"~~а дг \r ) дх~-~ г2 ' дх'
Однако г = л/х2 + y2-\-z2. Поэтому ~^- = —- ==¦== —.
дх <\х2 + у2 + z2 v
Следовательно,
Аналогичным образом легко установить, что
^ dU а _? dU _а_ ?_
~ду ""Т2 ' г у д7~"г2*г#
Эти равенства можно объединить в одно векторное соотио
шение:
Его правая часть при а = —ут\т2 определяет силу тяготения,
действующую на массу т\ со стороны массы т2, расположенной
в начале координат. При а = kq\q2 мы приходим к кулоновской
силе взаимодействия зарядов q\ и q2 при аналогичном их рас-
расположении. Следовательно, B.34) и B.35) действительно опре-
определяют потенциальную энергию в этих случаях.
Рассмотрим подробнее потенциальную энергию тела массы т
в поле тяготения Земли. Обозначим радиус Земли через R, а е?
массу через М. Пусть частица массы т находится на высоте h
над поверхностью Земли (рис. 2.20). Тогда согласно B.34)
потенциальная энергия частицы равна*)
тт/1\ шМ шМ
и Щ — - Y т^ртГ — ~~ Y R(\+h/R) '
*) Раз упоминается поверхность Земли, то Землю, конечно, никак нельзя
считать частицей. Мы заостряем на з^ом внимание в связи с тем, что закон
всемирного тяготения был сформулирован для частиц. Оказывается, однако,
что гравитационное взаимодействие частицы с телом сферической формы так-
также носит кулоновский характер, в чем мы предлагаем читателю убедиться
самостоятельно.

88
ДИНАМИЧЕСКИЕ ПРИНЦИПЫ МЕХАНИКИ
1ГЛ 2Л
Если h «С R, то h/R « 1, и в этом случае с очень большой точ«
ностью 1 * = 1 — ~. Тогда
тМ ,
Рис. 2.20.
~" Y D I Y D2 fl"
Первый член является постоянной величиной и, следовательно,
несуществен. Второй член хорошо знаком из курса средней
школы. Обозначив yM/R2 = g, мы получим знакомую формулу
для потенциальной энергии в поле тяжести Земли: U(h)= mgh.
Тем самым величина g является ускоре-
ускорением свободного падения.
Из проделанного вывода следует, что
эта формула имеет область применимости,
ограниченную неравенством h <C R.
Соотношение g = yM/R2 позволяет оце-
оценить массу Земли. Принимая g «
« 9,8 м/сек2, R « 6,4-106 м, получим: М =
= gR2ly& 6-Ю24 кг.
Вид потенциальной энергии сил межатомного и межмолеку-
межмолекулярного взаимодействий мы можем охарактеризовать только
качественно. Потенциальная энергия U частицы, находящейся
в поле силы B.23), изменяется в зависимости от расстояния г
до центра по закону, изображенному на рис. 2.21. На равновес-
равновесном расстоянии г0 потенциальная
энергия имеет экстремум, по-
поскольку сила (компоненты кото-
которой с точностью до знака равны
производным потенциальной
энергии) в этой точке равна ну-
нулю. Этот экстремум с необходи-
необходимостью должен быть минимумом.
Только в этом случае при смеще-
смещении влево от равновесного поло-
положения мы получим силу отталки- ип1п
вания, а при смещении вправо —
силу притяжения.
Действительно, при условии минимума в точке г0 потенциальная энергия
при г <; г0 с увеличением г0 уменьшается. Это значит, что dUjdr << 0. Взятая
с обратным знакам, эта производная характеризует силовое воздействие на
частицу в радиальном направлении. Следовательно, —dU/dr > 0 определяет
силу, направленную от силового центра, т. е. силу отталкивания FOTJ>
(рис. 2.21). Аналогичным образом нетрудно установить, что при г > г0 на ча-
частицу будет действовать сила притяжения Fnp (рис. 2 21).
Наглядно направление силы по виду потенциальной кривой
можно определять так. Сила в данной точке действует в ту
" > отталмиЬания
Рис. 2.21.

§ 2.4] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 89
сторону, в которую покатится шарик, положенный на горку в
форме этой кривой (рис. 2.21).
Рассмотрим теперь силу упругости. Она также является по-
потенциальной. Если эта сила действует вдоль лг-направления
(рис. 2.11), то ей соответствует потенциальная энергия
и = Ц-. B.36)
Действительно,
F — — ^L — 6U — Ь?- Р — dU — П- F — ELL — П
1 х~ ах —~~~ 01 —-"¦*&> ty~"~~~di'~'{J) tz~ dz~V>
что согласуется с формулой B.24).
Помимо рассмотренных, к числу потенциальных относятся
силы, действующие со стороны постоянного во времени элек-
электрического поля любой конфигурации на заряженную частицу.
Потенциальность взаимодействия зарядов с постоянным (или,
как его часто называют, электростатическим) полем является
следствием потенциальности кулоновской силы.
Несмотря на зависимость магнитной силы Лоренца от ско-
скорости, ее можно отнести к числу потенциальных. Ее работа от
формы траектории частицы не зависит просто потому, что все-
всегда равна нулю. Действительно, согласно B.22) магнитная
составляющая силы Лоренца всегда перпендикулярна скорости
частицы v. Следовательно, в любой точке траектории она пер-
перпендикулярна направлению перемещения частицы. А сила, пер-
перпендикулярная смещению, работы не производит.
4. В отличие от рассмотренных сил, силы трения, сопротив-
сопротивления среды, так же как силы действия на заряженные ча-
частицы со стороны переменных электрических полей, к числу
потенциальных не относятся.
Рассмотрим работу сил трения. По определению она направ-
направлена строго против движения. Следовательно, (F-dr)=*
= —|F| • \dr\ = —Fdr, где dr определяет длину элементарного
смещения. Для простоты рассмотрим случай силы трения, по-
постоянной по величине: F = const. Работа этой силы равна
I = J (F ¦ dr) = - J F dr = - Fl,
где / — длина пройденного участка траектории. Очевидно, что
при заданном начальном и конечном положениях / зависит от
формы траектории. Следовательно, тем же свойством будет
обладать и работа АЛ.
Подчеркнем, что свойство работы сил трения быть функцией
процесса обусловлено тем, что действие этих сил всегда сопро-
сопровождается выделением тепла. Особенности этих явлений будут
рассмотрены в следующей части этого тома. Переменные элек-
электромагнитные поля будут рассмотрены в следующем томе.

ГЛАВА 3
ЗАКОНЫ СОХРАНЕНИЯ
§ 3.1. Происхождение законов сохранения
1. Так же как и принцип относительности, законы сохранен
ния импульса, энергии и ряда других величин выделяются среди
всех физических законов своей всеобщностью, т. е. высшей сте-
степенью фундаментальности. Принцип относительности и законы
сохранения соблюдаются в нерелятивистской и релятивистской
физике классических и квантовых явлений.
Сначала принцип относительности и законы сохранения были
установлены опытным путем, как обобщение огромного коли-
количества экспериментальных фактов. Значительно позже пришло
понимание глубокой взаимосвязи этих законов, позволившее не
только осмыслить их всеобщность, но и предсказать, в каких
условиях тот или иной закон сохранения может нарушаться
или видоизменять свою форму.
Своим происхождением законы сохранения обязаны свой-
свойствам симметрии природы. Эти свойства выражаются в неиз-
неизменности вида физических законов, т. е, в их инвариантности,
при некоторых преобразованиях. Последние называются преоб-
преобразованиями фундаментальной симметрии.
Подчеркнем, что речь идет о свойствах законов, а не пред->
метов. Симметрия кристаллов, корпуса корабля, архитектурного
ансамбля, колец Сатурна, Галактики и т. д. — это не те свой-
свойства, которые мы здесь будем рассматривать.
В конце § 1.1 были определены пространственно-временные
преобразования фундаментальной симметрии. Остановимся бо^
лее подробно на физическом содержании симметрии по отноше-*
нию к каждому из них.
а) Симметрия по отношению к сдвигу начала координат,
или, как говорят, свойство однородности пространства, означает,
что все точки физического пространства эквивалентны. Эта
эквивалентность выражается в том, что явление, произошедшее
в одной области пространства, повторится без изменений, если
будет вызвано в другом месте. При этом необходимо перенести

§3 11 ПРОИСХОЖДЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ 91
в новое место всю совокупность факторов, существенно обу-
обусловливающих явление.
Например, два одинаковых лазера, выведенных на один и
тот же режим работы в Москве и Ленинграде, будут давать
одно и то же излучение. Если же в пределах точности измере-
измерений что-либо после переноса в пространстве не воспроизво-
воспроизводится, то это означает, что что-то существенное для данного
явления либо забыли, либо не смогли перенести, либо то и дру^
гое вместе. Так, ход настенных часов с маятником может из-<
мениться при их переносе из одной точки на Земле в другую.
Причина — изменение ускорения свободного падения — обусловь
лена неравномерным распределением массы вещества Земли.
Отметим, что именно благодаря однородности пространств?
можно сравнивать результаты одинаковых экспериментов, по-
поставленных в разных лабораториях.
б) Симметрия по отношению к сдвигу начала отсчета вре-
времени, или свойство однородности времени, проявляется в фи-
физической эквивалентности разных его моментов. Разные мо-
моменты времени эквивалентны в том смысле, что любой физиче-
физический процесс протекает одинаковым образом независимо от
того, когда он начался. При этом условия, существенные для
процесса, в будущем должны быть такие же, как и в про-
прошлом.
Например, с точки зрения свойств пучка протонов безраз-
лично, в какой день и час запустить Серпуховский ускоритель
протонов. Характеристики будут одинаковыми, если только
ускоритель будет работать в одном и том же режиме. Свойство
однородности времени позволяет сравнивать результаты опытов,
проделанных в разное время.
в) Симметрия по отношению к повороту координатных осей,
или свойство изотропности пространства, есть физическая экви-
эквивалентность разных направлений в пространстве. Она выра-
выражается в том, что в повернутой установке, агрегате, лаборато-
лаборатории и т. д. все процессы протекают точно так же, как и до
поворота. При этом повороту должно быть подвергнуто все,
определяющее течение процесса.
Так, работа черно-белого телевизора не изменится от того,
что он будет поставлен на бок. Однако если положить на бок
открытый сосуд с водой, то вода из сосуда выльется. Неэквива-
Неэквивалентность двух положений (вертикального и горизонтального),
выражающаяся в том, что в одном случае вода в сосуде по-
покоится, а в другом выливается, не свидетельствует об отсут-
отсутствии изотропии пространства. Для воды в сосуде существенной
является взаимная ориентация ускорения свободного падения g
и боковых стенок сосуда (фактор, не существенный для те-
телевизора), Если одновременно с поворотом сосуда также

92 ЗАКОНЫ СОХРАНЕНИЯ |ГЛ 3
развернуть g (что, увы, не в наших силах!), то с водой ничего
не случится.
г) Симметрия по отношению к переходу от покоя к состоя-
состоянию равномерного и прямолинейного движения, или свойство
галилеевской (нерелятивистские скорости) или лоренцевской
(релятивистские скорости) инвариантности, заключается в фи-
физической эквивалентности покоя и равномерного прямолиней-
прямолинейного движения. В любой системе все происходит независимо от
того, покоится система или движется равномерно и прямоли-
прямолинейно, если только переход от одного состояния к другому осу-
осуществляется со всем существенным окружением.
Так, любой опыт, проведенный в вагоне поезда на прямо-
прямолинейном участке железной дороги, на котором скорость поезда
постоянна, ничем не будет отличаться от такого же опыта,
поставленного в лабораторном корпусе.
2. В этом месте нам придется принять на веру вывод, вы-
вытекающий из исходных положений квантовой механики:
Каждому преобразованию фундаментальной симметрии соот-
соответствует закон сохранения определенной физической величины.
Классическая механика является предельным случаем кван-
квантовой. Поэтому указанная связь законов сохранения с фунда-
фундаментальной симметрией существует и в классической меха-
механике*).
Укажем для перечисленных выше симметрии соответствую-
соответствующие им законы сохранения.
а) Однородность пространства, т. е. симметрия по отноше-
отношению к преобразованию сдвига [см. A.16)], r = r' + r0, приводит
к закону сохранения импульса.
Закон сохранения импульса соблюдается только для изоли-
изолированных систем. Действительно, если исследуемая система по-
помещена во внешнее силовое поле, то для такой системы разные
области пространства будут физически неэквивалентными.
Внешнее поле в этих областях будет разным. Однако если ис-
исследуемую систему дополнить всеми физическими объектами,
являющимися источниками воздействия на систему, то будет
сохраняться импульс расширенной таким образом системы. Та-
Такая система уже «чувствует» фундаментальное свойство одно-
однородности пространства.
Отметим, что закон сохранения импульса может выполняться
частично для неизолированных систем. Если внешние условия
*) Интересно, что, не обращаясь к квантовой теории, связь законов со-
сохранения с симметрией Вселенной можно установить (Э. Нётер, 1918 г.),
только добавив к классическому понятию состояния постулат о существова-
существовании еще одного фундаментального закона, называемого принципом наимень-
наименьшего действия. В этом отношении квантовое понятие состояния является бо-
более мощным, чем классическое.

$311 ПРОИСХОЖДЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ 93
однородны е каком-либо одном направлении, то будет сохра-
сохраняться компонента импульса вдоль этого направления. Напри-
Например (в пренебрежении сопротивлением воздуха), при полете
камня сохраняется горизонтальная составляющая его импульса.
Вертикальная компонента меняется, так как с высотой изме^
няется потенциальная энергия камня в поле тяготения Земли,
которое по отношению к камню является внешним.
б) Однородность времени, т. е. симметрия по отношению к
преобразованию t = V + t0 [см. A.16)], приводит к закону со-
сохранения энергии. Этот закон выполняется для систем, нахо-
дящихся в неизменных во времени внешних условиях. Такие
условия создаются только потенциальными внешними полями и
называются стационарными.
Действительно, выбор начала отсчета времени несуществен,
если только неизменны во времени внешние условия, в которых
находится система. Приведем пример из школьного курса. Энер-
Энергия частицы в поле тяготения & = ^~ + mgh сохраняется по-
потому, что поле тяготения со временем не изменяется. Потен-
Потенциальная энергия mgh зависит только от высоты частицы h над
поверхностью Земли (га и v — масса и скорость частицы).
в) Изотропность пространства, т. е. симметрия по отноше-
отношению к поворотам, т. е. к преобразованиям вида A.17), приво-
приводит к закону сохранения момента импульса. За одним исключен
нием (см. ниже), закон сохранения момента импульса соблю-
соблюдается только для изолированных систем.
Момент импульса классической системы будет определен
в § 3.4. Необходимость изолированности системы для сохране-
сохранения ее момента импульса — того же свойства, что и для со-
сохранения ее импульса. Исключением, о котором упоминалось
выше, является движение частицы или системы частиц в цен-
центрально-симметричном внешнем поле. Очевидно, что по отно-
отношению к такому силовому центру пространство будет изотроп-
изотропным. Поэтому момент импульса частицы или системы частиц
в центральном силовом поле сохраняется.
г) Симметрия относительно перехода к движущейся системе
отсчета, т. е. по отношению к преобразованиям Галилея в не-
нерелятивистском случае и по отношению к преобразованиям
Лоренца в релятивистском, приводит к закону сохранения цен-
центра инерции. Он выполняется только для изолированных си-
систем. Справедливость этого закона была установлена в § 2.2
на примере системы нерелятивистских частиц.
Напомним весьма существенное обстоятельство: закона сохранения им-
импульса недостаточно для обоснования закона сохранения центра инерции. Не-
Необходимо знать связь между импульсом и скоростью. Эта связь устанавли-

94 ЗАКОНЫ СОХРАНЕНИЯ [ГЛ 3
вается только с привлечением требований галилеевской (нерелятивистские
движения) или лоренцевской (релятивистские движения) инвариантности, т. е.
с использованием фундаментальной симметрии относительно переходов от со-
состояния покоя к равномерному прямолинейному движению.
Отметим, наконец, что
для изолированной системы выполняются все перечисленные
выше законы сохранения, что является следствием принципа от-
относительности.
Действительно, изолированная система «чувствует» все виды
фундаментальной симметрии. Это означает независимость ее
свойств от выбора инерциальной системы отсчета, т. е. эквива-
эквивалентность всех инерциальных систем, провозглашаемую прин-
принципом относительности.
3. Важным является вопрос о зависимости сохраняющихся
величин друг от друга и от иных переменных. Вид этих зависи-
зависимостей во многих случаях определяется на основе исходных
положений квантовой механики*). Ряд зависимостей будет
выявлен в следующих параграфах. Здесь мы сформулируем
один из важнейших выводов квантовой теории, который также
придется принять без доказательства.
Энергия любой изолированной системы & зависит от ее
импульса P = {Px,Py,Pz} таким образом, что между &, Р и
скоростью центра инерции системы V = {Vx, Vyy Vz} существует
универсальная связь:
^Г' дРу ' дРГГ
Однако в классической механике C.1) выполняется не
только для изолированных систем. В этом мы убедимся в § 3.3.
§ 3.2. Закон сохранения импульса в классической механике
1. Проиллюстрируем связь однородности пространства с за-
законом сохранения импульса в области применимости класси-
классического понятия механического состояния, т. е. в классической
механике. Для упрощения вычислений ограничимся рассмотре-
рассмотрением изолированной системы двух частиц, способных переме^
щаться только в одном ^-направлении. Обозначим их коорди-
координаты через х\ и х2, а потенциальную энергию их взаимодействия
через U(x\,X2). Однородность пространства выражается в том»
что при изменении координат частиц на одну и ту же вели-
величину х0 = const (рис. 3.1) потенциальная энергия U(x\yx2) не
*) Или же (в классической механике) с привлечением упомянутого на
стр. 92 принципа наименьшего действия.

§ 3 2] ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА 95
изменяется:
При любой функции U это равенство возможно только в том
случае, если U зависит не от двух переменных Х\ и х2 порознь,
а только от их разности х — х\ — х2\
При этом условии силы, действующие на каждую частицу, со-
соответственно равны
р __ dU(xbx2) _ dU (х) _ дЦ(х) дх _ dU
12 dxi дх\ дх дх\ дх '
ь х2) __ _____ dU (х) __ __ дЦ (х) дх _ dU
21 дх2 дх2 дх дх2 дх
Мы получили не что иное, как третий закон Ньютона: F\2 =
= —F2\. Складывая теперь уравнения движения частиц
dp\ и dp2 п
где рх и р2 — импульсы частиц, получаем:
Следовательно, полный импульс системы Р = рх -\- р2 сохра-
сохраняется,
Р = Pi + P2 = COnst*).
Это соотношение показывает, что импульс аддитивен.
Рис. 3.1.
Это свойство выполняется для системы произвольного числа
N нерелятивистских частиц: сохраняющийся импульс равен
сумме импульсов частиц системы,
N
P = Pi+ ... +P;v=Sp; = const. C.2)
*) Здесь вместо стандартных обозначений векторов Fi2, F2b p{ и р% мы
писали просто F[2, F21, Ри р2, так как при одномерном движении векторы ори*
ентированы в одном направлении.

96 ЗАКОНЫ СОХРАНЕНИЯ [ГЛ 5
Отметим, что в такой формулировке закон сохранения им-
импульса справедлив и в квантовой области. Формулировка за-
закона сохранения импульса претерпевает изменение лишь в тех
случаях, когда существенной частью физической системы ока-
оказывается поле. В этих случаях сохраняется только суммарный
импульс частиц и поля. Сумма импульсов одних только частиц
постоянной во времени уже не является. Это наблюдается, на-
например, в системах, в состав которых входят электрические за-
заряды. Известно, что заряды могут излучать электромагнитные
волны и в свою очередь испытывать действие со стороны таких
волн. В этих случаях необходимо учитывать импульс электро-
электромагнитного поля, переносимый электромагнитными волнами. Им-
Импульс поля будет рассмотрен в следующем томе курса.
В некоторых случаях закон сохранения C.2) справедлив и
в релятивистской области: суммарный импульс изолированной
системы релятивистских частиц сохраняется в состояниях, в ко-
которых частицы очень удалены друг от друга. Причина ясна: на
большом расстоянии частицы перестают взаимодействовать и
становятся свободными. Поле — переносчик взаимодействия —¦
исчезает. Такие состояния реализуются, например, при осу-
осуществлении ядерных реакций. Ядерными называются реакции,
возникающие при столкновении атомных ядер и элементарных
частиц. Состояния, к которым можно применять законы сохра-
сохранения импульса в форме C.2), — это состояния частиц задолго
до и спустя много времени после столкновения. Эти состояния
принято называть асимптотическими.
2, Важным обстоятельством является следующее:
Универсальной формулы для импульса, пригодной во всех
случаях, не существует.
Так, в нерелятивистской теории импульс частицы р выра-
выражается через ее скорость v и массу m по формуле р = mv. Им-
Импульс р релятивистской частицы зависит от ее скорости уже
по иному закону:
mv
р = , =,
V1 - v-/c2
Рассмотрим еще примеры. Бесконечный (т. е., разумеется,
достаточно большой!) идеально выращенный монокристалл ча-
часто в хорошем приближении можно считать однородной средой,
в которой могут свободно двигаться электроны проводимости,
а также различные, как их называют, квазичастицы. Типичным
примером квазичастицы является квант звука — фонон. Физи-
Физическую сущность квазичастиц мы объясним в томе III, посколь-
поскольку для этого необходимы квантовые представления. Однако

§ 3.3] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 97
мощь современного подхода к законам сохранения проявляется
в том, что многие свойства квазичастиц можно понять, даже не
зная, как они устроены. Из-за строгой периодичности кристалл
переходит сам в себя при смещении на любое расстояние, крат-
кратное периоду решетки. Поскольку период решетки очень мал (по-
(порядка 10~10 м), то кристалл «почти» однороден относительно
пространственных смещений. Это означает, что как электроны
проводимости, так и квазичастицы обладают «почти» сохраняю-
сохраняющимися импульсами. Но движущийся кристалл явно физически
не эквивалентен покоящемуся. Поэтому уравнения движения
для электронов проводимости и квазичастиц не инвариантны
относительно преобразований Галилея. А это означает, что им-
импульс свободной частицы внутри кристалла не обязан иметь
привычный вид; и действительно, импульс фонона вообще не
зависит от абсолютной величины скорости. Импульс же элек-
электрона проводимости р во многих металлах имеет форму, по-
похожую на B.3):
p = m*v, C.3)
но величина т*, называемая эффективной массой электрона,
может быть даже отрицательной, а по абсолютному значению
может отличаться от массы свободного электрона на порядок
и более в обе стороны.
«Почти» сохранение импульса для частиц в кристалле про-
проявляется в том, что отдельные столкновения сопровождаются
процессами «переброса» части импульса от частиц кристаллу
в целом или наоборот. При этом величина перебрасываемого
импульса является строго определенной и зависит только от
геометрических характеристик кристаллической структуры.
§ 3.3. Закон сохранения энергии в классической механике
1. Рассмотрим систему N классических частиц, находящуюся
в стационарных внешних условиях. Ее состояние определим за-
заданием положений Г\, ..., rN и импульсов рь ,.., pN всех ча-
частиц. Следовательно, от этих переменных зависит энергия си-
системы: <§ = <§(г\, ..., rN; pu ..., pjv). В аналитической меха-
механике и теоретической физике энергия как функция координат
и импульсов называется функцией Гамильтона. Обычно функция
Гамильтона обозначается через Я. В этом томе такое обозна-
обозначение использоваться не будет.
В отношении энергии справедливо следующее замечательное
утверждение:
Задание энергии как функции координат и импульсов частиц
полностью определяет динамику системы. При этом уравнения
4 А. В* Астахов

98 ЗАКОНЫ СОХРАНЕНИЯ 1ГЛ. 3
движения имеют вид:
dx{ д& dy. ___ дШ dz.
dt ~ dp • dt др. • dt дри '
C.4)
ctf dx{ f d/ cty. э dt dzi ' v '
/ 19 ДУ
и в этом виде называются уравнениями Гамильтона.
Разъясним математический смысл функции и уравнений Гамильтона. Энер-
Энергия & частиц зависит от 6N переменных
xv У\у zf. •*•'» *N> yN> zN\ PlJe. Ply> Piz> • ••*> PNx> PNy* PNz>
т. е. является функцией многих переменных. По каждой переменной ее можно
дифференцировать. Каждая из производных снова будет функцией координат
и импульсов частиц. Эти функции как раз и стоят в правых частях равенств
C 4) и C.5). Теперь вспомним, что координаты и импульсы сами являются
функциями времени. Их можно дифференцировать по времени. Эти производ-
производные стоят в левых частях равенств C.4) и C.5). Из сказанного следует, что,
во-первых, энергия является сложной функцией времени. Во-вторых, произ-
производные по времени переменных, от которых зависит энергия, выражаются че-
через некоторые функции тех же переменных. Это означает, что уравнения C.4)
и C 5) являются дифференциальными уравнениями первого порядка относи-
юлыю неизвестных
хр у 1» г{* •••; *уу> ум> 2др р\х> р\у- P\2i •••; Рмх" Рмуу Pnz*
Уравнения Гамильтона приводят к закону сохранения энер-
энергии. Чтобы избежать излишних вычислений, убедимся в этом
на примере системы двух классических частиц, находящихся в
стационарных внешних условиях и способных перемещаться
только в я-направлении. Тогда радиус-векторы и импульсы ча*
стиц имеют отличными от нуля только ^-компоненты:
Ti — {Xu о, 0); pi = {piXJ 0, 0}; /=1, 2.
Следовательно, в этом случае функция Гамильтона зависит
всего от четырех переменных:
& = & (Хи #2*> PiXi P2x)'
Продифференцируем эту функцию по времени. По правилу
дифференцирования сложной функции
d<§ д<$ dx\ . д<$ dx2 , д& dp]x . д& dp2x
dt ¦"" dxv ТГ + ~дх7 dt "^ др1х dt + др2
C.6)

§ 3.3] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 99
Легко видеть, что правая часть C.6) обращается в нуль, и,
следовательно, энергия сохраняется, если справедливы уравне-
уравнения Гамильтона. Для рассматриваемой системы они имеют вид
dxx _ д% dx2 = д&
dt др\х % dt др2х '
dt дх\ * dt дх2
и обращают в нуль сумму членов в правой части C.6).
Теперь легко понять физический смысл уравнений Гамиль-
Гамильтона. Уравнения C.4) дают выражения скоростей через коорди-
координаты и импульсы частиц. Уравнения же C.5)—просто уравне-
уравнения Ньютона, причем для сил, действующих на соответствующие
частицы, из сравнения уравнений C.5) и B.18) получаем:
Возникает вопрос, что нового дает гамильтонова форма клас-
классической механики? Уравнения Гамильтона содержат большую
информацию о физической системе, чем уравнения движения
Ньютона. В частности, из факта существования функции Га-
Гамильтона можно получить приведенную в начале этой главы
связь между законами сохранения и симметрией пространства—
времени. Не имея возможности остановиться на этих глубоких
вопросах, поясним отличие ньютоновской формулировки от га-
мильтоновой на примере уравнения движения частицы, пере-
перемещающейся вертикально внутри жидкости. Направим ось z
системы отсчета по вертикали. Тогда уравнение движения Нью-
Ньютона запишется в виде:
d2z
m
В правой части записаны сила тяжести и сила сопротивления
Стокса. Но не зависящей явно от времени функции Гамильтона,
приводящей к такому уравнению, просто не существует! Это
видно уже из того, что энергия частицы не сохраняется, так
как действует сила трения. В результате ее действия механиче-
механическая энергия частицы превращается в тепло. Таким образом,
гамильтонов метод, в отличие от ньютоновского, «чувствует»
коренное отличие силы сопротивления среды от силы тяжести
и ей подобных.
Наконец, отметим (и это крайне важно), что уравнения
Гамильтона допускают обобщение на квантовые движения. При-
Причина заключается в том, что сила является классической вели-
величиной, не имеющей квантового аналога. Энергия, существование
которой связано с однородностью времени, определяется и в
4*

100 ЗАКОНЫ СОХРАНЕНИЯ ТГЛ. 3
квантовом случае. Поэтому существует квантовый аналог клас-
классических уравнений движения в форме Гамильтона.
2. Определим, как зависит энергия классической системы от
координат и импульсов составляющих систему частиц. Для
этого воспользуемся уравнениями Гамильтона, выполнение ко-
которых, как мы знаем, гарантирует сохранение энергии.
Рассмотрим изолированную систему, состоящую всего из
одной частицы. Такая частица, очевидно, является свободной.
Выберем систему отсчета так, чтобы частица перемещалась
только вдоль оси х. Это означает, что радиус-вектор частицы
г — {х, 0, 0}, а ее импульс р = {pXi 0,0}. Уравнения Гамильтона
в данном случае имеют вид
-^- = -^L C 8)
dt оРх ' v tO}
dp* dff_ C9)
dt dx f
где <§?— функция Гамильтона частицы. Импульс свободной ча-
частицы сохраняется: dpjdt = 0. Тогда из C.9) находим, что
д<о/дх = 0, т. е. энергия свободной частицы от ее положения
lie зависит: & = & (рх).
Рассмотрим теперь уравнение C.8) [отметим, что оно яв-
является частным случаем общего закона C.1)]. Предположим,
что частица может двигаться с любой скоростью, в том числе
и с близкой к скорости света с. Поэтому воспользуемся реля-
релятивистским соотношением между скоростью частицы vx = dx/dt
и импульсом рх — — г. Из этого равенства путем про-
стых преобразований находим:
dx pxc
__
х
Подставляя это выражение в C.8), получаем уравнение
d% рхс
Записывая его в виде d<§ == —срх Рх =- и интегрируя, полу
/22 + 2
/
чаем: % = а + с *sjp\ + гп2сгу где а — постоянная интегрирова-
интегрирования. Обычно ее полагают равной нулю, чем просто фиксируют,
начало отсчета по шкале энергий. Замечая также, что в рас-
рассмотренной задаче р = {рх, 0,0}, окончательный результат,

§ 3.3] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 101
представим следующим образом:
8{р) = с д/рЧ7^1". C.10)
В таком виде, в котором под р следует понимать абсолютное
значение импульса (р2 = р2х + р\ + р2г, где рх, ру, рг — компо-
компоненты импульса р), он справедлив для свободной частицы, дви-
движущейся в любом направлении. Формула C.10) определяет
энергию свободной релятивистской частицы.
Если масса частицы равна нулю, то в этом случае из (ЗЛОI
следует, что
8{р) = ср = с\р\. C.11)
Теперь легко проверить, что частица с т = 0 может дви-
двигаться только со скоростью света. Действительно, направим
ось х системы отсчета по импульсу частицы. Тогда р = рх и
<S = срх. На основании уравнения Гамильтона C.8) получаем:
_dx _ д& _
v*— dt ~ дРх —с-
Полагая в C.10) р = 0, находим, что энергия покоящейся
частицы равна
<Г@) = <Г0 = тс2. C.12)
Энергия &о так и называется — энергия покоя частицы. Раз-
Разность
Т(р) = & (р) -&0 = с Vp2 + пг2с2 -&о (ЗЛЗ)
определяет энергию движения и называется кинетической энер-
энергией релятивистской частицы.
Найдем нерелятивистский предел функции Гамильтона
(ЗЛО). При малых скоростях движения v импульс p = mv. По-
Поэтому первое слагаемое под радикалом в (ЗЛО) намного мень-
меньше второго, ибо и <С с. Представим функцию Гамильтона
в виде:
8 (р) = тс2л/1+(р/тсJ = тс2 [1 + (p/mcf]m
и воспользуемся разложением бинома Ньютона
Применив его к [1 +(/?/тсJ]1/2, найдем:
Так как р <С тс, то в скобках можно пренебречь всеми чле-
членами, за исключением первых двух. Тогда находим:

102 законы сохранения тгл з
Формула C.14) определяет энергию нерелятивистской сво-
свободной частицы. Величина
Г </>)=? C-15)
называется кинетической энергией нерелятивистской частицы.
Найдем теперь энергию фонона. В предыдущем параграфе
указывалось, что скорость фонона v постоянна и не зависит от
его импульса. По величине она равна скорости звука и ориенти-
ориентирована в направлении его распространения. Выберем ось х
в этом направлении и воспользуемся уравнением C.8), поло-
положив в нем dx/dt = v = const. Тогда d& = v dpx. Интегрируя
это уравнение, получим:
& = vpx = v\p\, C.16)
так как в выбранной системе отсчета импульс фонона р =
= {рху 0, 0}, причем рх = \р\.
Рассмотрим частицу, находящуюся в стационарных внешних
условиях. Для простоты ограничимся случаем, когда сила
внешнего поля, действующая на частицу, ориентирована в од-
одном направлении и движение также происходит только в этом
направлении. Назовем его х-направлением. Обозначим потен-
потенциальную энергию частицы во внешнем поле через U(x). Урав-
Уравнениями движения частицы являются уравнения Гамильтона
C.8) и C.9). В отличие от свободной частицы, импульс частицы
в стационарных внешних условиях изменяется. Поэтому соглас-
согласно C.9) энергия частицы во внешнем поле зависит от коорди-
координаты х частицы: &=.<8(х^ рх). Учитывая результаты, получен-
полученные в предыдущем пункте, а также связь силы, действующей
на частицу, с потенциальной энергией,
F — dP* — dU <*)
х dt дх '
прямой подстановкой легко убедиться, что уравнениям C.8)"
и C.9) удовлетворяет функция Гамильтона
Если внешнее поле изменяется по всем трем направлениям
в пространстве, т. е. U = f/(r), где г — радиус-вектор частицы,
то в этом случае
# = #(#-, р) = с^р* + т2с' +U{r). C.17)
Формула C.17) определяет энергию релятивистской частицы
во внешнем поле,

§3 3] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ЮЗ
В нерелятивистском пределе
g = g{r, p) = mc2 + ^-+?/(r). C.18)
Продифференцируем C.18), например, по рх, учитывая при
этом, что р2: = р\-\- Р2УЛ~ р\- Получаем:
дрх гп х*
Это равенство— частный случай закона C.1). Мы видим, что
он выполняется не только для свободной частицы.
Обобщением, формулы C.18) на систему произвольного чис-
числа N нерелятивистских взаимодействующих частиц с массами
Ш\у ..., mN является функция Гамильтона
N No
& = 8 {ги ..., rN; рь . . ., pN) = У mtc2 + ^
+ U(ru ..., rN). C.19)
Выражение C.19) определяет энергию системы N взаимодей-
взаимодействующих нерелятивистских частиц. В нем U(ru ..., ?n)—по-
?n)—потенциальная энергия взаимодействия частиц друг с другом и
с внешним полем. Первое и второе слагаемые в правой части
C.19) определяют соответственно суммарную энергию покоя и
суммарную кинетическую энергию частиц системы. Проверку
сохранения величины C.19) мы оставляем читателю в качестве
самостоятельного упражнения.
Отметим, что энергия взаимодействующих частиц не адди-
аддитивна. Свойство аддитивности нарушается из-за присутствия
в C.19) потенциальной энергии U. Последняя при наличии взаи-
взаимодействия частиц не может быть представлена суммой членов,
каждый из которых характеризует только одну частицу. Так,
при N = 2
U -С/ (г и r2) = Ux(rl) + U2{r2) + Ul2{ru r2).
Слагаемые 1/»(гг-) (i=lf 2) определяют потенциальные энер-
энергии частиц во внешнем поле, а член Ui2(t\tr2)—энергию их
взаимодействия друг с другом, которая зависит от состояния
сразу двух частиц.
Часто энергию выражают не как функцию импульсов, а че-
через скорости. Подставляя в C.10) р = m»/V I — v2lc2, получим
выражение для энергии свободной релятивистской частицы:
^°)-7г%' C-20)

104 ЗАКОНЫ СОХРАНЕНИЯ [ГЛ 3
Отсюда, кстати, следует, что импульс частицы представим
в виде
p = ^rv. C.21)
Кинетическая энергия релятивистской частицы равна
C'22)
Для нерелятивистской частицы
^(у) = шс2 + -у-, T(v)=—?-. C.23)
Для релятивистской и нерелятивистской частицы в стационар-
стационарных внешних условиях, соответственно,
5 = ё (г, v) = /г^т^ + U (г), C.24)
VI — v 2/с2
6 = %{r,v) = mc2 + JE!L + U{r). C.25)
Для системы нерелятивистских частиц
N
= & {ги ..., rN; vu ..., vN) =
C>26)
Так как составной частью энергии системы является потен^
циальная энергия взаимодействия составляющих систему ча-
частиц, то ясно, что энергия измеряется в джоулях (в СГС—•
в эргах).
В заключение отметим, что в тех случаях, когда существен^
ной составной частью системы оказывается поле (например, си-
системы релятивистских взаимодействующих частиц), энергию
уже нельзя рассматривать как функцию определенного ранее
механического состояния. Необходимо учитывать энергию поля.
Вопрос об энергии электромагнитного поля будет рассмотрен
в следующем томе курса.
3. Одним из важных приложений закона сохранения энергии
является вопрос о границах движения нерелятивистской частицы
в потенциальном поле. Он решается с помощью C.25). Опу«.
стим в C.25) энергию покоя тс2. Это означает, что начало от-»
счета энергии выбирается на уровне <^0 = я^2. Так как кине-*

§3.3]
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
105
таческая энергия частицы l/2tnv2
торых частица может находиться,
[/(r)<^ = const.
О, то во всех точках, в ко-
C.27)
Следовательно, если в некоторой области значение потенциаль-
потенциальной энергии превосходит величину &, то эта область оказы-
оказывается «запретной» для частицы. В частности, если полная энер-
энергия S меньше значения потенциальной энергии частицы в очень
удаленных областях пространства, то частица может переме-
перемещаться только в ограниченной области.
Движение частицы в ограниченной области называется фи-
финитным. Если частица способна удаляться на любое, сколь
угодно большое расстояние от начала системы отсчета, то дви-
движение частицы называется инфинитным. Примером финитного
движения является движение планет Солнечной системы. Инфи-
Инфинитным является движение заряда в поле другого заряда того
же знака.
Отметим, что правило запрета, о котором мы только что
говорили, действует только в классической механике. В кван-
квантовой механике, как будет показано в томе III, частица может
проникать сквозь области, «запретные» по классическим пред-
представлениям.
Рассмотрим некоторые свойства финитного движения на
примере одномерного движения частицы в потенциальном поле.
Направление движения будем считать ^-направлением. Пусть
график функции U(x) имеет вид, изображенный на рис. 3.2,
Шх)
с b
Рис. 3.2.
Такая кривая потенциальной энергии обычно называется потен-
потенциальной ялюй. Это название связано с тем, что, как будет по-
показано ниже, при некоторых условиях частица с такой потен*
циальной энергией ограничена в перемещении. Она оказывается
словно попавшей в яму.
Предположим, что полная энергия частицы отрицательна и
равна &\ < О (рис. 3.2). В этом случае неравенство C.27) вы-
выполняется лишь на отрезке между точками х = а и х = Ъ.

106
ЗАКОНЫ СОХРАНЕНИЯ
1ГЛ 3
Поэтому частица все время будет находиться внутри потен-
потенциальной ямы и ее движение будет финитным. Кроме того, оно
будет повторяться во времени, т. е. будет периодическим. Точки
а и 6, в которых выполняется равенство U = 8\, задают гра-
границы движения. Они называются точками поворота. Графически
эти точки определяются координатами мест пересечения гори-
горизонтальной прямой 8\ = const с графиком функции U(х)\
(рис. 3.2). Их положение задают корни уравнения U(x) — 8\.
В точке поворота, например в точке а,
Следовательно, в точках поворота скорость частицы v обра-
обращается в нуль.
Если изменить полную энергию частицы, то прямая, изо-
изображающая закон сохранения энергии 8 = const, либо опу-
опустится, либо поднимется. Поэтому изменятся точки пересечения
этой прямой с графиком функции U(x), т. е. изменятся точки
поворота. Следовательно, размер области, в которой движется
частица, зависит от значения ее полной энергии. В частности,
если окажется, что 8 = &2 > 0 (рис. 3.2), то,движение частицы
станет инфинитным.
Особого внимания заслуживает точка с (рис. 3.2). В ней
потенциальная энергия частицы минимальна. Поскольку дей-
действующая на частицу сила равна —dU/dx, то в точке с сила
\
а2 а, с, Ь, с2 д2
Рис. 3.3.
равна нулю, а при смещении частицы и влево, и вправо от
точки с частица испытывает действие возвращающей силы F =
= —dUjdx. Поэтому точка минимума потенциальной энергии
определяет положение устойчивого равновесия частицы.
Рассмотрим рис. 3.3. Потенциальная яма, расположенная
между точками а,\ и Ъ\% отделена здесь от правой части рисунка

$ 3.3] ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 107
горбом функции ?/(*), который обычно называют потенциаль-
потенциальным барьером. Поэтому движение частицы с полной энергией
<?\ внутри потенциальной ямы будет финитным с точками по-
поворота а\ и Ь\. Однако если частицу перенести правее барьера,
то ее движение станет инфинитным с единственной точкой по-
поворота &2- С другой стороны, движение частицы, обладающей
полной энергией <§Г2 (рис. 3.3), является инфинитным во всей
области от аг до +оо. Точка С\ представляет собой точку устой-
устойчивого равновесия. Отметим, что в точке Сг, где потенциальная
энергия V (х) максимальна, действующая на частицу сила также
равна нулю. Однако при смещении из точки с2 появляется сила
F = —dUjdx (рис. 3.3), стремящаяся еще дальше отодвинуть
частицу. Поэтому с2 называется точкой неустойчивого равно-
равновесия.
4. Поскольку энергия любого тела включает энергию покоя,
то любое уменьшение массы должно сопровождаться выделе-
выделением энергии. Оценим порядок величины энерговыделения.
Определим, например, энергию покоя одного грамма веще-
вещества. По определению она равна
1 г X Ю17 м2/сек2 = 10~3 кг X Ю17 м2/сек2 = 1014 Дж
A017 м2/сек2 — это порядок квадрата скорости света с2), Энергии
в 10м Дж достаточно, чтобы поднять груз в десять миллионов
тонн на высоту около одного километра! Как показывает эта
оценка, вещество содержит огромные запасы энергии.
Существуют процессы, в которых часть этой энергии выде-
выделяется. К их числу относятся, например, некоторые ядерные
превращения. Одним из них является распад ядер изотопа ура-
урана U235, активированных медленными нейтронами (энергия од-
одного нейтрона составляет величину около 4-10~~21 Дж). Уран-235
является ядерным топливом в атомных реакторах. Эта способ-
способность активированных ядер U235 обусловлена тем, что суммар-
суммарная масса продуктов распада каждого ядра меньше массы ядра.
Поэтому часть энергии покоя ядра превращается в энергию
движения продуктов распада. Действительно, пусть до распада
ядро покоилось и его масса равна пг. Обозначим массы про-
продуктов распада через ш\ и т2. Разность
Am = m1 + m2 — m C.28)
называется дефектом массы. Для рассматриваемого превращен
ния она отрицательна: Дт < 0. Полная энергия до распада
совпадала с энергией покоя ядра тс2. После распада эта же
энергия (энергия сохраняется!) перераспределяется следующим
образом. Часть ее, равная т\с2 + т2с2, составляет энергию
покоя продуктов распада. Так как Дт<;0, то должна

108 законы сохранения 1гл
выделяться еще положительная энергия А<^. Она реализуется
в виде кинетической энергии разлетевшихся продуктов распада.
Существуют и обратные процессы, в которых кинетическая
энергия частиц превращается в энергию покоя. К таким про-
процессам относятся реакции рождения элементарных частиц, ко-
которые часто встречаются в ядерной физике. Например, при
столкновении протона и нейтрона помимо исходных частиц мо-
может образоваться еще и новая частица, например, положительно
заряженный пион. При этом появляется дополнительная масса
покоя—масса пиона. Следовательно, энергия покоя продуктов
реакции оказывается больше энергии покоя исходных частиц.
Это увеличение идет за счет уменьшения кинетической энергии:
кинетическая энергия исходных частиц оказывается больше
кинетической энергии продуктов реакции на энергию покоя
пиона.
5. Мы уже отмечали, что при действии сил трения механиче-
механическая энергия тел не сохраняется. Говорят, что силы трения не
гамильтоновы. Однако это не означает, что мы сталкиваемся
с нарушением закона сохранения энергии. Специфика систем
с трением заключается в том, что в них всегда выделяется тепло.
В таких системах механическое движение тел и тепловое дви-
движение составляющих тела частиц не являются независимыми.
При этом механическая энергия упорядоченного движения тел,
т. е. движения по строго определенным траекториям, необра-
необратимо превращается в энергию беспорядочного теплового движе-
движения. (Природа необратимости будет выяснена в § 10.4.) Таким
образом, полной энергией любой замкнутой или находящейся
в постоянном внешнем поле системы, между составными частя-
частями которой действуют силы трения, является сумма энергии
механического и теплового движений, которая всегда сохра-
сохраняется.
§ 3.4. Закон сохранения момента импульса
в классической механике
1. В классической механике моментом импульса частицы на-
называется векторное произведение
L=[rp]9 C.29)
где г и р — радиус-вектор частицы и ее импульс. Согласно опре*
делению момент импульса имеет размерность постоянной План*
ка ft.
Рассмотрим свободную частицу. Это частный случай изоли-
изолированной системы. Согласно закону сохранения момента для)

ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
109
изолированной частицы L = const. Проверим это. Дифференци*
руя C.29) по времени, получаем:
Первое слагаемое в правой части равно нулю, так как ско*
рость dr/dt и импульс р коллинеарны. Второе слагаемое рав^о
нулю, поскольку сохраняется импульс изолированной частицы:
dp/dt = 0. Таким образом, dL/dt = 0 и L действительно яв-
является постоянным вектором.
Если частица движется в силовом поле, то \г ^^—I === [r"jP] =^=
=7^=0, где F— действующая на частицу сила. Величина
M = [rF] (З.ЗЭ
называется моментом силы, действующей на частицу. Таким
образом, для несвободной частицы
dL
C.31)
Из C.30) и C.31) вытекает сохранение момента импульса
частицы в центральном поле. Действительно, в этом случае
сила коллинеарна радиус-вектору г.
Следовательно,
Рассмотрим изолированную си-
систему нескольких нерелятивистских
взаимодействующих друг с другом
частиц. Для простоты ограничимся
двумя частицами. Пусть ?/(гьг2) —
потенциальная энергия взаимодей-
взаимодействия частиц, где гг- = {x{i yif Z{} —
радиус-векторы частиц (t=l, 2).
Из однородности пространства сле-
следует, что U может зависеть только
от г = г\ — г2. Свойство изотропности пространства наклады-
накладывает дополнительное ограничение: V может быть функцией
только абсолютного значения вектора г. Только при условии
U=U(\r\ — г2|) = ?/(г) потенциальная энергия не будет из-
изменяться при поворотах системы как единого целого (рис. 3.4).
Тогда силы, действующие на частицы, равны
Рис. 3.4.

ПО 3AKOVbI СОХРАНЕНИЯ 1ГЛ. 3
Убедимся в этом. Найдем, например, лг-компоненту силы Fi2, действую-
действующей на первую частицу со стороны второй:
dU dU дг
v J ;x дхх дг дх{ *
Так как г = У (*i — х2J + (tji — у2J + (^i — z2J, то
<^r Xi—x2 x
дхг V(*i — x2J + (yi — y2J + (zi — z2J г '
где ^ = Xi — x2 и определяет ^-координату вектора г. Следовательно,
Аналогичные равенства получатся для остальных компонент силы F\2, a
также компонент силы F2i, что и доказывает справедливость C.32).
Согласно C.30) моменты сил FX2 и F2\ равны:
Складывая эти равенства, находим:
М, + М, = —)¦¦§- {[г,г] - [V)) =
С другой стороны,
iM dL\ . dL2 dL
l
.
dt ^ dt dt '
где L = L\ -|- L2, a Ii и L2 — моменты импульсов частиц. Ре-
Результат таков:
dL О
т. е. суммарный момент со временем не меняется,
L = Lx + L2 = const. C.33)
Это и есть закон сохранения момента импульса для изо-
изолированной системы двух взаимодействующих нерелятивист*
ских частиц. Соотношение C.33) указывает также, что момент
импульса является аддитивной величиной.
Эти свойства справедливы для изолированной системы лю-
любого числа iV нерелятивистских частиц. Момент импульса изо-

§ 3.4] ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА 1 11
лированной системы нерелятивистских частиц р. вен сумме мо-
моментов импульсов частиц и сохраняется:
L = Lx + ... + LN = ? Lt = const. C.34)
Как и закон сохранения импульса, закон C.34) справедлив
лишь в нерелятивистской области и для систем невзаимодей-
невзаимодействующих релятивистских частиц.
Предположим, что система частиц не является изолирован-
изолированной. Обозначим через F2 силу внешнего поля, действующую на
частицу системы с номером L Суммарный момент импульса L
системы во внешнем поле не сохраняется. При этом
¦г—а-B)
где
М = Z [rtFt] C.36)
— суммарный момент только внешних сил (ги где i= 1, 2, ...
..., N, обозначают радиус-векторы частиц системы). Суммар-
Суммарный момент внутренних сил взаимодействия частиц друг с дру-
другом равен нулю. В противном случае при Fi = О (i= 1, 2, ...
..., N)f т. е. для изолированной системы, йЬ/сНфО, что проти-
противоречит закону сохранения момента.
2. Момент импульса обладает важным свойством:
Момент импульса в целом покоящейся системы может быть
отличен от нуля. Момент импульса при нулевом значении пол-
полного импульса системы называется собственным.
Собственный момент обозначим через S. Полный момент
связан с собственным так:
S, C.37)
где R — радиус-вектор центра инерции системы, а Р — ее сум-
суммарный импульс. Первое слагаемое в правой части C.37) опре-
определяет момент импульса, обусловленный движением системы
как единого целого. В системе отсчета, в которой начало коор-
координат находится в центре инерции, имеем R = 0 и Р = 0. Сле-
Следовательно, в этой системе L = S.
Убедимся в существовании собственного момента на при-
примере системы двух частиц. В этом случае
L = L{ + L2 = [rxp{\ + [r2p2\.
Перейдем в систему отсчета, в которой центр инерции системы
частиц покоится и в которой, как уже установлено ранее, L = S.

112
ЗАКОНЫ СОХРАНЕНИЯ
[ГЛ. 3
В этой системе р2 = —рь Поэтому
S =4pi ('1 - г2)]
0.
Хорошо всем знакомой системой, обладающей собственным
моментом, является волчок, вращающийся на одном месте
(рис. 3.5).
Физический смысл выделения из полного момента импульса
собственного момента состоит в следующем. Момент [RP] ха-
характеризует поступательное движение системы. Собственный
момент с поступательным движением не свя-
связан и является характеристикой происходя-
происходящих в системе вращений.
Замечательно, что собственный момент
изолированной системы всегда сохраняется.
Действительно, импульс изолированной си-
системы сохраняется: Р = const. Поэтому
Рис. 3.5. поскольку скорость центра инерции V и им-
импульс Р коллинеарны. Следовательно, [RP] =
= const. Так как полный момент L тоже сохраняется, то сохра-
сохраняется и собственный момент S.
Найдем уравнение, определяющее изменение собственного
момента системы, на которую действуют внешние силы. Из
C.37) с учетом коллинеарности векторов dR/dt = V и Р сле-
следует, что
dt
dt
d
dL
dt
Пользуясь уравнением поступательного движения системы
B.11), находим:
N
Так как F— ? Fh то на основании C.35) и C.36)
Выражение
C.38)
C.39)
рпределяет суммарный момент внешних сил в системе отсчета,
начало которой находится в центре инерции системы» или. как

§3.4]
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
113
грворят, относительно центра инерции. На рис. 3.6 эта система
изображена пунктиром. Следовательно,
¦^ = MS. C.40)
В заключение отметим, что не только система частиц, но и
отдельные частицы могут обладать собственным моментом. Соб-
Собственный момент элементарных частиц называется спином. Так,
абсолютное значение спина
электрона,
равно —«г—
протона, нейтрона
Ну где Й — постоян-
постоянная Планка. Природа спина
квантовая, на что указывает
пропорциональность спина Й.
В рамках классических пред-
представлений существование спи-
спина объяснить нельзя. Действи-
Действительно, для одной частицы ее
радиус-вектор и радиус-век-
радиус-вектор центра инерции — это одно и то же, а импульс центра инер-
инерции есть просто импульс частицы. Поэтому в этом случае L ='
= [RP] и, следовательно, S = 0.
Рис. 3.6.
На этом закончено рассмотрение наиболее общих представ-
представлений механики. Областью применимости некоторых из них
(второй закон Ньютона, зависимости между различными вели-
величинами, например, между импульсом и скоростью, между энер-
энергией и импульсами и координатами частиц и т. д.) является
классическая физика. Другие же (принцип относительности, за^
коны сохранения) справедливы и в квантовой области. В сле-
следующих главах будет показано, как развитые представления
позволяют проанализировать свойства некоторых систем, пред-
представляющих непосредственный практический интерес. Главным
образом будут рассмотрены классические движения. Однако
ряд вопросов (гл. 5 «Столкновения») выходят за рамки класси-
классической физики,,

ГЛАВА 4
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
§ 4.1. Движение заряженной частицы
в электромагнитном поле
1. Согласно § 2.3 при применении единиц измерения СИ дви-
движение классической заряженной частицы во внешнем электро-
электромагнитном поле обусловлено силой Лоренца B.22а). Поэтому
оно описывается уравнением движения
4L~qE + q[vB]. D.1)
В общем случае поля Е и В могут зависеть от координат точки
пространства и от времени. Практически уравнение D.1) ис-
используется только в применении к элементарным заряженным
частицам и к некоторым ядрам и ионам.
Движения заряженных частиц в электромагнитных полях
носят разнообразный характер в зависимости от вида полей ?,
В, а также от начального состояния движения частиц. Закон
действия силы Лоренца таков, что работу может производить
только электрическая компонента силы. Магнитная компонента
работы не производит. Таким образом, электрическое поле спо-
способно увеличивать или уменьшать абсолютное значение скоро-
скорости движения, а магнитная сила влияет лишь на направление
скорости. Эти свойства широко используются. Так, электриче-
электрические поля применяют для ускорения и замедления заряженных
частиц в ускорителях. При этом управление направлением дви-
движения частиц осуществляется с помощью магнитного поля.
Ниже мы рассмотрим закономерности движения частиц в
электромагнитном поле наиболее простого вида. Будем считать
поле, во-первых, постоянным во времени и, во-вторых, однород-
однородным, т. е. одинаковым во всей области пространства, в которой
движется частила. Все это выражается такими равенствами:
Е = const и В = const. Электрическое поле, однородное с вьь
сокой точностью, можно создать, например, с помощью пло-
плоского конденсатора, а однородное поле В реализуется в катуиь

§ 41] ДВИЖЕНИЕ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 115
ке постоянного тока (рис. 4.1). Если отношение расстояния
между пластинами d к их линейному размеру /, а также отно-
отношение радиуса витков катушки г к ее длине I будут намного
меньше единицы, то в центральных областях этих устройств
поля будут однородными с точностями, соответственно, djl и г/1.
2. Рассмотрим движение заряженной частицы в однородном
электрическом поле. В таком поле траектория частицы является
кривой, которая целиком может быть расположена в некоторой
плоскости (плоская траектория). Плоскость, в которой лежит
траектория, проходит через век-
вектор начального импульса части- и ? ^
цы и вектор Е. 1 j + |+Чг-+ + + * +\
Действительно, при В = О дТ ? ИИ И И
уравнение движения D.1) имеет Г1 П - - - -]
вид
&- = дЕ. D.2)
2г
Так как Е — постоянный вектор,
то за любой промежуток време-
ни dt импульс частицы получает Рис. 4.1.
приращение dp, лежащее в пло-
плоскости, в которой находятся вектор Е и импульс частицы в мо-
момент начала отсчета времени dt. Следовательно, частица дви-
движется в плоскости, ориентация которой в пространстве опреде-
определяется направлением поля Е и направлением движения частицы
в начальный момент времени.
Выберем систему отсчета так, чтобы траектория частицы ле-
лежала в координатной плоскости ху, а по оси у было направлено
поле Е = {0, ?, 0}. Начальный импульс частицы в этой системе
будет равен р0 = {рОх, рОу, 0}. Кроме того, начало отсчета вы-
выберем так, чтобы в начальный момент времени t = 0 частица
находилась в начале координат: г@) = {0, 0, 0} = 0.
В компонентах уравнение D.2) имеет такой вид:
dp г dp.,
ТГ-°. -Ш—ЯЕ. D.3)
Так как Е = const, то
Рх @ = Сх = const, ру (/) == qEt + С2.
Постоянные С\ и С2 определяются из начальных условий:
Рх @) = Рох = Сь ру @) = рОу = С2.
Следовательно, решение уравнений D.3) имеет вид
Рх @ = Рох, РУ (/) = qEt + рОу. D.4)

I 16 ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
В нерелятивистском случае
[ГЛ. 4
где т — масса частицы, v = {vx, vyi 0}— ее скорость, a x(t) и
y(t)—координаты частицы в момент времени t. Поэтому D.4)
определяет систему дифференциальных уравнений относительно
искомых функций ~x(t) и y{t):
dx(t)
т dt ~
т
dy (t)
dt
•- qEt +
D.5)
Ее решение, удовлетворяющее начальному условию г@) = 0,
определяется соотношениями
•/.
D.6)
Проанализируем это решение. Если рох = 0, т. е. если в на-
начальный момент частица перемещается в направлении поля Е,
то это направление ее движения сохранится и во все последую-
последующие моменты: x(t) = O при рОх = 0. Следовательно, в этом слу-
случае частица будет перемещаться по прямой вдоль оси у. Если
же рох Ф 0, то, исключив
У
У\
из D.6) время t, получим
уравнение траектории
Рис. 4.2.
Рох
Графиком такой зависи-
зависимости является парабола.
Оба случая (рОх = О и
Рох Ф 0) изображены на
рис. 4.2.
Остановимся подроб-
подробнее на случае р0 = 0, ко-
когда в начальный момент времени частица покоится в начале
координат. В этом случае она будет двигаться вдоль оси у. При
этом из D.4) следует, что py(t)=: qEt, или
vy(i) — ^-t. D.7)
Таким образом, скорость частицы будет неограниченно воз«
растать со временем. Мы знаем, однако, что скоростей, превьь
шающих с, не существует. Это означает, что зависимостью D.7)
можно пользоваться только до тех пор, пока vy(t)<& с, т. е. до
моментов времени / < mclqE. При рассмотрении движения на

§4.1]
ДВИЖЕНИЕ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
117
временах большей длительности необходимо применять реляти-
релятивистские законы. В релятивистской механике
mv
р,, = «^-т= * _ , если лп„ = пп„=0.
В этом случае из D.4) получаем:
mvtJ (t)
Отсюда находим:
— qEt.
qEt 1 с
т # Vl + (qEt/mcJ ^\+(mc/qEtJ '
D.8)
Мы видим, что скорость частицы по-прежнему возрастает.
Однако, в отличие от скорости D.7), она никогда не превосхо-
превосходит с, поскольку корень в знаменателе D.8) все время остается
больше единицы. Этот результат согласуется с требованиями
теории относительности. Зависимость скорости частицы от вре-
времени для случая ро = 0 изображена на рис. 4.3.
Рис. 4.3.
Вычислим расстояние уТ, на котором покоящаяся вначале
релятивистская частица приобретает заданную кинетическую
Энергию Т. Воспользуемся законом сохранения энергии. Посто-
Постоянной силе qE соответствует потенциальная энергия частицы
U = — qEy. D.9)
Поэтому полная энергия частицы в однородном электрическом
поле равна
— v2/c2
?/=¦
me*
Vl ~ v2/c2
— qEy — const.
Значение константы можно определить из начальных уело-
дий. По предположению в начальный момент времени частица

118 ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯ* \ТЛЛ
покоилась в начале координат. Следовательно, при t = 0 имеем:
у = 0 и v = 0. Отсюда получаем, что <§ = тс2. Таким образом,
мы можем записать равенство
тс2 „ о
—==== qEy = тс1.
Отсюда для уТ получим:
yr = J-{_Ж==г-шА^-^-. D.10)
Зависимость D.10) используется, например, для оценки па-
параметров линейных ускорителей электронов — установок, в ко-
которых сгустки электронов разгоняются до скоростей, близких
к с. По заданной энергии электронного пучка на выходе уско-
ускорителя и напряженности ускоряющего поля можно оценить
длину ускорителя. Пусть требуется, чтобы под действием поля
порядка 104 В/м ускоренные электроны достигли скорости около
0г9 с (заряд электрона равен 1,6-10~19 Кл). Тогда согласно
D.10) они должны пройти в поле путь длиной порядка 103 м.
3. Перейдем к рассмотрению задачи о движении заряженной
частицы в однородном магнитном поле. Выберем систему от-
отсчета таким образом, чтобы магнитное поле В было направлено
по оси z:
В = @, 0, В).
Рассмотрим случай, когда в начальный момент времени частица
обладает скоростью, перпендикулярной полю В. Тогда в вы-
выбранной системе отсчета v@) = vo = {vOx, uOy, 0}. Релятивист-
Релятивистское уравнение движения частицы получается из D.1) при
? = 0:
lL=±("*\ = q[vB]. D.11)
Магнитная сила Лоренца перпендикулярна вектору В.
довательно, за любой промежуток времени dt импульс частицы
получает приращение dp = q[vB]dt, лежащее в той же плоско*
сти ху, что и начальная скорость v0. Следовательно, вся траек-<
тория частицы является плоской и лежит в плоскости ху. Пер-
Перпендикулярность магнитной силы Лоренца скорости частицы
означает, что частица будет обладать только нормальным уско->
рением, а величина ее скорости будет оставаться неизменной:
v2(t) = vl = vlx + u^ = const. Поэтому корень в D.11) можно
вынести за знак производной. В результате получаем:

§ 4.1? ДВИЖЕНИЕ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 119
где а — ускорение частицы. Его абсолютное значение равно
V~ у/ 9 /" о~7 о"
1 — V С С
— Vn / С
а = -
¦v0B.
D.12)
Здесь мы воспользовались взаимной перпендикулярностью век-
векторов v и В и равенством v = v0. Как отмечалось выше, вели-
величина D.12) должна быть равна нормальному ускорению ча-
частицы. Следовательно, согласно A.14),
4Л/1 ~
т -«""/? R #
Отсюда находим, что радиус кривизны траектории равен
mv0 1
/?=¦
qB
= -^ = const,
D.13)
— 0,1 / с*
где ро — абсолютная величина импульса релятивистской ча-
частицы. В нерелятивистском случае, т. е. при vo/c <C 1,
D.14)
=^ = -??. = const.
qB qB
В этой формуле ро — абсолютная величина нерелятивистского
импульса. Плоское движение по траектории постоянной кривиз-
кривизны и с постоянной по величине скоростью является равномер-
равномерным вращением по окружности. Следовательно, траектория дви-*
жения заряженной частицы в
однородном магнитном поле с
начальной скоростью, направ-
направленной перпендикулярно по-
полю, является окружностью
(рис. 4.4).
Очевидно, что D.13) и
D.14) определяют радиус
окружности, соответственно, в
релятивистском и нереляти-
нерелятивистском случаях. Этот радиус называется циклотронным или
гироскопическим.
Определим угловую скорость со частицы. Воспользовавшись
A.7) v0 = coi?, получим:
Рис. 4.4.
« = т = .
В нерелятивистском случае (^о
не зависит от v0 и равна
т v- vl/cK D.15)
С с) угловая скорость вращения
D.16)

120
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
[ГЛ 4
В
Генератор
переменного злентри-
ченпого поля
Угловая скорость вращения заряженной частицы в однородном
магнитном поле, определяющая частоту и период обращения
Т = 2я/со, называется циклотронной или гироскопической ча-
частотой.
Независимость угловой скорости нерелятивистской частицы в магнитном
поле, а следовательно, и периода ее обращения Т = 2я/со от скорости дви-
движения сыграла решающую роль в открытии в 1932 г. Э. Лоуренсом и М. Ли-
вингстоном циклического способа ускорения заряженных частиц. Ускоритель,
действующий на этом принци-
принципе, был назван циклотроном.
Мы приводим выдержку из
оригинальной статьи Э. Лоу-
ренса и М. Ливингстона, со-
сопровождая ее поясняющим ри-
рисунком 4.5.
«... Метод состоит в сле-
следующем. Полукруглые полые
пластины, похожие на дуангы
электрометра, установлены в
вакууме в однородном магниг-
ном поле, перпендикулярном
плоскости этих пластин, таким
, образом, что их диаметральные
края находятся близко друг к
Рис- 4.5. другу. К этим пластинам, слу-
служащим электродами, подво-
подводится колеблющееся напряжение высокой частоты, создающее колеблющееся
электрическое поле в зазоре между их диаметральными краями. В резуль-
результате в течение одной половины периода электрическое поле ускоряет ионы,
образовавшиеся в диаметральном зазоре и направляющиеся во внутреннюю
полость одного из электродов, где под действием магнитного поля они дви-
движутся по круговым траекториям и в конце концов опять попадают в зазор
между электродами.
Магнитное поле задается таким образом, чтобы время, необходимое для
прохождения полуокружности по траектории внутри электрода, равнялось по-
полупериоду колебаний. Вследствие этого, когда ионы возвратятся в зазор ме-
между электродами, электрическое поле изменит свое направление, и, таким об-
образом, ионы, входя внутрь другого электрода, приобретут еще одно прираще-
приращение скорости. Поскольку радиусы траекторий внутри электродов пропорцио-
пропорциональны скоростям ионов, время, необходимое для прохождения таким ионом
полуокружности, не зависит от его скорости. Поэтому, если они затрачивают
точно половину периода на первую половину своего оборота, то они будут
двигаться и дальше в таком же режиме и, таким образом, будут описывать
спираль с периодом обращения, равным периоду колебаний электрического
поля, до тех пор, пока они не достигнут наружного края прибора. Их кинети-
wiu.ee „
устройство

§ 4 П ДВИЖЕНИЕ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 121
ческие энергии по окончании процесса ускорения будут больше энергии, соот-
соответствующей напряжению, приложенному к электродам, во столько раз,
сколько они совершили переходов от одного электрода к другому».
Как видно из текста, Лоуренс и Ливингстон использовали нерелятивист-
нерелятивистские закономерности движения заряженных частиц в магнитном поле. По-
Поэтому они смогли добиться успеха только потому, что разгоняли достаточно
тяжелые частицы, такие, например, как протоны и ионы гелия. Из-за сравни-
сравнительно большой массы эти частицы, завершая ускорение, все же не достигают
скоростей, сравнимых со скоростью света с. Например, протоны, которые Лоу-
ренсу и Ливингстону удалось разогнать до кинетических энергий порядка
10~13 Дж, обладали скоростями движения, отношение которых к скорости
света было порядка ОД. (Эта оценка получается из равенства — — —
Vl — v2/c2
-—тс = 10~13 Дж, где т — масса протона, по порядку величины она равна
Ю-27 кг.)
Если бы вместо протонов использовались, например, электроны, которые
приблизительно в 10~4 раза легче протонов, то циклотрон Лоуренса и Ливинг-
стона не мог бы работать. Являясь более легкими, электроны сравнительно
быстро достигали бы скорости, сравнимой со скоростью света. В этом случае,
как показывает формула D.15), циклотронная частота начинает зависеть от
скорости, уменьшаясь по величине. При этом период обращения возрастает.
Следовательно, для того, чтобы в зазорах между электродами электроны уско-
ускорялись, необходимо изменять частоту переменного электрического поля, уско-
ускоряющего частицы, что в установке Лоуренса и Ливингстона не предусматри-
предусматривалось. Частота определялась по формуле D.16). Для поля В = 1 Тл и для
протонов она равна
qB 1.6.1(Г19Кл.1Тл 1л8 -1 1л8г
со = —— = г= « Ю° сек = 10° Гц.
т 1,2.10~/7кг
Заряд протона равен 1,6 • 109 Кл, его масса составляет величину 1,2 • 10~27кг.
Отметим, наконец, преимущества циклотрона перед методами однократ-
однократного ускорения заряженных частиц электростатическим полем. При исполь-
использовании таких методов для получения частиц высокой энергии необходимо
создавать ускоряющие разности потенциалов очень большой величины. Так,
для получения протонов с той же кинетической энергией, какую впервые по-
получили Лоуренс и Ливингстон, необходимо приложить ускоряющее напряже-
напряжение порядка 106 В. При высоких напряжениях возрастает угроза электриче-
электрического пробоя, которая и лимитирует возможности прямых методов. Цикло-
Циклотронный метод ускорения от этого недостатка свободен.
В заключение отметим, что если начальная скорость частицы
v0 составляет с полем В угол, отличный от 90°, то в этом слу-
случае частица будет двигаться по винтовой линии (рис. 4.6).
В этом легко убедиться следующим образом. Разложим ско-
рость частицы на две составляющие: z> = t>i + t>2, где вектор v%
перпендикулярен полю В, а вектор v% полю параллелен» Тогда

122
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
[ГЛ. 4
В
Рис. 4.6.
магнитная сила Лоренца будет зависеть только от скорости V\\
F = q [vB] = q [(v{ + v2)-B]=q [vxB] + q [v2B] = q [vxB],
так как [v2B] = 0 вследствие коллинеарности векторов v2 и В.
Поэтому магнитное поле не будет влиять на движение частицы
вдоль поля. В этом направлении скорость частицы будет со-
z храняться, оставаясь равной vO2,
где Vo2 —составляющая начальной
скорости частицы вдоль поля. Сле-
Следовательно, в этом направлении ча-
частица будет двигаться равномерно
и прямолинейно. Составляющая
движения, связанная со скоростью
V\, будет равномерным вращением
по окружности. Сумма этих движе-
движений приводит к перемещению по
винтовой линии. При этом радиус
винтовой линии и частота обраще-
обращения будут определяться соответ-
соответственно формулами D.13) и D.15)]
[в нерелятивистском случае — формулами D.14) и D.16)], в ко-
которые вместо vo нужно подставлять vQ\ — абсолютное значение
СКОРОСТИ Vq\.
4. Движение пучков заряженных микрочастиц в электромаг-
электромагнитных полях широко используется в науке и технике. Область
физики, в которой изучается
структура пучков заряженных
частиц в электромагнитных по-
полях, называется электронной
оптикой. В основе всех примене-
применений лежит а) способность элек-
электрического и магнитного полей
изменять направление движения
заряженных частиц, б) способ-
способность электрического поля осу-
осуществлять ускорение заряженных
частиц. Благодаря этому удается
разделять частицы в пучке или,
наоборот, собирать, т. е. фокуси-
фокусировать их в малой области пространства, а также получать
потоки заряженных частиц высоких энергий.
Остановимся на некоторых применениях электромагнитного
поля.
В анализаторе или спектрометре импульсов происходит про-
пространственное разделение заряженных частиц в зависимости от
величины их импульса. Принцип работы этого устройства осно-
Однородное
магнитное поле
Пучон
Рис. 4.7.

§ 4 1] ДВИЖЕНИЕ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 123
ван на зависимости, определяемой формулой D.14). Разделение
частиц схематически изображено на рис. 4.7. Частицы, влетаю-
влетающие в область однородного магнитного поля, перпендикуляр-
перпендикулярного плоскости рисунка, движутся затем по окружностям, ра-
радиусы которых зависят от абсолютных значений импульсов ча-
частиц и от их зарядов. Если скорости частиц одинаковы, то их
разделение будет происходить в зависимости от отношения т/д
(т — масса частицы, q — ее заряд). В этом заключается идея
масс-спектрометрического анализа пучков заряженных частиц
(обычно ионов).
Создавая электромагнитные поля определенных конфигура-
конфигураций, удается решать обратную задачу — не разделения, а фо-
фокусировки пучка заряженных частиц в малое пятно. Эта за-
задача похожа на фокусировку света линзами. Поэтому выпол-
выполняющие ее устройства называются электромагнитными линзами.
Они имеются, например, в телевизионных трубках, электронно-
электроннолучевых трубках осциллографов и электронных микроскопах.
Фокусировка имеет особо важное значение для электронной микроско-
микроскопии, ибо от фокусировки зависит разрешающая способность. Приведем неко-
некоторые цифры.
Две точки, находящиеся перед объективом оптического микроскопа, бу-
будут неразличимы, если расстояние между ними б по порядку величины мень-
меньше X/sin 6, где % — длина волны света, которым эти точки освещаются. Угол 9
показан на рис. 4.8. Для лучших оптических
микроскопов 6 приближается к предельному зна-
значению в 90°. Поэтому б приблизительно равно К
Которое в свою очередь составляет величину по-
порядка нескольких тысяч ангстрем. \ j
Квантовая природа электронов проявляет- \ !-2>
ся в том, что они также обладают волновыми \ I /
свойствами. Например, электроны с энергией ^
8-10~16 Дж обладают длиной волны всего лишь
0,05 А! Поэтому если бы для объектива электрон- Рис. 4.8.
ного микроскопа 20 было равно хотя бы 30°, го
можно было бы различать объекты размером порядка десятых долей ангстре-
ангстрема. Атомы в молекулах находятся на расстоянии всего лишь 1—2 А. Следо-
Следовательно, можно было бы фотографировать молекулы!
Это очень сложная задача, ибо очень трудно создать электронную
линзу, фокусирующую в одном и том же месте электроны, идущие близко
и далеко от оси линзы. Такая расфокусировка называется сферической абер-
аберрацией. Вследствие этого явления только недавно на лучших современных
электронных микроскопах удалось различить детали размером в несколько
ангстрем.
Наконец, в ускорителях заряженных частиц используется
как ускоряющее, так и стабилизирующее траекторию пучка

124 ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПбЛЯХ [ГЛ 4
действие электромагнитного поля. В этих устройствах получают
пучки высокоэнергичных протонов, электронов, дейтронов (ядра
тяжелого изотопа водорода), а-частиц. Все ускорители делятся
на две основные группы: линейные и циклические. В линейных
ускорителях используется либо принцип однократного ускоре-
ускорения электростатическим полем, либо принцип увлечения частиц
волной электрического поля. Циклические ускорители работают
по принципу, который уже обсуждался в связи с рассмотрением
циклотрона. В этих системах частицы ускоряются, многократно
проходя через сильное электрическое поле. А на своей орбите
во время ускорения они удерживаются магнитным полем. К та-
такому типу относится один из самых мощных в мире ускорите-
ускорителей протонов, созданный в СССР в 1968 г. (г. Серпухов), на
котором получают пучки протонов с энергией порядка 10~8 Дж.
Напомним, что на первом циклотроне был получен пучок про-
протонов с энергией в 105 раз меньшей.
§ 4.2. Нерелятивистское движение частицы
в центральном поле
1. Как в классической, так и в квантовой механике очень
важной является задача двух тел, в которой рассматривается
движение изолированной системы из двух взаимодействующих
друг с другом частиц. Для физики эта задача важна тем, что
система двух тел — простейшая, в которой проявляются силы
взаимодействия между телами. Поэтому именно на таких си-
системах устанавливаются и проверяются фундаментальные за-
законы сил. Важность задачи двух тел для приложений обусловле-
обусловлена тем, что к ней могут быть сведены многие вопросы, представ-
представляющие практический интерес. Приведем примеры.
Планеты Солнечной системы взаимодействуют с Солнцем
и друг с другом. Однако масса Солнца на несколько порядков
больше массы любой из планет. Общая масса всех планет со-
составляет примерно 1/700 часть массы Солнца. Поэтому сила
гравитационного притяжения каждой планеты к Солнцу на*
много превосходит силу притяжения планеты к другим плане-
планетам Солнечной системы. Это означает, что законы движения
планет Солнечной системы в основном определяются силой тя-
тяготения Солнца. Силы взаимодействия планет друг с другом
приводят лишь к незначительным возмущениям движения, обу-
обусловленного тяготением Солнца. Следовательно, закон движе-
движения каждой планеты с большой точностью может быть опре-
определен как решение уравнений движения системы двух тел —
Солнца и планеты.
Движение искусственного спутника Земли в основном опре-
определяется силой тяготения Земли. Это обусловлено тем, что рас-

§ 4.2] НЕРЕЛЯТИВИСТСКОЕ ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 125
стояние от спутника до Земли неизмеримо меньше расстояния
от спутника до любого небесного тела. А ведь сила тяготения
убывает обратно пропорционально квадрату расстояния! По-
Поэтому характер движения спутника также с высокой точностью
может быть выяснен из рассмотрения задачи двух тел: спут-.
ник — Земля.
В газах молекулы сталкиваются друг с другом. Как мы
увидим в части II, столкновения молекул определяют многие
свойства газов. При этом основную роль играют парные столк-
столкновения. Одновременные столкновения сразу трех и большего
числа молекул происходят крайне редко и не существенны. По*<
этому многие свойства газов могут быть поняты из рассмотрев
ния задачи двух тел — задачи о движении двух молекул, взаи^
модействующих друг с другом через силы B.23).
В подавляющем большинстве представляющих практический
интерес задач двух тел силы взаимодействия являются цен-
центральными. Перечисленные примеры иллюстрируют этот факт.
Поэтому ниже мы рассмотрим общую формулировку классиче-
классической задачи двух тел с центральными силами взаимодействия
и выясним те общие свойства движения тел, которые не зави^
сят от конкретного вида закона действия центральной силы.
2. Рассмотрим две нерелятивистские частицы с массами тц
и т2. Если вторая частица действует на первую с силой
F(r\—г2), то по третьему закону Ньютона сила действия пер*
вой частицы на вторую будет равна —F(r\ — r2). Через Г\ и г%
обозначены радиус-векторы частиц по отношению к выбранной
инерциальной системе отсчета. Уравнения движения замкнутой
системы двух частиц имеют вид
^ ^r2). D.17)
Сила F(r\ — г2) предполагается центральной, т. е. коллинеарной
вектору Г\—г2. Вместо переменных Т\ и г2 гораздо удобнее ис-
использовать переменные
[см. B.10)]. О целесообразности перехода к переменным R и t
уже говорилось в § 2.2. Здесь это тем более уместно, что сила
взаимодействия зависит только от г. Выражая Г\ и г2 через
JR и г, находим:
Подставляя эти выражения в левые части уравнений D.17),
убеждаемся в том, что эти уравнения сводятся к закону

126
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
[ГЛ 4
сохранения центра инерции d2Rjdt2 = 0 и к одному нетривиаль-
нетривиальному уравнению
m~ = F{r)y D.19)
где
т = — D.20)
Эта величина называется приведенной массой задачи двух
тел.
Окончательный вывод оказывается следующим: задача двух
тел эквивалентна задаче о движении одного тела с приведенной
массой в центральном силовом поле.
Решив уравнение D.19), т. е. найдя зависимость r(t), можно
по формулам D.18) восстановить законы движения частиц. Так,
например, в системе отсчета, называемой системой центра инер-
инерции (СЦИ), начало которой связано с центром инерции частиц
(в ней /? = 0), частицы будут
пцу! двигаться по подобным траекто-
траекториям. При этом соединяющая их
прямая все время проходит через
и начало координат, а абсолютные
величины радиус-векторов обрат-
обратно пропорциональны массам ча-
частиц (рис. 4.9):
Подчеркнем, что СЦИ являет-
является инерциальной, так как центр
инерции изолированной системы
движется равномерно и прямо-
прямолинейно.
Заметим, что если ni\ = m<i,
то m = mxj2 = m2/2; приведен-
приведенная масса вдвое меньше массы каждой частицы. Если же одна
из масс намного больше другой, например гп\ > т2, то
tYl\TYl2 №2
Рис 4-9-
mi + m2 I + (m2/tni) 2#
В этом случае приведенная масса практически совпадает с
меньшей массой.
3. Так как частица с приведенной массой движется в цен-
центральном поле, то ее момент импульса будет сохраняться
(см. §3.4):
L = [rp]=m[rv] = const, D.21)
где р = mv и v =

§4.2]
НЕРЕЛЯТИВИСТСКОЕ ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ
127
Отсюда вытекают два важных следствия. Во-первых, траек-
траектории движения в центральном поле частиц с приведенной мас-
массой т и массами т\ и т^ в СЦИ являются плоскими.
Действительно, согласно D.21) радиус-вектор г перпенди-
перпендикулярен постоянному вектору L. Следовательно, в любой мо-
момент времени он находится в плоскости, перпендикулярной L,
А это и означает, что траектория движения частицы с приве-
приведенной массой является плоской, а следовательно, плоскими
являются и траектории частиц с массами т\ и т2.
Вторым важным следствием сохранения момента является
постоянство секториальной скорости. Секториальной скоростью
называется площадь, заметаемая радиус-вектором в единицу
времени. В центральном поле секториальная скорость частицы
с приведенной массой /п, так же как и секториальные скорости
частиц с массами пг\ и ягг, не изменяются. Этот закон назы-
называется вторым законом Кеплера.
Рассмотрим сначала частицу с приведенной массой т. Пусть
S(t) обозначает площадь, заметаемую ее радиус-вектором к
моменту времени t с начала движения. На рис. 4.10 эта пло-
площадь выделена штриховкой. Для движения в центральном поле
изображенная картина является
плоской вследствие плоского харак-
характера траектории. г@) —это радиус-
вектор частицы в начальный мо-
момент времени t = 0. Секториальной
скоростью является величина
S = -^-. D.22)
Рассмотрим, насколько к момен-
моменту времени t -j- dt изменится пло-
площадь S(t). Обозначим это измене-
изменение через dS. Из рис. 4.10 видно,
что dS равно площади треугольни-
треугольника ОАВ. В нем АВ = dr — величн- Рис. 4.10.
на вектора смещения частицы dr за
время dt Очевидно, что dr=v(t)-dt, где v(t) —величина ско-
скорости частицы в момент времени t Если принять сторону ОА =;
= r(t) за основание треугольника ОАВ, то высотой будет яв-
являться отрезок ВС = АВ sin ф = dr sin t|) = v (t) dt • sin гр. Следо-
Следовательно,
sin ^dt =

128
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
[ГЛ. 4
где L — абсолютное значение момента импульса. Так как мо-
момент импульса сохраняется, то
что и требовалось доказать.
Сохранение секториальных скоростей частиц с массами тх
и т^ следует из пропорциональности в СЦИ их радиус-векто-
радиус-векторов t\ и г2 радиус-вектору г.
4. Рассмотрим вопрос о границах движения в задаче двух
тел с центральным взаимодействием, т. е. найдем, в каких
пределах может меняться расстояние между частицами (пе-
(переменная г = |г|). Из § 3.3 мы знаем, как решается такая за-
задача в случае одномерного движения по прямой. В нашем слу-
случае движение происходит в плоскости, т. е. является двумерным.
Однако эта двумерная задача может быть сведена к одно-
одномерной»
Уравнению движения D.19) соответствует полная энергия
2
& = •§¦—h U (г) = const, D.23)
где U (г)—потенциальная энергия, отвечающая центральной
силе F(r). Выберем такую инерциальную систему отсчета, на-
начало которой в рассматриваемый момент времени совпадает
с положением массы т. При этом
ее ось у направлена вдоль радиус-
вектора г, а ось х ему перпендику-
перпендикулярна и лежит в плоскости движе-
движения. Эта система изображена на
рис. 4.11. В точке О находится
центр силы F(r), a n — единичный
вектор в направлении ее действия.
Обозначим проекцию импульса на
ось у через рГу а его проекцию на
^ ось х — через рф. Этими обозначе-
обозначениями подчеркивается, что компо-
компонента рг относится к движению
вдоль радиус-вектора, а компонента /?ф—к движению в пер-
перпендикулярном направлении, т. е. к вращению. Согласно D.21),
абсолютная величина момента равна
О
Рис. 4.11.
Пользуясь этой формулой и учитывая, что р2 = pj + Рф> D.23),
можно преобразовать к виду

§42] НЕРЕЛЯТИВИСТСКОЕ ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 129
Величина L2/2mr2 называется центробежной энергией^
а сумма
^ D.25)
•— эффективной потенциальной энергией.
Выражение D.25) получено при выборе специальной системы
отсчета. Но входящие в него величины L2 и г2 являются ска-
скалярами. Поэтому иЭфф(г)—также скаляр, т. е. имеет одинако-
одинаковый вид во всех инерциальных системах отсчета. Следовательно,
во всех инерциальных системах полная энергия & равна
Так как она зависит только от импульса частицы в направле-
направлении г и от |г| = г, то задача о трехмерном движении частицы
в центральном поле сводится к одномерной задаче движения
частицы в радиальном направлении с эффективной потенциаль-
потенциальной энергией. Поэтому границы движения можно найти так
же, как в одномерном случае.
Физическая причина отличия С/Эфф—U от нуля заключается
в следующем. Выделяя переменные, характеризующие радиаль-
радиальную составляющую движения, мы исключили составляющую р$
импульса, описывающую вращение частицы вокруг силового
центра. Ввиду сохранения момента импульса согласно D.24)
уменьшение г должно приводить к увеличению рф. Добавочный
член L2/2mr2 в эффективной потенциальной энергии одномерной
задачи как раз этот эффект и учитывает. Название этого чле-
члена— центробежная энергия — отражает тот факт, что при при-
приближении к силовому центру скорость вращательной компонен-
компоненты движения частицы возрастает и вследствие этого возрастает
центробежный эффект отбрасывания частицы от силового
центра.
Эффективная потенциальная энергия совпадает с энергией
взаимодействия U(r) в единственном случае, когда L = 0. При
ЬФО поведение U9$$(r) может существенно отличаться от
U(г) в области малых г, т. е. вблизи силового центра. Это раз*
личие особенно заметно в случае притяжения к силовому центру
(притяжения между частицами с массами Ш\ и т2). Пусть энер-
энергия взаимодействия U(r) ведет себя так, как это изображено
if а рис. 4.12 пунктирной линией. Такой потенциальной энергии
отвечает сила F = —dU/dr < 0, направленная к силовому
центру, т. е. сила притяжения. Если U(r) убывает недостаточна
быстро при г->О, так что
\U{r)\<L2t2mr\ D.27)
& А. В* Астахоз-

130
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ
1ГЛЛ
Рис. 4.12.
то при r>r* функция и&фф(г) имеет вид потенциальной ямы,
а при г <! г* — потенциального барьера. На рис. 4.12 график
изображен сплошной линией, При выполнении условия
D.27) центробежная
энергия L2/2mr2 как бы
создает потенциальный
барьер около силового
центра, который препят-
препятствует падению массы тл
на центр притяжения.
Так, на рис. 4.12 при лю-
любой полной энергии § от-
отвечающая ей горизон-
горизонтальная линия & = const
пересекается с графиком
'f/эфф {г). Следовательно*
возникает точка поворо-
поворота Гцйл и запретная для
частицы с массой т зона
от нуля до rmin. Это озна-
означает, что в этом случае
исходные частицы с массами тх и т2 не могут сблизиться до
расстояний, меньших rmin.
Если полная энергия & > О, то существует только одна точ-
точка поворота /mm. Следовательно, при & "> 0 движение инфи-
нитно. При & < О (нижняя
горизонтальная линия на
рис. 4.12) возникают две точки
поворота rmln и rmax. В этом
случае движение финитно. При
этом расстояние частицы с
массой т от центра или рас-
расстояние между частицами с
массами Ш\ и т2 периодически
изменяется в пределах от rmia
ДО Гтах.
Заметим, однако, что это
еще не означает, что движе-
движение является периодическим.
Действительно, мы пока рас-
рассматривали только радиаль-
радиальную составляющую движения.
Вращательная компонента
движения — движения в направлении, перпендикулярном ра-
радиус-вектору г,— может быть тако,й, что, приблизившись на ми-
минимальное расстояние к центру, удалившись затем на макси-
Рис. 4.13.

§4.3]
ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ
131
мальное от него расстояние и вновь вернувшись на минимальное
(расстояние, масса т будет обладать радиус-вектором, поверну-
повернутым уже по-другому. В этом случае ее траектория не замкнется
и периодичности, разумеется, не будет (рис. 4ЛЗ). Условие пе-
периодичности состоит в том, что за время одного цикла измене-
изменения расстояния между массой т и силовым центром (от rmin до
>тах и обратно) частица повернется на угол, кратный 2я. На-
Например, в кулоновском поле притяжения это условие всегда
выполняется. В этом мы убедимся в следующем параграфе, в
котором задача двух тел с взаимодействием, происходящим по
закону U(r)= а/г, будет рассмотрена подробно.
§ 4.3, Движение в кулоновском поло
1. Кулоновское поле является важнейшим частным случаем
центрального поля, поскольку кулоновскому закону подчинены
два вида фундаментальных сил — электростатические и грави-
гравитационные. Потенциальной энергии U{r)= а/г, как мы видели
<х>0
(г)
Рис. 4.14
в § 2.4, отвечает сила F = ar/г3. При а = —|а|<0 кулонов-
ский силовой центр является центром притяжения. График эф-
эффективной потенциальной энергии при а < О и L Ф 0 изобра-»
жен сплошной линией в левой части рис. 4.14. Здесь Го — это
точка минимума ?/Эфф(г). Она определяется из условия
L2
L2
и равна

132 ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХv [ГЛ. I
Значение эффективной потенциальной энергии в этой точке,
которое, очевидно, определяет и минимальное значение полной
энергии, составляет
с~ а | L2 а2т
n~^mln--+2/nr2- 2L2.
В точке г* эффективная потенциальная энергия -~ -\ •$> °б-»
ращается в нуль:
,_ L2 _ L2 _ го_
Г 2та 2т \ а | 2 #
При а > 0 кулоновский центр является центром отталкива-
отталкивания. График ?/Эфф(О при а>0 и ЬФО изображен в правой
части рис. 4.14.
Как во всяком центральном поле, в кулоновском поле ча-«
стица движется в неизменной плоскости с постоянной секто-<
риальной скоростью. Кроме того, движение в этом поле обла-
обладает рядом других закономерностей. Рассмотрим их.
Специфической особенностью движения в кулоновском поле
является сохранение вектора
а = [рЦ + ~-. D.28)
Убедимся в этом. При дифференцировании по времени выражения D.28)
учтем сразу сохранение момента. Тогда
da Г dp .1 та dr __ mar e dr_^
ТГ~~1!ГГ J+ г *~df г2 'dt***
a t r ... ma dr mar d , 4u»
mar
При выполнении этих преобразований мы использовали соотношения
dr * r r , dp ar
7- = Р> ^ = LrP]' уравнение движения —~- = -
т—^- = р, L == [гр], уравнение движения -~ = -у и векторное тождество
Сохранение вектора а дает возможность полного решения
задачи о движении частицы в кулоновском поле. Выберем спе-
специальную систему координат, изображенную на рис. 4.15. Ed
ось у направлена вдоль вектора [pt\ а ось х лежит в плосш*
сти движения и направлена вдоль вектора р. Это означает,
во-первых, что г лежит в координатной плоскости ху. Во-вторых,
как это следует из D.28), ей же-принадлежит и вектор а. Та^
как векторы р и L ортогональны, то абсолютное значение

§ 4.3]
ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ
133
вектора [pL] равно pL. Поэтому (рис. 4.15)
max __ г I то>У
г и г
Следовательно,
D.29)
= т2а2
may
.2 Г 2
p2L
2Lma
Учтем теперь, что у = г sin p, a L = г/? sin |3 (рис. 4.15), так что
ру = L. Поэтому
= т2а2 + 2mL2 (J~ + 7) = т2а2 + 2m%L2 = const. D.30)
Найдем, как меняется величина радиус-вектора частицы и
зависимости от угла ф, который г составляет с постоянным
вектором а (рис. 4.15). Эта зависимость и определит уравнение
траектории движения. Соглас-
Согласно D.29) у\
/ ч , та 2 ,
{О • Г) — ОХХ -f- ОуУ — -— X -+• _ 6Г
с другой стороны, та же ве-
величина равна or cos q>. Отсюда
окончательно находим:
где
г===
L2
1 + е cos ф э
D.31)
X X
--^Г- ^—-^Г. D-32)
Рис. 4.15.
причем постоянная а определяется выражением D.30). При
L Ф 0, т. е. 5 =т^= 0, в зависимости от значений sue уравнение
D.31) описывает одно из следующих конических сечений *)з
а) эллипс и как частный случай эллипса — окружность, б) ги-
гиперболу, в) параболу. Постоянная 5 называется фокальным
параметром, а е — эксцентриситетом конического сечения. Не
вникая в детали, относящиеся к курсу аналитической геомет-
геометрии, ограничимся графическими пояснениями к только что ска-
сказанному.
*) Напомним, что коническим сечением называется линия, по которой про-
произвольная плоскость пересекает прямой круговой конус.

134
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ 1ГЛ. %
В случае притяжения (ос < 0) все возможные виды траек*
торий частицы с ненулевым моментом импульса изображены
на рис. 4.16. Фокусы каждой из кривых (для эллипса — один
из фокусов) находятся в начале координат, т. е. там, где
Рис. 4.16а. Для эллипса: L > О, c7mjn < <*f < О, s > О, 0 < е < 1. rm\n :
s
О,
VI — е2
: 0. /"mla ™ '"max =
; для окружности: L > 0, ^ =
а = 5.
s
Рис. 4.166. L>0,
Рис. 4.16в. L>0,# = G, s> 0,^=1
rm[a « s/2.
расположен кулоновский силовой центр. В подписях приведены
области значений энергии и эксцентриситета, а также указаны
характерные для каждой из кривых размеры.
В случае силы отталкивания (а > 0) при L Ф 0 движение
может происходить только по гиперболической траектории. Она
изображена на рис. 4.17. Эллиптическая и параболическая
траектории невозможны. Причина заключается в следующем.
При сс>0 функция 1/эфф(*1, не имеет потенциальной ямы

§4,3]
ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ
135
Рис. 4.17. L>0, <Г>0, s<0>
(рис. 4.14). Поэтому при любом значении энергии под дей-
действием силы отталкивания частица будет уходить от силового
центра сколь угодно далеко. Параболическое движение может
осуществиться только в том слу-
случае, если энергия частицы & = 0.
При а > 0 существует единствен-
единственное состояние с таким значением
&. Это — состояние частицы, бес-
бесконечно удаленной от силового
центра (г—><»), с импульсом
р = 0. Очевидно, что к центру
отталкивания такая частица при-
приближаться не может. Она не
будет также от него и удаляться,
поскольку на бесконечности ку-
лоновская сила обращается в
нуль. Следовательно, частица не
может получить ускорения. Поэтому она будет пребывать в
покое на бесконечном удалении от центра сколь угодно
долго.
Для подтверждения того, что уравнение D.31) действительно описывает
траектории, изображенные на рис. 4.16 и 4.17 с теми значениями характерных
параметров, которые там приведены, проведем выборочную проверку.
Заметим, во-первых, что знаменатель выражения D 31) при любых конеч-
конечных значениях энергии & И момента L, т. е. конечных значениях е, является
величиной ограниченной. Поэтому г никогда в нуль не обращается. Таким
свойством обладают все траектории, изображенные на рис. 4.16 и 4.17.
Теперь рассмотрим случай силы притяжения (а <0).
Предположим, что 0 < е < 1. Тогда 1 +ecos<j ф 0 при всех значениях
<р. Это означает, что г — величина ограниченная, что характерно для эллипса.
Очевидно, что г = гт1п при cos ф = 1 и г = гтах при cos ф = —1. В этих
случаях из D.31) следует, что, соответственно, rmin ^ s/(l + e)i a rmax =j
= s/(l — e). Эти значения как раз и приведены в пояснении к рис. 4.16а.
При ф = dhJt/2 уравнение дает для г значение г = s, что также указано на
этом рисунке.
Если е = 0, то согласно тому же уравнению г — s = const при всех уг-
углах ф. Это означает, что эллипс вырождается в окружность радиуса s, кото-
которая также показана на рис. 4.16а.
Если е>.1, то в этом случае знаменатель выражения D.31) обращается
z нуль при значениях полйрных углов
Ф-0
= — arccos —,
е
: arccos —,
е
D.33)
Следовательно, при этих углах г-*оо. Удаление частицы на бесконечность
как раз характерно для траектории, изображенной на рис. 4.166. При ф == 0
знаменатель выражения D.31) принимает максимальное значение 1 + <?»

136 ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ Ш; Ъ
Следовательно, при этом значении ср имеем г = гт\п = ~г~т—» чт0 и отмечено
йод рис. 4.166.
Проверим, наконец, значения гтщ для гиперболического движения в слу-
случае силы отталкивания (а > 0). С учетом того, что в этом случае е < —1 й
* < 0, D.31) можно преобразовать к виду
- М Ы
г =
1 — | е | cos ф | е | cos ф — 1
Это выражение будет иметь минимальное значение при ф = 0, которое как
раз и указано под рис. 4.17.
Суммируя все вышеизложенное, сформулируем закон, на^
зываемый первым законом Кеплера. Траектория движения ча->
стицы в кулоновском поле является коническим сечением. В поле
притяжения частица с ненулевым моментом импульса может
совершать как финитное движение по гиперболической или кру-
круговой орбите, так и инфинитное движение по гиперболической
или параболической траектории. В поле отталкивания осуще-
осуществимо только движение по гиперболе. Во всех случаях частица
с ненулевым моментом импульса проходит на конечном рас-
расстоянии от силового центра. Расстояние наибольшего сближения
с центром называется перигелием орбиты, а наибольшего уда-
удаления— ее афелием.
Перигелий rmin и афелий rmax орбит определяются из условия
* = */.« (г) =-2^ +у-const.
2. Эллиптическое движение отличается от всех остальных
своей периодичностью. Обозначим период обращения через 7\
Определим его, используя для этой цели второй закон Кеплера.
За время dt радиус-вектор частицы заметет площадь
dS=2—dt. Интегрируя это равенство в пределах от 0 до Г,
получим:
S = -g-. D.34)
где S — площадь эллипса, которая, как известно, равна
S = nab. D.35)
В D.35) а и Ъ — большая и малая полуоси эллипса, выражения
для которых приведены в подписи к рис. 4.16а. Подставляя их
значения и учитывая D.32), из равенства выражений D.34)|
и D.35} находим:
J^ D.36)

,§ 4.3] ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ 137
Это равенство выражает третий закон Кеплера: квадрат пе-
периода обращения по эллиптической орбите пропорционален
кубу ее линейных размеров.
Исторически законы Кеплера были открыты эксперимент
тальным путем. Они были сформулированы Кеплером в 1609 г,
как обобщение опытных данных Тихо Браге о движении планет
Солнечной системы. Открытие Кеплера позволило Ньютону
сделать вывод о том, что силы тяготения изменяются обратно
пропорционально квадрату расстояния и что законы Кеплера
являются следствием кулоновского характера поля тяготения
Солнца.
Экспериментальные данные, которыми располагал Кеплер,
были не настолько точны, чтобы можно было зарегистрировать
небольшие возмущения движения планет, вызванные их взаим-<
ным притяжением. Эта неполнота картины, как это ни парадок-
парадоксально, сыграла благотворную роль, так как позволила Кеплеру
отыскать простые эмпирические закономерности. Если техника
экспериментальных наблюдений была бы более развитой, чем
это было в то время на самом деле, то скорее всего Кеплер
запутался бы в массе мелких деталей и не смог сформулиро-
сформулировать свои законы. А это надолго задержало бы открытие одного
из фундаментальных законов — закона всемирного тяготения—*
и развитие механики в целом.
В настоящее время в составе Солнечной системы известны
девять больших планет и около полутора тысяч малых планет,
называемых астероидами. Так как масса Солнца примерно
в 700 раз больше остальных тел Солнечной системы, то центр
инерции Солнечной системы находится достаточно близко к
центру Солнца. Поэтому с высокой степенью точности систему
отсчета, связанную с Солнцем, можно считать инерциальной.
По этой же причине (об этом мы уже упоминали в § 4.2) можно
пренебречь силами взаимного притяжения планет. Таким обра-
образом, силовое поле, в котором движется каждая планета, можно
считать кулоновским и приведенная масса системы Солнце —
планета почти совпадает с массой планеты. Поэтому все полу-
полученные выше соотношения для эллиптического движения при^
веденной массы с очень хорошей точностью могут быть приме-
применены к движению любой из планет. При этом под массой m
следует понимать массу планеты, а под г — ее радиус-вектор,
отсчитываемый от начала системы координат, в котором нахо-*
дится центр Солнца.
Планеты движутся вокруг Солнца по эллиптическим орби*
там, параметры которых приведены в таблице 2. Длины боль-"
ших полуосей выражены в астрономических единицах длины
(а. е.). Эта единица определяется как полусумма расстояний от
афелия и перигелия Земли до Солнца и равна 1,495» 10й м.

13$ ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ [ГЛ. 1
Таблица 2
Меркурий
Венера
Земля
Марс
Юпитер
Сатурн
Уран
Нептун
Плутон
Длина боль-
большой полуоси
орбиты,
а. е.
0,387
0,723
1,000
1,523
5,202
9,554
19,218
30,109
39,60
Период
обращения»
сек
7,60-106
1,94-107
3,16-107
5,94-107
3,74-108
9,3.108
2,66-109
5,20-109
7,82-109
Эксцент-
Эксцентриситет
0,205
0,006
0,016
0,093
0,048
0,055
0,046
0,008
0,246
Угол
наклона
орбиты
7°00'
3°23'
0
Г5Г
1°18'
2°29'
0°46'
Г46'
\ТТ
Масса
планеты,
кг
3,28-1023
4,83-102*
5,98-1024
6,37-1023
1,9-1027
5.67-1026
8,80-1025
1,03 -1028
5,4-1024
Эксцентриситеты орбит очень малы, и по своей форме орбиты
мало отличаются от круговых. Исключение составляют Мерку-
Меркурий и наиболее удаленная от Солнца планета Плутон, имеющие
довольно вытянутые орбиты. Любопытно, что в настоящее время
за счет значительного эксцентриситета орбиты Плутон нахо-
находится ближе к Солнцу, чем предпоследняя планета таблицы 2 —
Нептун. Эта картина будет существовать вплоть до 2009 г.
Плоскости вращения различных планет очень близки друг
к другу. И здесь исключением является Плутон, орбита кото-
которого наклонена примерно на 18° к длоскости вращения Земли.
Все планеты движутся в одну сторону — против часовой стрел*
ки, если смотреть на Солнечную систему со стороны Полярной
звезды.
Таблица 2 позволяет проверить, насколько точно движение
планет Солнечной системы подчиняется законам Кеплера. На-
Например, для проверки третьего закона сравним орбиту Урана
с орбитой Земли. Куб отношения длин больших полуосей равен
A9,22K: 1 ^ 71ДЫ02. Отношение квадратов периодов состав-
составляет (84«2J ^ 70,9-Ю2. Как видно, обе цифры совпадают с
точностью до 1 %.
3. Рассмотрим некоторые приложения теории движения в
кулоновском поле. Начнем с того, что определим первую и вто-
вторую космические скорости.
Первой космической скоростью называется минимальная
скорость, которую нужно сообщить телу у поверхности Земли,
чтобы превратить его в искусственный спутник. Второй косми-
космической скоростью называется минимальная скорость, двигаясь,
с которой тело покидает Землю, перемещаясь по незамкнутой
орбите.
Очевидно, первой космической скоростью i/ обладает спут«
ник, движущийся по круговой орбите в непосредственной бли«

§ 4.3} ДВИЖЕНИЕ В КУЛОНОВСКОМ ПОЛЕ 139
зости к земной поверхности. В этом случае эксцентриситет ра-»
вен нулю и тело движется по окружности, радиус которой равен
радиусу Земли R. Воспользуемся тем, что радиус круговой
орбиты равен фокальному параметру, и применим формулу
D.32):
Так как масса спутника ничтожно мала по сравнению с массой
Земли, то приведенная масса т системы Земля — спутник прак-
практически совпадает с массой спутника. |a| = Ym^> гДе М — мас"
са Земли. Эта величина может быть выражена через величину
ускорения свободного падения g у поверхности Земли по фор«
муле утМ = gmR2 (см. § 2.4). Учтем, наконец, что L = p$R ==
= mv'R. Тогда
Полагая g = 9,8 м/сек2, R = 6,4-106 м, получаем:
v'&&- 103 м/сек.
Как установлено выше, в поле притяжения движение ста*
новится инфинитным при достижении энергии S = 0. Следова*
тельно, вторая космическая скорость v" должна определяться
из этого условия. В частности, на уровне земной поверхности
с» р" утМ mvn утМ
где pn = mvff — импульс тела, обладающего второй космиче-
космической скоростью v". Приравнивая S нулю, находим:
х)" = л/2уM/R = ^2gR » 11,2- 103м/сек.
4. Рассмотрим теперь, какой угол составляют друг с другом
скорости частицы при времени t—+ — оо и f—>+°° в случае дви-»
жения по гиперболической траектории. Эта задача имеет важ-
важнейшее значение для изучения столкновений заряженных частиц
|(этой теме посвящена следующая глава). Искомый угол обо-
значим через Э. При t—>+<*> частица движется бесконечно
далеко от центра. Так как кулоновская сила убывает с рас-»
стоянием, то при t—>zhoo состояния частицы являются асимпто*
тическими, т. е. частица движется равномерно и прямолинейно.
Рассмотрим, например, гиперболическое движение в поле
Притяжения. Асимптоты к гиперболе на рис. 4.18 изображены
пунктиром. Показанные на рисунке углы
Ф =arccos —, ф OQ = — arccos — ,
Q

140
ДВИЖЕНИЕ ЧАСТИЦЫ В РАЗЛИЧНЫХ СИЛОВЫХ ПОЛЯХ [ГЛ. I
в чем легко убедиться с помощью D.31). При указанных зна*
чениях ф частица уходит на бесконечность, г—>оо. По абсолют-»
ным значениям углы ф+00 и ф_то равны. Учитывая симметрию
Рис. 4.18.
гиперболы относительно оси абсцисс, с помощью рис. 4.18 на-<
ходим: ф+оо + а = я и G + 2а = я. Отсюда следует, что искомый
(угол 0 = 2ф+оо —я. Учитывая D.30) и значение е из D.32),
получаем:
. 0 1 та
sin у = — cos ф+0О = — - = — =
та 1
B&L2/ma2) ' ' в '
Обратим внимание, что значение D.38) не зависит от зна*
ка а. Следовательно, углы рассеяния в полях кулоновского
притяжения и отталкивания с одним и тем же абсолютным зна-
значением а одинаковы при одних и тех же значениях <? и L2.
Отметим также, что при переходе на параболическую траек-
траекторию (<^->0) угол рассеяния стремится к я.

ГЛАВА 5
СТОЛКНОВЕНИЯ
§ 5.1. Упругие и неупругие столкновения
1. Во многих случаях взаимодействие частиц носит характер
столкновений.
Столкновением частиц называется процесс, в котором в на-
начальный момент частицы настолько удалены друг от друга, что
каждая из них является свободной. При этом импульсы частиц
ориентированы так, что со временем частицы начинают взаимо-
взаимодействовать друг с другом *) (рис. 5.1).
Сталкивающиеся частицы могут быть как элементарными
(например, протоны), так и имеющими внутреннюю структуру
(атомы, молекулы, биллиардные шары и т. д.). После столкно-
столкновения частицы разлетаются настолько, что каждая из них снова
становится свободной. При ^
этом частицы в конечном со- ,''
стоянии по своим внутренним п ^^'*' ^J^
свойствам могут отличаться И^***00*^"* ^~~~~~~ Р
от частиц в начальном состоя- ^"^ ^"'
нии. В связи с этим столкно- "'
вения подразделяются на упру- Рис. 5.1.
гие и неупругие.
Упругим называется столкновение, в результате которого
внутреннее состояние частиц не меняется. Если внутреннее со-
состояние изменяется, то столкновение называется неупругим.
Столкновениями обусловлены многие явления, важные для
науки и техники. Остановимся на некоторых примерах. Прежде
всего столкновения играют основную роль в структуре и дина-
динамике газов. Действительно, в газе среднее расстояние между
*) Приведенное определение столкновения шире общераспространенного
«житейского» понимания этого термина. Например, столкновением двух заря-
заряженных шаров мы называем не только процесс их удара друг о друга, но и
процесс, при котором шары, не касаясь, отклоняются от прямолинейных путей
кулоновским взаимодействием.

142 СТОЛКНОВЕНИЯ (ГЛ. б
молекулами намного превосходит радиус действия межмолеку-
межмолекулярных сил. Каждая молекула время от времени сталкивается
со своими соседями. Такие процессы, как передача тепла в га-
газах, диффузия газов, способность газов оказывать сопротивле-*
ние движущемуся в газе телу, определяются свойствами столк*
новений молекул друг с другом. Химические реакции в газовой
фазе происходят вследствие неупругих столкновений молекул
реагирующих веществ. Способность тел проводить электричек
ство, т. е. свойство электропроводности, зависит от столкнове^
fi электронов проводимости с частицами, составляющими тело,
Рис. 5.26. Рис. 5.2в.
Особо важное значение столкновения имеют для изучения
микроскопической структуры вещества. Свойства атомов, атом-
атомных ядер и элементарных частиц можно исследовать единствен-
единственным способом, анализируя их столкновения с различными ча-
ствдами. Эти частицы слишком малы, чтобы их свойства можно
было «прощупать» иными методами исследования. Так, на атом
нельзя «посмотреть». Длина волны видимого света (она по-
порядка нескольких тысяч ангстрем) огромна по сравнению с
этими частицами. А свет меньших длин вблн сам, как оказы-
оказывается, становится потоком квантовых частиц — фотонов. В этом
умысле метод наблюдения объектов микромира с помощью
электромагнитного излучения равноправен с другими способами
зондирования микроскопической структуры вещества потоками
частиц любой другой природы.
Процессы столкновений имеют два важных свойства, выхо-
выходящих далеко за рамки классической механики. Во-первых, до-
довольно детальную информацию о таких процессах можно полу-
получить из законов сохранения. А так как эти законы справедливы
не только в классической, но и в квантовой физике, то резуль-
результаты, полученные из законов сохранения, применимы к столк-
столкновениям квантовых частиц — молекул, атомов, ядер и даже
элементарных частиц. Во-вторых, задача о полном описании
столкновений формулируется в терминах сечения — понятия,

$5 4} УПРУГИЕ И НЕУПРУГИЕ СТОЛКНОВЕНИЯ 143
имеющего смысл как в классической, так и в квантовой обла-
области (оно будет определено ниже, в следующем параграфе).
Еще одно общее замечание касается выбора системы отсчета
при анализе столкновений. Система отсчета, в которой столк-
столкновение изучается опытным путем, называется лабораторной
(ЛС) (рис. 5.2а). Бывает так, что в этой системе одна из ча-
частиц может считаться покоящейся (рис. 5.26). В этом случае
она называется мишенью, а налетающая на нее частица — сна-
снарядом. Теоретический анализ столкновений удобнее проводить
в другой системе — системе центра инерции (СЦИ) (рис. 5.2в),
В этой системе исключается движение центра инерции частиц
и сумма их импульсов равна нулю, так что импульсы
сталкивающихся частиц равны по величине и обратны по на-
направлению.
2. Законы сохранения дают возможность получить ту часть
информации о столкновении, которая не зависит от конкрет-
конкретного вида взаимодействия между частицами. Рассмотрим роль
законов сохранения импульса и энергии.
а) Упругое столкновение двух частиц. Очень распространен-
распространенный процесс. Он осуществляется, например, в газах (столкно-
(столкновение молекул), в макроскопических ситуациях (столкновение
биллиардных шаров), в ядерных реакциях (например, столкно-
столкновение нейтрона с протоном). За исключением ядерных реакций
высоких энергий, упругие столкновения относятся к нерелятп-
вистским процессам. Для каждого из них законы сохранения
импульса и энергии выражаются уравнениями
= K + K, E.1)
2m, l 2m2 2tn{ ' 2m2 ' v '
в которых m\ и m2 — массы сталкивающихся частиц, pL =mi%yi и
р'. z=mivfi (i= I, 2)—импульсы частиц, а и? и v\ (I = 1, 2) —
их скорости соответственно до и после столкновения. Из E.2)
видно, что закон сохранения энергии сводится к постоянству
суммарной кинетической энергии. Это следствие того» что при
упругом столкновении массы частиц не изменяются.
Скорости частиц в ЛС можно выразить через скорость их
центра инерции V и скорости их относительного движения V-*>
и и+оо соответственно до и после столкновения, т. е. в асимпто-
асимптотических состояниях. Для этого нужно воспользоваться преоб-
преобразованиями D.18). Дифференцируя их по времени и устрем-
устремляя затем время к —оо и +°°> с учетом закона

144 столкновения 1гл, $
центра инерции —^- == V = const находим:
^1
Здесь 2_oo и v+oo — скорости относительного движения частиц в
асимптотических состояниях (до и после столкновения). Найдя
с помощью E.3) импульсы частиц, прямой подстановкой легко
убедиться в том, что E.1) обращается в тождество. Это озна-
чает, что в E.3) закон сохранения импульса учтен.
Перейдем теперь в СЦИ. В ней V = 0. Поэтому в этой си-
системе
Здесь m = т\гп2/(nil-\-ГП2)—приведенная масса частиц. Под-
Подставляя значения импульсов в СЦИ в E.2), получаем:
+ ОО
Следовательно, v-^ = u+Oo, т. е. в результате столкновения
скорость относительного движения изменяет только свое на-
направление, а по абсолютному значению остается постоянной.
Таким образом, в СЦИ картина столкновения выглядит так,
как это изображено на рис. 5.3. Здесь 0 — угол рассеяния ча-
частиц в этой системе и на его значения ограничений нет: он
может быть любым. В ЛС картина значительно сложнее, что
и подтверждает преимущество СЦИ для анализа столкновений.
б) Столкновение слипающихся частиц. В результате частицы
не разлетаются, а образуют новую единую частицу. Примером
может служить столкновение метеорита с Землей.
Пусть в ЛС одна из частиц покоится, т. е. является ми-
шенькк Обозначим ее массу через п%2. Массу и импульс снаряда
б соответственно через пгцм р. Массу частицы, воз-*

$5.1] УПРУГИЕ И НЕУПРУГИЕ СТОЛКНОВЕНИЯ 145
никшей в результате слипания первоначальных частиц, обо-
обозначим через т, а ее импульс — через q (рис. 5.4). По закону
сохранения импульса р = q. Закон сохранения энергии при
условии, что движение является нерелятивистским, выглядит
так:
п2
Q I 2 Р i 9 ,'
E.4)
Очевидно, что это соотно-
шение несовместимо с ра-
венством т = mi + /пг. Сле-
довательно, до и после
столкновения масса системы ^У1^ |/*|= I/71=1^ 1-1/^1
разная, т. е. различное зна^ Р2-~Р/
чение имеет внутренняя
энергия системы в началь- Рис. 5.3.
ном и конечном состоянии.
Обозначим через Q изменение внутренней энергии: Q
= (т — mi — m2)c2. Из E.4) следует, что
Эта энергия для частицы макроскопических размеров выде*
ляется в виде тепла. Если измерить Q, то, зная первоначальный
т,
Рис. 5.4.
импульс, можно найти т. В нерелятивистских столкновениях
отличие т от mi + m2— очень малое по сравнению с массам^
т\ и /П2- Оно заметно лишь в комбинации (т — т\ — m<i)c%
так как с2— очень большая величина, порядка 1017 м2/сек2. Та*
ким образом, можно записать:
т = Ш\ + т2 + Am, причем Дт < mi (i == 1,2).
Так как последнее выражение для Q не содержит с2, то с вы«
сокой точностью
Ei -f- тг Ч~ Am *

] 46 СТОЛКНО&ЕШЯ [ГЛ. 5
в) Неупругие столкновения двух частиц без слипания. При-
Примером может служить одна из самых важных термоядерных»
реакций, в которой два дейтрона (тяжелый изотоп водорода,
iH2) превращаются в нейтрон п и изотоп гелия Н3
Ограничимся опять нерелятивистским случаем. Вследствие
неупругого характера столкновения массы частиц в начальном
состоянии Ш\ и /7?2 не равны массам ш\ и mf2 частиц в конеч-
ном состоянии. Пусть частица с массой m<i является мишенью.
Обозначим импульсы остальных частиц через pv р[ и р'Г Тогда
в ЛС закон сохранения энергии будет иметь вид
^+^+-?;=<с2+<с*+^+ik- E>5)
Пусть
m[c2 + my — mLc2 - m/2 = Q. E.6)
Тогда E.5) преобразуется так:
^ + Д + д. E.7)
2/ttj 2m\ 2ап^ V ;
Энергия Q может быть как положительной, так и отрица-
отрицательной. Если Q > 0, то столкновение называется эндотермиче-
эндотермическим. Такой процесс осуществляется не всегда. Действительно,
если кинетическая энергия снаряда p2lj2ml < Q, то процесс не-
эозможен, так как в этом случае нарушается закон сохранения
энергии E.7). Поэтому говорят, что Q определяет порог реак-
реакции. Порогом называется минимальная кинетическая энергия
снаряда, которой достаточно для рождения продуктов реакции
с нулевыми импульсами. Для эндотермических столкновений
кинетическая энергия частиц в конечном состоянии меньше ки-
кинетической энергии начального состояния.
При Q < 0 столкновение называется экзотермическим. Для
него характерен переход части внутренней энергии в кинети-
кинетическую энергию продуктов столкновения: кинетическая энергия
конечного состояния превосходит кинетическую энергию на-
начального состояния.
Столкновения тел, размеры которых намного превышают раз-
размеры элементарных частиц, чаще всего являются эндотермиче-
эндотермическими. Экзотермические столкновения больших тел всегда не-
необычны и должны быть специальным образом подготовлены.
К числу столкновений такого типа относится удар бойка по

§ 5 1] УПРУГИЕ И НЕУПРУГИЕ СТОЛКНОВЕНИЯ 147
взрывчатому веществу. В результате взрыва запасенная во
взрывчатке химическая энергия переходит в энергию движения
продуктов взрыва. Экзотермические столкновения характерны
для ядерных реакций. Например, к их числу относится упомя^
нутая выше термоядерная реакция. Для нее Q = —5,3-10~13 Дж,
При этом реакция идет с наибольшей легкостью в том случае,
если кинетическая энергия дейтрона-снаряда составляет сотые
доли процента его энергии покоя. Это означает, что в этом слу-
случае скорость дейтрона является нерелятивистской и мы вправе
применять к этой реакции соотношение E.7).
3. Рассмотрим распады нестабильных частиц. Эти процессы
часто встречаются в микромире. Они родственны неупругим
столкновениям. Их отличие от ранее рас- 0
смотренных процессов заключается в том, ^
что в начальном состоянии присутствует
всего одна частица. Пусть ее масса рав- /
на т и импульс равен р. Предположим, ^ р ,\J?f
что частица распадается на две частицы ~~^^Щ
с массами Ш\ и тг, обладающими им-
пульсами р\ и р2 (рис. 5.5). Процессы
распада на две частицы часто ветре- %
чаются в физике элементарных частиц Рис. 5.5,
высоких энергий. При этом продукты
распада даже в СЦИ часто разлетаются с весьма высокими
скоростями движения. Поэтому в этих случаях законы сохра-
сохранения следует записывать в наиболее общем релятивистском
виде;
Р == Pi 4- Ръ E.9)
с УР2 + mV = caJp] + m]c2 + с aJp\ + т\с2. E:9)
Именно с помощью этих уравнений была открыта неста-
нестабильная частица лямбда-гиперон Л° йо ее распаду на протон р
и отрицательно заряженный пион я~. Произошло это следую-
следующим образом. Электрически заряженные частицы научились
наблюдать в специальных устройствах, таких, как, например,
камера Вильсона, пузырьковая камера, а также с помощью фо-
фотоэмульсий. Во всех этих устройствах заряженные частицы,
к числу которых относятся р и яг, оставляют следы в виде
треков. В одном из таких устройств было зарегистрировано сле-
следующее событие. Некоторая заряженная частица оставила след
с изломом. На рис. 5.6 он изображен ломаной линией АОВ. По
соседству с точкой О начинались два других следа О'С и O'D*
Выяснилось, что их оставили р и яг. Было сделайо предполо-"
жение, что они возникли в результате распада в точке О' не-
некоторой нейтральной частицы, родившейся в точке О. На

148
столкновения
1ГЛ. П
рис. 5.6 направление ее движения отмечено пунктиром. Изме-
Измерения позволили определить углы 9i и 62, а также величины
импульсов я-мезона р\ и протона рг- Тогда, проектируя вектор-
векторное уравнение E.8) на направле-
направление 00', нашли величину импульса
неизвестной частицы:
p = Pi cos 0, 4- Р2 cos 92.
Подставив затем это значение в за-
закон сохранения энергии E.9), по-
получили уравнение относительно
массы т неизвестной частицы. Ре-
Решив его, выяснили, что
mAo«218Ome,
где те—масса электрона. Так была определена масса Л°-ги-
перона и открыта сама эта частица.
§ 5.2. Сечение рассеяния
1. В физических применениях чаще всего приходится иметь
дело со столкновениями не одной частицы, а с рассеянием
потока частиц мишенью.
Рассеянием называется процесс столкновения потока одина-
одинаковых частиц, имеющих параллельные импульсы, с мишенью
при условии, что каждая частица-снаряд независимо взаимо-
взаимодействует не более чем с одной из частиц мишени, называемых
рассеивающими центрами (рис. 5.7а).
Рис. 5.7а.
Рис. 5.76.
Оговаривающее условие означает, в частности, что мишень
должна быть достаточно тонкой, чтобы был малым вклад дво©-
ного и вообще многократного взаимодействия с мишенш*
(рис. 5.76), и что радиус действия сил, обусловливающих рас-
рассеяние, должен быть меньше расстояния между соседними рас*
сеивающими центрами мишени.

СЕЧЕНИЕ РАССЕЯНИЯ
149
Поток падающих частиц называют пучком. Обычно опыт по
рассеянию стараются ставить так, чтобы падающие частицы
имели не только параллельные импульсы, но и одинаковые
энергии. В этом случае пучок называют моноэнергетическим.
Рассеивающие центры мишени обычно тоже являются одина-
одинаковыми. Моноэнергетические пучки широко используются в
атомной и ядерной физике. Их направляют на различные ми-
мишени с целью получить сведения о строении микрообъектов по
результатам наблюдаемых столкновений,
Ввиду важного значения процессов рассеяния необходимо
определить понятия, удобные для их описания. Все процессы
столкновений описываются с помощью сечений. Для разъясне-
разъяснения физического смысла сечения рассмотрим моноэнергетиче-
моноэнергетический пучок частиц, с импульсом р у каждой, падающий на си-
силовой центр. В результате столкновения с силовым центром
частицы-снаряды отклоняются от первоначального направления
своего движения. Пусть dN— число частиц, рассеиваемых в
единицу времени в малый телесный угол dQ. На рис. 5.8 он
Рис. 5.8.
показан заштрихованной площадкой на сфере единичного ра-
радиуса с центром в месте расположения центра рассеяния. Ве«
личина телесного угла dQ равна sinQdQdy. Углы 8 и ф ме-
меняются в пределах 0 < 8 ^ я; 0 ^ ф < 2я. Очевидно, что dN
будет пропорционально телесному углу dQ, а также плотности
гютока частиц в падающем на силовой центр пучке, которую
мы обозначим через /о. Плотностью потока называется число
частиц, пересекающих в единицу времени единичную площадку,
перпендикулярную направлению движения частиц-

150 СТОЛКНОВЕНИЯ [ГЛ. 5
Единичный акт столкновения частицы-снаряда с рассеиваю-
рассеивающим центром, в результате которого частица отклоняется в те-
телесный угол dQ, будет характеризоваться отношением
do = !?-. E.10)
Именно оно и определяет величину, удобную для описания
процессов рассеяния. Эта величина называется дифференциаль-
дифференциальным поперечным сечением рассеяния в телесный угол dQ. Из
E.10) и определений dN и /0 следует, что сечение имеет раз*
мерность площади.
Поскольку dN пропорционально dQ, то этим же свойством
обладает и da. Коэффициент пропорциональности записывают
в виде do/dQ, так что
По определению dN/dQ равно числу частиц, рассеиваемых
в единицу времени в единичный телесный угол в направлении,
которое задается углами 0 и ср. Следовательно, dN/dQ описы-
описывает угловое распределение рассеянных частиц (т. е. их рас-
распределение по углам б и ф). Из сравнения E.10) и E.11) по-
получаем:
*0
Таким образом, угловое распределение рассеянных частиц пол-
полностью характеризуется величиной do/dQ. Оно имеет смысл
дифференциального сечения рассеяния в единичный телесный
угол в направлении, заданном углами 0 и ср (рис. 5.8).
Помимо дифференциального сечения, существует понятие
полного сечения рассеяния. Полное сечение а определяется ин-
интегрированием дифференциального сечения по всей области
изменения углов 0 и ср:
Я 2Я
%)\\ (?)р. E.13)
Если рассеивающий центр является источником центрально-
симметричного силового поля, то рассеяние полностью харак-
характеризуется дифференциальным сечением рассеяния в заданный
интервал углов @, 0 + ^0). Действительно, на частицу-снаряд
действует сила центрального характера, поэтому распределение
рассеянных частиц будет зависеть только от 0 и не будет за-
зависеть от угла ф (рис. 5.8). Это означает, что do/dQ не зависит
от ф. Дифференциальное сечение рассеяния в интервал углов
@, 0 + d0) определяется отношением числа частиц, рассеянных

§5.2] СЕЧЕНИЕ РАССЕЯНИЯ 151
в единицу времени в интервал углов F, 0 + dQ) при всех
углах ф, к плотности потока частиц в падающем пучке. Обо-
Обозначим это сечение через -jQ-dQ. Очевидно, что оно является
интегралом от E.11) по всем углам ср, при вычислении которого
следует учесть, что do/dQ от <р не зависит. Поскольку dQ =
= sin 6 dQ Лр, то
2
^). E.14)
Это соотношение определяет связь между do/dQ и da/dQs.
-g-JtesIne-g. E.15)
Величина do/dQ имеет смысл дифференциального сечения рас-
рассеяния в единичный интервал значений 8 в заданном направ-
направлении.
Существенно, что
понятие сечения не опирается на классическое определение
состояния. Для определения сечений достаточно знать только
импульсы частиц. Координаты частиц знать не обязательно*
Поэтому понятие сечения не теряет смысла в квантовой обла-
области и действительно используется для исследования столкно-
столкновений микрочастиц.
Выбор единиц измерения сечений обычно связывают с ха-
характерным пространственным масштабом рассматриваемых
столкновений. Так, в ядерной физике используется единица,
величина которой составляет 10~24 см2. Эта единица называется
барном. Ее выбор связан с тем, что геометрические сечения
атомных ядер имеют порядок величины 10~~24 см2.
В классической физике для детального описания рассеяния
вводится величина, называемая прицельным параметром. Он
обычно обозначается через р. При-
Прицельный параметр равен наикратчай-
наикратчайшему расстоянию, на котором части-
частица-снаряд прошла бы от центра рас-
рассеяния в том случае, если взаимодей-
взаимодействие с ним было бы выключено -<§>- \
(рис. 5.9).
Рассмотрим рассеяние на сфериче* Рис> 5#9*
ски симметричном рассеивающем
центре. Ясно, что каждому интервалу углов рассеяния
(8, 6 + dQ) соответствует свой диапазон значений прицельного
параметра (р, p-\-dp). Это означает, что между р и 8 суще-
существует функциональная связь: р = р(8). При этом р является
убывающей функцией 8: чем ближе к центру летит частица-

152
СТОЛКНОВЕНИЯ
снаряд, тем на больший угол она рассеивается. Таким образом,
можно утверждать, что из всех падающих в единицу времени
на центр частиц только dN = I0-2npdp частиц попадут в интер-
интервал углов (9, 9 + d9) (рис. 5.10). Поэтому
йа = -у^ = 2ярф = 2лр(9) -^\dQ. E.16)
В последнем выражении знак модуля необходим, так как по
определению do величина положительная, а dp/dQ < 0. В ре-
результате имеем:
da
а полное сечение равно
-fg-
d9. E.18)
Рис. 5.10.
Вывод формул E.16),
E.18) вскрывает физиче-
физическое содержание рассмотренных величин. Полное сечение а
имеет смысл площади, затеняемой центром рассеяния в направ-
направлении падения пучка. Частицы-снаряды, нацеленные в эту тень,
будут рассеяны центром. Дифференциальное сечение — часть
площади а. В случае сферически симметричного рассеивающего
центра она имеет вид кольца. Частицы, нацеленные в кольцо,
Рис. 5.11.
рассеиваются в определенный интервал углов, который соот-
соответствует значениям прицельного параметра между внутренним
и внешним радиусами кольца (рис. 5.11).
Отметим, наконец, что существуют также сечения неупругих
столкновений, в результате которых может происходить рожде-

СЕЧЕНИЕ РАССЕЯНИЯ
153
ние новых частиц и поглощение мишенью частиц-снарядов. Се*
чения неупругих столкновений также имеют размерность пло^
щади. Частицы-снаряды, нацеленные внутрь сечения, связанного
с мишенью, вызывают соответствующий аеупругий процесс.
Так, например, сечение рождения нейтрального пиона я0 при
столкновении протона р с нейтроном п имеет смысл площадки а,
связанной спи ориентированной перпендикулярно направлен
нию движения р. Нейтрон при этом считается мишенью, а про^
тон — частицей-снарядом. Если р нацелен внутрь площади а,
то его столкновение с п приве- ,
дет к образованию пиона.
2. Получим сечение упру-
упругого рассеяния нерелятивист-
нерелятивистской частицы на неподвижном
твердом шаре радиуса R
(рис. 5.12). Из реальных си- —в
стем, для которых эта задача
имеет значение, укажем, на-
например, на газы. Напомним,
что силы отталкивания резко
возрастают при сближении
молекул газа, а силы притя- Рис. 5.12.
жения намного меньше сил от-
отталкивания. Поэтому взаимодействие между молекулами можно
моделировать следующим образом:
В!
с (/•)
= {
О
при
при
г < R,
r>R,
E.19)
где U(г)—потенциальная энергия взаимодействия двух мо-
молекул на расстоянии г. Приближение E.19) учитывает дей-
действие очень больших сил отталкивания на расстоянии, меньшем
некоторого критического значения R. Поэтому по смыслу R
характеризует наименьшее расстояние между двумя молеку-
молекулами, т. е. является суммой их радиусов. Закон взаимодействия
E.19) не учитывает действие сил притяжения между молеку-
молекулами. Он соответствует удару частицы о поверхность твердого
шара радиуса R.
Обозначим через р_оо и р+оо импульс частицы-снаряда в на-
начальном и конечном состояниях, а через т — ее массу. Тогда
из закона сохранения энергии pioo/2rn = p^oo/2m следует, что
р_оо = р+00 = рос. Вследствие центрального характера взаимо-
взаимодействия E.19) траектория частицы-снаряда будет плоской.
Сила F действует на частицу-снаряд в момент ее соприкосно-
соприкосновения с поверхностью шара и направлена по радиусу. Поэтому
составляющая импульса частицы, лежащая в плоскости,

154
СТОЛКНОВЕНИЯ
касательной к поверхности шара в точке удара, сохраняет-
сохраняется. Следовательно, р_оо sin a = p<x> sin a = р+оо sin р = /?«> sin f$
(рис. 5.12). Таким образом, угол падения а равен углу отра-
отражения р и угол рассеяния 6 = л; — а — |} = я — 2а. Поэтому
прицельный параметр равен
Следовательно,
| 46 I ~ 2 Sin 2 '
Подставляя эти выражения в E.17) и E.18), находим:
do
nR2
E.20)
E.21)
Формула E.21) иллюстрирует геометрический смысл сече-
сечения. Выражение E.21) определяет площадь круга радиусом R«
т. е. действительно определяет площадь поперечного сечения
тени, отбрасываемой шаром.
3. Найдем сечение рассеяния частицы с массой т в поле
кулоновского центра. В этом случае, так же как и в предыду-
предыдущем пункте, закон сохранения энергии приводит к равенству
абсолютных значений им-
импульсов частицы-снаряда
в начальном и конечном
состояниях: р-оо — р+оо =*.
= роо. Теперь выразим
абсолютное значение мо-
момента импульса L через
прицельный параметр р
(рис. 5.13). Для этого за-
заметим, что ввиду сохра*
нения момента импульса
Ряс. 5.13. достаточно знать его зна-
значение в одном каком-то
состоянии. Пусть это состояние будет начальным. Так как
X, = [гр], то L равно произведению величины импульса частицы
на величину проекции ее радиус-вектора на направление, пер-
перпендикулярное импульсу. Из рис. 5.13 (он соответствует куло-
новскому полю притяжения) видно, что эта проекция равна
дельному параметру р. Таким образом,

I 5.2]
СЕЧЕНИЕ РАССЕЯНИЯ
155
Подставляя значение L, а также S>==pl>j2tn в D.38), находим*,
1
. G
sin-тг = •
Отсюда следует, что
га2
^^ т2а2 ctgF/2)
pt, ' sin2 (9/2)
Поэтому
= m2a2 cos F/2)
sin3 F/2)
и дифференциальное сечение в кулоновском поле равно
da _ { та \2 cos F/2)
sin3 F/2) °
E.22)
Полученный результат называется формулой Резерфорда.
В отличие от рассеяния на твердом шаре, кулоновское диф«
ференциальное сечение зависит от энергии (импульса) частицы-*
снаряда и очень сильно меняется в зависимости от угла рас-
рассеяния G. Угловая зависимость дифферен-
дифференциального сечения показана на рис. 5.14.
При малых углах рассеяния do/dQ неогра-
неограниченно возрастает. Эта особенность куло-
новского рассеяния обусловлена законом
изменения потенциальной энергии части-
частицы U в зависимости от расстояния г до
центра: U(r)~ IJr. Так как потенциальная
энергия довольно медленно уменьшается с
увеличением г, то частицы даже с очень
большими прицельными параметрами все
же претерпевают отклонение от первона-
первоначального направления движения. Именно поэтому дифферент
циальное сечение рассеяния на малые углы оказывается очень
большим. С увеличением угла рассеяния дифференциальное се-»
чение быстро уменьшается, стремясь к нулю при 8-* я. Этот эф-
эффект обусловлен тем, что отклонение на большие углы возмож-*
но лишь для частиц с очень малыми прицельными параметрами.
А в соответствии с E.17) do/dQ уменьшается с уменьшением р.
Полное сечение рассеяния на кулоновском центре бесконечно
велико;
п
cos F/2) d\
Рис. 5.14.
-$*-¦ ml
sin3 F/2)
¦ оо

156
СТОЛКНОВЕНИЯ
[ГЛ 5
Расходимость интеграла обусловлена резким возрастанием
da в области малых Э, которое происходит там по закону 1/03
и связано со слабым убыванием кулоновской потенциальной
энергии с расстоянием. Поэтому заряженная частица является
по отношению к другой заряженной частице мишенью с беско^
нечно большой поперечной площадью.
В томе III мы узнаем, что с формулой Резерфорда связано
одно из величайших открытий XX века — открытие ядерного
строения атомов.
4. Дифференциальные сечения столкновений измеряют экс^
периментально по величине E.12). Если плотность потока ча-
частиц в падающем пучке известна, то тем самым можно опре-
определить de/dQ. Сечение зависит от характера взаимодействия
I-dl
Рис. 5.15.
частицы-снаряда с мишенью. В этом мы уже убедились выше.
Так, зависимость E.20) дифференциального сечения рассеяния
на твердом шаре от угла рассеяния 0 совсем не похожа на фор-
формулу Резерфорда E.22). Поэтому, измерив сечение, можно ста-
ставить вопрос: какие силы приводят к процессу с наблюдаемым
сечением? Именно таким образом изучаются взаимодействия
между микроскопическими частицами и исследуются свойства
микромира.
Через полное сечение а выражаются такие важные величи-
величины, как коэффициент поглощения [х и длина свободного про-
пробега I. Последняя будет рассмотрена в части II. Здесь мы оста-
остановимся на коэффициенте поглощения.
Пусть пучок частиц падает на мишень, представляющую
слой некоторого вещества малой толщины dx*). Предположим,
что плотность потока частиц в падающем пучке равна /, а после
*) Критерий малости будет рассмотрен в следующей части, в § 9.1.

§ 5.21 СЕЧЕНИЕ РАССЕЯНИЯ 157
прохождения слоя составляет / — dl (рис. 5.15). Относительное
изменение плотности потока равно dill и является величиной
отрицательной. Это обусловлено тем, что в результате взаимо-
взаимодействия с частицами мишени некоторые из частиц-снарядов
либо изменят направление своего движения, либо вообще ис-«
чезнут, если столкновения неупругие (в этом случае появятся
новые частицы). Рассмотрим часть мишени с поперечной по
отношению к падающему потоку площадью, равной S. Пусть
плотность частиц вещества, с которыми происходят столкнове-
столкновения, равна п. Тогда в рассматриваемой части мишени будет
n-dx-S частиц. Для частиц-снарядов они будут затенять сум-
суммарную площадь on-dx-S, где а — полное сечение. Очевидно,
что отношение этой площади ко всей площади рассматривае-
рассматриваемой части мишени будет равно относительному изменению плот-
плотности потока частиц-снарядов:
E.23)
Интегрируя это уравнение, получим:
/ = /ов-^, E.24)
где /о — плотность потока частиц-снарядов при х = 0, / — плот-
плотность потока частиц, проникших на глубину х, а
\х = п(У. E.25)
Эта величина называется коэффициентом поглощения. Форму-
Формула E.24) показывает, что этот коэффициент и, следовательно,
полное сечение а можно измерять экспериментально. Если
определены плотности потока частиц-снарядов, падающих на
мишень (при х = 0) и прошедших ее (при некотором заданном
значении х), т. е. величины / и /о, то

ГЛАВА б
ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
§ 6.1. Кинематика движения твердого тела
1. При решении разнообразных вопросов технической меха-
механики приходится рассматривать тела, размерами которых пре-
пренебрегать нельзя. Таковы, например, задачи о движении раз-
различных узлов станков, машин и механизмов. Очень часто от-
отдельные детали таких устройств можно считать неизменными
по объему и форме, т. е. абсолютно твердыми телами (в пре-
пределах, гарантирующих нормальную работу). Движения такого
рода объектов описываются механикой абсолютно твердых тел.
Для сокращения в этой главе такие тела мы будем называть
просто твердыми, а подчас будем опускать и это прилага-
тельйое.
ЗаЦача описания движений твердых тел значительно упро-
упрощается, если представлять их состоящими из отдельных мате-
материальных точек, разделенных пространственно. Другими сло-
словами, такой подход предполагает, что тело имеет дискретную
структуру. Мы увидим, что различные характеристики таких
образований выражаются суммами по местам сосредоточения
точечных! масс составляющих частиц. На практике чаще всего
твердые тела удобно рассматривать как сплошные среды, т. е*
такие, -в которых распределение массы вещества можно считать
непрерывным. Переход к формулам для сплошных твердых тел
осуществляется заменой суммирования по дискретным точкам:
интегрированием по объему тела. При этом в сплошном теле
роль Массы дискретной точки играет элементарная масса dm
вещества, заключенного в бесконечно малом объеме dV теля.
Если масса единицы объема вещества в данном месте, т. е.
плотность массы, равна р, то dm = р dV. Поэтому для сплош-
сплошных тел аналогом дискретных сумм вида

§ 6 il КИНЕМАТИКА ДВИЖЕНИЯ ТВЕРДОГО ТЕЛ^ 159
где mj, ..,, тп — массы частиц тела с дискретной структурой^
являются интегралы по объему тела
Пользуясь этим правилом, мы будем выписывать формулы для
сплошных тел без дополнительных разъяснений, сразу же после
получения соответствующих выражений для тел с дискретный
строением.
2. В § 1.2 было установлено, что абсолютно твердое тело
является системой с шестью степенями свободы. Поэтому число
уравнений движения твердого тела должно быть равно шести.
Для выяснения, какие именно уравнения характеризуют дви-*
жение твердых тел, рассмотрим их кинематику.
Подчеркнем, что имеет смысл обсуждать только нереляти-»
вистское движение. Действительно,, в абсолютно твердом теле
смещение любой группы частиц в одной из частей тела должно
мгновенно привести к такому же смещению частиц во всех
остальных частях. В противном случае произойдет изменение
расстояний между частицами тела и тем самым тело уже не
будет абсолютно твердым. Мгновенная реакция одних частей
твердого тела на изменения, происходящие в других его частях,
является движением с бесконечно большой скоростью. В этом
и заключается причина несовместимости
модели абсолютно твердого тела с реляти-
релятивистскими принципами.
Произвольное бесконечно малое пере-
перемещение твердого тела является результа-
результатом двух движений (рис. 6.1). Одно из /
них — это параллельный перенос тела, при /
котором центр инерции (ЦИ) тела сме- j /s—f /
щается на некоторое бесконечно малое рас- ч-'' ч-''
стояние dR без изменения ориентации тела Рис. 6Д.
в пространстве. Это поступательная состав-
составляющая его движения. Другое движение осуществляется в виде
малого поворота тела вокруг ЦИ. Эта составляющая является
вращательным движением тела и характеризуется вектором
угла бесконечно малого поворота dcp.
Радиус-вектор любой точки твердого тела г представим
суммой
г = Я + а, F.1)
где R — радиус-вектор ЦИ тела, а вектор а определяет рао
положение точки относительно ЦИ (рис. 6.2). В абсолютно
твердом теле \а\ = а = const, т. е. вектор а может только вра-
вращаться. Поэтому, согласно A.6), da = [d(p-a], где я?ф — вектор

160
ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
угла бесконечно малого поворота. Итак,
а].
1ГЛ. 6 *
F.2)
Если перемещение dr произошло за время dtt то скорость
рассматриваемой точки равна
Здесь V — скорость ЦИ тела, а о— угловая скорость его враще-
вращения относительно ЦИ. Согласно F.3) скорость любой точки
твердого тела выражается через скорость ЦИ (скорость поступа-
поступательного движения) и угловую ско-
скорость (скорость вращения). Поэтому
уравнения движения твердого тела
должны определять, как происходит
изменение скоростей V и со, т. е. шести
величин
11/1/1/ \ — V
Рис. 6.2. Существенно, что угловая скорость
<о является абсолютной характеристи-
характеристикой вращения твердого тела в том смысле, что она не зависит
от того, относительно какой точки вращение рассматривается.
Это означает следующее. В разложении F.1) R характери-
характеризует положение ЦИ тела. Вместе с тем допустимы и другие
разложения г = R' -\- а', где R' — радиус-
вектор любой точки тела, не совпадаю-
совпадающей с ЦИ, а а' характеризует относи-
относительное расположение точек с радиус-
векторами г и R' (рис. 6.3). Предполо-
Предположим, что R' = R + #о. Тогда из рис. 6.3
видно, что а0 = а — а'. Рассуждая так
же, как при выводе F.3), полу-
получим:
'' + [<»'*'], F.4)
dt
Рис. 6.3.
где V = dR'jdt определяет скорость точ-
точки с радиус-вектором /?', а со' — угловая
скорость вращения относительно этой точки. Положим г = R'*
При этом a = aot (рис. 6.3) n.v = drfdt = dR'/dt = V. В этом
случае из F.3) следует, что
V

6 2} УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 161
Подставляя это выражение в F.4), находим:
V = V+[(Mo] + №<*'].
Так как ао = а — а', то это выражение преобразуется к виду;
v = v + [а • {а - а')] + [©'а'] = V + [<оа] + [(©' - а). а'].
Сравнивая его с F.3), приходим к выводу:
т. е. действительно угловая скорость не зависит от выбора точ«
ки, относительно которой рассматривается вращательная состав-
составляющая движения.
§ 6.2. Уравнения движения твердого тела
1. Обычно центр вращения выбирают в ЦИ тела. Одно из
преимуществ именно такого выбора (другие выяснятся в даль-
дальнейшем) заключается в том, что перемещение ЦИ является
поступательным движением тела как единого целого и урав-
уравнение этого движения известно. Им является уравнение B.11).
В нем теперь следует понимать под Р импульс тела, т. е. сумму
импульсов составляющих его частиц, а под JF — сумму всех
внешних сил, приложенных к телу. Так как движение твердого
тела является нерелятивистским, то это уравнение может быть
записано в форме
dV d2R р ,а кх
где т — масса тела, V и R — соответственно скорость и ра-
радиус-вектор ЦИ тела. Отметим, что если для определения силы,
действующей на частицу, достаточно указать величину, направ-
направление силы и со стороны чего она действует, то сила, дей-
действующая на твердое тело, имеет еще одну характеристику:
точку приложения. Точка приложения определяется радиус-век-
радиус-вектором частицы тела, на которую действует данная сила.
Из F.5) следует, что уравнение поступательного движения
твердого тела имеет вид уравнения движения нерелятивистской
частицы с массой m под действием силы F. Поэтому специфи-
специфические особенности движения твердого тела связаны только с
вращениями. Сконцентрируем внимание на этом виде движе-
движения, избрав за центр вращения ЦИ тела.
2. Рассмотрим собственный момент импульса тела
Здесь через гп обозначены радиус-векторы частиц тела отно-
относительно ЦИ: гп = {Хп> Уп> zn). Отметим, что при вращении
6 А. В< Астахов

162 ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА {ТЛ 8
сумма x2n + y2n+z2n=r* остается постоянной. Через тп обо-
обозначены массы частиц. Скорости частиц тела равны vn—[®fn]t
где со —угловая скорость вращения. Направление этого вектора
определяет ориентацию оси вращения, которая при сделанном
выборе центра вращения проходит через ЦИ тела. Применяя
к произведению [г„[шгп]] векторное тождество [a[ftc]] =
= b(а-с) —с(а•&), преобразуем выражение для S к виду
S = ZmB{©ri-rn(©.rll)}. F.6)
Как видно, S зависит от со. Поэтому dS/dt зависит в том числе
и от углового ускорения е = d(o/dt. С другой стороны, согласно
C.40) dS/dt можно выразить через момент внешних сил от-
относительно ЦИ. Отсюда следует, что
уравнения вращательного движения твердого тела имеют вид
dSx ,л dSy dSz
где S — собственный момент импульса тела, a Ms — суммарный
момент всех приложенных к телу сил, определенный относи-
относительно ЦИ тела.
Выпишем выражения для компонент S. Учитывая, что
(&-гп]| = (ОзсЛГп + Ыууп + о>2гп, из F.6) получаем:
Sy - /1?Я + 1>у + С^ F.8)
где
*%=2 тп (г"п -4); i% = - Z «hw /S = -? «^.;
'%-'% W-ZM'l-vV)-' 4ai = -?wn; F.9)
/@) _ /@). /@) -« /@). /@) = У т (Г2 _ 22\
zx lxz> lzy lyz> Lzz ?-*mn\rn *пУ
Величины F.9) называются моментами инерции тела, опре-
определенными относительно ЦИ. Последнее подчеркнуто в обо-
обозначениях верхним индексом @).
Из F.9) следует, что моменты инерции зависят от распре-*
деления масс и, вообще говоря, изменяются при изменении
ориентации тела относительно координатных осей. (Напомним,
что при вращении хп% цп, ?п изменяются со временем.). Для

.- 6.2]
УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
163
сплошного тела (непрерывное распределение массы) моменты
инерции определяются согласно правилу, сформулированному
в начале § 6.1. Например,
Соотношения F.7) образуют систему сложных дифферен-
дифференциальных уравнений. Это говорит о том, что вращения твердых
тел не относятся к категории простых движений. Даже враще-
вращение свободного тела может быть весьма замысловатым. Сво-
Свободно вращающимся называется тело, которое в начальный мо-
момент обладает угловой скоростью и на которое не действуют
внешние силы.
Действительно, для тела произвольной формы S и <о, вообще
говоря, направлены по-разному, на что указывают формулы
F.8). Из них, например, следует, что Sx зависит не только
от со*, но и от соу и со2. Кроме того, в общем случае моменты
инерции изменяются со временем. Вследствие этого сох, со^, со2
оказываются переменными во времени
величинами, даже если на тело и не дей-
действуют внешние силы. При свободном
вращении закон изменения сох, (ду, coz
определяется условием постоянства Sx,
Sy, Sz. Из всего сказанного следует, что
в общем случае ось вращения свободно-
свободного тела меняет свою ориентацию в про-
пространстве, а также может меняться и
темп свободного вращения. И все это бу-
будет происходить без каких-либо внешних
воздействий!
Например, свободное вращение тела
конической формы происходит так, как
это показано на рис. 6.4. Тело вращается
вокруг собственной оси. При этом ось
вращения (она направлена вдоль со) обращается вокруг на-
направления вектора S. Такое движение получило название регу-
регулярной прецессии.
3. В ряде случаев вращение твердых тел носит простой ха-
характер. Рассмотрим эти случаи.
Простым является вращение однородных тел сферической
формы. В этом случае
г@) ,@) г@) п
1 ху — I xz — * yz — и.
Действительно, рассмотрим, например, шар с однородным
распределением массы. ЦИ такого шара совпадает с его гео-
геометрическим центром. Тогда каждой частице с координатами
Рис. 6 4.

164
ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
ТГЛ S
х, у, z всегда можно сопоставить другую частицу с той же мас-
массой, но с координатами, например, х, у, —г (рис. 6.5). Поэтому
сумму J]mnxnzn можно разбить
п
на пары слагаемых, которые
будут отличаться друг от друга
только знаком z-координат. По
величине они будут одинаковы-
одинаковыми. Это означает, что их сумма
будет равна нулю и, следова-
следовательно, /*i = /i°2 = 0. Аналогично
доказывается, что I{yl = Ixy=I{yl —
= /S/) = 0. Кроме того для одно*
родного шара
Рис. 6.5. у т Х2 _ у т j.2 _ у т Z2
п п п П п П
поскольку свойства шара по всем направлениям, исходящим из
его геометрического центра, одинаковы. Но
Следовательно,
? mnxi
&=т Z mnri-
Это означает, что
/?> = СУ = /<°> = /<0) = |-2 mnrl = const.
Величина /(°) называется просто моментом инерции шара отно-
относительно его центра инерции. Расчет дает:
/@) = -|т#2, F.10)
о
где R — радиус шара, am — его масса.
Формула F.10) получается так. Предположим, что распределение массы
является непрерывным. Тогда
г2р dV.
Интегрирование выполняется следующим образом. Рассмотрим шаровой слой
бесконечно малой толщины dr с внутренним радиусом г (рис. 6.6). Вклад в
интеграл от этого слоя равен массе слоя, умноженной на г2. Плотность массы

§ 6.2k УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 165
-. Следовательно, масса слоя равна 4яг2 dr * — (величина
т
4nr2dr определяет объем слоя). Умножая массу слоя на г2 и интегрируя
полученное выражение по г в пределах от О
до R, получим F.10).
Для однородного шара Sx =
Sy = №(oyt Sz = /(°)co2, т. е.
Рис. 6.6.
Следовательно, уравнение вращатель-
вращательного движения шара имеет вид:
dS r,m do 2 n2 dm %/t
где M8 — суммарный момент внешних
сил, действующих на шар, определен-
определенный относительно его центра. В частности, если шар свободно
вращается, т. е. если М8 = 0, то da/dt = 0. Это означает, что
ось вращения сохраняет свою ориентацию в пространстве и
вращение является равномерным.
К числу простых относятся вращения твердых тел вокруг
закрепленных осей. Движения такого типа происходят в меха-
механизмах, конструкция которых предусматривает вполне опреде-
определенное расположение осей вра-
вращения различных узлов.
Пусть твердое тело вращает-
вращается относительно закрепленной
оси, ориентированной вдоль ко-
координатной оси z (рис. 6.7). При
этом ось вращения может и не
проходить через ЦИ тела. Имен-
Именно этот наиболее общий случай
мы и рассмотрим. Аналогично
тому, как были получены форму-
формулы F.8), нетрудно рассчитать
компоненты момента импульса.
Рассмотрим компоненту Lz. С учетом того, что угловая ско-
скорость может быть направлена только вдоль оси г, т. е. о> =
|= {0, 0, со2}, получим:
12 = /ггсог> F.11)
Рис. 6.7.
где для тела с дискретной структурой

166
ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
[ГЛ О
а для сплошного
= V r,/V2 .
z2)dV.
Величина Izz называется моментом инерции тела относи-
относительно закрепленной оси вращения. Подчеркнем, что момент
инерции /22 отличается от /Ц?]. Теперь координаты точек тела
хп, Уп, Zn (для сплошного тела — х, у, z) отсчитываются от на-
начала координат, не совпадающего с ЦИ тела. Из рис. 6.7 видно,
что rjl — z2n = x2n + #2=/2, где 1п — расстояние точки тела до
заданной оси вращения. Очевидно, что для любой точки тела
это расстояние со временем меняться
не будет. Поэтому
«const.
F.12)
Для сплошного тела
. 6.8.
= const. F.13)
Приведем пример. Пусть однород-
ный сплошной стержень вращается в
плоскости ху относительно оси г, про-
проходящей через один из концов стержня (рис. 6.8). Ось z пер-
перпендикулярна плоскости рисунка. Пусть масса стержня равна /п,
а его длина L. Плотность стержня p — m/LS, где S — попереч-
поперечное сечение стержня. Элемент объема стержня dV = S dl
(рис. 6.8). Следовательно, для стержня
F.14)
Учитывая постоянство Izz, уравнение движения тела с за-
крепленной осью "-77" —Мг можно преобразовать к виду
/«^r- = Afz. F.15)
Величина Mz называется суммарным моментом внешних сил
относительно закрепленной оси, а соотношение F.15) —уравне-
—уравнением вращательного движения твердого тела относительно за-
закрепленной оси.
Рассмотрим подробнее величину Mz. Для простоты предпо-
предположим, что на тело действует одна внешняя сила F. Без огра^
ничения общности можно считать, что она направлена перпен^
дикулярно оси вращения. Действительно, составляющая силы
вдоль закрепленной оси может привести только к сдвигу тела

§ 6 21
УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
167
вдоль этой оси. Поэтому эта составляющая не оказывает влия-
влияния на вращение.
Рассмотрим рис. 6.9, на котором изображена картина в
плане. Ось z перпендикулярна плоскости рисунка и направлена
на читателя. Пусть точка при-
приложения силы имеет коорди-
координаты ху у, z. Тогда
у=Н\па\ -г—/.
Fy = F sin p.
Fx = — F cos
Поэтому
M2 =
= IF (cos a sin p + sin a cos P)
Рис. 6.9.
х >
Но a -f- р = я — y- Следова-
Следовательно, / sin (а + р) = / sin y =
= ft, где ft — расстояние от оси
вращения до прямой, вдоль которой действует сила. Эта вели-
величина называется плечом силы. Таким образом,
Mz = F-h. F.16)
Заметим, что сила F заставляет тело вращаться против ча-
часовой стрелки. Если бы она была направлена так, что вызван-
вызванное ею вращение происходило бы
в обратном направлении, то форму-
формула для Мг отличалась бы от выра-
выражения F.16) знаком.
Таким образом, величина момен-
момента силы относительно закрепленной
оси равна произведению величины
силы на ее плечо. Момент силы по-
положителен, если он вызывает вра-
вращение против часовой стрелки, если
смотреть с конца вектора угловой
скорости. В противном случае мо-
момент силы отрицательный.
Если на тело действует несколь-
несколько сил, то правая часть уравнения
F.15) содержит алгебраическую
сумму моментов сил. Знак каждого слагаемого определяется по
только что сформулированному правилу.
Подсчитаем, наконец, какую работу производит сила F, вра-
вращающая тело вокруг закрепленной оси. Пусть под действием
Рис. 6.10.

168 ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА [ГЛ 6
силы тело повернулось на малый угол dcp (рис. 6.10). Точка
приложения силы при этом сместится на расстояние dl=ld^y
где / — расстояние от точки приложения силы до оси вращения.
Совершенная силой работа будет равна
dA = F dl cos -ф = Fl dcp cos ty.
Вследствие малости с/ф угол между направлением смещения
точки приложения силы и направлением на эту точку можно
считать равным я/2. Поэтому -ф = я — (я/2) — у = (я/2) — у
(рис. 6.10). Следовательно, /cos\|) = /sinу = h. Таким образом>
dA = Fhdy = M2 dqp.
Если действующая сила является потенциальной, то dA =
— — dU, где dU — малое изменение потенциальной энергии
тела при повороте на угол Лр. Следовательно, dU = —Mzdq и
Мг = -^-. F.17)
Эта формула позволяет определить момент силы относи-
относительно заданной оси, если потенциальная энергия тела известна
как функция угла поворота.
§ 6.3. Кинетическая энергия твердого тела
1. Вычислим кинетическую энергию твердого тела. Скорость
любой точки тела запишем в виде F.3), считая V скоростью
ЦИ тела. Тогда в этой записи а будет радиус-вектором точки
относительно ЦИ. Переобозначим а на г. Тогда скорость точки
с номером п будет равна
Следовательно, кинетическая энергия тела будет равна
п п
=т (Z m*
\ п /
При выбранном разложении движения
Действительно,

§ 6 3] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА 169
Разделив Yu^nrn на массу тела m = Yumn-> получим выраже-
п п
ние, определяющее радиус-вектор ЦИ тела. Однако гп по опре-
определению— это радиус-векторы точек твердого тела в СЦИ. По-
Поэтому CLmnrn)ltn = O, так как определяет радиус-вектор ЦИ
относительно самого себя.
Таким образом, оказывается, что кинетическая энергия рас-
распадается на сумму двух членов:
¦* === ¦* п i -* вр>
где
^1 ^?ЛИ%г1J. F.18)
Величина Гп определяет кинетическую энергию поступатель-
поступательного движения твердого тела. Величина Гвр, зависящая от угло-
угловой скорости, определяет кинетическую энергию вращения твер-
твердого тела относительно ЦИ. В том, что кинетическая энергия
оказывается суммой энергий двух независимых движений — по-
поступательного и вращательного, заключается еще одно преиму-
преимущество выбора центра вращения в ЦИ тела.
Рассмотрим энергию Гвр. Воспользуемся векторным тож-
тождеством
([ab] . [cd] ) = (a-c){b'd)-(a.d)(b- с).
Полагая a = c = (dnb = d = rn, получаем:
(IX]Т=ОХ] • 1X1) = ш2г» - 0й • гпJ-
Подставляя сюда г\ = х2п + у\ + z\ и (© • гп) = <?>ххп + <аууп + сог2„,
после несложных вычислений преобразуем F.18) к виду
F.19)
В этом выражении моменты инерции определяются формулами
F.9).
2. В тех случаях, когда уравнения вращательного движения
имеют простой вид, упрощается и выражение для кинетической
энергии Гвр. Так, для однородных тел сферической формы, для
которых I'x] = 1{у1 == 1{х1 = 0, а 1{хх = 1% = I{zl = I , имеем:
1 /@)fr2
Гвр == -i /@) (ol>2 + а>1 + со|) = ^-^- , F.20)
где со — величина угловой скорости. Например, для однородного
шара массой т, радиус которого равен R [см. F.10)],

170
ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
[ГТТ 6
Получим кинетическую энергию вращения тела вокруг за-
закрепленной оси. Обсудим общий случай, когда ось не проходит
через ЦИ. Тогда энергия Гвр по-прежнему будет определяться
выражением вида F.19), однако с другими моментами инерции,
которые мы условились обозначать буквой / без верхнего ин-
индекса @). Пусть ось вращения совпадает с координатной осью
z. Тогда со = {0, 0, coz}. Следовательно, в этом случае
Гвр==1/2гсо2. F.21)
Например, энергия однородного стержня длиной L и массой т,
вращающегося вокруг закрепленной оси, проходящей через
один из концов стержня (рис. 6.8), равна
При этом мы воспользовались формулой
F.14).
3. Выше неоднократно подчеркива-
подчеркивалось, что моменты инерции зависят от
того, какая точка выбрана за центр вра-
вращения и где проходит закрепленная ось.
Рассмотрим, как изменяются моменты
инерции при параллельном переносе оси вращения. При этом
ограничимся случаем, когда оси являются закрепленными.
Пусть тело вращается вокруг закрепленной оси 2, которая
не проходит через ЦИ и удалена от него на расстояние а
Рис. 6.11.
-г :
/ци ! _ / ци//ш I \
\ / ~ / 77ю / + /
Рис. 6.12.
(рис. 6.11). Кинетическая энергия такого движения будет равна
¦* ==: ¦* вр === ~с? * zz® >
где со — величина угловой скорости, a Izz — момент инерции тела
относительно заданной оси. Вращение вокруг оси z можно пред-
представить как поступательное перемещение твердого тела со ско-
скоростью его ЦИ и вращение вокруг оси z', проходящей через ЦИ
и параллельной оси z._ При этом, вследствие абсолютного харак*

§ 6 3] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА 171
тера угловой скорости, вращение вокруг оси z' будет происхо<
дить с той же угловой скоростью, что и вращение вокруг оси г.
Такое разложение вращения вокруг оси z схематически изо-
изображено на рис. 6.12. На нем представлена картина в плане.
Кинетическая энергия поступательного движения ЦИ равна
т 1/2/2, где m — масса тела. При этом V — это скорость, с кото-
которой движется ЦИ, вращаясь вокруг оси г. Следовательно,
V = соа. Кинетическая энергия вращения твердого тела отно-
относительно оси z\ проходящей через ЦИ, равна 1^1 • со2/2. Таким
образом,
®^
Отсюда получаем:
1гг=1?)г + ™2- F-22)
Эта формула определяет искомую связь между моментом
инерции относительно произвольной оси и параллельной ей оси,
проходящей через ЦИ тела. Расстояние между осями равно а.
Формула F.22) показывает, что из всех моментов инерции на*ь
меньшим является момент, определенный относительно оси,
проходящей через ЦИ тела,

ГЛАВА 7
КОЛЕБАНИЯ И ВОЛНЫ
§ 7.1. Одномерный гармонический осциллятор
1. Колебания являются широко распространенным видом
движения и наблюдаются в системах самой разнообразной при-
природы. Колебания относятся к процессам, точно или приблизи-
приблизительно повторяющимся через одинаковые промежутки времени.
При механических колебаниях повторяются, например, измене-
изменения положений и скоростей тел. Электрические колебания — это
повторяющиеся изменения напряжений и сил токов в электри-
электрических цепях, изменения электрического и магнитного полей
вокруг этих цепей. Существуют также «смешанные» колебания.
Они происходят, например, в электроакустических преобразова-
преобразователях — устройствах, преобразующих энергию механических
колебаний в электрическую и наоборот. Примерами таких уст-
устройств являются громкоговорители и микрофоны.
Несмотря на разную физическую природу,
в колебаниях обнаруживаются одни и те же закономерности,
которые исследуются общими методами.
Важной кинематической характеристикой является форма
колебаний. Она определяется видом той функции времени t, ко-
которая описывает изменение той или иной физической величины
при колебаниях. Наиболее важными (в этом мы вскоре убе-
убедимся) являются гармонические колебания. Гармоническое ко-
колебание описывается периодическим законом
D/ + e0). G.1)
Здесь |со@ характеризует изменение какой-либо физической
величины при колебаниях. Например, la>(t) может быть смеще-
смещением маятника от положения равновесия, мгновенным значе-
значением заряда на конденсаторе в электрическом колебательном
контуре, плотности воздуха в поле звуковой волны, напряжен-
напряженности электрического поля в электромагнитной волне и т. д.
Система, закон движения которой имеет вид G.1), назы-
называется одномерным классическим гармоническим осциллятором

§ 7 11 ОДНОМЕРНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 173
или сокращенно классическим осциллятором. Ьго характери-
характеризуют следующие величины. Циклическая частота со определяет
период колебания, т. е. время одного колебания. Если Т — пе-
период колебания, то
7- = -^. G.2)
Легко проверить, что функция G.1) удовлетворяет условию пе-
периодичности: ?©(? + Т)= l«>(t) (рис. 7.1).
Очевидно, что отношение v = 1/Г определяет число колеба-
колебаний в единицу времени. Эта величина называется частотой коле-
колебаний и она равна
. Чю( Ч1 k
Размах колебаний опре-
определяется амплитудой а. Ам-
Амплитуда равна абсолютно-
абсолютному значению наибольшего
отклонения.
Аргумент косинуса 6 = Рис-
= cot + Во называется фазой
колебаний, а Во = const — начальной фазой. Фаза однозначно
определяет значение колеблющейся величины.
Частота v измеряется в сек*. Частота v == 1 сек назы-
называется герцем (Гц). Кроме этой единицы широко употребляются
килогерц (кГц) и мегагерц (МГц): 1 кГц = 103 Гц, 1 МГц =
= Ю6 Гц.
В технических приложениях всегда говорят о частоте v.
Именно ее имеют в виду, говоря, например, что радиопередача
ведется на частоте 1 МГц. При теоретическом рассмотрении
удобна циклическая частота со, которую в дальнейшем сокра-
сокращенно мы будем именовать просто частотой, хотя на самом
деле она в 2я раз больше той, о которой говорят инженеры. Об
этом надо постоянно помнить!
Дифференцируя дважды по времени G.1), находим:
-%*?¦ = - со2а cos М + во) = - <*%« (О-
Уравнение
-^%Д +@^@=0 G.4)
называется уравнением одномерного классического гармоничен
ского осциллятора с частотой со. Важным свойством этого урав-
уравнения является линейность. Оно содержит функцию ?•©(<) и ее
вторую производную по времени в первой степени. Для линей-
линейных уравнений справедлив принцип суперпозиции. Он гласит,

174 КОЛЕБАНИЯ И ВОЛНЫ [ГЛ 7
что если g<J> (/) и |^)@""Два решения линейного уравнения, то
решением является также и любая линейная комбинация
где С\ и С2 — произвольные (в том числе и комплексные!) по-
постоянные. Кроме того, если ?©@—решение уравнения, то и
Cgft)(/), где С = const, также является решением.
Уравнение G.4) имеет второй порядок. Поэтому у него есть
два независимых решения. Одно из них — это функция G.1).
Другим независимым решением является a sin (col + Оо), в чем
легко убедиться прямой подстановкой. Следовательно, согласно
принципу суперпозиции решением уравнения G.4) будет любая
линейная комбинация
Сха cos Ш + 60) + С2а sin (со/ + 60).
Часто полагают, 4toCi = 1, С2 = — У-— 1 = — /. Тогда ока-
оказывается, что решением уравнения G.4) является функция
Фю @ = а cos (®* + Go) — ш sin (со/ + Go)»
которая согласно формуле Эйлера e~ix — cosx—tsinx можег
быть записана в виде
г|)ш(/)==щг-'(<оЖH)# G.5)
Такой формой записи закона гармонического колебания ши-
широко пользуются. Это связано с удобством проведения вычисле-
вычислений с выражениями вида G.5), что обусловлено простыми свой-
свойствами экспоненциальной функции. Так, экспоненциальная
зависимость сохраняется при дифференцировании и интегриро-
интегрировании. Разумеется, наблюдаемые значения каждой физической
величины вещественны. Нетрудно видеть, что наблюдаемый за-
закон гармонических колебаний G.1) легко получить из пред-
представления G.5). Именно, первый является вещественной частью
второго. Это записывают так:
где Re — часто употребляемый символ для обозначения веще-
вещественной части комплексной величины.
2. Принцип суперпозиции не накладывает ограничений на
величину амплитуды колебаний. Однако они все же есть и обус-
обусловлены областью применимости гармонического приближения
к колебаниям. Эта область исчерпывается только малыми коле-
колебаниями. Разъясним, что это означает.
Осциллирующие системы достаточно широко распростра-»
нены. Этим они обязаны следующему свойству. Оказывается,
что потенциальная энергия многих систем имеет «провалы»

§711
ОДНОМЕРНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
175
типа потенциальных ям. Например, именно такова энергия вза-
взаимодействия нейтральных атомов и молекул (см. рис. 2.22).
А как мы знаем (см. § 3.3), в этих случаях возможны периоди-
периодические движения, к числу которых относятся и колебания.
Ограничимся рассмотрением одномерного движения в неко-
некоторой потенциальной яме. Она изображена на рис. 7.2, и на нем
х0 обозначает положение равновесия частицы. Потенциальную
энергию частицы U (х) можно пред-
представить степенным рядом:
Здесь | = х — хо — смещение частицы
от положения равновесия, а ап — по-
постоянные коэффициенты. Прямым вы-
вычислением нетрудно убедиться в том,
что
1 dnU
а*=ТГ\
dxn
Рис. 7.2.
Заметим теперь, что в точке х = х0 потенциальная энергия
U (х) имеет минимум (рис. 7.2). Поэтому
dU
dx
= 0.
Таким образом, оказывается, что
х=хй
Предположим, что отклонения g от положения равновесия
малы. Критерием является незначительность изменения при
этом потенциальной энергии. Тогда в разложении G.6) можно
пренебречь всеми членами, за исключением первых двух. В этом
случае получаем, что с высокой точностью
Следовательно, действующая на частицу сила равна
dU d2U
F =
dU
dx
и уравнение движения частицы имеет вид
d2x (/) ______ ??_
dt2 —г — dx2
m
G.7)

178 КОЛЕБАНИЯ И ВОЛНЫ ТГЛ 7
где т — масса частицы. Легко видеть, что уравнение G.7) при-
приводится к виду уравнения движения осциллятора с частотой
т
G.8)
Это приведение осуществляется путем подстановки в левую
часть уравнения # = | + *о и простых алгебраических преобра-
преобразований.
Таким образом, мы действительно убедились в том, что при
малых отклонениях от положения равновесия движение в одно-
одномерной потенциальной яме носит характер гармонических коле-
колебаний. Кроме того мы установили, что частота таких колебаний
зависит только от свойств самой системы. Именно поэтому ее
часто называют собственной частотой системы.
Если отклонения от положения равновесия не являются ма-
малыми в указанном выше смысле, то в разложении G.6) уже
нельзя ограничиваться только первыми двумя членами. Тогда
уравнение движения будет уже нелинейным. Например, при
сохранении в правой части G.6) первых трех членов получаем:
dx ~ dl dx2
2 dx*
X = XQ
В этом случае уравнение движения частицы приводится к виду
Уравнение G.9) содержит g2 и поэтому является нелиней-
нелинейным.
Колебания, описываемые нелинейными уравнениями, назы-
называются ангармоническими. Для таких колебаний принцип супер-
суперпозиции уже не выполняется. Например, заменив g на eg, где
с — произвольная постоянная, мы увеличим левую часть урав-
уравнения G.9) в с, а правую — в с2 раз и равенство G.9) нару-
нарушится.
Общим, т. е. справедливым для колебаний любой природы,
является следующее важное положение:
применимость гармонического приближения и принципа су-
суперпозиции к колебаниям ограничена областью малых колеба-
колебаний, энергии которых с высокой точностью квадратично зависят
от отклонений от равновесных состояний.
3. Рассмотрим некоторые из осцилляторов.
а) Движение частицы под действием силы упругости. Эта
система изображена на рис. 7.3. Предполагается, что силы тре-
трения малы и ими можно пренебречь. Согласно B.36) потенци-
потенциальная энергия частицы, смещенной на | от положения равно-

§7.1]
одномерный гармонический осциллятор
177
весия, равна U = &?2/2, где k — коэффициент упругости пру-
пружины. Следовательно,
d2u
dx2
и
со =
. G.10)
К задаче рассмотренного типа сводятся задачи о колебаниях
атомов в двухатомных молекулах. Каждая молекула является
оооо5
(
X
у/////////^
Очень хорошая —
смазма
Рис. 7.3.
системой двух тел и характеризуется приведенной массой га =
= гп1т2/(т{ + га2), где тх и га2 —массы атомов. Масса га и
определяет частоту колебаний. Например, для молекулы NaCl
m = 2,33-10-26 кг, а наблюдаемая частота со = 7,16-1013 сек-1.
По этим данным с помощью G.10) можно оценить коэффициент
упругости /г, характеризующий, насколько жесткой
является связь атомов в молекуле NaCl- k =
= 120 Н/м2.
б) Математический маятник. Им называется
система, изображенная на рис. 7.4. Она состоит
из частицы массой га, подвешенной в поле тя-
тяжести к определенной точке на невесомой нити
или невесомом стержне длиной L. Невесомость
означает, что масса нити или стержня намного
меньше га.
При отклонении на малый угол ф от положе-
положения равновесия потенциальная энергия маятника
равна
V (ф) = mgh = mgL (I — cos ф) =
2 _? ^ mgL 2
11 —• ^— • Ф ,
= 2mgL sin2
Рис. 7.4.
поскольку при малых ф можно положить sin(q>/2) « ф/2. В дан-
данном случае роль смещения играет длина дуги g = 1Ф, так что
2L

178
КОЛЕБАНИЯ И ВОЛНЫ
1ГЛ. 7
Отсюда находим, что
d2U
mg
Подставляя это значение в G.8), находим собственную частоту
математического маятника:
сэ = У?717- G.11)
в) Физический маятник. Его образует твердое тело, подве-
подвешенное в поле тяжести на закрепленной горизонтальной оси,
которую примем за ось z (рис. 7.5). Уравнением движения тела
является соотношение F.15). Так как сог =
= dq/dt, то F.15) пред ставимо в виде
Мы видим, что оно подобно уравнению одномер-
одномерного движения частицы. В нем роль массы ча-
частицы играет момент инерции тела Izz, роль ко-
координаты частицы—угол отклонения ф, роль
силы — момент силы Mz. Это означает, что мы
вправе воспользоваться формулой G.8), заменив
в ней массу на Izz и найдя вторую производ-
производную потенциальной энергии тела U по углу ср
при ф = 0. Эту производную найдем с помощью
F.17):
d2U I йМг
«Ф 1ф=0 аФ ф=0
Момент Мг создается силой тяжести (рис. 7.5), и при малых <р
он равен
Mz = — mgh = — mga sin ф « — j
где а — расстояние от центра инерции тела до оси подвеса, а
m — масса тела. Таким образом,
d2U
dMz
Ф=0
= mga.
Окончательный результат таков: собственная частота физи-»
ческого маятника равна
со = д/^. G.12)
Формула G.12) показывает, что колебания возможны лишь
в том случае, когда ось подвеса не проходит через центр инер-
инерции тела. Если известно значение момента инерции /J2 отно*
сительно оси, проходящей через центр инерции тела, то на

§7.1] ОДНОМЕРНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 179
основании (G.22) формулу G.12) можно записать в виде
->. G.13)
4. Характерной чертой гармонического осциллятора является
следующая:
Средние значения кинетической и потенциальной энергии
гармонического осциллятора равны друг другу и каждое из них
составляет половину полной энергии {отсчитываемой от значе-
значения энергии покоя).
Подтвердим это примером. Рассмотрим систему, изображен-
изображенную на рис. 7.3. Учитывая периодичность движения, средние
значения определяют как сумму всех мгновенных значений за
один период Г, отнесенную к его длительности. Обозначая сред-
ние значения потенциальной и кинетической энергии через й?2/2
и mv2/2t получаем:
т г
mv2 rff
T J 2 ULf 2 """ T J 2
о о
Воспользуемся формулой G.1). Тогда
т
ka2 cos2 (at + Эо)
2
о о
Т 2я/со
ma2co2 sin2 (со/ + 60) А4 _ со Г та2со2 sin2 (со/ + 60)
2 Ш~~2^ ) 2
о о
kl2 _ \ [ ka2 cos2 (со/ + е0) j4_ о f
"^^~TJ 2 ЙГ~1я" J
о о
т^2 _ 1 Г
Интегрируя и учитывая G.10), находим:
mv2 ша2(д2
&2
2 ~ 2 "" 4 #
Полная энергия осциллятора (без учета энергии покоя) равна
^ mv2 . kt2 ma2®2 . о / . , л ч . ^а2 9 / 7 i л \ та2со2
* = -у- + "f- = 2~ Sin ^ + 60) + -g- COS2 (СО/ + 80) = —у .
G.14)
Следовательно,
2 2 2 * v*lcV

180 КОЛЕБАНИЯ И ВОЛНЫ 1ГЛ. 7^
§ 7.2. Одномерный осциллятор с трением. Затухающие
и вынужденные колебания
1. Все рассмотренные в предыдущем параграфе осциллирую-
осциллирующие системы являются идеализированными, поскольку не при-
принимались во внимание силы трения. В реальных системах они
всегда действуют. Рассмотрим, к чему это приводит.
Пусть осциллятором является частица массы т, закреплен-
закрепленная на пружине (рис. 7.3). Предположим, что частица движется
вдоль оси х в вязкой среде — жидкости или газе, которая ока-
оказывает сопротивление, описываемое законом Стокса B.26). То-
Тогда помимо силы упругости F = — k\ на частицу будет дей-
действовать сила трения
п, dx dl
где v — скорость частицы. Поэтому уравнение движения осцил-
осциллятора с трением имеет вид
или
~rl- + 2y 4т + ®21 = 0, G.16)
dt2 1 * dt 1 ъ у ч '
где со2 = k/m и у = a/2/n. Уравнение G.16) однородно и его ре-
решение имеет вид еи. Действительно, подставляя еи в G.16),
получаем равенство
Оно справедливо при всех /, если
Корнями этого уравнения являются
^1,2 = — Y
Следовательно, вид общего решения уравнения G.16) таков:
l = l(t) = АеЫ + Ве%>* = е~У* {Ле-^17^ + Ве-^7*^1), G.17)
где А и В — произвольные постоянные интегрирования.
Соотношение между у и о определяет характер движения.
При y ^ со движение является апериодическим. Это случай так
называехмых больших сил трения (напомним, что y пропорцио-
пропорционально коэффициенту сопротивления а). В этом случае положе-
положение частицы монотонно приближается к равновесному. Действи-
Действительно, пои v ^ со показатели экспонент, стоящих в фигурных

§ 7 21 ОДНОМЕРНЫЙ ОСЦИЛЛЯТОР С ТРЕНИЕМ 181
скобках выражения G.17), являются вещественными числами.
Вещественными должны быть А и В. Иначе смещение | будет
комплексным, что физически абсурдно. Так как при у ^ со ве-
величина — у ± У Y2 — со2 < 0, то ?(/) будет монотонно убываю-
убывающей по величине функцией времени. Ее график при А + В > О
изображен на рис. 7.6. Физическая
причина такого поведения заклю-
заключается в том, что большая сила тре-
трения не позволяет развиться колеба-
колебательному процессу. Сила трения
столь «успешно конкурирует» с си-
силой упругости, что со временем ско-
скорость частицы только монотонно
убывает. Положение частицы изме- Рис- 7<6#
няется тоже монотонно, прибли-
приближаясь к равновесному. Никаких колебаний при этом не воз-
возникает. Этот эффект используют в различных демпфирующих
устройствах.
При у <. а движение частицы носит характер затухающих
колебаний с частотой
со^У^1"?. G.18)
Действительно, в этом случае Уу2 — со2 = к»/. Тогда G.17)'
определяет функцию
которая преобразуется к виду
?(/) = a(/)cos(co'/ + e0), GЛ9)
где
a(/) = aoe-* G.20)
и по и 0о — постоянные. Таким образом, при условии у < со за-
закон движения носит периодический характер. Движение заклю-
заключается в колебаниях с частотой со', но с амплитудой, убывающей
во времени (рис. 7.7). Закон убывания определен формулой
G.20) и на рис. 7.7 изображен пунктиром.
Докажем справедливость G.19). Смещение ? является вещественной ве-
величиной. Это означает, что | = ?*, где звездочкой обозначено комплексно со-
пряжеьное значение. Условие 5 = 1* будет выполнено, если
Aewt + Be'*®'* = (AeWf + Ве~ш'*)* = А'е'*"'* + В*еш'*.
Отсюда следует, что А = В*, Л* = В. Поэтому

182
КОЛЕБАНИЯ И ВОЛНЫ
\ТЯ 1
Представим комплексное число А в тригонометрической форме Л=-~е1
где ао/2 — модуль комплексного числа Л, a Go — его аргумент. Тогда
¦ а0 •
• а0 cos (со7/ + 00).
При апериодическом и периодическом затухающем движе-
движении закон затухания зависит от значения у. Поэтому постоянная
у называется коэффициентом
затухания.
Остановимся более подроб-
подробно на затухающих колебаниях.
Как показывает формула
G.18), частота осциллятора с
трением меньше частоты гар-
гармонического осциллятора со.
Следовательно, период зату-
затухающих колебаний
Причина очевидна: трение
Рис. 7.7. тормозит движение. Если, од«
нако, y<(o, то различием ме-
между о/ и со, а также между V и Т можно пренебречь. В этом
случае с точностью до величин второго порядка малости со' = со,
Г = Т.
Очевидно, что при наличии трения энергия осциллятора бу-
будет уменьшаться, превращаясь в тепло, выделяющееся в среде,
в которой происходят колебания. Величиной, характеризующей
энергетические потери такого рода, является добротность.
Добротностью называют умноженное на 2п отношение запа-
запасенной энергии к величине средней энергии, теряемой за один
период колебаний. Добротность безразмерна.
В качестве примера в таблице 3 мы приводим значения доб-
добротности некоторых осцилляторов.
Таблица 3
Осциллятор
Сейсмические колебания
Скрипичная струна
Колебания электронов в атомах
Лазер
Колебания в возбужденном атомном ядре Fe57
Добротность
25-1400
103
107
1012
3-Ю12

§7.2] ОДНОМЕРНЫЙ ОСЦИЛЛЯТОР С ТРЕНИЕМ 183
При достаточно малых потерях добротность выражается че-
через частоту о и коэффициент затухания у по формуле
G.21)
Докажем G.21). Для этого рассмотрим, как изменяется со временем сред-
среднее за один период значение энергии затухающего колебания в том случае,
когда потери можно считать малыми, т. е. при у <С со. Среднее за период зна-
значение энергии равно
г J
~ mv2 , Щ2 т
где & = -g— + -f- = ~
о
Подставляя сюда G.19) и G.20), а также
v = --— = — (aoe~yt cos cat) — — aoye~yt cos со/ — a^e"^ sin co^
(для упрощения начальную фазу Go мы положили равной нулю), получим
сумму четырех интегралов. Заметим теперь, что в каждом из них е~У* мож-
можно с высокой точностью считать постоянной величиной. Действительно, при
у <С со относительное изменение этого множителя за один период Т = 2я/ш
равно
e-\(t+T)_ -yt
1 -
Здесь мы воспользовались представлением ех = 1 + х + -~- + • • •
Таким образом, в интегралах, определяющих &\ множитель е~Ч* можно
вынести за знак каждого интегрирования. Выполняя уже после этого интегри-
интегрирование, получим:
9 2
ЖЩ.е~2*, где Г@)=-^~. G.22)
Из G.22) следует, что в единицу времени среднее значение энергии затухаю-
затухающих колебаний изменяется на величину
Уменьшение же энергии за каждый период будет происходить на величину
Т •
dt

184 КОЛЕБАНИЯ И ВОЛНЫ [ГЛ 7
Отсюда следует, что добротность равва
(t) I 2Y
dt
что и требовалось доказать.
2. Так как в реальных системах происходят потери энергии,
то для поддержания колебаний необходимо извне пополнять
энергию осциллятора. Особенности движения в этом случае
таковы. Рассмотрим, например, частицу, способную совершать
одномерное движение вдоль оси х. Пусть помимо силы упруго-
упругости и трения на нее действует еще внешняя или, как ее часто
называют, вынуждающая сила /?, изменяющаяся по гармони-
гармоническому закону:
Величина Q называется частотой, a Ro — амплитудным значе-
значением вынуждающей силы. Уравнение движения для частицы
массой т, испытывающей действие всех перечисленных сил,
имеет следующий вид:
т -jpr = F + F +R = — kl — a-jf-
Перепишем его иначе:
-§- + 2Y -§¦ + ш2Е = г0 cos Ш, G.23)
где
Y = a/2/n, со2 = k/tn, rQ = RQ/m.
Полученное соотношение является неоднородным дифферен-
дифференциальным уравнением. Его решение является суммой общего
решения однородного уравнения G.16) и частного решения не-
неоднородного уравнения. Решение уравнения G.16) было найдено
в предыдущем пункте. Оно описывает затухающее движение.
Поэтому по истечении достаточно большого промежутка вре-
времени решение уравнения G.23) будет совпадать с частным ре-
решением. Описываемый им режим движения называется устано-
установившимся режимом вынужденных колебаний. Найдем закон
этого движения.
Восполозуемся следующим приемом. Величина cos Q/ яв-
является вещественной частью е1Ш = cos Q/ + i sin Qt. Поэтому
решим сначала уравнение
= гое'0'. G.24)

§ 7 2] ОДНОМЕРНЫЙ ОСЦИЛЛЯТОР С ТРЕНИЕМ 185
Потом по известному \|) = i|)(/) найдем закон движения по фор*
муле g = ?(/)= Re Ч>(*).
Ищем решение уравнения G.24) в виде
Подставляя его в уравнение G.24), получаем равенство
eiQ% { - &2 + 2lyQ + со2} = гоет.
Следовательно,
G>25)
Умножив числитель и знаменатель этого выражения на со2 —
— Q2 — 2iyQ, получим:
_ со2 - Q2 - 2/yQ
(со2 - Q2 + 2*уО) (^ - G2 - 2iyQ) ~ Г° A22 - со2J
Теперь легко найти действительную (Re -ф0) и мнимую части
комплексной величины ф0. Для обозначения последней часто
используется символ Im. Это обозначение примем и мы. Из
G.26) следует, что
со2 — Q2 T ___ 2уп
1Ш ^ "" Г° (Qa ~ со2J + 4Y2Q2 *
Определим теперь модуль а0 и аргумент 6о комплексного
числа гро-
а0 = а0 (Q) = V(Re ^оJ + (Im Ч>0J = </<о, "° Тт^жГ' G>27)
у(№ — со2J + 4Y й
00 = 90 (Q) = arctg -^L = arctg -J^. G.28)
Через них г|э0 выражается так: /фо = аов1'е°. Поэтому
ф (/) = -фое*а* = а0 (Q) el l«+e» Wl,
и решение уравнения G.23) имеет вид
I = 6 (/) = Re г|) (/) = а0 (Q) cos [Q/ + 90 (Q)]. G.29)
Следовательно, в установившемся режиме вынужденные коле-
колебания происходят с частотой вынуждающей силы, причем ам-
амплитуда колебаний зависит от частоты Q. Величина 6o(Q) опре«
деляет разность фаз смещения |@ и вынуждающей силы R(t).
Рассмотрим эти зависимости. Из G.27) следует, что ao(Q),
имеет максимум. Точка максимума является точкой минимума

188
КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
выражения (Q2 — а2J-\-4y2Q2 и определяется из условия
4т {(Q2 - со2J + 4Y2Q2} = 4Q (Q2 - о2 + 2y2) = О
ао(щ
Это равенство выполняется при й = 0 и Q = йр = V^2 — 2\Х
Если co<yV2, to второе значение является мнимым и фи-
физического смысла не имеет. В этом случае максимальное значе-
значение амплитуды достигается при Q = 0, т. е. в отсутствие коле-
колебаний. При Q = 0 на частицу действует постоянная внешняя
сила, равная Ro, которая смещает частицу на расстояние
a0@)cos 60 @) = ао(О) =? г0/со2. Если Я ф 0, то с увеличением
частоты ao(Q) монотонно уменьшается. Это означает, что при
Q ф 0 движение носит характер гармонических колебаний, раз-
размах которых плавно уменьшается с возрастанием частоты вы-
вынуждающей силы. Такой характер носит движение при доста-
достаточно большом трении
(очень вязкие среды).
Качественно иной харак-
характер движение имеет при ма-
малом трении. В этом случае
ao(Q) достигает максималь-
максимального значения при Q = QP =
= VG>2—2у2(рис. 7.8). В слу-
случае очень слабого трения,
когда у/ы <С 1, значение Яр
практически совпадает с
собственной частотой осцил-
осциллятора со.
Явление резкого возра-
возрастания амплитуды выну-
вынужденных колебаний при приближении частоты вынуждающей
силы к частоте пр называется резонансом. Частота Яр назы-
называется резонансной, а ао(пр) = ар называется амплитудой коле-
колебаний в резонансе.
Амплитуда в резонансе равна [см. G.27)]
Рис. 7.8.
а =
При у
2Y Vco2 -
ap =
G.30)
G.31)
При установившемся движении энергия осциллирующей си-
системы остается неизменной. В то же время система непрерывно
поглощает от источника внешней силы энергию, которая вос«
полняет потери, расходуемые на преодоление трения. Найдем,
чему равна средняя энергия, поглощаемая в единицу времени.

^ 7J21 ОДНОМЕРНЫЙ ОСЦИЛЛЯТОР С TPFHHEM 187
При смещении частицы на dx = d\ внешняя сила совершит ра-
работу Rdx = R d\. Работа, совершенная в единицу времени,
будет равна Я-^|- = /?0, если dt— время, за которое произо-
произошло смещение. Следовательно, среднее значение поглощаемой
в единицу времени энергии будет равно
" ~ Т J 1Х dt •
о
Здесь усреднение производится по одному периоду колебаний
Т = 2jt/Q. Подставляя в этот интеграл выражение для R и для
dl/dt, которое согласно G.29) равно — ao(Q) -Q sin[Q/ + во(ЙI
получаем:
д> = д> (Q) = — R0Qa0 (Q) -1 ^ cos Q/ • sin [Qt + 90 (Q)] dt.
о
После интегрирования находим:
^ = ^ (Q) = -1 /?0Qa0 (Q) sin 90 (Q).
Согласно тождеству sinarctgx = xl^l-\-x:2 имеем:
sin 0O (Q) = sin arctg _?v?L = 2yQ
Поэтому с учетом равенства r0 = /?оМ получим:
^ = ^ (Q) = - ym [Qa0 (Q)]2. G.32)
Таким образом, поглощаемая в единицу времени энергия
зависит от частоты Q.
Так как ао(?2) имеет резонансный пик — максимум, то &(Q)
имеет резонансный пик — минимум (рис. 7.9). Поэтому изме-
измерения зависимости поглощенной энергии от частоты позволяют
обнаружить резонансные явления и установить собственные ча-
частоты осциллирующих систем.
Приведем пример. В инфракрасной области спектра частот
наблюдается поглощение электромагнитной энергии кристал-
кристаллами поваренной соли. Максимум поглощения приходится на
частоту v = 4,91-1012 Гц. Ширина полосы поглощения имеет
такой же порядок. Механизм этого явления заключается в сле-
следующем. Кристалл поваренной соли «сконструирован» из по*
«ложительно заряженных ионов Na и отрицательно заряженных

188
КОЛЕБАНИЯ И ВОЛНЫ
ТГЛ 7
ионоз С1. Эти частицы совершают тепловые колебания. Попав
в поле электромагнитной в^лны, ионы Na и С1 приходят в ре-
режим вынужденных колебаний. Наличие поглощения в указан-
указанной выше области частот говорит о том, что среди колебаний
частиц поваренной соли имеются такие, частоты которых груп-
группируются около значения
4,9Ы012 Гц.
Отметим, что на частотах
¦ инфракрасного диапазона
спектра, выходящих за преде-
пределы отмеченного интервала, по-
поглощение отсутствует. В свое
время это обстоятельство было
использовано при создании ла«
зеров (оптических квантовых
генераторов), излучающих
Рис. 7.9.
электромагнитную энергию на
частоте порядка 3-Ю13 Гц. Из
кристаллов NaCl изготовля-
изготовлялись окна, через которые осуществлялся вывод электромагнит-
электромагнитной энергии из рабочего объема лазера.
Рассмотрим поведение разности фаз 8o(Q). График функции
G.28) изображен на рис. 7.10. Он показывает, что смещение
Рис. 7.10,
отстает по фазе от вынуждающей силы. При резонансе
отставание близко к зт/2 и в случае очень малой силы трения,
т. е. при у/ы < 1, с очень большой точностью равно я/2. Такое
отставание по фазе в резонансе объясняется следующим обра-
образом. При у/о) <С 1 закон движения в резонансе имеет вид
Следовательно,
@ = ар cos
dx
y) = cli> sin Qt'
Сравнивая эту величину с R(t)y видим, что в резонансе фаза
внешней силы совпадает с фазой скорости. Иначе и быть не

§ 7 3] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 1 89
может! Только в этом случае должен резко возрастать размах
колебаний, ибо частица получает толчки в надлежащие моменты
времени и в надлежащих положениях. Например, когда по-
положение частицы нулевое, то скорость максимальна и именно
в этот момент в направлении движения частицы действует
максимальная сила Ro.
Следует иметь в виду, что к наблюдаемым резонансным яв-
явлениям установленные выше соотношения применимы в области
применимости гармонического приближения. Действительно, в
основу было положено уравнение движения G.23). Вид его
левой части записан в предположении, что при отсутствии
трения и внешней силы система является гармоническим
осциллятором. Для реально происходящих явлений это условие
часто нарушается. Возникают существенно нелинейные эффек-
эффекты, которые могут приводить даже к разрушению системы. На-
Напомним популярную историю о рухнувшем мосте, по которому
мерным шагом с резонансной частотой проходил полк солдат.
§ 7.3. Колебания в системах
с несколькими степенями свободы
1. Рассмотренные в двух предыдущих параграфах законо-
закономерности являются простейшими в том смысле, что они харак-
характеризуют свойства изолированного колебания. Такие колебания
происходят в системах с одной степенью свободы. Именно к
числу таких систем относятся все ранее рассмотренные осцил-
осцилляторы. Частица в поле силы упругости, способная переме-
перемещаться лишь в одном ^-направлении, имеет только одну
степень свободы, которая описывается х-координатой частицы.
Математический и физический маятники, колеблющиеся в за-
заданной плоскости, также имеют одну степень свободы. Она
характеризуется углом отклонения ф.
Переход от одного осциллятора к системе с несколькими
степенями свободы приводит к качественному изменению.
В системе с несколькими степенями свободы возможны ко-
колебания с разными частотами. Их совокупность образует ча-
частотный спектр системы.
Поясним сказанное примером одномерной цепочки двух
частиц, изображенной на рис. 7.11. Пружины предполагаются
одинаковыми с коэффициентом упругости k и равновесной дли-
длиной а. Силами трения будем пренебрегать. При малых откло-
отклонениях от равновесия силы, действующие на частицы, будут
пропорциональны изменению длин соответствующих пружин,
В этом отражается общее свойство малых возмущений! Сила,
действующая на первую частицу, равна
Л = - kh + k%2 - kh = k (g2 - 2|0,

[гл 7
190 КОЛЬБАНИЯ И ВОЛНЫ
а на вторую
Fft = - kh + klx - /fo = ft (lx - 2|2).
Переменные gi и g2 описывают две степени свободы системы,
и ее движение описывается системой линейных уравнений
* ^F = * & - 260, m^-^kfa- 2h) G.33)
(масса частиц предполагается одинаковой и равной т).
Рис. 7.11.
У этой системы есть два гармонических решения. Исполь-
Используя для них запись в виде комплексных величин, перейдем от U
к обозначениям г|)г-:
b = ate~M (*=1, 2).
Убедимся в том, что функции такого вида удовлетворяют
системе G.33). Подставляя их в G.33), после дифференциро-
дифференцирования, сокращения на е~ш и перегрупппировки членов получим
однородную алгебраическую систему уравнений относительно а{
(i= 1,2):
Bk — mco2) a{ — ku2 = 0, — ka{ + {2k — moo2) a2 = 0.
Она имеет решение, если равен нулю определитель коэффи-
коэффициентов системы, т. е. при условии
B/г — т02J-?2 = О.
Отсюда находим, что в системе двух связанных осцилляторов
колебания могут происходить уже с двумя частотами:
©1 = У k/т, со2 = л/Шфп.
С увеличением числа частиц (числа степеней свободы осцил-
осциллирующей системы) увеличивается и число возможных частот
колебаний. Частотный спектр становится богаче. Факт же ли«
нейности уравнений движения от числа частиц не зависит. Это
означает, что любая линейная суперпозиция возможных гар-
гармонических колебаний есть один из возможных видов движения
осциллирующей системы. В этом заключается физическое со-
содержание принципа суперпозиции колебаний в системах с не«
сколькими степенями свободы.

§7.3] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 191
В осциллирующей системе с несколькими степенями свободы
каждое из допустимых движений, вызванных малыми возмуще-
возмущениями, является некоторой линейной комбинацией гармониче-
гармонических колебаний со значениями частот из частотного спектра
системы, чем и определяется особая важность гармонических
колебаний.
Обнаруженное свойство проявляется в следующем. Допу-
Допустим, что в системе одновременно возбуждаются разные коле-
колебания. Тогда движение системы является результатом простого
наложения возбужденных колебаний. Для иллюстрации здесь
мы рассмотрим только один пример, отложив обсуждение ряда
важных эффектов сложения колебаний до следующего пара-
параграфа.
Допустим, что частица может совершать колебания в двух
взаимно перпендикулярных направлениях. Такая частица обла-
обладает двумя степенями свободы. Предположим, что частоты не-
независимых колебаний одинаковы и равны со. Частоту, одинако-
одинаковую для независимых колебаний, называют вырожденной.
Выберем систему отсчета так, чтобы ее оси а: и у были
ориентированы в направлении возможных колебаний, а начало
отсчета совпало с положением равновесия частицы. Отсчет вре-
времени условимся производить так, чтобы законы колебания вдоль
осей х и у были бы законом косинуса соответственно с нулевой
начальной фазой и начальной фазой 0о. Если амплитуда коле-
колебаний вдоль оси х равна а, а вдоль оси у равна 6, то значения
радиус-векторов частицы при каждом из колебаний будут опре-
определяться следующим образом:
гх = {a cos со/, 0, 0}, г2 = {0, Ь cos (со/ + во)э 0}.
Если оба колебания возбуждены одновременно, то, согласно
принципу суперпозиции, результирующее движение частицы бу-
будет описываться законом
r = ri + r2 = {a cos со/, Ь cos (со/ + %), 0}»
Он показывает, что частица движется в плоскости ху по траек-
траектории, уравнение которой имеет вид
X2 , I/2 2XU л . 9 г\
-^ + t^-^f cos9°===sln e°.
Из аналитической геометрии известно, что это соотношение опре-
определяет уравнение эллипса. Ориентация осей эллипса по отноше*
нию к координатным осям, а также величина осей эллипса за^
висят от значений а, Ь и 0о.
Справедливость сказанного устанавливается следующим образом. Обозна-
Обозначим ненулевые координаты г через х и у: х = a cos со* и y^b cos (со/ + 0о).

192 КОЛЕБАНИЯ И ВОЛНЫ
Следовательно, cos cot = x/af a sin Ш = Vl — (x/aJ. Кроме тогг>,
-г- = cos ((at + 60) = cos (at • cos 80 — sin со/ • sin Эо =
[ГЛ. 7
ИЛИ
Возводя последнее равенство в квадрат, получим выписанное выше уравнение
эллипса.
Рис. 7.12.
Рис. 7.13.
В качестве упражнения мы предлагаем читателю убедиться
в справедливости следующих утверждений.
а) При 0о = 0 и 9о = ±я эллипс вырождается в отрезки пря-
прямых, изображенных на рис. 7.12. В каждом из этих случаев
движением является гармоническое
колебание частицы вдоль соответ-
соответствующего отрезка, происходящее с
частотой со и амплитудой, равной
Уа2 + Ь2.
б) При 8о = ±я/2 частица дви-
движется по эллипсу с полуосями, рав-
равными а и Ь и ориентированными
вдоль осей х и у соответственно.
При 9о = я/2 движение происходит
по часовой стрелке, а при Во =
= —я/2 — в обратном направлении
(рис. 7.13).
Если частоты взаимно перпенди-
перпендикулярных колебаний не одинаковы,
то характер результирующего дви-
движения частицы оказывается более сложным. Частица описы-
описывает кривые, вид которых может быть весьма запутанным. Эти
Рис. 7.14.

§ 7,3] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 193
кривые называются фигурами Лиссажу. Оказывается, что чем
ближе к 1 отношение частот складываемых колебаний, тем
сложнее фигура Лиссажу. Для примера на рис. 7.14 мы приво-
приводим фигуру Лиссажу при отношении частот 4/3 и 0О = я/2.
2. Помимо богатого частотного спектра возможных колеба-
колебаний, системы со многими степенями свободы обладают еще
одним замечательным свойством: в них наблюдаются явления
передачи различных возмущений от одних частей системы к дру-
другим. Эти процессы обусловлены взаимодействием между раз-
различными частями системы.
Распространение в пространстве различных видов возмуще-
возмущения вещества и поля, проявляющееся в переносе энергии возму-
возмущения, называется волновым процессом или волной.
Примерами такого типа движений являются звук и электро-
электромагнитные волны. Звук может распространяться только в ве-
веществе. Имея атомно-молекулярную структуру, вещество в ма-
макроскопических масштабах является системой с очень большим
числом степеней свободы. Электромагнитные же волны есть не
что иное, как распространяющиеся возмущения электромагнит-
электромагнитного поля. А оно, как мы об этом узнаем в следующем томе
курса, обладает бесконечно большим числом степеней свободы.
Ниже мы рассмотрим свойства волн, пренебрегая их зату-
затуханием*). Реально это означает, что оно столь мало, что в те-
течение достаточно большого времени энергия волны мало изме-
изменяется.
Случается так, что возмущения бывают малыми. И эти слу-
случаи совсем не редки. В этих ситуациях решающую роль в по-
понимании происходящих явлений играет закон, установленный
ранее. Мы имеем в виду принцип суперпозиции, позволяющий
свести вопрос о свойствах такого движения к рассмотрению гар-
гармонических колебаний, определенным набором которых можно
составить любое малое возмущение. Пока мы ограничимся
именно такими возмущениями. Следовательно, закономерности
их распространения могут быть поняты из рассмотрения пе-
редачи гармонических колебаний от одних мест пространства
к другим. На этом вопросе мы и сосредоточим внимание в
дальнейшем. Соответствующие волны принято называть моно-
монохроматическими.
В первую очередь обратим внимание на то, что ориентация
колебаний может быть различной относительно направления их
распространения. Такая картина наблюдается, например, в мо-
монокристаллах. Другой пример: в волне на поверхности жид-
жидкости колеблющиеся частицы совершают круговые движения
*) Затухание звуковых волн будет рассмотрено в гл. 14 этого тома! a
электромагнитных волн — в следующем томе,
7 А, В, Астахов

194 КОЛЕБАНИЯ И ВОЛНЫ 1ГЛ. Я
(рис. 7.15). В этом легко может убедиться каждый, бросивший
в реку легкий предмет в погожий день. Если ориентация не ме-<
няется беспорядочно относительно направления распространения]
волны, то говорят, что волна определенным образом поляризо*
вана. Бывает так, что колебания происходят строго перпенди-
перпендикулярно направлению распространения волны или вдоль этого
Напрадлсние
распространения Ьольы
Рис. 7 15.
направления. В первом случае волну называют поперечной, а во
втором — продольной. Поперечными являются, например, волны
в упругих струнах и электромагнитные волны. Звук же в газах
и жидкостях относится к числу продольных волн.
Важнейшей характеристикой волны является скорость ее
распространения. Общим свойством рассматриваемых здесь
волн (малые возмущения) является
независимость скорости распространения от амплитуды коле-
колебаний. Скорость каждой монохроматической волны зависит,
только от свойств среды, в которой волна распространяется*).
Подробно это свойство будет рассмотрено в гл. 14 на при-
примере звуковых волн.
Рассмотрим волну, распространяющуюся только в одном на*
правлении. Такую волну называют плоской. Разъясним этот
термин. Пусть частота возбуждающего волну колебания рав^
на оз. Выберем систему отсчета таким образом, чтобы это коле-
колебание оказалось локализованным в начале координат, а ось х
указывала бы направление распространения волны. Запишем
закон колебательного движения в начале координат в виде
Ф« @, 0 = **-**,
где а = const — амплитуда колебаний. Записью аргумента функ-
функции фа, в виде @, t) мы подчеркиваем то обстоятельство, что
речь идет о колебании в начале координат. Очевидно, что по
сравнению с ним колебания в произвольной точке г = {х, у, z)
будут запаздывать. Обозначим закон колебательного движения
в точке г через ^©(г, О- Поскольку волна распространяется
*) Электромагнитные волны могут распространяться и в пустом простран*
стве. Скорость таких волн равна скорости света, Они будут рассмотрены в
следующем томе курса.

7,3}
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
195
только в ^-направлении, то время запаздывания будет равно
т = x/v (рис. 7.16). Следовательно, ф©(г,/ + т) = \|>©@, f) или,
что одно и то же,
Отсюда следует, что при данном выборе системы отсчета
ij;^ (г, t) зависит только от х-координаты вектора г через комби-
комбинацию t — x/v:
(х, t)
-=ае ^ v> = ае~ш
где
G.34)
G.35)
Эта величина называется волновым
числом.
Функция G.34) определяет за-
закон движения в каждой точке про-
пространства. Часто для сокращения
функцию, характеризующую дви- Рис. 7.16.
жение в волновом поле, называют
просто волной. Таким сокращением будем пользоваться и мы.
Ввиду этого выражение G.34) в дальнейшем будет имено-
именоваться плоской монохроматической волной, распространяю-
распространяющейся в ^-направлении.
Напомним, что выше мы задались целью разъяснить термин
«плоская волна». Он связан со свойством аргумента функции
G.34) быть постоянным при каждом фиксированном времени t
на любой плоскости, перпендикулярной направлению распро-
распространения волны, т. е. в данном случае оси х. Этот аргумент
называют фазой волны. Обозначим его через 9а>(#, t):
Отсюда прямо видно, что при фиксированном t фаза Q(d{xyt) =
= const при х = const. Последнее равенство есть не что иное,
как уравнение некоторой плоскости, перпендикулярной оси х
(см. рис. 7.16). Обнаруженное свойство фазы означает, что во
всех точках любой плоскости, перпендикулярной направлению
распространения волны, колебания происходят одинаковым об-
образом. Именно поэтому волну и назвали плоской.
Рассмотрим теперь вопрос об описании плоской моно-
монохроматической волны, распространяющейся в произвольном
направлении. Для его решения заметим, что закон G.34) можно
переписать иначе. Введем единичный вектор п (п2=\)у ука-
указывающий направление распространения волны. Очевидно, что
7*

196 КОЛЕБАНИЯ И ВОЛНЫ 1ГЛ. f
в рассмотренном выше случае п ={1,0,0} и, следовательно,
х равно скалярному произведению (г« п) (рис. 7.16). Через век-
вектор п определяется так называемый волновой вектор, равный
Физический смысл k заключается в том, что его ориентация ука-
указывает направление распространения волны, а абсолютное зна-
значение равно волновому числу. С учетом этих определений закон
G.34) можно записать в виде
ае-Ш+ ikx _ ae-tot + ik {n-r) _ ае-Ш+i (k-г)^
Заметим теперь, что скалярное произведение (kr), как вся-
всякое число, является величиной, не зависящей от ориентации
координатных осей. А это и означает, что плоская монохромати-
монохроматическая волна, распространяющаяся в произвольном относитель-
относительно данной системы отсчета направлении (произвольна ориен-
ориентация п по отношению к координатным осям), описывается
законом, вид которого мы только что
установили:
фю(г>*) = ае-/«н-М*-г>. G.36)
В этом случае плоскости, в точках кото-
которых колебания происходят одинаково,
как перпендикулярные вектору k, имеют
наклонное положение (рис. 7.17). Фаза
jr же волны равна 0со(г, 0= wf— (ft-r).
Зависимость фазы рассматриваемой
Рис. 7.17. волны и от времени, и от пространствен-
пространственных координат означает, что каждое дан-
данное значение фазы распространяется в пространстве. И это не-
неудивительно, ибо рассматривается процесс распространения
колебаний. Найдем скорость перемещения фазы. Эта величина
называется фазовой скоростью. То, о чем было только что сказа-
сказано, наводит на мысль, что фазовая скорость должна быть равна
скорости распространения волны. И это действительно так.
В самом деле, пусть в некоторой точке г в момент времени t
значение фазы равно С, т. е. Эо, (г, t)= С. В последующий мо-
момент времени t + dt то же значение фазы возможно только в
другой точке r + dr, т. е. 0©(r + rfr, t + dt)=C. Отсюда ясно,
что dr/dt определяет фазовую скорость.
Из условия Go*(r ~\-dr, t + dt) = б©(г, t) находим:
со dt — (k • dr) = 0.
Это равенство возможно лишь в том случае, если
dr
vn

t 7 3] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 197
Действительно, отсюда следует, что dr = vn dt. Поэтому
со dt - (k • dr) = dt ¦ [со - v {k • л)] = dt (со - kv),
что согласно G.35) тождественно равно нулю. Таким образом,
наша догадка оказалась верной: фазовая скорость имеет на-
направление распространения волны, а ее абсолютное значение
равно скорости волнового процесса.
Продолжим рассмотрение свойств этого процесса. Важней-
Важнейшим из них является его периодичность в пространстве. Она
обусловлена двумя факторами: периодичностью колебаний во
времени и их распространением. Пространственный период на-
называется длиной волны и имеет смысл расстояния между бли-
ближайшими точками, в которых фаза колебаний одинакова. Обо-
Обозначим его через X и найдем, используя закон движения G.34).
С этой целью запишем условие пространственной периодично-
периодичности %о(# + К t) = tya(x, t), которое приводит к равенству
eik(x+k) _ eikx.eihh _ е%кх% Последнее выполняется при условии
kX = 2к (имеем в виду, что e2!ti = cos 2n + i sin 2я = 1). Таким
образом, находим, что
Я = 2я/й G.37)
или с учетом G.35)
% ..= 2:гш/со. G.38)
С помощью G.2) последнее выражение преобразуется к виду
% = vT9 G.39)
где Т — период колебаний.
Характерным признаком плоской волны является постоян-
постоянство направления ее распространения и постоянство амплитуды
колебаний. Далеко не все волны обладают такими свойствами.
Однако очень часто произвольные (не плоские) волны можно
считать почти плоскими в каждой малой области пространства.
Условием применимости такого приближения является малость
изменения амплитуды и направления волны на расстояниях по-
порядка длины волны. В этом приближении волны классифици-
классифицируют по строению их волновых поверхностей.
Волновой поверхностью называется геометрическое место то-
точек в пространстве, в которых колебания происходят в одина-
одинаковой фазе.
Так, для плоской волны волновыми поверхностями являются
плоскости, перпендикулярные направлению распространения
волны. Часто приходится сталкиваться со сферическими и ци-
цилиндрическими волнами. Для сферической волны волновыми по-
поверхностями является семейство концентрических сфер. Легко
сообразить, что в их общем центре расположен излучающий

198
КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ 7
волну источник (рис. 7.18). Источники цилиндрических волн
имеют форму очень длинных цилиндров. В этом случае волно^
выми являются поверхности цилиндров, соосных с цилиндром —
источником излучения (рис. 7.19). И в том, и в другом случае
волны распространяются по радиальным направлениям.
и
и
Рис. 7,18.
Рис. 7.19.
Распространяясь от источника, волна проникает во всё более
отдаленные области. Очевидно, что в каждый момент времени
всегда можно указать поверхность, отделяющую в данный мо-
момент область пространства, в которой волновой процесс уже
развился, от остальной, невозмущенной области. По форме эта
поверхность будет волновой. Однако ее отличительным свой-
свойством является перемещение со скоростью распространения вол-
волны (рис. 7.18, 7.19). Эта движущаяся пограничная поверхность
называется волновым фронтом.
3. Скорость распространения волны может изменяться в за-
зависимости от частоты колебаний. Это явление наблюдается,
например, при прохождении электромагнитных волн через ве-
вещество. В некоторых случаях оно наблюдается и для звуковых
волн. В гл. 14 будут приведены соответствующие примеры, от-
относящиеся к звуку.
Зависимость скорости распространения волны от частоты на-
называется дисперсией.
Дисперсия приводит к нарушению простой линейной связи
между частотой со и волновым числом k [см. формулу G.35)].
Зависимость оа = о)(&) называется дисперсионным уравнением
или законом дисперсии. Вид этого закона является важнейшей
характеристикой, отличающей одни волны от других. Волны с
разными законами дисперсии обладают разными свойствами.

§ 7.3] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 199
Одно из различий (о других мы узнаем по мере того, как будем
с ними сталкиваться) заключается в следующем. При отсут-
отсутствии дисперсии распространение волн может быть описано на
основе волнового уравнения. При наличии дисперсии это уже
не так. Волновым называется уравнение вида
д^±д^дЧр_ 1_ дЧр_ ___ (
2 v2 dt2 ~и> \<-™>
дх2 п ду2 ^ dz2 v2 dt2
в котором v — скорость распространения волны, а г|э— функция,
описывающая закон волнового движения. Она зависит от вре^
мени /и от координат х, у, z точки пространства, определяющих
место интересующих колебаний.
В справедливости G.40) проще всего убедиться на примере
одномерного волнового движения, которое мы будем предпола-
предполагать происходящим в ^-направлении. Начнем с монохроматиче-
монохроматических волн. Возможны две такие волны,
-фН-) (х, /) = ае-ш+ik* и <фЫ (^ t) = ав'ш'1к\
Первая распространяется вдоль оси х слева направо, другая—•
в обратном направлении. Прямой подстановкой нетрудно уста-
установить, что при условии G.35) и та, и другая волна удовлетво*
ряют одномерному волновому уравнению
дх2 v2 dt2 ~U*
Вспомним теперь, что согласно принципу суперпозиции про*
извольная плоская волна, распространяющаяся в х-направле«
нии, может быть представлена линейной комбинацией волн
О)
Здесь через С^ обозначены коэффициенты этой комбинации,
а суммирование распространяется на весь частотный спектр той
системы, в которой наблюдается данный волновой процесс. Те«
перь нетрудно установить, что если v не зависит от со, то г|?(л;, t)
также удовлетворяет одномерному волновому уравнению:
Vfr<+>fdV+) ' dV+)Nj , r(->fay-> 1 аУ2>\1
СО
ох>-
dt2

200 КОЛЕБАНИЯ И ВОЛНЫ 1ГЛ 7
Все представленные здесь преобразования недействительны,
если и = и (со).
4. Частота не является инвариантной характеристикой вол-
волны. Мы имеем в виду здесь то обстоятельство, что частота
волны изменяется при переходе из одной системы отсчета в
другую, движущуюся относительно первой. Это явление назы-
называется эффектом Допплера.
Рассмотрим, как это происходит.
Ограничимся областью только нерелятивистских движений
(например, звуковые волны). Пусть в покоящейся системе от-
отсчета К частота плоской бегущей в х-направлении волны рав-
равна со. Определим, какую частоту будет воспринимать наблюда-
наблюдатель, находящийся в движущейся системе отсчета /('. Эту
частоту мы обозначим через со'. Предположим, что скорость си-
системы К' равна V7, причем ориентация осей систем К и К' оди-
одинакова, а движение системы К' происходит в ^-направлении.
Пусть закон волнового движения в системе К имеет вид
Воспользуемся теперь преобразованиями Галилея A.18) и пе-
перейдем в систему К'. Тогда получим такой закон движения:
Мы видим, что наблюдатель системы К' будет регистрировать
волновой процесс с иной частотой
о/ = со — W
и волновым числом
Так как k — со/и, где и — скорость распространения волны в си-
системе /С, то
<о' = шA-Х). G.41)
Отметим, что противоречия между изменением частоты и
неизменностью волнового числа нет. Действительно, скорость
распространения волны в системе К' равна v' = v— V, где v —
скорость волны в системе /(. Поэтому
к ~~~ v' ~ v-V ~~" v — V ~~J~tl%
При этом мы воспользовались соотношением G.41).
Формула G.41) позволяет оценивать, насколько регистри-
регистрируемая приемником волны частота соПр отличается от частоты
колебаний источника волны соИСт, если приемник и источник
движутся друг относительно друга. ^

§7 4] ЭФФЕКТЫ СЛОЖЕНИЯ ВОЛН 2U1
Предположим, что источник волны покоится, а приемник
удаляется от него со скоростью V (рис. 7.20). Тогда в G.41)
со = Оист, а со' = (Одр- Поэтому
1 — ~г)
= (Оист ( 1 — ~г) <
При изменении направления движения приемника на обратное
меняет знак скорость V. Следовательно, в этом случае
-77- > СОИ
Предположим, что движется источник волн, а приемник по*
коится (рис. 7.21). Тогда в G.41) о/ = о)ИСт, а со = сопр и, сле-
следовательно,
Если источник удаляется от приемника, то изменяется знак К.
В этом случае
^р = 1 +T/V < ®ист'
Эффект Допплера находит широкое применение, так как
благодаря ему существует возможность изменять частоту волны,
№,„„&,.
Рис. 7.20. Рис. 7.21.
меняя, например, скорость движения излучателя. Именно таким
способом во многих случаях добиваются резонансного погло-
поглощения энергии волны различными осциллирующими системами.
Например, протоны и нейтроны в атомном ядре совершают коле-
колебания. Если на ядро направить электромагнитную волну, то,
меняя скорость ее излучателя, можно добиться совпадения ча-
частот электромагнитных колебаний и колебаний частиц в атом-
атомном ядре. При этом произойдет резонансное поглощение элек-
электромагнитной знергии ядром.
§ 7.4. Эффекты сложения волн
1. Принцип суперпозиции волн утверждает, что движение,
вызванное распространением сразу нескольких волн, есть снова
некоторый волновой процесс. Таким процессом является* на-
например, звучание оркестра. Оно возникает от одновременного

202 КОЛЕБАНИЯ И ВОЛНЫ |ГЛ 7
возбуждения звуковых колебаний воздуха отдельными музы-
музыкальными инструментами. Замечательно, что при наложении
волн могут возникать особые явления. Их называют эффектами
сложения или, как еще говорят, суперпозиции волн. Среди этих
эффектов наиболее важными являются следующие.
Интерференция — явление устойчивого во времени перерас-
перераспределения колебаний в пространстве, в результате которого
в одних местах колебания усиливаются, а в других ослабляются.
Это явление возникает при сложении волн с сохраняющейся во
времени разностью фаз. Для монохроматических волн это тре-
требование сводится к условию равенства частот.
Наиболее ярко интерференция проявляется в оптике. Именно
там мы и рассмотрим детали этого явления. Здесь же мы огра-
ограничимся обсуждением только одного, но очень важного интер-
интерференционного эффекта, который заключается в образовании
стоячих волн. Предварительно сделаем одно замечание. По дав-
давно сложившемуся обычаю интерференцию большого числа волн
именуют дифракцией. Мы просим читателя запомнить, что прин-
принципиального различия между интерференцией и дифракцией
нет. Природа этих явлений одна и та же.
2. Рассмотрим стоячие волны. Каждая стоячая волна обла-
обладает следующими свойствами. Вся область пространства, в ко-
которой возбуждена волна, может быть разбита на ячейки таким
образом, что на границах ячеек колебания полностью отсут-
отсутствуют. Точки, расположенные на этих границах, называются
узлами стоячей волны. Фазы колебаний во внутренних точках
каждой ячейки одинаковы. Колебания в соседних ячейках (ими
являются ячейки с общей границей) совершаются навстречу
друг другу, т. е. в противофазе. В пределах любой ячейки ам-
амплитуда колебаний изменяется в пространстве и в каком-то ме-
месте достигает максимального значения. Точки, в которых это
наблюдается, называются пучностями стоячей волны. Наконец,
характерным свойством стоячих волн является дискретность
спектра их частот. В поле стоячей волны колебания могут со-
совершаться только со строго определенными частотами и пере-
переход от одной из них к другой происходит скачком.
Необходимым условием образования стоячих волн является
наличие границ, отражающих падающие на них волны. При
этом условия на границах со временем меняться не должны
(в таких случаях математики говорят о постоянных во времени
граничных условиях). Стоячие волны образуются в результате
сложения падающих и отраженных волн. Явления такого рода
встречаются довольно часто. Так, каждый тон звучания любого
музыкального инструмента возбуждается стоячей волной. Эта
волна образуется либо в струне (струнные инструменты), либо
в столбе воздуха (духовые инструменты). Отражающими гра-

§ 7.4] ЭФФЕКТЫ СЛОЖЕНИЯ ВОЛН 203
ницами в этих случаях являются точки закрепления струны и
поверхности внутренних полостей духовых инструментов. По*
лости, в которых образуются стоячие звуковые волны, назы«
ваются акустическими резонаторами. В замкнутых полостях
можно создавать и стоячие электромагнитные волны. Такие
волны образуются, например, в рабочем объеме каждого ла«
зера. Стоячие волновые процессы очень распространены в mvh
кромире. Они очень специфичны по природе, ибо связаны с ве^
роятностыо. Об этих волнах будет рассказано в последнем
томе курса.
Рассмотрим простой пример стоячей волны. Предположим,
что струна ограниченной длины L натянута вдоль оси х. Допу«
стим, что концы струны жестко закреплены, причем левый ко*
нец находится в начале координат. Тогда координата правого
конца будет равна L (рис. 7.22). Вообразим теперь, что в струне
удалось возбудить монохро-
монохроматическую волну
распространяющуюся вдоль
оси х слева направо. От
Риг
правого конца струны вол- rMU~
на отразится. Предположим,
что это произойдет без потери энергии. В этом случае отра-
отраженная волна будет иметь ту же амплитуду и ту же частоту,
что и падающая. Поэтому отраженная волна должна иметь вид
Ее фаза содержит некоторую постоянную 0, определяющую из-
изменение фазы при отражении. Ее значение будет установлено
ниже.
Поскольку отражение происходит на обоих концах струны
и без потерь, то в струне будут одновременно распространяться
волны одинаковых частот. Поэтому при сложении ф<+* и t|)<)"")
должна возникнуть интерференция. Посмотрим, как она выгля-
выглядит. Для этого найдем результирующую волну:
Здесь в последнем выражении
Как всякую комплексную величину, <p(jt) можно представить
в виде: ц> (х) = а (х) eia(x\ где а(х) и а(х) являются, соответ-*
ственно, модулем и аргументом ц>(х). С учетом этого представ-
представления имеем;

204 КОЛЕБАНИЯ И ВОЛНЫ [ГЛ. 7
Мы видим, что в каждой точке струны происходят колебания
с частотой со. При этом амплитуда колебаний в точке х равна
а(х). Очевидно, что а2(х) = (р{х)у*(х)у где ср*(х) —величина,
комплексно сопряженная <р(х) и равная a(e~ikx + eikx~iQ). От^
сюда получаем:
а2 (х) = a2 (eikx + e~ikx^iQ) {e~ikx + eikx~iQ) =
= a2 B + e2ikx~iQ + e~2ikx+iQ) =
=a2 [2+cos Bfot—9)+/ sin {2kx-Q) + cos Bfejc—0)—/ sin Bfex—9)] =
или
a(x) = 2a cos
= 2a2 f 1 + cos Bfex - 9)] = 4a2 cos2 (kx - -|),
Так как концы струны закреплены, то там колебания отсут-^
ствуют. Из условия а@) = 0 следует, что 9 = п. Поэтому окон-
окончательно находим, что
а (х) = 2а cos [kx — -|Л I = 2a | sin kx |.
Теперь ясно видно, что в точках, в которых sin kx — 0, коле-
колебания отсутствуют вовсе. Эти точки и являются узлами стоячей
волны i|)a>(#, t). Там же, где |sin?#|= 1, амплитуда колебаний
максимальна и притом вдвое больше амплитуд складываемых
волн t])W и ij^. Эти точки являются пучностями стоячей вол^
ны. В появлении пучностей и узлов как раз и заключается
интерференция: в одних местах колебания усиливаются, а в
других прекращаются совсем.
Расстояние Ал: между соседними узлом и пучностью нахо-
находится из очевидного условия: kx = я/2. Так как k = 2яД, где
К — длина волны, то оказывается, что Ал: = Я/4. Расстояние
между соседними узлами равно 2Ах = К/2.
Найдем теперь а (л:). С этой целью преобразуем выражение
для ф(л:) следующим образом:
ф (х) = a {eikx + e-ikx+tn) = a {eikx — e~ikx) =
= a (cos kx + i sin kx — cos kx + i sin kx) — i 2a sin kx.
При этом мы учли, что 9 = я.
Рассмотрим точки из интервала 0 ^ х ^ Я/2. Для них
sin kx = 51пBял:/Я) ^ 0, и поэтому в этой области
i • 2a-sin kx — i 2a I syi kx I — / a ix) == einl2 a (x)

§ 7 4] ЭФФЕКТЫ СЛОЖЕНИЯ ВОЛН 205
fetni2 _ cos IL -\- i sin ~- = Л . Следовательно, для 0 ^ х ^ Л/2
имеем: а(х) = const = я/2 и
Перейдем теперь к точкам струны, находящимся в интерва-
ле у^х^Я. Здесь sin Ъс = sin Bял;/Л) ^0, и, следовательно,
Ф (х) = i 2а sin kx = — г 2а | sin йл; | = — i а (х) = е
а
Таким образом, для ~^.х^Х имеем: а {х) = const = — — и
Сравнивая законы колебаний в точках двух рассмотренных
интервалов, мы видим, что в пределах каждого из них фазы
колебаний одинаковы и равны, соответственно, ю/— ~ и
co/+-f-. Разность же этих фаз постоянна и по абсолютному
значению равна я. Это и означает, что колебания в одном из
интервалов совершаются навстречу, т. е. в противофазе, коле-
колебаниям в другом.
Свойства, которые мы сейчас обнаружили у волны фа(х,/)
на участках струны О^х^-тг и у^*^^» повторяются с пе-
периодом Л для всех последующих участков длины Х/2. Мы пред-
предлагаем читателю убедиться в этом самостоятельно.
Таким образом, рассмотренный пример показывает, что пу-
путем сложения падающей и отраженной волн a|)J0+) и ij^-)
|)J0
ствительно можно получить картину волнового движения, оха-
охарактеризованную в начале настоящего пункта. При этом ячей-
ячейками, о которых там говорилось, в одномерном случае являются
отрезки, заключенные между соседними узлами и имеющие
длину Я/2.
Убедимся, наконец, в том, что рассмотренная выше волна
может существовать только при строго определенных частотах
колебаний. Это обстоятельство следует из условия отсутствия
колебаний на правом конце струны: а(х) = 0 при х = L. От^
сюда получаем, что sin kL = 0. Это равенство возможно, если
kL = n-n, где п — произвольное положительное число. Отрица-
Отрицательные п исключаются по смыслу волнового числа. Итак, ока-
оказывается, что k, а следовательно и частота со, связанная с k
соотношением G.35), могут принимать только следующие строго

206 КОЛЕБАНИЯ И ВОЛНЫ [ГЛ. 7
определенные значения:
k=skn = l?-, со^со.-^ (л-0э 1, 2, ...). G.42)
Еще раз подчеркнем, что дискретность спектра частот является
типичным свойством всех стоячих волн, резко выделяющимся
в классической физике, в которой, казалось бы, все обречено из-
изменяться непрерывным образом. Отметим, что именно эта «ано-
«аномалия» сыграла выдающуюся роль в разгадке природы кванто-
квантовых явлений.
3. Еще одним важным эффектом суперпозиции волн яв-
являются биения. Это явление заключается в периодическом во
времени усилении и ослаблении колебаний, возникающих при
сложении волн близких частот. Это явление можно наблюдать,
например, таким образом. Предположим, что имеются два ка-
камертона, частоты колебаний которых достаточно близки. При
одновременном возбуждении камертонов возникают две звуко-
звуковые волны близких частот. В результате их сложения слыши-
слышимое звучание периодически то затухает, то усиливается. Это
и есть биения, в данном случае биения звука. Отметим, что бие-
биения наблюдаются и при сложении отдельных колебаний с близ-
близкими частотами.
Рассмотрим образование биений на примере двух волн с
почти равными частотами coi и сог- Допустим, что обе волны
распространяются в одном и том же направлении, вдоль кото-
которого и ориентируем ось х. Тогда
^)(х> t) = a^-toiWfci*, ^B)(Xt t) = а2е-*ъ*+*ь*.
В результате сложения этих волн возникает движение, кото-
которое описывается законом
Введем величины
1
= со1 — со2; к =
Из-за близости частот coi и оJ имеем: со > Дсо и k > ДА». По-
Поэтому закон i|)(#, t) преобразуется так:
G.43)
где
L * i i
ф = ф (xy t) = п\в 2 2 -}- #2^ ^ ^ •
Последняя величина изменяется со временем с очень малой
частотой. Поэтому движение, происходящее по закону G.43),
обладает такими свойствами. В каждой точке х происходят

§ 7.4] ЭФФЕКТЫ СЛОЖЕНИЯ ВОЛН 207
колебания с большой частотой со (большой в сравнении с Aw).
Их амплитуда определяется модулем комплексной величины ф.
Обозначив эту амплитуду через а(х, t), находим:
аЦх, /) = <р(*, 0<Р*(*>0 =
»* J
= а; + а] + а,а2 {cos (Дсо • * — Aft •*) — *' sin (Дсо • f — Aft • *) +
4- cos (Дсо • / — Mi • jc) + / sin (Aco • / — Aft • a:)} ==
= aj + a| + 2aAa2 cos (Aco • t - Aft • x). G.44)
Мы видим, что квадрат амплитуды колебаний в каждой точ-
точке меняется с малой частотой Дсо. С такой же частотой будут
происходить и колебания энергии. Напомним, что энергия про-»
порциональна квадрату амплитуды. Это и есть как раз тот
эффект, который проявляется в опыте с двумя камертонами.
Заметим, что так как квадрат амплитуды, а, следовательно, и
энергия колебаний зависят и от времени, и от координаты х,
то это означает, что каждое значение энергии перемещается
в пространстве. Дальнейшая логика рассуждений такая же, как
и при выводе выражения для фазовой скорости. Только теперь
речь идет о скорости распространения энергии. Эта величина
называется групповой скоростью. Обозначим ее через vrp. Ясно,
что если за время dt некоторое значение энергии [или квадрата
амплитуды G.44)] переместилось на расстояние dx, то игр =
= dx/dt. Величины dt и dx связаны условием
Дсо • dt — Aft • dx = 0.
Из него находим:
Угр~~ dt ~~ ДА? ~~ dk ' V'qo'
Последнее выражение записано ввиду малости Дсо и Aft.
Если дисперсия отсутствует, то групповая скорость совпадает
с фазовой. Действительно, в этом случае со = kv, причем v не
зависит от со. Тогда угр = d(o/dk = v. При наличии дисперсии
положение меняется. В этом случае

208 КОЛЕБАНИЯ И ВОЛНЫ [ГЛ. 7
Решая полученное уравнение относительно игр, находим:
v (со) v (со) , / v
da)
da) v (со) day
В случае трехмерного волнового движения групповая ско-*
рость определяется соотношением
dkx • dky • a&2
где kXj kyy kz — компоненты волнового вектора k. Это соотноше-
соотношение является обобщением одномерного закона G.45).
Обращает на себя внимание сходство соотношений C.1) и
G.46). Они подобны: скорости г>гр соответствует скорость V
центра инерции системы, частоте со — энергия системы <§Г, волно-
волновому вектору k — импульс системы Р. Более того, если частоту
и волновой вектор умножить на постоянную Планка Й, то полу-
получим величины, которые имеют, соответственно, размерность энер^
гии и размерность импульса. Это подобие отнюдь не случайно
и имеет глубокий смысл, открытый с созданием квантовой фи-
физики. Подробно об этом речь пойдет в томе III. Здесь лишь
отметим, что Йсо и tik — это действительно энергия и импульс
особых частиц — квантов волны (фотонов для электромагнит-
электромагнитных волн, фононов для звука), a vTV — скорость их движения.
Оказалось, что все материальные объекты обладают и свой-
свойствами частиц, и свойствами волн. В одних случаях в большей
мере проявляются волновые свойства (например, электромагнит-
электромагнитные волны не слишком высоких частот — не более 1018Гц), в
других — свойства частиц (электроны, протоны, атомы, молекулы
и т. д.). Поэтому неудивительно, что, изучая законы волновых
движений, мы обнаруживаем свойства, которые привыкли отно-
относить только к частицам»

ЧАСТЬ II
КИНЕТИЧЕСКАЯ ТЕОРИЯ МАТЕРИИ
ГЛАВА 8
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
§ 8.1. Тепловое движение
I. Представление об атомном строении вещества существует
давно. Впервые оно было выдвинуто в древней Греции еще за
400 лет до нашей эры. Однако только на рубеже XIX и XX сто-
столетий оно получило прямое экспериментальное подтверждение.
Трудность заключалась в том, что атомы, как оказалось, имеют
весьма малые размеры. Их радиусы не превышают нескольких
ангстрем (см. § 1.1). Поэтому увидеть их непосредственно очень
трудно. Средства наблюдения были разработаны сравнительно
недавно. К их числу относится, например, прибор, называемый
ионным проектором, который позволяет получать фотографии
отдельных атомов. На рис. 8.1 изображена его схема и получен-
полученная с его помощью фотография поверхности вольфрама при
увеличении в 4-Ю6 раз.
Ионный проектор представляет собой сферический сосуд диаметром при-
примерно 10 см. В центр сосуда вставлена вольфрамовая игла. Игла делается
максимально острой, такой, как это только допускает современная обработка.
Сосуд заполнен гелием под давлением около 1 мм рт. ст. Внутренняя поверх-
поверхность оболочки сосуда покрывается пленкой. На оболочку подается отрица-
отрицательный потенциал, на иглу — положительный. Внутри сосуда возникает элек-
электрическое поле. У острия иглы его напряженность максимальна. Сталкиваясь
с острием, атомы гелия отдают ему электроны, превращаясь при этом в поло-
положительные ионы. Каждый ион, отталкиваясь от одноименно заряженного
острия иглы, летит к отрицательно заряженной оболочке. В результате к стен-
стенкам сосуда направляется поток ионов, который оставляет след, фиксируемый
на пленке. Каждый атом вольфрама образует на поверхности острия микро-
микроскопический «бугор». На этих «буграх» ионизация гелия максимальна. По-
Поэтому и пленка сильнее всего чернеет в тех местах, куда входят силовые
линии электрического поля, начинающиеся на «буграх». В этом и состоит
фотографирование атомов. Получаемое на ионном проекторе увеличение
имеет порядок 10е.
Все окружающие нас тела состоят из атомов- 92" видов.
Вещества, построенные из* атомов одного сорта, называются

210
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
ГГЛ. 8
химическими элементами. Элементами являются, например, во-
водород, гелий, углерод, железо, золото и т. д. При сближении в
результате действия сил взаимного притяжения атомы могут
объединяться в устойчивые группы, образуя связанные состоя-
состояния. Связанные состояния небольшого числа атомов*) назы-
называются молекулами. Вещество, образованное из одинаковых мо-
молекул, состоящих из разных атомов, называется соединением.
Оболочка
'ыррамобая
игла
Рис. 8.1а.
Рис. 8.16.
К числу соединений относятся, например, вода Н2О, метан СН4,
поваренная соль NaCl и т. д. Мельчайшую составную часть
вещества мы в этой части будем называть частицей. Частицей
может быть как атом, так и молекула **).
2. Все непосредственно наблюдаемые нами тела являются
макроскопическими, т. е. состоят из громадного числа частиц.
Очень большим является такое число N, для которого \nN > К
В физике среди всех больших чисел особо важная роль выпала
*) По сравнению с полным числом атомов, составляющих тело.
**) Вопрос о том, что именно считать частицей в каждом конкретном-
случае, ясен для газов, но для жидкостей, и особенно для твердых тел, да-
далеко не прост (см. Введение). Однако для целей этой части книги твердое
тело можно представлять состоящим из молекул.

$ 8J] ТЕПЛОВОЕ ДВИЖЕНИЕ 211
на долю числа Авогадро
NA = 6,02252- 1023. (8.1)
Число Авогадро равно отношению молекулярной массы ве-
вещества*), выраженной в граммах, к массе одной молекулы.
В настоящее время введена единая шкала, в которой молеку-
молекулярные массы определяются по отношению к молекулярной мас-
массе изотопа углерода С12. Последняя принимается равной 12.
С числом Авогадро связана единица измерения количества ве-
вещества. Она называется молем. Моль — это такое количество
вещества, в котором содержится NA частиц. В СИ за единицу
измерения принят киломоль: 1 кмоль = 103 молей. Так, масса
одного киломоля углерода С12 равна 12 кг.
Измерение числа Авогадро относится к числу особо важных
событий по той причине, что это число прямо связано с суще-
существованием атомного строения вещества. Число Авогадро свя-
связывает микроскопический масштаб с макроскопическим, ибо
моль любого вещества обычно составляет тело привычных для
нас размеров. Так, при атмосферном давлении и 0°С моль лю-
любого газа занимает объем 22,4 л.
3. С одной стороны, макроскопические тела и их составные
части (также макроскопические) могут перемещаться друг от-
относительно друга упорядоченным образом. Закономерности та-
таких перемещений называются динамическими и рассматри-
рассматриваются в механике. С другой стороны, макроскопические тела
обладают свойствами, которые невозможно объяснить на основе
только законов механики (в том числе и квантовой). Своим
происхождением эти свойства обязаны атомному строению ве-
вещества и обусловлены движением его микроскопических частиц.
Этот вид движения обладает качественно новым свойством —
беспорядочностью. Закономерности движений такого рода на-
называются статистическими. Беспорядочность присуща движению
частиц вещества каждого макроскопического тела по той при-
причине, что их необозримо много. Поэтому невозможно проследить
за всеми деталями движения частиц, и все происходящее с ними
выглядит как цепь случайных событий.
Беспорядочное движение частиц, составляющих макроскопи-
макроскопические тела, называется тепловым. Тепловое движение опреде-
определяет внутреннее состояние каждого макроскопического тела.
За исключением особых случаев, которые мы рассматривать
не будем, тепловое движение является нерелятивистским.
Фундаментальным свойством теплового движения является
его способность «заставлять» вещество макроскопических тел
«забывать» свое начальное состояние, Это свойство проявляется
*) Химики эту величину называют молекулярным весом.

212
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
ТГЛ. 8
всегда при соблюдении только одного условия: должны быть
исключены меры, специально направленные на поддержание
начального состояния. Образно говоря, в этих случаях макро-
макроскопические тела ведут себя как «склеротические» системы.
Разъясним сказанное следующим примером. Предположим,
что в прозрачную воду падает капля окрашенной жидкости*
В начальный момент вещество этой жидкости будет сконцен*
трировано у места падения. Однако со временем вещество кра-
краски равномерно распределится по всему объему. При этом окон^
чательное состояние смеси будет одинаковым, независимо от
того, в каком месте появилось окрашенное вещество в началь*
ный момент (рис. 8.2). Это и означает, что данная система
Начальное
состояние 1
Конечное
состояние
Рис. 8.2.
Начальное
состояние 2
в конце концов совсем забывает о своем начальном состоянии.
Разумеется, начальное состояние можно сохранить, но об
этом нужно специально позаботиться. Например, это можно сде-
сделать так. Сразу же после падения капли обернуть ее непрони-
непроницаемой пленкой. Если при этом будет обеспечена герметичность,
то окрашенное вещество можно будет удержать в заданном
месте сколь угодно долго.
Природа «внутреннего склероза», развивающегося в макро-
макроскопических системах, будет установлена в гл. 10. Здесь нам
достаточно знать лишь о факте его существования.
Предположим, что макроскопическое тело помещается в
условия, которые со временем не меняются. Тогда, каким бы ни
было внутреннее состояние тела до его помещения в данные
условия, в конце концов это состояние будет «забыто». Веще-
Вещество тела перейдет в новое состояние, которое по причине по-
постоянства внешних условий со временем меняться не будет. Та-
Такие состояния называются стационарными. Однако в стационар-
стационарном состоянии вовсе не исключается, что через границы тела
не будет осуществляться перенос вещества, энергии, импульса,
электрического заряда.
Рассмотрим два примера. Предположим, что между двумя
пластинами помещается газ. Пусть одна из пластин разогрета
больше другой, но температура каждой пластины поддержи-

§8.1] ТЕПЛОВОЕ ДВИЖЕНИЕ 213
вается постоянной. Тогда независимо от того, что было с газом
до его помещения в данные условия, в конце концов он придет
в состояние с неизменным во времени распределением темпера-
температуры. Именно, вблизи каждой из пластин температура газа
будет равна температуре пластины. В объеме газа температура
будет изменяться, убывая от большего значения у горячей пла-
стины до меньшего значения у холодной. Однако в таком ста-
стационарном состоянии все время происходит перенос энергии.
Действительно, участки газа с пониженной температурой будут
отбирать энергию от более нагретых участков. Для сохранения
заданной разности температур на пластинах этот процесс пере-
переноса необходимо постоянно поддерживать. Осуществляют это
путем ввода энергии в форме тепла через пластину с повышен-
повышенной температурой (одна из границ системы) и отвода энергии
из системы через пластину с пониженной температурой (другая
граница).
Рассмотрим другой пример. В металлическом проводнике,
подключенном к источнику постоянного напряжения, возникает
постоянный электрический ток. За счет выделения джоулева
тепла проводник будет разогреваться. Однако его температура
будет изменяться до тех пор, пока не установится равенство
между количеством джоулева тепла, выделяющегося в провод-
проводнике за единицу времени, и количеством тепла, которое провод-
проводник за тот же промежуток времени отдает окружающим телам.
После этого состояние проводника перестанет изменяться (ко-
(конечно, при условии, что состояние окружающей среды остается
неизменным). Однако в этом стационарном состоянии через
проводник осуществляется перенос электрического заряда, что
другими словами называют электрическим током.
Разбирая эти примеры, мы говорили о физических величи-
величинах (температура, количество тепла, джоулево тепло, напряже-
напряжение, электрический ток), которые в данном курсе не были еще
определены. Здесь мы рассчитываем на то, что читатель имеет
о них представление из школьного курса физики.
Бывает так, что макроскопическое тело помещается в неиз-
неизменные во времени условия и при этом еще исключается перенос
вещества, энергии, импульса, электрического заряда через гра-
границы тела. Такое тело называется термодинамически изолиро-
изолированной системой. Примерами таких систем являются газ, по-
помещенный между пластинами с одинаковой температурой, и
Проводник, не подключенный к источнику напряжения. В тер-
термодинамически изолированных системах также действует меха-
механизм, приводящий к «склеротическим явлениям». Но в этом
случае он приводит к состояниям, получившим название состоя-
состояний теплового или термодинамического равновесия. Сокращенно
их называют просто равновесными.

214 макроскопические состояния {гл. а
Состоянием теплового равновесия является стационарное со^
стояние термодинамически изолированной системы.
Приближение к равновесному состоянию называется релак*1
сацией, а длительность этого процесса — временем релаксации^
До истечения времени релаксации состояние термодинамически
изолированной системы является неравновесным. Неравновес^
ным является также любое состояние системы при отсутствии
термодинамической изолированности.
Вернемся к рис. 8.2. У изображенной системы равновесным
является состояние с равномерным распределением вещества
окрашенной жидкости в воде. Начальные состояния / и 2, так
же как и все промежуточные состояния, проходимые при уста*
новлении равновесного распределения окрашенного вещества,
являются неравновесными. Время релаксации определяет дли^
тельность перехода в равновесное состояние.
Процессы установления равновесного состояния бывают бы-
быстрыми и медленными. Примером быстрого процесса является
выравнивание давления в газе, если в начальном состоянии оно
было не одинаковым в разных частях газа. Этот процесс проис^
ходит со скоростью звука. К числу медленных процессов отно-
относится выравнивание температуры. Так, если неоднородность в
распределении давления в воздухе имеет размер порядка 1 м,
то она исчезает за время порядка 10~3 сек. Без принудительного
перемешивания температурная неоднородность такого же раз-
размера рассасывается за время порядка 105 сек.
§ 8,2, Макроскопические параметры
1, Независимость поведения частиц тела, находящегося в
равновесном состоянии, от начальных условий означает, что
точный вид закона движения каждой частицы теряет всякое
значение. (Напомним, что закон движения определяется урав-
уравнениями движения и начальными условиями.) Другими слова-
словами, состоянию теплового равновесия присущ полный хаос в дви-
движении частиц.
Поэтому
свойства равновесного состояния не зависят от деталей дви-
движения отдельных частиц и определяются поведением всего их
коллектива. Это поведение характеризуется небольшим число/.:
величин, названных макроскопическими параметрами. Устано-
Установившийся характер равновесного состояния проявляется в по-
постоянстве во времени макроскопических параметров.
Макроскопические параметры характеризуют общие тенден-
тенденции в поведении очень большого числа частиц или, другими
словами, определяют усредненную картину их движения. По-

18.2] МАКРОСКОПИЧЕСКИЕ ПАРАМЕТРЫ
этому они имеют смысл средних значений физических величин,
описывающих движение частиц тела.
Средние значения определяются следующим образом. Рас-
Рассмотрим какую-либо из физических величин. Обозначим ее
через g. Например, ? может быть скоростью частицы, ее энер-
энергией и т. д. В результате теплового движения переменная g
будет изменяться, причем ее изменения будут носить случайный
характер. Среднее значение переменной g, которое обозначим
через |, определяется как среднее арифметическое всех значе-
значений, которые она принимает вследствие теплового движения.
Это среднее арифметическое вычисляется с помощью вероятно-
вероятности. Смысл и свойства вероятности будут обсуждаться в сле-
следующей главе. Здесь мы ограничимся только формулировкой
правила вычисления средних значений.
Как подчеркивалось выше, изменения g носят случайный ха-
характер. При этом одни значения g будут встречаться чаще,
а другие реже. О первых говорят как о более вероятных, а о
вторых — как о менее вероятных. Количественной мерой частоты
появления того или иного значения как раз и является вероят-
вероятность. Пусть вероятность обнаружить значение физической ве-
величины в малом интервале (g; g + rfg) равна dU7(g). Тогда
). (8.2)
Интеграл вычисляется по всей области возможных значений g.
Правило (8.2) предполагает, что физическая величина изме-
изменяется непрерывно. В квантовой области физические величины
могут изменяться скачкообразно, принимая только дискретный
ряд значений. Если gi, g2, •., Ь — возможные значения физи-
физической величины, причем №< —вероятность обнаружения зна-
значения 1и то в этом случае среднее значение вычисляется по
правилу
l^ltWi. (8.3)
2. Рассмотрим важнейшие из макроскопических параметров.
Одним из них является плотность вещества. Плотностью назы-
называется количество вещества, приходящееся в среднем на еди-
единичный объем тела. Это количество можно определять по-раз-
по-разному. Если речь идет о числе частиц, то говорят о плотности
частиц. Эту величину условимся обозначать буквой п. В СИ
она измеряется в м~3. Если имеется в виду масса вещества, то
вводят плотность массы. Ее будем обозначать через р. В СИ р
измеряется в кг/м3. Между р и п существует связь. Так, если
тело состоит из частиц одного сорта, то
Р ass МП,
где m — масса одной частицы.

216
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
[ГЛ.
Плотности известных в настоящее время веществ составляют
весьма широкий диапазон значений (см, табл. 4).
Таблица 4
Вещество
Вгщество атомного
ядра
Сжатые газы в центре
самых плотных звезд
Золото
Ртуть
Сжатое железо в ядре
Земли
Сталь
Алмаз
Алюминий
Человеческое тело
р, кг/м3
1017
ю8
1,93-104
1,36-104
1,2- 104
G,6-7,8)-103
3,53-103
2,7-103
1,07-103
Вещество
Вода
Жидкий водород
Воздух у поверхности
Земли
Воздух на высоте 20 км
Наивысший искус-
искусственный вакуум
Газы межзвездного
пространства
Газы межгалактиче-
межгалактического пространства
р, кг/м3
1,00-103
0,07-103
1,2
9-10~2
ю-13
ю-20
ю-26
Примечательно, что, независимо от степени сжатия, плот-
плотности жидких и твердых тел лежат в весьма узком интервале
значений. Плотности же газов варьируются в весьма широких
пределах. Причина заключается в том, что как в твердых телах,
так и в жидкостях частицы вплотную примыкают друг к другу.
В этих средах расстояние между соседними частицами состав-
составляет величину порядка 1 А и сравнимо с размерами атомов и
молекул. По этой причине твердые и жидкие тела обладают
очень малой сжимаемостью, чем и обусловлено малое различие
в их плотности. В газах положение иное. Среднее расстояние
между частицами газа значительно превышает их размеры. На-
Например, для воздуха у поверхности Земли оно составляет 102А.
Вследствие этого газы обладают большой сжимаемостью, а их
плотность может изменяться в очень широких пределах.
Внутреннюю структуру твердых, жидких и газообразных тел
схематически иллюстрирует рис. 8.3. На этом рисунке частицы
вещества изображены кружками.
Во всех частях однородного тела, находящегося в равновес-
равновесном состоянии, плотность одна и та же. Однородным называют
тело, все части которого состоят из одного и того же вещества.
Из всех однородных тел исключение составляют газы, нахо-
находящиеся во внешних полях. Внешнее поле приводит к пере-
перераспределению частиц газа, в результате чего частицы концен-
концентрируются по-разному в разных местах. Это явление будет
подробно рассмотрено в следующей главе. В принципе внешние
поля должны приводить к перераспределению частиц также и
в твердых телах, и в жидкостях. Однако вследствие чрезвычайно

8 2]
МАКРОСКОПИЧЕСКИЕ ПАРАМЕТРЫ
217
малой сжимаемости твердых тел и жидкостей для них этот эф-
эффект оказывается ничтожно малым.
Внутри макроскопических тел действуют силы. В жидкостях
и газах они характеризуются одной скалярной величиной — дав-
давлением. Давлением называется абсолютное значение средней
силы, действующей со стороны вещества газа или жидкости
на каждую из поверхностей помещенной в них единичной пло-
площадки.
.иди.
4+1
Ш
ill ii
iT
1111
Тбердое тело
Жидкость
Рис. 8.3.
Очень сильно сжатый
газ
Обычно давление обозначается через Р (или р). В СИ оно
измеряется в Н/м2 (эта единица называется паскалем, сокра-
сокращенно Па). Часто используются специальные, внесистемные еди*
ницы измерения давления: бар, техническая атмосфера (ат),
нормальная атмосфера (атм), миллиметр ртутного столба
(мм рт. ст.):
1 бар = 105 Н/м2;
1 ат=1 кгс/см2 = 9,81 • 104 Н/м2 = 0,981 бар;
1 атм = 1,033 ат = 1,013 • 105 Н/м2 =1,013 бар;
1 мм рт. ст. = 1,333 • 102 Н/м2 = 1,333 ¦ 10~3 бар.
Для жидкостей и газов справедлив закон Паскаля:
В состоянии теплового равновесия сила давления, приложен-
приложенная к любому элементу поверхности, находящейся в контакте
с веществом газа или жидкости, пропорциональна площади эле-
элемента и ориентирована к нему по нормали.
Действительно, эта сила возникает в результате теплового
движения, которое заставляет частицы вещества газа или жид-
жидкости сталкиваться с поверхностью. Очевидно, что в заданный
промежуток времени соударений будет тем больше, чем обшир-
обширнее обстреливаемая площадь. Таково доказательство первой
половины закона Паскаля.
Заметим теперь, что согласно второму закону Ньютона при-
приложенная к данному элементу сила равна импульсу, котооый

218 МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ 1ГЛ. $
передает этому элементу в единицу времени вещество газа или
жидкости. Из требования же равновесности его состояния сле-
следует, что среднее значение энергии вещества не должно изме-
изменяться. В противном случае его состояние будет неустановив-
неустановившимся, т. е. неравновесным. Отсюда вытекает, что соударения
частиц вещества с любой площадкой в среднем носят упругий
характер. А при этом условии импульс передается площадке
только в нормальном к ней направлении (см., например, § 5.2,
п. 2). В этом заключается обоснование второй половины закона
Паскаля.
Силы, действующие внутри твердых тел, более разнооб-
разнообразны. Они определяются набором физических величин, назы-
называемых механическими напряжениями. В отличие от давления,
напряжения не являются скалярными величинами. Они имеют
более сложную геометрическую природу. Величины такого рода
называются тензорами. В твердых телах сила, действующая на
каждую поверхность любой площадки внутри тела, ориентиро-
ориентирована произвольно. Эту силу можно разложить на две взаимно
перпендикулярные составляющие, одна из которых действует
вдоль, а другая — перпендикулярно площадке. Первая приводит
к так называемому касательному, а другая — к нормальному на^
пряжениям. Более подробно эти величины будут рассмотрены
в гл. 13.
А сейчас вернемся к давлению. Этот параметр обладает
следующим важным свойством:
В жидкости или газе, не находящихся во внешнем поле, дав-
давление всегда одинаково во всех участках среды, если только ее
вещество достигло равновесного состояния.
В противном случае различные части среды придут в дви-
движение под действием некомпенсированных сил. Это движение
не будет установившимся. Оно будет происходить до тех пор,
пока давление в различных частях среды не станет одинаковым.
После этого оно прекратится. Такую картину можно наблюдать,
например, в газе, разделенном на две части подвижным порш-
поршнем. Если давление по обе стороны поршня не одинаково, то
поршень будет перемещаться в ту сторону, в которой давление
меньше. Это будет происходить до тех пор, пока давление,
оказываемое на поршень с разных сторон, не станет одина-
одинаковым.
Остановимся на содержании понятия нагретости тела. Его
степень характеризуется макроскопическим параметром, назван-
названным температурой. Температура характеризует интенсивность
теплового движения частиц тела. Если движение частиц тела
носит классический характер, то температура связана со сред.-
ней кинетической энергией поступательного движения одной ча-
частицы. В этом ?лучае средняя кинетическая энергия поступа-

§82] МАКРОСКОПИЧЕСКИЕ ПАРАМЕТРЫ 219
тельного двиоюения одной частицы тела пропорциональна тем-
температуре Т:
¦?-4*Г, (8.4)
где m — масса одной частицы, a v — ее скорость. Температура Т
называется абсолютной. Коэффициент пропорциональности k на-
называется постоянной Больцмана. В СИ
k = 1,38 • 10~23 Дж/град, (8.5)
а в системе СГС
k =1,38- КГ16 эрг/град. (8.6)
Наиболее общее определение температуры, справедливое и
в квантовой области, будет дано в гл. 10.
Температура измеряется в градусах. Температурная шкала,
связанная с определением (8.4), называется абсолютной или
шкалой Кельвина. Она не содержит отрицательных значений
температуры, ибо согласно (8.4) температура пропорциональна
положительно определенной величине — среднему значению ки-
кинетической энергии частицы. Значение Т = 0 называется абсо-
абсолютным нулем температуры.
Помимо шкалы Кельвина широко распространена шкала
Цельсия. Температура по шкале Цельсия обычно обозначается
буквой /. Между абсолютной температурой Т и температурой t
по Цельсию существует линейная связь:
Г = /° 4-273,16°.
Соотношение между шкалами Кельвина и Цельсия иллю-
иллюстрирует рис. 8.4.
Из (8.4) следует, что v2 = 3kT/m. Величина
(8.7)
называется тепловой скоростью частиц массы т. В теле, нагре-
нагретом до температуры Г, частицы движутся в среднем со скоро-
скоростями порядка vT. Например, молекулы водорода при комнат-
комнатной температуре движутся со скоростями около 2-Ю3 м/сек,
а молекулы кислорода — со скоростями около 470 м/сек.
Свойством равновесного состояния является равенство тем-
температуры различных частей тела.
В противном случае непременно будет осуществляться пе-
передача энергии от одних частей тела к другим. Там, где

220
макроскопические состояния
[ГЛ. 8
О
«2

§ 8.2] МАКРОСКОПИЧЕСКИЕ ПАРАМЕТРЫ 221
температура больше, частицы движутся быстрее. Сталкиваясь
с медленными, они передают им энергию. В результате быстрые
частицы замедляются*), а медленные начинают двигаться
быстрее. Это означает, что характер коллективного поведения
частиц изменяется, т. е. тело нельзя считать достигшим равно-
равновесного состояния. Отметим, наконец, что в неравновесном со-
состоянии разными температурами могут обладать не только раз-
разные участки тела, но и его разные компоненты в одном и том
же объеме. Так, в плазме нередко возникают состояния, в кото-
которых температура электронов на несколько порядков выше тем-
температуры ионов.
Согласно (8.4) при Г = 0 полностью прекращается тепловое
движение. Это, однако, не означает, что движение исчезает во-
вообще. При низких температурах классические представления
о движении теряют свою силу. В этой области действуют кван-
квантовые законы. Согласно им движение вообще остановить нельзя,
даже понизив температуру до абсолютного нуля. О том, почему
это так, мы расскажем в последнем томе курса.
3. Плотность (или объем, обратно пропорциональный плот-
плотности), давление (или напряжения) и температура не ис-
исчерпывают всего множества макроскопических параметров. Так,
состояния тел, находящихся в электромагнитных полях, опи-
описываются с помощью специальных величин, с которыми мы
познакомимся в следующем томе. Системы, в которых протекают
химические реакции, характеризуются концентрациями соответ-
соответствующих веществ. Концентрация — это отношение числа частиц
данного вещества к числу частиц какого-то другого вещества.
Однако какой бы природы ни был тот или иной макроскопи-
макроскопический параметр, он описывает внутреннее состояние тела с
точностью до флуктуации. Флуктуациями называются случайные
отклонения физической величины от ее среднего значения.
Флуктуации в равновесном состоянии всегда очень малы. Имен-
Именно поэтому макроскопические параметры с очень высокой точ*
ностью характеризуют внутреннее состояние макроскопического
тела.
Например, в газе из 1019 частиц, достигшем равновесного со-
состояния, величина силы, действующей на единичную площадку,
в результате флуктуации отклоняется от своего среднего зна-
значения, т. е. от давления, не более чем на 1СН° %!
Флуктуации имеют статистическую природу, которая будет
рассмотрена в следующей главе. Причина их малости в равно-
равновесном состоянии будет установлена в гл. 9.
*) Именно этот механизм обусловливает замедление нейтронов в ядер-
пых реакторах.

222 макроскопические состояния [гл -8
§ 8.3. Уравнение состояния
1. Различные макроскопические параметры не являются не-
независимыми. Закон, выражающий зависимость между парамет-*
рами, называется уравнением состояния тела.
Рассмотрим однородные газообразные и жидкие тела. В рав-
равновесном состоянии их свойства описываются плотностью п или
объемом 1/, давлением Р и температурой Т (с точностью до ма-
малых флуктуации). Если, например, при заданном объеме V по-
повышать температуру Т газа, то возрастет его давление. Это
свидетельствует о том, что между этими тремя величинами су-
существует зависимость, которую в общем виде можно записать
так:
F(P9 V, Г) = 0.
Установление вида функции Т7, т. е. уравнения состояния, на
основе представлений об атомном строении вещества является
чрезвычайно сложной задачей, точно разрешенной только в од-
одном случае, а именно, для идеального газа,
2. Представление об идеальном газе возникло при изучении
свойств разреженных газов. В движении каждой частицы лю-
любого газа всегда можно различить две фазы: свободное движе-
движение и столкновение. Некоторое время частица движется на-
настолько далеко от остальных, что ее движение можно считать
свободным. Среднее время т такого движения называется вре-
временем свободного пробега. Путь /, который частица в среднем
проходит за это время, называется длиной свободного пробега.
По истечении времени порядка т частица сближается с какой-то
другой и начинает с ней взаимодействовать. Среднее время т'
взаимодействия двух частиц называется временем столкновения.
Идеальным называется газ, в котором
т'/т«Ь (8.8)
При этом условии свойства газа, достигшего равновесного со-
состояния, практически не зависят от взаимодействия частиц друг
с другом. Поэтому их не учитывают вовсе.
Необходимо, однако, иметь в виду следующее. Время сво-
свободного пробега должно быть намного меньше времени, за ко-
которое частица газа проходит расстояние порядка размеров со-
сосуда, в котором газ заключен. Это означает, что длина свобод-
свободного пробега намного меньше этих размеров. Если это условие
не выполнено, то газ называется сильно разреженным или газом
Кнудсена. Давление кнудсеновских газов — менее 10-~7—10~8 бар
(Ю-4—10-5 мм рт. ст.).
При давлениях, близких к атмосферному, условие (8.8) вы-
выполняется для газов, молекулы которых имеют простое строе-

18.31
УРАВНЕНИЕ СОСТОЯНИЯ
223
ние, например для кислорода, водорода, углекислого газа. Мо<
лекулы этих газов при нормальных условиях движутся со
скоростями порядка 102—103 м/сек, и для них отношение вре^
мени одного столкновения ко времени свободного пробега
составляет около 10~3. Если же молекулы газа имеют сложное
строение (органические соединения), то столкновения происхо-*
дят гораздо чаще, что обусловлено относительно большим раз-*
мером молекул. С ростом давления такие газы (например, пары
спирта) перестают быть похожими на идеальный гораздо быст-
быстрее, чем газы, состоящие из молекул простого строения.
Получим уравнение состояния идеального газа. С этой целью
рассмотрим на поверхности сосуда, в который газ заключен,
малую площадку S. Вслед-
Вследствие малости ее всегда мож-
можно считать плоской. Выберем
систему отсчета с осью х, на-
направленной перпендикулярно S
(рис. 8.5). Тогда скорость
сближения каждой частицы с
площадкой будет равна vx
(ух>0). Напомним, что в
равновесном состоянии соуда-
соударения частиц газа со стенками Рис. 8 5.
сосуда носят упругий харак-
характер. Следовательно, при каждом соударении площадке будет
передаваться импульс
где т — масса одной частицы газа. Примем на время, что все
подлетающие к площадке S частицы имеют одну и ту же ско-
скорость vx. Из условия идеальности следует, что до соударения со
стенкой сосуда каждая частица газа движется свободно. Это
означает, что vx = const. Поэтому за время At с площадкой S
столкнутся только те частицы газа, которые к началу отсчета
времени А^ находились от площадки на расстоянии, не превьь
шающем vxAt, и занимали объем SvxAt. Это рассуждение спра-
ведливо для реально существующих разреженных газов на
временах At <С т. Если плотность газа равна л, то в указанном
объеме в среднем будет находиться nSvx At частиц. Столкнув-
цшсь с площадкой, все эти частицы передадут ей импульс
Др = nSv • At • 2mv = 2mnvlS Д/.
Предположение, что все частицы газа имеют скорости с од-
одной и той же компонентой vx, действительности, конечно, не
соответствует. Вспомним, однако, что нам необходимо оценить
только коллективный эффект, возникающий отг столкновений с,

224 макроскопические состояния тгл. з
площадкой большого числа частиц газа. Этот эффект описы-
описывается средним значением полученного выше выражения. Усред-
Усредняя это выражение по vx, примем во внимание, что не все
частицы с одним и тем же значением vx сталкиваются с площад-
площадкой. Столкновение претерпевают лишь те из них, у которых
vx > 0. Частицы с vx < 0 движутся в обратном направлении и
встретиться с площадкой не могут.
Учтем теперь, что в равновесном состоянии движение частиц
является полностью беспорядочным. Поэтому число частиц, ле-
летящих к площадке 5 и от нее, в среднем одно и то же. Это
означает, что среднее значение v\ для vx > 0 вдвое меньше
среднего значения vx для всех vx. Таким образом, оказывается,
что за время At площадка S со стороны газа получит импульс,
в среднем равный
Следовательно, на данную площадку газ действует с силой,
среднее значение которой равно
Отсюда получаем, что давление газа равно
P = n-mvl. (8.9)
Теперь учтем, что беспорядочное движение в среднем одина-
одинаково по всем направлениям. Это означает, что
Поскольку v2 = v\ + v°y + vl, то
^^ + Ъ1+?г = ЗЦ. (8.11)
Из (8.9) и (8.11) следует, что
Р = ^п^ = ^п™!19 (8.12)
Используя теперь (8.4), находим:
P = nkT. (8.13)
Это соотношение и является уравнением состояния идеального
газа.
Существует несколько других форм записи этого уравнения.
Они таковы. По определению плотность п = N/V> где N — число
частиц газа, а V — его объем. Следовательно, (8.13) моншо

§ 8.3] УРАВНЕНИЕ СОСТОЯНИЯ 225
переписать так:
V
(8.14)
Часто используется и такая запись:
PV = NkT==-^--NAk-T = vRT. (8.15)
^ А
В ней v = N/NA определяет число молей газа. Величина
R=NA- k (8.16)
называется универсальной газовой постоянной. В СИ
# = 8,31 • 103 Дж/кмоль. (8.17)
Число молей газа можно определить через его массу М:
_ N _ mN __ М
V~ NA~ mNA~ ц-
Здесь \х = mNA — масса одного моля газа. Таким образом, урав-
уравнение состояния идеального газа можно преобразовать к виду
PV^^-RT. (8.18)
В такой записи оно известно под названием уравнения Клапей-
Клапейрона — Менделеева,
Из уравнения состояния идеального газа вытекает ряд важ-
важных следствий.
а) Закон Авогадро: в равных объемах разных газов, нахо-
находящихся при одинаковых давлениях и температурах, содер-
содержится одинаковое число молекул.
Действительно, так как N = PV/kT, то для разных газов
при одних и тех же Р, V и Т значения N будут одинаковыми.
В частности, в 1 см3 любого идеального газа при f = 0°С и дав-
давлении в 1 атм содержится 2,7-1019 молекул. Это число назы-
называется числом Лошмидта.
б) Закон Дальтона: в состоянии теплового равновесия дав-
давление в смеси идеальных газов равно сумме давлений каждой
компоненты смеси.
Пусть смесь состоит из / газов, причем частиц первого газа
Nu второго — N2 и т. д. В равновесном состоянии температура
каждой компоненты смеси одна и та же. Допустим, что она
равна Г, Тогда выполняются соотношения
ptV = NX • kT, P2V = N2 • kT, ..., PtV=Nr kT,
каждое из которых является уравнением состояния одной из
компонент смеси. Рь Р2, ..., А — это давления первой, вто*
рой, третьей и т. д. компонент. Эти давления называются
8 А, В» Астахов

226 макроскопические состояния 1гл. 8
парциальными. Сложим теперь выписанные выше равенства,
В результате йолучим:
,?/¦) К?,"') а-
Сумма в правой части — это полное число частиц в смеси. Сле-
Следовательно, давление смеси равно
что и требовалось доказать.
в) Известные из средней школы законы Бойля — Мариотта,
Шарля и Гей-Люссака получаются, например, из (8.14) при
постоянстве, соответственно, Г, V и Р.
3. По мере увеличения плотности газ становится все менее
похожим на идеальный. Все большее значение приобретают
взаимодействия частиц газа друг с другом. Эти взаимодействия
обусловлены силами, описанными в § 2.3. Напомним, что на
малых расстояниях эти силы являются силами отталкивания,
а на больших — силами притяжения.
Получение уравнения состояния газа, в котором было бы
точно учтено взаимодействие частиц друг с другом, является
очень сложной задачей, которая навряд ли будет когда-нибудь
решена. Приближенный и довольно грубый учет основных осо-
особенностей этого взаимодействия приводит к уравнению состоя-
состояния Ван-дер-Ваальса.
Оно может быть получено так. Из уравнения состояния
идеального газа следует, что при конечных температурах давле-
давление становится неограниченно большим только при сжатии газа
в точку. Для реальных газов давление должно резко возра-
возрастать при конечном объеме, равном по порядку величины
объему всех частиц газа. Примем, что сжатие газа до меньшего
объема невозможно. Этот минимальный объем запишем в виде
JV6, где Ь— объем одной частицы, a N — их число. Следова-
Следовательно, грубый учет сил отталкивания между частицами, дей*
ствующих на малых расстояниях и проявляющихся в резком
возрастании давления уже при конечном объеме, приводит
к следующей корректировке уравнения состояния идеального
газа:
V - Nb *
Действие сил притяжения между частицами проявляется в
уменьшении давления газа по сравнению с приведенной вели-
величиной. Это уменьшение обусловлено тем, что на каждую ча-
частицу, находящуюся у стенки сосуда, действует сила, направ*

§ 8.4] ВНУТРЕННЯЯ ЭНЕРГИЯ 227
ленная внутрь сосуда. Она вызвана притяжением со стороны
частиц газа, находящихся в его объеме. В грубом приближении
эту силу можно принять пропорциональной плотности газа
п = N/V. Заметим, что давление уже само по себе пропорцио-
пропорционально плотности. Следовательно, эффект уменьшения давления
будет пропорционален п2 = N2/V2. Коэффициент пропорциональ-
пропорциональности обозначим через а. Таким образом, учитывая действие
сил притяжения, мы должны перейти к соотношению
NkT N*
г a,
г — у _ Nb V2
которое в форме
( + yr<*)(V- Nb) = NkT (8.19)
называется уравнением Ван-дер-Ваальса. Коэффициенты а и Ь —
это постоянные Ван-дер-Ваальса, учитывающие, соответственно,
действие сил притяжения и отталкивания при взаимодействии
частиц газа друг с другом.
4. В настоящее время еще не найдено надежных уравнений
жидкого состояния. Хотя и существует ряд приближенных тео-
теорий жидкости, однако все они носят еще предварительный ха-
характер, и пока трудно оценить степень их точности. Несколько
лучше обстоит дело с уравнением твердого состояния. Однако и
здесь исчерпывающего ответа еще не найдено. С простейшим
уравнением твердого состояния мы познакомимся в гл. 13.
Ввиду серьезных трудностей, стоящих на пути получения урав-
уравнений жидкого и твердого состояний на основе микроскопиче-
микроскопических представлений, наиболее перспективным является установ-
установление вида уравнений состояния опытным путем.
§ 8.4. Внутренняя энергия
1. Важнейшей характеристикой внутреннего состояния ма-
макроскопического тела является его внутренняя энергия. Эта ве-
величина определяется как среднее значение полной энергии всех
частиц тела. При этом обычно внутреннюю энергию отсчитывают
от суммарной энергии покоя всех частиц. В дальнейшем вну-
внутренняя энергия будет обозначаться через Е. Так, если тело со-
состоит из N классических материальных точек, то
Здесь «f — точное значение полной энергии системы N частиц
(за вычетом энергии покоя), т< и Vi — соответственно масса и

228 макроскопические состояния 1гл. 8
скорость i-и частицы, U — энергия взаимодействия частиц друг
с другом и с внешним полем. Черта обозначает усреднение.
Внутренняя энергия обладает следующими свойствами.
а) В состоянии теплового равновесия частицы макроскопи-
макроскопического тела движутся так, что их полная энергия все время и
с высокой точностью равна внутренней энергии тела: & = <%' =
р
Данное свойство следует из общего положения о малости
флуктуации в состоянии теплового равновесия. Другими сло-
словами, это свойство можно сформулировать так: флуктуации
энергии в равновесном состоянии ничтожно малы. Например,
в газе, количество которого равно 0,01 моля, относительное от-
отклонение энергии от среднего значения, т. е. от внутренней энер-
энергии, в среднем составляет всего 10~п.
б) Внутренняя энергия тела является функцией его макро-
макроскопического состояния, т. е. зависит от макроскопических па-
параметров тела.
Из предыдущего параграфа известно, что в отсутствие внеш-
внешних электромагнитных полей состояние теплового равновесия
газов и жидкостей можно характеризовать всего двумя пара-
параметрами, например объемом и температурой. При этом давление
однозначно определяется через уравнение состояния. Поэтому
внутренняя энергия однородных газов и жидкостей зависит
только от двух величин, за которые можно выбрать объем V
и температуру Т (ниже, в § 10.3, будет выяснено, что этот
выбор — не самый удачный). Зависимость от Т обусловлена
движением частиц тела, т. е. наличием у них кинетической энер-
энергии. Зависимость от V связана с взаимодействием частиц друг
с другом. С изменением V меняется плотность п и, как след-
следствие, среднее расстояние между частицами. В зависимости от
этого меняется и средняя энергия их взаимодействия. Для твер-
твердых тел внутренняя энергия зависит еще и от их формы.
Действительно, частицы жидкости и газа могут занимать
любые пространственные положения, поскольку они не огра-
ограничены в своих перемещениях. С этим как раз и связано свой-
свойство газов и жидкостей не сопротивляться изменению формы.
Это в свою очередь определяет их способность передавать дав-
давление во все стороны одинаково (закон Паскаля). В твердых
телах положение иное. Частицы твердого тела локализованы на
своих местах в кристаллической структуре. Кристаллическая
структура оказывает сопротивление не только сжатию и растя-
растяжению. Она противодействует и изменению своей формы, даже
если объем тела сохраняется. Следовательно, внутренняя энер-
энергия твердого тела будет меняться и при изменении его формы.
С этим, кстати, связано то обстоятельство, что действующие в
твердых телах силы нельзя описать одной скалярной величи-

§8.4] ВНУТРЕННЯЯ ЭНЕРГИЯ 229
ной—давлением и требуется введение набора величин более
сложной математической природы — напряжений.
Отметим, наконец, что именно благодаря свойствам (а) и (б)
удалось развить подход к рассмотрению внутренних свойств
макроскопических тел, принципиально отличный от механиче-
механического. В рамках последнего энергия макроскопического тела за-
зависит от необозримо большого числа величин. Так, если тело
состоит из N классических частиц, то энергия такой системы
зависит от 3/V координат частиц и 3iV компонент их скоростей
или импульсов. Чрезвычайное обилие этих переменных практи-
практически исключает возможность описания свойств макроскопиче-
макроскопических тел в рамках чисто механического подхода.
в) Внутренняя энергия обладает свойством аддитивности,
т. е. внутренняя энергия системы тел равна сумме внутренних
энергий каждого тела.
Обозначим внутреннюю энергию системы тел через ?, а
внутреннюю энергию тела с номером i — через Et. Тогда свой-
свойство аддитивности внутренней энергии выражается равенством
В его справедливости убеждают следующие рассуждения.
Энергия Е может отличаться от 2 E>t лишь на величину энер*
гии взаимодействия тел. Допустим теперь, что в теле с номе-
номером I содержится Ni частиц. Тогда по порядку величины число
частиц на поверхности тела равно N*!*. В самом деле, харак-
характерный линейный размер тела, содержащего Ni частиц, пропор-
пропорционален А/73. Поверхность же тела пропорциональна квадрату
этого размера. Отношение числа частиц на поверхности тела
ко всему числу частиц по порядку величины составляет
N'tjNi==NJ4\ Очевидно, что именно это отношение характери-
характеризует относительный вклад взаимодействия тела с номером I
с остальными телами во внутреннюю энергию системы тел. Так
как Ni — макроскопически большая величина, то отличие NT4*
от нуля — чисто теоретическое. В этом и заключается причина
того, почему взаимодействием тел можно пренебречь.
2. Рассмотрим идеальный газ, находящийся в равновесном
состоянии. Найдем внутреннюю энергию газа.
Заметим, что частицы газа помимо поступательных обладают
еще и внутренними степенями свободы. Так, если частицами
газа являются атомы, то внутренние степени свободы обуслоз-
лены наличием в атомах электронов. Если же частицами газа
являются молекулы, то помимо электронного движения воз-
возможно вращение молекулы как единого целого и колебания
входящих в состав каждой молекулы атомов. Поступательное

230 макроскопические состояния [гл. 8
движение частиц газа является классическим, а их внутренние
движения могут носить квантовый характер. Лишь дри выпол-
выполнении определенных условий, которые будут сформулированы
ниже, внутренние степени свободы можно считать классическими.
Проявление квантовых свойств существенно влияет на вели-
величину внутренней энергии тела. Поясним это.
Отличительной чертой квантовых движений является скач-
скачкообразный характер изменения энергии. Поэтому для возбу-
возбуждения квантового движения необходимо сообщить конечную
порцию энергии AS*. Эту величину мы назовем энергетической
щелью. Частица газа может получить эту энергию только в ре-
результате столкновения с какой-то другой частицей. При столк-
столкновении энергия поступательного движения частиц может быть
частично или полностью израсходована на возбуждение внутрен-
внутренних движений. Согласно (8.4) энергия поступательного движе-
движения частиц по порядку величины равна kTy где Т — температура
газа. Следовательно, энергетической щели А<§ отвечает харак-
характеристическая температура
При температурах порядка Го или превышающих это значение
возбуждается движение, характеризующееся щелью A<g\ При
этом общей закономерностью является следующая: с ростом
температуры внутреннее движение быстро приобретает класси-
классический характер.
Для электронных движений в атомах по порядку величины
Isjg = К)-18 Дж и Гол=Ю5°К. Поэтому, электронные степени
свободы возбуждаются при весьма высоких температурах:
Г^Гол= Ю5оК, При более низких температурах электронные
степени свободы «заморожены» и их учитывать не надо. Отме*
тим, что электронные возбуждения сопровождаются ионизацией
частиц газа (см. рис. 8.4, стр. 220). При температурах Т^
355 105°К возникает плазма. В плазме важную роль играют
дальнодействующие кулоновские силы. Поэтому при температу-
температурах порядка 105°К и выше газ перестает быть идеальным.
Для подавляющего числа молекул энергетическая щель, от-
отвечающая колебательным степеням свободы, по порядку вели-
величины равна Д<^кол = 10-20 Дж. Следовательно, характеристиче-
характеристическая температура возбуждения колебаний в молекулах Гкол
имеет порядок 103°К. Например, для кислорода О2
Го°л = 2230°К. Таким образом, колебания возбуждаются при
температурах Г^Го°л= Ю3°К. У сравнительно небольшого
числа молекул, например таких, как HgCb, Hgb, SnCl4, некото-
некоторые из колебаний возбуждаются при сообщении энергии по-

§8 41 ВНУТРГННЯЯ ЭНЕРГИЯ 231
рядка 10~21 Дж. Такие колебания возникают при меньших тем-
температурах, Г> 102°К.
Наконец, энергетическая щель Д<§Гвр для вращательных дви-
движений молекул не превосходит величины 10~21 Дж. Поэтому ха-
характеристическая температура ГоР, отвечающая этому виду дви-
движений, не превышает 102°К и, как правило, составляет величину
в несколько градусов Кельвина или величину порядка 10°К. На-
Например, для кислорода ГоР = 2,О7°К. Только у молекул Н2 и D2
(D — тяжелый изотоп водорода) Г*р имеет аномально большие
значения, равные, соответственно, 85°К и 43°К- У всех молекул,
кроме Н2 и D2, ГоР значительно меньше температуры конден-
конденсации соответствующих газов. Поэтому в газах, состоящих из
молекул, вращательные степени свободы всегда возбуждены.
При этом при обычных условиях, как правило, соблюдается не-
неравенство Т > ГоР> так что вращения молекул можно считать
классическим движением.
Для вычисления внутренней энергии идеального газа вос-
воспользуемся законом равнораспределения энергии по классиче-
классическим степеням свободы:
В состоянии теплового равновесия на каждую классическую
степень свободы движения частиц тела приходится кинетическая
энергия, в среднем равная ?772, где Т — температура тела. Клас-
Классической называется степень свободы, которой отвечает движе-
движение, подчиняющееся законам классической механики.
Этот закон имеет статистическое обоснование, изложение ко-
которого выходит за рамки данного курса. Поэтому мы ограни-
ограничимся иллюстрацией, подтверждающей его справедливость. Рас-
Рассмотрим газ, молекулы которого можно считать классическими
частицами. Если он находится в равновесном состоянии и масса
каждой частицы газа равна т, то согласно (8.10), (8.11) и (8.4)
mv2x
2
mvl
2
mv\
2
1
Я
9
mv
2
kT
2
В этой цепочке равенств первые три величины — средние значе-
значения кинетических энергий, приходящихся на каждую поступа-
поступательную степень свободы частицы. Как видно, они равны между
собой и каждое из них равно kT/2, что и утверждает закон рав-
равнораспределения энергии.
Пусть частицами газа являются отдельные атомы. Тогда
вплоть до температур Т = Гол = 105°К их можно считать мате-
материальными точками. Следовательно, каждый атом обладает
только тремя поступательными степенями свободы. Поэтому
каждый атом будет обладать в среднем кинетической энергией
3/2?7\ Следовательно, если газ состоит из N частиц, то его

232
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
1ГЛ 8
внутренняя энергия равна
(8.20)
Рассмотрим идеальный газ, состоящий из молекул. Пусть их
число также равно N. Вклад во внутреннюю энергию от посту-
поступательных степеней свободы молекул вычисляется так же, как
и для газа, состоящего из отдельных атомов. Этот вклад состав-
составляет величину ?пост _ zj2NkT. Если температура газа меньше
Го°л, то помимо поступательных степеней свободы вклад во
внутреннюю энергию дают только вращательные степени сво-
свободы молекул. Напомним, что при обычных и более высоких
температурах вращательные движения молекул можно считать
классическими. Для определения величины Явр необходимо знать
число а вращательных степеней свободы. Это число может иметь
два значения: а = 2 и а = 3. Для линейных молекул, к числу
которых относятся, например, молекулы Нг, N2, Ог, имеем а = 2.
Для таких молекул энергия затрачивается на вращение вокруг
осей, не совпадающих с линией расположения атомов в моле-
молекуле (рис. 8.6). Каждое из них допускает разложение на два
-€--/--
Рис. 8.6.
Рис. 8.7
независимых вращения вокруг двух взаимно перпендикулярных
осей. Эти оси перпендикулярны линии расположения атомов
(рис. 8.6). Для прочих молекул а = 3, поскольку в этом случае
число независимых вращений равно 3. На рис. 8.7 для примера
изображена структура молекулы метана СН4 и указаны три не-*
зависимых вращения.
На основании закона равнораспределения энергии находим,
что каждая молекула обладает энергией вращательных движе-
кТ
нии, в среднем равной а-о"» a вклад во внутреннюю энергию

§8 4] ВНУТРЕННЯЯ ЭНЕРГИЯ 233
идеального газа от этих степеней свободы равен
При приближении температуры к Го°л начинают возбуж-
возбуждаться колебательные степени свободы молекул. Вклад ?кол о г
колебательных степеней свободы во внутреннюю энергию газа
оценивается следующим образом. После достижения темпера-
температуры 7"окол и вплоть до температур порядка 104°К, при которых
начинается диссоциация молекул, колебания атомов в молеку-
молекулах являются гармоническими, с высокой точностью подчиняю-
подчиняющимися классическим законам. Каждое колебание обладает как
потенциальной, так и кинетической энергией. В § 7.1 было пока-
показано, что средняя кинетическая и средняя потенциальная энер-
энергия гармонического колебания равны. Поэтому согласно закону
равнораспределения энергии на одну колебательную степень
свободы будет приходиться в среднем энергия kT. Следователь-
Следовательно, одна молекула с р колебательными степенями свободы будет
обладать энергией колебаний, в среднем равной $kT. Вклад Екол
этого вида движений во внутреннюю энергию газа составит ве*
личину
кол Npk kT (8 22)
Число р определяется следующим образом. Если одна моле-
молекула состоит из г атомов, то она имеет Зг степеней свободы—-
при условии, что электронные степени свободы «заморожены»в
Из Зг степеней свободы три приходятся на поступательное дви-
движение, а a — на вращательное. Следовательно, р = Зг — 3 — а.
Мы видели, что вклад во внутреннюю энергию идеального
газа от различных степеней свободы пропорционален темпера-
температуре газа. Их суммарный вклад принято записывать в виде
(8.23)
Значение у зависит от числа возбужденных степеней свободы.
Так, для газа, состоящего из атомов, у = 5/з- Это значение полу-
получается путем сравнения (8.20) с (8.23). В гл. 10 будет показано,
что у легко определяется экспериментально. Именно по этой
причине внутреннюю энергию газа и записывают в виде (8.23).
Измерения зависимости у от температуры дают возможность
устанавливать температуры возбуждения различных внутренних
степеней свободы молекул. Допустим, например, что каждая
молекула газа состоит из двух атомов. Полное число степеней
свободы каждой такой молекулы равно 6. Три из них являются
поступательными, две — вращательными и одна — колебатель-
колебательная; a = 2 и р = 1. Тогда в соответствии с (8.20) и (8.21) при

234
МАКРОСКОПИЧЕСКИЕ СОСТОЯНИЯ
1ГЛ. 8
температурах, при которых колебательная степень свободы еще
«заморожена»,
Е в ?пост + ?вр = _| |
Сравнивая это выражение с (8.23), находим, что при Г<Го°л
у==7/5# Если же Т > ^о°л» то колебательная степень свободы
«размораживается». В этой области
Е = ?ПОСТ + ?ВР + ?КОЛ = ^ЫкТ + NkT + NkT L
и у = 9/7. График изменения у с температурой изображен на
рис. 8.8. По положению излома графика и определяют Т1°л.
7/5
9/7
Рис. 8 8.
Подчеркнем, что зависимость энергии идеального газа только
от температуры обусловлена отсутствием взаимодействия между
его частицами. Если этим взаимодействием пренебрегать нельзя,
то появляется еще и зависимость внутренней энергии от объема
газа.

ГЛАВА 9
СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
§ 9.1. Вероятность и флуктуации
1. В предыдущей главе отмечалось, что отличительным свой-
свойством внутреннего движения макроскопических тел является его
случайный характер. Так, нельзя быть уверенным в том, что при
измерении числа частиц в какой-либо части тела оно окажется
равным некоторому заданному значению. Производя измерения
несколько раз, в каждом случае будем обнаруживать разные
значения. Аналогично, невозможно точно предсказать, с какой
скоростью будет двигаться та или иная частица тела, какой она
будет обладать энергией, моментом импульса и т. д. Подобная
неопределенность характерна для микроскопического подхода к
внутреннему движению. В этих условиях имеет смысл поста-
постановка лишь одного вопроса: какова вероятность того, что какая-
либо физическая величина будет иметь то или иное значение?
Понятие вероятности является первичным. Оно не сводится
к иным, более простым, и по существу постулируется. Вероят-
Вероятность дает наиболее правдоподобную оценку доли случайных
событий с данным исходом при большом числе их повторений в
одних и тех же условиях и является величиной безразмерной.
Разъясним, что это означает, на двух примерах.
Во многих детских играх набор очков производится с по-
помощью игральной кости. При ее бросании выпадение какого-
либо числа очков является случайным событием (рис. 9.1). Если
материал, из которого сделана кость, однороден и по своей
форме она является кубом, то нельзя отдавать предпочтение
выпадению какого-либо определенного числа очков. Все они рав-
равновероятны. Следовательно, вероятность выпадения данного чи-
числа очков, как наиболее правдоподобная оценка доли исходов
с определенным результатом, будет равна 7б-
Рассмотрим другой пример. Пусть вещество, сосредоточен-
сосредоточенное в слое малой толщины dx и с поперечным сечением 5, под-
подвергается облучению потоком каких-либо частиц (см. рис, 5.15

236 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ТГЛ. 9
на стр. 156). Малость dx означает, что это расстояние ничтожно
в сравнении с длиной свободного пробега частицы-снаряда в ве-
веществе мишени. Каждое столкновение частицы-снаряда с части-
частицей-мишенью является событием случайным. Найдем вероят-
вероятность dW столкновения на пути длиной dx. Предварительно от-
отметим, что подобного рода столкновения наблюдаются довольно
часто. Они имеют место при взаимодействии: космического из-
излучения с атмосферой и различными породами Земли; пучка
выведенных из ускорителя заряженных частиц с поставленной
на пути пучка мишенью; нейтронов в атомных реакторах с ма-
материалом конструкций этих установок и в ряде других случаев.
Отметим, что взаимодействие частиц газа друг с другом также
Рис. 9.1.
осуществляется путем столкновений. Любая частица газа время
от времени бомбардирует все прочие его частицы.
В § 5.2 указывалось, что столкновения характеризуются сече-
сечениями, каждое из которых имеет смысл тени, отбрасываемой ча-
частицей-мишенью в направлении потока частиц-снарядов. Там же
было показано, что вещество мишени, сосредоточенное в слое
толщины dx и площади 5, затеняет площадь ondxS, где а — се-
сечение столкновения, an — плотность вещества мишени. Отсюда
следует, что при достаточно длительном облучении наиболее
правдоподобная оценка доли попаданий частицы-снаряда в
частицу вещества мишени при прохождении в этом веществе
пути dx будет даваться отношением площади тени ondxS ко
всей площади обстрела S. Следовательно, dW = ondx.
Зная эту величину, можно оценить длину свободного пробега
/ частицы-снаряда. Действительно, на пути, равном /, частица
испытает в среднем одно столкновение. Поэтому dx/l = dW =
= ondx. Отсюда находим:
Мы видим, что средняя длина свободного пробега зависит от
плотности вещества мишени я и от характера взаимодействия
частиц-снарядов с частицами мишени, что определяется сечением

§ 9.1] ВЕРОЯТНОСТЬ И ФЛУКТУАЦИИ 237
а. В обычных молекулярных газах средняя длина свободного
пробега при нормальных условиях составляет около 10~7 м, что
намного превышает размеры молекул и сравнимо с длиной вол^
ны видимого света.
2. Вероятность случайного события и экспериментально наб-
наблюдаемая доля исходов, когда событие осуществляется, —это не
одно и то же. Если, например, измерять долю случаев, когда при
бросании игральной кости выпадает, скажем, шесть очков, то
оказывается, что строго определенного значения эта доля не
имеет. На рис. 9.2 представлена ее зависимость от общего числа
Доля
дыпаденип^
тести
очкоЬ
I
6
О г 4 8 16 32 64 128 256 512 Число бросании
Рис. 9.2.
бросаний для конкретной серии испытаний. Как видно, резуль-
результаты наблюдений отличаются от оценки в 7е- Эти результаты
группируются вблизи 7б —и только. Нет никаких гарантий^ что
экспериментальная кривая при увеличении числа испытаний бу-
будет стремиться к значению 7е. Более того, может произойти (и
действительно наблюдается) резкое отклонение от 7е: Характер-
Характерным свойством каждой экспериментальной кривой является
наличие случайных отклонений от наиболее правдоподобной
оценки. Именно такого рода отклонения происходят в любых
макроскопических системах, и именно они и обуславливают,
флуктуации.
В теории вероятностей устанавливается, что с увеличением
числа испытаний N доля наиболее правдоподобных или, как го-
говорят, наиболее вероятных флуктуации уменьшается по закону,
l/УЛ/7. Наиболее вероятными являются малые флуктуации. Та-
Такие случаи, когда, например, при бросании игральной кости
много раз подряд выпадает одно и то же количество очков, к
числу наиболее вероятных не относятся. При достаточно боль-
большом jV суммарная вероятность всех флуктуации, превышающих
любую сколь угодно малую (но конечную) величину, стремится
к нулю. Это следует из закона больших чисел, доказанного в
теории вероятностей П. Л. Чебышевым. Именно закон больших
чисел объясняет, почему макроскопические законы, полученные

СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ 1ГЛ. 9
на основе статистических представлений о движении частиц ве-
вещества, оказываются точными. «Секрет» заключается в том, что
число частиц в любом макроскопическом теле очень велико.
Поэтому вероятность отклонения от наиболее правдоподобной
оценки всегда оказывается ничтожно малой и отсутствие откло-
отклонения можно считать практически достоверным. Например, ве-
вероятность найти (при однократном наблюдении) относительное
отклонение энергии 0,0! моля газа от своего среднего значения
порядка 10~6 является поразительно малой величиной ~10-3'1(I5.
3. Перечислим и поясним нужные для дальнейшего основные
законы теории вероятностей.
а) Вероятность нескольких взаимоисключающих событий
равна сумме вероятностей каждого из них.
Предположим, что в результате N испытаний осуществились
события Л, б, С и т. д., причем если произошло одно из них, то
в то же время все остальные события исключаются. Например,
если при каком-то бросании игральной кости выпало 5 очков,
то при данном испытании ни 2, ни 3 и т. д. очка появиться уже
не могут. Пусть из N испытаний в NA случаях осуществилось
событие Л, в NB случаях — событие В и т. д. Тогда доля слу-
случаев, в которых осуществилось, например, либо событие Л, либо
событие В, равна
N N Т N •
Каждое из отношений в правой части этого равенства опреде-
определяет долю исходов с соответствующим результатом — либо со-
событие Л, либо событие В. На этом основании требуют, чтобы и
вероятность обладала аналогичным свойством.
Важным следствием свойства (а) является условие норми-
нормировки: сумма вероятностей всех возможных событий равна 1.
Действительно, такая сумма дает оценку доли случаев, в ко-
которых осуществляется любое из возможных событий. Но при
любом испытании это происходит непременно. Так, при каждом
бросании игральной кости обязательно выпадает какое-то число
очков. Отсюда следует, что интересующая нас оценка должна
даваться единицей.
б) Вероятность одновременного осуществления нескольких
независимых событий равна произведению вероятностей каждого
из них.
Пусть одновременно происходят два независимых события:
Л1Л2, BiB2, CiC2 и т. д. С такой ситуацией мы сталкиваемся, на-
например, бросая сразу две игральные кости. Каждое из пары не-
независимых событий — это выпадение определенного числа очков
на одной из костей (рис. 9.3). Обозначим через Na{a, число ис-
исходов, когда одновременно осуществляются события А\ и А24

г 0 21
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
289
Например, на одной из костей выпадает 4 очка (событие AL)y a
на второй—1 очко (событие Л2). Доля этих случаев составит
величину NaxaJN> где N — полное число испытаний. Пусть Na
и NAt определяют число исходов, в которых происходят соот-
соответственно либо событие Аи либо событие Лг. При этом сопут*
ствующее каждому из них другое независимое событие может
быть любым. Так, при бросании двух игральных костей можно
подсчитать число случаев, когда, например, первая кость дает
четыре очка при любом числе очков на второй. Тогда из Na,
Рис. 9.3.
случаев лишь доля, равная NaJN, приведет к результату, когда
одновременно с А\ осуществится и другое независимое событие
А2. Таким образом, Na1a1 = Na1 • {NaJN). Следовательно,
Na.a. Na. NA
N
N
M2
Из этого равенства вытекает, что доля случаев одновременного
осуществления двух независимых событий представляется про-
произведением. Его сомножителями являются доли случаев осуще-
ствления каждого события. В этом и заключается причина, по-»
чему аналогичное требование предъявляется к вероятности неза-»
висимых событий.
§ 9.2. Распределение Больцмана
1. При тепловом движении изменения в положении каждой
частицы тела носят характер случайного процесса. Поэтому мо-
можно говорить о вероятности обнаружения частицы в том или
ином месте, т. е. вероятности обнаружения значений ее радиус-
вектора в той или иной области. Подчеркнем, что по размерам
эта область должна намного превышать характерный размер
микроскопического строения тела, которым является для газов
средняя длина свободного пробега его частиц, для жидкостей а

240
СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
1ГЛ. 9
твердых тел — среднее расстояние между соседними частицами
Иными словами, область должна вмещать макроскопически
большое число частиц. Только при этом условии движение каж-
каждой частицы в данной области проявит черты случайного про-
процесса, ибо на нее будет оказано гигантски большое число воз-
воздействий со стороны ее окружения.
В дальнейшем мы неоднократно будем прибегать к понятию
малой (бесконечно малой) области или участка тела, вкладывая
в него следующий смысл: малой (бесконечно малой) называется
область (или участок) макроскопического тела, по размерам
ничтожная в сравнении с размерами всего тела, но все же на-
намного превосходящая характерный размер его микроскопиче-
микроскопического строения. Каждая такая область или участок содержат
макроскопическое число частиц и поэтому часто называются ма-
макроскопически малыми.
Рассмотрим вероятность dW обнаружить частицу в области,
определяемой малым интервалом значений радиус-вектора ча-
частицы (г; г + dr), считая, что
тело достигло равновесного
состояния. Векторный интер-
dz вал (г; г + dr) эквивалентен
трем координатным (я; х + dx),
(У\ У + dy), (z; z + dz) и изме-
измеряется объемом dV — dx dy dz
параллелепипеда, изображен-
изображенного на рис. 9.4. Так как рав-
равновесное состояние является
установившимся, то dW не
будет меняться со временем
и может определяться только
Шоложением интервала (г; r-\-dr), т. е. dW = dW(r). Оче-
Очевидно, что чем больше объем, тем вероятнее обнаружить в нем
Частицу. Для малого объема это выражается в том, что ве-
вероятность оказывается пропорциональной объему, так что мы
можем записать равенство
Величина
Рис. 9.4.
называется плотностью вероятности или функцией распределе-
распределения значений радиус-вектора г. Она имеет смысл предела отно^
шения вероятности обнаружить частицу в некотором объеме к
величине объема при стягивании последнего в точку с радиус*
вектором г.

§9 2] РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА 241
Условие нормировки накладывает ограничение на f(r). Оче-
Очевидно, что нахождение суммарной вероятности обнаружить час-
частицу в любом возможном месте сводится к интегрированию
dW(r) по всему объему тела V. Отсюда следует, что функция
распределения f(r) должна удовлетворять равенству
2. Найдем функцию распределения f(r) для идеального газа
классических частиц. Пусть газ занимает объем V и находится
в равновесном состоянии с температурой Г. При отсутствии
внешнего поля все положения любой частицы равновероятны.
Именно поэтому газ распределяется по всему доступному объе-
объему с одинаковой плотностью. В этом случае f(r) = f = const.
Значение постоянной находится из условия нормировки
V
откуда следует, что
l_ jv /i_
N * V ~ N
где N — полное число частиц газа, а п — его плотность.
Таким образом, оказывается, что в отсутствие внешнего поля
вероятность dW(r) обнаружить частицу газа в заданном объеме
dV не зависит от места расположения dV и равна
Картина меняется, если частицы газа испытывают действие
внешнего поля. В результате происходит пространственное пе-
перераспределение частиц и f(r) Ф const. Плотность и давление
газа оказываются в различных местах разными. Они приобре-
приобретают смысл локальных (т. е. определенных в точке) величин.
Значением плотности п(г) в точке г называется предел отноше-
отношения &N/AV, где AiV — среднее число частиц в объеме ДУ, при
стягивании AV в точку г. Давлением Р(г) в точке г называется
предел отношения &F/&S, где AF—абсолютное значение сред-
средней силы, действующей на площадку AS, при стягивании AS
в точку г.
Определяя эти величины, мы должны помнить, что они яв-
являются макроскопическими параметрами. Поэтому стягивание
в точку следует понимать как доведение AV и AS до столь
малых значений, что они могут считаться бесконечно малым к
в смысле, разъясненном в предыдущем пункте,

242 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ |ГЛ. $
Пусть силы внешнего поля являются потенциальными. Для
простоты предположим, что они действуют только в одном на*
правлении. Выберем систему отсчета так, чтобы ее ось z была
ориентирована в этом направлении (см. рис. 9.4). При равнове-
равновесии сумма всех сил, действующих на частицы газа в объеме dVv
должна быть равна нулю. Этими силами являются силы давле-
давления газа, окружающего о.бъем dV, и силы внешнего поля. Силы
давления, действующие на боковые грани объема dV, должны
быть скомпенсированы. .В противном случае они вызовут поток
газа в направлении, перпендикулярном оси г, что противоречит
предположению о равновесности его состояния. Внешнее поле
не может воспрепятствовать возникновению потока, поскольку
силы поля действуют только вдоль оси г. По этой же причине
силы давления, действующие через верхнее и нижнее основания
объема dV, не могут быть равны друг другу. Их разность долж-
должна компенсировать действие сил внешнего поля, приложенных
к частицам, находящимся в объеме dV. Эти силы в сумме дают
величину
где G — сила, действующая на одну частицу, п — плотность газа
в месте расположения объема dV. Если разность давлений на
верхнем и нижнем основаниях параллелепипеда составляет dP,
то dF должно быть равно dPdxdy. Из этого условия следует,
что
Обозначим потенциальную энергию частицы газа во внешнем
поле через U. Тогда согласно B.31) G = —dU/dz. Следова-
Следовательно,
Поскольку в равновесном состоянии температура газа везде
одинакова, то согласно уравнению состояния идеального газа
(8.13) мы можем записать следующее равенство:
Из двух последних равенств следует, что
или
Постоянную интегрирования мы записали как In щ. Очевид^
но, что по определяет плотность в том месте, где U = О,

I 9 21 РАСПРЕДЕЛЕНИЕ БОЛЬЦМЛИА 243
Таким образом, оказывается, что в состоянии теплового рав-
равновесия плотность газа, подверженного действию внешнего поля,
изменяется по закону
U (г)
л (г) = Лов кт . (9.2)
Это соотношение называется формулой Больцмана.
Закону (9.2) отвечает функция распределения
U{r)
kT ¦ (9*3)
Вероятность обнаружить частицу газа в объеме dV, располо-
расположенном у точки г, равна
U (г)
dW(r) = f{r)dV = ^-e «г . (9.4)
Этот закон называется распределением Больцмана.
Для идеальных газов давление отличается от плотности по-
постоянным множителем kT (T = const). Поэтому для таких газов
и (г)
«" , где PQ =
3. Рассмотрим поле земного тяготения. Вблизи земной по-
поверхности потенциальная энергия частицы газа на высоте z
равна U = mgz, где га— масса частицы. Уровень z = 0 счи-
считается совпадающим с поверхностью Земли. Поэтому, если газ
находится в равновесном состоянии и обладает температурой Г,
то изменение его давления с высотой происходит по закону
Эта формула называется барометрической. Ее можно при-
применять и для достаточно разреженной смеси газов. В этом слу-
случае компоненты смеси практически не взаимодействуют друг
с другом. Поэтому каждую компоненту можно рассматривать
отдельно и применять барометрическую формулу к парциаль-
парциальному давлению каждой из них. В частности, согласно баромет-
барометрической формуле для земной атмосферы оказывается, что чем
тяжелее газ, тем быстрее его давление убывает с высотой. По-
Поэтому атмосфера по мере увеличения высоты должна все более
обогащаться легкими газами. Например, плотность кислорода
должна падать быстрее, чем плотность азота.
Хотя такая тенденция наблюдается в действительности, тем
не менее, применяя барометрическую формулу к земной атмо«
сфере, необходимо соблюдать осторожность. На самом деле

244 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ [ГЛ. 9
атмосфера не находится в равновесном состоянии. Ее темпера-
температура с высотой меняется. Поэтому при использовании баромет*
рической формулы правильные количественные оценки можно
получить лишь в том случае, если применять ее к участкам, на
протяжении которых изменениями температуры можно прене-
пренебречь.
Неравновесность атмосферы обусловлена тем, что гравита-
гравитационное поле Земли не может удержать атмосферу вблизи пла-
планеты. Атмосфера непрерывно рассеивается. Этот процесс идет
тем быстрее, чем слабее поле. В частности, земная атмосфера
рассеивается очень медленно. За все время существования Зем-
Земля потеряла очень малую часть своей атмосферы. Что же ка-
касается, например, Луны с ее гораздо более слабым полем тяго-
тяготения, то к настоящему времени она практически полностью
лишилась своей атмосферы. Плотность газа у лунной поверхно-
поверхности приблизительно в 1012 раз меньше средней плотности зем-
земного воздуха.
В неравновесности земной атмосферы легко убедиться сле-
следующим образом. Допустим, что атмосфера пришла в равновес-
равновесное состояние и имеет везде одну и ту же температуру Т. При-
Применим к атмосфере формулу Больцмана. Рассматривая атмо-
атмосферу в целом, мы обязаны пользоваться для потенциальной
энергии каждой ее частицы точным выражением, следующим из
закона всемирного тяготения:
r r Mm
где у — гравитационная постоянная, М — масса Земли, г — рас-
расстояние частицы газа с массой т от центра планеты. Так как
U = 0 при г—»оо, то формула Больцмана должна быть запи-
записана в виде
уМт
п (г) ^п^е кТг .
Здесь Доо обозначает плотность газа на бесконечном расстоянии
от Земли. Положив г = R, где R — радиус Земли, находим;
уМт
Следовательно, Псо Ф 0. Однако количество вещества атмосферы
конечное. Поэтому оно не может быть распределено по беско«
нечному объему с нигде не исчезающей плотностью. Это против
воречие обусловлено исходным предположением о возможности
установления состояния теплового равновесия в земной атмо-
атмосфере.

i 9.3]
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
245
§ 9.3. Распределение Максвелла
1. В § 8.2 мы отмечали, что в состоянии теплового равнове-*
сия частицы макроскопического тела движутся в основном со
скоростями, близкими к значениям тепловой скорости vT.
Выражением «в основном» подчеркивается, что тепловая ско<
рость характеризует картину движения частиц только в сред-
среднем. Разные частицы движутся, конечно, с разными скоростями.
В ряде случаев, однако, необходимо знать распределение частиц
по скоростям. Этот вопрос возникает всякий раз, когда рассмат-
рассматривается явление, характер которого определяется видом такого
распределения. Например, скорость рассеивания земной атмо-
атмосферы определяется числом молекул, скорости которых превы-
превышают вторую космическую.
Приведем еще пример. Как известно, атомы могут излучать
электромагнитную энергию. При этом вследствие эффекта Доп-
плера частота излучения зависит от скорости движения атома.
Поэтому, если источниками излучения являются атомы газа,
то распределение интенсивности излучения по частотам опреде-
определяется распределением излучающих атомов по значениям ско-
скорости их движения.
2. Найдем вид распределения частиц тела по скоростям,
предполагая, что тело находится в состоянии теплового равно-
равновесия и движение его частиц подчиняется законам классической
механики. Задача заключается в отыскании вероятности обнару-
обнаружить частицу, значение ско-
скорости которой заключено в
любом заданном интервале.
Выберем этот интервал ма-
малым. Обозначим его через
{v\ v + dv). Он определяет-
определяется тремя интервалами
(Vz\Vz-\- dvz) компонент ско-
скорости. Мерой его является рис д.5.
малый объем dT=dvxdvydvz
в пространстве скоростей (рис.9.5). В этом пространстве по ко*
ординатным осям откладываются компоненты скорости vXy vy, v&
Вероятность обнаружить частицу в интервале (v\v -\- dv) 060-4
значим через dW(v). Она зависит только от положения интер-
интервала, т. е. от v. Во времени эта величина постоянна, так как
равновесное состояние является установившимся. Вероятность
dW(v) будет пропорциональна dT, ибо чем больше интервал
(v\v -\- dv)y тем вероятнее обнаружить частицу со значением
скорости в пределах этого интервала. Таким образом, можно
записать, что dW(vI = f (v)dT.

246 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ {ГЛ. 3
Величина
называется плотностью вероятности или функцией распределе-
распределения по скоростям. Она имеет смысл предела отношения вероят-
вероятности обнаружить частицу со скоростью в некотором объеме
пространства скоростей к величине этого объема при стягивании
его в точку, определяющую скорость v.
Функция f(v) должна удовлетворять условию нормировки:
4-оо +оо +оо
\f(v)dr= 5 dvx J dvy \ dvz-f{v)=l.
— оо —оо —оо
Это соотношение выражает требование: вероятность обнаружить
частицу с любым значением скорости должна равняться единице.
Если тело в целом покоится, то все направления движения
его частиц равноценны. Беспорядочный характер движения ча-
частиц в покоящемся теле не позволяет отдать предпочтение ка-
какому-либо одному направлению их движения. Следовательно,
функция распределения не должна зависеть от направления ско-
скорости. Она может меняться лишь при изменении абсолютного
значения скорости |t/|=y. Как будет видно из дальнейшего,
ее удобно рассматривать как функцию и2, т. е. f(v) = ф(и2).
Для определения ф(и2) рассмотрим покоящийся в целом газ,
считая, что все его частицы одинаковы и имеют массу т. Про-
Проследим за двумя сталкивающимися друг с другом частицами
газа. Предположим, что до столкновения они двигались со ско-
скоростями, значения которых не выходили за пределы двух ин-
интервалов (vu Vi + dvi) и {v2\ v2 + dv2). Предположим также,
что столкновение является упругим. Пусть в результате скорости
Рис. 9.6.
частиц изменяются так, что их значения оказываются в преде*
лах двух интервалов (у[; v\ + dv'x) и (v'2; v'2 + dv'2\ (левая часть
рис. 9.6). Число таких соударений будет пропорционально ве-
вероятности dW{p\,v?) обнаружить две частицы газа со скоро-
скоростями в пределах интервалов (vx\ V\-\-dvx) и (v2; v2 + dv2). До
столкновения частицы движутся независимо. Поэтому согласно

§3 31 РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА 247
правилу вычисления вероятности независимых событий
dW (v{9 v2) = dW (*,) dW (v2) = Ф (vf) Ф (vl)dTx dT2,
где dF] —dv{x dv\y dv\Zf dY2 — dv2xdv2ydv2z,
Кроме рассмотренных столкновений, которые мы условно
назовем прямыми, происходят и обратные столкновения. В этом
случае две сталкивающиеся частицы до соударения имеют ско-
скорости в интервалах (у[\ v\ + dv\), (z^; v2 + dv2)t а после столк-
столкновения их значения оказываются соответственно в интервалах
(^ь Vi-\-dvi) и (v2\ v2-\-dv2) (правая часть рис. 9.6). Число
обратных столкновений пропорционально вероятности
dW (v\\ v'2) обнаружить две частицы газа со скоростями в пре-
пределах интервалов (у',\ v\ + dv\), (vr2\ v2 + dv2), которую по тем
же причинам, что и выше, можно записать в виде
dW (v' v') = dW (v\) dW ЫЛ = Ф (V2)cp (vf2) dT[ dY'
1 Ix \y lz* 2 2x 2y 2z*
Примем теперь во внимание основное свойство равновесного
состояния газа: в этом состоянии число прямых и обратных
столкновений одинаково. Действительно, в противном случае ве-
вероятность обнаружить частицу со скоростью, например, в ин-
интервале (v\\ Vi -}-dv\) будет со временем меняться. Число таких
частиц будет либо уменьшаться, либо увеличиваться в зависи-
зависимости от того, каких столкновений больше — прямых или обрат-
обратных. А как уже отмечалось, в равновесном состоянии этого быть
не может. Из сказанного следует равенство dW(yv v^ =
= dW (v'l9 v'2), или
Ф (v}) ф (v\) dYl dY2 = ф (of) ф (v2) dY[ dY2.
Оказывается, кроме того, что dY\ dY2-= dY\ dY2. В результате
мы приходим к функциональному уравнению
Его решением, удовлетворяющим условию нормировки, является
функция распределения
N3/2 mV*
где Т — температура газа, k — постоянная Больцмана, am —
масса одной частицы.
Поясним сначала, почему dV{ dT2 = dY[ dY2.
Заметим, во-первых, что систему двух сталкивающихся частиц газа мож-
можно считать замкнутой. Это обусловлено тем, что в газе тройные столкновения
чрезвычайно маловероятны и ими всегда можно пренебречь. Следовательно,
если какие-либо две частицы газа сближаются, то все остальные находятся
настолько далеко, что практически не влияют на процесс соударения.

248 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ 1ГЛ. 9
Далее, вместо скоростей vv v2, v\y v2 столкновение двух частиц можно
описать в других переменных, используя скорости движения центра инерции
частиц до столкновения V = (v{ + v2)/2 (частицы одинаковые!) и после
столкновения V = уу^ + V2//^» a также скорости относительного движения
частиц до столкновения fl-oo == V\ —1>2 и после него v_^_ oo = vl — v2. Пусть
dT = dVxdVydV2, dy = dv_ooxdv_xydv_ooz, dV' = dV'xdV'ydV'z, dy' -
= dv'+ooxdv+ooy dv+ooz—малые объемы в пространстве скоростей, изме-
измеряющие интервалы
(V; V + dV), {v_co;v_co + dv_0O), (V; V + dVf), (v'+ M; v'+ „ + dv'+ x),
в которых заключены соответственно значения скоростей центра инерции и
относительного движения до и после столкновения. Согласно закону сохране-
сохранения центра инерции V = V. Следовательно,^ = dY'. При упругом соуда-
соударении скорость относительного движения меняет только свое направление. Ее
величина остается неизменной (см. § 5 1). Поэтому объем в пространстве ско-
скоростей dy' есть просто повернутый объем dy. Значит, dy = dY и, следова-
следовательно, dY dy = dYf dyf. Очевидно, что не имеет принципиального значения,
какой набор переменных — V, v_oo, V', v'+oo или ti[( v2, v\, v2 — исполь-
используется для описания столкновения. Оба набора равноправны. Поэтому, если
для набора V, v_oo, V , т>+оо имеем dY dy = dYr dy\ то и для переменных
V], v2, v{, v2 должно выполняться аналогичное равенство: dT\ dT2 = dYl dT2.
Перейдем к решению уравнения (9.6). Вследствие сохранения полной энер-
энергии системы двух сталкивающихся частиц и для прямого, и для обратного
о п /2 /2
столкновений V\-\- V2== v\ "Ь V2 • Поэтому (9.6) можно переписать так:
ф (vf) ф D) = ф (of) ф (г? + v\- v f).
Положим в этом равенстве vх = 0 и продифференцируем его по v\. Получим:
4 dv2 dv2 dv(
Переобозначая V\ на v и устремляя v% к нулю, приходим к уравнению
¦аф(°2) = - аф (v2), где а = lim Ф \2' = const. (9.8)
av Ф @) v2~^o dv2
Решением уравнения (9.8) является функция
<v(v2) = Ae~av\ (9.9)
где Л—постоянная интегрирования Легко видеть, что постоянная а должна
быть положительной, ибо только в этом случае ф(и2)-^0 при и2-*-оо. По*
следнее условие физически очевидно: вероятность обнаружить частицу с бес^
конечно большой скоростью движения должна быть равна нулю. В (9.9)'
А « (а/лK/2. (9.10)
Это значение получается так. Применим к (9.9) условие нормировки:]
4-оо +оо +°°
А [ dvx \ dvy
J
-о
+ ОО 9\ / +0О N / +ОО
\
-1. (9.11)

§9 3] РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА 249
Следовательно,
Л = [/(а)]~3, пге /(а) =
[в (9.11) роль переменной ? поочередно играют vXy vv и vz\ Вводя новую пе-
переменную интегрирования х = | у а, выражение для /(а) представим в виде
-f-OO
/(
Интеграл в правой части является числом, равным *\/п. Поэтому
/ (а) = У л/а", (9.12)
и для А получаем значение (9.10).
Постоянная а определяется из требования, чтобы "\ v2 было равно
vT = л/ЗкТ/т, где среднее значение v2 вычисляется по правилу (8.2):
+ оо 4-°° +°°
(v>)dT = (^у2 J dvx J dvy J dv
y J dvz
— oo —oo —oo
-foo +oo -foo
—схэ —oo —c»
-foo n.
—c» ^
Интеграл в фигурных скобках в правой части полученного равенства мы уже
вычисляли ранее. Он равен /3(а), где /(а) определяется формулой (9.12),
Поэтому
Приравнивая эту величину yj = 3kT/m, получаем:
a = m/2kT. (9.13)
Из (9.9), (9.10) и (9.13) следует справедливость (9.7).
Хотя мы рассматривали газ, тем не менее полученный ре-
результат справедлив для любого тела, находящегося в состоянии
теплового равновесия, если только к движению его частиц при-
применимы законы классической механики. В этом мы убедимся
в следующем параграфе. Оказывается, что вид распределения
частиц тела по скоростям их движения не зависит от того, как
частицы взаимодействуют друг с другом. Он определяется лишь
одним фактором — способностью частиц обмениваться энергией
в процессе установления равновесного состояния. Закон заклю-
заключается в том, что в состоянии теплового равновесия вероятность

250
СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
1ГЛ. 9
обнаружить частицу со скоростью в пределах интервала
(#; v 4- dv) равна
.3/2 —-~5Г
w e 2kT dT. (9.14)
Рис. 9.7.
Этот закон называется распределением Максвелла. Справед-
Справедливость распределения Максвелла ограничена областью приме-
применимости законов классической нерелятивистской механики к
тепловому движению.
3. Распределение Максвелла позволяет рассчитать вероят-
вероятность dW(v) обнаружить частицу тела с абсолютным значением
скорости в пределах малого интервала (v\ v-\-dv). Область
применимости результата расчета
совпадает с областью применимо-
применимости распределения Максвелла.
В системе координат, по осям
которой откладываются компонен-
компоненты скорости, интервал {v\ v + dv)
изображается сферическим слоем
(рис. 9.7). Величина радиуса вну-
внутренней сферы равна v, внешней —-
и -f- dv.
События, заключающиеся в том,
что частица движется с различны-
различными скоростями, являются взаимоис-
взаимоисключающими: частица не может
двигаться сразу с двумя различными скоростями! Поэтому по
правилу сложения вероятностей dW(v) должна быть равна
сумме вероятностей dW(v) событий, каждое из которых со-
состоит в том, что частица движется со скоростью, лежащей
в пределах одного из элементарных интервалов, на которые
можно разбить сферический слой (v\ v + dv). Для примера на
рис. 9.7 изображены два таких интервала. По абсолютным зна-
значениям V\ и V2 находятся в пределах слоя (v; v-\-dv). Однако
эти векторы принадлежат различным элементарным интервалам
(v\\ v{ + dV[) и (v2\ v2-\- dv2).
Согласно (9.7) функция распределения Максвелла зависит
только от величины скорости. Поскольку толщина слоя
(v; v -f- dv) предполагается малой, то при суммировании вероят-
вероятностей dW(v) в пределах сферического слоя (v\ v-\- dv) функ-
функцию распределения Максвелла можно считать неизменной. То-
Тогда суммирование сведется к подсчету суммарного объема всех
элементарных объемов сферического слоя. Последний равен
объему слоя 4nv2 dv.
Окончательный результат таков: для тел, находящихся в со-
состоянии теплового равновесия, вероятность обнаружить частицу

§94] РАСПРЕДЕЛЕНИЕ ГИББСА 251
тела со скоростью движения, абсолютное значение которой на-
находится в пределах заданного малого интервала (о; v-\-dv)y
равна
dW (v) = 4я ( 2^гK/2^ 2kT dv'
mv*
Это выражение называется распределением Максвелла по аб-
абсолютным значениям скоростей. Оно характеризуется плот-
плотностью вероятности или функцией распределения
то2
''п*е~ш. (9.16)
л, dW(v)
функция имеет смысл предела отношения —-г2— вероят-
вероятности обнаружить частицу с абсолютным значением скорости
в пределах некоторого интервала при стягивании его в точку,
определяющую значение v.
Распределение (9.15) позволяет оценить долю частиц тела,
скорости движения которых по своей величине лежат в преде-
пределах любого интервала (v\> V2). Эта доля равна
Здесь интеграл определяет сумму вероятностей, каждая из ко-
которых является вероятностью обнаружения частицы с абсолют-
абсолютным значением из интервала (и; v-\-dv), принадлежащего об-
области значений от V\ до V2. Согласно правилу сложения вероят-
вероятностей эта сумма определяет вероятность обнаружить частицу
тела с абсолютным значением скорости из интервала (v\, i^)-
Из (9.15) можно получить распределение по значениям ки-
кинетической энергии частицы. Ниже кинетическая энергия обо-
обозначена через 8, а вероятность обнаружить частицу с кине-
кинетической энергией из интервала {&\&-\-d&) — через dW(<o).
Так как & = mv2/2, то 2v dv = d (v2) = -^-dS> и v = ^Wfin.
Поэтому из (9.15) следует, что
dW (%) = ,2 $ъ е~шт d%. (9.17)
Л/я/е3Г3
§ 9.4. Распределение Гиббса
1. Распределения Больцмана и Максвелла экспоненциально
зависят от энергии (первое от потенциальной, а второе — от
кинетической энергии частицы). Эта общая их черта не является
случайной. В ней проявляется самый фундаментальный и самый

252
СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
1ГЛ 9
важный для практики закон статистической физики, открытый
Д. Гиббсом в 1901 г. В этом законе используется понятие о чис-
числе состояний. Остановимся на его содержании.
С точки зрения классической механики состояние системы N
частиц задается 6N переменными —координатами и, например,
компонентами импульсов всех частиц. Значения этих переменных
можно откладывать по осям абстрактной бМ-мерной системы ко-
координат. Вводимое таким образом пространство получило на-
название фазового. В нем по классическим представлениям ка-
каждому состоянию системы отвечает одна точка. С созданием
квантовой механики выяснилось, что на каждое состояние при-
приходится не точка, а фазовая ячейка с объемом Bnh)q, где ft—
постоянная Планка A.2) (см. § 1.1), a q — число степеней сво-
свободы системы.
Пусть система состоит из N точечных частиц. Рассмотрим
состояния, энергии которых не выходят за пределы малого ин-
интервала (&\ & -\-d&). Обозначим число таких состояний через
u{<o)d<?. Этим состояниям в фазовом пространстве отвечает
некоторая область. Допустим, что ее объем равен dK{<?). По-
Поскольку в данном случае q = 3jV, to, учитывая сказанное выше,
находим:
Поясним изложенное примером. Рассмотрим одномерный
гармонический осциллятор (q=\). Его состояние можно за-
задать импульсом р и смещением от положения равновесия ?. Для
такой системы фазовое про-
пространство двумерно и в нем
каждая фазовая точка ха-
характеризуется двумя коор-
координатами р и |. Полная
энергия осциллятора равна
что можно записать и так:
П2
Рис. 9.8.
На фазовой плоскости, т. е. в осях р и ?, полученное соот-
ношение определяет эллипс с полуосями a = ^2mS и Ь =
«=V2^/fe (рис. 9.8). При разных <^ будут получаться разные
эллипсы. Эллипсы, отвечающие интервалу (&, S' + dS'), запол-
заполнят некоторый слой. Он будет заключен между двумя эллипса-
эллипсами, полуоси которых определяются граничными энергиями &,

$ <М] РАСПРЕДЕЛЕНИЕ ГИББСА 253
& + d&. На рис. 9.8 этот слой показан штриховкой. Для дан-
данного случая di\(&) равно площади этого слоя, а 0(8) d<g =
= dA(S>)/2nH.
Закон, открытый Д. Гиббсом, состоит в следующем:
В состоянии теплового равновесия вероятность обнаружить
любое состояние частиц макроскопического тела определяется
только их полной энергией. Вероятность обнаружить состояние
с полной энергией из интервала {&\ & + d&) равна
dW (8) = \ e~™kT Q (8) d8. (9.18)
Это распределение вероятностей было названо распределен
нием Гиббса или каноническим. В нем k — постоянная Больцма-
на, а Т — абсолютная температура; Z — не зависящий от энер-
энергии коэффициент, величина которого определяется условием
нормировки:
В статистической физике классических систем Z называется ста*
тистическим интегралом. Как следует из условия нормировки,
он равен
\&. (9.19)
Здесь интегрирование производится по всем возможным энер-
энергиям системы.
Для систем квантовых частиц распределение Гиббса имеет
вид, подобный (9.18). Однако в этом случае энергия меняется
скачком, а не непрерывно. Поэтому вместо интегрирования при-
приходится суммировать дискретные значения*). В связи с этим
в квантовой статистической физике Z получило название ста-
статистической суммы.
В распределении Гиббса величина
%§ = e~
определяет плотность вероятности или функцию распределения
Гиббса. Она имеет смысл предела отношения вероятности об-
обнаружить состояние с энергией в некотором интервале около
значения & к величине этого интервала при стягивании его
к значению &\
*) Для макроскопических систем квантовые скачки оказываются на*
столько малыми, что с очень хорошей точностью суммы можно заменять ин«
тегралами,

254 tf АТИСТИЧЕСКНЕ РАСПРЕДРЛРНИЯ 1ГЛ 9
Часто интересуются вероятностью того, что положения и
импульсы частиц лежат в малых интервалах
(/у, n+rfr,), ¦. .> (rN; rN+drN); (p,; p, + dp{), ..., {pN; pN+dpN)
(через ti обозначены радиус-векторы, а через р\ — импульсы
частиц; массы частиц будем предполагать одинаковыми и рав-
равными т). Обозначим эту вероятность через dW, Энергия рас-
рассматриваемых состояний будет равна
Здесь U(ru ..., rN) — потенциальная энергия взаимодействия
частиц друг с другом и с внешним полем, если оно есть. При
этом значения г{ и pi необходимо брать из соответствующих ин-
интервалов (гу тг -f- dr{) и (ри Pi + dpi); i = 1, 2, ..., N. Согласно
закону, установленному Д. Гиббсом, dW с множителем
1 1
^'7?
будет равно числу состояний, приходящихся на область фазо-
фазового пространства, задаваемую интервалами (ry, rt + dr{) и
(PuPi + dpi); ( = 1,2, ..., N. Объем этой области равен
dA. = dV\ ... dVN - d(u{ ... d($N9
где dVi = dxi dy{ dz{ — объем, приходящийся на интервал
(гиГг -f dti), a dan = dpixdpiydpiz — объем, приходящийся на
импульсный интервал (рг-; pi + rfpi).
Отметим, что ранее введенная величина dh(&) и dA не
совпадают, что подчеркнуто отсутствием у последней аргумента.
Таким образом, находим, что
— ехр| - —I У — + U \\
dA. (9.20)
Перебирая все фазовые точки, мы получим вероятности всех
возможных состояний. Сумма этих вероятностей, которая под-
считывается интегрированием по всему фазовому пространству,
по условию нормировки должна быть равна единице. Отсюда
находим, что статистический интеграл можно представить и так:
Из (9.20) следует, что для тел, движение частиц которых
подчиняется законам классической механики, выполняется еле-

§ 9.4] РАСПРЕДЕЛЕНИЕ ГИББСЛ 55
дующий закон: в состоянии теплового равновесия положения и
импульсы частиц статистически независимы. При этом распреде-
распределение по значениям импульса каждой частицы является маке-
велловским. Распределение частиц по различным положениям
в пространстве носит больцмановский характер.
Действительно, из (9.20) следует, что dW представимо в виде
произведения
u ..., rN)dW(Pl) ... dW{pN),
где
d\V{ru ..., rN) = ae-u^—r^kTdVl ... dVN,
dW(Pi)^be~p2iI2tnkT dan (/-1,2, ..., N).
В этих выражениях а и b — постоянные коэффициенты, связан-
связанные лишь единственным условием:
LL
L_._
BnhKN Z '
Ясно, что dW(ru ..., rN) определяет вероятность обнару-
обнаружить частицы в интервалах (г\\ r\-\-drx), ..., (rN\ rN-\-drN),
а каждое из dW(pi)—вероятность обнаружить импульс части-
частицы с номером i в интервале (рг; pi -f- dpi). Тот факт, что dW
есть произведение этих вероятностей, свидетельствует о стати-
статистической независимости положений и импульсов частиц (см.
в § 9.1 правило умножения вероятностей). Как видно, dW имеет
больцмановский вид, а каждое из dW(pi) является соответ-
соответствующим максвелловским распределением. В последнем легко
убедиться, выразив импульсы через скорости: pi = mVi. Тогда
d(ot = dpix dpiy dpiz = m3 dvix dviy dviz = m3 dTt
и dW(pi) преобразуется:
Постоянная bm3 определяется условием нормировки и оказы-
оказывается равной (m/2nkTK/*. Таким образом, распределение по
импульсам каждой частицы действительно максвелловское.
2. Распределение Гиббса дает полное описание состояния
теплового равновесия любого тела. Это означает, что оно позво^
ляет определить все макроскопические параметры и установить
связь между ними, т. е. найти уравнение состояния, а также
определить флуктуации. Конечно, речь идет о принципиальной
возможности, ибо в большинстве случаев расчеты не удается
довести до конца из-за чисто вычислительных трудностей. Од-
Однако в том, что нужно проделать, ясность имеется полная. На-
Например, для системы N классических частиц любая физическая

256 СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ [ГЛ 5
величина | есть функция состояния системы, т. е. зависит, во-
вообще говоря, от N радиус-векторов частиц и N их импульсов:
1 = Е(^ь ..., rN\ pi, ..., pN).
Согласно общему правилу вычисления средних (8.2) и с учетом
вида распределения (9.20) различных состояний системы сред-
среднее значение gравно
Ранее уже отмечалось, что в состоянии теплового равновесия
флуктуации ничтожно малы. Это свойство обусловлено следую-
следующей особенностью распределения Гиббса:
Распределение Гиббса имеет очень острый максимум при
значении энергии, равном внутренней энергии тела.
Действительно, входящее в распределение Гиббса число со-
состояний Q(&)d<%' является монотонно возрастающей функцией
энергии. Так, для гармонического осциллятора это выражается
в том, что с ростом & (при фиксированном d<S) увеличивается
площадь эллиптического кольца, изображенного на рис. 9.8. Об-
Общая закономерность состоит в том, что чем больше энергия,
тем обширнее множество состояний, обладающих данной энер-
энергией. Таким образом, оказывается, что распределение Гиббсз
содержит произведение монотонно убывающей и монотонно воз-
возрастающей функций энергии. Ими являются e~^lkT и Q>(8>)d&
А произведение таких величин всегда имеет экстремум.
Количественно острота пика характеризуется следующим об-
образом. Вводится величина, которую называют полушириной
пика. Ее часто обозначают через б и
dW
d€
J
определяют как расстояние по оси
энергии между двумя точками. Одной
из них является значение внутренней
энергии, т. е. точка максимума распре*
деления Гиббса. Другой является точ«
- ка, в которой вероятность уменьшает-
уменьшается в е раз по сравнению с максималь-
максимальным значением (рис. 9.9). Оказывает-
^———^ ся, что для системы N частиц отноше-
отношение 6/Е составляет ничтожно малую
Рис. 9.9. величину порядка л/l/N <, Здесь умест-
уместно вспомнить пример, приведенный в
§ 8.4. Относительное отклонение энергии 0,01 моля газа от своего
среднего значения составляет поразительно малое число поряд-
порядка 10"1. Но уже для возбужденных тяжелых атомных ядер, ко-
которые содержат сравнительно небольшое число частиц и к кото-

§9.4] РАСПРЕДЕЛЕНИЕ ГИББСА 257
рым тоже пытались применять статистические методы расчета,
отклонения от средней энергии порядка 10%, т.е. вовсе не малы.
Наличие необычайно острого максимума у распределения
Гиббса прямо следует из закона больших чисел и говорит о том,
что в равновесном состоянии не только энергия, но и другие
физические величины практически не отличаются от значений
в тех состояниях, энергии которых равны внутренней энергии.
В этом коренится причина малых флуктуации в равновесном
состоянии — свойства, сформулированного в § 8.3.
Убедимся в наличии максимума при значении & = Е на примере идеаль-
идеального газа N материальных точек. Энергия такой системы совпадает с кинети-
кинетической энергией всех частиц (предполагается, что внешнее поле отсутствует):
N 2 N
Этому выражению можно сопоставить геометрический образ. В абстракт-
абстрактной системе координат 3N измерений, по осям которой откладываются компо*
ненты всех импульсов pix, piy, Piz, ..., Pnx, PNy, Pnz, при фиксированном
значении & выписанное уравнение определяет сферу радиуса R = V2m#\ Со-
Соответственно, число возможных состояний частиц газа с полной энергией в
пределах интервала (<§Г, <§-\-d&) будет пропорционально объему сфериче-
сферического слоя, заключенного между сферами с радиусами
Vf
Он, очевидно, равен площади сферы радиуса R, умноженной на dR.
Зависимость площади многомерной сферы от радиуса легко установить
из соображений размерности. Любая поверхность в пространстве любого чис-
числа измерений имеет на одно измерение меньше по сравнению с числом изме-
измерений самого пространства. Отсюда следует, что площадь ЗУУ-мерной сферы
пропорциональна R3N~l = BmS')i3N~l^2i объем сферического слоя пропор-
пропорционален
пЗЛГ-1 jp _
что относится и к числу состояний cfQ(^). Сохраняя зависимость только о?
( 3W - 1 SM \
энергии и учитывая, что N очень велико I тогда ^ «* ¦ - - J, по»
лучаем, что dQ(&) - ^Nnd^ и
dW {*)
Максимум функции, стоящей в правой части этого соотношения коэффи-
коэффициентом при d&\ достигается при значении ^Г, для которого
е-шт . о.
Из последнего равенства находим, что это значение равно 3NkT/2. Согласно
(8.20) оно совпадает с внутренней энергией газа.
В качестве упражнения читатель может проверить, что 6/Е = л/ЩъШ
9 Ai Bg Астахов

ГЛАВА 10
ОСНОВЫ ТЕРМОДИНАМИКИ
§ 10.1. Тепловые процессы
1. При изменении внешних условий состояние тела также
изменится. При этом, если после изменения внешних условий
тело снова окажется термодинамически изолированным, то по
истечении времени релаксации оно снова придет в состояние
теплового равновесия, вообще говоря, отличное от исходного,
С микроскопической точки зрения при изменении внешних усло-
условий изменяется характер теплового движения частиц тела.
Всякое изменение хотя бы одного из макроскопических пара-
параметров тела называется тепловым или термодинамическим про-
процессом. Законы тепловых процессов составляют предмет раз-
раздела физики, называемого термодинамикой.
Все тепловые процессы разделяются на равновесные и не-
неравновесные.
Процесс называется равновесным, если состояние тела в ка-
каждый момент времени с требуемой точностью является равно-
равновесным. Происходит только последовательная смена во времени
одних равновесных состояний другими.
Равновесный процесс может происходить только при доста-
достаточно медленном изменении внешних условий. Условие медлен-
медленности состоит в том, что за время релаксации изменение усло-
условий, в которых находится тело, должно быть пренебрежимо ма-
малым. Например, пусть тело нагревается с поверхности (одина-
(одинаково на всех ее участках) и ее температура изменяется на неко-
некоторую малую величину за время t. Условием медленности яв-
является неравенство
т//<1,
где т — время температурной релаксации.
Важнейшим свойством всякого равновесного процесса яв-
является его обратимость во времени. Обратимость означает воз-
возможность возвращения тела в первоначальное состояние через
те же промежуточные состояния, которые в процессе были прой^
дсны%

§ 10 I] ТЕПЛОВЫЕ ПРОЦЕССЫ 259
Например, газ, нагретый равновесным образом, можно снова
довести до первоначальной температуры медленным охлажде-
охлаждением. При этом газом будут пройдены те же состояния, что и
при нагреве, но только в обратном порядке.
Так как при равновесном процессе в каждый момент времени
тело находится в состоянии теплового равновесия, то такой про-
процесс можно изобразить графически. Действительно, если ввести
систему координат, по осям которой откладывать значения не-
независимых параметров, то в этой системе координат равновес-
равновесный процесс изобразится кривой.
Точки этой кривой отвечают про- Р>
межуточным состояниям. Графи-
Графическое изображение равновесно- '
го процесса называется диаграм-
диаграммой состояний.
Для примера на рис. 10.1 изо-
изображена РУ-диаграмма состоя-
состояний, которые газ проходит при Я,
равновесном расширении от объе-
объема V] до объема Уг, в результа- ' у у у" У
те чего давление газа падает от
значения Р\ до значения Р2. Кро- Рис- 10>*-
ме РК-диаграммы можно рас-
рассматривать РТ- и УГ-диаграммы (диаграммы давление — темпе-
температура, объем — температура).
Если процесс не является медленным в том смысле, который
был отмечен выше, то он является неравновесным.
Неравновесным называется процесс, при котором хотя бы
одно из состояний, проходимых телом, является неравновесным.
Неравновесные процессы необратимы.
Так, во время быстрого нагрева тела, когда не выполняется
условие x/t <C 1, ни одно из промежуточных состояний не будет
равновесным. В каждом из них температура у поверхности тела
будет выше, чем в глубине. При обратном процессе картина бу-
будет иной: температура у поверхности будет ниже температуры
в глубине тела. Как показывает этот пример, необратимость не-
неравновесных процессов связана с тем, что при изменении условий
в обратном порядке промежуточные состояния тела не будут
совпадать с теми, которые тело проходило при прямом процессе.
В отличие от равновесных, неравновесные процессы графи-
графически изобразить нельзя. Неравновесное состояние не может
быть однозначно охарактеризовано значениями параметров, от-
относящихся ко всему телу в целом. Так, нельзя сказать, что
неравномерно нагретое тело имеет определенную температуру 7\
Поэтому неравновесному состоянию нельзя сопоставить точку,
а неравновесному процессу — кривую.
9*

260 основы термодинамики игл, то
2. Может случиться так, что в результате теплового процесса
тело возвращается в исходное состояние. Процесс, в результате
которого тело возвращается в исходное состояние, называется
круговым или циклическим. Для сокращения такие процессы
часто называют циклами. На любой диаграмме состояний рав-
равновесный цикл изображается замкнутой кривой.
Ряд тепловых процессов выделяют в группу изопроцессов*
В этих процессах один из параметров остается неизменным*
Изотермическим называется процесс, протекающий при постоян-
постоянной температуре. Процессы, протекающие при неизменных дав-
давлении и объеме, называются соответственно изобарическим и
изохорическим. Особое место занимает так называемый адиаба-
адиабатический процесс. Этот процесс будет охарактеризован ниже.
§ 10.2. Первое начало термодинамики
1. Внутренняя энергия макроскопических тел качественно от-
отличается от механической энергии системы составляющих тело
частиц. Это отличие проявляется в существовании двух форм
изменения внутренней энергии — работы и тепла. Первая из-
известна нам уже из механики. Работа совершается в тех слу-
случаях, когда в результате взаимодействия частиц данного тела
с окружающими его объектами возникают какие-либо упорядо-
упорядоченные движения. Например, данное тело заставляет переме-
перемещаться другие тела. Существование теплопередачи прямо свя-
связано с тем, что внутренняя энергия является средним значением
полной энергии составляющих тело частиц. Поэтому на внутрен-
внутренней энергии сказывается и изменение распределения вероятно-
вероятностей различных значений энергии этой системы. Изменение вну-
внутренней энергии, происходящее по этой причине, и измеряется
количеством тепла.
Поясним сказанное на примере. Рассмотрим газ, температура
которого увеличивается, а объем сохраняется неизменным.
В этом случае газ работы не производит, ибо для foro, чтобы
вызвать перемещение контактирующих с газом тел, его вещество
должно либо сжаться, либо расшириться. Однако внутренняя
энергия газа все же возрастает, поскольку с ростом температуры
увеличивается скорость теплового движения. Это как раз и про-
происходит в результате сообщения газу энергии в форме передачи
тепла.
Закон сохранения энергии, формулировка которого учиты-
учитывает особую форму ее передачи путем теплообмена, является
фундаментальным законом физики и называется первым нача-
началом термодинамики. Этот закон гласит, что
в тепловых процессах любое изменение внутренней энергии
состоит из приращения количества тепла и совершенной работы.

$ 10.2] ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 261
Областью применимости первого начала термодинамики яв-
являются все тепловые процессы. Для бесконечно малых измене-
изменений этот закон записывается так:
dE = 6Q-6A, A0.1)
где dE— малое изменение внутренней энергии, 6Q — количество
переданного при этом тепла, бЛ — совершенная работа.
Количество тепла 8Q считается положительным или отрица-
отрицательным, если оно, соответственно, сообщается телу или у него
отбирается.
Процесс, в котором 6Q = 0, называется адиабатическим.
Адиабатический процесс всегда сопровождается изменением тем-
температуры тела. Так, при адиабатическом расширении тело со-
совершает работу только за счет своей внутренней энергии. При
этом скорость теплового движения частиц уменьшается, т. е.
понижается температура тела.
Знак работы 8А определяется в зависимости от того, совер-
совершается ли работа телом или она совершается над данным телом
другими телами. В первом случае 6Л >» 0, а во втором 6/1 < 0,
Расстановка знаков в A0.1) определяется тем, что при 6Q > 0
FQ < 0) внутренняя энергия тела увеличивается (уменьшает-
(уменьшается), а при бА > 0 (бЛ<;0), наоборот, уменьшается (увеличи-
(увеличивается).
Равенство A0.1) можно рассматривать как определение ко-
количества тепла. Именно, количество тепла равно изменению
внутренней энергии тела, если при этом не совершается работа.
Как составные части изменения внутренней энергии, количе-
количество тепла и работа измеряются в единицах энергии, т. е. в
СИ — в джоулях. Однако по исторически сложившейся традиции
количество тепла часто измеряют в специальных внесистемных
единицах — калориях (кал) или килокалориях (ккал);
2. Хотя количество тепла и работа являются составными ча-
частями изменения внутренней энергии, тем не менее между dE
с одной стороны, и 6Q и 6Л, с другой, имеется принципиальное
отличие, важность которого подчеркнута различием в обозначе-
обозначениях (d и 6) приращений. Внутренняя энергия является функ*
цией состояния тела. Поэтому ее изменение зависит только от
начального и конечного состояний тела. Работа и количество
тепла зависят не только от этих состояний, но и от способа
проведения процесса. Говорят, что количество тепла и работа
яв'ляются функциями теплового процесса (а не функциями со*
стояния!) *).
*) Непотенциальный характер сил трения обусловлен как раз тем, что пе*
ремещение тел при наличии трения всегда сопровождается выделением тепла.,

262 ОСНОВЫ ТЕРМОДИНАМИКИ 1ГЛ. ТО
Для разъяснения этого утверждения выразим величины 6Л
и 6Q через параметры, характеризующие состояние системы, и
через их приращения. Начнем с работы. При этом ограничимся
частным, но важным случаем, когда состояние рабочего тела
может быть охарактеризовано только объемом и давлением.
Такими телами являются газы и жидкости, не находящиеся
в электромагнитных полях. В этих случаях работа совершается
только при изменении объема вещества рабочего тела и про^
изводится силами давления.
Пусть цилиндрический сосуд с поперечным сечением S пере*
крыт с одной стороны подвижным поршнем так, как это указано
на рис. 10.2. Предположим, что поршень очень медленно сме^
щается и заставляет равновесно расширяться газ, заключенный
в сосуде. При малом смещении
dx газ совершит работу б Л =
= F dx, где F = PS — сила, с ко-
которой газ действует на поршень,
Р — давление газа в начале пу-
пути dx. Следовательно,
6A = PSdx = P dV, A0.2)
где dV = 5 dx — малое измене-
Рис- 10-2- ние объема газа. Если работа
связана с конечным изменением
объема, то она определяется суммой элементарных работ на
всех этапах процесса. Обозначим эту работу через ДЛ (в даль-
дальнейшем все конечные изменения будем обозначать значком Д).
Тогда
I
V/A////////////77Z///////////////.
A0.3)
Пределы интегрирования определяются объемом тела в на-
начальном и конечном состояниях. Отмеченное в конце предыду-
предыдущего пункта свойство работы быть функцией процесса выра-
выражается в том, что величина интеграла в правой части A0.3)
зависит не только от пределов интегрирования, но и от формы
кривой, изображающей процесс на РУ-диаграмме, по которой
производится интегрирование.
Действительно, предположим, что тело может перейти из
состояния Л в состояние В в результате двух различных равно-
равновесных процессов. Пусть на PV-диаграмме, изображенной на
рис. 10.3, первому из них соответствует кривая АСВ, а второ-
второму— кривая ADB. В первом случае
i= ) PdV.
{АСВ)

10 2]
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
263
При этом Р меняется вдоль кривой АС В, что отмечено соответ-
соответствующим значком под знаком интеграла. Этот интеграл чис-
численно равен площади под кривой АС В. Во втором случае
ДЛ2= [ PdV.
v, v2
Рис. 10.3.
(ЛОВ)
Эта работа измеряется площадью под кривой ADB. Разность
работ Д^2 ¦— АА\ ф 0. Как видно из рис. 10.3, она численно
равна площади, покрытой двойной
штриховкой, что и доказывает за- Р>
висимость работы от способа про-
проведения процесса.
Отметим также правило, которое
попутно выяснилось: работа сил
давления при равновесном процес-
процессе численно равна площади под
кривой, изображающей процесс на
Р1/-диаграмме состояний.
Поскольку изменение внутрен-
внутренней энергии не зависит от способа
проведения теплового процесса, а
работа этим свойством не обладает, то согласно первому на-
началу термодинамики количество тепла также является функ-
функцией процесса.
В частности, при любом циклическом процессе изменение
внутренней энергии Д? = 0, так что совершенная телом за один
цикл работа равна количеству по-
полученного тепла: ДЛ = AQ.
Убедимся прямым расчетом в
зависимости работы от способа
проведения процесса. Пусть ра-
рабочим телом является идеальный
газ. Рассмотрим два равновесных
перехода из состояния с давле-
давлением Pi и объемом V\ в состоя-
^ ние Рг, ^2' Эти переходы изобра-
изображены на рис. 10.4, на котором на-
начальному состоянию отвечает
точка Л, а конечному — точка В.
Один из переходов является 'изотермическим расширением, про-
происходящим согласно изотерме АВ. Другой состоит из двух про-
процессов. Первым является адиабатическое расширение, которое
описывается кривой АС. Второй — изохорическим процессом,
которому на диаграмме состояний отвечает участок ВС. На
этой стадии давление должно обязательно возрастать; ибо
в
В
м
Рис. 10.4.

2В4 основы термодинамики 1гл. ю
адиабата АС спадает с ростом объема быстрее, чем изотер-
изотерма АВ. Действительно, при отсутствии теплопередачи с уве-
увеличением объема будет уменьшаться температура, что по
сравнению с изотермическим процессом является дополнитель-
дополнительным фактором, ускоряющим падение давления.
Так как на участке ВС (рис. 10.4) работа не совершается, то
работа второго перехода будет равна работе адиабатического
расширения ДЛад. Работу первого перехода обозначим через
А^изот- Для расчета АЛад необходимо знать зависимость давле-*
ния от объема. Допустим, что температурные изменения в дан-
ном процессе таковы, что внутреннее состояние частиц газа
остается неизменным. Это означает, что у в выражении (8.23),
определяющем внутреннюю энергию газа, остается неизменным*
Тогда на основании (8.23) и (8.14) получаем:
,р _ , / NkT \ _ d (PV) _ V dP + PdV _
Y- 1
Сравнивая последнее выражение с A0.1) и учитывая A0.2),
находим:
_ V dP + у PdV
*— Y~1 '
Следовательно, при равновесном адиабатическом процессе
V dP -f- yP dV = 0. Разделив обе части этого равенства на PV,
получим уравнение
dP . dV A
Интегрируя его, находим: In Р + y 'п ^ = \n(PVy) = const, от-
откуда следует, что искомая зависимость имеет вид
PVy== const. A0.4)
Это соотношение называется уравнением Пуассона,
Очевидно, что const = Pil/i'. Таким образом, Р — P\V]IVy.
Подставляя это значение в A0.3) и интегрируя, находим, что
при равновесном адиабатическом расширении от объема V\ до
объема V2 газ совершает работу

§ 10.2] ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ 266
При изотермическом расширении согласно (8.14) давление
меняется в зависимости от объема по закону Р = NkT/V =
= Pi Vi/V. Тогда
ЛЛ,зоТ= \ PdV^P.V, \ ^ = PlVl\nj±. A0.6)
Сравнивая A0.5) и A0.6), видим, что АЛад ф ДЛИЗот.
3. Различные тела, обладающие одной и той же массой, на-
нагреваются по-разному при сообщении им одного и того же ко-
количества тепла. Говорят, что они различаются теплоемкостями.
Теплоемкостью тела называется количество тепла, которое
телу необходимо сообщить, чтобы его температура изменилась
на 1°.
Теплоемкость можно отнести к единице массы, одному молю
и единице объема тела. Соответственно этому теплоемкость на-
называется удельной, молярной и объемной.
Единицами измерения теплоемкости являются в СИ
1 Дж/град и внесистемная единица 1 кал/град или 1 ккал/град.
Удельную, молярную и объемную теплоемкости в СИ измеряют
соответственно в Дж/кг-град, Дж/моль-град и Дж/м3-град. Вне-
Внесистемными единицами являются 1 кал/кг-град, 1 кал/моль-град,
1 кал/м3-град или 1 ккал/кг-град, 1 ккал/моль-град,
1 ккал/м3-град.
Поскольку количество тепла является функцией процесса, то
значение теплоемкости зависит от условий теплопередачи. Од-
Однако если условия теплопередачи фиксированы, то теплоемкость
выражается через функцию состояния тела. Так, различают теп-
теплоемкость при постоянном объеме Cv и теплоемкость при по-
постоянном давлении СР. В первом случае нагревание (или охла-
охлаждение) осуществляется при неизменном объеме тела. Во вто-*
ром случае поддерживается постоянным давление.
Теплоемкость Cv определяется через внутреннюю энергию
тела:
. (Ю.8)
Теплоемкость СР определяется через функцию состояния
где Е — внутренняя энергия тела, V — его объем, а Р — давле-
давление:
Функция W называется энтальпией.

266 основы термодинамики Тгл то
Значки V и Р в A0.8) и A0.9) означают, что производные
являются частными. Первая из них вычисляется при постоян-
постоянном объеме, вторая — при постоянном давлении. Определения
A0.8) и A0.9) являются следствиями первого начала термоди-
термодинамики в предположении, что работа производится только си-
силами давления. Действительно, при неизменном объеме работа
не совершается, т. е. 8А = 0. Поэтому согласно A0.1) dE = 6Q,
что и приводит к A0.8). При Р = const имеем 6Q = dE + бЛ =
= dE + P dV = d(E + PV), так что оказывается справедливо!"!
формула A0.9).
Отметим, наконец, что СР > Су. Причина заключается в том,
что при нагревании с сохранением давления часть энергии в
форме тепла расходуется на расширение тела. Только предо-
предоставив телу возможность расширяться, можно при нагревании
сохранить давление неизменным.
Вычислим теплоемкости идеального газа, предполагая, что
у = const. Тогда из A0.8) и (8.23) следует, что для газа, со-
состоящего из N частиц,
. ( NkT \
дЕ \ — V V- * / Nk
V~ If
Согласно (8.14) энтальпия
j~ + NkT ==
Подставляя это выражение в A0.9), находим:
Nkv
Р у-]
/ Таким образом, теплоемкости идеального газа Су и СР не
зависят от температуры в тех областях, где у = const. Кроме
того,
Первое из этих соотношений указывает на возможность
экспериментального определения числа у. Для этого достаточно
измерить СР и Су теплоемкости газа. Именно эта возможность
имелась в виду в § 8.4. Второе подтверждает общий вывод
6 том, что Ср > Су.
4. Первое начало термодинамики указывает на возможность
получать работу за счет перераспределения тепла. Такое превра-
превращение может происходить при циклических процессах, в кото-
которых, как мы знаем, совершенная работа равна количеству тепла,
полученного рабочим телом. Если цикл осуществляется так, что
в конечном счете тело получает некоторое количество тепла,

§ ю.з] энтропия 267
т. е. если AQ > 0, то тело совершит положительную работу.
На этом явлении основано действие всех тепловых двигателей,
в которых рабочее тело меняет свое состояние по замкнутому
циклу. Цикл, при совершении которого тело производит положи-
положительную работу, называется прямым. В противном случае он
называется обратным.
Среди всех циклических процессов особо важная миссия вы*
пала на долю цикла Парно. Исторически с его изучением свя-
зано открытие одного из фундаментальных законов физики —
второго начала термодинамики, который будет рассмотрен позд-
нее. Здесь мы остановимся только на характеристике равновес-
равновесного цикла Карно. Им является круговой процесс, состоящий из
последовательно чередующихся двух равновесных изотермиче-
изотермических и адиабатических переходов.
Прямой процесс начинается с изотермического расширения.
Пусть температура рабочего тела на этом участке равна Т2. На
этой стадии рабочее тело получает некоторое количество тепла
AQ2 > 0 от внешней системы, называемой нагревателем или теп-
тепловым резервуаром. При равновесном процессе температуры ра-
рабочего тела и нагревателя одинаковы. Поэтому Т2 называют
температурой нагревателя. Изотермическое расширение затем
сменяется адиабатическим. В это время прерывается контакт
нагревателя с рабочим телом и температура последнего начи-
начинает уменьшаться. По достижении некоторого значения Т\ адиа-
адиабатическое расширение прекращается и рабочее тело приводится
в контакт с другой внешней системой с той же температурой 7V
После этого начинается изотермическое сжатие тела. На этой
стадии оно отдает некоторое количество тепла AQi < 0 внешней
системе. Поэтому эта внешняя система называется холодильни-
холодильником, а Т\ — температурой холодильника. Наконец, изотермиче-
изотермическое сжатие прерывается и сменяется адиабатическим, возвра-
возвращающим тело в первоначальное состояние.
§ 10.3. Энтропия
1. Хотя количество тепла является функцией процесса, тем
не менее при равновесных процессах его можно выразить через
изменение функции состояния, называемой энтропией. Понятие
энтропии впервые было введено Р. Клаузиусом в 1862 г. Ока-
Оказывается, что при равновесной теплопередаче при температуре Т
малое количество тепла равно
A0.10)
где dS — малое изменение энтропии тела.
Из A0.10) следует, что энтропия измеряется в единицах
теплоемкости. Подставив A0.10) в (ЮЛ) и предположив, что

268 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ. 10
работа производится только силами давления, т. е. измеряется
величиной A0.2), первое начало термодинамики можно записать
в виде
dE = TdS — PdV. A0.11)
Энтропия является столь же полноправной величиной, ха-
характеризующей состояние физической системы, как и ее соседи
в формуле A0.11) ?, I/, T и Р. Однако, в отличие от них, по-
понятие энтропии не используется в повседневной жизни. Поэтому
с ним не связаны интуитивные представления, всегда облег-
облегчающие понимание. Нам и без точных определений понятно, что
такое высокое давление, малый объем или низкая температура.
Но далеко не каждый сможет определить, например, в какую
сторону отличается энтропия ведра с водой от энтропии окру-
окружающего воздуха.
Понятие энтропии имеет двоякое истолкование: макроскопи-
макроскопическое и микроскопическое. Соотношение A0.10) является ма-
макроскопическим определением энтропии. Если в исходном рав-
равновесном состоянии тела с температурой Т\ и давлением Pi эн-
энтропия равна Si, то согласно A0.10) для определения энтропии
S2 в любом другом состоянии с температурой Т2 и давлением Рг
надо перейти в это состояние из исходного путем любого равно-
равновесного процесса, непрерывно измеряя количество тепла 6Q,
передаваемого при каждой температуре Г. Тогда энтропия S2
вычисляется по формуле
J^-, A0.12)
в которой интеграл является криволинейным и вычисляется
вдоль кривой, изображающей процесс. Поскольку энтропия яв-
является функцией состояния, то интеграл в A0.12) не зависит от
формы этой кривой и его значение определяется только началь-
начальным и конечным состояниями, т. е. пределами интегрирования.
Свойство энтропии быть функцией состояния будет рассмотрено
ниже.
Рассмотрим свойства энтропии, которые следуют из ее опре-
определения A0.10). Прежде всего, энтропия является аддитивной
величиной:
Энтропия системы из нескольких тел является суммой эн-
энтропии каждого тела.
Действительно, в состоянии теплового равновесия темпера-
температура и давление всех тел одинаковы,

§ юз] энтропия 269
Поэтому первое начало термодинамики для каждого из тел и
всей их системы выражается, соответственно, уравнениями
— PdV.
В них Eif Si, Fz-— соответственно внутренняя энергия, энтропия
и объем тела с номером /, а ?, S, V — те же величины, но отно-
относящиеся уже ко всей системе тел. При этом Е = X Et и V = Y, Vt.
i i
Легко видеть, что приведенные соотношения совместны лишь
при выполнении условия
Отметим, что свойство аддитивности выполняется и при от-
отсутствии теплового равновесия, что будет показано ниже.
Второе свойство энтропии состоит в том, что
в равновесных процессах без передачи тепла энтропия не
меняется.
Поэтому равновесные адиабатические процессы называют
также изэнтропическими. Это! свойство прямо следует из опре-
определения A0.10).
Третье свойство энтропии выражается в том, что
при постоянном объеме энтропия является монотонно воз-
возрастающей функцией внутренней энергии тела.
Действительно, при dV = 0 имеем: 6Q — dE, так что dS —¦'
= dE/T. Но температура Т всегда положительна. Поэтому при-
приращения dS и dE имеют один и тот же знак, что и требовалось
доказать.
И, наконец,
энтропия определяется только с точностью до произвольной
постоянной.
Действительно, согласно A0.12) измеримой является лишь
разность энтропии в двух состояниях. Эта разность не изме-
изменяется от добавления к энтропии произвольной постоянной.
Из четырех величин Р, F, Т и S только две независимы. Мы
уже знаем, что Р, V и Т связаны уравнением состояния
F(P,V,T) = 0. Но уравнение состояния еще не дает полного
описания свойств равновесного состояния. Так, два разных иде-
идеальных газа, например газ, частицами которого являются атомы,
и газ, состоящий из такого же числа молекул, подчиняются
одному и тому же уравнению состояния, но дшрю^ разные вну-
внутренние энергии— (8.20) и (8.23) с у = 7fe
Для полной макроскопической характеристики равновесного
состояния тела необходимо задать уравнение, связывающее эн-
энтропию с остальными параметрами. Вместо этого обычно

570 ОСНОВЫ ТЕРМОДИНАМИКИ 1ГЛ ТО
поступают иначе, именно, задают внутреннюю энергию Е как
функцию объема V и энтропии 5.
Задание внутренней энергии как функции объема и энтропии
Е = E(V,S) полностью определяет термодинамические свойства
однородного тела.
Действительно, согласно правилу дифференцирования функ^
ции двух переменных
Индексы у скобок указывают величины, остающиеся при диф«
ференцировании постоянными. Сравнив это соотношение с
A0.11), получим:
Эти равенства определяют температуру и давление по внутрен-
внутренней энергии, если последняя задана как функция объема и эн-
энтропии.
Отметим, что первое из равенств A0.13) является самым об-
общим определением температуры, справедливым как для клас-
классических, так и для квантовых систем. Разрешив его относи-
относительно S, найдем зависимость S = S(VyT) энтропии от объема
и температуры. А подставив выражение S(V\T) во второе из
соотношений A0.13), получим уравнение состояния.
Проиллюстрируем сформулированные выше свойства на эн-
энтропии идеального газа. Чтобы найти ее, заметим, что согласно
A0.1) и A0.2)
,Q_ 6Q _ dE + PdV
G О ~™ Тр •
Дифференцируя (8.14), убеждаемся в том, что
PdV NkdT f. dP NkdT NkdP
T T v T T P •
Вычисляя dE с помощью (8.23) и считая у = const, находим:
Nk . Aru) dT хти dp \ruf У dT d
"Интегрируя это равенство, получаем:
S = Na + Nk yztt In T - Nk In P =
Здесь через Na обозначена постоянная интегрирования, при-
причем а не зависит ни от температуры, ни от дарления. Получен-

§ юз] энтропия 271
ная формула показывает, что энтропия является функцией со-
состояния газа, которое определяется температурой Т и давлен
нием Р.
Представим, что газ состоит из двух частей, одна из которых
содержит N{ частиц, а число частиц в другой равно N2. Так как
обе части находятся в равновесии друг с другом, то температура
и давление в них одинаковы и равны, соответственно, Т и Р,
Следовательно, энтропия каждой части газа будет равна
(/=1,2).
Очевидно, что N\ -f- N2 = N. Поэтому S\ -\- S2 = S.
Таким образом, мы убедились в свойстве аддитивности эн«
тропии.
Как показывает результат вычислений, в выражение для эн«
тропии идеального газа входит величина у, отсутствующая в
уравнении состояния. Поэтому измерение энтропии дает допол*
нительную информацию о свойствах газа. В частности для газа,
состоящего из отдельных атомов (у = 5/г), при постоянном дав-
давлении энтропия меняется в зависимости от температуры по за-
закону 1п(Г5/2). Для газа, состоящего из двухатомных молекул, эта
зависимость иная. Так, при Т < Го°л величина у = 7/s и, следо-
следовательно, закон изменения энтропии с температурой имеет вид
In (Г7/*).
Убедимся теперь в справедливости соотношений A0.13). Про-
Проверим первое из них. Проверку второго оставляем читателю
в качестве самостоятельного упражнения. Из выписанного выше
выражения для S следует, что
Заменив Р на NkT/V и решая затем получившееся уравнение
относительно Г, находим, что
Подставляя эту величину в (8.23), получаем:
(Y-U
Следовательно,
' Nk
что и должно получиться в соответствии с общим правилом
A0.13),

272 основы термодинамики \гл. то
Отметим, наконец, что выражение для S можно записать'
и так:
Y — 1
Отсюда видно, что при постоянном объеме энтропия является
возрастающей функцией внутренней энергии Е.
2. Рассмотрим микроскопический смысл энтропии. Л. Больц-
маном было установлено, что для любых состояний, равновес-
равновесных и неравновесных,
S=k\nQ(E). A0.14)
Здесь k — постоянная Больцмана, a Q(E)—число микроскопи-
микроскопических состояний частиц тела, каждое из которых в макроско-
макроскопическом масштабе воспринимается как наблюдаемое макроско-
макроскопическое состояние с внутренней энергией Е. Другими словами,
Q(E)—это число микроскопических способов, какими данное
Макроскопическое состояние может быть получено. Отсюда пря-
прямо следует, что энтропия является функцией макроскопического
состояния тела. Величина Q(E) называется статистическим ее-
Юм макроскопического состояния.
Зависимость A0 14) следует, например, из распределения Гиббса. Убе-
Убедимся в этом и гем самым докажем справедливость A0.14) для равновесны*
состояний.
Пусть движение частиц тела подчиняется законам классической механики.
Тогда в состоянии теплового равновесия внутренняя энергия тела равна
= [ Ж dW(8),
где dW(&) задается распределением (9.18). Рассмотрим малое и равновесное
изменение внутренней энергии, выбрав для его обозначения символ б:
dE = б И 8 dW (8) \ = \ б {% dW (8)} = \b8dW(8)+\8b [dW
Окончательный результат получен на основании обычного правила вычисле-
вычисления малого изменения произведения двух величин, в данном случае & и
dW(<?). Мы уже отмечали, что изменение энергии через теплопередачу свя-
связано с изменением вероятностей различных состояний. Следовательно, коли-
количество тепла равно
6Q
Представим 8 б {dW (8)} в виде б {& dW (&)} — б^ dW (8). Тогда с учетом
(9.18) получим:
б {8 dW (%)} — \ъ& dW {8) = б |\ 8 dW (<Г)| - \ б# dW (8) =
= dE - — \ Ь$е-Шт Q (8) d8. A0.15)

§ ю.з] энтропия 273
Воспользуемся тождеством
e " w \ш е~тт а (<Г) dS + it? \® е~шт п wd*- A0Л6)
Оно получается в результате применения обычных правил дифференцирова-
дифференцирования (напомним, что б обозначает малое изменение) к выражению
V e~^kT п (&) d<o. При этом в нем переменными считаются энергия частиц #i
и температура Т. Число же состояний Q(&)d& с энергией в заданном интер-
интервале, как характерную для каждого тела величину, мы должны считать по-
постоянным. Выражая из A0.16) \bf?e~°'Q(<?)d& и подставляя резуль-
результат в A0.15), получим:
= dE + kT ~ - ~ Е = dE + kT б (In Z) - ЕЬ (In Г) = kTb i-~r + In Z \.
A0.17)
При этом было учтено (9.19).
Вследствие существования у распределения Гиббса чрезвычайно острого
максимума в точке & = Е подавляюще большой вклад в статистический ин-
интеграл (9.19) дают состояния системы составляющих тело частиц с энергией
& = Е. Поэтому Z практически не отличается от значения е~Е!ктп(Е), где
Q(E)—число состояний с полной энергией, совпадающей с внутренней энер-
энергией тела Е. При этом относительная ошибка, которую мы совершаем, заме-
заменяя Z величиной e-ElhTQ(E), порядка l/Vw, где N — число частиц тела. Для
макроскопических тел, у которых N — колоссально большое число, ее отличив
от нуля чисто умозрительное. Подставляя Z = e~E'kTQ(E) в A0.17), полу-
получаем:
6Q = kTb i~ + In {е~ттп (E))\ = kT6 {In Q (?)} = Td {k In Q (?)}. A0.18)
Отсюда следует, что действительно справедлива зависимость A0.10), при-
причем энтропия определяется законом A0.14). В A0.18) мы в конце концов
значок малого изменения б изменили на d, поскольку /HnQ(<^) является
функцией состояния.
Заметим, что и A0:f8) определяет энтропию с точностью до произволь-
произвольной постоянной. Ее добавление к k\nQ(S>) не нарушает равенства A0.18).
В этом отношении микроскопическое определение энтропии не добавляет ни-
ничего нового па сравнению с макроскопическим.
Рассмотрим энтропию равновесного состояния. Мы уже
знаем, что энтропия является возрастающей функцией

274 ОСНОВЫ ТЕРМОДИНАМИКИ {ГЛ. 10
внутренней энергии. Следовательно, с уменьшением последней
энтропия должна убывать. Заметим, что при фиксированном
объеме обеспечить уменьшение внутренней энергии можно
только путем охлаждения тела. При абсолютном нуле энергия
принимает наименьшее значение. Оказывается, что равновесное
состояние с такой энергией может быть реализовано единствен^
ным способом, т. е. при Г —>0 будет Q—>1. Так, с классической
точки зрения такое единственное состояние достигается только
при условии прекращения движения всех частиц. При этом они
должны занять строго определенные положения в пространстве,
отвечающие минимуму энергии их взаимодействия друг с дру-
юм, образуя таклм образом кристаллическую структуру.
Из A0.14) следует, что при Q —> 1 энтропия S—>0. Таким об-
образом, при температуре абсолютного нуля энтропия любого
тела, достигшего равновесного состояния, обращается в нуль.
В этом заключается содержание закона, названного в честь
открывшего его ученого теоремой Нернста. Этот закон назы-
называется также третьим началом термодинамики.
Строго говоря, справедливым является лишь утверждение о
достижении при абсолютном нуле только минимума энтропии.
Это обусловлено тем, что энтропия может содержать произволь-
произвольную отличную от нуля постоянную. Однако выбором начала
отсчета энтропии на уровне, определенном этой постоянной,
последняя всегда может быть исключена. Тогда будет
справедлива теорема Нернста в приведенной выше формули-
формулировке.
Отметим, что ряд опытных фактов противоречил теореме
Иернста. Однако в конце концов выяснилось, что у веществ, с
которыми экспериментировали (например, Н2О, аморфные тела,
сплавы), время релаксации быстро возрастает с понижением
температуры. Поэтому их переход в равновесное состояние при
приближении температуры к абсолютному нулю резко замед-
замедлялся. Следовательно, эти вещества просто не годились для
проверки теоремы Нернста, которая справедлива лишь при усло-
условии достижения равновесного состояния.
Из A0.14) следует, что аддитивность является свойством
энтропии, не зависящим от характера состояния. Действительно,
рассмотрим, например, систему двух тел с разными темпера*
турами. Состояние такой системы является неравновесным.
Пусть Q2 — статистический вес состояния вещества тела с но-
номером i (i = I, 2). Очевидно, что статистический вес состояния
системы двух тел будет равен Q = Qi-Q2- Применяя теперь
A0.14) к этой системе и к каждому входящему в ее состав
телу, получаем:

§ 10 41 ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 275
Здесь 5г- — энтропия тела с номером и Мы видим, что и в не*
равновесном состоянии энтропия является аддитивной вели*
чиной.
§ 10.4. Второе начало термодинамики
1. В § 10.1 отмечалось, что равновесными или обратимыми
являются процессы, протекающие с очень малой (строго говоря,
с бесконечно малой) скоростью. Все реальные процессы проте-
протекают с конечной скоростью. Поэтому они являются обратимыми
только с определенной точностью. Наоборот, необратимость яв-
является характерным свойством, вытекающим из самой природы
тепловых процессов. В этом законы тепловых явлений принци-
принципиально отличаются от законов механики. В отличие от тепло-
тепловых процессов, любое механическое движение можно обратить.
Так, камень, брошенный под углом к горизонту, может дви-
двигаться по той же траектории в обратном направлении. Для этого
после падения камня на землю ему нужно сообщить соответ-
соответствующую скорость Vq, а именно |^о1 = |#о1, р = а
(рис. 10.5). Если заснять движение с начальной скоростью vQ на
кинопленку и затем, начи-
начиная с конца, пленку пустить uo^x0t "Ог^Ч?'
в обратном направлении, то ' *
мы увидим фильм об истин-
ном обратном движении с S^y
начальной скоростью v'o. Со-
всем по-другому дело об-
обстоит, если на кинопленку Рис< 10-5*
заснять какой-либо тепло-
тепловой процесс. Например, пусть снят фильм о том, как разли-
разливается капля чернил в сосуде с водой. При прокручивании
пленки в обратном направлении мы увидим процесс, который
реально никогда не происходит. Равномерно распределенные
по всему объему с водой чернила никогда самопроизвольно не
собираются в малую каплю.
Проявления необратимости могут быть различными. Так, при
остывании горячего чайника происходит необратимый процесс
выравнивания температуры воды в чайнике и окружающего воз-
воздуха. При растворении щепотки соли в стакане воды происходит
необратимый процесс образования однородной смеси молекул
воды, ионов натрия и ионов хлора. При зажигании спички про-
происходит необратимый процесс окисления, выделения тепла с по-
последующим выравниванием температуры, с рассасыванием обра-
образовавшихся газов.
Подчеркнем, что в физике и в обыденной жизни представлен
ния о необратимости разные. Так, с обыденной точки зрения из

27В ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ ТО
перечисленных выше процессов необратимым является только
последний, поскольку чайник можно снова нагреть, соль — вы-
выпарить, а в стакан опять налить воды. В физике процесс осты-
остывания чайника был бы обратимым, если чайник, «не сходя с ме-*
ста», без посторонней помощи смог бы самостоятельно нагреть*
ся, остудив при этом окружающий воздух. Процесс растворения
соли был бы также обратим, если ионы натрия и хлора в воде
могли бы самопроизвольно собираться в кристаллики поварен-
поваренной соли. Различие обыденного и физического представлений
обусловлено тем, что в физике под обратимостью понимают не
просто воспроизводимость начального состояния, а воспроизво*
димость через те же промежуточные состояния, но расположен-
расположенные в обратной последовательности *).
Решающий шаг к количественной формулировке свойства не^
обратимости тепловых процессов был сделан французским ин*
женером С. Карно в 1824 г., задолго до установления закона
сохранения энергии. Окончательная макроскопическая формули*
ровка была дана Р. Клаузиусом, который ввел понятие энтро-
энтропии и показал, что изменениями этой и только этой величины
определяются свойства необратимости любых макроскопических
процессов. Этот замечательный по глубине, общности и обшир-
обширности применений вывод называется вторым началом термоди-
термодинамики. Он применим ко всем макроскопическим телам, за ис-
исключением Вселенной в целом.
Далее в этом параграфе для сокращения термодинамически
изолированные системы будут называться просто изолирован-
изолированными.
Современная формулировка второго начала термодинамики
известна под названием закона возрастания энтропии и гла-
гласит, что
в каждой изолированной макроскопической системе измене-
изменение энтропии AS при любом реальном процессе удовлетворяет
неравенству
При этом с точностью, с которой процесс является обратимым
(равновесным),
AS = 0.
Для необратимых неравновесных процессов
AS>0.
Необратимые процессы приводят к установлению равновесного
состояния. В этом состоянии энтропия изолированной системы
*) См. определение равновесного процесса в § 10.1

§ ТО 4} ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 277
достигает максимума. Никакие макроскопические процессы в та-
такой системе невозможны. Величина изменения энтропии являет*
ся количественной характеристикой степени необратимости про-
процесса.
Часто бывает так, что изучаемое тело не является изолиро*
ванным. В таком случае закон возрастания энтропии приме-
применяется к системе, состоящей из данного тела и некоторого на-
набора других тел, для которой условие изолированности оказы-
оказывается выполненным.
К Вселенной закон возрастания энтропии неприменим по
следующей причине. При рассмотрении поведения вещества на
очень больших расстояниях порядка 1026 м (см. § 1.1) суще-
существенную роль играют силы гравитации. Согласно общей теории
относительности эти силы определяют свойства пространства и
времени. При этом пространство и время являются своеобраз-
своеобразными внешними условиями, в которых находится вещество Все-
Вселенной. Оказывается, что эти условия отнюдь не являются ста-
стационарными. Они изменяются. В этом смысле Вселенная по-
подобна любому привычному для нас телу, которое подвергается
внешним воздействиям. Следовательно, ее нельзя считать изо-
изолированной системой и закон возрастания энтропии к ней
неприменим. И действительно, не наблюдается никаких призна-
признаков приближения Вселенной к состоянию теплового равновесия
или, по словам Р. Клаузиуса, состоянию тепловой смерти, ко-
которому присущ наивысший хаос во всем.
2. Закон возрастания энтропии имеет два следствия, которые
исторически были первыми формулировками второго начала тер-
термодинамики. Первая из них, данная впервые Р. Клаузиусом,
такова:
Невозможен процесс, при котором тепло самопроизвольно
переходит от тел менее нагретых к телам более нагретым.
Рассмотрим изолированную систему двух тел. Допустим, что
вещество каждого тела находится в состоянии теплового рав-
равновесия, однако равновесия между телами нет, т. е. система
в целом находится в неравновесном состоянии. Пусть это выра-
выражается в том, что температуры тел различны и равны соответ-
соответственно Т\ и Т2. Предположим, что объемы тел V\ и V2 остаются
неизменными. Обозначим энтропии и энергии тел через Si и Е{
(i=l, 2). Полная энергия и энтропия системы равны Е —
= Е\ + Е2у S = S\ + S2. Вследствие изолированности системы
изменение внутренней энергии системы равно нулю: dE ==
= dE\ + dE2 — 0, так что dE2 = —dEu Согласно закону воз-
возрастания энтропии
ds = dst + as2 =

278
ОСНОВЫ ТЕРМОДИНАМИКИ
[ГЛ. Iff
Здесь мы использовали то свойство, что при неизменных
мах V\ и V2 энтропия каждого тела является только функцией
его внутренней энергии. Так как каждое из тел предполагается
находящимся в равновесном состоянии, то можно воспользо-
воспользоваться первым из равенств A0.13). Тогда с учетом того, что
dE2 = — dEu получаем:
dE ( J l\ > о
1 V Т1 Т2 J
Пусть Т\ < Т2. Тогда из полученного неравенства следует,
что dE\ > 0. Это означает, что первое тело получает энергию от
более нагретого второго тела. При неизменном объеме это осу-
осуществляется только путем теплопередачи. Следовательно, тепло
всегда переходит только от более нагретого тела к менее на-
нагретому. Именно в таком теплообмене заключается механизм
установления равновесного состояния в
системе нескольких тел, температуры ко-
которых различны.
Другой формулировкой второго нача-
начала термодинамики,предложенной Д.Том-
соном, является принцип запрета вечного
двигателя второго рода:
Невозможно получить работу за счет
систематического охлаждения одного те-
тела без каких-либо изменений во всех
других телах.
Рассмотрим замкнутую систему трех
тел (рис. 10.6). Предположим, что одно
из них, скажем, первое, является объек-
объектам, над которым производится только работа по перемещению
этого тела в пространстве. Внутреннее состояние тела при этом:
не изменяется. Второе тело является только источником тепла,
т. е. тепловым резервуаром. Его объем остается неизменным.
Предположим, что вещество теплового резервуара находится
в состоянии теплового равновесия и обладает внутренней энер-
энергией Е2, энтропией S2 и имеет температуру Г2. Третье тело яв-
является рабочим. Его состояние изменяется по замкнутому циклу.
Следовательно, внутренняя энергия и энтропия этого тела как
функции состояния не дают вклада в изменение внутренней
энергии и энтропии всей системы. Назначение этого тела со-
состоит в том, чтобы, отобрав от теплового резервуара некоторое
количество тепла, превратить его в работу по перемещению пер-
первого тела. Следовательно, изменение энтропии всей системы
будет равно изменению энтропии теплового резервуара. Тогда
согласно закону возрастания энтропии
AS2 > 0»
Рис. 10.6.

§ 10 4] ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 279
где Д52— изменение энтропии теплового резервуара за один
цикл. При этом изменение энергии теплового резервуара будет
равно
Д?2=_ДД
где АЛ — работа, совершенная над первым телом. Как источник
энергии, тепловой резервуар должен обладать большими энер-
энергетическими запасами (в виде энергии теплового движения ча-
частиц его вещества). За один цикл рабочему телу будет передана
относительно малая часть этих запасов. Следовательно, темпе-
температура резервуара практически не изменится и останется рав-
равной Т2, а сам процесс теплопередачи можно считать равновес-
равновесным. Поэтому согласно первому началу термодинамики при
]/2 = const
^E2^т2^s2.
Из выписанных соотношений и положительности Т2 следует, что
ДЛ = — Д?2 = — Т2 AS2 < 0.
Это неравенство показывает, что никакой положительной ра-
работы только за счет тепла, изымаемого из теплового резервуара,
осуществить нельзя. Так, например, нельзя создать двигатель,
который бы работал, отбирая лишь тепло у мирового океана *).
Более того, при неравновесном процессе (неравновесный цикл
рабочего тела) должна быть произведена дополнительная ра-
работа над самой системой. Она равна нулю только при условии
равновесности всех превращений.
Наконец, еще одним важным следствием закона возрастания
энтропии является следующее условие:
Работа, получаемая при тепловом процессе, максимальна,
если процесс обратим.
Чтобы иметь возможность произвестя работу, к системе, изо-
изображенной на рис. 10.6, необходимо добавить четвертое тело,
которое отбирает некоторое количество тепла от рабочего тела,
т. е. является холодильником. Пусть вещество холодильника на-
находится в состоянии теплового равновесия и обладает внутрен-
внутренней энергией Ей энтропией S\ и температурой Т\ <С Т2. Его
объем V\ не изменяется. Тепловой двигатель, изображенный на
рис. 10.7, осуществляет цикл Карно, описанный в конце § 10.2.
Для него будут выполняться следующие условия:
&sx + as2 > о
(здесь знак равенства относится к равновесному процессу),
Д?"! + Д?2 = — АЛ.
*) Если бы это было возможно, то человечество обладало бы практиче-
практически неиссякаемым источником энергии, способным удовлетворить все потреб*
ности в полезной работе.

280 ОСНОВЫ ТЕРМОДИНАМИКИ [ГЛ ТО
Эти соотношения учитывают, что, во-первых, энтропия всей си-
системы изменяется в результате изменений энтропии теплового
резервуара и холодильника, и, во-вторых, работа производится
также за их счет. Предполагая равновесность (обратимость) пе^
редачи тепла рабочему телу и учитывая, что V\ = const и V2 =i
= const, из первого начала термодина-
термодинамики находим: ASi = AE\jT\\ AS2 =i
= AE2/T2. Следовательно,
2
Теплобой
резербуар
T2i S2'f E2
у
[Рабочее^
l тело j
4
Холодильник
^догпа
=*>
Рис. 10.7.
То
Выражая АЕ\ через АЕ2 и АЛ и прини-
принимая во внимание положительность Т\, из
последнего неравенства получаем:
Тем самым доказано, что работа бу-
будет максимальной в том случае, если со^
стояние рабочего тела будет меняться
обратимым образом.
Так как —АЕ2 равно энергии, посту-
поступившей в рабочее тело из теплового ре-
резервуара, т. е. равно энергии, затраченной на совершение ра-
работы АЛ, то отношение
^ — (- А?2) ^ Т2 "~ Т2
определяет КПД двигателя Карно. Величина
t Г, Т2-Тх
равна наибольшему значению КПД, которое достигается только
в обратимых двигателях. Замечательной особенностью т]тах яв-
является его независимость от свойств рабочего тела и от кон-
конструкции двигателя. Значение т]тах определяется только темпе-
температурами теплового резервуара и холодильника. Следовательно,
двигатели, имеющие различные конструктивные решения и раз-
различные рабочие тела, но работающие по равновесному циклу
Карно с одинаковыми температурами Т\ и Т2, равноценны
по КПД.
3. Закон возрастания энтропии — статистический закон. Он
выражает следующее фундаментальное свойство природы:
Все макроскопические процессы обладают односторонней на-*
правленностью. Переход между двумя макроскопическими со-
состояниями возможен только в том случае, если конечное состоя^

§ 10 4) ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 281
ние является более вероятным, чем начальное. В этом заклю-
заключается природа необратимости тепловых процессов, которая
проявляется в стремлении всех макроскопических тел перейти
в равновесное состояние.
Разъясним сказанное. Заметим, что согласно A0.14) энтро-
энтропия является возрастающей функцией статистического веса. По-
Поэтому закон возрастания энтропии можно переформулировать
в закон возрастания статистического веса: при необратимык
неравновесных процессах статистический вес изолированной си-
системы возрастает. Существенно, что это свойство и энтропии, и
статистического веса обусловлено единственной причиной — фак-
фактом неравновесности процесса. Ведь энергия изолированной си-
системы не изменяется! Оказывается, что чем больше статистиче-
статистический вес состояния, тем более оно вероятно. Следовательно, тем
чаще оно должно встречаться. А это означает, что если воз-
возможны два состояния с разными статистическими весами и в
какой-то момент времени изолированная система оказалась
в состоянии с меньшим статистическим весом, то наиболее ве-
вероятным последствием теплового движения является переход
в будущем в состояние с большим статистическим весом. Имен-
Именно в этом заключается смысл понятия односторонней направ-
направленности макроскопических процессов. Психологически это свой-
свойство воспринимается как неумолимое течение времени только
в одну сторону от прошлого к будущему.
Из этих рассуждений следует и такой вывод: равновесное
состояние является наиболее вероятным. Именно поэтому мы
повсеместно наблюдаем стремление всех тел перейти в это со-
состояние. После этого в изолированных системах прекращаются
всякие макроскопические процес- ,
сы, а энтропия и статистический {
вес достигают своих предельно
высоких значений.
Поясним на простом примере,
-0*
N1
t
почему состояния с большим ста-
статистическим весом оказываются
более вероятными. Пусть изоли-
изолированной системой является иде-
идеальный газ. Его изолированность ]
может быть обеспечена абсолют-
абсолютной жесткостью стенок сосуда, Рис- 10-8-
в котором газ находится, при
условии, что стенки совсем не проводят тепло. Разделим мыс-
мысленно сосуд на две одинаковые части (рис. 10.8) и оценим ве-
вероятности различных распределений частиц.
Предположим, что всего частиц N. Очевидно, что вероятность
пребывания каждой частицы в любой из частей сосуда равна 1/2

282 ОСНОВЫ ТЕРМОДИНАМИКИ 1ГЛ ТО
(при беспорядочном движении пребывание частицы как в од-
одной, так и в другой части сосуда — события равновероятные).
Перенумеруем частицы. Картину пребывания частиц с опреде-
определенными номерами в одной части сосуда, а остальных — в дру-
другой назовем определенной пространственной конфигурацией
частиц. Вследствие статистической независимости частиц иде-
идеального газа вероятность обнаружить любую пространственную
конфигурацию будет равна произведению вероятностей пребы-
пребывания каждой частицы в соответствующей части сосуда. Для N,
частиц это произведение равно \/2N. Обозначим через W(NUN2)\
вероятность пребывания любых N{ частиц в левой, а остальных
N2 = N — N\ частиц в правой частях сосуда. События, состоя-
состоящие в реализации разных конфигураций с одним и тем же чис-
числом N\ частиц слева и А72 частиц справа, являются взаимоис-
взаимоисключающими. Поэтому W(N\,N2) определяется суммой вероят-
вероятностей всех возможных состояний, в которых N2 каких-то частиц
находятся справа, a Ari оставшихся частиц —слева. Эта сумма
равна произведению 1/2^ на число таких состояний. Обозначим
это число через Q(AfbiV2). Очевидно, что Q(NUN2) является
статистическим весом состояния, в котором Ari любых частиц
будут в одной части сосуда, a N2 оставшихся — в другой. Легко
сообразить, что Q(N\yN2) равно числу перестановок между Ari
и А^2 частицами:
Следовательно,
ттпг / 1 * X Г \ /™\ / \ Т 1 т \ 1 /V 1
Отсюда видно, что W(NUN2) тем больше, чем больше статисти-
статистический вес Q(N\,N2).
Покажем теперь, что переход от менее вероятных состояний
к более вероятным, т. е. в направлении, определяемом законом
возрастания энтропии, приводит к равномерному распределению
частиц по всему сосуду. Именно такая картина свойственна
газу, достигшему равновесного состояния. Для этого найдем
\n?l(Nu N2). Согласно замечательной формуле Стирлинга, ко-
которая провозглашает асимптотическое равенство In х\ = х\п х,
справедливое с высокой точностью при больших х,
In Q (Mu N2) = In ~j = In ЛП - In ЛГИ - In N2\ =
= N In N - Nt In Nx - N2 In N2.
Напомним, что в газе N\ и N2 — макроскопически большие чис-
числа. Пусть N2 ^> N\, так что весь газ в основном находится в пра-
правой части сосуда.Тогда \nU{Nb iV2) ничтожен в сравнении с In2^

§ Г0.4] ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ 283
(например, при N{ = О, N2 = N будет In Q = 0. Детальный ана-
анализ поведения \пп при N2"> N{ мы предлагаем читателю осу-
осуществить самостоятельно). Итак, при N2*>N\ число 0^2^,
а следовательно, W(NU N2) ~ 0 (N > 1!). Таким образом, резко
неравномерное распределение газа обладает небольшим (в срав-
сравнении с 2^) статистическим весом и поэтому маловероятно,
Допустим теперь, что по порядку величины N\ = N2 = N12.
В этом случае с высокой точностью
1пО(ЛГ,,ЛГ2) = ЛПпЛГ--у 1пТ - YlnT" = ln2"'
Следовательно, по порядку величины Q(NU N2) = 2N. Это очень
большое число. Такому статистическому весу отвечает вероят*
ность, очень близкая к единице. Таким образом, состояние с рав-
равномерным распределением газа по всему сосуду является наи-
наиболее вероятным. Именно поэтому изолированный газ всегда
приходит в это состояние и оно является для него равновесным.
Как всякий статистический закон, закон возрастания энтро*
пии выполняется с точностью до флуктуации. Однако в макро-
макроскопических системах они столь незначительны, что закон воз-
возрастания энтропии практически можно считать точным законом.
Для иллюстрации подсчитаем, какое время необходимо газу,
чтобы он самопроизвольно вышел из равновесного состояния
таким, например, образом, чтобы с вероятностью 0,9 все его N
частиц оказались только в правой части сосуда (рис. 10.8).
Вероятность обнаружить при одном измерении N частиц в
одной части сосуда равна, как мы знаем, 1/2^. Тогда вероят-
вероятность того, что при одном измерении в другой части вообще не
окажется частиц, составит 1—(l/2iV). Следовательно, вероят-
вероятность при п независимых измерениях не найти в левой половине
сосуда ни одной частицы, согласно правилу умножения вероят^
ностей будет равна [1 —A/2^)]п. Поэтому вероятность Wn(N)]
того, что после п измерений все N частиц газа окажутся только
в правой части, будет равна
Положив Wn (N) = 0,9 и прологарифмировав записанное выше
равенство, найдем:
(здесь логарифмы являются десятичными). Поскольку N очень
велико, то — <С 1. Как известно, In A —х) ~ ~х при малых х.
Поэтому lg А дЛ = In А дЛ lg e по порядку величины

284
ОСНОВЫ ТЕРМОДИНАМИКИ
1ГЛ. 10
равен —1/2^. Тогда оказывается, что
1
Если измерения производятся через каждые At сек, то все
N молекул газа с вероятностью 0,9 соберутся только в правой
части сосуда через время
Если, например, Д/ = 1 сек, то т = 2N сек и чрезвычайно
быстро растет с увеличением числа частиц:
N
т, сек
5
32
10
1024
100
1032
105
2!°5
1019
2ю19
Из этой таблицы видно, что для макроскопически больших N,
например таких, как N = 1019, время т очень велико. Поэтому
о возможности самопроизвольного перехода всей массы газа
в одну из частей сосуда, т. е. самопроизвольного макроскопи-
макроскопического процесса с понижением энтропии, говорить не прихо-
приходится. Наблюдаемыми проявлениями самопроизвольного откло-
отклонения от равновесного состояния являются только малые флук-
флуктуации различных физических величин около своих средних
значений.

ГЛАВА li
ЯВЛЕНИЯ ПЕРЕНОСА
§ 11.1. Общая характеристика явлений переноса
1. Всякий необратимый процесс вызывается внешними усло-
условиями, в которых состояние тела оказывается неравновесным.
Если течение процесса со временем не изменяется, то процесс
называется стационарным. В противном случае процесс назы-
называется нестационарным.
Стационарные необратимые процессы возможны только в
стационарных внешних условиях. Таким процессом является,
например, установившийся теплообмен в газе, помещенном ме-
между пластинами, нагретыми до разных, но постоянных во вре-
времени температур (см. § 8.1). Подчеркнем, что при стационарных
необратимых процессах одна величина все же со временем из-
изменяется. Ею является энтропия, возрастание которой обусловь
лено вторым началом термодинамики. При любом, даже стацио-
стационарном, но необратимом процессе всякое тело непрерывно про-
производит энтропию. В этом мы вскоре убедимся непосредственно.
Нестационарные необратимые процессы могут протекать как
в стационарных, так и нестационарных внешних условиях. В ста-
ционарных внешних условиях нестационарный необратимый
процесс развивается в том случае, если начальное состояние
тела не является стационарным, соответствующим данным усло-
условиям.
Приведем пример. Допустим, что между пластинами, о кото-
рых мы уже говорили выше, помещается газ, в начальный мо-
мент одинаково разогретый по всему объему. Такое состояние
газа не является стационарным в данных условиях. В резуль-
результате теплового движения в такой системе развивается необра-
необратимый процесс теплообмена, который протекает в два этапа.
На первом этапе теплообмен носит нестационарный характер*
При этом происходит перераспределение энергии таким образом,
что в результате возникает стационарное состояние: в объеме
газа температура плавно меняется и у каждой пластины ев
значение совпадает с температурой пластины, На втором этапб

286 ЯВЛЕНИЯ ПЕРЕНОСА 1ГЛ Ifi
процесс теплообмена продолжается, но он уже является ста*
ционарным (см. выше).
В любой термодинамически изолированной системе необра*
тимые процессы всегда нестационарны. Они возможны только
в том случае, если начальное состояние системы не является
равновесным, и направлены на установление этого состояния.
Раздел физики, изучающий необратимые процессы, назьь
вается физической кинетикой, а сами эти процессы часто назы-
называют кинетическими. Свойства каждого кинетического процесса
определяются внешними условиями, в которых находится веще-
вещество, и зависят от внутренних свойств вещества. Особенно
важной является зависимость от закона действия сил между
частицами вещества. Поэтому изучение кинетических процессов
позволяет получить дополнительные сведения о силах взаимо-
взаимодействия между частицами вещества.
Каждый кинетический процесс приводит хотя бы к одному
из явлений переноса, которые называются диффузией, теплопро-
теплопроводностью, вязкостью, электропроводностью. Первые три явле-
явления будут описаны в этой главе. Электропроводность будет рас-
рассмотрена в следующих частях курса.
Диффузия (перенос вещества), теплопроводность (перенос
энергии в форме тепла), вязкость (перенос импульса) являются
необратимыми процессами, возникающими самопроизвольно
вследствие теплового движения при отклонении вещества от
равновесного состояния. Это отклонение должно выражаться,
соответственно, в неоднородном распределении вещества, его
температуры, в различии скоростей движения макроскопических
частей среды.
Подчеркнем, что в чистом виде, т. е. как следствие исклю-
исключительно лишь одного теплого движения, эти процессы наблю-
наблюдаются только при отсутствии принудительного перемешивания
среды.
Отметим, что под диффузией обычно понимают взаимопро-
взаимопроникновение вещества в различных смесях. Примером диффузии
является процесс рассасывания вещества окрашенной жидкости
в чистой воде, приведенный в § 8.1. Специфическим случаем
диффузии является самодиффузия, т. е. перемешивание молекул
одного сорта. Для наблюдения этого процесса часть молекул
необходимо каким-то способом пометить. Существует только
один такой способ: включить в часть молекул меченые атомы,
включающие ядра другого изотопа. Так, если в обычную воду
Н2О капнуть каплю сверхтяжелой воды ТгО (или наполовину
сверхтяжелой ТНО), где Т — тритий — сверхтяжелый изотоп во-
водорода, то начнется самодиффузия воды. Процесс рассасывания
можно наблюдать, регистрируя радиоактивное излучение ато-
атомов трития.

5 П.Т] ОБЩАЯ ХАРАКТЕРИСТИКА ЯВЛЕНИЙ ПЕРЕНОСА 287
2. Чаще всего встречаются неравновесные состояния, достав
точно близкие к состоянию теплового равновесия. Их называют
состояниями локального равновесия.
В состоянии локального равновесия вещество каждой малой
части тела находится в состоянии теплового равновесия, однако
равновесия между различными частями еще нет. В связи с этим
состояние теплового равновесия тела называют также состоя*
нием полного равновесия.
Причина возникновения локально равновесных состояний со-
состоит в том, что при стремлении к равновесному состоянию по-
последнее быстрее достигается в областях с относительно неболь-
небольшим числом частиц (легче «уравнять шансы» среди небольшого
числа частиц, чем у всех частиц сразу!). Напомним, что оценка
малости должна производиться только по сравнению с полным
числом частиц тела. По значению малое число частиц должно
оставаться макроскопическим, чтобы к малой части тела можно
было применять макроскопическое понятие состояния теплового
равновесия.
Описание кинетических процессов, протекающих в условиях
локального равновесия, дается в разделе физической кинетики,
который называется термодинамикой необратимых процессов.
Законы термодинамики необратимых процессов применимы
во всех случаях, когда любая неоднородность, обусловленная не-
неравновесностью состояния, имеет размер, намного превышающий
характерный размер микроскопического строения вещества
(средний свободный пробег для газов, среднее расстояние между
ближайшими частицами для жидкостей и твердых тел).
Так, законы термодинамики необратимых процессов непри^
менимы к переносу энергии через газ Кнудсена (см. § 8.3).
Для описания состояний локального равновесия исполь-
используются те же величины, что и для описания состояний полного
равновесия. Однако эти величины а) определяются для каждой
точки тела, т. е. являются локальными; б) могут изменяться со
временем; в) характеризуют свойства тела только совместно
с дополнительными величинами, получившими названия кинети-
кинетических потоков.
Законы термодинамики необратимых процессов допускают
локальную формулировку благодаря свойству аддитивности
ряда характеризующих вещество величин. Таковы, например,
количество вещества, его внутренняя энергия, импульс, энтро-
энтропия. Упомянем среди них и электрический заряд. Аддитивность
позволяет определять значения этих величин для каждого ма-
малого (но макроскопического) участка вещества и, следовательно,
описывать их распределение по различным участкам, что как
раз и необходимо для выявления свойств состояний локального
равновесия. Локальные значения каждой аддитивной величины

288 ЯВЛЕНИЯ ПЕРЕНОСА 1ГЛ. 11)
определяются ее плотностью, т. е. соответствующим количе-
количеством, приходящимся в данный момент времени на единичный
объем вещества в данном месте. Например, плотностью энтро*
пии является то ее количество, которым в данный момент вре-
времени обладает единичный объем вещества в интересующем нас
месте.
Кинетические потоки являются величинами, дающими коли-
количественную оценку переноса той или иной величины.
Потоки диффузии, тепла и энтропии являются векторами.
Они указывают, в каком направлении осуществляется перенос
вещества, энергии и энтропии. По абсолютному значению ка-
каждый из этих векторов равен, соответственно, количеству веще-
вещества, энергии и энтропии, которое в единицу времени перено-
переносится через единичную площадку, ориентированную перпенди-
перпендикулярно направлению переноса.
Поток импульса — величина более сложной геометрической
природы, ибо он связан сразу с двумя направлениями: направ-
направлением импульса и направлением его переноса. Поток импульса
является тензором и определяется как полный импульс, пере-
переносимый в единицу времени через единичную площадку, ориен-
ориентированную перпендикулярно направлению переноса.
Все плотности, так же как и все потоки, имеют общее в раз-
размерности. Любая плотность измеряется отношением единицы
измерения данного количества к 1 м3 (в системе СГС — к 1 см3).
Любой поток измеряется отношением единицы измерения коли-
количества переносимой величины к 1 м2-1 сек (в системе СГС —
к 1 см2-1 сек). Например, плотность энергии измеряется в Дж/м3
(в системе СГС — в эрг/см3), а поток тепла — в Дж/м2-сек или
во внесистемных единицах кал/м2-сек (в системе СГС — в
эрг/см2-сек). Плотность вещества измеряется либо в 1/м3 (плот-
(плотность числа частиц), либо в кг/м3 (плотность массы), в системе
СГС, соответственно, в 1/см3 и в г/см3. Поток диффузии изме-
измеряется в 1/м2-сек, кг/м2-сек (в системе СГС — в 1/см2-сек и
г/см2-сек).
Учитывая общность в размерности, а также в характере свя-
связей изменения во времени плотностей с соответствующими пото-
потоками (мы в этом вскоре убедимся), целесообразно ввести еди-
единую систему обозначений. Мы будем обозначать плотности че-
через р, а потоки буквой /. В тех случаях, в которых потребуется
конкретизация, какие же именно плотности и потоки рассматри-
рассматриваются, мы будем это делать с помощью верхнего* индекса у р
и /. Этот индекс будет буквенным обозначением соответствую-
соответствующей величины. Например, плотности энергии и энтропии и, со-
соответственно, потоки тепла и энтропии будут выглядеть так: plE\
р(?) и fE\ j№. У этого правила будет только одно исключение:
поскольку плотность вещества ранее обозначалась через п, то

§ ИЛ] ОБЩАЯ ХАРАКТЕРИСТИКА ЯВЛЕНИЙ ПЕРЕНОСА 289
и теперь мы сохраним за ней это обозначение. Поток диффузии
будет обозначаться через /<п>.
Отметим, наконец, что в условиях локального равновесия по
аддитивным величинам определяются локальные значения дру-
других величин, не обладающих этим свойством. Например, локаль-
локальное значение температуры вводится так. В момент временив рас-
рассмотрим малый участок вещества, сконцентрированный около
точки с радиус-вектором г и занимающий неизменный объем dV.
Внутренняя энергия, энтропия этого вещества, а также малые
изменения указанных величин будут, соответственно, равны
p<E4r,t)dV, pW(r9t)dV и dpW(r9t)dV, dp<s)(r,t)dV.
Здесь плотности энергии и энтропии берутся в данном месте, т. е.
в точке г, и в данный момент времени /. В состоянии локаль-^
ного равновесия к каждому малому участку вещества приме-
применимо первое начало термодинамики в "форме A0.11). Учитывая
неизменность объема вещества, получаем:
dpW (r, 0 dV=TdpW(r, t)dV9
где Т = Т(г, /) —температура данного участка вещества. Мы
видим, что
Tir.o-
v dp{S)(r*t)
Это как раз и есть локальное (в точке г) значение температуры
в момент времени t. Если состояния частиц вещества можно опи-
описывать классическим образом, то в этом случае температура
T(ryt) пропорциональна средней кинетической энергии частиц
в малом объеме, расположенном у точки г.
3. Рассмотрим, от чего зависит изменение во времени плот-
плотности р любой из аддитивных величин. Для простоты ограни-
ограничимся одномерными явлениями переноса. При этом в каждом
случае будем выбирать систему отсчета так, чтобы ее ось х
была ориентирована в направлении переноса. Тогда поток бу-
будет иметь отличной от нуля только ^-компоненту, которую, сле-
следуя избранной ранее системе обозначений, мы будем записы-
записывать через /. Кроме того, и р, и / будут зависеть только от х и L
Выделим участок вещества в виде бесконечно малого парал-
параллелепипеда. Пусть площадь каждой его боковой грани, перпен-
перпендикулярной оси х, равна dS, а левая грань проходит через точ-
точку х (рис. 11.1); толщина параллелепипеда равна dx. В объеме
параллелепипеда в момент времени t мерой свойства, описы-
описываемого плотностью р, является количество p(x,t)dxdS. Здесь
dx-dS— объем параллелепипеда. Например, количество веще-
вещества в этом объеме равно n(x,t)dx dSt энергия, заключенная
Ю А, В* Астахов

29G
ДЕЛЕНИЯ ПЕРЕНОСА
[ГЛ. If
в том же объеме, равна p(E)(x%t)dxdS и т. д. Скорость измене-
изменения количества р(ху t)dx dS равна
В общем случае это изменение происходит по двум причи-
причинам. Во-первых, оно вызывается переносом свойства, описывае-
описываемого плотностью р. Так, при / > 0 в единицу времени после мо-
момента t за счет переноса через левую грань количество
р(х, t)dxdS увеличивается на величину j(xt t)dSy а в результате
Рис. 11.1.
переноса через правую грань уменьшается на
j(x-\-dx9 t)dS. Суммарное изменение будет равно
величину
дх
Во-вторых, в системе может действовать источник. Напри-
Например, вещество может впрыскиваться извне или каким-то обра-
образом удаляться из системы, извне может подводиться энергия
или, наоборот, может осуществляться ее отвод из системы. Ис-
Источник может быть обусловлен внутренними причинами. Именно
таким является: источник энтропии. Он действует в любом не-
неравновесном состоянии и своим существованием обязан фунда-
фундаментальному закону природы — второму началу термодинамики.
Внутренний источник всегда имеется в системе, в которой ро-
рождаются частицы, например, вследствие ядерных превращений.
Пусть в результате действия источника плотность р(х, t)
изменяется в единицу времени Ra a(x, t). При а>0 источник
называется положительным, а при ог< 0 — отрицательным.
В первом случае он заставляет р увеличиваться, а во втором —
уменьшаться. При действии источника количество p(x,t)dxdS
в единицу времени изменится на o(x,t)dxdS сверх изменения,
обусловленного переносом. Составляя теперь уравнение баланса

5 11 Ц ОБШЛЯ ХЛГМСТГРИГТИКЛ стипшПй ПЕРЕНОСА 291
и сокращая на объем dx dS, получаем:
Как неоднократно подчеркивалось выше, источник энтропии
представляет особый интерес. Покажем на примере, что этот
источник действительно функционирует при отклонении от рав-
равновесного состояния. Рассмотрим теплопроводность. В этом слу-
случае объем каждого участка вещества следует считать неизмен-
неизменным. Изменяются только внутренняя энергия, энтропия и, как
следствие этого, температура. Ранее мы уже определили, как
связаны между собой эти величины. Для одномерного случая
dpW(x, t) = dpW(x, t)/T{x,f). Отсюда следует, что
dplS) (x, t) _ 1 dpiE) (x, t) _ 1 dj{E) (x, t)
dt ~ T (x, t) dt T (x, t) dx
Здесь второе равенство записано на основании A1.1), в кото-
котором мы положили р = р<Е>, / = fE\ g = сКЕ) = 0, предполагая
тем самым, что источник энергии отсутствует. Применяя теперь
известные правила дифференцирования, находим:
(X
, t) д ( /(?) (,t, t) \ j{E) (x, t) дТ (х, t)
дх\Т (x, t) ) T2 (x, t) дх *
dt
С другой стороны, согласно A1.1)
dp{S) (x, t) ___ dj{S) (x, t)
dt ~ dx
+
где a(S) — источник энтропии. Сравнивая два последних равен-»
ства, находим:
j(S) _ J_ HE) MS) _ _ {Е fL
3 T l ' 0
T2 dx •
Во-первых, обратим внимание на соответствие связи между
потоками jW и /^ первому началу термодинамики: при неиз-
неизменном объеме изменение внутренней энергии с коэффициент
том, равном температуре, пропорционально изменению энтропии.
Во-вторых, мы видим, что при Т Ф const непрерывно произво-
производится энтропия, ибо a<s) > 0. Действительно, \№ и дТ/дх всегда
имеют разные знаки. Например, если с увеличением х темпера^
тура возрастает, т. е. дТ/дх > 0, то /^ < 0, поскольку тепло мо-
может передаваться только от более нагретых участков к менее
нагретым. Следовательно, fE)-j- ^ 0 и тем самым и a^S) ^ 0.
Знак равенства имеет место только при Т = const, т. е. в со-»
стоянии теплового равновесия.
10*

292 ЯВЛЕНИЯ ПЕРЕНОСА [ГЛ. It
При а = 0
dp (*» t) i d/ (*> ft _ л /t f оч
Это соотношение называется одномерным уравнением непре*
рывности. Если процесс переноса стационарен, то в этом
случае
д! (х)
дх
= 0. A1.3)
Следовательно, при одномерном стационарном процессе / =
= const.
Если перенос осуществляется по всем трем пространствен-
пространственным измерениям, то уравнение непрерывности модифицируется.
Трехмерное уравнение непрерывности будет рассмотрено в сле-
следующем томе.
4. Помимо состояний локального равновесия, хотя и редко,
но все же встречаются состояния, очень далекие от равновесных.
Они называются сильно неравновесными, существуют, как пра«
вило, очень короткое время и «приготавливаются» в специаль-*
ных условиях. Здесь мы не имеем в виду биологические (жи-
(живые) системы, для которых как раз типичным является пребы-
пребывание в сильно неравновесных состояниях за все время жизне-
жизнедеятельности. Что же касается физических систем, то, например,
сильно неравновесным является состояние электронов на выходе
ускорителя. Столкнувшись с мишенью, в течение некоторого
времени электроны «помнят» свое начальное состояние. Однако
в результате случайных столкновений с частицами вещества ми-
мишени электроны об этом состоянии скоро «забывают», быстро
приближаясь к состоянию теплового равновесия с веществом
мишени.
Вместе с тем существуют физические системы, состояние ко-
которых все время значительно отличается от равновесного и
вследствие этого их нельзя описывать в рамках термодинамики
необратимых процессов. Одну из таких систем образуют ней-
нейтроны в ядерном реакторе. Они рождаются с высокой энергией,
которой соответствует температура порядка 1010 градусов, в ре-
результате деления ядер вещества, называемого ядерным топли-
топливом. Затем нейтроны замедляются до тепловых скоростей
в веществе, которое называется замедлителем. При тепловых
скоростях нейтроны поглощаются. В работающем реакторе уста-
устанавливается стационарный режим. Нейтроны рождаются быст-
быстрыми и, замедлившись, поглощаются. При этом состояние
системы нейтронов сильно отличается от равновесного вслед-
вследствие того, что среди них заметную долю составляют нейтроны
с высокой энергией. При этом на расстояниях, сравнимых с рас-

§ 11.2] ДИФФУЗИЯ И ТЕПЛОПРОВОДНОСТЬ 293
стоянием между соседними нейтронами, встречаются нейтроны
и высокой, и тепловой энергии. Это означает, что энергия резко
меняется на расстояниях, сравнимых с характерным размером
микроскопического строения среды.
§ 11.2. Диффузия и теплопроводность
1. В термодинамике необратимых процессов потоки диффу-
диффузии и тепла определяются, соответственно, законами Фика и
Фурье. Согласно закону Фика
*) = _D^^>, A1.4)
где п(х, t) —плотность диффундирующего вещества. По закону
Фурье
/) в _ х E^JL § A1.5)
где Т(ху t) —температура неравномерно нагретого тела.
В формулах A1.4) и A1.5) D и к называются, соответствен-
соответственно, коэффициентом диффузии и коэффициентом теплопроводно-
теплопроводности. Они положительны и зависят от свойств тела. Первый из
них характеризует скорость переноса вещества, а второй — ско«
рость переноса тепла. В соответствии с A1.4) и A1.5) коэф-
коэффициент D измеряется в единицах отношения/(rt)/-~- ,т. е. в СИ —
в м2/сек (в системе СГС — в см2/сек), ах — в единицах отно-
отношения /(?)/-г"э т. е. в СИ в Дж/(м*сек-град) = Вт/м-град
(в системе СГС — в эрг/см -сек-град).
Законы Фика и Фурье отражают свойства, установленные
опытным путем. Оказывается, что потоки диффузии и тепла воз-
возрастают с увеличением степени неоднородности в распределении
плотности и температуры. Степень неоднородности характери-
характеризуется производными дп/дх и дТ/дх, и опыт свидетельствует, что
потоки им пропорциональны. Знак минус в правых частях A1.4J]
и A1.5) учитывает свойство потоков всегда быть ориентирован-
ориентированными противоположно направлению возрастания плотности и
температуры. Вскоре мы убедимся в справедливости законов
Фурье и Фика для газов, рассматривая микроскопический ме-
механизм диффузии и теплопроводности, и попутно выясним ми-
микроскопическую природу коэффициентов Оих.
Вспомним, что по количеству тепла, сообщенного телу, мож-
можно найти изменение температуры. Для этого количество тепла
нужно отнести к теплоемкости. При теплопроводности оценка
температурных изменений должна производиться с помощью
теплоемкости СР> ибо если давление меняется, то перенос энер-

ЯВЛЕНИЯ ПГРГГ'ОГД ГГЛ И
гии будет осуществляться не только за счет теплового движе-
движения. Его будет вызывать и механическое перемешивание веще-
вещества, возникающее в результате различия давлений в разных
частях среды. Таким образом, скорость температурных измене-
изменений при теплопроводности характеризуется отношением
A1.6)
Эта величина называется коэффициентом температуропро-
температуропроводности вещества. В A1.6) СР — теплоемкость при постоянном
давлении единицы объема вещества- Следовательно, в СИ % из-
измеряется в м2/сек (в системе СГС — в см2/сек), т. е. по размер-
размерности совпадает с, коэффициентом диффузии. Это свидетель-
свидетельствует о том, чтс при наличии в теле одной лишь температурной
неоднородности коэффициент температуропроводности выпол-
выполняет роль коэффициента диффузии энергии.
Положим в A1.1) p(x,t) = n(x,t); j(x, t) = ](пЦх, t) и вос-
воспользуемся законом Фика A1.4). Тогда получим дифференци-
дифференциальное уравнение
дп (*, t) _ д ( п дп (х, t)
dt дх V дх
Оно называется уравнением одномерной диффузии и в нем
0<п) — это источник вещества.
Если вещество диффундирует в однородной среде, то в этом
случае коэффициент диффузии не зависит от х. Если к тому же
нет источников, то и о<п> = 0. Тогда уравнение диффузии упро-
упрощается и принимает вид
дп (х, t) _ n d2n(x,t)
dt ~ дх2 #
Его решение определяет закон изменения плотности п(х, t) во
времени и в пространстве.
Предоставляем читателю самому убедиться в том, что од-
одномерная теплопроводность описывается дифференциальным
уравнением
ср '
которое при х = const и сКя) = 0 принимает вид
дТ (х, t) д2Т (*, t)
dt % дх2
Если процесс диффузии или теплопроводности не является
стационарным, то, решив соответствующее уравнение диффузии
или теплопроводности, можно определить диффузионное время
релаксации хп и время релаксации при теплопроводности хт (за
время хп и хт выравниваются, соответственно, плотность диф-
dT(x,t) _ д ( дТ\
dt ~ дх Vе дх ) "г

П 2Г
ДИФФУЗИЯ И ТЕПЛОПРОВОДНОСТЬ
фундирующего вещества и температура тела). Однако по по-
порядку величины эти времена можно оценить гораздо проще из
соображений размерностей. Действительно, хп и %т могут опре-
определяться только характером распределений в начальный мо-
момент и свойствами тела. Начальные условия определяют размер
области, в которой либо плотность вещества, либо температура
в начальный момент были распределены неравномерно. Пусть
соответствующий характеристический линейный размер равен L.
Свойства тела по отношению к диффузии и теплопроводности
определяются, соответственно, коэффициентом диффузии D и
коэффициентом теплопроводности х или температуропроводно-
температуропроводности %. Из этих величин можно составить только две комбинации,
имеющие размерность времени. Ими являются L2/D и L2/%. Сле-
Следовательно, по порядку величины
Tr = L2/x. A1.7)
Примеры с численной оценкой значений хп и тг будут даны
в следующем пункте.
2. Рассмотрим диффузию газов с микроскопической точки
зрения. Пусть в смеси двух газов давление Р и температура Т
везде одинаковы, а состав меняется в jc-направлении. Обозначим
через nQ полное число частиц обоих газов в единице объема, а
через п(х, t)—плотность одного из них. Поток диффузии /<п>
определяется избытком числа частиц, проходящих в единицу
времени в положительном направлении оси х через перпендику-
перпендикулярную ей единичную площадку, над избытком тех же частиц,
проходящих через эту же площадку в отрицательном направ-
направлении. Оценим и то, и другое число по порядку величины, счи-
считая, что координата площадки равна х. Каждое из них равно
Рис. П.2.
числу частиц, занимающих объем параллелепипеда высоты vTt
где vT — тепловая скорость частиц, с основанием единичной
площади (рис. П.2). Объем такого параллелепипеда численно
равен vT. Число же частиц в этом объеме по порядку величины
равно произведению vT на плотность, значение которой нужно

296 ЯВЛЕНИЯ ПЕРЕНОСА ?ГЛ. П
брать в том месте, где частицы испытали последнее столкнове-
столкновение перед тем, как пересечь единичную площадку. Для частиц,
пересекающих площадку в положительном направлении оси х9
этим значением будет п(х — /, t), а для частиц, пересекающих
площадку в отрицательном направлении, — величина n(x-\-l,t),
где I — средняя длина свободного пробега частиц (рис. 11.2),
Таким образом, по порядку величины
j(n) = vT • п{х — I, t) - VT - tl{x + I, *).
По определению в состоянии локального равновесия плот-
ность п меняется слабо на расстояниях, сравнимых с /. Поэтому
по порядку величины
Следовательно,
Сравнивая это выражение с законом Фика A1.4), находим, что
с точностью до численного множителя порядка единицы
Вспоминая (9.1), окончательно находим:
A1.8)
Остается уточнить, к каким частицам смеси относятся вели-
величины Vt и а. Этот вопрос несущественен, если частицы двух
газов мало отличаются друг от друга, как, например, при само-
самодиффузии. Если же различие заметное, то, как показывает де-
детальный анализ, под vT следует понимать большую из скоро-
скоростей, т. е. тепловую скорость частиц наименьшей массы, а под
а — наибольшее из эффективных сечений (в смеси происходят
столкновения частиц каждого газа друг с другом и столкнове-
столкновения разных частиц).
Зависимость A1.8) раскрывает микроскопический смысл ко-
коэффициента диффузии газов. Она показывает, что скорость пе-
переноса вещества в газовой фазе зависит от характера взаимо-
взаимодействия частиц, который сказывается на величине а. Кроме
того, формула (Н.8) определяет зависимость коэффициента
диффузии от состояния газа. Так, с повышением температуры
при постоянном давлении величина D увеличивается, так как
возрастает тепловая скорость vT и падает плотность щ. При
постоянной температуре с увеличением давления коэффициент
диффузии уменьшается, так как при этом увеличивается плот*
ность.

§ 11.21
ДИФФУЗИЯ И ТЕПЛОПРОВОДНОСТЬ
297
Для достаточно разреженных газов (но не для газа Кнуд-
сена!) можно предсказать с довольно высокой точностью, как
именно это происходит. Воспользуемся уравнением состояния
(8.13). При этом, конечно, мы делаем приближение, которое
будет тем точнее, чем более разреженным газ является. Из
(8.13) следует, что при постоянном давлении плотность обратно
пропорциональна температуре Т. Согласно (8.7) vT пропорцио-
пропорциональна уТ. Поэтому для разреженных газов коэффициент
диффузии возрастает с температурой примерно по закону ГЧ
Наблюдаемые небольшие отклонения от этого закона объяс-
объясняются тем, что при изменении Т незначительно уменьшается
сечение а. С ростом давления при постоянной температуре ко-
эффициент диффузии уменьшается по закону Р~1, так как со-
гласно уравнению состояния (8.13) плотность пропорциональна
давлению.
Значения коэффициентов диффузии некоторых газов при
нормальном давлении и температуре 0°С представлены в таб-«
лице 5. Таблица показывает, что по порядку величин коэффи-^
циенты диффузии различных газов совпадают.
Таблица 5
Диффундирующее вещество
Бром
Бром
Аммиак
Пары воды
Углекислый газ
Основной компонент
Аргон
Метан
Воздух
Воздух
Углекислый газ
D, м*/сек
0,86-10
0,15-Ю"
0,19-Ю
0,23 • 10~4
ол • ю-4
Оценим теперь диффузионное время релаксации в газах.
Рассмотрим, например, диффузию брома в аргоне. Предполо-
жим, что линейный размер первоначальной неоднородности
распределения брома составляет 0,1 м. Тогда согласно A1.7)
эта неоднородность исчезнет за время порядка тп =
= 0,01 м2/@,86-10~5 м2/сек) ^ 103 сек. Эта цифра показывает,
что диффузионное перемешивание в газах является довольно
медленным процессом.
Выше мы убедились в том, что коэффициент температуро-
температуропроводности имеет смысл коэффициента диффузии энергии не-
неравномерно нагретого тела. Поэтому по аналогии порядок коэф-
коэффициента температуропроводности газов также равен
X == vTl — vT/no.
(И.9)

208
ЯВЛЕНИЯ ПЕРЕНОСА
ТГЛ If
Здесь п — плотность газа. По тому же сходству диффузии и
теплопроводности можно заключить, что теплопроводность в га-
газах также является медленным процессом.
Определим порядок величины коэффициента теплопроводно-
теплопроводности газов. Из A1.6) и A1.9) следует, что с точностью до чис-
численного множителя порядка единицы
При плотности газа п в единице объема содержится n/NA молей
газа. Поэтому
где С*роль— теплоемкость одного моля при постоянном давле-
давлении. Итак, окончательно получаем:
/^МОЛЬ
_
N,
A1.10)
Если газ достаточно разрежен, то можно воспользоваться
приближением идеального газа. Напомним, что теплоемкости га-
газов остаются постоянными в очень широком диапазоне темпера-
температур. Так как скорость vT пропорциональна У?\ то оказывается,
что для разреженных газов закон изменения коэффициента теп-
теплопроводности в зависимости от температуры близок к Т1г. От-
Отклонения от этого закона обусловлены тем, что, во-первых, у>
входящее в выражение для СРу хотя и слабо, но все же с тем-
температурой изменяется. Во-вторых, с увеличением температуры
несколько уменьшается эффективное сечение а. Согласно A.1.10)
коэффициент теплопроводности разреженных газов не зависит
от плотности и давления.
В табл. 6 в качестве примера приведены значения коэффи-
коэффициентов теплопроводности некоторых газов при 0°С.
Таблица 6
Вещество
Хлор
Углекис-
Углекислый газ
х, Дж/м-сек-град
0,72- 1(Г2
1,45- 1(Г2
Вещество
Воздух
Водород
и, Дж/м-сек-град
2,4Ы0~2
16,8 -КГ2
3. Микроскопические механизмы диффузии и теплопроводно-
теплопроводности в жидкостях и твердых телах существенно отличны от рас*

§ 11.21 ДИФФУЗИЯ И ТЕПЛОПРОВОДНОСТЬ
смотренного выше, так как в этих средах взаимодействие частиц
не носит характера столкновений.
Диффузия в жидкостях происходит значительно медленнее,
чем в газах.
Для сравнения приведем значение коэффициента диффузии
поваренной соли NaCl в воде: он равен 1,Ы0~9 м2/сек, т. е. на
четыре порядка меньше, чем у газов.
Диффузия происходит и в твердых телах. Характер этого
процесса определяется дефектами кристаллической структуры
твердых тел и существенно зависит от температуры. Более по-
подробно об этом будет сказано в гл. 13. Здесь только отметим,
что при обычных температурах диффузия в твердых телах яв<
ляется очень медленным процессом. Однако ее скорость резко
возрастает при увеличении температуры. Так, при комнатной
температуре коэффициент диффузии золота в свинец равен
4-10~н м2/сек, а при 300°С его значение увеличивается на пять
порядков и становится равным 10~9 м2/сек. Это явление ис-
используется, например, для отжига металлов. Для достижения
однородности сплава его длительное время выдерживают при
высокой температуре.
Явление теплопроводности в жидких и твердых диэлектри-
диэлектриках обусловлено колебаниями частиц среды, образующими вол-
волны сверхвысоких частот. В квантовой теории таким волнам
сопоставляются квантовые частицы — фононы. Движением фо-
нонов и обусловлен перенос энергии. В твердых и жидких ди-
диэлектриках этот процесс осуществляется гораздо быстрее, чем
в газах. Например, коэффициент теплопроводности воды х =
= 0,6 Дж/м- сек -град, а у кварца к = 93,2 Дж/м- сек -град. Пер-
Первое значение на порядок, а второе на четыре порядка выще
значений, характерных для газов (см. табл. 6). Более высокие
по сравнению с газами скорости переноса тепла обусловлены
интенсивным взаимодействием частиц в твердых и жидких ди«
электриках.
В проводящих средах эта скорость может быть еще больше*
Так, у меди и = 380 Дж/м-сек-град. Высокие значения коэф-
коэффициентов теплопроводности металлических проводников объяс-
объясняются тем, что в них тепло проводится главным образом элек-
электронами проводимости, которые очень подвижны. Более деталь-»
но теплопроводность в твердых телах будет рассмотрена в
томе III.
Коэффициенты теплопроводности жидкостей подчиняются го«
раздо более сложным закономерностям, чем коэффициенты теп-*
лопроводности газов. В отличие от газов, коэффициенты тепло*
проводности жидкостей с увеличением температуры уменьшают*
ся. Это вызвано тем, что увеличение температуры делает менее
заметным влияние сил притяжения между частицами жидкости*

300 ЯВЛЕНИЯ ПЕРЕНОСА 1ГЛ. If
Эффективно это выражается в ослаблении связи между ними,
что затрудняет перенос энергии. Данных о влиянии давления
еще очень мало. Известно лишь, что до 30—40 бар оно ничтож-
ничтожно мало.
§ 11.3. Вязкость
1. Рассмотрим газ или жидкость, которые находятся с од-
одной стороны от бесконечной плоской поверхности и занимают
полупространство х > 0 (рис. 11.3). Допустим, что поверхность
движется со скоростью, которая лежит в плоскости поверхности
и имеет величину и@). Частицы газа
l'l!| у |] |' I' I It I j | или жидкости, примыкающие к по-
V ] 11 I I | | | || верхности, будут вовлечены в движе-
М| Ли I I.' ние силами притяжения к частицам
поверхности. Поэтому возникнет тече-
|'^ i i' |' 11 ние граничащего с поверхностью слоя
I i f tVf- ' т газа или жидкости. Его скорость бу-
и(о)~
«I . N I 1|'| I дет также равна и@). По мере уда-
11 | | |' | | | И . I 11 ления от поверхности скорость тече-
I I | I' I l M j | I ния будет убывать, обращаясь в нуль
'' ' ' ' ' ' lf ' при лс->оо. Это означает, что скорость
D .«о течения является убывающей функ-
* ис* ' ' цией расстояния до поверхности, и =
= и(х), и перенос импульса будет
осуществляться в направлении оси х. Так же как при диффузии
и теплопроводности, в термодинамике необратимых процессов
поток импульса /<р> (рис. 11.3) зависит от скорости изменения
в пространстве скорости течения, и в одномерном случае
(рис. 11.3) эта зависимость имеет вид:
Коэффициент г] называется динамической вязкостью среды.
Он является положительной величиной, характеризующей ско-
скорость переноса импульса в результате теплового движения, и
определяется свойствами среды. Динамическая вязкость изме-
измеряется в кг/сек-м. Широко употребляется и единица измерения
системы СГС. Она равна 1 г/сек-см и названа пуазом (Пз)
в честь французского ученого Ж. Пуазейля, впервые в середине
прошлого столетия исследовавшего течение вязкой жидкости.
Импульс единицы объема газа или жидкости равен произве-
произведению плотности массы р на скорость его перемещения. По-
Поэтому помимо потока импульса рассматривают еще поток ско-
скорости течения, определяя его так:

5 1131 ВЯЗКОСТЬ1 301
Согласно этой формуле в СИ поток скорости измеряется в
м2/сек2. С учетом A1.11) его можно представить в виде
Ни) — _ v —
Коэффициент
v = r)/p A1.12)
называется кинематической вязкостью. В СИ он измеряется в
м2/сек, а в системе СГС в см2/сек. Единица 1 см2/сек имеет
специальное название — стоке (Ст), в честь английского фи-
физика середины прошлого века Дж. Стокса.
Размерность кинематической вязкости позволяет заключить,
что эта величина играет роль коэффициента диффузии или тем-
температуропроводности для скорости течения. Отсюда, по анало-
аналогии с диффузией и теплопроводностью, можно сделать три вы-
вывода. Первый из них относится к времени вязкой релаксации.
Предположим, что в начальном состоянии пространственная не-
неоднородность скорости течения среды имеет размер L. Если эта
неоднородность не поддерживается внешними силами, то вслед-
вследствие вязкости движение затормозится. Порядок величины вре-
времени вязкой релаксации тв определяется равенством
Второй вывод касается микроскопической оценки коэффи-
коэффициентов вязкости газов. По порядку величины
v = vTt, v]=9vTt = mnvT — = -^-t A1.14)
где пг — масса одной частицы газа. Остальные величины нам
уже знакомы по предыдущему параграфу. Согласно A1.14) ди-
динамическая вязкость не зависит от давления газа. Она изме-
изменяется только при изменении температуры по закону, близкому
к VI* (по этому закону изменяется vT). Отклонения от этого
закона обусловлены небольшими изменениями эффективного се-
сечения а с температурой.
Третьим является вывод о том, что выравнивание скоростей
макроскопического движения различных частей газа вследствие
вязкости является медленным процессом.
В отличие от газов, динамическая вязкость жидкостей с уве-
увеличением температуры уменьшается. Причиной является возра-
возрастание с ростом температуры скорости теплового движения ча-
частиц жидкости. Их перемещения становятся более свободными и
внутреннее трение уменьшается. При понижении температуры
динамическая вязкость жидкостей возрастает. В ряде случаев
она становится настолько большой, что жидкость затвердевает

302
ЯВЛЕНИЯ ПЕРЕНОСА
ГГД и
без образования кристаллической решетки. В этом заключается
механизм образования аморфных твердых тел. Примером их
могут служить стекла,По существу аморфное твердое тело есть
не что иное, как жидкость с аномально высокой вязкостью.
В табл. 7 в качестве примера приведены значения коэффи-
коэффициентов вязкости некоторых газов и жидкостей при температуре
20 °С.
Таблица 7
Вещество
Водород
Воздух
Бензол
% кг/сек *м
0,88- 10"
1,8-10~25
6,5-10
v, м'/сек
0,95-10
0,15-10
0,72-10~4
Вещество
Вода
Ртуть
Глицерин
Ц, кг/сек-м
1 .ю-;
1,55-10
1,5
V, м2/сек
ю-76
l,4-10~3
1,2-10~3
2. Свойства течения вязкой среды зависят от плотности ее
массы р, динамической вязкости г\ или кинематической вязкости
v. Они определяются также характерными для данного течения
скоростью v и линейным размером г. Например, для течения,
вызванного движением шара, характерным линейным размером
является радиус шара, а характерной скоростью — скорость дви-
движения шара. Для течения жидкости по трубе характерным ли-
линейным размером является диаметр трубы, а характерной ско-
скоростью— средняя скорость потока. Во многих случаях среду
можно считать несжимаемой. Так, сжимаемость жидкостей, как
известно, очень мала. При движении газа изменения давления
существенно сказываются на плотности газа только при скоро-
скоростях, сравнимых со скоростью звука. При дозвуковых скоростях
газ ведет себя практически как несжимаемая среда. Учитывая
сказанное, в дальнейшем будем считать р = const.
Из величин р, ц или v, r и v можно образовать безразмерную
комбинацию, которая называется числом Рейнольдса и обозна-
обозначается через Re:
vr
V
A1.15)
Число Рейнольдса является одной из важных характеристик
течения вязкой среды. От его значения зависит характер тече-
течения, которое может быть ламинарным и турбулентным.
Для каждого вида течения существует такое критическое
значение Reo> что при Re < Reo возможно только ламинарное
течение. При Re > Reo течение турбулизуется.
Так, для течения, вызванного движением шара, Reo порядка
103. Для жидкости, протекающей в трубе, Reo =230.

§ !! з] вязкость 303*
Ламинарное течение носит слоистый характер. Ему свой-
свойственно отсутствие перемешивания вещества соседних слоев.
Специфика турбулентности заключается в вихреобразном дви-
движении среды, при котором, наоборот, происходит интенсивное
перемешивание вещества в макроскопических масштабах (см.
рис. 2.15 и 2,16, стр. 80). Размеры турбулентных вихрей под-,
час бывают сравнимыми с некоторыми характерными разме-
размерами самой среды и даже больше их. Так, в земной атмосфере
могут возникать гигантские вихри с радиусом в сотни и даже
тысячи километров, что намного превышает толщину самой ат-
атмосферы.
Каждый турбулентный вихрь претерпевает со временем сле-
следующие изменения. Он дробится на вихри меньших размеров.
Те в свою очередь разбиваются на еще более мелкие, и т. д. Этот
процесс длится до тех пор, пока масштаб турбулентных неодно-
родностей не станет равным некоторому минимальному значе-
значению. После этого турбулентное движение превращается в ла-
ламинарное и запасенная в турбулентном потоке энергия в
результате вязкого трения в среде выделяется в виде тепла,
Минимальный масштаб турбулентности в атмосфере составляет
величину порядка 10~3 м.
С помощью числа Рейиольдса формулируется также крите-
критерий подобия течений. Оказывается, что
течения вязкой среды подобны, если числа Re для них оди-
одинаковы. Подобными называются движения, которые отличаются
только масштабом всех своих характеристик.
Подчеркнем, что физическое понятие подобия шире геометри-
геометрического, В физике говорят о подобии, если подобны все характе-
характеристики движения, а не только геометрические свойства участ-
участвующих в движении тел. Например, кроме расстояний должны
быть подобны скорости, энергии, силы и т.д. Так, в поле тяготе-
тяготения большой и маленький шар, сделанные из одного и того же
материала, подобными не являются. Действительно, пусть отно-
отношение радиусов шаров равно 2. Тогда отношение абсолютных
значений сил тяготения, действующих на шары, будет равно
уже 8. Ускорения же шаров в ноле тяготения будут одинако-
одинаковыми.
Подобные физические явления встречаются не так-то часто.
Вязкая среда является одной из редких систем, в которой воз-
возможны физически подобные явления. С другим примером физи-
физического подобия мы встретимся еще в § 12.2. Существование
подобных течений имеет огромное практическое значение. На-
Например, можно выяснить поведение потока воздуха при об-
обтекании крыла самолета с определенным Re, не строя самого
самолета. Вместо этого можно сделать модель и провести ее
испытание в аэродинамической трубе со скоростью воздушного

304 ЯВЛЕНИЯ ПЕРЕНОСА [ГЛ IT
потока, которая дает то же самое Re. Результаты будут приме-
применимы к настоящему самолету.
3. Установим, с какой силой вязкая среда действует на дви-
движущееся в ней тело. Как уже отмечалось, в этом случае харак-
характерным является размер тела г, а характерной скоростью —
скорость движения тела v. Из анализа размерностей следует,
что единственной комбинацией, имеющей размерность силы, яв-
является pv2r2. Поэтому закон действия силы сопротивления F
может иметь единственный вид:
, A1.16)
где f(Re)—некоторая функция Re. Допустим, что скорость v
мала. Критерием малости является условие
Re< 1,
поскольку Re пропорционально скорости v и безразмерно. При
малых числах Рейнольдса течение среды ламинарное. В этом
случае сила сопротивления обусловлена переносом импульса.
В самом деле, потоки концентрируются вблизи поверхности тела,
исчезая на больших от него расстояниях. Вследствие этого воз-
возникает поток импульса от тела к среде. Согласно второму за-
закону Ньютона, изменение импульса в единицу времени есть сила.
Поэтому наличие потока импульса непосредственно у поверхно-
поверхности тела означает, что на среду со стороны тела действует сила.
Противодействующая ей сила, приложенная к телу, и является
силой сопротивления. Поскольку ноток импульса пропорциона-
пропорционален вязкости, то при малых скоростях движения шара сила со-
сопротивления должна быть пропорциональна коэффициенту вяз-
вязкости. Это условие будет выполнено в том случае, если функция
/в A1.16) будет иметь вид
где С — некоторая постоянная. При этом условии мы получаем
закон сопротивления Стокса
о котором речь уже шла в первой части (§ 2.3). Более деталь-
детальный анализ позволяет в каждом случае определить значение
постоянной С. Например, для шара С = бя и
F = Qnx\vrt
где г — радиус шара.
При турбулентном течении закон действия силы сопротивле^
ния иной. В этом случае вязкость практически никакой роли не
играет. Механизм вязкости заключается в молекулярном пере*
мешивании, обусловленном тепловым движением. При турбу*

§ Ti.35 вязкость 305
лентности перемешивание является макроскопическим. Поэтому
в этом случае (т. е. при больших Re) сила сопротивления не бу-
будет зависеть от вязкости вообще. Из A.15) и A.16) следует, что
это может быть лишь в том случае, если f(Re) = D = const. Сле-
Следовательно, при больших скоростях (но меньших скорости
звука!)
F
Мы получили закон сопротивления Ньютона, также упоми-
упоминавшийся ранее в § 2.3. В полученном выражении коэффициент
D очень сильно зависит от формы тела. Сила сопротивления
Ньютона оказывается минимальной только при определенной
форме тела, которая называется хорошо обтекаемой. Тело хо-
хорошо обтекаемой формы должно быть закруглено спереди и
удлинено сзади, плавно заостряясь к концу.

ГЛАВА 12
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
§ 12.1. Фазовые диаграммы
1. Среди макроскопических процессов особую группу состав-
составляют фазовые превращения или переходы.
Фазовым превращением называется процесс, в результате
которого свойства тела меняются скачком. Состояния, между
которыми осуществляется переход, называются фазами.
Удивительность существования фазовых переходов усколь-
ускользает от нашего внимания только потому, что мы с детства к ним
привыкли. А ведь на самом деле картина очень загадочна. Дей-
Действительно, начнем охлаждать воду. Охлаждаем на градус, де-
десять градусов — никаких видимых изменений не происходит.
И вдруг, при охлаждении на ничтожнейшую долю градуса, вода
переходит в совершенно иное состояние льда.
Фазовые превращения бывают двух типов. Фазовым превра-
превращением первого рода называется процесс, при котором скачком
изменяются плотность, внутренняя энергия, энтропия тела. При
этом выделяется или поглощается энергия, называемая тепло-
теплотой фазового перехода.
Примером фазовых превращений первого рода являются из-
изменения агрегатного состояния вещества. Превращение жидко-*
сти в газ и обратный процесс называются, соответственно, испа-
испарением и конденсацией. Переход твердого состояния в жидкое
называется плавлением, а обратный переход — кристаллизацией.
Превращение твердого тела в газ называется сублимацией или
возгонкой.
Различные агрегатные состояния — газообразное, жидкое и
твердое — являются разными фазами. При этом твердым счи-
считается только кристаллическое состояние. Аморфное твердое со-»
стояние на самом деле является жидкостью с аномально боль-
большой вязкостью (см. § 11.3 в предыдущей главе). Поэтому такие
тела приобретают свойство текучести не скачком, а путем посте-
постепенного уменьшения вязкости, которое вызывается повышением
температуры.

§15 1] ОАЧОРМГ ДИАГРАММЫ 307
При всех агрегатных превращениях выделяется или погло-
поглощается энергия. Например, для превращения килограмма воды
в пар необходимо затратить энергию 2,3-106 Дж. Эта энергия
необходима для преодоления сил притяжения, действующих
между молекулами воды. Металлы начинают плавиться только
тогда, когда начинает разрушаться их кристаллическая решетка,
на что также необходимо затрачивать энергию. К числу фазо-
фазовых превращений первого рода относятся и некоторые переходы
твердого тела из одной кристаллической модификации в другую.
Эти превращения называются полиморфными. Кристаллы раз*
ной модификации состоят из одного и того же вещества и отли^
чаются друг от друга лишь строением кристаллической решетки.
Примером являются кристаллы графита и алмаза, построенные
из одного и того же элемента — углерода.
Некоторые вещества способны образовывать особое, четвер-
четвертое агрегатное состояние вещества. Оно называется жидкцм
кристаллом*). Как видно из названия, это состояние по своим
свойствам занимает промежу-
точное место между жид- /\ __*,_/\
костью и обычным кристаллом. нзсо \ ) N "~v{ \ ) ° *
Жидкокристаллической фазой ^ ' JJ ^ '
обладает, например, соедине-
соединение, молекула которого изо- Рис. 12.1.
бражена на рис. 12. К Это ве-
вещество называется параазоксианизол. На рисунке шестиуголь-
шестиугольники изображают бензольные кольца. При нормальном давле-
давлении параазоксианизол является жидким кристаллом в диапа-
диапазоне температур 114—1U5°C.
Жидкие кристаллы схожи с обычными жидкостями по своим
механическим свойствам: они текучи. Вместе с тем они обла-
обладают упорядоченной структурой, что роднит их с кристаллами.
Жидкие кристаллы образуются из молекул, обладающих вытя-
вытянутой линейной неразветвленной формой. Именно такой струк-
структурой обладает молекула, изображенная на рис, 12.1. У таких
веществ возможны состояния, в которых молекулы могут сво-
свободно перемещаться поступательно в продольном направлении.
.Однако поворачиваться они не могут, так к.ак мешают друг
другу. Схематически структура жидкого кристалла изображена
на рис. 12.2. В жидкокристаллическом состоянии наблюдается
строгая упорядоченность ориентации молекул в макроскопиче-
макроскопических объемчиках. Каждый из таких объемчиков является ма«
леньким кристалликом.
*) Некоторые вещества могут образовывать несколько жидкокристалли*
ческих модификаций.

308
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
[ГЛ. 12
Вещества, существующие в жидкокристаллическом состоя-
состоянии, имеют также и обычные твердокристаллическую и изотроп*
ную жидкую фазы. При этом последовательность образования
фаз следующая. При низких температурах вещество находится
в твердокристаллическом состоянии.
Рис. 12.2.
вращения, переходы, в которых одна
из фаз является жидким кристаллом,
сопровождаются поглощением или
выделением энергии. Однако теплота
плавления жидких кристаллов мала
по сравнению с теплотой плавления
твердых тел. Так, теплота перевода
1 кг жидкого кристалла параазоксианизола в обычную жид-
жидкость равна 3,3-103 Дж, теплота плавления 1 кг свинца состав-
составляет 2,1 • 104 Дж.
Фазовым превращением второго рода называется процесс,
в результате которого скачком изменяется зависимость свойств
тела от температуры и давления. При этом плотность, внутрен-
внутренняя энергия и энтропия скачка не испытывают. Поэтому при
фазовых превращениях второго рода энергия не выделяется и
не поглощается.
К фазовым превращениям второго рода относится, например,
переход жидкого гелия в сверхтекучее состояние. При темпе-
температуре выше 2,2°К гелий ведет себя как обыкновенная вязкая
жидкость. Так, при течении в трубе он испытывает действие
силы вязкого трения. Однако при температуре 2,2°К его вязкость
скачком падает до нуля. Это яв-
явление было открыто П. Л. Капи-
Капицей в 1938 г. Первое объяснение
этого явления было дано
Л. Д. Ландау в 1941 г. Последо-
Последовательная математическая тео-
теория сверхтекучести было построе-
построена Н. Н. Боголюбовым в 1947 г.
Сверхтекучесть проявляется,
например, в эффекте образования
«ползущей пленки». Если жид-
жидкий гелий налить в два сосуда,
разделенные перегородкой, то со временем уровни в сосудах
самопроизвольно выравняются (рис. 12.3). Причина заключаетсй
в том, что гелий начинает перетекать по очень тонкой, толщиной
в несколько сотен ангстрем, пленке, играющей роль сифона^
Рис. 12.3.

§ 12.1]
OA^ORhTF ДИАГРАММЫ
309
В отличие от обычных жидкостей, в которых из-за вязкости
образование и распространение жидкой пленки происходит очень
медленно, движение пленки сверхтекучего гелия происходит
очень быстро. Ее скорость достигает десятков сантиметров в се-
секунду.
Разными фазами гелия являются вязкий и сверхтекучий ге-
гелий. При этом их агрегатное состояние одинаковое. Обе фазы
являются жидкими.
Другим примером фазовых превращений второго рода яв«
ляется переход проводников в сверхпроводящее состояние.
Сверхпроводимость была открыта Г. Камерлинг-Оннесом на
ртути в 1911 г. Микроскопическая теория сверхпроводимости
создана Д. Бардиным, Л. Купером и Д. Шриффером в 1956 г.
Значительный вклад в развитие последовательной математиче-
математической теории этого явления был сделан Н. Н. Боголюбовым. Суть
самого этого явления заключается в том, что вблизи абсолют-
абсолютного нуля сопротивление некоторых проводников электриче-
электрическому току скачком падает до нуля. При этом их агрегатное
состояние не меняется. Проводники по-прежнему остаются
твердыми телами той же кристаллической структуры. Раз-
Различными фазами являются обычный и сверхпроводящий про-
проводник.
К фазовым переходам второго рода относятся полиморфные
превращения особого типа, при которых скачком изменяются
свойства симметрии кристаллической структуры.
В дальнейшем будут рассмотрены только равновесные фазо-
фазовые превращения первого рода, происходящие в отсутствие
внешних полей. Это означает, что температура и давление во
всех частях тела, испытывающего превращение, одинаковы.
2. При заданном давлении фазовое превращение всегда про-
происходит при строго определенной температуре. Поэтому изотер-
изотермический фазовый переход одновременно является изобариче-
изобарическим процессом.
Таблица 8
Вещество
Водород
Кислород
Этиловый спирт
Эфир этиловый
Ртуть
Свинец
Температура
перехода,
°С
-259,2
-219
-117
-116
-38,6
327
Вещество
Алюминий
Поваренная соль
Серебро
Медь
Железо
Кварц
Температура
перехода,
°С
660
804
961
1083
1535
1728

310
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
\ТЛ. 12
Температуры превращений твердое тело — жидкость некото-
некоторых веществ при атмосферном давлении приведены в табл. 8.
Эти значения называются точками плавления при данном дав-
давлении.
При изменении давления изменяется и температура фазового
превращения. На РГ-диаграмме эта зависимость изображается
кривой фазового перехода Р = Р(Т). Здесь Т обозначает точку
плавления при давлении Р. По названию превращений говорят
о кривых испарения — конденсации, плавления — кристаллиза-
кристаллизации и т. д. Кривые фазовых переходов могут иметь как положи-
положительный, так и отрицательный наклон. Например, приведенные
50
40
50
20
10
5бар
80
60
40
20
/600 1700
Рис. 12.4.
то t;o
100
Рис. 12.5.
200
на рис. 12.4 кривые плавления железа и никеля имеют положи-
положительный наклон, а приведенные на рис. 12.5 кривые плавления
висмута и галлия — отрицательный. Причина разного наклона
будет объяснена ниже.
Кривая фазового превращения разделяет плоскость РТ на
две области. Точки внутри каждой области соответствуют одно-
однофазным состояниям. Точки, лежащие на кривой фазового пре*
вращения, отвечают состояниям, в которых обе фазы присущ
ствуют одновременно и находятся в равновесии друг с другом.
Поэтому кривую фазового превращения называют также кривой
равновесия фаз.
Фазовые превращения можно изображать не только на РТ*
диаграмме, но также и на PV- и ГУ-диаграммах состояния. Гра<
фическое изображение фазового превращения на одной из диа-
диаграмм состояния называют фазовой диаграммой. Фазовые диа-
диаграммы на плоскостях РТ и PV существенно отличаются друг от
друга. Это отличие обусловлено тем, что в процессе самого пере-
перехода постоянны и температура, и давление, в то время как
удельный объем изменяется.
Удельным называется объем, приходящийся в среднем на
одну частицу вещества. Если тело из N частиц имеет объем V*

$ 12.1] ФАЗОВЫЕ ДИАГРАММЫ
то удельный объем равен
311
где п — плотность вещества. Так как при фазовом превращении
плотность меняется скачком, то такой же характер имеет и из-
изменение V.
Рассмотрим процесс изотермического сжатия вещества.
Предположим, что в начальном состоянии существует только
одна фаза / с удельным объемом ио, температурой 7\> и давле-
давлением Р(ь Пусть на РГ-диаграмме состояний этому состоянию
Соответствует точка А (рис. 12.6), а на Яи-диаграмме — точка а
Фаза 2
фаза /
Т=Тп- const
То
Рис. 12.6.
Рис. 12.7.
(рис. 12.7). На РГ-диаграмме процесс изотермического сжатия
вещества изобразится прямой ABC, а на диаграмме Pv — изо-
изотермой серь Форма последней определяется тем, что с увеличен
нием давления удельный объем фазы / будет уменьшаться. Сна-
Сначала уменьшение будет происходить плавно. Однако так будет
до тех пор, пока вещество не придет в состояние, которому на
РГ-диаграмме соответствует точка В (рис. 12.6), а на Ри-диа«
грамме — точка Pi (рис. 12.7). После этого начнется образовав
ние новой фазы 2 с удельным объемом v2 < V\. Из-за скачка
плотности V2 отличается от v\ на конечную величину. С этого
момента состояние вещества станет двухфазным.
При образовании новой фазы с меньшим удельным объемом
будет выделяться энергия. Количество вновь образовавшейся
фазы зависит от величины выделившейся энергии. Например,
при замерзании воды количество образовавшегося льда опреде-
определяется количеством тепла, отобранного у воды. Изменение сред-
среднего удельного объема v двухфазной системы с увеличением
доли х фазы 2 @ ^ х ^ 1) будет определяться законом
v = xvl + (l—x)vl. A2.1)
На рис. 12.7 ему соответствует прямолинейный участок Pi02.
параллельный оси v, так как при заданной температуре То

312 ФАЗОВЫЕ ПРЕВРАЩЕНИЯ [ГЛ. 12
фазовый переход происходит только при давлении Рх (рис. 12.6).
Точке р2 отвечает снова однофазное состояние с удельным
объемом и2. При дальнейшем увеличении давления состояние
вещества будет меняться уже непрерывно в пределах фазы 2
согласно прямолинейному участку ВС на РГ-диаграмме и изо-
изотерме р2у на Ри-диаграмме.
Таким образом, существенное отличие фазовых РТ- и Ру-диа-
грамм состоит в том, что при заданной температуре двухфаз-
двухфазному состоянию на РГ-диаграмме соответствует точка, а на
Ри-диаграмме— отрезок. По РГ-диаграмме нельзя определить
количественное соотношение фаз в двухфазной системе; Pv-
диаграмма позволяет получить ответ на этот вопрос. Например,
пусть состояние двухфазной системы на Ри-диаграмме изобра-
изображается точкой р' (рис. 12.7). Ей соответствует удельный объем
v'. Зная его величину, а также V\ и у2, из A2.1) легко найти х.
Кривой фазового перехода на РГ-диаграмме (рис. 12.6) на
Р^-диаграмме соответствует заштрихованная область (рис. 12.7),
Эта область разделяет две другие, отвечающие однофазным
состояниям. Действительно, при изменении температуры изме-
изменяется и давление. Следовательно, отрезок PiP2 на Ри-диаграмме
(рис. 12.7) либо поднимается, либо опускается, заметая на Ри-
плоскости целую область. При этом отрезок может укорачи-
укорачиваться и удлиняться. Это зависит от значений удельных объемов
разных фаз, которые определяются величиной давления в си-
системе.
3. Установим, от чего зависит наклон кривой фазового пере-
перехода. С этой целью рассмотрим циклический процесс, изобра-
изображенный на Ри-диаграмме
(рис. 12.8). На участке ар фа-
фаза/с удельным объемом и\
при давлении Р полностью пе-
переходит в фазу 2 с удельным
объемом и2. Напомним, что
этот процесс не только изоба^
рический, но и изотермический.
Далее, фаза 2 претерпевает
бесконечно малое изменение, в
Рис. 12.8. результате которого давление
увеличивается на dP. Этот пе;-*
реход изображен участком Ру. Затем совершается обратный
изотермический фазовый переход по прямой уб. Наконец, при
бесконечно малом переходе 6а система возвращается в исход-
исходное состояние.
Этот круговой процесс можно считать равновесным циклом
Карно. Во-первых, участки Ру и 6а бесконечно малы, так что
теплопередачей на них можно пренебречь. Во-вторых, участки

§ 12 2] КРИТИЧЕСКАЯ ТОЧКА 313
ар и уб являются изотермами. Величина работы за один цикл
численно равна площади фигуры офуб- Так как цикл является
бесконечно узким, то эта площадь равна Av-dP, где Av = V\—v2.
На совершение этой работы энергия затрачивается только на
участке уд, на котором удельный объем возрастает. Обозначим
теплоту этого перехода через AQ. Тогда КПД цикла будет равен
Av-dPjAQ. С другой стороны, он же равен dT/T, где dT — раз-*
ность температур на изотермах у8 и оф, Т — температура на изо-
изотерме уб (см. § 10.4). Следовательно,
— = i-Afi A22ч
Это соотношение называется уравнением Клапейрона — Кла-
узиуса. Оно и определяет наклон кривой фазового перехода.
Так, при испарении и сублимации кривая фазового перехода
имеет положительный наклон. Действительно, в этих случаях
тело поглощает энергию: AQ > 0. Кроме того, Av > 0, так как
удельный объем газа всегда больше удельного объема жидкости
и твердого тела. Тогда согласно A2.2) dP/dT > 0.
При плавлении кривая фазового перехода обычно имеет по-
положительный наклон. Для большинства веществ удельный
объем жидкой фазы больше объема твердой фазы: Av > 0. По-
Поэтому для них, так же как и в случае испарения, dP/dT > 0.
Однако у ряда веществ, получивших название аномальных,
Av << 0. К их числу относятся вода, висмут, германий, некоторые
сорта чугуна. Для них dP/dT <0 и кривая плавления имеет
отрицательный наклон.
Отметим, наконец, что кривые плавления идут круче кривых
испарения и сублимации. Это связано с тем, что при испарении
и сублимации изменение удельного объема намного превышает
изменение объема при плавлении. Приведем пример. Для пони-
понижения точки кипения воды на Г необходимо уменьшить давле-
давление на 3,6-Ю бар. Добиться такого же эффекта для льда
можно, лишь увеличив давление на 1,3-102 бар.
§ 12.2. Критическая точка
1. Кривая испарения — конденсации Р = Р(Т) обладает за-
замечательным свойством: она не уходит в бесконечность, а имеет
конец, за которым различие жидкой и газовой фаз исчезает.
Этот конец называется критической точкой. Ее координаты Тк
и Рк называются, соответственно, критическими температурой
и давлением. Так, на рис. 12.9 критической является точка К. На
нем области, на которые кривая Р(Т) разделяет плоскость РТ,
сопоставлены однофазным жидкому и газообразному состояниям

814
ФАЗОВЫЕ ПРГПРЛЩПШЯ
\ТЛ
по очевидному признаку: при одной и той же температуре дав-
давление в жидкости всегда больше, чем в газе.
В качестве примера в табл. 9 приведены значения критиче-
критических значений температуры и давления некоторых веществ.
Вещество
Вода
Спирт
Эфир
ГК.ОК
647,2
516,6
467,0
Рк, бар
221,4
63,9
35,9
Вешество
Углекис-
Углекислый газ
Кислород
Водород
1
гк.°к
304,2
154,4
33,2
а б л ид а 9
Рк, бар
73,9
50,3
12,9
•
•
Жидкость/
Газ
i
К /
i *
*
*
Рис. 12.9.
Достижение критического состояния практически определяют
по исчезновению поверхности раздела фаз в двухфазной си-
системе— жидкость и газ, образовавшийся в результате испарения
некоторой части жидкости. Если этот
газ находится в равновесии с жид-
жидкостью, то его называют насыщенным
паром. Давление такого газа также
имеет особое название. Об этом дав-
давлении говорят как об упругости на-
насыщенного пара. Если суммарный
объем жидкости и насыщенного пара
остается постоянным, то с увеличе-
увеличением температуры упругость насыщен-
насыщенного пара будет возрастать, так же
как будет возрастать и его плотность.
Наконец наступит такой момент, когда
плотности насыщенного пара и жидкости сравняются. Это и
означает, что система достигла критического состояния. В этом
состоянии исчезает межфазная граница (поверхность раздела
фаз). В нуль обращается также и теплота испарения.
На Ри-диаграмме приближение к критической точке прояв-
проявляется в сближении удельных объемов газа и жидкости. При
Т = Тк и Р = Рк они становятся одинаковыми. Это общее их
значение мы обозначим через ик. На плоскости Pv область двух-
двухфазных состояний имеет вид, изображенный на рис. 12.10, на
котором она заштрихована.
С существованием критической точки связана возможность
непрерывного перехода жидкости в газ и наоборот. На рис. 12.9
и 12.10 один из таких процессов изображен пунктирными кри-
кривыми. При переходе из состояния / в состояние 2 вдоль этих
кривых никакого скачка наблюдаться не будет и теплота пре-

§,122] КРИТИЧГСКЛЯ ТОЧКА 315
вращения будет равна нулю. Возможность непрерывного пре-
превращения жидкости в газ свидетельствует об отсутствии принци-
принципиального различия между ними. Строго говоря, пользоваться
терминами «жидкость» или «газ» можно лишь в том случае, если
существует двухфазная система с поверхностью раздела между
жидкой и газовой фазами. При этом «опознание» жидкости и
газа производится по свойствам наблюдаемого состояния: плот-
плотности, сжимаемости, вязкости и т. д.
В критическом состоянии вещество обладает особыми свой-
свойствами. Так, в этом состоянии неограниченно большой оказы-
оказывается сжимаемость вещества. Эта величина определяется про-
производной (dV/dP)T, вычисляемой при постоянной температуре
(это обстоятельство отмечено индексом Т в обозначении произ-
производной). Сжимаемость характеризует способность вещества
изменять свой объем при изотермическом изменении давления.
При этом условии изменение объема, возникающее при изменении
давления на 6Р, равно 8V — (dV/dP)T6P. Неограниченное уве-
увеличение сжимаемости при приближении к критической точке опре-
определяется формой кривой, ограничивающей область двухфазных
состояний на Яу-диаграмме (рис. 12.10). В критической точке К
'г
В этой цепочке равенств N — число частиц вещества. Следова-
Следовательно, в критическом состоянии (dP/dV)T = 0 и поэтому
(dV/dP)T-+oo.
В критической точке обращаются в бесконечность также
коэффициент термического (теплового) расширения и теплоем-
теплоемкость СР вещества. Коэффициен-
Коэффициентом термического расширения
называют производную (dV/dT)Pj
вычисляемую при постоянном
давлении (значок Р в обозначе-
обозначении производной указывает на
это обстоятельство). Эта произ-
производная характеризует способ-
способность вещества изменять свой
объем при изобарическом изме-
изменении температуры. Именно, если
в таких условиях температура из-
изменилась на 6Г, то изменение Рис. 12.10.
объема составит величину 6V =
= (д]//дТ)р8Т. Обращение в бесконечность теплоемкости СР
связано с неограниченным возрастанием (dV/dT)P. Действитель-
Действительно, согласно A0.9)
"" +p(dV

316
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
1ГЛ. 12
U
Рис. 12.11.
где Е и W — соответственно энергия и энтальпия вещества. Да-
Далее,
dV \ N ( dV_\ _N (
Т )р~~~ \дТ
(N — число частиц вещества). Стремление (dV/dT)P к бесконеч-
бесконечности при Т->ТК видно из рис. 12.11. На нем область двухфаз-
двухфазных состояний заштрихована, а К — это критическая точка. Убе-
Убедиться в том, что фазовая иГ-диаграм*
ма для испарения — конденсации дей-
действительно имеет вид, изображенный
на рис. 12.11, мы предоставляем чита-
читателю в качестве самостоятельного
упражнения.
Наконец, в критическом состоянии
исчезает поверхностное натяжение
жидкости, поскольку жидкость стано-
становится неотличимой от пара.
Резкое увеличение сжимаемости и
коэффициента термического расшире-
расширения вещества вблизи критического состояния приводит к тому,
что весьма большими становятся флуктуации его плотности.
Это является причиной резкого возрастания рассеяния света
веществом — явления* названного крити-
критической опалесценцией.
Отметим, наконец, что в смесях двух 220-
веществ могут быть две критические точ-
точки. Примером является смесь вещества,
называемого гексаметиленимином, и во-
воды. Область его двухфазных состояний
ограничивается замкнутой кривой, изо-
изображенной на рис. 12.12. По оси абсцисс
отложено процентное содержание гекса-
метиленимина. Критическими являются
точки /С.
2. Рассмотрим, в какой мере законо-
закономерности испарения и конденсации отра-
отражаются уравнением состояния реальных газов — уравнением
Ван-дер-Ваальса (8.19). Для этого сначала преобразуем его
к виду
A2.3)
/80
140
WO
60
О
20 40
Рис. 12.12.
Разделив это равенство на Af3, получим:
kT
/, . kT \ о , а аЪ л
\Ь + -jr J o+jo —т = 0.

12 2]
КРИТИЧЕСКАЯ ТОЧКА
317
При каждом фиксированном значении температуры соотноше-
соотношение A2.3) определяет зависимость Р = P(v). Каждая такая за-
зависимость называется изотермой Ван-дер-Ваальса. Некоторые из
них изображены на рис. 12.13.
Нумерация изотерм на ри- pt
сунке соответствует убыва^
нию температуры.
Форма изотерм Ван-дер-Ва-
Ван-дер-Ваальса объясняется следующим об-
образом. При фиксированных Р и
Т A2.3) является уравнением
третьей степени относительно v.
Оно имеет три корня. При этом
либо все они вещественны и по-
положительны, либо один корень ве-
вещественный и положительный, а
два других — комплексные числа,
сопряженные друг другу. Отрица-
Отрицательными вещественные корни
быть не могут. При v < 0 все сла-
слагаемые в левой части A2.3) отрицательны и поэтому в сумме не могут дать
нуль. Комплексные корни появляются только при достаточно больших значе-
значениях Т. Физический смысл имеют только вещественные корни. Они являются
абсциссами точек пересечения изотермы Ван-дер-Ваальса с прямой Р = const*
Поэтому либо изотерма монотонно спадает (один корень), либо у нее есть
впадина и горб (три корня). На
рис. 12.13 к числу первых относятся
изотермы U 2, 3, ко вторым — изо-
изотермы 4, 5, 6.
Рис. 12.13.
А'
Жидкость
Рис. 12.14.
Выясним физический
смысл различных участков
изотермы Ван-дер-Ваальса, у
которой есть впадина и горб
(рис. 12.14). Участки api и РгР
описывают однофазные состоя-
состояния, соответственно, газа и
жидкости. В двухфазной обла«
сти изотерма имеет участок
Р^, на котором с ростом давления объем увеличивается. Та-
Таких изотермических процессов в действительности не существует.
Следовательно, уравнение Ван-дер-Ваальса не описывает
свойств двухфазных систем. Для этого оно оказывается слиш-
слишком грубым. Несмотря на это, уравнение Ван-дер-Ваальса пред-
предсказывает существование критической точки. Действительно, с
повышением температуры впадина и горб изотермы уменьшаются,

318 ФАЗОВЫЕ ПРЕВРАЩЕНИЯ ТГЛ \2
стягиваясь в точку К на изотерме 3 (рис. 12.13). Эта точка
и является критической. Вблизи этой точки уравнение Ван-
дер-Ваальса передает особенности поведения реальных газоз
и жидкостей.
Отметим, наконец, что уравнение Ван-дер-Ваальса приводит
к закону соответственных состояний, который утверждает, что
вид уравнения состояния, записанного в приведенных величи-
величинах, одинаков для всех веществ. Приведенными называются от-
отношения
Закон соответственных состояний выражает подобие свойств
различных веществ. Например, из этого закона следует, что
уравнение кривой испарения — конденсации должно иметь оди-
одинаковый для всех веществ вид
Пределы применимости закона соответственных состояний
определяются пределами применимости уравнения Ван-дер-Ва-
Ван-дер-Ваальса.
Для обоснования закона соответственных состояний выразим критические
величины vKy Тк и Рк через постоянные Ван-дер-Ваальса а и Ь. Так как в кри-
критической точке все три корня уравнения A2.3) равны vK> то
Сравнивая коэффициенты при одинаковых степенях v, находим:
1 . ЬТК п а п 9 ab *
Решая эти уравнения относительно ик, Рк, ТК} получим:
Отсюда, принимая во внимание определение приведенных величин, нетрудно
преобразовать уравнение Ван-дер-Ваальса к виду
В это уравнение уже не входят постоянные а и Ь, зависящие от природы
газа. Следовательно, в такой форме уравнение состояния справедливо для
всех газов. Это и есть закон соответственных состояний^

§ 12.3] МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ 319
§ 12.3. Метастабильные состояния
1. Как было только что установлено, в области перехода
жидкость — пар реальная изотерма резко отклоняется от ва*ь
дер-ваальсовской кривой, превращаясь в прямую линию. Несшь
тря на это, нанесенные на рис. 12.14 сплошной линией участки
$fi[ и р2^ имеют физический смысл. Каждый из них описывает
особые состояния, которые называются метастабильными.
Метастабильным называется равновесное состояние с огрши*
ченной устойчивостью. При отклонении от этого состояния ее*
щество не стремится к нему обратно, а легко переходит в дру-
другое, устойчивое состояние. Метастабильные состояния сущест*
вуют ограниченное время.
Фазы, отвечающие участкам f^p' и $$2, называются соответ^
ственно переохлажденным паром и перегретой жидкостью. Эти
названия отражают следующие свойства. Рассмотрим, напри-
например, участок f^Pj (рис. 12.14). После достижения состояния,
которому сопоставляется точка |3ir должна начаться конденсация
газа в жидкость. Однако это случается не всегда. Конденсация
может начаться только при наличии в газе инородных к притом
смачиваемых включений.
Если они есть, то около каждого такого включения начинают
концентрироваться частицы газа. Напомним, что смачиваемость
означает преобладание сил притяжения между частицами газа
и включения над силами взаимного притяжения между части-
частицами газа. Именно поэтому и начинается группирование частиц
газа около включения. Они образуют вокруг последнего очень
тонкую пленку жидкости, толщина которой обычно колеблется
в пределах 10~9—10~7 м. Включение совместно с образовавшейся
вокруг него пленкой является центром конденсации. Когда при
заданной температуре давление достигает значения, лежащего
на кривой испарения — конденсации, то каждый такой центр
провоцирует процесс бурного присоединения к себе частиц окру-
окружающего вещества, пребывающего с ним по соседству в газовой
фазе» В макроскопическом масштабе этот процесс выглядит как
скачкообразное превращение газа в жидкость.
Если же газ является абсолютно чистым, то положение су«
ществевшо меняется. В таком газе с самого начала отсутствуют
зародыши жидкой фазы, а самопроизвольно они образоваться
не могут, и вот почему. Предположим, что в результате флук-
флуктуации плотности в газе самопроизвольно образовалась капля
жидкости (рис. 12.15). Если состояние вещества не является
близким к критическому, то большие флуктуации плотности
исключены. Поэтому самопроизвольно образовавшаяся кайля
не может быть больших размеров. Поверхность же капли

320 ФАЗОВЫЕ ПРЕВРАЩЕНИЯ [ГЛ 12
Находится под напряжением, вызванным поверхностным натяже-
Нием. На рис. 12.15 выделен участок сферической поверхности
капли и стрелками указаны действующие на него силы поверх-
поверхностного натяжения. Складываясь, эти силы дают суммарную
рилу F, направленную внутрь капли. С ростом кривизны поверх-
поверхности величина F возрастает. Для маленьких капель F достигает
значительной величины. Таким образом,
оказывается, что внутреннее давление
капли превосходит давление окружаю-
окружающей среды. Поэтому сразу же после об-
образования такие капли быстро разру-
разрушаются.
Следовательно, в газе без инородных
включений нет условий для образования
жидкой фазы даже тогда, когда достиг-
достигнуто состояние, которому отвечает точка
на кривой фазового перехода (точка Pi
на рис. 12.14). Более того, конденсация
Рис. 12.15. не начинается и при более высоких дав-
давлениях (точки участка $i$'i), при кото-
которых газ уже «вторгаетсг» в область жидкой фазы. Такой газ
й называется переохлажденным, так как при достигнутых зна-
значениях давления и температуры он «обязан» был бы превра-
превратиться в жидкость, но с ним, однако, этого не произошло. Оче-
Очевидно, что такое состояние является весьма неустойчивым. По-
Появление в переохлажденном газе смачиваемых инородных ча-
частиц сразу же приведет к его конденсации. В реальных условиях
необходимы специальные меры предосторожности для того, что-
чтобы не допустить засорения газа. Поэтому получить газ в пере-
переохлажденном состоянии довольно трудно.
Механизм образования состояния, называемого перегретой
жидкостью, сходен с механизмом образования переохлажденного
пара. На изотерме, изображенной на рис. 12.14, состояниям пе-
перегретой жидкости отвечают точки участка Р2Р2. Перегретой мо-
может быть только очень чистая жидкость, в которой нет зароды-
зародышей газовой фазы. Как правило, они всегда присутствуют в виде
Мельчайших пузырьков газа на стенках содержащего жидкость
сосуда или на взвешенных в жидкостях пылинках. Поэтому для
Получения состояния перегретой жидкости необходимо прово-*
дить тщательную предварительную очистку жидкости и стенок
сосуда.
2. Метастабильные состояния переохлажденного пара и пере*
гретой жидкости используются в различных целях. Например,
переохлажденный пар является рабочим веществом в камере
Вильсона. Это устройство является старейшим следовым реги-
регистратором заряженных частиц. Она была создана в 1912 г.

§ 12 3]
МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
321
В следовых регистраторах заряженные частицы оставляют
следы, называемые треками, которые, как правило, фотографи-
фотографируются с целью дальнейшего их изучения.
Частица
Источнин сбета
Фотогрскричесное
устройство
Поршень
Рис. 12.16.
'Нейтральная тпля
Типичная схема камеры Вильсона изображена на рис. 12.16.
Объем камеры наполнен нейтральным газом, обычно гелием или
аргоном, в который добавлено необходимое количество паров
воды в смеси с парами спирта. С помощью поршня меняют дав-
давление в камере и таким образом создают состояние переохлаж-
переохлажденного пара. Если заряженная частица влетает в камеру, когда
в ней находится переохлажден- „*
ный пар, то она становится цен-
центром конденсации и оставляет в
камере след из капелек тумана.
Этот процесс возникает вслед-
вследствие того, что на поверхности
возникающих заряженных капель
действуют электростатические
силы отталкивания. Они компен-
компенсируют силы поверхностного на-
натяжения и уменьшают давление
в капле. Такие капли уже не раз-
разрушаются. Различие между ней-
нейтральной и заряженной каплей иллюстрирует рис. 12.17. По
оси ординат отложено давление в капле, а по оси абсцисс —
радиус капли. Кривые характеризуют зависимость давления от
радиуса для заряженной и нейтральной капель.
Камера Вильсона работает следующим образом. Вначале
давление в камере таково, что пар не пересыщен, но близок
Заряженная цапля
Рис. 12.17.
И А. В, Астахов

322
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
[ГЛ. 12
Рис. 12.18.
к насыщению. При этом в камере создают довольно сильное
(порядка 103 В/м) постоянное электрическое поле, отсасываю-
отсасывающее случайно возникшие в камере (за счет космических лучей
и других причин) ионы. Перед самым началом работы отсасы-
отсасывающее поле выключается. Иначе оно бу-
будет размазывать треки. Рабочий цикл на-
начинается быстрым расширением газа при-
примерно на 20%. Пар становится пересыщен-
пересыщенным. На траекториях частиц, прошедших
через камеру, образуются треки из тумана.
Треки освещаются и фотографируются. На
рис. 12.18 представлена фотография треков,
оставляемых а-частицами. Видно, что одна
из а-частиц претерпела столкновение.
Отметим, что камеру почти всегда поме-
помещают в сильное магнитное поле (П. Л. Ка-
Капица, 1923 г.; Д. В. Скобельцын, 1923 г.).
Это позволяет по кривизне треков опреде-
определять знак заряда и импульс частиц (см.
§4.1).
Перегретая жидкость является рабочим
веществом в следовой камере, которая на-
называется пузырьковой (Д. Глэзер, 1952 г.). В пузырьковой ка-
камере трек заряженной частицы образуется пузырьками пара.
Запускается пузырьковая камера резким сбросом давления,
переводящим жидкость в метастабильное перегретое состояние.
Механизм образования пузырьков
лара точно не известен. Видимо,
главными факторами являются
электростатические силы и ло-
локальный перегрев жидкости вдоль
трека. Как и в камере Вильсона,
в пузырьковой камере требуется
высокая чистота жидкости. Жид-
Жидкость, конечно, должна быть про-
прозрачной, чтобы треки можно было
фотографировать. Чаще всего ис-
используются жидкий водород, про-
пропан, ксенон.
Размеры пузырьковых камер та-
такие же, как и камер Вильсона. Они
варьируются от десятков сантимет-
сантиметров до двух метров. Однако эффективный объем пузырьковой
камеры на 2—3 порядка больше, чем камеры Вильсона, так как
жидкости гораздо плотнее газов. Поэтому пузырьковая камера
является уникальным инструментом исследования цепей рожде-
Рис. 12.19.

§ 12.41
ТРОЙНАЯ ТОЧКА
323
ния и распадов частиц высокой энергии. В качестве примера мы
приводим расшифровку фотографии, на которой была впервые
зафиксирована элементарная частица й~-гиперон (рис. 12.19).
Огромный эффективный объем здесь был нужен для того, чтобы
иметь на снимке не только трек самого &--гиперона, но и треки
различных заряженных частиц, возникающих при распаде й~-ги-
перона.
§ 12.4. Тройная точка
1. В однокомпонентном веществе только кривая испарения —
конденсации имеет конец (критическую точку). Кривые плавле-
плавления— кристаллизации, а также кривая переходов между кри-
кристаллическими состояниями разной структуры могут только
~——~
-0,01
8
_л
А
f
2
, Р, Ю"°бар
- ^^УКидиоспш,
Пар |
0 Ofli
Рис. 12.20.
У
0,02
4
2
Р,
/О3 бар
Лед II 1 Лед III
—¦ mi
-40 -20 t°C
Рис. 12.21.
либо уходить в бесконечность, либо заканчиваться в тройных
точках.
Тройной называется точка на РГ-плоскости, в которой воз-
возможно равновесие трех фаз однокомпонентного вещества. Рав-
Равновесие четырех и большего числа фаз однокомпонентного ве-
вещества, как оказывается, вообще невозможно.
Например, система лед, вода, пар может находиться в рав-
равновесии только при давлении 6,09-10~3 бар и температуре 0,01°С
(рис. 12.20). На рис. 12.21 изображена часть фазовой диаграммы
воды с одной тройной точкой, в которой находятся в равнове-
равновесии три разных модификации льда. Эти фазы льда условно обо-
обозначены как лед I, лед II и лед III. При этом обычно наблю-
наблюдаемым является лед I.
Тройная точка равновесия трех агрегатных состояний — газ,
жидкость, твердое тело — существует у всех веществ, за исклю-
исключением гелия. На рис. 12.22 изображена фазовая диаграмма
гелия в области низких температур. Ее исключительной особен-
особенностью является отсутствие пересечения кривых плавления и
испарения. Кривая плавления пересекает ось давлений при
11*

324
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
1ГЛ. 12
WO
50
Цбар
2 3 4 Tt°K
Рис. 12.22.
Р = 24,5 бар. Гелий остается жидким даже при 0°К, если дав-
давление не превышает указанной величины. При этом для изотопа
Не4 область жидкой фазы состоит из двух частей. В области /
(рис. 12.22) Не4 ведет себя как обычная вязкая жидкость. В об-
области // он находится в сверхтекучем состоянии. Поведение ге-
гелия при низких температурах являет-
является квантовым эффектом, в связи с чем
низкотемпературный гелий называют
квантовой жидкостью.
Отсутствие конца типа критиче-
критической точки у кривых плавления гово-
говорит о том, что жидкая и твердая фазы
принципиально отличаются друг от
друга. Главное в этом отличии заклю-
заключается в том, что жидкости изотропны,
в то время как характерным свой-
свойством кристаллов является их анизо-
анизотропия. Когда о среде говорят, что она изотропна или анизо-
анизотропна, то имеют в виду либо одинаковость, либо отличие ее
свойств по различным направлениям.
Анизотропия кристаллов обусловлена различным характе-
характером упорядочения частиц в кристаллической решетке по разным
направлениям. Поэтому в любых условиях кристалл всегда
можно отличить от жидкости. След-
Следствием этого и является отсутствие
критической точки у кривой плав- 8
ления.
2. Фазовые диаграммы, как пра-
правило, имеют несколько тройных то- ,
чек. Это связано с наличием не-
нескольких кристаллических модифи- ?
каций вещества. В качестве приме-
примера на рис. 12.23 приведена полная
фазовая диаграмма воды. На диа-
диаграмме цифрами /, 2, 3, 4, 5 отме-
отмечены различные модификации льда.
Область 1 описывает состояния обычно наблюдаемого льда. На
рис. 12.23 область пара не изображена, поскольку она соответ-
соответствует столь малым давлениям, что в масштабе рисунка оказы-
оказывается незаметной.
Переходы между различными кристаллическими модифика-
модификациями часто сопровождаются образованием метастабильных
состояний типа переохлажденного лара и перегретой жидкости.
В отличие от метастабильных газовых и жидких состояний, ко-
которые образуются только в достаточно чистых системах, мета-
стабильные кристаллические состояния встречаются сплошь и
Жидкость
-40 -20 0 20 t,°C
Рис. 12.23.

«§ 12 4]
ТРОЙНАЯ ТОЧКА
325
Жидность
рядом, причем часто оказываются практически устойчивыми.
•Объясняется это тем, что в кристалле частицы весьма ограни-
ограничены в своих перемещениях. Поэтому перестройка кристалли-
кристаллической структуры из одной модификации в другую затруднена,
особенно при низких и уме-
умеренных температурах, при ко-
которых скорости теплового дви-
движения частиц невелики. В свя-
связи с этим процессы перестрой-
перестройки кристаллической решетки
обычно стимулируют нагрева-
нагреванием.
Рассмотрим пример. На
рис. 12.24 изображена фазовая р / т,°К
диаграмма углерода. Из вида
диаграммы следует, что при
обычных давлениях и темпе- Рис. 12.24.
ратурах устойчивой модифика-
модификацией является только графит. Однако хорошо известно, что в
этих условиях и алмаз, и графит ведут себя как вполне устой-
устойчивые кристаллы. Этот полиморфизм связан с большими раз-
различиями в строении их решеток. Требуются весьма существен-
существенные изменения для превращения одного кристалла в другой.
Так, если алмаз нагреть до температуры порядка 1700°К, то
он быстро рассыпается в порошок графита (разумеется, нагре-
нагревание следует осуществлять в вакууме во избежание сгорания
•алмаза). Обратный же процесс может происходить только при
очень высоких давлениях. Область устойчивости алмаза лежит
выше 104 бар. Одновременно необходима и высокая температу-
температура, чтобы процесс протекал с достаточной скоростью. Оптималь-
Оптимальная область давлений и температур определяется значениями
4,9 • 104 бар < Р < 105 бар и 1500 °К <Т< 3000 °К,
причем необходим еще металлический катализатор (например,
железо, кобальт, никель).
Первые сообщения о синтезе алмазов появились в !955 г.
Б Советском Союзе первый искусственный алмаз был получен
группой исследователей под руководством Л. Ф. Верещагина.

ГЛАВА 13
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
§ 13.1. Строение кристаллов
1. Качественное отличие свойств кристаллов от свойств га-
газов и жидкостей обусловлено их различным строением.
Кристаллом называется тело, обладающее периодической
атомной, молекулярной или ионной структурой.
Здесь под периодичностью подразумевается повторяющееся
упорядоченное расположение вещества в трехмерном прост-
пространстве.
Отметим, что в жидкостях также наблюдается упорядочен-
упорядоченность в расположении частиц. Однако размеры областей упоря-
упорядоченности по порядку величины не превышают нескольких рас-
расстояний между соседними частицами жидкости. При этом
группы частиц с упорядоченным строением неустойчивы во вре-
времени. Они распадаются и возникают вновь, концентрируясь
около разных частиц. В связи с этим жидкости относят к так
называемым системам с ближним порядком в отличие от кри-
кристаллов, которые являются системами с дальним порядком.
Механизм образования кристаллического состояния таков.
При понижении температуры уменьшается скорость теплового»
движения частиц. В конце концов наступает момент, когда ки-
кинетической энергии не хватает, чтобы преодолеть действие сил
притяжения между частицами. Частицы переходят в режим
тепловых колебаний около определенных положений равновесия,
отвечающих минимуму потенциальной энергии взаимодействия
частиц друг с другом. Эти положения образуют упорядоченную
и повторяющуюся в пространстве систему точек, т. е. кристал-
кристаллическую структуру. Таким образом, возникновение кристалли-
кристаллической структуры связано с превалирующим влиянием энергии
взаимодействия частиц друг с другом ниже точки плавления и
сублимации.
В основе физики твердого тела лежит представление об
идеальном кристалле. Кристалл называется идеальным в тех
случаях, когда для рассматриваемого круга явлений несущест-

§ 13 1] СТРОЕНИЕ КРИСТАЛЛОВ 327
венны любые отклонения от правильности кристаллической
структуры. Другими словами, кристалл идеален, если его можно
считать правильным монокристаллом, не имеющим никаких по-
посторонних примесей или иных нарушений его макро- и микро-
микроструктуры.
Из сказанного не следует, что идеальный кристалл — абст-
абстрактная модель, не имеющая реальной области применимости.
Напротив, можно сказать, что основная масса твердого веще-
вещества земного шара находится в монокристаллическом состоя-
состоянии. Например, размер частичек мелкодисперсной глины состав-
составляет около 5 -10~6 м, а толщина поверхностного слоя этих ча-
частичек имеет порядок 5-10~10 м. Поэтому даже в глине около
99,99% атомов находятся внутри монокристаллов.
Идеальный кристалл совмещается сам с собой при трансля-
трансляциях. Трансляциями называются параллельные переносы в опре-
определенных направлениях и на определенные расстояния. Точки
кристалла, совпадающие при трансляциях, называются эквива-
эквивалентными. Множество эквивалентных друг другу точек образует
кристаллическую решетку Браве. Эквивалентные друг другу
точки называются узлами кристаллической решетки. Наи-
Наименьший по объему параллелепипед, повторением которого
можно составить весь кристалл, образует элементарную ячейку
кристалла. Величины и направления ребер элементарной ячейки
задают векторы, которые назы-
называются основными векторами кри-
кристаллической решетки.
Подчеркнем, что эквивалентные
точки могут быть «пустыми» и на-
находиться где-то между частицами,
образующими кристалл. Однако в
дальнейшем мы будем «привязы-
«привязывать» эквивалентные точки к поло-
положениям равновесия частиц. Так, в
кристалле NaCl (рис. 13.1) эквива-
эквивалентными являются точки А, В и С. Рис. 13.1.
Эквивалентными являются также
центры всех ионов С1. Структура NaCl совершенно одинакова
относительно этих точек. Все положения равновесия ионов С1
образуют решетку Браве кристалла NaCl. Элементарной
ячейкой является куб, в каждой вершине которого имеется
ион С1. Векторы я, Ь и с являются основными векторами ре-
решетки.
Решетка Браве представляет всю трансляционную симмет-
симметрию кристалла, т. е. всю ее периодичность.
Подчеркнем, что решетка Браве вовсе не обязана исчерпы-
исчерпывать положения всех частиц кристалла. Проиллюстрируем это

328
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 1*
реальных кристаллов. На рис. 13.2 изобра-
изобрази А н /Гп'п °ТРУКТУРа ЧаСТИЦ> К0Т0Рые могут занимать пози-
ными In ?РИ М ЧаСТИЦЫ МОгут быть и одинаковыми, и раз-
разными. В данном случае элементарной ячейкой является заштри-
хованныи параллелограмм (одинарная штриховка) основЗв.
векторами — векторы а и 6.
Как видно, при выбранной эле-
элементарной ячейке частицы, за-
занимающие позиции В, не вхо-
Дят в число узлов решетка
Ьраве.
В связи с этим говорят, что
в общем случае кристалл пред-
ставляет собой несколько ре-
решеток Браве, вдвинутых одна
Рис 132 в ДРУгУю. Так, на рис. 13.2
ис- 13*2- позиции В образуют другую-
шшшшт
также
¦„-—¦-=—•=':
боре основными векторами будут а'— а Ь' фЬ
Несмотря на неоднозначность, при любом выборе
одной такой частице. Следовательно, в объеме * кристалл»
число ячеек всегда равно числу т таких частиц Сходящихся
в этом объеме. Поэтому объем ячейки равен Wm СлГова
тельно, он не зависит от способа выбора Эту независимость
также иллюстрирует рис. 13.2. Очевидно, что Пощади парал
лелограммов с одинарной и двойной штриховкой равны Р
помимо пространственной периодичности, кристаллические-
решетки обладают симметрией относительно поворотов на0Пре-

«I 13 1]
СТРОЕНИЕ КРИСТАЛЛОВ
329
деленные углы и отражений в некоторых плоскостях. В этом
отношении они обладают симметрией некоторых многогранни-
многогранников. Эти вопросы, имеющие специальный интерес, мы рассмат-
рассматривать не будем.
2. Реальные кристаллические вещества обычно встречаются
«в виде поликристаллов. Каждый поликристалл является сово-
совокупностью маленьких монокристаллов, называемых зернами или
кристаллитами. Размеры зерен варьируются в широких преде-
пределах. Решетки зерен ориентированы беспорядочно друг относи-
относительно друга. В свою очередь зерна состоят из более мелких
единиц — блоков. Размеры блоков колеблются в пределах
10~5—10~7 м. Решетки соседних блоков очень слабо, в пределах
нескольких минут, разориентированы друг относительно друга,
так что каждое зерно часто можно рассматривать как монокри-
монокристалл. В масштабах, превосходящих размеры зерен, поликри-
поликристаллическое вещество оказывается изотропным. Но это свой-
свойство является вторичным и не исключает анизотропии отдель-
отдельных зерен.
Отличие строения реальных твердых тел от идеального огра-
ограничивает область применимости модели идеального кристалла.
Перечислим некоторые из важных свойств твердых тел, которые
объясняются в рамках модели идеального кристалла. К их числу
относится анизотропия свойств монокристаллов. Например,
опытным фактом является способность кристаллов раскалы-
раскалываться только по строго определенным плоскостям, которые
называются плоскостями спайно-
спайности. Причина этого явления за-
заключается в том, что силы сцеп-
сцепления между частицами зависят
от расстояний между ними, кото-
которые в кристаллической структу-
структуре в разных направлениях не
одинаковы.
Например, графит обладает
слоистой структурой (рис. 13.3).
Расстояние между соседними
слоями в 2,3 раза превосходит
расстояние между соседними ато-
атомами углерода внутри слоя.
В этом и заключается причина
легкого расслоения графита
(вспомните, как быстро стирается карандаш!). А вот другой
пример. Сопротивление магния электрическому току зависит от
взаимной ориентации структуры этого кристалла и направле-
направления, в котором приложено напряжение. Объяснение этого
^явления состоит в том, что узлы решетки магния занимают
Рис. 13.3

330 кристаллическое состояние 1гл. та
положения вершин правильной шестиугольной призмы с отно-
относительно вытянутыми ребрами. Отсюда и возникает анизотропия
свойств, которая, в частности, проявляется в том, что в направ-
направлении боковых ребер призмы сопротивление оказывается в
1,28 раза меньше сопротивления в перпендикулярном направ-
направлении. Наиболее ярко анизотропия монокристаллов проявляется
в оптических явлениях, которые будут рассмотрены в следую-
следующем томе курса.
К числу свойств поликристаллических тел, которые можно
объяснить на основе представлений об идеальном кристалличе-
кристаллическом строении, относятся и те, которые обусловлены взаимодей-
взаимодействием частиц в зернах. Оно определяет, например, теплоту
плавления. Очевидно, что эта величина связана с энергией связи
частиц в кристаллической структуре, которая, в свою очередь,
зависит от ее строения. Последнее влияет на самые разнообраз-
разнообразные свойства — упругие, тепловые, электрические, магнитные и
другие. Мы неоднократно будем возвращаться к этим вопросам
по мере изложения курса.
3. Главная трудность опытного изучения микроскопического
строения твердых тел заключается в том, что характерным мас-
масштабом кристаллических структур является малая длина по-
порядка 1 А. Поэтому наблюдать детали кристаллического строе-
строения с помощью обычных оптических методов невозможно, так
как длина волны видимого света имеет порядок 103 А ^> 1 А.
Для исследования микроструктур пользуются двумя груп-
группами методов. К первой группе относятся методы прямого
наблюдения, использующие коротковолновые излучения, у ко-
которых длина волны меньше межатомных расстояний. С этой
целью используются, например, потоки электронов, которые мож-
можно направлять и фокусировать с помощью электрических и маг-
магнитных полей. Это методы электронной микроскопии. Мы уже
отмечали в гл. 4, что с возрастанием энергии микрообъектов
начинают проявляться их волновые свойства. Но если энергия
электронов имеет порядок от 10~19 Дж до 10~18 Дж, то длина
связанной с электроном волны будет намного меньше расстоя-
расстояний между соседними частицами в кристалле. Предел чувстви-
чувствительности электронных микроскопов удалось довести до 2—3 А,
что позволило различать отдельные атомы. В качестве примера
на рис. 13.4 приведена электронно-микроскопическая фотогра-
фотография кристалла вируса мозаичной болезни табака. Другим при-
прибором, позволяющим непосредственно наблюдать отдельные ато-
атомы, является ионный проектор, описанный в начале § 8.1 (см.
рис. 8.1).
Вторую группу составляют дифракционные методы. Получе-
Получение излучений с длиной волны порядка межатомных расстояний
проще получения более коротковолновых излучений. С их помо-

13.1]
СТРОЕНИЕ КРИСТАЛЛОВ
331
щью получают дифракционную картину, возникающую после
прохождения излучения через кристалл. Сам кристалл при этом
играет роль дифракционной решетки. Среди дифракционных ме-
методов исследований наиболее распространены электроногра-
электронография, рентгенография, нейтронография. В них используется яв-
явление дифракции волн различной природы — электромагнитных,
электронных, нейтронных. Основная трудность этих методов
заключается в том, что получается информация не об отдельных
Рис. 13.4.
атомах, а обо всей кристаллической структуре просвечиваемого
участка. Поэтому отдельные детали на дифракционной картине
не видны (см. рис. 13.6).
Общие свойства дифракции на кристалле таковы, а) Отдель-
Отдельная частица рассеивает падающие на нее волны во все стороны.
Резко выделенных направлений рассеяния нет. б) Идеальный
кристалл рассеивает очень избирательно. Если имеется, напри-
например, направленный пучок монохроматических лучей, то на слу-
случайно ориентированном кристалле, как правило, дифракции не
будет. Она возникает только при определенной ориентации кри-
кристалла, причем дифрагированный луч является остро направ-
направленным. Это происходит вследствие того, что волны, рассеянные
разными частицами, гасят друг друга в результате интерфе-
интерференции.
Существует несколько разновидностей дифракционных мето-
методов. К их числу относится, например, метод Лауэ. В этом

332
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ.
методе монокристалл освещается немонохроматическим потоком,,
т. е. потоком частиц с различными длинами волн. При этом-
монокристалл определенным образом ориентирован (рис. 13.5) ^
Фотоплен па-
Образец
Рентгенобсиий
луч
f
Рассеянные
лучи
Рис. 13.5.
Дифрагированные волны попадают на фотопленку. Получаю-
Получающееся дифракционное изображение называется лауэераммой.
Лауэграмма состоит из отдельных пятен, по которым можно*
определить структуру кри-
кристалла. На рис. 13.6 пред-
представлена лауэграмма кри-
кристалла кремния.
Выбор вида излучения опре-
определяется целью структурного ис-
следования. Перечислим особенно-
особенности различных видов излучения,
а) Рентгеновские лучи. В ос-
основном взаимодействуют с элек-
электронами вещества. Поэтому рент-
рентгенограмма дает информацию о
распределении электронов внутри,*
кристалла. Рентгеновское излуче-
излучение является проникающим. По-
Поэтому оно позволяет получить от-
отражение от большого числа пло-
плоскостей. Недостаток заключает*
рис |2 б ся в том» что сечение рассеяния.
рентгеновских квантов сильно за-
зависит от порядкового номера
атомов вещества. Поэтому, если в кристалле есть легкие и тяжелые атомы,
то на фоне тяжелых атомов рентгеновские лучи не «замечают» легких.
б) Пучки электронов. Так как электроны заряжены, то электроны пучка
сильно взаимодействуют с электронами и электростатическим полем ядер ве-

§ П.2] ДЕФЕКТЫ КРИСТАЛЛОВ 333
щества. Поэтому электронная дифракция позволяет выяснить расположение
атомов в кристалле. Сечение рассеяния электронов слабо зависит от поряд-
порядкового номера атомов. Поэтому электронограммы позволяют выделить легкие
атомы на фоне тяжелых.
в) Пучки нейтронов. Обладают колоссальной проникающей способностью,
существенно большей, чем у рентгеновских лучей. Рассеяние происходит на
ядрах. Поэтому нейтронограмма дает информацию о расположении ядер, т. е.
центров атомов. Сечение рассеяния нейтронов на всех ядрах примерно од-
одного порядка. Поэтому нейтронная дифракция позволяет разделять легкие и
тяжелые компоненты, а также соединения. Одним из главных недостатков
является радиоактивное загрязнение, в частности появление вторичной (наве-
(наведенной) радиоактивности.
§ 13.2. Дефекты кристаллов
1. Реальные твердые тела, как правило, отличаются от иде-
идеальных. Отличия порождаются условиями образования кристал-
кристалла и внешними воздействиями на уже образовавшийся кристалл
и проявляются в дефектах. Дефектами называются области с
нарушенным порядком расположения частиц, занимающие ма-
малую часть объема монокристалла.
В основу классификации дефектов положен геометрический
признак. Дефекты подразделяются на нуль-мерные, т. е. распо-
расположенные в отдельных точках кристалла, одномерные, т. е. рас-
расположенные вдоль некоторых линий, и двумерные, занимающие
некоторые поверхности. При этом размеры точечных дефектов,
так же как толщина линий и поверхностей, являются микроско-
микроскопическими. Они сравнимы с расстояниями между соседними
частицами кристалла, т. е. имеют величины около нескольких
ангстрем. Точечные дефекты в свою очередь подразделяются на
два типа: решеточные и электронные. Электронные типы дефек-
дефектов будут рассмотрены в томе III.
Дефекты качественно меняют свойства кристаллов. Цаоюе в
очень малых количествах дефекты сильно влияют на те физиче-
физические свойства, которые совсем или почти отсутствуют в идеаль-
идеальном кристалле. Являясь, как правило, «энергетически невыгод-
невыгодными», дефекты создают вокруг себя области повышенной фи-
физико-химической активности.
Наука о дефектах в кристаллах сравнительно молода. Только
в середине тридцатых годов XX века стало ясно, что теория
идеальных кристаллов не может объяснить целого ряда так на-
называемых структурно-чувствительных свойств твердых тел. К та-
таким свойствам относятся, например, поведение твердых тел под
нагрузкой, явления роста кристаллов, диффузия в твердых телах
и ряд других. Например, в модели идеального кристалла диф-
диффузия практически невозможна. Связи между частицами.

334
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ 13
занимающими узлы идеальной кристаллической решетки, на-
настолько сильны, что частицы не в состоянии их преодолеть и
перенос вещества невозможен. Однако на опыте он наблюдается.
Такое явление переноса, как теплопроводность, которое может
быть описано в рамках модели идеального кристалла, не может
быть объяснено во всех деталях, если учитывать только тепло-
тепловые колебания решетки. Для этого необходимо принимать в рас-
расчет дефекты.
2. Решеточные дефекты подразделяются на вакансии, атомы
внедрения и примесные атомы.
Вакансией называется незанятый частицей узел кристалли-
кристаллической структуры. Если пустой узел образуется в результате
удаления частицы из объема кристалла на его поверхность, то
вакансия называется дефектом по Шоттки. Если частица пере-
перемещается из узла в междоузлие, то такое нарушение правиль-
правильности решетки называется дефектом по Френкелю (рис. 13.7).
По Френкелю
По Шоттни
Рис. 13.7.
Дефекты по Шоттки снижают плотность вещества кристалла.
Дефекты по Френкелю на величину плотности практически не
влияют.
Встречаются также вакансии более сложного вида. Напри-
Например, в ионных кристаллах нередко образуются связанные пары
вакансий, образованные удалением двух ионов противополож-
противоположного знака. Рождение такой пары вместо одиночной вакансии
может оказаться более выгодным, так как при этом не нару-
нарушается электронейтральность кристалла.
Дефекты по Шоттки чаще встречаются в кристаллах с доста-
достаточно плотной упаковкой частиц близких размеров. В этих слу-
случаях в междоузлиях кристаллической структуры нет места для
лишних частиц. Дефекты по Френкелю, наоборот, свойственны
кристаллам с неплотными упаковками и с частицами, заметно
отличающимися по своим размерам.

§ 13 21 ДЕФЕКТЫ КРИСТАЛЛОВ 335
В любом кристалле обязательно есть некоторое количество
равновесных вакансий, обусловленных тепловым движением.
Участвуя в тепловом движении, частицы обмениваются энер-
энергией. Некоторые из них могут получить энергию, достаточную
для преодоления сил, удерживающих частицы в узле решетки.
Минимальное значение энергии, при сообщении которой частица
покидает узел, называется энергией активации. Значения энер-
энергий активации составляют величины порядка 10~~19 Дж. Согласно
Гиббсу, равновесная доля вакансий должна быть пропорцио-
пропорциональна e~~E*lkT, где Еа — энергия активации, а Т — температура
кристалла. При комнатной температуре Т = 300 °К отношение
EJkT порядка 40. Следовательно, при комнатной температуре
равновесное число вакансий составляет очень малую величину
порядка е~40 « Ю-16. Однако с ростом температуры равновесное
число вакансий быстро увеличивается, достигая 1—2% от об-
общего числа частиц вблизи точки плавления.
К числу точечных дефектов относятся также и примесные
атомы. К ним относятся атомы, чужеродные по отношению к
тем, которые образуют идеальный кристалл. Примесные атомы
либо замещают атомы основных компонентов, либо распола-
располагаются в междоузлиях. Кристаллы с дефектами первого типа
называются твердыми растворами замещения, а с дефектами
второго типа — твердыми растворами внедрения.
Так, раствором замещения является сплав ZnCu с преобла-
преобладающим содержанием одного из компонентов. Примером твер-
твердого раствора внедрения являются растворы углерода в железе,
образующие различные марки чугуна и стали. В этих растворах
атомы С оказываются в междоузлиях решетки, образованной
атомами Fe.
Точечные дефекты определяют многие свойства твердых тел.
Остановимся на некоторых из них.
Точечные дефекты играют основную роль в процессах диф-
диффузии в твердых телах. Так, в твердых растворах внедрения
диффузия осуществляется путем перехода внедренных атомов
из одного междоузлия в другое. В растворах замещения с нена-
ненарушенной решеткой все узлы заняты частицами. Поэтому в та-
таком кристалле диффузия должна была бы происходить путем
одновременного обмена местами пары различных частиц. Од-
Однако в реальных кристаллах всегда есть вакансии. Вследствие
этого фактически диффузия осуществляется путем перехода на
вакантные места частиц из занятых узлов решетки.
В § 11.2 отмечалось, что коэффициент диффузии в твердых
телах быстро увеличивается с температурой. Причина заклю-
заключается в следующем. Каждая частица кристалла постоянно дви-
движется в силовом поле. Для осуществления единичного перескока
из одного места в другое при любом механизме миграции

336 КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ [ГЛ 13
частиц необходимо преодолеть потенциальный барьер, высота
которого определяется энергией активации Еа. Число частиц,
кинетические энергии которых достаточны для преодоления
барьера, пропорционально е~Е^ т. Поэтому коэффициент диф-
диффузии в твердых телах зависит от температуры по закону
где Do = const. Отсюда следует, что D является резко возра-
возрастающей функцией температуры*). Кроме того, этот закон ука-
указывает на то, что преобладающим механизхмом диффузии будет
тот, для которого энергия активации наименьшая.
Точечные дефекты оказывают влияние на теплоемкость твер-
твердых тел при высоких температурах, особенно вблизи точки пла-
плавления. В этой области температур теплоемкость кристалла
с точечными дефектами оказывается заметно больше теплоем-
теплоемкости идеального кристалла. Вызвано это тем, что с ростом
температуры увеличивается число дефектов. При этом на созда-
создание каждого из них затрачивается энергия в пределах от 10~18
до 10~19 Дж. В связи с этим возрастает внутренняя энергия
кристалла, а, следовательно, и его теплоемкость.
На механические свойства точечные дефекты, если только их
не слишком много, влияют слабо. При очень высокой плотности
вакансий кристалл становится более хрупким. Это обусловлено
взаимодействием точечных дефектов с одномерными дефектами,
которые будут рассмотрены ниже.
Отметим, наконец, что в природных и искусственных кри-
кристаллах число дефектов не остается неизменным. Под влиянием
внешних воздействий оно может изменяться. Например, дефекты
могут образовываться при облучении быстрыми частицами (ней-
(нейтронами, протонами, электронами, у-квантами и т. д.). При этом
обычно возникают дефекты по Френкелю. Появляющееся при
этом изменение кристаллической структуры называется радиа-
радиационным повреждением. Изучение этих явлений имеет большое
практическое значение для тех областей науки и техники, в ко-
которых часто приходится иметь дело с взаимодействием потоков
различных частиц с разными материалами. Таковы, например,
реакторостроение и космическая техника.
Часто дефекты создают намеренно с целью получения мате-
материалов с новыми нужными свойствами. Так, различия в проч-
прочности между железом, различными марками стали и чугуном
обусловлены разным содержанием в этих материалах угле-
углерода — всего в несколько процентов.
*) Ускорение диффузии при повышении температуры лежит в основе ме-
метода отжига металлов, о котором мы уже говорили в § 11.2.

13.2]
ДЕФЕКТЫ КРИСТАЛЛОВ
337
3. Одномерные дефекты кристаллической решетки назы-
называются дислокациями. Дислокации нарушают правильное чере-
чередование кристаллических плоскостей. Число дислокаций в теле
характеризуется числом дислокационных линий, пересекающих
единичную площадку, расположенную внутри тела Это число
колеблется в пределах от 106—107 м~2 в наиболее совершенных
монокристаллах до 1015-1016 м~2 в сильно деформированных
металлах. На рис. 13.8 представлена фотография фронта тре-
трещины в кристалле КС1. На фотографии ясно видны петли дис-
дислокаций.
Рис. 13.8.
Простейшими дислокациями являются краевые и винтовые.
Представление о краевой дислокации дает рис. 13.9. Такая дис-
дислокация возникает от «лишней» кристаллической плоскости,
вдвинутой в кристалл, край которой оканчивается в объеме кри-
кристалла. Этот край и образует дислокацию, которая на рисунке
обозначена значком 1. Искажение кристаллической решетки
при наличии винтовой дислокации изображено на рис. 13.10.
В этом случае кристалл напоминает сплющенный винт мясо-
мясорубки. Лопасть винта-—это искаженная кристаллическая
плоскость, а его ось —винтовая дислокация. На рис. 13.10 она
изображена пунктирной линией. Если в кристалле имеется вин-
винтовая дислокация, то его правильное строение нарушено только
в окрестности оси винтовой поверхности.

338
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
Краевая и винтовая дислокации — это частные случаи дисло-
дислокации общего вида. В случае краевой дислокации линия дисло-
дислокации параллельна нарушенной плоскости (плоскости, край
которой оканчивается в объеме кристалла). В случае винтовой
Рис. 13.9.
Рис. 13.10.
дислокации ее линия перпендикулярна нарушенным плоскостям.
В общем случае дислокации ее линия может находиться под
любым углом к нарушенным плоскостям.
Рис. 13.11.
Дислокация либо образует замкнутую линию (рис. 13.8),
либо оканчивается на поверхности кристалла. Концы дислока-
дислокаций на поверхности наблюдают с помощью травления поверхно-
поверхности специальными реагентами. Поверхность разрушается легче
в местах нарушенной структуры. Это приводит к образованию

§ 13.2]
ДЕФЕКТЫ КРИСТАЛЛОВ
339
видимых ямок травления в местах, где линии дислокаций вы-
выходят на поверхность кристалла. В качестве примера на
рис. 13.11 приведена фотография поверхности кристалла LiF
(увеличение в 500 раз). Каждая ямка травления определяет
место выхода дислокации на поверхность кристалла.
В прозрачных кристаллах дислокации наблюдаются путем
•образования пересыщенных твердых растворов определенных
веществ. Атомы примеси стремятся выпасть в виде коллоидных
частиц, причем их рост происходит преимущественно в местах
нарушения структуры. Поэтому коллоидные частицы примеси
концентрируются вдоль линий дислокаций, делая их визуально
наблюдаемыми.
Значение дислокаций определяется их главным свойством,
отличающим дислокации от остальных дефектов:
во многих кристаллах, особенно металлических, дислокации
сравнительно легко перемещаются и размножаются.
Перемещение дислокаций иллюстрирует рис. 13.12. Пусть
к кристаллу приложены отмеченные стрелками силы. Частица А
...... •*!?** •¦/
• ••••• •¦-¦-V<*4 • • ^'^"tj^° t •
• ••••• •• + #• *^- • • ф t ф •
Рис. 13.12.
находится почти посередине. Ее нужно совсем немного пододви-
пододвинуть влево, чтобы дислокация переместилась из положения /
б положение 2. Таким образом дислокация смещается к краю
кристалла.
1
А\
III!
/А\
1A11
О/лталнибание
Рис.
13.13.
it
[
Притяжение
Дислокации могут взаимодействовать друг с другом, с точеч-
точечными дефектами и с поверхностью кристалла. Так, параллель-
параллельные краевые дислокации одинаковой ориентации отталкиваются,
а разных ориентации — притягиваются (рис. 13.13). Механизм

340
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. VS
размножения дислокаций обусловлен их взаимодействием друг
с другом и с другими дефектами. В результате взаимодействия
движение дислокаций может быть приостановлено.
Пусть, например, дислокация встречает два дефекта Л и В,
которые ее останавливают (рис. 13.14). Однако в промежутках
Рис. 13.14.
между дефектами она продолжает двигаться под действием при-
приложенных к кристаллу сил. В результате дислокация начинает
вести себя подобно профилю капли воды в кране. Отрыв дисло-
дислокационной капли приводит к появлению дополнительной дис-
дислокационной петли. Такой генератор дислокаций называется ис-
источником Франка — Рида. На фотографии, приведенной на
рис. 13.15, показан источник Франка —Рида, наблюдаемый в
кремнии.
Рис. 13.15.
Движение и размножение дислокаций, их взаимодействие
друг с другом и другими дефектами определяют многие свой-
свойства твердых тел. Здесь мы остановимся на роли дислокации
в процессах кристаллизации. Возникновение кристаллической

13.21
ДЕФЕКТЫ КРИСТАЛЛОВ
34*
фазы, так же как жидкой и газообразной, начинается с образо-
образования зародышей. Возникновение нового слоя частиц на иде-
идеально правильной поверхности кристалла невозможно путем
оседания каждой частицы на поверхность. Частица, имеющая,
соседей только с одной стороны, оказывается в невыгодных
энергетических условиях. Поэтому на поверхности такие ча-
частицы не удерживаются. Например, вероятность того, что па
идеальной поверхности кристалла NaCl может удержаться одна
частица, имеет порядок 10~16. Если же на поверхность кристалла
выходит конец винтовой дислокации, то есть уже готовая сту-
ступенька, к которой новые частицы легко присоединяются. По-
Поэтому необходимости в одиночных зародышах нет. Кристалл
растет по спирали, так, как это изображено на рис. 13.16.
Рис. 13.16.
4. Двумерные дефекты образуются границами кристалла.
Границы нарушают периодичность строения кристалла. Одним
из самых важных дефектов кристаллической структуры является
внешняя поверхность твердых тел. Во-первых, именно через
поверхность кристалл взаимодействует со своим окружением.
Во-вторых, частицы на поверхности связаны с решеткой значи-
значительно слабее, чем частицы, находящиеся в объеме. Последние
со всех сторон окружены частицами, поверхностные частицы —
только с одной стороны. Поэтому поверхностный слой имеет
избыточную энергию, которая имеет в среднем порядок 10~19 Дж
на одну частицу, т. е. около 1 Дж/м2. Поверхностная энергия
различна для разных кристаллов. Так, она равна 0,15 Дж/м2
для NaCl и примерно 10 Дж/м2 для алмаза. Смысл поверхност-
поверхностной энергии состоит в том, что она должна быть сообщена кри-
кристаллу при увеличении его поверхности, т. е. при дроблении, по-
поскольку разрушение кристалла — это процесс образования но-
новых поверхностей.
Из-за поверхностной энергии поверхностный слой имеет по-
повышенную активность в отношении различных физико-химиче-
физико-химических процессов, таких, как адсорбция, адгезия, образование по-
поверхностных химических соединений (например, окисление по-
поверхностей).
Адсорбцией называется концентрирование вещества двухфаз-
двухфазной системы на поверхности раздела фаз. Например, если.

342 КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ [ГЛ. ТЗ
кристалл соприкасается с газом, то на его поверхности плот-
плотность газа оказывается повышенной.
Адгезией называется возникновение связи между поверх-
поверхностными слоями двух разнородных тел, приведенных в сопри-
соприкосновение друг с другом. Адгезия выражается в прилипании
одного тела к другому. Примером адгезии является холодная
сварка металлов.
В поликристаллах существуют внутренние поверхностные
дефекты. Они образованы поверхностями зерен. На границах
__^^_^^ зерен решетка сильно искажена. По-
\\ \ I I I I llll/ этому поверхность внутренней грани-
границы, как и внешняя поверхность кри-
кристалла, обладает некоторой энергией.
При больших углах между зернами
атомы на границе расположены хао-
хаотично, как в жидкости. Между блока-
блоками, а также между зернами при ма-
малых углах между ними границу трак-
Рис- I3-*7- туют как упорядоченный ряд дисло-
дислокаций (рис. 13.17). Такая трактовка
границ позволяет проводить некоторые оценки и давать каче-
качественные предсказания. Так, из этой модели следует, что мало-
малоугольная граница способна двигаться под действием приложен-
приложенных к кристаллу сил.
§ 13.3. Механические свойства твердых тел
1. Внешние силы вызывают смещения частиц твердого тела.
При изменении взаимного расположения частиц в теле возни-
возникают внутренние силы. Говорят, что тело переходит в напряжен-
напряженное состояние. Это состояние характеризуется следующим обра-
образом. Выделим бесконечно малый (но макроскопический!)
объем вещества в виде куба (рис. 13.18). Обозначим через dS
площадь боковых граней куба. Рассмотрим силы, действующие
на каждую грань куба со стороны окружающего его вещества.
В отличие от газов и жидкостей, эти силы ориентированы, во-
вообще говоря, произвольно. Однако при равновесии
а) силы, действующие на противоположные грани куба,
равны;
б) равен нулю полный момент всех действующих на куб сил.
Из первого условия следует, что для характеристики напря-
напряженного состояния достаточно рассмотреть силы, приложенные
только к трем граням с одной общей вершиной, например к гра-
граням У, 2, 3 с общей вершиной О (рис. 13.18). На каждой из них
указаны компоненты действующих сил. Например, dF\x — это

13.3]
МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
343'
jc-компонента силы dFu приложенной к грани 1. Девять величин
_ dF]x dF2x _ dF3x
dS '
dFly
dS '
dF]z
dF2y
~~dS~*
dF2z
dS '
dS '
dS '
dS
полностью характеризуют силы, действующие на вещества
твердого тела, заключенного в единичном объеме, со стороны
Рис. 13.18.
окружающего вещества (рис. 13.18). Они-то и называются
механическими напряжениями (см. § 8.2) и образуют тензор,
tiro обычно записывают в виде матрицы
I TyK Gy Tyz \ .
TZx "^zy &z
Из условия (б) вытекает, что из девяти компонент тензора
напряжений независимыми являются только шесть. Действи-
Действительно, рассмотрим, например, силы dF\y и dF^x- Каждая из них
стремится повернуть куб относительно оси г, но в разных на-
направлениях. Ясно, что момент этих сил будет равным нулю, если.
dFiy = dF2x- А это означает, что %ху = хух. Аналогично устанав-
устанавливается, что xxz = xzx, xyz = xzy.
Из рис. 13.18 видно, что компоненты ох, оу, oz в зависимости
от знака характеризуют растягивающие или сжимающие
усилия. Компоненты ох, оу, gz являются нормальными напря-
напряжениями. Напряжения хху, xxz, xzy действуют в плоскости
соответствующих граней и поэтому называются касательными

344
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
или скалывающими (рис. 13.18; см. также § 8.2). И те, и другие
измеряются в единицах давления.
2. Смещения частиц твердого тела вызывают его деформа-
деформацию. Деформации выражаются в изменении как объема, так и
формы тела. В зависимости от знака изменение объема при не-
неизменной форме называется всесторонним растяжением или
сжатием. Изменение формы при неизменном объеме называется
сдвигом.
Если внешние силы не превышают определенного предела, то
вызванные ими деформации обратимы. Они исчезают при снятии
внешних нагрузок. Обратимые деформации называются упру-
упругими. Наибольшие напряжения, при превышении которых де-
деформация перестает быть обратимой, определяют предел упру-
упругости. Он зависит от природы тела и его предварительной
обработки. Так, монокристалл алюминия является упругим
телом, если напряжения не превышают 4 бар. Для технического
алюминия предел повышается до 103 бар.
При превышении предела упругости деформации приобре-
приобретают необратимый характер. Необратимость выражается в пла-
пластичности и разрушении. Пластические деформации не исчезают
при снятии внешних нагрузок, а при разрушении происходит
разъединение тела на две или более частей.
Во многих веществах разрушению предшествуют пластиче-
пластические деформации. Они сопровождаются течением вещества без
нарушения сплошности материала. Такие материалы назы-
называются пластичными. Так, монокристаллы цинка удается растя-
растягивать в 10 раз до наступления разрушения. При этом цилин-
цилиндрический образец вытягивается в ленту.
В развитии пластического деформирования главную роль
играет движение дислокаций. Они перемещаются при возникно-
возникновении сдвиговых напряжений, согласно механизму, обсуждав-
обсуждавшемуся ранее (см. рис. 13.12). Если дислокации выходят на по-
поверхность, то это приводит к необратимой деформации. На
рис. 13.19 показано, как это происходит.
Рис. 13.19.
Подчеркнем, что сдвиг, приводящий к пластической дефор-
деформации, может происходить и при приложении к образцу сжи-
сжимающих или растягивающих сил. Эту возможность иллюстри-

§ 13 3]
МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
345
рует схема на рис. 13.20. На ней изображен образец, в котором
имеется дислокация, образованная наклонной дополнительной
кристаллической плоскостью. Сжимающие образец силы имеют
составляющие вдоль направления, отмеченного пунктиром. Эти
составляющие осуществляют «косой» сдвиг, который приводит к
пластической деформации при выходе дислокации на поверхность»
Рассмотренные примеры демонстрируют основное отличие де-
деформации сдвига от деформации растяжения и сжатия. Оно за-
заключается в том, что деформация сдвига обладает неустойчи-
неустойчивостью. При сдвиге напряжения могут быть сняты в результате
пластического деформирования. В отличие от сдвига, напряже-
напряжения растяжения и сжатия исчезают только при снятии вызываю-
вызывающих деформацию внешних сил. Причина заключается в том, что
при растяжении и сжатии
источником увеличения вну-
тренней энергии тела яв-
ляется изменение объема.
Такое изменение энергии
нельзя устранить никаким
перемещением частиц тела.
Из дислокационной при-
природы пластичности выте-
вытекает, что наименьшим пре-
пределом упругости обладают
кристаллы с малой плот-
плотностью дислокаций (т. е. они являются наименее прочными).
В этом случае дислокации не мешают друг другу передвигаться
и пластическая деформация возникает при сравнительно малых
напряжениях. Упрочнение таких материалов осуществляется
введением примесей, останавливающих движение дислокаций.
Например, чистое железо является очень мягким материалом.
Однако при добавлении к нему углерода (чугун, различные
марки стали) предел упругости значительно увеличивается.
Важным свойством является также следующее: пластическое
деформирование приводит к повышению предела упругости. При-
Природа этого эффекта заключается в том, что при деформировании
возрастает число вакансий и частиц, находящихся в междоуз-
междоузлиях. Так, при деформации на 10% число точечных дефектов
решетки металлов достигает 1024—1025 на 1 м3. Дополнительно
возникшие дефекты тормозят движение дислокаций, приводя к
деформационному упрочнению. Это явление используется для
упрочнения металлов холодной обработкой (наклеп). Упрочне-
Упрочнение выражается в том, что при повторном нагружении матери-
материала предел упругости будет определяться напряжениями, кото-
которые вызвали последнюю пластическую деформацию при преды-
предыдущем нагружении.
Рис 13.20.

346
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
Поясним сказанное графически. На рис. 13.21 слева изобра-
изображена типичная зависимость напряжения а от относительного
удлинения е при растяжении. (Для убедительности на том же
рисунке справа приведена зависимость а от е, выраженного в
процентах, для алюминия, снятая при 300°К. Загиб кривой вниз,
в, /0%р
e-
f
О"
? 12 3 4 5 6
Рис. 13.21.
отмеченный пунктиром, обусловлен образованием «шейки» у об-
образца.) Величина сто — это предел упругости. При о > о0 появ-
появляется пластическая деформация. Пластическое деформирова-
деформирование описывается участком кривой АВ. Если достигнуто состоя-
состояние, которому отвечает точка Л', то при снятии нагрузки пове-
поведение тела будет описываться уже участком А'О'\ параллельным
участку АО. Отрезок 00' измеряет пластическую деформацию:
€(n1j} = 00/. Если затем тело снова нагружать, то оно будет де-
деформироваться по закону, который описывается участком О'А'.
Только после достижения состояния, которому отвечает точка
А\ начнется пластическая деформация. Следовательно, при по-
повторном нагружении пределом упругости будет о^ > а0. При
третьем цикле нагружения, которое начинается с состояния с
пластической деформацией е{*1 = ОО", предел упругости еще
больше увеличится до значения о" > сг^ > сг0.
Деформационное упрочнение со временем исчезает. Происхо-
Происходит это потому, что устойчивым состоянием твердого тела яв-
является состояние с идеальной решеткой. Поэтому тепловое дви-
движение в твердых телах стремится «залечить» дефекты. Это явле-
явление называется рекристаллизацией. Процесс рекристаллизации
протекает наиболее активно вблизи точки плавления.
Упрочнение не беспредельно. После достижения некоторого
предела тело переходит в текучее состояние и ведет себя по-

§ 13.3] МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ 347
добно вязкой жидкости. Максимальное значение предела упру-
упругости называется пределом текучести. Ни при каких деформа-
деформациях, за исключением всестороннего сжатия, в теле не могут
возникать напряжения, превышающие предел текучести. Однако*
предел текучести не всегда достижим, поскольку еще до пере-
перехода в текучее состояние материал может разрушиться. Разру-
Разрушение является следствием возникновения в теле мельчайших
трещин. Около острых вершин трещин возникают повышенные
напряжения, значения которых могут значительно превосходить
те, которые соответствуют действующим внешним силам. В ре-
результате может произойти разрыв связей между частицами в
районе вершины трещины. При этом трещина начинает расти.
Если в этот процесс вовлекается сразу много трещин, то эта
приводит к разрушению тела.
Отметим, что разрушение может произойти и без заметной
предварительной пластической деформации. В этом случае раз-
разрушение называется хрупким. Однако резкой границы между
хрупкими и пластичными телами не существует. Причина за-
заключается в том, что на характер деформирования влияют мно-
многие факторы: температура, тип напряженного состояния, скоро-
скорости деформирования, окружающая среда и т. д. Например,
повышение температуры увеличивает пластичность, так как.
интенсивнее залечиваются точечные дефекты и дислокации ста-
становятся более подвижными. Этим широко пользуются при горя-
горячей обработке металлов давлением. Наоборот, с уменьшением
температуры пластичность уменьшается. А так как пластические-
деформации способны заглаживать острия трещин, снижая тем
самым концентрацию напряжений, то с понижением темпера-
температуры хрупкость возрастает. Например, сталь при обычных:
температурах обладает высоким сопротивлением разрыву, при
низких же температурах она становится ломкой. Другой примеру
свидетельствующий об отсутствии четкой границы между пла-
пластичными и хрупкими материалами: мрамор является хрупким
при сжатии или растяжении только в одном направлении, а в-
условиях объемно-напряженного состояния проявляет пластиче-
пластические свойства.
Если бы в кристаллах не было дислокаций вообще, то проч-
прочность твердых тел была бы максимально возможной. Для иде-
идеальных кристаллов пластическое деформирование вообще недо-
недоступно. Так, для соскальзывания сразу всей верхней части кри-
кристалла относительно нижней (рис. 13.19) требуется затратить
очень большую энергию на одновременное перемещение всех,
частиц верхней части, лежащих на плоскости скольжения. Кри-
Кристаллы, близкие по своим свойствам к идеальным, могут быть
выращены только при соблюдении особых мер, обеспечиваю-
обеспечивающих образование монокристалла с почти идеальной решеткой.

348
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
Такими кристаллами являются тонкие «усы». Каждый кристалл
содержит одну винтовую дислокацию, вокруг которой осуществ-
осуществлялся процесс кристаллизации. На рис. 13.22 приведена фото-
фотография «усов» железа, выращенных из паров путем восстанов-
восстановления железа водородом из бромистого железа при 710°С.
Рис. 13.22,
3. Упругие деформации многих материалов подчиняются за-
закону Гука: деформации пропорциональны вызывающим их на-
напряжениям (см. § 2.3). Однако есть и исключения. Существуют
материалы, у которых предел упругости лежит достаточно вы-
высоко. При приближении к этому пределу начинает проявляться
нелинейная зависимость между деформацией и напряжением.
Именно так ведут себя, например, поликристаллы чистой меди.
При растяжении этого материала на 0,01% его первоначальной
длины (напряжение до 1,5-103 бар) закон Гука выполняется.
При растяжении же в пределах от 0,01% до 0,06% первоначаль-
первоначальной длины (область напряжений от 1,5-103 бар до 4,5-103 бар)
деформирование остается упругим, но уже является нелинейным
процессом.
Областью применимости закона Гука, как правило, являются
очень малые деформации. Рассмотрим основные законы линей-
линейных упругих деформаций поликристаллических тел.
При всестороннем сжатии (растяжении) напряжение не от-
отличается от давления (рис. 13.23) и вызывает относительное
изменение объема тела, равное
К
A3.1)

I3.3J
МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
349
Здесь К — постоянный коэффициент, называемый модулем все-
всестороннего сжатия. При сдвиге (рис. 13.24)
<P = t/G, A3.2)
где G — также постоянный коэффициент, называемый модулем
сдвига.
—
•
Iе-
>- 1
*~ 1
*" \^
\
1
<5 1
/^ А |
' 1
1
I
1
!
,\
Рис. 13.23.
Рис. 13.24
Модули К и G характеризуют упругие свойства материала
по отношению к основным видам деформации, являются поло-
положительными величинами и измеряются в единицах давления.
Положительность К и G обусловливается требованием механи-
механической устойчивости твердых тел. Согласно этому требованию
знак деформации и знак вызывающих ее напряжений должны
быть одинаковыми. Так, при всестороннем сжатии объем тела
может только уменьшаться, но не увеличиваться. Это означает,
что при о <С 0 изменение объема AV может быть только отри-
отрицательным. Это возможно лишь в том случае, если в A3.1)
К > 0. Если бы это было не так, то тогда каждое сжимающееся
тело являлось бы источником положительной работы, что физи-
физически абсурдно. Положительность модуля G доказывается ана-
аналогичным образом.
Часто вместо К и G рассматривают модуль Юнга Е и коэф-
коэффициент Пуассона v. Модули J( и G выражаются через Е и v
по формулам
G =
3A-2v) '
Я
2(l+v) •
A3.3)
A3.4)
Их справедливость будет доказана позднее.
Модуль Юнга является положительным и измеряется в еди-
единицах давления. Коэффициент Пуассона является безразмерной
величиной, значения которой не могут выходить за пределы

350
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. ТЗ"
интервала
-l<v<{, A3.5)
что является следствием положительности /С, G и Е. В действи-
действительности материалов с отрицательным коэффициентом Пуас-
Пуассона не наблюдается. Значения, близкие к l/2j характерны для:
тел, у которых велик модуль всестороннего сжатия. Примером
является резина.
Модуль Юнга и коэффициент Пуассона отражают упругие
свойства по отношению к деформациям одноосного растяжения
г или сжатия. Эти виды деформации
являются комбинированными, со-
_ стоящими как из деформации все-
= б стороннего растяжения или сжатия,.
- так и из деформации сдвига. На
рис. 13.25 появление деформации
сдвига при одноосном сжатии иллю-
иллюстрируется превращением внутрен-
внутреннего прямого параллелепипеда в ко-
косой. При одноосном линейном упругом сжатии или растяжении
относительное изменение длины образца е равно
Рис. 13.25.
е = о/Е.
A3.6)
При этом происходит изменение толщины образца (рис. 13.25).
Коэффициент Пуассона как раз и определяет относительное
поперечное растяжение или сжатие б через относительное удли-
удлинение или укорочение е:
б = — ve.
A3.7)
Положительность v для всех
известных материалов озна-
означает, что они при удлине-
удлинении только уменьшаются в
поперечном сечении.
Рассмотрим процесс од-
одностороннего сжатия (рас-
(растяжения). Он реализуется в
следующих условиях. Пусть
вещество твердого тела со
всех сторон, кроме одной, зажато жесткими стенками
(рис. 13.26). Пусть на него действует сила, вызывающая напря-
напряжение ох. Тогда вследствие реакции жестких стенок появятся
сжимающие напряжения oz и ау (ось у перпендикулярна пло-
плоскости рисунка). Обозначим через е*, еу, г2 деформации вдоль
соответствующих осей. При этом, конечно, в условиях односто-
Рис. 13.26.

§ 13.3] МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ 351
роннего сжатия гу = е2 — 0. Однако на время забудем об этом.
Рассмотрим, например, деформацию е2. Она будет, во-первых,
вызвана напряжением gz, а во-вторых, изменением размеров
тела, являющихся поперечными относительно деформирования
в х- и ^/-направлениях. Поэтому, в соответствии с A3.6) и A3.7),
^z= —
Аналогично находим:
Оу — У (Ох + Gz)
Положив теперь гх = гу — 0, получаем:
V
о а
v- 1
OY.
Для деформации в ^-направлении справедливы те же рас-
рассуждения, поэтому
__ ах — у (ау + дг)
Подставляя сюда найденные выше значения оу и az, получим:
l-v-2v^ A +v) A — 2у)
*х - ?(l_v) a* E(\-v)°f
Коэффициент * (Т_ о ^ называется модулем одностороннего
сжатия. Равенство A3.8) характеризует процесс упругого про-
продольного сжатия твердого тела.
Установим справедливость A3.3) и A3.4). Рассмотрим всестороннее сжа-
сжатие. В этом случае деформация тела вдоль каждой оси х, у, z (рис. 13.23)
будет одной и той же. Обозначим ее через е'. Рассмотрим, например, дефор-
деформирование вдоль оси х. Его величина будет складываться из деформации
одноосного сжатия вдоль оси х и изменения поперечных размеров тела, воз-
возникающих по направлениям у и z. Рассуждая теперь так же, как это было
сделано выше при рассмотрении одностороннего сжатия, мы приходим к ра-
равенству [см. A3.6) и A3.7)]
/ о , о*, a — 2vor I — 2v
о .' — -1 vn = ______ —— re
E ^~zo — ? — e a'
где б' определяет относительное изменение поперечных размеров при сжатии
в у- и 2-направлениях. Обозначим длины ребер изображенного на рис. 13.23
параллелепипеда через /*, /у, /z. Тогда его объем равен V = lxlylz. Следова-
Следовательно, малое изменение объема можно представить в виде
ДV = Д Aх1у1г) = Д/ж • у, + /* My ¦ 1г + lxly Д/2.

352
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
Отсюда получаем:
1х
¦ +
3A- 2v)
и
-а.
Сравнивая это выражение с A3.1), приходим к A3.3).
Рассмотрим деформацию сдвига. На рис. 13.27 изображен куб твердого
вещества, который показан с конца оси у, перпендикулярной плоскости ри-
рисунка. Внутри куба выделен другой, наклонный куб, вершины которого нахо-
находятся на серединах ребер большого куба. Длину ребер малого куба обозна-
обозначим через /. Пусть к граням большого куба приложены скалывающие силы,
z'
т
уф \
= Т
/
\
У
Рис. 13.27.
создающие касательные напряжения т. Для малого куба эти силы будут соз-
создавать вдоль направлений х' и zf, соответственно, растягивающие и сжимаю-
сжимающие нормальные напряжения ох, и а2,. Заметим, что сумма двух скалываю-
скалывающих сил, приложенных к граням с общим ребром, по величине в у 2 раз
больше каждой из скалывающих сил и лежит в одном из диагональных се-
сечений куба. В другом диагональном сечении эта сила будет вызывать нор-
нормальное напряжение. Но площадь каждого из диагональных сечений в V 2
раз больше площади каждой грани куба. Поэтому нормальные напряжения
в диагональных сечениях, т. е. ох, и аг,, по величине также будут равны т.
В результате сдвига большой куб превратится в скошенный параллеле-
параллелепипед. Две его боковые грани будут ромбами. Малый куб превратится в пря-
прямой параллелепипед. Обозначим длины его сжатых и растянутых ребер соот-
соответственно через l'z и fx (рис. 13.27). На рисунке отмечены также необходи-
необходимые для дальнейшего углы. При этом угол ф является малым Из рисунка
видно, что
/я ф \ 1 - tg (ф/2) l'z
НТ Т/ 1 4- tg (ф/2) ~ /'/
При малых
1
г (ф/2) 1 + (ф/2)
I--2-
1 2 '

§ 13.3] МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ 353
Поэтому с точностью до ф2
Х)—' ¦
При сжатии lz = / A — е')- Деформация е' складывается из деформа-
деформации сжатия вдоль z'-направления, равной ог*/Е = т/?, и деформации доба-
добавочного сжатия \bx, = va^/JE1 = vx/2?, возникающего за счет растяжения
вдоль оси х'\
Аналогично, 1Х = / A + е')« Учитывая малость е', с точностью до г' на-
находим:
-| -—V « A - е') A - е7) ~ 1 - 2а7. (б)
1Х 1 + е
Сравнивая равенства (а) и (б), получаем:
ф = 2е = !_Ь±т.
Сопоставляя это выражение с A3.2), убеждаемся в справедливости A3.4).
При деформировании твердых тел совершается работа. Она
запасается в виде упругой энергии. Так, при одноосном растя-
растяжении (рис. 13.25) малое изменение удлинения стержня равно
Ids. Поэтому малое приращение упругой энергии стержня dU
составит величину Fld&, где F — абсолютное значение силы,
растягивающей образец. Если поперечное сечение образца S, то
F = oS9 где а — напряжение. Поскольку IS = V, где V — объем
образца, то
dU
При этом мы воспользовались соотношением A3.6). Упругую
энергию недеформированного стержня естественно положить
равной нулю. Тогда, интегрируя dU в пределах от нуля до неко-
некоторого значения е, находим упругую энергию U(e) при дефор-
деформации е:
Отсюда видно, что каждый единичный объем тела обладает
упругой энергией
Эта величина называется плотностью упругой энергии одно-
одноосного деформирования. С помощью A3.6) она может быть
12 А. В« Астахов

354
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
выражена еще двумя способами:
во
2
2?
При всестороннем растяжении или сжатии плотность упругой
энергии равна
_ Кг2 _ 3 _ _о^
"~ 2 """" 2 8СГ~" 2К •
где деформация е и напряжение а связаны друг с другом соот-
соотношением A3.1). Доказательство последних равенств мы остав-
оставляем читателю в виде самостоятельного упражнения.
В заключение приводим таблицу значений различных упру-
упругих характеристик ряда веществ (табл. 10).
Таблица 10
Вещество
Железо кованое
Сталь
Латунь
Бронза
/С, 10е бар
1.4
1,8
1
0,9
G, 10е бар
0,7—0,8
0,7-0,8
0,3
0,3
Я, 10е бар
U9-2
1,9-2
0,9-1
0,8
V
0,27
0,25—0,33
0,34—0,40
0,36
§ 13.4. Тепловое движение в твердых телах
1. Рассмотрим внутреннюю энергию твердых тел, обуслов-
обусловленную тепловыми колебаниями кристаллической решетки. Со-
Сосредоточим сейчас внимание исключительно на тех условиях, в
которых колебания частиц твердого тела можно описывать
классическими законами. Для этого оценим область примени-
применимости классического рассмотрения. Колебания частиц кри-
кристаллической структуры в результате их взаимодействия не
являются изолированными. Это означает, что в кристаллах рас-
распространяются волны тепловых колебаний. Так как с микроско-
микроскопической точки зрения кристалл имеет дискретное строение, то
по порядку величины длина волны X не может быть меньше
среднего расстояния между частицами а:
Из этого ограничения следует, что частота тепловых колеба-
колебаний не может превосходить некоторого критического значения
<отах- Его легко получить с помощью формулы G.38):
2яр 2nv
где v — скорость распространения волны.

§ 13.4] ТЕПЛОВОЕ ДВИЖЕНИЕ В ТВЕРДЫХ ТЕЛАХ 355
Волны с большой длиной волны или малой частотой яв-
являются обычным звуком (длина волны намного превосходит а!),
Для оценки примем, что и для коротких волн (высоких частот)
по порядку величины v совпадает со скоростью звука. Анало-
Аналогично свету, который можно рассматривать как газ особых кван-
квантовых частиц — фотонов, звуковые волны высоких частот пред-
представляют собой газ квантов звука — фононов. Энергия фононов
определяется по тому же правилу, что и для фотонов: фонон
с частотой сотах обладает энергией
ср + 2nvfi
® max = fi^max = ——,
где h — постоянная Планка A.2). Характерная энергия тепло-
теплового движения на одну степень свободы имеет, как мы знаем,
порядок kT, где Т — температура тела. Отсюда следует, что
отношение
определяет характеристическую температуру тела. Она назы-
называется температурой Дебая в честь ученого, впервые в 1912 г.
объяснившего поведение теплоемкости твердых тел в низкотем-
низкотемпературной области. Обозначим дебаевскую температуру через
TD. Тогда критерий применимости классических представлений
записывается в виде
T*>TD. A3.10)
Если температура тела становится сравнимой с дебаевской тем-
температурой или оказывается ниже ее, то необходимо принимать
в расчет микроскопическое строение кристаллов и учитывать
квантовые закономерности.
Дадим численную оценку TD. По порядку величины скорость
звука v в твердых телах равна 103 м/сек. Расстояние а между
соседними частицами по порядку величины равно 1СН° м. Под-
Подставляя в A3.9) значения h и 6, получаем, что по порядку вели-
величины rD=102°K. Из-за «игры» различных коэффициентов, за
которыми мы не следили, значение TD может увеличиться до
величины порядка 103°К. Таким образом, для различных твер-
твердых тел значения TD варьируются в пределах от 102°К до 103°К.
При этом общая тенденция такова: чем жестче материал, тем
выше значение TD. Действительно, из A3.9) следует, что темпе-
температура пропорциональна скорости звука v. А скорость звука тем
выше, чем больше жесткость материала.
В табл. 11 указаны значения дебаевской температуры неко-
некоторых кристаллов.
Опыт показывает, что вдали от точки плавления струк-
структура кристалла вполне устойчива. Это означает, что колебания
12*

356
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. 13
Таблица И
Кристалл
РЬ
I
Na
Ag
TD, °К
88
106
172
215
Кристалл
NaCl
Fe
Be
С (алмаз)
TD, °К
231
453
1000
1860
частиц малы. Как малые, они являются гармоническими. По-
Поэтому при выполнении условия A3.10) твердое тело, состоящее
из N частиц, является системой 3N классических одномерных
гармонических осцилляторов. Увеличение N втрое связано с тем,
Су j
6
50 /00 150 200/ 250 300 Т
Рис. 13.28.
что частицы могут колебаться в трех независимых направле-
направлениях. Согласно закону равнораспределения энергии по степеням
свободы на каждый классический осциллятор приходится в
среднем энергия йГ, где Т — температура тела. Следовательно,
внутренняя энергия кристалла, обусловленная колебаниями его
решетки, равна
Поэтому
Для одного моля вещества (N = NA)
Cv = 3NAk = 3R = 6,3 ккал/град • кмоль = 25 • 103 Дж/град • кмоль.
Последние формулы выражают закон Дюлонга — Пти: при
температурах выше дебаевской теплоемкость кристаллических

§ 13 4] ТЕПЛОВОЕ ДВИЖЕНИЕ В ТВЕРДЫХ ТЕЛАХ 357
решеток твердых тел постоянна. Ее значение зависит только
от числа частиц, составляющих тело. Молярная теплоемкость
для всех тел одинакова и равна 6,3 ккал/граД'Кмоль =
= 25-103 Дж/град-кмоль.
На рис. 13.28 в качестве примера приведена температурная
зависимость молярной теплоемкости серебра. График показы-
показывает, что выше дебаевской температуры (см. табл. 11) закон
Дюлонга — Пти выполняется с очень хорошей точностью. Откло-
Отклонения появляются при Г < 7V Они тем значительнее, чем
ближе температура к нулю шкалы Кельвина. Поведение тепло-
теплоемкости при низких температурах будет рассмотрено в томе III.
Оно может быть объяснено только в рамках квантовой теории.
2. Все твердые тела при охлаждении и нагревании изменяют
свои размеры. Обычно с повышением температуры размеры тел
увеличиваются. Это явление называется тепловым расширением.
Его механизм заключается в расталкивании частиц при усиле-
усилении теплового движения. Качественная сторона этого явления
следующая. Тепловое расширение является эффектом, происхо-
происхождение которого обусловлено ангармоничностью тепловых коле-
колебаний. Действительно, при гармоническом колебании среднее
положение частицы все время остается неизменным и совпадает
с ее положением равновесия. Поэтому гармонический характер
тепловых колебаний исключает возможность теплового расши-
расширения, которое в действительности наблюдается. Тем самым
этот эффект есть следствие от-
отклонения тепловых колебаний от
гармонического закона.
Учтем ангармоничность коле-
колебаний частицы. Поведение потен-
потенциальной энергии U любой ча-
частицы отклоняется от параболи-
параболического закона и имеет вид, изо-
изображенный на рис. 13.29 (см.
также рис. 2.22). На рисунке
пунктиром изображена парабола р -32д
ci2, учитывающая взаимодей-
взаимодействие частиц в гармоническом
приближении (I обозначает отклонение частицы от равновес-
равновесного положения). Более точным приближением к истинному по-
поведению потенциальной энергии вблизи равновесного положе-
положения является закон
где g" — положительная постоянная. Член с |3 описывает асим-
асимметрию взаимного расталкивания частиц. Этот член мы уже
получали в § 7.1.

358 КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ [ГЛ. ТЗ
Среднее смещение {• найдем с помощью распределения
Больцмана с указанной выше потенциальной энергией:
[+ОО -j-1
— оо J
Это распределение нормировано на единицу: \ dW(l) = 1. По
правилу (8.2) находим:
1=
Вычисление интегралов с учетом малости смещения | приводит
к следующему результату:
| = const- kT. A3.11)
Убедимся в справедливости A3.11). Для малых ? допустимы следующие
приближения:
-f-oo +°°
—оо
-}-оо
+ OO
= \
( Щ) d%
—oo
JL J 6ed6 = x.
—oo
Здесь было использовано действительное для малых ? приближение
а также учтено обращение в нуль интеграла
обусловленное нечетностью подинтегральной функции.

§ 13.4] ТЕПЛОВОЕ ДВИЖЕНИЕ В ТВЕРДЫХ ТЕЛАХ 359
Введем теперь новую переменную интегрирования х = | yc/kT. Тогда
получаем следующие равенства:
+ ОО +ОО
— оо —оо
+ ОО +00
[ zel{)
kT J с
+
4,e f x*e-*dx,
с/2 J
—oo
Стоящие в их правых частях интегралы являются числами. Обозначим их
через а и Ь. Тогда окончательно находим, что
о ь
т. е. соотношение A3.11), в котором const =-^ •
Из A3.11) следует, что учет ангармоничности тепловых коле-
колебаний приводит к линейной зависимости среднего смещения
частицы от температуры. Величина а = const-к называется ко-
коэффициентом теплового расширения. Он не зависит от темпера-
температуры и измеряется в град.
Свойство а = const выполняется до тех пор, пока колебания
частиц можно рассматривать классически. В области низких
температур а изменяется, стремясь к нулю при приближении
к 0°К. Можно ожидать, что это изменение должно происходить
следующим образом. Как известно, kT определяет среднюю
энергию одного классического осциллятора &. Поэтому выра-
выражение A3.11) можно переписать в виде 1 = const-<§F. Эта фор-
формула подсказывает, что в квантовой области зависимость коэф-
коэффициента теплового расширения от температуры определяется
зависимостью энергии квантового осциллятора от температуры.
Вид этой зависимости будет установлен в томе III.
О величине коэффициента теплового расширения в классиче-
классической области можно судить по таблице 12, в которой приведены
значения а некоторых веществ. В монокристаллах вследствие
анизотропии коэффициент теплового расширения по разным на-
направлениям может иметь разное значение. Для примера в
табл. 12 приведены значения а|( и а± для цинка: а(| характери-
характеризует тепловое расширение вдоль боковых ребер шестигранных
призм, из которых составлена решетка Zn, cti — в перпендику-
перпендикулярном направлении.
Наконец, ряд веществ с увеличением температуры сжимают-.
с# Этим свойством при комнатной температуре обладают,
например, кальций и уран. Аномалии теплового расширения

360
КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
[ГЛ. ТЗ
Таблица 12
Вещество
Ац
Li
Na
К
а«10б, град 1
14
56
71
83
Вещество
КС1
CsCl
Zn
Zn
f
a-106, град"
100
50
aR =64
ax = 14
Рис. 13.30.
объясняются тем, что кривая потенциальной энергии, отвечаю-
отвечающая силам притяжения, обладает очень крутым наклоном. Влия-
Влияние этого фактора иллюстрирует рис. 13.30. Повышение темпе-
температуры приводит к увеличению энергии частицы: <§\ —>&2- При
этом границы движения частицы сме-
смещаются: п\—>а2, bi—*b2. При наличии
аномального наклона среднее положе-
положение частицы смещается влево: С\ —>
—*С2<С\. Это и означает, что про-
происходит тепловое сжатие.
3. В отличие от газов, уравнение
состояния твердого тела нельзя запи-
записать в виде, который был бы справед-
справедлив для всех твердых тел. Причина за-
заключается в большом многообразии
условий, в которых движутся частицы
твердых тел (различные формы кри-
кристаллических решеток, различия в за-
законах взаимодействия между частицами, разнообразные усло-
условия на границах твердого тела и т. д.). Все возможные факторы
точному учету не поддаются. Тем не менее в некоторых случаях
эта задача все же разрешима. Например, пусть упругое поли-
поликристаллическое тело наряду с нагреванием на ДГ градусов
подвергается одноосному растяжению. В твердых телах роль
давления играют напряжения, а роль объема берут на себя де-
деформации. Поэтому при одноосном растяжении с одновремен-
одновременным нагреванием уравнение состояния твердого тела может
быть записано в виде
е=4 + аДГ, A3.12)
где Е — модуль Юнга, а — коэффициент теплового расширения,
е — деформация, а — напряжение; о/Е определяет деформацию
одноосного растяжения, а аДГ — удлинение при нагревании на
ДГ градусов. Уравнение A3.12) связывает изменение размеров
тела, его температуры и действующее в теле напряжение в усло-
условиях одноосного растяжения.

ГЛАВА 14
ЗВУК
§ 14.1. Скорость звука
1. В число широко распространенных макроскопических про-
процессов входят движения вещества, объединенные под общим
названием звуковые волны или просто звук.
Звук представляет собой макроскопические волны, образо-
образованные упорядоченными малыми колебаниями вещества.
Макроскопичность волны означает, что ее длина X намного
превосходит характерный линейный размер микроскопического
строения среды. Следовательно, в газе X ^> /, где / — длина сво-
свободного пробега частиц газа. При нормальных условиях по по-
порядку величины /= 10~7 м, так что X !Э> 10~7 м. В жидкостях
и твердых телах X >> а, где а — среднее расстояние между со-
соседними частицами среды. Оно является величиной порядка
1 А = 10~10 м. Таким образом, для этих сред X 3> 10"~10 м.
Ограничения снизу на длину волны приводят к ограничениям
сверху на частоту. Их легко установить с помощью формул
G.3), G.38). При этом под v следует понимать скорость звука.
В газах при нормальных условиях скорость звука меняется в
пределах от 102 до 103 м/сек (исключением является водород,
для которого v > 103 м/сек). В жидких и твердых телах ско-
скорость звука почти на порядок выше, чем в газах. Таким обра-
образом, на основании упомянутых формул получаем, что частота
звуковых колебаний в газах при нормальных условиях
V = — < 1Q2 М/С?К ^ 1Q9 рц
2я Ю м '
а в жидких и твердых телах
В настоящее время в твердых телах умеют возбуждать звуковые
колебания с частотами примерно до 10ш Гц.

362 звук [гл и
Своим происхождением свойство упорядоченности обязано
тому, что звук возникает под воздействием механических коле-
колебаний. Так, звуковая волна, распространяющаяся от радио-
радиотранслятора, возбуждается колебаниями диффузора. Упорядо-
Упорядоченностью звуковые волны отличаются от хаотических движений,
например от тепловых колебаний частиц кристалла. Малость
колебаний вещества означает, что в звуковой волне отклонения
всех величин, характеризующих макроскопические свойства
среды, от их равновесных значений незначительны. Например,
перепады давления, возникающие в газе при прохождении че-
через него звука, меньше давления газа, не возмущенного
волной.
В более узком смысле звуком называются колебания среды
в диапазоне частот, воспринимаемых человеческим ухом, т. е.
в пределах от 16 Гц до 2-Ю4 Гц. Колебания с частотами
ниже 16 Гц называются инфразвуком, а с частотами свыше
2-Ю4 Гц — ультразвуком. Колебания сверхвысоких частот по-
порядка 1010 Гц называются гиперзвуком. Раздел физики, в кото-
котором изучаются звуковые явления, называется акустикой. В свя-
связи с этим звуковые волны называют также акустическими.
Макроскопический характер движений в поле звуковой вол-
волны позволяет не учитывать микроскопическое строение среды и
считать среду сплошной.
Для акустических волн в
любой среде колеблющейся
величиной является каждая
компонента достаточно ма-
малого смещения |(г, /) беско-
бесконечно малого объема среды
А У от положения равнове-
равновесия (рис. 14.1).
К физике звуковых яв-
явлений относятся следующие
141 вопросы, а) Как зависит
ис* ' # скорость звука от свойств
среды? б) Какие физические
величины характеризуют акустические явления? в) Каковы пре-
пределы применимости волнового уравнения к звуковым явлениям
и какие важнейшие физические явления возникают вне этих
пределов?
2. Определим скорость звука в газообразной или жидкой
среде. Заметим, что в этих средах могут распространяться толь-
только продольные волны, ибо ни газ, ни жидкость не сопротив-
сопротивляются изменению формы. Другими словами, в них могут возни-
возникать упорядоченные макроскопические колебания вещества
только в результате сжатия и растяжения.

§ 14 1]
СКОРОСТЬ ЗВУКА
363
Рассмотрим простейший случай одномерных звуковых волн.
Они могут быть возбуждены, например, колеблющейся мембра-
мембраной, помещенной в одном из концов длинной трубы, содержащей
газ или жидкость. Волновой процесс будет заключаться в пере-
перемещении по среде зон сжатий и разрежений вещества, вызван-
вызванных колебаниями мембраны. В данных условиях ? определяет
смещение вдоль трубы бесконечно тонкого (но макроскопиче-
макроскопического!) слоя вещества. Величина смещения зависит от коорди-
координаты х слоя в невозмущенном состоянии и от времени: | =
= l(xyt) (рис. 14.2). Очевидно, что и плотность, и давление
-РШГ:
Нч-
Рис 14.2.
также будут функциями х и L Давление и плотность в точке х
в момент времени t обозначим соответственно через Р(ху t) и
п(х, t). Равновесные значения этих же величин обозначим через
Р и п (без указания аргументов).
Рассмотрим вещество, заключенное в слое малой толщины
dx (рис. 14.2). Оно будет обладать ускорением —,*' . Масса
вещества составит величину mndx-S = pdx-S, где т — масса
одной частицы, р = тп — плотность массы, а 5 — поперечное
сечение трубы. На выделенную порцию вещества действуют
силы давления, приложенные к сечениям, расположенным в точ-
точках с координатами х и x + dx (рис. 14.2). Результирующая
этих сил равна
F = -[P{x + dx, t)-P{x9 t)]S = ~^^ldx-S.
На основании второго закона Ньютона мы можем записать ра-
равенство
которое после сокращения на dx-S выглядит следующим образом:
»n>(x,t) _^ dP(Xit)
дх ' \м-Ч

364 звук [гл 14
Это соотнощение является уравнением упорядоченного движе-
движения заключенного в трубе вещества.
Выразим —~г— через Цх, t). При этом необходимо учесть,
что а) распространение звука является адиабатическим процес-
процессом и б) звуковые колебания являются малыми.
Адиабатичность распространения звука определяется самой
природой звуковых волн. Действительно, звуковые колебания
приводят к возникновению в среде температурных неоднород-
ностей. По порядку величины их размеры равны длине волны Я.
Предположим, что звук распространяется в газе. Согласно
A1.7) время рассасывания температурной неоднородности с
размерами порядка К равно
Я2 Я,2
%
где х — коэффициент температуропроводности вещества газа,
vT — тепловая скорость движения его частиц, а / — средняя
длина их свободного пробега. Характерным временем волнового
процесса является его период Т = %/v, где v — скорость звука.
Из опыта следует (в этом мы вскоре убедимся непосредствен-
непосредственно) , что v и vT — величины одного порядка. Так как для звуко-
звуковых волн Я >> /, то по порядку величины
Последнее означает, что звуковая волна проходит расстояния,
сравнимые с размером вызываемой волной температурной неод-
неоднородности, настолько быстро, что теплообмен между различ-
различными участками среды развиться не успевает.
Таким образом, в звуковой волне изменение давления веще-
вещества происходит в результате адиабатического изменения его
плотности. Так как эти изменения малы, то
ДР(л:,/)==^|~^ An (л:,/),
где Ап(х, t)= n(x, t) — n\ АР(х, t)= P(x, t)— P, а производную
(дР/дп)аД нужно вычислять при условии адиабатичности рас-
распространения звука.
Отметим, что давление АР(х, t) называется акустическим.
Найдем Ап(х, t). Очевидно, что вещество, первоначально за-
занимавшее объем dx-S, после возбуждения волны к моменту t
будет занимать уже иной объем, равный
[v I г?\> _,1 - ? (*г I г1 лг 4\ _— v ? ( Y /Yl Q ——
Л —| WА, ^^ С^ \Л/ ""Г" (ЛЛ9 I j "~~ Л "—'" ^ \Лу I )\ О ——

§ ИЛ] СКОРОСТЬ ЗВУКА 365
Следовательно,
Выражая теперь п(х, t) через Ап(х, t), после сокращения на
dx-S в результате простых преобразований получаем:
Так как ¦ п — < 1,а смещение | также мало, то в фигур-
фигурных скобках выписанного равенства можно пренебречь вторым
членом, который по сравнению с д%(х, t)/dx является величиной
второго порядка малости. С этой точностью
Используя это равенство, проведем следующие преобразования:
dP(x,t) д ,р( л^рх^А^
дх дх ^ \Х> 1) Г> дх
_ (дР\ д№п(х, Ж _ _ (д?\ д21 (х, t)
\ дп >/ад dx ~ V дп ;ад %П dt*
Подставляя окончательный результат в A4.1), получаем одно-
одномерное волновое уравнение:
a2g (х, t) [
Отсюда следует, что в жидкой и газообразной среде скорость
звука определяется таким равенством:
Эта формула показывает, что скорость звука в газе и жидко-
жидкости зависит только от свойств среды в состоянии теплового рав-
равновесия. Чуть позже мы убедимся в справедливости такого же
суждения и относительно твердых тел. (Напомним, что о дан-
данном свойстве мы уже упоминали в § 7.3.)
Определим скорость звука в разреженном газе. Для этого
воспользуемся адиабатой Пуассона. Разделив A0.4) на (Nm)^y
где N— число частиц газа, а т — масса одной частицы, по-
получим:
- — = const.

366 ЗВУК [ГЛ. II
Следовательно,
(w )„=const •Ypv~'=7const • pv=:t-
Используя теперь уравнение состояния идеального газа (8.13),
находим:
(дР\ _ ynkT _ ykT
V dp Лд р т
Подставляя этот результат в A4.2), получаем:
Из A4.3) следует, что по порядку величины скорость звука
в газе совпадает с тепловой скоростью движения частиц газа.
В табл. 13 приведены значения скорости звука в некоторых га-
газах при 0°С. Обращает на себя внимание аномально высокая
скорость звука в водороде. Это отклонение от «нормы» обус-
обусловлено относительно малой массой молекулы водорода.
Газы, состоящие из одиночных атомов, и газы многоатомных
молекул отличаются тем, что в последних наблюдается диспер-
дисперсия звука. Дисперсия обусловлена объемной вязкостью — свой-
свойством вещества необратимо превращать в теплоту механическую
энергию при неравновесной (необратимой) объемной деформа-
деформации. Механизм этого явления таков. При быстром сжатии (рас-
(расширении) происходит нарушение равновесного состояния среды
и в ней возникают необратимые процессы, стремящиеся восста-
восстановить состояние теплового равновесия. Они проявляются в виде
вязкого трения в веществе. При сжатии и растяжении зависи-
зависимость силы вязкого трения от относительного изменения объема
определяется с помощью коэффициента объемной вязкости ?,
который имеет ту же размерность, что и кинематическая вяз-
вязкость v, и обычно имеет тот же порядок величины, что и v.
Как следствие объемной вязкости, дисперсия звука возни-
возникает следующим образом. Звуковая волна непосредственно ме-
меняет только поступательное движение молекул газа. Перерас-
Перераспределение энергии по другим, внутренним степеням свободы
молекул происходит вследствие их столкновений друг с другом
и в пределах каждого периода успевает пройти лишь частично.
Для низких частот за время одного периода перераспределение
практически завершается. С увеличением частоты появляется
диспропорция в распределении энергии по разным степеням
свободы молекул, все возрастающая по мере роста частоты. При
высоких частотах перераспределение энергии практически не
происходит. Поэтому на этих частотах газ многоатомных моле-
молекул ведет себя, как одноатомный, так как внутренние степени

§ ИЛ]
СКОРОСТЬ ЗВУКА
367
свободы не успевают возбуждаться. От того, как распределена
энергия по степеням свободы, зависит значение у в A4.3). Это
означает, что при разных частотах скорость звука в газах мно-
многоатомных молекул разная.
Перераспределение энергии между поступательными и вну-
внутренними (вращательными и колебательными) степенями сво-
свободы молекул приводит к «дисперсионным скачкам» скорости
звука. Они обусловлены «включением» или «выключением» при
изменении частоты различных внутренних степеней свободы.
Поэтому исследование дисперсии звука в газах позволяет изу-
изучать молекулярные процессы, протекающие в газовой фазе.
В отличие от газов, рассчитать температурную зависимость
скорости звука в жидкостях теоретически не удается, так как
неизвестно уравнение состояния жидкой среды. Обычно ско-
скорость звука в жидкости выражают через ее адиабатическую
сжимаемость
где vyA= m/p = l/n — удельный объем жидкости, а производ-
производная (дЯ/<Эауд)ад вычисляется при условии адиабатичности изме-
изменений объема жидкости в звуковой волне. Выражение, опреде-
определяющее скорость звука в жидкости, имеет такой вид:
*=VP/p". о4-4)
Эта формула получается из A4.2), если учесть, что юуж = т/р,
и определение р.
В табл. 14 приведены значения скоростей звука в некото-
некоторых жидкостях.
Таблица 13 Таблица 14
Газ
Азот
Водород
Воздух
Гелий
Кислород
Углекислый газ
v, м/сек
334
1284
331
965
259
268
Жидкость
Ацетон
Бензол
Вода
Керосин
Ртуть
Спирт метиловый
V, м/сек
1192
1326
1480
2330
1451
1123
Дисперсия звука наблюдается и в жидкостях и также обус-
обусловлена объемной вязкостью. Механизм этого явления в неко-
некоторых случаях такой же, как и в газах. Например, в сероугле-
сероуглероде, бензоле, четыреххлористом углероде объемная вязкость
обусловлена главным образом процессом передачи энергии от по-
поступательных степеней свободы молекул к внутримолекулярным

368 ЗВУК [ГЛ. 14
колебательным. Однако в большинстве случаев механизм
объемной вязкости более сложен, чем в газах. Так, объемная
вязкость растворов связана с изменением степени диссоциации
растворенного вещества. Объемная вязкость может быть обус-
обусловлена сольватацией молекул (присоединением молекул рас-
растворителя к молекулам растворенного вещества) и рядом дру-
других причин. Например, дисперсия звука в морской воде вызвана
присутствием в ней растворенной соли MgSO4.
3. Перейдем к рассмотрению скорости звука в твердых телах.
Звуковой волне, распространяющейся по газу или жидкости в
трубе, в твердых телах соответствует волна односторонних сжа-
сжатий и растяжений. Она также является продольной. При этом
в твердых поликристаллических телах роль (дР/др)Лд играет мо-
модуль одностороннего сжатия, отнесенный к плотности массы ве-
вещества. Действительно, изменениям давления газа или жидко-
жидкости в твердых телах соответствуют напряжения: ДР-*а. Так
как плотность изменяется вследствие сжатия и растяжения, то
относительному изменению плотности газа или жидкости Др/р
в твердых телах отвечает деформация е, т. е. Др/р—*е, или
Ар—>ре. Следовательно, величине АР/Др соответствует отноше-
отношение а/ре, которое согласно A3.8) равно отношению модуля од-
одностороннего сжатия к плотности массы. Таким образом, ско-
скорость продольных звуковых волн в поликристаллических твер-
твердых телах оказывается равной
p(l+v)(l-2v) * A4>5)
Помимо продольных волн, в твердых телах могут распро-
распространяться и поперечные звуковые волны. Они возникают в тех
случаях, когда в твердом теле возбуждаются деформации сдви-
сдвига. Волновой процесс заключается в движении по телу зон с
повышенным значением напряжения сдвига, разделенных зо-
зонами пониженного напряжения. При этом, в отличие от про-
продольных волн, в поперечной волне колебания могут происхо-
происходить в двух независимых направлениях, перпендикулярных на-
направлению распространения волны. Скорость распрострайения
v± каждого из двух независимых поперечных колебаний одина-
одинакова и зависит от модуля сдвига так:
Здесь мы воспользовались формулой A3.1).
Из A4.5) и A4.6) вытекают два следствия. Во-первых,
flu > v±, так как согласно A3.5)
(l-2v) <К

Н.21
ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКА
369
Для подтверждения мы приводим табл. 15, в которой указаны
V\\ и Vj_ для некоторых поликристаллических материалов.
Таблица 15
Вещество
Алюминий
Железо
Никель
и^ м/сек
6260
5850
5630
о_1_» м/сек
3080
3230
2960
Вещество
Сталь
Чугун
Лед
i»jjf м/сек
6100
4500
3980
uj_, м/сек
3300
2400
1990
Во-вторых, поскольку v\\ и у± пропорциональны ?"/2, то чем
тверже материал, тем больше скорость звука в нем.
Законы A4.5) и A4.6) выполняются для не слишком высо-
высоких частот звуковых колебаний. Для гиперзвуковых колебаний
начинает сказываться микроскопическое строение твердых тел.
Его влияние выражается в дисперсии гиперзвуковых волн.
В монокристаллах волны носят гораздо более сложный ха-
характер, что обусловлено анизотропией этих сред. Оказывается,
что в монокристалле в каждом направлении могут распростра-
распространяться три волны с разными скоростями. Эти волны не яв-
являются ни продольными, ни поперечными. Колебания частиц
в них имеют составляющие как вдоль, так и поперек направле-
направления распространения волны.
Так же как и для света, различие в скоростях распростране-
распространения звука в средах с различной жесткостью приводит к пре-
преломлению звуковых волн на границе раздела сред. Поэтому,
комбинируя различные материалы и придавая соответствующие
формы границам их контакта, можно создавать устройства, по-
подобные оптическим системам, например акустические линзы.
Акустические линзы изменяют сходимость звукового пучка. Они
применяются для улучшения направленности акустических из-
излучателей и приемников,, для создания мощных ультразвуковых
пучков, употребляемых при разнообразных применениях ультра-
ультразвука в химии, биологии, технологии и т. д.
§ 14.2. Физические характеристики звука
1. При прохождении звуковой волны вещество приобретает
дополнительную энергию, обусловленную упорядоченными ко-
колебаниями среды. Рассмотрим плоскую монохроматическую зву-
звуковую волну с частотой со и амплитудой а. Вспомним, что ки-
кинетическая и потенциальная энергии гармонического колеба-
колебания в среднем равны. Средняя кинетическая энергия единицы

370 звук [гл и
объема вещества равна
асо'
где ? — смещение при колебаниях, ар — плотность вещества
(см. § 7.1, п. 4). Поэтому в единичный объем вещества звук при-
привносит энергию, в среднем равную
# = 1ра2со2. A4.7)
Эта величина называется плотностью звуковой энергии.
В СИ она измеряется в Дж/м3.
Распространяясь и вовлекая при этом в колебания всё но-
новые частицы вещества, звуковая волна осуществляет перенос
энергии. Этот процесс характеризуется силой или интенсив-
интенсивностью звука. Сила звука определяет поток звуковой энергии,
т. е. энергию упорядоченного движения вещества, которая в
единицу времени переносится волной через единичную площад-
площадку, перпендикулярную направлению распространения волны.
Обозначим силу звука через /. Согласно определению
русо2а2 A4.8)
Действительно, за время dt через площадку dS, перпендику-
перпендикулярную направлению распространения волны, пройдет вся энер-
энергия, заключенная в прямом параллелепипеде, длина боковых
ребер которого равна v dt, а основанием является dS. Величина
этой энергии равна vdt-dSS. Отсюда следует, что за единицу
времени через единичную площадку переносится энергия v&.
В СИ сила звука измеряется в Дж/м2-сек = Вт/м2. На прак-
практике часто пользуются специальными внесистемными единицами.
Основная из них называется белом (б). Широко применяется и
десятая доля бела, которая называется децибелом (дб). Эти
единицы связаны с логарифмической шкалой измерений интен-
интенсивности звука. Своим происхождением эта шкала обязана осо-
особенности человеческого слуха, которая заключается в том, что
человеческое ухо реагирует не на интенсивность звука, а на
логарифм этой величины. Именно по этой причине диапазон
воспринимаемых человеческим ухом интенсивностей очень ве-
велик. В логарифмической шкале интенсивность /0 = 10~12 Вт/м2
принята за нулевой уровень. Сила звука такой величины близка
к порогу слышимости человеческим ухом звука с частотой
103 Гц. Уровень интенсивности в децибелах определяется как
101(///)
g(/)
Сила звука связана с акустическим давлением. Найдем эту
связь, полагая, что ось х выбрана в направлении распростра-
распространения волны и звук распространяется в газе. Выражая по фор-

§ 14.21 ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКА 371
мулам предыдущего параграфа АР(ху t) через дЦдх и учитывая
A4.2), находим, что давление АР(х, t) отличается от д^/дх на
множитель, по абсолютной величине равный v2p, где v — ско-
скорость звука. Воспользуемся комплексной формой закона движе-
движения в поле звуковой волны. В связи с этим произведем пере-
переобозначение g на ip (см. гл. 7). Тогда от дЦдх мы должны пе-
перейти к д^/дху где
Отсюда с учетом формулы G.35) получаем:
дх v Y
Мы видим, что абсолютная величина коэффициента пропор-
пропорциональности между акустическим давлением и смещением
равна
со
—
Эта величина показывает, во сколько раз амплитуда акустиче-
акустического давления отличается от амплитуды колебания среды а.
Следовательно, обозначив амплитуду акустического давления
через АР (без указания аргументов!), находим, что
A4.9)
Произведение vp принято называть акустическим сопротив-
сопротивлением среды. Из A4.8) и A4.9) следует, что
Амплитуда акустического давления может достигать весьма
больших значений. Например, в воде при силе звука 10 Вт/м2
имеем АР = 5,9 бар.
При распространении ультразвуковых волн перепады аку-
акустического давления происходят на очень малых расстояниях,
составляющих половину длины волны. Так, например, в воде
при распространении ультразвука с частотой v = 107 Гц это
происходит на длине u/2v, которая порядка 10~3 м.
Резкие перепады давления на малых расстояниях приводят
к большим сжатиям и разрежениям вещества, т. е. к выходу
за пределы применимости волнового уравнения, описывающего
только малые колебания среды. Это нарушение проявляется в
возникновении явления акустической кавитации. Акустической
кавитацией называется образование разрывов сплошности жид-
жидкости с последующим захлопыванием полостей при возбужде-
возбуждении в жидкости достаточно интенсивных ультразвуковых коле-
колебаний. Полости образуются при разрыве жидкости во время

372 звук [гл. н
полупериодов растяжения на так называемых кавитационных
зародышах. Кавитационными зародышами являются плохо сма-
смачиваемые участки твердого тела, погруженного в жидкость,
твердые частицы, частицы с трещинами, заполненными газами,
микроскопические газовые пузырьки, ионные образования, воз-
возникающие под действием космических лучей. Если амплитуда
акустического давления становится выше некоторого значения,
называемого навигационным порогом, то начинается быстрый
рост на этих зародышах пузырьков пара жидкости, что и озна-
означает появление разрывов ее сплошности. Эти заполненные па-
паром полости захлопываются во время полупериодов сжатия.
Величина кавитационного порога может меняться в очень
широких пределах: от величины давления насыщенного пара до
десятков и даже сотен бар. В настоящее время кавитационный
порог рассчитывать не умеют. Экспериментально установлено,
что его величина повышается с увеличением гидростатического
давления жидкости, при ее очистке от инородных включений,
с увеличением частоты и с уменьшением продолжительности
озвучивания. При захлопывании кавитационных полостей разви-
развиваются чрезвычайно большие, до нескольких тысяч бар, им-
импульсы давления. Они способны привести к разрушению тел,
соприкасающихся с кавитирующей жидкостью. Так, например,
в ряде случаев наблюдалось разрушение лопастей быстро вра-
вращающихся гребных винтов и турбин, возбуждавших вращением
в жидкости интенсивные ультразвуковые колебания.
2. Помимо дисперсии и акустической кавитации явлением,
также выходящим за пределы применимости волнового уравне-
уравнения, является затухание звука. Напомним, что решениями вол-
волнового уравнения являются волны, существующие бесконечно
долго (см. гл. 1). Так, одномерное волновое уравнение
а2» (*, 0 1 ач (*, 0 _ п
дх2 v2 dt2 -~~и
имеет решение вида
-ф(х, /) = ае-ш+1кх, где а = const и о = kv.
В каждой фиксированной точке х этот закон описывает неза-
незатухающие колебания с частотой о). Затухание звука обуслов-
обусловлено взаимодействием упорядоченных колебаний с неупорядо-
неупорядоченным тепловым движением среды. Это взаимодействие раз-
разрушает звуковые колебания, переводя энергию упорядоченного
движения в тепло. Поэтому волновое уравнение применимо
к звуку только для интервалов времени и расстояний, на кото-
которых затухание звука незначительно.
Выясним, чем определяется затухание. Уменьшение силы
звука dl при распространении на расстояние dx пропорцжн

§ 14 2] ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКА 373
нально dx и интенсивности / в начале этого участка. Поскольку
dl < 0, то все сказанное выражается таким соотношением:
Здесь у — не зависящий от х коэффициент пропорциональности,
который называют коэффициентом затухания. В СИ он изме-
измеряется в м. Множитель 2 введен из соображений удобства,
которые станут понятными чуть ниже. Записанное выше соот-
соотношение является дифференциальным уравнением относительно
интенсивности 1 = 1(х). Решение этого уравнения имеет вид
где /о — сила звука в начальной точке х = 0. Поскольку сила
звука пропорциональна квадрату амплитуды колебаний, то, обо-
обозначив последнюю через а, приходим к такому выводу: ампли-
амплитуда колебаний на глубине проникновения х равна
а = а(х) =
Мы видим, что, так же как и интенсивность, амплитуда за-
затухает по экспоненциальному закону. При этом показатель
экспоненты не содержит численных коэффициентов. В этом и
состоит удобство введения коэффициента 2 в уравнение для
1(х)у о чем было сказано выше.
Существует несколько механизмов затухания звука. Однако
их роднит то общее, что в результате энергия упорядоченного
волнового движения вещества необратимо превращается в энер-
энергию теплового, т. е. беспорядочного, движения его частиц.
К этим последствиям приводят теплопроводность, обычная и
объемная вязкость.
Теплопроводность развивается в результате колебаний тем-
температуры, которые возникают в среде при распространении п
ней звука. Напомним, что распространение звука является адиа-
адиабатическим процессом. А при адиабатическом процессе темпе-
температура изменяется.
Другой механизм обусловлен обычной и объемной вяз-
вязкостью. Действительно, звуковые колебания могут приводить
к сдвигу одних частей среды относительно других и вызывать
растяжения и сжатия вещества. Из сказанного следует, что
коэффициент затухания можно представить в виде суммы у =
= Yi + Y2> где yi и Y2 — это коэффициенты затухания, своим
происхождением обязанные, соответственно, теплопроводности
и вязкости, как обычной, так и объемной.
Оценим из соображений размерностей порядки величин yi
и Y2- Для этого заметим, что искомые величины должны зави-
зависеть только от свойств среды и от характеристик звуковой вол-
волны. Свойства среды относительно перечисленных необратимых

374 звук [гл. и
процессов характеризуются температуропроводностью х> кине-
кинематической вязкостью v и объемной вязкостью ?. Все эти коэф-
коэффициенты имеют одинаковую размерность. Звуковую же волну
характеризуют скорость звука v и частота со. Из перечисленных
величин можно составить единственные комбинации, имеющие
размерность обратной длины:
СО2 СО2 (О2 _.
X v
Отсюда следует, что по порядку величины
СО2 СО2 / ,
Важным свойством установленных зависимостей является
пропорциональность коэффициентов затухания квадрату часто-
частоты звуковых колебаний. Оно означает, что с возрастанием ча-
частоты затухание быстро увеличивается. Так, инфразвук свобод-
свободно проходит даже через земной шар. А звуковые волны с ча-
частотой 106 Гц при температуре 20°С затухают уже на расстоя-
расстоянии порядка 50 м. Особенно сильно затухание звука на очень
высоких частотах. Именно это препятствие является основной
трудностью на пути получения гиперзвуковых колебаний.
Отметим, наконец, что в газах yi и у2 — величины одного по-
порядка, причем объемная вязкость существенна только для газов
многоатомных молекул. Для жидкостей yi существенно мень-
меньше Y2- В твердых телах затухание определяется как вязкостью,
так и теплопроводностью.
§ 14.3. Ударные волны
1. При взрывах, при движении в газе тел со сверхзвуковыми
скоростями, при мощных электрических разрядах, при ударах
о преграды происходят сильные возмущения среды. Например,
изменения плотности вещества могут оказаться сравнимыми с
^возмущенной плотностью. В этих случаях скорость распро-
распространения возмущения начинает зависеть от его величины и
возникает так называемая ударная волна. На рис. 14.3 приве-
приведена фотография ударной волны, образованной снарядом, дви-
движущимся быстрее звука.
Ударной волной называется распространяющаяся со сверх-
сверхзвуковой скоростью узкая переходная область волны сжатия,
s которой происходит скачок всех величин, характеризующих
состояние вещества, — плотности, давления, скорости движения
вещества, температуры и т. д. Ударные волны образуются во
всех средах — газах, жидкостях и твердых телах.

§ 14.3] УДАРНЫЕ ВОЛНЫ 375
Рассмотрим механизм образования ударной волны на еле-
дующем примере. Пусть газ в трубе подвергается сильному сжа-
сжатию со стороны поршня, который перемещается с очень большой
скоростью. В момент времени t0, близкий к началу движения,
плотность газа будет распределена так, как это показано на
рис. 14.4, а. Повышенной плотность будет только в конечной
Рис. 14.3.
области вблизи поршня. Вдали плотность будет иметь невоз-
невозмущенное значение ро. Распределение давления будет иметь га>
добную форму. Возникшая зона сжатия начнет распространять-
распространяться по газу со сверхзвуковой скоростью.
Действительно, скорость перемещения зоны сжатия относи-
относительно газа и скорость течения газа, вызванного движением
поршня, имеют одинаковое направление. Поэтому скорость зоны
сжатия относительно стенок трубы будет больше скорости ее
движения относительно газа на величину скорости течения газа.
Кроме того, быстрое сжатие всегда является адиабатическим.
За время сжатия теплопроводность развиться не успевает. По-
Поэтому температура газа в зоне сжатия повысится, причем тем
значительнее, чем выше степень сжатия. Напомним, что ско-
скорость звуковых волн в газах увеличивается с ростом темпера-
температуры по закону Г/2. Поэтому, во-первых, скорость распростране-
распространения зоны сжатия будет выше скорости звука в невозмущенном
газе, так как температура несжатого газа ниже температуры
сжатого. Во-вторых, скорость слоя Ах\ зоны сжатия будет пре-
превышать скорость слоя A#2 (рис. 14.4,а). Поэтому слой Ах\ будет
догонять слой Ах2 и газ у фронта волны сжатия будет уплот-
уплотняться. В результате, перемещаясь со сверхзвуковой скоростью»
зона сжатия оторвется от поверхности поршня и области тече-
течения газа. При этом со временем ее фронт будет становиться все

376
ЗВУК
[ГЛ. 14
более крутым (рис. 14.4,6). В конце концов в некоторой точке xq
сформируется ударная волна — очень узкая область с размером
порядка среднего расстояния между частицами газа. В этой
области плотность будет скачком изменяться на конечную ве-
величину Др (рис. 14.4,в),
которая называется скач-
,,х . .„ ком плотности на фронте
я) ;;\^ ударной волны.
На фронте ударной
волны вместе с плот-
плотностью испытывают раз-
разрыв давление, температу-
температура газа, скорость его дви-
движения. При этом через
поверхность разрыва про-
происходит течение газа: он
переходит из области с
меньшей плотностью в
область с большей плот-
плотностью.
В табл. 16 приведены
значения параметров
х° ударной волны, распро-
Рис. 14.4. страняющейся по возду-
воздуху, который находится
при нормальных условиях: Ро = 1,013 бар, Т = 0°С, р0 =
= 1,29 кг/м3. Обозначения Рь рь ^i соответствуют давлению,
плотности и температуре за фронтом; w — скорость ударной
волны. Как видно из таблицы, скорость ударной волны стреми-
стремительно возрастает с увеличением давления за ударным фронтом
и может во много раз превысить скорость распространения зву-
звука. Поэтому мощные ударные волны (они образуются, например,
при термоядерных взрывах) тем более ,коварны, что не преду-
предупреждают о своем приближении шумом и обрушиваются совер-
Ах, Ах2
'л
X
t,>t0
Pi, бар
1
5
10,1
50,6
128
568
Pi/Po
1
2,84
3,88
6,04
8,58
И
w, м/сек
330
700
980
2 150
3 350
6 970
ти °к
293
482
705
2 260
4 000
10 000
Рь бар
1013
3019
6 463
19 440
145 771
Pi/Po
11
9,75
8,97
8,62
6,27
Таб
wt м/сек
9310
15 900
23 300
40 100
114 000
лица 16
ти °к
14 000
30 000
50 000
100 000
500 000

§ 14.3}
УДАРНЫЕ ВОЛНЫ
377
шенно неожиданно. Так, если бы термоядерный взрыв не со-
сопровождался вспышкой, то узнать заранее о порожденной им
ударной волне было бы невозможно.
На формирование ударного фронта требуется время. Оно
тем больше, чем меньше степень первоначального сжатия. Во-
первых, от нее зависит, насколько в начальный момент газ
уплотнен у переднего фронта зоны сжатия. Во-вторых, степень
первоначального сжатия определяет, насколько повысилась тем-
температура и, следовательно, как быстро будет идти процесс
дальнейшего уплотнения. Если бы не действовали механизмы
затухания, то с течением времени ударный фронт мог бы раз-
развиться из любой волны сжатия, в том числе и из очень слабой.
Однако при слабом сжатии волна затухает раньше, чем сфор-
сформируется ударный фронт, и он образуется только при сильном
сжатии. Ударные волны, образующиеся при взрывах, обладают
огромной разрушительной силой. При этом чем больше мощ-
мощность взрыва, т. е. чем выше степень первоначального сжатия,,
тем дальше распространяется, не разрушаясь, ударный фронт.
2. Рассмотрим скачки физических величин на ударном
фронте в газе. Пусть AS — достаточно малый элемент фронта
ударной волны, такой, что его можно считать плоским. Введем
систему координат, жестко связанную с этим участком, и ее
ось х направим по скорости фронта (рис. 14.5). Из невозму-
невозмущенной области х > 0 за единицу
времени через AS пройдет газ, за-
занимавший объем УолД5. Масса это-
этого газа равна po^ooc'AS, где р0 —
плотность невозмущенного газа, а
^осс — его скорость вдоль оси х.
С другой стороны в область х < О
позади фронта за единицу времени
через AS поступает масса газа
piflixAS, где pi и V\x — плотность и
^-компонента скорости газа за удар-
ударным фронтом. Вследствие сохране-
сохранения массы po^oxAS = pi^AS, или
Эти равные количества обозначим через /. Импульс газа, вы-
вытекающего в единицу времени из невозмущенной области х > 0^
равен (potfo) vOxAS. Импульс газа, втекающего за единицу вре-
времени в область х <С 0 за ударным фронтом, соответственно со-
составляет (p\Vi)vixAS. В этих выражениях v0 и V\ обозначают
скорости газа в областях х > 0 и х < 0. Таким образом, измене-
изменение импульса равно
(р,Vi) vlx AS — (р0г>0) vOx AS = / (v{ — vQ) AS.
| РпР,
! *ы
у"
У
ч
W
W
г
У
У
РоЛ
) х
¦''

378 звук 1гл. u
Это изменение вызвано разностью сил давления перед и за
ударным фронтом, которая равна (Ро — P\)AS, где Ро и Р\ —
соответственно давления перед фронтом и за ним. Приравнивая
согласно второму закону Ньютона изменение импульса эле-
элемента газа действующей на него силе, получим в компонентах:
PX + P2+, j(vQyvlyH, J(vOzvlz) O.
Последние два равенства обусловлены тем, что сила направ-
направлена перпендикулярно площадке AS. Из них следует, что
Таким образом, параллельные ударному фронту компоненты
скорости газа скачка не испытывают. Скачок претерпевают
только нормальные составляющие.
Используем теперь * закон сохранения энергии. Изменение
энергии протекающей через AS массы газа должно быть равно
работе сил давления, перегоняющих газ через ударный фронт.
Кинетическая энергия газа, втекающего в единицу времени в
сечение AS из невозмущенной области х > О, равна
Кинетическая энергия газа, вытекающего за фронт волны, равна
Внутренняя энергия газа перед и за ударным фронтом:
?о (Pot>o*)Д5 = Eol AS, ?i (Pi*u) AS = Exj AS
(через ?о и E\ обозначены внутренние энергии единицы объема
иевозмущенного газа и газа за ударным фронтом). Наконец,
работа сил давления над единицей массы газа равна
PiVi-PqVo = Pi ^
М pt р0 '
где М — масса газа, а Уо и V\ — объемы, которые эта масса
газа занимает перед и за ударным фронтом. Приравнивая из-
изменение энергии работе сил давления, после сокращения на /
получаем:
+ ? + = + ?+
Итог таков: значения величин, характеризующих состояние
газа перед ударным фронтом и за ним, связаны системой ра-

§ Т4.31 УДАРНЫЕ ВОПНЫ 379
венств, выражающих закон сохранения массы, уравнения дви-
движения и закон сохранения энергии:
о A4П)
Щу — Щу = vOz — vlz = О,
Добавляя к этим соотношениям уравнение состояния газа,
можно определить значения всех характеризующих газ величин
за фронтом ударной волны, если известны значения этих вели-
величин перед фронтом, а также скачок любой из величин в ударной
волне. Если из уравнений A4.11) исключить скорость газа, то
между оставшимися величинами получается соотношение, свя-
связывающее их значения по обе стороны разрыва. Это соотноше-
соотношение называется ударной адиабатой или адиабатой Гюгонио.
Адиабату Гюгонио можно получить следующим образом.
Выразим плотность через удельный объем и исключим vOx и v\K
из первого и последнего уравнений системы A4.11). Получим *):
Исключая из этих равенств /2, находим уравнение ударной адиа-
адиабаты:
Eo^El + ^(vo-vl)(Po + Px) = O. A4.12)
Если газ достаточно разрежен и к нему применимы законы
идеального газа, то Е = Pv/(y —- 1). В этом случае уравнение
ударной адиабаты имеет вид
v0 (Y - 1) Л)+ (Y+l)Pi ' Vit.ioj
Так как в ударной волне давление только возрастает, та
имеет физический смысл лишь та часть адиабаты A4.13), ко-
которой соответствует Pi > Pq. График адиабаты Гюгонио A4.13)
изображен на рис. 14.6. Ее часть, имеющая физический смысл,
выделена на рисунке сплошной линией. Если Р\/Ро—>оо, та
адиабата A4.13) стремится к асимптоте, уравнение которой
имеет вид
-?Ls=3
vQ у +1
*) Везде в дальнейшем v обозначает удельный объем: Vq — перед удар-
ударным фронтом, vi — за ним.

380
ЗВУК
[ГЛ. 14
-1
ui/uo
Рис. 14.6.
Из этого уравнения следует, что с помощью ударной волны
нельзя достичь беспредельного увеличения плотности. Макси-
Максимально достижимая плотность
_ равна
° ll Y+1
Pi max = Ро Y__ j •
В этом заключается причина то-
того, что отношения pi/po, приве-
приведенные в табл. 16, не проявляют
тенденции увеличиваться с ро-
ростом давления.
3. Рассмотрим образование
ударных волн в газе при движе-
движении в нем тела со сверхзвуковой
скоростью. Выясним сначала,
в чем заключается разница движений в дозвуковом и сверхзву-
сверхзвуковом режимах.
Если скорость меньше звуковой, то тело излучает вперед
болны сжатия. Они как бы «предупреждают» газ о приближе-
приближении тела. «Заблаговременно предупрежденный», газ плавно
расходится, пропуская тело. Картину газового потока удобно
рассматривать из системы отсчета, жестко связанной с телом.
Относительно этой системы
вдали от ее начала поток газа
является плоскопараллельным.
Вблизи начала линии потока
плавно искривляются, огибая
тело. Если тело имеет хорошо
обтекаемую форму, то за ним
не возникает завихрений.
ударный фронт
Рис. 14.7.
ТолоЬной
Сверхзвуковой режим дает -f-^бостоЫ / УдпРный <РРонт
совершенно иную картину. Газ
не успевает расходиться перед
телом. Его настигают волны
сжатия и возникает так называемый головной ударный фронт.
У задней кромки тела образуется еще одна ударная волна
(рис. 14.7). Она называется хвостовой. Газ, сжатый в голов-
головной волне, затем расширяется до давления меньше исходного.
Возврат к первоначальному давлению как раз и осуществля-
осуществляется в хвостовой волне. На некотором расстоянии от тела обе
волны имеют вид конусов, вложенных один в другой (рис. 14.7).
Уплотнение газа в ударной волне является причиной изме-
изменения его показателя преломления. Поэтому ударную волну
можно фотографировать (см. рис. 14.3).

§ 14.3] УДАРНЫЕ ВОЛНЫ 381
Легко понять, что газ в ударной волне должен нагреваться.
Так, в выбранной нами системе отсчета поток газа, доходя до
тела, останавливается.
Следовательно, кинетиче-
кинетическая энергия его упоря-
упорядоченного движения, т. е.
энергия его потока, пере-
ХОДИТ В Иную форму. Она ^ХдостоЪ'й /^дарныйифронт
превращается в энергию
теплового движения, т. е.
во внутреннюю энергию р -
газа. После прохождения
ударного фронта газ про-
продолжает нагреваться и доходит до так называемой темпера-
температуры торможения. При этом может возникнуть свечение газа.
Подчеркнем, что свечение возникает вовсе не от трения тела
о газ, как это неверно иногда объясняют. Причиной его воз-
возникновения является разогрев газа в ударной волне. Это свече-
свечение наблюдается, например, при падении на Землю метеоритов,
при полете ракет. Если разогрев газа достаточно велик, то это
может привести к плавлению тела. Видимо именно это произо-
произошло с тунгусским метеоритом, который тщетно искали хмного раз.
Тело, движущееся в газе со сверхзвуковой скоростью, за-
затрачивает значительную часть своей кинетической энергии на
образование обычных и ударных волн. При этом оно испыты-
испытывает сопротивление, которое называется волновым. Волновое со-
сопротивление имеет иную природу, нежели сопротивление, кото-
которое испытывают тела, движущиеся с дозвуковыми скоростями.
При сверхзвуковых скоростях последнее значительно меньше
волнового. Для уменьшения волнового сопротивления выгодно
придавать спереди телу заостренную форму. Тогда на носу
образуется коническая ударная волна. Она преломляет парал-
параллельные линии набегающего потока. В хвостовой ударной волне
они преломляются, переходя опять в параллельный поток
(рис. 14.8). Обе эти волны заметны на значительном удалении
от тела. Так, громкие хлопки от пролетающих сверхзвуковых
самолетов слышны на расстояниях до 20 км и далее. Их источ-
источником являются образующиеся ударные волны.
В заключение, отметим, что ударные волны образуются во
всех средах: в газах (за исключением ультраразреженных), в
жидкостях, в твердых телах, в сверхплотной ядерной материи.
В макроскопических количествах ядерная материя встречается,
например, в виде нейтронных звезд. Плотность массы в таких
образованиях по порядку величины равна 1017 кг/м3.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно твердое тело 28, 158—171
Аддитивность 62
— внутренней энергии 229
— импульса 95
— массы 61—62
— момента импульса ПО—111
— энтропии 268, 274—275
Адгезия и адсорбция 341—342
Акустическое сопротивление 371
Амплитуда 173
Атмосфера (единица) 217
Бар 217
Барн 151
Барометрическая формула 243
Бел 370
Биения 206—207
Вакансии 334—336
Вероятность 215, 235, 238—239, 281—284
Взаимодействия фундаментальные 68—69
Волна 193
— монохроматическая 193
— плоская 194—196
— поперечная, продольная 194
— стоячая 202—203
— сферическая, цилиндрическая 197—198
Волновая поверхность 197—198
Волновое уравнение 199
— число 195
Волновой вектор 196
— фронт 198
Время 20, 24
— релаксации 214. 295, 364
— свободного пробега 222
— собственное 46
— столкновения 222
Всестороннее сжатие (растяжение) 344
Второе начало термодинамики 267, 275—284
Вязкость 286, 300—302, 373—374
— объемная 366, 373—374
Газ 216
— идеальный 222
— Кнудсена 222
Гиперзвук 362
Гравитационная постоянная 70
Давление 217-218, 224-227. 243, 363-366,
378-379
— акустическое 364
— критическое 313-
— парциальное 225—226
Движение 23
— в кулоновском поле 131—140
Дгижение заряженной частицы 114—124
— квантовое и классическое 21
— под действием упругой силы 176—177
—- релятивистское, нерелятивистское 20
— тепловое 211
— финитное, инфинитное 105
Дефект массы 107
Дефекты кристаллов 333—342
Деформации упругие 344
Джоуль (единица) 81
Диаграмма состояний 259
Динамическая закономерность 221
Дислокации 337—341, 344, 347
Дисперсионное уравнение 198
Дисперсия волн 198
— звука 366—369
Дифракция 202
Диффузия 286, 293—300
Длина волны 197
— свободного пробега 156, 236
Добротность 182—184
Задача двух тел 124—125
Закон Авогадро 225
— возрастания энтропии 276-—280
— Гука 76, 77, 348
— Дальтона 225
— Дюлонга — Пти 356
— Кулона 72—73
— независимости действия ^сил 60
— Паскаля 217
— равнораспределения энергии 231
— соответственных состояний 318
— сохранения импульса 58, 64—65, 92, 94—
96, 143, 145, 147-148, 153-154
момента импульса 93, 108—113, 126—
128, 132, 163
центра инерции 61—62, 93, 126, 144
энергии 93, 97—104. 143—147, 153—154
— Фика 293
— Фурье 293
Законы Кеплера 127. 136, 137
— Ньютона 25, 59, 60
Звук 361-362
Звука затухание 372—374
— сила (интенсивность) 370
Изотропность пространства 91
Импульс нерелятивистский 58
— релятивистский 63
— фон он а 97
Инвариантность 26—27, 38. 50
Интервал 51
Интерференция 202
Инфразвук 362
Источник Франка — Рида 340
—• энтропии 290—291

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
333
Кавитация 371—372
Калория 261
Камера Вильсона 147, 320—322
Колебания 172
— вынужденные 184—189
— гармонические 172, 193
— затухающие 180—183
Коэффициент диффузии 293 и д., 336
— затухания 182, 373
— объемной вязкости 366, 374
— поглощения 156—157
— Пуассона 349—353
— температуропроводности 294—295, 297,
364, 374
— (термического теплового) расширения
315, 35Р
— теплопровоаности 293—294, 298—299
— упругости 68, 78, 177, 179—184, 189—190
Кристалл 326—330
— жидкий 307, 308
— идеальный 326, 327
Кристаллит (зерно) 329
Кристаллическая решетка Браве 327
Критерий подобия 303
Критическая опалесценция 316
— точка 313—318
Макроскопические параметры 214—221
Масса 58
— гравитационная и инертная 71
— приведенная 126
Миллиметр ртутного столба (единица) 217
Модуль всестороннего сжатия 349, 351—353
— одностороннего сжатия 351
— сдвига 349, 351—353
— Юнга 349, 351—353
Моль 211
Момент импульса 93, 108, 126—139, 165
• собственный 111—113, 161—162, 165
— силы 109, 112, 162, 165—168, 178—179
Моменты инерции 162—166, 171, 178—179
Напряжения механические 218, 343—344
Насыщенный пар 314
Ньютон (единица) 66
Одноосное растяжение (сжатие) 350
Однородность времени 91
— пространства 90—91
Опыт Майкельсона — Морли 40—41
— Этвеша 71
Осциллятор гармонический 172—179
— с трением 180—189
Паскаль (единица) 217
Первое начало термодинамики 260—265
Перегретая жидкость 319—320
Переохлажденный пар 319—320
Период колебаний 173
Пластичность 344
Плечо силы 167
Плотность вероятности (функция распре-
распределения) 240, 243,246, 247, 253
— вещества 2J5—216
— потока частиц 149
— упругой энергии 353—354
Поле 55-56, 73-74, 96, 104
— кулоновское 85
— однородное электромагнитное 114
— центрально-симметричное 85
Полнморфн-ые превращения 307, 309, 324—
325
Поляризация волны 194
Порог реакции 146
Постоянная Больцмана 219
— Планка 21
— универсальная газовая 225
Постоянные Ван-дер-Ваальса 226—227
Постулат Эйнштейна 41
Потенциальная яма 105
Потенциальный барьер 107
Поток диффузии 288, 293
— импульса 288, 300
— скорости течения 300—301
— тепла 288, 293
— энтропии 288, 291
Предел текучести 347
— упругости 344, 346
Преобразования Галилея 38
— Лоренца 48—50
Принцип инерции 25
— относительности 26
— суперпозиции 173—174, 190—192
— эквивалентности 72
Прицельный параметр 151
Процесс 82
— адиабатический 260—261, 364
— кинетический 286
— круговой (цикл) 260
— неравновесный (необратимый) 258—260
— равновесный (обратимый) 258—260
— тепловой 258—260
Пуаз (единица) 300
Пузырьковая камера 147, 322
Пучности стоячей волны 202—204
Работа 81—83, 260—265
Распределение Больцмана 239—243, 358
— Гиббса (каноническое) 251—257, 272—273
— Максвелла 245—251
— угловое 150
Рассеяние 148
— в кулоновском поле 139—140, 154—156
— упругое на шаре 153—154
Резонанс 186—189
Релаксация 214
Свободное тело 24
Сдвиг 344-345
Сечение 142—143, 148—153
— дифференциальное 150—152, 154, 155
— полное 150, 152, 154—157, 236, 296—298,
301
Сжимаемость 216, 315, 367
Сила 59
— взаимодействия электронейтральных ча-
частиц 75—76
— вынуждающая 184
— действия и противодействия 60
— Лоренца 74
— непотенциальная (неконсервативная) 82,-
89
— потенциальная (консервативная) 82—84
— реакции опоры 78
— сопротивления Ньютона 80, 305
Стокса 80, 304
— сухого трения 79
— центральная 85
Силовой центр 85
Симметрия трансляционная 327
— фундаментальная 90—94
Система отсчета 24
—- — изолированная 57
инерциальная 25
лабораторная 113

384
ПРЕДМЕТНЫЙ УКАЗАТЕЛИ
Система отсчета неинерциальная 26
— термодинамически изолированная 213
— центра инерции 126, 143
Скорость 31
— вторая космическая 138—139
— групповая 207—208
— звука 365—368
— первая космическая 138—139
— распространения волны (фазовая) 193—
194, 196
—• секториальная 127
— тепловая 219
— угловая 31
Сложение колебаний 191—192, 201—208
— скоростей классическое 39
релятивистское 51—52
Сокращение времени 43—44
— длины 44—46
Состояние асимптотическое 96
— локального равновесия 287
— макроскопическое (внутреннее) 211—214,
221
— метастабильное 319—323
— механическое 54—55, 252
— неравновесное 214, 292—293
—• теплового равновесия 213, 287
Спектр частотный 189—190, 205—206
Спин 113
Статистическая сумма 253
Статистические закономерности 211
Статистический вес 272—273, 282—283
—+ интеграл 253
Столкновения 141
— неупругие 141, 144—148
— упругие 141, 143, 153—156, 218
— экзотермические и эндотермические 146
Стоке (единица) 301
Температура 218—221, 270
— Дебая 355
— критическая 313
— характеристическая 230—231
Тепловой резервуар (нагреватель) 267,
278-280
Теплоемкость 265—266, 356—357
Теплопроводность 286, 293—ЗЭО, 364
Термодинамика 258
— необратимых процессов 287
Течение ламинарное 80. 302—303
— турбулентное 80, 302—303
Точка поворота 106
— приложения силы 161
— тройная 393—325
Траектория 30
Третье начало термодинамики (теорема
Нернста) 274
Угол рассеяния 139—140, 149—151
Ударная адиабата (адиабата Гюгонио) 379
— волна 374—381
Узлы стоячей волны 202, 204
Ультразвук 362
Упругость насыщенного пара 314
Уравнение Ван-дер-Ваальса 226—227, 316—
318
Уравнение вращательного движения твер-
твердого тела 162
— Гамильтона 98
— движения 56—57
— диффузии 294
—* Клапейрона — Клаузиуса 313
— Клапейрона — Менделеева 225
— непрерывности 292
— поступательного движения системы
(твердого тела) 63, 161
— Пуассона 264
— состояния 222, 227, 360
идеального газа 222—225
— теплопроводности 294
Ускорение 32—35
Условие нормировки 238
Фаза 173, 195
Фазовое пространство 252
Фазовые диаграммы 310—312
— превращения (переходы) 306—309
Флуктуации 221, 237, 256—257, 284, 319
Фонон 96-97, 102, 355
Формула Резерфорда 155
Функция Гамильтона 97
— процесса 82, 261—265
— состояния 55, 59, 67, 228
Холодильник, 267, 279—280
Центр инерции 61, 159—165, 168—169
Цикл Карно 267, 279—280
Циклотрон 120—121
Частота вырожденная 191
— гироскопическая (циклотронная) 120
— колебаний 173
— собственная 176
— циклическая 173
Число Авогадро 211
— Рейнольдса 302
— состояний 252, 257
— степеней свободы 29, 159, 231—234
Элементарная ячейка 327
Энергетическая щель 230
Энергия активации 335
— безмассовых частиц 101
— внутренняя 227—234, 260—261, 289, 356,
378-379
— идеального газа 232—234
— кинетическая 100—102
~- покоя 101
— потенциальная 83
— — эффективная 129
— системы частиц 103—104
— твердого тела 168—170
— фонона 102
— центробежная 129
Энтальпия 265
Энтропия 267—275
Эрг 81
Эффект Допплера 200—201, 245