Автор: Девятков В.В.
Теги: деятельность и организация общая теория связи и управления (кибернетика) здравоохранение медицинские науки информатика искусственный интеллект информационные технологии
ISBN: 5-7038-1727-7
Год: 2001
Текст
Информатика в техническом университете
Информатика в техническом университете
Серия основана в 2000 году
РЕДАКЦИОННАЯ КОЛЛЕГИЯ:
д-р техн, наук И.Б. Федоров — главный редактор
д-р техн, наук И.П.Норенков — зам. главного редактора
д-р техн, наук Ю.М. Смирнов — зам. главного редактора
д-р техн, наук В. Ф. Горнее
д-р техн, наук В.В. Девятков
канд. техн, наук И.П. Иванов
д-р техн, наук А. А. Марков
д-р техн, наук В.А. Матвеев
д-р техн, наук В.В. Сюзев
д-р техн, наук Б.Г. Трусов
д-р техн, наук В.М. Черненький
д-р техн, наук В.А. Шахнов
В. В. Девятков
Системы
искусственного
интеллекта
Допущено Министерством образования
Российской Федерации
в качестве учебного пособия для студентов
высших учебных заведений, обучающихся по специальностям
«Информационные системы и технологии» и «Автоматизированные
системы обработки информации и управления» по направлениям
подготовки дипломированных специалистов «Информатика
и вычислительная техника» и «Информационные системы»
Москва
Издательство МГТУ имени Н.Э.Баумана
2001
УДК 007001.33(075.8)
ББК 5.05
Д26
Рецензенты: д-р техн, наук, профессор Г.В. Росс,
д-р техн, наук, профессор Е.И. Пупырев
Д26 Девятков В.В. Системы искусственного интеллекта: Учеб,
пособие для вузов. — М.: Изд-во МГТУ им. Н.Э. Баумана,
2001. — 352 с., ил. (Сер. Информатика в техническом
университете).
ISBN 5-7038-1727-7
Изложены современные вопросы теории и практики систем искусственного
интеллекта. Рассмотрены различные типы исчислений, используемых для
создания систем искусственного интеллекта, включая такие их свойства, как
мультиагентность, нечеткость, модальность и т.п. С помощью аппарата логики
показано, что входит в дисциплину искусственного интеллекта, начиная с
решения методами искусственного интеллекта простых задач синтеза дискретных
устройств и заканчивая задачами моделирования и анализа ситуаций,
возникающих в процессе управления предприятиями.
Содержание учебника соответствует курсу лекций, который автор читает в
МГТУ им. Н.Э. Баумана.
Для студентов, аспирантов, инженеров и научных работников технических
специальностей.
УДК 007001.33(075.8)
ББК 5.05
ISBN 5-7038-1727-7
© В.В. Девятков, 2001
© Московский государственный
технический университет
им. Н.Э. Баумана, 2001
© Издательство МГТУ
им. Н.Э Баумана, 2001
ОГЛАВЛЕНИЕ
Предисловие...................................................8
1. Искусственный интеллект...................................11
1.1. Что же такое искусственный интеллект?...............12
1.2. Агенты — носители искусственного интеллекта.........13
1.3. Среды и агенты......................................17
Вопросы и упражнения.................................19
2. Логические рассуждения....................................20
2.1. Рассуждения в пространстве состояний среды..........20
2.2. Логика высказываний.................................24
2.3. Исчисление высказываний.............................30
2.4. Рассуждения в терминах интервалов...................37
Вопросы и упражнения.................................51
3. Логика предикатов.........................................52
3.1. Синтаксис и семантика...............................53
3.2. Переход от естественного языка к языку логики
предикатов..............................................59
3.3. Постановка задачи для среды чудовища в логике
предикатов..............................................61
Вопросы и упражнения.................................63
4. Вывод в логике предикатов.................................65
4.1. Исчисление предикатов...............................65
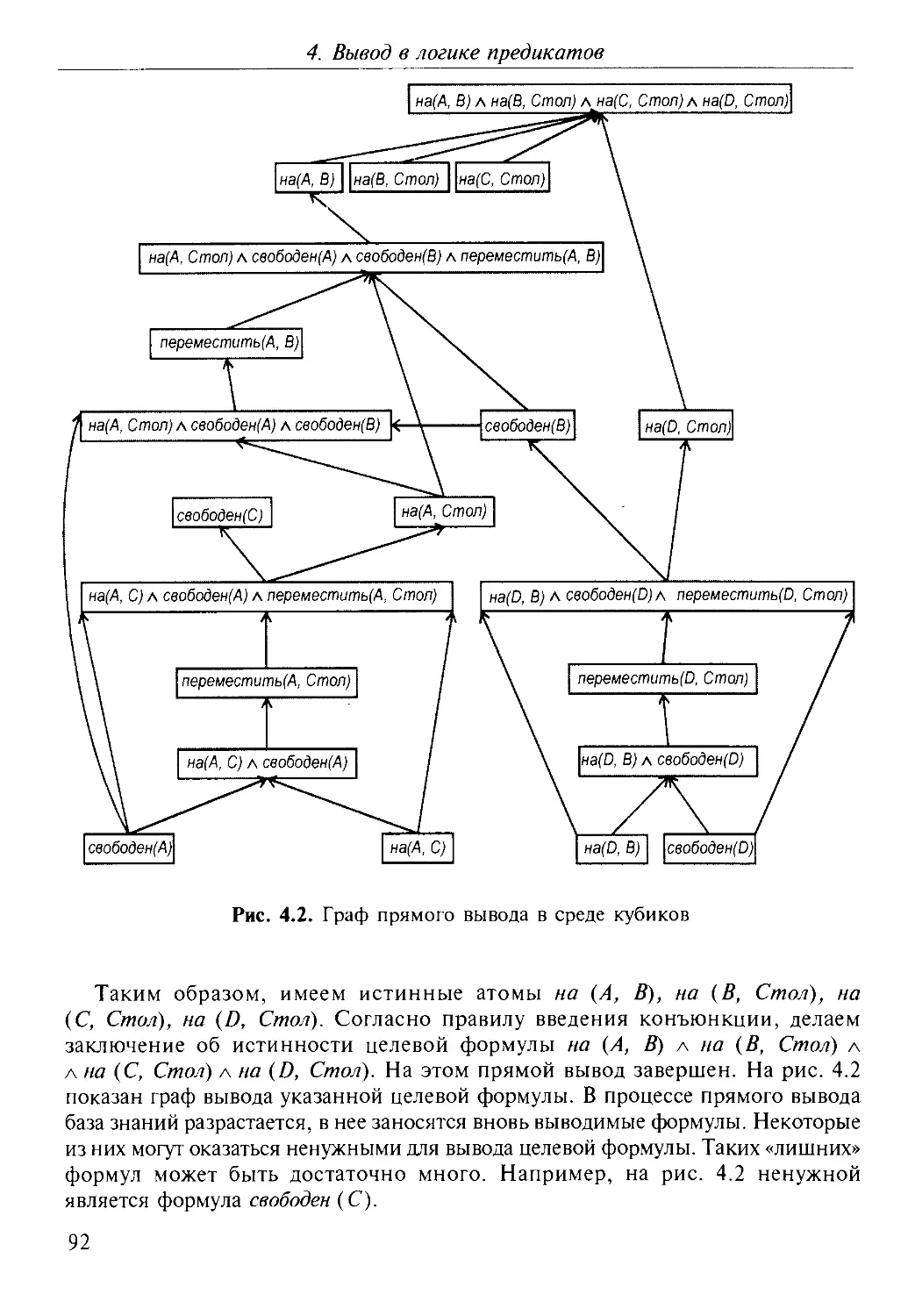
4.2. Прямой и обратный вывод.............................89
4.3. Полнота и непротиворечивость исчисления.............94
4.4. Вывод на основе правила резолюции...................96
Вопросы и упражнения................................103
5. Среды и языки............................................105
5.1. Автомат и среда....................................106
5.2. Язык и автомат.....................................107
5.3. Описание автомата на языке логики предикатов.......112
5.4. Построение автомата методом детерминизации.........116
5.5. Граф переходов состояний среды.....................119
5
Оглавление
5.6. Использование графа переходов для поиска в пространстве
состояний..............................................122
5.7. Построение графа состояний.........................123
5.8. Языки и грамматики.................................128
5.9. Грамматический анализ и автоматы...................130
5.10. Перевод с одного языка на другой .................133
Вопросы и упражнения................................135
6. Стратегии поиска.........................................136
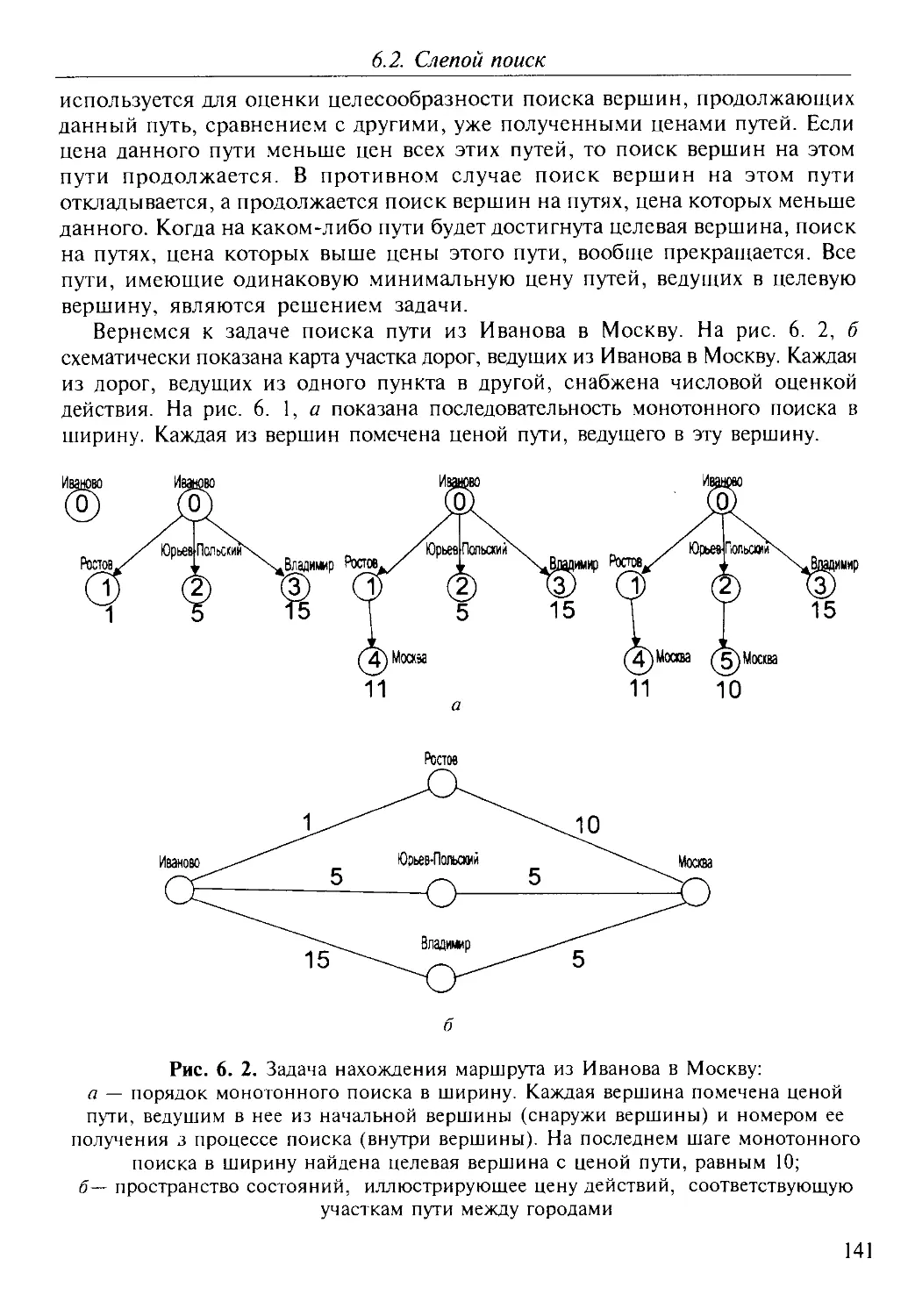
6.1. Оценки успеха при поиске цели .....................137
6.2. Слепой поиск.......................................138
6.3. Направленный поиск.................................146
Вопросы и упражнения.................................151
7. Ситуационное описание среды..............................153
7.1. Базовые понятия ситуационной модели................153
7.2. Среда логических электронных схем..................161
7.3. Среда обезьяны и банана............................164
Вопросы и упражнения.................................165
8. Ситуационное исчисление..................................167
8.1. Язык ситуационного исчисления......................168
8.2. Аксиомы ситуационного исчисления...................169
8.3. Охота на индейку...................................173
Вопросы и упражнения.................................176
9. Модальность в ситуационном исчислении....................179
9.1. Модальность и модальная логика.....................179
9.2. Язык временной модальной логики....................184
9.3. Модель параллельных процессов......................184
9.4. Мультипрограммное выполнение параллельных процессов.188
9.5. Модальная логика и анализ параллельных процессов...194
9.6. Инвариантные свойства..............................197
9.7. Свойства живости (осуществимости)..................203
9.8. Свойства предшествования...........................209
9.9. Доказательство свойств корректности................213
Вопросы и упражнения................................219
10. Дедуктивные базы данных..................................221
10.1. Реляционные базы данных...........................221
10.2. Реляционная алгебра...............................223
10.3. Триггеры..........................................227
10.4. Реляционная база данных и логические исчисления...229
10.5. Переход от Дейталога к SQL........................231
10.6. Ситуационное исчисление в дедуктивной базе данных.235
10.7. Проверка ограничений целостности..................240
Вопросы и упражнения..............................241
6
Оглавление
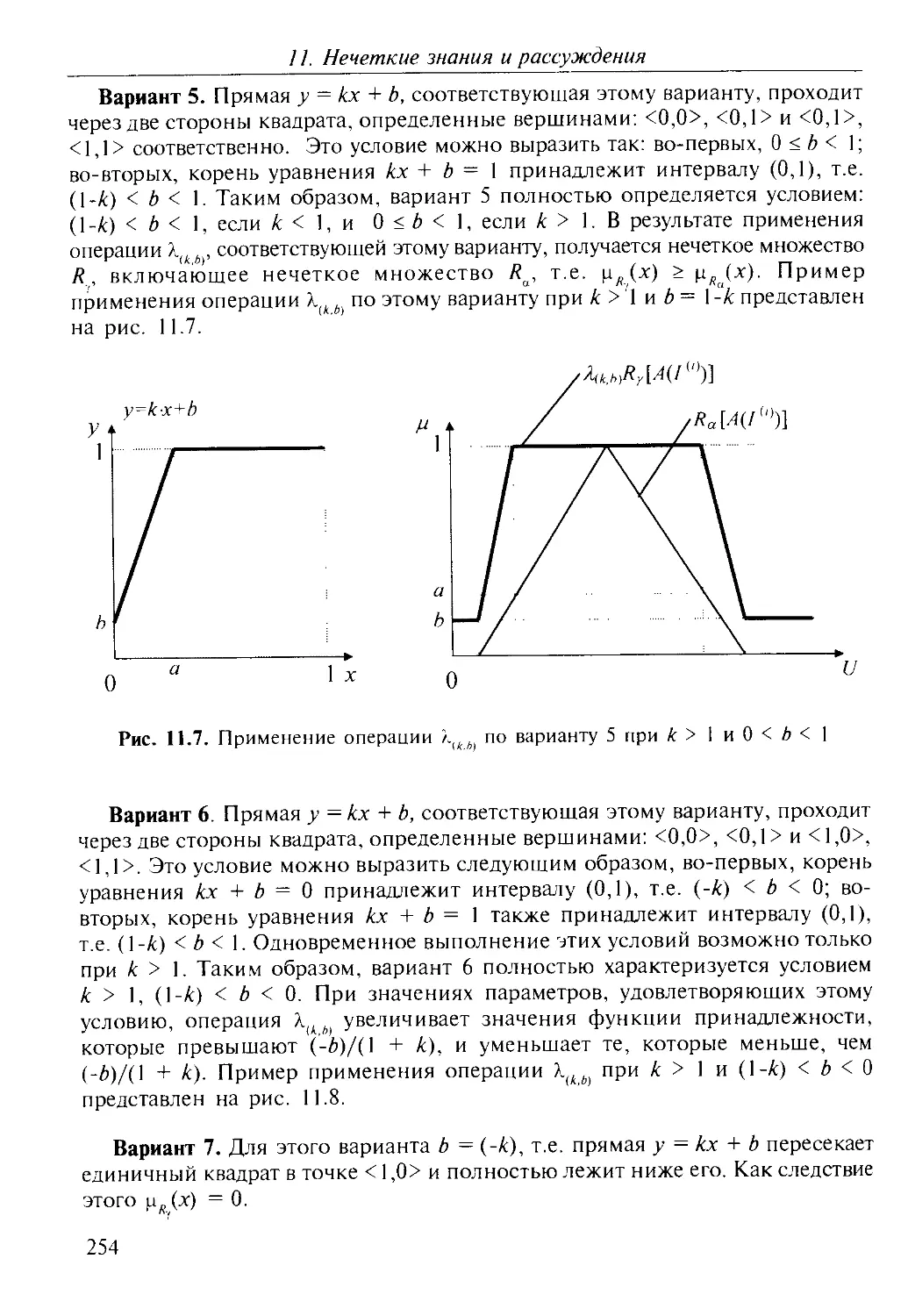
11. Нечеткие знания и рассуждения..........................242
11.1. Нечеткое множество и функция принадлежности......243
11.2. Принцип обобщения и степень совместимости........244
11.3. Нечеткая база данных.............................246
11.4. Нечеткие действия (операторы)....................248
11.5. Нечеткозначное исчисление........................259
11.6. Задача диагностики тепловых сетей................262
11.7. Проблемно-ориентированный язык...................264
11.8. Переход от проблемно-ориентированного языка к языку
нечеткозначного исчисления.............................279
11.9. Результаты решения задачи диагностики............281
Вопросы и упражнения...............................289
12. Планирование действий...................................291
12.1. Задачи планирования..............................291
12.2. Оценка плана.....................................297
Вопросы и упражнения...............................301
13. Онтологии и их применение..............................303
13.1. Введение в онтологию ............................303
13.2. Постановка задачи создания онтологии.............306
13.3. Использование онтологий..........................313
Вопросы и упражнения...............................315
14. Реализация систем......................................316
14.1. Архитектура......................................316
14.2. Извлечение знаний ...............................317
14.3. Формализация.....................................327
14.4. Выбор стратегии вывода...........................335
14.5. Реализация ......................................337
Вопросы и упражнения...............................339
Заключение.................................................341
Список литературы..........................................346
Предметный указатель.......................................347
ПРЕДИСЛОВИЕ
В мире имеется много специальной литературы, посвященной
искусственному интеллекту. До 90-х годов довольно часто появлялись публикации
на эту тему российских авторов, а также в переводе зарубежных специалистов.
В последнем десятилетии книги на русском языке, отражающие современное
состояние искусственного интеллекта, почти не издаются, несмотря на то что
в этой области происходят радикальные изменения. Искусственный интеллект
вторгается во все сферы деятельности, становится средством интеграции наук.
Развитые в экономическом отношении страны начали проводить интенсивные
исследования по созданию единого информационного пространства, создающего
условия для совместной дистанционной работы на основе однозначно
понимаемых баз знаний (онтологий). Многие аспекты этих исследований
базируются на идеях искусственного интеллекта.
Настоящая книга рассчитана на начинающего читателя. Автор на
протяжении многих лет читал курсы по различным разделам искусственного
интеллекта в техническом университете. Опыт общения со студенческой
аудиторией свидетельствует, что существующие отечественные издания
трудны для большинства читателей, не имеющих достаточной культуры в
области логики как математической дисциплины и склонных не к
исследованиям, а к разработке практических приложений на основе теории.
Помимо того, что современных отечественных книг на эту тему просто
нет, существующие чрезмерно формализованы, примеры решения задач
методами искусственного интеллекта зачастую слишком схематичны и не
доведены до детального разъяснения каждого шага. Переводы некоторых
книг неудачны и терминологически запутаны. Все это послужило стимулом
к написанию настоящего учебного пособия. Для его прочтения не требуется
дополнительных источников. Помимо стремления дать читателю современное
введение в искусственный интеллект, книга претендует на использование ее
в качестве учебного пособия для студентов и аспирантов, обучающихся
информатике в высших технических учебных заведениях. Поэтому в ней,
особенно в начальных главах, переходу к строгим определениям понятий
предшествует подробное изложение сути на простых примерах.
Предлагаемая книга имеет ряд принципиальных черт, отличающих ее от
ряда других.
8
Предисловие
Единообразие и взаимосвязь. Многие книги написаны с учетом
исторического развития искусственного интеллекта и разбиты на слабо связанные
между собой разделы, каждый из которых имеет свою специфику, понятия и
методы. В настоящей книге все главы взаимосвязаны, им присуща общая
терминология и последовательное изложение материала от простого к сложному.
Система искусственного интеллекта рассматривается как сообщество
агентов (носителей искусственного интеллекта). Концепция агента и системы
искусственного интеллекта как сообщества агентов положена в основу создания
современных систем искусственного интеллекта. Каждый агент имеет возможность
воспринимать состояния среды, в которой он находится, и воздействовать на нее
с помощью реакций. Иными словами, он отображает восприятия в реакции или
действия. Задача создания системы искусственного интеллекта в этом случае
представляет собой задачу построения такого отображения.
Ситуационные исчисления являются основой для представления знаний. В
основу способностей агентов рассуждать и приходить к умозаключениям положены
современные варианты ситуационных исчислений. Выбор того или иного варианта
исчисления зависит от особенностей среды, знания о которой представлены на
языке этого исчисления. Кроме того, в книге рассмотрен ряд наиболее характерных
и проработанных исчислений: четких, нечетких, модальных.
Применение теории на практике. Изложение теоретического материала
ведется не в отрыве от конкретных задач, а наоборот с широким использованием
примеров для конкретных сред. Наряду с теоретическими вопросами,
иллюстрируемыми простыми примерами, в книге приведены сведения о подходах
к реализации и решению реальных задач на базе излагаемой теории.
Предлагаемую книгу “Системы искусственного интеллекта” точнее было
бы назвать “Введение в искусственный интеллект на основе формальных
логических систем”. Область знаний искусственного интеллекта в настоящее
время не ограничивается разделами только настоящего учебного пособия.
Некоторые разделы, хотя и рассмотрены в книге, могут быть существенно
расширены. В частности, не включены главы по нейронным сетям,
интеллектуальной обработке сигналов и изображений, интеллектуальным
роботам и ряд других. Однако читатель, освоивший материал, получит весомый
багаж для изучения разделов искусственного интеллекта, не включенных в книгу.
Сознательно не дан исторический анализ развития искусственного интеллекта,
как правило, не указаны авторы — основоположники того или иного
направления или первоисточники каких-либо идей, используемых в данной
работе. Читатель сможет восполнить эти пробелы, воспользовавшись списком
литературы, который приведен в конце книги.
Настоящая книга состоит из 14 глав. Сложность материала возрастает с
ростом номеров глав и достигает максимума в 11 главе.
Первая глава является введением в искусственный интеллект. В ней
приведены краткие сведения о предмете искусственного интеллекта,
рассмотрены агенты различного типа и среды, с которыми им приходится
иметь дело. Во второй главе описана одна из наиболее простых логик — логика
9
Предисловие
высказываний, в рамках этой логики обсуждаются принципы рассуждений,
осуществляемых агентами на основе использования логики высказываний, введен
ряд важных понятий, обобщаемых и используемых в дальнейшем, приведены
простейшие примеры построения комбинационного и целенаправленного
агентов. Третья глава посвящена логике предикатов первого порядка. На
примерах из главы показано, почему логика предикатов первого порядка обладает
большими выразительными возможностями и более удобна для рассуждений,
осуществляемых агентами, по сравнению с логикой высказываний. Вопросы
вывода или рассуждения в логике предикатов первого порядка и примеры
построения целенаправленных агентов рассмотрены в четвертой главе.
В пятой главе предпринята первая попытка построения исчислений. Введено
понятие формального языка, рассмотрена связь языка и среды, приведены
примеры представления сред в формальном языке и построения по этому описанию
наилучшего в определенном смысле последовательностного агента, поскольку
любое исчисление — это прежде всего некоторый формальный язык
представления знаний. Процедуры рассуждений связаны с поиском цели,
поэтому в шестой главе показаны различные стратегии поиска и их* выбор в
зависимости от типа и доступных знаний о среде. В седьмой главе описана
достаточно универсальная ситуационная модель среды, которая может
использоваться для решения в различных прикладных задачах информатики.
В восьмой главе рассмотрено исчисление, называемое ситуационным,
которое можно использовать для создания агентов и их совокупностей,
решения различных прикладных задач, связанных с моделированием и
управлением в дискретных средах. Девятая глава посвящена исчислению,
называемому иначе модальной логикой, и вопросам применения его для
анализа корректности программ.
В десятой главе рассмотрены дедуктивные базы знаний. Показано, каким
образом строятся дедуктивные базы данных на основе исчислений различного
типа и как в них осуществляется поиск на основе этих исчислений.
Одиннадцатая глава посвящена вопросам планирования, т.е. нахождению
последовательностей действий, ведущих к достижению целей, построению
планов в процессе рассуждений на основе исчислений. В двенадцатой главе
показано представление нечетких знаний на основе соответствующего
исчисления, называемого нечеткозначным, построение и использование
языков пользователя для представления и использования нечетких знаний в
процессе решения практических задач.
Современный подход к решению задач на основе онтологий как средства
общепонимаемого формального представления знаний рассмотрен в
тринадцатой главе.
Четырнадцатая завершающая глава посвящена вопросам реализации систем
искусственного интеллекта для решения конкретных задач.
Автор глубоко признателен тем, кто внес свой вклад в обсуждение и
подготовку материала этой книги: В. Гайдукову, С. Косову, В. Румбешту.
Особую благодарность автор выражает своей жене Г.Н. Девятковой, без
долготерпения и помощи которой книга вряд ли могла быть написана.
10
1. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
В этой главе рассказано, что такое искусственный интеллект
в современном понимании и почему он заслуживает вашего внимания и изучения.
Введено понятие носителей искусственного интеллекта, называемых агентами,
представлены различные типы агентов и описаны свойства внешней среды,
с которыми агенты имеют дело.
Человек именует себя homo sapiens, что означает мудрое существо или
существо, обладающее умом (интеллектом), тем самым подчеркивая важность
именно умственных или интеллектуальных способностей. Область знаний
искусственного интеллекта пытается объяснить сущность этих способностей.
Одна из причин нашего интереса к искусственному интеллекту — это узнать
как можно больше о человеке как об интеллектуальном (мудром, умном)
существе, понять, что же такое интеллект. Искусственный интеллект в
отличие от психологии и философии занимается созданием интеллектуальных
искусственных существ (сущностей, объектов), которые принято называть
агентами или носителями. Поэтому другая причина нашего интереса — это
определить полезность таких интеллектуальных искусственных существ в
человеческой жизни, позволяющих, несмотря на раннюю стадию их
развития, уже сегодня делать много полезных и нужных вещей. Никто не в
состоянии точно предсказать будущее искусственного интеллекта, однако
ясно, что развитие информационных компьютерных систем с уровнем
человеческого интеллекта и выше будет оказывать огромное влияние на всю
нашу жизнь и будущее цивилизации.
Искусственный интеллект как дисциплина является очень молодой.
Формально считается, что ее развитие началось в 1956 г., когда было введено в
обиход понятие “искусственный интеллект”. В то же время изучение собственно
свойств интеллекта философами, которые пытались понять, как осуществляется
восприятие, обучение, запоминание и рассуждение, насчитывает уже не менее
2000 лет. Приход эры вычислительных машин (компьютеров) в начале 50-х
годов придал дисциплине искусственного интеллекта теоретически обоснованный
и экспериментальный характер. Общество почувствовало, что «электронный
мозг» таит в себе огромный потенциал для развития искусственного интеллекта.
Компьютеры позволили создать базу для экспериментальной проверки идей и
И
7. Искусственный интеллект
методов искусственного интеллекта. Многие из этих идей не выдержали
испытаний — создание агентов оказалось намного труднее, чем это
предполагалось на заре развития искусственного интеллекта. Современные идеи
намного богаче, тоньше и практичнее их ранних предшественниц.
В настоящее время ИИ объединяет большое число разделов. К
искусственному интеллекту относят как общую теорию очувствления или
восприятия, так и специальные методы типа игры в шахматы, доказательства
математических теорем, написания стихов или диагностики заболеваний.
Ученые, специальностью которых не является ИИ, находят в нем основу для
систематизации и решения интеллектуальных задач, которым они посвятили
значительную часть своей жизни. И наоборот, специалисты применяют методы
искусственного интеллекта в самых разнообразных областях, где без них не
удается достичь успеха. Именно поэтому искусственный интеллект является
воистину универсальной областью знаний.
1.1. Что же такое искусственный интеллект?
В общих словах мы рассказали, что такое искусственный интеллект, но
этого, конечно, недостаточно для того, чтобы понять, каковы же его задачи
и пути решения этих задач. Приведем несколько высказываний,
встречающихся в зарубежной и отечественной литературе и связанных с
определением искусственного интеллекта.
Восхищающие новые усилия заставить компьютеры думать...машины с
разумом в полном и языковом смысле (J.Haugeland, 1955 г.).
Автоматизация деятельности, которую мы ассоциируем с человеческим
мышлением, такой как принятие решений, решение задач, усвоение знаний
(R. Е. Bellman, 1978 г.).
Исследование умственных способностей с помощью ипользования
вычислительных моделей (Е. Charniak and D. McDermot, 1985 г.).
Теория эвристического поиска и вопросы создания решателей задач,
относящихся к разряду творческих или интеллектуальных (Г. С. Поспелов,
1986 г.).
Система, которая способна находить оригинальные и эффективные
ответы, часто неожиданные как для пользователя и конструктора ЭВМ, так
и для составителя программ, по которым работает машина
(А. Г. Ивахненко, 1986 г.).
Искусство создания машин, способных выполнять действия, которые
потребовали бы интеллекта от людей, если бы они эти действия выполняли
(R. Kurzweil, 1990 г.).
Область исследования, которая пытается понять и моделировать разумное
поведение в терминах вычислительных процессов (R. J. Schalkoff, 1990 г.).
Исследование того, как заставить компьютеры делать вещи не хуже людей
(Е. Rich and К. Knigpt, 1991 г.).
Изучение исчислений, которые позволяют понимать, рассуждать и
действовать (Р. Н. Winston, 1992 г.).
12
1.2. Агенты— носители искусственного интеллекта
Отрасль науки о компьютерах, которая интересуется автоматизацией
разумного поведения (J. I. Luger and W. A. Stubblefield, 1993 г.).
Этот список можно продолжить. Если считать, что все эти высказывания
или определения относятся к неким системам, обладающим искусственным
интеллектом, то можно заметить, что все они так или иначе связывают
искусственный интеллект с умением рассуждать и действовать (принимать
решения) на основании этих рассуждений. Из большинства определений
остается неясным, как все-таки заставить машины рассуждать и действовать
подобно человеку, а может быть и лучше. Например, можно пойти путем
наблюдения за поведением человека, а затем просто имитировать это
поведение на основе полученных экспериментальных данных. Такой путь
можно назвать имитационным.
В настоящей книге рассмотрен другой путь, опирающийся на
математический и инженерный подходы. В отличие от имитационного
назовем его логистическим (от греческого слова логистика (logistica),
означающего искусство вычислять, рассуждать). Основополагающая часть
теории искусственного интеллекта, изложенная в настоящей книге,
посвящена логистическому подходу, т.е. тому, как надо рассуждать,
используя логистику, чтобы в результате прийти к искомому выводу
(умозаключению) и на основании этого умозаключения принимать решение
о совершении тех или иных действий. С помощью аппарата логистики можно
изложить львиную долю того, что сегодня входит в дисциплину искусственного
интеллекта и о чем можно узнать после прочтения настоящей книги. В основе
логистики лежит определенный математический аппарат, оперируя которым
и удается формализовать процесс рассуждения и достижения решения (цели).
Это не означает, что человек рассуждает и действует точно так же. Мы этого
даже не знаем, но, воспользовавшись подобным аппаратом, будем в
состоянии построить агентов, обладающих интеллектом, т.е. способных
рассуждать и принимать на основании этих рассуждений решения. Рассмотрим
теперь подробнее типы агентов.
1.2. Агенты — носители искусственного интеллекта
1.2.1. Взаимодействие агента с внешней средой
Агент воспринимает внешнюю среду с помощью датчиков хг хт и
воздействует на нее посредством исполнительных органов zr , z„ подобно
тому, как человек воспринимает внешнюю среду или просто среду с помощью
органов чувств и воздействует на нее с помощью таких частей тела, как
руки, ноги и т.п. В понятия датчиков и исполнительных органов закладывают
самый широкий смысл. Например, датчиком может быть некий аналог уха,
воспринимающий речевые сообщения, а исполнительным органом — органы
речи, позволяющие передавать сообщения на каком-либо языке. Обычно
воздействие агента на среду называют реакцией, а восприятие агентом среды
13
1. Искусственный интеллект
— восприятием. Если каждый исполнительный орган z. сопоставить с
одноименной выходной переменной z, принимающей множество значений
у, и каждое такое значение назвать микрореакцией, то реакция будет
представлять собой набор значений у , уп. Аналогично, если каждый
датчик х. сопоставить с одноименной входной переменной хР принимающей
множество значений а., называемых микровосприятиями, то восприятие будет
представлять собой набор значений аг ..., ат. Поведение агента состоит в
переработке восприятий в реакции. Эта переработка осуществляется агентом
с помощью специального решателя, функционирующего на основе
заложенных в него знаний. Не существует какой-либо общепринятой
классификации агентов. В зависимости от сложности решаемых задач выделим
следующие четыре типа агентов: комбинационные; последовательностные;
целенаправленные; целевыбирающие.
1.2.2. Комбинационный агент
Поведение комбинационного агента внешне выглядит достаточно простым.
В определенный момент времени / агент получает с датчиков х;,..., хт
восприятие а;, ..., ат, характеризующее состояние среды. На основании
только этого восприятия и неизменяемых в процессе всего существования
агента знаний, хранящихся в его памяти, он в этот же момент времени с
помощью исполнительных органов z,, , Z„ формирует реакцию у у .
Конечно, при практической реализации агента на формирование реакции
по данному восприятию требуется время, но теоретически считается, что
все происходит мгновенно в момент времени /, и этот момент времени нас
может даже не интересовать. Существенно лишь то, что комбинационный агент
не порождает новые знания. Каждый раз, когда надо вырабатывать очередную
реакцию по вновь поступившему восприятию, он использует одни и те же
знания, хранящиеся в его памяти.
1.2.3. Последовательностный агент
Комбинационный агент может быть успешно использован в среде, в которой
одного восприятия в данный момент времени достаточно для выработки реакции
в тот же момент времени. Предположим, например, что агентом является
водитель автомобиля, движущегося по многорядному шоссе в крайнем правом
ряду. Впереди него движется другой автомобиль, который неожиданно начинает
резко тормозить (зажжены его тормозные огни). В этой среде правилами агента,
сформулированными на естественном языке, могли бы быть следующие.
• Если зажжены тормозные огни у движущегося впереди автомобиля и
левый ряд свободен, то обогнать его без торможения слева.
• Если зажжены тормозные огни у движущегося впереди автомобиля и
левый ряд занят, а скорость автомобиля агента невелика, то для того, чтобы
не врезаться в движущуюся впереди машину, затормозить и продолжать
движение в том же ряду.
14
1.2. Агенты— носители искусственного интеллекта
• Если зажжены тормозные огни у движущегося впереди автомобиля,
левый ряд занят, а скорость автомобиля агента такова, что любое собственное
торможение без съезда на обочину приведет к столкновению, то экстренно
затормозить и съехать на обочину.
Предположим, что вследствие критической ситуации комбинационный
агент способен в данный момент времени установить только факт наличия у
движущегося впереди автомобиля зажженных тормозных огней и факт наличия
помехи слева, но не в состоянии считать со спидометра и оценить скорость
своего автомобиля. В этом случае он может использовать только первое
правило из трех. Для того чтобы иметь возможность применить два других
правила, необходимо в подобной ситуации каждый раз успевать считывать
со спидометра скорость своего автомобиля. Тогда количество используемых
правил может быть увеличено.
Другой путь повышения числа используемых правил — регулярный
контроль в безаварийной ситуации скорости своего автомобиля по спидометру
и запоминание его последнего показания. Это нужно для того, чтобы извлечь
из своей памяти последнее показание спидометра, когда это понадобится.
Естественно, предполагается, что она с тех пор не изменялась. В момент
принятия решения определение скорости происходит за счет восприятия,
запомненного в некоторый предыдущий момент времени. Агентов, которые
используют запомненную в предыдущие моменты времени информацию,
называют последовательностными.
1.2.4. Целенаправленный агент
Поведение целенаправленного агента принципиально отличается от
комбинационного и последовательностного, поскольку их поведение основано
на восприятиях в настоящий или предыдущий момент времени и использовании
правил, учитывающих только эти восприятия или производные от них состояния.
Например, тот же комбинационный или последовательностный агент,
являющийся водителем автомобиля, должен попасть в определенное место по
известному ему адресу не позднее назначенного времени. Он плохо знает город,
но имеет карту и движется к нужному месту, ориентируясь по ней. Он видит,
что впереди перекресток, от которого улицы отходят только налево и направо,
и, повернув на любую из них, можно, в конце концов, достичь места
назначения. Оба маршрута кажутся равноправными, хотя по каким-то
непонятным для водителя причинам основной поток машин поворачивает
налево. Правый поворот всегда проще и водитель решает повернуть направо.
Однако он не знает, а на карте это не помечено, что, повернув направо,
из-за ремонта на одной из улиц, он столкнется с ситуацией, когда машины
вынуждены двигаться в один ряд, следовательно возникают постоянные
заторы. И именно поэтому большинство других машин, водители которых
лучше знают город, на перекрестке повернули налево. Таким образом
решение агента о повороте направо, скорее всего, приведет к тому, что он
опоздает к месту назначения.
15
/. Искусственный интеллект
Комбинационный или последовательностный агент в этой ситуации мог
бы принять правильное решение, если бы имел правило, учитывающее факт
поворота большинства машин на перекрестке налево, на основании которого
его реакцией также был бы поворот налево. Однако в реальной жизни, во-
первых, трудно предусмотреть абсолютно все правила, а во-вторых, среда
может изменяться, одни правила могут становиться излишними или даже
неверными, а других правил может недоставать. Поэтому сколько бы ни
пополнялась база правил комбинационного или последовательностного
агента, невозможно гарантировать достаточность числа правил для выработки
реакции в не предусмотренной заранее ситуации. Кроме того, их число может
стать слишком большим.
В этих условиях для того, чтобы не попасть впросак, агент должен как-то
предвидеть будущее. Комбинационный (или последовательностный) агент
использует информацию только о прошлом и настоящем и не способен
предвидеть ситуацию. Целенаправленный же агент прежде, чем принять
решение, на основании известной ему цели (в нашем примере места назначения
и времени, к которому он туда должен прибыть) заранее планирует свои
реакции. Иными словами, на основании имеющихся у него правил агент заранее
до того, как он начнет действовать, пытается построить план, гарантирующий
ему достижение цели, или обнаруживает, что такого плана не существует. В
случае обнаружения недостижимости цели он может запросить дополнительные
правила и продолжить или повторить процесс поиска. План является
последовательностью пар восприятие — реакция (или только реакций),
называемых также действиями и ведущих к цели. Если план найден, то
целенаправленный агент его выполняет и достигает цели.
Таким образом, решатель целенаправленного агента использует не раз и
навсегда данное ему множество правил, предписывающих, какие реакции
выдавать.в ответ на восприятия, а всякий раз для каждой вновь возникающей
цели порождает план достижения именно этой цели. Исходными для работы
такого решателя могут быть также правила, описывающие не реакции агента на
конкретные восприятия, а некие общие законы его поведения в среде, законы
поведения самой среды и законы порождения планов достижения целей.
1.2.5. Целевыбирающий агент
Целенаправленный агент в состоянии составить план достижения цели.
В принципе, планов достижения цели может быть несколько и из них надо
выбрать лучший по определенным критериям. Например, целенаправленный
агент—водитель может наметить несколько путей достижения места
назначения, но расход топлива при этом может быть различным.
Следовательно, желательно уметь оценить планы с точки зрения расхода
топлива и выбрать из них наилучший. Таким образом, целевыбирающий агент,
помимо возможности построения планов достижения целей, так же, как
это делает целенаправленный агент, способен на большее. Во-первых, при
наличии одной цели он может выбирать из множества всех конкурирующих
16
1.3. Среды и агенты
планов достижения цели наилучший, иногда и без полного построения всех
планов. Во-вторых, при наличии нескольких конкурирующих целей, достижение
каждой из которых заранее нельзя оценить с полной уверенностью, он способен
определить степень успеха достижения каждой цели в зависимости от ее
важности. В-третьих, на основании предшествующего опыта, он может
обучаться и корректировать или пополнять свои знания.
1.3. Среды и агенты
Агент всегда функционирует в некоторой среде. От свойств конкретной
среды зависит выбор типа агентов и всего, что ему необходимо для успешного
функционирования в этой среде.
Рассмотрим в общих чертах свойства сред в виде взаимоисключающих пар.
1.3.1. Дискретные и непрерывные среды
Дискретные среды таковы, что число различных восприятий и реакций,
которые требуются агенту при функционировании в среде, конечно, хотя и
может быть очень велико. Непрерывные среды могут порождать бесконечное
число восприятий, реакций или того и другого. Примером дискретной среды
является, например, среда шахмат, а непрерывной — среда агента-водителя,
если для его функционирования требуется восприятие значения, например,
скорости со сколь угодно высокой точностью. Если же все параметры среды
воспринимаются агентом (как это обычно бывает на практике) с определенной
точностью и в заданных пределах, например, скорость с точностью до 1 км/ч
в пределах от 1 до 200 км/ч, то такая среда с точки зрения агента также
может считаться дискретной.
1.3.2. Детерминированные и недетерминированные среды
В детерминированных средах по любому восприятию агент формирует
строго одну реакцию. Недетерминированные же среды таковы, что вследствие
каких-либо причин, например недоступности всех необходимых восприятий,
агент не в состоянии сформировать единственную реакцию.
1.3.3. Статические и динамические среды
Среда является статической, если за время, протекающее между получением
агентом любого восприятия и выработкой им реакции, в среде ничего не
изменяется. В противном случае среда называется динамической. При
функционировании агента в статической среде необязательно, чтобы он
наблюдал за ней, пока занимается выработкой реакции. Но даже если среда
является динамической, на практике чаще всего считается, что для агента
неважно, какие изменения в ней происходят, пока он вырабатывает реакцию.
Агент игнорирует эти изменения, считая динамическую среду статической.
Итак, в настоящей главе были рассмотрены три важнейших понятия:
17
7. Искусственный интеллект
искусственный интеллект, агент как носитель искусственного интеллекта и
среда, в которой агент функционирует. Типы сред определялись посредством
восприятия и реакции агента. Восприятия агента позволяют ему получать
сведения о среде, реакции — воздействовать на среду. В то же время среда
существует независимо от агентов и одним из важнейших понятий, связанных
со средой, является ее состояние. Полагая, что среда состоит из множества
объектов, каждый из которых, в принципе, может принимать бесконечное
число микросостояний (свойств, значений), состоянием среды назовем любой
набор всех этих микросостояний. Восприятие агента содержит информацию
(полную или неполную) о состоянии среды. Понятие состояния среды будет
далее широко использоваться и уточняться. Все дальнейшее содержание книги
будет направлено на то, чтобы научиться создавать агентов различного типа и в
какой-то степени сообщества этих агентов, которые позволяли бы решать
интеллектуальные задачи в конкретных средах.
Агент состоит из знаний и решателя, работающего с этими знаниями,
способен воспринимать информацию из внешней среды, в том числе и новые
знания, порождать внутри себя новые знания, используя уже ему известные
и реагировать (воздействовать) на внешнюю среду в результате рассуждений
на основе всех этих знаний. Предмет искусственного интеллекта в
предлагаемой книге рассматривается как наука о создании агентов, а под
системами искусственного интеллекта понимается сообщество агентов,
способных решать интеллектуальные задачи в средах.
Таким образом, наша главная цель — создание требуемого агента.
Спрашивается, с чего начинать процесс создания и кто это будет делать? Кто
будет формировать необходимые каждому агенту правила? В принципе,
поскольку эта задача относится к интеллектуальным, таким существом может
быть другой агент. Получается, что это уже какой-то суперагент или метаагент.
А кто научит метаагента? Какой-то вдвойне метаагент? А кто научит его? Если
идти этим путем, то перечень таких вопросов бесконечен. Чтобы выйти из
этой кажущейся неразрешимой ситуации, предполагается, что создание агента
любого типа осуществляется человеком, и он всегда способен решать задачи
суперагента любого уровня. Процесс создания агента сам по себе неформален
и качество описания, выражающееся в степени адекватности поведения
получаемого агента задуманному, зависит от учета создателем всех необходимых
аспектов его будущего поведения. Иначе говоря, создатель агента должен
включить в его описание все правила, необходимые для задуманного поведения.
Совокупность всех таких правил называют иногда базой знаний агента.
В действительности эту базу знаний можно представить в некотором
формальном языке, в частности, языке логики (понятие формального языка
будет введено позднее). Пока читатель может полагать, что таким языком
является некоторое подмножество естественного русского языка. В ответ на
свое восприятие агент с помощью логических рассуждений на основе знаний,
хранящихся в базе знаний, способен вырабатывать реакции. Механизм
рассуждений зависит от типа агента и от языка представления базы знаний. В
18
Вопросы и упражнения
случае комбинационного агента эти рассуждения простые, для других — более
сложные. Но в любом случае в основе рассуждений с использованием базы
знаний лежит логика. Именно поэтому наибольшее внимание в книге уделено
логикам, специальным языкам или исчислениям, создаваемым на их основе,
и процедурам рассуждений. Кроме того, наряду с введением необходимых
понятий даны примеры построения агентов для решения простых задач.
Вопросы и упражнения
1. Что такое искусственный интеллект?
2. Какая главная черта присуща агенту и какие бывают агенты?
3. Что такое среда и какие бывают среды?
4. Выберите одну из известных вам сред. Отнесите ее к одному из типов и
определите, какой из агентов наиболее подходит для вашей среды и почему?
5. Пусть агент является водителем со своими привычками и не всегда следует
правилам дорожного движения. Выбирите тип агента, который наиболее подходит
для каждого из следующих случаев поведения:
а) всегда использовать тормоза при спуске под гору, если впереди двигается другой
автомобиль, а скорость вашего автомобиля такова, что вы его быстро нагоняете;
б) никогда не использовать тормоза при спуске под гору, тормозить только
двигателем;
в) каждый раз при спуске под гору смотреть в зеркало заднего вида и при наличии
автомобиля сзади, который находится в пределах видимости, использовать тормоза,
а в отсутствие — не использовать. Тормозить двигателем, если в конце спуска видна
группа детей, стоящих на обочине.
6. Объясните понятия микровосприятие, микроситуация, микрореакция,
восприятие, реакция агента? Приведите примеры для каждого из них.
7. Что такое знания агента? Как они могут быть представлены?
8. Что делает решатель агента?
9. Что такое состояние среды и чем оно отличается от восприятия?
10. Что такое цель агента? Чем отличается целенаправленный агент от целе-
выбирающего?
11. Из каких двух главных частей состоит агент?
2. ЛОГИЧЕСКИЕ РАССУЖДЕНИЯ
В этой главе рассмотрена задача создания целенаправленного агента, имеющего
дело с дискретной средой, ее постановка и решение. Введены основные понятия
логики высказываний. Описан процесс рассуждений в этой логике, позволяющий
целенаправленному агенту достигать целей.
Рассуждением или умозаключением обычно называют ряд мыслей,
изложенных в логически последовательной форме. В предыдущей главе были
введены понятия состояний среды. Настоящая глава посвящена изучению
возможности агента находить интересующие его состояния среды (целевые
состояния), если он что-либо знает о других ее состояниях. Определение
целевых состояний осуществляется с помощью поиска или рассуждений в
пространстве состояний. Обсудим, как рассуждения подобного рода можно
формализовать в языке логики высказываний, т.е. как формально поставить
задачу на языке логики высказываний и затем ее формально решить,
пользуясь аппаратом логики высказываний. Рассмотрим также, предваряя
главу 6, что такое стратегия решения или поиска. Там, где это возможно,
введение необходимых понятий будем иллюстрировать простыми примерами.
В конце главы остановимся на трудностях, которые возникают при решении
задач с помощью только логики высказываний.
2.1. Рассуждения в пространстве состояний среды
В коммунальной квартире две старушки занимают по комнате. Комнаты
находятся в общем коридоре, который имеет выход на лестничную клетку.
Одна из комнат расположена слева (левая комната) от выхода, а другая —
справа (правая комната). В коридоре живет кот, которого обе старушки
одинаково любят и балуют, оставляя ему кусочки сыра. Каждая старушка
кладет кусочек сыра у двери своей комнаты. Кот отдыхает либо у левой комнаты
(слева), либо у правой (справа). Множество всех состояний этой среды (среды
кота) можно представить табл. 2.1, в столбцах которой для каждого состояния
среды указаны местонахождение кота (слева или справа), наличие или отсутствие
кусочка сыра (да или нет) у соответствующей комнаты.
Состояние b. означает, что кот находится около левой комнаты и около
обеих комнат лежит по кусочку сыра, состояние Ь2 — кот находится около
20
2.1. Рассуждения в пространстве состояний среды
Таблица 2.1
Состояние Местонахождение кота Наличие сыра
слева справа
Ь1 Слева Да Да
Ь2 Справа Да Да
Ьз Слева Да Нет
Ь4 Справа Да Нет
Ь5 Слева Нет Да
Ь6 Справа Нет Да
Слева Нет Нет
Ь8 Справа Нет Нет
правой комнаты и около обеих комнат снова лежит по кусочку сыра и т.д.
Кот может совершать в один и тот же момент времени только одно из
следующих действий: переходить к дверям левой комнаты, переходить к дверям
правой комнаты и съедать кусочек сыра около той комнаты, где он находится.
Эти действия обозначим с; = Идти налево, с2 = Идти направо и с? = Съесть
соответственно. Если среда находится в одном из состояний, перечисленных
в табл. 2.1, и кот совершает какое-либо из действий, то нетрудно определить,
в какое состояние после выполнения действия перейдет среда.
Будем полагать, что нам известно состояние, называемое начальным, с
которого могут начаться изменения среды при действиях кота. Пусть, например,
это будет состояние Ьг Будем изображать состояния кружочками с обозначением
состояния внутри кружочка.
Переход из одного состояния в другое,
Рис. 2.1. Допустимые переходы из начального состояния Ь1
21
2. Логические рассуждения
Рис. 2.2. Дерево переходов
происходящий в результате действия, будем изображать стрелкой, ведущей в
это другое состояние и помеченной соответствующим действием. Так, на рис.2.1
изображены все переходы из состояния Z>; в результате действий с;, с2, с3. На
рис. 2.2 показано дерево всех дальнейших переходов, являющееся продолжением
элементарного дерева на рис. 2.1. Построение каждой ветви дерева прекращено
на том состоянии, которое встречается повторно на пути, ведущем в него из
начального состояния.
2.1.1. Постановка задачи
Цель кота — не оставить ни одного кусочка сыра, где бы он изначально ни
находился. В терминах состояний среды целью кота является перевод ее с
помощью своих действий (реакций) в одно из состояний Ь7 или bg. Состояния,
в которые с помощью набора допустимых действий необходимо перевести среду,
называются целевыми. Процесс определения этих состояний называют
формулировкой цели. Будем полагать в рамках нашего примера, что каждое
восприятие совпадает с одним из состояний. Задачей агента (см. гл. 1) является
22
2.1. Рассуждения в пространстве состояний среды
нахождение последовательности действий или пар восприятие—действие,
ведущих на дереве переходов из начального состояния в целевые. Процесс
нахождения этих последовательностей называют поиском, выводом или
рассуждением. Постановкой задачи называют задание всех состояний и действий,
которые можно использовать для решения задачи, начального состояния и
целевых состояний, а также всех допустимых переходов между состояниями
при выполнении действий. Для среды кота постановка задачи уже осуществлена.
Все состояния, которые могут использоваться при решении задачи, перечислены
в табл. 2.1. Целевыми состояниями являются состояния b7, bg. Все допустимые
переходы между состояниями показаны на рис. 2.2. Из рисунка ясно, что
решениями задачи является последовательность bjc2, b2/c3, bjcp bjcv в
результате выполнения которой агент (кот) переведет среду в состояние Ь7,
и последовательность bjcp bjc? bjc3, в результате выполнения которой
среда окажется в состоянии bg
2.1.2. Поиск решения
Решения задачи для среды кота практически очевидны, когда построено
дерево переходов состояний среды, по которому легко проследить пути,
ведущие в целевые состояния из начального. В реальных задачах это дерево
может быть очень большим, вследствие чего нецелесообразно использовать
стратегию поиска, согласно которой необходимо сначала получать дерево
целиком. Вместо этого используются другие более эффективные стратегии
поиска, речь о которых пойдет далее. Однако, какая бы из этих стратегий не
применялась, элементарным шагом поиска является переход из одного
состояния среды в другое и анализ состояния, в которое переход был
осуществлен, на принадлежность к числу целевых. Каждый допустимый
переход из состояния й после совершения действия с в состояние bk можно
задавать с помощью правила перехода: « Если среда находится в состоянии
Аи совершается действие с, то она должна перейти в состояние Ьк».
Совокупность правил подобного типа используется в процессе поиска.
Одной из очевидных, но чрезвычайно неэкономных стратегий поиска,
позволяющей найти все решения для среды кота, может быть следующая.
1. Образовать множество В = {Ь7}, состоящее из одного начального
состояния ЬГ
2. Для каждого состояния множества В и каждого действия с найти,
согласно соответствующим правилам перехода, все состояния bk, в которые
переходит среда. Совокупность всех таких состояний, за исключением тех,
которые уже встречались в ранее образованных множествах В, принять за
новое множество В.
3. Проверить, нет ли среди элементов этого множества целевых состояний.
Если целевых состояний нет, то перейти к п. 2. Если целевые состояния есть,
то выписать в порядке использования правил все последовательности действий,
которые привели к целевым состояниям, удалить эти состояния из множества Ви
перейти к выполнению следующего пункта.
23
2. Логические рассуждения
4. Проверить, все ли целевые состояния найдены. Если найдены все, то
прекратить поиск. Если найдены не все, то перейти к п. 2.
Проиллюстрируем на примере среды кота применение этой стратегии.
Правила перехода выписывать не будем, поскольку в нашем распоряжении
уже есть дерево переходов (см. рис. 2.2).
Итак, вначале В = {Z>;}. После выполнения п. 2 имеем совокупность
состояний Ьр Ь2, Ь5. В этой совокупности нет ни одного целевого состояния,
а состояние Ь7 уже встречалось. Поэтому, согласно п. 3, принимаем
В = {b2, Ь,} и переходим к выполнению п. 2. В результате получаем
совокупность состояний Ьр Ь2, Ь4, Ь,, Ь6, среди которых опять нет целевых,
а Ьр Ь2, Ь6 уже встречались. Поэтому В = {Ь4, Ь6} и снова возвращаемся к
п. 2. После очередного выполнения этого пункта имеем совокупность
состояний b3, bp b5, b6, b8. Среди этих состояний bp Ь5, Ь6 уже встречались,
а состояние Ь8 является целевым. В это состояние ведет единственная
последовательность действий с3с2с3. Однако еще не все целевые состояния
найдены, а именно не найдено состояние Ь7. Поэтому в соответствии с п. 4
продолжим поиск, вновь переходя к п. 2 с множеством В= {Z>5}. В результате
получим совокупность состояний b3, b4, Ьг среди которых Ь3, Ь4 уже
встречались, а Ь7 целевое. Последовательностью действий, ведущих в
состояние Ь7, является c2c3ctc3 Итак, все целевые состояния найдены,
решение задачи в виде последовательности действий, ведущих в эти
состояния, получено. Поиск на этом прекращается.
2.2. Логика высказываний
В предыдущем параграфе показано, что рассуждения агента (поиск решений
задачи) сводится к определению правил перехода в соответствии с выбранной
стратегией. Каждый шаг состоит в проверке агентом истинности левой части
правила (факта нахождения среды в состоянии Ь. и допустимости действия с)
и, в случае ее истинности, признании факта перехода из состояния й в состояние
bk в результате действия с. Естественно, нам хотелось бы иметь математический
аппарат, на основе которого можно осуществлять постановку и поиск решения
задачи формально, используя наилучшую стратегию поиска. Логика
высказываний — это первый шаг к созданию такого аппарата.
Осуществить постановку задачи формально — значит, имея некий формальный
язык, выразить на нем все знания о среде, необходимые для решения задачи.
Формальный язык в соответствии с современными представлениями требует
рассмотрения двух его неотъемлемых частей: синтаксиса и семантики. Синтаксис
языка описывает допустимые в языке предложения, состоящие из цепочек
(последовательностей) символов, принадлежащих определенному множеству,
называемому алфавитом. Синтаксис языка позволяет отличать предложения,
принадлежащие языку, от предложений, ему не принадлежащих. Семантика
языка определяет смысл этих предложений, сопоставляя символы языка с
объектами реального мира, а предложения — отношения между объектами.
Без семантики предложения языка являются ничего не значащими для агента
24
2.2. Логика высказываний
цепочками символов. Семантика логики высказываний позволяет подразделять
все множество допустимых предложений на истинные и ложные. Истинные —
это те предложения, которые соответствуют имеющим место фактам или
отношениям, а ложные — не имеющим. Решать задачу формально — это значит
иметь множество правил и стратегию их использования, которые позволяют
осуществить вывод одних синтаксически правильных истинных предложений из
других синтаксически правильных истинных или предполагаемых истинными.
2.2.1. Синтаксис логики высказываний
Синтаксис логики высказываний прост и имеет прямые синтаксические и
семантические аналоги в естественных языках, что чрезвычайно облегчает нам
понимание логики высказываний. Символами языка логики высказываний,
составляющими ее алфавит, являются логические константы ИСТИНА и ЛОЖЬ.
сокращенно обозначаемые буквами И и Л, логические переменные х, у, z,--.,
обозначаемые строчными буквами латинского алфавита, логические связки л
(И), v (ИЛИ), (НЕ), = (ЭКВИВАЛЕНТНО), z> (ВЛЕЧЕТ) и круглые скобки.
Значениями логических переменных являются логические константы.
Предложения языка логики высказываний, называемые также формулами или
высказываниями, составляют в соответствии со следующими правилами:
логические константы являются простыми предложениями;
логические переменные также простые предложения;
сложные предложения формируются из простых с помощью связок
л (И), v (ИЛИ), -п (НЕ), = (ЭКВИВАЛЕНТНО), (ВЛЕЧЕТ)-
простые и сложные предложения, заключенные или не заключенные в
скобки, являются предложениями языка логики высказываний;
из предложений с помощью связок и скобок можно образовать новые
предложения языка логики высказываний;
связки имеют следующий порядок старшинства л, v, z>, =, т.е. связка
самая старшая, а связка = — самая младшая.
Формулы логики высказываний, составленные по этим правилам, называют
правильно построеннымим формулами или сокращенно формулами.
2.2.2. Семантика логики высказываний
Семантику логики высказываний можно пояснить смысловой
интерпретацией ее предложений или формул, под которой обычно понимают
процесс установления соответствия между логическими переменными и
изменяющимися свойствами объектов среды и между значениями переменных
(константами) и конкретными значениями свойств объектов. В примере со
средой кота — это соответствие между логической переменной хк и свойствами
кота находиться слева или справа и значениями логической переменной
х.= И и хк= Л, следовательно, одним из местонахождений кота (слева или
справа) и далее между отношениями свойств объектов и формулами, истинное
значение которых определяет наличие отношения, а ложное — его отсутствие.
25
2. Логические рассуждения
Иначе говоря, интерпретация определяет семантику формул
(предложений, высказываний) путем сопоставления переменных в формулах
со свойствами объектов среды, а отношений между этими свойствами — с
формулами. Это позволяет по значению формул после подстановки вместо
переменных конкретных значений свойств судить о наличии или отсутствии
у среды тех или иных совокупных свойств или отношений. Если дана какая-
либо формула, то подстановка в формулу констант вместо ее переменных
называется конкретизацией. Таким образом конкретизация является
результатом интерпретации. Замечательным свойством логики высказываний
является то, что семантика ее простейших формул, т.е. их истинностные
значения (И или Л) близки к соответствующим высказываниям на
естественном языке при любой интерпретации.
Так, например, если формула включает только одну связку, то ее
семантика очень близка к соответствующим высказываниям в русском языке.
Так семантика формул х v у, х л у, х, в которых встречаются соответственно
связки л, v, практически совпадает с отношениями, определяемыми
соответственно смыслом слов «и», «или», «не», употребляемых в русском
языке для выражения отношений между свойствами объектов, обозначаемых
переменными х, у, хотя некоторые различия имеются. Например, формула
х v у имеет истинное значение, если хотя бы одна переменная истинна, но
она истинна и при истинности обеих переменных. Говоря на русском языке
«х или у», обычно предполагаем, что это предложение истинно, если истинна
только одна переменная, т.е. это предложение русского языка по смыслу
ближе к формуле логики высказываний xv-.yv-.xv у.
Еще больше различий между семантикой формулы х z> у в логике
высказываний и похожему на нее высказыванию на русском языке «х влечет
у». Первое различие состоит в том, что в русском языке мы полагаем, что
предложение «х влечет у» истинно, если истинны х и у, т.е. предложение
русского языка по смыслу совпадает с формулой х лу, в то время как формула
х эу может быть истинной не только тогда, когда истинны обе переменные
х и у, но и когда обе ложны или когда х ложна, а у истинна. Кроме того,
семантика формулы х zj у вообще не предполагает какой либо связи между
переменными х и у. Чтобы не обсуждать в дальнейшем подобные
несоответствия, впредь будем полагать, что, употребляя формулу хэу, мы
вкладываем в нее смысл, вытекающий из следующего предложения: «Мы
заявляем, что истинность высказывания «х влечет у» означает, что истинность
х влечет истинность у, а больше мы ничего не заявляем».
Истинностные значения любой формулы, т.е. ее семантику, всегда можно
задать таблицей, состоящей из двух частей: в левой части таблицы перечислены
все наборы значений аргументов, а в правой соответствующие наборам
значения формулы. Задание таких таблиц для связок облегчается тем, что
значениями аргументов и формул являются только две величины — И или
Л. Такие таблицы в логике высказываний называют таблицами истинности
(табл. 2.2). Таблицы истинности можно построить для любой формулы,
поскольку любая формула является композицией формул для связок. Если
26
2.2. Логика высказываний
Таблица 2.2
X У —1 X х л у X V у х о у X = у
л л И Л л И И
л И И л И И л
И л л л И Л л
И И л И И И И
формула интерпретирована, то ее таблица истинности определяет семантику
интерпретированной формулы, поскольку по ней можем всегда определить,
какие же отношения между свойствами объектов, обозначаемых переменными,
имеют место (формула истинна) и не имеют места (формула ложна).
2.2.3. Общезначимые формулы н их роль
Формулы, истинные на всех наборах значений своих аргументов, называют
общезначимыми формулами. Если какая-либо формула а является
общезначимой, то этот факт обычно записывается с использованием знака
общезначимости |=, который ставится перед формулой: 1=а. Проверку формулы
на общезначимость можно осуществить с помощью таблицы истинности: если
формула истинна во всех строках таблицы истинности, которая содержит все
возможные наборы аргументов формулы, то эта формула общезначима.
Рассмотрим, например, формулу -> х л (-, у v у) о х. Таблицей истинности
для нее является табл. 2.3.
Таблица 2.3
X У —1 X у у) X Л у V у) —> X Л (—, у V у) ZD —1 X
л л И И И И
л И И И И И
И л л л л И
И И л л л И
27
2. Логические рассуждения
Из табл. 2.3 ясно, что формула х л (-. у vy)D-.i является общезначимой
(во всех строках последнего столбца стоит значение И). Ранее было заявлено,
что истинность высказывания z>a2 всегда означает, что истинность а влечет
истинность а2(здесь и отделяются формулами логики высказываний). Потому,
установив факт общезначимости формулы а^а2и истинности ар всегда можно
сделать заключение об истинности а2. Так, например, предположим, что
истинное значение логической переменной х в формуле -> х л (-. у v у) z> х
соответствует местонахождению кота слева (Слева), а ложное значение
логической переменной хсоответствует местонахождению кота справа (Справа),
истинное значение переменной у соответствует наличию сыра около левой
комнаты (Да), а ложное его отсутствию там (Нет). В этом случае при
истинности формулы —। х л (—। у v у) можно сделать заключение об истинности
формулы -л х, что соответствует нахождению кота у правой комнаты (Справа).
Таким образом, общезначимость формул вида a z> а2, называемых
импликативными формулами, является важным свойством для получения
заключения об истинности а2, называемого заключением, при истинности
а/; называемого посылкой. Для простоты импликативные формулы а, а2
будем называть так же, как и связку z>, импликацией. В логике высказываний
известно много общезначимых формул, называемых обычно законами логики
высказываний. Наиболее известными являются следующие законы:
коммутативные
ci] &а2 = а2 &<Х|,
о.] v а2 = а2 v а,;
дистрибутивные
<Х| &(а2 v а3) = (а, & а2) v (а, &а3),
а, v (а2 &а3) = (а, v а2)& (а, v а3);
ассоциативные
СС| &(аэ & а3) = (а] & а-,) & а3,
СС| v (a, v а3) = (а, v а2) v а3;
законы Де Моргана
—।(<Xj & а,) = (—।ос,) v (-ice,),
—|(СХ| v а2) (—.ос, )&(->а2);
закон двойного отрицания
28
2.2. Логика высказываний
В этих законах а обозначает любую правильно построенную формулу
логики высказываний.
Кроме общезначимых, существуют формулы выполнимые и невыполнимые.
Формула называется выполнимой, если существуют наборы значений ее
аргументов, на которых она принимает истинное значение, и наборы значений,
на которых она принимает ложное значение. Если формула на всех наборах
значений ее аргументов принимает ложное значение, то она называется
невыполнимой.
Установление истинности следствия по общезначимой импликативной формуле
достаточно универсальный способ для вывода заключений, но требует проверки
общезначимости последней. Если формула а, о а, не является общезначимой,
то подобного заключения делать нельзя. Проверку общезначимости можно
осуществить с помощью таблицы истинности. Однако построение таблиц
истинности слишком трудоемко для того, чтобы можно было решать реальные
задачи. Вместо этого используют специальные правила вывода, применение
которых базируется не на понятии общезначимости формулы, в частности
общезначимости импликативной формулы, а на понятии модели формулы.
2.2.4. Модель формулы
Любую среду, конкретизация в которой при соответствующей
интерпретации делает данную формулу истинной, называют моделью этой
формулы. Так, например, среда кота является моделью формулы хлхлхл
л z2 z) хк л xi л хп при конкретизации переменных хк, хр хр z2, хк
соответственно как высказываний «кот находится у левой комнаты», «у левой
комнаты лежит кусочек сыра», «у правой комнаты лежит кусочек сыра»,
«кот переходит к правой комнате», «кот находится у правой комнаты»
поскольку высказывание «если «кот находится у левой комнаты» и «у левой
комнаты лежит кусочек сыра» и «у правой комнаты лежит кусочек сыра» и
«кот переходит к правой комнате», то после этого «кот находится у правой
комнаты» и «у левой комнаты лежит кусочек сыра» и «у правой комнаты
лежит кусочек сыра», являющееся конкретизацией формулы хклх1лхплг2 z>
Хк Л Х1 Л X , истинно.
Понятие модели является важным в логике высказываний и других логиках,
поскольку позволяет удачно ввести понятие выводимости одних, истинных
при соответствующей интерпретации формул, из других истинных. Считают,
что формула а выводима из формул ар а2, ..., ат, если любая (но одна и та
же) модель всех этих формул ар а2, ..., ат является также моделью формулы
а. Иными словами, если формулы ар а2, ..., ат истинны на некотором
множестве конкретизаций в данной среде, то формула а выводима из них,
если она также истинна на всех конкретизациях этого множества. Факт
выводимости записывают с помощью символа выводимости h : ар ..., ак. |- а.
29
2. Логические рассуждения
2.3. Исчисление высказываний
Логическим исчислением,или просто исчислением^азыъакуг совокупность,
которая включает в себя: алфавит (совокупность используемых символов);
синтаксические правила построения формул в алфавите; аксиомы
(общезначимые исходные формулы); правила вывода по аксиомам
производных формул или теорем.
Правила вывода а |-р имеют дело непосредственно с формулами, а не с
таблицами истинности, позволяя по истинности одних формул делать
заключения об истинности других. Символы а и р в правиле вывода
обозначают одну или несколько формул; а называется условием, ар —
следствием. Если в условии или следствии формул несколько, то они
записываются через запятую. Нас прежде всего будут интересовать только
такие правила вывода, с помощью которых на основании истинности всех
формул, входящих в условие правила вывода, можно при любой
интерпретации сделать заключение об истинности всех формул, входящих в
следствие правила вывода. Обычно такие правила называют состоятельными.
Доказательство состоятельности правила вывода можно осуществить с
помощью таблицы истинности, каждая строка которой соответствует одной
из моделей условия, а общее число строк совпадает с числом всех моделей
условия. Если всем этим условиям соответствуют истинные следствия, то
правило является состоятельным.
2.3.1. Классическое исчисление высказываний
В предыдущем параграфе был рассмотрен язык логики высказываний. Если
в качестве алфавита логического исчисления взять алфавит логики высказываний,
в качестве синтаксических правил — синтаксические правила логики
высказываний, в качестве аксиом — некоторое множество общезначимых
формул, например законов, а в качестве правил всего два правила: модус поненс
и подстановки, указанные ниже, то в результате получим исчисление,
называемое обычно исчислением высказываний. Классическим исчислением
высказываний обычно называют исчисление, аксиомами которого являются
следующие общезначимые формулы:
а о (р а),
(аэр)э((а z> (р z>у)) э(аэу)),
(алР)э а,
(а л Р)э р,
а э( а v Р),
30
2.3. Исчисление высказываний
[3 о ( ос v (3),
а о ([3 о (ос л [3)),
(ос у) о (([3 э у) => ((ос v [3) о у)),
(ОС Z5 [3) Z) ((ОС —> [3) о —, ос),
—i —> ОС = ОС,
Обратим внимание, что все аксиомы логики высказываний включают в себя
только логические переменные и истинны при любой интерпретации. Поэтому,
если нам удастся достаточно адекватно интерпретировать эти законы в какой-
либо среде, то исчисление высказываний может служить основой для
рассуждений об этой среде.
Классическое исчисление высказываний использует два правила вывода.
Модус поненс. Из истинности условия импликации и истинности самой
импликации следует истинность следствия импликации:
а, а о [31- [3.
Правило подстановки. Из формулы а(/>) выводима формула а (Р),
получающаяся подстановкой в формулу а(р) вместо каждого вхождения
переменной р формулы Р\
а(р) |-а(Р).
Другие исчисления высказываний. Существуют и другие исчисления
высказываний. Так, например, при решении практических задач удобнее
использовать не законы логики высказываний, а правила, их заменяющие.
В этом случае логическое исчисление называют натуральным исчислением
высказываний. В натуральном исчислении высказываний обычно, помимо
правил модус поненс и подстановки, используют следующие правила.
Исключение конъюнкта. Из истинности конъюнкции следует истинность
любого ее конъюнкта:
а. л а, л ... л а На..
1 z nt
Введение конъюнкции. Из списка истинных формул следует истинность их
конъюнкции:
ар , ..., <у.п |- И] л а2 л ... л ап.
31
2. Логические рассуждения
Введение дизъюнкции. Из истинности формулы следует истинность ее
дизъюнкции с любыми другими формулами:
a h ос, v ос v ... v ос v ... v ос .
Исключение двойного отрицания. Из истинности двойного отрицания
формулы следует истинность ее самой:
—, —, ос ос.
Простая резолюция (удаление дизъюнкта). Из истинности дизъюнкции и
отрицания одного из ее дизъюнктов следует истинность формулы,
получающейся из дизъюнкции удалением этого дизъюнкта:
ос v [3, [3 h ос.
Резолюция. Из истинности двух дизъюнкций, одна из которых содержит
дизъюнкт, а другая — его отрицание, следует формула, являющаяся
дизъюнкцией исходных формул без упомянутого дизъюнкта и его отрицания:
ос v [3, [3 v yl-ocvy или эквивалентно ->осо[3, [ЗоуН-^осоу.
2.3.2. Формализация вывода средствами логики высказываний
Вернемся снова к нашему примеру — среде кота. Введем три логические
переменные хк, хл, хп, истинное значение первой из которых означает, что
кот находится у левой комнаты, а ложное, что он находится у правой комнаты;
истинное значение переменной хл означает, что кусочек сыра лежит около
левой комнаты, а ложное, что его там нет; истинное значение переменной
хп означает, что кусочек сыра лежит около правой комнаты, а ложное, что
его там нет. В результате таких обозначений табл. 2.1 можно заменить на
табл. 2.4. Каждое состояние среды можно рассматривать как комбинацию
(отношение) простейших свойств объектов, задаваемых значениями отдельных
логических переменных. Так, состояние соответствует комбинации свойств
кота и кусочков сыра, состоящей в том, что кот находится в левой комнате,
и в это же самое время около левой и правой комнат находится по кусочку
сыра. На русском языке эту комбинацию можно выразить предложением:
«Кот находится около левой комнаты, кусочек сыра лежит около левой
комнаты и кусочек сыра лежит у правой комнаты». В соответствии с уже
приведенной выше интерпретацией логических переменных хк, х, хп это
предложение можно представить формулой хк л хл хп, которая истинна в
единственном случае — все логические переменные, входящие в нее,
истинны, т.е. среда находится в. состоянии ЬГ Формулы такого типа,
являющиеся конъюнкцией переменных с отрицанием или без него, называют
элементарными конъюнкциями. Если среда находится в состоянии bv то
истинна формула-, хк л хл л хп и т.д.
Элементарную конъюнкцию, в которую входит по одному разу каждая
переменная, определяющую состояние среды, с отрицанием или без
32
2.3. Исчисление высказываний
отрицания, называют полной конъюнкцией, или конституентой. Аналогично
тому, как были введены логические переменные хк, х, хп, введем логические
переменные zt, Z2, Z3 для действий кота Идти налево, Идти направо, Съесть
соответственно. Переменная принимает истинное значение, если
выполняется соответствующее ей действие. В противном случае она
принимает ложное значение. Для простоты будем полагать, что кот не может
одновременно выполнять сразу более одного действия.
Рассмотрим теперь, как могут быть выражены в виде формул переходы
среды из одного состояния в другое при совершении котом того или иного
действия. Так, если кот находился в состоянии Ь, и выполнил действие Идти
направо, то среда перейдет в состояние Ь2. Факт нахождения кота в состоянии
Ь., и выполнение им в это время действия Идти направо означает истинность
формулы хк л хл л хп л z2, а факт перехода состояния Ь, при выполнении
действия Идти направо в состояние Ьг будем интерпретировать как истинность
формулы хк л хл л хп л z2 о - хк л хл л хп, что позволяет при истинности г Л X Л
л хп л z2 сделать заключение об истинности хк л хл л хп. Точно так же можно
выразить в виде аналогичных формул все остальные переходы, показанные
на рис. 2.2. Представим их в виде табл. 2.5. В первых трех столбцах этой
таблицы указаны переходы, имеющиеся на рис. 2.2, а в последнем —
формулы, соответствующие переходам.
Таблица 2.4
Состояние Переменные Формула, описывающая состояние
X к X п
bi И И И X Л X Л X К л п
bi л И И —i X Л X Л X к л п
\ И И л X Л X Л —1 X к л п
Ь4 л И л -1 X А X Л “1 X к л п
Ь5 И л И X А X Л X к л п
ь6 л л И —1 X Л —1 X Л X к л п
Ь1 И л л X А -1 X Л -1 X к л п
Ь* л л л -1 X А -1 X А —,Х к л п
2 - 1141
33
2. Логические рассуждения
2.3.3. Нахождение целевого состояния
Имея формулы для состояний и переходов, введенные в предыдущем разделе,
покажем теперь, как их можно использовать для нахождения одного из целевых
состояний. Целевыми состояниями являются Ь1 и Л8. Если среда находится в
состоянии Ь1, то это означает истинность формулы хк л -> хч л -> хп, а если в
СОСТОЯНИИ Й8, ТО ИСТИННОСТЬ формулы -1 Хк Л -1 Хд Л -I хп.
Имеем таким образом постановку задачи:
• начальное состояние среды представлено истинной формулой
х л х л хп;
• множество формул представляют все состояния среды в последнем
столбце табл. 2.4;
• множество допустимых переходов представлено импликациями в
последнем столбце табл. 2.5;
Таблица 2.5
Переход Импликация, соответствующая переходу
Исходное состояние Действие Ре зул ьти ру ющее состояние
Ь1 cj Ь! х л х л хп л Z. О X Л X А Х„ к л п 1 к л п
Ь1 С2 Ь2 X А X А X A 2L О X л X А X К л п 2 к л п
Ь1 С3 Ь5 X АХ AXAZ. ОХА-пХ АХ к я п З к л п
Ь2 С1 Ь1 —1 X А X А X A 2, О X А X А X к л п 1 к л п
Ь2 С2 Ь2 —7ХАХАХАД,О—i X Л X A X к л п 2 к л п
Ь2 С3 Ь3 —1 X А X А X А 2, О —1 X А X А ~1 X к л п 3 к л п
Ь4 Ь3 —1 X А X А —1 X A Z. OX АХ A—i X к л п 1 к л п
ЬА С2 Ь3 —1 X АХ А —1 X A Z, О —। X АХ А —i X к л п 2 к л п
Ь4 С3 Хк Л хл л -1 ХП Л Z3 =3 Хк л ХЛ л ХП
Ь3 С1 Ь3 ХК Л Хл Л -п Хп Л Z, 2Э Хк Л ХЛ л -П хп
34
2.3. Исчисление высказываний
Окончание табл. 2.5
Переход Импликация, соответствующая переходу
Исходное состояние Действие Ре зуд ьти р у ю ще е состояние
Ьз С2 ^4 X А X л—i X A Z, О —। X Л X Л —। X к л п 2 к л и
Ьз С3 Ь7 X Л X Л —1 X Л Z, ОХ Л —1 X Л -1 X кт п 3 к т п
Ьз С1 Ь5 XA-nXAXAZ, ОХА —। X Л X к л п 1 к ли
Ь5 С2 Ьв ХА—i X А X A Z-, О—। X А —1 X А X к ,т п 2 к т п
Ь5 С3 Ь5 ХА—। X А X A Z, ОХА—। X А X к л п 3 к л п
Ь6 Ь5 —1 X А —1 X А X A Z. О X А —। X А X к л п 1 к л п
Ьв С2 Ьв —। X А —। X А X A О —-1 X А —1 X А X к л п 2 к л п
Ьв С3 -п X А —• X А X A Z, О —1 X А — X А X к л п 3 к л п
• множество допустимых действий описывается формулами ’.л -
Zt л л —> Z3, -> Zt л л Z3,
• множество целевых состояний представлено формулами х. л -> л х. и
хк л -I хл л -I хп.
Решение задачи состоит в нахождении последовательности переходов, ведущих
из начального состояния в одно из целевых, и может быть следующим.
1. Выбираем начальное состояние й = />,. Это означает истинность
соответствующей ему формулы, которую будем обозначать Р(. В нашем случае
Pi = хклт лхп.
2. Выбираем одно из действий с, допустимых в состоянии Ь,, и
соответствующую ему логическую переменную zr например, с} и zr
3. Полагаем, что формула р.л Zj истинна (среда находится в состоянии />
и совершается действие с).
4. Находим по табл, 3.5 любую импликацию Р, л z z> Рр левой частью
которой является формула Р,л z. (При р.= р,, z = Zl и р, л z, = \ л х лхл?,
такой импликацией может быть, например, хк л х л хп л zt хк л xq л хп.)
5. Применяем правило модус поненс Р(л z, Р, л г => Р* h РА к истинным
формулам Р(л z, Р,л => Pt, заключая, согласно этому правилу, что формула
2*
35
2. Логические рассуждения
Таблица 2.6
Исключение конъюнкта а, л а. л ... л а 1- а -! Z) л —, Z2 Л Z3 1- Z3
Введение конъюнкта а,, а., ..., а 1- Р 2’ ’ н а. л а.л ... ла 1 2 н XAXAX,Z,kxAXAXAZ. к л п’ 3 к л п 3
Модус поненс а, а Zj Р Р хлх л х л z,, х лх л х л z, д к л п 3 ’ к л п 3 х л —1 х л х (-хл—.хлх к л п к л п
Исключение конъюнкта а. л а. л ... ла к а 12 н 1 —, Z, Л л -I z3 k z2
Введение конъюнкта а|; а2, ..., аф а, л осл ... ла 1 2 н XAXAX,Z,|-XA—iXAX AZ, к л гР 2 к л п 2
Модус поненс а, а дэ Р k Р X Л —\ X А X A Z,, X Л —i X А X A Z-, ZD к л п 2’ к л п 2 —1 х л —1 х л х I 1 х —1 л х л х к л п к л п
Модус поненс а, а Zj Р н Р —1 х л —! х л х л z,, —.хл—। х л х л z, з к л п З1 к л и 3 —> X Л —> X Л —i X к—1 X Л ~1 X Л —! X к л п к л п
Рк истинна. (При Р;= р7и z = z, РА= Р,= хклхчлхп, т.е. в этом случае среда
переходит из состояния bt снова в состояние Ь, в результате действия с .)
6. Проверяем, не является ли состояние bk, соответствующее формуле р
целевым. Если оно целевое и последнее из всех, которые надо найти, то на
этом поиск завершается. В противном случае, поиск следует продолжить,
возвращаясь к п.2 и начиная с состояния bk (в п.2 состояние Ь. принимается
равным bk) или возвращаясь к какому-либо состоянию, которое было
достигнуто, но переходы из которых еще не были рассмотрены.
Рассмотрим процедуру поиска решения для среды кота, в результате
которой будет найдена последовательность действий, ведущая в целевое
состояние />8, представляемое формулой -> хк л -> хч л -> х . Эту процедуру
представим в виде табл. 2.6, в первом столбце которой запишем название и
само правило вывода в общем виде из числа описанных ранее в этой главе, а
во втором — результат его конкретного применения.
36
2.4. Рассуждения в терминах интервалов
Таким образом, для примера со средой кота был осуществлен вывод формулы
X. Л X Л -I хп из исходных истинных формул Хк Л X Л Хп, г, Л £2 Л
ялхлхлг, ЭХЛ-нХ лх, хл-nX лхлг2 =>-х А-Х АХ,
хк л^х лхпл г3 з - хкл xqл -I хп, что можно записать в виде выражения
* А X Л Хп, -н Z, Л -n Z2 л Z3, - Z, л Z2 л -п гз, X Л X Л X Л Z3 - х л -п X Л X, X л
л-х лх AZ, 3-Х А-nX лх, -нХкл-нХ лхплг3 3 -х А^х Л.хк -X А
А — X А —i X .
л п
Приведенная задача со средой кота очень проста. В реальных задачах
число переменных, представляющих состояния среды, может быть гораздо
большим, что сделает практически нереальным представление состояний
конституантами. Выходом из этого положения может быть интервальное
представление состояний среды.
2.4. Рассуждения в терминах интервалов
Каждый из нас с детства знаком с настольными играми. Основным их
элементом является игральная доска, которая разбита на ячейки,
соединенные тем или иным образом путями. Играющие кидают кость и из
той ячейки, где они находятся, в зависимости от выпавшего числа очков
переходят в ту или иную ячейку. При этом можно попасть в «хорошую»
ячейку, которая расположена близко от целевой ячейки, но можно и в
«плохую», из которой бросавший кость может быть переведен назад и окажется
от цели дальше, чем был перед бросанием кости. Добравшийся до цели
раньше других выигрывает. Спектр таких игр велик: переходы из ячейки
зависят от встречающихся в ячейках различных препятствий и противников,
которые не только могут отбросить играющего назад, но и вообще вывести
его из игры, противники имеют возможность сами перемешаться по ячейкам
в ответ на ход бросающего кости и т.д.
Рассмотрим простой пример среды такого типа, называемой средой
чудовища. Среда имеет число ячеек, равное 4x4, расположенных по
вертикали и горизонтали. Каждая внутренняя ячейка имеет четыре соседних,
крайние ячейки могут не иметь соседних ячеек с одной или двух сторон.
Агент, выступающий в роли единственного играющего, может переходить в
одну из соседних ячеек. В одной из ячеек находится чудовище. Чудовище
издает зловоние, которое распространяется на соседние ему ячейки. В одной
из ячеек лежит золото, которое блестит. Кроме того, в ячейках могут быть
бездонные ямы. В ячейках, соседних ячейкам с ямами, ощущается сквозняк.
Задача агента, стартуя в ячейке (1, 1), добраться до ячейки с золотом, взять его
и благополучно вернуться назад.
Исходное состояние среды чудовища соответствует рис. 2.3, где буквы в
ячейках обозначают следующее: Ч — чудовище, 3— зловоние, С — сквозняк,
Б — блеск, Я — яма, Н — агент. Сопоставим каждую ячейку (/', у) среды с
шестью логическими переменными хч (/, у), хз (/, у), хс (/, у), х6 (/, у), хя (/, у),
хн (/, у). Будем полагать, что значение этих переменных истинно, если
37
2. Логические рассуждения
3 С я
Ч, 3 3, С, Б Я с
3 с
н С я с
12 3 4
Рис. 2.3. Исходное состояние среды чудовища
чудовище, зловоние, сквозняк, блеск, яма или агент присутствуют в
соответствующей ячейке, и ложно в противном случае. Введем дополнительные
логические переменные, характеризующие ориентацию агента на север, юг,
восток и запад: xn(i, j), х< (1, j), xe(i, j), xw(i, j). Истинное значение какой-
либо из них с индексами (/, J) означает ориентацию агента, находящегося в
ячейке (/, у) соответственно на север, юг, восток и запад; ложное значение
— отсутствие ориентации.
Естественно, такая интерпретация переменных означает, что только одна
из них может быть истинна. Понятно, что суммарное число переменных
равно 10 х 16 = 160, и набор значений всех переменных целиком задает
состояние среды чудовища. Так, например, начальное состояние среды,
показанное на рис. 2.3, определяется набором значений этих переменных,
в котором 17 переменных истинны: х (1, 1), х (1, 1), х (2, 1), х (3, 1),
х (4, 1), х (1, 2), х(3, 2), х (1, 3), хН(1, 3), х"(2, 3), х(2, 3), х“6 (2, 3),
хя (3, 3), хс (4, 3), хз (1, 4), хс (4, 3), хя (4, 4), а остальные ложны. Число
таких наборов, обычно называемых полными наборами значений, или
полными состояниями среды, астрономически велико и равно 2160. Конечно,
далеко не во всех полных состояниях может находиться среда вследствие
ограничений на значения каких-либо переменных в зависимости от значения
других. Например, как уже отмечалось, никакая переменная из хп (i, j),
xs(i,j), xe(i,j), xw(i,j) с одним и тем же индексом (z, j) никогда не может
быть истинной, если истинна какая-либо другая из этого множества. А
значит, и среда не может находиться в состояниях, где хотя бы две из них
одновременно истинны. Тем не менее, если рассуждать в терминах состояний
среды, то это число может быть слишком велико даже с учетом указанных
ограничений, а таблицу истинности практически невозможно построить.
К счастью, в реальных задачах чаще всего, во-первых, нет необходимости
знать значения всех переменных, а во-вторых, агент, зачастую, и не может
их знать. В нашем примере агент может воспринимать значения только тех
переменных, которые относятся к ячейке, в которой он находится (т.е. имеют
индекс, совпадающий с индексом ячейки местонахождения агента). При
этом восприятия агента определяются следующими факторами.
38
2.4. Рассуждения в терминах интервалов
В ячейке, где находится чудовище, и в соседних ей ячейках агент ощущает
зловоние чудовища.
В ячейках, соседних ячейке, в которой находится яма, агент ощущает
сквозняк.
В ячейке, где находится золото, агент видит яркий блеск.
Агент всегда стоит лицом к одной из соседних ячеек и может совершать
одно из следующих действий:
а) поворот к ячейке, в которой нет ни чудовища, ни ямы. Сопоставим
это действие с переменной zo, которая истинна, если действие поворота
совершается, и ложна в противном случае;
б) переход в соседнюю ячейку, к которой агент стоит лицом. Сопоставим
это действие с логической переменной zm, которая истинна, если действие
перехода совершается, и ложна в противном случае.
в) изъятие золота, если агент достиг ячейки, где оно находится. Это
действие сопоставим с логической переменной z3.
Теперь мы имеем достаточно полное представление о среде чудовища и
цели агента и можем перейти к формальной постановке задачи.
2.4.1. Интервальная постановка задачи
В начальном состоянии, показанном на рис. 2.3, агент находится в ячейке
(1, 1) и стоит лицом к ячейке (1, 2) (лицом на север). Это означает
истинность формулы хн (1, 1) л хп (1, 1). Правило для принятия агентом
решения о возможности совершения действия перехода в ячейку (1, 2) из
ячейки (1, 1) можно представить импликацией (2. 1)
хн(1, (1, 1)а->хз(1, 1)а-.хс(1, 1)=>ги. (2.1)
В левую часть этой импликации, являющуюся в данном случае
конъюнкцией, а в общем случае любой формулой, включены не все
переменные, характеризующие состояние среды чудовища, а только часть
из них, необходимая для принятия решения. В частности, в нее включены
переменная хн(1, 1), характеризующая местоположение агента, переменная
хп (1, 1), характеризующая ориентацию агента, переменная хз(1, 1),
характеризующая наличие или отсутствие зловония, и переменная хс(1, 1),
характеризующая наличие или отсутствие сквозняка. Обычно такие
переменные называют существенными.
Это правило задает условия допустимости совершения действия. Действие
может быть и не совершено. Но если оно совершилось, то среда перейдет в
какое-то другое состояние. Этот переход задается формулой
хн(1, 1)лх„(1, 1)л-.х(1, 1)л->хс(1, 1) л ги=>хн(1, 2)лх„(1, 2). (2.2)
Логически любая элементарная конъюнкция эквивалентна дизъюнкции всех
конституент (совершенной дизъюнктивной нормальной форме), в которых
существенные переменные имеют одно и то же значение, совпадающее с их
39
2. Логические рассуждения
значением в рассматриваемой конъюнкции, а несущественные переменные
пробегают все наборы значений. Множество всех полных состояний среды,
каждое из которых соответствует одной из конституент совершенной нормальной
формы, полученной по данной элементарной конъюнкции, называется
интервалом. Используя интервалы, можно перейти от рассуждения в терминах
конституент, представляющих состояния среды, к рассуждениям в терминах
элементарных конъюнкций, представляющих интервалы среды. Формулы
логики высказываний, в которых используются элементарные конъюнкции,
представляющие интервалы, будем называть интервальными формами.
Постановка задачи теперь состоит из следующих шагов.
Задание интервальных форм, определяющих начальные интервалы среды.
Задание в интервальной форме множества импликаций (правил),
определяющих условия местонахождения тех или иных объектов в ячейках
среды в зависимости от восприятий агента.
Задание в интервальной форме множества импликаций, определяющих
условия допустимости выполнения действий, которые агент должен совершать
в зависимости от местонахождения объектов.
Задание в интервальной форме множества импликаций, определяющих
допустимые переходы между ячейками при совершении агентом действия
перехода в зависимости от восприятий.
Задание интервальных форм, определяющих целевые интервалы.
Сформулируем теперь на основании сказанного задачу для среды чудовища
полностью.
Формулы, определяющие начальные интервалы. В нашем случае начальное
состояние можно представить следующей конституентой, содержащей все
160 переменных и определяющей тем самым одно начальное состояние:
Х(1, 1)лх(1, 1)лпХ(1, 1)л^х6(1, 1)а^Х(1, 1)ах(1, 1)лхп(1, 1)л
Л^х(1, 1) л х(1, 1) a^xJI, 1) л
л хч(2, 1)a-iX3(2, 1)лхс(2, 1)л-нХ6(2, 1)л-.хя(2, 1)лхн(2, 1)л-,хп(2, 1) л
л хД2, 1) л хе(2, 1) л —, xJ2, 1) а
л ->хч(3, 1) а —i х(3, 1) а —i хс(3, 1) а х6(3, 1) а хя(3, 1) а хн(3, 1) А
А Хд(3, 1) А х(3, 1) А --, X/3, 1) А XJ3, 1) А
л х(4, 1) а —1 х(4, 1) А х(4, 1) а —। х6(4, 1) а —1 х (4, 1) а хн(4, 1) л
А X (4, 1) А —। Х(4, 1) А —I X (4, 1) А —I х/4, 1) А
А -п хч(1, 2) А х(1, 2) а —1 хс(1, 2) А Х6(1, 2) а —1 хя(1, 2) а —i хн(1, 2) а
А^х(1, 2)а-1х(1, 2)а^х(1, 2)a-,xw(1, 2) А
40
2.4. Рассуждения в терминах интервалов
л хч(2, 2) л -1 хз(2, 2) л -1 хс(2, 2) л х6(2, 2) л хя(2, 2) л -> хн(2, 2) л
л хл(2,2) л хз(2, 2) л хе(2, 2) л xJ2, 2) л
л -1 хч(3, 2) л -1 хз(3, 2) л хс(3, 2) л х6(3, 2) л -> хя(3, 2) л хн(3, 2) л
л -> хл(3, 2) л -> xt(3, 2) л хе(3, 2) л -1 xw(3, 2) л
л -п хч(4, 2) л хз(4, 2) л хс(4, 2) а -> х6(4, 2) л хя(4, 2) л хн(4, 2) л
л хл(4, 2) л х/4, 2) л хе(4, 2) л xw(4, 2) л хч(1, 3) л хз(1, 3) л
A-,xc(l, 3) А-,х6(1, 3) л-,хя(1, 3) л-,хн(1, 3) л
Л -1 Хл(1, 3) Л -1 Хз(1, 3) Л -1 Хе(1, 3) А —1 Xw(l, 3) А
а хч(2, 3) л хз(2, 3) л хс(2, 3) л —1 х6(2, 3) а хя(2, 3) л хн(2, 3) л
а -> хл(2, 3) а —1 xt(2, 3) а -> хе(2, 3) а -1 xw(2, 3) а
а -1 хч(3, 3) а —1 хз(3, 3) а —1 хс(3, 3) а —1 х6(3, 3) а хя(3, 3) л хн(3, 3) а
а -1 хл(3, 3) а —1 х/3, 3) а хДЗ, 3) а х^З, 3) а
а -1 хч(4, 3) а —1 хз(4, 3) а хс(4, 3) а -л х6(4, 3) л -> хя(4, 3) а хн(4, 3) а
а -1 хл(4, 3) л -> xs(4, 3) а —1 хе(4, 3) а -1 хя(4, 3) а
а^хч(1, 4) ах(1, 4) а->хс(1, 4) а->х6(1, 4) а->хя(1, 4) л-,хн(1, 4) л
А хя( 1, 4) А х/1, 4) А х/1, 4) А xjl, 4) А
А х(2, 4) А -н х(2, 4) А X (2, 4) л —> х6(2, 4) а х(2, 4) а хн(2, 4) а
а -1 хл(2, 4) а -> хз(2, 4) а хе(2, 4) а -> xw(2, 4) а
а хч(3, 4) а -1 хз(3, 4) л хс(3, 4) а х6(3, 4) а хя(3, 4) а хн(3, 4) а
а -л хл(3, 4) а —1 хз(3, 4) л -> хг(3, 4) а xJ3, 4) а
а хч(4, 4) а —1 х(4, 4) а —1 хс(4, 4) а х6(4, 4) а х(4, 4)а хн(4, 4) а
А хл(4, 4) А х/4, 4) А хе(4, 4) а xJ4, 4).
Агент не знает всех значений переменных, входящих в эту конституенту.
Согласно его восприятию, он знает, что находится в ячейке (1, 1) и стоит
лицом на север, а также не ощущает в этой ячейке зловония и сквозняка.
Таким образом, начальная совокупность интервалов, определяемая
восприятием агента, задается формулой
Хн(1, 1) А х„(1, 1) А^х(1, 1) А^х(1, 1). (2.3)
41
2. Логические рассуждения
Формулы, определяющие условия местонахождения объектов среды. Если
в какой-либо ячейке (z, j) не ощущается зловония, то в соседних ей ячейках
чудовища нет. Точно так же, если в какой-либо ячейке нет сквозняка, то в
соседних ячейках нет ям. Импликации, с помощью которых можно выразить
эти знания, в общем случае имеют следующий вид.
х(/, у) ZD хч(/, У) Л хц(/-1, У) Л Хч(/+1, У) Л ХЧ(У у-1) л хч(/, У+1)
- п Хс(/, У) zd хя(Л У) л ХЯ(М, У) л -п хя(/ + 1, У) л -п Хя(/, у-1) л
- x(z,/ + 1). (2.4)
Для крайних ячеек вследствие отсутствия части соседних правая часть
подобных формул может не содержать каких-либо конъюнкций. Так, для
i = 1, у = 1 эта формула примет вид
- ,х(1, 1) =^х(1, 1) л-> хч(2, 1)л-.хч(1, 2).
Для ячеек (1, 2) и (2, 1) имеем формулы
- х(2, 1) zd —1 х (2, 1) л х (1, 1) л —1 х(3, 1) л —1 х(2, 2),
- х(1, 2) х(1, 2) л х(2, 2) л х (1, 1) л х(1, 3).
Понятно, что число формул типа (2.4) равно 32. Полезными могут оказаться
также знания о наличии чудовища или ямы в ячейках, соседних ячейке (/, j),
если в ней ощущается зловоние или сквозняк соответственно. Импликации, с
помощью которых можно выразить эти знания, имеют следующий вид:
x/z, у) хч(/, у) v хч(/-1, у) v хч(/+1, у) v x4(z, у-1) v x4(z, У+1)
x(z, у) x(z, у) v хя(/-1, у) v x(z + l,y) v хя(/, у-1) v хя(/,у + 1). (2.5)
При z = 1,у = 2 формула (2.5) примет вид
х/1, 2) zd Хч(1, 2) V хч(2, 2) V Хч(1, 1) V х(1, 3).
Число таких формул равно 16.
Формулы, определяющие условия выполнения агентом действий. Для того чтобы
достичь цели, агент должен совершать действия, которые бы привели его к этой
цели. В случае среды кота, рассмотренной ранее, предполагалось, что кот может
совершать одно из действий в любом состоянии и в любом порядке. Такое
поведение агента в среде чудовища неприемлемо, поскольку среда небезопасна,
и необходимо знать, в зависимости от обстановки, когда и какие действия можно
совершать. Для среды чудовища были введены три действия: действие перехода в
одну из соседних ячеек, действие по изъятию золота и действие поворота к ячейке,
в которой нет ни чудовища, ни ямы. Агент может перейти в соседнюю ячейку,
42
2.4. Рассуждения в терминах интервалов
если там его не подстерегает опасность в виде чудовища или ямы. Поэтому общий
вид импликаций, определяющих возможность совершения действия по переходу
в соседнюю ячейку, является следующим:
x„(j, У) а xn(i, у) л хч(/, У+1) л хя(/, У+1) о zm,
XS'J) лх(/,у)л-пХч(Уу-1)л^хя(УУ-1)=) zm> (2.6)
x„(i, 7) a xe(i, j) a -n X4(z+1, j) a xjz+l, j) z> zm,
xH(i, j) a xw(i, j) a хч(/-1, j) a хя(/-1, у) zm.
Одна из конкретных импликаций этого типа для перехода была введена
ранее (см. (2.1)). Число формул вида (2.6) равно 64. Соответственно,
возможные изменения интервалов (состояний среды), осуществляемые в
результате действия, связанного с переходом, задаются формулами
xH(i, У) a x„(z, у) а хч(/, У + 1) а хя(/, У + 1) a zm => xH(i, У+1) a xn(i, У+1),
xH(i, У) а х (z, у) л хч(/, У-1) а хя(/, у-1) a zm => xH(i, у-1) a xs(i, у-1), (2 ?
хн(/, У) a x/z, У) а хч(/+1, У) а хя(/+1, у) а хн(г+1, У) a xe(z+l, j),
x„(i, J) a xjz, y) a x4(z-l, У) a хя(/-1, У) a zm^> xH(z-l, у) Л xjz-l, j).
Формулы, определяющие условия выполнения действий по изъятию
золота, имеют вид
х„(6 7 ) Л х6(/, у) z, (2.8)
и их число равно 16.
Формулы, определяющие условия возможного выполнения действий
поворота агента, введем исходя из следующих соображений. Если агент стоит
лицом к какой-либо ячейке, и в результате своих рассуждений пришел к
выводу, что в этой ячейке может быть чудовище или яма , то он
поворачивается к той ячейке, в которой нет ни ямы, ни чудовища
(предполагается, что такая ячейка существует). Таким образом, формулы,
регламентирующие возможность выполнения действия поворота направо,
лицом к ячейке, в которой нет ни чудовища, ни ямы, если агент перед этим
находился в ячейке (z, У) и стоял лицом соответственно на север, восток,
юг и запад и перед ним находились чудовище и яма, имеют вид:
\(6 У) а хл(/, У) а хч(/, У + 1) а х (z+1, У) л хя(/+1, У) о го,
хнЦ, j) a xn(z, у) л хя(/, у + 1) л xq(z + l, у) л хя(/ + 1, j) zo,
х/i, У) a x/z, У)) а х (z+1, У) а хч(/, у-1) а хя(/, у-1) z> zo,
x/i, j) a x/z, j)) а хя(/+1, j) a -n x4(z, У-1) a хя(/, y-1) zo,
43
2. Логические рассуждения
xH(j, J) a x(i, j)) л xjz, j-1) л -n хч(/-1, j) л -n хя(/-1, j) zz> zo,
XH(i, j) a x(z, ;)) л xjj, j-\) a x(z-l, j) a -n xjz-l, j) zz> zo,
XS‘> J) A xjj, J)) A X4(z-1, j) A -n X4(z, j + 1) A -n X (z, /+1) ZD Zo,
xH(j, J) A xjz, /)) A x(z-l, J) A x4(z, j+1) A x/Z, / + 1) ZD Zo. (2.9)
Если же агент находится в ячейке (/, у), а чудовище иди яма в ячейках
(z, у + 1) и (z + 1, у), а в ячейкае (z, у-1) нет ни чудовища, ни ямы, то
можно воспользоваться формулой типа
XS‘> j) A xjz, У) А (хч(/, у + 1)) V x(z+1, У)) А x(z, у-1) А -л хя(/, у-1) ZD z0. (2.10)
Формулы, определяющие множество допустимых переходов. Агент может
перейти из ячейки (z, j) в соседние ячейки (z, у+1), (z, у-1), (z-1, у), (z+1, j)
в результате выполнения действия z При повороте он остается в той же ячейке.
Ориентация его при этом меняется. Поэтому импликациями, определяющими
местоположение и ориентацию агента после выполнения действия поворота в
соответствии с формулами (2.9), будут следующие:
7) a х (z, У) л x(z, У+1) а x(z+1, у) а х/z + l, у) a £ozd xh(z, У) a x(z, У),
x„(z, у) л x/z, У) л х (z, у+1) л -n xjz + l, у) л -п xjz + l, у) а £(>zd хн(/, У) a x/z, У),
X„(z, У) A x(z, У) А х (z + 1, j) А -n x(z, У-1) А -и x(z, у-1) a zo=> xh(z, У) a x(z, У),
xjj’ j) A xJJ, j) A x (z+1, у) А -и x (z, y-1) A -и x (z, y-1) A £O ZD xH(z, j) a x(z, y), (2. ] i)
x (z, У) a x(z, У) a x (z, У-1) a —i x(z-l, y) a -n x(z-l, ;) a £ozd xh(z, j) a xjz, j),
xH(i, j) a x(z, ;) a x(z, у -1) a —i x(z-l, У) a x (z-1, ;) az- xH(z, j) a xjz, j),
7) A +.(/, У) A x (z-1, У) A x(z, y + 1) A -n x(z, y+1) a;d xjz, y) a x/z, y),
x (z, У) A xjz, У) A x(z-1, У) A -n x(z, y + 1) A -n x(z, y + 1) a £ozd x (z, j) a xjz, j).
Если действие поворота выполняется в соответствии с формулой (2.10),
то импликация, определяющая местоположение и ориентацию агента, будет
следующая:
Л/'- л ХЛ У) а (\(9 У + 1)) v х (z + 1, У)) а -п x(z, у-1) а -п х (г, у-1) л го=з
У) Ax(z,y). (2.12)
Формулы (2.11), (2.12) предопределяют результат выполнения действия
поворота по ходу часовой стрелки при наличии чудовища или ямы в ячейке,
к которой агент стоит лицом.
Агент может совершать действие поворота и против хода часовой стрелки
в соответствии, например, с формулами типа
44
2.4. Рассуждения в терминах интервалов
xH(i, J) л x(z, у) л хч(/, у-1) л -и х(/+1, у) л -и x(z+1, у) л го=э х(/, у) л x(z, у),
х„(/, у) л x(z, у) л хя(/, у-1) л -и хч(/+1, у) л -п х/z + l, у) л
л £ozd хн(/, у) л x(z, у). (2.13)
В том случае, когда ячейка не имеет какой-либо соседней,
соответствующие условия и результат поворота модифицируются таким
образом, чтобы учесть отсутствие соседних ячеек.
Формулы целевых интервалов. Ограничим решение задачи нахождением
золота. Агент не знает, в какой ячейке находится золото. Только попав в
нее, он по блеску может определить, что оно в ней находится. Поэтому
стратегией агента является обследование всех ячеек, в которые он может
попасть и не погибнуть. Если ему удастся, блуждая таким образом, добраться
до ячейки (2, 3), то он увидит блеск и обнаружит там золото. Будем полагать
в настоящем примере, что целью агента является совершение действия по
взятию золота, т.е. его цель есть а решением задачи должно быть
нахождение последовательности действий (правил), в результате выполнения
которых цель будет достигнута.
С учетом того, что агент способен к восприятию сквозняка или зловония
только в ячейке, в которой он находится, а среда чудовища является
статической (местоположение чудовищ и ям не изменяется), то для
конкретных значений z и у в соответствии с рис. 2.3, по мере необходимости,
будем также использовать формулы вида
ХИ(‘, J) => - J),
xfj’ J) xjj, j),
x„(j> J) x^i, j),
xH(i, 7) 23 XS‘’
Например,
x(l, 2) D x(l, 2), XH(1, 2) zd —i x(l, 2), хн(2, 1) zd x(2, 1),
x(2, 1) x(l, 2),
x(2, 2) о x(l, 2), x(2, 2) zd x (2, 2), x(2, 3) z> x6(2, 3).
(2.14)
Правило, задающее условие совершения действия гз, описывается
следующей формулой:
xS'l<J) a XJJ,J) => гз. (2.15)
45
2. Логические рассуждения
2.4.2. Решение задачи
Рассмотрим вывод, приводящий к решению задачи нахождения агентом
золота в среде чудовища.
Начальный интервал задается формулой (2.3). Используя правило
исключения конъюнкта, по этой формуле агент может заключить, что
истинны формулы хн(1, 1), хп{\, 1), хД1, 1), хс(1, 1), т.е.
ХН(1, 1)лх(1, 1)л^х(1, 1)л^х(1, 1) F х(1, 1),
х(1, 1)лх(1, 1)л^х(1, 1) h х(1, 1),
Х(1, 1)лх(1, 1)л-,Х,(1, 1)л-нХ(1, 1) h ^х(1, 1),
х(1, 1)лх(1, 1)л^х(1, 1)л^х(1, 1) h ^х(1, 1).
Теперь агент может воспользоваться формулами (2.4) и правилом модус
поненс:
- .х/1, 1), -,*(1, 1) z? -> хч(1, 1) л -> хч(2, 1) Л
Л х(1, 2) I-- х(1, 1)Л. х, (2, 1) л-i х(1, 2),
- х(1, 1) -,х(1, 1) zd —1 х^( 1, 1) л —1 х^(2, 1) л
л X (1,2) х (1, 1) л X (2, 1) л -и X (1, 2),
заключая, что истинны формулы
- х (1, 1) Л х(2, 1) Л х( 1, 2) и X (1, 1) X (2, 1) Л х(1, 2).
Затем агент может вновь воспользоваться правилом исключения
конъюнкта, получая в результате истинные формулы
- х (1, 1), х (2, 1), X (1, 2), x(l, I), X (2, 1), X (1, 2),
которые означают, что чудовища и ям нет в ячейках, соседних ячейке (1, 1).
Далее агент может воспользоваться первой формулой из числа формул
(2.6) и правилом модус поненс:
х(1, 1) Л х (1, 1) л —1 х (1, 2) Л X (1, 2), хн(1, 1) Л х„(1, 1) Л
- хч(1, 2) Л —1 хя(1, 2) zd zm,
заключая, что формула zm истинна и, следовательно, он может совершить
действие перехода в ячейку (1, 2). Воспользовавшись этим фактом, правилом
модус поненс и первой формулой из (2.7), которая принимает следующий вид:
46
2.4. Рассуждения в терминах интервалов
х(1, 1) л О л хч(1, 2) л хя (1, 2) л zm => хн(1, 2) л х (1, 2),
агент может установить истинность формулы хн(1,2) лх(1, 2), означающей,
что он после совершения действия перехода находится в ячейке (1,2) лицом
на север к ячейке (1, 3). Теперь процесс исследования соседних ячеек на
существующие там опасности повторяется. В ячейке (1,2) агент ощущает
зловоние (истинна формула хз(1, 2)) и не ощущает сквозняка (истинна
формула хс(1, 2)).
Применяя формулы (2.4), правило модус поненс и правило исключения
конъюнкта, агент устанавливает, что в ячейке (2, 2) нет ямы (истинна
- х (2, 2)):
- х(1, 2), х(1, 2) zd -л х(1, 1) л -л х(2, 2) л —» х(1, 3).
Используя формулы (2.5) и правило модус поненс
х( 1, 2), х(1, 2) z> хч(1, 1) v хч(2, 2) v хч(1, 3) h хч(1, 1) v хч(2, 2) v х (1, 3),
агент получает истинную формулу хч(1, 1) v х (2, 2) v хч(1, 3), означающую,
что чудовище может находиться в одной из ячеек (1, 1), (2, 2) или (1, 3).
Но, согласно начальным условиям задачи, чудовища и ям нет в ячейке (1, 1)
(истинны формулы хч(1, 1), -> хя(1, 1)). Следовательно, чудовище может
находиться в одной из ячеек (2, 2) или (1, 3), что формально выводится с
использованием правила простой резолюции:
- х(1, 1), х (1, 1) V х (2, 2) V х(1, 3) hx(2, 2) v х(1, 3).
Далее на основании следующего варианта правила (2.10):
х(1, 2) л х (1, 2) л (х(2, 2) v х(1, 3)) л х(1, 1) л х (1, 1) zd zo
агент приходит к выводу, что у него есть единственная возможность
повернуться к ячейке (1, 1), что он и делает на основании следующего
варианта правила (2.12):
х(1, 2) л х (1, 2) л (х (2, 2) v х (1, 3)) л х(1, 1) л х (1, 1) л zo
хн(1, 2)лх(1, 2).
Затем агент устанавливает возможность выполнения действия перехода и
возвращается в ячейку (1, 1) на основании правил типа (2.6), (2.7):
х(1, 2) л х(1, 2) л —1 х(1, 1) л —1 х (1, 1) zd zm,
хн(1, 2) л xs(l, 2) л-> хч(1, 1)л-.х(1, 1)л;зх(1, 1)лх(1, 1).
Оказавшись вновь в ячейке (1, 1), агент последовательно устанавливает
возможность поворота к ячейке (2, 1), совершает этот поворот, устанавливает
возможность перехода в эту ячейку и совершает его. Все это он делает на
основании следующих правил, аналогичных по типу уже рассмотренным:
47
2. Логические рассуждения
хн(1, 1) л х(1, 1) л хч(2, 1) л хя(2, 1) =) zo,
xH(i, 1) л x/l, 1) л хч(2, 1) л Хя(2, 1) л го => хн(1, 1) л хе(1, 1),
Л/Н О л О л -п хч(2, 1) л хя(2, 1) => zm,
хн(1, 1)лх(1, 1)л^х(2, 1)л-,хя(2, 1)лгтохн(2, 1)лх(2, 1).
Очутившись в ячейке (2, 1), агент ощущает сквозняк и отсутствие зловония
на основании правил типа (2.14)
хн(2, 1) х(2, 1), хн(2, 1) э->хз(2, 1).
Так как зловония в ячейке (2, 1) нет (-,хз(2, 1) истинна), агент, используя
формулу типа (2.4)
-1 хз(2, 1) z> -I хч(1, 1) л —1 хч(2, 2) л -I хч(1, 3)
и правила модус поненс и исключения конъюнкта, заключает, что чудовища
нет в ячейке (2, 2) (-, хч(2, 2) истинна). Агент ощущает сквозняк в ячейке
(2, 1) (хс(2, 1) истинна), поэтому, используя формулу типа (2.5)
х(2, 1) => хя(1, l)vx(2, 2) vx(3, 1),
правило модус поненс и простую резолюцию, заключает, что в ячейке (3, 1),
к которой он стоит лицом, имеется яма (хя(3, 1) истинна). Отсюда на
основании правил типа (2.11)
х(2, 1) л х (2, 1) л х (3, 1) л —। х (2, 2) л -п х(2, 2)
хн(2, 1) л х(2, 1) а хя(3, 1) л —1 х (2, 2) л х(2, 2) хн(2, 1) л х (2, 1),
а затем правил (2.6), (2.7)
*н(2, О л *„(2’ О А X (2, 2) Л хя(2, 2) zm,
х(2, 1) л х (2, 1) л -п х(2, 2) л -> х (2, 2) л zm хн(2, 2) л х (2, 2)
агент сначала совершает поворот в сторону ячейки (2, 2), а затем и переходит
в нее. В ячейке (2, 2) на основании формул (2.14)
хн(2, 2) z> -1 х(2, 2), хн(2, 2) т) х(2, 2)
он обнаруживает, что в ней нет ни зловония, ни сквозняка (истинны формулы
- X (2, 2), X (2, 2)).
Далее по формулам (2.4), правилам модус поненс и исключения конъюнкта
он устанавливает, что чудовища и ямы в ячейке (2, 3) также нет (истинны
формулы -1 хч(2, 3), хя(2, 3)):
48
2.4. Рассуждения в терминах интервалов
- х (2, 2), х (2, 2) о х (2, 2) л х (1, 2) л х(2, 3) л х (3, 2) л х (2, 1) к
к ->хч(2, 2) л хч(1, 2) л хч(2, 3) л -> хч(3, 2) л х(2, 1),
- х (2, 2), х(2, 2) Z) —। хя(2, 2) л х (1, 2) л хя(2, 3) л х(3, 2) л х(2, 1),
к хя(2, 2) л -> хя(1, 2) л -> х(2, 3) л -1 х(3, 2) л х (2, 1)
После этого агент может воспользоваться одной из формул типа (2.6), одной
из формул типа (2.7) и правилом модус поненс для перехода в ячейку (2, 3):
хн(2, 2) л хя(2, 2) л хч(2, 3) л хя(2, 3), хн(2, 2) л хя(2, 2) л -п хч(2, 3) л
л х (2, 3) zm k zm,
хн(2, 2) л хя(2, 2) л хч(2, 3) л хя(2, 3) л zm z> хн(2, 3) л хя(2, 3) к
к хн(2, 3) л хя(2, 3).
В результате агент оказывается в ячейке (2, 3) (истинна хн(2, 3)) и видит
блеск золота (истинна хб(2,3) на основании правила хн(2,3) о хб(2,3)). Используя
формулу (2.8) и правило модус поненс, агент может сделать заключение о
возможности совершения действия г, по изъятию золота из ячейки (2, 3):
хн(2, 3) л х6(2, 3), хн(2, 3) л х6(2, 3)э z J г.
Схема, позволяющая проследить вывод решения для среды чудовища,
показана на рис. 2.4, где формулы вида сто Р изображены двумя жирными
прямоугольниками, соединенными жирной стрелкой. Внутри первого
прямоугольника записана формула а, а внутри второго — формула р. Стрелка
направлена от первого прямоугольника ко второму и соответствует знаку
импликации. Если в жирный прямоугольник с формулой р входят две жирные
скобки, выходящие из прямоугольников с формулами а, и сх2, то это
соответствует импликации а, лсх, э р.
2.4.3. Число формул в логике высказываний, требуемых
для представления знаний
Нетрудно заметить, что число формул, требуемых для постановки задачи,
растет довольно быстро, хотя среда чудовища имеет всего 16 ячеек и все ее объекты,
кроме агента, не изменяют своего местоположения. Так, число формул типа
(2.4) равно 32, (2.5) - 16, (2.6) - 64, (2.7) - 16, (2.8) - 16, (2.9) - 128,
(2.10) - 16, (2.11) - 128, (2.12) - 16, (2.13) - 32, (2.14) - 32, что в сумме
составляет 496.
49
2 Логические рассуждения
хя(2 3)
Рис. 2.4. Схема вывода решения в логике высказываний в среде чудовища
хя (2.2)
*я(2 1)
-^хч(1 1) л-^х„(1,1)
(1 1>УХЧ(2 2)у хч(1 3)
(2.2) Л хп(2 2)\
50
Вопросы и упражнения
В случае более сложной среды необходимо представить все возможные
изменения местоположения других объектов, например чудовища, в ответ на
действия агента и для действия каждого такого объекта предусмотреть свои
формулы. Занижая оценку, будем полагать, что число формул в среде с /ячейками
равно примерно Is. Тогда при / = 5, 6, 7, ... это будут числа 3125, 7776, 16807...
соответственно. Могут потребоваться также правила, учитывающие предысторию
действий агента. Все это может привести к огромному числу формул, для хранения
которых потребуется такой большой объем памяти, которой может не хватить
даже на современных компьютерах. Кроме того, сама постановка задачи,
требующая записи такого огромного числа формул, может стать практически
невыполнимой задачей. В то же время многие реальные задачи часто, несмотря
на большое число переменных, могут иметь сравнительно небольшое количество
формул в постановке задачи и достаточно успешно решаться с использованием
логики высказываний. К числу таких задач, например, относятся задачи анализа
логических схем.
Вопросы и упражнения
I. Используя таблицы истинности, докажите общезначимость следующих законов
логики высказываний:
а) (х л у) = —> х м у; б) -> (х v у) = х л -> у;
в) х л (у v z) = (х л у) v (х л г); г) х v (у л ф = (х v у) л (х v г);
д) х z> у = х v у; е) (х = у) = (х о у) л (у э х);
ж) х у = (х л у) v (-. у л х).
2. Определите, к какому типу (общезначимых, выполнимых или невыполнимых)
относятся следующие формулы и докажите это, используя таблицы истинности или
формулы из предыдущего упражнения:
а) Умный Z; Умный; б) Умный > Дурак;
в) (Умный z> -> Дурак) z> (-. Умный z> Дурак); г) Умный v Дурак v Дурак;
д) (Умный л Способный) z> Дурак = (Умный z> -> Дурак) v
v (Способный -> Дурак);
ж) (Умный Дурак) ((Умный л Способный) з -> Дурак).
3. Предполагая, что некоторая среда может быть описана с использованием только
четырех логических переменных х, у, z, и, определите сколько моделей может иметь
среда для следующих формул:
а) х л у; б) х л у л z; «) х v у.
4. Агент играет роль швейцара в отеле. В его обязанности входит открыть двери
отеля перед клиентом; помочь ему донести багаж до стойки администратора, если у
клиента есть багаж; открывать двери автомобиля, подъехавшего к отелю, если он в это
время свободен от других обязанностей, т.е. цель швейцара — обслужить всех клиентов.
Сформулируйте постановку задачи для среды клиента в пространстве состояний, если
начальным состоянием среды является состояние, в котором одновременно к дверям
отеля подошел клиент без багажа и подъехал автомобиль.
51
3. ЛОГИКА ПРЕДИКАТОВ
В этой главе рассмотрена логика предикатов первого порядка, являющаяся
существенно более выразительным, чем логика высказываний, языком
представления знаний агентов.
Во второй главе было показано, каким образом логику высказываний можно
использовать для представления знаний и логических рассуждений. Однако
выразительные возможности логики высказываний невысоки. Требуется
слишком много формул логики высказываний для описания даже простых сред.
Например, в случае простой среды чудовища (см. гл. 2) для того, чтобы
указать факт наличия или отсутствия любого объекта (чудовища, агента, ям,
золота) в какой-либо ячейке среды, пришлось ввести для каждого объекта
множество логических переменных, число которых совпадает с числом ячеек
среды, и сопоставить каждое местонахождение объекта в какой-либо ячейке с
координатами (/, у) истинному значению переменной, соответствующей
объекту и этой ячейке. Понятно, что число таких переменных равно числу
ячеек среды, умноженному на число объектов.
В настоящей главе изучим логику предикатов первого порядка, называя ее
в дальнейшем просто логикой предикатов, которая существенно более
выразительна, чем логика высказываний, и позволяет представлять знания о
среде гораздо более компактно. Выразительность логики предикатов является
следствием ее основополагающей идеи, заключающейся во взаимно-однозначном
сопоставлении каждого уникального (не совпадающего ни с каким другим)
объекта среды с индивидуальной объектной константой, обозначаемой именем
(названием) объекта, а класс однотипных по каким-либо свойствам объектов,
— с объектной переменной, значением которой являются объектные константы.
Объектные константы и переменные в литературе часто называют индивидными,
или предметными.
Предикатом называют высказывательную функцию, определенную на
множестве наборов значений объектных переменных. Эта функция может
принимать только два значения: Истина (И) и Ложь (Л), называемые
истинностными значениями. Отношения объектов среды представляются на
52
3.1. Синтаксис и семантика
языке логики предикатов, как и на языке логики высказываний, в виде
определенных предложений (высказываний, формул логики предикатов),
использующих объектные переменные и объектные константы, а также ряд
других конструкций, включая уже известные связки и скобки.
Рассмотрим подробнее язык логики предикатов.
3.1. Синтаксис и семантика
Синтаксис логики предикатов с использованием метаязыка Бэкуса Наура
приведен на рис. 3.1. Рассмотрим семантику всех синтаксических
конструкций, приведенных на этом рисунке.
Формула —>
Атом
| Предложение
| Предложение Связка Предложение
| Квантор {Переменная, Переменная) Предложение
| Предложение
| {Предложение),
Атом
Предикатный символ {Терм, ..., Терм)
| Терм = Терм,
Терм
Функциональный символ {Терм, ..., Терм)
| Константа
| Переменная,
Связка —> | л | v | =,
Квантор —> V | В,
Константа Строка символов, начинающаяся с прописной буквы,
Переменная Строка символов, начинающаяся со строчной буквы,
Предикатный символ Строка символов, начинающаяся со строчной буквы,
Функциональный символ Строка символов, начинающаяся со строчной буквы.
Рис. 3.1. Синтаксис логики предикатов в метаязыке Бэкуса-Наура
3.1.1. Объектные переменные
Объектные переменные или просто переменные обозначаются строкой
символов, начинающейся со строчной буквы и записываемой курсивом.
Областью значений каждой переменной является множество констант, в
общем случае даже бесконечное. Как эта область значений очерчивается,
будет ясно из дальнейшего.
53
3. Логика предикатов
3.1.2. Функции
Для того чтобы задать такие отношения между объектами, когда в точности
один объект соответствует множеству других объектов, используют функции.
Например, если объектами являются двоичные цифры 0 и 1 и десятичные
цифры 0, 1, ..., 9, то любому набору из трех двоичных цифр, представляющему
двоичное число, можно однозначно сопоставить десятичную цифру. Если
двоичные цифры сопоставить с переменными х, у, z, а десятичные с переменной
q, то рассмотренное отношение между двоичными и десятичными цифрами
можно представить в виде функции преобразование_2 в_10 (х, у, z). Выражение
преобразование_2_в_10 называют функциональным символом. Так при х =1,
у = 0, z = 1 с помощью функции преобразование_2_в_10 (х, у, z) получим
значение функции, равное q = 5. Следует заметить, что функция в логике
предикатов не предполагает обязательного наличия какого-либо алгоритма
вычисления значения функции по ее аргументам. Она лишь задает с помощью
констант и переменных определенное отношение между объектами,
соответствующими ее аргументам, и каким-то одним объектом.
3.1.3. Объектные константы
Каждая объектная константа, называемая в дальнейшем, если это не вызывает
путаницы, просто константой, взаимно однозначно сопоставляется в процессе
интерпретации с каким-либо одним объектом среды. Константа обозначается
строкой символов, начинающейся с прописной буквы, и, чаще всего, эта строка
символов совпадает с именем или наименованием объекта и записывается
курсивом, например, Владимир, Чудовище, Кот и т. д.
3.1.4. Термы
Константы, переменные и функции являются термами. Выбор констант,
переменных и функций для данной среды полностью является прерогативой
того, кто использует логику предикатов. Предположим, например, что наша
среда имеет такие объекты, как крылья и птицы, и нам известно, что “птицы
имеют крылья”. Спрашивается, как выразить это знание? Введем константы,
обозначающие конкретный вид птиц, например, Воробей, Синица, Соловей,
и константу Крылья, обозначающую объект крылья. Введем также переменную
х, обозначающую все объекты, которые являются птицами; функциональный
символ имееткрылья ставит во взаимно-однозначное соответствие любой птице
объект крылья. Тогда функция имеет крылья (х) задает отношение между
объектом крылья и птицей х.
Если, например, х = Воробей, то имеет крылья {Воробей) = Крылья. Но это
не единственная возможность выразить отношения между птицами и крыльями.
Функция может не содержать аргументов, т.е. иметь только один функциональный
символ. Термы, не содержащие аргументов, т.е. константы, переменные и
функции без аргументов, называют элементарными термами.
3.1.5. Предикатный символ
С помощью предикатов задаются отношения между объектами. Такие
отношения задаются выражением, начинающимся, как и в случае с функцией,
54
3.1. Синтаксис и семантика
строкой символов, записанных курсивом, первая буква которой строчная. Эта
строка символов называется предикатным символом. За ним в скобках следует
упорядоченный набор переменных или констант, соответствующих объектам,
находящимся в поименованном отношении. Так, например, если два человека
Владимир и Марина являются братом и сестрой, то это отношение родства
может быть выражено с помощью конструкции братисестра (Владимир,
Марина), где брат_и_сестра является предикатным символом, а (Владимир,
Марина) — упорядоченным набором объектных констант. Конструкция
брат_и_сестра (Владимир, Марина) является предикатом, способным принимать
одно из двух значений Истина или Ложь. В случае истинного значения
предиката будем говорить также, что отношение, задаваемое предикатом, имеет
место, а в случае ложного — не имеет места.
Отношение между птицами и крыльями, выраженное выше с помощью
функции, может быть выражено и с помощью предиката крылья (х), который
истинен, если это отношение выполняется. Это может быть, например, когда
х = Воробей, т.е. когда истинен предикат крылья (Воробей).
3.1.6. Атомы
Выражение предикатный_символ (терм, терм, ..., терм) называют атомом.
Атом представляет предикат. Особо выделяется атом, предикатным символом
которого является знак равенства, а аргументами два терма. Этот атом можно
было бы представить как равны (терм, терм) или = (терм, терм), но, как
правило, его записывают в обычной инфиксной форме терм = терм. Этот
атом истинен, когда значения обоих термов совпадают. Атомы без знака
отрицания или со знаком отрицания называют литералами.
ЗАЛ. Кванторы
Когда мы имеем дело с объектами, то возникает естественная потребность
выразить какие-либо общие свойства целого множества объектов. Кванторы
как раз служат этим целям. Таких кванторов в логике предикатов всего два.
Квантор общности V. Вспомним, что при решении задачи поиска золота в
среде чудовища для того, чтобы выразить правило “В какой бы ячейке агент не
находился, если он видит блеск золота, то он должен его взять”, было
использовано 16 однотипных формул (2.8) , число которых совпадает с числом
ячеек. Эти формулы имели вид
x(i, 1) лхб(1, 1) о
J) л x6(i, у) гз,
(3.1)
хн(4, 4) л х6(4, 4) z3.
55
3. Логика предикатов
Здесь хн(/, j), x6(i, j) — отдельные переменные. Каждая из них принимает
истинное значение, если соответствующий ей объект (в данном случае агент и
золото, точнее блеск золота) находится в ячейке (z, j). Обратим еще раз
внимание на то, что xH(i, j) и x6(i, j) — это индексированные логические
переменные с индексами н, б, i, j, каждая из которых считается единым
неделимым символом. Большое количество формул пришлось вводить из-за
того, что в логике высказываний нет возможности представить указанное
выше правило в виде одной формулы. В логике предикатов такая возможность
имеется и, вместо 16 формул в логике высказываний, в логике предикатов можно
написать одну:
V (i, j) xH(i, j) лх6(/, j) z> z3, (3.2)
где знак V называется квантором общности. Но в этой формуле хн(/, j),
x6(i, j) и уже не являются логическими переменными. Здесь хн, х6, z, —
предикатные символы, вид которых для удобства сохранен тем же, что и в
логических переменных, a i, j — числовые объектные переменные,
соответствующие координатам ячеек. На естественном языке это правило
формулируется следующим образом: “Для всех ячеек с координатами
(/, j) справедливо: если агент находится в ячейке с координатами (/, j) и
видит в ней блеск золота, то он должен его взять”.
Смысл квантора общности V совпадает с выражением естественного языка
“Для всех...”. Множество формул (3.1) логики высказываний эквивалентно
одной формуле (3.2) логики предикатов, т.е имеет место
(V (/, У) Xit(i, У) Л х6(/, У) о гз) = (хн (1, 1) Л х6(1, 1) о гз) Л (хн (1,2) Л
л х6(1, 2)37) л (хн (4, 4) л х6(4, 4) гз).
Квантор существования 3. Квантор общности позволяет формулировать
высказывания о свойствах целого множества объектов. В то же время часто
возникает необходимость высказываться о свойствах отдельных объектов из
какой-либо их совокупности. Для этого используют квантор существования
3. Вернемся к примеру со средой чудовища. Во второй главе для того, чтобы
выразить знания о наличии чудовища в ячейках, соседних ячейке с
координатами (i,J), если в ней ощущается зловоние, было введено 16 формул
(2.5), в которых индексы i, j пробегают множество значений от 1 до 4.
Вместо этих 16 формул с помощью квантора общности можно записать одну
формулу, помня, что теперь вместо логических переменных используются
предикаты, а индексы стали числовыми объектными переменными:
V (z, j ) х (/, j) хч(/, j ) v хч(/-1, j) v хч(/ +1, j ) v хч(/, у-1) v хч(/, У+1). (3.3)
На естественном языке высказывание, соответствующее этой формуле, звучит
так: “Для всех ячеек с координатами (i,j ) справедливо: если ощущается зловоние
в ячейке с координатами (/, У), то существует ячейка, соседняя ячейке с
56
3.1. Синтаксис и семантика
координатами (/, j), в которой находится чудовище”. Для того чтобы выразить
часть этого высказывания “...существует ячейка, соседняя ячейке с координатами
(/, у), в которой находится чудовище” в логике высказываний были
использованы формулы (2.5), в которых справа от знака импликации стоит
дизъюнкция пяти логических переменных. В логике предикатов имеется
возможность более короткой записи этой части высказывания с использованием
квантора существования 3:
3 (g, h) x4(g, h) л ((g = i л (h =j-l v h =j +7) v (h =j л (g = i-1 v g = z+1)).
Используя эту запись вместо 16 формул логики высказываний, в логике
предикатов можно ограничиться одной формулой (3.4)
V (z, j ) x/z, j ) => 3 (g, h) x4(g, h) л ((g = i л (h = j -1 v h = j +1) v
v (h =j л (g = z-1 vg = z+1)). (3.4)
Квантор существования произносится на естественном языке как
“Существует...”.
Взаимосвязь между кванторами. Считают, что квантор связывает
переменные, которые записываются за знаком квантора в скобках. Поэтому
их называют связанными. Переменные же, которые ни один квантор не
связывает, называют свободными. Взаимосвязь между кванторами
существования и общности можно легко выразить с помощью связки и она
основана на следующем соображении: если какая-либо совокупность
переменных связана квантором общности таким образом, что все объекты,
которым соответствуют эти переменные, не обладают каким-то общим
свойством, то не существует объекта (а следовательно, и соответствующей
ему переменной), который обладал бы этим свойством. Например, в случае
среды чудовища, если во всех ячейках нет чудовища, то это означает, что не
существует ни одной ячейки, в которой бы находилось чудовище и наоборот.
Эту взаимосвязь можно описать следующей формулой:
V (/, j) х (z, j) = -. 3 (/, j) x4(z, j).
Если же ямы находятся во всех ячейках, то это означает, что не существует
ячейки, в которой не было бы ямы. Эту взаимосвязь можно выразить
формулой
V (z, j ) x„(z, j ) = 3 (z, j) x„(z, j ).
Продолжая аналогичные рассуждения и обозначая /*(х) любую формулу,
переменная х которой связана кванторами, получаем следующие законы,
характеризующие взаимосвязь между кванторами:
V (х) Р (х) = 3 (х) Р (х),
57
3. Логика предикатов
V (х) Р(х)=3 (х) Р (х),
V (х) Р (х) = 3 (х) Р(х),
V (х) Р(х) = 3 (х) Р(х).
3.1.8. Равенство
Ранее рассматривался атом особого типа терм = терм, называемый
равенством, в котором используется знак равенства в инфиксной форме. Этот
знак, являющийся одновременно предикатным символом, свидетельствует о
том, что формула терм = терм истинна только в том случае, если оба терма
соответствуют одному и тому же объекту. Обозначая константы символами X,
Y, переменные символами х, у, функциональный символ символом F, это
можно пояснить с помощью табл. 3.1.
Использование равенства можно пояснить двумя примерами из мира
чудовища. Имеем формулу
3 (/, у) х(3, z) л х (3, у), (3.5)
которая на естественном языке читается следующим образом: “Существуют
/, у такие, что в ячейках с координатами (3, /), (3, у) находится яма”. Для
нашего примера (см. рис. 2.3) действительно существуют ячейки с
координатами (3, 1), (3, 3), в которых находится яма. Это означает, что
формула (3.5) истинна при значениях координат (3, 1), (3,3). Значения
переменных I, j могут быть как различными, так и одинаковыми. Если же
Таблица 3.1
Х = Y Формула истинна, если константы X и Y именуют один и тот же объект
х= Y Формула истинна, если переменная х принимает значение, равное константе Y
х= У Формула истинна, если значение переменной х совпадает со значением переменной у
X = F(Y) Формула истинна, если значение функции F(Y) совпадает с константой X
х = F(Y) Формула истинна, если значение функции F(Y) совпадает со значением переменной х
х = F(y) Формула истинна, если значение функции F(y) совпадает со значением переменной х
X = F(y) Формула истинна, если значение функции F(y) совпадает со значением константы X
58
3.2. Переход от естественного языка к языку логики предикатов
используется формула (3.6) с равенством, то она будет истинна только при
равных значениях / и/:
3 (6 j) хя(3, /) л х (3, j) л (/ =j). (3.6)
Формула (3.7) с отрицанием равенства, наоборот, будет истинна при
различных значениях координат (3,1)
3 (6 j) хя(3, i) л хя(3, j ) л (/ = j )). (3.7)
3.1.9. Аксиомы, теоремы, факты и цели
Определения таких понятий, как интерпретация, общезначимость, модель,
выводимость формул, введенных в главе 2 для логики высказываний, остаются
справедливыми и для логики предикатов. В математической литературе,
посвященной логике предикатов первого порядка, аксиомами обычно называют
формулы, истинные при всех интерпретациях в некоторой среде. Как и в случае
логики высказываний, это можно выразить и другими словами: аксиомами
называют такие формулы логики предикатов, для которых среда является
моделью при всех их интерпретациях. Как уже отмечалось, атомы с отрицаниями
или без них называют литералами. Аксиомы, являющиеся литералами, все
аргументы которых константы, часто называют фактами. Аксиомы, не
являющиеся фактами, часто называют правилами. Факты и правила
представляют собой формулы логики предикатов. Основная задача агента —
вывод на основании фактов и правил истинных формул, называемых обычно
теоремами, целями или целевыми формулами.
При описании аксиом и целей для конкретной среды возникает много
вопросов. Приведем некоторые из них.
Как определить, что сформулировано достаточно аксиом, относящихся
к данной среде, для того, чтобы можно было вывести все интересующие
нас цели?
Как избежать избыточного числа аксиом?
В каком виде аксиомы лучше всего формулировать?
3.2. Переход от естественного языка к языку логики предикатов
Переход от высказываний на естественном языке к высказываниям на
языке логики предикатов достаточно прост, хотя и требует определенной
аккуратности. Рассмотрим пример перевода на язык логики предикатов
первого порядка предложений естественного языка. Если мы хотим выразить
на естественном языке знания о том, что некоторое существо (объект),
которое имеет крылья, является птицей или что существо, которое летает и
несет яйца, также является птицей, то мы можем записать это в виде двух
следующих предложений русского языка.
Если существо имеет крылья, то это существо — птица.
Если существо летает и несет яйца, то это существо — птица.
59
3. Логика предикатов
Те же знания можно выразить на языке логики предикатов в виде таких
правил или формул:
имеет крылья (существо) о птица (существо),
летает (существо) л несетяйца (существо) zd птица (существо). (3.8)
Для того чтобы перейти к этой форме представления знаний в языке логики
предикатов сначала, глядя на предложения русского языка, определяем,
что же является объектом, который необходимо сопоставить с константой
или переменной. В данном случае речь шла о классе некоторых существ,
обладающих определенными свойствами. Поскольку речь идет не о конкретном
существе, а о классе существ, то вводим переменную существо для обозначения
всех представителей этого класса. Свойства существ задаются фразами русского
языка «имеет крылья», «летает», «несет яйца», «птица». Из этих фраз,
обозначающих свойства, построим соответствующие предикатные символы,
имееткрылья, летает, несет яйца, птица. С использованием этих обозначений
фразы «существо имеет крылья», «существо летает», «несет яйца», «это существо
— птица» заменяются соответственно на предикаты имеет крылья (существо),
летает (существо), несет яйца (существо), птица (существо). Из этих
предикатов образуются формулы или правила (3. 8), в которых слову «и»
соответствует связка л, а словам «Если ... то» — связка о.
Вид существа определяет наличие или отсутствие у него перечисленных
свойств. Если это существо синица, то она имеет крылья, а если этим
существом является кролик, то, естественно, у него нет крыльев. Иначе
говоря, фраза «синица имеет крылья» справедлива или истинна в русском
языке, а фраза «кролик имеет крылья» ошибочна или ложна. В соответствии
с этим предикат имеет крылья (Синица) принимает истинное значение И, а
предикат имеет крылья (Кролик) — ложное Л. Слова Синица и Кролик в данном
случае являются объектными константами. Подставляя значения объектных
констант, имеем теперь возможность вычислять истинность или ложность
формул (3.8).
В данном примере использованы так называемые одноместные предикаты,
имеющие по одному аргументу. Предикаты могут быть также многоместные
(имеют более одного аргумента). В случае одноместного предиката
предикатный символ соответствует какому-либо свойству объекта. В случае
многоместных предикатов предикатный символ рассматривается либо как
некоторое общее свойство объектов, соответствующих аргументам, либо,
чаще всего, как отношение, в котором эти объекты находятся, что, впрочем,
также является их свойством. Формулы задают отношения между такого типа
свойствами, но только с использованием связок.
Логика предикатов, как и логика высказываний, необходима для решения
задач. Постановка задачи на языке логики предикатов, даже если есть
соответствующее описание на естественном языке, далеко не простое дело.
Для облегчения этого процесса на основе логики предикатов разрабатываются
60
3.3. Постановка задачи для среды чудовища в логике предикатов
более удобные языки, учитывающие особенности конкретных сред. Этим
языкам будет уделено внимание в дальнейшем. Сейчас же вернемся к среде
чудовища и рассмотрим, как можно осуществить постановку задачи для среды
чудовища в логике предикатов.
3.3. Постановка задачи для среды чудовища
в логике предикатов
Осуществим последовательно введение термов, атомов, фактов, правил
и формул цели.
Термы:
константы Агент, Чудовище, Яма, Золото, Зловоние, Сквозняк, Блеск,
1, 2, 3, 4-,
переменные i, j, g, h, областью значения которых являются константы
Л 2, 3, 4',
переменная х, областью значений которой является множество констант
Агент, Чудовище, Яма, Золото.
Атомы:
находится (х, i, j), истинность которого свидетельствует, что объект х
находится в ячейке с координатами i, j, а ложность — он там не находится;
пахнет (i, j), истинность которого свидетельствует, что в ячейке с
координатами i, j агент ощущает зловоние, а ложность — не ощущает;
сквозит (/, j), истинность которого свидетельствует, что в ячейке с
координатами i, j агент ощущает4 сквозняк, а ложность — не ощущает;
блестит (i, j), истинность которого свидетельствует, что в ячейке с
координатами i, j агент видит блеск золота, а ложность — блеск ему
не виден;
ориентация (I, j), истинность которого свидетельствует, что агент стоит
лицом к ячейке с координатами (z, у) а ложность — он не стоит лицом к
ячейке с этими координатами;
перейти (J, j), истинность которого свидетельствует, что агент переходит
в ячейку с координатами (z, j), к которой он стоит лицом, а ложность, —
что он никуда не переходит;
повернуться (i, j), истинность которого свидетельствует, что агент
поворачивается направо на 90°, оставаясь в ячейке с координатами (z, j), а
ложность — не поворачивается;
взять (i, j), истинность которого свидетельствует, что агент берет золото в
ячейке с координатами (z, j), в которой он находится, а ложность, — что он
ничего не берет...
Постановка задачи в терминах логики предикатов теперь будет выглядеть
следующим образом.
61
3. Логика предикатов
Факты, определяющие начальные местоположения объектов. Начальная
ситуация показана на рис. 2.3 и с учетом введенных термов и атомов может
быть представлена формулой
находится (Агент, 1, 1) л ориентация (1,2) л
л -1 пахнет (1, 1) л -> сквозит (1, 1).
Правила, определяющие условия местонахождения объектов среды. Как и
прежде, если в какой-либо ячейке не ощущается зловония, то в соседних ей
ячейках чудовища нет. Точно так же, если в какой-либо ячейке нет сквозняка,
то в соседних ячейках нет ям. Импликации, с помощью которых можно выразить
эти знания, теперь приобретают следующий вид:
V (i, J) - пахнет (i, /)=?— находится (Чудовище, g, h) л
a ((g = i а (й =у-7 v h =j +1) v (h =j a (g = j-lv g = i +1)),
V (i, J ) -1 сквозит (i, j) zd -> находится (Яма, g, h) л
a ((g = i а (Й =j -1 v h =j +1) v (h =j a (g = i-l vg = i +1)).
Знания о наличии чудовища или ямы в ячейках, соседних данной ячейке,
если в ней соответственно ощущается зловоние или сквозняк, можно
представить в виде
V (i, j) пахнет (i, j) z> 3 (g, h) находится (Чудовище, g, й) a
л ((g = i а (й =y-1 v h =j +1) v (h =j л (g = i-l vg = z'+l));
V (i, j) сквозит (i, j) =)3(g, h) находится (Яма g, й)а
a ((g = i a (й =y-l v h =y-bl) v (h = j a (g = /-1 vg = /+1)).
Правила, определяющие условия выполнения агентом действий и допустимых
переходов. Агент может перейти в соседнюю ячейку, если там его не подстерегает
опасность в виде чудовища или ямы. Поэтому формулами, определяющими
действия по переходу в соседнюю ячейку, являются следующие:
V (/, у) находится (Агент, i, j) а ориентация (g, h) а
a ((g = i A(h =j-l v h =j +1) v (h =j a (g = / -1 v g = i +1))
a -i находится (Чудовище, g, h) л находится (Яма, g, й) z>
z> перейти (g, h) а находится (Агент, g, h) a ((g = i л (h =y-l) z>
z> ориентация (i, y-2)) v (g = i а (й = j +1) z> ориентация (i, j+2)) v
62
Вопросы и упражнения
v (g = z -1 л (й =j ) z> ориентация (i-2, у)) v (g ~ i +1 л (h = j) z>
z> ориентация (i+2, j)).
Формула, определяющая условия выполнения действий по изъятию
золота, имеет вид
V (i,j) находится (Агент, i,j) л блестит (i,J) z> взять (i, j).
Формулы, определяющие условия выполнения действий поворота агента
направо, имеют вид
V (/, у) находится (Агент, i, j) л ориентация (g, h) л
a ((g = i/\(h =J-l v h =/+l) v (h =j *(g = i-\ v g = z+1)) a
л (находится (Чудовище, g, h) v находится (Яма, g, й)) z>
z> повернуться (i, j) a ((g = i) a (h =j-1) z> ориентация (z-1, j) v
v (g = z) a (h =j +1) z> ориентация (z+1, j)) v (g = z-1) a (h =j) z>
z> ориентация (i, y+1)) v (g = z +1) л (ft =/) zj ориентация (i, /-!)).
Формулы цели. Цель агента — нахождение и изъятие золота, а решение
задачи — последовательность действий агента, приводящая его в ячейку, где
находится золото. Поэтому формулой цели будет просто взять (i, j).
Вопросы и упражнения
1. Представьте на языке логики предикатов следующие предложения русского языка:
а) не все студенты любят математику и физику;
б) только один студент любит историю;
в) только один студент любит как историю, так и электронику;
г) отставание по истории легче устранить, чем отставание по электронике;
д) любой охотник, не употребляющий дичь в пищу, вызывает удивление;
е) известны женщины, которые любят мужчин, не являющихся охотниками;
ж) живет в городе охотник, который знаком со всеми мужчинами-охотниками
этого города;
з) никто не любит охотника, который убивает дичь ради развлечения.
2. Запишите следующие условные предложения русского языка в виде правил
логики предикатов:
а) если вы любите детективы, то сегодня вечером можете посмотреть прекрасный
фильм из этой серии;
б) по утрам подают кофе и бутерброды с ветчиной;
в) может быть я заскочу к вам вечером, если успею;
г) я ее одновременно люблю и ненавижу;
д) если бы вы вовремя ушли с работы, вы бы успели к ужину. Если бы вы
успели к ужину, то попробовали бы прекрасное мороженое. Если бы вы попробовали
это мороженое, то всегда бы уходили с работы вовремя.
63
3. Логика предикатов
3. Сформулируйте на языке логики предикатов аксиомы, описывающие отношения
родства между внуками, бабушками и дедушками, родителями, сестрами, братьями,
дочерьми, сыновьями, зятьями, дядями и тетями.
4. Имеем среду, состоящую из стола и кубиков на нем. Каждый из кубиков
может лежать либо непосредственно на столе, либо на одном из других кубиков,
образуя с кубиками, лежащими под ним, столбик. Столбики могут быть любой
высоты. Сформулируйте на языке логики предикатов постановку задачи, исходя из
следующих условий:
а) кубик А лежит на кубике В, кубик В на кубике С, а кубик С на столе;
б) единственное действие, которое можно совершать в среде кубиков -- это
перемещать один кубик, на котором ничего не лежит, на стол или на другой кубик,
если он свободен от кубиков сверху;
в) необходимо перевернуть столбик из кубиков, используя это действие;
г) покажите формально, как получается решение в вашей постановке задачи.
5. Дополните постановку задачи, рассмотренную в настоящей главе для среды
чудовища, аксиомами, учитывающими возможность совершения агентом выстрела
из лука и поражения чудовища, если агент стоит к нему лицом в соседней ячейке и
в ней нет сквозняка. Объясните, как в этом случае может измениться стратегия
движения агента при условии, что после поражения чудовища зловоние, исходящее
от него, исчезает.
4. ВЫВОД В ЛОГИКЕ ПРЕДИКАТОВ
В настоящей главе рассмотрены процедуры вывода в логике предикатов
первого порядка, позволяющие осуществлять вывод целевых формул. Введены
основные понятия исчисления логики предикатов, отличающих его от
исчисления высказываний. Продолжается знакомство с более сложными
понятиями логических исчислений, базирующихся на логике предикатов первого
порядка, показаны различные типы выводов. В конце главы затронуты вопросы
полноты и непротиворечивости исчислений, основанных на логике предикатов
первого порядка.
Во второй главе определено понятие и изложена суть вывода (поиска,
рассуждения) в пространстве состояний с использованием логики
высказываний. В третьей главе рассмотрен язык логики предикатов первого
порядка, существенно более выразительный по сравнению с логикой
высказываний. Это большая выразительность языка логики предикатов
объясняется следующим. Вместо логических переменных логики
высказываний в логике предикатов используются предикаты. Предикаты
могут не иметь аргументов и тогда они являются полным аналогом логических
переменных. Но предикаты могут иметь в качестве аргументов объектные
константы и переменные, область значений которых может быть в принципе
даже бесконечной. Истинностное значение предикатов в этом случае зависит
от значения его аргументов. Кроме того, в логике предикатов используются
кванторы, которые позволяют делать высказывания в лаконичной форме о
множествах связанных определенными отношениями объектных переменных.
Следствием большей выразительности языка логики предикатов является более
сложная, хотя и схожая с логикой высказываний структура вывода.
4.1. Исчисление предикатов
В главе 2 было определено понятие логического исчисления. Одним из
таких исчислений является классическое исчисление предикатов. Как и любое
другое исчисление, оно построено на использовании:
алфавита (совокупности используемых символов);
3 — 1141
65
4. Вывод в логике предикатов
синтаксических правил построения формул в алфавите;
аксиом (общезначимых исходных формул);
правил вывода по аксиомам производных формул или теорем.
Алфавит и синтаксические правила построения формул в исчислении
предикатов определены в предыдущей главе. Множество аксиом классического
исчисления предикатов определяется следующим образом: каждая аксиома
классического исчисления высказываний трансформируется в аксиому
классического исчисления предикатов. Эта трансформация выражается только
в том, что все ее логические переменные рассматриваются как предикаты, а
формулы как формулы логики предикатов первого порядка.
К этому множеству аксиом, являющихся аналогом аксиом классического
исчисления высказываний, добавляются две следующие аксиомы:
V (х) а(х) а (у),
а(у)эЗ (х) а(х).
Общезначимость этих аксиом легко проверить с помощью таблиц
истинности.
Множеством правил классического исчисления предикатов является модус
поненс а, а р hp, в котором аир являются формулами логики предикатов
первого порядка, и два правила введения кванторов:
a zd р pa zz> V (х) р (х),
а zz> р h Э (х) а (х) р.
Классическое исчисление предикатов первого порядка не единственно.
Существует множество других исчислений, построенных на основе
классического, но использующих, помимо правил классического исчисления
предикатов, и другие правила. В частности, в главе 2 были введены такие
правила вывода в логике высказываний, как исключение конъюнкта,
введение конъюнкции, исключение двойного отрицания, простая
резолюция, резолюция. Эти правила справедливы и для логики предикатов,
с тем только отличием, что в них используются формулы логики предикатов,
а не логики высказываний.
Как и в случае классического исчисления высказываний, все аксиомы
классического исчисления предикатов не содержат констант. Кроме того,
все предикатные символы в классическом исчислении высказываний являются
абстрактными в том смысле, что любой предикатный символ в аксиомах
логического исчисления предикатов может быть переименован и от этого
ничего не изменится. Иными словами, аксиомы классического исчисления
предикатов, как и аксиомы классического исчисления высказываний,
остаются аксиомами при любой интерпретации.
Гфи использовании классического исчисления предикатов для описания
свойств какой-либо конкретной среды абстрактные предикатные символы
66
4.1. Исчисление предикатов
заменяют конкретными, называемыми также индивидуальными предикатными
символами. Кроме того, вводят факты, аксиомы и правила, не являющиеся
аксиомами классического исчисления предикатов и зависящие от той среды,
для которой осуществляется формализация постановки задачи. В результате
получается некоторое новое логическое исчисление. Формулы этого
исчисления по-прежнему строят по тем же правилам, показанным на рис.
3.1. С его помощью можно выводить формулы, которые нельзя получить в
классическом исчислении высказываний. С практической точки зрения нас
интересуют именно такие исчисления, учитывающие особенности конкретных
сред. В дальнейшем ряд таких исчислений и будет рассмотрен. Чтобы
отличать такие исчисления от классического исчисления логики предикатов
первого порядка, назовем их неклассическими исчислениями. К их числу
относятся также исчисления, которые строятся не на основе логики
предикатов первого порядка. В настоящей главе продолжим изучение
неклассических исчислений, построенных на основе логики предикатов
первого порядка.
Пусть, например, среди множества аксиом в неклассическом исчислении
для какой-либо среды имеется две аксиомы V(x) а(х) и а (Л) о р (В), где х —
переменная; А, В— константы; а, р — предикатные символы. Спрашивается,
можно ли на основании этих аксиом, используя правило модус поненс а, а
о р Н р, заключить, что формула Р(й) истинна. Если принять а = а(А),
Р = Р(й), то такое заключение можно было бы сделать, если бы среди
исходных аксиом имелась аксиома а (Л). Ее у нас нет. Имеется только аксиома
V (х) а (х). Эта аксиома гласит: «Для всех х имеет место истинность формулы
а (х)». Когда речь идет о всех х формулы а(х), то имеются в виду,
естественно, только те х, областью значений которых являются заранее
оговоренные константы, среди которых есть константа Л хотя бы потому,
что она встречается в предикате а (Л) формулы а (Л) р (5), т.е. в предикате,
предикатный символ «которого совпадает с предикатным символом предиката
в аксиоме V(x) а (х). Это означает, что предикат а (Л) истинен.
Следовательно, можно воспользоваться правилом модус поненс и заключить,
что формула р (В) истинна. Таким образом, чтобы воспользоваться правилом
модус поненс
а (Л), а (Л) z> Р(5) к р (Я),
пришлось по аксиоме V (х) а (х) получить аксиому а (Л). Это равносильно
использованию правила вывода, означающего, что при наличии аксиомы
V (х) а (х) вместо переменной х в предикат а (х) можно подставить константу
А (эта подстановка обозначается х -> А) и в результате получить аксиому
а (Л). Это правило называют правилом исключения квантора общности. Кроме
этого правила могут потребоваться также правила исключения квантора
существования, которые записывают в общем виде следующим образом:
з*
67
4. Вывод в логике предикатов
исключения квантора общности
V (х) а (х) Н а (х -> А);
исключения квантора существования
Э (х) а (х) h а (х -> А);
введение квантора существования
а (А) р- Э (х) а (х-> А).
Здесь а (х) — произвольная формула логики предикатов, имеющая
связанную квантором общности или существования переменную х; а (х -> А) —
формула а (х), в которой все вхождения переменной х заменены на константу А.
4.1.1. Снова пример со средой чудовища
Вернемся к решению задачи нахождения агентом золота в среде чудовища.
В предыдущей главе были сформулированы необходимые для решения задачи
аксиомы. Перечислим их в несколько ином виде и перенумеруем, вводя
дополнительно два атома: находится (Препятствие, i, 0), находится
(Препятствие, 0, у). Здесь используется дополнительная константа
Препятствие, соответствующая некоторому вымышленному объекту,
который ограничивает передвижение объекта в ячейки, хотя бы одна
координата которых равна нулю.
Предварительно напомним, что восприятие агента позволяет ему
определять наличие зловония, сквозняка или блеска только в той ячейке,
где он находится. Поэтому полное начальное состояние среды чудовища
(см. рис. 2. 3) агенту неизвестно. Находясь в ячейке (1, 1), он может
воспользоваться только восприятиями в этой ячейке.
Формулы, определяющие начальные знания агента:
находится (Агент, 1, 1) (4.1)
ориентация (1, 2) (4.2)
находится (Зловоние, 1, 1) (4.3)
-> находится (Сквозняк, 1, 1) (4.4)
-> находится (Яма, 1, 1) (4.5)
V (/) находится (Препятствие, i, 0) (4.6)
V (у) находится (Препятствие, 0, у) (4.7)
68
4.1. Исчисление предикатов
Для того чтобы выразить возможность восприятия агентом зловония,
сквозняка или блеска в ячейках (1, 2), (2, 1), (3, 1), соответственно введем
следующие формулы:
находится (Агент, 1, 2) находится (Зловоние, 1, 2), (4-8)
находится (Агент, 2, 1) z> находится (Сквозняк, 2, 1) л л находится (Зловоние, 1, 2), (4.9)
находится (Агент, 2, 3) zd находится (Блеск, 2, 3), (4.Ю)
находится (Агент, 1, 2) -1 находится (Сквозняк, 1,2), (4.11)
находится (Агент, 2, 2) z> -> находится (Зловоние, 2, 2), (4.12)
находится (Агент, 2, 2) z> —. находится (Сквозняк, 2, 2). (4.13)
Формулы, определяющие условия местонахождения объектов в зависимости
от восприятия:
V (i, J) находится (Зловоние, i, у) z> -i находится (Чудовище, i, J) л
л -1 находится (Чудовище, z, у-1) л -> находится (Чудовище, I, j +\) л
л -> находится (Чудовище, z-1, j ) л находится (Чудовище, z+1, у), (4.14)
V (i, j) находится (Сквозняк, i, у) zd
zd находится (Яма, i, у-1) л находится (Яма, i, j +1) л
л находится (Яма, i-1, у) л -> находится (Яма, i +1, у ), (4.15)
V (i, J ) находится (Чудовище, i, у) z>
zd находится (Зловоние, i, у) л -> находится (Зловоние, i, j -1) л
л -> находится (Зловоние, i, у+1) л
л -1 находится (Зловоние, z-1, j) л -> находится (Зловоние, z+1, у ), (4.16)
V (z, у) находится (Чудовище, i, у) zd
о находится (Зловоние, i, у) л находится (Зловоние, i, j -1) л
л находится (Зловоние, i, у+1) л находится (Зловоние, z-1, j ) л
л находится (Зловоние, z+1, у), (4.17)
69
4. Вывод в логике предикатов
V (z, j) находится (Зловоние, I, у) z> находится (Чудовище, i, /) v
v находится (Чудовище, i, j -1) v находится (Чудовище, i, j +1) v
v находится (Чудовище, z-1, j) v находится (Чудовище, z + 1, j), (4.18)
V (i, j) находится (Сквозняк, i, J) di
zd находится (Яма, i, j-1) v находится (Яма, i, j +1) v
v находится (Яма, z-1, j) v находится (Яма, z+1, J). (4-19)
Формулы, определяющие условия выполнения агентом действий:
V (z, j) находится (Агент, i, j) л ориентация (i, j-1) л
л находится (Чудовище, i, j -1) л находится (Яма, i, j -1) zd
zd перейти (I, j-1) л находится (Агент, i, j-1) л ориентация (i, j-2), (4.20)
V (z, j) находится (Агент, i, j ) л ориентация (i, j +1) л
л находится (Чудовище, i, j +1) л находится (Яма, i, j +1) zd
zd перейти (i, /+1) л находится (Агент, i, j+1) л ориентация (i, j+2), (4.21)
V (z, j) находится (Агент, i, j) л ориентация (z-1, j) л
л -i находится (Чудовище, z-1, j) л находится (Яма, i -1, j) zd
zd перейти (z-1, j) л находится (Агент, z-1, j) л ориентация (i-2, j), (4.22)
V (z, j) находится (Агент, i, j) л ориентация (z+1, j) л
л находится (Чудовище, z+1, j ) л находится (Яма, z+1, j ) =>
zd перейти (z+1, j) л находится (Агент, z+1, j) л ориентация (z+2, j), (4.23)
V (z, j) находится (Агент, i, j) л находится (Блеск, i, j) zd
zd взять (i, j), (4.24)
70
4.1. Исчисление предикатов
\/ (i, J) находится (Агент, i, j) л ориентация (i, j -1) л
л (находится (Чудовище, i, j-1) v находится (Яма, i, j -1) v
v находится (Препятствие, i, j -1)) о повернуться направо (i, j) л
л находится (Агент, i, j) л ориентация (Z-l, j), (4.25)
V (i, j) находится (Агент, i, j) л ориентация (z-l, j) л
л (находится (Чудовище, i-l, j ) v находится (Яма, z-l, j) v
у находится (Препятствие, z-l, /)) о повернутьсянаправо (i, j) л
л находится (Агент, I, j) л ориентация (i, J+1), (4.26)
V (z, j) находится (Агент, i, j) л ориентация (i, j+\) л
л (находится (Чудовище, I, j +1) v находится (Яма, i, j +1) v
v находится (Препятствие, i, j+1)) о повернуться направо (i, j) л
л находится (Агент, i, j ) л ориентация (z+1, /), (4.27)
V (z, j) находится (Агент, i, j) л ориентация (z+1, j) л
л (находится (Чудовище, z+1, j) v находится (Яма, z+1, j) у
у находится (Препятствие, z+1, j)) zd повернуться направо (i, j) л
л находится (Агент, i, j) л ориентация (I, у-1), (4.28)
V (z, j) находится (Агент, i, j) л ориентация (i, j -1) л
л (находится (Чудовище, i, j -1) v находится (Яма, i, j -1) v
v находится (Препятствие, i, j-1)) о повернутьсяналево (i, j) л
л находится (Агент, i, j) л ориентация (z+1, j), (4.29)
V (z, j) находится (Агент, i, j) л ориентация (z-l, j) л
л (находится (Чудовище, z-l, j) v находится (Яма, z-l, j) v
v находится (Препятствие, z-l, j)) zd повернутьсяналево (i, j) л
л находится (Агент, i, j) л ориентация (i, j'-l), (4.30)
71
4. Вывод в логике предикатов
V (i, j) находится (Агент, i, j ) л ориентация (i, у+1) л
л (находится (Чудовище, i, у+1) v находится (Яма, i, у+1) v
v находится (Препятствие, i, у+1)) о повернутьсяналево (i, j) л
л находится (Агент, i, j) л ориентация (z-1, у), (4.31)
V (i, j) находится (Агент, I, J) л ориентация (z+1, у) л
л (находится (Чудовище, z+1, у) v находится (Яма, z+1, у) v
v находится (Препятствие, z+1, у )) о повернутъся_ налево (i, у) л
л находится (Агент, i, у) л ориентация (i, у+1). (4.32)
Формула цели:
3 (i, j) взять (I, у). (4.33)
4.1.2. Вывод
Рассмотрим подробно вывод с использованием правил исключения
квантора общности, конъюнкта и введения конъюнкции. Вывод разобьем
на шаги, на каждом из которых будем применять только одно из
перечисленных правил, а в результате получать новую формулу.
Шаг 1. В соответствии с правилом исключения квантора общности и
формулой (4.14) получаем
находится (Зловоние, 1, 1) о -> находится (Чудовище, 1, 1) л
л находится (Чудовище, 1, 2) л -> находится (Чудовище, 2, 1). (4.34)
Шаг 2. В соответствии с формулами (4.3), (4.34) и правилом модус
поненс получаем
-1 находится (Чудовище, 1, 1) л — находится (Чудовище, 1, 2) л
л находится (Чудовище, 2, 1). (4.35)
Шаг 3. В соответствии с формулой (4.35) и правилом исключения
конъюнкта получаем
-1 находится (Чудовище, 1, 1), (4.36)
находится (Чудовище, 1, 2), (4.37)
-^находится (Чудовище, 2, 1). (4.38)
72
4.1. Исчисление предикатов
Шаг 4. В соответствии с правилом исключения квантора общности и
формулой (4.15) получаем
-> находится (Сквозняк, 1 ,1) о -> находится (Яма, 1, 2) л
л -> находится (Яма, 2, 1). (4.39)
Шаг 5. В соответствии с формулами (4.4), (4.39) и правилом модус
поненс получаем
-> находится (Яма, 1, 2) л находится (Яма, 2, 1). (4.40)
Шаг 6. По (4.40) и правилу исключения конъюнма получаем
находится (Яма, 1, 2), (4.41)
находится (Яма, 2, 1). (4.42)
Заметим, что поскольку ячеек хотя бы с одной нулевой координатой не
существует, то соответствующие им предикаты не включены в формулы (4.39)
и (4.40).
Шаг 7. В соответствии с формулами (4.1), (4.2), (4.37), (4.41) и
правилом введения конъюнкции получаем
находится (Агент, 1, 1) л ориентация (1, 2) л
л находится (Чудовище, 1, 2) л -> находится (Яма, 1, 2). (4.43)
Шаг 8. В соответствии с формулой (4.21) и правилом исключения
квантора общности получаем
находится (Агент, 1, 1) л ориентация (1, 2) л
л -1 находится (Чудовище, 1, 2) л -> находится (Яма, 1, 2) о
о перейти( 1, 2) л находится (Агент, 1, 2) л ориентация (1, 3). (4.44)
Шаг 9. В соответствии с формулами (4.43), (4.44) и правилом модус
поненс получаем
перейти (1, 2) л находится (Агент, 1, 2) л ориентация (1, 3). (4.45)
Шаг 10. В соответствии с формулой (4.45) и правилом исключения
конъюнкта получаем
перейти (1, 2), (4.46)
находится (Агент, 1, 2), (4.47)
ориентация (1, 3). (4.48)
73
4. Вывод в логике предикатов
Шаг 11. В соответствии с формулами (4.47), (4.8) и правилом модус
поненс получаем
находится (Зловоние, 1, 2). (4.49)
Шаг 12. В соответствии с формулами (4.11), (4.47) и правилом модус
поненс получаем
находится (Сквозняк, 1, 2). (4.50)
Шаг 13. В соответствии с формулой (4.18) и правилом исключения
квантора общности получаем
находится (Зловоние, 1, 2) о находится (Чудовище, 1, 1) v
v находится (Чудовище, 1, 2) v находится (Чудовище, 1, 3) v
v находится (Чудовище, 2, 2). (4-51)
Шаг 14. В соответствии с формулами (4.49), (4.51) и правилом модус
поненс получаем
находится (Чудовище, 1, 1) v находится (Чудовище, 1, 2) v
v находится (Чудовище, 1, 3) v находится (Чудовище, 2, 2). (4-52)
Шаг 15. В соответствии с формулой (4.52) и правилом резолюции (согласно
(4.36) истинен предикат -> находится (Чудовище, 1, 1), а по (4.37) — истинен
предикат находится (Чудовище, 1, 2); следовательно, находится (Чудовище,
1, 1) и находится (Чудовище, 1, 2) ложны) получаем
находится (Чудовище, 1, 3) v находится (Чудовище, 2, 2). (4.53)
Чудовище только одно и поэтому только один из предикатов в формуле (4.53)
должен быть истинным. Определить, однако, какой из них истинен, агент не
может. Поэтому попытаемся сформулировать действия, которые, находясь в
ячейке (2, 1), агент может совершать в предположении, что чудовище может
быть в любой из двух ячеек (1,3) или (2, 2).
Шаг 16. В соответствии с формулой (4.27) и правилом исключения
квантора общности получаем
находится (Агент, 1, 2) л ориентация (1, 3) л
л находится (Чудовище, 1, 3) повернуться направо (1, 2) л
л находится (Агент, 1, 2) л ориентация (2, 2). (4.54)
74
4.1. Исчисление предикатов
Шаг 17. В соответствии с формулами (4.47), (4.48), (4.53) и правилом
введения конъюнкции получаем
находится (Агент, 1, 2) л ориентация (1, 3) л
л находится (Чудовище, 1, 3). (4.55)
Шаг 18. В соответствии с формулами (4.54), (4.55) и правилом модус
поненс получаем
повернуться (1, 2) л находится (Агент, 1, 2) л ориентация (2, 2). (4.56)
Шаг 19. В соответствии с формулой (4.56) и правилом исключения
конъюнкции получаем
повернуться (1, 2), (4.57)
находится (Агент, 1, 2), (4.58)
ориентация (2, 2). (4.59)
Шаг 20. В соответствии с формулой (4.28) и правилом исключения
квантора общности получаем
находится (Агент, 1, 2) л ориентация (2, 2) л (находится (Чудовище, 2, 2) v
v находится (Яма, 2, 2)) zz> повернуться (1, 2) л находится (Агент, 1, 2) л
/\ ориентация (1, 1). (4.60)
Шаг 21. В соответствии с формулами (4.53), (4.58), (4.59) и правилом
введения коньюнкции получаем
находится (Агент, 1, 2) л ориентация (2, 2) л
л находится (Чудовище, 2, 2). (4.61)
Шаг 22. В соответствии с формулами (4.60) (4.61) и правилом модус
поненс получаем
повернуться (1, 2) л находится (Агент, 1, 2) л ориентация (1, 1). (4.62)
Шаг 23. В соответствии с формулой (4.62) и правилом исключения
конъюнкта получаем
повернуться (1, 2), (4.63)
находится (Агент, 1, 2), (4.64)
ориентация (1, 1). (4-65)
75
4. Вывод в логике предикатов
Шаг 24. В соответствии с формулой (4.20) и правилом исключения
квантора общности получаем
находится (Агент, 1, 2) л ориентация (1, 1) л
л -I находится (Чудовище, 1, 1) л находится (Яма, 1, 1)
о перейти (1,1) л находится (Агент, 1,1) л ориентация (1, 0). (4.66)
Шаг 25. В соответствии с формулами (4.5), (4.36), (4.64), (4.65) и
правилом введения конъюнкции получаем
находится (Агент, 1, 2) л ориентация (1, 1) л
л находится (Чудовище, 1, 1) л -> находится (Яма, 1, 1). (4-67)
Шаг 26. В соответствии с формулами (4.67), (4.66) и правилом модус
поненс получаем
перейти (1, 1) л находится (Агент, 1, 1) л ориентация (1, 0). (4.68)
Шаг 27. В соответствии с формулой (4.68) и правилом исключения
конъюнкта получаем
перейти (1,1), (4.69)
находится (Агент, 1,1), (4.70)
ориентация (1, 0). (4.71)
Таким образом, агент вернулся в ячейку (1, 1), но ориентация его
изменилась. Теперь он стоит лицом к несуществующей ячейке (1, 0).
Шаг 28. В соответствии с формулой (4.6) и правилом исключения
квантора общности получаем
находится (Препятствие, 1, 0). (4.72)
Шаг 29. В соответствии с формулой (4.29) и правилом исключения
квантора общности получаем
находится (Агент, 1, 1) л ориентация (1, 0) л
л (находится (Препятствие, 1, 0) v находится (Чудовище, 1, 0) v
v находится (Яма, 1, 0)) о повернуться_налево (1, 1) л
л находится (Агент, 1, 1) л ориентация (2, 1). (4.73)
76
4.1. Исчисление предикатов
Шаг 30. В соответствии с формулами (4.70), (4.71), (4.72) и правилом
введения конъюнкции получаем
находится (Агент, 1, 1) л ориентация (1, 0) л
л находится (Препятствие, 1, 0). (4-74)
Шаг 31. В соответствии с формулами (4.73), (4.74) и правилом модус
поненс получаем
повернуться налево (1, 1) л находится (Агент, 1, 1) л
л ориентация (2, 1). (4.75)
Шаг 32. В соответствии с формулой (4.75) и правилом исключения
конъюнкта получаем
повернуться налево (1, 1), (4 76)
находится (Агент, 1, 1), (4.77)
ориентация (2, 1). (4.78)
Шаг 33. В соответствии с формулой (4.23) и правилом исключения
квантора общности получаем
находится (Агент, 1, 1) л ориентация (2, 1) л
л находится (Чудовище, 2, 1) л — находится (Яма, 2, 1) о
zd перейти(2, 1) л находится (Агент, 2, 1) л ориентация (3, 1). (4.79)
Шаг 34. В соответствии с формулами (4.77), (4.78), (4.38), (4.42) и
правилом введения конъюнкции получаем
находится (Агент, 1, 1) л ориентация (2, 1) л
л находится (Чудовище, 2, 1) л — находится (Яма, 2, 1). (4.80)
Шаг 35. В соответствии с формулами (4.80), (4.79) и правилом модус
поненс получаем
перейти (2, 1) л находится (Агент, 2, 1) л ориентация (3, 1). (4.81)
Шаг 36. В соответствии с формулой (4.81) и правилом исключения
конъюнкта получаем
перейти (2, 1), (4.82)
находится (Агент, 2, 1), (4.83)
ориентация (3, 1). (4.84)
77
4. Вывод в логике предикатов
Шаг 37. В соответствии с формулами (4.83) и (4.9) и правилом модус
поненс получаем
находится (Сквозняк, 2,1). (4-85)
Шаг 38. В соответствии с формулой (4.19) и правилом исключения
квантора общности получаем
находится (Сквозняк, 2, 1) о находится (Яма, 2, 2) v
v находится (Яма, 1, 1) v находится (Яма, 3, 1). (4.86)
Шаг 39. В соответствии с формулами (4.85), (4.86) и правилом модус
поненс получаем
находится (Яма, 2, 2) v находится (Яма, 1, 1) v
v находится (Яма, 3, 1). (4.87)
Шаг 40. В соответствии с формулой (4.15), правилом исключения
квантора общности, получаем
находится (Сквозняк, 1, 2) о находится (Яма, 1, 1) л
л находится (Яма, 2, 2) л находится (Яма, 1, 3). (4.88)
Шаг 41. В соответствии с формулами (4.58), (4.1 1), (4.88) и правилами
модус поненс и исключения конъюнкта получаем
находится (Яма, 1, 1), (4.89)
-- находится (Яма, 2, 2), (4.90)
находится (Яма, 1, 3). (4.91)
Шаг 42. В соответствии с формулами (4.87), (4.5), (4.90) и правилом
резолюции получаем
находится (Яма, 3, 1). (4.92)
Шаг 43. В соответствии с формулой (4.30) и правилом исключения
квантора общности получаем
находится (Агент, 2, 1) л ориентация (3, 1) л
л находится (Яма, 3, 1) о повернутьсяналево (2, 2) л
л находится (Агент, 2, 1) л ориентация (2, 2). (4-93)
78
4.1. Исчисление предикатов
Шаг 44. В соответствии с формулами (4.92), (4.83), (4.84) и правилом
введения конъюнкции получаем
находится (Яма, 3, 1) л находится (Агент, 2, 1) л
л ориентация (3, 1). (4.94)
Шаг 45. В соответствии с формулами (4.94), (4.93) и правилом модус
поненс получаем
повернутъсяналево (2, 2) л находится (Агент, 2, 1) л
л ориентация (2, 2). (4.95)
Шаг 46. В соответствии с формулой (4.95) и правилом исключения
конъюнкта получаем
повернутьсяналево (2, 2), (4.96)
находится (Агент, 2, 1), (4.97)
ориентация (2, 2). (4.98)
Шаг 47. В соответствии с формулой (4.21) и правилом исключения
квантора общности получаем
находится (Агент, 2, 1) л ориентация (2, 2) л
л находится (Чудовище, 2, 2) л находится (Яма, 2, 2) zz>
zd перейти (2, 2) л находится (Агент, 2, 2) л ориентация (2, 3). (4.99)
Шаг 48. В соответствии с формулами (4.9), (4.14), (4.97), (4.98), (4.90)
и правилами исключения квантора общности, модус поненс и введения
конъюнкции получаем
находится (Агент, 2, 1) л ориентация (2, 2) л
л находится (Чудовище, 2, 2) л находится (Яма, 2, 2). (4.100)
Заметим, что шаг 48 не является таким простым, как все остальные. Его
детализацию предлагается выполнить самостоятельно.
Шаг 49. В соответствии с формулами (4.100), (4.99) и правилом модус
поненс получаем
перейти (2, 2) л находится (Агент, 2, 2) л ориентация (2, 3). (4.101)
Шаг 50. В соответствии с формулой (4.101) и правилом исключения
конъюнкта получаем
перейти (2, 2), (4.102)
79
4. Вывод в логике предикатов
находится (Агент, 2, 2), (4.103)
ориентация (2, 3). (4.104)
Шаг 51. В соответствии с формулами (4.103), (4.12) и правилом модус
поненс получаем
-- находится (Зловоние, 2, 2). (4.105)
Шаг 52. В соответствии с формулами (4.103), (4.13) и правилом модус
поненс получаем
находится (Сквозняк, 2, 2). (4.106)
Шаг 53. В соответствии с формулой (4.14) и правилом исключения
квантора получаем
находится (Зловоние, 2, 2) о находится (Чудовище, 2, 2) л
л -- находится (Чудовище, 2, 1) л находится (Чудовище, 2, 3) л
л находится (Чудовище, 1, 2) л -> находится (Чудовище, 3, 2). (4.107)
Шаг 54. В соответствии с формулами (4.105), (4.107) и правилом модус
поненс получаем
находится (Чудовище, 2, 2) л находится (Чудовище, 2, 1) л
л находится (Чудовище, 2, 3) л находится (Чудовище, 1, 2) л
л -- находится (Чудовище, 3, 2). (4.108)
Шаг 55. В соответствии с формулой (4.108) и правилом исключения
конъюнкта получаем
находится (Чудовище, 2, 2), (4.109)
находится (Чудовище, 2, 1), (4.110)
-1 находится (Чудовище, 2, 3), (4.1Н)
-> находится (Чудовище, 1, 2), (4.Н2)
находится (Чудовище, 3, 2). (4.113)
Шаг 56. В соответствии с формулой (4.15) и правилом исключения
квантора получаем
80
4. /. Исчисление предикатов
-> находится {Сквозняк, 2, 2) о -> находится {Яма, 2, 1) л
л -1 находится {Яма, 2, 3) л находится {Яма, 1, 2) л
л -> находится {Яма, 3, 2). (4.114)
Шаг 57. В соответствии с формулой (4.114) и правилом исключения
конъюнкта получаем
-> находится {Яма, 2, 1), (4.115)
находится {Яма, 2, 3), (4.116)
находится {Яма, 1, 2), (4.117)
находится {Яма, 3, 2). (4.118)
Шаг 58. В соответствии с формулой (4.21) и правилом исключения
квантора общности получаем
находится {Агент, 2, 2) л ориентация (2, 3) л
л -> находится {Чудовище, 2, 3) л -> находится {Яма, 2, 3) о
о перейти (2, 3) л находится {Агент, 2, 3) л ориентация (2, 4). (4.119)
Шаг 59. В соответствии с формулами (4.103), (4.104), (4.111), (4.116)
и правилом введения конъюнкции получаем
находится {Агент, 2, 2) л ориентация (2, 3) л
л -1 находится {Чудовище, 2, 3) л -> находится {Яма, 2, 3). (4.120)
Шаг 60. В соответствии с формулами (4.120), (4.119) и правилом модус
поненс получаем
перейти (2, 3) л находится {Агент, 2, 3) л ориентация (2, 4). (4.121)
Шаг 61. В соответствии с формулой (4.121) и правилом исключения
конъюнкта получаем
перейти (2, 3), (4.122)
находится {Агент, 2, 3), (4.123)
ориентация (2, 4). (4.124)
Шаг 62. В соответствии с формулами (4.123), (4.10) и правилом модус
поненс получаем
находится {Блеск, 2, 3). (4.125)
81
4. Вывод в логике предикатов
Шаг 63. В соответствии с формулой (4.24) и правилом исключения
квантора общности получаем
находится (Агент, 2, 3) л находится (Блеск, 2, 3) о взять (2, 3). (4.126)
Шаг 64. В соответствии с формулами (4.123), (4.125) и правилом
введения конъюнкции получаем
находится (Агент, 2, 3) л находится (Блеск, 2, 3). (4.127)
Шаг 65. В соответствии с формулами (4.127), (4.126) и правилом модус
поненс получаем
взять (2, 3). (4.128)
Шаг 66. В соответствии с формулой (4.128) и правилом введения
квантора существования получаем
взять (2, 3) о 3 (/, у) взять (i, j). (4.129)
Таким образом, была достигнута (выведена) цель (4.33).
4.1.3. Трудности процедуры поиска решения в среде чудовища
Процедура поиска решения сравнительно простой задачи в среде чудовища
потребовала 66 шагов. На каждом шаге применялось чаще всего какое-либо
одно правило вывода. (Некоторые шаги, например, шаг 48 вывода формулы
(4.100), были несколько укрупнены). Что можно заметить, анализируя эту
процедуру?
Несмотря на простоту задачи, число шагов кажется несоразмерно большим
(66 шагов).
Также кажется слишком большим количество новых истинных литералов,
которые были выведены в процессе поиска решения (130 литералов).
Выбор очередного шага неоднозначен. Количество новых истинных
литералов, которые можно вывести из уже известных, назовем степенью
ветвления.
На степень ветвления сильно влияют правила исключения квантора
общности, поскольку при его использовании осуществляется замена
переменных константами, а число таких замен в принципе может быть даже
бесконечным.
Приходится очень часто применять правила введения конъюнкции,
комбинируя литералы в целях получения формул, являющихся комбинацией
литералов, для использования их в правилах модус поненс. Также часто
приходится применять правило исключения конъюнктов в целях получения
литералов для использования их в правилах введения конъюнкции.
Итак, в выводе, который только что был продемонстрирован, все время
приходилось выводить истинность отдельных литералов, а затем, комбинируя их
82
4.1. Исчисление предикатов
в истинную конъюнкцию а и используя какую-либо истинную импликацию
юР, применять правило модус поненс а, аз р гР для получения новой истинной
формулы р, по которой затем снова приходилось выводить истинные литералы,
и так до тех пор, пока не получится требуемая нам истинная формула. Поскольку
в этом процессе все время приходилось спускаться на уровень отдельных литералов,
то естественным образом напрашивается идея ввести ограничения на вид
используемых в исчислении и правиле модус поненс формул так, чтобы не
приходилось постоянно и раздельно применять правила исключения квантора
общности, исключения конъюнкта и введения конъюнкции.
Для этого предлагается ввести обобщенное правило модус поненс а, а з р Кр,
в котором а и р не являются произвольными формулами логики предикатов
первого порядка. Отметим, что обобщенным его называют в связи с тем,
что оно позволяет избавиться от раздельного использования правил
исключения квантора общности, исключения конъюнкта и введения
конъюнкции, хотя с общей точки зрения это правило является частным
случаем правила модус поненс.
4.1.4. Обобщенное правило модус поненс
Обозначим в (8) некоторый атом, имеющий предикатный символ в и
множество вхождений переменных и констант 8. Тогда обобщенное правило
модус поненс принимает вид
Р (х₽), v (xv), а(ца)л Р(цр) л ... л v(pv) з у(цу), а(ха-> 0^) =
= а(ца-> 0Иа), р (Хр-> ezp) = Р(ц₽-> ецр),..., v(xv-> 9Xv) = v(K-> еи ) К у(ц,-> 9ц).
Смысл этого правила состоит в следующем. Формулы а(хц), Р(хр), •
v(xv) являются атомами и каждый из них имеет множество вхождений констант
и переменных у. В формуле а(ца)л р(цр) л ... л v(p ) оу(ц ), представленной
импликацией, а(ца), Р (цр), ..., v(p ), у(ц ) являются атомами, каждый из
которых имеет множество вхождений констант и переменных ц. Если
существуют подстановки 9 такие, что а(ха-> 9у ) = а(ц-> 0ц ), Р(хр-> 0 ) =
= Р(цр -> 9ц ), ..., v(xv-> 0 ) = v(pv-> 0 ), то будет истинным атом у(ц-»6 ).
Напомним, что е (8 -» 9) означает, что вместо аргументов 8 атома е подставляются
аргументы 9. При этом необходимо соблюдать следующие требования:
Вместо переменной в 8 можно подставлять переменную из 9. Такую
подстановку называют переименованием переменной.
Вместо переменной в 8 можно подставлять константу из 9. Такую
подстановку называют конкретизацией переменной.
Вместо переменной в 8 можно подставлять функцию из 9. Такую
подстановку называют заменой переменной.
Вместо одной и той же переменной везде следует подставлять одну и ту же
константу или функцию. Переименовываются одновременно все вхождения
одной и то же переменной.
83
4. Вывод в логике предикатов
Процесс поиска нужной подстановки 9 называют унификацией, а формулу,
в атомы которой осуществлена подстановка, называют унифицированной. В
некоторых исчислениях для подстановки, конкретизации и замены переменной
вводят отдельные правила. Подстановка называется наиболее общей, если
благодаря ей наименьшее число переменных замещается константами. В
обобщенном правиле модус поненс вместо V(x)a(x) записывают а(х), т.е.
кванторы общности подразумеваются, но не употребляются. Кванторы
существования в обобщенном правиле модус поненс вообще не используются.
Поскольку обобщенное правило модус поненс является единственным, которое
мы собираемся использовать в процессе вывода, то, следовательно, постановка
задачи изначально должна удовлетворять следующим условиям.
Формулы в постановке задачи не должны содержать кванторов
существования.
Если они все же есть, то, прежде чем решать задачу, от кванторов
существования следует избавиться с помощью, например, правила исключения
квантора существования или какими-либо другими способами, речь о которых
пойдет дальше.
Все формулы в постановке задачи должны быть атомами или
импликациями, левая часть (посылка) которых является конъюнкцией
атомов, а правая (заключение) — либо атомом, либо пустым символом.
Такие формулы называют хорновскими формулами.
Преобразование произвольных формул логики предикатов в хорновские
формулы непростая задача, причем не любую формулу можно преобразовать
к такому виду. В нашем примере со средой чудовища кванторов
существования, не считая формулы цели, вообще нет, тем не менее,
подобное преобразование всех формул невозможно. Например, это нельзя
сделать для формул (4.18), (4.19). Рассмотрим, как выполняется указанное
преобразование для формул (4.1) — (4.32). Для того чтобы можно было
легко сопоставить эти формулы с их преобразованиями, будем последние
нумеровать теми же числами, но со звездочкой, комментируя производимые
преобразования (если в преобразованиях нет необходимости, то
соответствующая формула переписывается без комментариев):
находится (Агент, 1, 1), (4.1)*
ориентация (1, 2). (4.2)*
Выполняя преобразования на основе закона а = a v Ложь =
= a zd Ложь, получаем
находится (Зловоние, 1, 1) zd Ложь, (4.3)*
находится (Сквозняк, 1, 1 ) zd Ложь, (4.4)*
находится (Яма, 1, 1) zd Ложь. (4.5)*
84
4. /. Исчисление предикатов
Простым удалением квантора общности (если он есть) или на основе закона
(а о р л у) = (-> a v р л у) = (а zd Р) л (а о у) получаем следующие формулы:
находится (Препятствие, i, 0), (4.6)*
находится (Препятствие, 0, j), (4.7)*
находится (Агент, 1, 2) => находится (Зловоние, 1, 2), (4.8)*
находится (Агент, 2, 1) zd находится (Сквозняк, 2, 1),
(4.9)*
находится (Агент, 2, !)=>—> находится (Зловоние, 2, 1),
находится (Агент, 2, 3) zd находится (Блеск, 2, 3). (4.10)*
Выполняя преобразования на основе закона a zd -> р = a v р = - v Ложь = а л р zd Ложь, получаем следующие формулы: (а л р) v
находится (Агент, 1, 2) л находится (Сквозняк, 1,2) zd Ложь, (4.11)*
находится (Агент, 2, 2) л находится (Зловоние, 2, 2) zd Ложь, (4.12)*
находится (Агент, 2, 2) л находится (Сквозняк, 2, 2) zd Ложь. (4.13)*
Вторая формула в (4.9)* может быть преобразована аналогично.
С помощью преобразования а эр л лу л ... л - 5 а v t р л
у л ... л -> 5 = (а v -> р) л (а v -> у ) л ... л (а v -> 5) =
= (р zd а) л (у zd а) л ... л(8з а), удаления квантора существования и правила
исключения конъюнкта, получаем следующие формулы:
находится (Чудовище, i, j) zd находится (Зловоние, I, j),
находится (Чудовище, i, j-1) о находится (Зловоние, i, j),
находится (Чудовище, i, j+1) о находится (Зловоние, i,j),
находится (Чудовище, z-1, j) zd находится (Зловоние, i, j),
находится (Чудовище, / + 1, j) zd находится (Зловоние, i, j)', (4.14)*
находится (Яма, I, /) zd находится (Сквозняк, i, j),
находится (Яма, i, j-1) о находится (Сквозняк, i, j),
находится (Яма, i,j + \) о находится (Сквозняк, i, j),
находится (Яма, z-1, J) zd находится (Сквозняк, i, j),
находится (Яма, z+1, j) zd находится (Сквозняк, i, j)', (4.15)*
85
4. Вывод в логике предикатов
находится {Зловоние, I, j) zd находится {Чудовище, i, j),
находится {Зловоние, i, j-\) zd находится {Чудовище, i, J),
находится {Зловоние, I, j +1) zd находится {Чудовище, i, j),
находится {Зловоние, /-1, j) zd находится {Чудовище, i, j),
находится {Зловоние, z+1, j) zd находится {Чудовище, I, j). (4.16)*
Следующие формулы преобразовать к требуемому виду невозможно.
Оставим их в прежнем виде, исключив квантор существования:
находится {Чудовище, i, j) zd находится {Зловоние, i, j) v
v находится {Зловоние, i, у-1) v находится {Зловоние, i, j) v
v находится {Зловоние, I, y + 1) v находится {Зловоние, z-1, j)
находится {Зловоние, z + l,y); (4.17)*
находится {Зловоние, i, j) zd находится {Чудовище, i, j) v
v находится {Чудовище, i, j -1) v находится {Чудовище, i, j +1) v
v находится {Чудовище, i-1, j) v находится {Чудовище, z + 1, j); (4.18)*
находится {Сквозняк, i, j) zd находится {Яма, i, y-1) v
v находится {Яма, i, y + 1) v находится {Яма, z-1, у) v
v находится {Яма, z + 1, у), (4.19)*
С помощью преобразования а л р л -> / л -п <5zd с л у л ф = a v pv у vSv
v £ л у л q> = (—avn pvy vo vc)a(- av - Pv vy v6v,')a (- к v-п Р v yv5 vo),
удаления квантора существования и правила исключения конъюнкта получаем
следующие формулы:
находится {Агент, I, у) v ориентация {I, у-1) v
86
4.1. Исчисление предикатов
v находится (Чудовище, i, j-1) v находится (Яма, i, j-1) v
v перейти (i, j-1);
находится (Агент, i, j) v ориентация (i, j-1) v
v находится (Чудовище, i, j -1) v находится (Яма, i, j-1) v (4.20)*
v находится (Агент, i, j-1);
находится (Агент, i, j) v —> ориентация (i, j-1) v
v находится ( Чудовище, i, j -1) v находится (Яма, i, j -1) v
v ориентация (i, j-2).
Число подформул в системе формул (4.20)* совпадает с числом литералов
вследствие импликативной формулы (4.20) и различаются они только
последним литералом. Поэтому для остальных формул (4.21)* — (4.23)*
выпишем только первую подформулу:
находится (Агент, I, j) v -> ориентация (i, j + 1) v
v находится (Чудовище, i, j +1) v находится (Яма, i, j +1) v
v перейти (i, j + 1); (4.21)*
находится (Агент, i, J ) v ориентация (z-l, j ) v
v находится (Чудовище, z-l, j) v находится (Яма, z-l, j) v
v перейти (z-l, j); (4.22)*
- i находится (Агент, i, / ) v ориентация (z + 1, j) v
v находится (Чудовище, z +1, j) v находится (Яма, z +1, j) v
v перейти (z+1, j); (4.23)*
находится (Агент, i, j) v —, находится (Блеск, i, j) v взять (i, j). (4.24)*
87
4. Вывод в логике предикатов
Подформулы системы формул (4.25)* — (4.32)* получаются аналогично,
но их еще больше. Выпишем, как и в предыдущем случае, только по одной
(первой) подформуле:
находится (Агент, i, j) v -> ориентация (i, j-1) v
v находится (Чудовище, i, y-1) v повернутьсянаправо (i, j); (4.25)*
находится (Агент, i, j) v -> ориентация (z-1, j) v
v -> находится (Чудовище, z-1, j) v повернуться_направо (i, j); (4.26)*
находится (Агент, i, j) v -> ориентация (i, j +1) v
v —> находится (Чудовище, i, y + 1) v повернуться направо (i, j)', (4.27)*
находится (Агент, i, J) v -> ориентация (z+1, j) v
v —i находится (Чудовище, z+1, j) v повернуться направо (i, j + 1); (4.28)*
находится (Агент, i, j) v -> ориентация (i, j-1) v
v находится (Чудовище, i, j-l) v повернуться_налево (i, j); (4.29)*
- > находится (Агент, i, /) v -> ориентация (z-1, j) v
v находится (Чудовище, v повернуться_налево (i, j)', (4.30)*
- > находится (Агент, i, у) v ориентация (i, y + 1) v
v находится (Чудовище, i, y + 1) v повернуться_налево (i, y); (4.31)*
находится (Агент, i, j) v ориентация (z+1, j) v
v-> находится (Чудовище, z + 1, j) v повернуться_ налево (i, j). (4.32)*
Применение обобщенного правила модус поненс вследствие того, что
в нем используются не отдельные атомы, а их конъюнкции, делает вывод
более эффективным. Это объясняется тем, что подстановка одних и тех же
88
4.2. Прямой и обратный вывод
констант осуществляется сразу для совокупности атомов, входящих в
конъюнкцию левой части импликации и, если необходимо, то правой.
4.2. Прямой и обратный вывод
Наиболее распространенными являются два типа вывода: прямой и обратный.
До сих пор как во второй главе, так и в настоящей в примерах со средой чудовища
использовался прямой вывод. Будем полагать, что все формулы, входящие в
постановку задачи, образуют некоторую начальную базу знаний.
Идея прямого вывода основана на следующих шагах. На первом шаге
подбирается правило вывода, условие которого можно образовать из формул
начальной базы знаний с использованием, если это необходимо, унификации.
Обычно начинается все с формул, представляющих знания о начальном состоянии
среды. По правилу вывода получаются новые истинные формулы, являющиеся
его унифицированным следствием. Эти формулы помещаются в начальную базу
знаний, в результате чего она превращается в другую базу знаний, из нее
извлекаются новые формулы, и все повторяется сначала до тех пор, пока на
очередном шаге унифицированное следствие не совпадет с целевой формулой.
Таким образом, в процессе прямого вывода на каждом его шаге база знаний
пополняется выведенными истинными формулами.
В обратном выводе все делается наоборот. На первом шаге обратного вывода
подбирается правило вывода, следствием которого является целевая формула,
а условие может быть образовано из формул начальной базы знаний, с
использованием, если это необходимо, унификации. Унифицированные
формулы, входящие в условие, принимаются за новые целевые формулы
(обычно называемые подцелевыми формулами) и все повторяется сначала, но
уже для каждой их них. И так до тех пор, пока все унифицированные подцелевые
формулы не окажутся аксиомами, входящими в начальную базу знаний. При
выводе на основе использования обобщенного правила модус поненс,
унификации и хорновских формул используется только один тип правила,
поэтому нет необходимости осуществлять выбор подходящего правила вывода.
Это типизирует процедуры прямого и обратного вывода, превращая их в
итеративную процедуру выполнения однотипных шагов. Рассмотрим прямой и
обратный вывод на простых примерах из среды кубиков.
4.2.1. Постановка задачи в среде кубиков
Формулы, определяющие начальные знания агента. Имеем среду,
состоящую из стола и кубиков на нем. Каждый из кубиков может лежать
либо непосредственно на столе, либо на одном из других кубиков, образуя с
кубиками, лежащими под ним, столбик. Столбики могут быть любой высоты.
Пусть начальное состояние среды кубиков следующее: кубики С и лежат на
столе, кубик А лежит на кубике С, кубик D на кубике В (рис. 4. 1).
89
4. Вывод в логике предикатов
Рис. 4.1. Начальное и целевое состояния среды кубиков
Начальное состояние среды кубиков можно описать следующими атомами:
на (А, С), (4.130)
на (С, Стол), (4.131)
на (D, В), (4.132)
на (В, Стол), (4.133)
свободен (А), (4.134)
свободен (D).
(4.135)
Атомы на (А, С), на (С, Стол), на (D, В), на (В, Стол) описывают положение
кубиков относительно друг друга, а атомы свободен (А), свободен (D) указывают,
что на кубиках А и В ничего не лежит.
Формулы, определяющие условия выполнения действий. Действия, которые
можно совершать в среде кубиков — это перемещать один кубик, на котором
ничего не лежит, на стол или на другой кубик, если он свободен от кубиков
сверху. Для обозначения этих действий введем атомы переместить (х, у) и
переместить (х, Стол). Тогда для нашего примера достаточно двух формул,
определяющих условия выполнения действий:
на (х, у) л свободен (х) переместить (х, Стол), (4.136)
на (х, Стол) л свободен (х) л свободен (z) переместить (х, z)- (4.137)
Формулы, определяющие условия перехода состояний среды:
на (х, у) л свободен (х) л переместить (х, Стол) гэ на (х, Стол), (4.138)
90
4.2. Прямой и обратный вывод
на (х, у) л свободен (х) л переместить (х, Стол) о свободен (у),
на (х, у) л свободен (х) л свободен (г) л
л переместить (х, z) о на (х, z),
(4.139)
(4.140)
на (х, у) л свободен (х) л свободен (z) л переместить (х, С) о свободен (у). (4.141)
Целевая формула. В соответствии с рис. 4.2 целевой будет следующая формула:
на (А, В) л на (В, Стол) л на (С, Стол) л на (D, Стол).
(4.142)
4.2.2. Прямой вывод
Начнем с формулы (4.136), унифицируя которую получим формулы
следующие формулы:
на (А, С) л свободен (А) о переместить (А, Стол),
на (О, В) л свободен (Z)) о переместить (D, Стол).
(4.143)
(4.144)
На основании обобщенного правила модус поненс и формул (4.130), (4.134),
(4.132), (4.135), (4.143), (4.144) делаем заключение о возможности выполнения
действия по перемещению кубиков А и D на стол: истинны атомы переместить
(А, Стол), переместить (D, Стол). Эти атомы помещаются в исходную базу
знаний. Далее можно воспользоваться формулами (4.138), (4.139), унифицируя
которые получим формулы
на (А, С) л свободен (А) л переместить (А, Стол) о на (А, Стол), (4.145)
на (А, С) л свободен (А) л переместить (А, Стол) о свободен (С), (4.146)
на (D, В) л свободен (D) л переместить (D, Стол) о на (D, Стол), (4.147)
на (D, В) л свободен (D) л переместить (D, Стол) о свободен (В). (4.148)
В результате кубики А и D оказались на столе. Кубики С и В никуда не
перемещались и, согласно начальному состоянию, остались на столе. Используя
формулу (4.137), получим унифицированную формулу
на (А, Стол) л свободен (А) л свободен (В) о переместить (А, В). (4.149)
Наконец, воспользовавшись формулой (4.138), получим унифицированную
формулу
на (А, Стол) л свободен (Л) л свободен (В) л переместить (А, /?) о
2d на (А, В).
(4.150)
91
4. Вывод в логике предикатов
Рис. 4.2. Граф прямого вывода в среде кубиков
Таким образом, имеем истинные атомы на (Л, В), на (В, Стол), на
(С, Стол), на (D, Стол). Согласно правилу введения конъюнкции, делаем
заключение об истинности целевой формулы на (А, В) л на (В, Стол) л
л на (С, Стол) л на (D, Стол). На этом прямой вывод завершен. На рис. 4.2
показан граф вывода указанной целевой формулы. В процессе прямого вывода
база знаний разрастается, в нее заносятся вновь выводимые формулы. Некоторые
из них могут оказаться ненужными для вывода целевой формулы. Таких «лишних»
формул может быть достаточно много. Например, на рис. 4.2 ненужной
является формула свободен (С).
92
4.2. Прямой и обратный вывод
4.2.3. Обратный вывод
Обратный вывод начинается с целевой формулы на (А, В) л на (В, Стол) л
/\ на (С, Стол) л на (D, Стол). Для нашего примера его можно проследить по
тому же графу на рис. 4. 2. Только в отличие от прямого вывода, который
осуществлялся в направлении стрелок, обратный вывод осуществляется против
направления стрелок. Кроме того, ненужных формул не выводится, что делает
его в ряде случаев более эффективным, особенно, если для вывода целевых
формул достаточно незначительной части базы знаний.
В настоящей главе были рассмотрены только принципы прямого и обратного
вывода. Возможны и комбинации прямого и обратного вывода. Во всех случаях
исходной для вывода является некоторая начальная база знаний. Для того
чтобы иметь возможность решения реальных задач на основе использования
исчислений, необходимо иметь ответ на ряд очень важных вопросов.
Первая группа вопросов связана с понятием полноты исчисления. Если
все общезначимые формулы выводятся в данном исчислении и только они,
то его называют полным. В противном случае исчисление называют неполным.
Если в нашем распоряжении (распоряжении агента) имеется некоторое
исчисление, то как определить, является ли оно полным?
Если исчисление является полным, то какая стратегия вывода обеспечивает
вывод любой общезначимой формулы этого исчисления? Стратегию,
обеспечивающую вывод всех общезначимых формул данного исчисления и
только их, называют полной. Если полная стратегия вывода существует и
она нам известна, но данная формула не выводима из начальной базы знаний,
то можно ли это .узнать без вывода?
Другой класс вопросов, важных для практического использования исчислений,
связан с понятиями их противоречивости и непротиворечивости. Исчисление
называют непротиворечивым, если не существует формулы, выводимой в этом
исчислении вместе со своим отрицанием. В противном случае исчисление
называют противоречивым. Из практических соображений нас интересуют
непротиворечивые исчисления. Исчисление нам необходимо для того, чтобы
осуществлять вывод для достижения определенной цели. Если же для одного
и того же исчисления существует некий вывод, позволяющий достичь цели, и
в то же самое время для этого же исчисления существует вывод,
свидетельствующий о том, что цель не достижима (достижимо ее опровержение),
то такое исчисление скорее всего неадекватно отражает свойства среды, в которой
оно интерпретируется. Главный вопрос, связанный с непротиворечивостью
исчислений звучит так: если данное исчисление противоречиво вследствие
того, что в нем выводится некоторая формула и отрицание этой формулы,
то можно ли обнаружить этот факт без вывода этих двух формул?
Прежде, чем переходить к ответу на перечисленные выше вопросы, ответим
на более простой. Если формула выводима в каком-либо исчислении (не
обязательно полном), то выводима ли она при использовании той же системы
93
4. Вывод в логике предикатов
аксиом и единственного правила вывода — обобщенного правила модус поненс?
Вернемся к примеру со средой кубика.
Предположим, что в начальной базе знаний имеются аксиомы
свободен (В),
свободен (В) переместить (В, Стол),
переместить (В, Стол) на (В, Стол).
Пусть целевой формулой является формула на (В, Стол). С помощью
обобщенного правила модус поненс сначала можно вывести формулу
переместить (А, В), а затем формулу на (В, Стол).
Если в базе данных имеются аксиомы
-л свободен (В),
—, свободен (В) освободить и переместить (В, Стол),
освободить_и_переместить (В, Стол) на (В, Стол),
то формулу на (В, Стол), несмотря на то, что она выводима с использованием
обычного правила модус поненс, нельзя вывести с помощью обобщенного правила
модус поненс, поскольку формулу свободен (В) освободить и переместить
(В, Стол) невозможно преобразовать в хорновскую формулу. Таким образом,
существуют исчисления, для которых не все общезначимые формулы можно
вывести с помощью только обобщенного правила модус поненс. Перейдем к
ответу на остальные вопросы.
4.3. Полнота и непротиворечивость исчисления
На основе введенных определений полноты и непротиворечивости
логические исчисления можно поделить на следующие группы: полные и
непротиворечивые; неполные и непротиворечивые; противоречивые.
Наша задача — построение неклассических исчислений, относящихся к
первым двум группам. Заметим, что на практике полнота исчисления является
желательным, но редко удовлетворяемым фактором. Объясняется это многими
причинами, среди которых доминирующими являются следующие две.
Размерность задач для конкретных сред (число переменных, констант,
предикатов, функций), для которых имеет смысл использовать логические
исчисления, как правило, велика. Полное исчисление требует полной
аксиоматизации. Это приводит к большому росту числа необходимых аксиом
даже для сравнительно простых сред и необходимости обоснования
достаточности этих аксиом.
Число типов выводимых формул (целей) для реальной среды ограничено
конкретными потребностями. Вывод только этих формул следует
гарантировать, ограничиваясь тем множеством аксиом, которые это
позволяют сделать.
94
4.3. Полнота и непротиворечивость исчисления
Проблемой полноты и непротиворечивости исчислений занимались и
продолжают заниматься. Для некоторых исчислений вопрос о полноте имеет
положительный ответ, например для классического исчисления высказываний
и для классического исчисления предикатов первого порядка. Для
классического исчисления предикатов вопрос полноты был решен немецким
математиком Куртом Геделем в 1930-1931 годах. Он доказал теорему, которая
называется теоремой о полноте классического исчисления логики предикатов
первого порядка. Согласно этой теореме любая общезначимая формула
классического исчисления логики предикатов первого порядка выводима в
этом исчислении. Это означает, что для классического исчисления логики
предикатов первого порядка существует полная стратегия вывода.
Гедель доказал теорему о полноте классического исчисления предикатов
первого порядка, но не привел полной стратегии вывода, которую можно
достаточно эффективно использовать на практике. Это сделал в 1965 г.
Дж. Робинсон, опубликовав полную стратегию вывода для классического
исчисления высказываний на основе правила резолюции. Заметим, что
упомянутые положительные ответы о полноте относятся к классическому
исчислению предикатов первого порядка. Нас же в практическом плане
интересуют, прежде всего, неклассические исчисления. Вопрос об их полноте
и непротиворечивости обсудим далее. Однако еще раз заметим, что
неклассические исчисления, использующие классическое исчисление предикатов
первого порядка, могут, наряду с другими, включать его правила вывода, в
частности правило резолюции. Вследствие теоретической и практической
значимости этого правила стратегию вывода на его основе рассмотрим детально
в следующем параграфе.
Отметим еще один важный момент, связанный с теоремой о полноте
классического исчисления логики предикатов первого порядка и вопросом об
установлении факта невыводимое™ формулы из начальной базы знаний без
вывода. Теорема Геделя гласит, что любая общезначимая формула логики
предикатов первого порядка выводима в классическом исчислении логики
предикатов первого порядка. Но в каждом конкретном случае до тех пор пока
вывод не осуществлен, мы не знаем, выводима ли данная формула. А если она
не выводима и, следовательно, вывод никогда не будет найден, то как отличить
ситуацию, когда мы еще не достигли вывода, от ситуации, когда он никогда
не будет достигнут? К сожалению, ответ на этот вопрос не утешителен:
невозможно различить эти две ситуации и выводимость формулы может быть
установлена только тогда, когда она выведена. Если же она не выводится, то
придется осуществить все варианты вывода и только после этого, если она все-
таки не была выведена, сделать заключение о невыводимое™. Это же считается
справедливым и для неклассических исчислений.
Как следствие, неутешительным остается ответ и на вопрос распознавания
противоречивости исчисления: для того чтобы установить непротиворечивость
исчисления в общем случае, придется осуществить вывод всех теорем и только
при отсутствии среди них любых двух, одна из которых является отрицанием
другой, сделать заключение о непротиворечивости исчисления.
95
4. Вывод в логике предикатов
4.4. Вывод на основе правила резолюции
Правило резолюции (или резолюция) уже рассматривалось во второй главе.
Это правило гласит, что из истинности двух дизъюнкций, одна из которых
содержит дизъюнкт, а другая — его отрицание, следует (выводима) формула,
являющаяся дизъюнкцией исходных формул без упомянутого дизъюнкта и его
отрицания. Резолюция записывалась в следующем виде:
a v р, -i^vyhavy или эквивалентно а о Р, р о у а о у.
В логике предикатов первого порядка она выглядит так же. Формулы а,
Р, у в ней являются формулами этой логики. Введем по аналогии с
обобщенным правилом модус поненс обобщенное правило резолюции, или
обобщенную резолюцию:
а,01 (х,) v ... v а. j0*'-” (х,..,) v а m (xz) v а,.+1о(,+|) (x;+1) v ... v amam(xm),
P,E1 (У>) v ... v p. (y, J v рч(у.) v P;+1e0+1) (yy.+1) v ... v P„“(y„),
V (z, j) (a.i = Py , о: * ej, Унификация (a’1 (x;), PyEy (yy.)) = 8) h
Подстановка (8 (a,01 (x,) v ... v a. (x.,) v aH.|a(H'1)(xH.|) v ... v (xj v
V p^1 (y,) V ... V p.;1 > () v P7+1e(/+1) (yy.+1) V ... v pn“ (y„)).
Здесь aai(x), i' = 1, ..., n обозначает литерал, такой, что am (х) = a (x),
при сп = 1 и a. °' (x;) =-,a;(xz.) при сп = 0. Аналогичный смысл имеет символ
еу в литерале Ру Еу (уу ), j= 1, п. Подстановка (8(f)) означает формулу,
получающуюся из формулы f в результате подстановки 5 во все ее атомы.
Суть обобщенного правила модус поненс можно выразить следующим
образом. Если существует истинная формула
a,n' (х,) v ... v a ,a('-1) (х.) v aai (х) v a„ 1a(''+1, (x..) v ... v a om (x),
являющаяся дизъюнкцией литералов af(xf i= 1, ..., n, и истинная формула
P,El (yt) V ... v p./<'-') (yy j) v pyy (y.) v Py+1E°+1) (yy+1) V ... v Р„Е"(ул),
также являющаяся дизъюнкцией литералов Руеу (у), j = 1, ..., л, и в этих
формулах предикатные символы литералов а°‘ (х.) и РуЕ; (у) одинаковы
(a, = Р), сп * еу, и для атомов aai (х.) и РуЕ? (уф существует унификация 5,
делающая их одинаковыми (записывается как Унификация а. ((х.), Ру (уф) = 8),
то можно вывести истинную формулу, получающуюся в результате
подстановки 8 в дизъюнкцию исходных формул после удаления в них литералов
а.” (х) и РуЕу (у). Выведенную таким образом истинную формулу называют
резольвентой. Так же как и в случае резолюции для логики высказываний,
обобщенную резолюцию можно выразить с использованием импликации.
96
4.4. Вывод на основе правила резолюции
Обратим внимание, что исходные формулы в обобщенной резолюции и
резольвента являются дизъюнкцией литералов. Обычно такие формулы
называют клаузалъными формами, или клаузами. Таким образом,
использование резолюции для вывода требует клаузальной формы
представления знаний. Это, в свою очередь, означает, что база знаний,
вывод для которой осуществляется на основе обобщенной резолюции, должна
представлять собой совокупность клауз, понимаемых в целом как формула,
являющаяся конъюнкцией клауз. Формулы такого типа обычно называют
конъюнктивными нормальными формулами.
4.4.1. Прямой вывод на основе резолюции
Вернемся теперь к примеру с кубиками и повторим прямой вывод той же
целевой формулы, но уже используя обобщенную резолюцию. Заметим,
что формулы (4.130), (4.135) уже являются клаузами. Остальные формулы с
помощью простейших преобразований на основе закона a v р = а о р легко
преобразуются в клаузы. В результате вместо (4.136) — (4.141) получим
следующие формулы.
Формулы, определяющие условия выполнения действий*.
- л на (х, у) v свободен (х) v переместить (х, Стол), (4.151)
- > на (х, Стол) v свободен (х) v свободен (z) v
v переместить (х, г)- (4.152)
Формулы, определяющие условия переходов состояний среды:
на (х, у) v -1 свободен (х) v переместить (х, Стол) v на (х, Стол), (4.153)
- > на (х, у) v —। свободен (х) v -> переместить (х, Стол) v свободен (у), (4.154)
-л на (х, у) v -1 свободен (х) v -> свободен (z) v
v переместить (х, z.) v на (х, z), (4.155)
на (х, у) v -л свободен (х) v свободен (z.) v
v переместить (х, z.) v свободен (у). (4.156)
Целевая формула. Целевая формула в соответствии с рис. 4.1 является
конъюнкцией литералов и при прямом выводе, как и в случае использования
обобщенного правила модус поненс, будет выводиться для каждого литерала,
входящего в ее состав, раздельно
на (А, В) л на (В, Стол) л на (С, Стол) л на (D, Стол). (4.157)
4 — 1141
97
4. Вывод в логике предикатов
Вывод. Используя унифицированные клаузы (4.130), (4.151), которые
после унификации превращаются в клаузы (4.158), (4.159), получаем
резольвенту (4.160):
на (Д Q, (4.158)
на (А, С) v свободен (A) v переместить (А, Стол), (4.159)
свободен (A) v переместить (А, Стол). (4.160)
Используя клаузы (4.134), (4.160), получаем резольвенту
переместить (А, Стол). (4.161)
Используя эту резольвенту и унифицированную клаузу (4.154), которая после
унификации превратилась в клаузу (4.162), получаем резольвенту (4.163):
на (А, у) v свободен (A) v -> переместить (А, Стол) v
v свободен (у), (4.162)
на (А, у) v -1 свободен (A) v свободен Ст). (4.163)
Затем, используя клаузы (4.130), (4.134) и унифицированный резольвент
(4.163), получаем резольвенту
свободен (С). (4.164)
Аналогично можем получить следующие резольвенты:
на (А, Стол), (4.165)
переместить (D, Стол), (4.166)
свободен (В), (4.167)
на (D, Стол). (4.168)
Итак, кубики А и D могут быть перемещены на стол, в результате чего
кубики В и С окажутся свободными. После этого, используя клаузы (4.134),
(4.135), (4.165) и клаузу (4.152), которая после унификации превращается в
клаузу (4.169), получаем резольвенту (4.170)
на (А, Стол) v -> свободен (A) м -> свободен (В) v переместить (А, В), (4.169)
переместить (А, В). (4.170)
Наконец, воспользовавшись клаузами (4.134), (4.135), (4.165), (4.170) и
клаузой (4.155), которая после унификации превращается в клаузу (4.171),
получим резольвенту (4.172):
98
4.4. Вывод на основе правила резолюции
на (А, Стол) v -> свободен (A) v свободен (В) v
v переместить (А, В) v на (А, В), (4.171)
на (А, В). (4.172)
Таким образом, снова имеем истинные атомы на (А, В), на (В, Стол),
на (С, Стол), на (D, Стол). Согласно правилу введения конъюнкции, вновь
делаем заключение об истинности целевой формулы на (А, В) л на
(В, Стол) л на (С, Стол) л на (D, Стол). На этом прямой вывод с
использованием обобщенного правила резолюции завершен.
Достоинством использования обобщенного правила резолюции для прямого
вывода является способность выводить большее количество формул по
сравнению с выводом на основе обобщенного правила модус поненс. В
процессе вывода база знаний по-прежнему разрастается за счет занесения в
нее вновь выводимых формул. Некоторые из этих формул могут оказаться
ненужными для вывода целевой формулы.
Как уже говорилось, Робинсон предложил использовать обобщенную
резолюцию для создания стратегии вывода, в основе которой лежит
опровержение доведение до противоречия. Идея этой стратегии вывода
состоит в следующем. Предположим необходимо вывести истинность целевой
формулы а. Делается опровержение этой формулы, т.е. предполагается
истинным ее отрицание -,а. Эта формула, являющаяся отрицанием целевой,
заносится в базу знаний. После этого, если, начиная обратный вывод с
формулы -л а, удастся установить противоречие, т.е. вывести пару литералов
Р и -> р, то считается, что сделанное предположение об истинности отрицания
целевой формулы ошибочно (опровергнуто) и делается заключение об
истинности целевой формулы а. Если в результате рассмотрения всех
возможных путей вывода такого противоречия установить не удастся, то
считается, что целевая формула является ложной.
Рассмотрим стратегию обратного вывода на основе опровержения для
примера с кубиками.
4.4.2. Обратный вывод на основе опровержения и обобщенной резолюции
Как уже отмечалось, вывод истинности целевой формулы может
осуществляться по очереди литерал за литералом. Поэтому рассмотрим его
только для одного литерала на (А, В) целевой формулы (4.157). Опровержением
литерала на (А, В) является литерал -> на (А, В). Обратный вывод начинается
именно с этого литерала. Для того чтобы можно было детально проследить
процесс вывода, будем записывать на каждом шаге вывода с помощью
обобщенной резолюции три формулы — две исходные и резольвенту, нумеруя
по ходу вывода получаемые резольвенты, а также указывая для каждого шага
используемые подстановки и подчеркивая те литералы, которые в резольвенту
не попадают:
99
4*
4. Вывод в логике предикатов
- п на (А, В): (4.173)
на (А, Стол) v -> свободен (A) v свободен (В) v
v переместить (А, В) v на (А, В); (4.174)
на (А, Стол) v свободен (/4) v -> свободен (В) v
v переместить (А, В); (4.175)
на (А, Стол) v свободен (A) v -> свободен (В) v
v переместить (А, В); (4.176)
на (А, Стол) v -> свободен (A) v свободен (В) у
v переместить (А, В)-, (4.177)
- > на (А, Стол) v свободен (A) v свободен (5); (4.178)
- > на (А, Стол) v свободен (/1) v -> свободен (5); (4.179)
свободен (/1): (4.180)
на (А, Стол) v свободен (В}: (4.181)
на (А, Стол) v свободен (5); (4.182)
- > на (А, у) v свободен (A) v переместить (А, Стол) v
у на (А, Стол): (4.183)
- > на (А, у) у -1 свободен (/1) v -> переместить (А, Стол) v
' Свободен (В); (4.184)
на (А, у) у свободен (А) у переместить (А, Стол) у
у свободен (В): (4.185)
100
4.4. Вывод на основе правила резолюции
свободен (А); (4.186)
на (А, у) v переместить (А, Стол) v свободен (В)\ (4.187)
-> на (D, В) v свободен (£>) v переместить (D, Стол) v
v свободен (В)', (4.188)
на (D, В) v свободен (D) v переместить (D, Стол)', (4.189)
-> на (D, В) v -> свободен (D) v свободен (В)', (4.190)
на (D, В)л- свободен (D) у свободен (В): (4.191)
свободен (Р)\ (4.192)
на (D, В) v свободен (В)', (4.193)
на (D, В) v свободен (/?); (4.194)
на (D, В); (4.195)
свободен (В)', (4.196)
свободен (В)', (4.197)
-> свободен (В); (4.198)
Nil. (4.199)
101
4. Вывод в логике предикатов
4.4.3. Преобразование произвольной формулы логики предикатов первого
порядка в клаузальную форму
Применение обобщенного правила резолюции требует представления
формул в клаузальной форме. В этом разделе покажем, с помощью каких
эквивалентных преобразований любая произвольная формула логики
предикатов первого порядка может быть преобразована в клаузальную форму.
Процедуру преобразования представим в виде отдельных шагов.
Исключение импликаций. Из логики высказываний известно, что a z> р =
= -> a v р. Поэтому на первом шаге с помощью этой формулы исключаем все
импликации.
Перемещения знака отрицания (->) непосредственно к атомам. В клаузах
отрицание допустимо только перед атомами. Поэтому используя
перечисленные ниже законы Де Моргана, эквивалентности кванторов и
двойного отрицания, перемещаем знак отрицания непосредственно к атомам:
-> (a v Ь) = а л р,
(а л Ь) = -> а v -> р,
-> V .х а (х) = 3 х а (х),
3 х а (х) = V х а (х),
-> а = а.
Переименование переменных. Во всех формулах, в которых встречаются
кванторы, использующие одни и те же связанные переменные, как,
например, в формуле V х а(х) v 3 х р(х), переименовываем связанные
переменные таким образом, чтобы они были индивидуальными для каждого
квантора. Например, для нашего примера это может быть использование
переменной у вместо переменной х для квантора существования. В результате
получится формула V х а(х) v 3 у р(у).
Перемещение кванторов влево. После предыдущего шага, в результате
которого каждый квантор использует свои связанные переменные,
обозначения которых не совпадают с переменными других кванторов, все
кванторы перемещаем влево. Так, например, простая формула a v V х р (х)
после перемещения квантора влево примет вид V х -> a v р (х).
Сколемизация. Сколемизацией называется специфический прием удаления
кванторов существования. В простейшем случае — это замена формулы 3 у
Р(у) на формулу Р(Д), где А является константой, ранее не встречавшейся.
В общем случае, когда переменная, связываемая квантором существования,
встречается в каком-либо литерале вместе с переменными, связанными
102
Вопросы и упражнения
квантором общности, приходится, чтобы избавиться от квантора общности,
вводить специальную функцию, зависящую от переменных, связанных
квантором общности, вместо переменной, связанной квантором
существования.
Так, если имеем формулу
- V X а(х) => 3 у (р (у) v у (X, у)),
то здесь литерал р (у) может означать, например, наличие некоторого
свойства, именуемого предикатным символом р, у объекта, именуемого
переменной у, а атом у (х, у) задает отношение между объектами х, у. Объект,
обозначенный переменной у, определяется в этом случае значением
переменной х и может быть заменен на ранее не встречавшуюся функцию
F(x), называемую обычно функцией Сколема. После такой замены квантор
существования может быть удален, а формула приобретает вид
V х а(х) z> р (F(x)) v у(х, F(x)).
Распределение конъюнкций относительно дизъюнкций. Это распределение
осуществляется на основе использования дистрибутивного закона
(а л р) v у = (а v у) л (Р v у).
Перемещение скобок к концу и началу. На этом шаге формулы со скобками
типа (a v р) v у или (а л р) л у приводятся соответственно к виду (а v р v у)
или (а л р л у). После этого шага исходная формула преобразуется в
нормальную конъюнктивную форму, являющуюся конъюнкцией дизъюнкций
литералов. Каждая дизъюнкция литералов является клаузой.
Вопросы и упражнения
1. Для каждой из следующих пар атомов приведите наиболее общую подстановку:
а) а(С, D, G), а(х, D,
ff) Р(у, F(A, 5)), Р(у, F(x, z));
в) x(F(x), у), х(Г(х), О;
г) 8(F(x), х, х), 8(F(y), у, у);
д) e(F(G(x, у), e(F(G(x, В), Н(у)\
2. Запишите аксиомы логики предикатов первого порядка, достаточные на ваш
взгляд для вывода с помощью обобщенного правила модус поненс следующих теорем:
а) собаки, кошки и козы являются животными;
б) котенок является потомком кота и кошки;
в) Васька является котом и отцом котенка;
г) каждая кошка имеет родителей.
3. Каким образом резолюция может быть использована для доказательства того,
что формула является
а) общезначимой?
б) выполнимой?
103
4. Вывод в логике предикатов
4. Известны истинные утверждения “Воробей имеет крылья”, “Воробей несет
яйца” и “Если животное имеет крылья и несет яйца, то это птица”. Требуется доказать
утверждение “Воробей является птицей”. Для этого выполните следующее:
а) переведите эти утверждения на язык логики предикатов первого порядка,
выделив все необходимые группы формул, включая целевую;
б) сделайте опровержение целевой формулы;
в) переведите все формулы в клаузальную форму;
г) используя резолюцию, докажите (выведите) истинность целевой формулы.
5. В среде кубиков начальное состояние показано на рис. 4. 1. Целевое состояние
должно быть таким, чтобы кубики в обоих столбиках поменялись местами. Для этого
выполните следующее:
а) переведите все необходимые для вывода формулы в язык предикатов первого
порядка;
б) используя модус поненс, выведите целевую формулу, используя прямой вывод;
в) используя резолюцию, выведите целевую формулу, используя прямой вывод;
г) используя резолюцию и опровержение, докажите истинность целевой формулы,
используя обратный вывод;
д) сравните число шагов, требуемое для каждого типа вывода.
6. Распишите подробно вывод формулы (4.100) в примере со средой чудовища.
5. СРЕДЫ И ЯЗЫКИ
В этой главе обсуждается роль языка как эквивалента среды. Рассмотрено,
как представление знаний на языке логики предикатов можно использовать для
вывода в пространстве состояний и как можно уменьшить число предложений
в этом представлении в результате разбиения множества состояний на классы
эквивалентности. Введен ряд понятий из теории автоматов, используемых в
настоящей главе для поиска классов эквивалентных состояний. Приведены
сведения из теории формальных грамматик, необходимые для определения и
использования языка.
Во второй главе введено понятие формального языка логики
высказываний, который используется для представления знаний о среде.
С помощью этого языка осуществлялось решение задач нахождения
последовательностей действий, ведущих в целевые состояния. Таким
образом, агент, решающий ту или иную задачу, фактически чаще всего
имеет дело не с самой средой, а с некоторым ее представлением или
описанием на каком-либо языке. Поэтому он должен знать, как этот язык
устроен, для того, чтобы понимать описание, составленное на нем. В
настоящей главе рассмотрены вопросы описания языков с помощью
формальных грамматик и использование такого описания агентом.
Стратегия поиска целевых состояний и ведущих в них последовательностей
действий примера со средой кота состояла в рассмотрении всех возможных
состояний и переходов из каждого состояния при выполнении каждого
действия. Для решения задачи поиска золота в примере для среды чудовища
применялась похожая стратегия, но с использованием не состояний, а
интервалов. Отмечалось, что стратегии подобного типа весьма неэкономны
по числу шагов, используемых для поиска цели.
Описанию различных стратегий поиска будет посвящена следующая глава.
Сложность поиска зависит как от объема описания знаний о среде на том
или ином языке, так и от стратегии поиска. Если описание избыточно, то
105
5. Среды и языки
часть времени поиска может расходоваться впустую на анализ избыточной
информации. В настоящей главе показано так же, как может быть сокращен
объем описания на языке в задачах поиска целевых состояний.
5.1. Автомат и среда
Конечным инициальным детерминированным автоматом называют объект,
определяемый следующими шестью понятиями.
Входной алфавит А = {at, а2, ..., ат}.
Внутренний алфавит (множество состояний автомата)
В = {Ьг ь2, ьп}.
Выходной алфавит С = {сг с2, ..., сф
Функция переходов f\ А х В -+ С, записываемая так же, как
f(a, b) = by где а е A, bt, bj е В.
Функция выходов ср: В С, записываемая так же, как
(р(Ь) = с, где £ е В, с\ е С.
Начальное состояние Ьо е В. Обычно будем полагать, что Ьо= Ь/
В дальнейшем для простоты вместо длинного словосочетания
«инициальный детерминированный конечный автомат» будем говорить просто
«автомат». Автомат можно рассматривать как эквивалент некоторой
абстрактной среды, имеющей множество состояний В и начальное состояние
Ьо е В. Когда среда находится в каком-либо состоянии Л , агентом может
быть совершено действие а. В результате среда перейдет в состояние Ь,
определяемое функцией переходов f(a, b) = />. В каждом состоянии Ь. может
быть определена функция выходов, называемая также иногда оценочной
функцией ср(й) — с:. Если автомат находится в состоянии ф, то считается,
что еще никакая входная последовательность на него не была подана. Для
удобства будем полагать, тем не менее, что на него была подана пустая
последовательность е.
Таким образом, автомат перерабатывает последовательности еа:]а/2... а,.в
последовательности b<}bAbi2 ... b:l, соспс.2 ... си, где аА, а.2 ,..., е А, Ьо, Ь.{,
b2,..., bit е В, са, cit, ci2 с^еС. Если на автомат была подана
последовательность е, то он перейдет в состояние Ьо. Если на него была
подана последовательность еа.}, то он перейдет в состояние bf и т. д. Если
на него была подана последовательность ea{ai2... а^, то он перейдет в состояние
Ь/Г Говорят при этом, что последовательность еа:]а.2... а:/ ведет в состояние
/>(/из начального состояния bg. Произвольную последовательность во входном
106
5.2. Язык и автомат
алфавите обозначим а*. Если она ведет в некоторое состояние й из некоторого
состояния />., то этот факт записывается так: f*(a*, b.) = b.
Последовательности действий подразделяют на допустимые и запрещенные.
Допустимыми называют последовательности, которые могут быть поданы на
автомат, а запрещенными — последовательности, которые на автомат никогда
не подаются. Условно считается, что все запрещенные последовательности ведут
в одно и то же фиктивное состояние Л t В и <р(Л) = 1. Функцию выходов
можно определить не на всех состояниях. Если она не определена, то будем
считать, что ее значение равно X. Если при этом f*(a*, b0) = b и функция
выхода <р(й) = с или ф(/>) = X , то этот факт запишем <р *(а *) = с или <р *(а *) = X
соответственно.
5.2. Язык и автомат
Множество (алфавит) А назовем множеством допустимых действий а;
а*= а1а2... а — произвольная, конечная или бесконечная последовательность
допустимых действий (входная последовательность) в алфавите А, А* —
множество всех последовательностей а*, е — пустое действие, еа* — а*,
<р*— функция на множестве А*” = А* и е, которая ставит в соответствие
последовательностям а*е А*" элементы множества С"=СоХ, где X — символ
неопределенного значения, т.е. <р*(а*) е С" или <р*: Л*"-> Л*" х С" = S*.
Обозначим Р с А*" множество допустимых последовательностей действий
агента, включая последовательность из одного пустого действия е. S —
множество последовательностей а*<р*(<з*) таких, что а* е Р, f*(a*') е В\
<р*(а*) е С". Очевидно, что 5 с S*.
Иначе говоря, множество последовательностей Р таково, что оно состоит
только из допустимых последовательностей действий и каждая такая
последовательность ведет в какое-либо состояние среды. Множество У получается
из множества Р приписыванием к концу каждой последовательности а* е Р
элемента множества С" (выходного символа), и наоборот, множество Р
получается из множества 5 удалением у каждой последовательности этого
множества последнего символа. Получаемое таким образом множество Рпо
множеству Sобозначается P(S).
Языком называют множество последовательностей символов в каком-либо
алфавите. Множества A*, A*", S*, S, Р являются множествами последо-
вательностей символов и, следовательно, каждое из них можно считать языком.
Говорят, что язык (множество последовательностей действий) 5 с 5*
реализуется инициальным автоматом, если любая последовательность
действий а* е P(S), такая, что <з*<р*(а*) е S ведет из начального состояния
Ьп в какое-либо состояние й этого автомата и <р*(а*) = <р(/>.). О входной
последовательности а* ведущей в состояние b при этом также говорят,
что она реализуется в данном автомате. Классический вопрос, давно решенный
в теории автоматов, — какие языки можно реализовать в автоматах? (Напомним,
что речь пока идет об инициальных детерминированных конечных автоматах.)
107
5. Среды и языки
Ответ на этот вопрос состоит в следующем. Если множество S с S*
удовлетворяет условиям полноты, непротиворечивости и регулярности, то
можно построить автомат, реализующий множество 5 (язык 5).
Сформулируем условия полноты, непротиворечивости и регулярности для
множества 5.
Условия полноты. Для всякой.порлелрвательности а*е S' всякое ее начало
также принадлежит 5.
Условия непротиворечивости. Не существует ни одной пары
последовательностей ах *а1к *, а2 *а2к *е 5, таких, что ах * = а2 * и ср *(ах *) ср’(о2 *).
Условия регулярности. Любая последовательность а*е S может быть получена
из пустой последовательности е только в результате последовательного
приписывания справа (конкатенации) конечных или бесконечных циклических
последовательностей в алфавите А.
5.2.1. Сокращение числа состояний
Итак полагаем, что исходным для построения автомата является язык
Sc S* = А*"х С". Нашей задачей является построение автомата, реализующего
этот язык. Введем на множестве А*" = А* о е отношение R, определяемое
следующим образом.
Отношение R. a, *Ra2*, если а, *,а2* е А*" и 'ср*(о, *«*) = ф*(а2*«*) для всех
а*, таких, что ах*а*, а2*а* е А*".
Нетрудно показать, что отношение R является отношением
эквивалентности и разбивает множество А*" на классы эквивалентности Qx,
Q2> > Qk+^ где Q\ — класс эквивалентности отношения R, которому
принадлежит пустая последовательность е. То, что R является отношением
эквивалентности, объясняется прежде всего полной определенностью
функции ср* за счет введения значения А. этой функции на запрещенных
последовательностях множества А*".
Множество классов эквивалентности можно использовать для построения
автомата, реализующего множество 5*, на основании следующих свойств
классов эквивалентности Qx, Q2, QkJrX, являющихся следствием условий
полноты, непротиворечивости и регулярности множества последова-
тельностей действий А*".
Свойство однозначной продолжаемости. Для всякого действия а * и всякого
класса эквивалентности 1 < г < А; Н- 1, существует единственный класс
Q I < t < k + 1, такой, что и Qa с Qt, где Qa — множество всех входных
последовательностей а *а таких , что последовательность а * е Qr.
Свойство связности. Для любого класса Qt, 1 < ? < £ + 1, существует хотя
бы одна последовательность действий а* = ata2... а1}, такая, что
Qxax с Q2, Q2a2 с Q2, ..., Qt la/l c Qt.
108
5.2. Язык и автомат
Свойство недоопределенности. Если множество допустимых последовательностей
Рне совпадает с множеством входных последовательностей А*", т.е. Ра А*", то
существует единственный класс эквивалентности Q., 1 < i < k + 1 , все
последовательности которого не принадлежат множеству Р, т.е. Q cz Р. Для
определенности будем считать, что этот единственный класс последовательностей
есть Qk+X. Из этого свойства также следует, что пересечение класса Qk+] с
множеством Р пусто (Qk+X n Р = 0), а все остальные классы Qr , I < г < к,
включаются в множество P(Qra Р). Построение автомата (обозначим его М *),
реализующего язык S*, может быть осуществлено следующим образом. Классы
эквивалентности Qx, Q2, ..., Qk, Qk+X отношения R объявляются соответственно
состояниями b'x, b'v ..., b'к, b'k+x автомата Л/ * Если Q a с Q то состояние b't
переходит в состояние Ь’., т.е. если Q.a с Q, то f(a, b') = Ь', где f — функция
переходов. Функция переходов однозначна вследствие свойства однозначной
продолжаемости. Функцией выходов автомата М* является функция <$(Ь') =
где а* е Q. Функция выходов автомата М* однозначна вследствие условия
непротиворечивости. Начальным состоянием автомата М* является состояние
Ь'х, соответствующее классу эквивалентности Qx, содержащему пустую
последовательность е. Вследствие свойства связности автомат Л/* будет связным.
Таким образом, автомат М* имеет к +1 состояние, каждое их которых
соответствует одному из классов эквивалентности. Поскольку состояние Ь' к+х
соответствует классу Qk+X, то это означает, что для любой последовательности
а* е Qk+X имеет место (р(а*) = к и этот класс единственный. Автомат Л/
реализующий язык S, отличается от автомата М* отсутствием в нем состояния
Ь'к+Х и соответственно переходов в него. Множество состояний автомата М
обозначим В, а автомата М * — В'.
ф
5.2.2. Пример сокращения числа состояний
Пусть задано следующее множество 5 простым перечислением
последовательностей а*<р*(а*). А= {а,, а2, а3}, <р*(а*) е С = {с,, с2, с3}:
5 = {есх, ахсх, ахахсх, аха2с2, аха2сх, а2с2, a2axc2, a2a2c2, a2a3cx, a2axaxc2,
a2axa2cx, aycx}.
Тогда, согласно определению,
P(S) = {е, ах, ахах, аха2, аха2, а2, а2ах, а2а2, a2av а2ахах, а2аха2, а2}.
Множество 5 содержит все начала своих последовательностей. В множество
входят последовательности, которые могут быть получены продолжением
последовательностей множества 5 с соблюдением свойства регулярности. Если
последовательность а* е S*\S, т.е. a* t 5, то <р*(а*) — к. Очевидно, что
множество P(S*), где 5* = 5 и 5*\5, содержит все собственные начала своих
последовательностей, т.е. удовлетворяет условиям полноты. Оно удовлетворяет
также условиям непротиворечивости и регулярности.
109
5. Среды и языки
Начнем построение классов эквивалентности с проверки отношения R для
двух первых последовательностей е, множества Р, проверяя последовательно
на равенство значения функции <р* сначала для продолжения длины 0 этих
последовательностей, затем длины 2, 3 и т.д., пока либо не получим неравенство
этих значений, либо пока не станет очевидным, что на всех последующих
продолжениях функции одинаковы. В первом случае последовательности
помещаются в разные классы, а во втором в один и тот же. Если при проверке
функций <р*(а*) и ф*(а*2) окажется, что ф*(а*) = с , а ф*(д*) = X, то будем
считать, что ср*(о*).
Проверка на продолжениях длины 0:
<р*(ф = ф*(о,) = с,.
Проверка на продолжениях длины 1:
<P*(^) = ф*(о1о|) = ср ф*(еа2) = ф*(а]а2) = с2, ф*(еа3) = ц>*(а^3) = с,.
Проверка на продолжениях длины 2:
Ф*(еа|а|) = ф*(о|а,«|) = ср = ф*(о1о,о2) = с2, ф*(ео,а3) = ф*(а|а1а3) = с,,
= ф*(а1а2о1) = с2, ф*(«?а2а2) = = с2, ф*(«?а2а3) = ф*(а,а2а3) = с,,
Ф*(еа3а,) = ф*(а,а3а,) = X, ф*(еа3а2) = ф*(а|а3а2) = X, ф*(еа3а3) = ф*(а]а3а3) = X.
Проверка на продолжениях длины 3:
Ф*(£>а|а,а1) = ф*(а(а1а,а|) = X, ^(ea^aj = ф*(а|а1а,а2) = X,
Ф*^,^) = ф*(о,о|о|о3) = X,
Ф*^,^) = ф*(а|а|а2а|) = X, ф^еа,^) = Ф*(а]а1а2а2) = X,
Ф*(^а,а2а3) = ф*(а)а|а2а3) = X,
Ф*(еа1а3а1) = ф*(а|с!1а3а|) = X, ^*(ea^a2) = ф*(а|а|а3а2) = X,
Ф*(га,а3а3) = ф*(а|а|а3а3) = X,
Ф^е-а^а.) = ф^а^од) = с2, ф*(еа2а,а2) = ф*(а|а2а|а2) = ср
Ф*(^2о1о3) = ф*(а(а2а,а3) = X,
^(еа2а2а}) = ф*(а,а2а2а,) = X, ф*(еа2а2а2) = ф^а^а^) = X,
Ф*(^а2а2а3) = ф*(а(а2а2а3) = X,
НО
5.2. Язык и автоматы
ц>*(еа2а3а}) = ф*(а|а2а3а1) = А., ф*(еа2а3а2) = ф*(а1а2а3а2) = А.,
Ф*(еа2а3а3) = ф*(а1а2а3а3) = А.,
Ф*(еа3а|а1) = ф*(а|а3а1а1) = А., ф^е^о^) = ф*(а1а3а1а2) = А.,
Ф*(еа3а1а3) = ф*(а|а3а1а3) = А,
Ф*(еа3а2а1) = ф*(а1а3а2а1) = А,
Ф*(еа3а2а2) = ф*(а1а3а2а2) = А, ф*(еа3а2а3) = ф*(а1а3а2а3) = А,
Ф*(еа3а3а1) = ф*(а|а3а3а|) = А, ф*(еа3а3а2) = ф^о^о^) = А,
Ф*(еа3а3а3) = tf>*(axa3a3a3) = А.
Проверку для последовательностей е, а1 можно не продолжать, поскольку
по условиям задачи множество Р содержит только последовательности длиной
не более трех, а следовательно, на всех еще не просмотренных их
продолжениях а*, длина которых будет уже более трех, функция ф*(а*) = А.
Значит, последовательности е, at находятся в отношении Л и их можно
поместить в один класс Qt и продолжить подобным образом проверку для
одной из последовательностей, помещенных в класс Qv и какой-либо
последовательности из множества Р, еще не помещенной в этот класс. После
того как все последовательности, для которых это можно сделать, будут
помещены в класс Q., перейдем к получению класса Q2 из числа оставшихся
непомещенными в класс Ql последовательностей, используя аналогичную
процедуру проверки отношения R. И так до тех пор, пока все
последовательности не будут распределены по классам. В результате для
нашего примера получим следующие классы эквивалентности:
Q\ ^2^3* ^3}’
03 = Ца2}.
Сопоставим классы эквивалентности Q,, Qv Q3 соответственно состояниям
b', b’v b' автомата M. Поскольку последовательности ах, ахах множества
Qtat принадлежат классу Qx, то f(av b[) = Ь[, т.е. автомат М, находящийся
в состоянии Ь\, при совершении действия а, остается в том же состоянии.
Остальные последовательности множества Qxax принадлежат классу, который
нас в данном случае не интересует (классу Qk+X при к = 3 для данного примера).
Далее, поскольку входные последовательности а2, аха2 множества Qxa2
принадлежат классу 02, то f(a2, Z>') = b2 и т.д. В результате получим автомат
М, граф переходов которого показан на рис. 5. 1. Начальным состоянием
111
5. Среды и языки
этого автомата является состояние Ь\.
Значение функции выхода указано рядом с
соответствующим состоянием.
Таким образом, для построения автомата
Л/ на рис. 5. 1 использовался следующий
алгоритм.
Алгоритм разбиения последовательностей
на классы эквивалентности:
а) принять i = 0. Задать множество /’=/’(5);
б) объявить множество Q. = 0;
в) если существует хотя бы одна
последовательность а* е Р такая, что Q.Ra* Рис. 5.1. Граф переходов
(Q'Ra* означает , что для каждой последо- автомата Л/,
вательности а* е Qt имеет место at*Ra* ,
причем если £? = 0, то всегда имеет место QRa*). то перейти к следующему
пункту. В противном случае перейти к пункту д);
г) считать Q. равным Qu а* , а Р равным Р\а * и перейти к выполнению
пункта в) с новыми Q. и Р,
д) если Р = 0, то перейти к пункту е). В противном случае принять i
равным (+1 и перейти к пункту б) с новым г,
е) отождествить полученные классы эквивалентности Qt, ...,Qk с
внутренними состояниями b\, b'v ..., Ь'к автомата М. Для каждого действия
а е А и каждого класса эквивалентности Q такого , что Qa с Q построить
на графе переходов автомата дугу (/>', />’). Дополнить полученный граф
переходов отметкой каждой вершины Ь'. значением функции ф(£'). Перейти
к следующему пункту,
ж) конец.
5.3. Описание автомата на языке логики предикатов
Рассмотренное в примере множество последовательностей действий 5
можно представить в виде дерева, показанного на рис. 5.2. Подобное дерево
мы уже строили при рассмотрении среды кота (см. рис. 2.1). Однако делали
мы это во второй главе, будучи еще незнакомыми с логикой предикатов.
Теперь мы можем воспользоваться ее возможностями для постановки задачи
нахождения последовательностей действий, ведущих в целевые состояния.
Напомним, что в главе 2 постановкой задачи называется задание всех
состояний и действий, которые могут использоваться для решения задачи,
начального состояния и целевых состояний, а также всех допустимых
переходов между состояниями при выполнении соответствующих действий.
Введем следующие атомы.
112
5.3. Описание автомата на языке логики предикатов
Рис. 5.2. Дерево последовательностей действий
Атомы действий для дерева:
действие (а,), действие (а2), действие (о,).
Эти атомы истинны, если совершается соответствующее действие,
находящееся в скобках.
Атомы состояний для дерева:
состояние (Ьх), состояние (Ь7), состояние (Ь2), состояние (ЙД,
состояние (Ь3), состояние (Z>9), состояние (Z>4), состояние (Ь]0),
состояние (tc), состояние (Ьи), состояние (Ь6), состояние (Ьх2).
Эти атомы истинны, если среда находится в соответствующем состоянии.
Формулы переходов между состояниями для дерева. Дерево на рис. 5.2
содержит И переходов между состояниями, каждый из которых происходит
при осуществлении соответствующего действия. Переходы описываются
импликациями:
состояние (Ь) л действие (е) о состояние (/>,),
состояние л действие (ах) о состояние (Ь2),
состояние (Ьх) л действие (а2) о состояние (Ь3),
состояние (/>,) л действие (а3) о состояние (Z>4),
состояние (Ь2) л действие (ах) состояние (Д),
ИЗ
5. Среды и языки
состояние (Z>2) л действие (а.) о состояние (Ь6),
состояние (Ь2) л действие (а3) о состояние (Z>7),
состояние (Ф) л действие (а,) о состояние (Z>g),
состояние (/>,) л действие (а2) о состояние (Ь9),
состояние (Z>3) л действие (а3) о состояние (Z>10),
состояние (Z>g) л действие (а,) о состояние (/>,,),
состояние (Z>9) л действие (а2) о состояние (й|2).
Легко заметить, что подобное описание можно осуществлять как по дереву,
так и по графу переходов автомата, реализующих множество S. Если
воспользоваться графом на рис. 5.1, то получим следующее множество формул.
Атомы действий для графа. Эти атомы, естественно, те же самые, что и
для дерева на рис. 5.2:
действие (а,), действие (а2), действие (а3).
Атомы состояний для графа. Граф переходов на рис. 5.1 содержит
существенно меньше вершин (состояний), чем дерево на рис. 5.2. Поэтому
и количество атомов для состояний меньше:
состояние (Ь'), состояние (Ь'), состояние (Ь').
Формулы переходов для графа. Переходов в графе также меньше, чем в
дереве. Поэтому и соответствующих импликаций также меньше:
состояние (/>') л действие (е) о состояние (/>'),
состояние (/>') л действие (а,) о состояние (Ь\),
состояние (/>') л действие (а3) о состояние (Ь\),
состояние (/>)) л действие(а2) состояние(Ь2),
состояние (/>') л действие (а,) о состояние (Ь'),
состояние (Ь') л действие (а3) о состояние (/>'),
состояние (6') л действие (а,) zd состояние (£'),
состояние (/>/) л действие (а2) zz> состояние (/>').
114
5.3 Описание автомата на языке логики предикатов
Атомы действий, состояний и формулы переходов являются основой для
постановки задачи. Легко подсчитать, что постановка задачи поиска целевого
состояния, если ее осуществлять по дереву на рис. 5.2, будет содержать 3
атома для действий, 12 атомов для состояний и 12 формул для переходов, в
то время как постановка задачи по графу на рис. 5.1 будет содержать 3 атома
для действий, 3 атома для состояний и 8 формул для переходов. Если
ограничиться только этими формулами, то в первом случае имеем суммарное
число формул, равное 27, во втором случае — 14, т.е. во втором случае
число формул уменьшилось почти вдвое. Это, конечно, не означает, что
сложность (трудоемкость) поиска при постановке задачи поиска с меньшим
количеством фактов будет всегда ниже, но, по крайней мере, объем памяти,
требуемый для запоминания формул, может быть значительно меньше.
Конечно, предварительное преобразование исходного описания постановки
задачи в другое, требующее меньшее количество формул, также требует
ресурсов (времени, памяти). Но если это преобразование осуществляется
один раз, а после этого решение задачи осуществляется многократно для
поиска различных целей, то затраты на преобразование могут оказаться
оправданными.
Возникает, конечно, вопрос, можно ли использовать для поиска цели
по графу ту же стратегию, что и по дереву. Легко заметить, что при поиске
по дереву не использовалось никаких соображений, которые учитывали бы
свойства дерева. На каждом шаге поиска состояние, в которое был
осуществлен переход после очередного действия, проверялось, не является
ли оно целевым. Если оно таковым оказывалось, то задача поиска (если
целевое состояние единственное) считалась завершенной. Таким образом,
рассмотренная в главе 2 стратегия поиска в пространстве состояний никак
не зависит от того, имеете ли вы граф или дерево.
Алгоритм разбиения последовательностей на классы эквивалентности требует
трудоемкой и утомительной процедуры проверки отношения R на множестве
последовательностей S. В постановке задачи, однако, вместо множества
последовательностей действий S имеем множество состояний и переходов.
Каждой последовательности действий а* ведущей из начального состояния,
соответствует на дереве последовательность переходов, ведущих из начального
состояния дерева в одно из промежуточных или целевых состояний. Каждая
последовательность ведет только в одно состояние, т.е. каждое состояние
взаимно однозначно соответствует последовательности переходов, ведущей в
него. Это означает, что если последовательность действий а*ведет из начального
состояния в состояние Ь, то можно считать, что <р*(а*) = q>(Z>). Исходя из
этого, вместо классов эквивалентности последовательностей действий можно
получать классы эквивалентности состояний на основе трансформации
отношения R в отношение, которое обозначим Rb, определяемое следующим
образом: bxRbbv если bv b2e В и q>(Z>") = cp(Z>"2) для всех а}*а*, а2*а* е А*"
таких, что а} * ведет в bt, а2 * ведет в Ь2, а* ведет из состояния Ь} в состояние
Z>", а из'состояния Ь2 в состояние Ь".
115
5. Среды и языки
5.4. Построение автомата методом детерминизации
Из определения отношения R непосредственно следует, что две
последовательности а{ *, а2 * множества Р тогда и только тогда находятся в
отношении R , когда ф*(а{ *) = ф *(<э2 *). Следовательно, если в одно множество
включать только те последовательности множества Р, для каждой пары а, *
а2* которых имеет место ф*(а,*) = ф*(а2*) , то множество Р разобьется на
конечное число подмножеств (классов), которые будем обозначать (J/01,
О т О (0)
5.4.1. Пример построения автомата
Пусть 5 = {OjCj, а^с^, а}а2с}, a2alc2, ес3, аха2ахс2, а{а2а2с}, a2a2atcp
axa[axa[cv а{а{а2а{ахс2, а2с2, а2а2с3, ахахахс2, а}аха2с^. Для этого множества
будем иметь классы
С?,"» = {е, а2, а2а2, а{а{а}, а{а{а2},
Q2W> = {а,, а,а2, ata2a2, а2а2а{},
= {0,0,, a2av а[а2а{, а^а^, а{а{а2а{}.
Сопоставим эти классы соответственно состояниям Ь\т, Ь'2т, Ь'3т
некоторого автомата Л/1<0), построив для него граф переходов точно так же,
как для автомата Л/ но используя классы <21<0), <22<0), <23<0). Тогда получим
автомат, граф переходов которого показан на рис. 5.3. Этот автомат является
недетерминированным, так как из состояния Ь\т исходят две дуги, помеченные
одним и тем же действием аг Если с помощью алгоритма разбиения
последовательностей на классы эквивалентных для того же множества .5 построить
классы эквивалентности, то их будет четыре Q = {е, а2а2}, Q2 = {а}, а}а2, аха2а2,
а2а2а{}, Q3 = {а{а{, а2а}, a^a2av аха{а{а{, а{а{а2а{},
Q4 = {а2, а}а}а{, а}а2а2}. Сравнивая Qv Qv Qv
Q4 и Qf\ Qf \ видим, что Q^}= Q, и QA,
= Qv Q}m ~ Qy те- Л701 того> чтобы no
классам (?<0) построить детерминированный
автомат M, достаточно разбить множество Qf’
на два непересекающихся подмножества Q и 04.
Эта процедура соответствует замене состояния Z//0’
недетерминированного автомата Л//0’ двумя
состояниями Ь'х и Ь'4, в результате чего он
превращается в детерминированный автомат Л/ .
В общем случае под детерминизацией будем
понимать итеративную процедуру (более
Рис. 5.3. Граф переходов
автомата
детально эта процедура будет рассмотрена чуть
позднее ) построения автомата Л/(,) по автомату
116
5.4. Построение автомата методом детерминизации
Л£'” с помощью разбиения некоторых классов Q^'\ соответствующих
состояниям автомата Л/"1’, на непересекающиеся подклассы Q(,),
соответствующие состояниям автомата Л/(,). Разобьем класс 0|<0’ = {е, а2,
а2а2, axa}av а}а{а^ автомата на подклассы по следующему принципу:
любые две последовательности а, * а2*е (2/°’ будем помещать в один и тот же
подкласс, если для них имеет место <$*(а3*а) = ф*(й2*й) для всех действий а.
Класс Q}(0) в этом случае можно разбить на два подкласса {е, а2а2] и
{а2, а{а{ау а^аха2}, так как
Ф*(еа,) = ф*(о2а2л,) = ср ф*(еа2) = ф*(а2а2а2) = с,,
Ф*(а2а,) =ф*(а,а|«1о1) = ф *(а}аха2а{) = с2,
Ф*(°2°2) = ф *(0,0,0,^) =ф *(0,0,0^,) = су
Введем новые обозначения классов
С/1’ = {е, а2а2},
Q2{Y} = {о,, а{а2, ala2a2, а2а2а{},
23(1) = {0,0), a2av а^а2ау а^а^, а{а{а2а}},
24"’ = °!0!0!’ aia'ai}-
Эти классы совпадают соответственно с классами Qv Q Q}, Q
полученными по алгоритму разбиения последовательности на классы
эквивалентности и, следовательно, автомат Л/(1), который можно построить
по этим классам, является детерминированным.
Настоящим примером был проиллюстрирован подход к процедуре
детерминизации. Перейдем к более строгой формулировке этой процедуры в
виде алгоритма. Рассмотрим отношение £<'* на множестве А*”: ах*Е{,'а2*, если
а, *, а2*& А*", ф*(а,*а*) = ф*(а2*а*) для всех а* е А*" длиной 1(а*) < i. Из
определения отношения Е1,) следует, что отношение £<0) как раз разбивает
множество последовательностей Р из рассмотренного примера на классы
С?/0’, 02|О), (23<О)- Действительно отношение Ет проверяется только для
последовательностей а*, длина которых равна нулю, а такая последо-
вательность существует только одна — пустая последовательность е. Тогда по
определению £•'> для любых двух последовательностей а{*, а2* е Р имеет
место ах*Е^}а2*, если ф*(о,*) = ф*(«2*). В то же время , если / выбрано
равным или большим длине р самой длинной входной последовательности
из множества Р, то из определения отношения £(,) следует, что отношение
£(’1) совпадает с отношением R, а отношение £(,+|) разбивает множество Р
на классы, каждый из которых является подклассом отношения £'< т.е. для
каждого класса Q<,+1* существует класс Q^’, такой, что Q(,+1,c Qh(l>. В общем
случае автомат Л/(,) = (A, B(i\ С(,\ f(l\ фм) строится аналогично автомату
117
5. Среды и языки
М. Состояниям Ь'^, V®, ... У k{i} этого автомата соответствуют классы
СЛ С2('Л ... Qh(l>-
Функцией переходов автомата Л/(,) является функция
У<'>) = {Z>7>| а* е Qf \ а*а е Qf>},
а функцией выходов
фЮ^т/Ю) = {ф*(а*а) = ф(')(/>'А(')) |<з*е £/<0, а*а е Qh(i}}-
Начальным состоянием автомата Л/(,) является состояние Ь'^\
соответствующее классу Q^\ который содержит пустую последовательность е.
Автомат Л/(,) в общем случае является недетерминированным, так как из одного
и того же состояния Ь'}‘\ по одному и тому же входному состоянию а
возможен переход в несколько различных состояний b'h(i}. При этом,
поскольку отношение Е™ совпадает с отношением R, то при выполнении
условий полноты, непротиворечивости и регулярности для множества S
автомат Л/(п) совпадает с автоматом Л/,, т.е. является инициальным,
детерминированным и конечным.
Создадим с использованием отношения £(,) алгоритм построения автомата
Л/, реализующего заданное множество S последовательностей.
5.4.2. Алгоритм детерминизации по множеству последовательностей
Запишем этот алгоритм в виде
а) принять i = 0;
б) разбить множество Р на классы ... по отношению £’(,),
где Qx{i} является классом, содержащим пустую последовательность е;
в) отождествить классы QV>, Q^'\ ... с внутренними состояниями
У2(‘\ ...Ук<‘> автомата Л/(,). Построить автомат Л/(,) с этими внутренними сос-
тояниями У<’\ Ь'}'\ функцией переходов /(,) и функцией выходов ф(,);
г) проверить, является ли автомат Л/(,) детерминированным. Если он
детерминированный, то перейти к пункту е), в противном случае перейти к
следующему пункту;
д) разбить каждый класс Qx(i\ Q2(i}, ... QJ1’ по отношению £(,+1) на
подклассы. Считать множество этих подклассов новым множеством классов
<2i(/+1), <22<'+|), > где является классом, содержащим пустую
последовательность е. Принять i = z + 1 и перейти к пункту в);
е) считать автомат Л/(,) автоматом Л/. Конец.
Рассмотренные алгоритмы построения автомата в качестве исходного
задания использовали множество (язык) последовательностей 5. В то же
время каждое такое множество однозначно представляется деревом, причем
каждой последовательности а* & P(S) однозначно соответствует состояние
дерева из множества всех состояний В, в которое она ведет из начального
состояния. Следовательно, эти алгоритмы могут быть модифицированы для
работы сразу с деревом и его состояниями без перехода к множеству 5. Для
118
5.5. Граф переходов состояний среды
этого достаточно заменить отношение E(i'> на множестве А*” следующим
отношением: D(l): b{D{r,bv если b{, е В, ф*(а*, bt) = <р*(а* Ь2) для всех
а*е А*” длиной /(а*) < L Тогда функции переходов и выходов будут иметь вид
f^(a, //(')) = bt е Qf\ b=f{a, b) e
ф«)(^)) = {ф(5 )|Z> e Q^}.
Следовательно, вместо алгоритма детерминизации по множеству
последовательностей действий можно использовать следующий алгоритм.
5.4.3. Алгоритм детерминизации по множеству состояний
Запишем этот алгоритм в виде
а) принять i - 0;
б) разбить множество В на классы Qf\ ..., по отношению
D{‘\ где <2,(,) является классом, содержащим начальное состояние Z>0;
в) отождествить классы Q^, Q2{i), ..., Си(/) с внутренними состояниями
Ь\('\ Ь'2{,), ..., Ь’к-‘> автомата Л/(0. Построить автомат Л/<0 с этими внутренними
состояниями b'f \ b'2{i\ ..., b'^‘\ функцией переходов/<ои функцией выходов
Ф(,);
г) проверить, является ли автомат Л/(0 детерминированным. Если он
детерминированный, то перейти к пункту е), в противном случае перейти к
следующему пункту;
д) разбить каждый класс С/'*, Q/‘\ ..., по отношению на
подклассы. Считать множество этих подклассов новым множеством классов
Ql<‘+>>, Q2(i+I>, ••• где <21('+|) является классом, содержащим пустую
последовательность е. Принять i = i + 1 и перейти к пункту в);
е) считать автомат Л/(,) автоматом Л/ . Конец.
5.5. Граф переходов состояний среды
Вернемся теперь снова к примеру со средой кота из второй главы и рис. 2.2,
на котором показано дерево переходов из начального состояния во все
состояния этой среды. От этого дерева легко перейти к графу переходов,
оставив только одну из повторяющихся вершин (ту, которая расположена
ближе к начальному состоянию) и направив дугу в оставшуюся вершину. В
результате получится граф переходов, показанный на рис. 5.4. На этом
графе каждая вершина имеет петлю. Это означает, что при действии
(действиях), соответствующем петле, состояние среды остается неизменным
и такие действия желательно не осуществлять. Устраним их на графе,
изображенном на рис. 5.4. В результате получим граф без петель, показанный
на рис. 5.5. Зададим на множестве состояний этого графа функцию ф(5). Будем
полагать, что на целевых состояниях ф(й7) = ф(58) = с,, а на всех остальных
ф(5) = с2. Построим автомат Л/ по последнему алгоритму. Получим классы
119
5. Среды и языки
Рис. 5.4. Граф переходов с петлями для среды кота
= {/>,, b2, by b4, b5, b6}, Q2{0> = {bv Z>g}. Если по этим множествам построить
граф переходов автомата Л?0), то он будет иметь два состояния и не будет
детерминированным, поскольку подмножества состояний {Z>|5 b2, Ь4, Ь5},
{/>,, Ьь} одного и того же класса (J^0’ переходят в состояния различных классов
2/0’ и 02(О>. Поэтому по этим классам не может быть построен автомат М и
класс необходимо разбить на подклассы 0/1’ = {/>,, Ь2, Ь4, Ь5},
= {b3, bb}, Q}(]> = 02(o*. Если построить по этим классам автомат Л/’1*, то
он будет иметь три состояния, но опять не будет детерминированным,
поскольку подмножества состояний {bt, b2}, {Ь4, Ь5}, одного и того же класса
(1 > переходят в состояния различных классов Qt(l) и <22(|). Это видно на рис. 5. 7.
Разобьем класс (J/1* на два подкласса. В результате получим классы
0/21 = {/>,, b2}, Q2(2> = {b4, b5}, Q3(2> = Q2('\ Q42' = С3(|). В соответствии с
этими классами уже может быть построен детерминированный автомат М,
поскольку все состояния каждого из классов переходят в состояния какого-
либо одного класса (?(|). Это видно из рис. 5. 8.
Автомат М построенный по множеству классов С?/2’, Q2(2>, Q3(2>, Q4(2\
показан на рис. 5. 9. На этом рисунке классы С/2’, <22(2), <23(2), <24<2)не
заменены на состояния Ь<2>, Ь2(2>, Ь}(2>, Ь4(2} для того, чтобы видеть, какие
исходные состояния среды их образуют.
120
5.5. Граф переходов состояний среды
Рис. 5.5. Граф переходов без петель для среды кота
Q<0> Q(0) QW> q|0> Q<") Q<»» Q<«> Q‘°> Q'»' 0'“»
Рис. 5.6. Переходы состояний классов 0/0’ и (7,"°’
О’0' О'0’ Q,0) О"" О*11’ О™ Q(0) Q*"1 Ql0) Q 2
Рис. 5.7. Переходы состояний классов 0,(|), Q;’
q<2> q«> q(2> qW q<2> qI2> Q^> Q<«
Рис. 5.8. Переходы состояний классов Qtm, Q2'2>, Q^-',
121
5. Среды и языки
5.6. Использование графа переходов для поиска
в пространстве состояний
В настоящей главе была рассмотрена взаимосвязь между языком,
автоматом и средой. Язык — это множество последовательностей символов,
в частности последовательностей действий агента. Постановка задачи поиска
целевых состояний требует формулировки знаний о среде. Язык используется
для формулировки этих знаний с явным или неявным упоминанием состояний
среды. Язык может быть реализован автоматом. В этом случае автомат может
рассматриваться просто как другая форма представления знаний. Более того,
автомат то же можно рассматривать как язык, более наглядный и компактный
в его графовом эквиваленте — дереве или графе переходов, особенно для
представления знаний о простых средах. Объем требуемых исходных знаний
и сложность поиска зависят от языка представления знаний. Автоматное
представление знаний позволяет оптимизировать исходное представление
знаний и даже упорядочивать их, как это видно из примера со средой кота.
Граф на рис. 5.9 имеет почти линейную структуру, что позволяет без лишнего
блуждания по дереву находить целевые состояния.
Рис. 5.9. Автомат М, построенный по множеству состояний классов
Ф G,12’, Q'\ Q,m,
122
5.7. Построение графа состояний
5.7. Построение графа состояний
5.7.1. Дерево состояний
Построение дерева состояний рассмотрим на примере простой среды.
Среда и дерево состояний среды для нас не различимы. Если дерево состояний
построено, то по нему можно построить автомат, который в этом случае
также адекватен среде. Поэтому мы сразу будем говорить не о среде, а о
дереве состояний и автомате, помня при этом, что речь все-таки идет об
объектах, в определенной степени адекватных среде. Итак, пусть требуется
построить автомат М, адекватный некоторой среде и имеющий один двоичный
вход х и один двоичный выход Z- На вход этого автомата (воздействие на среду)
поступает произвольная бесконечная последовательность нулей и единиц, т.е.
входной алфавит А = {0, 1}. Каждая подпоследовательность подряд идущих
входных символов а4а3а2а1 (а. е А) входной бесконечной последовательности
поступает на вход автомата соответственно в моменты времени /3, /2, /. р
Л, где /. — некоторый момент времени; /.ч — момент времени,
предшествующий моменту /; / 2 — момент времени, предшест-вующий
моменту Л р ti } — момент времени, предшествующий моменту / 2. Каждая
такая подпоследовательность а4а3а2а, рассматривается как четырехразрядное
двоичное число а423 + а322 + а22' + 0,2° (т. е. это число подается на вход
автомата, начиная со старших разрядов). Задачей автомата М является
классификация десятичных эквивалентов подпоследовательностей а4а3а2а15
подаваемых на его вход соответственно в моменты времени / 3, /. t t., на
две группы: меньших или равных 9 и больших 9. На выходе автомата должен
появляться 0 в первом случае и 1 — во втором.
Отметим, что рассматриваемый автомат является представителем
обширного класса автоматов, принадлежащих к декодирующим устройствам,
задачей которых является обнаружение во входной бесконечной
последовательности, подаваемой на их входы, некоторых подпоследо-
вательностей, обладающих тем или иным свойством. Для практических задач
естественно считать, что автомат, прежде чем начать свою работу, находится
в некотором начальном состоянии, через которое он может многократно
проходить в процессе своей работы. Пусть для рассматриваемого автомата М
это будет состояние Ьй. Очевидно, что существует всего 24 различные входные
последовательности а4а3а2а, длиной 4. Учитывая сказанное, дерево состояний
автомата можно строить следующим образом. Будем полагать, что в
начальном состоянии Ьй, находящемся на ярусе 0 дерева, нам неизвестны
значения переменных (неизвестные значения переменных обозначим знаком ?),
которые подавались на вход автомата в предыдущие моменты времени.
Состояния — последователи начального состояния (начальное состояние
находится на ярусе 0) получаются в результате действия, присваивающего
переменной сходно из возможных значений (0 или 1). В результате имеем
состояния яруса 1. Последователи состояний яруса 1 получаются в результате
123
5. Среды и языки
действия, присваивающего одно из возможных значений переменной ос,, и
т.д. Начальное дерево состояний, которое можно, как ранее, называть
деревом поиска состояний, показано на рис. 5. 10. Как всегда внутри вершин
стоят обозначения состояний (вместо записи Ь:записываем просто /). Слева
???? (о)
Рис. 5.10. Дерево поиска состояний автомата М
124
5.7. Построение графа состояний
от вершин указаны входные последовательности а4а3а2ар получающиеся
после подачи очередного входного символа. Еще неизвестные значения
переменной а обозначены знаком «?». Дуги помечены значениями 0 или 1,
означающими действие по присвоению соответственно 0 или 1 переменной
а, если эти дуги входят в вершины яруса i.
5.7.2. Построение неминимального графа переходов
Для того чтобы можно было от построенного дерева на рис. 5.10 перейти
к неминимальному графу переходов, будем полагать, что нам известна
подпоследовательность а4а3а2ар в результате которой автомат попал в
состояние Ьо. Вообще это может быть любая подпоследовательность из числа
допустимых. Пусть это будет подпоследовательность 0000. Тогда во всех
подпоследовательностях дерева, показанного на рис. 5.10, символ «?» следует
заменить на 0. В результате получим дерево, показанное на рис. 5.11. Каждой
вершине этого дерева соответствует одна конкретная подпоследовательность
a4a3a2aj, состоящая из 0 и 1. Все конкретные подпоследовательности
встречаются на дереве. Дерево, представленное на рис. 5.10, может быть
продолжено, поскольку на автомат подается бесконечная последовательность
из 0 и 1. Но новых подпоследовательностей и соответствующих им состояний
уже не появится. Для каждого из состояний на дереве рис. 5.10, из которого
дуги еще не выходят, найдется уже полученное состояние, в которое из этого
состояния может быть направлена дуга. Поэтому нет смысла продолжать
построение дерева, а во-вторых, можно удалить те поддеревья, которые
начинаются в состояниях, встречающихся повторно, перенаправив идущие к
этим поддеревьям дуги в ранее встречающиеся состояния. В результате из дерева
на рис. 5.11 получится граф переходов, показанный на рис. 5.12.
Рис. 5.11. Дерево поиска состояний после конкретизации начальной
последовательности a a3a2a.
125
5. Среды и языки
Рис. 5.12. Граф переходов автомата, полученный по дереву, показанному на рис. 5.11
о!"
'ОООдо г
©0 0® 0© 0© 0® 0® ®0 0® 0® 0®
ФСГ Q0,Q,:” Q;0,Q;0iQ,0)Q!Q| Qo1Q;o) Q0iQ01Q0|Q0) Q^^QrQ'01 QW
n(°)
0 0 0^*2 0 0®
А А, А А A A
0® 0® 0® 0® ©0 0®
Qo)qo: (TOT Q0!Q01Q01Q01 QM Q№
Рис. 5.13. Классы состояний (70) автомата, показанного на рис. 5.12
его!11 стог <теп та тата стог сгсгта та
та* ога" та
® 0 0 © ® ©
Рис. 5.14. Классы состояний (71* автомата, показанного на рис. 5.12
126
5.8. Языки и грамматики
Рис. 5.15. Классы состояний (72> автомата, показанного на рис. 5.12
Рис. 5.16. Классы состояний (73) автомата, показанного на рис. 5.12
Рис. 5.17. Состояния и переходы минимального автомата, полученные по
алгоритму детерминизации состояний
127
5. Среды и языки
5.7.3. Минимизация числа состояний
Перейдем теперь к минимизации числа состояний автомата, показанного
на рис. 5.12, по алгоритму детерминизации по множеству состояний. На
рис. 5.13 — 5.16 показаны совокупности классов состояний (70’, (71’, (721,
(73), полученные по этому алгоритму. В соответствии с классами (73) после
переобозначений классов символами состояний получаем автомат, граф
переходов которого показан на рис. 5.17.
5.8. Языки и грамматики
В предыдущих параграфах было дано понятие языка, используемого для
описания поведения среды. Был рассмотрен простейший вариант такого
языка в виде конечного множества последовательностей 5. Было показано,
как от такого простейшего описания, обладающего определенными
свойствами, можно перейти к графовому представлению этого языка в виде
автомата и представить этот автомат на языке логики.
Обратим внимание, что в реальных задачах агент, реализуемый как
программа, работа которой осуществляется на основе какого-либо исчисления
и стратегии вывода, имеет, как правило, дело не с физической средой, а как
раз с описанием свойств этой среды на каком-либо языке. Задать эти языки
простым перечислением конечного множества последовательностей 5
практически невозможно. Задание становится более сложным. Изучая именно
такого рода задания, можно перейти от них к формальной постановке задачи
на языке того или иного исчисления. Собственно, это задание или описание и
выступает чаще всего для агента в качестве эквивалента среды, за исключением
может быть агентов, реализуемых как роботы, которые обладают органами
восприятия и реакции. Кроме того, при мультиагентной реализации систем
агенты взаимодействуют друг с другом с помощью сообщений, передаваемых
на каком-либо языке. Именно поэтому важно знать, как могут быть формально
описаны свойства среды в языках, не являющихся логическими языками, и
как можно перейти от таких языков к формальной постановке задачи в том или
ином исчислении или как разобрать сообщение, поступающее данному агенту
извне. В настоящем разделе будут рассмотрены способы определения языков с
помощью формальных грамматик, будет показано, как можно перейти от такого
определения к аксиомам, определяющим свойства среды, и как можно разбирать
и выполнять действия на основе языковых сообщений.
5.8.1. Формальные грамматики
Назовем некоторое множество А, состоящее из элементов а, терми-
нальным алфавитом, а его элементы терминалами. Введем также конечное
непустое множество символов N, которые назовем нетерминалами.
Множества N и А не пересекаются. Объединение этих множеств обозначим
128
5.8. Языки и грамматики
символом V. Элементы множества А будем по-прежнему обозначать
строчными символами а, а элементы множества N— заглавными буквами.
Множество всех последовательностей в алфавите V обозначим И* Если к
множеству V* добавить пустой символ, то получим множество И*’.
Наконец, множество упорядоченных пар (у, w), где v является элементом
множества И *'х А х V *', a w — элементом множества И*, обозначим
символом.
Каждая упорядоченная пара (v, w) называется порождающим правилом.
Порождающее правило обычно обозначается v -> w. Из определения
порождающего правила следует, что w не может быть пустой последо-
вательностью.
Формальной грамматикой называют четверку:
G = (N, А, Р, S),
где Р является непустым конечным множеством порождающих правил, а
5 — специальный непустой символ, называемый начальным нетерминальным
символом. Н. Хомским предложена классификация формальных грамматик,
состоящая из четырех типов: 0, 1, 2 и 3, в зависимости от типа порождающих
правил. Классификация Хомского (/(у) означает длину последовательности
v) приведена в табл. 5.1.
Из этой таблицы следует, что любая автоматная грамматика является
одновременно контекстно-свободной, любая контекстно-свободная —
контекстно-зависимой, любая контекстно-зависимая — грамматикой типа 0.
Последовательность w*выводима из последовательности у*с помощью правила
v —> w, если последовательность v* содержит подпоследовательность у, замена
которой на и'дает w*. Вывод последовательности w*H3 последовательности у*
с помощью правила g обозначим у* => ы*. Последовательность w* выводима
из у* с помощью правил gl, g2, ..., gk, g(£+l), если существует множество
Таблица 5.1
Тип грамматики Название грамматики Вид порождающих правил
0 Типа 0 у е V*'x А XV*', w е V*
1 Контекстно-зависимая у е V*'x А х V*', w eV*, Цу) < l(w)
2 Контекстно-свободная у e N, ту e V*
3 Автоматная у e N, w е А х N или w е А у g N, w е N х А или n't А
5 - 1141
129
5. Среды и языки
последовательностей у.*, у* .... у* таких, что у*, => у *, у* => у*, ,
у * => у * у * —> уу *
yk gk^ vk+\ ’ ук+\ g(£+l) '
5.8.2. Языки
Язык L(G), порождаемый грамматикой G, является множеством всех
последовательностей а* множества А*, которые могут быть выведены из
начального нетерминального символа с помощью правил грамматики G.
Пример. Дана автоматная грамматика G;
А = {at, а2}, W = {Nt, NJ, S, Р = {S -+N{, N} -э atN2, N2 -> atN2, N2 -э aj
Язык, порождаемый этой грамматикой имеет вид
L(G) = {а”а2, т > 1}.
Здесь aja2 означает любую последовательность из идущих подряд т символов ор
за которыми следует единственный символ а2.
Пример. Дана контекстно-свободная грамматика G\
А = {о„ aj, N = {?/,}, 5, Р = {5 -э Nv Nx -э а^а2, N} -э ataj.
Порождаемый язык
А((7) = {ajaj, п > 1}.
Пример. Контекстно-зависимая грамматика
А = {а,, а2, aj, N = {W,, N2, NJ, S, Р = {5 -> Nx, Nt a^,
yVt —> a,N,—> a2a2a2, a,N,—> N2aJ.
Порождаемый язык
L(G) = {ajajaj, n > 1}.
5.9. Грамматический анализ и автоматы
В предыдущем параграфе рассматривались формальные грамматики и
порождение с их помощью, начиная с начального символа, языков или
отдельных последовательностей, принадлежащих языкам. В этом параграфе
решим обратную задачу. Дана грамматика и некоторая последовательность.
Требуется определить, принадлежит ли данная последовательность языку,
порождаемому данной грамматикой, или нет. Грамматика в этом случае
выступает как средство распознавания последовательностей языка. Ограничимся
случаем самой простой грамматики — автоматной. Для распознавания
последовательностей, порождаемых автоматными грамматиками, может быть
использована модель конечного автомата, рассмотренная в настоящей главе,
поскольку между автоматной грамматикой и конечным автоматом имеется тесная
связь. Суть этой связи состоит в том, что для любого языка, все последова-
тельности которого порождаются некоторой автоматной грамматикой, может
130
5.9. Грамматический анализ и автоматы
быть всегда построен конечный автомат (не обязательно детерминированный),
реализующий все эти последовательности, и этот автомат может быть
использован для распознавания последовательностей данного языка.
В модели конечного автомата, необходимого для распознавания
последовательностей языка и называемого распознающим, удобно выделить
из множества всех внутренних состояний подмножество F с В, состояния
которого называются финальными, и не использовать множество выходных
состояний и функцию выхода. Распознающий автомат определяется
следующим образом:
М = (А, В, f b0, F),
где А = {ар а2, ..., ат} — входной алфавит; В = {/>,, Ь2, ..., Ьп} — внутренний
алфавит (множество состояний автомата); /: А * В —> В —функция переходов,
записываемая так же, как f(a, b) = b, а е A, b., b е В\ F -— непустое
множество финальных состояний, Fс 3. Количество финальных состояний
выбирается из практических соображений. Мы ограничимся одним
финальным состоянием bF
Начальное состояние Ьд<= В.
Будем полагать, что Ьо = Ьх. Последовательности аха2 ... я языка,
порождаемого какой-либо автоматной грамматикой, поступают на вход
распознающего автомата. Если последовательность принадлежит языку, то
автомат после подачи последнего символа ах последовательности аха2 ... а.
должен оказаться в одном из состояний множества финальных состояний.
Если последовательность не принадлежит языку, то этого не произойдет, и
этот факт используется для распознавания последовательностей, не
принадлежащих языку.
Распознающий автомат построим по распознающей грамматике следующим
образом.
Каждому нетерминальному символу N грамматики сопоставим внутреннее
состояние b.
Каждому правилу N, -> aNj сопоставим дугу (переход) из состояния Ь, в
состояние b по входному состоянию а.
Каждому правилу Nx-> а сопоставим дугу (переход) из состояния bt в
состояние />Л по входному состоянию а.
Пример. Дана автоматная грамматика G:
А = {ах, а2, aj, N = {(V„ N2, NJ, S = Nx, P = {ДГ -+ axN2, N2 axN2,
N-,^ av Nx^axN3, N2^ aj.
Порождаемый язык
L(G) = {a,a3} u {ax"a2, n > 1}.
5*
131
5. Среды и языки
Конечный автомат, распознающий язык L(G) (рис. 5.18):
А = {a,, а2, а3},
В = {Ьр Ь2, Ь3, ЬД
Д Дар />,) = {Ь2, ЬД Да{, Ь2) = {Ь2}, Да2, Ь2) = {ЬД Да3, Ь3) = {/>4},
= bv
F =
Этот простой конечный автомат не является детерминированным. Можно
показать, что любой недетерминированный конечный автомат может быть
преобразован в эквивалентный детерминированный автомат или в систему
эквивалентных детерминированных автоматов. Под эквивалентностью автоматов
в данном случае понимается их способность распознавать одни и те же языки.
Системы автоматов способны распознавать и более мощные языки, например,
порождаемые контекстно-свободными грамматиками. Таким образом, модель
конечного автомата может служить основой для распознавания достаточно
широкого класса языков. Учитывая это, модель конечного автомата может быть
использована для создания агентов, способных выполнять следующие функции.
Распознавать языки (последовательности, предложения, сообщения в этих
языках), на которых описаны знания о среде, проверяя, таким образом,
синтаксическую правильность представления знаний о среде.
Конечный автомат, распознающий язык, на котором представлены знания
о среде, может рассматриваться как некий эквивалент этой среды. В этом
Рис. 5.18. Граф переходов распознающего автомата
132
5.10. Перевод с одного языка на другой
случае состояния автомата соответствуют состояниям среды, и автомат может
быть использован агентом для поиска целевых состояний в пространстве
состояний, как это было уже продемонстрировано ранее в настоящей главе.
В том и другом случае (распознавании и поиске цели), находя те или иные
состояния, агент может совершать определенные действия или выдавать сообщения
другим агентам. Например, в случае распознавания действия могут быть
направлены на перевод одних сообщений (последовательностей языка) в другие.
Рассмотрим на простейшем примере, как это может быть сделано.
5.10. Перевод с одного языка на другой
Рассмотрим на простейшем примере перевод с одного языка на другой.
Исходный язык задан грамматикой G.
А = {«,+}, N = {Nv Nv A.,}, S = Nv Р = {Nx -э aNp N2-> !,
N2-> +NV N3-> aNJ,
Применяя грамматику G, получаем язык
L(G) = {a(+a)"! , n >0}.
Автомат, распознающий язык L(G), будет следующим:
А = {«,+}, В = {/>,, Ь2, Ь3},
f:f(a, b}) = {b2},f(+, b2) = {Ь3}, Да, b3) = {/>,},/(’, Ь2) = {64},
Z>o =bt,
Р = {\}.
Рис. 5.19. Граф переходов автомата,
распознающего язык L(G)
Граф переходов автомата показан на
рис. 5.19.
Рассматриваемый язык состоит из
множества последовательностей, каждая из
которых представляет сумму чисел,
обозначаемых символом а. Символ «!»
означает конец последовательности. Перед
нами стоит задача перевода любой последо-
вательности в последовательность команд
Поместить а; (поместить число а в
сумматор), Сложить а; (добавить число а
к содержимому сумматора), Прекратить
(завершить процесс суммирования). Рас-
смотрим процесс перевода на примере,
133
5. Среды и языки
например, последовательности а + а + а\. Результатом перевода должна быть
последовательность Поместить а; Сложить а; Сложить а; Прекратить. Процесс
перевода состоит из следующих повторяющихся шагов.
На автомат слева направо поступает очередной символ последовательности
а + а + а\
Если этот символ допустим для данного языка, то автомат, воспринимая
его, переходит в какое-либо одно состояние автомата (в данном случае автомат
детерминированный). Если он не допустим, то выдается сообщение об ошибке.
Состояние сопоставлено с некоторым действием, которое и выполняется.
После этого все повторяется для следующего символа.
Введем единственное элементарное действие Соединить (и, г) над
последовательностями и, v. В результате выполнения этого действия получается
новая последовательность uv. Процесс перевода представим в виде таблицы
(табл. 5.2). В первом столбце таблицы указывается очередной символ,
поступающий на автомат, во втором столбце указано состояние, в которое
Таблица 5.2
Очередной входной символ Состояние автомата Действие Результат действия
и = Поместить
а Ь2 и = Соединить (и, а) и = Соединить' и, ;) и —Поместить а и = Поместить а;
+ Ьз и = Соединить (и, Сложить ) и = Поместить а; Сложить
а Ь2 и = Соединить (и, а) и = Соединить(и, ;) и = Поместить а; Сложить а и = Поместить а; Сложить а;
+ Ьз и = Соединить (и, Сложить ) и = Поместить а; Сложить а; Сложить
а Ь2 и = Соединить (и, а) и = Соединить(и, ;)) и = Поместить а; Сложить а; Сложить а и = Поместить а; Сложить а; Сложить а;
1 и = Соединить (и, Прекратить) и = Поместить а; Сложить а; Сложить а; Прекратить
134
Вопросы и упражнения
автомат переходит в результате поступления очередного входного символа, в
третьем столбце указаны действия, соответствующие состоянию и, наконец, в
последнем столбце указан результат каждого действия.
Вопросы и упражнения
1. Дайте формальное определение конечного инициального детерминированного
автомата.
2. Почему автомат называют конечным и как это проявляется в определении?
3. Почему его называют инициальным и как это проявляется в определении?
4. Почему его называют детерминированным и как это проявляется в определении?
5. Вспомните, что такое язык и объясните, почему множество входо-выходных
последовательностей в настоящей главе называют языком.
6. Что такое реализация языка автоматом?
7. Какими свойствами должен обладать язык, чтобы его можно было реализовать
в инициальном детерминированном автомате?
8. Дайте определение отношения эквивалентности R на множестве входо-выходных
последовательностей, реализуемых автоматом, и объясните, как это отношение может
быть использовано для минимизации числа состояний автомата.
9. В чем суть, связь, различие между алгоритмами сокращения числа состояний
автомата по множеству последовательностей с помощью проверки отношения R,
детерминизации по множеству последовательностей, детерминизации по множеству
состояний?
10. Нарисуйте простой граф переходов инициального детерминированного
конечного автомата.
11. Постройте инициальный детерминированный автомат по множеству последо-
вательностей 5 = {ее,, ахсх, а ахахсх, ахахахахсх, а2а2сх, ахахс2, а2с2, а2а2а2с2}, выразите
в виде аксиом условия перехода каждого состояния в другие состояния, а в виде
теоремы условие детерминированности автомата. Докажите теорему методом
резолюции.
12. Постройте инициальный детерминированный автомат по множеству последо-
вательностей 5 = {есх, ахсх, ахахахсх, ахахахахсх, а2а2сх, ахахс2, а2сг а2а2а2с2, ахахаха2с2,
аха2с2, а2а2ахс2, а2а2а2ахс2}. Минимизируйте число его состояний методом
детерминизации.
6. СТРАТЕГИИ ПОИСКА
В этой главе проанализированы различные стратегии, с помощью которых
можно осуществлять поиск целевых состояний.
Во второй главе рассматривались понятия, используемые при постановке и
решении задачи в пространстве состояний, в частности было введено понятие
вывода для нахождения цели. Вывод не является однозначным и после
очередного шага приходится определять, какой же следующий шаг целесообразно
сделать, чтобы поскорее достичь цели. Очередной шаг зависит от того, какая
стратегия вывода выбрана. Понятие «вывод» обычно используют вместе с той
или иной логической системой; понятие «поиск» — безотносительно к какой-
либо логической системе.
В настоящей главе описаны некоторые стратегии поиска, иллюстрируемые
простыми примерами из области нахождения подходящего маршрута. Напомним
некоторые ранее определенные понятия и введем ряд новых.
Состояние (или состояния) среды, с которого агент начинает решение
задачи, называют начальным состоянием.
Соответственно множество всех состояний, достижимых из начального с
помощью всех допустимых последовательностей действий, называют
пространством состояний и обозначают В.
Последовательность вершин, ведущих из начального состояния в другое в
данном пространстве состояний, называют путем. Длиной пути называют
количество вершин на этом пути.
Процесс нахождения целевого состояния (состояний) называют страте-
гией поиска цели, или поиском цели.
Агент, являющийся исполнителем той или иной стратегии, должен
действовать таким образом, чтобы при анализе состояний среды максимизировать
свой успех. Это требование носит слишком общий характер, чтобы его можно
было непосредственно воплотить в конкретную стратегию. Рассмотрим сначала,
какие оценки могут характеризовать успех.
136
6.1. Оценки успеха при поиске цели
6.1. Оценки успеха при поиске цели
Оценки успеха, характеризующие эффективность поиска, могут быть
самыми различными. Будем полагать, что оценка успеха является
положительным числом или нулем и чем больше число, тем успешнее
действует агент. Тогда самая очевидная оценка — это возможность
достижения цели вообще. Эта оценка носит двузначный характер: например,
она принимает некоторое максимальное значение, если цель достижима, и
минимальное в противном случае. Другая оценка может быть ценой пути,
вычисляемой с помощью функции цены пути. Третья оценка может быть ценой
поиска, характеризующейся объемом необходимых для поиска времени и памяти.
Наконец, еще одна оценка успеха может быть общей ценой, являющейся
некоторой функцией от цены пути и цены поиска.
Цена поиска зависит от многих обстоятельств. Так, например, если агент
сильно стеснен во времени, то цена поиска может быть пропорциональна
времени, затрачиваемому на поиск. Общая цена может зависеть от
пройденного расстояния и затраченного на поиск времени. Вычисление
общей цены непростая задача, поскольку выбор пути, а следовательно, и
пройденное расстояние могут определяться временем, затраченным на поиск.
Чем меньше времени потрачено на поиск, тем дальше от оптимального может
оказаться выбор пути. Зачастую в этих условиях приходится идти на некий
компромисс, далекий от оптимального решения.
Стратегии поиска различаются последовательностью или порядком просмотра
состояний или множеств состояний в пространстве всех состояний среды.
Стратегии поиска в пространстве состояний обычно сравнивают по ряду
критериев. Основными критериями являются следующие.
Полнота', стратегия является полной при условии, что она всегда
обеспечивает нахождение решения (целевого состояния или состояний), если
оно вообще существует в данном пространстве состояний.
Сложность по времени', время, необходимое для нахождения решения.
Сложность по памяти', объем памяти, необходимый для решения задачи.
Оптимальность: стратегию называют оптимальной при условии, что она
обеспечивает нахождение решения, которое может не быть наилучшим, но
известно, что оно принадлежит некоторому классу или подмножеству, все
элементы которого обладают неким общим свойством (или свойствами), согласно
которому мы их относим к оптимальным решениям.
Минимальность: стратегия является минимальной, если она гарантирует
нахождение наилучшего решения. Минимальность, таким образом, является
частным и более сильным случаем оптимальности.
Стратегии поиска разбивают на две большие группы: слепой поиск и
направленный поиск. Различие между слепым и направленным поиском можно
продемонстрировать на следующем простом примере. Представим себе, что
агент приехал в Россию по туристической путевке с целью совершить путешествие
по золотому кольцу России. Его самолет сел в аэропорту Шереметьево.
137
6. Стратегии поиска
Обратный вылет тоже из Шереметьева. Путешествие по золотому кольцу агент
совершал на автобусе. Посетив все города золотого кольца, агент самостоятельно
поехал в близлежащий город Иваново, где задержался и отстал от автобуса. В
отличие, например, от Ярославля, Иваново не имеет прямой автострады,
соединяющей его с Москвой. У агента есть обратный билет на самолет с датой
вылета на следующий день, билет не может быть продлен, да к тому же обратных
билетов вообще нет на ближайшие две недели. Срок визы также заканчивается
через два дня. Отправляясь в поездку, агент ставил перед собой, помимо
туристических, несколько других целей: улучшить знание русского языка,
завязать полезные деловые контакты, написать несколько пейзажей с видами
русской природы и т.п. Но, учитывая серьезность ситуации, главной его
целью теперь стало вовремя добраться до аэропорта Шереметьево, не опоздав
на свой самолет. После формулировки главной цели агент может принимать
во внимание и другие факторы, влияющие на ее достижение.
Прежде всего, следует решить, что мы будем понимать под действиями и
состояниями. Если бы вдруг нам пришло в голову в качестве действий выбрать
такие, как «повернуть руль на 10 градусов» или «продвинуться вперед на 1
метр», то решение задачи на таком уровне детализации стало бы практически
неразрешимой задачей. В нашем случае в качестве действий лучше всего
выбрать переезд из одного города в другой, а в качестве состояний нахождение
агента в том или ином населенном пункте. Целевым состоянием в этом случае
будет нахождение агента в аэропорту Шереметьево (в Москве).
Поиск будет слепым, если агент не имеет никакой информации о дорогах,
ведущих из Иванова в другие города, и будет перебирать все дороги подряд.
И наоборот, его поиск станет направленным, если он ознакомится с картой,
увидит, что Москва лежит на юго-западе от Иванова, и будет пытаться
выбирать дороги, ведущие в юго-восточном или близком к нему направлении.
6.2. Слепой поиск
6.2.1. Поиск в ширину
Одна из самых очевидных стратегий поиска называется поиском в ширину.
Поиск начинается с корневой вершины, определяются все последователи
корневой вершины, затем все последователи каждого из последователей
корневой вершины, далее все последователи каждого из последователей,
найденных на предыдущем шаге, и т.д. до тех пор, пока не будут найдены
все вершины, соответствующие целевым состояниям. Согласно этой
стратегии, вершины глубиной к ищутся после того, как будут найдены все
вершины глубиной Л-1. На рис. 6. 1 показана последовательность нахождения
138
6.2. Слепой поиск
Рис. 6.1. Деревья поиска в ширину при 1=2: нулевая вершина
(дерево глубиной к = 0), дерево после нахождения последователей
нулевой вершины (дерево глубиной Л =1), дерево после нахождения
последователей первой вершины, дерево после нахождения
последователей второй вершины (дерево глубиной к = 2)
вершин при поиске в ширину и при числе последователей каждой вершины,
равном 2. При поиске в ширину сначала рассматриваются все пути, длина
которых равна 1, затем длиной 2 и т.д. Очевидно, что поиск в ширину
удовлетворяет критерию полноты и минимальности, поскольку в процессе
этого поиска рассматриваются все пути, ведущие из начальной вершины
(состояния) во все остальные.
Оценим время и память, затрачиваемые в процессе поиска в ширину.
Будем полагать, что число последователей каждой вершины равно /. Тогда в
начале поиска в ширину мы имеем одну начальную вершину, затем /
последователей, потом /2 последователей и т.д. В общем случае при глубине
дерева поиска, равной к, число вершин, изучаемых в процессе поиска,
равно 1 + / + /2 + /3 + ...+ 1к.
При конкретных значениях / и к по этой формуле можно вычислить
максимальное число вершин дерева поиска, которое может быть получено в
процессе поиска в ширину. Естественно, решение можно найти раньше,
чем будут найдены все последователи. Однако для некоторых задач эта
величина может быть достигнута. Обычно вместо этой формулы употребляют
ее обозначение в виде О(1к), которое называют экспоненциальной оценкой
сложности. Если полагать, что получение каждого последователя требует
одной единицы времени, то O(lk) является оценкой сложности по времени.
В процессе поиска в ширину каждая вершина дерева должна сохраняться до
получения требуемого решения. Если полагать, что для этого сохранения
требуется единица памяти, то та же формула является одновременно и оценкой
сложности по памяти для поиска в ширину.
139
6. Стратегии поиска
Посмотрим, что это будут за величины при I = 10 для различных значений к
(табл. 6.1). Предполагается, что 1000 вершин-последователей могут быть
получены за 1 с, и что одна вершина требует 100 байт памяти. Эти значения
соответствуют средним затратам времени и памяти, требуемым для решения
многих иллюстративных задач типа головоломок. Из табл. 6.1 можно сделать
два важных вывода. Во-первых, рост требований к памяти для решения задач
поиском в ширину гораздо более серьезная проблема, чем рост требований
ко времени решения тех же задач. Так, например, вполне приемлемо
подождать решения задачи в течение 18 мин при / = 6, но необходимость
наличия 111 Мбайт памяти для решения таких сравнительно простых задач
кажется слишком высокой ценой. Во-вторых, для задач, в которых / > 10,
помимо катастрофического увеличения требований к памяти, наблюдается
стремительный рост временных затрат, не позволяющий решать реальные
задачи с помощью поиска в ширину даже на современных мощных
компьютерах. Это приводит к следующему заключению: Стратегии поиска,
имеющие экспоненциальные оценки сложности решения задач по времени
или памяти, в частности стратегия поиска в ширину, нельзя использовать
для решения задач большой размерности, т.е. задач, у которых 1 > 10.
6.2.2. Монотонный поиск в ширину
Поиск в ширину обеспечивает нахождение целевого состояния, находящегося
на минимальной глубине дерева поиска. Однако минимальность цены пути
при этом не гарантируется. Монотонный поиск в ширину является некоторой
модификацией поиска в ширину, заключающейся в том, что в процессе поиска
в ширину всякий раз, когда определяется очередная вершина-последователь,
одновременно вычисляется цена пути, ведущего в эту вершину. Эта цена пути
Таблица 6.1
Глубина дерева Количество вершин Требуемое для поиска время Требуемая для поиска память
0 1 1 миллисекунда 100 байт
2 111 0,1 секунды 11 килобайт
4 11.111 11 секунд 1 мегабайт
6 106 18 минут 111 мегабайт
8 10" 31 час 11 гигабайт
10 10'° 128 дней 1 терабайт
12 10'2 35 лет 111 терабайт
14 ю14 3500 лет 11111 терабайт
140
6.2. Слепой поиск
используется для оценки целесообразности поиска вершин, продолжающих
данный путь, сравнением с другими, уже полученными ценами путей. Если
цена данного пути меньше цен всех этих путей, то поиск вершин на этом
пути продолжается. В противном случае поиск вершин на этом пути
откладывается, а продолжается поиск вершин на путях, цена которых меньше
данного. Когда на каком-либо пути будет достигнута целевая вершина, поиск
на путях, цена которых выше цены этого пути, вообще прекращается. Все
пути, имеющие одинаковую минимальную цену путей, ведущих в целевую
вершину, являются решением задачи.
Вернемся к задаче поиска пути из Иванова в Москву. На рис. 6. 2, б
схематически показана карта участка дорог, ведущих из Иванова в Москву. Каждая
из дорог, ведущих из одного пункта в другой, снабжена числовой оценкой
действия. На рис. 6. 1, а показана последовательность монотонного поиска в
ширину. Каждая из вершин помечена ценой пути, ведущего в эту вершину.
Рис. 6. 2. Задача нахождения маршрута из Иванова в Москву:
а — порядок монотонного поиска в ширину. Каждая вершина помечена ценой
пути, ведущим в нее из начальной вершины (снаружи вершины) и номером ее
получения з процессе поиска (внутри вершины). На последнем шаге монотонного
поиска в ширину найдена целевая вершина с ценой пути, равным 10;
б— пространство состояний, иллюстрирующее цену действий, соответствующую
участкам пути между городами
141
6. Стратегии поиска
6.2.3. Поиск в глубину
При поиске в глубину, начиная с корневой вершины (корневая вершина
находится на уровне 1), рассматриваются все инцидентные ей вершины уровня
2, начиная слева направо. Если удается найти среди них все целевые вершины,
то на этом поиск прекращается. Если среди них не удается найти все целевые
вершины, а максимальная глубина дерева еще не достигнута, то берется самая
левая вершина уровня 2 и рассматриваются все инцидентные ей вершины уровня
3 слева направо. Если после этого все целевые вершины все еще не найдены,
то берется самая левая вершина из уровня 3. Затем снова рассмат-риваются все
инцидентные ей вершины уровня 3 слева направо и так до тех пор, пока либо
не будут найдены все целевые вершины, либо достигнута максимальная глубина
дерева, на которой в соответствии с рассматриваемой процедурой просмотрены
все вершины, инцидентные самой левой вершине предыдущего уровня, и все
целевые все еще не найдены. В последнем случае осуществляется подъем по
дереву на один уровень вверх, выбор на этом уровне самой левой вершины,
инцидентные которой вершины следующего уровня еще не рассмотрены, и
поиск дальше среди целевых вершин по тому же принципу. И так до тех пор,
пока все вершины дерева не будут рассмотрены. На рис. 6.3 показана
последовательность поиска в глубину для дерева с тремя уровнями и степенью
ветвления 2. Вершины на этом рисунке пронумерованы в соответствии с
последовательностью их просмотра.
Рис. 6.3. Стратегия поиска в глубину
142
6.2. Слепой поиск
Требования к объему памяти при поиске в глубину существенно меньше,
чем при поиске в ширину. Как видно из рис. 6. 3, в памяти необходимо
хранить все вершины, инцидентные вершинам на пути из корневой вершины
к любой другой, соседние вершины которой рассматриваются. Очевидно,
что при степени ветвления / и глубине дерева к оценка сложности по памяти
при поиске в глубину равна О(1к). Оценка сложности по времени для поиска
в глубину остается такой же, как и при поиске в ширину, а именно О(1к).
Для задач, дерево поиска для которых конечно, а число целей сравнительно
невелико, поиск в глубину может оказаться эффективным, так как имеет шанс
найти это небольшое число целей без просмотра всех вершин.
Для задач, имеющих большую или даже бесконечную глубину дерева, поиск
в глубину может оказаться крайне неэффективным, так как будет стремиться
все время в глубину, в то время как цель может оказаться близкой к корню
дерева, но на том пути, который еще не был просмотрен. Поиск же все время
уходит вниз и в случае бесконечной глубины дерева может никогда не вернуться
назад к просмотру вершин, среди которых находятся целевые. Вследствие этого
следует избегать использования поиска в глубину для решения задач с большой
или бесконечной глубиной дерева. Поиск в глубину, таким образом, нельзя
считать ни полным, ни оптимальным.
6.2.4. Ограниченный поиск в глубину
Ограниченный поиск в глубину является частным случаем поиска в глубину.
При этом поиске используется ограничение на глубину поиска. Например,
при поиске маршрута из Иванова в Москву при наличии информации о числе
населенных пунктов, которые могут встретиться на этом пути, глубину поиска
можно ограничить числом этих населенных пунктов. При ограниченном поиске
в глубину, как только достигается уровень, совпадающий с этим числом,
происходит возврат назад так же, как это делается при обычном поиске в
глубину. Ограниченный поиск в глубину полный, если ограничение на глубину
поиска выбрано таким образом, чтобы обеспечить просмотр всех вершин дерева.
Оценки сложности по времени и памяти при ограниченном поиске в глубину те
же, что и при обычном поиске в глубину.
6.2.5. Итеративный поиск в глубину
При ограниченном поиске в глубину сложность поиска зависит от выбора
ограничения. Например, при поиске маршрута можно использовать не число
всех населенных пунктов в районе поиска подходящего маршрута, а
максимальное число населенных пунктов, которые могут встретиться на каждом
из возможных маршрутов. Это число называют обычно радиусом поиска. Знание
радиуса поиска приводит к более эффективному ограниченному поиску в
глубину. Однако в большинстве задач радиус поиска не известен до тех пор,
пока задача не будет решена. Итеративный поиск в глубину использует
стратегию, основанную на итеративном применении ограниченного поиска в
143
6. Стратегии поиска
Рис. 6.4. Итеративный поиск в глубину
глубину сначала для радиуса поиска, равного 0, затем 2, после этого 3 и т.д.
Четыре итерации такого поиска для бинарного дерева иллюстрирует рис. 6. 4.
Итеративный поиск в глубину может показаться очень неэффективным,
поскольку некоторые вершины просматриваются многократно. Однако для
многих задач подавляющая доля вершин находится на низком уровне.
Напомним, что оценка сложности по времени при ограниченном поиске в
глубину вычисляется по формуле
0(/*) = 1 + / + /2 +....+ /*-2 + /*_| + /*.
Например, для / = 10, к = 5 будем иметь 0(/А) = 111111. При итеративном
поиске на глубину к вершины глубины к просматриваются один раз, глубины
к-\ — два раза, глубины к-2 — три и т.д. Корневая вершина просматривается
к + 1 раз. Таким образом, оценка сложности по времени при итеративном
поиске в глубину вычисляется по формуле
0(/Л) = {к + 1) /° + (к) /' + (Аг-1) /2+ .... + 3 Г2 + 2 /*-' + 1 /*.
Для / = 10, к = 5 будем иметь 0(/*) = 123456. По сравнению с оценкой
сложности по времени для ограниченного поиска в глубину сложность по
времени для итеративного поиска в глубину возросла только на 11%. Из
формулы, приведенной выше, видно, что чем выше степень ветвления,
тем ниже доля сложности, получающейся за счет повторного просмотра
вершин. Но даже для случая, когда 1 = 2, сложность по времени итеративного
поиска в глубину только в два раза превосходит сложность по времени простого
поиска в глубину. Это означает, что оценка сложности по времени
144
6.3. Направленный поиск
итерационного поиска в глубину по-прежнему равна O(Jk), а сложность по
памяти — O(lk). Итеративный поиск в глубину достаточно хорошо себя
зарекомендовал для задач с большим пространством поиска и неизвестной
его глубиной.
6.2.6. Двунаправленный поиск
Идея двунаправленного поиска основана на использовании сразу двух
стратегий — прямого поиска от корневой вершины и обратного от целевой
вершины. Процесс поиска прекращается, когда оба этих процесса встретятся
на середине глубины. Если считать, что степень ветвления при прямом и
обратном поиске одинакова, то оценка сложности по времени двунаправленного
поиска будет 0(2М/2) = 0(/^). Эта оценка существенно лучше, чем аналогичная
для рассмотренных стратегий поиска. Однако все это в идеале, т.е. при
условии, что цель только одна, степень ветвления и сложность нахождения
последователей и предшественников одна и та же. При решении практических
задач, однако, это условие может нарушаться. Кроме этого могут возникать и
другие проблемы. Например, установление факта появления одной и той же
вершины в той и другой половине поиска может потребовать значительных усилий
и составить значительную долю сложности. Если все эти проблемы можно решить
за постоянное время, не зависящее от числа вершин, то оценка сложности по
времени двунаправленного поиска останется равной 0(/*/2).
6.2.7. Сравнение стратегий поиска
Характеристики шести рассмотренных стратегий, где / — степень
ветвления, к — глубина поиска, d— максимальная глубина дерева поиска,
г — ограничение на глубину поиска, сведены в табл. 6.2.
Таблица 6.2
Критерии Поиск
В ширину Монотонный в ширину В глубину Ограни- ченный в глубину Итера- тивный в глубину Двуна- правлен- ный
Время 1к 1к ld 1’ 1к
Память 1к 1к ld 1’ 1к /V2
Оптималь- ность Да Да Нет Нет Да Да
Полнота Да Да Нет Да, если г > к Да Да
145
6. Стратегии поиска
6.3. Направленный поиск
Как было показано в предыдущем разделе, все стратегии слепого поиска
обладают экспоненциальными оценками сложности по времени поиска, а
некоторые и по памяти, и, вследствие этого, пригодны для решения
сравнительно небольших задач. В стратегиях слепого поиска знания,
используемые при выборе очередной вершины, определяют только общий
порядок выбора и никак не учитывают качество выбора, например, по
сложности поиска целевой вершины. В стратегиях направленного поиска
знания, используемые для выбора очередной вершины, более глубокие и
используют специальные функции, называемые критериями. Если для каждой
вершины Ь, участвующей в поиске, критерий может быть вычислен, а множество
всех вершин упорядочивается по этому критерию, то выбор очередной вершины
производится в соответствии со значением этого критерия. Чем лучше значение
критерия (например, выше или ниже), тем предпочтительнее выбор. Иными
словами, из множества альтернативных вершин выбирается та, для которой
критерий имеет наилучшее значение. Поэтому стратегии выбора подобного типа
называются стратегиями выбора по наилучшему критерию. Критерии обычно
выбираются таким образом, чтобы оптимизировать сложность поиска, найти
оптимальное решение или достичь того и другого. В настоящем разделе
рассмотрим некоторые стратегии направленного поиска, при котором
используются дополнительные знания о среде, позволяющие понизить сложность
поиска. Рассмотрим, как осуществляется направленный поиск при решении
оптимизационных задач.
6.3.1. Поиск по критерию близости к цели
Критерием близости к цели обычно является числовая функция h(b) > О,
вычисляемая для вершины b и характеризующая близость этой вершины к
целевой. При использовании критерия близости к цели, начиная с корневой
вершины, просматриваются все соседние ей вершины, выбирается та, для
которой h(b) минимальна, и все повторяется вновь для выбранной вершины.
И так до тех пор, пока не будет достигнута целевая вершина, для которой
h(b) = 0, т.е. выбирается та вершина, которая ближе всего находится к
цели. Вид критерия близости к цели зависит от среды (является проблемно
зависимым).
Чтобы получить достаточно полное представление об этом критерии, вернемся
к задаче поиска маршрута из Иванова в Москву. Критерием выбора в этом случае
будет минимальное расстояние по прямой (кратчайшее расстояние) от вершины
(населенного пункта) до Москвы. Естественно, чтобы значение критерия могло
быть вычислено, необходимо иметь карту или какой-либо другой источник
информации, содержащий сведения о кратчайших расстояниях от населенных
пунктов до Москвы. На рис. 6. 5 показана последовательность поиска по критерию
близости к цели для примера с поиском маршрута из Иванова в Москву,
использованного при рассмотрении монотонного поиска в ширину.
146
6.3. Направленный поиск
Иваново
Рис. 6.5. Поиск по критерию близости к цели
На первом шаге вычисляется кратчайшее расстояние от корневой вершины
(Иваново) до Москвы (А = 230). На втором шаге просматриваются все вершины
(города), в которые ведет дорога из Иванова и вычисляется кратчайшее
расстояние h от этих городов до Москвы. По этому критерию ближайшим по
прямой до цели (Москвы) оказывается Юрьев-Польский (А = 140). На третьем
шаге просматриваются все вершины, в которые ведет дорога из Юрьева-
147
6. Стратегии поиска
Польского. Для них снова вычисляется кратчайшее расстояние h до Москвы.
Кратчайшим оказывается расстояние от Киржача (А = 76). Наконец, на
последнем шаге вновь просматриваются все вершины, в которые ведет дорога
из Киржача, а также вычисляется кратчайшее расстояние до этих городов. Среди
этих городов оказывается город с кратчайшим расстоянием h = 0, т.е. целевая
вершина (Москва). На этом поиск по критерию близости к цели завершается.
Поиск по критерию близости к цели является поиском в глубину, но с
выбором на каждом шаге единственной вершины, от которой начинается
следующий шаг. Недостатки этой стратегии те же, что и для слепого поиска
в глубину, а именно, она неоптимальная и неполная, поскольку может
случиться, что поиск пойдет по бесконечному пути и никогда не вернется
назад. Оценка сложности по времени этой стратегии поиска равна 0(/Д, где
d— максимальная глубина пространства поиска.При поиске по критерию
близости к цели приходится хранить все вершины, рассматриваемые при
поиске. Поэтому оценка сложности по памяти для этой стратегии та же, что
и оценка сложности по времени. Если критерий близости к цели выбран
достаточно удачно, то сложность поиска может быть существенно уменьшена.
6.3.2. Поиск по критерию цены пути (А* - поиск)
Обозначим g(b) — критерий цены пути из корневой вершины в вершину
b, a h(b) — уже рассмотренный критерий близости к цели. Пусть оба критерия
имеют одну и ту же размерность. Функцию /(A) = g(b) + h(b) можно считать
критерием цейы пути из корневой вершины в целевую. С помощью этого
критерия можно находить пути с минимальной ценой. Рассмотрим стратегию
поиска на основе этого критерия и покажем, что она будет полна и
оптимальна, если ввести небольшие ограничения на критерий h(b). Идея
этого ограничения состоит в том, чтобы выбирать критерий h(b) таким
образом, чтобы не переоценивать близость к цели, т.е. не выбирать значение
h(b) меньше, чем оно есть на самом деле. Критерий h(b), выбираемый таким
образом, называется допустимым. Стратегия поиска, использующая критерий
/(А) и допустимый критерий h(b), известна как А* - поиск. Критерий близости
цели h(b), использованный в примере с поиском маршрута из Иванова в Москву,
является типичным примером допустимого критерия, поскольку не может быть
пути из одного населенного пункта в другой короче, чем кратчайший путь. На
рис. 6. 6 показаны первые четыре шага поиска пути из Иванова в Москву с
использованием критерия /(b) в А*- поиске. Заметим, что в результате
этого поиска, в отличие от поиска только по критерию близости к цели,
рассмотренного в предыдущем разделе, выбран путь к Москве не через Юрьев-
Польский, а через Владимир, хотя Юрьев-Польский ближе к Москве, чем
Владимир. Такой выбор объясняется тем, что цена пути g(b) от Иванова до
Юрьева-Польского выше, чем до Владимира вследствие очень плохой дороги.
Дальнейший выбор маршрута можно проследить по рисунку, где на любом
пути от корневой вершины значение критерия /(/>) нигде не уменьшается при
переходе к рассмотрению очередной вершины. Это не случайность и справедливо
148
6.3. Направленный поиск
Рис. 6.6. Поиск по критерию цены пути (А* - поиск)
почти для всех допустимых критериев h(b) близости к цели. Критерии/(/>), для
которых имеет место подобное свойство, называются монотонными. Если
монотонность нарушается, то путем незначительной коррекции это нарушение
может быть устранено. Рассмотрим, например, пару вершин Ь, Ь', где b
предшественник, а Ь' — последователь. Предположим, что g(b) = 3, h(b) = 4.
Тогда f(b) = 7, т.е. цена пути через вершину b самое меньшее равна 7.
Предположим также, что g(b') = 4, /i(b') = 2, т.е. f(b') = 6 . Ясно, что в
этом случае критерий /(/>) не является монотонным. К счастью, благодаря
тому, что любой путь через Ь’ является также путем через Ь, цена пути /(/>') =
6 является бессмысленной. Поэтому каждый раз, как рассматривается какая-
либо вершина Ь' и оказывается, что ее цена пути f(b') < f(b), мы полагаем,
что /(/>') = f(b), т.е. f(b') = max (f(b), fib')).
Таким способом немонотонность может быть всегда устранена, и критерий
f(b) никогда не будет уменьшаться вдоль одного и того же пути при условии,
что h(b) допустимое. Если же f(b) никогда не уменьшается вдоль одного и
того же пути, начинающегося от корневой вершины, то на пространство
состояний можно наложить контуры, каждый из которых охватывает
множество вершин Ь, для которых значение критерия f(b) меньше
определенной величины с. Процесс поиска можно представить как переход
149
6. Стратегии поиска
от просмотра еще не просмотренных вершин какого-либо внутреннего
контура, для всех вершин которого имеет место f(b{) < с, к просмотру
вершин некоторого внешнего контура, для всех вершин Ь2 которого имеет
место/(/>2) < с2 и < с2 . Это продолжается до тех пор, пока внутри очередного
контура не окажется целевая вершина с h(b) = 0. При удачном выборе
критерия f(b) контуры как бы растягиваются в сторону целевой вершины,
фокусируясь вокруг оптимального пути. Обозначим с* цену оптимального
пути. Тогда можно утверждать следующее:
А*- поиск просматривает вершины с /(/>) < с*.
А*- поиск осуществляет направленный просмотр вершин, стремясь к
просмотру вершин контура, для которых имеет место/(/>) = с*.
Решение, получаемое с помощью А*- поиска, является оптимальным,
поскольку находится вершина с максимальным значением f(b), а
следовательно, и максимальным g(/>), так как А(/>) = 0. А*- поиск является
также полным, поскольку увеличивая постепенно значение критерия f(b),
мы должны, в конце концов, найти путь к целевой вершине. Заметим также,
что для данного критерия /(/>) не существует никакой другой процедуры
поиска, которая давала бы более оптимальные решения, чем А*- поиск.
Все эти утверждения требуют более строгих доказательств, которые мы здесь
не приводим. Оценки сложности по времени и памяти для А*- поиска
аналогичны оценкам для поиска по критерию близости цели.
На идее А*- поиска построено много других методов поиска, учитывающих
особенности конкретной среды, которые влияют на выбор критериев, и
различные ограничения, например по доступным ресурсам (времени
выполнения и доступной памяти).
6.3.3. Оптимизирующий итеративный поиск
Во многих задачах поиск целевого состояния (состояний) в пространстве
состояний ставится как задача нахождения такого состояния (состояний),
которое в определенном смысле наилучшее (оптимальное). При этом не имеет
особого значения цена пути нахождения цели, если эта цель может быть
достигнута за приемлемые затраты времени и памяти. Идея оптимизирующего
итеративного поиска станет понятной, если полагать, что состояния — это
точки на поверхности некоторого горного ландшафта. Чем выше точка находится
над уровнем моря, тем лучше (оптимальнее) состояние, которое она
представляет. Точки, соответствующие пикам, являются оптимальными
точками. Задачей оптимизирующего итеративного поиска является такой
порядок просмотра точек, или иначе такое движение по поверхности ландшафта,
при котором в конце концов достигаются (находятся) оптимальные точки.
Имеется большое разнообразие процедур оптимизирующего итеративного
поиска. Одной из таких процедур является градиентный поиск. Рассмотрим
суть этой процедуры.
Идея градиентного поиска чрезвычайно проста — двигаться в направлении
подъема вверх, начиная с некоторого начального состояния. Дерево поиска
не хранится, а сохраняется только последнее найденное состояние b и оценка
150
Вопросы и упражнения
его качества L(b). Если попадаются несколько состояний с одинаковой оценкой
качества, то, как правило, выбирается одно из них. Градиентный поиск в
чистом виде обладает тремя известными недостатками.
Если вершин несколько, то поднявшись на одну из них, процесс поиска
остановится, полагая, что цель достигнута, хотя достигнутая вершина является
всего лишь локальным оптимумом и далека от наилучшей.
Если ландшафт имеет плато, то процесс поиска по нему становится
случайным.
Если ландшафт имеет гребни (хребты) со слабым наклоном, то легко
достигнув гребня, процесс поиска может очень долго идти по гребню, пока
не достигнет оптимальной вершины.
После остановки процесса градиентного поиска начинается следующая
итерация с другого начального состояния. Найденное оптимальное состояние
сохраняется до тех пор, пока не будет найдено лучшее. Этот итеративный
процесс поиска осуществляется конечное число раз или пока не будет найдено
устраивающее решение.
Ясно, что если провести достаточное число подобных итераций, то оптимальное
решение, в конце концов, будет найдено. Успех градиентного поиска сильно
зависит от вида пространства состояний. Если число локальных минимумов
невелико, то оптимальное решение будет найдено сравнительно быстро.
Процедуры градиентного поиска могут отличаться способом выбора очередной
вершины в процессе подъема на вершину, выбором очередной вершины для новой
итерации и т.д.
Вопросы и упражнения
1. В чем состоит главное отличие между слепым и направленным поиском?
2. Каковы критерии качества стратегий поиска?
3. Что такое сложность поиска?
4. Какие оценки сложности поиска чаще всего используются?
5. Выберите начальное состояние, целевое состояние, действия и цену действия
для каждой из следующих задач (расскажите, какую стратегию вы примените для
решения каждой из них):
а) найдите телефонный номер жителя Москвы Ивана Ивановича Иванова при
условии, что в телефонном справочнике все телефоны упорядочены сначала по
фамилиям, затем внутри одинаковых фамилий по именам и в последнюю очередь по
отчествам;
б) та же самая задача, но без отчества;
в) вы имеете четыре цветные краски и ваша задача — раскрасить карту таким
образом, чтобы никакие два соседних субъекта федерации не были раскрашены одним
цветом. Выберите стратегию раскраски и покажите, что раскраска с помощью этой
стратегии возможна;
г) вы потерялись в незнакомом маленьком городе и хотите вернуться на автобусную
станцию, откуда вы начали маршрут по городу. У вас нет никакой карты. Все жители
уже заперлись в своих домах, поскольку уже поздно, и спросить, куда идти, уже не у
кого. Какую стратегию поиска вы выберите?
151
6. Стратегии поиска
6. Сформулируйте известную задачу об охотнике, козе, волке, капусте и лодке
в терминах состояний и используйте поиск в ширину для нахождения самого короткого
по времени решения.
7. Придумайте среду, для которой итеративный поиск в глубину будет хуже, чем
просто поиск в глубину.
8. Сформулируйте процедуру двунаправленного поиска в ширину в том и другом
направлении таким образом, что в каждом направлении в каждую единицу времени
находится по одной вершине.
9. Было показано, что допустимый критерий h(b) позволяет получить
неуменьшающийся критерий f(b'). Можно ли показать, что монотонность f(b) всегда
влечет допустимость h(by>
10. Можно ли построить процедуру двунаправленного А*-поиска? Если можно,
то при каких условиях? Опишите процедуру поиска.
11. Некоторая среда имеет конечное множество состояний, каждое из которых
определяется набором значений п двоичных переменных х1; ..., х На множестве этих
переменных определена целочисленная функция/(хр ..., хл). Переходы возможны только
между соседними состояниями (состояниями, отличающимися значением только одной
переменной). Выберите подходящую стратегию поиска наборов значений переменных
хр ..., хл, на которых функция /(хг ..., хл) принимает максимальное значение.
7. СИТУАЦИОННОЕ ОПИСАНИЕ СРЕДЫ
В этой главе рассмотрены некоторые свойства ситуационной динамической
среды и их представление на языке логики предикатов первого порядка.
Логика предикатов первого порядка — это средство представления знаний
и рассуждений (см. гл. 1). Однако сама по себе она является общим
инструментом и не дает рекомендаций по выбору конкретных выразительных
средств (фактов, словаря, аксиом, целей) для описания знаний о конкретной
предметной области (среде). Для этих целей обычно применяют то или иное
ситуационное исчисление, имеющее свой выразительный язык.
Выразительные средства языка, как правило, зависят от вида среды и обычно
содержат ряд разделов.
Ситуационному исчислению в целом и языкам ситуационных исчислений и
посвящены следующие главы. При решении реальных задач дело имеют не с
физической средой, а с ее моделью. Как уже говорилось в главе 5, с точки
зрения агента физическая среда и модель среды неразличимы. Модель среды
сложно представить или описать на каком-либо языке. Мы будем использовать
язык логики предикатов первого порядка. В настоящей главе рассмотрено не
описание конкретной среды, а наиболее типичные языковые конструкции,
используемые для представления моделей сред.
7.1. Базовые понятия ситуационной модели
Формирование базовых понятий ситуационной модели осуществляется на
основе логики предикатов первого порядка с использованием ее синтаксиса
и семантики. Поэтому все базовые понятия ситуационной модели строятся
на основе термов, атомов, литералов, функций и формул логики предикатов
первого порядка. Если синтаксис какого-либо базового понятия совпадает с
синтаксисом в логике предикатов первого порядка, его семантика также
совпадает с семантикой аналогичного понятия в логике предикатов первого
порядка. Несмотря на то что логика предикатов в четвертой главе рассмотрена
достаточно подробно, некоторые понятия уточним для удобства чтения главы.
153
7. Ситуационное описание среды
7.1.1. Объекты
Объекты реального или вымышленного мира (последние называют
ментальными объектами) обозначают прописными буквами, словами или
предложениями русского языка, начинающимися с прописной буквы,
выделяемыми курсивом и написанными слитно вследствие употребления символа
подчеркивания между словами. Например, С, Стол, Столдеревянный.
1А.2. Объектные переменные
Объектные переменные или просто переменные определяют объекты и их
обозначают строчными буквами, словами или предложениями русского языка,
начинающимися со строчной буквы, выделяемыми курсивом и написанными
слитно вследствие употребления символа подчеркивания между словами.
Например, с, стол, стол деревянный.
1А.З. Категории
Часто рассуждения ведутся не на уровне конкретного объекта, а на уровне
множества, или категории, к которой этот объект относится. Имеется два
основных способа представления категорий в логике предикатов первого порядка.
Первый способ связан с использованием одноместного предиката,
характеризующего свойство объектов, относящихся к данной категории.
Предикат является истинным, если значение его аргумента совпадает с одним
из объектов, обладающих данным свойством или, иначе, принадлежащим
данной категории. Например, одноместный предикат томатыДеБарао (х)
истинен, когда х есть томат сорта Де Барао, т.е. предикат истинен, когда х
принадлежит множеству томатов сорта Де Барао, обозначаемых константами
X, Х2, Хт. Таким образом, этот предикат представляет категорию томатов сорта
Де Барао.
Второй способ основан на материализации категории и заключается в
представлении категории как объекта. В этом случае, например, категория
Томаты_ДеБарао выступает как объект, являющийся множеством всех томатов,
и мы можем использовать выражение Томаты_Де_Барао (Xt, Х2, ..., Хт) для
того, чтобы сказать, что данная категория состоит из конкретных сортов помидор
X i = 1, ..., т. Материализация категории позволяет рассуждать о самих
категориях, а не только об их членах, поскольку категория ТоматыДеБарао
выступает как объектная константа, обозначающая конкретный объект —
категорию томатов определенного сорта. Материализация категорий позволяет
также вводить переменные, обозначающие категории, и рассуждать с
использованием этих переменных.
Мы будем использовать оба способа представления категорий. Категории
выполняют важную роль для описания, систематизации и наследования
признаков объектов. Приведенные ниже примеры дают достаточно полное
представление о возможностях подобного описания.
154
7.1. Базовые понятия ситуационной модели
Объект х является элементом категории Томаты Де Барао (A), Х2, Ху.
элемент категории (х, Томаты_Де_Барао) = х = Х3 v х = Х2 v ... v х = Хт.
Категория Томаты_Де_Барао (Хр Х2,..., Хт) является элементом категории
Томаты, а категория Томаты — элементом категории Овощи'.
Овощи (Томаты (Томаты_Де_Барао (Xt, Х2, Ху Томаты Микадо
(У[, У2, Уп)), Огурцы (Изящные (U}, U2, ..., U), Вязниковские (Ир V2, И)).
Все элементы категории Томаты_Де_Барао имеют общие свойства
(являются красными и круглыми):
(V х) элементкатегории (х, Томаты_Де_Барао) гэ красный (х) л круглый (х).
Все элементы категории Арбузы могут быть распознаны по некоторым
свойствам:
(V х) красныйвнутри (х) л зеленый снаружи (х) л
/\ элемент-Категории (х, Бахчевые) гэ элемент_категории (х, Арбузы).
Категория Томаты имеет свойства томатов, районированных в
Московской области
томаты_районированные_в_Московской_области (Томаты).
Все категории, элементы которых обладают определенными свойствами,
входят в категорию Томаты.
(V х) (V у) красный внутри (х) л зеленый_снаружи (х) л
л элемент категории (х, у) зэ элемент категории (у, Томаты).
Категории к, и к2 не имеют общих элементов:
(V к к2) не_имеют_общих_элементов (kv к2) = (V э2)
(элемент-Категории (эр к.) л элемент_категории (э2, к2) лэ,/ э,).
Категории /ср к2, к} входят в одну категорию к4 (являются частью категории к4):
(V Кр к2, к3, к4) входят в одну-Категорию (кх, к2, к3, к4) = (V эх, э2, э3)
(элемент-Категории (эр /с^ л элемент категории (э2, к2) л
155
7. Ситуационное описание среды
л элемент категории (э3, к3) л (3 э4, э5, э6) (элемент-Категории (эА, кА) л
л элемент_категории (э5, к4) л элементкатегории (э6, к4) л Э] =
= ЭлЭ—.ЭгА = 3,.
4 2 5 3 6
Категории кх, к2 являются разбиением категории к3 на две категории, не
имеющие общих элементов, объединение которых совпадает с категорией к}:
(V кх, к2, к3) разбиение (кх, к2, /с) = не имеют общих элементов (к}, к2) л
л входят в-Одну категорию (кр к2, к}) л (V э) [элемент_категории (э, к}) о
о элемент категории (э, ks) v элемент категории (э, к2)].
Необходимые и достаточные условия для вхождения объекта х в одну и ту
же категорию Инженеры.
(V х) элемент категории (х, Инженеры) = высшее_образование (х) л
л закончил технический университет (х).
7.1.4. Сортовые категории
Для удобства и выразительности описания моделей сред вводят особые, заранее
предопределенные, непересекающиеся ни с какими другими категории объектов.
Чаще всего объекты этих категорий являются вымышленными. Обычно эти особые
категории объектов называют сортовыми категориями, или сортами.
7.1.5. Стандартные предикаты
Стандартными предикатами называют заранее определенные предикаты,
аргументы (термы), истинностные значения которых заранее предопределены.
7.1.6. Библиотечные функции
Библиотечными функциями называют заранее определенные функции, область
определения и область значений которых заранее предопределены. Собственно
фиксация сортовых категорий, стандартных предикатов, библиотечных функций
и вид ряда аксиом, описывающих отличительные свойства среды, и составляют
суть модели среды. Рассмотрим основные сортовые категории, стандартные
предикаты, библиотечные функции и вид некоторых аксиом, используемых
для описания ситуационных моделей сред.
156
7.1. Базовые понятия ситуационной модели
7.1.7. Микроситуации
Каждая сортовая категория микроситуаций содержит множество
вымышленных объектов, называемых микроситуациями. Среда может
находиться только в одной микроситуации данной категории. В то же время
среда может находиться сразу в нескольких микроситуациях различных
категорий. Микроситуация может изменяться при определенных действиях.
О микроситуациях приходится рассуждать. Переменная, соответствующая
микроситуации, обозначается символом у. Каждая категория микроситуаций
может быть материализованной и обладать всеми чертами обычного объекта.
Стандартный предикат микроситуация (у) вводится для того, чтобы определить
свойство объекта находиться в микроситуации у данной сортовой категории,
т.е. он истинен, когда объект находится в микроситуации у.
Микроситуация используется в качестве аргумента в различных предикатах.
Одним из таких предикатов является стандартный предикат достижима
(А, у). Он истинен, когда переменная у принимает определенное значение
из своей категории микроситуаций и этому значению соответствует объектная
константа R.
7.1.8. Состояния
В реальных задачах, которые мы хотели бы решать, число микроситуаций
может быть велико, причем приходится иметь дело с различными их
комбинациями, т.е. определять совокупные свойства наборов микроситуаций.
Так, например, одним из таких наборов является внешнее состояние, или
макроситуация', набор значений микроситуаций, в который входит по одной
микроситуации из каждой категории. Понятно, что число макроситуаций в
категории макроситуаций равно мощности декартова произведения всех
категорий микроситуаций. Понятно также, что в случае использования одной
категории микроситуаций, микроситуация является одновременно
макроситуацией. Внутренним состоянием среды называют набор значений
всех объектных переменных, не являющихся микроситуациями. Полным
состоянием среды называют пару внутреннее состояние — внешнее состояние.
Таким образом, внутреннее и внешнее состояния являются частью полного.
Среда всегда находится в одном из полных состояний, которые чаще всего
будем называть просто состояниями. Микро- и макроситуации используют
для того, чтобы наводить определенный порядок на множестве состояний и
рассуждать о состояниях среды с учетом этого порядка.
Стандартный предикат макроситуация (s) вводят для указания того, что среда
находится в макроситуации s. Макроситуацию, так же как и микроситуацию,
используют в качестве аргумента в различных предикатах. Одним из таких
предикатов является стандартный предикат достижима (R, s). Он истинен,
когда макроситуация s принимает определенное значение и этому значению
соответствует объектная константа R.
157
7. Ситуационное описание среды
7.1.9. Действия
Действия совершаются над объектами. В результате изменяются значения
объектных переменных, а следовательно, и состояния среды. Так, например,
если мы имеем такой объект, как автомобиль, который может быть заведен
или незаведен, то мы можем ввести действие завести (автомобиль), в
результате которого он заводится. Если при описании среды не используются
такие понятия, как микроситуация или макроситуация, то условие
совершения и результат этого действия можно записать в виде
-I заведен (автомобиль) л завести (автомобиль) о заведен (автомобиль).
Если же мы хотим, чтобы действия совершались только тогда, когда среда
находится в определенной макроситуации, то, обозначив ее символом 5, а
действие — символом d, условие совершения и результат этого действия можно
записать в виде
макроситуация (s.) л заведен (автомобиль) л действие (d)^>
макроситуация (s.) л заведен (автомобиль).
В обеих приведенных формулах использован предикат заведен (автомобиль).
Во многих случаях более удобно не вводить подобного рода предикаты, а
использовать категории свойств объектов. Например, в данном случае такой
категорией может быть (Заведен, Незаведен). Тогда, используя стандартный
предикат достижима, условие совершения и результат действия можно
записать в виде
достижима (Незаведен, s.) л действие (d) з достижима (Заведен, 5).
Еще один вариант формулы можно получить, если ввести функцию переход
(d, s). Значением этой функции является одна из макроситуаций среды, в
которую она переходит в результате действия d. Для нашего примера с
автомобилем можно считать, что s = переход (d, s.). С использованием этой
функции вышеприведенную формулу можно переписать в следующем виде:
достижима (Незаведен, s:) л действие (d) о
z> достижима (Заведен, переход (d, s.)).
7.1.10. Ситуация
Понятие ситуации является центральным в ситуационном исчислении. В
принципе, можно было бы его не вводить, а рассуждать в терминах состояний,
что иногда и делают. Однако, как уже отмечалось, для реальных задач большой
размерности состояния, необходимые для описания модели среды, даже
невозможно перечислить. Кроме того, во многих задачах нет необходимости знать
значение полного состояния. Достаточно знать, что наступило следующее
158
7. 7. Базовые понятия ситуационной модели
состояние и значения только некоторых переменных этого состояния. Каждая
ситуация по смыслу эквивалентна даже не одному состоянию, а какому-либо
подмножеству множества всех состояний среды, и задается не в виде перечисления
этого подмножества, а в виде формул предикатов первого порядка, определяющих
условия наступления этой ситуации.
Схема описания знаний и последующих рассуждений на основе этих знаний
с использованием ситуаций выглядит следующим образом. Есть некоторая
начальная ситуация, которая задается формулой или совокупностью формул,
определяющих условия наступления начальной ситуации. Эту ситуацию
обозначим символом So (переменные ситуации, так же как макроситуации,
обозначим символом s). Есть множество действий, применимых в этой ситуации
и переводящих ее в другие ситуации. Каждая из этих других ситуаций опять
может быть переведена с помощью действий в следующие ситуации и так до тех
пор, пока не появится ситуация, удовлетворяющая нас по условиям решения
задачи. При этом каждая последующая ситуация 5 вычисляется по
предыдущей st и действию d с помощью функции 5 = переход (d, s).
7.1.11. Мера, измеритель и единица измерения
В любой области знаний (среде) объекты имеют длину, вес, цену или
определяются какими-либо другими величинами, используемыми для
характеристики их свойств, называемых мерами. Для того чтобы указать тип
меры, используют одноместные предикаты, например длина, вес, цена,
аргументами которых являются измеряемые объекты. Если объект L имеет меру
длина, то предикат длина (£) истинен. Если объект не имеет этой меры, то
предикат ложен. С мерой связано ее значение, как правило, числовое,
называемое величиной меры и представляемое переменной величина меры. Для
того чтобы можно было определять численное значение меры, используют
объекты, называемые измерителями меры. Например, если требуется
измерять длину объекта L, то измерителем длины может быть объект Рулетка.
Для того чтобы выразить числовое значение меры, используют объектную
константу, представляющую используемую единицу измерения.
Например, если единицей измерения является Сантиметр, то для того,
чтобы выразить измеренную длину объекта L с помощью рулетки, запишем
Длина (L) zd Результат измерения (L, величина_меры, Рулетка, Сантиметр),
где переменная величина_меры приобретает значение результата измерения
рулеткой объекта L в сантиметрах. Аналогично можно записать
вес (томат) zz> результатизмерения (томат, величина меры, Весы, Килограмм),
цена (томат) zz> результат измерения (томат, величина меры,
Кассовый аппарат, Доллар),
159
7. Ситуационное описание среды
(V х) элементкатегории (х, Дни) z>
zd резулыпатизмерения (х, величинамеры, Хронометр, Час).
Величина меры не обязательно должна быть только числовой.
7.1.12. Время
Время в ситуационных моделях сред является важным фактором,
используемым для задания моментов времени начала и окончания свершения
действий, наступления состояний, ситуаций, а также указания интервалов
времени, в течение которых действия, состояния, ситуации не изменяются.
Для представления времени вводится категория Kt упорядоченных
положительных чисел t, называемых моментами времени или просто
моментами. С помощью моментов времени задаются интервалы времени [/
Г2], где у — моменты времени, < t2. С интервалом связана его
продолжительность, равная tt - ty Для того чтобы рассуждать во времени,
вводят функции начало (х), окончание (х), продолжительность (х), где х
обозначает действие, состояние или ситуацию. Эти функции принимают
следующие значения:
начало (х) = окончание (х) = t2,
продолжительность (х) = начало (х) - окончание (х).
Наряду с функциями вводят также предикаты соседние (х, у), до (х, у),
после (х, у), внутри (х, у), где х, у обозначают действие, состояние или
ситуацию. Истинность этих предикатов определяется следующими аксиомами:
(V х, у) соседние (х, у) = окончание (х) = начало (у),
(V х, у) до (х, у) = окончание (х)) < начало (у),
(V х, у) после (х, у) = до (у, х),
(V х, у) внутри (х, у) = (начало (у) < начало (х)) л
л(окончание (х) < окончание (у)),
(V х, у) перекрытие (х, у) = (начало (х) < начало (у)) л
л (начало (у) < окончание (х)) л (окончание (х) < окончание (у)).
Рассмотрим примеры представления нескольких простых сред с помощью
введенных понятий.
160
7.2. Среда логических электронных схем
7.2. Среда логических электронных схем
Рассмотрим широко известную схему одноразрядного сумматора С (рис.
7. 1). Она состоит из двух функциональных элементов ИСКЛИЛИ, двух И
и одного ИЛИ и имеет три входа х{, х2, х3 и два выхода zt, Zy На входы х|; х,
подаются складываемые двоичные значения (биты), на вход х, подается
значение переноса. На выходе zt появляется значение суммы, а на выходе
Zi — значение переноса.
7.2.1. Основополагающие соображения
Логическая схема состоит из логических элементов (в дальнейшем элементов)
и соединяющих их проводов, называемых обычно соединениями. Логические
элементы, так же как и вся схема С, имеют входы и выходы: каждый логический
элемент имеет по два входа и по одному выходу. На входы элементов поступают
сигналы (биты). Каждый сигнал может принимать два значения 0 и 1.
Наша задача состоит в анализе корректности схемы, т.е. в проверке
правильности выдачи ею выходных сигналов в ответ на входные. Для того
чтобы такой анализ осуществить, необходимо иметь модель этой схемы.
Желательно при этом, чтобы она не содержала лишних сведений, которые
не будут использоваться при анализе. Так, например, в данной задаче анализа
мы не собираемся использовать такие свойства схемы, как ее размер,
стоимость, цвет, форму, длину соединений, места пересечения этих
соединений, время распространения сигнала и т.п. В других задачах анализа
эти сведения могли бы потребоваться, т.е. описание модели зависит не только
Рис. 7.1. Логическая схема двоичного сумматора С с тремя входами х,,х2, х} и
двумя выходами г,, , состоящая из двух ИСКЛ ИЛИ, двух И и одного ИЛИ
6—1141
161
7. Ситуационное описание среды
от предметной области, с которой мы имеем дело, но и от постановки задачи
анализа, а это в свою очередь влияет на выбор выразительных средств из
числа тех, которые были рассмотрены в предыдущем параграфе.
7.2.2. Создание модели сумматора
Приступим к выбору имен функций, предикатов, переменных и констант,
которые мы будем использовать для описания схемы. Каждый проводник схемы,
соединяющий в единое целое группы входов и выходов логических элементов,
сопоставим со своей переменной (см. рис. 7. 1). Все такие соединения схемы
поделим на три группы, сопоставив им следующие переменные: переменные
х х2, х3, соответствующие соединениям, одновременно являющимся входами
схемы, переменные z,, Z2, соответствующие соединениям, являющимся
одновременно выходами схемы, переменные у,, у2, у3, соответствующие
соединениям, не являющимся входами или выходами схемы (все введенные
переменные показаны на рис. 7.1 рядом с соответствующими им соединениями).
Каждый логический элемент в схеме сумматора имеет два входа и один выход.
Поэтому для каждого типа логического элемента (И, ИЛИ, ИСКЛИЛИ)
определим свой трехместный предикат
элементИ (вход, вход, выход),
элемент ИЛИ (вход, вход, выход),
элементИСКЛИЛИ (вход, вход, выход),
где каждая переменная вход, вход, выход совпадает с одной из переменных
Х2, Х3, у,, У2, у3, z,, Z2, Т.е.
вход, выходе {%,, х2, х}, у,, у,, у,, zt, Z2}-
Переменные х,,х2, х3, у,,у2, У3, Z{, Z2 могут принимать только значения О
или 1. Каждый из предикатов, представляющих собой соответствующий
логический элемент, истинен, когда набор значений переменных вход, вход,
выход этого предиката совпадает со строкой таблицы истинности этого
логического элемента. Например, предикат элемент И (вход, вход, выход)
истинен только при следующих значениях своих переменных
элемент И (0, 0, 0),
элемент И (0, 1, 0),
элемент И (1, 0, 0),
элемент И (1, 1, 1).
Предикат элемент ИЛИ (вход, вход, выход) истинен только при следующих
значениях своих переменных:
162
7.2. Среда логических электронных схем
элементИЛИ (О, О, 0),
элемент ИЛ И (О, 1, 1),
элемент ИЛИ (1, 0, 1),
элемент ИЛИ (1, 1, 1).
Предикат элементИСКЛИЛИ (вход, вход, выход) истинен только при
следующих значениях своих переменных:
элемент ИСКЛ ИЛИ (0, 0, 0),
элемент ИСКЛ ИЛИ (0, 1, 1),
элемент ИСКЛ ИЛИ (1, 0, 1),
элемент ИСКЛ ИЛИ (\, 1, 0).
Теперь осталось представить весь сумматор как единое целое, имеющий в
соответствии со схемой на рис. 7. 1 три входа и два выхода. Для этого,
используя уже введенные переменные, введем предикат
сумматор (вход, вход, вход, выход, выход).
Предикат сумматор будет истинным, когда значения выходных переменных
вычисляются в соответствии со схемой соединений логических элементов
рис. 7. 1 и их таблицами истинности. Для строгого определения этого правила
вычисления значений выходных переменных по значениям входных введем
аксиому
элемент ИСКЛ ИЛИ (хр х2, у,) л элемент_ИСКЛ_ИЛИ (у,, х2, zt) л
л элемент ^ (хр х2, у2) л элемент И (х3, у,, у3) л
л элемент ИЛИ (у3, у2, z2) о сумматор (хр х2, х3, zv z2).
На этом описание двоичного сумматора завершается и можно его
использовать для анализа корректности схемы, для чего необходимо
сформулировать задачи анализа в виде целей, которые требуется достичь.
7.2.3. Формулировка целей анализа
Типичными целями (вопросами) анализа для логических схем являются
следующие.
Если известны значения сигналов на выходах схемы, то какие значения
сигналов на входах схемы?
Если известны значения сигналов на входах схемы, то какие значения
сигналов будут на выходах схемы?
6*
163
7. Ситуационное описание среды
Если известны значения сигналов на некоторых входах и выходах, то
каковы значения неизвестных сигналов на остальных входах и выходах?
Так, например, в более конкретном виде применительно к схеме нашего
примера вопрос первого типа мог бы выглядеть так: какие наборы сигналов
на входах схемы сумматора могут приводить к сигналу 0 на выходе г, и к
сигналу 1 на выходе схемы? Формально на языке логики предикатов вопрос
выглядит следующим образом:
сумматор (х х х , 0, 1)?
Как можно получить ответы на подобные вопросы для схемы на рис. 7.1 на
основе уже изученных процедур вывода в логике предикатов, подробно
рассмотрено в четвертой главе. Этот пример очень прост. В нем использовано
небольшое количество понятий из числа введенных в настоящей главе. Однако
он достаточно типичен для задач проверки корректности схем. Во многих других
средах может быть использован подобный подход к описанию знаний о среде.
7.3. Среда обезьяны и банана
Пример среды обезьяны и банана также достаточно известен и часто
используется в качестве простого примера задачи из области искусственного
интеллекта. Рассмотрим пример среды в следующем варианте.
Около двери комнаты на полу находится обезьяна, а в определенном месте
комнаты подвешен банан. Обезьяна голодна и хотела бы съесть банан, но не
может до него дотянуться с пола. Около окна на полу лежит ящик, который
обезьяна может передвинуть, залезть на него и схватить банан, если ящик
находится прямо под бананом. Создадим ситуационную модель среды
обезьяны и банана.
Будем полагать, что обезьяна может находиться в одном из четырех мест: у
двери на полу (константа Удвери), у ящика на полу (константа Уящика), на
ящике (константа На_ящике). Аналогично введем константы, характеризующие
местоположение ящика Под_бананом, У_окна, и константы, характеризующие
состояние банана Схвачен, Не схвачен. Обезьяна может совершать каждый раз
одно из следующих действий d. схватить банан (Схватить), залезть на ящик,
(Залезть), слезть с ящика (Слезть), передвинуть ящик под банан (Передвинуть),
отодвинуть ящик от банана к окну (Отодвинуть), перейти к ящику (Перейти_
к_ ящику), перейти к двери (Перейти к_ двери). Это, конечно, упрощенная
среда, поскольку в ней исключены промежуточные положения обезьяны и ящика.
Теперь можно описать условия изменения местоположений обезьяны:
(V .у) достижима (У_двери, переход (d, s)) = d = Перейти_ к_ двери v
v достижима (У двери), s) /\—<(d = Перейти_ к_ ящику),
(V .s') достижима (У_ящика, переход (d, s')) = d = Перейтикящику v
v достижима (У_ящика, s) /\—<(d = Перейти_ к_ двери),
164
Вопросы и упражнения
(V 5) достижима (Наящике, переход (d, s)) = л d — Залезть v
v достижима (На_ящике, s) л—,(д = Слезть).
Аналогично для ящика можно записать следующие утверждения:
(V 5) достижима (Уокна, переход (d, s)) = л d = Отодвинуть v
v достижима (У_окна, s) л -1 (4/ = Передвинуть),
(V .у) достижима (Под бананом, переход (d, s)) = л d = Передвинуть v
v достижима (Под_бананом, s) /\—,(d = Отодвинуть).
Для банана будем иметь следующие утверждения:
(V 5) достижима (Несхвачен, переход (d, s)) =
= достижима (Не_схвачен, s) л -i (4/ = Схватить).
(V .у) достижима (Схвачен, переход (d, s)) =
= d = схватить v достижима (Схвачен, s).
Кроме этих утверждений необходимо также описать условия совершения
действий и начальную ситуацию. Читателю предоставляется выполнить это
в качестве упражнения в следующей главе.
Один из вопросов, ответ на который нас может интересовать в настоящем
примере, теперь можно сформулировать следующим образом: существует ли
такая ситуация, когда банан схвачен? На языке логики предикатов этот вопрос
выглядит следующим образом
(3 5) достижима (Схвачен, s)?
Вопросы и упражнения
1. Дайте определения для теоретико-множественных операций над категориями:
пересечения, объединения, дополнения.
2. Используя описанный в главе одноразрядный сумматор опишите
четырехразрядный сумматор. Сформулируйте вопросы по проверке корректности
его функционирования.
3. Напишите множество аксиом, позволяющих вычислять цену какого-либо
предмета (например, томата), при условии, что известна цена за килограмм и все
томаты имеют одинаковый вес.
4. В процессе обучения на старшем курсе студенты должны выбрать 3 курса из 9,
которые им надлежит обязательно прослушать. Курсы разбиты на три группы. Каждая
группа содержит курсы с обязательным одинаковым свойством и различными
необязательными свойствами. Выбранные курсы в совокупности должны содержать все
165
7. Ситуационное описание среды
обязательные свойства. Необязательные свойства определяются по желанию студента.
Аксиоматизируйте процесс выбора подходящих курсов с учетом обязательных требований.
Сформулируйте вопрос по поиску подходящих курсов.
5. Аксиоматизируйте процесс выбора покупки в Елисеевском гастрономе в
Москве. В качестве отправной точки для аксиоматизации воспользуйтесь
предложением: «Вчера Галина зашла в Елисеевский гастроном в Москве и купила
огурцов и филе судака». Ваше аксиоматическое описание должно быть достаточным
для ответа на вопросы, связанные с предложениями подобного типа. Следующие
наводящие вопросы могут помочь вам в аксиоматизации.
а) какие категории продуктов и отношений между ними вам необходимы?
б) какая иерархия существует между этими категориями?
в) какие ограничения на эти отношения можно наложить?
г) какие свойства продуктов необходимо детально описать?
Формируемая вами система аксиом (база знаний) должна быть достаточной для
ответа на ваши вопросы, список которых вы должны составить заранее. Постарайтесь
сделать вашу базу знаний как можно более общей. Вопросы не должны быть
тривиальными. Например, вопрос «Галина купила филе судака?» тривиален, если в
базе знаний имеется аксиома, эквивалентная предложению «Галина купила филе
судака». Вопросы должны быть такими, чтобы для ответа на них требовалась цепочка
шагов вывода. Многое в описании модели процесса выбора покупки в гастрономе
может быть приблизительным, но должно позволять сделать вывод при ответе на
вопросы следующего типа.
а) Галина ребенок или взрослая?
б) Галина купила три огурца?
в) Галина купила сколько-нибудь филе судака?
г) если Варя была в магазине в это же время, то Галина видела ее?
д) огурцы растут в гастрономе?
е) можно ли в гастрономе купить шампунь?
ж) что Галина будет делать с огурцами?
з) Галина взяла с собой деньги в гастроном?
и) у Галины остались деньги после покупки?
8. СИТУАЦИОННОЕ ИСЧИСЛЕНИЕ
В этой главе рассмотрены основные выразительные средства языка
ситуационного исчисления
В настоящей главе продолжается начатое в предыдущей главе обсуждение
ситуационного исчисления. Ситуационное исчисление рассматривается более
строго как логический язык, содержащий ряд разделов. Развитием ситуационных
исчислений для моделирования динамического поведения различных сред
занималось много исследователей в различных странах. Некоторые ситуационные
исчисления очень похожи между собой. Различия между другими более заметны.
Существуют исчисления, не использующие понятие ситуации. Так, например,
следующая глава посвящена исчислению, называемому временной модальной
логикой, которое по сути относится к ситуационному исчислению.
Ситуационное исчисление является формальной системой, базирующейся
на логике предикатов первого порядка. В основе его лежит понятие ситуации,
рассмотренное в предыдущей главе. Как и в более простом случае, когда мы
рассматривали вопросы рассуждения в пространстве состояний на основе логики
высказываний (см. гл. 2) или логики предикатов первого порядка (см. гл. 3,
4), будем полагать, что среда переходит из одной ситуации в другую в результате
выполнения некоторого действия. И единственная возможность перехода в
другую ситуацию — это совершение действия. В настоящей главе рассмотрим
современный вариант довольно простого ситуационного исчисления, который
можно было бы назвать инициальным детерминированным ситуационным
исчислением, поскольку оно предполагает, что все изменения в среде начинаются
с некоторой начальной ситуации и переход из любой ситуации при совершении
любого действия возможен только в одну ситуацию. Все пространство ситуаций
и переходов между ними можно представить в виде дерева, корневой вершиной
которого является начальная ситуация. Степень ветвления дерева не превосходит
числа действий. В настоящей главе рассмотрены основные разделы,
составляющие это исчисление, не очень сложные примеры и процедуры решений
некоторых из них. Сначала напомним ряд уже введенных ранее обозначений и
введем некоторые новые.
167
8. Ситуационное исчисление
8.1. Язык ситуационного исчисления
Ситуационное исчисление является логическим языком для описания
динамики изменения среды. Интуитивно язык ситуационного исчисления
предполагает, что есть некоторая начальная ситуация 5^ и среда изменяется
от ситуации к ситуации по мере выполнения действий. При этом
предполагается, что других ситуаций, помимо тех, которые могут быть
достигнуты с помощью выполнения действий, не существует. В этом языке
используются следующие категории, предикаты и функции.
Три непересекающиеся категории: категория действий А, категория ситуаций
S и категория объектов среды D. По-прежнему строчные буквы (a, s, f d, х,
у, ... ) или слова, начинающиеся с этих букв, используются для обозначения
переменных этих категорий, а прописные буквы (A, S, F, X, Y, ...) или слова,
начинающиеся с этих букв — для обозначения констант. Элементами категории
действий являются простые или сложные константы, обозначающие действия.
Сложные константы этой категории, т.е. константы, сами являющиеся
категориями, могут содержать в качестве элементов только элементы категории
D. Элементами категории ситуаций являются простые константы, обозначающие
ситуации. Элементами категории D являются любые простые или сложные
константы, кроме именующих действия и ситуации. Сложные константы этой
категории могут содержать в качестве элементов только элементы категории D.
Стандартная функция переход'. Эх 5 -> S. Значением функции переход (a, s)
является ситуация s', в которую переходит ситуация з в результате действия
a. Sg — начальная ситуация.
Стандартный предикат до (s}, 52), который будет также записываться в
обычном инфиксном виде 5, < 52. Этот предикат истинен, если ситуация 51
наступает раньше ситуации s2; .v, < s2 означает 5, < s2 v s, — s2.
Стандартный предикат допустимо (a, s). Этот предикат истинен, если
действие а допустимо (может быть выполнено) в ситуации з.
Функторный предикат ф (dx, d2, dn, s), где d}, d,, ..., d„ — переменные
или константы категории D, ф — предикатный символ. Функторный предикат
содержит единственный аргумент s, значение которого принадлежит
категории ситуаций S. Смысл функторного предиката следующий: если
свойство или отношение ф между dr d2, ..., dn имеет место в ситуации 5, то
предикат ф (dv d,, ..., dn, s) истинен в этой ситуации 5, и наоборот.
Например, если предикат проданы (Чашка, Чайник. Тарелка, S) истинен в
ситуации 5, то это означает, что некоторые конкретные чашка, чайник и
тарелка с именами Чашка, Чайник, Тарелка проданы в ситуации S.
Функторная функция f(d}, d2, ..., dn, s), где dt, d,. dn — переменные
или константы категории D. Функторная функция также содержит
единственный аргумент 5, значение которого принадлежит категории ситуаций
168
8.1. Язык ситуационного исчисления
S. Значение функции принадлежит категории D. Например, значением функции
изготовлена {гончар, глина, S) может быть значение переменной чашка.
Остальные обозначения будем вводить по мере необходимости.
8.2. Аксиомы ситуационного исчисления
Все аксиомы рассматриваемого ситуационного исчисления подразделяют
на следующие группы:
базовые аксиомы;
допустимых действий;
перехода в следующие ситуации;
начальной ситуации;
ограничений.
8.2.1. Базовые аксиомы
К числу базовых относится сравнительно небольшое число аксиом,
устанавливающих отношения между ситуациями, действиями и переходами
между ситуациями в результате выполнения этих действий. Основными среди
них являются следующие аксиомы.
Аксиому
(V ф)1(‘Х>) Л (v а, 5)(<p(5) z> <р {переход {а, 5)))] z> (V 5)(ф(.у)) (8.1)
называют индукционной аксиомой. В таком виде она не является аксиомой
логики предикатов первого порядка, поскольку ф здесь обозначает некоторую
формулу и это обозначение формулы рассматривается в данном случае как
переменная, связанная квантором общности. Это не мешает, однако,
использовать ее в рамках ситуационного исчисления, основанного на логике
предикатов первого порядка, для доказательства истинности формулы ф по
следующей схеме: если удалось доказать, что в начальной ситуации 5
справедливо некоторое свойство, представляемое формулой ф, и если во
всех ситуациях 5 справедливость свойства ф влечет справедливость этого
свойства в ситуации s' = переход {a, s) для всех действий а, то свойство ф
имеет место дтя всех ситуаций 5. Эта аксиома позволяет доказывать свойства,
справедливые для всех ситуаций. Порядок доказательства при этом состоит
из трех шагов:
доказательства того, что ф(50) истинна,
доказательства того, что для любого действия а и любой ситуации 5 истинна
импликация ф(5) z> ^{переход {а, 5)),
заключения (вывода), что предикат ф($) истинен для всех 5.
Следующая аксиома говорит о том, что ни в одну ситуацию нельзя перейти
из двух различных ситуаций в результате различных действий, или, другими
словами, в каждую ситуацию ведет только один переход. Эта базовая аксиома
свидетельствует о том, что множество переходов между ситуациями можно
169
8. Ситуационное исчисление
представить в виде дерева, начинающегося в некоторой начальной ситуации
(V а а2, 5,, 52) переход (а}, 5,) = переход (а2, s2) zd
zd <у — а2 л = s2. (8.2)
К числу базовых относятся также следующие аксиомы:
(V 5) 5() < 5,
т.е. любая ситуация наступает позже начальной:
(V .$•) .? * 5() о (3 a, s')(s = переход (a, s')),
если некоторая ситуация s не является начальной, то существует действие а
и ситуация s', из которой при выполнении этого действия осуществляется
переход в ситуацию 5 (иными словами, в любую ситуацию можно попасть
из некоторой другой);
(V 5,, S2, S2) .5, < .S2 AS2 < 5, ZD < 53,
если ситуация .у, была до ситуации ,?2, а ситуация s2 до ситуации 53, то ситуация
была до ситуации 53;
(V at, а,, .у,, ,у2) переход (а}, .s,) < переход (а2, s2) zd < s2,
если переход из ситуации был до перехода из ситуации s2, то и ситуация 5!
была до ситуации />,;
(V a, s) (.? < переход (а, .?)),
т.е. любая ситуация наступает до ситуации, в которую она переходит;
(V a, s, s') (переход (a, s)) < s' zd s < s',
если ситуация, в которую был осуществлен переход из ситуации s, была до
или тогда же, что и ситуация s', то и ситуация 5 была до или тогда же, когда
и ситуация .s'.
Этот список базовых аксиом может быть расширен.
8.2.2. Аксиомы допустимых действий
В каждой ситуации может совершаться множество действий. Суммарное
число действий, используемых для различных задач, может существенно
превышать число действий, которые допустимы в тех или иных ситуациях.
Аксиомы допустимых действий определяют ту совокупность действий из числа
всех действий, которые допустимы в тех или иных ситуациях, позволяя
суживать пространство поиска решения. В общем, каждая аксиома
допустимых действий имеет следующий вид:
170
8.3. Охота на индейку
допустимо (a (dv d2, ..., d), s) = (dv d2, ..., dn, s),
где a(dv d2, ..., dn) — n — местный функциональный символ, задающий
действие с областью значения А, где dt, d2, ..., dn — переменные или
константы категории D, a d2, .... dn, s) — формула co свободной
переменной 5, не содержащая предикатных символов допустимо и имеющая
единственную ситуационную переменную 5. Такие формулы будем называть
простыми.
Например, если одним из действий, которые может совершать охотник в
ситуации 5, имея ружье, является выстрелить (Охотник, Ружье) и это
действие в любой ситуации 5 может быть совершено при условии, что ружье
заряжено, то одной из аксиом допустимых действий может быть аксиома
допустимо (выстрелить (Охотник, Ружье), s) = заряжено (Ружье, s).
8.2.3. Аксиомы перехода в следующие ситуации
Аксиомы перехода в следующие ситуации определяют значения
функторных предикатов и функций в ситуации, в которую среда попадает в
результате перехода из некоторой предыдущей ситуации после выполнения
некоторого действия.
Аксиома для функторного предиката:
Tin(dv d2, ..., dn, s) = <pn(^, d2, ..., dn, переход (a, s)).
Здесь фп(«У1, d2, ..., dn, переход (a, s)) является л+1-местным функторным
предикатом, a itn(dv d2, ..., dn, s) — простая формула, все переменные
которой свободные. Например, формулой для функторного предиката
заряжено (Ружье, 5) может быть следующая:
-1 заряжено (Ружье, s) л а = зарядить =
= заряжено (Ружье, переход (зарядить, s)).
Аксиома для функторной функции:
d2, ..., dn, s) = f^(dt, d2, ..., dn, переход (a, s)) = y.
Здесь/(dp d2, ..., dn, переход (a, s)) является я+1-местной функторной
функцией, а лф(^, d2, ...,dn, s) — простая формула, все переменные которой
свободные. Например, формулой для функторной функции может быть
следующая:
заряжено (Ружье, s) л а = зарядить =
= вес (Ружье, переход (зарядить, s')) = 2585.
171
8. Ситуационное исчисление
8.2.4. Аксиомы однозначности имен для действий
Действия а и а', названные по-разному, не могут совпадать. Это
определяется аксиомами однозначности имен действий, имеющих вид
a(dv dr ..., d) ф a'(dv d2, ..., dn).
8.2.5. Аксиомы начальной ситуации
Аксиомы начальной ситуации являются простыми формулами, которые могут
содержать единственную ситуационную переменную начальной ситуации Ао. Эти
аксиомы задают начальные условия для среды, описываемой с помощью
ситуационного исчисления. Заметим, что эти аксиомы могут вообще не
содержать символа начальной ситуации.
8.2.6. Аксиомы ограничений
Аксиомы ограничений позволяют ограничить пространство поиска решения
при наличии дополнительных знаний о динамике изменения действий и
ситуаций. Укажем некоторые из этих аксиом. Введем предикаты достижима
(.у), произойдет (a, s). Первый из них истинен, если заранее известно, что
ситуация .у всегда достижима, т.е. для данного описания среды нам известно,
что существует последовательность действий, начинающаяся в начальной
ситуации, которая ведет в ситуацию у. Второй предикат истинен, если
известно, что ситуация s достижима и в этой ситуации может быть выполнено
действие а. На основании сказанного справедливы следующие аксиомы:
достижима (А),
произойдет (a, s) = достижима (переход (а, Д),
(V a, s') достижима (переход (a, s)) достижима (s) л допустимо (a, s').
Для каждой конкретной среды совокупность перечисленных аксиом описывает
ее поведение в различных ситуациях или ее динамические свойства, являясь
тем самым моделью поведения этой среды. Формулируя те или иные вопросы,
интересующие нас и касающиеся поведения среды, а затем доказывая или
опровергая их на основе аксиом, можно моделировать те или иные ситуации,
т.е. определять возможность достижения этих ситуаций и соответствующих им
истинностных значений функторных предикатов или функций. Процесс
описания поведения среды по-прежнему остается нетривиальной задачей, требует
определенной аккуратности и обеспечения полноты и непротиворечивости
исходного описания. В процессе доказательства могут использоваться различные
стратегии поиска, и они должны гарантировать получение положительного
ответа, если он существует. Всем этим вопросам в специальной литературе
уделяется много внимания. В настоящей книге в целях избежания перегрузки
172
8.3. Охота на индейку
ее теоретическими проблемами эти вопросы полноты и непротиворечивости не
обсуждаются. Далее рассмотрим моделирование поведения ряда простых сред,
широко известных в области искусственного интеллекта.
8.3. Охота на индейку
Эта задача относится к классу широко известных задач о выстреле. В
данном варианте речь идет об охоте на индеек. Индейки могут быть глуховаты
или хорошо слышать. Если они хорошо слышат, то при зарядке ружья они
услышат звук закрываемого затвора и спрячутся. Если они глухие, то они не
слышат этого звука, не прячутся и могут быть поражены. Сначала представим
необходимые аксиомы, комментируя их по ходу дела. Аксиомы разобьем на
введенные ранее группы.
8.3.1. Исходные аксиомы
Аксиомы начальной ситуации:
живая (Индейка, 5),
спрятавшаяся (Индейка, А).
Эти аксиомы свидетельствуют, что в начальной ситуации все индейки
живые и они не спрятались.
Аксиомы допустимых действий:
допустимо (Зарядить, s) л допустимо (Выстрелить, s).
Эта аксиома гласит: в любой ситуации, независимо ни от каких условий,
можно зарядить ружье и выстрелить из него.
Аксиомы перехода в следующие ситуации:
допустимо (a, s) л а = Зарядить зэ заряжено (Ружье, переход (а, т)),
допустимо (a, s) л а = Зарядить л глухая (Индейка, s)
о спрятавшаяся (Индейка, переход (а, 5)),
допустимо (a, s) л а = Выстрелить л заряжено (Ружье, s) л
л спрятавшаяся (Индейка, л) живая (Индейка, переход (а, 5)),
допустимо (a, s) л а = Выстрелить л заряжено (Ружье, s) л
л спрятавшаяся (Индейка, 5) о живая (Индейка, переход (a, s)),
173
8. Ситуационное исчисление
допустимо (а, 5) л а = Разрядить zd заряжено (Ружье, переход (a, s)),
допустимо (a, s) zd [глухая (Индейка, s) = глухая (Индейка, переход (а, 5)],
допустимо (a, s) zd [спрятавшаяся (Индейка, переход (a, s)) =
= а = Зарядить л глухая (Индейка, s) v спрятавшаяся (Индейка, 5)].
Эти аксиомы указывают, что случится в следующей ситуации с ружьем
или индейкой, если то или иное действие допустимо в настоящей ситуации.
8.3.2. Поставленный вопрос
Если предположить, что помимо начальной ситуации существуют такие
ситуации SI, S2, S3, S4, что SO < SI < S2 < S3 < S4 и, соответственно, в
ситуациях SI, S2, S3 будут осуществлены действия Зарядить, Ждать,
Выстрелить, а ситуация S4 достижима, то спрашивается, будет ли жива в
этой ситуации индейка, если она не глухая, т.е.
(S0< SI < S2 < S3 < S4) л произойдет (Зарядить, S1) л
л произойдет (Ждать, S2) л произойдет (Выстрелить, S3) л
л достижима (S4) л -> глухая (Индейка, SI) живая (Индейка, S4)?
Таким образом поставленный вопрос означает, что формула
(SO < SI < S2 < S3 < S4) л произойдет (Зарядить, S1) л
л произойдет (Ждать, S2) л произойдет (Выстрелить, S3) л
л достижима (S4) л глухая (Индейка, S1)
априори предполагается истинной, а следовательно, на основании правила
исключения конъюнкта истинным должен быть каждый из следующих конъюнктов:
(SO < SI < S2 < S3 < S4),
произойдет (Зарядить, S1),
произойдет (Ждать, S2),
произойдет (Выстрелить, S3),
174
8.3. Охота на индейку
достижима (84),
глухая (Индейка, 81).
8.3.3. Получение ответа на поставленный вопрос (вывод)
Доказательство вследствие его простоты приведем без комментария и
ссылок на используемые аксиомы:
|- произойдет (Зарядить, 81) = достижима (переход (Зарядить, 81)),
|- достижима (переход (Зарядить, 81)) z> допустимо (Зарядить, 81) л
л достижима (S1),
F допустимо (Зарядить, S1) л Зарядить = Зарядить л
л глухая (Индейка, SI) z> спрятавшаяся (Индейка, переход (Зарядить , 81)),
|- спрятавшаяся (Индейка, переход (Зарядить, 81)) =
= спрятавшаяся (Индейка, 82) л S2 = переход (Зарядить, S1),
к спрятавшаяся (Индейка, 82),
h допустимо (Зарядить, S1) л Зарядить = Зарядить о
zd заряжено (Ружье, переход (Зарядить, 81)),
!- заряжено (Ружье, переход (Зарядить, 81)) = заряжено (Ружье, 82)) л
л 82 = переход (Зарядить, 81)),
Ь заряжено (Ружье, S2).
|- произойдет (Ждать, 82) гл допустимо (Ждать, 82),
допустимо (Ждать, 82) гл [спрятавшаяся (Индейка, переход (ждать, 82) =
н Ждать = Зарядить л глухая (Индейка, s) v спрятавшаяся (Индейка, 82)],
175
8. Ситуационное исчисление
h спрятавшаяся (Индейка, переход (Ждать, S2)) =
= спрятавшаяся (Индейка, 52)],
|- спрятавшаяся (Индейка, S3) л S3 = переход (Ждать, S2) =
= спрятавшаяся (Индейка, 52)],
спрятавшаяся (Индейка, S3)|,
произойдет (Выстрелить, S3) о допустимо (Выстрелить, S3),
|- допустимо (Выстрелить, S3) л Выстрелить = Выстрелить л
л заряжено (Ружье, S3) л спрятавшаяся (Индейка, S3) о
zd живая (Индейка, переход (Выстрелить, S3)),
\- живая (Индейка, переход (Выстрелить, S3)) = живая (Индейка, S4) л
л S4 = переход (Выстрелить, S3),
h живая (Индейка, S4).
Вопросы и упражнения
1. Что такое язык ситуационного исчисления?
2. Какие группы аксиом входят в язык ситуационного исчисления?
3. Перепишите вывод к задаче об охоте на индейку, приводя на каждом шаге
вывода используемые аксиомы.
4. Задача об автоматическом выстреле сформулирована на языке ситуационного
исчисления в виде следующей группы аксиом:
допустимо (Зарядить, s) л допустимо (Выстрелить, s).
допустимо (Разрядить, s) = заряжено (Ружье, .s);
живой (Индивидуум, s)\
произойдет (Зарядить, S1) л произойдет (Ждать, S2) л
л произойдет (Выстрелить, S3)',
SI < S2 < S3 < S4;
176
Вопросы и упражнения
достижима (S4)',
допустимо (a, s) z> [заряжено (Ружье, переход (a, s)) = а = зарядить л
л а = Зарядить л заряжено (Ружье, 5)];
допустимо (a, s) z> [живой (Индивидуум, переход (a, s)) =
= (а = Выстрелить л заряжено (Ружье, s) л живой (Индивидуум, л1)].
Разбейте аксиомы задачи об автоматическом выстреле на группы. Объясните
существо задачи на естественном языке. Сформулируйте на языке ситуационного
исчисления вопрос: существует ли ситуация S4, в которой Индивидуум может остаться
живым после выстрела. Дайте ответ на этот вопрос с помощью формального вывода на
языке ситуационного исчисления.
5. Задача о стенфордском преступлении отличается от задачи об автоматическом
выстреле тем, что в третьей аксиоме исключается литерал произойдет (Зарядить, S1) и
добавляется аксиома живой (Индивидуум, S4). Разбейте аксиомы этой задачи на
группы. Сформулируйте на языке ситуационного исчисления вопрос: было ли ружье
заряжено в ситуации S4. Дайте ответ на этот вопрос с помощью формального вывода
на языке ситуационного исчисления.
6. Задача о русской охоте на индейку отличается от задачи об охоте на индейку,
рассмотренной в настоящей главе, тем, что вместо ружья используется револьвер,
барабан которого заряжен не полностью. В зависимости от поворота барабана
возможны две ситуации. В одной из них патрон окажется напротив бойка, а в
другой патрон будет вне бойка. Будем полагать, что каждое из этих положений
барабана зависит от двух действий Повернуть_напротив и Повернуть_вне. Тогда
аксиоматизация этой задачи выглядит следующим образом:
допустимо (Повернутьнапротив, s) л допустимо (Повернуть вне, s).
допустимо (Зарядить, т) л допустимо (Выстрелить, s)\
допустимо (a, s) z [заряжен (Револьвер, переход (а, .$)) = а = зарядить v
v заряжен (Револьвер, $)];
допустимо (а, т) о |готов к выстрелу (Револьвер, переход (a, s)) =
= а — Повернуть напротив v готов к выстрелу (Револьвер, т) л
л а = Повернуть_напротив[',
допустимо (a, s) о [живая (Индейка, переход (a, s)) = живая (Индейка, s) л
л (а = выстрелить л заряжен (Револьвер, s') л
л готов к выстрелу (Револьвер, 5)];
произойдет (зарядить, S1) л произойдет (выстрелить, S3)\
произойдет (Повернуть напротив, S2) v произойдет (Повернуть вне, S2).
Разбейте аксиомы этой задачи на группы. Сформулируйте на языке ситуационного
исчисления вопросы: 1) может ли остаться индейка живой в ситуации S4, 2) может
177
8. Ситуационное исчисление
ли индейка быть подстреленной в ситуации S4. Дайте ответ на эти вопросы с помощью
формального вывода на языке ситуационного исчисления.
7. Задача об угоне автомобиля состоит в следующем. Владелец припарковал
автомобиль на улице в неположенном месте и удалился по своим делам. Когда он
вернулся, автомобиля на месте не было. Заключение владельца — автомобиль был украден
(угнан) после парковки или убран с улицы службами автоинспекции вследствие
неправильной парковки до его возвращения к месту парковки. Введем действия
Припарковать, Угнать и Убрать. Предположим, что автомобиль был припаркован в
некоторой ситуации Sm. На языке ситуационного исчисления это можно записать
следующим образом:
припаркован (Автомобиль, 8т) л достижима (Sm)\
факт исчезновения автомобиля чуть позже после парковки записывается следующим
образом:
достижима (5) л припаркован (Автомобиль, Sn) л S < Sn.
Введем аксиому перехода в следующую ситуацию:
допустимо (a, s) z> [припаркован (Автомобиль, переход (a, s}) =
= припаркован (Автомобиль, s) л а * Угнать л а * Убрать л
л а = Припарковать\.
Сформулируйте на языке ситуационного исчисления вопросы: 1) мог ли быть
автомобиль угнан? 2) мог ли быть автомобиль убран? Расширьте аксиоматизацию,
если введенных аксиом недостаточно. Разбейте аксиомы на группы. Дайте ответ на
вопросы с помощью формального вывода на языке ситуационного исчисления.
9. МОДАЛЬНОСТЬ
В СИТУАЦИОННОМ ИСЧИСЛЕНИИ
В этой главе рассказано, что такое модальность и какую роль она играет
в ситуационном исчислении, превращая его в модальное ситуационное
исчисление или модальную логику. Особое внимание уделено применению
модальной логики для анализа корректности поведения параллельных процессов.
Изложены основы использования модальной логики для анализа корректности
параллельных процессов. Описана используемая для этого анализа модель
параллельных процессов. Подробно рассмотрены наиболее типичные свойства
корректности параллельных процессов, их формальная запись в языке
модальной логики. Приведены сведения о принципах формального доказа-
тельства (проверки) свойств корректности.
9.1. Модальность и модальная логика
При развитии различных исчислений как формальной основы для
рассуждений о тех или иных явлениях нашей среды постоянно наблюдается
стремление по возможности полно и точно выразить и учесть динамику
изменений этой среды. Самым простым исчислением является логика
высказываний (см. гл. 2). Для того чтобы выразить динамику изменений среды,
например во времени, средствами логики высказываний, придется ввести
переменные, истинность которых будет означать наступление того или иного
момента времени. Если таких моментов много, то описание в логике
высказываний становится крайне неудобным. Логика предикатов первого
порядка (см. гл. 3) является более сложным, но и более выразительным
исчислением в результате введения кванторов, функций и предикатов. Функции
и предикаты могут зависеть от временных переменных, которые позволяют
описывать динамику среды. Ситуационные исчисления еще более удобны для
описания динамики среды, поскольку они основаны на использовании
специальных ситуационных переменных, значения которых могут зависеть от
времени или пространства.
179
9. Модальность в ситуационном исчислении
В некоторых случаях рассуждения о динамике изменения во времени
ситуаций и связанных с этими ситуациями фактов не требуют знания ни
точного времени наступления этих ситуаций, ни использования самих
ситуаций (ситуационных переменных). Достаточным является установление
истинности того, что та или иная формула, выражающая определенные
отношения между объектами среды, станет, в конце концов, истинной, не
станет истинной, станет истинной с какой-либо степенью уверенности и
т.п. при определенных значениях объектных переменных в некоторой
ситуации, явное значение которой нас не интересует. На естественном языке
для выражения этих отношений обычно используют слова типа “допустимо”,
“необходимо”, “возможно” и другие, выражающие определенную степень
уверенности наступления каких-либо событий во времени или пространстве,
но без указания точного времени или места. Возможность делать в логике
высказывания, содержащие выразительные средства, которые характеризуют
подобную степень уверенности или «силу» высказывания, называют
модальностью. Исчисления, в которых введены специальные символы или
слова (модальные операторы), с помощью которых это делается, называют
модальными исчислениями.
В настоящей главе рассмотрим пример одного из таких исчислений,
основанного на логике предикатов первого порядка и называемого обычно
временным модальным исчислением или временной модальной логикой.
Слово “временное” появляется здесь в связи с тем, что изменение
подразумеваемых ситуаций происходит во времени. В нашем случае время
течет линейно. Ситуации, естественно, тоже изменяются линейно в этом
времени. Обсудим более подробно концептуальную суть временного
модального исчисления.
Рассмотрим, например, утверждение: «Идет дождь». Очевидно, что
истинность этого утверждения зависит от двух факторов (параметров): даты и
места, которые подразумеваются, но не употреблены. Выбирая определенные
дату ?() и место /0 и уточняя с их помощью указанного утверждения, получаем
другое утверждение: «Идет дождь в месте / во время t». Это утверждение
полностью определено и должно быть либо ложным, либо истинным. Теперь
можно ввести атом дождь (I, t): «Идет дождь в месте / во время г», который
имеет равные приоритеты для обоих параметров / и I. Модальный подход
предполагает два различных приоритета или уровня для параметров / и t.
Параметр с более высоким приоритетом определяет ситуацию и не
употребляется явно в высказываниях. Так, если в качестве переменной,
полностью определяющей ситуацию, выбрать время, то вместо атома дождь
(I, t) будет использоваться атом дождь (/). Значение этого предиката зависит
как от ситуации (в данном случае времени или даты), так и от места. Но
точное значение ситуации нас не интересует, поскольку мы собираемся
рассуждать о таких вещах, как возможность дождя в месте / в принципе или
неизбежность дождя в месте / когда-либо вообще и т.п.
180
9.1. Модальность и модальная логика
Переход от логики предикатов к модальной логике не такой резкий, как
переход от логики исчисления высказываний к логике предикатов. При этом
выбор переменных, определяющих ситуацию, произволен и зависит от
субъективной точки зрения. Имеются очевидные преимущества введения
модального формализма. Он позволяет нам сделать переменные,
определяющие ситуацию, более важными, чем все остальные, и ввести
неявную зависимость формул модальной логики от ситуаций и тем самым от
переменных, ее определяющих. Временная модальная логика предполагает
наличие базисного отношения достижимости между ситуациями: R(s, s'),
которое определяет возможность перехода из одной ситуации 5 в другую
ситуацию s'. Это отношение имеет место, если ситуация s' достижима из
ситуации 5.
Вернемся снова к примеру о дожде. Как уже отмечалось, здесь ситуации
определяются датами (днями), т.е. ситуация и день или дата в данном случае
одно и то же. Между ситуациями можно установить отношение достижимости:
R(s, s'), если ситуация (день) s' следует за ситуацией (днем) 5. Главная
идея обозначений, принятых в модальной логике, состоит в стремлении
избежать обозначения ситуаций (дат в нашем примере) и отношения
достижимости. Вместо этого вводят два специальных модальных оператора,
описывающих свойства ситуаций, достижимых из данной ситуации: оператор
необходимости □ и оператор возможности 0.
Смысл этих операторов заключается в следующем. Пусть w является
некоторой формулой модальной логики. Тогда Dw и Ovv также формулы
модальной логики. Значение формул w, Dw и Ovv неявно зависит от некоторой
текущей ситуации 5. Формула Dw считается истинной в ситуации s, если
формула w истинна на всех ситуациях, достижимых из ситуации 5, включая
собственно ситуацию 5. Формула Ovv считается истинной в ситуации s, если
формула w истинна хотя бы в одной ситуации, достижимой из ситуации 5.
Обозначим w(5) значение формулы w в ситуации 5. Тогда правила вывода
истинных значений модальных формул □и'(а) и 0w(x) можно записать
следующим образом:
w(5), V(5')l^(5, s') Л w(-s')] 1”Пи'(5),
W(5), Э(5')1Д5, s') Л W(5')J I- Ои'(а). (9.1)
Эти правила введены только для того, чтобы пояснить смысл модальных
операторов. На самом деле, как уже говорилось, в формулах модальной
логики символ ситуации не используется, но подразумевается. Модальная
формула записывается с помощью пропозициональных символов,
предикатных символов (включая равенство), функциональных символов,
констант, переменных, классических операторов (связок) и кванторов, а
также модальных операторов.
Формулу без модальных операторов, являющуюся по существу формулой
логики предикатов первого порядка, называют иногда статической.
181
9. Модальность в ситуационном исчислении
Модальная формула, называемая иногда динамической, содержит статические
подформулы, к которым применены классические и модальные операторы.
Истинностное значение модальной формулы в некоторой ситуации можно
найти на основе правил (9.1). При этом предполагается, что в каждой
рассматриваемой ситуации все классические символы формулы можно
интерпретировать и конкретизировать таким образом, что ее истинностное
значение будет определено. Например, формула
дождь (/)=><>-> дождь (/)
эквивалентна утверждению «если в какой-либо день в каком-либо месте I
идет дождь, то наступит другой день, когда в этом же месте / не будет
дождя». Для того чтобы эта формула стала истинной при некотором
конкретном значении места /, должен существовать день 5, в который дождь
начался и затем прошел в этом же месте. Утверждению «если в какой-либо
день в каком-либо месте I идет дождь, то он будет идти и в любой другой
день в этом же месте /» соответствует формула
дождь (/) Z) Одождь (/).
Для того чтобы эта формула стала истинной при некотором конкретном
значении места /, должен существовать день 5, в который дождь начался и
затем уже никогда не прекращался в этом месте.
Приведем примеры формул модальной логики, поясняя на основе правил
(9.1), при каких условиях эти формулы будут истинными.
Формула O(EJw) истинна в ситуации s, если существует хотя бы одна
ситуация s’, достижимая из ситуации 5, в которой истинна формула Пж
Иными словами, истинность формулы O(EJw) означает, что существует
ситуация s', достижимая из ситуации 5, такая, что в ситуации s' и во всех
достижимых из нее истинна формула ж
Формула □(Ow) истинна в ситуации 5, если во всех ситуациях s', достижимых
из ситуации 5, истинна формула Ож Иными словами, истинность формулы
□(Ow) означает, что для всех ситуаций s', достижимых из ситуации 5, можно
найти хотя бы одну достижимую из s' ситуацию, в которой истинна формула ж
Формула □(w z) Dw) истинна, если для всех ситуаций s', достижимых из
s, истинна формула w Пж Истинность формулы w Dw в ситуации s'
означает истинность формулы w во всех ситуациях, достижимых из ситуации
s'. Таким образом, истинность формулы D(w Dw) означает, что формула
w становится всегда истинной в любой ситуации .s', достижимой из 5, и
остается истинной для всех ситуаций, достижимых из s'.
Модальная логика построена на базе логики предикатов первого порядка,
и в ней, естественно справедливы понятия, используемые в последней:
общезначимость, выводимость и др. В частности, формулы
□ -IV Z) Ow,
□ w = 0 vv
182
9.1. Модальность и модальная логика
общезначимы. Формула
□ (w zd w2) (Dw! zd Dw2)
также общезначима. Это означает (на основе правила модус поненс), что
истинность формулы □(и'| zd w2) всегда влечет истинность формулы □и'| zd Пи^.
Задавая различные ограничения на отношение достижимости R, можно
получать различные модальные исчисления. В нашем случае полагаем, что
отношение R всегда рефлексивно (sRs) и транзитивно {(stRs2 л s2Rs3) zd s}Rs2)).
Вследствие этого общезначимы все следующие формулы:
□ w zd w благодаря рефлексивности (если во всех ситуациях, достижимых из
s, истинна w, то w истинна и в ситуации а);
OOwzjOw благодаря транзитивности отношения R (если существует ситуация
5 достижимая из 5 которая в свою очередь достижима из ,v(), причем в
ситуации s2 формула w истинна, то существует sr достижимая из ,s0, в которой
формула w также истинна, и .sz = s2).
Как уже отмечалось, модальная логика, рассматриваемая в настоящей
книге, в своем названии имеет добавку «временная». В связи с этой добавкой
на модальную логику, а точнее на базовое отношение достижимости,
налагаются дополнительные условия, состоящие в том, что ситуация s'
достижима из ситуации 5, если ситуация 5 может перейти в ситуацию s'
благодаря изменениям среды во времени. В настоящей книге ограничиваемся
линейным и дискретным изменением ситуаций. Это означает, что
рассматриваемая нами временная модальная логика имеет дело с
последовательностями вида 50, ..., причем 5 достижимо из 5, тогда и
только тогда, если i < j, а 5() есть единственная начальная ситуация.
Благодаря дискретности последовательностей ситуаций мы можем
ссылаться не только на ситуации, которые являются далекими
последователями данной, но и на единственную следующую ситуацию.
Поэтому в ряде случаев целесообразно ввести оператор следующей ситуации,
обозначаемый °, и отношение непосредственного следования r(x, s').
Очевидно при этом, что транзитивное рефлексивное замыкание отношения
г дает отношение достижимости R , введенное выше. Последовательность
50, s2, для которой отношение r(st, 5+]) имеет место для всех i > О,
интуитивно соответствует развитию процессов во времени, наблюдаемому
как последовательность дискретных ситуаций.
Дадим теперь краткую характеристику языка временной модальной логики,
который мы частично уже рассмотрели и который будем использовать в
дальнейшем. В книге этот язык используется для рассуждений о процессах
и программах, и его детали вводятся постепенно и на примерах.
183
9. Модальность в ситуационном исчислении
9.2. Язык временной модальной логики
Язык временной модальной логики основан на языке логики предикатов
первого порядка и использует множество индивидуальных (объектных) и
пропозициональных переменных и констант, функциональных и предикатных
символов. Множество всех переменных разбивается на два подмножества:
глобальных и локальных переменных.
Глобальные переменные имеют одну область интерпретации. Локальные
переменные подразделяются на группы, каждая из которых имеет свою, отличную
от других групп, область интерпретации. Речь об этих группах пойдет позднее.
Формулы временной модальной логики строятся из атомарных формул
(атомов), к которым применяются логические (л, v, z>, =, ->) связки,
модальные операторы (□, 0, °, \л), скобки и кванторы (3, V) над
индивидуальными глобальными переменными. Формулу называют
классической, если она не имеет модальных операторов.
Для того чтобы уметь вычислять формулы временной модальной логики,
как и ранее, необходимо определить среду и интерпретировать в этой среде
множество переменных, констант, функций, предикатов, формул.
Интерпретация и вычисление значений формул будет подробно
проиллюстрировано применительно к конкретной среде параллельных
процессов или, точнее, модели параллельных процессов.
9.3. Модель параллельных процессов
Одной из популярных областей применения модальной логики является
формулировка условий корректности параллельных программ или процессов
и проверка истинности этих условий для конкретных параллельных программ.
Для того чтобы формулировать эти условия, необходимо четко знать, что же
собой представляют параллельные процессы. Для этого рассмотрим модель
параллельных процессов.
Модель параллельных процессов состоит из т, т >1, процессов Р}, Рт,
выполняющихся параллельно. Каждый процесс Р., i= 1, ..., т, представляет
собой граф переходов с вершинами, обозначаемыми /',, Г\, ..., Множество
£ = ..., Ре} называется также множеством мест процесса Р. Места
могут быть активными и пассивными. Переходом а в графе переходов
процесса называется дуга, помеченная условием и следствием перехода.
Переход вместе с инцидентными ему вершинами (местами) изображен
на рис. 9.1.
са(У>/ у:=/а(У)
Рис. 9.1. Переход а и инцидентные ему вершины (места) /, /'
184
9.3. Модель параллельных процессов
На рисунке обозначено: у = (_ур ..., у„) — множество локальных
индивидуальных и пропозициональных переменных, ca(j) — условие, при
истинности которого и активном месте / происходит выполнение перехода
а из места / в место у: = fa(y) — действие или константа перехода a', fa
— преобразование, ассоциируемое с этим действием. Если место активно и
са(й) истинно, то говорят, что переход а является допустимым для у = h.
Место I может иметь к инцидентных ему переходов (рис. 9.2).
Рис. 9.2. Совокупность переходов 1, ..., к
Полным входным условием для места / является Et(y) = Cj(j) v с2 (j) v ...
v ck{y). При этом c(j) л c(j) = Л, если i j, и не требуется, чтобы Et(y) = И.
Такие процессы называют обычно детерминированными. Если процесс Р
имеет хотя бы один переход а, который является допустимым, то процесс Р
называют допустимым.
Переменные множества у = (ур ..., уп) называют распределяемыми. Эти
переменные доступны всем процессам. Поэтому рассматриваемую модель
параллельных процессов называют моделью с распределяемыми переменными.
В такой модели связь и синхронизация между процессами осуществляется с
помощью распределяемых переменных. Совокупность параллельных
процессов будем также называть программой.
Часто будем представлять процесс в текстовой линейной форме вместо
графовой. Каждый переход и инцидентные ему вершины будем представлять
одним предложением, называя его иногда командой. Приведем примеры
предложений в текстовой форме и соответствующие им графы (рис. 9.3,
9.4), являющиеся частным случаем графического представления переходов,
приведенных на рис. 9.1, 9.2:
ЕСЛИ* СТО у: = f(y) НА Г\ или I; у: = f(y) НА Г; (9.2)
У- =f(y)
Рис. 9.3. Переход, соответствующий (9.2)
185
9. Модальность в ситуационном исчислении
ЕСЛИ* I* С(у) ТО НА т\ или /: ЕСЛИ С(у) ТО НА т\
ЕСЛИ * /* НЕ С(у) ТО НА Г; или I: ЕСЛИ НЕ С(у) ТО НА I'; (9.3)
ЕСЛИ * / * ТО (и,, ир): = f(V', v) НА /'.
Рис. 9.4. Переход, соответствующий (9.3)
Последнее предложение содержит программный сегмент (ир ,ирУ =
= f(vv деталями которого мы не интересуемся. Существенным для
нас является только следующее:
1) сегмент может изменять только переменные ир ..., и, р > 0 и может
использовать для этого только переменные v,, ...,v, 5 > 0;
2) выполнение сегмента должно обязательно завершиться.
Предложение, в результате которого происходит остановка выполнения
процесса в месте /, если оно до этого было активным, имеет вид
ЕСЛИ * I* ТО СТОП, или /: СТОП.
Пример. Рассмотрим параллельную программу вычисления биноминальных
коэффициентов Скп для чисел п и к, таких, что 0 < к < п:
ПРОГРАММА Биноминальные коэффициенты
ВХОДНЫЕ ЦЕЛЫЕ п, к, у, : = п, у2: = 0, у}: = 1
ВЫХОДНЫЕ ЦЕЛЫЕ
ПРОЦЕСС Числитель
ВХОДНЫЕ ЦЕЛЫЕ у v уг
186
9.3. Модель параллельных процессов
ВЫХОДНЫЕ ЦЕЛЫЕ у.
ЕСЛИ * /0* (у, = (п - к)) ТО НА 1е
ЕСЛИ * /0 * НЕ (j, = (п - /с)) ТО НА
ЕСЛИ * / * ТО у - = к у, НА I
ЕСЛИ* L* ТО у. = j -1 НА I
ЕСЛИ * I * ТО СТОП
С
КОНЕЦ Процесс Числитель
ПРОЦЕСС Знаменатель
ВХОДНЫЕ ЦЕЛЫЕ ух, у2
ВЫХОДНЫЕ ЦЕЛЫЕ у,
ЕСЛИ * тй * (j2 = к) ТО НА те
ЕСЛИ * т0* НЕ (у2 = к) ТО НА /и,
ЕСЛИ * т}* ТО у2. = у2+1 НА т2
ЕСЛИ * т2* (j, + у2 < п) ТО НА тъ
ЕСЛИ * т2* НЕ (у, + у2< п) ТО НА т2
ЕСЛИ * /и * ТО у= уЛу. НА тп
ЕСЛИ * т* ТО СТОП
е
КОНЕЦ Процесс Знаменатель
КОНЕЦ Процесс Биноминальные коэффициенты.
Как видно из приведенного описания, процесс Числитель, последовательно
используя значения уг равные п, п-1, ..., п-к + 1, вычисляет числитель в
уу Процесс Знаменатель, используя значения у2, последовательно равные
187
9. Модальность в ситуационном исчислении
1, 2, к, вычисляет знаменатель, присваивает значения у2, а затем делит
на у. Предложения
ЕСЛИ * т2* (у, + у2 < п) ТО НА т2,
ЕСЛИ * т2* НЕ (У[ + у2 < п) ТО НА т2
синхронизируют выполнение процесса Р2 (Знаменатель) с процессом Рх
(Числитель), чтобы обеспечить деление у на i только после того, как оно будет
умножено на n-i+1 без остатка. Основанием этому служит теорема, утверждающая,
что произведение i последовательных чисел к (к + 1)... (к + /-1) всегда делится
на i\ Рассмотрим теперь, как параллельные процессы вычисляются. Вместо
понятия «вычисление» будем использовать понятие «выполнение» как
соответствующее понятию процесса.
9.4. Мультипрограммное выполнение параллельных процессов
На уровне модели параллельных процессов предполагается, что процессы
выполняются параллельно. Физически это обусловливает наличие для каждого
процесса своего индивидуального процессора. В реальной жизни количество
процессоров компьютера ограничено и вместо дисциплины параллельного
выполнения процессов используются дисциплины квазипараллельного, в
частности на одном процессоре. В этом случае для эквивалентности
результатов необходимо учитывать дополнительные ограничения на
выполнение процессов и использовать специальные средства синхронизации.
В настоящей главе рассмотрен однопроцессорный вариант выполнения
параллельных процессов, называемый мультипрограммным, причем все
процессы предполагаются детерминированными. Его главное свойство состоит
в чередовании выполнения переходов различных процессов на одном процессоре
как последовательности дискретных шагов. На каждом шаге (такте) выбирается
один процесс, выполнение которого допустимо, и выполняется его допустимый
переход. (Заметим, что этот переход в каждом процессе единственный вследствие
детерминированности процессов.) Выбором процесса ведает специальный
планировщик или диспетчер. Диспетчер может осуществлять холостые такты,
в которых ни один процесс не выполняется, и значения всех переменных,
включая переменные места, остаются неизменными. В случае, когда ни один
из допустимых процессов не может быть выполнен и холостой такт является
единственно возможным выбором, будем говорить, что модель параллельных
процессов находится в дедлоке. Специальный случай такой ситуации
проявляется, когда все процессы остановились (находятся в терминальных
местах). Следует также отметить, что каждый переход выполняется без какого-
либо вмешательства со стороны других процессов, в связи с чем все операции,
относящиеся к переходу, называются неделимыми ити атомарными.
Рассмотрим условия, при которых мультипрограммное выполнение
параллельных процессов будет давать те же результаты, что и чисто
188
9.4. Мультипрограммное выполнение параллельных процессов
У = О
Процесс Р,
Процесс Р{
Рис. 9.5. Параллельные процессы
Р,иР2
параллельное. Предположим, что в нашем распоряжении имеется два
параллельных процесса Р} и Рг, имеющих соответственно допустимые
переходы (рис. 9.5).
Мультипрограммное выполнение этих
процессов дает единственный результат
у = 0, так как не имеет значения, что
мы сделаем вначале: прибавим 1 в
процессе Р}, а затем вычтем 1 в процессе
Р2 или поступим наоборот. Истинно
параллельное выполнение может дать
либо у = 1, либо у = -1 в зависимости от
реального времени выполнения
переходов. При этом предполагается,
что процессы одновременно получают
значение у = 0 и какой из них последним
положит вычисленное им значение у, тем
оно и будет, т.е. если Р, выдает результат
вычисления значения у позже Р2, то
будем иметь у = 1 в качестве результата,
если раньше, то у = -1.
Таким образом, мультипрограммное
выполнение не отражает реального
параллелизма. Это является следствием
выполнении команды у: = у+ 1, у =у - 1 содержат слишком много событий
и не являются «атомарными». (Атомарными мы называем те команды или
переходы, которые происходят без вмешательства каких-либо других.)
Выполнение каждой из этих команд включает в себя: выбор значения
того, что при мультипрограммном
распределяемой переменной, вычисление выражения, стоящего справа,
присвоение значения распределяемой переменной.
В реальном параллельном выполнении процессов эти события могут
чередоваться с событиями в других процессах, приводя таким образом к
взаимовлиянию. При тщательном изучении выполнения процессов
обнаруживается, что критическими событиями являются выбор и присвоение
значений распределяемым переменным.
Разделим все переменные на две группы:
локальные, или частные, переменные процесса Р — это те переменные,
которые изменяются только этим процессом;
распределяемые переменные — это те переменные, к которым имеют
доступ другие процессы.
Появление переменной в левой части команды назовем модифицирующей
ссылкой на переменную, в правой — ссылкой доступа к переменной.
Появление переменной в команде данного процесса назовем критической
ссылкой на переменную, если справедливо одно из следующих условий:
189
9. Модальность в ситуационном исчислении
Рис. 9.6. Модифицированные
параллельные процессы Р и Р2
модифицирующая ссылка на пере-
менную, к которой имеется ссылка
доступа со стороны другого процесса;
ссылка доступа к переменной, на
которую имеется модифицирующая
ссылка со стороны другого процесса.
Мультипрограммное выполнение
позволяет получить те же результаты, что
и при реальном параллелизме, если
справедливо следующее правило един-
ственности критической ссылки: каждая
команда может иметь самое большее одну
критическую ссылку. В предыдущем
примере команда у: = у +1 нарушает это
правило, так как она имеет две
критические ссылки. Модифицируем
рассмотренную выше программу следую-
щим образом (рис. 9.6). На рисунке
и /2 — локальные пере-менные
процессов Р и Р соответст-венно.
Теперь при мультипрограммном выполнении нашей модели возможно получение
в качестве результата {0, -1, +1} в зависимости от диспетчирования.
Подытожим обсуждение отношения между параллельным и мультипрог-
раммным выполнением параллельных процессов.
Модель параллельных процессов, подчиняющаяся правилу единственности
критической ссылки, может давать одно и то же множество результатов при
параллельном и мультипрограммном выполнении.
Для каждой модели параллельных процессов существует эквивалентная
модель, подчиняющаяся правилу единственности ссылки.
Таким образом, используя мультипрограммное выполнение параллельных
процессов, можно представить все возможные ситуации, возникающие при
параллельном выполнении. Однако следование только правилу единственности
критической ссылки при мультипрограммном выполнении еще не гарантирует
результата, эквивалентного результату параллельного выполнения. Для
достижения эквивалентности результатов необходимо должным образом
управлять (диспетчировать) выполнением процессов, в частности, запрещать
вмешиваться в выполнение определенного множества переходов (команд) одного
процесса до их завершения, прежде, чем переходить к выполнению переходов
другого. Управление такого типа обычно называют синхронизацией выполнения
процессов. Одним из средств такой синхронизации являются специальные
переходы или команды, называемые семафорами.
9.4.1. Семафоры
Семафоры являются особыми атомарными командами, для которых
делается необходимое в этом случае исключение из правила единственности
190
9.4. Мультипрограммное выполнение параллельных процессов
критической ссылки, поскольку они выступают как стандартный способ
синхронизации параллельных процессов и имеют дело со специальными
семафорными переменными. Этих команд две и их обозначают занять (у)
и освободить (у).
Команда занять (у) эквивалентна предложению
ЕСЛИ * / * у >0 ТО у. = у - 1 НА Г,
где Г — место перехода, следующего в записи процесса сразу за этим предло-
жением. Для краткости этот переход можно записывать в виде /: занять (у).
Команда освободить (у) эквивалентна предложению
ЕСЛИ * / * ТО у: = у +1 НА
где Г также место перехода, следующего в записи процесса за этим предло-
жением. Для краткости ее можно записать в виде /: освободить (у).
При преобразованиях процессов с целью удовлетворить правила един-
ственности критической ссылки семафоры не изменяют и всегда оставляют в
том виде, как они определены выше. Никакие другие операции над
семафорными переменными у, кроме указанных выше, не допускаются. Обычно
семафорным переменным вначале присваивается 1 или другое положительное
целое число. Процесс, достигший команды занять (у), будет выполняться
дальше только в том случае, если у > 0, после этого у уменьшиться на 1 и
получит значение, равное 0. Таким образом, место, которому соответствует
команда занять (у), является точкой, которая синхронизирует данный процесс
с другими процессами, содержащими команды занять (у) и освободить (у) с
той же самой переменной у.
Пример. Рассмотрим модель параллельных процессов следующего вида:
у: = 1
Процесс Р, Процесс Р2 ... Процесс Рк
/': занять (у) /2: занять (у) ... 1к: занять (у)
т'\ освободить (у) т2; освободить (у) ... тк: освободить (у)
Предположим, что Р{ первым достигает когда у = 1. Он проходит /‘ и
устанавливает у = 0. До тех пор пока Рх находится между /'и т1, у будет
оставаться равным 0 и любой другой процесс Р‘, который попытается идти
далее своего места i > 1, будет задержан здесь, поскольку условие у > 0
ложно. Он будет ожидать здесь до тех пор, пока у снова не станет
положительным, что может быть только после вызова процессом Рх своей
команды освободить (у) в т'. Даже если Рх и Р2 достигли /' и /2 одновременно,
неделимость команды занять (у) гарантирует, что только один процесс Р'
может получить доступ к своей области, лежащей между Ри т‘. Эта область
191
9. Модальность в ситуационном исчислении
называется критической секцией, и наше использование семафоров в этом
примере гарантирует взаимное исключение доступа к критической секции,
т.е. только один из процессов может выполнять критическую секцию в любом
такте. Взаимное исключение критических секций необходимо, когда двум
или более процессам необходим доступ к распределяемым переменным или
ресурсам, таким, например, как диски, и нам необходимо защититься от
взаимовлияния этих процессов или от попыток других процессов получить
доступ к тому ресурсу, с которым данный процесс уже имеет дело.
Пример. Вернемся еще раз к программе вычисления биноминальных
коэффициентов. Заметим, что у3 — критически распределяемая переменная,
т.е. переменная, которая встречается в команде ф уу = у3уу не удовлетворяющей
правилу единственности критической ссылки. Следовательно, мы должны
разбить команду
ЕСЛИ* I* ТО Уу = у^
на две:
ЕСЛИ * /, * ТО t- = уух НА 1\ ;
ЕСЛИ * /;* ТО у3: = tv
Подобным образом команду
ЕСЛИ * т3* ТО у3: = у3/у2
разобьем на две:
ЕСЛИ * т3* Т О tr = yjy2 НА т'3;
ЕСЛИ * т'3* Т0уу = Г2.
Если считать, что допустима последовательность /р т3, l'v т'у то это
означает, что I' запоминает некоторое значение в у3, а т'3 немедленно
перезаписывает туда другое значение, запомненное в t2. Таким образом,
значение у3, вычисляемое в /р будет полностью потеряно и результат будет
неверным. Чтобы предотвратить такую неудачу, мы должны защитить каждую
из последовательностей / Г и mv т\ от взаимного влияния с помощью
семафора у4. В результате программа вычисления биноминальных коэф-
фициентов принимает вид
192
9.4. Мультипрограммное выполнение параллельных процессов
у-. = п, у, = 0, у3: = 1, у.= 1
Процесс
Процесс Р2
/(|: ЕСЛИ у, = (п-к) ТО НА 1с
занять (_у4)
4- Ф = У.УХ
1у Уу = '1
/4: освободить (у4)
/5: : у= у,- 1
/6: НА /0
I : СТОП
е
ти: ЕСЛИу= кТО НА те
т\- Ут ~ Уз + 1
т2. ЕСЛИ у} + у2< п ТО НА т.
т.: занять (_у4)
"V С = У2/'У3
ту у2. = /2
т,: освободить (у.)
т.: НА т0
те: СТОП
Взаимно защищенными критическими секциями здесь являются (/,, /4) и
(w., т.. ть) соответственно. Введение этих секций гарантирует вычисление
значения у3 в каждом из процессов без какого-либо влияния друг на друга.
Результат работы этих процессов эквивалентен приведенным ранее процессам
вычисления биноминальных коэффициентов, которые не обеспечивали
единственность критической ссылки.
Помимо необходимости синхронизации выполнения параллельных
процессов, управление ими со стороны диспетчера при их мультипрограммном
выполнении должно обладать свойством справедливости. Рассмотрим
сущность этого свойства.
9.4.2. Справедливость
Рассмотрим сначала программу без семафоров с полным условием £(j)
для каждого нетерминального места / * 1е , т.е. £(_р) = Истина для любого
у. При этих условиях каждый процесс, который еще не окончился, допустим,
т.е. всегда имеет допустимый переход, который выполняется, когда выбран
диспетчером. Каждый процесс должен выполняться до тех пор, пока он не
достигнет терминального места. Для моделирования этого свойства в
мультипрограммном режиме мы требуем, чтобы диспетчер был справедливым.
Под справедливостью понимается такое поведение диспетчера, при котором
любой процесс, готовый к выполнению, т.е. допустимый, должен в конце
концов выполнить свой допустимый переход. Иными словами, запрещается
ситуация, в которой какому-либо процессу, еще не закончившему свое
выполнение, т.е. имеющему допустимые переходы и не находящемуся в
7-1141 193
9. Модальность в ситуационном исчислении
терминальном месте, никогда не будет предоставлена возможность
выполняться.
В общем случае требование справедливости формулируется следующим
образом: требование справедливости по отношению к процессу соблюдается,
если всякий раз, когда процесс готов выполняться, он в конце концов получит
такую возможность, даже если будет готов выполняться бесконечно часто.
Рассмотрим простой пример двух процессов Р{ и Р2, которые синхронизируются
с помощью семафора:
Процесс Р,
У = 1
/(): занять (у)
/,: освободить (у)
/2: на /0
Процесс Р2
т0: занять (у)
т.: освободить (у)
т2: на пг
Очевидно, что если бесконечное чередование мест образует последо-
вательность /,, /2, /0, mt, т2, т0, /,, /,, /0, т}, т2, т0, то требования
справедливости по отношению к процессам Р, и Р, соблюдаются. В то же
время, если чередование мест образует последовательность /г / / / 12,
/0,..., когда процесс Р2 постоянно находится в месте т0, то требования
справедливости не соблюдаются. На практике любой диспетчер удовлетворяет
требованию: никакой процесс, готовый к выполнению, не может быть
отвергнут им более чем £раз. Здесь к является константой, характеризующей
диспетчера.
9.5. Модальная логика и анализ параллельных процессов
Для того чтобы использовать модальную логику как средство описания и
анализа свойств параллельных процессов (программ), введем точное понятие
ситуации и последовательности ситуаций применительно к программе.
Ситуацией, или состоянием, назовем набор значений 5 = < X; г] >. Здесь
к — < X,, ..., кт > — вектор значений переменных места л = {л,, ..., лт}, в
котором л изменяется в пределах множества мест L.= {/'0, ..., /', ...,/(} процесса
Р. Значение переменной места л. указывает на место /' в процессе Р, которое
активировано, р = <р,, ..., r\n>eD" — вектор значений распределяемых
индивидуальных и пропозициональных переменных у в ситуации 5.
Выполняемой последовательностью ситуаций программы Р = Pj |..| \ Рт
называется в общем случае бесконечная последовательность ситуаций 5 = s0,
5|( s2, ...., такая, что каждая ситуация \+1 = <Х'; р'> получается из ситуации
sk = <?i; р >, начиная с начальной ситуации 50, согласно одному из следующих
правил:
194
9.5. Модальная логика и анализ параллельных процессов
холостой такт : sk+=sk,
i-Й рабочий такт : выбираем один из процессов Р, 1 < i < т, содержащий
допустимый переход,
ЕСЛИ * X, * c(j) ТО у': = f(y) НА
при некотором значении у = д, такой, что с(р) = Истина. Согласно этому
переходу получаем X' заменой Х; на X', для всех j * I имеем X' = X ; ^'получаем
по команде у’’. = f(y) допустимого перехода процесса Р'. т)': = /(р).
Выполняемая последовательность ситуаций ст является справедливой, если
для нее соблюдается сформулированное ранее по отношению к процессам
требование справедливости.
Таким образом, поведение параллельных процессов характеризуется
множеством его справедливых выполняемых последовательностей ситуаций.
Используя формализм временной модальной логики, будем устанавливать
свойства этих последовательностей для параллельных процессов, характеризуя,
таким образом, их динамическое поведение. Введем предварительно ряд
дополнительных обозначений и понятий. Формулы временной модальной логики
будем рассматривать, используя следующие переменные:
локальные распределяемые у ..., уп\
локальные мест л , ..., ли;
глобальные хр ..., хк, и{, и,. ...
Переменные у ..., уп называют также программными. Переменные х,, ..., хк
называют входными и их можно изменять только в определенные
оговариваемые заранее такты выполнения процессов извне (не могут
изменяться процессами). Будем полагать, что их значения задаются перед
началом выполнения процессов и после этого остаются неизменными.
Переменные uv и2, ... являются добавочными, остаются постоянными в
течение всего выполнения (не изменяются от состояния к состоянию) и
используются для задания отношений между локальными значениями в
различных состояниях. Например, формула
Vw[(y — и) 9(у = w+l)]
означает, что в будущем будет такой такт, в котором значение переменной у
будет больше на 1, чем ее текущее значение.
Для места / еЛ атомарную формулу л = / обозначим в месте (/), т.е.
в месте (/) = Истина, если л; = /. Таким образом для данной ситуации
5 = <Х; т)> и места / &L. формула в_месте (/) истинна в этой ситуации 5, если
процесс Р. находится в месте I, т.е. Т = I. В более общем случае для множества
мест L с £ формула в месте (Л) истинна, если процесс Pt находится в одном
из мест, принадлежащих множеству L, т.е. в месте (L) истинна, если
значение переменной места л; е L, т.е. если L = {1а, /и+|, ..., lh} для некоторых
О < а < Ь, то будем так же записывать в месте (L), как в месте (I / ..., /).
I = h
Таким образом в месте (L) = в месте (I I ..., I) = v в месте (I).
а а 7
7*
195
9. Модальность в ситуационном исчислении
Для данной совокупности параллельных процессов (программы) Р пусть ф(х)
будет предусловием входных переменных, задающим начальные значения и
ограничения для входных переменных х, a f0(x) — предусловием программных
переменных, задающим начальные значения для переменных у, vp0(n) —
предусловием, задающим начальные значения мест программы. Начальное
предусловие, ассоциируемое с допустимым вычислением, представляется
формулой
(х, у, 71) = ф(х) Л /0(х) Л ф0(л).
Выполняемая последовательность ситуаций ст является (Д,ф) —
инициализируемым вычислением, если она является справедливой выполняемой
последовательностью ситуаций программы Р, и ,$0 = <Х; т]> есть первая
ситуация последовательности ст, такая, что А, совпадает с множеством
начальных мест (/'0, ..., /"') процессов, а р = /0(х) для входных значений х,
таких, что имеет место предусловие ф(х). Выполняемая последовательность
ситуаций является (Р, ф)-вычислением, если она является суффиксом (Д, ф)-
инициализируемого вычисления. Множество F(P, ф) обозначает множество
всех (Р, ф)-вычислений. Множество F(P, ф) называют также допустимым
вычислением, а каждую последовательность этого множества — допустимой
выполняемой последовательностью.
Формула w временной модальной логики является F(P, ф)-правильной,
если она истинна для всех последовательностей множества F(P, ф). Такая
формула является свойством программы Р. Нас интересуют именно формулы
такого типа, выражающие правильные программные свойства. Введем
обозначение k w, которое означает, что формула w является F(P, ф)-
правильной, т.е. w истинна для каждого справедливого (А ф)-вычисления
программы Р. Иными словами, выражение k w означает, что формула w
истинна для любой допустимой выполняемой последовательности. Отметим,
что когда мы говорим об истинности формулы w для множества допустимых
выполняемых последовательностей, то полагаем, что формула w содержит
условия, позволяющие проверять свойства программы, относящиеся именно
только к этому множеству. Например, если речь идет о свойствах программы,
касающихся только последовательностей, ведущих в терминальные состояния,
то при формулировке этих свойств следует оговорить, что все допустимые
выполняемые последовательности, о свойствах которых идет речь, оканчиваются
именно в терминальных состояниях. Доказательство свойств ведется только
для этих последовательностей. Значение формулы w на остальных допустимых
выполняемых последовательностях может быть несущественным.
Выражения вида h w служат базовыми утверждениями свойств программы
(теоремами). Главной нашей целью является составление таких формул
(теорем) и рассмотрение процедур доказательства их истинности. Разработчик
программ, желающий убедиться, что его программы удовлетворяют
определенным свойствам, должен сформулировать эти свойства, а затем
доказать их.
196
9.6. Инвариантные свойства
Для дальнейшего рассмотрения важно следующее справедливое утверждение:
Н w zd к w.
Оно означает, что если w истинна для любой возможной последовательности,
то она истинна также для каждого (Р, ф)-вычисления. Это утверждение
позволяет нам записать общезначимые формулы временной модальной логики
1= w с использованием введенного обозначения И :
Н □ —> w = —। Ow,
И DCw, zd и>2) zd (Dw, zd Dw2),
Н D(w zd ° w) zd (w ZD Dw).
Справедливым является также следующее выражение:
h w zdH Qw.
Оно означает: если w истинна для всех (Р, ф)-вычислений, то Dw также
всегда истинна для них.
Перейдем теперь к главной цели настоящей главы — изучению свойств,
которым, как правило, должны удовлетворять программы. Естественно,
эти свойства не являются всеобъемлющими, могут пополняться или
модифицироваться, но являются достаточно характерными для
рассматриваемого типа программ. Их классифицируют в зависимости от вида
представляющих эти свойства формул. Принципы доказательства истинности
формул в принципе ничем не отличаются от изложенных в главе 4, за
исключением того, что в дополнение к уже изученным используются правила
вывода, содержащие модальные операторы. Принципам доказательства и
примерам доказательства будет посвящен отдельный параграф настоящей
главы. Сначала рассмотрим только программные свойства.
9.6. Инвариантные свойства
Программные свойства, которые всегда должны выполняться для данной
программы, называют инвариантными свойствами. Они описываются
формулой вида Н Dw.
Это означает, что формула w должна быть истинна для каждой
последовательности допустимого вычисления, определяемого начальными
условиями этой формулы, т.е. w — инвариант по отношению к такому
допустимому вычислению (исходя из этого, можно было бы вместо Н EJw
написать И w).
Чтобы подчеркнуть тот факт, что мы имеем дело с предусловием ^(х, у, л),
иногда будем записывать £(х, у, л) zd Dw. Формула в этом виде выражает
инвариантное свойство, известное как свойство безопасности, базирующееся
на предположении, что ничего плохого случиться не может, если выполнены
начальные предпосылки £(х, у, и). Чаще всего полное предусловие ^(х, у, к)
при формулировке того или иного свойства будем оговаривать отдельно,
записывая перед формулой свойства, его часть или вообще ничего не записывая.
197
9. Модальность в ситуационном исчислении
9.6.1.Частичная корректность
Это свойство имеет значение только для программ, в которых каждый процесс
содержит терминальное место Л Такие программы назовем терминальными в
отличие от нетерминальных программ, которые предполагают бесконечное
выполнение и поэтому не содержат терминальных мест. Пусть с,(х, у, л) —
предусловие, которое задает ограничения на множество значений входных и
программных переменных и переменных мест, для которого предполагается,
что программа является правильной. ф(х, у) — утверждение о корректности
программы, т.е. отношение, которое должно установиться между входными
переменными х и результирующими значениями у при приходе всех процессов
в терминальные места. Используя введенные обозначения, свойство частичной
корректности записывается следующим образом:
И с,(х, у, л) о Щвместе (/,) ф(х, у)),
где / = (![_, ..., 1те) — множество терминальных мест всех процессов. Эта
формула означает, что если начальная ситуация удовлетворяет
ограничивающему предусловию £,(х, у, л), то в любой терминальной ситуации,
достижимой из начальной, т.е. в такой, что А = Z, имеет место отношение
ф(х, у) между входными значениями х и полученными значениями у
Заметим, что х остается постоянным в течение всего времени вычислений,
но при этом окончание программы само по себе не гарантируется.
Пример. Программа вычисления факториала:
У>= х,у2=\
/„: ЕСЛИ у} = О ТО НА /
Оф Уф = (У, - О yty2)
/,: НА /(1
I: С ТОП.
(’
В результате выполнения этой программы после ее останова в месте / будем
иметь у2 = х! Утверждение частичной корректности для этой программы следующее:
И 8>(х, у, л) л Швместе (/) у2 = х!),
где начальные условия, ассоциируемые с допустимым вычислением, имеют
вид
Цх, j, л) = в месте (/()) л уt = х л у2 = 1 л х > 0.
198
9.6. Инвариантные свойства
Свойство частичной корректности как инвариантное свойство фактически
является частью совокупности инвариантов. Обычно для того, чтобы доказать
свойство частичной корректности, доказывают инвариантность более полной
формулы, из которой следует частичная корректность:
И (вместе (1а) л у, = х л у2 = х > 0) д> □{[ в месте (/()) о (у1 > 0) л
л G'jJ'r = *!)] л {в месте (1}) д> (у, > 0) л (у2у,! = х!)] л {вместе (/,) о
о (у, > 0) л (у,У|! = х ’)] л {вместе (1е) д> (у, = 0) л (у, = х!)]}.
Пример. Программа, подсчитывающая число вершин в двоичном дереве X.
5= (X). С = 0
/0: ЕСЛИ S = () ТО НА 1е
проверка стека 5 на наличие в нем вершин дерева X.
ф (Т, S): = (голова (5), хвост (S))
выбор головы голова (5) и хвоста хвост (S) стека S и помещение их в Ги
S соответственно.
ф ЕСЛИ Т = 0 ТО НА /0
проверка переменной дерева на отсутствие в нем вершин.
ф С: = С + 1
Увеличение счетчика на 1.
/4: 5: = левое (Т) правое (Т) S
Помещение левого и правого поддеревьев в стек 5.
I- НА /()
/: СТОП.
е
Здесь Т — переменная дерева; 5 — стек, содержащий вначале дерево X.
состоящее из поддеревьев; голова (S) — взятие головы стека 5; хвост (S) —
взятие хвоста стека 5; левое (Т) — дает левое поддерево; правое(Т) — дает
правое поддерево. Определяя |Т| как число вершин в дереве Т, можем
выразить утверждение частичной корректности:
Н П[в_месте (?е) д> С = |Х|].
Начальные условия, соответствующие допустимому вычислению для этого
случая, имеют вид
в месте (/0) л .8 = (X) л С = 0.
199
9. Модальность в ситуационном исчислении
Пример. Параллельная программа вычисления биноминальных коэффициентов:
Утверждение частичной корректности:
И (0 < к < п) о П[(в_месте (Г) л в месте (те) у = С"к)].
Полное начальное условие, ассоциируемое с допустимым вычислением:
в месте (/0) л в месте (т0) л yt = п л у2= 0 л у.= 1 л у, = 1 л 0 < к < п.
9.6.2. Чистое поведение
Свойство чистого поведения обусловливает правильность выполнения
переходов (команд) для каждого места процессов программы. Например, в
случае деления свойство чистого поведения может обусловливать, что делитель
не ноль и не слишком мал, чтобы не приводить к переполнению. Если
программа содержит ссылку на элемент массива, то свойство чистого
поведения может обусловливать попадание индекса в определенные границы.
Обозначив условие чистого поведения в месте / как ар будем иметь следующую
запись свойства чистого поведения:
И ^(х, у, л) zd □ л (в месте (/) z> а).
Конъюнкция берется по всем потенциально опасным местам программы.
Пример. Программа должна давать только целые числа в течение всего
времени вычисления. Тогда условие чистого поведения для программы
вычисления факториала в месте /р являющемся критическим, будет
следующим:
И (х > 0) о Щв месте (/,) э (у{ > 0)].
Пример. Если программа деление содержит команду
/: ЕСЛИ * / *у, > у} ТО у; = (5[/] - у2),
где ъ — оператор целого деления и изменение индекса / массива 5 лежит в
пределах от 1 до л, то условие чистого поведения в месте / будет следующим:
И ПЦвместе (!) л (у, > у2)] =э [(1 < I < п) л (у2* 0)]} .
Пример. Свойство чистого поведения для программы, считающей
вершины дерева, имеет вид
И ПЦв месте (/,) S # ( ) л (в месте (/4) Т # 0].
Это утверждение гарантирует, что не будет сделана попытка вытолкнуть
(взять) данные из пустого стека или декомпозировать пустое дерево.
200
9.6. Инвариантные свойства
Пример. Главное условие чистого поведения для программы вычисления
биноминальных коэффициентов будет следующим:
h п(0 < к < п ) \2{в месте (т.) 102* 0) л (у, mod у = 0)]}.
9.6.3. Глобальная инвариантность
Очень часто некоторые свойства программ не зависят от какого-либо
конкретного места. В этом случае говорят о глобальных инвариантностях.
Свойство глобальной инвариантности в общем виде выглядит следующим
образом:
h Пф(х) ZD пр,
т.е. свойство р всегда имеет место в течение допустимого выполнения.
Пример. Условие того, что у, всегда должно быть положительным для
программы вычисления факториала, выглядит следующим образом:
Н (X > 0) ZD П(у, > 0).
Другое условие глобальной инвариантности для этой программы может
быть следующим:
Н (х > 0) о П(у2у,! = х!).
Пример. Свойство глобальной инвариантности для программы вычисления
биноминальных коэффициентов имеет вид
И (0 < к < п) □!(«-£ < у, < п) Л (0 < у2 <)].
Те же самые обозначения можно использовать для локальной
инвариантности по отношению к определенному месту /:
Н ^(в месте (/) Р).
Пример. Условие, которое должно быть истинным, когда мы находимся
в месте /0, для программы подсчета вершин дерева выглядит следующим
образом:
И Щв месте (/)0=> (S \Т\ + С= |Д|)],
т.е. сумма вершин поддеревьев в стеке S плюс значение счетчика С есть
число вершин дерева X.
201
9. Модальность в ситуационном исчислении
9.6.4. Взаимное исключение
Понятие критической секции и взаимного исключения было введено ранее.
Вернемся к ним и сформулируем свойства корректности программ.
Рассмотрим два параллельных процесса Р, и Рг Предположим, что каждый
процесс содержит секцию С с L., i = 1,2, которая критична к попеременному
выполнению команд из секции другого процесса. Например, это может быть
доступ к распределяемому устройству (такому, как диск) или распределяемой
переменной. Как уже говорилось, если природа этих секций такова, что
они ни при каких обстоятельствах не могут выполняться одновременно, то
их называют критическими.
Свойство взаимного исключения для С{ и С, можно представить следующим
образом:
ф(х) □ -я (в месте (С,) л в месте (С,).
Это свойство означает, что всегда, когда активно хотя бы одно место
секции С{, то в секции С2 не может быть ни одного активного места, и
наоборот.
9.6.5. Отсутствие дедлока
Как уже отмечалось, параллельная программа, состоящая из т процессов,
находится в дедлоке, если ни один из процессов не является допустимым.
Это означает, что единственно возможным тактом для диспетчера является
холостой, в результате чего непрерывно повторяется одна и та же ситуация
дедлока. Ясно, что в ситуации дедлока каждый процесс Р заблокирован в
некотором месте / е£, полное входное условие для которого является все
время ложным при всех текущих значениях р переменных у. Следовательно,
единственными потенциальными источниками дедлока являются места /,
для которых полные входные условия £ остаются все время ложными. Такие
места называют ожидающими. Терминальное место 1е в этом смысле также
является ожидающим. Однако специальный случай, в котором все процессы
находятся в терминальных состояниях, считается остановом, а не дедлоком.
Рассмотрим набор I = (/', ..., /'”) ожидающих мест, lJ eL,, не все из
которых терминальные. Пусть £р ..., Ет являются полными входными
условиями, соответствующими этим местам. Чтобы предотвратить дедлок в
I, требуется выполнение следующего свойства:
Н ф(х) о □( V в месте (/') zd v £(у)).
/ = 1 м
Это означает, что в случае, когда процессы находятся в /, то по крайней
мере один из них допустим. Этот процесс может выполняться, и тем самым
дедлок предотвращается.
Для того чтобы предотвратить возможность дедлока во всей программе,
необходимо налагать подобные требования на каждый набор ожидающих мест,
исключая /, = (Р, ..., 1'1).
202
9.7. Свойства живости (осуществимости)
Пример. Условие отсутствия дедлока для программы вычисления
биноминальных коэффициентов является следующим:
И (0 < к < п) zd П{[(в_месте (/,) л в_месте (т3) zd (у4 > 0)] л [(вместе (I) л
л в месте (т) zd (у4 > 0)] л [(вместе (7) л в месте (т3) zd (у4 > 0)]}.
Это условие учитывает тот факт, что при нахождении в (/,, т3) имеет
место у4> 0 и один из процессов должен выполняться. Если один из процессов
оказывается в терминальном месте, то другой не должен попасть в дедлок
при выполнении команды занять.
9.7. Свойства живости (осуществимости)
Эта категория свойств выражается общей формулой:
Н ZD Ow,.
Эта формула означает, что для каждого допустимого вычисления, если
и1! является изначально истинной, w2 должна в конце концов также стать
истинной. В отличие от свойств инвариантности, которые описывают только
сохранение желаемых свойств при переходах от одного места к другому,
свойства живости говорят о том, что некоторые события в конце концов
должны осуществиться. Эта формула в определенном смысле формулирует
цель, которая обязательно должна быть достигнута после некоторого, в общем
случае неизвестного, числа тактов.
Заметим, что вследствие замкнутости оператора 0 относительно множества
суффиксов допустимых вычислений приведенная формула, выражающая
свойство живости, эквивалентна следующей:
Й □(и'| ZD 0w2).
9.7.1. Абсолютная корректность
Это свойство похоже на частичную корректность и имеет смысл только
для программ с терминальными местами. Говорят, что программа абсолютно
корректна, если для всех значений входных переменных х, удовлетворяющих
ф(х), ее окончание гарантировано и выходное значение у после окончания
выполнения программы удовлетворяет ср(х, у). Более того, пусть I обозначает
набор терминальных мест программы. Тогда абсолютная корректность
выражается так:
И ф(х) zd 9(в_месте (( ) л ф(х, у)).
Это означает, что если мы имеем допустимую выполняемую
последовательность, начинающуюся в ситуации, определяемой местами (
и значениями у =fn(x). в которой ф(х) истинна, то далее для этой выполняемой
203
9. Модальность в ситуационном исчислении
последовательности гарантированно будет иметь место ситуация, определяемая
1с и удовлетворяющая <р(х, у).
Пример. Программа вычисления факториала:
Н (х > 0) ZD ^вместе (/,) л у2 = х!).
Пример. Программа подсчета вершин дерева:
Н (S = (A)) zd <)(в_месте (1е) л С = |Х|).
Пример. Программа вычисления биноминальных коэффициентов:
Н (0 < к < п) > 0[(в_месте (1е) л в месте (те) л у3 = С*)|.
9.7.2. Гарантированное осуществление
Свойства живости позволяют выразить причинно-следственную связь между
любыми двумя событиями, возникающими в течение выполнения программы,
а не только между началом и окончанием программы. Такая возможность
особенно существенна, когда программа является циклической. Общий вид
формулы, выражающей свойство гарантированного осуществления, следующий:
И (в месте (/) л ср) z> 9(в_месте (/)' л ср').
Эта формула означает, что если <р истинна в месте /, то в конце концов
будет достигнуто место в котором <р' истинна.
Пример. Для программы подсчета числа вершин в дереве утверждение
гарантированного осуществления, которое служит основой для доказательства ее
корректности, имеет вид
Н [вместе (/()) л S = us л С = с] л 9\в_месте (/0) л S = 5 л С = с + [и |],
где и, s, с использованы в роли глобальных переменных, в то время как S и
С — локальные переменные. Это утверждение говорит о том, что нахождение
в 1п с непустым стеком гарантирует попадание в конце концов в одном из
последующих тактов снова в 1п. При этом верхний элемент стека и будет уже
взят и значение Сбудет увеличено на число вершин в этом верхнем элементе.
Следующие свойства живости имеют значение для параллельных программ,
содержащих более одного процесса.
9.7.3. Доступность
Рассмотрим снова процесс, который имеет критическую секцию С. В
предыдущем разделе при изучении свойства взаимного исключения было
204
9.7. Свойства живости (осуществимости)
показано, как установить защиту для такой секции от вмешательства со
стороны других процессов. Продолжающим и дополняющим свойством к
свойству взаимного исключения является свойство доступности, означающее
следующее: если процесс желает войти в свою критическую секцию, он, в
конечном счете, попадает туда, т.е. не будет неопределенно долго
удерживаться механизмом защиты. Очевидно, что защитный механизм
является бесполезным, если он не позволяет в конце концов процессу войти
в его критическую секцию.
Пусть 1Х — место перед критической секцией. Тот факт, что процесс
находится в (, отражает намерение войти в критическую секцию. Пусть С
является множеством мест в критической секции. Тогда выражение свойства
доступности выглядит следующим образом:
И в месте (I) zd 9в_ месте (С).
Правильная конструкция критической секции должна гарантировать
выполнение этих двух полезных свойств: взаимного исключения и
доступности.
9.7.4. Беступиковость
Более общий класс свойств живости связан с возможностью осуществления
продвижения процедуры вычисления любого процесса, находящегося в месте
I. Здесь мы не ограничиваемся только местами, содержащими семафорные
команды. Рассмотрим произвольное нетерминальное место I в некотором
процессе Р, т.е. / # L Если вычисление процесса должно развиваться таким
образом, что он обязательно должен покинуть место /, то он не может
оставаться блокированным в / вследствие ошибки диспетчера, который
управляет выполнением процесса Р Это означает, что процесс Р, находясь
в месте /, в котором истинна формула в месте (/), должен его обязательно
покинуть, в результате чего станет истинной формула в месте (/).
Следовательно, свойство беступиковости для любого места /, I # / может
быть выражено следующим образом:
И 0(—I в месте (/)),
или эквивалентной формулой
н- □<?_ месте (/),
которая означает, что мы никогда не будем заблокированы в месте /.
Свойство беступиковости так же известно как свобода от индивидуального
зависания, определяемого как ситуация, в которой некоторые процессы,
которые не находятся в терминальных местах, не могут продвигаться
(выполняться), несмотря на то, что программа в целом выполняется за счет
продвижения других процессов. Заметим, что это более сильное требование,
205
9. Модальность в ситуационном исчислении
чем отсутствие дедлока, поскольку считается, что программа не попала в
дедлок до тех пор, пока хотя бы один процесс выполняется.
9.7.5. Отзывчивость
Очень важным классом программ, относящихся обычно к параллельным
программам, являются операционные системы и такие программы реального
времени, как системы резервирования билетов в авиации или другие системы
баз данных, функционирующие в режиме on-line. Эти программы удобно
рассматривать как непрерывные или циклические программы, работающие
постоянно. Остановка выполнения этих программ обычно отражает
ошибочные условия. Следовательно, эти программы работают не на
получение конечного результата, а для результатов, производимых в течение
их бесконечного выполнения. Таким образом, понятия абсолютной и
частичной корректности здесь не применимы и должны быть заменены
утверждениями, учитывающими непрерывное выполнение программ. Одним
из важнейших свойств таких программ является отзывчивость.
Пример. Предположим, что программа, моделирующая операционную
систему G (диспетчер), обслуживает ряд программ (процессов)
пользователей А,, ..., Rt, управляя распределением между ними ресурсов.
Ресурсами могут быть жесткий диск, главная память и т.д. Пусть программы
пользователей взаимодействуют с диспетчером, запрашивая ресурсы через
булевы (пропозициональные) переменные {г, g}, i = !, ..., t. Переменная
г устанавливается истинной пользователем программы R,, чтобы
сигнализировать о запросе ресурса. Переменная g устанавливается истинной
операционной системой С, сообщающей тем самым пользователю А, что
он может взять ресурс. После использования ресурса пользователь А
возвращает ресурс обратно системе G, присваивая переменной г ложное
значение. Операционная система признает освобождение ресурса
присвоением переменной g ложного значения.
Итак, имеем
А выдает запрос zd г: = истина;
G предоставляет ресурс zDg: = истина;
R освобождает ресурс zd г: = ложь;
G признает освобождение zd g: = ложь.
Утверждением а, означающим, что диспетчер справедливо реагирует на
запросы потребителя, является
а,' г, -':'J S,,
т.е. когда бы г не стала истинной в конце концов g будет истинной. Заметим,
что это утверждение не требует, чтобы г становилась истинной, когда
диспетчер G находится в каком-либо определенном месте.
206
9. 7. Свойства живости (осуществимости)
Подобным образом необходимо обеспечить подтверждение Ь, освобождения
ресурса присвоением g, ложного значения:
Л: г 0(-,g).
Более того, система не сможет работать нормально, если не будет
обеспечено должного взаимодействия между программами пользователей.
Например, система не может обещать пользователю А, предоставления
ресурса, если пользователь Ар который в это время занимает его в конце
концов его не освободит.
Следовательно, требуется, чтобы поведение пользователя R удовлетворяло
определенным требованиям с , а именно:
С
Это утверждение говорит о том, что в случае предоставления потребителю R
ресурса г этот ресурс в конце концов будет освобожден. К сформулированным
утверждениям обычно добавляются утверждения, гарантирующие правильное
непрерывное поведение G. Одним из таких утверждений является следующее:
d- □( I g, < 1),
/ -i
означающее, что в любом такте диспетчер предоставляет ресурс самое большее
одному потребителю. Оно относится к типу утверждений взаимного исключения.
Введем теперь утверждение корректного поведения диспетчера G в целом:
£ = л а л л h л d.
/-1 ' /-1 '
Корректное поведение, ожидаемое от пользователей А, имеет вид
Проблема доказательства правильного поведения диспетчера G может быть
решена двумя различными путями.
В первом случае рассматривается параллельная программа, которая
состоит из одного диспетчера G. Переменные г и g рассматриваются как
входные и выходные переменные этой программы. Значения переменных г
устанавливаются внешними пользователями А,, ..., Rt. Для этой программы
необходимо доказать истинность формулы
Й Dip z> □£,
задающей свойство отзывчивости. Смысл этой формулы состоит в том, что
при условии непрерывно правильного поведения пользователей, формирующих
внешнее воздействие в соответствии с формулой <р, диспетчер G должен всегда
вести себя соответствующим образом в соответствии с формулой правильного
поведения
207
9. Модальность в ситуационном исчислении
Во втором случае рассматривается параллельная программа Р, которая
состоит из операционной системы G, работающей совместно с программами
Rt, А, т.е.
р= g На, II... II R.
Для каждого R устанавливается модель, которая гарантирует выполнение
условия с. В упрощенном виде такую модель можно представить как
следующую программу пользователя R. при начальном значении г = Ложь-.
1{- НА /,
г: = Истина
I - ЕСЛИ -gTO НА I
2 °i 2
12: ЕСЛИ ТО НА 12
I: занять ресурс
Iг: = Ложь
/' ЕСЛИ - gTO НА I,
/,: ЕСЛИ g, ТО НА L
1ь' на k-
Если полагать, что эта модель А хорошо представляет реального
потребителя R в части его взаимодействия с G, то для гарантии корректного
поведения программы необходимо доказать истинность формулы
Й □ (ср л ^),
также задающей свойство отзывчивости.
Таким образом, возможны две моделирующие ситуацию альтернативы:
рассмотрение диспетчера G в единственном числе и во взаимодействии с
внешними пользователями посредством переменных г, gt или рассмотрение
совокупной системы, состоящей из G и Rx, ..., Rr В первом случае
соответствующее поведение внешних по отношению к G пользователей
проверяется и обеспечивается отдельно посредством непрерывного сохранения
значения ф. Во втором случае поведение пользователей А проверяется вместе
с соответствующим поведением G.
Аналогичный анализ может быть распространен на другие ситуации,
где необходимо обеспечивать взаимодействие с внешними устройствами и
реагировать соответствующим образом на внешние сигналы.
208
9.8. Свойства предшествования
9.8. Свойства предшествования
Третий класс рассматриваемых нами свойств составляют свойства, которые
называются свойствами предшествования и выражаются с помощью оператора
«до тех пор пока» U и дополнительного оператора предшествования Р, который
можно рассматривать как частный случай оператора U. В простейшем случае
свойства предшествования описываются следующим выражением:
Н U w2.
Это выражение означает (истинно), что во всех допустимых вычислениях
программы, если в будущем наступит ситуация, в которой формула станет
истинной, причем до этого такта она была ложной, a w, была истинной, то
формула w перестанет быть истинной в этой ситуации. Этот оператор очень
полезен для выражения отношений предшествования между ситуациями.
Для дополнительного оператора предшествования Р выражение w Pw,
эквивалентно -> ((-> w,) U w2). Выражение и-Ри’2 читается как "и1! предшествует w2"
и является истинным, если w2 станет истинной в какой-либо ситуации, будучи
до этого ложной, а ситуация, в которой стала истинной наступила ранее.
Несколько очевидных свойств дополнительного оператора предшествования
Р можно получить из соответствующих свойств оператора U и определения
оператора Р:
1) иРи- = □ w;
2) h’jPh’j л WjPh’jZd H'jPb',;
3) w1Pw2 = w2 л [w, л° (и^Ри^)];
4) □ -i w2 zd WjPw2;
5) Ph\ v w Ph^ v 0(w л H'2).
Выражение 1 свидетельствует о том, что w всегда предшествует себе, если
w является всегда ложной: w не может предшествовать самой себе.
Выражение 2 означает транзитивность отношения предшествования: если
и1, предшествует w2, а последняя предшествует w то w предшествует и>3.
Выражение 3 дает индуктивную характеристику оператора Р. Оно говорит
о том, что и1! предшествует w2, если в настоящей ситуации w2 не истинно,
а и,, истинно, либо в настоящей ситуации w2 не истинно, а начиная со
следующей ситуации предшествует w.
Выражение 4 говорит о том, что если w2 никогда не становится истинной,
то и1! предшествует w2 для любого
209
9. Модальность в ситуационном исчислении
Выражение 5 характеризует линейность развития событий во времени для
любых двух w, и w2: или и,1 предшествует w2, или w2 предшествует или обе
истинные в одной и той же ситуации.
Рассмотрим некоторые из свойств предшествования, использующих
операторы U и Р.
9.8.1. Безопасность
Выражение типа nW' можно интерпретировать по отношению к программе
как свойство, выполнение которого мы хотим всегда иметь для определенной
гарантии правильности программы, выражение типа Он-, — как свойство,
выполнение которого нарушает указанную гарантию. Тогда для некоторых
случаев выражение h^Uh^ можно интерпретировать как комбинацию свойств
□и1! и 0и\. поскольку справедливо выражение
Н (□ W Л W2) ZD
которое и является одним из свойств безопасности. Однако более интересен
случай, когда w всегда имеет место вплоть до ситуации, в которой происходит
w, т.е. когда свойство имеет место вплоть до свойства w2, знаменующего
наступление нежелательных явлений, нарушающих правильность программы.
Другое свойство безопасности, использующее оператор U, является
уточнением свойства
Н (вместе (/) л ф) zd (вместе (/') л ф'),
используемого для того, чтобы выразить достижение программой в некоторой
ситуации места в котором формула ф' будет истинна, если в настоящей
ситуации программа находится в месте / и формула ф истинна. Место /' при
этом не обязательно должно достигаться первый раз.
В отличие от этого свойства выражение (также относящееся к классу
свойств безопасности)
Н (в месте (/) л ф) zd |(-> в месте (/')) U (в месте (/') л ф')]
говорит о том, что если программа находится в месте / и формула ф истинна,
то в некоторой ситуации она должна достичь места Г и при первом же
приходе в это место /' формула ф' будет истинной.
Пример. Для программы вычисления биноминальных коэффициентов
имеем
Н (0 < к < п) zd {\(в_месте (т4) zd (у2 * 0 ) л. (у} mod у2 = 0) л (п-к < yt < л)] л
л (0 < у2 < к) U (в месте (1е) л в месте (те) л у3 = Скп ]}.
Это свойство говорит о том, что до тех пор, пока не будет достигнуто окончание
программы с правильным результатом, должны выполняться свойства чистого
поведения и глобальной инвариантности.
210
9.8. Свойства предшествования
9.8.2. Предусмотренная реакция (отзывчивость)
Свойства, выражаемые формулой о 0и;2, относятся к числу свойств
отзывчивости, выполнение которых гарантирует, что на каждую ситуацию,
в которой формула w, истинна, программа отвечает в конце концов истинным
значением формулы w2. Часто желательно дополнить это свойство
требованием, чтобы формула w2 никогда не становилась истинной, если этому
не предшествует истинность формулы wf, т.е. чтобы программа не реагировала
на непредусмотренную ситуацию. Это свойство в общем случае можно
выразить с помощью оператора предшествования, но в каждом конкретном
случае требуется тщательно выбирать ситуации, после наступления которых
проверяется предшествование. Хорошим примером выражения, задающего
свойство предусмотренной отзывчивости, является следующее:
И [вместе (/0) о w, Р w2)] л |(w2a° w2) о" (и\ Р и>2)].
Этот пример иллюстрирует тщательный выбор ситуаций: предшествование
Wj по отношению к w2 проверяется либо начиная с ситуации, определяемой
начальным местом /0, либо после ситуации, в которой w, была истинна и
изменила свое значение на ложное в следующей ситуации.
В большинстве практических случаев имеется дополнительная информация
о Wj и w2, которая помогает сформулировать требования в более простой
форме.
Пример. Вернемся к примеру с операционной системой G, которая
распределяет ресурс между пользователями Я(, ..., /?,. Простейший протокол
взаимодействия между потребителем R и операционной системой
определяется следующими четырьмя выражениями:
1) h (г л -1 g) =>
Это выражение говорит о том, что если г истинна, a g, ложна, т.е. запрос
на ресурс со стороны rt имеется, но он еще не предоставлен, то пользователь
R обязан настаивать на своем требовании, подтверждая значение г в
следующем такте;
2) И (г Л g) ZD °gt.
Это выражение означает, что если ресурс был предоставлен пользователю
Я, то диспетчер не имеет права отнять его до тех пор, пока пользователь не
присвоит г ложное значение;
3) Н (г Л g_) -п г .
Это утверждение означает, что если диспетчер еще не признал отказа от
ресурса пользователя R, то R не может выставлять нового требования;
211
9. Модальность в ситуационном исчислении
4) Н (- С л -п g) о ° g.
Это утверждение означает, что если ресурс не занят пользователем Ли не
затребован им, то ресурс не предоставляется процессу, который его не
требует. Все это и есть описание свойства предусмотренной отзывчивости.
Выполнение перечисленных свойств вместе со следующими
дополнительными выражениями гарантирует правильное поведение
программы:
5) Н г о 0g;,
6) Н g, 0 -л г;
7) Н -п г о 0 -n gt.
Четыре первых утверждения характеризуют поведение программы в
соседних ситуациях. В глобальном стиле свойства предусмотренной реакции
можно выразить следующими выражениями:
а) Н г => |r U(g, л г)];
6) Н g,^ [g, U (г л g)];
в) Н -п г =>1-1 г U(-ig; Л -1 г)|;
г) н 1 g,^(r, Р g).
Эти выражения заменяют все остальные. Утверждение а) говорит о том,
что если г истинно, то оно должно оставаться истинным до тех пор, пока g
истинно. Утверждение б) говорит о том, что если ресурс предоставлен, то
он остается предоставленным до тех пор, пока от него не откажутся.
Утверждение в) говорит о том, что если от ресурса отказались, то он не
может быть затребован до тех пор, пока отказ от него не будет признан.
Утверждение г) говорит о том, что если ресурс не назначен, то его
назначению должен предшествовать запрос.
9.8.3. Справедливая отзывчивость
Во многих случаях предшествование двух ситуаций (ср, предшествует ср )
связано с предшествованием двух других ситуаций (ф предшествует ф ), когда
ф( предшествует событию ф2. Такой случай назовем условным предшествованием.
Его можно представить выражением
И (ф, Р ф2) (<р, Р <р2),
которое означает, что если ф] предшествует ф2, то ср предшествует ср2.
212
9.9. Доказательство свойств корректности
Вместе с выражениями отзывчивости
h Ф| о Оф,,
Н ф2 О 0ф2,
выражение условного предшествования называют справедливой отзывчивостью.
Иначе говоря, если Н ф, Оф, и Н ф2 => 0ф2 интерпретируются как ответ ф, на
требование ф(, то отзывчивость означает, что каждое требование будет
обязательно сопровождаться ответом. Справедливая отзывчивость устанавливает
порядок ответа и дополнительно требует: если ф, предшествует ф то ответ на
ф,, а именно ф, должен предшествовать ответу на ф , а именно ф2.
Пример. Рассмотрим распределение ресурсов для операционной системы
и обслуживаемых ею пользователей. Наложим требование справедливости
на свойства отзывчивости. Это требование может быть задано выражением
(г Р г) о (gi Р g), которое означает, что если потребитель R поместил свой
запрос раньше потребителя Я, то он раньше и будет обслужен. Однако
здесь необходимо быть осторожным, ставя жесткие условия. Например, если
g, истинно, в то время как оба г. и г ложны, то может иметь место ситуация,
когда нельзя обещать, что g. будет предшествовать g Для исключения такой
ситуации необходимо исходить из ложности g. Тогда выражение условного
предшествования будет выглядеть следующим образом:
Н (-1 g) =э [(г Р г) о (gt Р gy)J.
9.9. Доказательство свойств корректности
Из материала настоящей главы ясно, что временная модальная логика
является одним из видов ситуационного исчисления. Интерпретация формул
этой логики осуществляется посредством логики предикатов первого порядка.
Принципы доказательства в модальной логике те же, что и для других
исчислений, базирующихся на логике предикатов первого порядка.
Единственное отличие состоит в использовании при доказательстве правил и
формул, содержащих модальные операторы. Для доказательства свойств
корректности нам необходимо иметь следующие исходные данные.
Аксиомы собственно модальной логики, часть из которых была рассмотрена в
начале настоящей главы. Эти аксиомы, как обычно, назовем базовыми
аксиомами.
Правила вывода в модальной логике. Эти правила также по аналогии с
предыдущей главой назовем базовыми правилами.
Общие аксиомы, описывающие свойства модели параллельных процессов
(программы), не зависящие от конкретного типа программы, свойства
корректности которой необходимо доказать. Эти аксиомы, как обычно, назовем
модельными аксиомами.
213
9. Модальность в ситуационном исчислении
Частные аксиомы, описывающие свойства конкретной программы,
корректность которой необходимо доказать. Эти аксиомы, поскольку мы
имеем дело с программами, назовем программными аксиомами.
Формулировку свойства корректности, которое требуется доказать для
данной программы.
В настоящем параграфе ограничимся рассмотрением примера доказательства
корректности для простой программы (рис. 9.7), содержащей только один
процесс и, следовательно, являющейся последовательной детерминированной
программой. Мы не будем выписывать все известные к настоящему времени
базовые аксиомы и правила модальной логики. Будем вводить эти аксиомы
и правила по мере необходимости в ходе доказательства.
9.9.1. Модельные аксиомы
Нам потребуется только одна модельная аксиома М, на основе которой
будут порождены все программные аксиомы. Эту аксиому можно записать
следующим образом:
М‘. [в месте (/) л c(j) л у = «] о [в месте (Г = переход (c(j), 1)) л
л У =f(u) (х) =/2 (у)].
Она гласит: если процесс находится в активном месте / (истинен предикат
в месте (/)) и истинно условие перехода с(у), а текущее значение переменных
набора у есть и, то он переходит в место если значение условия с(у)
истинно. В месте /' выполняется присвоение переменным набора у значений
переменных набора/(«) и вычисляется (конкретизируется) (х) = /2 (j). Из
этой аксиомы видно, что проверка условия c(j) выступает здесь в роли
действия, в результате которого осуществляется переход в место
9.9.2. Программные аксиомы
Рассмотрим программу возведения в целую степень х2 >0 действительного
числа х т.е. программу вычисления х*г. Эта программа имеет три места /0,
/р / Место 1п является начальным и до начала вычисления истинно действие
Начать. Вычисление начинается в результате выполнения действия Начать.
Предположим, что 0°=1. Необходимо показать корректность этой
программы, т.е. что она действительно вычисляет указанную степень. Граф
переходов этой программы представлен на рис. 9.7.
Тогда программными аксиомами, полученными по модельной аксиоме
для каждого перехода программы, будут следующие:
Л/ : в_месте (/0) л -п Начать [вместе (/0 = переход (-, Начать, /0)) л
Л J = и Л и = (хр Х2, 1) Л X^2 = уз у/2],
214
9.9. Доказательство свойств корректности
М,: в_месте (/0) л Начатье [в месте (7, = переход (Начать, /0)) л
л у = и л и = (хр X,, 1) л х/2 = У3 у/2],
Л/2: [в_месте (/,) л у2 = 0 л у ~ и ] о [вместе (/2 = переход (у2 = 0, /,)) л
лу= и л хД = у2 уД],
М2. [в месте (Д л у2 > 0 л нечетный (у2~) л у = и ] о
о [в месте (/, = переход (у2 > 0 л нечетный (уД, 1Д) л у = (wp w2-l, д и}) л
Л Хр = у2 у/2],
Л/4: [в месте Ц) л у2 > 0 л четный (у2) л у = и ] о
о [в месте (/, = переход (у2 > 0 л четный (у2), /)) л у = (мД и2 4-2, w3) л
л V2 = У3 У,Ч
—I Начать /
6;, У2. уД := (xv х2,1Л
Сь)
Начать/ \ /у — 0 / уД
(У, ’ у2' ) := <Х1 ’ Хг’ 1 =у)'~ I /
( у > О Л нечетный (уД /
у > О А четный (уД/
6;2- yrD,
Рис. 9.7. Граф переходов программы возведения в целую степень х2 числа х .
9.9.3. Свойство корректности
Для того чтобы установить корректность программы вычисления степени,
необходимо доказать истинность выражения
215
9. Модальность в ситуационном исчислении
И в месте (/0) л Начать л х,> 0 з 9в_месте (/2) л у = xfi.
Согласно классификации свойств, приведенной ранее, это выражение
относится к числу свойств осуществимости. Напомним, знак Н говорит о
том, что доказательство истинности должно вестись только для справедливого
(Р, ф)-выполнения программы. Но поскольку наш пример простейший и
имеет дело только с одним процессом, то следует доказать истинность
выражения
1= вместе (/0) л Начать лх,> 0 з 9в_месте (/2) л у, = х^г.
9.9.4. Доказательство
Для того чтобы было удобно следить за процессом доказательства
корректности программы, каждый его шаг будем нумеровать. Как всегда,
формула со знаком |- впереди означает, что она стала истинной в результате
вывода на этом шаге. Выше будем указывать те правила или аксиомы, которые
использовались для доказательства ее истинности. Некоторые из этих правил
и аксиом ранее нигде не упоминались. Большинство из этих правил легко
вывести из правил и аксиом, рассмотренных в предыдущих главах. Если
потребуется, то будем давать также пояснения к доказательству на
соответствующем шаге. В соответствии с приведенным ранее определением
ситуация 5 есть состояние программы, когда она находится в месте I и ожидает
выполнения очередного действия для перехода в другую ситуацию (место
при этом может оказаться тем же самым). Обратим внимание, что как только
программа попадет в место I, переменным набора у присваиваются значения
промежуточного набора и и вычисляется очередное промежуточное значение
Уу У/2 = х,х2.
Начальное условие имеет вид
h (вместе (/0) л Начать л х2> 0. (9.4)
Используя программную аксиому Л/Ои подставляя вместо у3 ее значение,
равное 1, получаем
(в месте (10) л у = и л и = (хрх2, 1) л х*2 = 1- у >2 , (9.5)
т.е. имеем истинную формулу
216
9.9. Доказательство свойств корректности
= [вместе (/0) л у = «л и = (х,, _х2,1) л х,л2 = 1- у/'г].
Используя программную аксиому Мх, начальное условие (9.1), формулу
(9.5) и правило модус поненс, имеем
h вместе Д) л у = и ли = (х, х2,1) л хД = 1- уъ. (9.6)
Начальное условие х2 > 0 представляем в виде
Р(Д) = вместе Ц) л у = и ли — (хр х2, 1) л хД = 1- у *2.
Имеем
- х2 > 0 е А = 0 v х, > 0. (9.7)
Используя формулы (9.6)—(9.7) и правило введения конъюнкции, получаем
Н вместе (/,) л у = и л и = (хр х2, 1) л х*2 =1- у *2 л х2 = 0 v х2 > 0). (9.8)
Используя формулу (9.8) и правило (tt = Q h f(tt, Q = /(rp t2), имеем
j- вместе (/,) л у = ил и = (хрх2,1) л х1х2=1- уу2 л
лу3- УД = х^ л х2 = 0 v х2 > 0. (9.9)
Используя формулу (9.9), правило исключения конъюнкта и правило
(', = Q I’ /(ф = /(ф 9’ получаем
в месте (/,) л у = ил и = (хр х2,1) л х^г = у2уД л у2 = 0. (9.10)
Используя формулу (9.10), правило исключения конъюнкта и правило
« = t2) Ь /(ф Q = имеем
h в месте (lt) л у = и л и = (хр х2,1) л х^г = у3-у/2 л у2 > 0. (9.11)
Формула (9.11) для случая нечетного у2 имеет вид
Н в месте Ц) л у = и л и = (хр х2,1) л х^г = у2уД л нечетный (у2) л
лу2>0. (9.12)
Формула (9.12) для случая четного у2 имеет вид
h в .месте Ц) л у = ил и = (хрх,,1) л х^2 = y3-yty2 л четный (у,) л у2 > 0. (9.13)
217
9. Модальность в ситуационном исчислении
Используя программную аксиому М2, формулу (9.10) и правило модус
поненс, получаем истинную формулу Р(а, /,) для случая, когда
у2 = 0, и = (хр х2, 1)
|- в месте (/2) л у = и л и = (хр х2, 1) л ху2 = у3ур л у2 = 0. (9.14)
Используя программную аксиому Му формулу (9.12) и правило модус
поненс, получаем истинную формулу Р (а, /,) для случая, когда
у > 0, и = (хр х2,1) и нечетный (у2)
|- в месте (I) л у = и л и = (х,, х2 — 1, х,) л нечетный (у2) л
лу3- у >2 = х,л2А У2 > 0. (9.15)
Используя программную аксиому Л/4, формулу (9.13) и правило модус
поненс, получаем истинную формулу Р(а, /,)) для случая, когда у2 > 0,
и = (х,, х2,1) и четный (у2).
Ь в месте (lt) л у = и л и = (х,2, х2-ь 2, 1) л четный (у2) л
л у3- у/2 = х,л2 л у2 > 0. (9.16)
Предположим теперь, что формула
Р(/) = в месте (/,) л у = «л и = (и{, и2, и3) л х^ = УуУ/'г = и3и"г л
л и2 = 0 v и2 > 0)
истинна для любого места /.
Тогда используя программную аксиому М2, формулу (9.14) и правило
модус поненс, получаем истинную формулу Р(а, /,) для случая, когда
у2 = 0, и = (и,, и2, w3) = (йр 0, w3), четный (у2)
h вместе (/2) л у = и л « = (ир 0, w3) л х,л2 = у3-у/2 = и3и"2 = и3-и}° =
= и}\ = и3 = у3 л у2 = 0.
Используя программную аксиому М3, формулу (9.15) и правило модус
поненс, получаем истинную формулу Р (а, 1{) для случая, когда у2 > 0,
и = (ut, и2 -1, н,«3) и нечетный (у2)
Н в месте (/,) л у = и л и = (wp и2 -1, иу и3) л нечетный (у2) л = х*2 =
= у3-у/2 = и}-и3и‘‘^' = w3-w"2A у2 > 0. (9.17)
218
Вопросы и упражнения
Используя программную аксиому Л/4, формулу (9.16) и правило модус
поненс, получаем истинную формулу Р (a, /) для случая, когда у, > О,
и = (u,, w2 -1, и{ иъ} и четный (у2)
|- в месте (/; л у = и л и = (и,2, w2 + 2, 1) л четный (у2) л х*2 = у3-у/2 =
= 1-(«!2) 2 = и2-и"1 л у2 > 0. (9.18)
Других формул Р (а, /,) не существует. Таким образом, показана
истинность Р(1а) и истинность V(o, /) \Р(1)) Р(а, /)|. Из индукционной
аксиомы следует истинность формулы
V(/) Р(()) = V(/)(e_jwecme (/) л у = и ла = (мг м3) л х,л2 — у3-у>2 =
= и2-и"г) = ^(в месте (/) л у = и л и = (и и uj л
лх;2 = у3-у/2 = w3-m,“2). (9.19)
Используя аксиому модальной логики D/Ъ 0/ получаем
<)(в_месте (!) л у = и л и = (wp м2, и}) л х,л2 = у3-у}'2 = и^и^‘2). (9.20)
Начальным значением х,, присваиваемым промежуточной переменной
иг является положительное конечное число. Промежуточное значение
и2 = у2 согласно выполняемым действиям уменьшается до тех пор, пока не
станет равным 0 . При этом значении и2 — уг = 0 и формула (9.20) приобретает
следующий вид:
§(в_месте (/) л у = и л и = (и,, 0, и,) л х;2 = у). (9.21)
Используя правило исключения конъюнкта, получаем
<)(в месте (Г) л х,'2 = уз). (9.22)
Таким образом, имеем
1= в месте (/(|) л Начать л х, > 0 п <)в_месте (/,) л у= хр.
Корректность программы доказана.
Вопросы и упражнения
I. Что такое модальность?
2. Зачем вводятся модальные операторы во временной модальной логике9
3. Каков смысл модальных операторов?
4. Из каких конструкций состоит язык временной модальной логики?
219
9. Модальность в ситуационном исчислении
5. В чем содержательная суть модели параллельных процессов? Дайте формальное
определение модели параллельных процессов. Что такое программа?
6. В чем состоит мультипрограммное выполнение параллельных процессов?
7. Адекватно ли мультипрограммное выполнение параллельных процессов
параллельному выполнению? Если неадекватно, то в чем состоит неадекватность и
как ее избежать?
8. Что такое дедлок? Вследствие каких явлений параллельные процессы могут
попасть в дедлок? Как избежать дедлока?
9. Чем модальная временная логика удобна для описания и проверки правильного
выполнения программы?
10. Какие свойства программ вам известны? Дайте их содержательное толкование.
Запишите эти свойства на языке временной модальной логики.
11. Какова структура доказательства корректности (свойства) программы? Какие
типы аксиом применяются для доказательства корректности программ?
12. Постройте инициальный детерминированный автомат по множеству
последовательностей 5 = {ес,, ayv а{ахау}, а2а2с^ а1ау2, а2с2, а2а^а2с2}.
Сформулируйте свойство отсутствия перехода любого состояния в себя по любому
входу av Докажите или опровергнете это свойство.
13. Постройте инициальный детерминированный автомат по множеству
последовательностей 5 = {ес}, atct, а^а^, a2a2ct, а}а}с2, а2с2, а2ааЛсД.
Сформулируйте свойство детерминированности автомата. Докажите или опровергнете
это свойство.
14. Постройте инициальный детерминированный автомат по множеству
последовательностей 5 = {ect, atct, ара^, арарс a2a2ci’ a{aSv aic^ a2a2a2c2V
Сформулируйте свойство достижимости каждого состояния из начального. Докажите
или опровергнете это свойство.
15. Постройте инициальный детерминированный автомат по множеству
последовательностей 5 = {ее,, ау{, а{аха{с{, ауца{а,с{, a2a2cv ajalc2, а2с2, а2а2а2сД.
Сформулируйте свойство наличия циклического перехода по входу а, из начального
состояния через все остальные снова в начальное. Докажите или опровергнете это
свойство.
16. Постройте инициальный детерминированный автомат по множеству
последовательностей 5 = {ect, ау^ а^а^, ayiyiyi^, а2а2с{, а{а}с2, а2с2, а2а2а2с2}.
Сформулируйте свойство отсутствия перехода любого состояния в себя по любому
входу. Докажите или опровергнете это свойство.
10. ДЕДУКТИВНЫЕ БАЗЫ ДАННЫХ
В настоящей главе рассмотрены некоторые аспекты теории дедуктивных
баз данных, запросы к которым удовлетворяются на основе использования
исчислений.
Современный компьютеризованный мир трудно представить без баз данных,
хранящих огромные массивы информации, называемой данными. Эти базы
данных постоянно обновляются. К ним непрерывно поступают запросы на поиск
информации по определенным признакам и отношениям между данными.
Теоретическим и практическим вопросам баз данных посвящено много работ.
Базы данных различаются по структуре хранящихся в них данных и бывают
иерархическими, сетевыми (графовыми), объектно-ориентированными и
реляционными. После появления реляционных баз данных стали публиковаться
и теоретические работы, предлагающие строить теорию реляционных баз данных
на основе какой-либо формальной системы или исчисления. Запросы к
реляционным базам данных или поиск в базах данных в этом случае предлагалось
осуществлять как вывод в некотором исчислении. В настоящее время интерес к
этому направлению развития баз данных стал особенно ощутим в связи с бурным
развитием сетевых технологий и необходимостью работать с распределенными
данными различного типа. Именно базам такого типа посвящена настоящая глава.
Распространенной точкой зрения на реализацию дедуктивной базы данных является
подход, основанный на определенном расширении системы управления данными
в реляционной базе. Рассмотрим суть этого подхода.
10.1. Реляционные базы данных
Данные в реляционных базах хранятся в виде таблиц, задающих
определенные отношения между этими данными. Каждому столбцу таблицы
взаимно однозначно соответствует атрибут (имя столбца) а, а атрибуту —
множество значений переменных {х'г х'2, ..., х'Д = Xt. Переменные одного
и того же множества Xt принимают значения из одного универсума.
Множество значений d, = {о'р о'2,..., о'г(} переменных {х'р х'2, ..., х'л}
называют доменом.
221
10. Дедуктивные базы данных
Под схемой отношений подразумевают выражение «(zzJJQ, аДХт)), в
котором а является именем схемы отношений, а:(Х) — термы базы, i = 1, т.
Схему отношений, все термы которой конкретизированы а(ах(Д), ..., zzjz/j),
называют конкретизированной схемой отношенийгили таблицей a{ax(dx}, ...,
аДДД). Если нас не интересуют конкретные множества переменных и
доменов, то схему отношений обозначают a(zz(, ..., zzm), а соответствующую
ей таблицу Т(а).
База данных — это множество конкретизированных схем отношений или
таблиц, называемых также конкретизацией t ил и состоянием базы. Состояние
базы, т.е. ее конкретизация, может изменяться. Множество всех атрибутов
базы есть А = {а |/ e/V}, где N = N — количество атрибутов.
Подмножество атрибутов множества А, состоящее из / атрибутов, индексы
которых пробегают множество значений /(,), обозначим Л(/<,)). Будем
полагать, что атрибуты всегда упорядочены в соответствии с порядком
индексов в множестве /(,), а /(,)упорядочено по возрастанию. Таким образом,
Л(/(,)) = {a\J <= /(,)}. Множество Л(/(,)) будем называть основой схемы отношений.
В каждом состоянии базы данных каждому атрибуту соответствует один домен
z/ = {cz'j, ст'2, ..., о'г,} из некоторого конечного множества всех доменов D.
Соответствие между множеством атрибутов а и доменов z/ в каждом состоянии
S базы данных можно выразить в виде функции dom (at, S): А -» D,
отображающей множество атрибутов на множество доменов, т.е. dom (a., S) =
= dj = {су',, су'2, ..., о'Д. Символ состояния базы данных будем, как правило,
опускать, имея в виду, что база всегда конкретизирована, т.е. имеет состояние.
Множество всех различных подмножеств индексов /(,), где 1 < z < N,
содержащих / различных индексов из множества индексов N всех атрибутов,
обозначают J}N} = {/(,|| j = 1, ...,C‘N}, где C‘N — количество сочетаний из N
по z. С учетом введенных обозначений схему отношений можно обозначить
как а(Л(/(т))). Обозначим
= X бопАаД
Здесь X — знак операции декартова произведения всех доменов, атрибуты
которых принадлежат множеству Л(/(,)).
Строкой таблицы a(ax(dt), ..., am(dm)), где dt = {ст',, ст'2, ..., ст'г/}, z = 1, ..., т,
называют упорядоченное множество (кортеж) ц,(а) = ц, («(zz,)^), ..., zzm(z/m))) =
= {су1,, су2,, ..., cym,}, I е {1, ..., ri}. Конкретный элемент строки ц,(а), лежащий
на пересечении ее со столбцом, соответствующим атрибуту а., обозначим
ju,(cz) = су',. Множество всех строк ц,(а), / = {1, ..., ri} таблицы <Дах(Дх), ...,
zzm(z/J) обозначим ц(а).
222
10.1. Реляционные базы данных
Пример. Зададим конкретизированную схему отношений для данных о
поездах, следующих из начальных до конечных пунктов в центральной
России. Эту схему отношений назовем прямыемаршруты. Введем для нее
атрибуты номерпоезда, пунктотправления, пункт назначения,
день_отправления, время отправления и соответствующие им домены:
dom {номер поезда) = (МТ-100. ТК-200, КМ-300).
dom {пункт отправления) = {Москва, Тула, Калуга),
dom {пункт назначения) = {Тула, Калуга, Москва),
dom {день отправления) = {Понедельник, Среда, Пятница),
dom {время отправления) = {10.00, 14.00, 16.00).
Конкретизированную схему отношений прямые маршруты можно
представить в виде таблицы (табл. 2.1).
Таблица 2.1
номер _поезда пункт_отправ- ления пункт_назна- чения денъ_отправ- ления времяотправ- ления
МТ-100 Москва Тула Понедельник 10.00
ТК-200 Тула Калуга Среда 14.00
КМ-300 Калуга Москва Пятница 16.00
10.2. Реляционная алгебра
Реляционной алгеброй обычно называют язык, позволяющий
формулировать запросы к базе данных и вычислять ответы на эти запросы.
Этот язык содержит ряд операторов, основными из которых являются
следующие.
• Оператор выбора V, позволяющий выбирать строку из таблицы.
• Оператор проекции Д, позволяющий осуществлять проекцию таблицы
на определенные ее столбцы.
• Операторы пересечения о, объединения о и разности \, определенные
для таблиц одинакового формата.
223
10. Дедуктивные базы данных
• Оператор картезианского произведения х.
Рассмотрим эти операторы более формально.
10.2.1 . Оператор выбора V
Дана таблица a(at(ds), аДДД), в которой представлено множество
атрибутов А(Дт}), и выражение vQw, где Q е {<, <, =, >, >}, v,we {А(П1)) о
j dom (Л(/|т|))}, причем имеет место один из следующих случаев:
v, w е
v е А(Т""), w е dom (А(Д'п}У),
v е dom (Д(/('"’)), w е Л(/|т))-
В случае применения оператора выбора к таблице am(dm)),
где б/ = {ct'j, о'2, •••, ст'г,}, / = 1, tn, и выражению vQw получим таблицу,
имеющую то же множество атрибутов Л(/<га)) и множество строк ц,(а) =
= оиЦ„))) = {с?',, с2,, о™}, I е {1, ri}, исходной таблицы
a.(a\d{), ..., «,„(<„)), таких, что
V(/)p,(v) Q p/(w)), если v, w е
V(/)piz(v) Q w, если v е A(I{"'}), w <= dom (Л(/("'))),
V(/) v Q p^w)), если v е dom (Л(/("”)), w е Д(/|т’).
Пример. В результате применения операции выбора к табл. 2.2 при условии,
что v = пункт отправления, Q = “ = ”, w = Тула, получим табл. 2.3.
Таблица 2.2
номер-Поезда пункт_отправ- ления пункт_назна- чения денъ_отправ- ления время_отправ- ления
МТ-100 Москва Тула Понедельник 10.00
ТК -200 Тула Калуга Среда 14.00
КМ-300 Калуга Москва Пятница 16.00
М-150 Москва Калуга Вторник 12.00
МТ-200 Москва Тула Среда 17.00
224
10.2. Реляционная алгебра
Таблица 2.3
номерпоезда пункт_отправ- лення нунктназна- чения день отправ- ления в р смя_от прав- леная
МТ-100 Москва Тула Понедельник 10.00
МТ-200 Москва Тула Среда 17.00
10.2.2 . Оператор проекции А
Дана таблица a(a\d{), ..., ak(dk)), ..., am(dm)), имеющая множество атрибутов
А(Рт>), а также множество атрибутов такое, что Л(/(у’) с А(Рт>).
Применение оператора проекции к таблице а(а^), am(dm)) и множеству
атрибутов A(PJ>) дает новую таблицу, получение которой осуществляется в
два этапа. На первом этапе формируется таблица a'(a](d\), ..., a'(d), ...,
a'(rf')), такая, что {а', ..., а'} = A(/,J>) и V(z) (а'= ак) zd dom (а') = dom (ак).
На втором этапе в этой таблице все одинаковые строки заменяются одной
из них.
Пример применения операции проекции. Пусть дана табл. 2.2, а также
множество атрибутов {пункт отправления, пункт назначения]. Тогда,
применяя к ним операцию проекции, получаем табл. 2.4.
Таблица 2.4
пунктотпра вления пункт_на значения
Москва Тула
Тула Калуга
Калуга Москва
Москва Калуга
10.2.3 . Оператор пересечения о
Даны таблицы, имеющие одно и то же множество атрибутов, но,
возможно, разные домены. В результате применения оператора пересечения
8 - 1141
225
10. Дедуктивные базы данных
получается новая таблица, имеющая то же множество атрибутов и множество
всех строк, встречающихся как в первой, так и во второй исходных таблицах.
10.2.4 . Оператор объединения и
Даны таблицы, имеющие одно и то же множество атрибутов, но,
возможно, разные домены. В результате применения оператора объединения
получается новая таблица, имеющая то же множество атрибутов и множество
строк, являющееся объединением строк первой и второй исходной таблиц.
10.2.5 . Оператор разности \
Даны таблицы, имеющие одно и то же множество атрибутов, но,
возможно, разные домены. В результате применения оператора разности
получается новая таблица, имеющая то же множество атрибутов и множество
строк, встречающихся только в первой таблице, но не встречающихся во
второй.
10.2.6 . Оператор картезианского произведения х
Даны две таблицы, имеющие соответственно множество атрибутов
и A(I(J>). Оператор картезианского произведения позволяет получить по этим
таблицам новую таблицу, множество атрибутов которой является
объединением {Л(/("”) о A(JtJ>)} атрибутов двух исходных таблиц, а множество
строк получается как результат конкатенации каждой строки первой таблицы
с каждой строкой второй.
Пример. Даны две таблицы (табл. 2.5 и 2.6).
В результате применения к ним операции картезианского произведения
получим табл. 2.7.
Кроме перечисленных операторов в реляционной алгебре могут встречаться
и другие. Реляционная алгебра является вычислительной основой
пользовательских языков, на которых, собственно, и осуществляется контакт
пользователя (запросы, создание, модификация и т.п.) с базой данных.
Таблица 2.5 Таблица 2.6
номсрпосзда пункт_отправ- ления пункт_назна- чения
МТ-100 Москва Тула
ТК -200 Тула Калуга
денъ_отправ- ЛСНИЯ врсмя_отправлсния
Понедельник 10.00
Среда 14.00
226
10.3. Триггеры
Таблица 2.7
номер _поез да пункт_отправ- ления пункт_на зна- чения денъ_отправ- лсния Время_отправ- ления
МТ-100 Москва Тула Понедельник 10.00
МТ-100 Москва Тула Среда 14.00
ТК -200 Тула Калуга Понедельник 10.00
ТК -200 Тула Калуга Среда 14.00
Одним из таких языков является SQL (Structured Query Language), семантику
предложений которого можно легко истолковать с помощью введенных понятий
и операторов реляционной алгебры. Этот язык является своего рода стандартом
языка запросов для коммерческих баз данных. В задачу настоящей книги не
входит рассмотрение всех аспектов реляционной алгебры и пользовательских
языков типа SQL. Они нам нужны только для того, чтобы показать в дальнейшем
их связь и использование для построения дедуктивных баз данных.
10.3. Триггеры
Современные базы данных позволяют указывать и выполнять над базой
данных действия с помощью рассмотренных операторов реляционной алгебры
или их аналогов в языке SQL в зависимости от свершения таких изменений в
базе данных, как создание, удаление или модификация таблиц. Эти
изменения обычно называют событиями. Описание действий осуществляется
с помощью специальных правил, не очень удачно называемых триггерами.
События, приводящие к выполнению правил, называют обычно триггерными
событиями. В настоящем параграфе рассмотрим концепцию триггеров,
поскольку они могут быть использованы для реализации вывода в дедуктивных
базах данных. Триггеры не входят в определение понятия базы данных. Они
воспринимаются и выполняются системой управления базой данных.
Синтаксически триггер определяется следующим образом:
Триггер -» Указатель Триггер Имя триггера Для Имя таблицы Когда Событие
Режим выполнения Спецификация действия [ Список триггеров с большим
приоритетом} [ Список триггеров с меньшим приоритетом},
Указатель —> Создать I Заменить,
8*
227
10. Дедуктивные базы данных
Событие —> Ввести данные в таблицу I Удалить данные из таблицы |
Обновить значения в столбцах таблицы [Список столбцов таблицы],
Режим выполнения —> Для каждой строки | Для таблицы,
Спецификация действия —> Начало Если Условие То Действие Конец.
Каждый триггер определяется по отношению к таблице базы данных.
Событиями являются введение данных в таблицу, удаление данных из таблицы
и обновление значения в определенных столбцах таблицы. Совершение
событий дает возможность выполнить действия, указываемые в спецификации
триггера. Это выполнение может произойти, но может и не произойти. Все
зависит от условия, предшествующего действию в спецификации действия.
Режим выполнения указывает, будет ли действие выполняться отдельно для
каждой строки таблицы или для таблицы в целом. В списке триггеров с большим
приоритетом задаются триггеры, приоритет выполнения которых выше, чем
у данного. Список триггеров с меньшим приоритетом указывает триггеры,
приоритет выполнения которых ниже, чем у данного. Если сразу несколько
триггеров с одинаковым приоритетом могут выполняться, то система
управления базой данных выполняет один из них в произвольном порядке.
Пример. База данных некоторого предприятия содержит две таблицы
форматов
заказ (поставщик, изделие, количество, сумма, исполнитель, статус),
бюджет (исполнитель, сумма бюджета).
Таблица заказ хранит сведения о поставщиках изделий, которые заказал
исполнитель в некотором количестве на определенную сумму. Таблица
бюджет хранит информацию об исполнителях и суммах бюджета, которые
они могут потратить. На предприятии действуют три правила.
Сумма, которую может потратить каждый исполнитель, не должна
превосходить сумму его бюджета.
Заказы посылаются поставщику по электронной почте.
Если сумма заказа превышает 1000 руб., то исполнитель должен получить
разрешение на ее расходование от вышестоящего начальника.
Не используя введенный выше формализм для триггеров, рассмотрим
суть их использования для проверки выполнения этих правил. Первое и третье
правила могут быть реализованы триггерами, выполняемыми в результате
введения данных в таблицу заказ. Прежде всего должен выполняться триггер,
проверяющий, является ли сумма заказа исполнителя по данному изделию
228
10.4. Реляционная база данных и логические исчисления
менее 1000 руб. Если это так, то статус исполнителя по данному изделию
устанавливается разрешающим закупку. В противном случае выполняется
другой триггер, в результате чего по электронной почте посылается запрос
начальнику исполнителя на разрешение закупки, который в своем ответе
устанавливает соответствующий статус исполнителя. Триггер, реализующий
второе правило, выполняется, когда статус исполнителя является
разрешающим.
При использовании триггеров требуется решение двух главных вопросов.
Любое ли изменение в любой базе данных приводит к конечному числу
шагов выполнения триггеров?
Является ли выполнение триггеров детерминированным?
В большинстве существующих систем управления базами данных
положительного ответа на эти вопросы добиваются специальными
ограничениями на выполнение триггеров.
10.4. Реляционная база данных и логические исчисления
Таблица Г(а) (таблица с именем а) реляционной базы данных может
рассматриваться как хранилище фактов а{&'р сД, ..., o’"1,), / е {1, ..., ri},
каждый из которых взаимно однозначно соответствует строке цДа) = {сд,
сз1,, ..., с?"1,) таблицы а.
Пример представления таблицы как множества фактов. Пусть имеется
таблица преподаватели (табл. 2.8).
Таблица 2.8
фамилия зарплата должность
Па влов 3000 Профессор
Ивин 2500 Доцент
Селихов 2000 Старший_преподавателъ
Эту таблицу можно представить множеством фактов:
преподаватели {Павлов, 3000, Профессор),
преподаватели {Ивин, 2500, Доцент),
преподаватели {Селихов, 2000, Старший-Преподаватель).
229
10. Дедуктивные базы данных
Иными словами, таблицу преподаватели можно рассматривать как
интерпретацию атома преподаватели {фамилия, зарплата, должность). Запрос
к базе данных, звучащий как “Преподаватели с какой фамилией, зарплатой
и должностью делают атом преподаватели {фамилия, зарплата, должность)
истинным?”, можно рассматривать как поиск всех конкретизаций этого атома
при данной интерпретации.
Таким образом, схема отношений а{А{1{т})) может быть атомом с предикатным
символом а и множеством переменных А{1{т}). При этом предполагается, что все
строки конкретизированной схемы отношений (таблицы) Т{а) являются
конкретизациями атома а{А{1(т})), делающими его истинным. Используя атомы
по правилам того или иного исчисления, можно формулировать аксиомы, на
основе которых с использованием базовых аксиом этого исчисления осуществляется
вывод целевой формулы. Одним из таких исчислений может быть исчисление,
использующее только хорновские формулы и обобщенное правило вывода модус
поненс. Черты этого исчисления были рассмотрены в четвертой главе. Другим
исчислением может быть ситуационное исчисление, рассмотренное в восьмой
главе. Формулировку цели в постановке задачи применительно к базе данных
обычно называют запросом, а найденную (выведенную) цель — ответом на запрос.
Язык любого исчисления, используемого для формальной постановки
задачи запроса и дедуктивного вывода для получения ответа на запрос, обычно
называют Дейталогом (Datalog), а описание на нем Дейталог-программой.
Часть Дейталог-программы, не содержащую фактов, называют Дейталог-
правилами. Теперь реляционной базой данных назовем пару, состоящую из
множества таблиц (конкретизированных схем отношений) и Дейталог-правил.
Приведем пример реляционной базы данных, содержащей одну таблицу
пункты (табл. 2.9) и два Дейталог-правила.
Таблица 2.9
пункт_отправлсния пункт_назначения
Москва Тула
Тула Калуга
Калуга Москва
Дейталог-правила:
пункты {пунктотправления, пункт назначения) zd
z> маршрут {пункт отправления, пункт назначения),
пункты {пункт отправления, промежуточный пункт) л
230
10.5. Переход от Дейталога к SQL
л железнодорожный_маршрут (промежуточныйпункт, пункт назначения) л
л пункт отправления пункт назначения маршрут (пункт—Отправления,
пункт назначения).
Дейталог-программа, соответствующая этой реляционной базе данных,
будет следующей:
пункты (пункт—отправления, пункт__назначения)
zd маршрут (пункт—отправления, пункт назначения),
пункты (пункт_отправления, промежуточный_пункт) л
л маршрут (промежуточныйпункт, пункт назначения) л
л пункт_отправления # пункт назначения zd
zd маршрут (пункт отправления, пункт назначения),
пункты (Москва, Тула),
пункты (Тула, Калуга),
пункты (Калуга, Москва).
Множество всех атомов Дейталог-программы, являющихся фактами, называют
экстенсионалом. Множество всех остальных конкретизированных атомов,
выводимых с помощью Дейталог-программы, называют интенсионалом.
Дедуктивная база данных состоит из реляционной базы данных (т.е. множества
таблиц, соответствующих экстенсионалу, и Дейталог-правил) и множества
таблиц, соответствующих интенсионалу. Всем фактам экстенсионала, имеющим
один и тот же предикатный символ, соответствует одна таблица, атрибуты
которой совпадают с именами переменных факта, а строки являются наборами
значений этих переменных. Всем атомам интенсионала, имеющим один и тот
же предикатный символ, соответствует также одна таблица, атрибуты которой
совпадают с именами переменных атома. Строки этой таблицы могут заполняться
по-разному. Это зависит от интерпретации атрибутов, в частности от области
значений каждого атрибута. В крайнем случае, это может быть множество всех
возможных наборов значений атрибутов.
10.5. Переход от Дейталога к SQL
Вместо того, чтобы строить отдельную систему вывода для ответа на
запросы в языке Дейталог, покажем, как можно перевести эти запросы в
231
10. Дедуктивные базы данных
язык SQL и тем самым получить ответ на запрос с помощью вычислений в
реляционной алгебре, стоящей за операторами языка SQL. Вернемся к
приведенной выше Дейталог-программе, соответствующей реляционной базе
данных. Введем с целью наглядности следующие более короткие имена
аргументов в этой программе:
пунктотправления = по,
пункт назначения = пн,
промежуточный пункт = пп.
После введения этих обозначений Дейталог-программа будет иметь вид
пункты (по, пн) тэ маршрут (по, пн),
пункты (по, пп) л маршрут (пп, пн) л по # пн о маршрут (по, пн),
пункты (Москва, Тула),
пункты (Тула, Калуга),
пункты (Калуга, Москва).
Экстенсионалу этой программы соответствует таблица пункты (табл. 2.10).
Таблица 2.10
по пн
Москва Тула
Тула Калуга
Калуга Москва
Интенсионалу программы соответствует таблица маршруты (см. табл. 2.11),
имеющая те же атрибуты и те же строки, что и таблица пункты. Это
объясняется тем, что атом маршруты (по, пн) имеет в качестве аргументов то
же множество переменных, что и атом пункты (по, пн), наборы значений
которых определены одними и теми же фактами пункты (Москва, Тула),
пункты (Тула, Калуга), пункты (Калуга, Москва).
232
10.5. Переход от Дейталога к SQL
Таблица 2.11
по пн
Москва Тула
Тула Калуга
Калуга Москва
Если бы программа не содержала второго правила, то на запрос маршрут
{по, пн) должны быть выданы ответы
маршрут {Москва, Тула),
маршрут {Тула, Калуга),
маршрут {Калуга, Москва),
что соответствует табл. 2.12.
Таблица 2.12
по пн
Москва Тула
Тула Калуга
Калуга Москва
Очевидно, что в языке SQL для получения такого ответа должен быть
сформулирован запрос
Select пункты.по, пункты, пн from пункты.
Если бы программа не содержала первого правила, то на запрос маршрут
{по, пн) должны быть выданы также три ответа:
маршрут {Москва, Калуга),
маршрут {Тула, Москва),
233
10. Дедуктивные базы данных
маршрут (Калуга, Тула),
что соответствует формированию табл. 2.13.
Таблица 2.13
по пн
Москва Калуга
Тула Москва
Калуга Тула
Для получения такого ответа в языке SQL должен быть сформулирован
запрос
Select пункты.по, маршруты.пн from пункты, маршруты
Where пункты.пн = маршруты.по And пункты.по # маршруты.пн.
Если программа содержит оба правила, то на запрос маршрут (по, пн) должна
быть выдана табл. 2.14, являющаяся объединением таблиц, полученных для
каждого правила в отдельности.
Таблица 2.14
по пн
Москва Тула
Тула Калуга
Калуга Москва
Москва Калуга
Тула Москва
Калуга Тула
234
10.6. Ситуационное исчисление в дедуктивной базе данных
Для получения такого ответа в языке SQL должен быть сформулирован
запрос
Select пункты.по, пункты.пн from пункты
Union
Select пункты.по, маршруты.пн from пункты, маршруты
Where пункты.пн = маршруты.по And пункты.по * маршруты.пн.
Мы рассмотрели только принципы расширения реляционной базы данных,
в результате которых она становится дедуктивной базой данных, и
использования Дейталога путем перехода от него к реляционному языку
запросов типа SQL. Достоинствами такого расширения, которое приобретает
система управления реляционной базой данных в результате превращения ее
в дедуктивную базу данных, являются следующие.
База данных как хранилище фактов (экстенсионал) остается той же самой и
работа с ней, например с целью организации многопользовательского доступа,
обновления, управления транзакциями, восстановления, не изменяется.
Дейталог-программа, в особенности, если она допускает рекурсию как
язык запроса к базе данных, является более выразительным средством, чем
язык запросов типа SQL.
Ответы на запросы и подзапросы, получаемые в процессе вывода, не
обязательно помещать в базу данных и хранить там, что уменьшает риск
повреждения данных в базе и не приводит к ее переполнению.
Таким образом, превращение реляционной базы данных в дедуктивную
базу не изменяет структуры хранимых данных, а касается только изменения
системы управления базой данных, превращая ее в дедуктивную систему
управления базой данных. Иными словами, понятие дедуктивной базы
данных выражает не свойство структуры данных, а свойство дедуктивной
системы управления данными, состоящее в том, что она позволяет
осуществлять дедуктивный вывод. Конечно, переход от запроса Дейталог-
программы к запросу на языке типа SQL неоднозначен. В ряде случаев такой
переход целесообразно выполнять с использованием триггеров. Все эти
вопросы в настоящей книге не рассматриваются.
10.6. Ситуационное исчисление в дедуктивной базе данных
Преимущества дедуктивной базы данных становятся еще более заметными,
если в качестве основы для Дейталог-программы используется ситуационное
исчисление. Программы такого типа будем называть ситуационными
Дейталог-программами. Ограничимся демонстрацией на простом примере
студенческой ситуационной Дейталог-программы тех возможностей, которые
235
10. Дедуктивные базы данных
открываются перед нами в случае использования ситуационного исчисления,
черты которого рассмотрены в главе 8. При этом мы не будем рассматривать
структуру таблиц базы данных, соответствующих атомам ситуационного
исчисления или переход от запроса в языке ситуационного исчисления к
языку SQL. Ограничимся уровнем ситуационной Дейталог-программы.
При этом предполагается, что дедуктивная база данных находится в
некоторой ситуации (состоянии) до тех пор, пока не будет выполнено
некоторое действие, переводящее ее в другую ситуацию.
10.6.1. Категории
Студенческая среда для нашего примера содержит три категории:
фамилий студентов: Кст = {Светланова, Маринина, Борисов, Иванов},
читаемых курсов: К = {Физика, Механика, Математика, Химия,
электроника, Информатика, Программирование},
оценок К = {2, 3, 4, 5}.
Переменная, принимающая значение из категории студентов,
обозначается студент. Переменная, принимающая значение из категории
курсов, обозначается курс, а из категории оценок — оценка.
10.6.2. Отношения
Отношения в студенческой среде задаются следующими предикатами:
записан (студент, курс, s): предикат истинен, если студент студент
записан на курс курс, когда база находится в ситуации s.
экзаменован (студент, курс, оценка, s): предикат истинен, если студент
студент экзаменован по курсу курс с оценкой оценка, когда база находится
в ситуации s.
прослушан (студент, курс,, курс.,): предикат истинен, если прослушивание
курса курс, является обязательным для записи на курс курс, студента студент.
Заметим, что значение этого предиката не зависит от ситуации, в которой
находится база данных.
10.6.3. Действия
Действия, которые могут осуществляться в студенческой среде, являются
следующими:
236
10.6. Ситуационное исчисление в дедуктивной базе данных
Записать {студент, курс)', записать студента студент на курс курс.
Поставить {студент, курс, оценка)', поставить студенту студент оценку
оценка за сдачу курса курс.
Отчислить {студент, курс)', отчислить студента студент с курса курс.
10.6.4. Аксиомы начальной ситуации
Аксиомы начальной ситуации определяют содержимое базы данных в
начальной ситуации Ао:
записан {Светланова, Информатика, Sa) v записан {Светланова,
Электроника, 50),
(V студент, курс) прослушан {студент, курс, Электроника) =
= курс = Физика л курс = Математика,
(V студент, курс) -> прослушан {студент, курс, Информатика),
(3 курс) записан {Борисов, курс, 50),
(V курс) записан {Борисов, Информатика, 5)) = курс = Физика v
v курс = Математика v курс = Механика,
записан {Маринина, Информатика, 5),
записан {Иванов, Электроника, 5),
экзаменован {Светланова, Физика, 4, 5).
10.6.5. Аксиомы допустимых действий
Студент может быть записан на курс курс., только в том случае, если он получил
оценку не ниже 3 по курсу курс{, обязательному для записи на курс курс:.
допустимо {Записать {студент, курс,), s) = {V (курс:) прослушан {студент,
курс,. курс,) (3 оценка) экзаменован {студент, курс,. оценка, s) л
л оценка > 3.
237
10. Дедуктивные базы данных
Студенту может быть поставлена новая оценка, если она отличается от
старой:
допустимо {Поставить {студент, курс, оценка^), s) = (3 оценка^
экзаменован {студент, курс, оценка^ s) л оценка.,^ оценка{.
Студент может быть отчислен с курса, если он перед этим был на него
записан:
допустимо {Отчислить {студент, курс), s) = записан {студент, курс, s).
10.6.6. Аксиомы перехода в следующие ситуации
записан {студент, курс, переход {a, s)) = а = Записать {студент, курс) v
v записан {студент, курс, s)) л а * Отчислить {студент, курс).
Эта аксиома задает условия, при которых студент в следующей ситуации
окажется записанным на курс. Это происходит либо вследствие выполнения
действия записи студента, или вследствие того, что он уже был записан в
предыдущей ситуации, и действия по его отчислению не осуществлялись.
экзаменован {студент, курс, оценка {, переход {a, s)) = а =
= Поставить (студент, курс, оценка^ v экзаменован {студент, курс,
оценка,, 5) л (V оценка^) а * Поставить {студент, курс, оценкаД
Эта аксиома задает условия, при которых студент окажется
экзаменованным в следующей ситуации. Это происходит либо вследствие
выполнения действия по выставлению оценки, либо вследствие того, что
он уже был экзаменован, и никакая новая оценка не ставилась.
10.6.7. Запросы к ситуационной Дейталог-программе
Обратим внимание, что аксиомы начальной ситуации, представленные в
языке ситуационного исчисления и, вообще, любого исчисления, не
изменяются средствами того исчисления, которое используется. Их
изменение осуществляется извне. Кем и с помощью каких средств это делается
в настоящей книге, мы даже не интересуемся. Использование же действий
необходимо нам только для того, чтобы можно было запрашивать у
дедуктивной базы данных ответы на гипотетические вопросы типа: “Может
ли случиться некоторая ситуация, в которой истинны определенные
предикаты при определенных значениях их аргументов, если такие-то и такие-
то действия и в такой-то последовательности были бы выполнены?” Примером
запроса этого типа для нашего примера мог бы быть следующий: “Если была
выполнена последовательность действий Отчислить {Иванов, Математика),
238
10.6. Ситуационное исчисление в дедуктивной базе данных
Записать {Маринина, Математика), то в результате ее выполнения студент
Иванов записан на какой-либо курс?” Для положительного ответа на этот
гипотетический вопрос необходимо установить истинность формулы
(3 курс) {записан (Иванов, курс, переход (Записать (Маринина,
Математика), переход (Отчислить (Иванов, Математика), So)))
хотя бы для одного значения переменной курс.
10.6.8. Ограничения целостности дедуктивной базы данных
Таким образом, ответы на запросы к ситуационной Дейталог-программе,
несмотря на наличие действий, не изменяют начальной базы данных. В
процессе поиска ответа, конечно, устанавливаются новые отношения, но
все они выводятся только на основании аксиом начальной ситуации, аксиом
допустимых действий и аксиом перехода в следующие ситуации. Эти аксиомы
могут быть изменены с помощью операций добавления, удаления или
модификации, причем чаще изменяются аксиомы начальных ситуаций, а
не аксиомы допустимых действий и перехода в следующие ситуации. Новые
запросы к базе данных осуществляются после завершения этих операций.
Ограничением целостности ситуационной Дейталог-программы называются
такие ее инвариантные свойства, которые должны всегда выполняться, в
какой бы ситуации база не находилась или даже какие бы изменения
экстенсионала не произошли. Ограничения целостности задаются в виде
аксиом и проверяются всякий раз после изменения экстенсионала. Так,
например, ;ыя рассмотренной студенческой базы данных могло бы быть
введено следующее ограничение целостности: ни один студент не может иметь
сразу две оценки по одному и тому же предмету. Если предположить, что
ситуационная Дейталог-программа содержит информацию о стипендиях,
получаемых студентами в течение срока обучения, с использованием
предикатов типа стипендия (студент, размер стипендии, s), то ограничением
целостности могло бы быть следующее: стипендия каждого студента не может
уменьшаться в течение всего срока его учебы.
Если ввести действие Назначить (студент, размер стипендии), то
ограничение целостности можно задать формулой
(V 5, s', студент, размер стипендии, размерстипендии') л s < 5' л
л стипендия (студент, размер стипендии, s) л стипендия (студент,
размер стипендии', 5') размер стипендии < размер стипендии'.
Естественно, чтобы была возможность проверять это ограничение
целостности, т.е. устанавливать истинность инвариантных свойств Дейталог-
программы. необходимо ввести аксиому допустимых действий и аксиому
перехода в следующую ситуацию:
239
10. Дедуктивные базы данных
допустимо (Назначить (студент, размерстипендии), s) =
= (3 размер стипендии') стипендия (студент, размер стипендии', s) л
л размер стипендии ' < размер стипендии,
стипендия (студент, размер стипендии, переход (a, s)) = а = Назначить
(студент, размерстипендии) v стипендия (студент, размерстипендии) л
л V (размер стипендии') а Назначить (студент, размер стипендии').
Потребуется также следующая аксиома единственности имен:
Назначить (студент, размер стипендии) = Назначить (студент',
размер стипендии') зэ студент = студент' л размер стипендии =
= размер стипендии'.
Поиск ответов на запросы к ситуационной Дейтадог-программе осуществляется
традиционным прямым или обратным выводом, стратегии которого рассмотрены
в главе 8 и других главах. При доказательстве же целостности обычно используют
индукционные аксиомы, с одной из которых мы подробно ознакомились и привели
в главе 9 детальное доказательство на ее основе корректности программы.
Применяются и другие индукционные аксиомы. В частности, для проверки
целостности ситуационной Дейталог-программы часто применяется двойная
индукционная аксиома. Рассмотрим, как может быть использована эта аксиома
для доказательства целостности ситуационной Дейталог-программы.
10.7. Проверка ограничений целостности
Проверку ограничений целостности можно осуществить с помощью двойной
индукционной аксиомы второго порядка. Двойная индукционная аксиома очень
похожа на простую индукционную аксиому и использует не одну, а две
ситуационные переменные:
(V <р) ф (5(|, 5(1) л [(V а, х)(ф (j>, j>)) зэ ф(5, переход (а, 5))] л [(V a, s, s')
(х < s' л ф(х, s') зэ ф(л; переход (а, '>'))! => (V х')(ф(Т s')).
Двойная индукционная аксиома аналогична простой индукционной
аксиоме. Так, для нашего примера со стипендиями студентов надо доказать
истинность формулы
(V х, s') s < s' зэ [V (студент, размер стипендии, размер стипендии')
стипендия (студент, размер стипендии, s) л стипендия (студент,
размер стипендии', s') зэ размер стипендии < размер стипендии'],
240
Вопросы и упражнения
логически эквивалентной приведенной выше формуле, задающей
ограничение целостности. Если обозначить
ф(5, s').= V (студент, размер_стипендии, размер_стипендии')
стипендия (студент, размер стипендии, s) л стипендия (студент,
размер_стипендии', s') о размер_стипендии < размер_стипендии',
то схема использования двойной индукционной аксиомы для доказательства
целостности будет состоять из следующих шагов:
доказать истинность формулы ф(50, 50).
предположить истинность формулы (V a, s) ф (s, s). На основании этого
предположения показать, что истинна формула (V а, з)(ф(5, Переход (a, s)).
предположить истинность формулы (V a, s, s')(s < s' л ф(5, s')). На
основании этого предположения показать, что истинна формула [(V a, s, s’)
(s < s’ л ф (s, переход (a, s'))].
если удастся доказать истинность всех этих формул, то сделать заключение,
что имеет место истинность формулы (V s, 5')(ф(5, s')), что и требуется доказать.
Ограничение целостности является частным случаем ограничений на
ситуации (состояния), которые формулируются с помощью индукционных
аксиом различного типа. Индукционные аксиомы второго порядка могут
быть использованы для определения свойств различных сред, в которых
выразительных средств логики предикатов первого порядка недостаточно.
Вопросы и упражнения
1. Доказать ограничение целостности студенческой базы: “Стипендия каждого студента
не может уменьшаться в течение всего срока его учебы”, используя введенные выше аксиомы.
2. Используя индукционные аксиомы второго порядка, опишите свойства
следующих множеств.
а) Множество N натуральных чисел, такое, что 0 e N. Если х е N, то
s(x) е N, где s(x) — натуральное число, получающееся из числа х на следующем шаге
с помощью некоторого преобразования.
б) Множество D потомков Адама и Евы, таких, что Адам е D и Ева е D. Если
хе D и у является потомком х, то у e D;
в) Минимальное множество формул логики высказываний L, такое, что любая
переменная х логики высказываний принадлежит множеству L. Если формулы w
w2 е L, то формулы не (и^), влечет (w, w2) также принадлежат множеству L;
г) Множество всех состояний инициального детерминированного автомата,
находящихся в отношении эквивалентности R (см. главу 5).
3. Какое-либо подмножество Т множества всех состояний инициального
детерминированного автомата, находящихся в отношении эквивалентности R,
является примером так называемого транзитивного замыкания. Используя двойную
индукционную аксиому второго порядка, опишите свойства множества Т.
4. Пусть r(s, s') — атом, истинный, когда состояния s, s' инициального
детерминированного автомата находятся в отношении эквивалентности R, t(s, s') —
атом, истинный, когда состояния s, s' принадлежат транзитивному замыканию Т.
Показать, что следующее определение транзитивного замыкания на языке логики
предикатов первого порядка ошибочно:
t(s, s') = r(s, S') V (3 s”) t(s, s") A r(s", s').
241
11. НЕЧЕТКИЕ ЗНАНИЯ И РАССУЖДЕНИЯ
Рассматривается, как можно представлять знания о среде в условиях,
когда нет полной уверенности, что эти знания истинны, и как в этом
случае может быть организован вывод.
Любая формула логики высказываний или логики предикатов первого
порядка может быть только либо ложной, либо истинной. Это означает,
что при использовании этих логик агент имеет возможность делать только
одно из противоположных суждений о ложности или истинности каких-либо
событий, фактов, отношений в среде, с которой он имеет дело. Реальные
среды далеки от такого идеала, при котором о любом явлении, событии,
отношении в среде можно говорить с категорической уверенностью, что оно
имеет или не имеет места. Основными источниками такого рода
неопределенности являются следующие факторы.
Практическая невозможность или нежелание сделать описание знаний о
среде полным вследствие высокой размерности среды и, как следствие,
высокой сложности описания, например, по затратам времени и памяти.
В терминах состояний среды это означает неполное описание состояний
среды и переходов между ними в результате действий агента, требуемых для
решения задачи.
Недостаточная теоретическая изученность свойств среды, что не позволяет
описать ее достаточно адекватно. В терминах состояний и переходов между
ними получаем тот же результат, что и в предыдущем случае.
Недетерминированность переходов среды из одного состояния в другое.
Для описания знаний о таких средах средствами логики предикатов требуется
либо детерминизация этого описания, либо применение адекватных средств
описания, позволяющих учитывать и каким-либо образом представлять
недетерминированность среды.
Настоящая глава посвящена тому, как можно задавать такого рода
неопределенность и как осуществлять вывод в этом случае. Имеются
различные подходы и основанные на них методы задания и вычисления
неопределенности. Среди всех этих подходов можно выделить два
главенствующих.
242
/1.1. Нечеткое множество и функция принадлежности
Один из них основан на введении числовой оценки, характеризующей
степень уверенности или доверия к истинностным значениям вычисляемых
формул. По степени уверенности можно судить, как далеки формулы от
полной истинности или ложности. Иначе говоря, сначала формула
вычисляется так же, как и прежде, и определяется, истинна она или ложна,
а потом вычисляется степень уверенности в истинности этой формулы.
Существуют различные подходы к вычислению степени уверенности. Чаще
всего степень уверенности — это положительное число, изменяющееся в
диапазоне от 0 до 1. Чем больше это число, тем выше степень уверенности
в истинности формул. Математические аппараты для вычисления степени
уверенности также могут быть различными. Очень популярным является
аппарат теории вероятностей. В этом случае степень уверенности истинности
атомов задается как вероятность, а степень истинности формул, в которые
эти атомы входят, вычисляется по законам условной вероятности.
При другом подходе для каждого атома а(х,, ..., хи) или формулы вводятся
целый спектр возможных значений, лежащих между О (Л) и 1 (И), и правила
вычисления этих значений. Вычисленные таким образом значения определяют
степень истинности формул. В настоящей главе рассмотрен второй подход.
Фундаментом этого подхода является нечеткая логика, предложенная Л. Заде
в начале 60-х годов. Рассмотрим основополагающие понятия нечеткого
множества и функции принадлежности.
11.1. Нечеткое множество и функция принадлежности
Нечетким множеством А называют совокупность упорядоченных пар:
А = {< \iA(u)/u >} , где ip, — функция принадлежности нечеткого множества
А, ее значение £/ —> (0, 1] характеризует степень принадлежности
элемента «множеству U. Множество U называют универсальным множеством,
или универсумом. С нечетким множеством связан ряд следующих понятий и
определений, необходимых в дальнейшем.
Под основой Support (А) нечеткого множества А подразумевают подмножество
множества U, на всех элементах и которого функция принадлежности имеет
значение, большее 1, т.е.
Support (Л) = {и е U | pj(«) > 0}.
Ядром нечеткого множества А называют множество
Kernel (А) = {и е U | (м) = 1}.
Нечеткое множество А нормальное, если А 0, или, другими словами,
если в множестве А существует хотя бы один элемент, функция принадлежности
которого равна 1. В противном случае нечеткое множество является аномальным.
Для нечетких множеств на упорядоченных универсумах вводят понятие
выпуклости. Нечеткое множество А называют выпуклым, если его функция
243
11. Нечеткие знания и рассуждения
принадлежности выпукла, т.е. для любых трех точек и}, uv u^Uсправедливо
выражение
и} <и2 <и2 op/I(w2)>min[p/1(w1),p/)(w3)].
На множестве нечетких множеств некоторого универсума U, которое
обозначим S-R(Z7) = {и I ц : U [0,1]}, вводят следующие операции,
аналогичные обычным теоретико-множественным операциям.
Дополнением нечеткого множества А в универсуме U называют нечеткое
множество
-Л =^J(l-p4(w)/w).
utU
Объединением нечетких множеств А и В называют нечеткое множество
°в=U тах[ц 71 (р й (м)] /w'
uzl!
Пересечением нечетких множеств Ли В называют нечеткое множество
а п в=Umin^ а ц й и ’
uef/
Включение А с йдля нечетких множеств определяют с помощью отношения
линейного порядка функций принадлежности на интервале [0, 1]:
А с В = рА(и) < рДи), X/u^U.
11.2. Принцип обобщения и степень совместимости
Использование нечеткого множества позволяет обобщить обычные (четкие)
отображения, функции, операции, отношения и т.п. на случай, когда
аргументы нечетко определены.
Пусть f: X Y — четкое отображение из универсума X в универсум Y.
Если А — нечеткое множество, заданное на универсуме X, то его образом
будет нечеткое множество В, заданное на универсуме У:
5 = ^sup{p/x)|xeX,y = /(x)}/y,
где sup обозначает верхнюю границу (наибольшее значение) функции
принадлежности ц/х). Это выражение обычно называют принципом
обобщения. В случае, когда область определения функции f обладает
244
11.2. Принцип обобщения и степень совместимости
некоторой структурой, например является подмножеством декартова
произведения универсумов Xt х Х2 х ... х Хг на которых заданы соответственно
нечеткие множества Av А2, ..., Ап а универсумы независимы друг от друга,
принцип обобщения имеет следующий вид:
5 = ^sup{min[^(xJ,p/x2)>--M*/)l!*i е Хх,х-> е Xt,
yeY у = f(xx,X2,...,Xl)} / у.
Таким образом, с помощью рассмотренного принципа обобщения можно
осуществить переход от нечетких множеств, каждое из которых имеет свою
функцию принадлежности и задано на своем универсуме из множества
универсумов Хх, Х2, ..., Xt, к одному нечеткому множеству, заданному на
одном универсуме Xt х Х2 х ... х Xt, с одной функцией принадлежности:
5ир{т1п[ц/1(х|),ц4(х2),...,цл(х/)]},гдех1 е Х},х2 &Х2,...,х1 еХ,.
В настоящей книге принцип обобщения напрямую практически не
используется. Его роль является важной при определении так называемой
степени совместимости нечетких множеств. В дальнейшем, в результате
нечеткого вывода могут быть получены различные нечеткие множества,
которые необходимо сравнивать друг с другом с той или иной целью,
например, для оценки их близости. Степень совместимости нечеткого
множества В с нечетким множеством А, каждое из которых задано на одном
и том же универсуме U, определяется следующим образом.
Пусть цл: U -> [0,1], U [0,1] — функции принадлежности нечетких
множеств А и В соответственно. Функция / = |ig(w) определяет степень
принадлежности элемента и & Uнечеткому множеству В. Используя принцип
обобщения, можно получить нечеткое множество С(В, А):
С(В,А)= 5ир{цл(и)|ие А, Г = цй(и)}/г.
Это нечеткое множество и называют степенью совместимости нечеткого
множества В с нечетким множеством А. Универсумом нечеткого множества
С(В, А) является интервал [0, 1]. Чем ближе нечеткое множество В к нечеткому
множеству А, тем больше элементов множества С(В, А), в которых значение t
совпадает с цл (г). Если эти множества одинаковы, то t = цл(0 для всех t.
Во многих прикладных задачах, например, распознавание сигналов и
образов по эталонам, сравнение одной формулы с другой (эталонной),
семантика эталонов задается нечетким множеством А, а семантика вновь
полученного образа, сигнала или формулы — множеством В. В этом случае
степень совместимости используют для оценки степени близости вновь
полученного сигнала, образа или формулы, семантика которых выражается
нечетким множеством В, к эталонам, семантика которых выражается
нечетким множеством А. На основе степени совместимости могут быть
построены различные меры для оценки степени близости.
245
11. Нечеткие знания и рассуждения
11.3. Нечеткая база данных
Нечеткую базу данных можно рассматривать как обобщение реляционной
базы данных. Напомним сначала некоторые понятия реляционных баз
данных, введенные в предыдущей главе и используемые также для нечеткой
базы данных. Каждому столбцу таблицы взаимно однозначно соответствует
атрибут (имя столбца) о, а атрибуту — множество значений переменных
{х'р х'2, ..., х'г } = Хг Переменные одного и того же множества X, принимают
значения из одного универсума. Множество значений d, = {o',, о'2, ..., о'п}
переменных {х',, х'2, ..., x'J называется доменом. Схемой отношений
называют выражение а(о1(А'|), ..., ат(Хт)), в котором а является именем
схемы отношений, afX) — термы базы, / = 1, ..., т.
Схему отношений, все термы которой конкретизированы a.(at(d}),
ajdj), называют конкретизированной схемой отношений^или таблицей
a.(a\d), aj^dj). Если нас не интересуют конкретные множества
переменных и доменов, то схема отношений обозначается просто а(ар ...,
а ), а соответствующая ей таблица обозначается Т(а).
Под реляционной базой данных понимают множество конкретизированных
схем отношений или таблиц, называемых также конкретизацией, или
состоянием базы. Состояние базы, т.е. ее конкретизация, может изменяться.
Множество всех атрибутов базы есть А = {а, | I е N}, где N = {1,,7V}, А —
количество атрибутов. Подмножество атрибутов множества А, состоящее из
i атрибутов, индексы которых пробегают множество значений /('\
обозначается Л(/"’). Атрибуты всегда упорядочены в соответствии с порядком
индексов в множестве /"’, а /"’упорядочено по возрастанию. Таким образом,
Д(/"’) ={а |уе/"’}.
Множество Л(/"’) называют основой схемы отношений. В каждом состоянии
базы данных каждому атрибуту соответствует один домен J = о'р о'2, ..., <Уп
из некоторого конечного множества всех доменов D. Соответствие между
множеством атрибутов а, и доменов J в каждом состоянии 5базы данных может
быть выражено в виде функции dom (a., S)\ А -» D, отображающей множество
атрибутов на множество доменов, т.е. dom (at, S) = dj ={0',, о'2, ..., а'г/}. Символ
состояния базы данных, как правило, опускается, имея в виду, что база
всегда конкретизирована, т.е. имеет состояние. Множество всех различных
подмножеств индексов / '", где \ < i < N, содержащих I различных индексов
из множества индексов N всех атрибутов, обозначается J<N> ={/(,) | j =
где С'Л — количество сочетаний из Апо i. С учетом введенных обозначений
схема отношений может обозначаться как а(А(Гт))').
246
11.3. Нечеткая база данных
Нечеткой схемой отношений называют выражение «(аДЛ',, А,), ат(Хт,
AJ), где а по-прежнему является именем схемы отношений, R — имя
нечеткого множества, соответствующего атрибуту а и определенного на
множестве переменных Х:.
Нечеткой конкретизированной схемой отношений a(a}(dv А,), ..., am(dm, Aj)
называют нечеткую схему отношений «(а/ф, А,), .... am(dm, Rm)}, все термы
которой конкретизированы. Нечеткая база данных — это множество нечетких
конкретизированных схем отношений базы. Множество всех ее доменов
называют также состоянием нечеткой базы данных. Пару [Л(/(")> AJ, где
= {а,, ..., ат}, Аа = {цЛа(о)/о}, а е dom Аа = {ц^(о)/о} —
нечеткое множество, получаемое по нечетким множествам А,, ..., А ,
называют обобщенной нечеткой схемой отношений. В нечетком множестве
Ао функция принадлежности определена на всех о е dom т.е.
Аа = {ц^(о)/<з |о е dom (Л(/(0))}. Обобщенную нечеткую схему отношений
[^4(/(')), AJ обозначим так же, как Аа[Л(/('*)], опуская индекс а, если его
употребление не вызвано особой необходимостью, и называя обобщенную
нечеткую схему отношений просто схемой отношений. Получение Ац является
одной из важных задач настоящей главы. В частном случае Аи может быть
получено на основе принципа обобщения. Схему отношений [А(/('>), А ]
называют нормальной, если Аи является нормальным нечетким множеством,
т.е. (3 и)(и е dom (A(I{i})) л ps(«) = 1.
Схема отношений А[/1(/•'*)] сепарабельная, если для любого разбиения
А = {£, | j = 1, т} множества /*'>, такого, что
/=|
имеет место
А[Д(/<,))]= X Prop
/=| '
где проекция нечеткого множества R[A(/Iir)] на £ задана формулой
Prop Я[Л(/(,))].
4 I
Операция проекции подробно рассмотрена далее. Сепарабельная схема
отношений А| А(1{1))] обладает замечательными свойствами: 1) она может быть
получена как декартово произведение схем отношений A[£J, являющихся
проекциями схемы отношений А[Л(/0>)], которые соответствуют
непересекающимся подмножествам Е, е А множества образуют разбиение
А; 2) схемы отношений А|с ] могут быть получены в результате проекции
схемы отношений А[Л(/(/))] на
247
11. Нечеткие знания и рассуждения
11.4. Нечеткие действия (операторы)
Как и в случае реляционных баз данных, над нечеткой базой данных
совершаются различные действия. Эти действия совершаются для того, чтобы
достичь, как и ранее, определенных целей, но уже в условиях нечеткости
схем отношений. Множество всех действий распадается на следующие три
группы.
Действия, направленные на изменение состояния базы: модификацию
функций принадлежности и доменов.
Действия, направленные на изменение схем отношений (замена,
добавление, удаление или модификация схем).
Действия, направленные на формирование обобщенных схем отношений
на основе имеющихся в базе конкретизированных или вновь образованных
схем отношений без изменения состояния базы.
Первая группа действий может изменять состояние базы данных (изменение
доменов). Вторая группа действий изменяет схемы. Состояние базы при
этом может изменяться. Третья группа действий ничего не изменяет в базе,
порождая новые схемы и предназначена для вывода заключений по
фиксированному состоянию базы данных. Рассмотрение первых двух групп
не входит в задачу настоящей главы. Действия третьей группы соответствуют
в теории реляционных баз данных операторам или операциям, но в нашем
случае осуществляются не над четкими схемами отношений, а над нечеткими.
Таким образом, в нашем случае объектом третьей группы действий являются
конкретизированные нечеткие схемы отношений a(a}(dx, Rx), a^d, /?)).
Каждой такой нечеткой схеме отношений однозначно соответствует основа
схемы отношений Д(/('’) = {ах, ..., о.}, множество доменов d{, ..., d; и
нечеткие множества Rx, ..., /?. Введем также следующие обозначения.
Множество всех основ схем отношений {Э(/•'’)}:
й1(,|)1=й и
Множество всех основ схем отношений включает все возможные основы
схем отношений с любой арностью от унарных до jV-арных. База данных,
содержащая множество схем, соответствующих всем основам, называется
полной. В противном случае она неполная.
Множество всех схем отношений {/?[Э(/('))]}:
{/W")l} = I Л(/<") 6 М(/'Д}}.
Множество всех действий (операций) третьей группы над нечеткими
схемами отношений, в результате которых формируются новые нечеткие
схемы отношений и определяются соответствующие им нечеткие множества,
можно подразделить на следующие группы:
248
/1.4. Нечеткие действия (операторы)
теоретико-множественные операции дополнения, объединения,
пересечения: о. п, о};
операции линейного преобразования:{Л(А | к > 0, (-к) < b < 1};
пороговые операции: {г) | р е [0, 1]};
операции цилиндрического продолжения: {Cz(/)| I <eN, е
операции проекции: {Proj /(,)| / &N, /(,) е J)N>}.
11.4.1. Теоретико-множественные операции
Теоретико-множественные операции, рассматриваемые в настоящем разделе,
являются обобщением операций над нечеткими множествами для одного
универсума. Рассматриваемые операции применяются к исходным схемам
отношений /?и[у4(/('))|, нечеткое множество /?а которых известно и задано на
универсуме, являющемся множеством dom (А(!(‘)). В результате этих операций
получается новая нечеткая схема отношений, определенная на том же
универсуме. Таким образом, теоретико-множественные операции будем
рассматривать применительно к схемам (х)/х} = где =
{й |у е/*'*}, х е dom (А(1{1}У).
В результате применения операции дополнения, обозначаемой знаком
по схеме /?ДЛ(/*'’)] получаем схему /?^[у4(/(,))]:
= = [J i-p^w/x.
хе dom ( lll>))
Пример применения операции дополнения представлен на рис. 11.1, где
с помощью выносных линий показаны функции принадлежности и нечеткие
множества, в которые они входят. Основа схем отношений А(/{1) на рис.
11. 1 и всех последующих указана в общем виде, несмотря на то, что рисунки
иллюстрируют только случаи для основ, содержащих один или два атрибута.
Для рис. 11.1 это означает, что А(/{') = А(1а), причем U = dom (Л(/(|))).
Рис. 11.1. Операция дополнения
249
11. Нечеткие знания и рассуждения
Применяя операцию объединение, обозначаемую знаком о, получаем
Ra U Rp = J тах(ца (х), (х)) /(х).
хе d(>m{ ))
Выполняя операцию пересечение, обозначаемую знаком п, имеем
ЯаГЦ,= П тт(ца(х),цр(х))/(х).
Примеры операций объединения и пересечения показаны на рис. 11.2.
Рис. 11.2. Операции объединения (а); пересечения (б)
Применяя операцию следования, обозначаемую знаком с, получаем
(Лсд/?Р) = Ry = К (х)/х)},
где
1, Ц/?а(х)<цЛр(х);
= \ / х z х
' Ц/?а(х)>ц^(х).
250
11.4. Нечеткие действия (операторы)
Пример применения операции следования представлен на рис. 11.3.
Рис. 11.3. Операция следования
11.4.2. Операции линейного преобразования
Операции линейного преобразования определяются двумя параметрами к
и b (к > О, (-к) < b < 1) и являются унарными, т.е., как и операция
дополнения, совершаются над одним нечетким множеством. В результате
применения этих операций получается новое нечеткое множество R. Иными
словами, любая операция линейного преобразования является унарной
операцией, принимающей в качестве аргумента нечеткое множество R и
возвращающей в качестве результата в общем случае другое нечеткое
множество R , которому соответствует та же основа схемы отношений. Таким
образом, при этой операции преобразованию подвержена только функция
принадлежности. Другими словами, функция принадлежности чА, нечеткого
множества R является результатом линейного преобразования функции
принадлежности ps нечеткого множества Ry
а
м*) = (*)•
7 ' а
Каждая операция к определяется значением параметров к и Л, т.е.
зависит от взаимного расположения прямой у = кх + b и единичного квадрата
[0,1]х[0,1], внутри, которого расположена функция принадлежности p^(x).
При к > 0 (прямая у = кх + Ь монотонно возрастает) существуют семь
вариантов взаимного расположения этой прямой и единичного квадрата
(рис. 11.4). Рассмотрим каждый из этих вариантов.
251
11. Нечеткие знания и рассуждения
Рис. 11.4. Варианты (1—7) взаимного расположения прямой у = kx + b
и единичного квадрата
Вариант 1. к > 0, b = 1. В этом варианте прямая у = kx + b пересекает
единичный квадрат в точке <0,1 > и полностью лежит выше его. Как следствие
этого цЛ(х) = ц^(х).
Вариант 2. к > 0, (-к) < b < 1. Прямая у = kx + b в этом варианте
проходит через две стороны квадрата, которые определяются вершинами:
<0,0>, <0,1 > и < 1,0>, <1,1> соответственно, т.е. корни уравнений kx + b = 0
и kx + b = 1 не принадлежат интервалу (0,1) по оси абсцисс.
Пересечение прямой у = kx + Ь и единичного квадрата обеспечивается
при выполнении условия к > 0 и (-к) < b < 1. Корни уравнения kx + b = 0
не принадлежат интервалу (0,1), если или — £1 • Разрешая эти
неравенства относительно b и учитывая, что к > 0, получим b > 0 или b < {-к).
Заметим, что при b < (-к) прямая у = kx + b либо не пересекает, либо имеет
единственную точку пересечения с единичным квадратом, а значит, имеет
смысл рассматривать только условие b > 0. Аналогично, корни уравнения
kx + b = 1 не принадлежат интервалу (0,1), если или ’ т-е-
b >1 или b < (1 - к). Учитывая, что при b > 1 прямая у = kx + b либо не
пересекает, либо имеет единственную точку пересечения с единичным
квадратом, оставим только условие b < (1- к).
Таким образом, этот вариант полностью характеризуется условиями
0 < к < 1, ...,0 < b < (1 - к). Пример применения операции Х(А4|,
соответствующей этому варианту, представлен на рис. 11.5.
252
11.4. Нечеткие действия (операторы)
по варианту 2 при 0 < k < 1 и 0 < b < (]-£)
Вариант 3. Определяется условием к = 1 и Ь = 0 (частный случай варианта 2).
Операция ЛЦ4). соответствующая этому варианту, дает (х) = ц^(х).
Вариант 4. Прямая у = кх + Ь, соответствующая этому варианту, проходит
через две стороны квадрата, определенные вершинами: <0,0>, < 1,0> и < 1,0>,
< 1,1 > соответственно. Это условие можно выразить следующим образом: во
первых, корень уравнения кх + b = 0 принадлежит интервалу (0,1), т.е.
(-к) < b < 0; во вторых, корень уравнения кх + b = 1 не принадлежит интервалу
(0,1), т.е. Ь < (\- к). Таким образом, вариант 4 полностью определяется
условиями: (-к) < b < (1-£), если к > 1, и (-к) < b < 0, если к < 1. В
результате применения операции \кЬ), соответствующей этому варианту,
получается нечеткое множество Л , являющееся подмножеством нечеткого
множества R.. т.е. цЛ(х) < (х). Пример применения операции X по
этому варианту при к‘> 1 и b = \-к, представлен на рис. 11.6.
Рис. 11.6. Применение операции л по варианту 4 при к > 1 и b = \ -к
253
/1. Нечеткие знания и рассуждения
Вариант 5. Прямая у = кх + Ь, соответствующая этому варианту, проходит
через две стороны квадрата, определенные вершинами: <0,0>, <0,1 > и <0,1 >,
<1,1> соответственно. Это условие можно выразить так: во-первых, 0 < b < 1;
во-вторых, корень уравнения кх + b — 1 принадлежит интервалу (0,1), т.е.
(!-£)</>< 1. Таким образом, вариант 5 полностью определяется условием:
(1-£) < b < 1, если к < 1, и 0 < b < 1, если к > 1. В результате применения
операции \кь, соответствующей этому варианту, получается нечеткое множество
Я, включающее нечеткое множество Яа, т.е. цЛ(х) > (х). Пример
применения операции к по этому варианту при £ > 1 и Z> = 1-£ представлен
на рис. 11.7.
Рис. 11.7. Применение операции Z по варианту 5 при к > 1 и 0 < b < 1
Вариант 6. Прямая у = кх + Ь, соответствующая этому варианту, проходит
через две стороны квадрата, определенные вершинами: <0,0>, <0,1 > и < 1,0>,
< 1,1 >. Это условие можно выразить следующим образом, во-первых, корень
уравнения кх + Ь — 0 принадлежит интервалу (0,1), т.е. (-Л) < b < 0; во-
вторых, корень уравнения кх + b = 1 также принадлежит интервалу (0,1),
т.е. (1 -к) < b < 1. Одновременное выполнение этих условий возможно только
при к > 1. Таким образом, вариант 6 полностью характеризуется условием
к > 1, (1-Л) < b < 0. При значениях параметров, удовлетворяющих этому
условию, операция увеличивает значения функции принадлежности,
которые превышают (-/>)/( 1 + к), и уменьшает те, которые меньше, чем
(-/>)/(! + к). Пример применения операции к при к> 1 и (1 -к) < b < О
представлен на рис. 11.8.
Вариант 7. Для этого варианта b = (-к), т.е. прямая у = кх + b пересекает
единичный квадрат в точке < 1,0> и полностью лежит ниже его. Как следствие
этого пА, (х) = 0.
254
11.4. Нечеткие действия (операторы)
При k = G (у = kx + b(b — константа)) и 0 < b < 1 функция принадлежности
цЛ(х) = Л^ц^Ст) = b для любого элемента множества доменов dom (А(1{,}))
(рис. 11.9). В частности, при b = 1 получим нечеткое множество, функция
принадлежности которого на любом элементе универсума равна 1, а при b = О,
соответственно, нулю.
11.4.3. Пороговая операция
Пороговая операция г] имеет параметр р е [0,1 ], называемый порогом,
и может рассматриваться как предельный случай операции линейного
255
//. Нечеткие знания и рассуждения
преобразования при £ —> ® и р = — . В результате ее применения
получается нечеткое множество, функция принадлежности которого
« = П(Р1ЦЛ( U) - Р-
Пример применения операции т| представлен на рис. 11.10.
Рис. 11.10. Применение пороговой операции
11.4.4. Цилиндрическое продолжение
Операция цилиндрического продолжения, в отличие от уже
рассмотренных, имеет дело не с одной схемой отношений, а с двумя. Если
A(/il}) и A(KJ}) — основы этих схем отношений, то ее можно определить
следующим образом:
С>ЯМ(/,',)]=Я
где R — нечеткое множество, определенное на универсуме dom (А(/{,) и Аи))).
Функция принадлежности множества R определяется так: v) = pfc(w)
для всех и е dom (ACI'1’)), (и, v) е dom (A(Ill) о А01)). Пример применения
операции цилиндрического продолжения для нечетких множеств R [Л(/(,))| и
АрИ(А'7>)], в результате чего получено нечеткое множество ЯДЛ(/(,) и А17’)]
представлен на рис. 11.11.
11.4.5. Проекция
Операция проекции нечеткого отношения Ra[A(/(i} и А(П)Ь где Ra —
нечеткое множество, определенное на универсуме (и, v) е (dom (Л(/(,))) х
х dom (A(K{J})), на нечеткое множество dom (А(Г‘}) определяется следующим
образом:
ProjKm Ra\A(l" u А’7’)] = А [Л(/(,))1,
256
11.4. Нечеткие действия (операторы)
где R — нечеткое множество, определенное на универсуме dom (А(1и>)) с
функцией принадлежности
ця(и) = 5ир{цЛ (и, у) | и е dom {A{I[i)')> v е dom
(и, v) е {dom (A(l(,>)) х dom (A(Klj>)).
Пример применения операции проекции представлен на рис. 11.12.
Рис. 11.11. Применение операции цилиндрического продолжения
Рис. 11.12. Применение операции проекции нечеткого отношения
9 - 1141
257
11. Нечеткие знания и рассуждения
Посредством введенных операций можно получить другие операции над
нечеткими множествами, например, операции декартова произведения и
копроизведения.
11.4.6. Декартово произведение
Операция декартова произведения нечетких множеств ЯДЛ(/1,))| и
RГ![/4(А'и))], где /(,) n = 0, является пересечением цилиндрических
продолжений:
А,[Л(/(,))| х Яр[Л(^’)]=С>Я [Л(/('’)1 п С/(,)Яр[Ж01)]-
11.4.7. Копроизведение
Операция копроизведения тех же нечетких множеств является
объединением цилиндрических продолжений
Я |Л(/">)1 + Яр|Д^»)] = [Л(/(,))1 о С>Яр[Л(^>)1-
11.4.8. Выборка
Операция выборки Select^ позволяет сформировать новое нечеткое
множество R [Л(АЪ>)] по нечеткому множеству Ra|А(I{i})] на основе проверки
формулы 0:
Select^ = Я[Л(Я'ф].
В принципе формула 0 может быть любой формулой, построенной с
использованием связок л, v и операций сравнения доменов. В результате
операции выборки в множество dom отбираются только те домены
{сф, о'2, ..., оф, сф , оф ..., оф, ат2, оф} с dom (Л(/(,))), для которых
формула 0 истинна. Функции принадлежности этих доменов не изменяются.
11.4.9. Сравнение
Операция сравнения состоит в сравнении двух нечетких множеств.
Нечеткое множество Яр|т1(А'О))] равно нечеткому множеству ЯДЛ(/(,))], если
/(,) = и всех и е dom (А(Г‘>)) имеет место («). Операцию
сравнения двух нечетких множеств будем записывать как Яр[Л(А'01)] = /?а|Л(/(,|)|.
11.4.10. Включение
Операция включения состоит в проверке на включение одного множества
в другое. Нечеткое множество Яа[Л(/(,))] включается в Яр[Л(А'0’)], а нечеткое
множество Яр[Л(A'<J))| включает (содержит) ЯД^/0’)], если /(,) = К'!' и для
всех и е dom (Л(/(,))) имеет место ц^(и) < (w). Операцию включения будем
записывать как Яа[Л(/(,))] с Яр[Л(A'w)].
258
11.5. Нечеткозначное исчисление
11.5. Нечеткозначное исчисление
Введенные в предыдущих разделах понятия позволяют ввести нечеткозначное
исчисление, значениями формул которого будут не Истина или Ложь, а
конкретизированные нечеткие отношения. Сами формулы при этом называют
формулами нечеткозначного исчисления. Значения формул, являющиеся
конкретизированными нечеткими отношениями, определяют наличие или
отсутствие тех или иных нечетких отношений в среде (базе данных). Перейдем
к более конкретным определениям нечеткозначного исчисления.
Сделаем два необходимых для дальнейшего утверждения, которые
достаточно очевидны и могут быть легко доказаны.
Проекция нормальной схемы отношений Яа[Л(/(,))| на любую подсхему
Яр[Л(^>)1 cz является нормальной схемой отношений.
Проекция сепарабельной схемы отношений ЯДЛ(/(,))] на любую подсхему
с Аа[/1(/('))] является сепарабельной схемой отношений.
Рассмотрим предварительно некоторые свойства сепарабельных
нормальных нечетких схем отношений.
Имеем сепарабельную нормальную нечеткую схему отношений /?а[Л(/°1)],
где i е N = {1, 2, ..., N}. Пусть S = {/?|Л(/(11)] |, i е N, /('’ е J(,V)} — все
нечеткие схемы отношений, полученные с помощью всех возможных
проекций схемы включая саму эту схему. Согласно приведенным
ранее утверждениям, любая схема А[?1(/<'))] е S, как и схема Яа[Л(У1'1)],
является нормальной и сепарабельной. Отсюда следует, что схема
может быть получена с помощью использования одной из следующих операций.
Операция декартова произведения двух схем Я[Л(Л'(7’)| и R[A(H}\А',у))], т.е.
Операция проекции схемы А[/1(А'и))], такой, что У1'1 с K{J>, т.е.
АИ(/('’)| = Proj^ R[A(K(J))].
Операция включения в схему R'[Л(/(,))], т.е.
Я[Л(/(,))1 £ /?'[Л(/('’)1-
Множеством всех схем при фиксированном / является Т(1(1'):
Я'ИС/1'1)] с Г(У('>) = | 2 Я[Л(/1,))1}-
Множество схем Т(Г'У) в свою очередь входит в множество нормальных
сепарабельных схем Т:
T(l{li) с Т = |J
/
9*
259
/1. Нечеткие знания и рассуждения
Таким образом, все множество рассмотренных схем можно представить с
помощью диаграммы Венна так, как показано на рис. 11.13. Здесь Q —
множество всех нечетких схем отношений, L — множество нечетких схем
отношений, которые могут быть получены по сепарабельным нормальным
схемам множества Т с помощью операций, но не обязательно являются
сепарабельными и нормальными. Поскольку исходная схема отношений
Яс|Л(/(у))] является подмножеством множества Z, то ее вывод может быть
всегда осуществлен с помощью операций проекции, декартова произведения
и включения.
Рис. 11.13. Взаи мосвязь множеств нечетких отношений
Нечеткий вывод. На основании рассмотренных выше операций введем
следующие правила для осуществления нечеткого вывода.
11.5.1. Правило следования
Если известна нечеткая конкретизированная схема отношений Яи[Л(
и существует нечеткая конкретизированная схема Яр[Л(/(,,)|, такая, что
R (Д/’”)] з R [Л(/"*)], то можно вывести нечеткую конкретизированную схему
R„\A(Iil})\, Rfi\A(Яр[Л(/<'•)! Э Я \~Rfi\A(l^\.
11.5.2. Правило обобщения
Если известна нечеткая конкретизированная схема отношений Я [Л(/('’)]
и К(п з Г", то можно вывести нечеткую конкретизированную схему
отношений Яр|Л'и’)] = С’А / Я |\4(/")]-
я„И(/"’)Ь я'1" => I- сЛ.(7)ЯиИ(/'->)|.
260
11.6. Задача диагностики тепловых сетей
11.5.3. Правило проекции
Если известна нечеткая конкретизированная схема отношений Яа|Л(/"’)]
и К!1' с /(,), то выводима нечеткая конкретизированная схема отношений
АрМ(/<Д] = ProjKo>Ra
Яа[Л(/''’)], К’1'1 с /(,) h Proj^RJAW')].
11.5.4. Правило пересечения
Если известны нечеткие конкретизированные схемы отношений RrJA(/(,))|
и R Й(/<'Д], то выводима нечеткая конкретизированная схема отношений
R,= * И(/(,’)1 п я₽М(/(,))|:
я М(/(,,)Ь ЯрИ(/<>)] к я [Л(/('’)| П 7?р[^(/< ’)].
Под выводом в нечеткозначном исчислении будем понимать такую
последовательность применения перечисленных правил, в результате которого
выводится требуемая целевая формула, значением которой является
нормальная сепарабельная нечеткая схема отношений. При этом важным
является тот факт, что применение правил следования, обобщения, проекции
к любым элементам множества Т (сепарабельным нечетким нормальным
схемам) порождает только элементы множества Т. Таким образом, задавшись
некоторым конечным множеством нечетких конкретизированных схем
отношений, принадлежащих множеству Т (аксиом), и применяя правила
следования, обобщения, проекции, мы можем выводить новые нечеткие
сепарабельные нормальные конкретизированные схемы отношений
(теоремы). Однако, если заранее неизвестно, что все исходные нечеткие
конкретизированные схемы отношений таковы, что они принадлежат
множеству Г, то использование приведенных правил может привести к
результату, который не является нормальной сепарабельной схемой.
Следовательно, возникает проблема установления принадлежности всех
аксиом множеству Т.
Множество Т является множеством нормальных и сепарабельных схем
отношений. Поэтому все значения исходного множества аксиом также
должны быть нормальными и сепарабельными схемами, а в результате
применения к ним перечисленных правил должны выводиться также
нормальные и сепарабельные схемы отношений. Если все исходные
нормальные и сепарабельные схемы отношений являются таковыми, то они
называются согласованными. Для проверки множества схем на согласованность
могут быть использованы разные стратегии. Одной из них может быть
стратегия проверки на каждом очередном шаге вывода нормальности и
сепарабельности вновь выведенной схемы нечетких отношений. Если она
таковой не является, то следует возвратиться к предыдущему шагу вывода,
отказываясь от пути вывода, который привел к получению аномальной схемы
отношений.
261
7 7. Нечеткие знания и рассуждения
Использование нечеткозначного исчисления непосредственно в
рассмотренном виде неудобно, хотя и возможно. На практике используются
более выразительные языки, семантика которых определяется посредством
нечеткозначного исчисления. Эти языки учитывают особенности среды, с
которой приходится иметь дело и называются обычно проблемно-
ориентированными языками. Рассмотрим пример такого языка, правила
перехода от него к нечеткозначному исчислению и решение задачи с помощью
нечеткозначного исчисления.
11.6. Задача диагностики тепловых сетей
Среда состоит из простейшей тепловой сети (ТС), топология которой
показана на рис. 11.14. Здесь цифрой 1 обозначена котельная; 2 — узел
ветвления; 3 — центральный тепловой пункт 1 (ЦТП1); 4 — центральный
тепловой пункт 2 (ЦТП2). Ветви 1-2 и 2-1 — подающая и обратная магистрали
соответвенно; 2-3 и 3-2 — подающая и обратная линии ЦТП1; 2-4 и
4-2 — подающая и обратная линии ЦТП2.
Предположим, что имеется возможность q t
измерять величину подпиточного расхода,
а также величины давлений в подающем и
обратном трубопроводах на входе и выходе
котельной, ЦТП1 и ЦТП2. /V
Для характеристики подпиточного расхода / х.
будем пользоваться терминами: «маленький», / X.
«средний» и «большой», а величины давлений гуз 4
будут характеризоваться словами: «низкое»,
«нормальное» и «высокое». Нормальное Рис. 11.14. Топология тепловой
функционирование ТС (отсутствие повреж- сети
дений) можно определить как состояние, при
котором расход подпиточной воды
небольшой и все измеряемые давления в пределах нормы. В любом другом
случае функционирование нельзя считать нормальным. Одной из возможных
причин ненормального функционирования могут быть закупорка и порыв
трубопроводов. Эта информация может быть получена от эксперта или, как в
нашем простом примере, из соображений здравого смысла и поверхностных
знаний законов гидравлики.
Введем дополнительные обозначения: подпиточный расход обозначим
символом q\ давления на входе в подающую магистраль, на входе ЦТП1 , на
входе ЦТП2, на выходе ЦТП1, на выходе ЦТП2 и на выходе обратной
магистрали обозначим, соответственно, символами р\, р2, рЗ, р4, р5 и рб.
С учетом введенных обозначений следующее описание можно рассматривать
как неформальное описание функционирования тепловой сети:
262
11.6. Задача диагностики тепловых сетей
Если q - небольшой и р\, р2, рЗ, рб, р5, рб нормальные, то ТС
функционирует нормально,
Если имеет место повреждение - порыв или закупорка, то ТС функционирует
в аварийном режиме,
Если имеет место порыв, то q - большое,
Если имеет место порыв на подающей магистрали, то р\ - очень низкое, а
р2, рЗ, рб, р5, рб - низкие,
Если имеет место порыв на подающей линии ЦТП1, то р2, рб - очень
низкие, а р\, рЗ, р5, рб - низкие,
Если имеет место порыв на подающей линии ЦТП2, то рЗ, р5 - очень
низкие, а р\, р2, рб, рб - низкие,
Если имеет место порыв на обратной линии ЦТП1, то рб - очень низкое,
а р\, р2, рЗ, р5, рб - низкие,
Если имеет место порыв на обратной линии ЦТП2, то р5 - очень низкое,
а р\, р2, рЗ, рб, рб - низкие,
Если имеет место порыв на обратной магистрали, то рб - очень низкое,
а р\, р2, рЗ, рб, р5 - низкие,
С уверенностью 90%, если имеет место закупорка, то q - маленький,
Если имеет место закупорка на подающей магистрали, то р\ - очень
высокое, а р2, рЗ, рб, р5, рб - очень низкие,
Если имеет место закупорка на подающей линии ЦТП1, то р\, рб
нормальные, р2, рб - очень низкие, а рЗ, р5 - примерно нормальные.
Если имеет место закупорка на подающей линии ЦТП2, то р\, Р& *
нормальные, рЗ, р5 - очень низкие, а р2, рб - примерно нормальные,
263
11. Нечеткие знания и рассуждения
Если имеет место закупорка на обратной линии ЦТП1, то р\, рб -
нормальные, р2, р4 - высокие, а рЗ, р5 - примерно нормальные,
Если имеет место закупорка на обратной линии ЦТП2, то р\, рб -
нормальные, рЗ, р5 - высокие, а р2, р4 - примерно нормальные,
Если имеет место закупорка на обратной магистрали, то р\, р2, рЗ, рХ
р5 - очень высокие, а рб - очень низкое.
Задача диагностики тепловой сети состоит в обнаружении повреждений
на основе приведенного описания функционирования. Иными словами, в
процессе диагностики необходимо получить ответы на вопросы двух типов:
а) прямые вопросы (определение факта возникновения повреждения):
«Имеет ли место повреждение при текущем состоянии тепловой сети?»
б) обратные вопросы (определение типа и локализация места повреждения):
«Повреждение какого типа имеет место при текущем состоянии тепловой
сети и установленном факте возникновения повреждения?» и «В каком месте
находится повреждение при тех же исходных данных?»
Наша цель — это научиться решать подобные задачи формально, используя
нечеткозначное исчисление. Для этого необходимо перейти от неформального
описания функционирования тепловой сети сначала к формальному описанию
на проблемно-ориентированном языке, а затем к языку нечеткозначного
исчисления, на котором и осуществить вывод. Рассмотрим вариант такого
проблемно-ориентированного языка.
11.7. Проблемно-ориентированный язык
Плодотворным подходом, используемым для создания проблемно-
ориентированных языков, семантика которых зиждется на нечеткозначном
исчислении, является подход, основанный на понятии лингвистической
переменной.
11.7.1. Лингвистическая переменная
Лингвистическая переменная характеризуется пятеркой: <Х, 0(%), U, G, М>.
Здесь X — название лингвистической переменной; 0(%) — обозначает
множество лингвистических значений (лингвистических термов) переменной
X, каждое из которых представляет собой слово или выражение естественного
языка. Среди всех лингвистических значений множества 0(А") выделяется
специальное их подмножество 06(%), которое назовем базовым множеством
лингвистических значений. Оно считается заданным, а остальные лингвистические
значения (имена) порождаются синтаксическими правилами G.
264
11.7. Проблемно-ориентированный язык
Каждому лингвистическому значению ставится в соответствие нечеткое
множество, заданное на универсуме И. Нечеткое множество,
соответствующее лингвистическому значению, выражает его смысл.
Соответствие между лингвистическим значением из множества 0(АД и каким-
либо нечетким множеством задается с помощью отображений М, называемых
также семантическими правилами. Семантические правила ставят в
соответствие лингвистическим термам схемы нечетких отношений следующим
образом.
Каждому лингвистическому терму из базового множества взаимно однозначно
соответствует какой-либо атрибут а нечеткой схемы отношений. В этом случае
лингвистический терм обозначается так же, как атрибут а. Лингвистический
терм а соответствует также домену dom (а) = {o'j, о'2, ..., а'л} этого атрибута,
и значением лингвистического терма является нормальное сепарабельное
нечеткое множество R(a) = (ц(а'2)/с'2, ...,(p(o'rj)/o'n}, определенное
на этом домене.
Функции принадлежности нечетких множеств, задающих смысл
лингвистических термов одной и той же лингвистической переменной,
должны обладать определенными свойствами. К числу этих свойств относятся
следующие:
нечеткое множество, соответствующее каждому лингвистическому
значению, должно быть нормальным и выпуклым;
если упорядочить лингвистические значения одной и той же
лингвистической переменной по возрастанию носителей нечетких множеств,
то для двух любых смежных лингвистических термов д и а ( необходимо,
чтобы носители соответствующих им нечетких множеств Я , Я +1 пересекались
(Support (R) n Support (Я+1) * 0), а ядра этих множеств не пересекались
(Kernel (R) n Kernel (Я+|) * 0);
универсум лингвистической переменной должен иметь верхнюю и нижнюю
границы (Зхр х, = inft/; 3 х2, х2 = supt/), и эти величины должны принадлежать
ядрам нечетких множеств крайних термов.
Создание проблемно-ориентированного языка включает введение помимо
лингвистических переменных необходимых логических связок, модальностей,
формул. Значениями формул также являются схемы отношений. Часть
лингвистических переменных вводится естественным образом. В нашем
примере — это подпиточный расход, который, если временно опустить
синтаксические и семантические правила, можно определить как <q,
{маленький, средний, большой}, Q>, где Q — множество всевозможных
значений расхода подпиточной воды в данной ТС. Аналогично определяются
лингвистические переменные давления: <pt, {низкое, среднее, высокое},
Я >, / = 1, ..., 6, где Я — все возможные значения соответствующего давления.
Другие же переменные вводятся более «искусственно». Для обозначения вида
повреждения введем лингвистическую переменную -повреждение, {порыв,
нет, закупорка}, [-1, 1 ]>, в которой в качестве универсума примем отрезок
265
11. Нечеткие знания и рассуждения
[-1, 1]. В этом отрезке значение 0 будем трактовать как отсутствие
повреждений, интервал [-1, 0) — как шкалу тяжести порыва, а (0,1] — как
шкалу степени закупорки.
Режим функционирования ТС выразим с помощью переменной <авария,
{нет, да}, [0,1 ]>, которую можно рассматривать как аналог логической с
лингвистическими значениями ,истинности.! Для |Обозначения места
повреждения в ТС также нужно ввести лингвистическую переменную.
Учитывая, что для нашего примера повреждениям подвержены только участки
трубопроводов, место повреждения удобнее всего измерять в расстоянии до
какой-либо фиксированной точки в ТС, например до начала подающей
магистрали. Однако наша ТС имеет нелинейную структуру, следствием чего
оказывается, что универсум мест повреждений не будет линейно
упорядоченным, что, в свою очередь, затруднит дальнейшее манипулирование
с переменной места повреждения. Во избежание этого применим следующий
прием. Рассмотрим эквивалентную схему ТС (рис. 11.15), в которой выделим
два контура. Первый контур составляют котельная — подающая магистраль —
подающая линия ЦТП1 — обратная линия ЦТП1 — обратная магистраль.
Второй — котельная — подающая магистраль — подающая линия ЦТП2 —
обратная линия ЦТП2 — обратная магистраль соответственно. Если
рассматривать эти контуры по отдельности, то каждый из универсумов мест
повреждений окажется линейно упорядоченным.
3
2
Контур 1
Контур 2
Рис. 11.15. Контурное представление ТС (обозначения те же, что и на рис. 11.14)
Введем две лингвистические переменные: <МК\, {ПМ, ПЛ\, ОЛ\,
OM},L}> и <МК2, {ПМ, ПЛ?., ОЛ?, OM},L2>, где имена МК\ и МК2 означают
место в контуре 1 и контуре 2; ПМ, ПЛ\, ПЛ2, ОЛ\, ОЛ2, ОМ — подающая
магистраль, подающая линия ЦТП1, подающая линия ЦТП2, обратная линия
ЦТП1, обратная линия ЦТП2 и обратная магистраль соответственно; L, =
= [0, /,] и L, = ]0, /2] — расстояния от начала подающей магистрали по
контуру 1 и по контуру 2.
266
11.7. Проблемно-ориентированный язык
Особенностью многих реальных задач является то, что объекты, с
которыми они имеют дело, для описания функционирования используют
модальности. В нашем примере это предложение, в котором используется
модальность «с уверенностью 90 %».
Вид используемой модальности зависит от отношения индивидуума,
составляющего описание, к описываемой среде. Кроме того, модальности
одного и того же вида могут отличаться друг от друга «силой» отношения.
Так, если сравнить, например, модальности «возможно» и «очень
возможно”, то становится ясно, что вторая модальность в большей степени
определяет возможность суждения, чем первая.
Таким образом, любую модальность можно представить парой: <вид
модальности, градация модальности>, где вид модальности определяет
разновидность отношения между суждением и реальной средой, а градация -
силу этого отношения. Градацию модальности удобнее всего выражать
количественно, в виде процентного отношения между определяемой
модальностью и максимально возможной модальностью этого вида. Так,
вид встретившейся в нашем примере модальности можно определить как
процент уверенности, а ее градацию — как 90 %. Этот вид модальности
можно обозначить символом % и в результате получить обозначение «% 90»
для модальности «с уверенностью 90 %».
Введем обозначения для ряда других слов в неформальном описании
функционирования тепловой сети: есть — связка между именами
лингвистических переменных и их значениями; не, очень, почти, и, или —
лингвистические модификаторы и связки для получения новых
лингвистических значений; л, v, о, = — логические связки.
Если переписать приведенный выше неформальный текст с учетом
введенных лингвистических переменных и обозначений связок, то получим
пример формализованного описания повреждений в тепловой сети:
{q есть не большой л р\ есть нормальное л р2 есть нормальное л рЗ есть
нормальное а /И есть нормальное л р5 есть нормальное л рб есть нормальное)
{авария есть нет)',
(повреждение есть {порыв или закупорка)) {авария есть да);
{повреждение есть порыв) zd {q есть большой);
{повреждение есть порыв л МК\ есть ПМ л МК2 есть ПМ) zd (pl есть очень
низкое л р2 есть низкое л рЗ есть низкое л р4 есть низкое л р5 есть низкое л
л рб есть низкое);
267
11. Нечеткие знания и рассуждения
(повреждение есть порыв л МКА есть ПЛ\) zd (pl есть низкое л р2 есть
очень низкое л />3 есть низкое л рА есть очень низкое л р5 есть низкое л
л />6 есть низкое)',
(повреждение есть порыв л МК2 есть ПЛ2) zd (/>1 есть низкое л р2 есть
низкое л р2> есть очень низкое л рА есть низкое л р5 есть очень низкое л
л рЬ есть низкое)',
(повреждение есть порыв л МК\ есть 0Л\) лз (/>1 есть низкое л р2 есть
низкое л рЗ есть низкое л рА есть очень низкое л р5 есть низкое л рЬ есть
низкое)',
(повреждение есть порыв л МК2 есть 0Л2) zz> (pl есть низкое л р2 есть
низкое л р2 есть низкое л рА есть низкое л р5 есть очень низкое л рЬ есть
низкое);
(повреждение есть порыв л МК1 есть ОМ л МК2 есть ОМ) zd (pl есть
низкое л р2 есть низкое л р2> есть низкое л рА есть низкое л р5 есть низкое л
л рЬ есть очень низкое)',
% 90 ((повреждение есть закупорка) лз (q есть маленький))',
(повреждение есть закупорка л МК\ есть ПМ л МК2 есть ПМ) лз (pl есть
очень высокое л р2 есть очень низкое л р2> есть очень низкое л рА есть очень
низкое л р5 есть очень низкое л рб есть очень низкое)',
(повреждение есть закупорка л МК1 есть ПЛ\) о (pl есть нормальное л
л р2 есть очень низкое л р2> есть почти нормальное л рА есть очень низкое л
л р5 есть почти нормальное л рб есть нормальное)',
(повреждение есть закупорка л МК2 есть ПЛ2) лз (pl есть нормальное л
л р2 есть почти нормальное л />3 есть очень низкое л рА есть почти
нормальное л р5 есть очень низкое л рб есть нормальное)'.
268
11.7. Проблемно-ориентированный язык
(повреждение есть закупорка л МК\ есть 0Л\) о (р\ есть нормальное л
л р2 есть высокое л рЗ есть почти нормальное л рА есть высокое л р5 есть
почти нормальное л рб есть нормальное);
(повреждение есть закупорка л МКЛ есть 0Л2) л (р\ есть нормальное л
л р2 есть почти нормальное л рЗ есть высокое л рА есть почти нормальное л
л р5 есть высокое л рб есть нормальное);
(повреждение есть закупорка л МКА есть ОМ л МК2 есть ОМ) zd (р\ есть
очень высокое л р2 есть очень высокое л рЗ есть очень высокое л рА есть
очень высокое л р5 есть очень высокое л рб есть очень низкое).
Текущее состояние ТС описывается теми же средствами:
q есть большое л р\ есть очень низкое а р2 есть низкое л рЗ есть низкое л
л рА есть низкое л р5 есть низкое л рб есть низкое.
11.7.2. Синтаксис прооблемно-ориентированного языка
Основываясь на сказанном и приведенном примере, определим более
строго синтаксис проблемно-ориентированного языка L.
Алфавит Al языка L составляют следующие группы символов:
имена лингвистических переменных: X = {X, Х2, ..., Х.у;
термы лингвистических переменных: 0 = |^J Q(X ) i
/=i
символы модальностей;
логические связки: л, v,,
связка есть и скобки (, ).
Элементы множества 9 порождаются синтаксическими правилами
лингвистических переменных Х е X. Вообще говоря, синтаксические правила
различных лингвистических переменных могут отличаться друг от друга. Но
для простоты будем считать, что все они построены единообразно и в
соответствии со следующим определением.
Пусть имеется лингвистическая переменная <Х, б(Х), U, G, М>. Алфавит
А(.синтаксических правил G включает в себя:
базовые термы: 96(%);
269
II. Нечеткие знания и рассуждения
{Не, Очень, Почти, Или, И} — лингвистические модификаторы и связки;
скобки (,).
Л юбой терм из множества 0(А') представляет собой цепочку символов алфавита
А(,, удовлетворяющую следующему описанию на метаязыке Бэкуса Наура:
Терм —> Базовый терм | Не Терм I Очень Терм | Почти Терм I Терм Или Терм\
Терм И Терм,
где Базовый терм — терминальный символ, принадлежащий множеству
базовых термов 96(А).
Символы модальностей содержат префикс и следующее за ним число.
Префикс определяет конкретный вид модальности из некоторого заранее
заданного конечного множества видов, а число — количественное выражение
градации этой модальности.
Будем использовать модальности вида: невозможность, случайность,
возможность, необходимость и процент уверенности. Пусть им соответствуют
префиксы {Невозможно , Вероятно , Возможно , Необходимо , %}. Число,
следующее за префиксом и выражающее градацию соответствующей
модальности, должно быть натуральным и не должно превышать сотни. Кроме
этого для модальности процент уверенности допустимой градацией может быть
число 0. Построенные таким образом символы модальности читаются так:
Невозможно й — «с тУ-процентной невозможностью»; Вероятно й - «с N-
процентной случайностью»; Возможно N — «с тУ-процентной возможностью»;
Необходимо й ~ «с ^процентной необходимостью»; % N — «с уверенностью
N %», где N — выраженное в процентах значение градации.
Следовательно, при заданном алфавите АМм1, включающем следующие
группы символов:
виды модальностей: {Невозможно , Вероятно , Возможно , Необходимо , %};
цифры: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
символ модальности должен удовлетворять описанию на метаязыке Бэкуса-
Наура:
Цифра -> 112l3|4|5|6i 7|8|9,
Ноль 0,
N -> Цифра | Цифра 0 I Цифра Цифра I 100, (111)
Префикс —> Невозможно | Вероятно_ | Возможно_ | Необходимо_ | %,
т -> Префикс N I % Ноль.
270
11.7. Проблемно-ориентированный язык
Таким образом, любое правильно построенное выражение (формула)
языка L представляет собой цепочку символов алфавита Аг удовлетворяющую
следующему описанию на метаязыке Бэкуса-Наура:
Атом -> У есть Т,
Формула -> Атом | Формула | Формула л Формула | Формула v
v Формула | Формула о Формула | т Формула.
Здесь Y е X — имя лингвистической переменной; Те 0(E) — терм этой
лингвистической переменной; т — символ модальности.
11.7.3. Семантика проблемно-ориентированного языка
Семантика лингвистических переменных. Семантические правила М каждой
лингвистической переменной <Х, 0(Л), U, G, М> задают отображение
множества термов 0(А') в множество Fuzzy (U) нечетких подмножеств
универсума U:
М: Q(X) -> Fuzzy (U).
Это означает, что, если терм Т е 0(%), то М(Т) — нечеткое множество
М( Т) е Fuzzy (С), выражающее смысловое содержание терма Т.
Функции принадлежности нечетких множеств М(Т), где Т е 0i, чаще
всего определяются в диалоге с экспертом. Согласно определению нечеткого
множества, для любого терма Т е 0С¥):
= {pW(7)(w)/zr | и eU}.
Универсум U лингвистической переменной должен быть линейно
упорядочен. В частном случае универсум U можно рассматривать как отрезок
действительной прямой |х|Т х,|. где х, = inf U, хг = sup U.
Нечеткие множества, соответствующие каждой лингвистической
переменной, должны удовлетворять ряду перечисленных ниже условий.
а. Условие нормальности. Каждое нечеткое множество М{Т) должно
быть нормальным нечетким множеством.
б. Условие выпуклости. Каждое нечеткое множество М(Т) должно быть
выпуклым.
в. Условие полноты. Если множество всех нечетких подмножеств М( Т)
каждой лингвистической переменной упорядочить по возрастанию inf {Support
М(Т), то для любой пары соседних множеств М(Т) и М(Т+]) должно
выполняться
Support (М(Т) о Support (М(Т+1)) * 0.
г. Условие непротиворечивости. При выполнении условия полноты
должно выполняться
271
11. Нечеткие знания и рассуждения
Kernel (М(Т)) n Kernel (М(Т+1)) = 0.
В дальнейшем будем считать, что функция принадлежности каждого терма
имеет трапециевидную форму. Выбор такой формы функции принадлежности
обоснован следующими соображениями:
эта функция всегда выпукла (трапеция — выпуклая фигура);
график функции может быть построен по четырем точкам на
действительной плоскости, как показано на рис. 11.16.
Рис. 11.16. Трапециевидная форма функции принадлежности
Аналитически трапециевидную функцию принадлежности можно записать
следующим образом:
h <и <с,
(и) =
-----и------.а < и < h;
h-a h-a
-1 d
-----и ч----. с < и < d;
d-с d— с
О, (и < a) v (и > d).
(И.2)
Параметрически это можно выразить так: 5 = (a, b, с, d), где а < Ь < с < d.
Может показаться, что такое определение функции принадлежности
достаточно примитивно и приближенно представляет реальное смысловое
значение определяемого понятия. Однако существует мнение, что не
обязательно располагать точными значениями функции принадлежности.
Например, некоторые авторы полагают, что на практике достаточно
приближенного представления функции принадлежности, поскольку: ошибка
не будет возрастать при ее использовании вследствие применения в
большинстве случаев только операции нахождения максимума и минимума.
272
11.7. Проблемно-ориентированный язык
Нечеткие множества для термов, порождаемых синтаксическими
правилами, могут быть легко вычислены с помощью применения конечного
числа операций, каждая из которых соответствует конкретному
лингвистическому модификатору или связке. Семантические правила
построения нечетких множеств для термов следующие:
М(Т), где Т е Qh(X), определяется в диалоге с экспертом;
Пусть Т,,Т,е 0(АГ), тогда
М(неТ}) = -1 М(ТХ), где М(Т}) — дополнение нечеткого множества М(Т)'.
Vи е С, ц А(и) = 1- ц4(и) (здесь и далее М(ТХ) = В, М(Т2) = /1);
М(очень7\) = CON Т})), где CON(М(Т)) — операция концентрирования
нечеткого множества, которая в общем случае заключается в нахождении
подмножества М( 7\). Иногда эта операция определяется как Vw е U, раЛ(/))(«) =
= ц4(«)2. Будем ее определять так же с помощью операции X при k > 1 и
b = 1- к как V// е О, ^С0ЧА\и) = л(2 пцл(ц);
М^почтиТ^ = DIL(M( Г,)), где D1L (М(ТХ)) — операция растяжения
нечеткого множества, которая обычно определяется как Vw е U, ^Dll{4<(u) =
= ^ц4(и). Будем ее определять так же с помощью операции при к > 1 и
Ь = 0 как е U, цд//(.()(и) = \2,0)ц/«);
М( Т, или Т2) = M(Tt) 'j М( Т,), где Л/( Т}) о М( Т2) — объединение нечетких
множеств М(Т}) и М(Т2): \/и е U, a, g(w) = maxfp^w), цй(«)|;
МСГ и Т2) = М(Т{) п М(Т2), где М(ТХ) ' M(Tj — пересечение нечетких
множеств М(ТХ) и Л/( 7 \) : Vm е U, p^.g(«) = minlpjw), pg(w)|.
Семантика модальностей. Введем лингвистическую переменную
Суверенность, Mod, [0,1],б7, М>, значения которой будем трактовать как
модальности языка L. Эта переменная несколько отличается от обычных
лингвистических переменных следующими факторами.
Во-первых, базовое терм-множество переменной уверенность составляют
символы модальности, правила построения которых определяются
синтаксическими правилами (11.1). Хотя базовое терм-множество Mod и
конечно, но достаточно велико: содержит 501 терм (модальности вида
невозможно, вероятно, возможно и необходимо имеют по 100 градаций, а
модальность процент уверенности — 101 градацию). Во-вторых,
синтаксическое правило G порождает только элементы базового терм-
множества Mod. В-третьих, универсумом лингвистической переменной
уверенность является отрезок [0,1], причем, конкретная интерпретация
элементов универсума зависит от вида модальности. В-четвертых,
семантическое правило М отображает базовое терм-множество Mod в
множество нечетких подмножеств Fuzzy ([0,1]):
273
11. Нечеткие знания и рассуждения
М\ Mod -> Fuzzy (|0,ID-
Ввиду рассмотренных отличий, семантические правила лингвистической
переменной уверенность также отличаются от рассмотренных ранее
следующим.
1. Семантические правила М включают только один вид правил, поскольку
все термы переменной уверенность являются базовыми.
2. Семантика модальностей накладывает ряд ограничений на моделирующие
ее нечеткие множества. Например, невозможно линейно упорядочить базовое
терм-множество Mod лингвистической переменной уверенность в соответствии
с условием, рассмотренным выше. Очевидно, что линейный порядок
существует только среди модальностей одного вида, когда они сравниваются
по градации.
Таким образом, модальности одного вида следует рассматривать
независимо от остальных и, с учетом этого, необходимо несколько изменить
условие полноты базового терм-множества, а условие непротиворечивости
заменить условием согласованности. Условие полноты запишем так:
^\Support(M(ТУ) Ф 0.
1 elW
Это означает, что существует по крайней мере один элемент универсума,
принадлежащий всем носителям всех нечетких множеств Л/( Г). Если символ
модальности с градацией тУ обозначить Гуи упорядочить термы по возрастанию
градации, то условие согласованности будет иметь вид
М(1\) с М(ТУЧ),
где N = N ... 99; N =0 ;ыя модальности процент уверенности и N =1
для остальных видов.
Остальные условия для нечетких множеств, порождаемых семантическими
правилами для элементов базового терм-множества, остаются в силе. Следует
заметить, что рассмотренные ограничения не влияют на тип используемых
трапециевидных функций принадлежности.
3. Не требуется определять отображение М для каждого из 501 возможного
терма. Достаточно рассмотреть всего пять случаев, соответствующих видам
модальностей.
Модальности вида процент уверенности. Для этого вида модальности
отрезок [0,1] следует интерпретировать как шкалу уверенности, в которой
ноль означает отсутствие уверенности, а единица — абсолютную уверенность.
Все остальные оценки располагаются между этими двумя граничными
случаями и выражают степень уверенности. Любое модальное понятие вида
274
/ /. 7. Проблемно-ориентированный язык
«%N» содержит в себе оценку уверенности, которой на шкале [0,1 ]
соответствует определенная точка:
Kernel = Support = \n, 1].
В соответствии с методикой построения трапециевидных функций
принадлежности и формулами (11.2), получим
Модальности вида процент уверенности имеют функции принадлежности,
представленные на рис. 11.17.
0 Л7100 1 п
Рис. 11.17. Виды функций принадлежности модальности процент уверенности
Для остальных видов модальностей общими будут следующие замечания.
С каждым видом модальности связана своя собственная шкала (отрезок |0,1]).
Любое модальное понятие вида невозможность, случайность, возможность и
необходимость, имеющее градацию п, содержит оценку, которой на
соответствующей шкале соответствует точка п = N/\0Q. Между модальностями
невозможно, вероятно, возможно, необходимо существует определенная
взаимосвязь.
Невозможным является то, что не является возможным, и наоборот.
Следовательно, эти понятия антиподы, и оценке N на одной шкале
соответствует оценка 1-/7 на второй.
Необходимым является то, что не случайно, и наоборот. Как и в
предыдущем случае, необходимость и случайность — антиподы, и оценке п
на одной шкале соответствует оценка l-п на второй.
Необходимо все то, что возможно. Обратное не верно. Точнее, оценка
возможности всегда превосходит оценку необходимости, то есть точке п на
шкале необходимости может соответствовать точка из отрезка |п, 11 на шкале
возможности.
275
11. Нечеткие знания и рассуждения
Модальности вида возможность. Пусть п = N/\00 — точка на шкале
возможности. Если полагать, что, говоря о возможности чего-либо, мы
предполагаем также, что существует и большая возможность того же самого,
а говорить о возможности при ее полном отсутствии неверно, тогда модальное
понятие «Возможно_Ы» полностью совместимо со всеми оценками
возможности, которые не меньше п, а абсолютно не совместима единственная
оценка, равная нулю. Таким образом,
Kernel (М(Возможно_N)) = [я, 1];
Support (М(Возможно_N) = (0, 1].
Формула (11. 2) для этого случая приобретает вид
В Х4 ( Но зможно _.\ )(1<)
О, и = 0;
< — и, 0 < и <п\
п
1, п < и < 1 .
Модальности вида возможность имеют функции принадлежности,
представленные на рис. 11.18, а.
Модальности вида невозможность. Рассмотрим модальное понятие
Невозможно_N и противоположное ему понятие Возможно й', где N' = 100-М
Пусть п = М/100 — точка на шкале невозможности, а (1-я) = М'/ЮО —
соответствующая ей точка на шкале возможности. Поскольку Невозможно й —
антипод Возможно й', то с ним полностью совместима единственная оценка
возможности, равная нулю, а абсолютно не совместимы все те оценки,
которые не меньше 1-п. Таким образом,
Kernel (М(Невозможно К)) = {0};
Support (М(Невозможно_К) = [0, 1-я).
Следовательно, формула (11. 2) приобретает вид
1, w = 0;
В Л/ (Невозможно \)1<
— • и + 1,
1-я
0<я<(1 -я);
0,
(1-я) < и < 1.
276
11.7. Проблемно-ориентированный язык
Модальности вида невозможность имеют функции принадлежности
представленные на рис. 11.18, б.
Модальность вида необходимость. Пусть п = jV/100 — точка на шкале
необходимости. На шкале возможности ей может соответствовать любая точка
из отрезка [/?, 1|. Полагая, что все, что необходимо, должно быть возможно,
можно заключить, что с модальным понятием Необходимой полностью
совместима единственная оценка возможности, равная единице, а абсолютно
не совместимы все те оценки, которые меньше п. Таким образом,
Kernel (М(Необходимо НУ) = {1};
Support (М(Необходимо_К) = |/г. 1|.
Следовательно, формула (11.2) принимает вид
В М{ Необходимо Х)^ ~ <
-----и------, п < и <
1-я 1-я
Модальности вида необходимость имеют функции принадлежности,
представленные на рис. 11.18, в.
Модальности вида случайность. Рассмотрим модальное понятие Вероятной
и его противоположность Необходимо й', где N’ — 100-Л7 Пусть п = N/100 —
точка на шкале случайности, а (I-/?) = jV'/ЮО — соответствующая ей точка
на шкале необходимости, которой может соответствовать любая точка отрезка
[1-/7,1] на шкале возможности. Поскольку << Вероятной» - антипод
Необходимо й', то с ним полностью совместимы все те оценки возможности,
которые меньше 1-/?, а абсолютно не совместима единственная оценка, равная
единице. Таким образом,
Kernel (М(Вероятно Н)) — [0, I-/?);
Support (М(Вероятно_К) = [0, 1].
Следовательно, формула (11.2) приобретает вид
Модальности вида случайность имеют функции принадлежности,
представленные на рис. 11.18, г.
1,
0 < и<(\ -п);
В М (Вероятно _ ,V) (м )
— м+—, (1-«) < и < 1;
п п
0, и=\.
277
11. Нечеткие знания и рассуждения
зможно
Нозмо Ж'НО 1
возможно 100
О 0.1
^М(Нев<> з можно
о
0.99 *
\-п
Необходимо 1
О 0.1 п 1 л'
Рис. 11.18. Виды функций принадлежности для модальностей: а — возможность;
б — невозможность; в — необходимость; г— случайность
РмЛКроятпп X)
1
Необходимо 100
\-п 0.99 х
На рис. 11.18 сплошными линиями показаны функции принадлежности,
соответствующие граничным градациям модальности (1 и 100), а
пунктирными линиями — некоторой промежуточной градации 1 < N < 100;
п = Л7100.
Рассматривая параметрическое задание нечетких множеств, порождаемых
семантическими правилами переменной уверенность, можно заметить, что
модальности имеют три или два постоянных параметра, а остальные
параметры зависят от градации модальности. Причем для модальности
процент уверенности переменными параметрами являются первый и второй,
для невозможности — четвертый, для случайности — третий, для возможности —
второй и для необходимости — первый.
Семантические правила, определяющие смысл модальностей, выражаются
следующим набором правил:
M(%N) = (0.01-М 0.01-М 1,1), где W = 0,1 ..., 100;
М(Невозможно Х) = (0, 0, 0,1 -0.01 /V), где N — 1, 2 ..., 100;
278
11.8. Переход от проблемно-ориентированного языка к языку нечеткозначного исчисления
М(Вероятно_]У) = (О, 0,1 -0.01 • N, 1), где N = 1, 2 100;
М(Возможно_]У) = (0,0.01-tV, 1, 1), где N — 1, 2 .... 100;
М(Необходимо_]У) = (0.01-М 1, 1, 1), где N= 1, 2 100.
Таким образом, была определена семантика всех конструкций довольно
универсального проблемно-ориентированного языка. Теперь рассмотрим
процедуру перехода от описаний в проблемно-ориентированном языке к
семантически эквивалентному описанию на языке нечеткозначного
исчисления.
11.8. Переход от проблемно-ориентированного языка к языку
нечеткозначного исчисления
Определим переход от проблемно-ориентированного языка L к языку
нечеткозначного исчисления О как некоторое отображение S.
S: L -> Q. (11.3)
Будем полагать, что имена лингвистических переменных, встречающихся в
алфавите языка А, являются атрибутами нечетких схем отношений, и что с каждым
конкретным атрибутом связан свой домен, являющийся универсумом этой
лингвистической переменной. Отображение (11.3) можно рассматривать как набор
правил, называемых правилами перехода, каждое из которых устанавливает
соответствие между правильной формулой языка L и задающей ее смысл
правильной формулой языка О. Заметим, что любая формула языка L является
либо атомарной (состоящей из одного атома), либо построена из атомарных с
помощью символов модальностей или логических символов (связок) алфавита
Аг Поэтому определим правила перехода сначала для атомарных формул, а затем
для производных от них.
Если а — имя лингвистической переменной, а а <= 0(a) — ее
лингвистический терм, то:
S(a есть а) -» a(o, R),
где a(d, R) — нечеткий конкретизированный терм; R — нечеткое множество
R = M(d), определенное на d, т.е. смысл формулы а есть а языка L
представляется нечетким конкретизированным термом с атрибутом а,
доменом d и нечетким множеством M(d), определенном на этом домене.
Согласно обозначениям нечеткозначного исчисления,
a(d, R) = Я[Л(/(1))].
Правила перехода для остальных формул языка L определяются
индуктивно. Обозначим р и q произвольные формулы языка L. Тогда
279
11. Нечеткие знания и рассуждения
образами этих формул и формул, получающихся из них с помощью связок,
будут следующие нечеткие схемы отношений:
ад = ЛМ(Л’)], S(q) = я[Л(/ад],
адр) =
S(p л q) = Q/) ЯДЛ(/<'’)] п Ср,-, RqИ(Л'О’)], если /<'> п 0,
S(p л q) = Я [/!(/''’)] х Я [Л(/ад], если /<'> п =0, (11.4)
S(p -v q) = Ски) ЯД/Ц/’'1)] '.j Cpit Я</[Л(Я(у|)1, если /('’ n 0,
S(p v q) = ЯДЛ(/<-’)1 + Я |Л(/Г<'>)], если /<'> п /Г<'’=0,
S(p ^q) = ЯДЛ(/«’)] о Сро Rq[A(K^)].
Правила перехода для модальностей можно представить в виде
S( Возможно _Nb}P [A(/*'’)],
1 W
где k = —; b = 0; n =---
n 100
SU leooxodu.xtoNД = X(AWP[J(/<'))],
, 1 , n N
где к = —; b =-----; n =---
n 1 - n 100
5(Невозможно Нp) = b}P [Л(/“ ’)],
, 1 t » N
где k = —; b = 0: n =---
n 100
StBepoamHo Nkab)PlA(P‘})],
, 1 , i-« -V
где k = —; b =-----; n =---
n n 100
Здесь — схема отношений, полученная для формулы р согласно
правилам (11.4).
280
11.9. Результаты решения задачи диагностики
11.9. Результаты решения задачи диагностики
11.9.1. Схема гидравлической цепи
Вернемся к примеру сети теплоснабжения, показанной на рис. 11.15.
Гидравлическая цепь, соответствующая этому рисунку тепловой сети,
представлена на рис. 11.19.
Рис. 11.19. Схема гидравлической цепи
Из рисунка ясно, что гидравлическая цепь имеет 8 узлов и 9 ветвей. Узел
/ соответствует выходу из котельной в подающую магистраль; узел 2— точка
разветвления подающей магистрали на подающую линию ЦТП1 и подающую
линию ЦТП2; узел 3 — вход ЦТП1; узел 4 — выход ЦТП1 ; узел
5 — вход ЦТП2; узел 6 — выход ЦТП2; узел 7 — точка слияния обратной
линии ЦТП1 и обратной линии ЦТП2 в обратную магистраль; узел8
соответствует входу в котельную из обратной магистрали. Узлы 4и бявляются
потребителями, а расходы теплоагента в этих узлах (24 и характеризуют
среднее значение потребления сетевой воды на нужды горячего
водоснабжения. Узел 8 является источником притока, а расход теплоагента
в этом узле Q^ = Q4+ Q6 — расходом подпиточной воды. В качестве единицы
измерения расхода примем м3/с.
11.9.2. Определение нечетких множеств и переход
к нечеткозначному исчислению
Для иллюстрации результатов решения задачи диагностики системы
теплоснабжения возьмем часть приведенного описания на проблемно-
ориентированном языке, содержащую информацию только о повреждениях
и охватывающую только один контур ТС: подающая магистраль, подающая
281
11. Нечеткие знания и рассуждения
линия ЦТП1, обратная линия ЦТП1, обратная магистраль. Для описания
этой части системы теплоснабжения введем лингвистические переменные.
Давление на входе в подающую магистраль:
<pv е£(^), и, G, м>,
где = {низкое, нормальное,высокое} — базовое терм-множество
лингвистической переменной p^,U = [0 МПа, 1 МПа] — универсум,
означающий, что давление на входе в подающую магистраль может изменяться
от 0 до 1 МПа; G — синтаксическое правило; М — семантические правила,
определяющие следующее смысловое содержание базовых термов:
п , = (0, 0, 0.25, 0.5);
, = (0.25, 0.5, 0.6, 0.8);
г М(нормальное) 1 1 7
, = (0.6, 0.8, 1, 1).
Здесь и далее нечеткие множества, определяющие смысловое содержание
базовых термов переменной р{, заданы своими трапециевидными функциями
принадлежности и записаны в параметрическом виде. На рис.11.20
представлены графики функций принадлежности нечетких множеств,
соответствующих базовым термам лингвистической переменной pv
Рис, 11.20. Функции принадлежности базовых термов лингвистической
переменной р.
Описание остальных лингвистических переменных не такое подробное,
как для переменной рг Так, значения базового терм-множества и универсума
вносятся непосредственно в кортеж, определяющий лингвистическую
переменную; синтаксические и семантические правила дополнительно не
282
71.9. Результаты решения задачи диагностики
оговариваются, так как о них уже шла речь ранее. В определении лингвистической
переменной указывается только смысловое содержание базовых термов; графики
функций принадлежности базовых термов лингвистических переменных р„ ру р.
и р5 не приводятся, так как по внешнему виду они аналогичны изображенным на
рис. 11.20 и отличаются только параметрами.
Давление на входе ЦТП1:
<р2, {низкое, нормальное, высокое}, [0 МПа, 0.6 МПа\, G, М>'.
, = (0, 0, 0.2, 0.25);
цм , = (0.2, 0.25, 0.35, 0.4);
г Мкнормальное) ' 7 7 1 '
, = (0.35, 0.4, 0.6, 0.6).
Давление на входе ЦТП2:
<ру {низкое, нормальное, высокое], [0 МПа, 0.7 МПа\, G, М>\
, = (0, 0, 0.25, 0.3);
, = (0.25, 0.3, 0.4, 0.45);
‘ М(нормальное) ' 7 7 7 77
цм , = (0.4, 0.45, 0.7, 0.7).
Давление на выходе ЦТП1:
<р4, {низкое, нормальное, высокое], [0 МПа, 0.3 МПа\, G, М >;
,= (0, 0, 0.025, 0.05);
, = (0.025, 0.05, 0.15, 0.2);
г М(нормальное) ' 7 7 7 77
,= (0.15,0.2,0.3.0.3).
Давление на выходе ЦТП2:
<р5, {низкое, нормальное, высокое], [0 МПа, 0.3 МПа\, G, М>\
= (0, 0, 0.025, 0.05);
,= (0.025,0.05,0.15,0.2);
‘ М(нормальное) х 7 7 7 '7
,= (0.15,0.2,0.3,0.3).
Гм(<зысокое) \ 7 ’ , /
283
1 /. Нечеткие знания и рассуждения
Лингвистическим переменным р р2, р,, р4 и р5 соответствуют конкретные
узловые давления Р}, Pv Ру, Р4, Ps. Лингвистическая переменная авария:
<авария, {нет, да}, |0,1 ], G, М>'.
, = (0, 0, 0,1); = (0, 1, 1, 1).
Лингвистическая переменная авария при штатном (безаварийном) режиме
функционирования сети теплоснабжения принимает значение нет, а при
аварийном — да. На рис. 11.21 представлены графики функций
принадлежности базовых термов лингвистической переменной авария.
Рис. 11.21. Функции принадлежности базовых термов лингвистической
переменной авария
Место повреждения в контуре 1:
<МК1, {ПМ, ПЛ1, ОЛ1, ОМ}, \0 м, 2040 м], G, М>\
(0,0,520,524); = (520, 524, 1018, 1022);
0W(ft7/)= (Ю18, 1022, 1516, 1520); pM(0W) = (1516, 1520, 2040, 2040).
Графики функций принадлежности базовых термов лингвистической
переменной МК1 представлены на рис. 11.22.
Описание повреждений на языке L имеет вид
((/?, есть нормальное л (р2 есть нормальное л (р, есть нормальное л (р4 есть
нормальное л р. есть нормальное)))) = {авария есть нет))’,
284
11.9. Результаты решения задачи диагностики
Рис. 11.22. Функции принадлежности базовых термов
((/?, есть низкое л (р2 есть низкое л (р, есть низкое л (р3 есть низкое л
л р, есть низкое)))) = (авария есть да));
()МК1 есть ПМ) = (р. есть очень низкое л (р, есть низкое л (р, есть низкое л
л (р, есть низкое л р, есть низкое)))));
()МК1 есть ПЛ1) = (р, есть низкое л (р2 есть очень низкое л (р, есть низкое л
л (р4 есть очень низкое л р. есть низкое)))));
((МК! есть 0Л1) = (р. есть низкое л (р2 есть низкое л (р, есть низкое л
л (р4 есть очень низкое л р, есть низкое)))));
((МК1 есть ОМ) = (р, есть низкое л (р2 есть низкое л (р3 есть низкое л
л (р4 есть низкое л р5 есть низкое))))).
Предположим, что нас интересуют ответы на два вопроса (прямой и
обратный).
Имеет ли место повреждение? Этот вопрос на языке L выглядит так: Бавария
есть да.
Где находится повреждение? На языке L он выглядит так: ?МК1.
В приведенной части описания на языке L каждую формулу можно
представить в общем виде следующим образом:
285
11. Нечеткие знания и рассуждения
pfa) л р2(х2) л р3(х}) л р4(х4) л р,(х.) = авария (у,),
рх(Х\У л р2(х2) л р3(х3) л р4(х4) л р5(х5) = МК1 (_у2),
где х , х2, х3, х4, х5, ух, у2— значения соответствующих лингвистических
переменных. Согласно правилам перехода от формул проблемно-
ориентированного языка к формулам нечеткозначного исчисления, получим
С. , R\{p„ , д}| => С. . R [{авария}],
{авария} t ir'| ’ ’ г 5 J -I g ..., р$} авария1' • JJ’
........./41 Л с ,,>
где «,[(/>,.Пг:1 (/= I...5) - унарное нечеткое
/ = 1. .5
отношение, несущее информацию о значении давления pt; С 5| — операция
цилиндрического продолжения нечеткого отношения со схемой {р,} на схему
{Pi, , Р5}-
Функция принадлежности нечеткого множества /?, входящего в состав
нечеткого отношения /?[{/>}], принималась трапециевидной: = (Р - 5, Р - е,
Р + е, Р + 5), где Р — значение соответствующего узлового давления;
5, е(0 < е < 5) — оценки максимальной и минимальной абсолютной
погрешности вычислений. Значения узлового давления в реальных условиях
снимаются со специальных датчиков, 5 = 0,001 МПа, s = 0,0005 МПа. На
рис. 11.23 представлен график такой функции принадлежности.
Рис. 11.23. Функция принадлежности lis (/ =1...5)
Проверка на согласованность результата перехода от формул языка L к
языку нечеткозначного исчисления дала положительный результат, который
здесь не приведен.
286
11.9. Результаты решения задачи диагностики
11.9.3. Результаты решения
Аварийный режим функционирования возникает, когда появляется
повреждение на одном из участков тепловой сети. Авария в этом случае
характеризуется местом повреждения и степенью его тяжести, т.е. расходом
воды, вытекающей через место повреждения. Практика эксплуатации тепловых
сетей показывает, что степень тяжести может изменяться от 1 до 75 % расхода
воды, протекающей по поврежденному участку. Для диагностики мест
повреждений выберем середины подающей магистрали, подающей линии
ЦТП1, обратной линии ЦТП1 и обратной магистрали. В каждом из этих
мест для повреждений со степенью тяжести, равной 25, 50 и 75 % от расхода,
установившегося на соответствующей ветви гидравлической цепи при среднем
водопотреблении ((?4 = 0,024 м3/с, Qb = 0,0016 м3/с), определим
соответствующие значения узловых давлений (как уже отмечалось, в реальных
условиях эти значения, например, определяются с помощью датчиков).
После этого, пользуясь полученными формулами нечеткозначного
исчисления, вычислим ответы на вопросы Бавария есть да и 1МК1. Результаты
этих вычислений (процедуры вычислений и соответствующие им узловые
давления не приводим) показаны в таблице для середин подающей
магистрали (строки 1-3), подающей линии ЦТП1 (строки 4-6), обратной
линии ЦТП1 (строки 7-9) и обратной магистрали (строки 10-12).
Анализируя эту таблицу, можно сделать следующие заключения. Во всех
рассмотренных ответах на первый вопрос Возможно ]00 авария есть да, что
соответствует исходной посылке — режим функционирования аварийный.
При ответе на вопрос относительно повреждений любой степени тяжести,
произошедших в середине подающей магистрали, место повреждения определяется
формулой Возможно_!00 (МК! есть ПМ} л (ВероятноЮО (МК! есть ПЛ!) л
(Невозможно !00 (МК1 есть ОЛ 1) л Невозможно !00 (МК1 есть ОМ). В
переводе на естественный язык это означает: «С возможностью 100% повреждена
подающая магистраль, со случайностью 100% может оказаться поврежденной
подающая линия ЦТП1, но с невозможностью 100% повреждена обратная линия
ЦТП1 и с невозможностью 100% повреждена обратная магистраль», или более
коротко «С большой долей уверенности повреждена подающая магистраль, но
не исключено, что повреждена подающая линия ЦТП1». Очевидно, что этот
ответ согласуется с исходной посылкой.
При моделировании повреждений, имеющих степени тяжести 25 и 50% и
произошедших в середине подающей линии ЦТП1, место повреждения
определяется формулой %0 (МК1 есть ПМ) л (%0 (МК1 есть ПЛ!) л
(Невозможно_100 (МК1 есть ОЛ!) л Невозможно 100 (МК1 есть ОМ), что в
переводе на естественный язык означает: «С уверенностью 0% порыв
произошел на подающей магистрали и с уверенностью 0% порыв произошел
на подающей линии ЦТП1, но с невозможностью 100% повреждена обратная
линия ЦТП1 и с невозможностью 100% повреждена обратная магистраль»,
или более коротко «Повреждение где-то в подающих трубопроводах».
287
11. Нечеткие знания и рассуждения
Таблица 11.1
Степень тяжести Ответ на вопрос
повреждения, % ? авария есть да ?МК1
25 Возможно!00 авария есть да Возможно_100 (МК1 есть ИМ) л л (Вероятно_100 (МК1 есть ПЛ!) л л (Невозможно_100 (МК1 есть ОЛ!) л л Невозможно ! 00 МК! есть ОМ)
50 Возможио_ 100 авария есть да Возможно_100 (МК1 есть ИМ) л л (Вероятно_100 (МК! есть ПЛ!) л л (Невозможно_100 (МК! есть ОЛ1) л л Невозможно-!00 МК! есть ОМ)
75 Возможно_100 авария есть да Возможно_100 (МК1 есть ИМ) л л (Вероятно_100 (МК1 есть ШИ) л л (Невозможно_100 (МК! есть ОЛ1) л л Невозможно ! 00 МК1 есть ОМ)
25 Возможно_100 авария есть да %0 (МК! есть ИМ) л (%0 (МК1 есть ПЛ!) л (Невозможно-100 (МК! есть ОЛ1) л Невозможно_100 (МК1 is ОМ)
50 Возможно_100 авария есть да" %0 (МК! есть НМ) л (%0 (МК! есть ПЛ!) л (Невозможно-100 (МК! есть ОЛ1) л НевозможнО-100 (МК! есть ОМ)
75 Возможно_100 авария есть да Вероятно_100 (МК! есть НМ) л л (Возможно_100 (МК1 есть ПЛ 1) л л (Вероятно_100 (МК1 есть ОЛ1) л л Невозможно-100 (МК1 есть ОМ))))
25 Возможно_100 авария есть да Невозможно ! 00 (МК1 есть ПМ) л л (%0 (МК! есть ПЛ!) л (%0 (МК! есть ОЛ1) л %0 (МК1 есть ОМ)
50 Возможно_ 100 авария есть да Невозможно-100 (МК1 есть ПМ) л л (%0 (МК! есть ПЛ!) л (%0 (МК! есть ОЛ1) л %0 (МК! есть ОМ)
75 Возможно_100 авария есть да Невозможно-!00 (МК1 есть ПМ) л л (%0 (МК! есть ПЛ!) л (%0 (МК! есть ОЛ1) л %0 (МК! есть ОМ)
25 Возможно_100 авария есть да %0 (МК! есть ПМ) л (%0 (МК! есть ПЛ 1) л (%0 (МК! есть ОЛ1) л %0 (МК! есть ОМ)
50 Возможно_100 авария есть да %0 (МК! есть ПМ) л (°/о0 (МК! есть ПЛ!) л (%0 (МК! есть ОЛ1) л л %0 (МК! есть ОМ)
75 Возможно_100 авария есть да %0 (МК! есть ПМ) л (%0 (МК! есть ПЛ!) л (°/о0 (МК! есть ОЛ!) л j л %0 (МК! есть ОМ)
288
Вопросы и упражнения
Этот ответ менее точен, чем в предыдущем случае, но согласуется с
исходной посылкой. При моделировании порыва со степенью тяжести 75%,
произошедшего в середине подающей линии ЦТП1, место повреждения
определяется формулой Вероятно !00 (МК! есть ПМ) л (Возможно_100(МК1
есть ПЛ!) л (Вероятно,!00 (МК! есть 0Л1) л Невозможно 100 (МК! есть
ОМ), что означает «С большой степенью уверенности повреждение на
подающей линии цтп 1, но не исключено, что повреждена подающая
магистраль или обратная линия ЦТП1». Этот ответ также согласуется с
исходной посылкой и представляется более точным, чем при аналогичных
повреждениях с меньшей степенью тяжести. При моделировании порыва
любой степени тяжести, произошедшего в середине обратной линии ЦТП1,
место повреждения определяется формулой Невозможно 100 ( МК! есть ПМ)
л (%0 (МК! есть ПЛ!) л (%0 (МК! есть ОЛТ) л %0 (МК! есть ОМ), что
означает: «Повреждение может оказаться в любом месте за исключением
подающей магистрали». Очевидно, что этот ответ согласуется с исходной
посылкой, но очень неточен. При моделировании повреждений в середине
обратной магистрали место повреждения определяется формулой %0 (МК!
есть ПМ) л (%0(МК1 есть ПЛ!) л (%0(МК1 есть ОЛ!) л %0(МК1 есть ОМ),
что означает «Место повреждения не определено».
Вопросы и упражнения
1. Измерения магнитного поля производятся вблизи поверхности головы человека
в целях определения активности мозга с помощью двух датчиков. Колебания
магнитного поля наблюдаются в пределах от I до 3 с дискретностью 0,5 в некоторых
условных единицах измерения. Точность показаний каждого из датчиков оценивается
функцией принадлежности нечетких множеств D и Dr
a) D, = {1/1., 0.75/1.5, 0.3/3, 0.15/2.5, 0/3};
б) D,= {1/1, 0.6/1.5, 0.2/3, 0.1/2.5, 0/3}.
2. Для этих двух нечетких множеств найдете следующие нечеткие множества:
а) 2/ , £>2, Z) г D2;
б) -п Dt, D,;
в) ЛО^О2)-,
г) Z),, /),о. D-,
д) D, о D2, D2 о D2.
3. Банк, выдающий кредитные карты, хотел бы знать, каковы привычки клиента
при трате денег. Например, было бы желательно знать, сколько он обычно тратит
за определенный период, какова величина единовременной траты и т.п. Как правило,
эти привычки имеют значительный разброс даже для клиентов с одинаковым уровнем
доходов. Введем лингвистическую переменную клиент, лингвистическими
значениями которой будут термы бережливый, умеренный, щедрый, транжир. В
качестве универсума выберем отрезок от 0 до 10000 условных денежных единиц.
а. Постройте на введенном универсуме нечеткие множества, соответствующие
каждому терму и имеющие трапецеидальные функции принадлежности. Нечеткие
10 - 1141
289
11. Нечеткие знания и рассуждения
множества должны отражать ваш взгляд на семантику лингвистических термов и
обладать свойством нормальности.
б. Постройте графическое представление этих множеств.
в. Найдите графически для каждой пары введенных вами А, В соседних
(пересекающихся) нечетких множеств А, В множества
А г, 5, Аг, В,- (Аи В), -.(Ап В).
г. Сформулируйте на естественном языке смысл каждого из этих множеств.
4. Простейшая распознающая система должна обнаруживать среди множества
объектов те, которые обладают характерными признаками. Множество объектов
определим как множество термов {автомобиль, танк, корабль, гора} лингвистической
переменной объект, универсумом для которой являются упорядоченные наборы
значений некоторых признаков. В данном случае нас не интересуют эти признаки.
Для нас существенным является то, что для каждого терма лингвистической
переменной объект можно на этом универсуме построить совокупность нормальных
нечетких множеств. Объект распознается на основании сравнения его с образами
объекта, являющимися геометрическими фигурами. Геометрические фигуры
определим как множество термов {квадрат, восьмиугольник, треугольник, круг, эллипс}
лингвистической переменной образ, универсумом для которой также являются
упорядоченные наборы значений некоторых признаков.
а. Постройте гипотетические нечеткие множества для всех термов обеих
лингвистических переменных.
б. Изобразите их в графическом виде.
в. Постройте схемы отношений для предложений
образ (квадрат) z> объект (автомобнсчь). образ (квадрат) объект (танк),
образ (эллипс) объект (корабль), образ (треугольник) —. объект (корабль),
образ (круг) j объект (гора), образ (восьмиугольник) —. объект (гора).
г. Найдите схемы отношений для этих формул.
д. Постройте нечеткие множества для этих схем отношений.
5. Скорость вращения вала двигателя зависит от напряжения, поданного на него,
и от тормозящих усилий на валу двигателя. Пусть скорость измеряется в пределах от
I до 10, напряжение в пределах от 0 до 7, усилия — от 0 до 5.
а. Придумайте три терма для лингвистической переменной скорость, пять термов
для лингвистической переменной напряжение, три терма для переменной усилие.
б. Введите разумные с вашей точки зрения трапецеидальные функции
принадлежности и соответствующие им нечеткие множества для всех термов.
в. Введите формулы нечеткого проблемно-ориентированного языка, задающие
зависимость скорости от напряжения и тормозящих усилий на валу двигателя.
г. Приведите формулы нечеткозначного исчисления отношений, соответ-
ствующие этим формулам.
д. Вычислите значения этих формул нечеткозначного исчисления.
е. Постройте графическое представление значений формул нечеткозначного
исчисления.
290
12. ПЛАНИРОВАНИЕ ДЕЙСТВИИ
В настоящей главе рассмотрены принципы нахождения последовательностей
действий (планов) для достижения целей на основе аксиоматического описания
исходной постановки задачи. Оценка эффективности плана проведена с
использованием нечетких множеств, изученных в предыдущей главе.
В предыдущих главах книги описано решение задач достижения
определенных целей на основе использования определенных действий. Для
многих реальных задач нужно не просто найти целевое состояние, но и
построить план или последовательность действий, приводящих к цели, чтобы
его можно было многократно использовать для достижения подобных целей,
не повторяя вновь поиск решения, или реально выполнить его и достигнуть
цели. Желательным при этом является нахождение таких планов, которые
оптимальны в определенном смысле. По существу, вывод или поиск цели
всегда связан с нахождением какого-либо плана, и это означает, что неявно
мы уже занимались планированием почти во всех предыдущих главах,
отыскивая путь к достижению целей. Однако при этом не ставилась задача
извлечения и оценки плана в явном виде. В данной главе на простом хорошо
известном примере с двумя сосудами, наполняемыми водой, рассмотрим
принципы планирования (нахождения плана) на основе использования
ситуационного исчисления.
12.1. Задачи планирования
Пусть сосуды для воды А и В имеют различную емкость — 3 и 4 галлона
соответственно (рис. 12.1). Каждый сосуд наполняется из своего крана и
имеет свой сливной кран. Кроме того, каждый сосуд имеет трубу с краном
для перелива воды в другой сосуд. Допускается выполнение трех действий
над каждым сосудом: опустошение сосуда, наполнение сосуда и перелив из
одного сосуда в другой.
Введем две функции содержимое (сосуд). Если сосуд = А, то областью значений
функции является множество {0, 1, 2, 3}, а если сосуд = В, то областью значений
функции является множество {0, 1, 2, 3, 4}. Введем также предикат состояние
10’
291
12. Планирование действий
Опустошение Опустошение
сосуда А сосуда В
Рис. 12.1. Задача о поиске плана наполнения сосудов
(сосуд, содержимое (сосуд), s), характеризующий состояние сосуда. Этот
предикат истинен, если в ситуации .у содержимое сосуда равно одному из
значений функции содержимое (сосуд) из области ее значений.
Аксиомами ситуационного исчисления для нашей задачи будут следующие.
12.1.1. Аксиомы начальной ситуации
состояние (А, О, 50) л состояние (В, 0, 5).
12.1.2. Аксиомы допустимых действий
Аксиомы опустошения сосудов:
допустимо (Убавить (сосуд), s) с состояние (сосуд, содержимое (сосуд), s) л
л содержимое (сосуд) # 0.
Аксиомы наполнения сосудов:
допустимо (добавить (A), s) с состояние (А, содержимое (A), s) л
л содержимое (А) 3,
допустимо (добавить (В), s) с состояние (В, содержимое (В), s) л
л содержимое (5) * 4.
292
12.1. Задачи планирования
Аксиомы переливания из сосуда в сосуд:
допустимо (перелить (А, В), s) с состояние (А, содержимое (A), s) л
л содержимое (А) * 0 л состояние (содержимое (В), s) л содержимое (В) * 4,
допустимо (перелить (В, A), s) с состояние (В, содержимое (В), s) л
л содержимое (S) * 0 л состояние (содержимое (A), s) л содержимое (А) * 3.
12.1.3. Аксиомы перехода в следующие ситуации
Запишем эти аксиомы в виде
Допустимо (убавить (сосуд), s) л состояние (сосуд, содержимое (сосуд), s)
zd состояние (сосуд, содержимое (сосуд) -1, переход (убавить (сосуд), s)),
допустимо (добавить (сосуд), s) л состояние (сосуд, содержимое (сосуд),
s) zd состояние (сосуд, содержимое (сосуд) +1, переход (добавить (сосуд), s)),
допустимо (перелить (сосуд, сосуд’), s) л состояние (сосуд, содержимое
(сосуд), s) л состояние (сосуд’, содержимое (сосуд’), s) состояние
(сосуд, содержимое (сосуд) - 1, переход (перелить (сосуд, сосуд’), s)) л
л состояние (сосуд, содержимое (сосуд’) + 1, переход (перелить (сосуд,
сосуд’), s).
Наша цель в данном случае — нахождение плана (последовательности
действий), в результате которых сосуды окажутся в ситуации s, в которой
состояние сосудов будет определяться формулой
состояние (А, 2, s) л состояние (В, 2, s).
12.1.4. Процедура поиска плана
Стратегии поиска плана могут быть самыми различными. Часть из них
безотносительно к какому-либо языку описания поведения среды фактически
рассмотрена в главе 6. В настоящей главе используем процедуру обратного поиска,
основанную на резолюции (см. гл. 4). Эта процедура состоит в следующем:
опровержение цели, которая должна быть достигнута;
преобразование аксиом в клаузальную форму;
до тех пор, пока есть разрешимые клаузы, выполнение следующих шагов:
293
12. Планирование действий
нахождение пары разрешимых клауз, начиная с опровержения цели,
и разрешение их;
добавление результата разрешения (резольвенты) к списку клауз.
если достигнута пустая клауза (Nil), то прекращение процедуры и
констатация факта нахождения плана;
выписывание плана в явном виде и оценка возможности его
выполнения;
уели разрешимых клауз нет, а пустая клауза не достигнута, то
констатация, что при данном множестве аксиом цель не может быть
достигнута и план не может быть построен.
12.1.5. Клаузы
Для нашего примера отрицание цели будет следующим:
состояние (А, 2, s) v — состояние (В, 2, s). (12-1)
Начальные клаузы имеют вид
состояние (А, 1, 50), (12-2)
состояние (В, 3, 50). (12.3)
Клауза опустошения сосудов следует из аксиомы опустошения:
допустимо (убавить (сосуд), 5) v состояние (сосуд,
содержимое (сосуд), s) v содержимое (сосуд) * 0. (12.4)
Клауза наполнения сосуда А вытекает из аксиомы наполнения сосуда А:
допустимо (добавить (/1), 5) v -> состояние (А, содержимое (A), s) v
содержимое (А) 3. (12.5)
Клауза наполнения сосуда В получается из аксиомы наполнения сосуда В.
допустимо (добавить (В), s) v — состояние (В, содержимое (В), s) v
содержимое (В) * 4. (12.6)
Клаузы переливания из сосуда в сосуд можно получить, используя
соответствующие аксиомы переливания:
294
12.1. Задачи планирования
допустимо (перелить (А, В), s) v состояние (А, содержимое (/1), s) v
содержимое (/1) 0 v - состояние (содержимое (В), s) v содержимое
(В) * 4, (12.7)
допустимо (перелить (В, A), s) v ~ состояние (В, содержимое (В), s) v
содержимое (Я) * О v-> состояние (содержимое (A), s) м содержимое
(/1) * 3. (12.8)
Клаузы перехода в следующие ситуации:
допустимо (добавить (сосуд), ~ состояние (сосуд, содержимое
(сосуд), s) v состояние (сосуд, содержимое (сосуд) + 1, переход (добавить
(сосуд), s)), (12.9)
допустимо (убавить (сосуд), s) v состояние (сосуд, содержимое
(сосуд), s) v состояние (сосуд, содержимое (сосуд) -1, переход (убавить
(сосуд), 5)), (12.10)
допустимо (перелить (сосуд, сосуд'), s) v состояние (сосуд,
содержимое (сосуд), s) v состояние (сосуд', содержимое (сосуд'), s) v
v состояние (сосуд, содержимое (сосуд) - 1, переход (перелить (сосуд,
сосуд'), s)), (12.11)
допустимо (перелить (сосуд, сосуд'), s) v состояние (сосуд,
содержимое (сосуд), s) v состояние (сосуд', содержимое (сосуд'), s) v
v состояние (сосуд, содержимое (сосуд’) + 1, переход (перелить (сосуд,
сосуд')). (12.12)
12.1.6. Обратный вывод
Процедура вывода на основе опровержения и обобщенного правила
резолюции приведена ниже (см. гл. 4). Каждый шаг вывода состоит из трех
клауз — двух исходных и резольвенты с используемыми подстановками.
Литералы, которые не попадают в резольвенту, подчеркиваются:
295
12. Планирование действий
состояние (А, 2. переход (добавить (/1), .у)) v состояние (В, 2, s), (12.13)
допустимо (добавить (A), s) v состояние (А, 1, .у) v состояние
(А, 2, переход (добавить (/1), $)). (12.14)
допустимо (добавить (/1), .у) v состояние (А, 1, .у) v
состояние (В, 2, я), (12.15)
допустимо (добавить (/1). .у) v состояние (А, 1, s) v 1 3, (12.16)
состояние (А, 1, s) v состояние (В, 2, s'), (12.17)
состояние (А, 1, 50) v состояние (В, 2, s), (12.18)
состояние (А, 1, 50). (12.19)
состояние (В, 2, s), (12.20)
-> состояние (В, 2. переход (убавить (В}, .у)). (12.21)
допустимо (убавить (В), s) v состояние (В, 3, s) v состояние
(В, 2. переход (убавить (В), s(). (12.22)
допустимо (убавить (В), s) v состояние (В, 3, я), (12.23)
допустимо (убавить (В), s) v состояние (В, 3, s) v — 3*0, (12.24)
состояние (В, 3, s), (12.25)
состояние (В, 3, 50). (12.26)
состояние (В. 3, 50). (12.27)
Nil. (12.28)
12.1.7. Построение плана
Суть построения плана достаточно проста. Рассмотрим участок процесса
вывода (12.22) — (12.27). Преобразуем клаузы (12.22), (12.24), (12.27) этого
участка в эквивалентные формулы:
296
12.2. Оценка плана
допустимо (убавить (В), s) л состояние (В, 3, 5) zd состояние
(В, 2, Переход (убавить (В), s)), (12.29)
допустимо (убавить (В), s') с состояние (В, 3, j) л 3 * 0, (12.30)
состояние (В, 3, 50). (12.31)
Используя эти формулы и обобщенные правила модус поненс, можем
осуществить следующий прямой вывод:
состояние (В, 3, 50), состояние (В, 3, 50) л 3 * 0 z> допустимо (убавить
(В), So) \~ допустимо (убавить (В), 50),
допустимо (убавить (В), So), состояние (В, 3, 50), состояние (В, 3, 5) л
л допустимо (убавить (В), SQ) zd состояние (В, 2, переход (убавить (В),
50)) состояние (В, 2, переход (убавить (В), 50)).
На основании этого вывода приходим к заключению об истинности
формулы
состояние (В, 2, переход (убавить (В), 50)), (12.32)
интерпретация которой означает, что сосуд В переводится в состояние, когда
его содержимое равно 2, в результате действия Убавить (В), осуществленного
в ситуации 50. Точно так же можно установить истинность формулы
состояние (А, 2, Переход (Добавить (А), 50)), (12.33)
интерпретация которой означает, что сосуд А переводится в состояние, когда
его содержимое равно 2, в результате действия Добавить (А), осуществленного
в ситуации 50. Таким образом, план достижения цели определяется формулой
переход (убавить (В), So) л переход (добавить (А), 50)). (12.34)
Этот план не является единственным. Аналогично можно найти другие планы
достижения той же цели.
12.2. Оценка плана
Если планов достижения одной и той же цели может быть несколько, то
возникает задача выбора наилучшего из них. Эта задача отчасти аналогична
задаче нахождения наилучшей стратегии достижения цели (см. гл. 6),
297
12. Планирование действий
поскольку план можно рассматривать как путь, ведущий к достижению цели.
И тогда для оценки и выбора наилучшего пути можно воспользоваться
методами, описанными в главе 6. В настоящей главе рассмотрим другой
подход к выбору наилучшего плана, основанный на материале предыдущей
главы. Критерием оценки плана будем считать значение формулы нечеткого
проблемно-ориентированного языка, задающей путь достижения цели на
основании найденного плана.
Вернемся к примеру, приведенному в настоящей главе. План, полученный
ранее, является четким. Будем полагать, что вместо языка логики предикатов
первого порядка в этом примере используется какой-либо нечеткий
проблемно-ориентированный язык, в котором выражение состояние {сосуд,
содержимое {сосуд), s) эквивалентно выражению {состояние {сосуд, s) есть
содержимое {сосуд)), в котором состояние {соруд) — лингвистическая
переменная, а выражение Содержимое {сосуд) — это не функция,
принимающая целочисленные значения, а один из лингвистических термов
Нуль (А), Один {А), Два {А), Три (А) и Нуль {В), Один {В), Два {В), Три {В),
Четыре (В) соответственно лингвистических переменных состояние {А) и
состояние {В). Каждому из этих термов А. соответствует нечеткое множество
Л/(А), заданное на универсуме действительных чисел. Например, для сосуда
А могут быть следующие нечеткие множества (функции принадлежности для
них в данном случае не являются трапециевидными):
М{Нуль {А)) = {1/0, 0.7/0.25; 0.2/0.5; 0.1/0.75; 0/1; 0/1.25 4- 0/4},
М{Один {А)) = {0/0; 0.1/0,25; 0.2/0.5; 0.7/0.75; 1/1; 0.7/1.25; 0.2/1.5;
0.1/1.75; 0/2, 0/2.25 э- 0/3},
М{Два {А)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 0/1; 0.1/1.25; 0.2/1.5; 0.7/1.75; 1/2;
0.7/2.25; 0.2/2.5; 0.1/2.75; 0/3, 0/3.25 ч- 0/3),
М{Три {А)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 0/1; 0/1.25; 0/1.5; 0/1.75; 0/2;
0.1/2.25; 0.2/2.5; 0.7/2.75; 1/3}.
Содержательно носитель (основу) каждого из этих множеств можно
рассматривать как возможные отклонения реальных значений содержимого
сосудов от номинального значения, а функцию принадлежности как оценку
этого отклонения. Для сосуда В смысл нечетких множеств тот же самый, и
их можно получить аналогично:
М{Нуль {В)) = {1/0, 0.7/0.25; 0.2/0.5; 0.1/0.75; 0/1; 0/1.25 0/4},
298
]2.2. Оценка плана
М(Один (В)) = {0/0; 0.1/0,25; 0.2/0.5; 0.7/0.75; 1/1; 0.7/1.25; 0.2/1.5;
0.1/1.75; 0/2, 0/2.25 + 0/4},
М(Два (В)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 0/1; 0.1/1.25; 0.2/1.5; 0.7/1.75; 1/2;
0.7/2.25; 0.2/2.5; 0.1/2.75; 0/3, 0/3.25 0/4},
М(Три (В)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 0/1; 0/1.25; 0/1.5; 0/1.75; 0/2;
0.1/2.25; O.2/2.5; 0.7/2.75; 1/3, 0.7/3.25; 0.2/3.5; 0.1/3.75; 0/4},
М(Четыре (А)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 0/1; 0/1.25; 0/1.5; 0/1.75; 0/2;
0/2.25; 0/2.5; 0/2.75; 0/3; 0.1/3.25; 0.2/3.5; 0.7/3.75; 1/4 }.
Пусть вместо начальных состояний, определяемых формулами (12.2),
(12.3), имеют место следующие формулы нечеткого проблемно-
ориентированного языка:
состояние (А, Один (A), SQ),
состояние (В, Три (В), So).
Кроме того, вместо любой четкой формулы (атома) состояние (сосуд,
содержимое (сосуд), s) будем использовать формулу, в которой X является
термом лингвистической переменной состояние (сосуд, s) и ему соответствует
нечеткое множество М(к). Запишем это соответствие в виде
М(состояние (сосуд, X, s) = М(Х).
Тогда
М(состояние (А, Один (A), So) = М(Один (А)), (12.35)
М(состояние (В, Три (В), 50) = М(Три (В)), (12.36)
М(состояние (А, Два (Л), переход (добавить (А), 50)) = М(Два (А)), (12.37)
М(состояние (В, Два (В), переход (убавить (В), 50)) = М(Два (В)). (12.38)
299
12. Планирование действий
Так как план (12. 34) позволяет достичь цели, формулу, определяющую
достижение цели с помощью этого плана на нечетком проблемно-
ориентированном языке, можно представить в виде
(состояние (А, Один (А), 50) о состояние (А, Два (А), Переход (Добавить
(A), So)) л (состояние (В, Три (В), 50) => состояние (В, Два (В),
переход (убавить (В), 50)). (12.39)
Смысл первой импликации означает, что если содержимой сосуда А в
ситуации 50 было Один (А), то после выполнения действия добавить (/1)
сосуд А переходит в ситуацию переход (добавить (А), 50)) и его содержимое
становится равным Два (А). Смысл второй импликации аналогичен.
Используя формулы (12.35)—(12.39) и правила перехода от проблемно-
ориентированного языка к нечеткозначному исчислению (11.3), имеем для
оценки нашего плана формулу
В(М(Один (A)) =>,, М(Два (А)) л (М(Три (В)) zd,, М(Два (В)) = С{В}(М(Один
(А)) М(Два (A)) n CiA}(M(Tpu (В)) о М(Два (В)),
где {/1} и {5} — нечеткие схемы отношений соответствующие лингвистическим
переменным А и В. Подставив в нее соответствующие значения нечетких
множеств, получим следующие оценки нашего плана:
Л/, = (М(Один (А)) М(Два (А)) = {0/0; 0/0,25; 0/0.5; 0/0.75; 0/1; 0.1/1.25;
0.2/1.5; 0.7/1.75; 1/2; 1/2.25; 1/2.5; 1/2.75; 1/3)},
М2 = (М(Три (В)) ^g М(Два (В)) = {0/0, 0/0.25; 0/0.5; 0/0.75; 1/1; 1/1.25;
1/1.5; 1/1.75; 1/2; 0.7/2.25; 0.2/2.5; 0.1/2.75, 0/3, 0/3.25 + 0/4},
C{B}(MJ = {0/0,0; 0/0,25,0; 0/0.5,0; 0/0.75,0; 0/1,0; 0.1/1.25,0; 0.2/1.5,0;
0.7/1.75,0; 1/2,0; 1/2.25,0; 1/2.5,0; 1/2.75,0; 1/3,0;
0/0,0.25; 0/0,25,0.25; 0/0.5,0.25; 0/0.75,0.25; 0/1,0.25; 0.1/1.25,0.25; 0.2/1.5,
0.25; 0.7/1.75,0.25; 1/2,0.25; 1/2.25,0.25; 1/2.5,0.25; 1/2.75,0.25; 1/3,0.25;
300
Вопросы и упражнения
0/0, 4; 0/0,25,4; 0/0.5,4; 0/0.75,4; 0/1,4; 0.1/1.25,4; 0.2/1.5,4; 0.7/1.75,4;
1/2,0; 1/2.25,4; 1/2.5,0; 1/2.75,4; 1/3,4)},
СМ)(Л/2) = {0/0,0, 0/0,0.25; 0/0,0.5; 0/0,0.75; 1/0,1; 1/0,1.25; 1/0,1.5; 1/0,1.75;
1/0,2; 0.7/0,2.25; 0.2/0,2.5; 0.1/0,2.75, 0/0,3, 0/0,3.25 0/0,4;
0/0.25,0, 0/0.25,0.25; 0/0.25,0.5; 0/0.25,0.75; 1/0.25,1; 1/0.25,1.25; 1/0.25,1.5;
1/0.25,1.75; 1/0.25,2; 0.7/0.25,2.25; 0.2/0.25,2.5; 0.1/0.25,2.75, 0/0.25,3,
0/0.25,3.25 - 0/0.25,4;
0/3,0, 0/3,0.25; 0/3,0.5; 0/3,0.75; 1/3,1; 1/3,1.25; 1/3,1.5; 1/3,1.75; 1/3,2;
0.7/3,2.25; 0.2/3,2.5; 0.1/3,2.75, 0/3,3, 0/3,3.25 - 0/3,4}.
Остается вычислить нечеткое множество п С{А}(М2) (в следующем
разделе предлагается сделать это вычисление в качестве упражнения).
Функция принадлежности множества С (Mt) п С{ является
интегральной оценкой качества плана.
Вопросы и упражнения
1. Начальным состоянием в среде кубиков является следующее: кубики А и В
лежат на столе. Кубик С лежит на кубике А. В целевом состоянии кубик С должен
лежать на столе, на нем — кубик В, а на кубике В должен оказаться кубик А. Если
на кубике ничего не лежит, то его можно переместить на стол или на другой кубик,
на котором также ничего не должно лежать:
а) осуществите формальную постановку задач, используя язык ситуационного
исчисления;
б) найдите план, требующий наименьшего числа действий для достижения цели.
2. Вычислите нечеткое множество C|e)(A/,) n С (Л/2), получение которого не
завершено в предыдущем разделе. Дайте графическое представление этого множества.
Объясните, используя это графическое представление, почему функция
принадлежности этого множества может служить оценкой плана.
3. Используя задачу о среде обезьяны и банана, рассмотренную в главе 7,
выполните следующее:
а) завершите полностью формальное описание среды обезьяны и банана на языке
ситуационного исчисления;
301
12. Планирование действий
б) найдите два плана достижения обезьяной цели, когда банан схвачен;
в) введите лингвистические переменные и термы, характеризующие состояния
среды обезьяны и банана;
г) введите нечеткие множества, которые на ваш взгляд отражают семантику термов
лингвистических переменных;
д) вычислите нечеткие множества, оценивающие планы;
е) проанализируйте правдоподобность этих оценок.
13. ОНТОЛОГИИ И ИХ ПРИМЕНЕНИЕ
Настоящая глава представляет собой введение в область искусственного
интеллекта интересующуюся онтологиями. Определено понятие онтологии,
рассмотрены назначение онтологий, методология их создания. Особое
внимание уделено применению онтологий. Подробно описан подход к созданию
и использованию онтологии в области проектирования сложных систем.
В книге подробно рассмотрены языки исчислений, которые могут быть
использованы для описания свойств различных сред и выявления (вывода)
новых. Составление подобных описаний, особенно для сложных сред,
непростая задача. Описания подобного типа стали называть онтологиями.
Появился новый раздел искусственного интеллекта, посвященный созданию
и использованию онтологий. Возникают следующие вопросы:
Что означает термин «онтология»?
Какие перспективы связывают с использованием онтологий?
Что является теоретическим базисом онтологии?
Ответам на эти вопросы посвящен следующий раздел.
13.1. Введение в онтологию
13.1.1. Что означает термин «онтология»?
Люди, организации и программные системы взаимосвязаны между собой.
Способ выражения знаний даже об одних и тех же вещах и на одном и том
же языке может быть столь различным, что это приводит к непониманию
между людьми даже при разговоре об одном и том же предмете. Об этом
много написано, в том числе в литературе, не имеющей прямого отношения
к искусственному интеллекту. Непонимание становится еще более
значительным в случае обмена информацией между людьми, организациями
и программами. Возможности взаимодействия программных моделей,
созданных в различных организациях, возможности повторного
использования и распространения этих моделей весьма ограничены. Это в
свою очередь приводит к повторным усилиям по созданию программных
моделей, мало отличающихся от уже созданных. Такая ситуация напоминает
повторное изобретение велосипеда.
303
13. Онтологии и их применение
Спрашивается, как можно избежать такого рода изобретений?
Естественный ответ — это устранить или свести к минимуму концептуальную
и терминологическую путаницу и установить однозначное понимание языка,
используемого для формирования требований и спецификаций сложных
систем. Такой язык должен прежде всего служить средством коммуникации
между людьми, имеющими различный взгляд на одни и те же вещи,
взаимодействия между программными системами путем трансляции в него и
из него, инструментальной поддержки для повторного использования
благодаря формальной спецификации, унификации представления различных
моделей, автоматизации проверки корректности, переводимости различных
методов моделирования в унифицированное представление.
Онтологией называют представленные на некотором языке, обладающем
перечисленными ранее свойствами, знания о некоторой области интересов
(среде, мире). Онтологии непременно сопутствует некоторая концепция этой
области интересов. Чаще всего эта концепция выражается посредством
определения базовых объектов (индивидуумов, атрибутов, процессов) и
отношений между ними. Определение этих объектов и отношений между
ними обычно называют концептуализацией. На определенном этапе
концептуализация может быть неявной (или ментальной, т.е. существующей
только в чьей-то голове). Онтология является явным представлением
некоторой концептуализации и может иметь несколько форм представления:
неформальную на каком-либо естественном языке;
полуформальную на каком-либо структурированном подмножестве
естественного языка;
слабоформализованную на каком-либо языке из области искусственного
интеллекта с формальным синтаксисом;
формализованную на каком-либо языке из области искусственного
интеллекта с формальным синтаксисом, семантикой, значимым и полным
механизмом вывода.
Следующее определение онтологии, обобщает различные определения
онтологий: онтологией является общепринятая и общедоступная
концептуализация определенной области знаний (мира, среды), содержащая
базис для моделирования этой области знаний и определяющая протоколы
для взаимодействия между агентами, которые используют знания из этой
области, и наконец, включающая соглашения о представлении теоретических
основ данной области знаний.
13.1.2. Перспективы, связываемые с онтологиями
Литературные источники богаты описанием различных онтологий и
ожидаемых от их использования перспектив. Эти перспективы можно
подразделить на следующие категории:
улучшение взаимодействия;
унификация обмена данными;
304
13.1. Введение в онтологию
формализация процессов спецификации, повышения надежности и
обеспечения многократности использования.
Улучшение взаимодействия связывают с уже упомянутыми надеждами на
уменьшение терминологической и концептуальной путаницы и
неоднозначности понимания на основе осуществления следующих
мероприятий.
1. Создание в конкретной области человеческой деятельности (среде)
унифицирующего нормативного ядра понятий, которое позволило бы достичь
однозначного семантического толкования основных объектов и процессов
этой области. Предполагается, что это нормативное ядро является
семантической основой для порождения, переопределения и интерпретации
новых понятий.
2. Создание однозначно понимаемого множества отношений между
понятиями нормативного ядра, допускающего исследование динамических
и статических аспектов среды, влияния на нее различных факторов, вывод и
планирование ситуаций.
3. Обеспечение совместимости онтологий, разработанных различными
коллективами путем широкого использования полисинонимии и
ретранслируемости.
4. Обеспечение возможности коллективной работы по согласованию и
унификации онтологий и их нормативного ядра.
Унификацию обмена данными связывают с созданием интегрированных
инструментальных программных средств, построенных на основе
использования нормативного ядра и множества отношений. Эти средства
должны обеспечивать возможность обмена данными для созданных или
создаваемых на базе онтологий систем моделирования сред и выступают как
средство межъязыкового общения, как своеобразный декларативный язык,
на который переводятся другие языки и из которого перевод осуществляется
в индивидуальный язык пользователя. Эти средства должны иметь в своем
составе поддерживаемые, развивающиеся и доступные для использования
извне библиотеки онтологий.
Формализацию процессов спецификации, повышения надежности и
обеспечения многократности использования связывают с ролью онтологий,
которую они призваны играть для развития систем моделирования сред.
Язык онтологии выступает в этом случае как средство спецификации таких
систем и является декларативным. Роль онтологии зависит от степени
выразительности, формализованное™ и других свойств декларативного языка
онтологии. Повышение надежности систем моделирования связывают с
возможностью и удобством полуформального и формального анализа
декларативного описания на языке онтологии. При этом, говоря о
формальном анализе, полагают, что описание допускает формальный вывод
(доказательство) наличия тех или иных свойств среды. Обеспечение
многократности использования предполагает наличие в онтологии
305
13. Онтологии и их применение
метауровня, позволяющего настроить онтологию на конкретную задачу
применения, определить степень ее пригодности для решения конкретной
задачи и модифицировать или расширить ее, если это необходимо.
13.1.3. Создание онтологий
Несмотря на то что в литературе имеется много информации о создании
онтологий, какой-либо общепринятой или тем более стандартизованной
процедуры их создания не существует. Процесс разработки онтологий во
многом схож с развитием программных моделей сложных систем.
Типичными являются следующие этапы создания конкретной онтологии.
1. Постановка задачи. На этом этапе изучается среда, для которой
создается онтология, обдумывается, зачем нужна онтология, как и кем она
будет использоваться.
2. Построение онтологии. Этот этап разбивается на три подэтапа:
формализация понятий, кодирование и интеграция. В процессе
формализации понятий осуществляется: а) выявление основных объектов и
отношений предметной области (среды), б) текстовое описание этих объектов
и отношений, в) сопоставление этим объектам термов, а отношениям —
утверждений (аксиом). В процессе кодирования формируется описание на
каком-либо формальном языке результатов предыдущего подэтапа. Обычно
кодирование включает: а) выбор формального языка для кодирования, б)
кодирование в выбранном языке термов и базовых отношений, в) описание
с использованием введенных кодов термов и базовых отношений формул,
соответствующих утверждениям. Подэтап интеграции выполняется
параллельно двум упомянутым и требует тщательного обдумывания, каким
образом вновь создаваемая онтология будет интегрироваться с уже
существующими.
3. Формирование вопросов. На этом этапе осуществляется обдумывание
и формальное описание вопросов, на которые онтология должна давать
ответы, выбирается программная среда для реализации онтологии.
В следующем разделе на примере конкретной среды достаточно подробно
рассмотрим процесс разработки и использования онтологии. Еще раз
заметим, что принципиальным для создания онтологий является не
процедурный, а декларативный подход. Теоретической основой большинства
языков, используемых для кодирования онтологий, являются различные
исчисления, в основе которых, как правило, лежит логика предикатов
первого порядка с равенством. Используются и другие логики в качестве
теоретической основы для онтологий.
13.2. Постановка задачи создания онтологии
На обогрев зданий расходуется от 40 до 50% энергии, потребляемой
человечеством в развитых странах, и этот расход имеет тенденции к росту.
Так, например, доля потребления энергии на нужды отопления жилых зданий
306
13.2. Постановка задачи создания онтологии
в Западной Европе составляет 52% всей вырабатываемой энергии. Близкая
оценка (40%) приводится в США. Многие источники называют похожие цифры
для Канады, России, Южной Африки. Подсчитано, что только благодаря
проектированию более эффективных систем теплоснабжения зданий можно
высвободить до 30% энергии. Все это свидетельствует о том, что необходимы
средства эффективного проектирования систем теплоснабжения, позволяющие
осуществить необходимую человечеству экономию энергии.
13.2.1. Исходные соображения для создания онтологии
Отправным материалом для проектирования реальных систем
теплоснабжения здания является архитектурный проект, который определяет
размеры здания и его помещений, конструкции всех элементов здания, места
установки и размеры окон и дверей, расположение инженерных сооружений,
в частности систем теплоснабжения, канализации, вентиляции, т.е. всего,
что необходимо в соответствии с действующими строительными нормами и
правилами. Для того чтобы иметь возможность осуществлять оптимальное
автоматизированное проектирование систем теплоснабжения жилых зданий,
необходимо иметь формальную модель, с помощью которой можно было
бы решать задачу. Спрашивается, какие соображения должны быть положены
в основу подобной модели? С одной стороны, в настоящее время известны
различные математические модели, которые используются при
проектировании систем теплоснабжения зданий, основанные на законах
теплопередачи, например, дифференциальные уравнения, линейные
уравнения стационарного режима. Все было бы хорошо, если бы задача
выглядела как классическое совместное решение системы уравнений для
нахождения оптимальных переменных системы теплоснабжения по известным
исходным данным. К сожалению, для большинства реальных задач
использование классического подхода встречает серьезные препятствия,
связанные со следующим. Во-первых, в рассмотрение при оптимизации
должны быть включены показатели затрат, выраженные в виде эмпирических
формул для расчета, например, стоимости жизненного цикла здания и других
переменных, множество разнородных условий и требований, диктуемых
действующими нормами и правилами. Во-вторых, при классическом подходе
невозможно учесть требования, которые носят субъективный, присущий
только данному проекту характер и изменяются по мере продвижения
процесса проектирования. В-третьих, упомянутый классический подход не
охватывает метауровня, без которого современная автоматизация
проектирования вообще неосуществима, а именно уровня планирования
алгоритмов оптимального поиска в пространстве допустимых значений.
Возможным путем хотя бы частичного преодоления указанных препятствий
является логический подход к решению задачи оптимального автоматизированного
проектирования систем теплоснабжения жилых зданий, в основе которого лежит
комплексная онтология, которую назовем онтологией теплоснабжения,
включающая в себя весь багаж накопленных знаний.
307
13. Онтологии и их применение
В настоящей главе не ставится задача рассмотрения всех аспектов
онтологии теплоснабжения как формальной теории. Для этого понадобилась
бы отдельная книга. Рассмотрим лишь некоторые свойства онтологии
теплоснабжения и результаты ее применения.
Вопросы, на которые предполагается получать ответ с помощью
онтологий, обычно называют компетентными. Их формулируют как теоремы,
в результате логического доказательства которых и получают ответ на
поставленные вопросы. Как всегда выделяют два типа вопросов: прямые вопросы
(анализа) и обратные вопросы (синтеза). Пример вопроса прямого типа:
«Каковы будут эксплуатационные характеристики здания (комфортность и
стоимость) при заданных значениях переменных здания и системы
теплоснабжения (конструкции, применяемых материалах, ценах)?» Пример
вопроса обратного типа: «Каковы должны быть значения переменных
конструкции, чтобы обеспечить требуемые или наилучшие (оптимальные)
эксплуатационные характеристики здания при заданных условиях, определяемых
некоторыми константами (климатическими, стоимостными и т.п.)?»
13.2.2. Построение онтологии теплоснабжения
В данном случае онтология состоит из четырех групп аксиом. Вид этих
аксиом зависит от языка исчисления, на котором они представляются. В
настоящей главе нас интересует не столько язык, сколько смысл того, что
представляют эти группы аксиом. Поэтому для их представления ограничимся
языком логики предикатов первого порядка. Рассмотрим следующие довольно
типичные (и не только для данной среды) группы аксиом: а) аксиомы
идентификации, получаемые по известным математическим уравнениям
теплопередачи, формулам для расчета температуры, эмпирическим формулам
для расчета стоимости жизненного цикла систем теплоснабжения; б) аксиомы
вычислений, формулирующие правила вычисления значений искомых
переменных; в) аксиомы корректности, задающие порядок и условия
корректности вычислений, г) аксиомы оптимизации, позволяющие получать
ответы на обратные вопросы и определяющие правила поиска оптимальных
решений.
Аксиомы идентификации. Будем полагать, что здание в целом, включая
систему теплоснабжения, имеет множество объектных переменных Х= {%,, ...,
xv}, включая все известные и неизвестные, исходные и промежуточные,
оценочные и конструктивные и т. п. В реальном проектировании требуется
находить или уточнять значения части этих переменных, которые, как
правило, должны попадать в определенный интервал значений. Интервалом
в нашем случае называют множество действительных чисел г, таких, что
I < г < h, где I, h — границы интервала. Интервал значений переменной х
обозначим [х] = [/,/?], где /, h являются левой и правой границами интервала
соответственно, и будем его называть значением переменной х. Множество
308
13.2. Постановка задачи создания онтологии
интервалов значений множества переменных Хт с Xобозначим [AJ. Каждой
переменной х сопоставим предикат
параметр (х, |х])
истинный, когда переменная х лежит в интервале [/, А]. В дальнейшем все
переменные, как всегда, будем обозначать малыми буквами, константы —
большими, а множества переменных — большими полужирными.
Введем множество отношений {R{, ..., Rm}. Каждое отношение R.
связывает некоторое подмножество переменных Хт с X и используется для
вычисления неизвестных значений переменных X ™х с Хт по известным
значениям переменных X с Хт. Этот процесс называется вычислением
отношения R.. Как конкретно осуществляется вычисление неизвестных
значений в зависимости от множества известных значений, определяют
аксиомы вычислений, рассматриваемые чуть ниже. В самом общем случае
предполагается, что для вычисления любого неизвестного значения
переменной х, а точней — границ интервала ее значений всегда найдется
набор переменных Хтвх, значения которых известны и позволяют найти
значение х.
Введем переменную г, значением которой является одно из конкретных
отношений множества {Rt, ..., Rm}. Одно и то же отношение может связывать
различные подмножества Хт<^ X. Все появления одного и того же отношения
перенумеруем и введем переменную т, значениями которой будем считать
эти номера. Введем также предикат экземпляр (г, т, Хт, [Л^]) = экземпляр
(г, т, Хт). Этого предикат истинен, если отношение г с номером т
связывает множество переменных Хт значениями которых является множество
[XJ. Множество переменных Хт предиката экземпляр может совпадать,
пересекаться или не пересекаться с множествами переменных других
предикатов экземпляр. Вычисляемые (выходные) переменные одного
предиката экземпляр могут быть входными для других, в результате чего
получается некоторая сеть предикатов экземпляр, которую можно изобразить
в виде графа, если каждый такой предикат представить вершиной, а ребрами
представить переменные. Таким образом, все знания о проектируемой
системе теплоснабжения, будь то система уравнений или какие-либо
эмпирические формулы представляются в виде множества предикатов типа
параметр и экземпляр. Эти простейшие предикаты и составляют группу
аксиом идентификации.
Аксиомы вычислений. Следующий этап формирования онтологии — это
формулировка аксиом вычислений, задающих правила вычисления
отношений. Как уже отмечалось, каждое отношение г — г(Х^ связывает
множество переменных Хт и используется для вычисления неизвестных
значений переменных X ™х с X по известным значениям переменных
X °х с Хт. Разбиений множества Хт на подмножества X “х и Х°ых может быть
достаточно много (К). Каждому такому разбиению сопоставим оператор
309
13. Онтологии и их применение
fmk(Xmkx, ХтГ), к = 1, К, по которому осуществляется вычисление
неизвестных значений переменных. Введем предикат
оператор (fmk (Хтк“х, [X Хт™х, = оператор (fmk (Хтквх, Хт™х)),
который истинен, если известны значения переменных множества Хтквых с Хт
оператора/'^ , и в результате вычисляются значения неизвестных переменных
Хткеых с X. Тогда множество аксиом вычислений отношения г для одного
множества Хт = {хт|, xm?} с X выглядит следующим образом:
параметр (хт1, [/,, А,|) л ... л параметр (xmq, \lq, AJ) л
л (оператор (fm (Хткх, Хт"ыхУ) и экземпляр (г, т, Хт), где к = 1, ..., К.
Интервальная арифметика лежит в основе вычисления формул. Поэтому
напомним элементарные правила вычислений в этой арифметике. Операции
сложения, вычитания, умножения и деления над двумя интервалами [/,, AJ
и [/2, AJ имеют вид:
[/,, А,] + \12, AJ = [/, + Л„ /2 + AJ,
[/р А,1 - AJ = [/, - Ар - AJ,
|/р AJ * {lv AJ = [пипЦ-Ар /,А2, /2-Ар /2-А2}, тах{/| А|, /,А2, /2Ар /2-А2}],
[/,, А,|/[/2, AJ = [тт{/Д, /,/А2, /2/Ар /2/А2}, тах{/,/Ар /,/А2, /2/Ар /2/Л2}],
О i |/2, А2|.
Рассмотрим теперь пример аксиом вычислений для отношения сложения,
связывающего три переменные множества Х= {хр х2, х3} отношением сложения
А . Для отношения сложения возможны только три оператора: а) вычисляющий
по известным х, и х2 неизвестную х3, б) вычисляющий по известным х, и х3
неизвестную х2 и в) вычисляющий по известным х3 и х2 неизвестную х,. Аксиомы
вычислений для отношения R+ будут определяться следующим образом:
(параметр (хр |/р AJ) л параметр (х2, [/2, AJ) л параметр (х3, [/3, AJ) л
л |/3, AJ = [/„ А,] + |/2, А2| экземпляр (R+, 0, хр х2, х3, [/р AJ, [/2, AJ,
|/3, А3|),
параметр (х [/,, AJ) л параметр (х2, [l2, AJ) / параметр (х3, [73, А3]) л [/2, AJ =
= |/г А3| - |/р А,| zd экземпляр (R+, 0, хр х2, х3, [/р А,], \12, А2], [/3, А3]),
310
13.2. Постановка задачи создания онтологии
параметр (хр [/р AJ) / параметр (х2, [Z2, h2]) л параметр (х3, [l}, h ])л [/ , А ] =
= [l}, h}] - [l2, h2] о экземпляр (R_, 0, хр х2, х}, [/р AJ, [/,, h2], [l}, h}]).
Аксиомы вычислений должны быть заданы для всех отношений, участвующих
в онтологии, и их используют для вычисления значений переменных.
Аксиомы ограничений. Перед началом вычислений задается множество
начальных значений входных переменных в виде множества предикатов
параметр (х, [/, h]), где х, I, h соответственное имя переменной и границы
интервала ее значений. Обозначим множество начальных значений всех
переменных Ео. Первый шаг вычисления — это нахождение тех предикатов
типа экземпляр (г, т, Хт), отношения которых могут быть вычислены согласно
аксиомам вычислений с использованием множества Е Обозначим это
множество предикатов >У0. После нахождения множества S(j осуществляется
вычисление отношений и получается новое множество значений переменных
Et, и все повторяется сначала, но вместо множества Е используется
множество Ev Процесс получения множеств значений переменных Е Е{,
... и соответствующих им множеств 50, Sv ... в принципе может продолжаться
бесконечно. На практике останов происходит либо в результате появления
на некотором этапе вычислений пустого множества, что соответствует
отсутствию вычислимых отношений, либо в результате предписанного заранее
числа допустимых итераций, либо в результате достижения устраивающего
пользователя результата, либо в результате каких-либо других критериев
останова. В частности, поскольку в основе вычислений лежит интервальная
арифметика, то можно воспользоваться ее результатами, позволяющими при
определенных условиях осуществить сходимость итеративной процедуры
вычисления интервальных значений переменных к некоторым локализующим
интервалам, содержащим требуемые решения. Аксиомы, описывающие
условия останова или ограничивающие каким-либо образом область
вычислений (после решения), называют аксиомами ограничений.
Аксиомы оптимизации. Для того чтобы можно было получать ответы на
обратные вопросы, необходимо иметь возможность нахождения оптимальных
значений некоторых переменных, называемых критериями. Это означает,
что в онтологии должна быть группа соответствующих аксиом оптимизации.
Критериями, например, в нашем случае могут быть переменные
комфортности и стоимость здания, причем для достижения энергетической
эффективности стоимость должна учитывать все затраты жизненного цикла
здания, т. е. расходы на эксплуатацию, энергию, ремонт. Это означает,
что задача оптимизации является многокритериальной, а критерии
противоречивы. В теории математического программирования такая задача
ставится как векторная задача оптимизации с ограничениями.
311
13. Онтологии и их применение
Среди объектных переменных, описывающих здание, выделим те, которые
мы можем изменять в процессе поиска их оптимального сочетания. Они
образуют вектор переменных X, конкретное значение которого [А”] будем
называть решением. Решение представляет собой точку в пространстве
значений переменных. Будем полагать, что оптимальное решение
принадлежит множеству Парето ( решение [А”*] принадлежит множеству
Парето, если это допустимое решение и для любого другого решения [А”] из
допустимой области значение хотя бы одного критерия хуже, чем для [А”*]).
Множество Парето — это множество неулучшаемых решений, так как для
любого из них нельзя найти другого допустимого решения, в котором один
критерий бы улучшался, а остальные бы не ухудшались. Однако получение
множества Парето недостаточно для решения практических задач. Необходимо
применить дополнительные знания в конкретной постановке задачи для
выбора единственного [А"*] из множества Парето.
Возможны три типа постановок задачи оптимального поиска: а) значения
критериев комфортности задаются, а оптимизируется только стоимость,
б) задается верхняя граница стоимости, которую нельзя превышать, а
оптимизируются только критерии комфортности, в) совместно
оптимизируются все критерии для поиска компромиссного решения.
Первая задача является однокритериальной. Задачи б) и в) —
многокритериальные, из которых наиболее общая - последняя. Рассмотрим
сначала подход к ее решению. Существующие методы решения
многокритериальных задач связаны с тем или иным учетом системы
предпочтений человека и, на основе этого, с выбором какого-либо принципа
оптимальности. Методы делятся на несколько групп: методы назначения
весовых коэффициентов для каждого критерия, упорядочения критериев по
важности, оптимизации наихудшего критерия, минимизации суммы
отклонений критериев от идеальных значений и интерактивной оптимизации.
Не во всех методах легко выразить предпочтения проектировщика и не все
методы дают, в конечном итоге, оптимальное по Парето решение.
Популярными являются методы оптимизации наихудшего критерия, сущность
которых состоит в следующем. Решается задача оптимального поиска по
каждому критерию х отдельно, и определяются наилучшие [х]П1ах и наихудшие
[x],nin его значения. Далее, для каждого критерия определяется множество
его относительных значений, вычисляемых по формуле
|х|огн = [х] - [х]"1"’ / [х]",ах - [x],Min.
Очевидно, что среди всех относительных значений данного критерия
существует минимальное. Оптимальным считается решение [х*], имеющее
максимальное относительное значение критерия среди всех минимальных
относительных значений критериев в множестве всех допустимых решений.
Какой бы метод получения оптимального решения не применялся, в любом
случае — это некий ограниченный поиск в пространстве значений наборов
312
13.3. Использование онтологий
переменных X. Например, это может быть оптимизирующий интерактивный
поиск, рассмотренный в главе 6, или какой-либо другой из той же главы.
Конкретный вид аксиом оптимизации зависит от выбираемого вида поиска
и в настоящей книге не приводится.
Таковы основные типы аксиом онтологии теплоснабжения, предназначенной
для решения задач анализа и оптимизации. Конечно, это не онтология целиком.
Даже те предикаты, которые мы ввели, кроме аксиом идентификации, требуют
своих правил, выражающих их через более простые предикаты. Однако
приведенного материала достаточно, чтобы понять структуру онтологии и
основополагающие подходы к ее созданию. Теперь рассмотрим некоторые
результаты использования онтологии теплоснабжения.
13.3. Использование онтологий
Чтобы продемонстрировать возможности онтологии теплоснабжения,
рассмотрим характер тех наиболее типичных результатов анализа, которые
получаются на основе ее использования. В качестве практического примера
возьмем готовый типовой проект жилого индивидуального двухэтажного дома,
предназначенного для строительства в центральных районах Европейской части
России. Поставим задачу, во-первых, получить оптимальное решение, а
во-вторых, сравнить его с решениями типового проекта и исследовать влияние
различных факторов на оптимальность решения и найти главные. На основе
рассмотренных выше принципов была разработана онтология, позволяющая
рассчитывать температуры воздуха в зонах здания, температуры внутренних
поверхностей стен, тепловую устойчивость конструкции здания, нагрузку
системы отопления и размеры радиаторов, а также стоимость жизненного
цикла здания и отдельных компонент: стоимость строительства, величину
годовых отчислений на эксплуатацию и годовые затраты на топливо.
Из переменных проекта были выбраны двенадцать, это —- толщины и
материалы основных элементов ограждающих конструкций. Критериями,
по которым проводилась оптимизация, в различных вариантах решения
выступали температуры воздуха в жилых зонах, тепловая устойчивость,
первоначальная стоимость здания и, конечно, стоимость жизненного цикла.
Решение проводилось следующим образом. Значения переменных брались
из проекта, строительной справочной литературы и действующих СНиП. В
зависимости от варианта решения заполнялась база данных, потом искалось
оптимальное решение согласно описанной онтологии.
Была проведена серия экспериментов по оптимизации стоимости
жизненного цикла системы. На рис. 13.1 изображена зависимость различных
составляющих стоимости жизненного цикла от назначаемых температур в
помещении. Все стоимости приведены к одному году эксплуатации. Для
выявления зависимости диапазон изменения температур, 16-24 °C, взят
несколько шире, чем регламентируется СНиП.
313
13. Онтологии и их применение
Толщина
ограждающих
конструкций, м
Температура в жилых зонах. °C
Рис. 13.1. Зависимость составляющих стоимости жизненного цикла
от заданной температуры в жилых зонах: светлые значки — эксперимент;
темные — проектное решение
Температура
в жилых зонах. °C
Рис. 13.2. Зависимость температуры в жилых зонах от ограничений
стоимости жизненного цикла
Естественно, чем выше эта температура, тем лучше теплозащитные
свойства ограждения и выше комфортность здания. Видно, что все
компоненты стоимости возрастают. Наибольшую тенденцию к росту
проявляет толщина наружной стены. По-видимому, это и есть параметр,
314
Вопросы и упражнения
который наиболее тесно связан с температурой в зонах. Кроме того, на
рисунках показаны параметры решения, соответствующие исходному
типовому проекту. При прочих равных условиях оптимизированное проектное
решение, полученное с помощью рассмотренной онтологии, выявило
возможность сокращения стоимости жизненного цикла на 10% в основном
благодаря сокращению расхода топлива на 35 % при повышении
теплозащитных свойств здания.
Результаты другой серии экспериментов, в которой вводились ограничения
на стоимость жизненного цикла и исследовалось их влияние на температуру в
жилых зонах, показаны на рис. 13.2., подтверждают очевидный результат
для данного типа зданий — рост температуры с увеличением затрат.
Вопросы и упражнения
1. Что означает термин «онтология»?
2. Какие формы онтологий наиболее типичны?
3. Какие перспективы связывают с использованием онтологий?
4. Что является теоретическим базисом онтологий и какие программные средства
используют для реализации онтологий?
5. Каковы этапы создания онтологий?
6. Каковы наиболее типичные группы аксиом при создании онтологий?
14. РЕАЛИЗАЦИЯ СИСТЕМ
В настоящей главе рассмотрены этапы создания систем искусственного
интеллекта на примере конкретной среды.
Архитектуры реальных систем искусственного интеллекта, в особенности
многоагентных (или мультиагентных) систем, могут быть самыми
разнообразными. Для реализации подобных систем разрабатываются
специальные инструментальные программные средства. Эти средства
предполагают определенную технологию создания мультиагентных систем.
Подобная технология включает ряд крупных этапов, типичными из которых
являются следующие:
выбор архитектуры мультиагентной системы (числа и типов агентов;
локальных целей, стоящих перед каждым из них; принципов взаимодействия
и выработки глобального решения);
изучение свойств и поведения среды, с которой придется иметь дело
агентам, и представление этих знаний в виде неформальной онтологии. Этот
этап часто называют извлечением знаний о среде;
представление глобальных (доступных всем агентам) и локальных знаний
(доступных отдельным агентам), полученных на этапе извлечения знаний,
на формальном языке какого-либо исчисления в виде формальных глобальной
и локальной онтологий. Этот этап часто называют формализацией;
выбор стратегии вывода для каждого из агентов, на основе использования
которой агент будет достигать поставленной перед ним цели;
разработка программы и аппаратуры, реализующей мультиагентную
систему. Этот этап иногда называют реализацией.
В настоящей главе рассмотрены все эти этапы на примере построения
одноагентной системы искусственного интеллекта.
14.1. Архитектура
Архитектура системы показана на рис. 14.1. Агент получает сообщения
от телеметрической системы сбора информации сети распределения и подачи
воды. Задачей агента является анализ различных ситуаций в сети
распределения и подачи воды на основе этих сообщений и выдача оператору
результатов этого анализа.
316
14.2. Извлечение знаний
Восприятия
Сеть распределения и подачи воды агента > 4 Действия Агент
(реакции)
агента
Рис. 14.1. Архитектура одноагентной системы
14.2. Извлечение знаний
14.2.1. Источники приобретения знаний
Рассмотрим типичные источники знаний.
Оператор. Несмотря на указанные выше трудности извлечения знаний из
оператора, он является главным источником знаний.
Система наблюдения и контроля. Этот источник используется совместно
с оператором в процессе интервью с ним. Если система наблюдения и
контроля достаточно развита, то наблюдение с ее помощью за поведением
сети в реальном масштабе времени делает интервью с оператором более
легким, выразительным и эффективным.
Математическая модель поведения. Математические модели поведения
физической сети (в случае сети распределения и подачи воды — это
гидравлическая модель) реализуются в виде компьютерных программ. Путем
экспериментов с этими программами извлекаются дополнительные знания о
реакциях сети в ответ на определенные воздействия извне; проверяются знания
эксперта, извлеченные в ходе интервью с ним; формируются правила и
стратегии вывода и т.п.
Архив данных. В процессе наблюдения за поведением любой реальной
среды осуществляется накопление и архивация данных, характеризующих ее
поведение. В случае сети распределения и подачи воды — это телеметрическая
информация от датчиков давления и расхода воды, сведения о затратах
энергии, данные об уровне воды в резервуарах и т.п. Данные в архиде
структурированы по часам, дням, месяцам и доступны для анализа в процессе
извлечения и проверки знаний.
За работой сети распределения и подачи воды наблюдает группа
операторов, которые, если это необходимо, могут вмешиваться в ее работу.
Они ответственны за процесс управления сетью распределения и подачи воды,
экономию и качество воды, безопасную работу сети. Главная задача агента
состоит в том, чтобы помочь оператору принять правильные решения.
Операторы могут иметь многолетний опыт эксплуатации сети распределения
и подачи воды, хорошо знают ее поведение в различных ситуациях, типичные
причины возможных отказов и мероприятия по их устранению. Поэтому
317
14. Реализация систем
одним из источников знаний о сети являются именно операторы. Источником
более тонких знаний о поведении сети являются инженеры, обслуживающие
оборудование сети. Иными словами, весь персонал, участвующий в
эксплуатации, управлении, ремонте сети, может служить источником знаний
о ее поведении. Этот источник главный, но не единственный. Все, кто является
источником знаний, называются экспертами.
Процесс извлечения знаний не является хорошо определенным и
однозначным. Он является скорее искусством и набором приемов, чем
наукой. При извлечении знаний из персонала, обслуживающего сеть,
используется интервью. Того, кто занимается извлечением знаний (и не
только из персонала), будем называть аналитиком.
Одна из самых больших проблем, связанных с извлечением знаний на
основе интервью, состоит в неточности, приблизительности, а иногда и
ошибочности извлекаемых знаний. Источником этих неточностей чаше всего
является эксперт, для которого бывает трудно неформально на естественном
языке выразить те знания, обладателем которых он является, а другого способа
их выражения он не имеет. Вследствие этого довольно часто эксперты дают
ответы о своих действиях в той или иной ситуации, не соответствующие их
фактическому поведению. Типичная ситуация — это когда аналитик не знаком
с областью знаний эксперта, а эксперт не знаком с методами искусственного
интеллекта.
Идеальной является ситуация, когда экспертом и аналитиком является
одно лицо, хотя это случается крайне редко. В условиях разнополюсных
знаний эксперта и аналитика процесс извлечения знаний является трудоемкой
и длительной процедурой.
Другая проблема, связанная с процессом извлечения знаний, состоит в
субъективности аналитика. Ответы эксперта интерпретируются и
преобразовы-ваются аналитиком в понятную ему формальную онтологию.
Этот процесс преобразования субъективен. Аналитик может неправильно
понять или извратить знания эксперта, что впоследствии приведет к
ошибочной работе агента.
К сожалению, перечисленные проблемы никогда не могут быть разрешены
полностью, поскольку процесс извлечения знаний сильно зависит от
специфических особенностей среды. Накопление человечеством формальных
онтологий может сильно помочь в уходе от этих проблем. Целью аналитика
является не только извлечение знаний, но и представление их в виде
формальной онтологии. Процесс получения знаний от эксперта чаще всего
проходит путем многократных интервью с экспертом на естественном языке.
Аналитик обрабатывает эти знания, формализуя их. Будем полагать, что
аналитик проводит интервью на естественном языке, а формализацию
результатов интервью представляет в виде схем ситуаций. Схемой ситуаций
называется ориентированный граф с тремя типами вершин: вершин ситуаций,
восприятия, реакции. Вершины последнего типа позволяют образовывать
некоторую иерархию схем и разбивать процесс извлечения знаний по частям.
318
14.2. Извлечение знаний
14.2.2. Построение схем ситуаций
Построение каждой схемы ситуаций состоит из следующих простых шагов.
Вводится круглая залитая вершина начальной ситуации (начальная
вершина) с уникальным индексом.
Далее итеративно из каждой вершины ситуации, начиная с исходной,
проводятся дуги в овальные вершины восприятия, вводимые по результатам
интервью. Каждая из этих овальных вершин соответствует одному из
альтернативных высказываний, истинность которого в данной ситуации
следует установить. Внутри этой вершины записывается соответствующее
высказывание в виде формулы предикатов первого порядка а.
Из каждой овальной вершины восприятия проводится единственная дуга в
прямоугольную вершину реакции, внутри которой записывается действие d.
Из прямоугольной вершины реакции выходит единственная дуга,
направленная в какую-либо вновь вводимую незалитую или существующую
вершину ситуации данной схемы ситуации или в незалитую круглую
начальную вершину обозначающую начальную ситуацию другой схемы
ситуаций. В последнем случае рядом с этой вершиной записывается на
естественном языке название соответствующей схемы ситуаций, имеющей
эту вершину ситуации (залитую круглую) в качестве начальной. Из незалитой
круглой вершины, соответствующей начальной ситуации другой схемы, дуг
не выходит.
Любой путь, ведущий от вершины ситуации 5. через овальную вершину с
формулой а действие (г/) в прямоугольную вершину с действием dк вершине
ситуации 5, представляется парой формул
5 л а о действие (d),
переход (d, 5.) = 5.
Напомним, что запись 5 в первой из этих формул является сокращенной
записью атома
ситуация (5),
а затем переход (d, S) во второй формуле является функцией.
Таким образом, схема ситуаций является не чем иным, как некоторой
формой представления формул. Схема ситуаций используется для извлечения
знаний путем постепенного ее построения в процессе интервью, начиная от
начальной вершины. Извлечение знаний в этом случае состоит в получении
ответов на следующие вопросы и построении по результатам ответа
соответствующей схемы ситуаций.
Какова начальная ситуация для данной схемы ситуаций?
Если мы находимся в некоторой ситуации (вершине ситуации), то
истинность каких альтернативных высказываний а следует проверить в этой
ситуации?
319
14. Реализация систем
Если мы установили истинность высказывания а, соответствующего какой-
либо вершине восприятия, то какое действие d теперь следует совершить?
Если мы совершили действие d, соответствующее какой-либо вершине
реакции, то в какую ситуацию мы после этого попадем? Если это начальная
ситуация какой-либо схемы ситуаций, то каково ее название? В результате
ответа на каждый из этих вопросов может быть построен очередной участок
схемы ситуаций. Схема ситуаций может быть очень большой и избыточной,
схем может быть несколько. Глубина схемы может зависеть от начальной
ситуации, с которой начинается процесс ее построения. Число вершин и
дуг схемы характеризует сложность процесса извлечения знаний. Эта
сложность может быть уменьшена рядом приемов. Один из них — это
объединение вершин, все возможные пути из которых одинаковы, и переход,
таким образом, от дерева к графу.
Рассмотрим процедуру извлечения аналитиком знаний (построения схем
ситуаций) о поведении и управлении типичной сетью распределения и подачи
воды.
14.2.3. Сеть распределения и подачи воды
Упрощенно сеть распределения и подачи воды можно рассматривать как
разветвленную сеть трубопроводов разного диаметра, в определенных узлах
которой находятся так называемые контрольные точки, давление воды в
которых может быть измерено. Для нашей сети таких контрольных точек 12.
В других узлах этой сети находятся насосные станции, каждая из которых
содержит некоторое число насосов, подающих воду из резервуара,
соответствующего станции, в сеть. Число таких станций — 12. Большинство
насосов станций работает с постоянной частотой (скоростью) вращения.
Только две насосные станции (2 и 6) имеют возможность автоматического
регулирования частоты вращения (скорости насосов). Автоматическое
регулирование позволяет поддерживать постоянное давление в определенных
контрольных точках сети путем изменения скорости насосов. В нашем случае
такая точка единственная — 4. Потребителями воды являются жители города,
три тепловые станции и различные предприятия. Эти знания о сети довольно
скудные. Опустим важный, но простой этап перехода от определений и
понятий на естественном языке к термам и атомам языка логики предикатов
первого порядка. Введем некоторые из них сразу. Заметим только, что в
реальной ситуации процесс введения необходимых термов и атомов не является
единовременным и осуществляется в процессе построения схемы ситуаций.
14.2.4. Термы и атомы
Как правило, эксперт не знаком с терминологией логики предикатов
первого порядка, и формирование термов, атомов и формул осуществляется
аналитиком по результатам интервью с экспертом на естественном языке.
Аналитик, прежде чем определить необходимые термы и атомы, должен
320
14.2. Извлечение знаний
ознакомиться с принципами работы сети, терминологией, используемой
экспертом. После этого он сам выбирает термы и атомы, которыми будет
пользоваться. Введем некоторые их них.
Переменные и константы. Переменная точка, областью значений которой
является множество номеров от Точка_1 до Точка_12 всех контрольных точек
сети распределения и подачи воды.
Переменная станция, областью значений которой является множество
номеров станций от Станция_1 до Станция !2.
Переменная значение давления, принимающая значения Высокое, Низкое,
Нормальное.
Переменная значение_скорости, принимающая значения Высокая, Низкая,
Нормальная.
Переменная значениеровня, принимающая значения Высокий, Низкий,
Нормальный.
Атомы. Атом давление (точка, значение_ давления). Этот атом истинен,
если давление в контрольной точке точка принимает одно из значений
значение_ давления'.
атом скорость (станция, значениескорости),
атом уровень (станция, значение_уровня).
Функция. Функция насосная станция (точка) задается табл. 14.1.
Аргументом этой функции является одна из контрольных точек, а значением —
насосная станция, наиболее влияющая на давление в данной точке.
Перейдем теперь к формированию схем ситуаций.
14.2.5. Первичная схема ситуаций
Построение схем ситуаций начинается с первичной схемы. Выбирается
начальная ситуация 50, и эксперту задается вопрос: «Если мы находимся в
ситуации 5 то истинность каких альтернативных высказываний следует
проверить в этой ситуации?» Ответом на этот вопрос является перечень
следующих трех альтернативных высказываний на русском языке, подлежащих
проверке на истинность или ложность:
Наличие хотя бы одной контрольной точки, в которой давление высокое
или низкое.
Наличие хотя бы одной насосной станции, скорость вращения регули-
руемых насосов которой высокая или низкая.
Наличие хотя бы одного резервуара, уровень воды в котором низкий.
После формализации этих ответов получим часть схемы ситуаций,
показанную на рис. 14.2.
11 - 1141
321
14. Реализация систем
Таблица 14.1
Значение переменной точка Значение функции насосная_станция(точка)
Точка_1 Станция_10
Точка_2 Станция_7
Точка_3 Станция_6
Точка_4 Станция_6
Точка_5 Станция_6
Точка_6 Станция_3
Точка_7 Станция_6
Точка_8 Станция_12
Точка_9 Станция_7
Точка_10 Станция_7
Точка_11 Станция_7
Точка_12 Станция_7
Рис. 14.2. Исходный шаг в построении первичной схемы ситуаций
Затем следует продолжить опрос с учетом уже полученных ответов. Типы
возможных вопросов перечислены ранее при рассмотрении схем ситуаций.
В упрощенном виде на русском языке эти вопросы можно сформулировать
следующим образом.
Если наличие хотя бы одной контрольной точки, в которой давление
высокое или низкое, установлено, то что делать дальше?
322
14.2. Извлечение знаний
Если наличие хотя бы одной насосной станции, скорость регулируемых
насосов которой высокая или низкая, установлено, то что делать дальше?
Если наличие хотя бы одного резервуара, уровень воды в котором низкий,
установлено, то что делать дальше?
Возможными ответами на эти вопросы могут быть соответственно:
Регулировать давление. Схема ситуаций для регулирования давления в
контрольных точках.
Регулировать скорость. Схема ситуаций для регулирования скорости насосов.
Регулировать уровень. Схема ситуаций для регулирования уровня резервуаров.
Эти ответы позволяют завершить первичную схему ситуаций на рис. 14.2.
В результате получим схему, показанную на рис. 14.3.
для регулирования давления для регулирования скорости регулирования уровня волы
в контрольных точках вращения насосов в резервуарах
Рис. 14.3. Первичная схема ситуаций
14.2.6. Схема ситуаций для регулирования давления в контрольных точках
Построение схемы ситуаций для регулирования давлений в контрольных
точках начинается, как и в случае первичной схемы, с начальной ситуации
5р но уже предварительно определенной в первичной схеме ситуаций. После
этого следует вопрос к эксперту: «Если мы находимся в ситуации то
истинность каких альтернативных высказываний следует проверить в этой
ситуации?» Ответ может быть следующим.
Наличие контрольной точки, давление в которой высокое и не ниже,
чем во всех остальных контрольных точках.
Наличие контрольной точки, давление в которой низкое и не выше, чем
во всех остальных контрольных точках.
п*
323
14. Реализация систем
После формализации этих ответов получим часть схемы ситуаций для
регулирования давления в контрольных точках, показанную на рис. 14.4.
5,
(Эточка) давление (точка, Высокое) л
(Уточка_\, р,)(давление (точка.
Высокое) л давление (точка), pt) л
Высокое > рх)
(Э точка) давление (точка, Низкое) л
(Уточка), рх)(давление (точка,
Низкое) л давление (точка_), рх) л
Низкое < рх)
Рис. 14.4. Начальный шаг в построении схемы ситуаций для регулирования
давлений в контрольных точках ситуаций
Далее следует продолжить опрос с учетом уже полученных ответов. На
русском языке дальнейшие вопросы можно сформулировать следующим
образом.
Если установлено наличие контрольной точки, давление в которой высокое
и не ниже, чем во всех остальных контрольных точках, то что следует делать
дальше?
Если установлено наличие контрольной точки, давление в которой низкое
и не выше, чем во всех остальных контрольных точках, то что следует делать
дальше?
Ответами на них могут быть соответственно следующие:
Если установлено наличие контрольной точки, давление в которой высокое
и не ниже, чем во всех остальных контрольных точках, то выключить какой-
либо из включенных насосов на насосной станции, оказывающей наибольшее
влияние на найденную точку, и перейти к начальной ситуации.
Если установлено наличие контрольной точки, давление в которой низкое
и не выше, чем во всех остальных контрольных точках, то включить какой-
либо из выключенных насосов на насосной станции, оказывающей
наибольшее влияние на найденную точку, и перейти к начальной ситуации.
После формализации этих ответов получим окончательную схему ситуаций
для регулирования давления в контрольных точках, показанную на рис. 14.5.
Теперь можно перейти к построению схемы ситуаций для регулирования
скорости насосов.
14.2.7. Схема ситуаций для регулирования скорости насосов
Скорость вращения насосов, которая регулируется автоматически, является
важным показателем, знание которого позволяет принимать решения о
324
14.2. Извлечение знаний
(Зточка) давление (точка, Высокое} /•
(Чточка), р))(давление (точка,
Высокое) давление (точка ), р!) ,<
Высокое > pl)
(Зточка) давление (точка, Низкое) л
(Чточка_), р\)(давление (точка,
Низкое) давление (точка_1, р!)
Низкое < р!)
" ' ' "...~ ' ................. ''
выключить! насосная станция/точка) )
включить (насосная станция!точка)) \
Рис. 14.5 Схема ситуаций для регулирования давления в контрольных точках
включении или выключении тех или иных насосов. Мы не будем больше
описывать те вопросы аналитика и ответы эксперта, на основании которых
строится схема ситуаций. Возможность сделать это будет предоставлена
читателю в разделе «Вопросы и упражнения». Здесь же приведем результаты
интервью в описательной форме на естественном языке и представим
соответствующие схемы ситуаций.
Измеряется частота вращения (скорость) насосов только одной насосной
станции 6. Для принятия решений недостаточно знать, какова эта частота
вращения: нормальная, низкая или высокая. Необходимо знать характер
изменения частоты вращения и потребление населением воды. Характер
потребления воды можно представить графиком потребления, типичным для
данной сети и полученным путем многократных наблюдений. Такой график
показан на рис. 14.6.
Сведем все полученные в процессе интервью ответы эксперта в табл. 14.2.
На основании результатов интервью, сведенных в эту таблицу, получаем
схему ситуаций, показанную на рис. 14.7.
14.2.8. Схема ситуаций для регулирования уровня воды в резервуарах
Вода поступает в сеть из резервуаров. Резервуары наполняются с помощью
специальных насосов первичной подачи воды. Включением и выключением
этих насосов управляет специальная автоматика. Если уровень воды в
резервуарах низкий, то соответствующие насосы включаются на заполнение
резервуаров. Когда уровень воды высокий — насосы выключаются. Обычно
операторы не управляют этими процессами. Однако может оказаться, что
потребление воды из резервуаров выше поступления. Поэтому оператор
обязан предотвращать ситуацию, когда какой-либо из резервуаров окажется
пустым. Делает он это выключением насосов станции потребления,
325
14. Реализация систем
Птрсбленис воды
на одного жгпсля
Время
Рис. 14.6. Типичный график потребления воды (в л/ч)
на одного жителя в течение суток
Таблица 14.2
Скорость насосов станции 6 Давление в контрольной точке 4 Потребление воды населением Действия
Высокая Уменьшается - Включить дополнительный насос станции 10
Высокая Не уменьшается Увеличивается Включить дополнительный насос станции 12
Низкая Увеличивается - Выключить насос станции 10
Низкая Не увеличивается Уменьшается Включить дополнител ьный насос станции 12
326
14.3. Формализация
Рис. 14.7. Схема ситуаций для регулирования скорости насосов
забирающих воду из резервуара, и включением вместо выключенных других
насосов станции замещения. Станции замещения определяются заранее
эмпирически, расчетами или с помощью моделирования сети. Введем
функцию станциязамещения (станцияпотребления), значением которой
является номер замещающей станции, а аргументом — номер потребляющей
станции. Зададим эту функцию в виде табл. 14.3.
Схема ситуаций регулирования уровня воды в резервуарах показана на
рис. 14.8.
Итак, построение схем ситуаций завершено. Перейдем к следующему
этапу построения системы.
14.3. Формализация
Для удобства часть этапа формализации, заключающаяся во введении
термов и атомов, была выполнена при рассмотрении этапа извлечения
знаний. Оставшаяся часть этапа формализации состоит в переходе от схем
ситуаций к формулам, начиная с первичной схемы ситуаций на рис. 14.3.
В нашем случае этот этап облегчается благодаря тому, что в схемах ситуаций
уже использованы формулы логики предикатов первого порядка.
14.3.1. Формулы, получаемые по первичной схеме ситуаций
Первичная схема ситуаций имеет одну ситуацию So, из которой исходят
три дуги, ведущие в овальные вершины, помеченные соответственно
327
14. Реализация систем
Таблица 14.3
станция_потребления станция_замещения (ста нц ия_ потр ебления)
Станция_04 Станция_07
Станция_12 Станция_04
Станция_06 Станция_12
Станция_10 Станция_01
Станция_01 Станция_11
Станция_11 Станция_10
Станция_02 Станция_10
Станция_03 Станция_05
Станция^05 Станция_03
Станция_08 Станция_09
Станция_09 Станция_08
Станция_07 Станция_04
Рис. 14.8. Схема ситуаций для регулирования уровня воды в резервуарах
328
14.3. Формализация
выражениями (3 точка)[давление (точка, Низкое) v давление (точка,
Высокое), (3 насос) [скорость (насос, Высокая) v скорость (насос, Низкая),
(3 станция) уровень (станция, Низкий).
Из овальных вершин, помеченных этими выражениями, ведут дуги в
прямоугольные вершины, помеченные соответственно действиями
Регулироват ъдавление,
Регулироватьскорость,
Регулировать_уровень.
Из этих вершин дуги ведут в вершины ситуаций 5р 52, Это означает,
что истинность формул в овальных вершинах влечет истинность
соответствующих действий, а истинность действий — переход в
соответствующие ситуации. Следовательно, имеем формулы
50л (3 точка)[давление (точка, Низкое) v давление (точка, Высокое)] о
о действие (Регулировать_давлениё),
5 л (3 насос)[скорость (насос, Высокая) v скорость (насос, Низкая)] о
действие (Регулировать скорость),
5(| л (3 станция)[уровень (станция, Низкий)] о
z> действие (Регулировать_уровень),
переход (Регулировать давление, 50) = 5р
переход (Регулировать_скорость, 50) = S,,
переход (Регулировать_уровень, 50) =
14.3.2. Формулы регулирования давления в контрольных точках
На схеме регулирования давления в контрольных точках (рис. 14.5) из
ситуации 5 выходят две дуги, направленные в овальные вершины, которые
помечены соответственно формулами
(3 точка) [давление (точка, Высокое) л (V точка', р) давление (точка,
Высокое) л давление (точка', р) л Высокое > р] (14.1)
329
14. Реализация систем
(3 точка)[давление (точка, Низкое)) л (V точка', р) давление (точка,
Низкое) л давление (точка', р)| л Низкое <р. (14.2)
Из овальных вершин, соответствующих этим формулам, ведут дуги в
прямоугольные вершины, которым соответствуют действия
выключить (насос, насосная станция (точка)), (14.3)
включить (насос, насоснаястанция (точка)). (14.4)
Это означает, что истинность формулы (14.1) в ситуации 5 влечет
истинность формулы (14.3), а истинность формулы (14.2) влечет истинность
формулы (14. 4) в этой же ситуации. Следовательно, имеем формулы
5, л (3 точка) [давление (точка, Высокое) л (V точка', р) давление
(точка, Высокое) а давление (точка', р) л Высокое > р[ о действие
(выключить (насос, насосная станция (точка))), (14.5)
5, л (3 точка) [давление (точка, Низкое) л (V точка', р) давление
(точка, Низкое) л давление (точка', р) л Низкое < р\ э действие
(включить (насос, насосная станция (точка))). (14.6)
Из прямоугольных вершин, соответствующих действиям (14.3), (14.4),
дуги ведут вновь в ситуацию 5 Следовательно, имеем формулы
переход (выключить (насос, насосная станция (точка)), St) = 5р (14.7)
переход (включить (насос, насосная_станция (точка)), S}) = (14.8)
Таким образом, мы получили формулы (14.5)— (14.8) языка логики
предикатов первого порядка, аксиоматизирующие поведение оператора сети
распределения и подачи воды при регулировании давления в контрольных
точках. Две первые формулы включают кванторы. Вследствие конечного и
сравнительно небольшого числа контрольных точек эти формулы легко
преобразуются в эквивалентные, не содержащие кванторов формулы. Сначала
избавимся от квантора существования. В результате получим формулы
330
14.3. Формализация
[5, л (давление (Точка_ОХ, Высокое)) л (V точка', р) (давление
(Точка_0\, Высокое) л давление (точка', р) л Высокое > р) о действие
выключить (насос, насосная станция (Точка01)))] v
v [5, л давление (Точка_02, Высокое) л (V точка', р)(давление (Точка_02,
Высокое) л давление (точка', р) л Высокое > р) з действие (выключить
(насос, насосная станция (Точка_02)))] v
v [5) л давление (Точка_Х2, Высокое)) л (V точка', р)(давление (Точка_Х2,
Высокое) л давление (точка', р) л Высокое > р) действие (выключить
(насос, насосная станция (7bwa_12)))]; (14.9)
[5, л (давление (ТочкаОХ, Низкое)) л (V точка', р) (давление
(ТочкаОХ, Низкое) л давление (точка', р) л Низкое < р) действие
(включить (насос, насосная станция (ТочкаОХ)))] v
v л давление (Точка_02, Низкое) л (V точка’, р)(давление (Точка_02,
Низкое) л давление (точка', р) л Низкое < р) действие (включить (насос,
насосная станция (Точка_02)))\ v
v [5, л давление (Точка_12, Низкое)) л (V точка', р)(давление (Точка_12,
Низкое) л давление (точка', р) л Низкое < р) о действие (включить
(насос, насосная станция (Точка_ 12)))]. (14.10)
После избавления от квантора общности получим формулы
[5, л (давление (ТочкаОХ, Высокое)) л (давление (ТочкаОХ, Высокое) л
л давление (ТочкаОХ, р) л Высокое > р) л (давление (ТочкаОХ, Высокое) л
331
14. Реализация систем
л давление (Точка_02, р) л Высокое > р) л
л (давление (Точка_01, Высокое)л
л давление (Точка_\2, р) л Высокое > р) о действие (выключить (насос,
насоснаястанция (Точка_0\))] v
v л давление (Точка_02, Высокое) л (давление (Точка_02, Высокое) л
л давление (Точка_0\, р) л Высокое > р) л (давление (Точка_02, Высокое) л
л давление (Точка_02, р) л Высокое > р) /
л (давление (Точка_02, Высокое) л давление (Точка_\2, р) л Высокое > р)
з действие (выключить (насос, насосная_станция (Точка_()2))\ v
v [5j л давление (Точка_\2, Высокое) л (давление (Точка_\2, Высокое) л
л давление (Точка 01, р) л Высокое > р) /\ (давление (Точка_\2, Высокое) л
л давление (Точка_02, р) л Высокое > р) л
л (давление (Точка_\2, Высокое) л давление (Точка_\2, р) л Высокое > р) о
=> действие (выключить (насос, насосная_станция (Точка_\2))]-, (14.11)
[5, л (давление (Точка_0\, Низкое)) л (давление (Точка_0\, Низкое) л
л давление (Точка_0\, р) л Низкое < р) л (давление (Точка_()\, Низкое) л
л давление (Точка_02, р) л Низкое < р) л (давление (Точка О], Низкое)л
л давление (Точка_\2, р) л Низкое < р) действие (выключить (насос,
насосная станция (Tbwco Ol)))] v
332
14.3. Формализация
v [5, л давление {Точка_02, Низкое) л {давление {Точка_02, Низкое) л
л давление {Точка_01, р) л Низкое < р) л {давление {Точка_02, Низкое) л
л давление {Точка_02, р) л Низкое < р) л
л {давление {Точка_02, Низкое) л давление {Точка_\2, р) л Низкое >р) о
Z) действие {выключить {насос, насосная станция {Точка_{Т2)))] v
v [5, л давление {Точка_\2, Низкое) л {давление {Точка_\2, Низкое) л
давление {Точка_0\, р) л Низкое < р) л {давление {Точка 12, Низкое) л
давление {Точка_02, р) л Низкое > р) /\
л {давление {Точка_\2, Низкое) л давление {Точка_\2, р) л Низкое > р)
о действие {выключить {насос, насосная станция {Точка_\2)))]. (14.12)
Каждая из формул (14.11), (14.12) является формулой, состоящей из
дизъюнкции импликаций, левая часть которых является конъюнкцией атомов, а
правая состоит из одного атома. Очевидно, что для доказательства истинности
такой формулы достаточно доказать истинность хотя бы одной импликации. Для
доказательства же может быть использовано обобщенное правило модус поненс.
Аналогично можно получить формулы и по остальным схемам ситуаций.
Выпишем их без комментариев.
14.3.3. Формулы регулирования скорости насосов
Получение формул регулирования скорости насосов легко проследить по
рис. 14.7. Имеем
S2 л (3 насос) [скорость {Станция_6, насос, Высокая) л давление
{Точка_4, Уменьшается) о действие {включить {насос,
Насосная_станция_ 10))],
333
14. Реализация систем
S, л (3 насос) [скорость (Станция_6, насос, Низкая) л давление
(Точка_4, Не_уменьшается) л потребление (Уменьшается) действие
(включить (насос, Насосная_станция_)2))],
S2 л (3 насос) [скорость (Станция_6, насос, Высокая) л давление
(Точкой, Не_уменьшается) л потребление (Увеличивается) о действие
(включить (насос, Насосная_станция_)2))],
S2 л (3 насос) [скорость (Станция_6, насос, Низкая) л давление
(Точка_4, Увеличивается) действие (выключить (насос,
Насосная_станция_ 10))],
переход (включить (насос, Насосная_станция_(<д), S2) — S2,
переход (включить (насос, Насосная_станция_)2), S2) = S2,
переход (выключить (насос, Насосная_станция_\<д), S2) = S2.
14.3.4. Формулы регулирования уровня воды в резервуарах
Получение формул регулирования уровня воды в резервуарах легко
проследить по рис. 14.8:
53 л уровень (Станция ), Низкий) о действие (включить (насос,
станция замещения (Станция_\) л действие (выключить (насос,
Станция)),
S, л уровень (Станция_2, Низкий) о действие (включить (насос,
станция замещения (Станция_2) л действие (выключить (насос,
Станция _2),
334
14.4. Выбор стратегии вывода
S3 л уровень (Станция_)2, Низкий) действие (включить (насос,
станция_замещения (Станция_)2) л действие (выключить (насос,
Станция ) 2),
переход (включить (насос, станция замещения (Станция )), S.) = 53,
переход (включить (насос, станция замещения (Станция !), S,) = Sy
переход (включить (насос, станция замещения (Станция_)2), 53) = 53.
14.4. Выбор стратегии вывода
На этом этапе выбирается стратегия вывода, которая будет использоваться
в процессе нахождения агентом решений. Рассмотрим, как это делается на
примере первой формулы (14.11) из группы формул регулирования давления
в контрольных точках
[5 л (давление (Точка 01, Высокое)) л (давление (ТочкаО), Высокое) л
л давление (Точка_0\, р) л Высокое > р) л (давление (ТочкаО), Высокое) л
л давление (Точка_02, р) л Высокое > р) л
л (давление (Точка О), Высокое) л
л (давление (Точка_)2, р) л Высокое > р) действие (выключить (насос,
насосная станция (ТочкаО 1)))] v
[S, л давление (Точка_02, Высокое) л (давление (Точка_02, Высокое) л
л давление (Точка О), р) л Высокое > р) л (давление (Точка_02, Высокое) л
давление (Точка _02, р) л Высокое > р) л
335
14. Реализация систем
л (давление (Точка_02, Высокое) л давление (Точка_\2, р) л Высокое > р)
действие (выключить (насос, насосная станция (Точка _<Т2)))] у
v [S, л давление (Точка_\2, Высокое) л (давление (Точка_)2, Высокое) л
л давление (ТочкаО), р) л Высокое > р) л (давление (Точка_\2, Высокое) л
л давление (Точка_02, р) л Высокое > р) л
л (давление (Точка_\2, Высокое) л
л давление (Точка_\2. р) л Высокое > р) действие (выключить (насос,
насосная станция (Точка_\2)))]. (14.13)
В этой формуле используются атомы 5,, давление (точка, значениедавления),
действие (выключить (насос, насосная станция (точка)). Области значений
переменных точка, значение давления, насос и функции насосная станция
(точка) определены ранее.
Как уже говорилось, задачей агента является анализ ситуаций, в которых
находится сеть распределения и подачи воды и выдача соответствующих
реакций. Задача, сформулированная таким образом, не содержит цели,
поставленной агенту так, как это делалось раньше. Поэтому использование
стратегий обратного поиска, предполагающих, что цель определена,
исключается. Формула (14.13) состоит из хорновских импликаций
S, л давление (To4Ka_N, Высокое) л давление (точка_Ы, Высокое) л
л давление (ТочкаО1, р) л Высокое > р л давление (Точка Ы, Высокое) л
л давление (Точка_02, р) л Высокое > р) /\
л давление ( To4Ka_N, Высокое) л
л давление (Точка_\2, р) л Высокое > р выключить (насос,
насосная станция (To4Ka_N))],
где N = 1, 2, ..., 12.
336
14.5. Реализация
Предполагая, что все остальные формулы имеют такую же структуру и
являются аксиомами, определяющими взаимодействие среды и агента,
каждый шаг стратегии вывода можно сформулировать следующим образом.
Для всех текущих ситуаций S., начиная с начальной, получить восприятие
(множество значений входных переменных).
Конкретизировать, используя это восприятие, все импликации вида
5 л a z> действие (d).
Найти все импликации, левая часть которых S л а при осуществленной
конкретизации истинна.
Для каждой такой импликации считать выведенной ее ^правую часть
действие (d).
Сформировать реакцию агента, соответствующую конкретизированным
выведенным действиям d в правых частях импликаций 5 лаэ действие (d).
Использовать конкретизированные выведенные правые части (действия)
для нахождения следующих ситуаций по формулам переход (d, S) = 5.
Очевидно, что эта стратегия является стратегией прямого вывода в ширину
на основе обобщенного правила модус поненс со следующими отличиями:
часть, а может быть и все значения переменных, используемых для
конкретизации, берутся из восприятия агента, а не аксиоматизируются
заранее; процесс вывода может быть бесконечным.
14.5. Реализация
На этапе реализации решается множество практических вопросов
разработки выбранной архитектуры в виде конкретной программы или
аппаратуры. На этом этапе приходится осуществлять выбор инструментальных
программных и аппаратных средств для реализации системы, разработку
структуры системы, программирование, отладку. На рис. 14.9 показана
структура аппаратно-программных средств, реализующих архитектуру
одноагентной системы на рис. 14.1. Блоки системы, показанные на этом
рисунке, осуществляют следующие функции.
14.5.1. Блок управления
Телеметрические данные обновляются телеметрической системой сбора и
передачи каждые 10 с. Поэтому блок управления агента также обновляет свое
восприятие, получаемое от этой системы, каждые 10 с, синхронизируя это
обновление с телеметрической системой сбора и передачи. Делает он это,
используя таймер. Блок управления осуществляет также запуск программных
блоков системы, показанных на рис. 14.9: интерфейса с телеметрической
системой сбора, машины вывода, архиватора, интерфейса с оператором в
соответствии с определенной временной диаграммой между двумя соседними
восприятиями. Блок управления также синхронизирует свою работу с другими
программами, выполняемыми на том же процессоре (компьютере).
337
14. Реализация систем
Оператор
Рис. 14.9. Структура аппаратно-программных средств, реализующих архитектуру
одноагентной системы управления распределением и подачей воды
14.5.2. Интерфейс с телеметрической системой
Телеметрические данные, получаемые телеметрической системой сбора
и передачи, запоминаются ею в специальной области телеметрических
данных, доступ к которой агентом осуществляется на основе динамического
протокола обмена данными.
338
Вопросы и упражненеия
14.5.3. Блок значений
Блок значений хранит значения термов, вычисленных на очередном шаге
вывода.
14.5.4. Блок правил
Этот блок содержит все формулы (аксиомы), используемые для вывода.
14.5.5. Блок архива
В этом блоке, как и в блоке значений, хранятся значения термов,
полученных за несколько предыдущих шагов вывода.
14.5.6. Машина вывода
Этот блок осуществляет вывод, используя значения термов из блоков
значений и архива, на основе правил из блока правил. Полученные на
очередном шаге значения термов помещаются в блок значений.
14.5.7. Архиватор
Архиватор осуществляет перемещение значений из блока значений в блок
архива перед их обновлением в результате вывода и структуризацию этих
значений в архиве по времени и типам термов.
В случае мультиагентной системы каждый дополнительный агент может иметь
структуру, аналогичную структуре рассмотренного агента. Если агенты
взаимодействуют между собой, то для организации этого взаимодействия может
быть использован агент-менеджер. Агенты могут взаимодействовать и напрямую,
передавая сообщения друг другу, или через общие блоки значений.
Вопросы и упражнения
1. Назовите основные этапы реализации мультиагентных систем. Какие задачи
решаются на каждом этапе?
2. Сформулируйте перечень вопросов, которые могут быть использованы для
построения схем ситуаций на рис. 14.7, 14.8.
3. Вспомните задачу со средой чудовища, рассмотренную в главах 3, 4. В той
задаче был только один агент, целью которого являлось нахождение и вынос золота.
Чудовище все время находилось в одной и той же ячейке. Изменим условия задачи.
Будем считать, что чудовище является вторым агентом, способным блуждать по
ячейкам по тем же правилам, что и первый агент, с тем отличием, что он не может
определить местонахождение первого агента до тех пор, пока не окажется с ним в
одной ячейке. Он не может так же заходить в ячейку с золотом и теряет право
перемещаться, как только первый агент достигнет ячейки с золотом. Чудовище
съедает первого агента, если они оба оказываются в одной ячейке. Агенты совершают
действия по очереди, пока это возможно. Сделайте следующее.
339
14. Реализация систем
а) выберите архитектуру двухагентной системы для этой задачи;
б) постройте схемы ситуаций для каждого агента;
в) получите формулы, описывающие поведение каждого агента в среде;
г) сформулируйте цель первого агента, состоящую в достижении ячейки с золотом;
д) используя общий блок значений, покажите, существует ли вывод, в результате
которого первый агент достигает ячейки с золотом (из того же начального состояния,
которое приведено на рис. 2.3), если перывм действие совершает первый агент;
е) мформулируйте цель второго агента (чудовища), состоящую в уничтожении
или блокировании перемещений первого агента;
ж) используя общий блок значений, покажите, существует ли вывод, в результате
которого первый агент будет уничтожен или заблокирован, если первое действие по-
прежнему совершает первый агент.
4. Модифицируйте условия задачи со средой чудовища, введя дополнительную
возможность для первого агента застрелить чудовище, если оно находится в соседней
ячейке, первый агент знает об этом и стоит к чудовищу лицом.
ЗАКЛЮЧЕНИЕ
Обсуждается возможность создания думающих машин и некоторые требования
к мультиагентным системам искусственного интеллекта.
О возможности создания думающих машин
Предмет искусственного интеллекта тесно связан с вопросами, которыми
философы задаются на протяжении многих веков: «Как работает человеческий
мозг?», «Могут ли животные думать?», «Можно ли создать думающую машину?»
или «Может ли машина мыслить?» и т.п. Ответы на них волнуют философов и
до сих пор. Вопрос же о возможности создания мыслящей машины тесно связан
с искусственным интеллектом, а взгляд на него философов и специалистов в
области искусственного интеллекта зачастую не только неоднозначен, но даже
носит антагонистический характер. В настоящей книге детально не обсуждаются
большинство перечисленных вопросов, причины и суть упомянутого антагонизма.
Затронем лишь последний из них, непосредственно связанный с содержанием
учебника, а именно: «Может ли машина думать?» Прежде, чем отвечать на этот
вопрос, уточним смысл, вкладываемый в слово «думать», когда речь идет о
машине. Например, в нашем индустриальном мире вполне естественно услышать
такие фразы: «Самолет летает», «Автомобиль пожирает», «Корабль плавает»,
«Компьютер думает». Здесь глаголы «летает», «пожирает», «плавает», как и
глагол «думает», употребляются применительно к машинам различного типа и
означают совсем не то же самое, что в них вкладывается, когда речь идет не о
машинах, а о животном или человеке. Так, если мы говорим: «Птица летает»,
то это более или менее похоже на то, как это делает самолет, но если мы
говорим «Человек пожирает», то это совсем не похоже на то, как это делает
автомобиль, пожирая бензин. Аналогичная ситуация имеет место при
использовании слова «думать» по отношению к человеку и компьютеру.
При употреблении всех этих слов (думает, летает, плавает, пожирает) по
отношению к машинам очень много метафоричности. Когда мы говорим: «Мой
компьютер тупой. Он слишком долго думает, чтобы с ним можно было
нормально общаться», — то мы совсем не предполагаем, что машина способна
быть тупой, как человек, способна думать, как человек, и общаться, как человек.
341
Заключение
Появление у компьютеров свойств, напоминающих способность думать,
относится к 40-м гг. XX в. Но если определить способность думать как способность
рассуждать и принимать решения с помощью органического естественного мозга,
то следует заключить, что компьютеры не могут думать.
Алан Тьюринг в 1950 г. в своей известной книге «Вычислительные машины
и интеллект» предложил вместо того, чтобы спрашивать «Может ли машина
думать?», — разработать для нее некоторый тест на интеллектуальность. Он
предположил, что к 2000 г. компьютер с памятью 109 бит можно будет достаточно
хорошо запрограммировать, чтобы создавалось впечатление, что он думает. И
это оправдалось. Тьюринг также рассмотрел широкий спектр возражений,
касающихся возможности создания интеллектуальных (думающих машин).
Несмотря на то что эти возражения относились к середине 40-х гг. XX в.,
некоторые из них не сняты до сих пор. Рассмотрим ряд этих возражений.
Неспособность к творчеству
Под неспособностью к творчеству понимается отсутствие у машины
способности придумать что-нибудь заново, без указания свыше от программиста,
самостоятельно накапливать и обобщать данные, получаемые в процессе
наблюдения за средой. В настоящее время это возражение опровергается,
например, созданием современных программ для игры в шахматы, способных
самостоятельно совершенствовать свою игру, начиная с относительно слабой
квалификации.
Неспособность проявлять человеческие чувства
Под этой неспособностью понимается отсутствие у машины проявлений
доброты, дружбы, инициативы, юмора, склонности ошибаться, любить,
радоваться, размышлять о себе и т.п. Возражения по поводу неспособности
машины проявлять человеческие чувства во многом основаны даже на
современном этапе их развития с непониманием или неверием даже технически
образованных людей в способности машин извлекать с помощью датчиков,
имитирующих органы чувств человека, информацию из окружающей среды, а
также воздействовать на среду с помощью своих исполнительных органов подобно
человеку. На современном уровне развития компьютеров многие человеческие
чувства достаточно хорошо ими имитируются. Конечно, до создания полного
прототипа человека с его эмоциональным миром еще очень далеко, но это не
кажется чем-то нереальным.
Неспособность отвечать на определенные вопросы
Чаще всего это возражение основывают на так называемой теореме Геделя о
неполноте формальных систем (исчислений). Суть этой теоремы состоит в том,
что в любой непротиворечивой логической теории (формальном языке,
множествах аксиом и правил вывода) можно сформулировать истинное
предложение, которое в ней недоказуемо, т.е. недоказуемо с использованием
только исходных аксиом и правил вывода.
342
Неспособность отвечать на определенные вопросы
Более детально теорема Геделя о неполноте может быть пояснена на примере
логической теории натуральных чисел. В этой теории имеется единственная
константа 0 и единственная функция /, такая, что /(0) = 1, /(/(0)) = 2,
/(/(/(0))) = 3, ... Язык логической теории натуральных чисел содержит также
символы арифметических операций и обычный набор связок и кванторов. Любое
множество А истинных предложений а в языке этой логической теории можно
перенумеровать. Для этого достаточно упорядочить в лексикографическом
порядке сначала предложения длины 1, затем 2 и т.д., а затем присвоить каждому
из предложений а уникальный номер #а, который обычно называют геделевским
номером предложения. Доказательно теоремы Геделя в полном виде является
достаточно сложным. Но вполне убедительным рассуждением, свидетель-
ствующим о его справедливости, является следующее.
Предположим, что мы имеем множество А истинных предложений
(высказываний) относительно натуральных чисел. Помня, что каждое
предложение а е А имеет уникальный номер #а, обозначим #А множество всех
номеров предложений, входящих в А. Пусть а(#Ь, А) означает следующее
истинное высказывание: для доказательства предложения b с номером #Ь
недостаточно только аксиом рассматриваемой логической теории. Пусть теперь
b = а(#Ь, А) и b е А, тогда предложение b утверждает собственную недоказуемость
и является истинным в данной логической теории.
Допустим, что утверждение b доказуемо с использованием только аксиом
этой теории. Тогда наше исходное утверждение ложно. Следовательно, ложное
предложение b доказуемо в нашей теории. Но b е А, а это означает, что А
состоит не только из истинных предложений. Это противоречит определению
А. Следовательно, b недоказуемо в нашей логической теории. Но это именно
то, что утверждает Ь. Значит, предложение b истинно.
Поведение компьютера может быть представлено в некоторой логической
теории, поэтому на основе теоремы Геделя о неполноте логических систем можно
заключить, что всегда найдутся задаваемые машине вопросы, истинность которых
она установить не сможет. Это, конечно, справедливо. Но точно так же это
справедливо и по отношению к человеку, если считать, что при решении проблемы
(доказательстве теорем) он использует одну логическую теорию. На самом деле
наша интуиция подсказывает, что человек использует не одну логическую теорию,
а целый спектр теорий. При невозможности доказать теорему в одной из них он
переходит к другой, затем, если с ней ничего не получается, — к третьей и т.д. до
тех пор пока не удастся наткнуться на логическую теорию, которая позволяет
осуществить доказательство. Не видно никаких препятствий компьютеру делать
то же самое, перебирая или конструируя новую логическую теорию в попытке
доказать теорему (ответить на вопрос).
Мы затронули незначительную часть возражений, касающихся возможности
создания думающих машин. Грубо все возражения можно поделить на те, которые
выражают сомнения в технической осуществимости думающих машин, и те,
которые выражают принципиальную невозможность создания чего-то
эквивалентного по силе человеческому мозгу. Первые из этих возражений даже
на основании того, что уже было сказано, не очень убедительны и чрезмерно
пессимистичны. Зачастую, они высказываются людьми, не очень сведущими в
343
Заключение
теории искусственного интеллекта и современном уровне технологического
развития элементной базы компьютеров. Возражения второго рода на наш взгляд
также недостаточны. Зачастую их невозможно опровергнуть, но точно так же
невозможно строго доказать. К счастью, в наше время все эти возражения
практически не сказываются на развитии как практики, так и теории
искусственного интеллекта. И одна из важнейших тенденций его развития в
ближайшем будущем — это развитие мультиагентных систем. Какими же
главнейшими особенностями эти мультиагентные системы должны обладать?
Особенности мультиагентных систем
Мультиагентные системы должны помогать человеку в решении сложных
интеллектуальных задач и не проявлять своенравия в поведении там, где этого от
них не требуется. Для этого они должны удовлетворять ряду необходимых
требований. Наиболее значимыми из них являются следующие три.
Агент должен вести себя рационально. Под рациональным поведением
понимается такое поведение агента, когда на любое восприятие его реакция
является рациональной. Это очень расплывчатое определение. Что такое
рациональное поведение и реакция — определяет конструктор агента. Будем
полагать, что он это может всегда сделать. Конечно, рациональность поведения
зависит от типа среды и цели, поставленной агенту конструктором. Если агенту
поставлена цель ухаживать за газоном, то его поведение, когда он вместо того,
чтобы подстригать газон, начнет копать ямы на нем, не может считаться
рациональным.
Агент должен иметь такую стратегию вывода, которая расходует время,
необходимое для вычисления, рационально. Это требование менее субъективно,
чем предыдущее. Зачастую рациональный расход времени требует компромисса
между качеством решения и расходуемым временем. Иногда расход времени на
вывод считается рациональным, если он не превосходит некоторого предела.
Зачастую рациональным расходом времени считается такой расход, при котором
поведение агента происходит в реальном времени. Обычно, это означает, что
среда является динамической и ее состояния изменяются через определенные
интервалы времени. Агент должен воспринимать (распознавать) каждое из этих
изменяющихся во времени состояний среды и успевать вырабатывать реакцию
не позже, чем этот интервал закончится.
Агент должен иметь рациональную сложность реализации. Рациональная
сложность реализации предполагает, что число единиц (логических элементов,
программных команд, процессоров и т.п.), необходимых конструктору для
создания агента, либо оптимально, либо не превосходит некоторой величины,
либо еще каким-либо образом оценивается. Для того чтобы можно было
сконструировать агента, удовлетворяющего перечисленным требованиям,
необходимо иметь инструментарий, в основе которого лежат соответствующие
теоретические положения. Часть из них рассмотрена в настоящей книге. Чем
сложнее среда, с которой имеет дело агент, тем сложнее структура его знаний и
тем выше требуемый тип агента. Агент самого простого типа (комбинационный),
выдает реакцию в тот же момент времени, в который он осуществил восприятие.
Поэтому, если в задачу конструктора входит создание агента, поведение которого
344
Особенности мулътиагентных систем
должно происходить в реальном времени, то комбинационные и
последовательностные агенты — это то, что надо. Однако следует иметь в виду,
что как для четких, так и нечетких сред это может привести к увеличению
сложности реализации. Если же среда и структура знаний о ней очень сложные,
то представление этих знаний в виде, который требуется для комбинационного
и последовательностного агента, может оказаться непростым или даже
невозможным делом. Тем не менее, в любом случае путь от нерационального
расхода времени целенаправленными или целеустремленными агентами лежит в
направлении «переписывания» всей или части их базы знаний на язык
комбинационных или последовательностных агентов с учетом требований
рационального расхода времени и рациональной реализации. Это
«переписывание» связано с определенной структуризацией знаний, с
распределением задач между отдельными параллельно функционирующими
агентами, с введением некоторой иерархии и координацией поведения агентов
метаагентами.
В заключение хотелось бы сказать, что в настоящее время уже появился
современный инструментарий и технологии, использующие языки логических
исчислений для разработки онтологий и функционирующих на их базе
мультиагентных систем. Предлагаемая читателю книга является введением в
теоретическую подоплеку этих развивающихся технологий, яркую перспективу
которых в настоящее время уже никто не оспаривает. И наконец, автор считает
своим долгом отметить, что на стиль изложения материала книги и выбор ее
содержания оказала большое влияние книга Стюарта Русселя и Питера Норвига
«Искусственный интеллект. Современные методы».
Список литературы
I. Братко И. Программирование на языке Пролог для искусственного
интеллекта: Пер. с англ. М.: Мир, 1990.
2. Гаврилов М.А., Девятков В.В., Пупырев Е.И. Логическое проектирование
дискретных автоматов. Языки, методы, алгоритмы. М.: Наука, 1977.
3. Клини С. Математическая логика: Пер. с англ. М.: Мир, 1973.
4. Ковальски Р. Логика в решении проблем: Пер. с англ. М.: Наука,
1990.
5. Логический подход к искусственному интеллекту. От классической
логики к логическому программированию/ А. Тэйс, П. Грибомонт,
Ж. Луис и др.: Пер. с фр. М.: Мир, 1990.
6. Логический подход к искусственному интеллекту. От модальной логики
к логике баз данных/А. Тэйс, П. Грибомонт, Г. Халин и др.: Пер. с фр.
М.: Мир, 1998.
7. Лорьер Ж.-Л. Системы искусственного интеллекта: Пер. с фр. М.:
Мир, 1991.
8. Малпас Д. Реляционный язык Пролог и его применение: Пер. с англ.,
М.: Наука, 1990.
9. Новиков И.С. Элементы математической логики. М.: Физматгиз, 1959.
10. Переверзев В.Н. Логистика. Справочная книга по логике. М.: Мысль,
1995.
11. Поспелов Д.А. Ситуационное управление. Теория и практика. М.:
Наука, 1986.
12. Стерлинг Л., Шапиро Э. Искусство программирования на языке
Пролог: Пер. с англ. М.: Мир, 1990.
13. Хоггер К. Введение в логическое программирование: Пер. с англ. М.:
Мир, 1988.
14. Rich Е., Knight К. Artificial Intelligence. McGraw-Hill, New York, 1991.
15. Winston P.H. Artificial Intelligence. Addison-Wesley, Reading,
Massachusetts, Third Edition, 1992.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
А*- поиск 148
Агент 11
Аксиома 59
— ограничений 311
Алфавит 24
Аналитик 318
Аномальное нечеткое множество 243
Атом 55
Атрибут 221, 246
Б
База данных 222
— знаний 89
Базовое множество лингвистических
значений 264
Базовые
— аксиомы 213
— клаузы 97
— правила 213
Библиотечная функция 156
В
Введение квантора существования 68
Вершина восприятия 318
— реакции 318
— ситуации 318
Взаимное исключение доступа
к критической секции 192
Включение 244
Внешнее состояние 157
Внутреннее состояние 157
Внутренний алфавит 106
Возможность достижения цели 137
Восприятие 14, 318
Время 160
Входная переменная 14, 195
Входной алфавит 106
Вывод 23
Выводимость 29, 59
Выполнимая формула 29
Выполняемая последовательность 194
Выпуклое нечеткое множество 243
Выходная переменная 14
Выходной алфавит 106
д
Датчик 13
Двойная индукционная аксиома 240
Двунаправленный поиск 145
Дедлок 188, 202
Дедуктивная база данных 231
Действия 16, 158
Дейталог 230
Дейталог-правила 230
— программа 230
Детерминизации 116
Детерминированная среда 17
Динамическая среда 17
— формула 182
Дискретная среда 17
Добавочная переменная 195
Доведение до противоречия 99
Домен 221, 246
Дополнение 244, 249
Допустимая выполняемая
последовательность 196
Допустимая последовательность
действий 136
Допустимое вычисление 196
Допустимый критерий 148
— процесс 185
3
Заключение 28
Запрос 230
Законы логики высказываний 28
Замена переменной 83
Знания 14
И
Измеритель меры 159
Импликативная формула 28
347
Предметный указатель
Импликация 28
Имя схемы отношений 222, 246
Инвариантные свойства 197
Индивидная переменная 52
Индивидуальный предикантный
символ 67
Индукционная аксиома 169
Инициализируемое вычисление 196
Инициальное детерминированное
ситуационное исчисление 167
Интенсионал 231
Интервал 40
— значений 308
Интервальная форма 40
Интервью 318
Интерпретация 25, 59
Исключение квантора общности 67
--существования 67
Искусственный интеллект 11
Исполнительный орган 13
Истинностные значения 26, 52
Исчисление 30
— высказываний 30
Итеративный поиск в глубину 144
К
Категория 154
— действий 168
— объектов среды 168
— ситуаций 168
Квантор 55
— общности 56
— существования 56
Классическая формула 184
Классическое исчисление
высказываний 30
Классическое исчисление
предикатов 65
Клауза 97
Клаузальная форма 97
Комбинационный агент 14
Компетентные вопросы 308
Конкретизация 26, 222, 246
— переменной 83
Конкретизированная схема
отношений 222, 246
Конституента 33
Концептуализация 304
Конъюнктивная нормальная
формула 97
Критерий 146
Критическая секция 192, 202
Критическая ссылка на
переменную 189
Критическое событие 189
Л
Лингвистическая переменная 264
Лингвистическое значение
переменной 264
Литерал 55, 59
Логистика 13
Логическое исчисление 30
Локальный оптимум 151
м
Макроситуация 157
Материализация категории 154
Ментальные объекты 154
Мера 159
Микро восприятие 14
Микрореакция 14
Микроситуация 157
Минимальность 137
Многоагентная система 316
Многоместный предикат 60
Модальность 180
Модель 29, 59
— параллельных процессов
с распределяемыми
переменными 185
Модельные аксиомы 213
Модифицирующая ссылка 189
Монотонный критерий 149
Мультиагентная система 316
348
Предметный указатель
н
Направленный поиск 137
Натуральное исчисление
высказываний 31
Начальная ситуация 159
Начальное состояние 21, 106, 136
Начальный нетерминальный
символ 129
Невыполнимая формула 29
Недетерминированный автомат 118
Недетерминированная среда 17
Неклассическое исчисление 67
Неполная база данных 248
Неполное исчисление 93
Непрерывная среда 17
Непротиворечивое исчисление 93
Непротиворечивость 108
Нетерминал 128
Нетерминальная программа 198
Нечеткая база данных 247
— логика 243
— схема отношений 247
Нечеткозначное исчисление 259
Нормальное множество 243
Нормальная схема отношений 247
О
Обобщенная нечетная схема
отношений 247
Обобщенная резолюция 96
Обобщенное правило модус поненс 83
Обратный вывод 89
Общая цена 137
Общезначимость 59
Общезначимая формула 27
Объединение 244, 250
Объектная константа 52, 54
— переменная 52, 53
Ограничение целостности 239
Ограниченный поиск в глубину 143
Одноместный предикат 60
Ожидающее место 202
Онтология 303, 304
Операция концентрирования 273
— следования 250
— растяжения 273
Опровержение 99
Оптимальность 137
Основа 243
— схемы отношений 222, 246
Останов 202
Ответ на запрос 230
Отношение достижимости 181
Отношение эквивалентности 108
Оценочная функция 106
п
Переименование переменной 83
Пересечение 244, 250
План 291
Подцелевая формула 89
Поиск 23
— в глубину 142
— в ширину 138
Полная база данных 248
— конъюнкция 33
— стратегия вывода 93
Полное исчисление 93
— состояние 157
Полнота 108, 137
Порождающее правило 129
Последовательностный агент 11
Постановка задачи 23
Правила 59
— введения кванторов 66
— вывода 29
— единственности критической
ссылки 190
— перехода 279
Правильно построенная формула 25
Предикат 52
Предикатный символ 55
Предметная переменная 52
Предусловие входных переменных 196
— программных переменных 196
Принцип обобщения 244
Принципы планирования 291
349
Предметный указатель
Проблемно-ориентированный
язык 262
Программа 185
Программная переменная 195
Программные аксиомы 214
Простая формула 171
Пространство состояний 136
Противоречивое исчисление 93
Процент уверенности 267
Прямой вывод 89
— нечеткий вывод 246
Путь 136
Р
Равенство 58
Радиус поиска 143
Распознающий автомат 131
Распределяемое множество
переменных 185
Рассуждение 20, 23
Рациональная сложность реализации 344
Рациональное поведение 344
Рациональный расход времени 344
Реакция 13, 318
Реализация множества
последовательностей автоматом 107
Регулярность 108
Резольвента 96
Рекурсия 235
Реляционная база данных 230, 246
Решатель 14
С
Свободная переменная 57
Свойства доступности 205
Свойство безопасности 210
— беступиковости 205
— отзывчивости 206, 211
— предшествования 209
— программы 196
Связанная переменная 57
Семантика 24
Семафор 190
Сепарабельная схема отношений 247
Синтаксис 24
Синтаксические правила 264
Ситуационное исчисление 168
Ситуация 158, 194
Следствие 30
Слепой поиск 137
Сложность по времени 137
Сложность по памяти 137
Согласованные схемы 261
Сорт 156
Сортовая категория 156
Состояние 18, 157, 194
— базы 222, 246
— нечеткой базы данных 247
— среды 18
Состоятельные правила 30
Справедливая отзывчивость 213
— последовательность 195
Справедливость 193
Среда 13
Ссылка доступа к переменной 189
Стандартный предикат 156
Статическая среда 17
— формула 181
Степень ветвления 82
— истинности 243
— совместимости 245
— уверенности 243
Стратегия поиска 23, 137
— цели 136
Строка таблицы 222
Существенные переменные 39
Схема ситуаций 318
— отношений 222, 246
т
Таблицы истинности 26
Теорема 59
Терм 54, 176, 231
Терминал 128
Терминальная программа 198
— алфавит 128
Транзитивное замыкание 241
Триггер 227
Триггерное событие 227
350
У
Универсальное множество 243
Универсум 243
Унификация 84
Унифицированная формула 84
Условие 30
Условное предшествование 212
Ф
Факт 59
Финальное состояние 131
Формальная грамматика 129
Формальный язык 24
Формула 25
— нечеткозначного
исчисления 259
— временной модальной логики 184
Формулировка цели 22
Функторная функция 168
Функторный предикат 168
Функциональный символ 54
Функция 54
— выходов 106
— переходов 106
- Сколема 103
Предметный указатель
X
Хорновские формулы 84
ц
Целевая формула 59
Целевыбирающий агент 16
Целевые состояния 22
Целенаправленный агент 15
Цель 59
Цена поиска 137
э
Эксперт 318
Экспоненциальная оценка
сложности 139
Экстенсионал 231
Элементарная конъюнкция 32
Элементарный терм 54, 96
Я
Ядро 243
Язык 107
—, порождаемый грамматикой 130
Учебное издание
Информатика в техническом университете
Девятков Владимир Валентинович
СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА
Редактор ГА. Нилова
Художник С.С. Водчиц
Корректор О.Ю. Соколова
Компьютерная верстка И.Ю. Луканиной
Изд. лиц. ЛР№ 020523 от 25.04.97 г.
Подписано в печать 17.01.01. Формат 70x100/16. Печать офсетная.
Бумага офсетная. Гарнитура «Таймс». Усл. печ. л. 28.38. Уч.-изд. л. 29.
Тираж 3000 экз. Заказ № 1141
Издательство МГТУ им. Н.Э. Баумана.
107005, Москва, 2-я Бауманская ул., д. 5.
Отпечатано с оригинал-макета в ППП «Типография «Наука».
121099, Москва, Шубинский пер., 6.