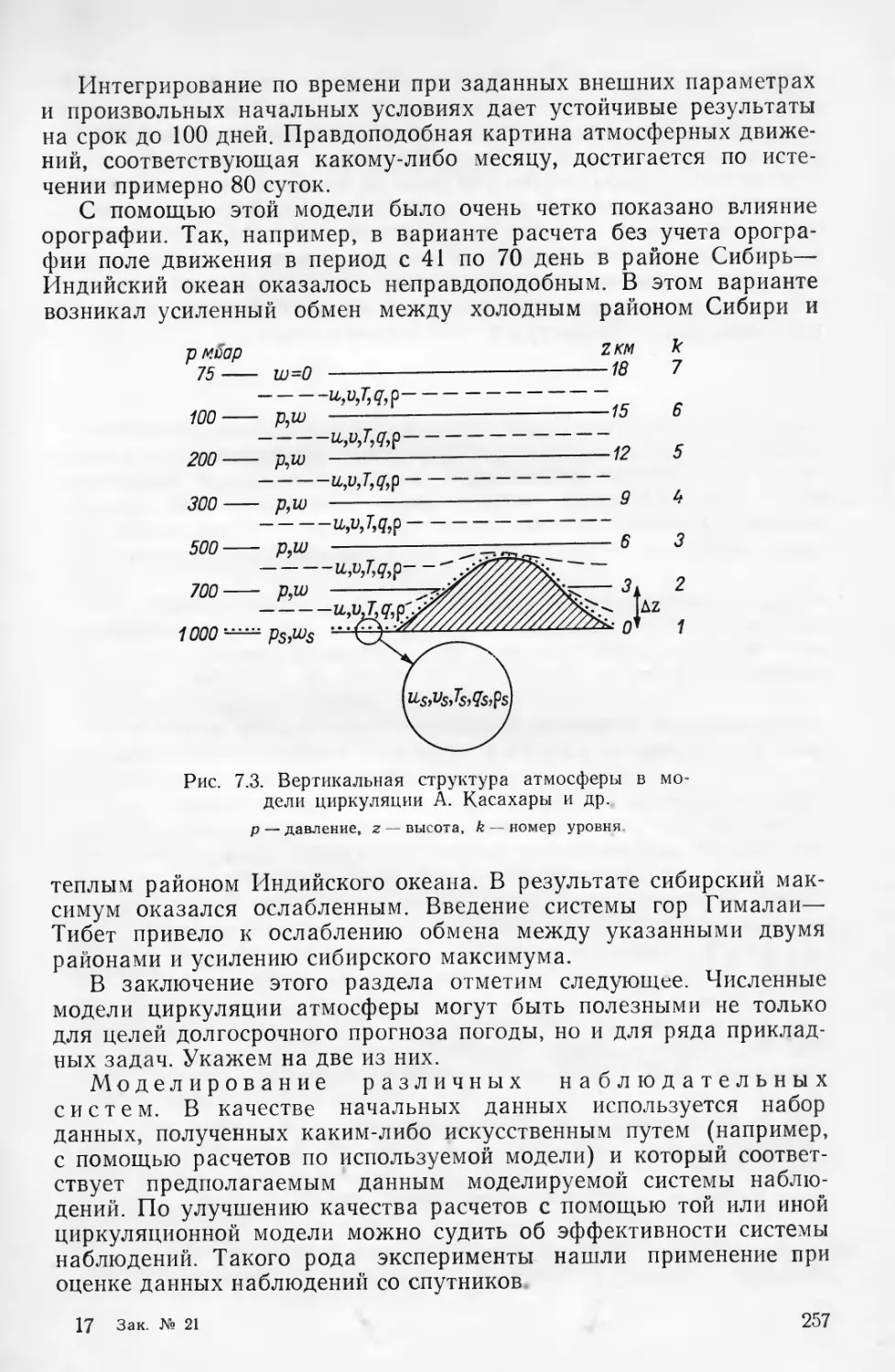
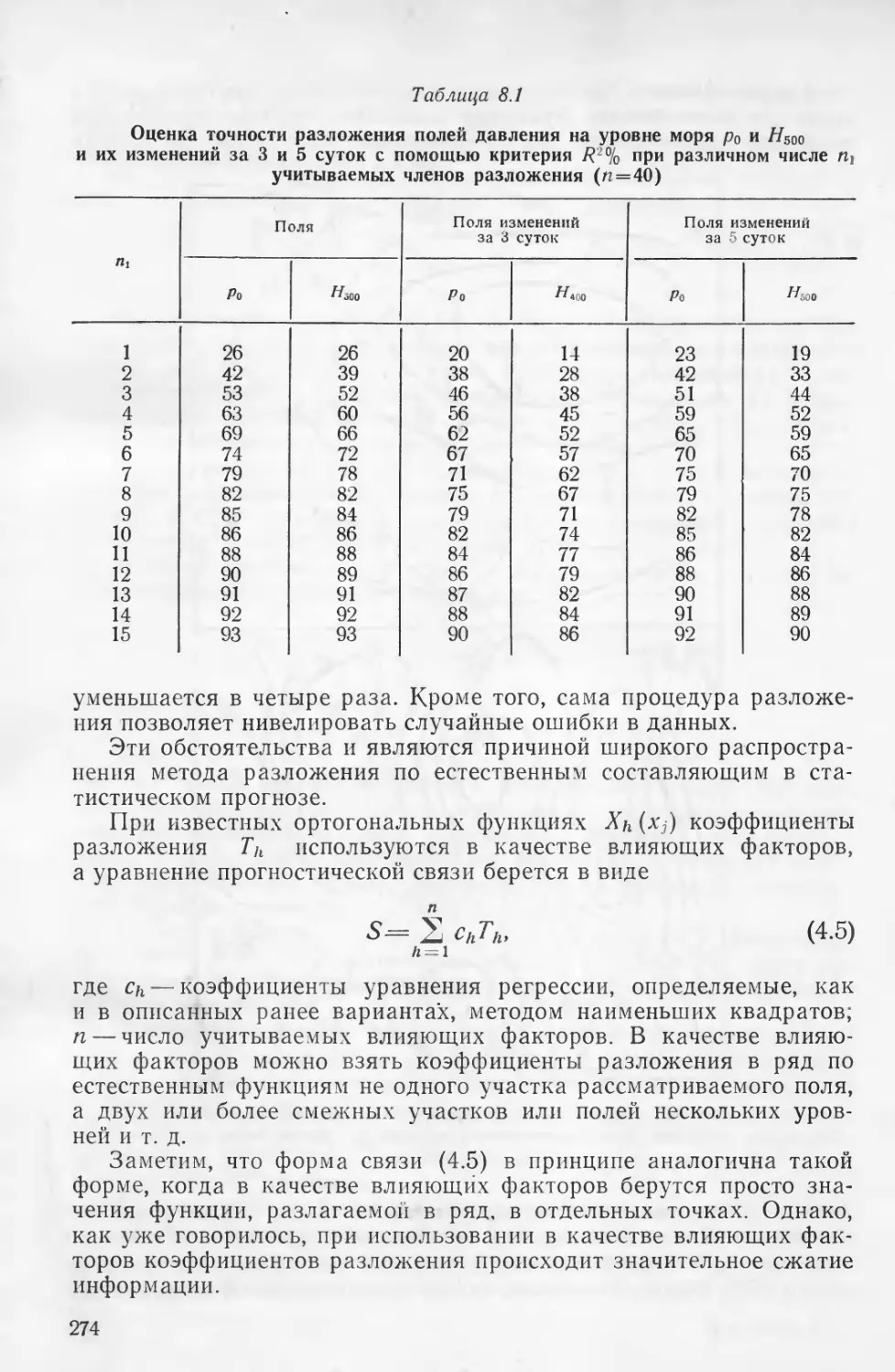
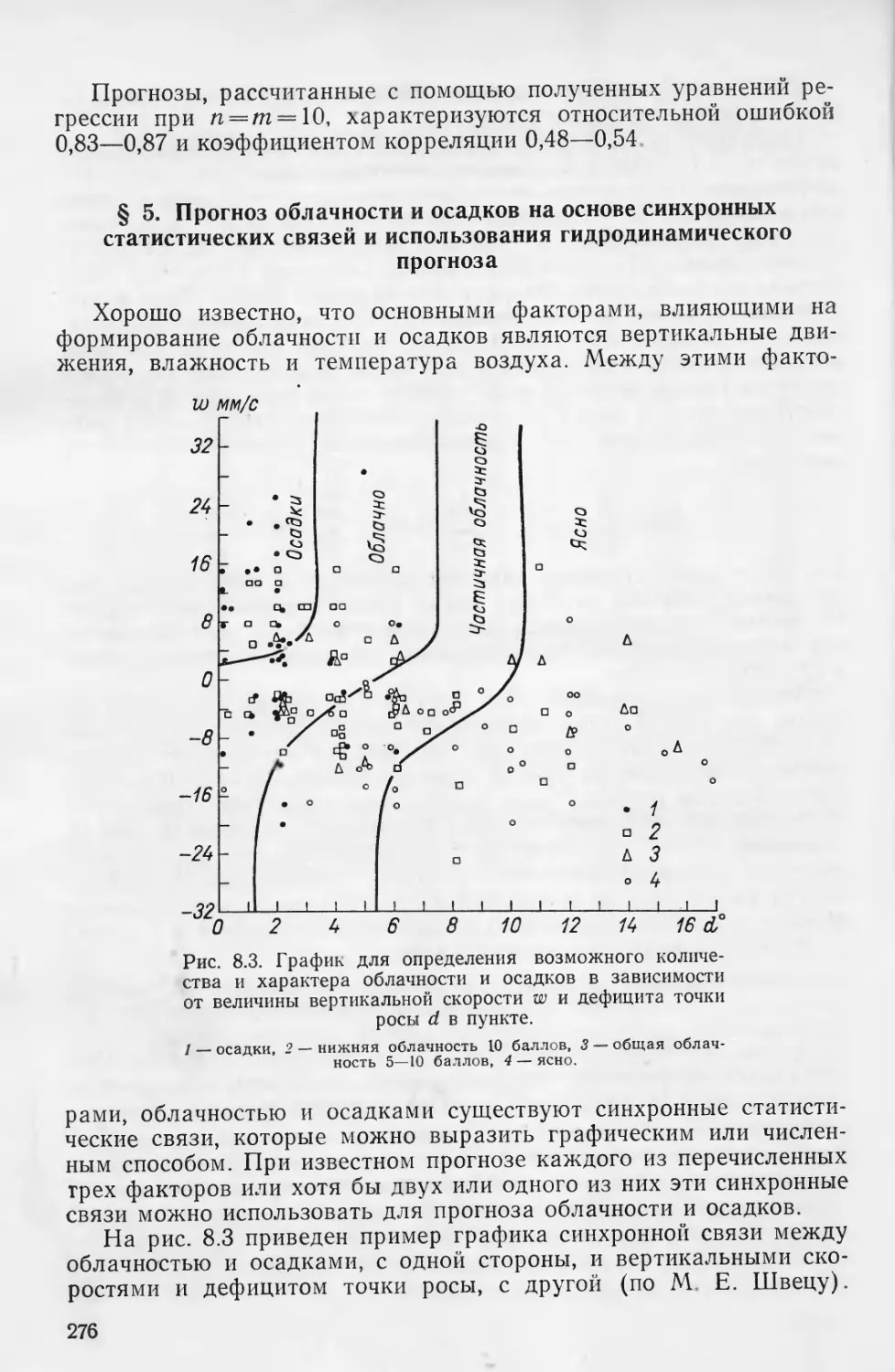
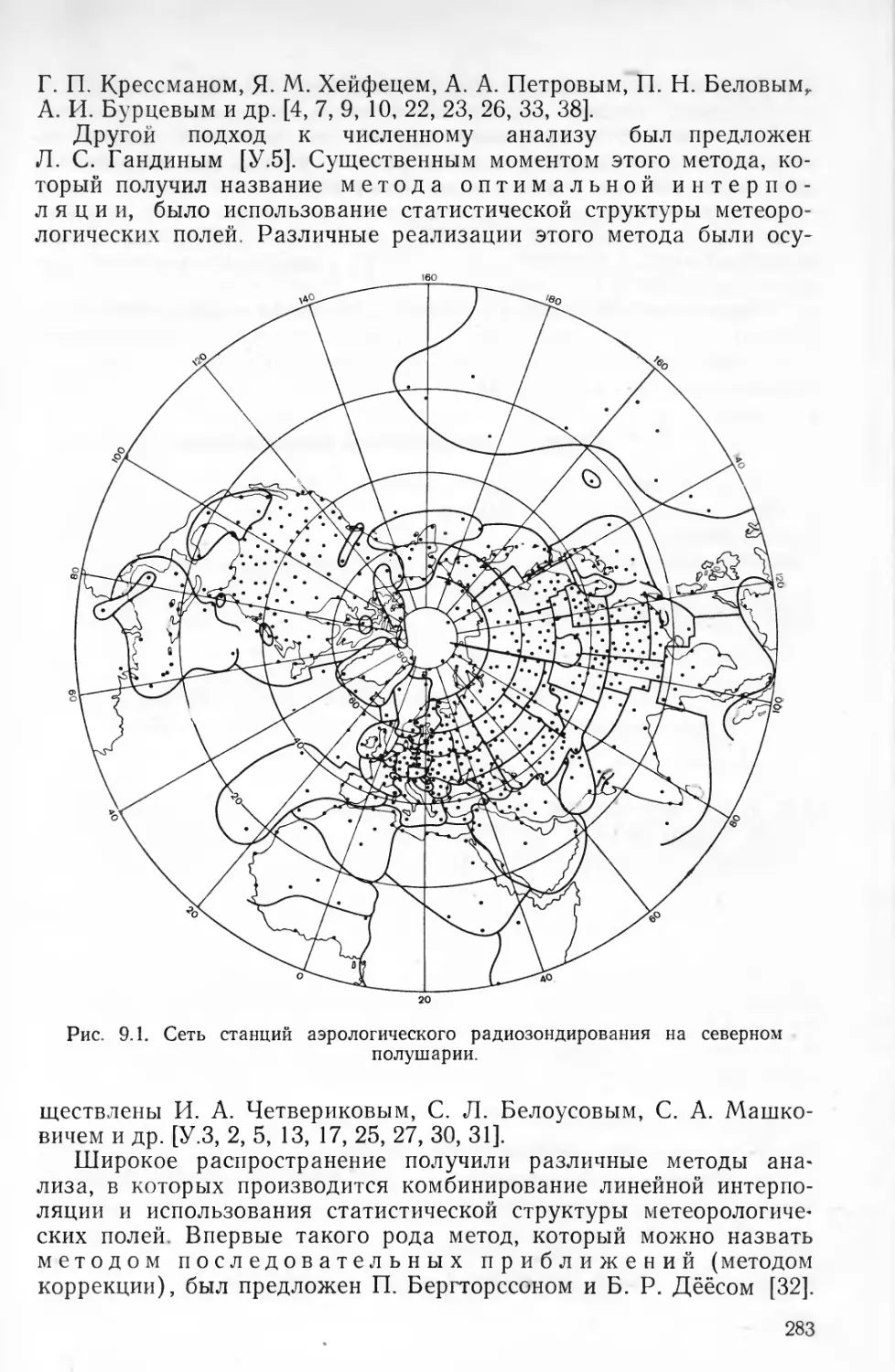
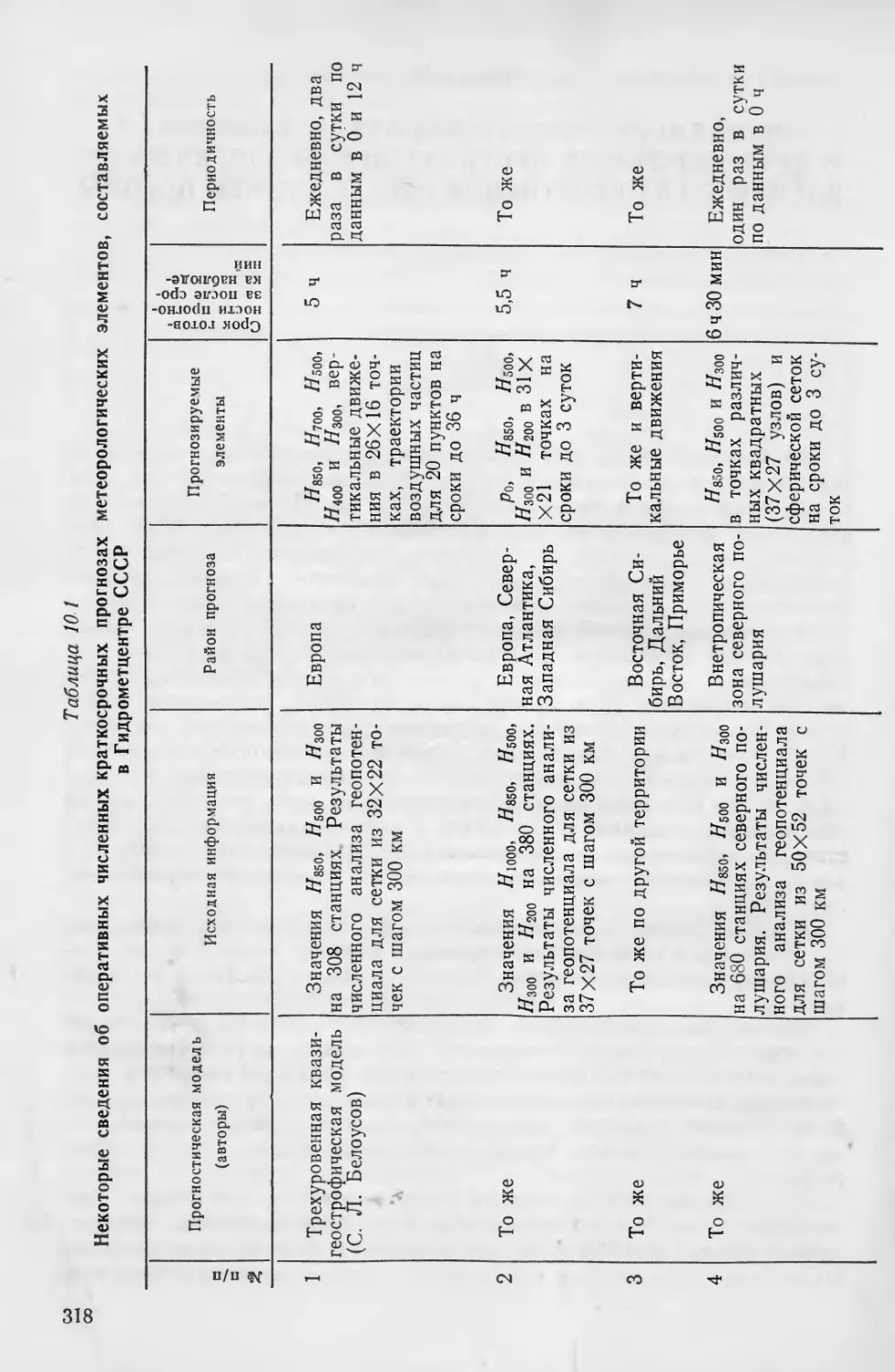
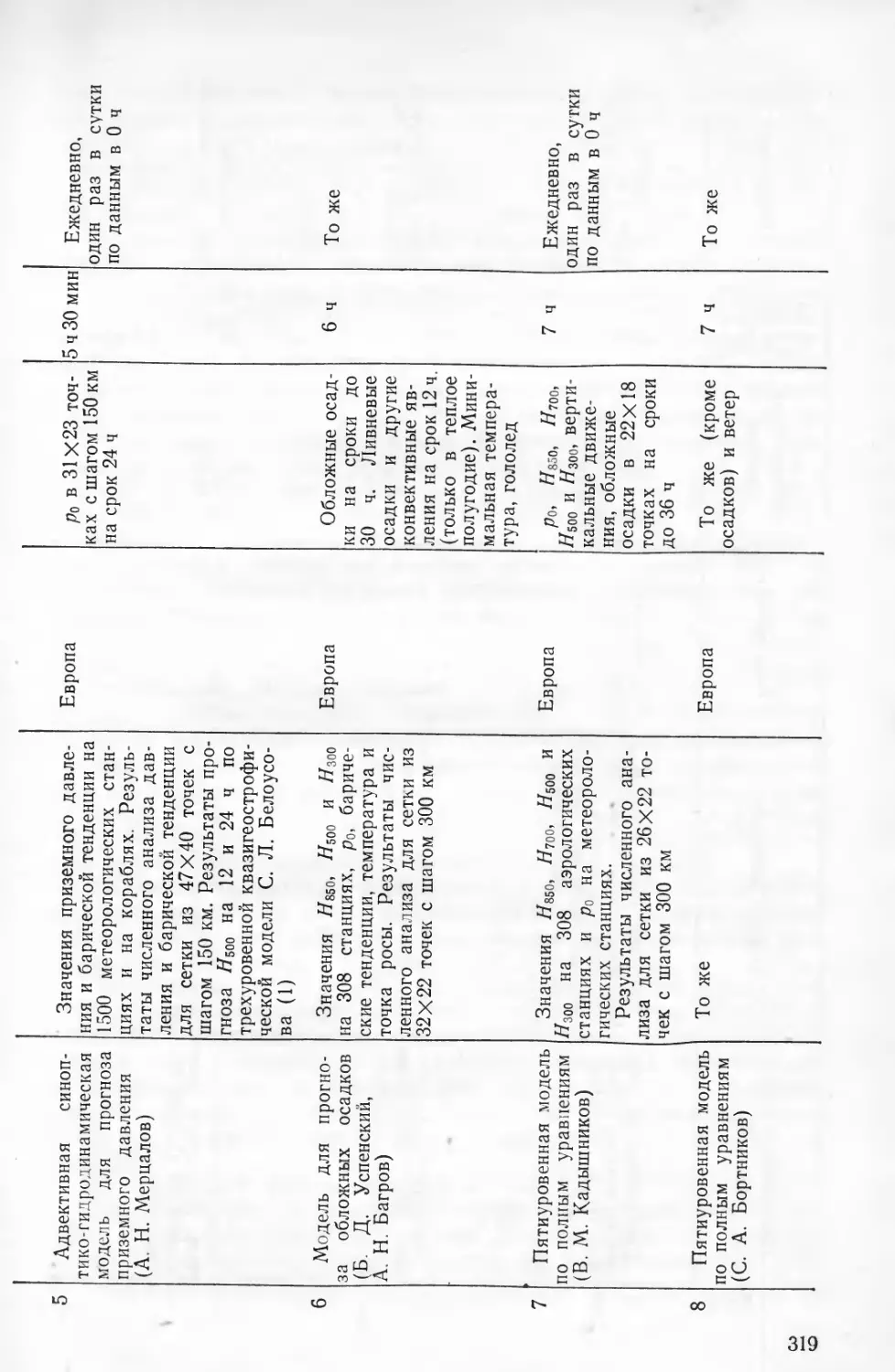
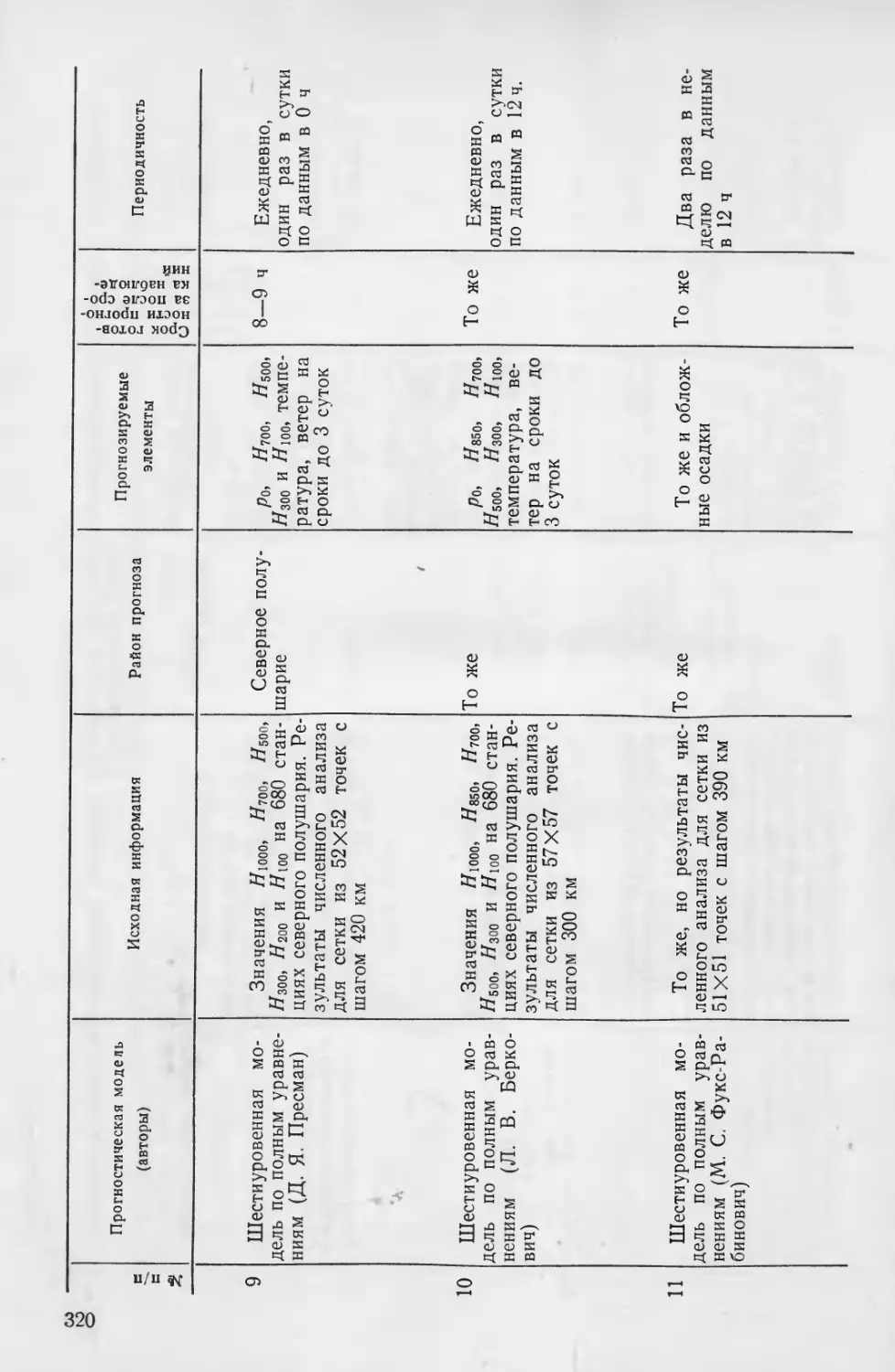
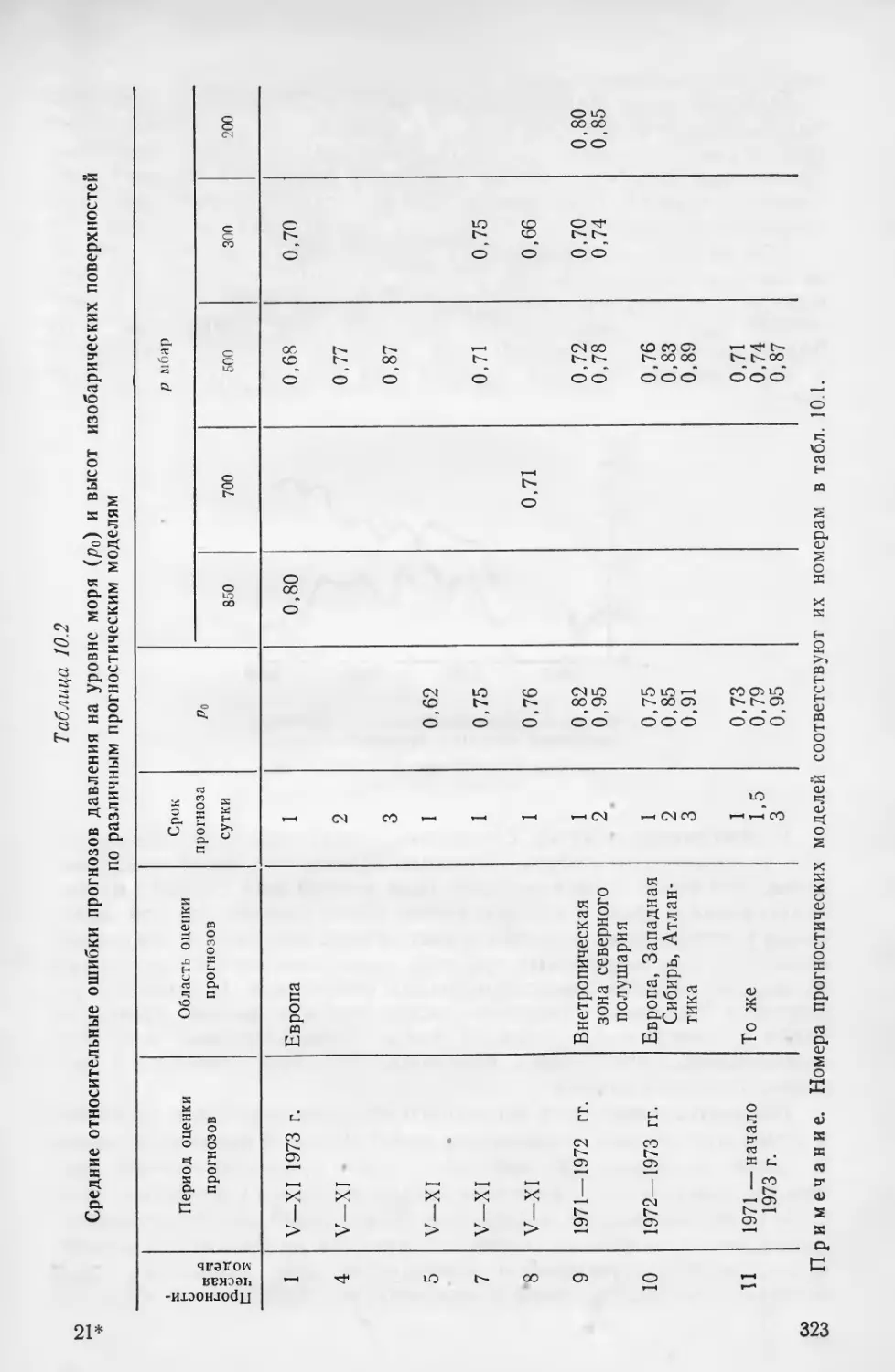
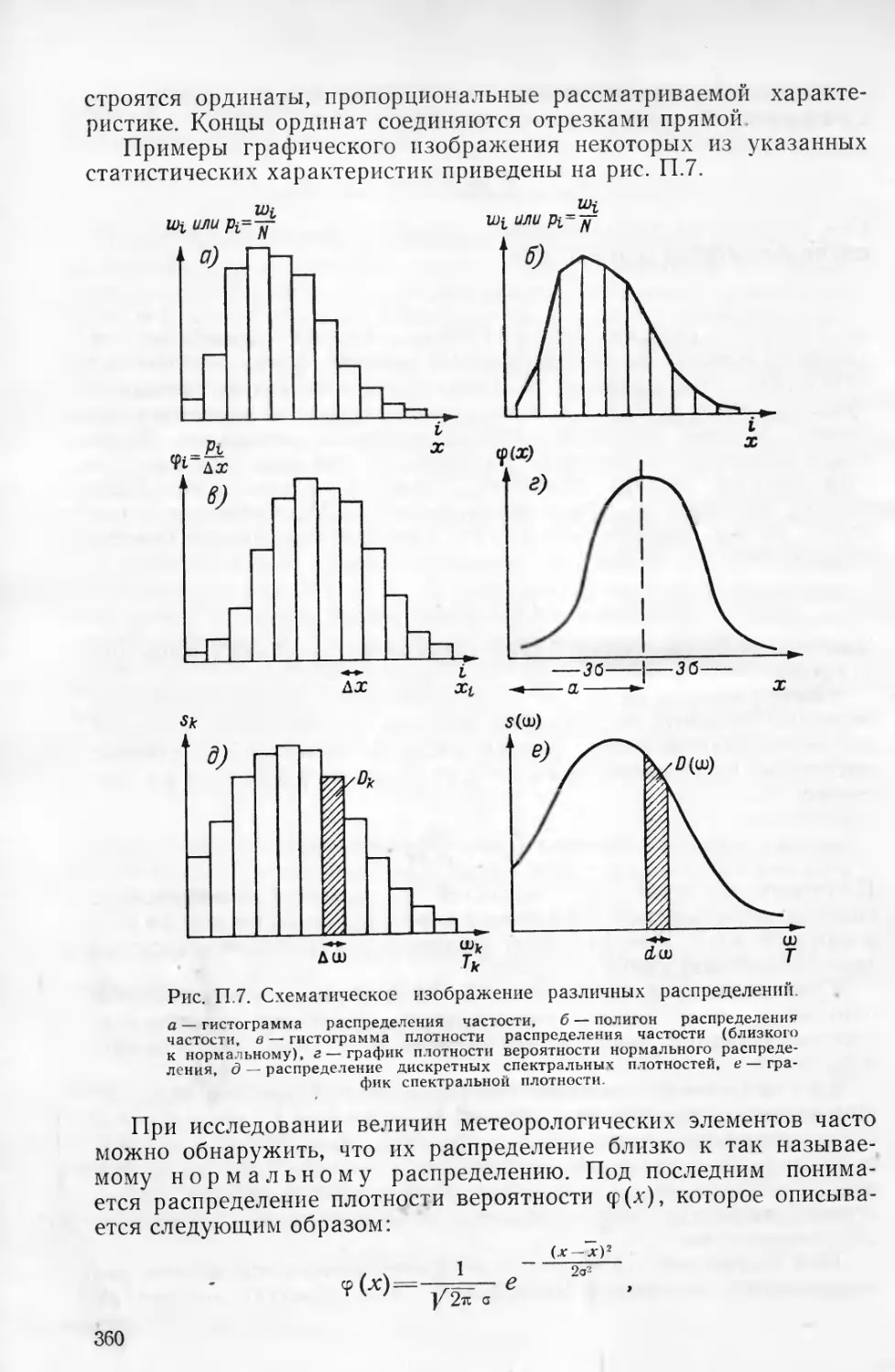
Текст
П.Н. БЕЛОВ
ЧИСЛЕННЫЕ МЕТОДЫ
ПРОГНОЗА ПОГОДЫ
П. Н. БЕЛОВ
ЧИСЛЕННЫЕ МЕТОДЫ
ПРОГНОЗА ПОГОДЫ
Допущено
Министерством высшего и среднего специального
образования СССР в качестве учебного пособия
для студентов университетов и гидрометеорологи
ческах институтов
ГИДРОМЕТЕОИЗДАТ • ЛЕНИНГРАД • 1975
УДК 551.509
Рецензенты:
Е. П. Борисенков (Главная геофизическая обсерватория им. А. И. Воейкова),
Л. С. Гандин, | А. С. Зверев | (Ленинградский гидрометеорологический
институт).
Ответственный редактор С. Л. Белоусов.
В книге изложены теоретические основы и методы численного прогноза погоды. Глав-
ное внимание уделено гидродинамическим методам. Из статистических методов рассматри-
ваются лишь те, которые по своей физико-математической основе и практической реализа-
ции имеют определенное сходство с гидродинамическими методами. Значительное внимание
уделено вопросам численного анализа метеорологической информации.
Для облегчения чтения книги, а также практического применения изложенных методов
в книгу включен ряд материалов справочного характера (единицы измерения физических
величин в различных системах, погрешности измерений метеорологических величин, данные
о пространственно-временном распределении и корреляционных зависимостях метеорологи-
ческих элементов, некоторые методы численного дифференцирования и интегрирования
и пр.).
Книга предназначена в качестве учебного пособия для студентов университетов и ги-
дрометеорологических институтов, аспирантов, слушателей курсов повышения квалификации,
инженеров метеорологов и пр Она может быть использована также и для самостоятельной
работы с целью изучения и применения на практике современных методов численного ана
лиза и прогноза погоды.
Предполагается, что читатель уже знаком с курсами высшей математики и метеоро-
логии в объеме программы для студентов гидрометеорологических институтов и географи-
ческих факультетов университетов.
This book deals with the theoretical foundations and methods of numerical weather
prediction. The main attention is paid to the hydrodynamic methods. From among the sta-
tistical methods only those are treated in the book which have certain similarity to the
hydrodynamic methods in their physico-mathematical basis and practical realization. Con
siderable attention is paid to the problems of numerical analysis of meteorological infor-
mation.
To facilitate the reading of the book and practical utilization of the methods discussed,
a number of reference aids have been included into the book (units for presentation of
physical values in different systems, errors in measuring meteorological values, the data on
time-space distribution and correlations of the meteorological fields, some methods of nu-
merical differentation and integration, etc.).
This book is intended as a training aid for students of universities and hydrometeorolo-
gical institutes, for postgraduates and for engineers in meteorology attending refresher
courses, etc. It might also be used for self-training to study the current methods of nume-
rical weather analysis and forecasting as well as to apply them in practice.
A reader is supposed to have a knowledge of the higher mathematics and meteorology
courses within the syllabi compiled for the students of the hydrometeorological institutes and
geographical faculties of the universities.
20807-133
Ь 069(02)-75 2"75
(6) Гидрометеоиздат, 1975 г.
ОТ АВТОРА
В основу данного учебного пособия положены лекции по числен-
ным методам прогноза погоды, читавшиеся автором на географиче-
ском факультете Московского государственного университета
в 1970—1974 гг. и на курсах повышения квалификации инженеров-
метеорологов при Гидрометцентре СССР в течение ряда лет.
На содержание учебного пособия оказали большое влияние на-
учные взгляды и труды чл.-корр. АН СССР И. А. Кибеля — осново-
положника численных методов краткосрочного прогноза погоды и
чл.-корр. АН СССР Е. Н. Блиновой, положившей начало числен-
ным методам долгосрочного прогноза погоды.
Автор пользовался советами и рекомендациями академика
АН УзССР В. А. Бугаева, педагогическая и организаторская дея-
тельность которого способствовала широкому внедрению числен-
ных методов прогноза в практическую деятельность службы по-
годы.
В связи с быстрым развитием нового раздела метеорологии,
каким являются численные методы прогноза погоды, автор стре-
мился делать упор на изложение общих теоретических основ ана-
лиза и прогноза погоды. Описание конкретных прогностических
моделей, число которых быстро растет, дается лишь в качестве
иллюстраций.
Отсутствие в учебниках по общей и динамической метеороло-
гии ряда эмпирических данных об атмосфере и специального ана-
лиза уравнений гидротермодинамики и их модификаций для целей
численного прогноза погоды потребовало включения их в данную
книгу.
Список литературы состоит из двух частей: в первой части при-
ведены сведения об учебниках, учебных пособиях, а также моно-
графиях, которые могут быть использованы в качестве учебных
пособий (ссылки на эту часть списка литературы снабжены бук-
вой У); во второй части списка приводятся сведения о работах,
посвященных тому или иному конкретному вопросу, рассматри-
ваемому в отдельных главах.
Нумерация формул двойная: на первом месте указан номер
параграфа данной главы, на втором — их порядковый номер вну-
три каждого параграфа. Рисунки и таблицы пронумерованы по
главам: на первом месте дан номер главы, на втором — номер
внутри главы.
§ 2—6 и 8—9 главы V написаны совместно с Л. В. Берковичем,
а § 6 главы IX и глава X — с С. Л. Белоусовым.
Автор признателен Ё. Н. Блиновой, В. А. Белинскому, Е. П. Бо-
рисенкову, М. И. Юдину, Л. С. Гандину, Л. В. Берковичу, В. В. Бы-
кову, А. Ф. Кивганову и другим лицам, сделавшим в процессе ра-
боты над рукописью ряд полезных замечаний, а также С. Л. Бе-
лоусову, взявшему на себя труд по редактированию книги.
1*
ВВЕДЕНИЕ
К началу шестидесятых годов влияние научно-технического про-
гресса серьезно изменило характер работы ряда звеньев службы
погоды. Созданы и действуют принципиально новые наблюдатель-
ные системы за погодой. Наиболее ярким примером является си-
стема наблюдений за погодой с метеорологических искусственных
спутников. Функционируют автоматические метеорологические
станции, на которых измерение метеорологических элементов, ко-
дировка и передача данных в радиометеорологические центры
производится без участия человека.
Наиболее глубокие изменения, имеющие далеко идущие послед-
ствия, произошли в самых главных звеньях службы погоды —
в прогностических центрах. От качественных методов прогнозиро-
вания был сделан переход к численным методам, основанным на
теоретических исследованиях И. А. Кибеля, Е. Н. Блиновой,
А. М. Обухова, Г. И. Марчука, Н. И. Булеева, А. С. Монина,
М. И. Юдина, Л. С. Гандина, Н. А. Багрова и др. в СССР, Н. Фил-
липса, Дж. Чарни, К. Хинкельмана, Дж. Смагоринского и др. за
рубежом.
Труды этих ученых и в первую очередь И. А. Кибеля составили
основу нового раздела метеорологии, получившего название чис-
ленных методов прогноза погоды. Его главной задачей является
разработка количественных методов анализа и прогноза атмосфер-
ных процессов п погоды, основанных на точных или приближенных
(численных) решениях уравнений гидротермодинамики и примене-
нии математической статистики.
В Советском Союзе с 1962 г. прогноз высотного барического
поля, являющийся основой всех прогнозов погоды, стал состав-
ляться исключительно численными методами на электронных вы-
числительных машинах. В дальнейшем этими же методами стали
рассчитывать барическое поле у земной поверхности, ветер и тем-
пературу по уровням и осадки.
Научно-технический прогресс глубоко затронул систему пере-
работки данных наблюдений. Эта система становится все более ав-
томатизированной.
Можно предполагать, что уже в недалеком будущем служба
погоды преобразуется еще более основательно. Специализирован-
ные измерительные комплексы будут автоматически производить
измерения метеорологических элементов, осуществлять их первич-
4
ную обработку и передавать в местные (региональные) радиоме-
теорологические центры. В этих центрах принятая информация
пройдет следующий этап обработки, будет комплектоваться для
передачи в другие радиометеорологические центры. Часть этой ин-
формации, а также информации, принятой от других радиометео-
рологических центров, будет использована для составления спра-
вок о текущей погоде, а также краткосрочных прогнозов по дан-
ному региону. Как справки, так и прогнозы будут готовиться
и передаваться вычислительным комплексом.
Справки о погоде и прогнозы по большим территориям или по
всему земному шару, а также долгосрочные прогнозы погоды бу-
дут составляться в наиболее крупных метеорологических центрах,
оснащенных высокопроизводительными вычислительными маши-
нами.
Службы погоды отдельных государств нуждаются в гидрометео-
рологической информации со всего земного шара (или же с его зна-
чительной части). Это обстоятельство привело к созданию Всемир-
ной службы погоды (ВСП), действующей в рамках Всемирной
метеорологической организации (ВМО).Всвязи с этим автоматизи-
рованные вычислительные комплексы отдельных стран должны
«стыковаться» между собой в смысле возможности обмена дан-
ными наблюдений и различной прогностической и другой инфор-
мацией.
Необходимо, однако, подчеркнуть, что как бы ни были совер-
шенны средства наблюдений и вычислительная техника и как бы
не была высока степень автоматизации, принятие решений оста-
ется за человеком, который должен иметь возможность в любой
момент вмешаться в работу автоматизированных систем, создан-
ных в стране и в рамках ВМО. Поэтому служба погоды требует
высококвалифицированных специалистов, хорошо знающих теоре-
тические основы и методы численного анализа и прогноза погоды,
а также практические стороны работы ее подразделений по опера-
тивному прогнозированию.
Глава I
НЕКОТОРЫЕ ХАРАКТЕРИСТИКИ АТМОСФЕРЫ
И АТМОСФЕРНЫХ ДВИЖЕНИЙ
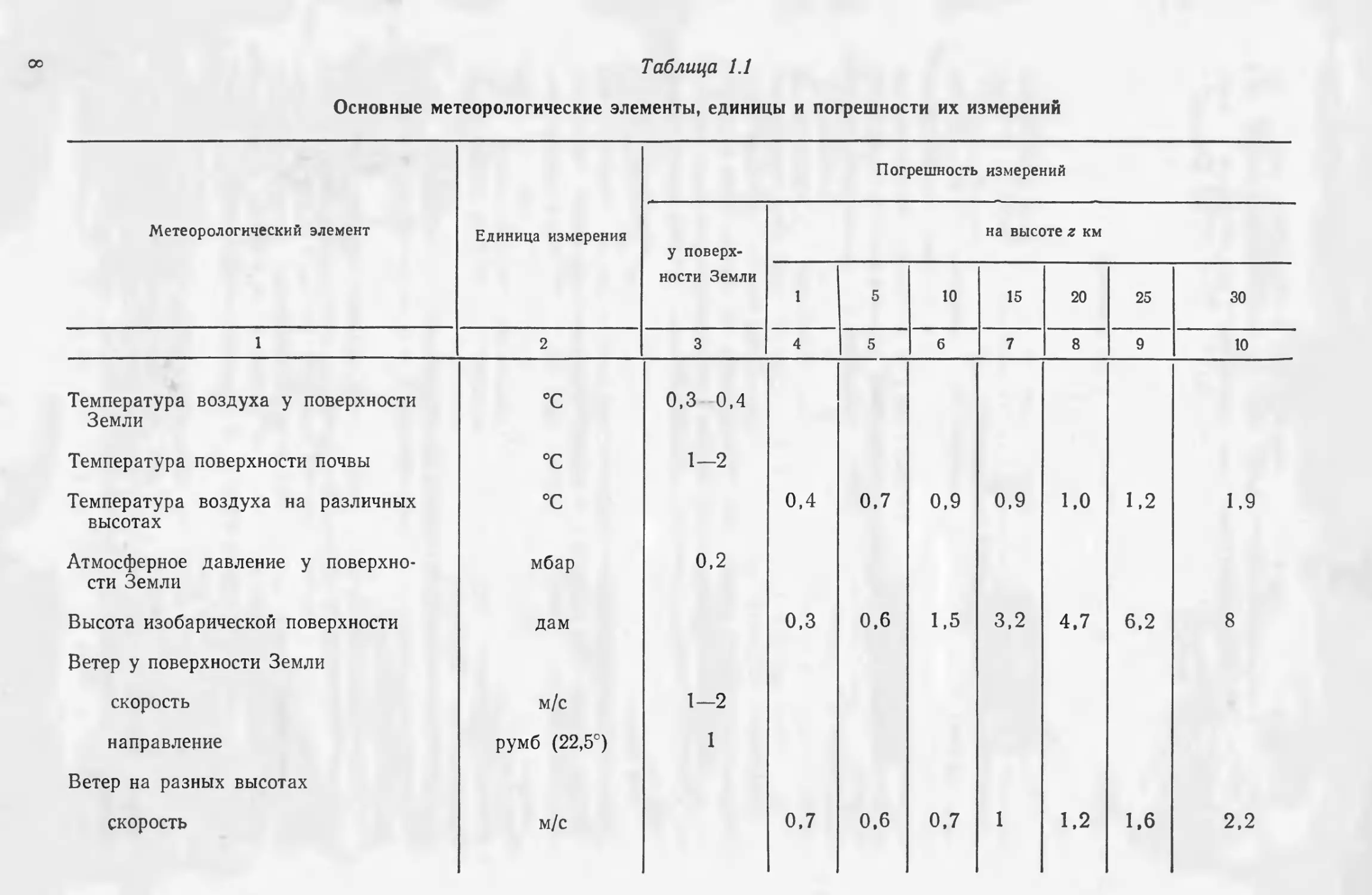
§ 1. Метеорологические элементы и точность их измерения
Состояние атмосферы и поверхности суши и моря можно оха-
рактеризовать с помощью ряда параметров, называемых метеоро-
логическими элементами. Перечень основных метеорологических
элементов, с которыми приходится иметь дело при прогнозе погоды,
приведен в табл. 1.1. Там же даны сведения о единицах и точности
измерений [10]. Под последней подразумевается средняя квадра-
тическая ошибка измерений.
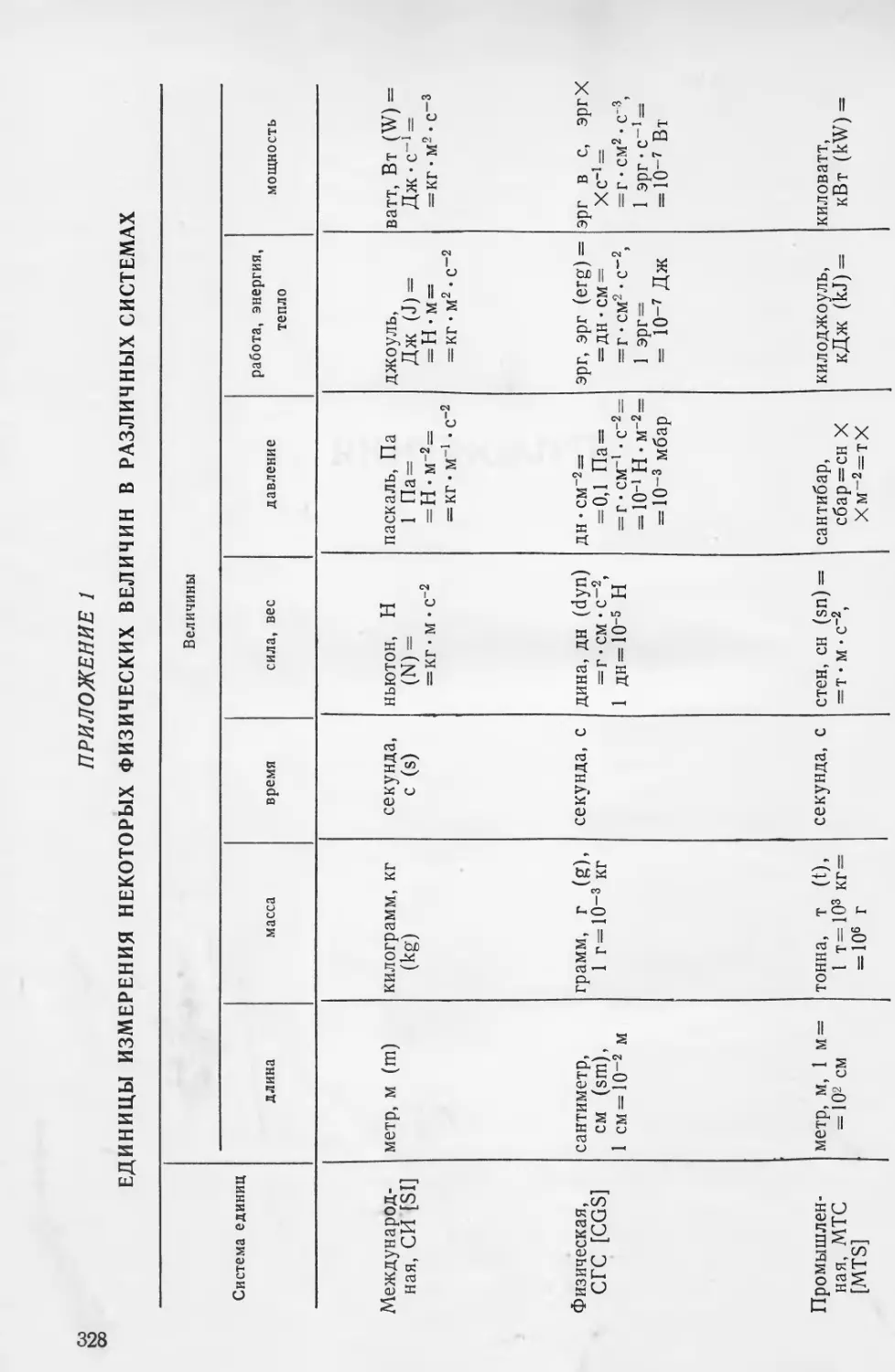
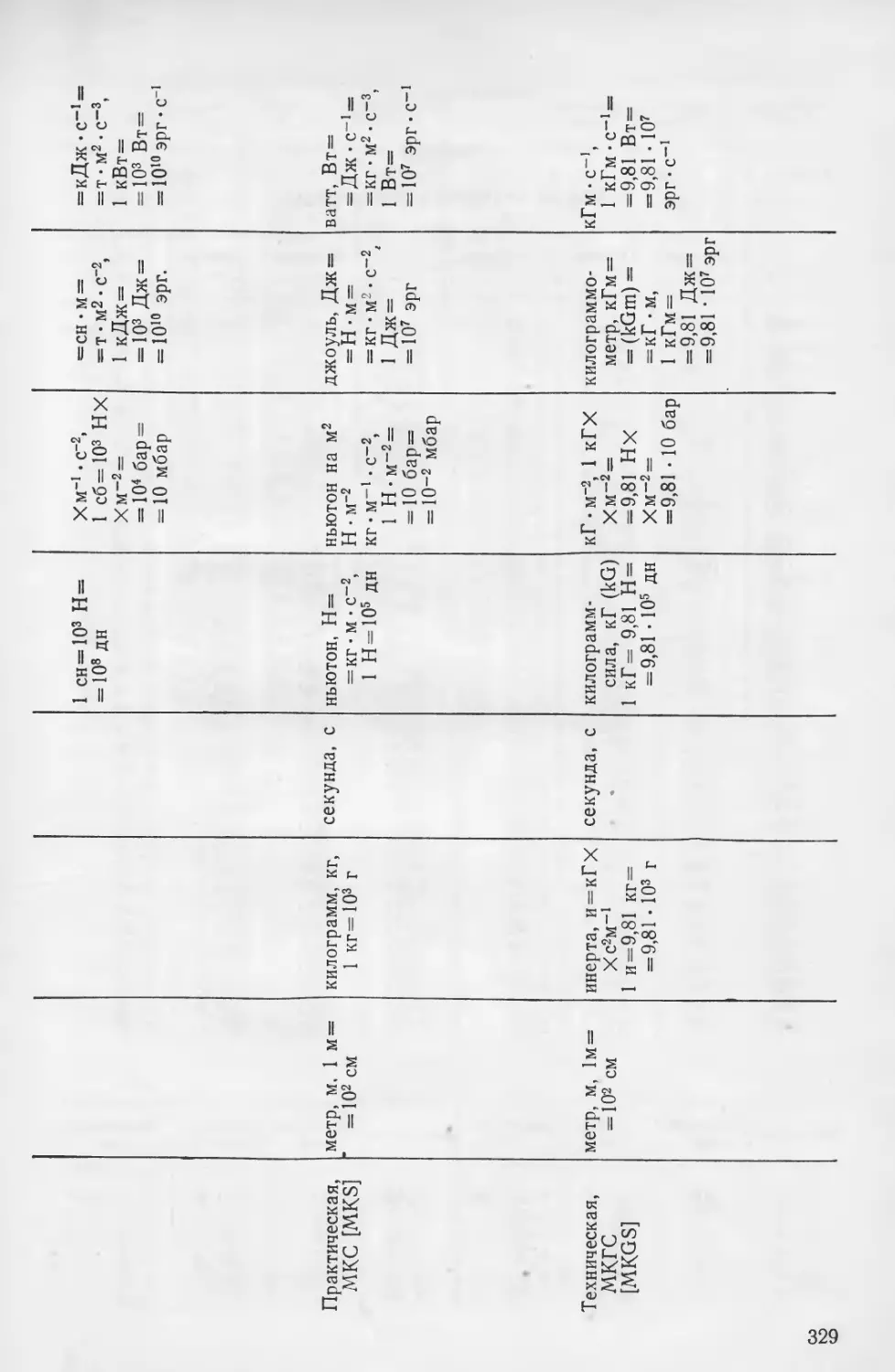
В качестве единиц измерения в табл. 1.1 приводятся единицы,
которые чаще всего используются в практике метеорологических
наблюдений в службе погоды СССР. Некоторые из этих единиц не
входят ни в одну из применяемых в науке и технике систем, т. е.
являются внесистемными. В задачах же численного прогноза по-
годы значения метеорологических элементов выражаются в какой-
либо системе единиц. Наиболее широко используются следующие
системы: промышленная—МТС (MTS), физическая — СГС (CGS),
техническая — МКГС (MKGS), а также международная система
СИ [4].
В приложении I приведены основные единицы указанных си-
стем, а также коэффициенты перехода от первых из этих систем
к Международной системе единиц СИ. С помощью приведенных
в приложении данных можно получить производные единицы,
а также осуществить переход от любой из указанных систем
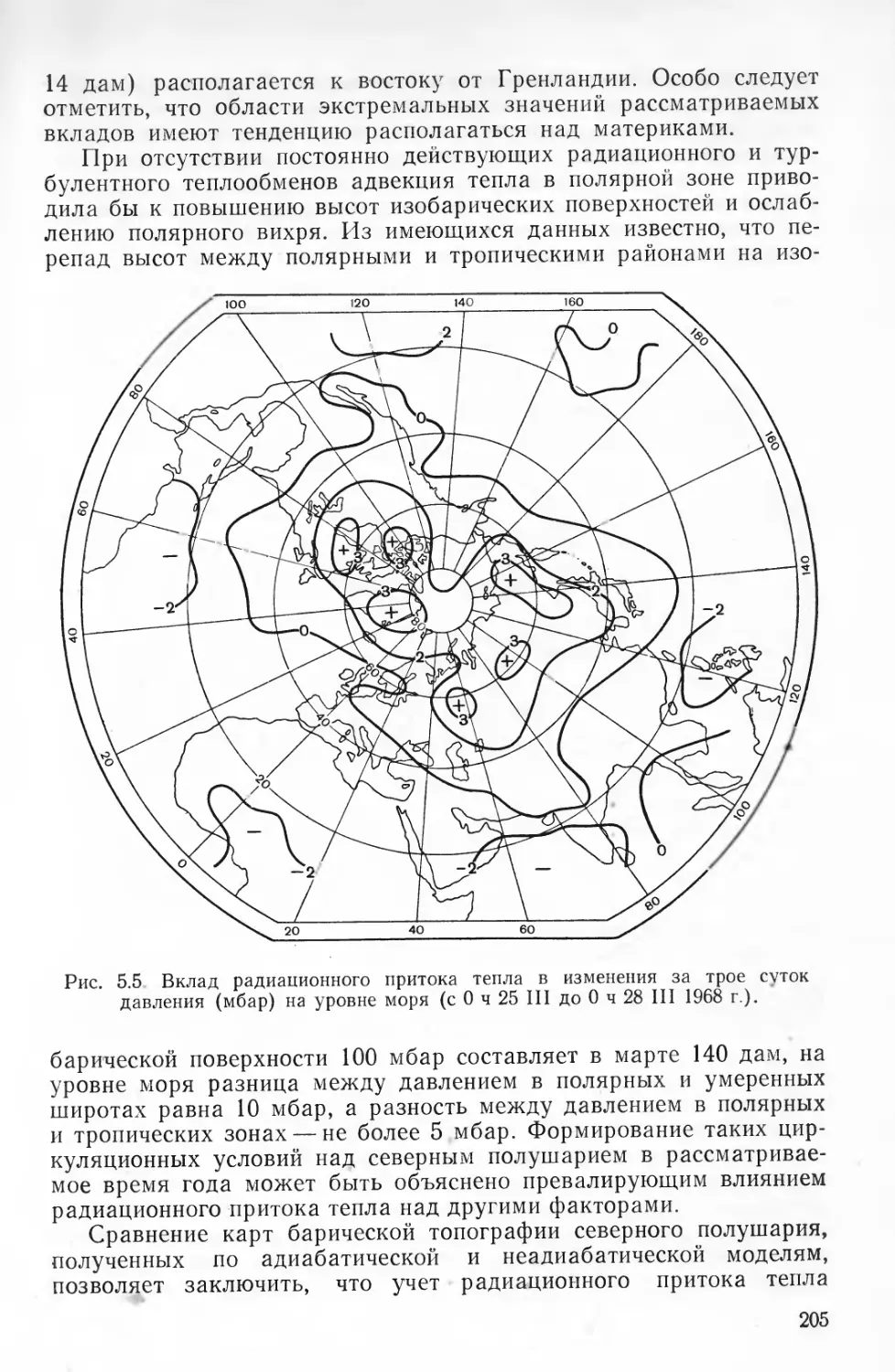
к другой.
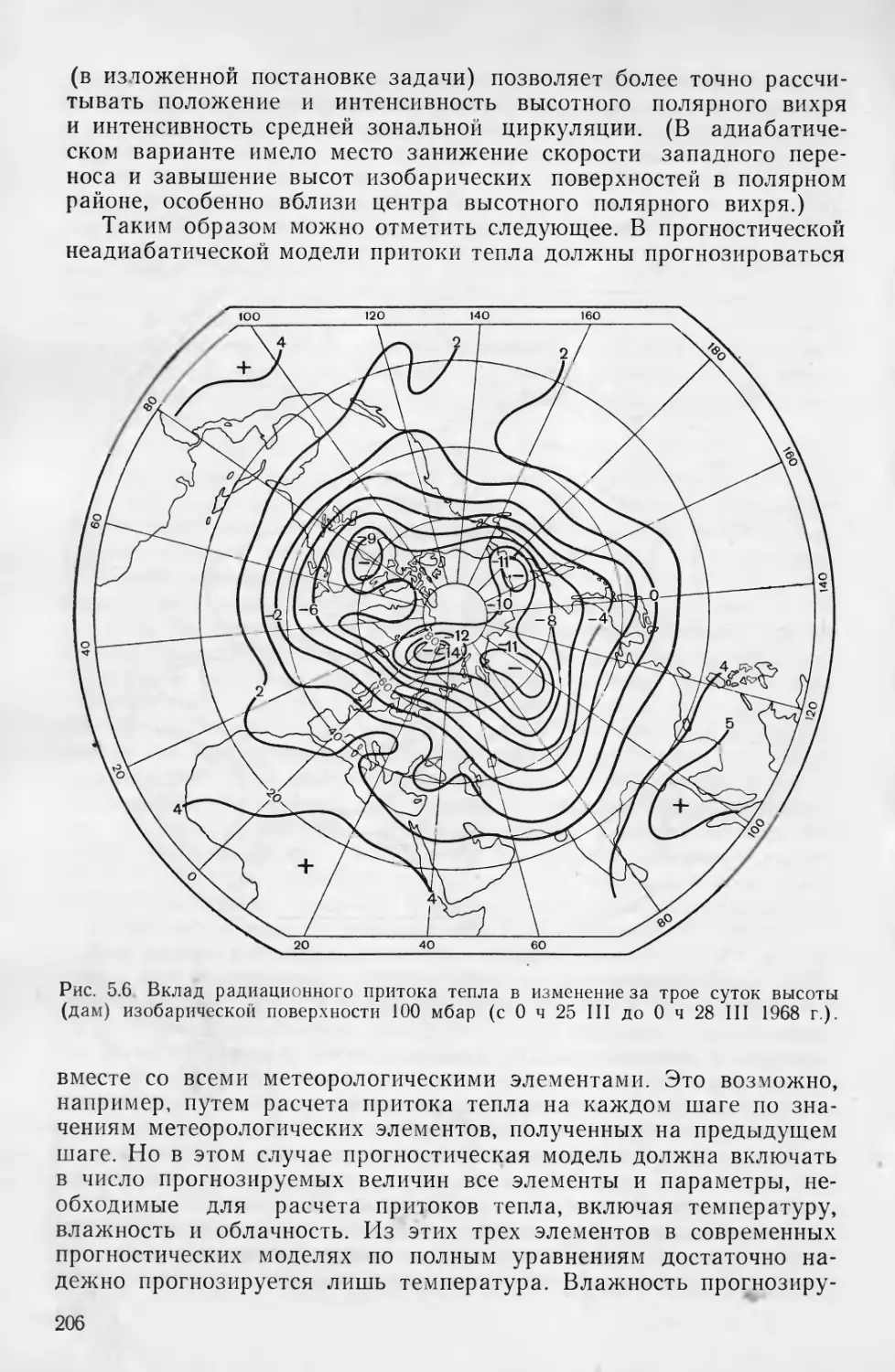
Ниже приводятся некоторые из применяемых внесистемных еди-
ниц измерения давления и дается их связь с единицами систем
и между собой:
мбар (миллибар) = 102 Н-м-2=103 дин• см~2 = 0,75 мм рт. ст.=
= 10”1 сбар (сантибар);
мм рт. ст. (миллиметр ртутного столба) = 133,3 Н • м~2 =
= 1,333 мбар;
атм (атмосфера физическая нормальная) = 1,013 • Ю5 Н-м~2 =
= 1013 мбар = 760 мм рт. ст. = 1,013 дин • см~2;
ат (атмосфера техническая) =9,81 • 104 Н«м-2 = 981 мбар =
= 735 мм рт. ст. = 1 кГ • см-2.
6
Энергия, или работа часто выражается в калориях (кал). При
этом 1 кал соответствует 4,187-107 эрг = 4,187 Дж = 0,427 кГм
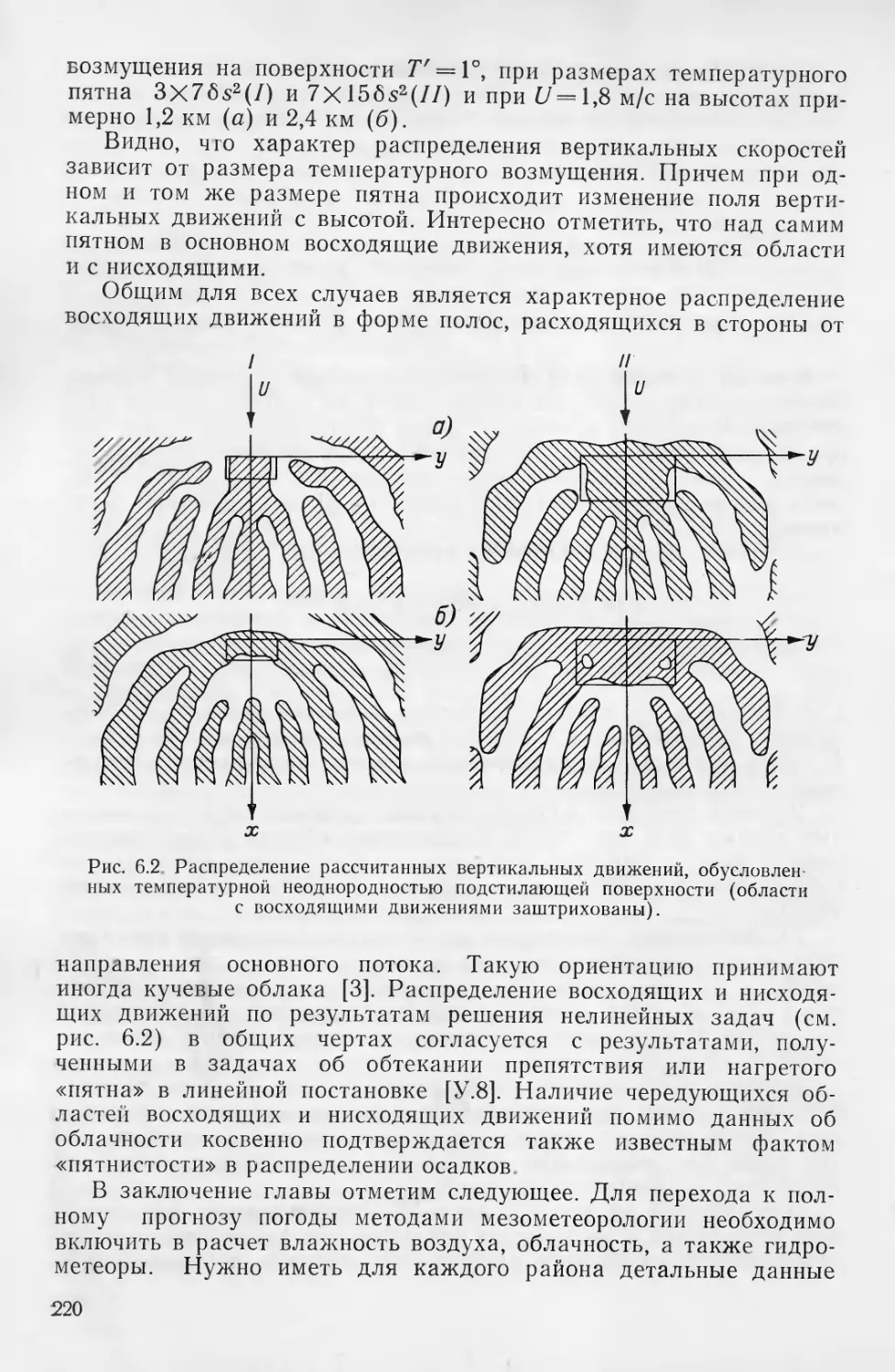
(1 ккал = 103 кал). Приток энергии, или тепла выражается в калХ
Хмин-1; 1 кал • мин-1 соответствует 0,0697 Вт = 0,0697 Дж-с-1 =
= 0,0697-107 эрг-с-1.
§ 2. Классификация атмосферных
движений
Все многообразие атмосферных движений условно можно раз-
бить на три основных типа: движения малого (микро), среднего
(мезо) и крупного (макро) масштабов.
Микромасштабные движения развиваются на простран-
ствах с горизонтальными размерами до нескольких сотен метров
и в течение времени до нескольких минут. Примерами микромасш-
табных движений являются движения, возникающие вблизи не-
больших препятствий: отдельных небольших неровностей земной
поверхности, строений, деревьев и пр. К микромасштабным движе-
ниям относятся также флуктуации, возникающие в воздушном по-
токе вследствие турбулентности. Последняя возникает при движе-
нии вблизи шероховатой поверхности, а также при наличии пере-
пада скоростей на небольших расстояниях. Турбулентный характер
атмосферных движений и связанные с этим микроколебания можно
зарегистрировать с помощью автоматических приборов, обладаю-
щих малой инерцией.
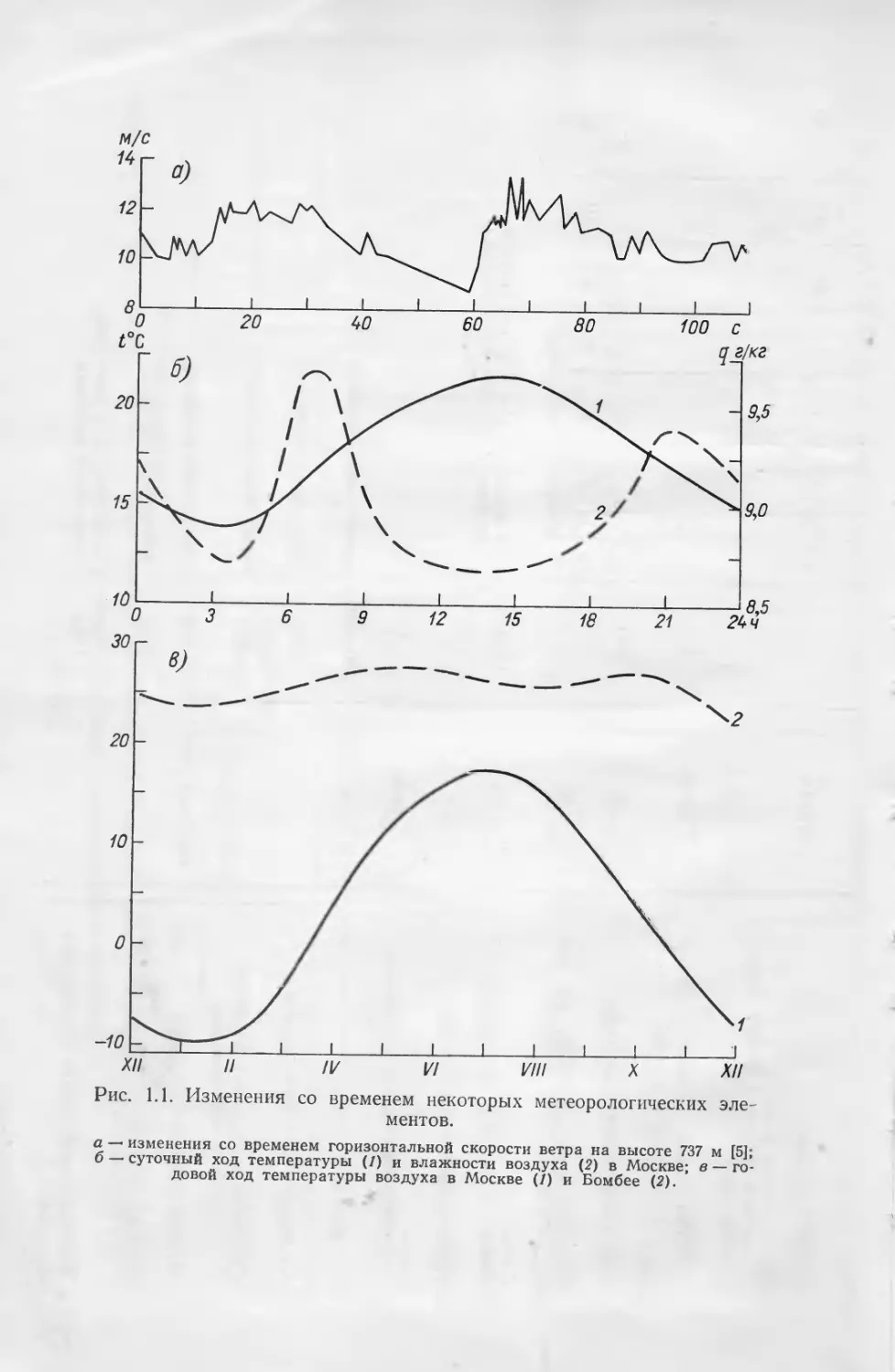
Из рис. 1.1 а можно видеть, что, например, за сравнительно ко-
роткое время (ПО с) скорость ветра изменялась от 9 до 14 м/с.
Вместе с тем этот график показывает, что короткопериодные коле-
бания скорости ветра происходят в небольших интервалах
времени. При осреднении за некоторый интервал времени
скорость принимает некоторое предельное значение. Ход изме-
нения со временем осредненной скорости имеет более плавный ха-
рактер.
Отметим, что к микромасштабным движениям относятся также
движения, связанные с акустическими и короткопериодными грави-
тационными волнами.
Мезомасштабные движения характеризуются горизон-
тальными размерами от нескольких сотен метров до нескольких со-
тен километров и промежутками времени порядка нескольких ча-
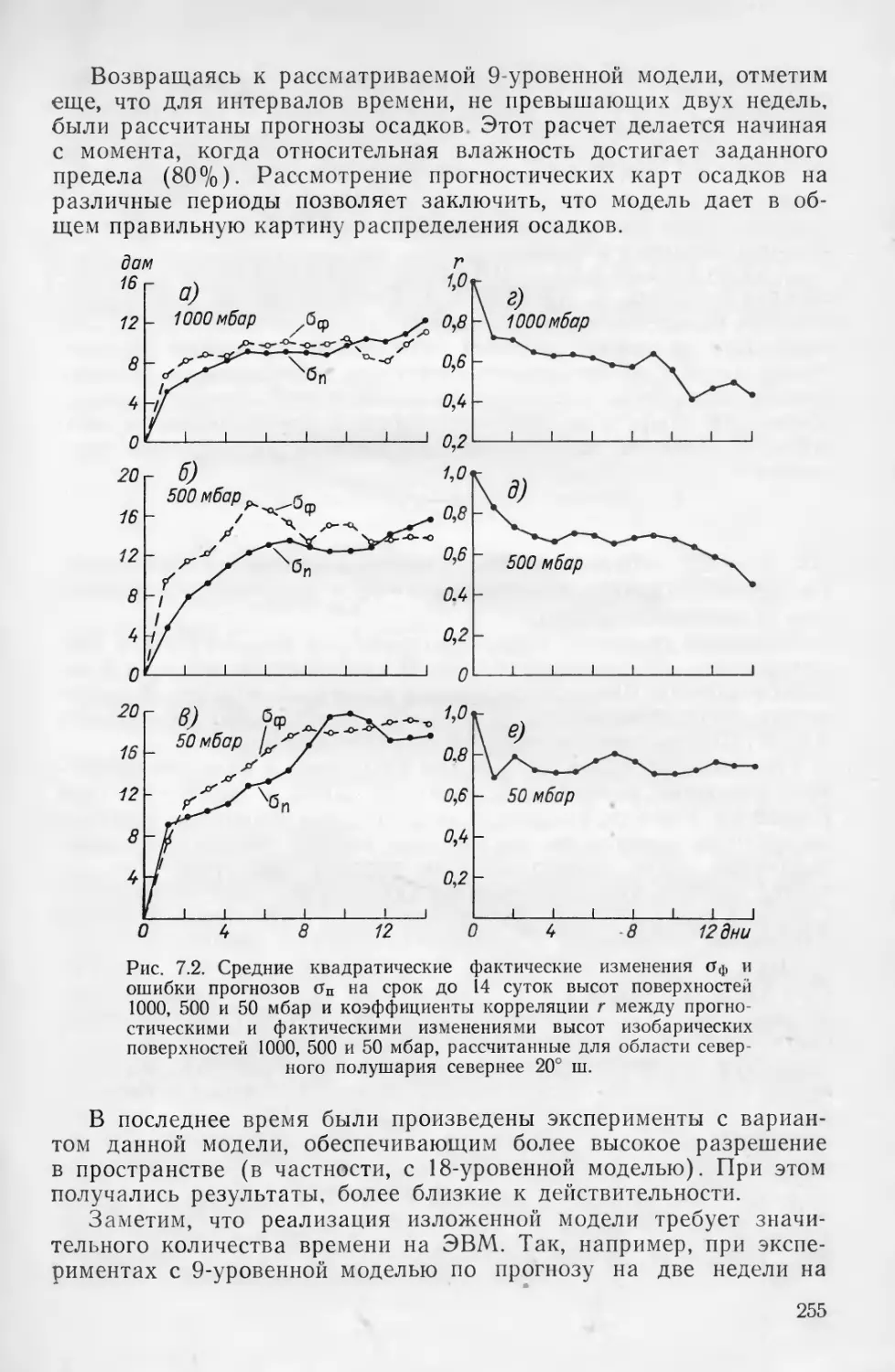
сов. Характерными примерами мезомасштабных движений явля-
ются развитие кучевого облака и процесс обтекания отдельной
горы. К этому типу движений относятся и гравитационные волны
с большими амплитудами.
Крупномасштабные движения характеризуются длинами
волн порядка тысячи километров и периодами колебаний порядка
суток. Вертикальный масштаб этих движений около 10 км. Приме-
ром крупномасштабных движений является циркуляция воздуш-
ных масс в областях циклонов и антициклонов. Крупномасштаб-
7
Таблица 1.1
Основные метеорологические элементы, единицы и погрешности их измерений
Метеорологический элемент Единица измерения Погрешность измерений
у поверх- ности Земли на высоте z км
1 5 10 15 20 25 30
1 2 3 4 5 6 7 8 9 10
Температура воздуха у поверхности Земли °C 0,3 0,4
Температура поверхности почвы °C 1—2
Температура воздуха на различных высотах °C 0,4 0.7 0,9 0,9 1,0 1,2 1,9
Атмосферное давление у поверхно- сти Земли мбар 0,2
Высота изобарической поверхности дам 0,3 0,6 1,5 3,2 4,7 6,2 8
Ветер у поверхности Земли
скорость м/с 1-2
направление румб (22,5°) 1
Ветер на разных высотах
скорость м/с 0,7 0.6 0,7 1 1,2 1,6 2,2
to
направление
Влажность воздуха у земной поверх-
ности
абсолютная влажность (упру-
гость водяного пара)
относительная влажность
Относительная влажность на раз-
ных высотах
Осадки
Облачность
количество
высота
Суммарная солнечная радиация
Отраженная солнечная радиация
Прямая солнечная радиация
Баланс длинноволновой радиации
(эффективное излучение)
Радиационный баланс (остаточная
радиация)
градус
мбар
%
%
мм
балл
м
кал • см-2 • мин-1
15—20о/о для жидких и 45—55% для твердых
осадков от измеряемой величины
10—20°/о измеряемой величины
5»/о измеряемой величины
5°/о измеряемой величины
Зо/о измеряемой величины
2Оо/о измеряемой величины
15о/о измеряемой величины
м/с
Рис. 1.1. Изменения со временем некоторых метеорологических эле-
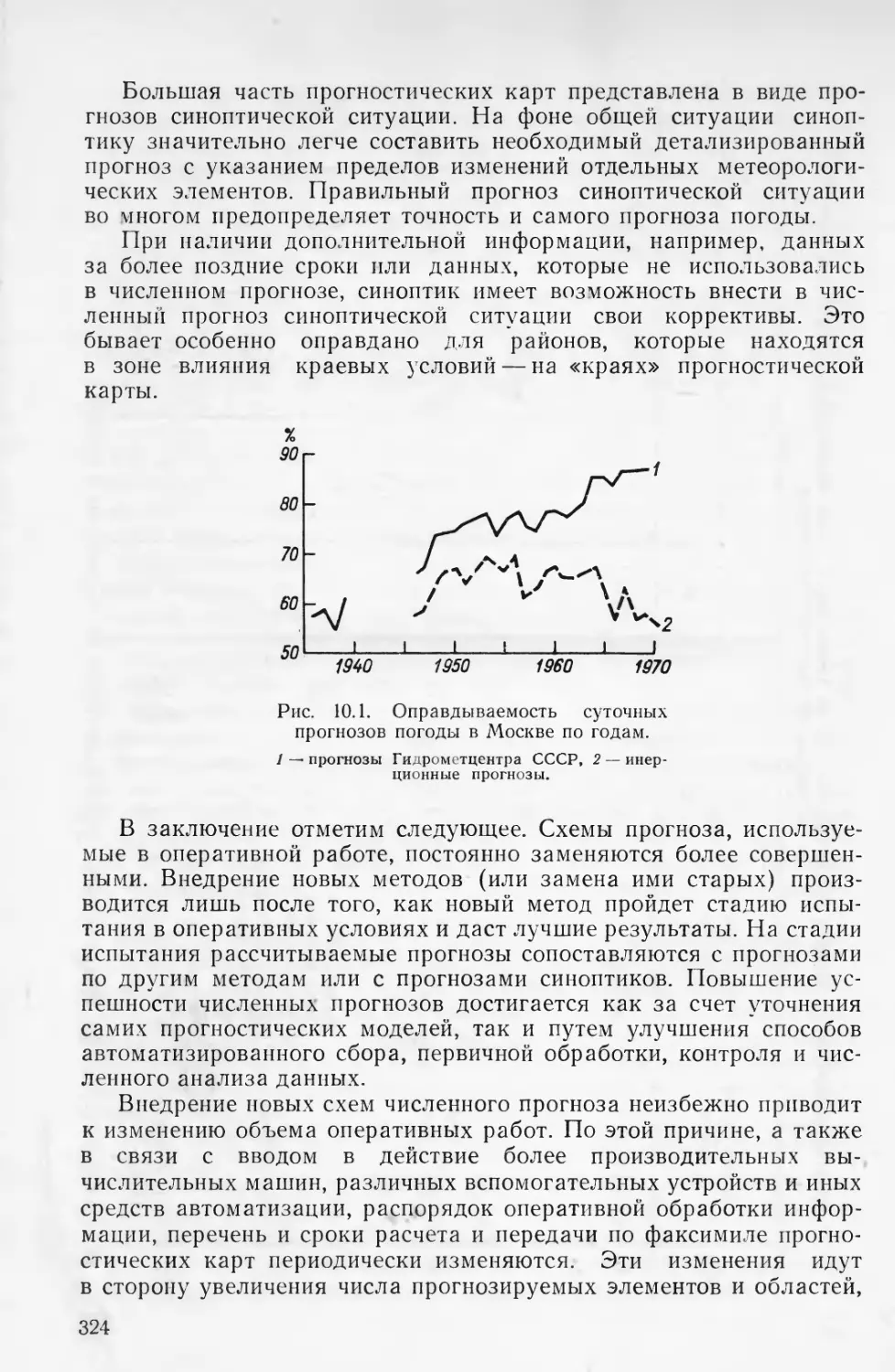
ментов.
а — изменения со временем горизонтальной скорости ветра на высоте 737 м [5];
б — суточный ход температуры (/) и влажности воздуха (2) в Москве; в — го-
довой ход температуры воздуха в Москве (/) и Бомбее (2).
ные движения называют часто движениями синоптических мас-
штабов.
Можно выделить еще и другие типы колебаний, например, су-
точные и годовые колебания (рис. 1.1 бив), глобальные колеба-
ния с периодами от недели до месяца, а также сезонные, междуго-
дичные и внутривековые колебания и др.
Наличие движений некоторых из указанных выше типов под-
тверждается эмпирическими данными, обработанными с помощью
методов спектрального анализа (см. приложение 7), что можно
увидеть на приводимых далее графиках (рис. 1.2).
На графиках спектральной плотности колебаний скорости ветра
и температуры (рис. 1.2) видны два резких максимума и один глу-
Рис. 1.2. Спектральная плотность колебаний скорости ветра
(/), температуры воздуха (2) [У 18] и индекса циркуля-
ции (5) [7].
бокий и обширный минимум. Максимум в области периодов около
0,016 ч (1 мин) соответствует движениям микромасштабов и обус-
ловлен в первую очередь микротурбулентными движениями. Дру-
гой максимум расположен вблизи периода 100 ч (~4 суток).
Кроме этих двух максимумов, имеется еще один частный максимум
вблизи периода 12 ч, который в основном связан с суточным ходом
метеорологических элементов.
Между указанными максимумами имеется глубокий минимум
с центром вблизи периода 20 мин. Это есть область мезомасштаб-
ных движений [У. 18]. Этот график подтверждает тот факт, что
движения данного масштаба относительно редки.
На графике спектральной плотности колебаний индекса цирку-
ляции атмосферы на поверхности 500 мбар, который представляет
собой отношение угловой скорости вращения атмосферы к угловой
скорости вращения Земли вокруг своей оси (см. гл. VII), отчетливо
11
виден максимум вблизи периода в 12 дней (см. рис. 1.2). Этот цикл»
несомненно, связан с известным в синоптической метеорологии ес-
тественным синоптическим периодом, длительность которого равна
примерно половине отмеченного на графике максимума спектраль-
ной плотности в 12 суток.
§ 3. Порядок величин метеорологических элементов
и их производных
Под порядком величины какого-либо элемента понимается зна-
чение этого элемента в диапазоне всех встречающихся величин
этого элемента (практически не менее 99%) при округлении ниж-
него и верхнего пределов значений до ближайшей степени числа
10 в принятой системе единиц. Например, скорость ветра изменя-
ется от 0 до 50 м/с. Поэтому в системе единиц МТС порядок ве-
личины скорости ветра составляет 10°—101. Давление воздуха у по-
верхности Земли колеблется от 940 до 1070 мбар или от 94 до
107 сбар. Значение нижнего и верхнего пределов после округления
оказывается одинаковым. Поэтому давление воздуха на уровне
моря имеет порядок 102. А. А. Фридманом и Г. Гессельбергом по
эмпирическим данным были составлены таблицы порядков величин
ряда метеорологических элементов и их производных [У. 10].
На практике, однако, удобнее оперировать не с диапазоном дан-
ного элемента, а с наиболее часто встречающимся или характер-
ным значением этого элемента [У.7]. Под характерным значением
какого-либо элемента или функции будем понимать их среднюю аб-
солютную или среднюю квадратическую величину, определенную
по данным измерений. Характерное значение какой-либо величины
или функции f будем обозначать с помощью символа О (f) и в даль-
нейшем выражать в единицах системы МТС.
Характерные значения непосредственно измеряемых метеороло-
гических элементов и их производных можно получить путем ста-
тистической обработки данных наблюдений. При этом производные
заменяются отношением приращения рассматриваемого элемента
к приращению времени б/ или координат 6s (6х, б у), 8z. Напри-
мер, полагают, что
dt It ' ds bs ’
где 6ft и 6fs — приращение элемента f по времени и горизонталь-
ным координатам. Приращения 6/ и 6s должны соответствовать
характерным масштабам тех процессов, которые исследуются. Для
исследования крупномасштабных атмосферных процессов харак-
терной горизонтальной длиной, как уже говорилось, является
1000 км, а характерным промежутком времени — сутки. Поэтому
при исследовании этих процессов обычно принимается, что б^ =
= 0,864-105 с = 1 сут., 6s=106 м и 6z = 2-103 м. Характерные
значения производных определяются, например, из соотношений
12
( df \ _ о (8Л) . n ( df \ _ О (5Д) .
\ dt J §t ’ \ ds ) &s
n(df \_ O(SA)
dz J bz
где О (6 ft), 0(6fs) и 0(6fz)—характерные значения приращений
функций за время 61 или на расстояниях 6s и 6г.
Характерные значения не измеряемых непосредственно величин
можно получить с помощью уже найденных характерных значений
измеряемых величин и известных соотношений. Например, харак-
терное значение плотности воздуха можно получить, используя
уравнение состояния p = p/RT и характерные значения р и Т,
В табл. 1.2 приведены характерные значения метеорологиче-
ских элементов и их производных, полученные М. И. Юдиным при-
менительно к крупномасштабным движениям в нижней половине
тропосферы во внетропических широтах при 6^=12 ч, 6s = 500 км
и 6г = 2,5 км [У.7]. В этой таблице приняты следующие обозначе-
ния: х, у, z — декартовы координаты, t — время, u, v, w — компо-
ненты скорости ветра вдоль осей координат, р—давление, Т —
Таблица 1.2
Характерные значения метеорологических элементов
и их производных (по М. И. Юдину [У.7])
Производная Метеорологические элементы
и, v м/с 7-10° р т/(м-с2) 102 г °C ЗЛО2 р т/м3 IO"3 W м/с 10-2 2г 1/с 2.10”с
d / d д \ ds \ дх * ду ) 1,2.10-5 8-10-7 7-10-6 3-10-11 2-10-8 4-10-п
д dt 1,2-10-4 8-10-6 7-10-5 3-10-ю 2-10-7 4-10-Ю
д 2-10-3 10-2 6-Ю-з 10-7 3-10-6 5-10-9
dz
d2 1,2.10-6 10-6 7-10-7 10-11
dz2 d2 3.10-п 1,5-10-12 2-10-п 8-10-17
ds2
d2 3-10-ю 1,5-10-И 2-10-ю 8-10-16
ds dt
d2 5-10-9 3-10-ю 3-10-9 6-10-15
ds dz
d2 5-10-8 3-10-9 3-10-8 6-10 и
dz dt
13
температура, р — плотность, Qz=-^---------вертикальная состав-
ляющая вихря скорости. Из данных этой таблицы следует, напри-
/ дТ \
мер, что О (и) = 7- Ю° = 7 и О{~—) =0,7- 10"5.
\ ds /
Ориентировочные оценки характерных значений метеорологиче-
ских элементов и их производных хотя бы с точностью до порядка
величины, т. е. до ближайшей степени числа 10 можно производить
и без использования готовых таблиц, а основываясь на опыте. Так,
например, известно, что скорость ветра у поверхности Земли изме-
няется от 0 до 20 м/с, достигая в редких случаях 40 м/с. Наиболее
часто скорость ветра колеблется в пределах 3—12 м/с. Поэтому
приближенно можно положить, что О(и) = Ю1. Другой пример. Из-
менение температуры воздуха на расстоянии 1000 км может со-
ставлять от 0 до 20° (хотя в исключительных случаях оно может
достигать и больших значений). Можно положить, что приращение
температуры на расстоянии 1000 км может быть равным 10, т. е.
О (8TS) = Ю1. Поэтому
о(")- ogn>.™_ ю-«.
\ ds / Ss 106
По данным табл. 1.2 О(и)=7- 10°, а =0,7 • 10-5, что бли-
\ us /
зко к найденным оценкам.
Следует иметь в виду, что эмпирические оценки порядков вели-
чин зависят от данных, которые используются при статистической
отработке. Сказанное относится также и к табл. 1.2.
§ 4. Некоторые данные о пространственно-временном
распределении метеорологических элементов и статистическая
структура метеорологических полей
Распределение метеорологических элементов по земному шару
является весьма сложным, а изменения метеорологических элемен-
тов во времени отличаются большим многообразием. Здесь будет
приведено лишь небольшое число данных по этому вопросу, знание
которых в первою очередь необходимо при решении задач числен-
ного прогноза погоды. При этом основное внимание будет уделено
полям давления и геопотенциала, поскольку они связаны с полями
ряда других метеорологических элементов: температуры, ветра
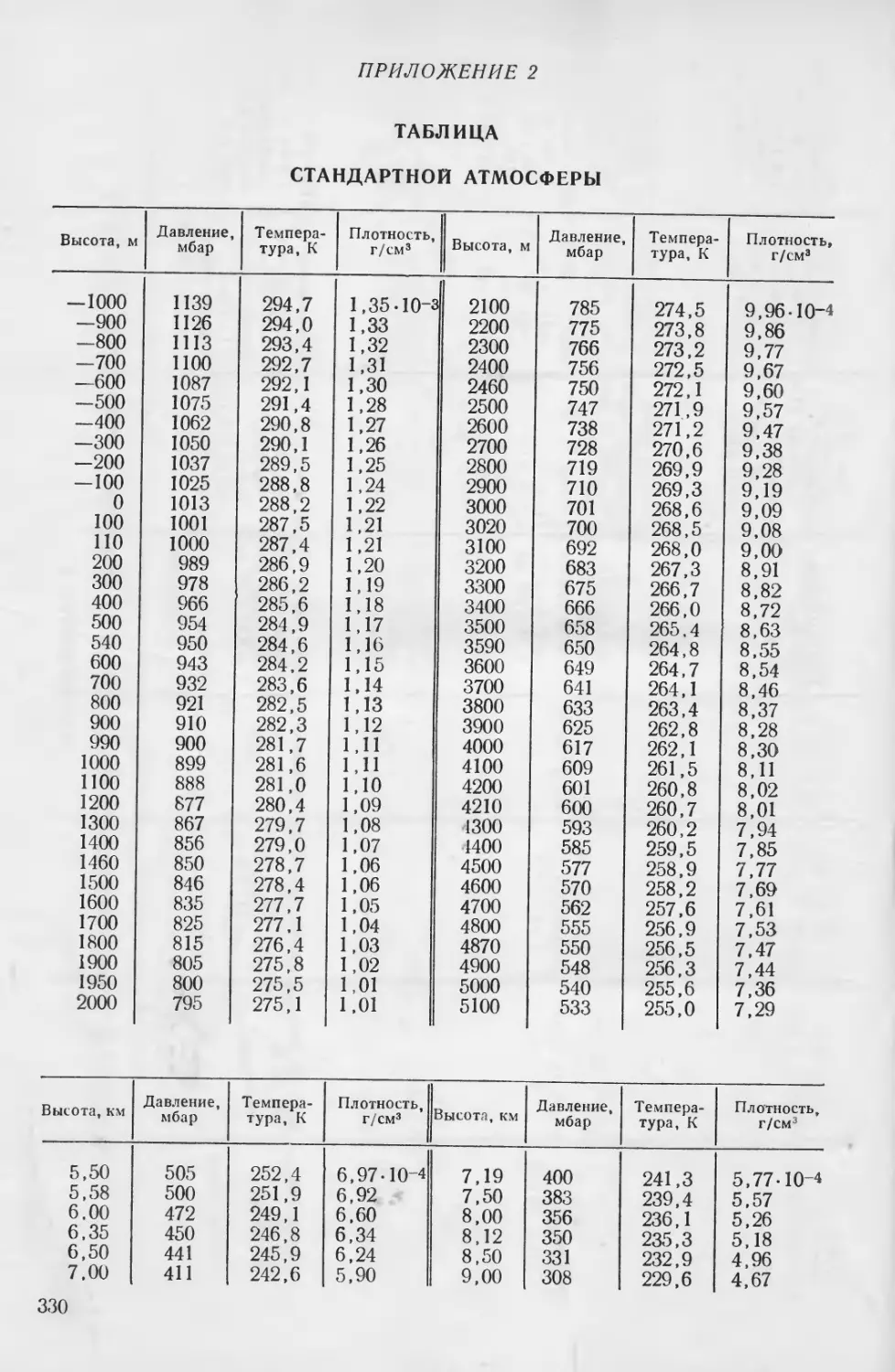
и пр. Наиболее общее представление о вертикальном строении ат-
мосферы можно получить по данным о стандартной атмосфере
[12] (приложение 2). Общее представление о меридиональном
распределении метеорологических элементов, а также об их годо-
вом ходе дают средние месячные и среднеширотные значения
(рис. 1.3). Именно этим данным здесь и уделено наибольшее вни-
мание.
14
Рис. 1.3. Изоплеты среднеширотных значений давления на уровне моря (а) [11] и высот изобарических
поверхностей 500 мбар (б), 200 мбар (в) и 100 мбар (г) [6].
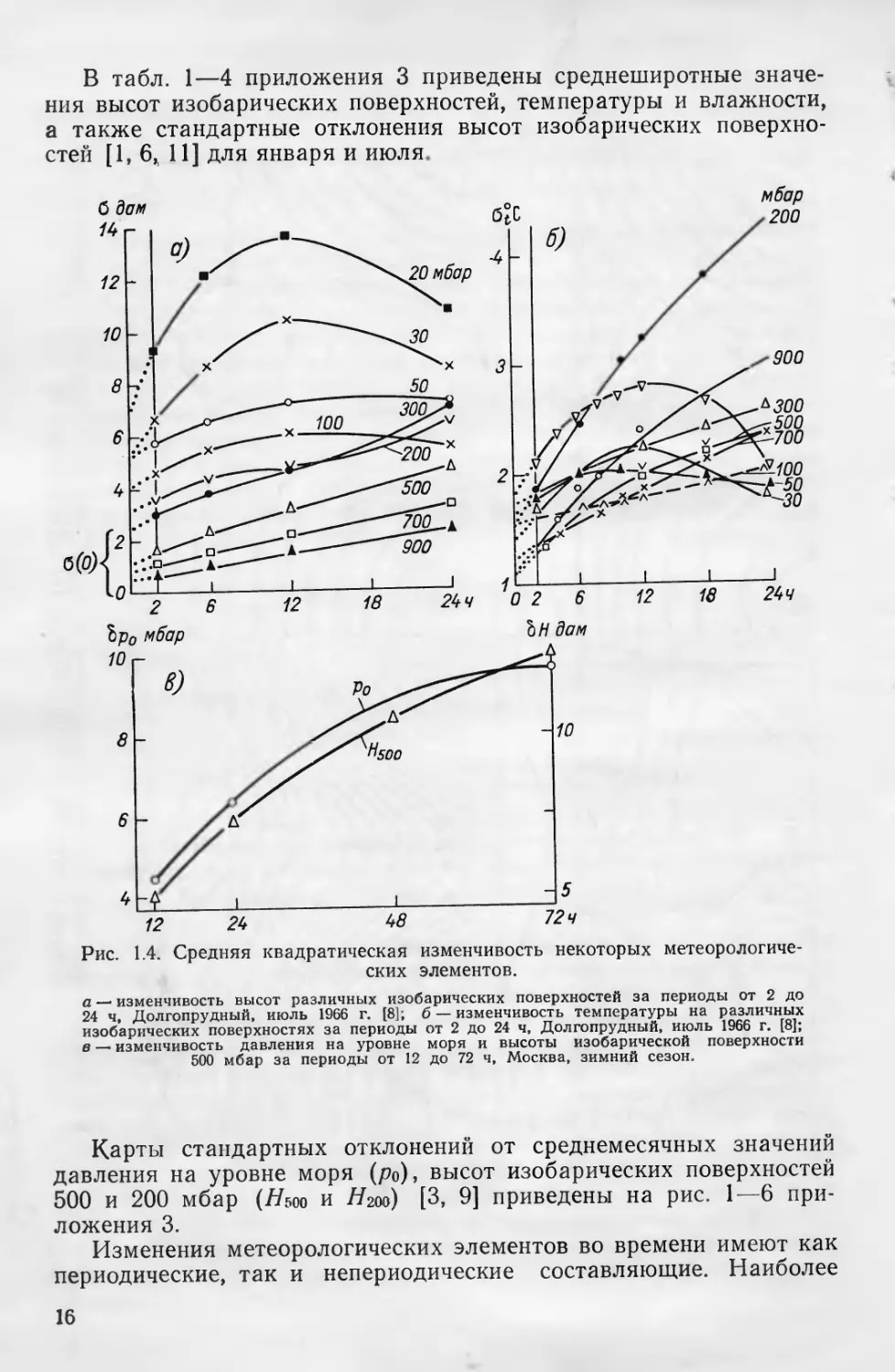
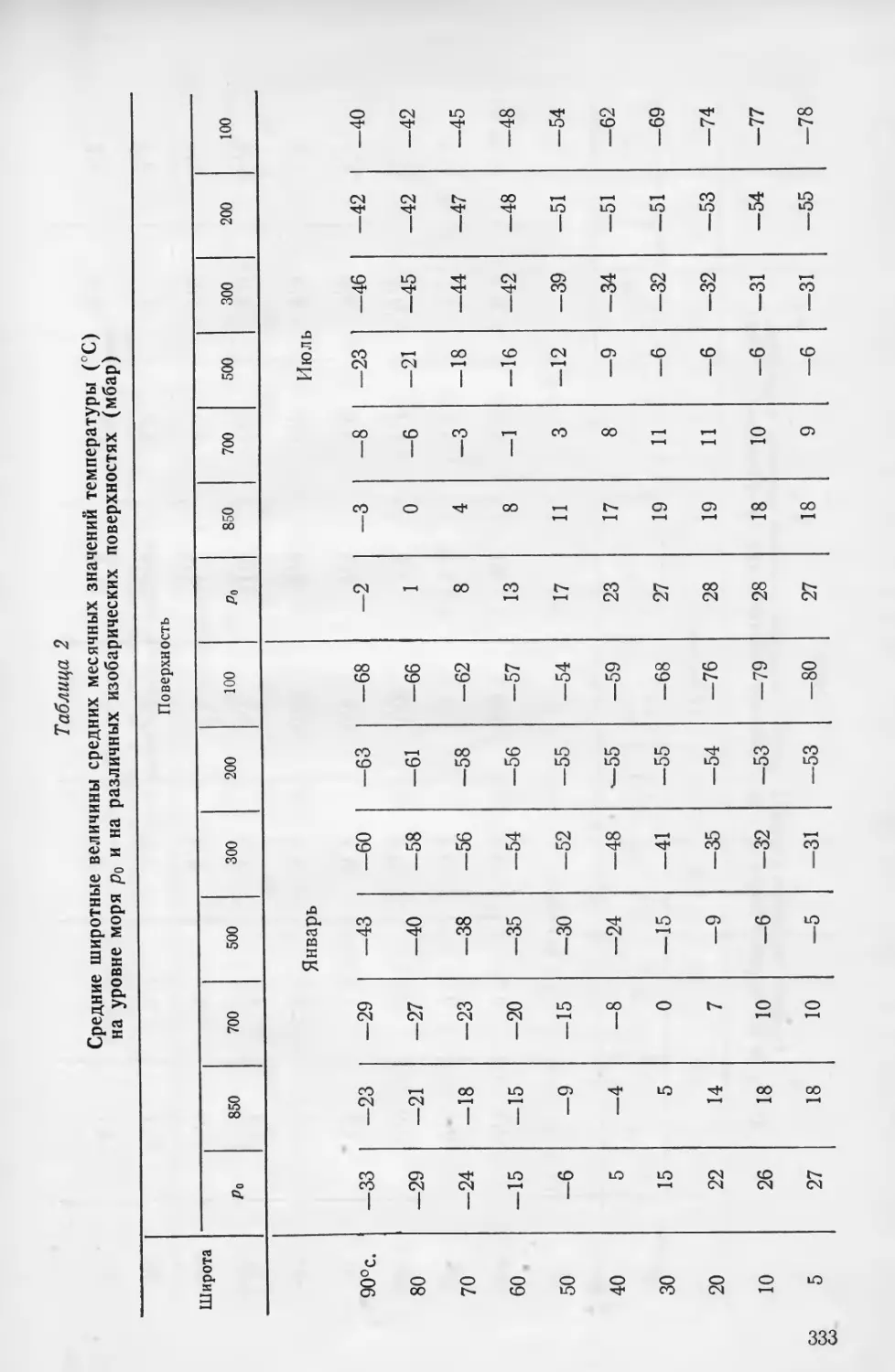
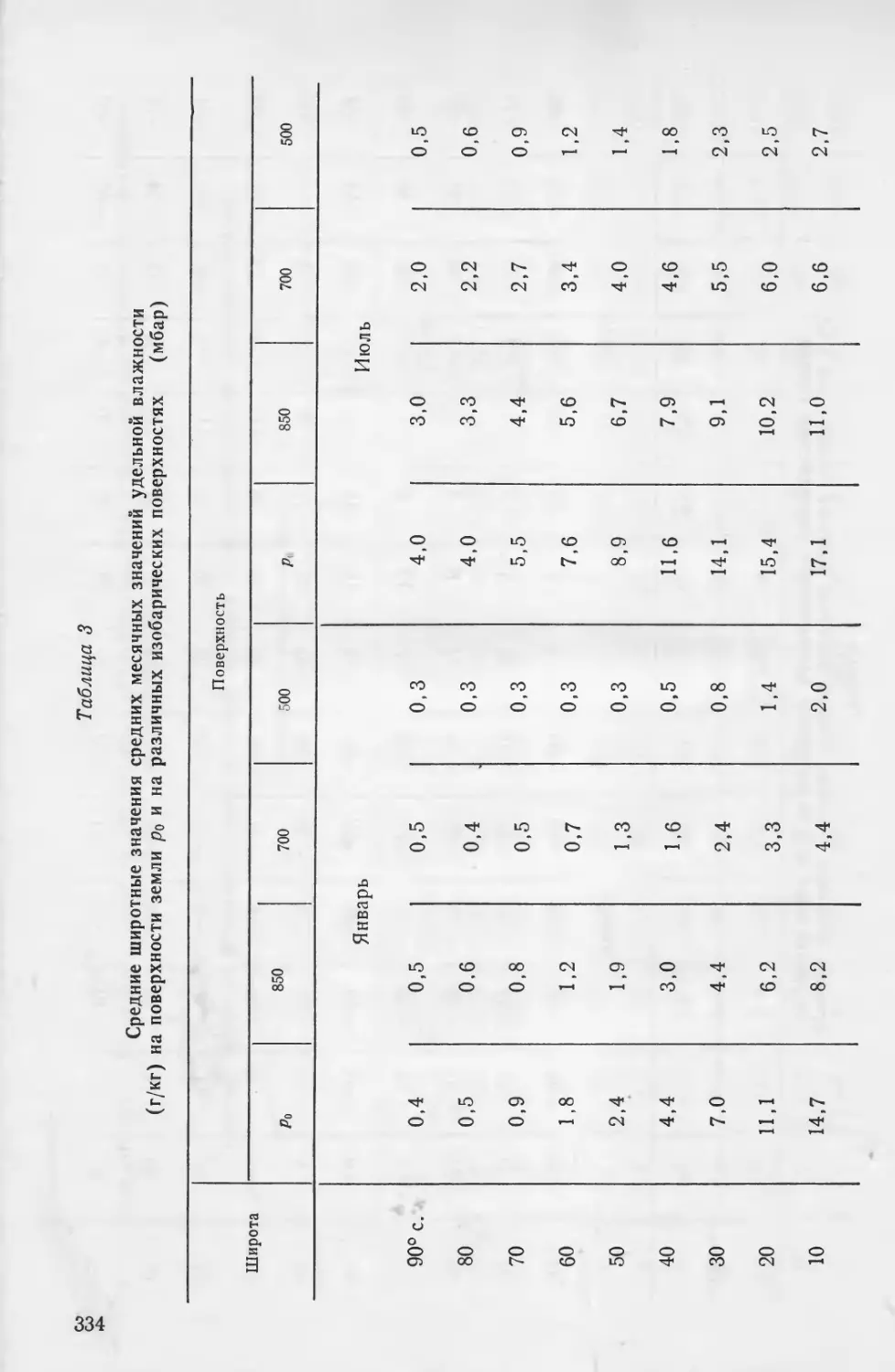
В табл. 1—4 приложения 3 приведены среднеширотные значе-
ния высот изобарических поверхностей, температуры и влажности,
а также стандартные отклонения высот изобарических поверхно-
стей [1, 6, 11] для января и июля
Рис. 1.4. Средняя квадратическая изменчивость некоторых метеорологиче-
ских элементов.
а — изменчивость высот различных изобарических поверхностей за периоды от 2 до
24 ч, Долгопрудный, июль 1966 г. [8]; б — изменчивость температуры на различных
изобарических поверхностях за периоды от 2 до 24 ч, Долгопрудный, июль 1966 г. [8];
в — изменчивость давления на уровне моря и высоты изобарической поверхности
500 мбар за периоды от 12 до 72 ч, Москва, зимний сезон.
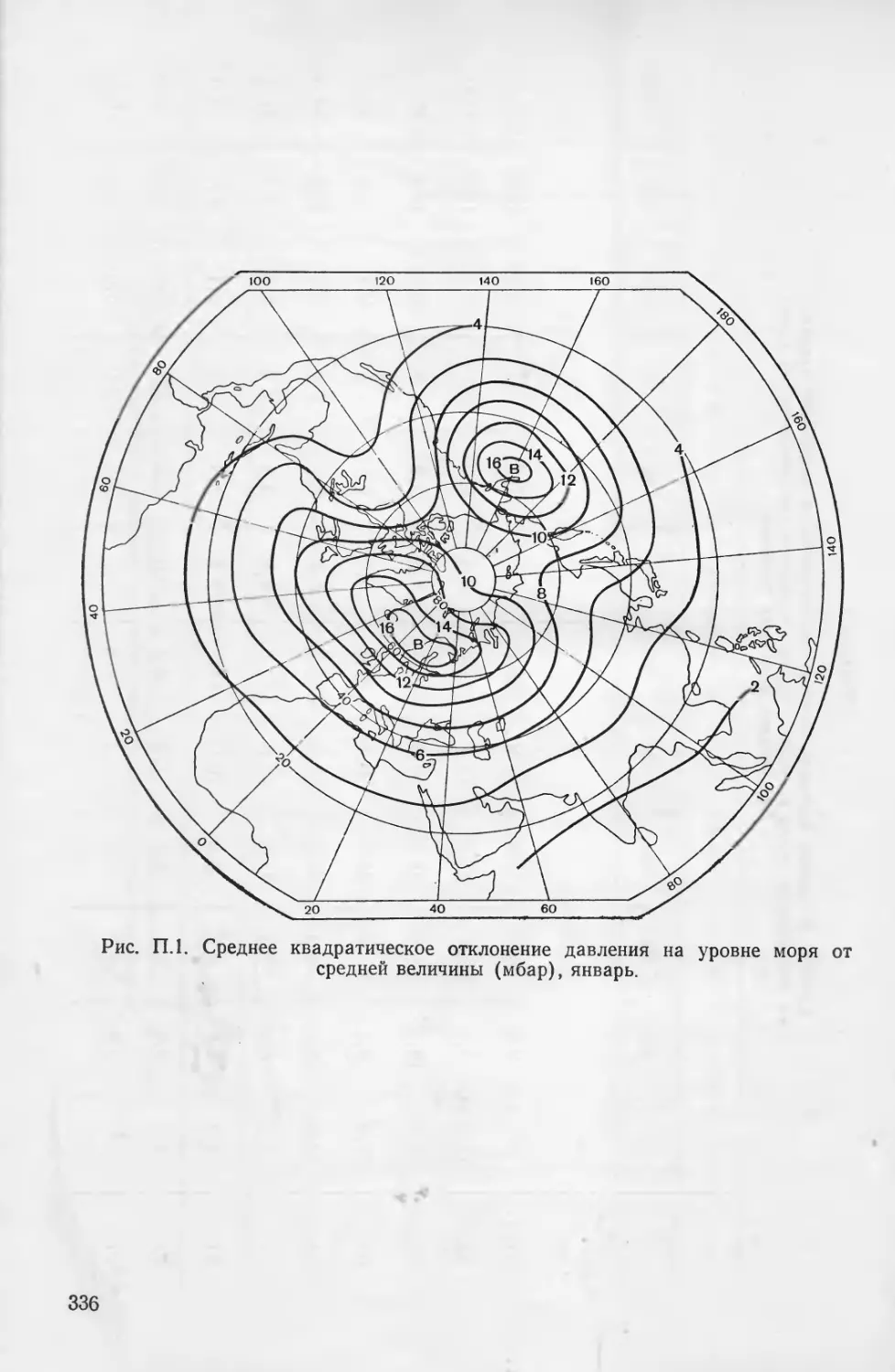
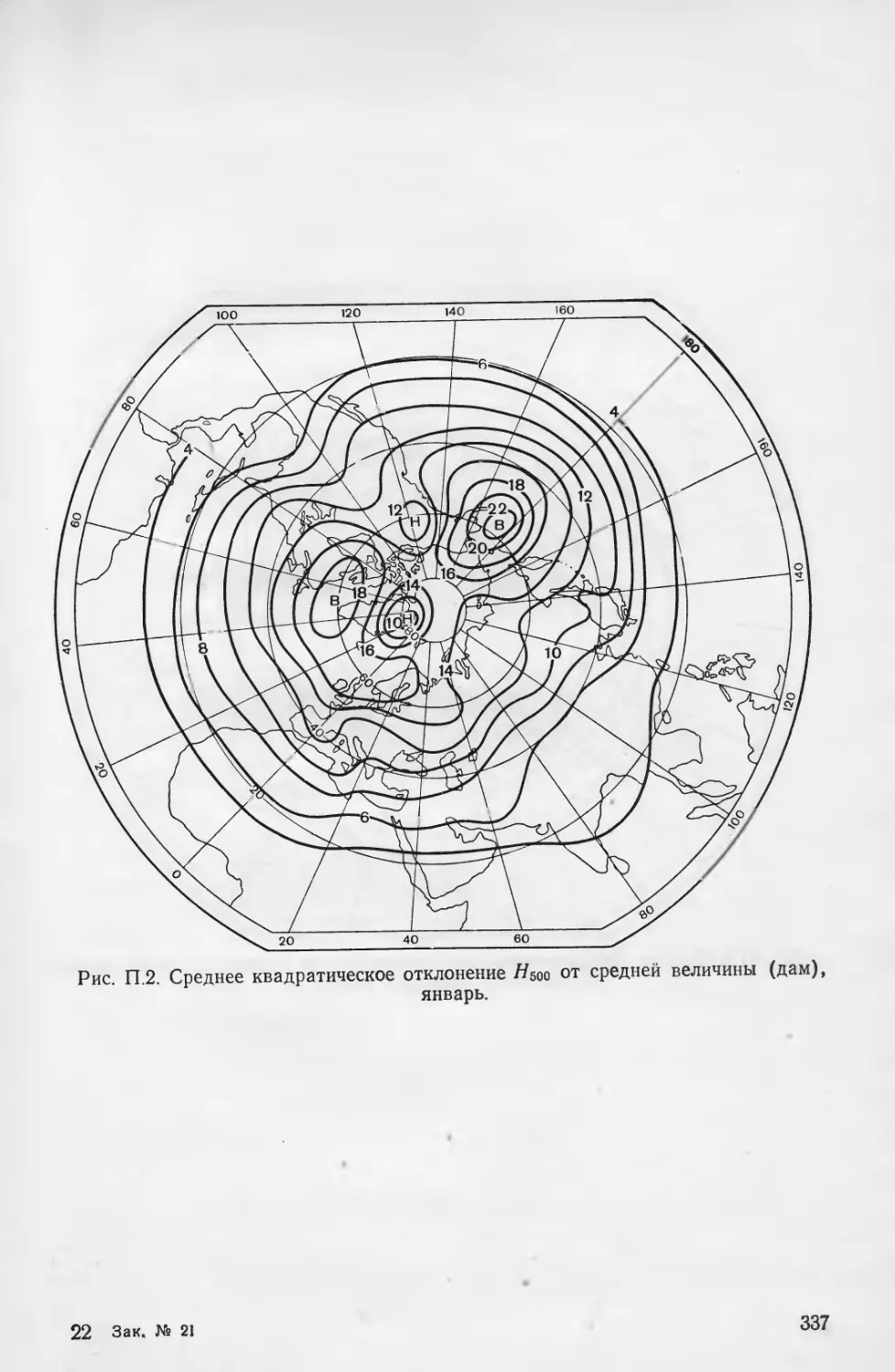
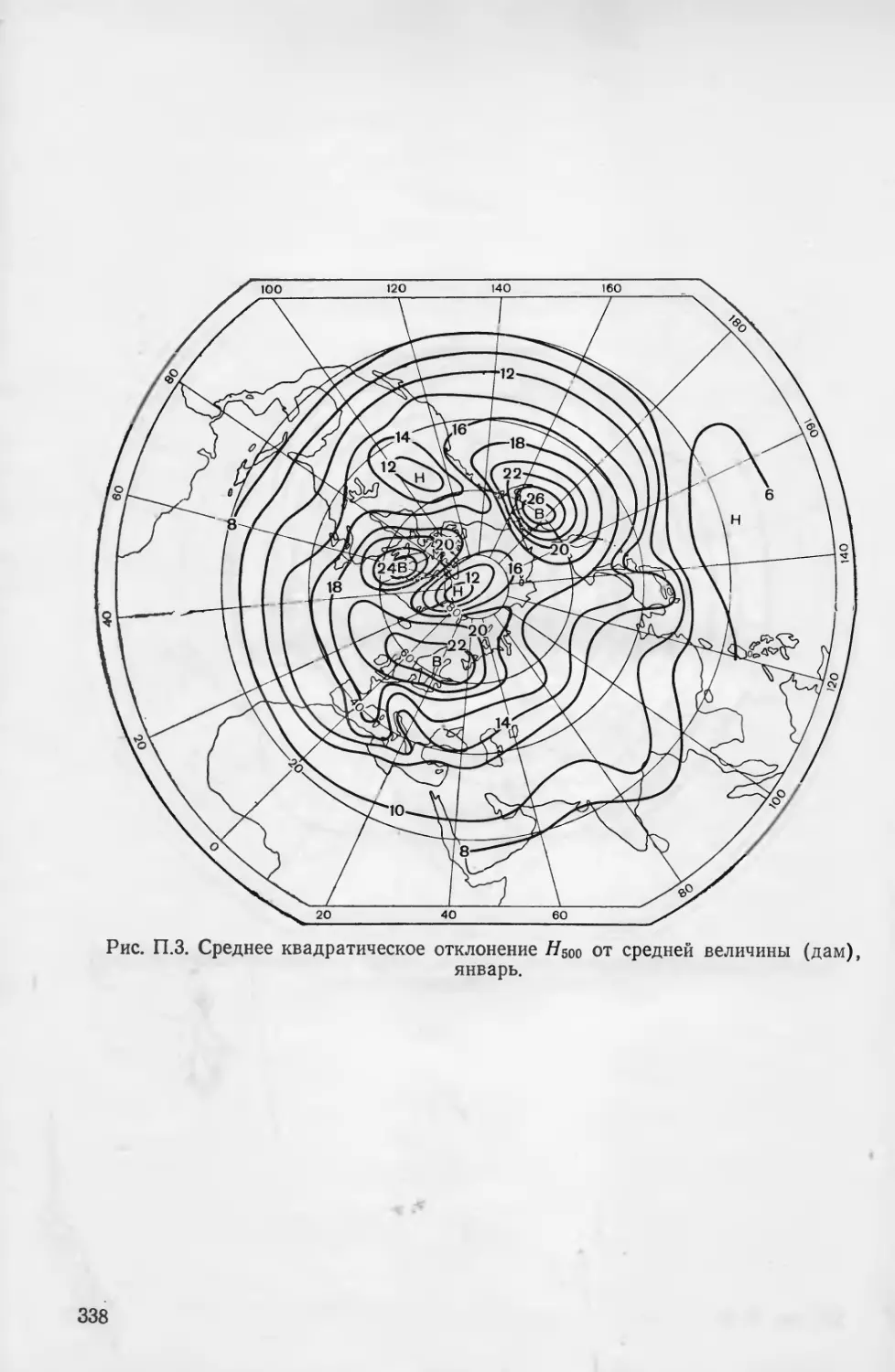
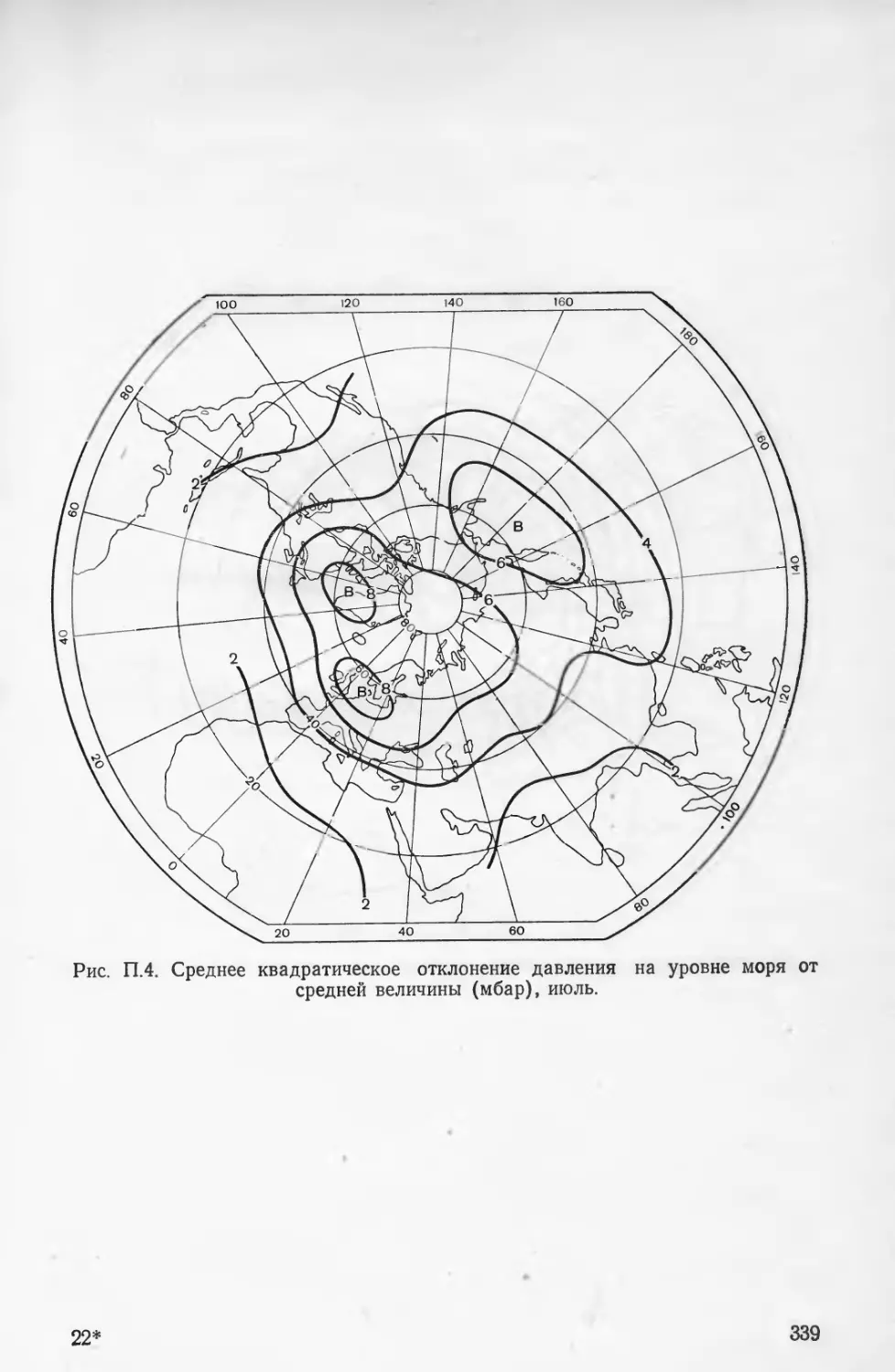
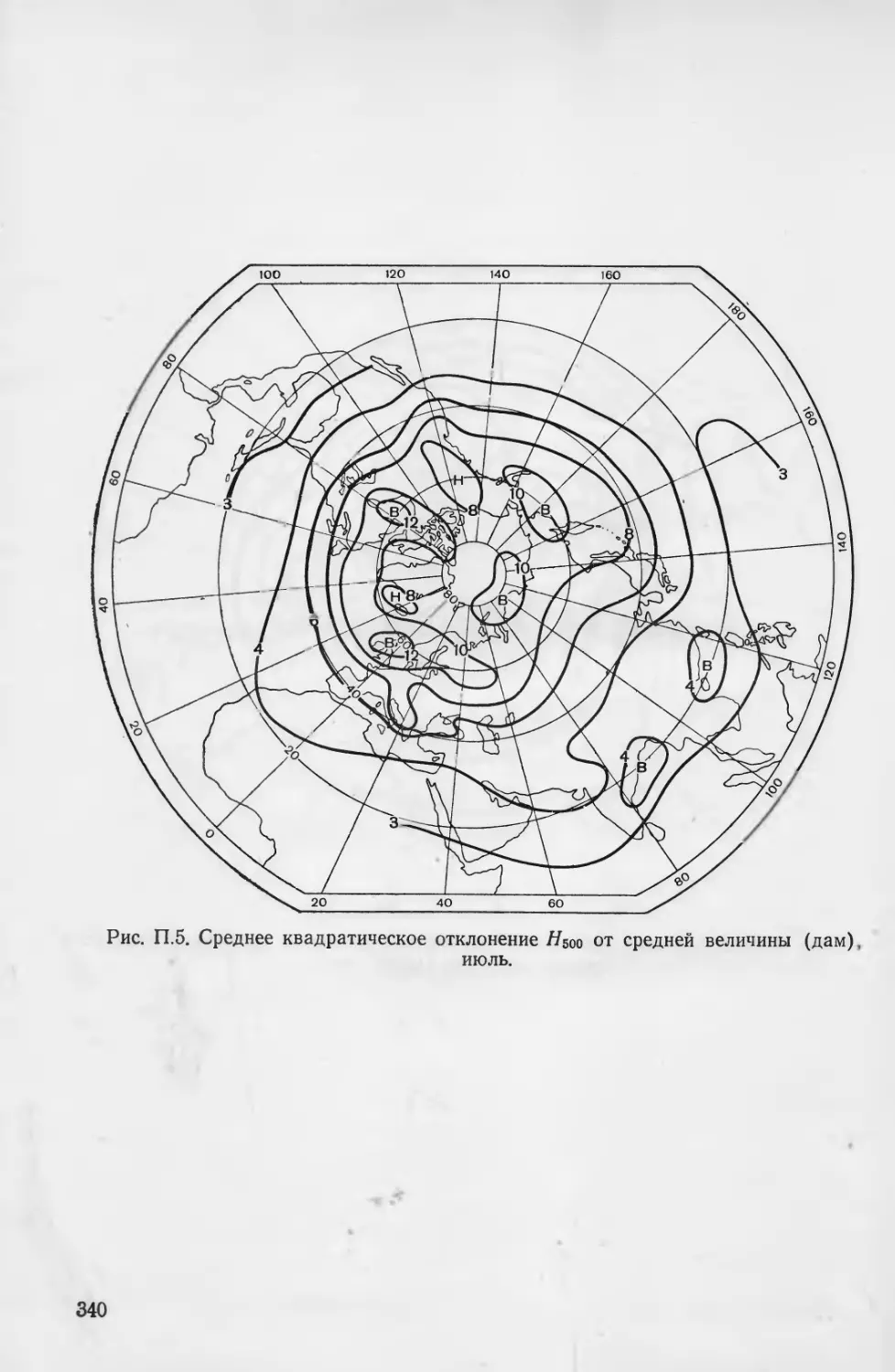
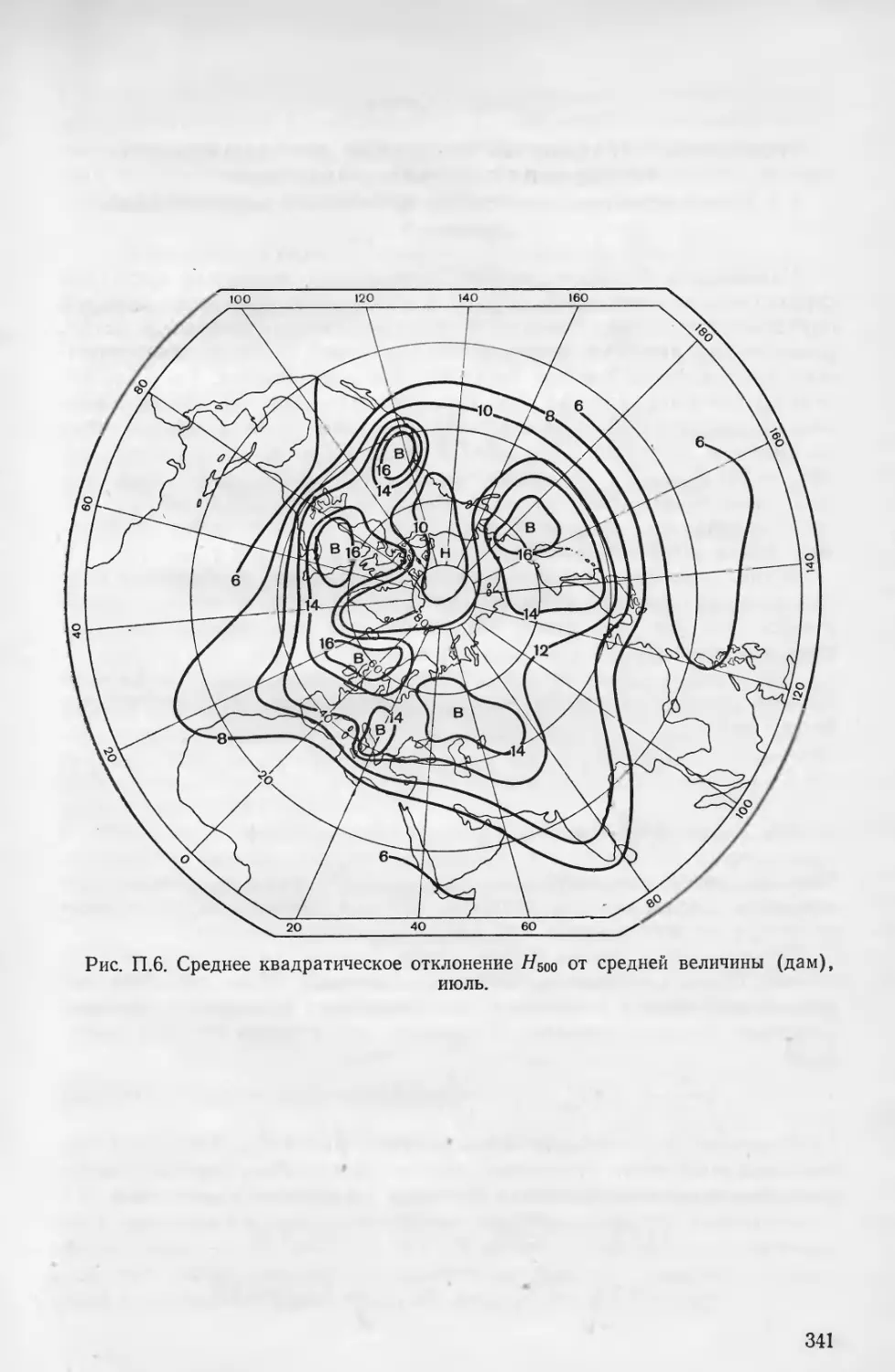
Карты стандартных отклонений от среднемесячных значений
давления на уровне моря (ро), высот изобарических поверхностей
500 и 200 мбар (Ньоо и //200) [3, 9] приведены на рис. 1—6 при-
ложения 3.
Изменения метеорологических элементов во времени имеют как
периодические, так и непериодические составляющие. Наиболее
16
важные периодические изменения связаны с суточным и годовым
ходом. Последние имеют различный характер как для отдельных
метеорологических элементов, так и для различных географических
районов и в разное время года (см. рис. 1.1). На этом рисунке
можно видеть, например, что кривые суточного и годового хода ме-
теорологических элементов могут иметь как по одному, так и по
два максимума и минимума.
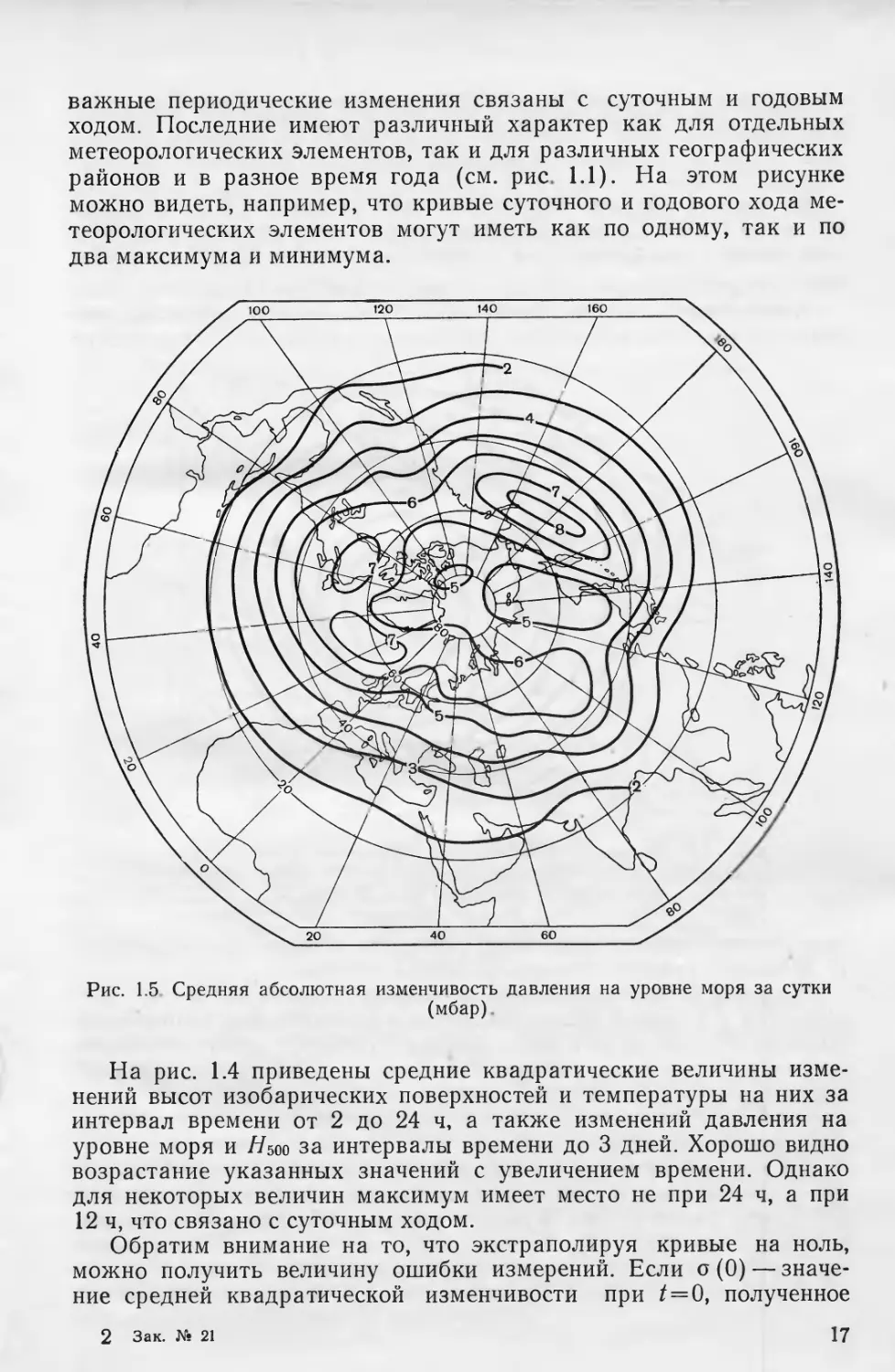
Рис. 1.5 Средняя абсолютная изменчивость давления на уровне моря за сутки
(мбар)
На рис. 1.4 приведены средние квадратические величины изме-
нений высот изобарических поверхностей и температуры на них за
интервал времени от 2 до 24 ч, а также изменений давления на
уровне моря и Я5оо за интервалы времени до 3 дней. Хорошо видно
возрастание указанных значений с увеличением времени. Однако
для некоторых величин максимум имеет место не при 24 ч, а при
12 ч, что связано с суточным ходом.
Обратим внимание на то, что экстраполируя кривые на ноль,
можно получить величину ошибки измерений. Если о (0) — значе-
ние средней квадратической изменчивости при t = 0, полученное
2 Зак. № 21
17
с помощью экстраполяции, то среднеквадратическая ошибка изме-
рения ои может быть найдена по соотношению [У.5]
% = °(0)Ц/2'.
На рис. 1.4 а видно, что для высоты изобарической поверхности
300 мбар о(0) = 2,5 дам. Отсюда следует, что среднеквадратиче-
ская ошибка измерения Язоо с помощью радиозондовой системы
РКЗ по приведенным данным составляет 2,5/f2 = 1,8 дам.
Изменчивость метеорологических элементов во времени, как
видно из рис. 1.5, на котором приведены данные об изменчивости
Рис. 1.6. Изолинии коэффициента корреляции между значе-
ниями высоты изобарической поверхности 700 мбар в различ-
ных точках и значением ее в Москве [2].
давления на уровне моря за 1 сутки по северному полушарию
[У.2], сильно зависит от географических условий.
Значения метеорологических элементов в различных точках про-
странства и в разное время находятся в определенной взаимозави-
симости, которая может быть описана статистическими методами,
например, с помощью корреляционных и структурных функций
(приложение 5). Рассмотрим некоторые наиболее важные с точки
зрения задач численного анализа и прогноза крупномасштабных
атмосферных процессов примеры этой взаимозависимости.
На рис. 1.6 приведена карта нормированной автокорреляцион-
ной функции высоты изобарической поверхности 700 мбар, получен-
ная путем расчета этой функции между значениями Я700 в Москве
и в ряде пунктов [2]. Рассматривая эту карту, можно отме-
тить, что значения автокорреляционной функции убывают с удале-
нием пунктов от Москвы. На расстоянии 1,5—2 тыс. км ее значение
18
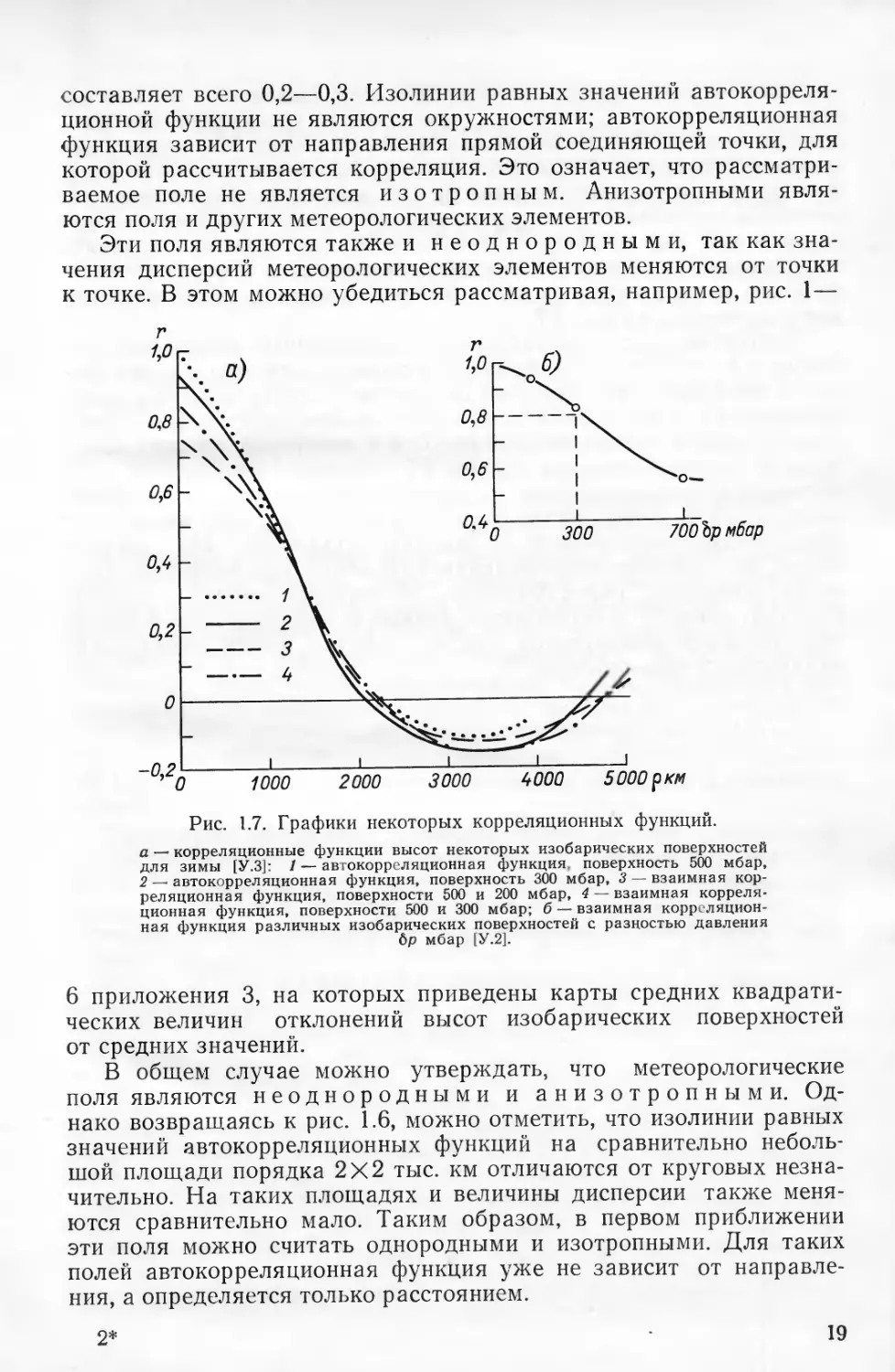
составляет всего 0,2—0,3. Изолинии равных значений автокорреля-
ционной функции не являются окружностями; автокорреляционная
функция зависит от направления прямой соединяющей точки, для
которой рассчитывается корреляция. Это означает, что рассматри-
ваемое поле не является изотропным. Анизотропными явля-
ются поля и других метеорологических элементов.
Эти поля являются также и неоднородными, так как зна-
чения дисперсий метеорологических элементов меняются от точки
к точке. В этом можно убедиться рассматривая, например, рис. 1—
Рис. 1.7. Графики некоторых корреляционных функций.
а — корреляционные функции высот некоторых изобарических поверхностей
для зимы [У.З]: 1 — автокорреляционная функция, поверхность 500 мбар,
2 — автокорреляционная функция, поверхность 300 мбар, 3 — взаимная кор-
реляционная функция, поверхности 500 и 200 мбар, 4 — взаимная корреля-
ционная функция, поверхности 500 и 300 мбар; б — взаимная корреляцион-
ная функция различных изобарических поверхностей с разностью давления
6р мбар [У.2].
6 приложения 3, на которых приведены карты средних квадрати-
ческих величин отклонений высот изобарических поверхностей
от средних значений.
В общем случае можно утверждать, что метеорологические
поля являются неоднородными и анизотропными. Од-
нако возвращаясь к рис. 1.6, можно отметить, что изолинии равных
значений автокорреляционных функций на сравнительно неболь-
шой площади порядка 2X2 тыс. км отличаются от круговых незна-
чительно. На таких площадях и величины дисперсии также меня-
ются сравнительно мало. Таким образом, в первом приближении
эти поля можно считать однородными и изотропными. Для таких
полей автокорреляционная функция уже не зависит от направле-
ния, а определяется только расстоянием.
2*
19
Зависимость нормированных автокорреляционных и вообще
нормированных корреляционных функций от расстояния для раз-
личных метеорологических элементов имеет более или менее оди-
наковый характер. При увеличении расстояния значения этих
функций вначале плавно убывают. На некотором расстоянии эти
величины переходят через нуль, а при дальнейшем увеличении рас-
стояния они, как правило, колеблются вблизи нулевых значений.
Примеры зависимости автокорреляционных и корреляционных
функций высот различных изобарических поверхностей от расстоя-
ния р приведены на рис. 1.7.
Особый интерес представляют нормированные автокорреляци-
онные и корреляционные функции в зависимости от разности вы-
сот. Зависимость этих функций от высоты в общем сходна с зави-
симостью их от расстояния, т. е. с увеличением разности высот зна-
чения функций уменьшаются, переходя в некоторых случаях через
нуль. В качестве примера на рис. 1.7 приведена зависимость нор-
мированной корреляционной функции геопотенциала различных
изобарических поверхностей в тропосфере от разности высот этих
поверхностей, выраженной в единицах давления На рисунке
видно, что значения этой функции при небольших величинах раз-
ности давления (бр< 100 мбар) близки к единице (г>0,90).
Из этого следует, что используя данные о геопотенциале близких
изобарических поверхностей, мы, по существу, имеем дело с взаи-
мозависящей информацией.
Глава II
УРАВНЕНИЯ ГИДРОТЕРМОДИНАМИКИ
И ИХ ПРЕОБРАЗОВАНИЯ ДЛЯ ЦЕЛЕЙ ЧИСЛЕННОГО
ПРОГНОЗА КРУПНОМАСШТАБНЫХ АТМОСФЕРНЫХ
ДВИЖЕНИЙ
§ 1. Уравнения гидротермодинамики идеальной жидкости
Атмосферные процессы могут быть описаны на основе трех из-
вестных законов физики: закона изменения количества движения,
закона сохранения массы и закона сохранения энергии Матема-
тическим выражением этих законов являются уравнения движения,
неразрывности и притока тепла соответственно. Наряду с этими
общими законами физики и вытекающими из них уравнениями при
исследовании атмосферных процессов должны быть привлечены
и другие соотношения, описывающие специфические свойства ат-
мосферы как некоторой вполне определенной разновидности сплош-
ной среды. К их числу относятся уравнение состояния и уравнение
переноса влаги.
Рассмотрим указанные уравнения применительно к идеальной
жидкости, какой считается атмосфера при отсутствии молекуляр-
ной и турбулентной вязкости и теплопроводности и лучистого теп-
лообмена. Эти же уравнения для модели атмосферы, более близкой
к реальной, мы рассмотрим в последующих параграфах этой
главы.
Уравнения движения. Уравнение движения в векторной
форме имеет вид
-^-=F—J-grad/?, (1.1)
где U — вектор скорости, dMfdt — вектор ускорения, F — вектор
сил, отнесенных к единице массы, gradp = Vp — вектор поверхно-
стных сил давления р, р — плотность, t — время.
Если и, v и w — проекции вектора скорости U, FXi Fv и Fz — про-
др др др
екции вектора силы F и и -----проекции вектора по-
верхностных сил или градиента давления на оси координат х, у и z,
21
то уравнения движения в координатной форме записываются
в виде:
du __р 1 др .
dt х р дх ’
dv __£, 1 др
~dF~py Г1)7’
Z7 1 дР /1 04
-dr==^~"T~d7t (L2)
где
d д . д . д . д
dt dt 1 дх 1 ду 1 дг
— символ индивидуальной производной.
Из массовых сил в атмосфере действует сила тяжести g, вклю-
чающая гравитационную силу притяжения Земли и центробежную
силу, и отклоняющая сила вращения Земли или сила Кориолиса,
которая выражается с помощью векторного произведения — 2(oXU,
где о — вектор угловой скорости вращения Земли, направленный
параллельно оси Земли к северному полюсу. Тогда векторное урав-
нение движения (1.1) применительно к атмосфере переписывается
в виде
grad— 2<oXU+g. (1.3)
Используя правила векторного анализа, для проекций силы Ко-
риолиса на оси х, у и z получим:
2 (соуw — wya); 2 (co^zz — ;
2 — wyzz),
где сох, со?/ и coz — проекции вектора со. Произведем ориентацию де-
картовой системы координат таким образом, чтобы начало коорди-
нат оказалось на поверхности Земли в некоторой точке, направле-
ние оси z совпало с направлением местной вертикали в этой точке
земной поверхности, а направления осей х и у остались произволь-
ными. В результате получим так называемую локальную де-
картову систему координат. В этом случае можно положить,
что проекции силы тяжести, направленной к центру Земли, gx =
= gy = 0> а gz=—gf где g— абсолютная величина силы тяжести.
Величина g зависит от высоты точки над уровнем моря и широты
места следующим образом:
g=9,80(l—0,0026 cos 2?) (1—3,14 • \0~7z) м/с2. (1.4)
Колебания величины g в зависимости от широты и высоты малы
(порядка десятых долей процента). Поэтому в численных прогно-
22
зах обычно полагают, что g = 9,8 м/с2. Учитывая сказанное, урав-
нения движения теперь можно записать в виде:
dv _ 1 dp OfO 1! I ‘701*
dt P dy
dw _ 1 dp Рот *7, 1 Pro и (у (1.5)
dt " P dz 1 Z/VJ у Ы, o’
Если теперь ось у направить по меридиану на север, а ось х по
параллели на восток, то
о)Л=0, o)y=o)COS^, 0^=0) sin ср,
где ср — широта места, со = 0,729- 10“4 1/с — абсолютная величина
угловой скорости Земли. Введем обозначения:
/=2о) sin ср, Zj = 2о) cos ср.
Переменная величина I называется параметром Кориолиса.
В этом случае уравнения движения принимают вид
du _ 1 dp J 7 m 7. mi*
dt " Р dx
dv _ 1 dp Ju’
dt ” Р dy 1'LL)
dw _ 1 dp 1 - /. it СГ (1.6)
dt ~~ Р dz
Уравнение неразрывности. В векторной форме это
уравнение имеет вид
др dt —f—div (pU)=O. (l.7)
Второй член уравнения описывает дивергенцию (расходимость) ко-
личества движения. Согласно формулам векторного анализа
div(pU) = V • (pU)
dpw » I dpw
dx ' dy ' dz
= U-~—"7Г- + Р div U,
dx 1 dy 1 dz 1 r
(1.8)
где
J- IT v, IT du , dv . dw
divU=V -^=^4--^ + ^-
— дивергенция скорости
23
С учетом выражения (1 8) уравнение неразрывности можно
записать теперь в двух различных видах:
dp ] dPw j dpv t dpw Z1 пч
dt + дх + ду + dz ~U’
т4+(4+-^+т)=«- <iio)
В случае несжимаемой жидкости dpldt^b и уравнение неразрыв-
ности принимает вид
^L + _^. + ^L=O. (1.11)
дх 1 ду 1 dz ' 7
Уравнения движения и неразрывности известны как уравнения
тидродинамики.
Уравнение состояния (уравнение Клапейрона) имеет
<вид
P=?RT, (1.12)
где Т — температура, /? = 2,8704• 106 эрг/(г-град)—удельная газо-
вая постоянная для сухого воздуха. Мы видим, что плотность есть
функция двух переменных: давления и температуры, так же, как и
давление есть функция двух переменных: плотности и температуры.
Однако в некоторых частных случаях плотность среды оказывается
зависящей только от давления (и наоборот). Такие среды называ-
ются баротропными. Для них справедливо соотношение
Р=Ф (Р), (1.13)
где символ Ф определяет вид функциональной зависимости р от р.
Характерный пример среды, для которой справедливо это соотно-
шение,— пресная вода в водоеме. Среды, в которых не выполня-
ется указанное условие, называются бароклинными.
Атмосфера лишь в некоторых частных случаях может рассмат-
риваться как несжимаемая жидкость с постоянной плотностью р =
= const. В общем случае она должна рассматриваться как сжимае-
мая жидкость.
Уравнение притока тепла есть примененное к атмо-
сфере выражение первого начала термодинамики. Оно может быть
записано в различных формах. Одна из них следующая:
где ср = 0,2405 кал/(г-град) — теплоемкость воздуха при постоян-
ном давлении, А = 2,3884 • 10~8 кал/эрг — термический эквивалент
работы, 8 — приток тепла к единице объема, о котором пойдет речь
дальше.
24
Используя уравнение состояния и уравнение Мейера
сР — cv=AR,
где с^=0,1719 кал/(г-град)—теплоемкость при постоянном объ-
еме, уравнение (1.14) можно переписать в виде
dT х — 1 Т dp__________ I
dt х р dt срр
(1-15)
где % = Cp/Cv «=» 1,4 или, учитывая, что Ag/cp=y& = 0,98- 10~2 гр а д/м—
сухоадиабатический градиент температуры,
——4т-=—• О-16)
dt gf dt срр ' '
Введем в рассмотрение потенциальную температуру 0 с помо-
щью соотношения
(1-17)
где Р= 1000 мбар — стандартное давление на уровне моря. Путем
простой подстановки можно убедиться, что уравнение (1.15) пере-
ходит в уравнение
б/0 _ 0 1 _ / Р 1
dt Т \ р / срр
(1.18)
где к = (сР — cv)/cp.
Вернемся теперь к притоку тепла е. В атмосфере имеют место
три вида притока тепла: лучистый ел, турбулентный ет и фазовый
8ф. Так что
е—ел4~ет4~еФ-
В идеальной атмосфере, в которой турбулентность отсутствует,
действуют только фазовый и лучистый притоки тепла.
Фазовый приток тепла связан с переходом влаги из одного
агрегатного состояния в другое. При конденсации, а также субли-
мации (переходе влаги из парообразного состояния в твердое, ми-
нуя жидкую фазу) происходит выделение тепла, а при испарении —
его затрата. Количество выделяемого (поглощаемого) тепла вы-
ражается соотношением
еф=^/п, (1.19>
где m — скорость конденсации (сублимации) или испарения влаги,
т. е. количество сконденсировавшейся или испарившейся влаги
в единице объема за единицу времени, 2"— теплота конденсации
(сублимации) или испарения (j?~600 кал/г).
Лучистый, а также турбулентный притоки тепла будут рассмот-
рены в следующих разделах.
Остановимся еще на уравнении первого начала термодинамики
для политропических процессов, т. е. процессов, протекающих
25
при постоянном значении теплоемкости сл = const. К политро-
пическим процессам относятся, в частности, изобарические (р =
= const), изостерические (р = const) и изотермические (Г=const)
процессы.
Уравнение притока тепла для политропических процессов мо-
жет быть записано в различных формах, например,
-4-=const или рр х=const или -4~=Х — -4т-; (1.20)
рА at р at ' х 7
Т dT X—1 Т dp п О1Ч
const или ---------------О-21)
р х
где X = (ср — сл) /(cv — сп) — показатель политропы.
Заметим, что последнее из уравнений (1.21) совпадает с урав-
нением притока тепла в форме (1.15) при в=0 и Х=х, т. е. с урав-
нением для адиабатического процесса, при котором сл=0. Кроме
того, положив в (1.21) %=1, мы получим dT/dt = O или Т=const,
т. е. мы приходим к изотермическому процессу. Приняв же в (1.20)
Л = оо, мы получаем р = const, т. е. условие изостерического про-
цесса в несжимаемой среде.
Уравнение переноса влаги. До сих пор шла речь об ат-
мосфере, в которой отсутствуют различные примеси и турбулент-
ность. Однако в реальной атмосфере почти всегда имеют место раз-
личные примеси, важнейшей из которых является водяной пар.
При отсутствии турбулентности изменение содержания водяного
пара в движущихся объемах воздуха происходит либо за счет кон-
денсации (сублимации), либо за счет испарения. Этот процесс опи-
сывается с помощью уравнения переноса влаги. Последнее запи-
шем применительно к удельной влажности qy равной отношению
массы водяного пара к массе влажного воздуха, в виде
Уравнения (1.6), (1.9), (1.12), (1.14) и (1.22) образуют замкну-
тую систему из семи уравнений для семи искомых величин u, v, w,
р, р, Т и q в случае атмосферы, рассматриваемой как идеальная
жидкость При этом в уравнении притока тепла (1.14) учтен при-
ток тепла только от конденсации; включение других видов притока
тепла требует введения новых искомых величин и соответственно
включения в построенную систему дополнительных уравнений. Эти
вопросы рассматриваются в трех последующих параграфах настоя-
щей главы.
§ 2. Уравнения гидротермодинамики для турбулентной
атмосферы
В предыдущем параграфе речь шла об уравнениях для так на-
зываемой идеальной жидкости, в которой отсутствует молекуляр-
ная вязкость, а движение является ламинарным. Такая стилизация
26
атмосферы может быть оправдана далеко не всегда. Дело в том,,
что если эффект молекулярной вязкости при исследовании атмо-
сферных движений является пренебрежимо малым, то эффект тур-
булентного характера движений может быть значительным.
Поэтому возникает проблема учета этого явления. В задачах динами-
ческой метеорологии и численного прогноза погоды наиболее ши-
рокое применение нашел приближенный учет турбулентности,
который производится с помощью перехода к уравнениям гидро-
термодинамики для осредненных значений рассматриваемых пере-
менных и использования результатов полуэмпирической теории
турбулентности.
Как уже говорилось, движение отдельных частиц в турбулент-
ном потоке носит хаотический характер и напоминает броуново
движение молекул. Описать эти движения с помощью гидродина-
мических уравнений невозможно. С другой стороны, при решении
метеорологических задач в этом и нет необходимости. Нам доста-
точно правильно описать некоторое среднее состояние переменных
и его изменение во времени. При этом эффект неупорядоченных
пульсаций может быть учтен суммарно.
Пусть f=f(x, у, z, t) — некоторая переменная, f — сглаженное
значение переменной, a f' = f— f — отклонение от этого сглажен-
ного значения или пульсация. Операция сглаживания может быть
определена различным образом. Здесь рассмотрим лишь сглажи-
вание по времени. Пусть т — период осреднения, выбираемый в ос-
новном на основании эмпирических исследований. Тогда операцию
сглаживания определим следующим образом:
f(x, у, Z, 0=4' У f^x> У’ z’ (2Л>
Путем элементарной проверки можно убедиться, что для сглажен-
ных функций справедливы следующие выражения:
J7=_^7. .
дх дх ’ ду ду 1 dz dz ’
7=7; 7=/-7=7~7=0 и т. д. (2.2)
Двойной чертой здесь обозначена двойная операция сглаживания.
При наличии двух функций f и мы имеем, например,
/4"?=/+?; /?=(/+7) (?+?')=
=/? +/'? +/?' +/V =/? +/V,
fy=fy и т. д. (2.3)
Применяя операцию сглаживания (2.1) и используя соотношения
(2.2) и (2.3) и аналогичные им к уравнениям гидротермодинамики
27
идеальной жидкости, приведенным в предыдущем параграфе,
мы получим уравнения для сглаженных переменных [10]. Проде-
лаем это по отношению к уравнениям движения в форме (1.2),
уравнению неразрывности (1.10) и уравнениям переноса тепла
(1.18) и влаги (1.22). Положим, что
u=u~\-ur; v=v-\-vr; w=w-|-w'; Р=р-\~Р' \
Т=Т-\-Т'-, р=р + р' и q=q-\-q’,
где величины с черточкой являются осредненными, а величины
оо штрихами — отклонениями от них.
Предварительно заметим, что каждое из только что перечис-
ленных уравнений может быть приведено к виду
£=7*’ (2Л)
где о — любая субстанция, a N— некоторая заданная функция.
Убедимся в этом, рассмотрев два примера. Первое из уравнений
движения (1.2) приводится к виду (2.4) при а = и, nN = pFx .
дх
Замечая, что
JL = _ р2 _± f JL \ - 02 а р \
dt dt \ р / ’ dx dx \ р )
и т. д., уравнение неразрывности можно переписать в виде
d ( 1 \ 1 / Эи . Эг/ . dw \
dt \ р / р \ dx *" dy *" Эг /
Но это уравнение принимает вид (2.4), если положить о= 1/р, а
__ du j dv ( dw
dx ’ dy * dz
Запишем теперь уравнение (2.4) в виде
(da . da . da . da \ /Л
(2-5)
Введем новые переменные:
mx=pu\ my=^v\ mz=yw. (2.6)
Можно убедиться, что уравнение (2.5) перейдет в уравнение
Эре t dmxa । dmya f
dt dx “Т" dy "Т" dz —yV-
Положим теперь, что
тх=тх-\-тх\ ту==ту-\-ту-, mz=mz-\-mz\
с' и N=N -\-N'
28
и сделаем предположение, что пульсации плотности р малы и ими
можно пренебречь, т. е. положим, что р = р.
Произведем теперь операцию сглаживания уравнения (2.7).
Учитывая соотношения (2.2) и (2.3), получаем:
dpG др (о °') ____ dpa | __дра
dt dt dt ' dt dt ’
dmxs
dx
dmxv ,
dx ' dx
T. Д.
В результате вместо уравнения (2.7) получаем
dps । dmx<s . дтуъ dmza
dt ' dx ' dy ' dz
dtnvv dm.,a
x____I_____у
dx * dy
dmc \ —
dz /
(2.8)
Произведя дифференцирование произведения, возвращаясь от
переменных тх, ту, mz к прежним, учитывая, что согласно урав-
нению неразрывности
-(др , дри , дру । dpw\_n
\ dt дх ‘ dy ‘ dz / ’
а также перенеся член уравнения (2.8), заключенный в скобки,
вправо, получаем
dv__ 1 д7 1 I дри'а' । dpv'a' ! dpw'a' \ /q qk
~dt~уА Тдх Ту 1 дГ~)•
Таким образом, вместо уравнения (2.4), справедливого для иде-
альной атмосферы, мы получили новое уравнение, которое отлича-
ется от первоначального наличием группы членов, содержащих
осредненные произведения пульсаций. Эти дополнительные члены
имеют смысл воздействия некоторой дополнительной силы, если
рассматривается поле скорости или дополнительного притока тепла
или влаги, если речь идет о распространении тепла или влаги. Сла-
1 дри'о' „
гаемые типа ——— представляют собой вызванные турбулент-
ностью изменения компонент ветра, температуры или влаги.
Учитывая полученные результаты, уравнения движения, нераз-
рывности, притока тепла и влаги для сглаженных величин можно
записать в виде
_ _ / 2* _ ________ \
du __дГ 1 dp 1 J dpuf L dpu'v' , dpu'w' |
dt x p dx p \ dx ' dy ' dz / '
_ / - 2 ___ \
dv__________________________________________1 др 1 | dpw't/' । dpv' । dpv’w' ]
dt y p dy p \ dx ' dy dz / ’
29
dw ___1 dp 1 ( dpu'w' j dpv'w' , dpw'2N| .
dt z p dz p \ dx dz )
dp , dpu j dpv j dpw _r.
dt * dx * dy * dz ’
d® _ 0 1- 1 / dpu'Q' . dpv'Q' . dpw’Q' \ *
dt ~T Cpp^ p \ dx * dy * dz / ’
dq __ m 1 Idpidq^ , dpv^f , dpi^7^ /о m\
dt ~ p p \ dx ' dy dz Г ( '
Три уравнения движения системы уравнений (2.Ю) содержат
шесть дополнительных переменных:
—7—7 —7
—ри =тХЛ; —puv='txy\ —?uw =ъХ2-
2 ____ 2
—ри' =хуу- —pu'w'=xyz; — pw’ = т2г, (2.11)
которые называются напряжениями турбулентного трения или на-
пряжениями Рейнольдса и имеют смысл потока количества движе-
ния, связанного с пульсациями.
При рассмотрении трех дополнительных членов уравнения при-
тока тепла введем величины:
^рц'б^Нд.; = fppw'0'=Hz, (2.12)
которые имеют смысл компонентов потока тепла Н, обусловлен-
ного турбулентностью. Поток тепла и его компоненты связаны
с турбулентным притоком тепла к единице объема вт следующим
образом:
<. и pH,
er=-d!VH=-^
<ЭНу
йН2 \
dz )
(2.13)
Аналогично переменные
pu'q'=Qx; pv'q'=Qy-, pw'q'=Qz, (2.14)
входящие в уравнение переноса влажности, можно интерпретиро-
вать как составляющие потока водяного пара Q. Связь между по-
токами водяного пара и его притоком к единице объема выража-
ется соотношением
.>__divQ=-(^ + ^ + >.). (2.15)
Все эти переменные являются новыми неизвестными. Таким об-
разом, операция осреднения, сохранив число исходных уравнений,
привела к появлению дополнительных неизвестных. Замыкания
системы можно достигнуть, привлекая какие-либо новые соотно-
шения.
Такие соотношения могут быть получены на основе полуэмпи-
рической теории турбулентности. Эта теория дает связи между ука-
30
занными переменными, содержащими произведения пульсаций,
и осредненными значениями рассматриваемых функций.
Так для напряжений турбулентного трения имеем:
ди ди . ди
ХХХ--РК \ ^Ху------ № i ZXZ-----РК ft? ’»
,, dv tdv . dw
— pk ~ду~ ’ Xyz—^k~dz~ ’ "zz—№ dz 9 (2.16)
где k и k' — коэффициенты турбулентной вязкости или обмена для
количества движения или просто коэффициенты турбулентности
в вертикальном и горизонтальном направлениях соответственно.
Последние, вообще говоря, являются неизвестными. Об их опреде-
лении будет идти речь в § 3. Пока же заметим, что коэффициент
k' обычно считается независящим от горизонтальных координат,
а коэффициент k — зависящим только от вертикальной коорди-
наты.
Турбулентные потоки тепла в этом случае выражаются в виде:
Н^=-срР^^; Ну=-срр4^-; Н2=-срр^-^-, (2.17)
где Л© и k'— коэффициенты турбулентного теплообмена в верти-
кальном и горизонтальном направлениях. Наконец, для турбулент-
ных потоков влаги справедливы соотношения:
Qx=-pkq^-, Qy=-pkq^-, Q^-pkQ-^-, (2.18)
где kq и Л'— коэффициенты турбулентного обмена для влаги в вер-
тикальном и горизонтальном направлениях. Коэффициенты турбу-
лентности &©, k'&, kq и k'q связаны с коэффициентами k и k' сле-
дующим образом:
Л0=ае£; £0=а0Л ; kq=aqk', kq=aqkf, (2.19)
где а© и aq— отношения коэффициентов турбулентности для тем-
пературы и влажности к коэффициенту турбулентности для коли-
чества движения. Эти коэффициенты, близкие к единице, могут
быть определены на основе эмпирических данных.
Имея в виду (2.19), пренебрегая изменениями плотности воз-
духа по горизонтали и вертикали как несущественным по сравне-
нию с изменениями соответствующих субстанций и учитывая (2.13)
и (2.15), турбулентные притоки тепла и влаги к единице объема
можно выразить в виде:
/./ а л । д .д®
4=a-^pPk AQ + a^pp-gy^-^-; •
= (2-20)
где Д = д2/дх2+д21ду2.
31
Значения коэффициентов а© и ад, как уже говорилось, опреде-
ляются с помощью эмпирических данных, обычно они близки к еди-
нице. В задачах численного прогноза принимается, что а© = ад=1.
Поэтому в дальнейшем, за исключением особо оговоренных слу-
чаев, эти коэффициенты будут опускаться.
Таким образом, учитывая силу Кориолиса и силу тяжести,
а также присоединяя к полученным уравнениям уравнение состоя-
ния. получим следующую систему уравнений для осредненных ве-
личин (знаки осреднения здесь и далее опускаются):
-4т-=-----4^—2coyw-}-2co^4-Af + ;
at р дх у 1 л 1 1 dz dz ’
dv 1 др n . n . .r л । d , dv
—rr=------—2(о^4-2сод/ге>4-£ ДгН—k-^—;
dt p dy z \ x \ ' dz dz 1
dp . dpu . dpv . dpw „
dz~~V'
p=R?T-,
~dT — \T) Д0+’йГ^"5г];
-g-=- —+k' ^q+-4~k-^. (2.21)
dt p 1 dz dz v 7
При использовании обычной температуры вместо потенциаль-
ной для турбулентных потоков и притоков тепла имеем:
Нх=—срр^ ; Ну = — cppk ;
нг= —cppk (4г+ь);
ет=Срр//Д7Ч-сРР^(4|- + ь). (2.22)
Тогда уравнение притока тепла принимает вид
4г-тг4г-7у<'-+‘ф)+*'47'+тл'(т+^- <2-23>
Величина фазового притока тепла 8ф определяется с помощью
соотношения, приведенного в предыдущем параграфе
§ 3. Пограничные слои в атмосфере
Действие сил турбулентной вязкости наиболее значительно
в пограничных слоях, которые связаны с зонами больших градиен-
тов скоростей. Так, например, пограничные слои возникают вблизи
фронтальных поверхностей или у береговой линии, где наблюда-
32
ется перепад скоростей. Это так называемые внутренние погранич-
ные слои атмосферы.
Наиболее важным является планетарный пограничный слой,
возникающий за счет влияния подстилающей поверхности и вра-
щения Земли.
Толщина пограничного слоя определяется рядом параметров
атмосферы и в первую очередь величиной коэффициента турбу-
лентной вязкости k. Произведем приближенную оценку толщины
планетарного пограничного слоя [У. 12]. Возьмем одно из уравне-
ний движения, например, уравнение, соответствующее оси х, и огра-
ничимся рассмотрением действия турбулентности только по верти-
д t ди тг
кали, т. е. члена ' Пусть в пограничном слое скорость
ветра изменяется от нуля у поверхности Земли до некоторого ха-
рактерного значения V при некоторой высоте d. Выше скорость ос-
тается неизменной. В таком случае при постоянном значении k
можно записать
\ dz dz ) d-
В пределах пограничного слоя преобладающей силой является
сила турбулентной вязкости, а вне его (в свободной атмосфере) —
сила Кориолиса, порядок которой
O(2a)Sincp) = O(/u) = /K
Следовательно, высота верхней границы пограничного слоя может
быть определена из условия равенства названных сил. Приравни-
вая выражения для этих двух сил, получаем
k~=lV.
d2
Отсюда
Полагая, например, k = 5 м2/с, /=1,2-10~4 1/с, находим d~200 м
В действительности, однако, действие силы турбулентной вязкости
проявляется до несколько большей высоты (мы убедимся в этом
несколько далее). Эта сила будет на порядок меньше силы Корио-
лиса примерно с высоты /1 — 600—1000 м. Слой атмосферы толщи-
ной 600—1000 м, прилегающий к земной поверхности, в котором
проявляется сила турбулентной вязкости, называют планетар-
ным пограничным слоем.
Внутри этого слоя различают еще нижний подслой (при-
земный или приводный слой), толщина которого составляет не-
сколько десятков метров В этом подслое сила турбулентной вяз-
кости на порядок больше силы Кориолиса и силы барического гра-
диента.
3 Зак. № 21
33
Рассмотрим теперь имеющий важное значение в теории
прогноза вопрос о распределении ветра с высотой
и о вертикальных движениях в планетарном погранич-
ном слое. Указанную задачу будем рассматривать вначале при за-
данном коэффициенте турбулентной вязкости для вертикального
направления k при условии стационарности и горизонтальной од-
нородности пограничного слоя, а также при пренебрежении малыми
членами w du/dz и w dv/dz в уравнениях движения.
При этих условиях уравнения движения имеют вид:
dz dz ' g >
<31>
1 dp 1 dp
где ug = ------—, vg=-— ---------компоненты геострофического
Zp dy Zp дх
ветра.
После введения комплексных переменных
M=u-\-iv и Mg=ug-\-ivgt
где i — мнимая единица, уравнения (3.1) можно записать в виде
одного уравнения
(3.2)
dz dz g v 7
(При этом было учтено, что \!i = —t).
Для случая k = const уравнение (3.2) принимает вид
(3.3)
Решая это уравнение при краевых условиях
при М ограничено,
при z=Q 714=0 (3.4)
(что означает ограниченность и и v на верхней границе атмосферы
и обращение их в нуль на земной поверхности — условие «прили-
пания») и возвращаясь к прежним переменным, получаем
1 дР (\ 1 др
— 7р—~ду~ ' * — COS ---------/р—~дх~ &
V (1 - cos —у е^г sin 8г> <3-5)
где
Найдем высоту z = h, при которой направление ветра будет со-
впадать с направлением изобар. Положим, что dp/dx = 0. Тогда при
z = h у = 0, если sin <5/г = 0. Но это выполняется при 6й = щп, где
34
п — целое число. Отсюда следует, что h = nnl&. При Z= 1,2- 10~4 1/с
и k = 5 м2/с 6=0,346- 10~2 1/м и тогда при п=1 получаем Л^910м.
Это более точная оценка высоты планетарного пограничного слоя
по сравнению с полученной ранее величиной d.
С помощью найденных выражений для и и v можно получить
вертикальную скорость, обусловленную турбулентной вязкостью.
Получим выражение для вертикальной скорости на высоте h. Ин-
тегрируя уравнения неразрывности по высоте от z = 0 до z = h, учи-
тывая, что при z = 0 w = 0, и опуская малые члены, получаем
h
1 С / дои . dov \ ,
wh—-------। -4——з—
" P/z J \ дх 1 ду )
о
Подставляя сюда и и v по (3.5) и обозначая А = д/дя2+д/дг/2, по-
лучаем
h
^н= —j Ape~Zzsin ozdz.
Принимая, что Ар = Ар0, где ро — давление на уровне моря, вынося
Аро за знак интеграла и производя интегрирование, получаем
^/г=аДр0, (3.6)
где
__ 1
а~ /РЛ» ’
В системе MTS при 2=1,2- 10~4 с“\ 6=0,346- 10~2 м-1 и рд =
= 1,1 • 10“3 т • м~3 (дляй=103м) а~2,19-109 м4 • т-1 • с-1 Отметим
еще, что О (Wh} = Ю~2 м/с.
Изложенная модель в основном правильно описывает измене-
ние ветра с высотой. Однако она дает слишком быстрое изменение
направления ветра с высотой вблизи земной поверхности. Несмотря
на это суммарный эффект пограничного слоя, выражаемый в виде
вертикальной скорости на его верхней границе, достаточно хорошо
отражает действительность Поэтому формула (3.6) нашла широ-
кое распространение в задачах численного прогноза.
Основным недостатком изложенной модели является предполо-
жение о постоянстве коэффициента турбулентной вязкости. Более
совершенные модели были получены при тех или иных гипотезах
относительно зависимости этого коэффициента от высоты. Так,
М. Е. Швец и М. И. Юдин [У.7] построили модель пограничного
слоя, задавая коэффициент k с изломом
kxz
kxhx
при
при
(3 7)
где /ii — высота приземного слоя, составляющая несколько десят-
ков метров, a kx — значение k при z = h\
3*
35
И. А. Кибелем [У 12] получено решение при задании коэффи-
циента турбулентной вязкости с изломом в виде
(, / Z \(1-е)
k =
при z < Aj;
при г>й1(
(3-8)
где O^e^I (при инверсии 1/4, при равновесных условиях, т. е.
при безразличной стратификации е^1/7, а при сверхадиабатиче-
ских градиентах е~ 1/10)
Так как в приземном подслое происходит очень быстрое увели-
чение скорости ветра с высотой, то оказывается, что в этом слое
сила турбулентной вязкости значительно превышает силу бариче-
ского градиента и силу Кориолиса. Действительно, если, например,
скорость ветра на верхней границе приземного слоя составляет
10 м/с, то при k = b м2/с и hi = 10 м
о \-4~k
\ аг
где М — значение М для приземного слоя.
В то же время при /=1,2-10“4 1/с О (1М) = 0 (1Мё) = 1,2 • 10~4Х
X 10= 1,2 • 10-3 м/с2. Поэтому для приземного слоя вместо уравне-
ния (3 2) будет справедливо
(3-9)
Из этого уравнения следует, что
a г +
k—=C1=const.
(3.10)
Это означает, что в приземном слое направление ветра не изменя-
ется с высотой, а изменение скорости обусловлено распределением
по высоте коэффициента k. Вне приземного слоя, как и ранее, бу-
дет справедливо уравнение (3.3). Таким образом, мы приходим
к необходимости решать двухслойную задачу. В качестве краевых
условий принимаем ограниченность решения на бесконечности, ус-
ловия «прилипания» у земной поверхности и условия «склейки» на
верхней границе приземного слоя, т. е. равенства здесь значений М
и М и их производных. Эти условия записываются в виде:
при г—оо М ограничено;
при г=г0 7И=0;
при z=hx М=М,
(3.11)
36
Высота го называется уровнем или параметром шеро-
ховатости. Она имеет смысл некоторой доли от средней вы-
соты мелких неровностей подстилающей поверхности, которые спо-
собствуют возникновению турбулентности. Значения го колеблются
в пределах О<го<1О см. Не производя соответствующих выкла-
док, приведем здесь окончательные выражения для М и Му полу-
ченные при условиях (3.8) и (3.11):
М1- 1+и‘(.+--> 11+11’'-’К
й-1Х+.->ди-^ <312>
^0
где
8=/7/2£, * = J -^-dz^25 м.
ZO
Возвращаясь к прежним переменным и разделяя действитель-
ные и мнимые части, получим выражения для и и v. С помощью
этих выражений можно получить формулу для вертикальной ско-
рости на верхней границе пограничного слоя. После незначитель-
ных упрощений это выражение записывается в виде
wh=a^p0, (3.13)
=_1___________1_______
ГДе ai~ lph 26 (1+266+26262) ”
При указанных ранее значениях рь / и 6 в системе MTS «1 =
= 109 м4 • т~4 • с-1, что в общем близко к значению а в (3.6).
Вернемся еще к вопросу о скорости ветра в приземном слое для
случая k = k\Z. Проинтегрируем уравнение (3 10) при условии Л1 = 0
при г=г0. В результате получим
где С — некоторая новая постоянная.
Полученное выражение показывает, что изменение скорости
в приземном слое происходит по логарифмическому закону. Подоб-
ное же выражение для скорости ветра получается и из общих по-
ложений полуэмпирической теории турбулентности. Так, например,
широко применяется следующее выражение для скорости ветра V:
где х = 0,4 — постоянная Кармана, a v*— так называемая динами-
ческая скорость. Последняя связана с силой турбулентного трения
т следующим образом:
37
Перейдем к рассмотрению такой постановки задачи, в которой
коэффициент турбулентной вязкости не задается заранее, а опре-
деляется в ходе решения уравнений пограничного слоя наряду
с другими метеорологическими параметрами, к числу которых
кроме компонентов ветра относятся также турбулентные потоки
тепла и влаги.
Впервые такая постановка задачи была рассмотрена А. С. Мо-
ниным, а затем С. С. Залитинкевичем и Д. Л. Лайхтманом. Изло-
жим здесь кратко постановку и решение этой задачи в основном по
работе [2].
В качестве исходных уравнений берутся уравнения движения,
притока тепла и баланса кинетической энергии турбулентных пуль-
саций в предположении их стационарности и однородности по го-
ризонтали, отсутствия лучистого и фазового теплообменов, а также
постоянства плотности внутри пограничного слоя.
Уравнения движения и притока тепла внутри пограничного слоя
берутся в виде:
(3-14)
(3.15)
где = 1, k®— коэффициент турбулентного обмена для
теплоты. Величины иё и vg считаются известными.
Проинтегрировав уравнение (3.16) по z и умножив результат на
сРр, получаем
где С — произвольная постоянная. Но левая часть полученного вы-
ражения равна турбулентному потоку тепла в вертикальном напра-
влении, взятому с обратным знаком, —Н. Полученное выражение
показывает, что в данной постановке задачи вертикальный поток
тепла не меняется с высотой. И мы можем записать
Н=— a@cppA-^-=const. (3.17)
Так как ^0/б/г = (8/7) (уа— у), то при &/Т=1 Н =
= — a®cPpk (уа —у).
Отсюда следует, что вертикальный поток тепла будет положи-
телен (направлен вверх) при неустойчивой (у>уа) и отрицате-
лен— при устойчивой (у<уа) стратификации. Величина потока
тепла будет зависеть от коэффициента k, который сам является
искомой функцией. При решении поставленной задачи применяется
метод последовательных приближений Если производную dQ/dz
заменить ее средним значением для всей толщи пограничного слоя,
38
а в качестве k задать какое-либо произвольное значение, то поток
Н будет в первом приближении определен. В последующих при-
ближениях, используя уже найденное значение k, получаем уточ-
ненные величины Н.
Рассмотрим теперь уравнение баланса кинетической энергии
турбулентных пульсаций pfe2, где b2 = (u'2 + v'2 + t^,2)/2, черта
сверху означает знак осреднения. При условии горизонтальной од-
нородности оно имеет вид
где ah = kblk\ kb — коэффициент турбулентного обмена для вели-
чины b; $=g/T — параметр плавучести. Это уравнение получается
путем умножения каждого из трех неосредненных уравнений дви-
жения на и. v и w соответственно (при этом сохраняются величины
пульсаций), осреднения и суммирования результатов, а также пре-
небрежения некоторыми малыми членами.
Первый член в правой части этого уравнения характеризует
переход кинетической энергии осредненного движения в энергию
турбулентности; он зависит от вертикальных градиентов скоростей
и всегда положителен. Второй член уравнения, который с учетом
сказанного можно записать в виде рН/сррили—а0р& (уа — у),опи-
сывает затрату энергии турбулентности на преодоление архимедо-
вых сил или сил плавучести или же переход этих сил в энергию
турбулентности. При устойчивой стратификации он отрицателен,
при неустойчивой — положителен. Третий член уравнения описы-
вает изменение кинетической энергии турбулентности в результате
турбулентной диффузии. Наконец, последний член уравнения е от-
ражает эффект диссипации или перехода кинетической энергии
турбулентных пульсаций в тепловую.
В случае стационарного процесса, который и рассматривается
в теории пограничного слоя, db2ldt = l0 и уравнение баланса прини-
мает вид
Система трех уравнений (3.14), (3.15) и (3.18) содержит пять
неизвестных: и, v, k, b и е. Присоединим сюда еще три уравнения,
следующие из полуэмпирической теории турбулентности:
1 з
k=b2 Ц &=cb2 Д;
Л==-7ф/-^-> (3 19)
где
= (Ju\2 ( dv \2 рЯ । ч d db
\ dz ) \\ dz ) ' kcpp I" k dz K dz 9
39
и — 0,37 и с~0,46-10-1— безразмерные константы. Новая, шестая
неизвестная переменная L имеет смысл среднего значения про-
странственного масштаба турбулентных пульсаций. Первое и вто-
рое из уравнений (3.19) дают связь между коэффициентом турбу-
лентности и скоростью перехода кинетической энергии турбулент-
ности в тепловую и значениями пространственного масштаба
и средней кинетической энергии турбулентности. Последнее из урав-
нений (3.19) показывает, что пространственный масштаб турбу-
лентности определяется распределением горизонтальной скорости
ветра и средней кинетической энергии турбулентных пульсаций,
а также величиной вертикального потока тепла.
Теперь мы имеем замкнутую систему шести уравнений (3.14),
(3.15), (3.18) и (3.19) с шестью неизвестными, включая перемен-
ную L.
Для решения данной системы уравнений требуется сформулиро-
вать краевые условия. Так как система содержит вторые производ-
ные от переменных и и v по г, то необходимо поставить по два ус-
ловия для каждой из этих переменных. В качестве таких условий
принимается обращение ветра в геострофический на бесконечности
и условие «прилипания» у земной поверхности, а точнее на высоте
го — так называемой высоте шероховатости подстилающей поверх-
ности. Эти условия записываются в виде:
при z—^oo u~^ug, v-^vg;
при z=zG и=0, v=0,
(3.20)
где ug и vg — компоненты ветра в свободной атмосфере. Наличие
второй производной переменной b по г требует задание двух крае-
вых условий относительно Ь. В качестве таких условий принима-
ются следующие:
0 при Н 0;
при г—*оо Ь~*
1
с2
2
3
при Н
>0,
(3.21)
1
г “22
при г=г0 b=c v*,
где х~0,4— постоянная Кармана, v*— скорость трения или дина-
мическая скорость, определяемая равенством
(3-22)
Смысл краевых условий для b сводится к тому, что значение b при
возрастании г стремится к нулю при нисходящем турбулентном по-
токе тепла и к некоторой величине, зависящей от параметра пла-
40
вучести, — при восходящем потоке тепла. На уровне шероховатости
значение b будет определяться скоростью трения. Последняя яв-
ляется новой переменной. Ее введение потребовало дополнитель-
ного соотношения (3.22).
Полученная система содержит ряд нелинейных уравнений. Ее
решение возможно лишь при применении приближенных или чис-
ленных методов. Численное решение системы было проведено в ра-
боте [2], где значения всех неизвестных, входящих в систему, были
получены в зависимости от следующих параметров: V — скорости
ветра в свободной атмосфере (на высоте 1—1,5 км), 60 = 0^—
— 0о — разности потенциальной температуры на высоте верхней
границы пограничного слоя (практически на высоте 1 —1,5 км)
и уровне шероховатости го (практически на высоте измерения при-
земной температуры), fi=g/T — параметра плавучести и Н — вер-
тикального потока тепла. Эти параметры называют внешними па-
раметрами пограничного слоя.
Решение данной системы уравнений производится методом пос-
ледовательных приближений. В первом приближении принимается,
что коэффициент k является линейной функцией высоты. Подстав-
ляя значение k для определенной высоты и выражая производную
d®ldz через известный параметр 60, находим с помощью (3.17)
первое приближение для Н. Вслед за этим путем численного реше-
ния рассматриваемой системы уравнений (3.14), (3.15), (3.18)
и (3.19) находятся значения всех искомых величин для различных
высот, в том числе и коэффициента турбулентности k. Имея это но-
вое значение k, расчет повторяют. И так до тех пор, пока разница
между переменными, найденными в двух соседних приближениях,
не окажется достаточно малой. После этого можно получить рас-
пределение по высоте метеорологических элементов (u, v и пр.),
определить параметры пограничного слоя, например, его высоту /г,
рассчитать вертикальную скорость на его верхней границе, турбу-
лентный поток тепла и т. д.
Численные эксперименты, проведенные по изложенной теории,
дали результаты, близкие к данным непосредственных измерений.
Отметим еще, что изложенная теория может быть применена
и для расчета турбулентных потоков влаги. В предположении ста-
ционарности, горизонтальной однородности и отсутствия конденса-
ции и испарения уравнение переноса влажности имеет вид
где aq = kq/k, kq — коэффициент турбулентности для q. Произведя
интегрирование данного уравнения по г и умножив результат на р,
мы убеждаемся в том, что вертикальный поток влаги
Q = -a//p^-^-= const
не зависит от высоты. Принимая в качестве еще одного внешнего
параметра пограничного слоя разность §q = qh— q0, где qh и qo—
41
значения q на высоте h (1,0—1,5 км) и 2о (практически на высоте
приземных метеорологических измерений), выражая производную
dqldz через этот параметр и используя значения k, найденные пу-
тем решения описанной ранее системы уравнений, можно рассчи-
тать величину вертикального потока влаги.
Найденные значения метеорологических элементов внутри пла-
нетарного пограничного слоя и на его границе можно теперь ис-
пользовать для уточнения прогноза по прогностической модели.
Это уточнение возможно различными путями. Один из возможных
путей заключается в замене ветра в планетарном слое, взятого
в квазигеострофическом или другом приближении, значением, по-
лученным в результате решения уравнений пограничного слоя.
Другой более простой путь сводится к введению в краевые условия
на нижней границе атмосферы вертикальной скорости, полученной
для верхней границы пограничного слоя wh. При учете неадиаба-
тических факторов в прогностическую модель вводится турбулент-
ный поток тепла с подстилающей поверхности, рассчитанный по из-
ложенной методике, и т. д.
Трудность такого подхода заключается в необходимости реше-
ния системы уравнений для пограничного слоя при учете внешних
параметров, которые прогнозируются по прогностической модели,
на каждом шаге по времени.
Рассмотрим теперь другой подход, при котором решение ука-
занной системы уравнений пограничного слоя на каждом шаге по
времени не требуется. Введем параметры
D V СО
R°— |/| г0 ’ S — Р |Z|V
Первый из этих параметров будем называть параметром Россби,
а второй — параметром стратификации. Как можно видеть, они
связаны с двумя параметрами прогностической модели: скоростью
ветра в свободной атмосфере и вертикальным градиентом потенци-
альной температуры. Чтобы иметь возможность вести расчеты
и для южного полушария, величина параметра Кориолиса взята
по модулю.
Таким образом, для вычисления величин Ro и S необходимо
знать скорость геострофического ветра V и разность потенциальных
температур на верхней и нижней границе пограничного слоя: 60 =
= 0д — 0о (остальные величины в формулах для Ro и S будем счи-
тать фиксированными параметрами точки расчета). Значения V,
&h и 0о с той или иной степенью приближения могут быть полу-
чены из прогностической модели Тогда характеристики турбулент-
ного режима — потоки тепла, влаги и количества движения — вы-
ражаются через универсальные функции от параметров Ro и S,
представленные в виде таблиц или номограмм. Например, зависи-
мость для турбулентного потока тепла имеет вид
H = -^pVB0/(Ro, S),
где f — известная функция
42
С помощью указанных зависимостей мы, в частности, можем по-
лучить величину угла между направлением ветра у земной поверх-
ности и в свободной атмосфере, величину коэффициента турбулент-
ности и т. д. Затем мы можем рассчитать компоненты ветра и тем-
пературу внутри пограничного слоя, вертикальную скорость на
верхней границе этого слоя.
Проведенные эксперименты по включению эффектов погранич-
ного слоя в прогностические модели показывают, что влияние тур-
булентности приводит к стабилизации потоков и перераспределе-
нию метеоэлементов в нижних слоях атмосферы, лучше соответст-
вующему реальным вертикальным профилям и т. д., и, в конечном
итоге, к более точному прогнозу метеоэлементов у поверхности
Земли и в свободной атмосфере.
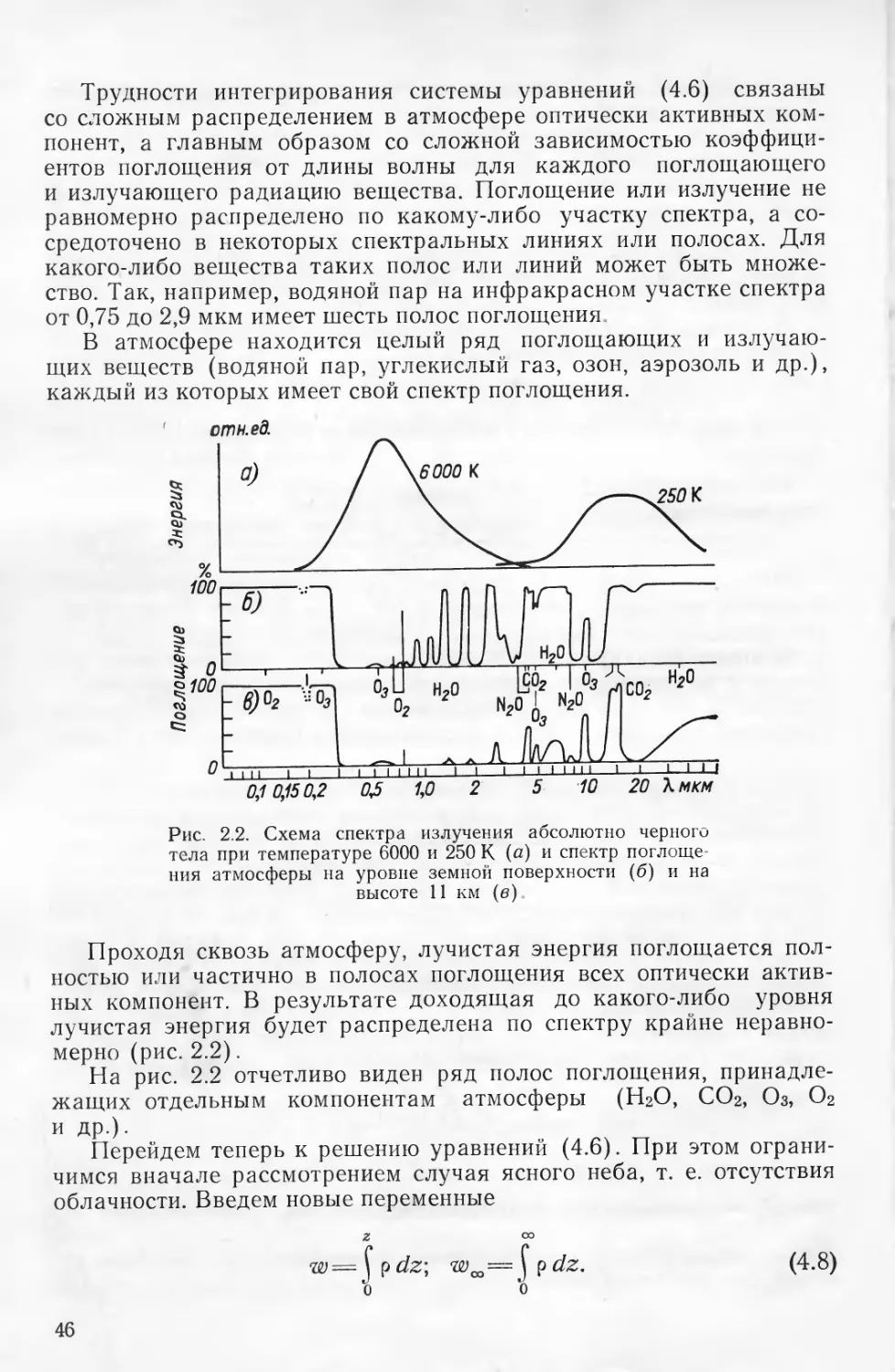
§ 4. Уравнения переноса лучистой энергии и радиационный приток
тепла в атмосфере
При турбулентном теплообмене в атмосфере обмен энергией
между ее отдельными частями осуществляется путем беспорядоч-
ных перемещений отдельных объемов воздуха. Этот же механизм
обеспечивает и распространение тепла конденсации, выделивше-
гося в каком-либо объеме.
Лучистый, или радиационный, теплообмен имеет другую при-
роду. Он связан с электромагнитными волнами, распространяю-
щимися в пространстве со скоростью света. При взаимодействии
частиц воздуха и примесей, содержащихся в атмосфере, и электро-
магнитных волн происходит поглощение частицами энергии этих
волн. В то же время частицы сами являются источниками электро-
магнитных волн. Поглощение и излучение электромагнитных волн
веществом сопровождается изменением уровней энергии колебаний
и вращения молекул и в конечном итоге — изменением темпера-
туры воздуха.
Из спектра электромагнитных волн, представленного на рис. 2.1,
в процессе обмена лучистой энергии, существенного для атмосфер-
ных условий, принимают участие волны оптического диапазона,
включающего инфракрасный (X >0,75 мкм) и ультрафио-
летовый (Х<0,4 мкм) интервалы спектра, а также участок
спектра видимого света (0,4 мкм<7<0,75 мкм).
Весь спектр электромагнитных волн, связанный с лучистым теп-
лообменом, удобно разбить на два диапазона, соответствующие
коротковолновой и длинноволновой радиации.
Коротковолновая радиация (Z~0,15—4 мкм)—это
излучение Солнца. 46% этого излучения приходится на долю ин-
фракрасной радиации, 9% — на долю ультрафиолетовой и 45% —
на долю видимого света.
Длинноволновая радиация ~4—80 мкм) пред-
ставляет собой излучение земной поверхности и частиц воздуха.
43
Этот вид лучистой энергии иногда называют также земной радиа-
цией.
Лучистая энергия может быть охарактеризована рядом пара-
метров. Прежде всего это интенсивность и поток радиации.
Интенсивность радиации — это полное количество лу-
чистой энергии, проходящей за единицу времени через единичную
площадку, перпендикулярную направлению луча, внутри единич-
ного телесного угла (стерадиана). Интенсивность излучения свя-
зана с длиной волны X и температурой Т излучающего тела фор-
мулой Планка
I he \—1
г 2hc% ~YkTr . ..
Е^~1Г-\е ~[1 ’ (4-1)
где с = 300 тыс. км/с — скорость света, /1 = 6,624 • 10-34 Дж • с— по-
стоянная Планка, 6=1,38- 10~23 Дж/град — постоянная Больцмана.
3-1Q20 3-Ю16 3-1016 3-10" 3-1012 3-1O10 3-108^r^(hc1)
Рис. 2.1. Спектр электромагнитных волн
Следует заметить, что приведенная формула относится к излу-
чению так называемого абсолютно черного тела, т. е. та-
кого тела, которое поглощает всю падающую на его поверхность
радиацию. Это означает, что такое тело не пропускает, а его по-
верхность не отражает падающую радиацию. Реальные тела, на-
ходящиеся на Земле, отличаются от абсолютно черного. Их излуче-
ние, как правило, меньше излучения абсолютно черных тел (такие
тела иногда называют серыми). Отношения интенсивности излуче-
ния реальных тел к интенсивности абсолютно черного тела 6^
имеют значения 0,9—1,0.
Полная или интегральная интенсивность излучения связана
с температурой излучающего тела или среды следующим
образом:
Е=]е^=^~, (4.2)
о
где о = 0,817-10-10 кал/(см2- мин)—постоянная Стефана—Больц-
мана.
Наиболее употребительной единицей интенсивности излучения
является 1 кал/(см2 - мин - ср).
44
Поток излучения в полусферу выражается через интенсив-
ность следующим образом:
7С
2к Т
F=J J £(6, ср) cos 6 sin С 4/0 (4.3)
о о
где 0 и ср — сферические координаты. Единицей потока излучения
является кал/(см2 • с) =0,06976 Дж/(см2 • с) =0,06976 Вт/см2. Вели-
чину, равную 1 кал/см2, называют ланглеем (1у).
В случае изотропного излучения, когда интенсивность не
зависит от направления лучей,
тс
2п “
Е=Е\ | cosG sin6 dft dy=itE. (4.4)
6 б
На основании (4.2) и (4.4) можно заключить, что для изотроп-
ного излучения
(4.5)
Перейдем теперь к изложению метода расчета интенсивности
и потоков радиации (см., например, [8, 12]). Введем в рассмотре-
ние интенсивности нисходящей (направленной сверху вниз) Ga
и восходящей (направленной снизу вверх) (А длинноволновой ра-
диации и интенсивность нисходящей коротковолновой радиации Sa-
(Величины Ga, Ga и Sa — положительны) В таком случае система
уравнений переноса лучистой энергии может быть записана в виде:
dG k о
dlE k. о
-^-=7^6^-^);
где p — плотность оптически активных компонент атмосферы, т. е.
поглощающих и излучающих лучистую энергию веществ Ек— мас-
совый коэффициент поглощения, 0 — угол между направлением
луча и вертикалью.
В качестве граничных условий принимается:
при z~*00 Ох—*0;
при 2=0
при 2 — 00 5X=S°(1-r)cos9. (4.7)
где —интенсивность солнечного излучения, приходящегося на
длину волны % на верхней границе атмосферы, Г - альбедо си-
стемы Земля—атмосфера.
45
Трудности интегрирования системы уравнений (4.6) связаны
со сложным распределением в атмосфере оптически активных ком-
понент, а главным образом со сложной зависимостью коэффици-
ентов поглощения от длины волны для каждого поглощающего
и излучающего радиацию вещества. Поглощение или излучение не
равномерно распределено по какому-либо участку спектра, а со-
средоточено в некоторых спектральных линиях или полосах. Для
какого-либо вещества таких полос или линий может быть множе-
ство. Так, например, водяной пар на инфракрасном участке спектра
от 0,75 до 2,9 мкм имеет шесть полос поглощения
В атмосфере находится целый ряд поглощающих и излучаю-
щих веществ (водяной пар, углекислый газ, озон, аэрозоль и др.),
каждый из которых имеет свой спектр поглощения.
Рис. 2.2. Схема спектра излучения абсолютно черного
тела при температуре 6000 и 250 К (а) и спектр поглоще-
ния атмосферы на уровне земной поверхности (б) и на
высоте 11 км (в)
Проходя сквозь атмосферу, лучистая энергия поглощается пол-
ностью или частично в полосах поглощения всех оптически актив-
ных компонент. В результате доходящая до какого-либо уровня
лучистая энергия будет распределена по спектру крайне неравно-
мерно (рис. 2.2).
На рис. 2.2 отчетливо виден ряд полос поглощения, принадле-
жащих отдельным компонентам атмосферы (Н2О, СО2, Оз, О2
и др.).
Перейдем теперь к решению уравнений (4.6). При этом ограни-
чимся вначале рассмотрением случая ясного неба, т. е. отсутствия
облачности. Введем новые переменные
Z СО
= ^оо— \?dz.
о о
(4.8)
46
Эти переменные характеризуют массу поглощающих и излучаю-
щих веществ в единичном столбе атмосферы Так как в соответст-
вии с правилами дифференцирования неявных функций
(z \
f , 1 д д
I р dz —5— = р—д—
J г \ ow r dw
а при 2 = 0 w = 0 и при z=oo ©=№«>, то уравнения и краевые усло-
вия (4.6) —(4.7) перепишутся в виде:
dG k\ k,. г
dw cos 9 х cos в х’
rftz. k k X i y JJ — x E * dw 1 cos 6 x cos 6 x’ (4.9)
6/S. k X X c . dw cosO x’ (4.Ю)
при ®=wco Gx=0;
при w=0 £7X = 8X£’X4-(1 —8X)GX; (4.11)
при ®=woo SX = S°(1 — r^cosO. (4.12)
Решение уравнений для длинноволновой радиации имеет вид:
b „---------(w —W)
W
, w
------W k (* -— W )
с08в +—A_Je“se
со ^Х
b Р---------(W -+-W)
+ c°se E.dW, (4.13)
где Exo — интенсивность излучения земной поверхности, wr — пере-
менная интегрирования.
Для определения притоков тепла необходимо еще совершить
переход к интегральной интенсивности (по всему спектру), а затем
от интенсивности к потокам радиации по формуле вида (4.3).
Таким образом, например, для нисходящего потока длинновол-
новой радиации мы имеем
2к 2
<ж)=П
о о
cos 6
_*х_
cos О
(wf — w)
E^dw'
d\
X sin 9 cos9 dy d 9.
(4.14)
47
Вычисление интегралов вида (4 14) при сложной зависимости
от л и при неизотропности излучения представляет собой весьма
сложную задачу.
Для целей численного прогноза оказывается достаточным при-
менение упрощенных вариантов расчета. Опишем здесь один из ва-
риантов упрощенного расчета, основанный на применении инте-
гральных функций пропускания Р (g), представляющих
собой отношение потока излучения абсолютно черного тела, про-
шедшего сквозь слой, содержащий массу оптически активных ком-
понент, равную g, к падающему потоку [У.7]. Из различных инте-
гральных функций пропускания для длинноволновой радиации,
определенных на основе эмпирических данных, приведем здесь
функцию пропускания по X. Нийлиск
— О 8VT — 2 oVT"
Р(е)=0 515е ’ + 0,485е ’ . (4.15)
Имея в виду определение интегральной функции пропускания,
вместо (4.14) можно записать:
Woo
О(лу)=- J BdP(w’-w). (4.16)
Для восходящего потока соответственно имеем
w W оо
U (w)^bBnP(w)-[- d J(w —w') —(1 —В) С В dP(w' Д-w). (4.17)
6 о
Здесь 6— интегральное значение бх для земной поверхности; В =
= о74; 5п = п74; Тп — температура земной поверхности.
Для падающего потока коротковолновой радиации можно по-
лучить:
-r)cos6Pfe[ -os6 ), (4.18)
где S°=l,94 кал/(см2-мин)—солнечная постоянная, Pk(%)—инте-
гральная функция пропускания для коротковолновой радиации, ко-
торая, по В. Меллеру и В. Г. Кастрову, имеет вид
Рк ($) = 1 - 0,090 е0-303. (4.19)
Имея величины потоков радиации, можно рассчитать для лю-
бого уровня радиационный баланс
/?=- 5 - Р= 5Д- G - U, (4.20)
представляющий собой разницу нисходящих и восходящих потоков
радиации.
48
Величина радиационного притока тепла к единице объема на-
ходится по соотношению
^=а(5 + <7--г/) (
л dz dz '
Изложенная методика может быть обобщена для случая облач-
ной атмосферы. Предположим, что облачные слои расположены
горизонтально и имеют по горизонтали бесконечные размеры. По-
лагая, что внутри облака радиационные потоки тепла F и S равны
нулю (что подтверждается экспериментальными данными), мы мо-
жем проинтегрировать уравнения (4.6) отдельно для надоблачной
и подоблачной частей атмосферы и для безоблачных слоев. После
этого, используя выражение (4.21), можем рассчитать притоки
тепла.
В случае частичной облачности расчет ведется два раза: для
ясного неба и для случая сплошной облачности. Приток тепла при
облачности N баллов найдем по формуле
•'V-Ts,o+(1-4r)*°. <4-22)
где 810 и 8° — притоки тепла для полной облачности и ясного неба
соответственно.
Из сказанного следует, что решение уравнений переноса лучи-
стой энергии связано с большими трудностями Поэтому для прак-
тических целей применяются упрощенные способы, подобные изло-
женному. Имеются и другие более простые способы, когда весь рас-
чет сводится к определению и использованию для вычисления
притока тепла небольшого числа параметров. Такие приемы полу-
чили название параметризации неадиабатических эффектов
§ 5. Упрощения уравнений гидротермодинамики
Ранее были выделены движения трех основных масштабов, су-
щественно различающиеся характерным порядком величин отдель-
ных метеоэлементов и рядом других особенностей. Эти различия,
естественно, должны быть учтены при построении системы уравне-
ний, пригодной для описания явлений соответствующего масштаба,
поскольку непосредственное использование уже полученной си-
стемы уравнений (2.21), пригодной, вообще говоря, для описания
явлений не одного какого-нибудь масштаба, а различных масшта-
бов, вызывает ряд неоправданных трудностей. Однако, чтобы при-
менить данную систему к описанию явлений одного какого-нибудь
масштаба, ее следует соответствующим образом упростить
Поставим своей целью получить систему уравнений гидротермо-
динамики, пригодную для описания крупномасштабных явлений,
т. е. таких, которые определяют погоду над сравнительно большими
районами с горизонтальным размером порядка 1000 км и характер-
ным временем 1 сутки. С этой целью произведем анализ порядков
4 Зак. № 21
49
величин отдельных членов системы уравнений гидротермодина-
мики. При этом будем пользоваться таблицей средних квадратиче-
ских значений метеорологических элементов и их производных (см.
табл. 1.2).
Рассмотрим в начале первые два уравнения движения системы
уравнений (2.21). Ввиду их идентичности ограничимся первым из
них. Примем, что k' = 5- 102, k = 5 м2/с и что при произвольном рас-
положении осей х и у O(o)z) =0(0)?/) =O(ojx) =cozsin<p^0,729X
X 10~4 0,707 ~ 0,5 - 10~4 с-1 (ср 45°).
Тогда, в соответствии с данными табл. 1.2, в системе МТС
=7 1,2 • 10-5^0,8 • 104; О (та/Ю*2 • 2 • !Q-3=2 • 10~5;
°(ттг) = т^8' Ю~’=0.8 - 10-»;
О(2оуау)=2 • 0,5 • 10-4 • 10~2= 10~6;
О (2<ог-и)=2 • 0,5 • 10“4 • 7=0,7 • 1СГ3;
О(£'Ди)=5 • 102 • 3 • 10-" = 1,5 • 10”8;
0 k -S-)-° I" -S-)-5 • '.2 • Ю--0.6 • 10-.
Сохраняя члены с характерными значениями, не меньшими чем
10-5, рассматриваемое уравнение можно записать в виде
ди j
~dt '
и
ди
дх
<V
ди
dz
др
дх
ди f
ду '
1
-J-Z'D,
где / = 2o)z=2o) sin ф — параметр Кориолиса, со — абсолютная вели-
чина вектора оэ. Производя аналогичные оценки, второе уравнение
движения получаем в виде
dv . ди . ди . dv
-хт--Н It -х----Н V -X-----k W
dt 1 дх 1 ду 1 dz
др
дУ
— III.
Р
Заметим, что члены и w~q— по крайней мере в несколько
раз меньше остальных членов рассматриваемых двух уравнений.
Поэтому в самом грубом приближении этими членами можно пре-
небречь, что довольно часто и делается в практических методах
численного прогноза погоды.
Обратим внимание, что в последних двух уравнениях члены, вы-
ражающие силу барического градиента и отклоняющую силу вра-
щения Земли, по крайней мере в 10 раз больше остальных членов
50
уравнений. Поэтому в самом грубом приближении можно поло
жить, что
0=- — 4^-+/®; о=-
р дх 1 ’
2
р
— la.
откуда и получаются известные выражения для компонентов гео-
строфического ветра:
1 др 1 др
11 -----------------— • 7) -------------—
/р ду 1 S /р дх •
(5-1)
Реальные поля ветра и давления таковы, что соотношения (5.1)
выполняются весьма приближенно. При конкретных ситуациях
всегда имеют место те или иные отклонения ветра от геострофиче-
ского. Однако в целом крупномасштабные атмосферные движения
можно считать близкими к геострофическим или квазигео-
строфическими. Это — так называемая гипотеза ква-
зигеострофичности крупномасштабных атмосферных дви-
жений, лежащая в основе квазигеострофических методов прогноза.
Перейдем теперь к рассмотрению третьего уравнения движения
системы уравнений (2.21). Согласно табл 1.2, при O(Aw)=0.5x
X 10~13 получаем:
O(^L)_2. Ю-';
° (“ ^)=о (^)=
о(«^)=3- IO->; O(g)-10':
0(2<оуу)==0(2«>у«)=0,7 10~3;
O(k' Дте>)=2,5 • 10-11;
о(~ *-7Г-)=°>8 • Ю-3.
\ dz dz ) ’
В этом уравнении два члена, выражающие силу барического
градиента и силу тяжести, по крайней мере на два порядка больше
остальных. Поэтому с высокой степенью точности при анализе
и прогнозе крупномасштабных атмосферных движений вместо
уравнения движения по оси z можно принять, что
1 др
(5-2)
Таким образом, вместо третьего уравнения движения мы получили
известное уравнение статики, которое обычно записывается в виде
dp
Реальные атмосферные движения не удовлетворяют этому соот-
ношению в точности Однако можно считать, что крупномасштаб-
ные атмосферные движения в среднем удовлетворяют этому
4*
51
соотношению. Если же в некоторый момент времени в каком-либо
локализованном районе возникло несоответствие соотношению
(5.2), то происходит быстрая перестройка поля давления таким
образом, что через очень короткое время (порядка минуты) оно
вновь начинает удовлетворять уравнению статики. В этом заклю-
чается так называемая гипотеза квазистатичности
крупномасштабных атмосферных движений.
Необходимо подчеркнуть, что уравнение статики будет спра-
ведливо лишь для крупномасштабных метеорологических процес-
сов, определяющих изменения погоды над сравнительно большими
районами (с горизонтальными размерами порядка тысячи километ-
ров). Для процессов меньших масштабов проделанные упрощения
могут оказаться неприменимыми, поскольку приведенные ранее ха-
рактерные значения относятся только к крупномасштабным про-
цессам.
Для иллюстрации сказанного оценим величины отдельных сла-
гаемых третьего уравнения движения применительно к мезомас-
штабным явлениям, например, к отдельному кучевому облаку, имею-
щему горизонтальные размеры порядка сотен метров (6s=102 м)
и развивающемуся за время порядка часа (6/ = 0,36- 104 с). Так как
вертикальные скорости в кучевом облаке достигают 10 м/с, то в ка-
честве характерного значения приращения вертикальной скорости
за время 6/ можно принять 10 м/с. Такую же величину будет со-
ставлять и приращение вертикальной скорости за один шаг по го-
ризонтальным координатам. То есть можно принять, что O(8wt) =
= 0 (8wx) = Ю1. Тогда получаем
п( dw О (bwt) _ lOi 1П_3.
dt It ~ 0,36 . 104 ‘ 1и ’
10».
dw
т. е. порядок величины члена и уже близок к порядку главных
членов рассматриваемого уравнения. Поэтому уравнение статики
для таких явлений оказывается неприменимым.
Обратимся теперь к анализу уравнения неразрывности (четвер-
тое уравнение системы уравнений (2.21)).
Сохраняя в самом грубом приближении члены с порядком ве-
личин 10~3, находим следующее соотношение:
-^+-^-=0. (5.3)
дх 1 ду 4 7
dw
Если еще сохранить член > имеющий порядок величины
10-6, то получим известное уравнение неразрывности для несжи-
маемой жидкости
+ (5.4)
дх ' ду * dz 7
52
Однако в общем случае уравнение неразрывности берется без
упрощений, что связано с некоторыми особенностями используе-
мых методов решения задачи.
В уравнении притока тепла (2.23) члены, стоящие в левой ча-
сти, имеют примерно одинаковый порядок. Поэтому это уравнение
используется в том же виде, в каком оно записывалось ранее.
Учитывая все сказанное, приходим к следующей упрощенной
системе уравнений гидротермодинамики, пригодной для целей ана-
лиза и прогноза крупномасштабных атмосферных процессов во вне-
тропических широтах и вне пограничных слоев:
ди
du , du , du
dt 1 dx 1 dy
dv . dv । dv
dt dx * V dy dz
0=-----
dz
dv
р дх
1
Р ду
р dz
dpv ( dpw n
“dy--*- ~дГ''~ЛУ,
дТ 7a dp
--------
g-p dt
dp । dpu
dt dx
dT . dT
dx * V dy dz
P=RpT.
Если ввести горизонтальный вектор скорости
дТ
dt
1
cp?
(5-5)
то два уравнения движения можно записать в виде одного вектор-
ного
4г=“т v^-Zkxv’ (5-6)
где i, j, k — единичные вектора, направленные вдоль осей х, у и z,
а знак X означает векторное произведение. В соответствии с пра-
вилами векторного умножения
kX V=k X(^i+^j)=икХ i+^kX j=^j —
Отсюда следует, что
/ (к X V)x= -lv\ I (к X V)y=lu.
§ 6. Уравнения гидротермодинамики для крупномасштабных
атмосферных движений в системах координат, связанных
с давлением
Система уравнений (5.5), а также формулы для расчета гео-
строфического ветра упрощаются, если от декартовой системы
координат перейти к системам координат, в которых вместо
53
вертикальной координаты используется давление или связанная
с ним переменная. Необходимость перехода к таким координатам
следует также и с другой точки зрения. Дело в том, что в службе
погоды высотные карты погоды составляются не в виде карт дав-
ления на стандартных высотах, а в виде карт барической топогра-
фии. Как известно, при построении карт барической топографии
в качестве анализируемой функции принимается геопотенциал
изобарической поверхности ср = gz или просто ее высота z. Дав-
ление р в этом случае играет роль независимой переменной.
Система координат хр, ур, р, 1Р (изобарическая
система координат). Если в декартовой системе координат незави-
симыми переменными являются %, у, г, /, то в изобарической си-
стеме координат такими независимыми переменными будут уР,
Р, tP,
При этом хр=х, уР = у и tp = t, а между координатами р и z су-
ществует соотношение
являющееся уравнением статики. В общем случае эту связь можно
записать в форме р = ф (г) или г = ф1 (р).
В качестве функций координат и времени в новой системе коор-
динат будут: и, v, Т, z = H (xPi yPl р, tp) и функция
(6.1)
dt dt 1 дх 1 ду 1 dz ' 7
которая является аналогом вертикальной скорости.
Произведя оценку порядков величин отдельных членов уравнения
др
(6 1), можно заключить, что —gpw. Отсюда следует,
в частности, что т положительно при нисходящих движениях и на-
оборот. Величина т в системе MTS выражается в сб/с.
Первые три функции соответствуют аналогичным функциям
в старой системе, а следующие две являются совершенно новыми.
Чтобы записать систему уравнений (5.5) в изобарической си-
стеме координат, необходимо произвести замену переменных в диф-
ференциальных уравнениях.
Воспользуемся правилом дифференцирования сложных функ-
ций многих переменных. Рассмотрим некоторую функцию Ф, явля-
ющуюся функцией четырех независимых переменных. В старой си-
стеме координат Ф = ф(х, уу г, /), а в новой системе Ф=Д (хр, ур, р,
tP). Частные производные в старой и новой системах координат
связаны следующим образом:
дФ дФ дхр дФ дур । дФ др f дФ dtp
дх дхр дх *" дУр дх * др дх 1 dtp дх
дФ дФ &хр I дФ дуР , дФ др । дФ dtp
ду дхр ду * дур ду * др ду “1 dtp ду
54
ЭФ ЭФ dxp . ЭФ дур . ЭФ др । ЭФ dtp
dz дхр dz ’ дур dz 'др dz * dtp dz ’
ЭФ ___ ЭФ дхр । ЭФ dyp ЭФ др . ЭФ dtp
dt дхр dt "г* дур dt ’ др dt * dtp dt
~ , дхр дуР dtp
Так как х=хр, у = уР и t = tp, то -^-=1, "^“=1 и ~^Г’==1,
а так как переменные уР и х, tp и х, хр и у, tp и у, хр и z, уР и г,
tp и г, Хр и /, ур и t не зависят друг от друга и, следовательно, при
частном дифференцировании могут считаться постоянными, то
дуР dtp _ dxp dtp _ dxp __ дур _ dtp _ дхр __ дур _
дх дх ду ду dz dz dz dt dt
В результате приведенные соотношения упрощаются и прини-
мают вид:
ЭФ ЭФ 1 ЭФ др
Эу дур 'др ду ’
ЭФ । ЭФ др
ЭФ ЭФ । ЭФ др
дх дхр 'др дх ’
ЭФ ЭФ Эр
dz др dz '
ЭФ
dt dtp 'др dt '
Полученные соотношения в дальнейшем используются для пре-
образования членов уравнений, содержащих производные от функ-
ций u, v, Т, р. Для преобразования выражений, содержащих пере-
менную р, запишем соотношения между старыми и новыми пере-
менными так, чтобы в левых частях стояли производные по новым
переменным хр, уР, р и tp:
ЭФ ЭФ дх । ЭФ ду 1 ЭФ dz , ЭФ dt
дхр дх дхр Г ду дхр ' dz дхр 1 dt дхр ’
дФ ЭФ дх । ЭФ ду . ЭФ dz , дФ dt
дуР дх дур 1 ду дур * dz дур 1 dt дуР ’
дФ _ ЭФ дх 1 ЭФ ду । ЭФ дг 4- дФ dt
др дх др * Эу др ’ dz др ’ dt др ’
дФ ЭФ Эх । ЭФ ду . ЭФ dz 1 ЭФ а/
dtp дх dtp ду dtp • dz dtp 1 dt dtp •
Если Ф = р, что то - дР дхР ^--0, дуР др 1. Приняв во внимание,
дх дхр = — дур dt dtp = 1
и
dy = dt дх dt дх . др -=0, ?
дхр dXp дУр dyp ~дГр dtp dt^
55
получим:
п__ др । др dz ' п___ др ,_др dz_.
дх ’ dz дхр ’ ду ' dz дур ’
1 _ др dz п_______ др dz j др
dz др ’ dz dtp dt
Если высоту изобарической поверхности р = const обозначить
через Н (в отличие от независимой переменной г), то:
др _ др дН _ дН
дх dz дхр 4Р дхр
др дН
ду dz дуР SP дуР
др = 1 - р'Г)*
dz с )/7
др
др _ др дН _ап дН
dt dz dtp dtp ’
Подставляя найденные соотношения между производными
в уравнение движения по оси х, получим
ди . ди др . / ди . ди др \ . (ди , ди др \
dtp 'др dt ‘ U \ дхр ' др дх ) ‘ \ дур ‘ др ду )
+4^)—
или после изменения порядка записи и сокращения членов
ди I ди , ди । ди ~ дН . z
Аналогично уравнение движения по оси у запишется следую-
щим образом:
dv . dv . dv . dv ~ дН ,
dtp ~^U дхр дур др & дур U'
Уравнение статики примет вид
дН RT
др ~ gP '
Для преобразования уравнения неразрывности запишем его
в виде
др . др . др I др . ( ди . dv . dw \ п
-^-+«-^+^-аг+да-Эг+р + -аг+^г)=0-
56
1 др _
Согласно уравнению статики, р =---~g~~dz' Подставляя это
выражение для р в уравнение неразрывности, получим
а2р 1и I V I эд а2р + (_gg_ д. д-ggJ—Q
dt dz dxdz'V dydz д2д2 T d2 \ dx dy dz ) v
Имея в виду, что
-JI du
и _ и dxdz ‘ dz \ dz dx ’
d^p Г7\ — =—1 ?<)- dv
dy dx dz \ dz dy ’
d^p w r— dz dz d dz dw dp dz dz
и что
dp dt 1 dp । dp । dp 1 dx 1 dy 1 dz = t;
дФ _ d^ дФ dp дФ дФ i дФ dp
dx dxp । 1 dp dx ’ dy dyp * dp dy
дФ <^Ф dp , dp dp dH
dz dp dz ’ dx dz dx 9
dp dp dH
dy dz dy 9
находим
dp dz du dp dp dv dp dp . dp / du . du dp \
dz dp dp dz dx dp dz dy ‘ dz \ dxp 'dp dx )
у dp { dv у dv dp \_n
~r~dr\~d^ ^~d^~d^)—U
или после сокращения подобных членов
dp t du dv । dz \ ~
dz \ dxp • dyp ‘ ~dp)
~ дР Л
1 ак как ——ф 0, то окончательно имеем
dz
du . dv . dz _~
dxp ' dyp ’ dp
Уравнение притока тепла примет вид
dT , dT . dT — . 1
-37-F W -3-Н'Я -3— = ———— T 4------£.
dtp dxp dyp pg 1 Cpp
Выразим еще величину т, являющуюся аналогом вертикальной
скорости wf через высоту Н.
57
Так как
т=-^
dt
dt 'и дх
др ।
ду ~*~
др
<W ~^—
dz
а
др дН др дН
dt dtp ' дх дхр ’
ТО
др _ дН
ду дур ’
др
dz ~~ё?>
„ / дН . дН , дН \ оч
х=^(-^г+ы1г^+^^7-®)- <6-2)
В итоге получаем систему уравнений гидротермодинамики
в изобарической системе координат (индекс р у переменных %, у и t
здесь и далее опущен):
-V7“ + ^~3 “3 hT -3—
dt 1 дх 1 ду 1 др
g—
® дх
j—Z-г»;
(6.3)
dv . dv . dv 1 dv dH
+ ----------H -3— =— g~3-
dt 1 dx 1 dy 1 dp b dy
lu\
(6-4)
g dH
^Р~дГ^
(6.5)
-&+^+ж=°; <6-6)
0T , д Т
dt дх
дТ = 7?Т(Та-Т) .__1_£
ду £Р сР?
(6.7)
В случае использования в качестве независимой переменной по-
тенциальной температуры 0 уравнение притока тепла запишется
в виде
дЮ 1 0_
dt Ср$ Т
(6.8)
Уравнения горизонтального движения (6.3—6.4) и неразрывно-
сти (6.6) можно записать в векторной форме. С этой целью введем
в рассмотрение единичные векторы i, j, к, направленные вдоль осей
х, у и р соответственно, и вектор горизонтальной скорости вдоль
изобарической поверхности
Уравнения горизонтального движения и неразрывности запишутся
теперь в виде
4^=-gVH-/kXV; W+^-=0, (6.9)
58
где
d
~dt
д
dt
1-V- v +
d
Уравнения гидротермодинамики в дивергент-
ной форме Используя уравнение неразрывности, уравнения
движения можно записать в форме:
du । du2 ( duv ! dux _ dH j
dt * dx "r dy "r dp & dx
dv . duv । dv2 . dv'z dH < /z? in\
-5Г- 4----5-----T“^-----------3--— ------(6.10)
dt 1 dx 1 dy 1 dp & dy 7
Убедимся в справедливости, например, первого из них. Для этого
преобразуем группу членов в левой части, которые подчеркнуты:
du । du . du
— U ------Н'У —s--Нт —S.
dx 1 dy 1 dp
То есть рассмотренная группа членов переходит в соответствую-
щую группу членов первого уравнения движения в обычном виде.
Вид уравнений статики притока тепла и неразрывности сохра-
няется.
Система координат (х, у, £, /). В качестве вертикальной
координаты принимается
о
(6.11)
где P = const (обычно Р = 1000 мбар). Между производными по р
и £ имеет место следующая связь:
а _ a dZ _ 1 d . d р d
dp ~ dZ dp ~ P dZ ’ dC ~И dp '
сг-система координат Системы координат х, у, г, t и
х, у, р, t обладают тем недостатком, что поверхность Земли не со-
впадает ни с уровнем z = const, ни с какой-либо поверхностью р =
= const. Это обстоятельство может вызвать затруднения при описа-
нии атмосферных движений вблизи земной поверхности
В этом отношении определенными преимуществами обладает
a-система координат. В этой системе вертикальной координатой
является
°=~Г> (6-12)
Ps
где ps — давление на уровне поверхности Земли, являющееся пере-
менной величиной.
59
Другие координаты этой системы:
Ха=Хр=Х; уо=ур=у; ta = tp = t. (6.13)
В качестве функций координат и времени в этой системе будут
функции U, V, Т, z=H (ха, уа, a, to) и функция
• da да । да
а dt dt ‘ дх
। </« ।
1 ду 1
да
dz
dt \ ps )
____________Р dps \= \ ( dps \
Ps \ dt ps dt ) ps \ dt )
являющаяся аналогом вертикальной скорости в о-системе коорди-
нат. Связь между о и т можно получить также в виде
____ dp __ d (aps) ___ da J dps _______ ' I dps /£ 1
dt dt ~~~Ps dt + dt + c dt • (o.lb)
Переход от системы координат хР, уР, р, tp к системе координат
хст, уо, о, to можно осуществить с помощью правил дифференциро-
вания сложных функций. В соответствии с этими правилами, при
учете соотношений (6.13) получаем, например, что
д _ д ! да д
дхо дх * дх да
Роа
или, так как
да _ д ( р \ 1 ( др р dps a dps
— (."77/ р7 ~р7 дха '
д д a dps д
дхп дх р. дх да
р а а
Аналогичные соотношения получаем и для производных д!дур
и dldtp.
Для вертикальных координат имеем
д да д д ( р \ д 1 д
др др да др \ ps / да ps да
Собирая полученные результаты вместе, получаем следующие
соотношения для перехода от одной системы координат к другой
д ___ д a dps д
дхр дх^ ps дх° да ’
д д a dps д
д _ д a dps д t д ____ 1 д /'С 1 ГА
dtp ~ dta Ps dto да ’ др~ Ps да * (0.10)
60
Индивидуальная производная в о-системе координат выразится
в виде
dt dt 1 дх 1 dy 1 da
а а а
(6.17)
где о выражается с помощью (6.14).
Получим теперь уравнения гидротермодинамики в новой системе
координат. Так как в соответствии с (6.16):
дН = _ дН а dPs дН
дхр дх а Ps дх а да
дН _ дН а dps дН
дуР дУ. Ps дУ. да
то уравнения движения перепишутся в виде:
dt & дх ps да дх ' '
AL=_ a AL jA __ i u
dt * d^ TS ps da dya Ul
где dGldt выражается no (6.17).
Уравнение статики с учетом (6.16) преобразуется к виду
т=____g_ Р дН g дН
R ps да R да •
Преобразуем теперь уравнение неразрывности. Учитывая (6.15)
и (6.16), получаем
dx 1 д ( • . dps \ да . 1 д ( dp,. \
др ps да \rs 1 dt / да ' ps да \ dt J
С учетом (6.16)
ди ди а dps ди
дхр дх a Ps дх a da
dv dv а dPs dv
дуР ' дУ, Ps дх а da
Подставляя эти результаты в (6.6), находим
да
да
ди । dv а / dps ди . dps dv
дх^ dya ps у дх^ да dya да
+77тИ^)=°- <6'18>
61
Но
д (г, -РЛ I - d / d£s I др^ | др; ) _
да \ dt / dt ' да \ dt ' дх ”• ду /
___ dPs dps du ! др^ dv \
dt ' \ дх да ' ду да ) ' ( • )
Учитывая (6.19) и производя сокращения, вместо (6.18) получаем
/ ди , dv । да \ , dps _п
Ps\ дх “г ду "т" да ) '” dt —v
или после перегруппировки членов
d_Ps । dups । dvp^ , daps „
dt dx ' ду ' da
a j а
Объединяя все полученные результаты, присоединяя сюда урав-
нение притока тепла, которое для случая использования потенци-
альной температуры в качестве независимой переменной формально
остается без изменения, и опуская индекс о, получаем систему
уравнений гидротермодинамики в виде:
_ a дН l_ а _А_ дН др°_1— lv•
dt ~ & dx ps да дх и'
dt ~ & ду ps да ду
T=-P.^L
R да
dps । dupg dvps , dap,
dt * dx ' dy ' da
JO __ 1 0
dt cpp T
(6.20)
где о определяется с помощью (6.14), а символ d/dt — с помощью
(6.17).
В векторной форме уравнения движения и неразрывности имеют
вид:
^-+ V (AV) + -^=0, (6.21)
где
^- = ^-+(V- v)+^.
Уравнения (6.3) —(6.7) и (6.20) называют полными уравне-
ниями гидротермодинамики. Они применяются непосредственно для
прогноза метеорологических полей. Однако, как будет видно из
62
дальнейшего изложения, целесообразно на основе этих уравнений
получить еще два дополнительных соотношения, которые окажутся
полезными как для уяснения физической сущности метеорологиче-
ских процессов, так и для составления прогноза погоды наиболее
удобными с точки зрения практического применения методами.
Такими уравнениями являются уравнения вихря скорости и дивер-
генции скорости.
§ 7. Уравнения вихря скорости и дивергенции
Уравнение вихря скорости. Вихрь скорости является
вектором Q = rot U, проекции которого на оси координат имеют вид:
о dw dv о _____ ди dw
"“•r dy dz ’ dz dx ’
0 ___ dv du o ________ dv du
dx dy ’ ~p dxp dyp
Численно вихрь скорости равен удвоенной угловой скорости
вращения частицы и направлен параллельно оси вращения в ту
сторону, откуда движение кажется совершающимся против часовой
стрелки. Нас будет интересовать лишь вертикальная слагающая
вихря Так как в циклоне движение совершается против, а в ан-
тициклоне— по часовой стрелке, то, как правило, вертикальная со-
ставляющая вихря в циклоне будет положительной, а в антицик-
лоне отрицательной величиной.
Уравнение для вихря скорости можно получить путем примене-
ния операции rot к уравнению движения (1.3)
-(QX V) U + Й div U= —2rot(®ХU)-------^-VT’XVp. (7.1)
Уравнение для вертикальной составляющей вихря скорости
можно получить путем преобразования уравнений движения Диф-
ференцируя уравнение (6.3) по у, а уравнение (6.4) по %, вычи-
тая из второго результата первый и делая некоторые преобразова-
ния, получаем
c)Q । dQ - dQ . dQ . dz dv dz du
-------“3------F T ------3---5-----S--4— =
dt----------------------------------------1 dx 1 dy 1 dp ' ox op dy dp
— + (7.2)
Оставляя в уравнении члены, имеющие наибольшую величину,
получим следующее упрощенное уравнение вихря скорости:
dQ . dQ. . dQ j / ди . dv \ dl dt
dt 1 дх 1 ду \ дх 1 ду ) дх ду
ИЛИ
„ d (Q + О I д (Q + /) _ . / ди dv \ (
dt U дх ' ду ~ \ дх > ду Г
63
В векторной форме указанное уравнение имеет вид
4t + V • V (2+Z)=-/V . V. (7.4)
Заметим, что выражение (Q + /) = Qa часто называют абсолют-
ным вихрем скорости Это название связано с тем, что сумма Q + /
характеризует вращательное движение частицы в абсолютной си-
стеме координат, не связанной с Землей. В этом аспекте величину
Q точнее было бы называть относительным вихрем, поскольку она
характеризует вращательное движение лишь относительно Земли.
Уравнение дивергенции скорости. Как уже говори-
лось, дивергенция скорости определяется выражением
п и du . dv > dw
4=divU = -^---к-л—Ь-л— -
dx 1 dy • dz
На основании уравнения неразрывности
д=—— —
f dt '
В случае несжимаемой среды, когда dp/dt = O, Д = 0.
Будем далее рассматривать лишь плоскую дивергенцию скоро-
сти в изобарической системе координат, т. е. дивергенцию вектора,
являющегося проекцией вектора скорости на горизонтальную пло-
скость
р. du । dv
dx ' dy ’
для которой получим специальное уравнение Для этого будем по-
ступать аналогично тому, как это было сделано при выводе урав-
нения вихря скорости. Продифференцировав уравнения движения
по х и у и сложив результаты, получаем
dD . dD . dD . dD . [ du \2 o du dv . ( dv \2 .
т+м-лг+г’+ + +
+ -^-?- + 4L-TL-Zi2 + w-^ v~=-gLH. (7.5)
1 dx dp 1 dy dp 1 dy dx ° v '
С помощью преобразования С. Петтерсена
( du \2 dv du । / dv \2 1 o2 . 1 ( dv . du \2 .
_i__L(2E_— V-b 1 П2
T 2 Ц dx J 2
уравнение дивергенции можно записать в виде
dD 1 । 1 ( dv j du \2 | 1 ( dv du \2 (
_ j 2 Эх J “г
। 1 « дъ du । Эт dv . dl dl A тг
-4—— -4—------1—--------IQ -4— и -"s-v —ч— — —g .
'2 ’ dx dp ' dy dp 1 dy dx ®
64
В векторной форме уравнение дивергенции имеет вид
. dD . дт ди . дт dv
—+V • +__+__
+ Vu-^ + Vv-^-kVXlV=-gbH.
Произведем теперь оценку порядка величин отдельных членов
уравнения дивергенции. Вначале определим порядок величины
плоской дивергенции D. На основании анализа данных табл. 1.2
можно принять, что
Отсюда делаем вывод, что слагаемые ди/дх и dvjdy на 90%
компенсируют друг друга. Следовательно, можно принять, что
O(O)-o(-g- + ^)=0(^)=l°-«.
Таким образом, оказалось, что величина дивергенции на поря-
док меньше каждого из составляющих ее двух членов. Это обстоя-
тельство приводит к трудностям вычисления дивергенции по дан-
ным о фактическом ветре.
Приближенно можно принять, что:
°(^)-°(-^)=4- 1СГ'!;
°(^)=о(^)=4
10- п;
0('тг)“0(®-^)=з-
В то же время
*ц = 1,4. 10- Ю;
\ дх ) \ ду ) \ ду дх J 9
О (Z2)=2,4 • 10 9; О (и -^-)= О (® -|£-)=0,9 • Ю"10;
О (g ДА/)=2,4 • IO"9.
Тогда, оставляя в уравнении дивергенции члены, имеющие порядок
10~9, мы получаем
lQ—gL.H.
5 Зак. № 21
65
Это выражение можно получить также на основании условия
геострофичности. Если же в уравнении дивергенции сохранить
члены с порядком 10~10, то оно переходит в соотношение
/ ди \2 dv ди . ( dv \2 . dl д1 7О Л 7/ z-
Ы)+2~dr-d7+(^r)+u-d7~v^r~lQ==-s^H- (7-6)
Полученное уравнение связывает горизонтальные компоненты
ветра и геопотенциал. Это уравнение и его разновидности часто
называют уравнением баланса. В векторной форме это
уравнение записывается так:
VX/V=_^A//- (7-7)
Это уравнение чает более точную связь между полями ветра и дав-
ления или геопотенциала по сравнению с геострофическими соот-
ношениями. Поэтому оно широко используется в прогностических
задачах.
§ 8. Уравнения гидротермодинамики в сферической системе
координат
Рис. 2.3. Сферическая система
координат.
До сих пор уравнения гидротермодинамики рассматривались
в локальной прямоугольной системе координат. Такая система ко-
ординат весьма удобна для исследова-
ния атмосферных процессов и решения
задачи прогноза в области, имеющей
ограниченные размеры. При рассмот-
рении же атмосферных процессов и для
решения задачи их прогноза в глобаль-
ном масштабе в ряде случаев оказы-
вается удобно использовать сфериче-
скую систему координат.
Пусть (рис. 2.3) г — расстояние от
центра Земли до некоторой точки N\
X— долгота места (положительная
к востоку); 0=-^------Ф— полярный
угол или дополнение широты ф (пе-
ременные г, Z и 6 и являются сфери-
ческими координатами). Тогда урав-
движения по осям 0Д и г, уравнение неразрывности и урав-
притока тепла записываются в виде [У. 13,1]:
, Уг ^9 ve <4 |
dt ' г дг ‘ г дб * г sin 6 д\
нения
нение
—^ctg— _----1— dp 2w cos + -О е >
г дг ди 1 1 °
66
d^x I Vr д_^\ I dvx ^'1- , Vi ct«°
dt ‘ r dr ' r dO * r sin 6 d\ * r
1 dp
prsinO d\
2w COS 4-2(0 sin 0vr 4~£\;
dvr i dvr ve dvr . v\ dvr________________ve + vx
* Z'r dr * r d6 rsln6 d\ r
= — 4 -^r — g — 2<o sin 6г>х+Dr;
д? I ,, dP , dP , dp , / i dJ^ , i
dt *" r dr * г Э6 * rsin6 cM r2 dr * r 06 *
VgCtgfl 1 dV± \_
”7" r ' r sin 0 Ok / ’
dT , d_T , dr , vx d?____7a / dp , I
dt * Vr dr •" r 06 * rsin6 d\ g? \ dt ' r dr '
dp . dp\ e
‘ r 06 ' r sin 6 dr / cpp
Здесь ve — составляющая скорости по меридиану (положитель-
ная к югу), vi — составляющая скорости по кругу широты (по-
ложительная к востоку), vr—вертикальная скорость (положитель-
ная вверх), De, и Dr — составляющие сил турбулентного трения
по осям 0, X и г соответственно.
Для задач метеорологии эти уравнения с самого начала не-
сколько упрощаются. При этом используется то обстоятельство, что
высота атмосферы намного меньше радиуса Земли (а = 6371 км).
В таком случае там, где значение г входит множителем, оно всюду
заменяется постоянным значением а. Далее вводится новая пере-
менная по соотношению z = r — а. Тогда очевидно, что t/r = yz,
(3 д '
а = • Приближенно принимают, что
1 drve dve 1 drv\ dv\
г dr ~ dr ’ г dr dr ’
1 dr^vr dvz
72 dr dz 9
С учетом указанных упрощений уравнения переписываются
в виде:
d^e । dve , ve dv6 dv„
dt * z dz * a d6 ‘ a sin 6 dX
2
— ctgO= —C£-4-2<j)COsei>x+.De;
a b ap do 1 a 1 в j
5*
67
дУ. . dV> . Vn dVX . Vl dv\ I VHVX . л
~dt ^Vz ST “1 a <Й asinO ~д\ 1 — Ctg 0 —
=-4 - 2(0cos +2(й sin e^+£»x;
dvz । дУг i dv, vx dv,
dt * z dz ’ a dO * я sin О d'K
9 9
2ф
a p dz ° л 1 z’
^p , dp , aP , ;’z d? , (dv, i «4
dt ' z dz ‘ a db * rz sin 0 dK * * \ dz ' a dO ‘
dT f dT } дТ \ дТ 7a ( dp . dp
dt * z dz * a dO * я sin О dA gp \ dt z dz
, dp , dp \ s
* a d6 * a sin 0 dK / cp%
Рассмотрев порядки величин членов уравнений подобно тому,
как это делалось ранее, и опустив сравнительно малые члены по-
лучим:
-----т?х=--------— cos 0т;х; (8.1)
dt а «р du 1 а» . \ /
-|~.ctg.L t;otjx=--к- -чу—2о) cos бг»6; (8.2)
dt 1 а 0 Л яр sin 6 dX °’ v 7
#=-^p; (8-3)
Ar p (. A ±i_+. J ±k+ vtg!LQ' (8 4)
dt * P \ dz a dO * a sin 6 dA * a ) ’ ' 7
P=R?T, (8.6)
где
। г, ±+ЛЛ+А______A (8 7)
dt ~ dt ^^z dz a dO tfslnO dX • x°*'7
Выведем уравнение вихря скорости в сферической системе ко-
ординат. В этой системе координат вертикальный компонент
вихря скорости выражается в виде
1 / d sin
1 ________________х
я sin 6 \ dO
dx / *
(8-8)
68
После некоторых преобразований уравнения движения по осям 0
и X принимают вид:
ve + vx
2
<4
<36
£_Э_
а ЭО
^-^г+(2«о50 + а)гч;
<4 ।
dz ‘
*>х ! . 1______<) / vij + г'л \ 1 др
dt ‘ "^г Qz ' a sin 6 дХ I 2 / ар sin 6 дК
— (2<в COS 04-2) Яо.
тт dve dv% „ .
Члены Vx- и v2 по крайней мере на порядок меньше
остальных. Поэтому уравнения приближенно можно записать так:
j4__> J_ д_ ( +
dt * а Э0 у 2
^--^-+(21ocos0+2)^; (8.9)
<4 । 1 д ( + "<
dt ‘ a sin 6 Эк \ 2
—4г- - (2« cos 6+2) v8.
ар sin 0 Эк v । / и
(8.10)
Умножим второе из этих уравнений на sin0 и продифференци-
руем полученный результат по 0. Из найденного выражения выч-
тем первое уравнение, предварительно продифференцированное
по X. Разделив найденное выражение на tzsinO и принимая во
внимание выражение для Q, получаем уравнение вихря скорости
в сферической системе координат
—(2 + 2« cos 8) 4---^4-4?
dt 1 а Э0 v 1 ' 1 л sin 6 dl
1 I dp dp
a2p2 sin 0 \ Э0 d\
dp dp \ _ 2a> cos 0 + a / I dve sin 6
Эк Э0 / #sin0 \ d\ ' Э0
(8.11)
Уравнение неразрывности (после перемены порядка дифферен-
цирования) запишем в виде
Эр . Эр . dp . dpvz .
dt * а Э0 ‘ a sin 6 Эк dz '
Ч-----г~(г 4^(^osine)4~~^]=0-
1 a sin О L Э0 v и 71 Эк J
В этом уравнении первые три члена на порядок меньше осталь-
ных. Поэтому приближенно уравнение можно записать так:
-4^-4----Р sin 9) 4-^-1=0. (8.12)
dz 1 a sin 0 [ ЭО v ° 7 'Эк J 4 7
69
Исключая из уравнения вихря плоскую дивергенцию с помощью
уравнения неразрывности, а также принимая во внимание, что, со-
гласно уравнению состояния
др dp др dp др д / р \ др д / р \ _
“dT’dX dF"dT d0 ~дГ\НТ) дк дв \ RT )
р [ др дТ др дТ \ р ( др дТ др дТ \
" \~d0~ ~dX dF'dT'j dX dX- d0 J’
получим следующее уравнение для вихря скорости:
dQ । ve д л? |-2cncos61 I dQ _ R
dt ' a d0 ' / 1 «sin 6 dX «2psin6
dp дТ \ . (2<d cos 0 H- Q) dpv2
dX de )' p dz
§ 9. Уравнения гидротермодинамики в системах координат,
связанных с картографическими проекциями
Ввиду того что поверхность земли близка к сферической, было
бы естественным задачу прогноза погоды решать в сферической
системе координат. Однако при непосредственном использовании
указанной системы возникает ряд дополнительных трудностей ма-
тематического характера, связанных с неравномерностью расстоя-
ний между меридианами, представлением производных в конечных
разностях в окрестности полюса и пр. По этой причине сфериче-
ская система координат имеет ограниченное применение. Она ис-
пользуется, например, в гидродинамическом долгосрочном прог-
нозе, где область решения охватывает всю сферу или полусферу
Земли. В задачах же краткосрочного прогноза, решаемых для
области, меньшей чем полушарие почти всегда применяется де-
картова система координат на плоскости карты, а точнее ее моди-
фикация с учетом особенностей той или иной картографической
проекции.
В последнее время, однако, наметилась тенденция к использо-
ванию в прогностических схемах систем координат на сфере с не-
равномерными промежутками между точками и, в частности, уже
рассмотренной сферической системы. Такой подход позволяет уст-
ранить некоторые трудности, возникающие при учете искажений,
вносимых картографическими проекциями.
Необходимость учета картографических проекций возникает
в связи с тем, что земную поверхность невозможно спроектировать
на плоскость без искажения. Эти искажения оказываются различ-
ными для разных типов картографических проекций.
Для процессов над сравнительно небольшими территориями
протяженностью, например, 2—3 тыс. км по меридиану эти иска-
жения небольшие, более или менее одинаковые на всей территории
и ими можно пренебречь. В этом случае плоскость географической
70
карты, на которую наносятся метеорологические данные или ре-
зультаты прогноза, можно отождествлять с плоскостью х, у декар-
товой системы координат или с плоскостью хр, ур изобарической
системы координат, а масштаб карты можно считать всюду посто-
янным. Именно при таком предположении и были получены пер-
вые численные прогнозы.
При рассмотрении процессов на большей территории, превы-
шающей, например, 3000 км по меридиану, искажения, возникаю-
щие при проектировании земной поверхности на плоскость, ока-
зываются уже значительными и различными для разных участков
карты и в этих случаях возникает необходимость их учета. Один
из возможных способов такого учета сводится к модификации
уравнений, записанных в декартовой системе координат, путем
введения в уравнения переменных множителей, определяемых па-
раметрами картографической проекции. Указанные множители мо-
гут быть получены в процессе перехода от сферической системы
координат к декартовой.
Прежде чем приступить к преобразованию уравнений, рассмот-
рим основные положения теории картографических проекций.
При этом ограничимся случаем, когда земная поверхность пред-
ставляется в виде сферы или поверхности шара радиусом а.
Картографические проекции получаются при отображении
земной поверхности на плоскость. В зависимости от способа
отображения получаются различные типы картографических
проекций.
Если отображение производится путем проектирования из ка-
кой-либо точки на плоскость по законам линейной перспективы,
то мы получаем перспективные проекции. Если проектиро-
вание осуществляется из центра земного шара, то получаем цен-
тральные проекции, а если из точки, находящейся на земной
поверхности, то стереографические. В случае, если линия
визирования (или проектирующий луч), исходящая из точки, на-
ходящейся на земной поверхности, и перпендикулярная к плоско-
сти, на которую производится проектирование, совпадает с осью
Земли, имеем прямую или полярную стереографиче-
скую проекцию.
При отображении земной поверхности на боковую поверхность
конуса, которая может быть либо внутренне касательной, либо
секущей, и при последующей развертке поверхности конуса в пло-
скость получаются конические проекции Если при этом ось
конуса совпадает с полярной осью Земли, то получаем прямую
коническую проекцию.
Путем отображения поверхности земного шара на поверхность
цилиндра, которая может быть либо внутренне касательной, либо
секущей, и последующего развертывания поверхности цилиндра
в плоскость получают цилиндрические проекции. Если при
этом ось цилиндра совпадает с осью земного шара, то будет иметь
место прямая цилиндрическая проекция. Цилиндрическую
проекцию можно рассматривать как частный случай конической
71
проекции, когда общий центр окружностей параллелей на плоско-
сти карты удален в бесконечность.
При отображении поверхности земного шара на плоскость ста-
вятся различные условия относительно искажений и масштаба изо-
бражения т, т. е. отношения длин на изображаемой поверхности
и на местности. В случае, если таким условием является подобие
бесконечно малых фигур на шаре и плоскости (а следовательно,
и равенство углов), то проекция называется равноугольной
или конформной. При этом масштаб оказывается независи-
мым от направления. Если же ставится условие постоянства отно-
шения площадей изображаемой и изображенных поверхностей, то
получаемая проекция является равновеликой. Наконец, при
условии равенства масштаба единице по одному из главных на-
правлений (вдоль меридианов или параллелей) мы получаем
равнопромежуточные проекции.
Под масштабом изображения (параметром увеличе-
ния) понимается отношение
где dl и dls — элементарные длины на плоскости изображения ина
местности. Это отношение, вообще говоря, зависит как от поло-
жения точки, так и от направления рассматриваемого бесконечно
малого отрезка dl. В дальнейшем, однако, мы будем рассматри-
вать лишь случаи независимости т от направления, что справед-
ливо для всех равноугольных (конформных) проекций. Отличие
масштаба изображения от единицы приводит к различию в вели-
чинах производных по координатам на плоскости изображения и
на местности. Между ними существует следующее соотношение
~дЦ==т~дГ •
где индексом s отмечены производные по координатам на мест-
ности.
При представлении картографических проекций в виде геогра-
фической карты вводится еще масштаб карты М, равный
отношению длип на бланке карты и на местности и меняющийся
от точки к точке (истинный масштаб) и главный или общий
масштаб карты Л1Г, равный отношению длин на карте и на мест-
ности в точках, для которых масштаб изображения т равен еди-
нице. Именно этот, т. е. главный масштаб и приводится всегда на
бланках географических карт. Очевидно, что М=тМТ и т=М/Мг.
Таким образом, масштаб изображения, или параметр увеличения
можно определить еще как отношение истинного масштаба карты
в рассматриваемой точке к главному.
При решении задач численного прогноза погоды, как и вообще
в синоптической метеорологии, наиболее широкое распространение
получили три типа картографических проекций: стереографическая
полярная, коническая прямая и цилиндрическая прямая (мерка-
72
торская) проекция. Все эти проекции являются конформными или
равноугольными. Рассмотрим эти проекции более подробно [3].
Стереографическая полярная проекция. Поверх-
ность земного шара проектируется из полюса на плоскость, про-
ходящую через широтный круг ерь При этом, например, для изо-
бражения на карте северного полушария проектирование произ-
водится из Южного полюса, а круг широты ф1, выбирается
в северном полушарии (рис. 2.4). На рис. 2.4 М — точка на поверх-
ности земного шара, М'— отображение этой точки на плоскости
картографической проекции. В этой проекции круги широт на по-
верхности Земли ф = const превращаются в концентрические окруж-
ности на плоскости, а меридианы Х = const — в радиальные прямые,
исходящие из точки изображения
полюса.
Введем на этой плоскости поляр-
ную систему координат р, %. При
этом полярную ось (х = 0) совме-
стим с проекцией на рассматривае-
мую плоскость меридиана М сфе-
рической системы координат. Тогда
р будет равно расстоянию от изоб-
ражения переменной точки М' на
этой плоскости до изображения на
ней полюса. Обозначим через k
расстояние от изображения полюса
до изображения точек экватора.
Рис. 2.4. Стереографическая поляр-
ная проекция
Тогда для данной проекции между сферическими координатами X,
б и полярными р, % имеют место следующие соотношения:
JL=tg4=tg(4r—т)’ Z=X“Xb
k=2a cos2 ---------TJ=a О +sin <?i);
д д д rfp д __________________
дк ду ’ д® dft dp dp ’
1 = * fi I ( р V] _ р 1
a dO а 1 + cos 6 2а [ ’ \ k / 1 л sin 6
Для карт погоды в стереографической проекции, составляемых
в СССР, главный масштаб принят для широты 60°. Подставляя
/ у“з\
это значение ф1 = 60° в (9.2), получим & = ( Н——\а^ 1,8660а.
Введем теперь на плоскости карты в стереографической проекции
декартову систему координат х, у. Ее начало поместим в точке
этой плоскости, соответствующей географическим координатам фо,
Хо, а ось у направим параллельно проекции на плоскость изобра-
жения меридиана М при его направлении к северному полюсу.
73
Тогда, если хп и уп — координаты полюса, то между декартовыми
и сферическими координатами существует следующая связь:
0
.. .оу —. •• „ Sin(X —X]);
1 + ^-т
0 1 - tg -f-
У=Уп — k tg -5- cos (X — х,)=уп - k-— cos (X — Xj). (9.3)
1+.81
Координаты хп и уп определятся из соотношений (9.3) при х = у =
= 0, <р = фо и Z = Z0. Здесь и далее <р положительно для северных
широг и отрицательно для южных. Имея в виду, что k = 1,8660а,
для параметра пг получаем
1,8660
1 -f- sin ср
Чтобы определить значения пг в любой точке, достаточно найти
широту места ф этой точки. Из первой формулы соотношений (9.2)
можно получить
(94)
1
sin ср=—
где p = f(x— хп)2+(у— г/п)2—расстояние между двумя точками,
одна из которых является переменной точкой с координатами х
и у относительно принятого начала декартовой системы координат,
а другая — изображением полюса с координатами хп и уп.
Стереографическая проекция используется при картировании
участков земной поверхности, имеющих значительную протяжен-
ность по меридианам (например, карты полушарий).
Равноугольная коническая проекция, называемая
также проекцией Ламберта, получается путем установления со-
ответствия между точками шара и секущего конуса. Затем конус
развертывается на плоскость. Круги широт на поверхности шара
переходят в дуги концентрических окружностей на плоскости, а ме-
ридианы— в радиальные прямые, исходящие из точки изобра-
жения полюса. При равноугольной конической проекции нет такого
наглядного соответствия между точками шара и конуса, как при
стереографической проекции. Зависимость между широтой точки
на шаре и полярным радиусом ее изображения на плоскости полу-
чается из условия подобия областей на шаре и на плоскости
карты, что равносильно равенству углов.
Пусть р — расстояние между изображением полюса на плоско-
сти и изображением переменной точки, k — расстояние между изо-
бражениями полюса и точек экватора. Тогда между сферическими
74
и полярными координатами в случае, когда полярная ось совпа-
дает с меридианом М, справедливы соотношения:
«cos <f3tg° +
k---- ~ ,
а
а==_____ lg (a cos ?з) — lg (a cos ?4) _ /95ч
где фз и ф4 — широты, для которых масштаб равен главному мас-
штабу. Для рассматриваемой проекции фз = 30°, ф4 = 60°.
Следовательно,
а= ----—^0,7156,
1g (2 4- КЗ) — Ig /3
k (]<3)“]^L а 1,7930а.
Далее можно записать
д __ д д _________ dp д ___ д
эГ~а "аГ’ _дГ~д? ~~та *»
Введем как и в случае стереографической проекции на плоско-
сти изображения декартову систему координат. Ось у направим
параллельно меридиану Лц при его направлении к полюсу Если
при этом координаты полюса относительно начала декартовой си-
стемы координат, находящейся в точке фо, Zo, будут хп и z/n, то
декартовы координаты любой точки выразятся через широту
и долготу следующим образом:
х=хг1-|-Л
l+tg-fJ
Sin (X — X,);
1 + tg /
cos(X —Xt).
(9.7)
Координаты хп и уп определятся из соотношений (9.7) при х =
= у = 0, ф = фо и Z = До.
Карты конической проекции применяются в основном при отоб-
ражении участков земного шара, имеющих сравнительно неболь-
шое протяжение по меридианам и параллелям.
75
Прямая цилиндрическая равноугольная (мер-
каторская) проекция получается путем отображения по-
верхности шара на боковой поверхности цилиндра внутренне ка-
сательной или секущей. При прямой цилиндрической проекции
ось цилиндра совпадает с полярной осью Земли. Боковая поверх-
ность цилиндра разрезается по одной из образующих и разверты-
вается в плоскость, что и дает цилиндрическую проекцию. В этой
проекции меридианы изображаются прямыми, параллельными ме-
жду собой и отстоящими друг от друга на расстояниях, пропор-
циональных разности соответствующих долгот, а параллели —
в виде прямых, перпендикулярных к линиям меридианов.
Введем на плоскости изображения декартову систему коорди-
нат. При этом ось у направим вдоль меридиана Ло при его направ-
лении к полюсу, а ось х- вдоль широты фо- Тогда:
Х=^(Х —Хо);
(1 \
--------|4-у3;
1
(9.8)
- k COS
k=a cos m =------------=-----—,
тя’ a cos т cos т
где X и Xo — выражено в радианах, фь— широта, на которой т=\
Значение являющееся декартовой координатой экватора, опре-
делится с помощью второго из соотношений (9.8) при у = 0 и
Ф = фо. Эта проекция применяется главным образом для карт тро-
пической зоны. Для таких карт, принятых в СССР, ф& = 22,5° и k =
= а cos 22,5°.
В табл. 2.1 приведены значения масштаба изображения т
на различных широтах для трех разобранных типов картографи-
ческих проекций. Там же приведены и значения параметра Корио-
лиса.
Все изложенное относительно проектирования на плоскость по-
верхности земного шара можно распространить и на изобариче-
ские поверхности, которые практически «параллельны» поверхно-
сти земного шара. Важно еще отметить, что преобразования, свя-
занные с картографическими проекциями, не касаются
вертикальной координаты, которая всегда направлена по местной
вертикали.
Переход к уравнениям в декартовой системе координат, свя-
занной с той или иной картографической проекцией, производится
на основе уравнений, записанных либо в векторной форме, либо
в сферической системе координат.
Рассмотрим сначала случай перехода от уравнений в векторной
форме. Возьмем уравнения горизонтального движения и нераз-
рывности в изобарической системе координат:
V, • Vs+-^=0,
(9-9)
76
Таблица 2.1
Значения масштаба изображения т для различных картографических проекций
и параметра Кориолиса Z для разных широт
Широта, град. Картографическая проекция Z-104 с-1
стереографи- ческая полярная = 60° коническая равноугольная <Рз = 30°, = 60° цилиндрическая прямая (Мерка- тора) ? k= 22,5°
0 1,866 1,282 0,924 0,000
5 1,717 1,211 0,927 0,127
10 1,580 1,151 0,938 0,254
15 1,474 1,099 0,956 0,378
20 1,408 1,057 0,983 0.499
25 1,312 1,026 1,019 0,617
30 1,244 1,000 1,067 0,729
35 1,185 0,984 1,128 0,837
40 1,136 0,971 1,206 0,937
45 1,094 0,964 1,307 1,031
50 1,057 0,968 1,437 1,117
55 1,026 0,980 1,611 1,194
60 1,000 1,000 1,848 1,263
65 0,979 1,033 2,186 1,321
70 0,962 1,084 2,702 1,371
75 0,949 1,161 3,570 1,408
80 0,940 1,291 5,322 1,436
85 0,935 1,567 10,595 1.452
90 0,933 оо оо 1,458
где
к — единичный вектор вдоль оси р, а индексом s отмечены ве-
личины, относящиеся к поверхности Земли. Между переменными
и операторами на сфере и на плоскости картографической проек-
ции (которые далее будут выписываться без индекса $) сущест-
вуют следующие соотношения:
V5=znV; V5=znV; • V5=/n2V • V;
DS=VS • Ns=m?\ • N=ni2D. (9.10)
Подставляя соотношения (9.10) в уравнения (9.9), получаем
_^Y-=_g/wV//-/kXmV, m2V • V4--^=0. (9.11)
77
Учитывая, что
Vs • VsVs=mV • mV (mV)=m2V • (mV • V+Wm)=
= m3V • VV+m2V • VVm.= m(m2V • VV +mV2Vm)=
= m[m2V VV-|—yVm2j,
где V2 = V • V = u2+v2,
на основании (9.9) получаем:
4У + lk\N-
m2V V-4—^=0,
1 dp
(9.12)
где
d d । 9<r _ । d
~аГ~~дГ^гт v ’ v
Записывая полученные уравнения движения и неразрывности
в координатной форме и присоединяя уравнения статики, притока
тепла и переноса влаги (при отсутствии конденсации и испаре-
ния), получаем следующую систему полных уравнений гидротер-
модинамики в декартовой системе координат, связанной с карто-
графическими проекциями:
du . w2 + v2 dm2 dH , ,
-тг+—2---------дТ=-ё-дг+1^
dv j и2 4- v2 dm2 _ dH ,
~dF 2 dy~~~~S~dy LU''
dT
dt
i 2( dT
^m\u^
dr \ <?- ,i
f-'tf-s— = -n— *4-------------£;
1 dy J Rp 1 cpp
#+m2(° ^+'v w)+^=m2k' ’ <9J3>
где
d d . 2 / d . d\. d
'-7ГГ = Г tn2, U + T “3— •
dt dt 1 \ dx 1 dy ) 1 dp
В приведенных уравнениях под и и v следует понимать состав-
ляющие ветра на плоскости картографической проекции, которые
можно получить по результатам измерения ветра следующим об-
разом.
78
Пусть c=|Vs|—абсолютная величина скорости фактического
ветра, А — азимут ветра (угол между направлением на север и
направлением, откуда дует ветер, отсчитываемый по часовой
стрелке); а— угол между осью х и направлением, куда дует ве-
тер; Xi — угол между направлением на север и осью у (рис. 2.5).
Тогда, учитывая, что абсолютная величина скорости ветра в соот-
ношениях, записываемых в системе координат, связанной с пло-
скостью картографической
с
проекции, равна —, для
проекций вектора ветра на
плоскости картографической
проекции получаем:
и= — cos а, т7= —sin а,
т 3 т
(9.14)
где
а=-|-тс—Xj —Л.
Если под и и v понимать
не проекции действительно-
го ветра на оси системы ко-
ординат, связанной с карто-
графической проекцией, а
компоненты действительного
Рис. 2.5. Проекции вектора ветра на плоско-
сти карты.
ветра на сфере или местно-
сти, то для них будут справедливы соотношения:
Vs • Ns=m\ • V/, V5 • \sNs=mNs • W5,
и уравнения движения и неразрывности в координатной форме
примут вид:
afw дН . z dv дН z
( ди . dv \ . дх п
(9.15)
На практике применяются оба изложенных варианта. Рассмот-
рим теперь переход к картографической проекции от уравнений
в сферической системе координат. Этот переход проделаем на при-
мере стереографической проекции для операторов Якоби и Лап-
ласа, которые в сферической и декартовой системах имеют вид:
1 /Л m 1 ( дА дВ дА дВ \
sin 6 sin6 дк об р
И, В)
дА дВ
дх ду
дА дВ
ду дх ’
79
л _ 1 д д д I 1 д2
sine dO SinU dO "Т" Sin2 0 dX2
л_ a2 j а2
дх2 + ду2 ’
а также для операторов, описывающих горизонтальную адвекцию:
A д ] д -
s а дв * a sin 0 дк ’
где индексом s помечены операторы на сфере.
Указанный переход будем производить в два этапа: на первом
этапе проделаем переход от сферической системы координат к по-
лярной, на втором этапе — от полярной к декартовой.
Используя соотношения (9.2), получаем
-ДтгИ, B)s=—
Sin 0 v ’ /s p
/ дА дВ
Р \ др ду
дА дВ дА
----5--------Б-
др ду ду
дА дВ \
ду др / ’
Переход от полярных
формулам:
координат к декартовым производим по
д , . д
—н sin 7 -т— ;
1 А ду
д , д \
---pCOS у -5— .
дх 1 Л ду )
д
dp C0S z дх
д
дх
Тогда для якобиана получаем
1 » » 9 9 Г ( дл4 । . дА \ / . дВ ।
-ет<Л’ ^=/ИЙ [(cos X -^-4-sin X -ajr) (-sin x -^4-
• дВ \ / дА . дА \ i дВ . дВ \1
+cos X - (—sin х -^+ cos х -^) (cos х т 4- sin х =
— т2а2
д^ дВ _____ дА дВ \____w2//2(А В}
дх ду ду дх ) ( » ) •
Делая аналогичные преобразования для оператора Лапласа
и оператора адвекции As, находим:
. та д ( р д \ . ( та \2 д2
Дс=----та— —та-^— 4- ---------- =
s р др \ та др / 1 \ р ) ду2-
= т2а? (— -^-р +-у ^-]=ni2a2^
\ р др г др 1 Р^ ду/ /
As=m2A.
80
Таким образом,
B)s=mW(A, В)-
Ls=ma2L\ As=m2A, (9.16)
что соответствует операторам в уравнениях (9.13).
§ 10. Постановка задачи о прогнозе крупномасштабных
атмосферных движений
Все три вида атмосферных движений—макро-, мезо- и микро-
масштабные движения — безусловно оказываются взаимосвязан-
ными. Однако с точки зрения прогноза погоды нас в первую оче-
редь будут интересовать крупномасштабные, а во вторую — сред-
немасштабные движения.
Так как макро- и мезомасштабные движения существенно раз-
личаются по ряду характеристик, то для их рассмотрения и прог-
ноза должны быть получены специальные отличные друг от друга
системы уравнений. Эти системы могут быть решены независимо.
При этом предполагается, что при рассмотрении и прогнозе
крупномасштабных движений учет мезо- и микромасштабных дви-
жений может быть осуществлен приближенно в виде поправок
к решению системы уравнений для крупномасштабных движений.
При этом влияние микромасштабных движений учитывается сум-
марно, без рассмотрения конкретных турбулентных пульсаций.
При прогнозе же мезомасштабных явлений учет крупномас-
штабных процессов может быть осуществлен параметрически, пу-
тем задания характеристик крупномасштабных движений вне об-
ласти мезомасштабного воздействия.
В этом параграфе будет рассмотрена постановка задачи о прог-
нозе крупномасштабных движений. Задача же о прогнозе мезо-
масштабных явлений и погоды будет рассмотрена в гл. VI.
Будем рассматривать атмосферу, состоящую из двух частей:
планетарного пограничного слоя (нижние 600—1000 м), в кото-
ром сила турбулентной вязкости и сила Кориолиса имеют одина-
ковый порядок, и всей остальной части атмосферы (свободная
атмосфера), где влияние вязкости мало. Ввиду сравнительно ма-
лой толщины пограничного слоя будем вначале решать задачу
прогноза без его учета. При этом пограничный слой как бы «стя-
гивается в пленку», не имеющую толщины. В решение, полученное
при таких условиях, потом может быть введена поправка на влия-
ние пограничного слоя.
В качестве исходной возьмем систему полных уравнений гид-
ротермодинамики (6.3) — (6.7) в изобарической системе координат:
ди . ди . ди . ди ~ дН . .
-37—i ^~з--г'^ “3-гт~з_~ = ~й'*з--
dt 1 дх 1 ду 1 др ь дх 1 ’
dv . dv . dv . dv дН ,
-37—г и —т-г -з---Н ---
dt 1 дх 1 ду 1 др ь ду ’
6 Зак. № 21
81
т
g дН
тгр дР ;
ди , dv . дт _
дх * ду ‘ др ’
дТ , дТ , дТ & . 1
Г U “3 Г ~3 = “п— т Ч---£,
dt-----------------------------1 дх-1 ду-Rp 1 срр
где
(ЮЛ)
С2^ ^2^(7а-7)
g
(Ю.2)
— некоторый параметр, называемый параметром статической ус-
тойчивости и считающийся известным Рассмотрим случай, когда е
задано (в частности, 8=0). В этом случае система пяти уравне-
ний содержит пять неизвестных: и, v, т, Т и Н. Так как она имеет
три производных по времени, то для ее решения необходимо за-
дание в начальный момент трех функций. В качестве таковых мо-
жно задать, например, и, v и Н. В таком случае две остальные
функции, т. е. Т и т определяются по данным первых трех с по-
мощью уравнения статики и уравнения неразрывности, не содер-
жащих производных по времени. Таким образом, мы полагаем, что
при Z=0 и=и0(х, у, р); v=vQ(x, у, р);
H=HQ(xf у, р). (10.3)
Можно, однако, в качестве начальной задать не Ну а Т. В этом
случае, кроме того, потребуется задать давление на уровне моря.
Для решения данной системы уравнений, кроме начальных, не-
обходимо задать граничные условия. Исходя из того, что в прин-
ципе область решения данной задачи может охватывать поверх-
ность всего земного шара, ограничимся рассмотрением краевых
условий по вертикали Так как система уравнений содержит две
производные по вертикальной координате р, то необходимо задать
два краевых условия.
В качестве одного из таких условий принимается непроникно-
вение масс воздуха сквозь земную поверхность что означает ра-
венство нулю вертикальной скорости w при z = 0. В изобарической
системе координат это условие, согласно (6.2), имеет вид
I дН - дН . дН \ /1П,Ч
при р=р ЯР1( аг+«-р7-+г'-^г) • (,0-4)
где Р = 1000 мбар, pi — средняя плотность воздуха у поверхности
земли.
Величина Ti по сравнению с т на других уровнях мала, поэтому
иногда вместо краевого условия (10.4) используется более простое:
при р=Р T=Ti=0.
(10.5)
82
В качестве второго краевого условия привлекается условие со-
хранения массы атмосферы. Это означает, что на верхней границе
атмосферы р^->0. В изобарической системе координат при допол-
нительном предположении, что и и v ограничены, это условие
имеет вид
при р-^0 т=т0--0. (10.6)
Краевые условия (10.4—10.6) могут быть переписаны в другом
виде. Согласно уравнению притока тепла (пятое уравнение си-
стемы (10.1)), имеем
_ Rp / drT 1 \__RP_ drT R?T _
Т С2 \ dt Ср? / с2 dt СрС^ £
Rp drT R
с2 dt аСр
где
а=^(ь-т)^-
Подставляя это значение т в (10.4), получаем
при р = Р
Rp drT _ R gp drH
cp dt aCp RT dt
или, учитывая уравнение статики,
п dr I дН . rr\ R2T
при p = P — e. (10.7)
Подставляя значение т в (10.6), получим
„ / дТ , дТ . дТ \ с? п
прир-^о
Из физических соображений положим, что при р->0 и и и огра-
ничены, а 8->0. Следовательно, для выполнения последнего ус-
ловия необходимо, чтобы при р->0 величина dT)dt была ограни-
чена. Тогда, используя уравнение статики, приходим к следующему
условию на бесконечности
при р ограничено. (10.8)
Полученные краевые условия в форме (10.7) — (10.8) эквива-
лентны условиям (10.4) — (10.6), но сформулированы для величины
dHjdt. В такой форме они оказываются необходимы, если решение
задачи ищется для dHIdt.
Система уравнений (10.1) и краевые условия (10.4) — (10.6)
или (10.7) и (10.8) представляют собой замкнутую систему и вме-
сте с начальными данными (10.3) служат основой численных мето-
дов прогноза крупномасштабных движений и погоды.
6*
83
В частном случае указанная система уравнений может быть су-
щественно упрощена. Это случай баротропной атмосферы, в кото-
рой, как уже говорилось, давление есть функция одной плотности
или температуры. В такой атмосфере при р = const будет и Т =
= const, а изобары и изостеры, а значит, и изотермы параллельны.
Из этого следует, что направление (но не скорость) геострофиче-
ского ветра с высотой не изменяется. Из сказанного следует, что
в данной модели атмосферы на любой изобарической поверхности
изменения температуры во времени и вдоль изобарической поверх-
ности отсутствуют. Следовательно, можно записать
дТ , дТ . дТ п
dt * дх 1 ду
или после замены температуры через высоты изобарических по-
верхностей с помощью уравнения статики
д дН , д дН , д дН
др dt dp дх др ду
Поставим еще более жесткое условие. Положим, что направление
и скорость действительного ветра с высотой остаются неизмен-
ными. Тогда, интегрируя приведенное соотношение по давлению
от р до Р и учитывая, что по условию скорость и направление
ветра с высотой не изменяются, получаем
В соответствии с краевым условием (10.4), второе слагаемое по-
следнего соотношения равно Ti/pig’ = /?TiTi/gP, где 1\— значение Т
при р=Р.
Тогда мы можем записать
dH
dt
дН
dx
dH
dy
R7\
gP
^=0.
Проинтегрировав уравнение неразрывности по давлению от р
до Р, учитывая неизменность ветра с высотой и краевые условия
(10.6), получаем
ду ) г \ дх ' ду )
Подставляя это выражение в предыдущее соотношение, получаем
следующее уравнение:
дН . дН . дН । du , dv \ /ш п\
+ -------------vQ --------F-TT- =0, (10.9)
dt 1 dx 1 dy 1 1 \ dx 1 dy / v 1
где q = c2lg, С = УР7\ = У287 • 300 —290 м/с — параметр, близкий
к скорости звука.
Полученное соотношение совместно с двумя уравнениями движе-
ния системы (10.1), которые в баротропном случае и при сделан-
84
ных предположениях справедливы для любого уровня, образуют
замкнутую систему из трех уравнений с тремя неизвестными:
ди I ди । ди дН . ,
~дГ + и -дГ + v ~ё ~dT+lv’
dv . dv . dv dH t
-jr+u'dr+'v-W=-s^y--------------
+ )=o. (10.10)
dt 1 dx 1 dy 1 v \ dx 1 dy ) v '
Это полная система уравнений гидродинамики для баротроп-
ной атмосферы. Она может быть применена к любому уровню.
Однако практика показала, что наилучшие результаты она дает
применительно к средней части атмосферы (изобарическая поверх-
ность 500 мбар).
К этой системе двухмерных уравнений мы вернемся в даль-
нейшем. А сейчас отметим, что система уравнений типа (10.10) мо-
жет быть получена также исходя из иных позиций. Рассмотрим
частный случай баротропности — однородную несжимаемую атмо-
сферу (р = const), ограниченную сверху свободной поверхностью
h(x, у, t). По-прежнему будем считать, что ветер не изменяется
с высотой. Интегрируя уравнение неразрывности для несжимаемой
атмосферы
ди ! dv ( dw __ n
дх *" ду * дг
по высоте z от 0 до h и учитывая, что при z = 0 w = 0, а также не-
изменность ветра с высотой, получаем
h
п J \ дх 1 ду J \ дх 1 ду J’
где Wh — вертикальная скорость перемещения свободной поверхно-
сти.
Для свободной поверхности справедливо соотношение dhjdt =
= 0, выражающее тот факт, что частицы жидкости при своем дви-
жении не проникают через эту поверхность, а перемещаются вдоль
нее, т. е. поверхность как бы всегда состоит из одной и той же со-
вокупности частиц. Из этого соотношения следует, что для свобод-
ной поверхности
dh . dh . dh
—\-U-5----•
п dt 1 дх 1 ду
Подставляя сюда полученное только что выражение для Wh, полу-
чаем
dh . dh , dh , [ ди , dv \ ,. ~ . ч
+ w ------рт, —— = —/г —--------U —— . (10.11)
dt 1 dx 1 dy \ dx 1 dy v 7
Для однородной атмосферы p=gp(h — z), следовательно,
1 dp dh 1 dp dh
p dx dx ’ p dy & dy
85
Подставляя эти выражения в уравнения движения и учитывая
условие неизменности ветра с высотой (du/dz = dv/dz = O), получим
два упрощенных уравнения движения Объединяя эти два уравне-
ния с уравнением (10.11), получаем следующую систему урав-
нений:
dv . dv . dv ~ dh
dt U dx dy & dy
lu\
dh . dh , dh , (du . dv \ < O4
dt 1 dx 1 dy \ dx 1 dy ) v 7
Легко видеть, что полученная система уравнений аналогична
системе (10.10). Различие же между ними состоит в том, что урав-
нения (10.10) записаны в изобарической, а (10.12)—в декартовой
системах координат.
Делая переход от декартовой системы координат к изобариче-
ской (аналогично тому, как это было сделано в § 6) и обозначая
высоту свободной поверхности через Н, вместо системы уравнений
(10.12) получим систему (10.10) при условии, что q = H. Можно
проверить что при с—300 м/с последнее условие справедливо для
высот порядка 5—9 км.
Решение системы уравнений для реальной атмосферы (10.1)
при условиях (10.3), (10.7) или (10.8), как и системы уравнений
для баротропной атмосферы (10.10) при q = c2lg или q = H и усло-
виях (10.3) связано с чрезвычайными трудностями. Эти трудности
обусловлены в первую очередь нелинейностью уравнений. Сущест-
венные трудности связаны также с тем, что рассматриваемые си-
стемы уравнений описывают не только медленные крупномасштаб-
ные процессы, но и быстрые волны, имеющие скорость, соизмери-
мую со скоростью звука. Но скорость перемещения волн,
описываемых уравнениями, в значительной мере предопределяет тре-
бования к способам решения этих уравнений: при больших скоростях
оказываются пригодными лишь более точные схемы решения спе-
циального вида. Так, например, допустимый шаг по времени при
численном решении задачи оказывается тем меньше, чем больше
скорость волн. В частности, при скоростях волн, соизмеримых со
скоростью звука, он не должен превышать 15 мин, т. е. интервала
времени на два порядка меньшего, чем характерное время круп-
номасштабных атмосферных движений (см. приложение 6, фор-
мулы (4.1) и (4.2)), что влечет за собой дополнительные труд-
ности.
В связи с этим, прежде чем перейти к решению прогностиче-
ских задач, рассмотрим вопрос о волновых движениях в атмо-
сфере.
Глава III
ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ
Все многообразие атмосферных движений можно рассматри-
вать, как наложенные друг на друга системы волн, имеющих раз-
личные длину, амплитуду и скорость. При этом одни типы волн
отражают и определяют крупномасштабные движения, другие —
мезомасштабные явления. Изучение этих типов волновых движе-
ний имеет непосредственное значение для правильного понимания
свойств атмосферы и разработки методов прогнозирования по-
годы. Однако существуют и такие типы волновых колебаний, ко-
торые не имеют какого-либо метеорологического значения. Тем не
менее знание свойств этих колебаний при численном прогнозиро-
вании также оказывается необходимым.
§ 1. Основные понятия о волновых движениях в атмосфере
При волновых движениях материальные частицы совершают
колебания около положения равновесия или около основного дви-
жения. Эти колебания могут происходить, например, параллельно
какой-либо прямой или по круговым орбитам, лежащим в парал-
лельных плоскостях.
Классическим и вместе с тем простейшим примером волнового
движения являются волны на поверхности воды. В этом случае
частицы воды совершают круговые движения. Вертикальный про-
филь образующейся при этом единичной волны хорошо описыва-
ется с помощью синусоиды, косинусоиды или экспонентной функ-
ции вида:
z(x, /)=Д sin(znx —а/);
z(x, /)=Xcos(ttix —о/);
z(xf t)=Aei{mx~at).
Здесь г (л, /) —высота поверхности воды по отношению к состоя-
нию покоя, А — амплитуда, m = 2nlL— волновое число, сг = 2л/Г —
круговая частота (v = o/2n = l/71— обычная частота, выражаемая
числом колебаний в секунду, т. е. в герцах), L — длина волны,
Т — период. Скорость перемещения волны выражается в виде с =
= 6jm, а ее абсолютная величина равна LIT.
87
Характерным для волновых движений является то, что при
сравнительно малых колебаниях материальных частиц имеют ме-
сто большие перемещения некоторых элементов волны, например
гребня или впадины волны. При этом скорость перемещения
волны не связана с поступательными движениями частиц. Заме-
тим еще, что изменения колебательного характера испытывают не
только координаты частиц, но все метеорологические параметры
(температура, плотность, давление, скорость и пр.).
Колебательные движения в атмосфере могут быть вызваны
проявлением «внешних» по отношению к атмосфере факторов. Та-
кими факторами могут быть, например, притяжение Луны, влия-
ние горных массивов и т. д. Волновые движения, вызванные внеш-
ними факторами, называют вынужденными колебаниями. Приме-
рами вынужденных волновых колебаний являются лунные
приливы, волны препятствий и т. д.
Однажды возникнув, волновые колебания могут существовать
в атмосфере довольно длительное время. При этом существующие
колебания могут претерпевать изменения и переходить из одной
формы в другую. В этом смысле атмосферу можно рассматривать
как замкнутую колебательную систему. Волновые явления, не свя-
занные непосредственно с внешними факторами, называют собст-
венными или свободными колебаниями. Эти колебания можно раз-
бить на три основных класса: крупномасштабные, гравитационные
и акустические волны.
Крупномасштабные волны являются проявлением инер-
ционных сил. Волны этого класса иногда называют инерционными,
а также длинными волнами или волнами Россби. Они возможны
лишь на вращающейся Земле. Волны этого класса имеют длину
порядка от сотен до нескольких тыс. км, скорость — до десятков
м/с и период — до нескольких суток; их амплитуда оказывается
значительной и составляет, например, в поле давления 20—
100 мбар. С точки зрения задач прогноза погоды движение и эво-
люция этих волн представляют наибольший интерес. Это метео-
рологически значимые волны. Их можно обнаружить на любой
карте погоды. Гребень волны в поле давления совпадает с цент-
ром антициклона или осью барического гребня, а впадина волны —
с центром циклона или осью ложбины.
Гравитационные волны связаны с проявлением сил тя-
жести, т. е. с влиянием гравитационного поля Земли (что и обус-
ловливает их название). Они возникают при изменяющейся с вы-
сотой плотности воздуха, когда вышедшая по каким-либо причи-
нам из состояния равновесия воздушная частица испытывает
действие архимедовой силы, стремящейся вернуть ее в прежнее
положение Колебания и смещения при этом происходят в верти-
кальной плоскости. Следовательно, равенство нулю вертикальной
скорости (w = 0) свидетельствует об отсутствии гравитационных
волн. Периоды колебаний, связанных с гравитационными волнами
в атмосфере, составляют около 330 с, а скорость перемещения
88
этих волн изменяется примерно от десятков до сотен м/с, дости-
гая в отдельных случаях 300 м/с
Амплитуды гравитационных волн невелики. Однако при нало-
жении ряда отдельных волн друг на друга может возникнуть зна-
чительное возмущение. Так, например, амплитуда возмущения
в поле скоростей, обусловленная гравитационными волнами, может
достигать 5—10 м/с. Длина гравитационных волн достигает не-
скольких десятков километров и более.
Акустические волны, или волны сжатия, обусловлены сжа-
тием или разрежением среды. В несжимаемой среде акустические
волны не возникают. Период колебаний для этих волн, являю-
щихся продольными, не превышает 300 с. Так как к этому классу
относятся и волны, воспринимаемые органами слуха человека
(с частотой от 20 до 20- 103 Гц), то эти волны называют также
звуковыми. Скорость перемещения акустических волн велика и
колеблется около 300 м/с (скорость звуковых волн, воспринимае-
мых органами слуха человека в сухой атмосфере, составляет около
330 м/с).
Амплитуды этих волн невелики и, например, для давления со-
ставляют всего десятые доли миллибара (за исключением случаев
взрывных волн, когда амплитуды резко возрастают).
Перейдем теперь к рассмотрению отдельных типов волн.
Предварительно изложим общий метод их математического ана-
лиза.
§ 2. Метод малых возмущений
Методы описания и изучения колебаний и волн существенно
зависят от того, являются ли амплитуды этих последних малыми
по сравнению с характерными величинами соответствующих па-
раметров основного состояния. В тех случаях, когда эти ампли-
туды действительно малы, математический анализ волновых дви-
жений удобно производить с помощью метода малых возмущений
[У.1, 10, 13]. Главным достоинством этого метода является воз-
можность перехода от рассмотрения нелинейных дифференциаль-
ных уравнений к линейным. Это достигается путем линеариза-
ции уравнений.
Если же амплитуды колебаний соизмеримы с величинами со-
ответствующих параметров основного состояния, метод малых воз-
мущений неприемлем, и исследование волновых движений приво-
дит к необходимости решения нелинейных уравнений. Это случай
так называемых нелинейных колебаний или колебаний с конечной
амплитудой. В этой главе мы ограничимся рассмотрением лишь
малых колебаний, исследование которых приводит к решению ли-
нейных уравнений.
Методику сведения нелинейных уравнений к линейным, т. е. ли-
неаризацию рассмотрим на частном примере. Запишем уравнение
89
движения относительно оси х, опустив члены, учитывающие турбу-
лентную вязкость,
ди . ди . ди . ди 1 др . , /о 1\
-^7- + ^-^— 4-W-4—=-------^-4-lv. (2.1)
dt 1 дх 1 ду 1 dz р дх 1 v '
Это уравнение является нелинейным, так как оно содержит ряд
членов с произведением неизвестных функций (эти члены подчерк-
нуты). Каждую из рассматриваемых функций представим в виде
суммы:
и=и-\-и', v=v-\-vr, w=^-f-w', Р—Р-\~РГ,
p=p+p'.
(2.2)
где функции, отмеченные чертой, описывают основное состояние
среды, а функции со штрихами — малые отклонения от этого ос-
новного состояния, такие, что
«1,
7
Для
зующие
простоты рассмотрим случай, когда функции, характери-
основное состояние, не меняются со временем. Положим
также, что величины и, v и w не изменяются в пространстве,
а функции р и р таковы, что для них всегда выполняется соотно-
шение
1
р
^4-/<у=о.
дх 1
(2-3)
Подставляя выражения (2 2) в уравнение (2.1), получим
‘У “-1 +(5+^) ^;+^-+
+(»+w) = 1 ; (5+„.),
Учитывая, что по условию ди/dt = ди1дх = ди1ду = 0, можно запи-
сать
fW , — ди'
dt дх
\-и'
ди'
дх
ди'
W
V'
ди'
dv
— ди' . , ди'
з----W —s =
dz 1 dz
1 др
р + р' дх
1 др'
р' дх
{-to-j-to' = 0.
{-77
90
Так как I pl <dp, то приближенно можно положить, что 1/(р-Н
+ р')~1/Р- Тогда последнее уравнение с учетом соотношения (2 3)
перепишется в виде
ди' . — ди' . , ди' . — ди' . , ди' . — ди' , , ди'
+ -^г+w + -gr
1 др'
р дх
lv'=0.
В этом уравнении есть члены (они подчеркнуты), содержащие про-
изведения величин отклонений или их производных, поэтому эти
члены являются малыми и ими можно пренебречь. В результате
приходим к следующему уравнению:
ди' . — ди' . — ди' . — ди' 1 др'
-dr+u-dr+v-dr+'w -дГ=-Т~дГ
(2.4)
Это уравнение уже не содержит произведений неизвестных (вели-
чины со штрихами), поэтому оно является линейным.
Для решения линейных уравнений могут быть применены раз-
личные известные способы. В методе малых возмущений широкое
распространение получили способы, использующие разложение
функций в ряды по тригонометрическим или показательным функ-
циям вида
со
2 A? sin msx\
s = 1
co
T As cos msx;
s 1
X Ase
s =1
1т$х
где As — амплитуда волны, ms = 2nlLs — волновое число, Ls —
длина волны, s — целые числа. Напомним, что в соответствии
с формулой Эйлера eiz =cos z+i sin z. Заметим также, что мни-
мая часть показательных функций вводится в рассмотрение в ос-
новном формально. Обычно нас будет интересовать лишь дейст-
вительная часть решения.
Применение рядов для решения линейных уравнений рассмот-
рим на примере уравнения
дЧ
dt2 дх2 9
(2-5)
где f(x, /)—любая функция, а2 = const. Если f есть отклонение
струны от состояния равновесия, то уравнение (2.5) характеризует
процесс колебания струны. Уравнение такого типа характеризует
и некоторые волновые движения в атмосфере. Пусть в начальный
момент
при /=0
оо
_ t v ХП . * /Л-X
f=<?(x)= X Ase ,
dt и-
(2.6)
91
Это означает, что начальные отклонения величины f от состояния
равновесия представлены в виде суммы волн с длинами LSi а на-
чальный импульс, т. е. сила, отсутствует. По аналогии с видом
отклонения струны в начальный момент решение уравнения (2.5)
будем искать в виде
(2.7)
Так как скорость перемещения волны cs, волновое число ms и кру-
говая частота crs связаны между собой соотношением
s
(2.8)
то можно видеть, что выражение (2.7) аналогично выражению
оо
/(х, /)= V AselmAx~Cst\ (2.9)
5= 1
Легко проверить, что
2V___ у 2д '(у-’Д
d/2 s = ] sAsS ’
<?2/ _ у w2« ч-z-V)
дх^ ^msAse
Подставляя эти выражения в рассматриваемое уравнение (2.5),
получаем
5 5 am2Ase ^х~^
s = l
ИЛИ
ОО
2 (o2-«2m2) Ase (^-^>=0.
S— 1
Данное равенство выполняется лишь при условии
2 2 2
os — a ms—0.
В результате мы получили выражение для неизвестной частоты
Gs. Решая его, находим для as два значения:
±ams.
Отсюда мы сразу можем формально определить скорость переме-
щения волн по соотношению (2.8). В результате для скорости по-
лучаем два значения
elt 2=±а.
92
Подставляя два найденные значения а в выражение (2.7), по-
лучим два решения рассматриваемого уравнения. Сумма этих ре-
шений будет общим решением. В результате получаем
itn (хat\ -ж—1 я ini (х —
Дх, Ase и Ле и \
5=1 5=1
или
/(х, /)_ (2.10)
5=1 L J
Используя формулы Эйлера, последнее выражение можно перепи-
сать в виде
f (х, f)=2 As {cos ms (хat)-}~ cos ms(x —at)
5=1
+ i [sin ms (x-\-at)-[-sin ms (x — af)\}.
Действительная часть решения имеет вид
оо
/(х, /)= 2 As [cos ms(x-^at)-\-cosms(x — at)]. (2.11)
5=1
Для определения коэффициентов разложения As, представляю-
щих собой амплитуды единичных волн с номером s, необходимо
воспользоваться начальным условием (2.6), т. е. заданной функ-
цией ср(х). Однако мы не будем делать этого, а ограничимся ана-
лизом полученного решения. Это решение показывает, что резуль-
тирующее значение функции f(x, t) определяется смещением и
наложением друг на друга волн в форме косинусоид, смещаю-
щихся со скоростью с = а в направлении оси х и в противополож-
ном направлении. Для двух единичных волн с номером s и дли-
ной Ls мы имеем
fs —As cos (х+аО+Л £'5 2tc z ,4 cos -j— (x — at). Ls (2.12)
Рассматривая трехмерное волновое уравнение вида d/2 a \ dx^ 1 dyt 1 dz^ J ’ (2.13)
можем положить, что
, S S \ V Л 1 (msX+nsy + k.Z)
при /=0 /(х, у, z)=^ 2 Ase v 5 5 ,
5 = 1
где ns и ks — волновые числа, соответствующие осям у и г, а ре-
шение уравнения искать в виде
, « I + 4- kz — ct )
Дх, у, z, /)= ZL Ase ( s s s . (2.14)
5= 1
93
В этом случае для определения os мы получим следующее соот-
ношение:
а2=й2 (m2+n2+A2).
Откуда
Sy=±&] ml^rn^-^ks (2.15)
или
где Lsx, Lsy, Lsz — проекции длины волны с номером s на оси х,
у, z. Составляющие скорости по осям х, у и z выражаются в виде
а а а
т~ ' СУ = ~ ’ Cz==~k ’
(2-16)
§ 3. Крупномасштабные волны
Для исследования этих волн возьмем уравнение вихря скоро-
сти в баротропном случае, т. е. при отсутствии вертикальной ско-
рости и при условии несжимаемости. Эти условия позволяют с са-
мого начала исключить из рассмотрения гравитационные и акусти-
ческие волны. При направлении оси у на север, а оси х на восток
уравнение вихря скорости при указанных условиях записывается
в виде
о dl 2<d cos q? ™ о
где р=—=“ — параметр Россби, а — радиус Земли
Это уравнение содержит произведения неизвестных и их произ-
водных. Поэтому оно является нелинейным. Для приближенного
решения уравнения произведем его линеаризацию. С этой целью
положим, что u = u + u', v = v + v', Q = Q + Q', где величины с чер-
точками характеризуют основное состояние. Так как и и v не за-
висят от времени и координат, то fi = dQ/<3/ = 0. Тогда
,, __ dv* ди*
дх ду ’
dQ dQ'
dt dt
Для простоты положим далее, что ^ = 0. Учитывая все сказан-
ное, уравнение вихря перепишем в виде
dQ' . — dQ* . о , . Г , dQ' . , dQ' 1 Л
—h W—5-----+ \u —s--------“3— =0.
dt 1 dx 1 r 1 L dx 1 dy J
94
Члены этого уравнения, заключенные в скобки, на порядок меньше
остальных. Поэтому ими можно пренебречь и записать
или
d t dv' ди' \ . — д ( dv' ди' \ . q , n
-дг\~д1——dr)+^=0-
Полученное уравнение не содержит произведений неизвестных
и, следовательно, является линейным. Ограничиваясь случаем не-
зависимости функций от координаты у, получаем уравнение вихря
в виде
d^vr I d^vf । q f z-s /q < \
dxdi ==0, )
Это уравнение имеет первый порядок дифференцирования по t.
Следовательно, для его решения достаточно иметь одно начальное
условие. Для простоты рассмотрим случай, когда при / = 0 v' вы-
ражается в виде ряда
оо
^'=2 V < (3.2)
5=1
В соответствии с видом начального поля, решение линеаризиро-
ванного уравнения вихря будем искать в виде
V д/('^-М)= v
5=1 5=1
Ограничимся рассмотрением одной гармоники 5.
Дифференцируя v' по х и по /, получим:
el
dt
dv„ , л i (mx-ct\
s=im Ase s s)\
dx s s ’
d2V„ „ i(tnx-at\
atnAe ,
dx dt s s s i
d^U n I (tn x— a
= ( s s <
Подставляя полученные выражения в линеаризированное уравне-
ние вихря и сокращая общий множитель (не равный нулю), по-
лучим следующее уравнение для os:
asms ““ + Р = 0.
95
Откуда
Р
as = ums-----—
5 s ms
и, значит,
cs=u------V- (3-3)
ms
Так как ms = 2n/£s, то
рд2
cs—u------(формула Россби). (3.4)
Окончательно для v' получаем
(3.5)
Действительная часть
^5=A(9cos-7—
Ls
Обратим внимание на случай постоянства параметра Кориолиса
/ = const. В этом случае |3=0, и мы получаем
^=A5cos-|^- (% — «/).
Ls
Это означает, что скорость перемещения волны в точности равна и.
Итак, мы получили, что имеющаяся в начальный момент волна,
в течение времени не меняя своей формы и амплитуды, смещается
вдоль оси х со скоростью cs, определяемой соотношением (3.3).
Из выражения для cs видно, что волна движется на восток (cs>
>0), если р£2/4л2<и, и волна движется на запад (cs<0), если
pL2/4n2>w.
В табл. 3.1 приведены рассчитанные по формуле (3.4) значе-
ния скорости перемещения волн различной длины L при и =
= 10 м/с = 36 км/ч для (р=50° и <р = 60°. Из анализа данных, при-
веденных в табл. 3.1, следует, что при определенных значениях и
существуют так называемые стационарные волны. Так, например,
при w = 10 м/с и <р = 60° стационарными будут волны, имеющие
длину около 6 тыс. км.
Аналогичным путем можно рассмотреть и более общие случаи
с основным движением, направленным произвольно, и при произ-
вольном начальном распределении и' и vr.
96
Таблица 3.1
Скорости перемещения (км/ч) волн длиной L при и=10 м/с
ч>° L 103/км
10 9 8 7 6 5 4 3 2 1
50 с —98 —73 —50 —30 —12 3 15 24 31 35
60 —68 —48 —31 —15 —1 10 17 27 32 35
Примечание. Положительные величины соответствуют перемещению вол-
ны на восток, отрицательные — на запад.
Подчеркнем, что если в начальный момент имеет место не одна
волна, а множество волн с различной длиной и амплитудой, то
вследствие суперпозиции (наложения) волн их результирующая
с течением времени может изменяться
§ 4. Гравитационные волны
Для анализа указанных волн рассмотрим случай баротропной,
однородной, несжимаемой (р = const) атмосферы высотой h. Усло-
вие несжимаемости позволяет сразу исключить акустические волны.
Как говорилось в предыдущей главе, для такой атмосферы спра-
ведлива следующая система уравнении:
dh . dh . dh , . / da . dv \ n /л i\
-нт-4-ц -3---3------3------h -3— 1=0. (4.1)
dt 1 dx 1 dy 1 \ dx 1 dy ) 7
Применяя метод малых возмущений положим, что
и=и(у)-\-и', v=vr, h=h(y)-\-hr. (4.2)
При этом пусть величины и и h связаны соотношением геострофич-
ности
dh
I dy
(4.3)
Произведем теперь линеаризацию исходной системы уравнений
(4.1) относительно основного состояния, за которое, как можно ви-
деть из поставленных условий, принято геострофическое движение
вдоль оси х. Подставляя соотношения (4 2) и (4 3) в уравнения
7 Зак. Хе 21
97
(4.1) и произведя линеаризацию, получаем' следующую систему
линеаризированных уравнений:
du' . — ди1 1 f . ~ dh' п
—\ги—^-----lv -\-g -s—=0;
dt 1 dx 1 dx ’
dv' . — dv' , r r , dh' ~
~dt 11~д5Г^и dy °’
^_+й_^_+А(_^1 + _^)=0. (4.4)
dt 1 dx 1 \ dx 1 dy ) 7
Рассмотрим вначале случай независимости движения от у,
а также отсутствия силы Кориолиса. Тогда
dh' dv' j
dy dy ’
и мы получаем:
dh! , — dh' . -г daT ~ г-ч
——Ьи—;-----\~h~*—=0. (4.5)
dt 1 dx 1 dx v 7
He решая полностью эту систему уравнений, ограничимся по-
лучением выражения для скорости перемещения волн. Для кратко-
сти записи будем рассматривать лишь одну волну с номером s.
Пусть:
/?;=/76.ez('v-0?), (4.6)
где Us, Vs и Hs—амплитуды колебаний переменных и', v' и h'.
Произведя соответствующие дифференцирования переменных
(4.6), подставляя найденные выражения в систему уравнений (4 5)
и сокращая в каждом из полученных уравнения общий множитель
iei(mx-at)^ получаем (индекс s опущен):
—a U -|- umU 4- gmH=0;
-aV 4-w/nV=0;
-aH-\-umH-\-hmU=Q. (4.7)
Перепишем полученную систему уравнений в виде:
(—a-\-utn) U-\- 0-17 4- mgH =0;
0 • Z74-(-a4-um) V4- 0 • Н =0;
mhU-\- 0-V 4-(-о4-мт)Н=0. (4.8)
98
Данную однородную систему алгебраических уравнений можно
рассматривать как систему трех уравнений для определения трех
неизвестных амплитуд: U, V и Н. Мы используем эту систему
лишь для определения частоты о.
Как известно из курса алгебры, однородная система линейных
уравнений имеет нетравиальное (ненулевое) решение лишь в том
случае, когда определитель системы равен нулю.
Напомним, что определитель третьего порядка раскрывается
следующим образом:
Ьх сх
А= #2 ^2 ^2 = Ct\b2C^ — — ^1^3^2“Ь^1^2^3 — £1#3^2«
#3 с3
В рассматриваемом случае определитель системы имеет вид
(—а-\-ит) 0 mg
А = 0 (—c-|-u/n) 0
nth 0 (—a-\-urn)
Приравнивая определитель нулю, получаем, следующее уравнение
для определения о:
(—mgh (--о-|-цт)=0
или
(—о—}-r/zzz) [(—— m2gA]=0.
Решая это алгебраическое уравнение, получаем
сх — ит, ^2, з = ит ± ni]f gh. (4.9)
Отсюда для скорости перемещения волн вдоль оси х (сх = о/т) на-
ходим три значения:
сх = и, с2, з=и±1 gb. (4.Ю)
Первое значение скорости соответствует простому переносу волн
основным потоком со скоростью и. Так как эта скорость невелика
(порядка 10 м/с), то это решение отражает возможность существо-
вания медленных волн в рассматриваемой модели атмосферы.
Второе и третье значения скоростей состоят из двух слагаемых:
и и gh. Рассмотрим вначаде случай и = 0. Тогда второе и третье
значения скоростей равны ±]^gh. Оценим возможные значения
этих скоростей. Прежде всего отметим, что произведение gh имеет
смысл потенциала силы тяжести. Следовательно, это значение ско-
рости волн связано с гравитационным полем Земли. В случае
7*
99
колебания воды в сравнительно неглубоких водоемах можно прибли-
женно положить, что /г=102 м. Тогда ]/gh = ^ 9,8- 102~30 м/с.
Атмосферу можно стилизовать как однородную жидкость
с плотностью ро=1,3*10-3 т/м3. Высота такой стилизованной одно-
родной атмосферы, как известно из курса общей метеорологии,
составляет ро/ро£= 102/1,3 • 10-3- 9,8 — 8000 м. Для такой атмосферы
скорость перемещения гравитационных волн составляет
У 9,8-8000 —280 м/с, что намного превышает скорость основного
переноса и. Волны рассмотренного типа иногда называют внеш-
ними гравитационными волнами. Скорость этих волн не зависит
от их длины, а определяется толщиной слоя жидкости. В океано-
логии они называются волнами мелкой воды.
Таким образом, проведенный анализ убеждает нас в том, что
система уравнений динамики атмосферы включает описание волн
со скоростями, во много раз превышающими характерную скорость
крупномасштабных атмосферных движений, что в свою очередь
является существенным для выбора метода решения этих уравне-
ний (см. приложение 7).
Для движения на вращающейся Земле при наличии силы Ко-
риолиса вместо системы уравнений (4.5) получим следующую си-
стему:
du' . — да' z , । dh' ~
-^7—----------iv +g -з—=0;
dt * дх 1 ь дх ’
dv' . — dv' i r г /у
—t Н и-^ \~1и —°;
(4.11)
dt 1 дх * dx 4 '
Соответствующая система уравнений для амплитуд теперь будет
иметь вид:
Z (—о-Ь-илп) гу— iv + imgH =0;
lU-\-i ( —а4- utn) V+ 0 • Н =0;
imhLJ-V 0- V
(4.12)
Приравнивая определитель этой системы нулю, получаем для о
следующее уравнение:
/3 (—о-|- utnf — Рт2 (—о 4-ит) gh-\-i (—□+ uni) /2=0.
или
(-а-]-ит) [(—а-\-итУ~ m2gh — Z2] =0, (4.13)
откуда находим
01 = шп, о2. 3 = шп±]/ m2gh-\-l2. (4.14)
100
Решение, соответствующее Oi отвечает переносу основным потоком,
а решение соответствующее 02,3 — гравитационным волнам, пере-
мещающимся в поле силы Кориолиса со скоростью
С2,3=Ы ± У gh+^fl-
(4.15)
Это выражение показывает, что скорость перемещения зависит от
длины волны (т2 в знаменателе) и что сила Кориолиса несколько
увеличивает скорость гравитационных волн. Однако абсолютная
величина этого увеличения невелика. Так, например, для волны
длиной 10 км, что соответствует волновому числу т = 2л/£ =
= 6,28- 10~4 м~\ при /г = 8000 м и /=1,2- 10-4 с-1 для абсолютной
величины скорости получаем
(/9,8 • 0,8 • Ю4+ 280,6 м/с.
При / = 0 получаем с—280 м/с. Следовательно, поправка состав-
ляет десятые доли процента.
Вернемся теперь к рассмотрению общего случая, т. е. к системе
уравнений (4.4) при 4=/=0, ...-=#0 и - =#0. При этом по-
прежнему будем полагать, что выполняется соотношение (4.3).
Полагая, что
и т. д.
(где ns = (2nlLys — волновое число, Lys— длина волны, отвечаю-
щие оси у), для амплитуд колебаний получаем следующую си-
стему уравнений (индекс 5 опущен):
I (—v-\-um) U— IV + imgH =0;
IU-Y/(—<?+ит) I/4- ingH =0;
imhU inhV 4-/(—H=0.
(4.16)
Приравнивая определитель этой системы нулю, получаем уравне-
ние для определения о
Z3 (—fnmlgh — fmnlgh — /3 (—о 4" um) t^gh-^r
4- i I2 — i3 (—о 4"urn) mngh—Q,
или
(—{(—о4“\gh +^2) + ) =0. (4.17)
101
Отсюда находим
а1==^/п, о2, з= и/n ± gh (/^2-|-^2)+/2 (4.18)
и для скорости перемещения волны вдоль оси х получаем
С\=и, с2,з=и ± +-5’) + -^-- (4-19)
Волны, скорости которых определяются соотношениями (4.19),
а также (4.15), называют инерционно-гравитацион-
ными.
В случае, если бы мы рассматривали уравнения баротропной
модели атмосферы в форме, когда третье уравнение берется в виде
(см. гл. II)
мы получили бы
Ct = «, Г2(3=ы± +
При и = 1 = 0 и независимости движения от координаты у
с2,з=± Ис2 =]<^Т7^1/287 • 300 ^290 м/с,
т. е. мы получили бы значение скорости, близкое к полученному
ранее.
Кроме рассмотренных типов гравитационных волн, характерных
для баротропной модели, в реальной атмосфере существуют гра-
витационные волны, движущиеся не только в горизонтальном, но
и вообще в любом направлении. Такие волны называют внут-
ренними гравитационными волнами. Их математический анализ
возможен при рассмотрении бароклинной модели атмосферы и бу-
дет сделан позже.
§ 5. Смешанные волны и отфильтрование внешних
гравитационных волн
В реальных условиях в атмосфере одновременно существуют
различные типы волн. Для примера рассмотрим простейший случай
одновременного существования знакомых нам крупномасштабных
и внешних инерционно-гравитационных волн.
Возьмем случай несжимаемой однородной жидкости (р = const).
Это означает, что акустические волны исключаются из рассмотре-
ния с самого начала. Для этого случая будет справедлива система
уравнений (4.1). Получив с помощью первых двух уравнений ука-
102
занной системы уравнение вихря скорости, рассмотрим вместо си-
стемы уравнений (4.1) следующую систему:
ди . ди . ди f . dh ~
dt 1 дх 1 ду 1 & дх '
д& . dQ . dQ . о । z / du . dv \ n
+w)=0;
dh^dh ( *£. + *L)=0. (5.1)
dt 1 dx 1 dy 1 \ dx 1 dy ) ' '
Для решения этой системы применим метод малых возмущений.
Пусть и = и(у)+u/;^v = v/; h = h(y) +h'. Кроме того, пусть, как
- g dh , , ,
и ранее, и =--a h , и и v не зависят от у.
Имея в виду, что в этом случае Q=----*, и опуская члены,
содержащие квадраты малых величин, получаем следующую си-
стему из трех линейных уравнений:
(duf ( — duf
~dt 'U~~dJT
d2vf j — d2v'
дГдх ‘U~dx^
^=0;
dx
^-=0;
dx
(Заметим, что индексом г здесь и далее отмечен дифференциаль-
ный оператор). Решение системы будем искать в виде:
«'-2 и/2
5=1 5=1
оо оо
. _ I ( 1П X — ст f Л ж’! _ I т „ (X — С
т'=2 Vse s =2 Vse и s}\
5=1 5=1
co co
/< = 2 ///<"-'-'>-2 (5.3)
5=1 5=1
где Us, Vs и Hs— амплитуды колебаний величин и', vr и h'. Для
сокращения записи далее будем рассматривать лишь один из чле-
нов каждого ряда. При этом индекс s будет опускаться. Путем
непосредственного дифференцирования соотношений (5.3) легко
проверить, что
д . д . д'* ? д д
-5t=-lmc^ -d7 = tm^ -дГ=~с^'
( д \ д \ с- \ д
+ С’ дх •
103
Учитывая эти соотношения и соотношение (4.3), систему (5 2) пе-
репишем в виде:
[₽ — тг (и — с)] v'+1 -^-=0;
-W+(^c),^+g^-O;
I — , । у диг . \ dh'
-uv +(ы-с)т=0.
Будем рассматривать эти уравнения как систему для определе-
, ди' dh' „
ния неизвестных: v' —г— и —~. Система имеет решение от-
дх дх
личное от нуля в случае, если определитель этой системы равен
нулю, т. е. если
[р — — с)]
-/
I
(и — с\
h
О
g
(и — с)
Раскрывая этот определитель получаем следующее уравнение для
нахождения скорости с:
[р — т2(и — с)] [gh — (и — с) (и — с)г] — /2 [(и — с) — и]=0. (5.4)
Это уравнение является уравнением третьего порядка. Ограничимся
рассмотрением приближенных решений, которые имеют вид:
с2, з=и ± 1 gh-\-l2lm2. (5.6)
Первое из этих соотношений получается при условии, что gh^>
(и— с)2, а второе при условии gh<^(u— с)2. Решение (5.5) со-
ответствует скоростям перемещения крупномасштабных (длинных)
волн. Оно сходно с выражением (3.3), которое было получено при
наличии только крупномасштабных волн.
Решения (5.6) соответствуют инерционно-гравитационным вол-
нам. Они сходны с решениями (4.15), полученными при наличии
только гравитационных волн. Скорости крупномасштабных и гра-
витационных волн, определяемые с помощью решений (5.5) и (5.6) >
равны или очень близки к скоростям, определяемым с помощью
решений (3.3) и (4.15). Как уже говорилось, интегрирование пол-
ных уравнений гидротермодинамики, описывающих одновременно
как крупномасштабные, так и гравитационные волны, является
чрезвычайно сложной задачей. Поэтому представляет практиче-
ский интерес получение таких преобразованных (или
104
«фильтрованных») уравнений, которые не содержали бы си-
ноптически мало значимых быстрых гравитационных волн и при-
том без существенных искажений описывали бы медленные синоп-
тически значимые инерционные волны.
Такие преобразованные уравнения получают двумя путями:
с помощью соотношений геострофичности и с помощью уравнения
баланса. На примере линеаризированных уравнений рассмотрим
здесь первый путь.
Возьмем линеализированную систему уравнений (5.2). Примем
g dh'
соотношение геострофичности и =“7-—^—• В таком случае one-
ратор, который в первом уравнении системы (5.2) отмечен буквой
г, должен обращаться в нуль. Это приводит к тому, что в после-
дующих соотношениях обращается в нуль множитель (и — с),
также отмеченный буквой г. Тогда вместо кубического уравнения
(5 4) для определения а мы получим следующее уравнение:
(и —с) (m2gA-|-Z2)4-(/2w + ₽g/z)=0.
Откуда
m2 + l2\gh'
Таким образом, введя геострофические соотношения, мы получили
лишь одно решение, совпадающее с решением (5.5) и отражающее
эффект перемещения длинных волн. Гравитационные волны оказа-
лись отфильтрованными.
Второй способ отфильтрования гравитационных волн основан
на использовании менее ограничительного условия, чем условие
геострофичности. Это условие заключается в равенстве нулю инди-
видуальной производной от горизонтальной дивергенции ветра
D = duldx+dv/dy
dD dD . dD . dD . dD n /c^
^Г==т+ы-^+г,-йГ+т-аГ=°- (5 7)
Как указывалось в гл. II, это условие приводит к уравнению
баланса
/ du V dv du .1 dv \2 . dl dl zo . „ /r O4
Последовательное применение данного диагностического соот-
ношения или его разновидностей позволяет исключать гравитаци-
онные волны.
§ 6. Внутренние акустические и гравитационные волны
Ранее на основе уравнений для баротропноп несжимаемой
среды был исследован ряд типов гравитационных волн, а также
крупномасштабные волны на вращающейся Земле.
105
В реальной атмосфере, которая является сжимаемой бароклин-
ной средой, имеет место более широкий спектр волн, который
включает внутренние акустические и гравитацион-
ные волны, а также так называемые двумерные волны. Под
внутренними акустическими и гравитационными волнами понима-
ются трехмерные волны, скорость перемещения которых имеет
вертикальную составляющую. В отличие от этих волн двумерные
волны перемещаются только в горизонтальном направлении
[У. 18, 4].
Для рассмотрения этих волн возьмем три уравнения движения,
уравнение неразрывности и уравнение политропического процесса
(см. § 1 гл. II), в простейшей форме описывающее бароклинность
атмосферы:
du 1 др . z dv 1 др f
-dT=~T^+lv' ^-=~TW~lu;
dw ___ 1 dp ___ dp__________ (du । dv dw \
dt p dz dt P \ dx ’ dy * dz J ’
dp л P dp
dt p dt ’
(6.1)
Произведем линеаризацию этих уравнений. В качестве основного
примем состояние покоя (w = u=w = 0), в котором значения р
И р удовлетворяют уравнению статики
др
dz
~gp-
Линеаризированные уравнения имеют вид:
диг 1 dpf .
dt jT дх
dvf ___ 1 dpr
dt dy
dwr
~dF
L^pL-sC--
p dz p ’
dp' ___ duf j dv*
dt —\ dx ‘ dy
dp'
~dt~
dz \ dt 1
(6.2)
где a2- = ^plp = ^RT — параметр, имеющий размерность квадрата
скорости. (В дальнейшем штрихи у отклонений всех переменных
будут опускаться.)
Получим вначале уравнение для чисто акустических колебаний.
С этой целью рассмотрим простейший случай горизонтального дви-
жения вдоль оси х сжимаемой жидкости при отсутствии силы Ко-
риолиса, т. е. мы положим v=w = l—0. Условие w=0 сразу ис-
ключает из рассмотрения гравитационные волны. При этих усло-
виях мы получаем следующую систему уравнений:
ди ____ 1 др df______________~ ди- . ___п2 df
dt р dx ’ dt " дх ’ dt dt ‘
(6.3)
106
Дифференцируя первое уравнение этой системы по х, а второе по
t и исключая d2uldtdx, получаем
д2р д2р
Дифференцируя теперь третье уравнение системы (63) по t и
исключая из полученного результата д2р/д/2, получаем
&Р _ z>2 д2Р
dt2 —а дх^ •
Это волновое уравнение является известным уравнением акус-
тики. Такое уравнение было рассмотрено в § 2, где было показано,
также, что круговые частоты о, соответствующие этому уравнению,
выражаются в виде
а= + ат.
(6.4)
Составляющие скорости волн получаются с помощью соотно-
шений (2.16), согласно которым, =
Таким образом, мы получили две волны, двигающиеся в проти-
воположных направлениях со скоростью а.
При Х = х = сР/си = 1,4 (адиабатический процесс), /? =
= 287 м2-с-2-град-1, Т = 273 К находим, что а = 330 м/с.
Перейдем теперь к рассмотрению общего случая, когда учтены
сила тяжести, сила Кориолиса и составляющие скоростей по всем
трем направлениям. При этом будем следовать А. С. Монину и
А. М. Обухову [4].
Введем параметр
₽=(X-l)g
da2
dz
(6-5)
Так как da2ldz = KR.dTldz, то параметр р будем называть пара-
метром статической устойчивости. Перепишем систему уравнений
(6.2) в виде:
dt дх 1 г 9 dt dy r ’
dpw ___ / dp । \ dp / dpu . dpv . dpw \ .
dt \ dz ’ dt \ dx dy "* dz / ’
_^.===_ppW_a2(^_+4!L+4^). (6.6)
dt rr \ dx 1 dy 1 dz ) v 7
Заметим, что в третьем уравнении движения введен параметр
g. В общем случае он равен единице Положив, что р = 0, полу-
чаем возможность перейти к статическому приближению.
107
Сделаем еще пояснение к выводу последнего уравнения си-
стемы (6.6). Непосредственно из последнего уравнения системы
(6.2) имеем
dt а Й + Р I р dz р dz I •
Учитывая, что р = Кр/а2 и dpfdz = —gp, а также соотноше-
ние (6.5), получаем
a2 dp 1 др _______________ а2 д р
~дГ "а2",
г?2 dp 1 др
1 dp
7 dz
р dz р dz
- У i
Подставляя это выражение в полученное соотношение и исключая
из результата dp/dt с помощью уравнения неразрывности, мы по-
лучаем последнее уравнение системы (6.6).
Введем функцию тока ф и потенциал скорости ср, а также функ-
цию х с помощью соотношений:
— дф . д<р — дф . д<р
р“=-^-+1г;
Легко проверить, что
dx 1 dy т дх ду *’
где A = д21дх2+д21ду2.
Дифференцируя первое уравнение системы (6.6) по х, а второе
по у, складывая результаты и учитывая соотношения (6.8), полу-
чаем
cP
pw=x-
(:6.7)
(6.8)
0.
д 4F=/ ~Lp или д HF ~+^)=°-
Аналогичным образом, произведя дифференцирование второго
уравнения системы (6.6) по х, а первого по у и вычитая резуль-
таты, находим
Д -Ц-=—/Дер или
Полагая, что функции ф, <р и р ограничены на бесконечности,
знак оператора “
опустить. Тогда
уравнений (6.6)
Лапласа
с учетом
имеем:
дф
dt ~
— а2 ~1Г~ ;
dt т гл дг ’
в полученных двух уравнениях можно
введенных обозначений вместо системы
1Т,
108
Для решения данной системы уравнений примем, что начальные
данные являются произвольными, а именно:
при /=0 ф=фо» ?=%. Х=Хо> Р=Ро, Р=Ро- (6.10)
В качестве краевых условий примем обращение в нуль потока ко-
личества движения у земли и на бесконечности, т. е. примем,
что
при z=Q /=0, при z~>оо х=0. (б.Н)
Система уравнений (6.9), имеющая пятый порядок по времени,
с начальными условиями (6.10) и (6.11) описывает как медленные,
синоптически значимые атмосферные движения, так и волновые
движения с большими скоростями — «быстрые волны». Одно из
решений данной системы уравнений, называемое иногда стацио-
нарным, соответствует медленным движениям и рассмотренным
ранее крупномасштабным волнам.
Отвлекаясь от этого решения, получим уравнения для атмо-
сферных движений с быстрыми волнами и рассмотрим их некото-
рые частные решения. Предварительно заметим, что выделение из
рассмотрения указанного решения с медленными волнами приво-
дит к снижению порядка дифференцирования по времени в соот-
ветствующей системе уравнений с пяти до четырех.
Продифференцируем по t второе и четвертое уравнения си-
стемы (6.9) и из полученных результатов с помощью остальных
уравнений этой системы исключим производные дф/д/, dp/dt,
dp/dt. В результате для ф. и / получим следующие два урав-
нения:
(-^ +/2) +^2 -&+"2 Д(р’
^-3-=^(^+а2-^+а2д^+^(^г+дФ <6-12)
Решение полученных уравнений будем искать в виде суммы волн
вида:
<?(х, у, z, 0=Ф(г)еНтх+лу-°о;
Х(х, у, z, t)=X(z)el(mx+ny~°‘\ (6.13)
где Ф(г) и X(z) —амплитуды колебаний.
Подставляя соотношения (6.13) в уравнения (6.12) и делая не-
которые преобразования (исключая из второго уравнения комби-
нацию д^/дг+Хц) с помощью первого уравнения), получим урав-
нения для амплитуд:
[Z2+<z2(m24-rt2)-a2] Ф=рХ+л2-^;
(Z2-^2 ^_ + go)=(pg_^2a2)X (6.14)
109
Одно из частных решенш! может быть получено при условии от-
сутствия вертикальных движений. В этом случае pw = X = 0 В со-
ответствии с первым уравнением системы (6.14), для о получаем
/2+а2(т2+п2) —о2 = 0.
Отсюда для частоты имеем
а= + J = ±а j/"(m2 + /z2)-]—. (6.15)
Учитывая соотношение (2.8), получаем
сх== ± a К( 1 Н ^2“) + а2т2 • (6.16)
В частном случае при движении только вдоль оси х (/г = 0) и
при отсутствии силы Кориолиса частота для этих волн по (6 15)
совпадает с частотой по (6.4).
Согласно второму уравнению системы (6.14), при Х = 0 имеем
«2-^-+^ф=о.
Решение этого уравнения можно записать в виде
где Ф* — постоянная. На основании этого выражения можно за-
ключить, что соответствующие данному решению волны охваты-
вают всю толщу атмосферы и распространяются по горизонтали.
Эти волны, перемещающиеся со скоростью, определяемой выраже-
нием (6.16), имеют акустическую природу и называются дву-
мерными.
Перейдем теперь к рассмотрению решений, для которых
При этом ограничимся случаем постоянства параметров а2 и р,
что имеет место при изотермии, т. е. при Т = const.
Получим уравнение для амплитуд, например, для Ф. Выразив
X через Ф с помощью второго соотношения системы (6.14) и под-
ставив результат в первое из них получаем
- 44-+4^ 4^+4 ® Н“!+'44 Мф=°-
(6.18)
Аналогичное уравнение можно получить и для X. Будем искать
частное решение уравнения (6.18) в виде Ф(г) =e^~M+ik)z, где М —
неизвестная постоянная, a k — волновое число. Подставляя это
частное решение в уравнение (6.18), получим следующее соотно-
шение:
(/2_а2)[(_Л1+^)2+1^(
-(т24-/г2)(^--р.а2)=0. (6.19)
НО
Имея в виду, что о вещественно, и приравнивая нулю мнимые ча-
сти, получаем 2Mk—($+g)kla2 = Q. Откуда М= (Р +g)/2a2.
Приравнивая нулю действительные части соотношения (6.19),
получаем
(Z2 - о2) рИ2 - £2 - - (т2+«2) (-g- - ^2)=о.
или после подставки значения М
(Р-о2) [ - ^2+И - («2+«2) - noV)=0. (6.20)
Это уравнение четвертого порядка. Решая его, найдем четыре зна-
чения о. Имея в виду выражения для Ф(г) и М, для величин ср и
% находим
, \ (mx + ny + kz-ot)
(?, X)m,n,k^e 2а
(6.21)
Рассматривая (6.21), можно убедиться, что амплитуда волн
с высотой убывает. Движение волн происходит по всем трем на-
правлениям. Поэтому волны, описываемые с помощью выражения
(6.21), являются трехмерными. Их называют также внут-
ренним и.
Для определения скорости перемещения волн найдем частоты о.
Для простоты ограничимся рассмотрением случая отсутствия
силы Кориолиса, когда Z = 0. В этом случае уравнение для частоты,
имеющее четвертый порядок, получает вид:
c4_[(m2+ft2) + _^ _|__L( ₽+jL )2]й202 + (т2 + /г2)^.=0.
Решая это уравнение, для о2 получаем
02=^ [(т2+/г2)4
4<gp m2 n2
(6.22)
Двум парам найденных значений о соответствуют определенные
типы волн. Для выяснения их природы рассмотрим случай изотер-
мического состояния атмосферы, при котором дТ/дг = 0 и, в соот-
ветствии с (6.5), р= (X—1)^.
Рассмотрим вначале изостерический процесс, при котором
плотность остается постоянной и, следовательно, акустические
волны невозможны. Для этого процесса Х->оо (см._§ 1, гл. II) и,
следовательно, р->оо. Имея в виду, что a2 = KRT, можно убе-
диться, что второй член подкоренного выражения в решении (6.22)
111
значительно меньше единицы. Тогда можно воспользоваться при-
ближенным соотношением вида
1
где 8 < 1. Имея это в виду, вместо (6.22) можно записать
Выпишем теперь выражения для каждой пары значений о, ко-
торые получаются после некоторых сокращений, а также опуска-
ния малых величин. При этом величины о, получающиеся при по-
ложительном значении радикала, снабдим индексом а, при отри-
цательном— индексом g. Тогда получаем
).# Т Г(/П2 4- Я2) + — -L -—
I
Н (2/? Г)2 J ’
trfi + и2
р-2 ~1
[х(т2+п2)+й2+_|_^
----------------------------------------- j
Можно убедиться, что при Х->оо (limx^-oo--—
/V
2_ g2(X-l)
Ci о- ~
Е \RT
(6.23)
1):
2 g2
°е~^ RT
2
ОО;
/И2 п2
Т2
1x(ot2 + „2) + ^ + __
(6.24)
2
Это означает, что волны с частотами оа исчезают. Следовательно,
они относятся к классу акустических. Вторая группа волн в несжи-
маемой среде остается. Их частоты определяются вторым соотно-
шением (6.24).
Рассмотрим теперь изотермический процесс, при котором вы-
талкивающая сила, т. е. сила Архимеда, отсутствует и, следова-
тельно, невозможны гравитационные волны. Для этого процесса
(см. § 1, гл. II) Х=1, а ₽ = (Z — 1)£ = 0. u
Легко видеть, что при р=0 второй член под знаком корня
в выражении (6.22) равен нулю, а значение корня — равно еди-
нице. Имея это в виду, на основании (6.22) для этого случая
получаем:
4=0.
(6.25)
112
Таким образом, при изотермическом процессе, когда сила Ар-
химеда отсутствует, исчезает вторая группа волн, называемых
внутренними гравитационными волнами. Акустические
волны при этом сохраняются.
Отметим, что адиабатический процесс, при котором X=z =
^Cpfcv, а также и другие политропические процессы занимают
промежуточное положение между двумя рассмотренными процес-
сами.
Определим теперь возможные значения частот оа и Gg для слу-
чая Х = х = 1,4 и ц = 1. На основании (6.23), можно убедиться, что
при Х = х=1,4, как и при 7->оо, второй член подкоренного выра-
жения в решении (6.22) значительно меньше единицы. Поэтому
для этого случая о2 и о2 определяются по (6.23). Анализируя это
выражение можно заключить, что
*£2
^RT 9
£2(*—О
Ор- —
ё kRT
(6.26)
Отсюда для периодов внутренних акустических и гравитационных
волн получаем:
гр ____ 2к 2я
При х=1,4, R = 287 м-2-с-2 • град-1, Т = 273 К имеем Га<300 с,
Tg>330 с.
Таким образом, частоты и периоды внутренних акустических и
гравитационных волн в изотермической атмосфере не перекрыва-
ются.
Произведем теперь оценку величины скорости перемещения
внутренних акустических и гравитационных волн при ц=1, Х = х.
При перемещении волн только вдоль оси к cx = Glm = LxIT. Для
примера возьмем случай Lx=10 000 м. В соответствии с (6.26)
Ст >330 м/с, а Сх£<300 м/с. При других длинах волн скорости бу-
дут иными, однако в любом случае для одинаковых длин волн
скорость акустических волн будет больше, чем скорость гравита-
ционных волн.
Рассмотрим еще случай перехода к квазистатическому вари-
анту, когда ц -> 0. В случае адиабатического процесса, как уже го-
ворилось, частоты Ga и Gg определятся с помощью (6.23). Делая
в этих выражениях предельный переход Ц“>0, получаем:
2
2 £2(Х-1)
ё \RT
m2 4- п2
£2 _|---—
+ (2RT)2
(6.27)
Мы видим, что квазистатическое приближение фильтрует внут-
ренние акустические волны (при этом двумерные волны, частоты
8 Зак. № 21
113
которых определяются с помощью (6 15) и которые также имеют
акустическую природу, сохраняются) В то же время это прибли-
жение приводит к искажению частот гравитационных волн (сравни
(6.23) и (6.27)). Причем это искажение тем сильнее, чем больше
волновые числа т и пу т. е. чем короче длины волн. Для волн
большой длины (малые значения чисел тип) это искажение не-
велико.
При учете вращения Земли (/=#0) количественные характери-
стики волн будут несколько отличны от полученных. Однако ос-
новные выводы, полученные при / = 0, сохраняются.
Учет термической стратификации [1] приводит к изменению ча-
стот (5а и Gg. При этом при падении температуры с высотой увели-
чивается интервал между оа и сё. Однако и в этом случае изло-
женные выводы относительно общих свойств акустических и гра-
витационных волн сохраняются.
§ 7. Адаптация полей давления и ветра
Поля некоторых метеорологических элементов находятся между
собой в определенной взаимозависимости или согласованы между
собой. Например, поля давления и плотности или поля геопотен-
циала и температуры довольно точно связаны между собой урав-
нением статики. Нарушение в каком-либо месте этого условия вле-
чет за собой перестройку полей таким образом, что указанное со-
отношение быстро восстанавливается.
Особый интерес представляет взаимосвязь между полями дав-
ления и ветра. В первом приближении можно считать, что эти поля
связаны между собой соотношениями геострофичности:
1 др _ g дН 1 др _ g дН
I? ду I ду ’ /р дх I дх ’
Нарушение где-либо этих соотношений приводит к взаимному при-
способлению, или адаптации указанных полей, в результате
чего условия геострофичности восстанавливаются.
Теория адаптации полей давления и ветра была разработана
для баротропной атмосферы А. М. Обуховым [5], а для бароклин-
ной— И. А. Кибелем [У.12; 2], А. С. Мониным и А. М. Обуховым
[4]. В этих работах было показано, что процесс адаптации связан
с эволюцией перемещением акустических и гравитационных волн.
Рассмотрим здесь процесс адаптации в бароклинной атмосфере,
в которой выполняется уравнение статики, по И. А. Кибелю
[У.12; 2].
В качестве исходных возьмем два уравнения движения без
учета турбулентности и малых членов xduldp, xdvjdp, уравнения
114
неразрывности и притока тепла в адиабатическом случае и уравне-
ние статики:
dTu
drv
dt
dt
дН ,
g—л----
ь ду
дН . ,
b dx 1 ’
du i &v i ______n.
dx ' dy ' dp ’ dt
c2
“ Rp
_ g dH
dr д д d
dt dt dx dy
В качестве краевых условий примем:
dW
Р ~дрдГ ограничено,
при p~^Q
при р=р -Й-(/’4г+а/У)=0,
где а=Я (Ya —Y)/g-
Произведем линеаризацию уравнений движения и притока
тепла. В качестве основного примем состояние покоя (и = и=т =
= 0). Величины Т(р) и Н(р) связаны соотношением
т £ „ дн
T=--rP-^
Вводя геопотенциал Q=gH и новую вертикальную координату
^ = р!Р и опуская штрихи у малых величин, запишем уравнения
в виде:
du
~dt
дФ . z dv дФ z
-ч-----н/'Щ -57" =-----з-tir,
dx 1 ’ dt dy ’
du j dv j 1 dz q. dT_____c2 . j,_ СдФ .к
dx '~ду"'~Р~д£'~u; ~di RPC 1 ~ ' RdC ' ' A’
Краевые условия после линеаризации в новых обозначениях
примут вид:
„ п г д2Ф
при С df- ограничено;
при С=1 4 (4г-+аф)=0- (7-2>
В дальнейшем для простоты положим, что а=0.
Продифференцируем уравнение притока тепла по получен-
ный результат подставим в уравнение неразрывности и исключим
оттуда температуру с помощью уравнения статики. Тогда вместо
последних трех уравнений системы (7.1) получим
d d дФ 9 ( du । dv \
df ~dT ~dT=c Ы + ~d7) •
(7.3)
8*
115
Полученное соотношение и первые два уравнения системы (7.1)
представляют собой систему из трех уравнений с тремя неизвест-
ными и, v и Ф. Начальные условия возьмем в виде
при /=0 и--=и0, v=vG, Ф = Ф0, (7.4)
где индексом 0 обозначены известные произвольные функции ко-
ординат.
Продифференцируем каждое из первых двух уравнений системы
(7.1) по х и у. Складывая и вычитая результаты, получим
Т-т--АФ+«. Р-5)
где
0_______________ dv _ ди ___ ди j ду
дх ду ’ дх ' ду ’
Введем функцию тока и потенциал скорости с помощью соот-
ношений
ду ' дх ’ дх ’ ду
Очевидно, что £2 = Дф, Д=Аф, где А = д21дх2+д21ду2 Подставляя
эти выражения в уравнения (7.5), получаем:
Д-|^=-/Д? ИЛИ д(-^ + /?)=0;
Д -f^=—ДФ 4-ZДф или д(4+Ф-^)=0. (7.6)
С/ 4- \ С/ L J
Если считать, что функции ф и ф ограничены на бесконечности, то
оператор Лапласа в последних уравнениях можно опустить. Тогда
можно записать:
тг=-^ > = -РР)
Дифференцируя второе из этих уравнений по t и исключая из по-
лученного результата dty/dt с помощью первого из этих уравнений,
получаем
д2? дФ п ( д2? । /2 \ । дФ п
dt2 ~ dt У’ ИЛИ ( dt2 dt О’
После соответствующего дифференцирования полученного соотно-
шения и исключения из результата функции Ф с помощью уравне-
ния (7.3) получаем следующее уравнение для потенциала скоро-
сти:
^(^+Р,)=0. (7.8)
В качестве начальных условий вместо (7.4) теперь возьмем
при t=0 ср=ср0, ф=фо, Ф = Фо- (7.9)
116
Введем в рассмотрение новую функцию
(7.10)
о
Проинтегрируем соотношение (7.8) по £ от 0 до £ и результат по-
делим на У£. Тогда получим
с» J 4 [₽ 4 О+₽»)] «=о,
или
с2Д7?+е _^.(_g_+Z2?)=o. (7.Н)
Дифференцируя (7.10) по получаем
Подставляя этот результат в (7.11), получаем уравнение для R
‘?!д«+(е4-+;4-т)(4-+'’)Л=0- <712>
Введем новую независимую переменную £ =—1п£. Можно убе-
диться, что
г д д г2 д2 д2 . д
Тогда вместо (7.12) получаем
^^+(-5—г)(^-+₽)«-°- <713>
Получим краевые условия для R. Выразим в (7.3) горизонтальную
дивергенцию через ср, проинтегрируем результат по £ от 0 до £
и разделим полученное на ]/£. В итоге получаем
-уг/4 (₽4 44=-,ту $
ИЛИ
Учитывая это, краевые условия (7.2) при а = 0 запишем в виде
1
при £-*оо (С-*0)С2 ДТ? ограничено.
при$=0(С=1) /?=0. (7.14)
117
Начальными условиями для R будут:
при t-О dR\dt—RXf
где /?0 и Вл находятся по (7.9) и (7.10).
Решение уравнения (7.13) будем искать с помощью функций
вида
(mx + ny+kt — vt)
(7-15)
Подставляя (7.15) в (7.13) получаем следующее уравнение для ча-
стоты:
С1 2(от24-П2)+(Л2+-^)(-а24-/2)=0.
Решая его, получаем
<з =
m2 + л2
^+4-
4--
С2
(7.16)
— частоту внутренних гравитационных волн (внутренние акусти-
ческие волны были отфильтрованы в результате применения урав-
нения статики).
Произведем приближенную оценку скорости этих волн. Возьмем
случай атмосферы с линейным падением температуры с высотой
при у = 0,005 град/м, Тогда
f2=/?2r(Ta-T)/g-^2872 • 273 • 10~2 • 0,5/9,8.
Отсюда с~100 м/с. Ограничиваясь рассмотрением перемещения
волн вдоль оси х и полагая /=0, находим сх~200 м/с.
Вернемся к уравнению (7.13). Это уравнение волнового типа.
Его решение при заданных краевых и начальных условиях и най-
денных значениях о можно найти в [2]. Это решение имеет вид
Ж*, у, С, 0=4г
1 2- 411
ООО
1 2к 2Z/
4-JJ f <S>xGdrdbdt
ООО
(7.17)
где г и 6 — полярные координаты, G — функция влияния или
функция Грина, являющаяся известной функцией пространствен-
ных координат и времени.
Анализ решения (7.17) и функции Грина G позволяет сделать
следующие выводы. Если в начальный момент функции ср и dq/dt
всюду равны нулю за исключением некоторой ограниченной обла-
сти, то, согласно (7.17), функция R будет с течением времени стре-
миться к нулю. Это следует из того, что верхний предел одного
из интегралов в (7.17) пропорционален времени, т. е. область инте-
грирования растет, а подынтегральное выражение остается неиз-
118
менно отличным от нуля лишь в некоторой малой области Но это
значит, что с течением времени будут стремиться к нулю и функ-
ции ср и dy/dt. Но согласно (7.7) в этом случае при t-^oo мы по-
лучаем
—0 и - Ф+/ф —0. (7.18}
Дифференцируя последнее равенство по х и у и учитывая, что, со-
гласно (7.6), при <р = 0 и = —д^/ду и v = dty/dx, получаем, что
при t-^оо и—
1 дФ _ 1 дФ
Z ду ’ I ду *
Таким образом, при нарушении геострофичности в ограничен-
ной области пространства с течением времени движение стре-
мится стать геострофическим. Оценки показывают, что время,
необходимое для установления геострофичности, составляет 1 —
1,5 ч.
Процесс адаптации сопровождается уменьшением кинетической
энергии, так как часть ее идет на генерацию волновых колебаний.
Важно подчеркнуть, что в процессе адаптации происходит изме-
нение как полей давления так и ветра. Однако изменение поля
давления происходит более интенсивно, чем поля ветра.
Обсудим пример расчета адаптации в бароклинной атмосфере,
взятый из работы А. С. Монина [3]. В этом примере за исходное
состояние взята ситуация, напоминающая начальный момент фрон-
тообразования. По обе стороны от некоторой линии имеют место
119
два потока параллельные данной линии, но имеющие противопо-
ложное направление Возмущения в поле давления отсутствуют.
Геострофические соотношения нарушены.
В процессе адаптации геострофические соотношения были вос-
становлены. При этом поле ветра изменилось несущественно, в то
время как поле давления изменилось значительно. Практически
произошло приспособление поля давления к полю ветра.
Произошедшие изменения хорошо видны на рис. 3.1, на котором
на оси абсцисс отложены расстояния от указанной линии, а на оси
ординат — значения компоненты скорости в м /с и высота изобари-
ческой поверхности в дам. Индексом 0 отмечено начальное состоя-
ние. В процессе адаптации кинетическая энергия в данном примере
уменьшилась на 3%.
В реальной атмосфере непрерывно происходят два противопо-
ложных процесса. С одной стороны, в результате ряда причин
(влияние рельефа, неадиабатичность и пр.) происходит нарушение
геострофических соотношений и порождение волновых движений.
С другой стороны, волновые движения приводят к адаптации. В ре-
зультате поля давления и ветра находятся в соотношении, близком
к геострофическому. Предположение о близости движения к гео-
строфическому или гипотеза квазигеострофичности лежит
в основе квазигеострофической теории изменения метеорологиче-
ских элементов и ряда методов прогноза.
В заключение главы отметим следующее. Крупномасштабные
движения в атмосфере можно рассматривать в основном как ре-
зультат распространения и эволюции длинных волн. Следова-
тельно, любая прогностическая модель атмосферы должна пра-
вильно учитывать эти волны.
Вследствие малости амплитуд вклад гравитационных и акусти-
ческих волн в формирование поля ветра мал и при рассмотрении
поля движения эти волны можно рассматривать, как шумовые ко-
лебания, подлежащие фильтрованию.
Однако мы видели, что волновые колебания этих типов явля-
ются тем механизмом, который приводит к адаптации при наруше-
нии геострофичности Из этого следует, что в негеострофических
прогностических моделях атмосферы учет гравитационных и неко-
торых акустических волн является необходимым.
При практической реализации негеострофических моделей
вследствие ошибок в начальных данных, а также при применении
приближенных методов интегрирования конечно-разностных урав-
нений, возникают ложные колебания, при которых скорости пере-
мещения и периоды близки к соответствующим значениям для
реальных гравитационных и акустических волн. В процессе ин-
тегрирования по времени амплитуды этих ложных волн могут
расти.
На основании сказанного становится понятным, что в негеостро-
фических прогностических моделях атмосферы необходимо учиты-
вать реальные волновые процессы и подавлять или фильтровать
ложные.
Глава IV
МЕТОДЫ КРАТКОСРОЧНОГО ПРОГНОЗА, ОСНОВАННЫЕ
НА ИСПОЛЬЗОВАНИИ КВАЗИГЕОСТОФИЧЕСКОГО
И КВАЗИСОЛЕНОИДАЛЬНОГО ПРИБЛИЖЕНИЙ
Как уже говорилось, по целому ряду причин задача прогноза
погоды не может быть решена путем непосредственного интегриро-
вания исходных уравнений гидротермодинамики, приведенных
в гл. II. Для решения этой задачи эти уравнения должны быть пре-
образованы таким образом, чтобы они достаточно точно описывали
физический процесс формирования погоды и вместе с тем были бы
освобождены от несущественных деталей.
Основное преобразование исходных уравнений гидротермодина-
мики связано с использованием гипотезы квазистатичности
крупномасштабных атмосферных движений. В результате приме-
нения этой гипотезы мы приходим к так называемым полным
уравнениям гидротермодинамики, рассмотренным в гл. II и лежа-
щим в основе современных методов численного прогноза.
Однако в первых методах прогноза первоначальные или ис-
ходные уравнения гидротермодинамики были подвергнуты еще бо-
лее сильным преобразованиям на основе гипотез квазигео-
строфичности и квазисоленоидальности.
Гипотеза квазигеострофичности заключается в том, что движе-
ние считается близким к геострофическому, таким, что горизон-
тальные компоненты ветра выражаются в виде
U=Ug-\~u', V = Vg-]-v',
где
g дН g дН
us=--T-^~ и v^-T~dT
— компоненты геострофического ветра, и' и v' — малые отклоне-
ния от них.
Впервые гипотеза квазигеострофичности была теоретически обо-
снована с помощью метода разложения функций в ряд по степеням
некоторого малого параметра и успешно применена для прогноза
И. А. Кибелем в 1940 г. который разработал теоретический метод
прогноза давления и температуры [18]. В дальнейшем эта гипотеза
была подробно исследована А. М. Обуховым [26]. На ее основе
121
Н. И. Булеевым и Г. И. Марчуком [7, 8], а затем А. С. Мониным
[25] была создана квазигеострофическая теория изменения метео-
рологических элементов.
Эта теория и ее обобщения явились основной большого числа
работ по численному прогнозу погоды. К их числу относятся ра-
боты С. Л. Белоусова, С. А. Машковича, А. И. Бурцева, П. К. Душ-
кина и Е. Г. Ломоносова, П. Н. Белова, В. В. Быкова, И. 3. Лут-
фулина, Г. П. Курбаткина и др. [2, 3, 5, 6, 9, 13—17, 20, 21].
В 1962 г. в СССР квазигеострофические прогнозы были внед-
рены в оперативную практику.
За рубежом квазигеострофическая теория и квазигеострофиче-
ские прогностические модели развивались Дж. Чарнеем, Н. Фил-
липсом, К. Хинкельманом и др. [33, 35—38].
Почти одновременно с разработкой квазигеострофических мо-
делей происходило развитие и применение для прогноза и гипо-
тезы квазисоленоидальности. Последняя заключается
в том, что горизонтальное движение принимается таким, что
и=1ц-\-ит,
дф дф
где =-------— и ^=—-------компоненты соленоидального ветра,
ду дх
ф — функция тока. Применение этой гипотезы обосновано мало-
стью горизонтальной дивергенции ветра, по сравнению с вихрем
скорости.
Гипотеза квазисоленоидальности впервые была применена
Е. Н. Блиновой для долгосрочного прогноза в 1943 г. Для кратко-
срочного прогноза эта гипотеза была использована В. В Быко-
вым, И. Г. Ситниковым, М. С. Фукс-Рабиновичем и др. [12, 29, 31],
а за рубежом — Б. Волиным и др. [34].
Исследования по отысканию возможно более точных соотноше-
ний между ветром и давлением привели к созданию агеострофиче-
ских прогностических моделей. Такие модели были предложены
впервые М. И. Юдиным, а затем А. И. Бурцевым и И. П. Ветло-
вым и др. [У.22; 10, 11].
Рассмотрению квазигеострофических, квазисоленоидальных
и агеострофических моделей и посвящена данная глава. Как пра-
вило, изложение тех или иных теорий и методов будет начинаться
с простейшего варианта — случая баротропной атмосферы.
§ 1. Разложение по малому параметру и квазигеострофичность
атмосферных движений
Установлено, что действительный ветер в среднем близок к гео-
строфическому. При нарушении геострофических соотношений, как
показано в гл. III, наступает процесс адаптации, в результате чего
происходит восстановление геострофичности. Однако под дейст-
вием ряда физических факторов нарушение геострофического
122
равновесия происходит все вновь и вновь. Близость действитель-
ного ветра к геострофическому и обусловлена этими двумя проти-
воположными процессами. Возникающие при этом движения назы-
вают квазигеострофическими.
В случае квазигеострофичности движения между ветром и дав-
лением существуют определенные соотношения. Эти соотношения
были установлены И. А. Кибелем в 1940 г. [18] путем разложения
компонент ветра в ряды по степеням некоторого малого параметра.
Выведем эти соотношения, пользуясь для простоты декартовой си-
стемой координат.
Возьмем два уравнения движения без учета сил турбулентной
вязкости:
du . du , du
-or+u-^+z'W
dv । dv i dv
%-=-.1-эр_+1
dz p dx 1
dv \ dp .
~5Г—Т~д7~1и-
Введем безразмерные координаты:
x=x/L, y=y/L, z=z/H, /=///0,
где L, H и /о — характерные значения горизонтального, вертикаль-
ного и временного масштабов и безразмерные переменные
u=u\U, <и=ъ\и, <w=‘wlW,
где Z7, W — характерные значения горизонтальной и вертикальной
скорости, /о — характерное значение параметра Кориолиса (для
внетропических широт). Тогда первое уравнение движения можно
записать в виде
U du . № - du . - du \ . WU — du
- — 4—— H'U—>— 4 ~
tQ dt ' L \ dx ' ду / 1 Н dz
1 dp
р dx
lQUlv.
Поделим полученное выражение на Ulo и примем, что Ь = В ре-
зультате получим
1 ( du . - du , — du \ . W — du 1 1 dp . \-
Wo I dt dx dy j 4)^ dz P dx
Заметим теперь, что все безразмерные переменные и производные
безразмерных переменных по безразмерным координатам имеют
порядок единицы. Учитывая это, произведем оценку порядков ве-
личин отдельных членов полученного уравнения. При этом мы бу-
дем иметь в виду крупномасштабные движения в тропосфере и ча-
стично ориентироваться на эмпирические данные о характерных
значениях и порядках величин метеорологических элементов, при-
веденных в гл. 1. Все величины будем приводить к системе единиц
МТС. В соответствии со сказанным принимаем, что L= 106, Н= 104,
/о=Ю5 (около суток), О (t7) = 10, О(Ц7) = 10~2, О(р) = 10"3, /о=1О~4,
О(др/дх)=8- 10~7—10~6.
123
Прежде всего рассмотрим правую часть уравнения. Так как
все безразмерные переменные имеют порядок единицы, то, легко
видеть, что O(lv) = l. Ориентируясь на приведенные ранее эмпири-
ческие данные, получаем
---i____IQ-з= 1
101 . Ю4 1
и тогда
_1____1 др\
. UIq р дх )
Таким образом, оба члена правой части рассматриваемого урав-
нения имеют одинаковый порядок величины, равный единице.
Перейдем теперь к оценке членов левой части уравнения. Пре-
жде всего рассмотрим параметр 1//о/о = 8 = 10”1. Этот параметр был
введен И. А. Кибелем и по его имени называется параметром Ки-
беля.
Группа членов уравнения, заключенная в скобки, входит в урав-
нение с множителем e=Vio.
Рассмотрим теперь последний член левой части уравнения. Он
входит в уравнение с множителем lF//0/7 = 8lF/0/#=8 • 10"1. От-
сюда следует, что О (WllH)=z2.
Проделывая аналогичные оценки для второго уравнения дви-
жения, учитывая все сказанное, уравнения движения получаем
в виде:
ди . — ди . — ди \ . 9— ди 1 1 др . I -
——Н ——=-----775---— t-V
dt дх ду I dz UIq % дх lQ
dv . - dv , ~ dv \ , 9— dv 1 1 dp
dt dx ду I dz 6^0 P
I
z0
(1.1)
Эти уравнения используются для определения и и v по заданным
значениям р, р и /. Ориентируясь на то, что отдельные члены вхо-
дят в уравнения с различными множителями (1, 8, 82), для опре-
деления и и v воспользуемся методом последовательных прибли-
жений. В соответствии с этим методом значения и и v представим
в виде:
'у='у1+£^2+е2'уз+ • • •
Подставляя эти выражения в уравнения (1.1) и опуская члены, со-
держащие 8, в первом приближении имеем:
— 1 1 dp — 1 1 dp
щ~~7Г7^~ду' ’ ‘Vl~7Tli~dx '
124
Используя найденные значения щ и щ и ограничиваясь учетом
членов со множителем 8, для следующего, второго приближения
получаем:
- 1 1
Ы2— и I
dt 1 дх ' ду I
- 1 1
г’2— и I
ди\ . ~ ди\ । — ди\ \
+«i •
dt дх ду 1
(1-2)
Ограничиваясь двумя приближениями, возвращаясь к прежним
переменным и обозначая ui = ugf vi = vgi и,2=и' и v2=v', получаем:
в первом приближении:
1 др
и=и<г=----;
Zp дх ’
1 др
V =V<т=-г~ ,
g Zp дх ’
(1-3)
во втором приближении:
zz=ttg+^'; v=vg-{-v', (1.4)
где
, 1 / dvg dvg ! 1 Г д2р , 1 др 'll
U I \ dt дх ду J Pf L дх dt "г /р \Р’ дх /];
, 1 ( dug dug dug \
~ I dt дх
1
/2р
cftp
ду dt
, , х да дЬ да дЬ
(а, Ь) = -^-----------ч----якобиан.
4 1 дх ду ду дх
В изобарической системе координат соответственно получаем:
в первом приближении:
и= — - g дН -; v = £ dH (1.5)
1 ду l dx
и во втором приближении:
дН д^Н 1 g («. dJL \1.
и~ 1 ду /2 1 дх dt ' / dx /] ’
дН sir д?Н , -S-l (1-6)
V— 1 дх Z2 1 ду dt * I I ду Л’
Таким образом, мы получили, что действительный ветер можно
представить в виде двух составляющих: геострофической и агео-
строфической (отклонения от геострофического). Величины по-
следних по сравнению с геострофическими составляющими малы
(порядка 1/ю), поэтому в первом приближении ветер можно счи-
тать геострофическим.
Приведённые соотношения между компонентами ветра и полем
давления позволяют рассчитывать ветер по полю давления и ши-
роко используются в квазигеострофических прогностических мо-
делях.
125
§ 2. Теория изменения давления в баротропной атмосфере
в квази геострофическом приближении
Как уже говорилось, баротропной называется среда, в которой
давление является функцией одной плотности или одной темпера-
туры. В баротропной среде изобары и изотермы или изостеры па-
раллельны. В этом случае система прогностических уравнений су-
щественно упрощается, а в предположении квазигеострофичности
движения сводится к одному уравнению для давления или высоты
изобарической поверхности. Это уравнение может быть получено
различными способами.
Наиболее простой путь сводится к следующему. Возьмем
упрощенное уравнение вихря скорости
)№ + /) .^.ЗД + О (21)
dt 1 дх 1 ду \ дх 1 ду ) v 7
и уравнение неразрывности, из которого следует, что горизонталь-
ная дивергенция выражается в виде
ди j dv дт
дх * ду др '
(2.2)
Исключая дивергенцию из уравнения вихря скорости, получаем
№ , д(& + 1) , d(Q + Z) дг
dt дх ду др *
(2.3)
В соответствии с краевыми условиями на верхней и нижней гра-
ницах атмосферы т = 0. Но в этом случае в атмосфере должен су-
ществовать уровень, для которого дх/др = 0. В таком случае урав-
нение вихря скорости получает вид
дй , „ d(Q+t) , д (Q1)
dt дх ду —
(2.4)
Воспользуемся теперь результатами, полученными в предыду-
щем параграфе при разложении компонент ветра по степеням ма-
лого параметра е. Ограничиваясь только первым членом разложе-
ния, т. е. полагая, что и' = v' = 0, имеем:
(2.5)
где Д = д21дх2+д21ду2.
Подставляя эти соотношения в уравнение (2.4), получаем
,ая м *(£*"+') , “+')
dt ду дх * дх ду
Последнее выражение можно записать сокращенно
д-^-+(я,дя+/)=°. (2‘6)
126
Введем обозначение
Л ____1
2~ g L
d(Hg + l) , d(Qg + l)
us dx ду
- (н, ДЛУ-j-z), (2.7)
где ug, vg и Qg — геострофические значения ut v и Q.
Введенная функция пропорциональна геострофической ад-
векции вихря скорости. При адвекции положительного (циклони-
ческого) вихря она положительна, при адвекции отрицательного
(антициклонического) вихря — отрицательна.
Запишем теперь уравнение (2.6) короче, в виде
Д^- = Д„.
dt
(2.8)
Мы получили уравнения вихря скорости (2.6) и (2.8)
фическом приближении. Из уравнения неразрывности
в геостро-
(2.2) сле-
дует, что при ди/др = 0 горизонтальная дивергенция
ди
дх
ду
ду
об-
ращается в нуль. Поэтому уровни, для которых справедливо полу-
ченное уравнение вихря в форме (2.6) и (2.8), а также сами урав-
нения называют бездивергентными.
В действительности уровней, где предположение о бездивергент-
ности выполнялось бы во всех точках, не существует. Однако об-
работка данных о фактическом ветре показала, что в среднем ве-
личина дивергенции от земли до некоторой высоты убывает, а за-
тем возрастает. Высота с минимальной дивергенцией колеблется
от 2 до 8 км. Наиболее часто она составляет 3—5 км.
Уровень с минимальной дивергенцией называют средним
уровнем, а соответствующие прогностические модели — моделями
среднего уровня.
Уравнение, аналогичное (2.6), (2.8), можно получить другим
путем, не делая предположения о наличии бездивергентного уро-
вня, а исходя непосредственно из системы уравнений баротропной
атмосферы (уравнения (10.10) гл. II). Первые два уравнения этой
системы позволяют получить уравнение вихря скорости (2.1).
Из последнего уравнения указанной системы уравнений следует, что
ди
дх
dv
ду
дН
дх
дН \
ду / *
Н \ dt 1
и
Подставляя это выражение для дивергенции в уравнение вихря
скорости (2.1), получаем
dQ , d (Q +/) . (Q-|-/) I ( дН , дН . дН \ /о m
—г;—\-и— v Т - = -ft -V7—\-u-z---, (2.9)
dt 1 дх 1 ду Н \ dt ' дх 1 ду / ’ ' 7
или с учетом геострофических соотношений,
<21°)
где a?=l2/gH — известный параметр, Н — среднее значение Н
127
Это уравнение получено без предположения об отсутствии ди-
вергенции. Поэтому в отличие от уравнения (2.8) оно называется
дивергентным уравнением вихря скорости.
Поскольку одним из условий, при которых было получено урав-
нение (2.10), является условие баротропности, то его, а также и
прогностические уравнения, основанные на этом и подобных ему
уравнениях, называют баротропными.
Итак, мы получили баротропное уравнение вихря скорости
в двух видах (2.8) и (2.10). Оба уравнения содержат одну искомую
функцию Н — высоту изобарической поверхности, отождествляемой
со «средним» уровнем или уровнем, свойства которого эквива-
лентны свойствам атмосферы в целом в баротропном приближении.
Уравнение в любой из полученных форм может быть использовано
как прогностическое для определения будущих значений Н по их
начальным значениям. Уравнение это является нелинейным и имеет
пространственные производные третьего порядка. Получить точное
решение этого уравнения в аналитической форме относительно Н
как функции координат и времени оказывается невозможным. По-
этому применяются приближенные, или численные методы их ре-
шения, которые будут рассмотрены в следующем разделе.
Здесь же получим решение этих уравнений в аналитическом
виде относительно дН/dt. Для этого уравнение (2.8) будем
рассматривать как линейное уравнение типа уравнения Пуассона,
а уравнение (2.10)—типа уравнения Гельмгольца. Решения урав-
нений подобного типа хорошо известны. Применительно к уравне-
ниям (2.8) и (2.10) решения можно записать в виде:
2л я
2л R
рого производится интегрирование;
где г, ф — полярные координаты; R— радиус круга, внутри кото-
1 К <
и In —---функции
Грина или функции влияния. Контурный интеграл равен среднему
значению функции дН/dt вдоль окружности радиусом R. При
R I г \
In —=0, а функция Ко I-5-) — близка к нулю.
г \ R J
Обработка большого материала показала, что при надлежащем
выборе R средняя величина дН/dt по окружности мала по сравне-
нию со значением дН/dt в центре круга. В таком случае получаем:
2л R
дН * ~ ~
1,1 " - 6.
-4-J j ln -y-^rdrdr.
2л R
(2.П)
(2.12)
128
Из этих уравнений следует, что изменение давления на среднем
уровне обусловлено одним физическим фактором — адвекцией
вихря скорости. Анализ этих выражений показывает, что падение
(рост) давления на среднем уровне происходит при уменьшении
(увеличении) циклонического вихря или, что то же, при увеличении
(уменьшении) антициклонического вихря вдоль потока. Напомним,
что циклонический вихрь положителен, а антициклонический — от-
рицателен. Важно подчеркнуть, что на изменение давления в дан-
ной точке влияет адвекция вихря не только в этой же точке, но во
всей плоскости круга радиусом R. Однако с увеличением расстоя-
ния это влияние уменьшается.
§ 3. Квазигеострофические одноуровенные прогностические модели
Выше получены уравнения (2.8) и (2.10) для производной гео-
потенциала по времени и их решения относительно этой производ-
ной, выраженные в виде интегралов (2.11) и (2.12). Но для про-
гноза погоды необходимы значения геопотенциала на некотором
пространстве в определенный срок. Рассчитать значения геопотен-
циала с помощью полученных уравнений или их решений на неко-
торый промежуток времени вперед можно только путем примене-
ния приближенных или численных методов интегрирования. Дадим
представление об этих методах на примере решения уравнений
типа (2.8) и (2.10) для некоторой ограниченной области.
Все данные, необходимые для расчетов, должны быть заданы
в узлах некоторой правильной регулярной сетки точек. Расчет про-
изводных dHIdt и искомых функций Н делается в этих же самых
узлах. Чаще всего сетку точек получают на основе прямоугольной
декартовой системе координат. Для этого вводятся безразмерные
координаты по соотношениям i = x/8s и j = y/8s, где х, у — декар-
товы координаты i,j переменной точки, 6s — шаг сетки, или расстоя-
ние между соседними точками (/, /). Если область расчета пред-
ставляет собой прямоугольник со сторонами, равными (п—l)6s
и (/—l)6s, то в ней окажется nl узлов (рис. 4.1). Размер шага
сетки 6s выбирается таким образом, чтобы данные в узлах сетки
достаточно хорошо (с необходимой детальностью) представляли
исходное поле. Если сеть точек будет слишком редка, то можно бу-
дет «пропустить» небольшие циклоны, ложбины и гребни, что не-
сомненно будет сказываться на качестве прогнозов.
Известно, что барические образования имеют горизонтальные
размеры порядка 1000—3000 км, а самые небольшие из них — 500—
600 км. Исходя из этого можно считать, что максимально допусти-
мый шаг по координатам не должен превышать 250—300 км. Шаг
по координатам, равный 300 км, принят в большинстве прогности-
ческих схем. Однако в некоторых схемах шаг по координатам уве-
личен до 500 км, а в других уменьшен до 150 км.
Период прогноза Т также делится на определенные интервалы
6/, называемые шагами по времени. Если t — время, то номер шага
9 Зак. № 21
129
по времени равен отношению //W Между шагами по времени и ко-
ординатам должно выполняться следующее неравенство:
(3.1)
где ит — максимальная скорость ветра. При выполнении этого
неравенства воздушные частицы за один шаг по времени переме-
стятся на расстояние не большее, чем расстояние между сосед-
ними точками принятой сетки. В случае несоблюдения указанного
условия прогноз оказывается невозможным, так как возникает яв-
ление так называемой вычислительной неустойчивости (см. при-
1-2 —
1-3 —
1-4 —
3 —
2 —
+ + + +
I- + + + -
П~4 YL-3 п-2 п-1 I X
д + -+ + 4-
0 12 3
hj+1
4
1-1,J-1 i+1, i-1
Рис. 4.2. Сетка точек, используе-
мая для численного дифференци-
рования.
Рис. 4.1. Сетка точек на плоскости карты
для численного прогноза.
+ + + +
ложение 6), приводящее к резкому, нереальному возрастанию рас-
считываемых величин. Если 65 = 300 км, а ит = 50 м/с, то dt<
<4250 с (71 мин). При краткосрочном прогнозе по квазигеостро-
фическим схемам 6/ принимают обычно равным 1 или 1,5 ч.
Чтобы произвести численное интегрирование уравнений задачи
и получить значения dHfdt и прогностические значения И в узлах
сетки, необходимо иметь величины Н в начальный (исходный) мо-
мент во всех nl узлах.
Рабочие формулы для расчета по значениям Н в узлах
сетки получаются по правилам численного дифференцирования
функций (см. приложение 6). В простейшем случае можно запи-
сать (рис. 4.2):
I дН \ + I дН \ + \
\ дх )tj 25s ’ \ ду Jtj 25s ’
/ га ( да \ ( db \ I да \ [ дЬ \
(а> — \ дх )ij ’
130
( g g Н1 + У.) + Н1-Ь] + Н1.} + \+Н1,}-]—4ИИ,,
\~r^+lhj~Tj (M* H li'
(3.2)
И T. Д.
С помощью этих формул по значениям Н рассчитывают вели-
чины в узлах сетки. В двух крайних строках и столбцах сетки
получить величины Лй оказывается невозможным. Если значения
Н заданы в nl узлах сетки, то величины Лй могут быть рассчитаны
лишь в (п- 4) (/ — 4) внутренних узлах (см. рис. 4.1).
Следующий этап прогноза на среднем уровне заключается
в расчете dH/dt по найденным значениям правой части уравнения,
т. е. Лд. Существуют два различных способа решения этой задачи.
В первом способе для вычисления dHIdt используется решение
прогностического уравнения в интегральной форме вида (2.11) или
(2.12). В этом случае двойной интеграл с помощью формул чис-
ленного (приближенного) интегрирования записывается в виде
суммы парных произведений величин Лй в отдельных точках на
числовые коэффициенты, называемые весами, которые определя-
ются функциями Ко (г//?) или In/?/г и показывают, каким образом
значения AQ в различных точках обусловливают изменение давле-
ния в данной точке. В общем виде такую сумму можно записать так:
где AQk — значения величин Лй в некоторой точке k\ N — число то-
чек, окружающих точку £ = 0, в которой рассчитывается dHIdt.
Чаще всего число N принимается равным восьми. Заметим, что
dH/dt может быть определено не для всех точек области решения
задачи, в которых имеются вычисленные значения Лй. В самых
крайних рядах и столбцах dHIdt не может быть рассчитано. Таким
образом, если значения Н были заданы в nl узлах сетки, то вели-
чины Ла могут быть рассчитаны в (п— 4) (Z — 4), а величины
dHIdt— лишь в (п — 6) (/ — 6) внутренних узлах сетки (см.
рис. 4.1).
Второй способ вычисления dHIdt заключается в непосредствен-
ном решении прогностических уравнений (2.8) или (2 10) на вы-
числительной машине (без использования решения для dHIdt
в форме двойных интегралов). В этом случае дифференциальное
уравнение для dHIdt записывается в так называемой конечно-раз-
ностной форме Рассмотрим это на примере уравнения (2.8).
Умножим это уравнение на (6s)2 6/ и для краткости примем,
что
4^-8/ q, ^a(SS2)8f=F.
9*
131
Тогда, записывая оператор Лапласа для точки ij по пятиточеч-
ной схеме в виде
л fT)_ ф<- 1, j + ф/ + ь j + ;-1 4- Ф/, y + i — 4Ф0-
(£?)2 > У6-6)
получим следующее конечно-разностное уравнение для определе-
ния q:
Qi-\, j-\-qi+\, rVqt, y + 1 — (3.4)
Если исходные значения Н заданы в nl точках, то это уравнение
решается для точек с индексами / = 2, 3, ..., и— 3; / = 2, 3, ..., I—3.
В качестве краевых условий принимается q = 0 в точках с индек-
сами / = 0, \,п— 1, и — 2; / = 0, 1, I— 1, I — 2, т. е.
^o,j = 7i,;=^-i,;=7n-2,/=^,o=^i = ^ /-1 = ?/,/-2=0. (3.5)
Выписанное уравнение и краевые условия можно записать
в виде системы (п — 4) (Z — 4) линейных алгебраических уравне-
ний, где в качестве неизвестных будут величины q в (п— 4) (/— 4)
узлах. Системы уравнений с большим числом неизвестных реша-
ются итерационными способами, например, экстраполированным
методом Либмана (см. приложение 4).
После расчета dHjdt необходимо получить значение Н в сле-
дующий момент времени. Для этого используются конечно-разно-
стные выражения для производных, с помощью которых мы полу-
чаем:
(3.6)
или
Я<+5<=М_6<+2(^8Л (3.7)
Формула (3.6) получается при использовании односторонней раз-
ности, а формула (3.7) — центральной разности по времени t.
Формулы (3 6) и (3 7) используются для предвычисления значе-
ний Н в момент /4-6/ по найденным значениям дН/dt. Чтобы полу-
чить прогноз на более длительный срок, все операции повторяют
несколько раз. А именно, после нахождения значений HtM снова
рассчитываются величины Aq, относящиеся к моменту /4-6/, и де-
лается еще один шаг по времени. В результате получим величины
Нмы- Чтобы получить значения Н через Т ч, очевидно, необхо-
димо сделать 7/6/ шагов по времени. Например, если 7 = 24 ч,
6/= 1,5 ч, то 7/6/= 16, т. е. для получения прогноза на сутки все
указанные операции нужно выполнить 16 раз или, как говорят,
надо сделать 16 шагов по времени.
При выполнении одного шага прогностические значения Н по-
лучаются не во всех nl точках, в которых заданы значения Н в на-
чальный момент, а лишь в (п— 6) (Z — 6) точках. После выполне-
132
ния второго шага по времени прогностические значения будут по-
лучены только в (п — 12) (Z—12) узлах. Таким образом, область
прогноза при каждом шаге очень быстро сокращается. Если, на-
пример, исходные значения заданы в 26x22 узлах, то уже после
четырех шагов область прогноза оказалась бы сведенной к нутю.
Чтобы избежать этого, приходится полагать, что в крайних двух
или трех рядах и столбцах величины Н известны в течение всего
срока прогноза. Тогда расчет и дН/St, а следовательно, и Ht+&t
на каждом шаге можно производить для всех внутренних точек
без сокращения области прогноза. В действительности, конечно,
значения Н на краях сетки неизвестны. Поэтому приходится, как
это уже упоминалось выше при рассмотрении итерационного спо-
соба решения задачи, делать предположение о том, что в течение
всего срока прогноза величины Н на краях не изменяются, т. е. что
там dH/dt = 6. Несомненно, что такое искусственное условие на
краях сетки сказывается на качестве прогнозов. Особенно сильно
это отражается на прогнозе в точках, близких к краям сетки.
В центральных же точках сетки, удаленных от крайних рядов на
1000—1500 км, это влияние невелико.
При реализации схемы численного прогноза по большой терри-
тории, достигающей до 3000 км по меридиану, нельзя пренебречь
изменениями масштаба карты, возникающими при изображении
поверхности Земли на плоскости географической карты (см. § 9
гл. II). Один из простейших способов учета указанного эффекта со-
стоит во введении так называемого масштабного множителя т в по-
лученные уравнения.
Практически это сводится к замене выражения для на вы-
ражение вида
Л>=-(я,
При прогнозе на длительные сроки (порядка суток) в некото-
рых случаях возникает явление вычислительной неустойчивости,
которое искажает прогностические поля. Это явление можно «пога-
сить», применяя специальную операцию, которая получила назва-
ние сглаживания. В простейшем случае сглаживание сводится
к расчету значений Н в каждом узле сетки по прогностическим зна-
чениям Н в ближайших точках, по формулам вида
М;=аоМ;+а1 (M-i, ;+i)~b
Ц-а2 (M-i, y-i + M+i, y+i+M+i, ;+i)> (3.8)
где а0, а2— коэффициенты, подбираемые эмпирическим путем
(например, по [2] ао = 5/э, сц = 2/д, «2 =—7э), и замене рассчитан-
ных значений сглаженными.
Отметим еще следующее обстоятельство. При прогнозе по огра-
ниченной территории важен также вопрос о выборе местоположе-
ния границ области расчета. При прочих равных условиях жела-
тельно, чтобы границы области расчета проходили через области
133
с небольшой изменчивостью метеорологических элементов, по-
скольку обычно на границах принимается постоянство искомых
функций. Это обстоятельство приводит к увеличению ошибок про-
гноза до 20%. Влияние таких фиктивных условий на границе на
прогноз можно уменьшить путем учета климатических данных об
изменчивости прогнозируемых элементов. Целесообразно, напри-
мер, границы области расчета проводить по районам с небольшими
градиентами давления и с наименьшей фактической изменчивостью
во времени.
Одноуровенные квазигеострофические модели широко приме-
нялись в 50-е годы. Начиная с 60-х годов они стали заменяться бо-
лее совершенными квазисоленоидальными и многоуровенными ква-
зигеострофическими моделями, а затем и моделями с полными
уравнениями. В последние годы одноуровенные квазигеострофиче-
ские модели применяются лишь как вспомогательные.
§ 4. Теория изменения метеорологических элементов
в бароклинной атмосфере в квазигеострофическом приближении
Рассмотрим эту теорию в предположении квазигеострофично-
сти, квазистатичности и адиабатичности крупномасштабных атмо-
сферных движений. Это означает, в частности, что предполагается
соблюдение уравнения статики и близость движения к геострофиче-
скому. В начале рассмотрим применения этой теории к процессам
в свободной атмосфере. Влияние пограничного слоя, а также осо-
бенности подстилающей поверхности будут рассмотрены отдельно.
В качестве исходной принимается система полных уравнений
гидротермодинамики (см. (10.1) гл. II), которая после введения пе-
ременной £ и опускания малых членов, содержащих ди/д^ и dvjd^,
получает вид:
ди
dt
ди . ди дН . ,
-ч—-з— =
дх 1 ду дх 1 ’
dt дх ‘ V ду
rr дН 1
S ду
g г дН . ди ( dv j I dt
~дх~ ~ду~ ~д^
дТ . дТ , дТ &
dt +“ дх ду ~ RPt.
(4.1)
Первые два уравнения системы (4.1) используются для получе-
ния соотношений между ветром и давлением (см. соотношения
(1.6)). С помощью полученных соотношений для горизонтальной
дивергенции находим
дх 1 ду /2 [ dt 1 \ ’ I 1 /]
134
(4.2)
Подставляя это выражение в уравнение неразрывности и учитывая
выражение (2.7) для Ай, получаем
л л
dt Pg дС *
Преобразуем теперь уравнение притока тепла. С помощью урав-
нения статики выразим температуру через геопотенциал, а компо-
ненты скорости ветра и и v заменим геострофическими (опустив
малые члены и' и v') В результате
Г2 Г Д _ с2
4 dt dt g Pg
(4-3)
где
Ат=— = Й-Ч", тг) <44>
— геострофическая адвекция температуры. Функция Ат такова,
что при адвекции тепла она положительна, а при адвекции хо-
лода — отрицательна.
В результате мы получили систему двух уравнений (4.2) и (4.3)
с двумя неизвестными: Н и т. Эти два уравнения совместно с урав-
нением статики и соотношениями квазигеострофичности (1.6) и яв-
ляются уравнениями квазигеострофической модели. Приведенный
вывод уравнений данной прогностической модели принадлежит
И. А. Кибелю [У.12].
Другой вывод уравнений этой же прогностической модели был
дан ранее Н. И. Булеевым и Г. И. Марчуком [7]. Этот вывод также
основан на гипотезе квазигеострофичности, хотя соотношения (1.6)
в явном виде и не используются Воспроизведем этот вывод. С по-
уравнений движения, в которых опускаются малые члены
т dv
мощью
т ди
и
Р
получаем уравнение вихря скорости
dQ ( d (Q 4-1) । d (Q + I) _____________ z ( du f dv \
dt * dx * V dy \ dx ' dy )'
Исключая отсюда дивергенцию с помощью уравнения неразрыв-
ности, получаем
„ d(Q + l) । d (Q-4-Z) _ l dz
dt ‘ w dx ' dy ~ P dC *
Используя теперь геострофические соотношения, получаем уравне-
ние (4.2). Уравнение (4.3) выводится, как и ранее.
Теперь исключим из полученной системы уравнений (4.2) — (4.3)
неизвестное т. Для этого преобразованное уравнение притока те-
пла (4.3) разделим на с2 й продифференцируем по £. Подставляя
полученное в результате этого выражение для drfdp в преобразо
ванное уравнение вихря скорости (4.2), получим
K^L-A /2 д С2 d dH 2 /? d С л
а dt д dC dC dt g dt c2
135
Итак, получается одно уравнение для определения одного неиз-
вестного Н. Однако оно является настолько сложным (нелинейное
уравнение в частных производных третьего порядка с четырьмя не-
зависимыми переменными), что современные методы математиче-
ского анализа не позволяют получить его решение в виде функции
координат и времени Н (х, у, £, /). Поэтому данное уравнение ре-
шается численно. Как и при решении прогностического уравнения
на среднем уровне, искомой функцией будем считать dHIdt. Члены,
содержащие dHIdt, перенесем влево, а остальные члены — вправо.
В результате получим следующее уравнение:
» 1^, (4.5)
dt 1 dC с2 dt а g dt, с2 т v '
где правую часть можно считать известной. В самом деле, если
в данный момент известны поля давления и температуры, то по ним
dA
можно определить Лд, Ат и —. Относительно неизвестной dHIdt
данное уравнение является линейным уравнением второго порядка.
Для однозначного решения этого уравнения необходимо задать
граничные условия. Ввиду того что уравнение имеет второй поря-
док относительно трех независимых переменных (х, у, £), для ре-
шения на ограниченной территории нам необходимо задать крае-
вые условия по всем трем координатам. Однако если это уравне-
ние решать на бесконечной плоскости или на всем земном шаре, то
достаточно ограничиться заданием краевых условий лишь по вер-
тикальной координате £. В качестве одного из таких условий при-
нимается непроникновение воздушных частиц через поверхность
земли, которое при условии геострофичности принимает вид (см.
(10.4) и (10.7) гл. II)
при С=1 (р=Р)
или с учетом (4.3)
д дН . дН _ R . ..
dt +а dt g Ат’ И-6)
где а=с2//?7'1.
В качестве второго применяется краевое условие на верхней
границе атмосферы (см. (10.8) гл. II), т. е.
при (р-*0) С ограничено. (4.7)
Уравнение (4.5) и краевые условия (4.6) и (4.7) в случае по-
стоянных значений / и с2 позволяют получить выражение для
dHIdt в некоторой точке на любой изобарической поверхности
[У.12]
— ~ ° = t J J G°Aedx'd?'dA' + .Ш °TATdx' dy' dV, (4.8)
0 —co 6 —co
136
где Gq — функция влияния, показывающая, каким образом адвек-
ция вихря на разных уровнях влияет на dHIdt в рассматриваемой
точке; GT — функция влияния, характеризующая влияние на
dH)dt адвекции температуры на разных уровнях; х', у', £'— пере-
менные интегрирования, а интегрирование распространяется прак-
тически на всю атмосферу.
Решение (4.8) показывает, что величина dHIdt в некоторой
точке зависит от двух факторов: адвекции вихря скорости и ад-
векции температуры Ат. Характер влияния на dHIdt опреде-
ляется функцией влияния Oq, которая выражается весьма слож-
ным образом через координаты рассматриваемых точек и пара-
метры уравнения. Примеры функций G& приведены на рис. 4.3 и 4.4.
На этих рисунках ось ординат соответствует координате £', а ось
абсцисс — расстоянию переменной точки интегрирования с коор-
динатами х', у' от топки расчета, помещенной в начале координат
(г\=х'2 А-у'2). Величины даны в условных единицах. Функция
Go всюду отрицательна. Максимальное значение она принимает
в точке прогноза; по мере удаления от точки прогноза как в гори-
зонтальном, так и в вертикальном направлении функция влияния
убывает. Все качественные правила, которые были получены отно-
сительно влияния на dHIdt ранее, сохраняются и в данном слу-
чае. Однако теперь необходимо рассматривать и вертикальное рас-
пределение адвекции вихря. При этом следует иметь в виду, что
влияние дальних уровней невелико. Например, на dHIdt поверх-
ности 1000 мбар влияние адвекции вихря на поверхности 100 мбар
будет мало, но влияние А& на поверхности 500 мбар еще значи-
тельно.
Функция GT (рис. 4.5 и 4.6) такова, что адвекция тепла (хо-
лода) выше точки расчета приводит к падению (росту), а ниже
ее — к росту (падению) давления.
Уравнение для вертикальных движений. Зная
величину dHIdt, легко рассчитать значения dTfdt и т. В самом
деле, дифференцируя уравнение статики по времени, получим
формулу для изменения температуры во времени
dT _ g г д / дН \
dt ~ R^ d^ \ dt )'
Величина т определяется из уравнения притока тепла (4.3).
Выражения для т и dTIdt можно получить также путем состав-
ления и решения соответствующих дифференциальных уравнений.
Тогда величины т и dT/dt аналогично dHIdt будут выражены через
адвекцию вихря и адвекцию температуры. Построим уравнение
для т. Применим оператор Лапласа к правой и левой частям
уравнения (4.3) и умножим результат на Р. Тогда
4 Д f К ЬАТ=-^- Дт.
137
Рис. 4.3. Функция влияния Gq для изменения вы-
сот изобарической поверхности 1000 мбар.
Рис. 4.4. Функция влияния GQ для изменения вы-
сот изобарической поверхности 500 мбар
Рис. 4.5. Функция влияния GT для изменения
высот изобарической поверхности 1000 мбар.
Рис. 4.6. Функция влияния GT Для изменения
высот изобарической поверхности 500 мбар.
Дифференцируя уравнение (4.2) по g и умножая результат на
Pg2, получаем
рп д . дН р^2 dAs _____ 12 «2
~дГа dt ~ g дС2 •
д дН
Исключая Pg2-—-А ——- из последнего выражения, находим
dg dt
Ат.
Оставляя члены с т в левой части и умножая результат на g/c2,
получим
Л I 72 £2 d2z — д Д № АД М СП
A'C-’M с2 с2 дС С2 (4- )
Решение этого уравнения при указанных ранее краевых усло-
виях имеет вид [У. 12]
т = У J у OTsAsdx dy' dt +$ J У GxTATdx dy' Л, (4.10)
0 —оо 0 —оо
где интегрирование распространяется на всю атмосферу, а функ-
ции и GXT характеризуют влияние на т величин адвекции вихря
и адвекции температуры соответственно.
Для перехода от величины т к вертикальной скорости w и об-
ратно достаточно вспомнить, что
pg
— g?W ИЛИ -------Вт W-
Если р выразить в миллибарах, т — в мбар/12 ч, w — в см/с, то
при /? = 287 м2 • с-2 • град-1, получаем
т=_ 9* 12 • 3600 • 10-2=4-®'
2о/ 1
ИЛИ
где а=14,8-у-.
Например, при р = 700 мбар и Г=250К <2 = 41,4, так что вертикаль-
ной скорости w=l см/с соответствует значение т=—41,4 мбар/12 ч.
§ 5. Учет турбулентной вязкости и орографии
До сих пор речь шла о прогнозе в свободной атмосфере над
плоской земной поверхностью Рассмотрим теперь влияние турбу-
лентности в пограничном слое и крупных неровностей земной по-
верхности, т. е. орографии, в рамках постановки задачи прогноза
139
в квазигеострофическом приближении. Учет обоих названных фак-
торов производится аналогичным образом, путем изменения крае-
вого условия на нижней границе атмосферы при сохранении усло-
вия на верхней границе, где по-прежнему принимается, что т = 0.
Краевое условие на нижней границе атмосферы должно быть по-
лучено независимо от основной системы прогностических уравне-
ний. Рассмотрим подробнее, каким образом производится учет тур-
булентного трения.
Учет турбулентной вязкости. При решении прогно-
стического уравнения для dHIdt в бароклинной атмосфере (4.5)
без учета указанного фактора в качестве краевого условия прини-
малось, что при 2 = 0 w = 0. В изобарической системе координат
это условие приближенно записывалось в виде
приС=1 (р=Р) ™
(условие (4.6)). Теперь мы будем считать, что вертикальная ско-
рость на нижней границе атмосферы равна той скорости, которая
возникает на верхней границе планетарного пограничного слоя,
т. е. мы будем считать, что при 2 = 0 w=Wh. Этим и будет учтено
суммарное влияние на процессы в свободной атмосфере погранич-
ного слоя, как бы стянутого в прилегающую к Земле пленку.
В качестве Wh можно принять значение w, которое получается
из теории пограничного слоя. Мы можем принять, например, что
<wh=akpQ=b Д770 или 'Wh=axLpb=bx (5.1)
где ро — давление на уровне моря, Hq — высота изобарической по-
верхности 1000 мбар, а и czi — коэффициенты (см. § 3, гл. II), Ь =
=g-pa~l,08- 10“2а, bi = gQU\^ 1,08• 10“2ai. Найденное выражение
для Wh и используется для уточнения краевого условия на нижней
или в форме (4.6)
Подставляя в выражение для т (6.2) гл. II значение w=wh и ис-
пользуя геострофические соотношения, получаем
пРиС=1 ----*д^о)
или в форме (4.6)
4 т+а 4г= -т Ат+аЬ дя°- (5-2)
Теперь прогностическое уравнение (4.5) решается с этим новым
краевым условием. В результате получаем [У.12]:
44=1 J J GsAa dx' dy' dt,' + f f J' GTATdx' dy' dt' +
0 —co 0 — co
+ O^Hodx’dy'. (5.3)
140
Это решение отличается от решения (4 8) наличием третьего
интеграла, описывающего эффект приземного трения. Интегриро-
вание распространяется на изобарическую поверхность 1000 мбар,
а функция влияния GAH характеризует влияние лапласиана ДЯ
на изменение давления. Функция бдн всюду положительна. Вблизи
точки расчета она больше, вдали — меньше. Знак изменения дав-
ления зависит от знака Д//.
В циклоне Д//>0, следовательно, и произведение 6ДН Д//о>О,
в антициклоне Д//<0, значит, и бдн Д//о<О. Таким образом, фак-
тор приземного трения приводит к росту давления в циклоне
и к падению — в антициклоне Расчеты показывают, что в интен-
сивном циклоне рост давления благодаря этому фактору может
достигать 10—15 мбар/сутки.
Учет орографии. Подобно учету приземного трения, учет
орографии производится с помощью замены краевого условия на
уровне моря. Сформулируем это условие.
Пусть высота горы z есть функция координат хи у
у).
Этой же функцией описывается и положение воздушных частиц,
прилегающих к неровной поверхности земли. Пусть далее коорди-
наты частиц х, у и z являются функциями параметра t. Продиффе-
ренцировав приведенное выражение для z по /, получим следую-
щее соотношение:
dz д$ dx ] д% dy
dt дх dt ' ду dt
Так как
то для вертикальной скорости воздушных частиц, обусловленной
орографией, получаем
<5-4>
С помощью полученного выражения производится изменение крае-
вого условия на нижней границе атмосферы. В результате в выра-
жении для dHIdt будет получен дополнительный член, отражаю-
щий влияние орографии. По структуре он аналогичен последнему
слагаемому в (5.3) и содержит соответствующую функцию
влияния.
Анализ этого члена показывает, что на наветренной стороне гор
влияние орографии приводит к восходящим движениям и росту
давления, а на подветренной стороне гор влияние орографии при-
водит к нисходящим движениям и падению давления. Действие
орографии значительно проявляется лишь в близких к поверхности
горы слоях воздуха. В слоях, удаленных от поверхности горы на
3—5 км, влияние гор незначительно.
141
Данный метод пригоден для учета влияния на крупномасштаб-
ные процессы лишь достаточно протяженных горных массивов, ха-
рактерный горизонтальный масштаб которых соизмерим с соответ-
ствующим масштабом изучаемых атмосферных движений. Соответ-
ственно этому под высотой горы Цх, у) понимается некоторая
сглаженная характеристика рельефа, отражающая крупномасш-
табные особенности последней. Следует также иметь в виду, что
в данной постановке задачи условие (5.4) фактически приписыва-
ется нижней изобарической поверхности //=1000 мбар, а не вы-
соте реальной горы Следовательно, влияние гор большой высоты
(более 2—3 км) не может быть достаточно точно описано этим ме-
тодом. Указанное ограничение можно устранить, если использовать
в качестве вертикальной координаты переменную о (см. формулу
(6.12) гл. II).
§ 6. Квазигеострофические многоуровенные прогностические
модели
Основой для построения многоуровенных квазигеострофических
методов прогноза является уравнение для dHIdt (4.5) и его реше-
ние в виде тройных интегралов типа (4.8) или с помощью конеч-
ных разностей. Так же, как и в случае одного уровня, прогноз
рассчитывается с помощью приближенных, или численных, ме-
тодов.
Прежде всего необходимо выбрать число уровней. Этот выбор
производится, с одной стороны, исходя из практических потребно-
стей, в соответствии с которыми в прогностическую схему включа-
ются те уровни, для которых необходимо получать прогноз. В не-
которых случаях это сделать не удается и тогда в прогностическую
схему включают какие-то другие уровни, по которым можно бу-
дет получить прогноз и для интересующих нас уровней. С другой
стороны, учитываемые в схеме уровни должны возможно более
полно отражать состояние атмосферы. Это, однако, не означает,
что простое увеличение числа уровней будет всегда улучшать по-
лучаемые результаты, так как введение в схему коррелированных
данных не увеличивает истинную информацию, но зато перегру-
жает схему В прогностических схемах, основывающихся на ква-
зигеострофическом приближении, счетные уровни берутся обычно
таким образом, что разность на них оказывается не меньше
100 мбар. Однако в пограничном слое, а также в стратосфере уро-
вни можно брать и чаще. Это связано с быстрым изменением ме-
теорологических элементов с высотой в пограничном слое или при
переходе от тропосферы к стратосфере.
С учетом выбранных уровней вводятся безразмерные коорди-
наты: i=x/8s, j = y/6s, £ = £/6£. Выбор шагов по горизонтальным
координатам 6s и по времени б/ производится также, как и в слу-
чае одного уровня. Что же касается шагов по вертикальной коор-
динате б£, то они в значительной мере определяются выбором
142
счетных уровней. В соответствии с этим он может быть перемен-
ным по высоте.
Область прогноза определяется исходя из практических потреб-
ностей, а также из реальных возможностей (вычислительная тех-
ника и пр.). Исходные данные Н должны быть заданы в узлах вы-
бранной сетки. Если число уровней составляет s, то мы должны
иметь tils значений Н.
Первым этапом численного прогноза является расчет влияющих
факторов, т. е. Лй и Ат. Вычисление Лй производится также, как
в случае одного уровня.
Для расчета адвекции температуры между уровнями необхо-
димо записать производные в конечных разностях. Если шаг по
вертикали равен 6£, то формулы численного дифференцирования
дают
1 J_— ВС ^k + l ( дС )
+ 2
k~~2
Так как вычисленные таким образом производные относятся к се-
редине слоев, расположенных между уровнями А, &+1 и k— 1, то
г. 1 , 1
им присвоены индексы kA—— и k<--— /
Теперь, например, для точки (t, /,
можно записать
I. J.
2
_ g2 (( дН \ г_д_ / +
- ri 4+4 (\ A, j. *+± U? \
(дН_\ г д ]
Uy A, j, *+± Idx \ Лор
этому необходимо производные (дН/дх)
и (дН/ду)
~2
2
Значения H в промежуточных точках i, j, k-\—g- неизвестны, no-
t, J. k
выразить через Hi, j, к и Hi, j, k+i. Для этого положим, что
(дН\ _1 д(Нк + Нк+х) (дН\ _ 1 д(Нк + Нк+})
дх )k+^~ 2 дх ’ \ду /к+±~ 2 ду
Учитывая эти выражения, получим
» у,
-44 , {(Нк, яй+1)-(/4, яА)+(яА+1, яй+1)-(яй+1, /Ш/,
=-^-С
*4 ** -4
Иг)
I
где b = g2IRl.
Имея в виду, что (Л, Л)=0 и (Л, В)=—(В, Л), получим
Иг).. ,=4^ 1(^, яй+1)о.
t-i j> 2 2
143
После нахождения Лй и Ат необходимо вычислить dHIdt Как и
в случае прогноза на одном уровне, это можно сделать двумя пу-
тями: путем расчета интегралов с помощью приближенных, или
численных методов интегрирования решений вида (4.8) или путем
решения прогностического уравнения (4.5) непосредственно итера-
ционным способом.
После расчета тем или иным способом значений dH[dt во всех
точках сетки с помощью соотношения (3.6) или (3.7) делается шаг
по времени. Затем вновь рассчитываются Aq и Ат и т. д.
Общая последовательность операций при численном прогнозе
на нескольких уровнях очень близка к соответствующей последо-
Рис. 4.7. Сетка точек, используе-
мая для вычисления простран-
ственных интервалов.
вательности при прогнозе на среднем уровне.
Как и в случае прогноза на среднем уровне, в крайних двух или
трех рядах и столбцах значения Н принимаются постоянными.
Существует ряд конкретных мно-
гоуровенных прогностических мо-
делей. Эти модели отличаются
друг от друга во многих отноше-
ниях: выбором уравнений, приме-
нением итерационных или инте-
гральных способов расчета dHIdt,
учетом трения или орографии,
особенностями численной схемы
и т. д. Остановимся на некоторых
из них.
Трехуровенная прогно-
стическая модель, основан-
ная на использовании
функций влияния. Эта мо-
дель, разработанная С. Л. Белоусо-
вым [6], в течение ряда лет приме-
няется в оперативной практике
в качестве основной модели числен-
ного краткосрочного прогноза. В качестве счетных уровней при-
няты изобарические поверхности 850, 500 и 300 мбар. Шаг по го-
ризонтальным координатам составляет 300 км, а по времени —
1,5 ч. Для прогноза на сутки или 36 ч используется сетка из 32X
Х22 узлов, а для прогноза на более длительные сроки (до трех
суток)—сетка 37x27 узлов. На трех крайних рядах сетки зна-
чения Н задаются постоянными. Экстраполяция по времени произ-
водится с помощью односторонних разностей (соотношение
(3.6)).
Расчет dHIdt производится путем приближенного вычисления
тройных интегралов решения (4.8). Для этого в горизонтальной
плоскости вокруг точки расчета с помощью концентрических ок-
ружностей образуются четыре кольца (рис. 4.7). При этом всего
используются значения Н в 7X7 узлах сетки. Интегрирование по
вертикали производится по данным трех уровней для Aq и двух
слоев для Ат методом трапеций.
144
В результате тройные интегралы сводятся к суммам парных
произведений вида
4 3 _ 4 2
(“^7") = Zj Zj A$.rmakrmAr Zj Zj ^Trs^krs^
К 01 /k r=0m=\ r = 0s=l
где k — номер уровня, для которого вычисляется прогноз; т и s—
соответственно номер уровня или слоя, для которых рассчитыва-
ются Aq и АТ\ г — номер кольца; и Ат — конечно-разностные
выражения Ля и Ат в точках сетки, осредненные по окружностям
указанных выше радиусов; akrm, bkrs — весовые коэффициенты,
получающиеся с помощью функций влияния Go и GT соответ-
ственно.
В качестве исходных данных используются значения высот по-
верхностей 850, 500 и 300 мбар в узлах указанных сеток. Эти зна-
чения получаются в результате численного анализа методом опти-
мальной интерполяции высот изобарических поверхностей по из-
мерениям на аэрологических станциях. Рассмотренная прогностиче-
ская модель позволяет получить прогноз высот изобарических по-
верхностей 850, 500 и 300 мбар во всех узлах сетки, за исключением
трех крайних рядов с каждой стороны. При этом достоверность
прогноза увеличивается по мере удаления от этих крайних рядов.
Кроме высот поверхностей 850, 500 и 300 мбар с помощью уравне-
ния (4.3) прогнозируются вертикальные движения на разных уров-
нях и на разные сроки, значения высот поверхностей 700 и 400 мбар,
получаемые путем интерполяции прогностических значений основ-
ных высот, и некоторые другие параметры атмосферы.
Относительная ошибка прогнозов высот изобарических поверх-
ностей на 24 ч вперед по этой методике в среднем за ряд лет со-
ставляет около 0,7.
Результаты прогноза высотного барического поля по изложен-
ной методике используются для прогноза траекторий воздушных
частиц, осадков (см. § 9), а также давления на уровне моря.
Прогноз давления на уровне моря производится по так назы-
ваемой адвективной синоптико-гидродинамической схеме, разрабо-
танной А. Н. Мерцаловым [24]. Основу этой схемы составляет мно-
голетний синоптический опыт, который показывает, что небольшие
барические образования и некоторые другие особенности бариче-
ского поля у земной поверхности перемещаются в основном в со-
ответствии с ведущим потоком, несколько отклоняясь от него как
по скорости, так и по направлению. Эти отклонения могут быть уч-
тены на основе эмпирических правил. Эмпирические данные пока-
зывают также, что правилу ведущего потока подчиняются и изал-
лобарические области, определяемые по трехчасовым изменениям
давления (барические тенденции). Указанные правила были
взяты в основу алгоритма и программы расчета на ЭВМ полусу-
точных и суточных изменений давления. Направление и скорость
ведущего потока определялись по полю функции В (х, у) =
= АН (6s)2+ 47/, где 6s — шаг сетки.
10 Зак. № 21
145
Испытание данной методики дало положительные результаты:
относительная ошибка прогноза суточных изменений давления со-
ставляет менее 0,7.
Трехуровенная прогностическая модель, ос-
нованная на решении конечно-разно стных урав-
нений, разработана П. Н. Беловым [2, 3]. В ней используется ите-
рационный метод решения конечно-разностных уравнений. В каче-
стве исходных уравнений модели берутся преобразованные уравне-
ния вихря скорости (4.2) и притока тепла (4.3), а в качестве
граничных условий принимаются условия (4.7) и (5.2). С помощью
краевого условия (5.2) учитывается турбулентная вязкость в по-
граничном слое.
На основе уравнений (4.2) и (4.3) выводится уравнение для
dHIdt (4.5). Запишем это уравнение с учетом переменности масш-
таба картографической проекции в виде
<61>
где q=St dHfdt\ т — масштабный множитель:
F=A2-P^±^AT\, Ай=-(н,
St — шаг по времени.
Краевые условия (5.2) и (4.7) перепишем в виде
при С=1 —\-aq=fbt; (6.2)
при С=0 C2-g-=0, (6.3)
где
г т2 * т_т । m2 ( TJ дН \
f=sK~MI+g-r(H, т).
Краевое условие на верхней границе (6.3) получается из условия
(4.7) с учетом следующих соображений. Так как при £ = 0 т=0, то
в соответствии с преобразованным уравнением притока тепла (4.3)
мы должны принять, что
при с=о
Из физических соображений мы должны принять, что на верх-
ней границе атмосферы и, v, dTIdx и dTjdy ограничены и,
следовательно, %АТ = 6. В результате мы приходим к условию
(6.3).
146
Для численного решения уравнения (6.1) разделим атмосферу
на ряд слоев путем введения уровней где /г = 0, 1, 2, ... — номер
уровня. Разделение на слои может быть произведено различным
образом. В результате мы можем получить TV-уровенную модель
атмосферы. Здесь мы рассмотрим модель с тремя слоями одина-
ковыми по массе воздуха, и тремя основными уровнями (k =
= 1, 2, 3), находящимися в середине этих слоев. Слои отделим друг
от друга промежуточными уровнями (рис. 4.8).
Введем в рассмотрение шаг по вертикали 6£ = 1/3 = 0,333. Тогда
индекс k будет иметь смысл новой безразмерной переменной k =
Рис. 4.8. Вертикальная структура атмо-
сферы. Прогностическая модель П. Н. Бе-
лова [2].
Запишем теперь уравнение (6.1) в конечных разностях. Прежде
всего рассмотрим член уравнения (6.1), содержащий производные
по вертикали. Этот член представим в виде
д & dq \ _ 1 Г/ Р dq\ ( С2 dq \
. dC с2 dt, )k~ К \ е2 dt )k. _1_ \с2 4___1
'2 2
Учитывая это соотношение, записав в конечных разностях член
и отнеся правую часть уравнения к узлу сетки ijk, получим сле-
дующее конечно-разностное уравнение:
^Z-l, у, j, j-\, k /4-1, j, ^4-14“
^btjk Qijk+Ctjk К j, k-i=Fijk< (6-4)
10*
147
где
CiJ'k~\ m2 )и\ вс ) ( C2)k_ j.’
Fijk=Fijk (M28^-
Краевые условия в конечных разностях примут вид:
при Л=3-2~ ^/уз)_Ь 1 —f 1 °Л (6.5)
/-'3 2 '3~2
при k=l (ди1~Яцо)=О. (6.6)
Заметим, что фиктивный уровень k = 4 при решении будет ис-
ключей.
При практической реализации было принято:
^й=з2_==Р1^з"_?2^2» (А^)й=_3_^ = (А^О*=з’
где |31= 1,312, р2 = 0,312. Первое из этих выражений было получено
путем интерполяции. Параметр статической устойчивости с2 при-
нимается зависящим только от высоты и рассчитывается по фак-
тическим данным.
Решение уравнения (6.4) по данным высот изобарических по-
верхностей 850, 500 и 200 мбар в 26X22 узлах сетки с шагом 300км
производится итерационным способом. При этом уровни £ = 0,167
и С = 0.
Величина невязки для очередного приближения выражается
в виде
я(^;+1)=сц л д й+^_ у+1, *+
J, ijk^ljk^ С*-1 FIjk’
а значение q следующего приближения определяется по соотноше-
нию
Наиболее быстрая сходимость получается при следующей комбина-
ции коэффициентов перерелаксации:
xj=0,275; х2=0,237; х3=0,244.
В результате серии экспериментов было показано, что перемен-
ность параметров I и т достаточно учитывать лишь при вычисле-
нии правой части прогностического уравнения. В левой же части
уравнения можно принять //m = const.
148
Переход к следующему шагу по времени производится по соот-
ношению (3.6). Вертикальные скорости определяются после нахож-
дения q с помощью уравнения притока тепла (4.3).
Данная прогностическая модель дала удовлетворительные ре-
зультаты при испытании. Средняя абсолютная ошибка суточных
прогнозов высот поверхности 850, 500 и 200 мбар составила около
3, 4 и 5 дам соответственно, а коэффициент корреляции для про-
гнозов изменений высот составлял около 0,75.
Малопараметрическая прогностическая мо-
дель [28]. Как уже говорилось, с одной стороны, для более де-
тального описания вертикальной структуры атмосферы жела-
тельно включение в численную модель большого числа уровней,
а с другой стороны, данные близлежащих уровней оказываются
коррелированными и потому их одновременное включение не вносит
существенно новой информации. В связи с этим делаются попытки
описания вертикальной структуры атмосферы с помощью тех или
иных аппроксимаций таким образом, чтобы эта структура была бы
наиболее полно отражена с помощью малого числа параметров.
В качестве примера такой аппроксимации можно привести по-
литропную атмосферу. В этом случае состояние атмосферы описы-
вается с помощью данных на двух уровнях. Такая аппроксимация
была использована, в частности, С. А. Машковичем при разработке
двухуровенной прогностической модели [23].
Следуя идее А. М. Обухова, Л. В. Руховец для выбора опти-
мального описания вертикальной структуры атмосферы в прогно-
стической модели предложил использовать разложения в ряды по
так называемым эмпирическим (оптимальным) ортогональным
функциям, или естественным составляющим (см. гл. VIII). В этом
случае вертикальный профиль какого-либо метеорологического эле-
мента, в частности профиль изменений высот изобарических по-
верхностей, можно описать с достаточной точностью с помощью
всего нескольких параметров.
Пусть q(ph) = qh — производная по времени, или изменение за
какой-либо интервал времени высот изобарических поверхностей
k=\, 2, ..., и; фг(рь)=фг& — естественная составляющая, или опти-
мальная функция с номером i= 1, 2, ..., п. Тогда значение qu. можно
представить в виде ряда
1 = 1
где
п
at= 2 Qk^ik (6.8)
k=l
— коэффициенты разложения, называемые статистическими векто-
рами.
Для точного представления qk на всех заданных уровнях необ-
ходимо взять п членов разложения. Однако проведенная статисти-
ческая обработка для суточных изменений высот пяти и шести
149
изобарических поверхностей (от 1000 до 200 мбар) показала, что
достаточная точность получается уже при учете всего двух членов
разложения. (Два члена разложения описывают более 85% факти-
ческой междусуточной изменчивости высот всех рассматриваемых
поверхностей.)
Учитывая это обстоятельство, можно, используя разложение
(6.7), преобразовать прогностические соотношения квазигеострофи-
ческой модели к такому виду, чтобы они содержали в качестве не-
известных не функции dHIdt, а коэффициенты разложения Есте-
ственные составляющие при этом должны быть получены
заранее в результате статистической обработки эмпирического мате-
риала. Однако подобного рода функции могут быть получены и не-
посредственно, исходя из уравнений прогностической модели. В та-
ком случае мы вместо функции будем иметь функций Xik, кото-
рые называют составляющими динамического вектора Xi (Хгк),
а вместо (6.7) и (6.8) получим:
п
qk-^XiXlk- (6.9)
1 = 1
п
Х= 2 qkxik. (6.10)
fc=l
Введя уровни k=\, 2, ..., п, произведя замену вертикальных
производных конечными разностями, делаем переход от уравнения
(6.1) к системе уравнений вида
^QkJrak-\Qk-\A'akQk-]rakA-^k + \=Pk (^=L 2, п), (6.11)
где q = dHldt, коэффициенты а определяются параметрами модели
(шаг по вертикали и пр.), а функция F — величинами AQ и Ат.
Матрице коэффициентов этой системы уравнений соответствует
п значений собственных чисел М и п собственных, или динамиче-
ских векторов Xi с составляющими Xik.
В результате ряда преобразований [28] вместо системы урав-
нений (6.11) для q получается новая система уравнений для дина-
мических векторов Xi
+ G’=1> 2, п), (6.12
где Fi определяется по значениям Fk.
Это уравнения типа уравнения Гельмгольца. Решая их, мы на-
ходим Xi, затем с помощью (6.9) — величины а затем делаем
шаг по времени.
Однако переход от Xi к qh не обязательно делать на каждом
шаге; его достаточно сделать лишь в конце прогностического пе-
риода.
Практическая реализация изложенной модели была осуществ-
лена применительно к прогнозу высот изобарических поверхно-
стей 1000, 850, 700, 500, 300 и 200 мбар. При этом в соответствии
150
с упоминавшимися уже результатами статистической обработки
эмпирических данных разложение в ряд ограничивалось двумя чле-
нами, содержащими Xi и Х3, как наиболее значимыми Следова-
тельно, модель оказалась двухпараметрической.
Испытание модели дало удовлетворительный результат. С це-
лью улучшения прогноза давления на уровне моря модель была до-
полнена учетом приземных барических тенденций [17]
§ 7. Квазисоленоидальные прогностические модели
Уравнение неразрывности в самом грубом приближении (кото-
рое строго выполняется только в случае несжимаемой атмосферы
и плоского движения) можно записать в виде
да । dv п
дх ду
Это случай бездивергентного, или соленоидального движения Пу-
тем простой подстановки легко убедиться, что в этом случае суще-
ствует такая функция ф, для которой справедливы следующие со-
отношения:
Эту функцию в гидродинамике называют функцией тока (она
имеет размерность квадрата длины деленного на время), а ветер,
определяемый приведенными соотношениями, называют соле-
н о и д а л ь н ы м.
Функцию тока можно выразить через высоту изобарической по-
верхности с помощью уравнения баланса (см. (7.6) гл. II)
(4±Г+24Е--^ + (4£-Г+«^-----------У 4^-/2=-^ АН. (7.2)
\ дх ) 1 дх ду 1 \ ду / 1 ду дх ° 47
Пользуясь выражениями и и v через ф, можно получить;
ди __ d2<p * dv_____д2ф . ()__ dv ди ___.
дх дх ду 1 ду дх ду ' дх ду
Подставляя эти и подобные выражения в уравнение баланса, по-
лучим преобразованное уравнение баланса в виде
/А, оГ^Ф ^Ф ( <?2Ф VI I д1 ^Ф , dl д^
^[дх2ду2 \дхду) |+ дх дх + ду ду ~ё
Если Н известно, то ф находится путем решения данного урав-
нения.
Следует отметить, что это уравнение является нелинейным. По-
этому оно решается приближенным методом [У.22].
Произведенные расчеты показали, что представление ветра с по-
мощью функции тока является более точным, чем представление
151
его с помощью геострофических соотношений. При этом наиболь-
шее уточнение имеет место в областях интенсивных циклонов.
Приведем краткое описание некоторых конкретных прогности-
ческих моделей, в которых используется предположение о близости
поля ветра к квазисоленоидальному.
Соленоидальная бездивергентная модель. Про-
гностическое уравнение этой модели в баротропной атмосфере
имеет вид
^ + 0- <7-4)
Это уравнение получается путем подстановки приведенных соот-
ношений соленоидальности в бездивергентное уравнение вихря
скорости (2.4).
Квазисоленоидальная дивергентная модель
получается путем подстановки соотношений соленоидальности
в уравнение (2.10) в предположении, что
дН I dty дН . дН ~
IF—i-dF’ ыЧг + г’^Г=0-
Прогностическое уравнение этой модели записывается следующим
образом:
д^г-а2-|г=-(Ф> дФ+0- <7-5)
При учете изменения масштаба карты соответствующее уравне-
ние принимает вид
'»!дф+'). (7.6)
Методы численного прогноза, основанные на приведенных уравне-
ниях, аналогичны методам численного прогноза по соответствую-
щим квазигеострофическим уравнениям. Отличие заключается
в том, что перед первым шагом по времени по известному полю Н
путем решения уравнения баланса находят функцию тока ф. Полу-
чив прогноз ф на интересующий нас момент времени, делают пере-
ход от функции ф к Н. Для этого вновь решают уравнение баланса,
но на этот раз относительно функции Н по известной функции ф.
Полученное поле Н и является прогностическим.
Квазисоленоидальная дивергентная модель прогноза получила
широкое распространение как в нашей стране, так и за рубежом.
Прогноз по этой модели рассчитывается для северного полушария
на срок до 5 суток.
Квазисоленоидальная бароклинная модель
при частичном использовании потенциальной
слагающей ветра. Модель была разработана и применялась
в прогностической работе в США. В этой модели определение ком-
понент ветра производится в несколько этапов На первом этапе
полагается, что и = —ф^, и=фх. При этом функция тока находится
152
по данным Н путем решения уравнения баланса. (Здесь и далее
нижний индекс означает дифференцирование по соответствующей
переменной).
На последующих этапах предполагается, что
«= — фу+?х. ^=Фл-+ъ>
(7.7)
где ср — потенциал скорости. При этом всегда Н=Аф, D=A<p.
Функция потенциала определяется последовательными прибли-
жениями путем решения уравнения для вертикальной скорости
и уравнения неразрывности.
Диагностическое уравнение для аналога вертикальной скоро-
сти т типа (4.9) выводится с помощью уравнения вихря скорости
и уравнения притока тепла. При этом принимается, что в уравне-
нии вихря скорости й=Аф, а в уравнении притока тепла (4.3)
дН I дф „
~~&T=Z—~dt‘ Rajiee из П0ЛУченных Двух уравнении исключается
dty/dt. С этой целью уравнение (4.2) с учетом указанной замены й
дифференцируется по £, а над уравнением (4 3) (после умножения
его на g/tpl) выполняется операция А После исключения из полу-
„ л д дф
ченных уравнении Л-^—,
получается следующее уравнение
для т:
Лт . р £2 й2х — £2 Ра дА* RK КА (7К\
где
Л--V[<“»+“’) 1><Д1+'> +<^+^> 'Т'1 1:
Ат=-^ t ] (7-9)
В качестве краевых условий принимается, что т = 0 при р = 0
и при р=Р.
Уравнение неразрывности с учетом того, что £>=Аф, записыва-
ется в виде
*=—£• (7.10)
На первом этапе принимается, что и = и^=и^ v = v^ = v^, и^=
= а<р=0. Подставляя эти выражения в и Ат и решая уравнение
(7.8), находим первое приближение для т. Подставляя найденное
значение т в уравнение (7.10) и решая его как уравнение Пуас-
сона, находим первое приближение для потенциала ф<1). Теперь
компоненты ветра принимаются следующими: и ——Ф^ + ф^» D =
=фх + ф(^. Подставляя эти компоненты в выражение для и Ат,
решая уравнения (7.8) и (7.10), определим второе приближение
функции потенциала и т. д. После нескольких приближений опреде-
ляется окончательное выражение и и v.
153
Далее определяется тенденция вихря скорости путем решения
уравнения вихря
_ _ д (Дф + /) д(Дф + /) _ z д
dt и дх v ду
(7.11)
и делается шаг по времени с помощью центрированной разности
^+8/=(Л-б^4"2 8/
(на первом шаге используется односторонняя разность).
С помощью найденного значения Qt+ы находится функция тока
путем решения уравнения Пуассона Дф = £2. Далее, решая
диагностические уравнения (7.8) и (7.10), определяют функции
Ъ+ы и фибь а затем с помощью (7.1) находят компоненты ветра.
По найденным компонентам и и v определяют Нг+ы путем решения
уравнения баланса относительно Н. Теперь делается переход к сле-
дующему шагу по времени для Н.
Вариант изложенной схемы использовался в оперативной про-
гностической работе в США. В этом варианте в качестве исходных
используются данные о высотах изобарических поверхностей 850,
500 и 200 мбар. Расчет вертикальных движений производится
с учетом влияния рельефа и приземного трения для поверхностей
650 и 350 мбар. Прогностические значения Н получаются для по-
верхностей 850, 500 и 200 мбар, а также для поверхностей 1000
и 300 мбар (с помощью интерполяции и экстраполяции).
Средняя квадратическая ошибка прогнозов по Северной Аме-
рике, составляемых по этой схеме в оперативном порядке, для по-
верхностей 850, 500 и 300 мбар в 1962—1963 гг. составляла соот-
ветственно 2,6; 3,4 и 5,1 дам. Коэффициенты корреляции составили
0,6—0,8.
Возможен другой вариант схемы, согласно которому в каче-
стве начальных привлекаются также данные о фактическом ветре.
В этом случае начальное приближение для функции тока опреде-
ляется путем решения уравнения Aa|?i = Qi, где Qi определено по
фактическому ветру. С помощью найденного значения ф1 и уравне-
ния баланса находится первое приближение для Н (Hi). Далее вы-
числяется новое значение Q с помощью соотношения
Й2—Д (Н} —Hq),
где Но — фактическое значение Н Затем снова находятся ф2 и Н2
и т. д.
§ 8. Методы прогноза, основанные на расчете агеострофических
составляющих ветра
Указанные методы, первые варианты которых были разрабо-
таны М. П. Юдиным [У.22], известны как агеострофические.
154
Одним из важнейших этапов в этих методах является расчет агео-
строфических составляющих ветра:
, \ g дН
U =u-ug=u+-^--^-,
V =V — Vg = V
g
I дх
Для этих составляющих выводятся специальные уравнения. Изло-
жим кратко основные положения, используемые при их выводе.
Продифференцируем по времени выражения для и' и v'. В ре-
зультате получим:
ди’ ди . g д%Н
dt dt I ду dt 1
dv’ dv g d%H
~dF = ~dt Г dx dt *
du' dv'
Сделаем предположение, что члены ——— и ——
значительно
меньше каждого члена правых частей
последних уравнений. Тогда:
ди g д2Н . dv g д2Н
dt I ду dt ' dt I dxdt
Подставив эти выражения в уравнения движения без учета сил
du
трения и членов вида т-^-, получим:
г / g д
1и — 7 эз
™ I ду
dv dv
дх ду '
ди . ди
Из этих уравнений исключим производную dHIdt с помощью урав-
нений притока тепла, статики и неразрывности. Последнее вслед-
ствие того, что
ди । dv __ д
дх * ду дх
/ , g дН \ . д I , .
g дН \__ ди’ . dv’
I дх ) дх ' ду ’
имеет вид
ди’ ] dv’ , dt
дх * ду др
В конечном счете получаем дифференциальные уравнения для
и' и v' с известными правыми частями. Эти уравнения сходны
с уравнением для dHIdt в квазигеострофической теории. Решая эти
уравнения с помощью интегралов или численным путем, получаем
значения и' и v'.
Существует несколько конкретных методик прогноза, основан-
ных на расчете агеострофических составляющих. Рассмотрим для
примера методику прогноза ветра и температуры К- В. Пятыги-
ной [27].
155
В качестве исходных используются уравнения движения и при-
тока тепла, записанные в виде:
дТ ( дТ , дТ \ . с2
л7"= — и Ч-'У-ч— +-77— т.
dt \ дх 1 ду / 1 Rp
Кроме этих уравнений, используются уравнение неразрывности
в приведенном ранее виде, а также выражения для и' и v'. Рассчи-
тав значения и' и у', мы можем найти значения т с помощью про-
интегрированного по высоте уравнения неразрывности
Зная в начальный момент поля и', v', т, а также и и v, мы можем
теперь с помощью приведенных уравнений рассчитать производные
по времени. После этого значения и, v и Т в каждой узловой точке
регулярной сетки в момент времени Z+б/ определяются следую-
щим образом:
7’(/ + 8/)=Г(/) + [^8/.
Далее процесс вычислений повторяется, т. е. по известным значе-
ниям ц, v, Т в момент времени /+6/ вычисляются
uf (/ + &/), v' (/+«), т (/ + &/),
а затем значения горизонтальных составляющих ветра и темпера-
туры в момент времени /4-26 / и т. д.
Начальные значения и и v, необходимые для расчета и', v',
ди dv дТ .
и могут быть взяты по данным наблюдений
dt dt dt
о ветре или предварительно вычислены по геострофическим соот-
ношениям. Заметим, что непосредственное определение и' и v' по
приведенным соотношениям вследствие больших ошибок в измере-
ниях ветра привело бы к большим погрешностям.
156
§ 9. Прогноз влажности и обложных осадков
Изложенные в предыдущих разделах методы позволяют про-
гнозировать лишь часть метеорологических элементов, а именно:
давление или высоты изобарических поверхностей, температуру
и плотность воздуха, а также направление и скорость ветра в гео-
строфическом или соленоидальном приближении. Для полной ха-
рактеристики погоды этого недостаточно. Более того, с точки зре-
ния влияния погоды на практическую деятельность человека ука-
занные элементы не всегда являются главными Чтобы полностью
охарактеризовать погоду, необходимо знать такие ее элементы, как
облачность, осадки, влажность, а также такие явления, как туман,
гололед и пр. Кроме того, необходимо знать не только крупномасш-
табные погодные условия, но и местные (локальные) особенности.
Расширение числа прогнозируемых элементов требует увеличе-
ния количества прогностических соотношений. Некоторые из таких
соотношений сформулированы и будут рассмотрены далее. С по-
мощью этих соотношений удается получить прогноз крупномасш-
табных полей влажности и обложных осадков.
Дальнейшее расширение числа прогнозируемых элементов,
а также их детализация во времени и в пространстве связаны
с переходом к движениям мезомасштаба (см. гл. VI).
Рассмотрим сначала физические основы прогноза крупномас-
штабных полей влажности и осадков в рамках предположения
о квазигеострофичности атмосферных движений. При этом ограни-
чимся лишь случаями обложных осадков.
Как известно, влага в атмосфере может находиться в состоянии
водяного пара, воды и льда. Образование облачности и осадков
связано с переходом влаги из одного состояния в другое. Поэтому
полное решение указанной задачи должно учитывать эти переходы.
Ограничимся здесь упрощенным вариантом учета этих явлений.
Положим, что испарение с водяных капель отсутствует, конден-
сация (сублимация) начинается сразу по достижению состояния
насыщения, выпадение осадков — сразу по наступлению конденса-
ции, а вся сконденсированная влага выпадает в виде осадков. При
таких условиях прогноз осадков в значительной мере будет опре-
деляться прогнозом влажности, к рассмотрению которого мы и пе-
реходим.
Из различных характеристик влажности (абсолютная и относи-
тельная влажность, точка росы и т. д.) рассмотрим удельную влаж-
ность (содержание влаги в единице массы влажного воздуха)
4=0,622^-, (9.1)
где е — упругость водяного пара в миллибарах, которая связана
с температурой точки росы Та формулой Магнуса
*(^~ 273)
е=6.Ц.10*+(Г--!”> . (9.2)
157
Здесь коэффициенты а и b в зависимости от фазового состояния
влаги (вода, лед) принимают следующие значения: а = 7,63, b =
= 241,9 для воды; а = 9,5, 6 = 265,5 для льда.
Далее будет удобным одновременно рассматривать еще и мак-
симальную удельную влажность (которая возможна при заданной
температуре Т)
qm=0,622^f , (9.3)
где ет — максимальная упругость водяного пара определяется по
формуле Магнуса, в которой вместо температуры точки росы взята
температура воздуха.
Приведенные соотношения позволяют по известным значениям Т
и Та, полученным в результате измерений или прогноза, рассчи-
тать q и qm. (Возможен также и обратный переход от q и q^
к 7 и Td.)
Процесс изменения удельной влажности может быть описан
уравнением переноса влаги (см. (2.21) гл. II)
4т"= Д7+4- , (9.4)
dt р 1 1 dz dz ’ v 7
где k' и k — коэффициенты турбулентной вязкости, m — абсолют-
ная скорость конденсации (сублимации) водяного пара, т. е. коли-
чество воды или льда, образовавшихся за единицу времени в еди-
нице объема.
Для простоты будем полагать, что турбулентный обмен отсут-
ствует.
Рассмотрим два случая: 1) Td<T, q<qm и 2) Td = T, q = qm.
Тогда в первом случае удельная влажность в движущейся ча-
стице будет оставаться неизменной и уравнение переноса влаги
приобретет вид
или
^-+-4+» >-+’>=» м
Во втором случае, когда q = qm, будет происходить конденсация
(т#=0) и уравнение переноса влаги примет вид
dqm =__
dt р
С помощью уравнения притока тепла, записанного с учетом теп-
лоты конденсации, и уравнения Клаузиса—Клапейрона, можно
найти выражение для скорости конденсации, которая оказывается
пропорциональной вертикальной скорости и некоторой функции
158
давления и температуры F (7, р). Тогда последнее соотношение
можно записать в виде
^=F(T, р)х (9.6)
или
L-^.=/7(7, р)х. (9.7)
dt 1 дх 1 ду 1 др 4 ' 7
Если dq-mldt определено, то количество осадков Q, выпавших
из единичного столба воздуха, ограниченного поверхностями pi
и р2, за время между t\ и t2 можно рассчитать по формуле А. Ф. Дю-
бюка
<2 Р2
<м>
tl Pl
Прогноз влажности и осадков может быть осуществлен следую-
щим образом. Пусть мы имеем какую-либо прогностическую схему
(назовем ее основной), которая позволяет получать на каждом
шаге по времени прогноз и, v, Т и т. Имея данные о влажности
и температуре, определяем, достиг водяной пар состояния насыще-
ния или нет.
Если состояние насыщения не достигнуто, то для расчета изме-
нения удельной влажности используется уравнение переноса влаж-
ности в форме (9.5) и с помощью полученных по основной прогно-
стической схеме значений и, v и т рассчитывается q на один шаг
времени вперед.
Если же состояние насыщения достигнуто, то рассчитывается
функция F (Т, р), а затем с помощью прогностического значения т
и скорость конденсации dqmldi на разных уровнях. Затем опреде-
ляется количество осадков, выпавших из единичного столба всей
атмосферы за шаг по времени б/.
Прогноз влажности теперь составляется с помощью соотноше-
ния (9.7), в котором значения u, v и т берутся по основной про-
гностической схеме. Далее делается следующий шаг по времени,
который начинается с проверки на состояние насыщения и т. д.
Изложенные здесь общие принципы прогнозов осадков лежат
в основе нескольких конкретных методик [1, 30].
В этих методиках используется прогноз высот изобарических
поверхностей по квазигеострофической трехуровенной модели
С. Л. Белоусова (см. § 6). Дополнительно прогнозируются бариче-
ское поле у поверхности земли по способу [24], траектории воздуш-
ных частиц, температура и вертикальные движения. В качестве ис-
ходных данных, помимо полей давления на уровне моря, его тен-
денций и высот изобарических поверхностей 850, 700, 500
и 300 мбар, необходимых для прогноза поля геопотенциала и дав-
ления на уровне моря, используются данные о температуре и тем-
пературе точки росы у поверхности земли и на поверхностях 850,
159
700, 500 и 300 мбар, полученные на станциях. Численный анализ
этих данных производится методом оптимальной интерполяции для
сетки с шагом 300 км.
Расчет осадков выполняется упрощенным способом. Прибли-
женно принимается, что в соотношении (9.8)
^Qm.
dt др
Тогда, производя в (9.8) интегрирование по р методом трапеций,
при использовании данных на поверхностях 850, 700 и 500 мбар
для одного шага по времени получаем [1]
Q=a{ &<785оЧ“#2 ^?7ОоЧ“^3 ^<7500,
где ai, аз — коэффициенты, 6q = q'm — q'^ — разность между мак-
симальными значениями удельной влажности в начале и конце
подъема насыщенного воздуха. Значения qr и q" вычисляются
с помощью (9.3) по значениям Т и Та для данного шага по вре-
мени.
Прогноз осадков рассчитывается на срок до 30 ч отдельно для
ночного и дневного времени суток. Оправдываемость прогноза об-
ложных осадков по факту их выпадения составляет около 80%.
§ 10. Учет неадиабатичности атмосферных процессов
Как уже говорилось, в атмосфере существует три вида притока
тепла: лучистый (радиационный) ел, турбулентный 8Т и фазовый
8ф. Каждый из этих видов притока тепла может быть выражен
через значения некоторых метеорологических элементов, а также
ряда параметров атмосферы и подстилающей поверхности (содер-
жание примесей в атмосфере, альбедо и т. п.). Если бы значения
необходимых метеорологических элементов и параметров были до-
статочно точно известны, то учет неадиабатических факторов
в прогностических моделях атмосферы можно было бы произвести
также достаточно точно путем расчета на каждом шаге по времени
всех составляющих притока тепла и введения их в уравнение при-
тока тепла и в соответствующие краевые условия.
В действительности целый ряд параметров атмосферы и подсти-
лающей среды, необходимых для расчета притока тепла, таких, как
содержание аэрозоля, альбедо и пр., практически остаются неизве-
стными, а значения таких элементов, как влагосодержание, тем-
пература воздуха и подстилающей поверхности, определяются
в процессе интегрирования прогностических уравнений весьма не-
точно.
Из сказанного ясно, что учет притоков тепла в численном про-
гнозе может быть произведен лишь приближенным образом
Рассмотрим некоторые из таких приближенных методов учета
притоков тепла в прогностических квазигеострофических моделях.
160
Радиационный приток тепла наиболее точно рассчитывается
путем интегрирования уравнений переноса лучистой энергии при
использовании функций пропускания. Такой способ расчета радиа-
ционного притока тепла применен, например, в работах [4, 32].
Серьезную трудность представляет собой вычисление турбу-
лентного притока тепла. Непосредственный расчет по формулам
вида
д г, д&
не дает желаемого результата вследствие недостаточности данных
о вертикальном профиле температуры и отсутствия данных о коэф-
фициенте турбулентности.
Если говорить о турбулентном притоке тепла в нижнем слое ат-
мосферы, прилегающем к земной поверхности, то наиболее досто-
верный результат можно получить на основе теории пограничного
слоя. Однако на практике широкое распространение получил при-
ближенный способ расчета турбулентного притока тепла от под-
стилающей поверхности, который реализован в квазигеострофиче-
ских моделях.
В соответствии с этим способом турбулентный поток тепла от
подстилающей поверхности вычисляется по соотношениям вида
Ят=АУо(Л-^о) или H^(a + bVQ)(Ts-T0),
где Ts — температура подстилающей поверхности, То и Уо— темпе-
ратура воздуха и скорость ветра у земной поверхности, А, а и b —
коэффициенты, подбираемые эмпирическим путем. Приток тепла
к единице объема атмосферы на высоте с давлением р вычисля-
ется по соотношению
ет=рК0(^-Г0)(-£-У ,
где Р и у — некоторые коэффициенты. Учет турбулентного притока
тепла по такому способу производится только в случаях, когда
Ts>To.
Фазовый приток тепла рассчитывается с помощью соотношения
где т — количество сконденсировавшейся или испарившейся влаги
в единице объема за единицу времени.
Сложность задачи заключается в определении величины т,
В работах по численному прогнозу учитывается лишь тепло конден-
сации. Испарением же влаги и соответствующим расходом тепла
вследствие его малости пренебрегается. На основе уравнения пе-
реноса влаги при отсутствии турбулентного обмена, а также при
условии, что конденсация начинается сразу после достижения со-
стояния насыщения, можно записать, что
11 Зак. № 21
161
где 7/П = 0,622в7П/р — соответствующая данной температуре макси-
мальная удельная влажность, ет=Е(Т)— максимальная упругость
насыщения, определяемая по температуре по формуле Маг-
нуса (9.2).
Дифференцируя функцию qm по t и подставляя результат в вы-
ражение для т, получаем
т= -0,622 ——^г\=- 0,622
* р \ dt р dt )
Р I dem
р \ dT dt
ejn dp \
p dt ) '
Используя это выражение, находим
еф=-0,622^-^-№-4^------------------
ф р \ dT dt р dt /
Возьмем теперь уравнение притока тепла при учете только фазо-
вого притока тепла в виде
dT = 7а dp . £ф
dt gp dt "Г Срр •
Если положить, что dp 1 dt известно, то последние два уравне-
ния можно рассматривать как систему для определения перемен-
ных dT/dt и 8ф. Исключая из этой системы dT/dt и делая затем не-
которые преобразования, получаем:
ср (7а 7ва) dp .
6ф i dF ’
dT_ 7ва dp
dt g$ dt ’
где ya=Ag/cP — адиабатический,
, 0,622.5%
ARpT
0,622.2* dem
cpp dT
(10.1)
— псевдоадиабатический (т. e. имеющий место при отсутствии ра-
диационного и турбулентного притоков тепла) градиенты темпе-
ратуры (уа~1 град/100 м, ува~0,6—0,9 град/100 м).
В изобарической системе координат
£Ф—
ср (7а 7ва)
------------------т-
g
(Ю.2)
дТ , дТ
dt 1 дх
дТ
ду
(7ва —7) т
(10.3)
Из выражения (10.2) следует, что для расчета £ф в зоне кон-
денсации достаточно иметь значения т и ува. Величина т может
быть получена с помощью прогностической модели, а ува— вычис-
лена по формуле (10.1).
162
урав-
(Ю.4)
вели-
тепла
Обратим внимание на то, что уравнение притока тепла с уче-
том фазовых превращений в форме (10.3) внешне сходно с
нением адиабатичности, взятым в виде
дТ . дТ . дТ (ъ-7)
—Г U -з--- V -3— = ---— Т.
dt 1 дх 1 ду др
Как видно, различие заключается в наличии в уравнениях
ЧИНЫ Уа ИЛИ Ува.
Указанное обстоятельство позволяет производить учет
конденсации без непосредственного определения 8ф. Для этого до-
статочно найти зоны с конденсацией и в этих зонах в уравнении
притока тепла вместо уа подставить ува. Такой способ учета тепла
конденсации применяется в ряде работ.
Проведенные различными авторами оценки [4, 32] показывают,
что роль каждого из всех трех видов притоков тепла в изменениях
метеорологических элементов является различной при разных ус-
ловиях. При некоторых условиях роль этих факторов может быть
существенной. Так, например, вклад притоков тепла в суточное
изменение давления и температуры может достигать 10—20%.
Рассмотрим это более подробно на примере учета радиацион-
ного притока тепла по работе [4]. В этой работе была произведена
оценка роли радиационного притока тепла в изменении давления
на основе квазигеострофической модели с применением итерацион-
ного метода решения, рассмотренного в § 6 наст, главы.
Радиационный приток тепла рассчитывался путем интегрирова-
ния уравнений переноса лучистой энергии при использовании ин-
тегральных функций пропускания.
Рассчитанные через каждые 6 ч по фактическим данным о тем-
пературе, влажности и облачности величины радиационного при-
тока тепла использовались далее в процессе интегрирования по
времени прогностического уравнения. Вычитая из полученных
величин изменений геопотенциала те изменения, которые полу-
чаются по соответствующей адиабатической модели, мы получаем
вклады притока тепла и таким образом получаем оценку роли при-
токов тепла в формировании полей метеорологических элементов
(табл. 4.1 и 4.2).
Таблица 4.1
Радиационные изменения температуры (°С/сут) в различных слоях
при различной высоте и мощности облачности
Слой, мбар Ясно Облачность задана в слое, мбар
1000900 900-500 700-500
200-0 —0,17 —0,19 —0,26 —0,26
500—200 —0,24 —0,34 —0,96 —0,79
700—500 —1,20 —1,75 —3,12 1,92
900—700 —1,20 —1,80 —0,58 —0,14
1000—900 —1,68 1,44 —0,05 —1,90
11*
163
Таблица 4.2
Изменения высот изобарических поверхностей (дам/сут), связанные
с радиационным притоком тепла при различной высоте
и мощности облачности
Поверхность, мбар Ясно Облачность задана в слое, мбар Фактическая облачность
1000-900 900-500 700-500
200 —1,40 —1,73 —3,47 —1,32 -1,76
500 —0,93 —1,29 —1,62 0,69 —1,30
700 0,00 —0,03 0,88 —0,07 —0,15
1000 1,12 1,23 0,44 —0,64 1,17
Из анализа данных этих таблиц можно сделать ряд интересных
выводов. Так, в случае ясного неба во всех слоях имеет место ра-
диационное выхолаживание, особенно сильное в нижнем слое.
В результате такого распределения притока тепла наблюдается
рост давления в нижних слоях и падение — в верхних. При этом
указанные величины составляют 10—20% общего изменения дав-
ления. В средней тропосфере влияние притока тепла на изменения
давления невелико.
Наличие облачности в нижнем слое (900—1000 мбар) приводит
к прогреву этого нижнего слоя и к усилению выхолаживания вы-
шележащих слоев. Характер изменения давления остается таким
же, как в случае ясного неба. Однако рост давления у земли и па-
дение на высотах усилены.
Увеличение высоты облаков резко меняет картину радиацион-
ного притока тепла и изменения давления. Так при облачности
в слое 700—500 мбар наблюдается падение давления в нижних
слоях. При реальной облачности в среднем по всему полю имеет
место такой же эффект, как и при ясном небе, хотя поля величин
изменений давления, обусловленных радиационным процессом,
сильно различаются.
В заключение отметим следующее. Роль каждого из видов при-
тока тепла (радиационного, турбулентного и конденсационного),
как уже говорилось, является существенной. Однако в реальных
условиях различные виды притоков тепла частично компенсируют
друг друга. Так, например, преобладающее радиационное выхола-
живание в нижних слоях частично компенсируется турбулентным
притоком тепла от более теплой подстилающей поверхности. В ре-
зультате, совместное влияние всех видов притока тепла может
оказаться даже меньше влияния какого-либо одного из них.
Из сказанного следует, что улучшение прогнозов можно получить
лишь при совместном учете всех или хотя бы главных видов при-
тока тепла.
Опыт совместного учета основных видов притока тепла в четы-
рехуровенной квазигеострофической прогностической модели, при-
менявшейся в оперативной службе погоды в Японии [38], показал,
что улучшение прогнозов составило 5—10%.
Глава V
МЕТОДЫ КРАТКОСРОЧНОГО ПРОГНОЗА, ОСНОВАННЫЕ
НА ИНТЕГРИРОВАНИИ ПОЛНЫХ УРАВНЕНИЙ
ГИДРОТЕРМОДИНАМИКИ
Основной недостаток методов прогноза, рассмотренных в преды-
дущей главе, связан с неточностью описания поля движения с по-
мощью квазигеострофического и других приближений. Особенно
отчетливо этот недостаток проявляется при процессах образования
новых возмущений в полях ветра и давления, а также при пере-
стройке барического поля. Именно при этих процессах имеют ме-
сто наибольшие отклонения фактического ветра от геострофиче-
ского или соленоидального.
Уже в 50-х годах наряду с интенсивным развитием квазигео-
строфических и других так называемых фильтрованных прогности-
ческих моделей начались поиски новых путей решения задачи
гидродинамического прогноза. Эти поиски привели к появлению но-
вого направления, в котором не используется никакого приближе-
ния относительно действительного ветра. Делается только предпо-
ложение о квазистатистичности крупномасштабных атмосферных
движений. В качестве основных уравнений при этом используются
непреобразованные («примитивные») или полные уравнения
гидротермодинамики.
Наиболее важный вклад в создание нового направления в тео-
рии прогноза был сделан И. А. Кибелем. Им было указано на необ-
ходимость учета процесса адаптации при интегрировании полных
уравнений и предложена наиболее общая прогностическая модель
на основе полных уравнений [14—16]. В то же время И. А. Кибель
показал, что в процессе интегрирования полных уравнений благо-
даря адаптации движение должно оставаться близким к геостро-
фическому.
Для разработки новых прогностических моделей важное значе-
ние имели новые методы интегрирования дифференциальных урав-
нений, предложенные Г. И.*Марчуком [У. 17].
Идеи И. А. Кибеля и Г. И. Марчука легли в основу целого ряда
прогностических моделей, разработанных советскими исследовате-
лями: С. А. Бортниковым, И. И. Булеевым, С. В. Немчиновым
и В. П. Садоковым, В. В. Быковым, В. М. Кадышниковым,
Л. В. Берковичем, Д. Я. Прессманом, М. С. Фукс-Рабиновичем,
165
В. И. Воробьевым, В. М. Дымниковым и Г. Р. Контаревым и др.
[3, 5, 6, 8—13, 19—22, 24, 25].
Интенсивное развитие методов прогноза, основанных на инте-
грировании полных уравнений гидротермодинамики, проводилось
также зарубежными исследователями. Можно указать, например,
на работы Дж. Смагоринского, Н. Филлипса, Дж. Чарни, К. Хин-
кельмана, Г. Райзера, Ф. Г. Шумана и др. [У.16; 27—36].
Создание новейших быстродействующих ЭВМ, работающих
со скоростью порядка миллиона операций в секунду, способство-
вало быстрому доведению новых прогностических моделей до ста-
дии применения в оперативной работе.
В этой главе будут изложены общие принципы, лежащие в ос-
нове методов прогноза с помощью полных уравнений. Эти прин-
ципы будут иллюстрироваться конкретными методами прогноза,
причем в начале будут рассматриваться баротропные модели, как
наиболее простые для восприятия, а затем более сложные — баро-
клинные.
§ 1. Постановка задачи прогноза метеорологических элементов
на основе полных уравнений
гидротермодинамики
Под полными уравнениями гндротермодинамики будем пони-
мать уравнения, в которых вместо уравнения движения по верти-
кальной оси принимается уравнение статики. При отсутствии тур-
булентной вязкости и притоков тепла в изобарической системе ко-
ординат эти уравнения имеют вид (см. (6.3—6.7) гл. II).
ди . ди . ди . ди дН . ,
-зт- + ^-з-Ит -з—=- £ ~з
dt 1 дх 1 ду 1 др ь дх 1 ’
dv , dv . dv . dv дН 1
—h^-з------------“3—=—------------tu:
dt 1 дх 1 ду 1 др ь ду ’
£ дН
ди . dv . дт ____~
дх ' ду ' др ’
дТ । дТ . дТ & Z1
dt ~^U дх +'1’ ду ~ Rp Т-
В качестве краевых условий по вертикали принимается непро-
никновение воздуха через верхнюю границу атмосферы и сквозь
земную поверхность, т. е.
при р=0 т=0,
п „ (дН . дН . дН\ Z1
при р=р = (1.2)
166
Рассмотрим теперь условие на границе области интегрирова-
ния Г. Необходимость в постановке таких условий возникает при
интегрировании уравнений не на всем земном шаре, а на ограни-
ченной территории.
Простейшие граничные условия при неизменности всех рас-
сматриваемых функций на границе области интегрирования не
дают удовлетворительных результатов. Наиболее обоснованно эти
условия можно поставить для случая, когда граница области ин-
тегрирования проходит вдоль экватора В этом случае можно при-
нять, что на границе нормальная составляющая скорости ветра Vn
и производные по нормали от касательной составляющей вектора
скорости Vr и от высот изобарических поверхностей обращаются
в нуль, т. е. ।
У„|г=0, 4М =°> =0- <L3>
п *г ’ дп |г • дп |г 4 7
Краевые условия (1.3) отражают известные эмпирические
факты о малости обмена воздуха между северным и южным полу-
шариями.
Рассматриваемая система уравнений содержит три производные
по времени. Это означает, что в начальный момент должно быть
задано распределение в пространстве трех функций. Эти три функ-
ции из пяти могут быть выбраны произвольно. Если, например, из-
вестными принять и, v и Н, то Т найдется с помощью уравнения
статики, а т — из'уравнения неразрывности. Действительно, ин-
тегрируя уравнение неразрывности по р и учитывая первое из гра-
ничных условий (1.2), находим
р
<и>
о
Обычно принимается, что
при /=0 и=и°, v=vG, H=HQ. (1.5)
Система уравнений (1.1) является весьма сложной, так как она
содержит ряд нелинейных членов. Получить ее точное решение
в аналитическом виде оказывается невозможным. Поэтому она ре-
шается численными (приближенными) методами.
Один из возможных путей приближенного решения данной си-
стемы заключается в следующем. Перепишем уравнения движения
и притока тепла таким образом, чтобы в левой части остались
только производные по времени, а в правой части все остальные
члены, суммы которых обозначим через fu, fv и fT:
->=л, 4=л, ^-=fr. (1.6)
Если в некоторый (в том числе начальный) момент времени функ-
ции u, v и Н известны, то можно определить Т и т, а затем и функ-
ции fu, fv и fr, а следовательно, и производные du!dty dvjdt, dTfdt.
167
Теперь, используя какое-либо приближение для производных,
можно сделать шаг по времени и найти будущие значения и, v, Т
и Н. Далее вновь рассчитывается функция т и т. д.
При таком подходе уравнения системы (1.1) никак не преобра-
зуются, поэтому такой путь решения условно можно назвать п р я -
м ы м методом интегрирования уравнений.
Несмотря на кажущуюся простоту, реализация этого под-
хода требует особой тщательности в выборе конечно-разностной
аппроксимации производных и специальной подготовки исходных
данных. Использование простейших конечно-разностных соотноше-
ний и данных непосредственных измерений, содержащих ошибки,
не могут привести к цели. Причина заключается в следующем. Рас-
сматривая правые части первых уравнений системы (1.1), а также
величин} £>, можно заключить, что они представляют собой малые
разности больших величии. В самом деле, если
o[g~)=o(k.^\o-\
то o(-g4x-+fo)=O(Z#)==10“4
(v' = v-—vg — отклонение ветра от геострофического) и если
™ о(эг+-ву)-°(с)=10^
Тогда при наличии даже относительно небольших ошибок в и
и v (независимо от причины) мы можем получить относительно
большие ошибки в величинах и', v' и D, а значит, и в величинах
правых частей уравнений (1.6) и выражения (1.4), а в конечном
счете — в определении производных по времени. В дальнейшем мы
увидим, каким образом преодолеваются указанные трудности.
И. А. Кибель [14—16] предложил такие способы интегрирова-
ния полных уравнений, при которых указанные малые разности
больших величин исключаются с самого начала. Проиллюстрируем
это на двух примерах. Рассмотрим вначале способ, когда решение
ищется для производных по времени в виде пространственных ин-
тегралов.
Введем новую независимую переменную £ = р/Р, исключим из
уравнения притока тепла температуру с помощью уравнения ста-
тики и перепишем полученные уравнения таким образом, чтобы ли-
нейные члены оказались в левой, а нелинейные — в правой части
уравнений, т. е. в виде:
ди / . дН (ди . ди . т ди \ п
dt 1 ь дх \ дх 1 ду 1 Р dl /
dv . , . дН ( dv . dv . т dv \ D
-^-+^+^-^-=-(«-^+^-37+^^)=-^;
168
d^H । __ rjf Д
dUdi + ~P X —R^T,
ди . dv । 1 дг __р
~д^~^~~д^^"Р~ дС ’
(1-7)
где
/I7'=
дТ
дх
д^Н । д^Н \
и дхдС dydt. )
— адвекция температуры.
Произведя дифференцирование уравнений движения и комби-
нируя результаты, получим уравнения вихря скорости и диверген-
ции. Кроме того, преобразуем уравнение притока тепла, исключив
из него т. В результате получим следующие три уравнения:
i /л__д .
^-^g^-lQ=AD-
д „ дШ &
R & (^т)
g Я
(1.8)
где
ди I
дх ду ’
dv du
дх ду ’
й
А - L d(Q+Z) I у d(Q+Z)
Лв—— [W дх -1-^ ду
1 г д / ( Л
Р [ дх \ д^ ) ду \ с
]_£)2_
dl , dl 1
и ду +10 дх Р
В самом общем случае можно считать, что
дФ I д?
и~ ду А дх'
(1-9)
так что
с
2=Д<|>, £) = Д?> т/Р=-(д<рЛ.
О
Предположим, что величины Ат, Aq и Ad. содержащие нелинейные
члены, в некоторый момент времени (например, в начальный)
(110)
л _ ( dD
А° дх
дх ' ду ’
169
известны. В таком случае систему (1.8) можно рассматривать
как систему из трех уравнений с тремя неизвестными: dHIdt, Q, D.
Исключая из полученной системы уравнений две какие-либо пе-
ременные, можно получить уравнение для любой из них. Так, на-
пример, уравнение для dHfdt имеет вид
Л дН . /2 д р2 д / 1 д^Н ।
л dt «2 г dz /2 а/з -г dt Я-
d [ R ^(^г)
dt [ gc2 d’Qdt
R Р
h
। i A ,lln
g c2 dt + g U-11)
Решая это уравнение и учитывая краевые условия, мы можем
получить dHfdt в виде интегралов по переменным х, yf £, t. Огра-
ничиваясь лишь изложением общего подхода к решению задачи,
мы не будем здесь выписывать эти интегралы, а дадим лишь гид-
родинамическую трактовку полученных уравнений и их реше-
ний.
Система уравнений (1.8), а также уравнение вида (1.11) описы-
вают перемещение и эволюцию как медленных крупномасштабных,
так и быстрых внутренних гравитационных волн. При этом быст-
рые волны при своем перемещении и затухании способствуют адап-
тации метеорологических полей. В то же время наличие в уравне-
ниях нелинейных членов /4q, AD и Ат отражает процесс непрерыв-
ной генерации новых волн. В результате рассмотренная система
уравнений будет описывать процесс, движения в котором имеют
характер колебаний вблизи квазигеострофического. Решая задачу
шагами по времени, мы получаем прогноз крупномасштабных дви-
жений при учете процесса адаптации и близости движения к гео-
строфическому.
Рассмотрим теперь второй подход И. А. Кибеля к интегрирова-
нию полных уравнений, когда вначале производится замена произ-
водных по времени конечными разностями, а решение ищется отно-
сительно значений искомых функций в будущий момент времени.
Исключив из уравнения притока тепла т с помощью уравнения
неразрывности, перепишем систему уравнений (1.7) в виде:
т du , dH \__
'P'~dC'S~Sx)~
dv . dv
dx 1 dy
т dv , dH \_________ j-,
~Р dZ ^£~dy~)
d„2 d_dH___c2_[_du R а(£Лг)
dC dZ dt g\dx'dy) g dC
(1-12)
Произведем теперь замену производных по времени с помощью со-
отношений:
(1-1з>
170
где dt— шаг по времени; и°, v° и HQ — значения функций в началь-
ный, п1, vl и Я1— в конечный моменты времени. Отнесем
теперь силу Кориолиса и горизонтальную дивергенцию к буду-
щему моменту времени, а силу барического градиента представим
в виде полусуммы сил в начальный и конечный моменты времени,
дН g д(Н'+Н°) дН g d(FF+H°)
т. е. положим, что g——=—---------------> g-^—=~^--------------•
дх 2 дх ду 2 ду
В результате вместо уравнений (1.12) получим;
их — I = ц° — ;
ф1 -j-1 =ф° — %tFv;
д г2 дН1 сШ / ди1 ! dv1 д cWO R д (£АТ)
dt dt g \ дх + ду )— dt dt g dt
Мы можем теперь найти решение системы (1.14) относительно
w1, v1 и FF. С помощью первых двух уравнений системы получаем:
ц1== -+ bw
'Р1= ! (ZB<)2 k0 -1 ^tu° — — 1 S^u)l • (1-15)
С учетом этих соотношений можно найти выражение для дивер-
генции. Найденное выражение подставим в третье уравнение си-
dFB
стемы (1.14). Выделив из функций Fu и Fv производные
дН1 ,
и и вернувшись к функциям Ви и Bv, получаем следующее
уравнение для искомой функции FF:
(4+“'4-+^^г+оз,4р4)("' "")=л. с-16)
где czi, а2 и аз — коэффициенты, А— комбинация функций Ат, Ви,
Bv, а также начальных значений и0, vQ и Я0.
Решив уравнение (1.16), получим будущие значения Я1. Теперь
с помощью (1.15) определяются будущие значения и1 и и1. Далее
может быть сделан следующий шаг по времени и т. д.
Идеи, содержащиеся в изложенных подходах И. А. Кибеля, на-
шли широкое применение при разработке конкретных прогности-
ческих схем. Особенно важным оказалось предложение о выраже-
нии линейных членов (силы Кориолиса и силы барического гради-
ента) через их значение не только в начальный, но и в конечный
моменты времени, т. е. предложение о применении так называе-
мых неявных конечно-разностных схем (см. приложение 6).
171
§ 2. Интегрирование полных уравнений гидродинамики
для баротропной атмосферы при использовании явных схем
Полные уравнения гидродинамики для баротропной атмосферы
возьмем в виде:
ди . ди . ди
“33--Н и -3-Г “3—
dt 1 дх 1 ду
dv . dv . dv
-dr+u-d^+v-d^
дН . дН . дН
-dr + u-dF+v~W
(2.1)
дН , f
ь дх 1 ’
дН ,
ё ду и’
\ дх 1 с
Перепишем уравнения таким образом, чтобы в левой части ос-
тались только производные по времени, т. е. в виде:
ди . ди
dv . dv
“-dr+v-df
дН
U
дх
ди
~дГ
dv
~дГ
дН
dt
ди । dv
дх ‘ ду
(2-2)
Зная и, v и Н в какой-либо момент времени t, мы можем рас-
считать значения fu, fv и fH, а следовательно, и производные по
времени. Чтобы получить значения и, v и Н в некоторый будущий
момент времени /+б/, необходимо заменить производные по вре-
мени с помощью конечных разностей. При использовании явных
конечно-разностных схем возможно несколько вариантов конечно-
разностных аппроксимаций. В табл. 5.1 приведены данные о неко-
торых из них [26].
Рассмотрим свойства и примеры применения некоторых явных
схем интегрирования.
Метод односторонних разностей вперед обеспечивает первый
порядок точности аппроксимации производных, а метод централь-
ных разностей — второй порядок (см. приложение 6). Учитывая,
что первый из этих методов дает небольшую точность аппрокси-
мации и обладает вычислительной неустойчивостью, его примене-
ние ограничивается в основном первым шагом по времени Наи-
более широкое распространение получил второй метод. К явным
схемам примыкают так называемые итерационные, или полунеяв-
ные (см. табл. 5.1). В этих схемах один шаг по времени делается
с помощью промежуточного этапа. Однако всегда правая часть,
уравнения берется явно.
В некоторых случаях для численной аппроксимации использу-
ется метод Адамса, в соответствии с которым
= (2.3>
Здесь X — любая функция, a f=dX)dt
172
Таблица 5.1
Возможные схемы конечно-разностной аппроксимации производных
по времени в прогностических уравнениях (по [26])
Методы Аппроксимация Условие устойчивости
Явные
1. Односторонних разно- Х' + ь‘ — X1 Неустойчив
стей вперед 2. Центральных разно-
xt+K_xt-*t=ftlt
стей c 8s <'1
Явные, и т е р а ц и-
о н н ы е
1. Эйлера с пересчетом х* — х‘ = /‘ы Ы С-Г7" <1
xt+it_xt== fit OS
2. Разностей назад х*—х1~^ = fu Xt+St—X‘ = f*U It C^<0.8
3. Центральных разно- X*— x‘-&t = 2f‘u
стей (трапеций) 1 / \ c Bs ’
х‘+*‘-х‘=^-(/* + /‘)ы
Неявные
1. Односторонних раз- XZ + 6Z —Xz = f‘ + &l 6/ Абсолютно устой- чив
ностей назад
2. Трапеций xz + sz— x' = 4-(/ + SZ + /0®/ Абсолютно устой-
z \ / чив
3. Частично неявный X t -f- s/ a — 8f Слабая неустой-
= 2(yz + s/ +4) Ы чивость для круп- номасштабных
волн
Примечание. X — любая функция; f=dX!dt\ St и 6s — шаги по времени
и горизонтальным координатам; с — максимальная скорость перемещения волн;
f 1 и f 2 — нелинейная и линейная части f.
Метод Адамса имеет третий порядок точности аппроксимации.
Однако для его реализации необходимо иметь значение f не
только на текущем шаге, но и на предыдущем.
Подчеркнем, что при любом из упомянутых методов конечно-
разностной аппроксимации можно выразить будущее значение
функции через известные функции непосредственно, т. е. в явном
виде.
Перейдем теперь к рассмотрению конечно-разностной аппрок-
симации правых частей уравнений (2.2). Для квадратной сетки
173
точек с безразмерными координатами i и / в простейшем случае,
например, первое уравнение системы (2.2) запишется в виде
( ‘2bS ' + j —1» j) y + 1 j — l)”t“
+g (^4-1. j — /)] +4/^7-
Такая простейшая аппроксимация при использовании явных
схем оказывается недостаточной, так как она не обеспечивает не-
обходимой точности и не фильтрует ошибки в исходной информа-
ции. Поэтому были разработаны специальные способы конечно-
разностной аппроксимации уравнений.
Для примера рассмотрим систему конечно-разностной аппрок-
симации, предложенную Ф. Г. Шуманом [34, 35]. Пусть п — любая
безразмерная координата (f, j и т. д.). Введем в рассмотрение
основные точки координатной системы, имеющие целые значения
индексов и, и промежуточные точки с полуцелыми значениями п.
Обозначим
где X имеет смысл осреднения, а Хп — конечно-разностная про-
изводная, (6Z) п — приращение координаты, соответствующей ин-
дексу п.
Можно проверить, что
X —X —(An + 1-[-2Arn4-Arn_i);
(2.5)
Применим соотношения (2.4) и (2.5) к простейшему одномер-
ному уравнению
ди . ди дН
<2-6)
и рассмотрим для примера два способа конечно-разностной ап-
ди 1 д(ии)
проксимации этого уравнения Так как и ——==—---------------, то по-
С/АС С/АС
следнее уравнение может быть записано в так называемой ди-
вергентной форме
da , 1 d (ии) _ „дН (С) 7х
dt ‘ 2 дх дх ' v '
Заменив производные на конечные разности и применив осредне-
ние, получим уравнение (2 7) в так называемой полумомент-
ной форме
—f 1 --------X —х
Ut 2~{uu)x— —gH х*
(2.8)
174
Если i и s — конечно-разностные координаты по осям х и t соот-
ветственно, то последнее уравнение с учетом (2.5) запишется в виде
। 1 Ы / 2 2 \
5 +1 5 — 1 Ч 2 • Ч-1> 5 — 1, s)
= -g*L(Hi+bs-H._b J. (2.9)
Произведем теперь в (2.6) замену производных по (2.4) и про-
изведем осреднение; причем, функцию а, стоящую перед производ-
ной по горизонтальной координате, для фильтрации ошибок осред-
ним дважды. В результате вместо (2.8) получим
u‘t + uxxuxx = -gHxx (2.10)
или, учитывая (2.5),
Щ, 5+1 “ Ui> 5-14-К^'+Ь ^4~2W/, s4“^/-1. 5) (^i4-l, 5“^i-l, 5)] =
= -g|-(//i+1>i-//z_1,s). (2.11)
Это так называемая адвективная форма с фильтрующим
множителем.
Существуют и другие конечно-разностные аппроксимации урав-
нений, но рассмотренные выше способы получили наиболее широ-
кое распространение. Отметим, что в приведенных примерах мы
можем выразить искомые (будущие) величины, в данном случае
Ui, s+i, через известные величины непосредственно, т. е. в явной
форме.
Рассмотрим теперь три прогностические модели, в которых при-
меняются явные схемы.
Прогностическая модель баротропной атмо-
сферы Ф. Г. Шумана [34]. В этой модели используются урав-
нения (2.1). Однако они записываются с учетом переменности мас-
штаба карты в виде:
Применяя адвективную форму с фильтрующим множителем, по-
лучаем следующие конечно-разностные уравнения:
«М- йху -H'v y®T;
-7жуйхуГ;
{-тлу + (й+^)] Г. (2.12)
175
Данная модель была реализована для прогноза АТ5оо в тропи-
ках, а также в северном полушарии. В последнем случае исполь-
зовалось граничное условие на экваторе (1.3).
Прогностическая модель баротропной атмо-
сферы М. С. Фукс-Рабиновича [24]. В качестве исходных урав-
нений в этой модели берутся уравнения (2.1). При этом в урав-
нениях движения производится учет горизонтальной турбулентной
вязкости, что делается путем добавления к первому и второму
уравнениям движения членов k'k'&v.
Для аппроксимации производных по времени используется ме-
тод Адамса.
Аппроксимация правых частей уравнений выполняется по ме-
тоду Ф. Шумана, изложенному ранее, а оператор Лапласа выра-
жается в виде
/+^/4-h J >4-1 “
— 2 (XV’+XI/1)]. (2.13)
176
Рассматриваемая прогностическая модель реализована для
прогноза АТ5оо по большей части северного полушария. Область
расчета представляет собой восьмиугольник с центром симметрии
на северном полюсе (рис. 5.1). Шаг по координате составляет
390 км на широте 60°. В самой короткой строке восьмиугольника
расположены 23 точки сетки, а в самой длинной строке — 51 точка.
Всего в восьмиугольнике 2181 точка. На границе области принима-
ется условие (1.3). Модель дает удовлетворительные результаты
на срок до 5 суток.
Прогностическая модель Д Я. Пресмана [21].
В этой модели в качестве исходной принимается система уравне-
ний (2.1). Конечно-разностная аппроксимация уравнений произво-
дится на основе схемы Лакса—Вендроффа. По этой схеме наряду
с основными точками сетки с безразмерными координатами ц /,
s рассматриваются промежуточные точки с полуцелыми значени-
ями координат. Аппроксимация уравнений производится при це-
лых s для промежуточных точек, а при полуцелых s — для основ-
ных. При этом недифференцируемые функции в какой-либо точке
заменяются их средними значениями в четырех окружающих точ-
ках, производные по х и у вычисляются по четырем точкам, а про-
изводные по времени заменяются односторонними разностями впе-
ред при целых s и центральными — при полуцелых s.
В соответствии со сказанным, получаем для целых s и полу-
целых z, /:
X 1 1 + s+^G + 1,/ + + h 5)»
(2.14)
для полуцелых s и целых z’, /:
(Выражения для dXjdy не приводятся, так как они аналогичны
выражениям для dXjdx.) Заметим, что аппроксимация производ-
ных'по горизонтали имеет второй порядок точности.
12 Зак. № 21
177
Модель была применена для прогноза высоты изобарической
поверхности 500 мбар для квадратной сетки из 50x50 точек (ос-
новные точки) с шагом 300 км на широте 60°. На границе прини-
малось условие (1.3). Удовлетворительные результаты получаются
при прогнозе на срок до трех суток.
§ 3. Интегрирование полных уравнений гидродинамики
для баротропной атмосферы при использовании неявных схем
При интегрировании уравнений гидродинамики методами, опи-
санными в предыдущем параграфе, все члены уравнений относи-
лись к одному исходному моменту времени. После замены произ-
водной по времени конечными разностями мы получали возмож-
ность найти выражение для искомых функций через известные
величины в явной форме.
Теперь рассмотрим другой подход к интегрированию уравне-
ний, при котором часть или все члены прогностических уравнений
относятся не только к исходному, но и к последующему моменту
времени. В результате мы получим неявную схему. Неявные схемы
по сравнению с явными обладают большей вычислительной устой-
чивостью, что в свою очередь позволяет учитывать в соответствую-
щих моделях различные эффекты без потери устойчивости счета.
Существует много разных вариантов неявных схем. Некоторые
сведения о них приведены в табл. 5.1. На практике широкое при-
менение нашел метод трапеций. Так как значения ft+Qt не могут
быть вычислены непосредственно по исходным данным, то для реа-
лизации таких схем применяется метод последовательных прибли-
жений. В качестве fMt в первом приближении принимаются зна-
чения р, а во втором — значения f, вычисленные по данным, по-
лученным в первом приближении, и т. д.
Применение неявной схемы проиллюстрируем на примере од-
ной прогностической модели
Прогностическая модель баротропной атмо-
сферы 3. И. Цквитинидзе [25]. Уравнения прогностической
модели берутся в форме (2.1). Уравнения движения перепишем
в виде (1.12) (без учета членов, содержащих производные ди!д^,
dvldt^, производные по времени заменим с помощью соотношений
(1.13), а составляющие силы Кориолиса в функции F заменим
полусуммами их значений в начальный и конечный моменты вре-
мени. В результате получим:
1 1 о I 1Ы о /г1 ।
и----2“ v =и Н—2“^------2’(rw + rJ;
li / В/ 1 о I 0 I Е7О \
V + -у- и =<v----2~и----
где F1 и F0 — значения F в конечный и начальный моменты вре-
мени.
178
Решая полученную систему уравнений, получаем:
«' {(1 - S2) «°+1 - 4 [(+F°«)+в (/ЭД};
= ТТТТ {(1 - г2) - z Ыи° - ~ [(Fxv 4- - 8 (Fxu+F°„)]), (3.1)
где & = lSt)(2.
Третье уравнение системы (2.1) перепишем в виде
дН
dt
/ диН . dvH \___ р
\ дх * ду / н ’
Заменив производную по времени конечными разностями, а функ-
цию FH полусуммой ее значений в начальный и конечный моменты
времени, получим
(3.2)
Соотношения (3.1) и (3.2) и служат основными прогностиче-
скими уравнениями модели. Так как в правых частях этих соотно-
шений стоят неизвестные функции , F1 и F1, то используется
метод последовательных приближений. В соответствии с этим ме-
тодом значения u1, v[ и FF для последующего v 4-1-го приближе-
ния определяются с помощью выражений:
(ui)4 + i = T-L_-{(l -e2)u°+/8^°-
(г)1) ' + 1=_1_|(1 — £2) —
-4[(F^+^+s (W+^l};
(3.3)
В качестве краевого условия применяется условие (1.3), а в каче-
стве начального приближения для функций F1 — их значение в на-
чальный момент времени, т. е. величины F0.
Методика была реализована для прогноза АТ5оо для квадрат-
ной области с 52X52 точки с центром симметрии на полюсе с ша-
гами по координатам 300 км и по времени 10 мин. Удовлетвори-
тельные результаты получаются на срок до трех суток.
Наряду с требованием устойчивости счета при построении раз-
ностных схем должны выполняться и другие требования, обеспе-
чивающие соответствие разностного уравнения исходному диффе-
ренциальному. Среди этих требований важнейшим является
12*
179
выполнение в разностных схемах тех законов сохранения различных
величин, которым удовлетворяют дифференциальные уравнения за-
дачи. Для баротропной модели атмосферы, описываемой системой
уравнений (2.1) с краевыми условиями (1.3), одной из таких со-
храняемых величин является сумма кинетической Я=(и2 + а2)/2
и потенциальной Ф = ^Я энергий в области интегрирования По-
кажем, что эта величина остается постоянной. С этой целью ум-
ножим первое уравнение системы (2.1) на и, второе на v, третье
на g и результаты сложим. Тогда получим
или
d ( и? 4- и2 । гТД ( । дгФ \
~dF\ 2 гф) — + "дГ")-
Проинтегрируем теперь обе части уравнения по площади S, огра-
ниченной кривой Г, на которой удовлетворяются условия (1.3)
(S) (S)
В силу краевых условий (1.3) интеграл в правой части последнего
равенства обращается в нуль. Это легко показать для частного
случая, когда граница Г представляет собой квадрат со стороной
2а, вписанный в окружность экватора на плоскости карты. Тогда
а а а а | а а
J J (-^r)dxdy= f J ^rdxJ <ыф) | ^’=°-
—а —а —а (—а j — а —а
В результате получим
Отсюда следует, что
J Г(ц2^2-+Ф)^ = const.
(«$)
Результаты численного интегрирования уравнений баротропных
моделей показывают, что приведенное соотношение в основном вы-
полняется.
Заканчивая рассмотрение баротропных моделей, отметим сле-
дующее. Предполагается, что при реализации прогностических мо-
делей по полным уравнениям в качестве начальных данных дол-
жны быть использованы значения u, v и Н в узлах сетки. Однако
ввиду практически полной невозможности получения достаточно
180
точных величин и и v по фактическим измерениям приходится
ограничиваться применением каких-либо приближений для них.
Так, например, для прогностической модели Ф. Г. Шумана в ка-
честве и и v берутся их соленоидальные составляющие, а для
прогностических моделей М. С. Фукс-Рабиновича, Д. Я. Пресс-
мана и 3. И. Цквитинидзе — геострофические.
Отсюда ясно, что необходимы поиски более точных приближе-
ний для и и v. Кроме того, для прогностических моделей по пол-
ным уравнениям исходные данные и, v и Н должны быть опреде-
ленным образом согласованы друг с другом. Это относится и
к бароклинным моделям.
§ 4. Интегрирование полных уравнений
гидротермодинамики
для бароклинной атмосферы при использовании полунеявных схем
Рассмотрим интегрирование полных уравнений гидротермоди-
намики для бароклинной атмосферы при использовании полуне-
явных схем на примере прогностической модели, разработанной
Л. В. Берковичем [3]. Особенностью этой схемы является то, что
в ней сочетаются преимущества записи силы Кориолиса в урав-
нениях движения в неявной форме с простотой реализации явных
схем.
Уравнения движения, неразрывности, статики и притока тепла
запишем в виде (см. гл. II):
ди — lv = ( du? I —m —; b \ dx 1 duv ! dun e™_\.
dt dy * dp 1 g dx Г
dv \-lu= I duv . dv2 ! dvn g¥L\.
dt m\ dx du 1 dv dx * dy 1 dy + — * dp । dp = 0; ' & dy )'
сЮ ( du® । dv® . dn® \ । / Р \х е
др pg \ р) ’
(4.1)
где 0 — потенциальная температура, Z=(cP — cv)lcP. Заметим, что
уравнения движения и притока тепла записаны в так называемой
дивергентной форме, получающейся из обычной с помощью урав-
нения неразрывности.
В качестве краевых условий по вертикали принимается:
при р=Р
при /7=0 т=0;
дН . / duH . dvH . diH \
=~5г+m Ьзг++-аг}=
(4.2)
181
На боковых границах, проходящих вблизи экватора, как и ранее,
принимается
17 । дут I п дН ~
vn г=о- —=0; -з— —о.
п ,г дп |г дп г
(4.3)
Исключив из уравнения притока тепла 0 с помощью уравнения
статики и приняв 8=0. получаем
д дН г д / диН । dvH . дтН \ дН
dt др ™ L др \ дх * ду др у~Гас др
(дН ди . дН dv . дН ди \1_____~
где а=(1—Л) 1р. В результате мы получили четыре уравнения,
т. е. первые три уравнения системы (4.1) и уравнение (4.4) с че-
тырьмя неизвестными: и, v, Н и т.
Введем конечно-разностные координаты f, /, Л, s и следующие
операторы:
^п-11’
(4.5)
где г принимает значения х, у, р, t; п — значения соответствую-
щей безразмерной координаты, а X — значения u,v,Hu т.
Конечно-разностную аппроксимацию первых трех уравнений
системы (4.1), уравнения (4.4) и второго из краевых условий (4.2)
произведем следующим образом:
Щ— lv‘-=— /n[(«2)x+(«u)y + (ul-\)P4-g-//i] = —7nFu; (4.6)
vt-\-lu= — m [(и'у)х4-(‘И2)у+(^хут:)р4-§-Яу] = — mFv; (4.7)
«xP+'i»y/’+'tp=0; (4.8)
Hpt+m [(и//).г+(®Я)у + (Яут)р]р =
= /n [H7uxPy+HxMy-VHxp\p - (4.9)
при p =--P Ht+m [c^77)^+(^77)?+(Яхут)^]=0. (4.10)
Учитывая операторы (4.5), уравнения движения можно запи-
сать в виде:
us+i~ us_x— /S/(^s+1-4-^(S_1) = — 2UmFu\
(^+1 + ^-1) = —-2btmFv.
182
Решая эту систему уравнений относительно us+i и vs+i, находим
Us + \— 1 (/^)2 { И G°02l us— 14“2/ btvs_\
— 2l(bt)2 tnFvs —2btmFus\\ (4.11)
1 = i + (767)2- (11 ~ G M2] 1 - 2/ Vus_, +
+2/ (W)2 mFus - 2ltmFvs\. (4.12>
Итак, мы получили четыре конечно-разностных уравнения
(4.9) — (4.12), которые вместе с краевыми условиями по вертикали
и условиями по боковой границе полностью определяют задачу.
Реализация выписанных уравнений производится с помощью шах-
матной пространственно-временной сетки (рис. 5.2), которую мо-
жно представить себе как комбинацию из двух вложенных с двой-
ставлена сплошными линиями, а вторая — пунктирными). При
этом на четных шагах по времени (s = 0, 2, 4, . ..) функции u, v
и Н определяются в узлах с четными г, j (i, j = 0, 2, 4, ...), а в не-
четные моменты — в узлах с нечетными /, / (г, / = 1, 3, 5, ...).
Функция т, наоборот, в четные моменты времени определяется
в нечетных узлах и т. д. При этом в начальный момент доста-
точно задать значение функций и, v и Н только в четных узлах.
Это обстоятельство позволяет производить расчеты при меньшем
числе исходных данных, чем при использовании обычной (не шах-
матной) пространственно-временной сетки.
Последовательность счета заключается в следующем. Имея
значения и и v в четных узлах, мы с помощью уравнения нераз-
рывности (4.8) с учетом первого из краевых условий (4.2) по-
лучаем значения т в нечетных узлах Далее зная значения и, v и Н
в четных узлах и значения т в нечетных, рассчитываем Fu и Fv,
а затем us+i и vs+i с помощью соотношений (4.11) и (4.12) в не-
четных узлах.
Теперь с помощью краевого условия у поверхности земли
(4.10) определяем Hs+i для изобарической поверхности
183
.Р=1000 мбар, а затем с помощью соотношения (4.9), представляю-
щего собой комбинацию уравнений притока тепла и статики,—
значения f/s+i для всех основных уровней. Далее переходим к сле-
дующему шагу по времени. Теперь, определив функции т в чет-
ных узлах, вычислим все остальные функции для четных узлов
и т. д.
Условие вычислительной устойчивости, полученное на основе
соответствующей линейной модели, имеет вид
ы2+г>2+2 J/g//). (4.13)
Изложенная методика была реализована для случая f, / = 0,
1, .. ., 56; Л = 0, 1, . . ., 10; 6s(6x, 6z/)=300 км на широте 60°;
6р^100 мбар и 6/=15 мин. Квадратная сетка точек такова, что
угловые узлы оказываются лежащими на экваторе. Прогноз ц, v
л Н рассчитывается для поверхностей 1000, 900, 700, 500, 300 и
100 мбар, а расчет т производится для уровней, расположенных
между этими поверхностями.
В качестве начальных значений и и v берутся их величины,
полученные по данным Н с помощью геострофических соотноше-
ний.
Удовлетворительные результаты получаются при прогнозе до
3—5 суток.
§ 5. Прогностические бароклинные модели при использовании
неявных схем
В прогностической модели атмосферы, рассмотренной в пре-
дыдущем параграфе, производные по времени в какой-либо точке
выражаются через те или иные функции в этой же точке с помо-
щью алгебраических соотношений. Рассмотрим теперь другой под-
ход, при котором для производных по времени будут получены но-
вые уравнения, в которые они, как и в квазигеострофической
теории, будут входить под знаком тех или иных линейных диффе-
ренциальных операторов.
Этот подход будет проиллюстрирован на примере двух прогно-
стических моделей. Общим для них является стремление путем
тех или иных преобразований получить систему «плоских» ко-
нечно-разностных уравнений, не содержащих разностей по верти-
кальной координате.
Прогностическая модель С. А. Бортникова [5].
В качестве исходных принимаются следующие уравнения (см.
(6.5 6.8) и (6.10) гл. II):
ди ) I ац2 | duv j доля дФ _ 1—
dt 1 дх 1 ду 1 dt, ' dx 1 L U
dv ! duv 1 dv2 1 dv<& дФ 111
dt дх ' ду di ду I'
184
<)2ф
~дШ
ди ! dv ! да
дх ' ду * дС
д2ф
дх дС
с)2ф \
(5.1>
где Ф=§Н, (i>=x/P. В качестве краевых условий принимается
io=0 при С=0 и С=1. (5.2)
Разобьем атмосферу на пять слоев с помощью шести уровней
k = 0, 1, 2, 3, 4, 5, которым соответствуют £ = 0; 0.3; 0,5; 0,7; 0,85
и 1,00, и запишем уравнения движения и неразрывности для уров-
ней £ = 0,3; 0,7 и 1,0, а уравнение притока тепла — для уровней
£ = 0,5 и 0,85. В результате получим 11 уравнений. Для примера
выпишем здесь первое из уравнений движения
+ (Л=1, 3, 5).
dt ‘ дх k дх ду \ дС )k v 7
Производные по вертикали, входящие в уравнения движения,
неразрывности и притока тепла заменим конечными центральными
разностями вида
где = — Zk-i- При этом учтем краевые условия (5.2).
Примем в качестве расчетных уровни 1, 3 и 5, положим, что:
^2=~g” (^i+^з); ^2="2" (^i+^з); ф2="2- (ф1+фз);
и4=-^-(и3-[-и5); У4=4'(г’3+'г'5): ф4—+фз)
и введем новые неизвестные:
t7=aiUi4“a2^3~ba3^5;
1 , ч
tt 2 (^3 ^5/’
У=а^ 4- «г^+аз^;
^=-4- (^3—^5);
Т/=И1Ф1-]-®2Ф3_ЬаЗФ5> Л = “2-(Ф1 Фз)»
л=4-(ф3—ф5),
где ai, а2, аз — коэффициенты для соответствующих уровней
185
Для новых переменных, а также для со2 и С04 получаем 11 урав-
(5.3)
dt 1 дх 1 dt 1 ду 1 z ' 7
-F+^=o; (5.4)
дх 1 ду ’ v 7
ди । dh , dv . dh . z л z- r\
-ar + ^F-to=O1’ -Эг + -^-+/ы=°2; (й-5)
4т—г Г2 (4^ + -^-}=а3-, (5.6)
dt ' \ дх 1 ду ) г’ 7
ди 1 dh dv 1 dh > z /г-
-зт-4--^-1^—ал, -хт“ + ~х—\-lu=a5- (5.7)
dt 1 dx 4 dt 1 dy 1 °’ v 7
d/z 1 rv> I du 1 dv 1 zr o\
“XT—Г™ -3--—5— =^6i (5.o)
dt 1 у dx 1 dy ] °’ 7
0'5[(тг+тг)+°’3(-^+4)]; (5-9)
°.15[(-й-+^)+1'7(#+-^)]. <s'°)
где Г2 и Г2 — постоянные, А и а — некоторые известные функции.
Принимая во внимание уравнение (5.4), можно ввести такую
функцию тока, что
U=—^=4г-- (5-11)
ду 9 дх х 7
Дифференцируя соотношения (5.3) по х, а затем по у, скла-
дывая и вычитая результаты, получаем уравнения типа уравнения
вихря скорости и баланса. После замены U и V через функцию
д (dU dV\ „
тока при условии, что ===^1 они ПРИМУТ ВИД:
12Л_ Mil в (5.12)
dt L дх ду J Lv 7
(5.13)
\ dx dy / 1 \ dx 1 dy / dy 1 dx v 7
Для численного решения уравнений (5.5—5.8) применим неяв-
ную схему. Производные по времени представим в виде
jgL=-L(Afi-Afo), (5.14)
где М — любая функция, Л4° — функция в начальный момент, АР —
функция в момент времени б/.
186
Уравнения (5.5—5.6) и (5.7—5.8) после замены в них произ-
водных по времени будем рассматривать как две системы уравне-
ний с тремя неизвестными. Рассмотрев вначале уравнения движе-
ния и применив прием, описанный в § 1 при выводе формул (1.15)
настоящей главы, получим выражения для u1, v1 и u1, vl через h
и h соответственно вида (1.15). Подставив эти формулы в уравне-
ния (5.6) и (5.8), мы получим следующие выражения для h и h
в будущий момент времени, т. е. для ft1 и h':
(5.15)
где Xi и л2— постоянные, a fi и f2— известные функции
Уравнения (5.15) являются уравнениями типа уравнения
Гельмгольца. Решая их, мы находим hl и /г1, а используя преды-
дущие уравнения — и все остальные искомые функции.
Примененная неявная схема позволяет использовать большие
(до 3 ч) шаги по времени.
Изложенная методика была реализована для прогноза давле-
ния на уровне моря и высот изобарических поверхностей 850, 700.
500 и 300 мбар, а также вертикальных движений для сетки из
26x22 точек с шагом 300 км на срок до 36 ч.
Прогностическая модель В. М. Кадышникова
[12—13]. Введя новую переменную g=l—£, заметим, что для
любой функции М справедливо равенство
(1~0 +М. (5 16)
Уравнения движения, статики, неразрывности и притока тепла пе-
репишем в виде:
дим ди । dtfi . duv । дФ /«г, f 1 •
д£ dt ‘ дх * ду ’ дх г и J ,
dv<* di dv j dt 1 duv дх , av2 1 ду 1 дФ dy +/Ы=/2;
<5(1- 6)Ф _ =RT- Ф = =/3;
v 7 \ дх 1 ду / J ’
д (1—£) (аТ _,< I дТ . диТ j диТ
дЬ ~~ ' дх 1 дуГ)~
—1_ г]=/5
L g 1 J У ‘
187
В качестве краевых условий примем:
при В=1 со—О,
с. п — 1 ( дФ । дФ . дФ \ /г 1 о\
при $=0 (5.18)
где Ti — средняя температура атмосферы.
Применим теперь метод интегральных соотношений, который
позволит получить уравнения, не содержащие дифференцирования
по вертикальной координате. Поясним идею этого метода. Легко
видеть, что каждое из уравнений (5.17) имеет вид
-g-=/0), (5.19)
где z— любая функция. Имея в виду решение задачи для п уров-
ней, представим функцию f (g) в виде ряда
п
(5.20)
k = 0
и разделим промежуток интегрирования по g на п отрезков с по-
мощью точек go = O, gi, .. ., gn = l. Значения функций z в точке gt-
обозначим через Zi. Для определения п-Ы коэффициентов за-
пишем равенство (5.20) для каждой из и+1 точек. В результате
получим п+1 уравнений, которые запишем в виде
(s=0, 1, .... /г).
/г = 0
Решив эту систему уравнений, получаем
п
^ksfsi
5 = 0
где bks—числовые коэффициенты. Подставляя найденные коэф-
фициенты ah в (5.20), а затем в (5.19), находим
-$-= % (2 В*.
04 k = 0 \s = 0 /
Интегрируя эю выражение по g от 0 до gi, получаем
п / п \ ^4-1
^0 = 2L I bksfs j ’ । .
fc = 0 \5 = 0 / R • 1
Изменяя порядок суммирования и обозначая
П
ct'is== 2 bks , . 1 ,
k = 0 “ *" 1
получаем
^0 & is/s 1 • • •> fl).
5 = 0
188
Последнее соотношение можно рассматривать как систему п урав-
нений для определения функций fs по значениям Zi, а также fo-
Решая эту систему, получаем
iPiA+p./o (/=1. 2, .... «),
5^0
где Pi — некоторые новые коэффициенты.
Полученное соотношение применим теперь к каждому из урав-
нений (5.17) по п раз (к уравнению статики п—1 раз). Приэтом
учтем краевые условия (5.18), а также, что гп==0 (так как в этом
случае 1—g = 0). В результате вместе с краевым условием у зем-
ной поверхности мы получим 5Хп уравнений.
Выпишем для примера уравнение, получающееся из первого
уравнения движения
duj . dw* dujVj . дФг
dt ’ дх ду дх
lVi~s^Q + ду ) >
где А и В — коэффициенты.
Для решения полученной системы уравнений производные по
времени заменяются односторонними разностями по формуле
(5.14). В уравнениях движения слева оставляются только будущие
значения и и v, а также члены, содержащие силу Кориолиса. Ре-
шая полученную систему двух уравнений относительно и и v,
получаем для них выражения вида (1 15) и, таким образом, при-
ходим к неявной схеме.
Подставляя полученные выражения для и и v в другие урав-
нения системы и исключая последовательно неизвестные, в конеч-
ном итоге получим п уравнений для какого-либо одного неизвест-
ного.
Отметим, что полученные уравнения будут содержать диффе-
ренциальные операторы Так, например, уравнение для изменения
геопотенциала 6Ф = 6/дФ/д/ получается в виде
\ дх ду } 1 1
+ 1 +sg5Z2 (/=0, 1. .... я-1), (5.21)
где а, Ь — коэффициенты, a, j — числовая матрица, — некото-
рая комбинация линейных-и нелинейных членов исходной системы
уравнений. То, что правая часть уравнения (5.21) не содержит
производных по вертикали, и является главным достоинством дан-
ного метода.
После нахождения геопотенциала находим и остальные функ-
ции. Неявность схемы позволяет получить устойчивое решение при
шаге по времени в 1 ч.
189
Изложенная методика была реализована для сетки из 26X
Х22 точек с шагом 300 км применительно к трем и пяти уровням,
включая уровень моря, на срок до 36 ч. Модель была дополнена
расчетом влажности и осадков [12] с помощью соотношений
(9.1-9.3) и (9.5—9.8) гл. IV
§ 6. Прогностические модели при использовании сг-системы
координат
До сих пор мы рассматривали уравнения гидротермодинамики
атмосферы в изобарической системе координат. Эта система коор-
динат удобна при разбиении атмосферы на слои в зависимости от
содержания в них массы воздуха. Кроме того, измерения метео-
рологических элементов относятся к стандартным изобарическим
поверхностям, непосредственно связанным с указанной системой
координат. Следовательно, начальные данные могут быть заданы
непосредственно для выбранных координатных плоскостей.
Однако эта система неудобна при разбиении атмосферы наслои
с различной массой воздуха. Такое деление атмосферы необходимо
при учете особенностей слоев атмосферы, обладающих какими-
либо специфическими свойствами. К числу таких слоев можно от-
нести, например, стратосферу с ее изотермией, тропосферу с более
или менее постоянным вертикальным градиентом температуры,
планетарный пограничный слой и т. д. В этом отношении
более удобной является так называемая о-система координат,
введенная впервые Н. А. Филлипсом [32] (см. подробнее § 6,
гл. II).
В качестве вертикальной координаты в этой системе принима-
ется e = plps, где ps — давление на какой-либо фиксированной по-
верхности. В качестве такой поверхности может быть взята зем-
ная поверхность или поверхность тропопаузы. В частном случае,
когда ps = P =1000 мбар, о = £ = р/Р.
Уравнения гидротермодинамики и краевые условия в этой си-
стеме координат (см формулы (6.20) гл II) возьмем в виде:
ди , (ди , ди . дН . дп \ . • ди / । г? п
-з-—\-т и -з——кй’-з— /^4-/7х=0;
dt 1 \ дх 1 ду 1 ь дх 1 р дх ) 1 да 1 х ’
dv . [ dv . dv . дН . дп \ . • dv . z . — п
д I /-\ дп
g^+cpQ^=0;
дв . / d0 . d0 \ । • d0 10 п
~з-—\-т и -з—-------тг е=0;
dt 1 \ дх 1 ду ) 1 да срр Т
4Ш+» [4(“»+^(^)]<)=» <6 •>
190
где п= (p/P)r/cp; Fx и Fy — ускорения, обусловленные турбулент-
ной вязкостью; e^deldt.
о=0 при о=1 и о=0 при p=ps и /7=0. (6.2)
Рассмотрим теперь несколько вариантов интегрирования дан-
ной системы уравнений.
Прогностическая модель Национального ме-
теорологического центра (НМЦ) США (модель Ф. Г. Шу-
мана и Дж. Б. Ховермейла) [35]. Атмосфера разбивается на че-
б -р~Ро
^"Рг-Ро
Стратосфера
180
Рис. 5.3. Вертикальная структура атмосферы прогностиче-
ской модели Национального метеорологического центра
США [35].
тыре основных слоя: тропосферу, стратосферу, планетарный по-
граничный слой и слой постоянной потенциальной температуры
(рис. 5.3). Для каждого из этих слоев вводится собственная вер-
тикальная координата о=(р — рв)/рн— рв, где рн — давление на
квазигоризонтальной нижней поверхности рассматриваемого слоя,
Рв— давление на верхней поверхности слоя (см. рис. 5.3). С по-
мощью координатных плоскостей о = const тропосфера делится
еще на три, а стратосфера — на два слоя. Всего таким образом
вводится в рассмотрение восемь поверхностей, включая поверх-
ность земли, верхнюю границу планетарного пограничного слоя,
тропопаузу и фиктивную поверхность с нулевым давлением.
На плоскости карты стереографической проекции вводится сеть
из 2621 точки (53x57) с шагом 381 км на широте 60° (рис. 5.4).
191
На линиях, проходящих между последними и предпоследними
строками и столбцами сетки, ставится условие жесткой стенки,
т. е. условие непроникновения воздуха и условие симметрии для
некоторых элементов Практически принимается, что на этих ли-
ниях
. г д\\ д® д (др \ р
п дп дп дп \ да / ’
Рис. 5.4. Сетка точек прогностической модели Национального метеоро-
логического центра США [35].
Сила турбулентной вязкости учитывается только в пограничном
слое и описывается приближенно с помощью выражений:
1
Fx=-g-CD(U2+z-2)2 и-
1
Fy=-gi-CD(U2+^2)2^,
где pi — стандартная плотность воздуха на уровне моря, 6pi =
= 50 мбар, CD — коэффициент, подбираемый эмпирически.
192
Из всех видов притока тепла учитывается только турбулентный
приток тепла от поверхности океана в пограничный слой, для ко-
торого приближенно принимается
срг 1
где Tw— температура поверхности океана, @ — потенциальная тем-
пература воздуха у этой поверхности, К—10~4 с-1 — коэффициент,
подбираемый эмпирически.
Исходные данные для прогностической модели готовятся в два
основных этапа. На первом этапе производится численный анализ,
в результате которого получают значения высот основных изоба-
рических поверхностей, а также температуры на некоторых из них
для точек, входящих в восьмиугольную область (рис. 5.4). Значе-
ния геопотенциала и температуры для точек, не входящих в вось-
миугольник, берутся на основании климатических данных. На вто-
ром этапе по исходным значениям в указанных точках с помощью
специальной интерполяции находятся соответствующие значения
метеорологических элементов для поверхностей в о-системе коор-
динат. При этом производится специальный анализ высоты тропо-
паузы.
Начальные значения компонент бездивергентной части ветра
находятся с помощью уравнения баланса, а дивергентной части —
с помощью уравнения для т в квазигеострофической модели. В дру-
гих вариантах используются также и данные о фактическом
ветре.
Конечно-разностная аппроксимация уравнений (6.1), а также
краевых условий производится по способу Ф. Г. Шумана, описан-
ном в § 2.
Прогностическая модель позволяет рассчитывать прогнозы на
несколько суток.
Прогностическая модель Д. Я. Пресмана [22].
В качестве исходных уравнений берутся уравнения, аналогичные
уравнениям системы (6.1) (при Fx = Fy = z =0). Используя верти-
кальную координату о = р/Р«, атмосфера делится на 10 равных
слоев плоскостями ok = const (о0 = 0,05, 05= I; & = 0, 7г, 1, 3Д, •
.. ., 5), а на плоскости карты стереографической проекции нано-
сится квадратная сетка из 52X52 точек с центром симметрии
в Северном полюсе и с шагом 420 км на широте 60°.
Вычислительная схема аналогична схеме, описанной в § 2 на-
стоящей главы. В качестве исходных данных используются геопо-
тенциал и скорость градиентного (геоциклострофического) ветра.
Прогноз на срок до трех суток рассчитывается для поверхностей
100, 200, 300, 500 и 700 мбар и для уровня моря.
Прогностическая модель М. С. Фукс-Рабино-
вича и С. О. Крич а ка [18]. Исходные уравнения модели ана-
логичны уравнениям системы (6.1) (при Fx = Fy = &=0). Атмо-
сфера делится на два слоя: стратосферу и тропосферу, внутри
которых в качестве вертикальной координаты принимается
13 Зак. № 21
193
соответственно <з=р1рт и от = (р— РтЖрв — рт), где рт — давле-
ние на уровне тропопаузы.
Стратосфера и тропосфера делятся на два и четыре слоя соот-
ветственно. Всего, таким образом, в рассмотрение вводится шесть
уровней, включая уровень земной поверхности (04=1).
Интегрирование производится для восьмиугольной области
(рис. 5.1), охватывающей большую часть северного полушария.
Шаг сетки составляет 390 км на широте 60и.
Вычислительная схема аналогична соответствующей схеме ба-
ротропной модели М. С. Фукса-Рабиновича, описанной в § 2.
В качестве исходных данных принимаются высоты основных
изобарических поверхностей и геострофический ветер
Удовлетворительные прогнозы получаются на срок до трех
суток.
10-уровенная прогностическая модель Ф. Буш-
би и М. Тимпсон [27]. Эта модель разработана и применяется
в метеослужбе Англии для прогноза метеорологических элементов,
в частности фронтальных осадков. Система полных уравнений гид-
ротермодинамики, включая уравнение переноса влаги в атмосфере,
записывается с учетом членов, учитывающих горизонтальный и
вертикальный турбулентный обмен, притоки тепла вследствие кон-
денсации и конвекции, а также приземное трение и орографию.
Атмосфера разбивается на 10 равных по массе слоев. Горизон-
тальная сетка включает 95X63 узла на карте стереографической
проекции для каждого уровня с шагом 50 км. Для аппроксимации
горизонтальных производных применяется экономичная шахматная
сетка. Подготовка начальных данных для 10-уровенной модели
состоит из следующих этапов:
1) анализ геопотенциала и относительной влажности для стан-
дартных поверхностей от 1000 до 100 мбар.
2) интерполяция значений этих метеоэлементов для уровней,
используемых в модели,
3) расчет составляющих ветра с помощью уравнения баланса,
4) определение вертикальной скорости из диагностического
уравнения для этой функции.
Модель дает хорошие результаты при прогнозе барического
поля и осадков на срок до 36 ч.
§ 7. Интегрирование полных уравнений гидротермодинамики
методом расщепления
До сих пор в этой главе рассматривались прогностические мо-
дели, в которых интегрирование уравнений производилось без ка-
кого-либо их существенного преобразования. Рассмотрим теперь
другой подход, когда перед интегрированием исходная система
полных уравнений разбивается на несколько более простых систем,
решаемых последовательно, причем каждая из них описывает не-
которую вполне определенную часть изменений метеорологических
194
элементов. Этот подход был предложен и развит Г. И. Марчуком
[У.17].
Рассмотрим этот метод на примере адиабатической модели без
учета турбулентной вязкости, а также малых членов, содержащих
производную dxldp. Уравнения модели запишем в виде:
gHx\
ut-\-uvx-\-vVy — lu= —gHy;
Tt+uTx+vTy=c\\Rp-
T=-gpHp\R. (7.1)
Здесь и далее индексы х, у, р, t означают частные производные
по соответствующим переменным.
В соответствии с методом расщепления система уравнений
(7.1) заменяется двумя системами уравнений:
щ-\-иих-]-х)иу=0\
Tt+uTx+vTy==Q (7.2)
и
ut-\-lv= — gHx;
Ъ1 — 1и=—ёНу-,
Tt=c^lRp-,
«х+^у+1:р=0; Т-— gpHp\R. (7.3)
Система уравнений (7.2) описывает горизонтальный перенос
метеорологических субстанций вдоль потока, а система уравнений
(7.3) —адаптацию метеорологических полей. Заметим, что каждая
из систем уравнений (7.2) и (7.3) проще, чем исходная система
уравнений (7.1): при этом система уравнений (7 3) оказывается
линейной.
Если сложить соответствующие уравнения этих систем, то по-
лучим систему, которая будет отличаться от (7.1) лишь тем, что
члены с производными по времени окажутся в ней удвоенными.
Это различие будет учтено в ходе решения систем путем соответ-
ствующего изменения величины шага по времени.
Рассмотрим вначале систему уравнений (7.2), которую запи-
шем в виде
(7.4)
где вектор ср имеет вид
и
13*
195
Для простоты рассмотрим вначале следующее уравнение
(7.5)
При этом вначале и будем считать известным. Решая задачу ша-
гами по времени, каждый шаг по времени $t = ts+i— ts разобьем
на два равных интервала.
На первом из них 1 уравнение (7.5) аппроксимируем
разностным уравнением первого порядка точности по обеим пере-
менным с односторонне-направленными разностями
при
при
(7.6)
где d//2dx. Обратим внимание на то, что член ф.х записан
неявным образом. Легко убедиться, что уравнение (7.6) можно за-
писать в виде
-2^+v+cz?^iT=-^> (7-7)
где
ai=\ l+iv, 1 “hli1/1;
^=Ы-н;
Полученное соотношение представляет собой алгебраическую
систему уравнений (/ = 0, 1, .. ., и), являющуюся разностным ана-
логом линейного обыкновенного дифференциального уравнения на
некотором отрезкедля функции ф 2 .Это уравнение имеет
второй порядок по переменной, отвечающей индексу i, и решается
при заданных на концах отрезка значениях ф(0) и ф(%п).
Число алгебраических уравнений системы (7.7) равно числу то-
чек сетки на рассматриваемом отрезке; каждое из уравнений си-
стемы, отвечающих внутренним точкам отрезка, содержит значе-
ния искомых величин в трех соседних точках, а уравнения, отве-
чающие крайним точкам, — в двух.
Существует весьма экономичный способ решения на ЭВМ ал-
гебраических систем уравнений данного специального вида, на-
зываемый методом факторизации. Решение системы уравнений
этим методом состоит в том, что сначала во всех точках сетки по-
следовательно от меньших номеров i к большим рассчитываются
и запоминаются значения некоторой вспомогательной функции Zi
по рекурентной формуле
г* + 1= 2^/—Д/ ’ z=1, 2’ •••’ ^i=cp(O),
196
а затем, используя найденные значения z-i, от больших номеров
i к меньшим находятся значения искомых величин ци по рекурент-
ной формуле
?i=₽i+i'fi+i+^+i; Z=/z —I. «-2, .... 0; ?„=?(л„).
Входящие в эти формулы коэффициенты не зависят от <р{
и рассчитываются заранее по рекурентной формуле:
.....»"'! ₽‘=°-
Метод решения будет устойчивым, если ai + d^2bi. Это условие
выполняется, так как щ + d = 21 pd .
Можно показать, что формально разностное уравнение (7.7)
аппроксимирует уравнение
ш?х=- kyXX)
где
, w2 В/ . I и I
Таким образом, аппроксимация уравнения (7.5) разностной схе-
мой (7.7) приводит к появлению эффекта фиктивной или счетной
вязкости, причем величина коэффициента вязкости k может быть
очень большой, что приводит к сглаживанию метеорологических
полей.
На втором интервале t производится коррекция
полученного решения с помощью схемы с центральными разно-
стями, имеющей второй порядок точности
l?* + 1=V-tJ-z(?z+i2(7.8)
В целом комбинация схем (7.7) и (7.8) приводит к аппроксима-
ции второго порядка точности по переменным t и х и является
счетно-устойчивой. При этом (7.8) ликвидирует эффект фиктивной
вязкости.
Рассмотрим теперь вопрос о граничных условиях. Простой ана-
лиз показывает, что если на обеих границах, т. е. при х = 0 и х =
=хп вектор скорости направлен из области расчета, то граничные
условия оказываются излишними. Если же на какой-либо из гра-
ниц или на обеих вектор скорости направлен внутрь этой области,
то требуется задание искомой функции. В том случае, когда это
оказывается необходимым, граничные условия ставятся следую-
щим образом:
<Рл=<Р (*«)>
где —заданная функция.
Рассмотренная схема с двумя этапами называется схемой
«предиктор — корректор».
197
Вернемся теперь к решению системы уравнений переноса (7.2)
или соответствующему ей уравнению (7.4) и системы уравнений
адаптации (7.3). Разбивая шаг по времени на две части, сначала
решим уравнение переноса, в результате чего получим значения
элементов <p(u, v, Т) для момента S + V2. После этого, решая урав-
нения адаптации, находим значения всех элементов в момент вре-
мени 1.
В соответствии с методом расщепления первую часть задачи
решаем в два этапа по уже рассмотренной схеме «предиктор —
корректор». Рассмотрим сначала этап предиктора, охватывающий
промежуток времени 6Z/4 между моментами s и S + V4. Имея
в виду зависимость искомой функции от двух переменных прост-
ранственных координат х и у — разобьем рассматриваемый интер-
вал времени 6//4 еще на два, каждый длительностью по St/8.
В пределах первого из этих интервалов будем учитывать перенос
только по оси х, а в пределах второго — по оси у. Тогда расчет
на этапе предиктора сведется к последовательному решению двух
одномерных уравнений адвекции типа (7.5): сначала по перемен-
ной х, а затем по у.
Введем конечно-разностные операторы
V*?=?*+!— <р*-ь
где k — любая из конечно-разностных координат i или /.
Тогда на этапе предиктора последовательно решаются следую-
щие конечно-разностные уравнения:
s+4 * » s. *+-4
? 8=? — 457 и М 8;
ср 4=<р 8___^Ara? 4, (7 9)
где оператор Д^ имеет вид
f А-й при ^>0;
| при us <0.
Аналогичный смысл имеет и оператор Д™. При решении каж-
дого из уравнений (7 9) используется метод, рассмотренный на
примере уравнения (7.5). В результате мы получаем значения ср
для момента S + V4.
На втором этапе решается разностное уравнение схемы кор-
ректора, которое имеет вид
? =?-----48Г'“ Vm<f> /• (7-10)
Имея значения ср + 2 т. е. и, v и Т для момента времени
198
s + V2 (или t+ д//2), мы можем теперь перейти к решению второй
части нашей задачи, т. е. к решению уравнений адаптации (7.3)
и получению значений всех рассматриваемых переменных для мо-
мента времени s+1. Для этого запишем систему уравнений (7.3)
в конечных разностях, используя неявную схему. Производные по
времени запишем с учетом того, что значения переменных в мо-
мент S + V2 уже определены на этапе «предиктор — корректор».
Члены уравнений, не содержащие производных по времени, отне-
сем к моменту s+1. Соответствующие системе уравнений (7.3)
конечно-разностные соотношения примут вид:
54-1 +
WS+1— V + 2 , s + 1 + 1
-----_----------lu = gHy ;
5 . _L
7's + 1 _ T + 2_C2 J + L
It Rp T ’
Wx+1+^+1+^+1=O; Ts'+'=-^pHs+}. (7.11)
Данная система из пяти уравнений содержит пять неизвестных.
Из этих пяти уравнений получим одно уравнение для Hs+l. С по-
мощью первых двух уравнений системы выразим us+i и vs+1 через
Hs+i. Затем, заменив в третьем уравнении Ts+i на Hs+i с помощью
уравнения статики, выразим ts+1 через Hs+i. Подставив получен-
ные выражения для us+i, vs+i и ts+1 в уравнения неразрывности,
получим уравнение для Hs+i
-h (•£ тг)+-AF [д"‘+'+и м;; ‘’ >1-
g др \ с2 ) 1 g№ L i у ।
/ . 1 . 1 \ / ,1 , 1 \1
—|— lb£\Uy —Vx —lx^ )J >
где d2=l + (/до-
полученное линейное дифференциальное уравнение в частных
производных по х, у, р для ns+1 сходно с уравнением для — -
в квазигеострофических моделях прогноза. Оно решается методом
биортогонализации при соответствующих краевых условиях. С по-
мощью найденных значений Hs+l и уравнений системы (7.11)
определяются все остальные неизвестные.
Изложенная методика была реализована в ряде работ, напри-
мер, в работах [11, 19].
199
§ 8. Учет неадиабатических
факторов
В связи со сложностью учета неадиабатических факторов
в прогностических моделях исследования в этой области носят
главным образом поисковый характер
Здесь, как и в § 10 гл. IV, будет рассмотрена такая постановка
задачи, при которой величина притока тепла рассчитывается не-
зависимо от системы прогностических уравнений, а затем учиты-
вается при решении этой системы путем подстановки найденной
величины в соответствующий член уравнения притока тепла. Если
при этом расчет притоков тепла проводится при использовании
изменяющихся со временем фактических значений метеорологиче-
ских элементов, то неадиабатическая модель может быть только
диагностической.
Рассмотрим, следуя работам [1, 2], сначала влияние радиаци-
онного, а затем турбулентного притока тепла на изменение давле-
ния и формирование барических полей на северном полушарии.
Это влияние изучалось на основе шестиуровенной прогностической
модели по полным уравнениям гидротермодинамики, описанной
в § 4, при интегрировании по времени до трех суток. В уравнении
притока тепла системы уравнений (4.1) принималось, что е=ел +
+ ет, причем для изучения влияния каждого из притоков тепла
в отдельности полагалось последовательно ет = 0 и сл = 0.
Радиационный приток тепла для отдельных слоев прогности-
ческой модели рассчитывался заранее по фактическим данным
о температуре, влажности и облачности при учете альбедо подсти-
лающей поверхности и облачности путем интегрирования уравне-
ний переноса лучистой энергии при использовании интегральных
функций пропускания (см. § 4 гл. II).
При интегрировании уравнений по времени (до трех суток),
приток тепла рассчитывался только для одного момента в каждые
сутки. При этом использовались средние для данных суток значе-
ния температуры, влажности и облачности.
Интегрируя уравнения при одних и тех же начальных данных
о геопотенциале один раз по неадиабатической модели, а второй —
по адиабатической и производя вычитание полученных значений
метеорологических элементов, получаем величины вкладов притока
тепла.
В табл. 5.2 приведены средние величины вкладов радиацион-
ного притока тепла в изменение за трое суток давления на уровне
моря и высот изобарических поверхностей 500 и 100 мбар, вы-
численных для всего полушария и отдельно по широтным зонам,
а также величины изменений средней температуры слоя, располо-
женного между изобарическими поверхностями 100 и 1000 мбар.
Из данных таблицы следует, что вследствие радиационного при-
тока тепла в среднем по полушарию давление на уровне моря ос-
тается неизменным, а изобарические поверхности понижаются и
тем сильнее, чем выше поверхность. При рассмотрении вкладов
200
Таблица 5.2
Средние величины вкладов различных видов притока тепла в изменение
давления на уровне моря (мбар), высот изобарических поверхностей (дам)
и средней температуры (°C) слоя 100—1000 мбар за трое суток в период
с 0 ч 25 по 0 ч 28 марта 1968 г.
Приток тепла Величина Северное полушарие п = 1625 Тропическая зона (<р < 40°) п = 1093 Умеренные широты п = 414 Полярная зона (<р" 67°) 118
Радиационный Н 100 —8,6 - 7,3 -11,1 -12,8
^500 - 3,8 -3,6 -4,3 —5,0
А) 0,0 - 0,3 0,4 0,7
Т -1,5 1,2 -2,0 -2,3
Турбулентный ^100 - 1,7 2,3 0,9 -0,9
А) 0,1 - 0,7 0,7 2,2
Т 0,3 0,5 0,0 -0,5
Радиационный и ^100 -0,4 2,0 -0,9 -9,2
частично турбу- ^500 -0,1 0,3 0,6 —2,3
лентный РЬ -0,1 -0,6 0,7 2,0
Т 0,0 0,4 -0,8 -1,9
Примечание, п — число точек.
по широтным зонам видно, что давление на уровне моря понижа-
ется в тропиках и повышается в высоких широтах. Изобарические
поверхности понижаются на всех широтах, однако их понижение
в полярной зоне наиболее сильное.
Такое распределение вкладов радиационного притока тепла
легко объясняется качественно. В табл. 5.3 приводятся рассчитан-
ные величины радиационного притока тепла ко всей толще атмо-
сферы, обусловленные длинноволновой и коротковолновой радиа-
цией, для разных широтных зон, времен года и при различной
облачности. Видно, что радиационный приток тепла при любых
условиях приводит к выхолаживанию атмосферы, причем в холод-
ное время года выхолаживание в полярной зоне наибольшее.
Таблица 5.3
Радиационное выхолаживание атмосферы в кал/мин для единичного столба
атмосферы с основанием 1 см2
Зона Теплое полугодие Холодное полугодие
ЯСНО облачно ясно облачно
Тропическая —0,078 -0,056 -0,082 -0,094
Полярная —0,072 -0,053 -0,106 —0,177
201
Легко понять, что при отсутствии меридиональных перемеще-
ний такое положение должно было бы приводить к понижению
изобарических поверхностей, причем наиболее сильному в поляр-
ных областях. Меридиональный обмен частично компенсирует этот
эффект таким образом, что в верхних слоях возникает перенос
масс, направленный из тропической зоны к полюсу. Это приводит
к некоторому ослаблению понижения высот изобарических поверх-
ностей в полярной зоне и повышению давления на уровне моря.
В то же время такой меридиональный обмен должен сопровож-
даться понижением давления на уровне моря в тропической зоне.
На основе данных табл. 5.2 о радиационном притоке тепла мо-
жно заключить, что должны существовать факторы, которые при-
водят к нагреванию атмосферы, хотя бы в некоторых широтных
зонах. Очевидно, что такими факторами являются турбулентный
и фазовый притоки тепла.
Фазовый приток тепла в атмосфере возникает всюду, где про-
исходит конденсация, и приводит к некоторому прогреву атмо-
сферы в целом, особенно в экваториальной зоне, где очень сильно
развита конвекция.
Более значительным является прогрев атмосферы за счет тур-
булентного обмена. Наиболее интенсивен турбулентный обмен при
прогреве подстилающей поверхности и возникновении при этом
у земной поверхности сверхадиабатических градиентов. Такие ус-
ловия существуют над континентами в тропической зоне, а в лет-
нее время года и в умеренных широтах. В процессе турбулентного
обмена при сверхадиабатических градиентах от подстилающей по-
верхности в атмосферу передается значительное количество тепла.
В то же время в полярной зоне, особенно в зимнее время года,
происходит радиационное выхолаживание подстилающей поверх-
ности, наиболее интенсивное при наличии снежного покрова,
и турбулентный теплообмен здесь приводит к охлаждению нижних
слоев атмосферы.
Для оценки обмена теплом между подстилающей поверхно-
стью и атмосферой, связанного с турбулентным обменом, был про-
делан следующий численный эксперимент. Наряду с расчетом ра-
диационного притока тепла производился расчет турбулентного
притока тепла, точнее той его части, которая обусловлена непо-
средственно обменом с подстилающей поверхностью При этом
предполагалось, что указанный вид турбулентного обмена имеет
место только в планетарном пограничном слое, практически в слое
850—1000 мбар.
Величина турбулентного потока тепла от подстилающей поверх-
ности определялась с помощью уравнения теплового баланса под-
стилающей поверхности
Qn+ QH=o,
где R — радиационный баланс, т. е. разность между приходящей
к поверхности и отраженной от нее и излучаемой ею радиацией;
QT — турбулентный поток тепла в атмосферу (или из атмосферы);
202
Qn — поток тепла в почву или в глубь океана; Qn— поток тепла,
связанный с испарением.
Если положить Qh+Qh = 0, что приближенно имеет место в хо-
лодное время года, то из уравнения теплового баланса следует,
что
QT=-/?.
Последнее равенство означает, что радиационное прогревание
или охлаждение подстилающей поверхности полностью передается
в нижний слой атмосферы.
Производя расчеты с учетом и без учета этого вида притока
тепла, мы получаем оценку его влияния на изменения давления,
высот изобарических поверхностей и температуры (см. табл. 5.2).
Видно, что турбулентный обмен с подстилающей поверхностью
приводит к прогреву атмосферы в тропиках и в целом по полуша-
рию. В полярной же зоне турбулентный обмен приводит к выхо-
лаживанию. Температура слоя 850—1000 мбар за трое суток в тро-
пической зоне повышается на 6,1°, а в полярной — понижается
на 5,7°.
За счет этого фактора давление на уровне моря в тропиках по-
нижается на 0,7 мбар, а в полярной зоне увеличивается на
2,2 мбар. Изобарические поверхности в тропиках повышаются.
Таким образом, в тропической зоне турбулентный обмен и ра-
диационный приток тепла действуют в противоположном направ-
лении и в значительной мере компенсируют друг друга.
Ориентируясь на наличие тенденции к взаимной компенсации
радиационного и турбулентного притоков тепла, можно предло-
жить методику совместного учета радиационного и турбулентного
притоков тепла. Положим, что величина радиационного и турбу-
лентного притоков тепла в любом слое атмосферы представляется
в виде
£л = £лН“£л, £т = £т+ £Т>
тогда
£ = £л4“£т = £л4~£т“Ь£л4“£т.
Здесь 8л и 8Т — стандартные или «постоянно действующие», не
зависящее от времени части притоков тепла. Положим далее, что
стандартные части радиационного и турбулентного притоков тепла
компенсируют друг друга, т. е., что
£л'4“£t=z: о*
В таком случае
е=£л+£т.
Отвлечемся пока от турбулентного притока тепла, т. е. бу-
дем считать, что е' =0, и допустим, что стандартная часть
203
'радиационного притока тепла равна его климатической величине.
Последнюю можно рассчитать, используя климатические данные
о температуре, влажности и облачности При этих предположениях
£ ®л •
Очевидно, что указанная компенсация стандартных частей ра-
диационного и турбулентного притоков тепла имеет место не во
всех зонах. В полярной зоне радиационный и турбулентный при-
токи тепла не только не компенсируют, но даже усиливают друг
друга. Частично такой же эффект имеет место в умеренных ши-
ротах. Можно положить, что граница зоны компенсации проходит
вблизи линии снежного покрова или льдов: севернее этой линии
турбулентный обмен, так же как и радиационный, приводит к вы-
холаживанию атмосферы.
На этом основании было принято, что над районами, покры-
тыми снегом или льдом, е = ел, а в остальных районах 8 = 8Л— 8Л.
Результаты расчетов изменений за трое суток давления на
уровне моря, высот изобарических поверхностей 500 и 100 мбар,
а также средней температуры слоя 100—1000 мбар, выполненных
при таком предположении, приведены в нижней части табл. 5.2.
Видно, что в этом варианте учета притока тепла в среднем по по-
лушарию изменения всех рассматриваемых величин малы, как и
должно быть. Давление на уровне моря в тропиках слабо пони-
жается, в полярной зоне — повышается. Высоты изобарических
поверхностей, наоборот, в тропиках повышаются, а в полярной
зоне понижаются. Таким образом, совместное действие радиаци-
онного и турбулентного притоков тепла способствует созданию
в тропической зоне пониженного давления у поверхности земли и
повышенного на высотах, а в полярной зоне — повышению давле-
ния у поверхности земли и понижению на высотах и, следова-
тельно, образованию у полюса высотного полярного вихря.
На рис. 5.5 и 5.6 приведены карты вкладов притока тепла, полу-
ченного указанным способом, в изменения за трое суток давления
на уровне моря и высот изобарической поверхности 100 мбар.
Как видно из рисунков, поля вкладов притока тепла имеют
весьма пеструю картину, характеризующуюся чередованием обла-
стей положительных и отрицательных значений. На приземной
карте обширные области положительных вкладов расположены
над большей частью Евроазиатского и Североамериканского ма-
териков. Области наиболее интенсивного роста давления (до
3 мбар) наблюдаются над Сибирью, Гренландией и Канадой. Об-
ласти падения давления расположены в основном к югу от ши-
роты 30°. Область максимального падения давления (до 3 мбар)
отмечается над Африкой.
На карте вкладов притоков тепла в изменение высоты поверх-
ности 100 мбар (рис. 5.6) наблюдается иная картина. Область от-
рицательных вкладов занимает все полярные и большую часть
умеренных широт. Область максимального понижения высот (до
204
14 дам) располагается к востоку от Гренландии. Особо следует
отметить, что области экстремальных значений рассматриваемых
вкладов имеют тенденцию располагаться над материками.
При отсутствии постоянно действующих радиационного и тур-
булентного теплообменов адвекция тепла в полярной зоне приво-
дила бы к повышению высот изобарических поверхностей и ослаб-
лению полярного вихря. Из имеющихся данных известно, что пе-
репад высот между полярными и тропическими районами на изо-
Рис. 5.5 Вклад радиационного притока тепла в изменения за трое суток
давления (мбар) на уровне моря (с 0 ч 25 III до 0 ч 28 III 1968 г.).
барической поверхности 100 мбар составляет в марте 140 дам, на
уровне моря разница между давлением в полярных и умеренных
широтах равна 10 мбар, а разность между давлением в полярных
и тропических зонах — не более 5 мбар. Формирование таких цир-
куляционных условий над северным полушарием в рассматривае-
мое время года может быть объяснено превалирующим влиянием
радиационного притока тепла над другими факторами.
Сравнение карт барической топографии северного полушария,
полученных по адиабатической и неадиабатической моделям,
позволяет заключить, что учет радиационного притока тепла
205
(в изложенной постановке задачи) позволяет более точно рассчи-
тывать положение и интенсивность высотного полярного вихря
и интенсивность средней зональной циркуляции. (В адиабатиче-
ском варианте имело место занижение скорости западного пере-
носа и завышение высот изобарических поверхностей в полярном
районе, особенно вблизи центра высотного полярного вихря.)
Таким образом можно отметить следующее. В прогностической
неадиабатической модели притоки тепла должны прогнозироваться
Рис. 5.6 Вклад радиационного притока тепла в изменение за трое суток высоты
(дам) изобарической поверхности 100 мбар (с 0 ч 25 III до 0 ч 28 III 1968 г.).
вместе со всеми метеорологическими элементами. Это возможно,
например, путем расчета притока тепла на каждом шаге по зна-
чениям метеорологических элементов, полученных на предыдущем
шаге. Но в этом случае прогностическая модель должна включать
в число прогнозируемых величин все элементы и параметры, не-
обходимые для расчета притоков тепла, включая температуру,
влажность и облачность. Из этих трех элементов в современных
прогностических моделях по полным уравнениям достаточно на-
дежно прогнозируется лишь температура. Влажность прогнозиру-
206
ется менее успешно, а облачность, как правило, вообще не прогно-
зируется. Между тем именно облачность является главным регуля-
тором радиационного притока тепла. Выход из этого затруднения
заключается в определении облачности по значениям прогнозируе-
мых элементов. В ряде работ для этой цели предлагается исполь-
зовать корреляционные зависимости между облачностью, темпера-
турой и влажностью и вертикальными движениями. Возможно ис-
пользование более простой зависимости только между облачностью
и вертикальными движениями типа Л^ = /(т), где f — некоторая
функция. Пример использования такой зависимости в неадиабати-
ческой прогностической модели можно найти в работе [18].
§ 9. Подготовка и согласование начальных данных
для прогностических моделей по полным уравнениям
гидротермодинамики
В квазигеострофических адиабатических моделях в качестве
исходного использовалось поле только одного метеорологического
элемента — геопотенциала. В прогностических моделях, основан-
ных на интегрировании полных уравнений при условии адиабатич-
ности в качестве начальных требуются поля трех метеорологиче-
ских элементов. Чаще всего это две горизонтальные компоненты
ветра и геопотенциал. Вообще говоря, ветер и геопотенциал изме-
ряются независимо друг от друга. По этой причине поля каждого
из этих элементов представляют существенную и независимую ин-
формацию для прогностической модели.
В идеальном случае абсолютно точных измерений начальные
поля отражали бы наличие в рассматриваемый момент всего спек-
тра волн, существующих в атмосфере. В случае, если прогности-
ческая модель достаточно хорошо описывает поведение со време-
нем всех волн, мы получим прогноз погоды одновременно с прогно-
зом акустических и гравитационных колебаний.
Однако измерения метеорологических элементов производятся
с погрешностями (см. гл. I). В прогностической модели эти по-
грешности могут быть восприняты как некоторые фиктивные вы-
сокочастотные волны. Если вычислительная схема прогностической
модели является недостаточно устойчивой, то в процессе интегри-
рования по времени амплитуды этих ложных высокочастотных
волн могут резко возрасти. В результате метеорологический смысл
решения будет утрачен.
По этой причине желательно ошибки измерения, а также фи-
зически реальные возмущения, но имеющие масштаб меньше до-
пустимого для данной прогностической модели, исключить из ис-
ходных данных (т. е. убрать «шумы», отделив их от «сигнала»).
Сделать это полностью невозможно. Существуют, однако, методы,
с помощью которых можно, используя неточную информацию о не-
скольких полях, существенно уменьшить ошибки измерений в каж-
дом из них. В соответствии с этими методами по исходным
207
полям производится расчет измененных полей. В этих новых полях
ошибки измерения будут существенно уменьшены. Тем самым
в значительной мере произойдет и фильтрация ложных волн.
Вместе с тем применяемый при этом математический алгоритм
может быть направлен на исключение или уменьшение амплитуд
реальных волн, например, гравитационных. Последнее достига-
ется путем специального согласования рассматриваемых полей
с помощью некоторых гидродинамических или статистических со-
отношений Полученные в результате этого новые метеорологиче-
ские поля, в которых ложные волны практически устранены, а амп-
литуды фактических высокочастотных колебаний существенно
уменьшены, являются для прогностических моделей по полным
уравнениям наиболее приемлемыми. Процедура получения началь-
ных данных по данным непосредственных измерений или по дан-
ным численного анализа получила название согласования
(или инициализации) полей.
Существует несколько конкретных методов согласования, к ко-
торым относятся методы, предложенные в работах Г. И. Марчука
[У. 17], М. С. Фукс-Рабиновича и Н. Г. Федоровой [23], Т. Нитты
и Дж. Ховермейла [31], Ю. Сасаки [У.23] и др.
Рассмотрим для примера методику согласования полей геопо-
тенциала и вегра для баротропной модели атмосферы, разрабо-
танную М. С. Фуксом-Рабиновичем и И. Г. Федоровой. Она осно-
вана на расчете «псевдопрогнозов». По этой методике в одном из
ее вариантов делаются шаги по времени поочередно вперед и на-
зад. При этом используется метод Эйлера с пересчетОхМ (см.
табл. 5.1), который сводится к следующим двум этапам расчетов:
шаг вперед
шаг назад
X** = XZ+8Z — /+8Х Xz=Xz + 8/-/**^,
где под X понимается любая из функций и, v или Н, a f = dXjdt.
После многократного повторения этих этапов поля и, v и Н ока-
зываются согласованными между собой в смысле их соответствия
системе уравнений (2 1) баротропной модели. Время, соответст-
вующее сделанным шагам, имеет порядок нескольких часов.
Реализация изложенной методики может быть различной. На-
пример, в процессе согласования могут изменяться все три рас-
сматриваемых элемента. Возможен расчет при «закреплении» ка-
кого-либо элемента. В случае, если «закрепленным» принять гео-
потенциал, то с помощью описанной процедуры мы фактически
восстанавливаем поле ветра по полю геопотенциала.
В любом случае согласованные поля содержат меньше значи-
тельных ошибок. В силу этого они практически не включают в себя
ложных волн. Вследствие того, что рассмотренная прогностическая
модель обладает свойством уменьшать амплитуды высокочастот-
ных колебаний, согласованные таким образом поля не включают
208
в себя также и фактических высокочастотных колебаний с боль-
шими амплитудами.
Экспериментально показано, что прогнозы, рассчитываемые по
согласованным данным, оказываются лучше прогнозов, получае-
мых по первоначальным данным. Улучшение прогнозов H5w по
нескольким случаям составило для первых и вторых суток 10—
12%, для третьих — 20—40%. Еще более важно отметить, что если
по несогласованным данным прогноз на пятые сутки оказывается
вообще невозможным, то по согласованным данным прогноз ока-
зывается удовлетворительным.
Изложенный метод согласования начальных данных о геопотен-
циале и ветре может быть распространен и на бароклинные мо-
дели.
Перейдем теперь к рассмотрению вопроса о подготовке данных
для прогностических моделей, включающих расчет осадков,
а также учитывающих неадиабатические факторы.
Как мы видели, для простейших моделей, включающих прог-
ноз осадков, необходимы данные о влажности Между тем сущест-
вующие традиционные средства метеорологических наблюдений
могут обеспечить такими данными только сравнительно малую
часть земного шара. Кроме того, измерения влажности являются
недостаточно точными, а в верхней части атмосферы (выше 5 км)
вообще ненадежными.
Радикальным решением этой проблемы будет создание новых
средств наблюдений, позволяющих получать данные о влажности,
а также водности над земным шаром. Прообраз таких средств мо-
жно видеть, например, в спутниковой системе наблюдений за
влажностью с помощью спектрометрических измерений в микро-
волновом диапазоне.
Пока же, как мы видели, приходиться прибегать к различного
рода гипотезам относительно распределения влажности в атмо-
сфере. Одной из таких гипотез является предположение о полной
насыщенности воздуха в исходный момент. С первого взгляда та-
кая гипотеза может показаться слишком далекой от реальности.
Однако практика показала, что при расчетах на небольшой срок
порядка суток, такая гипотеза дает удовлетворительные резуль-
таты. Это можно объяснить тем, что завышение содержания влаги
в атмосфере в начальный момент, которое получается в моделях,
использующих эту гипотезу, в некоторой мере компенсируется от-
сутствием поступления влаги в атмосферу от подстилающей по-
верхности за счет испарения. Ясно, однако, что с течением времени
в такой модели будет происходить «высушивание» атмосферы и
прогноз будет становиться неудовлетворительным.
Для учета неадиабатических факторов необходимо знать рас-
пределение в атмосфере не только влажности, но и облачности,
а также аэрозоля, углекислого газа и озона. По-видимому, в на-
стоящее время о содержании в атмосфере трех последних элементов
можно говорить лишь в среднем для каких-либо периодов. Для на-
чального момента данные об облачности мы имеем со спутниковых
14 Зак. № 21
209
систем наблюдений. Однако для расчета радиационных и фа-
зовых притоков тепла необходимо знать распределение облачности
не только в исходный момент, но и в течение всего периода прог-
ноза. Но это может быть обеспечено лишь в случае, если прогно-
стическая модель будет включать облачность в качестве одного
из элементов прогноза.
Наконец, для расчета турбулентного теплообмена необходимы
данные о температуре подстилающей поверхности, а также о тем-
пературе почвы или воды на некоторой глубине вблизи поверхно-
сти. Можно надеяться, что данные о температуре подстилающей
поверхности могут быть получены с помощью спутниковых систем
измерения. Однако данные о температуре почвы или воды со зна-
чительных территорий в ближайшее время вряд ли могут быть по-
лучены.
Кроме упомянутых данных, используемых как начальные, при
реализации неадиабатических прогностических моделей необходим
и еще целый ряд данных, которые в общем можно рассматривать
как параметры атмосферы. Сюда относятся данные об отражатель-
ной (альбедо) и излучательной способности различных подстилаю-
щих поверхностей, в том числе облачности, о распределении сне-
гового покрова, состоянии растительности и пр.
Можно заключить, что современная система наблюдений за
метеорологическими элементами и параметрами атмосферы не
обеспечивает гидродинамические методы прогноза всеми необхо-
димыми данными. Имеются определенные возможности улучшения
наблюдательных систем. Однако эти возможности ограничены. По-
этому одной из важнейших проблем прогноза является воспол-
нение недостающих начальных данных с одновременным исклю-
чением различного рода ошибок. Принципиальная возможность
этого на примере расчета начальных полей ветра была показана
в начале этого параграфа.
Глава VI
ЗАДАЧА ДЕТАЛИЗИРОВАННОГО ЛОКАЛЬНОГО ПРОГНОЗА
ПОГОДЫ МЕТОДАМИ МЕЗОМЕТЕОРОЛОГИИ
До сих пор речь шла о прогнозе крупномасштабных атмосфер-
ных процессов. Прогноз погоды, полученный на основе предвы-
числения таких процессов, по существу является только фо-
новым.
Фактическая погода на какой-либо территории часто сильно
отличается от общего фона. Это обусловлено в первую очередь
влиянием на погоду особенностей подстилающей поверхности мезо-
метеорологического масштаба. К таким особенностям подстилаю-
щей поверхности относится рельеф местности и ее температурная
неоднородность, приводящие к значительным отклонениям ветра,
вертикальных движений, осадков и других метеорологических эле-
ментов от фоновых значений.
В формировании погодных особенностей мезометеорологиче-
ского масштаба существенную роль играет вертикальное ускоре-
ние dw/dt. Поэтому учет мезометеорологических явлений в рам-
ках гипотезы квазистатичности является невозможным. Здесь
возникает необходимость перехода к исходным уравнениям гидро-
термодинамики с сохранением члена с вертикальным ускорением.
Это обстоятельство делает задачу прогноза весьма сложной как
в физическом, так и в математическом отношении.
Задача о прогнозе погоды методами мезометеорологии была
поставлена И. А. Кибелем, который наметил основные пути к ее
решению [4, 5]. Задача эта до сих пор не решена. Однако уже по-
лучено решение целого ряда частных вопросов, что привело к бо-
лее полному пониманию физических процессов, формирующих
локальную погоду, и подводит нас к решению задачи в це-
лом. Здесь можно отметить работы Л. Н. Гутмана, Е. М. Пе-
келиса, В. В. Шершкова, Н. Ф. Вельтищева и др. [У.8; 2, 3,
6, 7].
В этой главе будут получены уравнения для описания мезопро-
цессов и рассмотрены две частные, но весьма важные для реше-
ния задачи локального прогноза погоды задачи: об обтекании пре-
пятствий и о вынужденной конвекции.
14*
211
§ 1. Уравнения гидротермодинамики мезопроцессов
В качестве исходных используем уравнения гидротермодина-
мики— уравнения (2.21) гл. II. Опуская в уравнениях движения
по горизонтали члены 2со^ и 2<oxw, в уравнении движения по вер-
тикали— члены, содержащие силу Кориолиса, а в уравнении не-
разрывности— член dp/dt в виду их малости и полагая k = const,
указанную систему уравнений перепишем в виде:
—7-эг+/г+*' Ды+^ й:
1 др
V ~ду
1 др
du
~dF
dv
~dF ~~
dw
dt p dz
d$u । d^v
dx ‘ dy 1 dz
lu-\- k' Дг»-|-Л ;
i 0;
p=R?T-,
4Г+‘-5- ;
-Й-=~т-+4’4’+4-»-' (LI>
где
Л d2 , d2 d d , d , d . d
dx2 1 dy2 ’ dt dt 1 dx 1 dy 1 dz
Заметим, что считая в уравнении неразрывности др/д/ = О, мы с са-
мого начала исключили из рассмотрения акустические волны.
Положим, что:
Г(х, у, г, /) = 7(г)Ц- Т' (х, у, г, /);
р (х, у, г, t)=p (z)-\-pr (х, у, г, /);
р(х, у, z, О=р(г) + р'(х, у, z, t);
<?(х, У, z, = Q (г) + <7' (х> У> z> (1-2)
где функции с чертой являются известными (стандартными или
фоновыми) величинами, зависящими только от высоты, а функции
со штрихом — возмущениями, зависящими от всех координат и вре-
мени, и что
I Tf I pf р' I qf
|~ «1. «I. у«1. Iv«i. (1.3)
Для стандартных значений принимаем:
i#+s-=0; ^L=-7; (1.4)
212
Имея в виду соотношения (1.2) и (1.3), произведем упрощения
уравнений, которые называют упрощениями теории конвекции
[У.13]. Прежде всего заметим, что разлагая функцию 1п(1+х)
в ряд Тейлора, имеем
In (1 + л) » х —л2 4—х3 ...
При | х | 1 можно принять, что In (1+х)~х Преобразуем те-
перь члены уравнений движения, описывающие силу барического
градиента. Проделаем это подробно для члена
1 дР тя
---Имеем
р дх
Г1п =
р дх р дх дх дх \ Р I
ГТ 1 дР
Проделывая аналогичные преобразования для члена —по‘
ложив T = TCV, где ТСр — средняя температура атмосферы, и введя
обозначение
Ф = /?Гср-^-, (1.5)
р
получаем:
1 др дФ 1 др дФ /,
р дх дх ’ р ду ду \ • /
Для силы барического градиента в вертикальном направлении
имеем
ттг=«г4[1л(|+1)+|"?]ет^-+'?7'^-(|лй-
Но при учете соотношений (1.4)
пт д . - RT др RT - Т „Т+Т'
RT-^-\np= —^^p=-g^=-g—=—=
02 р 02 р т т
рг рг
= -g-g^p-^~g-g—f
Т 7 ср
поэтому
J__др _ дФ - Т’
р dz ~ dz g g Тср
Остальные члены в уравнениях движения остаются без изменения.
Займемся теперь преобразованием уравнения неразрывности.
Предварительно представим его в виде
ди । dv . dw , г 1 / dp , dp . др \1 п
тй + + -дГ + 1т \ w T>r)J=°-
213
Рассмотрим сумму членов этого уравнения, заключенных в квад-
ратные скобки. Перепишем ее в виде
и ln p+^ ln p+w ln P
или, учитывая, что In p — p'/p + ln p,
d / p' \ । d / p' \ . d / p' \ . w dp
U |4r- -3— -V H—— -S~- .
dx p у 1 dy p ) 1 dz p ) 1 p dz
Первые три члена этой суммы, содержащие малую величину р',
малы, а в последнем члене
1 dp
р dz
RLJL- ( р I дР Р_ \= ( р-~ | £ ~
р д2 \ RT) р \дг Т dz j р ‘ Т 1
= ( £ I 1 ) = ~ ^7 g— #7
RT ‘ Т ) RT ЯГср ’
Учитывая
в виде
сказанное, уравнение неразрывности перепишем
du । dv . dw
-----U—--L =a^
dx 1 dy 1 dz
где
°=(я-Ят).ЖР.
В уравнении притока тепла:
dT _ _ dT' I , dT _ _ dT’ i , dT dTr - dt
dt dt “1 dt dt ' u dz
dp' i dp_ _ dp dz = — wgp;
dt dt 1~ dt ""
7a g dp. -- —Taw.
g? dt g? dz ~
В уравнении переноса влаги
dt dt ‘ dt dt ‘ dz ~ dt
Учитывая все сказанное, приходим к следующей системе уравне-
ний гидротермодинамики мезопроцессов:
dzz d<!> . z । ,, л . , d2zz
4?-=-w-Zu+A'^S;
^=-4+^+^'д®+^
214
ди , dv . dw
+ Ga- l) ™ = 7^- (ел+®ф) + ^ + k -—-;
^—^w=-^+k'^+k^, (1.7)
где P = 77?1cp — параметр конвекции или плавучести Член |3g
в третьем уравнении движения выражает силу Архимеда. Если
Т'>0, то этот член положителен и значит сила Архимеда направ-
лена вверх, если Т' <0 — вниз.
Заметим, что, если не делать предположения о постоянстве
коэффициента турбулентности, то последние члены в уравнениях
движения, притока тепла и переноса влаги примут вид:
д 1 ди д , dv д , dv
~дГ“~дГ’ ~д1“~дГ> ~д?-^->
Применительно к потенциальной температуре уравнение при-
тока тепла запишется в виде
т+®5=(т)‘ Ь7<*-+е*)+*' дй'+4 [» +s)]| •
где
S = дв/д2, 0 (х, у, zt /) = 0 (z)4-0'(х, у, г, /).
Отметим еще, что представление метеоэлементов в форме (1.2)
можно использовать и для и и -о. Однако так как возмущения и'
и v' по сравнению с и и v, характеризующими основное или не-
возмущенное движение, не являются малыми, такое представление
не приводит к упрощениям.
К числу мезометеорологических задач, решаемых на основе
приведенной системы уравнений, относятся задачи об обтекании
препятствий воздушным потоком, о локальных ветрах, вынужден-
ной конвекции в пограничном слое, ячейковой конвекции и др
Первые решения некоторых из этих задач были получены при
использовании метода линеаризации. Стремление к получению ре-
шений в аналитическом виде приводило к ряду ограничений в по-
становке задачи. В силу этого результаты, полученные на основе
линеаризованных уравнений, носили ограниченный характер, хотя
и способствовали пониманию ряда важных мезометеорологических
процессов.
В последнее десятилетие уравнения мезометеорологии реша-
ются почти исключительно как нелинейные при применении чис-
ленных методов решения для той или иной сетки точек. При этом
в одних случаях путем исключения из рассмотрения производных
215
по времени (d/dt = O) задача сводится к стационарной, в других —
мезометеорологическая задача решается как нестационарная.
В последнем случае производится интегрирование уравнений по
времени до того момента, пока не будет достигнут так называемый
установившийся режим, при котором рассчитываемые по соответст-
вующим уравнениям изменения во времени не станут пренебре-
жимо малыми.
При решении любой мезометеорологической задачи величины,
характеризующие основное состояние, считаются известными, на-
пример, по наблюдениям или из прогноза. Должны быть заданы
также распределения таких мезометеорологических факторов, как
рельеф местности и ее температурная неоднородность.
В случае, если мезометеорологическая задача решается как не-
стационарная, т. е. путем интегрирования уравнений по времени
и отыскания установившегося режима, должны быть заданы еще
и начальные условия. В качестве последних обычно принимаются:
отсутствие всех возмущений в полях метеоэлементов, равенство
и и v их фоновым значениям и w = 0.
Найдя тем или иным путем мезометеорологические возмущения
метеорологических элементов и сложив эти величины с их фоно-
выми значениями, мы и получаем уточнение или детализацию прог-
ноза для конкретного района.
Постановку и методы решения мезометеорологических задач
рассмотрим более подробно на примере задач обтекания препят-
ствий и вынужденной конвекции. Эти задачи имеют прямое отно-
шение к детализированному локальному прогнозу, так как они
позволяют получить для сравнительно небольших площадей (по-
рядка 50x50 км) распределение возмущений в полях темпера-
туры, влажности, ветра и вертикальных движений. С помощью по-
следних возможен переход к расчету облачности и осадков.
Первая из указанных двух задач будет решаться как стацио-
нарная, в то время как при решении второй задачи будет приме-
нен метод стационирования.
§ 2. Обтекание препятствий воздушным потоком
Этот вопрос уже давно привлекал к себе внимание ученых.
В последние годы он связывается с задачей локального прогноза
погоды. Как уже говорилось, неровности земной поверхности обус-
ловливают весьма сложную систему движения, которая приводит
к разнообразию погодных явлений даже в близких друг к другу
пунктах. Зная особенности рельефа в каком-либо небольшом райо-
оне с горизонтальными размерами порядка десятков километров,
например, в районе какого-то города, а также характеристики ос-
новного состояния атмосферы (фона погоды), можно рассчитать
детальное распределение метеорологических элементов или хотя
бы некоторых из них и тем самым осуществить детализацию прог-
ноза погоды.
216
Рассмотрим один из вариантов решения подобной задачи по
работе Е. М. Пекелиса [6].
В качестве исходных примем уравнения (1.7) (кроме уравнения
переноса влаги) при о = 0 (условие несжимаемости), при отсутст-
вии турбулентного обмена, в случае адиабатичности и при 1 = 0,
Последнее условие справедливо при рассмотрении движений не-
больших масштабов. Будем решать задачу как стационарную, т. е.
при условии, что все производные по времени равны нулю (djdt =
= 0), для области пространства, заключенной между некоторой
горизонтальной поверхностью раздела z = // = const («крыша») и
земной поверхностью, уравнение которой z=6(x, у). Скорость не-
возмущенного потока будем счи-
тать не зависящей от координат.
Направим ось у вдоль основ-
ного невозмущенного потока и
положим, что при у-+—оо рель-
еф становится равнинным. Бу-
дем считать, что на высоте Н
движение является горизонталь-
ным, а на земной поверхности
выполняются условия обтекания.
В таком случае краевые условия
задачи при решении системы
уравнений (1.7) при перечислен-
ных предположениях записыва-
ются в виде:
Рис. 6.1. Распределение рассчитан-
ных вертикальных движений при
обтекании небольшого холма.
Т' = Ф = ‘&) = ц=0, V=U при у—*-----ос;
п lj дЪ . дЪ
W = 0 При Z = H, при Z = b.
(2.1)
(2.2)
Последнее из приведенных соотношений (2.2) выражает усло-
вие обтекания. Для практического решения поставленной задачи
краевое условие (2.1) несколько упрощается, а именно принима-
ется, что возмущения отсутствуют не при у-*—оо, а в области,
находящейся на некотором конечном удалении от препятствия
в направлении, противоположном основному движению, и по сто-
ронам от препятствия.
Вводятся новые переменные и некоторая сеть точек. Дифферен-
циальные уравнения (1.7) записываются в виде конечно-разност-
ных уравнений, решая которые и находятся значения возмущений
искомых величин, т. е. Т', w и пр.
Анализ результатов расчетов приводит к выводу, что неровно-
сти рельефа приводят к значительным возмущениям как в полях
и, v и w, так и в поле Т' При этом конфигурация изолиний воз-
мущений разных элементов оказывается весьма сложной, имеющей
волновой характер и зависящей от принятых параметров модели
В качестве примера на рис. 6.1 приведено поле ш, рассчитанное
при наличии одиночного холма, поверхность которого была задана
217
в виде параболлоида вращения 6 (х, у) =с — Ь(х2+у2), где с —
высота параболлоида, принятая равной 800 м, b — постоянная, за-
висящая от горизонтальной протяженности холма (8 км). Расчет
проделан при Н=8 км для высоты z = 4 км. Орографическое
препятствие на рисунке показано в виде заштрихованной об-
ласти.
Вдоль направления основного потока за холмом на рис. 6.1
видно чередование областей восходящих (знак +) и нисходящих
(знак —) вертикальных движений, имеющее волновой характер.
В то же время на рисунке можно обнаружить зоны восходящих
движений, имеющих вид полос, напоминающих облачные полосы,
обнаруживаемые со спутников [3].
Согласно расчетам, выполненным другими методами и при дру-
гих условиях, зоны восходящих движений имеют спиралевидный
характер. Возможность существования таких систем подтвержда-
ется также наблюдениями за облачностью, производимыми со
спутников.
§ 3. Вынужденная конвекция в пограничном слое атмосферы
Помимо вертикальных движений, возникающих при крупномас-
штабных движениях и обтекании препятствий, в атмосфере суще-
ствуют конвективные вертикальные движения. Эти движения об-
условлены проявлением силы Архимеда, которая возникает при
горизонтальной температурной неоднородности подстилающей по-
верхности, обусловленной неодинаковыми отражательными и по-
глощательными способностями различных участков земной поверх-
ности и растительности, а также агротехническими мероприяти-
ями. Особенно велика температурная неоднородность в городах,
где значительные парковые зоны чередуются с участками, покры-
тыми асфальтом и занятыми строениями.
Зная распределение температурных неоднородностей на какой-
либо площади, мы, вообще говоря, можем рассчитать детальное
распределение метеорологических элементов над данной площа-
дью и тем самым перейти к детализированному прогнозу погоды.
Рассмотрим указанную задачу по работе В. В. Шершкова [7].
В качестве исходных уравнений принимается система уравне-
ний (1.7) без последнего уравнения и в предположении, что ел +
+ Еф = 0 и / = 0 (последнее предположение при рассмотрении про-
цессов малого масштаба является вполне оправданным).
Возмущение в поле температуры у земной поверхности счита-
ется известной функцией координат, т. е. при г = 0 Т' = 7о(х, у)
(это есть возмущающий мезометеорологический фактор). Примем,
что поля метеорологических элементов являются симметричными
-относительно плоскости у = 0.
Решение задачи будем искать внутри прямоугольной области,
'Ограниченной плоскостями х = 0, х = а, z/=0, у = а, а сверху —
плоскостью z = H.
218
В качестве краевых условий примем:
при z=Q u=v=ew=G, T' = TQ(x, у);
при z=H u=U, Т' = Ф=г>=0;
п ди dTf дФ n
при x=Q 'u=(w=-^— — —^— = ~s—=0;
1 dx dx dx ’
du dv dw dTr дФ
при x=a = -3— = ~s— = —i— = -v—=0:
K dx dx dx dx dx
~ du dw дФ dTr ~ /о i\
при y = 0, a ‘u=-r-= -?—=-7—= ——=0. (3.1)
r ’ dy dy dy dy v z
Краевые условия (3 1) означают следующее У земной поверх-
ности принимается условие «прилипания», на верхней границе рас-
сматриваемого слоя атмосферы задан невозмущенный поток, на-
правленный вдоль оси х. На горизонтальных границах рассматри-
ваемой прямоугольной области принимается отсутствие потока
вдоль оси у и равенство нулю градиентов рассматриваемых пере-
менных.
В качестве начальных данных принимается
при /=0 ^=^—Тг = Ф=0,
u(z}=U-^ ,
(32)
т. е. считается, что существует только движение вдоль оси х, рав-
номерно усиливающееся с высотой до своего предела U на высоте
Н, а вне указанной прямоугольной области возмущения отсутст-
вуют.
Решение системы (1.7) при краевых условиях (3.1) и началь-
ных данных (3.2) производится численным образом. В рассматри-
ваемой области вводится сетка из 32x32x9 точек с шагами по
горизонтали 6s = 500 м, по вертикали 6г = 300 м и по времени
61 = 15 с.
По выполнению некоторого числа шагов по времени (порядка
200) получаемые значения рассматриваемых переменных прини-
мают устойчивые значения (устанавливается стационарный ре-
жим). Эти значения зависят от заданных условий, т. е. от скоро-
сти потока V и от размера и величины температурного возмуще-
ния 7о(х, у) на поверхности.
Из всех рассматриваемых величин (и, v, w, Т', Ф и р) наи-
больший интерес представляет вертикальная скорость. Оказыва-
ется, что ее распределение в пространстве носит волновой харак-
тер. При этом чередование восходящих и нисходящих движений
имеет место по всем направлениям.
Для примера на рис. 6.2 приведено распределение рассчитан-
ных восходящих и нисходящих движений для указанной, а также
симметричной ей области расчета при величине температурного
219
возмущения на поверхности Т' = 1°, при размерах температурного
пятна 3X7 6s2 (7) и 7Х 156s2(77) и при U =1,8 м/с на высотах при-
мерно 1,2 км (а) и 2,4 км (б).
Видно, чго характер распределения вертикальных скоростей
зависит от размера температурного возмущения. Причем при од-
ном и том же размере пятна происходит изменение поля верти-
кальных движений с высотой. Интересно отметить, что над самим
пятном в основном восходящие движения, хотя имеются области
и с нисходящими.
Общим для всех случаев является характерное распределение
восходящих движений в форме полос, расходящихся в стороны от
Рис. 6.2 Распределение рассчитанных вертикальных движений, обусловлен-
ных температурной неоднородностью подстилающей поверхности (области
с восходящими движениями заштрихованы).
направления основного потока. Такую ориентацию принимают
иногда кучевые облака [3]. Распределение восходящих и нисходя-
щих движений по результатам решения нелинейных задач (см.
рис. 6.2) в общих чертах согласуется с результатами, полу-
ченными в задачах об обтекании препятствия или нагретого
«пятна» в линейной постановке [У.8]. Наличие чередующихся об-
ластей восходящих и нисходящих движений помимо данных об
облачности косвенно подтверждается также известным фактом
«пятнистости» в распределении осадков.
В заключение главы отметим следующее. Для перехода к пол-
ному прогнозу погоды методами мезометеорологии необходимо
включить в расчет влажность воздуха, облачность, а также гидро-
метеоры. Нужно иметь для каждого района детальные данные
220
о рельефе местности и о распределении температуры земной по-
верхности.
Данные о рельефе, вообще говоря, имеются и включение их
в расчет возможно [1]. Поэтому учет рельефа в мезометеорологи-
ческом прогнозе вполне реален. Вполне реальной задачей является
и учет влажности.
Что же касается учета распределения температуры подстилаю-
щей поверхности в какой-либо момент, то здесь существуют серь-
езные трудности. Дело в том, что прогноз температуры подсти-
лающей поверхности является сам по себе сложнейшей задачей,
Поэтому здесь можно говорить о каких-либо приближенных реше-
ниях в некоторых особых случаях, например в случаях чередова-
ния суши и водных площадей или в случаях резкого различия
в характере подстилающей поверхности. В связи со сказанным
учет температурных неоднородностей подстилающей поверхности
в мезометеорологическом прогнозе представляется делом буду-
щего.
Еще сложнее обстоит дело с прогнозом облачности, осадков,
тумана, а также опасных явлений погоды: шквалов, смерчей и др.
Здесь предстоит еще большая работа в теоретическом плане и
изучении этих явлений по эмпирическим данным.
Глава VII
ТЕОРИЯ И МЕТОДЫ ГИДРОДИНАМИЧЕСКОГО
ДОЛГОСРОЧНОГО ПРОГНОЗА ПОГОДЫ
Проблема долгосрочного прогноза погоды имеет важное народ-
нохозяйственное значение. Это одна из труднейших проблем со-
временной науки, однако в ее решении уже достигнуты определен-
ные успехи.
Еще в 1943 г. Е. Н. Блиновой была впервые предложена теория
атмосферных движений планетарного масштаба и долгосрочного
прогноза [2]. В этой теории использовались гипотеза квази-
соленоидальности атмосферных движений, метод линеа-
ризации и математический аппарат разложения полей в ряды
по сферическим функциям, т. е. спектральный метод. Кроме
того, впервые было применено соотношение, связывающее поля
давления и функции тока. Впоследствии такого рода соотношение
стало применяться и в краткосрочном прогнозе и получило на-
звание уравнение баланса. На основе указанной теории
уже в 1946 г. был получен прогноз давления на среднем уровне
и уровне моря и прогноз наземной температуры на 20 дней впе-
ред по северному полушарию [3]. С 1952 г. было начато состав-
ление опытных прогнозов средней месячной температуры воздуха
у поверхности земли по территории Евразии с заблаговременно-
стью 40 дней, а с 1958 г. стали регулярно составляться прогнозы
температуры по северному полушарию [7]. В 1954—1956 гг.
Е. Н. Блиновой была создана теория гидродинамического долго-
срочного прогноза [6], не связанная с линеаризацией уравнений,
которая легла в основу ряда прогностических моделей, разрабо-
танных Е. Н. Блиновой, С. Л Белоусовым, Г. П. Курбаткиным
[15, 17]. Основные уравнения этой теории были использованы
также для создания ряда линеаризированных прогностических мо-
делей, предложенных С. А. Машковичем и Я. М. Хейфецем,
Ш. А. Мусаеляном, М. Б. Галиным [16, 22, 24].
Дальнейшее развитие гидродинамической теории долгосрочного
прогноза шло по пути совершенствования физической постановки
задачи. В 1961 г. был сделан переход к интегрированию полных
уравнений гидротермодинамики и более точному
учету неадиабатических факторов [8, 9, 11, 12]. Впоследствии был
разработан и применен новый метод интегрирования нелинейных
222
уравнений — метод выделения главных волн [13].
Весьма существенным моментом теории, созданной Е. Н. Блино-
вой, является то, что эта теория позволяет одновременно рассчи-
тывать как прогноз, так и климатические поля метеорологи-
ческих элементов [12].
В последние годы теория климата и общей циркуляции атмо-
сферы привлекает все большее внимание. Ряд исследователей по-
лагает, что создание физико-математических моделей циркуляции
атмосферы должно способствовать разработке надежных методов
долгосрочного и сверхдолгосрочного прогноза погоды. Можно от-
метить работы Г. И. Марчука, М. Е. Швеца и др. [19, 27] в СССР,
Н. Филлипса, Дж. Смагоринского, Е. Минца, А. Аракавы, А. Ка-
сахары, У. Вашингтона и др. [23, 25, 26, 28—30] за рубежом.
На основе такого рода исследований К Миякодой и др. [31] была
разработана многоуровенная прогностическая модель, позволяю-
щая получать прогноз метеорологических элементов по северному
полушарию на срок до двух недель.
Построение моделей общей циркуляции атмосферы необходимо
также для выполнения расчетов по оценке возможных метеороло-
гических последствий! преднамеренных и непреднамеренных воз-
действий деятельности общества на окружающую среду.
Успешному решению задачи долгосрочного прогноза погоды
несомненно способствуют новые методы и алгоритмы решений диф-
ференциальных уравнений, разрабатываемые Г. И. Марчуком
[У.17].
§ 1. Теория атмосферных движений планетарного масштаба
и долгосрочного прогноза, основанная на интегрировании
линеаризированных уравнений гидродинамики в соленоидальном
приближении и использовании спектрального метода
Данная теория [2,3] представляет особый интерес, так как в ней
впервые было применено квазисоленоидальное приближение,
предложен первый вариант уравнения баланса и применен метод
разложения переменных в ряды по сферическим функциям, т. е.
спектральный метод.
В этой теории используется важная особенность атмосферы,
заключающаяся в том, что все атмосферные движения развиваются
на фоне западного переноса, который принимается за основное
состояние атмосферы. Интенсивность этого переноса часто бывает
столь велика, что все остальные движения можно рассматривать
как малые отклонения от этого основного потока. В этих случаях
оказывается возможным применение метода малых возмущений
(см. § 2 гл. III). Тогда нелинейные уравнения гидротермодина-
мики можно будет преобразовать в линейные.
Здесь и далее в настоящей главе используется система уравне-
ний термогидродинамики в сферических координатах (см. § 8
гл. II).
223
В рассматриваемой задаче принимается, что движение атмо-
сферы слагается из зональной циркуляции и возмущений послед-
ней. В свою очередь возмущения зональной циркуляции представ-
ляются в виде стационарных (не зависящих от времени) и неста-
ционарных частей. В соответствии с этим положим:
vx(0, X, /)=^(6)+^(0, К t)-
^(0, k, k)+^(0, к, /);
Г(о, к, /)=г(0)+г(0. к,)-|-г'(е( к, /);
р(0, /)=р(0)+У(0, Ч+р"(0. 0. (1-1)
где величины с чертой соответствуют зональной циркуляции атмо-
сферы, величины с одним штрихом — стационарным, а с двумя
штрихами — нестационарным возмущениям. Характеристики зо-
нальной циркуляции полагаются известными (например, по кли-
матическим данным).
Стационарная часть возмущений зональной циркуляции обус-
ловлена распределением материков и океанов и описывает общую
циркуляцию атмосферы и в частности центры действия атмосферы.
Нестационарная часть связана с перемещающимися и развиваю-
щимися барическими образованиями, фронтами и пр. Для прог-
ноза важны именно нестационарные возмущения, а стационарные
возмущения имеют значение в теории общей циркуляции атмо-
сферы и климата.
Зональные части и р определяются через индекс цирку-
ляции а, который представляет собой угловую скорость враще-
ния атмосферы относительно земной поверхности (см. § 3 наст,
главы). Из тригонометрических построений получаем
^x = a^sinO. (1.2)
где а — радиус Земли.
Принимая в первом приближении для и р геострофическое
соотношение
- 1 др
х 2со cos 0 яр дО
и интегрируя последнее, находим
р (G)=A)4“Ptf2aw$in2 А. (1-3)
где ро — давление на полюсе.
Аналогично этому положим, что
7(6)^r0+Alsm2e, (1.4)
где То — температура на полюсе, а М — разность температур на
экваторе и полюсе.
224
Далее принимается гипотеза квазисоленоидальности, согласно
которой движение является бездивергентным. Тогда уравнение не-
разрывности может быть записано в виде (см. (8.12) гл. II)
a dv.
-a0-(^sine)+T=o.
Это соотношение позволяет ввести функцию тока ф, такую, что
1 Эф 1 Эф /1
Для функции тока примем также, что ф(0, X, /)=ф (0)+ф/ (6, М +
+ф,,(0, К /). Примем далее, что для абсолютных величин справед-
ливы соотношения:
^х » ^х » ^х, v'e » tjq,
"р»рг»р\ Т» Г» Т".
(1.6)
В таком случае оказывается возможным применение метода линеа-
ризации.
Возьмем теперь уравнение вихря скорости без члена d(pyz)/dz,
что справедливо для средней тропосферы, и уравнение движения,
соответствующее оси X, без члена vzdvjdz как обладающего наи-
меньшим порядком величины, а также без учета силы турбулент-
ной вязкости (см. формулы (8.13) и (8.2) гл. II).
ЭЙ , Эй . dQ
dt ' a dti ' a sin 0 ЭХ
1 / dp dT
cP sin ОрГ \ ЭО ЭХ
dvx , ve dvi , vx
а
—— 2ojsin 9=
а
dp dT \
эГ“эог
^х । ctgO
dt "l” а ЭО "Г «sin 0 ЭХ а
=-------~ cos >
a sin Op ЭХ °’
(1.7)
где
Э sin Огл dv.
________л и
эо______эх
<)_____1_
a sin
Используя представления (1.1), применяя метод линеаризации,
считая функции, соответствующие зональной циркуляции, извест-
ными и вводя по (1.5) функцию тока, мы можем теперь получить
системы уравнений для стационарных возмущений, а затем и для
нестационарных.
Решая вначале систему уравнений для стационарных возмуще-
ний, мы находим поля метеорологических элементов, соответствую-
щие рассчитанной теоретически зональной циркуляции атмосферы.
Зная их, можем теперь перейти к задаче долгосрочного прогноза
путем решения уравнений для нестационарных возмущений.
15 Зак. № 21
225
Рассмотрим вначале задачу о стационарных возмущениях по-
лей давления и функции тока, отвлекаясь от нестационарных воз-
мущений и считая поле температуры известным (например, по кли-
матическим данным). Подставляя в уравнения (1.7) значения vq,
vk и р по (1.1), учитывая, что
sin 0, 2=2а cos О, dV)JdQ=aa cos 9,
2а sin О,
дТ др dQ dQ dQ' " n
^-^=-дК==-дГ=~1Г=-дГ==-дГ=-дГ=^^==р =0’
и производя линеаризацию, получаем
dQ' 2 (a + w) . n ' 1 (др дТ' др' dT \
a ~d7. a S1П >г’° <z2 sin 0? Г ("dF дГ дб ) ’
dv'^ lo/ix fl 1 др'
a т+2 <э C0S ~ apsinT^T •
Полагая (на основе анализа эмпирических данных) второй член
правой части первого из приведенных двух уравнений малым, прини-
мая в соответствии с (1.3) dp/dQ = 2acopcz2 sin 6 cos 6, используя со-
отношения соленоидальности (1.5), на основании которых
__ 1 дУ
a sin 6 дк ’
1 / д (sin 6vx)
a sin О I дб
1 ду
-5Г’
д\
#2 1
где
д 1 д д | 1 <)2
a sin 0 dO Sin dO sln2 0 д№ ’
a
приходим к следующей системе уравнений для г|/ и р':
д ДФ' I п/ I \ дФ' 2aco^2Cos6 ATI
—г?--f-2 (a rn))-y—=-----=-----
дк 1 v 1 ' дк р
д2Ф' q , . \ х л дФ'
a W “ 2 <а+0>) ctg6 т= -
дк
1 др'
sin 6 р дк ’
(1-9)
где Т и р — средние для атмосферы значения Тир. Заметим, что
второе из уравнений (1.9) дает связь между функцией тока и дав-
лением. По существу это или подобные ему уравнения, получен-
ные Е. Н. Блиновой в 1943 г. [2], являются линеаризированным
вариантом уравнения баланса.
Зная распределение температуры, а значит и Т', решая первое
из уравнений (1.9), мы можем получить величины ф', а затем
с помощью второго уравнения и значения р'. Используя далее
соотношения соленоидальности, можно рассчитать и нестационар-
ные возмущения v'Q и .
226
Таким образом, задавая для каких-либо времен года или ме-
сяцев климатическое распределение температуры, мы теоретически
рассчитываем поля скоростей и давления на некотором среднем
уровне. Используя барометрическую формулу, можно сделать пе-
реход к полю давления на уровне моря [5].
Изложенная теория позволила в основном правильно описать
основные черты общей циркуляции атмосферы, в частности, уда-
лось получить сибирский максимум, исландский минимум и дру-
гие особенности общей циркуляции атмосферы. Е. Н. Блиновой
была решена задача и о распределении температуры в атмосфере
[4, 12]. Изложенная теория и упомянутые работы и составляют
гидродинамическую теорию климата.
Используя найденные значения стационарных отклонений, мы
можем теперь решить уравнения для нестационарных частей рас-
сматриваемых переменных, т. е. решить задачу прогноза.
Можно, однако, несколько упростить задачу. С учетом соот-
ношений (1.6) при получении уравнений для нестационарных воз-
мущений можно опустить члены, содержащие стационарные воз-
мущения, т. е. произвести линеаризацию только относительно
западного переноса. В этом случае стационарные отклонения необ-
ходимы только для того, чтобы найти начальные значения неста-
ционарных частей. Если же при этом в качестве стационарных ча-
стей использовать климатические данные (включающие как зо-
нальные составляющие, так и стационарные части незональных
отклонений), то задача о предвычислении нестационарных воз-
мущений, т. е. собственно задача прогноза оказывается отделенной
от задачи теории климата.
Произведем теперь линеаризацию уравнений (1.7) относительно
зонального потока и получим уравнения для нестационарных ча-
стей. Прежде всего заметим, что для средней части тропосферы,
для которой мы хотим получить решение, можно не учитывать ба-
роклинные факторы (их учет был необходим при решении задачи
теории климата). Поэтому правую часть первого уравнения (1.7)
можно приравнять нулю.
Подставляя в уравнения (1.7) значения и vq по (1.1), учиты-
вая принятые обозначения и производя линеаризацию, для неста-
ционарных возмущений получаем:
dQ" , v'o dQ ^х
dt * a dO * a sin 0 d\
'а
— 2(o sin 6=0,
dv"\ dvy „ i
—pa ---—2 (aш) COS 6^o=------------=--— -y
dt 1 (П 1 v 1 ' л? sin 0
В соответствии с условиями (1.5)
*__________________ 1 dy
a sin 0 dk
1 dty”
а Э0
^x
a"=—nr
a sin 0 \
d sin 0vx
d0
dk
=4-дфг.
fl2 T
(1.10)
15*
227
Имея это в виду, получаем следующие уравнения:
(4+’тК+2<“+“)т-°-
дф"
<Э6
2 («+<о) ctg6-^2-=
1 др"
р sin 6 д\
(1.11)
В результате мы имеем систему из двух уравнений с двумя не-
известными гр" и р". Прежде всего заметим, что линеаризирован-
ное уравнение вихря скорости (первое из уравнений (1.11)) содер-
жит лишь одну переменную гр". Следовательно, оно может быть
решено независимо от другого.
Для его решения применяем метод разложения полей в ряды
по сферическим функциям, т. е. спектральный метод. Пусть иско-
мая функция представляется в виде ряда
П
ф"= I] [D^cos(mX+4"z)-|-r)?sin(mX+a^)]P™ (1.12)
п — 1 т = 1
где п и т — волновые числа (принимающие целые значения),
P™ = P™(cosf))—присоединенные полиномы Лежандра, о™ — ча-
стоты волн. Для определения частот подставим выражение для
гр" в первое из уравнений (1.11), предварительно произведя со-
ответствующее дифференцирование. В результате получаем
И /
п = 1 /п = 1 '
cos(mX-|-a^/)]x
(1 дР^ 2 \ 1
liHT-^sin0T-liSo рп) (^+“те)+2т(а+“)Л7]) =0-
Отсюда следует, что
1 д о д/ п
sin о до sin0 dfl
'»2 рт I 2w О + м) рш=л
sin2 в "Т + п
Полагая cos6=x и учитывая, что
• П 3
sin О——, вместо по-
дх
следнего уравнения получаем
(1-х2)
d2Pm
п
dx2
2х
dPm
dx
2т (а со)
<# + ат
т%
1 -Х2
р™=о.
Но это уравнение совпадает с известным уравнением для присо-
единенных полиномов Лежандра
(I -V2)
d2Pm
п
dx^
dP™
2х—Т^~
dx
л-2 \
1 -Х2/
Р-=0
228
при
p=n(«+l)
2/7z (a -j- w)
an ”b am
Отсюда следует, что
—a/zz-f
2m (a 4- w)
n (n 4- 1)
(1.13)
Итак, мы видим, что частота волн зависит от угловой скорости
вращения Земли, индекса циркуляции и волновых чисел п и т.
Зная частоту, мы можем теперь определить угловую скорость от-
дельных волн
т ап 2 (а 4~ <•>)
=----------- = а-----7—г 1
п т п (п 4- 1)
(1-14)
Первый член правой части полученного выражения дает вос-
точную составляющую скорости, а второй — западную. Величина
второго члена зависит от волнового числа гг. чем меньше это
число, тем больше абсолютная величина этого члена. Так как
крупные (длинные) волны имеют малые значения волновых чисел,
то они будут иметь тенденцию к смещению на запад.
Вернемся теперь к решению первого из уравнений (1.11). Оче-
видно, что необходимо еще определить коэффициенты D™ и D'™.
Для этого мы воспользуемся начальными данными. Положим, что
в исходный момент возмущение давления представляется в виде
ряда
р" (0, к) = 2 2 [ATcossin тл] Р™ (cosO). (1.15)
п — 1 tn = 1
Дифференцируя выражение (1.12) для ф" по 6 и X, полагая
затем / = 0 и подставляя результаты в первое из уравнений (1.11),
получаем соотношение для определения неизвестных коэффициен-
тов и по известным коэффициентам А™ и Д'™.
Для того чтобы получить решение только на северном полу-
шарии, считалось, что функция тока антисимметрична относи-
тельно экватора, т. е., что
ф(Х, к-0, /)=-ф(Х, 0, /). (1.16)
Применение условия (1.16) приводит к тому, что ряд членов
разложений (1.12) и (1 15) обращается в нуль. Например, в вы-
ражении (1.12) остаются члены, содержащие присоединенные по-
линомы Лежандра только с нечетной разностью индексов п— т.
После того как будут определены коэффициенты D™ и D'™ у чтобы
получить прогноз ф", достаточно в выражение (1.12) подставить
время t и значение о™ по (1.13). Величины скоростей и'' и у''
229
можно получить с помощью соотношений (1.10), а р" или Н"— пу-
тем решения второго из уравнений (1.11), считая, что гр" известно.
Зная величины нестационарных отклонений, переход к истин-
ным значениям метеоэлементов осуществляется путем прибавле-
ния отклонений к климатическим значениям.
Рассмотренные выше решения позволяют прослеживать поведе-
ние и рассчитывать различные характеристики отдельных волн
в общем спектре атмосферных движений. В этом одно из несом-
ненных достоинств методов прогноза, основанных на применении
спектральных разложений функций типа (1.12).
§ 2. Метод долгосрочного прогноза средних месячных аномалий
температуры
Полученное решение для гр" используется далее для решения
задачи о прогнозе температуры на долгий срок [7]. Для этого при-
влекается уравнение притока тепла, в котором учитывается верти-
кальный и крупномасштабный горизонтальный турбулентный теп-
лообмен. Ограничиваясь задачей прогноза температуры у земной
поверхности, в уравнении притока тепла можно положить vz = 0.
В соответствии со сказанным уравнение притока тепла берется
в виде
дГ . дТ dT d . dT . k'
dt * а d(J ‘ a sin О dz dz ‘ а2 '
где k и k'—коэффициенты турбулентности для вертикального и
горизонтального направлений.
Производя линеаризацию этого уравнения относительно основ-
ного состояния и выражая v" с помощью функции тока ф", для
нестационарных возмущений получаем
Id_____। d \ Tr __ 1 dT d<T
\ dt * а d'K ) я2 sin 0 dft dK
d dT" kr
----(2.1)
dz dz 1 «2 v '
Линеаризированное уравнение притока тепла (2.1) содержит
вертикальную производную второго порядка. Это значит, что необ-
ходимо поставить два краевых условия. В качестве одного из них
применим условия ограниченности решения на бесконечности, т. е.
Т" -*0 при г-*оо, (2.2)
а в качестве второго — условие теплового баланса на подстилаю-
щей поверхности
-X-Г+=А+-S -8®тк
dz 1 dz 1 ’
где А и S— нисходящие потоки длинноволновой и коротковолно-
вой радиации, 6оТ4— излучение земной поверхности, X— коэффи-
циент температуропроводности, знаком * помечены величины, от-
носящиеся к земной поверхности.
230
Это уравнение является нелинейным (член 6оТ4). Получим на
его основе линейное уравнение для нестационарных возмущений.
Полагая Т = Т+Т", где Т — климатическое значение Т, и приме-
няя формулу бинома Ньютона, получим
П=(г+ 7’")4=Г4+473Г"4-6Г2Г'2+ . . .
Принимая во внимание малость Г", можно положить, что
у4 ^4 । 4 уз у"'
Отделяя теперь в уравнении баланса нестационарные возмущения,
положив для этого, что для климатических значений Т справедливо
соотношение
-х 4^-+х* -4?-=А+5 - 5о^4>
dz 1 dz 1
и обозначив 4Т3бо = р, получаем следующее линеаризированное
уравнение теплового баланса:
2£L=-i17’"- (2-3>
Но это уравнение содержит новую неизвестную — температуру под-
стилающей поверхности (суши или моря). Поэтому необходимо
ввести в рассмотрение дополнительное уравнение. Таким уравне-
нием является уравнение теплопроводности для подстилающей по-
верхности, которое для нестационарных отклонений имеет вид
<2-4)
dt с*р* dz dz х 7
Введение этого уравнения требует постановки еще двух краевых
условий для 7*" В качестве таковых принимается, что
при г-*—оо Г*" ограничено,
при z=0 Т" = Т*" (2.5)
(условие «склейки» решений для Т" и Т*").
В качестве начальных условий примем, что при / = 0
Г'(0, X, г, 0)=/7(6, X, г),
Г*" (е, X, г, 0}=F*(P, X, г), (2.6)
где F и F* — известные функции.
Подставляя найденное ранее решение для ф" в уравнение при-
тока тепла (2.1), используя краевые условия (2.2) и (2.5) и на-
чальные данные (2.6), мы получаем решения для Т" и Т*".
Если полученное решение проинтегрировать по времени для ка-
кого-либо интервала /2—ti и поделить полученное выражение на
231
t2—h, то мы получим величину отклонения, или аномалии, сред-
нюю для этого интервала.
Если, например, /2—h равно месяцу, то выражение
Т- (6, х, 5 Г'(е, х, t)dt
будет означать прогностическую величину средней для этого ме-
сяца аномалии температуры воздуха.
Вернемся к вопросу о начальных данных для Т" и Т"* Анализ
решения и проведенные расчеты показали, что начальные поля Т"
и 7"* имеют значения для прогноза только на первые 10—15 дней.
При увеличении срока прогноза их влияние уменьшается, а роль
меридионального обмена, при котором главное значение имеет раз-
ность температуры полюс—экватор, увеличивается. В частности,
как было показано Е. М. Добрышманом, при прогнозе на месяц
влиянием начальных полей Т" и Т*" можно пренебречь, а доста-
точно ограничиться учетом начального поля движения в средней
тропосфере.
На основе изложенной теории была составлена расчетная
схема и с 1958 г. регулярно составляются прогнозы средних ме-
сячных аномалий температуры воздуха для северного полушария.
В качестве начальных данных используются высоты изобарической
поверхности 500 мбар, осредненные по нескольким дням, отстоящим
от начала месяца, для которого составляется прогноз, на 40 дней.
Функция тока берется приближенно в виде ty=-gH/l.
Для оценки прогнозов используются критерии р и Q (см. § 6
гл. VIII).
В среднем р и Q имеют значения примерно 0,2 и 1,1 соответст-
венно.
§ 3. Расчет индекса циркуляции
Под индексом циркуляции понимается угловая скорость дви-
жения воздуха относительно земной поверхности. При этом счи-
тается, что атмосфера движется как единое целое. Имея в виду
соотношение геострофичности и выражение (1.2), для зональных
значений высоты изобарических поверхностей получим
^х(0 z)=—о—-—г------_==а^а sin 6. (3.1)
А v ' 2am cos 0 dO v
Интегрируя по 0 от 0i до 02, находим
Н (^2, z)=H ,г)-[—* •— [sin202 — sin2 61]. (3.2)
Отсюда
п , drt(02, г)-~Л/(6г, z)]
V [81112 02 — 81112 09
232
Таким образом, формально для определения индекса циркуля-
ции среднего для широтного пояса достаточно иметь зональные
значения Н для двух широт.
Более точный способ расчета индекса циркуляции предложен
Е. Н. Блиновой. Этот способ предусматривает нахождение такой
линейной функции для величины //(6) sin2 6, которая бы наимень-
шим образом отклонялась от фактических значений Я (6) sin20
на всех широтах. Так может быть найдено значение индекса цир-
куляции а, наименьшим образом отклоняющееся от «локальных»
значений этого индекса, отвечающих каждому из широтных
поясов.
Ориентируясь на соотношение (3.2), для какого-либо уровня
можно записать Hh = A+Bxh, где Xfe = sin20fcj А и В неизвестные
коэффициенты, А = 1, 2, .. — порядковый номер широты. Коэффи-
циенты А и В определим методом наименьших квадратов (см. при-
ложение 7) из условия минимума величины
2 [A-YBxk-Hk]\
/2=1
Условием экстремума является обращение в нуль частных произ-
водных по параметрам:
^-2 [А-Н?ха-/Л]2=2 2 [A4-£?xft-/7j=0,
0Л Л=1 Л=1
- п __ п
2 [А+Вхь-Н^Ч 2 [д+вхй-//Л]хЛ=о.
Решая эту систему двух уравнений, находим
п \2
у
k I
k=l /
n ___ n n.
Я I X^H ft У Xk У। Hk
D fe=l /2=1 fel|=l
3=-------——------------------
- Z4
k=l
dH dxk
Подставив значение —^-=—= 2B sin 0 cos 0 в (3.1), получаем
a = Bg7coa2.
Часто, однако, оказывается удобнее иметь дело не непосредст-
венно с индексом циркуляции а, а с безразмерным индексом cz/co.
На практике расчет индекса сх/со производится по значениям зо-
нальных величин Я на шести широтах (40, 45, 50, 55, 60, 65°). Для
этого случая расчетная формула, полученная на основе решения
для В, имеет вид [12]
-£-= IO-3 [-0,7752^5-0,4952/Убо-0,1854//55+0,1448^+
+0,4853^45+0,8258^0],
233
где, например, //65— среднее значение высоты изобарической по-
верхности (дам) на широте 65°. Средние широтные значения вы-
числяются по 24 величинам Н для долгот, кратных 15°.
По этой формуле производятся расчеты индексов а/со для ос-
новных изобарических поверхностей как ежедневных, так и сред-
них для определенных периодов. Значения индекса циркуляции
слабо меняются ото дня ко дню. Однако он имеет годовой ход.
Для примера укажем, что в среднем за 20 лет (1949—1968 гг.)
для поверхности 700 мбар индекс циркуляции принимал значения
в январе 0,025, в июле — 0,017, а для поверхности 300 мбар —
0,054 и 0,055 соответственно.
§ 4. Теория прогноза на среднем уровне атмосферы,
основанная на интегрировании нелинейных уравнений
гидродинамики в соленоидальном приближении
Метод линеаризации позволяет свести нелинейные уравнения
к линейным, а затем получить решение в аналитическом виде. При
этом прогноз на заданный срок получается как бы с помощью од-
ного шага по времени. Такой способ позволяет избежать накопле-
ния разного рода погрешностей, возможных при многошаговых рас-
четах. В то же время реальные атмосферные движения часто бы-
вают таковы, что нестационарные возмущения в поле скоростей по
абсолютной величине оказываются соизмеримыми со скоростью ос-
новного потока. В таких случаях применение метода малых воз-
мущений и линеаризации оказывается невозможным и, следова-
тельно, возникнет необходимость решения нелинейных уравнений.
Теория прогноза атмосферных движений в средней тропосфере
на основе нелинейных уравнений была предложена Е. Н. Блино-
вой в 1954 г. Изложим ее, следуя работе Е. Н. Блиновой и
С. Л. Белоусова [15]. В качестве основного уравнения берется
уравнение вихря скорости в виде
-^-4—^- -^-(Й4-2(0 cos 6)4-----(4.1)
dt 1 а дО ' 1 7 1 a sin 6 дХ v '
где
1 / d sin dv. \
о___ .. ______А_____L
л sin 6 \ d§ d\ Г
В качестве второго соотношения используется уравнение нераз-
рывности, которое для среднего уровня имеет вид
<?sinOve dvx
эе + д/. и-
Это уравнение позволяет выразить компоненты скорости Уо и
vk через функцию тока
__ 1 дф __________ 1 дф
a sin 6 дХ ’ а дО
234
Таким образом, принимается гипотеза квазисоленоидальности.
Подставляя выражение для Q, Уе и в уравнение (4,1) и учи-
1
а2
тывая, что Q
Лф, получаем уравнение для определения ф
4--Л-й-(Ф. Дф)+2<о-^=О, (4.2)
1 a2 sin 0 1 дХ 47
где символ (Л, В) выражает якобиан в сферической системе коор-
динат.
Как и в случае декартовой системы координат, данное уравне-
дф
ние решается относительно —
а прогноз получается шагами
по времени. Уравнение (4.2) записывается в виде
д4г=-[ дф)+2ю ч-
dt L я2 sin О 1 dX I J ’ 7
Последнее уравнение можно рассматривать как уравнение Пу-
ассона на сфере с известной правой частью. Его решение имеет
вид
2х тс
4^=4- f f Ini 2(1 - cos т)/ (О', X') sin О' dO' dk', (4.3)
°* о о
где 0' и V— переменные интегрирования (интегрирование распро-
страняется на поверхность всего земного шара), а
cos y=cos 9 cos 9' —sin 9 sin 9' cos (X — X'),
причем у есть угловое расстояние на сфере между точками с ко-
ординатами 0, X и 0', X'.
Чтобы избежать интегрирования по всему земному шару и све-
сти его к интегрированию по одному северному полушарию, пред-
полагается, что поля функции тока в северном и южном полуша-
риях антисимметричны, т. е. что
ф(9, Х)=-ф(гс-9, X) и /(9, Х) = -/(т:-9, X). (4.4)
Представим интеграл (4 3) в виде суммы двух интегралов
2тс тс
J J 1п]/2(1 — cosy)/(9', X')sin9'd9dX' =
о о
ТС
2- “ __________
= j* J In 1^2(1 — cos у)/(9', X')sin9'rf9'rfX' +
0 о
2тс тс
+ J J In V2(l -cost)/(9', k')sinO'dO'dk'.
0 2L
2
235
Во втором интеграле произведем замену переменных, введя
0" = л— 0'. Тогда, имея в виду, что sin 0'=sin 0", d0'=—d0",
f(0', A')=f(jx — 0", X') =—f(Q", V) и меняя пределы интегриро-
вания, вместо указанного интеграла получим
тс
2гс 2 ____________________
| j In у2 (1 - cos 7) f (0", X') Sin 0" M" d\',
где cos у =—cos 0 cos 0' +sin 0 sin 0'cos (Z — V), а интегрирование
распространяется только на одно полушарие
Возвращаясь к переменной 0' и объединяя два интеграла, по-
лучим
?2тс 2
^=4- f In i-cosj; rjsinO'rfO'rfX'.
dt 4r. J J 1 + cos 7 ’
(4-5)
Полученный результат интерпретируется так же, как и в слу-
чае решения аналогичной задачи в декартовой системе координат.
Именно функция f(0', V) отражает перенос вихря скорости,афунк-
1 1 — cos у , „ , „ _
ция In--------— является функцией влияния, или функцией Грина.
1 +cos у
Общая схема прогноза аналогична схеме для случая декарто-
вых координат. Вначале определяются начальные значения функ-
ции тока, далее с помощью решения уравнения (4.5) рассчитыва-
дф
ется производная и делается шаг по времени.
После выполнения необходимого количества шагов по времени
можно сделать переход от функции ф к функции Н путем решения
уравнения баланса относительно Н.
§ 5. Теория прогноза в бароклинной атмосфере, основанная
на интегрировании нелинейных уравнений гидротермодинамики
в квазисоленоидальном приближении
Излагаемая далее теория прогноза разработана Е. Н. Бли-
новой в 1956 г. [6]. В этой теории используются гипотезы ква-
зисоленоидальности и адиабатичности атмосферных про-
цессов.
В качестве основных уравнений принимаются уравнения дви-
жения, неразрывности, вихря скорости и притока тепла в предполо-
жении адиабатичности (уравнения (8.9) и (8.10), (8.12), (8.13) и
(8.5) гл. II), а также уравнение статики. Рассмотрим приведение
этих уравнений к виду, в котором они используются в данной мо-
236
дели. Предполагаем, что имеют место следующие соотношения:
р(6, X, г, /)=Р(г)+Рг (°, 0;
Г(6, X, г, /)=7(г) + Г'(0, X, г, /);
р(б, X, г, /)=p(z)4-p'(e, К z>
где р(г), T(z) и p(z) —известные стандартные или климатические
значения р, Т и р, являющиеся функциями только высоты г; р',
Т' и р' — отклонения от этих стандартных значений.
Так как для всех трех названных элементов отклонения суще-
ственно меньше стандартных значений, то отношения pip, Т'/Т
и р7р по абсолютной величине всегда значительно меньше еди-
ницы. Это позволяет применить метод линеаризации уравнений.
Разлагая функцию 1/р в ряд по степеням малой величины р'/р,
получаем
1 _ 1 _ 1 1 ~ 1 Л _ pr \ 1
р Р + Р' р 1 + ~ р \ р ) Р
р
Аналогичным образом:
1 = RT . ]П Л I
Р р’р Р р ’ \ р } р
В таком случае, например,
1 др _ RT др ___prp d In р ~ prp
р дЪ~~~р ЭГ —7x7 дО
д In р ] д
~дО * >
1 др Г <9 In р . ( р’
У dz L дх \ ~р
но
dz
ainp _ 1 др_^__Lp-^=_ р
р р ёР RP '
Следовательно,
J_ др q ji _____
p dz dz
237
Отсюда, имея в виду, что
получаем
1 др
р dz
±g = 0 (уравнение
статики),
RT-?-(-C-}-g-^=0.
дг \ р ) Т
Далее полагаем, что
d?vz d?vz
dz ~ dz
а в уравнении неразрывности (8.12) гл. II величину р, стоящую
в качестве множителя перед скобкой, заменяем на р. Имея в виду
все сказанное, пренебрегая малыми членами, а также учитывая,
что
dT дТ'
06 06 ’ ОХ 0Х ’ 06 06
dT or dT or
ОХ ох ’ dt dt 9
получим следующую систему уравнений:
_ _ 2LL * ZL+,х (2„, cos «+а); (5.!)
« C/v р
RT d
a sin 6 d\
dt ‘ a 06 2
।___1__L
dt ' «sin 6 d\
— Т’6 (2оз cos 64“^)-
(5.2)
(5-3)
2
P
RT-£--£—g^
dz р у
0;
d?Vz
_______P
dz T a sin 6
dv^
~dV
=0;
(5-4)
W I । дЛ- i-fr _.\v =0-
dt + а ЙО + a sin 0 д\ {}г U’
(5-5)
I д /о । 2(о cos 6) I
dt ' a 06 ‘ ' «sin 6 OX
( pt I 2(0 c°s 6 + Q d^vz_
sin 0 ( ~p ’ j ’* p dz
Тщательный анализ показывает, что в уравнении (5.4) первый
член меньше каждого из двух остальных. Поэтому очень грубо
для всех уровней можно положить, что
O^0sin0 0vx
06 ‘ 0Х
238
Последнее соотношение позволяет ввести функцию тока гр,
а компоненты vq, а также Q выразить через гр следующим об-
разом:
<’.=--жг4- <5-7>
где А — оператор Лапласа на сфере. Таким образом, принимается
гипотеза квазисоленоидальности на всех уровнях. С другой сто-
роны, сравнение порядков величин членов уравнений (5.1) и (5.2)
позволяет приближенно записать
_ ^ср- —|-^,2(ocosO>^0,
а дб р 1 А
------------------cos 0 °’ (5.8)
a sin 0 дА р ° v '
где ТСр — осредненное по всей атмосфере значение температуры.
Сравнение соотношений (5.7) и (5.8) позволяет сделать вывод, что
^4-=l^2»cos(,t.
^^2<ocos0-^- (5-9)
Отсюда можно заключить, что с точностью до произвольной по-
стоянной
/?Тср ~ 2<о cos №.
И,мея это в виду и полагая в уравнении статики (5.3) Т—Тср,
получаем это последнее уравнение в виде
тг 2со cos 0 rj. db /г i п\
Г=------g---- ГСР^Г- (5Л°)
Подставляя соотношения (5.7) и (5.9) в уравнение вихря ско-
рости (5.6) и уравнение притока тепла (5.5) и пренебрегая ма-
лыми членами, получаем:
дДф । 1 /• л.ч 1 о дф 4w2cos20 dfy \ ।
~dt Ь «2sine ДФ) + 2(Й д\ ~ gsine V’ dz
। 2(0 cos Оа2 dpvz . (5 11)
р dz
Н—7-^-й (ф, р^=0. (5.12)
dzdt * л2sin 6 V’ dz / ‘ 2(о cos r v '
»
Введем новую независимую переменную £=—-, где Р =
= 1000 мбар. Так как
д _______________ д _ д ( р \ д __________ ^р д
dz dt dz dz \ Р J dt P dt ’
239
то
/ дф \ £Р / dty \ dpvz _ £Р dpvz
дг Р Г дг ~ Р dt '
Уравнения вихря скорости (5.11) и притока тепла (5.12) теперь
принимают вид:
дДф . 1 /1 л 1 \ । о дф 4о>2 cos2 6 fc (, дф \
~дГ~^ л2sin О АФ) + 2с0"ЗГ— sin0/?rcp dz )
2со cos Ол2^ dpvz . /с; iq\
Р д£ ’ (0.1 о)
д2ф , 1 дЬ \ Я2Лф(Ъ — 7) _п
d^dt * tf2sin0 v’ dz / 2со cos O/^2
(5.14)
В результате получаем два уравнения с двумя неизвестными гр
и vz. Для среднего уровня правая часть уравнения (5.13) мала и
уравнение принимает вид (4.2).
Для решения полученной системы уравнений построим вначале
одно уравнение для гр. Для этого умножим уравнение (5.14) на
и результат продифференцируем по g. При этом величину
Г= ^2Уср ( 7а —7
4co2#2g- у COS2 6 /ср
будем считать постоянной (г~—. Тогда получим
2со cos Oa2g р dpvz _ d fc2 д дф । 1 fc2( h дф \
Р д£ Э; * д^ dt "4" a2sin0 дб * V ’ /
Подставляя это выражение в уравнение (5.13), находим
^+т^е!44=-^пг«''
4Н- <5-15>
Для сокращения письма введем функцию
Тогда уравнение (5.15) переписывается в виде
4-£24--^-+г^4т-= 2!й-(ф> а)-2<йг4г- <5-16)
dz dz dt 1 dt a2 sin 6 VT ' d\ v 7
В качестве краевых условий принимаются:
при г=0 (В=1) ^2=0,
при г-*оо (£~*0) p^-*0 (5.17)
240
Решение уравнения (5.16) относительно дф/д/ при краевых ус-
ловиях (5 17) ищется для северного полушария. Вводится допол-
нительное условие. Именно, считается, что на экваторе ф = 0. Это
соответствует слабым ветрам в экваториальной зоне В таком слу-
чае решение получается в виде
тс
1 2тс Т
-Jr=S S f [<*’ ^)+2^2sin6 -|r]rf6rfX^+
1 2тс 2
+И
ООО х 7
(5.18)
где gi и g2 — функции Грина, указывающие на характер влияния
на dty/dt величин
[(Ф, Дф)+2«ш2з1п 9 и (ф,
соответственно, а интегрирование распространяется на северное
полушарие.
Полученное решение было использовано С. Л. Белоусовым для
прогноза высот изобарических поверхностей 850 и 500 мбар [1].
Функция тока приближенно бралась в виде ф = gH/I.
Исходные данные были взяты в 505 точках северного полуша-
рия через каждые 10° долготы и 5° широты (от полюса до 20° с. ш.).
Подынтегральные функции в решении (5.18) вычислялись в декар-
товой системе координат. При этом принималось, что:
1 д _ д 1 д _ д
a sin 6 дК дх ’ а дЬ ду ’
л 1 . д д , 1 д2 а2 . а2 \
Sint) Э0 Sln6 Й0 + Sin2 0 <П2 —а \ <)л-2 + ду2 ) ’
1 / л ох о ( дА дВ дА дВ \
B)s—a д^'^дГ)’
где индексом s обозначены операторы на сфере. Шаг по коорди-
натам As принят равным 555 км.
В другом варианте реализация теории Е. Н. Блиновой была
выполнена Г. П. Курбаткиным [17]. В качестве исходных уравне-
ний принимаются уравнения притока тепла (5.14) и уравнение
вихря скорости (5.13), в котором с самого начала пренебрегается
первым членом правой части, являющимся относительно малым.
Уравнение вихря скорости записывалось для изобарических по-
верхностей 300 и 700 мбар, уравнение притока тепла — для поверх-
ности 500 мбар, а вертикальные производные заменялись конеч-
ными разностями.
16 Зак. № 21
241
В результате было получено три уравнения, содержащие dty/dt
для поверхностей 300 и 700 мбар и vz — для поверхности 500 мбар.
После решения этих уравнений, являющихся уравнениями типа
Пуассона и Гельмгольца, делается шаг по времени.
При составлении прогнозов по данной модели обнаружилось,
что ультрадлинные волны (с длиной волны более 5 тыс. км), свя-
занные с сезонными (климатическими) областями высокого и низ-
кого давления, на прогностических картах оказываются смещен-
ными на запад В действительности эти волны являются квази-
стационарными. Это обстоятельство приводило к ухудшению
прогнозов. Они заметно улучшились после того, как в качестве на-
чальных стали использоваться данные, из которых указанные длин-
ные волны предварительно «убирались». Результаты прогноза на
необходимый срок складывались с величинами Я, соответствую-
щими длинным волнам, «убранным» на первом шаге.
Отметим еще, что исходные уравнения (5.13) и (5.Г4) были
использованы С. А. Машковичем и Я. М. Хейфецем, а также
М. Б. Галиным для разработки линейных прогностических моделей
[16, 22].
§ 6 Теория долгосрочного прогноза, основанная на интегрировании
полных уравнений гидротермодинамики при учете
неадиабатических факторов
Излагаемая далее теория была разработана Е. Н. Блиновой
в 60-х и начале 70-х годов [8—14]. В ней учитываются все основ-
ные погодообразующие факторы: все основные виды притока
тепла, теплообмен атмосферы с подстилающей поверхностью, из-
менения альбедо, связанные с облачностью и состоянием подсти-
лающей поверхности и т. д. Для скоростей принимается
_ 1 дф । 1 дер 1 дф , 1 д<р
«sin 0 дЛ * а дб ’ а дб «sin 0 дк ’
где ср — потенциал скорости.
Очевидно, что включение в эти соотношения потенциала скоро-
сти и означает переход в постановке задачи от квазисоленоидаль-
ного приближения к использованию системы полных уравнений
гидротермодинамики.
В этом случае вертикальная компонента вихря скорости и го-
ризонтальная дивергенция скорости представляются в виде
2=-^- Дф, D =-к- Д<р.
Вместо вертикальной скорости vz вводится в рассмотрение
функция W=-^-gp (z)vz, вместо р — функция &=-p-RTcpp', где
р'=р — p(z), а вместо Т будет рассматриваться функция Т' =
242
— Т— T(z). В качестве исходных уравнений принимаются урав-
нения вихря скорости, дивергенции, неразрывности, притока тепла,
статики и переноса влажности. Как и в § 5 наст, главы, в каче-
стве вертикальной координаты примем величину В соот-
ветствии со сказанным, эти уравнения записываются в виде:
дАФ . 1 ,, * , . о 9 m , 1 ду д (ДФ 4- 2со«2 cos 6) .
Н---о--" тг (Ф, АФ+2с°я2 cos 0) И-у- ---
dt 1 a2 sin 6 т * ' 1 #2 ди
дб
। 1 дАф аДф 2 dW . a dW dvQ =
• ^2 sin 6 dX дХ d£ а дб d£ ‘ sin 6
=Т^Г=<ф, r)-(^+2<rfcoSe)^
(6.i)
д Д<р ,г/ <ЗД<р dW dvb a dW ,
dt W di а <30 <3$ sin 0 dk di +
2 dv.
(Д?)2-----Дер —™
v *7 a ‘du
1
Д2
2
a
dv
I 1-^ |
a dG + asinO <3X
— 2o) cos 0 Дф-}~2ош sin Огц=0;
(6-2)
(6-3)
4-д?
dw
dTf । dt 1 ve дТ' , а дб 1 dT’ asin0 dk 7a g дФ j dt 1 RTcp Г /, g (la 7) g
(6.4)
T’=- £ дФ di ’ (6.5)
dq_ , ve <3<? , v k dq n7 dq <3 , <3?
dt * a de a sin 0 <33. <3$ dz dz
(6-6)
Здесь q — удельная влажность, a F — функция, учитывающая при-
ток тепла Она включает в себя приток тепла, связанный с корот-
коволновой и длинноволновой радиацией, которая считается диф-
фузной, и турбулентный теплообмен по вертикали FT. Для послед-
него принято
/г 1 д . дТ
д Л ,
bpv
где X — коэффициент турбулентной теплопроводности. Приток
тепла за счет конденсации учитывается путем замены в случае со-
стояния насыщения в уравнении притока тепла уа на уВа-
В качестве краевых условий принимаются следующие:
на верхней границе атмосферы
при В=0 W=0 и -^-=0, (6.7)
16*
243
у земной поверхности
при £=1 V7=0 и — Х-^-
--X^L_JL=/?. (6.8)
dz ср dz v 7
Здесь А? — радиационный баланс, а последний член в левой части
учитывает затрату тепла на испарение.
Введение новой неизвестной функции 7* требует дополнитель-
ного уравнения. Таким уравнением является уравнение теплопро-
водности для подстилающей среды
дГ* _ dW*
dt —к dz^
(6.9)
(для океана здесь следует еще учесть горизонтальную адвекцию
тепла, что достигается добавлением к левой части (6 9) членов
* *
ve dT* vx
a dft * a sin О
dT*
d\ 9
где v*Q и у* — средние значения скоростей воды в океане, которые
могут быть взяты, например, по климатическим данным)
Для замыкания полученной системы уравнений принимаются
еще два граничных условия:
при z-^—oo при z=0 Г*=Т. (6.10)
В качестве начальных данных должны быть заданы Ф, vq
и q.
Система уравнений вместе с краевыми условиями (6.1—6.10)
представляет собой замкнутую систему полных уравнений. Ввиду
ее сложности она может быть решена только приближенными (чис-
ленными) методами.
Рассмотрим ход такого решения, отвлекаясь пока от уравнения
переноса влаги.
Производные по времени в уравнениях (6.1), (6.2) и (6.4) за-
меняются конечными разностями:
4^=4-44-4 ^'+“-
дт' _ 1 _ 1 —
dt ~ Ы u dt ~
Аналогично конечными разностями заменяются и производные по
g. При этом атмосфера делится на ряд слоев с помощью введения
уровней gi, ^2, . .in- Далее все функции, входящие в (6.1) и (6.2)
линейно, берутся в момент t+6t (неявно), а все нелинейные члены
в этих уравнениях — в момент t+§tl2. В уравнении (6.4) член
с Г и все члены правой части запишем в момент t+8t, а нели-
244
нейные члены в левой части — в момент Z+6//2. Положим далееу
что все функции в моменты t и известны. В таком случае
мы можем сделать шаг по времени и определить искомые функции
для момента /+ 6Л
Вначале с помощью уравнения (6.4) определяем Wt+&t через
фн-st и известные функции. Найденное выражение для
деч+б* подставляется в уравнение неразрывности (6.3). В резуль-
тате получаем выражение для Д<р*+б*. Подставив теперь все най-
денные функции в уравнение вихря скорости (6.1), мы определим
Дф<+6* и ф*+б*. Теперь на основании уравнения дивергенции и ста-
тики можно получить уравнения для определения Ф*+б* и T't+bt.
В результате мы получаем замкнутую систему уравнений. После
определения и T't+6t легко получить значения ф*+*6
и т. д.
При реализации изложенной схемы возникает целый ряд труд-
ностей, к числу которых относится вычисление пространственных
производных высокого порядка и нелинейных членов уравнений
вида (ф, Дф).
Е. Н. Блинова [13] предложила такой метод, в котором частич-
но преодолены указанные трудности и сочетается учет физических
факторов, описываемых с помощью нелинейных членов, с преи-
муществами математического аппарата разложения переменных
в ряды по сферическим функциям. Этот метод получил название
метода выделения главных волн или частичной линеа-
ризации. Идею его поясним на примере.
Пусть, например, поле некоторой переменной представляется
в виде
Ф(е, х, /)=ф(о, /)+ф(о, х, /)+Ф(0, х, /), (6.11)
где функция ф(0, t) —характеризует зональный поток, ф(6, X, t) —
наиболее крупные возмущения — главные волны, а ф(0, X, t) —
сравнительно малые возмущения. При этом
ф=ф-|-£ф-[-£2ф, (6.12)
где 8 — некоторый параметр малости.
Рассмотрим теперь якобиан вида (ф, Дф). С учетом (6.11) и
(6.12) получаем
(ф, Дф) = [(ф4-еф-ф-£2ф), А{ф4-еф4-е2ф)] = (ф, Дф)-|-
+е(ф, Дф)-]-£2 (ф, Дф)-}“£(ф, Дф)-|-£2 (ф, Дф)-[-£3 (ф, Дф) —
Ц-£2(ф, Дф)-1-£2 (ф, Дф)-ф-е4 (ф, Дф).
245
Частичная линеаризация заключается в том, что мы пренебре-
гаем членами, содержащими произведения малых величин, т. е.
членами с е3 и е4. В таком случае, учитывая еще, что (гр, А гр) =0,
получаем
(Ф, Дф)^(ф, Дф) + (ф, Дф) + (ф, Дф)+(ф, Дф). (6.13)
Далее зональные части и члены, описывающие главные волны,
представляются в виде простых выражений, например, вида
ф = — Л2 а (/) Рг (cos 6) = — а2 а (/) COS 9,
ф= [Я? (/) cos {ХЛ + //? (/) sin рЛ] Pt (cos 0), (6.14)
где а(/), Яц(/) и H'v(t) —коэффициенты, зависящие от времени;
v и ц — волновые числа (заметим, что если гр — описывает поле
скоростей, то a(t) — является индексом циркуляции).
Здесь мы сталкиваемся с новой трудностью: как правильно опи-
сать главные волны, которые будут иметь место в прогнозируемый
период.
Малые возмущения выражаются в виде ряда по сферическим
функциям со значительным числом членов, т. е. в виде
ф = S S [Нп (t) cos тк-]-Нпт (/) sin Ы] р™(cos 9), (6.15)
п > т гп
где Hm(t) и —зависящие от времени коэффициенты раз-
ложения.
Подставляя теперь соотношения вида (6.14) и (6.15) в наши
прогностические уравнения, производя частичную линеаризацию
с помощью соотношений вида (6.13) и делая еще ряд преобразова-
ний, мы получаем вначале уравнения для определения коэффици-
ентов а, и Н'». Хотя при этом все полученные уравнения или
некоторые из них оказываются нелинейными, иногда их можно ре-
шить до конца в аналитической форме [13]. В противном случае
они решаются численно. Тогда задача должна решаться шагами
по времени. После определения указанных коэффициентов реша-
ется задача нахождения коэффициентов Н™ и Н'™ разложения
(6.15). Но это уже линейная задача, поскольку, как это видно из
(6.13), величины гр нигде не входят в виде произведения. Ее реше-
ние производится обычными для таких задач методами. Оконча-
тельное решение получается путем суммирования всех трех волно-
вых компонент, т. е. членов вида гр(0, /), гр (6, X, /) и гр (6, X, /).
246
§ 7. Четырехуровенная квазисоленоидальная нелинейная
прогностическая модель
Данная модель разработана С. А. Машковичем и И. Г. Вейль
[21] Постановка задачи здесь близка к рассмотренной в § 5.
Для решения прогностических уравнений развита методика спек-
тральных разложений полей в нелинейнОхМ случае. Уравнения мо-
дели получаются на основе уравнения вихря скорости и притока
тепла в квазисоленоидальном и адиабатическом приближении.
После введения в качестве независимой переменной £ = р(6, Х)/Р
и использования уравнения статики, которое при условии ф =
= gHll берется в форме
т _ __ g_ r
1 ~ R dt ’
эти уравнения принимают вид:
A -Jr + 21. fl- (Ф, Аф)+2ю -Jb = -±- аЧ ,
dt 1 a2 sin 6 VT’ * dl Р dt 1
d^
dt dt
Исключив из этой системы уравнений т, получим
дф
dt
А-17 X- (ф, Аф)4-2со
«2sin6 VT’ 1
А
W I Р п2 (г2 д2ф \
dK с2 U dt V dtdt J
+^еттг'?^-гг)=°- <7Л>
На верхней границе атмосферы принимаем т-^0 при £->0 От-
сюда следует, что
<7-2>
На нижней границе атмосферы принимается w = 0. Полагая при-
ближенно, что
и что получаем
при С=1
_ Р1 дф
RT. dt ‘
Подставляя это выражение для т в уравнение притока тепла, за-
писанное для нижней границы атмосферы, получаем следующее
краевое условие:
„риС=1 (7.3)
где ai=/?(Ya —у)/^-
247
В качестве начального условия берется:
при 1=0 ф(Х, О, С, 0)=фоОч в, Q- (7.4)
Для получения решения на северном полушарии для функции
тока принимается условие антисимметрии относительно экватора
ф(к, -я —О, С, /)=-ф(л, 9, С, /). (7.5)
Кроме того, принимается условие ограниченности ф(21, 0, £, /) на
полюсе и периодичности по долготе, что выражается в виде
ф(Х+2тс, О, С, /)=ф(Х, О, С, /). (7.6)
Для решения поставленной задачи применяется спектральный
метод. Решение нелинейного уравнения (7 1) ищется с помощью
рядов по сферическим функциям вида
ф(Х, °, 12[фл(^ /)со8тХ4-ф,Г (С, /)sinЫ] Р™(cos9),
п т
где т и п — волновые числа, ф™(£, t) и ф'ш(?, t) —коэффициенты
разложения, зависящие от времени и высоты.
Если ввести волновой вектор у(тъ п^), определяемый волно-
выми числами ту и пу (y = nv + fmv), то можно использовать дру-
гую, более короткую форму записи разложения в ряды по сфери-
ческим функциям
ф(Х, 9, С. 0=2Х(С- О (cos 9), (7.7)
т
где Pv(cos0) =P™(cos0).
После подстановки выражения (7.7) в уравнение (7.1) и неко-
торых преобразований получаем следующее уравнение:
“ЭГ ~дГ dUdi ^~а~ — а 2 [^а — +
/2 а / дФо дф \1 1
(7-8)
где av = nv(nv+1),
If ( dP
^7pa — 2~ J ШрРр J dB
0 4
— коэффициенты, не зависящие от времени и вычисляемые зара-
нее, а и р — волновые вектора, связанные с волновыми числами
тип. Правая часть полученного уравнения содержит произведе-
ния искомых коэффициентов разложения ф и, следовательно, урав-
нение (7.8) является нелинейным Ввиду трудностей решения не-
линейных уравнений будем решать его относительно dtyy/dt, пола-
гая правую часть в некоторый момент известной.
248
Далее производится замена производных по вертикали конеч-
ными разностями. С этой целью атмосфера разбивается на четыре
слоя поверхностями £ = 0; 0,17; 0,50; 0,83 и 1,0. Уравнение (7.8)
запишем для уровней £ = 0,17; 0,50 и 0,83 при учете граничного ус-
ловия (7.2), а кроме того, учтем условие при £ = 1. В результате
вместо одного уравнения (7.8) получим систему из четырех ко-
нечно-разностных уравнений, содержащую в качестве искомых ве-
личин коэффициенты рядов по сферическим функциям.
Теперь делается переход к конкретному количеству членов
ряда и тогда вместо упомянутых четырех уравнений, мы получаем
систему линейных алгебраических уравнений, число которых будет
зависеть от числа учтенных членов ряда.
При конкретной реализации данной модели вместо ряда (7.7)
использовался ряд вида
М | т | = N — 1
Ф(х, е, с, /)= 2 2 Ф« 0^z"iXA7(cos6)
т = —/VI п = 1 т |4-1
при 7H=7V=1O. В этом случае полученная система для определе-
ния коэффициентов ряда содержала 440 уравнений; число коэф-
фициентов /Стра составило 8323.
В качестве исходных данных используются высоты изобариче-
ских поверхностей 850, 500 и 200 мбар и давление на уровне моря,
заданные в узлах регулярной сетки с шагами 66 = 5° и 6Х=1О°,
охватывающей северное полушарие.
Интегрирование по времени производится методом Адамса по
соотношению
при шаге по времени, равном 1,5 ч. Рассмотренная методика позво-
ляет прогнозировать поля давления на уровне моря и высот ука-
занных изобарических поверхностей на срок до 10 суток
Возможность интегрирования нелинейной задачи на долгий срок
здесь обеспечивается тем, что расчетная схема предусматривает
достаточно точное выполнение условия сохранения энергии и дру-
гих инвариантных величин и свободна от нелинейной неустойчи-
вости.
Модель обобщена на случай учета неадиабатических факторов
[20]. Это обеспечивается, в частности, включением в расчеты ос-
новных климатообразующих факторов. Воздействие последних на
энергетику модели описано приближенно в форме закона Ньютона,
согласно которому приток энергии к некоторой системе пропорцио-
нален величине отклонения системы от равновесного состояния.
Благодаря этому уточнению в ходе прогноза обеспечивается под-
держание реального «климатического фона», который обычно ис-
кажается в адиабатических вариантах задачи (ложное смещение
длинных волн к западу и др.)
249-
§ 8. Численное моделирование циркуляции атмосферы
и долгосрочный прогноз погоды
Модель атмосферы, предназначенная для долгосрочного прог-
ноза погоды, должна правильно описывать общие черты циркуля-
ции атмосферы за длительный период. Более того, можно считать,
что для долгосрочного прогноза погоды могут быть применены
лишь те модели, которые правильно воссоздают атмосферную цир-
куляцию, хотя, разумеется, не всякая циркуляционная модель мо-
жет быть использована для прогноза.
Этим обстоятельством объясняется особое внимание исследо-
вателей к созданию гидродинамических моделей циркуляции ат-
мосферы и климата. Первая работа в этом направлении была вы-
полнена в СССР Е. Н. Блиновой [2], построившей гидродинами-
ческую теорию волн давления, температурных волн и центров
действия атмосферы в линейной постановке. Дальнейшие работы
в этом направлении, выполнявшиеся с конца 50-х годов, позволили
построить гидродинамические модели других явлений и процессов
планетарного масштаба и привели к созданию ряда моделей об-
щей циркуляции атмосферы и океана. За рубежом такие модели
были построены Н. Филипсом, Е. Минцем и А. Аракавой, Дж. Сма-
горинским и др., А. Касахарой и У. Вашингтоном [23, 25, 26, 28—31]
и другими авторами. В СССР циркуляционные модели были раз-
работаны Г. И. Марчуком, М. Е. Швецом и др. [19, 27].
Характерным для этих исследований является стремление на-
ряду с созданием устойчивых вычислительных схем, позволяющих
интегрировать нелинейные уравнения на долгий срок, ввести в мо-
дели наиболее точное описание внешних источников и стоков энер-
гии, питающих циркуляцию атмосферы — неадиабатических эф-
фектов. При этом задание начального состояния оказывается
несущественным. Аналогичная ситуация, как мы видели, имеет ме-
сто при долгосрочном прогнозе средних месячных температурных
аномалий (§ 2 наст, главы). Однако идеальной была бы такая
постановка задачи, когда с помощью одной и той же основной
модели атмосферы можно было бы рассчитывать как погоду, так
и климат.
Дадим краткое описание некоторых из созданных и разви-
ваемых в настоящее время моделей общей циркуляции атмо-
сферы.
Девятиуровенная модель циркуляции атмо-
сферы [25, 31]. Эта модель разрабатывалась около 10 лет
Дж. Смагорииским, С. Манабе, Дж. Холлоуэйем, К. Миякодой и др.
в Принстонском университете (штат Нью-Джерси, США), а затем
в Лаборатории геофизической гидродинамики Бюро Погоды США
в г. Принстоне
В качестве исходных уравнений принимаются полные уравне-
ния гидротермодпнамики при учете турбулентной вязкости и не-
адиабатичности, которые записываются в о-системе координат
250
в дивергентной форме при учете картографической проекции (на-
чало координат помещено в полюсе):
dpsU_______ 2 TjL ____д I PsUV Y| dau .
dt [ дх \ т )' ду \ т /J *s ds ~
2u)Sin6
dpsv _
dt
— ps |2<osin6
(vx — ну) — mgps — mRT-^-}-psDx-,
2^2- - чу)] и - mgps -^--mRT -^+psDy-,
dH _ RT
da ga ’
dPs _ „,2 Г ,_d ( PsV do .
dt L дх \ m /~*~ dy \ m /] de ’
dps? _ [ d ( p£iT \ dt psvT_ Y]
dt L dx \ m ) ' dy \ m /1
deT
Ps da
dt
P^r \ d / ppvr \|
in / ’ dy \ m /]
^4г+^Г<=-- + =.+'«^
UV1 I
-Ps -^-YPs^A-PsTk,
где m — масштабный множитель; Dx и Dy — компоненты силы тур-
булентной вязкости; г = 0,622е/(р — е)—отношение смеси; е — аб-
солютная влажность; гт — приток влаги, обусловленный горизон-
тальной и вертикальной турбулентной вязкостью; — приток влаги
вследствие конденсации.
В качестве граничных условий принимается
о=0 при о=0 и о=1.
Величины Dx, Dy, ет и гт — определяются через производные
переменных и, v, Т, г и коэффициенты турбулентной вязкости,,
а ел — по способу, основанному на использовании интегральных
функций пропускания.
У земной поверхности вертикальные потоки количества движе-
ния, тепла и влаги задаются следующим образом:
T,=-PAC|Vft|VA;
^s=PhcPC\Vh\(Ts-Thl^-,
Qs=PhC\Vh\[r(Ts)-rh],
где С — некоторый коэффициент; индексом h помечены величины,
относящиеся к высоте верхней границы нижнего (приземного) слоя
(/z^75 м), u = RJcp.
251
На земной поверхности (на суше) принимается условие тепло-
вого баланса в виде
(1 -As)S-\-G=^+Hs+^Qs,
где 3—тепло конденсации, — альбедо подстилающей поверх-
ности. В этом уравнении не выписан член, учитывающий тепло-
обмен с почвой. Поэтому оно будет справедливым лишь для хо-
лодного времени года, когда этот теплообмен мал. Данное
краевое условие используется, в частности, при расчете темпера-
туры поверхности суши. Температура же водной поверхности счи-
тается известной и равной климатической. Поэтому над океаном
условие теплового баланса не ставится. В случае, если в резуль-
тате решения уравнений переноса влаги и притока тепла на оче-
редном шаге относительная влажность окажется больше критиче-
ского значения (100 или 80%), то принимается, что наступает
процесс конденсации и вся сконденсировавшаяся влага выпадает
в виде осадков, количество которых для всего столба атмосферы
вычисляется по формуле
о
^rdp,
ps
где 6г — изменение отношения смеси водяного пара.
Для численного интегрирования уравнений в атмосфере выде-
ляются девять поверхностей (рис. 7.1) со значениями коорди-
наты О'
.....9>-
Кроме того, рассматривается верхняя граница атмосферы п = 0 и
поверхность земли о'=1(р = р«). Обратим внимание на то, что
координатные поверхности расположены по вертикали не равно-
мерно: наиболее часто они расположены в стратосфере и вблизи
земной поверхности. При этом уровень о3 соответствует верхней
границе нижнего приземного слоя, а уровень о8— верхней границе
планетарного пограничного слоя.
Интегрирование исходных уравнений производится либо для
северного полушария, либо для всего земного шара.
В первом случае уравнения записываются в конечных разно-
стях на плоскости карты стереографической проекции. При этом
вводится прямоугольная сетка точек, охватывающая полушарие.
Шаг сетки может быть различен. В одном из вариантов он состав-
ляет 640 км у полюса. В другом варианте шаг сетки у полюса со-
ставляет 320 км. Тогда на полушарии оказывается 5025 точек.
При интегрировании по полушарию у экватора ставится условие
непроникновения масс воздуха через экватор, т. е. там принима-
ется, что Кп = 0.
252
Во втором случае, при интегрировании по всему земному шару
уравнения записываются в сферической системе координат с ша-
гом по широте и долготе в 2°. В этом случае число точек на зем-
ном шаре составляет 9216.
При расчетах потоков и притоков тепла температура поверх-
ности океана, граница снегового покрова и облачность принима-
ются известными по климатическим данным.
В первых экспериментах по исследованию формирования цир-
куляции начальные данные задавались весьма искусственным обра-
к рмбар.
0,000 0,5---------------------------------------------------- 0 (6=0)
0,009 1 ---------------------------------------------- 9
0,074 2 74
500
б(к=1,5;
2,5;...8,5)
664
0,500
0,664
0,811 7
0,926 8
0,991 9
1,000 9,5
Рис. 7.1. Вертикальная структура атмосферы в модели цир-
куляции Дж. Смагоринского и др.
зом. Полагалось, например, что в начальный момент атмосфера
является неподвижной, а ее температура всюду равна 289 К. Внеш-
ние параметры (приток тепла от Солнца и пр.) задавались близ-
кими к действительным для какого-либо месяца.
Оказалось, что по истечении достаточно длительного времени
порядка нескольких месяцев возникает циркуляция, близкая к фак-
тически наблюдаемой средней картине циркуляции для месяца,
к которому относятся внешние параметры.
Данная модель была использована не только для исследования
циркуляции атмосферы, но и для прогноза различных метеоро-
логических полей по северному полушарию. В этом случае
253
в качестве начальных были использованы фактические данные
о температуре, давлении и влажности воздуха, полученные с помо-
щью численного анализа для стандартной сетки по северному по-
лушарию. Скорость ветра для этой цели представлялась в виде со-
леноидальной и потенциальной частей:
г, —_ J*L_i у — ду
и~ ду дх ’ и~дх'ду
Значения ф находились с помощью уравнения баланса, ср — из
уравнения неразрывности, взятого в виде Дф+дт/др = 0, ат — из
уравнений квазигеострофической модели.
Анализ рассчитанных прогнозов показал, что удовлетворитель-
ный результат получается на сроки, не превышающие двух недель.
Это хорошо видно на рис. 7.2 а, б, \в, где приведен ход средней
квадратической ошибки прогноза высот изобарических поверхно-
стей 1000, 500 и 50 мбар на сроки до 14 суток. Там же приведены
соответствующие данные о фактической изменчивости за соответ-
ствующие интервалы времени. Мы видим, что с некоторого мо-
мента времени ошибка прогноза начинает превышать фактическую
изменчивость. О значительном ухудшении качества прогнозов на
срок более двух недель свидетельствуют также и графики хода
коэффициентов корреляции между прогностическими и фактиче-
скими изменениями высот (рис. 7.2 г, д, е).
Полученные результаты, по-видимому, частично подтверждают
гипотезу о существовании предела предсказуемости
крупномасштабных атмосферных процессов. Под последним неко-
торые исследователи понимают интервал времени прогноза, при
котором его средняя квадратическая ошибка остается меньше при-
родной изменчивости. На основании ряда проведенных экспери-
ментов эти исследователи определяют верхний предел предсказуе-
мости индивидуальных крупномасштабных процессов в три-четыре
недели. Здесь следует, однако, отметить, что результаты численных
экспериментов в значительной мере зависят от самой численной
модели, а также от качества начальных данных.
Вопрос о характере начальных данных для долгосрочного
прогноза, особенно большой заблаговременности, нуждается в спе-
циальном исследовании. Возможно, что начальные данные для
долгосрочного прогноза должны отличаться от начальных данных
для краткосрочного прогноза меньшей детализацией, включать
в себя сведения только о наиболее крупных атмосферных ано-
малиях.
В любом случае ясно, что при долгосрочном прогнозе должны
возможно более полно учитываться постоянно действующие не-
адиабатические факторы
Можно полагать, что при переходе к прогнозу некоторых ос-
редненных характеристик атмосферных движений (как это пред-
лагается, например, в работе Е. Н. Блиновой [10]) или ансамблей
индивидуальных процессов предел предсказуемости увеличивается.
254
Возвращаясь к рассматриваемой 9-уровенной модели, отметим
еще, что для интервалов времени, не превышающих двух недель,
были рассчитаны прогнозы осадков Этот расчет делается начиная
с момента, когда относительная влажность достигает заданного
предела (80%). Рассмотрение прогностических карт осадков на
различные периоды позволяет заключить, что модель дает в об-
щем правильную картину распределения осадков.
Рис. 7.2. Средние квадратические фактические изменения Оф и
ошибки прогнозов сгп на срок до 14 суток высот поверхностей
1000, 500 и 50 мбар и коэффициенты корреляции г между прогно-
стическими и фактическими изменениями высот изобарических
поверхностей 1000, 500 и 50 мбар, рассчитанные для области север-
ного полушария севернее 20° ш.
В последнее время были произведены эксперименты с вариан-
том данной модели, обеспечивающим более высокое разрешение
в пространстве (в частности, с 18-уровенной моделью). При этом
получались результаты, более близкие к действительности.
Заметим, что реализация изложенной модели требует значи-
тельного количества времени на ЭВМ. Так, например, при экспе-
риментах с 9-уровенной моделью по прогнозу на две недели на
255
полушарии при 5025 точках и шаге по времени 10 мин время счета
прогноза на 24 ч на ЭВМ UNIVAC-1108, работающей со скоростью
600 тыс. операций в секунду, составило 10 ч.
С начала 70-х годов расчеты по данной модели производятся
на ЭВМ IBM 360/95 с быстродействием в 5 млн. операций в се-
кунду, а в 1974 г. для этой цели в Лаборатории геофизической
гидродинамики была установлена ЭВМ TI-ASC с быстродействием
50 млн. операций в секунду.
Двухуро венна я модель циркуляции атмо-
сферы Е. Минца, А. Аракавы и А. Катаямы [23, 28] (метеороло-
гическое отделение Калифорнийского университета в США). Это
была одна из первых моделей циркуляции, численные экспери-
менты по которой проводились для всего земного шара. Верхняя
граница атмосферы идентифицировалась с изобарической поверх-
ностью 200 мбар, а нижняя — совпадала с поверхностью земного
шара. В качестве вертикальной координаты применялась пере-
менная
0=
Ps — Рт ’
где рт = 200 мбар — среднее значение давления на тропопаузе.
На верхней границе атмосферы (о = 0) и у земной поверхности
(о—1) принималось о = 0.
Исходные уравнения гидротермодинамики записывались в сфе-
рической системе координат с учетом турбулентной вязкости и не-
адиабатичиости. Шаги сетки брались различным образом. В одном
из вариантов принималось, что 6Х = 9°, бф = 7°, в другом — 6Z = 5°,
6ф=4°. Шаг по времени принимался равным 12 мин.
При моделировании циркуляции атмосферы в качестве началь-
ного состояния принималось состояние покоя и изотермия (при
Г = 250 К). Расчетная циркуляция атмосферы становится похожей
на среднюю циркуляцию месяца, для которой задаются внешние
параметры, через период времени порядка 250 суток. Так, на
карте, соответствующей внешним параметрам (приток тепла от
Солнца и пр.) за январь, хорошо отражены сибирский и азорский
максимумы, исландский и северотихоокеанский минимумы.
Ш е с тиуровенна я модель циркуляции атмо-
сфер ы А. Касахары и У. М. Вашингтона [29, 30] (модель Нацио-
нального центра исследования атмосферы — NCAR). Вертикальная
структура модели атмосферы приведена на рис. 7.3. Исходные
уравнения гидротермодинамики, включающие уравнение переноса
влаги, записываются в сферической системе координат с сохране-
нием z в качестве вертикальной координаты. При этом в уравне-
ниях введены члены, учитывающие турбулентную вязкость и не-
адиабатичность. Учет орографии производится с помощью крае-
вого условия на нижней границе атмосферы при z = g a>=tos =
= V-Vg. На верхней границе атмосферы (zt=18km) принимается,
что w = 0. Шаги сетки составляют дА=дф = 5°, dz = 3 км, а шаг
по времени — 6 мин (имеется также вариант с 6%=бф=2,5°).
256
Интегрирование по времени при заданных внешних параметрах
и произвольных начальных условиях дает устойчивые результаты
на срок до 100 дней. Правдоподобная картина атмосферных движе-
ний, соответствующая какому-либо месяцу, достигается по исте-
чении примерно 80 суток.
С помощью этой модели было очень четко показано влияние
орографии. Так, например, в варианте расчета без учета орогра-
фии поле движения в период с 41 по 70 день в районе Сибирь—
Индийский океан оказалось неправдоподобным. В этом варианте
возникал усиленный обмен между холодным районом Сибири и
рмйар zkm к
75-- w=0 --------------------16 7
-------------------u,vj\q,p-----------
100---------------- p,w --—--15 6
----u,,v,T,q,p-------
200- p.w —————————— 12 5
--------щи,Т&р----------
300--------------------- p,w ————————- 9 4
Рис. 7.3. Вертикальная структура атмосферы в мо-
дели циркуляции А. Касахары и др.
р — давление, z — высота, k — номер уровня
теплым районом Индийского океана. В результате сибирский мак-
симум оказался ослабленным. Введение системы гор Гималаи—
Тибет привело к ослаблению обмена между указанными двумя
районами и усилению сибирского максимума.
В заключение этого раздела отметим следующее. Численные
модели циркуляции атмосферы могут быть полезными не только
для целей долгосрочного прогноза погоды, но и для ряда приклад-
ных задач. Укажем на две из них.
Моделирование различных наблюдательных
систем. В качестве начальных данных используется набор
данных, полученных каким-либо искусственным путем (например,
с помощью расчетов по используемой модели) и который соответ-
ствует предполагаемым данным моделируемой системы наблю-
дений. По улучшению качества расчетов с помощью той или иной
циркуляционной модели можно судить об эффективности системы
наблюдений. Такого рода эксперименты нашли применение при
оценке данных наблюдений со спутников
17 Зак. № 21
257
Исследование влияния на климат антропоген-
ных факторов, т. е. промышленной и прочей деятельности че-
ловека. Деятельность человека и использование им природных ре-
сурсов нашей планеты ведет к изменению окружающей среды.
В качестве примера можно говорить об изменениях под влиянием
деятельности человека концентрации в атмосфере углекислоты,
озона, аэрозоля и пр. или об изменении альбедо подстилающей
поверхности. Можно произвести расчеты, вводя в модель предпо-
лагаемые изменения этих параметров. В таком случае мы полу-
чим оценку влияния этих факторов на атмосферные движения,
распределение температуры и т. п., т. е. на климат.
Глава VIII
СТАТИСТИЧЕСКИЕ МЕТОДЫ ЧИСЛЕННОГО ПРОГНОЗА
ПОГОДЫ
Гидродинамическими методами удовлетворительно предсказы-
ваются циркуляционные условия (общая синоптическая ситуация).
Собственно же прогноз погоды, включающий прогноз всех метео-
рологических элементов, а также опасных явлений погоды, до сих
пор составляется в основном с помощью качественных способов,
при которых существенную роль играют опыт и интуиция синоп-
тика.
Это обстоятельство делает необходимыми дальнейшие глубокие
исследования в области применения гидродинамических методов
и в то же время заставляет искать и применять и другие пути
решения проблемы. К таким путям можно отнести применение
математической статистики.
В прогнозе погоды статистическими методами наиболее широ-
кое применение получил метод множественной линей-
ной регрессии (см. приложение 5).
Этот метод используется в метеорологии уже длительное время.
Однако удовлетворительные методики прогноза, основанные на
этом методе, стали появляться лишь в последние два десятилетия.
Это связано в первую очередь с возможностями ЭВМ.
Первые работы по применению метода множественной регрес-
сии к прогнозу погоды с использованием ЭВМ были основаны на
вычислении так называемых эмпирических функций
влияния. К таким работам относятся исследования П. Н. Бе-
лова, Е. П. Борисенкова и др. [5—8]. В этих работах форма связи
между рассматриваемыми метеорологическими элементами при-
нималась, исходя из гидродинамической теории, которая дает зна-
чение искомого метеорологического элемента в виде интегралов
с функциями влияния.
В ряде работ, например, в работах К. А. Васюкова, Н. И. Зве-
рева, Д. А. Педя, А. Л. Каца и др. [11, 15—18] вид уравнения
связи и влияющие факторы выбирались, исходя из общих синоп-
тических представлений. Такие прогностические методики полу-
чили название синоптико-статистических.
В последние десятилетия широкое применение получили такие
методы прогноза, в которых в качестве влияющих факторов
17*
259
брались не сами метеорологические элементы или их простейшие
комбинации, а некоторые обобщенные характеристики состояния
атмосферы. В качестве последних используют коэффициенты раз-
ложения переменных в ряды по каким-либо ортогональных функ-
циям, например, полиномам Чебышева, сферическим функциям
и др. [2, 3, 15].
В самое последнее время наиболее широкое применение полу-
чило использование для статистического прогноза коэффициентов
разложения полей в ряды по так называемым естественным
составляющим.
Использование метода разложения полей по естественным ор-
тогональным функциям для анализа и прогноза было предложено
в СССР А. М Обуховым и Н. А. Багровым [1, 20]. Наиболее об-
стоятельные исследования по применению этого метода к прогнозу
погоды выполнены М. И. Юдиным и Г. И. Груза [12, 19, 22].
Наконец, особо следует сказать еще об одном подходе, в ко-
тором при статистическом прогнозе используются результаты прог-
нозов, рассчитанных гидродинамическими методами [17, 18].
Перейдем теперь к краткому изложению перечисленных подхо-
дов к статистическому прогнозу, а также к описанию некоторых
конкретных прогностических моделей.
§ 1. Метод эмпирических функций влияния
Главной особенностью этого метода статистического прогноза
является то, что выбор формы связи, влияющих факторов, а также
области, в которой они должны учитываться, производится на ос-
нове гидродинамической теории.
Для примера рассмотрим, как решаются эти вопросы на базе
квазигеострофической гидродинамической теории краткосрочного
прогноза поля давления. Согласно этой теории, изменение давле-
ния на разных уровнях связывается с тремя физическими факто-
рами: адвекцией вихря скорости Aq, адвекцией температуры Ат и
приземным трением АЯ0 (лапласиан). Соответствующая формула
для изменения высот изобарических поверхностей имеет вид
4г = J f J GsAsdV-\-^ J J GTATdV-\-$ J G^HodS, (1.1)
где Gq, Gt, G&Ho—функции влияния, указывающие на характер
влияния на dH/dt величин Ай, Ат и АЯ0 соответственно, dV и
dS — элементы объема и площади. В первых двух членах интегри-
рование распространяется на часть атмосферы, а в третьем — на
часть поверхности Земли.
При практической реализации выписанного решения производ-
ные заменяются конечными разностями, а интегралы — суммами.
Если i — номер точки на плоскости, j — номер уровня, &Н — ко-
нечное приращение Н в течение некоторого промежутка времени,
260
например, в течение суток, то формула (11) после перехода от
интегралов к суммам записывается так:
т п tn п п
2 2 May+2 2 Mrv+2 (1.2)
/=1/ = 1 х=1
где т — число уровней; п — число точек на плоскости, в которых
берутся значения указанных факторов; ац, Ьц, а — веса или коэф-
фициенты влияния.
Если ограничиться учетом главных частей выражений для Лд
и АТ, которые описываются линейной комбинацией значений Я,
относящихся к разным уровням / и различным точкам i на этих
уровнях Л то мы придем к соотношению
т п
(1.3)
7=1i=l
или, учитывая, что для точки прогноза 8Н = Ны— Н,
т п
2«W (1-4)
;=1х=1
где dij — коэффициенты.
Исходя из гидродинамической теории, можно записать еще и
такую форму связи:
т п т п
я= 2 2 (4) + ,2 .2 (4- в/). (1.5)
В этом варианте для прогноза используются не только начальное
состояние барического поля в момент /о, но и его состояние в пред-
шествующий (/о—б/).
Кроме выбора влияющих факторов и формы уравнения связи
между прогнозируемым элементом и влияющими факторами, на
основе анализа полученного решения в форме (1.1) можно уста-
новить также размер области влияния и число точек в этой обла-
сти, данные в которых необходимо учесть при прогнозе. Как сле-
дует из теории и практики гидродинамического прогноза, область
влияния при прогнозе на сутки представляет собой круг радиусом
около 1000 км, а число учитываемых уровней должно быть не ме-
нее двух. Легко подсчитать, что при шаге по горизонтальным ко-
ординатам около 500 км число точек, данные в которых учитыва-
ются при прогнозе, должно составлять 50 (5x5x2). Это, однако,
не означает, что число учитываемых точек i, j в уравнениях связи
типа (1.2) — (1.5) в точности должно равняться числу точек, учиты-
ваемому в гидродинамических соотношениях.
Дело в том, что статистические методы накладывают условие
«независимости» всех учитываемых переменных. На практике это
условие обычно сводят к тому, чтобы разные влияющие факторы,
а также значения факторов в соседних точках не имели бы силь-
ной корреляционной связи между собой.
261
Выражения (1.2) — (1.5) отличаются влияющими факторами,
количеством уровней и точек, в которых эти влияющие факторы
учитываются. Общим между ними является то, что во всех случаях
между прогнозируемым элементом и влияющими факторами имеет
место линейная зависимость. В наиболее общем виде эта зависи-
мость представляется так:
п
(1.6)
i=l
где S — прогнозируемый элемент («предиктант»), F — влияющий
фактор («предсказатель» или «предиктор»), индекс i характери-
зует вид влияющего фактора и положение точки в пространстве.
К аналогичной зависимости можно прийти и в случае прогноза
других элементов, однако влияющие факторы могут оказаться
другими. Так, например, для прогноза высоты нижней границы об-
лачности в качестве одного из влияющих факторов принимается
адвекция влажности.
Отметим здесь одно обстоятельство. Соотношения вида (1.6)
используются как в гидродинамических, так и в статистических
методах прогноза. Различие заключается в способе определения
весов или конечно-разностных функций влияния Ci. В первом слу-
чае они получаются теоретически с помощью функции влияния G.
Во втором случае веса получаются эмпирически, путем
математической обработки данных. Это обстоятельство и послу-
жило поводом к тому, что по аналогии с теоретическими функци-
ями влияния определенные эмпирическим путем веса стали назы-
вать эмпирическими функциями влияния, а сам ме-
тод прогноза — методом эмпирических функций
влияния.
Заметим, что соотношения вида (1.6), в которых коэффициенты
определяются статистическим путем, называются линейными урав-
нениями регрессии.
Рассмотрим теперь некоторые конкретные прогностические мо-
дели, основанные на методе эмпирических функций влияния.
Метод прогноза давления на трех уровнях.
Изменение давления или высот изобарических поверхностей в точке
s = l представляется в виде [5]
2 14 2
1=А)+Е ^AskHsk + ^ Bk(Hk, Нк_^=ь (1.7)
= = l /г = 1
где HSk — значения высот изобарических поверхностей (& = 0, 1, 2)
в пунктах (s=l, 2, .. ., 14) в некоторый начальный момент вре-
мени; якобианы (Hk, Hk-i) характеризуют перенос температуры
в слое, расположенном между изобарическими поверхностями k
и k—1, в точке $ = 1; и Bk — коэффициенты, называемые эм-
пирическими функциями влияния.
262
Выбор формы связи был произведен на основании квазигеост-
рофической теории. Однако из сравнения соотношений (1.2) и
(1.7) видно, что связь взята более простой, чем это следует из
теории. В качестве влияющих факторов приняты адвекция темпе-
ратуры, высоты изобарических поверхностей и температуры Сами
величины температуры в соотношение (1.7) в явном виде не вхо-
дят, а входят разности высот изобарических поверхностей, пропор-
циональные средней температуре
Соотношение (1.7) позволяет учитывать приземное трение. Это
следует из того факта, что АН является линейной функцией Н.
Учет адвекции вихря с помощью соотношения (1.7) произво-
дится лишь частично: учитывается только перенос вихря (АН) по
изолиниям поля Н. Действительно, в этом случае
(Я, ДЯ)^(77,
i
где коэффициенты Р; зависят от градиентов поля Я и от распо-
ложения точек I.
С учетом зависимости (1.7) были рассчитаны эмпирические
функции влияния, необходимые для прогноза на 24 и 36 ч изме-
нений давления на уровне моря и высот изобарических поверхно-
стей 700 и 300 мбар для зимнего сезона (декабрь—февраль) в 20
пунктах Европейской территории СССР. В качестве исходных дан-
ных использовались давление на уровне моря и высоты изобари-
ческих поверхностей 700 и 300 мбар для 170 ситуаций на 44 стан-
циях территории Евразии. При вычислении эмпирических функций
влияния для прогноза давления в одной точке использовались дан-
ные не всех 44 станций, а лишь 14 станций (включая точку прог-
ноза), находящихся друг от друга на определенном расстоянии
(600—700 км), выбранном на основе специального исследования.
Эмпирические функции влияния, в отличие от теоретических,
не являются симметричными (рис. 8.1). Это обстоятельство объяс-
няется, по-первых, тем, что эмпирические функции влияния учи-
тывают особенности местных условий, а, во-вторых, тем, что с их
помощью прогноз делается одним шагом по времени на значитель-
ный срок, в то время как теоретические функции влияния требуют
многошаговых расчетов.
В работе [6] в качестве влияющих факторов используются дан-
ные о полях геопотенциала как в исходный момент, так и за про-
шедший срок. Соотношение для прогноза изменений давления на
уровне моря и геопотенциала 500 мбар на разные сроки берется
в виде
Sk= 2 aikH^°°24)+ 2 bikH^(-24) +
i = 1 i = 1
+ 2 ^°°(0)+2^яГ(0),
i=l 1=1
263
где Я500(0) и //500(—24), 7/1000(0) и Я1000(—24) —некоторые линей-
ные функции высот изобарических поверхностей 500 и 1000 мбар
в исходный момент времени и в прошедший момент, отстоящий
от исходного на 24 ч; Sk — значение прогнозируемого элемента на
срок k; a, b, с, d — коэффициенты влияния; i — номер точки; N—•
число точек.
В работе Е. П. Борисенкова [7] для прогноза изменений дав-
ления на 3 и 5 суток в качестве влияющих факторов были взяты
изменения давления за прошедшие 5 суток (гц) в 25 точках, рав-
Рис. 8.1. Карта распределения коэффициентов ASk
(эмпирических функций влияния) уравнения регрес-
сии (1.7) для прогноза давления на уровне моря на
24 ч в Москве (веса для вклада АТ1000)
номерно расположенных на северном полушарии. Соответствую-
щее уравнение регрессии было взято в виде
25
1 = 1
где ц—-дополнительный влияющий фактор, учитывающий харак-
тер термического поля в районе северного полюса, aij— эмпириче-
ские функции влияния.
С помощью данной и подобной прогностических моделей был
исследован вопрос о целесообразности применения функций влия-
ния, вычисленных отдельно для какого-либо класса процессов.
Оказалось, например, что лучшие результаты получаются в том
случае, когда производится учет сезонных особенностей циркуля-
ции. Результаты статистического прогноза улучшаются еще более,
когда расчет функций влияния и их применение осуществляется
раздельно для различных форм циркуляции.
264
§ 2. Синоптико-статистические методы прогноза
Выбор формы связи, влияющих факторов и пр. может быть
сделан на основании синоптического опыта. В этом случае в ка-
честве влияющих факторов принимаются такие характеристики
атмосферных процессов, о существенности влияния которых на
формирование погоды или изменение метеорологических элементов
синоптик или исследователь убедился в процессе синоптического
анализа. Приведем несколько примеров.
Из синоптического анализа процессов можно заключить, что
характер погоды в течение месяца на Европейской территории
СССР связан с интенсивностью центров действия атмосферы
(азорский, северотихоокеанский и сибирский максимумы, исланд-
ская, алеутская и среднеазиатская депрессии) Исходя из этого
предположения в работе [И] уравнение регрессии для прогноза
месячной аномалии температуры (Д4) в пункте k, расположенном
на Европейской территории СССР, принимается в виде
Д/ k=^Qk Д^4“2Е aik
i
где Д/&, Д^ — аномалия температуры в точке прогноза и в центре
действия атмосферы, — коэффициенты регрессии.
Важным фактором формирования длительных аномалий темпе-
ратуры является интенсивность зональной и меридиональной цир-
куляции. Следовательно, объективные характеристики этой цирку-
ляции могут быть использованы в качестве влияющих факторов.
Рассмотрим некоторые из этих характеристик.
Индекс зональной циркуляции а представляет собой угловую
скорость движения атмосферы относительно Земли (см. гл. VII).
На практике используется не непосредственно этот индекс, а его
отношение к угловой скорости вращения Земли оз, т. е. отношение
а/ы (оз = 0,729. 10~4 с”1).
А. Л. Кацем для характеристики движения атмосферы пред-
ложены зональный (/3) и меридиональный (7М) индексы циркуля-
ции. Индекс зональной (меридиональной) циркуляции представ-
ляет собой среднее по площади абсолютное приращение давления
или высоты изобарической поверхности вдоль меридиана (парал-
лели) в расчете на 1 градус широты (долготы). Индексы 13 и /м
могут быть рассчитаны как для всего полушария, так и для ка-
кого-либо одного сектора полушария или района.
Индексы 13 и /м были использованы в качестве влияющих фак-
торов для прогноза давления и температуры на срок 5—10 дней
[16]. Так, например, для прогноза аномалии температуры
в пункте k на срок т использовалось следующее уравнение регрес-
сии:
akJbkJckx &tk,
265
где /' и Гм—-величины отклонений индексов циркуляции в атлан-
тико-евразийском секторе от соответствующих средних значений,
Atkx — аномалия средней суточной температуры в пункте прогноза,
подсчитанная в исходный для прогноза день, — некоторая
постоянная поправка.
Для долгосрочного прогноза важное значение имеет учет не
только интенсивности атмосферной циркуляции, но и других по-
казателей состояния атмосферы, а также подстилающей поверхно-
сти. Так, в работе [14] было показано, что для прогноза средних
декадных значений температуры, кроме индексов зональной и ме-
ридиональной циркуляции, необходимо учитывать облачность и
радиационный баланс, состояние снежного покрова и ледовитость
океана. Как показал М. И. Юдин [19, 21], учет последних двух
факторов является особенно важным, поскольку они характери-
зуют состояние подстилающей поверхности и сравнительно слабо
меняются со временем.
§ 3. Применение обобщенных показателей состояния атмосферы
В последние годы все большее распространение получают та-
кие методы статистического прогноза, в которых в качестве влияю-
щих факторов используются не непосредственно измеряемые вели-
чины или простейшие функции от них, а некоторые обобщенные
характеристики состояния атмосферы. Это связано со следующими
обстоятельствами. Увеличение заблаговременности прогноза со-
провождается увеличением области учета влияющих факторов.
Последнее же влечет за собой увеличение числа точек, в которых
они должны учитываться, и, следовательно, увеличение числа пе-
ременных, что в свою очередь требует резкого увеличения вы-
борки, используемой для получения коэффициентов уравнения ре-
грессии. Однако существующий метеорологический архив, как пра-
вило, не содержит еще необходимого объема данных. Кроме того,
и это пожалуй главное, увеличение числа переменных ведет
к тому, что вследствие различного рода ошибок коэффициенты
уравнения регрессии вычисляются не точно. В результате расчет
по полученному уравнению регрессии оказывается излишне чувст-
вительным к небольшим ошибкам в исходных данных. Это непри-
ятное следствие можно устранить путем исключения переменных,
характеризующихся тесной корреляционной связью с другими пе-
ременными. Последнее достигается с помощью предварительной
специальной статистической обработки исходных данных.
Другой путь исключения факторов, имеющих взаимные корре-
ляционные связи, заключается в переходе в уравнениях регрессии
от характеристик, являющихся результатами непосредственных из-
мерений или простых операций над ними, к некоторым обобщен-
ным показателям, характеризующим атмосферные процессы в це-
лом. В качестве таких обобщенных показателей могут быть при-
266
няты коэффициенты разложения полей в ряды по некоторым
функциям. Такие обобщенные показатели и характеристики и при-
нимаются в качестве влияющих факторов, или предсказателей.
Веса, с которыми будут входить эти предсказатели, как и ранее,
находятся путем составления и решения системы нормальных
уравнений. При рациональном выборе обобщенных показателей
мы получаем возможность иметь достаточно детальную характери-
стику процесса при малом числе самих предсказателей. Методика
нахождения обобщенных показателей должна заранее исключить
всякую корреляцию между ними.
Рассмотренный подход к решению задачи статистического прог-
ноза развивается в работах Н. А. Багрова, Н. И. Зверева и др.
[2, 15].
В указанных работах в качестве обобщенных показателей при-
нимались коэффициенты разложения поля того или иного метео-
рологического элемента в ряды по полиномам Чебышева.
Рассмотрим для примера, каким образом функцию F (х) можно
представить в виде ряда по полиномам Чебышева. Пусть значения
функции F нам известны в п дискретных точках xlf Х2, ..хг-, • ..
. . ., хп. Тогда разложение в ряд по полиномам Чебышева v-того
порядка имеет вид
(х)=А0+А1ф1-|- . . . -ф-А^-ф- . . . -|-AV<J)V = п),
k —О
где Ak — коэффициенты разложения, подлежащие определению,
а фк(х, п)—полиномы Чебышева, зависящие от координаты х и
от числа точек п таким образом:
фо=1, ф1=х-------2—> Ф2=Ф1------(2— 11 т’ д*
Каждый полином высшей степени выражается через полиномы
низших степеней с помощью следующего рекуррентного соотноше-
ния:
Л2(Л2_£2)
Фл+1—4 (4^2—1) Фл-Р
Коэффициенты разложения Ah определяются по формуле
У F^Xi^k^Xi)
Д __ * = 1
у Ф2 Сч)
i 1
где фь(*г)—числовое значение ф& при x = Xi, a F (х^—числовое
значение функции F в точке x=Xi. Цля. данных значений г = 1,
2, ..., п и k полиномы ф/1(Хг), а также (%г) вычисляются за-
ранее.
267
На практике разложение функций приходится производить по
координатам х и у, т. е. в двойной ряд по полиномам Чебышева.
Если известны значения функции F (х, у) в точках (xb уА, (х2,
У2) и т. д.» то это разложение имеет вид
к s
F(x, у) = 2 2 ЛА(*М(У/)>
k=- 0 5 = 0
где
2 2 F {Xi, yf) (Xi) (yj)
л _ г = 1 j=i
п
1 = 1
Опыт показывает, что для описания крупномасштабной цирку-
ляции, например, для территории, охватываемой сеткой из 7Х
Х7 узлов с расстоянием между ними около 500 км, достаточно
около 10—15 членов. При этом главными членами разложения
оказываются члены низшего порядка.
Коэффициенты разложения Aks и принимаются в качестве пред-
сказателей.
В работе Н. А. Багрова и Н. И. Зверева [2] разложение по
полиномам Чебышева было применено для прогноза АТ500 на срок
до 7 дней. Разложение полей по полиномам производилось не
только по координатам х, у, но и по времени t
Н (Л-, у. 0=2 2 2 Aksrtyk (x,) (у,) (0). (3.1)
k S г
Коэффициенты разложения Aksr— характеризуют не только
форму циркуляции, но и ее изменение во времени. Для определе-
ния коэффициентов Aksr необходимо иметь данные Н в 7X7 =
= 49 точках за семь последовательных сроков наблюдений с су-
точным интервалом. На основании предварительного исследова-
ния связей коэффициентов разложения поля АТ500 за две последо-
вательные недели было отобрано только восемь коэффициентов
разложения, относящихся к исходной неделе; они и были приняты
в качестве предсказателей.
В качестве обобщенных показателей атмосферной циркуляции
можно принять также коэффициенты разложения полей в ряды
по сферическим функциям
Н (б, a)=2S У \Р™ cos sin mX] P™ (cos 6),
n m
где 0 и % — широта и долгота, P™(cos0)—присоединенный поли-
ном Лежандра, D'" и D'™— коэффициенты разложения, пит —
целые числа.
Наконец, возможно применение разного рода смешанных поли-
номов, например полиномов Чебышева вдоль меридиана и триго-
268
нометрических функций вдоль параллелей. Так, в работе [3] для
прогноза АТ500 на северном полушарии было применено следующее
разложение
Я(х, Z)=2 Zj cos a/k| фДх),
k i
где ky I — целые числа, x = 0, 1, 2, . . — индекс широт, X = 0, 1,
.. ., m — 1 — индекс долгот, a = 2л/m, (m = 36, a = 10°).
Коэффициенты разложения находятся по формулам:
п т -1
Aki=~ 2 —1 Н(-Х' Х) Ы*) COS а/Х;
т х = о Х=0
п т-1
Bki = — 2 2 X) (x)sin а//..
т х = 0 Х = 0
Как уже говорилось, найденные значения коэффициентов раз-
ложения и используются в качестве влияющих факторов, или пред-
сказателей. В таком случае, например, для ряда (3.1) искомое зна-
чение прогнозируемого элемента представляется в виде
S—^CkSrAksri (3.2)
ksr
коэффициенты Cksr находятся методом наименьших квадратов.
При этом искомой функцией может быть не само значение какого-
либо элемента, а коэффициенты разложения поля искомого эле-
мента в соответствующий ряд.
Здесь важно отметить следующее. В уравнении регрессии вида
(3.2) могут быть учтены не все коэффициенты разложения, а лишь
главные из них, т. е. те, которые несут наибольшую информацию
о влияющих факторах. При этом число таких главных коэффи-
циентов может быть в несколько раз меньше их общего коли-
чества.
В последние годы все большее распространение получает ис-
пользование разложений в ряды по так называемым естественным
ортогональным составляющим.
§ 4. Использование разложения метеорологических полей
по естественным составляющим
Наряду с рассмотренными в § 3 представлениями метеорологи-
ческих полей в виде рядов по некоторой системе заранее выбран-
ных ортогональных функций (полиномов Чебышева, сферических
функций и др.) для целей статистического прогноза и в некоторых
других разделах метеорологии нашли применение представления
этих полей в виде рядов по естественным составляющим. В этом
случае система функций, по которым ведется разложение,
269
не задается заранее, а подбирается соответственно специфическим
свойствам структуры рассматриваемого метеорологического поля.
Поэтому каждая из составляющих поля при таком способе разло-
жения имеет вполне определенный метеорологический смысл и мо-
жет изучаться как некоторый реальный объект.
В связи с рассмотрением малопараметрической гидродинами-
ческой модели прогноза (см. § 6, гл. IV) был дан пример приме-
нения представления метеорологических параметров (в частности,
вертикальных профилей изменений геопотенциала) в виде рядов
по естественным составляющим. Здесь подробнее рассмотрим ме-
тодику таких представлений и ее использование в статистических
методах прогноза.
Пусть [1] FXj)=Fij — функция времени U (i=l, 2, . . ., m)
и пространственных координат Xj (/=1, 2, .. ., и), характеризую-
щая какое-либо метеорологическое поле, Xh (xj) — собственная
функция с номером h заданной совокупности Fij. Функция Xh на-
зывается также естественной ортогональной функцией, или есте-
ственной составляющей. Тогда имеет место следующее
разложение:
F ij—— ThiXhj,
(4.1)
где Thi — коэффициенты разложения, a Xhj— значение функции Xh
в точке с номером /. В этом разложении неизвестными будут как
коэффициенты Thi, так и функции Xhj. Их определение произво-
дится методом наименьших квадратов, исходя из условия мини-
мума функции
4-2 2 И,- -2
I j L л J
где величины F^ считаются известными из наблюдений в п пунк-
тах для т ситуаций.
Функции X и Т будем определять последовательно, начиная
с /г = 1. Тогда в соответствии с условием минимума для нахожде-
ния X и Т получаем следующие уравнения (индекс h здесь и да-
лее опускается):
= - 2 2 FijXj 4-2^2 Х2=0;
J J
2 2 Л/^4-2Ху2 Л2=о.
i i
Перепишем эти две системы уравнений в виде:
2 X} (Z=l, 2, . . m);
2 0=1 > 2- • • - «)•
270
Из первой системы уравнений найдем
T^FikXk\^X\ (4.2)
к I k
(для удобства индекс / здесь заменен на индекс & = 1, 2, ..п)*
Подставляя это выражение в левую часть второй системы урав-
нений, получаем
X Xk V V X2k.
k i i k
Введем обозначения:
i-4-v mi;
m i k
A,,-^ F„Fit.
Тогда приходим к системе
2 A)kXk=\X} (/=1, 2, . . п) (4.3)
k
или в развернутом виде
(Ап—X) А^А^Н- • • • A-A\nXn=Q',
^21^1 (^22 — Х)Х2Ч“ • • • 4“^2п^л = 0;
Ап\Х\-\- Ап2Х2-\- • • • —Х)ХЛ = О.
То есть мы получили однородную систему линейных уравнений
для определения Хь Л2, ..Хп. Условием существования решения
такой системы является обращение в нуль ее определителя. Это
условие в матричной форме запишется в виде
|| А-ХЕ ||=0,
где Е — единичная матрица.
Решая последнее уравнение, мы найдем п значений чисел X,
называемых собственными (или характеристическими) числами
матрицы Ajk. Подставляя найденные значения X в уравнения (4.3),
мы получим п различных решений нашей задачи:
^11^12 • • • Х\п Для
^21-^22 • • • Х2п ДЛЯ Х2;
Хп\Хп2 • • • Хпп ДЛЯ Хл.
Каждое из этих решений называется собственным вектором мат-
рицы А. Последний представляет собой совокупность п чисел.
271
Всего имеется п собственных в'екторов. Для каждого собственного
вектора Х^(х) можно теперь рассчитать соответствующую функ-
цию времени Th(t) по формуле (4.2), которая после восстановле-
ния индекса h запишется в виде
2 FlkXhk
--- (//=1,2,..., //<//). (4.4)
—
;г
Естественные функции Xh (х) описывают возмущения разных
масштабов, наиболее характерные для рассматриваемого поля (по-
этому данные функции и получили название естественных). Стар-
шие составляющие (функции Xh с меньшими номерами й) описы-
вают самые крупные возмущения. По мере увеличения номера h
масштаб соответствующего возмущения уменьшается.
Для примера на рис. 8.2 приведены первая и десятая состав-
ляющие поля изменения давления на уровне моря за 5 суток, по-
лученные при разложении поля, заданного значениями давления
в 40 точках (м = 40) по 180 ситуациям [10].
Точность представления полей в виде разложения (4.1) удобно
характеризовать с помощью отношения
h. = 1
где п — общее количество членов разложения, п^п— часть из
них. Знаменатель приведенного выражения характеризует диспер-
сию рассматриваемого поля, заданного в п точках, числитель —
часть этой дисперсии, отраженную первыми щ членами разложе-
ния. Очевидно, что R2 есть отношение части дисперсии, отражен-
ной первыми ni членами, к общей дисперсии.
Анализ показывает, что для удовлетворительного представле-
ния какого-либо поля с помощью ряда (4.1) можно не брать все
п членов разложения, а ограничиться учетом лишь нескольких
старших членов ряда.
Для примера в табл. 8.1 из [10] приведены значения /?2, полу-
ченные при разложении полей давления на уровне моря и высот
изобарической поверхности 500 мбар, а также их изменений за 3
и 5 суток при различном числе th учитываемых членов разложе-
ния. Данные получены путем разложения соответствующих полей,
заданных в 40 точках Северной Атлантики, Европы и Западной
Сибири, для 180 ситуаций.
Из рассмотрения таблицы следует, что учет около 80% общей
дисперсии обеспечивается при 8—10 членах разложения (из об-
щего числа 40), а 15 членов разложения обеспечивают учет около
90% общей дисперсии
272
Таким образом, мы приходим к заключению, что разложения
полей по естественным функциям позволяют, во-первых, выделить
наиболее характерные для рассматриваемого поля составляю-
Рис. 8.2. Первая (а) и десятая (б) естественные состав-
ляющие поля изменения давления на уровне моря за
5 суток.
щие, а, во-вторых, существенно сократить объем учитываемой ин-
формации. Так, например, при разложении какого-либо поля по
данным в 40 точках и учете первых 10 составляющих, дающих
около 80% общей дисперсии, объем первоначальной информации
18 Зак. № 21
273
Таблица 8.1
Оценка точности разложения полей давления на уровне моря р0 и Я5Оо
и их изменений за 3 и 5 суток с помощью критерия У?2 % при различном числе щ
учитываемых членов разложения (п = 40)
Поля Поля изменений за 3 суток Поля изменений за 5 суток
Ро ТУзоо Ро 7/ 4оо Ро 77 о
1 26 26 20 14 23 19
2 42 39 38 28 42 33
3 53 52 46 38 51 44
4 63 60 56 45 59 52
5 69 66 62 52 65 59
6 74 72 67 57 70 65
7 79 78 71 62 75 70
8 82 82 75 67 79 75
9 85 84 79 71 82 78
10 86 86 82 74 85 82
11 88 88 84 77 86 84
12 90 89 86 79 88 86
13 91 91 87 82 90 88
14 92 92 88 84 91 89
15 93 93 90 86 92 90
уменьшается в четыре раза. Кроме того, сама процедура разложе-
ния позволяет нивелировать случайные ошибки в данных.
Эти обстоятельства и являются причиной широкого распростра-
нения метода разложения по естественным составляющим в ста-
тистическом прогнозе.
При известных ортогональных функциях Xh (Xj) коэффициенты
разложения Th используются в качестве влияющих факторов,
а уравнение прогностической связи берется в виде
п
5= 2 chTh, (4.5)
Л —1
где Ch — коэффициенты уравнения регрессии, определяемые, как
и в описанных ранее вариантах, методом наименьших квадратов;
п — число учитываемых влияющих факторов. В качестве влияю-
щих факторов можно взять коэффициенты разложения в ряд по
естественным функциям не одного участка рассматриваемого поля,
а двух или более смежных участков или полей нескольких уров-
ней и т. д.
Заметим, что форма связи (4.5) в принципе аналогична такой
форме, когда в качестве влияющих факторов берутся просто зна-
чения функции, разлагаемой в ряд, в отдельных точках. Однако,
как уже говорилось, при использовании в качестве влияющих фак-
торов коэффициентов разложения происходит значительное сжатие
информации.
274
Для иллюстрации применения указанного подхода рассмотрим
две конкретные методики прогноза.
О. В. Батырева [4] предложила способ прогноза наземного дав-
ления на 3 и 5 суток. В качестве влияющих факторов взяты ко-
эффициенты разложения поля давления на уровне моря и поля
геопотенциала 700 мбар. При этом разложение полей производи-
лось для двух районов: I — Европейская территория СССР и За-
падная Сибирь, II — Западная Европа, Северная Атлантика и во-
сточная часть Северной Америки. По каждому району были взяты
значения давления и геопотенциала в 40 точках. Путем экспери-
ментов и анализа было установлено, что для прогноза давления
на 3 суток достаточно учесть 8 и 6 членов разложения поля дав-
ления на уровне моря в I и II районах (коэффициенты А и С со-
ответственно) и 4 члена разложения поля геопотенциала в I рай-
оне (коэффициенты В). Соответствующее уравнение регрессии
имеет вид
8 4 6
^Pi= Z. aihAh “F Zj Zj
h l h=l h-1
где dpi— прогностическое значение давления в точке Z; ацъ,
сцъ — коэффициенты влияния Всего, следовательно, было учтено
18 обобщенных показателей состояния атмосферы, для определе-
ния которых использовались значения давления и геопотенциала
в 120 (40X3) точках.
Аналогичное уравнение было взято и для прогноза давления на
уровне моря на 5 суток. Испытание предложенного метода дало
удовлетворительные результаты. Так, средняя абсолютная ошибка
прогнозов давления на уровне моря составила 5,8—7,2 мбар, а со-
ответствующая относительная ошибка равнялась 0,84—0,86.
Рассмотрим методику прогноза приземного давления и /Лоо на
несколько суток, предложенную Т. П. Борисенковой [10]. В этой
методике в качестве влияющих факторов использовались коэффи-
циенты разложения по естественным ортогональным составляющим
величин изменений приземного давления ро и /Лоо за 3 и 5 суток.
Уравнение регрессии бралось в виде
п т
§S\k — Zj ^ihkPh^T Zj bihkHh,
h=l h=l
где dSxik — изменение высот изобарической поверхности 500 мбар
(& = 1) или приземного давления (k = 2) в точке i за период т,
равный 3 или 5 суткам; Рх , Нх —коэффициенты разложений по ес-
тественным ортогональным составляющим изменений полей ро и
/Лоо; h — номер составляющей; и, т — число учитываемых членов
разложения; axhh , bxhk—коэффициенты уравнения регрессии.
Исходные данные учитывались по территории первого естест-
венного синоптического района. Поля давления и геопотенциала
характеризовались их значениями в 40 пунктах зондирования,
равномерно освещающих данный район.
18*
275
Прогнозы, рассчитанные с помощью полученных уравнений ре-
грессии при n = m = 10, характеризуются относительной ошибкой
0,83—0,87 и коэффициентом корреляции 0,48—0,54
§ 5. Прогноз облачности и осадков на основе синхронных
статистических связей и использования гидродинамического
прогноза
Хорошо известно, что основными факторами, влияющими на
формирование облачности и осадков являются вертикальные дви-
жения, влажность и температура воздуха. Между этими факто-
Рис. 8.3. График для определения возможного количе-
ства и характера облачности и осадков в зависимости
от величины вертикальной скорости w и дефицита точки
росы d в пункте.
1 — осадки, 2 — нижняя облачность 10 баллов, 3 — общая облач-
ность 5—10 баллов, 4 — ясно.
рами, облачностью и осадками существуют синхронные статисти-
ческие связи, которые можно выразить графическим или числен-
ным способом. При известном прогнозе каждого из перечисленных
трех факторов или хотя бы двух или одного из них эти синхронные
связи можно использовать для прогноза облачности и осадков.
На рис. 8.3 приведен пример графика синхронной связи между
облачностью и осадками, с одной стороны, и вертикальными ско-
ростями и дефицитом точки росы, с другой (по М. Е. Швецу).
276
На этом графике три кривые разграничивают четыре области, от-
носящиеся к различным состояниям погоды: ясно, частичная об-
лачность, облачно, осадки. Различными знаками изображены дан-
ные, которые использовались при построении графика.
Допустим, что при прогнозе получили: w=12 мм/с, d = 2°. С по-
мощью графика определяем, что данным значениям w и d соот-
ветствуют осадки. При прогнозе w =—16 мм/с и d = 2° следует
прогнозировать частичную облачность.
Прогнозирование облачности и осадков с помощью статистиче-
ских связей возможно также на основе уравнений регрессии. Для
этой цели Р. Л. Алпатова в качестве влияющих факторов исполь-
зовала аналог вертикальной Скорости т, дефицит точки росы d
и температуру Т на четырех уровнях. Уравнение связи принима-
лось в виде
S = C\d\-\- C2d2 4~ 4“ ^4^4 + 4“ CQX2 4“ £?т3 4~ ^8Т4 4~
4“^9^ 14_^10^24~б;11^3“Ьб;12Л,
где 5— характеристика облачности и осадков (5 = 1 при 0—5 бал-
лах, S = 2 при 6—8 баллах, 5 = 3 при 9—10 баллах, 5 = 4 при
10 баллах облачности с выпадением осадков), индексы 1, 2, 3,
4 соответствуют изобарическим поверхностям 850, 700, 500 и
300 мбар, Ci — Ci2 — коэффициенты уравнения регрессии (эмпири-
ческие функции влияния), определяемые методом наименьших
квадратов. При этом величины 5, d, т и Г выражаются в отклоне-
ниях от их средних значений.
Средняя квадратическая ошибка определения 5 по приведен-
ному уравнению регрессии для облачной системы As—Ns состав-
ляет около единицы. Это означает, например, что если при расчете
получено 5 = 3, то возможными значениями 5 являются 5 = 2 и
5=4; т. е. возможна облачность 6 баллов и более.
На основании анализа величин коэффициентов с можно заклю-
чить, что наибольшее влияние на формирование облачности и
осадков оказывают влажность и вертикальные движения на по-
верхности 700 мбар. Влияние этих факторов на поверхности 850
и 500 мбар еще значительно, а на поверхности 300 мбар — не су-
щественно.
Статистические связи могут быть получены не только для от-
дельных метеорологических элементов, но и для коэффициентов
разложения полей в ряды по ортогональным функциям.
Так, в работах А. Л. Каца, Ш. А. Мусаеляна и др. [17, 18]
такие связи были получены и использованы для прогноза пяти-
дневных сумм осадков. Предполагается, что осадки определяются
в основном циркуляционными условиями поля Я500 для средних
дней пентад, для которых ведется расчет осадков. Эти поля раз-
лагались в ряды по естественным составляющим. Для составления
уравнения регрессии использовались 15 членов указанного разло-
жения.
277
Применение изложенной методики при использовании гидро-
динамического прогноза Я5оо на 3 суток позволило получать прог-
нозы пятидневных сумм осадков с абсолютной ошибкой в 3,1 мм
и относительной ошибкой, равной 0,82.
Заканчивая рассмотрение статистических методов прогнозиро-
вания, отметим следующее. Для того чтобы найденные по какому-
либо материалу коэффициенты уравнений регрессии были устой-
чивы во времени и, следовательно, применимы к прогнозу, необ-
ходимо включение в статистическую обработку весьма большого
ряда наблюдений. По некоторым оценкам, для получения устой-
чивых статистических связей необходимо Я/п>15, где N — число
использованных ситуаций, п- количество переменных в уравнении
регрессии.
Однако существует и другой подход к получению пригодных
для прогноза статистических связей. Этот подход заключается
в постоянном обновлении материала, включаемого в статистиче-
скую обработку, таким образом, чтобы уравнения регрессии уточ-
нялись непосредственно перед составлением прогноза. В этом слу-
чае мы получим так называемую адаптивную прогностическую
модель [13]. В такой системе для получения положительного ре-
зультата необходимо лишь, чтобы N было больше или равно п.
§ 6. Определение качества численных прогнозов
Объективная оценка качества прогнозов имеет существенное
значение как для непосредственного определения эффективности
прогнозов, так и для сопоставления различных методов прогноза
с целью отбора наилучшего.
Приведем основные количественные критерии, применяемые для
определения успешности численных прогнозов. Почти все они но-
сят статистический характер и поэтому имеют реальный смысл
лишь при наличии достаточно длинных рядов испытываемых пе-
ременных.
Рассмотрим вначале методы оценки, относящиеся только к эле-
ментам, прогнозируемым в форме скалярных величин, т. е. в виде
чисел, каждое из которых относится к одной точке i в простран-
стве или времени. Если, например, ЯИ1, Яи2, . .., Я1Ьу— исходные,
ЯП1, ЯП2, •.Япдг — прогностические и ЯфЬ Яф2, ..., ЯфЛг— факти-
ческие (в срок прогноза) значения Я в точках 4=1, 2, .. ., Я, то
точность прогноза можно оценить с помощью следующих характе-
ристик:
1) средней абсолютной ошибки прогноза
2) средней относительной ошибки прогноза
_ b
£~ 8ф ’
278
1 w
где бф = — У, |Нф — Ни\г — средняя абсолютная фактическая из-
г = 1
менчивость;
3) стандартной (средней квадратической) ошибки прогноза
где (8ЯП);=(ЯП - Яф)£; 8ЯП=-Т г2 №);;
4) средней квадратической относительной ошибки прогноза
а
е1==---,
°Ф
где
Оф=}/ Z [0ЯФХ-877Ф]2^ ,
’ i ~ 1
_____________________ , *
(8//ф)г=(Яф-Яи);; 8//ф=-^- 2 (8Яф)/;
i — 1
5) коэффициента корреляции между прогностическими измене-
ниями б//п = #п — и фактическими изменениями 8Нф = Нф—
И и
N
2 (»яп)' (8/7);
r= f = 1 _________
ЛЧ’Ф
где
(Шп)'=(8Яп)г-оЯп;
(8Л7ф)'=(8/7ф)/-8Яф;
Оп=]/
Точность прогноза вектора ветра V с компонентами и и v вдоль
осей хну может быть оценена путем расчета
1) среднего модуля векторной разности между прогностиче-
ским и фактическим векторами ветра
7 N Л- ______________________
с=-м- 2 |vn—¥<{,^=-^2 1 (ип—«фЯ+С^п-^ф)1
i = l i = l
279
2) среднего квадратического отклонения модуля векторной раз-
ности между прогностическим и фактическим изменениями векто-
ров ветра
°г=1/ 77 2j (SVn — &Уф)?— l/\r 2 [(8«п — 8«фЯ+(8г>п — ^ф)/Ь
r i = 1 r i=1
где
SVn=Vn —V„; 5Уф=Уф —VH; 8wn=tzn —ми;
^Иф=Мф — ии; Zv„=v„ — vtl; 8-иф=г>ф —г»и.
При оценке долгосрочных прогнозов широко используются так
называемые качественные коэффициенты корреляции, или пара-
метры р, р<р, (>>., а также параметр Q, определяемые соотношени-
ями:
«+ — п- . = пт+ ~пу- .
«+ + «- ’ ? «<р+ + ’
__ пх+ пх-
Рх «х++”х_
Здесь п+— количество совпадений, п- — количество несовпадений
знака фактической и прогностической аномалии или фактического
и прогностического изменения во времени рассматриваемого эле-
мента F; пф+, Агф_, — количество случаев для совпадений
и несовпадений знаков градиентов dF/dcp и dF/dK в сравниваемых
полях; Лш, Лфг- и о2—прогностическая и фактическая аномалии
и дисперсия рассматриваемого элемента в точке I.
Для оценки прогнозов полей геопотенциала в службе погоды
США (и в некоторых других странах) используется показатель Si,
равный средней по карте величине отношения абсолютной ошибки
разности прогностических значений в двух соседних точках поля
к фактической или прогностической (в зависимости от того, ко-
торая из них больше) разности значений поля в той же паре то-
чек:
с _ 100 V IЪН11
1— N тах{|8Л7ф|; |6//п|)г
где ЪНг — ошибка в прогнозе разности значений геопотенциала
в i-той паре точек, бЯф и 6ЯП — фактическая и прогностическая
изменчивость в той же паре точек, N — число пар точек.
При идеальном прогнозе, очевидно, Si=0. Этот критерий, как
и р£ = рф + фк, дает оценку подобия градиентов сравниваемых по-
лей, но одновременно позволяет проверить и правильность прог-
ноза изменений со временем, учитываемую, например, путем на-
хождения относительной ошибки е.
280
Величины средних абсолютных б и относительных 8 ошибок
легко доступны для ручного счета. Они очень распространены при
оценке краткосрочных прогнозов. При использовании этих крите-
риев для оценки долгосрочных прогнозов вместо средней абсолют-
ной изменчивости вычисляется средняя абсолютная величина ано-
малий (отклонений от нормы).
Легко также рассчитываются критерии р, рф, рь Q и Si. Ос-
тальные критерии могут быть рассчитаны лишь с применением вы-
числительной техники и применяются в основном для оценки крат-
косрочных прогнозов и прогнозов малой заблаговременности.
При оценке прогнозов в ряде случаев может быть полезным их
сопоставление с «псевдопрогнозами». К числу последних можно-
отнести:
1) климатический прогноз — прогнозируются значения метео-
рологических элементов, равные их норме, т. е. климатическим
значениям;
2) инерционный прогноз — прогнозируются значения метеоро-
логических элементов, наблюдавшиеся в исходный момент времени
(«погода не меняется»);
3) случайный прогноз — прогнозируются значения метеороло-
гических элементов, соответствующие некоторому набору случай-
ных чисел.
Прогнозы, полученные по какому-либо методу (т. е. методиче-
ские прогнозы), можно признать удовлетворительными лишь в тех
случаях, когда приведенные количественные критерии (или часть
из них) для этих прогнозов будут выше, чем соответствующие
критерии для псевдопрогнозов.
Глава IX
ЧИСЛЕННЫЙ АНАЛИЗ
МЕТЕОРОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
Для численного прогноза погоды необходимо иметь в качестве
начальных данных значения метеорологических элементов в уз-
лах регулярной сетки. Между тем метеорологические измерения
производятся на метеорологических станциях, размещенных по тер-
ритории крайне неравномерно. Всего (на сентябрь 1973 г.) в се-
верном полушарии насчитывается 693 метеорологических станции,
на которых производятся аэрологические наблюдения с помощью
радиозондов (рис. 9.1).
Прежде всего бросается в глаза то, что распределены они
крайне неравномерно. Большая часть этих станций расположена
на хорошо обжитой территории. На акватории же океанов их по-
чти нет. Кроме того, число аэрологических станций явно недоста-
точно.
На первом этапе развития численных методов прогноза значе-
ния метеорологических элементов в узлах сетки находились сле-
дующим образом. На карту с проведенными на ней изолиниями
накладывалась прозрачная палетка с нанесенными на ней узлами
сетки. Далее путем визуальной интерполяции определялись значе-
ния метеорологических элементов, которые записывались на спе-
циальные бланки, а затем набивались на перфокарты или перфо-
ленты. Такой способ занимает много времени и приводит к искусст-
венному нарушению автоматического процесса прохождения ин-
формации через технические устройства.
За последние десятилетия значительное внимание было уделено
вопросам автоматизации указанного процесса. В первую очередь
была решена задача получения значений метеорологических эле-
ментов в узлах регулярной сетки по их значениям на станциях.
Эта задача получила название численного или объектив-
ного анализа.
Впервые метод численного анализа был предложен X. А. Па-
новским в 1949 г. [44]. Метод сводился к представлению поля
какого-либо элемента в виде некоторого полинома. Этот метод
стал называться методом полиномиальной интерпо-
ляции. Различные варианты этого метода позднее были предло-
жены В. В. Быковым и Г. П. Курбаткиным, Б. Джилкристом и
282
Г. П. Крессманом, Я- М. Хейфецем, А. А. Петровым, П. Н. Беловым,
А. И. Бурцевым и др. [4, 7, 9, 10, 22, 23, 26, 33, 38].
Другой подход к численному анализу был предложен
Л. С. Гандиным [У.5]. Существенным моментом этого метода, ко-
торый получил название метода оптимальной интерпо-
ляции, было использование статистической структуры метеоро-
логических полей. Различные реализации этого метода были осу-
Рис. 9.1. Сеть станций аэрологического радиозондирования на северном
полушарии.
ществлены И. А. Четвериковым, С. Л. Белоусовым, С. А. Машко-
вичем и др. [У.З, 2, 5, 13, 17, 25, 27, 30, 31].
Широкое распространение получили различные методы ана«
лиза, в которых производится комбинирование линейной интерпо-
ляции и использования статистической структуры метеорологиче*
ских полей. Впервые такого рода метод, который можно назвать
методом последовательных приближений (методом
коррекции), был предложен П. Бергторссоном и Б. Р. Дёёсом [32].
283
Вариант такого метода был разработан Г. П. Крессманом [35].
Развитие новых средств наблюдений, таких как, например,
спутниковые системы, привело к тому, что метеорологические из-
мерения стали несинхронными. Это обстоятельство потребовало
разработки нового подхода к проблеме численного анализа и при-
вело к созданию четырехмерного численного ана-
лиза [2, 11, 14—16, 19, 24, 30, 31, 34, 36, 40, 41, 47], который пра-
вильнее было бы называть пространственно-временным
численным анализом.
Перечисленным вопросам и будет посвящена данная глава. Вна-
чале будут изложены методы численного анализа, а затем обсуж-
дена общая проблема автоматизации сбора, обработки и анализа
метеорологической информации.
§ 1. Метод полиномиальной интерполяции
Метод основан на описании участка поля какого-либо элемента
в окрестности точки регулярной сетки полиномом (многочленом).
Эти полиномы могут быть алгебраическими, тригонометрическими,
сферическими и т. д. и могут иметь разные порядки. Например,
в случае плоскости (один уровень) алгебраические полиномы пер-
вого, второго и третьего порядка соответственно имеют вид:
Р\ (X, y)=«o+«i^+o2y;
Р2 (*, у)=а0+«1х+а2У++о4х2+«вУ2;
Pi (*. у)=flo+atA-+а2у4- о,ху+п4х2+а5у2+о6х2у+
+ «7Ху2+<28Х3+О9у3,
где %, у — координаты, &о — а9— коэффициенты Указанные поли-
номы можно записать в более компактном виде. Например, по-
лином третьего порядка записывается в виде
/4-/=з
Рз(*. У)= Z а1}х1у\ (1.1)
z, j=о
Основы метода рассмотрим на примере анализа поля геопотен-
циала одного уровня при использовании полинома первого по-
рядка. Поместим начало координат в рассматриваемый узел сетки
и положим, что в окрестности этого узла поле геопотенциала пред-
ставляется в виде
Я(х, у)=^о + «1^+^2У-
Если бы мы каким-либо образом определили коэффициенты а0, fli,
а2, то значение геопотенциала в любой точке х, у легко было бы
рассчитать по приведенному соотношению. В частности, при х =
у = 0 Я(0, 0) =ао Это значение и можно принять в качестве ис-
комого, т. е. в качестве значения геопотенциала в узле или точке
сегки, найденного в результате численной интерполяции.
284
Содержание задачи заключается в определении коэффициен-
тов а Последние вычисляются методом наименьших квадратов по
значениям геопотенциала в нескольких пунктах (станциях) наблю-
дений (5 = 1, 2, N), расположенных в окрестности узла (влия-
ющие точки). Число пунктов (станций) может быть невелико. Од-
нако в любом случае их число должно быть равно или превышать
число членов взятого полинома. В данном случае принятый нами
полином первого порядка содержит три члена. Следовательно, не-
обходимо взять не менее трех пунктов (7V^3). Приближенное зна-
чение геопотенциала в любом пункте i с помощью принятого поли-
нома можно выразить в виде
Я(хь У/)=«о+«1^ + а2Уь
где Xi и yi — координаты пункта i. Например, для пункта i=l
с координатами Xi и yi
У1) = Яо4~Я1-*14“Я2Уь
Найденное таким путем значение геопотенциала будет содер-
жать ошибку = у г) — Hi, где Hi — фактическое значение
геопотенциала в пункте i.
Согласно методу наименьших квадратов (см. приложение 7),
коэффициенты а должны быть такими, чтобы сумма квадратов
ошибок б i по всем пунктам была бы минимальна, т. е. коэффици-
енты а должны быть найдены из условия минимума следующего
выражения:
1 = 1 i — 1 i = 1
Условием экстремума является обращение в нуль производных
Q по всем коэффициентам а. В результате мы получим следую-
щую систему нормальных уравнений с тремя неизвестными:
an N
== 2 (ao+Й1 xt + «2У/ ~ -fy) У«=0.
После выноса коэффициентов а из под знака суммирования и пе-
реноса членов, не содержащих неизвестные, в правую часть си-
стема уравнений примет вид:
#0^11 4“ #1^21 4" #2^31 = П1',
Я 0^12 4- ^22 4“ ^2^32 — ^2 \
^0^13 4" а14" «2^33^= ^3,
285
где
N N N
mn=l, xb т31=-дг2 У>’ ni=-N~^ Hl'
i = 1 i = 1 i = 1
NN N
1 V 1 V 1 V
= 2^ Xi> m22=-j^- 2 *Z*Z, ^32=-^^ Х*Уь
4 = 1 Z = 1 Z = 1
N N
1 v 1 v
^13=^7- 2 У/, т23=-дг 2 У^ь
I = 1 Z = 1
N
fl^ = n~ У[Нь
z = 1
Легко заметить, что матрица из коэффициентов тц симмет-
рична и что, следовательно, пц^т^.
Рассчитав значения т и п и решив полученную систему урав-
нений, находим искомые коэффициенты а. Значение ао = //(О, 0)
и будет искомой величиной Н в узле или точке сетки.
Проделав такую операцию для всех заданных точек сетки
(влияющие станции для каждой точки будут разными), мы полу-
чаем в них значения геопотенциала, которые далее используются
для численного прогноза либо автоматического расчерчивания
диагностических полей.
Изложенная схема интерполяции дает хорошие результаты
в случаях одинаковой достоверности данных во всех пунктах i.
Реальная же метеорологическая информация имеет различную до-
стоверность в разных пунктах, что может быть связано с использо-
ванием приборов разных конструкций, с ошибками измерений и пр.
В этом случае интерполяция по приведенной схеме может дать
неудовлетворительные результаты. Учесть различия в достоверно-
сти данных можно путем введения в схему дополнительных весов
gi, о которых речь пойдет далее.
Определив каким-либо путем эти веса, мы можем учесть их
при составлении и решении системы нормальных уравнений для
определения коэффициентов аь В рассматриваемом нами примере
эти коэффициенты должны быть определены из условия минимума
следующего выражения:
Q= 2 2 gi [Н(хь
Z = 1 Z = 1
N
= 2 ^(«о+^л+«2У<—М)2-
Z = 1
286
Система нормальных уравнений теперь будет иметь вид:
1 4“ ^1 ^21 4“ #2^31 — 1 >
^0^124” ^1^224“ ^2^32 == ^2»
#0^1з4“ ^1^23 4“^2^33-^3,
где
N N
~ 1 v ~ 1 V
^11-- дт 2 gb ^21--- у jgjj giXi,
Z = 1
N
m^~N~
l = \
N
^12 = ^- 2 SiXi,
Z = 1
N
~ 1 v
^32=7y- 2 gi^yb
i. 1
N
^13 pj giVi)
Z= 1
N
~ 1 V 2
m'^=~N~ ZiStyb
i = 1
Z = 1
TV
~ 1 V LT
п'=~!Г It Si^b
Z = 1
N
— 1 V1 2
77Z22== yy gi^b
Z = 1
^2=4г
i-1
N
m23=-7r 2 gixiyi>
i = l
N
«3=-^ 2 SiVi^i-
i 1
Аналогичным образом может быть получена система уравнений
для других случаев интерполяции.
Рассмотрим схемы численного анализа, в которых в качестве
исходных используются не только данные об анализируемом эле-
менте на одном уровне, но и другие данные
Так, например, при использовании данных различных уровней
и применении для аппроксимации полей полиномов второго по-
рядка пространственное поле геопотенциала может быть представ-
лено в виде
У> Q=^o4_/2ix4"<22y4"^3^y+
4~ С1^Х“ &зу2 —[— 4- dyXZ —|— &8.У^ 4“
где ^==р/Р. Минимизации в этом случае подлежит функция
X gik \H(.xh yit Q —Я,й|2,
Z, k
где i — индекс пункта на плоскости, k — индекс вертикальной ко-
ординаты, Hih — значение измеренной величины Н в точке прост-
ранства ik, gik — вес данных измерений в этой точке.
287
Наряду с данными измерений анализируемого элемента можно
использовать значения этого элемента, полученные по прогнозу.
Обозначим такие данные через Н. В этом случае, например, при
учете данных одного уровня минимизируется функция
<2=3<7НЯ(хг, У()-М]2+2а[я(х/, у/)-Д]2,
где индексы i и / относятся к пунктам, содержащим данные по
наблюдениям и по прогнозу соответственно, qi и pi — соответству-
ющие веса фактических и прогностических данных.
При анализе поля геопотенциала возможно использование дан-
ных о ветре в предположении геострофичности последнего. Исполь-
зуя геострофические соотношения
и, например, полином второго порядка для Н, получаем:
и (х, у) =-f- («2+азх+2«3у);
v(x, У)=^(«1+«зУ+2л4х).
В общем случае использования фактических и прогностических
данных о геопотенциале и данных о ветре минимизируется следу-
ющее выражение
Q- X у<)-^]2+2 уу)-Я]2+
+ 2тл ([«(**> Уй)-«Л2+[^(^, Ул)-^]2).
k
где индексы f, /, k характеризуют положение пункта на плоскости
с измеренными и прогностическими значениями геопотенциала и
измеренными значениями компонент ветра, аг-, Pj, у& — соответст-
вующие веса.
При записи полиномов в форме (1.1) выражение для Q преоб-
разуется к виду
Q=S
" tn + n=3
у,
т, п = 0
^mn^i У '1 — Hi *4“
288
g д
l ду
tn -f- n — 3
у
m, n — 0
O'tnnXk yk
g d
I dx
где bmn — коэффициенты полинома, аппроксимирующего поле Н.
Система нормальных уравнений для определения коэффициен-
тов а и b получается путем дифференцирования выражения для
Q по всем коэффициентам а и b и приравнивания результатов
к нулю.
Еще одно обобщение метода полиномиальной интерполяции
заключается в использовании каких-либо ортогональных функций,
например полиномов Чебышева или тригонометрических функций.
В последнем случае поле одного уровня может быть представлено,
например, в виде
Я (9, >-)=^ S Dnkeksinn\,
т k п k
где 6, Л — полярный угол и долгота, т и п — номера гармоник,
k — целые числа (0, 1, 2, ...), С и D — коэффициенты разложения,
которые находятся из условия минимума выражения
Q=2 [Я(бг,
i
где i — номер точки на плоскости.
На основе изложенной теории был разработан и внедрен в прак-
тику ряд конкретных методик.
Так, например, в СССР практическое применение получила ме-
тодика численного анализа, предложенная В. В. Быковым,
Г. П. Курбаткиным и др. [9, 10]. В одном из вариантов этой мето-
дики, разработанной применительно к численному анализу одно-
временно для нескольких изобарических поверхностей, был ис-
пользован принцип последовательного послойного анализа, при-
меняющийся при составлении карт барической топографии.
Численный анализ изобарических поверхностей (1000, 850, 700, 500
и 300 мбар) производится последовательно снизу вверх. Вначале
производится анализ высоты поверхности 1000 мбар. При этом
в окрестности каждого узла поле высот поверхности 1000 мбар
(Hr) представляется в виде полинома второго порядка.
После получения поля Hi производится численный анализ от-
носительной топографии изобарических слоев Н^ (1000—850,
850—700 мбар и т. п.). Высота каждой следующей поверхности
(&+1) находится по соотношению
яА+1=яй+/4+1.
19 Зак. № 21
289
Ввиду гладкости полей Hh+l оказалось возможным представ-
лять эти поля с помощью билинейного полинома
//*+1(х, у)=Ь0-\-Ь}х-\-Ь2у-\-Ь3ху,
где b — коэффициенты.
Такой принцип, при котором анализ данных на некотором
уровне производится с учетом результатов анализа на нижележа-
щих уровнях, обеспечивает получение согласованных анализов на
разных уровнях и одновременно позволяет при анализе на более
высоких уровнях косвенным образом использовать более полные
данные на нижних уровнях (в частности, на уровне 1000 мбар).
Данная методика была реализована для сетки из 26X22 точки
с шагом 300 км. При практической реализации данной методики
предусмотрен оптимальный выбор последовательности точек сетки,
в которых производится анализ, а именно: в первую очередь вы-
полняется анализ в хорошо освещенных районах и результаты его
используются при анализе в прилегающих районах с меньшим ко-
личеством данных. Предусмотрено также использование данных
о приземном давлении на синоптических станциях для анализа по-
лей приземного давления и высоты изобарической поверхности
1000 мбар.
Метод полиномиальной интерполяции применяется для объек-
тивного анализа в практике английской метеорологической службы.
Интерполяция производится с помощью полинома третьего порядка
вида (1.1).
В заключение этого параграфа отметим два весьма существен-
ных момента.
Во-первых, реализация метода полиномиальной интерполяции
возможна лишь при наличии определенной сети станций внутри
некоторой заданной площади. Поясним это на примере.
Пусть мы производим анализ поля Я (%, у) на плоскости. При
этом используем полином второго порядка, содержащий шесть
неизвестных коэффициентов а. Для их определения необходимо
использовать данные не менее, чем в шести пунктах. Однако из-за
ошибок в наблюдениях нам необходимо обеспечить определенное
сглаживание полей. Для этого число пунктов наблюдений должно
быть больше шести, например десять. Эти пункты должны нахо-
диться в окрестности рассматриваемого узла сетки и обеспечить
необходимую точность аппроксимации поля. Последнее обстоя-
тельство приводит к некоторым условиям в отношении густоты и
расположения станций. Эти условия могут меняться в зависимости
от требуемой точности аппроксимации.
На основании многочисленных опытов можно утверждать, что
методом полиномиальной интерполяции невозможно получить
удовлетворительный результат при расстояниях между пунктами
с данными наблюдений (или данными, их заменяющими) более
700 1000 км.
290
При наличии «густой» сети с расстоянием между пунктами
в 300—600 км точность метода полиномиальной интерполяции
оказывается достаточно высокой. Так, например, средняя абсо-
лютная ошибка интерполяции АТэоо составляет 1—2 дам.
Второй существенный момент метода полиномиальной интер-
поляции заключается в выборе весов отдельных наблюдений (gi,
pi и Др.). Ввиду отсутствия какой-либо общей методики их опре-
деления, пригодной к любому варианту, подбор весов, как пра-
вило, производится на основе эмпирических данных и численных
экспериментов.
Так, например, при использовании в анализе данных одного
и того же метеорологического элемента веса можно принять про-
порциональными средней квадратической ошибке данных рассмат-
риваемого пункта (Ог), т. е. принять, что [7]
1
Для придания большего веса пунктам, находящимся ближе
к узлу сетки, принимается, например, что [7, 9]
gi=T7^T’
где г — расстояние от узла до пункта f, а — коэффициент.
§ 2. Метод оптимальной интерполяции
Этот метод основан на использовании характеристик статисти-
ческой структуры метеорологических полей, которые должны быть
получены заранее путем обработки данных наблюдений за про-
шедшие сроки. Поэтому прежде чем излагать существо метода
рассмотрим некоторые статистические характеристики (см. при-
ложение 7) метеорологических полей.
Пусть f — значение метеорологического элемента в некоторой
точке, f — среднее значение этого элемента (норма), f' =f — f —
отклонение от среднего значения (аномалия или вариация). Здесь
и далее черта сверху означает осреднение. Средняя величина
квадрата аномалии f', т. е. D = f'2 называется дисперсией элемента
f; средняя величина произведения значений f' в двух каких-либо
точках i и /, т. е. = —ковариационной функцией (иногда
эти функции называют просто корреляционными функциями);
а отношение ковариационной функции к корню квадратному из
произведения дисперсии в этих точках
’ V717; ',D‘D‘
(2.1)
19*
291
— нормированной ковариационной функцией (или нормированной
корреляционной функцией). В дальнейшем эти функции будем на-
зывать нормированными автокорреляционными функциями или
просто коэффициентами корреляции.
Поле элемента f называется изотропным, если функция
= f'. зависит лишь от положения середины прямой, соединяю-
щей точки i и /, и ее длины и не зависит от направления этой
прямой. Поле называется однородным, если дисперсия эле-
мента f постоянна для всего поля (Di = Dj = d2), а значение mtj
не зависит от положения середины прямой, соединяющей точки i
и /, а зависит только от длины этой прямой, т. е. от расстояния
между точками i и j (rij).
Следовательно, в случае однородного и изотропного поля для
нормированной ковариационной функции получаем
№ij ^2 Р* (ri/)-
Для практических целей используются корреляционные функ-
ции, определенные по эмпирическим данным за прошлые сроки.
Такие функции неоднократно подсчитывались для различных эле-
ментов и имеются в форме таблиц или в аналитическом виде. На-
пример, нормированная корреляционная функция для АТ500, по-
лученная М. И. Юдиным, имеет следующий вид:
[х(г)=(14-О,98г)е-о’98г
(г выражено в тыс. км).
Измерения метеорологических элементов производятся с опре-
деленной ошибкой. Это обстоятельство учитывается при расчете
корреляционных функций по данным наблюдений следующим об-
разом. Пусть f — измеренная величина метеорологического эле-
мента, содержащая ошибку измерения б; f — истинное значение
этого элемента; o2 = f'2, где f' =f — f.
Тогда, принимая ошибки случайными, т. е. считая, что:
1) среднее значение ошибки в каждой точке равно нулю, т. е.
6^=0,
2) ошибки в разных точках некоррелированы, т. е. бгб^ = О
GV/),
3) ошибки не коррелируют с истинными значениями элемента
в любых точках, т. е. бг-/' =0,
имеем следующие соотношения:
/=/; fifj=
fifj a^j),
^,2
=// =
(2-2)
292
С учетом этих соотношений эмпирические значения нормиро-
ванной автокорреляционной функции, определяемой по данным
наблюдений со средней квадратической ошибкой о, находятся сле-
дующим образом:
где
1
Nd?
N
V
k=l
(2.3)
d2=—
a N
fikfjk,
(2.4)
— дисперсия элемента f'ik и f'.h — отклонения элементов от
нормы в точках i и /; k — номер случая (ситуации); N — число
случаев, вошедших в статистическую обработку. Чем больше
число N, тем надежнее определяется величина ц.
На практике для получения значения ц(г), соответствующего
некоторому заданному расстоянию г, выбираются такие пары пунк-
тов /, расстояние между которыми близко к г, и по данным во
всех этих пунктах за большое число сроков производится расчет
Цг; по формуле типа (2.3). Такие расчеты производятся не для
одного, а для большого числа различных значений расстояний.
В результате этих расчетов получаем значения р для различных г.
Найденная таким путем функция р (г) после проверки выпол-
нения некоторых критериев может быть далее аппроксимирована
аналитической формулой типа приведенной выше или записана
в виде таблицы значений с постоянным шагом по г. В таком виде
эти функции могут быть использованы для практических расчетов
при численном анализе.
После этих предварительных замечаний перейдем к изложению
существа метода оптимальной интерполяции. В соответствии с этим
методом отклонение f' истинного значения элемента f в узле сетки
от нормы f выражается в виде
/о= 5 Р if i —P\f\ +Р2/2+ . . . -\~Pnfп, (2.5)
1= 1
где f\ = fi — fi — есть отклонение измеренного элемента от нормы
в пунктах i (г = 1, 2, .. ., и), pi — интерполяционные веса. Для оп-
ределения pi в соответствии с методом наименьших квадратов со-
ставляется система нормальных уравнений из условия минимума
среднего квадрата ошибки б, с которой выполняется приведенное
соотношение для большого числа ситуаций и числа точек, в кото-
рых производится расчет f', т. е. из условия минимума функции:
п I2
/о - X Plfi
i = l J
--2 п
/о -2/0 S pji + (ЗлЛ)2 .
/=1 J
(2.6)
293
Функция Е будет иметь минимум, если ее частные производные по
pi будут равны нулю, т. е. при условии
-^-=0 (/=1,2,..., п). (2.7)
Дифференцируя каждый член выражения для Е, получаем:
44=0; + (/++)=7iZ;
, / п \2 п _ / п \
=2i^7;7;=2.iip/Z7;.
С учетом полученного вместо (2.7) имеем
-247+2 2 a7/7J=O (/•=!, 2, ..., «).
7=1
Поделив это выражение на дисперсию в районе расположения
узла сетки, для которого делается интерполяция, учитывая соот-
ношения (2.2) в предположении, что средняя квадратическая
ошибка данных в каждой точке i известна и равна о+ найдем
1 кл —'•—7 °? I —'•—7
Д Pjfifj+Pi (*=+ 2, . . ., П).
Пусть T\i = o2./d2, — отношение среднего квадрата ошибки к дис-
персии в дальнейшем будем называть относительной ошибкой на-
блюдения. Тогда, вспоминая определение функции р, приходим
окончательно к следующей системе уравнений:
3 РЛ»у+т=Нм (/=1, 2, . . ., п). (2.8)
В развернутом виде эта система нормальных уравнений запи-
сывается так:
Р\ (Нп~Ь7?1)+/721112+ • • • -\~Рп№\п = Рчи;
Р№\2-*ГР2 (tt22“h722)+ • • • +Ри112л = 1102;
Р1Нл+/721х2п+ • • • "\~Рп (l1nn + 7]n) = FL0rt-
Поделив выражение (2.6) для Е на дисперсию d2, для относи-
тельной ошибки интерполяции е получим
Е 1 + 2
£— d2 — &
294
В данном случае имеем:
-&-f* = 1 > f* .2 Pi f l = 2 P^'
n / n \
= ^2 Pi ^2 PjV-aA-Pi^ •
Тогда
n n / n \
s = i — 2 2 Pi\^i 4- 2 pa 2 р^иЛ- рл
i=l i=\ \j=l /
Но на основании (2.8) выражение в круглых скобках равно рол
Поэтому
п
е= 1 —2лНо/- (2-9)
1 = 1
Величина относительной ошибки интерполяции заключена
в пределах
0<е<1.
Очевидно, что чем ближе 8 к нулю, тем лучше интерполяция.
Квадрат абсолютной ошибки интерполяции 6 связан с относи-
тельной ошибкой е следующим образом: d2 = 8d2, где d2— дис-
персия.
Если все значения и гц известны, то для данного располо-
жения станций вокруг узла величины 6 и 8 можно рассчитать за-
ранее. В табл. 9.1 приведены величины средних квадратических
ошибок интерполяции (6) АТ500 для густой и редкой сети (сред-
ние расстояния между станциями составляют соответственно около
400 и 1300 км) при различных значениях т]. Эти значения могут
быть получены при различной комбинации величин о и d. Так,
например, полагая, что для АТ500 d = 150 дам2 и учитывая, что
средняя квадратическая ошибка высот АТ5оо, полученных по дан-
ным радиозондирования, составляет 1,7 дам [У.5], находим q =
= (1,7)2/150~0,02. Как следует из данных табл. 9.1, ошибка ин-
терполяции минимальна в случае густой сети станций при т) = 0
Таблица 9.1
Теоретическое значение средйих квадратических ошибок интерполяции 6 дам
значений АТ5Оо при различных ц для густой 6Г. с и редкой др. с сети станций
У 0 0,02 0,05 0,10
&г. С 1,8 2,0 2,3 2,6
вр. С 4,6 4,8 5,1 5,4
295
(6 = 1,8 дам). При т]=0,02 в случае густой сети станций 6=2,0,
а в случае редкой—6=4,8 дам. Из этого следует, что лучшие
результаты метод оптимальной интерполяции, как и другие ме-
тоды, будет давать в районах, хорошо освещенных метеорологи-
ческими данными, и худшие — в районах, плохо освещенных ме-
теорологическими данными.
Рассматривая поле относительной ошибки интерполяции е для
северного полушария по С. А. Машковичу (рис. 9.2) и сравнивая
Рис. 9.2. Поле относительной ошибки интерполяции е для высоты
изобарической поверхности 500 мбар на северном полушарии
(по С. А. /Машковичу).
его с расположением аэрологических станций (см. рис. 9.1), мо-
жно заключить, что наименьшие относительные ошибки интерпо-
ляции порядка 0,02 (им соответствует средняя квадратическая
ошибка порядка 1,7 дам) имеют место в районах с густой сетью
станций (Европа, Северная Америка). Наибольшие относитель-
ные ошибки (е более 0,9) имеют место в районах с очень редкой
сетью станций (океаны). Этой относительной ошибке соответст-
вует абсолютная ошибка интерполяции порядка 10 дам.
На основании общей теории метода оптимальной интерполяции
были разработаны конкретные схемы численного анализа для раз-
личных сеток точек и разных областей. В СССР наиболее широкое
практическое применение получила методика численного анализа
поля геопотенциала на нескольких уровнях, реализованная
296
С. Л. Белоусовым. В этой методике для интерполяции использу-
ются данные восьми точек, ближайших к узлу. В конкретных про-
граммах шаг сетки, число узлов и прочие параметры сетки могут
быть заданы произвольно. Частными случаями являются прямо-
угольные области, содержащие 26x22 или 37X27 точек с шагом
сетки в 300 км, или восьмиугольная область, изображенная на
рис. 5.1 (см. гл. V).
Метод оптимальной интерполяции был применен также для
численного анализа полей приземного давления, барической тен-
денции, температуры и точки росы для учащенной сетки с шагом
в 150 км по данным сети метеорологических станций. Соответст-
вующая методика была разработана и реализована А. Н. Багро-
вым, С. Л. Белоусовым и А. Г. Тарнопольским [2]. Одна из харак-
терных особенностей этой методики связана с тем, что плотность
сети метеорологических станций значительно выше плотно-
сти аэрологических станций. Так, например, число метеорологиче-
ских станций, относящихся к области анализа, включающей 47 X
Х40 узлов сетки с шагом 150 км с центром в Европе, составляет
1304, в то время как при анализе поля геопотенциала для не-
сколько меньшей области, включающей 26x22 узла с шагом
300 км, число аэрологических станций составляет около 300.
Наличие достаточно густой сети метеорологических станций
позволяет использовать только те станции, которые удалены от
узла на небольшие расстояния. Достаточная точность интерполя-
ции обеспечивается при учете данных всего четырех станций.
В свою очередь уменьшение числа учитываемых станций и связан-
ное с этим уменьшение порядка системы уравнений (2 8) обеспе-
чивает более надежный расчет интерполяционных весов pi. При
этом отношение квадрата ошибки наблюдений к дисперсии эле-
мента, т. е. величина т], как и при анализе аэрологических данных,
принималась постоянной и равной 0,02.
Проведенные эксперименты показали, что рассмотренная ме-
тодика для упомянутой территории дает удовлетворительные ре-
зультаты. Так, например, расхождения между результатами чис-
ленного и синоптического анализов давления на уровне моря для
районов с самой густой сетью станций в среднем составили
0,6 мбар. Для районов же с редкой сетью станций результат чис-
ленного анализа этим методом ухудшается.
Отметим еще один подход к численному анализу пространст-
венных полей, предложенный Г. И. Марчуком [У. 17]. В этом под-
ходе в качестве первоначального этапа предлагается разложение
вертикального профиля рассматриваемого элемента в ряд Фурье.
На втором этапе производится интерполяция на узлы сетки коэф-
фициентов разложения. При этом в качестве одного из возможных
методов принимается метод оптимальной интерполяции. Достоин-
ство такого подхода заключается в возможности учета при гори-
зонтальной интерполяции наличия возмущений разных масштабов
(старшие члены разложения в ряд Фурье имеют больший горизон-
тальный масштаб по сравнению с младшими)
297
За рубежом различные варианты метода оптимальной интер-
поляции предложены Л. Бенгтссоном и Н. Густавсоном, М. А. Ала-
кой и др. [29, 31].
§ 3. Метод последовательных приближений
В оперативной работе метеорологических служб ряда стран
применяется метод интерполяции, который условно можно назвать
методом последовательных приближений или методом коррекций.
Первый вариант такого метода первоначально разрабатывался
применительно к анализу карт барической топографии П. Берг-
торссоном и Б. Р. Дёёсом в Швеции [32].
Изложим этот метод в его первоначальном виде. Вначале по-
лучают так называемое предварительное поле, представляющее со-
бой комбинацию климатического и прогностического (на срок ана-
лиза) полей. Пусть Нп, Н и Н — значения высот изобарической
поверхности предварительного, климатического и прогностического
полей соответственно в узловой точке. Тогда принимается, что
Н
где ц и |л = 1 —ц — веса, определенные заранее. Эти веса различны
для различных районов. В среднем ц«0,80.
Полученное таким образом предварительное поле подправля-
ется с помощью фактических значений высот и ветра на станциях.
По фактическим значениям высот и скорости ветра на станциях,
а также с помощью предварительного поля получают несколько
новых значений высот в узле по соотношениям:
^1 = ^с+(//п-Япс); Я2=Яс+(^-)сГ;
где величины с индексом «с» относятся к станции, а с индексом «п»—
к предварительному полю; градиенты (дН1дп)с определены по
скорости ветра на станции с помощью геострофического соотноше-
ния; величина (дН/дп)и — градиент в узле, определяемый по пред-
варительному полю; г — расстояние между станцией и узлом.
Полученные промежуточные величины Н2 и Нз будут вхо-
дить в окончательное поле Н с определенными весами ц, которые
являются следующими функциями расстояния станции от рассмат-
риваемого узла г:
30 97
!*=-ИШ"°’04; IW—;^70-.
298
где единицей измерения г является 300 км. Из последних соот-
ношений можно заключить, что p>i приближается к нулю при г =
= 1500 км, а Ц2 и цз — при г = 900 км. Поэтому данные о высотах
использовались лишь со станций, удаленных от узла не более чем
на 1500 км, а данные о ветре — лишь со станций в радиусе до
900 км.
Для пунктов, удаленных от узла сетки более чем на 900 км, но
менее чем на 1500 км, а также для пунктов, где данные о ветре
отсутствуют, вычисление промежуточных полей Н2 и Н3 не про-
изводилось, а значения Hi бралось не с весом pi, а с весом Ц4,
равным
2,25
fJ'4~ г8 + 5
10
г4 + 20
0,01.
Если п — число станций, на которых используются данные и
о высотах и о ветре, а т — число станций, на которых использу-
ются данные только о высотах, то окончательная формула для
расчета Н в узле сетки имеет вид
„_______ * т
-j- р. Н 4“ у1, -1 + Р-2^2 + Р-З^з)/ + 2 -----(р4^i) J
____________t = i Р* j=i Pj
n j m i
p + p + 2 — 112 + ^3) S — (r)j
i=i pz p;
где pi и pj — дополнительно вводимые веса станций, определяемые
их плотностью (числом станций в круге радиусом 375 км). Учет
плотности делается для того, чтобы уменьшить действие взаимно-
коррелированных значений Н для близких станций.
Наиболее широкое распространение метод последовательных
приближений получил в США. В оперативной практике там при-
меняется вариант этого метода, разработанный Г. П. Крессма-
ном [35].
Рассмотрим этот вариант применительно к полю геопотен-
циала.
В качестве предварительного используется прогностическое
поле на 12 ч вперед. Далее в это поле последовательно вводятся
поправки. При наличии данных о высоте изобарической поверх-
ности Н в предварительное поле Нп вводится поправка
Ся=1Г(г;)(Я-//п)г .
При наличии данных о высоте и ветре поправка берется
в виде
U7(r0 [М—^0+-^(г|Дх-и Дух].
299
Здесь i — индекс пункта с измерениями, а 0 — индекс узла сетки,
т — масштабный множитель, k — эмпирический коэффициент
(равный 1,08), W(ri)—весовая функция, которая берется в виде
W (г)—
при г /?,
при r>R,
о
где г — расстояние между узлом и точкой измерения, R— некото-
рое предельное расстояние, и и v — составляющие скорости ветра,
Дх и Ду — проекции расстояния между узлом сетки и пунктом
наблюдения на оси х и у соответственно.
Окончательная поправка в предварительное поле берется
в виде
AnH + mv
где пн и mv — число точек с наблюдением о геопотенциале и ветре,
а А — относительный вес данных о геопотенциале.
Далее в соответствии с методом последовательных приближе-
ний описанная процедура повторяется несколько раз, причем при
каждом последующем приближении в качестве предварительного
поля принимается поле предыдущего приближения При этом зна-
чение R каждый раз уменьшается. При первом приближении R =
= 4,75x300 км, а далее оно принимает значения 3,6x300, 2,2x300
и 1,8x300 км
Это делается с целью учета более мелких возмущений в факти-
ческом поле. Процедура оканчивается после того, как разности
значений геопотенциала двух соседних приближений не будут пре-
вышать некоторой заданной величины.
При численном анализе поля давления на уровне моря и вы-
сот изобарических поверхностей в качестве предварительного поля
используется прогностическое поле на 6 и 12 ч вперед соответст-
венно.
Изложенная методика применяется в США также для числен-
ного анализа поля температуры, влажности и других метеоэле-
ментов.
Существуют модификации методики, в которых в результате
анализа получается поле функции тока ф и поле соленоидального
ветра.
При этом используются соотношения:
а также уравнение баланса в виде
л, 1 ( л । п 17 V <?2Ф <?2Ф 1 „,Т
ДФ =—у— I Д/У4-2 (-л—ч— I----з—п—ч—о— — • V/ к
т I ( 1 Цдлгду ) дх% ду?- J ‘ J
300
Сетка точек может быть произвольной. В Национальном ме-
теорологическом центре США численный анализ по северному по-
лушарию производится для восьми изобарических поверхностей
для сетки точек с шагом 381 км на широте 60°, изображенной на
рис. 5.5 (см. гл. 5). Внутренняя (восьмиугольная) область ана-
лиза содержит 1977 точек. Используются также схемы анализа
по той же методике для ограниченной территории с шагом, со-
ставляющим 7г и 7s от шага основной сетки.
Остановимся теперь на сравнении трех рассмотренных методов
численного анализа. Прежде всего следует подчеркнуть, что не-
возможно категорически утверждать о безусловном преимуществе
какой-либо одной схемы. Каждая из рассмотренных схем обладает
определенными преимуществами и недостатками. Рассмотрим ос-
новные из них.
Основной недостаток метода полиномиальной интерполяции
связан с тем, что реальные поля иногда плохо описываются с по-
мощью выбранного полинома. В таких случаях при редкой сети
станций некоторые значения коэффициентов а оказываются сильно
зависящими от ошибки измерения. Это в свою очередь приводит
к большим ошибкам интерполяции.
Достоинствами метода оптимальной интерполяции являются
учет структуры метеорологических полей и возможность предва-
рительной оценки качества интерполяции для различных районов,
вместе с тем использование гипотезы об однородности и изотроп-
ности поля аномалий оказывается не всегда оправданным, что не-
сомненно снижает качество интерполяции.
Определенным недостатком метода последовательных прибли-
жений является некоторый произвол при построении предваритель-
ного поля, а также в выборе зависимости весов станций от рас-
стояния и от плотности сети станций.
§ 4. Использование в численном анализе дополнительной
информации
Изложенные ранее методы численного анализа дают эффектив-
ные результаты в районах, хорошо освещенных данными наблюде-
ний. В районах же с редкой сетью станций качество численного
анализа резко снижается. Поэтому для таких районов возникает
необходимость получения и использования какой-либо дополни-
тельной информации (под последней будем понимать метеорологи-
ческую информацию, получаемую не с помощью обычных наблю-
дений на метеорологических станциях).
Дополнительная информация может быть получена с помощью
новых наблюдательных средств: спутники, уравновешенные шары-
зонды, буи и пр. Из этих средств несомненно наиболее важными
являются спутниковые системы наблюдений, позволяющие полу-
чать данные об облачности, интенсивности лучистой энергии в раз-
личных диапазонах длин волн и пр.
301
Первоначальные измерения со спутников не дают непосредст-
венных значений метеорологических элементов, пригодных для чи-
сленного анализа. Поэтому перед использованием таких данных
для анализа необходим переход от измеряемых параметров к инте-
ресующим нас метеорологическим элементам. Такой переход может
быть сделан различными путями, важнейшим из которых является
статистический. После этого может быть применен один из спосо-
бов анализа, изложенных ранее, или какой-либо другой способ.
Рассмотрим теперь это более подробно на некоторых примерах.
Использование в численном анализе данных
об облачных системах спиралевидного харак-
тера. Такие облачные системы, называемые облачными вих-
рями, как правило, наблюдаются в циклонических областях
и определенным образом связаны с полем ветра и давления. Уста-
новив эти связи и применяя их к конкретному облачному вихрю,
можно получить значения скорости и направления ветра или вели-
чину давления в ряде точек. Полученные данные затем можно
включить в какую-либо схему численного анализа.
Так в работе Л. А. Анекеевой [1] получены средние величины
направления и скорости ветра у поверхности земли и на поверх-
ностях 850, 700, 500 и 300 мбар в различных частях облачного
вихря.
Область облачного вихря делилась на восемь секторов с цент-
ральным углом в 45° и на пять равных частей вдоль радиуса.
Всего в области оказалось 40 частей, в которых могут быть
определены скорость и направление ветра.
Данные о ветре, получаемые таким путем, использовались в чис-
ленном анализе поля ветра методом полиномиальной интерполя-
ции. Компоненты скорости ветра при этом представлялись полино-
мом второго порядка в виде:
z+;=2 /+/=2
и= У Ян-кУ; S Ьих1у\
i'J — O I, j = 0
где а и b — коэффициенты.
Результаты проведенных экспериментов показали, что при на-
личии в рассматриваемой области облачного вихря поле ветра вос-
станавливается вполне удовлетворительно. Имея значения компо-
нент ветра в узлах сетки, можно путем решения уравнения баланса
относительно Н получить и значения геопотенциала.
В ряде работ, например [42, 43], были установлены связи между
особенностями облачных систем и значениями давления в их ха-
рактерных точках. Эти значения можно использовать в численном
анализе поля геопотенциала наряду с данными аэрологических
наблюдений.
Однако более эффективным является другой способ использо-
вания таких данных, применяющийся в США и получивший назва-
ние программы SINAP (применение спутниковых данных в чис-
ленном анализе и прогнозе). В соответствии с этой программой
302
данные об облачности первоначально используются для уточнения
синоптического анализа барического поля, производимого вручную
по всем имеющимся данным. Особое внимание уделяется районам
с плохой освещенностью обычными данными. Для этих районов при
наличии облачных систем вихревого характера с помощью стати-
стических связей между облачностью и высотой изобарической по-
верхности определяются значения высот в ряде характерных точек
облачной системы (центр вихря и пр.). Эти точки рассматриваются
далее как некоторые искусственные станции и вводятся в ЭВМ для
использования в окончательном численном анализе наряду с дан-
ными радиозондирования. Эта система позволяет заметным обра-
зом улучшить анализ для малоосвещенных районов.
Использование данных об общей облачности.
Ш. X. Мусаелян [17, 18] применил подход, не связанный с нали-
чием облачных вихрей. Этот подход основывается на предположе-
нии о наличии связей между облачностью и вертикальными, а также
и горизонтальными движениями. Можно предположить, что суще-
ствует связь и между облачностью и некоторыми характеристиками
ветра, в частности вихрем скорости или же его геострофическим
значением, пропорциональным ДЯ. Однако ищется не непосредст-
венная связь между указанными величинами, а связь между коэф-
фициентами разложений указанных элементов в ряд Фурье.
С этой целью значение количества общей облачности S, а также
поле рассматриваемого элемента, например ДЯ, на некоторой ши-
роте (или иной линии на карте) представляется в виде рядов типа
5 (X)=-^- + 2 COS 7?гХ;
кН (Х)=-^—р У <om cos mX,
где Sm и сот — коэффициенты разложения, X — долгота.
Далее по фактическим данным об S (X) и ДЯ (X) строятся ли-
нейные уравнения регрессии для коэффициентов разложения вида
== Przz,
где ат и pw — коэффициенты, определяемые методом наименьших
квадратов.
Имея данные наблюдений за облачностью для рассматриваемой
ситуации, мы можем определить коэффициенты разложения Sm,
а с помощью полученных уравнений регрессий найти и коэффици-
енты разложения com. С помощью последних определяются вели-
чины AH=f(x, у). Решая данное уравнение, мы находим значения
Я для заданной сетки точек.
Полученные таким образом поля Я можно существенно улуч-
шить, используя данные редкой сети станций. Здесь возможны раз-
ные подходы. Один из них заключается в следующем [17]. Пусть
Я — значения высоты изобарической поверхности на аэрологиче-
ских станциях редкой сети, Hi — соответствующие величины,
303
найденные путем линейной интерполяции значений геопотенциала
в узлах сетки, восстановленных по данным об облачности, а б =
= // — Hi. Построим теперь ряд треугольников с вершинами в точ-
ках расположения станций таким образом, чтобы любой из узлов
сетки оказался внутри одного из треугольников.
Положим далее, что внутри треугольников разности б можно
представить в виде линейной функции
В (%, у)=ах-\-Ьу-\-с,
тдх а, b и с—некоторые коэффициенты. Последние определим
из условия, что величины б в вершинах треугольника известны.
Если 61, 62 и бз — значения б в вершинах треугольника, хь Х2, х3
и yi, У2, уз — координаты хну этих вершин, то для нахождениям,
b и с получим следующую систему линейных алгебраических урав-
нений:
•^1«+У1^+^==5ь
4“ у2Ь + С = &2,
+С—*з •
Теперь с помощью выражения для б с найденными коэффици-
ентами м, 6, с мы можем для каждого из узлов сетки, лежащих
в данном треугольнике, по их координатам х, у рассчитать вели-
чину поправки б. Сложив найденные таким путем величины б
с величинами Hi, получим окончательные значения геопотенциала
во всех узлах сетки.
В результате применения изложенной процедуры согласования
значений геопотенциала, найденных по данным наблюдений за об-
лачностью, с их значениями на редкой сети станций окончатель-
ные величины геопотенциала в узлах сетки оказываются более
точными по сравнению с данными восстановления только по дан-
ным наблюдений за облачностью. Ошибки в определении АТ500 та-
ким методом составляют 2—3 дам, в то время как без процедуры
согласования они составляли 5—12 дам.
Использование данных дистанци онно г о зонди-
рования. Рассмотрим теперь некоторые возможности использо-
вания данных дистанционного зондирования атмосферы со спутни-
ков. При этом мы ограничимся данными о вертикальном профиле
температуры, получаемыми с помощью спектральных измерений,
например, в полосе поглощения углекислого газа (Z,~15 мкм). Эти
измерения позволяют получить значения температуры в тропосфере
с точностью 1—2° при ясном небе и 3—4° при облачности [20, 45].
Зная вертикальный профиль температуры и значение давления
на каком-либо уровне, можно рассчитать давление на любом
уровне [8].
Значения давления на разных уровнях можно получить также
по данным непосредственных измерений со спутника с помощью
полученных заранее статистических связей [46].
304
В любом случае мы можем получить значения давления на раз-
ных уровнях или высот изобарических поверхностей с некоторой
точностью, например, для АТ500 средняя квадратическая ошибка со-
ставляет 2—4 дам при ясном небе и 3—6 дам при облачности.
Полученные данные можно использовать в численном анализе
наряду с основным, т. е. данными наблюдений на метеорологиче-
ских станциях. При этом возможен учет как несинхронное™ на-
блюдений (см. следующий параграф), так и различий в точности
наблюдений, производимых различными средствами. Последние
могут быть учтены с помощью весов gi, приписываемых данным
наблюдений в отдельных точках. Эти веса можно принять, напри-
мер, обратно пропорциональными известной средней квадратиче-
ской ошибке наблюдений. При использовании метода оптимальной
интерполяции переход к весам типа gi не потребуется, так как зна-
чения средней квадратической ошибки наблюдений, разделенные
на дисперсию, непосредственно входят в расчетные формулы. В лю-
бом случае при использовании измерений со спутника необходимо
иметь в виду, что ошибки измерений в отдельных пунктах дистан-
ционного зондирования уже не являются независимыми (как в слу-
чае измерений с наземных станций), поскольку они производятся
одним и тем же прибором. Для учета такой корреляции ошибок
вносятся изменения в ранее рассмотренные интерполяционные
формулы.
В самом простейшем случае включение данных, полученных
с помощью наблюдений со спутников, возможно без учета несин-
хронное™ и различия в точности наблюдений [45].
Проведенные эксперименты показали, что использование такого
рода данных позволяет заметным образом улучшить численный
анализ. Так, в работе [28] показано, что включение в численный
анализ данных измерений спутниковым инфракрасным спектромет-
ром (СИКС) со спутника «Нимбус» при разности в сроках наблю-
дений не более 7 ч позволило уменьшить ошибку анализа //500
в районе редкой сети станций более чем на 2 дам.
В качестве дополнительной информации могут быть использо-
ваны данные измерения скорости и направления ветра, производи-
мые на самолетах гражданской авиации с помощью доплеровского
радара или инерционно-навигационной системы. В перспективе
можно ориентироваться на одновременное использование наряду
с основной всей дополнительной информации, что несомненно явля-
ется весьма сложной задачей. Работы в этом плане только начаты
[37].
§ 5. Четырехмерный численный анализ
До сих пор речь шла о численном анализе метеорологических
полей на плоскости или в трехмерном пространстве по данным син-
хронных наблюдений. Между тем, как уже говорилось, для новей-
ших наблюдательных метеорологических систем характерной
20 Зак. № 21
305
является несинхронность наблюдений. В то же время для числен-
ных методов прогноза погоды необходимы данные, отнесенные
к некоторым единым срокам.
В связи со сказанным возникает необходимость в таком методе
численного анализа, в котором учитывались бы данные наблюде-
ний за разные сроки. Такой анализ можно назвать пространст-
венно-временным или четырехмерным численным
анализом.
При решении такой задачи возможны различные подходы [3,11,
14, 15, 19, 36]. Один из них заключается в том, что время рассмат-
ривается в качестве независимой переменной наряду с пространст-
венными координатами. В этом случае возможно обобщение всех
рассмотренных в § 1—3 методов численного анализа.
Второй подход заключается в предварительном приведении не-
синхронных данных к единому сроку с последующим применением
какого-либо метода пространственного численного анализа. Для
приведения несинхронных данных к единому сроку используется
прогностическая модель.
В обоих из указанных подходов в качестве дополнительных дан-
ных могут быть использованы также результаты прогноза.
В зависимости от способа использования данных несинхронных
наблюдений возможны два основных варианта реализации про-
странственно-временного численного анализа. В первом из них пре-
дусматривается проведение расчетов распределения метеоэлемен-
тов в пространстве и выдача соответствующих полей лишь для
некоторой последовательности заранее заданных дискретных сро-
ков /1, ^2, ... (например, для синоптических), к которым путем тех
или иных преобразований приводятся данные наблюдений, относя-
щиеся к моментам, не совпадающим с дискретными сроками ана-
лиза. В этом случае мы имеем так называемую дискретную
схему пространственно-временного анализа, обеспечивающую по
существу получение последовательности обычных пространствен-
ных анализов.
Однако выполнение пространственно-временного анализа для
использования его результатов в численном прогнозе возможно
и целесообразно не только для некоторых заранее заданных сро-
ков, но и, вообще говоря, непрерывно — по мере поступления каж-
дой новой серии данных наблюдений. В этом случае мы имеем так
называемую непрерывную схем у пространственно-времен-
ного анализа и прогноза, обеспечивающую получение для любого
момента времени (а не только для заданных сроков) наиболее пол-
ной модели распределения метеоэлементов в атмосфере.
Рассмотрим теперь некоторые из указанных подходов и пред-
ложенные способы их реализации более подробно. Для простоты
рассуждения будем вести применительно к численному анализу
одного скалярного метеорологического элемента на одном уровне.
Метод полиномиальной интерполяции обобщается следующим
образом. При представлении поля скалярного элемента, например
геопотенциала, в виде какого-либо полинома время t рассматри-
306
вается в качестве одной из независимых переменных. Так, при ис-
пользовании полинома второго порядка принимается, что
Я(х, у,
+о8^+«</2- (5.1)
Коэффициенты а, как и ранее, находятся из условия минимума
выражения
I, S
где индексом i отмечено положение точки на плоскости, индексом
s — момент времени, а суммирование распространяется на все рас-
сматриваемые точки на плоскости и моменты времени. Значение
весовой функции giS может быть выбрано из каких-либо дополни-
тельных соображений (в простейшем случае gis = 1).
Численные эксперименты по учету несинхронных данных с по-
мощью полинома вида (5.1) показали, что учет несинхронных дан-
ных уменьшает ошибку численного анализа поля /Лоо на 1—2 дам
по сравнению с анализом, выполненным только по синхронным дан-
ным редкой сети (при сохранении только первых четырех членов
выражения (5.1)).
Рассмотрим теперь каким образом обобщается метод опти-
мальной интерполяции. При этом вновь будем рассматривать ска-
лярный элемент на плоскости. Если индекс i по-прежнему характе-
ризует положение точки на плоскости, a s — время, то согласно
методу оптимальной интерполяции значение любого скалярного эле-
мента в узле сетки хо (в отклонениях от нормы) выражается через
значения этого элемента в других пунктах пространства и в другие
моменты времени в виде их линейной комбинации вида [15]:
^0 Zu 2 ('is^’isy (5*2)
I-15=1
где п — число точек на плоскости, т — число моментов времени.
Коэффициенты Cis находятся из условия минимума выражения
~ п т “12
Zj Zj Cis^is Хо >
_/ = 1 5 = 1
где черта сверху означает осреднение. Это условие при предполо-
жении об однородности и изотропности полей, а также об отсутст-
вии корреляции между ошибками измерений в случае двух момен-
тов времени наблюдений ti и /2 (т = 2) приводит к следующей си-
стеме линейных алгебраических уравнений:
V \ci\B(riki ti)-\-ci2B (rik, f2)] = B(r0kt /2);
z = i
Zj \ci\B(riki t2)-\-ci2B (rikt /i)]=S(r0A:, /J, (5.3)
i = 1
20*
307
где k = 1, 2, . . п — индексы точек (пунктов) на плоскости; rik и roh—
расстояния между точками k и i и точкой k и узлом сетки соответ-
ственно; В = В (гikt ts)—значения пространственно-временной кор-
реляционной функции метеорологического элемента. Если функция
В нам известна, то решая систему уравнений (5.3), мы получим
искомые коэффициенты с. Подставляя их в выражение (5.2), по-
лучаем значения элемента в узлах сетки для заданного момента
времени, т. е. %о.
Одна из трудностей реализации изложенного метода заключа-
ется в получении пространственно-временных корреляционных
функций и их аппроксимации. В работе С. М. Олевской простран-
ственно-временная корреляционная функция для высоты изобари-
ческой поверхности 500 мбар представляется в виде
в(г, т)=л(х) 51п^(;)г1 е~^г,
' ’ 7 ' 7 р(т)г
где т = /т— ts — сдвиг по времени; Л, р, у — коэффициенты, зави-
сящие от т. Для ATsoo эти коэффициенты при различных т прини-
мают следующие значения (при г, выраженном в тыс. км): при
т = 0 (нет сдвига по времени) Л = 172 (дам)2; 0 = 1,51; у = 0,25; при
т=1 сут. Л = 134 (дам)2; р = 1,52; у = 0,14; при т = 2 сут. Л =
= 90 (дам)2; р = 1,50; у = 0,02.
Проведенные эксперименты показали, что использование дан-
ных наблюдений за прошедший срок, отстоящий от момента ана-
лиза на 24 ч, в случае редкой сети станций снижает ошибку интер-
поляции на 7%.
Использование наряду с данными в основной срок данных за
один предшествующий дополнительный срок, отстоящий от мо-
мента анализа на 12 ч, даже при больших ошибках наблюдений
снижает ошибку анализа на 36%, а за два срока — на 52%.
В изложенных обобщениях методов полиномиальной и опти-
мальной интерполяции данные несинхронных наблюдений включа-
ются в численную процедуру анализа без каких-либо дополнитель-
ных преобразований. Как уже говорилось, другой подход к реше-
нию задачи четырехмерного численного анализа заключается
в предварительном приведении несинхронных данных анализируе-
мого элемента к единому сроку с последующим применением про-
цедуры пространственного анализа.
Рассмотрим один из вариантов такого приведения данных
к единому сроку [4], Пусть, например, Hs — значение Н в мо-
мент времени ts в некоторой точке, Hs и На — прогностические зна-
чения Н на моменты времени ts и ta для этой же точки, где ta —
момент, для которого нужно произвести численный анализ, а Н“—
приведенное к сроку ta значение Hs. Тогда величина Has с исполь-
зованием прогноза может быть определена следующим образом:
Has =Hs+(Ha-Hs),
308
где разность в скобках представляет собой величину прогностиче-
ского изменения Н за время ta— ts.
Проведенные эксперименты показали, что включение в числен-
ный анализ данных за прежний срок при ta — ts=V2 ч (после их
приведения к стандартному сроку), позволило заметно улучшить
качество анализа.
Изложенное относилось к дискретным схемам анализа Рас-
смотрим теперь непрерывную схему анализа-прогноза.
Представим себе, что для расчетов мы используем две одновре-
менно работающие вычислительные машины: «медленную» и «бы-
струю». Первая машина рассчитывает анализы и прогнозы в таком
режиме, при котором прогноз на некоторый момент времени бывает
готов к тому же моменту реального времени, без опережения или
отставания. Другими словами, в памяти этой машины постоянно
имеется некоторая модель состояния атмосферы на текущий мо-
мент времени.
Вторая («быстрая») машина, работая в соответствии с распо-
рядком выдачи прогностической продукции данного метеорологи-
ческого центра, периодически получает от первой машины мгно-
венную картину состояния атмосферы за очередной синоптический
срок и, используя ее как анализ, производит обычный расчет про-
гноза на различные сроки с большим опережением реального вре-
мени. (Разумеется, что такое разделение задачи на два этапа или
на две задачи не требует использования двух ЭВМ, так как при до-
статочной производительности вычислительной машины обе задачи
могут попеременно решаться на одной и той же ЭВМ )
Решение второй задачи не нуждается в специальных поясне-
ниях, поэтому рассмотрим лишь методику решения первой.
Пусть по каким-либо данным мы рассчитали прогноз на некото-
рый срок ts, в который поступила очередная серия дополнительных
(несинхронных) данных. По получении таких данных расчет про-
гноза прекращается и производится совместный численный анализ
вновь полученных и прогностических данных. В результате получа-
ется некоторое новое поле. Оно и используется как исходное для
дальнейшего расчета прогноза впредь до поступления новой серии
дополнительных данных. Таким образом, происходит как бы не-
прерывная корректировка прогноза при использовании каждой но-
вой серии дополнительных данных. При этом каждая такая серия
может не охватывать всю рассматриваемую область, а относиться
к какому-либо отдельному (пусть даже небольшому) району. По-
следовательное восполнение и включение в анализ такого рода
данных с различных районов, выполняемое за значительный интер-
вал времени, в итоге позволяет существенно улучшить численный
анализ по области, соизмеримой с размерами полушария. В ре-
зультате этого, находящаяся в памяти «медленной» машины мо-
дель атмосферы в любой момент является наиболее полной, по-
скольку в ней учтены все данные, поступившие до этого момента.
Такого рода эксперименты [16, 30, 31, 34, 40, 41, 47] показали
перспективность непрерывной схемы анализ—прогноз.
309
В заключение отметим следующее Значения метеорологиче-
ских элементов, полученные в узлах прогностической сетки потому
или иному способу численного анализа, обычно и используются
в качестве исходных данных для численного прогноза. Однако при
наличии результатов численного анализа полей нескольких метео-
рологических элементов (например, давления и ветра) имеется воз-
можность улучшить качество анализа каждого из этих элементов
путем специального согласования результатов анализа между со-
бой. Такое согласование делается исходя из того, что поля различ-
ных элементов в среднем должны соответствовать тем или иным
соотношениям, используемым в данной прогностической модели, на-
пример, соотношениям геострофичности.
Из различных методов указанного согласования можно отме-
тить вариационный метод согласования, предложенный Ю. Сасаки
[У.23].
Другой способ согласования метеорологических полей, предназ-
наченный для прогностических моделей с полными уравнениями
гидротермодинамики и основанный на расчете «псевдопрогнозов»,
был описан в § 9, гл. V.
Проведенные численные эксперименты показали, что использо-
вание в качестве начальных данных метеорологических полей, по-
лученных в результате согласования, улучшает качество прогнозов.
§ 6. Автоматизация сбора, обработки и анализа
метеорологической информации
Широкое внедрение автоматизации на всех этапах обработки
метеорологической информации в настоящее время является необ-
ходимостью, обусловленной требованиями в метеорологическом
обслуживании народного хозяйства страны и все возрастающим
объемом данных наблюдений. Объем информации, поступающей по
линиям связи в прогностические центры, достигает огромных раз-
меров и с каждым годом он продолжает увеличиваться. Это увели-
чение происходит за счет расширения наблюдательной сети стан-
ций, увеличения сроков наблюдения, а главное за счет внедрения
новых наблюдательных средств, например, метеорологических
спутников. Ясно, что эффективное использование такого по-
тока метеорологической информации с сохранением прежней прак-
тики ее обработки вручную, без автоматизации, просто невоз-
можно.
Впервые необходимость в автоматизации обработки данных
возникла при подготовке исходной информации для численных
прогнозов. Но вскоре стало ясно, что оперативное применение но-
вых методов возможно только при автоматизации всех звеньев об-
работки метеорологической информации, начиная от наблюдений
и кончая выдачей прогноза потребителю. Программа такой автома-
тизации в нашей стране получила название комплексной автома-
тизации Гидрометслужбы СССР.
310
В глобальном масштабе в рамках Всемирной метеорологиче-
ской организации (ВМО) намечается осуществить согласованную
систему сбора, передачи и переработки информации метеорологи-
ческими центрами. Такие центры есть в нашей стране и в ряде дру-
гих стран (США, Англия, ФРГ, Япония, Швеция и др.).
Круг задач, выполняемых этими центрами в области оператив-
ной обработки информации весьма широк. Он включает:
1. Сбор по линиям связи и первичную автоматическую обра-
ботку с помощью вычислительных машин метеорологической ин-
формации (включая информацию с метеорологических спутников.
Земли), выдачу обработанной информации для последующей пере-
дачи потребителям, а также для ее дальнейшей обработки (рас-
чета численных анализов и прогнозов, получения климатических
характеристик). В первичную обработку входит опознавание, рас-
кодирование и предварительный контроль данных аэрологических
и наземных наблюдений с приведением их к некоторым стандарт-
ным формам для последующего этапа автоматической обработки,,
а также наноска данных наблюдений на карты с помощью ЭВМ,,
совмещение на картах различных видов информации и др.
2. Проведение численного анализа, т. е. выполнение расчетов
по проконтролированным данным наблюдений на станциях, в ре-
зультате которых будут определены значения метеорологических
элементов в точках регулярной сетки.
3. Прогнозирование метеорологических полей с использованием
результатов численного анализа. Выдачу потребителям через ли-
нии связи результатов расчета и прогнозов в виде карт, бюллете-
ней, таблиц, графиков.
Как упоминалось выше, сбор и обмен метеорологической инфор-
мации осуществляется радиометеорологическими центрами в соот-
ветствии с регламентом сроков и объема, установленным ВМО,
а также национальными метеорологическими службами. При этом
каждый вид метеорологических сводок должен быть соответствую-
щим образом стандартизирован, т. е. иметь определенную струк-
туру и код в соответствии с принятыми соглашениями. Поступаю-
щие от нескольких радиометцентров сводки могут содержать ин-
формацию по одним и тем же станциям. Поэтому первичная
обработка прежде всего должна предусматривать специальную
сортировку сведений, в частности, исключение повторных сооб-
щений.
В большинстве оперативных подразделений закодированная ме-
теорологическая информация принимается и передается по теле-
графным и радиоканалам, причем регистрация поступающих дан-
ных производится посредством телетайпа. Скорость передачи
информации выражается в бодах (число двоичных разрядов, пере-
даваемых в одну секунду). Большинство каналов связи, используе-
мых для передачи метеорологической информации, работает со
скоростью 50 бод (около 10 телеграфных знаков в секунду) и лишь
в некоторых случаях используются скоростные каналы на 1200 бод.
Планами автоматизации Гидрометслужбы СССР, а также
311
планом создания Всемирной службы погоды (ВСП) предусмотрена
организация новой автоматизированной системы связи, в которой
обмен будет осуществляться главным образом со скоростью
1200 бод. При этом распределение потоков информации и все упра-
вление работой системы связи будет осуществляться с помощью
специальных ЭВМ.
При скорости 50 бод одна телеграмма СИНОП передается за
5 с, а телеграмма ТЕМП — примерно за минуту. Поступающую по
каналу связи информацию телетайп регистрирует не только в виде
-печатного текста, но и в виде бумажной перфорированной ленты,
;на которой информация зафиксирована с помощью пробивок (от-
верстий). Полученная таким путем перфолента может быть ис-
пользована, в частности как промежуточное звено между линиями
связи и ЭВМ. С помощью специального устройства ввода в ЭВМ,
носящего название фотоввода, информация с перфоленты может
вводиться в ЭВМ.
Все более широкое применение находит метод непосредствен-
ного обмена информацией между линиями связи и ЭВМ. В этом
случае информация параллельно с поступлением по линиям связи
записывается на магнитные ленты, а затем с них считывается в опе-
ративную память ЭВМ. Такой способ наиболее приемлем в опера-
тивной практике, так как сокращает время между поступлением
и использованием информации. По мере осуществления планов
автоматизации такой способ ввода данных в ЭВМ станет
основным.
Следующий этап работы предусматривает предварительную об-
работку информации по программам. Он состоит в формировании
массива ячеек-групп, логическом анализе, поиске и раскодировании
сообщений, в контроле телеграмм и исправлении ошибочных дан-
ных. Рассмотрим, например, каким образом с помощью вычисли-
тельной машины производится раскодирование метеорологических
телеграмм с данными о температурно-ветровом зондировании с на-
земных станций, передаваемых по международному коду FM-35.
Предположим, что в машину непосредственно по линии связи
поступают телеграммы с различных станций за различные сроки
и с различной информацией. Необходимо из этого большого коли-
чества телеграмм отобрать лишь те, которые относятся к какой-то
определенной территории, например к Европе и Западной Сибири,
и к одному сроку, например к 0 ч, и только с информацией о верти-
кальном зондировании. Поиск таких телеграмм осуществляется как
по опорным знакам индикатора заголовка, так и по отличительным
цифрам. Если обнаружен индикатор заголовка, то две ближайшие
пятизначные группы испытываются на время и на индекс.
При наличии в системе периферийных устройств ЭВМ специ-
альных средств визуального отображения данных на экране име-
ется возможность в ходе первичной обработки корректировать при-
нимаемые ЭВМ решения. Так, если из-за каких-либо искажений
телеграмма не могла быть опознана программой, то соответствую-
щий участок исходного текста высвечивается на экране. Тогда
312
в ряде случаев дежурный оператор может обнаружить искажение
и, внеся необходимое исправление, отправить исправленный текст
обратно в память ЭВМ для повторной обработки по обычным пра-
вилам.
Чтобы отобрать лишь нужные станции, необходимо предусмот-
реть в программе блок сравнения очередного индекса станции с на-
бором индексов станций, располагающихся на данной территории.
Этот набор индексов играет роль своего рода «словаря». Пятизнач-
ной группе, испытываемой на индекс станции, должен быть найден
эквивалент в словаре. Это будет означать, что станция входит
в данный район и что все группы, следующие за индексом, должны
быть обработаны. Если же данный индекс не совпал ни с одним
из индексов словаря, то данные этой станции должны быть опу-
щены, так как станция не расположена на рассматриваемой тер-
ритории.
Далее необходимо отобрать информацию по сроку наблюдения.
Если закодированное время наблюдения отличается от рассматри-
ваемого срока больше, чем, например, на ±2 ч, то станция из даль-
нейшего рассмотрения исключается. Если же срок совпадает, то все
последующие группы в телеграмме, содержащие данные о высоте,
температуре и т. д., направляются в определенные ячейки памяти
машины. Эти ячейки будут хранить данные одной телеграммы. Да-
лее проверяется на совпадение индекса и срока следующая теле-
грамма и т. д. В результате такой обработки всех телеграмм, по-
ступивших в машину, в ячейках памяти машины в определенном
порядке будут храниться данные о высотах изобарических поверх-
ностей, температуре, дефиците точки росы и ветре со всех стан-
ций, расположенных в заданном районе.
Чтобы использовать эти данные для анализа и прогноза, необ-
ходимо знать координаты (географические или декартовы на пло-
скости карты) каждой станции. Для этого в машине нужно иметь
второй словарь, который содержал бы эти координаты. В таком
случае индекс каждой станции должен сравниваться с индексами
словаря. В случае совпадения индекса обрабатываемой станции
с одним из индексов словаря в ячейку памяти, содержащую индекс
данной станции, засылаются координаты этой станции, хранящиеся
в словаре. В результате данные каждой станции, занимающие
группу ячеек, будут содержать и координаты.
Как уже говорилось, ошибки в исходных данных ухудшают ка-
чество численного анализа, а следовательно, и прогнозы. Поэтому
еще до численного анализа (или в ходе его) ошибочные данные
должны быть исправлены или исключены.
Можно предложить много путей решения этого вопроса. Можно,
например, использовать принцип согласования различных метеоро-
логических элементов на одной и той же станции. Например, оче-
видно, что дефицит точки росы не может быть отрицательным
числом.
Рассмотрим один из простейших способов контроля, основан-
ный на использовании климатических данных. Допустим, что
31а
в машине имеется еще один словарь, содержащий климатические
нормы для высот изобарических поверхностей. В таком случае
высоты всех изобарических поверхностей каждой станции необхо-
димо сравнить с нормой. В случае, если расхождение превысит не-
которую допустимую величину, то данные этой станции из даль-
нейшего рассмотрения исключаются. Конечно, такой способ конт-
роля слишком груб: он позволяет избавиться лишь от больших
ошибок.
Для ликвидации мелких ошибок применяются более детальные
способы контроля.
При этом широко используются методы, позволяющие не только
обнаружить, ио и при определенных условиях исправить ошибоч-
ные или не согласующиеся с окружающими данные. Это оказыва-
ется возможным, в частности, благодаря наличию известной избы-
точности информации. К числу таких методов относится статиче-
ский контроль аэрологических телеграмм, предусматривающий
проверку соответствия сообщаемых значений температуры и гео-
потенциала на разных уровнях уравнению статики. Проверка со-
стоит в сравнении разностей сообщенных высот соседних изобари-
ческих поверхностей (толщин слоев) с толщинами слоев, вычис-
ленными по сообщенным значениям температуры на двух соседних
изобарических поверхностях. Если для некоторого слоя расхожде-
ние (невязка) между этими величинами превосходит некоторый за-
данный предел, то считается, что хотя бы одна из четырех величин
(геопотенциал или температура на двух изобарических поверхно-
стях) ошибочна. Тогда по соотношению невязок в соседних слоях
в большинстве случаев удается обнаружить и исправить ошибоч-
ную величину.
Другие способы обнаружения и исправления ошибочных дан-
ных основаны на использовании известной статистической струк-
туры метеорологических полей. Так, при горизонтальном контроле
данных, который предусматривает интерполяцию в точку располо-
жения проверяемой станции, используются сведения об автокорре-
ляционных функциях, зависящих от расстояния по горизонтали.
Разность между сообщенной и вычисленной (проанализированной)
величиной метеоэлемента на проверяемой станции сравнивается
с некоторой допустимой невязкой, зависящей от взаимного распо-
ложения окружающих станций, точности измерений метеоэлемента
и характеристик статистической структуры поля этого элемента
в горизонтальной плоскости (в частности, дисперсии). Если полу-
ченная разность оказывается выше допустимой невязки, то прини-
мается, что имеет место ошибка на проверяемой или на одной или
нескольких окружающих станций. Для окончательного суждения
о том, имеется ли ошибка на проверяемой станции, производится
серия дополнительных проб, каждая из которых состоит в том, что
повторяется расчет анализа для пункта расположения проверяемой
станции, причем каждый раз одна из первоначально учитывав-
шихся окружающих станций заменяется некоторой более удален-
ной станцией.
314
Аналогично производится контроль вертикальной согласован-
ности данных в одном пункте. Именно, величины геопотенциала1
или температуры на каком-нибудь одном уровне сравниваются с их.
значениями, вычисленными по данным о геопотенциале или темпе-
ратуре на остальных уровнях с помощью оптимальной интерполя-
ции по высоте, основанной на использовании автокорреляционных
функций, зависящих от расстояния по вертикали. Если сообщен-
ная величина отклоняется от вычисленной более чем на некоторую
допустимую невязку (зависящую, в частности, от взаимного рас-
положения уровней, точности измерений и некоторых характерис-
тик статистической структуры соответствующего метеоэлемента по
вертикали), то считается, что имеет место ошибка, и при некоторых
условиях ошибочная величина может быть заменена вычисленной.
При комбинированном использовании вертикального и горизон-
тального контроля геопотенциала и температуры, а также статиче-
ского контроля, предусматривающего проверку взаимной согласо-
ванности этих элементов, в большинстве случаев удается уверенно
локализовать ошибку (т. е. найти ту станцию и тот уровень, где
данные неверны) и исправить ошибку. Другим вспомогательным
средством контроля является сравнение сообщаемых величин
с прогнозом, рассчитанным на тот срок, к которому относятся эти
величины. Такой способ контроля особенно важен при использова-
нии данных, относящихся к нестандартным срокам наблюдения
(данные спутников, рейсовых самолетов и др.). Наибольшие труд-
ности для контроля представляют данные в области с редкой сетью
станций, малой изменчивостью (дисперсией) метеоэлементов и не-
надежными измерениями. К таким областям относится, в частности,
зона тропических широт. В этих случаях ошибочные (или несогла-
сующиеся с окружающими) данные удается обнаруживать лишь
по результатам объективного анализа, где их влияние сказыва-
ется в появлении ложных весьма интенсивных возмущений.
Дальнейший анализ метеорологической информации может
быть различным в зависимости от поставленной задачи. Важней-
шей задачей является подготовка данных для численного прогноза,
т. е. численный или объективный анализ, а также автоматическое
составление диагностических карт с расчерченными изолиниями.
Полученные в результате численного анализа значения метеороло-
гических элементов в узлах регулярной сетки точек удобно ис-
пользовать и для расчета координат положения изолиний (изогипс,
изобар, изотерм). Это экономичнее, чем вычисление указанных ве-
личин непосредственно по данным наблюдений на станциях.
При наличии соответствующих устройств отображения в ходе
численного анализа, как и при первичной обработке данных, не-
редко применяется ручная корректировка в районах с редкой сетью
станций. При этом, в частности, могут быть эффективно использо-
ваны данные спутниковых наблюдений.
Другой целью автоматической обработки оперативной инфор-
мации может быть преобразование информации к виду, удобному
для длительного хранения. Эта информация в последующем
315
используется для составления различных справочных сведений
и для режимных обработок.
К численному анализу для целей прогноза, как и ко всем ос-
тальным этапам оперативной обработки информации, предъявля-
ется очень важное требование — минимальная затрата времени на
его проведение, а также необходимость его проведения в жесткие
заранее заданные сроки.
Заключительным этапом автоматической обработки данных на-
блюдений, а также результатов численного прогноза является по-
Рис. 9.3. Пример прогностической карты АТ5Оо для ограниченной области,
вычерченной автоматически двухкоординатным регистрирующим прибором
(ДРП) в Гидрометцентре СССР.
строение диагностических и прогностических карт с проведенными
изолиниями. Такие карты составляются широкоформатным алфавит-
но-цифровым печатающим устройством либо двухкоординатным ре-
гистрирующим построителем (ДРП). Пример прогностической кар-
ты для Евразии, расчерченной автоматически, приведен на рис. 9.3.
Возможны и другие пути выдачи как промежуточных, так и
окончательных результатов, например, на экран катодно-лучевой
трубки, на котором можно видеть своеобразную карту с изолини-
ями, либо на запоминающее устройство — магнитную ленту,
а также непосредственно в линии связи в виде факсимильного
изображения карты с изолиниями и любыми иными символами
и обозначениями.
Глава X
ПРИМЕНЕНИЕ ЧИСЛЕННЫХ МЕТОДОВ АНАЛИЗА
И КРАТКОСРОЧНОГО ПРОГНОЗА МЕТЕОРОЛОГИЧЕСКИХ
ЭЛЕМЕНТОВ В ОПЕРАТИВНОЙ РАБОТЕ СЛУЖБЫ ПОГОДЫ
Численные методы прогноза ряда метеорологических элементов
прочно вошли в практическую деятельность службы погоды. Это
стало возможным в связи с освоением и внедрением оперативной
обработки метеорологической информации с помощью ЭВМ. Од-
ним из этапов оперативной обработки информации является пред-
вычисление полей метеорологических элементов. Расчеты прогно-
стических карт производятся в крупных прогностических центрах
ряда стран мира, в том числе в СССР, США, ФРГ, Англии, Фран-
ции, Японии, Швеции и др. Рассчитываемые карты и другие про-
гностические материалы распространяются по факсимиле или с по-
мощью цифрового кода и применяются теми прогностическими
центрами, которые не имеют возможности производить расчеты.
Кроме того, между различными центрами производится взаимный
обмен прогностической информацией. Можно определенно утверж-
дать, что те или иные виды прогностических карт, рассчитываемые
численными методами, могут иметь у себя подавляющее большин-
ство прогностических подразделений. Выполнению этой задачи бу-
дет способствовать осуществление плана Всемирной службы по-
годы (ВСП).
В СССР расчет прогностических карт численными методами
производится в ряде центров страны: в Москве, Новосибирске, Ле-
нинграде, Ташкенте, Минске, Ростове-на-Дону, Тбилиси, Хабаров-
ске и др.
Рассмотрим кратко объем и распорядок работ по обеспечению
службы погоды прогностическими картами и другими данными
в Гидрометцентре СССР по состоянию на 1973 г. В табл. 10.1 ука-
заны прогностические схемы, применявшиеся в оперативной ра-
боте, а также сведения, характеризующие исходные данные, об-
ласть и сроки прогноза, сроки изготовления прогностических карт
и пр.
Последовательность подготовки прогнозов по различным схе-
мам определяется в первую очередь тем обстоятельством, что чис-
ленный анализ и прогноз по заданной территории возможны только
после получения данных наблюдений с этой и смежных областей.
317
co
I—t
00
Таблица 10 1
Некоторые сведения об оперативных численных краткосрочных прогнозах метеорологических элементов, составляемых
в Гидрометцентре СССР
1 П/П Прогностическая модель (авторы) Исходная информация Район прогноза Прогнозируемые элементы Срок готов- ности прогно- за после сро- ка наблюде- ний Периодичность
1 Трехуровенная квази- геострофическая модель (С. Л. Белоусов) Ч Значения #sso, #soo и #ЗОо на 308 станциях Результаты численного анализа геопотен- циала для сетки из 32x22 то- чек с шагом 300 км Европа #850, #700, #500, #4оо и #зоо, вер- тикальные движе- ния в 26X16 точ- ках, траектории воздушных частиц для 20 пунктов на сроки до 36 ч Ежедневно, два раза в сутки по данным в 0 и 12 ч
2 То же Значения #юоо, #850, #500, #зоо и Я200 на 380 станциях. Результаты численного анали- за геопотенциала для сетки из 37X27 точек с шагом 300 км Европа, Север- ная Атлантика, Западная Сибирь Ро, #850, #500, #300 И #200 В 31X Х21 точках на сроки до 3 суток 5,5 ч То же
3 То же То же по другой территории Восточная Си- бирь, Дальний Восток, Приморье То же и верти- кальные движения 7 ч То же
4 То же Значения #85о, #500 и #ЗОо на 680 станциях северного по- лушария. Результаты числен- ного анализа геопотенциала для сетки из 50x52 точек с шагом 300 км Внетропическая зона северного по- лушария #850, #500 И #300 в точках различ- ных квадратных (37X27 узлов) и сферической сеток на сроки до 3 су- ток 6 ч 30 мин Ежедневно, один раз в сутки по данным в 0 ч
Адвективная
синоп-
тико-гидродинамическая
модель для прогноза
приземного давления
(А. Н. Мерцалов)
6
Модель для прогно-
за обложных осадков
(Б. Д. Успенский,
А. Н. Багров)
Значения приземного давле-
ния и барической тенденции на
1500 метеорологических стан-
циях и на кораблях. Резуль-
таты численного анализа дав-
ления и барической тенденции
для сетки из 47x40 точек с
шагом 150 км. Результаты про-
гноза Я5оо на 12 и 24 ч по
трехуровенной квазигеострофи-
ческой модели С. Л. Белоусо-
ва (1)
Значения //gso. ^Аоо и //зоо
на 308 станциях, р0, бариче-
ские тенденции, температура и
точка росы. Результаты чис-
ленного анализа для сетки из
32x22 точек с шагом 300 км
7
Пятиуровенная модель
по полным уравнениям
(В. М. Кадышников)
Значения Н85о, Я700, //500 и
#зоо на 308 аэрологических
станциях и ро на метеороло-
гических станциях.
Результаты численного ана-
лиза для сетки из 26X22 то-
чек с шагом 300 км
8
Пятиуровенная модель
по полным уравнениям
(С. А. Бортников)
То же
оо
S
Европа
Ро в 31X23 точ-
ках с шагом 150 км
на срок 24 ч
5 чЗО мин
Ежедневно,
один раз в сутки
по данным в 0 ч
Европа
Европа
Европа
Обложные осад-
ки на сроки до
30 ч. Ливневые
осадки и другие
конвективные яв-
ления на срок 12 ч.
(только в теплое
полугодие). Мини-
мальная темпера-
тура, гололед
РО» #850, H70Q,
#500 и //300, верти-
кальные движе-
ния, обложные
осадки в 22X18
точках на сроки
до 36 ч
То же (кроме
осадков) и ветер
6ч То же
7 ч
7 ч
Ежедневно,
один раз в сутки
по данным в 0 ч
То же
№ п/п
Прогностическая модель
(авторы)
Исходная информация
9 Шестиуровенная мо- дель по полным уравне- ниям (Д. Я. Пресман) Значения #юоо, #700, #500, #зоо, #200 и #100 на 680 стан- циях северного полушария. Ре- зультаты численного анализа для сетки из 52X52 точек с шагом 420 км
Ч
10
Шестиуровенная мо-
дель по полным урав-
нениям (Л. В. Берко-
вич)
Значения #юоо, #850, #700,
#500, #зоо и #юо на 680 стан-
циях северного полушария. Ре-
зультаты численного анализа
для сетки из 57X57 точек с
шагом 300 км
11
Шестиуровенная мо-
дель по полным урав-
нениям (М. С. Фукс-Ра-
бинович)
То же, но результаты чис-
ленного анализа для сетки из
51X51 точек с шагом 390 км
Район прогноза Прогнозируемые элементы Срок готов- ности прогно- за после сро- ка наблюде- ний Периодичность
Северное полу- шарие Ро, #700, #500, #300 И #100, темпе- ратура, ветер на сроки до 3 суток 8-9 ч Ежедневно, один раз в сутки по данным в 0 ч
То же Ро, #850, #700, #500, #300, #100, температура, ве- тер на сроки до 3 суток То же Ежедневно, один раз в сутки по данным в 12 ч.
То же То же и облож- ные осадки То же Два раза в не- делю по данным в 12 ч
Данные наблюдений с разных районов поступают в прогностиче-
ские центры неодновременно. Так, например, по территории СССР,
Европы и по акватории северной части Атлантического океана дан-
ные наблюдений поступают в Гидрометцентр СССР не позднее 3 ч
с момента наблюдений, в то время как данные с территории Север-
ной Америки — после 6 ч, а с Тихого океана еще позже.
По этой причине целесообразен такой распорядок автоматизи-
рованной оперативной обработки информации, который обеспечи-
вал бы последовательное расширение области анализа и прогноза
по мере поступления данных. В соответствии с этим в Гидромет-
центре СССР вначале рассчитывается прогноз для территории Ев-
ропы по результатам численного анализа для регулярной сетки
из 32X22 точки при использовании наблюдений на 308 аэрологиче-
ских станциях. Для этой территории прогноз составляется по не-
скольким прогностическим схемам. В первую очередь расчет про-
изводится по квазигеострофической трехуровенной схеме С. Л. Бе-
лоусова. По этой схеме рассчитываются прогнозы на 18, 24 и 36 ч
карт изобарических поверхностей 850, 700, 500, 400 и 300 мбар,
а также диагноз и прогноз вертикальных токов и прогноз траекто-
рий воздушных частиц на разные сроки на уровнях 850, 700
и 500 мбар. Поскольку счетными (основными) уровнями схемы яв-
ляются поверхности 850, 500 и 300 мбар, то значения Я700 и //400
находятся путем интерполяции значений 7785о, //500, /7зоо- Расчет
всех указанных величин по данной схеме на ЭВМ типа М-220 (при
быстродействии 20 тыс. операций в секунду) занимает всего
15 мин. С учетом времени, требуемого на первичную обработку
данных и выполнение численного анализа методом оптимальной
интерполяции, прогностические карты оказываются готовыми для
дальнейшего использования и для передачи по факсимиле не позже
5 ч после срока наблюдений. Прогноз по данной схеме для терри-
тории Европы рассчитывается дважды в сутки. Часть рассчитывае-
мых прогностических карт расчерчивается автоматически.
На основе прогноза по этой схеме и результатов анализа полей
температуры и точки росы у поверхности земли и на ряде изобари-
ческих поверхностей один раз в сутки составляются численные про-
гнозы обложных осадков на сроки до 30 ч.
Прогнозы поля АТ500 на 24 ч по упомянутой прогностической мо-
дели используются также для предвычисления карты приземного
давления с помощью адвективной синоптико-гидродинамической
модели А. Н. Мерцалова. В качестве исходных данных при
этом используются результаты численного анализа полей при-
земного давления и приземной барической тенденции для сетки
с шагом 150 км, производимого по данным синоптической сети
станций.
По указанной прогностической модели С. Л. Белоусова после
прогноза по Европе рассчитываются прогнозы по Северной Атлан-
тике, а также по Восточной Сибири, Дальнему Востоку и приле-
гающим акваториям на срок до 3 суток на поверхностях 1000, 850,
500, 300 и 200 мбар.
21 Зак. № 21
321
Для получения прогностических карт по указанным областям,
частично используются результаты расчетов, производимых по
значительно большей области, включающей всю внетропическую
зону на карте северного полушария (сетка анализа содержит 50X
Х52 точек с шагом 300 км). Такой способ подготовки прогности-
ческих карт позволяет устранить нежелательные искажения полей
на краях области, возникающие из-за использования фиктивных
граничных условий.
Не все рассчитываемые поля наносятся на бланки карт. Так,
прогнозы по району Восточной Сибири, Дальнего Востока, При-
морья и по прилегающим морям в виде значений в точках сетки
в цифровом коде передаются по телеграфу в Хабаровск, где ис-
пользуются в оперативной работе. Рассчитанные значения полей
геопотенциала поверхностей 500, 300, 200 мбар в Гидрометцентре
СССР используются для выполнения на ЭВМ навигационных рас-
четов по нескольким авиатрассам большой протяженности. Резуль-
таты этих расчетов в виде буквенно-цифровых сводок с планами
полетов передаются в соответствующие аэропорты.
После прогнозов по квазигеострофическим моделям (и ча-
стично одновременно с ними) рассчитываются прогнозы для огра-
ниченной области и по ряду моделей, основанных на интегрирова-
нии полных уравнений гидротермодинамики. С помощью этих моде-
лей прогнозируются давление на уровне моря, ветер на основных
изобарических поверхностях, а также количество обложных осад-
ков. Ежедневно рассчитываются прогнозы на сроки до 36 ч по пя-
тиуровенной модели С. А. Бортникова и пятиуровенной модели
В. М. Кадышникова. Прогноз по этим схемам производится по
данным геопотенциала в узлах сетки из 26X22 точек с шагом
300 км, получаемым с помощью численного анализа методом
полиномиальной интерполяции. Подготовка данных для этих
схем и прогнозы по ним требуют большего времени. Поэтому
эти прогнозы бывают готовы через 6—7 ч после срока наблю-
дений.
Вслед за указанными прогнозами, которые можно назвать р е -
г и о и а л ь н ы м и, рассчитываются прогнозы на срок до 3 суток по
северному полушарию по шестиуровенным прогностическим моде-
лям Д. Я. Прессмана, Л. В. Берковича и М. С. Фукс-Рабиновича,
основанным па интегрировании полных уравнений. Прогнозы по
этим моделям включают уровень моря и все основные изобариче-
ские поверхности до 100 мбар. Получаемые карты расчерчиваются
автоматически.
Всего за сутки в Гидрометцентре СССР рассчитывается более
50 прогностических карт.
Полученные прогностические карты передаются в прогностиче-
ские отделы Гидрометцентра СССР, а также по факсимильным ли-
ниям связи в местные прогностические подразделения.
В табл. 10.2 приведены данные об оправдываемое™ прогнозов
по некоторым из перечисленных прогностических моделей.
322
Таблица 10.2
Средние относительные ошибки прогнозов давления на уровне моря (р0) и высот изобарических поверхностей
по различным прогностическим моделям
to
*
со в Прогности- ческая модель Период оценки прогнозов Область оценки прогнозов Срок прогноза сутки Ро р мбар
850 700 500 300 200
1 4 5 7 8 9 10 И П; V—XI 1973 г. V—XI V—XI V—XI V-XI 1971—1972 гг. 1972—1973 гг. 1971 — начало 1973 г. римечание. Ном Европа Внетропическая зона северного полушария Европа, Западная Сибирь, Атлан- тика То же ера прогностических 1 2 3 1 1 1 1 2 1 2 3 1 1,5 3 : моделей 0,62 0,75 0,76 0,82 0,95 0,75 0,85 0,91 0,73 0,79 0,95 соответствук 0,80 )Т их ном 0,71 ерам в табл. 0,68 0,77 0,87 0,71 0,72 0,78 0,76 0,83 0,89 0,71 0,74 0,87 10.1. 0,70 0,75 0,66 0,70 0,74 0,80 0,85
Большая часть прогностических карт представлена в виде про-
гнозов синоптической ситуации. На фоне общей ситуации синоп-
тику значительно легче составить необходимый детализированный
прогноз с указанием пределов изменений отдельных метеорологи-
ческих элементов. Правильный прогноз синоптической ситуации
во многом предопределяет точность и самого прогноза погоды.
При наличии дополнительной информации, например, данных
за более поздние сроки пли данных, которые не использовались
в численном прогнозе, синоптик имеет возможность внести в чис-
ленный прогноз синоптической ситуации свои коррективы. Это
бывает особенно оправдано для районов, которые находятся
в зоне влияния краевых условий — на «краях» прогностической
карты.
Рис. 10.1. Оправдываемость суточных
прогнозов погоды в Москве по годам.
/ — прогнозы Гидрометцентра СССР, 2 — инер-
ционные прогнозы.
В заключение отметим следующее. Схемы прогноза, используе-
мые в оперативной работе, постоянно заменяются более совершен-
ными. Внедрение новых методов (или замена ими старых) произ-
водится лишь после того, как новый метод пройдет стадию испы-
тания в оперативных условиях и даст лучшие результаты. На стадии
испытания рассчитываемые прогнозы сопоставляются с прогнозами
по другим методам или с прогнозами синоптиков. Повышение ус-
пешности численных прогнозов достигается как за счет уточнения
самих прогностических моделей, так и путем улучшения способов
автоматизированного сбора, первичной обработки, контроля и чис-
ленного анализа данных.
Внедрение новых схем численного прогноза неизбежно приводит
к изменению объема оперативных работ. По этой причине, а также
в связи с вводом в действие более производительных вы-
числительных машин, различных вспомогательных устройств и иных
средств автоматизации, распорядок оперативной обработки инфор-
мации, перечень и сроки расчета и передачи по факсимиле прогно-
стических карт периодически изменяются. Эти изменения идут
в сторону увеличения числа прогнозируемых элементов и областей,
324
охваченных численными прогнозами, а также сокращения времени
между моментом наблюдений и получением прогностических карт.
Использование в оперативной работе численных методов про-
гноза ряда метеорологических элементов позволило поднять общий
уровень оправдываемое™ прогнозов погоды. Об этом можно, на-
пример, судить по данным, приведенным на рис. 10.1, где представ-
лен ход средней годовой оправдываемое™ суточных прогнозов по-
годы для Москвы [1] и приведены для сравнения данные об оправ-
дываемое™ инерционных прогнозов («завтра будет то же, что и
сегодня»). Значительный рост оправдываемое™ прогнозов в начале
60-х годов объясняется в основном тем, что именно в этот период
происходила наиболее быстрая замена синоптических методов про-
гноза высотного барического поля на численные.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
ЕДИНИЦЫ ИЗМЕРЕНИЯ НЕКОТОРЫХ ФИЗИЧЕСКИХ ВЕЛИЧИН В РАЗЛИЧНЫХ СИСТЕМАХ
Система единиц Величины
длина масса время сила, вес давление работа, энергия, тепло мощность
Международ- метр, м (т) килограмм, кг секунда, ньютон, Н паскаль, Па 1 Па = = Н-м-2= = кг • м-1 • С’2 джоуль, Дж (J) = = Н-м = = КГ • М2 • С’2 ватт, Вт (W) = Дж • с~1== =кг • м2 • с-3
ная, СИ [SI] (kg) с (s) (N) = = КГ • М • С"2
Физическая, сантиметр, грамм, г (g), секунда, с дина, дн (dyn) ДН • СМ"2 = эрг, эрг (erg) = эрг в с, эргХ
СГС [CGS] см (sm), 1 см = 10-2 м 1 г = 10_3 кг = г • см • с-2, 1 дн=10-5 Н IIIIIIII S . аз g's А II "О м м II II = дн • см = = г • СМ2 • С”2, 1 эрг= = 10~7 Дж Хсч = = Г • СМ2 • С’3, 1 Эрг • С“1 = = 10-7 Вт
Промышлен- метр, м, 1 м = = 102 см тонна, т (t), секунда, с стен, сн (sn) = сантибар, килоджоуль, киловатт, кВт (kW) =
ная, МТС [MTS] 1 т= 103 кг= = 106 г = т • м • с~2, сбар = сн X Хм“2=тХ кДж (kJ) =
Практическая,
МКС [MKS]
метр, м, 1 м =
’ = 102см
килограмм, кг,
1 кг=103 г
секунда, с
Техническая, метр, м, 1м = = 102 см инерта, и = кГХ секунда, с
мкгс [MKGS] Хс2м~! 1 и=9,81 кг= •
= 9,81 • 103 г
1 сн=103 Н=
= 108 дн
X м"1 • с-2,
1 сб=103 НХ
Хм~2 =
= 104 бар =
= 10 мбар
=сн • м =
=т • м2 • с-2,
1 кДж =
= 103 Дж =
= 1010 эрг.
= кДж • с-1 =
= Т • М2 • С“3,
1 кВт=
= 103 Вт =
= 1010 эрг • с-1
ньютон, Н= = КГ • М • С"2, 1 Н=105 дн ньютон на м2 Н-М-2 кг • м-1 • с~2, 1 Н • М~2 = = 10 бар = = 10~2 мбар джоуль, Дж = = Н • м = = кг • м2 • с~2г 1 Дж= = 107 эрг ватт, Вт = = Дж • с~! = =кг • м2 • с~3, 1 Вт= = 107 эрг • с~
килограмм- сила, кГ (kG) 1 кГ = 9,81 Н = = 9,81 • 105 дн кГ • м-2, 1 кГХ Хм-2= = 9,81 НХ Хм~2 = =9,81 • 10 бар килограммо- метр, кГм = = (kGm) = =кГ • м, 1 кГм = = 9,81 Дж = = 9,81 ’ 107эрг кГм • с"1, 1 кГм • с-!= = 9,81 Вт= = 9,81 • Ю7 эрг•С"1
ПРИЛОЖЕНИЕ 2
ТАБЛИЦА
СТАНДАРТНОЙ АТМОСФЕРЫ
Высота, м Давление, мбар Темпера- тура, К Плотность, г/см3 Высота, м Давление, мбар Темпера- тура, К Плотность, г/см3
—1000 1139 294,7 1,35.10-3 2100 785 274,5 9,96-10-4
—900 1126 294,0 1,33 2200 775 273,8 9,86
-800 1113 293,4 1,32 2300 766 273,2 9,77
—700 1100 292,7 1,31 2400 756 272,5 9,67
—600 1087 292,1 1,30 2460 750 272,1 9,60
—500 1075 291,4 1,28 2500 747 271,9 9,57
-400 1062 290,8 1,27 2600 738 271,2 9,47
-300 1050 290,1 1,26 2700 728 270,6 9,38
-200 1037 289,5 1,25 2800 719 269,9 9,28
-100 1025 288,8 1,24 2900 710 269,3 9,19
0 1013 288,2 1,22 3000 701 268,6 9,09
100 1001 287,5 1,21 3020 700 268,5 9,08
110 1000 287,4 1,21 3100 692 268,0 9,00
200 989 286,9 1,20 3200 683 267,3 8,91
300 978 286,2 1,19 3300 675 266,7 8,82
400 966 285,6 1,18 3400 666 266,0 8,72
500 954 284,9 1,17 3500 658 265,4 8,63
540 950 284,6 1,16 3590 650 264,8 8,55
600 943 284,2 1,15 3600 649 264,7 8,54
700 932 283,6 1,14 3700 641 264,1 8,46
800 921 282,5 1,13 3800 633 263,4 8,37
900 910 282,3 1,12 3900 625 262,8 8,28
990 900 281,7 1,11 4000 617 262,1 8,30
1000 899 281,6 1,11 4100 609 261,5 8,11
1100 888 281,0 1,10 4200 601 260,8 8,02
1200 877 280,4 1,09 4210 600 260,7 8,01
1300 867 279,7 1,08 1300 593 260,2 7,94
1400 856 279,0 1,07 1400 585 259,5 7,85
1460 850 278,7 1,06 4500 577 258,9 7,77
1500 846 278,4 1,06 4600 570 258,2 7,69
1600 835 277,7 1,05 4700 562 257,6 7,61
1700 825 277,1 1,04 4800 555 256,9 7,53
1800 815 276,4 1,03 4870 550 256,5 7,47
1900 805 275,8 1,02 4900 548 256,3 7,44
1950 800 275,5 1,01 5000 540 255,6 7,36
2000 795 275,1 1,01 5100 533 255,0 7,29
Высота, км Давление, мбар Темпера- тура, К Плотность, г/см3 Высота, км Давление, мбар Темпера- тура, К Плотность, г/см3
5,50 505 252,4 6,97-10-4 7,19 400 241,3 5,77-10-4
5,58 500 251,9 6,92 7,50 383 239,4 5,57
6.00 472 249,1 6,60 8,00 356 236,1 5,26
6,35 450 246,8 6,34 8,12 350 235,3 5,18
6,50 441 245,9 6,24 8,50 331 232,9 4,96
7,00 411 242,6 5,90 1 9,00 308 229,6 4,67
330
Высота, км Давление, мбар Темпера- тура, К Плотность, г/см3 Высота, км Давление, мбар Темпера- тура. К Плотность, г/см3
9,18 300 228,5 4,57-10-4 21,0 47,25 216,7 7,60-10-5
9,50 286 226,4 4,40 22,0 40,40 216,7 6,50
10,0 265 223,1 4,14 23,0 34,55 216,7 5,55
10,4 250 220,6 3,93 24,0 29,54 216,7 4,75
10,5 245 219,9 3,89 25,1 25,00 216,9 4,06
11,0 227 216,7 3,65 26,0 21,62 219,4 3,43
11,5 210 216,7 3,37 27,0 18,54 222,1 2,91
11,8 200 216,7 3,22 28,0 15,94 224,8 2,47
12,0 194 216,7 3,12 29,0 13,72 227,6 2,10
12,5 179 216,7 2,88 30,0 11,84 230,4 1,79
13,0 166 216,7 2,66 35,0 5,802 244,0 8,28-10-6
13,5 153 216,7 2,46 40,0 2,959 257,7 4,00
13,6 150 216,7 2,39 45,0 1,564 271,3 2,01
14,0 142 216,7 2,28 50,00 0,846 274,0 1,08
14,5 131 216,7 2,11 55,0 0,458 270,6 5,89-10-7
15,0 121 216,7 1,95 60,0 0,241 253,4 3,31
15,5 112 216,7 1,80 65,0 0,122 236,3 1,79
16,0 103 216,7 1,66 70,0 0,058 219,2 8,27-10-8
16,2 100 216,7 1,60 75,0 0,026 202,0 4,55
16,5 95.7 216,7 1,54 80,0 0,011 185,0 2,10
17,0 88,4 216,7 1,42 85,0 0,004 185,0 8,53-10-9
17,5 81.8 216,7 1,31 90,0 0,002 185,0 3,43
18,0 75.62 216,7 1,22 95,0 0,001 185,0 1,42
18,5 69,92 216,7 1,12 100 0,0003 209,2 0,54
19,0 64,65 216,7 1,04 105 0,00015 233,4 0,23
19,5 59,77 216,7 9,61-Ю"5 ПО 0,00008 257,4 0,11
20,0 55.27 216,7 8,89 115 0,00004 295,0 0,05
20,6 50,00 216,7 7,90 120 0,00003 332,2 0,03
ПРИЛОЖЕНИЕ 3
СТАТИСТИЧЕСКИЕ ДАННЫЕ О ПРОСТРАНСТВЕННО-ВРЕМЕННОМ РАСПРЕДЕЛЕНИИ МЕТЕОРОЛОГИЧЕСКИХ
ЭЛЕМЕНТОВ
Таблица 1
Средние широтные величины средних месячных значений высот изобарических поверхностей (дам)
Широта Изобарическая поверхность, мбар
1000 850 700 500 300 200 100 1000 850 700 500 300 200 100
Январь Июль
90° с. 12 130 270 506 840 1090 1512 6 136 290 540 899 1175 1648
80 12 129 270 507 842 1094 1520 8 139 292 548 906 1177 1646
70 11 132 275 514 852 1107 1540 8 142 297 556 919 1187 1649
60 И 134 280 523 864 1121 1561 8 143 301 563 928 1196 1653
50 13 139 288 535 882 1141 1585 10 147 307 571 942 1212 1660
40 15 145 298 552 906 1167 1608 11 151 314 582 959 1232 1670
30 16 151 308 570 937 1203 1633 11 152 317 589 969 1244 1672
20 13 152 314 582 958 1229 1650 10 151 316 588 969 1244 1665
10 10 150 314 585 965 1238 1656 9 150 314 586 966 1239 1657
5 9 149 313 585 966 1240 1656 10 150 314 586 966 1239 1655
Таблица 2
Средние широтные величины средних месячных значений температуры (СС)
на уровне моря р0 и на различных изобарических поверхностях (мбар)
Широта Поверхность
Ро 850 700 500 300 200 100 Ро 850 700 500 300 200 100
Январь Июль
90°с. -33 -23 -29 -43 -60 -63 -68 2 3 -8 -23 46 -42 -40
80 -29 -21 -27 -40 -58 -61 -66 1 0 -6 -21 -45 -42 -42
70 -24 -18 -23 -38 -56 -58 -62 8 4 -3 -18 -44 -47 -45
60 -15 -15 -20 -35 -54 -56 -57 13 8 —1 -16 -42 -48 -48
50 -6 -9 -15 -30 -52 -55 -54 17 11 3 -12 -39 -51 -54
40 5 —4 -8 -24 -48 —55 -59 23 17 8 -9 -34 -51 -62
30 15 5 0 -15 -41 -55 -68 27 19 11 -6 -32 -51 -69
20 22 14 7 -9 -35 -54 -76 28 19 11 -6 -32 -53 -74
10 26 18 10 -6 -32 -53 -79 28 18 10 -6 -31 -54 —77
5 27 18 10 -5 -31 -53 -80 27 18 9 -6 -31 -55 -78
Таблица 3
Средние широтные значения средних месячных значений удельной влажности
(г/кг) на поверхности земли р0 и на различных изобарических поверхностях (мбар)
Широта Поверхность
Ро 850 700 500 Pi 850 700 500
Январь Июль
90° с. 0,4 0,5 0,5 0,3 4,0 3,0 2,0 0,5
80 0,5 0,6 0,4 0,3 4,0 3,3 2,2 0,6
70 0,9 0,8 0,5 0,3 5,5 4,4 2,7 0,9
60 1,8 1,2 0,7 0,3 7,6 5,6 3,4 1,2
50 2,4 1,9 1,3 0,3 8,9 6,7 4,0 1,4
40 4,4 3,0 1,6 0,5 11,6 7,9 4,6 1,8
30 7,0 4,4 2,4 0,8 14,1 9,1 5,5 2,3
20 11,1 6,2 3,3 1,4 15,4 10,2 6,0 2,5
10 14,7 8,2 4,4 2,0 17,1 11,0 6,6 2,7
Таблица 4
Средние широтные значения среднего квадратического отклонения давления
на поверхности земли р0 мбар и высот изобарических поверхностей (дам)
от средних месячных значений
Широта Поверхность
Ро 850 700 500 300 200 Ро 850 700 500 300 200
Январь Июль
90° с. — 9,0 10,2 13,5 12,0 12,7 — 7,0 7,7 9,5 12,5 9,8
80 12,5 9,6 11,1 13,5 14,8 16,3 8,5 6,8 7,7 9,7 12,9 11,0
70 13,5 10,3 11,9 15,3 19,6 18,9 7,6 5,9 6,9 9,4 13,3 12,8
60 12,0 10,2 11,7 15,6 20,4 19,1 6,6 6,1 7,1 9,7 14,1 13,8
50 9,8 8,7 10,0 13,8 18,3 16,7 5,5 5,1 6,0 8,4 12,5 14,0
40 7,8 6,9 7,8 11,0 14,6 14,1 4,5 3,8 4,4 5,9 8,8 11,3
30 5,2 4,9 5,9 8,4 10,9 11,1 3,7 2,9 3,3 4,1 6,1 8,0
20 2,5 3,3 3,9 5,1 7,3 8,1 3,0 2,2 2,4 3,4 5,2 6,6
оо со СЛ 10 — 2,3 3,1 — 5,3 6,8 — 2,1 2,0 3,0 4,4 6,5
Рис. П.1. Среднее квадратическое отклонение давления на уровне моря от
средней величины (мбар), январь.
336
Рис. П.2. Среднее квадратическое отклонение от средней величины (дам),
январь.
140
22 Зак. № 21
337
140
Рис. П.З. Среднее квадратическое отклонение Я5оо от средней величины (дам),
январь.
338
Рис. П.4. Среднее квадратическое отклонение давления на уровне моря от
средней величины (мбар), июль.
22*
339
140
Рис. П.5. Среднее квадратическое отклонение 7/soo от средней величины (дам)
июль.
340
Рис. П.6. Среднее квадратическое отклонение Н500 от средней величины (дам),
июль.
341
ПРИЛОЖЕНИЕ 4
НЕКОТОРЫЕ СВЕДЕНИЯ ПО ЧИСЛЕННЫМ МЕТОДАМ РЕШЕНИЯ
УРАВНЕНИЙ ГИДРОТЕРМОДИНАМИКИ
§ 1. Конечно-разностная аппроксимация производных и дифференциальных
уравнений
Рассмотрим функцию четырех переменных, например трех про-
странственных координат х, у, z и времени /, значения которой
определены в точках некоторой пространственно-временной сетки,
разделенных равными интервалами (шагами) вдоль соответствую-
щих направлений. Введем безразмерные координаты: i=xldx, j=
= y/dy. k=z[dz, s = tldt, где dx= dy = ds — шаг по горизонталь-
ным координатам, dz — шаг по вертикальной координате, dt — шаг
по времени. Значение функции X в точке Xi, yj, Zh, ts будем обозна-
чать через Xijks, т. е. положим, что Xijks = X (хг-, y-j, zkl ts). При рас-
смотрении зависимости функций только от одной, двух или трех ко-
ординат индексы остальных координат будут опускаться. Напри-
мер, будем полагать, что X (xt) = Xi, X (Xi, Уз) = Хц и т. д.
Существует ряд способов замены производных от функций при-
ближенными конечно-разностными соотношениями; выбор подхо-
дящего способа разностной аппроксимации производных опреде-
ляется особенностями конкретной решаемой задачи.
Рассмотрим два из них на примере функции одной из коорди-
нат, например х. Приближенные значения производных записыва-
ются в виде:
<L2>
Первый способ аппроксимации производных будем называть двух-
точечным (одностороняя разность вперед), второй способ — трех-
точечным (симметричная или центрированная разность).
Существуют и другие более точные конечно-разностные соотно-
шения. Приближенные значения производных более высоких по-
рядков получаются с помощью приближенных выражений для про-
изводных первого порядка. Например, для второго способа полу-
чаем
(1.3)
Приведенные соотношения легко распространяются на случай не-
скольких координат. Например, для оператора Лапласа на плоско-
сти с помощью второго способа замены производных мы имеем
==_(В^)2’^/ + 1’ y+i+X-.y-i (1-4)
342
Оценим точность конечно-разностной аппроксимации производных
по рассмотренным двум способам. С этой целью определим поря-
док величины разности между приближенным и точным значени-
ями производных е, = 8хХ — dXJdx в точке I. Воспользуемся форму-
лой разложения функций в ряд Тейлора
ул / । л\_ v/ \ । дХ L, 1 1 д^Х .g . 1 д^Х .о ।
X(x-±-h)=X(x)-]—/?+~оГ + + •••
v 1 ' v ' 1 дх 1 2! дх2- 1 3! дх% 1
Применяя эту формулу при х=хг, получаем (й = бх):
1 1 1 1 \ дх h 1 2! \ дх2 Ji 1 3! \ дхЗ Ji 1 ’
' 1 1 \ дх Ji 1 2! \ дх2 Ji 3! \ дх% Ji 1
Используя полученные выражения для точки Z, находим
1 д2Х , । 1 д*Х
2! дх2 3! дх*
=0(Л),
е„=8ИХ-^ = Л- ... =0(F).
Рассматривая полученные разности, мы видим, что старший
член рядов, выражающий разность е, имеет множителем в первом
случае Л, а во втором — А2. Поскольку шаг сетки h мал (по сравне-
нию с общей длиной рассматриваемого отрезка вдоль оси х) то
можно говорить, что указанные ряды имеют в первом случае пер-
вый порядок точности, а во втором — второй, что обозначается с по-
мощью символов О (h) и О (А2).
Используя приближенные выражения для производных, можно
произвести замену дифференциальных уравнений их конечно-раз-
ностными аналогами. Проделаем это на примере уравнения типа
уравнения Гельмгольца
LX —a?X = f, (1.5)
где а2 = const, a f — известная функция координат х и у. Данному
дифференциальному уравнению соответствует конечно-разностное
ДгА-а2^у=//у. (1.6)
Применив соотношение (1.4), получаем
—(4+a2)Arzy=/?Zy, (1.7)
где Fij= (Ss)2fij, a2 = a2(6s)2.
Так как соотношение (1.7) получено с помощью замены производ-
ных конечными разностями второго порядка точности, то и конечно-
разностные уравнения (1.6) и (1.7) аппроксимируют соответствую-
щее ему дифференциальное уравнение (1.5) с точностью до вто-
рого порядка малости.
343
§ 2. Некоторые способы решения конечно-разностных уравнений
Рассмотрим некоторые способы решения конечно-разностных
уравнений на примере уравнения Пуассона
&X=f, (2.1)
которое является частным случаем уравнения Гельмгольца при
а2 = 0. Соответствующее дифференциальному уравнению (2.1) ко-
нечно-разностное уравнение при использовании второго способа за-
мены производных конечными разностями записывается в виде
ij. (2.2)
Пусть мы решаем задачу Дирихле, когда заданы значения ис-
комой функции на границе.
Для простоты положим, что область расчета является прямо-
угольником со сторонами х = хг=о, y = yj=o, х=Хг=м+1, У = Уз w+ь
где М и N — целые числа, а на границах искомая функция равна
нулю. Таким образом, граничные условия можно записать в виде
Х/у=0 при Z=0, Л1+1; /=0, 7V+1. (2.3)
Запишем конечно-разностное уравнение (2.2) в виде системы
линейных алгебраических уравнений. Для этого индексам i и / бу-
дем придавать конкретные значения, соответствующие каждой
внутренней точке данного прямоугольника (f=l, 2, . .., М\ j =
= 1, 2, ..., X). Задав, например, i = 1, / = 1, получаем
Xoi+X2i+Xio+X12 —4Хц=77 Ц.
Так как в соответствии с краевыми условиями Xoi и Хю известны,
то их перенесем вправо. В результате получим
Х21+%12 — 4XU=F и — Х01 — X10=F Ц.
В данном случае в силу условия (2.3) Xoi = Xio=O, а значит Fu =
= Fu. Для точки f = 2, j = 4 имеем
Х14 + Х34 + Х23 + Х25 — 4X24=^24,
и т. д.
В результате получаем столько линейных алгебраических урав-
нений, сколько точек содержится внутри заданной области, т. е.
MN уравнений. Решая эту систему, находим искомые значения X
во всех внутренних точках области.
Если число точек невелико, то, как правило, применяются точ-
ные методы решения; при большем же числе точек применяются
приближенные методы.
Приведем пример точного решения. Возьмем случай Л4 = Х=3.
Положим, что на границах рассматриваемой области искомая функ-
ция равна нулю. Записывая соотношение (2.2) последовательно
для точек (11), (12), (13), (21) и т. д., мы получаем следующую
344
систему из девяти линейных алгебраических уравнений с девятью»
неизвестными Хп, Xi2, Х13, Х21 и т. д.
+^21
4^22
4^23
—4X2i+ Х22
-}-Х21 — 4Х224-Х23
+^22 —4Х2з
21
^22
=Л1
=7^ 12
=F 13
4~^31 =^21
-J-X32 = ^22
+^33 = ^23
—4Х31 4~ Х32 —Р31
+%31 — 4X32-j~ Х33=/?32
4"^32“"4Х33=/733
Решим эту систему относительно Х22 методом исключения Для
этого сложим второе, четвертое, шестое и восьмое уравнения, а за-
тем первое, третье, седьмое и девятое.
Переписав два полученных результата, а также пятое уравне-
ние и обозначив F22=Fq, Fi2+/?2i + F23+/?32=/?i и F11 + F13+F31 +
+ /?зз=Т?2, получим систему из трех уравнений:
Xj2 4“ -У21 + ^23 4" ^32 — 4Х22-Fо;
—4 (Х12 4-^214“ ^23 4“ ^32) 4“ 2 (Хп 4~ Azi3 4-Лз14“ ^зз) 4“
4“4Х22=/?[;
2 (Х12 4~ ^214- ^23 4- -Х’зг) ~ 4 (Хп 4- ^13 4" *314“ *зз)=F2.
Из последнего уравнения имеем
Хп 4“Х134"*31 4-^33 = ”2“ (*124-*214“ *234"*32)--4~F2 .
Подставив это выражение во второе уравнение выписанной си-
стемы и переписав первое уравнение, получим
*12 4- *21 4- Х23 4- Х32— 4Х22=/7 о;
4Х22 — 3 (Х124’^21 4“^234’^32) = ^ 14"“2-^72-
Исключим отсюда (Х12+Х21 + Х23+Х32), тогда
— 4Х224—3-Х22—з-^7!—2—о,
- 3 VT 1
22=--^-Го---8~П
1 р
16
откуда
345
или
^22— g- F22 §“(^ 12 + Л21+^2332)“
—1б"(^ п + ^ 1з + Л31+^зз)«
В общем виде
Xij= --8“(Л-1,/ + ^ + 1,; + ^? bj-i+Z7 —
“""щ (Л-1,/-1 + ^z + i,j-i + ^’i-ij + i + Z7/ + 1,y + 1).
Метод исключения удобно применять при небольшом числе то-
чек. При большом же их числе для решения системы алгебраиче-
ских уравнений, аппроксимирующих дифференциальное уравнение
разностным, целесообразно применять приближенные, или итера-
ционные методы решения.
Из приближенных методов решения конечно-разностных урав-
нений рассмотрим один из вариантов метода последовательных
приближений, или итерационного метода — так называемый экс-
траполированный метод Либмана. Сделаем это снова на примере
уравнения Пуассона (2.1) и соответствующего ему конечно-разно-
стного уравнения (2 2) при краевых условиях (2.3).
Уравнение (2.2) при учете краевых условий (2.3) позволяет по-
лучить систему из MN уравнений с MN неизвестными Х^.
Если величинам Xij придать некоторые произвольные значения,
то соотношения (2.2) не будут выполняться. Левая и правая части
каждого из этих соотношений будут отличаться на некоторую ве-
личину Rij, называемую невязкой. Для каждой точки ij значение
Rij является невязкой того уравнения системы (2.2), которое отве-
чает данной точке. Если величины Xij далее изменять не произ-
вольным, а вполне определенным образом, то невязку Rij в каждой
точке можно сделать как угодно малой. Чем меньше будет величина
невязки, тем ближе будут приближаться значения Х^ к истинным,
т. е. соответствующим точному решению разностного уравнения
(2.2). Процесс изменения Xij будем производить последовательным
приближением. Обозначим номер очередного приближения через
v +1. Расчет значений Xij будем вести, увеличивая последовательно
индексы i и j. В таком случае весь расчет производится следующим
образом.
Вычисляется невязка (v+l)-го приближения в точке ij по соот-
ношению
/?;+1”==^±1,>у4-?г;+1>у+^;+11+?г;>7+1 -4А7,-Fi}.
(2.4)
Заметим, что значения X в точках с индексами f+1 и / + 1 берутся
по предыдущему v-му приближению, а в остальных — по текущему
-346
(v+l)-My приближению Обозначение невязки (v+l)-ro прибли-
жения с использованием двух верхних индексов указывает на это
обстоятельство. Найденные значения используются для по-
лучения поправок к значениям X предыдущего приближения
Значения X для (v+l)-ro приближения находим по соотноше-
нию
(2-5)
где х — некоторый коэффициент, называемый коэффициентом пере-
релаксации.
Процесс заканчивается по условию, которое обычно задается
в виде
^?тах
(2-6)
где /?тах — максимальная для всех точек ij абсолютная величина
/?, а е — заданная величина.
На практике при значениях М и N порядка 50 удовлетвори-
тельная точность решения достигается после нескольких прибли-
жений.
Существуют и другие, более экономичные методы решения урав-
нения типа (2.2), в частности, не требующие выполнения итераци-
онной процедуры.
§ 3. Явные и неявные конечно-разностные схемы
Для решения прогностических задач особый интерес представ-
ляет конечно-разностная аппроксимация дифференциальных урав-
нений, содержащих производные по времени. Из различных схем
аппроксимации рассмотрим здесь две схемы: явную и неявную. Для
простоты изложения сделаем это на примере простейшего линей-
ного дифференциального уравнения
да , ди ~
--Н “л— = 0.
dt 1 ду
(3.1)
где с — постоянная.
Явные схемы получаются в случаях, когда искомые пере-
менные можно выразить через известные явным образом. Запи-
шем конечно-разностный аналог дифференциального уравнения
(3.1), отнеся его к точке js.
=0.
Применяя для производной по координате второй способ ап-
проксимации (формула (1.2)), а к производной по времени как
первый (формула (1.1)), так и второй способ аппроксимации,
347
получим следующие два варианта конечно-разностного урав-
нения:
^у. 5 +1 1, 5 и у—i, s) === 0, (3-2)
^у, 5+1 ^у, 5—1 *4“а (^у+к ^у—1»^)==0> (3-3)
где a = cftt/Ss.
Полагая, что значения функции и в данный и предшествующий
моменты времени, т. е. при s и s — 1 известны, с помощью любого
из соотношений (3.2) и (3.3) можно выразить значения функции и
в будущий момент времени, т. е. величину щ, s+i через известные
функции явным образом. Например, на основе соотношения (3 2)
получим
^у. 5-Г1===^У5 2~ (^/-|-1> 5 и j _ 1, 5).
По этой причине подобные конечно-разностные аппроксимации
и называют явными.
Неявные схемы получаются в основном в случаях, если
производные по времени и остальные члены дифференциального
уравнения отнести к разным моментам времени. При этом искомые
переменные через известные явным образом не выражаются. Воз-
можны различные варианты аппроксимации.
Один из них имеет место, например, если производную по вре-
мени отнести к моменту s, а другие члены уравнения — к моменту
<s + 1, тогда
Применяя, например, второй способ аппроксимации производных,
получаем следующее конечно-разностное уравнение:
му, 5 + 1 — ^у, s-i 4-а — и y__b s+i)=0. (3.4)
Другой вариант аппроксимации получается в случае, если про-
изводную по времени отнести к моменту s, а остальные члены урав-
нения выразить через значения функций в разные моменты вре-
мени, включая момент s+ 1. Положив, например, что
ди \ ______ 1 [7 ди \
\ ду /у,5-4-1
и применив к производным по t и по у второй способ аппроксима-
ции производных, получаем
Uj, 5+1 5-1 Ч 2” (^У+ 1 5+ 1 «/-1, 5+1 + ^У + 1, 5-1 «У-1, 5-1) =0.
(3-5)
348
Обратим внимание на то, что соотношения (3.4) и (3.5) дают
связь между будущим значением и в момент $+1 и значением
функций в прошедший момент времени. При этом оказывается,
что искомую функцию в точке /, s+1 нельзя выразить через другие
функции явно. Поэтому подобные конечно-разностные соотношения
и называют неявными.
Поскольку конечно-разностные соотношения, отвечающие неяв-
ным схемам, не позволяют вычислять последовательно значения ис-
комых величин для различных моментов времени, то на практике
для расчетов эти соотношения представляют в виде систем разно-
стных уравнений, решаемых специально построенными методами
(в том числе итерационными). Выбор схемы для аппроксимации
уравнений, содержащих производные по времени, существенно
определяется особенностями решаемой задачи.
§ 4. Вычислительная неустойчивость
При решении конечно-разностных уравнений приходится много-
кратно выполнять сходные вычислительные процедуры. В частно-
сти, при гидродинамическом прогнозе на сутки по современным
прогностическим моделям приходится делать сотни шагов по вре-
мени. Если не предпринимать специальных мер, то при таком мно-
гократном повторении аналогичных вычислений может возникнуть
такое положение, когда имеющиеся в начальных данных или воз-
никающие в процессе счета небольшие ошибки (например, ошибки
округления) могут усилиться и совершенно исказить решение. Это
явление называют вычислительной неустойчивостью.
Рассмотрим его на примере двух простейших линейных уравне-
ний. Одно из них возьмем в виде (3.1). Заметим, что такой вид при-
нимает одномерное уравнение вихря скорости при отсутствии силы
барического градиента и силы Кориолиса и в случае, если скорость
переноса вихря вдоль оси у равна с.
Получим вначале точное решение этого уравнения при условии,
что в начальный момент функция и (у) имеет вид волны, т. е. при-
мем, что при t = 0
u(y) = Aein\
где Л — амплитуда волны, п — волновое число, f = y—1.
В соответствии с видом и (у) для начального момента решение
уравнения (3.1) будем искать в виде
я (у, /) = Ае1<пу~°*\
где сг — частота. Легко убедиться, что
да . л l(ny-at) ди . /(пу_с/)
—изАе , —;— = щАе
dt ’ ду
349
Подставляя эти выражения в уравнение (3.1), получаем
1Ае1<пу~^{~с+сп\=Ъ,
откуда о = бтг и, значит,
и (у, t)=Aein^-ct\
Полученное решение отражает эффект перемещения крупномас-
штабных волн. Имеющаяся в начальный момент волна смещается
вдоль потока со скоростью су = а1п = с. При этом важно отметить,
что амплитуда волны остается без изменения, что означает устой-
чивость решения.
Перейдем теперь к соответствующим конечно-разностным урав
нениям. По аналогии с предыдущим рассуждением положим, что
в начальный момент s = 0 данная функция представлена в виде
волны типа
ujQ=Aein^\
Решение конечно-разностных уравнений будем искать в аналогич-
ном виде
ujs=Aei^nj^'-^t\
Легко проверить, что
uy+1, s=ujselnty\ Uj_x, s=Ujse~My;
4j+\, s+i=K^ez<"8y~’8Z>; s+1=tt7^<-n8y-°w>.
Рассмотрим теперь явную схему с разностями вперед, т. е. схему
(3.2). Подставляя в соотношение (3.2) только что полученные вы-
ражения, приходим к уравнению
uJse~hit — uJs-\—(ujseinSy — uJse~My)=O
ИЛИ
tijs - 1 Г -т (ez”Sy - e~in 8у)]=0.
Так как ujs^ 0, то отсюда следует, что
е~/а s/ __ j зу _ е-т Ов
Учтем, что по формуле Эйлера eiz— e~iz=2isinz9 положим, что
сг=(Уг-|-шй где ог и <Уг — действительные и мнимые части о, и заме-
тим, что
—iatt — — iabt a, st Q.Sf _
e =e =e e =e [cos (ar8/) - isin (a//)]
350
Тогда получаем
CT/SZ г 1
е [cos (згВ /) — i sin (sr B^)J —-1 Ц-/a sin п By=0.
Отделив действительную и мнимые части, находим:
ст . Zt
е cos(or3/)=l;
ст .6/
е sin(arB/)=a sin (п^у).
Возведя обе части равенств в квадрат и складывая, находим
2ст.г/
е 1 =1+ о? sin2 (п By).
Так как всегда правая часть данного равенства >1, то е2стгб/>1,
а значит, 2<уг-6/>0. Следовательно, всегда Ог>0. Проанализируем
теперь полученное решение
i(fijZy-csZt) i [nj ZyisЛ s Zt]
ujs—Ae =Ae =
a^sZt i (nJ Zy — afs Zt}
=Ae e
Мы видим, что первый множитель при амплитуде А при ог>0
будет расти с увеличением времени. Это значит, что будет увели-
чиваться амплитуда первоначальной волны.
Возрастание амплитуды будет тем сильнее, чем больше шаг по
времени 6/. При бесконечно малом шаге (6/—>-0) возрастания ам-
плитуды не будет — в соответствии с точным решением.
Отсюда заключаем, что явная схема (3.2) с односторонней раз-
ностью вперед обладает вычислительной неустойчивостью.
Возьмем теперь схему с центральной разностью (3.3). Проделы-
вая аналогичные выкладки, получаем
lt~eh 8/) “ 7 ^~in *y-ein 5у)] =0
Учитывая формулы Эйлера, находим
sin (a sin (п By).
Откуда
о B/=arcsin [a sin (п By)].
Мы видим, что если а sin (п&у) > 1, то о будет мнимым числом
и тогда решение будет иметь сомножитель eais6*} который показы-
вает, что амплитуда волны растет со временем и, следовательно,
вычислительная схема будет неустойчивой. Если же a sin (пб//)^1,
то рост амплитуды со временем не будет иметь места. Так как
351
всегда sin (п6у) 1, то для выполнения последнего неравенства
необходимо, чтобы имело место неравенство 1, т. е.
Ы 1 /И
(4*)
Это есть условие вычислительной устойчивости для явной схемы
с центральными разностями (3.3). При 6s = 300 км и с = 40 м/с по-
лучаем для шага по времени 6/^7500 с, т. е. шаг по времени не
должен превышать 2 ч.
Наконец, рассмотрим неявную схему (3.5). Подставляя значе-
ния и в соотношение (3.5) и сокращая общий множитель UjSy полу-
чаем
& -is St eiv St a yei (n 8y —a St) (n 8y_f-a M) j ^i(n Sy-{.a St)
_e~i(n Sy-a ___q
или после некоторых преобразований и использования формул
Эйлера
sin a В/—y sin п Ъу • 2 cos a В/ = 0.
Произведя сокращения, поделив все выражения на cos об/ и пе-
ренеся член, содержащий sin п бу вправо, получаем
tgsB/=asin (п By)
или
a8/=arctg [a sin (nBy)].
При любом nd у и а правая часть последнего выражения является
действительным числом. Отсюда следует, что о также является
действительным числом. Значит, данная схема является устойчивой
при любом значении выражения c6t/6s.
Рассмотрим еще вопрос с вычислительной неустойчивости ре-
шения волнового уравнения
_____ 2 д2и
д& С '
Используя центральные разности, получаем следующее конечно-
разностное уравнение:
uj, 5+1 —5-1 = а2(w/ + l, 5 — sY
Разыскивая решение конечно-разностного уравнения в виде
и^=Ае1<п^у~^\
для о получаем
e-i.st , ^8/_2=а2(^лбу-4-в-/лйу—2).
352
Отсюда
cos (а 3/)— 1=а2 [cos (« By) — 1 ].
Так как 1 —cos2z=2 sin2(z/2), то
sin2 —g—=a2 sin2 .
Откуда
. а bt . п Sy
Sin—2~ = ± a Sin —2^- ,
и, значит,
aS/ . . г /2 Sy 1
—2~ = ± arcsin asm...2 - .
Вычислительная схема будет устойчивой, если о — действительное
число. Но это возможно в случае, если
I • и Sy I
asm —2~ <5 1.
Так как | sin (n6r//2) | ^1, то необходимым условием вычисли-
тельной устойчивости является
^<1. (4.2)
Внешне это условие совпадает с условием (4.1). Однако, если в ус-
ловии (4.1) под с подразумеваем скорость перемещения крупно-
масштабных волн, то в условии (4.2) с имеет смысл скорости аку-
стических волн. При скорости волн 330 м/с и при 6s = 300 км дол-
жно быть 6/ меньше 15 мин.
§ 5. Операции с векторами
Пусть i, j, k — единичные вектора, направленные вдоль осей
х, у и г. Тогда любые вектора А и В могут быть представлены
в виде
A=Axi-4-Ayj+A,A B=^i + 5yj+^k,
где Ах, А у и Az, BXi Ву и Bz — проекции векторов А и В на оси х, у
и 2 соответственно.
Модули векторов являются скалярами и выражаются в виде
|А|=Д = -|/-Д2+А2+А2, |B|=5 = j/52 + S2+52.
Сумма (разность) векторов есть новый вектор
С=А±В=(ЛЛ±5х)|-+(Ау±5у)Л-(Дг±5г)к.
23 Зак. № 21
353
Скалярное произведение векторов есть скаляр
А • В=| А | | В | cos 6=АВ cos О,
где 0 — угол между векторами А и В.
Для единичных векторов
i . i=j . j=k . k = l, i . j=j . k=i • k=0.
Поэтому
a • b=-b А=(дл-ду]-;-д2к)(^+^+ад=
—AxBx^AyBy~\~AZBZ •
Векторное произведение двух векторов АXВ есть новый
вектор, имеющий длину АВ sin0, а направление которого совпадает
с направлением движения правого винта в направлении от А к В.
Для единичных векторов
iXi=jXj=kXk=O,
iXj= -jXi=k, kXi= -iXk=j, j\k=-kXi=i.
Применяя эти результаты, получим
AXB=(AJ+Ayj+A2k)X(£J+£yi+W==
=(АуВ2— AzBy)\-\-{AzBx~- АхВ^\-\-(АхВу~- AyBJ) к
или в виде определителей третьего и второго порядков
АХВ =
i
Ах
J к
А у Az
By Bz
Ay Az
Bz
Az Ax
Bz Bx
i+
A.
В
Ay
By
k.
’ +
Смешанное произведение векторов
A
(AXB)C=
Ay
By
Cy
Az
Bz
Cz
(AXB)XC=(C • A)B —(C • B)A,
AX(BXC)=(A • C)B —(A • B)C.
Оператор набла
_ . д . . д . , д
1 дх ду + дг '
Применив оператор набла к скаляру, например, давлению, получим
градиент
gradp= Vp=-i-^-4-j-g- + k .
Применив оператор набла к вектору скорости
[J=zz i Ц-тг|-j-w к,
354
получаем дивергенцию вектора
divU=V • U
ди । dv t dw
dx ’ ду ’ dz ’
Вихрь вектора
Q=rotU=VXU =
i
д
dx
U
j k
д d
dy dz
dw dv \ . .
Ту +
+(-Й—
где Qy, — компоненты вектора Й.
Примеры применения векторных операций:
1) U Vp_(«i + «J+»k)(-^i+-^-J+-fck)=
™“Х । г‘ Х! ,'Х (скаляР);
о\ I т ж—1 д I д I д
' дх 1 ду 1 дг ’
3) и • VU=(U • V)U=(ui+^j + wk)X
х0^+^+к^)^+^+дак)=
лг+г’-7>г+®’-агР+
• / dw . dw , dw \ , z 4
+(““£r+r~ar + w^F)k (BeKT°P);
4) /(kXU)=/kX(«i+®j-|-®k)=-Zd-|-/uj (вектор);
5) щ=кХ?ф=кх(|^ЧЧ#+к4М=-#1+-^] =
' * T /x \ dx 1 J dy 1 dz / dy 1 dx J
где г|? — функция тока,
дф дф
мч-=--1Г> ^=~дГ
— компоненты вектора соленоидального ветра U^;
23*
355
6) Ug=-^kXW=
dH у dH . dH
dx 'J dy "* dz
g дН . . g дН . . ।
=----T~~5 >4—7 л j = -4-tL,
I dy 1 I dx J • 6*
где H — высота изобарической поверхности,
н==__£__^_
us I dy ’ Ug I dx
— компоненты вектора геострофического ветра Ug;
= k •
dw
~dy
7) k • VXU=k • rotU =
dv \ . t / du dw ( dv
dz J 1 \ dz dx P ' \ dx
_ dv du q
dx dy *’
du
~ду
8) k • -^"XV®=k • [-^-(«i+®j+wk)X
4 .( dw . . dw . . dw t \1 i [( dv dw
xUr'+-drj+^k)l==4hr^7-
dw dw \ . .
dz dy J 1
dw dw
dz dx
du dw \ 4 । ( du dw
dz dz J 3 T у fiy
dv dw
dz dx
du dw dv dw
dz dy
dz dx
ПРИЛОЖЕНИЕ 5
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Все процессы и явления, наблюдаемые в природе, можно раз-
бить на две основные группы, детерминированные и случайные про-
цессы. Детерминированными называют такие процессы,
которые обусловлены рядом известных факторов. Детерминирован-
ные процессы удается описать с помощью математических уравне-
ний, отражающих известные законы Примером детерминирован-
ных процессов являются движения планет. Эти движения с помо-
щью расчетов удается предсказать на много лет вперед с большой
точностью.
В отличие от детерминированных, случайные процессы не
поддаются какому-либо объяснению в рамках имеющихся физиче-
ских теорий и гипотез. Они не описываются точными математиче-
скими уравнениями и поэтому не могут быть точно предсказаны.
К числу таких случайных процессов или явлений можно отнести
броуновское движение молекул или выпадение орла или решетки
при бросании монеты. Такого рода процессы или явления называют
иногда чисто случайными. Однако при многократном воспроизве-
дении некоторых явлений, которые следует причислить к случай-
ным, удается все же установить некоторые общие закономерности,
имеющие вероятностный характер. Так, например, при многократ-
ном бросании монеты вероятность появления орла оказывается
близкой к V2.
Реальные объекты сложны и в большинстве случаев не явля-
ются ни чисто детерминированными, ни чисто случайными. Они со-
держат как детерминированную, так и случайную составляющие.
К таким объектам относится и атмосфера. Можно предположить,
что крупномасштабные атмосферные движения являются в основ-
ном детерминированными. Движение же отдельных частиц в тур-
булентном потоке является случайным и непредсказуемым процес-
сом. Значительная часть атмосферных движений занимает про-
межуточное положение и может быть описана с помощью
теоретико-вероятностных и статистических методов.
При решении задачи прогноза погоды гидродинамическими ме-
тодами делается предположение о том, что атмосферные движения
и изменения погоды являются в основном детерминированными
процессами. В действительности же уравнения гидротермодина-
мики, с помощью которых производится гидродинамический про-
гноз погоды, могут полностью описать сложные метеорологические
процессы лишь в рамках того или иного приближения, зависящего
от нашего уровня познания этих процессов. Кроме того, уравнения
гидротермодинамики решаются не точными, а приближенными ме-
тодами. По этим причинам задачу прогноза погоды нельзя считать
полностью детерминированной. Следовательно, закономерно ис-
пользование в задачах прогноза погоды теоретико-вероятностных
и статистических методов.
357
С учетом этих общих замечаний рассмотрим теперь основные
понятия математической статистики, которые широко используются
при исследовании атмосферных процессов и при прогнозе погоды.
1. Некоторые статистические характеристики
Теория вероятностей и математическая статистика имеют дело
со случайными величинами. Под случайной величиной понимают
переменную величину, которая в результате испытания может при-
нять то или иное значение. Совокупность случайных величин или их
последовательность в пространстве или времени можно рассматри-
вать как случайную функцию пространственных или временных
координат или как случайный процесс. Значения метеорологиче-
ских элементов в дискретных точках пространства и времени,
которые они принимают в результате какого-либо метеорологиче-
ского процесса, можно рассматривать как своего рода результат
испытаний со многими переменными. Этот результат можно опи-
сать с помощью основных понятий математической статистики
и теории вероятностей.
Пусть мы имеем выборку некоторых случайных элементов или
переменных хг-, где i=l, 2, ..., N — некоторый параметр, фиксирую-
щий номер элемента, время или значение какой-либо пространст-
венной координаты, N — общее число переменных, входящих в вы-
борку. Чтобы каждый раз не оперировать со всеми элементами вы-
борки, ее описывают с помощью небольшого числа статистических
характеристик («статистик»). Рассмотрим некоторые из них.
Среднее значение. Определяется следующим образом
Среднее значение, определенное таким образом, является эмпири-
ческой оценкой теоретической средней или математического
ожидания а.
Дисперсия и среднее квадратическое значе-
ние. Пусть х'. = Хг — х— отклонение переменной л от средней, или
вариация. Тогда дисперсия D или о2 переменной х выразится в виде
Найденная таким образом дисперсия является эмпирической оцен-
кой теоретической дисперсии, равной математическому
ожиданию квадрата вариации. На практике для оценки отклонений
значений переменных от средней часто используется не дисперсия,
а положительный квадратный корень из нее, называемый сред-
ним квадратическим, или стандартным отклонением
358
В качестве характеристики отклонений иногда пользуются
средним абсолютным отклонением
При нормальном распределении отклонений (см. далее) имеет ме-
сто приближенное соотношение
□=1,258.
Частота (частость) распределения. Разобьем все
элементы выборки на группы, каждый элемент которых отличается
каким-либо общим признаком. Пусть, например, таким признаком
будет величина элемента х, а все группы состоят из элементов, ве-
личины которых заключены внутри заданного интервала. Тогда
число элементов Шг, входящих в группу i, будем называть часто-
той (иногда частоту называют повторяемостью). Если
частоту поделить на общее число элементов N, входящих в вы-
борку, то мы получим частость (называемую иногда относи-
тельной повторяемостью)
Частость является эмпирической оценкой теоретической вероятно-
сти р (х).
Пусть разбивка на группы производится по равным интервалам
величины элемента Дх. Поделив частость на выбранный интервал
Дх мы получим величину, равную частости отнесенной к единице
интервала, называемую плотностью распределения ча-
стости
(р.=_£щ=_Л1-
Дх ЛгДх ’
Плотность распределения частостей является эмпирической
оценкой теоретической плотности распределения веро-
ятности ф(х). При Ax = const плотность распределения частости
пропорциональна самой частости.
Существуют различные способы графического представления
описанных статистических характеристик. Наиболее распростра-
ненным являются графики распределения в виде гистограммы
и полигона.
Гистограмма распределения строится следующим образом.
Над каждым отрезком оси абсцисс, изображающим интервал Дх,
строится прямоугольник, площадь которого пропорциональна рас-
сматриваемой характеристике (частоте, частости или плотности
распределения частости). Если при этом ширина интервала Дх по-
стоянна, то высоты прямоугольников пропорциональны указанным
характеристикам.
При построении полигона распределения на оси абсцисс от-
кладываются интервалы значений х, а в середине интервалов
359
строятся ординаты, пропорциональные рассматриваемой характе-
ристике. Концы ординат соединяются отрезками прямой
Примеры графического изображения некоторых из указанных
статистических характеристик приведены на рис. П.7.
Рис. П.7. Схематическое изображение различных распределений.
а — гистограмма распределения частости, б — полигон распределения
частости, в — гистограмма плотности распределения частости (близкого
к нормальному), г — график плотности вероятности нормального распреде-
ления, д — распределение дискретных спектральных плотностей, е — гра-
фик спектральной плотности.
При исследовании величин метеорологических элементов часто
можно обнаружить, что их распределение близко к так называе-
мому нормальному распределению. Под последним понима-
ется распределение плотности вероятности <р(х), которое описыва-
ется следующим образом:
<Р (*)= е
у а
(х-х)2
2а2
360
где х— математическое ожидание величины х, а о2 — дисперсия.
При нормальном распределении плотности вероятности (см.
рис. П.7г) оказывается, что 90% всех значений отклонений (х— х)
заключены внутри интервала —Зо<(х — х)<3о. Пример распре-
деления близкого к нормальному приведен на рис. П.7 в.
Ковариационные и корреляционные функции.
До сих пор мы рассматривали лишь одну переменную х. Перейдем
теперь к рассмотрению двух переменных: х и у. Пусть обе пере-
менные являются функциями одного параметра г=1, 2, ..., /V, ко-
торый, как и ранее, фиксирует номер элемента, время или значение
какой-либо пространственной координаты. Пусть далее у =
1 А —
=— Х1Уг — среднее значение у, у\=Уг — У — вариация, о2 =
г = 1
1 N 2
=— 22/ —дисперсия переменной у, о2—дисперсия перемен-
ной х. Тогда ковариационная функция переменных х и у (иногда ее
называют просто корреляционной функцией) выражается в виде
I n
Ковариационную функцию называют кроссковариационной,
если х и у — разные элементы, и автоковариационной, если х и у —
один и тот же элемент, относящийся к различным точкам простран-
ства или времени.
Если ковариационную функцию разделить на ОхОу, то мы по-
лучим нормированную ковариационную или просто корреляцион-
ную функцию
тху 1 Ki ' '
Гху '
Последнюю часто называют коэффициентом корреляции.
Ковариационные функции называются пространственными, если
переменные х и у относятся к разным точкам пространства, и вре-
менными, если х и у относятся к разным моментам времени.
Структурные функции. Под структурной функцией не-
которого метеорологического элемента f понимается средний квад-
рат разности значений этого элемента в двух точках пространства
Bf(r, r+p)=[/(r)-/(r+p)]2,
где г и г+р—радиусы-векторы двух точек, причем р есть вектор,
соединяющий эти две точки, а черта сверху означает осреднение
по большому числу ситуаций (наблюдений). Такая структурная
функция является пространственной. Аналогичным образом вво-
дится понятие временной, а также пространственно-временной
структурной функции.
361
На практике необходимо уметь вычислять значения струк-
турной функции для каких-либо конкретных точек простран-
ства и времени. Пусть /=1, 2, ..N — порядковые номера отдель-
ных наблюдений (измерений) какого-либо метеорологического
элемента х в двух точках с пространственными (или временными)
координатами / и k, а х?-7 и хд^— значения данного элемента в двух
указанных точках, полученные при /-том наблюдении (измерении).
Тогда значение структурной функции для переменной х, относя-
щейся к точкам / и k, выразится в виде
i -- 1
Если рассматривать не сами значения х, а их вариации, т. е. от-
клонения от средних, то для значения структурной функции полу-
чим другое выражение
b)k=
Если индекс i соответствует номеру измерения (реализации),
а индексы / и k фиксируют две точки в пространстве, то получаем
значения пространственной структурной функции для пары
точек с координатами / и k; если же i соответствует пространст-
венной координате или номеру некоторого пункта, а индексы j и k
фиксируют два момента времени, то получаем значения времен-
ной структурной функции для данного пункта.
Фиксируя положение точки j и меняя положение точки k, мы
можем получить ряд значений структурной функции, соответствую-
щих различным расстояниям I или интервалам времени т между
точками / и k. Нанеся полученные значения на график, получим за-
висимость структурной функции от расстояния или интервала вре-
мени.
Между структурной и автоковариационной функциями, а также
дисперсией существует следующее соотношение:
bik=^+^k-^fnjk,
где о2 и q2 — дисперсии элемента х в точках j и nijk — значения
автоковариационной функции элемента х, относящиеся к точкам
j и k.
В случае однородного поля, когда g2.=g2 = о2, последнее соот-
ношение принимает более простой вид
bjk=2a2 — 2nijk.
Все описанные здесь статистические характеристики случайных
переменных являются выборочными. Они зависят от объема
выборки /V, а также от самой выборки. Если, например, исследуе-
мая переменная х зависит от времени, то выборки могут отно-
362
ситься к различным периодам. Вообще говоря, чем больше объем
выборки, тем выборка лучше характеризует так называемую гене-
ральную совокупность. Однако на практике объем выборки при-
ходится ограничивать. Поэтому статистические характеристики, по-
лученные для данной выборки часто оказываются несправедли-
выми для другой выборки и недостаточно хорошо отражают
соответствующие характеристики для генеральной совокупности.
Эти характеристики остаются устойчивыми лишь в случае так на-
зываемого стационарного процесса.
Метеорологические процессы, вообще говоря, нельзя считать
стационарными. В качестве примера, подтверждающего нестацио-
нарность атмосферных процессов, приведем известный факт потеп-
ления Арктики в последние годы. В этом случае средние величины
метеорологических элементов, а также и все другие статистические
характеристики, определенные за различные периоды, включающие
десятки лет, оказываются неустойчивыми. Несмотря на это при ре-
шении многих метеорологических задач, в том числе и задач про-
гноза статистическим методом, предполагается, что метеорологиче-
ские процессы являются стационарными. При этом используется
гипотеза об эргодичности, согласно которой статистические
характеристики при переходе от одной выборки к другой изменя-
ются слабо.
Заметим, что приведенные ранее выражения для среднего зна-
чения, дисперсии, ковариационных и структурных функций спра-
ведливы в случае осреднения ряда величин или их произведений,
входящих в выборку. При этом указывается объем выборки В прин-
ципе, однако, способ осреднения можно не указывать. Это об-
стоятельство может быть отражено с помощью изменения формы
записи для осреднения. Так, например, выражения для ковариаци-
онной и структурной функций могут иметь вид:
*ул = (х'— x'k)2,
где черта сверху означает осреднение. При этом, если осреднение
распространяется на все элементы генеральной совокупности, то
полученные величины практически будут равны соответствующим
теоретическим характеристикам.
Ковариационные и структурные функции являются частными
случаями моментов связи, введенных в 1924 г. Л. В. Келле-
ром и А. А. Фридманом.
Гармонический анализ и спектральная плот-
ность колебаний. Если какая-либо функция f (f) представля-
ется в виде суммы гармонических колебаний различных частот
(гармоник), то ее можно охарактеризовать спектром, т. е. функ-
цией, описывающей распределение амплитуд по частотам Подобно
световому спектру, этот спектр будет показывать, с какой амплиту-
дой отдельные гармонические составляющие содержатся в рас-
сматриваемой функции.
363
Пусть функция f (t) б промежутке времени от 0 до Ti (величину
71 назовем основным периодом функции) представляется в виде
ряда Фурье
f («* COS ^kt-\-bk sin
z /г = 1
где k= 1, 2, 3, ... — целые положительные числа; (Ok = 2nk/Ti— кру-
говые частоты, соответствующие этим числам (величину coi = 2n/Ti
назовем основной частотой, соответствующей основному периоду
71); ah и Ьк — коэффициенты Фурье, определяемые по соотноше-
ниям:
ак=-^ f (f) cos ukt dt при k = 0, 1,2,3, . . .;
о
bk=-^ j*/(/)sin akt dt при k= 1, 2, 3, ...
b
С помощью простейших преобразований выражение для f (t) можно
привести к виду
Qsin(co^4-^),
где ерь — фаза колебания, определяемая с помощью соотношения
tgqh = ak/bk, а
^=/4+^
— амплитуда колебания, соответствующая частоте со& или й-той
гармонике. Определив значение коэффициентов ак и Ьь, а затем
и ск, мы тем самым получаем распределение или спектр амплитуд
ck по частотам со& или же по периодам Tk = 2n/d)h отдельных гармо-
ник. При этом периоды гармоник связаны с основным периодом Ti
соотношением Th = T]jk.
При практическом применении приведенных соотношений бес-
конечный ряд заменяется суммой по ограниченному числу членов
ряда, а интегрирование по t заменяется суммированием. При этом
на отрезке времени 71 с помощью интервалов А/ вводятся точки
ti = i\t, где г = 0, 1, 2 а функция f (t) в этих точках должна быть
определена.
С помощью амплитуды Ck можно найти дисперсию Dk, т. е.
среднюю для гармоники с номером Л, частотой и периодом Th
величину квадрата отклонений функции f (/) от среднего для дан-
ной гармоники значения f (t). Очевидно,
, Tk _ , Tk с2
о 0
364
Откладывая на оси абсцисс номера гармоник k или соответствую-
щие им значения периодов Tk, а на оси ординат — величины ампли-
туд, получаем график спектра амплитуд, найденного с помощью
гармонического анализа.
Более наглядный результат мы можем получить с помощью
определения и анализа спектральной плотности колебаний различ-
ной частоты. Эта последняя характеристика может быть применена
лишь к анализу стационарных случайных функций.
Пусть x(t) и х(/+т) — значения переменной х в моменты t
и /+т, где т — некоторый интервал времени, х' (t) и х' (Л-т) — от-
клонения указанной переменной от средней,
т (т)=х' (/) х'
— автоковариационная функция. Последняя может быть выра-
жена в виде
со
пг (т)= j*5 (t0)cos do),
6
где & = 2tiIT — круговая частота, T — период колебаний,
s (со) =— I пг (т) cos ок dx,
о
Функция s (со) называется спектральной плотностью или просто
спектром колебаний. Смысл последней легко уяснить из предель-
ного выражения
где Дсо — приращение частоты, a D(co)— дисперсия, т. е. средний
квадрат колебаний на участке Дсо. Спектральная плотность коле-
баний какой-либо переменной имеет размерность дисперсии этой
переменной, деленной на размерность частоты.
Часто вместо спектральной плотности s(co) рассматривается
нормированная спектральная плотность
5(у))=^ио_,
где D — суммарная дисперсия, т. е. средний квадрат отклонений
функции от ее среднего значения для всего рассматриваемого ин-
тервала. Функция S определяется следующим образом:
2
S (ш)=—- С г (х) cos ок dx,
о
где
Г(х)=^-Х' ^х' и+т)
365
— нормированная автоковариационная функция, для которой спра-
ведливо соотношение
со
Г (т) = J S (со) cos сот dco.
о
Легко видеть, что произведение S(co)co — является величиной без-
размерной.
Если в качестве независимой переменной использовать частоту
f = co/2n, то выражения для т (т) и 5 (f) можно записать в виде:
т (т)=2к J $ (/) cos (2к/т) df\
о
s (f)~=4 J т (т) cos (2тс/т) dx.
о
Аналогично этому
оо
О
5 (/) =4 j* г (т) cos (2к/т) d'z.
б
Рассмотрим теперь, каким образом производится расчет спект-
ральных функций на практике. Сделаем это на примере расчета
функции 5 (f). Прежде всего рассчитывается автокорреляционная
функция т(т) для ряда значений т. Пусть в исследуемом интер-
вале времени рассматриваемая функция x(t) задана в дискретных
точках ti (f = 1, 2, ..., /V), а также в точках /г + т, (/ = 1,2,..., N).
Тогда для интервалов т7- корреляционная функция рассчитывается
по соотношению
1 N
i1
где
(^/) x(ti) x(t^
Х' (ti 4“ т/) = Х (ti + т/) — Х (ti + Д
а л (Л) их(С + т7)—средние значения.
Для расчета спектральной функции s (Д) при частотах Д инте-
грал заменяется суммой подынтегральных функций по всем зна-
чениям / = 0, 1, ..., N при различных tj.
Положим, что fk = k/^f и т; = /Дт, где А/ и Ат — заданные ин-
тервалы частоты и времени. Тогда, учитывая, что cos (2л/0) = 1,
366
a m(xo) = Z). где D — дисперсия элемента x при т=0. для значения
спектральной плотности при частоте fk получаем
*л=«(Л)=4
т (ty)cos(2Vft'tj)
или
sfc=4
D -|- У т (j Дт) cos (2nk i\fj Дт)
7=1
Дт.
Аналогичным образом для нормированной спектральной функ-
ции получаем
$k—4
1 + У r(T?)cos(2V*^/)
/=1
Ат.
Для получения графической зависимости Sr или Sr от частоты на
оси абсцисс откладывается частота /&, круговая частота со& или со-
ответствующие им периоды колебаний Tr, а на оси ординат — зна-
чения Sr или Sr. Внешне полученный график похож на гистограмму
плотности распределения частости (рис. П.7 д). При этом высота
прямоугольника при fh или численно равна средней плотности
дисперсии на участке Д/ или (Дю). Уменьшая интервалы частот
Д/ или Дсо, мы можем в пределе получить непрерывный график
спектральной плотности (рис. П.7 е).
Отметим, что на графике площадь, заключенная между кривой
s((jd) и осью абсцисс численно равна суммарной дисперсии D =
оо
= 22^- Действительно, рассматривая выражение для т (т) при
fe=i
т = 0, мы видим, что левая часть его оказывается равной дисперсии,
так как т (0) = D и мы получаем, что
03
D= J s((o) dm.
о
Но последний интеграл численно равен указанной ранее площади
При рассмотрении нормированной спектральной плотности пло-
щадь, заключенная между кривой S (со) и осью абсцисс, равна
единице. Это следует из того факта, что при т=0 г=1 и
1 = j 5* (<о) бАо.
6
При графических построениях на оси абсцисс иногда отклады-
вается не частота, а логарифм частоты In f. В этом случае по оси
ординат обычно откладывают произведение f-s(f), имеющее раз-
мерность дисперсии рассматриваемой величины х
Максимумы спектральной плотности будут соответствовать наи-
более значимым и часто встречающимся частотам.
367
Если в качестве переменной х взята скорость, то автоковариа-
ционная функция оказывается пропорциональной кинетической
энергии движения. Поэтому спектральную функцию иногда назы-
вают энергетическим спектром (спектральной плотностью энер-
гии) .
Отметим, что в литературе для спектральной плотности встре-
чаются и другие выражения, которые отличаются от приведенных
постоянными множителями. Например, выражение для s (f) иногда
записывается в виде
<$(/)= J /п (т) cos (2^/т) dz.
о
Однако это обстоятельство не имеет существенного значения, так
как основной целью спектрального анализа является получение не
абсолютных значений спектральной плотности, а зависимости ее от
частоты или периода колебаний.
Примеры спектральной функции некоторых метеорологических
процессов приведены в гл. I. Заметим еще, что для получения спек-
тральной функции, характеризующей значимость или повторяе-
мость волн различных длин, достаточно рассмотреть пространст-
венную автоковариационную функцию, для чего вместо времени t
можно взять длину /, а вместо круговой частоты о — волновое чи-
сло /г = 2л/£, где L — длина волны.
2. Метод множественной линейной регрессии
Из всех известных методов математической статистики в зада-
чах прогноза погоды наиболее широкое распространение получил
метод множественной линейной регрессии, который в метеорологии
называют также методом эмпирических функций влияния. Другие
методы применяются меньше. Рассмотрим кратко основы этого
метода.
Пусть из физических соображений известно, что искомая пере-
менная S (назовем ее предсказуемым) определяется рядом пере-
менных f, <р, ... (назовем их влияющими факторами, которые ино*
гда называют также предсказателями), каждая из которых может
быть задана в некоторой системе точек пространства и времени.
Тогда, согласно рассматриваемому методу, между приближенным
значением искомой переменной S и переменными f, ср, ... предпо-
лагается наличие линейной связи вида
5=ао+ • • •> (2-0
i J
где fi, (рд .. — значения переменных f, (р, ... в точках i и /; сумми-
рование распространяется по всем заданным точкам i и /; а, b и с —
368
числовые коэффициенты регрессии, подлежащие определению. По-
следние находятся путем обработки фактических данных о пере-
менных S, /, ф, ... за прошедшие сроки методом наименьших квад-
ратов.
Рассмотрим это на примере зависимости искомой переменной S
от переменной F, заданной в точках 4=1, 2, ..п. Для простоты
примем, что переменные S и F представляют собой отклонения от
их норм, определенных как средние по большому ряду наблюдений.
Тогда можно записать
5= V ^F(=C1F14-C2F24- . . . -\-cnFn. (2.2)
1 = 1
Будем полагать, что выражение (2.2) применимо для любого слу-
чая (ситуации) k с одними и теми же коэффициентами С{. Однако
в каждом случае значение S с помощью соотношения (2.2) будет
получено с различной ошибкой 6^ = (5 — S)k. Для нахождения не-
известных коэффициентов Ct методом наименьших квадратов необ-
ходимо по прошедшим (архивным) данным отобрать достаточно
большой ряд случаев (ситуаций) Л=1, 2, ..., N, Для каждого слу-
чая необходимо выписать фактические значения переменной S
и влияющих факторов Fi. В результате получим выборку из N зна-
чений переменных S и nN значений F, которые могут быть сведены
в таблицу вида:
F11, ^21, • • •» ЛпЪ ^1
F12, ^22, • • •, Fn2\ S2
F\k> F2k, • • •, Fnk; Sk
(23)
F\n> F2Nj . . FSN
Данные этой таблицы (назовем ее основной выборкой) исполь-
зуются далее для составления так называемой системы нормаль-
ных уравнений. Последняя, согласно методу наименьших квадратов,
составляется из условия минимума суммы квадрата ошибки 6k по
всем N случаям, т. е. минимума функции
N 7V / хч Лг Г /г
Q=X 2 c^~s
Л=1 k = l k=l L 1
Условием экстремума функции является обращение в нуль всех
ее частных производных. В результате мы получим следующую
24 Зак. № 21
369
систему из п уравнений с п неизвестными коэффициентами сд
dQ dci N =22 /? = 1 n ^4 _ i = l CtFik ~sk Flk =0
dQ дс2 N = 2 v Г- 1 n 2 _ i 1 -sk F2k 0
dQ дсп CM • II n V Ci Fik -sk Fnk =0
k — 1 i — 1
После изменения порядка суммирования, сокращения и переноса
членов, не содержащих неизвестных G, в правую часть полечим
систему уравнений
аПс\Л~а2\с2~\~ • • • ~\~ап\сп — Ь\
а22с2~\г • • • 4"^я2^л = ^2
а\пс\ а2пс<1Л~ • • • +^/г/?Лг = ^п .
где
аЧ= 4" 2 FikFjk, SkFik-
k = l k=\
Рассчитав по данным f и S коэффициенты а и b системы урав-
нений (2.4) и решив ее каким-либо способом (например, способом
исключения), получим числовые значения искомых коэффициентов
Сг уравнения регрессии (2.2). В случае трех—пяти переменных ре-
шение системы можно произвести вручную, при большом числе пе-
ременных — с помощью ЭВМ. Оценку точности полученного
уравнения регрессии (2.2) по отношению к данным, входящим в вы-
борку (2.3), можно произвести путем расчета средней квадратиче-
ской ошибки (То, сводного (множественного) коэффициента корре-
ляции /? и относительной ошибки 8 с помощью соотношений:
где
2 5*~2 g A
k1 i 1
£==0о/°ф,
(2.5)
370
В случае, если точность оказывается удовлетворительной, полу-
ченное таким образом уравнение регрессии далее может быть при-
менено к другим данным. Например, если уравнение регрессии было
получено по данным за прошедшие годы, то оно может быть ис-
пользовано для прогнозов в текущем и последующих годах. Однако
здесь необходимо заметить, что коэффициенты регрессии, опреде-
ленные по одной выборке, могут дать плохие результаты для дру-
гой, т. е. может иметь место «неустойчивость» коэффициентов. Ве-
роятность возникновения такого явления уменьшается по мере
уменьшения отношения числа учитываемых переменных п к числу
случаев N, т. е. отношения n/N. С другой стороны, уменьшение чи-
сла п ведет к увеличению средней квадратической! ошибки. Поэтому
должно существовать некоторое оптимальное значение отношения
n/N, при котором сохранялись бы сравнительно небольшие вели-
чины Оо и имелась возможность применения найденных коэффици-
ентов уравнений регрессии к другой выборке и, в частности, к про-
гнозу. Для некоторых вариантов задачи прогноза поля давления
малой заблаговременности оптимальное отношение n/N составляет
приблизительно Vis.
Общего метода построения нелинейных уравнений регрессии не
существует. Однако в некоторых случаях нелинейную зависимость
удается свести к линейной. Пусть, например, мы выявили, что за-
висимость 2 от х и у выражается с помощью трансцендентной
функции
С2х ч- С3у
г = Схе
где е — основание натуральных логарифмов, a С\, С2, Сз— неиз-
вестные коэффициенты. После логарифмирования получаем видо-
измененную зависимость
in z = in Cj 4- С2х Ц - С3у.
Таким путем мы перешли от нелинейной (трансцендентной) за-
висимости к линейной, к которой можно применить метод наимень-
ших квадратов.
24*
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ПОСТОЯННЫЕ
А = 2,3884 • 10~8 кал/эрг— термический эквивалент работы; амплитуда волны
а= 6371 км — средний радиус Земли; абсолютная влажность; ско-
рость звука в изотермической атмосфере (330 м/с)
с —скорость перемещения волны
ср~ 0,2405 кал/(г-град)—удельная теплоемкость воздуха при постоянном дав-
лении
cv = 0.1719 кал/(г-град) — удельная теплоемкость воздуха при постоянном объ-
еме
с2 = R2T (7д — *f)/g — параметр статической устойчивости
Д — дивергенция скорости
D — горизонтальная дивергенция скорости
d — дефицит температуры точки росы
е — упругость водяного пара
F — вектор сил, отнесенных к единице массы
Р — поток длинноволновой радиации в полусферу
G—функции Грина (функции влияния), нисходящий по-
ток длинноволновой радиации
g — сила тяжести
Д = grad — градиент
Н —высота изобарической поверхности; амплитуда
h — высота
__i — единичный вектор, направленный по оси х
i = V — 1 — индекс точки на оси х
J (А, В)=(А, В) —якобиан
JS(A, В) = (А, B)s —якобиан на сферической поверхности
j —единичный вектор, направленный по оси у
j — индекс точки на оси у
К — кинетическая энергия
к — единичный вектор, направленный по вертикали
k — коэффициент турбулентной вязкости, соответствую-
щий вертикальному направлению; волновое число, со-
ответствующее оси z\ индекс точки на оси z (р)
k' — коэффициент турбулентной вязкости соответствующей
горизонтальной плоскости
L —длина волны
—теплота конденсации или испарения влаги (£«600
кал/г)
/ = 2о) sin ср — параметр Кориолиса
М — масштаб карты
т — масштабный множитель; волновое число, соответству-
ющее оси х; значение ковариационной функции; ин-
декс
N — балл облачности
п — волновое число, соответствующее оси р; индекс
О —символ порядка величины или характерного значения
Р-1000 мбар — стандартное давление воздуха на уровне моря
Р™ —присоединенный полином Лежандра
372
р — давление воздуха; независимая переменная по верти-
кали
Q — поток субстанции, количество осадков
q — удельная влажность воздуха
/^=2,87-106 эрг/(г-град) =
= 287 м~2 • с-2 • град-1—удельная газовая постоянная сухого воздуха, радиа-
ционный баланс
/?п—4,615-106 эрг/(г- град)—
= 1,102-10-1 кал/(г-град) — удельная газовая постоянная водяного пара
г — радиус-вектор
г — расстояние; коэффициент корреляции
S — нормированная спектральная плотность, поток сол-
нечной радиации
s—расстояние, спектральная плотность, индекс точки на
оси времени t
Т — температура по абсолютной шкале; период колеба-
ний *
Td — температура точки росы по абсолютной шкале
t — время; температура по шкале Цельсия
td — температура точки росы по шкале Цельсия
U — трехмерный вектор скорости
U — скорость основного потока; восходящий поток длин-
новолновой радиации
и — составляющая скорости по оси х
V — вектор горизонтальной скорости ветра
v — составляющая скорости по оси у
w — составляющая скорости по оси z
х — декартова горизонтальная координата по оси ОХ
у — декартова горизонтальная координата по оси OY
z — декартова вертикальная координата
« — индекс циркуляции атмосферы
о 1 dl „
р = — параметр Россби
7 — вертикальный градиент температуры
7 а = 0,98-10-2 град/м — сухоадиабатический градиент температуры
7ва — влажноадиабатический градиент температуры
Д — оператор Лапласа на плоскости
Д5 — оператор Лапласа на сферической поверхности
S — разность; средняя абсолютная ошибка; полярный
угол
s — приток тепла к единице объема; невязка; относитель-
ная ошибка; параметр малости
С = р/Р — вертикальная координата
Н — турбулентный поток тепла
0 — потенциальная температура
те
0~2---? — полярный угол
х — CpjCv = 1,4 — постоянная Кармана; отношение теплоемкостей при
постоянном давлении и объеме
X — длина волны; долгота места; коэффициент темпера-
туропроводности; показатель политропы --------^0,289
373
р. — значение нормированной ковариационной функции
v — частота колебаний (герц или колебаний в секунду)
$ = р Р, где р (z) — стандартное давление, Р= 1000 мбар
р — плотность воздуха
о — среднее квадратическое отклонение; вертикальная
координата (p[ps)
dp
т =. ----аналог вертикальном скорости
ср—широта места; потенциал скорости
ф функция тока
О — вихрь скорости
О — вертикальная составляющая вихря скорости
(о -< 0,729-Ю 4^1 — угловая скорость вращения Земли; угловая частота
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоковариационные функции 361
Агеострофическая прогностическая модель 154
Адаптация метеорологических полей 114
Адвекция 80
Адвекция вихря скорости 127
— температуры 135, 169
Аналог вертикальной скорости 54, 139
Аппроксимация производных 342
Бароклинность 24
Баротропность 24, 126, 128
Векторные операции 353
Вертикальная скорость 13, 54, 139
Вихрь скорости 13, 14, 63
Волны в атмосфере 87
— акустические (звуковые) 89, 105
— гравитационные 88, 97, 105
----внешние 100, 102
----внутренние 102, 105, 111
— двумерные 106, ПО
крупномасштабные (Россби) 88, 94
Вычислительная неустойчивость 349
— схема неявная 173, 178, 348
----полунеявная 173, 181
----явная 172, 173, 347
Геострофический ветер 51, 121
Гистограмма 359
Дивергенция скорости 64
Естественные составляющие 149, 269
Изотропность метеорологических полей 19, 292
Индекс циркуляции 224, 232
375
Инициализация 208
Итерационный метод 132, 148, 346
Картографические проекции 71
Квазигеострофическое приближение 51, 121, 122
Квазисоленоидальное приближение 121, 122, 151, 152, 225
Квазистатическое приближение 52, 121
Ковариационные функции 291, 361
Конвекция 218
Конденсация 25
Корреляционные функции 291, 361
----пространственно-временные 308
Коэффициент корреляции 361
Кроссковариационные функции 361
Линеаризация 89, 225
Масштабный множитель 72
Метод множественной линейной регрессии 368
Метод полиномиальной интерполяции 284
— последовательных приближений 298
— оптимальной интерполяции 291
Метод статистического прогноза:
Багрова Н. А. и Зверева Н. И. 268
Багрова Н. А., Стеблянко В. А. 269
Батыревой О. В. 275
Белова П. Н. 262, 263
Борисенкова Е. П. 264
Борисенковой Т. П. 275
Васюкова К. А., Зверева Н. И., Педя Д. А. 265
Каца А. Л. 265
осадков 276
Модель общей циркуляции атмосферы:
Касахары А. и Вашингтона У. М. 256
Минца Е. и др. 256
Смагоринского Дж. и др. 250
Неадиабатические факторы 25, 31, 43, 160, 200
Неоднородность метеорологических полей 19
Неявная вычислительная схема 113, 178, 348
Обтекание препятствий 216
Объективный анализ 282
Однородность метеорологических полей 292
Оператор Лапласа (лапласиан) 31, 79, 80, 132, 342
— Якоби (якобиан) 79
Оценка качества прогнозов 278
Параметр Кибеля И. А. 124
— конвекции (плавучести) 215
376
— Кориолиса 23
— стратификации 42
— Россби 42, 94
—увеличения 72
Параметризация 94
Первичная обработка метеорологической информации 310
Пограничный слой 32
Политропический процесс 25
Полные уравнения гидротермодинамики 62, 165, 166, 242
Полунеявная вычислительная схема 181
Порядок величин 12
Приток тепла радиационный 49, 163, 200, 243
---турбулентный 25, 31, 161, 200, 230, 243
---фазовый 25, 161
Прогностическая модель атмосферы агеострофическая 154
------бароклинная 134, 166, 184, 190, 230. 236
------баротропная 84, 126, 172, 178, 234
------без дивергентная 127, 234
------квазигеострофическая 121
------квазисоленоидальная 151, 236
------малопараметрическая 149
------неадиабатическая 160, 200, 230, 242
Прогностическая модель атмосферы:
Белова П. Н. 146
Белоусова С. Л. 144
Берковича Л. В. 181
Блиновой Е. Н. 223, 230, 234, 236, 242
Бортникова С. А. 184
Булеева Н. И. и Марчука Г. И. 135
Бушби Ф. и Тимпсон М. 194
Кадышникова В. М. 187
Кибеля И. А. 122, 134, 168
Марчука Г. И. 194
Машковича С. А. 149
Машковича С. А., Вейль И. Г. 247
Мерцалова А. Н. 145
Шумана Ф. Г. и Ховермейла Дж. Б. (НМЦ США) 191
Прессмана Д. Я. 177, 193
Руховца Л. В. 149
Фукс-Рабиновича М. С. 176
Фукс-Рабиновича М. С. и Кричака С. О. 193
Цквитинидзе 3. И. 178
Шумана Ф. Г. 175
Юдина М. И. 154
Радиационный баланс 202
Ряды Фурье 364
— по полиномам Чебышева 267
— по сферическим функциям 228
Сглаживание 133
Согласование метеорологических полей 208
Спектр электромагнитных волн 43
Спектральная плотность 11, 363, 365
Спектральный метод решения прогностических уравнений 223
Средний уровень в атмосфере 127
Стандартная атмосфера 330
377
Структурная функция 361
Сублимация 25
Сферические функции 228
Тепловой баланс 202
Теплота испарения 25
- конденсации 25
Теории конвекции упрощения 213
Точность измерения метеорологических элементов 6.8
Уравнение баланса 66
---кинетической энергии турбулентных пульсаций 39
— вихря скорости 63, 69, 126
— Гельмгольца 128, 343
— дивергенции скорости 64
— неразрывности 23, 57
— переноса (притока) влаги 26, 158
— притока тепла 24
— Пуассона 128, 344
-состояния (Клапейрона) 24
— статики 51
Уравнения гидротермодипамики 21
---в изобарической системе координат 54
---в сферической системе координат 66
---в дивергентной форме 59
---мезопроцессов 212
Уравнения движения 21
— - осредненные 26
— переноса лучистой энергии 43
Фильтрованные уравнения 105
Формула Планка 44
• —Магнуса 157
— Россби 42, 94
Функции влияния (Грина) 118, 128, 139, 141, 236, 241
— пропускания 48
Частота, частость 359
Четырехмерный численный анализ 305
Численный анализ 282
Эмпирические функции влияния 260
Явная вычислительная схема 172, 173, 347
378
СПИСОК ЛИТЕРАТУРЫ
Учебники, учебные пособия и монографии, которые могут быть использованы
в качестве учебных пособий [У]
1. Белинский В. А. Динамическая метеорология. Л., Гидрометеоиздат, 1948,
703 с.
2. Белов И. И. Практические методы численного прогноза погоды. Л., Гид-
рометеоиздат, 1967, 335 с.
3. Белоусов С. Л., Гандин Л. С., Машкович С. А Обработка опе-
ративной метеорологической информации с помощью электронно-вычислитель-
ных машин. Л., Гидрометеоиздат, 1968. 280 с.
4. Березин И. С., Жидков Н. П. Методы вычислений. Т. 1. М., Физмат-
гиз, 1962, 464 с.
5. Г а н д и н Л. С. Объективный анализ метеорологических полей. Л., Гидро-
метеоиздат, 1963. 287 с.
6. Г а н д и н Л. С., Дубов А. С. Численные методы краткосрочного прог-
ноза погоды. Л., Гидрометеоиздат, 1968. 427 с.
7. Г а н д и н Л. С., Лайхтман Д. Л., Матвеев Л. Т., Ю д и н М. И
Основы динамической метеорологии. Л., Гидрометеоиздат, 1955. 647 с.
8. Гутман Л. Н. Введение в нелинейную теорию мезометеорологических про-
цессов. Л., Гидрометеоиздат, 1969, 293 с.
9. Демидович Б. П., Марон И. А., Шувалова Э. 3. Численные
методы анализа. АГ, «Наука», 1967. 386 с.
10. Динамическая метеорология. Под ред. Б. И. И з в е к о в а и Н. Е. К о ч и н а.
Ч. 1. М.—Л., Редиздат ЦУБГМС, 1935. 351 с. Ч. 2. М—Л., Гидрометеоиздат,
1937. 279 с.
11. Зилитинкевич С. С. Динамика пограничного слоя атмосферы. Л., Гид-
рометеоиздат, 1970. 291 с.
12. Кибель И. А. Введение в гидродинамические методы краткосрочного прог-
ноза погоды. Изд-во технико-теоретической литературы, 1957. 375 с.
13. Коч ин Н. Е., Кибель И. А., Розе Н. Е. Теоретическая гидромехани-
ка. Ч. 1. Изд. 6, М., Изд-во физико-математической литературы, 1963. 583 с.
14. К о н д р а т ь е в К. Я- Актинометрия. Л., Гидрометеоиздат, 1965. 691 с.
15. Л а й х т м а н Д. Л. Физика пограничного слоя атмосферы. Изд. 2-е, Л., Гидро-
метеоиздат, 1970. 341 с.
16. Лекции по численным методам краткосрочного прогноза погоды. Л., Гидро-
метеоиздат, 1969. 734 с.
17. Марчук Г. И. Численные методы в прогнозе погоды. Л., Гидрометеоиздат.
1967. 356 с.
18. М о н и н А. С. Прогноз погоды как задача физики. М., «Наука», 1969. 184 с.
19. Пановский Г. А., Брайер Г. В. Статистические методы в метеоро-
логии. Л., Гидрометеоиздат, 1967. 242 с.
20. Смирнов Н. В., Дунин-Барковский И. В. Курс теории вероят-
ностей и математической статистики для технических приложений. М., «Наука»,
1965, 511 с.
21. Томпсон Ф. Д. Анализ и предсказание погоды численными методами. М.,
Изд-во иностр, лит., 1962. 239 с.
22. Ю д и н М. И. Новые методы и проблемы краткосрочного прогноза погоды.
Л., Гидрометеоиздат, 1963. 404 с.
23. Haltiner G. J. Numerical weather predic’ion. 1971. 317 p
379
К главе I
1. Аэроклиматический атлас северного полушария. Л., Гидрометеоиздат, 1963.
213 с.
2. Б е л о в П. Н. Краткосрочный прогноз полей давления с применением элек-
тронной счетной машины «Погода».— «Труды ЦИП», 1959, вып. 86, с. 3—41.
3. Беляева В. Н., Мерцалова О. Б., Пашкова 3. Д. Об исполь-
зовании среднего квадратического отклонения температуры и высоты изобари-
ческой поверхности в аэроклиматологии.— «Труды НИИАК», 1962, вып. 16,
с. 20—27.
4. Г л а г о л е в Ю. А. Справочник по физическим параметрам атмосферы. Л.,
Гидрометеоиздат, 1970. 211 с.
5. Девятова В. А. и др. Исследование пульсаций горизонтальной составляю-
щей скорости ветра до высоты 5 километров.— «Труды ЦАО», 1958, вып. 21,
с. 52—120.
6. Заставенко Л. Г. Барическое поле тропосферы северного полушария.
М., Гидрометеоиздат, 1972. 237 с.
7. К о л е с н и к о в а В. Н., Монин А. С. О спектрах микрометеорологиче-
ских, синоптических и климатических колебаний метеорологических полей. Ме-
теорологические исследования. М., «Наука», 1968, с. 30—57.
8. М а р ф е н к о О. В. Оценка точности результатов радиозондирования на
аэрологической сети Советского Союза.— «Метеорол. и гидрол.», 1969, № 3,
с. 14—21.
9. Мерцалова О. Б. Стандартизация вертикальных корреляционных связей
давления.— «Труды НИИАК», 1972, вып. 79, с. 37—53.
10. Наблюдения на гидрометеорологической сети СССР. Определение понятий
гидрометеорологических элементов и оценка точности наблюдений. Л., Гидро-
метеоиздат, 1970. 71 с.
11. Стехновский Д. И. Барическое поле земного шара. Л., Гидрометеоиз-
дат, 1962. 147 с.
12. Таблица стандартной атмосферы. ГОСТ 4401-64. М., Изд-во стандартов, 1964.
43 с.
К главе II
1 Блинова Е. Н. Гидродинамическая теория волн давления, температурных
волн и центров действия атмосферы.— «ДАН СССР», 1943, т. 7, с. 284—287.
2. Бобылева И. М., Зилитинкевич С. С., Лайхтман Д. Л. Тур-
булентный режим в термически стратифицированном планетарном пограничном
слое атмосферы.— В сб.: Атмосферная турбулентность и распространение ра-
диоволн (Труды международного коллоквиума, Москва 15—22 июня 1965). М.,
«Наука», с. 179—190.
3. Г р а у р А. В. Математическая картография. Изд. 2. Изд-во МГУ, 1956,
372 с.
4. Хинкельман К. Г. Полные уравнения.— В кн.: Лекции по численным
методам краткосрочного прогноза погоды. Л., Гидрометеоиздат, 1969, с. 317
390.
5. Фейгельсон Е. М. Лучистый теплообмен и облака Л., Гидрометеоиздат,
1970. 230 с.
К г л а в е III
1. Дикий Л. А. Об акустических и гравитационных колебаниях в атмо-
сфере.— «Изв. АН СССР», сер геофиз., 1959, № 8, с. 1186—1194.
2. К и б е л ь И. А. О приспособлении движения к геострофическому.— «ДАН
СССР», 1955, т. 104, № 1, с. 60—63.
3. М о н и н А. С. Изменения давления в бароклинной атмосфере.— «Изв. АН
СССР», сер. геофиз., 1958, № 4, с. 497—513.
380
4. М о н и н А. С., Обухов А. М. Малые колебания атмосферы и адаптация
метеорологических полей.— «Изв. АН СССР», сер. геофиз., 1958, № 11, с. 1360—
1373.
5. О б у х о в А. М. К вопросу о геострофическом ветре.— «Изв. АН СССР»,,
сер. геогр. и геофиз., 1949, т. 13, № 4, с. 281—306.
К г л а в е IV
1. Багров А. Н. Оперативная численная схема прогноза конвективных явле-
ний (кучевообразной облачности, ливней, гроз и шквалов) и обложных осад-
ков.— «Труды ГМЦ», 1972, вып. 91, с. 25—46.
2. Б е л о в П. Н. Численный прогноз барического поля по трехуровенной мо-
дели атмосферы.— «Труды ЦИП», 1961, вып. 111, с. 29—38.
3. Б е л о в П. Н. Сравнение точности численных прогнозов, рассчитанных по-
бароклинной и баротропной схемам.— «Метеорол. и гидрол.», 1963, № 7, с. 40—42.
4. Б е л о в И. Н., К и в г а н о в А. Ф. Об изменениях температуры и геопо-
тенциала, обусловленных радиационным притоком тепла.— «Труды ММЦ», 1965,
вып. 8, с. 55—67.
5. Белоусов С. Л. Краткосрочный прогноз давления с помощью быстродей-
ствующих вычислительных машин.— «Труды ЦИП», 1957, вып. 60, с. 10—16.
6. Б е л о у с о в С. Л. Многоуровенные квазигеострофические модели прогноза.
В кн.: Лекции по численным методам прогноза погоды. Л., Гидрометеоиздат,
1969, с. 294—316.
7. Булеев Н. И. иМарчук Г. И. О динамике крупномасштабных атмо-
сферных процессов.— «Труды ИФА», 1958, № 2, с. 66—104 (работа выполнена
в 1951 г.).
8. Булеев Н. И., Марчук Г. И. Влияние приземного трения на эволюцию
метеорологических элементов в свободной атмосфере. В сб.: Вопросы динамиче-
ской метеорологии, М., Изд. АН СССР, 1960, с. 55—66 (работа выполнена
в 1951 г.).
9. Б у р ц е в А. И. Метод расчета вертикальных скоростей воздуха при учете
изменения вертикального градиента температуры с высотой.— «Труды ЦИП»,
1958, вып. 77, с. 82—102.
10. Бурцев А. И. Схема численного прогноза ветра и геопотенциала в ниж-
ней половине тропосферы.— «Труды ЦИП», 1961, вып. 100, с. 32—41.
11. Бурцев А. И., Ветлов И. П. Схема численного прогноза ветра в сво-
бодной атмосфере.— «Метеорол. и гидрол.», 1962, № 11, с. 4—11.
12. Быков В. В. Об уравнениях динамики атмосферы при гипотезе квазисоле-
ноидальности.— «Метеорол. и гидрол.», 1956, № 11, с. 8—14.
13. Быков В. В. Об учете отклонения ветра от геострофического в кратко-
срочном прогнозе.— «Изв. АН СССР», сер. геофиз., 1962, № 3, с. 418—423.
14. Вейль И. Г. Гидродинамические схемы краткосрочного прогноза погоды.—
«Труды ГМЦ», 1973, вып. 124. 119 с.
15. Дубов А. С. Об учете приземного трения при прогнозе давления у Земли.—
«Труды ГГО», 1957, вып. 71, с. 66—71.
16. Душкин П. К., Ломоносов Е. Г. Результаты прогнозов барического
поля на трех уровнях с помощью вычислительной машины.— «Труды ЦИП»,
1960, вып. 106, с. 20—31.
17. Ильин Б. М. Об одной схеме прогноза поля давления у Земли.— «Труды
ГГО», 1968, вып. 226, с. 89—97.
18. К и бель И. А. Приложение к метеорологии уравнений механики бароклин-
ной жидкости.— «Изв. АН СССР», сер. геогр. и геофиз., 1940, № 5, с. 627—638.
19. К и б е л ь И. А., С а д о к о в В. П. О краткосрочном прогнозе погоды в не-
адиабатических случаях. В кн.: Некоторые проблемы метеорологии. М., Изд.
АН СССР, 1960, с. 7—12.
20. Л о м о н о с о в Е. Г. К использованию функций влияния при гидродинами-
ческом прогнозе погоды. В сб.: Материалы совещания координационной комис-
сии по численным прогнозам. Л., Гидрометеоиздат, 1961, с. 44—52.
381
21. Л у тф ул ин И. 3. Новые методы предвычисления метеорологических по-
лей. Л., Гидрометеоиздат, 1966. 196 с.
22. М а р ч у к Г. И. и др. Оперативная квазигеострофическая схема краткосроч-
ного прогноза для пяти уровней атмосферы.— «Изв. АН СССР», Физика атмо-
сферы и океана, 1965, т. 1, № 2, с. 129—135.
23. М а ш к о в и ч С. А. Прогноз наземного давления с помощью быстродейст-
вующих электронных вычислительных машин - «Метеорол. и гидрол.», 1957,
№ 1, с. 8—18.
24. М е р ц а л о в А. Н. К прогнозу барического поля в нижнем слое атмосфе-
ры.— «Труды ГМЦ», 1969, вып. 57, с. 3—30.
25. Монин А. С. Изменение давления в бароклинной атмосфере.— «Изв. АН
СССР», сер. геофиз., 1958, № 4, с. 497—514.
26. О б у х о в А. М К вопросу о геострофическом ветре.— «Изв. АН СССР»,
сер. геогр. и геофиз., 1949, № 4, с. 281—306.
27. Пятыгина К В. Агеострофическая модель прогноза полей метеорологиче-
ских элементов на большом числе уровней.- В кн.: Труды симпозиума по чис-
ленным методам прогноза погоды. Л., Гидрометеоиздат, 1964, с. 132—142.
28. Руховец Л. В. Оптимальная малопараметрическая модель прогноза поля
геопотенциала па большом числе уровней.— В кн.: Труды симпозиума по чис-
ленным методам прогноза погоды. Л., Гидрометеоиздат, 1964, с. 98—115.
29. Сит н и к о в И. Г., К р и ч а к С. О. Опыт численного решения уравнения
баланса в рамках квазисоленоидальной схемы прогноза геопотенциала на север-
ном полушарии «Труды ГМЦ», 1968, вып. 19, с. 22—30.
30. Успенски й Б. Д. Количественный прогноз обложных и ливневых осад-
ков. -«Метеорол. и гидрол.», 1970, № 1, с. 11 -18.
31. Фукс-Рабинович М. С. Соленоидальная баротропная прогностическая
модель с учетом диффузионных эффектов.— «Труды ГМЦ», 1970, вып. 54,
с. 51—55.
32. Ш в е ц М. Е., Шпееров Б. Е. Об использовании результатов радиацион-
ных измерений со спутников в модели крупномасштабных атмосферных дви-
жений.— «Труды ГГО», 1964, вып. 166, с. 173—181.
33. Bergthorsson Р. е. a. Routine forecasting with the barotropic model.—
“Tellus”, 1955, vol. 7, N 2, p. 272—274.
34. Bolin B. An improved barotropic model and some aspects of using the
balance equation of three-dimensional flow.— “Tellus”, 1956, vol. 8, N 1, p. 61—
75.
35. Charney J. G.. Phillips N. A. Numerical integration of the quasigeo-
strophic equation for barotropic and simple baroclinic flows.— “Journ. Meteor.”,
1953, vol. 10, N 2, p. 71—99.
36. H a 11 i n e r G. J Numerical weather prediction, 1971. 317 p.
37. H i n k e 1 m a n n K. Zur numerischen Wettervorhersage mittels Relaxations-
methode unter Einbeziehung barokliner Effekten.— “Tellus”, 1953, vol. 5, N 3,
p. 251—259, N 4, p. 499—512.
38. S a i t о N. The results of numerical forecasting with the 4-level baroclinic
model. Proc, of the International Symposium on Numerical Weather Prediction
in Tokyo, 1960. Meteorological Society of Japan, 1962, p. 35—46.
К главе V
1. Белов П. Н. и др. Эксперименты по учету радиационного притока тепла
в численном прогнозе- «Труды ГМЦ», 1971, вып. 89, с. 120—131.
2. Б е л о в П. Н., Беркович Л. В. Исследование влияния притоков тепла
на формирование приземного и высотных барических полей северного полуша-
рия.— «Метеорол. и гидрол.», 1973, № 3, с. 22—32.
3. Беркович Л. В. Шестиуровенная схема прогноза метеоэлементов по пол-
ным уравнениям для большой территории. «Труды ГМЦ», 1972, вып. 100,
с. 108—115.
4. Беркович Л. В., Катаев В. В., Фукс-Рабинович М. С. Об учете
стратифицированного пограничного слоя атмосферы в схемах численного прог-
ноза метеорологических элементов. «Труды ГМЦ», 1972, вып 103, с. 42- 50.
382
5. Бортников С. А. Построение многоуровенной прогностической модели на
основе опыта оперативного краткосрочного прогноза по полным уравнениям для
двух уровней атмосферы.— «Труды ГМЦ», 1968, вып. 16, с. 21—32.
6. Б у л е е в Н. И., Марчук Г. И. Некоторые вопросы теории краткосроч-
ного прогноза полей метеорологических элементов.— В кн.: Труды Всесоюзного
научного метеорологического совещания, т. 11, 1963. с. 12—20.
7. Б у р ц е в А. И. О предвычислении ветра и температуры.— «Труды ММЦ»,
1965, вып. 6, с. 41—45.
8. Быков В. В. Некоторые результаты расчета прогностических значений гео-
потенциала.— «Труды ММЦ», 1965, вып. 6, с. 19—24.
9. Б ы к о в В. В., Бортников С. А., Кадыш ников В. Н. Опыт опе-
ративного краткосрочного прогноза погоды с помощью полных уравнений гид-
родинамики.— «Метеорол. и гидрол.», 1971, № 8, с. 3—14.
10. Вейль И. Г. Гидродинамические схемы краткосрочного прогноза погоды.—
«Труды ГМЦ», 1973, вып. 124, 119 с.
11 Дымников В. П и др. Неадиабатическая оперативная схема краткосроч-
ного прогноза погоды.— «Труды ГГО», 1972, вып. 272, с. 15—23.
12. Кадышников В. М. Псевдоадиабатическая модель обложных осадков
в краткосрочном прогнозе погоды.— «Метеорол. и гидрол.», 1968, № 12, с. 33—40.
13. Кадышников В. М. Использование направленных разностей в численном
решении задачи краткосрочного прогноза погоды.— «Труды ГМЦ», 1970, вып. 48,
с. 34—51.
14. Кибель И. А. Способ краткосрочного прогноза метеорологических элемен-
тов—«ДАН СССР», 1958, т. 118, № 4, с. 687—690.
15. Кибель И. А. Конечно-разностная схема решения системы уравнений крат-
косрочного прогноза погоды и соотношения квазигеострофичности.— «ДАН
СССР», 1960, т. 132, № 2, с. 319—322.
16. Кибель И. А. Сведение системы дифференциальных уравнений, исполь-
зуемых при краткосрочном прогнозе погоды, к системе алгебраических уравне-
ний,— «ДАН СССР», 1962, т. 143, № 6, с. 1336—1339.
17. Кибель И. А. Гидродинамический (численный) краткосрочны?! прогноз по-
годы.— В сб.: Механика в СССР за 50 лет. Т. 2, М., 1970, с. 561-—583
18. Крич а к С. О., Фукс-Рабинович М. С. Бароклинная модель прог-
ноза по полным уравнениям гидротермодинамики для внетропических широт
северного полушария с учетом процессов влагообмена.— «Метеорол. и гидрол.»,.
1972, № 1, с. 26—36.
19. Марчук Г. И., Контарев Г Р., Ривин Г С. Краткосрочный прог-
ноз погоды по полным уравнениям на ограниченной территории.— «Изв. АН
СССР», Физика атмосферы и океана, 1967, т. 3, № 11, с. 1166—1178.
20. Н е м ч и н о в С. В., Сад ок о в В. П. Построение устойчивой по началь-
ным данным схемы расчетов для прогноза метеорологических элементов на
основе решения полных уравнений термогидродннамики.— Труды ВНМС, т 2,
1963, с. 80—91.
21. Прессман Д. Я- Об одной разностной схеме краткосрочного прогноза
погоды.— «Труды ММЦ», 1965, вып. 6, с. 33—40.
22. П р е с с м а н Д. Я- Шестиуровенная схема краткосрочного прогноза погоды
по полным уравнениям.— В кн.: Труды Всесоюзной конференции молодых уче-
ных Гидрометслужбы СССР. Л., Гидрометеоиздат. 1971, с. 12—20.
23. Федорова Н. Г., Фукс-Рабинович М. С. О динамическом согласо-
вании исходных полей для моделей по полным уравнениям гидротермодина-
мики.— «Метеорол. и гидрол», 1972, № 5, с. 3—11.
24. Фукс-Рабинович М. С. Об оценке влияния точности исходной инфор-
мации на прогноз геопотенциала и скорости ветра с использованием примитив-
ной баротропной модели атмосферы.— «Труды ГМЦ», 1970, вып. 71, с. 98—108.
25. Ц к в и т и н и д з е 3. И. К численному прогнозу геопотенциала и ветра.—
«Метеорол. и гидрол.», 1969, № 2, с. 37—43.
26 Численные методы решения задач динамики атмосферы и океана. Перев.
с англ. Л. Гидрометеоиздат, 1968, 367 с.
27. В u s h b у F. Н. and Timpson М. S. A 10-level atmospheric model and
frontal rain.— “Quar. J. of the Royal Meteorological Society”, 1967, vol. 93,
N 395, p. 1—17.
383
-28. Charney J. G. The use of the primitive equations of motion in numerical
prediction.— “Tellus”, 1955, vol. 7, N 1, p. 22—26.
29. Charney J. G. Integration of the primitive and balance equations. Proc, of
the Intern. Symp. on Numerical Wea. Prediction in Tokyo, 1960. Met. Soc. of
Japan. 1962, p. 131—152.
30. H i n к e 1 m a n n K. Ein numerisches Experiment mit den primitiven Gleichun-
gen. The atmosphere and sea in motion. Rossby Memorial volume. The Rockfeller
Inst. Pres. New York, 1959, p. 486—500.
31. Nitta T. and Hovermale J. B. A technique of objective analysis and
initialization for the primitive forecast equations.— “Monthly Weather Review”,
1969, vol. 97, N 9, p. 652—658.
32. P h i 11 i p s N. A. Numerical integration of the primitive equations on the
hemisphere.—“Monthly Weather Review”, 1959, vol. 87, N 9, p. 333—345.
33. Reiser H. Baroclinic forecasts with the primitive equations. Proc. Intern.
Symp. on Numerical Wea. Prediction in Tokyo. 1960, Met. Soc. of Japan, 1962,
p. 77—84.
34. S h u m a n F. G. Numerical experiments with the primitive equations. Proc.
Intern. Symp. on Numerical Wea. Prediction in Tokyo. 1960. Met. Soc. of Japan,
1962, p. 85—107.
35. Shuman F. G. and Hovermale J. B. An operational six layer primitive
equation model.— “J. Appl. Met.”, 1968, N 7, p. 525—547.
36. Smagorinsky J. On the numerical integration of the primitive equations
of motion for baroclinic flow in a closed region.— “Mon. Wea. Rev.”, 1958,
vol. 86, N 12, p. 457—466.
К главе VI
1. Быков В. В., П е к е л и с Е. М., Шершков В. В О требованиях к ме-
теорологической информации для численного решения задач мезометеороло-
гии.— «Труды ГМЦ», 1972, вып. 99, с. 72—79.
2 Вельтищев Н. Ф Ячейковая конвекция в поле вихря скорости.— «Труды
ГМЦ», 1971, вып. 73, с. 3—16.
3. Использование данных о мезомасштабных особенностях облачности в анализе
погоды. Под ред. Н. Ф Вельтищева. Л., Гидрометеоиздат, 1973. 150 с.
4. К и б е л ь И. А Некоторые новые задачи гидродинамического краткосрочного
прогноза погоды.— «Труды ГМЦ», 1964, вып. 3, с. 3—18.
5. К и бель И. А. Гидродинамический краткосрочный прогноз в задачах мезо-
метеорологии.— «Труды ГМЦ», 1970, вып. 48, с. 3—33.
<6. П е к е л и с Е. М. Численное решение пространственной нелинейной задачи
обтекания препятствия воздушным потоком.— «Труды ММЦ», 1966, вып. 14,
с. 36—47.
7. Ш е р ш к о в В. В. Пространственная задача о вынужденной конвекции в по-
граничном слое атмосферы.— «Метеорол. и гидрол.», 1971, № 1, с. 22—31.
К главе VII
1. Белоусов С. Л. К прогнозу геопотенциала на северном полушарии в слу-
чае бароклинной атмосферы.— «Труды ЦИП», 1960, вып. 93, с. 25—34.
2. Б л и н о в а Е. Н. Гидродинамическая теория волн давления, температурных
волн и центров действия атмосферы.— «ДАН СССР», 1943, т. 39, № 7, с. 284—
287.
3. Б л и н о в а Е. Н. Опыт долгосрочного прогноза погоды при помощи гидро-
динамики.— «Труды ГМЦ», 1973, вып. 86, с. 63—79 (работа выполнена в 1946 г.).
4. Б л и н о в а Е. Н. К вопросу о среднем годовом распределении температуры
в земной атмосфере с учетом материков и океанов.— «Изв. АН СССР», сер.
геогр. и геофиз., 1947, т. 11, № 1, с. 3—14.
5. Б л и н о в а Е. Н. К вопросу об определении давления на уровне моря.—
«ДАН СССР», 1953, т. 92, № 3, с. 557—560.
6. Б л и н о в а Е. Н. Метод решения нелинейной задачи об атмосферных дви-
жениях планетарного масштаба.— «ДАН СССР», 1956, т. 111, № 6, с. 975—977.
7. Блинова Е. Н. Гидродинамический прогноз средних месячных аномалий
384
температуры для северного полушария Земли с использованием данных Меж-
дународного геофизического года.— «ДАН СССР», 1960, т. 131, № 2, с. 293—296.
8. Б л и н о в а Е. Н. Гидродинамические исследования нестационарных атмо-
сферных процессов планетарного масштаба.— «ДАН СССР», 1961, т. 140, № 2,
с. 354—357.
9. Блинова Е. Н. Гидродинамическая теория климата и долгосрочного прог-
ноза погоды.— «ДАН СССР», 1961, т. 140, № 3, с. 571—574.
10. Блинова Е. Н. Трехмерная задача о прогнозе сглаженных значений ме-
теорологических элементов.— «ДАН СССР», 1962, т. 147, № 6, с. 1355—1358.
11. Блинова Е. Н. К гидродинамической теории климата и долгосрочного*
прогноза погоды. В кн.: Гидродинамический долгосрочный прогноз погоды. М.,.
«Наука», 1964, с. 5—18.
12. Блинова Е. Н. Динамика атмосферных движений планетарного масштаба
и гидродинамический долгосрочный прогноз погоды.— «Труды ГМЦ», 1967,
вып. 15, с. 3—25.
13. Блинова Е. Н. Метод решения нелинейной планетарной задачи долго-
срочного прогноза метеорологических элементов.— «Труды ГМЦ», 1968, вып. 31,
с. 3—25.
14. Б л и н о в а Е. Н. Научно-исследовательская и оперативная работа по гидро-
динамическому долгосрочному прогнозу погоды.— «Труды ГМЦ», 1973, вып. 86,
с. 3—8.
15. Б л и н о в а Е. Н., Белоусов С. Л. Нелинейная нестационарная задача
определения полей давления планетарного масштаба на среднем уровне атмо-
сферы.— «ДАН СССР», 1958, т. 120, № 2, с. 281—284.
16. Галин М. Б. Гидродинамический прогноз малой заблаговременности с по-
мощью линейной теории.— «Труды ММЦ», 1964, вып. 2, с. 21—32.
17. Курбаткин Г. П. Двухуровенная схема прогноза геопотенциала и верти-
кальных токов (малой заблаговременности). В кн.: Гидродинамический долго-
срочный прогноз погоды. М., «Наука»; 1964, с. 19—41.
18. Марчук Г. И. Теоретическая модель прогноза погоды малой заблаговре-
менности.— «Изв. АН СССР», сер. геофиз., 1964, № 5, с. 754—764.
19. Марчук Г. И., Курбаткин Г. П., Цветков В. И. Численная модель
глобальной циркуляции атмосферы. В кн.: Численные методы решения задач
прогноза погоды и общей циркуляции атмосферы. Новосибирск, 1970, с. 98—
142.
20. Ма шкович С. А., Блинкова Е. Д. О воспроизведении климатического
распределения метеорологических элементов на основе неадиабатической спект-
ральной модели атмосферы.— «Меторол. и гидрол.», 1972, № 8, с. 3—14.
21. Машкович С. А., Вейль И. Г. О прогнозе на средние сроки крупно-
масштабных компонентов циркуляции на основе нелинейной спектральной мо-
дели.— В сб.: Труды V Всесоюзного метеорологического съезда. Т. 2. Л., Гидро-
метеоиздат, 1972, с. 42—54.
22. Машкович С. А., Хейфец Я- М. Опыт численного прогноза наземного
давления на несколько дней вперед.— «Труды ЦИП», 1963, вып. 126, с. 8—19.
23. Минц Е. Интегрирование полных уравнений движения атмосферы на про-
должительный срок для всего земного шара.— В кн.: Теория климата. Пер.
с англ. Л., Гидрометеоиздат, 1967, с. 230—257
24. Мусаелян Ш. А. О прогнозе влажности.— В кн.: Гидродинамический дол-
госрочный прогноз погоды. М., «Наука», 1964, с. 62—74.
25. Смагоринский Дж., Манабе С., Холлоуэй Дж. Л. Результаты
численных опытов с девятиуровенной моделью общей циркуляции атмосферы.—
В кн.: Теория климата. Пер. с англ. Л., Гидрометеоиздат, 1967, с. 117—184.
26. Филлипс Н. А. Общая циркуляция атмосферы: численный эксперимент.—
В кн.: Теория климата. Пер. с англ. Л., Гидрометеоиздат, 1967, с. 6—60
27. Ш в е ц М. Е. и др. Численная модель общей циркуляции атмосферы на по-
лушарии.— «Труды ГГО», 1970, вып. 256, с. 3—44.
28. А г a k a u a A., Katayama A. and Mintz Y. Numerical simulation of the
general circulation of the atmosphere. Proc. WMO/IUGG Symp. on Numerical
Wea. Prediction in Tokyo, 1968, Japan Met. Agency, Tokyo, 1969. p. IV—7—IV—
8—11.
25 Заказ № 21
385
29. К a s a h a r a A. and Washington W. M. NCAR global general circula-
tion model of the atmosphere.— “Mon. Wea. Rev.”, 1967, vol. 95, N 7, p. 389—
402.
30. К a s a h a r a A. and Washington W. M. General circulation experiments
with a six-layer NCAR model, including orography, cloudiness and surface tem-
perature calculations.— “J. Atmos. Sci.”, 1971, vol. 28, N 5, p. 657—701.
31. Mi ya ko da K. e. a. Experimental extended predictions with a nine-level he-
mispheric model.—“Mon. Wea. Rev.”, 1969, vol. 97, N 1, p. 1—76.
К главе VIII
1. Багров H. А. Аналитическое представление последовательности метеоро-
логических полей посредством естественных ортогональных составляющих.—
«Труды ЦИП», 1959, вып. 74, с. 3—24.
2. Б а г р о в Н. А., Зверев Н. 14. Способ прогноза геопотенциала Н5Оо на
средние сроки.—«Труды ЦИП», 1961, вып. 108, с. 3—22.
3. Багров Н. А., Стебля нко В. А. О прогнозе поля Н500 на полушарии.—
«Метеорол. и гидрол.», 1969, № 11, с. 27—35.
4. Б а т ы р е в а О. В. Статистический прогноз приземного давления на 1, 3,
5 дней.— «Метеорол. и гидрол.», 1969, № 7, с. 56—63.
5. Б е л о в П. Н. Прогноз атмосферного давления с помощью эмпирических
функций влияния.— «Метеорол. и гидрол.», 1958, № 2, с. 10—16.
6. Белов П. Н. Использование эмпирических функций влияния для прогноза
погоды в одном пункте.— «Труды ЦИП», 1961, вып. 111, с. 44—49.
7. Б о р и с е и к о в Е. П. Физико-статистические методы анализа и предвычи-
сления метеорологических полей.— «Труды ААНИИ», 1963, т. 263. 243 с.
^8 . Борисенков Е. П и Борисова Л. Е. Физико-статистическая схема
предвычисления средних месячных аномалий температуры воздуха на полуша-
рии. Труды ААНИИ, 1967, т. 275, с. 310—318.
9. Б о р и с е п к о в Е. П , Романов М. А. Алгоритмы и программы стати-
стической обработки информации на ЭВМ. Л., Гидрометеоиздат, 1969. 354 с.
10. Борисенкова Т. П. Статистическая схема прогноза малой заблаговре-
менности, учитывающая историю процесса.— В кн.: Анализ и прогноз погоды.
Труды Всесоюзной конференции молодых ученых Гидрометслужбы СССР, Л.,
1971. с. 118—126.
11. Васюков К. А., Зверев И. И.. Педь Д. А. О прогнозе аномалии
средней месячной температуры воздуха с 10-дневной заблаговременностью.
Труды ЦИП, 1966, вып. 147, с. 3- 9.
12. Груза Г. В. Опыт применения статистических главных компонентов (есте-
ственных ортогональных составляющих) в технике корреляционного анализа.
Труды САНИГМИ, 1969. вып. 40 (55), с. 19—36.
13. Груза Г. В. Адаптивные системы статистического анализа и прогноза по-
годы в метеорологии.— В кн.: Применение статистических методов в метеороло-
гии. Л., Гидрометеоиздат, 1971, с. 4—11.
14. Еса ков а Н П., Афанасьева В. Б., Титов В. М Статистическая
схема прогноза средних декадных температур с учетом данных о радиацион-
ных потоках, облачности, ледовитости и снежного покрова. Труды ГГО, 1968,
вып. 201, с. 8—13.
15. Зверев Н. И. Применение статистики в предсказании погоды. Труды ГМЦ,
1970, вып. 66, 195 с.
16. Кац А. Л. Опыт построения синоптико-статистической методики прогноза
декадной аномалии температуры.— «Метеорол. и гидрол.», 1965, № 5, с. 14—22.
v17. Кац А. Л. Схема синоптико-гидродинамико-статистического прогноза по-
годы за 3—10 дней.— «Метеорол. и гидрол.», 1973, № 6, с. 15—25.
18. Кац А. Л. и др. Модель численного прогноза осадков на пять дней — «Ме-
теорол. и гидрол.», 1970, № 10, с. 11—22.
19. Мещерская А. В. и др. Естественные составляющие метеорологических
полей. Л., Гидрометеоиздат, 1970, 199 с.
386
20. О б у х о в А. М. О статистически ортогональных разложениях эмпирических
функций. Изв АН СССР, сер. геофиз., 1960, № 3, с. 432—439.
21. Юдин М. И. Физико-статистический метод долгосрочных прогнозов погоды
Л., Гидрометеоиздат, 1968, 28 с.
К главе IX
1. Анекеева Л. А. Эффективность использования данных об облачности, по-
лученных со спутника, в объективном анализе поля ветра.— «Труды ГМЦ»,
1971, вып. 89. с. 50—59.
2. Багров А. Н., Белоусов С. Л., Тарнопольский А. Г. Схема
объективного анализа полей давления, барической тенденции, температуры и
точки росы по данным синоптической сети станций.— «Труды ГМЦ», 1972,
вып. 91, с. 58—76.
3. Б е л о в П Н. Применение данных наблюдений со спутников в четырехмерном
численном анализе.— «Метеор, и гидрол.», 1974, № 6, с. 107 111.
4. Б е л о в П. Н., Бурцев А. И., Алпатова Р. Л. Методика учета дан-
ных несинхронных наблюдений в численном анализе поля геопотенциала.—
«Труды ГМЦ», 1974, вып. 132, с. 41—51.
5. Б е л о у с о в С. Л., Артанова А. К- Автоматизированная первичная
обработка аэрологической информации в Гидрометцентре СССР. Технологиче-
ская схема и опыт оперативной эксплуатации.— «Труды ГМЦ», 1970, вып. 71,
с. 59—76.
6. Борисенков Е. П. Физико-статистические методы анализа и предвычи
сления метеорологических полей.— «Труды ААНИИ», 1963, т. 263. 243 с.
7. Бурцев А. И., Белов П. Н., Бушуева Л. С Численный анализ ме-
теорологической информации, имеющей различную точность, основанный на по-
линомиальной аппроксимации.— «Труды ГМЦ», 1974, вып. 132, с. 30—40.
8. Бурцев А. И. и Мусаелян Ш. А. Методы использования спутниковой
информации в численном анализе и прогнозе погоды. В сб.: Труды 5-го Всесо-
юзного метеорологического совещания. Т. 2, 1972, с. 174 184.
9. Быков В. В. Применение полных уравнений гидродинамики к прогнозу
метеорологических элементов и опыт оперативной работы. В кн.: Лекции по
численным методам краткосрочного прогноза погоды. Л., Гидрометеоиздат. 1969,
с. 391—449.
10. Быков В. В, Курбаткин Г. П. Анализ метеорологических и аэроло-
гических данных с помощью электронно-вычислительной машины. «ДАН
СССР», 1960, т. 134, № 5, с. 1065—1068.
И. Ган дин Л. С. Проблема четырехмерного усвоения данных метеорологиче-
ских наблюдений.— «Метеорол. и гидрол.», 1971, № 3, с. 15—21.
12. Г андин Л. С., Смирнова Л. В. Об автоматическом контроле опера-
тивной метеорологической информации.— «Труды ГГО», 1973, вып. 508, с. 60—
73.
13. Машкович С. А. Об объективном анализе карт барической топографии
северного полушария.— «Труды ММЦ», 1964, вып. 4, с. 3—10.
14. Машкович С. А. О четырехмерном анализе данных наблюдений.— «Ме-
теорол. и гидрол », 1971, № 11, с. 97—102.
15. Машкович С. А .Применение в целях четырехмерного анализа методов
согласования метеорологических полей и оптимальной интерполяции.— «Труды
ГМЦ», 1972, вып. 103, с. 3—12.
16. Машкович С. А., Вейль И Г. Численные эксперименты по четырех-
мерному объективному анализу на основе спектральной прогностической мо-
дели.— «Метеорол. и гидрол.», 1972, № 3, с. 3—15.
17. М у с а е л я н Ш. А., А п р а у ш е в а Н. Н. О совместном использовании
данных наблюдений со спутника и редкой сети аэрологических станций для
восстановления полей метеорологических элементов.— «Труды ГМЦ», 1968,
вып. 30, с. 93—95.
18 Мусаелян Ш. А. и др. Вопросы использования данных метеорологиче-
ских спутников в численном анализе и прогнозе.— «Метеорол. и гидрол.», 1970,
№ 12, с. 3—11.
25* 387
19. М у с а е л я н Ш. А., Хорошилов А. Ф. О пространственно-временном
анализе асинхронных метеорологических данных.— «Метеорол. и гидрол.», 1973,
№ 2, с. 36—46.
20. П а х о м о в А. А. и др. Опыт термического зондирования на ИСЗ «Мете-
ор.»— «Метеорол. и гидрол.», 1971, № 12, с. 25—30.
21. Петриченко И. А. Использование данных о геопотенциале и скорости
ветра на нескольких уровнях при объективном анализе карт барической топо-
графии.— «Труды ЦИП», 1962, вып. 102, с. 20—26.
22. П е т р о в А. А. О привлечении различных источников информации и учете
зависимости исходных данных при полиномиальной аппроксимации полей.—
«Труды ГМЦ», 1971, вып. 58, с. 87—97.
23. П е т р о в А. А. О методе объективного анализа, основанном на полиноми-
альной аппроксимации полей.— «Метеорол. и гидрол.» 1968, № 6, с. 21—28.
24. Сонечкин Д. М. Обоснование четырехмерного (непрерывного) усвоения
данных метеорологических наблюдений на основе динамико-статистического под-
хода.— «Метеорол. и гидрол.», 1973, № 4, с. 13—20.
25. Успенский Б. Д., Галахова Т. А. О детализированном анализе ме-
теорологических полей.— «Труды ГМЦ», 1972, вып. 108, с. 9—19.
26. Хейфец Я- М. Схема восьмиуровенного объективного анализа поля гео-
потенциала.— «Труды ГМЦ», 1969, вып. 39. с. 25—40.
27. Ч е т в е р и к о в И. А. Схема объективного анализа карт барической топо-
графии методом оптимальной интерполяции — «Труды ЦИП», 1962, вып. 102,
с. 3—12.
28. Ч у з а в к о в а Н. А. и А р т а н о в а А. К. Некоторые вопросы использо-
вания данных дистанционного зондирования атмосферы в анализе барического
поля.— «Труды ГМЦ», 1972, вып. 104, с. 56—64.
29. А 1 a k а М. А., Е 1 v a n d е г R. С. Optimum interpolation from observations of
mixed quality.— “Mon. Wea. Rev.”, 1972, vol. 100, N 8, p. 612—624.
30 Bengtsson L., Gustavsson N. An experimental in the assimilation of
data in dynamical analysis.— “Tellus”, 1971, vol. 23, N 4—5, p. 328—336.
31. Bengtsson L. and Gustavsson N. Assimilation of non-synoptic observa-
tions.— “Tellus”, 1972, vol. 24, N 5, p. 383—399.
32. В e r g t h о r s s e n P., Doos B. R. Numerical weather map analysis.— “Tellus”,
1955, vol. 7, N 3, p. 329—340.
33. Bush by F. H., HuckleV. M. Objective analysis in numerical forecasting.—
“Quart. J. Roy. Met. Soc.” 1957, vol. 83, N 356, p. 232—247.
34. Charney J. G., H a 1 e m M. and Jastrow R. Use of incomplete historical
data to infer the present state of the atmosphere.— “J. Atmos. Sci.”, 1969, vol. 26,
N 5, P. 2, p. 1160—1163.
35. Cressman G. P. An operational objective analysis system.— “Mon. Wea.
Rev.”, 1959, vol. 87, N 10, p. 367—374.
36. D о 6 s В R. Numerical experimentation related to GARP.— “WMO GARP publ.
ser.”, 1970, N 6, 68 p.
37. E n d 1 i c h R. M. a. o. Computation of upper tropospheric reference heights from
winds for use with vertical temperature profile observations.— “Mon. Wea. Rev.”,
1972, vol. 100, N 11, p. 808—816.
38. Gilchrist B. and Cressman G. P. An experiment in objective analysis.—
“Tellus”, 1954, vol. 6, N 4, p. 309—318.
39. H a 11 i n e r G. J. Numerical weather prediction. 1971. 317 p.
40. J a s t г о w R. and H a 1 e m M. Simulation studies related to GARP.— “BAMS”,
1970, vol. 51, N 6, p. 490—513.
41. Kasahara A. Simulation experiments for meteorological observing systems
for GARP.—“BAMS”, 1972, vol. 53, N 3, p. 252—264.
42. M с С 1 a i n E. P., R u z e s к i M. А., В г о d r i c h H. J. Experimental use of
satellite pictures in numerical prediction.— “Mon. Wea. Rev.”, 1965, vol. 93, N 7,
p. 445—452.
43. H a g 1 e R. E. and Hayden С. M. The use of satellite-observed cloud patterns
in northern hemisphere 500-mb numerical analysis.— ‘NOAA Tech. Rep. NESS”,
1971, 55, Washington, D. C., 25 p.
44. P a no f sky H. A. Objective weather-map analysis.— “J. of Met.”, 1949, vol. 6,
N 6, p. 386—392.
388
45. Smith W. L. and Fawcett E. B. Operational use of SIRS data. Satellite
and computer applications to synoptic meteorology. WMO, N 283. Secretariat of
the Meteorological Organization. Geneva—Switzerland, 1971, p 39—62.
46. Smith W. L., Woolf H. M. and Jacob W. J. A regression method for ob-
taining real-time temperature and geopotential height profiles from satellite spec-
trometer measurements and its application to Nimbus 3 “SIRS” observations.—
“Mon. Wea. Rev.”, 1970, vol. 98, N 8, p. 582—603.
47. Williamson D. and Kasahara A. Adaptation of meteorological variables
forced by updating.—“J. Atmos. Sci.” 1971, vol. 28, N 8, p. 1313—1324.
К г л а в e X
l. Бугаев В. А. Прогнозирование погоды в недавнем прошлом, в настоящее
время и в ближайшем будущем.— «Метеорол. и гидрол.». 1972, № 9, с. 19—30.
ОГЛАВЛЕНИЕ
От автора . . . . . . 3
Введение . . ................................................. 4
Глава I. Некоторые характеристики атмосферы и атмосферных движений 6
§ 1. Метеорологические элементы и точность их измерения . —
§ 2. Классификация атмосферных движений.................... 7
§ 3. Порядок величин метеорологических элементов и их про-
изводных ............................................... 12
§ 4. Некоторые данные о пространственно-временном распре-
делении метеорологических элементов и статистическая
структура метеорологических полей......................... 14
Глава II. Уравнения гидротермодинамики и их преобразования для целей
численного прогноза крупномасштабных атмосферных движе-
ний ................................................................. 21
§ 1. Уравнения гидротермодинамики идеальной жидкости . . —
§ 2. Уравнения гидротермодинамики для турбулентной атмо-
сферы .................................................... 26
§ 3. Пограничные слои в атмосфере......................... 32
§ 4. Уравнения переноса лучистой энергии и радиационный
приток тепла в атмосфере............................ . 43
§ 5. Упрощения уравнений гидротермодинамики............... 49
§ 6. Уравнения гидротермодинамики для крупномасштабных
атмосферных движений в системах координат, связанных
с давлением............................................... 53
§ 7. Уравнения вихря скорости и дивергенции .... . 63
§ 8. Уравнения гидротермодинамики в сферической системе
координат.............. ................... 56
§ 9. Уравнения гидротермодинамики в системах координат,
связанных с картографическими проекциями . . 70
§ 10. Постановка задачи о прогнозе крупномасштабных атмо-
сферных движений ............... ... ... 81
Глава III. Волновые движения в атмосфере . 87
§ 1. Основные понятия о волновых движениях в атмосфере —
§ 2. Метод малых возмущений................ . . 89
§ 3. Крупномасштабные волны . . . ....... 94
§ 4. Гравитационные волны............................. 97
§ 5. Смешанные волны и отфильтрование внешних гравитаци-
онных волн ................................
§ 6. Внутренние акустические и гравитационные волны 105
§ 7. Адаптация полей давления и ветра . U4
Глава IV. Методы краткосрочного прогноза, основанные на использовании
квазигеострофического и квазисоленоидального приближений
§ 1. Разложение по малому параметру и квазигеострофич-
иость атмосферных движений...............................
§ 2. Теория изменения давления в баротропной атмосфере
в квазигеострофическом приближении ......................
§ 3 Квазигеострофические одноуровенные прогностические мо-
дели ....................................................
§ 4. Теория изменения метеорологических элементов в баро-
клинной атмосфере в квазигеострофическом приближении
§ 5. Учет турбулентной вязкости и орографии . .
§ 6. Квазигеострофические многоуровенные прогностические
модели ..................................................
§ 7. Квазисоленоидальные прогностические модели..........
§ 8. Методы прогноза, основанные на расчете агеострофиче-
ских составляющих ветра..................................
121
122
126
129
134
139
142
151
154
390
§ 9. Прогноз влажности и обложных осадков .... 157
§ 10. Учет неадиабатнчности атмосферных процессов . 160
Глава V Методы краткосрочного прогноза, основанные на интегрировании
полных уравнений гидротермодинамики . . . . 165
§ 1 Постановка задачи прогноза метеорологических элемен-
тов на основе полных уравнений гидротермодинамики 166
§ 2. Интегрирование полных уравнений гидродинамики для
баротропной атмосферы при использовании явных схем 172
§ 3 Интегрирование полных уравнений гидродинамики для
баротропной атмосферы при использовании неявных схем 178
§ 4. Интегрирование полных уравнений гидротермодинамики
для бароклинной атмосферы при использовании полуне-
явных схем ............................................... 181
§ 5. Прогностические бароклинные модели при использовании
неявных схем.............................................. 184
§ 6. Прогностические модели при использовании п-системы ко-
ординат .................................................. 190
§ 7. Интегрирование полных уравнений гидротермодинамики
методом расщепления..................................... 194
§ 8. Учет неадиабатических факторов . .... 200
§ 9 Подготовка и согласование начальных данных для прог-
ностических моделей по полным уравнениям гидротер-
модинамики ......................... . . . ........ 207
Глава VI. Задача детализированного локального прогноза погоды мето-
дами мезометеорологии................................................ 211
§ I. Уравнения гидротермодинамики мезопроцессов 212
§ 2. Обтекание препятствий воздушным потоком.............. 216
§ 3. Вынужденная конвекция в пограничном слое атмосферы 218
Глава VII Теория и методы гидродинамического долгосрочного прогноза
погоды . ................................. 222
§ 1. Теория атмосферных движений планетарного масштаба
и долгосрочною прогноза, основанная на интегрировании
линеаризированных уравнений гидродинамики в соленои-
дальном приближении и использовании спектрального ме-
тода ................................................... 223
§ 2. Метод долгосрочного прогноза средних месячных анома-
лии температуры................................ . . 230
§ 3. Расчет индекса циркуляции . . . 232
§ 4. Теория прогноза на среднем уровне атмосферы, основан-
ная на интегрировании нелинейных уравнений гидродина-
мики в соленоидальном приближении ........................ 234
§ 5. Теория прогноза в бароклинной атмосфере, основанная
на интегрировании нелинейных уравнении гидротермоди-
намики в квазисоленоидальном приближении.................. 236
§ 6. Теория долгосрочного прогноза, основанная на интегри-
ровании полных уравнений гидротермодинамики при
учете неадиабатических факторов .......... 242
§ 7. Четырехуровенпая квазисоленоидальная нелинейная прог-
ностическая модель ....................................... 247
§ 8. Численное моделирование циркуляции атмосферы и дол-
госрочный прогноз погоды .... ... 250
Глава VIII. Статистические методы численного прогноза погоды 259
§ 1. Метод эмпирических функции влияния . . 260
§ 2. Синоптико-статистические методы прогноза ............ 265
§ 3. Применение обобщенных показателей состояния атмо-
сферы .................................................... 266
391
§ 4. Использование разложения метеорологических полей по
естественным составляющим................................. 269
§ 5. Прогноз облачности и осадков на основе синхронных ста-
тистических связей и использования гидродинамического
прогноза ................................................. 276
§ 6. Определение качества численных прогнозов............. 278
Глава IX. Численный анализ метеорологической информации............... 282
§ 1. Метод полиномиальной интерполяции.................... 284
§ 2. Метод оптимальной интерполяции................... . 291
§ 3. Метод последовательных приближений................... 298
§ 4. Использование в численном анализе дополнительной ин-
формации ................................................. 301
§ 5. Четырехмерный численный анализ....................... 305
§ 6. Автоматизация сбора, обработки и анализа метеорологи-
ческой информации 310
Глава X. Применение численных методов анализа и краткосрочного прог-
ноза метеорологических элементов в оперативной работе слу-
жбы погоды............................................................ 317
Приложения:
1. Единицы измерения некоторых физических величин в раз-
личных системах................................ .... 328
2. Таблица стандартной атмосферы . . ................ 330
3. Статистические данные о пространственно-временном рас-
пределении метеорологических элементов.................... 332
4. Некоторые сведения по численным методам решения урав-
нении гидротермодинамики.................................. 342
§ 1. Конечно-разностная аппроксимация производных и
дифференциальных уравнений ............................. —
§ 2. Некоторые способы решения конечно-разностных урав-
нений ................................................. 344
§ 3. Явные и неявные конечно-разностные схемы........... 347
§ 4. Вычислительная неустойчивость...................... 349
§ 5. Операции с векторами............................... 353
5 Некоторые сведения из математической статистики . . . 357
§ 1. Некоторые статистические характеристики............ 358
§ 2. Метод множественной линейной регрессии............. 368
Основные обозначения и постоянные.......................... 372
Предметный указатель . . . 375
Список литературы.......................................... 379
ПАВЕЛ НИКОЛАЕВИЧ БЕЛОВ
ЧИСЛЕННЫЕ МЕТОДЫ ПРОГНОЗА ПОГОДЫ
Редактор Е. И. Ильиных. Техн, редактор Л. М. Шишкова.
Художник С. Н. Исакова. Художественный редактор В. А. Баканов.
Корректор Г. С. Макарова
Сдано в набор 7/1 1975 г. Подписано к печати 27/VI 1975 г. М-17259. Формат 60Х907!6. Бумага
тип. № 1. Печ. л. 24,5. Уч.-изд. л. 25,44. Тираж 3000 экз. Индекс МЛ 10. Заказ № 21.
Цена 1 руб 13 коп.
Гидрометеоиздат. 199053. Ленинград, 2-я линия, д. 23.
Ленинградская типография № 8 Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств, полиграфии и книжной торговли.
190000, Ленинград, Прачечный пер., 6.