Автор: Монии А.С. Питербарг Л.И.
Теги: климат погода метеозависимость
Текст
5^< 5??< 7®< $“< fS?< -4?< 7??S: 7Ъ<^^'№<уЪ<
ПРЕДЕЛЫ
ПРЕДСКАЗУЕМОСТИ
ЖЖЖЖЖЖЖ^Ж^жЖЖЖ^
ПРЕДЕЛЫ
ПРЕДСКАЗУЕМОСТИ
КЛИМАТОЛОГИЯ
А.С.Монин, Л.И.Питербарг
ПРЕДСКАЗУЕМОСТЬ ПОГОДЫ И КЛИМАТА
Введение
Обсуждаемый здесь предмет хорошо знаком читателю по еже-
дневным сообщениям Гидрометцентра. А центральные газеты пу-
бликуют прогнозы погоды даже на неделю вперед, и они совсем
неплохо оправдываются. Наверняка у читателей возникал вопрос,
а почему не дается прогноз на месяц или два вперед. Потребность
в таком прогнозе особенно велика для народного хозяйства. Имея
надежные предсказания погоды на такие сроки, мы могли бы пра-
вильно планировать сроки сева сельскохозяйственных культур, вне-
сения удобрений и сбора урожая, квалифицированно составлять гра-
фики воздушных перевозок, оптимальным образом осуществлять
запуски космических кораблей и еще многое другое.
А разве не заманчиво знать, какая погода будет на Земле че-
рез сто или тысячу лет? Здесь, конечно, уместнее говорить лишь
о некоторой «средней» за длительный промежуток времени погоде,
которую мы примем за определение климата (это определение бу-
дет уточнено через несколько абзацев). Вопрос о прогнозе климата
представляется одним из важнейших и с точки зрения фундамен-
тальных научных задач. Так почему же Гидрометцентр не дает нам
прогнозы на длительные сроки — месяцы, годы, столетия? Может
быть, не хватает современных компьютеров, или недостаточна ква-
лификация сотрудников?
Увы, причина лежит гораздо глубже, и серьезный взгляд на про-
блему сроков надежного прогноза неизбежно приводит к фундамен-
тальным вопросам нашего мироздания, находящимся в поле зрения
современной теоретической физики. Понимание сложности этой про-
блемы невозможно без экскурса в современные математические ме-
тоды исследования предсказуемости динамических и стохастиче-
ских систем. Одна из целей настоящей работы — показать, сколь
короток путь от наших повседневных забот («будет ли завтра
дождь?») до проблем, волнующих лучшие умы человечества.
Когда мы говорим о прогнозе некоторой физической величины
х (в случае прогноза погоды ею может быть температура воздуха,
скорость ветра, количество осадков и т.д.), то подразумеваем, что
эта величина зависит от времени: х = x(t). Задача прогноза за-
ключается в том, чтобы вычислить, предсказать, угадать значение
х для некоторого будущего момента времени t + т по информации
о поведении (истории) этой величины и других величин, определя-
ющих эволюцию х или влияющих на нее, до момента времени t, ко-
торый мы ассоциируем с настоящим. Величина т будет называться
сроком прогноза.
Такая постановка задачи предполагает, что эволюция x(t) долж-
на подчиняться определенным закономерностям. Эти закономерно-
сти могут выражаться в детерминистской форме, тогда это дела-
ется чаще всего с помощью эволюционных дифференциальных (или
более сложных интегродифференциальных, операторных) уравне-
ний или же в статистической форме, когда задаются статистиче-
ские характеристики x(t), неизменные по времени или же изменяю-
щиеся в соответствии с известными законами. Как было совершенно
верно отмечено в работе [1], один и тот же процесс в зависимости от
поставленной задачи или степени осведомленности о закономерно-
стях его протекания может рассматриваться как детерминирован-
ный или как случайный. Например, прогноз температуры воздуха
в данном месте на определенной станции) на срок 1-3 сут. осуще-
ствляется путем интегрирования уравнений движения и переноса в
атмосфере. При указанных сроках атмосферные процессы можно
считать адиабатическими, т.е. пренебрегать притоком энергии из-
вне и ее диссипацией за счет вязкости. Эти уравнения очень точно
описывают динамику в адиабатическом случае, и нет никакой ну-
жды прибегать к альтернативному способу описания.
Однако при исследовании вопроса о предсказании температу-
ры на длительные сроки, усредненной по значительной площади
и продолжительному временному промежутку, детерминированное
описание этой величины теряет свою привлекательность. Дело в
том, что усредненные гидродинамические величины уже не опи-
сываются точными замкнутыми уравнениями. В силу нелинейно-
сти уравнений гидротермодинамики усредненные уравнения пере-
носа включают в себя турбулентные потоки тепла, а усредненные
уравнения движения — турбулентные потоки импульса (напряже-
ния Рейнольдса). Проблема замыкания усредненных уравнений яв-
ляется одной из сложнейших в теории турбулентности и в общем
случае не имеет удовлетворительного решения [2]. Существующие
полуэмпирические методы параметризации потоков тепла, влаги и
импульса далеки от совершенства и вряд ли способны помочь в за-
даче прогноза на длительные сроки. Причины того, что указанные
потоки невозможно предвычислять на большие промежутки вре-
мени, мы обсудим ниже.
Между тем длительные наблюдения за температурой воздуха,
которые на многих станциях ведутся более 100 лет, дают доста-
точно богатую информацию для анализа статистических (т.е. сред-
них) характеристик исследуемой величины, что может послужить
основой для создания статистической модели долгопериодного по-
ведения температуры воздуха в данном месте, или в определенном
регионе, или же в глобальных масштабах (Например, средняя тем-
пература воздуха северного полушария). В этом случае чисто ста-
тистическое описание может оказаться предпочтительнее детерми-
нированного. Эта простая идея о рассмотрении процессов в атмо-
сфере и океане на коротких (погодных) масштабах времени как
детерминированных, а на длительных (климатических) как случай-
ных процессов, определяет принятый ниже план изложения.
Вначале мы приведем основные необходимые сведения из теории
динамических систем и вкратце обсудим то, что препятствует их
предсказуемости: неустойчивость и стохастизацию (разд. 1). Эти
сведения помогают понять, почему ограничена предсказуемость ре-
альных атмосферных процессов в рамках моделей гидродинамики
(разд. 2). Разд. 3 содержит элементы математической теории про-
гноза случайных процессов и полей в рамках линейной модели и
служит необходимым подготовительным этапом для исследования
предсказуемости климата (разд. 4). В разд. 5 обсуждаются возмож-
ности улучшения статистического прогноза, а также некоторые об-
стоятельства, ограничивающие его эффективность (даже в линей-
ных процессах). Разд. 6 посвящен проблеме использования резуль-
татов прогноза погоды в экономике.
В качестве временной границы, условно разделяющей погоду и
климат, примем величину то = 1 мес. Процессы с характерным
временным масштабом т„, много меньшим, чем то(тп то), бу-
дем относить к погоде, а процессы с масштабом изменчивости тк,
много большим то(тк то), будем называть кинематическими. Под
«характерным масштабом изменчивости» тп, тк можно понимать,
например, время корреляции. Из этого определения следует, что,
усреднив погодный процесс по длительному промежутку времени
(месяц и больше), мы получим климатический процесс. Примеры:
ежечасные измерения температуры воздуха, его влажности и ско-
рости ветра имеют характерное время корреляции 1-3 сут. и посему
суть временные ряды, представляющие погодные процессы; темпе-
ратура поверхности океана (ТПО), т.е. температура, усредненная
в пределах верхнего, перемешанного ветром слоя с толщиной в де-
сятки метров, имеет характерное время изменчивости 3-6 мес. и,
следовательно, ее временная эволюция есть климатический процесс.
1. Динамические системы и их свойства
Наиболее универсальной математической моделью природных
процессов служат динамические системы. Предположим, что состо-
яние исследуемого объекта в каждый момент времени можно задать
с помощью числовых значений параметров, pi,P2> • • совокупность
которых обозначим через р = (pi,P2, • • •) и будем называть состоя-
нием. Множество всех возможных (допустимых) состояний р = {р}
образует фазовое пространство. В случае если изменение состояния
системы в последующие моменты времени можно вычислить, исходя
из эволюционного уравнения
p = $(t,p), (1)
где точка означает производную по времени, а Ф (t, р) — некоторая
функция на фазовом пространстве, будем говорить о динамической
системе, задаваемой уравнением (1).
Если исследователя интересует состояние системы лишь в дис-
кретные моменты времени (или он вынужден ограничиться только
такими наблюдениями), ее эволюция записывается в виде
p(n + 1) = Фп[р(п)],
где р(п) — состояние системы в момент времени tn, п = 0,1,2,...,.
Далеко не всегда при изучении природных процессов удается
ограничиться конечной (или даже счетной) совокупностью пара-
метров pi ,р2,..., задающих состояние системы. Чаще всего прихо-
дится рассматривать фазовое пространство, элементами которого
служат функции или совокупности функций времени и простран-
ственных координат. Системы такого вида называются контину-
альными или бесконечномерными в отличие от конечномерных, со-
стояние которых описывается конечным набором параметров. Так,
например, математическое описание состояния движущейся жидко-
сти осуществляется с помощью функций, определяющих распреде-
ление скорости жидкости v(r, t), где г — координата в простран-
стве, и каких-либо ее двух термодинамических характеристик, на-
пример, давления р(г, t), и плотности р(г, t). Уравнения, задающие
эволюцию этих полей (уравнения Навье-Стокса в совокупности с
уравнением сохранения массы) уже настолько сложны, что в общем
случае для них даже не доказаны теоремы существования и един-
ственности решения. Во многих задачах гидродинамики, океаноло-
гии, метеорологии достаточно ограничиться исследованием лишь
первых членов разложения указанных полей по некоторой полной
системе функций. Эти функции нумеруются в порядке возрастания
сложности их аналитической структуры, и первые из них имену-
ются низшими модами, а процесс редукции континуальной системы
к конечномерной, охватывающей лишь низшие моды, называется
методом Галеркина.
Динамические системы разделяют на автономные (Ф не зависит
от t в непрерывном случае и от п — в дискретном) и неавтономные
(в противном случае); линейные (Ф есть линейная функция от р в
конечномерном случае или линейный оператор на функциональном
пространстве в континуальном случае) и нелинейные (указанные
условия не выполняются). В дальнейшем ограничимся автономными
системами, так как в большинстве случаев модели, применяемые в
механике, гидродинамике и геофизике, автономны. К тому же не-
автономные системы можно сводить к автономным путем расши-
рения фазового пространства. Более пристального внимания заслу-
живает деление систем на линейные и нелинейные. Сама эта терми-
нология не совсем удачна. Дело в том, что строго линейных систем
в природе не существует вообще. Линейная система есть лишь неко-
торый воображаемый предел нелинейной системы при допущении
малости определенных параметров или, что то же самое, при пре-
небрежении некоторыми вполне реальными процессами. Так, ли-
нейное уравнение колебаний маятника получается в результате до-
пущения малости отклонения маятника от положения равновесия.
Допуская малость числа Рейнольдса, т.е. пренебрегая силами инер-
ции по сравнению с вязкостью, приходим к линейным уравнениям
течения вязкой жидкости. Список таких примеров можно было бы
продолжить. Чем же вызвано стремление заменить нелинейные си-
стемы линейными? Только одной причиной — удобством аналити-
ческого исследования: задачи, связанные с линейной динамикой, ре-
шаются несравненно проще, чем задачи нелинейные.
Между линейными и нелинейными системами можно провести
вполне четкую физическую границу. Перейдем в уравнении р = Ф(р)
где р = р(г, t) — функция, описывающая состояние непрерывной си-
стемы, для простоты — скалярная (пусть, например, это давление
в точке пространства г), а Ф — линейный оператор, инвариантный
относительно сдвигов пространства (или, другими словами, опера-
тор с постоянными коэффициентами), к преобразованию Фурье
р(г, t) = f p(k, t)e^k,r^dk (2)
(k — волновой вектор), т.е. представим меняющиеся по времени
поле р(г, t) в виде суперпозиции элементарных синусоидальных волн
с амплитудами р(к, t). Тогда в пространстве Фурье (в пространстве
волновых векторов к) уравнения динамики примут особенно про-
стой вид
-£p(k,t) = $(k)p(k,t), (3)
at
где Ф(к) — изображение оператора Ф в пространстве Фурье. Таким
образом, мы получили совокупность (хотя и непрерывную) ничем
не связанных между собой уравнений, каждое из которых можно ре-
шать по отдельности, что, кстати, сделать совсем нетрудно. Дру-
гими словами, волны, образующие в результате суперпозиции ис-
следуемое поле р(г, t), никак между собой не взаимодействуют —
каждая из них эволюционирует независимо от остальных и ее по-
ведение определяется лишь волновым вектором к. Конечно, пред-
ставление вида (2) имеет место и для поля, описываемого нелиней-
ным уравнением, однако уравнения для амплитуд в таком случае
получатся уже «сцепленными» между собой, и это обстоятельство
является принципиальным, элементарные гармонические составля-
ющие взаимодействуют между собой. Эти взаимодействия приво-
дят к значительно более сложному асимптотическому поведению
нелинейных систем по сравнению с линейными. Как видно, напри-
мер, из формулы (3), стационарное состояние линейной системы
PooQt) = limt_>oop(k, t), если таковое существует, не может дать
«сплошного» спектра в пространстве волновых чисел, так как этот
спектр отличен от нуля лишь на множестве тех к, для которых
Ф(к) = 0, т.е. наверняка имеет размерность не выше 2 для опе-
раторов Ф общего вида. Весьма небогат в линейном случае и запас
вариантов приближения к стационарным или периодическим состо-
яниям. В то же время сценарии асимптотического поведения нели-
нейных динамических систем чрезвычайно разнообразны и сложны,
хотя и подчиняются некоторым общим закономерностям, к изложе-
нию которых мы и перейдем.
Отметим, что впервые «необычное» поведение нелинейной дина-
мической системы было открыто именно в связи с задачей прогноза
погоды крупнейшим американским метеорологом-теоретиком
Э.Н.Лоренцом. Изложим вкратце историю этого открытия, следуя
книге [3]. Появившееся в середине 50-х годов первые численные
схемы гидродинамического краткосрочного (несколько суток) про-
гноза погоды оказались мало эффективными, что заставило многих
исследователей обратиться к статистическим методам прогноза,
основанным на представлении о линейной регрессии (подробно эти
методы будут обсуждаться дальше). В немалой степени это напра-
вление стимулировалось появившимися примерно в то же время ра-
ботами Н. Винера (см., например, статью [4]), посвященными пред-
сказанию стационарных случайных процессов.
Казалось, что использование большого числа предикторов мо-
жет заменить гидродинамические схемы прогноза, несмотря на су-
щественную нелинейность атмосферных процессов. Лоренц скепти-
чески отнесся к идее статистического прогноза и решил проверить
ее путем численного эксперимента на какой-либо динамической мо-
дели. В результате непростых поисков, связанных с желанием по-
лучить апериодические движения (понятно, что предсказание пери-
одических или близких к ним движений по наблюдениям прошлых
состояний системы легко осуществить, не прибегая даже к какому-
либо более или менее сложному математическому аппарату), Ло-
ренц остановился на двухуровневой модели атмосферы, которая
методом Галеркина с удержанием только наиболее крупномасштаб-
ных мод была сведена к системе обыкновенных дифференциальных
уравнений. Для найденной таким образом системы 12-го порядка
действительно удалось показать полную несостоятельность стати-
стического прогноза в рамках линейной модели. Однако попутно
было сделано куда более значительное открытие. Исследуя одно из
численных решений системы, Лоренц вывел промежуточные зна-
чения фазовых переменных на печать по формату «три знака по-
сле десятичной запятой» при точности представления «шесть зна-
ков после запятой» в памяти машины. Использовав эти значения в
качестве начальных данных для последующего счета, Лоренц обна-
ружил, что после расчета на время около двух месяцев результаты
резко отличались от тех, которые были получены путем интегриро-
вания системы без промежуточного вывода значений переменных
на печать, т.е. без отбрасывания трех последних знаков в промежу-
точных результатах. Вначале он даже заподозрил машинный сбой,
однако тщательная последующая проверка убедила его в том, что
невинное на первый взгляд округление начальных данных действи-
тельно приводит к драматическим последствиям для конечных ре-
зультатов счета. Подробный анализ показал, что начальный шум
порядка 103 рос, удваиваясь примерно каждые четыре модельных
дня, и увеличился, таким образом, за два месяца в 215 « 3.3 -104 раз,
достигнув десятков единиц. В дальнейшем изучаемая модель была
существенно упрощена, в ней осталось всего лишь три независимые
переменные, и получилась известная система Лоренца
X = -аХ + стУ,
Y = гХ - Y - XZ (4)
Z = -bZ + XY.
Смысл переменных заключается в следующем: X характеризует
интенсивность конвективных движений, Y — разница температур
восходящих и нисходящих конвективных струй, Z — отклонение
вертикального профиля температуры от линейного; фиксирован-
ные параметры: г — относительное число Рэлея, ст — число Пранд-
тля, b — число, характеризующее геометрию вертикального сече-
ния конвективных валов.
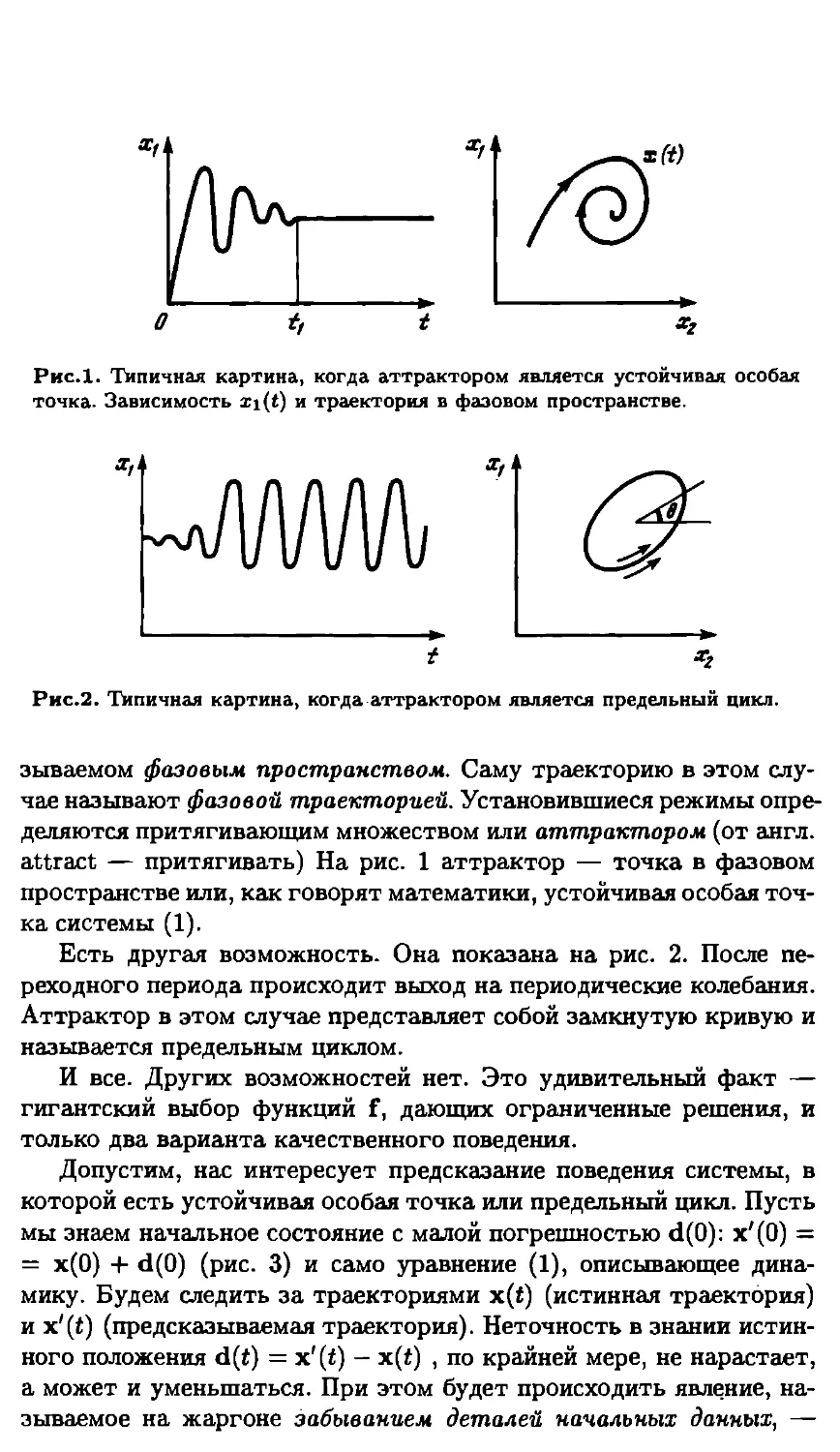
Лоренц не ограничился констатацией неустойчивости решений
системы (4). Под устойчивостью здесь и далее мы понимаем устой-
чивость по А.М.Ляпунову: фазовая траектория р = р(ро, t) (т.е. ре-
шение уравнения (1)), отвечающая начальному значению р0, назы-
вается устойчивой, если для всякого положительного сколь угодно
малого числа е существует положительное число <5 такое, что для
любой траектории р = р(ро,^)> с начальным условием ро, удовле-
творяющим условию р(ро> Ро) < <5, где р — расстояние между точ-
ками ро,Ро> в любой момент времени имеет место неравенство
р(р, Р) < £, т.е. близким начальным условиям соответствуют близ-
кие фазовые траектории. Более тщательный анализ поведения ре-
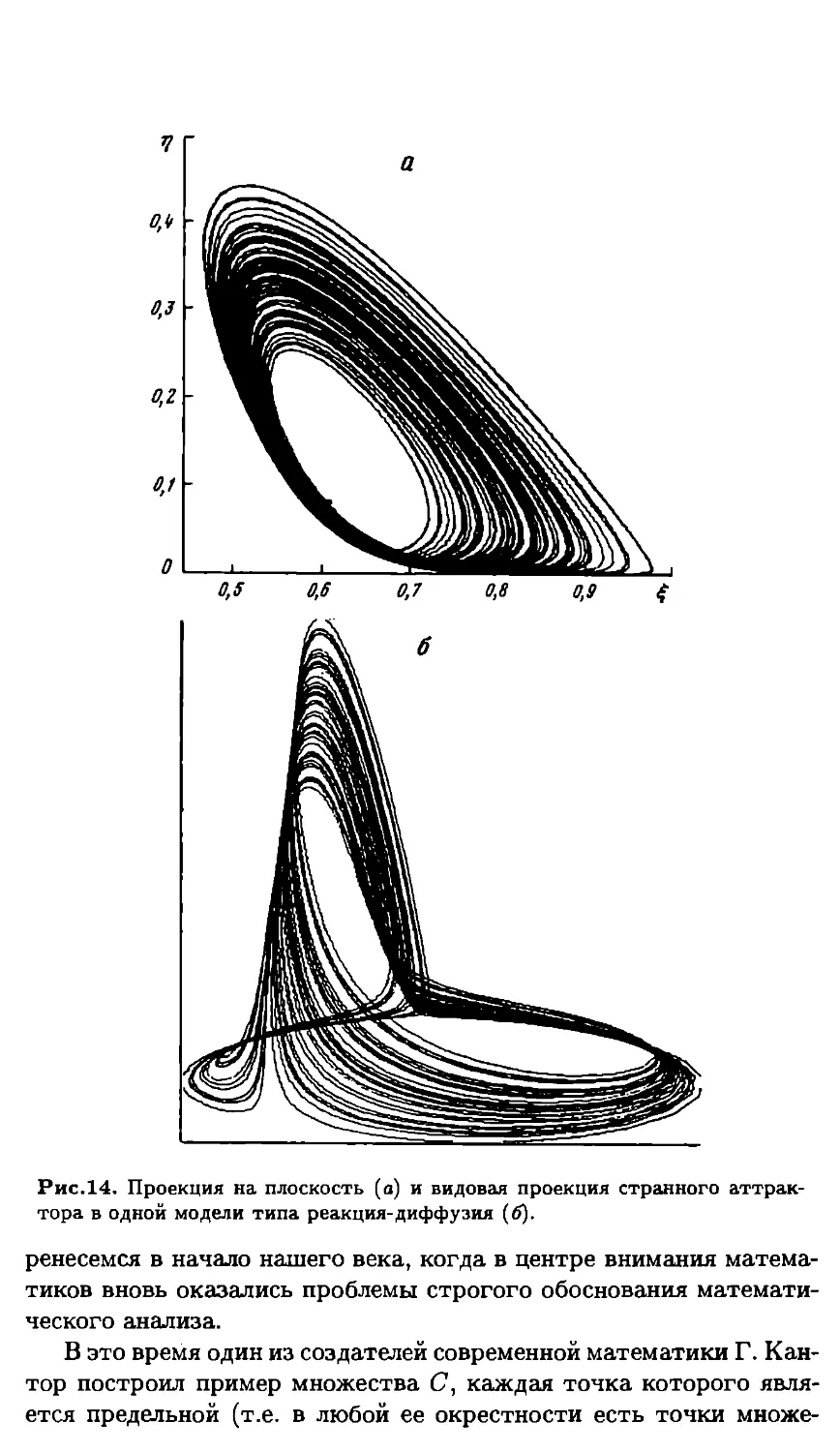
шений системы (4) привел к открытию странного аттрактора —
подмножества фазового пространства, на котором фазовые траек-
тории ведут себя удивительным образом.
Для более подробного пояснения необходимо провести несколько
определений, которые мы дадим, слегка поступившись математиче-
ской строгостью. Назовем точку фазового пространства Р неблу-
ждающей, если фазовая траектория, выйдя из любой ее окрестно-
сти, по крайней мере, еще один раз вернется в эту же окрестность.
Неблуждающими являются, например, стационарные точки, в ко-
торых траектория удерживается при любых t, или точки, принад-
лежащие предельным циклам (такие точки соответствуют перио-
дическим траекториям). Если фазовая траектория p(po,t)> выйдя
из любой точки ро некоторого подмножества N С Р фазового про-
странства, остается в нем при всех t > 0, т.е. p(p0,t) 6 N, то
такое множество называется инвариантным. Примеры инвариант-
ных множеств: стационарная (предельная) точка, замкнутая тра-
ектория (предельный цикл). Если у N нет подмножеств, обладаю-
щих тем же свойством, то N называют минимальным инвариант-
ным множеством, а минимальные инвариантные множества, состо-
ящие из неблуждающих точек, называются аттракторами. Нако-
нец, странным аттрактором называется аттрактор, отличный от
неподвижной точки или замкнутой траектории. Таким образом, по
своему определению странный аттрактор является «пристанищем»
периодических траекторий динамической системы.
Странные аттракторы, встречающиеся в системах гидродина-
мического типа (в том числе и в системе Лоренца), характеризу-
ются тем, что на них газовые траектории обнаруживают свойства
стохастичности, а именно:
1) очень чувствительную зависимость от начальных условий (не-
устойчивость), создаваемую экспоненциальной расходимо-
стью начально близких траекторий (и приводящую к их не-
предсказуемости или невоспроизводимости при заданных на-
чальных условиях со сколь угодно высокой, но конечной точ-
ностью);
2) плотность почти всех траекторий на аттракторе, т.е. их сколь
угодно близкое прохождение около любой его точки (и, зна-
чит, бесконечнократную возвращаемость к ней), причем лю-
бое начальное неравновесное распределение вероятностей
(мера) в фазовом пространстве (точнее, в области притяжения
странного аттрактора) стремится к некоторому предельному
равновесному распределению Р(Л) на аттракторе (инвариант-
ной мере);
3) перемешивание, означающее, что для любых (измеримых) под-
множеств аттрактора А и В вероятность после выхода из А
через большое время оказаться в В пропорциональна мере В:
lim Р{(Г‘Л) П В] = Р(Д)Р(В),
t—kOO
где FlA — множество точек фазового пространства, в кото-
рое перейдут точки множества А за время t под действием ди-
намики системы. Следствием перемешивания являются неза-
висимость от начальных условий ро (при почти всех ро) сред-
него значения по времени (P[p(t)]) любой функции F(p) на
странном аттракторе и его совпадение со средним значением
по инвариантной мере Р(р) (эргодичность).
Признаком перемешивания является достаточно быстрое зату-
хание при больших временах (т —> оо) корреляционных функций
= ([pi(t) - (pi(t))] [pj(t + т) - (pj(t + r))J)
и, значит, непрерывность их преобразований Фурье по т — спек-
тральных функций.
Рассматриваемые в гидродинамике системы (в том числе и си-
стемы Лоренца) являются диссипативными, т.е. в них происходит
сжатие фазового объема. Экспоненциальная расходимость близких
траекторий при сжатии фазового объема возможна, если по одним
направлениям рк в фазовом пространстве Р происходит расшире-
ние, а по другим — сжатие, т.е. неблуждающие фазовые точки
должны быть подобны двумерным седлам. Такие точки называют
гиперболическими, а окрестность гиперболической точки предста-
вляет собой объединение устойчивого многообразия, на котором
фазовые траектории сближаются, и неустойчивого, где фазовые
траектории экспоненциально расходятся. Сколь типично наличие
такого рода гиперболических множеств у фазовых пространств ди-
намических систем? Может ли малое изменение такой системы при-
водить к исчезновению гиперболических множеств? В связи с этим
полезно использовать введенное А. А. Андроновым и Л. С. Понтря-
гиным понятие грубой (теперь предпочитают говорить — струк-
турно устойчивой) системы, формулируемое следующим образом:
при любом е > 0 имеется такое 5 > 0, что для любой измененной
системы р = Ф1(р), отстоящей от исходной по некоторой метрике
ЦФ1 — Ф|| не более чем на 6, существует взаимно однозначное и вза-
имно непрерывное преобразование фазового пространства на себя,
сдвигающее его точки не более чем на е и переводящее траектории
неизмененной системы в траектории измененной.
В одно- и двумерных фазовых пространствах структурной устой-
чивостью обладают так называемые системы Морса-Смейла, у ко-
торых множества неблуждающих точек состоят лишь из конечного
числа неподвижных точек и замкнутых траекторий, причем все
они гиперболические, и отвечающие любым таким точкам устой-
чивые и неустойчивые многообразия либо не пересекаются, либо в
сумме образуют полное касательное пространство (свойство транс-
версальности).
Однако в фазовых пространствах большего числа измерений
системы Морса-Смейла структурной устойчивостью уже не обла-
дают, и для их грубости по гипотезе С. Смейла (1965), необходимо
и достаточно, чтобы у каждого осуществляемого фазовым потоком
преобразования фазового пространства множество Я неблуждаю-
щих точек было гиперболическим, а множество периодических то-
чек — всюду плотным в Я (это так называемая аксиома А) и, кроме
того, каждое устойчивое и каждое неустойчивое многообразия то-
чек из Я были бы трансверсальными. Для систем, удовлетворяю-
щих аксиоме А, доказана стохастичность аттракторов (Р. Боуэн,
О. Рюэлль). Таким образом, при размерности фазового простран-
ства, большей 2, для него в определенном смысле типично наличие
бесконечного множества Я гиперболических неблуждающих точек
со всюду плотным в нем множеством периодических траекторий.
О. В. Аносов обнаружил даже такие потоки, у которых гиперболи-
ческим множеством является все фазовое пространство.
Характерной особенностью странного аттрактора является так-
же то, что его мера Лебега, как подмножества фазового простран-
ства (или, грубо говоря, объем), равна нулю. Таким образом, это
подмножество имеет структуру канторовского множества — всюду
плотного замкнутого множества лебеговой меры нуль. Для иден-
тификации размеров множества канторовского типа используется
более тонкая характеристика — размерность Хаусдорфа.
Образование структуры странного аттрактора можно предста-
вить следующим образом. Через малое время начальный малый куб
фазового пространства растягивается по неустойчивым направле-
ниям и сжимается по устойчивым, превращаясь в длинный тонкий
лист, который затем из-за ограниченности диаметра аттрактора
начинает складываться. Эта операция с течением времени повто-
ряется много раз, и в пределе больших времен начальный фазовый
объем превращается в бесконечно тонкую пленку с бесконечным чи-
слом складок. Хаусдорфова размерность такого образования весьма
просто выражается через относительные числа затухающих и ра-
стущих траекторий в окрестности данной точки и экспоненциаль-
ные скорости их роста и затухания.
Переход динамических систем в стохастическое состояние про-
исходит путем последовательных бифуркаций, т.е. резких измене-
ний характера движения, вызванных изменениями параметров си-
стемы. Наиболее правдоподобные гипотезы о последовательностях
бифуркаций, ведущих к стохастичности, называются сценариями
стохастизации. К настоящему времени таких сценариев существует
несколько, и они достаточно хорошо изучены [5], хотя вопрос о со-
ответствии этих гипотез реальной картине зарождения турбулент-
ности в жидкости или газе остается открытым.
2. Предсказуемость погоды
Перейдем к вопросу о предсказуемости погоды и дадим количе-
ственные оценки возможностей прогноза. Экскурс в теорию стоха-
стизации динамических систем понадобился нам для того, чтобы
понять ограниченность этих возможностей.
Речь будет идти о долгосрочном прогнозе погоды (несколько
недель) в рамках уравнений динамики атмосферы. Мы уже слегка
затрагивали вопрос о разделении движений на крупномасштабные
и мелкомасштабные в связи с обсуждением понятий погоды и кли-
мата. Такое разделение приносит большую пользу во многих обла-
стях метеорологии. При таком подходе крупномасштабные движе-
ния описываются индивидуально, а действие мелкомасштабных дви-
жений учитывается лишь статистически. Например, при описании
распространения в воздухе примеси, выбрасываемой через фабрич-
ную трубу, крупномасштабное движение воздуха — ветер — зада-
ется индивидуально, а мелкомасштабная турбулентность, создаю-
щая нерегулярные завитки на дымовой струе, учитывается лишь
статистически (скажем, путем введения коэффициентов обмена).
К таким же областям метеорологии относится, конечно, и дол-
госрочный прогноз погоды. Мы хотим индивидуально предсказы-
вать на долгие сроки крупномасштабные характеристики погоды,
но ясно, что практически невозможно (да и ненужно) индивиду-
ально предсказывать на долгие сроки мелкомасштабные движения,
например, создающие завитки на дымовых струях. Поэтому воз-
никает естественный вопрос: какая же грань должна разделять
крупномасштабные процессы («погоду»), предсказываемые индиви-
дуально, и мелкомасштабные процессы («турбулентность»), описы-
ваемые лишь статистически?
Эта грань может быть различной при разных сроках прогноза.
Действительно, при наименьших сроках (скажем, до суток) мы ста-
раемся прослеживать индивидуально даже за мезомасштабными
процессами (используя данные учащенной сети метеостанций на
синоптических картах, называемых «кольцовками»); наоборот,
при многолетних обобщениях все синоптические процессы целесо-
образно описывать статистически (рассматривая их, по идее Де-
фанта [6, с. 143], как макротурбулентность).
Выбор разделяющего масштаба означает выбор определенной
модели из совокупности моделей, отличающихся степенью подроб-
ности изучаемых явлений. Таким образом, мы имеем иерархию мо-
делей, порождающую иерархию степеней детерминированности [7].
Практическая непредсказуемость мелкомасштабных движений
на долгие сроки требует пояснений. Если бы мы могли точно фик-
сировать начальное состояние всех мелкомасштабных движений и
точно решать точные уравнения их динамики, то, абстрактно го-
воря, сроки предсказуемости не были бы ничем ограничены. Даже
континуальность гидродинамических полей не была бы здесь прин-
ципиальным препятствием: поскольку непрерывные поля на очень
малых расстояниях меняются линейно, было бы достаточно фикси-
ровать начальные значения гидродинамических полей лишь в точ-
ках пространственной сетки с расстояниями меньше внутреннего
масштаба турбулентности, имеющего в атмосфере значения поряд-
ка миллиметров.
Но мы можем фиксировать начальные значения метеорологиче-
ских полей лишь в точках гораздо более грубой сетки (с шагом по
горизонтали в 107 —108 раз больше внутреннего масштаба), так что,
очевидно, индивидуальные движения с масштабами меньше шага
сетки вообще не фиксируются; кроме того, определенную погреш-
ность вносят измерительные приборы («измерительные шумы»), да
еще мы совершаем ошибки округления. Из-за этих начальных оши-
бок даже при точном решении точных уравнений динамики неиз-
бежны ошибки прогноза, которые будут, вообще говоря, расти с
увеличением срока прогноза, а мы, кроме того, используем лишь
приближенные уравнения динамики, да еще приближенно аппрок-
симируем их в целях численного решения, например, разностными
уравнениями.
Очевидно, прогноз индивидуальных процессов будет давать до-
полнительную информацию сверх той, которую дает их статисти-
ческое (климатическое) описание, лишь до тех пор, пока ошибки
прогноза не превысят средних климатических вариаций прогно-
зируемых величин. Соответствующий срок можно назвать преде-
лом предсказуемости рассматриваемых процессов. Он зависит от
типа процессов (в частности, их масштабов) и формы рассматрива-
емых их количественных характеристик, от характера и величины
начальных ошибок, от качества прогностического метода. Задачу
определения пределов пред< казуемости можно назвать проблемой
предсказуемости.
Возможность того, что малые изменения начального состояния
атмосферы (начальные ошибки) могут привести за долгие сроки к
существенным изменениям конечного состояния атмосферы (и соз-
дать проблему предсказуемости), указывалась еще 40 лет назад в
ряде выступлений известного математика А. Н. Колмогорова в сле-
дующей образной форме: представим себе две одинаковые планеты
с совершенно идентичными состояниями атмосферы. Если на одной
из них выйти на крылечко и махнуть платочком, а на другой этого
не сделать, то через какое время погода на этих планетах станет
совершенно различной?
При формализации проблемы предсказуемости в качестве меры
ошибки прогноза в метеорологии обычно принимается среднее ква-
дратичное отклонение прогнозируемых значений от истинных. По-
ступим таким образом и мы. Пусть xi(t) — истинное состояние
компоненты атмосферы масштаба L в момент времени t. Мы пред-
полагаем, что эволюция хь(€) задается некоторой динамической си-
стемой, и под «истинным» значением понимаем значение, вычислен-
ное по точным начальным условиям. В силу неизбежности ошибок
в начальных данных, о природе которых говорилось выше, про-
гнозируемое значение zt(t) будет отличаться от истинного. Усред-
ним прогнозируемые значения по ансамблю всех возможных началь-
ных условий (распределение которых описывается некоторой веро-
ятностной мерой) и в результате получим среднее прогнозируемое
значение zi,(t). Среднюю квадратичную ошибку прогноза опреде-
лим равенством
d = P2[xL(t),zL(t)],
где черта означает усреднение по ансамблю начальных условий.
Расстояние р — это евклидово расстояние в случае конечномерных
систем и расстояние в пространстве квадратично интегрируемых
функций в случае непрерывных систем.
Пусть, кроме того, на множестве возможных состояний атмо-
сферы задано климатическое распределение вероятности, так что
известна и климатическая дисперсия компонент масштаба L, т.е.
величина
здесь угловые скобки обозначают климатическое усреднение (прак-
тически это означает усреднение наблюдений за длительный про-
межуток времени). Тогда пределом предсказуемости ti компонент
масштаба L будет верхняя грань значений t, при которых выпол-
няется условие сг£,(^) < Это определение, появившееся почти
30 лет назад в работе одного из авторов [6, с. 145], близко к пред-
ложенному недавно понятию горизонта предсказуемости [7], но не
идентично ему.
В метеорологической литературе проблема предсказуемости
впервые была изложена Томпсоном (см. [6, с. 146}), предприняв-
шим также попытку аналитически рассчитать функцию ^(t) в
рамках простейших (квазигеострофических) прогностических мо-
делей. Более аккуратно такой расчет был проделан Новиковым
(см. [6, с. 146]): в случае, когда основное начальное поле и началь-
ное поле ошибок суть статистически независимые однородные и
изотропные случайные поля с радиусами корреляции L и Li, он по-
лучил
2 Z.X __ 1 2 1 , 2 (У^1)2____,
16 L |.1 + 2[1 + (Ь/Ь1)2]2 +"J ’
где Т — типичный временной масштаб синоптической изменчиво-
сти. Полагая Т = 1 сут. и L = 2Lj, убеждаемся, что время t^, в
течение которого ошибка прогноза достигает ошибки случайного
выбора, оказывается равным 2 нед. Уравнения для полного стати-
стического описания эволюции поля ошибок получены Татарским
(см. [6, с. 147]).
Первый численный эксперимент по предсказуемости был выпол-
нен Диким и Коронатовой (см. [6, с.147]), которые сопоставляли 24-
и 49-часовые прогнозы при помощи баротропной модели с фактиче-
скими начальными данными и с такими же данными с добавлением
случайной ошибки. Бралось как пространственно-некоррелирован-
ное поле ошибок, так и поле с радиусом корреляции в два шага
сетки, средняя квадратичная ошибка — как 10, так и 20 м. В разных
сериях прогнозов результаты получались различными, но в среднем
ошибка возрастала на 30-50% за 24 час, причем пространственно-
коррелированные ошибки возрастали несколько быстрее некорре-
лированных.
Гораздо более полные численные эксперименты по предсказуе-
мости осуществил Д. Чарни с помощью моделей Д. Смагоринского,
С. Лейтса и И. Минца [6, с. 147]. Наиболее показательны измене-
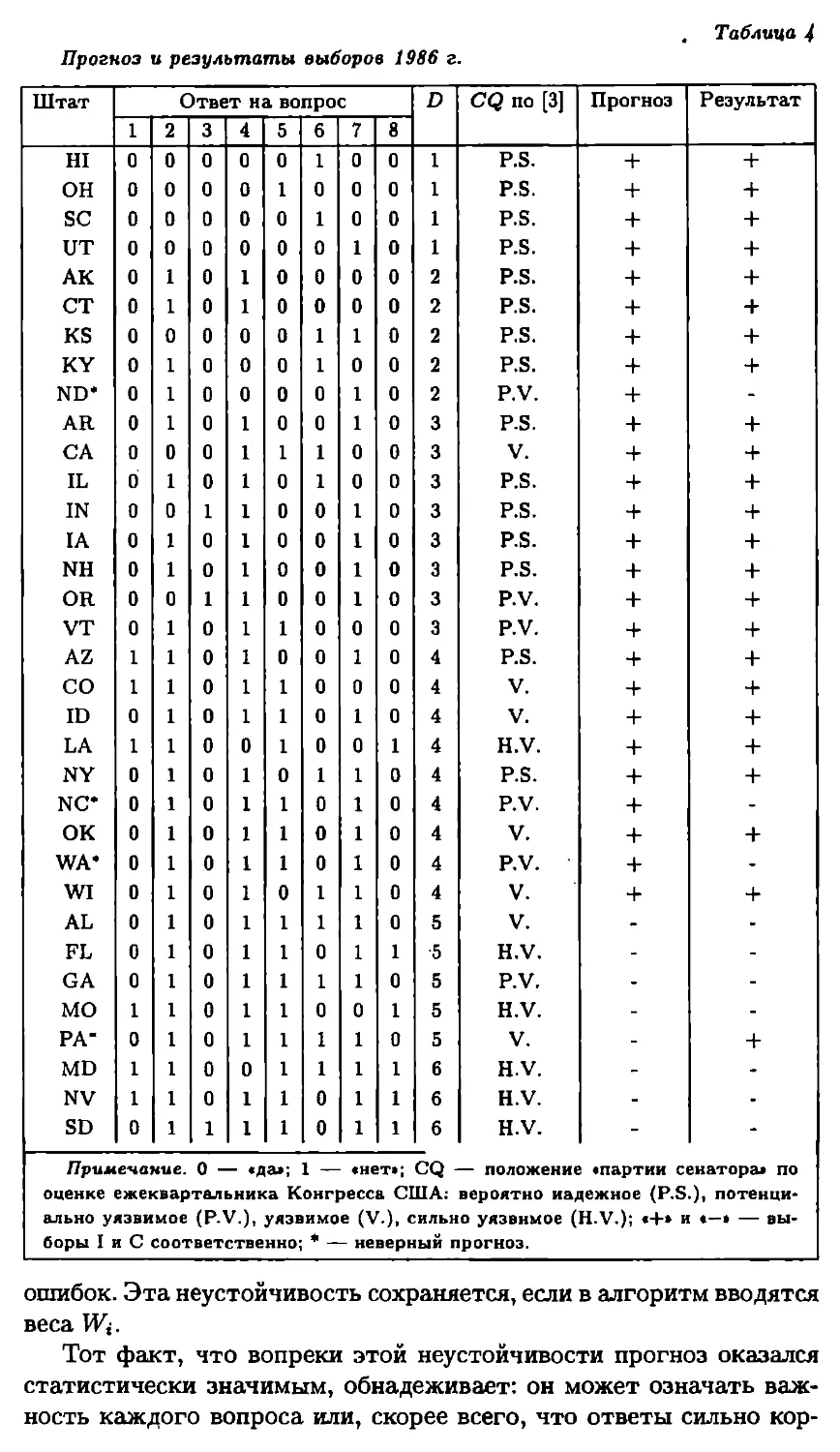
ния ошибок в модели Минца; на них мы и остановимся. Началь-
ные ошибки здесь вводились в поле температуры, а результирую-
щие ошибки прогноза в поле температуры подсчитывались на 234-е
сутки на двух уровнях; 1 (около 400 мбар) и 2 (около 800 мбар)
— отдельно для Северного (N) и Южного (S) полушарий. При на-
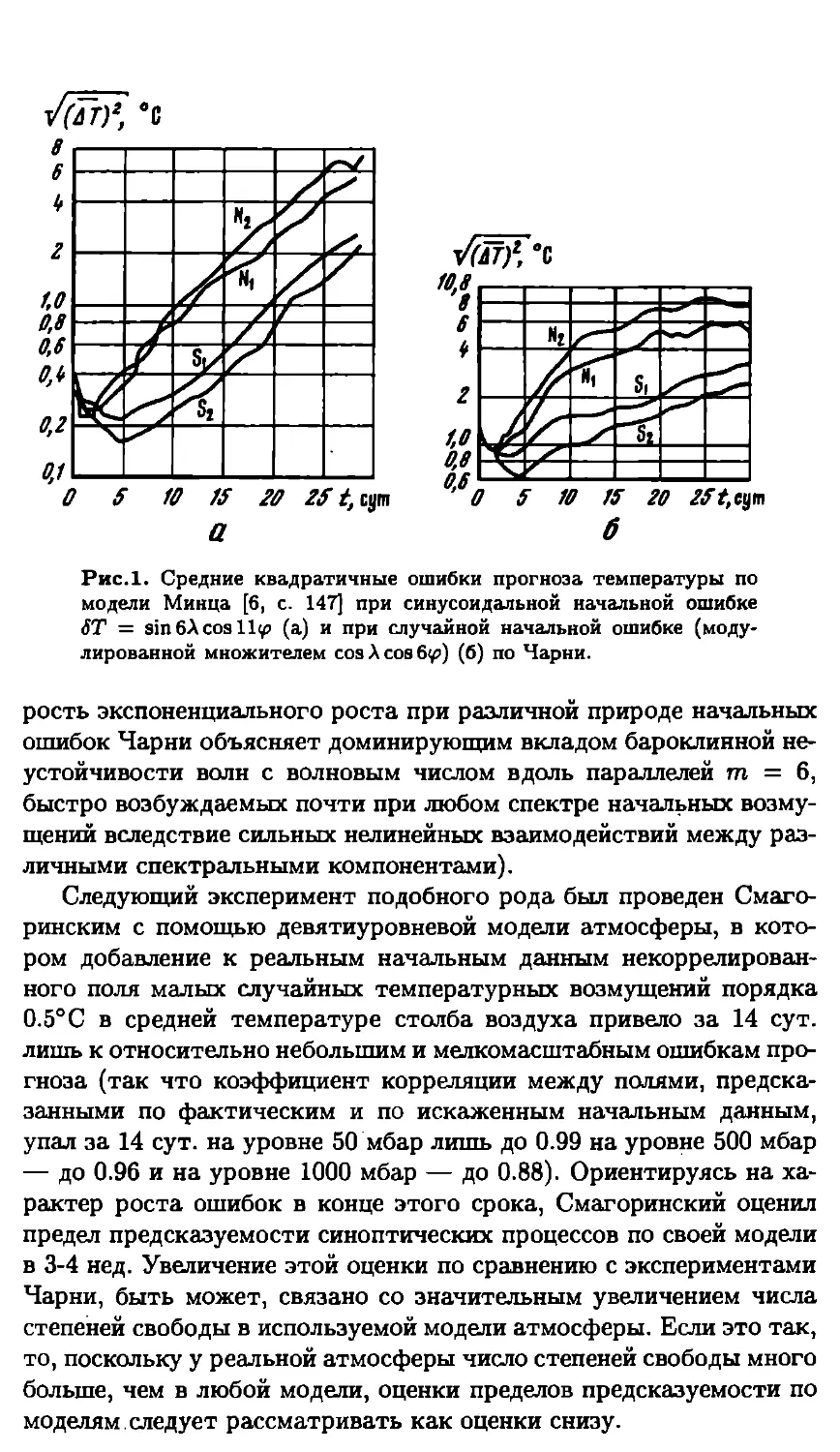
чальном синусоидальном поле ошибок ST = sin6Аcosily с ампли-
тудой 1° — широта, А — долгота) изменения средней квадра-
тичной ошибки прогноза температуры показаны на рис. 1а, из ко-
торого видно, что сначала в процессе адаптации поля скорости к
возмущению в поле температуры ошибка убывает, затем она экс-
поненциально растет (удваиваясь каждые 5 сут.) в соответствии
с линейной теорией неустойчивости малых возмущений, и затем
доросшие до конечной величины возмущения входят в режим не-
линейных осцилляций. Эволюция ошибки прогноза при случайной
начальной ошибке показана на рис. 16, а при начальной ошибке, ло-
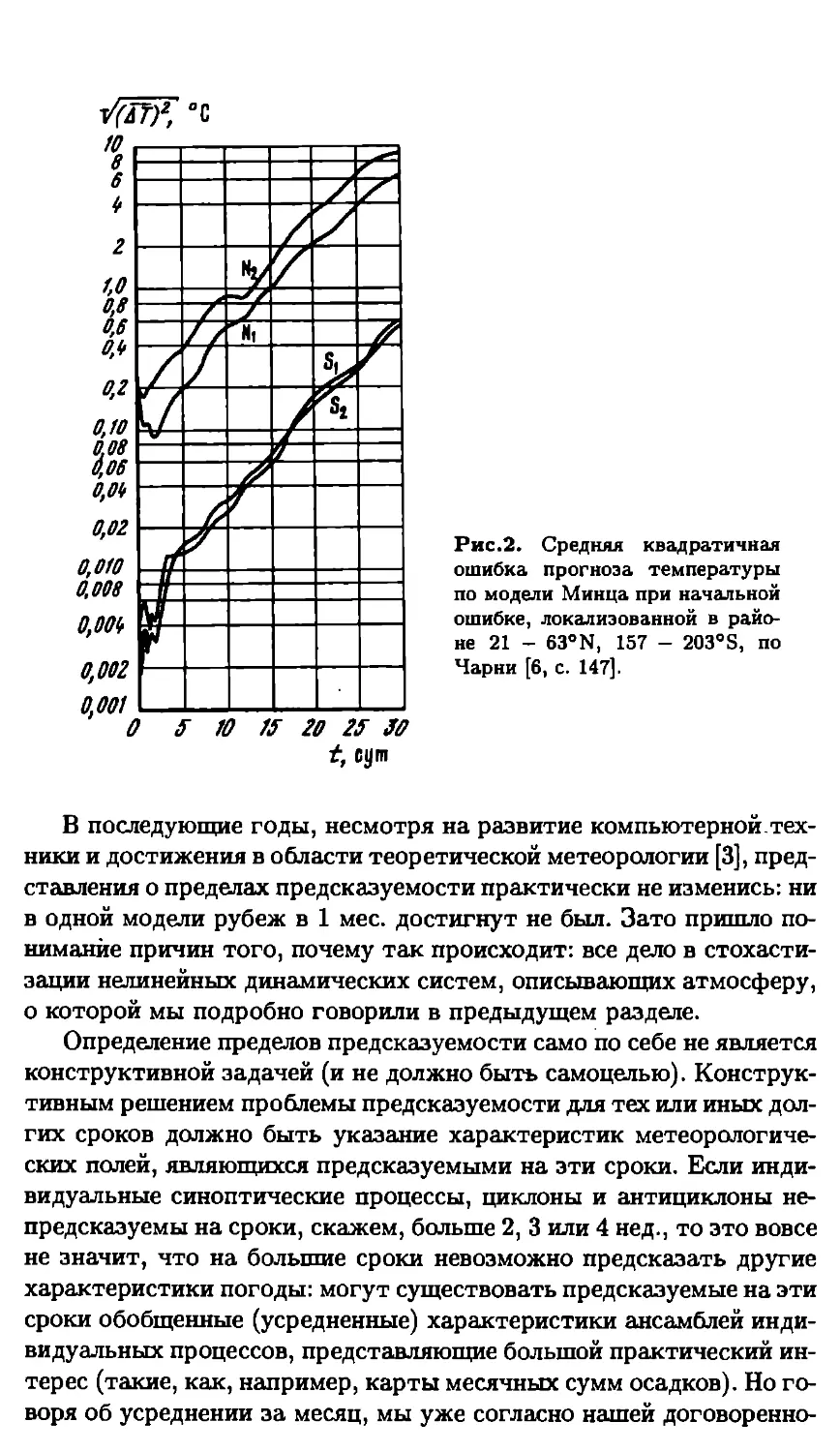
кализованной в пространстве (квадрат 21 — 63°, N, 157 — 203° S), —
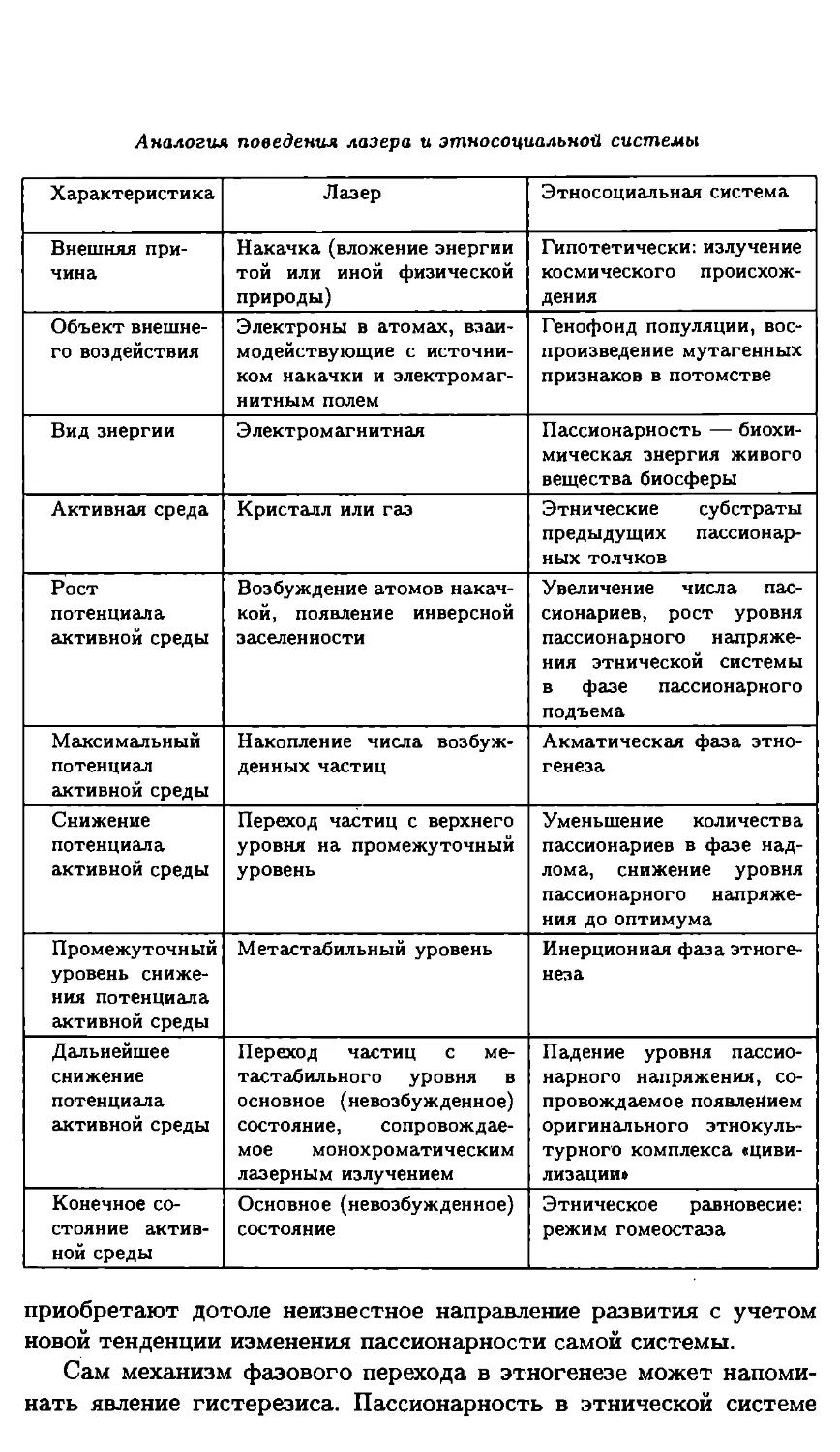
на рис. 2. Из рис. 2 видно, что порожденные возмущением в Север-
ном полушарии в процессе адаптации полей скорости и давления,
гравитационные волны достигают Южного полушария за 1-2 сут.,
создавая в нем возмущения с энергией на три порядка меньше, чем
у начального возмущения.
За предел предсказуемости Чарни принимает срок, в течение
которого ошибка прогноза достигает значения, равного средней
квадратичной разности двух случайных полей температуры (или
двух фактических полей: при разности времени больше 3 сут. их
средняя квадратичная разность оказывается приблизительно по-
стоянной, равной 5° С в Северном и 4° С в Южном полушарии на
уровне 1 и, соответственно, 8 и 3°С на уровне 2, откуда видно, в
частности, что предельный срок инерционного прогноза поля тем-
пературы равен 3 сут.). При значении этой разности 8°С (на уровне
800 мбар в Северном полушарии), при сроке удвоения ошибки 5 сут.
и начальной средней квадратичной ошибке 1°С предел предска-
зуемости получается равным 51og2B = 15 сут. (одинаковую ско-
Рис.1. Средние квадратичные ошибки прогноза температуры по
модели Минца [6, с. 147] при синусоидальной начальной ошибке
ST = sin6Аcosily (а) и при случайной начальной ошибке (моду-
лированной множителем cos А cos бу) (б) по Чарни.
рость экспоненциального роста при различной природе начальных
ошибок Чарни объясняет доминирующим вкладом бароклинной не-
устойчивости волн с волновым числом вдоль параллелей т = 6,
быстро возбуждаемых почти при любом спектре начальных возму-
щений вследствие сильных нелинейных взаимодействий между раз-
личными спектральными компонентами).
Следующий эксперимент подобного рода был проведен Смаго-
ринским с помощью девятиуровневой модели атмосферы, в кото-
ром добавление к реальным начальным данным некоррелирован-
ного поля малых случайных температурных возмущений порядка
0.5°С в средней температуре столба воздуха привело за 14 сут.
лишь к относительно небольшим и мелкомасштабным ошибкам про-
гноза (так что коэффициент корреляции между полями, предска-
занными по фактическим и по искаженным начальным данным,
упал за 14 сут. на уровне 50 мбар лишь до 0.99 на уровне 500 мбар
— до 0.96 и на уровне 1000 мбар — до 0.88). Ориентируясь на ха-
рактер роста ошибок в конце этого срока, Смагоринский оценил
предел предсказуемости синоптических процессов по своей модели
в 3-4 нед. Увеличение этой оценки по сравнению с экспериментами
Чарни, быть может, связано со значительным увеличением числа
степеней свободы в используемой модели атмосферы. Если это так,
то, поскольку у реальной атмосферы число степеней свободы много
больше, чем в любой модели, оценки пределов предсказуемости по
моделям следует рассматривать как оценки снизу.
Рис.2. Средняя квадратичная
ошибка прогноза температуры
по модели Минца при начальной
ошибке, локализованной в райо-
не 21 - 63°N, 157 - 203°S, по
Чарни [6, с. 147].
В последующие годы, несмотря на развитие компьютерной.тех-
ники и достижения в области теоретической метеорологии [3], пред-
ставления о пределах предсказуемости практически не изменись: ни
в одной модели рубеж в 1 мес. достигнут не был. Зато пришло по-
ниманйе причин того, почему так происходит: все дело в стохасти-
зации нелинейных динамических систем, описывающих атмосферу,
о которой мы подробно говорили в предыдущем разделе.
Определение пределов предсказуемости само по себе не является
конструктивной задачей (и не должно быть самоцелью). Конструк-
тивным решением проблемы предсказуемости для тех или иных дол-
гих сроков должно быть указание характеристик метеорологиче-
ских полей, являющихся предсказуемыми на эти сроки. Если инди-
видуальные синоптические процессы, циклоны и антициклоны не-
предсказуемы на сроки, скажем, больше 2, 3 или 4 нед., то это вовсе
не значит, что на большие сроки невозможно предсказать другие
характеристики погоды: могут существовать предсказуемые на эти
сроки обобщенные (усредненные) характеристики ансамблей инди-
видуальных процессов, представляющие большой практический ин-
терес (такие, как, например, карты месячных сумм осадков). Но го-
воря об усреднении за месяц, мы уже согласно нашей договоренно-
сти выходим за рамки погоды и приближаемся к климату, поэтому
перенесем это обсуждение в последующие разделы.
3. Элементы теории прогноза стационарных
случайных процессов
Здесь мы предполагаем, что поведение интересующей нас фи-
зической величины х (для простоты скалярной) описывается слу-
чайным процессом x(t), т.е. можно говорить лишь о вероятности, с
которой величина x(t) принадлежит тому или иному интервалу чи-
словой прямой. Совокупность таких совместных вероятностей, от-
вечающих всем возможным наборам моментов времени, называется
конечномерными распределениями процесса. Для полного описания
случайного процесса необходимо задать все его конечномерные рас-
пределения.
Предположим, что наблюдение y(t) процесса z(t) проводится до
момента времени t. В общем случае y(t) не совпадает с x(t) из-за
ошибок измерения. Обозначим через Yq совокупность всех значе-
ний процесса y(t) до момента to- Таким образом, вся информация
о поведении процесса в прошлом заключена в множестве Yj. За-
дача оптимального прогноза на срок т в соответствии с принятой
нами ранее средней квадратичной мерой ошибки формулируется
так: требуется найти величину z(to,T), зависящую лишь от пере-
менных из множества Уо, такую, что среднее квадратичное откло-
нение
ао(т) = {(z(to,r) ~ z(to + т))2)
минимально, где угловые скобки означают усреднение по ансам-
блю реализаций x(t). Искомая величина z[to,T) представляет со-
бой условное математическое ожидание (среднее значение) вели-
чины- x(to + г) относительно совокупности случайных величин Уо
и в общем случае может быть выражена в терминах конечномер-
ных распределений процессов z(t) и y(t). Однако практическая цен-
ность этих формул невелика из-за их громоздкости и из-за того, что
конечномерные распределения реально не известны эксперимента-
тору.
Чтобы упростить задачу, ограничимся классом величин z, ли-
нейно зависящих от переменных из совокупности Уо- Конечно, это
ограничение резко снижает эффективность прогноза. Ситуация
близка к тому, как если бы мы условились приближать реальные
динамические системы линейными. Приведем простой пример, ко-
торый хорошо иллюстрирует уровень возможной ошибки. Пусть
наблюдается случайная величина х с нулевым средним значением,
причем вероятность, с которой х принимает значения, большие а,
равна вероятности, с которой она принимает значения, меньшие
—а. Предполагается, что ошибки наблюдения отсутствуют. Требу-
ется построить наилучшую линейную оценку (прогноз) величины
и = х2 - {х2}, т.е. найти такой коэффициент к, при котором сред-
нее квадратичное отклонение величины z = кх от и минимально.
Другими словами, требуется найти регрессию z на х. Воспользо-
вавшись стандартной формулой, выражающей факт некоррелиро-
ванности и — кх и х, получим к = (их}/(х2) = 0. Парадоксальный
результат, когда в качестве прогноза точно предвычисляемой ве-
личины получается нуль, возникает из-за подмены понятия «зави-
симость» понятием «коррелированность».
И все же существует довольно широкий класс процессов, для
которых наилучший линейный прогноз совпадает с наилучшим во-
обще, — это гауссовские процессы [8]. Как мы увидим в дальней-
шем, в весьма общей ситуации климатическую систему можно рас-
сматривать как линейную, поэтому для исследования климата при-
менение линейной теории прогноза оправданно. Обратимся, следо-
вательно, к вопросу построения наилучшего линейного прогноза.
Введем в пространстве случайных величин скалярное произведе-
ние (предполагая, без ограничения общности, что (z(t)) = (y(t)) =
= 0).
(У(*1)»У(*2)) = <У(*1)У(*2)>-
Это скалярное произведение превращает совокупность случай-
ных величин, состоящую из значений процесса в разных точках, их
линейных комбинаций и пределов этих комбинаций по норме || • || =
= (’, )1/2, в гильбертово пространство £. Если, например, процесс
y(t) порождается конечным числом гармоник, т.е. его спектр лока-
лизован в конечном числе точек, то соответствующее пространство
£ конечномерно.
Пусть £о — линейное подпространство из £, порождаемое лишь
случайными величинами из совокупности Yq. В конечномерном слу-
чае £о — некоторая гиперплоскость. Тогда задача состоит в на-
хождении точки, принадлежащей гиперплоскости £о, ближайшей к
точке x(to +т). Для этого надо «опустить перпендикуляр» из точки
i(to + т) на гиперплоскость £о, что, как известно, делается с помо-
щью циркуля и линейки. Однако в нашей ситуации этих инструмен-
тов недостаточно, хотя геометрический язык оказывается весьма
полезным при решении этой задачи, относящейся скорее уже не к
теории случайных процессов, а к одной из областей функциональ-
ного анализа. Средняя квадратичная ошибка оптимального про-
гноза Oq(t) представляет собой длину указанного перпендикуляра,
а его основание, обозначаемое z(f0)'r), и есть искомое прогнозиру-
емое значение.
Задача прогнозирования имеет относительно полное решение в
случае статистически стационарного случайного процесса. Здесь
мы рассматриваем стационарные в широком смысле процессы, т.е.
корреляционная функция R(ti — tz) = (x(ii)x(t2)) зависит лишь от
разности моментов времени. Ошибками наблюдения пренебрегаем,
т.е. отождествляем x(t) и y(t). При достаточно общих условиях,
смысл которых сводится к тому, что спектр процесса x(t) сплошной,
процесс x(i) представляется в виде (разложение Вольда)
t
x(t) = j G(t — s)b(s) ds,
—oo
где 6(s) — стационарный белый шум с единичной дисперсией, а
ядро G(u) определяется по корреляционной функции. Решение за-
дачи прогноза дается формулой
to
z(to,r) = j G(r — u)b(u) du.
— OO
Таким образом, оптимальный линейный прогноз можно постро-
ить, зная корреляционную функцию процесса.
Рассмотрим, например, случайный процесс с корреляционной
функцией R(t) = где а > 0 — параметр. При дополнитель-
ном предположении гауссовости этот процесс является марковским;
он известен в математической литературе как процесс Орнштейна-
Уленбека. Физикам он более известен как решение уравнения Лан-
жевена
х + ах = b(t).
В этом случае G(u) - е~аи, и, следовательно, z(0, г) = е-от2:(0),
т.е. прогноз зависит лишь от последнего наблюдаемого значения
(в этом и состоит свойство марковости). Ошибка прогноза также
легко вычисляется: О’2 (г) = 1—е~2аг. Отметим, что решение уравне-
ния <т2 (г) = 7 для предела предсказуемости при заданной точности
прогноза 7 дается формулой
= -^-1п(1 -7).
Za
Точное аналитическое решение задачи имеется в более общем
случае, когда спектральная плотность процесса равна единице, де-
ленной на многочлен степени 2р. В этом случае оптимальный про-
гноз на любой срок выражается через значения процесса и его
производных до порядка р — 1 включительно. Такие процессы на-
зываются /^марковскими и являются решениями дифференциаль-
ных стохастических уравнений с постоянными коэффициентами по-
рядка р, в правой части которых стоит белый шум. Также явно
решается задача прогноза в случае, когда спектральная плотность
процесса является дробно-рациональной функцией частоты [9]. Та-
кие процессы носят название сложно-марковских и характеризу-
ются тем, что могут быть вложены в качестве компоненты в век-
торный марковский процесс. Сложно-марковский процесс также
удовлетворяет стохастическому дифференциальному уравнению с
постоянными коэффициентами, однако в его правой части могут
фигурировать и производные от белого шума. Множество предик-
торов такого процесса также конечномерно, однако не все из этих
предикторов совпадают с производными процессами в «настоящий»
момент времени — часть из них зависит от всего «прошлого» про-
цесса [10].
Аналогом сложно-марковских процессов в случае дискретного
времени служат процессы авторегрессии - скользящего среднего
(АРСС), широко используемые ныне и моделирования многих при-
родных процессов, в том числе и в климатологии. Эволюция такого
процесса {хп} описывается разностным уравнением
•^п 4" 4“ ... 4“ СКр—l^n—р+1 = £п 4" 1 4- • . /31£п—д> (5)
где ai,...,ap_i — постоянные коэффициенты авторегрессии;
/31,...,/3, — постоянные коэффициенты скользящего среднего;
{еп} — дискретный белый шум. Пару (р, д) называют порядком
процесса. В случае когда все коэффициенты /3< равны нулю, говорят
просто о процессе авторегрессии.
Весьма важным для приложений оказывается процесс авторе-
грессии 1-го порядка (р = 1). Оптимальный прогноз такого про-
цесса (при отсутствии ошибок наблюдения) дается простой форму-
лой 2n+i = aiXn- Заметим также, что если x(t) процесс Орнштейна-
Уленбека, то последовательность {хп}> полученная из x(t) выбором
значений, разделенных равными промежутками времени, является
процессом авторегрессии 1-го порядка.
Для определяемых уравнением (5) АРСС-процессов хорошо раз-
вита техника оценки коэффициентов авторегрессии (а^аг,-• •) и
скользящего среднего (/31, /З2,...) по наблюдениям процесса, а также
имеются явные формулы прогноза [11]. Отметим, что если x(t) —
сложно-марковский процесс, т.е. процесс с рациональной спектраль-
ной плотностью, то последовательность {x(nAt)}, где At — неко-
торый шаг дискретности по времени, есть АРСС-процесс. Однако
если x(t) — р-марковский, т.е. процесс со спектральной плотно-
стью «единица, деленная на многочлен», то x(nAt) не обязательно
процесс авторегрессии. Тем самым устанавливается связь между
стохастическими дифференциальными уравнениями, которые мо-
гут возникать в различных физических задачах, с моделями АРСС,
введенными как средство обработки временных рядов произволь-
ной природы. Оказывается, что такого же рода связь существует
между стохастическими дифференциальными уравнениями с част-
ными производными и векторными процессами авторегрессии.
Однако эта связь довольно сложна и по этой причине здесь обсу-
ждаться не будет. Соответствующие формулы и выкладки приво-
дятся в монографии одного из авторов [12]. Польза от результатов
такого рода состоит в том, что статистические модели процессов
можно строить, исходя из физических моделей, описываемых соот-
ветствующими дифференциальными уравнениями. Попутно можно
оценивать неизвестные или неопределенные параметры физических
моделей по наблюдениям процесса, используя хорошо развитую ста-
тистическую технику оценивания неизвестных коэффициентов ав-
торегрессии. Этот путь использовался при исследовании климати-
ческой изменчивости [12], к которой мы сейчас переходим.
4. Предсказуемость климатических процессов
Точка зрения на климатическую изменчивость, излагаемая в
данной статье, развита Хассельманом [13] и не является общепри-
нятой или доминирующей в климатологии. Суть ее состоит в том,
что долгопериодные колебания (больше месяца) в системе океан —
криосфера — суша — атмосфера являются откликом линейной
инерционной системы на короткопериодные погодные возмущения,
связанные с синоптическими атмосферными процессами и рассма-
триваемые в качестве белого шума. При таком подходе причины
климатической изменчивости ищутся внутри самой климатической
системы, а не в изменении внешних параметров (связанных, на-
пример, с вариациями солнечной активности), хотя сами эти из-
менения при таком подходе вполне могут быть учтены. Данный
подход привлекателен тем, что в его рамках удобно исследовать
проблему предсказуемости. Грубо говоря, простые стохастические
модели климата сводятся к некоторому подобию уравнения Лан-
жевена, в котором белый шум — синоптические атмосферные про-
цессы, а переменная, описывающая состояние, — это какой-либо па-
раметр климатической системы: ТПО, толщина ледового покрова,
растительный покров земли и т.д. Удобство такого подхода также
состоит в. том, что не надо долго искать причину случайных ко-
лебаний климата (а их наличие не может отрицать никто): эта
причина заключается в стохастичности поведения атмосферы, а
последняя обусловлена нелинейностью динамических процессов в
ней. Таков самый короткий путь к пояснению нерегулярной измен-
чивости климата, видной, например, из спектров долгопериодных
колебаний гидрометеорологических характеристик, имеющих вид
красного шума [14]. Заметим еще, что далеко не все исследователи
отождествляют климатическую изменчивость с изменчивостью, ха-
рактеризуемой временным масштабом более месяца. При изложе-
нии концепции простых стохастических моделей климата мы будем
пользоваться терминологией статьи [13].
Состояние климатической системы в каждый момент времени
характеризуется набором полей W = {u>i(г, t),Тог(г, £),-..}, гДе I —
время, г — точка пространства. Совокупность W можно разделить
на две части: набор медленно меняющихся (климатических) пере-
менных U = {ui,U2,...} и быстро меняющихся (погодных) пере-
менных V = {t>i, V2,...}. В группу V входят не только атмосфер-
ные поля, но и ряд полей океана: аномальные дрейфовые течения,
глубины залегания сезонного термоклина и т.д., изменчивость ко-
торых непосредственно индуцируется синоптическими атмосфер-
ными процессами. Типичные временные характеристики перемен-
ных из группы V составляют несколько суток (синоптический мас-
штаб в атмосфере), а характерное время изменчивости переменных
групп U, таких, например, как средняя температура воды в верхнем
перемешанном слое океана, равно нескольким месяцам или больше.
Таким образом, для существующих временных масштабов изменчи-
вости ти и tv имеем
Разница величин и ти обусловлена различием основных фи-
зических характеристик воды и воздуха: удельной теплоемкости,
плотности и кинематической вязкости. Эволюция климатической
системы может быть записана в виде
щ = Р(У,1Г), (6)
Vi = Gi(V,U), (7)
где Pi, Qi — вообще говоря, нелинейные операторы от многокомпо-
нентных функций У, U. Система уравнений (7) представляет собой
модель общей циркуляции атмосферы, а система (6) описывает из-
менчивость температуры поверхности океана и других медленно
меняющихся климатических характеристик, как отклик на «слу-
чайное» возбуждение «погодными переменными». При современном
развитии компьютерной техники интегрирование системы уравне-
ний (7) на времена порядка О(ти) невозможно. Модель с высоким
разрешением используется обычно для интегрирования (7) на про-
межуточном периоде то, rv << то ти, в течение которого медлен-
ные переменные могут рассматриваться как постоянные, но кото-
рый уже достаточно велик для того, чтобы набрать подходящую
статистику для погодных переменных. Следовательно, хотя модели
общей циркуляции атмосферы и дают важную информацию для ис-
следования климатической изменчивости, они, тем не менее, не мо-
гут моделировать ее как таковую.
Традиционное изучение динамики долгопериодной изменчиво-
сти основывалось на усреднении системы (6) по периоду то- В ре-
зультате усреднения получаем статистическую динамическую мо-
дель
d{ui)/dt = {Pi(V,U)). (8)
Операцию усреднения в (8) формально предпочтительнее трак-
товать как усреднение по ансамблю реализацией быстро меняю-
щихся полей V. В силу предполагаемой эргодичности такое усред-
нение совпадает с временным. Поскольку операторы Р, в общем
случае нелинейны, средняя скорость изменчивости (Pi) параметра
(щ) будет зависеть как от статистических характеристик и V и U
по отдельности, так и от их совместных статистических характери-
стик. Для замыкания уравнений, следовательно, нужно прибегать к
некоторым гипотезам. В этом уже состоит некоторая ущербность
применения статистических динамических моделей. Хотя класс мо-
делей (8) и называется статистическим, а силу присутствия опе-
рации усреднения и включения гипотез замыкания, редуцирован-
ное уравнение в действительности является детерминированным, а
не статистическим. Уже отмечалось, что асимптотические реше-
ния нелинейных детерминированных уравнений, содержащих отно-
сительно малое число степеней свободы, могут представлять собой
непериодические осцилляции случайного типа, подобные наблюда-
емым погодным или климатическим флуктуациям [15]. Однако в
своем большинстве хорошо известные простые статистические ди-
намические модели предопределяют единственное, не зависящее от
времени, асимптотическое состояние для любого заданного началь-
ного условия. Такие модели по своей сути не могут породить реше-
ния с непрерывным спектром, наблюдаемые в природе.
В прошлом долгопериодная изменчивость появлялась в рамках
классической статистической динамической модели как отклик си-
стемы (8) на изменения внешних граничных условий, как солнечная
радиация и мутность атмосферы, в большей мере, чем как резуль-
тат внутренних взаимодействий.
Однако если отказаться от усреднения системы (6) и рассматри-
вать ее как систему стохастических дифференциальных уравнений,
то причины долгопериодной изменчивости могут быть выведены
непосредственно из внутренних взаимодействий (это, конечно, не
исключает возможной значимости дополнительных, внешне инду-
цированных изменений климата). При таком подходе медленные
климатические переменные рассматриваются уже как случайные
поля с временными масштабами корреляции ти и больше. В част-
ности, свойственный долгопериодной изменчивости временной
спектр, характерный для «красного» шума, может быть получен
из (6) в результате следующих действий.
Функционал Р в (6) зависит, вообще говоря, от всего прошлого:
й = {i)(r, s),s < t},Ut = {u(r, s),s < t}. Считая отклонения v' =
= v — v, и' = и — й от среднего состояния небольшими, линеари-
зуем (6):
., 6Р , 6Р ,
и = ----V -I----и',
SVt 6Ut '
где 5P/5Vt и 6P/6Ut — вариационные производные в точке (Й, (7t),
являющиеся, как известно, линейными операторами от v' и и' со-
ответственно. В простейшем предположении, что эти операторы
зависят лишь от настоящего, из (9) получаем уравнение Ланжевена
(9)
й' = av! + av’
(аист — постоянные). С учетом малого времени корреляции «бы-
строго» процесса u'(t) это уравнение дает «красный» спектр
для u'(t).
Отметим, что линеаризация уравнения (6) необязательна. Усло-
вие короткокоррелированности позволяет исследовать статистиче-
ские свойства решения уравнения теплового баланса, так как урав-
нения для первого и второго моментов оказываются замкнутыми и
линейными [12]. В [13] неусредненные модели типа (6) получили на-
звание моделей стохастической генерации. Следуя [13], связь между
статистической динамической моделью, моделями атмосферной
циркуляции и стохастической генерации можно установить, исполь-
зуя аналогию с броуновским движением. Климатические U и погод-
ные V переменные могут интерпретироваться в аналогичной кар-
тине как большие и маленькие частицы соответственно, точнее как
их координаты и импульсы. Анализ климатической изменчивости
в рамках статистической динамической модели тогда эквивалентен
определению траекторий крупных частиц путем рассмотрения вза-
имодействия только крупных частиц между собой и со средними
полями давления и напряжения, создаваемыми движением малых
частиц (плюс влияние внешних сил). Численные эксперименты с мо-
делью общей циркуляции атмосферы соответствуют в этой картине
точному вычислению всех траекторий малых частиц при фиксиро-
ванном положении больших частиц. Если даже допустить, что на
протяжении эксперимента крупные частицы могут менять свое по-
ложение, то, как правило, невозможно провести интегрирование на-
столько далеко, чтобы увидеть ощутимые отклонения больших ча-
стиц от их начального положения. Наконец, модели стохастической
генерации соответствуют классическому статистическому рассмо-
трению броуновского движения, когда закономерности флуктуаций
крупных частиц выводятся из статистики малых частиц, с кото-
рыми они взаимодействуют.
В противоположность задаче броуновского движения перемен-
ные V{ в действительной климатопогодной системе, конечно, не на-
ходятся в состоянии термодинамического равновесия, и статисти-
ческие свойства V{ не могут быть выведены из статистической тер-
модинамической теории энергетически замкнутых систем; однако
их можно описать, исходя из численных экспериментов или реаль-
ных данных. Посредством статистического рассмотрения достига-
ется большое сокращение объема вычислений, так как требуется
относительно небольшая статистическая информация относитель-
но V. Она может быть получена путем экспериментирования с мо-
делью общей циркуляции атмосферы на относительно коротких
промежутках времени то ти.
С первого взгляда может показаться удивительным, что ста-
тистическая редукция полной климатопогодной системы возможна
без каких-либо гипотез замыкания; каждому специалисту, знако-
мому с системами, включающими турбулентные течения жидко-
стей, хорошо известно, что их эволюция связана с необратимыми,
сильно нелинейными процессами. Все дело в том, что редукция в
данном случае есть следствие временного(ударение на «но») разде-
ления масштабов. Это свойство теряется в обычных турбулентных
системах. Так, например, простая квазистационарная модель сто-
хастической генерации для атмосферы, связанная с моделью оке-1
ана, невозможна. Одна из главных трудностей состоит в выводе
линейных передаточных функций атмосферного отклика, которые
должны включать флуктуации нелинейных вихревых течений.
Идею Хассельмана о простых стохастических моделях клима-
та можно рассматривать как альтернативу концепции усреднения,
господствовавшей до недавнего времени в статистической физике.
В широком смысле эта концепция означает, что крупномасштаб-
ные процессы могут быть описаны детерминистскими уравнени-
ями, учитывающими случайные мелкомасштабные флуктуации в
виде эффективных коэффициентов, зависящих от статистических
характеристик «микромира».
Экспериментальное изучение статистической предсказуемости
климата, начатое В. Е. Привальским в 70-х годах [16,17] еще до по-
явления работы Хассельмана, в общем привело к тем же неутеши-
тельным результатам, которые следуют из теоретического анализа
на основе уравнения Ланжевена. В упомянутых работах (см. также
[18]) исследовалась, в частности, предсказуемость последовательно-
сти средних годовых значений ТПО в северной части Атлантиче-
ского океана за период с 1881 по 1970 г. Ряды аппроксимировались
моделями АРСС с использованием оптимальной процедуры выбора
порядка модели (р, q). В большинстве случаев оптимальной оказы-
валась модель авторегрессии 1-го порядка, а относительная ошибка
прогноза на один шаг вперед (год) была равна 75-80%. В тех слу-
чаях, когда оптимальной оказывалась другая модель, предсказуе-
мость по модели авторегрессии 1-го порядка практически совпа-
дала с предсказуемостью, оцененной по оптимальной модели. Таким
образом, наблюдалось полное согласие с выводами, основанными на
простой стохастической модели климата. В качестве предела пред-
сказуемости автором указанного исследования принималось время,
при котором относительная ошибка прогноза s(r) = ст2(т)/<т2 (где
ст2 — климатическая дисперсия) достигает 80%. Для средних го-
довых значений ТПО такой предел, следовательно, равен одному
году-
Более оптимистичными выглядят оценки предсказуемости ря-
дов средних месячных значений аномалий ТПО [12]. Под анома-
лиями понимается отклонение средней месячной температуры от
нормы, вычисляемой по длительным рядам наблюдений. На боль-
шей части акватории Северной Атлантики средняя квадратичная
ошибка прогноза s на один шаг вперед составляла 50-60%, что со-
ответствует пределу предсказуемости 3-4 мес. В отдельных райо-
нах предсказуемость оказывалась заметно выше или заметно ниже
указанного среднего значения, что связано с характерными гидро-
логическими особенностями этих районов. Отметим, что приведен-
ная цифра 3-4 мес. и есть примерная величина длительности суще-
ствования аномалий, известная задолго до исследования их пред-
сказуемости. Для северной части Тихого океана благодаря более
длительным рядам наблюдений (32 года по сравнению с 18 годами
в Атлантике) удалось оценить предсказуемость аномалий темпе-
ратуры отдельно для летних (май, июнь, июль, август) и зимних
(ноябрь, декабрь, январь, февраль) месяцев. Если в летние месяцы
предсказуемость оставалась невысокой (примерно такой же, как и
средняя сезонная для Атлантики), то в зимние месяцы з снизилась
до 30-50%, чему соответствует предел предсказуемости 6-10 шагов.
Это связано с тем, что зимой из-за большой интенсивности ветров
верхний перемешанный слой гораздо толще, чем летом, а поэтому
он более инерционен.
Приведенные оценки получены в рамках «многомерных» (век-
торных) моделей авторегрессии, в которых «состоянием» счита-
лась температура на фиксированной географической сетке (кон-
кретно с 5-градусной ячейкой) вкупе с температурой поверхности
в четырех ближайших точках сетки. Это позволило учесть про-
странственные связи в поле температуры (адвекцию и крупномас-
штабную диффузию тепла). Однако выигрыш в предсказуемости
по сравнению с одномерными моделями оказался небольшим: всего
5-10%. Отметим, что и совместный статистический анализ рядов
средней годовой температуры по упоминавшимся данным, привед-
ший к обнаружению обратной связи в системах теплых и холод-
ных течений в Атлантике, дал примерно такое же незначительное
увеличение предсказуемости [18]. Высокие значения ошибки про-
гноза обусловлены также значительной погрешностью использовав-
шихся данных. По некоторым оценкам «шум» в них составлял около
20% по дисперсии. Связано это с тем, что в один массив были со-
браны весьма разнородные данные, полученные с попутных торго-
вых судов. По специальной методике, позволяющей отфильтровы-
вать шум, была проведена оценка потенциальной предсказуемости,
т.е. той, которая имела бы место при отсутствии шума [12]. Ми-
нимальный предел ошибки прогноза з оказался равным 20-50% в
зависимости от района Северной Атлантики. Такие расчеты позво-
ляют составить представление о горизонте предсказуемости ано-
малий ТПО.
Это важное понятие было ведено Дж. Лайтхиллом на качествен-
ном уровне и уточнено Ю. А. Кравцовым в статье [7], где под го-
ризонтом предсказуемости подразумевается время т);т, при кото-
ром корреляция между предсказанным значением z(to+r) процесса
x(t) и его наблюденным значением у (to + г) в отсутствие ошибок
и при идеальной (адекватной) модели достигает 0.5. Отметим, что
этот же термин в ином смысле использовался в работе [19]. Так
как указанный коэффициент корреляции £>(т) взаимно однозначно
выражается через относительную среднюю квадратичную ошибку
прогноза s(t), а последняя в случае процесса авторегрессии 1-го по-
рядка равна sT где з — ошибка прогноза на один шаг вперед, то к
упомянутой ситуации, о горизонте предсказуемости можно судить
по величине з. Здесь уместно заметить, что использованная выше
статистическая модель аномалий ТПО была получена из эволюци-
онного уравнения теплового баланса верхнего перемешанного слоя
океана, и поэтому модель можно считать адекватной (удовлетвори-
тельно описывающей реальные процессы). Для минимальных значе-
ний з = 20% горизонт предсказуемости riim равен примерно 12 мес.,
а при з = 50% имеем тцт ~ 4 мес. Эти оценки следуют из простого
соотношения £>(т) = 1 — з(т), справедливого в случае авторегрессии
1-го порядка.
Весьма важной для океанологов величиной представляется уро-
вень моря. В монографии [18] приводятся результаты обработки
рядов средних годовых значений уровня моря длиной 70-100 лет
для 35 прибрежных пунктов. Оптимальными оказывались модели
авторегрессии порядка р — 0 (белый шум), 1 и 2, а величина з варь-
ировала в пределах 70-80% для колебаний уровня, обусловленных
муссонным нагоном, и достигала 90% для колебаний уровня, свя-
занных с зональной циркуляцией атмосферы. В этом случае пра-
вильнее говорить о непредсказуемости, чем о предсказуемости, ибо
предел предсказуемости по самым заниженным стандартам едва до-
тягивает (а иногда и не дотягивает) до длины шага дискретности.
Еще более пессимистичными оказались результаты исследова-
ния предсказуемости средних годовых значений температуры воз-
духа [18], которые отражают упоминавшуюся короткокоррелиро-
ванность локальных атмосферных процессов. Обработке были под-
вергнуты около 100 рядов продолжительностью от 80 до 315 лет.
Ошибка одношагового прогноза колебалась в диапазоне 85 4- 99%
при оптимальных порядках модели авторегрессии р = 0 4- 7. Предел
предсказуемости получился меньше одного года.
Поиск процессов, обладающих более высокой статистической
предсказуемостью, привел к выводу о ее возможном возрастании
при пространственном усреднении процессов в атмосфере и океане.
Так, ошибка одношагового прогноза средней годовой температуры
воздуха Северного полушария составляет около 60%, а предел пред-
сказуемости достигает 5 лет.
При усреднении годовой температуры воздуха в пределах 5-гра-
дусных широтных зон в Северном полушарии (1891-1976 гг.) от-
носительные ошибки прогноза з для тропической эоны (35° N) и
высоких широт (75° N) оказались равными 60-70%, а соответству-
ющие пределы предсказуемости — 4-5 лет. Не исключено, что такой
результат связан с уменьшением в этих зонах меридионального пе-
реноса теплосодержания и потенциальной энергии (рис. 3).
Во всей области от 75 до 15° N, т.е. там, где данные о темпе-
ратуре сравнительно надежны, ошибка прогноза с широтой меня-
ется так же как и Е. Если считать, что совпадение кривых на ри-
сунке не случайно, то оно означает, что статистическая предсказуе-
мость температуры воздуха имеет локальный характер: с уменыпе-
у' till.
Рис.З. Относительная ошибка
прогноза средней зональной
температуры воздуха с годо-
вым упреждением з и средний
меридиональный поток суммы
теплосодержания и потенциаль-
ной энергии в атмосфере Е.
нием меридионального переноса ошибки прогноза средней зональ-
ной температуры убывают, а ее предсказуемость растет. Наимень-
шие ошибки прогноза с одношаговым упреждением отмечаются для
областей от 30 до 40 и выше 65° N. Возможно, что повышение пред-
сказуемости в зоне 30 — 40° связано с расположением здесь двух
устойчивых центров высокого давления: Азорского и Гавайского
антициклонов. Кроме того, минимуму относительной ошибки про-
гноза на широте 75° N примерно отвечает положение Гренландского
антициклона. Предел предсказуемости в умеренных и низких широ-
тах с сильным меридиональным переносом равен примерно одному
году. Похожие выводы были получены и для среднего зонального
давления воздуха [18].
Отметим также, что даже при относительно низкой средней ква-
дратичной ошибке прогноза температуры воздуха на один шаг до-
верительный интервал для прогнозируемого значения, соответству-
ющий доверительной вероятности 0.9, слишком велик — он суще-
ственно превышает два средних квадратичных отклонения, рассчи-
танных по всему ряду наблюдений.
Некоторый рост статистической предсказуемости наблюдается
и для одного пространственно-усредненного процесса в океане: пло-
щади льдов в Баренцевом море в летние месяцы 1899-1981 гг. Для
этого ряда относительная ошибка одношагового прогноза составля-
ет всего 53%, а предел предсказуемости — 3 года [18].
С приведенными результатами резко контрастируют результа-
ты исследования предсказуемости уровня бессточных озер. Однако
метод оценки предсказуемости здесь был совершенно иным. Автор
работы [18] исходил из модели авторегрессии 2-го порядка уровня,
которая получается непосредственно из уравнения водного баланса,
записанного после некоторых упрощений в виде
x(t) = aiXt-i + a2vt + a3lt, (10)
где x(t) — уровень озера в t-м году; Vt — объем притока за год;
It — толщина годового слоя видимого испарения; ai = 1 — i>i(Z);
а2 = 1/F, F — средняя площадь озер; аз = -1; bi — коэффициент
пропорциональности в регрессивном соотношении F = a + bw, w —
средний объем озера. Исходя из оцененных по данным наблюдений
моделей видимого испарения и притока, были получены следующие
оценки коэффициента авторегрессии ар Каспийское море — 0.97;
Балхаш — 0.91; Мертвое море —- 0.98; Большое Соленое озеро —
0.87. Эти оценки предопределили весьма высокий предел предска-
зуемости уровня бессточного озера: от 10 лет в случае Большого
Соленого озера до 50 лет для Мертвого моря (чем круче берега
озера и меньше средний приток, тем лучше предсказуемость).
Такая высокая предсказуемость связана с большой инерционно-
стью колебаний уровня больших бессточных озер. Результаты рас-
четов предсказуемости по реальным данным оказались близкими к
приведенным оценкам предсказуемости, полученными из теорети-
ческой модели (10).
5. Пути улучшения статистического прогноза
Из обсуждавшихся примеров можно сделать вывод, что усред-
нение по времени или по пространству исследуемой гидрометеоро-
логической характеристики приводит, как правило, к повышению
предсказуемости. Так обстоит дело, в частности, с температурой
воздуха. Такая же картина наблюдается и в случае ТПО [20], где
трехмесячное сглаживание аномалий температуры заметно увели-
чило предел предсказуемости. Однако силы всеобщности указан-
ное правило не имеет. Известны случаи, когда усреднение данных
наблюдений на площади не приводило к улучшению качества про-
гноза [18].
Может сложиться впечатление, что, привлекая все большее число
предикторов, можно добиться существенного улучшения результа-
тов прогноза. Так, рассматривая в случае аномалий ТПО наряду с
температурой в соседних точках также температуру в более уда-
ленных точках и привлекая данные о температуре и важности воз-
духа, скорости ветра и т.д., казалось бы, можно получить гораздо
лучший прогноз, поскольку все указанные факторы, безусловно,
влияют на изменение температуры воды в рассматриваемой точке.
Однако простые численные эксперименты, в которых число предик-
торов увеличивалось с 5 до 9, показали, что это совсем не так: за-
метного увеличения предсказуемости не происходило, а зачастую
она даже ухудшалась. Подробно эта ситуация анализировалась в
статье А. М. Яглома [21]. Приведем вкратце результаты этого ана-
лиза.
Пусть мы хотим найти методом наименьших квадратов наилуч-
шую оценку величины х (предиктант) по значениям предикторов
yi,... ,у к, т.е. требуется найти коэффициенты ...,а*, обеспечи-
вающие минимальный средний квадрат отклонения {(х — aiyi —
—ofc?/fc)2)- Используемые при расчете эмпирические значения коэф-
фициентов корреляции ТЦ и между величинами х и yi, i = 1,..., к,
и между парами yi и yj,i,j = 1,..., к, являются неточными и зави-
сят от объема (и качества) тех данных, которые имеются в распо-
ряжении наблюдателя. Поэтому и оптимальные значения щ,..., а*
не являются точными, т.е. наилучшими для всей генеральной сово-
купности случайных величин (3/1,..., у к, х), и в применении к после-
дующей независимой выборке эти коэффициенты могут оказаться
гораздо менее удачными. Чтобы этого не происходило, подбор пре-
дикторов должен удовлетворять нескольким требованиям, важней-
шие из которых состоят в следующем: чтобы добиться достаточно
высокой точности оценок коэффициентов регрессии, число предик-
торов к не должно быть слишком большим. Если объем выборки
имеет порядок одной или нескольких сотен, то число к не должно
превосходить нескольких единиц. Ограничение на число предикто-
ров Лоренц назвал «табу статистического прогноза» [22].
Второе требование, к которому привлек внимание А.Н. Колмо-
горов [23], состоит в запрещении перебора большого числа систем
предикторов (пусть даже каждая из них и содержит лишь неболь-
шое число величин) для отбора лучшей из этих систем. Дело в том,
что если мы перепробуем множество разных систем предикторов,
то хотя бы для одной из них с большой вероятностью значение коэф-
фициента корреляции предикторов с величиной х окажется сильно
завышенным. В таком случае эта система предикторов будет вы-
брана в качестве наилучшей. Однако уже в следующем экспери-
менте выбранная система предикторов дает результаты гораздо
хуже ожидаемых.
Как указывает Яглом [21], соображения Колмогорова делают до-
вольно проблематичными и преимущества некоторых сравнительно
новых методов статистического прогноза погоды, предложенных
позже опубликования статьи Колмогорова. Типичным примером
является так называемый метод просеивания. Этот метод состоит
в том, что вначале рассматривается большая совокупность предик-
торов, а затем из них последовательно выбираются «наилучшие».
Сначала отбирается тот (для определенности yi), которому отве-
чает наибольший эмпирический коэффициент корреляции с х, за-
тем тот (уг), который дает наибольший вклад в сводный коэффи-
циент корреляции пары (3/1,3/2) с а:, и т.д. После нескольких шагов
вклад оставшихся предикторов оказывается весьма незначитель-
ным, и процедуру просеивания можно прекратить. Однако уже упо-
минавшиеся аргументы позволяют сделать вывод, что «наилучший»
набор предикторов является таковым лишь для данной выборки и
может дать весьма неудовлетворительный результат при переходе
к другой независимой выборке. Примерно так же обстоит дело с
широко распространенным методом эмпирических ортогональных
функций [24], совпадающим, в сущности, с методом главных компо-
нент многомерного статистического анализа [25]. Хотя этот метод
довольно часто используется для прогноза океанологических [20] и
метеорологических [22] полей, результаты оказываются не всегда
удовлетворительными в том случае, когда «старшие» эмпирические
моды выбираются методом, подобным просеиванию [22].
Один из полезных путей улучшения прогноза состоит в поиске
функционала от исследуемых величин, наиболее успешно прогно-
зируемого по данным наблюдений этих же величин в прошлом или
других величин, связанных с исследуемыми. Формально задача ста-
вится так. Имеется совокупность наблюдений Y = (j/i,...,Уп), тре-
буется найти функционал F(xi,... , тт) от случайных величин
Xi,..., хт оптимальный средний квадратический прогноз которого
по наблюдениям Y был бы наилучшим среди прогнозов, отвечаю-
щим всей совокупности функционалов F. В линейной постановке
(т.е. когда рассматривается множество линейных функционалов)
математические приемы решения этой задачи были даны в рабо-
тах Обухова и Хотеллинга [26,27]. Согласно этой теории, для ука-
занных совокупностей случайных величин можно найти такие ли-
нейные комбинации щ,г — 1,... ,п и vj,j = величин у'к
и х'{ соответственно, где штрих означает отклонение от среднего,
что щ некоррелированы между собой, Vj некоррелированы между
собой, щ некоррелированы со всеми Vj\j / г. Пусть р\ > Рг ••• —
коэффициенты корреляции uj c»i, «г cvjh т.д. В таком случае
коэффициенты Pi,P2, • • называются каноническими корреляциями
совокупностей Y и X, а случайные величины щ и V{ соответству-
ющими каноническими величинами. Очевидно, величина г>1 и дает
решение поставленной задачи. Нахождение канонических корреля-
ций и величин может быть сведено к некоторой алгебраической (ма-
тричной) задаче на собственные значения.
В [28] приводятся примеры применения метода канонических
корреляций в случае, когда Y — это данные наблюдений за полем
атмосферного давления на определенной сети станций в некоторый
день. Было показано, что некоторые усредненные характеристики
поля давления могут быть предсказаны по данным наблюдений в
предыдущий день заметно точнее, чем значения давления в одной
точке, причем общий характер «оптимально предсказуемых харак-
теристик поля давления» (отвечающих первой и второй канониче-
ским корреляциям) для европейской части СССР и для террито-
рии США оказался примерно одинаковым. Интересен также при-
мер применения метода канонических корреляций к реальному ряду
средних годовых приземных температур воздуха Т, усредненных по
широтному поясу, заключенному между 30 и 80° N [28]. По климати-
ческому ряду значений за 1892-1976 гг. были подсчитаны временные
корреляционные функции при длине выборки, равной 86, которые
затем использовались для расчета первой канонической корреля-
ции pi, и первых канонических величин щ и щ для совокупностей
{T(t),T(t -1),...,T(t - п + 1)} и {T(t + 1), T(t + 2),...,T(t + n)}
при п = 1,5. При этом оказалось, что с ростом п значение pi
монотонно возрастает от 0.6 до 0.8, причем по значениям T(t),
T(t — 1),..., T(t—4) точнее всего предсказывается не значение T(t+
+1), а линейная комбинация значений T(t + l),T(f+ 2),... , T(t + 5),
приближающаяся к среднему арифметическому всех этих значений.
Полученный вывод коррелирует с упоминавшимися результатами
и гипотезами о лучшей прогнозируемости усредненных характе-
ристик. Метод канонических корреляций развит также для случая
непрерывных совокупностей {it}, {у*} [29], что весьма полезно для
тех метеорологических задач, где важно проследить за временным
ходом атмосферных полей и их прогнозов.
6. Использование результатов прогноза
Дж. К. Томпсон в 1972 г. рассчитал, что при оптимальном ис-
пользовании метеорологической информации в США можно полу-
чить экономический эффект в размере 739 млн. долл, ежегодно.
Эта цифра складывается из выигрыша, обусловленного внедрением
в прогностическую практику новых научных достижений, повы-
шающих успешность предсказаний (примерно 60% от указанной
суммы), и выигрыша, связанного с совершенствованием оператив-
ного использования прогнозов путем перехода к экономически
оптимальным хозяйственным решениям. Львиная доля приведен-
ной суммы приходится на сельское хозяйство — 567 млн. долл.,
на коммунальное хозяйство — 112 млн. долл., строительство — 32
млн. долл., авиацию — 4 млн. долл, и т.д. Цифры взяты из моно-
графии Жуковского [30], в которой последовательно развивается
подход к оптимальному использованию метеорологической инфор-
мации при принятии экономических решений.
Рассмотрим простой пример. Пусть Некто предсказал, что уро-
вень Каспия в будущем году понизится с вероятностью р = 0.9, а
повысится соответственно с вероятностью q = 0.1. Должно ли Лицо,
принимающее хозяйственные решения, реагировать так, чтобы
ориентировать все проводимые мероприятия на понижение уровня?
Было бы нормально, если бы Лицо проделало следующие простень-
кие вычисления. Допустим, что повышение уровня Каспия приведет
к затоплению прибрежных нефтяных сооружений и нанесет тем
с ущерб в С руб., а перенос этих сооружений в безопасное место
стоит с руб. (очевидно, что С с). Тогда если принимается ре-
шение спасать оборудование (решение 1), то ожидаемые затраты
составят S\ = с-р + с- q = с, а если принимается решение оставить
все на своем месте (решение 2), т.е. довериться более вероятному
с точки зрения прогнозиста событию, то ожидаемые затраты ока-
жутся равными S2 = О р+С q = cq. Таким образом, S2/Si = qC/c.
И если, например, С/с = 100, то S2 в 10 раз больше, чем Si, и,
конечно, следует предпочесть решение 1 и эвакуировать оборудо-
вание из опасной зоны, несмотря на то что вероятность затопления
невелика. К сожалению, в жизни все произошло наоборот.
Этот простой пример показывает также, что при оценке каче-
ства любых метеорологических прогнозов возникают две в извест-
ной степени самостоятельные задачи [30]. Первая состоит в оценке
успешности прогноза. Этот вопрос обычно интересует разработ-
чика прогностической методики и синоптика, пользующегося дан-
ной методикой в оперативной практике. При этом преследуется
цель безотносительно к хозяйственному использованию прогноза
дать оценку непосредственно самому искусству предсказания по-
годы. Вторая задача, которая имеет первостепенное значение для
потребителя, заключается в определении хозяйственной ценности
прогноза. Последнюю необходимо знать, чтобы решить вопрос, ис-
пользовать этот прогноз или нет, а если использовать, то как, и
какой экономический эффект в результате этого может быть полу-
чен. Вопрос о мерах успешности прогноза и мерах его экономиче-
ской полезности подробно обсуждается в упомянутой монографии.
Рассмотренный пример приводит к следующей схеме принятия
решения по результатам прогноза. Пусть результатом прогноза
служит набор вероятностей pi,... ,рп, с которыми осуществляется
одно из состояний погоды Fi,..., Fn. В эту схему легко поместить
и наблюдения непрерывно распределенных величин, понимая под
событием Fi, попадание ее значения в некоторый интервал с но-
мером г. Собственно только такие события и интересуют потреби-
теля, а не конкретные значения величин. Предположим еще, что в
распоряжении потребителя имеется набор действий (мероприятий)
di,...,dm, причем для каждой пары diyFj задана сумма ущерба
U(di, Fj), получаемого в результате появления погоды Fj после при-
нятия решения о проведении мероприятия di. Разумеется, это мо-
жет быть не только ущерб, а и доход: в этом случае условимся счи-
тать величину U отрицательной. Имеется громадное количество на-
званий функций U, некоторые из них мы здесь приведем: в экономе-
трике и социологии — функция полезности, в теории игр — функ-
ция выигрыша, а теории принятия решений — функция потерь. Мы
будем пользоваться последним термином. Знание функции потерь
необходимо для построения правильной стратегии использования
информации. В результате действия dk ожидаемые потери будут
п
равны Sk = 52 PiU(dk,Fi) и потребителю разумно выбрать такое
1=1
мероприятие dk, которое дает минимальное значение потерь Sk-
В приведенном выше примере di — это решение 1, с?2 — решение 2,
Fi — повышение уровня Каспия, F2 — понижение, U(Fi,di) = с,
U(Fi,d2) = С, U(F2,di) = с, U(F2,d2) = 0.
Более гибкая стратегия состоит не в выборе конкретного дей-
ствия из набора возможных (di,..., dm), а в задании вероятностей
91 > • • • > Чт', 91 + • • • + Qm + 1> с какими принимается то или иное ре-
шение. Это так называемая рандомизированная стратегия приня-
тия решений. В реальной практике применение рандомизированной
стратегии может осуществляться чередованием действий di,..., dm
с частотами qi,..., qm соответственно. Иногда рандомизацию мож-
но применять в единичном эксперименте. Например, если действие
dk означает внесение удобрения к-го вида, то это удобрение вно-
сится на площади, пропорциональной qk- При рандомизированной
стратегии средние потери являются уже функцией от распределе-
ния q = (91,--.,9m):
S^^^PiqiUlF^. (11)
i i
Поиск оптимальной стратегии сводится теперь к поиску вектора q,
компоненты которого доставляют минимальное значение функцио-
налу (11).
Еще более полезно считать принятие решения и появление того
или иного варианта погоды событиями зависимыми. В этом случае
стратегия есть набор условных вероятностей рц = P(dj\Fi) приня-
тия решения dj при условии состояния погоды Е). Первоначально
такой подход был предложен в работе А.С.Монина, а затем уже
развит в работах Н.А.Багрова и Г.В.Грузы (см. [6, с. 180]), а также
в упоминавшейся монографии [30].
Математический аппарат решения задач выбора оптимальной
стратегии в условиях неопределенности к настоящему времени ши-
роко развит, и центр тяжести проблемы использования гидрометео-
рологической информации должен быть перенесен, по-видимому, в
область проблемы построения (оценивания, вычисления) функции
потерь U(F, d). Насколько нам известно такая работа еще не ор-
ганизована. Одна из наиболее существенных трудностей на этом
пути состоит в количественном описании потерь, связанных с теми
или иными антропогенными действиями и реакцией природы на
них. Не все можно измерить в деньгах. Если доход от улучшения
орошаемости земель, связанный с возрастанием стока рек и озер,
можно оценить в рублях, то возможную потерю отдельных видов
рыб (пусть даже и не особенно ценных с утилитарной точки зре-
ния) в результате таких действий оценить гораздо сложнее.
По-видимому, один из выходов в данной ситуации состоит в
обращении к методам статистики объектов нечисловой природы,
интенсивно развивающимся в последнее время [31]. При таком под-
ходе вместо абсолютных количественных характеристик объектов
(или действий) используются сравнительные качественные оценки:
«лучше», «предпочтительнее» и т.д., и оптимизация функции потерь
проводится на основе такой качественной информации.
Вряд ли в небольшой статье можно дать полную картину состо-
яния проблемы предсказуемости погодных и климатических про-
цессов. Мы, однако, надеемся, что читатель получил представле-
ние об основных методах прогноза, количественных характеристи-
ках предсказуемости и факторах, препятствующих успешному про-
гнозу на длительные сроки, в обсуждаемой области науки.
Авторы благодарят Ю.А.Кравцова и В.Е.Привальского за ряд
полезных замечаний, способствовавших улучшению рукописи.
ЛИТЕРАТУРА
1. Татарский В.И. О критериях степени хаотичности // УФН. 1989. Т.158,
Вып.1. С.123-128.
2. Монин А.С., Яглом А.М. Статистическая гидромеханика. М.: Наука, 1956.
564 с.
3. Сонечкин Д.М. Стохастичность в моделях общей циркуляции атмосферы.
Л.: Гидрометеоиздат, 1984. 277 с.
4. ИЧ'епег N., Mazani Р. The prediction theory of multivarite stochastic process
// Acta Math. 1957. Vol.98. P.111-150.
5. Монин A.C. Теоретические основы геофизической гидродинамики. Л.: Ги-
дрометеоиздат, 1988. 423 с.
6. Монин А.С. Прогноз погоды как задача физики. М:: Наука, 1969. 184 с.
7. Кравцов Ю.А. Случайность, детерминированность, предсказуемость //
УФН. 1989. Т.158, Вып.1. С.93-122.
8. Ибрагимов И.А., Розанов И.А. Гауссовские случайные процессы. М.: На-
ука, 1970. 384 с.
9. Яглом А.М. Экстраполяция, интерполирование и фильтрация стационар-
ных случайных процессов с рациональной спектральной плотностью // Тр.
Моск. мат. о-ва. 1955. С.237-278.
10. Питербарг Л.И. О прогнозе одного класса случайных полей // Теория
вероятностей и ее применения. 1983. № 1. С.176-182.
11. Бокс Дж., Джеккинс Т. Анализ временных рядов. М.: Мир, 1974. 242 с.
12. Питербарг Л.И. Динамика и прогноз крупномасштабных аномалий темпе-
ратуры поверхности океана. Л.: Гидрометеоиздат, 1989. 206 с.
13. Hasselmann К. Stochastic climate models. Pt.I. Theory // Tellus. 1976. Vol.28,
№ 6. P.473-485.
14. Вулис И. А., Монин А.С. О спектрах долгопериодных колебаний метеоро-
логических полей // ДАН СССР. 1971. Т.197, № 2. С. 328-331.
15. Lorenz E.N. A study of the predictobility of a 28-variable atmospheric model
// Tellus. 1965. Vol.17, № 5. P.321-333.
16. Привальский B.E. Об оценивании спектральной плотности крупномасштаб-
ных процессов // Изв. АН СССР, Физика атмосферы и океана. 1976. Т.12,
№ 9. С.979-988.
17. Привальский В.Е. О статистической предсказуемости крупномасштабных
гидрометеорологических процессов // Физика атмосферы и океана. 1977.
Т.13. № 4. С.371-377.
18. Привальский В.Е. Климатическая изменчивость (стохастические модели,
предсказуемость, спектры). М.: Наука, 1985. 189 с.
19. Parzen Е., Newton J. Forescasting and time series model types of 111 economic
time series // The forecasting accuracy of major time series methods. N.Y.:
Willey, 1984. P.267-288.
20. Davis R.E. Predictability of sea surface temperature and sea level pressure
anomalies over the North Pacific Ocean // J. Phys. Oceanogr. 1976. Vol.6, № 3.
P.249-266.
21. Яглом A.M. Статистическое прогнозирование // Колмогоров A.H. Теория
вероятностей и математическая статистика. М.: Наука 1986. С.523-526.
22. Lorenz E.N. Prospects for statistical weather forecasting // Statist. Forecasting
Proj. Final Rept. Cambridge (Mass.), 1959. P.388.
23. Колмогоров A.H. К вопросу о пригодности найденных статистическим
путем формул прогноза // Колмогоров А.Н. Тория вероятностей и матема-
тическая статистика. М.: Наука, 1986. С.161-167.
24. Мещерская А.В., Руховец Л.В., Юдин М.И., Яковлева Н.И. Естественные
составляющие метеорологических полей. Л.: Гидрометеоиздат, 1970. 160 с.
25. Андерсон Г. Введение в многомерный статистический анализ. М.: Физмат-
гиз, 1963. 502 с.
26. Обухов А.М. Нормальная корреляция векторов. // Изв. АН СССР. Сер.
мат. и естеств. наук. 1938. № 3. С.339-370.
27. Hotelling Н. Delation between two sets of variables // Biometrika. 1936. Vol.28.
P.321-377.
28. Обухов A.M., Фортус М.И., Яглом A.M. Метод канонических корреляций
для анализа случайных процессов и его применения в метеорологии // Тез.
I-Всемир. конгресса о-ва матем. статист, и теор. вер. им. Бернулли. Т.1.
Сек.1-19. М.: Наука, 1986. С.398-400.
29. Гельфанд И.М., Яглом А.М. О вычислении количества информации о слу-
чайной функции, содержащейся в другой такой функции // УМН. 1957.
Т.12, № 1. С.3-52.
30. Жуковский Е.У. Метеорологическая информация и экономические реше-
ния. Л.: Гидрометеоиздат, 1981. 304 с.
31. Орлов А.Н. Статистика нечисловых объектов // Статистика. Вероятность.
Экономика. М.: Наука, 1985. С.99-114.
Г.Р.Иваницкий
КАК АКТИВНАЯ АВТОВОЛНОВАЯ СРЕДА
ПРЕДСКАЗЫВАЕТ БУДУЩЕЕ
Бактерия стала добычей фага; мотылек сгорел в пламени свечи;
заяц оказался жертвой рыси; погиб во время шторма экипаж яхты;
погребено население поселка под пеплом проснувшегося вулкана;
исчезло государство в порожденной им экологической катастрофе.
У всех этих и многих других трагедий причина одна — неправиль-
ная оценка и прогноз ситуации. Очевидно, что предвидение есть
фактор выживания.
Предсказание независимо от того сделано оно с помощью вычи-
слений на ЭВМ или с помощью биологической системы, например,
такой, как наш мозг, — это физический процесс. К нему приме-
нимы те же понятия, что и к другим физическим процессам. Пред-
сказание заключается в том, что выводы о возможности будущего
события либо ряда событий делаются на основании анализа и обоб-
щения предыдущего опыта. В различных условиях объем сведений
о прошлом неодинаков. Хотя подавляющее большинство событий
имеет периодическую повторяемость (как будет показано ниже),
тем не менее, наряду с синфазностью циклических природных про-
цессов также периодически возникает их десинхронизация. Тогда
процесс имеет хаотический, случайный характер. Поведение хаоса,
как правило, непредсказуемо, хотя и в хаосе часто скрыта упоря-
доченность [1].
Самые неожиданные на первый взгляд предсказания также ба-
зируются на памяти, содержащейся, например, в истории матери-
альной культуры, в фольклоре, в дошедших до нас письменных ис-
точниках или в космических процессах. Значительную часть опыта
прошлого составляет информация, заложенная в живом организме
генетическим путем. По оценкам приблизительно 1 /3 информации,
необходимой для выживания человека, носит генетическую окраску,
2/3 — связаны с обучением и воспитанием. Эти данные были полу-
чены на основе интеллектуального тестирования однояйцевых близ-
нецов, по разным причинам разделенных в раннем возрасте и воспи-
тываемых приемными родителями. У животных доля генетической
памяти больше.
Наша цель — показать, что активные автоволновые среды мо-
гут предсказывать будущее для определенного класса природных
явлений, носящих циклический характер. Мы рассмотрим пример
одной из возможных прогнозирующих систем, во многом напоми-
нающей работу нашего мозга.
Активные автоволновые среды
Все многообразие сред можно представить в виде двух боль-
ших групп: консервативные и активные. Первые не имеют внутрен-
него запаса энергии; вторые, напротив, содержат распределенный
по среде запас потенциальной энергии, которая может быть акку-
мулирована разными способами. Между этими группами иногда
трудно установить границу. Тем не менее, такое деление сред на
два вида оправданно, что будет ясно из дальнейшего изложения.
Автоволны — это обобщенное понятие, позволяющее системати-
зировать экспериментальные факты и теоретические представле-
ния о некоторых нелинейных процессах, наблюдаемых в активных
средах в биологии, химии и физике [2-4]. Простейшие автоволны —
это волны горения, например, огненный фронт во время лесного по-
жара. Распространение автоволн сопровождает многие процессы:
передачу информации в живом организме, сокращения сердечной
мышцы, начальные этапы морфогенеза у некоторых простейших
организмов, активацию катализаторов в химической промышлен-
ности и т.д.
Подчеркнем, что автоволны возникают только в активных сре-
дах и по своим свойствам существенно отличаются от волн, распро-
страняющихся в консервативных средах, например, от электромаг-
нитных или механических волн.
Чтобы возбудить волны в консервативных средах, необходимо
создать начальное возмущение, которое затем будет распростра-
няться в виде волн. Для таких волн выполняется закон сохранения
энергии. Если мы бросаем камень в воду тихого озера, то часть ки-
нетической энергии камня переходит в энергию возмущения кру-
говых волн на поверхности водоема. Законы взаимодействия вол-
новых возмущений выглядят просто для низкоамплитудных сину-
соидальных волн в консервативных средах: такие волны свободно
проходят одна сквозь другую, и их взаимодействия сводятся к ал-
гебраическому суммированию колебаний в каждой из точек среды
(принцип суперпозиции). Этим, в частности, объясняется класси-
ческая интерференционная картина — муаровый узор, образован-
ный колеблющимися (там, где амплитуды суммируются) и спокой-
Рис.1. Взаимодействие волн от двух источников, а — интерференция волн
на поверхности воды; б — отсутствие интерференции для автоволн в актив-
ной среде (видно, что автоволны при столкновении не проходят одна сквозь
другую, как на рисунке слева, а аннигилируют).
Таблица 1
Сравнение свойств волн в консервативных средах и автоволн в активных
средах
Свойство Волны Автоволны
Приток энергии — +
Сохранение амплитуды и формы волны — +
Отражение от препятствий + —
Аннигиляция — +
Интерференция + —
Дифракция + +
Примечание. Знак «+» показывает наличие соответствующего свойства, знак «—» — отсутствие.
ними (там, где амплитуды вычитаются) участками среды (рис. 1а).
Тот же фундаментальный принцип суперпозиции обусловливает два
других характерных свойства обычных волн в консервативных сре-
дах — их способность к отражению от препятствий и границ среды
и к дифракции (огибанию препятствий).
Хотя в консервативных средах энергия начального возмущения
сохраняется, передавать сигналы на большие расстояния в такой
среде сложно: плотность энергии в дву- и трехмерных средах падает
с увеличением расстояния от источника, а форма сигнала искажа-
ется из-за дисперсии — разных скоростей распространения различ-
ных спектральных составляющих сигнала.
Итак, в отличие от обычных волн автоволны распространяются
в средах с распределенным запасом энергии, т.е. активных средах.
Из приведенной таблицы видно, что единственное общее свойство
тех и других — способность к дифракции. Простейший пример
активной среды — бикфордов шнур. Энергия запасена в порохо-
вой начинке, а автоволна, бегущая вдоль шнура, — волна горения.
В процессе ее распространения вещество шнура переходит из вы-
сокоэнергетического устойчивого состояния (несгоревший порох)
в низкоэнергетическое (пепел и газы, остающиеся после горения),
причем часть энергии, высвобождающейся в области горения, рас-
сеивается, а остальная расходуется на розжиг следующих, еще не
сгоревших элементов шнура.
Рассмотренный пример поясняет следующее общее определение:
автоволны представляют собой наблюдаемые структуры (в нашем
примере — пламя), которые поддерживаются процессами локаль-
ного высвобождения запасенной в среде энергии, идущей на запуск
аналогичных процессов в соседних областях. Такие наблюдаемые
структуры принято называть диссипативными, так как их наличие
связано с рассеянием (диссипацией) энергии.
Автоволны на значительные расстояния распространяются как
бы по эстафете: сигнал заново воспроизводится в каждой точке
среды. Энергия среды не сохраняется, а расходуется на поддержа-
ние автоволны, поэтому понятны два первых свойства автоволн,
указанные в таблице. Автоволны черпают энергию из среды. Две
автоволны, сталкиваясь, аннигилируют: ведь за фронтом бегущей
автоволны, где происходит переход среды из высокоэнергетиче-
ского состояния в низкоэнергетическое, тянется «выжженная» (в
случае бикфордова шнура в буквальном смысле зона, в которой та-
кой переход уже произошел. В результате две столкнувшиеся авто-
волны уничтожают друг друга (рис. 16). Это их важное свойство
нам потребуется в дальнейшем изложении. Аналогичные причины
объясняют невозможность интерференции и отражения автоволн
от границ среды и препятствий. Что же касается их способности
огибать препятствия, т.е. дифрагировать, то автоволны обладают
ею в полной мере. Дифракцию можно объяснить здесь, как в слу-
чае обычных волн в консервативных средах, принципом Гюйгенса
(рис. 2).
Существенные отличия автоволн от других типов волн и опре-
делили их выделение в особый класс явлений.
Распространение автоволн в активных средах
с восстановлением энергии
Наиболее интересны автоволны, распространяющиеся в актив-
ных средах при восстановлении запаса энергии. Именно такие среды
Рис.2. Дифракция автоволн.
а — построение Гюйгенса:
каждая точка среды, которой
достиг в данный момент фронт
автоволны, становится источ-
ником элементарных круговых
автоволн; б — огибание авто-
волной границы активной среды
(последовательные положения
фронта отмечены цифрами)
Рис.З. Закручивание спирального фронта пламени на горелке.
Слева на последнем кадре схематически изображены фазы за-
кручивания фронта пламени (М.А.Морозов, Г.И.Иваницкий).
нам в дальнейшем потребуются для создания прогнозирующей си-
стемы. Медленные процессы восстановления переводят среду из низ-
коэнергетического состояния (после пробега автоволны) в исход-
ное высокоэнергетическое. В таких средах могут возникать локаль-
ные самоподдерживающиеся источники автоволн различных типов.
Рассмотрим три примера активных сред с восстановлением: го-
релку с медленно проводящими топливо фитилями, химическую ак-
тивную среду и биологическую возбудимую ткань. Закономерности
распространения и взаимодействия автоволн в активных средах не
зависят от способа физической реализации среды.
Активная среда в виде горелки. Для демонстрации про-
стейшего механизма возникновения и распространения автоволн в
1979 г. М. А. Морозовым и автором статьи была придумана спе-
циальная горелка. В листе металла на близком расстоянии одно от
другого были просверлены отверстия, в которые вставили полосы
асбеста, соединенные между собой. Концы этих полос опустили в
ванну с густым маслом. Сам по себе асбест не горит, но когда он
пропитается маслом, то становится уже фитилем и его можно под-
жечь. Скорость горения асбестового фитиля, пропитанного маслом,
выше скорости поступления горючего вещества (масла). Поэтому
фитиль через некоторое время погаснет. После этого за счет диф-
фузии он впитает масло, и его вновь можно поджечь и т.д. Таким
образом, фитиль может находиться в трех состояниях: горение; па-
уза (рефрактерный период), когда засасывается масло; готовность
вновь вспыхнуть после поджога.
Если в такой демонстрационной горелке поджечь один из фити-
лей, то от него загорится соседний. Первый фитиль вскоре погас-
нет (выгорит масло), но к этому времени по горелке уже побежит
фронт пламени. Так технически просто можно создать активную
среду с восстановлением: каждый ее элемент (фитиль) может в от-
личие от бикфордова шнура вспыхнуть не один, а сколько угодно
раз. Отметим, что повторно поджечь можно не только внешним
источником, но и пламенем, подведенным по среде. Для этого до-
статочно линию фитилей, вдоль которой бежит пламя, замкнуть
в кольцо, и пламя начнет вращаться по ней. Если же фитили за-
полняют плоскость, то на ней при определенных условиях также
будет вращаться огненный вихрь или распространяться круговые
волны (рис. 3).
Активная среда на основе химической реакции. Хими-
ческая активная среда была создана в Институте биофизики АН
СССР А. М. Жаботинским и А. Н. Заикиным в 1970 г. и предста-
вляет собой тонкий слой жидкости, где протекает окислительная
реакция Белоусова (позднее эта реакция в научной литературе по-
лучила название реакции Белоусова-Жаботинского). Реакция имеет
циклический (колебательный) характер. В отличие от большинства
известных окислительных процессов, которые идут до исчерпания
одного из субстратов (окислителя или восстановителя), в ходе этой
реакции выделяется ингибитор, тормозящий реакцию на некоторое
время после того, как исчерпана лишь небольшая доля реагентов.
Состав реакционной смеси следующий (он был описан Б. П. Бело-
усовым в середине 50-х годов): лимонная кислота — 2.00 г, суль-
фат церия — 0.16 г, бромат калия — 0.20 г, серная кислота (1:3) —
2.0 мл, вода — до общего объема 10.0 мл. Церий (металл переменной
валентности) играет роль маятника: он появлялся то в окисленной,
то в восстановленной форме.
Рис.4. Автоволны в химически активной среде (А.М.Жаботинский,
А.Н.Заикин).
Обобщенно реакцию можно представить следующим образом:
сначала бромат окисляет ионы Се3+ до Се4+, а сам превращается в
гипобромит; гипобромит окисляет лимонную кислоту, а бром вос-
станавливает Се4+ в Се3+ , давая бромид ион, способный тормозить
реакцию ионов Се с броматом. Попеременное изменение степени
окисления церия проявляется в периодическом изменении окраски
раствора. Для получения периодической реакции можно использо-
вать и иные субстраты (сегодня известно около 50 подобных ко-
лебательных химических реакций). Описание аналогичной реакции
позднее было уточнено Р. Ноейсом, Р. Филдом (США) и Э. Керо-
шем (Венгрия).
Если указанную реакционную смесь налить тонким слоем в плос-
кий сосуд, то за счет ухудшения перемешивания каждый малый
объем жидкости можно рассматривать как элемент активной воз-
будимой среды с восстановлением, по которой автоволны окисления
могут пробегать столько раз, насколько хватит запасов субстратов
(рис. 4). В реакции Белоусова-Жаботинского за один раз окисля-
ется приблизительно 0.01 субстрата и волна окисления может про-
бежать около 100 раз. Механизм распространения волн окисления в
принципе тот же, что и волн горения (горение — частный случай
окисления): возбужденные («горящие») элементы среды возбуждают
(«поджигают») соседние.
Рис.5. Распространение импульса возбуждения (фронта волны) по нервному
волокну. Вверху — параметры импульса (римскими цифрами обозначены пе-
риоды, в которых живая ткань находится в разных состояниях: I — период
покоя; II — период восстановления (рефрактерности); III — период возбу-
ждения (значение потенциала действия равно амплитуде импульса); внизу —
схематическое изображение деполяризации нервной ткани в момент прохо-
ждения импульса.
Активная среда в виде возбудимой биологической ткани.
Систематическое исследование активных сред биологической при-
роды было начато в 1966 г. в Институте биофизики АН СССР
В. И. Кринским с соавторами.
Наиболее известный пример такой среды — нервное волокно.
Распространяющийся по нему импульс также оказывается авто-
волной; он представляет собой электрохимическую волну перехода
между двумя состояниями: покоя, когда разность потенциалов на
мембране волокна велика (приблизительно —0.08 В), и активного со-
стояния — возбуждения, когда разность потенциалов мала (около
+0.04 В). При распространении нервного импульса в каждой точке
возбудимой мембраны высвобождается энергия, исходно запасен-
ная в виде неравновесных концентраций ионов калия и натрия по
обе стороны мембраны (рис. 5). В живых организмах, помимо од-
номерных активных сред — нервных волокон, существуют дву- и
трехмерные активные среды, построенные из возбудимых клеток,
функционирующих так же, как и нервные волокна.
Примеры таких сред — головной и спинной мозг, гладкомышеч-
ные стенки кишечника, матки, мочевого пузыря, а также сердеч-
ная мышца.. Распространяющиеся по ним автоволны имеют ту же
физическую природу, что и нервный импульс, отличаясь от послед-
него лишь длительностью и скоростью; однако в процессах жиз-
недеятельности организма их роли различны. Если импульс, бегу-
щий вдоль нервного волокна, служит для передачи информации,
то, например, идущая по сердцу волна возбуждения запускает кас-
кад биохимических процессов, инициирующих сокращение сердеч-
ной мышцы, на режиме которого отражается изменение в распро-
странении автоволн возбуждения.
Принципы функционирования всех активных сред (физических,
химических и биологических) оказываются похожими и могут быть
описаны на языке математики одними и теми же уравнениями. Эти
уравнения имеют вид дифференциальных уравнений параболиче-
ского типа:
du/dt = duau + f(u, v),
dv/dt = DvAV + <p(U,V), (1)
где U — энергия горения (в модели распространения пламени в
горелке), или концентрация активных радикалов (в модели хими-
ческой реакции), или разность потенциалов на мембране клеток (в
модели возбуждения биологических тканей); V — необходимое ко-
личество горючего вещества (в модели распространения пламени),
или концентрация окисленной формы катализатора (в модели хими-
ческой реакции), или трансмембранная проводимость клеток (в мо-
дели возбуждения биологической ткани); DU,DV — коэффициенты
диффузии волн возбуждения и волн восстановления (рефрактерно-
сти); t — время; Д — оператор Лапласа; /([7, V) и V) — функ-
ции, определяющие связь между параметрами U и V. Вид этой связи
зависит от поведения системы в точке. К характеристике связи мы
вернемся в следующем разделе.
Во всех случаях активная среда может рассматриваться как дву-
уровневая система, которая может находиться в двух существенно
различных состояниях: высоко- и низкоэнергетическом. При рас-
пространении автоволны на ее переднем фронте элементы среды пе-
реходят с высокоэнергетического уровня на низкоэнергетический.
Выделяющаяся при этом энергия расходуется, как уже было ска-
зано, на запуск аналогичных переходов на участках среды, распо-
ложенных непосредственно перед фронтом автоволны.
Активные среды без восстановления после перехода остаются на
низкоэнергетическом уровне, и автоволна повторно по ним распро-
страняться не может (например, бикфордов шнур, волны фазовых
переходов). В активных средах с восстановлением автоволны могут
распространяться в принципе сколько угодно раз, так как каждый
элемент такой среды возвращается на высокоэнергетический уро-
вень вследствие медленных процессов восстановления — накачки
энергии.
Повторим: для горелки с медленно подводящими топливо фити-
лями высокоэнергетический уровень соответствует фитилям, про-
питанным горючим, низкоэнергетический — состоянию, когда
a
г
Рис.6. Различные типы автоволн, возникающих в активной среде с восста-
новлением запаса энергии, а — концентрические автоволны; б— спиральные
автоволны; в — ячеистые автоволны; г — простые пространственные авто-
волны — вихри; д — скрученные пространственные автоволны; е — вихревые
пространственные кольца
горючего в фитилях нет (но оно есть в емкости, куда погружен
фитиль). В возбудимых клетках высокоэнергетическому состоянию
соответствует большая разность энергетических потенциалов
между внутренней и внешней сторонами мембраны клетки
(—0.08 В), а низкоэнергетическому — малые значения этой разно-
сти (+0.04 В). Пока не окончился процесс, возвращающий систему
в высокоэнергетическое состояние, элемент среды обычно невозбу-
дим; соответствующее время называется временем рефрактерности
(термин, заимствованный из физиологии).
Динамика взаимодействия автоволн. В активных средах
существуют одинаковые конфигурации автоволн, которые можно
классифицировать по сходству их формы и механизму возникно-
вения. Можно выделить, по крайней мере, четыре типа автоволн:
концентрические волны, или, как их еще называют, ведущие центры
(пейсмекеры), спиральные волны (ревербераторы), ячеистые волны
(например, ячейки Бенара) и пространственные вихри (рис. 6).
Отметим три основных свойства динамики взаимодействия ав-
товолн. Во-первых, существуют два режима работы источников
волн — ждущий и автоколебательный, и возможен переход от од-
ного к другому. Во-вторых, между источниками автоволн возни-
кает конкуренция за пространство, в котором распространяются
испускаемые ими автоволны. В-третьих, имеется возможность
управления частотой излучения автогенераторов.
Уравнение (1) описывало поведение активной среды в простран-
стве. Соответствующую этому уравнению сосредоточенную систе-
му можно записать так:
U = f(U,V), V = ip(U,V)\ (2)
она представляет собой нелинейную релаксационную систему с
N-образной характеристикой (рис. 7) (обобщенная модель Ван-дер-
Поля), которая может быть как ждущим генератором одиночных
импульсов (режим 1), так и автогенератором концентрических волн
(режим 2 на рис. 76). Изменяя взаимное положение функций U и V
на фазовой плоскости, можно переводить систему из ждущего ре-
жима в автогенераторный. Этот переход достигается увеличением
скорости подачи энергии в систему после возбуждения или увеличе-
нием скорости потребления энергии во время возбуждения, другими
словами, увеличением коэффициента усиления в цепи возбуждения
и уменьшением коэффициента усиления в цепи торможения.
Допустим, что имеется два автогенератора, создающих концен-
трические автоволны, распространяющиеся в активной среде. Один
из них излучает их с частотой wi, другой — шг- Волны, как уже
отмечалось, при столкновении уничтожают друг друга (аннигили-
руют). Генератор, испускающий волны с большей частотой, шаг за
шагом (с каждым циклом испускания волны) будет «отвоевывать»
пространство у низкочастотного автогенератора и через некото-
рый промежуток времени поглотит этот автогенератор. Время, за
которое произойдет поглощение, равно
VW1 - 0)2
где I — расстояние между генераторами; v — скорость распростра-
нения автоволны, v = comst для данной среды; wi и о>2 — соответ-
ственно круговые частоты испускания автоволн первым и вторым
Рис.7. Фазовая плоскость, отражающая связь между возбуждающей и
тормозящей (рефрактерной) компонентами в активной среде в модели,
описываемой уравнением (2). а — траектория представляющей точки на
фазовой плоскости сосредоточенной системы, порождающая автоволну
возбуждения в нервном волокне (см. рис. 5), участок БВ траектории со-
ответствует состоянию возбуждения, участок ВГА — рефрактерности;
точка А и ее окрестность соответствует состоянию покоя; б — фазовая
плоскость для двух режимов: I — ждущий генератор одиночных импуль-
сов, II — автогенератор; в — профиль изменения потенциала в нервном
волокне, соответствующий траектории движения представляющей точки
по фазовой плоскости; я — схематическое изображение фрагмента ав-
товолны, соответствующего профилю изменения потенциала на рис. 10в
(возбужденные участки зачернены, рефрактерные — заштрихованы).
автогенераторами. Если = h>2, то это время станет бесконечно
большим. Другими словами, два равночастотных автогенератора
не могут поглотить друг друга. Если близко к нулю, то время
захвата территории у второго автогенератора' первым будет мини-
мальным.
На рис. 8а показана геометрическая интерпретация взаимодей-
ствия автоволн от двух автогенераторов, имеющих одновременный
старт, но работающих с разными частотами. Их можно предста-
вить в виде двух круговых конических поверхностей. Чем вьппе ча-
стота генератора, тем больше угол между осью конуса и его обра-
зующей. На рис. 86 изображена временная динамика увеличения
территории захватываемой высокочастотным генератором. Пока-
заны два сечения конусов. Первое соответствует моменту встречи
Рис.8. Геометрическая интерпретация взаимодействия автоволн от
двух автогенераторов, испускающих волны с разными частотами. По
вертикальной оси отложено время, по горизонтальным осям — коор-
динаты на плоскости; а — взаимодействие автоволн двух генераторов,
расположенных на расстоянии I; б — динамика захвата территории
высокочастотным автогенератором у низкочастотного вследствие ан-
нигиляции сталкивающихся автоволн.
Рис.9. Уничтожение низкочастотного автогенератора автовол-
нами высокочастотного автогенератора в реакции Белоусова-
Жаботинского.
автоволн, второе — моменту подавления высокочастотным автоге-
нератором низкочастотного. В последнем случае центр испускания
автоволн второго автогенератора оказывается накрытым волной
первого высокочастотного автогенератора. Рис. 9 иллюстрирует
этот процесс в химической активной возбудимой среде.
Частотой работы автогенераторов в активных средах можно
управлять, т.е., увеличивать или уменьшать ее, например, путем
изменения скорости расхода энергии в цепи возбуждения или ско-
рости восстановления энергии через цепь торможения. В нервных
сетях этот процесс обеспечивается в возбуждающих или тормозя-
щих синаптических окончаниях за счет выделения соответствую-
щих медиаторов, влияющих на работу ионных каналов нейрона.
В описанной выше горелке такое управление можно обеспечить, на-
пример, путем изменения вязкости масла, подавая периодически на
фитиль растворитель или изменяя сечение фитиля, пережимая его.
Однако при технической реализации лучше искать такие среды, в
которых можно в цепях управления частотой автогенераторов ис-
пользовать электрические или световые сигналы. Один из таких
вариантов реализуется, например, в химической среде на основе ре-
акции Белоусова-Жаботинского при добавлении в среду светочув-
ствительного катализатора на основе рутения, другой — на основе
фотодиодов, включаемых в цепь обратной связи активных элемен-
тов среды; по-видимому, возможно для изготовления активных сред
использовать жидкокристаллические матрицы, белковые светочув-
ствительные молекулы или специальные фотохромные стекла [5-8].
Важен принципиальный момент, что существуют такие активные
автоволновые среды, состоящие из матриц автогенераторов, час-
тота которых меняется пропорционально интенсивности попадаю-
щего на них сигнала.
Модель внешней среды и ее фурье-обраэ. Чтобы делать
прогноз, нужно иметь модель поведения внешней среды. Если при
построении модели отдать предпочтение каким-либо постулатам,
то необходимо составить комментарий. Однако он сужает свободу
выбора (ограничения всегда связаны с некоторым произволом). В
реальной природе, как правило, этих ограничений нет. Поэтому во-
прос: сколько моделей может иметь окружающий нас мир? — лишен
смысла. Их бесчисленное множество. Если разные явления суще-
ствуют вместе, то правильнее говорить не о приоритете того или
иного, а лишь об их связях и дополнительности.
Мы отдадим предпочтение модели циклической структурной ор-
ганизации внешней среды, поскольку она отличается достаточной
простотой и в то же время содержит в себе большое разнообразие
форм поведения. Кроме того, она обладает предсказательной си-
лой, но не требует жестких причинно-следственных ограничений.
В цикле причины и следствия периодически меняются местами и
зависят от момента или места, с которого мы начали наблюде-
ние. Процессы, протекающие вокруг и внутри нас, действительно
имеют существенную периодическую компоненту. Когда мы гово-
рим о «стреле времени», то и в этом случае мы можем рассматри-
вать развитие процесса как периодическое, но с большим периодом.
При движении макротел отдельные циклы, легко наблюдаемые
в микропроцессах, из-за дефазировки сливаются вместе, и движе-
ние описывается в терминах непрерывно возрастающего времени.
На этом основывается детерминированность законов классической
механики. В таких процессах предсказание возможно на большие
временные интервалы. Возникает вопрос: что такое большой вре-
менной интервал? Он большой по сравнению с чем? Приведем при-
меры.
Существующая сегодня небесная механика Ньютона с поправ-
ками релятивистского уточнения закона всемирного тяготения
Эйнштейна обладает предсказательной силой на миллионы лет.
Масштаб эволюции Вселенной — это миллиарды лет. На таких вре-
менных интервалах влияние так называемых малых параметров мо-
жет оказаться весьма существенным, и возможно, что в этом случае
Вселенная выйдет на циклический процесс с очень большим пери-
одом по сравнению, например, со временем существования нашей
планетной системы.
Итак, за временной интервал предсказания («горизонт предска-
зания») следует принять отрезок времени, меньший, чем период на-
хождения системы в данном устойчивом состоянии (другими сло-
вами интервал между двумя бифуркационными точками траекто-
рии ее развития). Если достаточно полно известна периодичность
смены траекторий развития системы, т.е. имеется обширный мате-
риал наблюдения за ее поведением между многими бифуркацион-
ными точками, то интервал предсказания может быть расширен.
Приведем пример, связанный с меньшими, но тоже достаточно
большими временными интервалами —- 600 млн. лет, которые от-
деляют нас от первых живых организмов. Палеонтологические на-
ходки говорят о существовании периодов массового вымирания жи-
вотных, чередующихся внутри этого диапазона с длительностями
около 26-28 млн. лет. Так, 65 млн. лет назад вымерли динозавры.
Однако прогнозировать периоды макропроцессов из-за ограничен-
ности доступного для изучения реликтового материала сложно.
Наличие более коротких периодов в процессах развития внеш-
ней среды очевидно. Периодическое движение Земли вокруг Солнца
дает период 365.25 сут. Движение Луны вокруг Земли — пример
ритма с периодом 29.53 сут. 7-суточная неделя — это пример пе-
риодичности колебаний атмосферы, коррелируемых с флуктуаци-
ями ионосферы Земли под влиянием изменения потока заряженных
частиц, излучаемых Солнцем (солнечного ветра). Вращение Земли
вокруг своей оси дает суточный (или циркадный) ритм. Вся био-
сфера — это также набор разных ритмов, определяемых жизнен-
ными циклами популяций, состоящих из отдельных особей. Суще-
ствуют волны поколений в городах с периодом 25-27 лет, связанные
с репродуктивным периодом людей. Это пример социальных рит-
мов. Перечень циклических процессов можно продолжать, но и при-
веденных достаточно, чтобы сделать вывод — мы живем в мире,
моделью значительной части которого может быть взаимодействие
периодических процессов. Если это так, то возникает вопрос: по-
чему же так сложно делать предсказания в этом гармонично устро-
енном мире?
Неизохронность циклических процессов. В подавляющем
большинстве циклических систем амплитуды и частоты движения
различных «маятников», формирующих циклы, зависят от энергии,
поступающей извне в выделенную для исследования систему. Из-
менение величины энергии, в свою очередь, зависит от движения
«маятников» других иерархических уровней. Свойство зависимости
частоты от энергии называют неизохронностью. Причем зависи-
мость частоты от энергии имеет разный характер. Частота может
расти пропорционально энергии в степени 3/2,1,1/2. Эта зависи-
мость определяется организацией системы.
Неизохронность колебаний характеризуется изменением часто-
ты на единицу изменения энергии, поступившей в систему. Чем
больше эта величина dw/dE, тем меньше инерция движения «маят-
ников», тем быстрее они входят в резонанс и выходят из него (тем
короче интервал между бифуркационными точками) и тем сложнее
делать предсказание в такой системе.
В системе маятников резонансы могут возникать не только при
соотношении частот их движения 1 : 1 (колебания в унисон), но и
при других значениях кратности — 1 : 2, 2 : 5, 1 : 3, 1 : 4, 1 : 5,
3 : 5, 3 : 7 и т.д. Именно этим фактом объясняется наличие у ряда
планет многочисленных спутников, устойчиво вращающихся с раз-
ными периодами вокруг них. Однако если система неизохронная и
энергии в нее поступает извне много, а связь между маятниками
слабая, то может начаться миграция частот маятников по различ-
ным резонансным соотношениям. Такая миграция по шкале частот
была известна еще А. Пуанкаре. Он писал по этому поводу: «Слож-
ности этой картины движения настолько поражает, что я даже и
не пытаюсь изобразить ее» [9]. Траектории частотного движения
пересекаются друг с другом в фазовом пространстве, и возникает
неограниченное блуждание системы по резонансам, позднее полу-
чившее название диффузии В. И. Арнольда, описавшего в первом
приближении динамику этого процесса [10]. В этом случае движе-
ние маятников между резонансами будет несинхронизовано по фа-
зам.
Если связь сильная, а энергии мало, то движения происходят
синхронно. Все другие варианты будут приводить к промежуточ-
ным случаям. На рис. 10 показаны результаты машинного модели-
рования движения двух неизохронных маятников при сильной связи
между ними. При малых значениях энергии маятники колеблются
Хаос
Рис.10. Изменение частоты и> и фазы колебаний в при взаимодей-
ствии двух маятников в зависимости от энергии Е, поступающей в
систему (Г.Р.Иваницкий, М.А.Морозов).
синхронно, затем по мере увеличения частоты может измениться
фаза их взаимных колебаний. Маятники начинают колебаться в
противофазе. Далее по мере увеличения энергии они начинают ра-
ботать независимо со случайным изменением фаз, наступает хаос.
Обратное движение по пути уменьшения энергии приводит к ги-
стерезису, ширина петли которого зависит от du/dE — показа-
теля частотно-энергетической инерционности системы, состоящей
из двух маятников.
Если число осцилляторов увеличить, то разнообразие форм по-
ведения возрастет [11]. На рис. 11 приведена диаграмма такого ма-
шинного эксперимента. В некоторой среде помещается п неизохрон-
ных генераторов, исходно имеющих разброс параметров, другими
словами, генетическую вариацию (изменяется в относительных еди-
ницах от 0 до 10). Эта вариация определяется конструктивными
параметрами генераторов и разбросом частот их начальных осцил-
ляций. Генераторы связаны через источник совместного питания,
который, в свою очередь, получает энергию от другого источника,
объем которого неограничен. Исходное наполнение источника сов-
местного питания (разнообразие внешней среды) может изменяться
в пределах от 0.063 до 1 (в отн. ед.). Поведение таких осциллято-
ров демонстрирует любопытное свойство. При бедном источнике
совместного питания через определенное число циклов наблюдения
(показаны внутри диаграммы цифрами) неизохронные генераторы
синхронизуются и пульсируют в унисон (светлые кружки сектор А,
зоны 1-5). При богатом источнике питания и большой генетической
вариации синхронизации вообще не возникает (черные кружки —
сектор В-Д, зона 1-2). Система в этом случае проявляет свойства
хаотического поведения. Наконец, при других параметрах генети-
10,0
Секторы
А Б В ' г Д
7бЬо fs'oo 1 1 г
-оэеее
060 7600
/
i
2
800 1»0 2720 2720 2720
8
720 720 НЮ 7320 1/80
I
600 7360 7360 020 360
рооээ-
0,063 0,725 0,25 0,5 7
Разнообразие внешней срейы
О
Рис.11. Диаграмма машинного моде-
лирования изменения фаз в системе из
п маятникой-генераторов (Г.Р.Ива-
ницкий, М.А.Морозов, Л.Ф.Русанова).
ческой вариации и разнообразии внешней среды возникают проме-
жуточные формы поведения. Происходит синхронизация осцилля-
торов с набегающим сдвигом фаз (секторы — зоны Б-1; Г-4,5; Д-5).
Возможна также синхронизация с разбивкой на группы генерато-
ров, колеблющиеся в унисон. Сами группы имеют между собой фа-
зовый сдвиг (секторы — зоны Б-5; В-3,4,5). Наконец, имеет место
частичная синхронизация, когда между группами, колеблющимися
в унисон и имеющими фазовый сдвиг, появляются генераторы —
«конформисты», имеющие удвоенную частоту и присоединяющиеся
то к одной, то к другой группе. Они создают картину частичной
синхронизации, приближающейся по своему виду к полной десин-
хронизации, имеющей вид хаоса (секторы — зоны Б-2, Г-3, Д-3,4).
Гармоническая модуляция и модуляция гармоник. Любой
физический процесс можно описать изменяющейся в пространстве
и во времени функцией, которую, в свою очередь можно разложить
на сумму других функций. Как известно, для периодических про-
цессов наиболее удобной формой разложения является разложение в
ряд по гармоническим составляющим — в ряд Фурье. Такой ряд бы-
стро сходится и ограничен наивысшей частотой, имеющей место в
периодическом процессе. Всегда можно сделать прямой и обратный
переход от пространства реального времени в фурье-пространство,
где переменной является частота.
Теперь мы можем сформулировать одну из задач предсказания:
как будет себя вести в будущем неизохронный осциллятор, нахо-
дящийся в системе других, связанных с ним осцилляторов? Какие
частоты изменения его поведения являются существенными и наи-
более полно характеризуют систему осциллятор-среда? Чем огра-
ничена точность прогноза?
Начнем с ответа на последний вопрос. В одномерном случае
периодический неизохронный процесс можно записать, например,
так:
y(t) = щ sin[wi« + 0(f)], (4)
где 0(t) — изменение фазы этого процесса. Если мы знаем закон
изменения функции 0(t), то мы можем осуществлять прогноз с вы-
сокой точностью на любой временной интервал. Если принять пред-
ставление о структуре нашего мира как о наборе сообщающихся со-
судов с разной емкостью энергии и соответственно с разным набо-
ром циклов ее обмена, то моделью поведения внешней среды может
быть, например, выражение
y(t) = ai sin[wit + 01 (t)],
0(t) — a2 sin[w2i + 02(t)],
0г(С = a3 sin[w3t + 03(f)],
©n(i) = an+i sin[wn+11 + 0n+i(t)], (5)
где a2,a3,a4 — амплитуды модулирующих частоту основного рит-
ма сигналов или, другими словами, девиация частоты. Выбор ча-
стоты основного ритма зависит от временного интервала, в кото-
ром мы стремимся сделать предсказание.
Ограничим рассмотрение двумя иерархическими уровнями. На
рис. 12 показаны примеры изменения поведения процесса во вре-
мени, когда частоты неизохронного осциллятора изменяются по
гармоническому закону
y(t) = а± sin[wit + а.2 sin (6)
На рис. 13 даны фрагменты фурье-образов, соответствующие
этим процессам.
Если близко к иг, а е = a3/wi больше единицы, то про-
цесс приближается к хаотическому, например, на рис. 12в е = 5,
W2/W1 = 3.45. Если частоты шу и и>2 отличаются в десятки раз, то
даже при больших значениях £ наблюдается периодический харак-
тер изменения процесса (рис. 12а): £ = 50,шг/^1 = 0.034. Ана-
логичная картина и при обратном соотношении частот: Шг/^1 =
36000, е = 10 (рис. 126).
в
Рис.12. Развитие во времени фрагментов синусоидального про-
цесса с модулируемой по синусоидальному закону фазой с пара-
метрами. а — е = 50,0)2/011 = 0.034; б— е = 10,012/0)1 = 36000;
в — е = 5,012/0)1 = 3.45.
Вывод очевиден — к видимости хаоса приводит сравнительная
близость частот самого процесса и источника питания, модули-
рующего его частоту. Когда шг много больше или меньше основ-
ной частоты процесса, то рассматривая процесс в заданном диапа-
зоне, можно пренебречь сверхбыстрыми или сверхмедленными мо-
дулирующими компонентами. Следует заметить, что выбор диапа-
зона предсказания задается и конструктивными параметрами са-
a
Рис.13. Фрагменты фурье-образов в частотной области, соот-
ветствующие процессам, изображенным на рис. 12.
мой системы, делающей прогноз. Живые организмы, в том числе и
человек, не исключение.
В анализаторно-исполнительных системах живых организмов
быстрые явления, следующие одно за другим, сливаются вместе и
воспринимаются как одно целое. Например, если произвести две
вспышки света с интервалом 100 мс, то человек воспринимает их
как одну. Временная разрешающая способность живых организмов
эволюционно сопряжена с реакцией их двигательного аппарата и
изменчивостью среды в их экологической нише, которую необхо-
димо отслеживать для выживания.
Регистрирующие и анализирующие системы живых организмов
— это биохимические машины, где носителями информации явля-
ются потоки ионов — сравнительно крупных частиц с низкой энер-
гией. Они обеспечивают работу автогенераторов в активных сре-
дах мозга. Поэтому пространственно-временные анализирующие
возможности автоволновых активных сред в мозгу животных огра-
ничены сверху областями, занимаемыми сравнительно крупными
осцилляторами (минимальное расстояние между ионными каналами
на мембранах нервных клеток ~ 80-i- 100А). Активные среды из ин-
формационных частиц с низкой энергией могут реагировать лишь
на суммарное изменение высокоэнергетических частиц, например,
фотонов, так как в каждой точке пространственно-временных ко-
ординат активной среды, анализирующей внешний процесс, пере-
крывается множество волновых пакетов от разных легких высоко-
энергетических частиц. Таким образом, исходя из этого элементар-
ного квантовомеханического принципа, частотные анализирующие
возможности нашего мозга ограничиваются сверху величиной, при-
близительно 10 Гц.
Такую оценку сверху дает и другое рассуждение. Длительность
импульса возбуждения нейрона около 3 мс плюс рефрактерный
«хвост», приблизительно в 2 раза превосходящий по длине сам им-
пульс (см. рис. 5). Таким образом, быстродействие в точке вычи-
слительной системы на активной автоволновой среде, составленной
из нейронов, не более 102 on./с. Скорость распространения нерв-
ного импульса по аксону порядка 20 м/с. Средняя длина путей
от анализирующих до исполнительных элементов около 1.5 м, при-
близительно 75 мс. Таким образом, мы получаем верхнюю частоту
около 10 Гц.
Кроме того, альфа-ритм — основной ритм нашего мозга, про-
являющийся на электроэнцефалограммах уже у детей в 5-6 лет и,
по-видимому, характеризующий основную частоту автогенерато-
ров активной среды мозга, — также лежит в диапазоне от 8 до
13 Гц. Резюмируя, отметим, что верхней частотой прогноза, для ко-
торого приспособлен мозг человека (не вооруженный приборами),
является частота 10 Гц.
Нижняя предельная частота мозга определяется продолжитель-
ностью памяти организма, т.е. продолжительностью его жизни.
Подчеркнем, что мы не рассматриваем социально-технические спо-
собы расширения этого диапазона в человеческом обществе (пись-
менные источники, памятники культуры, научные архивы и т.д.).
Память человека и приобретаемые человеком знания имеют лю-
бопытное отличие. Например, для современных юношей события
войны 1941-1945 гг. и события войны 1812 г. являются практиче-
ски одинаково далекими событиями. Исторические события, про-
исшедшие до рождения человека, имеют тенденцию к нивелировке
различий между ними. В то время как для живущих участников
Великой Отечественной войны этот временной период, насыщен-
ный разными событиями, составляющими часть их жизни, расцве-
чен эмоциональными переживаниями.
Активная автоволновая среда очищает фурье-образ. Пе-
рейдем к описанию процесса работы, предсказывающей будущее ак-
тивной автоволновой среды. На активную двумерную автоволновую
среду, состоящую из матрицы автогенераторов (рис. 14), проекти-
руется в рамках некоторого интервала времени фурье-образ внеш-
него процесса. Среда должна синтезировать с наибольшей досто-
верностью развитие этого процесса в будущем. Частоты автогене-
раторов пропорциональны интенсивности гармоник фурье-образа.
Таким образом, раструбы конусов (см. рис. 8) будут отражать рас-
пределение интенсивностей гармоник в фурье-пространстве. Дина-
мика взаимодействия автогенераторов в активной среде, как уже
отмечалось, такова, что через некоторый интервал времени вблизи
высокочастотных генераторов (гармоник фурье-образа с большой
интенсивностью) будут подавлены низкочастотные генераторы
(гармоники фурье-образа с малыми интенсивностями). Испускае-
мые автогенераторами расходящиеся по поверхности среды авто-
волны можно интерпретировать как растущие во времени кони-
ческие поверхности (см. рис. 14). Ось времени перпендикулярна
к плоскости двумерной координатной сетки. В данном случае мы
имеем четырехмерное пространство — две координаты на плоско-
сти и две координаты на поверхности каждого конуса. Таким обра-
зом, двумерная активная среда по размерности пространства со-
впадает с четырехмерным окружающим нас миром (три простран-
ственных координаты и четвертая координата — время) и может
служить местом формирования его модели. Наш мозг, если рас-
сматривать его как стопки плоских активных автоволновых сред,
будет пятимерным. Еще в 1926 г. В. А. Фок и О. Клейн предло-
жили модификацию уравнения Шрёдингера, в котором вместо че-
тырех было использовано пять переменных. Решение такого урав-
нения можно интерпретировать как волны, распространяющиеся в
обычном четырехмерном пространстве-времени, но в присутствии
модулирующих гравитационного или электромагнитного поля. Та-
ким образом, мозг живых организмов комплементарен по размерно-
сти пространства пятимерному миру Фока-Клейна и, по-видимому,
1
Рис. 14. Двумерная активная автоволновая среда, состоящая из автогене-
раторов, расположенных в каждой точке координатной сетки.
эволюционно ориентирован на взаимодействие с процессами в пя-
тимерном пространстве.
Площадь Si подавления в г'-й зоне в фурье-пространстве за время
t будет расти в соответствии с выражением
(7)
где t — текущее время наблюдения; — момент времени встречи
автоволны г-го генератора с первой волной fc-ro генератора; и
— соответственно частоты испускания автоволн г-м и к-м автогене-
раторами; v — скорость распространения автоволн по поверхности
среды; п — количество генераторов, контактирующих своими ав-
товолнами в г-й зоне среды с г-м генератором. Очевидно, что со
временем периметр зоны контактов г-го автогенератора с другими
автогенераторами будет расти. В конце концовка достаточно боль-
шое время вся площадь активной зоны будет занята автоволнами
наиболее высокочастотного автогенератора. Остальные автогене-
раторы будут ими поглощены.
Однако если делать обратное преобразование Фурье, последова-
тельно задавая временной интервал очистки локальных зон, то мы
будем получать сигнал от прошлого процесса, проходящий последо-
вательные стадии очистки. Он будет освобождаться от шума и от
гармоник разложения, которые, находясь рядом с пиками высокой
интенсивности, являются модуляторами главных частот процесса.
Рис.15. Компьютерный модельный пример очистки одномерного процесса с
помощью операций, осуществляемых активной автоволновой средой. На верх-
нем графике показан фурье-образ процесса (по горизонтальной оси отложены
частоты, по вертикальной — интенсивности гармоник разложения процесса в
ряд Фурье). Под графиком звездочками помечены гармоники, которые оста-
ются после последовательных четырех стадий очистки фурье-образа с по-
мощью активной автоволновой среды. Ниже показано изменение реального
процесса, разворачивающегося во времени, соответствующего последователь-
ным четырем стадиям очистки фурье-образа. На графике 2 уже проявляется
скрытая ранее (график 1) закономерность. Максимальные значения процесса
имеют упорядоченность, повторяясь через 7, 14, возможно 24-26 циклов. Окон-
чательно прогноз выявляется на графике 4 — через каждые семь циклов про-
исходит смена фаз в процессе. Набег смены фаз за четыре периода дает не-
определенность в периоде 24-26-го цикла, наблюдающуюся на графике 2. По
графику 3 можно обнаружить еще ряд более мелких особенностей процесса 1
(Г.Р.Иваницкий, А.А.Деев).
Описанный здесь нелинейный динамический фильтр, основан-
ный на логике активных автоволновых сред, обладает свойством
самоочистки и отличается за счет локальности действия от извест-
ных технических методов фильтрации сигналов в фурье-области.
Создание технических систем для оптимальной частотной фильтра-
ции требует предварительного знания о характере сигнала и шума.
В данном случае таких знаний не требуется. Активная автоволно-
вая среда из автогенераторов обладает самонастройкой, поэтому
она сама выбирает траекторию очистки фурье-образа по реперным
гармоникам и тем самым выделяет наиболее существенные гар-
10
Рис.16. Одна из возможных блок-схем устройства, осуществляющего
предсказание будущего по прошлому с помощью очистки фурье-образа
от шумов и гармонических составляющих, модулирующих основные ча-
стотные гармоники процесса. 1 — источник лазерного излучения; 2 —
лазерное излучение; 3 — плоскость представления изменения функ-
ции, отражающей поведение внешней среды в прошлом; 4 — первая
линза, осуществляющая перевод функции прошлого в фурье-образ; F —
фокусное расстояние линзы; 5 — фурье-плоскость, где формируется с
помощью первой линзы фурье-образ функции, отражающей поведение
внешней среды в прошлом (в этой плоскости располагается активная ав-
товолновая среда, очищающая фурье-образ от шумов и гармонических
составляющих малой интенсивности и делающая обратное преобразова-
ние частот генераторов в интенсивности в фурье-образе); 6 — блок пи-
тания активной автоволновой среды; 7— вторая линза, осуществляющая
обратный перевод преобразованного с помощью активной автоволновой
среды фурье-образа поведения этой функции в будущем; 8 — плоскость
отображения будущего поведения процесса как функции времени; 9 —
устройство регистрации этой функции; 10 — устройство измерения и
визуализации возможного будущего поведения функции, описывающей
процесс.
ионические компоненты, характеризующие процесс. Однако и для
нее существуют ограничения точности прогноза, определяемые со-
отношением сигнала к шуму. Предрассудок — это есть нечто иное,
как неправильно сделанный человеком прогноз, когда за сигнал его
мозгом был принят шум.
На рис. 15 показано несколько последовательных временных ин-
тервалов для компьютерного модельного примера очистки одно-
мерного процесса с помощью операций, осуществляемых активной
автоволновой средой. Единственным переменным критерием, кото-
рым определяется качество прогноза системы при заданных пара-
метрах самой автоволновой среды, является время очистки фурье-
образа. Если его выбрать очень малым, то активная автоволновая
среда не успеет самоочиститься от шумов. Если его выбрать очень
большим, то могут быть уничтожены существенные компоненты
сигнала. Из графиков рис. 15 видно влияние динамики очистки на
изменение вида процесса. На рис. 16 дана одна из возможных схем
технического устройства, осуществляющего последовательность
операций прогноза с помощью активной автоволновой среды и на-
бора оптических преобразователей [12].
Возможно, что по похожему алгоритму, но в другом физико-
химическом исполнении работают и структуры нашего мозга. Од-
нако матрицы автогенераторов мозга—это не гомогенная система,
подобная описанной выше. В структуру автоволновой среды на-
шего мозга генетически уже заложены исходные различия между
конструктивными параметрами нейронов. Это и есть генетическая
память о прошлом. Об этом можно судить и по их морфологиче-
скому разнообразию и по разнообразию модулей, образуемых из
них. Это разнообразие является априорной моделью, отражающей
усредненные параметры внешней среды, в которой около 40 тыс. лет
назад эволюционно сформировался наш мозг. Рассмотренная нами
исходно гомогенная автоволновая среда из автогенераторов — это,
образно говоря, мозговая структура без генетического опыта про-
шлого. Наблюдение за ритмами изменения электрической активно-
сти различных зон мозга дает основание для того, чтобы принять
главный тезис — мозг является разновидностью активной автовол-
новой среды, сформировавшейся для прогноза процессов, развива-
ющихся в пространстве и во времени как вне, так и внутри нас.
Эта активная среда оптимальным образом приспособлена к про-
гнозу ситуаций в пространственно-временном диапазоне нашего су-
ществования. Поэтому если мы из-за поспешности выводов или из-
за плохой памяти ошибаемся в прогнозе каких-либо событий, то
адресовывать эти ошибки следует лишь к самим себе.
ЛИТЕРАТУРА
1. Иваницкий Г.Р. Ритмы развивающихся сложных систем. М.: Знание, 1988.
48 с. (Математика, кибернетика, N* 9).
2. Иваницкий Г.Р., Еринский В.И., Селькор Е.Е. Математическая биофизика
клетки. М.: Наука, 1978. 310 с.
3. Кринский В.И., Михайлов А.С. Автоволны. М.: Знание, 1984. 64 с. (Физика;
№ 10).
4. Иваницкий Г.Р. Автоволны вокруг и внутри нас. // Наука и человечество:
(Междунар. сб.). М.: Знание, 1989. С.211-226.
5. Иваницкий Г.Р. Биологические микроустройства. // Вести. АН СССР.
1984. К* 3. С.118-128.
6. Всеволодов Н.Н., Иваницкий Г.Р. Биологические светочувствительные
комплексы как технические носители информации // Биофизика. 19Я5. Т чи,
вып.5. С.883-887.
7. Светочувствительные биокомплексы и оптическая регистрация информа-
ции: (Сборник). Пущино: ОНТИ, 1985. 220 с.
8. Биотехника — новое направление компьютеризации / Под ред. 1 . 1*. Ива-
ницкого. М.: Наука, 1990. 145 с.
9. Пуанкаре А. Избранные труды. М.: Наука, 1972. Т.2. 339 с.
10. Арнольд В. И. О неустойчивости динамических систем со многими степе-
нями свободы. // ДАН СССР. 1964. Т.159, № 1. С.9-29.
11. Иваницкий Г.Р., Гайда Б.А., Деев А.А. и др. Внешние или внутренние
причины определяют синхронность деления клеток на ранних стадиях эм-
бриогенеза? // Биофизика. 1991. Т.36, вып.2. С.358-364.
12. Иваницкий Г.Р., Куниский А.С. Исследование микроструктуры объектов
методами когерентной оптики. М.: Энергия, 1981. 166 с.
СИНЕРГЕТИКА
Г. Г. Малинецкий
СИНЕРГЕТИКА, ПРЕДСКАЗУЕМОСТЬ
И ДЕТЕРМИНИРОВАННЫЙ ХАОС
Хотя об этом и не принято говорить
вслух, мы все знаем, что с общечело-
веческой точки зрения цели нашей на-
уки намного скромнее, чем цели, напри-
мер, древнегреческой науки, и что наша
наука с большим успехом увеличивает
нашу мощь, чем наделяет нас знаниями,
4 представляющими чисто человеческий
интерес.
Е. Вигнер
Начиная с древних времен возможность предсказывать воспри-
нималась как удел мудрецов и одна из основных целей развития
науки. Предсказание жрецами солнечных и лунных затмений счи-
талось чудом. Плутарх, излагая биографии героев Греции и Рима,
полагал, что, оглянувшись в прошлое, можно понять будущее от-
дельных людей, государств, народов. Однако построение алгорит-
мов прогноза он оставлял проницательному уму своих читателей.
Ситуация кардинально изменилась после математической фор-
мулировки законов природы. Оказалось, что движение небесных
тел можно рассчитывать, решая дифференциальные уравнения. Эти
уравнения могут быть достаточно сложны. Их решение и исследова-
ние может потребовать много усилий, изобретательности, создания
совершенно новых математических инструментов. Однако в прин-
ципе это всегда можно сделать. Эта захватывающая идея на много
лет увлекла ученых. В самом деле, возникла большая область ис-
следований, где можно рассчитывать на научный прогноз. В ней,
казалось, единственным препятствием являются чисто математи-
ческие сложности, которые со временем будут преодолены.
Блестящий французский математик Пьер Симон Лаплас, кото-
рый внес большой вклад в преодоление этих сложностей, полагал,
что главная задача современной и будущей науки состоит в получе-
нии следствий из законов Ньютона. Сколько веры в неограниченные
возможности разума и в рациональное начало в его ответе Напо-
леону. На вопрос императора, почему в его системе мира нет места
Богу, математик с гордостью ответил: «Я не нуждаюсь в этой ги-
потезе».
Дальнейшее развитие науки обычно характеризуют как цепь
триумфов, каждый из которых расширял наши возможности, повы-
шал точность описания различных явлений, а с ней и возможности
что-либо предсказывать.
Но не менее оправданным представляется и диаметрально про-
тивоположный взгляд. Большинство фундаментальных теорий, из-
менивших стандарты научных исследований (меняющих парадигму,
по выражению историка науки Куна), связано с осознанием все но-
вых и новых ограничений. И, прежде всего, с ответом на вопрос,
чего нельзя сделать, какие цели мы в принципе не можем ставить
перед научным исследованием.
В самом деле, заменив знак у временной переменной, в урав-
нениях, описывающих систему, которая идеально описывается за-
конами Ньютона, мы не изменим самих уравнений. Пленку, на ко-
торой снято развитие системы, можно крутить и в прямом, и в
обратном направлении. Законы механики не позволяют, просмо-
трев фильм, установить, какой из двух вариантов реализуется в
природе. Но появились термодинамика и статистическая физика, и
в естественные науки вошла необратимость. Во многом стало по-
нятно, почему пленка в природе не прокручивается назад и почему
нельзя построить вечный двигатель.
Квантовая механика наглядно продемонстрировала, что мы прин-
ципиально лишены возможности измерить с наперед заданной точ-
ностью одновременно координату и импульс элементарной частицы.
Не поддаются одновременному измерению и многие другие вели-
чины. Множество непреодолимых барьеров позволила обнаружить
теория относительности. Все эти теории, в сущности, сузили круг
тех вопросов, которые можно задавать Природе.
И в этом ряду большое место занимают работы последних лет,
связанные с предсказуемостью и так называемым динамическим
хаосом. Они позволили осознать еще один барьер. Оказалось, что
мы в принципе не можем дать «долгосрочный прогноз» поведения
огромного количества даже сравнительно простых механических,
физических, химических и экологических систем. Можно предполо-
жить, что предсказуемое на малых и непредсказуемое на больших
временах поведение характерно для многих объектов, которые изу-
чают экономика, психология и социология.
Обычно передний фронт фундаментальных исследований свя-
зывают с гигантскими астрофизическими масштабами или микро-
структурой материи. Работы по динамическому хаосу показали,
что парадоксальными свойствами, которые, по существу, только
начинают изучаться, обладают объекты, прекрасно описываемые
классической механикой.
Попробуем сформулировать главное из того, что внесла в про-
блему прогноза новая наука, называемая нелинейной динамикой.
Впрочем, английский термин nonlinear science — нелинейная на-
ука — здесь, наверное, удачнее.
Раньше думали, что есть два класса объектов. Одни — детерми-
нированные. Прогноз их поведения может быть дан на любое же-
лаемое время. Другие — стохастические. Ими занимается теория
вероятностей. Типичный пример — бросание костей или монетки.
То, что выпадет в этот раз, никак не связано с предысторией. Здесь
нельзя говорить о детерминированном прогнозе и можно иметь
дело лишь со статистическими характеристиками; средними зна-
чениями, дисперсиями, распределениями вероятностей.
В последние 20 лет было показано, что есть еще один важный
класс объектов. Формально они являются детерминированными,
точно зная их текущее состояние, можно установить, что произой-
дет с системой в сколь угодно далеком будущем. И вместе с тем
предсказывать ее поведение можно лишь в течение ограниченного
времени. Сколь угодно малая неточность в значении начального со-
стояния системы нарастает со временем, и с некоторого времени мы
теряем возможность что-либо предсказывать. На этих временах си-
стема ведет себя хаотически. Тут вновь приходится говорить лишь
о статистическом описании. Такие системы были обнаружены в ги-
дродинамике, физике лазеров, химической кинетике, астрофизике и
физике плазмы, в геофизике и экологии. Поистине огромна область,
в которой наши возможности предсказывать весьма ограничены.
Однако в некоторых случаях осознанный барьер не только ли-
шает иллюзий, но и помогает увидеть в одних случаях обнадежива-
ющие перспективы, а в других - истинный масштаб стоящих про-
блем.
О роли динамического хаоса и рассказывает эта статья. Она на-
писана таким образом, чтобы все основное было понятно без фор-
мул. Картинки в ней более существенны. Пожалуй, роль формул
в ней можно сравнить со значением жестикуляции в устной речи.
Если следить за ней, многое становится нагляднее.
Возможно, что взгляды, появившиеся в нелинейной динамике,
заинтересуют людей, работающих в самых разных областях.
Нелинейность и поведение открытых систем
Так разум среди хаоса
явлений
Распределяет их по ступеням
Причинной связи, времени
пространства
И укрепляет сводами числа.
М. Волошин
Одним из своих самых важных достижений И. Ньютон считал,
говоря современным языком, использование в качестве математи-
ческих моделей обыкновенных дифференциальных уравнений
11
dxjdt = f(x, А),
х(0) = Хо, х =
(1)
Такие уравнения определяют скорость изменения вектора х, име-
ющего N компонент. В начальный момент этот вектор имеет зна-
чение xq. Этот вектор может определять скорость и положение ма-
териальных точек, набор скоростей и положений планет Солнечной
системы, напряжение в электрической цепи и еще множество раз-
ных величин.
Остается удивляться изяществу законов природы, оказавшихся
достаточно простыми: проведя сравнительно несложные выкладки,
связанные с исследованием уравнения (1), можно предсказать дви-
жение небесных тел и существование неизвестных планет, струк-
туру электромагнитного поля в резонаторе или спектр излучения
атома водорода.
Парадигма классической механики, опирающаяся на исследова-
ние уравнения (1), включала две ключевые идеи.
Первая может быть пояснена таким примером. Если
f =
—Ш2Т1
то эти уравнения можно переписать как
±1 = х2
, 2
Х2 = “WI1.
Исключив х2 можно привести их к виду
+ w2ii = 0.
Такое уравнение возникает в поразительном множестве самых
разных ситуаций — от задачи о колебаниях грузика на пружинке до
изменения численности хищников и жертв в каком-нибудь регионе.
Его решения имеют вид ii = Asinut + Bcosuit.
Важная деталь — функция f линейно зависит от неизвестных
xi и Х2, т.е. f(ax + /Зу) = af(x) + /3f(y). Такие уравнения реша-
ются очень просто. Их решения - синусы, косинусы и показатель-
ные функции. Замечательный американский физик Ричард Фейн-
ман как-то сказал, что основная часть теоретиков большую часть
жизни проводит за решением линейных уравнений. И одна из глав-
ных причин этого — линейные уравнения, в сущности, единствен-
ный класс математических моделей, который можно детально про-
анализировать. Они похожи на тот фонарь, около которого ученые
особенно любят вести поиск.
Естественно рассуждать так. Решив одно уравнение, описыва-
ющее движение маятника, мы получили очень простые и полезные
функции, которые могут быть использованы и во многих других
задачах. Поищем другие линейные уравнения. Возможно их реше-
ние приведет к другим полезным функциям. По этому пути и пошли
математики. Замечательные функции были введены Эрмитом, Ла-
герром, Лежандром, Бесселем, Якоби.
Вторая идея связана с использованием асимптотических мето-
дов. Ее смысл также очень прост. Пусть мы умеем решать уравне-
ние (1) для функции f = f0(x), при этом х — y0(t), а нас интересует
ее решение при f = fb + cfi, где е — небольшая величина (или, как
говорят математики, малый параметр). Тогда естественно искать
оо
решение в виде ряда x(t) = $2
fc=O
Для каждой функции У1,уг>-- - будут получаться свои уравне-
ния, но они могут оказаться намного проще исходного. Кроме того,
возможно, уже несколько первых членов ряда позволят определить
решение с высокой точностью. Этот подход оказался во многих за-
дачах очень эффективен и продолжает активно развиваться и в
наши дни. Спектр задач, где он был с блеском использован, чрез-
вычайно широк — от небесной механики, где именно с его помощью
и были решены наиболее интересные задачи, до квантовой электро-
динамики и общей теории относительности.
Эти две идеи и их впечатляющее использование в астрономии
стали основой для детерминизма — концепции, проникнутой ве-
рой в безграничные возможности разума, открывшего все фунда-
ментальные законы природы и способного получить весь набор их
следствий.
Однако на рубеже нынешнего столетия стало ясно, что число
линейных уравнений, для которых полезно ввести и детально ис-
следовать некоторые специальные функции (аналоги синусов) неве-
лико. Сравнительно небольшой класс задач доступен и асимптоти-
ческому методу. Использование численных методов без довольно
точных представлений об изучаемом решении даже в настоящее
время при наличии огромного арсенала компьютеров напоминает
поиски в темной комнате. Нужна была новая концепция.
Такая концепция появилась на рубеже нашего века. Ее автором
стал выдающийся французский математик Анри Пуанкаре. Он кар-
динально изменил постановку вопроса. Во многих случаях основ-
ной интерес представляет не все решение, а некоторый предельный
(асимптотический) режим, на который система выходит на боль-
ших характерных временах. (Формально — при стремлении вре-
менной переменной t к бесконечности.) И этому асимптотическому
поведению, качественному исследованию решений и должно быть
уделено основное внимание.
Такая формулировка проблемы и привела к созданию новой па-
радигмы, которая стремительно развивается и сейчас. Дело не толь-
ко в том, что эта идея принципиально изменила облик математики.
Математика перестала быть наукой о числах и фигурах. В ней по-
явились такие разделы как топология, теория катастроф, теория
бифуркаций, где основными являются не количественные, а каче-
ственные свойства изучаемых объектов. Гораздо важнее, что среди
множества самых разных систем уравнений, имеющих совершенно
разный вид, описывающих различные процессы, удалось обнару-
жить глубокое внутреннее единство.
Приведем один пример. Пусть уравнение (1) описывает какую-
нибудь открытую (т.е. способную к обмену энергией, веществом
или чего-либо еще с окружающей средой) систему. Такими являются
большинство объектов экологии, химии, радиотехники, но не явля-
ются традиционные модели небесной механики, для которых энер-
гия сохраняется. Понятно, что если в систему поступает энергия, то
в ней она может рассеиваться, диссипировать. Такие системы на-
зывают диссипативными. Замечательный результат состоит в том,
что какие бы функции f при N = 2 мы не взяли, в конце будут на-
блюдаться только две различные картины, показанные на рис. 1 и 2.
Возьмем какую-нибудь компоненту вектора х, например ii(t).
После некоторого переходного режима (от t — 0 до t = <i на рис. 1)
она выходит на постоянное значение, так же как и остальные ком-
поненты вектора.
Можно считать, что уравнение (1) описывает траекторию точки,
определяющей состояние системы в пространстве {zi,... ,zjv}, на-
Рис.1. Типичная картина, когда аттрактором является устойчивая особая
точка. Зависимость xi(t) и траектория в фазовом пространстве.
Рис.2. Типичная картина, когда аттрактором является предельный цикл.
зываемом фазовым пространством. Саму траекторию в этом слу-
чае называют фазовой траекторией. Установившиеся режимы опре-
деляются притягивающим множеством или аттрактором (от англ,
attract — притягивать) На рис. 1 аттрактор — точка в фазовом
пространстве или, как говорят математики, устойчивая особая точ-
ка системы (1).
Есть другая возможность. Она показана на рис. 2. После пе-
реходного периода происходит выход на периодические колебания.
Аттрактор в этом случае представляет собой замкнутую кривую и
называется предельным циклом.
И все. Других возможностей нет. Это удивительный факт —
гигантский выбор функций f, дающих ограниченные решения, и
только два варианта качественного поведения.
Допустим, нас интересует предсказание поведения системы, в
которой есть устойчивая особая точка или предельный цикл. Пусть
мы знаем начальное состояние с малой погрешностью d(0): х'(0) =
= х(0) + d(0) (рис. 3) и само уравнение (1), описывающее дина-
мику. Будем следить за траекториями x(t) (истинная траектория)
и x'(t) (предсказываемая траектория). Неточность в знании истин-
ного положения d(t) = x'(i) — x(t) , по крайней мере, не нарастает,
а может и уменьшаться. При этом будет происходить явление, на-
зываемое на жаргоне забыванием деталей начальных данных, —
с целого класса начальных состояний будет происходить выход на
один и тот же установившийся режим.
Можно ввести и количественные характеристики скорости стрем-
ления близких траекторий одна к другой. Выберем две близкие тра-
ектории x(t) и x't и посмотрим, как меняется расстояние d(t) =
= |x'(t)—x(t)| (это просто длина вектора d(t)). Если две траектории
сходятся, то d(t) ~ еА/,Л < 0. Величина А называется ляпуновским
показателем. Ее формальное определение таково:
A(x(0), d(0)) = lim lim In .
t-юо d(o)->o [ t a(0)
Можно сказать, что ляпуновский показатель, если он положите-
лен, характеризует среднюю скорость разбегания двух бесконечно
близких траекторий (или сближения, если он отрицателен).
Понятно, что выбирая различные точки х'(0) вблизи х(0) и раз-
личные точки х(0), мы, вообще говоря, будем получать различные
числа. Однако в 1968 г. советский математик В. Оселедец пока-
зал, что при весьма общих условиях почти все точки х'(0) и х(0) в
окрестности странного аттрактора в 7V-мерной системе вида (1) бу-
дут давать один и тот же набор N ляпуновских показателей Ai,...
..., Ajv- Смысл их очень прост. Показатель Ai характеризует изме-
нение длины отрезка |x(t) -x'(t)|, где x(t) и x'(t) — две бесконечно
близкие траектории. Изменение площади параллелограмма с верши-
нами x(t), x'(t), x"(t) (рис. 4) определяется величиной exp[(Ai+A2)t],
объем параллелепипеда — exp[(Ai + А2 + Аз)£], и т.д. Поскольку мы
рассматриваем TV-мерные системы, у которых есть аттрактор и,
следовательно, TV-мерный объем сокращается, Ах + ... + Адг < 0.
У устойчивой особой точки Ai < 0, i = 1,..., АГ; у предельного ци-
кла Ai = 0, Aj < 0, i = 2,..., N.
Если нас интересуют только установившиеся режимы, то задача
еще более упрощается. В самом деле, подождем достаточно долго:
до тех пор, пока произойдет выход на установившийся режим. Если
все происходит как на рис. 1, то важны будут только предельные
значения и вместо уравнения (1) достаточно будет решить алгебра-
ическую систему f(x) = 0. В случае показанном на рис. 2, можно
ввести одну координату, характеризующую положение точки на ци-
кле (например, угол 0), и вместо (1) решать более простое уравне-
ние, определяющее изменение угла в. Только от этого угла и зави-
сят все остальные переменные xi = ii(0),... ,x(N) = x(N)ff. Таким
образом, в этой идеализированной постановке у нас есть все воз-
можности получить «глобальный прогноз» — на любое желаемое
время с высокой точностью.
Рис.З. К предсказанию поведе- Рис.4. Сумма двух первых ляпу-
ния системы, в которой есть новских показателей характеризует
устойчивая особая точка или изменение с течением времени пло-
предельный цикл. Если величина щади параллелограмма S(t).
d(t) уменьшается, то близкие
траектории z(t) и z'(t) стре-
мятся друг к другу.
При N > 2 был бы возможен еще один аттрактор, описыва-
ющий двухчастотный режим и называемый инвариантным тором
(рис. 5). Аттрактор похож на бублик, на который намотана траек-
тория. В простейшем случае изменение функции ii(t) напоминает
биения. Здесь Ai = 0, Аз = О, А, < 0, г = 3,.... Следовательно, также
возможен прогноз.
Разумеется, все просто только в принципе. При анализе реаль-
ных систем основные усилия уходят на установление функции f,
что и эквивалентно построению математической модели явления.
Далеко не всегда просто измерить начальное х(0) и текущее x(t)
состояния системы.
Кроме того, изучаемое уравнение может иметь несколько ат-
тракторов. Типичный пример такой ситуации показан на рис. 6. Ат-
тракторы здесь — устойчивые неподвижные точки 01 и 02. У ка-
ждого из них есть своя область притяжения: в этом случае соответ-
ственно А и В. Все траектории из А стремятся к 01, из В — к 02.
Допустим, мы знаем все возможные аттракторы — их можно
условно назвать целями развития процессов в системе, знаем на-
чальное состояние х(0). Но, чтобы понять, что произойдет, в конце
концов, или как-то управлять ходом процесса, этого недостаточно.
Нужно знать еще и области притяжения различных аттракторов.
Мы можем найти замечательный аттрактор 01 и искренне же-
лать, чтобы система со временем его достигла. Но исходное со-
стояние может оказаться далеко от области А и тогда аттрактор
01, будет для нас недостижим. С такими задачами часто прихо-
дится сталкиваться в экологии и химической технологии. Правда,
возможна и другая ситуация, когда точка х(0) находится на гра-
Рис.б. Возможный вид инвариантного тора в фазовом пространстве и
соответствующая зависимость xi(t).
Q
Рис.6. Иллюстрация того, что неболь-
шие изменения начальных данных на
границе притяжения G аттракторов
(здесь это ось симметрии) могут каче-
ственно изменить поведение системы.
нице области притяжения Q. Тогда немного изменив х(0), мы смо-
жем выбрать цель развития системы.
Аттракторы, предельные циклы, области притяжения — ключе-
вые слова в нелинейном языке, на котором ученые самых разных
дисциплин все чаще формулируют свои результаты. Роль же са-
мого языка и связанных с ним образов очень возросла.
Просматривая журналы, где публикуются статьи по нелиней-
ной динамике, сразу замечаешь, как много работ посвящено каче-
ственным особенностям нелинейных процессов. Бросается в глаза
резкий контраст между стилем научных работ по математической
физике конца и начала нашего века. Видимо, причина в том, что
большинство задач, которые сейчас приходится решать ученым, не-
линейны. О свойствах нелинейного мира известно очень немного.
Кроме того, с появлением компьютеров появилась новая технология
научных исследований — вычислительный эксперимент. Открылись
новые возможности проверять смелые и неожиданные гипотезы, го-
раздо детальней просчитывать возможные варианты, прежде чем
переходить к натурному эксперименту. Это привело к возрастанию
роли интуиции, аналогий, образов, предлагаемых математической
физикой, а порой и совсем далекими дисциплинами. Наверно, можно
сравнить нынешний этап исследований с древнегреческой наукой.
Ученые того времени опирались при объяснении мира и его изу-
чении на мифы, аналогии, неожиданные образы и получали порой
удивительные результаты. Так же и современные ученые пытаются
понять сложность нашего мира, опираясь на простейшие нелиней-
ные модели.
Синергетика и параметры порядка
Заметим, прежде всего, что всякое
обобщение до известной степени пред-
полагает веру в единство и простоту
природы. Допущение единства не пред-
ставляет затруднений... Поэтому мы
должны задавать вопрос не о том, едина
ли природа, а о том, каким образом она
едина.
А. Пуанкаре
В книгах писателей, пишущих о науке и знании, часто возникает
образ гигантской библиотеки. У того, кто попадает в нее, нет воз-
можности ознакомиться даже с ее небольшой частью и узнать, где
в этом лабиринте истина соседствует с заблуждением. И только
счастливый случай помогает разгадать одну из загадок библио-
теки. Ощущение сокровища, которым неясно как распорядиться,
есть в книгах Борхеса, Германа Гессе, Умберто Эко.
Причины нарастающего беспокойства многих исследователей за
судьбу науки удачно сформулировал один из создателей квантовой
механики Е. Вигнер в статье «Пределы науки». В начале работы он
так определяет область знаний, которую можно отнести к сфере
научной деятельности: «Я считаю, что некий запас знаний разумно
назвать «нашей наукой» в том случае, если найдутся люди, кото-
рые бы жаждали овладеть каждой частью, даже сознавая, что это
выше их сил, при условии, что есть достаточная уверенность, что
отдельные части свода знаний не противоречат друг другу, а обра-
зуют единое целое». И далее он делает неутешительный прогноз:
«Нетрудно представить себе, что наступит и такое время, когда
изучающий физику утратит интерес или будет попросту не в си-
лах пробиться сквозь уже накопившиеся слои к переднему фронту
науки, к самостоятельному исследованию...»
Разумеется, есть и стабилизирующие эффекты — исключение
целых разделов науки из области активных исследований, возмож-
ность найти более короткие пути в лабиринте наших знаний:
«... чем глубже мы понимаем открытия, тем лучше можем объяс-
нить их».
Конечно, со времени написания статьи оба фактора не утратили
свою роль. И все же сейчас многие исследователи свои надежды свя-
зывают с разработкой междисциплинарных подходов. Можно наде-
яться, что такие подходы - совокупность идей, методов, приемов,
применимых для анализа различных проблем, — помогут увидеть
единство во многих явлениях природы. Возможно, именно им су-
ждено сыграть роль нити Ариадны в лабиринтах науки.
Синергетика исследует общие закономерности возникновения
упорядоченности в открытых нелинейных диссипативных систе-
мах. Она существенно изменила взгляд на многие явления. В ее
рамках удалось показать, что многие сложные системы, описание
которых требует огромного, а в некоторых случаях и бесконечного
числа степеней свободы, могут вести себя просто. И напротив, по-
ведение совсем простых систем всего лишь с тремя степенями сво-
боды может быть очень сложным, хаотическим. И то и другое са-
мым тесным образом связано с проблемой прогноза. Остановимся
на ключевом понятии синергетики — понятии самоорганизации.
Напомним, что число степеней свободы определяется тем, сколько
величин нужно задать, чтобы полностью охарактеризовать состоя-
ние системы. Например, для объектов, которые описываются обык-
новенными дифференциальными уравнениями, это просто N. Но
сейчас ученых все больше интересуют задачи, в которых изучаемые
величины изменяются во времени и в пространстве. Формально у
них N = оо.
Пусть, например, нас интересует, как меняется распределение
реагентов в химическом реакторе. При этом вместо /V-мерного век-
тора х в уравнении (1) нам придется иметь дело с набором М функ-
ций и, (г, t), i = 1,..., М, описывающих концентрацию г-го реагента
в точке с координатой г в момент времени t. Их для краткости
можно записать как некий вектор u(r, t). Этот вектор в каждой
точке г в момент времени t, естественно, свой.
Если считать, что поведение реагентов определяется химиче-
скими реакциями и диффузионными процессами, то уравнения, опи-
сывающие эволюцию u(r, t), можно символически записать в виде
u< = Durr -I- F(u, A), 0 < r < I. (2)
Член Durr описывает диффузионные процессы (матрицу D со-
ставляют коэффициенты диффузии), член F(u, А) — кинетику хи-
мических реакций. Мы считаем, что реактор имеет длину I. Реше-
ние этого уравнения — функции, зависящие от двух переменных г
и t. В уравнение (2) входят производные по переменным г и t или,
как говорят, частные производные, а уравнения, в которые такие
производные входят, это уравнения в частных производных.
Физики, химики, занимающиеся-моделированием технологиче-
ских процессов, инженеры, применяющие теорию упругости, гидро-
динамики очень привыкли к таким уравнениям. Со времен Лапласа,
впервые написавшего уравнения такого типа, они глубоко вошли в
фундамент естествознания. Если F — линейная функция, то эти
уравнения могут быть сравнительно просто решены. И о них почти
все известно. Если F нелинейна, то уравнение (2) (его обычно на-
зывают системой типа реакция-диффузия) представляет собой объ-
ект, который сейчас активно исследуется современными методами.
О таких уравнениях написаны тысячи работ.
Само введение u(r, t) — смелый и непростой шаг. Фейнман на
вопрос о наглядном образе электромагнитного поля ответил, что
у него нет наглядного образа. Проще всего представлять, что в
каждой точке пространства задано шесть чисел, характеризующих
электрическое и магнитное поля. Здесь та же ситуация. u(r, t) —
это М чисел в каждой точке пространства, которые меняются со
временем. Интуитивно хочется иметь более простое описание.
Одна из возможностей, которую предлагает синергетика, со-
стоит в следующем. Вернемся к идее аттрактора и к уравнению (1).
При t -> оо у нас возникало более простое описание. Например, если
в системе происходит выход на предельный цикл, то состояние си-
стемы определяют одной величиной — положением точки на цикле
(угол в на рис. 2). Все остальные переменные зависят только от нее
х = х(0).
Так же дело обстоит и во многих задачах с частными производ-
ными. Не все степени свободы играют одинаковую роль. В нели-
нейной диссипативной системе обычно удается выделить конечное,
а иногда и небольшое число переменных, к которым «подстраива-
ются» остальные. Эти переменные называют иногда параметрами
порядка. Это можно пояснить на таком примере. Возьмем функ-
цию и(х), заданную на интервале от 0 до I. Ее можно разложить по
гармоникам (математики говорят, разложить в ряд Фурье) и найти
амплитуду каждой гармоники.
Другими словами, представить функцию и(х) в виде
ОО
u(l) = Cm cos(nmx/l).
m=Q
Эта операция становится совершенно понятной, если вспомнить
школьный опыт с треугольной призмой. Проходя через нее, луч бе-
лого света дает замечательную «радугу». Призма разделяет свет на
составляющие с разной длиной волны. Близкая процедура много-
кратно осуществляется в телевизорах или радиоприемниках.
и(х)
Рис.7. Функция u(z) и ее коэффициенты Фурье (чем более изрезанной явля-
ется функция, тем больше коэффициентов имеют близкую амплитуду).
Или другая аналогия. В школьной физике вектор разлагается на
составляющие х и у. В пространстве функций эти составляющие —
функции cos(jrmx/l), т = 0,1,2.... Их уже бесконечно много. А ве-
личина проекции на каждую из них определяется амплитудой гар-
моники Ст,.
Пусть функция и(х) имеет сложный изрезанный вид (рис. 7а).
В ее поведении не видно какой-либо закономерности или упорядо-
ченности. При этом амплитуды многих гармоник сравнимы между
собой. Обратим внимание на зависимость к-го коэффициента Фу-
рье ак от номера к (см. рис. 7а). Напротив, гладкая функция и(х)
на рис. 76 ведет себя очень просто, в ней легко заметить законо-
мерность: она близка к периодической. Для того чтобы передать ее
профиль, достаточно задать амплитуды всего нескольких гармоник
(см. рис. 76). Если процесс идет так, что количество гармоник боль-
шой амплитуды уменьшается, то в системе будет возникать некото-
рая упорядоченность, будет происходить самоорганизация. Такую
упорядоченность часто называют диссипативными структурами,
чтобы подчеркнуть ту роль, которую играют диссипативные про-
цессы в ее образовании.
Сам термин «диссипативная структура» был введен бельгийским
ученым И. Пригожиным. Работы ученых его школы помогли понять
связь возникающих структур с представлениями термодинамики.
Они сыграли большую роль как в теоретическом, так и в экспери-
ментальном изучении упорядоченности в открытых системах. Вот
как пишут Г. Николис и И. Пригожин о возникающих структурах:
«... как удаленность от равновесия, так и нелинейность могут слу-
жить причиной возникновения упорядоченности в системе. Между
упорядоченностью, устойчивостью и диссипацией возникает в выс-
шей степени нетривиальная связь. Чтобы четче выделить эту связь,
мы будем называть упорядоченные конфигурации, появляющиеся
вне области устойчивости термодинамической ветви, диссипатив-
ными структурами... Такие структуры могут существовать вдали
от равновесия лишь за счет достаточно большого потока энергии
и вещества... Диссипативные структуры являют собой поразитель-
ный пример, демонстрирующий способность неравновесности слу-
жить источником упорядоченности».
Под областью устойчивости термодинамической ветви здесь по-
нимается область параметров, в которой применимы методы клас-
сической термодинамики.
Самоорганизация, формирование диссипативных структур
дают надежду на то, что сложные системы можно описать просто.
В самом деле, у нас появилась возможность говорить о сложных
объектах на простом языке.
Можно попробовать найти аналогии тем образам, которые суще-
ствуют в простейших системах, в распределенных (т.е. зависящих
от пространственной координаты) системах.
Простейшим аттрактором в системах вида (1) является устой-
чивая особая точка, при этом все величины стремятся при t —> оо
к постоянным значениям. Ее аналог — решение уравнения (2), не
зависящее от времени, в частности, стационарная диссипативная
структура. Типичный пример такой структуры показан на рис. 8.
Это установившееся распределение реагентов в некоторой хими-
ческой реакции, в которой участвуют два вещества X и Y, и =
= (X, У). Компоненты вектора и в каждой точке стремятся к по-
стоянным значениям: u(r, t) -> и'(г). При этом сама функция и'(г)
может иметь достаточно сложный вид. Тем не менее, она является
только устойчивой особой точкой в некотором фазовом простран-
Рис.8. Типичный вид стационарной
диссипативной структуры. Функции
X(r,t),Y(r, t) определяют распреде-
ление концентраций в одной модели,
описывающей химическую реакцию.
Рис.9. Вид решения, соответствующего периодическому режиму в некоторой
модели, описывающей колебательные химические реакции.
стве. Можно найти и аналоги предельных циклов. Один из них, воз-
никающий в некоторой модельной системе, играющей важную роль
при исследовании уравнения (2), показан на рис. 9. Не правда ли
красиво?
Но, пожалуй, наибольшее впечатление производит не сопоста-
вление отдельных типов упорядоченности, аттракторов разных си-
стем, а их эволюция при изменении параметров задачи.
Одно из замечательных представлений нелинейного мира —
представление о ветвлении решений или о бифуркациях. Бифурка-
цией называют изменение числа или устойчивости решений опреде-
ленного типа.
Простейший пример бифуркации дает обычное квадратное
уравнение
ах2 + Ьх = А(а > 0).
Рис.10. Зависимость х(А). Устойчивые
решения лежат на ветви, показанной
сплошной линией, неустойчивые — штри-
ховой.
Будем менять параметр А. При А < А* = — Ь2/4а оно не имеет
решений. При А = А* у него появляется одно, а при А > А* — два
решения. В точке А = А* происходит бифуркация. Ее иллюстрирует
рис. 10 где по оси абсцисс отложено значение А, по оси ординат —
значения корней уравнения. Такие рисунки называют бифуркаци-
онными диаграммами.
Если бы мы рассматривали некоторую химическую реакцию, в
которой изменение концентрации некоторого вещества X опреде-
ляется дифференциальным уравнением
dx/dt = ах2 + Ьх — А,
то установившиеся режимы (при которых х не зависит от времени)
также определялись бы квадратным уравнением. В этом случае
приходится следить не только за числом решений, но и за их устой-
чивостью. Из двух решений, как видно на рисунке, здесь устойчиво
только одно.
Поразительная особенность нелинейных диссипативных систем,
которая и сделала возможным создание синергетики, состоит в том,
что в исходных системах, в моделях, связывающих параметры по-
рядка, и в самых простых уравнениях происходят одни и те же би-
фуркации. Несколько самых простых показано на рис. 11. Наличие
нескольких элементарных бифуркаций — одно из проявлений един-
ства природы. Осознание этого факта породило многие разделы
науки. Одним из них является теория катастроф. Об общности и
большом значении этих представлений говорит обширный список
ее приложений: остойчивость судов, механика жидкости, оптика и
теория рассеяния, термодинамика и фазовые переходы, лазерная
физика, экология и эмбриология, социологическое моделирование.
Если бы не было ничего известно, кроме того, какие бифуркации
происходят в системе, то и это было бы очень полезно. Поясним это
на примере одной простой модели социологии.
Рис.11. Типичные бифуркационные диаграммы в случае, когда хотя бы одна
из вторых производных функции F(x.X) в точке (z*,A*) не равна нулю.
Рис.12. Типичное поведение состояний равновесия в модели формирования
общественного мнения, а — случай, когда ни одно из мнений не является
изначально более предпочтительным; б— одно из мнений изначально имеет
преимущество. Сплошная линия соответствует устойчивым состояниям рав-
новесия, штриховая — неустойчивым.
Пусть нас интересует голосование сообщества по определенному
вопросу. Систему характеризует величина X — разница между
тем, сколько людей готовы голосовать «за» и «против». Остроту
вопроса, его важность для сообщества характеризует параметр А.
Типичная бифуркационная диаграмма, возникающая в этой за-
даче, показана на рис. 12а. Опишем происходящее, считая, что ни
оно из мнений изначально какого-либо преимущества не имеет. При
А < Ао вопрос безразличен большинству. Когда А = Ар сообщество
делает выбор. И в зависимости от него большинство сообщества
укрепляется в этом мнении (число тех, кто поддерживает его, ра-
стет). Система движется по верхней или нижней ветви. Типичная
картина в случае, когда одно из мнений предпочтительнее, пока-
зана на рис. 126. Пусть мы хотим изменить общественное мнение
относительно небольшими возможностями I. (Это число сторонни-
ков, которое мы на краткий срок можем привлечь на свою сторону.)
Если ничего не предпринимать, общественное мнение будет ме-
няться так, как показывает верхняя кривая на рис. 126. При А Ар
воздействие бесполезно — вопрос не важен. При А Ар это также
бесполезно — мнение уже сформировано. Однако вблизи точки Ар
небольшое воздействие может определить всю дальнейшую судьбу
сообщества. Это типично для многих бистем, изучаемых синергети-
кой. Напрашивается аналогия с вопросом «о роли личности в исто-
рии».
Во многих случаях ученые любят экстраполировать. В обсужда-
емой модели это звучит так: «завтра будет примерно так же, как
сегодня». Нижняя картинка на рис. 126 показывает, что это далеко
не всегда оправданно. Пусть общественное мнение уже в достаточ-
ной мере поляризовано, но параметр А уменьшается. Пусть состоя-
ние системы определяется точками на нижней ветви кривой. Тогда
при малом изменении параметра А вблизи точки Ао общественное
мнение меняется скачком. Происходит «перескок» с нижней ветви
на верхнюю. Подавляющее большинство сообщества резко меняет
свой взгляд. Подобное в реальных системах неоднократно наблю-
далось. Такие аналоги «фазовых переходов» активно исследуются в
настоящее время.
Подведем итоги. Синергетика предлагает следующий путь ис-
следования сложных систем. Поиски параметров порядка, устано-
вление связи между ними. Анализ возникающих уравнений. Если
эти уравнения вновь окажутся слишком сложными, то и в них также
следует искать параметры порядка и строить другие модели. По-
сле построения такой иерархии моделей и их анализа можно начать
восхождение вверх к исходной системе. На этой основе можно по-
пытаться дать прогноз ее поведения.
Рецепт очень общий, не связанный с каким-либо конкретным
видом систем или уравнений и поэтому очень привлекательный для
многих исследователей, занимающихся самыми разными проблема-
ми. Но в этом и его слабость. Неясно, как для данной системы найти
параметры порядка, как их измерить. Однако если уж мы их знаем,
то очень сложные процессы удается очень просто описать. К при-
меру, большинство проблем при математическом моделировании в
социологии, психологии, политике связано с тем, что параметры
порядка неизвестны.
Вместе с тем довольно много известно о том, каковы параме-
тры порядка для уравнения (2), описывающего распределенные си-
стемы. В одних случаях это амплитуды некоторых фурье-гармоник,
в других — самые медленные или самые быстрые переменные. На
этом пути было получено много важных результатов. В частности,
в ряде случаев удалось понять, как у целого, состоящего из многих
взаимодействующих подсистем, возникают свойства, которыми ни
одна из подсистем не обладает.
До недавнего времени было неясно, является ли выделение пара-
метров порядка полезной процедурой, за которой стоят интересные
эвристические соображения, или со временем удастся обосновать ее
строго. Таким обоснованием является доказательство того, что ат-
тракторы уравнений вида (2) (формально описывающих системы с
бесконечным числом степеней свободы) описываются конечномер-
ной системой (1). Мне кажется, до недавнего времени большинство
специалистов придерживались первой точки зрения.
Работы последних лет, и в частности исследование американ-
ских математиков С. Фояша, Дж. Селла и французского матема-
тика Р. Темама, показали, что для многих уравнений, к примеру,
для ряда систем реакция-диффузия, строгие результаты могут
быть получены. Концепция параметров порядка оказалась еще бо-
лее глубокой, чем это казалось раньше.
Странность странных аттракторов
Если наши результаты, касающиеся не-
устойчивости непериодического тече-
ния, применить к атмосфере, которая
явно не периодична, то получается, что
предсказать погоду на достаточно от-
даленное будущее невозможно никаким
методом, если только теперешнее со-
стояние не известно точно. Из-за не-
избежной неточности и неполноты на-
блюдений погоды точное предсказание
на очень долгий срок, видимо, невоз-
можно.
Э. Лоренц
Обсуждая крупное научное достижение, рождение новой идеи,
всегда интересно посмотреть, что думали по этому поводу предше-
ственники и современники автора. И часто оказывается, что они
высказывали близкие мысли. Идея «витала в воздухе». Не является
исключением и открытие хаоса в детерминированных системах.
Суть идеи прекрасно сформулирована в рассказе Рэя Брэдбери
«И грянул гром». Одна из компаний устраивает с помощью машины
времени для своих клиентов сафари, охоту на доисторических жи-
вотных. Компания тщательно выбирает животных для отстрела и
специальные маршруты передвижения охотников, чтобы происшед-
шее практически не имело последствий. Однако по случайности ге-
рой рассказа во время неудачной охоты сошел с маршрута и раз-
давил золотистую бабочку. Затем он возвращается в свое время и
осознает, как драматически повлияла судьба бабочки на дальней-
ший ход событий. Неуловимо изменился химический состав воздуха,
оттенки цветов, изменились правила правописания и, наконец, ре-
зультаты последних выборов. К власти пришел режим, жестоко рас-
правившийся со своими противниками. В свой последний миг герой
рассказа понимает, что гибель бабочки нарушила хрупкое равно-
весие; повалились маленькие костяшки домино, большие костяшки,
гигантские костяшки...
Образ падающих костяшек увеличивающегося размера прекрас-
но иллюстрирует важнейшее свойство детерминированных систем
с хаотическим поведением — чувствительность к начальным дан-
ным. Начальные отклонения с течением времени нарастают, малые
причины приводят к большим следствиям. Это явление иногда на-
зывают эффектом бабочки, так объясняя название: взмах крыльев
бабочки в неустойчивой системе может со временем вызвать бурю,
изменить погоду в огромном регионе.
А вот какое рассуждение, посвященное предсказуемости, приво-
дится в фейнмановских лекциях по физике.
«Обычно думают, что недетерминированность, невозможность
предсказать будущее — это особенность квантовой механики, и
именно с ней связывают представление о свободе воли и т.д. Но если
бы даже наш мир был классическим, т.е. если бы законы механики
были классическими, все равно из этого не следует, что те же или
какие-то аналогичные представления не возникли бы. Да, конечно,
с точки зрения классики, узнав местоположение и скорость всех ча-
стиц в мире (или в сосуде с газом), можно точно предсказать, что
будет дальше. В этом смысле классический мир детерминирован.
Но представьте теперь, что наша точность ограничена и что мы не
знаем точно положение только одного из атомов; знаем, скажем, его
с ошибкой в одну миллиардную. Тогда, если он столкнется с другим
атомом, неопределенность в знании его координат после столкно-
вения возрастает. А следующее столкновение еще сильней увеличит
ошибку. Так что если сначала ошибка и была еле заметной, то все
равно вскоре она вырастает до огромнейшей неопределенности.
Ясно, что мы не можем по-настоящему предвидеть положение
капель, если мы не знаем движения воды абсолютно точно.
Правильнее будет сказать, что для данной точности (сколь угод-
но большой, но конечной) можно всегда указать такой большой про-
межуток времени, что для него становится невозможным сделать
предсказания. И этот промежуток (в этом вся соль) не так уж ве-
лик. .. Время с уменьшением ошибки растет только логарифмиче-
ски, и оказывается, что за очень и очень малое время вся наша
информация теряется».
Американское издание фейнмановских лекций вышло в 1963 г. В
том же году в «Journal of the Atmospheric Sciences» появилась статья
га -
w -
о -
-w -
-га -
-за -
га t
Рис.13. Типичная зависимость некоторой компоненты в непериодическом
решении (здесь она характеризует изменение одной из компонент магнит-
ного поля в модели солнечного динамо; такие кривые определяют изменение
солнечной активности).
американского метеоролога Эдварда Лоренца, положившая начало
новому направлению в естествознании — исследованию хаоса в де-
терминированных системах.
Тем не менее, можно только удивляться научной смелости Ло-
ренца, выбравшего простейшую модель — систему всего лишь трех
обыкновенных дифференциальных уравнений, просчитавшего ее на
компьютере и сумевшего понять, что он имеет дело не с ошибками
вычислений, а с новым явлением.
Проиллюстрировать сделанное Лоренцем несколькими нагляд-
ными образами можно так. Наряду с аттракторами, показанными
на рис. 1, 2 и 5 есть еще один тип аттракторов. Он соответствует
процессам, при которых изучаемые величины даже при t —> оо не
выходят ни на постоянные значения (как на рис. 1), ни на перио-
дический (рис. 2), ни на квазипериодический режим (рис. 5). Они
продолжают меняться непериодическим образом, сколько бы мы за
ними не наблюдали, например, так, как на рис. 13.
Предельный цикл внешне похож на петлю (см. рис. 2), которая
может быть сложным образом изогнута в фазовом пространстве,
инвариантный тор — на бесконечную нить, намотанную на глад-
кую поверхность. В отличие от них странный аттрактор обладает
необычной геометрией и внешне может быть похож на клубок тра-
екторий, как на рис. 14а. Аттрактор, представленный на этом ри-
сунке, был обнаружен в одной задаче, возникшей в теории систем
реакция-диффузия. В этом случае, как и в системе Лоренца, N = 3
[см. формулу (1)]. Удивительный мир странных аттракторов ока-
зался совсем близко.
Видовая проекция этого аттрактора в трехмерном фазовом про-
странстве представлена на рис. 146. Она напоминает две ленты,
склеенные одна с другой.
Чтобы в полной мере оценить замечательную геометрическую
структуру этого и большинства других странных аттракторов, пе-
a
7
Рис.14. Проекция на плоскость (а) и видовая проекция странного аттрак-
тора в одной модели типа реакция-диффузия (б).
ренесемся в начало нашего века, когда в центре внимания матема-
тиков вновь оказались проблемы строгого обоснования математи-
ческого анализа.
В это время один из создателей современной математики Г. Кан-
тор построил пример множества С, каждая точка которого явля-
ется предельной (т.е. в любой ее окрестности есть точки множе-
I—I I—I
Рис.15. Схема построения канто-
рова множества.
М м М М Н м М М
ства). Кроме того, это множество не содержит ни одного отрезка
и является несчетным (все его точки нельзя перенумеровать нату-
ральными числами). Способ его построения показан на рис. 15: на
п + 1-м шаге из каждого отрезка выбрасывается открытый интер-
вал, составляющий треть этого отрезка. Множество, полученное
после бесконечного количества шагов, и аналогичные множества
называются канторовыми. Такое множество обладает масштабной
инвариантностью. Представим, что у нас есть набор увеличитель-
ных стекол. Если мы будем рассматривать множество в крупном
масштабе (стекло с малым увеличением), то увидим два отрезка.
В более мелком масштабе каждый из них расщепляется на два.
В еще более мелком — каждый из этих четырех отрезков также
расщепляется и т.д.
А теперь рассечем ленты аттрактора на рис. 146 некоторой по-
верхностью. Мы видим множество точек, лежащих вблизи двух не-
прерывных кривых (рис. 16а). Будем рассматривать его в более
мелком масштабе (рис. 166). В еще более мелком масштабе лента
расщепляется на две (рис. 16в), при дальнейшем увеличении раз-
решения — еще на две и т.д. Странный аттрактор в этом сечении
устроен так же, как канторово множество. Необычный геометриче-
ский объект, построенный в начале века, чтобы служить аргумен-
том в абстрактных математических рассуждениях, оказался типич-
ным для большинства странных аттракторов.
Часто говорят, что множество, подобное себе на меньших мас-
штабах (как обсуждавшееся множество С), обладает канторовой
структурой. Анализируя такие множества, можно убедиться, что
обычные понятия длины, площади, объема здесь неэффективны.
В самом деле, посчитаем, переходя к пределу, длину канторова
множества. Она равна нулю. Если выбрасывать не по одной трети,
а по одной р-й части, то длина все равно будет равна нулю. Но полу-
чившиеся множества будут разными. Нетрудно построить пример,
на каждом шаге выбрасывая все меньшую часть остатка, когда
получившееся, в конце концов, множество будет иметь конечную
длину. Это тем более парадоксально — ведь в нем нет ни одного
отрезка.
Рис.16. Канторова структура аттрактора, показанного на рис. 14.
Другой интересный математический объект — остров Коха.
Схема его построения показана на рис. 17. Можно проверить, что
площадь фигуры, которая получится в пределе (она и называется
островом Коха), будет ограничена, а периметр будет неограниченно
расти. Допустим, что мы хотим померить его периметр, пользу-
ясь линейкой размера е. Из схемы построения ясно, что измеренная
длина периметра L будет зависеть от е : L(e) « Се~а, а > 0. Есте-
ственно предположить, что величина а и будет наиболее существен-
ной при анализе объектов, обладающих канторовой структурой.
Такие величины, как а, были введены в 1919 г. В. Хаусдорфом.
В самом простом случае для «хороших» множеств идея сводится
Рис.17. Схема построения острова
Коха.
к следующему. Будем покрывать изучаемое множество в р-мерном
пространстве р-мерными шарами радиуса е. Их число будет раз-
ным для разных покрытий. Выберем покрытие, при котором число
шаров минимально, и обозначим это число через N(e). Пусть при
е —> ON ~ e~dc, de назовем емкостью множества и будем рассма-
тривать как существенную характеристику изучаемого объекта.
Для отрезка в одномерном пространстве (Р = 1) минимальное
покрытие совпадает с разбиением на отрезки длины e,N ~ е-1 и
dc = 1. Для квадрата de = 2, для куба de = 3. Величина dc здесь
совпадает с обычной размерностью.
Для канторова множества естественно поступить так. Выберем
Е = 1/3. Чтобы покрыть С, нужно два таких отрезка. При е =
— 1/9 — четыре. При е = (1/3) — 2П отрезков, а значит, dc =
= In 2/In 3.
Если мы будем выбрасывать не 1/3, а l/s-ю часть, то dc =
= In 2/1ns. Видимо, de лучше отражает канторову структуру, чем
обычная длина. Множества, для которых емкость (или ее аналогии)
дробны, получили название фракталей (от англ, fractal — дробный).
Большинство странных аттракторов - фрактали.
С точки зрения прогноза знание фрактальной размерности
очень полезно. Пусть изучаемый объект описывается системой
вида (1). Ее важнейшей характеристикой является величина N.
Если у нас есть заниженная оценка М (т.е. мы считаем систему
проще, чем она есть на самом деле), то, во-первых, будем измерять
не все ее параметры порядка. Систему в двух разных состояниях
мы будем принимать за одну и ту же. Во-вторых, с ней время от
времени могут происходить неожиданности.
Это можно пояснить на примере мифических двумерных су-
ществ, живущих на сфере (М = 2). Они могут не догадываться
о существовании третьего измерения (N = 3). И появление нового
Рис.18. Восприятие «плоскатиками»,
живущими на сфере; появления звезды
из третьего измерения.
предмета из третьего измерения на своей сфере они будут воспри-
нимать как чудо (рис. 18). В таком же положении мы можем ока-
заться, недооценив N. Незнание N, возможно, в основном и сдержи-
вает использование динамических систем вида (1) в нетрадицион-
ных областях моделирования — социологии, психологии, политике
и др.
Простейшая связь между N ndc такова. Если оказалось, что ат-
трактор, соответствующий какому-либо реальному процессу, имеет
размерность dc, то в его модели вида (1) N > dc, если de — це-
лое, и N > [dc] + 1 в противном случае (квадратные скобки здесь
обозначают целую часть). В действительности связь является еще
более глубокой. Обусловлена она другим фундаментальным свой-
ством странных аттракторов — чувствительностью к начальным
данным.
Для странных аттракторов характерно наличие хотя бы одного
положительного ляпуновского показателя Ai!
Положительные ляпуновские показатели заставляют совершенно
иначе взглянуть на саму возможность предсказывать явления при-
роды. В самом деле, когда аттрактор — цикл или точка, то, наблю-
дая за системой достаточно долго, можно дать достоверный про-
гноз, даже если x(t) мы знаем с небольшой ошибкой (ведь |x(t)—
—x'(t)| не будет расти). Но у странного аттрактора через время
т ~ 1/Ai две близкие вначале траектории перестанут быть близ-
кими. Как бы мала ни была ошибка, мы принципиально не можем
предсказать, что произойдет с системой через время т.
На гораздо меньших временах система предсказуема. Если нас
интересует ее статистические свойства, то, проследив ее поведение
на больших временах, мы сможем выяснить такие характеристики,
как среднее значение x(t), дисперсию и т.д. Однако возможности
прогноза величины х(£) оказываются ограниченными.
Именно с чувствительностью системы к начальным данным
Э.Лоренц и связывал проблемы, возникшие со среднесрочным (на
несколько недель) прогнозом погоды. Ученые столкнулись с тем,
что совершенствование математических моделей, использование
компьютеров с большим быстродействием и памятью, разработка
новых численных методов в течение десятков лет не позволили раз-
работать эффективную методику такого прогноза. Если атмосфера
может быть описана некоторой динамической системой [т.е. моде-
лью вида (1)], и ее старший ляпуновский показатель А ~ 1/неделя,
то это объясняет трудности, с которыми столкнулись метеорологи.
У TV-мерной диссипативной динамической системы, описывае-
мой уравнением вида (1), вообще говоря, существует TV ляпунов-
ских показателей, характеризующих данную траекторию x(t) на
аттракторе. Обычно эти числа оказываются одними и теми же по-
чти для всех траекторий. Если аттрактор странный, то среди них
есть определенное число положительных А1,...,А* > 0 (они соот-
ветствуют близким траекториям, разбегающимся от данной), один
нулевой Ajt+i = 0 и У - k — 1 отрицательных (они характеризуют
близкие траектории, стремящиеся к x(t)) показателей.
Очень интересным является вопрос о связи динамических ха-
рактеристик (например, А*,г = 1,...,2V) с геометрическими (на-
пример, de). Американские математики Дж. Каплан и Дж. Йорке
выдвинули гипотезу, в соответствии с которой
3
где j — наибольшее число, такое, что £) > 0.
г=1
Для большого класса систем вида (1) с непрерывным временем,
у которых N = 3, и с дискретным временем
Хп+1 = y(xn),xi = х',х =
XN
у которых N — 2, эта формула строго обоснована. При больших N
ситуация сложнее, она сейчас активно изучается, но и здесь фор-
мула Каплана-Йорке обычно дает хорошее приближение.
Тем не менее, поразительно, что геометрия и динамика стран-
ных аттракторов так тесно связаны. Измерив ляпуновские пока-
затели, можно судить о геометрии, а померив емкость, получить
информацию о значениях ляпуновских показателей.
Еще один важный вопрос: в какой же мере случайно поведение
системы со странным аттрактором? Вернемся к рис. 146.
Если мы будем следить на экране дисплея за тем, как точка,
характеризующая состояние системы, «бегает» по аттрактору, то
увидим, что она случайным образом попадает то на левую, то на
правую ленту. Это наводит на мысль дать символическое описание
такой траектории в виде бесконечного набора нулей и единиц. Если
на к-м витке точка двигается по левой ленте, на к-м месте после-
довательности будем писать нуль, если по правой — единицу. Это
даст нам бесконечную последовательность нулей и единиц, вообще
говоря, для каждой начальной точки хо свою.
А теперь обратимся к теории вероятностей. Излюбленная мо-
дель этой теории — бросание монеты. Допустим, мы бросили мо-
нету бесконечно много раз. Результаты такой серии удобно запи-
сать в виде последовательности {bjt}. Если в fc-й раз выпал «орел»,
будем на к-м месте писать нуль, если «решка» — единицу. Последо-
вательность {б*} также определяет некоторое число в двоичной си-
стеме. Каждой возможной серии бесконечных последовательностей
соответствует свое число. (Среди всех возможных последователь-
ностей {б*} будет несчетное количество непериодических после-
довательностей. Интересно, что существует взаимно однозначное
соответствие между бесконечными последовательностями нулей и
единиц и всеми точками канторова множества.)
Можно доказать, что найдется начальная точка xq, определя-
ющая последовательность {с*}, совпадающую с любой выбранной
нами бесконечной последовательностью бросаний монеты {6^}.
Это удивительный факт. В самом деле, представим прибор, ко-
торый измеряет только знак х. Тогда сколько бы измерений мы ни
провели, определить, является ли этот процесс чисто случайным
(как, например, при бросании монеты) либо детерминированным,
как в модели (1) или (2) невозможно.
Оказалось, что системы со странными аттракторами могут
быть моделями самых разных явлений — колебательных химиче-
ских реакций и изменений численности популяций животных, ги-
дродинамических систем и некоторых процессов в экономике. Хаос
ожидает нас на каждом шагу в самых простых системах.
Приведем два примера.
1. Солнечная активность проявляется в виде локализованных
явлений: пятен, вспышек протуберанцев, время жизни которых не
превышает нескольких оборотов Солнца. Но процесс активности
не является полностью случайным. Он модулируется механизмом,
обладающим крупномасштабными и долговременными характери-
стиками. Главная из них — 22-летняя повторяемость магнитного
поля и связанная с ней 11-летняя вариация числа пятен по Воль-
фу W(t). На этот цикл накладывается заметная модуляция, про-
исходящая с характерным временем около 57 лет. Наблюдаются
также глобальные ослабления активности на времена, превышаю-
Ы)
Рис.19. Типичный вид аттрак-
тора в одной модели солнечного
динамо.
щие несколько десятков лет. Наиболее известное ослабление актив-
ности носит название минимума Маундера. Ослабление такого ти-
па, описываемое некоторой математической моделью, представлено
на рис. 13. Долговременная модуляция хорошо прослеживается по
концентрации изотопа 14 С в кольцах деревьев и, по-види-
мому, имеет хаотический характер, что позволило высказать ги-
потезу о наличии странного аттрактора в динамической системе,
определяющей солнечную активность.
Типичную проекцию аттрактора в модели долговременных ва-
риаций солнечной активности, имеющей вид (1), иллюстрирует
рис. 19. В этой модели N = 7. Первые четыре уравнения характери-
зуют магнитное поле Солнца, остальные три - его гидродинамиче-
ское движение. Безразмерный параметр D пропорционален угловой
скорости вращения. При сравнительно малых D аттрактор может
быть инвариантным тором (рис. 19а). При больших — он явля-
ется странным, но лежит в окрестности тора (рис. 196). С этим
может быть и связана 57-летняя модуляция. Однако далее емкость
аттрактора de, растет и движение на нем усложняется (рис. 19в).
Эта модель качественно согласуется с результатами наблюдений и
Рис.20. Схема динамо Рикитаки.
предсказывает эффекты типа минимума Маундера. Поскольку она
обладает чувствительностью к начальным данным, a TV’(t) меря-
ется довольно грубо, то можно рассчитывать на прогноз только
нескольких долговременных колебаний солнечной активности.
2. Человечество всегда стремилось заглянуть как в далекое бу-
дущее, так и в далекое прошлое. В некоторых случаях это уда-
ется сделать. Например, измеряя, в каком направлении намагни-
чены образцы пород, появившихся в далеком прошлом, можно
узнать, как были расположены магнитные полюса Земли миллионы
лет назад, как менялось их положение. Эти данные показывают,
что, вероятно, в последние 600 млн. лет расположение магнитных
полюсов менялось хаотическим образом. Объяснить такое поведе-
ние очень важно. Возможно, это поможет понять процессы, проис-
ходящие в ядре Земли.
Для моделирования этого удивительного явления Т. Рикитаки
в 1958 г. предложил оригинальную физическую модель, известную
сейчас как динамо Рикитаки. Она представляет собой два диска
динамо, соединенных так, что ток от каждого диска проходит через
катушку другого (рис. 20). На валы действует одинаковый момент
силы. Диски могут в этой модели рассматриваться как имитация
двух больших вихрей в ядре Земли.
Уравнения, описывающие эту систему, настолько просты, что
их стоит выписать:
Х1 = -flXi + х2х3,
Х2 = —/2X2 +Х1Х4,
Х3 = 1 - XiX2 - V1X3,
Х4 = 1 — Х1Х2 — V2X4,
где Ji и 12 — токи; д — сопротивление проводника; х3 и Х4 —
угловые скорости дисков; Pi и р2 — коэффициенты трения.
Строго говоря, это уравнения для обобщенной модели Рики-
таки, где учитывается трение валов. Есть основания полагать, что
она лучше передает реальную ситуацию. В этой модели при всех
значениях параметров существуют состояния равновесия — устой-
чивые точки. Иногда с ними сосуществуют предельные циклы и в
большой области параметров — странные аттракторы. Это озна-
чает, что при одних начальных данных т1(0),2:2(0))2:з(0)>а:4(0) по-
лярность магнитного поля сохраняется, при других — меняется пе-
риодически или хаотическим образом.
Вид одной из проекций аттрактора при нескольких значениях
параметра р показан на рис. 21. Видно, что картина оказалась до-
статочно запутанной. В ней есть и предельные циклы, и странные
аттракторы. В одних случаях они симметричны, в других — нет.
Каждый из странных аттракторов — сложный объект, деталь-
ный анализ которого при современном уровне математики является
далеко не простой задачей. Если предположить, что один из пара-
метров системы (например р.) очень медленно меняется (гораздо
медленней, чем в ней происходит выход на аттрактор), то вопрос
об эволюции аттрактора при изменении параметра становится за-
дачей прогноза.
Как подойти к этой проблеме? Исходя из предыдущего раздела,
естественным представляется такой путь: нахождение параметров
порядка и построение упрощенных моделей. На этой основе ана-
лиз проводят анализ того, как происходит переход от простейших
аттракторов к более сложным, хаотическим при изменении пара-
метров задачи, и затем выясняют последовательности бифуркаций,
приводящих к усложнению аттрактора.
Анализ механизмов перехода от порядка к хаосу при измене-
нии параметров в различных моделях и в реальных системах сей-
час часто называют изучением сценариев перехода к хаосу. Работы
последних лет позволяют предположить, что в природе обычно реа-
лизуется всего несколько универсальных сценариев. Возможно, от-
крытие и исследование этого удивительного факта войдут в исто-
рию как один из наиболее важных результатов прикладной матема-
тики нашего века. Ведь это огромный шаг к пониманию внутрен-
него единства нелинейных явлений.
В качестве упрощенных моделей в этой ситуации часто возни-
кает поразительно простой на первый взгляд объект — так назы-
ваемые одномерные отображения
Zn+1 = f(xn, А), Х1=х'. (3)
Если f(x, А) = х + А, то эта формула определяет последова-
тельность чисел {хп}, составляющих арифметическую прогрессию.
Рис.21. Эволюция аттрактора в обобщенной модели Рикитаки при измене-
нии параметров (pi = 0.004, Р2 = 0.002).
Если /(х,А) = Ах, то последовательность {хп} — геометрическая
прогрессия. Однако когда f — нелинейная функция, пусть даже са-
мая простая, например, квадратичная парабола f(x, А) = Ах(1 — х),
одномерное отображение, задаваемое формулой (3), является очень
интересным объектом. Большинство задач, связанных с этой мо-
делью, могли быть сформулированы еще во времена Евклида. Од-
нако их анализ потребовал широкого использования вычислитель-
ного эксперимента, разработки совершенно новых математических
инструментов. Он начал активно проводиться только в 70-е годы
нашего века.
Изучение одномерных отображений, у которых f(x, А) = Ai(l —
—я), позволило найти два универсальных сценария перехода от по-
рядка к хаосу в динамических системах. Позже экспериментаторы
обнаружили, что именно они реализуются во многих гидродинами-
ческих, химических и радиоэлектронных системах. Знание таких
сценариев очень полезно с точки зрения прогноза. Принципиальное
значение этих результатов в синергетике и нелинейной динамике
неоднократно обсуждалось.
Менее известен другой любопытный аспект. Анализ одномер-
ных отображений показывает, с какой ситуацией мы можем столк-
нуться в проблеме предсказания в реальных системах. Пусть ото-
бражение (3) генерирует последовательность {in}, принадлежащую
единичному отрезку. При п —> оо ее поведение также определяется
притягивающим множеством или аттрактором.
Для этих аттракторов можно ввести ляпуновский показатель р.
Поскольку отображение одномерное, то и показатель будет один.
Если р < 0, то можно дать прогноз поведения системы. При р > О
мы вновь сталкиваемся с чувствительностью к начальным данным.
Представление об аттракторе одномерного отображения можно
получить, пользуясь следующим несложным приемом. Разобьем
единичный отрезок на М маленьких отрезков длины е(е — У-/М)
и будем смотреть, в какие отрезки попадают первые N элементов
последовательности {in}- Каждому отрезку сопоставим число эле-
ментов, попавших в него. В результате получится ступенчатый гра-
фик, называемый гистограммой, например, такой, как на рис. 22а.
Переходя к пределу М —> oo,N —> оо,е —> оо и отнормировав пло-
щадь под графиком на единицу, получим зависимость величины,
называемой плотностью вероятности р от х.
Какие же функции р(х) будут у аттракторов одномерных ото-
бражений? Самая простая возможность: {in} стремится к периоди-
ческой последовательности {ап}, в которой ап = an+p+i. Это ана-
лог предельного цикла в непрерывной системе. Он описывает пери-
одический режим и называется устойчивым циклом. Зависимость
p(i) при этом представляет собой р одинаковых пиков (рис. 226).
(Можно сказать, что каждый из пиков имеет бесконечную высоту,
нулевую ширину и конечную площадь, равную 1/р). Ляпуновский
показатель отрицателен и возможен глобальный прогноз.
Другой случай реализуется при А = 4. Элементы последователь-
ности {in} заполняют весь отрезок, хотя и с разной плотностью
(рис. 22в). Ляпуновский показатель положителен и долговремен-
ный прогноз невозможен. Это аналог странного аттрактора. С по-
хожими ситуациями мы уже сталкивались, и они уже не кажутся
удивительными.
Рис.22. Пример гистограммы для М = 10, е = 1/10, N — 30 (а) и инвари-
антные меры одномерных отображений (б-г).
Но оказывается при некоторых значениях параметра А будет су-
ществовать иной режим. Типичная зависимость р(т) в этом случае
представлена на рис. 22г. Здесь р(т) / 0 только в пределах несколь-
ких «островов» (в этом случае трех). Все элементы хп с п = Зк,
к = 1,2..., принадлежат первому острову, с п = Зк + 1 — второму,
с п = Зк + 2 — третьему, т.е. порядок обхода островов строго фик-
сирован.
Ляпуновский показатель здесь строго положителен и, казалось
бы, нам не приходится надеяться на глобальный прогноз. Однако
если требуется ответ о состоянии системы с точностью L > I =
= тах{/1,/2,^з} (см. рис. 22г), то из-за неизменного порядка обхода
мы такое предсказание в состоянии сделать. Такие аттракторы сей-
час часто называют шумящими циклами. Если они характерны для
многих реальных систем, то у исследователей появятся новые воз-
можности для предсказаний.
Другая особенность нелинейных систем, которую иллюстриру-
ют одномерные отображения, связана с зависимостью от параме-
тра. В отображении (3) с функцией f(x,X) = Ат(1 — х) область
изменения параметра — отрезок 0 < А < 4. Грубо говоря, можно
выяснить, наблюдается ли при каждом значении параметра хаос
или упорядоченный режим.
Естественной представляется следующая ситуация. Когда при
А = Ао имеет место хаос, то и при близких значениях Ао — <5 <
< А < Ао + 6 также реализуется хаотический режим. В этом случае
можно было бы говорить, что система устойчива относительно из-
менения параметра А. Однако дело обстоит совершенно по-другому.
В любой, сколь угодно малой окрестности точки Ао есть значения
параметра А, отвечающие устойчивым циклам, а, следовательно,
порядку.
Вместе с тем если наугад задать значение А на интервале 0 <
< А < 4, то с положительной вероятностью в системе будет хаоти-
ческий режим. Этот парадоксальный факт был доказан советским
математиком М. Якобсоном, а само явление американский ученый
Дж. Фармер назвал чувствительностью к параметрам.
Поставим следующий мысленный эксперимент. Пусть изучаемая
система точно описывается известным одномерным отображением
и пусть точно задано ее начальное состояние А. Однако если само
значение параметра А известно со сколь угодно малой погреш-
ностью, то предсказание вновь может стать вероятностным. С не-
которой вероятностью в системе будет наблюдаться хаос, с неко-
торой — порядок.
Динамический хаос и реальность
Tia из одной Десятку строй, А двойку скрой, - О ней не вой, Дай тройке ход, Чтоб стала чет, И ты богач. Четверку спрячь, О ней не плачь, А пять и шесть С семеркой свесть, И до восьми Их подыми. Девятка — кон, Десятку — вон. Вот ведьмина таблица умноженья. И. В. Гете
Поставим следующий мысленный эксперимент. Допустим, что
изучаемое явление идеально описывается некоторым дифференци-
альным уравнением, у которого есть странный аттрактор. Как в
этом случае сравнивать результаты теории с экспериментом?
Пусть система обладает чувствительностью к начальным данным,
и две близкие траектории быстро удаляются одна от другой. Тогда
можно ожидать, что различие между вычисленной траекторией и
экспериментальными данными с течением времени также будет ра-
сти. И причиной этого являются не недостатки модели, а природа
изучаемых явлений.
Зачастую при проверке физических теорий сравнивалось не-
большое число измеряемых величин (частоты, длины, времена и
т.д.), либо величины, усредненные по большому интервалу времени.
Однако есть большой класс задач, где интересны не только кон-
кретные численные значения величин в данный момент в данной
точке, не только величины, усредненные по большому временному
интервалу, а сама динамика процесса. Таковы, например, задачи,
связанные с прогнозом поведения нелинейных систем (например, с
предсказанием погоды).
Здесь об эффективности модели нужно судить по тому, насколь-
ко точно и на каких временах она дает прогноз поведения системы,
а не по тому, насколько хорошо с ее помощью определяются средние
значения на больших интервалах.
Итак, открытие странных аттракторов кардинально изменило
саму постановку вопроса о сравнении теории и эксперимента. Как
же сравнивать свойства одного хаотического режима с другим?
Раньше большинство ученых считало, что нужно сравнивать
некоторые величины, которые широко используются в теории ве-
роятностей, — средние значения, дисперсии, плотность вероятно-
сти р(т). Но в последние годы было показано, что даже в простей-
шем случае все не так просто. Было доказано, что у одномерного
отображения rr(n +1) = /(тп) существует бесконечно много различ-
ных функций / (определяющих динамику), которым соответствует
одна и та же плотность вероятности р(т) (статистическая харак-
теристика). Чтобы соответствие стало взаимно однозначным, надо
указать не только число максимумов у функции р(т), но и нетри-
виальную информацию о симметрии f.
Другой ответ, который предпочитают сейчас, таков: нужно
сравнивать характеристики аттрактора в модели (такие, как ем-
кость, ляпуновские показатели и т.д.) и аттрактора, который опи-
сывает экспериментальные данные. Последнее понятие далеко не
очевидно, и ниже мы его обсудим.
Вернемся к нашему мысленному эксперименту. Поговорим
о том, что и как надо измерять, чтобы исследовать хаотические
режимы в нелинейных средах, и какие характеристики по ним вы-
числять.
Будем считать, что у нас есть прибор, измеряющий одну из ха-
рактеристик изучаемой системы в разные моменты времени с ин-
тервалом At. Результаты измерений дают ограниченную последо-
вательность {dt},0 < i < оо. Возникает вопрос: можно ли по этой
последовательности выяснить, имеем мы дело со сложным детерми-
нированным процессом, который описывается дифференциальным
уравнением dx./dt = f в n-мерном фазовом пространстве, или со
случайной функцией? Ответ был дан в 1980 г. Ф. Такенсом. Этот
математик является в настоящее время одним из самых извест-
ных специалистов по хаотической динамике. Именно он вместе с
Д. Рюэллем ввел в 1971 г. термин «странный аттрактор*.
Будем говорить, что результаты измерений могут быть опи-
саны с помощью гладкой детерминированной модели, если суще-
ствуют дифференциальное уравнение с гладкой функцией f(x) и
гладкая функция д, такие, что
1) для каждой наблюдаемой последовательности {а<} экспери-
ментальных данных существует точка х0 такая, что at =
= р[х(гД£)], где x(i) — решение дифференциального уравне-
ния с начальным условием х(0) = Хо;
2) для каждой начальной точки хо решение x(t),x(0) = хо при
t > 0 ограничено.
Бели для некоторой последовательности {а<} удается построить
функции f и д, а также x(t), будем говорить, что результаты дан-
ного эксперимента могут быть объяснены с помощью гладкой де-
терминированной модели.
Чтобы сформулировать критерий Такенса, введем несколько
определений. Пусть {а<} — ограниченная последовательность дей-
ствительных чисел (экспериментальные данные). Для каждого
е > 0 и целого положительного п определим множество целых по-
ложительных чисел Сп>е следующим образом: 0 6 Сп<£ при i > Oi 6
6 Сп,£ в том и только в том случае, если для всех j <i,j 6 СП)Е
тах{|а* aj |, Oj+i |, • • •, |o»4-n aj+n|} —
Обозначим через СП1Е({а,}) число элементов в Спл. Так как по-
следовательность {а,} ограничена, Сп,е конечно.
В работе Такенса были сформулированы следующие утвержде-
ния.
Результаты эксперимента, определяющие последовательность
{а<}, могут быть объяснены с помощью гладкой детерминирован-
ной модели, если величина In Сп,£({а*})/(п — 1ns) равномерно огра-
ничена при п — 1ns —> оо. Если же эта последовательность не огра-
ничена, то последовательность измерений не может быть описана с
помощью гладкой детерминированной модели.
В принципе последняя формула позволяет выяснить, имеем ли
мы дело с хаосом в детерминированной системе или изучаемый про-
цесс является чисто случайным, и ответить на вопрос, есть ли в
наблюдаемом хаосе порядок.
Теорема Такенса, область ее применимости, ряд важных дета-
лей, связанных с ней, требуют отдельного обсуждения. Но даже
в идеальном случае, когда есть бесконечно длинная последователь-
ность точно измеренных значений, между теорией и экспериментом
лежит пропасть. В теореме Такенса фигурирует предел при е -> О
и величина С(п>е). Естественно ожидать, что компьютеру, если он
будет непосредственно вычислять предел, потребуется бесконечное
время.
Через эту пропасть в 80-х годах удалось перекинуть мостик, ко-
торый условно можно назвать вычислительными алгоритмами ана-
лиза экспериментальных данных для систем с хаотическим поведе-
нием. От того, насколько прочен и надежен этот мостик, во многом
зависит, имеет ли ряд изящных результатов хаотической динамики
отношение к реальности.
По страницам книг и брошюр кочует фраза одного из созда-
телей квантовой механики о роли «безумных идей» в познании. Со
времени, когда говорилась эта фраза, прошло более 50 лет, и ситу-
ация существенно изменилась. Развитие формализма, возможность
использовать компьютеры, создание новых экспериментальных ме-
тодов становятся все важнее. Именно они часто и приводят к более
глубокому пониманию Природы.
Роль «кухни» исследователей быстро возрастает. Достаточно
просмотреть список работ, удостоенных Нобелевской премии, что-
бы убедиться — оценку все чаще получает не блестящая идея, а
виртуозное исполнение. По-видимому, представления синергетики
и хаотической динамики не нашли такого воплощения, после кото-
рого многое, являющееся предметом научных исследований, стано-
вится рутинной операцией.
Вернемся к «мостику», обратим внимание на несколько основных
идей и алгоритмов, а потом обсудим проблемы и трудности.
Выше была введена емкость множества de. Однако естественно
ожидать, что одного этого числа недостаточно, чтобы полно оха-
рактеризовать «клубок траекторий», и что оценить его по данным
эксперимента будет непросто. Поэтому сейчас для характеристики
странных аттракторов вводится бесконечное число фрактальных
размерностей.
Точки, характеризующие странный аттрактор, вообще говоря,
с разной вероятностью «посещают» разные области фазового про-
странства. Чтобы учесть этот факт, будем покрывать изучаемое
множество в р-мерном пространстве кубиками с ребром е. Кубику
с номером i сопоставим вероятность, с которой точки множества в
рего попадают, Pi. Далее можно ввести набор величин D4, называ-
емых обобщенными размерностями, по формуле
Dq = 1/(9- l)lim[(log£p?)/(loge)],
Рис.23. Набор обобщенных размер-
ностей для аттрактора Фейгенбаума.
В отображении zn+i = Azn(l — Xn)
при А —> Лоо = 3.5699456 происходит
переход от циклов к непериодиче-
ским траекториям. Аттрактор при
Л = Лоо называется аттрактором
Фейгенбаума.
где суммирование ведется по всем кубикам покрытия. Величины
D4 обычно определены при любых действительных q, и можно по-
казать, что Dq > Dq>, если q' > q. Такой набор обобщенных раз-
мерностей позволяет охарактеризовать изучаемое множество более
полно, чем каждая размерность в отдельности. Обобщенные раз-
мерности были введены в 1985 г. для некоторого класса «хороших»
множеств. При определенных значениях q они совпадают с размер-
ностями, известными ранее. Например, при q = 0 — это емкость,
поскольку тогда сумма в числителе совпадает с числом кубиков, по-
крывающих изучаемое множество. Di называют информационной
размерностью, D2 — корреляционным показателем (его обычно
обозначают буквой р).
Для нескольких аттракторов можно выяснить весь набор Dq,
—00 < q < 00, или, как говорят, рассчитать а-спектр, и убедиться,
что отличие dcv от других размерностей и величин, которые нужно
вычислять в теореме Такенса, невелико (рис. 23). Поэтому можно
оценить одну из величин Dq, наиболее доступную для расчета на
ЭВМ.
Сейчас такой величиной является корреляционный показатель.
Он был введен в 1983 г. П. Грассбергером и И. Прокаччо. Ими был
предложен способ его оценки.
Возьмем наугад N точек изучаемого множества в р-мерном про-
странстве и вычислим расстояния между всеми N точками р(х<, Xj),
а затем функцию (7(e) = N~2 (число расстояний р < е).
Корреляционный показатель определяется числом
и = 1пп[1п/(е)/1пе].
Чтобы определить фрактальную размерность аттрактора,
обычно пользуются следующим рецептом.
При получении экспериментальных данных для анализа процес-
сов в нелинейной среде будем измерять некоторую зависящую от
времени характеристику процесса а< в одной точке (если а, — век-
тор, то будем брать любую из его компонент) через фиксирован-
ные интервалы времени At. По этим данным построим набор т-
мерных векторов & = (ak,a,k+i, ,а,к+т-1) (например, (i = (ai,
Эти векторы называются (-векторами, а простран-
ство, в котором они лежат, — (-пространством. Затем определяем
фрактальную размерность (обычно корреляционный показатель)
множества (-векторов. (Слова «фрактальная размерность* взяты в
кавычки потому, что размерность — предел при е —> 0 любого мно-
жества, состоящего из конечного числа точек, — равна 0. На прак-
тике определяется не предел, а наклон графика зависимости In С(е)
от In е в некотором интервале изменения е. Эту процедуру проделы-
ваем для т = 1,2. .-. Если размерность аттрактора конечна и равна
р, можно ожидать, что при достаточно больших т > то (обычно
при т > 2р + 1) полученные значения уже не будут зависеть от т.
Это означает, что существует набор то параметров порядка,
к которым «подстраиваются» все остальные степени свободы си-
стемы.-Такое поведение характерно для многих математических
моделей, изучаемых синергетикой, в том числе для нелинейных си-
стем с бесконечным числом степеней свободы, которые описыва-
ются уравнениями в частных производных.
Построение (-векторов и определение р получили название ре-
конструкции аттрактора. Обычно она применяется и в некоторых
ситуациях, выходах за рамки тех, для которых была обоснована.
Это приводит к ряду интересных математических задач.
Подчеркнем парадоксальность этого рецепта. Чтобы исследо-
вать количество параметров порядка у сложной многомерной си-
стемы, достаточно измерять одну величину в дискретные моменты
времени.
Размерность странного аттрактора дает представление о его
геометрии и числе параметров порядка, но не позволяет оценить,
насколько быстро расходятся близкие траектории. Для такой оцен-
ки нужно уметь по экспериментальным данным вычислять ляпу-
новские показатели.
Самым простым и полезным алгоритмом в этой области оста-
ется алгоритм, предложенный в 1985 г. Условно его можно назвать
методом аналога. Его суть ясна из рис. 24а (этот рисунок можно
сравнить с рис. 3 и 4). Выбирается вектор (,• (это может быть (-
вектор в некоторый момент времени) и ищется его сосед ('•, распо-
ложенный достаточно близко к на расстоянии £(to). Если раз-
ность j—jo достаточно велика, то можно считать, что мы имеем две
различные близкие траектории. Поскольку в системе есть положи-
тельный показатель, расстояние между образами ('• и (? растет и в
Рис.24. Определение ллпуновского показателя с помощью метода аналога.
момент времени ti становится равным когда его уже нельзя
считать малым, а траектории близкими. В этот момент ищется дру-
гой близкий вектор , такой, чтобы ориентация векторов С"—Cj(<i)
и Cj(ti) — Cj(ii) была близка. Если таких векторов нет, выбирается
любой близкий сосед. Далее траектории прослеживаются, пока рас-
стояние между ними не станет равным £'(£г), потом ищется новый
вектор на расстоянии L(t2) и т.д.
При таком подходе максимальный ляпуновский показатель опре-
деляется по формуле
А1 = 7----Г > > log2 777—V
tM - to
Чтобы вычислить сумму двух наибольших показателей, нужно
рассматривать пары близких траекторий и изменение площадей со-
ответствующих треугольников (рис. 246):
х , х _ 1 A'(th)
Al + Аг - ----— У , log2 -ту--г.
tM ~ to A(ifc-i)
Когда ищутся новые соседние векторы, также надо следить,
чтобы ориентация треугольников была близка.
L
Рис.25. Течение между вращающимися ци-
линдрами — излюбленный объект анализа
в синергетике и гидродинамике.
Обычно, пользуясь методом аналога, больше двух ляпуновских
показателей не вычисляют.
Полезность обсуждавшихся вытпе алгоритмов наглядно иллю-
стрирует следующий пример из гидродинамики.
Одной из систем, в которой наблюдается переход от упорядочен-
ного ламинарного режима к хаотическому турбулентному, является
течение Куэтта-Тейлора. Это течение между двумя цилиндрами вы-
соты L, радиусы которых равны а и b (рис. 25). Внешний цилиндр
вращается с угловой скоростью Q, внутренний неподвижен. Дви-
жение жидкости в этой задаче определяется безразмерным параме-
тром — числом Рейнольдса Re = Па(Ь—а)р-1 (м — кинематическая
вязкость).
При небольших числах Рейнольдса движение жидкости лами-
нарно, его можно описать явной формулой. Далее при увеличении
частоты П возникают диссипативные структуры — так называе-
мые вихри Тейлора. При увеличении частоты вращения вихри Тей-
лора теряют устойчивость, движение жидкости становится пери-
одическим (аналог предельного цикла). При еще больших числах
Рейнольдса возникает двухчастотный режим (аналог инвариант-
ного тора) и далее при Re = Rec движение становится турбулент-
ным.
Для анализа этого течения была предложена эффективная экспе-
риментальная техника, связанная с лазерной доплеровской спектро-
скопией. Измеряя доплеровский сдвиг лазерного луча, проходящего
через жидкость, можно определить одну из компонент скорости в
данной точке. Последовательные измерения этой компоненты дают
массив а.1,.. .,ац.
По этим данным вычислялся корреляционный показатель и поло-
жительные ляпуновские показатели при Rec < Re < 1.3Rec.
tg£fc)
Рис.26. Оценка фрактальной раз-
мерности по данным натурного
эксперимента для течения Куэтта-
Тейлора [24] (Re/Rec = 12.4, где
Rec — значение числа Рейнольдса,
при котором теряет устойчивость
простейшее течение). Анализирова-
лась выборка из 16384 элементов.
Аттрактор вложен в 6-мерное прост-
ранство. На нижнем рисунке показана
зависимость s(lge).
Типичная зависимость логарифма величины С(е), называемой кор-
реляционным интегралом, от In е в этой задаче и тангенса наклона
касательной к этой кривой s = dlgC(s)/dlg£ приведена на рис. 26.
На кривой s = s(ln е) можно выделить четыре области, они типичны
для гидродинамических задач и ряда других.
Область А. В этом интервале масштабов размеры ячеек слиш-
ком малы. В каждую ячейку (кубик с ребром Е) попадает всего
несколько точек, что не позволяет оценить вероятности Р,, кото-
рые фигурируют в определении размерности.
Область В. В этой области выборка недостаточна, чтобы пере-
дать канторову структуру аттрактора. Кроме того, в ней обычно
существенна погрешность эксперимента или точность, с которой
известны точки аттрактора.
Область С. Точки кривой в этом интервале характеризуют кор-
реляционный показатель и. Чтобы расширить область С, можно
увеличить размер выборки, повысить точность эксперимента, наи-
лучшим образом выбирать переменные, которые будут анализиро-
ваться, или применять специальные методы обработки эксперимен-
тальных данных.
Область D. Размеры ячеек разбиения стремятся к размерам ат-
трактора, и кривая In С = InC(lnE) не характеризует его фрак-
тальную структуру.
При исследовании странных аттракторов более высокой размер-
ности картина оказывается близкой, однако с увеличением размер-
ности уменьшается длина участка С.
Проведенный анализ показал, что в изучаемом интервале чисел
Рейнольдса значение и не превышает 5.4. Это убедительно пока-
зало, что в такой бесконечномерной системе существует маломодо-
вый хаос. Предположение о наличии странного аттрактора неболь-
шой размерности, описывающего это течение, оказывается справед-
ливым. В этой задаче также удается установить положительность
старшего ляпуновского показателя.
Представители гуманитарных дисциплин, искусствоведы часто
пишут о смене стилей (в архитектуре, живописи, литературе, оде-
жде). Однако для современников смена стилей часто воспринима-
ется как мода. Наверно можно, употребляя математический образ,
сравнить стиль с медленно меняющейся переменной, а моду с нало-
женными на нее колебаниями довольно большой амплитуды.
По-видимому, важную роль играет мода и в точных науках.
В этом легко убедиться, пролистав подшивки научных журналов и
выделив «голодные» слова, темы, характерные картинки. Лет 20 на-
зад редакции охотно принимали статьи, в которых было слово «со-
литон». Десять лет назад для публикации статьи о динамическом
хаосе вполне достаточно было приложить картинку с «клубком тра-
екторий». Сейчас и у нас, и за рубежом охотно печатают работы,
где вычисляются корреляционные показатели и показатели Ляпу-
нова. Нет, это пишется не в осуждение. Позицию редакций можно
понять — среди «информационного шума* вполне могут быть важ-
ные й глубокие работы в перспективном, как сегодня кажется, на-
правлении. Блестящее произведение, претендующее на место в Веч-
ности, может скрываться под маской мимолетной моды.
Описанные выше алгоритмы позволяют обработать любую вы-
борку и получить некоторый набор чисел. Количество задач, где
они применялись, огромно и продолжает быстро расти. Вот не-
сколько недавних примеров. Вычисление корреляционного показа-
теля для выборки, характеризующей интенсивность излучения из
окрестности нейтронной звезды. Ляпуновский показатель для по-
следовательности криков новорожденных. Корреляционный покат
затель для некоторых типов солнечной активности. Ляпуновский
показатель для выборки, определяющей расположение простых чи-
сел в натуральном ряду. Анализ неравномерности вращения Земли.
Корреляционный показатель для среднесуточных изменений тем-
пературы и для глобальных вариаций климата. Корреляционные
показатели для выборок, описывающих деловую активность, кар-
диограммы и энцефалограммы. И так далее...
По одним названиям, да часто и по самим работам, непросто
судить, где знание и и А может привести к глубоким и интересным
результатам, а где является данью моде. Это тем более непросто,
поскольку для большинства таких работ результатом является не-
сколько чисел. Видимо, сейчас в этой области самое важное не по-
лучить число, а понять, что же оно означает и как его использовать
дальше.
Отношение к работам, где этого нет, один из создателей хаоти-
ческой динамики Д. Рюэлль в красноречиво названной статье «Де-
терминированный хаос: наука и фантазия» выразил в следующих
словах: «Читатели «Путеводителя для путешественников по галак-
тике», этого шедевра английской литературы, написанной Д. Адам-
сом, знают, что громадный суперкомпьютер решил «великую про-
блему» жизни, Вселенной и всего. Ответ, полученный после многих
лет вычислений, был 42. К сожалению, никто не знал точно, на какой
же вопрос это был ответ и что с ним делать. Я думаю, что произо-
шло следующее. Суперкомпьютер взял очень длинный ряд, содержа-
щий все, что он знал о «жизни Вселенной и обо всем», и начал вы-
числять корреляционный показатель аттрактора соответствующей
динамической системы, используя алгоритм Грассбергера-
Прокаччо. Этот ряд имел длину, несколько большую чем 1021. И вы
можете представить себе, что произошло. После многих лет вычи-
слений пришел ответ: размерность приблизительно равна 2 lg10 N «
«42».
Динамический хаос. Двери в сказку
Хороши ваши стихи,
скажите сами?
Чудовищны! — вдруг смело и
откровенно произнес Иван.
М. Булгаков
Далее много будет сказано о несовершенстве существующих под-
ходов и непростых задачах, вставших при анализе проблемы про-
гноза в синергетике. Поэтому вначале поговорим, как дело может
обстоять в идеальном случае.
Пусть изучаемый процесс описывается одномерным отображе-
нием:
Zn+i =д(хп), п = 1,2,...
Для простоты будем считать, что д(х) = 1 — 2|х|. Пусть из-
вестны значения xi,...,xm, где длина выборки М = 104. В этом
отображении взятое наугад число xi в интервале — 1 < xi <1 дает
непериодическую последовательность, поэтому будем полагать, что
xi,..., хм часть такой последовательности. Теперь изменим точку
зрения. Рассмотрим обратную задачу. Допустим, что числа ii,...
...,хм получены в результате эксперимента, и спросим себя, мо-
жем ли мы по этим данным восстановить динамическую систему
(р-мерное отображение)?
Применяя обсуждавшиеся алгоритмы, можно убедиться, что
фрактальная размерность аттрактора (у или dc) близка к единице, а
единственный положительный ляпуновский показатель равен Ai =
In 2. При такой длине выборки можно достаточно точно оценить
обе величины.
Это позволяет предположить, что в некотором отображении
Хп+1 = f(xn), хп =
п = 1,2,...,
определяющем динамику системы, р = 1, т.е. существует единствен-
ный параметр порядка, и моделью изучаемого процесса может быть
одномерное отображение.
Проблему прогноза для этой системы можно поставить следую-
щим образом. По результатам предыдущих наблюдений ii,...,хм
предсказать значения ijw+i, ^м+2> и т.д.
При ее решении можно действовать так. Исходя из имеющейся
выборки, построим зависимость xn+i = xn+i(xn), т. е. зависимость
п + 1-го элемента последовательности от n-го на плоскости
{in,xn+i} (рис. 27а). Это будет ни чем иным, как функцией /.
Разумеется, на этой плоскости будет конечное число точек, а для
прогноза потребуется функция при каждом значении х, — 1 < х < 1.
Поскольку М достаточно велико, можно воспользоваться стан-
дартным алгоритмом интерполяции, известным еще со времен Нью-
тона и работающим быстро и достаточно точно. В результате при-
менения этого алгоритма получится функция /, позволяющая да-
вать прогноз и поэтому называемая предиктором (от англ, to pre-
dict — предсказывать).
Способ получения прогноза таков. Пусть мы знаем хм с точ-
ностью <5. Это будет «измеренное значение» хм = хм + <5- Тогда
предсказываемое значение гм+i (см. рис. 27) будет хм+i = y(xjn)i
ZM+2 - хм+2 = И Т.д. (см. рис. 276).
В силу чувствительности к начальным данным погрешность
прогноза на каждом шаге возрастает, в нашем случае, по крайней
Рис.27. Принципиальная схема построения предиктора f по наблюдаемым
данным.
мере, в 2 раза, так как Ai = In 2. На самом деле она возрастает еще
больше, так как вместо функции д мы знаем только приближен-
ную зависимость /. Следовательно, можем предсказать в лучшем
случае на к шагов к < 1 + log2 6. (В самом деле, предположив, что
через к шагов погрешность 5eXlk будет сравнима с характерными
размерами аттрактора S, получим <5eAlfc = S, к = (In S — In <5)/Ai).
В нашем случае S = 2, Aj = In 2, к = 1 - log2 5.
Действуя аналогичным образом, можно построить предикторы
и в случае, когда х является вектором. Дж. Фармер сделал это
для нескольких дифференциальных уравнений и эксперименталь-
ных данных, описывающих одну из компонент скорости при турбу-
лентном течении жидкости.
В теореме Такенса фигурирует бесконечно длинная выборка
идеально точных данных, измеренных с интервалом At. Допустим,
мы можем распорядиться временем дискретизации At. Как это сде-
лать наилучшим образом? Естественно требовать, чтобы по вы-
борке данной длины N можно было наиболее точно оценить харак-
теристики аттрактора.
Есть несколько хорошо зарекомендовавших себя рецептов. Один
из них особенно прост. Если At очень мало, то проекция аттрак-
тора на какую-нибудь плоскость в ^-пространстве будет близка к
диагонали (рис. 28а). Если величина At велика, то аттрактор мо-
жет стать слишком сложным. В оптимальном варианте аттрактор
должен быть и достаточно простым, и наиболее удобно разверну-
тым (рис. 286). Чтобы получить наибольшую информацию, последо-
вательные ^-векторы должны быть «наиболее независимы». Этого,
например, можно добиться, рассмотрев автокорреляционную функ-
Рис.28. Типичная картина, когда At
слишком мало (а), и реконструкция
аттрактора по экспериментальным
данным для колебательной химичес-
кой реакции Белоусова-Жаботинского
(б). Обрабатывалась выборка из
32762 элементов. Нижняя кривая
соответствует автокорреляционной
функции Ь(т), верхняя — функции
взаимной информации. Вверху пока-
зан реконструированный аттрактор,
в котором At соответствует первому
нулю Ь(т); внизу — первому минимуму
7(т). Нижний аттрактор «развернут»
удачнее.
Т
цию Ь(т) = f x(t)x(t + r)dt и взяв At, соответствующее первому
о
нулю (см. рис. 286, левый аттрактор).
Можно ввести более сложную функцию, называемую взаимной
информацией 1(т), и с ее помощью выбрать At (см. рис. 286, пра-
вый аттрактор). Если нужно измерить ляпуновские показатели, то
At можно выбрать и иначе. Одним словом, значением At можно
распорядиться разумно.
Сложнее обстоит дело с длиной выборки N. В работе П. Грасс-
бергера и И. Прокаччо, в которой и предлагалось рассчитывать
корреляционный интеграл, были приведены примеры тестовых рас-
четов для одномерных и двумерных отображений, систем диффе-
ренциальных уравнений и уравнений с запаздыванием. Последний
класс математических моделей сейчас широко используется в эко-
логии, нелинейной оптике, теории иммунитета. Они имеют вид
u(t) = /((u/t - г)) - ff(u(t)).
Это уравнение потенциально обладает бесконечным числом сте-
пеней свободы — чтобы задать его решение, нужно знать функцию
на целом интервале от 0 до т. При большом времени запаздывания
т такие уравнения могут описывать хаотические режимы. С уве-
личением т фрактальная размерность аттрактора обычно линейно
растет.
В упоминавшейся работе по сравнительно небольшим выбор-
кам, включавшим от 10 до 30 тыс. элементов, довольно точно уда-
валось определить значение корреляционного показателя. Это вы-
звало большой оптимизм. В самом деле, есть масса интересных заг
дач, в которых выдвигалась гипотеза о существовании детермини-
рованного хаоса: задача о солнечном и земном динамо, проблема
климатического и погодного аттрактора. В каждом из этих слу-
чаев выборка не очень большая, например, при анализе изменений
климата за последние тысячи лет длина выборки не превышает
500-700 элементов, в задаче о геодинамическом аттракторе (нерав-
номерность скорости вращения Земли за последние века) известно
700 элементов, в задаче о погодном аттракторе доступно не более
60 тыс. ежесуточных измерений температуры. Достаточно ли этого
для обоснованных заключений о природе этих явлений? Дискуссия
по этому поводу активно ведется на страницах научных журналов
«Nature», «Journal of the Atmospheric Sciences» и других изданий.
Например, один из наиболее очевидных доводов. Пусть аттрак-
тор имеет размерность v и может быть вложен в р-мерное про-
странство. Чтобы охарактеризовать его геометрию и оценить ве-
роятности Pi, фигурирующие в формуле для обобщенных размер-
ностей Dq, нужно, чтобы в каждый р-мерный кубик, где есть точки
аттрактора, попало хотя бы п точек. При реконструкции аттрак-
тора каждая из компонент ^-вектора будет принимать все значения
от £тах до £min. Пусть £max - £min - L. В р-мерном кубе с ребром
L содержится (Ь/е)р кубиков с ребром е, а значит, длина выборки
должна быть N = п{Ь/е)р, т.е.р ~ ln.1V. Максимальная размерность
аттрактора, которая может быть оценена, исходя из выборки в N
элементов, зависит от N по логарифмическому закону. Обычно с
этим легко соглашаются.
Но каков коэффициент, определяющий эту зависимость? В од-
ной из работ, получивших известность, утверждается, что для
оценки хаусдорфовой размерности djj с погрешностью в несколько
процентов нужно иметь выборку длины, превышающей 42“, где
а — целая часть du, либо целая часть плюс единица. То есть для
анализа аттрактора с фрактальной размерностью 3 нужно иметь
100 тыс. элементов, а с размерностью 6 — более 10 млрд. Но если
это так, то почему же в некоторых случаях хорошие результаты по-
лучаются в результате обработки гораздо меньших выборок? Про-
стого и ясного ответа на этот вопрос пока нет.
Другая проблема — малый шум и ограниченная точность дан-
ных. В определения фрактальных размерностей входят пределы при
е 0 или при N —> оо. Разумеется, их непосредственная оценка
при анализе конкретных данных недоступна. Типичная картина
будет следующей. При исследовании странного аттрактора в иде-
альном случае, неограниченно уменьшая масштаб, мы бы видели
одну и ту же, повторяющую себя структуру. Однако при нали-
чии шума мы можем увидеть всего лишь несколько уровней та-
кой структуры. Если же шум слишком велик или точность изме-
рений слишком мала, то реконструированный странный аттрактор
вообще может утратить необычные геометрические свойства. По-
этому приходится оценивать в каждой конкретной системе уровень
шума и продумывать процедуру оценки размерности по конечной
выборке.
Любимыми способами обработки данных для многих экспери-
ментаторов являются сглаживание данных и численное дифферен-
цирование. С точки зрения теории динамических систем обе про-
цедуры являются достаточно опасными. В зависимости от параме-
тров используемых алгоритмов они могут как уменьшить, так и
увеличить размерность реконструированного аттрактора.
Как правило, в каждом конкретном случае эти проблемы воз-
никают в собственном обличье, они требуют детального анализа
всей вычислительной «кухни» и изучения многих методических во-
просов. В ходе исследования с коллегами результатов наблюдений
в проблеме геодинамического аттрактора, метеорологических дан-
ных и вычислительного эксперимента по моделированию трехмер-
ных турбулентных течений жидкости мне пришлось убедиться, что
в каждом из этих случаев даже сама постановка задачи об оценке
количественных характеристик аттрактора должна быть разной.
Без тщательного изучения особенностей каждой конкретной си-
стемы в этой области нас ждут много замечательных «открытий»
и следующих за ними «закрытий». В качестве примера можно при-
вести дискуссию о погодном аттракторе. Постановка задачи та-
кова: нужно выяснить, описывается ли изменение средней дневной
температуры некоторой динамической системой со странным ат-
трактором. Ход этой дискуссии очень интересен. Вначале стали по-
являться статьи, в которых на основе анализа выборок в несколько
тысяч элементов утверждалось, что для реконструированного ат-
трактора 1/ ss 3 4- 4. Позже следовали возражения, и на основе близ-
кой выборки делался вывод, что и = 6 4- 8. И наконец, стали по-
являться работы, в которых корреляционный показатель погодного
аттрактора оценивался как и = 10 4-11. Похожим образом развива-
лись события и в связи с проблемой климатического аттрактора.
Разумеется, чтобы утверждать, что по этим данным нельзя по-
лучить тех или иных значений или указать на методические неточ-
ности, нужно иметь те же самые выборки (обычно данные Берлин-
ской обсерватории). Мне и сотруднику ИПМ им. В. Келдыша АН
СССР А. Б. Потапову они были недоступны. Однако мы проана-
лизировали с этой точки зрения данные Пражской обсерватории
Клементина (длина выборки N « 6 • 104). Если не принимать во
внимание каких-либо ограничений и никак предварительно не обра-
батывать выборку, то действительно значение и будет близко к 10,
хотя и с невысокой точностью. Кривая S(e) = din C/dlne имеет не-
большой плоский участок, по которому и определяется значение и.
А теперь поступим иначе. Вычисляя корреляционный интеграл,
посмотрим, каковы соседи взятой наугад точки х^ (рис. 29). Что
дает наибольший вклад в С(е)? Ответ прост — наибольший вклад
дают соседи по траектории. Понятно, что к структуре аттрактора
они не имеют никакого отношения. Если At очень мало, а соседей
по траектории очень много по сравнению с остальными точками, то
аттрактор воспринимается как одномерная кривая (у = 1). Чтобы
исследовать структуру аттрактора, обычно при анализе окрестно-
сти данной точки соседей по траектории убирают (рис. 296). Эта
процедура довольно широко известна специалистам. Если ее прове-
сти, то плоский участок у кривой S(e) исчезает. Становится ясно,
что конечное значение и для этой выборки было связано лишь с
несовершенством методики.
Конечно, проанализировав гораздо большую выборку (пока та-
кой в гидрометцентрах мира нет), исследователи, возможно, полу-
чили бы достоверное значение и. Взяв выборку еще большей длины,
возможно, удалось бы оценить ляпуновские показатели и построить
предикторы. А может быть и нет. Сегодня мы этого не знаем.
Проблемы погодного и климатического аттрактора, а также
других задач такого типа обладают еще одной принципиальной чер-
Рис.29. К вычислению корреляционного показателя погодного и климати-
ческого аттрактора, а — точки, попавшие в шар радиуса е; б — удалены
соседи по траектории точки х.
той. В этих случаях мы имеем дело с многочастотными колебани-
ями со сплошным гладким спектром, в котором не удается выделить
несколько «наиболее важных» частот (разумеется, кроме годичного
хода). Грубо говоря, мы не можем сказать, где кончается погода и
начинается климат. Это обстоятельство намного усложняет анализ
данных.
После сказанного в этом разделе создается впечатление, что про-
блема прогноза погоды и предсказания динамики других открытых
нелинейных систем являются клубком неразрешимых загадок.
Возможно, некоторые читатели подумают, что исследования в
обсуждаемой области зашли в тупик, а специалистам, занимаю-
щимся этими вопросами, лучше сменить работу. Такой взгляд сей-
час порой высказывается и на научных конференциях.
Если перспективы использования идей синергетики в проблеме
прогноза не кажутся собеседнику заманчивыми, если конкретные
задачи, решенные до сих пор, не убеждают в перспективах этого
подхода, то остается одно. Рассказать о надеждах и мечтах. Ведь
будущее в науке, да и не только в ней, определяется как прошлым
и настоящим, так и нашими представлениями о будущем.
Об этом проще всего сказать, сформулировав несколько точек
зрения, иногда взаимоисключающих, на причины сегодняшних
трудностей и ближайшие перспективы, намеренно упрощая, а ино-
гда и утрируя их.
1. Задача предсказания температуры в одной точке бесперспек-
тивна. Предсказывать надо не среднесуточную температуру,
а некие функционалы, которые и надо найти, например, усред-
ненное давление или температуру в каком-либо регионе или
другие функционалы, связанные с усреднением не только по
пространству, но и по времени. Может быть, вообще следует
рассчитывать на прогнозы вроде: «... если январь снежный, а
февраль холодный, то июль сухой», разумеется, с количествен-
ными определениями понятий «сухой», «снежный», «холодный»,
оценкой погрешности и всеми необходимыми атрибутами.
2. Ляпуновский показатель характеризует некоторую усреднен-
ную скорость разбегания близких траекторий по большому
временному интервалу. Однако он ничего не говорит о пове-
дении отдельных траекторий в отдельных областях фазового
пространства. Почему бы время от времени не сталкиваться с
ситуацией, показанной на рис. 30. В области Gi близкие тра-
ектории долго и медленно сходятся, в области Gj — быстро
расходятся.
Тогда мы имеем все возможности для прогноза, если наша си-
стема попала в область Gi, до того момента как она покинет
ее. Предсказания тогда могли бы выглядеть так. Если над
районом А давление лежит в интервале Д, температура 1г,
влажность 13, в районе В - ... и т.д., то в течение времени си-
туация будет развиваться так... Некоторые явления в физике
атмосферы хорошо согласуются с этим взглядом.
3. Изящная возможность, связанная с наличием шумящих цик-
лов, уже обсуждалась ранее.
4. Нужны новые методики учета априорной информации. В са-
мом деле, расчет «в лоб» фрактальной размерности и ляпунов-
ского показателя часто не дает желаемого результата. Вместе
с тем удаление тренда, сглаживание или, напротив, усиление
различных участков спектра существенно меняют структуру
реконструированного аттрактора.
Возможно, этот модифицированный аттрактор и несет наибо-
лее важную информацию о системе. Близкая программа, связанная
с выделением медленных переменных, в свое время была очень по-
пулярна в метеорологии. Большие усилия были вложены в проверку
гипотезы, в соответствии с которой состояние атмосферы и океана
в небольшом числе ключевых точек достаточно полно характери-
зует состояние атмосферы Земли и позволяет дать прогноз. Обе
программы не принесли желаемых результатов. Но это не значит,
что кто-то другой не добьется на этом пути успеха.
Не исключено, что каждая из этих возможностей не имеет отно-
шения к прогнозу в данной конкретной системе. Возможно, в этом
случае ключ будет связан с одним из двух других подходов, кото-
рые сейчас интенсивно развиваются в рамках синергетики.
Рис.30. Поведение близких траекто-
рий в отдельных участках фазового
пространства.
Первый подход возник в теории алгоритмов. Пусть мы распо-
лагаем гигантским компьютером (цифровой вычислительной ма-
шиной) с огромными памятью и быстродействием. Нетрудно пове-
рить, что с его помощью можно смоделировать процессы в боль-
шинстве нелинейных диссипативных систем нашего мира, поведе-
ние которых мы желаем предсказывать. Во всяком случае, это пред-
положение готово принять большинство специалистов в области
естественных наук.
Но что такое компьютер? Это машина, которая меняет содержа-
ние ячеек в моменты времени Д<, 2Д£ в соответствии с определен-
ными правилами. Каждая из ячеек может быть в конечном числе
состояний р. Правила, по которым меняется состояние ячеек, со-
держатся в них самих.
Обычно, чтобы выполнить ту или иную операцию, существует
несколько алгоритмов. Пусть, например, в компьютере запрограм-
мирован алгоритм сложения целых чисел, записанных в двоичном
коде (т.е. в виде множества 00,01,03,..., где число х = oq + 2ai +
+22аз + ...; а» могут быть равны нулю или единице).
Допустим, нам нужно умножить число х на 2*. Самый простой и
долгий способ для этого состоит в том, чтобы число х раз сложить
с самим собой 2*. Но можно сделать это быстрее. Нужно только
последовательность ...030100 сдвинуть на к элементов влево. Чи-
слу 2кх соответствует последовательность ... Oia00... 0. Вместо 2к
операций понадобилась одна.
Все алгоритмы, для которых существует более короткий обход-
ной путь, будем называть приводимыми, для которых не сущест-
вует — неприводимыми.
Можно сказать и иначе — приводимость алгоритма и возмож-
ность получить прогноз тесно связаны. Если исходный алгоритм
определяет, что произойдет с состоянием системы через Ni шагов,
а второй переводит ее в это состояние через .Уз шагов (Ns < Ni),
то последний можно рассматривать как алгоритм прогноза для си-
стемы, эволюцию которой имитирует первый алгоритм.
На эту связь обратил внимание американский исследователь
С. Уолфрэм. Его гипотеза состоит в следующем. Задачи, в решении
которых теоретическая физика добилась больших успехов, отно-
сятся к вычислительно приводимым. Для них типичны либо возмож-
ность выделить несколько степеней свободы, описывающих дина-
мику системы, либо наличие многих одинаковых подсистем. В этом
случае обычно эффективны процедуры усреднения и вновь пере-
ход к сравнительно простым соотношениям. Однако турбулентные
течения в гидродинамике, биологическая эволюция, многие явле-
ния в физике атмосферы относятся к вычислительно неприводи-
мым системам. И единственный способ проанализировать их разви-
тие — имитация, т.е. непосредственный расчет систем, сравнимых
по сложности. На построение эффективных упрощенных моделей
здесь надеяться не приходится. Концепция аттрактора здесь непри-
менима. С разных начальных данных может происходить выход на
совершенно различные установившиеся режимы. Эту парадоксаль-
ную возможность иллюстрирует игра «Жизнь», предложенная ан-
глийским математиком Дж. Конвеем. Она показывает, как просты
могут быть правила, определяющие вычислительно неприводимые
системы.
В игре «Жизнь» рассматривается бесконечная плоская решетка
квадратных ячеек-клеток. Время в этой игре дискретно (t =
= 1,2,...). Клетка может быть живой или мертвой. Изменение ее
состояния в момент t + 1 определяется состоянием ее соседей в мо-
мент t (соседей у каждой клетки восемь, четыре имеют с ней об-
щие ребра, а четыре — только вершины). Правила таковы: если
клетка мертва в момент времени t, она оживает в момент t + 1
тогда и только тогда, когда трое из ее восьми соседей были жи-
выми в момент t. Эти правила очень просты. Имея лист бумаги
в клетку, можно проследить эволюцию простейших конфигураций.
Компьютер позволяет следить за поведением больших сообществ на
больших временах.
Есть глубокая аналогия между процессами в нелинейных дисси-
пативных средах и этой дискретной системой. Поэтому естественно
поставить следующие вопросы: какие основные типы структур
(т.е. конфигураций, определяющих поведение сообществ клеток на
больших временах) могут существовать в такой системе? Каковы
здесь законы организации структур? Могут ли они взаимодейство-
вать и к чему это приводит?
Простейшие структуры здесь — стационарные, т.е. не завися-
щие от времени. Их примеры показаны на рис. 31а (в центре живой
клетки мы ставим черный кружок, по краям квадрата нанесены
деления с интервалом в две клетки). Главное состоит в том, что
эти структуры локализованы. Будучи разделенными двумя белыми
клетками, они не влияют друг на друга.
Можно считать, что стационарные структуры повторяют себя
на каждом шаге по времени. А если через 2, 3 или р шагов? Такие
конфигурации будем для краткости называть циклами. Они описы-
вают периодические процессы в сообществах клеток.
Циклы 2 показаны на рис. 316. Смотреть здесь нужно по стро-
кам. Поскольку циклы 2 тоже локализованы, то все они предста-
влены в одной области. При эволюции различных сообществ часто
встречается цикл 2, показанный во второй строке. Его называют
семафором.
Посмотрим, какие типы упорядоченности еще есть в игре
«Жизнь». На рис. 31в показана замечательная конфигурация, назы-
ваемая «планер» (стационарная структура здесь поставлена в каче-
стве точки отсчета). Через каждые четыре шага планер повторяет
себя, но сместившись на одну клетку вниз и вправо (понятно, что
в силу симметрии есть планеры, распространяющиеся вдоль любой
диагонали клеток-квадратов в обоих направлениях). На рисунке по-
казаны четыре различные фазы планера.
Столкновение двух планеров или планера со стационаром может
приводить к их аннигиляции (рис. 31г). В других столкновениях
может рождаться целый набор стационаров и семафоров.
Чем большую площадь занимает сообщество, тем сложнее оно
может себя вести. Поэтому интерес вызывают неограниченно ра-
стущие в пространстве конфигурации. Одну из них, называемую
катапультой или планерным ружьем, предложил в 1970 г. Р. Госпер-
младший. Видно, что катапульта через каждые 30 шагов повторяет
себя и выпускает планер (рис. 31д). Планерное ружье заполняет
пространство потоком планеров.
Наличие такой конфигурации, как планерное ружье, играет
принципиальную роль. В самом деле, ЭВМ можно рассматривать
как конечный набор простейших логических элементов, осущест-
вляющих операции И, ИЛИ, НЕ, определенным образом соединен-
ных проводами, по которым распространяется набор импульсов,
кодирующих последовательность нулей и единиц.
В качестве генератора таких импульсов в игре «Жизнь» высту-
пает планерное ружье. Наличие планера в потоке естественно ин-
терпретировать как единицу, отсутствие — как нуль. Столкнове-
ния планеров, приводящих к их аннигиляции, позволяют построить
элемент НЕ, направив два потока под прямым углом (если планер
в определенном месте есть в первом потоке, то после столкнове-
д
Рис.31. Различные конфигурации в игре «Жизнь», а — стационарные струк-
туры; б — примеры циклов; в — планер; г — столкновение и аннигиляция
двух планеров (представлены конфигурации в последовательные моменты вре-
мени); д— планерное ружье.
ния планер в другом потоке на этом месте исчезнет). Более слож-
ным образом в игре «Жизнь» конструируются другие элементы.
Однако они могут быть сконструированы, и игра «Жизнь» оказы-
вается эквивалентной универсальной вычислительной машине — в
ней при определенных начальных данных возможны процессы лю-
бой сложности, которые могут быть смоделированы на ЭВМ.
Альтернативный подход к проблеме прогноза, находящий все
больше приверженцев, связан с нейронными сетями. Бросающееся в
глаза отличие мышления человека от работы современных компью-
теров состоит в следующем. Мы имеем массу неформальных инту-
итивных представлений, которыми пользуемся для быстрой оценки
ситуации и принятия эффективных приближенных решений. Кроме
того, человек имеет возможность чему-либо научиться, отбирая из
потока информации то, что нужно для решения поставленной за-
дачи. Последняя способность связана с великим даром многое за-
бывать и удерживать в памяти ключевые фрагменты и важные де-
тали.
Именно поэтому многие стороны интеллектуальной деятельно-
сти, доступные маленькому ребенку, представляют для компьюте-
ров огромные проблемы. Среди них узнавание лиц, обучение речи,
решение несложных неформализованных задач, поиск закономерно-
стей. Большие усилия, вложенные в шахматные компьютеры, до сих
пор не вывели их на уровень, превышающий человеческие возмож-
ности.
Однако в последние годы появился новый класс вычислительных
систем, называемых нейрокомпьютерами, которые ориентированы
на решение проблем, сложных или недоступных для традиционных
компьютеров. Грубо говоря, это вычислительные системы, кото-
рые могут менять свою структуру в соответствии с поступающей
информацией, разумеется, исходя из поставленной задачи. Можно
сказать, что эти машины конструируют сами себя, отражая доступ-
ную их восприятию реальность. Это открывает возможности для
обучения: развития, поиска аналогий, восстановления целого по от-
дельным фрагментам и научного прогноза.
В самом деле, допустим, что для некоторой сложной системы
не известны ни параметры порядка, ни связывающие их соотноше-
ния, но зато можно достаточно долго наблюдать за ее поведением.
Хочется надеяться, что нейрокомпьютер с определенными параме-
трами будет в состоянии отобрать информацию, «относящуюся к
проблеме», найти взаимосвязи, которые легко «проходят через сито»
всех описанных в этой статье и многих других алгоритмов, и на
этой основе построить соответствующую вычислительную струк-
туру. Такой подход сейчас активно развивается в связи с пробле-
мой прогноза землетрясений, обработки космической информации,
созданием «разумных» робототехнических систем, способных про-
анализировать ход определенных процессов.
К сожалению, сейчас нет возможности рассказать о конкрет-
ных системах в этой области, основных алгоритмах, важных и ин-
тересных деталях и тем более о достигнутых целях и успехах. Но,
возможно, это дело нескольких ближайших лет. Видимо, тогда и
станет ясно, что специалистам в области прогноза поведения слож-
ных систем не следовало менять работу, что использование идей
синергетики в этой области оказалось плодотворным, что большие
усилия, вложенные в исследование обсуждавшихся вопросов в 90-е
годы, были не напрасны.
В тексте статьи нет ссылок, однако, внимание читателей, кото-
рых заинтересуют детали или иной взгляд на обсуждавшиеся про-
блемы, можно обратить на следующие работы.
Проблемы, связанные с развитием науки, математическим мо-
делированием нелинейных процессов и созданием междисциплинар-
ных подходов, обсуждаются в книгах Н. Н. Моисеева [1], И. При-
гожина, И. Стенгере [2] и сборнике под редакцией А. А. Самар-
ского [3].
Представление о синергетике и концепции параметров порядка
дают книги Г. Хакена [4], Г Николиса, И. Пригожина [5] и сборник
«Компьютеры и нелинейные явления» [6]. Ряд строгих результатов
содержит статья [7].
О фракталях рассказывают книги [8, 9], а об их размерностях —
статьи [10, 11].
Примеры численных алгоритмов оценки фрактальных размер-
ностей дает работа [12].
Странные аттракторы рассматриваются в книге Г. Шустера [13],
замечательном сборнике оригинальных статей «Странные аттрак-
торы» [14] и книге, содержащей обзор строгих результатов [15]. Об-
зор нескольких направлений хаотической динамики и теории дис-
сипативных структур дан в статье [16].
Обобщенная модель Рикитаки анализируется в работе [17], мо-
дель солнечного динамо — в [18].
Одномерные отображения рассматриваются в книге А. Н. Шар-
ковского, Ю. А. Майстренко, Е. Ю. Романенко [19]. Задача о связи
динамики с вероятностными характеристиками для одномерных
отображений решается в статье С. В. Ершова, Г. Г. Малинецко-
го [20].
Чувствительность к параметрам рассматривается в работе [21].
Алгоритмы вычисления ляпуновских показателей по эксперимен-
тальным данным обсуждаются в статье [22]. Алгоритм реконструк-
ции аттракторов приведен в [23], а применение этого алгоритма для
анализа течения КуэттагТейлора рассматривается в статье [24] из
которой и взят рис. 26. Пессимистичный взгляд на перспективы
этого подхода развиваются в статье [25]. Способ построения пре-
дикторов предлагается в работе [26]. Один из способов выбора, ши-
роко используемый в настоящее время, рассмотрен в статье [27]. Из
этой работы и взят «красивый» странный аттрактор на рис. 286.
Примеры вычисления корреляционного показателя для двух кон-
кретных систем приведены в работах [28, 29]. Традиционные до-
воды «за» и «против» можно найти в дискуссии о погодном и клима-
тическом аттракторе [30, 31]. Алгоритм удаления ближайших сосе-
дей описан в работе [32].
Гипотеза о связи предсказуемости с приводимостью или непри-
водимостью алгоритмов рассматривается в статье [33].
С нейрокомпьютерами знакомит книга [34].
В заключение считаю приятным долгом поблагодарить А. А. Са-
марского, С. П. Курдюмова, А. Б. Потапова, Т. С. Ахромееву и
Е. С. Ершова за помощь, поддержку и полезное обсуждение про-
блем синергетики.
ЛИТЕРА ТУРА
1. Моисеев Н.Н. Математика ставит эксперимент. М.: Наука, 1979. 224 с.
2. Пригожин И., Стенгере И. Порядок из хаоса. М.: Прогресс, 1986. 432 с.
3. Компьютеры, модели, вычислительный эксперимент / Под ред. А.А. Са-
марского. М.: Наука, 1988. 176 с.
4. Хакен Г. Синергетика. М.: Мир, 1980. 404 с.
5. Николис Г., Пригожин И. Самоорганизация в неравновесных системах.
М.: Мир, 1979. 512 с.
6. Компьютеры и нелинейные явления. М.: Наука, 1988. 192 с.
7. Foias С., Sell G.R., Тетат R. Inertial manifolds for nonlinear evolutionary
equatione // J. Different. Equat. 1988. Vol.73, № 2. P.309-353.
8. Mandelbrot B.B. Fractals, form, chance and dimension. San-Francisco:
Freeman, 1977. 365 p.
9. Фракталы в физике. M.: Мир, 1989. 672 с.
10. Fazmer J.D., Ott Е., Yorke J.A. The dimension of chaotic attracters // Physica
D. 1983. Vol.7, № 1/3. P.153-180.
11. Crassberger P., Procaccia T. Measuring the strangeness of strange attractors
// Ibid Vol.9. № 1/2. P.189-202.
12. Малинецкий Г.Г., Потапов А.Б. О вычислении размерностей странных
аттракторов // Журн. вычисл. математики и мат. физики. 1988. Т.28. 7.
С.1021-1037.
13. Шустер Г. Детерминированный хаос. М.: Мир, 1988. 240 с.
14. Странные аттракторы. М.: Мир, 1981. 256 с.
15. Итоги науки и техники. Сер. Современные проблемы математики. Фунда-
ментальные направления. М.: ВИНИТИ, 1985. Т.2.
16. Akhromeyeva T.S., Kurdyumov S.P., Malinetskii G.G., Samarskii A.A. Non-
stationary dissipative structures and diffusion-induced chaos in nonlinear media
// Phys. Repts. 1989. Vol.176. № 5/6. P.179-372.
17. Ershov S. V., Malinetskii G. G., Ruzmaikin A.A. A generalized two-disk dynamo
model // Geophys. Astrophys. Fluid. Dyn. 1989. Vol.47. P.251-277.
18. Малинецкий Г.Г., Рузмайкин А.А., Самарский А.А. Модель долговремен-
ных вариаций солнечной активности. М., 1986. 28 с. (Препр. / Ин-т прикл.
математики им. М. В. Келдыша АН СССР; № 170).
19. Шарковский А.Н., Майстренко Ю.А., Романенко Е.Ю. Дифференциаль-
ные уравнения и их приложения. Киев: Наук, думка, 1986. 280 с.
20. Ершов С.В., Малинецкий Г.Г. О решении обратной задачи для уравнения
Перрона-Фробениуса // Журн. выч. математики и мат. физики. 1988. Т.28
К* 10. С. 1491-1497.
21. Farmer J.D. Sensitive dependence on parameters in nonlear dynamics // Phys.
Rev. Lett. 1985. Vol.55 № 4. P.351-354.
22. Wolf A., Swift J.B., Swinney H.L., Vastano J.A. Determining Lyapunov
exponents from a time series // Physica D. 1985. Vol.16. 3. P.285-317.
23. Tokens F. Distinguishing deterministic and random systems // Nonlinear
dynamics and turbulence. Boston etc., 1983. P.366-381.
24. Brandstater A., Swinney H.L. Strange attractors in weakly turbulent Couette-
Taylor flow //Phys. Rev. A. — Gen. Phys. 1987. Vol.35. K’ 5. P.2207-2220.
25. Ruelle D. Deterministic chaos: the science and the fiction // Proc. Roy, Soc.
London A. 1990. Vol.427. P.241-248.
26. Farmer J.D., Sidorowich J. J. Predicting chaotic time series // Phys. Rev. Lett.
1987. Vol.59. X« 8. P.845-848.
27. Fraser A.M., Swinney H.L. Independent coordinates for strange attractors from
mutual information // Phys. Rev. A. — Gen. Phys. 1986. Vol.33. X1 2. P.1134-
1140.
28. Малинецкий Г.Г., Потапов А.Б., Приймак В.Г. О возможности описания
турбулентности течений вязкой жидкости аттрактором конечной размер-
ности // ДАН СССР. 1991. Т.326, № 5. С.1101-1106.
29. Malinetskii G.G., Potapov А.В., Gizzatulina S.M. et al. Dimension of geo-
magnetic attractor from data on length of day variations // Phys. Earth and
Planet. Inter. 1990. VoL59. P.170-181.
30. Fraedrich K. Estimating the dimensions of weather and climatic attractors //
J. Atmos. Sci. 1986. Vol.43, № 5. P.419-432.
31. Grassberger P. Do climatic attractors exist // Nature. 1986. Vol.323. P.609-612.
32. Theiler J. Spurious dimensions from correlation algorythm applied to limited
time-series data // Phys. Rev. A. — Gen. Phys. 1986. Vol.34, X* 3. P.2427-2432.
33. Wolfram S. Universality and complexity in cellular automata // Physica D.
1984. Vol.10, № 1/2. P.1-35.
34. Итоги науки и техники. Сер. Физические и математические модели ней-
ронных сетей. М.: ВИНИТИ, 1990. Т.1. 385 с.
КИБЕРНЕТИКА И ИНФОРМАТИКА
В.А.Лисичкин
ТЕОРЕТИКО-ИНФОРМАЦИОННЫЙ ПОДХОД
К ОЦЕНКЕ ДОСТОВЕРНОСТИ ПРОГНОЗОВ
Введение
Прогнозирование за последние 20-25 лет перестало быть заня-
тием только научных работников, оно переросло в профессиональ-
ную деятельность специалистов разных отраслей промышленности,
техники, технологии и других сфер социума. Чтобы деятельность
была эффективной (а потому целесообразной и полезной для обще-
ства), необходимо иметь возможность оценить достоверность ре-
зультатов этой деятельности. Что является результатом деятельно-
сти человека во время его занятия прогнозированием? Это некото-
рая вероятная информация о будущем или некоторая совокупность
сигналов, содержащих информацию о будущем [1].
Данная информация в отечественной и зарубежной литературе
интерпретируется на основе двух подходов — семантического и
статистического. Семантический подход достаточно полно описан
в работах И. Земана [2], К. Морозова [3], У. Р. Эшби [4], А. А. Харке-
вича [5, 6], В. Майлса [7], Р. Аккофа и Ф. Эмери [8] и др. Статисти-
ческий подход базируется на фундаментальных работах К. Шен-
нона [9], Т. М. Рида и К. Е. Габбинса [10], Д. Кеньона и Г. Стей-
мона [11], А. Рапопорта [12], А. Н. Кочергина и 3. Ф. Цайера [13],
Байеса и др. и описана в многочисленных книгах и статьях со-
временных авторов. Не рассматривая здесь достоинства и недо-
статки этих подходов для нашей постановки задачи, отметим, что
нами сделана попытка теоретико-информационного подхода, кото-
рый более адекватно описывает процесс прогнозирования. Поэтому
постановка задачи оценки достоверности прогноза формулируется
как задача оценки достоверности передачи сигнала по каналу связи
с шумами.
1. Прогнозирование как задача теории информации
Разработка прогноза предполагает переработку информации,
полученной из определенных источников и приведенной в опреде-
ленную систему. Поэтому прогнозирование можно рассматривать
как передачу информации по каналам связи. Для технических ка-
налов связи справедливы известные теоремы Шеннона [9], напри-
мер, такая: «Пусть имеется источник информации х, энтропия ко-
торого в единицу времени равна Н(х), и канал с пропускной спо-
собностью С. Тогда если Н(х) > С, то при любом кодировании пе-
редача сообщений без задержек и искажений невозможна. Если же
Н(х) < С, то всегда можно достаточно длинное сообщение закоди-
ровать так, чтобы оно было передано без задержек и искажений с
вероятностью, близкой к единице».
Рассматривая предсказание как сигнал, естественно обобщить
понятие канала связи на такие системы. Пусть канал связи соеди-
няет две точки четырехмерного континуума (ri, ti) и (гг, ^)- Будем
интересоваться частным случаем, когда координаты х, у, z фикси-
рованы, а переменной величиной является время.
Передачу по каналу связи, соединяющему точки (и, ti) и (гг,£2),
можно интерпретировать как передачу информации из прошлого в
настоящее (ti < <2) или из будущего в настоящее (<i > £2)- Разу-
меется, физическая реализация канала связи возможна только для
передачи информации из прошлого в будущее. Рассмотрим, однако,
передачу информации из будущего, считая, что это равносильно
прогнозированию.
Для конкретизации состояния системы в точке (ri,ti), где ti —
некоторый будущий момент времени, введем понятие «прогности-
ческого демона», передающего информацию по временнбму каналу
связи из будущего в настоящее. Польза от такого понятия опреде-
ляется ценностью полученных результатов. На первый взгляд идея
прогностического демона совпадает с идеей Лапласа. Однако ла-
пласовский демон обладает абсолютным знанием начального состо-
яния в прошлый или в настоящий моменты времени, осведомлен о
законах всяческого развития и поэтому способен предсказывать аб-
солютно точно, на сколь угодно далекий срок в будущем. Невозмож-
ность существования лапласовского демона более или менее оче-
видна. Она доказывается, например, с помощью негэнтропийного
принципа информации. В отличие от лапласовского, прогностиче-
ский демон осведомлен о состоянии некоторой системы в будущем
и сообщает о ней нам сегодня.
Очевидно, прогностический демон, который абсолютно точно
определял бы будущие состояния и передавал информацию о буду-
щем без искажений, явился бы простым обращением лапласовского
демона, и поэтому его существование невозможно. Но если догово-
риться, что прогностический демон определяет состояние системы
в будущий момент времени с некоторой неопределенностью, так что
количество информации I, с которым он вступает в жизнь, не равно
бесконечности, и что А/ < оо (при передаче теряется какое-то ко-
личество информации из-за прогностического шума во временном
канале связи), то прогностический демон приобретает право на су-
ществование в качестве модели прогноза.
Введем понятие прогностического шума. Трудно представить
себе прогноз, который полностью отражал бы состояние системы
в будущем. Более реалистичным будет предположить, что при ги-
потетической передаче сообщений из будущего часть информации
теряется из-за помех, которые назовем прогностическим шумом.
Рассмотрим систему, состоящую из источника информации X,
канала связи К и приемника Y. Источник информации предста-
вляет, в свою очередь, систему, состояние которой в общем слу-
чае описывается несколькими случайными величинами xi,xz,... ,ха
с плотностью вероятности fx (zi,X2,... ,^s). Ограничимся рассмо-
трением простого варианта, который описывается одной случай-
ной величиной X с плотностью вероятности А(т)- Пусть состояние
приемника также характеризуется одной случайной величиной у с
плотностью вероятности fy(y)-
Предположим, что канал связи К расположен не в простран-
ственном, а во временном континууме. Иными словами, источник
информации X, состояния которого с некоторыми вероятностями
определяются демоном, разделен с приемником временным интер-
валом t. Состояние приемника Y есть прогноз состояния источ-
ника X. Таким образом, интервал прогнозирования соответствует
длине канала связи. Можно получить несколько соотношений, свя-
зывающих прогностические параметры.
Бели бы шума не было, то количество информации, пришедшее
в систему Y, равнялось бы энтропии Н(х) системы X. Но в дей-
ствительности оно будет меньше на величину Н(z|y), где Н(z|y) —
условная энтропия системы X.
Выразив Н(х) через одномерную плотность вероятности /г(т),
a 7f(j/|z) - через двумерную плотность fxy(x,y) и условную вероят-
ность f(y\x), представим 1Х_>У в виде
оо оо
Ix^y = -j fХ(х) \og fx(x)dx + J у fxy(x,y)\ogf(x\y)dxdy.
—оо —оо
Определить плотность вероятности fix') систем в любой буду-
щий момент времени и условную плотность f(x\y) чрезвычайно
трудно. Однако используя формулу ДЛЯ 1Х->У, можно подсчитать,
например, максимальную информацию maxlx_>y, которую пропус-
кает канал связи при помехах. Эта величина представляет собой
максимальную информацию о будущем, которую можно получить
в момент времени t при данном состоянии системы с помощью вы-
бранного метода прогноза. Качество метода, собственно говоря, и
характеризует качество временного канала связи.
Определить максимальную информацию в общем случае непро-
сто. Эта величина зависит от природы помех, от того, какова веро-
ятность искажения символов при подобных помехах. Существенно
также, коррелируют ли между собой эти помехи, каковы условные
вероятности и корреляционные функции помех и т.д. Задачу можно
решить, предположив шум белым и нормально распределенным, и
предположив, что вероятность искажения р зависит от качества и
длины канала связи, т.е. в конечном счете, от качества прогности-
ческого метода и времени упреждения прогноза /3. Запишем зави-
симость д от/3 и от времени t в виде д = p(t,/3). Максимальное
время упреждения прогноза или, что то же самое, прогностиче-
ский горизонт определяется качеством теории или метода прогно-
зирования. Его можно оценить, приравнивая тах1х_>у к нулю, т.е.
рассматривая предельный случай, когда информация полностью те-
ряется в канале связи, что не позволяет судить о будущем состоянии
системы.
Проведем подобные вычисления для одного из простейших слу-
чаев.
Пример. Попытаемся предсказать два несовместимых события,
образующих полную группу событий, которые могут произойти к
определенному времени, скажем, откроют ли природу гравитации к
2000 г., или нет. Здесь может возникнуть дискуссия о правомерно-
сти примера «открытие к 2000 г.». Во-первых, пример с открытием
с точки зрения статистического подхода на первый взгляд трудно
описать, так как вероятность р невозможно измерить. Проще было
бы придумать какую-то более простую модификацию. Например,
р — это «истинная» доля «очкариков» (людей в очках) или доля ин-
фицированных СПИДом и т.д., ат — это прогнозируемая доля.
Однако этот пример дает возможность применить теорию субъек-
тивной оценки вероятности события и тем самым расширить разви-
ваемый здесь подход. Во-вторых, здесь просматривается параллель
с баесовским подходом. Можно построить достаточно изящную мо-
дель прогноза, пользуясь баесовскими соотношениями. Но это уже
дело будущих исследований. Присвоим событию «не откроют» сим-
вол 0, событию «откроют» — символ 1. Пусть демон оценивает эти
события вероятности р и 1 — р и передает сведения нам, закодировав
их соответственно символами 0 и 1. В процессе передачи каждый
символ может быть искажен, т.е. заменен противоположным, с ве-
роятностью /z(/3,t). В итоге событие «не откроют» предсказывается
с вероятностью г, событие «откроют» — с вероятностью 1—т / 1— р.
Итак, прогноз можно представить как передачу с помехами эле-
ментарных символов 0 и 1 от источника X к приемнику Y через
канал связи К. Нетрудно вычислить потерю информации при пере-
даче или условную энтропию Н(j/|z). Она будет зависеть только от
вероятности искажения д(/3, t):
#(j/|z) = р logр - (1 - р) log(l - д).
Тогда полная информация, передаваемая одним символом, опреде-
ляется выражением
1^х = {-Г logr - (1 - г) log(l - г)} -
- {-/Hog Р - (1 - р) log(l - р)} =
= fo(r) + *1(1 - г)] - Ь(м) + № - м)] ,
где для краткости обозначено i](x) = х log х.
Информация на один символ достигает максимума при г = 1/2
и равна
max 1 - 1п(р) + т/(1 - д)].
Для определения свойства канала связи, который теряет всю ин-
формацию, приравняем максимальную информацию нулю:
тах/^Х = 0.
Решение этого уравнения дает
7/(д) + 7/(1 -р) = 1, (1)
откуда находим р = 1/2.
Зависимость вероятности искажения р от времени t примем в
виде
M(/3,t) = (l-e-^), (2)
где /3 — время упреждения, характеризующее скорость деградации
информации. При t = 0 вероятность искажения прогноза равна 0, а
при t -+ оо она стремится к единице, т.е. вероятности достоверного
события. Зависимость р от /J имеет противоположный характер.
При плохом качестве теории, когда /3 —> 0, прогноз ложен практи-
чески на любом интервале времени. Напротив, при /3 —> оо точность
прогноза растет, а р —> 0. Это модель качественно правильно со-
гласуется с эмпирическими данными.
Прогностический горизонт thor (максимальная дальность про-
гноза) можно определить, приравняв дк 1/2:
откуда имеем
thor = /31п2.
Выражение для вероятности искажения можно записать, исполь-
зуя прогностический горизонт, в виде
/о .\ (thor А -< ( tln2\
ММ = д —,t = 1 - exp —----------- .
\1п2 ) \ thor )
Если бы величина /7 не зависела от времени, то ее можно было
бы определить, исходя из стационарных свойств прогностической
теории, выразив, например, через сложность объекта прогнозиро-
вания или через количество негэнтропии, затраченной на прогноз.
Для практически важного конкретного случая прогноза двух несо-
вместимых событий, рассмотренного выше, прогностический гори-
зонт thor не зависит от точности прогноза. Это положение имеет об-
щий характер, ибо за прогностическим горизонтом точность пред-
сказания падает настолько, что говорить о качестве прогноза уже
бессмысленно. Таким образом, если мы знаем качество теории, ис-
пользуемой для прогнозирования, то можем определить прогности-
ческий горизонт.
Естественно ставить перед собой задачу выбора такой теории,
которая давала бы максимальный прогностический горизонт. Если
общий вид зависимости, определяемой теорией (законом), известен,
а неизвестны только параметры (или константы) теории, то для
определения параметров может быть предложен следующий метод.
2. Оптимизация методов прогнозирования
Пусть мы наблюдаем какую-либо величину xt+T в определенные
дискретные моменты времени t+тв прошлом (т = 0,1, —2..., —п),
т.е. имеем дискретный временной ряд (it, xt-i,xt-2, • • • , zt-n)- При-
мем полиномиальную прогностическую модель и представим xi+r в
виде суммы неслучайного степенного ряда и случайной величины et:
т
zt+r = ^^(t + rr + et+i-. (3)
Предположим, что £t+r представляет нормальный стационарный
случайный процесс с нулевым средним и корреляционной функцией
А:1(т) (нестационарный процесс будет рассмотрен позже). Тогда
xt+r тоже является нормальным стационарным случайным процес-
сом со средним значением
xt+т = $2тг^+т)<- <4)
i
Задача прогнозирования заключается в отыскании коэффициен-
тов at, образующих в совокупности вектор параметров а =
= {ai, аг,...,am}. Обычно такую задачу решают методом наимень-
ших квадратов так, чтобы сумма квадратов отклонений экспери-
ментальных точек от сглаживающей кривой была минимальной:
<&+т ~ xt+т)2 = 22 £t+r = min •
r=0 r=0
Опираясь на гауссовский закон распределения вероятности для е
и исходя из признака максимума правдоподобия, из условия £ е2 =
= min можно найти некоторое разумное число коэффициентов am.
Такой подход в основном обращен на согласование с предшествую-
щими данными. Между тем можно исходить и из других соображе-
ний.
Пусть т = 0,1,2,... ,п — отсчеты будущих моментов времени.
Рассмотрим два таких момента времени: текущий момент t и какой-
нибудь момент t + т в будущем. Тогда мы имеем две непрерыв-
ные системы случайных величин xt и xt+T с нормальным законом
распределения. Поставляем вопрос: какое количество информации
можно получить о системе it+T, если известна система xt?
Очевидно, что прогноз о состоянии системы Xt+T будет доста-
точно полным только тогда, когда количество информации о нем
будет отличаться от нуля (естественно, что мы делаем прогноз
только на основании прошлых значений it).
Выражение для полной взаимной информации между системами
xt и xt+г записывается в виде
ОО
«,+т = [ [ f(xttxt+T) log dxt dxt+т-
J J f\xt)j\xt+T)
—oo
Полная взаимная информация IXt <_,It+r является неотрицатель-
ной величиной и обращается в нуль только тогда, когда системы xt
и xt+T независимы. При нормальном законе распределения величин
xt и xt+T для их независимости необходимо и достаточно, чтобы
корреляционный момент обращался в нуль:
k(xt,xt+r) = 0.
(5)
Рассматривая фиксированное т в предположении о стационарно-
сти случайного процесса it, условие (5) можно записать как урав-
нение для определения горизонта предсказуемости т:
k(xt,xt+T) = k(t,t + т) = кх(т) = 0. (6)
Разумеется, практически мы можем определить функцию только
для прошлых значений времени (т = 0, —1, —2,..., —п), но вслед-
ствие четности корреляционной функции для стационарного про-
цесса (кх(т) = кх(—т)) появляется возможность использовать име-
ющуюся информацию при т > 0. Уравнение (6) дает тот прогности-
ческий временнбй горизонт 7Ъог> за которым прогноз невозможен,
поскольку информация о состоянии величины х в момент времени
t + т + 1 (при отсутствии периодической зависимости) обращается
в нуль.
Запишем выражение для корреляционной функции:
kx(t, t + т) = M[x(t)x(t + т)] = M(et, £t+r) =
= M{[xt - i(t)][xt+T - x(t + -r)]}
или, учитывая (4),
m m
kx(t, t + r) = M{[xt - £ %(ty^t+r - E %(t + r)f]}. (7)
i i
Для стационарного процесса корреляционная функция1 зависит
только от т и а:
fcx(t, t + т, а) = кх(т, а).
Приравнивая кх к какой-нибудь малой заранее заданной вели-
чине т] (уровню доверия прогноза), получим уравнения для интер-
вала тл
кх(т,а.) = т). (8)
Решив (8) относительно тл:
^=^,7/), (9)
найдем выражение для прогностического горизонта в зависимости
от вектора коэффициента регрессии а и доверительного уровня
прогноза т).
Если нужно определить вектор а, отвечающий максимальному
прогностическому горизонту, то выражение (9) можно написать в
виде
тл = ¥>(а, т]) = max.
1 Может быть описана в виде уравнения регрессии.
Приравняв частные производные по а; нулю:
{d</>(a,7f)/dai} = О,
найдем а, в функции т] и прошлых значений величины
а = f(xt+T,vj),T - 0,-1,-2,
Когда мы имеем только одну реализацию стационарного случай-
ного процесса на достаточно большом участке времени Т и пред-
полагаем у этого процесса эргодическое свойство, корреляционную
функцию можно найти, проведя усреднение не по множеству наблю-
дений, а по времени. Иными словами, (7) можно записать так:
Т-т
кх(т) - 7^-— [ + т) dt.
1~Т J
о
Ограничив число членов степенного ряда в (3) двумя, приводим
уравнение (8) к виду
^(т.ох.аг) = а? + ^02(7 - т) + ^а2(Т - т)2+
О
Т-т
2 f
+ ™---- / xt • xt-т dt—
1 — Т J
о
Т-т
- ~ dt~
о
Т-т
- J12 / t(xt + Xt-.,} dt = 7].
1 — Т J
о
Уравнение относительно т можно довести до численного реше-
ния, определив ах и аг по описанной выше процедуре. Данный метод
прогнозирования будет оптимальным в смысле дальности прогноза.
3. Общие свойства методов прогнозирования
Пусть Р — мощность метода прогнозирования, т.е. максималь-
ное количество информации о единице пространства на определен-
ное время упреждения прогноза, которое можно получить с помо-
щью данного метода. Так, если метод может давать к элементарных
символов информации на единице пространства, то
Р = ктпах.1,
где max I — максимальная информация на один символ, она всегда
меньше единицы и равна ей только в отсутствие прогностического
шума, что, увы, невозможно.
Если прогноз выдается в виде некоторой случайной функции
с корреляционной функцией, изменяющейся по пространству, то
мощность метода можно записать наподобие одного из известных
результатов теории информации:
/ д \ / д \
Р = filog2 (1 + — J =к- 2/cfclog2 ( 1 + — } ,
где П — пространственная частота2; S — средняя мощность сиг-
нала; N — средняя мощность шума.
Относительно Р можно высказать некоторое достаточно общее
утверждение. Применим прогностический метод с мощностью про-
гнозирования Р к событиям у с удельной энтропией h, которые
могут произойти через некоторое время. Оказывается, что если
h > Р, то прогноз невозможен, т.е. нельзя предсказать события с
удельной энтропией, большей, чем мощность метода прогноза. До-
казывается это утверждение подобно второй теореме Шеннона в
теории информации.
Предположим, что сообщение о событии зашифровано прогно-
стическим демоном т единичными символами и не содержит избы-
точной информации. Для того чтобы расшифровать это сообщение
без искажений, необходимо, чтобы выполнялось неравенство
к > т/тах.1,
где к — число элементарных символов, которым может обладать
метод прогнозирования на единицу пространства.
Задачу об оценке прогнозирования количественных величин
можно решать следующим образом.
Если известны спектральная плотность сообщения о будущем
Sc и спектральная плотность прогностического шума Sm (практи-
чески достаточно знать отношение их интегральных значений), то
спектральную плотность прогноза Sn($l) можно найти по формуле
Дп(П) = Н-1
Sm(Sl)dSl)
(Ю)
2 Пространственная частота — это некоторая априорно заданная характери-
стика класса методов прогнозирования, связанная, например, с шириной полосы
пропускания метода прогнозирования.
где Н-1 — обратная функция от Н = Я[5(П)]. Среднеквадратич-
ную ошибку прогноза а2 можно найти, проинтегрировав выраже-
ние (10):
ОО
a2 = I S„(O)dO.
о
Для иллюстрации рассмотрим пример с белым шумом, допуска-
ющий определение функции Н~1 в явном виде.
Предположим, что значения прогноза х распределены по нор-
мальному закону:
1 х2
Тогда энтропия этой системы будет равна
y/2irean
НМ = log
(11)
В качестве модели прогностического шума возьмем гауссовый
белый шум с постоянной спектральной плотностью Sm = const и
дисперсией Dm, вообще говоря, зависящей от времени упреждения
прогноза, но постоянной по пространству: Dm = = ’тИ- Изме-
рение, проделанное прогностическим демоном, будем характеризо-
вать постоянным среднеквадратичным разбросом ас = const. Тогда
из (10) и (11) следует:
log
у/2яеап
Да:
-2
Среднеквадратичное отклонение прогноза будет равно
= Д£ кт(*) + *с'
Ж .
а мера точности прогноза h = стп/х/2 составит
д* +<г2.
где П — ширина полосы пропускания метода прогноза.
Выразив Да: через П:
Да: = Т/2П,
где L — длина передаваемой функции, получим
_ 2П>/7гё [ am(t) ]П
L •
Для прогнозирования нужно определить константы тех законо-
мерностей, которым подчиняется прогнозируемая величина. Про-
гноз состоятелен только в той пространственно-временнбй области,
в которой константы действительно сохраняют постоянное значе-
ние. Найти константы можно различным путем, но всегда необхо-
димо использовать информацию, заключенную в прошлых данных.
В качестве примера упомянем тривиальные в современной фи-
зике преобразования Лоренца, которые охватывают все кинема-
тические эффекты специальной теории относительности. Струк-
тура преобразований была подсказана логикой, базирующейся на
усреднении многократно повторявшихся в прошлом соотношений.
Практически все общие законы получены с оглядкой на эмпириче-
ские данные. Постоянство входящей в преобразование Лоренца ве-
личины с (скорости света) проверено пока только в четырехмерном
объеме IO"17 < х < 1028 см и 10-27 < At < 3 • 1017. Эта величина
найдена в результате многочисленных измерений и экспериментов.
В настоящее время для формализованного определения констант,
линейно входящих в закономерность, которой подчиняется измене-
ние прогнозируемой величины, чаще всего применяются корреля-
ционный и регрессивный анализы.
При выборе данных, на основе которых определяется закон из-
менения прогнозируемой величины, возникает вопрос: следует ли
руководствоваться некоторыми общими правилами?
Рассмотрим временной ряд прогнозируемой величины х. Обыч-
но вариации х существенно зависят лишь от немногих причин и в
то же время подвержены слабому воздействию множества второ-
степенных факторов. Задача исследования — суметь отличить су-
щественное от несущественного, т. е. пренебречь второстепенными
обстоятельствами и найти «единственно возможную» зависимость
между прогнозируемой («зависимой») величиной и независимыми
величинами, численно выражающими причины. Если это удастся,
то константы, которые входят в прогностическую модель, опре-
деляются одновременной подстановкой зависимой и независимых
величин со значениями из некоторой пространственно-временной
области. Величина в области, в которой прогноз удовлетворителен
характеризует устойчивость отношений между следствием и при-
чинами.
Наблюдаемый процесс можно рассматривать как сумму квазиде-
терминированной части (прогноза) и случайного шума. Неустойчи-
вость отношения между следствием и причинами (в число последних
входят и упомянутые выше многочисленные второстепенные фак-
торы) отражается на неустойчивости характеристик этого случай-
ного шума. Например, неустойчивость проявляется в увеличенном
разбросе эмпирических данных. Чем больше они разбросаны по ве-
личине, тем меньше они заслуживают доверия и тем меньше не-
сут информации об истинном отношении между причинами и след-
ствием.
4. Связь между дисконтированием и нестационарностью
Имеющиеся эмпирические данные можно дисконтировать, т.е.
осуществить по отношению к ним некоторую дискриминацию, про-
водя измерения с некоторыми пространственно-временным интер-
валом. Это приведет к потере точности, с которой определяются
константы в модельном законе, а, следовательно, и сокращению
дальности прогноза при заданной точности, поскольку дисконти-
рование влечет за собой уменьшение количества данных, принима-
емых к рассмотрению (напомним, что любое уменьшение выборки
увеличивает дисперсию величин, которые находят при усредненных
данных из этой выборки).
Таким образом, если информацию, которую дает каждое наблю-
дение, представлять как сумму истинной и ложной, то относитель-
ная доля ложной информации будет увеличиваться по мере удаления
от времени составления прогноза как в прошлое, так и в будущее.
Скорость увеличения (уменьшения) этой доли зависит от несимме-
трии функции, описывающей закон изменения дисперсии отклоне-
ний от сингулярной зависимости и от правомерности ее распро-
странения на будущее. Из опыта известно, что чем короче время
упреждения прогноза, тем более близкие по времени данные мы
должны использовать.
Для того чтобы прогнозировать какую-либо величину, необхо-
димо установить зависимость ее от времени. Один из наиболее раз-
работанных математических методов определения этой зависимо-
сти — сглаживание эмпирических данных, основанное на принципе
максимума правдоподобия. Необходимое условие применения ме-
тода — наличие прошлых временных рядов эмпирических значений
прогнозируемой величины, т.е. какого-либо количества информа-
ции о ее поведении.
Пусть т увеличивается при движении по временной оси в про-
шлое. Если имеется ряд из п точек на графике, отображающем эм-
пирические данные, то это дает возможность провести кривую, вы-
ражаемую полиномом п — 1 степени и проходящую через все эти
точки. Однако такое решение вряд ли можно признать удовлетво-
рительным, так как коэффициенты полинома будут испытывать
неустойчивость. Нестабильное поведение коэффициентов полинома
объясняется тем, что на регулярное изменение прогнозируемой ве-
личины, которое происходит под действием устойчивых факторов,
накладывается множество относительно слабых случайных возму-
щений. Каким бы вероятностным законам ни подчинялись отдель-
ные возмущения, совокупное возмущение оказывается распределен-
ным по закону, близкому к нормальному. Эта особенность использу-
ется для нахождения параметров прогнозируемой закономерности
в методе наименьших квадратов.
Пусть истинная зависимость х от т выражается формулой х =
= <р(т). Рассмотрим какое-либо значение аргумента т, когда х имеет
значение хт. В силу указанных выше причин случайная величина хт
распределена почти по нормальному закону с математическим ожи-
данием £(т) и Со среднеквадратичным отклонением ат. Нормаль-
ный закон, по которому распределена величина хт, можно записать
в виде
Установим вероятность того, что система, вообще говоря, за-
висимых (или, по крайней мере, коррелированных) случайных ве-
личин ii,Х2,...,хп примет совокупность значений, лежащих в пре-
делах (хт,хт + dxr)(r = 1,2, ...,п). Эту вероятность вычислили с
помощью нормального закона в пространстве п измерений:
У (xi, Х2 j • • • j^n) dx 1 dx2 ...dxу, —
V\c]
(гтг)1^
rr(r)]2 dxi dx2 ..., dxn,
(12)
где [(7] — определитель матрицы С, С — ||(7rt 11 — матрица, обрат-
ная корреляционной матрице К. Если элементы корреляционной ма-
трицы К равны К = Ц-Krtll, то
CTt = (-1)т-4^ = • [С];
здесь [К] — определитель корреляционной матрицы; MTt — ми-
нор этого определителя, получаемый при вычеркивании из него т
строки и t столбца. Корреляционная матрица в общем виде записы-
вается так:
кик12 ... К1П
_ ^21^22 •••
1<ГП11<ГП2 . . . Кпп
где Krt = MiTit — корреляционные моменты, характеризующие
попарную корреляцию величин хт = хт — хт, входящих в систему.
Можно представить ||К|| в другом виде:
ин =
fll0"! • • • J'lnO’lO’n
••• r2n^2fn
о
Fnl^l^n ••• Гпп0пп
Используя принцип максимального правдоподобия, выберем сред
ние значения ё(1), т(2),..., х(п) так, чтобы максимизировать выра-
жение (12). Для этого достаточно доставить максимум выражению:
r=Ot=O
= max. (13)
Из (13) следует требование
Ст^Хт ~х^2 = i2tCrt=111111 • (14>
r=Ot=O r=Ot=O
Если величины хт и it при т / t некоррелированы:
Krt = M(xrxt) = О,
выражение (14) принимает вид
т _2
E^=min- (15)
т=0 т
В частном случае, когда случайный процесс хт стационарен, т.е.
все ат одинаковы, условие (15) отвечает традиционному методу
наименьших квадратов:
т
х^ = min.
г=0
(16)
Используя определенным образом информацию, фиксированную
в единичном наблюдении, удается определить доверительный ин-
тервал для истинного значения х(т) при заданной доверительной
вероятности. В предположении, что количество информации в еди-
ничном наблюдении не зависит от момента времени, в который
проводится наблюдение, правомерно выражение (16). Однако такое
предположение не вполне отвечает существу дела, так как количе-
ство информации от близких по времени наблюдений, безусловно,
не равно количеству информации от наблюдений, проведенных в
далеком прошлом. Иными словами, информация с течением вре-
мени обесценивается, дисконтируется. Такое дисконтирование мно-
гие авторы учитывают в (16) с помощью весовых дисконтирующих
факторов wT, которые приводят в соответствие вклад каждого на-
блюдения со времени, когда оно сделано:
т
WTx2 = min. (17)
r=0
Попытаемся установить связи между весовой функцией и старе-
нием информации. Для этого найдем количество информации, со-
держащееся в наблюдении хт.
В нашем случае энтропия наблюдения хт в момент времени т
будет:
а изменение энтропии АН за время Дт равно
А „ , Ог+Дг , СГг+ДсГг
ДНТ = log —= log —-----------.
<ГГ (Г?
Когда процесс стационарен, имеем ДЯГ = 0, так как Д<тг = О,
иными словами, в предположении, что разброс эмпирических дан-
ных от некоторого среднего х(т) не зависит от времени, дискон-
тирование информации не происходит и весовая функция тожде-
ственно равна 1. Исходя из этого, можно сформулировать следую-
щее утверждение.
Вместо того, чтобы искать математическое ожидание произ-
вольного нестационарного процесса с некоррелированными откло-
нениями методом наименьших квадратов, можно найти математи-
ческое ожидание стационарного процесса (тоже с некоррелирован-
ными отклонениями) методом наименьших взвешенных квадратов,
причем весовые коэффициенты определяются по правилу
wr = (о-о/^г)2-
Справедливо и обратное утверждение.
Введение дисконтирующих весов в метод наименьших квадра-
тов равносильно гипотезе о нестационарное™ временного ряда эм-
пирических данных, причем = o^/wT.
Справедливость этих утверждений следует из сравнения условий
(15) и (17).
Так как энтропия наблюдения хт равна Нт = С\ log оу, а оу =
= aQw~1^2, то Нт = С - l/21ogwr или wT = 22^с~Нт\
Отметим еще, что из выражения Нт = Ci + 1/2 log для энтро-
пии наблюдения хт следует, что
Ят = Ci + | logo-o - | log= С - j logwT.
В результате получается удобная оценка для дисконтирующего
фактора:
Wr = 24(с"я<
Заключение
В современной литературе проблема оценки достоверности про-
гноза рассматривается как одна из слабо разработанных проблем
прогностики. Трудности подхода к ее решению вытекают из огра-
ниченности применяемых для интерпретации процесса прогнозиро-
вания семантической и статистической теорий информации. Разви-
ваемый в статье теоретико-информационный (шенноновский) под-
ход к описанию прогнозирования как передачи сигнала по каналу
связи с шумами позволяет получить ряд полезных выражений, опи-
сывающих общие свойства методов и моделей прогнозирования. При
этом следует помнить ограничения и шенноновского подхода, свя-
занные с природой и характеристиками прогнозируемого процесса
и спецификой используемых прогностических моделей. Дальнейшее
развитие полученных теоретических результатов может пойти по
двум направлениям. Во-первых, связать энтропийный характер мо-
дели прогноза как теории, адекватной в той или иной мере про-
гнозируемому процессу (объекту), с теорией субъективных веро-
ятностей. Это позволит значительно расширить область интерпре-
тации полученных в статье результатов. И, во-вторых, построить
модель прогноза, используя байесовский подход. Попытки байесов-
ского подхода были сделаны, но без увязки с теоретико-информаци-
онным подходом.
В заключение хочу выразить глубокую признательность про-
фессору Ю.А.Кравцову за ценные замечания, которые помогли
улучшить текст статьи, и коллегам за обсуждение результатов.
ЛИТЕРАТУРА
1. Лисичкин В.А. Прогностика. Терминология. М.: Наука, 1990. 47 с.
2. Земан Й. Познание и информация. М., 1965. 224 с.
3. Морозов К.Е. Философские проблемы теории информации // Философия
естествознания. М.: Наука, 1966. С.56-84.
4. Эшби У.Р. Введение в кибернетику. М.: Наука, 1959. 231 с.
5. Харкевич А.А. О ценности информации // Проблемы кибернетики. М.,
1960. Вып.4. С. 6-11.
6. Харкевич А.А. Очерки общей теории систем. М.: Наука, 1965. 428 с.
7. Майлс В. Измерение ценности научной информации // Зарубеж. радио-
электроника. 1965. X" 1.
8. Акофф Р., Эмери Ф. О целенаправленных системах. М.: Наука, 1974. 257 с.
9. Шеннон К. Работы по теории информации и кибернетике. М.: Наука, 1963.
443 с.
10. Reed Th.M., Gubbins К.Е. Applied statistical mechanics. N.Y., 1973. 271 p.
11. Кеньон Д., Стеймон Г. Биохимическое предопределение. М.: Наука, 1972.
238 с.
12. Рапопорт А. Различные подходы к общей теории систем. // Системные
исследования. М.: Наука, 1979. С.530.
13. Кочергин А.Н., Цайер З.Ф. Информациогенез и вопросы его оптимизации.
Новосибирск; Наука, 1977. 135 с.
14. Zeman Знание и информация. М.: Наука, 1965. С.320.
15. Ashby Введение в кибернетику. М.: Радио, 1959.
16. Miles Измерение ценности информации. Зарубежная радиоэлектроника,
1965.
17. Ackoff, Р. Emery Goal-oriented System. М.: Наука, 1974.
18. Shannon The theory of Information. M.: Наука, 1963.
19. Kenyon, G. Steinman Biochemical predestination. M.: Наука, 1972.
КИБЕРНЕТИКА И ИНФОРМАТИКА
М.А.Садовский, В.Ф.Писаренко
О ПРОГНОЗЕ ВРЕМЕННЫХ РЯДОВ
Введение
Классическая постановка задачи прогноза стационарного вре-
меннбго ряда x(t) [1, 2] формулируется следующим образом. Цен-
трированный стационарный случайный процесс x(t) считается за-
данным на полуоси t fE (0, оо). Среднее значение процесса для упро-
щения ситуации можно считать равным нулю:
Ex(t) = 0.
Зная реализацию x(t) до момента t = 0, надо предсказать значе-
ние х(т) процесса в будущем (т > 0), причем оптимальный прогноз
х(т) по определению должен минимизировать среднеквадратичную
ошибку прогноза
Е|т(т) - £(т)|2.
В общем виде ответ на эту задачу известен: оптимальный про-
гноз имеет вид
x(r) = E[x(r)|x(t),t<0], (1)
где последнее выражение обозначает условное математическое
ожидание прогнозируемой случайной величины х(т) при условии
заданных значений реализации x(t), t < 0.
Изложенная постановка задачи имела многочисленные естествен-
ные обобщения: рассматривались задачи прогноза для многомер-
ных процессов и полей, задачи фильтрации и прогноза, задачи ин-
терполяции, прогноз обобщенных процессов и т.д. В данном случае
для нас существенно лишь то, что случайность при такой поста-
новке задачи предполагается заданной априори, и вопрос о том,
какова ее природа, не обсуждается. Зададимся вопросом: а как
формируются на практике те величины и процессы, которые есте-
ственно принимать в качестве случайных?
1. Формирование случайных величин
С точки зрения обсуждаемой здесь проблемы предсказуемости
можно выделить следующие три типа случайных величин [3].
1. Величины f/т образующиеся в результате взаимодействия боль-
шого числа независимых (или слабо зависимых) и соизмеримых по
диапазону принимаемых значений слагаемых
= & +& + ••• + £п- (2)
Отдельные слагаемые & могут иметь и неслучайную природу.
Независимо от природы факторов & в силу центральной предель-
ной теоремы теории вероятностей величина т;п будет принимать
такие значения, какие могла бы принимать некоторая гауссовская
случайная величина. Примерами такого рода случайных величин
может служить поле напряжений в нагруженном образце горной
породы, пронизанном многочисленными микротрещинами, или поле
сейсмических волн в среде с многочисленными неоднородностями
плотности или упругих скоростей.
Заметим, что в указанных случаях иногда можно (по крайней
мере, в принципе) индивидуально измерить все случайные факторы
(трещины или неоднородности) и таким образом для каждого об-
разца предсказать значение поля. Однако это бывает совершенно
нерентабельно с технической и вычислительной сторон и удобнее
считать поле случайным.
Такие случайные величины можно назвать явлениями с боль-
шим числом степеней свободы (независимых, образующих факто-
ров). Среди случайных величин с большим числом степеней сво-
боды встречаются и такие, для которых практически невозможно
индивидуализировать все факторы. Примером служит броуновское
движение микрочастицы вещества в жидкости или дробовой шум в
радиолампе.
2. Величины или процессы, порождаемые неустойчивыми, нели-
нейными отображениями или динамическими системами [4,5]. При
отображении получается последовательность величин хп (вообще
говоря, векторных):
xn = F(xn_i;A), п = 1,2,..., (3)
где F — некоторая нелинейная функция; Л — параметр, характери-
зующий режим; хо — начальное значение последовательности, кото-
рое может задаваться произвольно. В случае динамических систем
с непрерывным временем функция x(t), которую можно считать
векторной функцией, является решением нелинейного дифферен-
циального уравнения
F(d/dt;A;a:(t)) = 0, (4)
коэффициенты которого зависят от параметра А; начальные усло-
вия для x(t) задаются при t = 0. Для некоторых F последователь-
ности хп выглядят как случайные процессы, хотя и являются реше-
ниями неслучайных дифференциальных (разностных) уравнений.
Указанное явление получило название «динамического хаоса» [4,5].
Оказывается, что случайности типа динамического хаоса не так
уж редки в природе и в технике. Например, почти все алгоритмы
псевдослучайных чисел, получаемых на ЭВМ, имеют вид (3) и от-
носятся к динамическому хаосу.
Для случайностей второго типа также можно определить поня-
тие числа степеней свободы. Известно, что динамические системы
удобно описывать, используя так называемое фазовое простран-
ство. Например, в качестве фазового пространства можно взять
многомерное пространство, у которого по осям откладываются зна-
чения x(t),x (t),... ,xm(t), где тп — порядок дифференциального
уравнения. Через каждую точку фазового пространства (за исклю-
чением некоторых особых точек) проходит одна траектория дина-
мической системы. Эволюция такой системы изображается кривой
в фазовом пространстве. Таким образом, в качестве числа степеней
свободы для хаотической динамической кривой можно взять число
т. Иногда траектория кривой при t —> оо занимает не все про-
странство, а «наматывается» на некоторый «аттрактор» меньшей
размерности d < т. Размерность d может быть дробной. Случай-
ность в хаотической динамике, по существу, характеризуется лишь
конечным числом независимых факторов. Впрочем, это число мо-
жет достигать больших значений (в несколько десятков, сотен и
более).
Динамический хаос возникает при определенных условиях в тур-
булентных течениях, при конвекции вязкой жидкости, в магнито-
гидродинамических потоках и т.п.
3. Случайность квантовых явлений. К таким явлениям отно-
сятся, например, радиоактивный распад или дифракция электро-
нов. Этот тип случайности является наиболее совершенным (не-
предсказуемым) и природа его неясна. Здесь мы ограничимся толь-
ко упоминанием этого источника случайности.
Укажем теперь новые особенности в постановке задачи прогно-
за временных рядов, которые появились недавно в научной литера-
туре. Эти особенности связаны: а) с развитием теории динамиче-
ского хаоса, б) с новыми задачами прогноза точечных процессов (в
частности, в применении к прогнозу землетрясений [6,7] и в) с но-
вым взглядом на природу помех, затрудняющих прогноз [8].
2. О прогнозе временных рядов с использованием теории
динамического хаоса
За последнее время были развиты эффективные методы про-
гноза временных рядов, порожденных динамическими система-
ми [9,10]. При этом существенно, что сама система, т.е. функция
F в (3) или (4) не предполагается известной, а восстанавливается
(конечно, с некоторой погрешностью) по конечной реализации про-
цесса x(t) в прошлом. Собственно задача прогноза разбивается на
две части: восстановление фазового пространства по реализации
x(t) и построение с помощью некоторых методов интерполяции про-
гноза для каждой точки (точнее, для окрестности каждой точки)
фазового пространства. Первая часть задачи решается на основа-
нии теоремы Паккарда-Такенса [11,12], позволяющей по одной ре-
ализации x(t) построить конечномерное пространство, которое со-
держало бы внутри себя фазовое пространство системы. Можно
сказать, что фазовое пространство восстанавливается по теореме
Паккарда-Такенса «с некоторым запасом».
После этого применяются некоторые методы интерполирования
в многомерных пространствах. В результате оказывается, что даже
не зная уравнений динамической системы F(x;X) или F(d/dt\ Л; х),
можно получить достаточно хорошее приближение F(x;A),
F(d/dt; А; х), которое и дает при использовании соотношений (3),
(4) приемлемый прогноз на некоторый ограниченный интервал вре-
мени.
Во многих случаях прогноз с использованием оценок F(x;A),
F(d/dt‘, А; х) гораздо лучше традиционного оптимального, линей-
ного прогноза, основанного на корреляционной функции Вт(т) про-
цесса x(t}:
о
Вт(г) = У х(и)х(и - т) du.
-т
Так, в работе [13] приведен пример, когда нелинейный, дина-
мический прогноз в задаче конвекции подогреваемой снизу вязкой
жидкости дает среднеквадратичную ошибку на малых временах
прогноза в 50 раз меньше, чем стандартные методы оптимального
линейного прогноза. В работах [9,10] приведены весьма впечатля-
ющие примеры прогноза неизвестной наблюдателю динамической
системы. Так, в [9] даны примеры удовлетворительного прогноза и
восстановления странного аттрактора и предельной инвариантной
меры на этом аттракторе по 75, 50, 25 и даже по 10 (!) точкам.
Конечно, не при всех условиях нелинейный динамический прогноз
намного лучше оптимального линейного. Возможны ситуации, ко-
гда эти способы дают примерно одинаковый результат. Однако,
по-видимому, всегда стоит затратить дополнительные усилия на
нелинейный динамический прогноз и сравнить его с линейным.
По сути дела, нелинейный прогноз с использованием интерпо-
ляции траекторий в фазовом пространстве напоминает прогноз по-
годы в «докомпьютерные» времена. Тогда для прогноза, скажем, да-
вления на высоте 1000 м метеоролог отбирал из прошлой истории
карты изолиний давления, напоминающие карту на сегодняшний
день. Затем он смотрел, что было «в прошлом» на следующий день,
и давал примерно такой же прогноз на завтра. Здесь роль фазо-
вого пространства играла карта изолиний давления — двумерная
картинка. Конечно, с появлением компьютера возникает возмож-
ность использовать не только двумерные пространства, но и про-
странства с гораздо большей размерностью, а также и различные,
изощренные методы многомерной интерполяции.
3. Прогноз точечных процессов
Значительный прогресс был достигнут в прогнозах точечных
процессов [6,7]. В этом случае на основании наблюдений процесса
y(t),t < 0, требуется спрогнозировать моменты времени ti,t2,...,
в которые наступает связанный с процессом y(t) точечный процесс
x(t). Говоря нестрого, точечный процесс x(t) можно представить в
виде набора <5-функций:
i
и вся информация о процессе заключена в моментах времени t,, ко-
торыми могут служить моменты сильных землетрясений в задан-
ной области.
Прогноз значений {£,},i = 1,2,..., можно осуществлять различ-
ными способами. Например, можно предсказывать время tj ближай-
шего к t = 0 события точечного процесса, затем при t = tr прогно-
зировать следующее событие t2 и т.д. Можно брать другую форму
прогноза, а именно, прогнозировать наступление и ненаступление
точечного события ti в ближайший малый интервал времени At.
Такой способ прогноза принят, например, в работе [6], где точеч-
ный процесс ti, t2,... обозначает моменты сильных землетрясений в
некоторой области. При этом могут возникать ошибки двух типов:
«пропуск цели» (когда не предсказывалось событие в интервале At,
а оно произошло) и «ложная тревога» (когда предсказывалось собы-
тие в интервале At, а оно не произошло). Для стационарных процес-
сов эти ошибки можно характеризовать независящими от времени
вероятностями а,/3. Для постановки задачи об отыскании опти-
мального прогноза необходимо вместо двух параметров а, /3 ввести
одну функцию потерь 7(0, /3). Оптимальным, по определению, будет
называться тот прогноз, который минимизирует среднее значение
функции потерь.
Как мы видим, ситуация с прогнозом здесь сложнее, чем в случае
предсказания стационарного случайного процесса и использования
минимума среднеквадратичной ошибки в качестве критерия опти-
мального прогноза. И хотя среднеквадратичная ошибка прогноза
характеризует в среднем прогнозную ситуацию, прогноз, миними-
зирующий среднее значение функции потерь у(а,/3), будет, вообще
говоря, отличаться от оптимального в среднеквадратичном смысле
прогноза и может полнее учитывать запросы практики, отражае-
мые в выборе функции потерь у(а,/3).
Описанный выше подход можно было бы обобщить, вводя до-
полнительно новые характеристики качества прогноза. Например,
можно было бы прогнозировать в интервале (t, t+At) три ситуации:
нет событий, одно событие, более одного события. В применении к
прогнозу землетрясений это соответствовало бы раздельному про-
гнозу одиночного толчка и двукратных толчков и более примерно
одинаковой силы. Для практики такое различие может быть су-
щественным: вопрос о возможности повторных СИЛЬНЫХ толчков
является жизненно важным. Напомним, что парные толчки при-
мерно одинаковой силы не являются редкостью в сейсмологической
практике. Например,, два сильных землетрясения в районе Гаэли
(Узбекистан) в 1976 г. с магнитудами около 7,2 были разделены
интервалом в 40 сут.
В качестве дополнительной характеристики качества прогноза
можно было бы взять и его заблаговременность. Введение дополни-
тельных характеристик приводит к новым типам ошибок или к но-
вым количественным характеристикам прогноза. Для определения
оптимального прогноза, в конечном счете, опять необходимо вве-
сти одну функцию потерь от средних значений его характеристик
или вероятностей ошибок различного типа и считать оптимальным
тот прогноз, который ее минимизирует.
4. Природа помех, затрудняющих прогноз
В классической задаче прогноза ошибка характеризовалась од-
ним числом — величиной среднеквадратичного отклонения про-
гноза от истинной реализации (для фиксированного времени про-
гноза т). Это весьма грубый, усредненный способ характеристики
прогноза. Гораздо более детальная и информативная характери-
стика точности прогноза получится, если мы зададим условную
локальную среднеквадратичную ошибку прогноза, т.е. ошибку для
окрестности произвольной точки в фазовом пространстве. В прин-
ципе такая информация может быть получена при конструирова-
нии динамического прогноза с неизвестной функцией F методом
интерполяции в фазовом пространстве [9,10,13]. Обычная средне-
квадратичная ошибка при этом будет равна среднему значению по
всему фазовому пространству (по натуральной инвариантной мере)
от условных локальных ошибок. Таким образом, указанная детали-
зация среднеквадратичной ошибки прогноза может дать полезную
дополнительную информацию в задаче прогноза.
Другая детализация среднеквадратичной ошибки прогноза пред-
ложена Ю. А. Кравцовым в работе [8]. Эта детализация относится
к прогнозу динамических систем. Она подразделяет помехи, содер-
жащиеся в динамической системе, на три типа в соответствии с их
происхождением:
— помехи типа измерительных шумов; они могут быть в прин-
ципе уменьшены путем снижения шумов в приборах регистра-
ции, более частой дискретной выборкой из непрерывного про-
цесса и т.д.;
— помехи, обусловленные неточностью модели динамической си-
стемы, на основании которой строится прогноз; эти помехи
также могут быть в принципе уменьшены путем усложнения
модели и ее более точной подгонки к истинной динамической
системе;
— помехи, которые не могут быть уменьшены, какие бы усилия
мы не прикладывали («влияние всей Вселенной на нашу дина-
мическую систему» [8]).
Зная соотношение этих трех типов помех, можно, вообще говоря,
определить, какая из них является основной и ограничивает глав-
ным образом точность прогноза. Так, например, если указанные
три типа помех входят активно в динамическую систему, то диспе-
рсия их суммы определяется приближенно наибольшей дисперсией
из трех слагаемых. Поэтому для улучшения прогноза необходимо
уменьшить именно помеху с наибольшей дисперсией.
Помехи третьего типа в соответствии с их определением не мо-
гут быть уменьшены при данном уровне развития техники и науки.
Поэтому Ю. А. Кравцов называет определяемое этими помехами
время эффективного прогноза «горизонтом предсказуемости» [8].
Обобщая этот подход, можно предложить расчленение полной
помехи £ в динамической системе на ряд составляющих £i, - . ,£т.
В простейшем случае, когда помехи аддитивны
£ = £1 + • + £т
и независимы, составляющие дисперсии также аддитивны:
ст| = ст? + ... + ст^. (5)
В общем случае составляющие £i,..., £т могут входить в раз-
ные места динамической системы и по-разному влиять на качество
прогноза.
Помехи целесообразно подразделять на компоненты в зависи-
мости от того, каковы затраты на снижение помех данного типа.
Эти затраты можно задавать некоторыми монотонно убывающими
функциями дающими стоимость уменьшения дисперсии ст?
помех г-го типа в 1/д раз. При этом естественно считать, что <р,(1) =
= 0. Если дисперсию ст| практически невозможно уменьшить, то
можно формально положить
= °°. Д < 1-
Если дисперсия помех г-го типа уменьшена в 1/in раз, то сум-
марная стоимость такого уменьшения помех равна ip:
ч
¥’ = ф1(Д1) + --- + фт(Мтп)- (6)
Используя формулу (5), получим для полной дисперсии выражение
ст| = ^ст?-|-...+^тст^. (7)
Естественно выбирать значения ,..., р,т так, чтобы при фик-
сированных затратах <р минимизировать полную дисперсию ст^.
Рассмотрим в качестве примера случай, когда
<p,(z) = l/xai — 1, г‘=1,...,тп,
где а» — заданные положительные константы. В этом случае опти-
мальные «веса» помех p,i, минимизирующие суммарную помеху (7)
при заданных затратах (6), даются выражениями
щ = (Аоа,/ст?)1/(1+ои),
(8)
где Ао — корень уравнения
+ + A1/(l+“m)(Qm/tr2i)l/(l+am) = v + т
Таким образом, затраты tp на уменьшение дисперсии суммарной
помехи ст| целесообразнее всего распределить по компонентам с ве-
сами Hi, определяемыми формулой (8). Разделение помех на соста-
вляющие по предложенной методике является, по нашему мнению,
полезной операцией.
5. Проблемы прогноза сильных землетрясений
В заключение остановимся на перспективах использования из-
ложенных выше новых подходов в проблеме прогноза временных
рядов к задаче прогноза сильных землетрясений.
Подход, изложенный в разд. 3, фактически уже предложен для
использования в прогнозе землетрясений [6,7]. Упоминавшиеся выше
ошибки «пропуска цели» и «ложной тревоги» являются содержатель-
ными примерами ошибок разного типа, связанных с прогнозом. Ми-
нимизация функции потерь от условных вероятностей этих ошибок
определяет оптимальный прогноз. В принципе таких условных ве-
роятностей может быть не две, а больше. Это позволит более полно
характеризовать оптимальный прогноз.
Расчленение помехи на три составляющие, предложенное в [8],
и изложенное в разд. 4 обобщение этого подхода, по-видимому, ра-
зумно применять в задачах прогноза землетрясений, как, впрочем,
и во многих других практических задачах. Этот метод, по суще-
ству, дает анализ природы помех и указывает наиболее простой
способ понижения суммарной помехи.
Наиболее сложный и неясный вопрос заключается в том, можно
ли использовать достижения динамического хаоса и нелинейного
прогноза в задачах прогноза землетрясений. Приведем сначала не-
которые соображения, которые заставляют скептически относиться
к такой возможности.
Прежде всего, для землетрясений в отличие от задач конвекции,
гидродинамики или магнитогидродинамики не установлены урав-
нения, которым подчиняется процесс. В то время как для перечи-
сленных задач, по крайней мере, в некоторых частных случаях тео-
ретически (или численно) доказано, что их решения обладают свой-
ствами динамического хаоса с небольшим числом степеней свободы,
для землетрясений неясно даже, для какого физического поля нужно
пытаться найти уравнения. Землетрясения происходят в блочной,
пересекаемой многочисленными разломами, сильно неоднородной
твердой оболочке Земли — литосфере — в результате ее деформи-
рования под действием тектонических сил. Есть основания пола-
гать, что на сейсмический режим оказывают сильное влияние раз-
личные физические и химические процессы: тепловые, электриче-
ские, движение флюидов по разломам и т.д.
Насколько реально установить адекватные уравнения для поля
напряжений в такой сложной среде? И как выглядит поле прочно-
стей при этих условиях? Ответы на эти вопросы непросты.
Отметим еще, что даже для движений, описываемых нелиней-
ными уравнениями, имеющими свойства динамического хаоса, при-
менение развитых методов прогноза [9,10,13] может быть совер-
шенно неэффективным из-за большого числа степеней свободы.
Если это число превосходит, скажем, 50, то объем наблюдений,
необходимых для оценки динамики и конструкции прогноза, ста-
новится огромным и нереальным в большинстве практических за-
дач. Надежда на маломерную динамическую систему, управляю-
щую землетрясениями, пока не имеет серьезных оснований.
Вторая особенность задач прогноза землетрясений состоит в
том, что уровень помех в них очень высок. Если во впечатляю-
щих примерах динамического прогноза уровень помех на 1-2 по-
рядка ниже уровня полезного сигнала (поля), то для сейсмических
событий ошибки соизмеримы с полезным сигналом, если говорить,
скажем, о поле напряжений и методах его регистрации. Ясно, что
если в самой благоприятной для прогноза динамической системе
внешние шумы соизмеримы с сигналом, то прогноз будет очень не-
надежным.
На что же можно надеяться в применении достижений динами-
ческого хаоса к задачам прогноза землетрясений?
Прежде всего, отметим, что благодаря целенаправленным рабо-
там по прогнозу землетрясений сейсмологам удалось выявить не-
сколько более или менее эффективных предвестников землетрясе-
ний (действующих неоднозначно, но статистически) и построить
методы долгосрочного (на 1-3 года вперед) прогноза, обладающего
хотя и ограниченной точностью и надежностью, но, тем не менее,
вполне годного для использования в целях уменьшения потерь от
землетрясений [14]. Статистическая значимость этих методов дол-
госрочного прогноза несомненна. Имеются также отдельные слу-
чаи успешного краткосрочного прогноза [15]. Это наводит на мысль
использовать при реконструкции фазового пространства для сей-
смического процесса наиболее надежные из предвестников. Если
будет найдена такая совокупность предвестников, состояние кото-
рой определяет с приемлемой надежностью прогноз сильного земле-
трясения, то дальше можно воспользоваться развитыми в нелиней-
ной динамике методами интерполяции траекторий в фазовом про-
странстве.
Разработанные В.И.Кейлис-Бороком и его коллегами мето-
ды долгосрочного прогноза сильных землетрясений [14] выдаются
с неопределенностью в 1-3 года по времени и порядка 200-400 км
по пространству. Разумеется, такой долгосрочный прогноз нельзя
сопоставлять по его полезности с краткосрочным прогнозом с не-
определенностью, скажем, в одни сутки по времени и в 10-20 км по
пространству. Но именно за счет большей неопределенности в дол-
госрочном прогнозе удается добиться большей надежности. Сле-
дует отметить, что дискретизация фазового пространства динами-
ческих систем может значительно «уменьшить хаос» и даже приво-
дить к детерминированному поведению в огрубленном, дискретизо-
ванном пространстве. Это явление называют «шумящие циклы» [16].
При этом невозможно предсказать траекторию системы внутри
огрубленных частей, хотя порядок их следования детерминирован.
Вопросы дискретизации фазового пространства очень сложны и
интересны, но пока еще мало разработаны. Они относятся к так
называемой символической динамике [17].
Заметим, что при вынесении суждения о возможности или невоз-
можности эффективного прогноза землетрясений следует соблю-
дать осторожность. В самом деле, любое уравнение или матема-
тически доказанное утверждение, которое свидетельствует о не-
возможности прогноза, всегда базируется на каких-то предполо-
жениях и упрощениях природного сейсмического процесса. Ска-
жем, рассматриваются только явления в рамках принятых пред-
ставлений механики разрушения и при определенных условиях да-
ется заключение о невозможности эффективного прогноза. Однако
помимо явлений, рассматриваемых механикой разрушения матери-
алов, в реальной жизни происходит еще масса других: электриче-
ских, химических, магнитных и т.д. Кроме того, диапазон частот,
которым оперирует механика разрушения, ограничен, а полезная
для прогноза информация может содержаться в инфра- или ульт-
развуковых колебаниях, лежащих вне этого диапазона. На такие ко-
лебания могут реагировать животные, либо специальные приборы.
Поэтому делать вывод о невозможности вообще эффективного про-
гноза землетрясений с определенной точностью явно неосторожно
и преждевременно. Речь может идти лишь об ограниченной способ-
ности прогноза конкретных методов при принятых упрощениях.
ЛИТЕРАТУРА
1. Колмогоров А.Н. Интерполирование и экстраполирование стационарных
случайных последовательностей // Изв. АН СССР. Сер. мат. 1941. Т.5.
С.3-14.
2. Wiener N. Exyrapolation, inyerpolation and smoothing of stationary time series.
Cambridge (Mass): MIT press, 1949. 163 p.
3. Садовский M.A., Писаренко В.Ф. Случайность и неустойчивость в геофи-
зических процессах // Изв. АН СССР. Физика Земли. 1989. М* 2. С.3-12.
4. Шустер Г. Детерминированный хаос. М.: Мир, 1988. 240 с.
5. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания.
М.: Наука, 1987. 423 с.
6. Молчан Г.М. Стратегии в прогнозе сильных землетрясений // Компью-
терный анализ геофизических полей. М.: Наука, 1990. С.3-27.
7. Molchan G.M. Structure of optimal strategies in earthquake prediction // Pure
and Appl. Geophys. 1991. Vol. 129. P.375-387.
8. Кравцов Ю.А. Случайность, детерминированность, предсказуемость //
Успехи физ. наук. 1989. Т.158, № 1. С.93-122.
9. Casdagli М. Nonlinear prediction of chaotic time series // Physica D. 1989.
Vol.35. P.335-346.
10. Abarbanel H., Brown R., Kadtke B. Prediction in chaotic nonlinear systems;
methods for time series with broadband Fourier spectra // Phys. Rev. A. 1990.
Vol.41, № 4. P.1782-1807.
11. Packard N., Crutchfield J., Farmer J., Shaw R. Geometry from a time series
// Phys. Rev. Lett. 1980. Vol.45, № 9. P.712-716.
12. Takkens F. Detecting strange attractors in turbulence // Leet. Notes in Math.
Berlin; Heidelberg: Springer, 1981. № 898. P.366-381.
13. Farmer J., Sidorovich J. Predicting chaotic time series // Phys. Rev. Lett.
1987. Vol.59, № 8. P.845-848.
14. Габриэлов A.M., Дмитриева О.Д., Кейлис-Борок В.И. и др. Долгосроч-
ный прогноз землетрясений: Методические рекомендации. М.: Наука, 1986.
127 с.
15. Моги К. Предсказание землетрясений. М.: Мир, 1988. 382 с.
16. Bowen R. Equilibrium states and the ergodic theory of Anosov diffeomorphisms
// Leet. Notes in Math. Berlin; Heidelberg: Springer. 1975. М» 470. P.280-341.
17. Компьютеры и нелинейные явления: Информатика и современное естество-
знание / Предисл. А.А. Самарского. М.: Наука, 1988. 192 с.
КИБЕРНЕТИКА И ИНФОРМАТИКА
Ю.А.Кравцов
ФУНДАМЕНТАЛЬНЫЕ И ПРАКТИЧЕСКИЕ
ПРЕДЕЛЫ ПРЕДСКАЗУЕМОСТИ
Введение
Колоссальный интеллектуальный прорыв, совершенный в XX в.
и подготовленный всем развитием науки в предшествующие сто-
летия, не мог не создать иллюзию о всемогуществе научных зна-
ний, о способности науки решить сколь угодно сложные проблемы
техники, медицины и т.д. Наука и сейчас продолжает оставаться
фундаментальным фактором прогресса. Однако по одному вопросу
научный прогресс явно замедлился и наука едва ли может проде-
монстрировать свое прежнее могущество, несмотря на, безусловно,
возросшие возможности регистрировать, накапливать и анализиро-
вать данные с помощью современных компьютеров. Таким вопро-
сом является проблема предсказуемости. Что ограничивает время
прогноза? Почему возможностей современных ЭВМ часто недоста-
точно, чтобы обрисовать даже ближайшее будущее? Чего именно
не достает современному научному подходу для эффективного про-
гноза? Почему способность человеческого общества предсказывать
будущее растет отнюдь не пропорционально вложенным средствам?
В данной статье мы обсудим вопросы предсказуемости на срав-
нительно простом примере динамических процессов колебательного
типа, т.е. процессов, которые осциллируют по более или менее слож-
ному закону относительно какого-то уровня. Уже на примере ко-
лебательных динамических систем можно углядеть основные фак-
торы, ограничивающие предсказуемость. Таких факторов сущест-
вует, увы, достаточно много, и свою задачу автор видит в том,
чтобы выявить только основные, если не очевидные препятствия
удовлетворительному прогнозу.
Итак, что же ограничивает предсказуемость?
1. Реальный, наблюдаемый и модельный процессы
Любой прогноз начинается с анализа наблюдаемого процесса
y(t), под которым мы будем подразумевать процесс, регистриру-
емый физическими приборами. Наблюдаемый процесс y(i) отнюдь
не тождествен реальному, физическому процессу x(t). Дело в том,
что наблюдение (измерение) всегда подвергается искажениям.
Прежде всего, физические приборы обычно осуществляют филь-
трацию сигнала, т.е. вносят определенные спектральные искаже-
ния. К этому типу искажений относится, в частности, простая вре-
менная задержка, y(t) = x(t — г), характерная для многих систем:
технических, экономических, метеорологических и т.д. При силь-
ном сигнале или при использовании неадекватного измерительного
устройства могут проявиться нелинейные искажения. Далее, прин-
ципиальную роль играют шумы и помехи при измерениях, которые
ради краткости мы будем называть просто измерительными шу-
мами и обозначать Измерительные шумы ограничивают воз-
можности измерить, а в некоторых случаях — даже обнаружить
слабые сигналы.
Наконец, вектор наблюдаемых данных y(t) может иметь мень-
шую размерность qy, чем размерность реального процесса qx, по-
скольку число измеряемых параметров всегда меньше, чем общее
число степеней свободы, вовлекаемых в движение. Такие искаже-
ния можно назвать размерными.
В простейшем случае, когда спектральные, размерные и нели-
нейные искажения пренебрежимо малы, а шум имеет аддитивный
характер, наблюдаемый процесс y(t) связан с реальным процессом
x(t) соотношением
y(t) =x(t) + v(t). (1)
Прогноз всегда составляется на основе модельных представле-
ний и возникает как результат упрощенного (приближенного, иде-
ализированного) описания реальной системы. Дифференциальное
уравнение, которому подчиняется реальная динамическая система,
символически запишем в виде
Mx(d/dt,x',Qk,fj) = 0, (2)
где Мх — оператор, отвечающий данной системе; d/dt — символ
дифференцирования, х — набор переменных, существенных для
данной задачи при принятом уровне описания; а*, — параметры
реальной системы; fj(t) — все несущественные, малозначащие и
флуктуационные переменные.
В разбиении переменных на существенные и несущественные
уже содержится определенный произвол. В зависимости от того,
Рис.1. Процессы, рассматриваемые при предсказании. z(t) — реальный фи-
зический процесс (пунктир); y(t) — наблюдаемый (регистрируемый) про-
цесс (тонкая линия), z(t) — модельный, предсказываемый процесс (толстая
линия).
как он решается, возникает то или иное приближенное модельное
уравнение
M2(d/dt,z-,ak,Q) = 0. (3)
Здесь ak — оценки параметров (в идеале at — а символ
«О» поставлен там, где в реальной системе (2) находились малозна-
чительные факторы fj. Пренебрежение этими факторами и соста-
вляет существо идеализации.
При рассмотрении проблемы предсказуемости мы вынуждены
иметь дело фактически с двумя процессами: наблюдаемым y(t) и
модельным z(t), тогда как реальный процесс x(t) остается как бы
на заднем плане: он не подвергается прямой регистрации, не имеет
определенной размерности, подвержен влиянию флуктуационных
факторов Все три процесса схематически изображены на
рис. 1. В качестве начального условия z° для модельного процесса
z(t) естественно взять значение у° наблюдаемого процесса y(t) в
начальный момент времени t°:
х° = У°, z° = z(t°), y° = y(t°). (4)
Именно в силу этого соотношения измерительные шумы i/(t) ока-
зывают существенное влияние на прогноз. Действительно, из (4) и
(1) следует, что начальное значение модельного процесса отлича-
ется от начального значения реального процесса: z° = х° + i/°, и
если уравнение (2) для x(t) обладает свойством локальной неустой-
чивости, как для большинства динамических систем, то начальная
невязка v° = z° — х° породит экспоненциально нарастающую раз-
ницу \z — т| ~ i>° ехр(А+т), где А+ — наибольший ляпуновский пока-
затель, а т = t — t° — интервал времени после начала наблюдения.
Вторая причина погрешности прогноза — действие флуктуаци-
онных сил Даже в отсутствие измерительных шумов флуктуа-
ционные силы fj(t) вызывают слабое начальное расхождение между
процессами z и х, после чего включится механизм экспоненциаль-
ного роста возмущений. Этот механизм появления погрешностей
прогноза присущ всем без исключения физическим системам.
Третий, наиболее важный источник погрешности прогноза —
неточность модельного оператора Mz относительно реального опе-
ратора Мх. Именно от выбора модельного оператора Мг и зависит
в основном успех прогноза.
Из каких соображений следует выбирать оператор ЛГ2? Что огра-
ничивает время предсказуемого поведения? Почему прогноз так
редко бывает удачным? Чтобы ответить на эти вопросы, введем
количественную меру качества прогноза и обсудим ряд понятий,
связанных с предсказуемостью динамических процессов: степень
предсказуемости, время предсказуемого поведения, горизонт пред-
сказуемости и др.
2. Степень предсказуемости. Горизонт предсказуемости
Общепринятой характеристикой качества прогноза служит сред-
ний квадрат ошибки Т] = у — z:
<Т?2) = ((У-^)2). (5)
Угловые скобки означают здесь эмпирическое усреднение. Если
Уз = + т) — значение процесса y(t) спустя время т после мо-
мента начала j-ro наблюдения, a Zj = z(t® + т) — соответствую-
щий прогноз на интервале (t°, £° + т), удовлетворяющий начальному
условию (4) (г® — у®), то средний квадрат ошибки (5) дается выра-
жением
1 N
= дг S + т')~ + г)]2 • (6)
j=i
Считается, что чем больше проведено наблюдений, тем надеж-
нее оценка погрешности (6).
Для того чтобы характеризовать потенциальную предсказуе-
мость, удобнее использовать безразмерную характеристику
которая представляет собой коэффициент корреляции между про-
гнозом и наблюдением спустя время т после начала наблюдения.
Рис.2. Характер зависимости степени предсказуемости D от времени
т = t — t°, протекшего после начала наблюдения.
Эта величина равна единице при т = t — t° = 0, поскольку началь-
ное значение прогноза z° берется равным у°. Если значения у и z
отсчитывать от среднего уровня, то с течением времени величина
D будет уменьшаться до нуля.
Общий ход зависимости D{t) показан на рис. 2. Значения D(t),
близкие к единице, отвечают удовлетворительному прогнозу, тогда
как малые значения соответствуют несогласованному ходу наблю-
дения и прогноза. Поэтому величину £>(т) естественно назвать сте-
пенью предсказуемости, а время, за которое D{r) падает до уровня
1/2 — временем предсказуемого поведения Tpred- Степень предска-
зуемости D однозначно связана с абсолютной погрешностью про-
гноза {if):
= (y2) + {z2) Г _ {if) 1
<1/2> + <г2>Г W
Времени предсказуемого поведения rpred отвечает абсолютная
погрешность {if) порядка 1/2((у2) + {z2)) и {у2}, т.е. порядка дис-
персии наблюдаемого процесса.
С общей точки зрения степень предсказуемости D{r) можно
рассматривать как степень сходства между наблюдением и про-
гнозом. Если высокую степень сходства (D » 1) рассматривать
как свидетельство определенного, детерминированного поведения,
а малые значения D{r) приписать непредсказуемому, случайному
поведению, то D{r) можно трактовать как степень детерминиро-
ванности наблюдаемого процесса y{t) по отношению к модельному
процессу z(t). Именно такая трактовка была принята в статье [1].
Отожествление случайности с непредсказуемостью лежит в основе
концепции частично детерминированных процессов и полей, кото-
рая была развита в работах [1-3]. Согласно этой концепции, процесс
y{t) рассматривается как полностью детерминированный (полно-
стью предсказуемый) на временах, малых по сравнению со време-
нем предсказуемого поведения rpred, как полностью случайный на
больших временах т 2> тргеа и как частично детерминированный на
промежуточных временах т » Tpred-
Трактовка случайности как непредсказуемости является лишь
одним из многих соглашений о случайности, принятых в совре-
менном научном обиходе. Теоретико-множественный подход, соста-
вляющий основу современной теории вероятности, связывает слу-
чайность с существованием вероятностной меры (вероятностных
распределений), относя к случайным любые величины, процессы и
поля, снабженные вероятностной мерой. Колмогоровский алгорит-
мический подход отождествляет случайность с алгоритмической
сложностью. В экспериментальной физике случайность часто свя-
зывают с потерей корреляции. Так, для процесса y(t), характери-
зуемого коэффициентом корреляции
Ку(т) =
- т))
<2/2>
О)
значения процесса, разделенные временем, превышающим время кор-
реляции тс, считаются случайными.
Важно, что один и тот же процесс может быть случайным с
точки зрения одного соглашения и детерминированным — в рам-
ках другого. Так, процесс, имеющий сложный известный алгоритм,
является случайным в рамках алгоритмического подхода и детер-
минированным в рамках теории частичной детерминированности,
поскольку при известном алгоритме мы в состоянии построить про-
гноз z(t) на достаточно больших интервалах времени с гаранти-
рованным значением степени предсказуемости D = 1. Еще один
пример относится к случаю, когда время предсказуемого поведе-
ния Tpred превышает время корреляции тс. В интервале тс < т <
< Tpred один и тот же процесс y(t) следует классифицировать как
случайный, если действовать в рамках соглашения, отождествля-
ющего случайность с потерей корреляции, и как детерминирован-
ный о точки зрения теории частичной детерминированности, ото-
жествляющей случайность с непредсказуемостью.
Соотношение тс < rpred является довольно типичным для многих
динамических систем (несколько примеров будут приведены ниже).
Более того, по отношению к системам, допускающим хотя бы в
принципе динамическое прогнозирование, можно утверждать, что
время корреляции тс является наименьшим (наихудшим) временем
прогнозируемого поведения, а коэффициент корреляции Ку(т) —
наименьшей (наихудшей) степенью предсказуемости. Низший пре-
дел Tpred = тс реализуется в условиях, когда мы не располагаем
динамическим уравнением и для прогноза используем принцип
«завтра будет как сегодня». В этом случае в качестве прогноза
z(t) — z(t° + т) берется значение y(t°), наблюдаемое в данный мо-
мент t°:
z(t + т) = y(t°) или z(t) = y(t - т). (10)
В итоге степень предсказуемости (7) превращается в коэффи-
циент корреляции (9). Очевидно, все сказанное справедливо и в от-
ношении степени и времени когерентности, поскольку мерой коге-
рентности служит как раз коэффициент корреляции (7).
Отметим попутно тщетность попыток получить время предска-
зуемости ТрГе<1, заметно превышающее время корреляции тс, с помо-
щью статистических методов прогноза, опирающихся на линейные
алгоритмы авторегрессионого типа. Сопоставимость Tpred со вре-
менем корреляции тс можно установить из весьма общих соображе-
ний. В качестве примера рассмотрим линейный прогноз размерно-
сти m + 1:
z(t° + т) = aoy(t°) + aiу(t° - г) + ... + amy(t° - тт), (11)
составленный из ттг + 1 предшествующих значений наблюдаемого
процесса.
Если выбрать оптимальные коэффициенты ат из условия мини-
мальности среднего квадрата ошибки прогноза (5), то все коэффи-
циенты ат выразятся через значения функции корреляции Ку(пт),
п = 0,1,..., пг. В то же время степень предсказуемости (7) выража-
ется через те же самые значения Ку[пт). В итоге уравнение D(r) =
= 1/2, из которого надлежит определить rpred, содержит только
значения функции корреляции и не может дать значения Tpred, су-
щественно отличные от тс. Мне представляется, что эти простые
соображения еще не осознаны в должной мере разработчиками ли-
нейных статистических предикторов авторегрессионого типа, не-
смотря на то что в литературе имеются убедительные свидетель-
ства этому.
Один из примеров относится к зашумленному динамическому
хаосу [1,4]. Пусть А+ — наибольший положительный показатель
Ляпунова. Тогда средний квадрат ошибки прогноза нарастает по
экспоненциальному закону
<^2) = (<$ + <*/ + <^дм) ехр<2А+т\ (12)
где величины <т£, aj и <7дМ отражают соответственно вклад инстру-
ментальных шумов, вклад физических шумов в системе и влияние
неточности модели ДМ = Mx — Mz. Последнее слагаемое можно ин-
терпретировать как вклад «шумов незнания» (термин используется
в теории обнаружения слабых сигналов). Приравняв средний ква-
драт ошибки (12) дисперсии наблюдаемого процесса (у2), получим
оценку времени предсказуемого поведения
т 1 1-
Tpred ~ in 2 , „2 i „2 '
2Л+ av +<Tf + <тдм
По порядку величины 1/(2А_|_) отвечает времени корреляции си-
стемы: тс « 1/2А+- Поэтому отношение тргеа/тс характеризуется
значением величины, стоящей под знаком логарифма. Если, напри-
мер, шумовые слагаемые и <тдм составляют одну тысячную
от среднеквадратичной амплитуды Ау ~ (j/2)1^2, то тргеа «
» тс In 103 ~ 7тс, т.е. в 7 раз превышает время корреляции. Если
же шумовые слагаемые составляют 10-6 от Ау, то время предска-
зуемости возрастает до 14тс.
Важным является понятие горизонта предсказуемости 7Ъог> вве-
денное Дж. Лайтхиллом [5] для обозначения времени, в течение ко-
торого микроскопически малое различие в начальных условиях на-
растает до макроскопических величин порядка Ау. Мы будем трак-
товать горизонт предсказуемости несколько иначе — как предель-
ное время предсказуемого поведения, которое нельзя превзойти ни
усовершенствованием измерительных приборов, ни усовершенство-
ванием предсказательной модели z(t) [1]. Иными словами, горизонт
предсказуемости Thor отвечает пределу пренебрежимо малых изме-
рительных шумов и шумов незнания:
7Ъог — Цр}х Tpred’
м—>O,AJW—>0
В только что рассмотренном примере зашумленного динамиче-
ского хаоса этому условию отвечает пренебрежение вкладами а2 и
Одм по сравнению с вкладом физических шумов aj, влияние кото-
рых невозможно устранить полностью ни при каких условиях:
71,01 2А+ 1П а2
(15)
Представленные здесь соображения позволяют составить общую
картину изменения степени предсказуемости по мере совершенство-
вания прогностической модели z(t). На малых временах, не превы-
шающих время корреляции тс, удовлетворительный прогноз дается
принципом «завтра как сегодня» (11). Степень детерминированно-
сти (7) в этом случае совпадает с коэффициентом корреляции (9),
временной ход которого изображается кривой 1 на рис. 3. При
Л(т), Ка(т)
Рис.З. Характер изменения степени предсказуемости по мере совершенствова-
ния модели процесса. Кривая 1 отражает качество прогноза по принципу «зав-
тра как сегодня»; кривые 2 и 3 отвечают более или менее удовлетворительным
моделям zi(t) и Z2(t), а кривая 4 дает предельно достижимое значение степени
предсказуемости («горизонт предсказуемости»). Переход А —> В от модели zi
к более совершенной модели zi переводит процесс из разряда случайных (не-
предсказуемых) к детерминированным (предсказуемым).
Tpred ~ тс некоторое улучшение могут дать линейные статистиче-
ские модели авторегрессивного типа (11), но радикальное преодо-
ление порога возможно только за счет модельных процессов, полу-
чаемых на основе динамических уравнении.
По мере совершенствования модели степень предсказуемости,
а вместе с нею и время предсказуемого поведения увеличиваются
(см. рис. 3). На этом этапе процесс y(t) может превратиться из
случайного, непредсказуемого (точка А на кривой 2, отвечающей
модели zi (t)) в детерминированный, предсказуемый (точка В на
кривой 3, отвечающей улучшенной модели ^(i)). Переход из слу-
чайного в детерминированное состояние возможен только в рамках
концепции частично детерминированных процессов, отождествля-
ющей случайное с непредсказуемым, и характерен для практики
физического эксперимента. В сущности, речь идет о переходе «не-
понятого» в «понятое». В рамках аксиоматической теории вероят-
ностей такой переход невозможен в принципе, поскольку в теории
вероятностей случайный процесс остается таковым независимо от
того, существуют или нет модели для его предсказания.
Наконец, существует предельное время предсказания — гори-
зонт предсказуемости Thor, начиная с которого никакая модель не
может обеспечить удовлетворительное предсказание. Предельная
степень предсказуемости изображена на рис. 3 кривой J.
Оценка предельного времени предсказания 7hor имеет принципи-
альное значение: бессмысленно даже пытаться строить прогнозы на
времена, превышающие 7hor- Такие прогнозы не могут дать ничего,
кроме потерь времени и средств, не говоря уже о моральном ущербе
от несбывшихся прогнозов.
Если окажется, что все испытанные модельные процессы z(t)
не в состоянии вывести степень предсказуемости D(r) за контуры
коэффициента корреляции Ку(т), т.е. если Tpred < тс, то попытки
построить ритмическую модель исследуемого процесса j/(t) следует
признать безуспешными, а сам процесс y(t) целесообразно квалифи-
цировать как шум. Иными словами, шум — это случайный (в обыч-
ном теоретико-вероятностном смысле) процесс, для которого не
удается подобрать динамическую предсказательную модель. В то
же время процессы, допускающие предсказания на времена, пре-
вышающие время корреляции, следует отнести к классу частично
детерминированных (частично предсказуемых) процессов.
Выше мы говорили об алгоритмах эволюции, описываемых диф-
ференциальными уравнениями. Между тем во многих системах дей-
ствуют конечно-разностные алгоритмы (отображения). Приведем
краткие сведения об этих алгоритмах, поскольку следующие ниже
примеры основаны именно на конечно-разностном описании.
Пусть хт — динамическая переменная, F(xm-i, /т-1) — не-
линейная функция, осуществляющая преобразование хт-1 в тт, а
fm — флуктуационные влияния. Реальная последовательность под-
чиняется, таким образом, уравнению
хт = F(Xm—1, fm—1)- (16)
Наблюдаемая последовательность ут отличается от хт вслед-
ствие нелинейных, спектральных и шумовых искажений. В простей-
шем случае, когда действуют только аддитивные шумы, ут и хт
связаны между собой соотношением ут = хт + ит, подобным (1).
В качестве модельного уравнения возьмем «бесшумное» отобра-
жение
zm = F2(zm_!,0), (17)
которое заменяет теперь модельное дифференциальное уравне-
ние (3). В качестве начального условия для модельной последова-
тельности z° возьмем начальное значение наблюдения у° : z° = у°.
Проиллюстрируем общие утверждения этого раздела некоторыми
расчетами для кусочно-линейных отображений (рис. 4). Эти рас-
четы демонстрируют исключительно важную роль шумов и не ме-
нее важную роль модели в вопросе о предсказуемости локально не-
устойчивых систем. На рис. 5-7 представлены результаты вычисле-
ния степени предсказуемости D и коэффициента корреляции Ку,
полученные в работе [2] для системы, которая описывается одно-
мерным кусочно-линейным отображением отрезка (0,1) в самого
себя:
•^т — •^'(•Ет—1) "Ь fm— li ^'(з-) — {^^}i Ут — -^т-
(18)
Рис.4. Кусочно-линейное отображение, а — слабый наклон; б — уме-
ренный наклон; в — сильный наклон.
Рис.Б. Зависимости степени предсказуемости (а) и коэффициента
автокорреляции (6) от дискретного времени ц для разных значе-
ний уровня шума. Степень предсказуемости существенно зависит от
уровня шума, тогда как чувствительность коэффициента автокорре-
ляции Ку(ц) к шуму незначительна.
Здесь F(x) = {Ля} — дробная часть числа Ах (графики F(x)
при А = 1.1, Л = 2.0 и Л = 9.9 приведены на рис. 4); fm — аддитив-
ное флуктуационное воздействие с равномерной плотностью веро-
ятности в интервале —10_р < f < 10“р, р — показатель, характе-
ризующий силу флуктуаций: чем больше р, тем слабее флуктуации
(в наших примерах 2 < р < 6). Значения fm п fn при т / п счи-
таются некоррелированными: В данном случае, когда при-
нята модель аддитивных шумов fn, введение измерительных шумов
представляется излишним, так что в (18) различение между наблю-
даемой и реальной последовательностями не проводится: ут = хт.
Что касается модельной последовательности zm, то мы подчиним
ее незашумленному уравнению
zm = F(zm-1), F(z) = {Az}. (19)
На рис. 5,а показаны полученные численным моделированием
зависимости степени предсказуемости Р(д) от дискретного вре-
мени р = т — тп°, прошедшего после начала испытания. Серия кри-
вых на рис. 5 в отвечает значению коэффициента наклона А = 2
(см. рис. 4,6) и пяти значениям показателя р — 2 -? 6, т.е. пяти зна-
чениям уровня шумов ст/ от 10“2/л/3 до 10-6/\/3.
Кривые на рис. 5,в показывают, что степень предсказуемости
близка к единице в течение 5-15 тактов, а затем довольно быстро
спадает до нуля. Время предсказуемого поведения оказывается
сильно зависящим от уровня шумов оу и подчиняется логарифми-
ческим соотношениям типа (15) с показателем Ляпунова А+ = А.
По порядку величины при А = 2ppre(j » (1/2 А) 1п(1/о2), что неплохо
согласуется с фактическими значениями ppred, которые можно из-
влечь из рис. 5,а.
Между тем коэффициент корреляции Ку(р} спадает до уровня
~ 1/2 практически уже на первом шаге, при этом Ку(р) обнаружи-
вает весьма слабую чувствительность к уровню шумов (рис. 5,6).
Этот результат свидетельствует о глубоком различии между вре-
менем корреляции и временем предсказуемости.
Изменение параметра А в отображении (17) существенно вли-
яет на качество предсказания. На рис. 6, в и б показаны зависимости
Л(д) для отображений с малой (А = 1.1), средней (А = 2) и большой
(А — 9.9) крутизной при двух значениях уровня шума: рис. 6,в от-
вечает умеренному уровню шума (р — 2), когда помеха составляет
около 1% относительно типичного значения у ~ 1, а рис. 6,6— силь-
ному шуму (р = 1), достигающему 10% наблюдаемых осцилляций.
Рис. 6,а, 6 показывают, как уменьшается время предсказуемости
при увеличении крутизны отображения А. Так, из рис. 6,6 следует,
что при сильном шуме (р = 1) время предсказания ppred падает с
4.7 при А = 1.1 до 1.4 при А = 9.9. В то же время из рис. 6,в,г,
иллюстрирующих поведение коэффициента корреляции Ку(р}, сле-
дует, что при переходе от малой крутизны А = 1.1 к большому
значению А = 9.9 и от меньшего уровня шума (<т/ ~ 10-2) к боль-
Рис.6. Зависимости степени предсказуемости (а, б) и коэффициента авто-
корреляции (в, г) от дискретного времени д для различных наклонов А и
для умеренного и сильного уровней шума, а, в — р = 2, а/ = 0.01/л/З; б, г —
р= 1.
тему (ст/ ~ 10-1) время корреляции практически не меняется и
составляет всего лишь один такт.
Если в модельном уравнении (19) коэффициент А подвергнуть
малым вариациям ДА, то время предсказуемого поведения «почув-
ствует» неточность модели при ДА > ст/, поскольку в этом случае,
согласно (13), дрге<1 « (1/2А) 1п[1/ст2 + (ДА)2]. Изучая зависимость
Ppred от гипотетического значения А = А+ДА или же, что практи-
чески более удобно, зависимость степени предсказуемости Л от А
при фиксированном д (рис. 7), можно решить две практически важ-
ные задачи: во-первых, оценить параметр А в физической системе,
скажем, по значению, обеспечивающему максимальное время пред-
сказания /iPred> а во-вторых, определить уровень шумов в системе
ст/ по ширине кривой на рис. 7. Обе эти задачи чрезвычайно часто
встречаются в практических исследованиях, причем не только в фи-
зике. Эффект принципиальной важности состоит в том, что рост
шумов ст/ и неточность параметров модели ДА входят в рассмо-
трение как бы на равных, и если в реальной физической системе не
удается изменить никакие параметры, то такую неопределенность
Рис.7. Зависимость степени предска-
зуемости D от величины наклона А
(ширина кривой определяется уровнем
шума).
следует признать неустранимой. В этом случае никакое уточнение
модели не может дать сколько-нибудь ощутимого эффекта.
3. Поиск предсказательных моделей
С точки зрения математики проблема предсказуемости сводит-
ся к решению обратной задачи, а именно, к восстановлению динами-
ческого уравнения, которому подчинялся бы наблюдаемый процесс
y(t) [6]. Располагая таким уравнением, можно было бы построить
его решение при t > t°. Это решение и послужило бы прогнозом z(t).
Трудности решения такой обратной задачи огромны. Прежде
всего, существует бесконечно много уравнений, которым удовле-
творял бы наблюдаемый процесс y(t) с определенной точностью,
диктуемой флуктуационными условиями задачи. В этом проявля-
ется свойство неполноты любой системы гипотез, моделей, идеа-
лизаций, что тесно связано с теоремой Гёделя о неполноте любой
системы аксиом.
Ясно, что обратная задача вообще не разрешима, если не при-
бегнуть к сужению класса пробных уравнений. В этом сужении
и состоит, собственно говоря, основная трудность решения про-
блемы. Хорошо, если структура исследуемой системы в основных
чертах известна. Тогда задача сведется к определению коэффици-
ентов этих уравнений.
Если же структура системы неизвестна, целесообразно испы-
тать те или иные модели для объяснения наблюдаемого поведения.
Общие требования к моделям неоднократно обсуждались в лите-
ратуре: модель должна адекватно передавать основные свойства
системы, не будучи ни чересчур сложной, ни чересчур упрощенной.
В сущности, выработка моделей — это то, чем занимается есте-
ствознание. Особенность обратных задач рассматриваемого типа
состоит разве что в том, что речь идет не о поиске фундаменталь-
ных закономерностей, а о выяснении динамической структуры ис-
следуемой системы с использованием уже известных закономерно-
стей.
Наряду с индивидуальным подходом к каждой конкретной за-
даче с глубоким изучением физических процессов в системе (до
недавнего времени это был единственно возможный путь) можно
предложить также формальный математический подход, ориенти-
рованный на использование суперкомпьютеров. Речь идет о соста-
влении библиотеки типичных динамических уравнений с автома-
тической подгонкой коэффициентов под наблюдаемый процесс. Не-
смотря на значительные ожидаемые затраты машинного времени,
задача подгонки не представляется чересчур реалистичной.
Говоря о выборе типичных динамических уравнений, следует
ориентироваться прежде всего на уже исследованные системы, до-
пускающие хаотическое поведение (строго периодические системы
практически мало интересны). Сейчас изучено уже не менее сотни
таких систем. К ним относятся, например, аттрактор Лоренца, не-
автономное уравнение Дуффинга, нелинейный осциллятор под дей-
ствием сильной периодической силы и др.
Далее, каждое из типичных уравнений содержит несколько, ска-
жем, п = 3-г5 параметров, вариацией которых можно осуществлять
подгонку под наблюдаемый процесс. Пусть Да* — разумный шаг
изменения параметра А* = шах а* — min а* — общий диапазон изме-
нения этого параметра. При использовании метода перебора необ-
ходимо вычислить S = П*=1(А*/Да*) решений данного типичного
уравнения.
Полученное таким путем число вариантов, которые необходимо
испытать на близость к наблюдаемому процессу, может оказаться
огромным. Так, если Ак/^аь = 100 (это вовсе не преувеличенная, а
скорее преуменьшенная оценка), а число варьируемых параметров
равно пяти, то S к 10Б = 1О10. Это число следует умножить еще на
число типов испытываемых уравнений Q. При Q = 100 общее число
вариантов составит Si = QS = 1012.
Перебрать подобное число вариантов на суперкомпьютерах
представляется невозможным. Поэтому необходимо сделать все воз-
можное, чтобы уменьшить число испытываемых вариантов. Ука-
жем здесь две более или менее очевидные возможности.
Предварительный выбор более узкого класса уравнений на осно-
ве экспертных оценок. Нам представляется, что на этом пути
можно уменьшить число испытываемых уравнений в 3-10 раз. Ко-
нечно же, это очень мало по сравнению с 1012, но для начала и это
неплохо.
Использование адаптивных и самоусложняющихсл алгоритмов.
Вместо исчерпывающего перебора всех возможных параметров за-
дачи можно попытаться подобрать грубую модель, работающую на
сравнительно коротких интервалах времени, а затем уточнять уже
меньшее число параметров в сравнительно узком диапазоне их зна-
чений. В сущности, речь идет об алгоритмах типа тех, которые ис-
пользуются при создании искусственного шахматного интеллекта.
Главнейшая черта этих алгоритмов — отбрасывание заведомо бес-
смысленных вариантов — представляет первостепенный интерес
для проблемы предсказания.
В одном отношении задача предсказания динамических систем
проще, чем задача шахматных алгоритмов, поскольку в проблеме
предсказания отсутствует активный соперник, который может на-
вязать свою линию поведения. Впрочем, роль активного противо-
действия здесь играют шумы, которые вносят значительный эле-
мент неопределенности.
Имея в виду общую проблему восстановления динамической
структуры исследуемой системы, укажем несколько приемов, ко-
торые могут оказаться полезными при построении динамических
моделей.
Во-первых, вместо локальных значений среднего квадрата ошиб-
ки прогноза (гр) и степени предсказуемости £>(т) на практике целе-
сообразно использовать значения, усредненные еще и по интервалу
наблюдения Т. Если комбинированное (по реализациям и по вре-
мени) среднее обозначить фигурными скобками, например
е°+т
{yz} = У W'W')) dt',
то речь идет об использовании величин
b2} = Ш - *|2} и ОД = {yz}/{y2}^2{z2}^, (20)
которые как бы фильтруют наблюдаемый процесс y(t) относитель-
но модельного процесса z(t). В результате появляется даже возмож-
ность обнаруживать слабый сигнал x(t), скрытый в шумах.
Во-вторых, в качестве критерия качества подгонки можно ис-
пользовать модельное уравнение (3), если подставить в него наблю-
даемый процесс y(t), т.е. оценить величину
si = |M2[d/dt,y(t)]|
или же квадрат этой величины, усредненный по времени Т:
1
в2 = т
(21)
(22)
Величина s% осуществляет своеобразную «фильтрацию моде-
лей»: если наблюдаемый процесс y(t) плохо «вписывается» в модель-
ное уравнение M2(d/dt,z) = 0, то величина s2 оказывается недопу-
стимо большой, что и позволяет исключить соответствующую мо-
дель из рассмотрения.
Может оказаться, что минимизацию {г/2} удобнее проверить на
первоначальном, грубом этапе подгонки, тогда как поиск мини-
мума величин si или s2, более чувствительных к изменениям па-
раметров, целесообразно осуществлять на последующих этапах.
В-третьих, можно рекомендовать некоторые приемы так назы-
ваемого дискриминантного анализа, который используется для вы-
явления внутренних изменений в тех или иных процессах, не об-
наружимых «на глаз» или же при помощи примитивных критериев
типа постоянства дисперсии. Речь идет об анализе нелинейных ком-
бинаций, содержащих наблюдаемый процесс y(t), его степени
у2, у3,...,, а также его производные у1, у и т.д. Наиболее инфор-
мативными оказываются комбинации, которые обнаруживают при-
ближенное постоянство (являются приближенными инвариантами)
на некотором интервале времени, скажем
у" + а^у' + а2(у')2 + азУУ' + а^У + а$У3 - const. (23)
Изменения таких комбинаций свидетельствовали бы о вариациях
параметров а*, т.е. об изменениях внутри системы. Применительно
к рассматриваемой проблеме поиск инвариантов сводится, в сущно-
сти, к определению приближенного дифференциального уравнения
для данной системы и потому заслуживает пристального внимания.
В-четвертых, отметим противоречивую роль шумов в решении
обратной задачи. Как это ни парадоксально, чем больше уровень
шума, тем проще построить предсказательную модель. Дело в том,
что многие слагаемые в дифференциальном уравнении с ростом
флуктуационных сил становятся малозначительными и их можно не
принимать во внимание, благодаря чему резко (на порядки!) сни-
жаются затраты машинного времени на перебор параметров. Разу-
меется, при большом уровне шума время предсказуемого поведения
уменьшается.
В связи с этим можно рекомендовать введение слабого шума
в процесс подбора коэффициентов дифференциального уравнения.
Такой шум может служить регуляризирующим фактором в про-
цессе последовательных приближений.
Важно, что введение искусственного шума позволяет оценить
уровень внутренних флуктуаций в системе. Для этого следует за-
фиксировать уровень шума, при котором коэффициенты восста-
новленного дифференциального уравнения начинают демонстриро-
вать относительную независимость.
Разумеется, многое зависит от спектральной плотности (окра-
шенности) искусственного шума, от того, куда именно (в какое сла-
гаемое уравнения) он вводится и т.д. Тем не менее сама возмож-
ность хотя бы грубо оценить уровень флуктуационных сил пред-
ставляется привлекательной.
В-пятых, следует обратить внимание на возможность предсказа-
ния без восстановления дифференциального уравнения. Речь идет
о предсказании по похожим образцам из прошлого. Пусть, напри-
мер, поведение системы накануне интересующего нас момента вре-
мени t° похоже на то, как вела себя система перед моментом i,
в прошлом. В качестве предсказания при t > t° мы берем тогда
z(t° + т) = y(t, + т). В этом случае задача восстановления динами-
ческой структуры системы не ставится, а информация о предыду-
щем поведении используется, в сущности, как аналоговое решение.
Именно так поступают иногда при долгосрочном (на полгода и бо-
лее) предсказании погоды по метеоданным предыдущих лет.
Совсем недавно такой метод прогноза был испытан на несколь-
ких хаотических системах, описываемых отображениями, в рабо-
те [7]. Основной результат работы состоял в том, что фактическое
время предсказуемого поведения оказалось значительно (в 3, 10 или
даже в 100 раз в зависимости от изучаемого отображения) больше
времени корреляции те. Нам представляется, что эти весьма обнаде-
живающие результаты нуждаются еще в дополнительном анализе
и осмыслении. В частности, не вполне ясно, чем именно опреде-
ляется время предсказуемости: шумами /(t), действующими в си-
стеме, измерительными шумами i/(t), или же неточностью началь-
ных условий в моменты t° и t.. Кроме того, еще предстоит выяс-
нить, как влияет на предсказуемость общая нестационарность (из-
менчивость) внешних условий.
Разумеется, этот вопрос может быть поставлен для всех без ис-
ключения методов предсказания, мы кратко обратимся к нему в
следующем разделе. Здесь же отметим настоятельную необходи-
мость выработки критериев стационарности системы, подвергаю-
щейся прогнозированию на основе стационарной (не зависящей от
времени) модели. Такие критерии помогли бы понять действитель-
ную ценность алгоритмов, выбранных на «испытательном» интер-
вале, и их применимость вне этого интервала времени.
В-шестых, целесообразно кратко обсудить достоинства и недо-
статки «прогноза в прошлое», который иногда рекомендуется для
проверки алгоритмов прогноза на ограниченном фактическом ма-
териале. В этом случае сравнению подвергаются значения наблю-
дения y(t° — т) и прогноза z(t° — т) в момент времени t° — т, пред-
шествующий моменту наблюдения t°. Разумеется, «прогноз в про-
шлое» возможен только при условии, что алгоритм допускает вза-
имно однозначное соответствие между прошлым и будущим. Это
условие сразу же исключает из рассмотрения взаимно неоднознач-
ные отображения в случае конечно-разностных уравнений и си-
стемы с гистерезисами в случае сильно нелинейных дифференци-
альных уравнений.
Но даже в условиях взаимной однозначности время прогноза «на-
зад» не обязательно равно времени прогноза «вперед», потому что
флуктуации нарастают вперед и назад во времени по разным за-
конам. Это видно из формулы типа (13), которая дает оценку вре-
мени предсказуемого поведения в локально неустойчивой системе
с наибольшим положительным показателем Ляпунова А+. Исполь-
зуя эту формулу для прогноза в прошлое, вместо А+ следует под-
ставить модуль наименьшего отрицательного показателя |А_ |, по-
скольку именно этот показатель характеризует рост возмущений
в обращенном времени. Кстати, с конечностью времени прогнози-
руемого поведения в прошлом приходится иметь дело многим спе-
циалистам — историкам, археологам, следователям. Определенную
роль в ограниченности такого прогноза играет и нестационарность
динамических уравнений движения, о чем говорилось выше.
В-седьмых, в некоторых задачах удается перейти от алгоритма
в виде дифференциальных уравнений к конечно-разностному ал-
горитму. Такой переход осуществляется отображением Пуанкаре,
которое устанавливает связь между последовательными точками
£т пересечения фазовой траектории с выделенной поверхностью —
секущей плоскостью Пуанкаре. Ясно, что отображение Пуанкаре
понижает размерность задачи: размерность вектора £ на секущей
плоскости Пуанкаре на единицу меньше, чем размерность про-
странства.
Если исходную задачу удается свести к одномерному отобра-
жению, то это фактически равносильно полному решению задачи,
поскольку свойства зашумленного одномерного отображения доста-
точно хорошо изучены. В качестве примера можно привести одну
из первых (если не самую первую) задач, в которых динамическая
структура восстанавливается на уровне отображения [8].
Система, о которой идет речь, — это автогенератор с туннель-
ным диодом, который генерирует отрезки (цуги) экспоненциально
нарастающих синусоид, рост которых прекращается в момент от-
пирания туннельного диода. Вид генерируемой последовательности
импульсов схематически показан на рис. 8. Вся задача описыва-
ется дифференциальным уравнением третьего порядка. Однако при
Рис.8. Типичный вид последовательности импульсов в генера-
торе Кияшко-Пиковского-Рабиновича (КПР).
определенных условиях ее можно свести к исследованию отображе-
ния, связывающего последовательные значения локальных макси-
мумов ут. На плоскости (ут, Ут-i) экспериментальные точки обра-
зуют характерные конфигурации (рис. 9), располагаясь вблизи не-
которых средних линий ут = F(ym_i), которые могут быть при-
няты в качестве основы для прогноза zm =
Практически построение кривой осуществлялось с помощью по-
линомиальной аппроксимации (отдельно на каждом из двух участ-
ков), при этом коэффициенты полиномов определялись по методу
наименьших квадратов. Степень достоверности прогноза zm, по-
строенного на основе сглаженной кривой F(zm_i), изображена на
рис. 10 (кривая 1) для случая естественного шума, действующего
в автогенераторе (см. рис. 9,а). Время предсказуемого поведения
составляет при этом около 10 тактов. Если ввести в генератор до-
полнительный шум, то разброс экспериментальных точек на плос-
кости (ут,Ут-1) увеличивается (см. рис. 9,6), хотя модельная кри-
вая ут = F(ym-i) практически не деформируется. Как и следовало
ожидать, введение дополнительного шума снижает время предска-
зуемого поведения примерно вдвое, т.е. с 10 до 5 тактов (кривая 2
на рис. 10).
В заключение этого раздела отметим, что информация о фрак-
тальной размерности динамического хаоса также может быть по-
лезной для построения предсказательных моделей. В частности,
фрактальная размерность может указать ориентировочное число
степеней свободы, вовлеченных в движение, и тем самым — по-
рядок модельного дифференцированного уравнения. Тем не менее,
к данным, извлекаемым из фрактальной размерности, следует от-
носиться критически. Так, например, за размерностью единица,
которой обладает предельный цикл, может скрываться довольно
сложная система, обладающая многими степенями свободы. Иными
словами, фрактальная размерность характеризует скорее тополо-
гические, чем динамические свойства системы, и именно это об-
стоятельство вынуждает внимательно изучать всю совокупность
доступных данных, прежде чем остановиться на размерности мо-
дельной системы.
Рис.9. Отображение в случае генератора КПР (уровень шума на рис. 9,6
примерно вдвое больше, чем на рис. 9,а. Точки — экспериментальные зна-
чения; сплошные линии — модельные значения.
4. Что мешает предсказанию?
Выше мы сосредоточили внимание на методах построения пред-
сказательных моделей в динамических системах и перечислили
трудности, подлежащие преодолению преимущественно с помощью
компьютеров. Несмотря на важную роль компьютеров, трудности
предсказания все же нельзя целиком отнести к недостаточной мощ-
ности ЭВМ. Правильнее было бы видеть основные препятствия в
природе прогнозируемых явлений. Что же именно в природе вещей
мешает прогнозированию?
в
1,0
0,5
О
V X
_|__-hb._ I**--
5-10 15/i
Рис.10. Степень предсказуемости
£>(д) для генератора КПР. 1 —
естественный шум; 2 — увеличен-
ный шум.
Перечисление причин, которые так или иначе мешают прогно-
зированию, может занять достаточно много места. Тем не менее,
нельзя обойти молчанием причины, которые носят фундаменталь-
ный характер. К ним относятся: локальная неустойчивость многих
исследуемых систем; влияние измерительного прибора на прогно-
зируемое явление; эволюционные процессы в открытых системах;
прохождение точек бифуркации при наличии шумов и стоимость
прогноза. Обсудим эти факторы.
Локальная неустойчивость. Практически все сколько-нибудь
сложные физические системы обладают свойством локальной не-
устойчивости. В таких системах малые возмущения не затухают,
а наоборот, нарастают хотя бы в течение ограниченного времени.
Это свойство наблюдается в гидродинамических и воздушных по-
токах, в системах многих тел, включая газ и Солнечную систему,
в электрических и механических колебательных системах со мно-
гими степенями свободы и т.д. Временные и пространственные
масштабы, характеризующие такие неустойчивости, варьируют в
огромных пределах — от миллионов и миллиардов лет в космиче-
ских масштабах до миллиардных долей секунды в движении моле-
кул в газовой среде.
Локальная неустойчивость в колоссальной степени усложняет
прогнозирование процессов, особенно, если нарастание возмущений
происходит по экспоненциальному закону, как это характерно для
динамического хаоса. В этом случае, как следует из формул типа
(13) и (15), время предсказуемого поведения зависит от динамиче-
ских и флуктуационных параметров по логарифмическому закону.
Это означает, например, что для увеличения времени предсказуемо-
сти тргес1 на порядок, т.е. в 10 раз, отношение сигнал/шум (t/2)/crJ
должно возрасти в е10, т.е. примерно в 10 000 раз! Этот пример
показывает, почему так медленно отодвигается горизонт предска-
зуемости по мере увеличения сигнала или уменьшения шума.
С общих позиций локальная неустойчивость классических си-
стем может рассматриваться как причина случайности в физиче-
ском мире. Микроскопически слабые возмущения, скажем, тепло-
вой природы, воздействуя на локально неустойчивые хаотические
системы, за конечное время могут достигнуть макроскопических
значений. Иными словами, динамический хаос выполняет функцию
гигантского усилителя микрофлуктуаций, при этом внешний на-
блюдатель в состоянии проследить разве что за поведением резуль-
тирующих макрофлуктуаций. С этой точки зрения выявление свой-
ства локальной неустойчивости в исследуемой системе имеет пер-
востепенное значение: горизонт предсказуемости таких систем осо-
бенно мал.
Этот вывод можно проиллюстрировать на примере больцманов-
ского газа, т.е. совокупности маленьких упругих сфер, моделиру-
ющих молекулы реального газа. При типичных для земной атмо-
сферы условиях длина свободного пробега молекул I превышает
диаметр молекул а в q = l/a = 104 раз. Это число показывает,
во сколько раз увеличится угловое возмущение авт частицы при
соударении с другой молекулой, т.е. а9т = q<j9m-\. При соверше-
нии нескольких соударений угловое возмущение достигает авт ~
~ qma0Q. Легко видеть, что при q = 104 <70m достигнет любой вели-
чины за конечное и при этом весьма умеренное число соударений.
Например, если принять авт и 1, что отвечает полной потере па-
мяти о первоначальном направлении движения частицы, то для т
получим оценку
1п(<Т0т/<Т0о) In CT0Q
771 ~ In q ~ In q
Каким бы не было первоначальное возмущение аОо, число соуда-
рений всегда будет составлять несколько единиц или, в крайнем
случае, несколько десятков единиц. Этот пример показывает, что
предсказуемое поведение больцмановского газа простирается всего
лишь на несколько соударений, а если учесть, что интервал между
последовательными соударениями составляет около 1О10 с, то гори-
зонт предсказуемости тног не превышает Ю-9 с. Эта оценка, кстати,
имеет отношение и к проблеме необратимого поведения реального
газа: обратимость движения молекул характерна лишь для интер-
валов At < Thor после обращения скоростей всех молекул, тогда как
при At > Thor частицы неизбежно потеряют память о своих ско-
ростях в момент обращения, например, под воздействием слабого
теплового электромагнитного поля.
В гидродинамических потоках горизонт предсказуемости, ра-
зумеется, значительно больше, чем в больцмановском газе, но по
отношению ко времени корреляции тс превышение невелико: оно по-
прежнему определяется логарифмом отношения сигнал/шум. Это
объясняет, в частности, медленность прогресса в предсказании по-
годы.
Искажающее воздействие прибора (измерения) на про-
гнозируемое явление. Проблему предсказуемости можно сфор-
мулировать не только на классическом, но и на квантовомеханиче-
ском языке. Очевидно, в этом случае предсказанию должна подвер-
гаться волновая функция исследуемой системы.
Казалось бы, это не вносит ничего принципиально нового по
сравнению с классической системой: просто одна предсказываемая
величина (классическая траектория) заменяется другой (волновая
функция). Однако различие, хотя и не столь принципиальное, как
это считалось ранее, все же имеется и связано оно с измерением
начальной волновой функции i/>°, без которой прогноз немыслим.
Как известно из теории квантовых измерений, показаниям при-
боров и состоянию исследуемой системы отвечают разные началь-
ные волновые функции, и поэтому прогноз, основанный на показа-
ниях приборов, может отличаться от реального поведения системы.
Отличие начальных состояний — реального и измеренного — свя-
зано с возмущающим действием прибора.
До недавнего времени считалось, что с воздействием прибора
следует считаться только при рассмотрении квантовомеханических
систем. Между тем воздействие измерения или, точнее, измеритель-
ного прибора, понимаемого здесь в широком смысле, оказывается
существенным и в классических системах, если последние обладают
свойством локальной неустойчивости [1]. Дело в том, что в локально
неустойчивой системе малое возмущение, вносимое прибором, мо-
жет быстро усилиться и кардинально изменить наблюдаемый про-
цесс. Показания приборов в этом случае уже не характеризуют не-
возмущенный процесс, который мы собирались измерить. Такое ис-
кажающее воздействие прибора на измеряемый классический про-
цесс, насколько нам известно, детальному анализу еще не подвер-
галось.
Возмущающее действие прибора может проявиться, например,
при попытке проследить мелкомасштабные движения воздуха или
жидкости с помощью малых датчиков. Ясно, что увеличение числа
датчиков рано или поздно приведет к искажению самого потока еще
на классическом уровне. По всей вероятности, следует найти опти-
мальный уровень взаимодействия прибора с исследуемой классиче-
ской системой, при котором достигается определенный компромисс
между количеством извлекаемой информацией и ее искажением. Со-
ображения о «компромиссном» измерении можно высказать и в от-
ношении квантовомеханической системы.
Эволюция открытых систем. Особенность больших откры-
тых систем состоит в том, что они в состоянии претерпевать эволю-
ционные изменения: в них постоянно возникают неустойчивости тех
или иных масштабов, рождаются новые и исчезают старые струк-
туры, т.е. происходят метаморфозы самоорганизации. В отноше-
нии эволюционных, самоорганизующихся систем возникают специ-
фические вопросы.
Во-первых, в случае систем, испытывающих эволюцию, прихо-
дится считаться с трансформацией модельных уравнений и/или с
изменением характера решений этих уравнений. Разумеется, фун-
даментальные уравнения движения не меняются, но модельные
представления о поведении системы на разных этапах эволюции
могут быть различными. Различным может быть и характер реше-
ния уравнений, описывающих систему. Например, уравнение Эйри
х — tx — 0 имеет ограниченные осциллирующие решения при t < О,
тогда как при t > 0 оно приобретает экспоненциально нарастающие
и затухающие решения.
Во-вторых, имеются трудности выработки критериев качества
прогноза в условиях эволюции. В стационарных, не эволюционных
условиях обычно удается выработать более или менее удовлетво-
рительные критерии качества прогноза, скажем средний квадрат
погрешности (т/2) или степень предсказуемости D(r). Такие крите-
рии можно оправдать, используя многократные сравнения прогноза
с наблюдением в течение длительного промежутка времени Т.
Иначе обстоит дело в условиях эволюции. Общепринятые кри-
терии пригодны здесь только для относительно малых временных
масштабов: общее время наблюдения Т, складывающееся из тп суб-
интервалов At = T/m, должно быть мало по сравнению с харак-
. терным временным интервалом эволюции Atev, Если же Т > Atev,
то экспериментатор не в состоянии отработать критерии качества
«на ходу» и вынужден ограничиваться одноразовыми сравнениями
наблюдения с прогнозом.
В-третьих, особое беспокойство вызывает проблема выявления
неустойчивостей, возникающих в процессе эволюции. Характерное
время неустойчивых процессов Tinst обычно меньше типичного вре-
мени эволюционных изменений Ate„ (если это было бы не так, т.е.
если Tinst ~ &tev> то сам процесс развития неустойчивости был бы
не отличим от фонового эволюционного процесса). В первые мо-
менты после зарождения неустойчивости быстро растущая экспо-
нента скрывается под шумами. Этот процесс становится обнару-
жимым только через некоторое время после того, как он превысит
уровень шума. После этого неустойчивый процесс стремительно
развивается и достигает макроскопических значений за конечное
время порядка нескольких Tjnst (для неустойчивостей так называе-
мого взрывного типа это время может быть еще меньше).
В этих условиях неустойчивость часто регистрируется только
a posteriori, когда первоначальный прогноз, составленный без учета
экспоненциальной неустойчивости, уже потерял силу.
В-четвертых, в открытых системах в процессе совершенство-
вания прогноза можно ожидать иерархического расширения мо-
дельных уравнений за счет привлечения в модель все новых и но-
вых подсистем и эффектов, которыми пренебрегалось на малых
пространственно-временных интервалах.
Для грамотного прогноза одинаково важны как малые, так и
большие масштабы изменения ближайшего окружения. Мелкомас-
штабные процессы в окружающих системах могут проявиться как
короткодействующие шумы, тогда как крупномасштабные движе-
ния могут быть ответственными за медленное изменение параме-
тров изучаемой подсистемы.
Иерархический характер предсказательных моделей отражает
важную черту физического мира, в котором ВСЕ СВЯЗАНО СО
ВСЕМ. Этот принцип всеобщей взаимосвязанности должен посто-
янно ощущаться всеми, кто связан с прогнозами.
Прохождение точек бифуркации при наличии шумов.
Пусть бифуркация происходит при значении управляющего пара-
метра Г(>. Предположим также, что если при г < тъ система имела
только одно состояние равновесия у(г), то после бифуркации по-
являются два устойчивых состояния j/i(r) и уг(г)1 При очень мед-
ленном изменении параметра г вероятность обнаружить систему в
любом из этих состояний равна 1/2, так что при медленном про-
хождении точки бифуркации выбор нового состояния происходит
по закону случая. К этому надо добавить, что при приближении к
бифуркационной точке наблюдается существенное усиление флук-
туаций в системе - это явление имеет такую же природу, как пре-
досциляционный шум, резко усиливаются перед началом генерации
в осцилляторах, в частности в лазерах, или же, как шум, возра-
стающий в момент фазовых переходов (явление типа критической
опалесценции).
Можно было бы думать, что при прохождении бифуркационных
точек выбор нового состояния всегда происходит под доминирую-
щим воздействием шумов. Между тем при быстром изменении па-
раметра дело обстоит иначе: определяющим оказывается не дей-
ствие шумов, а динамические процессы [3]. В этом заключается
один из парадоксов предсказуемости: в нестационарных, быстро
меняющихся условиях прогноз может оказаться более успешным,
чем в медленно меняющихся условиях, близких к стационарным.
Пусть tb — момент прохождения бифуркационной точки. В ок-
рестности этой точки можно принять, что управляющий параметр
меняется по линейному закону: r(t) 2; rb+rb(t-tb), где гъ = dr(tb)/dt
— скорость изменения в момент бифуркации. Оказывается, что
если скорость тъ достаточно велика, тъ Gbf, то влиянием шумов
можно пренебречь и система с вероятностью, близкой к единице,
окажется в каком-то определенном состоянии равновесия, а именно
в том, какое диктуется уравнениями движения с переменным па-
раметром r(t). Наоборот, при тъ G&f выбор стационарного со-
стояния происходит исключительно под влиянием шумов, как это
описано в начале раздела.
Критическое значение скорости тъ — Gaj, пропорционально
уровню шумов в системе ст/, было найдено как аналитически, так и
путем численного моделирования. В частности, О. Я. Бутковский
провел численное моделирование для логистического отображения
в момент первого удвоения периода.
Стоимость прогноза. Как бы банально это ни звучало, но
прогноз стоит денег. Например, прогресс в прогнозе погоды упира-
ется в проблемы развития сети метеостанций, совершенствования
автоматических приборов, развития систем передачи информации,
увеличения мощности компьютеров и т.д.
Стоимостный аспект проблемы приходится принимать во вни-
мание при любом прогнозировании. Стоимостные ограничения мо-
гут проявиться в любых факторах, вовлекаемых в прогноз: от сто-
имости зависит и уровень измерительных шумов (при использова-
нии недостаточно совершенных приборов), и количество первич-
ных данных, на основе которых вырабатывается модель прогноза,
и мощность компьютера, на котором проводятся расчеты.
Сказанное позволяет отнести стоимость к фундаментальным
ограничениям прогноза: это просто иная форма выражения слож-
ности изучаемых явлений. Во всяком случае, ссылки на недостаточ-
ность финансирования звучат гораздо чаще, чем на другие, более
«фундаментальные» факторы.
5. Динамические аналогии в социально-экономических
явлениях
Схема прогноза, опирающегося на динамические уравнения, мо-
жет показаться привлекательной не только для физических, но и
для многих других явлений, в том числе экономических и социаль-
ных. Обсудим некоторые аспекты проблемы.
Прежде всего, следует отметить, что далеко не все социально-
экономические явления имеют динамическую природу, т.е. могут
описываться динамическими дифференциальными уравнениями.
Например, больше всего на принадлежность к динамическим си-
стемам претендуют макросистемы материального производства и
товарного обращения. В этом случае речь идет о больших массах
товаров и об усредненных (по времени или по регионам) величинах.
Чем меньше масштаб рассматриваемого процесса, тем сильнее от-
клонения от чисто динамических процессов и тем меньше шансов
построить динамический прогноз. Еще меньше шансов построить
динамический прогноз для социальных систем, поскольку в этом
случае существенным становится не усредненное, а индивидуаль-
ное поведение, особенно поведение лидеров, которым делегируются
полномочия отдельных членов коллектива.
Далее, даже в тех случаях, когда уравнения могут быть запи-
саны, надо иметь в виду некоторые отличительные особенности
этих уравнений, не имеющие аналога в естественных науках. Дело в
том, что отдельные члены в обсуждаемых уравнениях или некото-
рые коэффициенты в них могут меняться в зависимости от множе-
ства социально-политических факторов. В частности, в модельных
уравнениях в той или иной степени должна отражаться массовая
психология (и даже крайние ее проявления — фанатизм, заблужде-
ния), степень доверия к лидерам, зависимость от предыстории, тра-
диции и т.д. и т.п. Более того, коэффициенты даже «самых обоб-
щенных» уравнений, скажем, уравнений, описывающих динамику
добычи топлива в мировом масштабе, могут зависеть от решений,
принимаемых отдельными странами или даже отдельными дикта-
торами.
Многое зависит от законов, действующих в той или иной стране,
от ресурсов, от гибкости и мудрости руководителей, от привержен-
ности народа догмам. Все эти факторы, конечно же, снижают пред-
сказательную силу динамических моделей в социально-экономичес-
кой области. Это не означает, разумеется, что следует вообще отка-
заться от динамических моделей. Скорее всего, они должны играть
роль частных сценариев, по которым может пойти социально-эконо-
мическое развитие. Роль таких сценариев может оказаться весьма
ценной в моменты, когда нужно принимать серьезные решения.
Несмотря на ограниченную ценность модельных уравнений, сам
динамический подход к социально-экономическим явлениям может
породить полезные аналогии с явлениями, уже изученными в есте-
ственных науках. Например, переживаемый нашей страной переход
от одной экономико-политической системы к другой имеет много
сходного с фазовыми переходами. Аналогия касается как струк-
турной стороны вопроса (разрушение одних структур и появление
других), так и некоторых деталей, например роста флуктуаций в
момент перестройки, рассматриваемой как фазовый переход.
При определенных условиях динамическая структура экономики
может приобрести свойство локальной неустойчивости. В условиях
свободной рыночной экономики это не следует рассматривать как
катастрофу: просто рынок адекватно реагирует на различные воз-
мущения, быстро уходя от невыгодных отношений. Такая неустой-
чивость в малом может привести к выбыванию из игры отдельных
предприятий при сохранении глобальной устойчивости. Напротив,
в системе жесткого управления экономикой (да еще при наличии не-
компетентного руководства, которое постоянно запаздывает с при-
нятием нужных структурных решений) вероятность срыва в глубо-
кий хаос резко возрастает. В литературе уже обсуждается вопрос
о динамическом хаосе в экономике, появились даже публикации по
близкой проблеме хаоса и предсказуемости в вопросе о стратегии
национальной безопасности [9].
Вообще, вопрос о роли флуктуаций в экономике представляется
очень важным. Создается впечатление, что так называемые боль-
шие циклы в развитии экономики порождены первоначально сла-
быми толчками (открытие паровой машины и ткацкого станка, за-
тем электромотора, компьютера и т.д.), которые быстро меняли ха-
рактер производства и за исторически короткое время приводили к
новой технологической цивилизации. Не исключено, что нормальная
экономика обладает свойством локальной неустойчивости к ценным
изобретениям и нововведениям, тогда как ненормальная экономика
отторгает их.
Обсуждаемые здесь процессы быстрого внедрения вновь изо-
бретенных машин, технологий, принципов, приводящие к измене-
нию «технологического лица» экономики за сравнительно короткие
времена (порядка 50-80 лет), возможно, характерны и для других
сфер жизни: геополитики, демографии, этногенеза и т.д., но с дру-
гими временными и пространственными масштабами. Можно ду-
мать, что такие процессы более или менее прогнозируемы на этапах
уверенного роста и насыщения, но не на этапе зарождения. Все это
несколько напоминает судьбу больших пузырей воздуха в бурно ки-
пящей воде: когда пузырек стал уже достаточно большим, он про-
должает уверенный и прогнозируемый рост и движется вверх, к
поверхности жидкости, но процесс зарождения и становления пу-
зырька вряд ли предсказуем.
Что же касается предсказания «траекторий» отдельных пред-
приятий, машин, людей, то их можно уподобить отдельным молеку-
лам в кипящей жидкости: рано или поздно теплице и гидродинами-
ческие процессы вовлекут данную молекулу в движение очередного
пузыря, но заранее этот пузырь указать нельзя.
Тем более невозможно предсказать судьбу отдельных людей, на-
деленных волей и страстями, погруженных в социальную среду и
приверженных определенным принципам. В этом отношении можно
только присоединиться к мнению А. Д. Сахарова, который сказал:
«В судьбу как раз я не верю. Я считал, что будущее непредсказуемо
и не определено, оно творится всеми нами — шаг за шагом в нашем
бесконечно сложном взаимодействии».
Заключение
Сформулируем основные выводы из проведенного рассмотре-
ния, сделав это в «ученической» форме, чтобы подчеркнуть скром-
ность достигнутых результатов на фоне по настоящему сложных
проблем.
1. Любой процесс имеет ограниченное время предсказуемого по-
ведения, которое определяется неточностью модельного урав-
нения, уровнем измерительных шумов и уровнем флуктуаций
в исследуемой системе. Максимальное значение этого времени,
отвечающее действию только неустранимых флуктуаций в са-
мой системе, представляет собой горизонт предсказуемости,
за пределы которого выйти невозможно.
2. В поисках предсказательной модели хороши любые средства,
но на наибольший успех можно рассчитывать там, где удачная
модель сочетается с мощным компьютером.
3. Среди множества факторов, препятствующих успешному про-
гнозированию, можно выделить несколько фундаментальных
причин: локальная неустойчивость исследуемых систем; воз-
мущающее действие прибора на исследуемое явление; эволю-
ционные процессы в исследуемой системе; бифуркации в ходе
эволюции и стоимостные ограничения.
4. Многие понятия и модели, выработанные в естественных на-
уках, видимо, могут оказаться полезными при рассмотрении
социально-экономических явлений, однако обнаруженные сей-
час аналогии носят пока что поверхностный характер и тре-
буют внимательного изучения.
ЛИТЕРАТУРА
1. Кравцов Ю.А. Случайность, детерминированность, предсказуемость //
Успехи физ. наук. 1989. Т.158, №. 1. С.93-115.
2. Илькова Л.Ш., Кравцов Ю.А., Мергелян О.С., Эткцн В.С. Степень ча-
стичной детерминированности динамического хаоса // Изв. вузов. Радио-
физика. 1985. Т.28, № 7. С.929-932.
3. Kravtsov Yu. A. Randomness and predictability in dynamic chaos // Nonlinear
waves / Ed. A.V. Gaponov-Grekhov. Berlin; Heidelberg: Springer, 1989. Vol.2:
Dynamics and evolution. P.44-46.
4. Кравцов JO.А., Эткцн B.C. К вопросу о роли флуктуационных сил в
динамике автостохастических систем // Изв. вузов. Радиофизика. 1981.
Т.24, № 8. С.992-999; Степень динамической корреляции и проблема выявле-
ния динамической природы случайных процессов // РЭ. 1984. Т.29, № 12.
С.2358-2364.
5. Lighthill J. The recently recognized failure of predictability in Newtonian dyna-
mics // Proc. Roy. Soc. London A. 1986. Vol.407. № 1832. P.35-50.
6. Crutchfild J.P., McNamara B.S. Equation of motion from a data series //
Complex System. 1987. Vol.l, № 2. P.417-425.
7. Farmer K.D., Sidorovich J. Predicting chaotic time series // Phys. Rev. Lett.
1987. Vol.59. P.845-848.
8. Илькова Л.Ш., Кравцов Ю.А., Пиковский А.С. Определение степени де-
терминированности экспериментально наблюдаемых хаотических режимов
// Кратк. сообщ. по физике ФИАН. 1986. № 11. С.7-9.
9. Saperstejn А.М., Mayer-Kress G. Chaos versus predictability in formulating
national strategic security policy // Amer. J. Phys. 1989. Vol.57, № 3 P.217-223.
социология
И.В.Бестужев-Лада
БУДУЩЕЕ ПРЕДВИДИМО,
НО НЕ ПРЕДСКАЗУЕМО:
ЭФФЕКТ ЭДИПА В СОЦИАЛЬНОМ
ПРОГНОЗИРОВАНИИ
1. Исторический экскурс
У истории современного научного прогнозирования — много-
тысячелетняя предыстория. Она включает в себя религиозную эсха-
тологию (учение о «конце света») в его индуистско-буддистско-
джайнистском и иудаистско-христианско-мусульманском вариантах,
социальные утопии разного типа с древнейших времен до наших
дней, философию истории с ее концепциями циклического разви-
тия, регресса и прогресса человечества, борьбу марксизма против
различных немарксистских концепций отношения к возможности
познания будущего, из которых ведущую роль до сих пор играет по-
зитивизм. У всех главнейших идейных течений — действующих лиц
этой предыстории — отношение к будущему покоилось на убежден-
ности в принципиальной возможности его предсказания. Эта убе-
жденность, закрепившаяся в обыденном сознании и дающая непло-
хой хлеб многочисленным гадалкам, прорицателям и пр., и сегодня
свойственна едва ли не всем лицам, принимающим решения, от глав
правительств до глав семей, не исключая и наших отечественных.
В 1927 г. Советское правительство дало задание группе эконо-
мистов во главе с В. А. Базаровым (Рудневым) разработать про-
гноз развития СССР к исходу первой пятилетки 1928-1932 гг. —
первого плана развития народного хозяйства страны. Результатом
работы группы явился вывод, который можно было бы отнести
к числу наиболее выдающихся научных открытий XX в., если бы
хоть одно такое открытие получило в истории человечества свое-
временное признание. Вывод был сформулирован следующим обра-
зом: «Всякий перспективный план народного хозяйства, будет ли
это генеральный план, пятилетка или контрольные (погодовые) ци-
фры, должен представлять собой синтез директивы и прогноза,
т.е. должен иметь определенную целевую установку и генетиче-
ское научное обоснование ее осуществимости. Часто возникающие
среди плановых работников прения о том, какому из двух элементов
должно быть отдано преимущество, по нашему мнению, являются
сплошным недоразумением, вытекающим из неправильной поста-
новки вопроса. Телеология и генетика (по-современному, целевой и
трендовый подходы, И. Б.-Л.) — не конкурирующие между собой
антагонисты, а диалектически связанные друг с другом моменты
единого гармонического целого» [1, с. 38-39].
Иными словами, в исследовании перспектив развития управля-
емых в принципе явлений авторы предлагали заменить тщетные
попытки безусловных предсказаний предсказаниями сугубо услов-
ными: одним, основанным на экстраполяции в будущее наблюдае-
мых тенденций при сугубо условном допущении их неизменяемо-
сти средствами управления («генетика»), другим — основанным на
столь же условном допущении некоторых желательных изменений
средствами управления («телеология»). В обоих случаях смыслом
исследовательских операций являлось повышение уровня научной
обоснованности плановых и иных решений: «Перефразируя извест-
ное изречение Канта, можно сказать, что телеологические уста-
новки перспективного планирования без генетического их обосно-
вания пусты, а генетические исследования без целевых установок
слепы. План народного хозяйства должен быть зрячим и вместе с
тем реальным, научно обоснованным» [1, с. 38-39].
Статья из погребенного в сталинских «спецхранах» журнала
«Плановое хозяйство», где был опубликован излагаемый материал,
оставалась неизвестной позднейшим читателям до 80-х годов [2] и
практического значения не имела.
Ровно 30 лет спустя, в 1957 г., в аналогичную ситуацию по-
пали американские специалисты, получившие задание разработать
прогноз-предсказание высадки человека на Луну по программе
«Аполлон». Не зная ничего об опыте своих русских коллег, они при-
шли к тем же выводам. Сначала тоже возникла дилемма: либо про-
гноз, либо план-программа. Затем родилась идея так называемого
технологического прогнозирования, составляющего суть современ-
ной научной прогностики. Эта идея предусматривает замену тщет-
ных попыток безусловных предсказаний, с одной стороны, сугубо
условным поисковым (эксплораторным) прогнозом, основанным,
как и «генетический» прогноз у русских, на анализе трендов, с це-
лью выявить или уточнить проблемы, подлежащие решению сред-
ствами управления, а с другой — столь же условным нормативным
(у русских — «телеологическим»), основанным на анализе контр-
трендов, идущих от дерева целей по заранее заданным критериям
и представляющих, по сути, оптимизацию наблюдаемых трендов.
Смысл исследовательских операций прежний: как бы предваритель-
ное «взвешивание» ожидаемых и желательных последствий намеча-
емых целевых, плановых, программных, проектных, текущих упра-
вленческих решений.
На сей раз научное открытие не оказалось погребенным в «спец-
хранах» по политическим соображениям, а было использовано на
практике, обнаружило колоссальный экономический эффект (до
800% прибыли в результате оптимизации решений по данным сопо-
ставления поисковых и нормативных прогнозов) и породило «бум
прогнозов» 60-годов — появление сначала на Западе, а затем, во
второй половине десятилетия, также в СССР и почти всех странах
Восточной Европы сотен исследовательских центров разного мас-
штаба, занявшихся разработкой «технологических прогнозов» [3-7].
Любопытно, однако, что чисто психологическая установка лю-
дей на прогноз-предсказание (в обыденном сознании формулиру-
емая как страстное желание «знать свое будущее», хотя это ало-
гично и противоестественно, поскольку лишает смысла жизнеде-
ятельность любого организма, до человека включительно, — мы
специально остановимся на этом вопросе ниже) оказалась настолько
сильной, что в чистом виде «технологическое прогнозирование» про-
явило себя преимущественно лишь на прикладном уровне научно-
технического характера, там, где требовались исследования пер-
спектив развития систем человек-техника и их подсистем.
Между тем в социальном прогнозировании — от перспектив
развития человечества в целом до частных социально-политических
прогнозов — по-прежнему преобладал либо «телеологический», либо
«генетический» подход, несмотря на поистине катастрофические
результаты. На Западе это выразилось сначала в конструировании
чисто утопических концепций «постиндустриального общества», ко-
торое якобы «произрастет» из современного «индустриального» без
политической борьбы, результаты которой не поддаются безуслов-
ным предсказаниям (60-е годы), а затем — чисто экстраполяци-
онных концепций грядущей «глобальной катастрофы», опять-таки
независимо от непредсказуемых результатов политической борьбы
(70-е годы). В итоге в 80-е годы, когда восторжествовала идеоло-
гия неоконсерватизма, западная футурология оказалась в затяжном
кризисе, из которого не вьппла доселе.
В Советском Союзе «технологическое прогнозирование», бурно
развивавшееся в 1967-1970 гг. в ожесточенной борьбе с догматиз-
мом после провала хрущевской утопии «коммунизма к 1980 году»,
было в 1971 г. тотально разгромлено по ходу свертывания «косы-
гинских реформ» 1966-1969 гг. и заменено «Комплексной програм-
мой научно-технического прогресса» на 1990 г. (затем ее продле-
вали на 5 лет каждую пятилетку). Последняя не являлась ни про-
гнозом, ни программой, ни планом, а представляла собой, по сути,
чисто спекулятивные построения, долженствовавшие «подкрепить»
планирование, но абсолютно игнорировавшиеся плановиками. Та-
ким образом, полностью фиктивное, как теперь ясно, планирова-
ние (поскольку планы не имели ничего общего с действительно-
стью) «подкреплялось» своеобразной помесью столь же фиктивных
квазипрогнозов и псевдопрограмм, несших сугубо идеологическую
функцию, хотя и остававшихся — в силу своей фиктивности — се-
кретными. В 1990 г., все это было упразднено как заведомо не-
состоятельное и в научном, и в политическом отношении, но еще
пока не заменено ничем более конструктивным, так что проблема-
тика особенностей исследования будущего (сам этот термин лишь
начинает проникать в официальную терминологию) остается для
нашей страны исключительно актуальной, так же, впрочем, как и
для всех остальных стран «победившего» (точнее не победившего)
социализма.
Из этой проблематики выделяется по своему значению научная
проблема пределов и особенностей предсказуемости в обществове-
дении, которая еще в 60-х годах нередко сводилась к так называе-
мому эффекту Эдипа — по имени легендарного древнегреческого
царя, тщетно пытавшегося видоизменить предсказанное ему буду-
щее.
2. Эффект Эдипа в социальном прогнозировании
Понятие «социальное прогнозирование» имеет несколько значе-
ний. В узком смысле это прогнозы собственно социальных отноше-
ний, за рамками экономических, политических и др.; в широком —
прогнозы в обществоведении в отличие от прогнозов в естествове-
дении, включая технические науки. Есть и промежуточные значе-
ния. Ниже это понятие используется в широком смысле общество-
ведения в целом, включая экономические, политические, историче-
ские, психологические, педагогические, правовые и тому подобные
науки.
Все объекты прогнозирования, с известной точки зрения, можно
расположить по условной шкале, которая характеризует взаимодей-
ствия предсказания с решением, действиями на основе которого
можно видоизменить предсказанное. На одном полюсе шкалы ока-
жутся объекты, где такое взаимодействие мало, тогда как на дру-
гом, напротив, велико и приближается к условной единице. В по-
следнем случае решение вмешивается, компенсирует или даже от-
меняет предсказание. Не первом полюсе окажутся объекты есте-
ствоведения, на другом — обществоведения.
Теоретически взаимодействие ни в каком случае не может быть
равно нулю. Так, например, умозрительно можно представить себе
вмешательство даже в предсказания солнечных затмений, которые
считается образцом точности в настоящее время. Для этого доста-
точно взорвать на одной стороне Луны крупный заряд ядерных бое-
припасов, способный сместить орбиту Луны, скажем, на несколько
микрон (пример, разумеется, сугубо условный). Применительно к
объектам естествознания, включая технику, мы лишены возможно-
сти существенно изменять что-либо, чтобы видоизменить предска-
занное. Примером могут служить прогнозы погоды. Да, в каком-то
(очень незначительном) диапазоне мы способны менять погодные
условия в рамках ограниченного региона, однако это безумно до-
рого и сравнительно малоэффективно. Поэтому на практике оста-
ется только пытаться предсказывать и затем приспособляться к
предсказанному. Подобная ситуация типична для естествознания,
техники.
Совершенно иначе выглядит взаимодействие решения с пред-
сказанием в обществоведении, как это можно продемонстрировать,
скажем, на примере личного поведения или политической борьбы.
Что бы я ни предсказал вам на вечер, на следующий день или год,
скурпулезнейше изучив особенности вашего характера, образа жиз-
ни, внешних обстоятельств, — услышав мое предсказание, вы вполне
в состоянии «саморазрушить» его действиями на основе решения с
учетом предсказанного. Или, напротив, вы даже не подозревали о
возможности предсказанного, но, услышав предсказание, «самоосу-
ществили» его соответствующими действиями. Точно так же в обла-
сти политики можно, допустим, с высокой точностью предсказать
на послезавтра мятеж какого-нибудь генерала, вознамерившегося
стать диктатором. Но ведь ничто не мешает завтра же на основе
такого прогноза-предсказания сместить генерала и подавить тем
самым мятеж в зародыше. Или, напротив, нагнетать истерию гря-
дущего мятежа до тех пор, пока самый тугодумный генерал не до-
гадается «самоосуществить» подобное предсказание.
В современной прогностике это и называется эффектом Эдипа.
Он детальнейше описан в прогностической литературе 60-х годов, а
в нашей стране фундаментально обобщен в монографии А. М. Ген-
дина [8, с. 236-290]. Тем не менее, заказчики прогнозов до сих пор,
как правило, требуют, по сути, предсказания заказываемого, а раз-
работчики под их давлением делают вид, будто никакого эффекта
Эдипа не существует. Чтобы преодолеть психологический барьер
на пути от вожделенного прогноза-предсказания к прогнозу, «взве-
шивающему» последствия принимаемых решений, приходится вновь
и вновь возвращаться к этому вопросу. В данном случае развивая
основные методологические положения современной научной про-
гностики, мы предлагаем
Постулат 1. О принципиальной невозможности безусловного
предсказания будущих состояний объектов, поддающихся видоиз-
менению действиями на основе решений, принимаемых с учетом
подобного предсказания.
Этот постулат, в свою очередь, покоится на постулате о прин-
ципиальной непредсказуемости будущего состояния любого орга-
низма, способного реагировать на такое предсказание соответству-
ющим видоизменением своего поведения, потому что «знание буду-
щего» в подобной ситуации делает бессмысленной жизнедеятель-
ность организма, т.е. является физически невозможным.
В самом деле, представьте себе, что, скажем, какая-нибудь рыба
точно «знает», что, разинув пасть утром, она наверняка, при лю-
бых обстоятельствах, заглотает червяка, а разинув пасть вечером,
тоже наверняка, при любых обстоятельствах, попадется на крючок.
Ясно, что на месте рыбы раньше или позже появится некий кибер-
нетический организм, ничего общего не имеющий с земной флорой
и фауной, мало того, — вообще с законами бытия в нашем домене
Вселенной.
Подобно этому, трудно представить себе человека, который
точно «знает», что завтра его ждет, скажем, счастливая свадьба,
а послезавтра — несчастная гибель. Ясно, что он оказывается в си-
туации, многократно описанной в художественной литературе —
от «Египетских ночей» Пушкина до «Мастера и Маргариты» Бул-
гакова, и либо пассивно ожидает свершения предсказанного, либо
пытается видоизменить его, либо превращается в киборга, в сверх-
естественное существо, которому все человеческое чуждо. Напо-
мним в связи с этим лишь один момент, хорошо иллюстрирующий
обсуждаемый тезис. Насколько бессмысленным было с человеческой
точки зрения все поведение, вообще все существование Воланда и
его свиты в «Мастере и Маргарите», заранее знавших все, что про-
изойдет с ними на страницах романа и за этими страницами!
С этой точки зрения предвидение будущего — а то, что буду-
щее предвидимо, не подлежит сомнению в свете достаточно много-
численных фактов истории — на практике может осуществляться
либо в форме приспособления к безусловно предсказанному (там,
где последнее физически невозможно видоизменить), либо в форме
анализа тенденций, условно экстраполированных в будущее (трен-
дов), закономерности развития которых в прошлом и настоящем до-
статочно хорошо известны, включая как выявление перспективных
проблем, подлежащих решению средствами управления, в случае со-
хранения неблагоприятных тенденций на будущее, так и оптимиза-
цию трендов для выявления возможных решений проблем, обнару-
женных прогнозным поиском.
Если на основе предлагаемого (увы, напрасно предлагаемого!)
постулата последовательно переориентировать ведущиеся прогноз-
ные разработки управляемых в принципе объектов, то, думается,
эффективность прогнозирования значительно повысится.
Для упрощения изложения мы сознательно опустили два важ-
ных момента. Во-первых, помимо крайних значений предложенной
выше шкалы («нулевого» и «единичного»), существует бесконечное
множество промежуточных значений, где взаимодействие предска-
зания и решения осуществляется лишь частично или лишь при из-
вестных обстоятельствах. Во-вторых, возможное в принципе взаи-
модействие предсказания и решения отнюдь не означает наличие
такой возможности на практике. И не только в тех случаях, когда
у нас для этого «коротки руки», но и когда, казалось бы, ничего
не стоит видоизменить предсказанное. Посмотрите, как многое, в
принципе вполне рационально управляемое, у нас — человечества —
пущено на самотек, развивается подобно любым стихийным процес-
сам. Это относится не только к природным явлениям или к техно-
сфере, но и, практически, почти к любым явлениям социосферы —
от экономики, культуры, политики до семьи и быта нашей с вами
личной жизни.
Разве мы научились, например, рационально управлять демогра-
фическими процессами? Нет, они проходят совсем как стихийные,
скажем, климатически-погодные. То же самое в той или иной сте-
пени относится ко всем почти явлениям или процессам, которые
изучает обществоведение. В данном отношении их можно без боль-
шой натяжки назвать стихийными, естественными. Но так как, в
принципе, они все же управляемы, их в современной прогностике
принято называть квазиестественньми, квазистихийными. Людям
от такой квазистихийности плохо, а разработчикам прогнозов хо-
рошо, потому что дает возможность как бы минимизировать эф-
фект Эдипа, условно абстрагироваться от него и тем самым значи-
тельно упростить разработку прогноза.
Сказанное позволяет нам сформулировать
Постулат 2. Квазистихийность, т.е. практическая неупра-
вляемость подавляющего большинства социальных процессов или
явлений, в принципе поддающихся управлению, позволяет отно-
ситься к ним в известном смысле как к природным явлениям и
до известной степени абстрагироваться от принципиальной воз-
можности их видоизменения средствами управления, что суще-
ственно упрощает и облегчает как трендовый анализ, так и опти-
мизацию трендов, максимально раскрывая огромный научный по-
тенциал технологического прогнозирования, ориентированного не
на безусловное предсказание, а на повышение эффективности ре-
шений посредством сугубо условных предсказаний, как бы «взве-
шивающих» последствия намечаемых решений.
Практически речь идет о принципиальной возможности деле-
ния исследовательского процесса разработки прогноза на два этапа:
первый — в абстрагировании от возможных решений, способных
видоизменить наблюдаемые тенденции (поисковый прогноз), вто-
рой — в абстрагировании от возможных решений, способных по-
мешать оптимизации трендов (нормативный прогноз). Разделение
процесса прогнозирования на эти два этапа с обязательным про-
хождением каждого из них и столь же обязательным сопоставле-
нием полученных в том и другом случае результатов дает возмож-
ность избежать наблюдавшегося до сих пор уклона то в утопиче-
скую (апологетическую, оправдывающую проводимую политику),
то в антиутопическую (алармистскую, критикующую проводимую
политику) сторону. Иными словами, дает возможность существенно
поднять уровень объективности и, следовательно, эффективности
(в смысле научной обоснованности) прогнозов, напрочь отрешив-
шись от соблазна тщетных попыток повторения разработки скан-
дально проваливающихся прогнозов-предсказаний.
Попытаемся проиллюстрировать сказанное на двух примерах.
Один относится к глобалистике — комплексу глобальных проблем
современности, другой — к перспективам перестройки в России
(без региональных различий, учесть которые в рамках настоящей
статьи нет практической возможности.)
3. Проблема предвидения и предсказания в современной
глобалистике
Безвозвратно отошли в прошлое времена, когда обозримое буду-
щее человечества представлялось на Западе предсказуемым перехо-
дом развитых стран мира в идиллическое состояние «постиндустри-
ального общества», как бы автоматически преодолевающего гло-
бальные проблемы современности — растущий разрыв между стра-
нами принципиально разного уровня развития, растущие мировые
энергетический, сырьевой, продовольственный, торговый, транс-
портно-коммуникационный, экологический, демографический, во-
енный (гонка вооружений) и другие дисбалансы, кризис мировой
культуры, систем образования и здравоохранения, кошмарные про-
цессы гиперурбанизации, с одной стороны, и деградации дере-
вень — с другой, цунами антиобщественных явлений (преступность,
«теневая экономика», наркотики, включая алкоголь), бессилие меж-
дународных организаций, призванных содействовать преодолению
перечисленных проблемных ситуаций. Нет больше возврата и к алар-
мистским видениям неизбежной глобальной катастрофы при пере-
ходе названных проблемных ситуаций в критические и далее в ка-
тастрофические: человеческая психология не мирится с бесконеч-
ным нагнетанием подобного рода страхов, она «привыкает», затем
«устает» и настоятельно требует «смены пластинки».
Вот уже более десятка лет ясно, что существующая мировая ци-
вилизация вряд ли переживет XXI в., что выжить в сложившихся
условиях способна только качественно новая, альтернативная ци-
вилизация, менее энергоемкая и более устойчивая в экологическом,
демографическом и культурологическом отношениях. Более или ме-
нее прояснены и важнейшие конкретные контуры такой цивилиза-
ции: свертывание индустриализации, урбанизации, массовых пере-
возок грузов и пассажиров любым моторным транспортом, всемер-
ное повышение в мировом энергобалансе удельного веса так на-
зываемых чистых источников энергии (Солнце, вода, ветер, под-
земное тепло Земли, разница температур верхних и нижних слоев
морской воды и т.п.), всемерное повышение в мировом сырьевом
балансе вторсырья на основе замкнутых циклов производства, вы-
ход всех стран мира на «демографический оптимум»: три ребенка в
среднем на каждую женщину фертильного возраста, оптимизация
образования с ликвидацией разрыва между поколениями, стабили-
зация культуры путем преодоления разрушительного «наркотиче-
ского эффекта» современных «контркультур», минимизация основ-
ных антиобщественных явлений, начиная с преступности и кончая
наркотизацией общества, выход на такие определяющие ценности,
как семья, наука, искусство, содержательный досуг и, прежде всего,
развитие личности. Однако психологические барьеры, стоящие на
пути к альтернативной цивилизации, весьма высоки. Они подкреп-
ляются социально-экономическими и социально-политическими
барьерами (экономическая отсталость, социальные традиции, по-
литическая борьба и т.п.). Поэтому такие барьеры вот уже второй
десяток лет практически неодолимы, а их преодоление требует уде-
сятирения усилий, в том числе и в плоскости научного предвидения.
Сравнительно недавно, в 60-70-х годах, на первых этапах соб-
ственно истории современного научного предвидения сложилось ра-
циональное эшелонирование условных технологических прогнозов-
предсказаний: текущие, (ожидаются лишь детальные количествен-
ные изменения), краткосрочные (существенные количественные из-
менения), среднесрочные (количественно-качественные), долгосроч-
ные (качественно-количественные), наконец, сверхдолгосрочные
или, как их еще называют, дальнесрочные (общие качественные из-
менения). Конкретно годы упреждения определялись по-разному, в
зависимости от особенностей характера объекта прогноза. Так, в
нашей стране, где прогнозирование ориентировалось на пятилетки
планирования, текущие социально-экономические прогнозы ограни-
чивались обычно текущим годом или предстоящим сезоном, крат-
косрочные — грядущей пятилеткой, среднесрочные — следующим
за ней пятилетием, долгосрочные еще на одну-две пятилетки далее
(но не больше чем на 20 лет), сверхдолгосрочные — за пределами
этого периода времени.
За последнее десятилетие темп социально-экономических и соци-
ально-политических изменений в мире еще более ускорился. Ныне
вряд ли осуществимы долгосрочные прогнозы с 20-летним перио-
дом упреждения. Диапазон долгосрочности в общем и целом сокра-
тился по меньшей мере в полтора-два раза и ныне в среднем почти
целиком укладывается в ближайшее 10-летие. Соответственно сред-
ний диапазон среднесрочного прогнозирования сужается до 3-7 лет,
краткосрочного -— до года-двух, а текущие прогнозы все чаще из-
меряются не столько месяцами, сколько неделями или даже днями.
Все остальное в пределах грядущего столетия оказывается в диа-
пазоне сверхдолгосрочности, который ныне все более настоятельно
требует подразделения на эшелоны, но эта работа, по существу, вся
еще впереди.
При этом все более резко намечается принципиальная разница
между прогнозами в диапазонах долгосрочности и сверхдолгосроч-
ности: в первом случае речь идет об условных прогнозах-предска-
заниях изменений количественно-качественных и качественно-ко-
личественных характеристик исследуемых процессов и явлений, во
втором — об общих качественных оценках с сугубо ориентиро-
вочными количественными иллюстрациями. Временной диапазон за
рамками максимум первого 10-летия грядущего столетия в социаль-
но-экономическом и социально-политическом прогнозировании все
более явно остается в такой же тени прогностической неопределен-
ности, в какой было грядущее столетие на заре современной про-
гностики четверть века назад.
Все без исключения количественные прогнозные данные XXI в.
носят преимущественно условно-вероятностный характер, ничего
общего не имеющий с предсказаниями в собственном смысле слова.
Даже такие сильно инерционные социальные процессы, как, до-
пустим, рост мирового народонаселения, невозможно описывать в
чисто предсказательном ключе. Да, по динамическим рядам точно
просчитано, что в первой четверти грядущего столетия числен-
ность населения земного шара поднимется с существующих пяти
с лишним миллиардов и почти наверняка шести с лишним в 2000 г.
примерно до восьми с лишним, а затем, на протяжении последу-
ющих пятидесяти лет — при наблюдаемых тенденциях снижения
рождаемости — может стабилизироваться на уровне десяти с лиш-
ним миллиардов, плюс-минус два-три миллиарда при отклонении
тренда в ту или другую сторону. Но и два-три по отношению к
десяти — разве это можно считать хорошим предсказанием? При
этом мы не приняли во внимание высокой вероятности катастрофи-
ческих «всплесков» типа крупной истребительной войны или панде-
мии СПИДа, с одной стороны, прихода к власти в какой-нибудь
крупной стране (странах) «третьего мира» клерикально-фашист-
ских сил, способных существенно притормозить тенденцию сни-
жения рождаемости и в два-три раза удвоить население за какие-
нибудь полвека — с другой. В обоих случаях отклонение может
достичь плюс-минус пяти миллиардов, что так же далеко от удо-
влетворительного предсказания, как прогноз погоды типа «либо
солнце — либо дождь».
Еще менее «предсказательны» процессы с ярко выраженным дис-
кретным характером, а таких подавляющее большинство. Что
можно предсказать, например, в отношении перспектив развития
мирового энергетического баланса, кроме определенной вероятно-
сти открытия способа управления термоядерной реакцией, что спо-
собно качественно изменить данный баланс? Только одно: в XXI в.
невозможно каждые несколько лет удваивать производство и по-
требление энергии, как в XX в., тем более что в грядущем столетии
к этому процессу гораздо более энергично, чем ныне, подключатся
страны «третьего мира» — девять десятых населения земного шара
к 2100 г. Правда, и такое предсказание имеет колоссальное значе-
ние для политических решений глобального, регионального и даже
локального характера. Что можно предсказать касательно перспек-
тив развертывающейся информационной революции, когда откры-
вается возможность обмениваться информацией как бы «вне вре-
мени и пространства», плюс возможность сублимации транспорт-
ных потребностей общества заменой их электронно-коммуникаци-
онными. Такого рода перспективы, коренным образом меняющие не
только образ жизни людей, но саму психологию (во всякЪм случае,
социальную психологию) особей и всего рода Homo sapiens, впору
начать хотя бы осмысливать.
Все основные характеристики возможной и необходимой альтер-
нативной цивилизации XXI в., носят принципиально «непредсказа-
тельный», сугубо нормативный характер: чтобы суметь пережить
XXI в., человечество должно выйти на демографический оптимум
в среднем трех детей на одну женщину, должно максимально свер-
нуть моторный транспорт и столь же максимально развернуть бе-
зотходное производство, должно минимизировать катастрофиче-
ский сегодня разрыв поколений, проявления разрушающей личность
и общество «антикультуры» и т.д. Здесь мы вновь возвращаемся к
историческому значению научного открытия возможности замены
тщетных попыток предсказания управляемых в принципе процес-
сов технологическими прогнозами, ориентированными на повыше-
ние эффективности управления.
В меньшей, но все же в существенной мере сказанное относится
к диапазону долгосрочности в перспективе ближайшие 10-20 лет.
Конечно, инерционные процессы намного раздвигают здесь рамки
возможности прогнозов предсказаний. Например, никакие земные
или небесные силы не в состоянии существенно отклонить наметив-
шийся тренд роста мирового народонаселения с пяти до шести мил-
лиардов на протяжении грядущего десятилетия, кроме разве ядер-
ного Армагеддона (который при существующих обстоятельствах
может сегодня явиться только результатом в ничтожной степени
маловероятной чудовищной провокации либо сбоя технических си-
стем) и тому подобных глобальных катастроф, близких по своему
характеру к стихийным. Но, в свою очередь, диапазон подобных
процессов — не в пример дискретным — весьма ограничен и за
ним простирается сплошное поле «непредсказуемости».
Что можно предсказать, допустим, в отношении такого типично
дискретного явления, как мировые цены на нефть? Сколько ни рас-
считывай, а всегда может возникнуть конфликт, в значительной
мере определяющийся личным характером того или иного госу-
дарственного деятеля, конфликт, способный наполовину и более
поднять или снизить цены на нефть. Как сложатся, в частности,
на протяжении 90-х годов отношения между Ираном, Ираком, Ку-
вейтом, Объединенными эмиратами, Саудовской Аравией и дру-
гими арабскими странами?1 Предсказать тут ничего невозможно.
Можно только либо гадать понапрасну, либо разрабатывать поис-
ковые и нормативные прогнозы для оптимизации внешнеполитиче-
ских решений того или иного правительства. И так в подавляю-
щем большинстве случаев, по всем основным аспектам социального
(социально-экономического, социально-политического и т.д.) про-
гнозирования.
1 Отмечу, что эта фраза была написана до войны в Персидском заливе и до
августовского путча в Москве.
4. Проблема предвидения и предсказания в
прогнозировании дальнейшего развития России
Все только что сказанное в полной и даже еще большей мере
относится к прогнозам регионального масштаба (относительно гло-
бальных), в том числе и к прогнозам дальнейшего развития России.
Тут чем менее масштабен и сложен объект прогнозирования, чем
меньше в нем взаимоуравновешивающих трендов, тем меньше диа-
пазон «предсказуемости», несмотря на кажущуюся сравнительную
простоту прогнозных разработок.
Можно ли было, например, в первой половине 80-х годов пред-
сказать перестройку второй половины того же десятилетия? Ко-
нечно, перестройка назревала и можно было с относительно вы-
сокой долей уверенности предсказать, что она почти наверняка
произойдет в ближайшие одно-два, максимум два-три десятилетия,
тем более что назревавшая — шестая по счету, считая первой ле-
нинскую «новую экономическую политику» 1921-1929 гг. (практи-
чески 1927 г.), второй — хрущевские реформы 1956-1964 гг. (прак-
тически 1962 г.), третьей — косыгинские реформы 1966-1971 гг.
(практически 1968 г.), четвертой — оставшийся на бумаге про-
ект реформ 1979 г., пятой — андроповскую попытку 1983 г. вы-
рваться из стагнации (застоя). Все пять имели целью преодоле-
ние нежизнеспособности реализованной утопии казарменного соци-
ализма (административно-командной системы, бюрократического
централизма, тоталитаризма и т.п.), и все пять разбились о порази-
тельную живучесть — при полной нежизнеспособности — этой си-
стемы, цементированной самой мощной в мире бюрократией, срос-
шейся с мафией «теневой экономики», подавившей и разложившей
народ тотальным террором и длительным оболваниванием всех и
вся, с тяжелейшими сдвигами в области морали, психики, интел-
лекта едва ли не каждого элемента системы. Так что достаточно
было метода простой исторической аналогии, чтобы предсказать в
обозримом будущем неизбежность очередной перестройки и высо-
кую вероятность очередного провала. Но вот в конкретном плане
такого рода предсказание было бы сильно затруднено.
Не забудем, что верхние эшелоны системы были достаточно
сильно напуганы волюнтаризмом Хрущева и, казалось, сделали все
мыслимое, чтобы избежать возможности повторения чего-нибудь
подобного — не то что хрущевского, но даже андроповского. Члены
действительного правительства страны — Политбюро ЦК КПСС
— кооптировались по клановому принципу личной доверительно-
сти (хотя формально избирались на Пленуме ЦК КПСС), любые
отклонения в личных характерах взаимоуравновешивались балан-
сом тесно связанных между собой клановых групп правящей верх-
ушки и подкреплялись монолитной консервативной массой первых
секретарей обкомов партии и глав ведущих ведомств — действи-
тельных хозяев страны «на местах». При таких обстоятельствах
Горбачеву — протеже Громыко и Андропова — никогда в жизни не
стать бы не то что генсеком, но даже кандидатом в члены Полит-
бюро, если бы он хоть раз допустил высказывание — пусть даже
устно-неофициальное — позволявшее заподозрить его в реформа-
торских намерениях. Его избрали генсеком только как одного из
самых молодых и потенциально здоровых, активных членов Полит-
бюро в обстановке замешательства, вызванного тремя смертями
генсеков подряд на протяжении всего лишь каких-нибудь двух лет,
что делало выработанную систему «престолонаследия» по степени
близости очередного претендента к прежнему генсеку смехотвор-
ной в глазах всего мира и разом отводило большинство соперников
М.Горбачева. Но даже и при таких обстоятельствах новый генсек
прошел буквально чуть ли не одним голосом, волею случая аппарат-
ных игр, которые вполне могли бы дать иной расклад.
Зная такие обстоятельства, можно было с высокой долей веро-
ятности предсказать возможность очередной перестройки где-то
на протяжении 90-х годов плюс-минус пять лет (с убыванием веро-
ятности в ту или эту сторону), причем скорее всего аппаратного
типа, по образцу 1979 г., максимум — повторения андроповской в
смягченном варианте, без малейшего посягательства на самодержа-
вие партократии, вообще на незыблемость существующей системы.
Горбачев казался стопроцентно типичным партократом, взращен-
ным в коридорах обкома, хотя оказался нетипичным, а логикой со-
бытий сделался даже как бы «антитипичным». Но каким бы он ни
был, его практические возможности в роли реформатора сильно
ограничены не только его личностью (обнаружившей поразитель-
ную способность к эволюции в отличие от типичных «твердокамен-
ных» партократов), но прежде всего политическим окружением, в
котором поначалу полностью, стопроцентно господствовали кон-
сервативные силы, и даже затем среди «подобранных» лично Гор-
бачевым все как на подбор, за исключением буквально двух-трех
лиц, оказались консерваторами, даже воинствующими консервато-
рами. При такой ситуации можно понять и объяснить мучительную
медлительность, половинчатость хода перестройки в 1985-1991 гг.,
когда даже тихоходный паровоз Горбачева рисковал то и дело ото-
рваться от допотопных вагонов партократии с неизбежно следую-
щими засим катаклизмами.
Но предсказать хотя бы в общих чертах перипетии минувших
лет — это за рамками возможностей науки. Правда, это не ис-
ключало и не исключает условных предсказаний поискового и нор-
мативного характера — но кто же даже в те времена, не говоря
уже о более ранних временах, отважился бы на них? Да просто сло-
жившаяся социальная психология не позволила бы.
Можно ли было предсказать любой исход начавшейся перестрой-
ки, хотя бы из числа тех, что несколько лет назад открыто обсужда-
лись в западной литературе того времени? Например, продолжение
ситуации второй половины 80-х годов (относительное «равновесие»
перестроечных и антиперстроечных сил, не дающее развертывать
перестройку, но и не позволяющее свернуть ее, при продолжаю-
щемся медленном сползании от критической ситуации в народном
хозяйстве и внутриполитическом положении страны к катастрофи-
ческой и столь же медленном ослаблении партократических струк-
тур с усилением очень слабых пока еще оппозиционных сил) на про-
тяжении по меньшей мере первой, а то и второй половины 90-х
годов или даже следующего десятилетия — дальше не позволяла
глобальная ситуация. При таком варианте СССР попадал на ми-
ровой арене в положение Индии, Бразилии, Мексики, что означало
при существовавших условиях решение его судьбы внешними или
центробежными силами за пределами Кремля.
Другой вариант — «План Маршалла» для Советского Союза, с
помощью которого страна на рельсах рыночной экономики повто-
рила бы германское или японское «чудо» рывка в ряды наиболее вы-
сокоразвитых стран мира (ныне такого рода прецеденты довольно
многочисленны). Или военный переворот с реставрацией неоста-
линистского режима — иных вариантов при наличной верхушке
армии и КГБ в поле зрения не имелось. Или распад Советского
Союза на полностью автономные регионы — процесс шел, но сдер-
живался дислокацией вооруженных сил, на штыках которых держа-
лась империя. Или вдруг (!) цепь высокоэффективных социально-
политических и социально-экономических решений правительства,
выводящих страну из кризиса, — оснований для такой перспективы
в силу парализующего политику противоборства указанных пере-
строечных и антиперестроечных сил также в поле зрения исследо-
вателя, увы, не имелось. Можно добавить сюда любой другой мы-
слимый вариант.
По нашему мнению, на весь диапазон перспектив подобного рода
полностью распространяется упомянутое выше методологическое
положение о принципиальной непредсказуемости управляемых в
принципе процессов и явлений. Да, при наличии соответствующей
информации мы могли бы предсказать срок и форму реализации
советского аналога «Плана Маршалла», бу де в поле зрения оказался
подобный документ, так и не родившийся; можно было, абстрактно
говоря, предсказать также срок и характер государственного пе-
реворота, отпада от страны каких-то регионов, эффективного го-
сударственного решения комплекса перестроечных проблем (тоже
тогда исследователю неизвестного). Но это означало бы лишь рез-
кую активизацию борьбы перестроечных и антиперестроечных сил
вокруг «маршалльного» варианта, исход которой существенно от-
далит или приблизит срок столь радикального шага плюс столь же
существенно изменит его форму и содержание. То же самое отно-
сится к предсказанию военного переворота, распада империи или
эффективного решения проблемы. Иными словами, вместо научно-
прогностического документа мы получим политико-пропагандист-
ский, со всеми полагающимися последствиями.
Сказанное полностью относится и ко всем прочим перспектив-
ным социальным проблемам советского общества, будь то преобра-
зование экономики, судьба партократии или, что то же самое, дебю-
рократизация, демократизация общества, стабилизация двух про-
тивоположных демографических проблемных ситуаций («демогра-
фический взрыв» в Средней Азии с перспективой еще одного удво-
ения там численности населения на протяжении каких-нибудь 20-
30 лет и начинающаяся депопуляция, выморочность в большинстве
остальных регионов страны), модернизация анахроничных систем
народного образования и здравоохранения, торможение гибельных
для общества процессов разложения культуры, гиперурбанизация с
деградацией села, разрушение окружающей природной среды, вве-
дение половодья преступности (включая латентную преступность в
сфере «теневой экономики») в «естествененные» берега, дезалкого-
лизация общества с достаточно эффективными преградами на пути
грядущего массового вторжения собственно наркотиков и т.д.
Зато в том же плане растет актуальность технологического со-
циального прогнозирования, позволяющего путем сопоставления
данных поисковых и нормативных условно-предсказательных про-
гнозов «взвешивать» возможные последствия намечаемых или уже
принимаемых по каждому из перечисленных аспектов решений, по-
вышая уровень их объективности и, следовательно, эффективности.
Иное дело — сама научная проблема особенностей и характера
условности предсказаний в поисковых и нормативных прогнозах.
Но эта проблема требует специального обсуждения.
5. Прогнозы спустя пять лет после августовского путча
1991 г.
Кто бы мог осмелиться дать точные предсказания тех собы-
тий, которые произошли, скажем, в Кувейте или Москве, в совсем
недавнем прошлом? Тем не менее, прогноз развития СССР, сделан-
ный независимо друг от друга разными группами прогнозистов в
различных странах мира в конце 1987 — начале 1988 г., в наше
время почти полностью оправдался, при этом события лета и осени
1991 г, как мирового, так и нашего внутригосударственного харак-
тера убедительно продемонстрировали эффективность основного
постулата технологического прогнозирования.
Напомним, что наиболее вероятный вариант продолжения на-
чавшейся в 1985 г. очередной «перестройки» согласно прогнозам не
мог продолжаться более 4-5 лет, после чего неизбежно должен был
быть совершен переход к качественно иному сценарию развития со-
бытия.
И действительно, к осени 1990 г, т. е. через 5 лет после ее на-
чала, перестройка полностью зашла в тупик, и начался переход к
«сценарию номер два» — к военной диктатуре. Затем несколько ме-
сяцев ушло на попытки реализации «сценария номер три», а именно,
на поиски аналога «плана Маршалла» для СССР как единственной
практической возможности вывода страны из кризиса.
В августе 1991 г, снова произошел возврат к «сценарию номер
два», а затем — вторичный поворот к «сценарию номер три», но
уже на фоне «сценария номер четыре», предусматривающего рас-
пад СССР на самостоятельные регионы. И только «сценарий номер
пять», как и было запрогнозировано в 1988 г., остался наименее
вероятным. Этот сценарий предусматривал появление харизмати-
ческого лидера, который повел бы за собой все республики бывшего
СССР к выходу из кризиса ценой значительных, хотя и временных
лишений, как это имело место, например, в Польше.
Как видим, технологический прогноз, не претендуя на безуслов-
ность предсказаний, позволяет довольно объективно оценивать кон-
кретное содержание и степень вероятности ожидаемых событий.
Еще более предвидимым и еще менее предсказуемым выглядит
будущее России и других республик бывшего СССР спустя пять
лет после августа 1991 г.
Выясняется, что из состояния реализованной утопии выбраться
гораздо труднее, чем войти в него. Даже для восточных земель
Германии (бывшая Германская Демократическая Республика), как
утверждают специалисты, потребуется смена поколений, чтобы эти
земли окончательно интегрировались с западными. Что же гово-
рить о республиках СССР, которые увязли в этой утопии гораздо
глубже?
Самым крупным и самым неприятным открытием явилось то,
что, оказывается, процесс падения производства и распада госу-
дарства имеет сильную инерцию. Должно пройти несколько лет,
прежде чем распадающиеся принудительные экономические связи
«сверху» будут перекрыты зарождающимися рыночными связями
«снизу». Прежде чем миллионы людей, привыкших к «видимости ра-
боты за видимость зарплаты» начнут работать, как этого требует
рыночная экономика, пройдя чистилище массовой безработицы.
Прежде чем центробежные силы «бегства от Москвы» будут пере-
крыты центростремительными силами экономической кооперации
и политической интеграции, как в Западной Европе. Специалисты
утверждают, что для завершения периода упадка и для периода ста-
билизации положения хотя бы на уровне 1985 г. (разумеется, в ином
экономическом и политическом качестве) потребуется не менее 10-
15 лет, т.е. чуть ли не до середины 1-го десятилетия XXI века. После
этого ожидается подъем.
Поскольку многие бывшие «социалистические» страны ушли по
этому пути гораздо дальше России, можно прибегнуть к прогнозу
по аналогии и образно сказать, что к 2000-2005 г. — если все время
принимать оптимальные решения — Россия имеет шанс выйти на
уровень Польши 90-х годов (индикатор: примерно вдвое более вы-
сокая средняя месячная зарплата). И потребуется минимум еще
столько же времени, чтобы выйти на уровень Турции 90-х годов
(втрое больше средняя зарплата плюс относительная адаптация к
мировому рынку).
Так выглядит предвидимое будущее России и других республик
бывшего СССР. Его можно резко ухудшить неоптимальными ре-
шениями — вплоть до экономического краха и гражданской войны
по югославскому сценарию. Но его невозможно сделать очередным
«чудом» типа южнокорейского или тайваньского — слишком велики
инерционные силы наследия недавнего прошлого. Впрочем, Южной
Корее, Тайваню и другим дальневосточным «тиграм» тоже потре-
бовалось для их «чуда» немало лет.
А вот насчет предсказаний труднее. Произойти хоть завтра мо-
жет что угодно: от военного путча и возврата к тоталитаризму до
кровавой междоусобицы, как в Югославии. Но это только замед-
лит объективно неизбежный процесс движения от социальной пато-
логии (тоталитаризм) к социальной норме (демократия 4- рынок).
Только не надо, разумеется, идеализировать эту «норму». Здесь свои
проблемы, только «нормальные», а не «патологические».
Сегодня, в середине 90-х годов, Россия вот уже шестой год
в смятении — в третьей Великой Смуте русской истории, считая
первой конец XVI — начало XVII века, а второй — 1917-21 гг. —
топчется на распутье трех путей.
Прямо поедешь — тем путем, которым шли, точнее, кружили,
последние пять лет - неизбежно попадешь не куда-нибудь, а пря-
миком в ... Колумбию. Да-да, в типичную «банановую республику»,
жалкий «сырьевой придаток» современного мирового рынка, вот-
чину транснациональных корпорации и американских монополии,
с засильем уголовной и чиновной мафии, с непрестанной грызней
среди верхушки военщины и, соответственно, непрестанной чере-
дой дворцовых переворотов, с процветанием кучки компрадоров и
нищетой подавляющего большинства населения, с постыдными ма-
рионетками вместо правительства. Мы в России уже далеко про-
двинулись по этому пути. Налицо и кучка компрадоров («новые рус-
ские» — 2% населения), и обнищание подавляющего большинства
(свыше 80%) населения. И срастание уголовной мафии с коррум-
пированной частью госаппарата. И падение производства. И нара-
стающее засилье верхушки военщины. И постепенное превращение
страны в сырьевой придаток Запада с подавлением отечественной
промышленности и сельского хозяйства западными монополиями.
В дворцовых переворотах, а также чисто мафиозных «разборках»
среди правящих кругов тоже недостатка нет. Все это называется
«идти по пути реформ». И конца этому «пути» пока что не видно.
Налево свернешь — туда, куда зовут реваншисты-коммунисты —
наверняка попадешь в КНДР с ее марксизмом-ленинизмом-стали-
низмом-чучхеизмом, с ее массовым голодом населения, в то время
как точно такие же корейцы на юге полуострова не знают, куда де-
вать излишки продовольствия и промышленных товаров, буквально
«наступают на пятки» Японии и США. Не забудем, что все тотали-
тарные режимы всегда держались и сегодня держатся только мас-
совым террором внутри страны и беспрерывными авантюрами в
войне. Для России в геополитической обстановке 90-х гг. такая «чу-
чхеизация» неизбежно обернулась бы новым гигантским Ираном, а
то и Афганистаном от Смоленска до Владивостока.
Направо свернешь — туда, куда зазывают социал-либерал-демо-
краты (не путать с элдэпээровцами!) — со временем, как уже гово-
рилось, доберешься и до Польши, и до Чехии, и до Венгрии. Но для
этого требуются действительные реформы, а не разговоры о них.
И, в первую очередь, — режим наибольшего благоприятствования
для массового предпринимательства (напомним: исчезновение и по-
явление целого миллиона фирм в США ежегодно!). Режим, прямо
противоположный существующему порядку вещей. Ну и, разуме-
ется, переход от фиктивной «демократии» к действительно партий-
ной системе правящей и оппозиционных партий и к действитель-
ному разделению властей вместо традиционного авторитаризма на
всех уровнях государственного управления. Понятно, это означало
бы сильнейший удар по засилью чиновной и уголовной мафии, дела-
ющей все, от нее зависящее, чтобы не допустить такого поворота
событий.
По какой дороге двинется конь былинного русского витязя? Ко-
гда он, образно говоря, доберется хотя бы до Варшавы? Или до
Боготы? Или до Пхеньяна? Какие препятствия встретит? Как одо-
леет их? И одолеет ли?
Все это — хороший хлеб для гадалки или прорицателя. Или не
менее хороший сюжет для писателя-фантаста. Все это — тот слу-
чай, когда любая потуга на предсказания автоматически оборачи-
вается домыслом.
Научная прогностика в состоянии выявить при такой перспек-
тиве лишь назревающие проблемы и возможные пути их решения.
Но разве такая информация не представляет интереса для лиц,
эти решения принимающих? Равно как и для самых широких кругов
населения?
ЛИТЕРАТУРА
1. Базаров В.А. Принцип построения перспективного плана // План, хоз-во.
1928. № .2. С.38-39.
2. Каким быть плану: дискуссии 20-х годов. Л.: Лениздат, 1989. 166 с.
3. Бестужев-Лада И.В. Окно в будущее. Современные проблемы социального
прогнозирования. М.: Мысль, 1970. 269 с.
4. Бестужев-Лада И.В. Поисковое социальное прогнозирование. М.: Наука,
1984. 272 с.
5. Бестужев-Лада И.В Нормативное социальное прогнозирование. М.: На-
ука, 1987. 214 с.
6. Бестужев-Лада И.В Прогнозное обоснование социальных нововведений.
М.: Наука, 1993. 236 с.
7. Бестужев-Лада И.В Россия 1904-2004. От колосса к коллапсу и обратно.
М.: Изд. Роспедагенства, 1997 (в производстве). 292 с.
8. Гендин А.М. Предвидение и цель в развитии общества. Красноярск, 1970.
436 с.
социология
В.И.Кейлис-Борок, А.Дж.Лихтман
САМООРГАНИЗАЦИЯ АМЕРИКАНСКОГО
ОБЩЕСТВА ПРИ ВЫБОРАХ ПРЕЗИДЕНТА
И СЕНАТОРОВ США
Введение
Контингент избирателей (электорат) можно рассматривать как
нелинейную иерархическую систему «избирательных групп», кото-
рые различаются по своим интересам и по своей реакции на те
или иные приемы избирательной борьбы. Здесь имеются в виду
группы, которые складывают весь электорат. Они так или иначе
представлены в общественно-политических организациях, но от-
нюдь не совпадают с ними. Разделение на эти группы обусловлено
множеством факторов: социально-экономических, территориаль-
ных, этнических, культурных и др. Система этих групп — иерар-
хическая в том смысле, что каждая группа неоднородна и последо-
вательно подразделяется на более мелкие группы, вплоть до неде-
лимого элемента — индивидуального избирателя.
Эти представления в различных терминах общеприняты и, ви-
димо, не нуждаются в комментариях. Число обычно рассматривае-
мых групп — до нескольких сотен.
Обширная литература посвящена попыткам понять, почему аме-
риканская избирательная система приходит к выбору того или ино-
го кандидата, или предсказывать исход выборов, хотя бы и не вни-
кая в их механизм (например, путем опроса избирателей). Однако,
несмотря на предельно острый интерес к этим проблемам, много-
численные предсказания остаются противоречивыми. Некоторые из
них поразительно точны, но они пока что не воспроизводимы, в зна-
чительной мере интуитивны и их трудно выбрать заранее из всей
массы предсказаний.
Традиционную концепцию американских выборов можно резю-
мировать следующим образом.
Задача кандидата — оптимизировать предвыборную платфор-
му и тактические приемы так, чтобы привлечь на свою сторону
максимальное число избирательных групп, минимально оттолкнув
остальные.
Платформа (обещания по острым в год выборов вопросам) опти-
мизируется в соответствии с интересами избирательных групп, а
тактика — в соответствии с их психологией.
Стремление к такой оптимизации доводится до крайности в раз-
гар борьбы, что делает предвыборную кампанию поверхностной,
оторванной от реальных интересов общества; поэтому исход выбо-
ров зависит от внезапных поворотов судьбы, сенсаций, риторики и
т.п.
Эта концепция при внешней убедительности оставляет извест-
ную неудовлетворенность: хотя в природе, вообще говоря, и встре-
чаются бифуркации, нужны конкретные доказательства, чтобы по-
верить, будто огромная масса избирателей (108 для президентских
выборов, 106 — 107 для сенатских) легко меняет свое коллективное
решение под влиянием преходящих факторов, не относящихся к су-
ществу избирательной дилеммы.
Кроме того, эта концепция представляет американскую демо-
кратию, при всех ее недостатках, уж чересчур беспомощной; тради-
ционный коллективный портрет американского избирателя выгля-
дит гигантским простофилей, легко возбудимым и по-детски довер-
чивым. Он похож на того, к кому обращены коммерческие рекламы.
Проблема американских выборов заслуживает альтернативной
гипотезы. Такая гипотеза рассмотрена в работах [1-3]. Согласно
этой гипотезе коллективное решение американского электората
(в пределах страны в целом при выборе президента или каждого
отдельного штата при выборе сенаторов) определяется долговре-
менными, с характерным масштабом в несколько лет факторами и
тем самым предсказуемо за много месяцев вперед.
В работе [2] мы попытались найти такой набор характеристик
состояния общества, который в сумме достаточен для предсказа-
ния исхода выборов президента или сенаторов (аналогичная задача
для выборов в сенат рассмотрена в работе [3]). Ввиду отсутствия
адекватной теоретической модели обе задачи решались феномено-
логически, путем анализа предвыборных ситуаций прошлого. Это
может представлять интерес в нескольких отношениях:
— для понимания избирательного процесса;
— для построения его теоретической модели;
— собственно для прогнозов.
Мы пришли к выводу, что при выборе президента или сенатора
электорат решает, сохранять ли выборную должность за той же
партией, которая занимала ее в предыдущий срок. При этом безраз-
лично, что это за партия — демократическая или республиканская.
Выбор президента определяется коллективной оценкой того, как
правительство США справлялось со своей работой в предыдущие
4 года и, отчасти, как ему везло. Если не было особенно крупных
неудач, то при современной системе выборов партия останется у
власти. В противном случае она будет отстранена. Этот принцип
остается неизменным, начиная, по крайней мере, с выборов А. Лин-
кольна в 1860 г., несмотря на огромные перемены за последующие
30 лет.
Выбор сенатора, напротив, зависит от оценки электоратом по-
литического влияния кандидата.
Логика и алгоритмы предлагаемого здесь анализа соответству-
ют работам школы И.М.Гельфанда по распознаванию. Мы исполь-
зовали здесь опыт исследований в области прогноза землетрясе-
ний [4].
1. Выборы президента США. Формальный анализ
В качестве исходных данных на основе здравого смысла и
опыта прошлого были выбраны интегральные характеристики аме-
риканского общества, которые могут влиять на исход выборов. Эти
характеристики определены на минимальном уровне разрешения —
как ответы «да» или «нет» на некоторые вопросы, перечисленные
в табл. 1. На них можно ответить перед выборами, как только
обе партии выдвинут своих кандидатов. Вопросы сформулированы
так, что ответ «да» благоприятен для победы правящей партии.
Часть из них пока что определяется интуитивно. Их влияние на ис-
ход выборов известно. Представляется неожиданным, что их ока-
залось достаточно, чтобы предсказать исход выборов.
Определенные по историческим данным ответы на эти вопросы
даны в табл. 2. Они и составляют использованные исходные данные.
Постановка задачи — обычная для распознавания. Разделим
предвыборные ситуации на два класса: I (icumbent) и С (chellenger).
Ситуация I заканчивается победой кандидата от той партии, кото-
рая занимала Белый дом в предыдущее четырехлетие; ситуация С
заканчивается его поражением. Это определение сохранено и для
тех двух выборов 1876 и 1888 гг., в которых коллегия выборщи-
ков отвергла кандидата, получившего большинство голосов изби-
рателей.
Таблица 1
13 вопросов для прогноза президентских выборов
1. Количество мандатов: после последних промежуточных выборов правя-
щая партия увеличила число мест в палате представителей.
2. Конкуренция: не было серьезной борьбы при выдвижении кандидата от
правящей партии.
3. Преемственность: кандидат правящей партии — теперешний Президент.
4. Третья партия: нет серьезной третьей партии или независимой предвы-
борной кампании.
5. Экономическое положение во время избирательной кампании: страна не
испытывает экономического спада.
6. Долгосрочное экономическое положение: реальный рост дохода на душу
населения за истекающий президентский срок не меньше среднего при-
роста за предыдущие два срока.
7. Изменение политики: правящая администрация осуществила серьезные
перемены в национальной политике.
8. Социальные волнения: эа период нахождения у власти не было серьезных
социальных волнений.
9. Скандал: правящая администрация не запятнана крупным скандалом.
10. Международные или военные неудачи: правящая администрация не имеет
крупных международных или военных неудач.
11. Международные или военные успехи: правящая администрация имела
крупный успех в военной или международной политике.
12. Обаяние Президента: кандидат оппозиции харизматичен или является
национальным героем.
13. Обаяние соперника: кандидат конкурирующей партии ие харизматичен
или не является национальным героем.
Примечание. Победа предсказывается, если число ответов «нет» не превышает
пяти, в противном случае предсказывается ее поражение.
Задача формулируется так: дан «материал обучения» (табл. 2) —
примеры выборов I и С с ответами на вопросы из табл. 1. Требуется
найти «решающее правило»; оно указывает, как предсказать исход
конкретных выборов по ответам на вопросы для этих выборов.
Ввиду ограниченности материала обучения мы выбрали для ре-
шения этой задачи простейший алгоритм — «распознавание по Хе-
мингу» [2]. Он состоит в следующем: определяется ядро — набор
ответов, которые встречаются в классе I относительно чаще, чем в
классе С. Для этого вычисляются числа
К(г) = п(г/1) : п(1) - п(г/С) : п(С).
Здесь г = 1,2,..., 13 — номер вопроса из табл. 1; п(г/1) и п(г/С)
показывают, сколько выборов I и С в материале обучения имеют
ответ «да» на г-й вопрос; п(1) и п(С) — число выборов I и С в
Таблица 2
Разделение президентских выборов по вопроснику, 1860-1988 гг.
Год 1 2 3 4 5 6 7 8 9 10 11 12 13 Кол-во «нет»
Победа правящей партии
1864 0 0 0 0 0 X 0 X 0 0 0 X 0 3
1868 0 0 X 0 0 0 0 X 0 0 0 0 0 2
1872 X 0 0 0 0 0 X X 0 0 0 0 0 3
1880 0 X X 0 0 0 0 0 0 0 X X 0 4
1888 X 0 0 0 0 0 X X 0 0 X X 0 5*
1900 X 0 0 0 0 0 0 0 0 0 0 X X 3
1904 0 0 0 0 0 0 0 .0 0 0 0 0 0 0
1908 0 0 X 0 0 X 0 0 0 0 0 X 0 3
1916 X 0 0 0 0 X 0 0 0 0 0 X 0 3
1924 X тГ 0 X 0 0 0 0 X 0 0 X 0 4
1928 0 0 X 0 0 0 X 0 0 0 0 X 0 3
1936 0 0 0 0 0 0„ 0 0 0 0 X 0 0 1
1940 X 0 0 0 0 0 0 0 0 0 X 0 0 2
1944 X 0 0 0 0 0 а- 0 0 X 0 0 0 2
1948 X 0 0 X 0 X 0 0 0 X 0 X 0 5
1956 0 0 0 0 0 0 X 0 0 0 0 0 0 1
1964 X 0 0 0 0 0 0 0 0 X . 0 X 0 3
1972 X 0 0 0 0 X X 0 0 0 0 X 0 4
1984 0 0 0 0 0 X 0 0 0 0 X 0 О' 2
1988 0 0 X 0 0 0 X 0 0 0 0 X 0 3
Победа оппозиции
1860 0 X X X 0 0 X X 0 0 X X 0 7
1876 X X X 0 X X X 0 X 0 X X 0 9*
1884 X X X 0 X X X 0 0 0 X 0 0 7
1892 X X 0 X 0 0 0 X 0 0 . X X 0 6
1896 X X' X 0 X X X X 0 0 X 0 0 8
1912 X X 0 X 0 0 X 0 0 0 X X 0 6
1920 X X X 0 X X 0 X 0 X 0 X 0 8
1932 X 0 0 0 X X X X 0 0 X X X 8
1952 0 X X 0 0 X X 0 X X 0 X X 8
1960 X 0 X 0 X X X 0 0 X X X X 9
1968 X X X X 0 0 0 X 0 X X X 0 8
1976 X X 0 0 0 X X 0 X X X X 0 8
1980 X X 0 X X 0 X 0 0 X 0 X X 8
Примечание. Номера вопросов соответствуют табл.1: 0 - - «да*; X - — «нет».
Звездочкой отмечено, что коллегия выборщиков изменила результаты народного
голосования.
материале обучения. Следующий ответ входит в ядро: «да», если
А'(г) > к-, «нет», если К(г) < -к. Если |А"(г)| < к, то г-й вопрос не
используется для распознавания.
Расстояние D от данных выборов до ядра определяется так:
£> = £ Wi, где Wi — вес г-го вопроса, W, = |&(г)| : max|k(i)|. Сум-
мирование проводится по тем вопросам, ответ на которые противо-
положен ответу в ядре. При Wi = ID есть просто число ответов, не
совпадающих с ответами в ядре (т.е. не благоприятных для победы
правящей партии). Решающее правило формулируется так: выборы
относятся к I, если D < L и к С, если D > L, где L — некоторый
порог. Если D близко к L, можно для осторожности отказаться от
прогноза, но мы это условие не вводим.
При анализе данных мы приняли Wt = I и к = 0.1. Включив
все выборы за 1860-1880 гг. в материал обучения, получаем ядро,
состоящее из одних нулей (все ответы — «да»). Оно соответствует
здравому суслу. Разделение наборов с помощью этого ядра показано
в последнем столбце табл. 2, который определяет апостериорный
выбор порога L = 5.
Как и во всех задачах на распознавание, успех определяется на-
дежностью решающего правила. В конце концов, хорошее разделе-
ние выборов в табл. 2 было предопределено алгоритмом. В пользу
решающего правила говорят успешные заблаговременные прогнозы
выборов 1984 и 1988 гг. [1]. Для его статистической оценки необхо-
димо больше заблаговременных прогнозов.
Устойчивость полученных результатов подтверждается вариа-
цией материала обучения. Основной численный эксперимент в этом
направлении аналогичен эксперименту «сейсмическая история» из
работы [4]. Мы определяли исход каждых последовательных выбо-
ров, начиная с 1900 г., используя в качестве материала обучения все
предыдущие выборы (но, разумеется, не те выборы, исход которых
«предсказывается»). Этот эксперимент воспроизводит следующую
ситуацию: наблюдатель выполняет описанный выше анализ с 1900
по 1980 г. перед каждыми выборами и после выборов выясняет,
ошибся он или нет. Этот эксперимент дает правильный результат
для 19 из 21 выборов.
Итак, сформулированное выше феноменологическое различие си-
туаций перед выборами I и С мало изменялось в течение последних
130 лет.
Проводилась также дополнительная обработка. В частности, ис-
ключался один из пяти вопросов и добавлялся один из следующих
ниже: какая из двух партий — республиканская или демократиче-
ская — находилась в оппозиции; была ли серьезная борьба за выдви-
жение кандидата оппозиции; вели ли США войну во время предвы-
борной кампании; существовали ли особенно острые внешнеполи-
тические проблемы; то же для внутренних проблем. Исключались
5 выборов, при которых число голосов за две основные партии раз-
личалось менее чем на 1% (1880, 1884, 1888, 1960, 1968 гг.). Оста-
влены в обучении только выборы XX в. (ядро при этом не измени-
лось).
При всех этих экспериментах добавлялось не более двух ошибок
(подробнее см. [1,2]).
Мы использовали также алгоритм «распознавание по Бонгарту»
или КОРА-3 [4], который может формировать комплексные вопросы
из двух или трех первоначальный. Это не дало пока лучших или
дополнительных результатов. Преимущество распознавания по Хе-
мингу в том, что оно меньше подвержено влиянию случайных ком-
бинаций тех или иных ответов в материале обучения.
2. Промежуточные выборы в сенат. Формальный анализ
Сенаторы выбираются на шесть лет. Каждые два года пере-
избирается примерно треть сенаторов. Тем самым часть выборов
(«промежуточные») проводится в середине срока полномочий Пре-
зидента США, а часть одновременно с выборами Президента.
Выборы в сенат, проводящиеся между президентскими, рассма-
тривались нами потому, что работа [3] делалась в 1985 г., и мы
хотели проверить полученные результаты на предсказании исхода
выборов 1986 г.
Логика и алгоритмы анализа оставались теми же, что и для
президентских выборов.
Исходные данные были взяты из истории трех предыдущих про-
межуточных выборов - 1974, 1978 и 1982 гг. Каждый из 50 штатов
США участвовал в них, по крайней мере, один раз. Для анализа
были отобраны интегральные характеристики предвыборного со-
стояния штатов (табл. 3). Вопросы в табл. 3 сформулированы так,
что ответ «да» благоприятствует «партии сенатора», т.е. той пар-
тии, представитель которой занимает оспариваемое место. Ее по-
беда предсказывается, если число ответов «нет» не больше четырех;
в противном случае предсказывается ее поражение.
Вопросы 2, 3 и 6 были уточнены так, чтобы ответы на них не
являлись бы интуитивными (см. [3]).
Постановка задачи и алгоритм распознавания — те же, что для
президентских выборов.
Результаты голосования отражены на рисунке. Они приводят
к следующему решающему правилу: место сенатора сохранится за
той же партией (I), если D < 5, и перейдет к другой партии (С),
если D > 5. Поскольку, как и раньше, хорошее разделение выбо-
ров I и С (см. рисунок) обусловлено процедурой обучения, это пра-
вило нуждается в проверке. Для этой проверки использован прогноз
выборов 1986 г., опубликованный за неделю до них [5]. Этот про-
Таблица 3
8 вопросов для прогноза промежуточных выборов в сенат
Кандидат ^партии сенатора»:
1. Теперешний сенатор?
2. Деятель национального масштаба?
3. Выдвинут без серьезной борьбы (собрал не менее двух третей голосов в
первом же туре)?
»Партил сенатора»:
4. Собрала не менее 60% голосов на предыдущих выборах.
5. Собрала для проведения компании, по крайней мере, на 10% больше
средств, чем оппозиция.
Кандидат оппозиции:
6. Не деятель национального масштаба и не был ни губернатором штата,
ни членом Конгресса США.
7. Принадлежит той же партии, что Президент США.
8. Выдвинут без серьезной борьбы.
гноз дан в тайл. 4 вместе с предсказаниями экспертов и фактиче-
ским исходом выборов. Мы видим, что наш прогноз подтвердился в
30 штатах из 34. Статистическая значимость оценивалась для двух
утверждений:
а) использованные данные сильно коррелированны с исходом вы-
боров;
б) использованные данные позволяют предсказывать исход вы-
боров (т.е. давать нетривиальные предсказания).
Для проверки утверждения а) можно использовать результаты
прогноза выборов 1986 г. в 34 штатах. Для проверки утвержде-
ния б) следует исключить из рассмотрения выборы, исход которых,
по мнению экспертов, был предсказуем; мы исключили группу P.S.
из табл. 4.
Конкурирующая гипотеза следующая: место сенатора сохранит-
ся за той же партией (I) с вероятностью Р<(£ = 1.2) и перейдет к
другой партии с вероятностью 1 - Pi. (Р, соответствует случаю,
когда предыдущий сенатор принадлежит той же партии, что и пре-
зидент США; Ръ - противоположному случаю.) Известно, что при
промежуточных выборах в сенат Рг > Pi, т.е. президентская пар-
тия в менее благоприятном положении. По данным о прежних вы-
борах Pi = 0.67; Р2 = 0.87. Уровень значимости оценивался в [3].
Конкурирующая гипотеза отвергается на уровне выше 99,9% для
SC78I
IL78I
LA74I
ID74I
HI74I
GA74I
О
WV82I
WI82I
WA82I
ND82I
MT82I
MS82I
TH78I
OR78I
WI74I
WA74I
SC74I
MO74I
IN74I
IL74I
CT74I
AL74I
1
OH82I
NY82I
ME82I
НОВ 21
FL82I
NM78I
NC78I
ID78I
AK78I
SD74I
KS74I
IA74I
CA74I
AZ74I
2
WY82I
UT82I
TX82I
TN82I
RI82I
РАВ 21
MN82I
MI82I
MA82I
HIB2I
DE82I
CTB2I
AZB2I
WV78I
VA78I
TX78I
RI78I
LA78I
NC74I
NY74I
ND74I
МА78С
1
VT82I
NJ82I
NEB 21
MOB 21
INB2I
HT78I
KY7BI
KS78I
GA78I
DE7BI
AR78I
AL78I
PA74I
OR74I
OK74I
MO74I
AR74I
AK74I
MI78C
NV82C
IA78C
4
WY7BI
NM82C
NJ78C
NH78C
HE7BC CA82I
ME78C UT74I
CO78C OK7BC SD78C
VT74C MN78C MS7BC
KY74C NV74C OH74C
CO74C NH74C FL74C
5 6 7
Разделение промежуточных выборов (1974-1982 гг.) по расстоянию
Хеминга D (нижняя строка) от ядра (т.е. по числу ответов «нет»
на вопросник в табл. 3). Первые две буквы — индекс штата; цифры
указывают год выборов; латинские буквы: I — победа «партии сена-
тора», С — победа оппозиции.
утверждения а) и на уровне выше 97% для утверждения б). Эти
оценки подробно обоснованы в [3].
Чтобы получить представление об устойчивости этих оценок,
мы определяли Pi, Р2 по другим ансамблям промежуточных выбо-
ров, по некоторым показателям, сходным с 1986 г., а именно: 1) в
тех же 34 штатах после 1945 г. (все выборы или только при респу-
бликанской администрации) и 2) выборы во всех штатах при рес-
публиканской администрации (1974 и 1982 гг.). Кроме того, мы
уменьшали на 1 число успехов. Во всех случаях оценки доверитель-
ного уровня менялись несущественно.
Прогноз промежуточных выборов 1990 г., также опубликован-
ный заранее [6], дал верные результаты в 32 случаях из 35. Тем
самым в целом из 69 предсказаний 62 оказались правильными. Вы-
боры 1990 г. интересны тем, что «партия сенатора» осталась у вла-
сти в 32 штатах, что для промежуточных выборов необычно много.
Даже в этой необычной ситуации алгоритм прогноза дал весьма
удовлетворительный результат.
Устойчивость решающего правила исследовалась путем тех же
численных экспериментов, что и для президентских выборов, и ока-
залась достаточно высокой (конкретные числа приведены в [3]).
Единственный серьезный источник неустойчивости — это по-
рог D = 5 при разделении выборов на I и С. Его изменение на ±1
вызывает, как видно из рисунка, слишком много дополнительных
Таблица 4
Прогноз и результаты выборов 1986 г.
Штат Ответ на вопрос D CQ no [3] Прогноз Результат
1 2 3 4 5 6 7 8
HI 0 0 0 0 0 1 0 0 1 P.S. + +
ОН 0 0 0 0 1 0 0 0 1 P.S. + +
SC 0 0 0 0 0 1 0 0 1 P.S. + +
UT 0 0 0 0 0 0 1 0 1 P.S. + +
АК 0 1 0 1 0 0 0 0 2 P.S. + +
СТ 0 1 0 1 0 0 0 0 2 P.S. + +
KS 0 0 0 0 0 1 1 0 2 P.S. + +
KY 0 1 0 0 0 1 0 0 2 P.S. + +
ND* 0 1 0 0 0 0 1 0 2 P.V. + -
AR 0 1 0 1 0 0 1 0 3 P.S. + +
СА 0 0 0 1 1 1 0 0 3 V. + +
IL 0 1 0 1 0 1 0 0 3 P.S. + +
IN 0 0 1 1 0 0 1 0 3 P.S. + +
IA 0 1 0 1 0 0 1 0 3 P.S. + +
NH 0 1 0 1 0 0 1 0 3 P.S. + +
OR 0 0 1 1 0 0 1 0 3 P.V. + +
VT 0 1 0 1 1 0 0 0 3 P.V. + +
AZ 1 1 0 1 0 0 1 0 4 P.S. + +
CO 1 1 0 1 1 0 0 0 4 V. + +
ID 0 1 0 1 1 0 1 0 4 V. + +
LA 1 1 0 0 1 0 0 1 4 H.V. + +
NY 0 1 0 1 0 1 1 0 4 P.S. + +
NC* 0 1 0 1 1 0 1 0 4 P.V. + -
OK 0 1 0 1 1 0 1 0 4 V. + +
WA* 0 1 0 1 1 0 1 0 4 P.V. + -
WI 0 1 0 1 0 1 1 0 4 V. + +
AL 0 1 0 1 1 1 1 0 5 V. - -
FL 0 1 0 1 1 0 1 1 5 H.V. - -
GA 0 1 0 1 1 1 1 0 5 P.V. - -
MO 1 1 0 1 1 0 0 1 5 H.V. - -
PA* 0 1 0 1 1 1 1 0 5 V. - +
MD 1 1 0 0 1 1 1 1 6 H.V. - •
NV 1 1 0 1 1 0 1 1 6 H.V. - -
SD 0 1 1 1 1 0 1 1 6 H.V. - -
Примечание. О — «да»; 1 — «нет»; CQ — положение «партии сенатора» по
оценке ежеквартальника Конгресса США: вероятно надежное (P.S.), потенци-
ально уязвимое (P.V.), уязвимое (V.), сильно уязвимое (H.V.); «+» и «—» — вы-
боры I и С соответственно; * — неверный прогноз.
ошибок. Эта неустойчивость сохраняется, если в алгоритм вводятся
веса Wi.
Тот факт, что вопреки этой неустойчивости прогноз оказался
статистически значимым, обнадеживает: он может означать важ-
ность каждого вопроса или, скорее всего, что ответы сильно кор-
релированны. Это отражает некоторую тенденцию электората, ко-
торую нам не удалось диагностировать проще.
Предельная дискретизация характеристик («да» или «нет») —
весьма распространенный прием эвристического анализа сложных
данных, особенно в случае малых выборок. Он ведет к «потере ин-
формации», но зато делает результаты более надежными.
Выборы сенаторов в годы, когда избирается и президент, анали-
зировались аналогично [1]. Полученные результаты нельзя считать
проверенными, поскольку прогноз выборов 1988 г. не был заранее
опубликован. Однако для полноты картины мы эти результаты при-
ведем.
Первые шесть вопросов из табл. 3 остались прежними, два по-
следних вопроса были заменены следующими.
7А. Для президентских выборов предсказывается, что правящая
партия останется у власти (I).
8А. Выносимое на выборы место сенатора занято той же пар-
тией, которой принадлежит большинство в Ассамблее штата.
По этому вопроснику, при том же пороге D = 5 правильно опре-
деляется исход 30 из 33 сенаторских выборов 1988 г.
3. Обсуждение результатов
В естественных науках часто встречаются сложные хаотические
системы, в поведении которых после правильного усреднения обна-
руживаются устойчивые закономерности, в том числе и предска-
зуемость. Эти закономерности трудно (и часто невозможно) выве-
сти из поведения элементарных компонент системы. Изложенные
здесь результаты означают, что в такую систему самоорганизу-
ется и американское общество при выборах президента и сенаторов.
Иерархическая система американских избирательных групп обла-
дает закономерным устойчивым и предсказуемым поведением с вы-
сокой степенью интеграции на уровне страны или штата.
В процедуре выборов эта интеграция преодолевает противоре-
чия и в интересах групп, и в их социальной психологии. Закономер-
ности в исходе выборов остаются устойчивыми от 1860 до 1988 г.,
т.е. в предельно широком диапазоне всех условий и с предельно
различным электоратом. В 1860 г. он не включал группы, соста-
вляющие три четверти теперешнего электората: женщины, негры,
подавляющее большинство выходцев из Латинской Америки, Азии,
Восточной и Южной Европы.
Эти выводы в свете опыта изучения хаотических систем, встре-
чающихся в естественных науках, не кажутся необычными. Их
сравнение с традиционным представлением о каждых конкретных
президентских выборах с 1860 г. проведено в работе [1].
Чем обусловлен коллективный выбор электората? Об этом мож-
но судить по достаточным для прогноза характеристикам состоя-
ния общества (см. табл. 1 и 3). Заметим, прежде всего, что, несмо-
тря на до наивности простое определение этих характеристик, они
отражают с сильным усреднением весьма широкий круг глубоко
затрагивающих общество явлений. Рассмотрим, например, первую
характеристику (вопрос), использованную для президентских вы-
боров (см. табл. 1). Она зависит от того, как изменилось отно-
шение электората к правящей партии (что выражено в реальном
голосовании, а не в менее надежных опросах); насколько эффек-
тивна партийная машина; как изменилась способность администра-
ции справляться со своими задачами в два предвыборных года, в
том числе ее способность не разочаровывать своих сторонников и
т.п. Вторая характеристика отражает наличие лидерства и дисци-
плины в правящей партии и снова ее удовлетворенность деятельно-
стью правительства. Средства, собранные на избирательную кам-
панию (последняя характеристика для выборов в сенат, см. табл. 3),
отражают отношение избирателей, взвешенное по их реальной (де-
нежной) поддержке. Разбор всех характеристик для президентских
выборов можно найти в работе [1]; некоторые соображения для се-
наторских выборов приведены в [3].
Напомним, что наши выводы состоят в достаточности, но не
единственности или оптимальности рассматриваемых характери-
стик. Напротив, у нас сложилось впечатление, что другие характе-
ристики могут быть столь же, если не более, важны. Например, в
работе [1] набор характеристик был изменен по сравнению с перво-
начальным [2]. На прогнозе вперед это не отразилось.
Что мы узнали об американских выборах? Обычно при анализе
выборов принимают во внимание: партийную принадлежность кан-
дидатов (республиканец или демократ); их позиции и обещания по
актуальным в год выборов проблемам; стратегию и тактику пред-
выборной борьбы, драматизируемые события последних месяцев.
Согласно нашим выводам эти факторы не существенны. 13 ха-
рактеристик, достаточных для прогноза президентских выборов,
показывают, что исход президентских выборов определяется кол-
лективной оценкой деятельности правительства за истекшие 4 года.
Оценка включает все стороны правительственной деятельности,
включая экономику. Если эта оценка положительна, кандидат пра-
вящей партии будет избран; в противном случае он потерпит пора-
жение. Иными словами, исход выборов зависит не от обещаний, а
от результатов деятельности правительства и не зависит от идео-
логии, поскольку она не отразилась на результатах.
Восемь характеристик, достаточных для прогноза выборов в се-
нат, интерпретируются сложнее, что и естественно для менее силь-
ного усреднения. Значительную роль играет политическое влияние
кандидата и его партийной машины в штате. Оценка результатов
проявляется лишь косвенно, а состояние экономики, вопреки ожи-
даниям, играет небольшую роль.
Как победить на выборах? Если принять изложенные вьппе вы-
воды, то исход выборов предопределен вскоре после выдвижения
кандидатов и изменить его могут лишь перемены, не зависящие от
борющихся сторон (исключая разве что скандал).
Это противоречит традиционным представлениям о выборах.
Вспомним, например, традиционную версию выборов президента
Буша [1].
За четыре месяца до выборов, в июле 1988 г., его поражение счи-
талось несомненным, поскольку в опросах избирателей он отставал
от М. Дукакиса на 17%; ни один из кандидатов не побеждал при
таком разрыве накануне выборов. Через месяц Буш произнес бле-
стящую речь в Новом Орлеане, и его популярность сразу возросла.
Он продолжал блестящие выступления (что связывалось с помощью
Пегги Нунан) и начал очень эффективно (при помощи П. Атуотера
и Р. Эйлса) разоблачать ошибки М. Дукакиса на посту губернатора
штата Массачусетс: загрязненность Бостонской гавани, мягкий ре-
жим для опасных преступников. В результате при опросе избирате-
лей накануне выборов он опередил М. Дукакиса на 8%, и примерно
с этим перевесом победил.
Таким образом, согласно традиционной версии несколько бле-
стящих помощников и неудачи соперника в его штате неожиданно
изменили решение национального электората.
Из наших выводов вытекает другая версия. За полгода до вы-
боров (т.е. за три месяца до начала «новой тактики» Буша) был
опубликован следующий прогноз: «Если между нынешним момен-
том и выборами не произойдет неожиданный спад экономики или
национальная катастрофа, то Буш уверенно победит независимо от
того, кто будет его соперником» [1]. Этот прогноз был основан на
значении D = 3, т.е. на сильно усредненной и устойчивой оценке
состояния общества.
Это не значит, конечно, что любая из сторон может сразу же
прекратить предвыборную борьбу. Наши выводы получены для
условий, когда она ведется именно так, как последние 130 лет: стра-
тегия и тактика соперников не существенны, но остается пока не
ясным, просто ли они бесполезны или взаимно компенсируют друг
друга. Следствия для президентской предвыборной кампании оче-
видны.
Для победы существенны только достижения национальной ад-
министрации за истекшие 4 года; тем самым бесполезны и предвы-
борные коалиции, и попытки манипулировать общественным мне-
нием, и негативные высказывания в адрес соперника.
Что делать партии, которой, если верить полученным здесь кри-
териям, предстоит поражение?
Если это партия президента — попытаться добиться серьезных
успехов в экономике (вопрос 5, см. табл. 3) внутренней политике
(вопрос 7), внешней политике (вопросы 10,11). Иными словами, при-
носить управление в жертву пропаганде бесполезно, единственный
шанс — улучшить управление.
Если это не партия президента, у нее нет возможностей суще-
ственно изменить состояние дела. Нам кажется, что ее единствен-
ный шанс — попытаться повернуть содержание предвыборной кам-
пании к существу дела, предложив будущей администрации про-
екты основных решений: бюджета, основных международных до-
говоров, новых законов, кабинета министров.
При выборах в сенат политические факторы и партийная ма-
шина играют значительную роль, а требования к сенатору, занима-
ющему этот пост к моменту выборов, кажутся менее конкретными.
Изложенные результаты иллюстрируют, как мы надеемся, воз-
можности сильного («глобального») усреднения для понимания и
прогноза поведения сложной хаотической системы, какой является
современное общество.
Исход выборов президента и сенаторов США определяется про-
стыми по формулировке предельно усредненными характеристика-
ми социальной, политической и экономической обстановки в год
выборов.
В случае президентских выборов эти характеристики усреднены
по США в целом. Один и тот же набор характеристик удовлетвори-
тельно коррелирует с исходом выборов, начиная, по крайней мере,
с 1860 г. В случае выборов в сенат эти характеристики усреднены
по штату в целом. Один и тот же набор характеристик оказывается
коррелированным с исходом выборов для каждого штата, начиная
с 1974 г.
Вместе с тем исход выборов оказывается слабо коррелирован-
ным с рядом факторов, которым традиция придает большое зна-
чение: принадлежность кандидата к республиканской или демокра-
тической партии; его позиция по актуальным проблемам; тактика
предвыборной борьбы, ее сенсации и перипетии.
Полученные выводы подтверждены успешными заблаговремен-
ными прогнозами выборов в сенат в 1986 и 1990 гг. и президент-
ских выборов в 1984 и в 1988 гг. Для выборов в сенат число успехов
(62 из 69) достаточно, чтобы считать результат статистически зна-
чимым.
ЛИТЕРА ТУРА
1. Lichtman A., DeCell К. The thirteen keys to the Presidency. Lanham; New-
York; London Madison books, 1990. 449 p.
2. Lichtman A., Keilis-Borok V.I. Pattern recognition applied to presidential elec-
tions in the United States 1860-1980; Role of integral social, economic and po-
litical traits // Proc. Nat. Acad. Sci. USA, 1981. Vol.78. P.7230-7234.
3. Lichtman A., Keilis-Borok V.I. Aggregate-level analysis and prediction of
midterm senatorial elections in the United States, 1974-1986 // Ibid. 1989.
Vol.86. P.1076-1080.
4. Гельфанд И.М., Губерман Ш.А., Кейлис-Борок В.И. и др. Условия возник-
новения сильных землетрясений (Калифорния и некоторые другие регионы)
// Вычислительная сейсмология. М.: Наука, 1976. № 9. С.3-90.
5. DeCell К. Interview// Washingtonian. 1986. Nov. Р.142-145.
6. Lichtman A., DeCell К. Interview // Ibid. 1990. Oct. P.115-119.
этнология
Л.Н.Гумилев, В.Ю.Ермолаев
ПРОБЛЕМЫ ПРЕДСКАЗУЕМОСТИ
В ИЗУЧЕНИИ ПРОЦЕССОВ
ЭТНОГЕНЕЗА
Проблема предсказуемости в самом общем виде порождается
фактом существования прошлого, настоящего и будущего. Для че-
ловека предсказуемость, вероятно, стала проблемой с того момента,
как он начал ощущать это различие. Разность прошлого, настоя-
щего и будущего, очевидно, ощущалась уже предками современного
человека из рода Hominides, однако имеющиеся данные не дают
оснований для однозначных выводов на сей счет. Различие субстан-
ций времени — факт установленный для людей так называемой
фиксированной исторической эпохи, т.е. последних 3-4 тыс. лет.
Столь широкие хронологические рамки свидетельствуют, что по-
требность заглянуть в будущее, попытаться его определить у Ното
sapiens имеет довольно сильные стимулы.
В самом деле, мы живем в сложном, изменяющемся мире, накла-
дывающем на нашу жизнь множество внешних ограничений, кото-
рые отнюдь не всегда делают эту жизнь легче и приятнее. И не
стоит думать, будто наши предки располагали более широкой по-
лосой свободы: просто их ограничения были качественно иными.
Короче говоря, у «простого человека» поводов для визита к гадал-
кам и прорицателям и тогда было ничуть не меньше, чем поводов
сегодня для общения с экстрасенсами.
Существенно, что рост или спад бытового интереса к будущему
оказывается никак не связанным с успехами науки или достижени-
ями технического прогресса: XX в., век высоких технологий и по-
трясающих воображение прорывов в самых разных областях зна-
ния, вместе с тем стал и столетием реанимации для астрологии,
хиромантии и самой примитивной эсхатологии. И как это не пара-
доксально, но в поведенческом плане современный обладатель уни-
верситетского диплома, старающийся определить судьбу по звез-
дам или папиллярным линиям руки, ничем не отличается от средне-
вековых клиентов знаменитого Нострадамуса или античного рим-
лянина, вопрошавшего авгуров о дне грядущем. Во всех случаях
остается непреложной бытовая уверенность в принципиальной воз-
можности предсказания будущего, а успех прогноза ставится в ис-
ключительную зависимость от квалификации специалиста.
Но как только мы уходим от бытового понимания предсказу-
емости и начинаем говорить о научном ее понимании, мы обязы-
ваем себя к ответу на ряд принципиальных вопросов. Первый из
них: «О предсказуемости чего идет речь?» Ведь прогнозирует-то
каждый в своей сфере компетенции: экономист пытается опреде-
лить по конъюнктуре рынка ожидаемый объем продаж и связан-
ную с ним прибыль, политик — будущую расстановку сил в борьбе
за власть, врач — тенденцию развития болезни и т.д. Но самые
разные объекты предсказуемости объединяет нечто общее: человек
пытается предсказать поведение системы, ее возможную поведен-
ческую реакцию на внешние воздействия. Иначе говоря, предсказу-
емость — это всегда предсказуемость поведения объекта. Однако
понимание универсального характера категории поведения распре-
делилось по разным областям знания неравномерно. В естественных
науках обоснованно считается, что «естественнее или, по меньшей
мере, менее двусмысленно говорить о СЛОЖНОМ ПОВЕДЕНИИ
(выделено авторами — Л.Г., В.Е.), нежели о сложных системах»
[1, с. 12].
В гуманитарных (а тем более в так называемых общественных)
науках дело обстоит иначе. Там описанию по универсальной моде
поведения традиционно предпочитаются расчлененные, классифи-
кационные описания по способам производства, языкам, культурам
и т.п. Разумеется, расчлененные описания необходимы, но дума-
ется, что они все же являются не самоцелью, а лишь необходимыми
этапами в уяснении общих механизмов поведения для систем, раз-
личных по уровням структурной организации. И потому страшна
не сама приверженность гуманитариев к символам языка или куль-
туры, а то, что многие попытки применить категорию «поведе-
ние» к «двуногому без перьев» почитаются недопустимой ересью.
Но, увы, понимание основной задачи науки — поиска и объясне-
ния общего в темпоральном океане разнообразия — не составляет
атрибута мышления всех, кто наукой занимается. Не является ис-
ключением из правила и классическая этнография.
И здесь мы поневоле должны отвлечься от основной темы дан-
ной работы и объяснить некоторые специфические нюансы. До са-
мого последнего времени в отечественной этнографии полностью
господствовал традиционный взгляд на этнос как на социальную
общность, в развитии которой превалирующую роль играют исто-
рически сложившиеся условия материального производства, рамки
общественно-экономических формаций, культурные и лингвистиче-
ские детерминативы [2, с. 26-31 и след.; 3, с. 10-15; 246-250]. Аль-
тернативная этнологическая концепция этногенеза с несоциальной
парадигмой возникла сравнительно недавно [4, с. 112-120; 5] К на-
стоящему времени сходства и различия между двумя подходами к
изучению этногенеза получили достаточное освещение и вряд ли
нуждаются в дополнениях [6, с. 231-239]. В дальнейшем, говоря об
этносах и этногенезе, мы будем иметь в виду исключительно этно-
логическое значение этих терминов.
Этнология квалифицирует этногенез как несоциальный природ-
ный процесс, происходящий в биосфере Земли. Энергетическую ос-
нову этногенеза составляет открытая В. И. Вернадским биохимиче-
ская энергия живого вещества биосферы [7, с. 284]. Применительно
к этногенезу эффект этой энергии назван Л. Н. Гумилевым пасси-
онарностью. Пассионарность обеспечивает создание и существова-
ние в биосфере Земли отдельных этнических систем — природных
коллективов людей, обладающих общностью стереотипа поведения
на заданном уровне этнической иерархии и противопоставляющих
себя всем другим таким же коллективам, исходя из ощущения ком-
плиментарности [5, с. 93-94]. Именно комплиментарность (от фр.
compliment — приветливость) является первичным для формирова-
ния любого этноса ощущением этнической совместимости [5, с. 262].
Природа комплиментарности гипотетически связывается с колеба-
ниями этнического поля [5, с. 291-293].
Как и всякая другая, этническая система иерархична. Иерар-
хию этносферы составляют: 1) консорции: небольшие группы лю-
дей, объединенные общностью судьбы (например, творческие объ-
единения, банды, религиозные секты и т.п.); 2) субэтносы: подси-
стемы этносов, видимые как довольно крупные этнографические
или территориальные группы с бытом и культурой, отличающи-
мися от «столичных» (старообрядцы, поморы, сибиряки, интелли-
генты); 3) этносы: основные этнические таксоны, именуемые в со-
циальной системе отсчета народами, народностями или нациями;
4) суперэтносы: высший таксон этнической иерархии, включающий
в себя группу этносов с общей этнокультурной доминантой («Хри-
стианский мир», «Великая степь», «Античный мир» и т.д.)
Связь между биосферой и этнической системой можно схема-
тично очертить следующим образом. Под действием внешнего по
отношению к биосфере фактора (предположительно космического
излучения) в некотором ареале среди населяющих его человеческих
особей происходит мутация (пассионарный толчок). Она опреде-
ляет появление в исходной для этногенеза популяции наследуемого
признака — пассионарности. Носители признака (пассионарии) от-
личаются при физиологической полноценности способностью к по-
вышенной абсорбции энергии живого вещества из внешней среды и
выдаче ее в виде работы в физическом смысле. Поскольку признак
передается по наследству, то в последующих поколениях наблюда-
ется увеличение «количества» деятельности, выражаемое, скажем, в
числе событий. События эти своеобразны. Избыточная (свободная)
энергия пассионарности по вектору противоположна инстинкту са-
мосохранения индивида. Следовательно, пассионарии часто дей-
ствуют во вред себе — своим организмам и своему потомству. Но
действуя согласованно друг с другом и координируя действия всех
остальных людей, они вкладывают свою избыточную энергию в со-
здание и развитие новой поведенческой структуры — нового эт-
носа [5, с. 262].
Уровни пассионарности отдельных людей также различаются
между собой, как и уровни пассионарности разных этносов, изме-
няясь с течением времени. Величина пассионарности отдельного че-
ловека может по-разному соотноситься с величиной его инстинкта
самосохранения. Если пассионарность больше инстинкта, то чело-
век обладает за счет избыточной энергии способностью к сверх-
напряжениям, к деятельности сверх витальной потребности ради
разнообразных отвлеченных идеалов: это воин, писатель, админи-
стратор, авантюрист, мистик — каждый может представить себе
множество иных инициативных фигур [5, с. 255-259]. Когда пассио-
нарность равна инстинкту, это уравновешенный трудолюбивый че-
ловек, не расположенный драться за что-либо, а склонный добиться
своего постепенно и неуклонно — «честным трудом» [5, с. 273-274].
И наконец, еще один экстремальный стереотип связан с превыше-
нием инстинкта над уровнем пассионарности. Это тип безыници-
ативного человека с жизнелюбивыми, несложными устремлениями,
мало склонного не только к деятельности ради прозаичной цели, но
и к труду, направленному на самообеспечение — тип наркомана, ал-
коголика, профессионального нищего и им подобных [5, с. 275-277].
Временное изменение количества людей с разными стратегиями по-
ведения в данном этносе определяет, таким образом, общий уровень
его пассионарности. Вообще говоря, содержание упомянутых выше
четырех терминов (этнос, пассионарность, комплиментарность, эт-
ническое пассионарное поле) позволяет описать феноменологически
любой процесс этнического поведения во всех его фазах, к которым
можно отнести пассионарный подъем, акматическую фазу, надлом,
инерцию, обскурацию и гомеостаз (этноландшафтное равновесие)
[5, с. 355-431].
Приведенное выше пространное, но неизбежное вступление дает
повод думать, что этнологическая концепция этногенеза, по край-
ней мере, исходит из объективной основы, необходимой для пред-
сказуемости этнических процессов, а именно, опирается на челове-
ческое поведение. Но достаточно ли этого? Ведь для предсказуе-
мости мало иметь в виду сам феномен поведения: необходимо еще
и уточнить механизм процесса, типологизировать изучаемую си-
стему. Применительно к этносу встает, прежде всего, задача опре-
деления функциональных различий его с социумом. Различия эти
совершенно отчетливы. Этнос — природный коллектив, посред-
ством которого социальная жесткая система, лишенная способно-
сти к саморазвитию, получает необходимую ей для работы энер-
гию. Взаимодействие этноса с социумом создает этносоциальную
систему, где этнос сохраняет самостоятельное и жизненно важ-
ное значение. Такая функция этноса сообщает этносоциальной си-
стеме фазу развития, в которой отражается количество имеющей-
ся энергии.
Видимая нами непосредственно история идет не в рамках обще-
ственно-экономических формаций, а в дискретных этносоциальных
системах. И потому факты этой истории есть результат, в кото-
ром сопрягаются равноправно этническое и социальное направле-
ния развития. Следовательно, каждый факт истории отражает на-
ряду с социальной также и этническую динамику. Вместе с тем
сам человек, выступающий как исследователь бытия, является су-
ществом социальным и потому не может получать информацию
иначе, чем через явления социальные. Понятно, однако, что форма,
в которой получена информация, не исчерпывает того комплекса
абсолютных причин, результатом коих является ее существование.
Иначе говоря, хотя мы и можем наблюдать лишь социальные явле-
ния, факт их наблюдения не означает, что они имеют только и ис-
ключительно социальные причины.
Но если этносоциальная система — явление на границе между
этническим и социальным, то она должна демонстрировать осо-
бенности поведения, связанные с ее сопряженным характером. На-
блюдаются ли такие аналогии поведения этносоциальной системы
с поведением других пограничных структур, работающих на иных
формах энергии?
Обратимся к физике. Одним из наиболее популярных ее дости-
жений последних десятилетий является лазер — устройство, осу-
ществляющее генерацию света с помощью индуцированного излу-
чения. Поскольку лазерная генерация в микроволновом диапазоне
обнаружена в межзвездном пространстве, сам лазер можно рассма-
тривать как систему, находящуюся на границе между природными
феноменами и искусственными техническими устройствами [8, с. 21].
Это делает принципы его работы интересными для нашей темы.
Оставим в стороне математическое описание этих принципов и оста-
новимся на намеренно упрощенном описании, поскольку нам важно
уловить общие изменения в поведении лазера и попытаться соотне-
сти их с динамикой поведения этносоциальной системы.
Общая схема излучения лазерного импульса состоит в том, что
длительное воздействие накачки (внешнего источника энергии) на
активную среду системы увеличивает внутреннюю энергию систе-
мы. Последующая отдача накопленной энергии электромагнитному
излучению происходит в результате флуктуации и приводит к ви-
димому эффекту, обладающему уникальными свойствами: большая
световая мощность и высокая согласованность (когерентность) элек-
тромагнитных колебаний. В конце концов, атомы вновь возвраща-
ются в основное (невозбужденное) состояние. Такой динамике ла-
зера качественно можно поставить в соответствие поведение этно-
социальной системы. Обсудим это динамическое соответствие.
Если говорить об этносоциальной системе суперэтнического
ранга, то ее активную среду оставляет соответствующий суперэт-
нос, демонстрирующий поведенческое единство. Например, в основе
этносоциальной системы Западной Европы лежит суперэтнос, из-
вестный под названием Христианский (позднее Цивилизованный)
мир, история которого прослеживается с IX в.н.э. Этнический со-
став любой суперэтнической системы неоднороден и включает суб-
страты разного происхождения и разной этнической принадлежно-
сти. Как видим, и здесь активная среда является смешанной.
Вообще говоря, любая этническая система может находиться в
одном из двух состояний. Основное (статическое) состояние — это
этнический гомеостаз, где нет фазовой динамики и отсутствуют
изменения в стереотипе поведения. По отношению к гомеостазу эт-
ногенез является флуктуацией. В ходе этногенеза одна фаза сме-
няет другую и соответственно деформируется свойственный си-
стеме стереотип поведения. Таким образом, у этнической системы
также как и у лазера, есть свое «невозбужденное» состояние.
Переход от статического состояния к динамическому связан с
тем обстоятельством, что генофонд популяции подвергается му-
тагенному воздействию. По гипотезе Л. Н. Гумилева, источником
такой микромутации (пассионарного толчка) может служить кос-
мическое излучение [5, с. 473]: внешнее излучение играет такую же
роль, какую в лазере выполняет внешний источник накачки.
Сама микромутация соответствует зарядке лазерной лампы.
Разрядке лампы в лазере аналогичен процесс воспроизведения в
генофонде экстремального генотипа — признака пассионарности,
появившегося вследствие мутации.
Имеются и другие аналогии. То, что делают в лазере зеркала,
способствующие возвращению фотонов и активную среду, в супер-
этносе осуществляется создаваемой людьми системой поведенче-
ских моногамных запретов. Именно они налагают ограничение на
этнические контакты и тем самым поддерживают усилия по дви-
жению всей этносоциальной системы в определенном направлении.
Такое направление определяется комплексом идей, называемым эт-
нической доминантой.
Возбуждение атомов накачкой соответствует росту пассионар-
ности системы. Такой рост характеризуется воспроизведением пас-
сионарного признака и рождением его носителей — пассионариев.
Накопление частиц на верхних энергетических уровнях активной
среды лазера легко сопоставить с акматической фазой этногенеза,
когда пассионарность этносоциальной системы максимальна. Бы-
стрый переход частиц с верхних энергетических уровней на мета-
стабильный уровень соответствует в этногенезе резкому падению
пассионарности в короткой фазе надлома. Применительно к супер-
этносу метастабильному уровню с долгим временем жизни соот-
ветствует инерционная фаза, в которой пассионарность изменяется
довольно плавно. И наконец, переходу от метастабильного уровня
к основному, связанному с основным потоком когерентного лазер-
ного излучения, соответствует падение пассионарности в инерци-
онной фазе этногенеза. Результатом этой фазы служит появление
новой социально-культурной общности — «цивилизации».
В обоих случаях наблюдается сходная зависимость режима ра-
боты системы от уровня ее энергетического наполнения. При ма-
лых мощностях накачки лазер работает как некогерентный источ-
ник, излучение его хаотично, а время когерентности мало. Этни-
ческая система в инкубационном периоде фазы подъема также от-
личается слабой координацией: она существует в виде консорций
или субэтносов, т.е. таксонов сминимальным временем жизни. При
достижении пороговой мощности накачки в лазере начинаются ос-
цилляции, обусловленные согласованным излучением атомов. Так
появляется лазерное излучение, а время когерентности увеличива-
ется. При дальнейшем росте мощности накачки поведение лазера
снова изменяется: он начинает испускать световые вспышки корот-
кой продолжительности [8, с. 22-24].
Подобным образом ведет себя и этническая система. При до-
стижении определенного уровня пассионарного напряжения проис-
ходит создание нового этноса и связанной с ним этносоциальной
системы, в рамках которой осуществляется координация поведе-
ния консорций и субэтносов, составляющих этнос. Таким образом,
длительность существования этнического единства в данном слу-
чае также увеличивается, ибо этнос живет дольше субэтноса и тем
более консорции.
Последующее повышение уровня пассионарности этнической си-
стемы ведет к смене фазы развития. В новой акматической фазе из-
менение пассионарности уже не характеризуется прежней довольно
устойчивой тенденцией роста. Происходят частые и резкие чередо-
вания коротких подъемов с такими же спадами, что аналогично
генерации коротких импульсов в лазере.
Как видно, в поведении лазера и этносоциальной системы на-
блюдается значительное сходство (таблица). С этой точки зрения
этногенез можно было бы назвать усилением энергии живого веще-
ства биосферы под действием внешнего космического излучения.
Косвенно аналогия поведения подтверждает и принятую в этно-
логии гипотезу о космическом происхождении источника мутаций
[5, с. 473].
Таким образом, отталкиваясь от примера, приведенного Г.Хаке-
ном, легко увидеть типологическое единство поведения лазера и эт-
носоциальной системы. Такое единство говорит о принадлежности
этносоциальной системы к ряду диссипативных структур, описы-
ваемых в терминах синергетики [9, с. 31]. Но коль скоро этническая
система представляет собой диссипативную структуру популяцион-
ного ранга, на предсказуемость ее поведения должны распростра-
няться все ограничения, имеющие место для названных структур.
На наш взгляд, в изучении этногенеза наиболее существенным
ограничением является принципиальная невозможность достаточно
«точного» определения точек бифуркации этнического процесса.
В этногенезе в качестве бифуркаций выступают моменты так на-
зываемых фазовых и подфазовых переходов, т.е. смены тенденций
пассионарного напряжения системы. Существование таких перехо-
дов вполне объяснимо. В этногенезе работают два основных фак-
тора. Первый из них — старение, запрограммированное в воспро-
изведении генофонда изменение уровня пассионарного напряжения
системы во времени. Вторым является смещение, наступающее как
результат внешнего воздействия на данную этническую систему со
стороны других систем такого же ранга. В реальной этнической
истории мы никогда не наблюдаем идеального «закрытого» этноге-
неза, а видим непрерывную интерференцию этнических контактов
между представителями различных этнических систем. Контакты
также требуют отнюдь не малых затрат пассионарности. Как след-
ствие, ортогенное развитие этнических систем нарушается, и они
Аналогия поведения лазера и этносоциальной системы
Характеристика Лазер Этносоциальная система
Внешняя при- чина Накачка (вложение энергии той или иной физической природы) Гипотетически: излучение космического происхож- дения
Объект внешне- го воздействия Электроны в атомах, взаи- модействующие с источни- ком накачки и электромаг- нитным полем Генофонд популяции, вос- произведение мутагенных признаков в потомстве
Вид энергии Электромагнитная Пассионарность — биохи- мическая энергия живого вещества биосферы
Активная среда Кристалл или газ Этнические субстраты предыдущих пассионар- ных толчков
Рост потенциала активной среды Возбуждение атомов накач- кой, появление инверсной заселенности Увеличение числа пас- сионариев, рост уровня пассионарного напряже- ния этнической системы в фазе пассионарного подъема
Максимальный потенциал активной среды Накопление числа возбуж- денных частиц Акматическая фаза этно- генеза
Снижение потенциала активной среды Переход частиц с верхнего уровня на промежуточный уровень Уменьшение количества пассионариев в фазе над- лома, снижение уровня пассионарного напряже- ния до оптимума
Промежуточный уровень сниже- ния потенциала активной среды Метастабильный уровень Инерционная фаза этноге- неза
Дальнейшее снижение потенциала активной среды Переход частиц с ме- тастабильного уровня в основное (невозбужденное) состояние, сопровождае- мое монохроматическим лазерным излучением Падение уровня пассио- нарного напряжения, со- провождаемое появлением оригинального этнокуль- турного комплекса «циви- лизации»
Конечное со- стояние актив- ной среды Основное (невозбужденное) состояние Этническое равновесие: режим гомеостаза
приобретают дотоле неизвестное направление развития с учетом
новой тенденции изменения пассионарности самой системы.
Сам механизм фазового перехода в этногенезе может напоми-
нать явление гистерезиса. Пассионарность в этнической системе
р”^1
Р6
Жертвенность
пЫ5
Pf
п+3
<
г!
Г500
Фазы:
<2zJOO 600\900__________________
- Неспособность рееулоробать 6o#c\j
- Меслосовноеть удовлетво- Рвения
рять вожделения
„ Подъен Анпати- Надлоп Инерци-
чесная онная
Овсну-
рация
Регене- Релинт
рация
t
Качественное изменение пассионарности со временем.
может иметь два критических уровня. Если пассионарность сна-
чала растет, то с достижением первого критического значения тен-
денция роста может сменяться тенденцией падения, например, в ре-
зультате взаимного истребления: резня может унести жизни наибо-
лее активных пассионарных особей (рисунок). Некоторое ослабле-
ние доставляет оставшимся персонам возможность выбора, и при
достижении второго (меньшего) критического значения они осво-
бождаются от давления энергичных сограждан и довольно быстро
(«скачком») переводят систему к новому состоянию. В поведении
людей начинают доминировать уже не старые стереотипы поведе-
ния, а новые, дотоле казавшиеся не только неприемлемыми, но и
просто невообразимыми. Например, при переходе от фазы подъ-
ема к акматической фазе императив коллективной ответственно-
сти: «Будь тем, кем ты должен быть!» — сменяется на императив
чисто индивидуалистический: «Будь самим собой!» Свои импера-
тивы приносит и фаза надлома («Все будет иначе!»), и инерционная
фаза («Будь таким как я!»), и обскурация («Будь таким как мы!»)
[1, с. 475]. Сложность предсказуемости состоит здесь в том, что
принципиально невозможно определить, к какому именно импера-
тиву произойдет переход, поскольку роль случайности в момент
выбора чрезвычайно возрастает. Но как только выбор сделан, т.е.
новый императив навязан системе и принят подавляющим больший-
ством ее членов, детерминизм этнического развития вновь вступает
в свои права до момента следующего фазового перехода.
Как и в других диссипативных структурах, выбор этнической
системы в точке бифуркации очень сильно зависит от прошлой
истории системы. Например, очень быстрый рост управляющего
параметра — пассионарного напряжения — в фазе подъема делает
более вероятным столь же резкое падение пассионарности в момент
спада, а значит, и смещение ортогенного процесса этногенеза на
фоне имеющихся этнических контактов. Так, совершившие стре-
мительные пассионарные взлеты арабы в VI-VII вв. и монголы в
XII-XIII вв. не смогли пережить своих побед: созданные ими огром-
ные империи с полиэтничным населением оказались неуправляемы,
ибо на это не хватало даже растущей пассионарности завоевателей.
Совершившиеся фазовые переходы уже через 200 лет превратили
потомков арабских ансаров и монгольских нойонов в притесняемое
меньшинство населения.
Точно так же стимулируется этническое смещение и в случае
предшествующего нарушения связей этноса с ландшафтом. Самым
ярким примером тому служит античный Рим. Все римские гра-
ждане «героической эпохи» (фазы пассионарного подъема и акмати-
ческой фазы) были земледельцами и воинами, сражавшимися с вра-
гами «Pro aris et focis» — «За святилища и очаги». После того как в
непрерывных войнах акматической фазы количество пассионариев
уменьшилось, пришлось начать комплектовать армию субпассиона-
риями сражавшимися за плату благодаря железной дисциплине. Ре-
форма Мария (107 г. до н.э.), утвердившая новый порядок, фактиче-
ски закрепила уже сложившуюся ситуацию, при которой земля кон-
центрировалась в руках латифундистов и обрабатывалась рабами.
Легионеры, даже вернувшиеся из походов, легко расставались со
своими земельными наделами, ибо не видели смысла работать, по-
корив провинции и приобретя богатство. Таким образом, римляне
утратили контакт с ландшафтом и потеряли как этнос лидирую-
щее положение уже в инерционной фазе — в эпоху Августа, а с ее
окончанием не сохранились даже как реликт фазы гомеостаза.
Приведенный пример показывает что в изучении этногенеза мы
не можем предсказывать будущее с точностью, сохраняющей за
нашим прогнозом практическое значение. Этнического будущего
нет, ибо не совершены поступки, определяющие это будущее, и мы
не можем сказать — будут ли они совершены. Последнее не уди-
вительно, так как поступки лежат в стихии поведения отдельного
человека и определяются множеством случайных величин. Но зна-
чит ли это, что изучение этногенеза бесполезно? Отнюдь нет и
вот почему. Не имея возможности предсказать ближайшую пер-
спективу этногенеза из-за наличия фазовых переходов, мы, тем не
менее, имеем возможность сделать это для более длинных отрезков
времени. Скажем, ход этногенеза современной Японии позволяет
считать, что при прочих равных условиях к концу XXI - началу
XXII в. этнос Страны восходящего солнца перейдет к следующей
фазе развития — акматической. Такой переход, без сомнения, су-
щественно изменит экономическую и социально-политическую рас-
становку сил не только в Азиатско-Тихоокеанском регионе, но и во
всем мире. Однако у нас нет никаких оснований быть уверенными,
что вход японского этноса в акматическую фазу состоится навер-
няка, и это произойдет в 2090 г., а не в 2105. Конечно, в масштабах
жизни этноса, длящейся 1200-1500 лет, разницей в 30 и даже 50 лет
можно пренебречь, но для практических рекомендаций такая вели-
чина крайне существенна.
Итак, в изучении этногенеза предсказуемость поневоле ограни-
чена и специфична. Мы не можем, изучая этногенез, оперировать
прогнозами и утверждать, что выполнение определенных стандар-
тов поведения приведет к определенным результатам. В лучшем
случае мы можем говорить о том, что соблюдение определенных
ограничений в этническом поведении повышает? вероятность про-
дления жизни этноса. Но любое предсказание может быть опро-
кинуто при наступлении очередного фазового перехода, ибо его
хронология и событийная канва в значительной мере определяются
случайностью. И потому предсказуемость в изучении этногенеза
ставит своей целью не предугадывание будущего, а изучение про-
исходящего в природе глобального процесса с целью эффективной
адаптации к нему.
ЛИТЕРА ТУРА
1. Николис Г., Пригожин И. Познание сложного: Введение. М.: Мир, 1990.
2. Бромлей Ю.В. Современные проблемы этнографии. М.: Наука, 1981.
3. Бромлей Ю.В. Этнос и этнография. М.: Наука, 1973.
4. Гумилев Л.Н. По поводу предмета исторической географии: (Ландшафт и
этнос). III // Вести. ЛГУ. Геология. География. 1965. № 18.
5. Гумилев Л.Н. Этногенез и биосфера Земли. Л.: Изд-во ЛГУ, 1989.
6. Иванов К.П. Взгляды на этнографию, или есть ли в советской науке два
учения об этносе // Изв. Всесоюз. геогр. о-ва. 1986. Т.117. Вып.З.
7. Вернадский В.И. Химическое строение биосферы Земли и ее окружения.
М.: Наука, 1965.
8. Хакен Г. Синергетика. М.: Мир, 1980.
9. Ермолаев В.Ю. Самоорганизация в природе и этногенез // Изв. Всесоюз.
геогр. о-ва. 1990. Т.121. Вып.1.
10. Хакен Г. Синергетика: Иерархии неустойчивости в самоорганизующихся
системах и устройствах. М.: Мир, 1985.