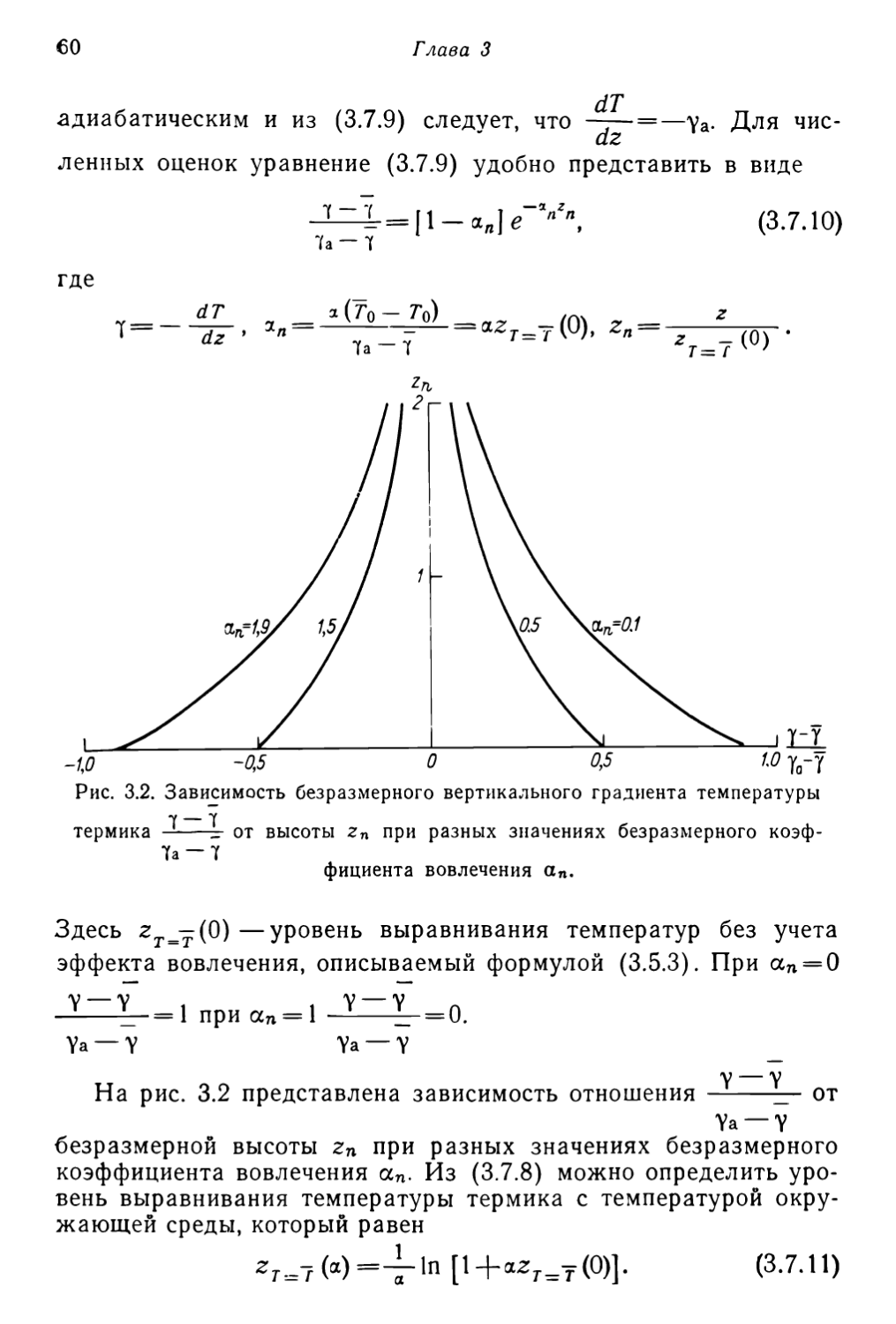
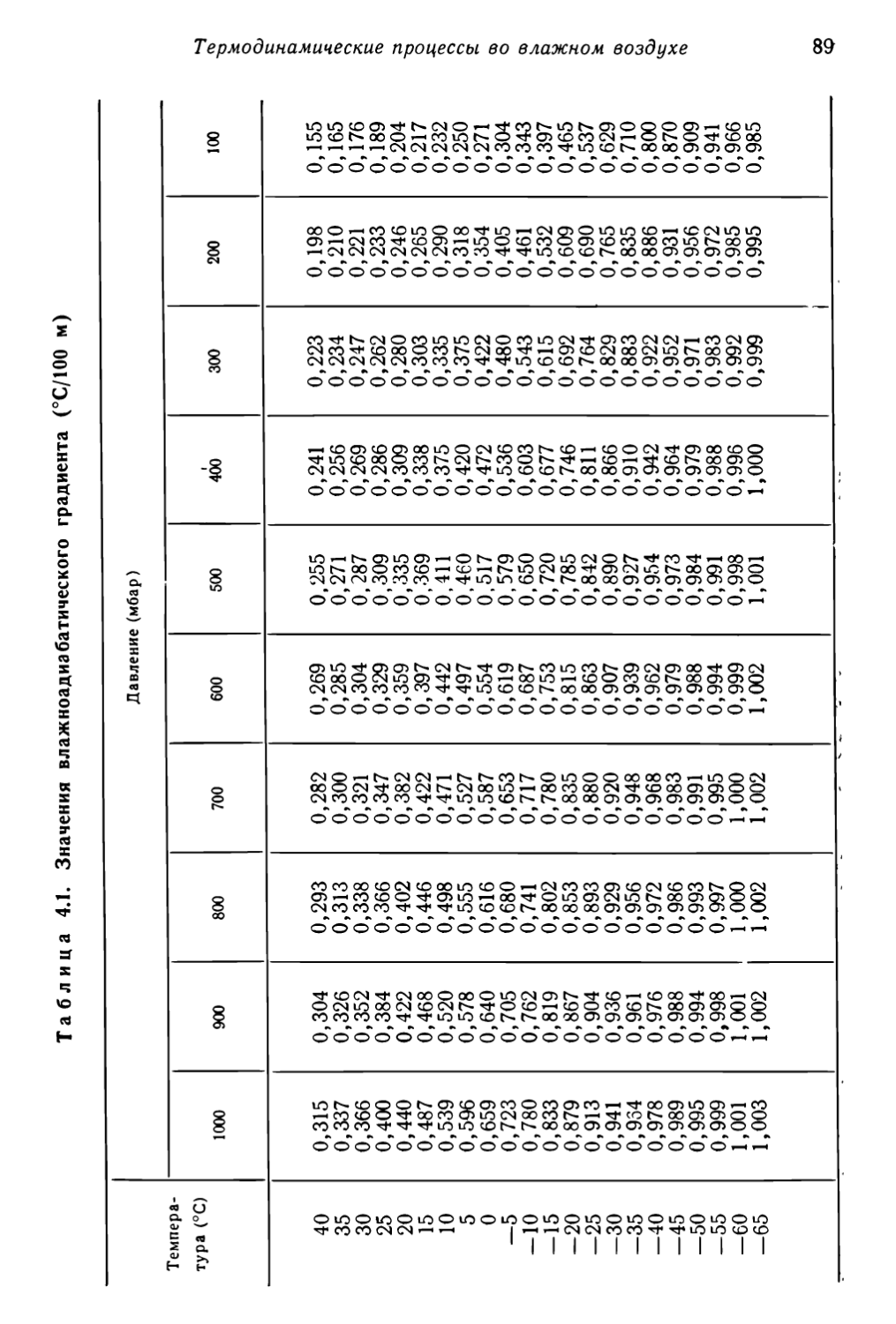
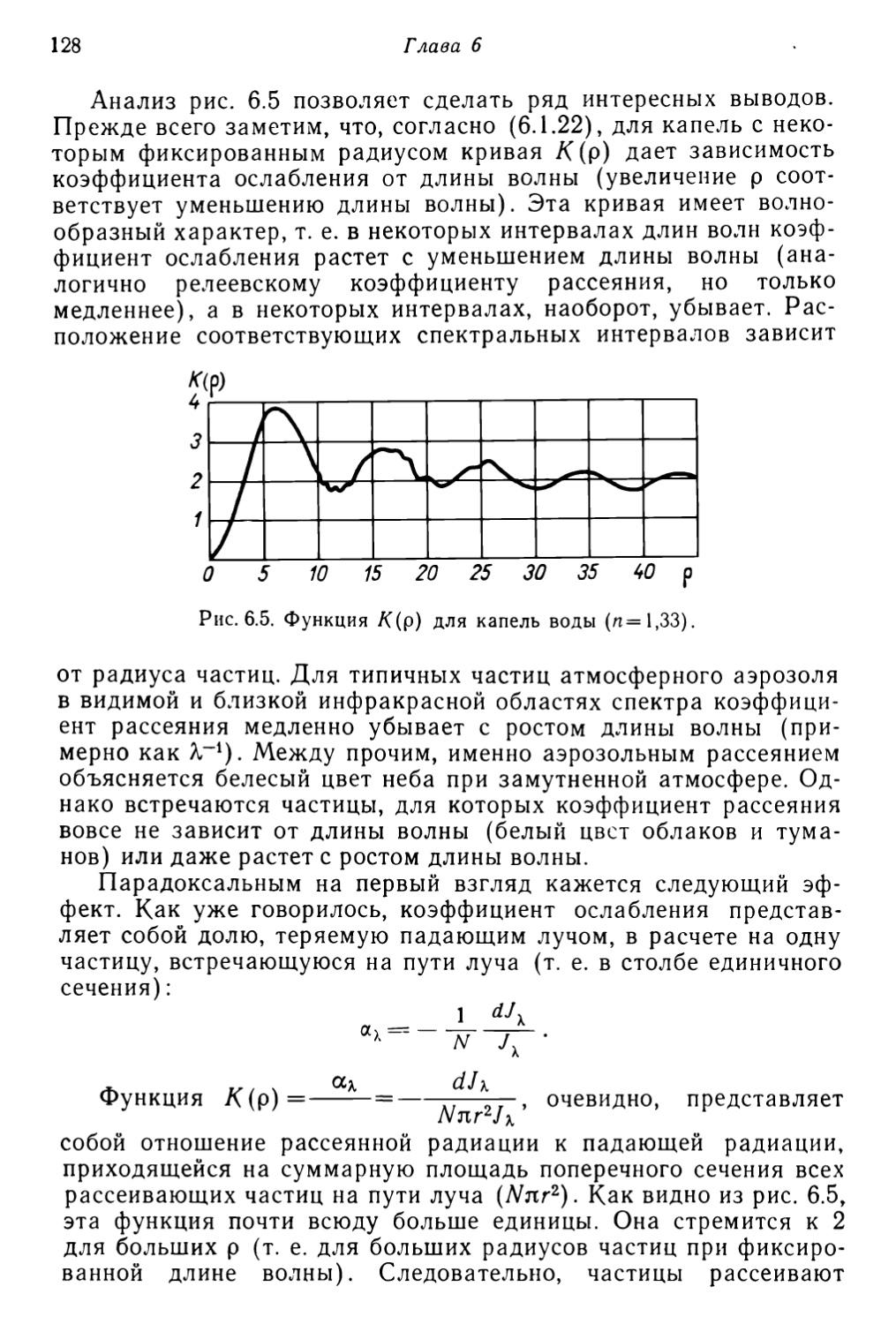
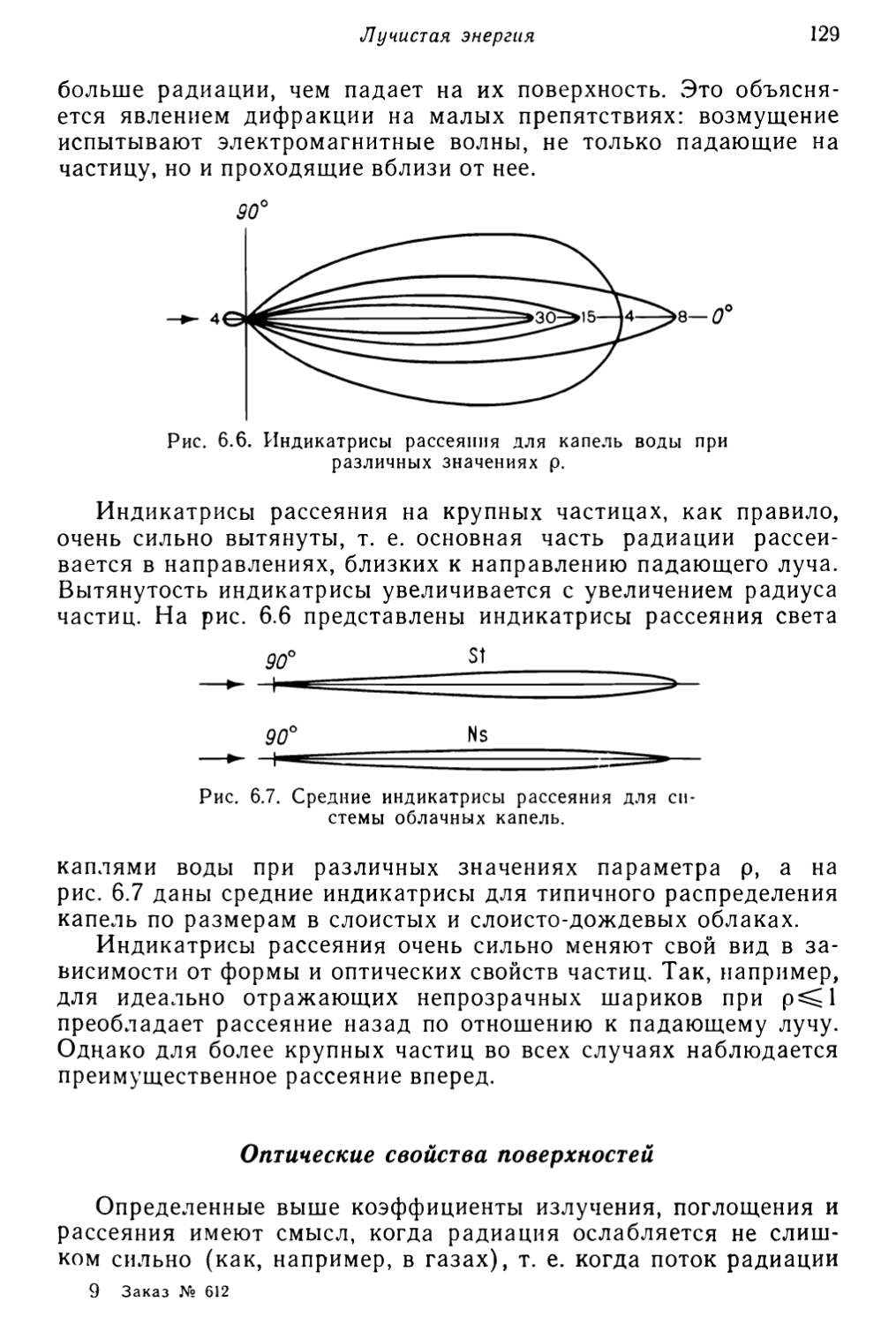
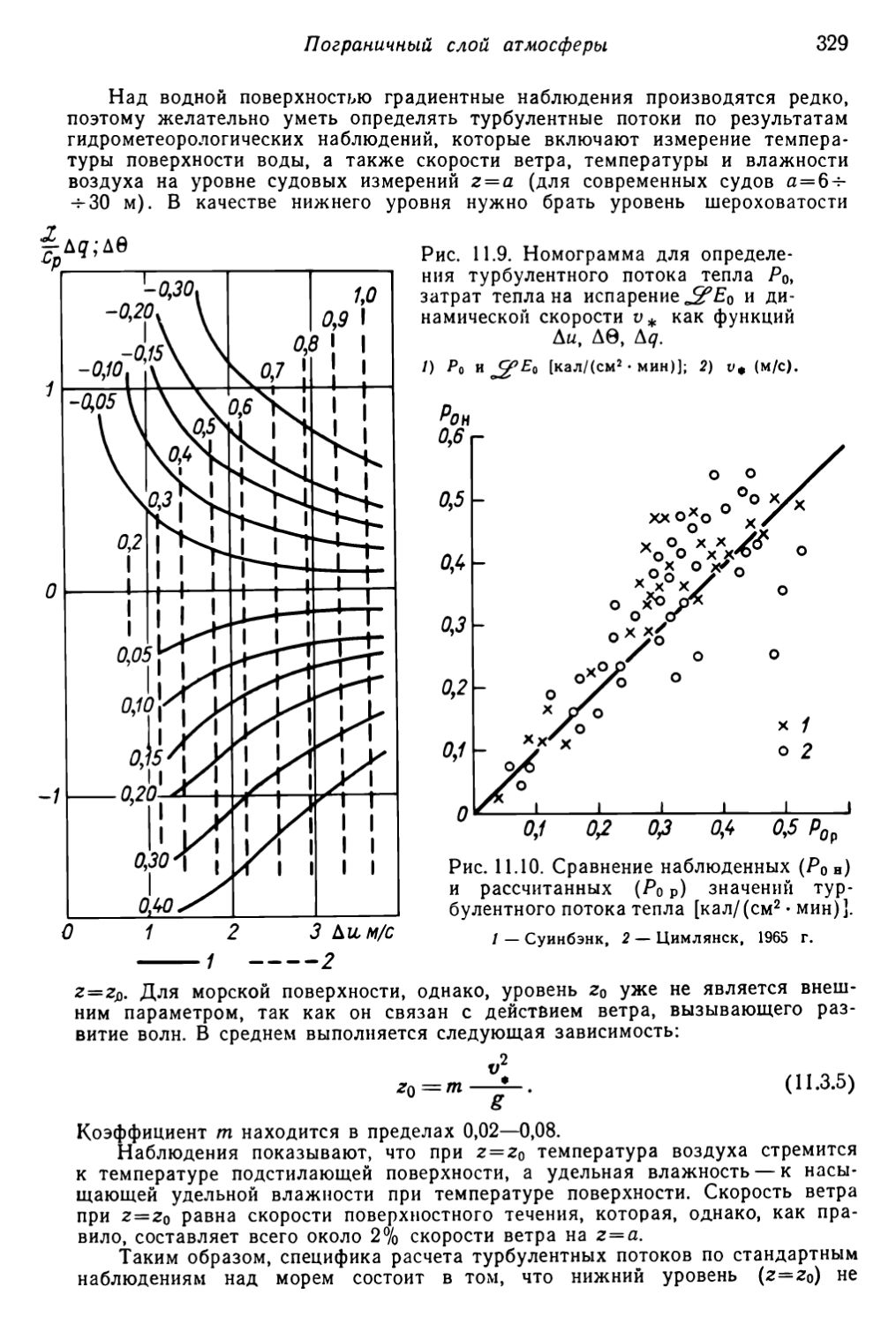
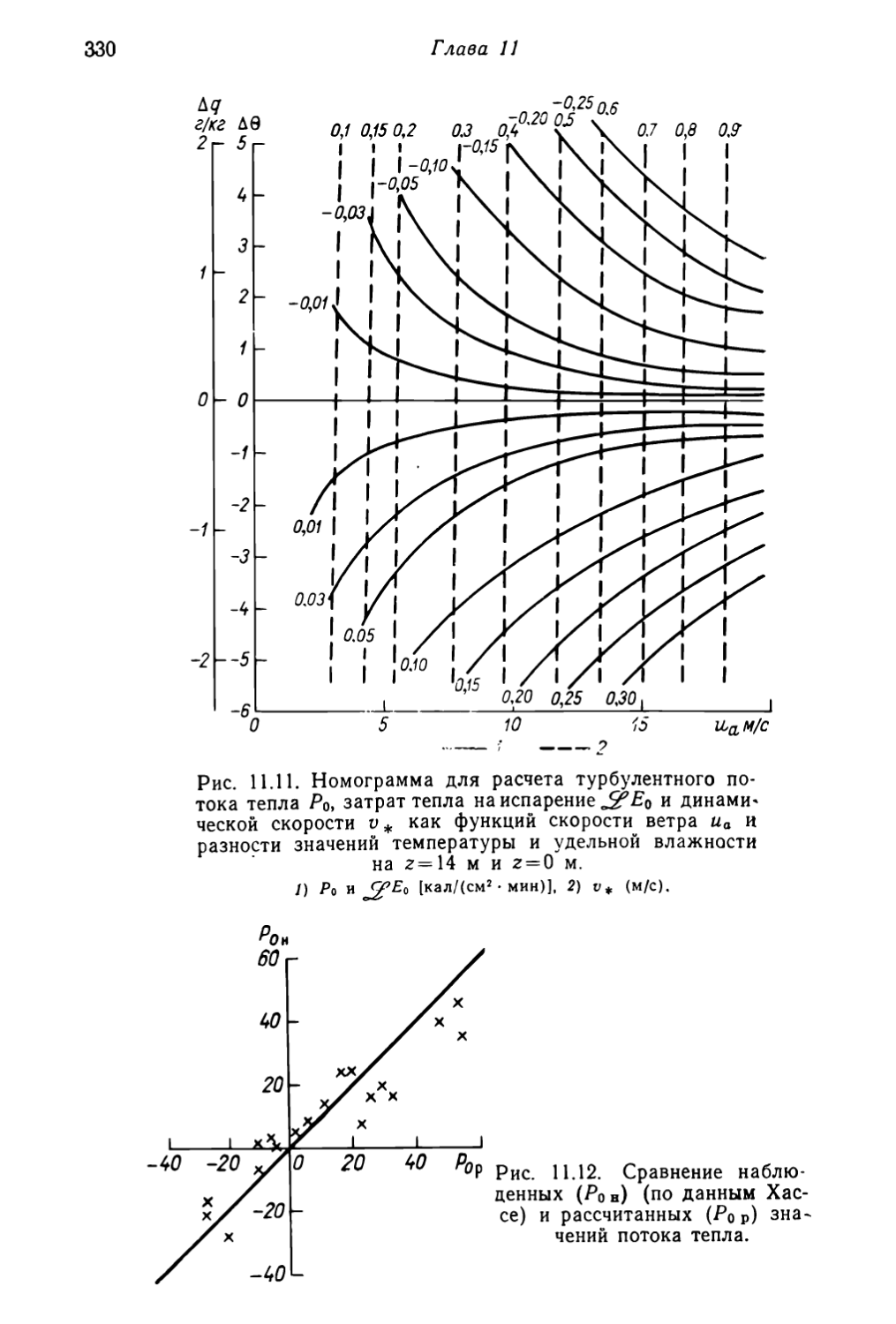
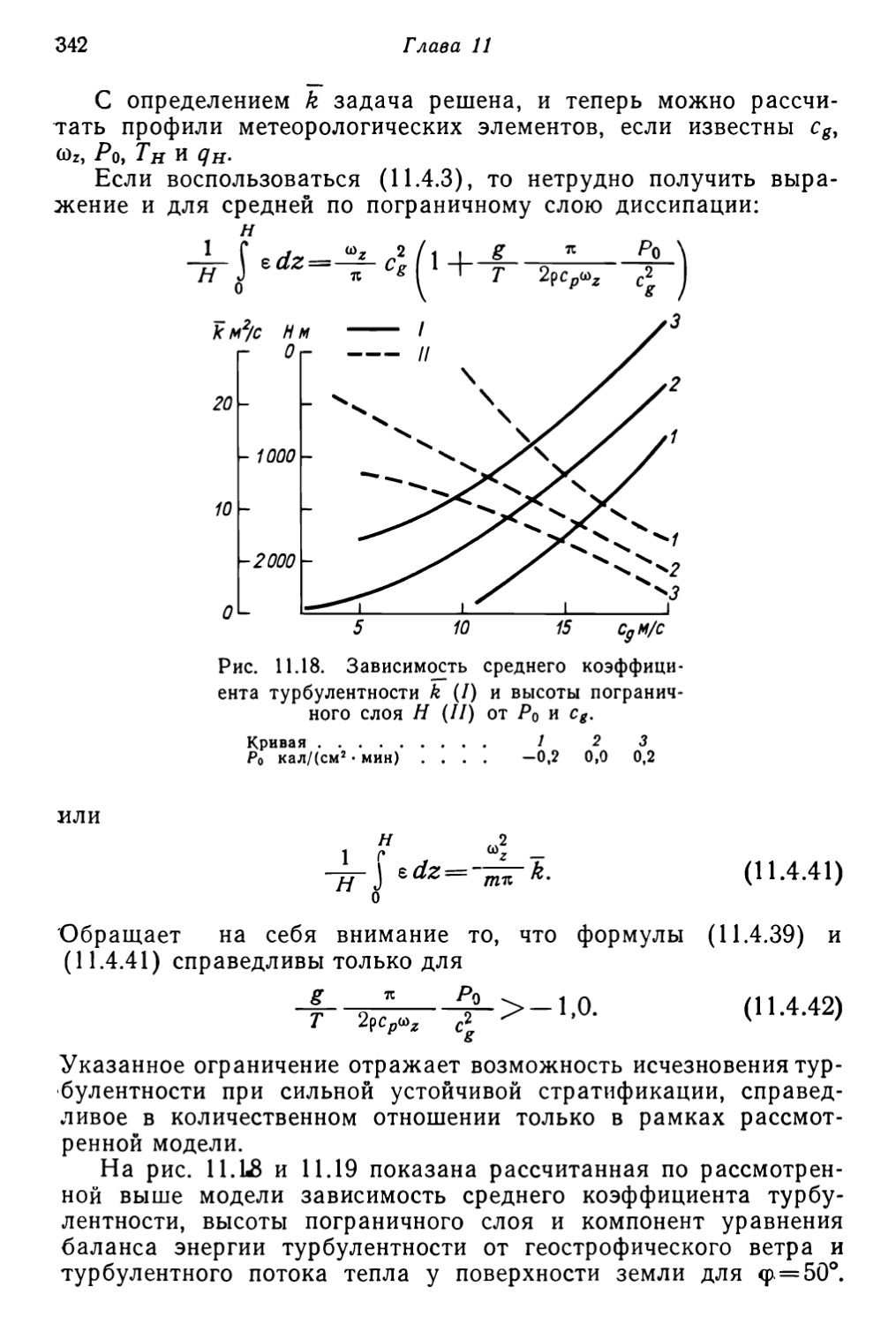
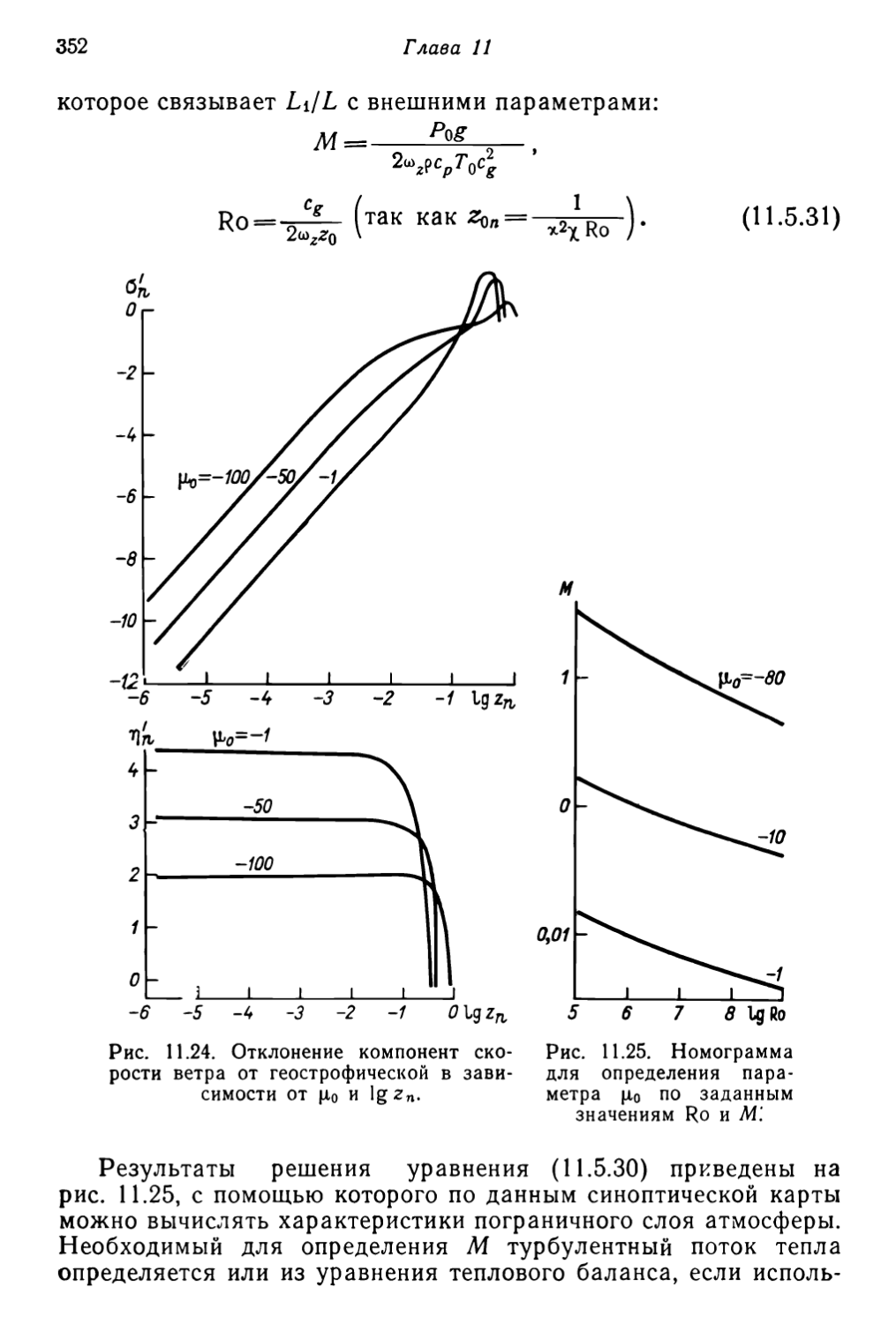
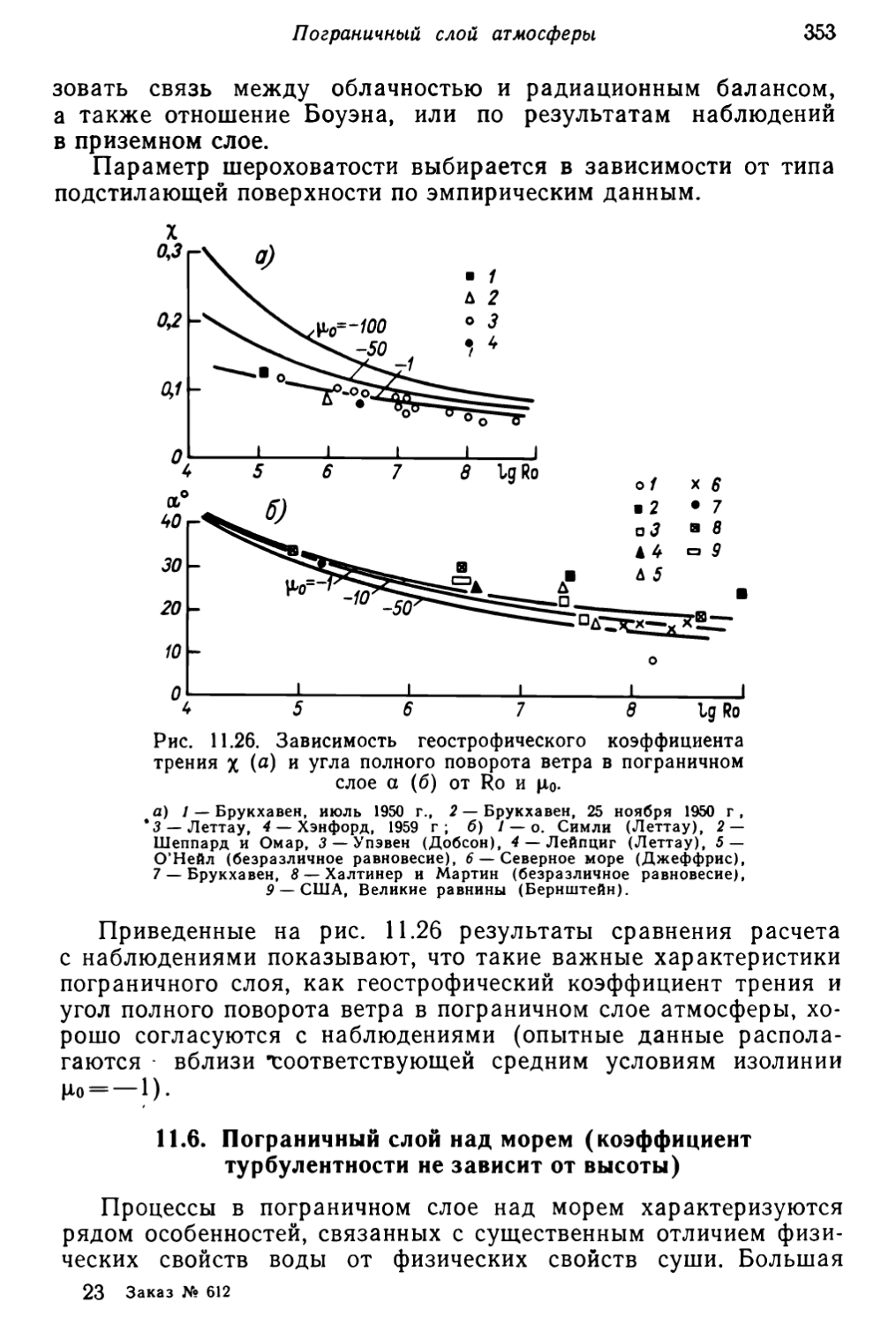
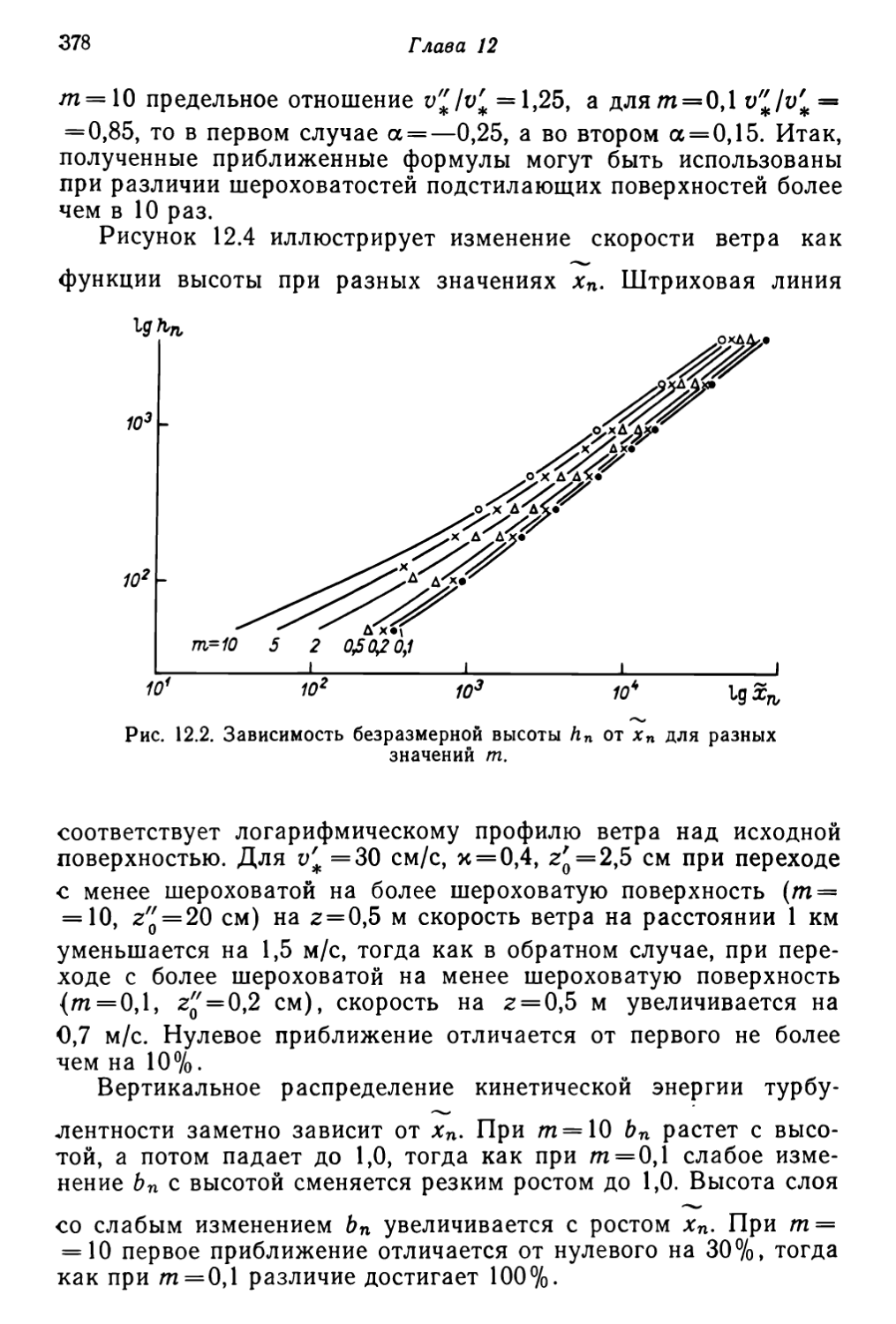
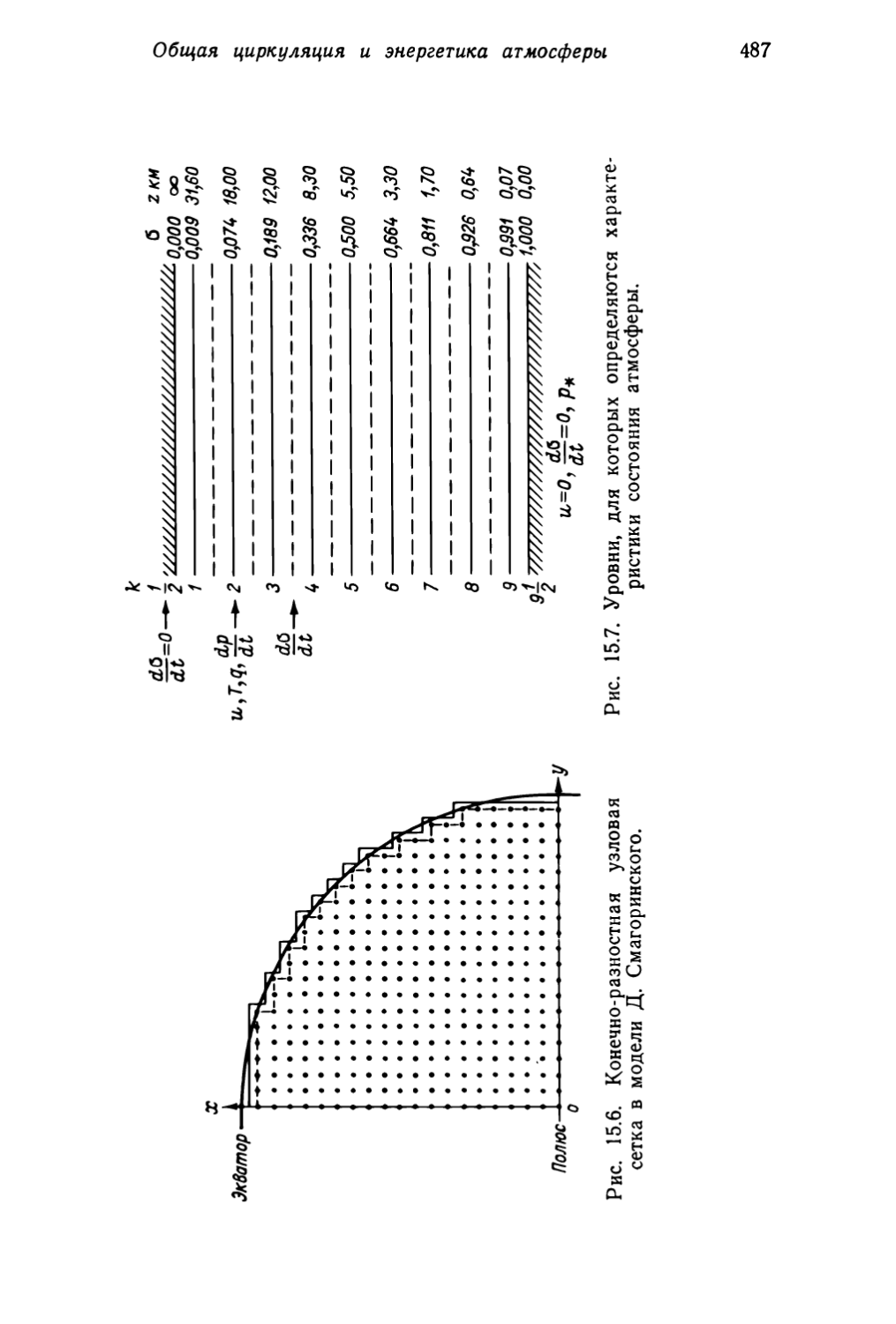
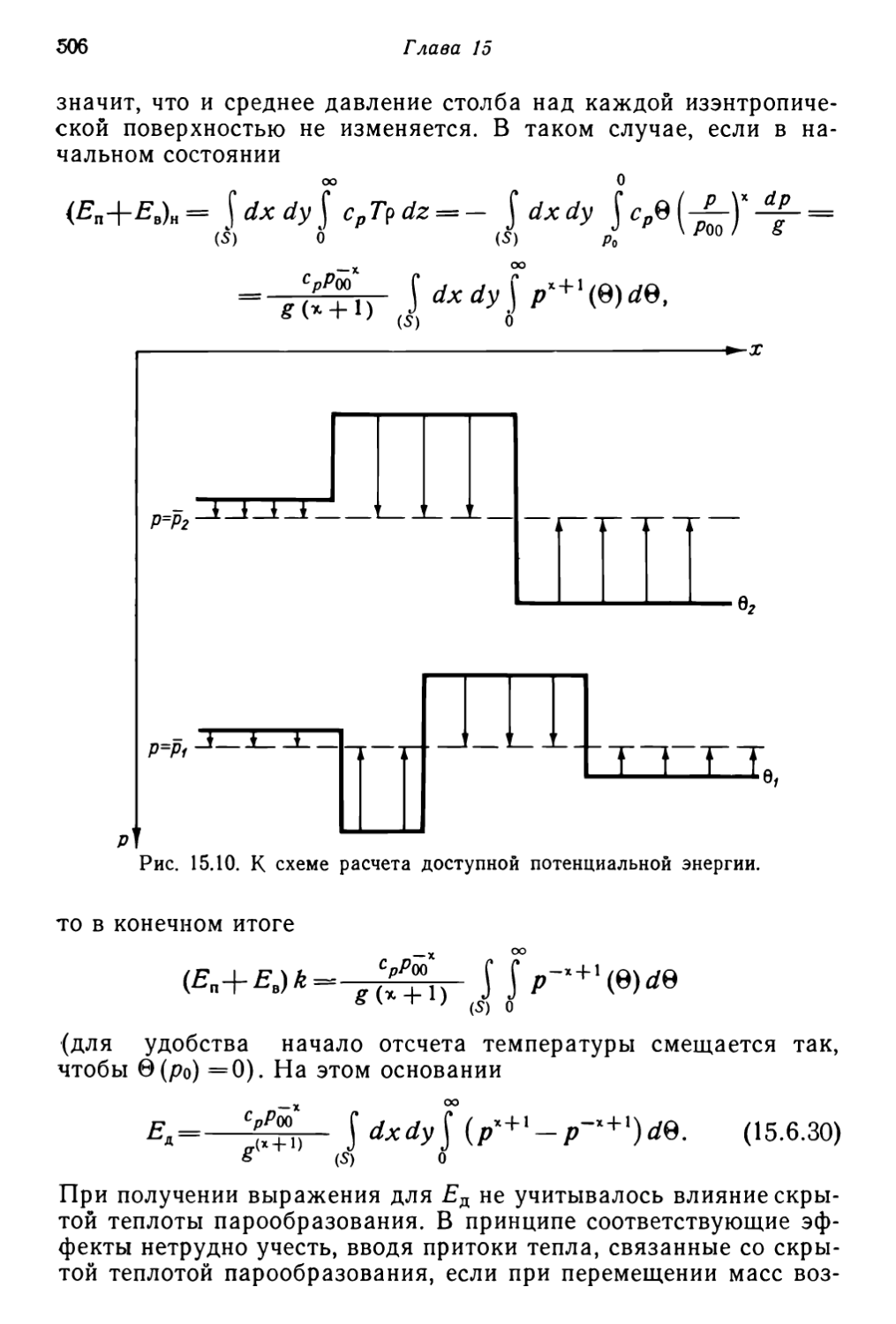
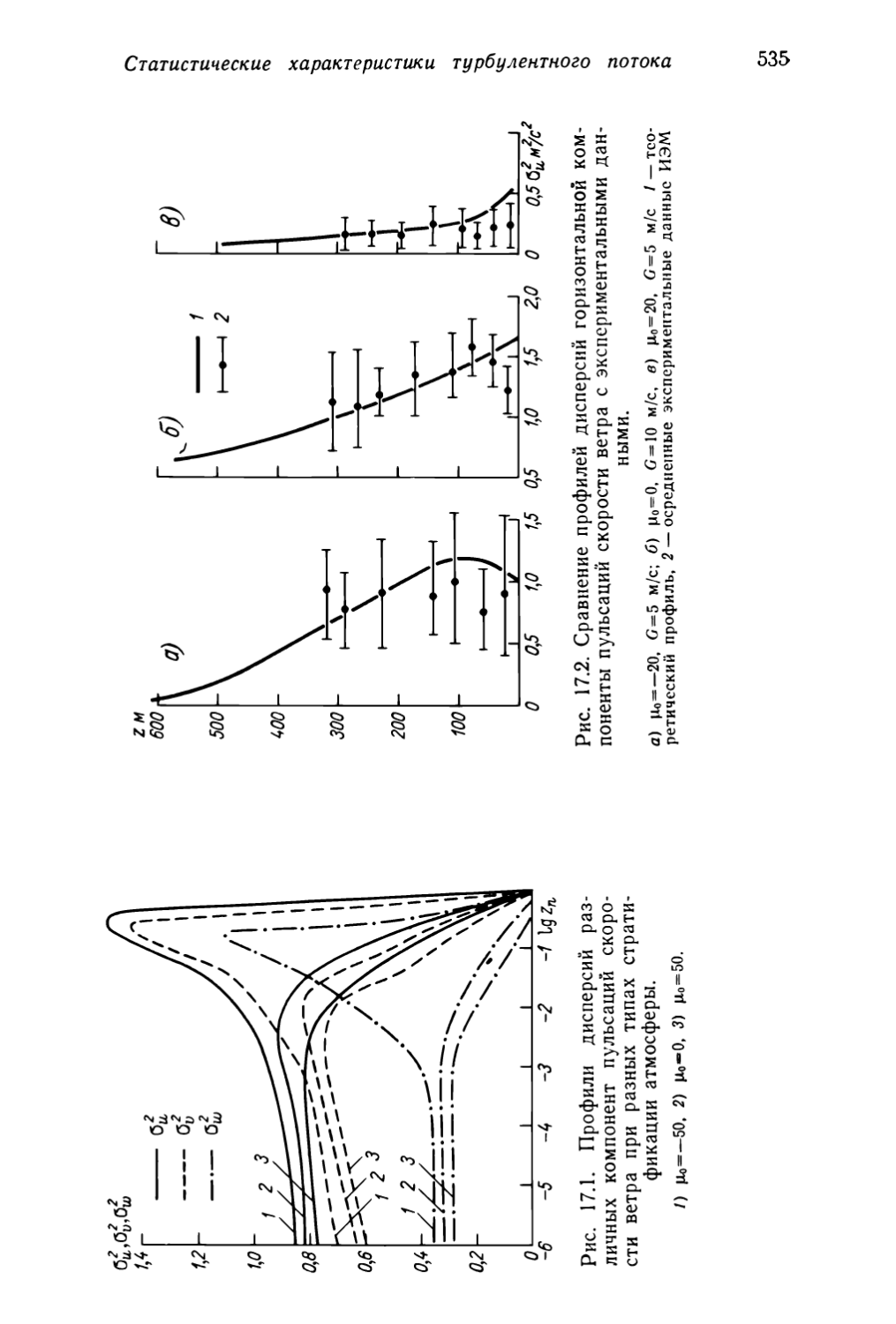
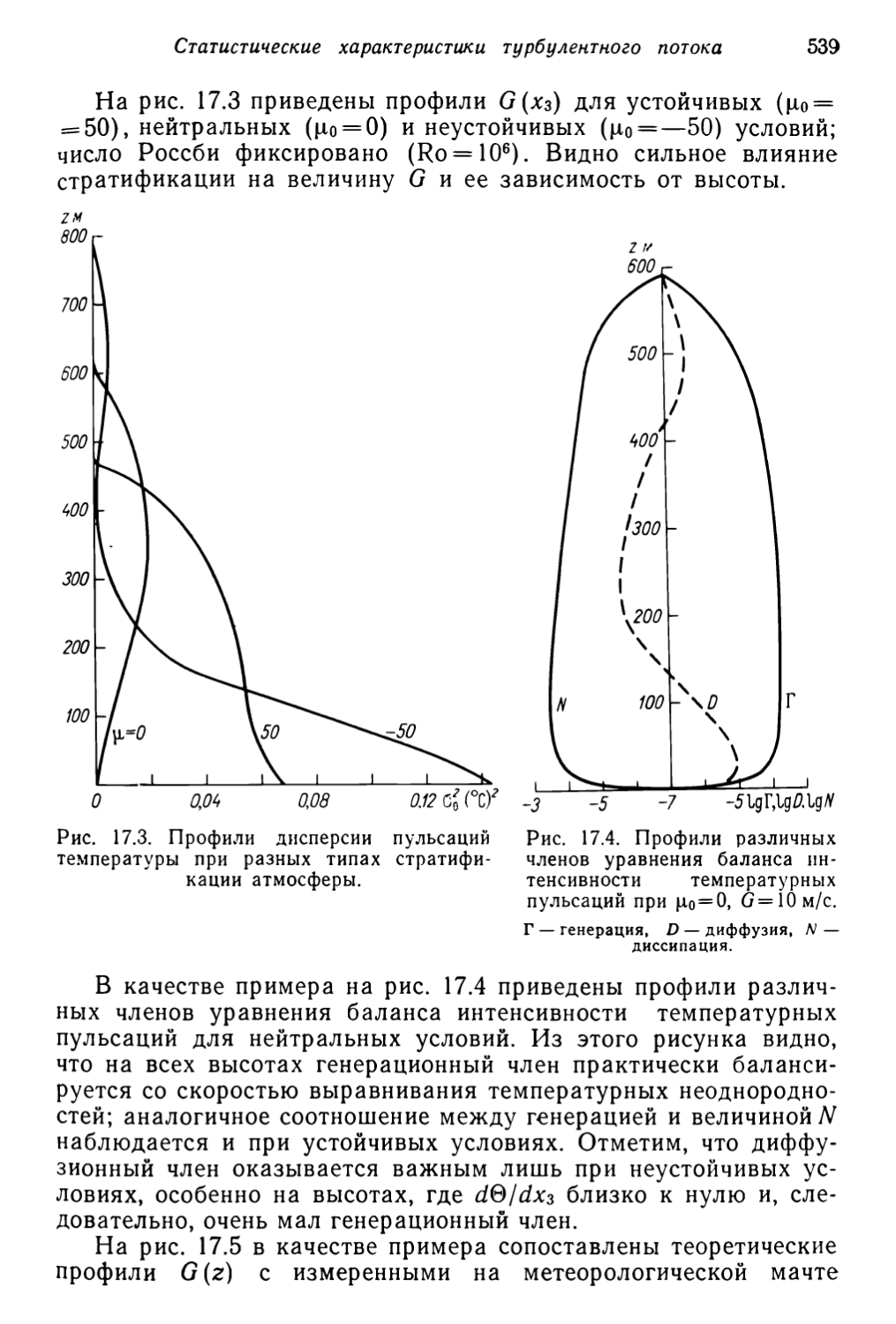
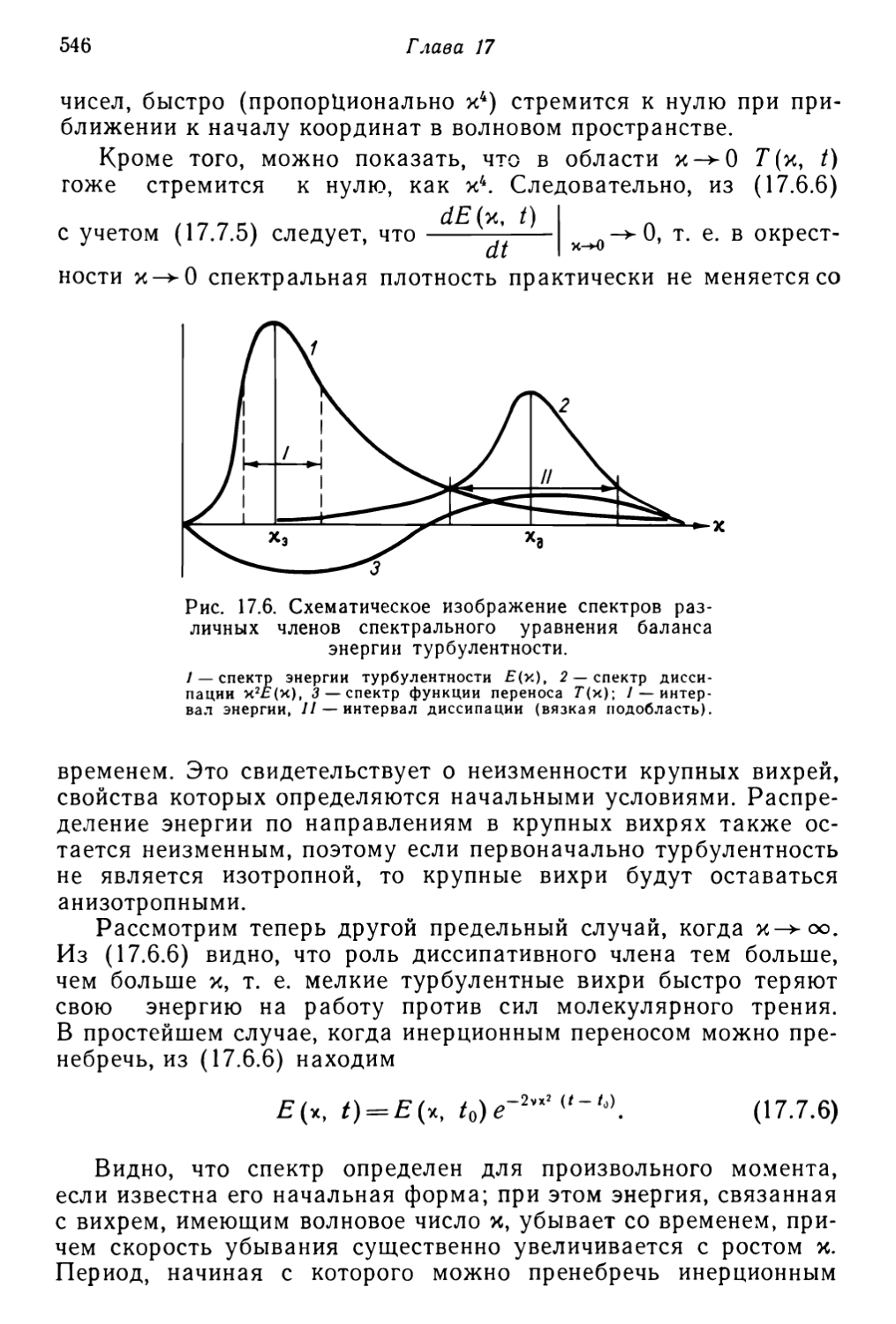
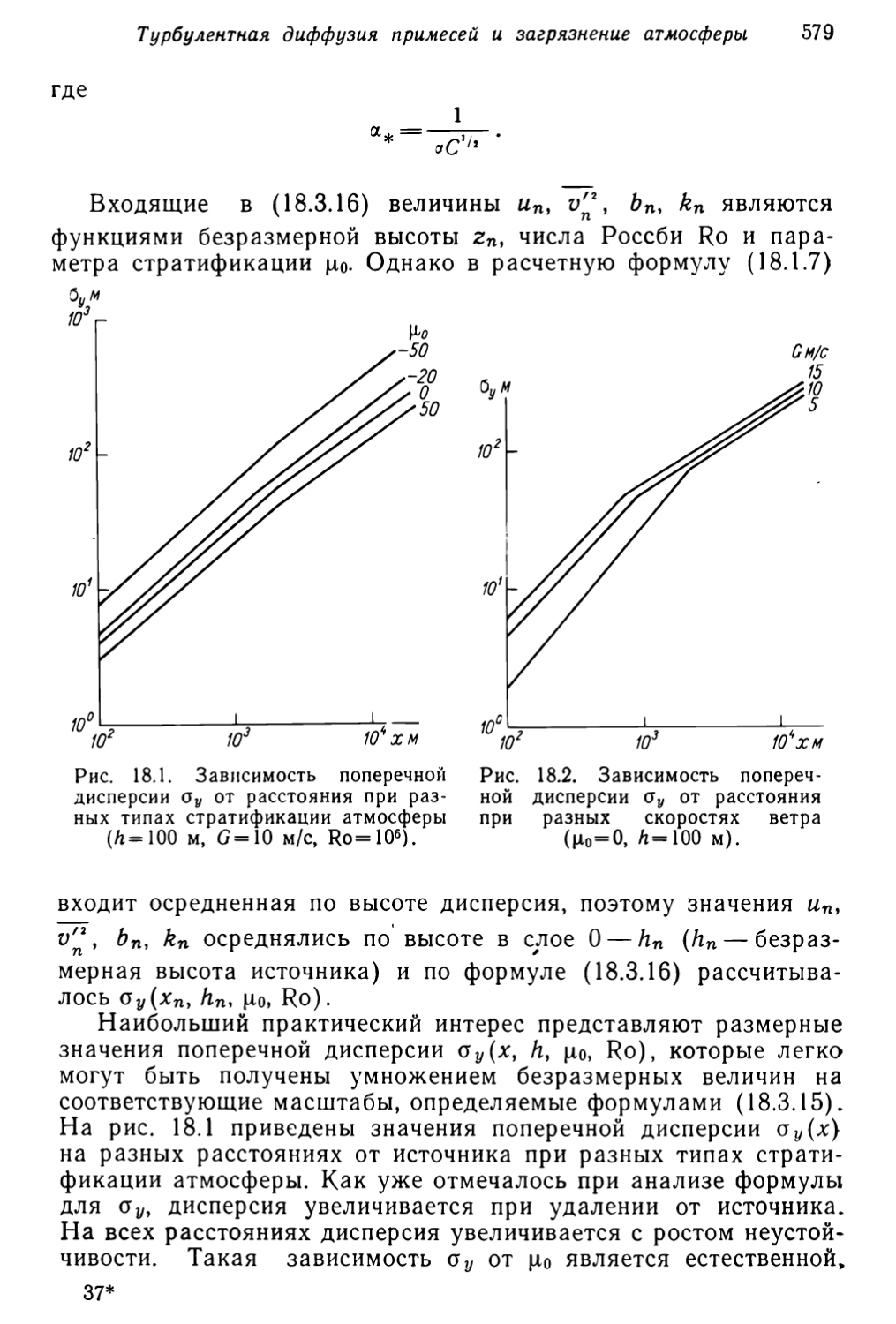
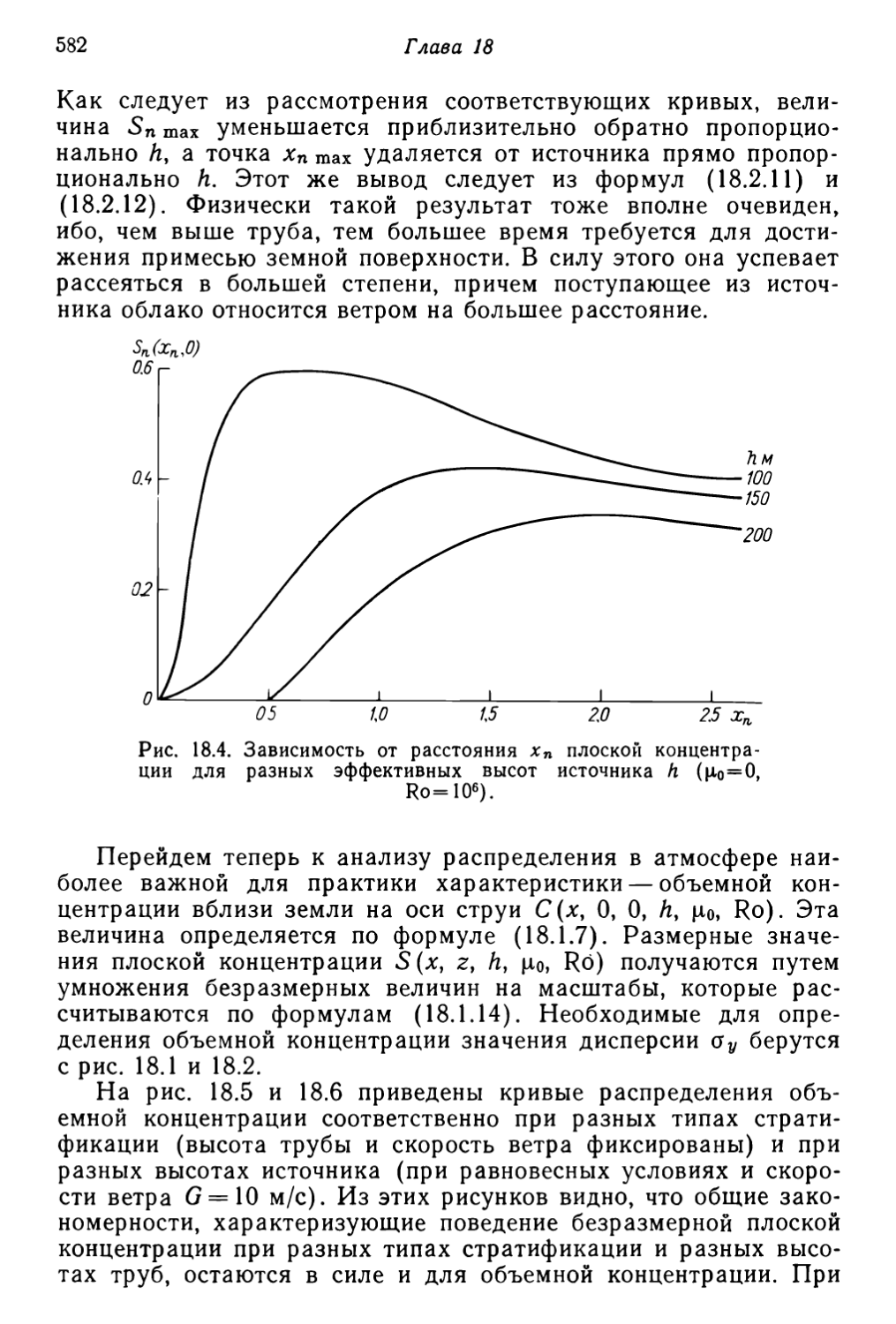
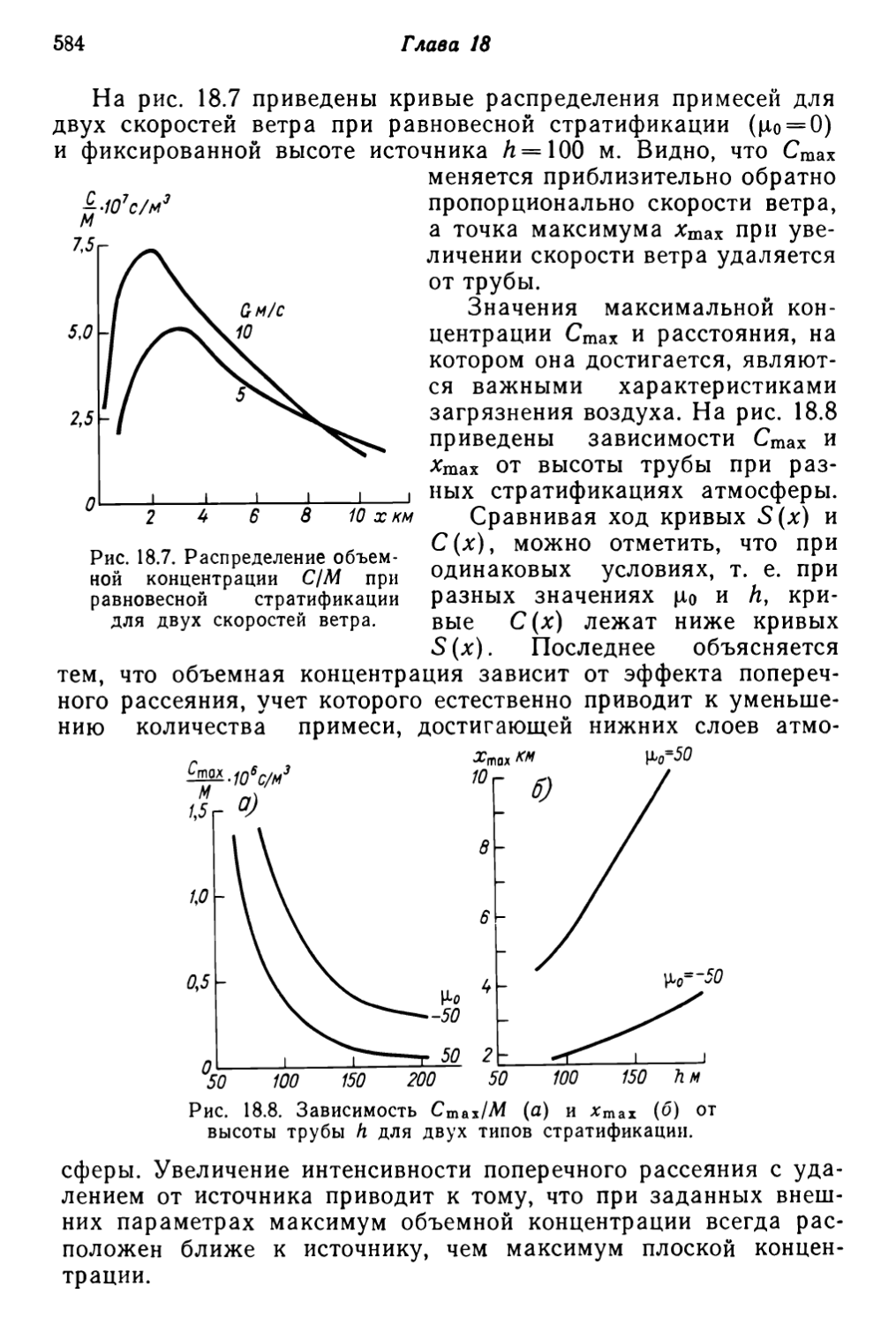
Текст
ДИНАМИЧЕСКАЯ
МЕТЕОРОЛОГИЯ
Теоретическая метеорология
Допущено
Министерством высшего и среднего специального
образования СССР в качестве учебного пособия
для студентов гидрометеорологических специальностей вузов
Под редакцией Д. Л. Лайхтмана
ГИДРОМЕТЕОИЗДАТ • ЛЕНИНГРАД • 1976
УДК 551.51(075.8)
Ф. А. Гисина, Д. Л. Лайхтман, И. И. Мельникова,
Э. Г. Палагин, Э. Л. Подольская, В. М. Радикевич,
А. П. Юргенсон
Рецензенты:
А Ф. Кивганов, В. А. Шнайдман, JI. Н. Герасименко (кафедра теоретической
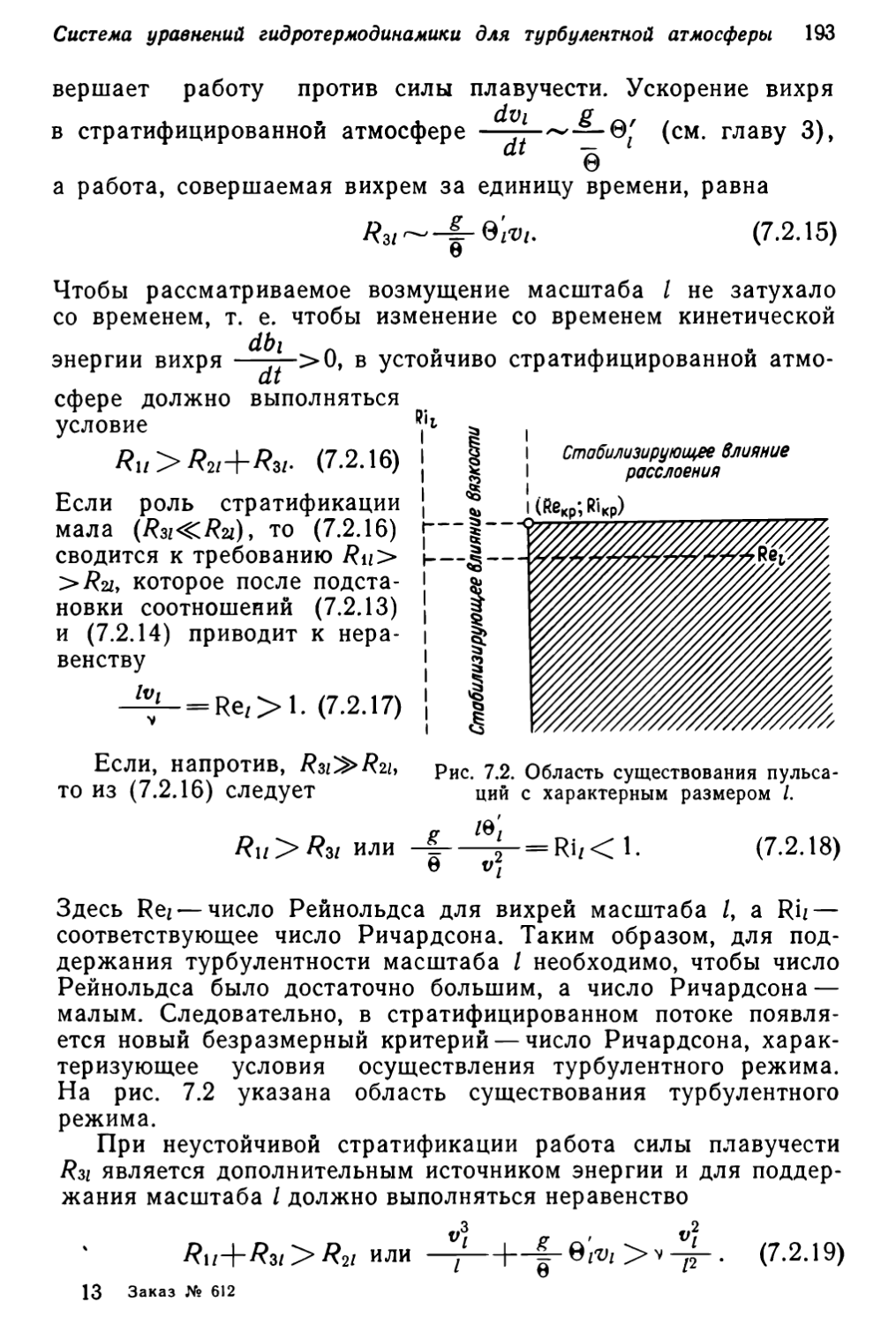
метеорологии и метеорологических прогнозов Одесского
гидрометеорологического института)
С. И. Титов, Б. Д. Панин, В. В. Клемин (кафедра синоптической и динамической
метеорологии Военного инженерного Краснознаменного института
им. А. Ф. Можайского).
В книге рассмотрены общие принципы механики, термодинамики и
теории переноса радиации применительно к условиям атмосферы. Анализируются
особенности полей давления, ветра, температуры и влажности в атмосфере,
а также связь между ними. Излагается теория глобальных процессов, включая
основные результаты численных экспериментов по общей циркуляции
атмосферы. Специальная глава посвящена некоторым актуальным проблемам
прикладной метеорологии.
Книга предназначается в качестве учебного пособия для студентов и
аспирантов гидрометеорологических институтов и университетов. Может быть
использована специалистами, интересующимися вопросами динамической
метеорологии.
In this book fundamental principles of mechanics, thermodynamics and
the theory of radiative transfer concerning atmospheric processes are treated.
Specific features of pressure, wind, temperature and humidity fields in the
atmosphere and their interconnexion are considered.
The theory of global dynamics including essential results of numerical
experiments in the general circulation of the atmosphere is discussed
A special chapter deals with some actual problems of applied meteorology.
This publication is intended as a text-book for undergraduate and
postgraduate students of hydrometeorological institutes and universities. It may be
of interest to specialists engaged in dynamic meteorology.
069(02)-76
(g) Гндрометеоиздат, 1976 г.
ПРЕДИСЛОВИЕ
Последнее учебное пособие по динамической метеорологии
издано в Советском Союзе более 20 лет тому назад. За эти годы
целый ряд разделов физики атмосферы получил существенное
развитие. Заметно изменились и методы теоретических
исследований. Классические способы аналитического интегрирования
уравнений, описывающих атмосферные процессы, все больше
вытесняются численным интегрированием. Благодаря этому
появилась возможность эффективного решения нелинейных задач.
Естественным следствием развития науки было возникновение
новых актуальных проблем, не привлекавших ранее внимания
или вообще неизвестных.
Все это привело к тому, что существующие курсы
динамической метеорологии, в свое время обеспечившие повышение
уровня метеорологического образования, теперь в значительной
мере устарели. Возникла потребность в новом учебном пособии.
В периоды интенсивного развития любой дисциплины
обычные трудности написания учебного пособия — изложение
материалов на современном уровне с использованием
математического аппарата, доступного студентам, ограничение объема
пособия рамками учебного плана — весьма усугубляются.
Авторам надлежит выделить из большого потока научных работ,
появляющихся в периодических изданиях, новый материал,
который следует включить в книгу. Отобранный материал нужно
изложить в доступной форме, подчас совершенно отличающейся
от использованной в оригинале.
При всех ограничениях, которые упоминались выше, мы
пытались использовать наиболее существенные результаты
исследований последних лет. В первую очередь это относится к
исследованиям по теории общей циркуляции атмосферы и
физическим основам численных прогнозов погоды. Нам
представлялось целесообразным обратить основное внимание на
физические принципы, а не на чисто вычислительную сторону, хотя
часто идеи, использованные при построении удачного
вычислительного алгоритма, бывают подсказаны сущностью процесса
и эта сторона вычислений должна быть по возможности
отражена.
Значительное место уделено проблемам пограничного слоя.
Не говоря уже о том, что учет процессов, происходящих в
планетарном пограничном слое — «слабое место» современных
численных прогнозов, решение многих прикладных задач (таких,
1*
4
Предисловие
как загрязнение атмосферы промышленными выбросами,
расчеты, связанные с деятельностью авиации, рациональный учет
метеорологических условий при мелиорации и строительстве)
основано на глубоком понимании процессов в пограничном слое,
в частности режима турбулентности в нижних слоях атмосферы.
В пособие включены также новые исследования по радиации,
теории облаков и турбулентности в свободной атмосфере.
При современных исследованиях с учетом возможностей
вычислительной математики и электронных вычислительных
машин главная задача теоретика заключается в корректной
формулировке задач, введении обоснованных упрощений и
интерпретации результатов расчетов. Мы считали возможным
обратить внимание на формулировку некоторых задач, даже если
их решение не может быть приведено в виде обозримых и ясных
формул. В связи с этим гораздо больше места, чем в
предыдущих курсах динамической метеорологии, отведено методам
теории подобия и анализа размерности, которые представляют
собой эффективный аппарат для рационального упрощения
конкретных задач и интерпретации результатов.
Учебное пособие составили следующие авторы: Н. Е. Воль-
цингер (п. 14.4), Ф. А. Гисина (главы 2—5, 17, пп. 1.1, 7.1, 7.2),
Д. Л. Лайхтман (главы 9, 10, 14, за исключением п. 14.4, а также
пп. 7.8, 11.7, 15.6), И. И. Мельникова (главы 8, 12, за
исключением п. 12.3, а также главы 13 и 16), Э. Г. Палагин (глава 1,
за исключением п. 1.1, глава 7, кроме пп. 7.1, 7.2, 7.8), Э. Л.
Подольская (глава 6), В. М. Радикевич (глава 11, за исключением
п. 11.7, и п. 12.3), А. П. Юргенсон (глава 15, за исключением
п. 15.6). Глава 18 написана Ф. А. Гисиной, Д. Л. Лайхтманом
и Э. Г. Палагиным совместно.
При работе над книгой мы многократно обращались к
исследованиям и идеям И. А. Кибеля, одного из
основоположников динамической метеорологии. Его светлой памяти мы
посвящаем свою книгу.
Глава 1. ОБЩИЕ ПРИНЦИПЫ
Атмосфера как сплошная среда. Общая формулировка уравнения баланса.
Уравнение баланса массы. Уравнение движения. Баланс импульса. Закон
сохранения энергии. Уравнение баланса внутренней энергии. Уравнение
состояния сухого воздуха. Сводные результаты.
Настоящая глава посвящена уточнению смысла
используемых в дальнейшем макроскопических характеристик сплошной
среды и формулировке уравнений гидротермодинамики как
уравнений баланса различных субстанций.
1.1. Атмосфера как сплошная среда
Атмосфера, являющаяся смесью газов, представляет собой
систему, состоящую из огромного числа элементарных частиц
(молекул в нижнем слое, атомов и молекул в верхнем),
находящихся в непрерывном хаотическом движении. При
математическом описании большинства атмосферных явлений возникает
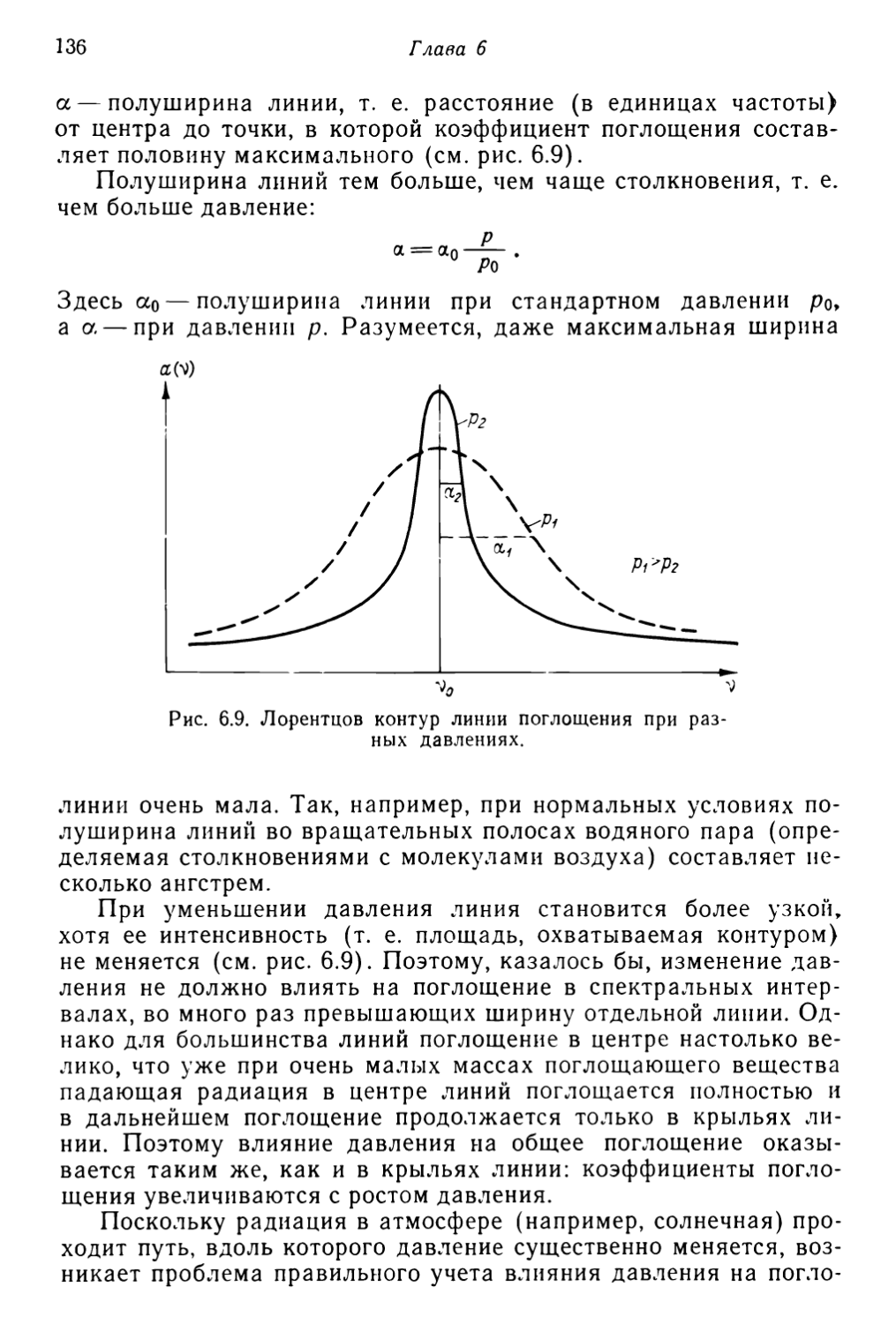
важный вопрос: можно ли отвлечься от дискретной структуры
атмосферы и рассматривать ее как сплошную среду?
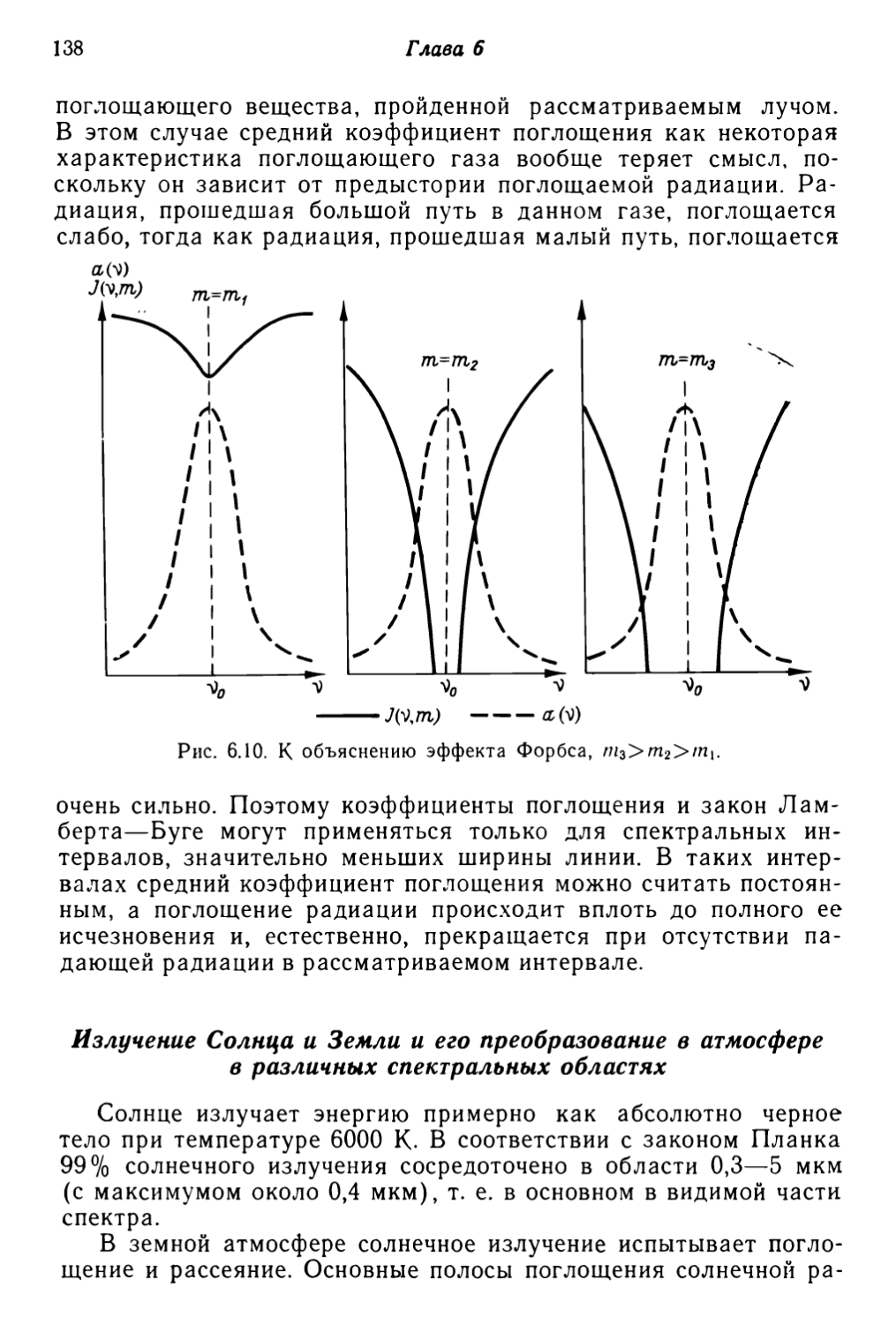
Использование гипотезы сплошности позволяет ввести в рассмотрение ряд
макроскопических величин, таких, как скорость движения
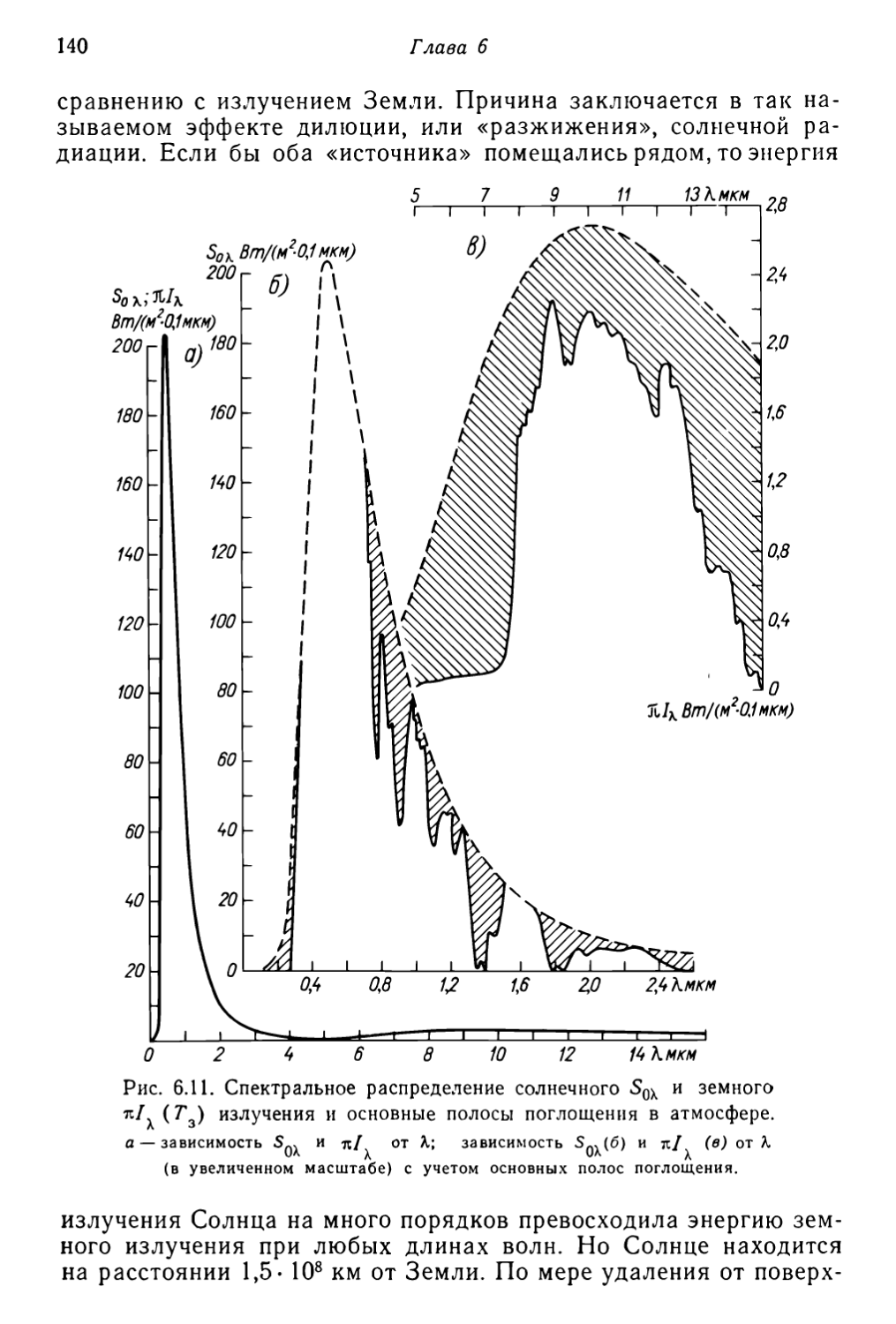
воздуха, его температура, плотность, давление, и сформулировать
уравнения, описывающие изменение этих величин в
пространстве и во времени.
Для введения макроскопических характеристик нужно
осуществить осреднение по элементарному объему системы,
который должен удовлетворять определенным требованиям:
линейные размеры этого объема /о должны быть велики по сравнению
с длиной свободного пробега молекул /, но малы по сравнению
с характерным масштабом рассматриваемого явления1 L^
^b/gradb (b— любая макроскопическая величина), т. е. /<С
<С/о<^£. Первое условие необходимо для того, чтобы исключить
флуктуации, обусловленные молекулярным движением; второе
позволяет пренебречь изменениями осредненных величин в
пределах выделенного объема. Поскольку /4С/о, в объеме V~/J
1 Более подробно вопрос о характерных масштабах различных явлений
рассмотрен в главе 7.
6
Глава 1
число молекул настолько велико, что при осреднении по
рассматриваемой совокупности флуктуации, обусловленные
движением отдельных молекул, пренебрежимо малы. Вследствие этого,
например, средний вектор скорости теплового движения
практически равен нулю. В то же время рассматриваемый
элементарный объем достаточно мал, что позволяет проследить изменение
в пространстве всех осредненных величин при переходе от
одного объема к другому.
При выяснении возможности рассмотрения атмосферы как
сплошной среды необходимо иметь в виду, с одной стороны,
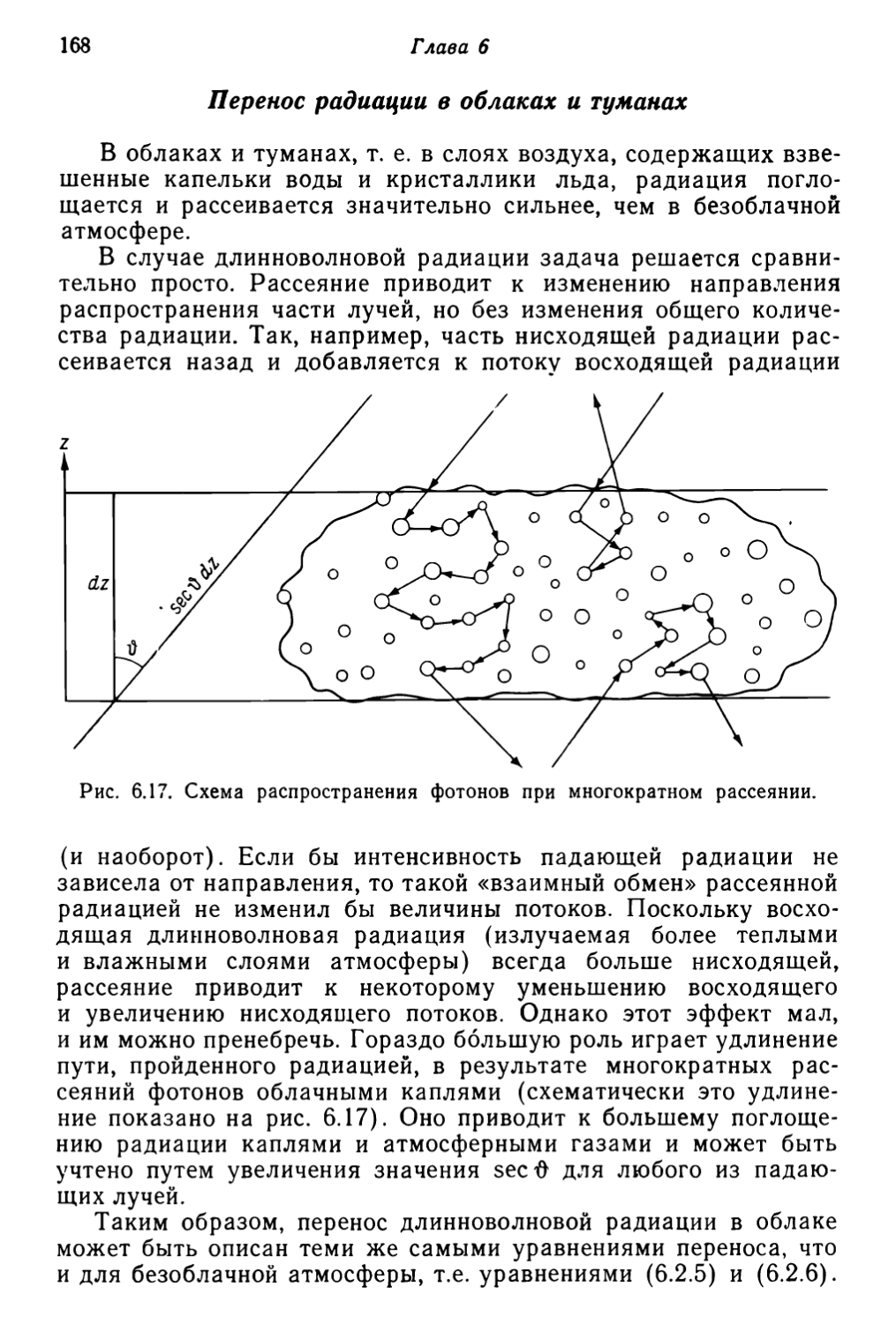
что длина свободного пробега существенно увеличивается с
высотой, а с другой, что атмосферные движения характеризуются
широким диапазоном масштабов. Поэтому выполнение гипотезы
сплошности зависит как от рассматриваемой высоты, так и от
специфики исследуемого явления.
Как правило, если не иметь в виду какие-либо специальные
задачи, характерный масштаб L больше 1 м, поэтому при
описании большинства явлений на высотах г<100 км атмосферу
можно трактовать как сплошную среду. На высотах г>100 км,
характеризующихся масштабами, соизмеримыми с длиной
свободного пробега, гипотеза сплошности не выполняется. В этом
случае необходимо исходить из дискретной структуры
атмосферы.
Наконец, отметим, что в ряде случаев, даже когда описание
атмосферы как сплошной среды допустимо, рассмотрение ее
свойств на микроскопическом уровне (с учетом дискретной
структуры) позволяет более детально исследовать специфику
явления.
1.2. Общая формулировка уравнения баланса
При изучении динамики атмосферных процессов интерес
представляют поля давления, температуры, скорости и
некоторых других характеристик. Для исследования изменения этих
полей в пространстве и во времени необходимо сформулировать
соответствующие уравнения. Они основаны на трех
фундаментальных законах сохранения — массы, количества движения и
энергии.
Первый из них дает возможность сформулировать уравнения
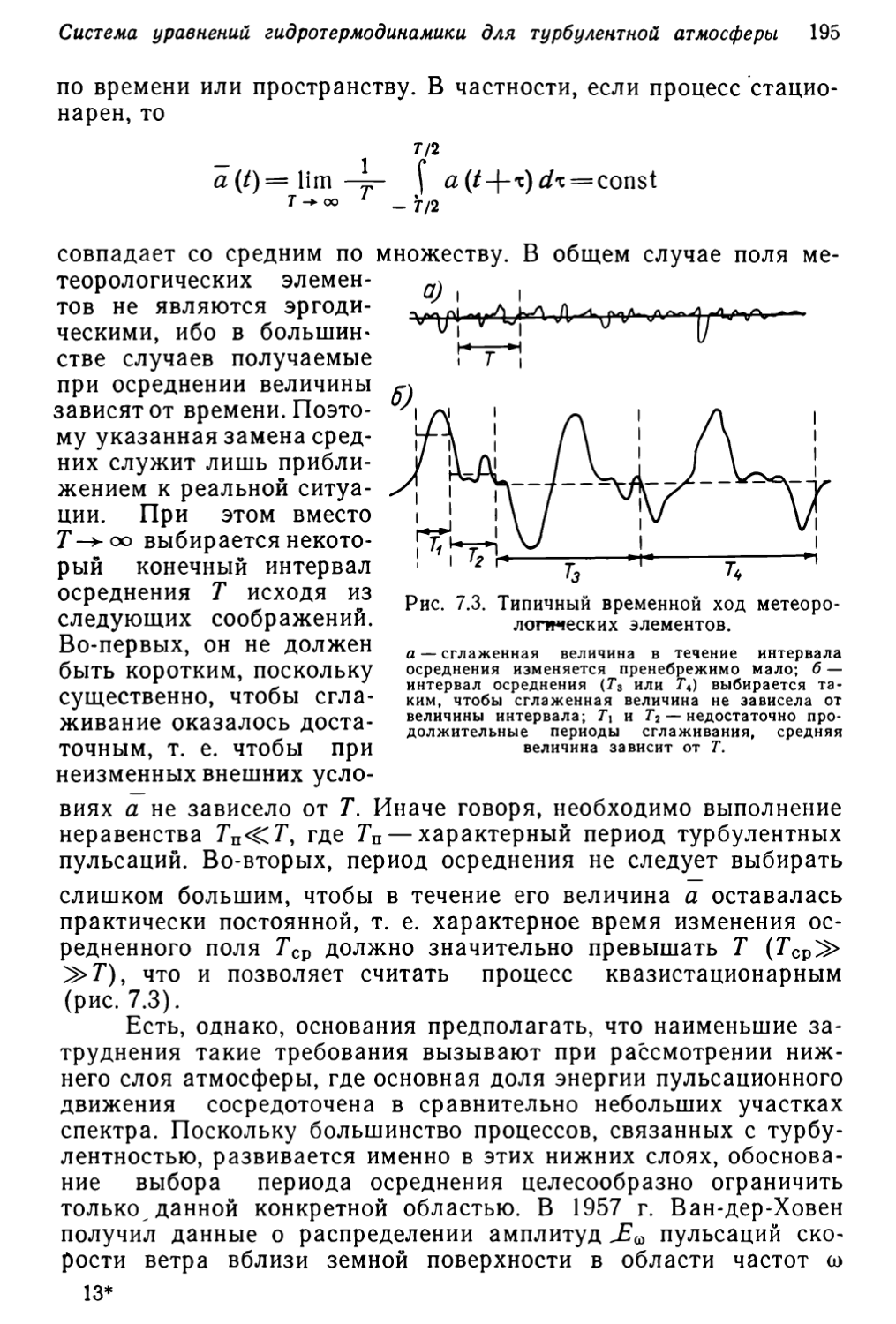
неразрывности и диффузии различных компонент воздуха.
Закон сохранения количества движения позволяет записать
уравнения движения, а закон сохранения энергии — уравнение
притока тепла.
При формулировке соответствующих уравнений удобно
руководствоваться следующими общими соображениями. Рассмот-
Общие принципы
7
рим движущуюся массу воздуха плотностью р. Пусть а —
некоторая интересующая нас удельная, т. е. отнесенная к единице
массы, скалярная величина. Тогда в единице объема будет
содержаться количество субстанции, равное ра. Изменение
количества субстанции в фиксированной точке за единицу времени
дра
будет , в элементарном объеме dV оно составляет
—-—dl/, а во всем объеме V: —-—dV. Это изменение мо-
жет быть обусловлено притоком рассматриваемой субстанции
через поверхность рассматриваемого объема yypavandS и на-
личием источников (стоков) JJJ I dV внутри объема. Здесь S —
v
поверхность, стягивающая рассматриваемый объем; / —
мощность источника, т. е. количество субстанции, возникающей
(исчезающей) в единице объема за единицу времени; pavan —
поток через единицу поверхности (п — нормаль к поверхности);
va = -— макроскопическая скорость движения рассмат-
риваемой субстанции; Nai — число молекул, обладающих
скоростью Vi.
Общее условие баланса для любой субстанции можно запи-
,е*
\\\^dV=-§f^ndS^\\ldV.
Перед двойным интегралом стоит знак минус, ибо поток
принимается положительным, если его направление совпадает
с внешней нормалью. При таком выборе знака положительный
поток означает отток вещества из рассматриваемого объема,
откуда и следует, что —тг~ и pavan имеют разные знаки.
Используя формулу Гаусса—Остроградского, получим
\$ $(■*%-+№ 9av„-l)dV=0.
V Х '
Если подынтегральная функция непрерывна и
дифференцируема, то полученное соотношение справедливо для любого
Уравнения такого типа часто называют уравнениями переноса.
8
Глава 1
объема и возможна запись в дифференциальной форме,
а именно
д$а
dt
-=-(11урат>вл + /. (1.2.1)
В тех случаях, когда нас интересуют разрывные поля, что
может быть связано, например, с наличием фронтальных
поверхностей, необходимо сохранять интегральное представление.
Уравнение (1.2.1) показывает, что изменение со временем
содержания данной субстанции в единичном, фиксированном
в пространстве объеме обусловлено наличием источников (или
стоков) субстанции и притоком ее извне.
Поток в (1.2.1) можно представить в форме двух слагаемых:
pavfl = pav + pa(vfl — v) = JK+JA. (1-2.2)
Здесь v — средняя скорость движения воздуха (скорость центра
масс смеси).
Первое слагаемое в (1.2.2) представляет собой перенос
субстанции а общим средним потоком. Это так называемый
конвективный поток JK. Второе слагаемое — поток, обусловленный
тем, что средняя скорость распространения субстанции а
отличается от общей скорости. Второе слагаемое пропорционально
разности между общей скоростью и скоростью распространения,
рассматриваемой субстанции. Эта часть полного потока
обусловлена неравномерностью распределения а в пространстве. Так,
если слева от плоскости, например, х = с а = а^фОу а справа
а = 0, то вектор va — v будет направлен, разумеется, вправо
независимо от направления общего потока. Второе слагаемое
в (1.2.2) называется диффузионным потоком Лд; по смыслу он
должен быть связан с величинами, характеризующими
пространственную неравномерность а. Подставив (1.2.2) в (1.2.1),
получим
-^=-divpav-divPa(vfl-v)+/. (1.2.3)
Полученное уравнение представляет собой уравнение баланса
субстанции а в дивергентной форме. Его можно записать еще
в виде
д^а
dt
= — (v grad pa) — pa div v — div JA-\-I,
откуда
-^-=-padivv-divJA+/. (1.2.4)
dt
Здесь использована формула векторного анализа
div pav = (v grad pa) -\- pa div v
Общие принципы
9
и понятие индивидуальной производной
dt dt
(vgradpa).
1.3. Уравнение баланса массы
Воздух является смесью различных газов. Пусть рг —
плотность /-того газа, а £г = рг/р — его массовая концентрация. По-
к
скольку ^Pi = p (k — число газовых компонент в воздухе), то
2с=1. (1-3.1)
/ = 1
Полагая, что в (1.2.3) а = си получим уравнение баланса /-той
компоненты воздуха в виде
-*£*-=-(Нуру^-ШуХ.+Л. (1.3.2)
Уравнение (1.3.2) показывает, что изменение концентрации
данной компоненты в единичном объеме происходит в
результате притока массы в данный объем и наличия источников (или
стоков). Когда речь идет о компонентах воздуха, то источники
(стоки) могут быть обусловлены фазовыми переходами воды,
химическими реакциями и процессами ионизации. Последние
необходимо учитывать при рассмотрении явлений, протекающих
в верхних слоях атмосферы. Уравнение (1.3.2) описывает также
изменение концентрации примесей, которые поступают в
атмосферу из различных источников (промышленные выбросы,
взрывы, естественная радиоактивность и т. д.).
Суммируя (1.3.2) по всем i, получим уравнение баланса
массы. При этом нужно учесть, что в результате фазовых
переходов, химических реакций и других процессов может
изменяться только масса данной компоненты, полная масса смеси
остается постоянной, т. е.
k
2 л=о. (1.3.3)
Если, кроме того, иметь в виду, что
k k
v =
x = l
10
Глава 1
то из (1.3.2) следует уравнение неразрывности, выражающее
закон сохранения массы:
^=-divPv, (1.3.4)
dt
или в другой форме
d? bpdivv = 0. (1.3.5)
dt
Если предположить, что воздух несжимаем, т. е. —— = 0, то
at
из (1.3.5) следует
divv = 0. (1.3.6)
Запишем (1.3.4) и (1.3.5) в проекциях на оси прямоугольной
декартовой системы координат, обозначив
Соответственно имеем:
В заключение заметим, что для ^-компонентной смеси только
k — 1 диффузионных потоков независимы и соответственно мы
имеем только k—1 уравнений баланса, &-тым уравнением
является общее уравнение неразрывности (1.3.4).
1.4. Уравнение движения. Баланс импульса
Уравнения движения сплошной среды имеют следующий
вид:
РТ—^"+Р^ << = 1.2,3). (1.4.1)
Здесь S?ji — компонента тензора напряжений; Ь\ — i-тая
компонента внешней силы, отнесенная к единице массы. Покажем,
1 Знак суммы допущен. В (1.3.7) и далее предполагается, что по
дважды повторяющемуся индексу производится суммирование, так что,
например,
dxf = 2d дхг
J 7 = 1 J
Общие принципы
11
что уравнения движения можно представить в форме
уравнения баланса импульса. Для этого воспользуемся следующим
тождеством:
р dt — dt Vi dt • v-*-z>
Исключим из (1.4.2) с помощью уравнения неразрывности
(1.3.5) —jj- и развернем индивидуальную производную:
_*m x_*wj (14>3)
dt ' dxj
Теперь, подставив (1.4.3) в (1.4.1), получим искомое
выражение
Полученное уравнение по структуре совпадает с общим
уравнением баланса (1.2.3). В левой части стоит изменение
импульса единицы объема за единицу времени; в правой части
pviVj+£Pji — полный поток импульса, pFi — источник i-той
компоненты импульса. Таким образом, внешние силы, не связанные
непосредственно с молекулярным взаимодействием
соприкасающихся объемов жидкости, можно рассматривать как источники
импульса. К указанным силам относятся сила тяготения,
центробежная сила и сила Кориолиса. Появление двух последних
сил обусловлено тем обстоятельством, что наиболее
употребительная в метеорологии система координат жестко связана
с земной поверхностью. В силу вращения Земли она не
является инерциальной. Поэтому движение воздушных масс
относительно поверхности Земли зависит не только от силы
тяготения FT, но и от сил инерции; центробежная сила ¥ц связана
только с переносным ускорением, а ускорение Кориолиса FKOp
обусловлено суммарным эффектом перемещения Земли
относительно квазинеподвижных звезд и относительным перемещением
частицы.
Согласно закону тяготения Ньютона, две частицы с массами
Wi и т2 притягиваются друг к другу с силой
р m\m2R
где у — поСтшшная тяготения; R = | R | — расстояние между
12
Глава 1
центрами масс. На частицу воздуха единичной массы (mi=l)
со стороны Земли (т2 = М) действует сила
F =а —_ MR
Гт-gx Т £2|R| '
При этом частица и Земля считаются материальными точками
(в данном случае |R|—расстояние между рассматриваемой
точкой и центром Земли).
ю
Рис. 1.1. К распределению сил, действующих на
Землю.
Центробежная сила, действующая на единицу массы, равна
Fu = gu = co2r = co2r=a)2^COScp,
где со — угловая скорость вращения Земли; г — радиус-вектор,
направленный перпендикулярно земной оси к центру
рассматриваемой частицы; ф — широта.
Составляющая центробежной силы gn8, касательная к
поверхности земной сферы, вызывает ее деформацию, которая
продолжается до тех пор, пока возникающая в свою очередь проекция
силы тяготения gTS не уравновесит g4S. В итоге поверхность
Земли становится эллиптической (из-за неоднородности земной
коры Земля имеет менее правильную форму, именуемую
геоидом).
Общие принципы
13
Угол а (рис. 1.1) весьма мал. Поэтому можно полагать, что
сила тяжести g, равная разности проекций сил gns и gTS на
ось г, может быть рассчитана по формуле
g = Stz - g-цг = giz — M2R COS2 ср.
Напомним, что удельная (т. е. отнесенная к единице массы)
сила Кориолиса равна
FKop=-2[«DXvI.
Если ось Хз направить по линии действия силы тяжести, т. е.
перпендикулярно земной поверхности, то FTi = FT3=—g. Что
касается тензора напряжений, то, как известно из
гидромеханики, он сводится к сумме гидростатического давления рбг^ и
вязкого напряжения Пц, так что
&и=рЪи + Пи. (1.4.5)
Тензор вязких напряжений связан с неоднородностью поля
скорости и, как известно, выражается через производные от
скорости по координатам:
п„
'->(■%+%■)• <'-4-6>
где |ы — коэффициент динамической вязкости.
Теперь уравнения движения (1.4.4) можно записать в виде
d?vt
dt дх
-^[pwj+Pbj+v (^7+^7)
—gphi—
— 2p(ujvk — «>kvi). (1.4.7)
Отметим, что индексы i, /, k в выражении для проекции силы
Кориолиса образуют циклическую перестановку чисел 1, 2, 3.
Введя в (1.4.7) значение индивидуальной производной, после
несложных выкладок получим уравнения движения в форме
Навье—Стокса:
dvt 1 dp * , 2 fi. d^vi , p. d^vt
dt p~ dxi li"■ 3 ~p dxt dxj * ~p dxjdx~j
— ghi — 2 (u>jVk — u>kVj). (1.4.8)
Utt 2 (я d2Vi
член — —-— в обычных условиях, учитывая квазинесжи-
3 р oxidxj
маемость воздуха (divv = 0), можно опустить, поэтому в
дальнейшем он фигурировать не будет.
14
Глава 1
1.5. Закон сохранения энергии. Уравнение баланса
внутренней энергии
Согласно закону сохранения энергии, изменение полной
энергии системы может быть связано только с притоком ее через
границы, ибо источники и стоки существовать не могут.
Поэтому для полной удельной энергии уравнение баланса следует
записать в виде
-^=-div(Pv£+JE) (1.5.1)
или
p4f=-divJ£. (1.5.2)
В динамике атмосферы основную роль играют следующие
главные виды энергии: кинетическая EK = v2/2, потенциальная
£п, внутренняя ЕВу лучистая £л и энергия фазовых переходов
Еф. Следует отметить, что на самом деле в атмосфере, кроме
перечисленных, имеют место и другие виды энергий, как,
например, химическая, магнитная, электрическая и т. п. Однако в
атмосферных процессах, о которых ниже будет идти речь,
наиболее важные взаимные превращения энергии практически
ограничены только главными видами. В связи с этим при
формулировке закона сохранения в полную энергию можно
включить только упомянутые выше главные виды.1 Тогда (1.5.2)
можно представить следующим образом:
P^-(£K-|-fn+^B+£1 + ^)=-div(JfK+JEn+J£B+J£(l)).
(1.5.3)
В (1.5.3) конвективный и диффузионный потоки лучистой
энергии отсутствуют, ибо электромагнитная энергия конвективным
и молекулярным движением не переносится.
В данном случае нас интересует уравнение баланса
внутренней энергии. Его можно получить из (1.5.3), если известно
уравнение баланса для отдельных видов энергии.
Уравнение баланса механической энергии получим, умножив
обе части уравнения (1.4.8) на v\ и просуммировав по всем
компонентам:
d ( i/2 \ 1 / др \ , fi d^vt
1 В верхней атмосфере могут быть существенны эффекты, связанные
с протеканием химических реакций, в связи с чем может оказаться, что
необходимо рассматривать химическую энергию.
Общие принципы
15
Вводя скорость в правой части полученного уравнения под знак
производной, умножая обе части его на р и учитывая, что 1>з =
dxz
=—-—, можно записать это уравнение в следующем виде:
at
р-^-(£к+£п)=- -^-(pvj-m-^+p-^— diss=
= - dlv (JfK+Jfn)+p div v - diss. (1.5.4)
Здесь
Уравнения баланса лучистой энергии и энергии фазовых
переходов в соответствии с общей формой записи и учетом того,
что Лел = 0, можно записать следующим образом:
""Ел=/л. 0.5.5)
r dt
PT=-dlvJ^+V О'5'6)
Вычитая из (1.5.3) уравнения (1.5.4) — (1.5.6) и поделив
результат на р, получим
dE° -^-(divJ^+A+^-^divv + diss). (1.5.7)
dt р
В (1.5.7) первые три слагаемых—-- = (div Jeb +/л + /ф)
в правой части отражают изменения внутренней энергии,
связанные с диффузией внутренней энергии, лучистым и фазовым
притоком.1 Член —pdivv отражает превращение внутренней
энергии в другие формы энергии вследствие сжатия или
расширения. Из уравнения неразрывности следует равенство
dlv v 1_ _rfp_ _ _d_ I J_\ _ dV
p ~~ p2 dt dt { p j dt »
где V— удельный объем. Поэтому
— div v = — р
р «" •— v dt •
Наконец, величина diss/p отражает переход механической
работы во внутреннюю энергию вследствие трения. Ее вклад
весьма мал, и в дальнейшем членом diss/p пренебрегаем.
1 Следует иметь в виду, что dQ не является полным дифференциалом,
но в дальнейшем в целях удобства будем использовать это обозначение.
16
Глава 1
Таким образом, уравнение баланса внутренней энергии
можно окончательно записать в виде
dEB dQ dV
-W-=^t P~dT- О-5-8)
В такой форме это уравнение носит название «первое начало
термодинамики».
Как будет показано в главе 3, величина Ев в случае
идеального газа однозначно связана с температурой 71, т. е. ЕВ = ЕВ(Т).
1.6. Уравнение состояния сухого воздуха
Опытным путем установлено, что свойства газов, входящих
в состав воздуха, с достаточной точностью описываются
законами идеальных газов *, а сам воздух можно считать смесью
идеальных газов.
Термодинамическое состояние воздуха может быть
однозначно определено тремя параметрами: давлением р,
температурой Т и плотностью р, причем они связаны соотношением
Р=Р(Р, Т). (1.6.1)
Соотношение (1.6.1) называется уравнением состояния, явный
вид которого можно определить либо на основе кинетической
теории газов, либо исходя из опытных законов Бойля—Мари-
отта и Гей-Люссака. Первый из них формулируется следующимч
образом: при неизменной температуре произведение давления
на удельный объем является величиной постоянной, т. е.
J- = -^. (1.6.2)
Р Ро v '
Закон Гей-Люссака связывает давление и температуру. При
постоянном объеме их отношение для фиксированной массы
газа также сохраняется постоянным, т. е.
-f=^. о-6-3)
Указанные законы справедливы и для реальных газов, у
которых пренебрежимо малы силы взаимодействия молекул и
собственный объем молекул. Опытные данные подтверждают, что
1 Под идеальным газом понимается среда, состоящая из сферических
молекул, расстояние между которыми значительно превышает их собственный
размер. Взаимодействие между ними сводится к соударениям, подчиняющимся
законам абсолютно упругого тела.
Общие принципы
17
в атмосфере эти условия выполняются с достаточной точностью,
если воздух не насыщен.
Явный вид зависимости р(р, Т) может быть найден методом
определения неизвестной функции по ее частным производным.
Дифференцируя (1.6.1), имеем
*-(-Jt)r * + (#),-Г. U.6.4)
На основании (1.6.2) и (1.6.3)
( др \ _ ро р ( др\ _ ро _ р п ~ гч
Подставив (1.6.5) в (1.6.4), получим
dp=fdp+-$rdT.
Интегрируя последнее равенство, имеем
Р = Ро
Р^ ро^о
-R. (1.6.6)
Постоянная интегрирования R носит название газовой
постоянной. Ее легко определить на основании закона Аво-
гадро, согласно которому одна грамм-молекула любого газа
при нормальных условиях (ро= 1,013249- 106 дин/см2, Го =
= 273 К) занимает объем У0 = 22 414 см3. Поэтому для одной
грамм-молекулы
р^ Ро _ Ро м- 1 _ Ро^о 1 Л*
Ро7\) 7о Ро f* То н- н-
(\х — относительная молекулярная масса газа).
Таким образом, можно записать, что
Определим газовую постоянную воздуха на основании закона
Дальтона, который гласит, что давление в смеси газов равно
сумме парциальных давлений этих газов. На основании
указанного закона, если смесь состоит из п газов, получаем
/> = 2 Рь
i = \
а поскольку
R т* mi то
(М — масса смеси, /л; — массы отдельных компонент), то
18
Глава 1
Обозначая
/Хс —^ \ М jii ^ М м-2 "* ' ' ' "■ М рп }'
уравнение состояния для сухого воздуха можно записать в виде
p = R?T, (1.6.7)
Здесь газовая постоянная сухого воздуха вновь обозначена
через R.
1.7. Сводные результаты
Таким образом, общие принципы механики атмосферы
можно сформулировать в виде трех законов сохранения — массы,
количества движения и энергии. Они могут быть записаны в виде
пяти скалярных уравнений. Шестым уравнением, замыкающим
систему, является уравнение состояния воздуха, выведенное
выше.
Чтобы сконцентрировать внимание, выпишем всю систему,
В тензорной форме указанные уравнения имеют вид:
4И-/-£+р-£-°- <'-71>
dvi j_ dvi 1 dp » j [i d^Vj
VJ dx, ~~ о dx: °lJ
dt l J dxj p dxi lJ ' p dxj dxj
-gb3l-2(ujVk-i»kVj), (1.7.2)
д£в , дЕв _ dQ dV (] ?ov
p = R9T. (1.7.4)
Из этой системы необходимо найти следующие величины:
компоненты вектора скорости vu давление /?, плотность р и
внутреннюю энергию ЕВ = ЕВ(Т). Таким образом имеем шесть
неизвестных величин при наличии шести уравнений (полагая что
—- известно).
Контрольные вопросы
1. Может ли тензор напряжений быть равен нулю? Чему он
равен в случае пренебрежения трением?
2. Чем сила тяжести отличается от силы тяготения?
3. За счет чего может меняться внутренняя энергия в
несжимаемой, лишенной трения жидкости?
Глава 2. ГАЗОВЫЙ СОСТАВ АТМОСФЕРЫ
Газовый состав атмосферы на разных высотах (теория
диффузионно-гравитационного разделения газов). Распределение плотности газа по высоте при
наличии турбулентного перемешивания. Время установления
диффузионно-гравитационного разделения газов. Диссипация газов из атмосферы. Уровень
диссипации газов. Интенсивность и время диссипации газов из атмосферы.
В этой главе рассматриваются некоторые общие вопросы
строения атмосферы, представляющие интерес при изучении
различных проблем теоретической метеорологии: изменение
газового состава воздуха с высотой, диссипация газов и
вертикальная протяженность атмосферы.
Существование атмосферы, ее вертикальная протяженность,
распределение плотности и газовый состав на разных высотах
обусловлены в значительной степени притяжением Земли, но
зависят также от большого числа других факторов.
Экспериментально установлено, что, за исключением таких компонент, как
водяной пар, озон и двуокись углерода, содержание которых
в воздухе очень мало и подвержено значительным вариациям,
концентрация основных газовых компонент вблизи Земли
практически не изменяется со временем и не зависит от местных
условий. Важным является изучение вопроса о газовом составе
воздуха на разных высотах: остается ли относительное
содержание различных газов в воздухе постоянным по высоте или
изменяется? Такие сведения необходимы для решения целого
ряда задач теоретической метеорологии. Достаточно вспомнить,
что условия распространения радиации существенно зависят от
газового состава воздуха. Интерпретация некоторых
спутниковых данных также требует информации о составе воздуха на
разных высотах. Например, при определении температуры по
измеренным значениям плотности и давления нужно знать
среднюю относительную молекулярную массу воздуха, значение
которой зависит от относительного содержания различных
газовых компонент. Состав атмосферы изменяется с высотой как
вследствие различий в уменьшении плотности разных газов, так
и в результате химических и фотохимических реакций и
ионизационных процессов, приводящих к диссоциации молекул на
атомы, образованию новых молекул, созданию положительных
и отрицательных ионов. Хотя фотохимические и ионизационные
процессы играют важную роль в целом ряде явлений,
протекающих в атмосфере, здесь рассматриваются такие аспекты
2*
20
Глава 2
проблемы строения атмосферы, когда влиянием этих процессов
можно пренебречь.
2.1. Газовый состав атмосферы на разных высотах
(теория диффузионно-гравитационного разделения газов)
При исследовании изменения с высотой газового состава
атмосферы обычно исходят из следующих соображений.
Предполагают, что атмосфера находится в равновесии, т. е.
макроскопическое движение отсутствует. Согласно закону Дальтона, при
равновесных условиях каждый газ, входящий в состав смеси,
ведет себя так, как если бы других газов не было, поэтому для
описания изменения с высотой парциального давления ра каж-,
дой а-компоненты можно использовать уравнение статики
dpa=-9agdz. (2.1.1)
Здесь ра — парциальная плотность а-компоненты воздуха; g —
ускорение свободного падения. Комбинируя (2.1.1) с
уравнением состояния для данной компоненты газа
pa = -^R*T, (2.1.2)
найдем распределение с высотой парциального давления и
плотности:
рЛ*)=РЛ0)е ° , (2.1.3)
Уд С S
7(0) ** * 1{Z)
dz
рЛ*)=рЛ0)-^-* • (2Л-4>
В (2.1.2) — (2.1.4) \1а — относительная молекулярная масса
а-компоненты смеси; /?* — универсальная газовая постоянная;
Г(0) и T(z)—температура воздуха у поверхности земли при
2 = 0 и на уровне z соответственно.
Если ввести в рассмотрение среднюю барометрическую
температуру Тт с помощью соотношения
"Г—Frf-fTiH*' (2Л-5)1
1 На небольшой высоте, где можно пренебречь изменением с высотой
ускорения свободного падения, введенное здесь определение средней
барометрической температуры совпадает с общепринятым.
Газовый состав атмосферы
2Г
то (2.1.3) и (2.1.4) можно записать в виде:
я
/>.(*)=/>«(0)е R*Tm =РЛ0)е * . (2.1.6)
РЛг) = РЛ0)-^^^Г = РЛ0)^-е"^, (2.1.7)
где Яа= характерный масштаб высоты,
показывающего
щий, на какой высоте плотность данного газа убывает в е раз;
go — ускорение свободного падения вблизи земли.
Уравнения, аналогичные (2.1.6) и (2.1.7), могут быть
получены и для всей смеси газов, из которых состоит воздух, если
использовать выведенное в главе 1 уравнение состояния
воздуха
p=J_$*T (2.1.8)
и уравнение статики
dp=-pgdz. (2.1.9)
Из этих соотношений следует:
где
p(z) =
р(г) = Р
N
а = 1
= Р
(0)
Ра.
Ф)е
ПО)
. Р =
Z
Н
е
N
а=1
г
Н
Ра.
(2.1.10)
(2.1.11)
= характерный масштаб высоты, определяющий
Vogo
уровень, на котором плотность воздуха убывает в е раз. Этот
масштаб часто называют высотой однородной атмосферы.
При получении (2.1.10) и (2.1.11) введено более общее, чем
в (2.1.5), определение средней барометрической температуры,
учитывающее, что на больших высотах средняя относительная
молекулярная масса воздуха |li изменяется с высотой, т. е.
1 _ 1 f е (*)*(*) ^
Из (2.1.7) видно, что плотность а-компоненты убывает с
высотой в соответствии с ее относительной молекулярной массой;
22
Глава 2
следовательно, чем тяжелее газ, тем быстрее убывает его
плотность с высотой. Вертикальное распределение газов в смеси,
связанное с их индивидуальными свойствами, называется
диффузионно-гравитационным разделением газов или просто
разделением газов.
Из приведенных рассуждений следует, что газовый состав
воздуха должен заметно изменяться с высотой: при увеличении
высоты воздух должен обогащаться легкими компонентами за
счет тяжелых. Согласно оценкам, выполненным по формуле
(2.1.7), уже на высоте 5 км содержание кислорода в воздухе
должно было бы уменьшиться до 19,60% (по сравнению
с 20,95% У земли), а выше 60 км атмосфера должна была бы
почти целиком состоять из водорода. Однако измерения,
выполненные с помощью шаров-зондов, ракет и искусственных
спутников, показали, что газовый состав атмосферы остается
постоянным до высот 100—120 км, т. е. , ч =—а\/ = const. Только
Р(г) 9(0)
выше этого уровня, называемого уровнем
диффузионно-гравитационного разделения, плотность различных компонент убывает
с высотой в соответствии с формулой (2.1.7), т. е. действительно
наблюдается изменение состава воздуха с высотой.
Важно выяснить, почему процесс разделения газов
происходит только на больших высотах, а не начинается с более низких
уровней, как это следует из приведенных соображений. Чтобы
объяснить реальную ситуацию, необходимо детально
исследовать механизм процесса разделения. С этой целью получим
формулу, описывающую изменение с высотой плотности данной
компоненты смеси, другим способом, учитывающим
молекулярную структуру газа. Рассмотрим, как распределяется в
атмосфере некоторый газ, имеющий плотность ра. Будем
по-прежнему полагать, что атмосфера находится в равновесии и что
молекулы газа движутся по вертикали только под влиянием
молекулярной диффузии и силы тяжести. При равновесии
полный поток частиц данного газа через единичную
горизонтальную площадку (Да) равен нулю, т. е.
Aa=-Da4^-*V,Pa = 0. (2.1.12)
Первый член этого уравнения описывает диффузионный,
а второй — гравитационный поток частиц; Da — коэффициент
молекулярной диффузии частиц a-компоненты в данной смеси;
^др. a — скорость их дрейфа, которую они приобретают под
действием силы тяжести. Скорость дрейфа можно найти из
следующих соображений. На фиксированную молекулу действует сила
тяжести и сила сопротивления, обусловленная столкновениями
«с другими молекулами. Поскольку столкновения являются слу-
Газовый состав атмосферы
23
чайными, при отсутствии внешней силы все направления
движения после столкновения равновероятны. Но, кроме случайного
движения, молекула имеет дополнительную скорость,
обусловленную влиянием силы тяжести FTnm. Среднее значение этой
скорости, которая и называется скоростью дрейфа, можно найти,
интегрируя уравнение движения
dw„n
Др. а р
а аЧ 'тяж
по времени от нуля до т (та — масса молекул данного газа,
т — среднее время между столкновениями). Таким образом,
приходим к соотношению
W
др. а
= J^L=Bamag. <2.1.13)
Величина Ва, равная ртношению среднего времени между
столкновениями к массе молекул (Ва = х/та), называется
подвижностью. Для частиц, находящихся в равновесии в поле
силы тяжести, справедливо соотношение Эйнштейна,
связывающее подвижность с коэффициентом молекулярной диффузии:
*. = -&-. (2-1.Н)
где k — постоянная Больцмана.
Подставив (2.1.13) с учетом (2.1.14) в (2.1.12), получим
do те
—гг—£Г'-=°- <2-1Л5>
В результате интегрирования (2.1.15) при использовании
(2.1.5) находим
mg0z
Pa(z) = ?A0)e т . (2.U6)i
Поскольку та = )ыа/Л^А (Л^а — число Авогадро) и kNA=R*> то
легко убедиться в том, что формула (2.1.16) практически совпа-
770)
дает с (2.1.7). Отсутствие в (2.1.16) отношения _, [
объяснять)
ется тем, что при выводе не учтен эффект термодиффузии. Этот
вопрос более детально обсуждается дальше.
Таким образом, если бы атмосфера находилась в
равновесии, то под действием силы тяжести и молекулярной диффузии
1 Формула (2.1.16), показывающая, что частицы в пространстве
распределены в соответствии со своей потенциальной энергией magoZt является
частным случаем общей формулы Больцмана, характеризующей
пространственное распределение газа в любом потенциальном поле.
24
Глава 2
должно было бы наблюдаться изменение газового состава
воздуха с высотой. В этом заключается сущность теории
диффузионно-гравитационного разделения газов. Вывод формулы для
ра(г) на основе уравнения (2.1.12) подсказывает, в чем следует
искать причину несоответствия полученного соотношения
(2.1.16) действительному распределению газа в слое атмосферы
до высоты около 100 км. В уравнении (2.1.12) учтена только
молекулярная диффузия частиц. Хорошо известно, что в
атмосфере существенную роль играет турбулентная диффузия
частиц, которая препятствует диффузионно-гравитационному
разделению газов. Крупные турбулентные вихри переносят по
вертикали большие массы воздуха, которые, перемешиваясь в
конечном счете с окружающей средой, сохраняют неизменным
•соотношение отдельных компонент смеси в слоях с развитой
турбулентностью.
Прежде чем перейти к рассмотрению влияния турбулентного
перемешивания на изменение с высотой плотности данного газа,
целесообразно сопоставить два приведенных выше вывода
формулы для ра(г). Предположив, что температура не изменяется
-с высотой, перепишем (2.1.15) в виде
-в-(^)-».-о- <*■■■»>
Здесь ра/^а = Яа — концентрация данного газа, т. е. число
частиц в единице объема. В статистической физике показывается,
что парциальное давление газа ра = ПакТ. Подставив это
соотношение в (2.1.17), убеждаемся в том, что оно эквивалентно
уравнению статики, записанному для данной компоненты смеси.
Следовательно, уравнение статики для данной компоненты смеси
можно использовать только тогда, когда в атмосфере
устанавливается равновесие под влиянием молекулярной диффузии и
гравитационного оседания.
Можно доказать эквивалентность двух приведенных выводов
формулы (2.1.16) и в том случае, когда температура воздуха
изменяется с высотой. В этом случае в уравнение (2.1.12) нужно
.ввести член, учитывающий термодиффузию — поток частиц,
обусловленный наличием вертикального градиента температуры
,(см. главу 5).
2.2. Распределение плотности газа по высоте при наличии
турбулентного перемешивания
Влияние турбулентного перемешивания на изменение
газового состава воздуха с высотой можно пояснить с помощью
следующих простых рассуждений. Если предположить, что
Газовый состав атмосферы 25»
равновесие в атмосфере устанавливается при участии
турбулентного перемешивания, то в правую часть уравнения (2.1.12)
нужно ввести член, описывающий поток частиц, обусловленный
турбулентной диффузией:
Угтурб— ^ dz у р J.
Тогда получим
Л.--А.-%--*др..р.-А-£(-7-)в0- (2-2.1)
Здесь, как это обычно делается, турбулентный поток записан
по аналогии с потоком, обусловленным молекулярной
диффузией.1 Необходимо, однако, иметь в виду, что турбулентное
движение является движением существенно большего масштаба,
чем молекулярное, поэтому при турбулентном движении
хаотически перемещаются не отдельные молекулы, а конечные массы
воздуха. При этом в движущейся массе воздуха сохраняется
массовая концентрация (напротив, плотность диффундирующего
вещества в вихре может меняться). Поэтому турбулентный
поток пропорционален не градиенту плотности данной компоненты
воздуха, а градиенту массовой концентрации ра/р (р —
плотность воздуха).
Если допустить, что при наличии турбулентного
перемешивания выполняются (2.1.13) и (2.1.14), то (2.2.1) с учетом
Т(0)
(2.1.11) при _. . ~ 1 после несложных преобразований можно
T(z)
записать в виде
J!*j± = -b{z)dz, (2.2.2)
и, следовательно,
где
- ] Ь(г) dz
P.W-P.(*i)« *' . (2-2.3)
" +4
1 1
н '
1
н
а
1 + -
1
77
К
Здесь /С= коэффициент турбулентности, Zi<z.
1 Вопрос о турбулентных потоках различных субстанций подробно
рассматривается в главе 7.
26
Глава 2
Как видно из (2.2.4), учет турбулентности приводит к тому,
что величина b{z)y характеризующая скорость убывания с
высотой плотности данной компоненты, зависит от двух масштабов
длины, связанных индивидуальными свойствами газа и всей
атмосферы, а также от отношения коэффициента турбулентности
к коэффициенту молекулярной диффузии. Каждый из этих
коэффициентов зависит от высоты, поэтому и соотношение между
ними меняется с высотой. Коэффициент молекулярной диффузии
обратно пропорционален давлению газа и растет с высотой по
показательному закону [см. формулу (2.1.10)]; коэффициент
турбулентности меняется с высотой в связи с изменением
средних градиентов скорости ветра и температуры.
Если в слое гг- — z турбулентное перемешивание преобладает
К (у\
над молекулярным, т. е. _ . ч ^>1, то
ui v 1 . /)(г) / 1 1 \ 1 ,
W Н ' К (г) \ Н% и ) И
Тогда из (2.2.3) следует
Pa(z) = ?a(zi)e н ==9a(zde h*'m '. (2.2.5)
Таким образом, если преобладающую роль играет
турбулентный обмен, плотность данной компоненты смеси изменяется
с высотой в соответствии со средней относительной
молекулярной массой воздуха, т. е. плотность всех компонент смеси
убывает с высотой по одинаковому закону. Из (2.1.11) видно, что
точно так же изменяется с высотой и плотность воздуха р (z).
Ра (?) Ра(0) ,
В этом случае, следовательно, —-V- = Л^ = const, т. е. га-
р(г) р(0)
зовый состав воздуха с высотой не изменяется.
Поскольку коэффициенты турбулентности и молекулярной
диффузии изменяются с высотой по разным законам (при этом
Ах (г) очень быстро увеличивается с ростом г), то начиная с
некоторой высоты Zi = h молекулярная диффузия начинает играть
К (г) ,
основную роль. В слое п—z, где _ . ч <С1,
Da(z)
b (z) « —п— = const,
а
и из (2.2.3) находим
(г-h)
_ (z-h) _ t1^
Р.(г) = Р.(А)е "" =Р.(А)« ^ - (2-2-6)
т. е. плотность данной компоненты смеси убывает с высотой
Газовый состав атмосферы
27
в соответствии с собственной относительной молекулярной
массой. В этом случае имеет место диффузионно-гравитационное
разделение газов и газовый состав воздуха, а следовательно, и
относительная молекулярная масса воздуха \х с высотой
изменяются.
Область постоянного газового состава воздуха называется
гомосферой, переменного — гетеросферой. Уже отмечалось, что
уровень, отделяющий гомосферу от гетеросферы, расположен на
высоте примерно 100—120 км. Можно думать, что на этой
высоте коэффициент молекулярной диффузии становится больше
коэффициента турбулентности. Поэтому уровень разделения
газов называется еще турбопаузой. В настоящее время
значительное внимание уделяется определению высоты турбопаузы в связи
с разработкой некоторых прикладных задач.
2.3. Время установления диффузионно-гравитационного
разделения газов
Известно, что бывают периоды более или менее интенсивной
турбулизации атмосферы. В свободной атмосфере турбулентный
режим является, как правило, перемежающимся. Казалось бы,
вследствие этого высота уровня разделения газов должна была
бы изменяться в широких пределах. Между тем из наблюдений
известно, что диапазон ее изменений невелик. В связи с этим
в рассматриваемой проблеме важным является вопрос о
времени установления диффузионно-гравитационного разделения.
Оценка этого времени необходима, в частности, и для
объяснения большой протяженности гомосферы. Задача об определении
времени установления равновесного распределения газов
формулируется следующим образом.
Предполагается, что к моменту t = 0 вследствие интенсивного
перемешивания воздух оказался однородным по составу
—— = const), а затем перемешивание прекратилось. Нужно»
определить, за какое время под влиянием молекулярной
диффузии и гравитационного оседания возникнет равновесное
распределение газов, соответствующее их относительной молекулярной
массе. Для получения ответа на поставленный вопрос
используется уравнение баланса массы данной компоненты смеси
-^--dlvJ.--Zr(D.4r- •"*■•'•)• (2-ЗЛ)
Скорость дрейфа частиц определяется по формуле (2.1.13); Ва
28
Глава 2
•определяется соотношением Эйнштейна (2.1.14). Задаются
начальные и граничные условия:
рЛг)|/=о = Р.(0)е-г/77,
Ра(2)|г==0 = Ра(0),
Р.Ю^со-О.
Задача может быть решена только численно, так как
коэффициент молекулярной диффузии и температура воздуха —
функции высоты. В результате численного решения из (2.3.1)
определяется зависимость плотности данного газа от времени и
высоты: ра (/, z). Время достижения стационарного режима
оказывается существенно зависящим от высоты: чем больше высота,
тем меньше время, необходимое для установления равновесного
распределения газов. Расчет этого времени был выполнен
несколькими учеными, при этом использовались разные модели
•атмосферы. Хотя количественные результаты, полученные
разными авторами, несколько отличаются друг от друга, основной
вывод одинаков: в нижних слоях атмосферы до высот, меньших
100—120 км, разделение происходит очень медленно — время
разделения исчисляется годами; в то же время на больших
высотах при z^h разделение газов устанавливается очень
быстро— в течение нескольких часов и даже минут, т. е. на этих
высотах эффекты турбулентного перемешивания очень быстро
ликвидируются после прекращения турбулентности.
Приведенные оценки объясняют, почему ниже уровня разделения
атмосфера, как правило, является однородной по составу, а выше
этого уровня происходит разделение газов.
2.4. Диссипация газов из атмосферы
При изучении газового состава воздуха и баланса массы
атмосферы в целом важным является вопрос о возможности
ускользания частиц из атмосферы. Эта проблема связана с
вопросом о вертикальной протяженности атмосферы.
Молекулы газа находятся в состоянии беспорядочного
движения, средняя скорость которого возрастает с ростом
температуры. Скорость отдельных молекул может достигать столь
больших значений, что они вылетают за пределы атмосферы и
уходят в межпланетное пространство. Это явление называется
ускользанием или диссипацией газов из атмосферы.
Очевидно, что пределы атмосферы могут покинуть лишь та-
_. mv2
кие частицы, кинетическая энергия которых tK=—-— превы-
Газовый состав атмосферы 29
ш'ает их потенциальную энергию Еи в гравитационном поле,
равную
оо оо оо
mGM I mMG
Еп= j mgdr=GMm J -7^=-
где G — универсальная постоянная тяготения; M — масса Земли;
m — масса молекулы; /?i — расстояние от молекулы до центра
Земли.
Из условия равенства кинетической и потенциальной энергии
частицы определяется так называемая критическая скорость
£кр, или скорость ускользания, достижение которой необходимо
для диссипации из атмосферы:
/2^М~
-^-. (2.4.1)
Для частиц, находящихся на поверхности земли, vKV~
— 11 км/с; эта скорость незначительно уменьшается с
увеличением расстояния частиц до поверхности земли.
По формуле (2.4.1) можно также рассчитать скорость
ускользания частиц из атмосфер других планет. Как будет
показано ниже, существование атмосферы в большой степени
определяется значением критической скорости. В частности, для
Луны уКр = 2,5 км/с; отчасти этим объясняется тот факт, что
Луна практически лишена атмосферы.
Итак, необходимым условием для диссипации газа из
атмосферы является наличие частиц со скоростями, превышающими
критическую. Возникает вопрос: имеются ли в атмосфере такие
частицы? Для ответа на него необходимо знать, какими
скоростями могут обладать молекулы в атмосфере. В статистической
физике показывается, что при термодинамическом равновесии
молекулы газа распределены по скоростям в соответствии
с формулой Максвелла
d/z=47m(^|^)3/2 v2e~~^FT~ dv, (2.4.2)
где dn — число молекул в единице объема, обладающих
модулем скорости в интервале от v до v + dv\ п — концентрация
молекул данного газа; m — их масса (остальные величины
вводились раньше). Величина F(v2) = , характеризующая
вероятность того, что частица будет иметь заданное значение
скорости в единичном интервале скоростей (dv = l)y называется
Функцией распределения. На рис. 2.1 представлена максвеллов-
ская функция распределения для трех значений
температуры Т.
30
Глава 2
Хотя атмосфера не находится в состоянии полного
термодинамического равновесия, можно считать, что в каждом малом
объеме, содержащем, однако, достаточно большое количество
молекул, осуществляется локальное термодинамическое
равновесие и имеет место максвелловское распределение молекул по
скоростям, соответствующее температуре этого объема.1
Важным следствием формулы (2.4.2) является то, что dn-+
->0 только при и->-оо, т. е. на любой высоте всегда имеются
Рис. 2.1. Распределение молекул газа
по скоростям для трех значений
температуры.
молекулы, скорость которых превышает критическую. Из (2.4.2)
и рис. 2.1 видно, что скоростями и^икр обладает тем большее
число молекул, чем выше температура газа.
Зная функцию распределения молекул по скоростям, можно
определить ряд важных характеристик молекулярного
движения, например наиболее вероятную скорость частиц vu. в =
■у-
2kT , dF
(она находится из условия
._~ „_«^~*~* — т , , =0), среднюю
т v J dv \v=v* в y *_
квадратическую или тепловую скорость молекул vT=y v2~
3kT t 2
(последняя определяется соотношением и2т =
-у-
оо
= J v2F (v2) dv).2 Кроме того, из (2.4.2) можно определить число
о
частиц, обладающих скоростью v^vKV.
1 Вследствие того что распределение по скоростям устанавливается
благодаря столкновениям молекул, происходящим при достаточной плотности газа
очень часто, время установления этого распределения мало. Поэтому в
атмосфере даже на больших высотах имеет место максвелловское распределение
молекул по скоростям. Но, как было показано в предыдущем параграфе,
время равновесного пространственного распределения молекул (больцманов-
ское распределение), которое устанавливается благодаря молекулярной
диффузии, очень велико.
2 Напомним, что с тепловой скоростью связана кинетическая энергия по-
mv\ з
ступательного движения молекул £к=—о— = -лкТ. Определяемая этой
формулой температура называется кинетической температурой.
Газовый состав атмосферы
31
Формула (2.4.2) описывает долю молекул, обладающих
заданным модулем скорости. В дальнейшем нам понадобится
формула, описывающая число молекул, имеющих заданные
компоненты скорости в различных направлениях:
m («2+ и^-\- те/2)
dnUt VtW = n ("2^t-)3/2 е ш da dv dw. (2.4.3)
Здесь dnu>v,w — число молекул данного газа в единице объема,
компоненты скорости которых в направлении осей х, у, z лежат
в пределах иу u + du\ v, v + dv\ w, w + dw соответственно.
2.5. Уровень диссипации газов
Наличие у молекул скорости v>vKp является необходимым,
но не достаточным условием для диссипации из атмосферы. Это
связано с тем, что в результате столкновений изменяются
скорость и направление движения молекул. Для того чтобы
движущаяся вверх молекула, имеющая v>vKp, могла покинуть
атмосферу, она не должна испытывать столкновений с другими
молекулами. В нижних слоях атмосферы вследствие большой
плотности воздуха вероятность столкновений велика и,
следовательно, возможность диссипации ничтожно мала. С ростом
высоты плотность уменьшается, увеличивается длина свободного
пробега молекул и возрастает вероятность пройти значительный
путь без столкновений.
Найдем уровень, начиная с которого частицы имеют
определенную вероятность пройти* бесконечный путь, не испытав ни
одного столкновения. Для этого нужно найти закон
распределения вероятностей столкновения молекул. Рассмотрим для
простоты случай, когда молекулы движутся только по вертикали.
Обозначим через W(z) вероятность того, что частица пройдет
путь г, не испытав ни одного столкновения. Тогда вероятность
того, что молекула не испытает столкновений на пути z + dz,
будет равна W(z + dz). Для того чтобы молекула прошла без
столкновений путь z + dz, она не должна испытать столкновений,
пролетев путь г, а затем путь dz. Оба эти события являются
независимыми. Поэтому величина W(z+dz) равна произведению
вероятностей прохождения без столкновения отрезков г и dz:
W(z-{-dz) = W(z) W(dz). (2.5.1)
Если через P(dz) обозначить вероятность того, что частица
испытает столкновение на пути dz, то
P(dz)+W(dz)=\,
откуда
W-(dz) = \-P(dz). (2.5.2)
32
Глава 2
Вероятность того, что молекула испытает столкновение за
время dt, в течение которого она пройдет путь dz, равна
P(dz) = Ndti (2.5.3)
где N — число столкновений, испытываемых движущейся
молекулой за единицу времени. Значение N нетрудно определить из
следующих соображений.
Предположим, что из-за малой вероятности можно
пренебречь столкновениями, при которых одновременно вступают
Рис. 2 2. К расчету вероятности столкновения молекул.
в контакт больше чем две молекулы. Для исследования
столкновения двух молекул друг с другом нужно рассмотреть их
относительное движение; скорость и направление движения каждой
из молекул сами по себе не играют никакой роли. Рассмотрим
молекулу Л1, сближающуюся с другой молекулой А2 с
относительной скоростью v0TH. Предположим, что молекулы
сталкиваются как упругие шары. Тогда молекулы столкнутся лишь
в том случае, если расстояние между их центрами b^ri + rz
(Г{ и гг — радиусы первой и второй молекул) (рис. 2.2). Число
столкновений можно рассчитать, представив, что молекула Ai
несет на себе диск радиусом ri + гг, центр которого совпадает
с центром молекулы. Столкновение произойдет только тогда,
когда центр молекулы А2 окажется внутри объема, вырезаемого
при движении молекулы Ль За единицу времени молекула Ai
вырезает в пространстве цилиндр, объем которого равен
я(г1 + /-2)2Уотн- При этом она испытает столкновение со всеми
молекулами, центры которых окажутся внутри цилиндра. Если
в единице объема имеется п2 молекул Лг, то число^столкнове-
ний, испытываемых за единицу времени, равно
i
7V = 7T(r1+r2)2^OTHA72
(2.5.4)
Газовый состав атмосферы 33
dz
Подставив (2.5.4) в (2.5.3) и заменив dt = , получим
Ptdz)= Mn + ^tw^ ^ (255)
Относительную скорость двух молекул, движущихся со
скоростями Vi и V2, можно найти с помощью функции распределе-
.. г- / \ dnu, v, w
ния Максвелла F (v) = :
i)2Q1H = j J | V! — v212 F(V\) F(v2) dux dvx dv)x du2dv2 dw2.
Перейдя к сферической системе координат, в которой dudvdw =
= v2dv этФЛЫф, и выполнив интегрирование по углам д и ср
(# — полярный угол, ф — азимутальный), получим
ОО 00
V20TH= J v\F{v\)dvx+\ v\F{vl)dv2 = v\?+vl. (2.5.6)
о ' о
Для молекул, имеющих одинаковую массу, Vii = v2i = vT. Тогда
из (2.5.6) следует
Подставив это соотношение в (2.5.5), находим
P(dz) =к(гх+г2)> Y2 n2dz = ^r, (2.5.7)
где
/=—т= = ——. (2.5.8)
/27с(п4-г2)2Л2 сп>
Величина / называется длиной свободного пробега.
Действительно, за единицу времени молекула проходит путь vT\ за это
время она испытывает N столкновений. Следовательно, путь,
проходимый между двумя последовательными соударениями и
называемый длиной свободного пробега, равен ' = _тт~ =
= —= . Величина а = у2л(г1 + г2)2 = 4у2лг2 (если
У2л(п + г2)2А1
молекулы одинаковы) называется поперечным сечением
столкновения.
Формулы (2.5.7) и (2.5.8) получены для случая, когда
молекула At сталкивается с молекулами Л2. При применении этих
формул к атмосфере необходимо учесть, что воздух представляет
собой смесь различных газов. Когда имеются молекулы
3 Заказ № 612
34
Глава 2
разных газов, то необходимо учесть столкновения молекулы
а-компоненты со всеми другими молекулами данного газа и
с молекулами всех других газов. Вероятность того, что
молекула а-компоненты газа испытает столкновение на пути dzy
Pa(dz) определяется в этом случае соотношением, аналогичным
(2.5.7):
Р,(</г) = -£-, (2.5.9)
а
а длина свободного пробега в соответствии с (2.5.8) равна
L=^ , (2.5.10)
2
\knk
k = \
где cra/i = У2я(га + гь)2 — поперечное сечение столкновений
молекул а-компоненты с молекулами ^-компоненты смеси.
Суммирование выполняется по всем компонентам смеси. С достаточной
точностью можно, однако, считать, что сечение
столкновений для разных газов одинаково и равно а; тогда длина
свободного пробега одинакова для всех компонент смеси и равна
l. = l—z --S-. <2-5Л1>
k = \
N
где п=^пк — число молекул в единице объема воздуха, свя-
занное с плотностью воздуха р соотношением р/т (т — средняя
I] nhmk \
масса молекулы, т= ) . В атмосфере в соответствии
с (2.1.11) число частиц в единичном объеме уменьшается с
высотой по формуле
n(z) = n(0)e-z/". (2.5.12)
Из (2.5.11) тогда следует, что длина свободного пробега
увеличивается с высотой по показательному закону:
l(z)= 1-^ = 1(р)ег'"у (2.5.13)
где /(0) —длина свободного пробега у Земли.
Подставив (2.5.2) с учетом (2.5.9) и (2.5.11) в (2.5.1),
получим I
W(z+dz)=W{z)(\—fe). (2.5.14)
Газовый состав атмосферы
35
Раскладывая W(z + dz) в ряд Тейлора с точностью до первого
члена разложения, преобразуем (2.5.14) к виду
d\V _ dz
W ~~ l{z) '
Найдем вероятность того, что частица, находящаяся на уровне
zu пройдет без столкновений путь z=zz — zt:
- J / (о
W=Ce "
При Zi=z2 W(z) =1; следовательно, C= 1.
Наибольший интерес представляет определение вероятности
того, что частица, находящаяся на уровне z, пройдет
бесконечный путь, не испытав ни одного столкновения:
оо
W(z)=*e А . (2.5.15)
На основании формулы (2.6.15) можно определить уровень
диссипации 2Д. Назовем уровнем диссипации высоту, начиная
с которой вероятность прохождения молекулой без
столкновений бесконечного пути равна е'1 (е — основание натурального
логарифма). Положив в (2.5.15) W{z) =е~1, найдем уравнение
для определения уровня диссипации
J-Пгг-1- (2-5Л6)
д
После подстановки в (2.5.16) соотношения (2.5.13) для l(z) и
выполнения интегрирования в предположении, что Н = const,
получим
z^Hln-^y. (2.5.17)
Приняв # = 20 км и /(0) = 10—5 см, находим гд~500 км.
Отметим, что более строгий расчет дает для уровня диссипации
числовое значение, близкое к полученному нами: гд«500-^600 км.
Из экспериментальных данных следует, что на такой высоте
Длина свободного пробега молекул достигает примерно 100 км,
т- е. действительно, начиная с уровня гд у частиц с v>vKV
появляется реальная возможность уйти за пределы атмосферы.
3*
36
Глава 2
2.6. Интенсивность и время диссипации газа из атмосферы
Считая уровень диссипации известным, можно определить,
какое число молекул покидает пределы атмосферы за единицу
времени и сколько времени требуется для диссипации данного
газа из атмосферы.
Назовем интенсивностью или скоростью диссипации число
частиц, диссипирующих из атмосферы за единицу времени через
единичную горизонтальную площадку на уровне диссипации.
Очевидно, что за единицу времени единичную площадку
пересекут частицы, находящиеся в слое толщиной до : до dnu, v, w, а дис-
сипируют из атмосферы только те частицы, скорость которых
больше критической. Следовательно, интенсивность диссипации
/ равна
I=)twdnUtVtW. (2.6.1)
Здесь интегрирование распространяется только на те частицы,
модуль скорости которых v>vKp.
В (2.6.1) величина dnu,v,w определяет число молекул в
единице объема, имеющих составляющие скорости в пределах и,
u + du\ v, v+dv; до, w + dw\ она описывается формулой
Максвелла (2.4.3). Для расчета / перейдем к сферической системе
координат, в которой роль радиуса-вектора играет скорость v:
u = vsinb cos ср, v = v sin & sin cp, w = v cos ft,
da dv dw = v2 dv sin & db dcp,
x^yV + ^+w2. (2.6.2)
Пределы интегрирования следующие: по Ф от 0 до я/2, по ф от
О до 2л, по v от иКр до оо.
Подставив в (2.6.1) вместо utiu, v, w
формулу (2.4.3) с
учетом (2.6.2) и выполнив интегрирование, получим
где п(гд) —концентрация частиц данной компоненты воздуха на
уровне диссипации. Формулу (2.6.3) можно переписать в другом
виде, если ввести в нее тепловую скорость молекул:
з vlp
Из (2.6.4) видно, что интенсивность диссипации существенно
зависит от тепловой скорости молекул: она тем больше, чем
Газовый состав атмосферы
37
больше vTl т. е. чем легче газ и чем выше температура. При
фиксированном значении тепловой скорости / тем больше, чем
меньше критическая скорость, т. е. при прочих равных условиях
интенсивность диссипации больше для атмосфер тех планет,
у которых уКр меньше.
При изучении происхождения атмосферы интерес
представляет определение времени диссипации данного газа из
атмосферы. Для оценки этого времени предполагается, что воздух
состоит только из данного газа. Под временем диссипации /д
понимается время, за которое газ, находящийся в цилиндре
с единичным поперечным сечением и высотой, равной высоте
уровня диссипации гд, диссипирует из атмосферы. В таком
цилиндре заключено
(2.6.5)
Wa = j nMdz
молекул данного газа. Изменение со временем числа молекул
в рассматриваемом цилиндре вследствие диссипации равно
-1 v2
3 КР
dN п (z\
dt U у^ Ut
1 +
"кр
2 v2
. (2.6.6)
Поскольку принимается, что атмосфера состоит только из
одного газа, то
-z/Ha
na(z) = n0e
-Vя*
яа(гд)=я0е
Подставив эти соотношения в (2.6.5) и (2.6.6), получим
dN
N
dt
(2.6.7)
где
'д =
]/6л#
На.
1 +"
'кр
»к2Р
2 V2
-I в
2 v2
(2.6.8)
Интегрируя (2.6.7) по времени, находим
ЛГ.(0=ЛГ.(0)е
-</',
(2.6.9)
36
Глава 2
т. е. число частиц вследствие диссипации убывает со временем
по экспоненциальному закону. Из (2.6.9) следует, что ^д —
время, за которое в рассматриваемом цилиндре число частиц
уменьшается в е раз. Это время и называется временем
диссипации.
Из (2.6.8) видна сильная зависимость времени диссипации
от свойств данного газа и температуры (через значения На и
vT. а). Чем легче газ, тем больше На и vT, а и тем, следовательно,
меньше время диссипации (табл. 2.1).
Таблица 2.1. Время (годы) диссипации некоторых газов
из атмосферы Земли
Газ
Водород
Гелий
Кислород
т к
500
3-108
6-1022
10108
1000
210
3-105
1039
1500
0,1
12-103
Ю29
2000
0,01
1,5
1021
Из табл. 2.1 видно, что при достаточно больших
температурах, характерных для верхних слоев атмосферы, только для
легких газов (водород, гелий) время диссипации из земной
атмосферы меньше возраста Земли (около 6- 109 лет). Для
тяжелых газов время диссипации существенно больше возраста
Земли, и для них эффект диссипации является пренебрежимо
малым.
Особый интерес в связи с этим представляет вопрос о
содержании гелия в воздухе. В результате радиоактивного распада
веществ в земной коре гелий непрерывно поступает в атмосферу.
Вследствие химической инертности он не может исчезать в
результате химических реакций. При отсутствии диссипации в
атмосфере накопилось бы значительное количество гелия,
существенно превышающее его действительное содержание. Именно
эффектом диссипации объясняется малое количество гелия
в земной атмосфере. В современных условиях содержание гелия
в атмосфере остается примерно постоянным. Это означает, что
скорость диссипации гелия практически уравновешивается
скоростью его поступления в атмосферу.
При выяснении значимости эффекта диссипации водорода,
который является самым легким газом, входящим в^остав
воздуха, необходимо учитывать, что он химически активен и может
исчезать и возникать в результате различных химических
реакций, протекающих в атмосфере. Тем не менее расчеты
Газовый состав атмосферы
39
указывают на важную роль
диссипации в балансе
водорода в земной атмосфере.
Для сравнения интересно
привести результаты оценки
времени диссипации кислорода
из атмосферы Луны:
7К . .
t« годы
. 500 1000 1500 2000
. 3-108 7,6 0,1 0,09
Из этих данных видно, что
лри всех значениях Т время
диссипации кислорода из
атмосферы Луны существенно
меньше возраста Луны. Этим,
в частности, объясняется
отсутствие у Луны атмосферы.
Следует, однако, иметь в виду,
что диссипация является
только одним из эффектов,
влияющих на химический состав
атмосферы, и только ею нельзя
объяснить различия в газовом
составе атмосфер разных
планет.
Отметим также, что
уровень диссипации иногда
условно принимается за верхнюю
границу атмосферы, хотя и на
значительно больших
расстояниях от Земли плотность
атмосферы достаточна, чтобы
вызывать заметные эффекты.
Над уровнем диссипации
расположена экзосфера, в
которую попадают атомы и
молекулы, имеющие на уровне
диссипации скорости, меньшие
критической. В этом слое
нейтральные частицы описывают
баллистические траектории
под действием только силы тя-
*^ис. 2.3. Вертикальная структура
атмосферы.
Классификация атмосферы
по свойством нейтрального газа
температурная
химическая
Экзосфера
Уровень диссипации
8*
Мезосфера
f Стратосфера
{~ТрЬрЬсфера {
ZKM\
500
•5
\100
I
в-
о
шоносфера
400
300 \
200 \
0 200 400 600 800 К
Таблица 2.2. Основные характеристики атмосферы на разных высотах по данным CIRA—1965 (международная
стандартная атмосфера)
Высота z (км)
0
50
100
150
200
250
300
400
500
600
Давление р (мбар)
1,02-103
7,91-10-1
2,9110-4
5,08-10-6
1,36
4,34-10-7
1,59
3,04-10-8
8,20-10-»
3,40
1
Температура
Т (К)
289
269
212
1014
1226
1296
1398
1436
1474
1474
Плотность
р (г/см3)
1,23-Ю-з
1,02-10-6
4,78-10-ю
1,69.10-12
3,61
1,03-10-13
3,34-10-н
5,09-10-15
1,17
3,45-10-16
Концентрация
п (см~3)
2,55-1019
2,13-1016
9,98-1012
3,63-ЮЮ
8,05-109
2,42
8,48-108
1,53
4,03-107
1,72
Относительная
молекулярная
масса (х
28,97
28,97
28,85
28,09
27,00
25,68
23,74
20,00
17,48
15,70
1
Ускорение
свободного
падения g
(см/С)
980,66
9С5,42
950,52
935,97
921,75
907,85
894,27
867,99
842,86
818,00
Длина свободного
пробега 1 (м)
3,92-10-7
4,70-10-4
1,01-10-)
2,83-102
1,24-103
4,15
1,18-104
6,55
2,48-105
6,85
Примечание. Длина свободного пробега вычислялась по формуле / = 1/сш, где о — поперечное сечение
рассеяния, которое принималось равным 10"15 см2. Следует указать, что .значения / на высотах 2^200 км нужно
рассматривать лишь как ориентировочные, так как вследствие анизотропии атмосферы длина свободного пробега
существенно зависит от направления.
Газовый состав атмосферы
41
жести, практически не испытавая столкновений друг с другом,
возвращаются в более плотные слои. Среднее время
пребывания частиц в экзосфере составляет всего несколько минут. За эк-
зосферой земная атмосфера (по крайней мере ее нейтральная
составляющая) переходит в межпланетный газ. На рис. 2.3
приведена схема вертикальной структуры атмосферы. В табл. 2.2
представлены экспериментальные данные о вертикальном
распределении некоторых важных характеристик атмосферы.
Контрольные вопросы
1. Какие процессы приводят к изменению газового состава
воздуха с высотой?
2. Как физически объяснить, почему турбулентное
перемешивание препятствует разделению газов по массе?
3. Оцените критическую скорость для Марса и Юпитера.
Существует ли атмосфера у этих планет?
4. Из каких соображений определяется уровень диссипации?
5. С каким временным масштабом нужно сопоставлять время
диссипации газов из атмосферы?
Глава 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
В СУХОМ ВОЗДУХЕ
Первое начало термодинамики для идеальных газов. Связь между
термодинамическими характеристиками при заданном притоке тепла. Изменение
температуры перемещающейся по вертикали массы сухого воздуха. Условия
статической устойчивости атмосферы. Уровень термической конвекции. Энергия
неустойчивости. Влияние вовлечения воздуха на свойства перемещающейся
по вертикали воздушной массы.
Основной причиной движений атмосферы является
неравномерный приток тепла к разным ее частям. Атмосферная «машина»
функционирует по следующей схеме: неравномерный
приток тепла -> контраст температуры -^неравномерное
распределение плотности —^неравномерное распределение давления
—^возникновение движения -►- перераспределение притока тепла. Эта
обстоятельство определяет важное значение уравнения притока
тепла — основного термодинамического уравнения — в полной,
системе уравнений гидротермодинамики. В связи с этим в
настоящем курсе значительное внимание уделено рассмотрению-
некоторых вопросов термодинамики применительно к специфике
атмосферных процессов.
Хотя, как было показано в главе 1, для определения всех
характеристик воздушной массы нужно решить полную систему
уравнений гидротермодинамики, существенным является то, что*
для изучения целого ряда важных атмосферных процессов
(изменения температуры в движущейся по вертикали воздушной
массе, условий статистической устойчивости, конденсации
водяного пара и др.) достаточно рассматривать только изменение
термодинамических характеристик массы воздуха под влиянием
внешних воздействий, отвлекаясь от решения полной
динамической задачи.
Атмосферный воздух является смесью сухого воздуха и
водяного пара. Содержание водяного пара и происходящие при
его насыщении фазовые переходы оказываются очень важными
для многих атмосферных процессов. Однако, вследствие того»
что влагосодержание воздуха всегда мало, то, как будет
показано ниже, до достижения состояния насыщения ТГри
исследовании многих термодинамических процессов, протекающих
в атмосфере, можно не считаться с наличием водяного пара и
рассматривать воздух как однокомпонентную газовую среду.
Начнем поэтому с изучения термодинамических процессов в
сухом воздухе, а затем перейдем к исследованию свойств
влажного воздуха.
Термодинамические процессы в сухом воздухе
43
3.1. Уравнение первого начала термодинамики
для идеальных газов
Чтобы использовать полученное в главе 1 уравнение первого
начала для определения изменения состояния системы под
влиянием внешних воздействий, необходимо установить зависимость
внутренней энергии от термодинамических характеристик. Уже
отмечалось, что внутренняя энергия Ев в случае однокомпонент-
ной системы может быть функцией двух термодинамических
величин, например объема и температуры. Однако теоретически1
и экспериментально (опыты Джоуля) было установлено, что
внутренняя энергия идеальных газов является функцией только
температуры и не зависит от объема, т. е. ЕВ=ЕЪ(Т). Считая
воздух идеальным газом, перепишем уравнение (1.5.8) в виде
-?b-dT=dQ-pdV. (3.1.1)
Имея в виду применение этого уравнения к выделенной
фиксированной воздушной частице, следует учесть, что в него входит
внешнее2 давление и для его определения нельзя использовать
уравнение состояния частицы, так как последнее связывает
внутренние термодинамические величины. Однако практически
всегда атмосферные процессы можно считать
квазистатическими, т. е. можно полагать, что внутреннее давление и
внешнее совпадают (более точным является термин «механическая
квазистатичность»).
Напомним, что квазистатическим называется процесс, при
протекании которого параметры рассматриваемой системы на
каждом шаге достаточно мало отличаются от параметров
окружающей среды. В действительности такие процессы
приближенно реализуются в тех случаях, когда изменения в системе
происходят достаточно медленно, чтобы при каждом
промежуточном состоянии система успела приспособиться к
изменившимся внешним условиям. Термин «медленно» имеет вполне
определенный смысл: скорость перехода из одного состояния
в другое должна быть меньше скорости выравнивания
термодинамических характеристик (в дальнейшем будем иметь в виду
температуру и давление). Поскольку давление выравнивается
Теоретическое доказательство независимости внутренней энергии
идеальных газов от объема может быть получено с помощью второго начала
термодинамики.
При исследовании атмосферных процессов, как и во многих других
случаях, удобно разбить термодинамические величины на внешние и внутренние,
нешние величины определяют состояние окружающей среды; в этой главе
°ни отмечены чертой сверху. Внутренние параметры характеризуют состояние
выделенной воздушной массы.
44
Глава 3
со скоростью звука, то в отношении давления естественные
атмосферные процессы можно считать квазистатическими
(механическая квазистатичность). Температура же выравнивается
значительно медленнее давления, поэтому очень часто
температура воздушной массы заметно отличается от температуры
окружающей среды, т. е. термическая квазистатичность не имеет
места.
Итак, предположим, что протекающие процессы
квазистатические в смысле равенства внешнего и внутреннего давления
(р=р). Поэтому используем для члена с давлением, входящего
в (3.1.1), соотношение, следующее из уравнения состояния
частицы:
pdV=RdT-Vdp. (3.1.2)
Подставив (3.1.2) в (3.1.1), получим
dQ = [^+R}dT-Vdp. (3.1.3)
Уравнения (3.1.1) и (3.1.3) —эквивалентные записи первого
начала, но еще не удобные для конкретных применений, поскольку
dE* _
неясно, как рассчитывать . Рассмотрим два частных
процесса: изохорический (dV = 0) и изобарический (dp=0). В
случае изохорического процесса из (3.1.3) получим
■#-=(#).-'- <з-'-4>
где cv — удельная теплоемкость при постоянном объеме.
Для изобарического процесса из (3.1.3) следует
где ср — удельная теплоемкость при постоянном давлении.
Подставив (3.1.4) в (3.1.5), найдем связь между ср и cv:
cP = cv+R. (3.1.6)
Используя формулы (3.1.4) — (3.1.6), запишем (3.1.3) в двух
эквивалентных формах, удобных для конкретных применений:
dQ = cpdT-RT^y (3.1.7)
dQ = cvdT-\-pdV. (3.1.8)
Уравнения (3.1.7) и (3.1.8), которые часто называются
уравнениями притока тепла, справедливы только для идеальных
газов, в отличие от уравнения (15.8), выполняющегося для лю-
Термодинамические процессы в сухом воздухе
45
бых веществ. Как отмечалось в главе 1, входящий в эти
уравнения приток тепла может быть обусловлен различными
причинами. Существенными для атмосферных процессов являются
следующие три типа притоков тепла: 1) лучистый, или
радиационный, приток тепла, 2) турбулентный приток тепла, 3)
приток тепла, обусловленный фазовыми переходами.
3.2. Связь между термодинамическими характеристиками
при заданном притоке тепла
В этом параграфе, не затрагивая вопроса о конкретном типе
притока тепла, установим связь между различными
термодинамическими характеристиками воздуха, считая приток тепла
заданным.
Интегрируя уравнения (3.1.7) и (3.1.8) с учетом уравнения
состояния, получим
2 2
-k=№K" ' -(*Г« ' • *•*'>
где Го, ро, Ро — значения параметров системы в начальном
состоянии (1), а Г, р, р — их значения в конечном состоянии (2).
Часто бывает удобно рассмотреть процесс, при котором
приток тепла пропорционален приращению температуры:
dQ = cdT. (3.2.2)
Такой процесс называется политропическим. Подставив (3.2.2)
в (3.2.1) и выполнив интегрирование, получим
Из (3.2.3) следует соотношение
pVn = const, (3.2.4)
где п=—- есть показатель политропы.
С\) — с
Формулы (3.2.3) и (3.2.4) представляют определенный
интерес, так как, придавая величине с (которая может быть
названа политропической теплоемкостью) любые положительные
и отрицательные значения, можно в некоторых случаях
достаточно точно аппроксимировать реальные атмосферные процессы.
Для простейших процессов величина с принимает следующие
значения:
46
Глава 3
Процесс Адиабатический Изохорический Изобарический Изотермический
(dQ = 0) (dV = 0) (dp = 0) (dT = Q)
с . . . О с
v
При изучении атмосферных явлений большое значение имеет
рассмотрение адиабатических процессов, для которых приток
тепла равен нулю, т. е. нет теплообмена между частицей
воздуха и средой. Хотя в атмосфере чисто адиабатических
процессов не бывает, но реальные процессы можно считать
адиабатическими тогда, когда приток тепла значительно меньше работы
внешних сил. В частности, при вертикальных движениях
воздушных масс вследствие значительных изменений давления,
наблюдающихся в реальной атмосфере, работа расширения
намного превышает приток тепла извне, и такой процесс
приближенно можно считать адиабатическим. Отклонения наблюдаются
вблизи поверхности земли (из-за больших контрастов
температуры между рассматриваемой массой и средой, следствием чего
является интенсивный приток тепла) и в верхних слоях
атмосферы (здесь существенным оказывается лучистый приток
тепла). Важность рассмотрения адиабатических процессов
обусловлена также тем, что адиабатическое приближение, как
показано в главе 14, с определенным основанием используется
в теориях краткосрочного прогноза погоды.
Адиабатический процесс, как следует из предыдущего,
является частным случаем политропического процесса. Полагая
в формуле (3.2.1) dQ=0 или в (3.2.3) и (3.2.4) с = 0, получим
связь между основными термодинамическими величинами при
адиабатическом процессе:
pVe',Cv =const. (3.2.7)
Эти формулы можно использовать для оценки изменения
состояния данной воздушной массы или для сравнения
термодинамических характеристик различных воздушных масс при
адиабатических процессах. Однако в последнем случае приходится
сопоставлять две пары термодинамических величин,
характеризующих состояние воздушных масс, что затрудняет
интерпретацию результатов. В связи с этим целесообразно использовать
еще одну очень удобную характеристику состояния воздушной
массы — потенциальную температуру, которая находит широкое
применение в метеорологических исследованиях. Напомним, что
Термодинамические процессы в сухом воздухе
47
потенциальной температурой в называется температура,
которую будет иметь частица сухого воздуха, если ее из начального
состояния с давлением р и температурой Т адиабатически
привести к стандартному давлению ро=ЮОО мбар. Из формулы
(3.2.5), которая называется уравнением Пуассона, следует
в
-г(-^)''. (3.2.8)
Ясно, что для сравнения состояния различных воздушных масс
достаточно сопоставлять только их потенциальные
температуры.
3.3. Изменение температуры перемещающейся по вертикали
массы сухого воздуха
Для определения изменения температуры перемещающейся
по вертикали воздушной массы используем уравнение первого
начала, которое запишем в виде
dT^ _ J_ dQ RT dp
dz cn dz p dz
(3.3.1)
Будем считать процесс квазистатическим (р = Р, -z—=-;—) и
\ dz dz I
используем для определения изменения с высотой давления
окружающей среды уравнение статики
Подставив (3.3.2) в (3.3.1), получим
dT _ 1 dQ g Т
dz с„ dz
(3.3.3)
Эта формула позволяет оценить изменение с высотой
температуры вертикально перемещающейся воздушной массы, если
известен приток тепла; при этом отношение температуры частицы
к температуре окружающей среды можно с достаточной точно-
Т
стью принять равным единице, т. е. -^«1.
Т
48
Глава 3
Если перемещение воздушной массы происходит
адиабатически (~"^— = 0), то из (3.3.3) следует
-£«--£—т.. (3.3.4)
Величина уа, определяемая формулой
Та = —^1°С/Ю0 м, (3.3.5)
ср
называется сухоадиабатическим градиентом и является одной
из важных метеорологических констант.
Из (3.3.4) следует, что поднимающая воздушная масса {dz>
>0) охлаждается, а опускающаяся (dz<0), напротив,
нагревается на величину уа на единицу высоты. Охлаждение
вызывается тем, что при подъеме воздушная масса, перемещаясь в
область более низкого давления, расширяется. Поскольку приток
тепла отсутствует, то работа расширения совершается за счет
внутренней энергии, что естественно приводит к ее уменьшению,
а следовательно, и к понижению температуры, так как d£B =
= CydT. При опускании вследствие сжатия внутренняя энергия
увеличивается и воздушная масса нагревается.
Т
Уравнение (3.3.3) с учетом (3.3.4) и при =-«1 можно за-
Т
писать в виде
dT _ 1 dQ
dz cD dz
Та- (3-3.6)
Это уравнение позволяет оценить возможность использования
предположения об адиабатичности процесса. Если приток тепла
—^-<SCpYa^0,98 Дж/(г- 100 м), то процесс приближенно можно
считать адиабатическим.
Когда поднятие воздушных масс происходит
неадиабатически, из уравнения (3.3.6) следует, что в зависимости от
величины притока тепла возможны различные ситуации:
а' ср dz >Та' dz ->u»
в этом случае приток тепла больше, чем охлаждение из-за
работы расширения, и поднимающаяся воздушная масса будет
нагреваться; *~
в этом случае приток тепла компенсирует охлаждение из-за ра-
Термодинамические процессы в сухом воздухе
49
боты расширения, и температура воздушной массы при
перемещении не изменяется;
ч 1 dQ , dT .n
в) -^-гг<ь> ~1Г<Ъ
в этом случае приток тепла недостаточен для того, чтобы
скомпенсировать охлаждение поднимающейся воздушной массы.
Легко получить формулу для изменения с высотой
температуры перемещающихся по вертикали частиц, если приток
тепла происходит политропически. Подставив в (3.3.6) -—— =
НТ ( Т
= с-г-, найдем при допущении —^ 1
dz 1 —с/Ср '
dz
(3.3.7)
При политропических процессах возможны различные ситуации
в зависимости от значения политропической теплоемкости с.
Из (3.3.7) следует линейное изменение температуры воздушной
массы с высотой при политропических процессах:
Г(г)=Г0-Тг, (3.3.8)
где
T = -r^7 = const.
Полезно получить формулу для изменения с высотой
потенциальной температуры частицы воздуха. С помощью
соотношения (3.2.8), используя (3.3.2), получим
de 8 dT , в g _ dT , п« q.
^ 6,0,
•ь точностью -y~U —~1 вертикальный градиент потенциальной
Т
температуры частицы отличается от градиента абсолютной
температуры на значение сухоадиабатического градиента. Если
dT
перемещение частиц происходит адиабатически, то —— = —7а
dz
и ~~~7~ = ®у т. е. в этом случае потенциальная температура
является консервативной характеристикой. При р = 1000 мбар
потенциальные и абсолютные температуры равны по определению,
а аппроксимация
Q(z)=T(z)+bzt (3.3.10)
4 Заказ К» 612
50
Глава 3
следующая из (3.3.9), вполне удовлетворительна для не очень
больших значений г, во всяком случае для нижнего
100-метрового слоя.
3.4. Условия статической устойчивости атмосферы
В неподвижной атмосфере могут возникать вертикальные
перемещения отдельных воздушных масс, обусловленные либо
случайным начальным смещением, либо флуктуациями
термодинамических величин, вызывающих вертикальные ускорения.
Вопрос о том, будут ли развиваться указанные движения в
атмосфере, является очень важным для метеорологии, так как ими
в значительной мере определяется вертикальный перенос
различных субстанций, образование и развитие конвективных
облаков и выпадение осадков.
В зависимости от того, способствует или препятствует
окружающая среда развитию таких вертикальных движений,
различают три типа состояния устойчивости (или стратификации)
атмосферы: неустойчивое, равновесное и устойчивое. Состояние
атмосферы, при котором вертикально смещающаяся частица
воздуха получает ускорение, совпадающее с направлением
движения, называется неустойчивым; если же при движении частицы
возникает отрицательное ускорение, то состояние атмосферы
называется устойчивым; если вертикальные смещения происходят
без ускорения, то состояние атмосферы называется
равновесным. Из определения типов стратификации атмосферы ясно, что
неустойчивая стратификация способствует развитию
вертикальных движений, а устойчивая — напротив, их затуханию.
Чтобы исследовать условия осуществления различных типов
стратификации атмосферы, запишем третье уравнение динамики
для вертикально перемещающейся частицы воздуха в виде
— = -— -^--* (34 1)
dt р dz ё' yo.t.i)
Считая процесс квазистатическим и используя для атмосферы
уравнение статики, получим
4B--;-*(f-l). (3.4.2)
Переходя с помощью уравнений состояния«лля частицы и
окружающей среды от плотностей к температурам, запишем
*L = -^(T-T) = $(T-T). (3.4.3)
Термодинамические процессы в сухом воздухе
51
Правая часть уравнений (3.4.1) — (3.4.3) представляет собой
разность между силой Архимеда и собственным весом
воздушной частицы; эта разность называется силой плавучести.1
Величина $=g/T называется параметром плавучести. Из (3.4.3)
следует, что тип стратификации зависит от знака разности
температур перемещающейся массы воздуха и окружающей среды.
Если температура частицы больше температуры окружающей
среды, то она испытывает положительное ускорение, т. е.
стратификация атмосферыч является неустойчивой; если Т = Т, то
= 0, и стратификация будет равновесной, а при Т<Т —
dt
устойчивой. При исследовании стратификации атмосферы
целесообразно предположить, что на исходном уровне, с которого
частица начинает свое движение, ее температура совпадает с
температурой окружающей среды. Поэтому соотношение между
температурами частицы и среды на некотором уровне зависит от
значения соответствующих температурных градиентов. Считая
слой, в котором движется частица, достаточно тонким,
запишем:
T{z0±bz)=T(z0n
dT
dz
dT
Az,
T(z0-\-Az)=T(z0)+^-lbz.
(3.4.4)
Если температуры частицы и окружающей среды изменяются
линейно, то соотношения (3.4.4) справедливы и для больших
значений Дг. Подставив (3.4.4) в (3.4.3), при условии T(zo) =
= T(zo) получим
dw a/ dT
/it г 1 "
dt
dz
(3.4.5)
Из этого соотношения следует, что стратификация атмосферы
будет:
неустойчивой, если -^~>~^-
dT df
равновесной, если "7г"==_5Г~
dT . df
устойчивой, если -^~<-^j-
(3.4.6)
] Нужно отметить, что во многих учебных пособиях и монографиях сила
Архимеда отождествляется с силой плавучести.
4*
52
Глава 3
Иногда вводят в рассмотрение параметр статической
устойчивости
dw
~dF п( dT df
'/3 =
Az
dz
dz
■)■
(3.4.7)
Параметр устойчивости x\ — это ускорение, испытываемое
движущейся воздушной массой на единице высоты. Если т]>0, то
состояние неустойчивое, г]=0 — равновесное, т)<0 — устойчивое.
При получении соотношений (3.4.6) и (3.4.7) не
накладывалось никаких ограничений на изменение с высотой температуры
перемещающейся воздушной массы, поэтому они справедливы и
при перемещении по вертикали влажного воздуха. Отметим
также, что полученные критерии имеют место как при
уменьшении, так и при увеличении с высотой температуры.
В том случае, когда воздушная масса перемещается
адиабатически, критерии устойчивости записываются так:
dT
dz
-fo-= —Та (равновесие),
dT
dz
< —Та (неустойчивость),
>—Та (УСТОЙЧИВОСТЬ).
(3.4.8)
Запишем теперь критерии устойчивости для адиабатических
процессов, используя понятие потенциальной температуры. В
отличие от потенциальной температуры поднимающейся
воздушной массы, которая, как было показано в п. 3, остается
постоянной при адиабатическом процессе, потенциальная
температура окружающей среды изменяется по вертикали, и характер
ее изменения может определять термическую устойчивость
атмосферы. Для градиента потенциальной температуры
окружающей среды легко получить соотношение, аналогичное (3.3.9):
1 d% I f df ,
"Та
е
dz
= 4г(^ + Та),
с помощью которого критерии (3.4.8) перепишутся в следующем
виде:
-^-<0 (неустойчивость),
—— = 0 (равновесие), \
-т— >0 (устойчивость).
(3.4.9)
Термодинамические процессы в сухом воздухе
53
Мы видим, что условия устойчивости в случае
адиабатического поднятия (или опускания) наиболее просто
формулируются в терминах потенциальной температуры. Атмосфера будет
неустойчива, если потенциальная температура уменьшается с
высотой, равновесна, если потенциальная температура не меняется,
и устойчива, если в увеличивается. Параметр г\ также можно
выразить через 0:
Г1==_Ппв_ (ЗА10>
Следует иметь в виду, что полученные здесь условия
устойчивости определяют интенсивность вертикальных движений,
обусловленную только температурной неоднородностью
атмосферы, при отсутствии или малости динамических эффектов.
3.5. Уровень термической конвекции
При выводе условий устойчивости предполагалось, что на
исходном уровне температура частицы совпадает с температурой
окружающей среды. В этом случае при устойчивой
стратификации частица испытывает отрицательное ускорение и
возвращается на исходный уровень. Однако в реальных условиях из-за
пульсаций, обусловленных турбулентностью, или местного
перегрева температура перемещающейся по вертикали воздушной
массы на исходном уровне может отличаться от температуры
окружающей среды. В этом случае объем воздуха может иметь
положительное ускорение и при устойчивой стратификации,
когда под влиянием архимедовой силы более теплые объемы
воздуха всплывают вверх, а более холодные опускаются вниз.
Вертикальные движения, обусловленные неустойчивостью
или начальным перегревом (или переохлаждением) воздушной
массы на исходном уровне, т. е. чисто тепловыми причинами,
называются термической конвекцией. Иногда эти движения
называют свободной конвекцией, так как они развиваются только
благодаря плавучести.
Вертикальное ускорение перегретой или переохлажденной
на исходном уровне воздушной массы в соответствии с
формулами (3.4.3) и (3.4.4) равно
-^ = НГ(г)-Г(г)] = [г„-Т0+(4^-^)дг], (3.5.1)
Где Г0 и Го — температуры воздушной массы и среды на исход-
AT rlT
ном уровне 2о, а —— и — средние в слое вертикальные
градиенты температуры для частицы и окружающей среды.
54
Глава 3
Из (3.5.1) видно, что даже при устойчивой стратификации,
dT df п
когда — ;—<0, частица будет иметь положительное уско-
dz dz
рение, если
Т°-Т°>(-7Г-^)Ь2- (3-5-2>
При решении различных задач, связанных с конвективными
движениями в устойчиво стратифицированной атмосфере,
представляет интерес определение уровня, где температура частицы
становится равной температуре окружающей среды, а также
уровня, где обращается в нуль вертикальная компонента
скорости частицы. В метеорологической литературе и тот, и другой
уровень называется уровнем термической конвекции. Получим
формулы для определения этих уровней.
Обозначим Лг = г — z0 = h). Из (3.5.1) видно, что на высоте,
где Т = ТУ вертикальное ускорение частицы обращается в нуль.
dw
Положив —— = 0, находим из (3.5.1)
at
I = Jo-"7** . (3.5.3)
т=т JJi_dT_
На этом уровне воздушная масса не останавливается, так как
ее вертикальная скорость здесь не равна нулю. Для получения
формулы для уровня, где w = 0, перепишем (3.5.1), подставив
W
W
4f=p[r0-:r0+(4f-4r)s]. <3-5-4)
Интегрируя (3.5.4) и считая -—- и —— постоянными, находим:
^.-p[(r.-T.)j+(4J~-^)4-]. (3-5.5)
Из (3.5.5), положив ш = 0, получим:
U=o=2^°-g=2Sr=T. (3.5.6)
Уровень, где w = 0, представляет собой максимальную
высоту, до которой может подняться перегретая воздушная масса
Термодинамические процессы в сухом воздух?
5S
(или опуститься переохлажденная) в устойчиво
стратифицированной атмосфере. Из (3.5.6) видно, что этот уровень в 2 раза
превышает уровень, где температура частицы выравнивается
с температурой окружающей среды.
Легко найти, что скорость частицы максимальна на уровне,
где температуры частицы и среды выравниваются.
Максимальное значение вертикальной компоненты скорости частицы равно
^тах = 33
dT dT
dl dl
,2 3
^=7 = -f^|w=0(r0-ro). (3.5.7)
Следует иметь в виду, что в действительности в устойчиво
стратифицированной атмосфере воздушная масса совершает
колебания около уровня 1Т=—. Вопрос о колебаниях воздушной
частицы рассматривается в главе 10. Нужно также отметить,
что приведенные выше оценки уровня конвекции получены при
пренебрежении работой, которую воздушная масса совершает
против силы трения. Поэтому полученные значения высоты
уровня конвекции завышены.
3.6. Энергия неустойчивости
Выше было локазано, что при определенных условиях в
атмосфере могут развиваться конвективные движения
термического происхождения. Рассмотренные выше критерии
устойчивости, основанные на сравнении вертикальных градиентов
температуры перемещающейся воздушной массы и окружающей
среды, в ряде случаев оказываются неудобными для оценки
интенсивности таких вертикальных движений. С одной стороны,,
это связано с тем, что указанные критерии характеризуют
состояние атмосферы в тонком слое (за исключением случая,
когда градиенты температуры постоянны), в то время как
конвективные движения могут развиваться в слоях значительной
протяженности. В общем случае трудно использовать
меняющееся с высотой значение вертикального температурного
градиента как характеристику устойчивости большого слоя. С другой
стороны, полученные ранее критерии устойчивости не учитывают
начального перегрева и, наконец, они не являются
количественной мерой кинетической энергии конвективных движений, кото-
Рая представляется более адекватной характеристикой
конвективного процесса.
В связи с этим для описания запасов энергии конвекции
в стратифицированной атмосфере введена интегральная
характеристика состояния устойчивости атмосферы — энергия
неустойчивости, которая широко используется при решении
различных метеорологических задач.
.56
Глава 3
Энергией неустойчивости некоторого слоя атмосферы
принято называть отнесенную к единице массы работу, которая
совершается при вертикальном перемещении воздушной массы
лод влиянием силы плавучести. Неустойчивой стратификации
соответствует положительная энергия неустойчивости,
устойчивой— отрицательная. Энергия неустойчивости при равновесной
стратификации равна нулю.
Получим формулу для расчета энергии неустойчивости Е.
Работа, совершаемая при перемещении единицы массы воздуха
.на высоту dz, равна ——dz. Если ускорение обусловлено только
•силой плавучести, то, по определению, эта работа равна
приращению энергии неустойчивости, т. е.
dE=^rdz = § [T(z)-T(z)] dz. (3.6.1)
Здесь для —— использована формула (3.4.3). В (3.6.1) удобно
выразить приращение высоты через изменение давления с
помощью уравнения статики:
dz=-4^ = - Ж- d~p. (3.6.2)
?g Pg
Тогда
dE=-R [T(z)-T(z)] din p. (3.6.3)
Ла основании (3.6.3) энергия неустойчивости некоторого слоя
атмосферы от ро до р определяется соотношением
р
Е = Х$[Т(р)-Т(р)]сЦПр. (3.6.4)
Ро
Таким образом, энергия неустойчивости зависит от разности
температур частицы и окружающей среды на всем пути от /?о до р.
Лри этом, если при подъеме (d\np<0) Т(р)>Т(р), то £>0
и состояние атмосферы является неустойчивым.
Из (3.6.4) следует, что в системе координат (Г, In р)
энергия неустойчивости пропорциональна площади, заключенной
между двумя изобарами (ро = const и /?i = const) и кривыми,
характеризующими изменение с высотой температуры
окружающей среды T(z) (кривая стратификации) и температуры
перемещающейся воздушной массы T(z) (кривая подъема). График
<: координатами Т и In р называется эмаграммой (рис. 3.1).
При расчетах энергии неустойчивости кривая стратификации
проводится по результатам зондирования. Кривая подъема стро-
Термодинамические процессы в сухом воздухе
57'
ится с помощью семейства сухих и влажных адиабат, которые
нанесены на эмаграмме. Посредством эмаграммы можно
вычислить не только энергию неустойчивости, но и целый ряд
важных метеорологических характеристик. Известны и другие не
менее удобные графические методы вычисления энергии
неустойчивости и других характеристик, например тефиграмма.
Inp
Рис. 3.1. Вычисление энергии
неустойчивости с помощью
эмаграммы.
Можно получить связь энергии неустойчивости с
кинетической энергией, которую приобретает движущаяся по вертикали
воздушная масса.
Если пренебречь трением, то
,п dw , dw i, , ( w2 \
dE=-dTdz=w-drdt==d[—)-
Полагая, что на исходном уровне ш=шо, получим
.«,?
Е=-
(3.6.5)
(3.6.6)
Если начальная вертикальная скорость равна нулю, то имеем
W2
Е=-
(3.6.7)
Таким образом, энергия неустойчивости непосредственно
связана с кинетической энергией вертикально перемещающейся
воздушной массы.
3.7. Влияние вовлечения воздуха на свойства перемещающейся
по вертикали воздушной массы
До сих пор при рассмотрении изменения с высотой
температуры перемещающейся частицы воздуха и расчете уровня
конвекции не учитывалось изменение массы перемещающейся воз-
Душной частицы (перемещающиеся частицы воздуха часто
.58
Глава 3
называют термиками или «пузырями»). В действительности из-за
вовлечения окружающего воздуха масса термика при
перемещении меняется. Поскольку вовлекаемый воздух имеет
температуру, отличную от температуры частицы, то в результате
вовлечения изменяется не только масса, но и температура
термика, а также другие характеристики. Оценим влияние
вовлечения на изменение температуры и ускорения термика,
предполагая, что на каждой высоте z присоединенная порция
окружающего воздуха сразу смешивается с поднимающимся воздухом,
так что радиальный градиент температуры отсутствует.
В п. 3.3 из уравнения первого начала было получено
выражение для изменения с высотой температуры воздушной массы
при заданном притоке тепла [см. уравнение (3.3.6)].
Предположим теперь, что приток тепла обусловлен только
вовлечением окружающего воздуха, вследствие чего масса
рассматриваемой частицы изменилась на dm. Естественно, что
приток тепла будет пропорционален разности (Т — Т) dm. Если
.считать, что приток тепла происходит при постоянном давлении,
то коэффициент пропорциональности равен сР. В (3.3.6) входит
приток тепла, отнесенный к единичной массе, поэтому
-g-^-TO^-g-. (3.7.1)
Подставив (3.7.1) в (3.3.6), получИхМ
dT
dz
аГ=аГ-Та, (3.7.2)
где а — коэффициент вовлечения, определяемый соотношением
1 dm
m dz
(3.7.3)
В общем случае а является функцией высоты, определение
которой представляет самостоятельную сложную задачу.
В настоящее время предложено несколько различных
моделей процесса вовлечения воздуха в перемещающейся термик, из
которых следует, что коэффициент вовлечения обратно
пропорционален линейному размеру / термика, т. е. а=—. Числовые
значения коэффициента пропорциональности а, полученные из
наблюдений, по данным разных авторов несколько отличаются
друг от друга. Для оценок можно принять, что а— 0,15.
Показано, что этот коэффициент зависит от стратификации,
увеличиваясь с ростом неустойчивости. Имеются также эмпирические
данные о среднем значении коэффициента вовлечения для тер-
миков разных размеров. Для численных оценок можно принять,
что а меняется от 10~7 до 10~5 см-1.
Термодинамические процессы в сухом воздухе
59
Для приближенной оценки эффекта вовлечения рассмотрим
самый простой случай, когда коэффициент вовлечения не
меняется с высотой, т. е. а = const. Это означает, что масса термика
растет с высотой по экспоненциальному закону:
m = m0eaz. (3.7.4)
Напишем теперь уравнение для определения ускорения
термика. Для термика постоянной массы, ускорение которого
обусловлено только силой плавучести, было получено соотношение
(3.4.3). В случае если масса частицы меняется, третье
уравнение движения запишется так:
dt
или
dt ' dt
±-{тт) = т?(Т-Т)
m-%h+w-%—n${T-T). (3.7.5)
dz
Подставив в (3.7.5) dt= , получим
dwt
-2aw2 = 2$ (Т-Т). (3.7.6)
dt
Чтобы из (3.7.2) и (3.7.6) найти T(z) и w(z), нужно знать
распределение по высоте температуры окружающей среды Т(г).
Задавая различные модели Г (г), можно получить T(z) и w(z)
для различных ситуаций. Наиболее просто определить их для
политропной атмосферы, когда
T(z) =70-Т?, (3.7.7)
где
<£Т
T=__ = const.
В этом случае нетрудно получить решение уравнения (3.7.2)
при граничном условии T(z) \ z=o = Tq:
Т(г) = Т0е~"+(Т0- Jizi) (1 -ё~") -?г. (3.7.8)
Изменение с высотой температуры поднимающейся частицы
равно
-|f =[а(Го-Г0)-(та-7)] <Г"-7. (3.7.S)
Если вовлечение отсутствует (<%=0), то процесс является
€0
Глава 3
адиабатическим и из (3.7.9) следует, что —:— = —va. Для чис-
dz
ленных оценок уравнение (3.7.9) удобно представить в виде
7~7
±=\\-*п]е пп,
где
Т =
dT
dz
7а-7
. * (То - То)
(3.7.10)
7а-7
= агг=т(0), zn =
*г-7<°> '
-%0 -0,5 0 0,5
Рис. 3.2. Зависимость безразмерного вертикального градиента температуры
7 — 7
термина — — от высоты zn при разных значениях безразмерного коэф-
Та~Т
фициента вовлечения ап.
Здесь zT=-(0)—уровень выравнивания температур без учета
эффекта вовлечения, описываемый формулой (3.5.3). При ап = 0
У~У_ =1 приап = 1 V~!_ =0.
Ya — У
Ya — Y
Y — Y
Ha рис. 3.2 представлена зависимость отношения — от
Ya — Y
безразмерной высоты zn при разных значениях безразмерного
коэффициента вовлечения ап. Из (3.7.8) можно определить
уровень выравнивания температуры термика с температурой
окружающей среды, который равен
*г=7(а)=-!г1п [1+«2г=г(°)]- (3-7Л1)
Термодинамические процессы в сухом воздухе 61
Подставив (3.7.7) и (3.7.8) в (3.7.6) и выполнив
интегрирование при граничном условии w (z) |2=о = 0, получим
wHz, a) = JL (2 [а (Го-7Ь) + (Т.-7)] *""-
-[2a(7'o-fo) + (T.-:r)]e~2" + (T.-7)}- (3.7-12)
При а = 0 получаем выведенную ранее формулу (3.5.5) для
изменения с высотой кинетической энергии термика единичной
массы при отсутствии вовлечения. Для этого в (3.5.5) вместо
dT df , -
и —— нужно соответственно подставить —Ya и —у:
dz dz
w*(z, 0) = 2?[(Г0-Г0)г-^т-^22]. (3.7.13)
Максимальное значение кинетической энергии при а = 0 равно
»'«.«(0) = р (Та - Т) 4=7 (0). (3-7.14)
Для графического представления удобно (3.7.14) записать в
безразмерной форме:
w4z„ .„) =_^_[2(ап + 1)е-апгЯ-(2ая+1)б~2а"г"-1]- (3.7.15)
<„ (°)
/I
На рис. 3.3 приведены профили безразмерной вертикальной
. wlzn, &п)
скорости термика wn(zn, an) =—-—— при разных значе-
^тах(О)
ниях безразмерного коэффициента вовлечения аЛ. Видно, что при
w(zn, »п)
всех значениях безразмерной высоты zn отношение т~-
КУщах (0)
уменьшается с увеличением аЛ, а точка максимума
располагается ниже.
Из (3.7.12) можно определить уровень, где вертикальная
скорость термика равна нулю:
zw=0(*) = ^rln[\+oLZw=0(0)]. (3.7.16)
Здесь г^=0(0) —уровень обращения в нуль вертикальной
скорости при отсутствии вовлечения, определяемый формулой (3.5.6).
На рис. 3.4 приведена зависимость безразмерного уровня
конвекции zn, 1|?=0(а*)=—^=0 от безразмерного коэффици-
zw=o (U)
ента вовлечения a* =azw=o(0). Чем больше коэффициент
вовлечения, тем ниже расположен уровень конвекции. Нетрудно
видеть [см. формулу (3.7.11)], что аналогичная зависимость от
62
Глава 3
безразмерного коэффициента вовлечения аЛ = агг=—(0)
характерна и для безразмерного уровня выравнивания температуры
ЛпгО
Рис. 3.3. Профили безразмерной
вертикальной скорости термика wn(zn, ап) при
разных значениях безразмерного коэффициента
вовлечения ап.
zn,w=0 &п)
W
0.5 h
L
О 1 2 с£
Рис. 3.4. Зависимость безразмерного уровня
конвекции Zn,w=o Ып) от безразмерного коэффициента
вовлечения ап .
термика с температурой окружающей среды 2Я,7=7 = - /Пч .
2т = 7 vu)
Из (3.7.12) можно определить высоту, где вертикальная
скорость термика максимальна:
1 14-2а* (0)
1 ' т~т (3.7.17)
*г = ?00
^max(a) = — ln-f
+ «rr=7(0)
Термодинамические процессы в сухом воздухе 63
Подставив (3.7.17) в (3.7.12), найдем максимальную скорость
термика:
г
1 -(0)
<£«(«) = ?(Та -т) x+lZC _m ■ (3-7.18)
Из (3.7.18) видно, что wmSiX(a) уменьшается с ростом
коэффициента вовлечения. Из (3.7.18) с учетом (3.7.14) получим
«'max (°0 1
^тах(О) 1/"1-Н2а<г/._Т (0)
(3.7.19)
Полученные соотношения (3.7.11), (3.7.12), (3.7.16), (3.7.17)
связывают величины, которые могут быть найдены из
экспериментов, с параметром вовлечения а.
Контрольные вопросы
1. Почему можно считать, что давление в воздушной частице
и окружающей среде совпадают, в то время как другие
термодинамические характеристики (температура и плотность)
отличаются?
2. Когда реальный процесс можно приближенно считать
адиабатическим?
3. Почему при адиабатическом поднятии воздушной массы
ее температура уменьшается?
4. Что понимается под термической, или свободной,
конвекцией?
5. В чем удобство введения такой характеристики
стратификации атмосферы, как энергия неустойчивости? Какие
исходные данные нужны для определения энергии неустойчивости?
6. Как влияет процесс вовлечения окружающего воздуха на
температуру и ускорение перемещающейся по вертикали
частицы?
Глава 4. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
ВО ВЛАЖНОМ ВОЗДУХЕ
Основные характеристики влажного воздуха и соотношения между ними.
Уравнение состояния реальных газов и фазовые переходы. Второе начало
термодинамики. Второе начало термодинамики и условия устойчивости
атмосферы. Условия равновесия фаз. Уравнение Клаузиуса—Клапейрона.
Изменение характеристик перемещающейся по вертикали массы влажного воздуха.
В предыдущей главе изложены некоторые важные для
метеорологии результаты изучения термодинамических процессов,
протекающих в сухом воздухе. В действительности в воздухе всегда
содержится водяной пар, роль которого в атмосферных
процессах очень велика. Это связано с тем, что при наблюдающихся
в атмосфере температурах вода может существовать в
различных фазах — газообразной (водяной пар), жидкой (вода),
твердой (лед, снег), которые часто встречаются одновременно. При
этом имеют место фазовые переходы, в результате которых
формируются такие важные элементы погоды, как туман, облачность
и осадки. Поскольку фазовые переходы сопровождаются
выделением (или поглощением) тепла, они приводят к изменению
хода термодинамических процессов. Эффекты, связанные с
выделением и поглощением тепла при фазовых переходах,
существенно сказываются на энергетике атмосферы и важны для
прогноза погодных процессов. Оценки показывают, что
энергетическая роль влажности в атмосфере весьма существенна: затраты
тепла на испарение в среднем равны 3- 103 кВт, что составляет
примерно 30% поглощаемого Землей солнечного тепла. Опасные
явления погоды, такие, как грозы и град, тоже связаны с
фазовыми переходами. Нельзя не упомянуть о существенной роли
водяного пара и облачности в процессах распространения лучистой
энергии; этот процесс обсуждается в главе 6.
Влагосодержание можно рассматривать как один из
специфических параметров, определяющих состояние воздуха, подобно
температуре и давлению. В результате испарения, конденсации
и выпадения осадков содержание воды в газообразной, жидкой
и твердой фазах изменяется в довольно широких пределах. Для
полного описания свойств влажного воздуха нужно ввести в
рассмотрение некоторые новые характеристики и получить
соответствующие соотношения для их определения. При изучении
влажного воздуха необходимо знать условия перехода воды из одной
фазы в другую, условия равновесия фаз и т. д. Для этого тре-
Термодинамические процессы во влажном воздухе 65
буется привлечь новый фундаментальный принцип — второе
начало термодинамики. Обсуждение этих вопросов составляет
содержание данной главы.
4.1. Основные характеристики влажного воздуха
и соотношения между ними
Влажный воздух, представляющий собой смесь сухого
воздуха и водяного пара, можно считать двухкомпонентной
системой. Вследствие особой роли водяного пара в атмосферных
процессах введено несколько различных характеристик для
определения его количества в воздухе. В зависимости от
рассматриваемой задачи могут оказаться более удобными те или иные из них.
Напомним определения основных характеристик. Плотность
водяного пара рп называется обычно абсолютной влажностью
воздуха. Отношение массы водяного пара к массе влажного воздуха
в фиксированном объеме называется удельной влажностью;
обозначим ее q. Отношение массы водяного пара к массе сухого
воздуха в фиксированном объеме называется отношением смеси;
обозначим его т. Обычно q и т измеряются в г/кг. Парциальное
давление водяного пара е называется упругостью. Парциальное
давление насыщенного водяного пара es называется
максимальной упругостью или упругостью насыщения. Относительная
влажность воздуха / — отношение фактической упругости
водяного пара к максимальной упругости при данной температуре,
Получим основные количественные соотношения,
позволяющие рассчитывать указанные характеристики. До достижения
насыщения водяной пар можно с достаточной точностью считать
идеальным газом, поэтому упругость связана с плотностью
водяного пара рп уравнением состояния
e = pa-^T=PnRnT, (4.1.1)
где /?*—универсальная газовая постоянная; Rn — газовая посто-
янная водяного пара, Rn= ; \iu — относительная молекуляр-
ная масса водяного пара. Так как газовая постоянная воздуха
/?*
/? = , то
У?п = ^/?^1,6/?, (4.1.2)
66
Глава 4
т. е. газовая постоянная пара примерно в 1,6 раза больше
газовой постоянной воздуха.
Получим теперь формулы для расчета удельной4 влажности
и отношения смеси, используя для сухого воздуха и водяного
пара уравнения состояния идеальных газов, соотношение (4.1.2)
и закон Дальтона
pw=P+e, (4.1.3)
где pw и р — соответственно давление влажного и сухого
воздуха.
По определению,
д=~Ы= р + Рп ^/?п Р + 0.622* ^°>622 Pw-0.378* • №ЛА)
т=-^ = -§ * ^0,622 - . (4.1.5)
Р Rn Pw — е pw — e v '
Поскольку e<^pWt #<Cl, m<Cl, то с большой точностью можно
принять
q^m^0,622—. (4.1.6)
Pw
Формулы (4.1.4) — (4.1.6) позволяют рассчитывать q и т, если
известны упругость водяного пара и давление влажного воздуха.
Точные формулы, связывающие отношение смеси и удельную
влажность, легко получить из определения этих величин:
?=-ГТ7Г' от=т^7- <4Л-7>
Запишем уравнение состояния ненасыщенного влажного
воздуха, считая его идеальной двухкомпонентной смесью газов:
Pw=P+e = pRT+9nRnT=9wRT(\+016q)- (4.1.8)
Из (4.1.8) следует важный для метеорологии вывод: плотность
влажного воздуха при одинаковых температуре и давлении
меньше плотности сухого воздуха в (1+0,6 q) раз. Это связано
с тем, что относительная молекулярная масса водяного пара
меньше относительной молекулярной массы сухого воздуха.
Уравнение состояния (4.1.8) можно записать в более удобной
форме, введя виртуальную температуру
Г,-741+0,60. (4.1.9)
Тогда для влажного воздуха уравнение состояния запишется
в таком же виде, как и для сухого:
Pb = pwRTv. (4.1.10)
Термодинамические процессы во влажном воздухе 67
В соответствии с (4.1.10) виртуальная температура — это
температура, которую имел бы при данном давлении сухой воздух
с плотностью, равной плотности влажного воздуха. Обычно
виртуальная добавка (0,6 q) невелика, поскольку q<^\. Однако
различие между температурой Т и виртуальной температурой Tv
может оказаться важным при определении вертикальной
статической устойчивости.
Действительно, как уже отмечалось в предыдущей главе,
полученные критерии устойчивости (3.4.6) будут справедливы и при
вертикальных перемещениях влажного воздуха. Эти критерии
получены из уравнения (3.4.2) для вертикального ускорения
частицы; применительно к влажному воздуху р и р в (3.4.2)
следует заменить pw и р^, соответственно. Поскольку для влажного
воздуха уравнение состояния можно записать в таком же виде,
как и для сухого, то легко видеть, что в случае влажного воздуха
для определения типа стратификации нужно сравнивать
вертикальные градиенты виртуальной температуры поднимающейся
частицы и окружающей среды. Согласно (4.1.9), вертикальный
градиент виртуальной температуры равен
Таким образом, соотношение между градиентами виртуальной
температуры среды и частицы, определяющее тип стратификации
/ dT dT\
атмосферы, зависит не только от разности I — —J , но и от
разности градиентов удельной влажности частицы в
окружающей среде. Добавка за счет вертикального градиента влажности
оказывается особенно важной над морем.
Напишем теперь уравнение первого начала для влажного
воздуха. Для единицы массы любого идеального газа уравнение
первого начала имеет вид
dQ = cpdT-RT^- = cpdT-^
р
Записав соответствующие уравнения для (1 — q) грамм сухого
воздуха и q грамм водяного пара и сложив их, получим
"Pw л ЛТ" _ DT "ри
Pw
dQ=cpwdT-^^=cpwdT-RTv^-t (4.1.12)
гДе cPw — теплоемкость влажного воздуха при постоянном
давлении, связанная с теплоемкостями сухого воздуха ср и водяного
пара сРП при постоянном давлении следующим соотношением:
cpw = cp[\+q[-^--\^\. (4.1.13)
5*
68
Глава 4
Отношение теплоемкостей водяного пара и сухого воздуха при
постоянном давлении равно примерно 1,9 и слабо меняется при
изменении температуры. Следовательно,
cpw**cp(\+0,9q). (4.1.14)
Поскольку q<^lj теплоемкость влажного воздуха практически
не отличается от теплоемкости сухого воздуха.
Таким образом, уравнение первого начала термодинамики и
основанные на нем выводы, полученные в главе 3 для сухого
воздуха, сохраняют силу и для влажного ненасыщенного воздуха.
4.2. Уравнение состояния реальных газов и фазовые переходы
При наблюдающихся в атмосфере давлении и температуре
уравнение состояния идеальных газов достаточно хорошо
отражает поведение водяного пара. Однако некоторые свойства
водяного пара в состоянии насыщения, когда имеют место фазовые
переходы, не описываются этим уравнением. В таком случае для
правильного описания свойств требуется модель, более точно
отражающая свойства газов, чем модель идеального газа, согласно
которой газ можно представить как совокупность материальных
точек, не занимающих никакого объема и не
взаимодействующих друг с другом.
Уравнение состояния с учетом конечного объема молекул и
сил притяжения между молекулами впервые было получено Ван-
дер-Ваальсом (1890 г.).1 Для одного моля газа это уравнение
может быть записано в виде
(p+-^)(V-b) = R*T. (4.2.1)
Постоянная а характеризует силы притяжения между
молекулами, а Ь — собственный объем молекул. Силы притяжения при-
а
водят к появлению добавочного внутреннего давления -т^—,
величина которого растет с уменьшением объема (увеличением
1 Обычно уравнения состояния либо определяются эмпирически, либо
выводятся методами статистической физики. Для описания поведения реальных
газов предложен целый ряд уравнений состояния. Широкое применение
получило уравнение Ван-дер-Ваальса вследствие того, что оно качественно верно
отражает поведение реальных газов, описывает возможность образования
двухфазной системы, переход в жидкое состояние, указывает на наличие
критической точки. Количественно это уравнение удовлетворительно описывает
поведение многих веществ в широком интервале температуры и давления.
Уравнение Ван-дер-Ваальса выводится теоретически в статистической физике
для малых плотностей газа, когдаЧвойства газа мало отличаются от свойств
идеального газа.
Термодинамические процессы во влажном воздухе
69
плотности). При -^-«Р и b«.V формула (4.2.1) переходит
в уравнение состояния идеальных газов. При V<b уравнение
(4.2.1) теряет смысл: нельзя сжать газ до объема, меньшего
собственного объема молекул.
Постоянные а и Ъ зависят от рода газа. При этом величины а
сильно различаются для разных газов. Это означает, что
средняя энергия взаимодействия молекул разных газов весьма
различна (например, средняя энергия взаимодействия для гелия
Рис. 4.1. Изотермы реального газа (кривые Ван-дер-Ваальса).
б — при разных температурах (7'|<7,2<7,кр<
<Т3<Т4).
а — при данной температуре,
в 160 раз меньше, чем для водяного пара). В то же время
величина b варьирует мало, что указывает на примерное постоянство
объемов молекул различных газов. Для водяного пара а = 5,47Х
ХЮ9 мбар-см6/моль2, 6 = 30,52 см3/моль. Для воздуха опытные
значения коэффициентов а и b приблизительно равны
3-Ю-3 ро/р2 и 3-Ю-3 1/ро соответственно, причем величины ро
и ро берутся при стандартных условиях.
Уравнение Ван-дер-Ваальса является уравнением третьей
степени относительно объема и имеет три действительных корня.
Изотермы p = F(V) имеют два экстремума (рис. 4.1а), так что
некоторому значению давления, например p = ps, соответствуют
три разных значения молярного объема: Vu V2> Vs.
Минимальному из этих трех значений объема (Vi) соответствует жидкое
состояние вещества, а максимальному (Уз) —газообразное. Для
b<V^Vi зависимость p(V) при данной температуре
соответствует жидкому состоянию, а для V^Vs — газообразному. Таким
образом, уравнение Ван-дер-Ваальса описывает как однофазное
(причем и жидкости, и газа), так и двухфазное состояние.
70
Глава 4
Необходимо, однако, отметить, что в действительности
переход из жидкого состояния в газообразное (и обратный переход)
осуществляется не вдоль участка изотермы Ван-дер-Ваальса
ABCDE, а вдоль изобары АСЕ, которая одновременно является
и реальной изотермой. Точки горизонтального участка АСЕ
описывают двухфазное состояние, при котором газ находится в
равновесии с жидкостью. Газ, находящийся в равновесии с
жидкостью, называется насыщенным; давление, соответствующее
этому состоянию, называется давлением насыщения (ps). Чем
ближе рассматриваемое состояние к точке Л, тем больше в
системе жидкости; напротив, при приближении к точке Е в системе
увеличивается количество вещества в газообразной фазе.
Посмотрим, описывает ли какие-либо реальные процессы
участок изотермы Ван-дер-Ваальса ABCDE. Участку BCD
соответствует необычная зависимость давления от объема: (-^тт-) >,
>0 (т. е. при увеличении объема давление также
увеличивается). Это область абсолютно неустойчивого состояния вещества,,
которое не наблюдается в реальных условиях. Что касается
участка DE, то он соответствует газообразному состоянию, но в
любой точке этого участка давление газа больше, чем давление
в состоянии насыщения. Такое состояние называется
пересыщенным газом. Оно может быть осуществлено реально при
определенных условиях и называется метастабильным состоянием.
Участок АВ соответствует другому метастабильному состоянию
вещества— перегретой жидкости.
Таким образом, различия между реальным фазовым
переходом и кривой Ван-дер-Ваальса объясняются тем, что состояния»
соответствующие кривой ABCDE, при обычных условиях не
наблюдаются экспериментально из-за их нестабильности (или ме-
тастабильности). При данной температуре (для данной
изотермы) только при определенном значении давления, а именно
при давлении насыщения, объему Vi соответствует устойчивое
состояние — состояние пара, находящегося в равновесии с
жидкостью, т. е. двухфазное состояние. В этом состоянии, как видно
из рис. 4.1 а (участок АСЕ), давление насыщения ps не зависит
от объема. При данной температуре ps имеет определенное
значение, которое изменяется только при изменении температуры.
На рис. 4.1 б представлены кривые Ван-дер-Ваальса при
разных температурах. Чем выше температура, тем выше
располагаются изотермы^ максимумы и минимумы становятся меньше
и сближаются; наконец, при определенной температуре
максимум и минимум сливаются в одну точку перегиба, которая
называется критической точкой. Это означает, что при увеличении
температуры различия между тремя корнями уравнения (4.2.1)
Термодинамические процессы во влажном воздухе 71
уменьшаются до тех пор, пока все три корня не совпадут в
критической точке. При критических значениях параметров рКр> 7кр>
ККр, соответствующих этой точке, различие между агрегатными
состояниями вещества исчезает. Изотермы Ван-дер-Ваальса при
Т>ТкР описывают состояния однофазной системы — газа, и чем
выше температура, тем ближе эти изотермы к изотермам
идеального газа. Значения рКр, 7кр, Ккр можно определить из уравнения
/л о i\ др дгР
(4.2.1), вычислив -~z и JL и приравняв их нулю:
Ркр
1 а гр 8 а чт л.
Для воды эти величины имеют следующие значения: ркр = 2,2бХ
ХЮ5 мбар, ГКр = 647 К, VKp = 55,8 см3/моль. Отметим, что в кри-
1 / dV \ <
тическои точке изотермическая сжимаемость %=~тт[~^~)т
обращается в бесконечность. Это обстоятельство играет важную
роль при изучении рассеяния света при его прохождении через
вещество. Если ввести в рассмотрение безразмерные величины
р Т V
рп=—[—у Тп=-^—, Vn = Tj—, то уравнение Ван-дер-Ваальса
Ркр Т кр V кр
можно записать в универсальном виде:
('«+^)(V'---r)=-3-7'" (4-2-2)
Более общим уравнением состояния реальных газов является
уравнение состояния в вириальной форме. Это уравнение
выражает отклонения от уравнения состояния идеальных газов в виде
бесконечного степенного ряда по плотности:
-^=1+5р+Ср2+Др3+£р4+ • • • (4-2.3)
Коэффициенты В, С, Д Е и т. д. этого уравнения называются
вириальными коэффициентами; они зависят от температуры и
природы рассматриваемого газа, но не зависят от плотности
и давления. Если все вириальные коэффициенты равны нулю, то
из (4.2.3) следует уравнение состояния идеальных газов. При
В = Ь 7^г> C = b2, D = b3 и равенстве нулю остальных ви-
риальных коэффициентов из (4.2.3) получается уравнение Ван-
дер-Ваальса. Важность вириального уравнения заключается
в том, что это уравнение имеет строгую теоретическую основу.
Каждый вириальный коэффициент можно вполне определенно
72
Глава 4
интерпретировать на основании молекулярных свойств.
Коэффициент В учитывает отклонение от уравнения состояния
идеального газа, обусловленное взаимодействием двух молекул, С —
взаимодействием трех молекул и т. д.
4.3. Второе начало термодинамики
Второе начало термодинамики аналогично первому началу
является результатом обобщения экспериментальных фактов,
оно не выводится, а постулируется. Известно много различных,
но по существу эквивалентных формулировок второго начала.
Изложим его содержание в общей форме, что позволит нам
наиболее простым путем получить важные для термодинамики
атмосферы соотношения (условия равновесия фаз, зависимость
максимальной упругости от температуры и др.).
1. Для каждой термодинамической системы можно ввести
функцию состояния, называемую энтропией, полное изменение
которой dS обусловлено производством энтропии внутри системы
diS и потоком энтропии deS, возникающим за счет
взаимодействия с окружающей средой:
dS=dtS-\-deS. (4.3.1)
По существу, (4.3.1) представляет собой уравнение баланса
энтропии, в котором не раскрыт явный вид источников d{S и
потоков deS.
2. Второе начало утверждает, что производство энтропии diS
равно нулю для обратимых1 (равновесных) процессов и больше
нуля в случае необратимых процессов, т. е. всегда
^5>0. (4.3.2)
Для изолированных систем (т. е. систем, которые не
обмениваются с окружающей средой ни теплом, ни веществом и для
которых, следовательно, deS = 0) из (4.3.1) и (4.3.2) следует
dS^O. (4.3.3)
Это неравенство означает, что энтропия изолированной системы
1 Напомним, что обратимым называется процесс, при протекании которого
система на каждой стадии находится в равновесии с окружающей средой,
т. е. его можно провести в пр5^мом и обратном направлении по одному и
тому же термодинамическому пути. Процессы, которые нельзя провести по
одинаковому термодинамическому пути в прямом и обратном направлении,
называются необратимыми. Все реальные процессы являются необратимыми.
Понятие обратимого процесса представляет собой очень важную идеализацию.
Некоторые реальные процессы можно, однако, считать приближенно
обратимыми. Необходимым условием для этого является медленное протекание
процесса, чтобы время, за которое существенно меняется состояние системы,
было велико по сравнению с временем установления равновесия.
Термодинамические процессы во влажном воздухе 73
никогда не убывает. Если система переходит из состояния 1 всо-
2
стояние 2, то, согласно (4.3.3), jdS = S2 — Si>0.
i
3. Для замкнутых систем, т. е. систем, которые обмениваются
с окружающей средой только теплом, но не веществом, поток
энтропии равен притоку тепла dQ, деленному на температуру:
deS=^-. (4.3.4)
Из (4.3.4) с учетом (4.3.2) и (4.3.1) следует, что в замкнутой
системе
dS>^_. (4.3.5)
Это соотношение представляет собой основную форму записи
второго закона термодинамики.
Чаще всего вывод о наличии такой функции состояния, как энтропия,
следует из более простых, кажущихся самоочевидными, но по существу не
доказуемых формулировок второго начала. Одной из наиболее распространенных
является формулировка Клаузиуса: тепло не может самопроизвольно перейти
от системы с меньшей температурой к системе с большей температурой.
Используя эту формулировку, можно с помощью мысленного эксперимента с
циклом Карно доказать существование функции состояния и получить
соотношения (4.3.4) и (4.3.5). В то же время из приведенных выше соотношений
вытекает формулировка Клаузиуса и некоторые другие важные следствия.
Рассмотрим два тела Л и Б, имеющие разные температуры ТА и ТБ и не
находящиеся в равновесии друг с другом, которые вместе составляют
изолированную систему, так что
dQA dQR
dS=dSA + dSB= -£±- + -f^~> °-
Так как система изолирована, то dQ=dQA+dQs =0, поэтому
НтГ-Т7Н>0-
Если ТА>ТБ, то приведенное соотношение выполняется только при dQA<0
(т. е. тепло переходит от тела с более высокой температурой к телу с
меньшей температурой).
Для того чтобы в рассматриваемой системе установилось равновесие, т. е.
dS = 0, необходимо, чтобы TA — TBi т. е. температуры тел, находящихся в
равновесии друг с другом, должны быть равны. Можно показать, что давления
находящихся в равновесии тел также должны быть одинаковыми: рА=рв-
Для открытых систем, т. е. систем, которые могут
обмениваться с окружающей средой как теплом, так и веществом, deS
содержит член, связанный с потоком вещества. Общее
утверждение второго начала, содержащееся в неравенстве (4.3.2),
остается справедливым и для открытых систем. Поступление же
энтропии извне (deS) может быть положительным, равным нулю
74
Глава 4
или отрицательным в зависимости от характера взаимодействия
системы с окружающей средой. Отметим, что энтропия является
экстенсивной величиной. Если система состоит из нескольких
частей, то полная энтропия равна сумме энтропии этих частей.
Из соотношений (4.3.2) — (4.3.5) следует, что второе начало
указывает направление протекания процессов. В системе могут
протекать только такие процессы, при которых производство
энтропии diS^O. В результате любого процесса, протекающего
в изолированной системе, энтропия конечного состояния больше
энтропии начального состояния. Поэтому в состоянии равновесия
энтропия системы максимальна.
Подставив (4.3.5) в общую формулу первого начала
термодинамики (1.5.8), получим совместную запись первого и второго
начал термодинамики для замкнутых систем:
dEB+pdV^TdS. (4.3.6)
Для обратимых процессов, протекающих в идеальных газах,
легко получить следующие уравнения:
dS=cv^f-R^, (4.3.7)
откуда следуют соотношения:
S = CplaT-R\np-\-S0t
S=cv\n T-R\n V+S0. (4.3.8)
Если использовать определение потенциальной температуры,
то первое из уравнений (4.3.7) можно записать в форме, часто
применяемой в различных метеорологических исследованиях:
dS=cpdlnQ. (4.3.9)
Рассмотрим, какие выводы следуют непосредственно из
второго начала термодинамики для атмосферы. При изучении
эффектов за длительные промежутки времени атмосферу—океан—
сушу можно рассматривать как единую систему, все части
которой взаимодействуют друг с другом. Эта система является
неизолированной: она получает энергию от Солнца и отдает
избыток энергии в космическое пространство. Поскольку система
атмосфера—океан—суша не претерпевает заметных изменений за
большие промежутки времени, то изменение энтропии всей
системы в целом равно нулю:
$(dS)vdV=0
Термодинамические процессы во влажном воздухе 75
{индексом V отмечены величины, относящиеся к конкретной
области пространства).
В то же время в системе происходят неравновесные
процессы — перенос тепла, количества движения и других
субстанций, поэтому производство энтропии внутри системы больше
нуля:
${dtS)vdV>0.
Тогда из соотношения (4.3.1) следует
j(^-)^K<0. (4.3.10)
С другой стороны, поскольку обмен энергией между системой и
окружающей средой происходит только вследствие излучения
и за длительные промежутки времени полная энергия системы
заметно не изменяется, то можно считать, что полный приток
тепла к системе равен нулю:
§(dQ)vdV=0. (4.3.11)
При этом важно, что баланс осуществляется лишь глобально;
для отдельных же областей пространства нет баланса между
поступлением и потерей тепла: (dQ)V¥=0. Чтобы одновременно
выполнялись (4.3.10) и (4.3.11), необходимо, чтобы, во-первых,
распределение температуры в пространстве было неравномерным,
а во-вторых, приток тепла должен быть положительным в
областях с более высокой температурой.
4.4. Второе начало термодинамики и условия устойчивости
атмосферы
Полученные в п. 3.4 условия статической устойчивости
атмосферы можно интерпретировать с помощью второго начала
термодинамики и для определенных условий сформулировать их
в терминах энтропии. Применяя уравнение (4.3.9) к атмосфере
и учитывая соотношения (3.4.9), можно для случая
адиабатического перемещения воздушных масс записать критерии
устойчивости следующим образом:
-т— <0 (неустойчивая стратификация),
-^- = 0 (равновесная стратификация),
-з— >0 (устойчивая стратификация).
(4.4.1)
76
Глава 4
Поскольку, как уже отмечалось, возможность осуществления
каких-либо процессов диктуется вторым началом
термодинамики, исследуем с этой точки зрения возникновение
вертикальных конвективных движений в атмосфере. Рассмотрим
некоторое состояние атмосферы, характеризующееся распределением
температуры T(z). Вычислим изменение энтропии в слое dz,
вызванное тем, что две единичные массы воздуха, расположенные
соответственно на уровнях z и z + dzy будут взаимно перемещены.
p(z+dz), T(z+dz)
W,p(z)
T(z)+j¥dz, p(z+d,z)
T(z+dz)-^dzyp(z)
Рис. 4.2. К расчету изменения энтропии при вертикальном перемещении
воздушных масс.
На рис. 4.2 изображено распределение температуры и давления
для начального и конечного состояния системы, которая в целом
предполагается изолированной. Энтропия системы складывается
из энтропии двух рассматриваемых воздушных масс (Si и S2)
и энтропии окружающей среды (S). Энтропию единичных масс
воздуха в начальном (SH) и конечном (SK) состоянии можно
рассчитать по формуле (4.3.8). Поскольку процесс состоит лишь
в перемещении дв^Х воздушных масс, то S при таком процессе
не изменяется. Легко найти полное изменение энтропии системы:
ок — он — Ср 1П
[т (,) +*£*,
dz
Г (г)
П*) + 4г&-
dT
dz
dz
Т(г) +
dT * 1
(4.4.2)
Мы предположили, что на исходных уровнях температура
рассматриваемых воздушных частиц совпадает с температурой
среды. В изолированных системах могут осуществляться только
Термодинамические процессы во влажном воздухе
77
такие процессы, при которых SK — 5Н^0, т. е. процесс может
осуществиться при условии
[Т(г)+4^ dz] [Т(г) ^dz-^dz] > Т(г) [щ+*. dz],
(4.4.3)
которое сводится к следующему неравенству:
Так как в изолированной системе температура частицы умень-
(AT \
——<0] , то (4.4.4) выполняется только при
условии
dT dT
dz dz
>0. (4.4.5)
Знак «больше» (>) в формуле (4.4.5) соответствует
неустойчивому состоянию, знак равенства — равновесному.
Приведенные рассуждения показывают, что в
рассматриваемом случае, при отсутствии локального перегрева, вертикальные
конвективные движения могут возникать только при
неустойчивой и равновесной стратификации атмосферы. При устойчивой
стратификации, когда неравенство (4.4.5) не выполняется, такой
термодинамический процесс невозможен. В этом случае
возникновение вертикальных движений может быть обусловлено либо
начальным перегревом, либо динамическими факторами.
4.5. Условия равновесия фаз. Уравнение Клаузиуса—Клапейрона
Из термодинамического соотношения (4.3.6), являющегося
следствием первого и второго начал, записанного в виде
dEB+pdV-TdS^O, (4.5.1)
следует, что при постоянных температуре и давлении можно
ввести новую функцию, называемую термодинамическим
потенциалом,
G=EB+pV-TS, (4.5.2)
дифференциал которой удовлетворяет неравенству
rfG<0. (4.5.3)
Это неравенство означает, что необратимые процессы,
протекающие при постоянных р и 7, сопровождаются уменьшением
78
Глава 4
термодинамического потенциала. Соответственно в состоянии
теплового равновесия термодинамический потенциал минимален.
Соотношение (4.5.1) записано для замкнутых систем, в
которых масса (или число частиц) не изменяется. Однако, когда речь
идет о фазовых переходах или равновесии фаз, следует
учитывать обмен массой между различными фазами. В частности,
когда жидкость и пар находятся в равновесии, молекулы с
поверхности жидкости переходят в пар (испарение), а частицы пара
конденсируются на поверхности жидкости. При равновесии число
частиц, переходящих из жидкости в пар и обратно, одинаково.
Другим примером системы с переменным числом частиц может
служить система, в которой происходят химические реакции. Для
систем с переменным числом частиц в соотношении (4.5.1)
появится дополнительный член, который наиболее просто получить
следующим образом. Поскольку внутренняя энергия, энтропия
и объем обладают свойством аддитивности, то равенство,
аналогичное (4.5.1), может быть написано для молярных величин, т. е.
величин, отнесенных к одной частице. Пусть в системе
содержится N частиц. Тогда, предполагая процесс обратимым,
запишем (4.5.1) в виде
Последнее равенство имеет место и при переменном числе
частиц. Учитывая это, перепишем (4.5.4) следующим образом:
1 ,^ с- dN TdS rpQ dN p лт/ i „\r dN
Отсюда, введя в рассмотрение химический потенциал \i с
помощью соотношения
?_E.-TS+PV f {455)
получим
dEB= TdS-p dV+p dN. (4.5.6)
Приведенное термодинамическое соотношение, пригодное для
открытых систем, часто называется соотношением Гиббса.
Легко видеть, сравнивая (4.5.2) и (4.5.5), что
HP. Т) = Щ±±- (4.5.7)
и, следовательно,
dG(LT) -i*(p. П (+.5.8)
Термодинамические процессы во влажном воздухе 79
Из (4.5.5) с учетом (4.5.4), получим
d\i = -SdT+Vdp, (4.5.9)
откуда следует
Здесь волной сверху обозначены молярные величины:
^— N ' V — N '
Напишем теперь условия равновесия между двумя фазами
одного вещества. Поскольку при фазовых переходах внутренняя
энергия зависит от числа частиц каждой фазы (N± и N2), то
термодинамический потенциал будет функцией от р, Г, Ni и Afo
G(p9 Т, Nu N2). Общее условие минимума термодинамического
потенциала при равновесии тогда запишется так:
При равновесии фаз температура, давление, а также полное
число частиц в системе N = Ni + N2 остаются постоянными (т. е.
dT = 0, dp = 0, dNi = —dN2). При этих условиях из (4.5.11)
получим
dG dG /Л г ю\
wr = w (4-5Л2)
откуда с учетом (4.5.8) вытекает следующее условие равновесия
фаз:
М/>. Т) = МР. П (4.5.13)
Итак, равновесие двух фаз вещества требует, помимо равенства
давлений pi = p2 и температур 7,i = 7,2, еще равенства химических
потенциалов.
Уравнение (4.5.13) позволяет выразить один из аргументов
через другой, т. е. найти р(Т) или Т(р) (например найти
упругость насыщения водяного пара как функцию температуры или
температуру точки росы как функцию давления и т. д.), и,
следовательно, определяет, на графике р, Т кривую равновесия фаз.
Чтобы найти р(Т) в конкретном случае, нужно знать вид
функций |ii и fX2. Можно, однако, даже не зная явного вида
выражений jlxi(р, Т) и |яг(р, Г), найти дифференциальное уравнение
кривой равновесия фаз. Дифференцируя (4.5.13) и используя
соотношение (4.5.10), получим
-^= j-fr . (4.5.14)
80
Глава 4
Из формулы dS=—— находим
L = $dQ = T (s2-Sx). (4.5.15)
Таким образом, фазовый переход сопровождается выделением или
поглощением некоторого количества тепла L, называемого
скрытой теплотой перехода.i К таким фазовым превращениям
относятся все изменения агрегатного состояния вещества
(конденсация, плавление, кристаллизация).
Выразив в (4.5.14) изменение энтропии через скрытую
теплоту перехода с помощью (4.5.15), получим уравнение Клаузиу-
са—Клапейрона, описывающее изменение давления находящихся
в равновесии фаз при изменении температуры:
~^ = i~L ~ч - (4-5-16>
*т t{v2-Vx)
Знак ■ а ■ зависит как от знака разности объемов обеих фаз
Vi—Vi, так и от знака L. Фазовый переход, происходящий при
повышении температуры (испарение, плавление), всегда сопро-
вождается поглощением тепла, т. е. L>0. Напротив, фазовый
переход, происходящий при понижении температуры
(конденсация, кристаллизация), сопровождается выделением тепла, т. е.
L<0.
Применим полученные выше соотношения к исследованию
равновесия различных фбз воды, что представляет значительный
интерес для физики атмосферы.
Запишем уравнение Клаузиуса—Клапейрона (4.5.16) для
случая равновесия воды и водяного пара. Если пренебречь
объемом воды по сравнению с объемом пара (Уп3>^в, считаем
водяной пар второй фазой, т. е. рассматривается испарение) и
предположить, что поведение насыщенного водяного пара близко
1 Отметим, что L — молярная теплота перехода, т. е. количество тепла,
выделенного при конденсации одного моля вещества. Удельная величина L,
т. е. количество тепла, выделенного при конденсации 1 г вещества, равна
N ~
L = L (NA — число Авогадро, \i — относительная молекулярная масса).
Термодинамические процессы во влажном воздухе
81
к поведению идеального газа \ то получим зависимость
упругости насыщения es от температуры в виде
dex
^в-п£?
dT
RnT*
При испарении
des Л
тельно, л_ >0, т. е
аТ
скрытая теплота перехода LB-n>0,
при уменьшении температуры
(4.5.17)
следова -
(dT<0)
упругость насыщения, также
уменьшается (кривая ОА на
рис. 4.3). При применении
уравнения Клаузиуса—Клапейрона
к фазовому переходу вода—лед
нужно иметь в виду важное
аномальное свойство воды,
отличающее ее от большинства
других жидкостей: вода при
замерзании расширяется, AV =
= VB— Ул<0 (при Г = 273К
AV——0,091 см3/г). Это
обстоятельство имеет чрезвычайно
важное значение: лед плавает
на воде. Поскольку при
плавлении Lb-л > 0, из формулы
(4.5.16) следует, что при плавлении (или кристаллизации)
-~<0 (кривая ОВ на рис. 4.3). Соответственно температура
плавления понижается при увеличении давления.
Предположим теперь, что имеются три фазы воды — лед,
вода и водяной пар. Если записать условия равновесия между
водой и паром как \1\ = \х2 и между водой и льдом в виде ^2 = ^3,
то тем самым оказывается выполненным и условие равновесия
первой и третьей фазы: |Я1 = |Яз. Так как каждое из этих равенств
приводит к определенной зависимости между давлением и
температурой, то равновесие трех фаз характеризуется на
То Т
Рис. 4.3. Кривые равновесия фаз.
1 Хотя свойства насыщенного водяного пара более точно описываются
уравнением Ван-дер-Ваальса, можно показать, что в диапазоне температур
и давления, характерных для атмосферы Земли, поправки, связанные с
использованием этого уравнения, оказываются несущественными. Поэтому с
хорошим приближением в уравнении Клаузиуса—Клапейрона можно заменить
R Т
объем насыщенного пара Vns= —-— с помощью уравнения состояния иде-
es
альных газов; при этом, однако, нужно иметь в виду, что е8 зависит только
от температуры.
6 Заказ № 612
82
Глава 4
диаграмме р, Т определенной точкой ро, Го, в которой
пересекаются все три кривые, описываемые соответствующими
уравнениями Клаузиуса—Клапейрона. В этой точке, называемой тройной
точкой, выполняется условие \ii = ^2 = |Ыз. Параметры тройной
точки воды следующие: температура 0,0078°С, давление ро =
= 6,11 мбар. При таких температуре и давлении вода, лед и
водяной пар находятся в равновесии. При давлении, меньшем ро,
лед при нагревании превращается непосредственно в пар, минуя
жидкое состояние (кривая ОС). Этот эффект наблюдается
ранней весной при небольшом морозе в солнечный день, когда
значительное количество снега исчезает без таяния, превращаясь
в водяной пар. В физике этот и обратный ему процесс именуют
сублимацией. В метеорологии сублимацией называется только
процесс непосредственного превращения водяного пара в
твердую фазу/Этот процесс наблюдается при отрицательных
температурах. В частности, в свободной атмосфере при низких
отрицательных температурах сублимация преобладает над
конденсацией, так как упругость насыщения водяного пара над льдом
меньше, чем над водой.
К кривым равновесия двух фаз вещества примыкают области
существования метастабильных состояний (штриховые линии на
рис. 4.3). Например, в области /, где устойчивым является
газообразное состояние, при некоторых условиях может
существовать в метастабильном состоянии жидкость (перегретая
жидкость). В области //, где устойчива жидкость, может при
определенных условиях существовать в метастабильном состоянии
пар (пересыщенный пар). Это обстоятельство уже отмечалось
при анализе уравнения Ван-дер-Ваальса. Наконец, в области ///,
где устойчива кристаллическая фаза, может существовать в
метастабильном состоянии переохлажденная жидкость. Наличие
метастабильных состояний в атмосфере (переохлажденные
облака) имеет существеннее значение при разработке проблемы
искусственного воздействия. По данным аэрологического
зондирования, в атмосферных условиях переохлажденная водяная
фаза отмечается до температуры —40°С, причем
переохлажденное состояние капель имеет место в большинстве исследуемых
облаков.
Для получения кривых равновесия различных фаз нужно знать
зависимость скрытой теплоты соответствующего перехода (LB-m
£в-л, £п-л) и молярных объемов (Уш Ув, У л) от температуры и
давления. Обычно эта зависимость определяется
экспериментально и является довольно сложной, поэтому производится
численное интегрирование уравнений Клаузиуса—Клапейрона и
результаты представляются в соответствующих таблицах.
Ситуация упрощается, когда речь идет об определении температурной
Термодинамические процессы во влажном воздухе 83
зависимости упругости насыщения водяного пара по формуле
(4.5.17), поскольку для Vn использовано уравнение состояния
идеального газа. Для интегрирования (4.5.17) нужно знать
только LB-n как функцию температуры. В обычных для
атмосферы интервалах температуры LB-n достаточно точно
аппроксимируется линейной функцией температуры:
Тогда из формулы (4.5.17) получается следующая зависимость
упругости насыщения от температуры:
es=cT пе \ (4.5.18)1
Иногда для определения es(T) используется эмпирическая
формула Магнуса
7,45/
es = es0- 10235+', (4.5.19)
где eso = 6,l мбар, t — температура.
4.6. Изменение характеристик перемещающейся по вертикали
массы влажного воздуха
1. Ниже уровня конденсации вертикально перемещающийся
влажный воздух является ненасыщенным, поэтому (при
пренебрежении эффектом вовлечения) относительное содержание
водяного пара в поднимающейся воздушной массе остается
постоянным:
q «/n« const. (4.6.1)
Тогда из формул (4.1.4) и (4.1.5), связывающих удельную
влажность и отношение смеси с упругостью водяного пара и
давлением влажного воздуха, следует, что ниже уровня конденсации
— = ^- = const. (4.6.2)
Р Ро
Беря логарифмическую производную и используя уравнение
статики (квазистатическое приближение), находим из (4.6.2)
е dz р dz RT ' ^.o.oj
Формула (4.6.3) показывает, что относительные изменения
1 Точность, даваемую этой формулой, можно оценить путем сравнения
вычисленных величин с табличными данными, полученными численно с учетом
более точной температурной зависимости L, или с измеренными значениями.
84
Глава 4
упругости и давления равны между собой и обратно
пропорциональны температуре окружающей среды. Приняв Г = 270 К, g =
* 1 de
= 9,8 м/с2 и/? = 287 м2/(К-с), получим —^—1%/100 м, т. е.
е dz
в среднем упругость водяного пара до уровня конденсации
убывает с высотой примерно на 1 % на каждые 100 м.
Максимальная упругость зависит только от температуры и
описывается уравнением Клаузиуса—Клапейрона, из которого
следует
J de^ _L d_T_
es dz RnTi dz m ^.o.t;
В главе 3 было получено соотношение (3.3.6) для изменения
температуры поднимающегося сухого воздуха при заданном
притоке тепла. Как уже отмечалось, это соотношение можно
использовать и при подъеме ненасыщенного влажного воздуха, понимая
под Т виртуальную температуру. В зависимости от величины
dT.
притока тепла величина ——, а следовательно, и относительные
dz
изменения максимальной упругости могут принимать разные
значения. Если предположить, что подъем влажного воздуха
происходит адиабатически, то тогда до уровня конденсации его
температура меняется по сухоадиабатическому закону ( —— = —уЛ
и из (4.6.4) следует
1 des __ ^7а
dz " RnT*
(4.6.5)
Хотя температура воздуха и скрытая теплота испарения
изменяются с высото^, можно получить приближенную оценку
относительного изменения упругости насыщения с высотой, приняв
£в-п = 2,5 кДж/г, Г = 270 К- Из (4.6.5) при этом получим
—?-~—7%/100 м, т. е. упругость насыщения убывает с
высоте dz
той примерно на 7% на каждые 100 м. Следовательно, в
реальной атмосфере соотношение между выражениями (4.6.3) и (4.6.5)
таково, что максимальная упругость уменьшается с высотой
быстрее, чем упругость водяного пара, что приводит к росту с
высотой относительной влажности f до тех пор, пока на уровне
конденсации она не достигает 100%. Из определения f находим
1 df 1 de 1 des g L dT
f dz e dz es dz RT RnT2 dz
(4.6.6)
В случае адиабатического процесса получим, используя прибли-
Термодинамические процессы во влажном воздухе 85-
женные оценки
1 de
1 de8
и
1 df
«6%/ЮО м, т. е. отно-
е dz " es dz f dz
сительное увеличение с высотой относительной влажности
составляет 6% на 100 м. Схематически изменения характеристик
влажного воздуха представлены на рис. 4.4.
2. Получим теперь формулу для определения уровня
конденсации. Уровнем конденсации называется высота z = hKy на
которой в поднимающемся влажном воздухе водяной пар достигает"
•г=К
■1=0
Рис. 4.4. Схематическое изображение изменения
характеристик влажного воздуха с высотой.
состояния насыщения и температура воздушной массы
становится равной температуре точки росы т:
T(z)\z=h=,(z)\z=hK. (4.6.7).
Если ввести средние в слое 0—hK градиенты температуры
(-—j и точки росы (—*—) » то можно получить
приближенное соотношение для определения Ак, записав
Г(Ак) = Г0+(4^)с/к,
х(Ак) = -о+(-£г)срЛк.
(4.6.8) •
где Т0 и То — температура воздуха и температура точки росы на
начальном уровне. Подставив (4.6.8) в (4.6.7), получим
(Л.) -(JL)
\ dz /ср \ dz /ср
86
Глава 4
Разность Т — т называется дефицитом температуры точки росы.
Из формулы (4.6.9) следует, что уровень конденсации зависит от
начального дефицита температуры точки росы и от средних
в слое градиентов температуры и точки росы.
При практическом использовании формулы (4.6.9) возникают
трудности, связанные с тем, что градиенты температуры не
измеряются на метеорологических станциях. В то же время
определение уровня конденсации представляет значительный интерес,
поскольку этот уровень обычно близок к нижней границе вну-
тримассовых конвективных облаков. Поэтому важно получить
соотношение для вычисления уровня конденсации по данным
стандартных метеорологических наблюдений. С этой целью
выполним приближенную оценку среднего градиента температуры
точки росы. Уравнение Клаузиуса—Клапейрона (4.5.16),
записанное в виде
dT T(V2-V\)
dp
(4.6.10)
определяет изменение температуры перехода из одной фазы
в другую при изменении давления (например, точки замерзания
или точки росы). Применяя (4.6.10) к описанию изменения
температуры точки росы ——, пренебрежем объемом жидкости Vi
ае
по сравнению с объемом водяного пара Уг и используем уравне-
D т
ние состояния идеальных газов Уг=—-—. Тогда (4.6.10)
запишется так:
dz zRnT
(4.6.11)
de Lb-ne
Из (4.6.11) с учетом формулы (4.6.3) находим
dz Z.B_n е dz RLB-n v '
Для получения приближенной оценки примем т^270 К, £в-п =
= 597 кал/г. Тогда
-^г^-0,17 К/100 м. (4.6.13)
AT
Подставив (4.6.13) и —р-=—Ya (считаем процесс адиабатиче-
dz
ским) в (4.6.9), получим следующее соотношение для
приближенной оценки уровня конденсации:
Лк«122(Го-<с0), (4.6.14)
Лк — в метрах.
Термодинамические процессы во влажном воздухе 87
Попытки применить формулу (4.6.14) для определения
высоты нижней границы облаков показали, однако, существенное
расхождение с фактическими данными. В некоторых случаях
удается уменьшить ошибку введением в формулу (4.6.14)
добавки аДГ, учитывающей как понижение температуры воздуха
ниже температуры точки росы, необходимое для появления
избытка влаги, так и влияние ядер конденсации. Предложены
также и другие методы определения высоты нижней границы
облаков, изложение которых выходит за рамки настоящей книги.
3. Рассмотрим изменение характеристик поднимающегося
влажного воздуха выше уровня конденсации. Поскольку при
подъеме насыщенного влажного воздуха происходит
конденсация, плотность пара убывает с высотой быстрее плотности
влажного (или сухого) воздуха, так что удельная влажность и
отношение смеси с высотой уменьшаются. Если предположить, что
насыщенный водяной пар в первом приближении можно
описывать уравнением состояния идеальных газов, то можно и для
насыщенного влажного воздуха использовать соотношение
qs*zmsfi* 0,622-^-, (4.6.15)
из которого следует
1 dqs 1 des 1 dp L dT g
qs dz es dz p dz RnT* dz RT
(4.6.16)
Из полученного выражения видно, что для определения
относительного изменения с высотой удельной влажности и
максимальной упругости нужно выяснить, как меняется с высотой
температура поднимающегося насыщенного влажного воздуха.
Используем для этой цели уравнение первого начала
термодинамики, которое с учетом уравнения статики запишется так:
dQ = cpdT+g^dz. (4.6.17)
Уже отмечалось, что приток тепла может быть обусловлен
различными причинами. При перемещении насыщенного
влажного воздуха удобно выделить приток тепла, связанный с
фазовыми переходами, который в соответствии с (4.5.15) можно
написать в виде
dQ^=-Ldqs. (4.6.18)
Подставив в (4.6.17) dQ = dQ* + dQ$M=dQ* — Ldq& и разделив
все члены уравнения на cpdz, получим
-88
Глава 4
Здесь через dQ* обозначены все виды притоков тепла, кроме
й!(2фаз.
-Используя для формулу (4.6.16), найдем
dT
dz
1
ср
1+-
dQ*
dz
D /> TO.
1 +
^—• (4.6.20)
Для влажноадиабатического процесса, т. е. процесса, при
котором отсутствует теплообмен между системой и окружающей
/ ^Q* \
средой I ——=01 , но имеется приток тепла, связанный с фазо-
(йЮфаз \
—-т^—=—Ldqs¥=0 I , из (4.6.20) находим
1+-
■£—Т^у^—Те. (4.6.21)
RnCpT
Градиент температуры, определяемый формулой (4.6.21),
называется влажноадиабатическим градиентом. Легко убедиться
в том, что в (4.6.21) знаменатель дроби больше числителя и,
следовательно, увл<Уа, что является очевидным из физических
соображений. Таким образом, при адиабатическом перемещении
•объема воздуха до достижения состояния насыщения его
температура изменяется с высотой по сухоадиабатическому закону:
dT . .
——=—Ya. После достижения насыщения дальнейший подъем
dz
сопровождается выделением скрытой теплоты и, следовательно,
скорость изменения температуры будет меньше, чем Ya. Важно
•отметить, что, в отличие от Ya, Yen является переменной
величиной. Расчеты показывают, что при больших положительных
температурах Увл может существенно отличаться от Ya, достигая
0,5°С/100 м. При отрицательных температурах qs-+0 и увл~>Уа-
В табл. 4.1 приведены значения влажноадиабатического
градиента для разных значений температуры и давления.
Зная увл, можно определить относительные изменения с
высотой удельной влажности, отношения смеси и максимальной
упругости. Относительная влажность выше уровня конденсации
остается постоянной. Схематически изменение характеристик
поднимающегося влажного воздуха ниже и выше уровня
конденсации представлено на рис. 4.4. Можно оценить изменение с высо-
Термодинамические процессы во влажном воздухе 89
о.
О
S
S
а>
ю
со
8
8
1
*
■
•
1
i
1
1
ее О
О. о
о» >-'
£ о.
Ю CD Г«- 00 О ^ 00 Ю С- О т£ СЛ СО СО СМ г—< О Г^- О Tf СО QO
_ __ _ _ о) CM csj £М СМ со со со ^ ю СО t^- 00 00 о сл сл сл
о" о" о" о" о" о" о" о" о" о" о" о" о* о" о" о о" о" о* о" о" о*
0О О 1—• со со Ю О 00 ^ Ю ^ СМ СЛ О Ю Ю СО ~н со СМ ю ю
а5г^счсо^соо5^юоюсоос7)сосооосо10^соо>
1—• см см см см см см со го ^ т*< ю со со t^ оо оо сл сл о сл сл
о о о*4 о" о* о" о" о" о* о" о" о* о" о" о* о" о" о" о" о" о" о*
СО тГ t^ СМ О СО Ю Ю СМ О СО Ю CM rf СЛ СО СМ СМ у—• СО СМ СЛ
см со ^ СО 00 О СО t^ СМ 00 ^ 1—' ОЭ СО СМ ОО СМ ю ь- 00 О? сл
СМ CM СМ CM СМ СО СО СО ^ т*« Ю СО СО t^ ОО 0О СЛ СЛ Сл сл сл сл
о*о*о о*о"о"о"о"о*о*о"о"о"о"о*о*о"о*о"о"о"о"
1—• СО О СО СЛ 00 Ю О CM СО СО h- СО i—' СО О СМ ^ Сл 00 СО О
^ ю со оо о со t4-. cn t^ со о t^. ^ 1—< со ^н ^ со i^ оо а> о
см см см см со со со ^ ^f ю со со ь- оо оо о сл сл сл сл ел о
о"о о~о о о о о^о^о^о^о о~о*о о~о~о о'о'о"^
lO'-'SOJiOCT^ONOOOiOfNOS^COTj'FHOOi-' |
ю t^- оо о со со i—• со ^ t^. ю см оо -^ а> см ю t^- оо а> сл о
СМ СМ см со ГО СО ^ "Ф Ю in СО h- h- 0О 00 О) Сл Сл СЛ СЛ СЛ О
о*о о о о о о о оо о о о" о" о* о" о* о" о" о* о" »-•
СЛ Ю Tf СЛ Сл Ь- CM t^ Tf СЛ Is- со Ю СО Ь- 05 СМ Сл 00 т*« Сл см
СО 00 О СМ Ю СЛ "^ СЛ Ю 1—' оо Ю 1—• со О СО СО f^ 00 СЛ Сл о 1
СМ СМ СО СО СО СО rf ^- Ю СО СО Г^. 00 00 СЛ СЛ СЛ СЛ О СЛ СЛ О
о о" о* о" о" о" о" о" о" о" о" о" о" о о о" о~ о" о~ о" о" *-н Г
(NO^NCSC4^NSC0SOiOOO0000C0^iOOiN
OOOCMTfOOCMt^CMOOlOi—iOOCOOOCMTfC00005Q500
CM CO CO СО СО Tf ^ Ю Ю СО h- t^ 00 00 Сл Сл Сл О Сл сЬ о о
о~ о* о" о" о* о* о" о" о" о* о* о" о" о" о" о* о" о" о" О ^ ^н
со СО 00 СО СМ СО 00 Ю СО О 1—• СМ СО СО Сл со см со СО ь- о см
СЛ ^ СО СО О ^ Сл Ю 1—• 00 ^ О Ю CD СМ Ю h- 00 Сл ф О О
см со со со ^ ^ ^ ю со со t^ оо оо оо сл а> сл сл ел ел о о
о о о о о"о о о о о о о о о о о о о о о"^н ^
tJ* СО CM Tf СМ 00 О 00 О Ю СМ СЛ t^ Tf СО ^н СО 00 Tf 00 у-1 см
О СМ Ю 00 CM СО CM С^ Tf о СО у—< СО О СО СО h- оо СЛ СГ5 о о
со со со СО тГ ^ Ю Ю СО I"- 1^ 00 00 СЛ СЛ Сл СЛ Сл сл сл о о
о"о"о о do о"о о о о о'оЪ оЪ"© о о"о г-, м
Ю Ь- со О О Ь- Сл со СЛ со О СО Сл со *—• rf оо Сл Ю Сл »—• СО
^нСОСОО^ООСОСЛЮСМООСО^!—'TfcOb-ООСЛСЛОО
СО СО СО ^f ^f ^t4 Ю Ю СО t^- h* 00 00 СЛ СЛ СЛ СЛ О) <J5 Сл О о
о" о" о* о о" о" о" о" о* о" о" о" о" о" о" о" о" о" о" о".-».-•
о ю о ю о ю о ю о ю о ю о ю о ю о ю о ю о ю
^ со со СМ СМ •—"—• 1 1—I 1—1 см см со со ^ ^t* Ю Ю СО СО
1 1 1 1 1 1 1 1 1 1 1 1 1
90
Глава 4
той количества конденсирующегося водяного пара. Из уравнения
состояния насыщенного водяного пара рд= находим
1 rfpn 1 rfg5 4Г 1 ^Г
Рп dz es dz dz T dz
^-^(^r-1)-^6-22)
В этом выражении ^>1, поэтому можно написать
1 d?n Ъл£
ИЛИ
dn W^l_ (4.6.23)
dz /?2Г3 " '
Рассчитав по (4.6.23) —j-^- и предположив, что вся сконден-
аг
сированная влага остается во взвешенном состоянии, можно
оценить водность облака б (количество влаги в единичном объеме
воздуха), задав среднюю толщину облака. Ниже приведены
результаты расчета ——^- и б (при dz = 500 м) для разных
температур:
t °С -20 -10 0 10
-^-г/(м3.100 м) 0,03 0,14 0,25 0,34
г г/мз 0,4 0,7 1,2 1,7
Из этих данных следует, что водность увеличивается при
повышении температуры. Отметим, что полученная температурная
зависимость и порядок величины б согласуются с данными
наблюдений, хотя значения водности, как и следовало ожидать,
оказываются завышенными.
Контрольные вопросы
1. Чем отличаются условия равновесия перемещающейся
массы ненасыщенного и насыщенного влажного воздуха?
2. Каким состояниям соответствуют участки АВ и DE кривой
Ван-дер-Ваальса? Наблюдаются ли такие состояния в
атмосфере?
Термодинамические процессы во влажном воздухе 9 К
3. Чему равен приток тепла к частице при влажноадиабати-
ческом процессе?
4. Почему до уровня конденсации удельная влажность и
отношение смеси не меняются с высотой?
5. Какие предположения делаются при выводе формулы
(4.6.14)?
6. Вывести формулу для влажноадиабатического градиента,
* д.д. I dm
в которой учитывался бы эффект смешения, причем сс= —=
т dz
= const.
Глава 5. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ
ТЕРМОДИНАМИЧЕСКИХ ФЛУКТУАЦИИ
К АТМОСФЕРНЫМ ПРОЦЕССАМ
Термодинамические флуктуации. Статистический смысл энтропии. Вероятность
термодинамических флуктуации. Вычисление флуктуации термодинамических
величин. Условия образования новой фазы. Вероятность образования
зародышей новой фазы. Вычисление потоков различных субстанций.
В главах 3 и 4 рассмотрены некоторые процессы,
протекающие в сухом и влажном воздухе, на основе соотношения
равновесной термодинамики без прямого учета внутреннего строения
газов. В то же время имеется ряд явлений, обусловленных
молекулярным движением, изучение которых представляет большой
интерес для метеорологии. К таким явлениям относятся, в
частности, рассеяние света в атмосфере на флуктуациях плотности,
•образование зародышей новой фазы и др. Вообще, динамика
образования и развития облаков, процессы кристаллизации, а
также такие важные прикладные вопросы, как обледенение
самолетов, образование конденсационных следов за самолетами и др.,
не могут быть исследованы без детального изучения
микрофизических процессов, протекающих в дискретной среде.
В настоящей главе рассмотрены некоторые вопросы,
выходящие за пределы равновесной термодинамики, в частности
термодинамические флуктуации и их вероятность, образование
зародышей новой фазы в результате флуктуации, процессы переноса
различных субстанций молекулярным движением.
5.1. Термодинамические флуктуации. Статистический
смысл энтропии
Уже отмечалось, что при термодинамическом описании
отвлекаются от внутреннего строения систем, которые
рассматриваются как сплошные среды; при неизменных внешних условиях их
термодинамические характеристики (температура, давление
и др.) должны иметь определенные постоянные значения. В
действительности, однако, вследствие хаотического движения
молекул термодинамические характеристики замкнутой системы
испытывают случайные колебания около некоторого среднего
значения. Отклонения параметров от их среднего значения (/' =
= / — /) называются флуктуациями. Наличие флуктуации не мо-
Приложения теории термодинамических флуктуации 93
жет быть объяснено в рамках термодинамики, так как для этого
необходимо учесть внутреннее строение системы. Исследование
свойств макроскопических тел в состоянии равновесия на
основании известных свойств молекул, из которых они состоят,
является предметом статистической физики.
Чтобы понять причину возникновения флуктуации, а также
выяснить статистический смысл энтропии, рассмотрим, как
характеризуется равновесное состояние газа в замкнутой системе
с термодинамической и статистической точки зрения. При
термодинамическом описании температура, давление, плотность,
внутренняя энергия и другие макроскопические характеристики
газа в состоянии равновесия должны иметь постоянные значения.
Энтропия газа при этом максимальна. Как будет показано ниже,
в равновесном состоянии наиболее вероятным является
равномерное распределение молекул газа по объему. При этом
макроскопические характеристики с большой точностью равны своим
средним значениям. Но вследствие хаотического движения
молекул возможны случаи, когда при равновесии распределение
молекул по объему будет неравномерным. Это приводит к
отклонениям значений макроскопических величин от средних, т. е.
к их флуктуациям.
Рассмотрим более подробно вопрос о статистическом
описании равновесного состояния изолированной системы (газа). Газ
состоит из огромного числа молекул, каждая из которых в
данный момент времени занимает фиксированное положение и имеет
определенную скорость (а следовательно, импульс и энергию).
Поэтому в каждый момент времени состояние всего газа, которое
называется его микросостоянием, определяется совокупностью
значений всех параметров, характеризующих состояние каждой
молекулы. Следовательно, если в газе имеется N молекул, то его
микросостояние определяется заданием 6/V параметров — для
каждой молекулы нужно задать три координаты и три
компоненты скорости (для простоты мы отвлекаемся от квантовой
природы молекулярного движения). В то же время
макроскопическое состояние газа, характеризующее его средние свойства,
зависит от существенно меньшего числа параметров. Это связано
с тем, что оно, в частности, определяется средней концентрацией
и средней суммарной кинетической энергией молекул, которые
вследствие тождественности молекул не меняются при
перестановке координат последних; направление скорости молекул также
не влияет на суммарные средние характеристики. Из этого
следует, что заданное макроскопическое состояние может быть
реализовано с помощью большого числа микросостояний, ибо
любые микросостояния, приводящие к заданным средним
значениям параметров системы, но отличающиеся набором 6N
координат и импульсов, будут макроскопически неотличимы.
94
Глава 5
Число микросостояний W, при котором реализуется данное
макроскопическое состояние системы, называется
термодинамической вероятностью.
Не вдаваясь в некоторые детали, связанные с квантовыми
эффектами, вычислим термодинамическую вероятность
пространственного распределения молекул в фиксированном объеме
идеального газа, содержащем TV молекул. Разделим объем на М
равных ячеек. Пусть молекулы совершенно произвольно
распределены по этим ячейкам. Микросостояние газа характеризуется
набором величин пи определяющих число частиц, содержащихся
в i-той элементарной ячейке; l^i^M. Естественно, что
м
2 Щ = Ы. (5.1.1)
Термодинамическая вероятность, т. е. число способов,
которыми можно распределить N молекул по М элементарным
ячейкам, определяется соотношением
y-vv"'-..--jrT- (5,-2)
11 nt\
i = \
Считая, что число частиц, заключенных в каждой элементарной
ячейке, достаточно велико, можно с помощью формулы
Стерлинга
Л|!=(-^_у\ 1п/г£ ! = /г, (ln/г^ —1)
переписать (5.1.2) в виде
м
In W=A — 2 я, In я,. (5.1.3)
i= 1
Здесь под А понимаются все члены, не зависящие от /гг-, т. е.
A = JV(ln7V-l)-f 2 nt = NlnN.
Выясним теперь, какое распределение молекул является
наиболее вероятным, т. е. при каких значениях щ величина W имеет
максимум. С учетом (5.1.1), из которого следует
м
2 8л£=0, (5.1.4)
i = l
условие максимума W можно записать в виде
м
IW=- 2 8л* In л* = 0. (5.1.5)
i = \
Приложения теории термодинамических флуктуации 95
В силу (5.1.4) это соотношение выполняется только при
пх = п2= . . . =пм. (5.1.6)1
Таким образом, наиболее вероятным является равномерное
распределение молекул газа по объему. Однако, как следует из
(5.1.2), вероятность неравномерного распределения частиц по
объему не равна нулю. При этом можно показать, что
вероятность малых отклонений от равномерного распределения
довольно велика, в то время как вероятность значительных
отклонений в системах, содержащих большое число частиц,
чрезвычайно мала. Ничто не препятствует всем молекулам, заключенным
в сосуд, собраться в малой его части, однако вероятность такого
состояния ничтожна.
Следовательно, в результате хаотических движений молекул
газ в замкнутой системе может находиться в различных
микросостояниях, но наиболее вероятным является состояние
равномерного распределения молекул, которому соответствует
максимум термодинамической вероятности. В этом состоянии
изолированная макроскопическая система находится наиболее часто.
При этом макроскопические величины (температура, давление
и др.) с большой точностью равны своим средним значениям,
энтропия и, как выше было показано, термодинамическая
вероятность системы максимальны. Такое состояние системы
называется статистическим или термодинамическим (или просто
тепловым) равновесием. Если в какой-либо момент времени система
не находилась в состоянии равновесия, а затем была
предоставлена самой себе, т. е. стала замкнутой, то через определенный
промежуток времени, называемый временем релаксации, она
перейдет в состояние статистического равновесия. Переход из
неравновесного состояния в равновесное сопровождается
увеличением термодинамической вероятности.
Из приведенных рассуждений видно как сходство, так и
различие между чисто термодинамической и статистической
трактовками. Различие, по существу, состоит в том, что утверждения
термодинамики имеют категорический характер, а статистической
1 В (5.1.5) величины бл* не являются независимыми, поскольку они
связаны соотношением (5.1.4). Из этого соотношения можно выразить 6rii через
м
все остальные вариации: 6aii= — 2^/2*' где ^п* тепеРь независимы. Тогда
(5.1.5) можно переписать в виде
м м
Ъп\\пп\-\- ^Ьш\пп1= ^ bni (1пп/ — ln/*i) = 0.
i=2 i=2
Вследствие независимости 6яг- это соотношение выполняется лишь при
In tii — In rti = 0, т. е. при /i»=ni.
96
Глава 5
физики — вероятностный. Статистическая физика
рассматривает все микроскопические состояния системы, а
термодинамика ограничивается исследованием только характеризующих
ее макроскопических величин, соответствующих наиболее
вероятным микроскопическим состояниям. (По образному
выражению Я. И. Френкеля, термодинамика как бы дает фотографию
системы, снятую с очень большой выдержкой, тогда как
статистика дает отдельные кадры фильма, расположенные, однако,
случайным образом.)
В то же время подобный характер поведения таких функций
состояния как энтропия S и термодинамическая вероятность W
(S и W максимальны при равновесии, переход из
неравновесного состояния в равновесное сопровождается увеличением S и
W)y указывает на взаимосвязь этих величин. Функциональная
связь между энтропией и термодинамической вероятностью
дается формулой Больцмана
S = kln W+C, (5.1.7)
представляющей основу статистического толкования
термодинамики (k — универсальная постоянная Больцмана). Соотношение
(5.1.7) показывает, что энтропия системы прямо
пропорциональна логарифму термодинамической вероятности. Изменение
энтропии системы при переходе из состояния 1 в состояние 2
равно
где Wi и Wi, Si и 5г — термодинамические вероятности и
энтропии состояний 1 и 2 соответственно. Если система переходит из
неравновесного состояния в равновесное, то W2>Wi и S2>Si.
Таким образом, увеличение энтропии связано с переходом
системы из менее вероятного в более вероятное состояние. Однако
возможны процессы, протекающие с уменьшением энтропии, хотя
для макроскопических систем их вероятность мала. Такие
процессы приводят к флуктуациям термодинамических величин,
которые играют важную роль в целом ряде явлений.
5.2. Вывод формулы для вероятности термодинамических
флуктуации
Пусть I — некоторый параметр, характеризующий состояние
изолированной системы (например, объем, температура и т. п.),
£ — его значение в состоянии равновесия, £' = 1 — £ есть
флуктуация; при равновесии £' = 0. Энтропия системы будет функцией |,
Приложения теории термодинамических флуктуации
97
т. е. S(l)\ при равновесии S0 = S(l). В соответствии с (5.1.7)
термодинамическая вероятность при равновесии равна
W0 = Cek =Ces{l)!k. (5.2.1)
Термодинамическая вероятность состояния, характеризующегося
мгновенным значением параметра g, равна
W=CeS{i)lk. (5.2.2)
Вероятность Я(£') флуктуации \' в системе, т. е. вероятность
состояния, при котором значение \ отличается от равновесного
значения |, пропорциональна отношению W/Wo* т. е.
s(S)-s(!)
р$)=Схе k . (5.2.3)2
Разложим S(l) в ряд около положения равновесия с
точностью до членов второго порядка:
S(9=s(D +
dS
di
Az-iH
a">S
d&
(Z-W
Так как энтропия максимальна при равновесии, то
dS
d\
. = 0,
d^S I
<o.
Следовательно,
где
5(0 = 5®-
a£S'2
1 rf2S
_ >
a — некоторая положительная величина.
в (5.2.3), находим
(5.2.4)
(5.2.5)
Подставив (5.2.4)
Р(\') = С}е 2 .
Постоянная Сь определяемая из условия нормировки
сю ,
}P(l')d£' = 1, равна у——. Подставляя значение Ci, получаем
1 Пропорциональна, а не равна, так как W0 не полное число
микросостояний, а число микросостояний, соответствующее равновесию.
2 Отметим, что формула (5.2.3) может быть получена также из более
общих положений статистической физики. Она часто называется формулой
Эйнштейна.
7 Заказ № 612
98
Глава 5
следующую формулу для вероятности флуктуации:
Распределение вероятностей такого вида называется
нормальным или гауссовым распределением. Оно имеет максимум
при !■' =0 (т. е. наиболее вероятным является состояние
равновесия) и быстро спадает с увеличением |' симметрично в обе
стороны (одинаковые значения положительных и отрицательных
флуктуации равновероятны).
Поскольку для получения величины а по (5.2.5) нужно знать
вид функции 5(g), что обычно оказывается затруднительным,
удобно выразить ее через легко определяемую характеристику.
Для этой цели вычислим с помощью (5.2.6) средний квадрат
флуктуации |/2, называемый дисперсией случайной величины:
оо оо <х£'2
— оо — оо
Следовательно, формулу для вероятности флуктуации можно
записать в виде
С'2
рм=тте 2"- (5-2J)
Величина дисперсии является единственным параметром
нормального распределения. Чем меньше дисперсия, тем более
острый максимум имеет функция Р (£').
5.3. Вычисление флуктуации термодинамических величин
Применим полученные выше соотношения для определения
средних квадратов флуктуации термодинамических величин, из
которых для нас наибольший интерес представляют флуктуации
плотности в газе, так как именно ими обусловлен один из видов
рассеяния света в атмосфере.
Обычно интерес представляют флуктуации, происходящие не
во всей замкнутой системе, а в достаточно малой, но
макроскопической ее части.2 Так, применительно к атмосфере можно рас-
1 Хотя при получении Р (£') флуктуации |' считались малыми, область
интегрирования можно распространить на все значения |' от —оо до +оо,
так как подынтегральная функция быстро убывает при увеличении |£'|;
можно полагать, что искажения функции Р(£') для больших £' будут поэтому
мало влиять на результат.
2 В частности, при исследовании рассеяния нужно знать флуктуации
в объеме, линейные размеры которого порядка длины волны.
Приложения теории термодинамических флуктуации
99
смотреть некоторый малый, но макроскопический объем
воздуха. Этот объем можно считать некоторой замкнутой
подсистемой, а окружающую среду с постоянной температурой Го можно
рассматривать как термостат. Будем считать, что флуктуации
происходят только в выделенном объеме, а окружающая среда
все время находится в равновесном состоянии.
Можно представить, что подсистема искусственно переведена
в новое равновесное состояние, в котором термодинамические
величины имеют флуктуационные значения, например, под
влиянием работы АЛ, совершаемой над подсистемой внешним
источником. В действительности флуктуации происходят
самопроизвольно, но, чтобы можно было использовать
термодинамические соотношения, удобно представить, что система переведена
в новое состояние под влиянием работы АЛ.1 При этом
предполагается, что параметры изменяются достаточно медленно,
вследствие чего в каждый данный момент успевает установиться
равновесное состояние.
Поскольку термостат и подсистема вместе составляют
замкнутую систему, то применима формула (5.2.3), но в ней AS =
= S(£)—S(l) теперь означает полное изменение энтропии
системы, складывающееся из изменения энтропии термостата AS0,
которая изменяется только вследствие флуктуации в подсистеме,
и изменения энтропии подсистемы ASn, происходящего в
результате флуктуации, т. е. AS=AS0 + ASn. Формула для вероятности
флуктуации теперь запишется так:
AS0+ASn
Р$) = Се * . (5.3Л)
В силу предположения о медленности изменения параметров
подсистемы справедливы термодинамические соотношения,
полученные для равновесных систем. Из основного
термодинамического соотношения (4.3.6) следует
А5„= А£»-" + ^"-^ , (5.3.2)
где Го и ро — равновесные температура и давление подсистемы,
равные соответствующим величинам термостата. Из этой
формулы ясно видно, что АЛ — работа, совершаемая внешним
источником, а не термостатом, ибо последняя равна poAVu. Для
термостата
Д50= А£в.о + Р0АКР ^ (533)
1 Такой подход иногда называют полутермодинамической теорией
флуктуации.
7*
100
Глава 5
В силу замкнутости системы (термостат +подсистема)
внутренняя энергия и полный объем остаются постоянными:
Д£'в.о+А£,в.п = оГ
AVr0 + Al/„ = 0. (5.3.4)
Поэтому, подставив (5.3.2) и (5.3.3) в (5.3.1), получим
_ АЛ
Р(£) = Се *У°. (5.3.5)
Таким образом, можно сказать, что мерой вероятности
флуктуации является работа, которую нужно совершить над
системой для перевода ее во флуктуационное состояние.
Подсчитаем теперь работу, которую нужно совершить для
того, чтобы имела место флуктуация объема V = Vn—1/п = АКп
при постоянной температуре. Для простоты представим себе газ,
заключенный в сосуд под поршнем. При равновесии давление
в сосуде равно внешнему давлению. При флуктуационном
изменении объема происходит изменение давления на величину Др =
= (—— ) AV, причем AV = 5z, где s — площадь поршня, а г —
\ OV I т
смещение поршня. Элементарная работа 6Л, совершаемая при
смещении поршня на величину dzy равна
bA=-bpsdz=-(-l$r)T0zdz=-(-lf)TLVdW.
Работа АЛ, совершаемая при изменении объема на величину V,
равна
w— \№),mw— (#),-£-• <**■*>'
Подставив АЛ из (5.3.6) в (5.3.5), получим формулу для
вероятности флуктуации объема при постоянной температуре:
/_др_\ у*
P(V>)=Ce[dv}r2kT\ (5.3.7)
Сравнивая эту формулу с (5.2.7) для вероятности флуктуации,
найдем выражение для среднего квадрата флуктуации объема
1 При малых изменениях объема величину \~Ayj можно считать не
зависящей от ДУ и вынести за знак интеграла.
Приложения теории термодинамических флуктуации 101
Зная флуктуации объема, можно найти флуктуации
плотности. Поскольку р = —, то
ут и у2^-уг= у% • (5.3.9)
ьт
yi уч Kl
Относительная флуктуация плотности равна
р'2 _ «' \дР )т _ krx /*<um
-£Г— у-2 у~> (0.3. 1UJ
1 /dv \ I
где X = —— (—д—) т — изотермическая сжимаемость I заметим,
что I —— ) .<01 . Интересно отметить, что относительные
средние квадратические флуктуации плотности обратно
пропорциональны размеру (объему) подсистемы, в которой они происходят.
Как уже отмечалось, именно флуктуациями плотности
обусловлен один из видов рассеяния света в атмосфере — так
называемое релеевское рассеяние (см. главу 6).
5.4. Условия образования новой фазы
Фазовые превращения воды оказывают существенное
влияние на атмосферные процессы. Остановимся поэтому на
рассмотрении некоторых вопросов, связанных с образованием
новой фазы.
Из анализа условий равновесия различных фаз, описанных
в предыдущей главе, следовало, что как только химический
потенциал существующей фазы, например водяного пара, окажется
выше химического потенциала другой фазы, например воды,
должен произойти фазовый переход, в данном случае конденсация.
Однако экспериментально было установлено, что если среда
является однородной (т. е. водяной пар является чистым, в нем не
содержится посторонних примесей), то при e = es конденсация не
происходит даже при температурах, значительно меньших
температуры точки росы. В чистом водяном паре затягивается
конденсация, при этом пар из устойчивого состояния переходит в мета-
стабильное состояние (переохлажденный или пересыщенный
пар). Совершенно аналогичная ситуация возникает и при других
фазовых переходах.
Экспериментальные исследования показали, что переход
через метастабильное состояние представляет не исключение,
а общее правило для фазовых переходов, происходящих
102
Глава 5
в однородных средах. В этой связи целесообразно рассмотреть
возникновение новой фазы в простейших условиях, когда среда
является однородной.
Возможность существования метастабильных состояний
связана с поведением молекул, находящихся в тонком
поверхностном слое, разделяющем обе фазы. Детальное изучение
поверхностного слоя представляет весьма сложную задачу, выходящую
за рамки термодинамики, так как требует учета взаимодействия
молекул. В термодинамике учет поверхностного слоя
производится чисто феноменологически, при этом слой считается
бесконечно тонкой поверхностью раздела, разграничивающей обе
фазы. Площадь 5 поверхности раздела является новым
параметром, характеризующим состояние системы. При данном объеме
система может иметь разную поверхность раздела, причем
каждому значению 5 соответствует свое состояние системы.
Изменение поверхности раздела сопровождается
производством или затратой работы. Работа, необходимая для изменения
поверхности раздела на величину ds при постоянной
температуре, равна
dA=-ods. (5.4.1)1
Знак минус указывает, что увеличение поверхности (ds>0)
требует затраты работы. Величина а является основной
характеристикой поверхности раздела, она называется коэффициентом
поверхностного натяжения. Из (5.4.1) следует, что коэффициент
поверхностного натяжения измеряется работой, необходимой
для увеличения поверхности на 1 см2 при постоянной
температуре.
Остановимся теперь на важном вопросе об изменении
условий равновесия фаз при наличии поверхности раздела.
Рассмотрим равновесие пара с жидкостью. Благодаря поверхностному
натяжению объем жидкости стремится принять форму с
минимальным отношением площади к объему. Небольшие количества
жидкости явно обнаруживают стремление принять сферическую
форму; в случае больших количеств жидкости влияние других
сил (например, силы тяжести) может нарушить сферическую
форму. Капли жидкости вследствие поверхностного натяжения
испытывают добавочное поверхностное давление рп, которое
может быть вычислено из следующих соображений. Формула
(5.4.1) описывает работу dA, необходимую для изменения
поверхности капли на величину ds. Поскольку при изменении
поверхности меняется и объем капли, эту работу можно с другой
1 Выражение (5.4.1) по внешнему виду напоминает формулу для работы
расширения ЬА = —pdV. Можно сказать, что а играет для поверхности такую
же роль, как давление для объема.
Приложения теории термодинамических флуктуации 103
стороны рассматривать как работу сжатия (или расширения),
производимую поверхностным давлением рп, т. е.
eds^pndV,
откуда
ds
Pn = *^V- (5.4.2)
Величина —— представляет собой кривизну поверхности раз-
а\
дела. В случае сферической поверхности
ds d(4r.ri) _ 2
dV ~~ Ji 4
d
(■§■-) '
Л,—T", (5.4.3)
где r — радиус капли.
Таким образом, при наличии сферической поверхности
раздела для равновесия жидкости и пара должно выполняться
соотношение
Р* = е+^-, (5.4.4)
где рж — давление в жидкости. В случае плоской поверхности
раздела (г-+оо) из (5.4.4) следует обычное условие равенства
давлений двух фаз при равновесии. Добавочное давление,
связанное с криволинейной поверхностью капли, оказывает
существенное влияние на равновесное давление пара над каплей и
скорость испарения капли. Связь между равновесными давлениями
пара над плоской (es) и сферической (ег) поверхностями можно
установить, записав условие равенства химических потенциалов
пара (первая фаза) и воды (вторая фаза):
Me. Т) = ъ[е+-%-, Т). (5.4.5)
Продифференцировав (5.4.5) при Т = const, получим
Заменив в (5.4.6) ( * J =Vn и ( 2 ) =Vm [см. формулу
(4.5.10)], найдем
(vn-VM)de=-2oVM-%-. (5.4.7)
104
Глава 5
Пренебрегая в левой части (5.4.7) молярным объемом
жидкости по сравнению с молярным объемом пара и используя
уравнение состояния Vn = RnT/e9 получим
de 2а 17 dr ,- Л оч
Интегрируя (5.4.8) от r-^oo (e = es) до г (е = ег), получим
^=^exp(wr)» (5А9)
1
где Рв=-г^ плотность воды.
V ж
Уравнение (5.4.9) показывает, что при малых размерах капли
давление еГу требуемое для конденсации, может быть
существенно больше упругости насыщения es. Отношение er/es
называется пересыщением. Следует иметь в виду, что г не может
быть меньше среднего расстояния между соседними молекулами
жидкости. Этому предельно малому значению г соответствует
зародышевая капля, состоящая всего из нескольких молекул.
Под зародышем понимается такая частица новой фазы, которая
при имеющемся пересыщении находится в равновесии с
окружающей средой. По формуле (5.4.9) можно оценить
пересыщение, необходимое для создания зародышей разного размера.
Оценим сначала предельное пересыщение, необходимое для
образования зародышевой капли, состоящей всего из нескольких
молекул. Приняв г = 4- 10~8 см, коэффициент поверхностного
натяжения воды сг = 74,22 дин/см2 при Г = 293 К, получим rmax =
= 13. Только при такой высокой степени пересыщения
зародышевые капли, состоящие всего из нескольких молекул, оказываются
жизнеспособными, т. е. способными не только сохраняться в
присутствии пара, являющегося по отношению к ним насыщенным,
но и расти путем его конденсации. Пересыщение существенно
уменьшается с ростом г: при г = 10~7 см = 2,8, а при г =
вг
= 10~6 см =1,1. Следует, однако, отметить, что в атмосфере
€s
пересыщение обычно составляет только доли процента, а в этом
случае такие мелкие зародышевые капли не могут быть
устойчивыми.
Ситуация меняется, если в веществе имеются посторонние
примеси достаточно большого размера, которые становятся
центрами образования новой фазы. В таком случае образование
новой фазы начинается практически сразу после достижения насы-
Приложения теории термодинамических флуктуации 105
щения. Этот факт имеет фундаментальное значение при изучении
проблемы образования облаков. Ниже вопрос образования
капель рассматривается более детально.
5.5. Вероятность образования зародышей новой фазы
Для того чтобы выяснить механизм образования новой фазы,
необходимо иметь в виду, что ее возникновение не может
начаться сразу во всем объеме, занимаемом прежней фазой.
Формирование новой фазы 2 в метастабильной фазе 1 начинается
с возникновения зародыша (маленькой капельки жидкости, если
рассматривается переход пара в жидкость) и его последующего
роста. Поэтому нужно рассмотреть условия образования
зародышей новой фазы в старой фазе. Чтобы в паре образовался
зародыш новой фазы, в некотором объеме должно возникнуть
сгущение молекул, вступающих во взаимодействие друг с другом
и образующих микроскопическую каплю. Соответственно для
образования в жидкости пузырька должно произойти разрежение
молекул в небольшом объеме жидкости. Такие сгущения или
разрежения можно рассматривать как флуктуации плотности.
Эти флуктуации, однако, отличаются от рассмотренных в п. 5.3
небольших флуктуации плотности, при которых сохранялось
данное агрегатное состояние системы. Флуктуации плотности, не
приводящие к изменению агрегатного состояния, называются
гомофазными. Наряду с гомофазными во всяком веществе могут
происходить флуктуации, приводящие к образованию плотных
молекулярных комплексов, которые можно трактовать как
зародыши новой фазы. Такие флуктуации называются гетерофаз-
ными. Они должны быть особенно резко выражены вблизи
кривой равновесия фаз.
Вычислим вероятность флуктуации плотности, приводящих
к образованию зародышей новой фазы. В соответствии с (5.3.5)
формула для вероятности образования зародыша новой фазы
может быть записана в виде
А (г)
P(r) = Ce kr , (5.5.1)
где А (г) —работа, необходимая для образования зародыша
радиусом г. Из основного термодинамического соотношения
следует, что эта работа равна изменению термодинамического
потенциала, возникающему при образовании в одной фазе
зародышей другой. Изменение термодинамического потенциала для
этого случая можно получить из следующих соображений.
Без учета поверхностных эффектов основное
термодинамическое соотношение для системы, состоящей из двух фаз одного
106
Глава 5
и того же вещества, при заданном объеме всей системы V
записывалось в виде dEB = T dS + \idN (в равновесии температуры,
давления и химические потенциалы обеих фаз одинаковы).
Чтобы учесть наличие поверхности раздела, в правую часть этога
соотношения нужно включить член, описывающий работу,
затрачиваемую на изменение поверхности раздела [см. (5.4.1)]:
dEB=TdS+\idN+ads. (5.5.2)
Соответственно дифференциал термодинамического потенциала
при r = const запишется
dQ = \idN + ads. (5.5.3)
Полный термодинамический потенциал системы, состоящей из
двух фаз, на основании (5.5.3) равен
G = [x1yV1 + lA2^2+a5» (5.5.4)
где juli, jut2 — химические потенциалы, а jVi, N2 — число частиц
соответственно первой и второй фазы. Изменение
термодинамического потенциала при возникновении в одной фазе
(термодинамический потенциал которой Gi = \XiN) другой фазы можно
представить в виде
bG=G-Gi = {p2-\><\)N2+GS. (5.5.5)
При получении (5.5.5) использовано очевидное условие N =
= 7Vi + yV2. Это и есть работа А(г)у идущая на образование новой
фазы. Предположив, что зародыш является сферическим,
выразим N2 и 5 через его радиус г с помощью очевидных соотношений
V 4 пг3
5 = 4яг2, N2=——=———1 где Уг — объем, приходящийся на
К2 О V2
одну частицу новой фазы. Тогда получим
A{r) = ^G = ~ (a2 - \н) -£-+W. (5.5.6)
Из (5.5.1) видно, что, чем меньше Л (г), тем больше
вероятность образования зародыша. При этом следует также иметь
в виду, что возникший зародыш должен быть устойчивым. Если
образование новой фазы приводит к уменьшению
термодинамического потенциала всей системы, то зародыш будет устойчивым.
Если же ——>0, то новая фаза будет неустойчивой. Из (5.5.6)
следует, что возможны два случая, изображенные на рис. 5.1.
В первом случае (кривая /) химический потенциал новой
фазы больше, чем старой, т. е. |ы2>Ц1. Образование новой фазы
является термодинамически невыгодным. Этому случаю
соответствует монотонный рост AG и А (г) с увеличением радиуса за-
Приложения теории термодинамических флуктуации 107
родыша. Максимальная устойчивость и максимальная
вероятность достигаются при г = 0, т. е. при отсутствии флуктуации.
Возникающие в результате флуктуации зародыши являются
неустойчивыми и через короткое время распадаются.
Во втором случае (кривая 2), когда Ц2<Ць с
термодинамической точки зрения устойчивой является вторая фаза. Однако
и в этом случае А (г) сначала растет с увеличением г, пока г<г0,
A(D=bG 4
Рис. 5.1. Зависимость работы, идущей на
образование зародыша, от его радиуса.
т. е., несмотря на то что в макроскопическом масштабе
устойчивой является новая фаза, малые зародыши новой фазы являются
неустойчивыми. Происхождение этой неустойчивости связано
с тем, что на образование новой фазы нужно затратить работу
А (г). Эта работа, как видно из (5.5.6), складывается из работы,
затрачиваемой на образование поверхности раздела (4яаг2),
и работы, идущей на изменение состояния системы в объеме W
При |Д2<щ эти два вида работы имеют разные знаки и
конкурируют друг с другом. При очень малых размерах зародышей
преобладающей является работа, идущая на образование
зародышей. Чем больше размер зародышей, тем большая работа
должна быть затрачена средой на их создание и тем меньше
вероятность их образования. Ситуация изменяется при г^г0: выигрыш
в работе за счет первого слагаемого в (5.5.6) начинает
преобладать над проигрышем. Чем больше г (при г>г0), тем больше
вероятность образования такого зародыша и тем он
устойчивее. Радиус г0, соответствующий максимуму А (г), определяет
108
Глава 5
минимальный размер зародыша, который оказывается устойчи-
лл dA I
еым. Из условия —— =0 находим
r0 = , 2°V2 , . (5.5.7)
Работа, затрачиваемая на образование зародыша радиусом г0г
в соответствии с (5.5.6) равна
Ifi па V0 4 о
Выразим в (5.5.8) разность jui—\х2 через степень
пересыщения с помощью соотношений (5.4.5) и (5.4.9):
H4-P2=V*-y-=tf„nn-J-. (5.5.9)
Подставив (5.5.8) с учетом (5.5.9) в (5.5.1), получим формулу
для вероятности образования зародыша радиусом г0:
Я(г0) = Сехр
16 ™*У\
3 Л/?2г31п2-^
п ех
(5.5.10)
Из (5.5.10) следует, что, чем больше степень пересыщения,
тем больше вероятность образования зародыша. Коэффициент
пропорциональности С вычислен в кинетической теории газов.
Приняв для водяного пара С = 1025, можно вычислить
вероятность образования зародышей при разной степени пересыщения,
или, что то же самое, число зародышей новой фазы,
образующихся в единицу времени. Для двукратного пересыщения
(—т— = 2\ Р(г)=10~69, т. е. в 1 см3 одна капля образуется за
10~69 с, или 1063 лет. При —^— = 3 среднее время образования
капли оказывается равным нескольким тысячам лет. При
изменяющемся от 4 до 5, число зародышей, образующихся в 1 с,
повышается от 1 до 1010. Таким образом, в гомогенной среде
спонтанная конденсация возможна лишь при наличии не менее
чем четырехкратного пересыщения. Этот теоретический вывод
согласуется с экспериментальными данными. В частности, опыты
в камере Вильсона показали, что в системе воздух—водяной пар
(без посторонних примесей) образование тумана происходит
только при восьмикратном пересыщении. Можно с уверенностью
заключить, что в свободной атмосфере никогда не имеют места
Приложения теории термодинамических флуктуации 109
столь большие пересыщения. Следовательно, спонтанная
конденсация водяного пара в атмосфере невозможна.
В действительности конденсация происходит на
присутствующих в воздухе посторонних примесях, называемых ядрами
конденсации, размеры которых близки к г0. При этом отпадает
необходимость в затрате работы на образование первичной
ассоциации молекул, а нужна лишь работа на рост капель от размеров
ядра конденсации до размера, соответствующего равновесию со
средой. Согласно (5.5.8), на образование зародыша радиусом г0
при спонтанной конденсации затрачивается работа А(г0) =
=— пог20 . При конденсации на ядре радиусом г на рост капли
о
от г до го затрачивается работа
Л(г)-Л(г0) = 4-™(г2-^) = -^-е ±™г\.$.ЪЛ\)
Роль ядра конденсации проявляется, следовательно, в
уменьшении работы образования зародыша. Каждому ядру
конденсации радиусом г соответствует определенное пересыщение er/es,
определяемое формулой (5.4.9), при котором работа образования
зародыша близка к нулю, т. е. на таком ядре может происходить
спонтанная конденсация при данном er/es. Оценки показывают,
что нижняя граница размеров ядер конденсации в атмосфере
порядка 10~6 см, т. е. 0,01 мкм.
Приведем пример, иллюстрирующий влияние ядер
конденсации на образование облаков в атмосфере. Предположим, что
масса воздуха, содержащего водяной пар, находится у
поверхности земли и имеет температуру Т0. В силу каких-то внешних
причин (например, под действием масс более холодного воздуха,
вытесняющих рассматриваемую массу воздуха вверх) она начинает
подниматься. При этом масса воздуха адиабатически
охлаждается, так что на уровне h ее температура
T(h)=T0-bfi. (5.5.12)
При адиабатическом подъеме справедливо уравнение
Пуассона
_ZJ*Le[^i*Lff", (5.5.13)
из которого при использовании (5.5.12) следует
p(h)=p0(^^!L)CpR. (5.5.14)
Кроме того, ниже уровня конденсации отношение упругости
по
Глава 5
водяного пара к давлению влажного воздуха сохраняется
постоянным, так что
e(h) = p(h)
(5.5.15)
Из (5.5.15) с учетом (5.5.14)
e(h) ( Го-таЛ VPl*
<о
-(-w
(5.5.16)
Из (5.5.16) можно по известному значению упругости
насыщения над плоской поверхностью eSOo{h) рассчитать отношение
М01Оэрг
16
12
Ш
1500 1600 1700 1800 1900 Км
Рис. 5.2. Зависимость работы,
идущей на образование зародышевых
капель в атмосфере, от высоты при
отсутствии (/) и наличии ядер
конденсации разных радиусов (2, 3 и 4)
2) л=б,5-10-7 см, 3) г=1,0-10-6 см, 4) г=
= 1,2- Ю-6 см.
es(h)/eSoo(h), т. е. пересыщение на любой высоте /г.1 Зная
пересыщение и определив Т (h) из (5.5.12), можно вычислить работу
образования зародыша. Если принять Г0~303 К и
относительную влажность воздуха вблизи земли / = 50%, т. е. е0=П,7 мбар,
то оказывается, что пересыщение наступает на высоте /г> 1400 м.
Рисунок 5.2 иллюстрирует зависимость работы образования
зародыша А(г) от высоты (начиная с Л = 1500 м) как при
отсутствии, так и при наличии ядер конденсации разных размеров.
Вероятность конденсации становится заметной, когда А(г)^0.
В рассмотренном примере заметная конденсация при отсутствии
ядер конденсации может происходить лишь при /i—Ю км. При
наличии ядер конденсации радиусом 6,5-10~7, 1,0- 10~6 и 1,2Х
X Ю-6 см заметная конденсация наступает соответственно на
высотах 1760, 1655 и 1625 м.
1 Можно допустить, что использование формулы (5.5.16) для
насыщенного влажного воздуха не приводит к существенным погрешностям.
Приложения теории термодинамических флуктуации 111
5.6. Вычисление потоков различных субстанций
Ниже будут получены формулы для потоков различных
субстанций, обусловленных молекулярным движением.
Необходимость рассмотрения этого вопроса связана с тем, что
диффузионные потоки входят в основные уравнения гидротермодинамики
(см. главу 1). Хотя, как будет показано ниже (глава 7),
интенсивность молекулярного переноса существенно меньше
интенсивности турбулентного переноса, в некоторых процессах,
представляющих интерес для метеорологии, перенос субстанций
молекулярным движением играет важную роль. В частности,
диффузионный молекулярный поток водяного пара определяет
начальный рост облачных капель. Кроме того, изучение
теплового режима верхней атмосферы указывает на то, что
молекулярная теплопроводность является важным фактором теплового
баланса термосферы.
Направленные потоки субстанций возникают только при
нарушении равновесия в системе, вызываемом неоднородностью
распределения макроскопических величин (плотности,
температуры, скорости). Экспериментально были получены формулы для
потоков различных субстанций, показывающие, что потоки
линейно связаны с градиентами макроскопических величин. Для
потоков массы 1р и тепла \Q известны эмпирические законы
Фикка и Фурье:
Ip = _DgradP, 1
IQ=-xgradr.| (5'6Л>
Коэффициенты пропорциональности D и х называются
соответственно коэффициентами диффузии и теплопроводности.
Теоретически формулы для потоков могут быть получены
в кинетической теории газов. Хотя вывод, основанный на
использовании кинетического уравнения, является более общим, мы
приведем простой и наглядный метод вычисления потоков,
исходя из принятых в статистической физике модельных
представлений. Выбор данного метода связан также еще и с тем,
что аналогичные рассуждения используются при получении
соотношений для турбулентных потоков различных
субстанций.
Исследуем сначала процесс переноса при отсутствии средней
макроскопической скорости. Для простоты рассмотрим случай,
когда неоднородность имеется только в одном направлении,
например, в вертикальном. Пусть в этом направлении изменяются
концентрация молекул n(z), температура T(z) и некоторая
молярная субстанция а (г). Поток субстанции а, создаваемый п
молекулами, равен nvTa (vT — вектор тепловой скорости,
112
Глава 5
|vT| = у ——) • Такое значение потока сохраняется только на
длине свободного пробега /. Чтобы рассчитать поток субстанции,
переносимой через уровень z молекулами, движущимися под
углом 0, нужно рассмотреть их перемещение с уровней z — l± и
z + l , где / =/cos0 (рис. 5.3). Проекция вектора тепловой
скорости на ось г для этих молекул будет vT cos 0. Тогда поток
субстанции, переносимой движущимися вверх молекулами через
единичную площадку в элементарном телесном угле dQ за еди-
z+lLf n,(z+lx), T(z+l±), aiz+lj
z-l±,ri(z-l±),T(z-l±),cL(z-l±)
Рис. 5.3. К расчету вертикальных потоков массы и тепла.
ницу времени, будет —nvTa\z-i± cos0dQ, а полный поток вверх
л 2
/] =— nvTa\z-i cos0sin0d0 (предполагается, что вверх дви-
Z О
жется половина молекул, находящихся на уровне г). Аналогично
л 2
поток субстанции вниз Iz =-^-\nvTa\z+i± cos0sin0rf0. Поток че-
z о
рез уровень z будет равен разности потоков, направленных вверх
и вниз:
/, = /]_/!= 4- f (^ra\z_t -nvTa\z+l )cos9sin0tf9. (5.6.2)
Раскладывая выражение в скобках в ряд Тейлора и
ограничиваясь первыми членами разложения, получим
г/2 1 d
/z=- J -±- (nvTa) I cos2e sin 0 d8=--3- / -j^(tiv,a). (5.6.3)
Приложения теории термодинамических флуктуации 113
В том случае, когда неоднородность имеется во всех трех
направлениях, поток молярной субстанции а описывается соотношением
1 = —g-/ grad (nvTa). (5.6.4)
На основе этой общей формулы можно получить выражения
для потоков массы и тепла, заменяя а массой молекул m и кине-
9
тическои энергией поступательного движения молекул ——
соответственно. Напишем сначала формулу для потока массы:
Ь = 2~/grad (nmvT) = j- / (vT grad ?+p grad vT). (5.6.5)
Здесь p=nm — плотность.
Используя выражение для градиента тепловой скорости
молекул
grad vT = -£^ grad Т=~т ]/^grad r=-^^Tgrad In T, (5.6.6)
преобразуем (5.6.5) к виду
IP = 3- tvT (grad p + -g- p grad In T\. (5.6.7)
Это уравнение показывает, что поток массы возникает при
наличии градиентов плотности и температуры. Поток массы,
обусловленный градиентом плотности, называется самодиффузией
или просто диффузией, а поток, обусловленный градиентом
температуры, называется термодиффузией. Наиболее важными
явлениями в атмосфере, при рассмотрении которых используется
уравнение (5.6.7), являются процессы диффузии в воздухе газов,
имеющих малую концентрацию, в том случае, когда их
концентрация неравномерно распределена в пространстве. При этом
обычно с достаточной точностью термодиффузией можно
пренебречь. При пренебрежении термодиффузией поток массы
описывается формулой
1Р = g- lvr grad р, (5.6.8)
совпадающей с эмпирической формулой Фикка. При этом
коэффициент диффузии D можно выразить через характеристики
молекулярного движения:
D = -g-/x>T. (5.6.9)
8 Заказ № 612
114
Глава 5
Получим теперь формулу для потока тепла. Как было
определено в главе 1, поток тепла, обусловленный молекулярным
движением, равен диффузионному потоку внутренней энергии.
Внутренняя энергия идеальных газов — это кинетическая
энергия поступательного движения молекул. Поэтому выражение для
потока тепла можно получить, подставив в (5.6.4) вместо а
кинетическую энергию поступательного движения молекул Етт =
= —-— (га — масса молекул):
1<? = —з"grad (^^кин) = 2~/grad (pvT) =
= 2rlvTp (grad In/7 -1—2~ grad In 7j. (5.6.10)
2
При выводе (5.6.10) использована формула р=—пЕшиь извест-
ная из статистической физики, и соотношение (5.6.6).
Из (5.6.10) видно, что поток тепла обусловлен как градиентом
температуры, так и градиентом давления. Для частного, но очень
важного случая отсутствия потока массы поток тепла может
быть выражен только как функция градиента температуры.
Приравняв к нулю поток массы (1р = 0), находим из (5.6.7):
grad In Р = ~2 grad In Т.
Используя это соотношение, получим
IQ= 2~toTP grad In T=—2~/TjTp/?*grad Г, (5.6.11)
где R*—универсальная газовая постоянная. Формула (5.6.11)
совпадает с эмпирической формулой Фурье.
Коэффициент теплопроводности х может быть выражен через
характеристики молекулярного движения:
х = ~2~ lvTpR* =-д- lvTpcv, (5.6.12)
где cv — удельная теплоемкость при постоянном объеме, которая
3
для одноатомных идеальных газов равна сг = — /?*. Из (5.6.12)
и (5.6.9) находим связь между D и к:
D = ^—. (5.6.13)
Приложения теории термодинамических флуктуации 115
Получим теперь формулу для потока количества движения,
переносимого молекулами. Для этого рассмотрим случай, когда
имеется макроскопическое движение, причем скорость
неравномерно изменяется в пространстве. Для простоты будем считать,
что отлична от нуля только составляющая скорости вдоль оси ох,
которая изменяется с высотой (ситуация, типичная для
атмосферы) (рис. 5.4). Очевидно, что для рассматриваемого случая
можно использовать формулу (5.6.3). Подставив в нее вместо
а х-вую составляющую количества движения ти, напишем
выражение для потока количества движения:
/* ти = - "з" I -^ (™лти).
(5.6.14)
Предположив, что концентрация молекул и температура
постоянны, запишем (5.6.14) в виде
* z ти
1 , du
(5.6.15)
z=0 V//////////////////////////////////////////////// *
о
Рис. 5.4. К расчету вертикального потока количества
движения.
Таким образом, видно, что вертикальный поток количества
движения прямо пропорционален вертикальному градиенту
макроскопической скорости. Коэффициент пропорциональности
т) = ^Рг-г/ (5.6.16)
называется коэффициентом динамической вязкости. Отношение
v = T]/p — кинематическая вязкость. Легко видеть, что
кинематическая вязкость совпадает с коэффициентом молекулярной
диффузии D.
8*
116
Глава 5
В заключение следует отметить, что наши вычисления были
основаны на самой простой модели. В рамках этой модели не
делалось различий между средней и средней квадратической
скоростями молекул и использовались некоторые другие упрощения.
При более точном расчете числовые коэффициенты, входящие
в формулы (5.6.7) — (5.6.16), могут оказаться несколько иными.
Общие закономерности, однако, получены правильно.
Контрольные вопросы
1. Чем различаются условия равновесия фаз для плоской
и сферической поверхностей раздела?
2. Что такое пересыщение? Как эта величина зависит от
радиуса капли?
3. Какая характеристика является мерой вероятности
образования зародышевой капли?
4. Почему в атмосфере невозможна спонтанная конденсация?
5. В чем состоит роль ядер конденсации?
Глава 6. ЛУЧИСТАЯ ЭНЕРГИЯ
Основные понятия. Законы взаимодействия радиации с веществом. Уравнение
переноса радиации. Их упрощение и интегрирование в разных спектральных
областях. Радиационный баланс системы Земля—атмосфера.
Метеорологические приложения.
Описание термодинамических процессов в значительной мере
основано на уравнении притока тепла, однако в главах,
посвященных термодинамике, сами притоки тепла обычно
рассматривались как заданные внешние факторы. В настоящей главе
исследуется один из главных источников (и стоков) тепла в
атмосфере— лучистый приток тепла, возникающий в результате
поглощения и излучения радиации.1
Хорошо известно, что первопричиной всех атмосферных
движений является солнечная радиация — ее неравномерный приход
к поверхности земного шара (неравномерный в пространстве
и во времени). Однако цепь физических процессов,
начинающаяся с поглощения солнечной радиации и приводящая в
конечном итоге к атмосферным движениям, оказывается чрезвычайна
сложной. В численных экспериментах, моделирующих
атмосферные движения, корректный учет влияния лучистого притока
тепла на динамику атмосферы стал возможным лишь в самое
последнее время.
В целом Земля и атмосфера получают от Солнца столько же
энергии, сколько сами излучают ее в мировое пространство,
поскольку многолетняя средняя температура на земном шаре
остается постоянной. Таким образом, процессы лучистого
теплообмена обеспечивают равновесный тепловой баланс Земли как
планеты в целом. Кроме того, лучистый теплообмен играет
немаловажную роль в атмосферных процессах в качестве
внутреннего механизма перераспределения энергии.
1 Как известно из курса физики, радиация (или излучение) представляет
собой электромагнитные колебания различной частоты, распространяющиеся
со скоростью с = 299 793 км/с в вакууме и с несколько меньшей скоростью*
в различных средах. Чем выше частота (меньше длина волны)
электромагнитных колебаний, тем больше переносимая ими энергия. В атмосферных
процессах существенную роль играет радиация в диапазоне длин волн 0,3—
60 мкм, т. е. в ультрафиолетовой, видимой и инфракрасной областях спектра.
Очень часто радиация проявляет себя как поток отдельных частиц — фотонов.
Особенно удобно такое представление при описании процессов поглощения и
излучения.
Д18
Глава 6
Главными источниками радиации, распространяющейся в
атмосфере Земли, являются Солнце, земная поверхность, облака
и сама атмосфера. При этом основные компоненты атмосферы
играют незначительную роль в процессах лучистого теплообмена.
С энергетической точки зрения главную роль в поглощении и
излучении радиации в атмосфере играют углекислый газ, озон и
особенно водяной пар. С биологической точки зрения важным
обстоятельством является поглощение кислородом и озоном
ультрафиолетовых солнечных лучей с длиной волны меньше 0,3 мкм,
губительно действующих на живые организмы.
В настоящей главе рассматриваются различные
теоретические аспекты лучистого теплообмена в атмосфере.
6.1. Основные понятия. Законы взаимодействия радиации
с веществом
Напомним некоторые понятия и законы, необходимые для
дальнейшего.
Основные характеристики радиации
Пусть 6/ч—количество лучистой энергии с длиной волны от
X до X + dXy поступающей из телесного угла do и проходящей за
время dt через плоудадку йоПу нормальную к направлению луча.
•Очевидно, что 6Fx пропорционально doni du>, dX и dt\
bFx = Jxdondiodldt. (6.1.1)
Коэффициент пропорциональности Д называется интенсивностью
монохроматического излучения (или спектральной
интенсивностью). Как видно из формулы (6.1.1), J\ представляет собой
количество лучистой энергии в единичном интервале длин волн,
проходящее за единицу времени в пределах единичного
телесного угла через единичную площадку, нормальную к
распространению луча. Если направление падения радиации составляет
некоторый угол О с нормалью к площадке, то это же самое коли-
чество энергии о/ч распределяется по площадке ао =
cos О
(рис. 6.1).
В дальнейшем мы будем рассматривать количество энергии
dF\, отнесенное к единичным интервалам времени и длин волн,
а также к единичной горизонтальной площадке, так что под
углом О будем понимать угол, образуемый направлением луча
с вертикалью. Кроме того, учтем, что элемент телесного угла
Лучистая энергия
119
в сферических координатах (О, \|?) равен отношению элемента
площади на сфере dS к квадрату радиуса г, т. е.
о«) = —р2Г == ~рт = sin Ъ d§ d'b. (6.1.2>
Тогда количество лучистой энергии в элементарном телесном
угле clco равно
dFx = Jx(z9 0, <flcos8sin»d8flty. (6.1.3)
В этом выражении явно указана зависимость интенсивности
радиации от координат точки,
поскольку излучение в атмосфере меняется
в пространстве. Вообще говоря,
интенсивность излучения может
меняться также и во времени, однако
скорость любых нестационарных
процессов в атмосфере настолько
меньше скорости распространения света,
что в любой фиксированный момент
времени поле излучения можно
считать установившимся, а зависимость
от времени можно учитывать
параметрически.
Количество лучистой энергии в
единичном интервале длин волн,
приходящей в единицу времени на
единичную горизонтальную
площадку из всей полусферы, называется монохроматическим или
спектральным потоком радиации. Оно равно
2тс 1С/2
FX = J dty \ Jx(z, 0, ^)cos»sin»d». (6.l.4>
6 о
В том случае, если радиация изотропна, т. е. интенсивность /х
не зависит от направления распространения,
2тс tJ2
/=,Х = УХ(2) j £/ф f cos8sin»rf0 = ic/x(e). (6.1.5)
о 6
Полный, или интегральный, поток радиации F — это количество
лучистой энергии, приходящей за единицу времени на
единичную горизонтальную площадку из всей полусферы и во всем
диапазоне длин волн. Он равен
Рис. 6.1. Количество лучистой
энергии, падающей на
нормальную и горизонтальную
площадки.
оо 2л
я г...
F=§ Fxdk= f Л J db j Jx(z, 0, «|») cos 0 sin 0 d». (6.1.б*
Я20
Глава 6
Нагревание или охлаждение атмосферы происходит в
результате взаимодействия радиации с веществом, поэтому необходимо
напомнить основные характеристики и законы этого
взаимодействия.
Закон Ламберта—Буге. Характеристики ослабления
и излучения радиации
Прежде всего, всякая радиация возникает именно вследствие
се излучения веществом. Кроме того, при распространении
радиации в среде частицы вещества под влиянием падающего
излучения приходят в возбужденное состояние, при этом они
поглощают падающую радиацию и сами становятся излучателями
электромагнитных волн. В результате единичного акта
излучения возбужденной молекулой или атомом испускается фотон,
или квант, излучения, энергия которого пропорциональна частоте
излучения. Аналогичным образом поглощение фотонов также
имеет дискретный характер. При наличии большого числа
излучающих молекул или атомов поглощается и испускается
множество фотонов и падающее излучение заметно трансформируется.
Можно сформулировать ряд макроскопических
закономерностей, описывающих излучение и поглощение радиации, не
вдаваясь в детали процессов на молекулярном уровне. (Более
подробно взаимодействие радиации с веществом рассмотрено
в конце настоящего параграфа.)
Согласно закону Ламберта—Буге, уменьшение
монохроматической интенсивности радиации линейно зависит от самой
интенсивности радиации и от количества ослабляющего вещества dm
.на пути луча:
dJx = — ах/х dm. (6.1.7)
Коэффициент ослабления а^ представляет собой
относительное уменьшение монохроматической интенсивности падающей
радиации в расчете на единичное количество
ослабляющей субстанции. Иногда удобно рассчитывать коэффициент
ослабления на единицу массы, иногда — на единицу объема, на
одну молекулу или еще какую-либо единицу, характеризующую
количество вещества. Точнее говоря, здесь имеется в виду
количество вещества в некотором столбе единичного сечения,
поскольку рассматриваемый луч имеет единичное сечение и может
взаимодействовать только с веществом, находящимся на его
пути.
Таким образом, массовый коэффициент ослабления имеет
размерность (—— I =L2M~[, объемный (-т^~) =^-1; раз-
Лучистая энергия
121.
мерность коэффициента, рассчитанного на одну частицу,
(-72") =^2. Произведение же ctxdm, как видно из формулы
(6.1.7), должно быть безразмерной величиной.
В общей формулировке закона Ламберта—Буге (6.1.7)
физический механизм ослабления не конкретизируется. Если речь-
идет о поглощении радиации (иногда его называют чистым
поглощением), т. е. о переходе электромагнитной энергии в
другие виды энергии, то следует употреблять термин «коэффициент
поглощения» (ая). В случае рассеяния радиации, т. е. в том
случае, когда общее количество лучистой энергии не меняется, но
интенсивность падающего пучка лучей уменьшается вследствие
изменения направления распространения части фотонов,
употребляется термин «коэффициент рассеяния» (сгх).
Аналогичным образом количество излучаемой энергии
пропорционально количеству излучающего вещества:
dJx = exdm. (6.1.8>
Здесь е%—коэффициент излучения. Таким образом,
коэффициентом излучения называется интенсивность монохроматической
радиации, излучаемой единичным количеством вещества
(единичной массой, единичным объемом, одной молекулой и т. д.). Часто>
выражение (6.1.8) записывают в форме, аналогичной закону
Ламберта—Буге:
dJx = axexdm, (6.1.9)
Величина ех = называется функцией источника. Она имеет
а\
размерность интенсивности радиации. Для так называемого
абсолютно черного тела, поглощающего всю падающую на него
радиацию, а^=\ и интенсивность излучаемой радиации как раз
и представляет собой функцию источника. Для реальных тел
всегда ах<1 и интенсивность излучаемой радиации меньше, чем
функция источника.
Обычно в атмосфере протекают одновременно все три
процесса— поглощение, рассеяние и излучение. При этом излучение
Солнца, излучение (поглощение) земной поверхности и облаков,
а также рассеяние радиации имеют сплошной спектр, тогда как
излучение (поглощение) газов сосредоточено в дискретных
спектральных интервалах (в так называемых линиях и полосах
поглощения).
122
Глава 6
Полное термодинамическое равновесие. Основные законы
теплового излучения. Локальное термодинамическое равновесие
Полное термодинамическое равновесие — это состояние, к
которому со временем должна прийти система, заключенная
внутри замкнутой полости. Такая полость представляет собой
модель абсолютно черного тела, поскольку любой луч, проникший
внутрь сквозь бесконечно малое отверстие, будет полностью
поглощен в результате многократных отражений внутри полости,
\\з какого бы материала ни состояли стенки или находящиеся
внутри полости частицы. Соответственно установившиееся при
термодинамическом равновесии излучение называется
равновесным тепловым излучением или излучением абсолютно черного
тела. При полном термодинамическом равновесии температура
и радиация внутри полости не меняются ни в пространстве, ни
во времени, радиация не зависит от направления. Поэтому
каждый элемент объема или поверхности излучает столько же
энергии, сколько получает, и радиационный приток тепла
отсутствует. Для равновесного теплового излучения выполняется ряд
фундаментальных физических законов.
Закон Кирхгофа
При термодинамическом равновесии отношение
коэффициента излучения вещества к его коэффициенту поглощения
(функция источника) не зависит от индивидуальных свойств вещества,
а является универсальной функцией температуры и длины
волны. Очевидно, что это отношение равно также интенсивности
излучения абсолютно черного тела 1\\
^-=h(T). (6Л.10)
Иными словами, при термодинамическом равновесии функции
источника для любых поглощающих веществ одинаковы и равны
интенсивности излучения абсолютно черного тела.
Коэффициенты излучения любых нечерных тел exi = ax\h(T)y e\2 = axih{T)
и т. д. оказываются меньше коэффициента излучения абсолютно
черного тела.
Закон Планка
Интенсивность излучения абсолютно черного тела 1\
определяется функцией Планка:
мп=2*Г м*т ,. (6.1.U)
Лучистая энергия
123-
Здесь Л — постоянная Планка; с — скорость света в вакууме;
k — постоянная Больцмана; Т — абсолютная температура. Часто
бывает удобнее пользоваться функцией Планка в шкале частот
с
V=T:
МП~^ eJT_l ■ (6-1.12).
Зависимость интенсивности излучения абсолютно черного
тела от длины волны для различных температур показана на
1\ кал/(см2-мин-мкм)
50 у , ,
10 20 30 ^ 0 50 60?^мкм
Рис. 6.2. Интенсивность излучения
абсолютно черного тела в зависимости от длины
волны и температуры.
рис. 6.2. Энергия излучения тем больше, чем выше температура.-
Излучение максимально при некоторой промежуточной длине
волны и становится исчезающе малым при Я—>~0 или X—>-оо.
Закон смещения Вина
Дифференцируя формулу (6.1.11) по длине волны, можно-
найти условие для определения максимума функции Планка 1:
КмТ= const = 0,2897 см - К. (6.1.13).
Из этой формулы, а также из рис. 6.2 видно, что при увеличении
температуры максимум кривой смещается в сторону более
коротких волн.
1 Законы Вина и Стефана—Больцмана можно вывести также иным
способом, не зная явного вида функции Планка. Исторически они были открыты
раньше закона Планка.
124
Глава 6
Закон Стефана—Больцмана
Выражение для интегральной интенсивности излучения
абсолютно черного тела можно получить, проинтегрировав формулу
(6.1.11) по всем длинам волн:
оо со
/=[ /xtfX = j/vdv=-!L7\ (6.1.14)
6 о
2л5&4
Здесь о=————-—постоянная Стефана—Больцмана. Соответст-
15с2 А3
венно интегральный поток излучения абсолютно черного тела
(т. е. полное количество энергии, излучаемое в полусферу) равен
F4,>t = tz[ = iT\ (6.1.15)
поскольку излучение абсолютно черного тела изотропно.
Локальное термодинамическое равновесие
Все перечисленные законы справедливы при наличии полного
термодинамического равновесия. Возникает вопрос, можно ли
пользоваться ими для описания радиационных процессов в
атмосфере.
Атмосфера безусловно не находится в состоянии
термодинамического равновесия. Она не является ни изотермической, ни
замкнутой, в нее проникают излучения от внешних источников —
ют Солнца и земной поверхности. Эти излучения не могут
находиться в равновесии с собственным атмосферным излучением,
поскольку температуры атмосферы и внешних источников сильно
различаются.
Тем не менее в атмосфере обычно существует так называемое
локальное термодинамическое равновесие, при котором в
данной точке различные виды энергии молекул распределяются так
же, как и при полном термодинамическом равновесии. В таком
случае, прежде всего, существует средняя кинетическая
температура газа (см. п. 1.5), а также справедливы закон Кирхгофа и
другие законы, связывающие характеристики излучения газа
с его температурой. Однако очень важно отметить, что при
локальном термодинамическом равновесии лучистый приток тепла
•отличен от нуля. Атмосфера может как нагреваться, так и
охлаждаться в результате радиационного обмена.
Перераспределение энергии между молекулами осуществляется при
столкновениях, поэтому для установления локального термодинамического
равновесия необходима достаточно большая частота
столкновений молекул, т. е. достаточная плотность воздуха (более под-
Лучистая энергия
125
робно этот вопрос будет рассмотрен ниже). В земной атмосфере
условия локального термодинамического равновесия
выполняются вплоть до высот примерно 70 км.
Рассеяние света. Релеевское рассеяние и рассеяние
на крупных частицах
При распространении света в неоднородной среде (в которой
имеются флуктуации диэлектрической проницаемости)
происходит рассеяние, т. е. изменение направления распространения
некоторой части фотонов.1 Согласно закону Ламберта—Буге
dJKy
*^х
Рис. 6.3. Рассеяние радиации в элементарном
объеме.
(6.1.7), интенсивность падающего света изменяется
(уменьшается) на величину
dJx = -axJxds. (6.1.16)
Коэффициент рассеяния о% обычно рассчитывают на единицу
объема (1 • ds) вдоль пути падающего луча ds.
Рассеянная радиация распространяется во всех возможных
направлениях (рис. 6.3), так что интенсивность радиации dJxVf
рассеянной под некоторым углом у по отношению к падающему
лучу, равна
rf/XT = x(7)-^-. (6.1.17)
Здесь x(y) —индикатриса рассеяния, характеризующая долю
радиации, рассеянной в данном направлении. Из формулы (6.1.17)
1 Помимо изменения направления, имеет место также поляризация
рассеянного света — явление, очень существенное для атмосферной оптики.
Однако эти вопросы выходят за рамки настоящего курса, так как поляризация
не влияет на приток тепла.
-**
Г~РЪ
\ Ч1(
^1 \
/v \ '
Ч* \ /
126
Глава 6
видно, что для изотропного рассеяния, когда к (у) = 1, полное
количество рассеянной радиации равномерно распределяется па
всем направлениям (на телесный угол 4л). Интенсивность
рассеянного света, как правило, не зависит от направления в
плоскости, перпендикулярной падающему лучу, тогда как
зависимость от угла у может быть очень сильной.
Подставив (6.1.16) в (6.1.17), для интенсивности радиации,
рассеянной на пути ds под углом у, окончательно получим
*Л7 = -J!l£L°xA<fc. (6Л.18)
Коэффициент рассеяния и индикатриса рассеяния зависят от
диэлектрической постоянной рассеивающих частиц и от
соотношения между размером частиц и длиной волны падающего света.
Если размер неоднородностей значительно меньше, чем длина
волны падающей радиации, и если, кроме того, частицы и среда
имеют близкие коэффициенты преломления, не содержат
свободных зарядов и не проводят электричество, то наблюдается так
называемое молекулярное, или релеевское, рассеяние (впервые
исследованное Релеем).
В атмосфере релеевское рассеяние происходит на флуктуа-
циях плотности воздуха (см. п. 5.4). При этом объемный
коэффициент рассеяния равен
8*3 („2 _ 1)2
ах = Щ4 • (Ъ.ЫУ)
Здесь п — показатель преломления для воздуха; N — число
молекул в единице объема.
Индикатриса при релеевском рассеянии описывается
формулой
^(T)=4(1+cos2f)- (6Л-20>
Как видно из формулы (6.1.19), релеевский коэффициент
рассеяния обратно пропорционален четвертой степени длины волны,
следовательно, преимущественно рассеивается коротковолновая
радиация. Этим эффектом объясняется, с одной стороны, голубой
цвет неба, т. е. рассеянного света, а с другой стороны,
покраснение диска Солнца или Луны вблизи горизонта, когда прямая
радиация проходит в атмосфере очень большой путь, и поэтому ее
коротковолновая часть почти полностью рассеивается.
Индикатриса рассеяния, описываемая формулой (6.1.20) г
изображена на рис. 6.4. Максимальные (и одинаковые) значения
рассеяния наблюдаются в направлениях «вперед» и «назад» па
отношению к падающему лучу. В направлении, перпендикуляр-
Лучистая энергия
127
ном падающему лучу, рассеяние минимально (и составляет
половину от максимального).
В том случае, когда размеры рассеивающих частиц сравнимы
с длиной волны падающей радиации (крупные частицы),
зависимость коэффициентов и индикатрис рассеяния от размеров и
свойств частиц, а также от длины волны оказывается очень
сложной. Встречающиеся в атмосфере крупные частицы — это
либо частицы пыли, либо мельчайшие капли воды. Причем, если
твердые частицы гигроскопичны и покрыты хотя бы тонкой
пленкой воды, они в оптическом отношении ведут себя как водяные
капли.
Рис. 6.4. Релеевская индикатриса рассеяния.
Крупные частицы могут как рассеивать, так и поглощать
радиацию. В зависимости от свойств частиц, а также от
соотношения между их размерами и длиной волны коэффициент
ослабления ах и индикатриса рассеяния очень сильно меняются.
Коэффициент ослабления в случае крупных частиц обычно
рассчитывают на одну частицу (приходящуюся на единицу
площади) и представляют следующим образом:
«х = кг>К(р), (6.1.21)
где г — радиус частицы; К(р)—некоторая функция от
параметра
Р = ^. (6.1.22)
Для водяных капель в видимой области спектра (где
отсутствует поглощение) функция К(р) представлена на рис. 6.5. Для
непрозрачных отражающих частиц кривая Л'(р) качественно
имеет такой же вид. В случае прозрачных, но поглощающих
частиц (например, для капель в инфракрасной области спектра)
максимумы и минимумы на кривой сглаживаются, притом тем
больше, чем сильнее поглощение.
128
Глава 6
Анализ рис. 6.5 позволяет сделать ряд интересных выводов.
Прежде всего заметим, что, согласно (6.1.22), для капель с
некоторым фиксированным радиусом кривая К(р) дает зависимость
коэффициента ослабления от длины волны (увеличение р
соответствует уменьшению длины волны). Эта кривая имеет
волнообразный характер, т. е. в некоторых интервалах длин волн
коэффициент ослабления растет с уменьшением длины волны
(аналогично релеевскому коэффициенту рассеяния, но только
медленнее), а в некоторых интервалах, наоборот, убывает.
Расположение соответствующих спектральных интервалов зависит
О 5 10 15 20 25 30 35 40 р
Рис. 6.5. Функция /С(р) для капель воды (л=1,33).
от радиуса частиц. Для типичных частиц атмосферного аэрозоля
в видимой и близкой инфракрасной областях спектра
коэффициент рассеяния медленно убывает с ростом длины волны
(примерно как Л-1). Между прочим, именно аэрозольным рассеянием
объясняется белесый цвет неба при замутненной атмосфере.
Однако встречаются частицы, для которых коэффициент рассеяния
вовсе не зависит от длины волны (белый цвет облаков и
туманов) или даже растет с ростом длины волны.
Парадоксальным на первый взгляд кажется следующий
эффект. Как уже говорилось, коэффициент ослабления
представляет собой долю, теряемую падающим лучом, в расчете на одну
частицу, встречающуюся на пути луча (т. е. в столбе единичного
сечения):
1
dJ,
Функция /((р)=-
а*
dJx
очевидно, представляет
Nnr4x'
собой отношение рассеянной радиации к падающей радиации,
приходящейся на суммарную площадь поперечного сечения всех
рассеивающих частиц на пути луча (Nnr2). Как видно из рис. 6.5,
эта функция почти всюду больше единицы. Она стремится к 2
для больших р (т. е. для больших радиусов частиц при
фиксированной длине волны). Следовательно, частицы рассеивают
Лучистая энергия
129
больше радиации, чем падает на их поверхность. Это
объясняется явлением дифракции на малых препятствиях: возмущение
испытывают электромагнитные волны, не только падающие на
частицу, но и проходящие вблизи от нее.
8-0°
Рис. 6.6. Индикатрисы рассеяния для капель воды при
различных значениях р.
Индикатрисы рассеяния на крупных частицах, как правило,
очень сильно вытянуты, т. е. основная часть радиации
рассеивается в направлениях, близких к направлению падающего луча.
Вытянутость индикатрисы увеличивается с увеличением радиуса
частиц. На рис. 6.6 представлены индикатрисы рассеяния света
90°
St
90°
Ns
Рис. 6.7. Средние индикатрисы рассеяния для
системы облачных капель.
каплями воды при различных значениях параметра р, а на
рис. 6.7 даны средние индикатрисы для типичного распределения
капель по размерам в слоистых и слоисто-дождевых облаках.
Индикатрисы рассеяния очень сильно меняют свой вид в
зависимости от формы и оптических свойств частиц. Так, например,
для идеально отражающих непрозрачных шариков при р^1
преобладает рассеяние назад по отношению к падающему лучу.
Однако для более крупных частиц во всех случаях наблюдается
преимущественное рассеяние вперед.
Оптические свойства поверхностей
Определенные выше коэффициенты излучения, поглощения и
рассеяния имеют смысл, когда радиация ослабляется не
слишком сильно (как, например, в газах), т. е. когда поток радиации
9 Заказ № 612
130
Глава 6
трансформируется в результате взаимодействия с частицами
вещества, распределенными в некотором объеме. Если в какой-
либо среде радиация ослабляется очень сильно, то весь поток
излучения генерируется (либо поглощается) в тонком
поверхностном слое. В этом случае вводятся понятия «излучательная
способность» и «поглощательная способность», а также
«коэффициент отражения» и «альбедо». Они аналогичны коэффициентам
излучения, поглощения и рассеяния соответственно, но отнесены
к единице поверхности тела.
Рис. 6.8. Направленное отражение радиации иеортотропной
поверхностью, / (#', \J/) =гх (#, ф, #', г|/) J (ft, \|)).
Излучательной способностью называется интенсивность
радиации, излучаемой единицей поверхности. В отличие от
изотропного теплового излучения газов, а также абсолютно черного
тела, излучение поверхности может существенно зависеть от
направления; таким образом, излучательная способность является
функцией температуры, длины волны и направления. Часто
вводится также понятие «коэффициент серости» (бх, о, \j>); он
представляет собой отношение спектральной излучательной
способности к спектральной интенсивности излучения абсолютно черного
тела, находящегося при той же температуре, что и
рассматриваемая поверхность. Если излучение данной поверхности
изотропно, то коэффициент серости бх также не зависит от
направления и равен отношению спектральных потоков излучения
данной поверхности и черного тела. Если, сверх того, излучательная
способность не зависит от длины волны, то такая поверхность
называется серым телом, а коэффициент серости не зависит от
Лучистая энергия
131
длины волны и равен отношению интегральных потоков
излучения серого и черного тел.
Поглощательной способностью называется отношение
интенсивности радиации, поглощаемой телом, к интенсивности
падающей радиации. В общем случае поглощательная способность
может зависеть от направления, температуры и длины волны. Для
интенсивности монохроматической радиации, согласно закону
Кирхгофа, поглощательная способность равна коэффициенту
серости. Для интегрального потока радиации это равенство
справедливо только в случае серого тела.
Спектральным коэффициентом направленного отражения
r\ (ft. i|>, Ъ\ ty') называется доля спектральной интенсивности
радиации, падающей в направлении О, г|), отраженная в
направлении #', г|/ (рис. 6.8).
Доля спектрального потока падающей (из полусферы)
радиации, отраженная во всех направлениях (т. е. в полусферу),
называется спектральной отражательной способностью или
альбедо {А\). Очевидно, что
2- 2* тс, 2 it/2
f d<|" \ d<\> \ sin V cos V db* J /x (&, ty) rx (%. <J/. &'. <|/') X
6 /о о о
A Xsinftcosfttfft
Л* — 2~= ^2 '
f dty i Jx (ft, ^)sinucos&tf&
о о
(6.1.23)
Если r\ не зависит от направлений падающего и отраженного
лучей, поверхность называется оротропной. Для оротропной
поверхности из выражения (6.1.23) легко получить
Л=*гх. (6.1.24)
Помимо спектрального альбедо А\, часто употребляется также
интегральное альбедо
оо
А=\ Axdl.
6
Из закона сохранения энергии следует, что для
непрозрачных тел 6х-Мх=1, так как падающая радиация либо
поглощается, либо отражается. Для полупрозрачных тел 6х+Ля<1,
поскольку часть радиации пропускается. Для серых тел альбедо
не зависит от длины волны. Часто употребляется также понятие
«абсолютно белое тело», для которого альбедо не зависит от
длины волны и равно единице. Таким образом, в
противоположность абсолютно черному телу, поглощающему всю падающую
радиацию, абсолютно белое тело отражает всю радиацию.
9*
132
Глава 6
В отношении естественных подстилающих поверхностей и
облаков следует различать инфракрасную и видимую области
спектра. В инфракрасной области спектра различные типы
подстилающих поверхностей практически можно считать серыми
телами. Их поглощательная способность колеблется в пределах
0,80—0,95, т. е. весьма близка к единице. Поэтому очень часто
подстилающую поверхность приближенно считают абсолютно
черным телом. Приближение абсолютно черного или серого тела
оказывается удовлетворительным также и для облачных слоев
(если рассматривать поток радиации вне облака). Поскольку
в инфракрасной области спектра облака и различные
подстилающие поверхности близки к абсолютно черным телам, их
альбедо мало, а направленные коэффициенты отражения вообще не
имеет смысла рассматривать.
В видимой области спектра альбедо может достигать очень
больших значений (например, 0,7—0,8 для свежевыпавшего
снега или облаков). Соответственно поглощательная (излуча-
тельная) способность этих поверхностей очень мала. При этом
излучательная способность в видимой области спектра вообще
не представляет интереса, поскольку при температурах Земли
и атмосферы коротковолновая радиация практически не
излучается. Для ряда поверхностей отражение сильно зависит от
направления (так, например, для воды и снега характерно
заметное зеркальное отражение).
Весьма существенна также спектральная зависимость
альбедо, чем и определяются различные цвета отражающих
поверхностей. Все формы облаков по отношению к видимой радиации
полупрозрачны, ибо, как известно из опыта, даже при самой
плотной облачности «день не становится ночью».
Взаимодействие радиации с веществом
Выше были формально определены количественные характеристики
излучения и ослабления радиации веществом. Рассмотрим качественно основные
физические процессы, приводящие к излучению, поглощению и рассеянию
радиации.
Как известно, радиация излучается молекулами и атомами вещества в
результате перехода с одного из возбужденных уровней (верхних) на более
низкие энергетические уровни (вплоть до основного невозмущенного
состояния). Энергия излучаемого кванта (фотона) Д£, определяющая его частоту
(длину волны), равняется разности энергий соответствующих уровней Е\ и
Е2:
/zv = f^ — Ео.
При этом в принципе процессы излучения и поглощения различаются лишь
знаком разности Е{ — £2. При Е\>Е2 происходит излучение фотона
возбужденным атомом или молекулой. Напротив, при Е\<.Е2 происходит процесс
поглощения и возбуждения атомов и молекул.
Лучистая энергия
133
При распространении радиации (рассматриваемой как поток фотонов или
как электромагнитная волна) возникает взаимодействие между волной и
молекулами вещества. Характер этого взаимодействия зависит от структуры и
энергии молекул и от частоты излучения (т. е. от энергии падающих
фотонов).
Молекулы вещества обладают различными видами внутренней энергии *,
связанными с движениями электронов в атомах, колебательными движениями
атомов в молекулах и вращением молекул. Кроме того, необходимо
учитывать энергию взаимодействия молекул. В газах молекулы взаимодействуют
лишь в моменты «столкновений», тем не менее это взаимодействие играет
решающую роль в радиационных процессах. Наибольшей энергией обладает
электронный спектр частот, т. е. частот, излучаемых при переходах между
разными уровнями электронной энергии (выше 1014 Гц). Затем следует
область колебательных частот, затем вращательных (1010—10п Гц). Еще
меньше энергия взаимодействия молекул. Все виды внутренней энергии молекул
имеют дискретные значения, тогда как энергия межмолекулярных
взаимодействий (по крайней мере в газах) имеет непрерывный спектр, так что ее роль
сводится к расщеплению (размытию) дискретных уровней внутренней энергии.
Непосредственное взаимодействие радиации с молекулой (или атомом)
может приводить к возбуждению только уровней внутренней энергии, но не
изменяет кинетической энергии движения молекул.
Если энергия падающего фотона достаточно велика, поглощение фотона
может вызвать переход электронов на верхние возбужденные уровни и даже
отрыв электронов, т. е. ионизацию атомов. Достаточной для этого энергией
обладает лишь ультрафиолетовое излучение Солнца, поглощаемое полностью
в самых верхних слоях, поэтому при радиационных процессах в большей
части атмосферы (особенно в тропосфере) электронные переходы играют
незначительную роль. Кванты с меньшей энергией могут вызвать переходы на
возбужденные уровни колебательного или вращательного спектра. -
Необходимо подчеркнуть, что эта возможность осуществляется только
в том случае, когда энергия кванта совпадает с разностью энергий двух
каких-либо квазистабильных уровней. В противном случае поглощение кванта
сопровождается переходом на нестабильный (виртуальный) уровень, и
практически молекула мгновенно возвращается к невозмущенному уровню. В
результате фотон немедленно излучается. Если этот процесс происходит в
однородной среде, то излученный фотон тождествен поглощенному и поле
падающей радиации не испытывает никакого изменения. Если же в среде имеются
неоднородности (например, взвешенные частицы или флуктуации плотности и
скорости молекул в газах), то невозмущенный уровень внутренней энергии
молекул оказывается размытым (т. е. может слегка меняться) в связи с
неравномерным распределением энергии взаимодействия. Тогда излучаемые
фотоны не вполне идентичны поглощаемым. Направление распространения
излучаемых фотонов отличается от направления падающих и подчиняется
строго определенному закону. Этот процесс называется рассеянием (иногда
простым рассеянием). Подчеркнем еще раз, что при рассеянии общее
количество электромагнитной энергии не меняется, изменяется только направление
распространения некоторой части фотонов.
1 Понятие «внутренняя энергия молекул» не следует путать с внутренней
энергией газа. Внутренняя энергия идеального газа Eb = cvT представляет
собой среднюю кинетическую энергию поступательного движения молекул.
Однако каждая молекула, помимо кинетической энергии, обладает
определенной энергией, характеризующей ее внутреннее строение, причем в общем
случае эта внутримолекулярная энергия трактуется тоже как часть
внутренней энергии неидеального газа. В данном случае существенно именно
различие между кинетической энергией и энергией внутреннего строения
молекул.
134
Глава 6
Теперь рассмотрим подробнее, что происходит в том случае, когда фотон
поглощается, т. е. когда осуществляется переход между какими-либо
квазистабильными уровнями внутренней энергии молекул. Время жизни молекулы
в возбужденном состоянии ограничено. Рано или поздно должно произойти
спонтанное (т. е. самопроизвольное) излучение фотона. При спонтанном
излучении поглощенный квант переизлучается без потери энергии. В некоторых
случаях излучение может произойти в результате одного перехода с
возбужденного уровня на основной. При этом будет излучен фотон той же частоты,
что и поглощенный. Такое переизлучение практически не отличается от
простого рассеяния. Что касается направления рассеяния, то в некоторых
случаях оно зависит от направления падающего света, а в некоторых случаях
оказывается совершенно случайным. Иногда процесс переизлучения может
произойти в результате нескольких переходов с возбужденного уровня через
промежуточные на основной. При этом будет излучено несколько квантов
меньшей частоты, чем поглощенный, однако суммарная излученная энергия
равняется энергии поглощенного кванта. И наконец, если фотон был поглощен
возбужденной молекулой, то в результате перехода на основной уровень
может быть излучен квант большей энергии, чем поглощенный. Такое рассеяние
(с изменением частоты по сравнению с частотой падающей радиации)
называется комбинационным.
Но тем не менее все рассмотренные случаи спонтанного переизлучения
поглощенной радиации, по существу, относятся к явлениям рассеяния, а не
чистого поглощения, поскольку электромагнитная энергия не переходит в
тепловую, т. е. в энергию поступательного движения молекул. И только в том
случае, если между актами поглощения и излучения успевает произойти одно
или несколько столкновений между молекулами, осуществляется чистое
поглощение.
Таким образом, судьба поглощенного фотона зависит от частоты
столкновений. Дело в том, что переход между различными видами внутренней
энергии (вращательной, колебательной, электронной), а также в кинетическую
энергию молекул возможен только в моменты столкновений. Поэтому среднее
время перехода энергии одного вида в энергию другого вида обратно
пропорционально числу столкновений в 1 с. Это время называется временем
релаксации. Если время релаксации значительно меньше продолжительности
жизни молекулы в возбужденном состоянии, то любой поглощенный квант
энергии от «внешнего» источника успевает перераспределиться между
молекулами газа, прежде чем произойдет спонтанное излучение. При этом, с
одной стороны, часть поглощенной энергии пойдет на увеличение средней
кинетической энергии поступательного движения молекул (т. е. на нагревание
газа), а с другой стороны, собственное излучение молекул, возникающее при
переходах с возбужденных уровней на основной, также будет однозначно
связано со средней кинетической температурой газа, поскольку установится
равновесие между различными видами энергии для всех молекул.
Для разных видов энергии время релаксации различно. Поэтому могут
существовать такие случаи, когда некоторые виды энергии (например,
кинетическая и вращательная) уже пришли в равновесие, а остальные еще нет.
Для справедливости сформулированных выше законов излучения и
поглощения достаточно, чтобы в состоянии равновесия находились не все
энергетические уровни молекул, а лишь те, которые принимают существенное участие
в лучистом теплообмене. Такое состояние называется локальным
термодинамическим равновесием. Условия его существования определяются плотностью
атмосферы (числом столкновений), спектральным составом «внешней»
солнечной радиации, а также концентрацией и молекулярной структурой
основных поглощающих газов. Таким образом, радиация одной и той же длины
волны может как рассеиваться, так и поглощаться молекулами данного газа
в зависимости от его плотности. В большинстве случаев процессы излучения,
поглощения и рассеяния происходят одновременно, однако количественное
Лучистая энергия
135
соотношение между ними различно для разных длин волн, разных веществ и
их состояний и для различных плотностей вещества, находящегося в
газообразном состоянии.
Контур спектральной линии. Зависимость коэффициентов
поглощения от давления и температуры. Эффект Форбса
Структура спектров поглощения в газах чрезвычайно сложна.
Число отдельных линий поглощения огромно. Группы линий
образуют полосы и системы полос. Для некоторых газов
(например, для углекислого газа) расположение линий в полосах более
или менее регулярно. Для ряда газов (например, для водяного
пара) расположение и интенсивность отдельных линий,
составляющих полосу, кажутся совершенно случайными. И хотя в
принципе, зная структуру молекулы, можно точно рассчитать
положение и интенсивность каждой линии, практически их можно
рассматривать только как набор случайных величин. Даже
каждая отдельная линия имеет достаточно сложный характер.
Линии поглощения не являются в буквальном смысле
линиями. При переходах между двумя определенными
дискретными уровнями излучаются не строго монохроматические кванты
с частотой \>о, а некоторый спектр частот. Это объясняется
«размытием» уровней, т. е. небольшим различием в энергии одних
и тех же уровней в разных молекулах. Иными словами, линия
поглощения формируется в результате поглощения многих квантов
различными молекулами и эти поглощенные кванты слегка
отличаются по частоте. Линия растягивается в полоску с центром
около основной частоты \>о, причем линия имеет строго
определенный контур. Существует несколько причин «размытия»
уровней. В тропосфере, где плотность воздуха достаточно велика,
основной причиной являются столкновения молекул. Контур
линии, определяемый столкновениями, обычно называется лорент-
цовым контуром и приближенно описывается сравнительно
простой формулой
"(^(.-voV + a^ (6-1.25)
Здесь a(v)—коэффициент поглощения при частоте v; v0 —
частота, соответствующая центру линии (т. е. переходу с
«неразмытого» возмущенного уровня); 5 — интенсивность линии, т. е.
суммарное поглощение во всей линии или же площадь,
охватываемая контуром линии (рис. 6.9);
+ оо
S= j a(v-v0)rf(v-v0); (6.1.26)
136
Глава 6
а — полуширина линии, т. е. расстояние (в единицах частоты)
от центра до точки, в которой коэффициент поглощения
составляет половину максимального (см. рис. 6.9).
Полуширина линий тем больше, чем чаще столкновения, т. е.
чем больше давление:
Здесь а0 — полуширина линии при стандартном давлении р0>
а а — при давлении р. Разумеется, даже максимальная ширина
Рис. 6.9. Лорентцов контур линии поглощения при
разных давлениях.
линии очень мала. Так, например, при нормальных условиях
полуширина линий во вращательных полосах водяного пара
(определяемая столкновениями с молекулами воздуха) составляет
несколько ангстрем.
При уменьшении давления линия становится более узкой,
хотя ее интенсивность (т. е. площадь, охватываемая контуром)
не меняется (см. рис. 6.9). Поэтому, казалось бы, изменение
давления не должно влиять на поглощение в спектральных
интервалах, во много раз превышающих ширину отдельной линии.
Однако для большинства линий поглощение в центре настолько
велико, что уже при очень малых массах поглощающего вещества
падающая радиация в центре линий поглощается полностью и
в дальнейшем поглощение продолжается только в крыльях
линии. Поэтому влияние давления на общее поглощение
оказывается таким же, как и в крыльях линии: коэффициенты
поглощения увеличиваются с ростом давления.
Поскольку радиация в атмосфере (например, солнечная)
проходит путь, вдоль которого давление существенно меняется,
возникает проблема правильного учета влияния давления на погло-
Лучистая энергия
137
щение. Если в каждой точке пути контур линии поглощения
является лорентцовым, т. е. определяется формулой (6.1.25),
-с соответствующим а(р), то контур линии, формирующейся в
результате поглощения на всем пути, вообще говоря, уже не будет
лорентцовым. Тем не менее оказывается, что он достаточно
близок к лорентцовому контуру при некотором среднем давлении.
Это приближенное описание называется приближением Кур-
тиса—Годсона. Однако на практике часто пользуются другим
(еще более простым и грубым) приближением, а именно
считают, что не полуширина линии, а сами коэффициенты
поглощения пропорциональны некоторой степени давления:
ах(Р) = ах(Ро)(-^)П.
Показатель степени п различен для разных газов и для разных
участков спектра, а также зависит от поглощающей массы. Если
рассматривать интегральный поток радиации, то в среднем
наиболее подходящими являются, по-видимому, следующие
значения п : 1 для водяного пара и 0,8 для углекислого газа.
Контур линии и особенно ее интенсивность зависят также и
от температуры поглощающего (излучающего) газа. Однако
зависимость от-температуры оказывается еще сложнее, чем
зависимость от давления, она даже может менять знак для разных
участков спектра: в некоторых полосах поглощение растет с
ростом температуры, а в некоторых убывает. Зависимость от
температуры поглощающей среды 0 либо не учитывают совсем,
либо учитывают приближенно, в виде степенной функции (так
же как зависимость от давления), т. е. считают, что
ах(р, в) = ахо(/>о, 90) (-£-)" (-£-)', (6.1.27)
причем показатель / различен для разных участков спектра.
Остановимся еще на одной существенной особенности
поглощения радиации — на так называемом эффекте Форбса.
На рис. 6.10 показано, как при прохождении радиации в
атмосфере полное поглощение излучения сначала наблюдается
только в самом центре линии, а затем постепенно
распространяется к краям. Помимо рассмотренной выше зависимости от
давления, это обстоятельство вызывает еще один эффект:
средний коэффициент поглощения уменьшается с увеличением
пройденной массы т. Пока в поглощении участвует вся линия,
средний коэффициент поглощения остается постоянным. После того
как наступает полное поглощение в центре линии, из
осреднения начинают выбывать максимальные значения коэффициентов
поглощения вблизи от центра и средний коэффициент
поглощения все больше и больше уменьшается с увеличением массы
138
Глава 6
поглощающего вещества, пройденной рассматриваемым лучом.
В этом случае средний коэффициент поглощения как некоторая
характеристика поглощающего газа вообще теряет смысл,
поскольку он зависит от предыстории поглощаемой радиации.
Радиация, прошедшая большой путь в данном газе, поглощается
слабо, тогда как радиация, прошедшая малый путь, поглощается
a(v)
-J(V,rn) tf(V)
Рис. 6.10. К объяснению эффекта Форбса, тъ>т2>т{.
очень сильно. Поэтому коэффициенты поглощения и закон
Ламберта—Буге могут применяться только для спектральных
интервалов, значительно меньших ширины линии. В таких
интервалах средний коэффициент поглощения можно считать
постоянным, а поглощение радиации происходит вплоть до полного ее
исчезновения и, естественно, прекращается при отсутствии
падающей радиации в рассматриваемом интервале.
Излучение Солнца и Земли и его преобразование в атмосфере
в различных спектральных областях
Солнце излучает энергию примерно как абсолютно черное
тело при температуре 6000 К. В соответствии с законом Планка
99% солнечного излучения сосредоточено в области 0,3—5 мкм
(с максимумом около 0,4 мкм), т. е. в основном в видимой части
спектра.
В земной атмосфере солнечное излучение испытывает
поглощение и рассеяние. Основные полосы поглощения солнечной ра-
Лучистая энергия
139
диации (имеющие энергетическое значение для тропосферы)
принадлежат водяному пару и углекислому газу и расположены
в близкой инфракрасной области спектра (от 0,7 до 5 мкм).
В верхней атмосфере существенную роль играет поглощение
ультрафиолетовой радиации озоном и кислородом.
Рассеяние солнечной радиации происходит на флуктуациях
плотности и на аэрозолях, т. е. на частицах пыли или каплях
воды. В соответствии с законами релеевского и аэрозольного
рассеяния наибольшую роль рассеяние играет в
ультрафиолетовой и видимой областях спектра и становится исчезающе малым
при длинах волн, превышающих 1 мкм.
Земная поверхность, облака и атмосфера тоже являются
источниками излучения, которое обычно называется
длинноволновым, в отличие от коротковолнового солнечного. Излучение
земной поверхности и облаков (за исключением перистых) близко
к излучению абсолютно черного тела при соответствующих
температурах (т. е. при температурах 200—300 К); 99% этого
излучения сосредоточено в области 5—50 мкм (с максимумом около
10 мкм). Если для солнечного излучения на длины волн больше
5 мкм приходится меньше 0,4% общей излучаемой энергии, то
для земного излучения, наоборот, меньше 0,4% энергии
приходится на'излучение с длинами волн меньше 5 мкм.
Собственное излучение атмосферы также соответствует
излучению черного тела при температуре 200—300 К, однако, как
уже упоминалось выше, спектр этого излучения не сплошной,
а состоит из большого числа линий и полос. Область 4—7 мкм
занята сильными полосами поглощения водяного пара,
а также полосами углекислого газа. В области 8—12 мкм имеет
место довольно слабое поглощение (так называемое окно
прозрачности). Около 15 мкм центрирована сильная полоса
углекислого газа. Частично перекрываясь с нею, а также в более
далекой инфракрасной области располагаются полосы водяного
пара.
На рис. 6.116 и в схематически изображены указанные
полосы поглощения на фоне спектрального распределения энергии
солнечного и земного излучения.
При сравнении солнечного и земного излучения необходимо
подчеркнуть еще одно обстоятельство. Из формулы Планка
следует, что при увеличении температуры излучающего тела его
излучение увеличивается при всех длинах волн (см. рис. 6.2).
Кривая Планка, соответствующая 6000 К, при всех длинах волн
лежит намного выше кривой Планка для 300 К. Порядки величин
интенсивности для обеих кривых настолько несоизмеримы, что
эти кривые невозможно изобразить на рисунке в одинаковом
масштабе. Тем не менее приходящее на Землю излучение Солнца
в длинноволновой области спектра (при А,>5 мкм) мало по
140
Глава 6
сравнению с излучением Земли. Причина заключается в так
называемом эффекте дилюции, или «разжижения», солнечной
радиации. Если бы оба «источника» помещались рядом, то энергия
Рис. 6.11. Спектральное распределение солнечного 50Х и земного
тс/ (Г3) излучения и основные полосы поглощения в атмосфере.
а — зависимость Sm и %[ от К; зависимость 5т (б) и я/ (в) от к
ил х ил X
(в увеличенном масштабе) с учетом основных полос поглощения.
излучения Солнца на много порядков превосходила энергию
земного излучения при любых длинах волн. Но Солнце находится
на расстоянии 1,5 • 108 км от Земли. По мере удаления от поверх-
Лучистая энергия
141
ности Солнца излучаемая им энергия перераспределяется на все
большую площадь, и поэтому энергия, приходящаяся на
единицу площади, становится все меньше (рис. 6.12). Интегральный
поток, излучаемый единичной площадкой поверхности Солнца,
равен о Г4 , а всей поверхностью Солнца 4яг2аГ4 (гс — радиус
Солнца). На расстоянии, равном радиусу земной орбиты г0у этот
поток распределяется на площадь 4яг*. Стало быть, на верхней
границе атмосферы (при среднем
расстоянии между Землей и Солнцем) на
единичную нормальную площадку
приходится количество солнечной энергии
50 =
4*Аг4
4*/\1
X
ХзГс4^2,27 кал/(см2 • мин).
Величина So называется солнечной
постоянной1. Отношение г2с/г20,
показывающее, во сколько раз солнечная
постоянная меньше, чем энергия, излучаемая
единичной площадкой поверхности
Солнца, называется фактором дилюции.
Таким образом, при сравнении кривых Планка для обеих
температур нужно умножить интенсивность излучения при
6000 К на фактор дилюции. Поэтому соотношение спектральных
величин солнечной и «земной» радиации в атмосфере
оказывается примерно таким, как изображено на рис. 6.11 а.
Земля
Рис. 6.12. Эффект
дилюции солнечной
радиации.
6.2. Уравнения переноса радиации. Их упрощение
и интегрирование в разных спектральных областях
Изменение интенсивности излучения, распространяющегося
в поглощающей, излучающей и рассеивающей среде,
описывается уравнениями переноса радиации, которые могут быть
сформулированы с помощью основных законов поглощения,
излучения и рассеяния. Получим эти уравнения для так называемой
плоскопараллельной атмосферы, т. е. для плоского,
горизонтально однородного и бесконечно протяженного по горизонтали
слоя атмосферы. Иными словами, для простоты пренебрегаем
1 В действительности излучение Солнца не вполне идентично излучению
абсолютно черного тела при 6000 К. По данным различных измерений,
солнечная постоянная равняется 1,95—2,05 кал/(см2 • мин), и ее значение
подлежит дальнейшему уточнению.
142
Глава 6
кривизной Земли и атмосферы (рис. 6.13). Такое рассмотрение
приводит к заметным ошибкам для очень больших зенитных
углов (больше 85°).
Рассмотрим изменение интенсивности монохроматической
радиации, распространяющейся в направлении, характеризуемом
зенитным углом О и азимутом г|) (азимут обычно отсчитывается
против часовой стрелки от направления на Солнце). Если угол #
■—.
Рис. 6.13. К выводу уравнений переноса.
острый, радиация распространяется снизу вверх и называется
восходящей. Обозначим ее интенсивность через Л (д, г|?). При
dz
прохождении плоского слоя от z до z + dz на пути ds=
интенсивность изменяется на величину
,ло.».;)-- "("с:;Г" Л(».».*)-
-•'"У Л9. t. *)+"^}->"У'иг +
COS i
°х (*) РР (*) dz
cos Ъ
2* п
Согласно закону Ламберта—Буге, первый и второй члены
в правой части этого выражения описывают ослабление
радиации в результате поглощения и рассеяния в рассматриваемом
слое; рп(г) и рр(г) —плотности поглощающего и рассеивающего
Лучистая энергия
143
вещества.1 Третий член описывает излучение радиации в слое dz,
В тех случаях, когда существует локальное термодинамическое
равновесие и справедлив закон Кирхгофа, функция источника
равна интенсивности излучения абсолютно черного тела, т. е.
Ч(г) = 1х(ТЩ.
Заметим, однако, что при наблюдающихся в атмосфере
температурах излучающего газа для коротких волн h{T) пренебрежимо
мало и, следовательно, мало также е\, тогда как а^ отнюдь не
мало. В этом случае при наличии полос поглощения будет
наблюдаться только поглощение высокотемпературной солнечной
радиации и отсутствовать собственное излучение.
Последний член в уравнении учитывает еще один механизм
изменения радиации, а именно ее усиление в результате
рассеяния в направлении Ф, г|? лучей, идущих во всех других
направлениях. Действительно, помимо рассматриваемого нами луча с
направлением ft, if>, сквозь слой dz проходят лучи всех других
направлений О', г|/ (Ф' меняется от нуля до л, а \|/ — от нуля до
2л, т. е. учитываются как восходящие, так и нисходящие лучи).
Для каждого произвольного луча с направлением Ф', г|/ (точно
так же как. и для рассматриваемого нами луча с направлением
dz
О, г|э) в цилиндре — рассеивается по всем направлениям
количество радиации
dJx(b', f, z) = -ax(z)Pp{z)-^¥Jx(b', f, г).
Из этого общего количества рассеянной радиации в направлении
О, г|) рассеивается доля, пропорциональная индикатрисе
рассеяния хх(г, й, i|), О', ф'), зависящая от угла между направлениями
О, г|) и Ф', г|/, а также от высоты г, поскольку с высотой меняется
соотношение между релеевским и аэрозольным рассеянием.
Таким образом, луч с направлением Ф, г|) испытывает в результате
рассеяния луча с произвольным направлением тУ, г|/ усиление,
равное
<b(z)?P{*)-£rW. f. *К(&. ф. *', </, г),
1 Для простоты рассматриваем только одну поглощающую и одну
рассеивающую субстанцию. На самом деле следовало бы учесть все
поглощающие и рассеивающие компоненты в атмосфере. Тогда вместо двух написанных
выше членов получились бы суммы нескольких соответствующих членов с
различными коэффициентами поглощения и рассеяния и плотностями
поглощающих и рассеивающих субстанций.
144
Глава 6
а в результате рассеяния всех лучей — суммарное усиление
2гс
Опуская для простоты записи явную зависимость от
аргументов д, \|?, Г, г, получим окончательно
dJ\ 1 ж р ах
2г. х
j <*|>'|*х(&, ф, »', ф')Л(»'. f) sin &'</&'. (6.2.1)
Гр X
COS &
о о
Для нисходящей радиации Д, распространяющейся сверху
вниз, все рассуждения остаются прежними, только угол О,
составляемый направлением луча с осью г, тупой, его косинус
отрицателен. Однако можно по-прежнему брать в качестве О
острый угол (т. е. отсчитывать угол от отрицательного направления
оси г), но необходимо учесть, что при распространении
нисходящей радиации в направлении луча изменение высоты dz
отрицательно. Тогда для нисходящей радиации уравнение переноса
может быть написано в таком виде:
dz COSU VKn"A-TI'pVJX/-'A cos»
(pnax + Pp*a) Л - -^~y 4 -
PPax
2%
j **'J*x(&. Ф, »', f)A(»'. Wsin&'d»'. (6.2.2)
costt
О и
Интегрирование уравнений переноса в общем случае
представляет чрезвычайно сложную задачу. Однако из рис. 6.11а
видно, что спектральные области, в которых сосредоточена
коротковолновая солнечная и длинноволновая земная радиация,
практически не перекрываются, следовательно, перенос
коротковолновой и длинноволновой радиации можно рассматривать
отдельно. При таком подходе уравнения переноса можно
упростить. Для длинноволновой радиации пренебрежимо мало
рассеяние, тогда как в коротковолновой области ничтожно мало
собственное излучение Земли, облаков и атмосферы.
Перенос длинноволновой радиации в атмосфере
В случае длинноволновой радиации пренебрегаем
рассеянием. Кроме того, будем считать, что выполняются условия ло-
Лучистая энергия 145
кального термодинамического равновесия. Тогда уравнения
(6.2.1) и (6.2.2) примут вид:
dJt _ РА /и / \
dz ~~ cost* wx xh
~^ = ^oTГ^л_Уx>,•
Разделим обе части этих уравнений на рп и обозначим pndz =
= dm. Действительно, поглощение зависит не от геометрической
толщины слоя, а от количества поглощающего вещества.
Поэтому вместо высоты z удобно ввести новую переменную —
поглощающую массу
= 1 Pn«fef (6.2.3)
m
о
т. е. количество поглощающего вещества в столбе воздуха
единичного сечения от земной поверхности до уровня г.1 Более того,
если считать справедливой степенную зависимость коэффициента
поглощения от давления и температуры
а*=аА-к)*Ш'-
то удобнее поправки на давление и температуру отнести не к
коэффициентам поглощения, а к поглощающей массе, т. е. ввести
так называемую эффективную массу
^ШШ***- (6-2-4)
Тогда коэффициенты ах0 = ах(р0, 0О) в уравнениях переноса не
будут зависеть от высоты, а значит, и от т.
Окончательно уравнения переноса могут быть записаны
в виде:
(A-h), (6.2.5)
Л;-/х). (6.2.6)
При этом т следует понимать как эффективную поглощающую
массу. Индекс «эф» в дальнейшем опускаем.
dm
d4
dm
cos ft
a\0 (
cos & v
1 Согласно определению (6.2.3), поглощающая масса имеет размерность
ML~2 (обычно г/см2). Однако на практике ее часто выражают в других
единицах, например в сантиметрах столба осажденной (сконденсированной) воды
единичного сечения или в сантиметрах единичного столба газа, приведенного
к нормальным условиям.
10 Заказ № 612
146
Глава 6
Сформулируем граничные условия. Будем считать, что Земля
излучает, как серое тело. Тогда на уровне земной поверхности,
т. е. при г = 0, т = 0,
2* я/2
Л*(0) = 33МТ;) + 0-&з)^|' fltyf A(0)cos*sinbdb. (6.2.7)
6 о
Здесь Т3 — температура подстилающей поверхности; б3 —
коэффициент серости; Л3=1 — б3 — альбедо. Первый член в правой
части описывает излучение земной поверхности, а второй —
отраженную от земной поверхности нисходящую радиацию.
На верхней границе атмосферы нисходящая длинноволновая
радиация отсутствует, поскольку ее источником является сама
атмосфера, а приходящая «извне», от Солнца длинноволновая
радиация пренебрежимо мала. Таким образом, при г->-оо и
jj>(M) = 0. (6.2.8)
При наличии облачности задача усложняется. Перенос
радиации внутри облачного слоя представляет отдельный, весьма
сложный вопрос. Однако в большинстве задач, имеющих
значение для динамической метеорологии, облачность можно
рассматривать как непрозрачную перегородку, излучающую как серое
(почти черное) тело. В таком случае необходимо рассматривать
перенос излучения в каждом безоблачном слое атмосферы,
ограниченном облачными слоями (или облачным слоем и
подстилающей поверхностью). На верхней или нижней границе облачности
задаются граничные условия, совершенно аналогичные условию
(6.2.7) на подстилающей поверхности, только в этом случае под
температурой поверхности следует понимать температуру на
границе облака, а под излучательной способностью — излуча-
тельную способность облака. Так, например, вместо условия
(6.2.8) на нижней границе облака при z = zu. обл, т = тн.0бл
получим
А (/Ян. обл) = &обл^Х (^н. обл) 4"
2* */2
+ 0 - &обл) 4- 1 ^ j Jl (^н. обл) cos Ь sin & db. (6.2.9)
о 0
Уравнения переноса длинноволновой радиации (6.2.5) и
(6.2.6) описывают изменение интенсивности монохроматической
радиации в слое атмосферы толщиной dz на произвольной
высоте г. Знание спектральных (монохроматических) интенсивно-
стей радиации представляет интерес для целого ряда специаль-
Лучистая энергия
147
ных задач атмосферной оптики, в частности для определения
температуры, влажности и других метеоэлементов с помощью
искусственных спутников Земли. Однако для динамики атмосферы
первостепенный интерес представляет тепловой эффект
радиации, т. е. интегральные потоки восходящей и нисходящей
радиации на разных уровнях. Для этого необходимо проинтегрировать
уравнения (6.2.5) и (6.2.6) по всем высотам, телесным углам
и длинам волн. Выполним это интегрирование на примере
уравнения (6.2.5) [уравнение (6.2.6) интегрируется совершенно
аналогично].
Уравнение (6.2.5)—это обыкновенное неоднородное
дифференциальное уравнение первого порядка. Свободный член
описывает собственное излучение атмосферы. Однородное
уравнение справедливо для поглощающей, но неизлучающей
атмосферы. Решение этого уравнения имеет ясный физический смысл
и позволяет ввести понятие функции пропускания (имеющее
решающее значение для всех последующих выводов). Поэтому
сначала проинтегрируем однородное уравнение.
Интегрирование уравнений переноса в неизлучающей
атмосфере. Функции пропускания
Для неизлучающей атмосферы в уравнении (6.2.5)
отбросим 1%. Проинтегрировав уравнение по массе, получим
jl(rn) = Ce C0SV (6.2.10)
Постоянную С определим из граничных условий на земной
поверхности (6.2.7), причем для упрощения выкладок положим
б3=1, т. е. будем считать подстилающую поверхность абсолютно
черным телом. Тогда
аХ0т
Jt(m) = Ix(T3)e "15fr. (6.2.11)
Отношение количества радиации, прошедшей через слой
ослабляющего вещества, к количеству радиации, падающей на
границу этого слоя, называется функцией пропускания. В данном
случае мы имеем дело с функцией пропускания для
монохроматической или спектральной интенсивности. Обозначим ее <г?\ь.
Согласно (6.2.11),
^n(m)^^f = e' cosS>. (6.2.12)
10*
148
Глава 6
Далее, используя уравнение (6.2.11) с учетом (6.2.12), получим
поток радиации:
2те тс /2 2т, тс/2
j d^ j y>t(m)cosOsinOdO = /x(r3) j dty J <^X&("0COS& sin daft.
о 0
Левая часть этого уравнения, по определению, есть
монохроматический поток восходящей радиации на уровне т. Обозначим
его Fx (m):
it,2
Я!(/я) = /х(Г3)21с j ^(m)cos»sin»rf». (6.2.13)
о
Но nIx{T3) =Fx4. т(Т3) =F\ (0) есть монохроматический поток
излучения черного тела при температуре Земли, т. е. восходящий
поток на уровне подстилающей поверхности Fx (0). Тогда
тс /2 ахот
= 2 f ^~"^Tcos&sin&rf&. (6.2.14)
6
Очевидно, что с7\ (т) == —^ есть не что иное, как функция
F\ (0)
пропускания для потока монохроматической радиации.
И наконец, проинтегрируем уравнение (6.2.13) по всем
длинам волн. При этом для сокращения записи учтем (6.2.14):
оо с»
F< {т) s j pi {т) dX=\ Fx ^ Лтз) #>x (m) dl.
0 6
Умножим и разделим правую часть на интегральный поток
излучения абсолютно черного тела при температуре земной
поверхности:
оо оо
/Ч т (Т3) = f Fx,. т (Т3) Ok = * j А (Г,) Л=0Гз4.
В результате получится
оо
5 ^ч.т(7з)
Поскольку Fh. т (Гз) = jF (0) есть интегральный поток восходя-
Лучистая энергия
149^
щего излучения на уровне подстилающей поверхности, то из
(6.2.15) получим
^(0) б' ^ч.т(Гз) V ^ V '
Здесь <ъР(т) —функция пропускания для интегрального потока
радиации, или, как ее обычно называют, интегральная функция
пропускания. Весовая функция Fx4.T(T3)/F4.T(T3) определяет
долю интегрального потока излучения абсолютно черного тела,
приходящуюся на интервал длин волн dX при данной длине
волны X.
Таким образом, интегральная функция пропускания есть не
просто сумма спектральных функций пропускания, а сумма,
учитывающая «вес» каждой из них, пропорциональный доле
излучения абсолютно черного тела. Это вполне понятно из
качественных физических соображений. Действительно, пропущенная
радиация определяется главным образом спектральными
функциями пропускания в области максимума излучения, тогда как
пропускание в областях, где интенсивность падающей радиации
мала, очевидно, не имеет значения.
Если учесть выражения для соответствующих функций
пропускания (6.2.12), (6.2.14) и (6.2.16), то монохроматическую
интенсивность, монохроматический поток и интегральный поток
радиации можно выразить совершенно аналогичными
формулами. Действительно, вместо (6.2.11), (6.2.13) и (6.2.15)
получим:
А (щ) = Л (0) &и (го), (6.2.17}
Ft (m) = Ft (0) ^х (го), (6.2.18>
F*(m) = F*(0)&(m). (6.2.19)-
Существенно различаются при этом лишь сами функции
пропускания для монохроматической интенсивности &%?>, для
монохроматического потока <&*х и для интегрального потока &.
Интегрирование уравнений переноса в излучающей атмосфере
Вернемся к интегрированию неоднородного уравнения (6.2.5).
Его решение будет суммой общего решения однородного уравнения и
частного решения неоднородного уравнения. Общее решение однородного
уравнения определяется выражением (6.2.10). Частное решение неоднородного-
уравнения получим путем вариации произвольной постоянной С (метод Ла-
гранжа):
о
150
Глава 6
Общее решение неоднородного уравнения имеет вид
_ ахот _ а\от ™ ахои
Л(т)=Л0+Л„о = Се cos»+e cos» j_io е-^т/х(Г)^и>
о
В отличие от переменного верхнего предела, переменную
интегрирования обозначаем буквой и. Постоянную С определим из
граничного условия на земной поверхности (6.2.7). Кроме того,
аХ0т
внесем множитель е cos0 , не зависящий от переменной
интегрирования, под знак интеграла. В итоге получим
ах0т т а\о (т - и)
Л* H = /x(7',)e"'^"+J /^ТЩ-^-е ^^du, (6.2.20)
о
или
ax0m т / ак0(т-и) \
А(т)=/,(Т3)е~^^Л-\ /X(7-(B))-A_U ^^)du.
0
(6.2.21)
Но, согласно формуле (6.2.12), е~ awmcos °= <^Xft (m). Совершенно
axo(m - и)
аналогично е со% ь = <^ я# (т — и) — функция пропускания
для интенсивности монохроматической радиации, прошедшей
слой толщиной га—и. Таким образом, выражение (6.2.21) можно
записать в виде
Л(тп) = 1х(Т3)&п(т)+\ Л (7») dr'*au~U) du- <6-2'22)
6
Теперь выполним интегрирование по всем телесным углам
и длинам волн точно так же, как и в случае неизлучающей
атмосферы.
Умножим выражение (6.2.22) на cos Ф и проинтегрируем по всем
телесным углам:
2л: те/2 2тс я/2
j rf+ f Н («О cos ft sin bdb = j d<\> J /x (Гз) *n (m) cos ъ sln * db +
0 0 0 0
2ic 7i/2 m
+ \ d<\> I cos&sin&d& Ix(T(u)) bkl —da.
0 0 0
Левая часть, по определению, есть монохроматический поток восходящей
радиации на уровне т, т. е. F\(m). Функция е/ х^ не зависит от азимута.
Лучистая энергия
151
Излучение абсолютно черного тела не зависит ни от ф, ни от Ф- Учитывая
это, а также меняя порядок интегрирования по О и по и, получим
«/2
F\(m)=2TiIx(T^ j* ^u(m)cosftsin&rf& +
6
m Гтс/2 "I
4- 2r f I} (T (u)) JL- f tf)b (m — и) cos » sin e rf& rfa.
6 Lo J
Учтем полученное выше -выражение для функции пропускания
монохроматического потока радиации (6.2.14), а также тот факт, что
*'х (Тэ) = ^х ч. , (^ *'х Г (")) -^,т (Г («)).
Окончательно получим для монохроматического потока
радиации на уровне га:
Я? (/я) = Fx,. т(Г3) ^х (т) + j Fx ч. т(7») ' х "~ *«.
6
(6.2.23)
И наконец, проинтегрируем (6.2.23) по всем длинам волн.
Посде интегрирования получится
оо оо оо тп
J^(m)dX = j^4_t(r3)^x(m)rfX+jf dX |^Хчт(Г(и))Х
0 0 0 0
d&, (m — и)
х^ du-
Левая часть, по определению, есть интегральный поток восходящей радиации
на уровне т, т. е. Fi(m). Для того чтобы привести к более удобному виду
интегралы в правой части, умножим и разделим каждый из них на
интегральный поток излучения абсолютно черного тела при соответствующей
температуре:
оо
Кроме того, поменяем во втором члене порядок интегрирования по X и по и„
В результате получим
? Г Г° Л „ т (Т (и)) d?,(m—u) 1
+J ^ * с7») у ;;•/(}• (У *« dl\du-
Согласно (6.2.16), интеграл в первом члене представляет
собой интегральную функцию пропускания. Что касается второго
152
Глава 6
члена, то его тоже можно выразить через интегральную
функцию пропускания. Действительно, полный дифференциал от
интегральной функции пропускания
оо
X ш dud\ + \ ■5Г[ Ду(Г) ^x(rn-u)^-dad\.
Только первый из двух членов содержится в полученном выше
выражении для интегрального потока восходящей радиации.
Следовательно, интегральный поток восходящей радиации на
уровне т выражается через частный дифференциал
интегральной функции пропускания по массе1:
т
^ (m) = F4. т (Т3) SP (т) + j Fx,. т (Г (и)) d^%~U) da. (6.2.24)
Обычно пренебрегают зависимостью интегральной функции
пропускания от температуры излучающего газа (температуры
источника), что приводит к ошибкам, не превышающим 10—15%.
В таком случае частный дифференциал совпадает с полным.
Сравнение выражений (6.2.22), (6.2.23) и (6.2.24)
показывает, что при сделанных упрощающих предположениях
монохроматическая (спектральная) интенсивность восходящей
радиации, монохроматический поток и интегральный поток в случае
излучающей атмосферы также выражается совершенно
аналогичными формулами с учетом соответствующих функций
пропускания— для интенсивности, для монохроматического потока и
для интегрального потока. Во всех случаях первый член
описывает излучение подстилающей поверхности, дошедшее до уровня
га, а второй член — собственное излучение слоя атмосферы,
заключенного между земной поверхностью и уровнем т. Это
излучение складывается из излучений всех нижележащих уровней
и(т — и>0), причем вклад каждого уровня пропорционален
излучению черного тела при соответствующей температуре
(температуре источника) и приращению функции пропускания в
бесконечно тонком слое du. Для наглядности схема формирования
потоков излучения (как восходящего, так и нисходящего)
представлена на рис. 6.14.
1 При численном интегрировании использование частного дифференциала
не представляет никакой трудности, однако при графическом вычислении
интеграла это невозможно. В связи с этим в ряде работ исследовался данный
вопрос и предлагалось вводить поправки к интегральной функции
пропускания либо вообще использовать иное выражение для интегрального потока.
Лучистая энергия
153
Заметим, что при любом профиле температуры собственное
излучение слоя атмосферы, доходящее до уровня га, всегда дает
некоторый положительный вклад; отрицательное собственное
излучение не имело бы физического смысла. Вместе с тем вклад
собственного излучения атмосферы практически всегда меньше^
чем поглощение радиации, поступающей от земной поверхности.
Поэтому суммарный поток восходящего длинноволнового
излучения убывает с высотой, т. е. приращение отрицательно.
П-нобл-ТЬ
m=0,z=O
^н обл
М-пг
cLil
m-u
гт
ii
V//////////////////////////////////////////////////////////////////////
Рис. 6.14. Схема формирования потоков длинноволновой радиации
в атмосфере.
Заметим также, что функция пропускания и ее производная-
очень быстро убывают с увеличением поглощающей массы,
поэтому вклад ближайших к рассматриваемому уровню слоев
максимален, тогда как излучение удаленных слоев почти не
достигает рассматриваемого уровня.
Уравнение переноса нисходящей радиации (6.2.6) может быть
проинтегрировано точно таким же образом, как и уравнение
(6.2.5). Если на верхней границе слоя имеется сплошной
облачный покров [граничное условие (6.2.9)], то решение должно быть
совершенно аналогичным (6.2.24), поскольку единственное
различие в постановке задачи определяется знаком перед правой
частью уравнения (6.2.6). Учитывая это различие в знаке, можно
по аналогии с (6.2.22), (6.2.23) и (6.2.24) записать выражения
для интенсивности нисходящей радиации Д, для нисходящего^
164
Глава 6
спектрального потока Fy, и нисходящего интегрального потока
радиации F на уровне т. Так, для интегрального потока
получим
Г^(т) = /\. т (Гн. обл) & Нн. обл — гп) -f
т
+ J /ЧТ(7») ^(l~m) <***■ (6.2.25)
тн. обл
Здесь предполагается, что облако излучает, как черное тело.
Схематически вклад излучения облака и вышележащих слоев
атмосферы в нисходящее излучение на уровне т изображен на
рис. 6.14.
В случае безоблачной атмосферы первый член в выражении
(6.2.25), естественно, отсутствует, а весь поток нисходящей
радиации на уровне т определяется собственным излучением
вышележащих слоев. При этом интегрирование распространяется
вплоть до верхней границы атмосферы [условие (6.2.8)]: z->-oo,
и=М. Тогда
т
F' (т) = 1>ч. т (Т(и)) ^iu-m) da. (6.2.26)
М
Совершенно аналогично можно получить восходящие и
нисходящие потоки для любых надоблачных, межоблачных и
подоблачных слоев.
Перенос коротковолновой радиации в атмосфере
Для коротковолновой (солнечной) радиации уравнения
переноса получают из уравнений (6.2.1) и (6.2.2), если пренебречь
собственным излучением атмосферы. Целесообразно
преобразовать последний член в этих уравнениях, описывающий усиление
радиации за счет рассеяния. Среди всех переменных
направлений Ф', г|/, в которых распространяется радиация, резко
выделяется одно — направление распространения солнечных лучей.
Из-за очень большого расстояния от Земли до Солнца видимые
угловые размеры Солнца, как известно, очень малы и солнечные
лучи практически можно считать параллельными. Поэтому
солнечная радиация в данный момент времени распространяется
в каком-то фиксированном направлении Ф^Ф©, i|/=ij)©, и, стало
быть, радиацию, возникающую при рассеянии прямой солнечной
радиации, нет необходимости интегрировать по направлениям
Ф' и я|/. Это так называемое первичное рассеяние.
Лучистая энергия
155-
Однако, помимо прямой солнечной радиации, в атмосфере
имеется также и рассеянная солнечная радиация,
распространяющаяся во всех возможных направлениях. Эта радиация
дает вклад так называемого многократного рассеяния (т. е.
рассеяния рассеянной радиации). Поскольку прямая радиация
Солнца обычно значительно больше, чем рассеянная, вклад
многократного рассеяния мал и часто им можно пренебречь по
сравнению с первичным рассеянием (т. е. рассеянием прямой
солнечной радиации). Но в некоторых задачах, когда рассеяние очень
велико, рассеянная радиация может быть сравнима с прямой
и даже превышать ее. В этом случае необходимо рассматривать
именно многократное рассеяние. Наглядным примером такого
сильного рассеяния является рассеяние радиации в облаках и
туманах. При достаточно плотной облачности диск Солнца
становится невидимым. Это означает, что вся первоначальная прямая
радиация рассеяна в облаке и в нижнем подоблачном слое
распространяется (а значит, и рассеивается) только рассеянная
радиация.
Учитывая различие в рассеянии прямой и рассеянной
радиации, удобно разделить последние члены в уравнениях (6.2.1) и
(6.2.2) на две части — на первичное и многократное рассеяние.
При этом прямую солнечную радиацию принято обозначать
через S\. Окончательно уравнения (6.2.1) и (6.2.2) примут вид:
+^Vi d*'.f **(*• *• »'• ЯЛОЛ </Ka'. (6-2.27)
6 6
£j[ , р а
а 2% *
Р Г I W I *х (*• Ф. *'• Ф') А (»', f) <*»'• (6-2.28)
COS
Для различных конкретных задач уравнения (6.2.27) и
(6.2.28) могут быть еще более упрощены. Эти случаи будут
рассмотрены в дальнейшем.
Сформулируем граничные условия. На верхней границе
атмосферы нисходящая рассеянная радиация отсутствует, так как
рассеяние возможно только в атмосфере. Но, как уже
говорилось, в коротковолновой области спектра главную роль играет
прямая солнечная радиация, которая максимальна именно за
пределами атмосферы. Таким образом, при z-> оо
Л (z)= с . * , , (6.2.29)
w 15X0 при 8 = »э, ф = ф®.
156
Глава 6
На земной поверхности восходящая радиация представляет
собой нисходящую суммарную радиацию (т. е. сумму прямой и
рассеянной радиации), отраженную от земной поверхности,
4(0, Ъ, ф) = 5х(0, V ф0)гх(&, 6, »0> <b)cos&0 +
2* тс/2
+ J £/•/ j Ух1 (0, »', ф')гх(0, 6, &', f)cos&'sin»'d&\ (6.2.30)
и о
Здесь Sx(0, О®, <>©) —прямая солнечная, а Л (О, О', г|/)
—рассеянная нисходящая радиация на уровне земной поверхности;
г\ — спектральный коэффициент яркости (или коэффициент
направленного отражения) подстилающей поверхности. В
большинстве случаев можно считать отражение изотропным. Тогда
л
г\= и выражение (6.2.30) значительно упрощается:
Л(0, 8, 4)=^[SX,(0, ft0i *0)cos»0+Di(O)]. (6.2.31)
Здесь
2тс тс/2
Dx40) = f rff f Л;(0, ft', f) cos»'sin &'*/&'
6 6
— нисходящий спектральный поток рассеянной радиации на
уровне земной поверхности.
При наличии облачности задача чрезвычайно усложняется
(в гораздо большей степени, чем для длинноволновой радиации).
Облачность частично отражает, частично поглощает и частично
пропускает радиацию. При этом коэффициенты отражения и
поглощения сильно меняются в зависимости от формы и мощности
Таблица 6.1. Радиационные характеристики облачности
в коротковолновой области спектра
Форма
облаков
Ci
As
St
Ns, Cb
Видимая обл
пропущенной
0,79
0,46
0,34
0,24
асть спектра
отраженной
0,21
0,54
0,66
0,76
Близкая инфракрасная область спектра
доля радиации
пропущенной
0,77
0,34
0,20
0,10
отраженной
0,19
0,46
0,50
0,60
поглощенной
0,04
0,20
0,30
0,30
Лучистая энергия
157
облаков. Более того, при прохождении облачного слоя прямая
радиация трансформируется в рассеянную, что также необходимо
учитывать. В задачах динамики атмосферы обычно используется
довольно грубая схематизация задачи. При этом облачный слой
рассматривается как полупрозрачная пластинка с заданными
характеристиками отражения, пропускания и поглощения.
В табл. 6.1 приведены осредненные радиационные
характеристики различных форм облаков.
При более строгом подходе рассматривается перенос
радиации внутри облака. В самых общих чертах такая постановка
задачи изложена ниже.
Интегрирование уравнений переноса коротковолновой радиации
Сформулированные выше уравнения переноса
коротковолновой радиации (6.2.27) и (6.2.28) описывают все возможные виды
радиации — прямую солнечную, рассеянную вверх и вниз,
отраженную от земной поверхности. Интегрирование этих уравнений
для самого общего случая представляет чрезвычайно сложную
задачу. Более того, в тех случаях, когда существенную роль
играет как поглощение, так и многократное рассеяние,
возникают принципиальные трудности. Уравнения переноса
справедливы для строго монохроматической радиации, т. е. для
спектральных интервалов, значительно меньших, чем ширина
спектральной линии. При интегрировании по длинам волн (даже
в сравнительно узких спектральных интервалах) вследствие
эффекта Форбса средний коэффициент поглощения уменьшается
с увеличением пройденной массы. С другой стороны, в
рассматриваемом направлении на данном уровне будут распространяться
лучи, прошедшие различный путь (в результате случайных
блужданий при рассеянии). Эти лучи будут поглощаться в разной
степени. В таком случае необходимо прослеживать путь для
каждой отдельной группы лучей, что, разумеется, нереально,
и задача обычно решается методом Монте-Карло. Здесь
будут рассмотрены лишь наиболее простые и важные частные
случаи.
Прямая солнечная радиация
Уравнение для интенсивности прямой солнечной радиации
получим из уравнения (6.2.28), положив J\=Sx, O = fto, ^=i|>0
и отбросив два последних члена, характеризующих усиление
луча за счет рассеяния, поскольку рассматривается именно
158
Глава 6
прямая радиация. Кроме того, учтем оба возможных механизма
рассеяния — релеевское и аэрозольное рассеяние:
dSi 1
^ = ^^(рпЯх+Р*хр + Ра*ха)5х. <6'2-32>
0
Здесь а^р и а^а — релеевский и аэрозольный коэффициенты
рассеяния соответственно; р — плотность воздуха; ра — плотность
аэрозоля. Остальные обозначения прежние.
При рассмотрении длинноволновой радиации отмечалось, что
удобно ввести эффективную поглощающую массу [см. формулу
(6.2.4)]. Аналогично в случае рассеяния удобно ввести релеев-
скую и аэрозольную оптические толщины единичного столба
атмосферы от поверхности земли до уровня z или до верхней
границы атмосферы1, а также их сумму, т. е. полную оптическую
толщину:
z оо
*хР = \ po^dz, ЕХр = j paXpdz; (6.2.33)
6 о
г оо
4* = §Pa?x*dz, ЕХа=| P*4*dz\ (6.2.34)
о 6
^Х = ^Хр + ^ХР» SX = SXa-T-Xa- (6.2.35)
С учетом введенных поглощающей массы и оптических толщин
уравнение (6.2.32) примет следующий вид:
dSx
—± = 8ес »0 (ах0 Лю+*/тХр-1-ЛХа). (6.2.36)
°х
Проинтегрировав это уравнение по высоте (т. е. по т, т?.р, xxah
получим
S —С max°sec0® T>>sec03
Постоянную С определим из граничного условия (6.2.29),
учитывая, что при z-> оо т=М, тх = 3*,:
С = Охо^ в
И окончательно получим
5x = 5xor('M-m)^°Sec!>^-(Hx-T")Sec0i. (6.2.37)
1 При рассмотрении коротковолновой радиации обычно отсчитывают
поглощающие массы вниз от верхней границы атмосферы. Здесь в целях
единообразия отсчет всюду ведется от земной поверхности. Кроме того, на
практике обычно пользуются не массовым, а объемным коэффициентом рассеяния.
z
В таком случае оптическая толщина т =- Га dz.
о
Лучистая энергия 159
Из формулы (6.2.37) видно, что ослабление солнечной радиации
тем сильнее, чем больше масса поглощающих и рассеивающих
субстанций на пути луча и чем больше зенитный угол Солнца,
т. е. чем больше геометрический путь луча в атмосфере.
_ (/Vf _ m) flX0 sec &0 - (3X ~ "^sec &©
Экспоненты e we представляют
собой не что иное, как функции пропускания для
монохроматической интенсивности в рассматриваемом слое от верхней
границы атмосферы до уровня z. При этом первая из функций
пропускания характеризует поглощение, а вторая — рассеяние
радиации.
Проинтегрируем выражение (6.2.37) по всем длинам волн.
Интегральный поток1 солнечной радиации равен
5= J Sx 0е~ (M-m)a"°sec V (Вх~tx) Sec Ч Л. (6.2.38)
О
Как уже упоминалось, коэффициент поглощения меняется в очень
•больших пределах даже на протяжении ничтожно малых
спектральных интервалов, охватывающих одну линию поглощения.
Коэффициенты рассеяния (и пропорциональные им оптические
толщины) изменяются в зависимости от длины волны
значительно медленнее (тяр~Х-4, Txa~A,-1). Поэтому некоторое сред-
-(2^-xx)sec&0
нее значение е можно вынести за знак интеграла.
00
Кроме того, умножим и разделим интеграл на S0 = jSxodX. Тогда
о
S=5o^-(Sx~Tx)sec°0c^[(M-/7z)sec^0I. (6.2.39)
Здесь
^|(M-/n)sec&0]4 J*_e-»w-m)«c*@ ^ (6240)
есть интегральная функция пропускания в коротковолновой
области спектра, обусловленная поглощением радиации [ср. с
аналогичной функцией пропускания для длинноволновой радиации
(6.2.16)].
1 Напомним, что под потоком радиации понимается полное количество
лучистой энергии, поступающей из всей полусферы (см. п. 6.1). Прямая
солнечная радиация распространяется в пределах очень малого телесного угла
(порядка 32'), однако это и есть полное количество поступающей солнечной
радиации. Поэтому оно обычно называется потоком.
160
Глава 6
,. ~ <SX-T)sec&0
Множитель е при надлежащем выборе средних
значений Ех и ~х\ представляет собой интегральную функцию
пропускания, обусловленную рассеянием.
Выражение (6.2.39) дает значение прямой солнечной
радиации в самом общем случае — при сочетании поглощения и
рассеяния. Оно годится как для безоблачной атмосферы, так и для
межоблачных слоев, только при этом следует учесть долю
прямой радиации, прошедшей сквозь облако (при плотных облаках
в подоблачном слое вообще нет прямой радиации).
Обычно при расчетах пользуются более простыми
выражениями. В видимой области спектра (л<0,7 мкм) в тропосфере
практически отсутствует поглощение, т. е. £Р[(Ь\— m)secde ] =
= 1. В близкой инфракрасной области спектра (0,7—4 мкм)
имеет место поглощение водяным паром и углекислым газом, но
рассеяние становится очень малым, и им можно пренебречь,
особенно при Я> 1 мкм.1
Рассеянная солнечная радиация в безоблачной атмосфере
Как отмечалось выше, в общем случае решение уравнений
переноса является чрезвычайно трудным. Однако в видимой
области спектра (где существенно рассеяние) можно пренебречь
поглощением. В большинстве задач, связанных с определением
притоков тепла, можно пренебречь также и многократным
рассеянием. Тогда решение оказывается сравнительно простым
даже при наличии крупных частиц. Получим такое решение для
интенсивности рассеянной радиации. Преобразуем уравнение
(6.2.27) следующим образом. Во-первых, отбросим члены,
учитывающие поглощение и многократное рассеяние. Во-вторых,
при однократном рассеянии выпишем отдельно релеевскую и
аэрозольную составляющие и введем соответствующие
оптические толщины (6.2.33) — (6.2.35). И, наконец, подставим
выражение для прямой солнечной радиации (6.2.37) также без учета
поглощения (т. е. при а?,о = 0).
В результате получим
/t y.v dz. -1-х. dz.n
I «/>. Xp ар да Xa
COS ft v /чр ''a/ ' COS Ь
XSxoe~(*x~^),ec*3.
1 В любом случае учет ослабления прямой солнечной радиации в
результате рассеяния имеет смысл лишь тогда, когда наряду с прямой радиацией
рассматривается также перенос рассеянной радиации.
Лучистая энергия
161
Разделим обе части уравнения на приращение полной
оптической толщины dxx = dxxj,+dxxai:
Здесь
dJ{
*\ "
4
i
cos & l
*Хср — ХХ р
ХХср
COS&
*Хр
dxx
с -(вХ-«Х)»*с»®
охое
, dxx»
1 -л. ^
(6.2.41)
(6.2.42)
есть средневзвешенная индикатриса, учитывающая релеевское
и аэрозольное рассеяние. Средневзвешенная индикатриса в
нижних слоях атмосферы в основном определяется аэрозольной
составляющей, которая оказывается намного больше релеевской.
С ростом высоты концентрация аэрозолей убывает и
увеличивается роль релеевского рассеяния. На больших высотах
индикатриса приближается к релеевской. Однако данные наблюдений
показывают, что и в верхних слоях атмосферы встречаются
замутненные слои, в которых индикатриса рассеяния сильно
вытянута вперед.
Вообще изменчивость индикатрисы и оптических толщин
наряду с чисто математическими трудностями приводит к
практической невозможности корректного решения уравнений переноса
рассеянной радиации. К счастью, изменение индикатрисы с
высотой не очень сильно влияет на поток рассеянной радиации (в
отличие от интенсивности). Поэтому реальную средневзвешенную
индикатрису можно заменить осредненным по высоте значением
клер. В таком случае обыкновенное неоднородное
дифференциальное уравнение (с постоянными коэффициентами) (6.2.41)
легко решается методом Лагранжа, аналогично тому, как это
было выполнено для уравнения переноса длинноволновой
радиации. Его решение имеет вид
О
Здесь через т' обозначена переменная интегрирования (т. е.
переменный уровень, на котором происходит рассеяние), в отличие
от произвольного, но фиксированного верхнего предела, т. е. от
уровня расчета. Интеграл во втором члене легко берется.
Постоянную С определим из граничного условия (6.2.31). При z =
= 0,тя=0
А Г -Вч sec» 1
А(0) = С=—MSxoCOsV А S+£x(0)J.
И Заказ JSfe 612
162
Глава 6
Окончательно получим
-(5X-^)secO0
it L
+
5X 0XX cp
sec$
+Ях(0)]
,-тЛ sec <
+
— e
-Bxseca0-xxsec(
(6.2.43)
secd + secft0
Аналогично для нисходящей радиации из уравнения (6.2.28)
получим
di,
cosu
*cp С p
(6.2.44)
Уравнение (6.2.44) отличается от уравнения (6.2.41) только
знаком в правой части. Его решение имеет вид
sx / 'Ч '
, TXsecO 5хохх <txsecO С - {8Х- тх) secO0 - xxsec» .
*х
cos$
Постоянную интегрирования определим из граничного условия
(6.2.29). Получим С = 0. И окончательно
л-
Sxo*icpsec»
sec Ь& — sec *
— (8\ — til sec ft
(*х-*х)
— е
(Sx-^X) sec^0
(6.2.45)
Формулы (6.2.43) и (6.2.45) дают спектральную
интенсивность восходящей и нисходящей рассеянной радиации на
произвольном уровне xx(z) в
безоблачной атмосфере.
Интенсивность рассеянной
радиации на рассматриваемом
уровне складывается из
интенсивности лучей,
рассеянных всеми вышележащими
/>/™ л> ™- или нижележащими слоями.
—р Схематически расположение
различных уровней
рассеяния и формирование
интенсивности изображены на
рис. 6.15.
Для того чтобы получить
интегральные потоки
рассеянной радиации, необходимо
проинтегрировать (6.2.43) и
у///////////////>/////////////////////////////////>//, (6.2.45) по всем телесным уг-
Рис. 6.15. Схема формирования интен- лам и Длинам волн- Однако,
сивности рассеянной радиации в атмо- учитывая сложную зави-
сфере. симость характеристик рас-
Лучистая энергия
163
сеяния от угла рассеяния и от длины волны, это
интегрирование можно выполнить только численно.
Изучение закономерностей рассеяния в атмосфере имеет
очень большое значение для ряда прикладных задач (не
связанных с тепловыми эффектами), таких, как определение дальности
видимости и естественной освещенности, определение
характеристик аэрозоля и облачных капель по наблюдениям рассеянного
света, интерпретация спутниковых наблюдений и т. д. В
настоящем курсе эти вопросы не рассматриваются.
Интегральные функции пропускания
Выше были получены выражения для интегральных потоков
длинноволновой и коротковолновой радиации на любом уровне
в атмосфере. В эти выражения входят интегральный поток
излучения черного тела (или интегральная солнечная постоянная)
и соответствующие интегральные функции пропускания,
зависящие от эффективной массы. Такое представление чрезвычайно
упрощает расчеты лучистых потоков и притоков, уменьшает их
трудоемкость. Действительно, громоздкое интегрирование по
направлениям и длинам волн выполняется заранее при
вычислении функций пропускания. А для каждой конкретной
стратификации ^остается выполнить два численных интегрирования по
высоте— вычисление эффективных поглощающих масс и затем
вычисление потоков радиации в зависимости от массы (высоты).
Поэтому интегральные функции пропускания широко
применяются при расчетах, несмотря на некоторые погрешности,
связанные с их введением.1
На примере длинноволновой радиации рассмотрим
подробнее некоторые детали. Функция пропускания для
монохроматической интенсивности (6.2.12) представляет собой простую
экспоненту. Скорость ее убывания с увеличением поглощающей массы
зависит от коэффициента поглощения а^о, который может
изменяться в очень широких пределах. Так, в некоторых участках
спектра аяо = 0 и радиация вообще не поглощается, а в
некоторых участках радиация практически полностью поглощается
водяным паром, количество которого эквивалентно сотым и
тысячным долям сантиметра столба осажденной воды. (Напомним для
1 В зарубежной литературе обычно употребляется не функция
пропускания с^(ш), а функция поглощения, или излучательная способность е=1 —
— <?(т). При этом часто при интегрировании по длинам волн используется
несколько иная весовая функция, а именно
\ df )l\ dT *
11*
Лучистая энергия
165
для интегральных функций пропускания характер зависимости
от пройденной массы оказывается совсем иным, чем для
спектральных функций пропускания. Интегральные функции
пропускания в противоположность спектральным очень быстро
убывают при малых массах, а с увеличением массы их убывание
замедляется. Это объясняется рассмотренным выше эффектом
Форбса.
Для удобства вычислений на ЭЦВМ функции пропускания
аппроксимируются приближенными аналитическими
формулами. Приведем некоторые примеры.
#| i i i i i i i i i i i i i i i i i i i I,
Q2 0,4 0,6 0,8 1,0 tf 1,4 1,6 1,8 тп г/см2
Рис. 6.16. Интегральные функции пропускания для коротковолновой (/,
2, 3) и длинноволновой (4, 5) радиации по данным различных авторов.
/ — Мюгге и Мёллер, 2 — Краснокутская и Фейгельсон, 3 — Евсеева и
Подольская, 4 — Ковалева и Шехтер, 5 — Градус, Нийлиск, Фейгельсон, 5—^ (т) —
— е а при а ^ —1.15.
При расчетах потоков длинноволновой радиации в
тропосфере (при ясном небе или в межоблачных слоях) очень удобна
функция пропускания (кривая 4), учитывающая две основные
поглощающие компоненты (водяной пар и углекислый газ):
^(m)=-0,539e-7,75/i;r+0,461e-0'674^ (6.2.48)
Здесь m — масса водяного пара (в г/см2 или в сантиметрах
столба осажденной воды). Поглощение углекислым газом учтено
путем соответствующего увеличения коэффициентов поглощения
для водяного пара, при этом принято среднее типичное
соотношение между количествами водяного пара и углекислого газа
в атмосфере. Такое предположение значительно упрощает
расчеты потоков радиации, однако в случае очень «сухой» или очень
166
Глава 6
«влажной» атмосферы приводит к некоторым погрешностям (не
слишком большим ввиду сравнительно малой роли углекислого
газа).
Для потоков длинноволновой радиации в случае облачной
атмосферы следует пользоваться интегральной функцией
пропускания (кривая 5), учитывающей поглощение водяным паром,
углекислым газом и капельно-жидкой водой. Эта функция
пропускания годится для тропосферы, как в безоблачных, так и
в облачных слоях. Естественно, что такая функция пропускания
описывается гораздо более сложной формулой:
3 3
+ П 2 аРе
п =2Л=1
-1,6б(ат3+а<1Ц)
2d а*е +
-l.«(«*3+«i"4-l)l
(6.2.49)
Здесь mi и гпз — поглощающие массы водяного пара и
капельножидкой воды в г/см2 (сантиметры столба осажденной воды);
mi — поглощающая масса углекислого газа, выраженная в
сантиметрах единичного столба, приведенного к нормальным
условиям. Значения коэффициентов, входящих в формулу (6.2.49) „
приведены в табл. 6.2.
Таблица 6.2. Коэффициенты afjp и а ^в формуле (6.2.49) при гп\ < 1 см,
ш2^300 см (в скобках при 1 cm<wi^10 см, 300 см<т2^500 см)
п
1
2
3
,(->
■(;}
к
1
0,192
(0,192)
0,044
0,322
2
0,210
(0,261)
0,192
0,400
3
0,347
(0,294)
0,000
0,278
1
474
(431,6)
2,900
0,562
2
11,2
(10,5)
0,226
0,012
3
0,300
(0,147)
0,00015
а
1100
Изложенные выше соображения справедливы также по
отношению к функциям пропускания для коротковолновой радиации
с одним лишь исключением. Выбор среднего значения sec^
в случае рассеянной радиации оказывается гораздо труднее. Это
объясняется тем, что длинноволновое излучение элементарного
объема изотропно (т. е. не зависит от направления). Зависимость
интенсивности радиации от зенитного угла определяется только
Лучистая энергия
167
геометрическим различием пройденных в атмосфере путей. При
рассеянии радиации, помимо указанного геометрического
эффекта, появляется физический эффект: рассеяние элементарным
объемом ни в коем случае не изотропно и определяется
соответствующей индикатрисой рассеяния. На практике для
безоблачных слоев1 часто пользуются тем же самым значением secfr =
= 1,66, однако это приводит к гораздо большим ошибкам, чем
в случае длинноволновой радиации.
Для коротковолновой (солнечной) радиации в безоблачных
слоях тропосферы может быть предложена интегральная
функция пропускания (кривая 3), учитывающая поглощение водяным
паром и углекислым газом:2
/-л / о ч ^ л~* . Л ЛЛ^ —2,99 Vmsec&f;x . _ , _ _ —0,0922 Ym secft^
S?(m sec d@)=0,463+0,062^ ° -f-0,450e 0 .
(6.2.50
Здесь m — масса водяного пара; поглощение углекислым газом
также учтено путем небольшого увеличения коэффициентов
поглощения водяного пара. (В коротковолновой области спектра
такое приближение оказывается весьма точным, поскольку роль
углекислого газа очень мала.) Более того, коэффициенты
функции пропускания учитывают поглощение солнечной радиации
в вышележащем слое озона (действительно, при пг = 0 <^ = 0,975,
т. е. солнечная радиация на перпендикулярную поверхность
равна так называемой подозонной солнечной постоянной).
Рассеяние данной функцией пропускания не учитывается. При учете
рассеяния удобнее рассматривать отдельно видимую часть
спектра, где поглощение практически отсутствует, а рассеяние
велико, и близкую инфракрасную область спектра (Х>0,7 мкм),
где мало рассеяние (во всяком случае, многократное), но
велико поглощение. В выражении (6.2.50) видимой области
спектра соответствует первый (постоянный) член, а близкой
инфракрасной— два остальных.
Из формул (6.2.48) и (6.2.50) видно, что часть радиации
очень сильно поглощается (первая экспонента), так что ее «путь
пробега» в атмосфере весьма мал. Часть же радиации
ослабляется сравнительно медленно и проникает сквозь всю толщу
земной атмосферы (вторая экспонента).
1 Для облачных слоев определение среднего пути, пройденного радиацией
(как коротковолновой, так и длинноволновой), представляет особую, весьма
сложную задачу. Этот вопрос рассмотрен ниже.
2 Эта функция годится также и для рассеянной радиации, только при
этом надо учитывать суммарную массу, пройденную лучом до момента
рассеяния на уровне гп' [(М — m'JsecO©] и после него:
г*сум
= (М — т') secft^ + (\m — m' |) sec ft .
168
Глава 6
Перенос радиации в облаках и туманах
В облаках и туманах, т. е. в слоях воздуха, содержащих
взвешенные капельки воды и кристаллики льда, радиация
поглощается и рассеивается значительно сильнее, чем в безоблачной
атмосфере.
В случае длинноволновой радиации задача решается
сравнительно просто. Рассеяние приводит к изменению направления
распространения части лучей, но без изменения общего
количества радиации. Так, например, часть нисходящей радиации
рассеивается назад и добавляется к потоку восходящей радиации
Рис. 6.17. Схема распространения фотонов при многократном рассеянии.
(и наоборот). Если бы интенсивность падающей радиации не
зависела от направления, то такой «взаимный обмен» рассеянной
радиацией не изменил бы величины потоков. Поскольку
восходящая длинноволновая радиация (излучаемая более теплыми
и влажными слоями атмосферы) всегда больше нисходящей,
рассеяние приводит к некоторому уменьшению восходящего
и увеличению нисходящего потоков. Однако этот эффект мал,
и им можно пренебречь. Гораздо большую роль играет удлинение
пути, пройденного радиацией, в результате многократных
рассеяний фотонов облачными каплями (схематически это
удлинение показано на рис. 6.17). Оно приводит к большему
поглощению радиации каплями и атмосферными газами и может быть
учтено путем увеличения значения sect} для любого из
падающих лучей.
Таким образом, перенос длинноволновой радиации в облаке
может быть описан теми же самыми уравнениями переноса, что
и для безоблачной атмосферы, т.е. уравнениями (6.2.5) и (6.2.6).
Лучистая энергия
169
Граничные условия при этом задаются на земной поверхности
и на верхней границе атмосферы, а вся атмосфера, включая
облачные и безоблачные слои, рассматривается как непрерывная
среда с заданным вертикальным распределением всех
поглощающих субстанций — газов и капельно-жидкой воды.
Соответственно выражения для интегральных потоков радиации будут
иметь такой же вид, как и для безоблачной атмосферы
[формулы (6.2.24) и (6.2.26)], только следует пользоваться
интегральной функцией пропускания, учитывающей поглощение
водяными каплями (6.2.49), а также увеличить seed для облачных
слоев. По данным различных авторов, в облаке secO = 2^-5.
Проведенные для слоистых облаков расчеты показали, что
резкие изменения потоков (и следовательно, большие притоки
радиации) имеют место в тонких пограничных слоях (примерно
100 м) в окрестности верхней и нижней границ облака. На
верхней границе наблюдается сильное выхолаживание, а на
нижней — нагревание. Внутри облака притоки радиации отсутствуют.
Такая картина получается в результате очень сильного
поглощения длинноволновой радиации облачными каплями, т. е.
качественно достаточно плотное облако (с водностью больше 0,05 г/м3)
близко к абсолютно черной пластинке, поглощающей и
излучающей радиацию только на поверхности. Количественно «черное
приближение» дает большие погрешности в притоках (примерно
50%) вблизи границ облака и в подоблачном слое, где приток
вообще очень мал. Притоки тепла над облаком, а также к
самому облачному слою и ко всей атмосфере в целом достаточно
хорошо описываются «черным приближением». (Как
упоминалось выше, именно такой подход обычно используется в
задачах динамики атмосферы.) Что касается более корректного
непрерывного рассмотрения, то оно совершенно необходимо при
решении задач, связанных с эволюцией облачности, а также в тех
случаях, когда требуется знание детального профиля притоков
тепла.
При распространении в облаке коротковолновой солнечной
радиации отсутствует собственное излучение, а роль рассеяния
и поглощения очень велика. Действительно, в облаке, как
правило, падающая солнечная радиация рассеивается полностью.
Около половины радиации рассеивается назад (отражается),
часть поглощается, а часть рассеивается вперед, т. е.
пропускается облаком, но уже не в виде параллельного пучка лучей,
а в виде рассеянной (диффузной) радиации.
Удобно рассматривать отдельно видимую и близкую
инфракрасную области спектра. В видимой области отсутствует
поглощение атмосферными газами. Радиация поглощается только
каплями. Спектр поглощения капельно-жидкой воды сплошной,
170
Глава 6
коэффициенты поглощения меняются плавно с изменением длины
волны. Поэтому отсутствует эффект Форбса, т. е. средний
коэффициент поглощения не зависит от пройденной массы. В этом
случае основная трудность состоит в учете многократного
рассеяния. [Как видно из выражений (6.2.43) и (6.2.45), даже для
однократного рассеяния без учета поглощения решение
получается достаточно громоздким.] Однако интегрирование
уравнений переноса всегда может быть выполнено численно или с
помощью приближенных аналитических методов.
В близкой инфракрасной области спектра (А,>0,7 мкм)
радиация поглощается каплями, водяным паром, углекислым
газом и озоном. Многократное рассеяние осуществляется каплями.
Как говорилось выше, в этом случае приходится прослеживать
пути отдельных лучей (что абсолютно нереально для всех лучей)
и задача обычно решается методом Монте-Карло.
Прослеживаются пути и определяются вероятности рассеяния и
поглощения для достаточно большого числа случайно выбранных
фотонов. Полученные закономерности обобщаются на весь поток.
Таким способом (при ряде упрощающих приближений) были
определены вероятности прохождения фотонами различных
путей (т. е. распределение фотонов по пробегам в отраженном
и пропущенном свете), а затем найдены эффективные средние
пути фотонов в слоистых облаках. В табл. 6.3 приведены
значения отношения среднего пути /, пройденного радиацией в облаке,
к геометрической толщине облака h (—= secT}j в зависимости
от оптической толщины облака т = акррй. Здесь ак — коэффициент
рассеяния облачными каплями; плотность рассеивающего
вещества рр есть не что иное, как водность облака б.
Таблица 6.3. Значения sec Ф = -г- в зависимости от оптической толщины
облака т и зенитного угла Солнца Ф
Поток
Отраженный
Пропущенный
Отраженный
Пропущенный
Отраженный
Пропущенный
sec $0
1
2
4
т
2
—
2,0
2,1
1,6
3,0
5
1,5
1,3
1,5
1,6
1,1
1,8
10
1,4
1,8
1,2
2,3
0,9
2,4
30
1,5
2,2
0,9
2,3
0,6
2,7
50
1,4
3,5
0,7
3,6
—
—
1000
—
0,6
6,6
—
—
Лучистая энергия
171
Пользуясь данными табл. 6.3, значениями вероятности
пропускания и отражения облаком *, а также интегральной
функцией пропускания, учитывающей все поглощающие субстанции,
можно рассчитать потоки нисходящей и восходящей радиации
в безоблачных слоях атмосферы и на границах облачных слоев.
Так, например, в надоблачном слое нисходящий поток — это
прямая солнечная радиация, определяемая формулой (6.2.39).
Рассеянием в безоблачных слоях можно пренебречь. Восходящий
поток — это отраженная от облака радиация. Он может быть
также вычислен по формуле (6.2.39), если внести поправки.
Во-первых, солнечную постоянную надо умножить на
альбедо облака; тем самым будет учтена отраженная доля
падающей радиации. Во-вторых, следует корректно учесть суммарную
массу поглощающих веществ, пройденную отраженными лучами.
Она представляет собой сумму масс водяного пара на пути
прямой радиации от верхней границы атмосферы до верхней
границы облака, в облачном слое на пути l = h secfr (см. табл. 6.3)
и над облаком — от верхней границы до рассматриваемого
уровня. При этом в безоблачных слоях для отраженной и
пропущенной диффузной радиации можно взять sec Ф= 1,66. Кроме
того, «средний» отраженный луч внутри облака прошел массу
капельно-жидкой воды /б = h seer) 6.
Аналогичным образом можно рассчитать пропущенную
(нисходящую) радиацию на любом уровне от нижней границы
облака до поверхности земли. В этом случае солнечную
постоянную надо умножить на вероятность пропускания облаком и точно
таким же образом учесть суммарную массу выше облака, в
облаке и ниже облака. Изменение с высотой потока внутри
облачного слоя рассчитать нельзя, поскольку эффективные
средние пути пробега фотона определены для всего облачного слоя.
Можно вычислить только полное количество радиации,
поглощенной в облаке, как разность входящих в облако и выходящих
из него потоков на верхней и нижней границах.
6.3. Радиационный баланс системы Земля—атмосфера.
Метеорологические приложения
Расчет потоков и притоков лучистой энергии в атмосфере
Используя полученные в предыдущем параграфе выражения,
можно рассчитать интегральные потоки коротковолновой и
длинноволновой радиации на произвольном уровне.
1 Очевидно, альбедо облака представляет собой сумму вероятностей
выхода для всех отраженных фотонов (при любых пробегах в облаке).
Аналогично определяется пропускание.
172
Глава 6
Вычисление потока прямой солнечной радиации по формуле
(6.2.39) с любой из интегральных функций пропускания
[например, (6.2.50)] не представляет особого труда. Интегральные
функции пропускания для коротковолновой радиации при
стандартных условиях в настоящее время получены с удовлетворительной
точностью. Об этом свидетельствует, в частности,
незначительное различие кривых (см. рис. 6.16), рассчитанных на основе
разных экспериментальных данных. Главные трудности здесь
связаны с определением профилей концентрации поглощающих
субстанций в реальной атмосфере. Кроме того, влияние
давления на поглощение радиации учитывается приближенно, путем
введения эффективных масс, а влияние температуры не
учитывается вовсе. До настоящего времени нет достаточно надежных
оценок точности такого приближения.
Вычисление потоков рассеянной радиации оказывается
гораздо сложнее [см. формулы (6.2.43) и (6.2.45)]. Однако, если
иметь в виду тепловые эффекты, рассеянием в безоблачной
атмосфере можно пренебречь. Действительно, в результате
рассеяния ослабляется поток прямой солнечной радиации и
соответственно на 10—15% уменьшается его поглощенная доля. Но это
уменьшение в значительной мере компенсируется поглощением
рассеянной радиации.
В облачных слоях рассеяние играет решающую роль.
Приближенный метод расчета потоков коротковолновой радиации
в облачной атмосфере был рассмотрен выше, но в целом эта
проблема почти не исследована. Сведения о радиационных
характеристиках различных типов облаков (особенно
кристаллических) крайне скудны и ненадежны. Задача чрезвычайно
сложна с математической точки зрения и требует трудоемких
расчетов, доступных только современным электронным
вычислительным машинам.
Для вычисления потоков длинноволновой радиации обычно
используются формулы типа (6.2.24) — (6.2.26) либо выражения,
полученные из указанных формул путем интегрирования по
частям *. Например, вместо (6.2.24) можно получить эквивалентное
выражение
т
F\m) = F4.r(T{m))-\ SP(m-u)-±^dti. (6.3.Г)
о
В любом случае необходимо выполнить численное
интегрирование по поглощающим массам. При ручных расчетах обычно при-
1 При этом необходимо, чтобы под знаком интеграла стоял полный диф
ференциал d&(m— и)\ в противном случае преобразованное выражение
содержит не функцию пропускания, а несколько иную функцию.
Лучистая энергия
173
меняются графические методы интегрирования. С этой целью
предложено свыше 10 радиационных диаграмм. Они основаны
на формулах типа (6.2.24) или (6.3.Г), рассчитаны с разными
интегральными функциями пропускания и, кроме того,
различаются в некоторых других деталях. Однако расчеты с помощью
радиационных диаграмм все же слишком трудоемки. В задачах
динамики атмосферы вычисления, как правило, осуществляются
на ЭЦВМ. При этом могут применяться любые стандартные
методы численного интегрирования, однако вследствие очень
быстрого изменения функции пропускания при малых массах и ее
медленного изменения при больших массах возникают некоторые
трудности при выборе шага интегрирования.
Помимо вычислительных трудностей, существуют трудности
принципиальные. Интегральные функции пропускания для
длинноволновой радиации определены менее надежно, чем для
солнечной (это подтверждается большим разбросом различных
функций пропускания на рис. 6.16). Как и в случае
коротковолновой радиации, встает проблема точности исходных профилей
температуры и концентраций поглощающих субстанций, а также
корректного учета зависимости функций пропускания от
давления и температуры. Потоки длинноволновой радиации,
рассчитанные с помощью различных радиационных диаграмм и
численных методов, отличаются весьма значительно: в некоторых
случаях, различие достигает 50%. В настоящее время проводятся
интенсивные исследования с целью уточнения методов расчета.
С другой стороны, даже при использовании современной
электронной вычислительной техники расчеты подчас требуют
слишком много времени. Поэтому не прекращаются поиски
оптимальных приближений, уменьшающих затраты машинного времени
без существенной потери точности. Приведем пример такого
приближения.
Интеграл в формуле (6.2.24) по теореме о среднем можно
выразить следующим образом:
m m
1 Л. х(Т(и)) ^(2~Ц) du =КМТЩ| [^ (0)- ^ («)] •
6 о
Для каждой конкретной стратификации наверняка можно
подобрать такое значение F4.T, при котором равенство будет
точным. Однако надо указать правило отыскания среднего в общем
случае. Можно представить его как линейную комбинацию
значений F4,T на границах интервала. Тогда
m
Г с /Т-/ w d& (m — и) ,
J ^.т(П«)) *25 —du =
6
= 1^ч. т ("0 + 0 - !*) /\. т (0)) [ 1 - ^ («)] •
174
Глава 6
Весовой множитель (i указывает относительный вклад слоев,
близких к уровню расчета т и удаленных от него. Так, при \х =
= 7г они дают равнозначные вклады. Величина ^ч. т есть просто
среднее арифметическое. При jut —>-1 поток излучения
практически формируется в ближайших к уровню расчета слоях. Расчеты,
проведенные для среднезональных профилей температуры и
влажности, показывают, что для нисходящей радиации такое
приближение весьма близко к истине. В пределах тропосферы
jli— 0,9-^0,98. Для восходящей радиации \i^0,6-^0,8, т. е. вклад
ближайших слоев относительно больше, однако и удаленные
нижние слои (более теплые и влажные) играют заметную роль.
При надлежащем выборе средних значений ц в пределах
тропосферы погрешность потоков в результате такой приближенной
замены интегралов не превышает 10%.
Основной целью радиационных расчетов является
определение радиационного баланса на разных уровнях и для системы
Земля—атмосфера в целом, а также лучистых притоков тепла
в атмосфере.
Радиационный баланс на произвольном уровне
/?(«)=.5(z)sec»0+Dl(e)-Dt(2)+/7l(2;)-/;,t(^ (6.3.1)
представляет собой разность нисходящих и восходящих потоков
(здесь через D и D обозначены потоки рассеянной вниз и
рассеянной вверх, т. е. отраженной, радиации). Его физический
смысл становится очевидным, если применить равенство (6.3.1)
к границам атмосферы. Так, при 2 = 0 радиационный баланс
равен количеству лучистой энергии, которая поступает за единицу
времени на единицу площади земной поверхности. При /?>0
Земля получает энергию путем лучистого теплообмена, при R<0
Земля теряет ее. Аналогично для z->~oo радиационный баланс
означает приход (потерю) энергии к системе Земля—атмосфера
в целом. В общем случае это приход лучистой энергии ко всему
слою (включая земную поверхность), расположенному ниже
уровня г. Можно определить радиационный баланс для слоя
произвольной толщины как разность радиационных балансов на
границах слоя. Наиболее интересен радиационный баланс всей
атмосферы: /?а = Ж°°) —#(0).
Обратная по знаку величина F = —R называется
результирующим потоком, а его длинноволновая часть 9 = F —F
—эффективным излучением. Результирующий поток
(положительный) направлен вверх, поскольку /7>0, когда преобладают
восходящие потоки.
Приток лучистой энергии £р (как и любой другой энергии)
представляет собой дивергенцию результирующего потока. По-
Лучистая энергия
175
скольку радиационные потоки существенно меняются только по
вертикали, в выражении дивергенции остается лишь один член
dF
——. Таким образом, в единицу времени приток тепла к единице
объема равен
dQp dEp dF
d\r dV dz
(6.3.2)
Физически знак минус означает следующее: если поток
увеличивается в направлении распространения (dF>0), то собственное
излучение среды преобладает над поглощением, среда теряет
эквивалентное количество тепла.
Наиболее показательной характеристикой лучистого притока
тепла является радиационное изменение температуры, т. е.
изменение только за счет лучистого притока. Очевидно, что
dQP 1 dQ
с
'( dt )р —
"Р\ dt )р dmB03R р dV
или, согласно (6.3.2),
\ dt ;р рс„ dz $ср dz v '
Часто бывает удобнее пользоваться шкалой давлений. В таком
случае
J_Jf_= g dR
ср dp ср dp
I dt )p —"
(6.3.4)
Заметим, что поглощают (излучают) радиацию водяной пар,
углекислый газ, озон, аэрозоли, плотность которых ничтожно мала
по сравнению с плотностью воздуха. Однако при условии
локального термодинамического равновесия нагревается (охлаждается)
вся смесь газов, т. е. воздух.
Выражения для лучистых притоков на данном уровне (т. е.
к бесконечно тонкому слою) можно получить путем
дифференцирования соответствующих выражений для потоков. Так,
например, из (6.2.24) получим
dF* _ dF* dm _ ( р \п ( е У Г с /Гч d& (п
dz dm dz ~ Рп\ ро / \ в0 I I Гч-Т^3' dm
+F,.AT(m))Um "•%—> +
+J
г? /т/ w d*<F (т — и) ,
dudm
176
Глава 6
Однако на практике удобнее рассчитывать притоки методом
конечных разностей через потоки на заданных уровнях.
Во-первых, как правило, представляет интерес изменение температуры
именно в слоях конечной толщины. Во-вторых, расчетные
формулы для потоков проще, чем для притоков. И наконец, весьма
нежелательно вычислять производные от функций пропускания.
Если сами функции определяются приближенно с какими-то
ошибками, то ошибки в производных оказываются значительно
больше.1 Вообще здесь следует подчеркнуть одно очень важное
обстоятельство. Основная часть атмосферы (выше пограничного
слоя) близка к состоянию лучистого равновесия. Поэтому
радиационные притоки малы, они представляют собой малую
разность больших величин. Так, уже радиационный баланс является
разностью нисходящих и восходящих потоков и оказывается
в несколько раз меньше последних. Поэтому ошибки в
определении потоков приводят к значительно большим ошибкам в
притоках. Иными словами, для надежного определения
радиационных изменений температуры требуется вычислять потоки с
большой точностью.
Теории лучистого равновесия атмосферы и термического
равновесия с учетом конвекции
Рассмотрев особенности переноса радиации и методы
расчета лучистых потоков и притоков в атмосфере, можно перейти
к основному (и наиболее трудному) вопросу: какова роль
лучистого теплообмена в динамике атмосферы? Полный ответ на
этот вопрос дает только решение проблемы общей циркуляции
атмосферы. Однако существенные частные выводы могут быть
получены в рамках теории лучистого равновесия. Лучистое
равновесие— это стационарное состояние, в котором находилась бы
атмосфера, если бы единственным механизмом теплообмена был
лучистый теплообмен. (При этом пренебрегают также лучистым
теплообменом в горизонтальном направлении, поскольку он
безусловно мал.) Очевидно, что в условиях лучистого равновесия
притоки радиации на всех высотах равны нулю, а
результирующий поток постоянен по высоте (в противном случае состояние
атмосферы не было бы стационарным). Если определить про-
1 Так, например, формулы (6.2.48) и (6.2.50) дают правильные значения
функций пропускания при крайних значениях массы (т=0 и т—юо) и вполне
удовлетворительно описывают изменение & (т) внутри интервала. В то же
время —-±—-—•> оо при т —► 0, что не имеет физического смысла и
вызвано ошибками аппроксимации.
Лучистая энергия
177
филь температуры, удовлетворяющий условиям лучистого
равновесия, и сравнить его с реальным, можно судить, где (и в
какой мере) лучистый теплообмен играет решающую роль и где
велика роль других факторов.
Одно из первых решений такого типа принадлежит Эмдену.
Несмотря на грубость некоторых исходных предположений, оно
дает качественно правильную и физически ясную картину,
позволяющую понять сущность проблемы. Получим это решение,
слегка видоизменив его в соответствии с предыдущим
материалом. Примем следующие предположения: 1) атмосфера
(водяной пар) поглощает длинноволновую радиацию, как серое тело,
т. е. ам = ао = const; 2) солнечная радиация поглощается только
земной поверхностью. Атмосфера в коротковолновой области
спектра абсолютно прозрачна.1 Воспользуемся исходными
уравнениями переноса длинноволновой радиации (6.2.5) и (6.2.6).
Учтем, что пропускание потока радиации эквивалентно
пропусканию направленного пучка лучей, распространяющегося под
углом О, для которого sec #=1,66. Далее умножим уравнение
(6.2.5) на cos $ и проинтегрируем по всем телесным углам в
пределах полусферы, а также по всем длинам волн. В итоге
получим
= — До
I dX\ а'Л d cos»sinOtf» =
обо m
оо 2тс т/2
1,66 j d\ j* d<b j [7xf (*>) - h (T)] cos & sin Ь dO.
0 0 0
Поменяв порядок интегрирования и дифференцирования,
а также учтя определение интегрального потока радиации
(6.1.6), получим
dm
= -\,ma0[F^-F4^(T)]. (6.3.5)
Аналогично уравнение (6.2.6) примет вид
-^-= 1,66а0 [F* - Л. т (Г)]. (6.3.6)
Условие постоянства результирующего потока при лучистом
равновесии
F = F*-F*=C (6.3.7)
замыкает систему уравнений для определения F , F и F4. т =
= аГ4.
1 В одном из вариантов Эмден учитывал поглощение солнечной радиации
в атмосфере. Это несколько усложняет задачу, но не меняет качественных
выводов.
12 Заказ № 612
178 Глава 6
Граничные условия запишем при следующих
предположениях. Пусть поток тепла в глубь почвы отсутствует, земная
поверхность поглощает всю падающую длинноволновую радиацию
и некоторую долю солнечной: (1 —A)So cos #© (здесь А —
альбедо системы Земля—атмосфера для коротковолновой
радиации). Тогда, согласно закону сохранения энергии, при 2 = 0,
т = 0
Ft(O)-Fl(O)=(l-A)5ocos&0, (6.3.8)
при 2->- оо, т=М
р*(М) = 0и (6.3.9)
Требуется найти профиль Т. Потоки F и f надо
исключить из системы (6.3.5) —(6.3.7). Вычтем (6.3.6) из (6.3.5):
d{F[-F^ = -\,66ao(F*+F>-2oT*).
Согласно (6.3.7), левая часть этого уравнения равна нулю.
Тогда
оГ4=-1-(/^+/^). (6.3.10)
Уравнение для определения F + F получим, сложив (6.3.5)
и (6.3.6):
d(F'd + Fi) --1,66а. (F*-/*). (6.3.11)
Учитывая (6.3.7), проинтегрируем (6.3.11):
Ff-f/^ = - ЬббаоСт+Сь (6.3.12)
Определим постоянные С и С\. Из (6.3.7) и (6.3.8) сразу же
следует:
C=F(0) = (l-A))SoCosV (6.3.13)
Постоянную С\ определим с помощью граничного условия
(6.3.9) и уравнения (6.3.7). Поскольку при m = M /^(Af)=0,
то
/?t (Л1)+/^ {M)=F* (Ж)-/71 (УИ) = С.
Тогда, согласно (6.3.12)
d = C(l + l,66M«). (6.3.14)
Лучистая энергия 179
Подставив С и d в (6.3.12), а (6.3.12) в (6.3.10), получим
аГ4= l~A S0cosft@[l + U6to0(AI-JH)l. (6.3.15)
Распределение плотности водяного пара по высоте (по Эм-
дену) задается формулой
где Я=2 км. Зависимостью коэффициентов поглощения от
давления и температуры пренебрегаем. Тогда
сю
M-m = l 9adz=?nuHe~ZIH.
Z
Окончательно
T(z) = [ l~A 50cos»@ (1 + 1,66а0рпо//^-г/я)],/4. (6.3.16)
Профиль T(z), рассчитанный по формуле (6.3.16) при
ЯорпоЯ = 1 и (1—A)So cos О0 =0,3 кал/(см2-мин), изображен
на рис. 6.18 (кривая 1). Его характерная особенность состоит
в том, что вблизи земной поверхности температура понижается
очень быстро, а с высотой градиент уменьшается. Так, при 2 = 0
—т—=—19,5 К/км, при 2 = 3,2 км —т—= —6,5 К/км и при 2>
>10 км ——«0. На земной поверхности имеет место скачок
температуры. Действительно, в условиях лучистого равновесия
излучение земной поверхности F (0) можно найти из уравнений
(6.3.8) и (6.3.12). Если положить т = 0 и подставить в
уравнение (6.3.12) постоянные С и G согласно (6.3.13) и (6.3.14),
получим
^t(o)+F*(0) = (l-A))S0cos»@(l + 1.66flo^).
Для того чтобы исключить F (0), сложим это уравнение с
уравнением (6.3.8):
2Fj (0) = (1 - A,) S0 cos »0 (2+1,66а0М).
Далее учтем, что Ff (0) =оТ\, а М=рпоН. Тогда
71.- [ 1ьЛ ^оС05^@(2+1,66а0рпоЯ)]</4.
12*
180
Глава 6
В то же время, согласно формуле (6.3.16), температура воздуха
у земной поверхности равна
T(0) = {-^-S0cosbe(l + l,66a0pBQH)\U.
При заданных значениях параметров температура земной
поверхности равна 283 К, а температура воздуха 261 К. Таким
образом, в нижней тропосфере лучистый теплообмен приводит
к заведомо неустойчивой стратификации и, следовательно,
должны развиваться конвекция и
-,*„ турбулентность (что и наблю-
Льо дается в действительности).
Переход к изотермической
стратосфере обеспечивается за
счет лучистого теплообмена.
\зо Разумеется, столь упрощенная
теория не может точно
описать реальные профили
температуры. Так, например, в при-
\20
Рис. 6.18. Вертикальные профили
температуры при лучистом
равновесии и при термическом равновесии
с учетом конвекции.
Ч Ю
1000
/ — теория Эмдена; 2 — лучистое
равновесие в безоблачной атмосфере; 3 —
термическое равновесие с учетом конвекции в
безоблачной атмосфере; 4 — термическое
равновесие с учетом конвекции в облачной
атмосфере. Кривые 2, 3 и 4 — по данным
Манабе и Стриклера.
ближении серой атмосферы невозможно получить инверсию
в районе тропопаузы, а также правильный широтный ход
высоты тропопаузы.
После исследований Эмдена был выполнен ряд работ,
рассматривающих лучистое равновесие в селективно поглощающей
атмосфере. При более корректной постановке задачи, когда
потоки F и F выражаются формулами типа (6.2.24) и (6.2.26),
а также учитывается поглощение коротковолновой радиации и
многие другие детали, система уравнений для определения
профиля температуры оказывается очень сложной и может быть
решена только численно.
В настоящее время разработан новый, нестационарный
метод решения. Задаются необходимые «внешние» условия:
профили поглощающих субстанций, среднее за сутки значение
инсоляции Socosd0, а также условия радиационного баланса на
Лучистая энергия
181
подстилающей поверхности. Для произвольного начального
профиля температуры (обычно изотермического) рассчитываются
радиационные изменения температуры на всех высотах и
соответствующие приращения температуры за некоторый интервал
—— ) ДЛ Рассчитанные приращения
температуры прибавляются к начальным значениям, и расчеты
производятся для вновь полученного профиля температуры. Эта
процедура повторяется до тех пор, пока радиационные изменения
температуры на всех уровнях не становятся меньше заданной
малой величины. При достаточно малом временном шаге (не
больше 8 ч) решение сходится для любого начального профиля.
Такой метод решения, по существу, моделирует физический
процесс, который протекал бы в неподвижной среде под действием
только лучистого теплообмена. Он демонстрирует развитие
картины во времени, а также инерционность атмосферы по
отношению к радиационным процессам. Эта инерционность
оказалась очень большой: для установления лучистого равновесия
требуется 1—2 года в зависимости от начального профиля.
В работе Манабе и Стриклера «Термическое равновесие
с учетом конвекции» использованы наиболее точные
современные данные и методы расчета радиационных изменений
температуры. Расчеты производились при среднезональных профилях
поглощающих субстанций, для разных широт и сезонов, для
безоблачной и облачной атмосферы. Облачные слои
рассматривались как полупрозрачные серые пластинки с заданными
радиационными характеристиками. Среднее количество и средние
высоты верхней и нижней границы задавались согласно средне-
зональным данным. Исследовалось влияние различных
начальных профилей температуры, относительные роли разных
поглощающих субстанций и многие другие детали, вплоть до таких,
как влияние различных способов учета зависимости функций
пропускания от давления и температуры.
Кроме того, помимо лучистого равновесия, рассматривалось
так называемое термическое равновесие с учетом конвекции.
В последнем случае на каждом временном шаге производилась
оценка градиента температуры во всех слоях. Считалось, что
в тех слоях, где градиент превышает заданные критические
значения (10 или 6,5°С/км), развивается перемешивание.
Принималось, что градиент температуры равен критическому, а избыток
тепла передается вышележащим слоям, в которых
соответственно также изменяется профиль температуры.
На рис. 6.18 (кривые 2, 3 и 4) приведены результаты
расчетов для следующих условий: 5о = 2 кал/(см2-мин), cos<ft0 =
= 0,25, альбедо подстилающей поверхности равно 0,102.
182
Глава 6
В качестве критического градиента температуры принято
значение 6,5°С/км. Кроме того, при расчетах предполагалось, что
вертикальное распределение содержания водяного пара и озона,
количество и высота облаков соответствуют среднезональным
значениям для апреля на широте 35° с. (эти значения можно
считать характерными средними значениями для земного шара).
При лучистом равновесии, как и в решении Эмдена,
получаются очень большие градиенты температуры в тропосфере,
однако скачок температуры на земной поверхности практически
отсутствует. Наблюдаются инверсии температуры в области
тропопаузы и выше 27 км (последняя обусловлена поглощением
в слое озона). Температура у земной поверхности оказывается
завышенной, а в стратосфере — слегка заниженной по
сравнению со стандартной атмосферой.
Учет конвекции сильно изменяет профиль температуры в
тропосфере и незначительно — в стратосфере. Температура земной
поверхности оказывается значительно ниже, чем при лучистом
равновесии, особенно для облачной атмосферы. В облачной
атмосфере с учетом конвекции рассчитанная температура
подстилающей поверхности совпадает с температурой в стандартной
атмосфере. Естественно, что при этом совпадает весь
температурный профиль в пределах тропосферы, поскольку
задается стандартное значение градиента. Выше 10 км
температура оказывается на 5—10°К ниже, чем в стандартной
атмосфере.
Аналогичные расчеты производились для разных широт.
Закономерности широтного распределения температуры и особенно
высоты тропопаузы значительно хуже совпадают с
реальными данными. Это вполне понятно, поскольку при указанной
постановке задачи практически не рассматривается динамика
атмосферы. Вертикальные движения (конвекция) и
турбулентный обмен учитываются весьма схематично: по сути дела, это
«подгонка» под экспериментальные данные. Горизонтальные
движения не учитываются вовсе. Скорее даже, наоборот,
требует объяснения «сверхъестественное» совпадение рассчитанных
и среднезональных профилей температуры. Выше отмечалось,
что профиль температуры крайне медленно меняется под
действием радиационного теплообмена. В то же время лучистый
теплообмен действует всегда в одном направлении (в среднем
за год). Конвекция и вертикальный турбулентный теплообмен
также в среднем переносят тепло от земной поверхности к
свободной атмосфере. Изменения температуры, вызываемые
горизонтальными движениями, относительно велики, происходят
значительно быстрее, но их знак часто меняется. Поэтому
радиационный обмен совместно с конвекцией определяет картину,
получающуюся при осреднении за длительный интервал времени
Лучистая энергия
18$
(климатические данные). Напротив, изменения температуры
за короткий интервал времени определяются динамикой
атмосферы.
Контрольные вопросы
1. При каких условиях собственное излучение газа
определяется его температурой?
2. Чем объясняется зависимость коэффициентов поглощения:
от давления?
3. Почему излучение Солнца в инфракрасной области
спектра мало по сравнению с собственным излучением Земли и
атмосферы?
4. В чем заключается эффект Форбса и какими физическими
процессами он обусловлен?
5. Как видоизменяются уравнения переноса в случае
длинноволновой и коротковолновой радиации?
6. Что такое интегральная функция пропускания? Как она
зависит от поглощающей массы и давления?
7. В чем состоят основные трудности расчета потоков и
притоков радиации в облачной атмосфере?
8. Как изменяются с высотой интегральные потоки прямой
солнечной радиации, восходящей и нисходящей длинноволновой
радиации, а также эффективное излучение?
9. Что такое лучистое равновесие? Каков профиль
температуры в атмосфере при лучистом равновесии?
10. Каковы основные особенности радиационного баланса
системы Земля—атмосфера?
Глава 7. СИСТЕМА УРАВНЕНИИ
ГИДРОТЕРМОДИНАМИКИ ДЛЯ ТУРБУЛЕНТНОЙ
АТМОСФЕРЫ
Понятие о турбулентности. Возникновение турбулентности. Методы
осреднения. Вывод уравнения для осредненных величин. Связь турбулентных потоков
с осредненными полями. Осредненные уравнения гидротермодинамики
атмосферы. Баланс кинетической энергии турбулентных пульсаций. Упрощение
уравнений динамики атмосферы. Классификация атмосферных движений.
7.1. Понятие о турбулентности
В главе 1 была сформулирована система уравнений
гидродинамики для определения полей скорости, температуры,
давления и влажности, которая является замкнутой,-если известен
приток тепла как функция времени и координат. Применение
этих уравнений для описания изменения в пространстве и во
времени метеорологических полей связано, однако, с
принципиальными трудностями, обусловленными турбулентным
характером атмосферных движений.
Чтобы выяснить сущность этих трудностей, остановимся
сначала на определении и основных особенностях турбулентных
течений. Турбулентным называется движение, характеристики
которого нерегулярно, беспорядочно изменяются в пространстве
и во времени при практически неизменных внешних условиях.
Именно случайный характер изменения параметров является
главной особенностью турбулентных течений, отличающей их от
плавных, ламинарных движений, свойства которых в любой
момент времени однозначно определяются внешними
условиями.
О турбулентном характере атмосферных движений
свидетельствуют записи изменений во времени и в пространстве
метеорологических элементов (скорости, температуры, влажности
и др.), полученные с помощью специальной малоинерционной
аппаратуры, а также наблюдения за распространением дыма от
промышленных источников. На рис. 7.1 в качестве примера
представлены типичные записи изменений во времени температуры Т
и вертикальной компоненты скорости ветра i/з, сделанные при
фиксированных внешних условиях. Наблюдающееся на
представленных кривых T(t) и vz(t) множество колебаний с разными
периодами и амплитудами указывает на сложную внутреннюю
структуру атмосферных движений.
Система уравнений гидротермодинамики для турбулентной атмосферы 185
Атмосферные движения, однако, не являются единственным
примером турбулентных течений. Большинство течений,
встречающихся в природе и технике, оказываются турбулентными.
При определенных условиях турбулентными являются течения
в океанах, морях, реках, в водопроводных трубах, газопроводах,
движения в пограничных слоях, образующихся при обтекании
различных поверхностей, в следах за движущимися телами
и т. п. Отличительными чертами атмосферной турбулентности
Рис. 7.1. Типичные записи изменений во времени
температуры и вертикальной компоненты скорости ветра.
являются многомасштабность и существенное влияние
стратификации.
Как будет показано в п. 7.2, турбулентный режим создается
в результате того, что при определенных условиях движение
становится неустойчивым по отношению к малым возмущениям.
Это означает, что случайные, неконтролируемые изменения
начальных или граничных условий приводят к кардинальным
изменениям поля скорости, так что эволюция поля носит
случайный характер и мгновенные значения вектора скорости
невозможно предвидеть. Вследствие этого математическое описание
турбулентных и ламинарных течений должно быть
принципиально различным. В случае ламинарного режима система
уравнений гидродинамики позволяет однозначно определить
значения всех характеристик в любой момент времени по их
начальным значениям при соответствующих граничных условиях. При
турбулентном режиме начальные значения соответствующих
характеристик также в принципе определяют их будущие
значения. Однако эти будущие значения зависят от неконтролируемых
возмущений начальных и граничных условий, задать которые
точно невозможно; поэтому интегрирование соответствующих
186
Глава 7
дифференциальных уравнений, описывающих мгновенные
реализации турбулентных полей, оказывается практически
невыполнимым. Могут быть заданы лишь распределения
вероятностей этих полей, а не их точные значения. Поэтому в случае
турбулентных потоков уравнения гидротермодинамики можно
использовать только для исследования соответствующих рас-
лределений вероятности или определяемых этими
распределениями осредненных характеристик случайных полей. Таким
образом, единственно возможным является лишь статистическое
описание турбулентных движений, заключающееся в
исследовании статистических закономерностей, характерных для большой
совокупности течений, находящихся при фиксированных
внешних условиях.
Ситуация, возникающая при турбулентном режиме
движения, качественно аналогична положению, с которым
встречаются в кинетической теории газов, изучающей системы из очень
большого числа хаотически движущихся и взаимодействующих
друг с другом молекул. Точное описание движения отдельной
молекулы практически невозможно; изучаются лишь средние
статистические свойства совокупности. Хотя между движением
большого числа молекул в газе и турбулентным движением
имеются принципиальные различия, на которые будет указано
позднее, тем не менее отмеченная аналогия часто оказывается
полезной и используется при описании турбулентных движений.
В практическом плане наибольший интерес представляет
изучение осредненных характеристик случайных
метеорологических полей. Сформулированная выше система уравнений
гидродинамики не может быть непосредственно использована для их
описания. В данной главе будет получена система уравнений,
описывающая средние поля скорости, температуры и других
характеристик турбулентной атмосферы. Прежде чем перейти
к выводу этих уравнений, необходимо остановиться на
некоторых важных для решения поставленной задачи вопросах,
связанных с основными свойствами турбулентных течений,
условиями их возникновения и правилами осреднения.
7.2. Возникновение турбулентности
Ламинарные и турбулентные течения представляют собой
два вида движений, свойства которых существенно отличаются
и которые при определенных условиях переходят один в
другой. Различия между ними проявляются в целом ряде
процессов, имеющих большое практическое значение. Достаточно
указать на то, что при турбулентном режиме воздействие потока на
обтекаемые жидкостью или газом тела оказывается значительно
Система уравнений гидротермодинамики для турбулентной атмосферы 187
большим, чем при ламинарном. Важным также является то, что
в турбулентных потоках гораздо интенсивнее происходит
диффузия тепла и примесей. Вследствие этого определение условий
перехода ламинарного режима в турбулентный оказывается
очень важным для решения многих прикладных задач. В то же
время выяснение механизма возникновения турбулентности
должно способствовать пониманию природы турбулентного
движения, поэтому изучение этого вопроса представляется интересным
и для физики атмосферы.
Критерий возникновения турбулентности был получен
английским физиком О. Рейнольдсом в 1883 г. при изучении
движений жидкости в круглых стеклянных трубах. Рейнольде показал,
что ламинарное движение переходит в турбулентное тогда, когда
безразмерное число Re= , которое впоследствии было
названо его именем, становится больше некоторого критического
значения ReKp (и и L — соответственно характерные масштабы
скорости и длины, v — кинематическая вязкость). Число Рей-
нольдса характеризует относительную роль сил инерции и
молекулярной вязкости в динамике течения. Это следует из оценки
по порядку величины соответствующих членов в уравнении На-
вье—Стокса
dv
V ds ui/L uL _p
Силы инерции, роль которых состоит в пространственном
переносе количества движения, способствуют возникновению не-
однородностей в потоке. Силы вязкости, напротив, сглаживают
возникающие неоднородности. При малых числах Re, когда силы
вязкости успевают рассасывать возникающие вследствие
действия сил инерции неоднородности, движение является
ламинарным. При больших Re, когда преобладающими становятся силы
инерции, в потоке возникают резкие неоднородности,
характеристики потока испытывают нерегулярные изменения, движение
становится турбулентным. Приведенные соображения поясняют,
почему именно число Re может служить критерием
возникновения турбулентности.
Критические значения ReKp были установлены
экспериментально для различных типов турбулентных течений. Было
обнаружено, что величина ReKp, в частности, существенно зависит
от степени возмущенности ламинарного потока — начальной тур-
булизации потока; оно тем меньше, чем больше начальная тур-
булизация.
Теоретический подход к проблеме возникновения
турбулентности основывается на следующих соображениях. В соответствии
188
Глава 7
с определением установившиеся ламинарные течения
описываются стационарными решениями гидродинамических
уравнений при заданных внешних условиях. Можно полагать, что
такие решения принципиально должны существовать при любых
числах Рейнольдса. В то же время из наблюдений известно, что
ламинарные течения имеют место лишь при Re<ReKp. Это дает
основание считать, что решения, соответствующие
осуществляемым реально движениям, должны не только удовлетворять
уравнениям гидродинамики, но и быть устойчивыми. Для
устойчивости движения необходимо, чтобы возникающие в потоке
возмущения затухали со временем. Если же неизбежно возникающие
в потоке жидкости сколь угодно малые возмущения будут
возрастать со временем, то это приведет к фундаментальным
изменениям исходного движения; движение в этом случае является
неустойчивым. Поскольку турбулентный режим возникает при
Re>ReKp, то можно думать, что ReKp характеризует условия
потери устойчивости. Поэтому теоретическое изучение
возникновения турбулентности сводится к математическому исследованию
вопроса об устойчивости решений уравнений гидродинамики.
Изучение математической теории устойчивости ламинарных
течений представляет самостоятельную важную проблему,
которой посвящена обширная литература. Здесь остановимся лишь
на качественной стороне вопроса и осветим некоторые
принципиальные моменты, основываясь на соображениях, высказанных
Ландау.
Математическое исследование вопроса об устойчивости
движения по отношению к малым возмущениям проводится по
следующей схеме. На основное стационарное движение с
распределением скорости Vio(x) накладывается малое возмущение
i>ii(x, t) [va(x, t) «С^го(х)], которое определяется таким
образом, чтобы результирующее движение Vi{x, t) =Vio(x) +vu(x9 t)
удовлетворяло уравнениям движения и неразрывности:
dvi J-*» dVl — ! др 1 у d2ttl Г7 2П
Ч£г=°- <7-2-2>
Поскольку Vio(x) является решением системы стационарных
уравнений (7.2.1) и (7.2.2), то (в линейном приближении) для
возмущения получаем:
-^- = 0. (7.2.4)
1 Возмущениями плотности здесь пренебрегаем.
Система уравнений гидротермодинамики для турбулентной атмосферы 189
Возмущение поля скорости vu(x, t) удовлетворяет системе
линейных дифференциальных уравнений с коэффициентами,
независящими от времени. Общее решение таких уравнений может
быть представлено в виде суммы частных решений типа
*п(х, t) = A{t)f(x), (7.2.5)
где A(t)—амплитуда, периодически меняющаяся со временем:
Ау) = е-ш = еТ-ш. (7.2.6)
Допустимые значения «собственных» частот Q определяются
в результате решения (7.2.3) после подстановки в него (7.2.5)
при соответствующих граничных условиях. В общем случае
собственная частота й является комплексной (у, со —
действительные величины). Если у<0> то возникшее малое возмущение
затухает со временем и движение является устойчивым
(ламинарное движение). При у>0 амплитуда возмущений растет со
временем, что означает потерю устойчивости. Поскольку движение
становится неустойчивым при Re>ReKp, то естественно считать
Y функцией Re и определить ReKp как величину, при которой для
одной из частот й мнимая часть обращается в нуль; пусть это
будет частота Qi = coi + /yi- При Re<.ReKp Yi<0> ПРИ Re = ReKp
Yi = 0, а при Re>ReKp Yi>0- При малых значениях разности
(Re — ReKp) Yi можно представить в виде
Tl = const (Re -ReKp). (7.2.7)
Поскольку множитель eyit быстро растет со временем, то
(7.2.3), (7.2.5) и (7.2.6) справедливы лишь для небольших
промежутков времени после потери устойчивости. Для этого
интервала из (7.2.6) имеем
-^-=2Т1|Л|». (7.2.8)
Правая часть (7.2.8), по существу, является лишь первым
членом разложения в ряд по степени Л и Л*. При больших t, т. е.
при увеличении модуля | А |, нужно учесть следующие члены
разложения. Интерес, однако, представляет не точное значение
d\A\* dA*
, а средняя по времени величина —-г— , причем осредне-
dt at
ние проводится по промежутку времени, большому по сравнению
2я _
с интервалом периодом изменения амплитуды. При осред-
COi
нении члены третьего порядка, содержащие периодический
190
Глава 7
множитель, пропадут, и с точностью до членов четвертого
порядка можно получить
d\A\2
dt
-=2Т1|Лр-а|Л|4, (7.2.9)
где коэффициент а, вообще говоря, может быть как
положительным, так и отрицательным. Общее решение (7.2.9) имеет вид
п 12 се1^
\А«)\ = ~а Г^> <7-2Л0>
1 + 27i се
где с — постоянная интегрирования. Если а>0, то амплитуда
Q
в начальный момент |Л(0)|2 = достаточно мала, за-
2yi
тем она возрастает довольно быстро с ростом t, потом рост
амплитуды замедляется, и при /—>-оо она стремится к конечному
пределу
л(оо)=(4Ч'/2, <7-211>
не зависящему от А (0).
Подставив в (7.2.11) vi из (7.2.7), получим
А (сю) ~ KRe-ReKp . (7.2.12)
Таким образом, неустойчивость течения при Re>ReKp приводит
к появлению нестационарного периодического движения. При Re
больших, но близких к ReKp, это движение может быть
представлено в виде наложения на стационарное движение Uto(x)
периодического движения i>ii(x, t) с малой, но конечной амплитудой,
величина которой при /-*оо растет пропорционально
У Re — ReKp.
Необходимо указать на следующую важную особенность
нестационарного периодического решения vu(x, t). Дело в том,
что уравнение (7.2.9) определяет лишь абсолютную величину
амплитуды. Фаза <pi = coi£+pi периодического движения, по
существу, остается неопределенной, она зависит от случайных
начальных условий. Таким образом, рассматриваемое
периодическое движение не определяется однозначно стационарными
граничными условиями. Можно сказать, что это движение обладает
одной степенью свободы (в отличие от стационарного
ламинарного движения, однозначно определяемого граничными
условиями и не обладающего степенями свободы).
Таким образом, наличие случайного малого возмущения
приводит при числе Рейнольдса Re большем, но близком к крити-
Система уравнений гидротермодинамики для турбулентной атмосферы 191
ческому значению ReKp, к появлению нестационарного
периодического движения, в котором одна из компонент с частотой Qi
становится неустойчивой. При дальнейшем увеличении числа Re
наступает момент, когда становится неустойчивым по
отношению к малому возмущению vn{x, t) и установившееся
периодическое движение Vio (x) + vu (х, t)} Исследование неустойчивости
в этом случае проводится аналогично описанному выше. Для
возмущения i^2(x, /) снова получится линейное
дифференциальное уравнение, коэффициенты которого будут теперь зависеть
не только от координат, но и от времени, так как начальное
течение теперь является нестационарным. Решение такого
уравнения следует искать в виде
*и(х, 0=Л(х, t)e~iSt,
где /2(х, t)—периодическая функция времени (с периодом
2я/о). Неустойчивость наступает тогда, когда появляется частота
^2 = co2+t'Y2, для которой Y2>0. В результате возникает
квазипериодическое движение, характеризующееся двумя различными
периодами и двумя степенями свободы (так как теперь
произвольны две фазы).
При дальнейшем увеличении числа Рейнольдса появляются
все новые и новые случайные колебания с различными
периодами и неопределенными фазами, т. е. движение приобретает
сложный и нерегулярный характер с огромным числом степеней
свободы. Такое движение является турбулентным. При этом
можно думать, что интервалы между соответствующими
критическими числами Reoj, возбуждающими новые колебания,
становятся все меньше и меньше и, следовательно, возникающие
колебания будут все более высокочастотными и
мелкомасштабными. Таким образом, при больших Re возникает развитое
турбулентное движение, являющееся суперпозицией движений
разных периодов и масштабов. Движение данного масштаба или
периода принято называть турбулентным вихрем (или
турбулентным молем).
Выше был рассмотрен тип движения, возникающего в случае,
когда в (7.2.9) коэффициент а>0. Принципиально возможен
1 Фактически это означает, что можно ввести число Рейнольдса не только
/ а
для всего течения в целом, но и для движения данной частоты со: Re=—^—-
v
(и , / — соответственно скорость и пространственный масштаб этого дви-
и \
жения, / = —— I, Неустойчивость движения и должна наступать при
Re >ReKP. Видно, что число Re тем скорее будет превышать критическое
значение, чем больше масштаб ^о-Из этого следует, что в первую очередь
теряют устойчивость движения большого масштаба.
192
Глава 7
еще один тип потери устойчивости, когда а<0. В этом случае
при Re<ReKp член Yil^l2 отрицателен, но член а|Л|4
положителен; следовательно, при достаточно большом значении ампли-
d\M2
туды | А |, когда а | А |4 > 2yi IА |2, производная ——— стано-
at
вится положительной. Это означает, что движение становится
неустойчивым по отношению к достаточно большим
возмущениям уже при Re<ReKp. В этом случае наряду с ReKp,
определяющим неустойчивость по отношению к малым возмущениям,
должно существовать более низкое критическое значение Re,
определяющее потерю устойчивости по отношению к конечным
возмущениям.
Таким образом, из приведенных соображений следует
наглядная качественная картина возникновения турбулентного
движения. Приведенные рассуждения относились к течению
с постоянной плотностью.
Другой подход, позволяющий исследовать условия
существования турбулентного режима, связан с использованием
энергетического метода. Сущность. этого метода состоит в изучении
баланса энергии вихревого возмущения соответствующего
масштаба и в определении условий, при которых энергия данного
возмущения не будет убывать со временем (т. е. возможно
длительное существование возмущения). Рассмотрим применение
этого метода в типичной для атмосферы ситуации. Пусть в
горизонтально однородном потоке возникло возмущение
масштаба /, имеющее скорость v\ и потенциальную температуру,
отличную от температуры окружающей среды на величину 6'.
Характерное время существования такого вихря ti~l/vi. В
таком случае от кинетической энергии основного потока (или от
вихря более крупного масштаба) на создание кинетической
энергии турбулентного движения масштаба I отнимается за
единицу времени энергия
R4~-i{ г". (7.2.13)
Кинетическая энергия вихря тратится на работу Ru против
вязкого трения. Сила трения описывается последним членом
в уравнении Навье—Стокса (7.2.1). Для вихря размером / она
имеет порядок v —, и, следовательно, работа, совершаемая
против сил вязкого трения за единицу времени, будет равна
/?2,~v-g-zv (7.2.14)
Кроме того, в устойчиво стратифицированном потоке вихрь со-
Система уравнений гидротермодинамики для турбулентной атмосферы 193
вершает работу против силы плавучести. Ускорение вихря
в стратифицированной атмосфере —;jt~~ ®i (см- главУ 3),
dt
0
а работа, совершаемая вихрем за единицу времени, равна
/?3/ ^-Q'lVi. (7.2.15)
«i
Стабилизирующее влияние
расслоений
Чтобы рассматриваемое возмущение масштаба / не затухало
со временем, т. е. чтобы изменение со временем кинетической
энергии вихря —37~>0» в устойчиво стратифицированной
атмосфере должно выполняться
условие
/?1/>/?2/ + *81- (7.2.16)
Если роль стратификации
мала (/?3z</?2z), то (7.2.16)
сводится к требованию Ru>
>/?2z, которое после
подстановки соотношений (7.2.13)
и (7.2.14) приводит к
неравенству
-^- = Re,> 1.(7.2.17)
Если, напротив, /?зг>/?2*,
то из (7.2.16) следует
Ru>Rzi или
Рис. 7.2. Область существования
пульсаций с характерным размером /.
/ez
= Ri/<l.
(7.2.18)
Здесь Re/ — число Рейнольдса для вихрей масштаба /, a Ri* —
соответствующее число Ричардсона. Таким образом, для
поддержания турбулентности масштаба I необходимо, чтобы число
Рейнольдса было достаточно большим, а число Ричардсона —
малым. Следовательно, в стратифицированном потоке
появляется новый безразмерный критерий — число Ричардсона,
характеризующее условия осуществления турбулентного режима.
На рис. 7.2 указана область существования турбулентного
режима.
При неустойчивой стратификации работа силы плавучести
/?зг является дополнительным источником энергии и для
поддержания масштаба I должно выполняться неравенство
3 2
/?./+Яз<>#2/ или -^-+^-e'^>v-^-. (7.2.19)
13 Заказ № 612
194
Глава 7
Когда преобладающим является термический фактор (Rzi^>
^>Ru), из (7.2.19) следует неравенство
\v[ >1. (7-2.20)
выполнение которого необходимо для существования данного
возмущения.
7.3. Методы осреднения
Поскольку все величины в турбулентном потоке испытывают
нерегулярные изменения, количественное описание процессов
целесообразно проводить по отношению к осредненным
характеристикам. Для этого необходимо, как предложил еще
Рейнольде, представлять интересующие нас гидродинамические
величины в виде а = а + а/. Здесь а, а и а' — соответственно
мгновенные, осредненные и пульсационные значения величины а
(а — унифицированное обозначение vu р, р, Т).
Однако здесь встает вопрос о смысле получаемых средних
и, следовательно, о принципах самого осреднения. Как уже
отмечалось, мгновенные поля всех гидродинамических
элементов в турбулентном потоке являются случайными. Это означает,
что при постановке ряда экспериментов при идентичных
внешних условиях каждая реализация будет осуществляться с
некоторой степенью вероятности. (Для сравнения вспомним, что
в ламинарном потоке при неоднократном воспроизведении
одного и того же опыта результаты будут тождественны.) Средним
в турбулентном потоке будет являться среднее по множеству
реализаций, образующих статистический ансамбль. При этом
устойчивые средние значения величин могут быть получены при
достаточно большом числе испытаний. Иными словами, под
средним значением следует понимать предел, к которому
стремится та или иная пульсирующая величина при неограниченно
возрастающем числе наблюдений, когда внешние условия для
всех случаев сохраняются неизменными (осреднение по
ансамблю).
Однако при изучении атмосферных процессов практически
невозможно получить средние по статистическому ансамблю,
так как невозможно осуществить множество опытЪв при
неизменных внешних условиях. Поэтому в действительности
используется осреднение во времени или в пространстве. При этом для
полей метеорологических элементов предполагается
справедливой эргодическая гипотеза. Она утверждает, что при
определенных условиях возможна замена средних по множеству средними
Система уравнений гидротермодинамики для турбулентной атмосферы 195
по времени или пространству. В частности, если процесс
стационарен, то
Т/2
a(<)=lim—- \ a(/+x)rfx = const
совпадает со средним по множеству. В общем случае поля
метеорологических
элементов не являются эргоди-
ческими, ибо в
большинстве случаев получаемые
при осреднении величины
зависят от времени.
Поэтому указанная замена
средних служит лишь
приближением к реальной
ситуации. При этом вместо
Т-+оо выбирается
некоторый конечный интервал
осреднения Т исходя из
следующих соображений.
Во-первых, он не должен
быть коротким, поскольку
существенно, чтобы
сглаживание оказалось
достаточным, т. е. чтобы при
неизменных внешних
условиях а не зависело от Т. Иначе говоря, необходимо выполнение
неравенства ГП<Г, где Гп —характерный период турбулентных
пульсаций. Во-вторых, период осреднения не следует выбирать
слишком большим, чтобы в течение его величина а оставалась
практически постоянной, т. е. характерное время изменения ос-
редненного поля Гср должно значительно превышать Т (Гср>
>Г), что и позволяет считать процесс квазистационарным
(рис. 7.3).
Есть, однако, основания предполагать, что наименьшие
затруднения такие требования вызывают при рассмотрении
нижнего слоя атмосферы, где основная доля энергии пульсационного
движения сосредоточена в сравнительно небольших участках
спектра. Поскольку большинство процессов, связанных с
турбулентностью, развивается именно в этих нижних слоях,
обоснование выбора периода осреднения целесообразно ограничить
только данной конкретной областью. В 1957 г. Ван-дер-Ховен
получил данные о распределении амплитуд jE© пульсаций
скорости ветра вблизи земной поверхности в области частот о>
13*
Ф .
Рис. 7.3. Типичный временной ход
метеорологических элементов.
а — сглаженная величина в течение интервала
осреднения изменяется пренебрежимо мало; б —
интервал осреднения (Т3 или Г4) выбирается
таким, чтобы сглаженная величина не зависела от
величины интервала; 7, и Т2 — недостаточно
продолжительные периоды сглаживания, средняя
величина зависит от Т.
196
Глава 7
0,0007—900 цикл/ч. На рис. 7.4 в системе (©£„, In со) приведены
эти результаты. Накопленные к настоящему моменту
дополнительные данные в общем подтверждают результаты Ван-дер-
Ховена. Площадь, ограниченная кривой, дает истинное значение
средней в любом интервале частот амплитуды пульсаций
у j£c)dG)= J соЕсодЛпсо). Имея это ввиду, нетрудно заметить, что
главные вклады в энергию флуктуационного движения
сосредоточены в двух четко разделенных областях: в области
крупномасштабных пульсаций
(так называемая
синоптическая область) с
центром вблизи частоты coi =
= 0,01 цикл/ч и в области
мелкомасштабных пульса-
ю'2 w4 ю° ю1 ..-10*ш$ши1/ч дий с центром около (о2 =
b-b-tr-ir-irri ^ко^отна, „б-
Рис. 7.4. Спектр скорости ветра в призем- ласть соответствует изме-
ном слое атмосферы. нениям скорости ветра,
вызванным прохождением
циклонов и антициклонов. Разумеется, эти изменения следует
рассматривать как вариации основного движения. В то же время
высокочастотная часть спектра, соответствующая
мелкомасштабной области, должна рассматриваться как область,
соответствующая турбулентным пульсациям, которые следует сгладить при
осреднении.1 Существование двух указанных областей,
разделенных широким участком промежуточных частот с относительно
малыми амплитудами пульсаций, по-видимому, указывает на
возможность выбора некоторого периода 7\ при котором
сформулированная выше эргодическая гипотеза выполнялась бы с
достаточным приближением. Это можно проиллюстрировать с
помощью простого примера. Действительно, как следует из
приведенного на рис. 7.4 спектра, отклонения скорости ветра от нормы
как функцию времени при грубой аппроксимации можно
представить в виде двух гармоник:
v(t)=Alsinu>lt-\rA2s\nu2t. (7.3.1)
Из (7.3.1) следует
^/А—Л, 2sln(°i^slno>1r/2 , - 2sinG)2*sino>2772
U l *lT +A2 ^f •
Если выбрать T так, чтобы
Ш1Г=^Ь^=е»Ь (7.3.2)
1 Здесь и далее речь идет только о мелкомасштабной турбулентности.
Система уравнений гидротермодинамики для турбулентной атмосферы 197
то
v (t)« Ах sin o>i/
и не зависит от Т. Это означает, что величина сглаженной
скорости мало зависит от периода осреднения, если рассматривать
интервалы частот, соответствующие мелкомасштабной области
спектра. Отсюда в свою очередь вытекает возможность выбора
периода осреднения, так как в указанном случае можно с
достаточной степенью точности считать выполняющимся равенство
v = v, где v отвечает повторному осреднению v. Эти
соображения, разумеется, в равной степени справедливы и для других
величин, подлежащих осреднению.
Из (7.3.2) и данных Ван-дер-Ховена нетрудно оценить
оптимальный период осреднения:
1 1
Т=
V
(i>lG>2
/0,01 • &0
= 67.
Эта величина хорошо согласуется с эмпирически найденными
периодами сглаживания. Более точный учет спектра пульсаций,
по-видимому, мало изменит полученное выше значение Т.
При конечном периоде осреднения выражение для средних
по времени величин будет иметь вид
Г/2
a(xh 0=4- f a(xh t+*)d*. (7.3.3)
-7/2
Если период осреднения Т удовлетворяет выше
сформулированным условиям, то с помощью (7.3.3) легко убедиться в
справедливости следующих соотношений:
а-\-а,\ =а-\-а\,
да да
дх.
dxi
а' =а — а=а—а=а — а=0,
аа\ =а (а\-\-а\) = аа\-\-аа\ = аа\-\-аа,\ =аа\,
аа,\ =(a-j-a') (а,\ -\-a'\) = aai-\-aa'i.
(7.3.4)
Ход доказательства, общий для всех соотношений, можно
продемонстрировать на примере вывода формулы a + ai = a + ai.
198
Глава 7
Учитывая (7.3.3), имеем
7/2
а+а,=^г- j [a(xh t-\-%)+ax(xh *+т)]Л —
- Г/2
7/2 7/2
= -f- \ a(*h t+^dx-]—=- J ax(xi% *+т)Л = а+аь
- 7/2 - 7/2
что и доказывает первое из соотношений (7.3.4). Аналогичным
образом можно получить и прочие формулы (7.3.4).
7.4. Вывод уравнения для осредненных величин
Как показано в главе 1, все уравнения, входящие в полную
систему уравнений гидротермодинамики, имеют вид уравнений
баланса для соответствующих субстанций. Выпишем полученное
там же общее выражение и проведем по отношению к нему
процедуру осреднения, следуя идеям Рейнольдса. Исходное
соотношение (см. главу 1) записывается в виде
д?а __ dp?;* Mjlj . .
dt ~~ dxj dxj п '* С7-4-1)
Представим все входящие в это уравнение величины в виде
суммы средней и пульсационной составляющей. При этом будем
иметь в виду, что атмосферные движения, как правило, можно
считать несжимаемыми, так что пульсациями плотности можно
пренебречь (р — р).1
Тогда (7.4.1) можно записать в виде
а[р(д + д')1 __ d[?(vj + vj)(a+a')]
dt dxj
dxj
\-1+Г. (7.4.2)
Используя соотношения (7.3.4), проведем процедуру осреднения
по отношению к уравнению (7.4.2). В итоге получим
(7.4.3)
дра
dt
dpavj
dxj
d?a Vj
dxj
dJRj
dxj
^«/
dXj
1 / 1 -/'
3
1 Отметим, что в уравнениях динамики это вполне допустимо, а в
уравнении баланса турбулентной энергии пульсации плотности играют
существенную роль, что в дальнейшем рассмотрено отдельно.
Система уравнений гидротермодинамики для турбулентной атмосферы 199
Обратим внимание на то, что в уравнении (7.4.3) появились
дополнительные члены (они подчеркнуты), связанные с
турбулентными пульсациями. При этом первый из подчеркнутых
членов в правой части описывает приток свойств, обусловленный
переносом посредством турбулентных вихрей. Его появление
в формальном отношении связано с осреднением нелинейных
членов, отражающих конвективный перенос. Второе и третье
подчеркнутые слагаемые описывают турбулентные флуктуации
дивергенции молекулярного потока (второй член) и источника
(третий член). Полагая, что для источника справедливы все
сформулированные выше правила осреднения, будем считать,
что //=0.1 Кроме того, как уже упоминалось, интенсивность
турбулентного переноса, осуществляющегося за счет движения
отдельных вихрей (молей), на несколько порядков выше
интенсивности молекулярного переноса, посредством которого
происходит обмен всеми свойствами в ламинарном потоке. Поэтому
dJnj dip* ^
величинами —-г-=^- и — можно пренебречь в сравнении
OXj OXj
dpavj doa'vj' ^
" соответственно. С учетом высказанного
dxj dxj
уравнение (7.4.3) может быть переписано в более простой
форме:
д9а d?avj dyav) -
dt dxj dxj
I. (7.4.4)
7.5. Связь турбулентных потоков с осредненными полями
Система дифференциальных уравнений для сглаженных
величин незамкнута, так как сглаживание, не увеличивая числа
уравнений, приводит к появлению новых неизвестных членов,
содержащих пульсации метеорологических элементов. Как
образно выразился Л. Ф. Ричардсон, такова «расплата» за
осреднение. Замыкания системы можно достигнуть, найдя
дополнительные соотношения для неизвестных функций, в частности,
можно попытаться связать пульсации с соответствующими
сглаженными величинами. При этом будем исходить из следующей
простой модели.
1. Рассмотрим турбулентный поток с неравномерно
распределенными свойствами. Через фиксированную точку в
пространстве, заполненном турбулентным потоком, непрерывно проходят
1 Это означает, что нелинейные эффекты в источниках либо отсутствуют,
либо пренебрежимо малы.
200
Глава 7
дискретные частицы воздуха — вихри, выделившиеся из
основного потока на самых различных расстояниях от места
наблюдения. Непрерывная смена вихрей вызывает пульсации
соответствующих величин в рассматриваемой точке.
2. Характеристики вихря (температура, влажность, скорость
и т. п.) в месте возникновения равны средним значениям
соответствующих величин в окружающей среде.
3. Движение вихрей на протяжении некоторого расстояния
/, называемого путем смешения, происходит квазистатически
(р = р) и без смешения с окружающей средой. В конце пути
вихри внезапно и полностью перемешиваются.1
Результатом такого движения будет поток различных
субстанций из областей с высокой их концентрацией в область, где
их концентрация ниже. Следовательно, турбулентность
приводит к выравниванию неравномерно распределенных свойств.
Таким образом, турбулентный обмен является важным звеном
в формировании полей метеорологических элементов.
Рассмотренная схема турбулентного обмена развита
Л. Прандтлем на основании некоторых аналогий между
молекулярным и турбулентным обменом. Несмотря на ее простоту,
она приводит к вполне приемлемым результатам, поскольку
погрешности модели при описании каждого элементарного акта
сглаживаются при осреднении.
Исходя из изложенной выше схемы перемешивания,
выведем формулы для турбулентных потоков различных свойств.
Начнем с рассмотрения частного, но важного случая, когда ос-
редненное значение рассматриваемого параметра распределено
в горизонтальной плоскости равномерно и существуют лишь
вертикальные градиенты средней величины. Выделим на
некотором уровне х3 единичную горизонтальную площадку. В
турбулентном потоке эту площадку пересекают вихри, движущиеся
с некоторой вертикальной скоростью v$(t, хз). Полный поток
субстанции а через эту площадку равен
ра^3 = pav3-\-pa vz. (7.5.1)
Здесь первое слагаемое описывает поток, вызванный средним
1 На самом деле процесс перемешивания непрерывен, и если вихрь
пересекал среду с меньшими значениями параметра а, то фактическое значение а
в нем будет меньше рассчитанного по изложенной схеме, и наоборот. Легко
понять, что в монотонном поле а вычисленные значения а для вихрей,
движущихся в противоположные стороны, будут иметь ошибки разных знаков.
В связи с этим при расчете суммарного турбулентного переноса погрешность
изложенной «схемы разрывного перемешивания» будет незначительной.
Система уравнений гидротермодинамики для турбулентной атмосферы 201
движением, а второе — турбулентный поток. На основании
условий 1 и 2
a'=Z{tt Xz-la)-a(tt xj=-ia^+±£Jj!*-t (7.5.2)
где la — путь смешения для свойства а. В (7.5.2)
хз—U(t)—исходная координата вихря, пересекающего в момент t
рассматриваемую площадку; /а>0 для вихрей, движущихся вверх,
и /а<0 для вихрей, движущихся вниз.
Из (7.5.1) и (7.5.2) после ограничения первыми членами
разложения находим
pa v'z = — р1аъ'г —j^- • (7.5.3)
Если на пути 1а величина а меняется из-за происходящих
в движущемся вихре внутренних процессов (например, если а —
температура вихря, то при адиабатическом расширении она
будет понижаться; если а — удельная влажность насыщенного
воздуха, то в вертикально перемещающемся вихре она может
меняться вследствие конденсации или испарения капель воды),то
a'=a(t, *з —/в)+/«-^ a(t, xz). (7.5.4)
Здесь — индивидуальная производная (изменение в
движущемся вихре, отнесенное к единице пути). В этом случае
ра%— р(-е| ёт)1*"*- (7-5,5)
В формуле (7.5.3) коэффициент при градиенте ——, равный
иХз
р/Лг>з = р*в(*. *з). (7.5.6)
аналогичен коэффициенту молекулярной диффузии; он
называется коэффициентом турбулентного обмена. В (7.5.6) ka =
= Uv,3— коэффициент кинематической турбулентной вязкости
(если а — количество движения), коэффициент
температуропроводности (если а — температура), коэффициент турбулентной
диффузии (если речь идет о любой пассивной примеси).
_> da 6 а —т~т" л
В тех случаях, когда —;—=—-—, ao'sO; такой верти-
& бхз 3
da
кальныи градиент —-— естественно называть равновесным. Как
202
Глава 7
следует из (7.5.6), ka растет с увеличением пути, который
проходят вихри, и с ростом их скорости. Поскольку обе эти
величины зависят от координат и могут меняться во времени, то.
разумеется, и ka = ka{t, xiy х2> хз). Заметим также, что в
движущемся вихре разные физические свойства могут с различной
скоростью выравниваться со свойствами окружающей среды
(/ = /а), в связи с чем ka может быть разным для разных
субстанций. При адиабатическом перемещении вихрей
консервативными в каждом вихре сухого воздуха (6а/6*3 = 0) остаются
потенциальная температура, удельная влажность и компоненты
скорости.1 Кинетическая температура и плотность водяного пара
из-за расширения (при перемещении вверх) или сжатия (при
перемещении вниз) изменяются. Если в перемещающемся вихре
воздух насыщен водяным паром на всем пути, то ни одна
из упомянутых характеристик не остается
консервативной, поскольку при перемещении происходят фазовые
переходы воды, сопровождающиеся выделением или поглощением
тепла.
Полученные выше формулы для турбулентных потоков
нетрудно обобщить для случая, когда средняя концентрация
является функцией всех трех координат. Тогда приходится
рассматривать вызванные турбулентностью потоки в трех
направлениях: III — вдоль охи П2 — вдоль 0X2 и Пз — вдаль охз.
Формула (7.5.2) при этом должна быть представлена в следующем
виде:
Я (t, Х\, Х2* X^)^(l(tt Х\, Х2, Х%)—1\ \t, Х\, Х2, Хъ)
да
дх\
— l2(t, Х\, Х2, Хъ) 0 /3(Г, Х\, х2, хг) ф -\-
-Мз('> Х\> Х2> Хз) §х *
Тогда
п>=- р {-щ- 1^+-щ-kVx +~йг ^ —ёг kVx) • (7-5J)
П2 = - Р (-fer/lZ,2+-e"^2+-^-/3x'2 ^-W). (7-5.8)
П3=-р(^-й+^^ + ^^-^^). (7-5.9)
1 Количество движения вряд ли можно считать консервативной
характеристикой, но часто это свойство для него постулируется в целях упрощения.
Система уравнений гидротермодинамики для турбулентной атмосферы 203
Поскольку здесь корреляция между U и v\, k и v'z , /3 и
v'3 значительно больше корреляции между остальными
переменными, то обычно малые слагаемые отбрасываются, после чего
получаем:
ni= — Р^-/1^1=— bia?
дхх *1"1 '"1аг дхх
да
дх3
(7.5.10)
(7.5.11)
Ъа \
Ьхг )■
(7.5.12)
дх2 "^ "ж дх2 •
Пз= - Р (~Щ~ ^з щ- Ж) = - Р*;
На основании полученных выражений для потоков
различных субстанций, вызванных турбулентностью, нетрудно найти
притоки соответствующих субстанций, а тем самым и локальные
изменения их концентрации, обусловленные турбулентностью:
<■»■-- -S—g—ё—гг(*--£-)+
дхч
Заметим, что вертикальные градиенты в атмосфере намного
больше горизонтальных,1 т. е.
д чч д д чч д
» -^г" и -1г— »
длг3 d*i дх$ " дх2
Поэтому члены, отражающие горизонтальный турбулентный
обмен, могут быть опущены. Тогда
„*!!-,-£-[* (-*-_*.)]. (7.5.14)
Здесь принято k=ksa-
Теперь с учетом (7.5.14) общее уравнение баланса (7.4.4)
может быть записано в виде
-$-~4?-+-£-(*-&-)+'■ («■'«>
Здесь и далее черта осреднения над всеми сглаженными
величинами в целях упрощения записи опущена.
1 Мы сейчас не рассматриваем случая резкого изменения свойств
подстилающей поверхности, где в узкой зоне могут иметь место значительные
горизонтальные градиенты.
204
Глава 7
Мы видим, что, в отличие от (7.4.1), уравнение (7.5.15)
содержит член —— \pk~-z—), появляющийся в результате опе-
ОХз V ОХь I
рации сглаживания. Он отражает вертикальный перенос
свойства а за счет турбулентного перемешивания. Процессы
турбулентного обмена значительно интенсивнее процессов молеку-
лярного обмена, в силу чего членом , который описывает
OXj
изменение свойства а за счет молекулярного обмена, в
дальнейшем будем пренебрегать.
7.6. Осредненные уравнения гидротермодинамики атмосферы
Всю систему уравнений легко получить, подставляя в (7.5.15)
вместо а соответствующие субстанции и используя полученные
в главе 1 выражения для источников. Полагая а=са, получим
уравнения диффузии какой-либо примеси:
doc d?cavf д I дс \
k
Суммируя (7.6.1) по всем а и учитывая, что Д]са=1 и
к
^/а = 0, получим уравнение неразрывности
Заметим, что (7.6.2) совпадает с (1.3.7), т. е. уравнение
неразрывности при сглаживании своего вида не меняет. Это
является следствием того, что мы пренебрегли пульсациями
плотности, считая воздух квазинесжимаемой средой.
С учетом (7.6.2) уравнение (7.6.1) может быть переписано
в виде
'4~&>-&-)+'.. <7-6-3>
В частности, для удельной влажности (ca=q) будем иметь
уравнение
'-S—Е5>-£-)+'г (7в-4>
С учетом уравнения неразрывности (7.6.2) общее уравнение
баланса (7.5.15) можно переписать в виде
Р-
da д /, да
dt dxz
(k?4St)+f- <7-6-5>
Система уравнений гидротермодинамики для турбулентной атмосферы 205
Уравнения движения получим, полагая в (7.6.5) a = Vj (/=1,
2, 3). Вид источника получен ранее (см. главу 1). Поэтому
окончательно уравнение движения примет вид
-fr—7"Й-+Т5-(*-ё-)-Л+-Я1-^ С-**»
Напомним, что при выводе этого уравнения мы пренебрегли
молекулярным трением в сравнении с турбулентным, а также
полагали р = const. Оба эти допущения по отношению к плотности
в уравнениях горизонтального движения вполне оправданы.
Наконец, уравнение притока тепла получим, полагая
в (7.6.5) а = сРв:
В (7.6.7) член с молекулярной теплопроводностью опущен,
ибо он мал по сравнению с турбулентным переносом тепла.
Кроме того, диссипативные эффекты в атмосфере не дают
ощутимого вклада в баланс внутренней энергии, и ими можно
пренебречь.
Уравнение (7.6.7) можно переписать еще в виде
?ср -^- = ?ср -}- (*е*-||-) + Л+/ф. (7.6.8)
Здесь введено ae=ke/k — отношение коэффициентов
турбулентности для тепла и количества движения.
Итак, нами получены сглаженные уравнения движения,
неразрывности, притока тепла и диффузии. В каждом из них, за
исключением уравнения неразрывности, фигурирует величина k.
По сути дела, введя коэффициент турбулентности, мы
выразили неизвестные величины турбулентных потоков через новую
неизвестную, причем последняя существенно зависит от
структуры турбулентного потока, масштабов течения и т. д., а в
конечном итоге является искомой функцией координат и времени.
Как уже упоминалось, исследование процессов диффузии
представляет собой самостоятельную задачу, к которой мы
обратимся в главе 18. Пока же мы ее рассматривать не будем. Тогда,
присоединяя к выведенным уравнениям уравнение состояния
p=RpT, которое при осреднении своего вида не меняет (при
сделанных приближениях), а также выражение для
потенциальной температуры
cp~~cv
0 = 7,р5оо_рГ
в итоге получим систему из семи уравнений. Они связывают
206
Глава 7
восемь неизвестных величин: Vu р, р, Т, 0, k. Таким образом,
задача незамкнута. Число уравнений на единицу меньше числа
неизвестных, т. е. возникает вопрос о замыкании, решение
которого сводится к отысканию дополнительных соотношений,
которые позволили бы уравнять число уравнений и число
неизвестных. Одним из таких дополнительных соотношений
является уравнение баланса энергии турбулентности, к выводу
которого мы обращаемся ниже.
7.7. Баланс кинетической энергии турбулентных пульсаций
Вывод уравнения баланса кинетической энергии
турбулентных пульсаций позволяет глубже понять факторы, которыми она
определяется, и, как сказано выше, дает возможность
сформулировать еще одно соотношение, необходимое для замыкания
системы уравнений.
Рассмотрим баланс средней удельной кинетической энергии
пульсационных составляющих скорости 6, т. е.
b=-^-{v\V\-\-V2V2JrVzVz).
Все рассуждения проведем по отношению к частному случаю,
полагая, что осредненные значения потоков турбулентной
энергии и ее источники зависят только от высоты, т. е. являются
функциями хз. Именно таким является поток в нижних слоях
атмосферы над однородной подстилающей поверхностью. При
этом будем пренебрегать влиянием пульсаций давления на
баланс кинетической энергии флуктуации. Это допущение не
приводит к существенным погрешностям, поскольку пульсации
давления вызывают главным образом перераспределение
кинетической энергии флуктуации между отдельными компонентами и
мало влияют на баланс полной энергии.
В стационарном турбулентном потоке кинетическая энергия
основного движения непрерывно переходит в кинетическую
энергию флуктуации, а последняя — во внутреннюю и в
гравитационную потенциальную энергию (в процессе совершения работы
против силы плавучести или с ее помощью). Суммарное
изменение энергии пульсаций равно полной работе, совершаемой,
во-первых, вихрями против вязкого трения и, во-вторых, силой
плавучести.
В общем случае нестационарного движения изменение в
единице объема за единицу времени dpb/dt определяется
уравнением баланса
_^___ d*bvJ dJbJ , r /77П
Система уравнений гидротермодинамики для турбулентной атмосферы 207
Приток энергии турбулентных пульсаций определяется
формулой типа (7.5.13), т. е.
dJl
bi
дхз
TSr(a**
4
дЬ
дх*
дх\
~ (аЛзР
)+^г(аЛр^) +
дХ2
дЬ
дх*
)•
Отсюда с учетом того, что поток турбулентной энергии зависит
только от хз, получим
6J
Ъ)
dJt
ьз
дх»
дх*
дх*
(a^p~d^~) (*з=*. ab = kblk)-
Су ихг охъ \ " ■ охг
Источниками энергии, как уже выяснено, являются: 1)
переход осредненного движения в энергию турбулентности (/i);
2) переход во внутреннюю энергию
за счет диссипации (diss); 3)
работа силы плавучести, дающая
положительный вклад при неустойчивой
стратификации и отрицательный —
при наличии устойчивого
расслоения (/2). Таким образом,
/^ = /i+/2 + diss.
Вычислим прежде всего
кинетическую энергию основного потока,
которая за единицу времени
превращается в энергию турбулентности,
т. е. Л. Вычисление проведем
исходя из следующих соображений.
Благодаря турбулентному обмену
количеством движения между
отдельными слоями на каждый
элемент жидкости действует
касательное напряжение (рис. 7.5). Часть работы, совершаемой этими
поверхностными силами, сообщает элементу ускорение, изменяя
кинетическую энергию его осредненного движения, другая часть
превращается в энергию турбулентности. Таким образом,
поступление энергии турбулентности за единицу времени равно
разности между полной работой касательных напряжений и
приращением кинетической энергии элемента, вызванной силами
турбулентного трения. На основании (7.5.12) получим
следующее выражение для работы касательных напряжений за
единицу времени, отнесенной к единице объема жидкости:
+~Хл
Рис. 7.5. Схема касательных
напряжений, действующих на
элементарный объем.
/ — средняя скорость, 2 —
касательные напряжения.
208 Глава 7
- *р -g- «* L **• ^2+ftp -§- ** I *+<*dXi dX2)x
Приращение кинетической энергии осредненного движения
единицы объема за единицу времени, вызванное турбулентным
обменом, равно
ЬННла+ЧтН,,.]-
Используя эти формулы, находим
Вычислим теперь работу, совершаемую против силы
плавучести /г. При вертикальном перемещении молей (вихрей) в
устойчиво расслоенном потоке работа (см. главу 3), отнесенная
к единице объема и совершаемая за единицу времени, равна
Р-Ж"^з=| -?g 1^1 ^3=[g(p-p)]%=-pg 8^e v*
Здесь р и 0 — плотность и потенциальная температура в
частице, а р и 0 — то же в окружающей среде. Движение молей
происходит квазистатически, т. е. р = р.
Выписанная формула относится к некоторому уровню Хз и
моменту времени /. Выполнив над ней операцию осреднения,
получим
**м ___ £ Гот— g
Здесь Г0 — средняя температура воздуха (Го—300 К). Тогда
на основании (7.5.12) получим
Из (7.7.3) видно, что при неустойчивой стратификации (v>Ya)
сила плавучести способствует развитию турбулентности, а при
устойчивой стратификации (v<Ya), наоборот, стремится ее
погасить. При нейтральной стратификации (—j—=01 никакого
вклада в рассматриваемый процесс она не вносит.
Система уравнений гидротермодинамики для турбулентной атмосферы 209
Таким образом, уравнение баланса энергии турбулентности
для единицы объема можно записать в следующей форме:
+"'*+тгг(«.*^г)- <"-4>
Заметим, что уравнение (7.7.4) не является следствием ос-
редненных уравнений движения и может рассматриваться как
дополнительное уравнение для определения коэффициента
турбулентного обмена. Однако в нем появились новые неизвестные
(Ь и diss), так что в итоге теперь имеем восемь уравнений и
десять неизвестных.
Система осталась незамкнутой. Существуют различные
гипотезы, которые позволяют в принципе уравнять число
уравнений и неизвестных. В главе 11 будут рассмотрены некоторые
из них и приведены те дополнительные соотношения, которые
позволяют замкнуть всю систему гидротермодинамики
турбулентной атмосферы.
7.8. Упрощение уравнений динамики атмосферы.
Классификация атмосферных движений
Основные идеи теории подобия
Общая система уравнений динамики атмосферы является
существенно нелинейной. Она описывает сложный механизм
притока тепла, эффекты турбулентности и сжимаемость. Все это
весьма усложняет математическую сторону исследований.
Несмотря на значительный прогресс, который наметился
в этом плане после внедрения численных методов с
использованием ЭВМ, подчас решение задач метеорологии приводит к
большим математическим трудностям. В связи с этим существенным
оказывается развитие приближенных методов интегрирования
уравнений, с одной стороны, и упрощение системы, которое тем
не менее обеспечивало бы достаточную для приложения
точность,— с другой.
Имея в виду последнее обстоятельство, целесообразно при
исследовании конкретных явлений провести предварительный
качественный анализ общих уравнений, который позволил бы
оценить вклад каждого слагаемого, а затем отбросить малые члены.
По существу, это означает упрощение уравнений, основанное
на пренебрежении второстепенными эффектами. Такого рода
14 Заказ № 612
210
Глава 7
анализ, не всегда тривиальный, выполняется методами теории
подобия на основании сведений о масштабах величин,
характеризующих изучаемое явление. Как мы увидим далее, техника
теории подобия основана на переходе в уравнениях к новым
переменным, при котором последние измерялись бы в естественных,
характеризующих исследуемое явление масштабах. Заметим,
кстати, что такое «физическое масштабирование» целесообразно
выполнять и как этап подготовки задач к решению на ЭВМ.
Иногда в безразмерных уравнениях выделяется малый
параметр, по степеням которого раскладываются искомые функции.
Самый простой способ упрощения уравнений динамики
можно основать на найденных из эмпирического материала
значениях метеорологических элементов и их производных.
Соответствующие данные приведены в табл. 7.1, подготовленной в свое
время Гессельбергом и Фридманом.
Таблица 7.1. Порядок величин метеорологических элементов
и их производных
д
ds
д.
dz
д
dt
д2
ds*
vs
10°-101
10-5—10-4
Ю-3-10-2
10-4-Ю-з
Ю-Ю-10-9
w
Ю-2-10-1
10-7—10-6
10-5 — Ю-4
Ю-б-Ю-5
10-9-Ю-9
P
105
Ю-4-10-2
101
10-2-Ю-1
10-9-Ю-8
1/P
10°
lO-S-io1?
10-4
10-7-Ю-6
10-13-Ю-12
T
102
10-5-Ю-4
Ю-3-10-2
10-4-Ю-з
10-1о_ю-9
В таблице даны наиболее часто повторяющиеся значения
горизонтальной (vs) и вертикальной (w) компонент скорости
ветра, давления (р), удельного объема (а=1/р) и температуры
в абсолютной шкале (Т) и их производных по горизонтали
(d/ds), вертикали (d/dz) и по времени (d/dt). Все величины
приведены в единицах килограмм, метр, секунда и характерны
для нижнего слоя тропосферы.
Воспользовавшись табл. 7.1, можно оценить порядок
различных слагаемых в уравнениях и выделить таким образом
главные. На ранних этапах развития метеорологии таблицы Гессель-
Система уравнений гидротермодинамики для турбулентной атмосферы 211
берга и Фридмана оказали неоценимую помощь теоретикам.
До сих пор они могут быть с успехом использованы для
некоторых предварительных оценок.
Однако приведенные в табл. 7.1 порядки величин отражают
все разнообразие атмосферных процессов, без какой-либо
классификации, и, разумеется, каждая из рассмотренных величин
характеризуется чрезвычайно большой дисперсией (разбросом).
Как следует из таблицы, даже наиболее часто повторяющиеся
значения меняются в 10—100 раз, в связи с чем таблица
позволяет лишь очень грубо оценивать разные слагаемые. Более
точные оценки можно получить, рассматривая порядки величин для
близких по физической природе явлений. Для подобной
совокупности каждая величина находится в сравнительно узком
интервале, для нее может быть дана лучшая оценка и тем самым
более основательное упрощение системы уравнений.
Однако составление таблиц для каждой совокупности
сходных (подобных) явлений на основании эмпирических данных
затруднительно, так как в каждой группе оказалось бы
недостаточно материала для того, чтобы получить, например,
надежные значения вторых производных, весьма «чувствительных»
к погрешностям измерений. Еще хуже может обстоять дело при
теоретическом исследовании совершенно новых проблем,
возникающих в процессе развития науки; в таком случае в наличии
имеются лишь единичные измерения, из которых можно
получить весьма предварительную информацию.
Как же найти специфические для рассматриваемого явления
оценки характерных величин на основании простейшей
информации, скажем, по данным о пределах, в которых могут
изменяться искомые величины? Мы подошли теперь к методам
теории подобия по существу.
Величины, характеризующие процессы в атмосфере,
являются функциями координат и времени и меняются в
определенных пределах. Для различных физических процессов сами
величины и пределы, в которых они изменяются, разные. В связи
с этим необходимо выбрать рациональную процедуру получения
величин, типичных для каждой группы сходных процессов;
обычно их называют характерными масштабами.
Условимся считать переменную величину f порядка единицы
и обозначать f = 0(l) (ordo по-латински — порядок), если 0^
^|/|^1. Если, например, ф1^|ф|^1ф2, то, очевидно, 0^
IФ — ф11 IФ — ф11
^ ^1, т. е. = 0(1).1 В этом случае будем
ф2 ф! ф2 ф1
1 Толкование этих неравенств в задачах физики имеет определенную
специфику. Во-первых, их следует рассматривать как приближенные соотношения;
например, если верхним пределом f является не 1, а 2 или 3, то это,
14*
212
Глава 7
говорить, что характерным масштабом функции ср — <pi является
величина
<Р2 — <Pi = <Po. (7.8.1)
Поскольку А (ф — фО =Аф, то при оценке производных ф2 — ф1 =
= фо является характерным масштабом для ф. Так, например,
характерным масштабом давления в циклоне (при оценках
градиента давления) является не значение давления в какой-либо
его точке, а перепад давления между периферией и центром.
Именно перепад давления является существенной
характеристикой циклона, определяющей основные процессы в нем. Точно
так же разность температур суши и воды, а не средняя
температура или температура в какой-либо точке определяет
свойства бризовой циркуляции (эта разность и должна приниматься
в качестве масштаба температуры для оценки горизонтальных
температурных градиентов). Определенные указанным способом
характерные масштабы используем для записи
дифференциальных уравнений в безразмерной форме.
Нетрудно понять, по какой причине после такого
масштабирования дифференциальных уравнений они начинают отражать
особенности конкретного, подлежащего исследованию явления.
Ведь характерные масштабы, явно фигурирующие в
безразмерных уравнениях, вносят в систему уравнений информацию о
характерных свойствах явления.
Рассмотрим выражения для первой и второй производных по
какому-либо аргументу \—^-\ "лг •••) * Пусть
? = <Р0<Рл.
х=х0хП1 (7.8.2)
где фо, Хо — характерные масштабы в указанном выше смысле.
Тогда
дер _ ср0 дуп
дх х0 дхп
дЦ _ <ро дЦп
<**2 ~~ А дх2
■*0 илп
(7.8.3)
(7.8.4)
Ограничимся классом функций, удовлетворяющих следующим
условиям:
разумеется, не меняет порядка величины, так что все равно /=0(1). Во-вторых,
имеется в виду, что среди множества значений ф обязательно встречаются
значения, достаточно близкие к предельным значениям, и речь идет о выборе
характерной количественной оценки для всего множества. И наконец, /=0(1}
вовсе не означает, что /»1.
Система уравнений гидротермодинамики для турбулентной атмосферы 213
°<|4Н*°<ср2_ср1=сро' (7*8-5)
°Я~^Г°^ Х2-ХХ ~W (7в8-6>
Поскольку из (7.8.3) следует, что
|-&Ь-*1-&-|. (^.7)
то на основании (7.8.5) имеем
0<<ро|
дхп
дЧп
дхп
<То
или
т. е.
о<-Й-<'-
Совершенно аналогично на основании (7.8.4)
(7.8.8)
дЦ | „ ч>о
"3*П °—^Г
дх\
Подставив это соотношение в (7.8.6), получим
0<
ТО
*0
дЦп
dxi
<
?0
*0
или, разделив на постоянный множитель <ро/*о, находим
0.
дЦп
дЛ
<1.
(7.8.9)
Эти выводы проиллюстрируем простейшим примером. Пусть
в рамках предыдущих обозначений
<Р = <р0е
Тогда
дер
<ро
дх х0
дЦ _ <р0
*о
?0 <*ря
*0 <**„
длг2
(7.8.10)
(7.8.11)
(7.8.12)
214
Глава 7
Из трех уравнений (7.8.10) — (7.8.12) следует:
°<М<?о. О(ср) = ср0,
о<|
о<
дх
д<? \^ То п( д<? \ То
d*2
То
о<Ы<1, оы=1,
} (7.8.13)
0<
о<
<?Тл
д2Тл
***
<'-°(-fc-)-i.
Для негладких, или разрывных, функций приведенные оценки
непригодны. В таких случаях всю область можно разделить на
отдельные участки, в которых выполняется уравнение (7.8.5).
Определенные трудности возникают тогда, когда искомые
функции имеют волновую природу, что часто является характерным
для атмосферы. Масштабы, выбранные по разным гармоникам,
пропорциональны длине волны и естественно будут разными.
В таких случаях выбор масштаба определяется особенностями
и целью поставленной задачи. Если по существу задачи интерес
представляют все флуктуации, включая и мелкомасштабные, то
масштаб нужно выбирать минимальным; и наоборот, если
основная цель — крупномасштабные свойства процесса, то выбор
масштабов по низким гармоникам и соответствующие
упрощения приводят к отфильтрованию несущественных
высокочастотных флуктуации. Так, например, для получения уравнений,
описывающих общую циркуляцию атмосферы, нет надобности
учитывать, локальные неоднородности атмосферы и даже отдельные
барические образования могут сглаживаться. Горизонтальный
масштаб в рассматриваемом случае имеет порядок радиуса
Земли.
Из-за нелинейности уравнения динамики сглаживание
мелкомасштабных флуктуации «оставляет след» (об этом уже
говорилось в п. 7.3) в форме вторых моментов от пульсаций.
Величина и свойства этих слагаемых зависят от того, какая часть
спектра флуктуации сглаживается.
Главный результат, вытекающий из приведенных выкладок,
заключается в том, что при переходе к безразмерным
переменным с помощью указанных масштабов (поскольку все
неизвестные величины в безразмерной форме имеют порядок единицы)
оценкой порядка величины каждого слагаемого в уравнении
Система уравнений гидротермодинамики для турбулентной атмосферы 215
служит стоящий при нем постоянный коэффициент,
составленный из масштабов, характерных для исследуемого явления.
Поскольку каждый класс подобных явлений характеризуется
своими масштабами, то соответственно главные члены уравнений
будут одинаковыми для подобных явлений. Если каждое
уравнение разделить на один из постоянных множителей, стоящих
при каком-либо из слагаемых, то в преобразованных уравнениях
коэффициенты при отдельных слагаемых будут безразмерными
величинами, составленными из характерных масштабов. Эти
безразмерные коэффициенты называются критериями, а
соответствующие уравнения — критериальными.
Явления принадлежат к одному классу, т. е. описываются
тождественной системой безразмерных уравнений, если
критерии для них равны по величине.
Очевидно, что критерии могут быть одинаковыми и тогда,
когда характерные масштабы различаются; важно лишь, чтобы
их комбинации, составляющие критерии, были равны. Это
обстоятельство является основой для лабораторного
моделирования.
Разумеется, что при рассмотрении нового явления мы можем
иметь лишь ориентировочные представления о характерных
масштабах. В таких случаях анализ уравнений представляет собой
лишь некую довольно грубую оценку. Тем не менее он всегда
является*крайне полезным для предварительного осмысливания
задачи. Из приведенных выкладок следует важный вывод,
который часто используется весьма эффективно: если известно, что
в заданной системе уравнений все слагаемые имеют одинаковый
порядок величины, то соответствующие критерии в безразмерной
системе равны, а соотношение между ними можно использовать
для оценки характерных масштабов.
Приведенные довольно общие рассуждения проиллюстрируем
на простейшем физическом явлении. Рассмотрим изменение
температуры в потоке воздуха, движущемся над поверхностью,
температура которой — периодическая функция времени. Пусть
для простоты скорость ветра и и коэффициент
температуропроводности k не зависят ни от координат, ни от времени, а
вертикальная компонента скорости w линейно растет с высотой.
Процесс описывается следующей системой уравнений:
дТ , z дТ и д*Т дТ .- Q - ,v
Щ, х, z)\g=Q = T0+Asta»t. \
T(t,x,z)\Xss0=T0(z)9 | (7-8Л5)
T(t, х, 2)|z=oo = r0(oo) = const. (7.8.16)
216 Глава 7
В рассматриваемом случае
/i-Поо).
Л-7о+А
/0 = Г0-Г0(оо)+Л;
fo — характерный масштаб для температуры.
Перейдем к безразмерным переменным. Полагая
Т— Т
получим:
* п\?п> *п, Zn)\Zn = 0 = Т —Т—Т~А ' (1-оЛЪ)
О оо '
Tn(tn. ха, zn)\Xn=0=Tln(tnt zn)t (7.8.19)
Tn(tnt zn)\Zn^Q=0. (7.8.20)
Класс подобных (в узком смысле) явлений определяется
следующими тремя критериями:
Пх —,
Если для двух процессов Яь Я2, Я3 одинаковы, то оба процесса
описываются одинаковой системой уравнений.
В уравнении (7.8.17) четыре слагаемых имеют
соответственно порядок величины:
1 п — w^ п — ktQ п — ut°
1, Пх —, "2—^7. Я3 —.
По известным значениям масштабов вычисляются Яь Я2, Я3;
если одно из них много меньше единицы, то им можно
пренебречь и соответственно упростить уравнения. Так, например,
если о>1 = 0,02 м/с, и = 10 м/с, zt = 100 м, г0=100 м, х0=100 км,
£=20 м2/с, то
ПХ _ *>А 1 Я3 _ и4 1
Я2 *i* 40 и Я2 "~ kx0 16 •
Система уравнений гидротермодинамики для турбулентной атмосферы 217
Стало быть, вторыми слагаемыми в левой и правой частях
(7.8.17) можно пренебречь. Легко понять, что в данном примере
to = 0(—7-)«4 ч, поскольку в упрощенном уравнении оба
слагаемых имеют одинаковый порядок величины. Из приведенного
примера видно, что в безразмерных переменных целый класс
явлений может описываться тождественными уравнениями, если
разные для каждого явления исходные параметры приводят тем
не менее к одинаковым значениям #i, Я2, Яз. Ясно также, что
для полного подобия явления равными должны быть еще два
критерия, которые входят в граничные условия, а именно:
Л4 = -^= ^— и Я5 = о)/0.
Таким образом, подобие в узком смысле является необходимым,
но недостаточным условием полного подобия.
Примеры упрощения уравнения динамики. Классификация
атмосферных движений
Рассмотрим первое уравнение движения (7.6.6):*
ди , ди , ди | ди рх , д ixz ,
dt '" дх ~v ду ' w dz p * dz p r
Здесь ради общности эффекты горизонтального турбулентного
обмена не отброшены и введены обозначения:
/=2a>sincp, -^**- = k -gj- = — u'w',
Пусть
p ду ' p ox
U = UoUnt v = v0vn, W = W0Wnt
dP _ „ dPn
Ps> ~^-=PsPl
dx rs> dXn
nx>
Ww* WV WW xq
(u'w')n (u'v')n (u'u')n PO
1 Выводы, которые следуют ниже, можно совершенно так же получить и
из второго уравнения.
218
Глава 7
да I дап tip да I дап да I дап а0
dt I dtn ~~h~* ~djT\~dx^ ~~ду~\~дуп ~Ц »
да
/т&—?■• <7-8-22»
dz i v*n /-з
Поскольку изменения турбулентных потоков обусловлены
изменением средних компонент скорости, то естественно
предположить, что соответствующие масштабы для координат (при обез-
размеривании производных и от потоков) одинаковы, т. е.
да г- д —,—j/—,—- 1 да /— da'w' /—.—у 1
(7.8.23)
Воспользовавшись масштабами, введенными в (7.8.22),
перепишем уравнение (7.8.21) в безразмерных переменных:
lt0 dtn "Г цх \U» дхп ^Vn дуп /T 1Ц Wn dzn —
Ps Pnx I т0 Г d*nzx I ^3 / dznxy . dznxx \"|
= ?>/,
PO^O Pn
(7.8.24)
Во всех" атмосферных движениях Ьз/Ь{<1. На этом основании
эффекты горизонтального турбулентного обмена
(мелкомасштабного) пренебрежимо малы по сравнению с
соответствующим влиянием вертикального турбулентного обмена. Поэтому
в правой части (7.8.24) почти всегда можно пренебречь вторым
членом в квадратных скобках.
Поскольку безразмерные величины, как показано выше,
имеют порядок единицы, то относительная значимость каждого
слагаемого в (7.8.24) определяется числовым значением
стоящего при нем коэффициента. Таким образом, вид уравнения,
описывающего конкретное явление, определяется значением пяти
следующих безразмерных коэффициентов:
1 цр wp ps TQ
lt0 ' ILX » IL3 ' ро/но ' Ро'ио^з *
Если на основании предварительных экспериментов известны
характерные масштабы и средние значения искомых функций,
то в (7.8.24) могут быть легко выделены главные слагаемые,
которые только и оставляются при приближенном исследовании
конкретного процесса.
1 Здесь черта сверху означает операцию сглаживания, при которой
отфильтровываются мелкомасштабные флуктуации ( см. п. 7.4).
Система уравнений гидротермодинамики для турбулентной атмосферы 219
Приведенные выше пять коэффициентов являются
критериями для классификации атмосферных движений.
Укажем прежде всего на одну особенность вертикальной
структуры атмосферы, заключающуюся в том, что при всех
ситуациях вертикальные градиенты метеоэлементов вблизи
земной поверхности намного больше соответствующих значений на
высоте. Это означает, что L"1, а стало быть, и слагаемое,
отражающее влияние турбулентного трения, в нижних слоях
атмосферы существенно больше, чем в верхних. В связи с этим
целесообразно разделить атмосферу на два слоя: пограничный
слой, в котором то/ро/ио£з^1, и свободную атмосферу, где
то/ро/^о^з<1. Естественно также выделить нижнюю часть
пограничного слоя, где то/ро/«о£з^>1, которую называют приземным
слоем.1 В пределах каждого из трех указанных слоев можно
выделить стационарные и нестационарные, горизонтально
однородные и горизонтально неоднородные явления в зависимости
от числового значения критериев 1///0 (число Кибеля) и Uo/Lil.
Нетрудно понять, что при стационарных горизонтально
однородных процессах в свободной атмосфере l//£o<Cl, uo/lLi^l,
ps/poluo = 0(l), так как только последнее слагаемое может
сбалансировать член порядка единицы (vn), остающийся в
уравнении. Указанный тип движений носит название «геострофические
движения».
Поскольку средний горизонтальный градиент давления и
характерная скорость в различных процессах сохраняют свой
порядок, то можно без заметных ограничений принять, что всегда
p$/poluo = l (за исключением, разумеется, приземного слоя, для
которого ио — малая величина).
Что касается слагаемого, которым определяется влияние
вертикальных движений, то, как следует из уравнения
неразрывности и близости ветра к геострофическому, wo/L3^tio/Li. Это
означает, что оно может оказаться существенным только при
горизонтально неоднородных процессах. Критерии, положенные
в основу классификации атмосферных движений, представлены
в табл. 7.2.
Форма приближенных уравнений, которыми описывается
каждый класс явлений, очевидна.
Рассмотрим несколько примеров. Для нестационарных
движений в пограничном слое атмосферы уравнение можно
использовать в следующем виде:
^ = Vn--^-^±~. (7.8.25)
1 Приведенные неравенства указывают на относительную роль силы
трения и силы Кориолиса в разных слоях атмосферы.
220
Глава 7
т
Критерий
1
"о
*0
Ро^о^з
а б л и ц а 7.2. Классификация атмосферных движений
Свободная
атмосфера
Пограничный
слой
Приземный слой
Тип движений
а
«1
«1
в
1
«1
в
«1
1
' «I1
а
«1
«1
в
1
«1
в
«1
1
0(1)
а
«1
«1
б
W«0^3/
«1
в
«1
о ММ
Ps
Ро^о
Примечание. Здесь а — стационарное горизонтально однородное
движение, б — нестационарное горизонтально однородное движение, в —
стационарное горизонтально неоднородное движение.
Локальные изменения скорости в течение небольших
промежутков времени в свободной атмосфере обусловлены главным
образом адвекцией и пестротой метеорологических полей. Это
означает, что в задачах краткосрочного прогноза можно принять
l/lt0 = uo/lLi. Поскольку здесь, кроме того, ветер близок к
геострофическому и эффекты турбулентности относительно малы,
то при формулировке задач краткосрочного прогноза уравнение
может быть записано в следующем виде:
1 ( дип {
ди„
Но
дхп*
Рпх
?п
(7.8.26)
Остановимся еще на уравнениях, описывающих бризовые
ветры. Нетрудно понять, что бризы характеризуются большой
горизонтальной неоднородностью потока (uo/lLi^>l) и
обладают небольшой мощностью по вертикали (то/ро/#о£з^>1).
На этом основании при построении теории бриза уравнение
«(7.8.24) следует записать в виде
дип
дхп
-Vn
дип
dzn
дУп
dzn
(7.8.27)
В упрощенных уравнениях влияние отброшенных слагаемых,
когда это требуется, может быть учтено во втором приближении,
«ели искать решение задачи как разложение по
соответствующему малому параметру.
Так, например, в задачах краткосрочного прогноза для
свободной атмосферы иногда необходимо учесть влияние упорядо-
Система уравнений гидротермодинамики для турбулентной атмосферы 221
ченных вертикальных движений, которые являются основным
механизмом взаимодействия между слоями по вертикали. В этом
случае компоненты скорости можно искать в виде разложения
по безразмерному параметру wq/ILz, т. е. искать решение
в форме
/.-/«■ +7Zr/"»+(-g-)V2-+ • • • <7-8-28>
Рассмотрим теперь третье уравнение динамики, одним из
слагаемых которого является сила тяжести. Поскольку
ускорение Кориолиса и силы трения всегда много меньше силы
тяжести, то на основании (7.6.5) имеем
dw.dw.dw. dw 1 dp .- 0 опч
т+"^г+*^г+а'^-=—г-яг~8' (7'8,29)
Обозначим характерное значение вертикального градиента
давления через рн и воспользуемся принятыми выше
обозначениями для остальных функций. Тогда (7.8.29) в безразмерных
переменных можно записать в следующем виде:
w0 dwn , ыо^о / д^п I &wn
tog dtn ^ Lxg
■(--е-+'.-й-)+
^o_ dwn PH Pm i (7.8.30)
«я^5—-^r^^-l.
' hg П fen ?0g ?n
В крупномасштабных атмосферных процессах uo=W м/с, wq =
= 10~2 м/с, /о=Ю5 с, Li = 106 м, L3=103 м. Тогда w0/t0g=l0-\
uoWolLig=\0-%, w20/Lsg=\0~s. Ясно, что при таких процессах
всеми слагаемыми в левой части (7.8.30) можно пренебрегать
и третье уравнение с большой точностью можно применять
в форме уравнения статики
-у~т£—*-0. (7.8.31)
Однако известны процессы, когда приближения статики
оказываются недостаточными. К ним относятся, например, мезомас-
штабные движения в грозовых облаках, где ускорения
воздушных масс иногда сравнимы с ускорением силы тяжести.
Другим примером, для которого приближения статики
неприемлемы, является задача о вертикальных мелкомасштабных
движениях. В этой задаче главный интерес представляет
вертикальная скорость отдельных частиц, плотность которых
отличается от плотности окружающей среды. Непосредственное
использование уравнения (7.8.29) в таком случае не может
привести к цели, поскольку искомая величина из него определяется
как малая разность больших величин. При решении таких задач
222
Глава 7
целесообразно преобразовать уравнение (7.8.29),
воспользовавшись близостью распределения давления в окружающей среде
к условиям статического равновесия. Например, полагая для
1 дР
окружающей среды —- g = 0, а для частицы, скорость
р dz
которой ищется, р=р + р', р = р, получаем из (7.8.29)
dw 1 др ^ р — р' др
dt ?-+-?' ^ Т2 ^
= \ др . р' др
J dz р2 dz
Т. е.
dw р'
Это уравнение оказывается вполне пригодным для
определения w.
Мы рассмотрели технику упрощения уравнений динамики.
Она, разумеется, пригодна и для других уравнений, в частности
для уравнения притока тепла. Однако из анализа уравнения
притока тепла не вытекают легко обозримые и характерные для
атмосферы свойства, как это следует, например, из уравнений
динамики (квазигеострофичность и статическое равновесие).
В уравнении притока тепла в зависимости от конкретной задачи
любое из слагаемых может оказаться главным, а часто все
слагаемые близки по значению.
Применение принципов теории подобия и приведенные
иллюстрации основаны на некоторой априорной, известной из
экспериментального материала информации о свойствах
исследуемого явления. Возможна и другая ситуация, когда опытные
данные, даже самые предварительные, отсутствуют, но налицо
замкнутая система дифференциальных уравнений и краевые
условия задачи. Очевидно, в заданной математической
формулировке задачи содержатся в специфической форме все свойства
исследуемого явления, в том числе и характерные масштабы.
В связи с этим естественно предположить, что существуют
какие-то способы, позволяющие получить эти масштабы и
сформулировать задачу в безразмерном виде, основываясь
исключительно на системе уравнений и условиях однозначности. Такой
предварительный качественный анализ проблемы основан на
идеях анализа размерности, он является весьма полезным и
обычно позволяет понять важные особенности рассматриваемого
процесса.
(7.8.32)
Система уравнений гидротермодинамики для турбулентной атмосферы 223
Ниже кратко излагается соответствующая методика. Пусть
в сформулированной задаче (система уравнений и краевые
условия) содержатся независимые переменные *i, хг, хз, ..., хп
и размерные параметры аи #2, аз, ..., аш. В таком случае
каждая из искомых функций fi = fi{xu ..., хп, аи ..., аш). На
основании П-теоремы анализа размерности это соотношение,
связывающее n + m+l размерных величин, можно представить
в форме зависимости между n + m+l—k безразмерных
комплексов, составленных из исходных аргументов, если k — число
величин в рассматриваемой совокупности, которые имеют
независимую размерность. Это значит, что уравнение для f* можно
переписать в форме
fi,n=fi,n(A\n> Аъп> • • •» Ai + m_*)' (7.8.33)
Безразмерное соотношение, полученное указанным способом,
будет содержать все критерии подобия и характерные масштабы
для функций fi и для независимых переменных. Часто на
основании полученного соотношения можно попытаться еще больше
упростить задачу. Для этого надо вычислить значения
безразмерных комплексов, после чего безразмерное соотношение
можно разложить в ряд по малым безразмерным комплексам.
В приближенной постановке задачи можно ограничиться
первым членом разложения; это дает основание для пренебрежения
соответствующими слагаемыми в исходной задаче. Иногда
найденное разложение представляет достаточно конкретный
результат, которым и можно ограничить решение задачи в целом.
Следует, однако, иметь в виду, что формально найденное
разложение основано на предположении о том, что искомая
функция не имеет особенностей вблизи нулевого значения комплекса,
по которому ведется разложение. Эффективность качественного
анализа задачи на основании П-теоремы связана с числом
аргументов (число независимых переменных плюс число
параметров) и в большой степени зависит от научной эрудиции и
творческих способностей исследователя.
В заключение приведем систему уравнений
гидротермодинамики в форме, которая в настоящее время используется в
задачах динамической метеорологии:
du 1 dp Л , ч , д и да
= — -±-^£ 2(<Dy«> —<0Д>)-}"jr-k
dt ~ р дх -vwy~ «*"/ т д2 -> д2
dv I dp 0, ч , д и dv , , d*v , , d2t/
(7.8.35)
224
Глава 7
1 dp
р dz
О—i--g—». (7.8.36)
-?-'.-?"§-■ С7АМ»
p = 9RT, (7.8.39)
e = r(^P\ (7.8.40)
(7.8.41)
Здесь —г- обозначает полный приток тепла.
Для процессов, в которых эффекты турбулентности пренеб-
режимы, можно полагать k = ky = kx = 6 = 0 = diss = diff; тогда при
заданном притоке тепла для семи неизвестных (и> v> w> р, р*
7\ в) получаем семь уравнений [в уравнении (7.8.41) все
слагаемые равны нулю, оно выполняется тождественно]. В противном
случае необходимы дополнительные соотношения для
определения слагаемых, описывающих турбулентность и приток тепла,
обусловленный радиацией и фазовыми переходами воды. Эти
вопросы будут рассматриваться в последующих главах.
Контрольные вопросы
— да да
1. Доказать справедливость равенства ~~^г=~~^г-
2. Может ли возникнуть турбулентность при отсутствии
градиента средней скорости?
3. В силу каких причин может затухать турбулентность в
невязкой жидкости?
4. Что такое порядок величины меняющегося
метеорологического элемента?
5. Определить порядок величины функции ф(0=<ро \т~~) »
ее первой и второй производных (0^п^2).
Глава 8. ДИНАМИКА СВОБОДНОЙ АТМОСФЕРЫ
Движения в поле изобар, близких к окружностям. Движение при чисто
круговых изобарах. Геострофический ветер. Изменение геострофического ветра
с высотой. Отклонение ветра от геострофического.
Анализ основных уравнений динамики, выполненный в п. 7.9,
показал, что с высоты 1—2 км непосредственное влияние
подстилающей поверхности на метеорологический режим
оказывается пренебрежимо малым. Атмосферу, расположенную выше
этого уровня, называют свободной атмосферой. В ней, если не
рассматривать области, примыкающие к поверхностям раздела,
облачным слоям и струйным течениям (о них речь пойдет
отдельно), из-за термической устойчивости и малых сдвигов
скорости ветра (большие Ri) вертикальный турбулентный обмен,
как правило, отсутствует. Поэтому обмен количеством движения
и водяным паром между различными слоями в свободной
атмосфере осуществляется только благодаря упорядоченным
вертикальным токам. Учитывая сказанное, остановимся на
особенностях движения в свободной атмосфере.
В данной главе рассматривается ограниченная задача —
определение вектора скорости при заданном поле давления.
Целесообразность такой постановки обусловлена тем, что
измерение давления в настоящее время не связано с существенными
трудностями и выполняется с достаточной точностью, в то время
как характеристики ветра определяются с большими
погрешностями, а вертикальную компоненту можно определить только
расчетным путем.
8.1. Уравнения движения в поле изобар, близких
к окружностям
Выпишем уравнения движения для свободной атмосферы.
Поскольку траектории частиц в большинстве случаев
криволинейны, удобнее записать эти уравнения в цилиндрической
системе координат (см. приложение 2 и рис. 8.1):
dvr dvr t/0 dvr dvr
„2
—г-зИ-^' (8ЛЛ)
226
Глава 8
dt
-Vr
dvb
dr
-vz
dvB
dz
vv
rwB
1 dp
?r
db
•lvr.
(8.1.2)
При этом результаты для прямолинейных траекторий будут
получаться как частный случай.
В уравнениях содержатся три неизвестные величины: vn ve, vz.
Для замыкания системы воспользуемся уравнением
неразрывности, считая, что с
достаточной точностью
движение удовлетворяет условиям
несжимаемости;
следовательно,
dva
дЬ
к4&-=0. (8.1.3)
Рис. 8.1.
Вектор скорости в полярной
системе координат.
Система нелинейных
уравнений (8.1.1) —(8.1.3) в
принципе может быть
решена численными методами.
Однако наблюдающиеся
в природе поля давления весьма разнообразны, и для каждого
отдельного случая получаются свои численные результаты.
Выявить общие свойства движения и связь поля скорости с полем
давления по таким материалам трудно.
Между тем некоторые упрощения позволяют получить
аналитическое решение и сравнительно простые формулы, удобные
для анализа, которые могут рассматриваться как
удовлетворительное приближение. В частности, в таких формулах
явно видна связь компонент скорости с параметрами поля
давления.
Рассмотрим движение на фиксированной высоте. Пусть поле
давления характеризуется изобарами, форма которых близка
к окружности. Тогда давление в любой точке (г, 8) может быть
представлено в виде суммы
Р(г, 6, t)=p0(r> t) + apx(r, 0, *),
где po(r, t) —давление на изобаре круговой формы с радиусом
го (начало координат в центре окружности); api(r, 6,
/)—поправка за счет отличия формы изобары от окружности
(рис. 8.2).
Близость изобар к окружности означает, что a — малая
величина; при а=0 изобара в точности имеет форму окружности.
Динамика свободной атмосферы
227
Решение системы уравнений (8.1 Л) — (8.1.3) в
рассматриваемом случае естественно искать в виде разложения в ряд по
параметру а, а именно:
vr = v0(rt t)-\-avx(r, б, *)+ . . .
vb = u0(г, t)-\-aux(r, е> <)+•••
^ = а^(г, 0, 0+---1 (8Л-4)
Здесь Wo и Уо — компоненты
скорости при круговых
изобарах; U\y vi и Wi — поправки,
связанные с отличием формы
изобары от окружности.
Подставив (8.1.4) в
уравнение (8.1.1), получим
дур
dv\
dt
dt
-fao + Wi) X
x(
dvo
dr
dv\
~dF
■)+
Рис. 8.2. Пример барического поля.
(uo + aui)
dv\
(tto + a^i)2
db
__ 1 ( дро | м dpi \ .
+/(«o+aai). (8.1.5)
Если проделать аналогичную процедуру с равенствами (8.1.2)
и (8.1.3), то получится система уравнений, в которые будут
входить множителями а в разных степенях. Поскольку все
уравнения должны выполняться при любых а, то слагаемые,
содержащие а в одинаковых степенях, должны быть тождественно
равны. Это дает возможность получить системы сравнительно
легко решаемых уравнений для определения каждого из членов
разложения. Так, приравнивая члены, содержащие а в нулевой
степени, получим:
dvo
dt
du0
dt
-щ
dv0
-V0
dr
dup
dr
__ 1 dp0 ■ ,
Цр^о
lv0t
(8.1.6)
(8.1.7)
dr
(rv0) = 0.
(8.1.8)
1 Предполагаем, что при круговых изобарах вертикальная компонента
скорости равна нулю.
15*
228
Глава 8
Если приравнять слагаемые, содержащие а в первой степени,
то получится система уравнения для определения вторых
членов разложений:
dv\ | „% dvp , dv\ , и0 <fai 2щц0 1 ^ , ,
(8.1.9)
дщ | дао | ди\ , mq d^i
■Vl -l>7—t-v0
dt т"1 dr ^"u dr ' г de
r ~——d lVi> (8.1.10)
Аналогично могут быть выписаны соответствующие системы
уравнений для любого члена разложений.
8.2. Движение при чисто круговых изобарах
Согласно (8.1.4), движение при чисто круговых изобарах
оцисывается уравнениями (8.1.6) — (8.1.8). Эти три уравнения
содержат две неизвестные величины; требуется найти такие
значения и0 и Уо, при которых удовлетворялись бы все три
уравнения.
Из равенства (8.1.8) следует, что vor = c, где с — некая
постоянная. Поскольку иофоо, в том числе и при г = 0, то с
должно быть равно нулю и, следовательно,
v0 = 0. (8.2.1)
dtio
В таком случае из (8.1.7) вытекает, что ^ =0, т. е. что Wo
не зависит от времени: движение при чисто круговых изобарах
стационарно.
Выражение для определения и0 получается из (8.1.6) при
условии (8.2.1):
——\-lUo -—Тг U.
Это равенство означает равновесие трех сил, отнесенных к еди-
Динамика свободной атмосферы
229
/ 2 \
нице массы: центробежной ( — ] , Кориолиса (luo) и гради-
ента давления I —I. Его решение дает
Очевидно, что при заданном градиенте давления в
фиксированной точке при определенном значении р скорость ветра должна
определяться однозначно. Следовательно, один из корней
полученного решения лишен физического смысла.
Поскольку движение вызвано градиентом давления, то при
—■— = 0 скорость также равна нулю, а, следовательно,
соответствующее решение должно иметь вид
lr
У(4-Г+f 4?- •
или
и0
-Т-Ь'+У+ТЯГ-*-]" »■*■*>
Движение, описываемое формулой (8.2.2), носит название
градиентного ветра. Скорость его увеличивается с увеличением
градиента давления; направление совпадает с направлением
касательной к изобаре (поскольку Уо = 0). В северном полушарии,
где />0, в циклонах ( !* >0 J Uq — положительная величина,
т. е. скорость направлена против часовой стрелки так, что
область низкого давления остается слева от направления
движения (рис. 8.3 а). В антициклоническом поле (——<,0) Ио<0,
т. е. движение происходит по часовой стрелке и область низкого
давления также остается слева (рис. 8.3 б).
Итак, в поле круговых изобар скорость движения зависит от
величины барического градиента и направлена по касательной
к изобаре таким образом, что область низкого давления
оказывается слева от направления скорости.
В южном полушарии, где /<0, градиентный ветер имеет
противоположное направление, т. е. он направлен так, что слева
от него оказывается область высокого давления.
230
Глава 8
Из формулы (8.2.2) видно, что градиент давления в
антициклонах не может быть больше некоторого критического значения.
Если
дро
дг
>
/2Г2
то при
_дро
дг
<0 uq становится мнимым числом.
Следовательно, при антициклоническом поле
Ро+5
Рис. 8.3. Направление градиентного ветра в циклоне (а) и в антициклоне
(б) при чисто круговых изобарах.
В циклоническом поле такого ограничения не существует.
Поэтому в среднем в циклонах наблюдаются большие значения
градиентов давления, а следовательно, и скорости ветра.
Для точек, расположенных на достаточно большом удалении
от центра барического образования, формула (8.2.2) может быть
записана в упрощенном виде:
1 др0 \ др0
гр/2 дг ) дг '
и0
-м
(8.2.3)
поскольку при больших г
V
1 +
дро
рг/2 дг
= 1
2 др0
гр/2 дг
(гр/2)2
т+
Выражение (8.2.3) позволяет заметить, что при одном и том
же значении модуля градиента давления, при прочих равных
условиях, скорость градиентного ветра в циклоне меньше, чем
в антициклоне.
Динамика свободной атмосферы
231
8.3. Геострофический ветер
В частном случае, когда радиус кривизны изобар настолько
велик, что их можно считать прямолинейными, действие
центробежной силы становится пренебрежимо малым. Стационарное
движение, скорость которого определяется равновесием двух
сил — силы барического градиента и силы Кориолиса, называют
геострофическим движением. Формула для скорости
геострофического ветра может быть получена у
из (8.2.3), если положить г->-оо:
1 др0
u0 = G = -
/р дг
(8.3.1)
или, поскольку в данном случае не
имеет смысла пользоваться
криволинейной системой координат,
1 др
/р дп •
G=-
(8.3.2)
Рис. 8.4. Вектор градиентного
ветра в системе ху.
где п — направление нормали к
изобаре.
Получим выражения для
проекций ug и vg вектора G на
соответствующие оси в декартовой системе координат. Пусть
др
0—угол, который образует барический градиент -^г— с осью ох.
дп
Тогда, согласно рис. 8.4 и формуле (8.3.2),
ug= — #0sinp = -
/р дп
sin р,
vg = и0 cos р =
1 др
Поскольку
/р дп
др . п др
cos р.
ду •
^cos?= "■
дп
дх
то
1 др
/р ду
(8.3.3)
v
1 др
z~ /р дх
(8.3.4)
232
Глава 8
Из формулы (8.3.2) и рис. 8.5 а следует, что скорость
геострофического ветра пропорциональна силе барического
градиента, а его направление совпадает с изобарами так, что область
более низкого давления находится слева от направления
движения. Последнее справедливо только при условии, что />0, т. е.
Рис. 8.5. Направление геострофического ветра
в северном (а) и южном (б) полушарии.
в северном полушарии. В южном полушарии направление будет
противоположным (рис. 8.5 б).
В экваториальной зоне (->0 и соотношение (8.3.2) не
выдр
полняется, поскольку здесь градиент давления —— не может
уравновешиваться силой Кориолиса. В этой зоне условия
равновесия могут достигаться только при круговых изобарах, когда
сила барического градиента уравновешивается центробежной
силой. В этом случае из уравнения (8.2.2) получается выраже-
Динамика свободной атмосферы
233
У г дро
-г-, из которого следует, что в рам-
ках рассматриваемого приближения в экваториальной зоне
могут существовать только циклонические образования (——
должно быть положительной величиной).
QQOQC3 О Q ^ О >0
^СМООэ^ «О Ю ^ nj- cvj
Скорость
Рис. 8.6. Номограмма для определения скорости
геострофического ветра (линейка Погосяна).
При практических расчетах по формуле (8.3.2) производную
др Ар
-д— можно заменить отношением конечных разностей —— и вы-
оп . дп
нислять скорость геострофического ветра G по формуле
27 ро
0 =
Ansincp р
(8.3.5)
где An — расстояние между двумя соседними изобарами по
нормали к ним, выраженное в сотнях километров; р0 и р —
соответственно стандартная (при р = 1000 мбар, Т= 273 К) и
фактическая плотность; скорость G выражена в метрах в секунду.
Вычисления по формуле (8.3.5) удобно производить с
помощью номограммы, представляющей собой семейство изолиний
скорости, нанесенных в системе координат (ф, An) (рис. 8.6).
Поскольку в синоптической практике для характеристики
высотных полей давления строятся не карты изобар, а карты
барической топографии, целесообразно преобразовать формулу
(8.3.2), заменив градиент давления градиентом абсолютного
геопотенциала.
Из постоянства давления на изобарической поверхности
следует, что
dp
дп
М£-*«°.
234
Глава 8
откуда
Поскольку —^— = —pg и, согласно определению геопотенциала,
9 8
dz=——dH (если Н — геопотенциал, измеряемый в
геопотенциальных метрах), то
дп >^ дп '
Таким образом, равенство (8.3.2) может быть переписано в
следующем виде:
G9,8 дН 9,8 . 0 /0 о «v
=—г—дГ~— *gPo. <8-3-7>
где Ро — угол наклона изобарической поверхности к плоскости
горизонта.
Из связи Н и р следует, что вектор геострофического ветра
перпендикулярен градиенту абсолютного геопотенциала и
направлен в северном полушарии так, что слева остается область
более низких значений Я.
Для практического применения формула (8.3.7) приводится
к виду
О = (R 3 8Ъ
Дл1 sin ср ' V • • /
где Ani — расстояние между двумя соседними изогипсами по
нормали к ним, выраженное в сотнях километров.
Сравнивая формулы (8.3.5) и (8.3.8), нетрудно убедиться,
что при одинаковом масштабе карт расстояние между
изобарами, проведенными через 5 мбар, эквивалентно расстоянию
между изогипсами AT, проведенными через 4 гп. дам. Это дает
возможность использовать номограмму, представленную на
рис. 8.6, и для вычислений по формуле (8.3.8).
8.4. Изменение геострофического ветра с высотой
В предыдущих параграфах рассматривалось движение на
фиксированном уровне. Теперь остановимся на вопросе об
изменении геострофического ветра от уровня к уровню. Поскольку
геострофический ветер определяется барическим градиентом,
рассмотрим сначала причины изменения с высотой
горизонтального поля давления.
Динамика свободной атмосферы
235
Согласно уравнению статики, давление в холодной
воздушной массе понижается с высотой быстрее, чем в теплой. Поэтому
при изменении температуры по горизонтали давление над
разными пунктами изменяется с высотой по-разному. Это приводит
к перестройке поля давления, а следовательно, и к изменению
горизонтального барического градиента с высотой.
Пусть в пунктах 1 и 2 (рис. 8.7), имеющих температуры 7\
и Тг соответственно, давление у поверхности одинаково: /?i(0) =
= рг(0). Если Ti = T2y то равенство давлений сохраняется на
z
♦ о)
Pi(z)
P2(z)
РАО) р2(о)
У//////////////////////Л
1 2
ТгТ2
б)
№
P2(z)
pJO) р2(0)
V////////////////W//////
1 2
Ti>T2
Рис. 8.7. Изменение поля давления под влиянием
температуры.
всех высотах: pi(z) = pi(z) (рис. 8.7 а). В этом случае
изобарические поверхности на всех высотах (штриховые линии)
параллельны плоскости горизонта, -~— = 0 и, согласно
(8.3.2), G = 0.
Если 71>Г2 (рис. 8.7 б), то давление над пунктом /
изменяется с высотой медленнее, чем над пунктом 2, и на уровне
z^O оказывается, что p\(z) >p2(z). Изобарические поверхности
на высотах проходят наклонно к плоскости горизонта, и
градиент давления на высотах з=^0 отличен от нуля. При этом с
увеличением z разность Pi(z)—pi{z) увеличивается и, следова-
др
тельно, увеличивается горизонтальный градиент -^—, а также
пропорциональный ему геострофический ветер.
Мы рассмотрели несколько частных случаев изменения
геострофического ветра с высотой, обусловленного
неоднородностью поля температуры.
Приращение вектора геострофического ветра в слое zi — zi,
связанное с горизонтальным градиентом температуры, называют
термическим ветром GT:
GT=G(*2)-G(zi). (8.4.1)
236
Глава 8
Для получения общего вида зависимости между термическим
ветром и горизонтальным градиентом температуры,
характеризующим температурную неоднородность, продифференцируем по
2 соотношения (8.3.3) и (8.3.4), воспользовавшись при этом
уравнением состояния. Тогда
д I ">g \ R д l a In
дг \ Т ) I дг \ ду
( Vg \ {^jL( дХпР
Л Т )— I дг \
д
дг
Из уравнения статики следует, что
д / д\п р \ g
д ( д\пр \
дг \ dxt )
дх
дТ
■)•
RT* дх.
где i= 1, 2.
Таким образом,
д ( Н \
дг V^TJ-
д ( Vg \
дг { Т )— I
g
дТ
IT* ду
g дТ
m дх •
Проинтегрировав последние соотношения по z, получим:
(8.4.2)
*2
I J
1 дТ
Г2 ду
аг=-т1-ът{-т-)аг'
(8.4.3)
Из (8.4.3) следует, что компоненты геострофического ветра на
двух уровнях различаются на некоторую величину, зависящую
от градиента температуры.
Рассмотрим частный случай, когда температура убывает
с высотой по линейному закону: Т(г) =То — yz. Тогда
f -ТО-" Г 1^Г = т][1п(7'о-^)-1п(Го-тг2)].
yz
Поскольку очевидно, что —!=— <С1, последнее соотношение можно
Го
преобразовать, представив логарифм в виде ряда
1п(Г0 —Тг) = 1п Г0(1 —^-) = lnr0+ln(l —^) =
Динамика свободной атмосферы
237
Тогда
f dz = гг-г\ h ( Т (
*2+*l)
Ф
*2 —*1
На основании полученного можно принять, что
dz
1
T(z)
g
i
т2
т2
'о
Tl d*i
дП д„
ду Л-
dTo-(z2-z{)
Zi z2
и переписать (8.4.3) в виде:
т
ug(z2)-ug(z1)^-=
где Дг=гг — £ь
Т 7*
Нетрудно показать, что -=—«—=—«1. Действительно,
i i i о
Г2
7*0 — Т^2
поскольку
То - v\
yAz
1 -
1-
J£2_
7*1
To
To
1,
Го
<Cl. На этом основании
ug(z2) — ug(zx) =
vg{z2)-vg{zx)
g
дТ0
IT0 ду
Аг,
g дТ0
Az.
(8.4.4)
Модуль вектора термического ветра определяется выражением
1Т0 дп\
dTo
Вычислив скалярное произведение векторов GT и -г-^-, можно
убедиться, что эти векторы перпендикулярны, поскольку
(°- -4SH—
<Э7о
дТо
дх
V , —
<ty
Ох
<Э7*0
dm
COS 04=0,
где cci — угол между векторами.
Таким образом, модуль вектора приращения
геострофического ветра в слое Az пропорционален горизонтальному
£тл
+G?
G0 Gji
—£
-u2
i
7
A
/
6) / /
/
/ .
/
/
GJit Gt,
/
/
^y
Oo
/- -/
/
/
z +
&13
Go
/ /
/ /
/
/
GT7
G2
/
/
y/
c7.~
L^
,
■ »
Oi
00
d]_
' dn,
' dn, /
Oo
/^o3 /
/
/
/
/ /
/
/
/
/
/
/ / / /
V Jr* /
^o^^ /
\ / ^ -—
dp drL
dn
Динамика свободной атмосферы
239
градиенту температуры и толщине слоя. Его направление
параллельно изотермам, причем область более низких температур в
северном полушарии остается слева.
Из равенства (8.4.1) следует, что
G (z2) __ G {zx) L1
Это значит, что при увеличении толщины слоя Дг G(22)->GT,
т. е. что по мере удаления от исходного уровня вес термической
добавки увеличивается и геострофический ветер все больше
приближается к термическому. Изобары перестраиваются и в
конечном счете становятся параллельными изотермам. И
действительно, наблюдения показывают, что на больших высотах в
свободной атмосфере области повышенного давления совпадают
с областями высоких температур, в то время как циклонические
центры совпадают с очагами холода.
Рассмотрим несколько частных случаев изменения ветра
с высотой при различных соотношениях между градиентом
давления на исходном уровне и горизонтальным градиентом
температуры.
1. Оба градиента параллельны (рис. 8.8 а). Векторы
геострофического Go и термического GT(z) ветра направлены в одну
сторону, и, следовательно, на уровнях, расположенных выше
исходного, геострофический ветер представляет собой
алгебраическую сумму Go и GT(z). Он увеличивается по модулю и остается
постоянным по направлению. В природе такая схема может
наблюдаться, например, в теплом секторе циклона,
перемещающегося с запада на восток, в котором температура понижается
с юга на север (см. рис. 8.9).
2. Градиент давления на нижнем уровне и градиент
температуры параллельны, но направлены в противоположные стороны
(рис. 8.8 6). В этом случае геострофический ветер на исходном
уровне и термический ветер направлены в противоположные
стороны и их векторная сумма равна алгебраической разности
их модулей, т. е. геострофический ветер уменьшается по
величине, не меняя своего направления до тех пор, пока модуль
термического ветра не станет равным модулю ветра на исходном
уровне. На уровне, где термический ветер равен по величине
начальному значению геострофического ветра, скорость
геострофического ветра равна нулю. Этот уровень получил название
уровня обращения. Выше этого уровня ветер меняет
направление на противоположное, а его скорость возрастает. Очевидно,
что высота уровня обращения z06p зависит от градиентов
Рис. 8.8. Изменение геострофического ветра с высотой в поле температуры.
240
Глава 8
давления и температуры. Действительно, поскольку на этом
уровне GT(z)=G0, то, имея в виду (8.3.2) и (8.4.5), получим
JPo
То
Д^обр — -
?g
дп
~дТо~
дп\
В циклоне, изображенном на рис. 8.9, такая схема имеет
место в его северной чзсти.
3. Градиент давления на нижнем уровне перпендикулярен
градиенту температуры и отклонен от него влево (рис. 8.8в).
дп
Go \£ G2 ~~ G1yG2 G3
Рис. 8.9. Изменение ветра с высотой в циклоне.
В этом случае вектор геострофического ветра на уровне z>zo
представляется диагональю параллелограмма, построенного на
векторах G0 и GT(z). Как видно из рисунка, он увеличивается по
модулю и поворачивает вправо. При этом угол между
векторами G(z) и GT(z) (а следовательно, угол между изобарой и
изотермой) с высотой уменьшается, стремясь к нулю. В циклоне
(см. рис. 8.9) такое изменение ветра наблюдается в его
передней части.
4. Градиенты перпендикулярны, но вектор
вправо от вектора —-
дп
отклонен
дп\
(рис. 8.8г). В этом случае скорость
ветра увеличивается с высотой и поворачивает влево, снова
приближаясь к вектору термического ветра. Такое изменение
геострофического ветра наблюдается обычно в тыловой части
циклона (см. рис. 8.9).
Стремление геострофического ветра с высотой приблизиться
к термическому наблюдается при любых соотношениях между
Динамика свободной атмосферы
241
термическим и барическим градиентами. Если угол между
градиентами тупой, то геострофический ветер сначала убывает по
величине до того уровня, на котором он становится
перпендикулярным термическому ветру, а затем увеличивается.
Выявленные закономерности позволяют решить такую
важную для практики задачу, как оценка локальных изменений
температуры в свободной атмосфере, обусловленных адвекцией, по
изменению ветра с высотой. Действительно, если температура
каждой частицы при движении не изменяется, а вертикальная
компонента скорости близка к нулю, то
дТ ( дТ \ ( дТ , дТ \ /о л с\
Согласно (8.4.2),
дТ IT dvi
g
дх g dz
дТ IT dug
ду g dz
Таким образом, если считать движение геострофическим, то
дТ \ IT I dvg dug \
При практических расчетах удобнее пользоваться не
проекциями вектора скорости ug и vg, а его модулем G и
направлением, в связи с чем равенство (8.4.7) приведем к виду
(-SF-L-f0"-*-- <8-4-8»
да
где — изменение направления геострофического ветра с
высотой.
Величина (-^г—) может быть вычислена и по данным
V dt /адв
о градиентах давления и температуры. Так, если в уравнении
(8.4.6) полагать u = ug и v = vg9 то на основании (8.3.3) и (8.3.4)
/ дТ \ = 1 / др дТ0 др дТ0 \
I dt /адв /р \ дх ду ' ду дх )
^^-^^sinS, (8.4.9)
/р дп дп\
где б—угол между градиентом давления и градиентом
температуры, отсчитываемый от градиента давления к градиенту
температуры против часовой стрелки (рис. 8.10).
J6 Заказ № 612
242
Глава 8
*-*
--^}ь<о
Рис. 8.10. Угол
дТ0
дп
ждТо
между
градиентами давления и
температуры.
Из формул (8.4.8) и (8.4.9) следует вывод, что, если ветер
/ да \
с высотой поворачивает вправо (-г—>>0 или 6<0) ,
температура в фиксированной точке повышается,
т. е. имеет место адвекция тепла. При
левом вращении ветра с высотой (что
имеет место, согласно рис. 8.10, при б>
>0) наблюдается адвекция холода. Этот
вывод представляет интерес для
практики, так как позволяет даже на основании
наблюдений в одной точке делать
обоснованные предположения о качественном
изменении температуры.
Формула (8.4.9) позволяет вычислить
изменение температуры по данным
синоптической карты.
8.5. Отклонение ветра от геострофического
В предыдущих параграфах были рассмотрены
закономерности, которым подчиняются движения, если поле давления
выражается семейством концентрических окружностей. Поправки,
связанные с отличием конфигурации изобар от чисто круговых,
могут быть получены из решения уравнений (8.1.9) — (8.1.11).
Следует отметить, что речь идет не только о формальных
поправках к решению задачи. С отклонением ветра от
геострофического связаны качественно новые процессы. В частности, из-за
отличия изобары от окружности, в потоке возникает
дивергенция массы и развиваются вертикальные движения, играющие,
как известно, важную роль в эволюции облачности и
образований осадков. Получим выражения для ии Vi и W{ для
стационарного движения.
Имея в виду (8.2.1), уравнения (8.1.9) — (8.1.11) можно
записать в виде:
-$-*««,—£-.$-• <8-5л>
■%-+»1')ъ—±-%-. (8-5.2)
где
Af(r) = 2+—. W(r)=l+-^-f—-^
Динамика свободной атмосферы 243
Заметим, что величины М(г) и N(r) вычисляются на основании
(8.2.2) и теперь могут считаться известными.
Если умножить (8.5.2) на i у — (t = V—1) и сложитьсурав-
нением (8.5.1), то получим линейное дифференциальное
уравнение первого порядка:
(1Ф
где
Ф
lYlAN Ф = П(г, в), (8.5.4)
"<'••>—-s-('-^+'^F*)-
В качестве граничного условия следует использовать
периодичность функции Ф(8), а именно
Ф(0) = Ф(6+2«),
так как
И, (Г, в) = И,(Г, 6 + 2*),
Mr, 8)=г;,(г, G+2-).
Решение уравнения (8.5.4) при таком граничном условии
имеет вид
Ф (в)-е" m Ц- (1 -1 ctg irNp) f П (г, х) eN{u Лс+
+.[П(г, eOe^'de'l, (8.5.6)
где
Р = '/^Г' .-^ = 9'-2^.
Приравняв вещественные и мнимые части выражения (8.5.6),
можно получить Ui и Vi. Согласно (8.5.5),
-V-тг^*.
t), = ReO.
Если теперь значения Ui и ui подставить в уравнение (8.5.3)
и проинтегрировать его от 2i до z%, получим выражение,
J 6*
244
Глава 8
позволяющее оценить скорость вертикальных движений,
возникающих за счет горизонтальной неоднородности поля давления:
Можно показать, что за счет меняющейся кривизны изобар
в циклонах могут формироваться области нисходящих
движений, а в антициклонах, наоборот — восходящих.
Величины ui и Vi представляют собой компоненты
отклонения ветра от градиентного (или геострофического), связанного
с отличием формы изобар от окружностей.
Наблюдения показывают, что разница между фактической
скоростью ветра и скоростью, вычисленной, например, по
формуле (8.3.2), в большинстве случаев составляет 5—10%
(табл. 8.1).
Таблица 8.1. Скорость (м/с) фактического и геострофического ветра
на разных изобарических поверхностях
Ветер
Фактический
Геострофический
Изобарическая поверхность (мбар)
850
11,1
10,7
700
14,9
14,0
500
16,9
17,8
Хотя сами по себе различия приведенных значений и невелики,
однако, как уже говорилось, они играют существенную роль
в эволюции барических образований, развитии вертикальных
движений в свободной атмосфере и тому подобных процессах.
Для того чтобы дать общую оценку отклонений ветра от
геострофического, вызванных как горизонтальной неоднородностью,
так и нестационарностью поля давления, запишем уравнения
движения в виде:
du it \
— = l(V-Vg)i
Тогда соответствующие проекции вектора отклонений V (их
называют агеострофическими отклонениями) будут определяться
следующими выражениями:
■»*-—г-зг- <8-5-7>
U .=11-
Динамика свободной атмосферы 245*
f'=*>-^=-j-4r- (8-5-8>
„ du dv
Поскольку —— и — проекции вектора ускорения на соот-
dt dt
ветствующие оси, то из равенства
следует, что вектор агеострофических отклонений
перпендикулярен вектору ускорения. Нетрудно показать, что в северном
полушарии он направлен влево от вектора ускорения.
fv'
-1—ft
^^^-ft-5 ^~^ ^-Po+5
Рис. 8.11. Направление вектора агеострофических
отклонений.
По величине отклонение ветра от геострофического
пропорционально модулю ускорения:
dV
VI—г
dt
(8.5.9)
Рассмотрим два примера, иллюстрируемые рис. 8.11.
В случае, изображенном на рис. 8.11а, частица движется
в область с большим градиентом давления. Поэтому скорость
dV
ее увеличивается, вектор —г-- направлен в сторону движения,
а вектор агеострофических отклонений — в сторону низкого
давления.
В поле изобар, представленном на рис. 8.116, скорость
частицы в направлении ее движения уменьшается, а вектор
агеострофических отклонений направлен в сторону высокого
давления.
Рассмотренные примеры позволяют сделать вывод, что
вектор агеострофических отклонений может быть направлен в
сторону как низкого, так и высокого давления. В зависимости от
того, куда отклоняется фактический ветер от геострофического —
влево или вправо, скорость его соответственно увеличивается
или уменьшается во времени.
246
Глава 8
Рассмотрим теперь пример, иллюстрирующий влияние агео-
строфических отклонений на развитие вертикальных движений.
Для этого получим выражение для вертикальной компоненты
скорости из уравнения неразрывности, записанного в декартовой
системе координат:
-Ф— HE-+-£-)~SS- <8-510>
Поскольку
u = ug-{-u\
v = vg-\-v',
то, согласно (8.3.3) и (8.3.4),
Id/?, ,
р«:—"Г ^Г+Р"'
Подставив эти выражения в (8.5.10) и выполнив
дифференцирование, получим
dpw / дуй' , d?v' \ , 1 / dl dp dl dp \ д?
~~дГ~ "" ~~ \dx~~ ~T"~dj~~ )*~W\dy~~dx~~ dx ~&Г) дГ'
(8.5.11)
На основании уравнения (8.5.11) можно сказать, что поле
вертикальных скоростей в свободной атмосфере определяется
•следующими тремя факторами: 1) агеострофичностью потока;
2) локальным изменением плотности; 3) изменением параметра
Кориолиса.
Сделаем некоторые оценки. Если полагать, что ось ох
направлена по касательной к широтному кругу, то
_}_(_Ы__др_ dl dp \ _ 1 dl dp
/2 \ dy dx . dx dy )~ /2 dy dx ~
_ ctgy 1 dp ctgcp
~ a I dx ~~pve a •
Здесь ф — широта места, a — радиус Земли.
Оценим порядок величины этого выражения:
Для оценки порядка величины локального изменения
плотности воспользуемся таблицей стандартов метеорологических
элементов и их производных:
0(-^-) = 3 • 10"7 кг/(м3- с).
Динамика свободной атмосферы
247
На основании этой же таблицы
О(^)=10-3кг/(м3.с).
Выполненные оценки показывают, что в реальных условиях
локальное изменение плотности и изменение параметра Корио-
лиса играют незначительную роль в формировании
вертикальной скорости, а главный вклад дает агеострофичность потока.
На рис. 8.12 приведен пример барического поля, при котором
развиваются вертикальные движения.
I
1G
I
I
I
I
! I \
Pb РЗ 'Р2
I
Р1
I
Ро
I
I
Р-1
Р-2
-*~х
\
Р-з
Рис. 8.12. Поле изобар, в котором могут развиваться
вертикальные токи.
В левой части поля градиент давления заметно увеличивается
в направлении движения частиц. Поэтому частицы здесь
движутся с довольно большим ускорением, а значит, согласно
(8.5.9), велики и значения V. С увеличением х в силу аналогич-
ных соображении величина V уменьшается, т. е. — <0.
Согласно (8.5.11), при такой ситуации скорость
вертикальных движений увеличивается с высотой, если на нижней границе
свободной атмосферы наблюдается восходящий поток
(связанный, например, с процессами в пограничном слое), и
уменьшается, если движение направлено вниз. Если на нижнем уровне
вертикальные токи отсутствуют, за счет агеострофичности будут
развиваться восходящие движения.
Контрольные вопросы
1. Вывести уравнения движения при круговых изобарах.
2. Какое движение называется градиентным? Чем
определяется скорость такого движения? Как оно направлено?
3. Как и почему изменяется с высотой вектор
геострофического ветра?
4. За счет чего могут развиваться упорядоченные
вертикальные токи в свободной атмосфере?
Глава 9. ПОВЕРХНОСТИ РАЗДЕЛА В АТМОСФЕРЕ
•Общие свойства поверхностей раздела (сильный разрыв). Наклон поверхности
раздела двух воздушных масс. Упорядоченные вертикальные движения,
обусловленные поверхностью раздела.
При рассмотрении результатов аэрологических зондирований
часто обнаруживаются тонкие слои, в которых резко изменяется
монотонный ход одного или нескольких метеорологических
элементов. Такие особенности в структуре атмосферы возникают:
1) вдоль поверхности соприкосновения воздушных масс с
разными свойствами; 2) вблизи верхней границы облаков; 3) около
поверхности раздела слоев с различной интенсивностью
турбулентного обмена.
На рис. 9.1 схематически представлены нерегулярности в
профиле температуры для трех упомянутых случаев.
Механизм возникновения неоднородностей в вертикальном
ходе температуры в виде инверсии при соприкосновении теплой
и холодной воздушных масс (рис. 9.1а) очевиден и не требует
пояснений. Инверсия вблизи верхней границы облака (рис. 9.1 б)
обусловлена большим эффективным излучением. Аномально
быстрое падение температуры вблизи поверхности соприкосновения
двух воздушных слоев (рис. 9.1 в) с разной интенсивностью
турбулентного обмена — результат выравнивания потенциальной
температуры (приближение градиента к адиабатическому)
в слое с интенсивным вертикальным перемешиванием. Часто
нарушения «гладкого» хода температуры сопровождаются нере-
гулярностями вертикального распределения удельной влажности,
концентрации пыли -и т. п. В некоторых случаях
горизонтальная протяженность указанных слоев достигает сотен
километров, с ними связано возникновение ряда явлений, которые
могут существенно влиять на динамику атмосферы, в частности,
в этих слоях развиваются волновые движения подобно волнам
на поверхности раздела между водой и воздухом. Барические
образования и специфические системы облаков — примеры
важных атмосферных объектов, возникновение которых связано
с такими волнами. В соответствии с указанным изучение свойств
областей нерегулярности и корректный учет разнообразных
эффектов, обусловленных ими, является важной частью ряда
проблем теоретической метеорологии.
Поверхности раздела в атмосфере
249'
При исследовании относительно крупномасштабных
процессов тонкий слой с большими градиентами метеорологических
элементов можно рассматривать как поверхность, на которой
терпят разрыв соответствующие функции. Принцип такой
схематизации иллюстрируется рис. 9.2. Можно предполагать, что
z а) б) В)
Рис. 9.1. Схема формирования нерегулярностей в профиле
температуры.
а — инверсия в области соприкосновения теплой (г>0) и холодной
воздушной массы (z<0); о — инверсия вблизи верхней границы
облака (облако расположено в области г<0). Заштрихована область
падения температуры вследствие выхолаживания, в —
возникновение инверсии на границе слоев с интенсивным (г<0) и слабым
(z>0) вертикальным перемешиванием В области интенсивного
перемешивания (z<0) градиенты близки к сухоадиабатическим,
падение температуры нормальное (6°С/км).
У —первоначальный ход температуры.
замена слоя конечной толщины поверхностью раздела не
исказит его влияния на крупномасштабные процессы,
математическая сторона соответствующей задачи при этом упростится^
а результаты окажутся более обозримыми. Разумеется, если
речь идет о явлениях, характерные масштабы которых сравнимы
с толщиной указанного слоя, или меньше ее, то возможность
такой схематизации исключается.
Поверхности раздела, на которых терпят разрыв сами
функции, называются поверхностями с сильным разрывом (рис. 9.2 а) у
в отличие от поверхностей со слабым разрывом (рис. 9.2 6), на
которых функции непрерывны, а разрыв терпят градиенты.
Напомним, что линия пересечения поверхности раздела с
горизонтальной плоскостыр называется фронтом.
250
Глава 9
Г(г)
Рис. 9.2. Схематизация реального профиля температуры путем
введения поверхностей разрыва.
1 — фактический ход метеорологического элемента с высотой, 2 —
схематизация реального вертикального распределения путем введения
поверхности разрыва.
9.1. Общие свойства поверхностей раздела (сильный разрыв)
Поверхность раздела в воздушном потоке является
некоторым гидродинамическим объектом, и естественно искать ее
свойства как следствие законов гидродинамики.
Для сокращения выкладок рассмотрим следующий простой
случай: ""
1) движение является одномерным, поэтому все искомые
функции зависят только от одной координаты, например х\
2) поверхность раздела перемещается вдоль оси ох, ее коор-
дината л: = ^(0, причем--7^-=g<oo;
3) при переходе через поверхность раздела скорость и,
плотность р и давление Р меняются скачкообразно, но в каждой из
областей однородности все величины не зависят ни от
координат, ни от времени. Это значит, что любая из рассматриваемых
функций может быть представлена в виде
/<=
/+ при х>\,
/_ при х<%;
(9.1.1)
Поверхности раздела в атмосфере 251
4) все изменения, связанные с перемещением поверхности
в потоке воздуха, происходят адиабатически.
Не следует думать, что рассматриваемый случай (в
частности, его одномерность) связан с сильными ограничениями.
Общий случай можно привести к данному, если применять
уравнения гидродинамики к достаточно малому цилиндру,
образующие которого параллельны нормали к поверхности в
фиксированной точке.
Рассмотрим цилиндр Sdx (рис. 9.3), пересекающий
поверхность раздела (5 — его поперечное сечение, dx — длина). Пусть
> А % А—% «
Рис. 9.3. Положение перемещающейся по
частицам воздуха поверхности раздела в два момента
времени.
AD = \bt, AB = u_6t, CD=u^bt\ ox — координатная ось,
относительно которой производится отсчет положения
всех элементов движения; Л, D — положение поверхности
раздела в моменты t0 и U+Ы соответственно; В, С —
положение частиц, по которым проходит поверхность
раздела в моменты *о и t0 + 6t.
относительно неподвижной оси координат ох положения
поверхности раздела в два момента времени t0 и /0+6* изображены
точками А и D, положение частиц, находящихся на поверхности
раздела в указанные моменты времени,— точками В и С
соответственно (в общем случае скорости движения частиц воздуха
и распространения поверхностей раздела — величины, никак не
связанные, поэтому в разные моменты времени поверхность
раздела может состоять из разных частиц). Для фиксированной
массы, расположенной между сечениями (А; С) в момент U
и (£; D) в момент U+8tt запишем уравнения сохранения
количества движения, массы и энергии. Поскольку рассматривается
область, в которой по крайней мере некоторые из физических
характеристик терпят разрыв, использовать уравнения динамики
в дифференциальной форме нельзя. (Напомним, что при выводе
уравнений Эйлера предполагается непрерывность всех функций
в пространстве и во времени.) В связи с чем мы можем
применять уравнения динамики только в форме интегралов. Для
рассматриваемого случая они имеют вид:
[(SSpudx)\tQ+u-(SSpudx)\t]=S(p_-p+)lt, (9.1.2)
252
Глава 9
(Sjprfx)|/e+8/ = (Sjprf*)|/e,
№)L.-K4
=o.
(9.1.3)
(9.1.4)
Уравнение (9.1.2)—закон сохранения количества движения,
(9.1.3)—массы, а (9.1.4)—уравнение адиабаты, являющееся
в данном случае следствием закона сохранения энергии. Если
функции непрерывны, то при 6^-^0 уравнения (9.1.2) — (9.1.4)
переходят в соответствующие дифференциальные уравнения.
Как видно из рис. 9.3, рассматриваемая масса в момент to
лежит справа от поверхности раздела, а в момент U+8t —
слева, все функции равны соответственно /+ или /_. Объем,
занимаемый массой, равен
[5. AC = S{AD-CD)=S(k-u+)bt при t = t0y
Sdx = { / • \
IS- BD = S(AD-AB)=S(t-u_)bt при t = t0+bt.
Подставив значения функций и выражения для объемов
б (9.1.2) —(9.1.4), получим:
Sp_u_(k — u_)bt — Sp+u+(k — u±)tt = S(p_ — p+)bt, (9.1.5)
S?_(k-u_)bt = S?+ (|-tt+)«f (9.1.6)
(рУ*1'р
(P-)
:v/c
(9.1.7)
p+ p- v '
Эти соотношения представляют собой вытекающие из законов
гидродинамики связи между кинематическими и динамическими
параметрами поверхности раздела. Преобразуем уравнения
(9.1.5) и (9.1.6) так, чтобы в каждом из новых уравнений
содержалось или только и-у или только и+. Для этого подставим
в (9.1.5) найденные из (9.1.6) значения:
Р+«+ = ?-и_ — (р_ — р-0 6,
5-a-u=-|Mi-iO.
Тогда имеем
и-о2-
Р4
Р--
Р- Р- — Р +
'Совершенно аналогично легко получить:
Р+ Р
Уравнение (9.1.7)
Р- — Р
— р+ • " Р- — Р+
(9.1.8)
(9.1.9)
(9.1.10)
3- —р+
используем теперь для определения
Для этого введем средние значения давления и плот-
Поверхности раздела в атмосфере 253
- р+ + р- - Р+ + Р-
ности р = , р= и отклонения от средних
величин бр=(р_— р+), бр = (р_—р+). Тогда из (9.1.7) следует
Iе р — Р-
Ш'1
Откуда имеем
- Ьр ( - Ьр
1с
у р
Р+ Т 5Р \ "^ 5Я
(9.1.11)
Разложим это соотношение в ряд по степеням -zr- и -^—, огра-
Р Р
ничимся малыми величинами первого порядка, полагая при этом
бр , бр
1>-^-, 1 >-гг-, и найдем
Р \ Р
Р- — Р+
ь? Р- — Р+ Cv р
В таком случае из (9.1.9) и (9.1.10) получаем
= _^Я7\ (9.1.12)
Сг
Сп
{\-u+r = ^^RT
?+ cv
Ср
-^RT. (9.1.13)
Величина }' -f- RT = 20,\ |/г—
__,_ . скорость звука при темпера-
cv
туре Т. Таким образом, поверхность разрыва давления
перемещается в атмосфере со скоростью, близкой к скорости звука.
Такие возмущения действительно возникают в атмосфере при
движении тел со сверхзвуковой скоростью (сверхзвуковые
самолеты, ракеты) или при грозовых разрядах. В области, которая
пересекается такой поверхностью разрыва, давление за весьма
малый промежуток времени меняется на конечную величину,
при этом частицы воздуха, пересекающие поверхность,
испытывают удар. Возмущения такого типа носят название «ударные
волны». Эти редкие явления мало влияют на режим атмосферы,
в связи с чем не представляют интереса для метеорологии.
Поскольку тем не менее в некоторых задачах метеорологии
целесообразно рассматривать тонкие слои как поверхности
разрыва температуры или плотности, причем они, разумеется,
254
Глава 9
перемещаются в пространстве со скоростями, близкими к
скорости ветра (составляющей лишь несколько процентов от
скорости звука), то в соответствии с уравнениями (9.1.9) и (9.1.10)
необходимо полагать, что на этих «метеорологических»
поверхностях: а) р- — р+ = 0, б) \ = и~ = и+, т. е. давление не терпит
разрыва, а скорость перемещения поверхности раздела совпадает
с нормальной составляющей скорости ветра. Последняя не
терпит разрыва, а это значит, что метеорологически значимые
поверхности раздела состоят все время из одних и тех же частиц.
Непрерывность давления называют динамическими условиями,
а непрерывность нормальной компоненты скорости —
кинематическими.
Заметим, что непрерывность давления не исключает сильных
разрывов в атмосферных полях плотности и температуры.
Однако из-за непрерывности давления на соответствующих
поверхностях должно выполняться следующее условие:
Важным примером использования полученных динамических
и кинематических условий являются задачи динамики системы
океан—атмосфера или задачи теории атмосферных волн на
поверхности раздела различных воздушных масс. При
интегрировании соответствующих систем дифференциальных уравнений
необходимо, чтобы искомые решения удовлетворяли условиям
непрерывности давления и нормальной компоненты скорости на
границе вода—воздух в первом случае или на границе двух
воздушных масс во втором.
Рассмотренные выше условия на поверхности раздела
получены при пренебрежении вязкостью. Более общий анализ
показывает, что вязкость и теплопроводность очень мало меняют
результат. С достаточной точностью сформулированные выше
динамические и кинематические условия можно использовать для
реальных движений в атмосфере и океане.
Отметим, наконец, что в принятомПвыше приближении часта
наблюдающиеся в атмосфере поверхности слабого разрыва
также обладают свойствами субстанциональности, т. е. состоят
все время из одних и тех же частиц.
9.2. Наклон поверхности раздела двух воздушных масс
Непрерывность давления накладывает определенные условия
на пространственную ориентацию поверхности раздела
соприкасающихся воздушных масс с разной температурой. Очевидно,
Поверхности раздела в атмосфере
255
например, что поверхность раздела не может быть
вертикальной, так как из-за различия температур воздушных масс
давление в них убывает с высотой по-разному (в теплой массе
давление убывает медленнее) и, следовательно, не может оставаться
одинаковым с обеих сторон. Можно предположить, что
непрерывность давления выполняется при определенном наклоне
поверхности раздела к горизонту, если при этом различие
вертикальных градиентов давления в рассматриваемых воздушных
массах компенсируется различием горизонтальных градиентов.
Каким должен быть соответствующий угол наклона?
Пусть в плоскости уог уравнение поверхности раздела z =
= h(y), в таком случае из условия непрерывности давления
следует, что
[p+(z, y)-p-(z, у)]|*=/му)=/МА. y)-P-(h, у)=0. (9.2.1)
Необходимо отсюда найти —7—. Дифференцируя (9.2.1) по у>
имеем
dz
dh
:=h dy
dy
др+ др.
ду
dz
dh
= h dy
dp-
dy
= 0, (9.2.2)
откуда следует
dh =
dy
dp+
dp-
dp+
dp-
dp+
dz
dy
z=h
dy
dp.
dz
z=h
dy dy
£(P+ —P-)
RT+T-
д In /?+
dy
д In /?_
- g т+-т- • <9-2-3)
Уравнение (9.2.3) пока не связано с какими-либо
ограничениями. Более простой вид ему можно придать, рассматривая
различные частные случаи. Так, например, при геострофических
др+,-
условиях — = —/(рн)+,~_ подставив соответствующие выра-
иу
жения для градиентов в (9.2.3), получим
dh Z р+н+ — p_w_ / T-U+ — Г+и_
dy
g
?+ — ?-
g
TV
(9.2.4)
Формула (9.2.4) принимает более удобный вид, если ввести
среднюю температуру обеих воздушных масс Т=—-——; тогда
dh
dy ~
Т_ = Т-
1 (-^ и+ — и_
ЬТ гр Тр • ЬТ
2 J~ g
■ и _
Т+— Т-
(9.2.5)
256
Глава 9
Легко показать, что второе слагаемое в круглых скобках
представляет собой средний тангенс угла наклона изобарических
поверхностей, оно намного меньше первого и может быть
отброшено.
Оценим порядок величины тангенса угла наклона. Для этого
воспользуемся значениями исходных параметров, характерными
z для поверхности раздела двух
воздушных масс: Т+ — Г_ = 5 К;
и+— а-=10 м/с; Г+ + Г_ =
= 550 К; /=1,2. Ю-4 с"1; g =
= 9,8 м/с2.
Тогда
dh
dy
1.2 • 10-4 . 550 10
9,8-5
= 0,0067.
Таким образом, 10~2 — порядок
тангенса угла наклона
поверхности раздела в свободной
атмосфере, где, как правило,
условия довольно близки к
геострофическим.
Рис. 9.4. Поверхность раздела в поле
давления.
/ — сечение фронтальной поверхности
плоскостью yoz, 2 — сечение изобарических
поверхностей плоскостью yoz, 3 —
наземные изобары, 4 — компоненты скорости
геострофического ветра.
Из анализа уравнений (9.2.3) и (9.2.5) следуют важные
выводы о ходе изобар и некоторых свойствах поля ветра в районе
фронта. Для этого обратим внимание на то, что при стабильном
режиме теплый воздух должен находиться выше поверхности
раздела, а холодный — ниже. Если принять, что индексы + и —>
относятся к теплой и холодной массе соответственно, и если ось
оу направить-так, чтобы холодный воздух располагался в обла-
—7— <0. Тогда из (9.2.3) и (9.2.5) следует, что
^ , a u+<u-. Нормальная к фронту составляющая
скорости, равная у-компоненте скорости, v<0y а х-компонента,
как показано выше, меняется на величину и-—и+>0, и, следо-
сти */<0, то
др+ др-
->-
Поверхности раздела в атмосфере
257
вательно, при прохождении фронта через определенную точку
происходит правое вращение ветра.
На рис. 9.4 представлен пример расположения фронта в поле
давления в соответствии с указанными условиями. На рисунке
изображено сечение фронтальной и изобарической поверхностей
плоскостью yoz, а также схема изобар в горизонтальной
плоскости. Как видно из рисунка, изобары в области фронта имеют
изгиб типа ложбины.
Несмотря на ограничения, при которых получены
приведенные здесь формулы, указанные особенности довольно хорошо
согласуются с эмпирическими данными.
9.3. Упорядоченные вертикальные движения, обусловленные
поверхностью раздела
В предыдущем параграфе показано, что при пересечении
поверхности раздела резко изменяется горизонтальный градиент
давления. Это естественно обусловливает возникновение верти-
кальнок^градиента скорости ветра. Сдвиг вектора скорости, как
правило, настолько значителен, что в окрестности поверхности
раздела происходит заметная генерация энергии
турбулентности, вследствие чего здесь возникает турбулизированный слой
толщиной в несколько сотен метров. Внутри этого слоя
благодаря эффектам турбулентности ветер отличается от
геострофического и непрерывно меняется по вертикали, приближаясь
1 др+ 1 др-
к геострофическим значениям —: г— и — г— на верх-
/р+ ду /р_ ду
ней и нижней границах соответственно.
Благодаря наклону поверхности раздела соответствующий
наклон имеет и связанный с ней турбулизированный слой. Этим
обусловлено существование горизонтальной неоднородности
в поле вектора скорости, в связи с чем возникают
упорядоченные вертикальные движения.
Полагая, что на большом расстоянии от фронта
вертикальные движения должны затухать, для плоского движения имеем:
z
—оо
Рассмотрим простейшую модель турбулизированного потока
в области поверхности раздела. Имеются в виду следующие
упрощения:
1) движение предполагается установившимся и однородным
вдоль оси ох;
17 Заказ № 612
258
Глава 9
2) зависимость искомых функций от ^/-координаты можно
учитывать параметрически;
3) вертикальный турбулентный поток количества движения
много больше переноса количества движения упорядоченной
dv
l\u du
вертикальной компонентой скорости I \k—-—
>иш, k——»
az
4) коэффициент турбулентной вязкости можно заменить ос-
редненной по вертикали величиной.
Тогда задача сводится к интегрированию системы
уравнений:
*-g-+2u)z*, = 0, (9.3.2)
Если начало оси oz расположить на поверхности раздела, то
граничные условия [см. (9.2.3)] задачи примут следующий вид:
«l^tco-0.
"|г^+0О = и+ = -
Т-
+
g (r+-
/ Т-
1
If*
Т-)
dh
ду
др+
ду
- S»
и
_ 1 др. Г+ . g (Т+-Т-) dh _ . g АГ dh
If- ду T- "т" / Т- ду — ^-т / т_ dy .
Решение уравнений (9.3.2) и (9.3.3), удовлетворяющее
условиям на внешних границах, найти нетрудно. Оно имеет
следующий вид:
(_1)'я(1 + г)г
u-\-iv = Uj-\-cJe . (9.3.5)
Здесь и далее /=1 для верхнего слоя,\/ = 2 для нижнего, [Д =
= £/+, t/2=£/-, £ = f—Г, г<0.
Произвольные постоянные d и Сг найдем, требуя
непрерывности вектора скорости и его вертикального градиента на z = 0,
которая достигается в результате сглаживания, обусловленного
турбулентным перемешиванием. Это значит, что
-СХ = С2. (9.3.6)
164
Глава 6
сравнения, что при средних условиях в единичном столбе всей
атмосферы содержится 2—3 см столба осажденной воды.)
Функция пропускания для монохроматического потока
(6.2.14) выражается через специальные (интегроэкспоненциаль-
ные) функции, для которых имеются подробные таблицы.
Однако далее следует выполнить интегрирование по длинам волн.
Поэтому при расчетах формулу (6.2.14) обычно заменяют более
простым приближенным выражением. Действительно, в этой
« —ах tin
формуле вынесем за знак интеграла е при некотором
cos#
1 —Г^
среднем значении =secth Тогда
cos#
^Am)^2e'axom4^ fcosbsinbdb=e-4om1^ . (6.2.46)
О
Оказывается, что при правильном выборе среднего значения sec Ф
упрощенная формула дает весьма малую погрешность (примерно
5—10%) по сравнению с точным выражением (6.2.14). В
результате многочисленных исследований было выбрано наилучшее
среднее значение sec О = 1,66. Следовательно,
^x(m) = e'axo'lMm. (6.2.47)
Таким образом, функция пропускания для
монохроматического потока в принципе не отличается от функции пропускания
для монохроматической интенсивности, т. е. пропускание потока
радиации, состоящего из лучей всех возможных направлений
(в пределах полусферы), эквивалентно пропусканию
направленного пучка лучей, распространяющегося под некоторым средним
углом.
Функция пропускания для интегрального потока радиации
(6.2.16) может быть получена в результате численного
интегрирования с учетом экспериментальных значений #4 в узких
спектральных интервалах либо путем непосредственных
измерений ослабления интегрального потока радиации. Интегральные
функции пропускания для длинноволновой (а также
коротковолновой солнечной) радиации, предложенные разными авторами,
приведены на рис. 6.16. Как видно из этого рисунка,
интегральные функции пропускания, полученные на основе различных
экспериментальных данных, довольно сильно различаются.
Эксперименты, проведенные в последнее десятилетие, можно
считать наиболее надежными. Для сравнения на рис. 6.16
изображена спектральная функция пропускания при некотором
среднем коэффициенте поглощения. Из сравнения кривых видно, что
Поверхности раздела в атмосфере 259
Из (9.3.6) и (9.3.4) найдем
С2 = —Сх =~2f- -fT ~аУ • (9.3.7)
Если поверхность раздела смещена относительно начала
координат на величину h(y), то соответствующее решение получается
элементарным обобщением (9.3.5). В этом случае
u-\-tv = Uj-\-Cje . (9.3.8)
Законность такого обобщения очевидна, поскольку (9.3.8)
удовлетворяет исходным уравнениям, граничным условиям на
\z\ =оо и условиям непрерывности на z = h.
dv
Из (9.3.8) найдем -г—, полагая, что функция h(y) задана:
*L = -\mCj(-\ya^(\ + L)e(-l)Ja(, + i)iz-h) . (9.3.9)
На основании (9.3.1) и (9.3.9) найдем
(z) = ImC,(-1)>a-f-(l + /) j e{-l)iaii+iuz-h)dz =
— оо
-4гЩ-^)е^а^-"^ша{г-Щ. (9.3.10)
Формула (9.3.10) принимает удобный для практического
использования вид, если из нее на основании (9.2.5) исключить ——.'
dy
Тогда
W(z)^^^r(^iye(-1)ia{z'h)sin(z-h)a. (9.3.11)
Как следует из (9.3.10), вертикальная скорость достигает
па
максимума на расстоянии —— от поверхности раздела, причем
— '_ \dy )e Sin 4 ~ U^ 4a>zr_ \ dy ) *
(9.3.12)
При ДГ=10 К, -^-=-^о"» / = 2(o2=10-4 с"1, Г-=280 К, g=
= 9,8 м/с2, дотах~4 см/с, что хорошо согласуется с
общепринятыми оценками.
Воспользовавшись уравнением баланса энергии
турбулентности, можно получить выражение для оценки коэффициента
17*
"чг
тах • 4«,Г.
260
Глава 9
турбулентности в области фронтальной зоны, под которой есте-
ственно понимать полосу шириной . Осредняя уравнение
баланса по такой полосе и пренебрегая диффузией вихревой
энергии через границы, получаем
2%/а
2] k *<« + '"> *<a-iv) dz_
о
2п/а 2тс/я
- j k^h(-lirJr4*)dz-a I dissflfe=0. (9.3.13)
Если предположить, что полная вязкая диссипация — функция
двух параметров рассматриваемой турбулентной зоны [к и а),
то должно быть
2*/а
J diss dz = C№a\ (9.3.14)
-2к/а
Легко показать, что
2п/а
С к djuj-iy) d(u-iv) d k ( agbT dh \2
J dz dz ~~ a \ 4uzTh dy ) *
T*-fr(-S-+T.)*-*-ft-[-7-h.-'»+i'-|-
—2k./a
Подставив значения интегралов в (9.3.13), нетрудно получить
^2=со2 \4»ЖТН dy ) То V шя (9 g
q | 4^(7а~Т) V '
Полученная формула, по крайней мере качественно, отражает
влияние основных внешних параметров на режим турбулентного
обмена в области фронта.
Контрольные вопросы
1. Можно ли использовать дифференциа/льные уравнения
динамики атмосферы для области, в которой имеется поверхность
раздела?
2. Вывести уравнение для угла наклона фронта, если
движение происходит при заданном притоке тепла.
3. Вывести уравнения для тангенса угла наклона
изобарической поверхности в поле геострофического ветра.
Глава 10. ВОЛНОВЫЕ ДВИЖЕНИЯ В АТМОСФЕРЕ
(ЛИНЕЙНАЯ ТЕОРИЯ)
Простейшие примеры образования волновых движений в атмосфере.
Параметры волн. Малые возмущения относительно состояния покоя. Краевые
условия в задачах теории волн. Энергетика малых возмущений. Связь
параметров волн с характеристиками основного состояния. Некоторые краевые
задачи. Волны в движущейся атмосфере.
Нетрудно привести примеры волновых движений. Так,
типичными волновыми движениями являются волны на воде;
специфические формы облаков делают видимыми волны в
атмосфере. Тем не менее дать общее и точное определение волнового
процесса затруднительно. Будем считать волновыми
специальный класс нестационарных движений, характеризующихся
периодичностью в пространстве и во времени (в общем случае).
Соответствующие поля метеорологических элементов, как
правило, можно записать в форме ряда Фурье. Волновые свойства
часто присущи атмосферным движениям, в связи с чем теория
волн составляет важный раздел метеорологии.
10.1. Простейшие примеры образования волновых движений
в атмосфере
Атмосферные волны являются или следствием периодически
меняющегося внешнего воздействия (например, приливные
волны), или результатом эволюции небольших возмущений,
которые накладываются на определенное исходное состояние. Его
обычно называют основным состоянием и предполагают
известным.
Возникновение волновых процессов в атмосфере под
влиянием периодической внешней силы представляется достаточно
ясным, по крайней мере качественно. Менее очевиден механизм
волновых процессов, являющихся эволюцией тех или иных
возмущений внутри самой системы. В связи с этим разберем один
пример, который является типичным.
Рассмотрим изменение свойств частицы воздуха, смещенной
по вертикали с некоторого исходного уровня г = 0 в устойчиво
стратифицированной атмосфере. На рис. 10.1 а представлен
график оазности плотностей частицы и окружающего воздуха
262
Глава 10
(Лр = р — р), на рис. 10.16 — вертикального ускорения
/ dm \
\dt )'
на рис. 10.1 в — вертикальной скорости (до), на рис. 10.1 г —
отклонения вертикальной координаты частицы от исходного
положения z(t) как функции времени. В начальный момент свойства
частицы совпадали со свойствами окружающей среды, а
действующие на нее силы (ускорение свободного падения и
вертикальный градиент давления) уравновешивались. Движение
начинается под влиянием направленного вверх внешнего импульса.
Рис. 10.1. Изменение параметров состояния частицы,
смещенной из равновесного положения при устойчивой
стратификации.
Вертикальные штриховые прямые — нулевое значение соответствующей
величины.
На стадии АВ частица движется вверх (до>0), поскольку
стратификация устойчива, Др>0, вследствие чего
dw
= -g^-<o.
Скорость при этом убывает и в положении В оказывается равной
о л \ dw\
нулю. Здесь Др и \^тг\ максимальны, частица соответственно
I at I
направлению и значению ускорения начинает двигаться вниз.
Изменения Ар, —— и ш на этой стадии представлены на
at
рис. 10.1 линиями ВС.
В положении С \ w \ = | wm3iX \; crajfo быть, на исходном уровне
частица не остановится и будет продолжать двигаться
вниз (до<0). Изменение указанных параметров состояния ча-
dw
стицы изображено линиями CD. На этом участке Др<0, —тг>
at
Волновые движения в атмосфере (линейная теория) 263
d W2
dt 2
>0, скорость и ускорение имеют разные знаки, т. е.
=ш—— <0, \w\ уменьшается. В точке D скорость равна нулю,
dw
при этом, однако, Лр^=0 и —— =^0, вследствие чего частица нач-
dt
нет двигаться вверх, и т. д.
*-£
Рис. 10.2. Колебания частицы в поле силы барического
градиента и силы Кориолиса.
du dv
-_ =/(у — ug), —-=—l(u — ug), в начальный момент
меридиональная составляющая скорости больше соответствующего
геострофического значения; w=-«^=»(u0 — vg)s\n It, v — vg = (v0 — vg)cos It,
v0-va
y-vet+
sin It.
Таков механизм, посредством которого небольшие
возмущения вызывают колебания частиц около исходного положения.
Разумеется, в рассматриваемом случае колеблется не только
плотность, но и остальные термодинамические характеристики.
В реальных условиях движения всегда связаны с трением
и соответственно с диссипацией кинетической энергии в тепло.
Поэтому колебания затухают, и в конечном счете частица
остановится на исходном уровне.
Аналогичный колебательный процесс возникает при
смещении массы воздуха, состояние которой определяется
равновесием любых других сил.
Вполне подобен, например, механизм колебания частицы
в поле горизонтального градиента давления и силы Кориолиса,
возникающих под влиянием мгновенного импульса. На рис. 10.2
264
Глава 10
приведен соответствующий временной ход v — vg, —гг> "тг"»
at at
и — Ug, y(t)- Указанный характер изменения всех параметров
частицы можно получить из анализа уравнения движения.
В рассмотренных примерах речь шла о колебаниях
фиксированной частицы воздуха, смещенной из равновесного положения.
Однако нужно иметь в виду, что благодаря связи между
соседними частицами, которая всегда существует в сплошной среде,
колебания одной частицы постепенно передаются окружающей
среде. Таким образом, возмущения начинают распространяться
во все стороны, возникают волновые движения, подобно тому
как удар камня вызывает волновые движения на всей
поверхности воды.
Параметры колебания — длина волны, период, скорость
распространения и т. д.— зависят от характера основного состояния
(структуры исходных физических полей и граничных условий),
от сил, которые определяют равновесное состояние частицы, и от
физических параметров (сжимаемости, теплоемкости и т. д.)
атмосферы или любой другой среды, колебания которой
изучаются.
Помимо чисто волнового развития возмущений, возможен
и другой ход процесса при некоторых условиях. Например, если
амплитуда возмущения растет со временем, то говорят о
неустойчивости основного состояния. Это означает, что небольшие
случайные импульсы приводят к фундаментальному
преобразованию исходных полей. Иногда, наоборот, возмущения довольно
быстро затухают; это свидетельствует об устойчивости
основного состояния.
Волновые движения часто имеют небольшую амплитуду и
играют незначительную роль в крупномасштабных процессах, но
их учет существенно усложняет математическую часть
метеорологических задач. В связи с этим при изучении
крупномасштабных явлений целесообразно вводить в уравнения динамики
упрощения (отбрасывая, например, некоторые слагаемые), при
которых незначительно искажались бы крупномасштабные
метеорологические поля, но исключались те свойства атмосферы,
благодаря которым в ней могут возникать определенные (не
существенные для рассматриваемого процесса) типы волн. Эти
упрощения, распространенные в современных моделях
численных прогнозов, получили название «фильтрации».
Однако некоторые типы волновых движений имеют
значительные амплитуды и вызываю^ колебания метеорологических
полей, сравнимые по величине с изменениями, обусловленными
синоптическими процессами. Разумеется, такие волны должны
тщательно изучаться.
Волновые дёижения в атмосфере (линейная теория) 265
Независимо от метеорологической значимости волн прежде
всего необходимо выяснить основные факторы, которые
определяют их свойства (частоту, длину, скорость распространения),
и механизм формирования того или иного типа волн, после чего
станут видны способы, посредством которых волны можно
отфильтровать. Типы волн, которые существенно влияют на
рассматриваемый процесс, необходимо исследовать и, в частности,
выяснять их наиболее важные свойства и эволюцию при разных
внешних условиях.
10.2. Параметры волн
Напомним основные понятия теории волн в сплошной среде.
Отдельная движущаяся гармоническая волна описывается
следующим уравнением:
F=Asin(mx-{-ny-\-qz — <st-\-a) =
-Asln(ni^-a/+a)-jim^l(m^_4 (10.2.1)
где a равно л/2 или нулю; соответственно следует брать или
вещественную, или мнимую часть показательной функции.
В (10.2.1) / = 1, 2, 3; mi = m, m2 = n, rri3=q; Xi = x, x2 = y, Xz=z
по повторяющемуся индексу производится суммирование. Здесь
же F— волновое приращение рассматриваемого элемента в
точке М(х, у, z) в момент t\ Л, т, /г, q, о — параметры волны.
Во всех последующих выкладках вместо тригонометрических
будем использовать показательные функции. Переход в
окончательных формулах к вещественным переменным осуществляется
по формуле Эйлера.
В (10.2.1) mjXj = mx+ny + qz можно рассматривать как
скалярное произведение вектора m(m, я, q) на радиус-вектор
г(х, у, г). Тогда
Р=АеЦт'г~°п; (10.2.2)
m называется волновым вектором; т, л, q — волновые числа.
Определенней фазе волнового процесса соответствует
фиксированное значение функции F в выражении (10.2.1). Так,
очевидно, что в вершине волны F имеет максимальное значение,
во впадинах — минимальное. Придавая в уравнении F = C\
разные значения константе Си получим разные фазы. Из условия
F = d = const следует
rrijXj — ot = mx-\-ny-{-qz — o/ = C2 = const. (10.2.3)
Формула (10.2.3) —уравнение плоскости. Таким образом, точки
равной фазы лежат на одной плоскости (фазовая плоскость),
266
Глава 10
в связи с чем говорят, что уравнение (10.2.1) описывает
распространение плоской волны.
Разделив уравнение (10.2.3) на ijm^m^ получим
mjXj zt — Сч
Ут jfn j УТП]ТП]
= 0. (10.2.4)
Поскольку (10.2.4) —уравнение плоскости в нормальной форме,
ot—Ci
то, как известно, — =о —расстояние плоскости от начала
irrijmj
координат (по нормали). Линейная зависимость б от времени
означает, что фазовая плоскость перемещается в пространстве
с постоянной скоростью
'♦-S--7=-w' <10^)
Сф называется фазовой скоростью.
Умножив Сф на косинусы соответствующих углов
п, ох) =
Vm? + л2 + $2
cos (я, оу) =
У ml + rfl + qt '
cos(^, oz) = —r q ,
V ' /m2 + /22 + ?2
получим проекции фазовой скорости на оси координат (сх, су,
cz):
У ТП]ГП]
Разумеется, фазовая скорость не имеет отношения к
скорости движения определенной частицы воздуха. В (10.2.4) Xj(t) —
координата, соответствующая положению определенной фазы
волны в момент t. В разные моменты времени в точке Xj
находятся разные частицы (в выражении для скорости частицы Uj =
=——j- под Xj понимается координата фиксированной частицы
в разные моменты времени).
Период волны т найдем из условия
i (m .х ,-оП I (m .х . — at — ах)
е / =е
откуда следует, что
ах = 2тг. (10,2.7)
Волновые движения в атмосфере (линейная теория) 267
После этого нетрудно определить длину волны (расстояние,
на которое фиксированная фаза перемещается за один период):
X = V = 2^=^p (10.2.8)
2я
Из (10.2.7) следует, что а= круговая (циклическая) ча-
т
стота.
Наряду с круговой частотой иногда используется
пропорциональная ей величина f — число колебаний в единицу времени:
Обычно существует связь между частотой и длиной волны,
так что
a = a(m, nt q) = a(mj). (10.2.9)
Формула (10.2.9) носит название дисперсионного уравнения,
поскольку из него следует зависимость фазовой скорости [см.
(10.2.6)] от длины волны, благодаря чему и происходит
дисперсия волн разной длины.
Как правило, в реальных атмосферных движениях
наблюдается не одна, а ряд волн с различающимися параметрами
(или, как говорят, ряд гармоник). В этом случае вместо фазовой
скорости можно говорить о так называемой групповой скорости
Сгр.1 Выведем формулу для групповой скорости. Рассмотрим
колебание, вызванное, например, двумя близкими гармониками.
Для простоты будем считать, что их амплитуды равны. Ось ох
выберем в направлении распространения волн. Для суммы двух
колебаний воспользуемся следующим представлением:
Де1 (("* + Ып) х-(° + Ь°)*\\Де1 [(m-Дт) лг-(а-Да) t] =
=2Acos(bmx-bat)el{mx-at). (10.2.10)
Функция e*(m*-<rt) правой части уравнения описывает гораздо
более высокочастотные колебания, чем cos (Дтх — Да^), так как
а^>Да. Это дает основание утверждать, что сумма двух близких
по своим параметрам волн (рис. 10.3) также является волной
со средними параметрами
(т 4- Ал*) -f (т — Am) (а 4- Да) + (<* — Д<0
т = 2 » а== 2 •
1 При внимательном наблюдении за морскими волнами можно различать
отдельные группы волн, движущихся со скоростью, существенно отличной от
скорости отдельных волн.
268 Глава 10
но медленно меняющейся амплитудой
А = 2A cos (ктх — До*).
(10.2.11)
Скорость, с которой перемещается в пространстве
рассматриваемая группа волн, найдем из условия А = const. Отсюда
следует, что
А/пх —Да/= const.
и, стало быть,
flfjC
Сг*>— dt —
Да
Am
(10.2.12)
Для достаточно близких
гармоник можно получить
в пределе
Да да
Am
сг? = lim
Дт -► 0
дт *
п ,ао г * - (10.2.13)
Рис. 10.3. График групповой скорости волн. v '
Групповую скорость СГр
нетрудно связать с
фазовой скоростью Сф,
которая в рассматриваемом случае равна —. Дифференцируя вы-
/ — результат сложения близких по своим пара
метрам волн; 2 — медленно меняющаяся ампли
туда.
т
ражения а = тсф, имеем
£гР — Сф-Гт~дт~
(10.2.14)
Производная
дсф
находится из соответствующего дисперсион-
дт
ного соотношения.
Из (10.2.14) следует, что в зависимости от характера
дисперсионного соотношения групповая скорость может быть как
больше, так и меньше фазовой скорости и даже различаться по
знаку.
Проанализированный результат сложения двух гармоник
равной амплитуды сохраняется качественно при рассмотрении
любого количе<ггва гармоник с близкими параметрами.
Волновые движения в атмосфере (линейная теория)
269
10.3. Вывод уравнений для малых возмущений
относительно состояния покоя
Примитивная форма уравнений
Будем считать процессы адиабатическими и пренебрежем
вязкостью. Для этих условий запишем уравнения
гидротермодинамики в декартовой системе координат:
du
dt
dv
~аТ~
dw
p ox '
1 dp
dy
dp
-lu,
d?
dt
dQ
dt p dz
_ I da * dv * dw \
" ~ P \~dx~ » "57 T -$2-) *
I dp 1 dp _ 1
rfe
cpT
dt
dt
dt
cpQ
dt
(10.3.1)
(10.3.2)
(10.3.3)
(10.3.4)
= 0. (10.3.5)
Любую из искомых функций fj представим в виде суммы
fj=7j-\-fj. (ю.3.6)
Здесь fi — величина функции в основном течении; /'—
приращение, возникающее в результате возмущений основного
состояния.
Если: а) возмущения характеризуются малой амплитудой,
так что слагаемые, которые содержат f в степени выше первой,
пренебрежимо малы (точнее сказать, 1^-^—1 , б) основное
состояние, на которое накладываются возмущения, определяется
следующими соотношениями:
u = v = w = 0y
p=p(z) = R-9T = R-9W( Р
-W л \*/Ср
причем
1000/
P=p(z)f T=T(z)t
j (10.3.7)
270
Глава JO
din р
din p
dine
dz
CpRT
^"£-
dz
din p
dz
__ g
= Г =
din p
dz
C2
dz
(10.3.7)
то для любой искомой функции из системы (10.3.1) — (10.3.5)
получим
df
df
dt
dt
-w
, df
dz
(10.3.8)2
Градиенты давления с учетом условия «а» могут быть
линеаризированы следующим образом:
1 др __ 1 д(р+р') ^
р дх
_ Р — Р'
Р2
1
Р
1 dp =
р dz
, 1 dp
1 J dz
P + P'
d(J+p')
dx
dp _ 1
dy ~ 7
1 dp'
7 dz
Pf
p
d*
_ 1 dp'
~ 7 a* »
dp'
P' <^ .
p2 <?2Г '
^^ 7 dz
(10.3.9)
/ _ l = _p —p' _ p-pf \
\ p + p' p2-p'2 "p2 )'
На основании (10.3.1) — (10.3.9) для определения малых
возмущений получаем следующую систему:
да
dv
dt ~
dw
dt "
dp' ,
дх "г"
dp'
dy
dp'
dz
(10.3.10)
(10.3.11)
(10.3.12)
1 Последнее уравнение системы отражает специфику вертикальной
структуры средних полей и неплохо описывает реальные условия нижней
тропосферы.
о о / df df
2 Здесь на основании условия «а» отброшены слагаемые и' -? \- v'-^—
как величины второго порядка малости.
Волновые движения в атмосфере (линейная теория)
dp' , ди , dv , dw
dt
dp'
dt
dx п ду
dt
dz
\-c2Tw=o
= 0,
271
(10.3.13)
(10.3.14)
Здесь
ьр *~
u=ou', v = pv', w = ow', c2= -^~=-r- RT.
Cv p Cv
Линейная система (10.3.10) — (10.3.14) содержит пять
неизвестных (и, v, w, р', р') и является, следовательно, замкнутой.
Введение функции тока и потенциала скорости
Для рассмотрения некоторых случаев волновых движений
вместо горизонтальных компонент количества движения удобно
ввести аналоги функции тока г|? и потенциала скорости ср, так что
d<\>
dy *
^ d<?
v --
dy
dx
(10.3.15)
Из (10.3.15) следуют выражения для вертикальной компоненты
вихря Q и дивергенции D:
о.
dv
du
D =
dx
da
dy
dv
■=ц,
Далее всюду
dx
A/ = -
-r dy
d*f , dy
= Acp.
(10.3.16)
dx*
dy2
Переход к функциям <p и г|) в системе (10.3.10) — (10.3.14)
выполним вычитанием и сложением продифференцированных по
соответствующим переменным уравнений (10.3.10) и (10.3.11).
В полученные уравнения вместо Q и D подставим их значения
на основании (10.3.16). Тогда имеем:
*-3—
д4?—
/4»-K-g-+-S-).
(10.3.17)
dt
^'-H-l-f)+/At' о°-3-18)
272
Глава 10
,1-*+д?+-«|—0. (10.3.20)
^Т-^-+Г-=0- 00.3.21)'
r> 0 d/ 2со cos ф . о ч 9
В этой системе р=-— = — (а —радиус Земли).2
В системе (10.3.17) — (10.3.21) явно выражено изменение
параметра Кориолиса, в связи с чем ее удобно использовать при
исследовании волн, свойства которых существенно связаны с
зависимостью ускорения Кориолиса от широты.
В рамках принятых выше приближений множители г, |х, v
равны единице. Как показано ниже, они введены ради удобства
анализа полученной системы. Если считать, что p=const
(приближение р-плоскости), то выписанные уравнения имеют
решения волнового типа.
Полученная система является довольно общей: в линейном
приближении ею учитывается влияние сжимаемости3 воздуха,
сила тяжести, сила Кориолиса и эффекты, обусловленные
отклонением метеорологических полей от гидростатического
равновесия. Можно, однако, предполагать, что упомянутые факторы
1 Можно показать, что
1 dp' dp' 7 дв'
~с2~ dt dt ~ в dt #
2 Параметр Кориолиса в окрестности широты <р0, на которой помещено
начало координат, можно разложить в ряд по степеням у (расстояние от
начала координат по меридиану):
0 dl 2о) | sin ср0 у cos 9о / У \2 . 1
Отсюда следует, что если для рассматриваемой области у/а<^\, то / и р можно
считать постоянными и равными соответственно 2о> sin фо и 2со cos фо/я.
В дальнейшем мы будем пользоваться этими приближениями.
3 Под сжимаемостью обычно понимается мера изменения плотности
движущейся массы; соответствующий эффект отражен в уравнении
неразрывности. С другой стороны, в процессе сжатия или расширения изменяется
давление, что сопровождается преобразованиями энергии. Это
обстоятельство отражено в уравнении притока тепла; соответствующее слагаемое в этом
уравнении 1 j! \ истолковывается как динамический эффект сжимаемости.
Волновые движения в атмосфере (линейная теория) 273
по-разному сказываются на волновых движениях разных типов.
Так, например, длинные волны подвержены большому влиянию
силы Кориолиса. Наоборот, короткие высокочастотные волны
зависят главным образом от сжимаемости воздуха. Удобно при
выполнении выкладок и исследовании решений проследить
влияние каждого из упомянутых эффектов в отдельности, введя три
упомянутых множителя г, \i, v при слагаемых, отражающих роль
вертикальных ускорений (г), кинематический эффект
сжимаемости (|ы) и энергетический эффект сжимаемости (v).
Для того чтобы пренебречь любым из указанных эффектов,
достаточно соответствующий множитель положить равным нулю,
в противном случае его следует заменить единицей. Очевидно,
что если необходимо учесть сжимаемость, то нужно принять
|x = v = l, а заменив их нулями, мы тем самым пренебрегаем
соответствующими эффектами. Аналогично выбором г можно
выяснить влияние отклонений состояния атмосферы от
гидростатического равновесия. Параметрами I, Р; g, Г соответственно
учитывается влияние силы Кориолиса, силы тяжести и
стратификации. Роль этих параметров становится ясной из
окончательных формул.
Заметим, что выводы, касающиеся влияния упомянутых
факторов на волновые движения в разных участках спектра, можно
использовать как подходящие оценки их роли в непериодических
атмосферных движениях, масштабы которых имеют порядок
длины соответствующих волн.
О пределах применимости теории малых колебаний
Полученная выше система уравнений (10.3.17) — (10.3.21)
применяется для изучения волновых движений в атмосфере. При
рассмотрении конкретных случаев важно быть уверенным в том,
что исходные приближения (пренебрежение нелинейными
членами, притоком тепла и вязкостью) допустимы. При упрощении
уравнений, по существу, предполагалось, что три неравенства
0(du'j/dt)
0\и dU
J dXj
O(dS'ldt)
О (du'j/dt)
»1,
»1.
»1 (10.3.22)
18 Заказ № 612
274
Глава 10
выполняются с достаточной точностью (х — коэффициент
вязкости).
Для выяснения пригодности указанных приближений при
изучении различных волновых процессов выразим приведенные
неравенства через параметры волн. Пусть
us = v0se J J '(s-1, 2, 3, y = l, 2, 3),
((m.xj-ot)
Тогда
01
О
01
дис
dt
л*:
-J=O\ — v0sie ) = -
2kVqs
^) = 0(-^V'^-ff/)) = ^^ j (Ю.3.23)
Y\ = 0{v,sm)ei(m^xr^)=J^. \
j J XJ J
Подставляя (10.3.23) в первое из уравнений (10.3.22),
получаем
^о^
»1,
(10.3.24)
т. е. линеаризированные уравнения оказываются достаточно
точными, если длина волны много больше произведения
амплитуды колебаний скорости на период. Выполняя аналогичные
оценки, второе неравенство (10.3.22) запишем в форме
2и/т
dQ
-»1.
(10.3.25)
dt
Это означает, что процесс можно считать адиабатическим, если
приращения температуры за единицу времени, обусловленные
/1 dQ'\
Up dt J '
баний температуры, деленной на период колебания.
Наконец, из третьего неравенства получим условия, при
которых можно пренебрегать вязкостью:
притоком тепла
много меньше амплитуды
колену _
CQfii
2гст%
2tix
»1.
(10.3.26)
Оно означает, что произведение фазовой скорости на длину
волны должно быть много больше коэффициента вязкости.
Волновые движения в атмосфере (линейная теория) 275
Неравенства (10.3.24) — (10.3.26) по крайней мере «задним
числом», после того как волновая задача уже решена, могут
быть использованы для обоснования исходных упрощений.
Разумеется, постановка задачи будет более основательной, если
значения величин, входящих в неравенства, получены из
экспериментов.
10.4. Краевые условия в задачах теории волн
Решения полученной системы уравнений должны
удовлетворять начальным и граничным условиям, которые определяются
спецификой поставленной задачи. Начальными условиями
задаются поля искомых функций, иногда их производные в
начальный момент. Вид начальных полей может быть самым
разнообразным, и невозможно указать какие-нибудь функции,
которые были бы типичными как начальные условия в задачах
теории волн. Что касается граничных условий, то дело оказывается
сравнительно простым. Условия на твердой поверхности, на
свободной поверхности жидкости и на поверхности раздела двух
жидкостей (или двух воздушных масс) исчерпывают
постановку большинства задач, представляющих интерес для
метеорологии. Сформулируем условия, которые должны выполняться
на указанных границах.
Условия на твердой поверхности
Пусть z = F(x, у) —уравнение твердой поверхности, с
которой соприкасается воздушный поток. Поскольку система
уравнений основана на приближениях идеальной жидкости, то
воздух или жидкость должны скользить вдоль твердой поверхности.
Это значит, что координаты движущейся частицы Xj(t) =Xjo +
t
+ J Uj(t') dt' должны для любого значения t удовлетворять урав-
и
нению заданной поверхности, если частица в какой-то момент
t0<t соприкасалась с поверхностью в точке Xjo. На этом
основании
г0+ f wdt = F\xQ + \tidt\ у0+ $vdt'). (10.4.1)
Более удобна обычно используемая дифференциальная форма
18*
276
Глава 10
кинематических условий. Дифференцируя (10.4.1) по времени,
получим искомое выражение:
•~ЖГ" + -ЗГ«- <10-4-2>
Этому уравнению должны удовлетворять только частицы,
расположенные на поверхности, т. е. (10.4.2) должно выполняться
при условии z = F(x, у).
Нетрудно убедиться, что условие (10.4.2) означает равенство
нулю нормальной к поверхности составляющей скорости.
Действительно, последнее означает, что скалярное произведение век-
/ l dF
тора скорости с(ы, v, w) на нормаль к поверхности п("п~-^—*»
T^f' —зг) равнонУлю [*=V 1+(if )2+(lf)2]' т-е-
dF . dF Л
Если, например, поверхность — горизонтальная плоскость, то
F(*> y)=z = const, ^=0, -^"=а
и, ст&ло быть, в этом частном случае
w\z=c = 0. (10.4.3)
Кинематические условия на поверхности раздела и
на свободной поверхности
Свободная поверхность, по существу, является частным
случаем поверхности раздела двух разных по своим свойствам
потоков жидкостей, при котором динамические и кинематические
элементы одного из потоков являются константами. В связи
с этим кинематические условия (см. главу 9) отражают то
обстоятельство, что поверхность раздела все время состоит из
одних и тех же частиц. Различие сводится лишь к тому, что для
поверхности раздела эти условия выполняются с обеих сторон,
а для свободной поверхности — только с одной.
В отличие от твердой поверхности, форма которой, а
соответственно и уравнение, не могут зависеть от времени, так что
——=1)7 форма поверхности раздела и свободной поверхности
меняется с течением времени.
Если уравнение поверхности раздела или свободной
поверхности записать в форме
г=Ф(х, у, t)t (10.4.4)
Волновые движения в атмосфере (линейная теория) 277
то условие сохранения частиц, составляющих поверхность,
выразится следующим уравнением:
zo-f j w(t')dt'=0\xo+$ ti{t')dt\ y*±lv(t')dt'% t).
(10.4.5)
Здесь, как и ранее, Uj — компоненты скорости частицы
М (хо, t/o, 20), которая находилась на поверхности в момент to.
Дифференцируя (10.4.5) по времени, получим
дФ . дФ . дФ
dt
дх
ду |г = Ф±0'
(10.4.6)
Для поверхности раздела уравнение (10.4.6) должно
выполняться с обеих сторон. Это имеется в виду при записи г = Ф±0
и при вычислениях соответствующей переменной величины
находится как ее значение на г=Ф при приближении к Ф сверху
(Ф + 0) или снизу (Ф — 0). Уравнение свободной поверхности
или поверхности раздела не задается apriori, а входит в число
искомых величин. Это дополнительные трудности по сравнению
с задачами, в которых граничные условия задаются на твердой
поверхности.
Если Ф = # + £(*, у у t) представляет собой уравнение
невозмущенной поверхности (a=const), то с точностью до малых
высшего порядка кинематическое условие можно записать в виде
<эс ,
дх ' ду
z = a±0
(10.4.7)
В том случае, когда исходное состояние задано условиями
(10.3.7) и соответственно £ — малая величина, то
w =-
Я'
dt
z = a±0
(10.4.8)
При
дФ
dt
= 0 из (10.4.6) как частный случай вытекают
полученные выше условия на твердой поверхности. Уравнение (10.4.7) —
следствие приближений идеальной жидкости. Для вязкой
жидкости положение совершенно иное: в то время как для
поверхности раздела (10.4.6) остается без изменений и для вязкой
жидкости, кинематические условия на твердой поверхности в этом
случае должны отражать факт «прилипания» жидкости (u = v =
=ш = 0).
278 Глава 10
Динамические условия на поверхности раздела
Поскольку при переходе через поверхности раздела,
представляющие интерес для метеорологии, давление не терпит
разрыва, то
Р(Х> У> *, ')и = Ф(х, у. О+О "/>(*• У> Z> ')|«Ф(х,у,О-0.
(10.4.9)
Выделив величину давления в основном состоянии, (10.4.9)
можно записать в виде
р(Ф+0)+р'(х, у, ф+о. *)«р(ф-0)+/>'(*. у, ф-о> ').
(10.4.10)
Если Ф = а+£, где а и £ сохраняют прежний смысл, то из
(10.4.10) в силу малости £ следует
Здесь отброшены малые высшего порядка (-т—£) . Исполь-'
зуя уравнение статики, получим окончательное выражение:
-g^ |,=в+о+/>'(*■ У- а+°> 0 = ~^p|z=fl_0+
+/>'(*. У. л-0, t). (10.4.11)
Для свободной поверхности (10.4.11) должно быть записано
в следующем виде:
-gCP\2=a_0+p'(x, у, а-0, 0=0. (10.4.12)
10.5. Энергетика малых возмущений
При получении системы уравнений для малых возмущений
ряд слагаемых по ходу выкладок отброшен из соображений
малости, в связи с чем встает вопрос, удовлетворяет ли
приближенная система уравнений закону сохранения энергии. Если это
не так, то уравнения не исключают ситуаций, при которых
искомые функции могут быть сильно искажены из-за фиктивных
источников или стоков энергии. Следует всегда иметь в виду,
что выполнимость закона сохранения энергии является важным
Волновые движения в атмосфере (линейная теория) 279
условием корректности упрощений по крайней мере в задачах,
связанных с отысканием стационарного режима. При анализе
энергетики процессов нет надобности рассматривать полную
энергию, которая включает и энергию основного состояния;
достаточно и целесообразно рассматривать баланс всех видов
энергий, вызванных только возмущениями.
Будем исходить из системы уравнений (10.3.10) — (10.3.14),
в которую удобно ввести энтропию
S = cp In 6-f-Ci =cv \np—Cp In p+const.
Отсюда следует:
При помощи (10.5.1) из уравнений (10.3.12) —(10.3.14)
после введения множителей г, ji, v исключим р'. Тогда имеем:
(10.5.3)
=0, (10.5.4)
(10.5.5)
Из (10.3.10) — (10.3.12) умножением соответственно на и, v,
w, используя при этом (10.5.2), получим уравнение для
кинетической энергии:
d и* 4-7/2 + г^2 - dp' ^ dp' —dp' g ~ , ,
Заменим здесь дивергенцию потока количества движения,
воспользовавшись (10.5.4), и введем скорости согласно
соотношениям:
u = pu't v=pv', Т0=р<а>'.
с2
dw __ dp' g ,
1 dt ~~ dz c* F
dp' 7 № \ . du ,
dt cp dt )* dx +
v —1 dp' | p" dS'
c2 dt ■" cp dt
dt; , dw
~сЦ > ЪТ
frS=o.
&*
280 Глава 10
Тогда имеем
—2 д u'2-{-v'2-{- w'2r —( ди'р' , dv'p' , dw'p' \
р dt 2 р \ d* "+"—5^ I 57~j~~
Р * \ С2 dt Ср dt ] J dz С2 ^Р + Ср W* "
Воспользовавшись (10.3.7), подставим в это уравнение
1 dp ^ —
—Г=———|—^- и исключим w при помощи (10.5.5). Тогда
Р
после несложных преобразований получим искомое уравнение
д
dt
и'2 + г/'2 4- гс''г i v + p. —1 ^,» , g с'1^
Р I ~9TV2"° J""
2 Т 072^2 ^ • 2Гс2
2р2С2
1 г дц'р' | dv'p' . dw'p' l , fx-
И- — 1 n, dS'
~?cp P *<
<*-i)g S'-*g-. (10.5.6)
Из полученного уравнения следует, что при jii = r = v = l (это
соответствует полной системе уравнений для малых колебаний),
закон сохранения энергии выполняется; при интегрировании
(10.5.6) по замкнутой массе (М) получаем
JJi(JSL+-^L+J*L)****-«.
(.И) J
и, стало быть,
"" + 1 + "" +^+TA^"-'°ns.. (Ю-5.7)'
Второе и третье слагаемые в (10.5.7)—приращения энергии,
обусловленные пульсациями давления и температуры соответст-
р'2 S
венно; —-— = ЕР есть энергия упругости, а 2 г S2=E8 —
2pW Р
термобарическая энергия; последняя связана с работой против
силы плавучести.
Из (10.5.7) видны и погрешности, которые могут возникать
из-за пренебрежения сжимаемостью (^ = 0) или упругостью
(v = 0). При этих упрощениях, как легко заметить, интеграл пол-
1 Заметим, что (10.5.6) имеет интегральный инвариант при любом \i=vt
если только £/Гс2=1.
Волновые движения в атмосфере (линейная теория) 281
ной энергии по всей массе, вообще говоря, не равен нулю. Так,
полагая ^i=v = 0, из (10.5.6) имеем
^-1П[°" + 1 + "' +-£-+-$-]*««-
dx dy dz.
-ш
dp' ■ _g s, dp' 1 , dS'
dt p2c2 ' рСрГс2 dt ?cp У dt
Выражение справа, если оно оказывается не равным нулю,
эквивалентно существованию источников энергии. При этом
полная энергия может возрастать безгранично с течением времени.
10.6. Связь параметров волн с характеристиками
основного состояния
Выше была получена система уравнений и краевых условий,
описывающих волновые движения малой амплитуды в
атмосфере. Несмотря на упрощения, которые были использованы при
ее выводе, ряд важных свойств атмосферных волн удается
выяснить в рамках предлагаемой модели.
Изложение теории волн начнем с общих свойств, которые им
«предписываются» характером дифференциальных уравнений,
не привлекая каких-либо краевых условий, отражающих
специфику частных задач. Это позволит выяснить существенные
особенности спектра волновых движений при разных состояниях
атмосферы. Целесообразность такого подхода объясняется, во-
первых, тем, что сравнительно простой анализ позволяет понять
важные черты «физики» волн, и, во-вторых, возможностью
конструировать решение любой конкретной задачи суммированием
частных решений в силу свойств линейных уравнений.
Начнем с рассмотрения волновых движений, которые мало
зависят от вращения Земли.
На основании (10.3.17) и (10.3.18) можно выяснить условия,
при которых пренебрежимы соответствующие эффекты. Для
простоты дадим необходимые оценки для зонально однородных
условий [—-г—=0). Из уравнений (10.3.17) и (10.3.18)
следует, что пренебрежение ^-эффектом (изменением параметра
Кориолиса с широтой) допустимо, если
в д'*
, дЦ U
ду*
282
Глава 10
Поскольку речь идет о волновых движениях, то ф~\|>~
~e4ny-ot)t на этом основании из предыдущего неравенства
следует
it-НЙ-^- осел)
откуда Xy^atgqx) (я— радиус Земли, сро — широта места).
На этом основании можно полагать, что (3-эффектом
допустимо пренебрегать при исследовании относительно коротких
волн (Va«Cl) всюду, за исключением экваториальной области.
Чтобы пренебречь вращением Земли (членами,
содержащими /), исключим из уравнений (10.3.17) и (10.3.18) Дг|х
Тогда получим
dt dt ^ dt Р dt \ дх ду J ^
+илт+ц(^.+^)-а
Отсюда (поскольку / содержится только в этом уравнении)
следует, что влияние вращения Земли становится относительно
малым, если
|/2Ау| «1 или -f «1, (Ю.6.2)"
dt dt
а
т. е. в высокочастотной области спектра атмосферных волн
можно не учитывать вращение Земли. Из (10.6.2) видно, что
именно в данном случае понимается под высокочастотной
частью спектра.
Таким образом, выяснены те ограничения, которые нужно
иметь в виду при анализе результатов настоящего параграфа.
Полагая в исходной системе (10.3.17) — (10.3.21) /=р=0,
получим:
Д^г=0, (10.6.3)
-w+p'=o. <10-6-4)
1 Поскольку Сф близка по числовому значению к скорости ветра, нетрудно
оценить длины волн, для которых допустимо пренебречь вращением Земли:
2ясф/а=^<2ясф//«600 км.
Волновые движения в атмосфере (линейная теория) 283
до'
др'
-Дер-
. dw
' ~дГ
= 0,
до'
4-Г^ = 0.
(10.6.6)
(10.6.7)
с* dt dt
Решения будем искать в виде простой гармоники
f(t,x,y,z)=f1(z)el(mx+ny-et).
Смысл параметров m, п и а известен из предыдущего,
варьируя их, мы исследуем волны разных типов. Очевидно, для
любой из искомых функций
-^ = ^Нр А/—(»»+«»)/. -£—/■/.
На этом основании из (10.6.3) — (10.6.7) получаем систему
обыкновенных дифференциальных уравнений:
ъ = о,
— k<Pi+/>i=0,
-lorw1-\--^—\-g9l=0,
- /ofxcp, - (rrfl+Я2) <p, -f -^g-=0,
(10.6.8)
(10.6.9)
(10.6.10)
(10.6.11)
(10.6.12)
Исключая последовательно pi, (pi и o>i, сведем систему к одному
дифференциальному уравнению:
&РХ
+(ъ+-$)-%-+р.№~ч*+*>[г-
dz*
Остальные функции выражаются через pi:
(10.6.13)
?1
«>1 =
а
г*
■Гз
Р\=-Л~Р\
dP\ I ^ „ \
-5r + -^2-Pij.
г / dp,
HF--)
(10.6.14)
284 Глава 10
Решение уравнения (10.6.13) легко находится:
Pl = Ape-ihilv+g"/c2)z±i4\ (10.6.15)
где
(10.6.16)
g I dp
Поскольку ГЧ — = —, в устойчиво стратифицирован-
Р
ной атмосфере \~г<^ ) амплитуда коротких волн убывает
с высотой по показательному закону. Правда, убывание
происходит сравнительно медленно. При средних условиях
-т— «Ю-4, т. е. амплитуда убывает в е раз в слое толщиной
Р
около 20 км.
Уравнение (10.6.16) связывает параметры колебаний q, т, п,
<т с состоянием атмосферы. Остановимся на наиболее важных
частных случаях.
Звуковые волны
Рассмотрим волновой процесс, в котором параметры волн
практически не зависят от ускорения свободного падения и
стратификации. Это значит, что имеются в виду волновые процессы,
определяющиеся только упругими свойствами воздуха
(сжимаемостью) и силами инерции. Из (10.6.16), положив jbi = r = v=l,
видим, что такое предположение допустимо, если
-g-» <»' + *>г* , (10.6.17)
4»i(r+^F = i(^4H2< 00.6Л8)
^~"*2+я2+?2 = ^?-. (Ю.6.19)
сф
=330 м/с есть
Cv Р
скорость звука.
Волновые движения в атмосфере (линейная теория) 285
Стратификация потока и гравитационное поле являются
основными факторами, обусловливающими анизотропность
волнового процесса. Поскольку в рассматриваемом случае влияние
указанных эффектов мало, нет оснований предполагать, что
волновые числа разные, и естественно принять m = n = q = \. Тогда
из (10.6.17) и (10.6.19) следует
»VirTg •
а из (10.6.18)
л« ^-. (10.6.20)
1 dp
Р
dz
Полученные неравенства, к сожалению, не могут быть
использованы для количественных оценок. Ясно лишь, что
звуковые волны должны обладать высокой частотой и малой длиной.
Важной особенностью звуковых волн является то, что их
фазовая скорость не зависит от волновых чисел. Это значит, что
волны распространяются без дисперсии. Из (10.6.16) видно, что
при г = 0 или при ц. = 0, или, наконец, при v = 0 m должно быть
равно нулю, т. е. система уравнений не имеет волновых решений
рассмотренного типа. Отсюда следует способ фильтрации
трехмерных звуковых волн. Для этого достаточно, например,
жидкость считать несжимаемой.
Гравитационные волны
Здесь речь пойдет о другом предельном случае, когда g и Г
являются характеристиками основного состояния, от которых
существенно зависят параметры волн, и, наоборот, эффекты
сжимаемости малы. В рассматриваемом случае проявляется
анизотропность атмосферы, так как ускорение свободного падения
и стратификация влияют только на вертикальные смещения.
Можно предположить, что вертикальная проекция волнового
вектора в рассматриваемом случае существенно отличается от
двух других проекций. Полагая в (10.6.16) jx = v = 0, получим
дисперсионное уравнение для гравитационных волн:
т2 + л2
Отсюда находим выражение для частоты:
^--г. (10.6.21)
.-у.
Г* (10.6.22)
r + 92/(m2 + „2)
286
Глава 10
Если (10.6.21) выполняется достаточно точно, то, поскольку
г = 1, пренебрежение эффектами упругости и сжимаемости [как
следует из (10.6.16)] означает, что
(т2 + л2)с2
«1,
г+-&-«1.
(10.6.23)
Второе неравенство всегда выполняется в атмосфере, а
первое указывает на то, что фазовая скорость гравитационных волн
много меньше скорости звука. Из (10.6.21) следует, что для
^4ж«' Ч-от.
Такие частоты наблюдаются в атмосфере и называются
частотами Вяйсяла. Поскольку q = Q эквивалентно Я2 = оо, o = ^Tg —
частота колебаний всего столба атмосферы в поле силы
тяжести.
Из (10.6.22) видно, что гидростатическое приближение
приводит к увеличению отношения вертикальной компоненты
волнового вектора (q) к горизонтальным компонентам (т, п) и к за-
Q2
вышению частот волн. Для —^—r^U как следует из (10.6.22),
можно без заметных погрешностей пользоваться
гидростатическим приближением. Этот вывод можно рассматривать как
основание для использования гидростатического приближения при
исследовании атмосферных движений с горизонтальными
масштабами, много большими вертикальных. Такими являются, в
частности, крупномасштабные атмосферные движения.
Выясним влияние целиком отброшенных эффектов —
сжимаемости и упругости — на соотношение между параметрами
гравитационных (а точнее, смешанных) волн. Воспользуемся
при этом тем, что фазовая скорость много меньше скорости
звука. Полагая |i=v = r=l, можно записать (10.6.16) в виде
*+М*+-Й
=-1+
г*
nP + rfl * (Щ2 + Л2) С2
Поскольку
Волновые движения в атмосфере (линейная теория) 287
среднее слагаемое справа можно отбросить, после чего найдем
■/
Г"П ТТ~ ' (Ю-6-24)
Из сравнения (10.6.22) и (10.6.24) следует, что пренебрежение
сжимаемостью эквивалентно занижению вертикальной
компоненты волнового вектора и завышению частот. Укажем, наконец,
что при Г = 0 из (10.6.16) имеем
= с
1 р-2
я2 + -^г^
]/7л2 + Я2
}/ '+ „,;„,* =оы-
Таким образом, в нейтральной атмосфере фазовая скорость волн
близка к скорости звука. Гравитационных волн в ней не может
быть.
Волны, связанные с вращением Земли. Волны Россби
Из физических соображений ясно, что сила Кориолиса влияет
главным образом на горизонтальные движения. Это позволяет
получить достаточно полное представление о волновых
движениях в поле силы Кориолиса, если ограничиться случаем
горизонтальных волн. Математическая сторона задачи при этом
станет значительно проще. Итак, в исходной системе уравнений
положим ш = 0. Будем считать пренебрежимо малым влияние
сжимаемости и силы тяжести. Для горизонтальных волн такое
упрощение представляется вполне оправданным.
f)nf
Из (10.3.19) следует при этом, что - =0, р'=р'(х, */, t)t
а из (10.3.21) р'=р'(х, у, t). Оставшиеся три уравнения
сводятся к следующему виду:
*-^--"*-?(-£ + -£-). 00-6.25)
A-£--Ap'-p(-g---St-)+/At, (Ю.6.26)
Дср=0. (10.6.27)
Из трех полученных уравнений могут быть найдены три
функции: ф, t|), р'. Будем искать их в виде
/=/0в'(т*+"у-").
288 Глава 10
Тогда
д/= - (т*+п2)/. (10,6.28)
На основании (10.6.27) получаем ф0 = 0 и, стало быть, <р=0.
Из оставшихся уравнений имеем:
(т2+п2) h% = - 1$т%, (10.6.29)
0 = (т2+/г2)/70+^фо-/(^2+^2)фо. (10.6.30)
Из (10.6.30) следует я = 0. Тогда на основании (10.6.29)
получаем дисперсионное соотношение
a=-JL, (10.6.31)
воспользовавшись которым найдем компоненты фазовой
скорости [см. (10.6.2)]:
"-таг—-&-• <>°«2>
с'—?тж-0- <10-6-33>
Отсюда видно, что относительно воздушной массы волны Россби
движутся на запад (сх<0).
Из указанного дисперсионного соотношения получим
групповую скорость [см. (10.2.13)]:
Из (10.6.30) следует соотношение между амплитудами
искомых функций
/?о = й0. (10.6.35)
Влияние вращения Земли на гравитационные волны
Из общей системы уравнений (10.3.17) — (10.3.21), полагая
|i = v = p=0, получим уравнения для гравитационных волн на
вращающейся Земле при пренебрежении эффектами
сжимаемости:
Д-*Ь=-/Д<р, (10.6.36)
Д-^=/Дф-Д/Л (10.6.37)
Волновые движения в атмосфере (линейная теория) 289
Д?=--^-. (10.6.39)
-^-=Гда. (10.6.40)
Как и в предыдущих случаях, решение будем искать в виде
f(t, х, у, z)=fl(z)eiimx+ny-°t). (10.6.41)
Тогда имеем:
/аф, = /<р,, (10.6.42)
/«?, = -/ф,+р,, (10.6.43)
irow^-^+gpu (10.6.44)
(OT2+rt2),fi=__^L> (Ю.6.45)
—/ор,=Гда,. (10.6.46)
После подстановки в (10.6.43) — (10.6.45) значений цч и pi из
(10.6.42) и (10.6.46) получим три уравнения для ij>i, pi и w\\
1»,(-7— l) = -Pu (10.6.47)
tall(ra__^) = ^L, (Ю.6.48)
/(Я.2 + Я2)а ,b=jgj_. (Ю.6.49)
Подставим теперь г|п и a>i из (10.6.47) и (10.6.48) в (10.6.49).
Тогда получим дифференциальное уравнение для рс
dz*
где
^-И2/>1=0, (Ю.6.50)
?2 = (rg_ra2)^±^i> (Ш.6.51)
Найдя из (10.6.50) pi, можно на основании (10.6.47) и (10.6.48)
определить t|?i и a>i, а затем, воспользовавшись (10.6.42) и
(10.6.46), найдем cpi и pi.
Решение (10.6.50) имеет вид
px = Ape±iqz. (10.6.52)
19 Заказ Хо 612
290 Глава 10
Дисперсионное соотношение (10.6.51), решенное относительно
а, дает
-/г, \ [i+Tdfed- с»-6-53)'
Из (10.6.53) следует, что вращение Земли стабилизирует
волновые движения, так что даже при неустойчивой стратификации
могут существовать стационарные волновые движения (Ima =
= 0), если только
-Г< gJln2) ^-у-^- ^*М- 00-6-54)
Критическое значение градиента, как легко заметить, растет
с широтой. Поскольку возникновение конвективных явлений
часто связано с потерей устойчивости гравитационных волн, то
очевидно, что в экваториальных широтах условия наиболее
благоприятны для развития таких процессов. Из (10.6.53) вытекает
также и то, что особенно существенно влияние вращения Земли
т2+п2
на динамику длинных горизонтальных волн (когда ►■
—>-0). Это обстоятельство сохраняет свою силу для любых
крупномасштабных движений.
Разделим обе части (10.6.53) на I. Тогда имеем
a
т _ t ^
' """ mZ + n*
Из этого уравнения следует, что безразмерная частота —
является функцией двух аргументов: безразмерной стратификации
I—~- = 5) и параметра анизотропии волнового вектора
(-£—).
\ т2+п2 I
Связь трех указанных величин согласно (10.6.55) иллюстри-
Q2
руется рис. 10.4. По осям ох и оу отложены значения —^——
т2 + п2
и — соответственно; кривые на графике представляют собой
изолинии параметра стратификации 5. Кривая s = 0 отделяет
область устойчивой стратификации (вверху) от области неустой-
1 Нетрудно видеть, что из (10.6.53) как частный случай вытекает
(10.6.22).
Волновые движения в атмосфере (линейная теория) 291
чивой стратификации. Как видно на рис. 10.4, вдоль линии
— =1 качественно меняется характер дисперсионного соотно-
ду_
дх Js==cons^"
шения: —-I ronst>0 при s<l и
ду_
дх
S=conet<0 ПРИ 5>1.
Прямая х = 0 на графике является шкалой частот Вяйсяла, на
ней —-г=—гУ*ё независимо от горизонтальных компонент
волнового вектора.
б
1\-
\
-о
1
\
^
-.
_—————— ^ о
^— ^ §•
Рис. 10.4. График дисперсионного соотношения для волн
в стратифицированном потоке на вращающейся Земле.
Сильная зависимость частот колебаний от стратификации
в области малых х (включая и х = 0) объясняется тем, что здесь,
по существу, имеют место квазивертикальные колебания.
По мере увеличения х волны приближаются к чисто
горизонтальным колебаниям. При этом зависимость частот от
стратификации ослабевает, и в пределе при
m2+n2
= оо из (10.6.55)
следует, что —=1 независимо от стратификации.
Влияние вращения Земли на звуковые волны
Рассмотрим характер горизонтальных двумерных волн (до =
= 0), которые могут иметь место в атмосфере. Будем
пренебрегать зависимостью параметра Кориолиса от широты и влиянием
19*
292
Глава 10
силы тяжести (это соответствует предположению g=0). В
данном случае система (10.3.17) — (10.3.21) упрощается, она
принимает следующий вид:
-Й-+АР-0.
v др'
~Ж~дГ
др'
dt
= 0.
(10.6.56)
(10.6.57)
(10.6.58)
(10.6.59)
Решения будем искать в виде
/ {тх + пу — ot)
Тогда имеем:
/-/о*'
ia\>0 — /?о=0,
Ьсро — Ро — /фо = 0, j
/a(xp0-[-(m2-f/г2)ср0 = 0, (
-^гРо — Ро = 0.
(10.6.60)
Отсюда, исключая последовательно ро, 'фо, ро, находим
следующее дисперсионное уравнение:
(т2 + П2) С2
„2__
M-V
-/2.
(10.6.61)
Сравнение (10.6.61) и (10.6.19) позволяет выяснить
характер влияния вращения Земли: оно может заметно увеличивать
фазовую скорость длинных волн, так что Сф>с. Интересно
отметить, что групповая скорость оказывается в рассматриваемом
случае меньше скорости звука. Из (10.6.61) следует и способ
фильтрации двумерных звуковых волн; для этого необходимо
положить \х=0 или v = 0, т. е. считать воздух несжимаемым.
10.7. Некоторые краевые задачи
Стационарный волновой режим на поверхности раздела
двух несжимаемых жидкостей разной плотности
(jx = v=0, Г = 0, г = 1)
Допустим, что две воздушные массы простираются
безгранично в обе стороны от поверхности раздела. Индексами I и II
Волновые движения в атмосфере (линейная теория) 293
обозначим физические величины, характеризующие верхнюю и
нижнюю воздушные массы соответственно. Предположим, что
массы нейтрально стратифицированы и допустимо пренебречь
сжимаемостью. Для решения задачи воспользуемся
результатами предыдущего параграфа. На основании (10.6.16) и
(10.6.15) для рассматриваемого случая имеем:
?2 = _(Щ2+Аг2)э (10.7.1)
q=±i \fm2+n2 = ±/Q.
Тогда
pUi = Aie-Qz+BieQz. (10.7.2)
Выражения для остальных функций найдем, используя
формулы (10.6.14):
'Pl.t
i dP\, i
W^= Г ST
\
(10.7.3)
Произвольные постоянные At и B\ определим на основании
граничных условий. Поскольку по физическому смыслу все
величины ограничены, мы должны потребовать, чтобы
Hmpi,i ic=oo, |
(10.7.4)
Пусть поверхность раздела расположена на 2 = 0, а уравнение
возмущенной поверхности имеет вид
С=С0е'(т*+Л>'-°'>. (10.7.5)
Поскольку все искомые функции ищутся в виде
f=fx(z)ei{mx+ny-9t\
кинематические условия (10.4.8) и динамические условия
(10.4.11) примут следующий вид:
®i,iL = o=- fe'oPi l*=°»
wx, „ | z^0 = - «opи I z=o, (10.7.6)
— Pi^o+Pi,i(0)=- Ph«Co+Pi.ii(0). (Ю.7.7)
(нужно иметь в виду, что w = pw'). Таким образом, для того
чтобы удовлетворить пяти граничным условиям, мы можем
распорядиться величинами А{, Аг, В\у В2, т, /г, а.
294
Глава 10
На основании условия (10.7.4) должно быть
P\,\ = A\e~Qz
Рии=В2е
Q, i (Ю.7.8)
A,
в,
Q
a
_Q_
a
=
— <£<)Pl,
a*oPib
Анализируя уравнения (10.7.3), нетрудно убедиться, что с
удалением от поверхности раздела возмущения всех физических
полей затухают. Подставим теперь pi, г- и w\ *, использовав (10.7.3),
в (10.7.6) и (10.7.7). Тогда
(10.7.9)
A-S2=£Co(pi-Pii). (10.7.10)
Полученные уравнения удовлетворяются при любом £о=?*=0. Это
легко понять, подставив в (10.7.10) значения А\ и Вг из (10.7.9).
Однако при этом должно
o* = gQ _p"~_Pl =gVm2+n2 !""!' . (10.7.11)
Рц + Pi Pn+Pi
Следовательно, мы нашли дисперсионное соотношение для
данной краевой задачи. Из (10.7.11) получаем выражение для
фазовой скорости:
СФ ym<i + n<L у утг + пъ 2Р V 2Р
gM
утЧ + Л2
(10.7.12)
Поскольку в задаче не учитываются какие-либо факторы,
обусловливающие различие процессов вдоль осей оу и ох,
естественно принять т = п. Тогда фазовая скорость
<*-+-'/-&-£-'/-&-¥-+■ <,о-7-1з>'
Легко оценить значение фазовой скорости. Например, при ДГ =
= 7 К, Г~=280 К, Х = 2800 м, # = 9,8 м/с2 сф~2,8 м/с. Таким
образом, фазовая скорость рассматриваемых гравитационных волн
близка к скорости ветра.
Выражение (10.7.13) легко обобщить и учесть влияние
стратификации и ускорения Кориолиса. Для этого вместо формул
1 Из (107.13) как частный случай вытекает соотношение для
гравитационных волн на свободной поверхности, достаточно положить в нем pi =0.
Волновые движения в атмосфере (линейная теория) 295
(10.6.15) и (10.6.16) нужно использовать эквивалентные
выражения (10.6.50) и (10.6.51). Элементарные выкладки, совершенно
аналогичные предыдущим, приводят в этом случае к
дисперсионному уравнению
gAT УпУ + гР 1
2Г
/(■--£■)('--£)
(10.7.14)
Отсюда видно, что пренебрежение стратификацией, так же как
и влиянием вращения Земли, приводит к завышению частоты.
Из выражения (10.7.14) можно найти предельный вид
дисперсионного соотношения при о-+0. Это случай так
называемых стационарных волн, т. е. волн, движущихся вместе с
воздушной массой. Для таких волн
2Т
gAT
Vm? + ti> |a=0 = _^-/yrg . (Ю.7.15)
Волны такой длины, вероятно, возникают на фронтальных
поверхностях с достаточно малым наклоном.
В случае сравнительно коротких волн может оказаться
существенным эффект сжимаемости и упругости. Известно, что
именно такого типа гравитационные волны на поверхностях
раздела в атмосфере являются причиной образования волнистых
облаков. При развитии коротких волн в условиях значительной
относительной влажности в вершинах волн вследствие
адиабатического охлаждения поднимающихся частиц воздуха
возникает конденсация, которая приводит к образованию облачных
гряд. Дисперсионное соотношение для рассматриваемого случая
может быть получено повторением выкладок, основанных на
формуле (10.6.15), которая при
|лП>з2
-(w2+^)(r-J^)--L(i>+-^)2<o
С2
должна быть записана в виде
причем
\2 (J./*va2
?=/(^ + ^)(г-^) + ^-(г,+^)2
С2
(10.7.17)
Только при этих условиях на поверхности раздела могут
возникать волновые движения, амплитуда которых затухает на
296
Глава 10
большом удалении. После выполнения указанных расчетов
получим
Л =
gfol-PlH"*2^) 1- С2(^+Л2)
х V* с2 ) РИ —Pi
2д Ри + Pi
(10.7.18)
Эволюция волнового возмущения в поле силы Кориолиса.
Фильтрация эффектов, обусловленных погрешностями
начальных полей
Во многих отношениях интересно рассмотреть задачу об
эволюции во времени заданного начального возмущения. В
зависимости от состояния атмосферы это возмущение может затухать
во времени или увеличиваться более или менее интенсивно.
В последнем случае возникают явления, с которыми приходится
считаться в прогнозах погоды. Другой существенный аспект
такой задачи связан с влиянием погрешностей начальных полей,
которые в численных прогнозах проявляются как некие
фиктивные возмущения. В связи с этим важно предусмотреть такой
путь решения проблемы, при котором погрешности начальных
данных не приводили бы к «паразитным» явлениям, не
имеющим отношения к действительности.
Рассмотрим случай, когда допустимо пренебречь эффектом
сжимаемости и изменением параметра Кориолиса (ji = v = p=0).
Соответствующая система уравнений нами рассматривалась
в п. 10.6 [формулы (10.6.36) — (10.6.40)]. Поскольку речь идет
об удовлетворении условиям, которые отражали бы характер
произвольного начального возмущения, то естественно искать
теперь выражения для всех функций в виде:
f=f0(i)el{mx+ny+q'\ *
bf=-.(m?+n?)ei{mx+ny+qz\
df _ _dfo_ i {mx + ny + gz) \ (10.7.19)
dt ~ dt *
df /„/ J (mx + ny + qz)
На основании (10.6.36) —(10.6.40) с помощью (10.7.19)
получаем систему обыкновенных уравнений:
-^-—/То. (Ю.7.20)
Волновые движения в атмосфере (линейная теория) 297
-^f- = l%-Po, (Ю.7.21)
г-*%?- = -tiPo-gPo. (Ю.7.22)
(m2-\-n2)<?0=Lqw0, (10.7.23)
-^-=Tw0. (10.7.24)
Исключая последовательно фо, ^о, Ро, Ро, получим
дифференциальное уравнение для w0:
-rf72"+ ,2 + г(т2 + л2) ^о-О. (Ш.7.25)
причем
<Ро = ^Ьг™о, (Ю.7.26)
/>o = C/-^4^-^-j^. (Ю.7.27)
Фо = С—s^rJ«o*. (Ю.7.28)
р0 = С, + Г J да0 Л- (10.7.29)
Здесь С и Ci — постоянные интегрирования.
Из (10.7.25) находим
чой=Аем+Ве-ш, (10.7.30)
где
Остальные функции по полученному выражению для Доо
определяются формулами (10.7.26) — (10.7.29). Найденное
решение системы дифференциальных уравнений (10.7.20) — (10.7.24)
используем для решения общей задачи, которая задана
начальными полями функций <р, г|), р', р'. Для этого воспользуемся тем,
что полученные частные решения удовлетворяют исходной
системе при любых значениях волновых чисел m, п> q и
произвольных постоянных Л, 5, С, Ci. В таком случае в силу
298
Глава 10
линейности исходной системы можно записать общее выражение
для wy например, в виде
+оо
W
= jj f [Л К п, д)еы-\-В(т, пу q)e'bt]X
Хе
l (mx + ny + qz)
dmdndq.
В аналогичной форме можно выписать остальные искомые
функции. После чего задача сводится к определению четырех
произвольных функций A(mt п, q), В(т} п, q)y С(т, n, q), Ci(m, n, q).
Они выражаются через начальные поля после обращения
соответствующих интегралов. Так, например,
А(ту п, q)-\-B(m, п, q) =
--(hfll^\^~Hmx+ny+qz)dxdydz-
Ограничимся простой задачей, которая при весьма
элементарных выкладках позволяет получить важные результаты.
Допустим, что
,п\ —A J {ТПХ + Пу+qZ)
.и л J {mx + ny + qz)
?i/=o — льв
пм Л J {mx + ny+qz)
Р \t=o — лре у
i (mx + ny + qz)
(10.7.32)
Здесь ЛФ, А^у АРу Лр — заданные константы. Используем их для
отыскания Л, 5, С, Си
В соответствии с принятыми обозначениями для любой из
искомых функций Af = fo\ 0. Имея это в виду, на основании
(10.7.26) — (10.7.30) находим <ро, ^о, ро, ро при ^ = 0, а затем,
воспользовавшись (10.7.32), выпишем систему алгебраических
уравнений для отыскания произвольных постоянных:
Л.=-
1Я
(^qbr(A+B>-
Лф= с -
Ар=а-
1Я
(А-В) —
mi + «2
1^Ьг(Л-В)*
/г
А, = Сх-^+{А-В).
(10.7.33)
Волновые движения в атмосфере (линейная теория)
Из этой системы найдем:
299
2а v"p
1
1z
B=-4r(Ap-lA,+teA9)-?*±*-
(10.7.34)
С=А*+-^-(Ар-1А*),
Cx = Af+^(Ap-lA,)^±*_
Искомые решения получим, отбросив в окончательных
выражениях мнимые части. Подробные вычисления проделаем для w.
На основании (10.7.19) и (10.7.30) имеем
5= (Aeiat + Be-iat)ei{mx+ny + qz).
Значения А и В подставим из (10.7.34), после чего получим
- е~
ч
Ар-1А
1/\<р
(еш + е~^)
Ф (еш-е-ш)
l {mx + ny + qz)
Воспользуемся теперь формулами Эйлера для перехода к
тригонометрическим функциям и отбросим мнимую часть. Тогда
найдем окончательное выражение:
w
__ -(т2^_п2) / Ар - 1\
sin at — А? cos at J sin (mx-\-ny-\-qz).
(10.7.35)
Аналогичная процедура позволяет получить вид остальных
функций:
pf = {Ap-(l--J)[(^-M^(l-COSa0-aA,Sina^]}x
\cos(mx-\-ny-\- qz)t
ф = [Лф + -^- [(Ар — /Аф) (1 —COS а*) —аЛср Sin at] JX
X cos (tfu:+fty+<72:),
cp = [(Ар —/A^sin a/ —aAcpCOSa^] cos (mx-^-ny+qz),
9' = A?cos(mx-\-ny+qz)—r(m2 + *2> [(Лр-/Лф) (1-cosa*)-
?g2
— aAcpSino^j sin (mx-\-ny-\-qz).
(10.7.36)
300
Глава JO
Рассматривая полученные формулы, нетрудно обнаружить,
что параметры начальных полей Ар— 1А$ и Л<р определяют
амплитуду возмущения, в связи с чем важно понять физический
смысл этих величин. Покажем, что они пропорциональны
отклонениям начальных значений скорости ветра от
геострофического.
Действительно, линеаризируя геострофические соотношения
получаем
и =
ри =и =
1
/р
1
др
ду
др'
v =
1 др
/р дх
I ду
pv =v =
1 dp'
I дх
Введя же функцию тока и потенциал скорости согласно
(10.3.15), можно полученные соотношения записать в виде:
ду
дх
ду
ду
д<\>
ду
д<\>
дх
1 др1
I ду
1 др'
I дх
(10.7.37)
Отсюда следует, что
<?2
дх*
И^-*)+^(^-*)-°'
дЦ , дЦ _а
дх*
ду*
(10.7.38)
(10.7.39)
Если начальные поля удовлетворяют геострофическим условиям,
то уравнения (10.7.32) должны быть решениями уравнения
Лапласа, т. е. (10.7.38); подставляя значения <р, р' и \|) из (10.7.32)
в (10.7.38), получаем:
-(m2-\-n2)A,ei{mx^ny+gz)=0.
Это значит, что
-^—Л^0, А,^0. (10.7.40)
Вернувшись теперь к решениям нестационарной задачи
(10.7.36), легко обнаружить, что при условии (10.7.40), т. е. при
«геострофическом» начальном состоянии, все
метеорологические поля не будут меняться с течением времени. Начальное
состояние в этом случае не вносит никакого вклада в эволюцию
полей во времени.
Волновые движения в атмосфере (линейная теория) 301
Таким образом, фильтрация паразитных явлений, которые
могут возникать в задачах прогноза из-за ошибок начальных
данных, достигается операцией согласования начальных полей
давления и ветра, в результате которой удовлетворяются
геострофические условия.
Рассматривая формулы (10.7.36), нетрудно заметить, что
амплитуда некоторых волновых возмущений может быть сколь
угодно больше начальной амплитуды при достаточно больших
значениях l/о. Таким образом, даже небольшие погрешности
начальных полей могут в процессе эволюции полностью исказить
реальный процесс.
В рассмотренном весьма простом случае агеострофичность
начальных полей, периодически меняющаяся в пространстве
согласно (10.7.32), вызывает незатухающие волны [выражения
(10.7.36)]; их частота [выражение (10.7.31)] определяется
параметрами начальных полей (га, пу q) и свойствами атмосферы
(g, г, /).
Более типичной является ситуация, при которой
агеострофичность сконцентрирована в ограниченной части пространства.
Исследование этого случая показывает, что при такой ситуации
возникает апериодический (затухающий) процесс, который в
конечном счете приводит к стационарному состоянию,
удовлетворяющему геострофическим условиям. Происходит адаптация
(приспособление) полей давления и ветра. Процесс адаптации
представляет собой тот механизм, благодаря которому почти во
всей атмосфере поддерживается геострофичность.
10.8 О волнах в движущейся атмосфере
Рассмотренные до сих пор волновые движения относились
к неподвижной атмосфере. Такое состояние наблюдается в
реальных условиях крайне редко, и вряд ли стоило ему уделять
внимание, если бы получаемые при этом свойства волн нельзя
было легко обобщить на случай движущейся атмосферы. Какие
новые обстоятельства возникают при волновых движениях в
потоке воздуха? Пусть существует конечная, не зависящая ни от
координат, ни от времени скорость, направленная вдоль оси ох;
обозначим ее через и. Тогда при выводе уравнений для малых
колебаний формула (10.3.8) должна быть записана следующим
образом:
dt dt ' и дх ^w dz # iiu.o.ij
Это значит, что все индивидуальные производные содержат
302
Глава 10
дополнительное слагаемое —и^—. Введем новые независимые
ох
переменные t'y х', y't zr вместо ty х, у, г, причем ti = t, хх =
= х—ut, у\ = у, zi=z. Тогда очевидно, что
д д - д д д д д д д
-U
dt ~- dtx " дхх ' дх дхх ' ду дух ' dz дг\ '
а в новых переменных
-^=^+-4- <1о-8-2>
Таким образом, использованная в предыдущих параграфах
система уравнений сохраняет свой вид, если ввести новые
независимые переменные, и, стало быть, все полученные выше
выводы остаются пригодными для потока, движущегося с
постоянной скоростью. Смысл новой системы координат ясен: она
движется со скоростью ветра, а поскольку эта скорость постоянна,
то она не может приводить к каким-нибудь изменениям в
физических процессах.
Совершенно иначе обстоит дело, если скорость зависит от
координат или от времени. Это вызывает фундаментальные
изменения в характере происходящих физических явлений, и в
частности в свойствах волн. Остановимся на одном простом
случае. Вернемся к задаче о волновых движениях на поверхности
раздела, рассмотренной в п. 10.7. Однако теперь предположим,
что обе воздушные массы движутся с разными, но постоянными
скоростями: верхняя — со скоростью и,\, нижняя — со скоростью
иц. Если для каждой воздушной массы ввести свою
подвижную систему координат так, чтобы скорость движения системы
координат соответствовала скорости ветра в ней, то в
собственной для каждой воздушной массы системе координат
дифференциальные уравнения и соответственно их решения будут иметь
одинаковый вид. Что касается параметров волновых движений,
то волновые числа будут, разумеется, одинаковыми в обеих
системах координат, а фазовые скорости и частоты волн —
разными, поскольку в обеих воздушных массах ось ох движется
с разной скоростью. На основании этих соображений запишем
формулы (10.7.2) и (10.7.3) для обеих воздушных масс:
р\ = (Aie-Qz+ BteQz) el <""+">'+">, \
^ = -J^' } (10.8.3)
~ i dpi
a; dz
Волновые движения в атмосфере (линейная теория)
303
Запишем граничные условия (10.4.7) и (10.4.11) для
данного случая:
w dV , - <%'
а\ дх »
Pi
<И
w" dC' j_;7 dv * при z = 0.
Ри
(10.8.4)
Pi— Pii = (?i — Pn)g" j
Пусть по-прежнему
V(t, х, y)=Z<>ei{mx+ny-ot).
Уравнения (10.8.4) написаны в системе координат,
скрепленной Землей. При подстановке в них искомых функций нужно
(10.8.3) записать в первоначальной системе координат. В этом
случае имеем:
V
in
^B2Qei^mx'mu^ny-^ = l^(a-muu)ei{mx+ny''at)t
л i (mx- muxt -f ny - jjf) о f (я1х-Шц+яу"ац<)
Л /~ " \/ * (/шг + лу —a/)
= grlPl — РнДо^ •
Отсюда следует, что должно быть
После этого получаем:
(10.8.5)
AXQ
(a— ma|)pi
S2Q
= — C0(a — /na,),
=C0 (a — /гшп), |
(10.8.6)
(a — man)pn
Л — ^2 = ^(р1 — Pn)Q). ]
Найдем из двух первых уравнений ;4i—Вг и подставим
в третье; после чего получим дисперсионное соотношение
(a — muiYpl + {G-muu)2pu = gQ(pn — р,). (10.8.7)
Можно положить в (10.8.7) u\ = Vy иц =—V; это не нарушает
общности. Очевиден смысл V: оно равно половине скачка
304
Глава 10
скорости на поверхности раздела (и\ — tiu = 2V). Решив (10.8.7)
относительно а, получим
2рсР V 2Рср \ 2рср /
(10.8.8)
Сравнивая полученное уравнение с аналогичным уравнением
для неподвижной атмосферы (10.7.11), видим, что параметры
волн существенно различаются в этих случаях. Из (10.8.8)
следует важное обстоятельство: при больших значениях V
подкоренное выражение в (10.8.8) может стать отрицательной
величиной, а о — комплексной. Это значит, что амплитуда некоторых
волн может возрастать с течением времени. Состояние с таким
разрывом скорости будет неустойчивым. Волны будут
трансформироваться в вихри, на поверхности раздела разовьется
турбулентность, обусловленное ею перемешивание вызовет
выравнивание скоростей ветра, скачок уменьшится, и в конечном счете
установится новый профиль скорости ветра. Это конечное
состояние, разумеется, нельзя получить как некий предел в рамках
линейной теории.
Из рассмотренной частной задачи следует вывод, который
оказывается общим свойством движений в атмосфере и океане:
неоднородность поля скорости (в рассмотренном случае это
означает УфО) может вызывать неустойчивость волн и
приводить к образованию вихрей. Рассмотренная задача — простейший
пример возникновения турбулентности.
Контрольные вопросы
1. Что такое групповая скорость волн? Чем отличается
фазовая скорость от групповой скорости?
2. При каких волновых движениях можно пренебрегать:
а) вязкостью, б) нелинейными эффектами, в) притоком тепла?
3. Каков физический смысл кинематических и динамических
условий на поверхности раздела?
4. В какой части спектра атмосферных волн можно
пренебрегать вращением Земли?
5. Каковы главные особенности упругих волн,
гравитационных волн и волн Россби?
Глава 11. ПОГРАНИЧНЫЙ СЛОИ АТМОСФЕРЫ
Система уравнений для пограничного слоя атмосферы. Метеорологические
элементы и характеристики турбулентности вблизи поверхности земли. Расчет
турбулентных потоков тепла, влаги и количества движения. Однопараметри-
ческая модель (/г=const). Нелинейная модель. Пограничный слой над морем
(коэффициент турбулентности не зависит от высоты). Параметризация
планетарного пограничного слоя атмосферы.
Пограничным слоем атмосферы называется нижний 1,5—
2-километровый слой, в пределах которого распределение
метеорологических элементов определяется непосредственным
влиянием подстилающей поверхности и турбулентностью. Наиболее
четко это можно проследить в вертикальном распределении
скорости ветра. Скорость ветра всегда равна нулю на
подстилающей поверхности1 и стремится к геострофической скорости
на верхней границе пограничного слоя атмосферы (для
горизонтально однородных условий и прямолинейных изобар).
Характер вертикального распределения скорости ветра между
этими двумя уровнями в значительной степени определяется
турбулентностью, которая вызывает обмен количеством
движения между различными слоями и сглаживает профиль ветра
(рис. 11.1).
Влияние подстилающей поверхности на вертикальный
профиль температуры и влажности в пограничном слое атмосферы
выражено менее четко в связи с значительным влиянием
других меняющихся в широких пределах факторов, мало
связанных со свойствами подстилающей поверхности. Так, например,
суточные колебания радиации качественно меняют
распределение температуры, тогда как профиль ветра, по крайней мере
качественно, не изменяется.
В теплом и влажном по сравнению с подстилающей
поверхностью воздухе температура и удельная влажность могут не
уменьшаться с высотой, а увеличиваться. Как и в случае
скорости ветра, турбулентность приводит к сглаживанию
профилей температуры и влажности.
При оценке влияния турбулентности следует, однако,
помнить, что она не только определяет характер вертикальных
профилей метеорологических элементов, но и в свою очередь
1 Вблизи водной поверхности скорость ветра равна скорости
поверхностного течения, обычно составляющей около 2% скорости ветра на уровне
стандартных наблюдений.
20 Заказ № 612
306
Глава И
z м
2000
зависит от градиентов этих элементов. В действительности поля
метеорологических элементов и турбулентный обмен изменяются
взаимосвязанно под влиянием внешних факторов. К числу
внешних факторов можно отнести приток солнечной радиации,
горизонтальный градиент давления, интенсивность обмена
свойствами между пограничным слоем, свободной атмосферой и
верхними слоями почвы.
Изменена ние внешних факторов, приводя
к изменению профиля одного из
метеорологических элементов
благодаря взаимодействию полей,
вследствие турбулентности или
в результате лучистого
теплообмена, сказывается на
вертикальном распределении других
элементов. Например,
увеличение притока солнечной
радиации к земной поверхности
приводит к повышению температуры,
при этом возрастает
вертикальный градиент температуры и
увеличивается турбулентность;
^^/^ ^^*~—х за счет увеличения турбулентно-
j сти происходит уменьшение гра-
1000
4 6 8 Ю им/с диентов температуры и скорости
Рис. 11.1. Профиль средней месяч- ветра, а это приводит к ослаб-
скорости ветра.
Воейково.
Станция лению турбулентности.
Взаимосвязанные изменения полей
температуры, влажности, скорости
ветра и турбулентности будут продолжаться до тех пор, пока
не установятся такие их распределения, которые обеспечат
тепловое и динамическое равновесие системы воздух—деятельная
поверхность для данного притока радиации и скорости
поступления водяного пара в атмосферный пограничный слой.
Наличие тесной взаимосвязи между полями
метеорологических элементов и турбулентности делает необходимым
определение их из решения совместной системы дифференциальных
уравнений и граничных условий.
11.1. Система уравнений, описывающих строение пограничного
слоя атмосферы
Рассмотрим случай, когда выполняются условия
стационарности и горизонтальной однородности. В п. 7.7 было показано,
что в этом случае уравнения движения принимают следующий
вид:
Пограничный слой атмосферы 307
д и ди , 0 1 др
дг дг ' г р дх '
д , dv а 1 др
дг dz z р ду
Или, считая градиент давления внешним параметром и
выражая его через геострофический ветер, получим:
^r*-g--2M«-"*) = 0. (И.1.1)
Для замыкания системы используем уравнение баланса
энергии турбулентности (см. п. 7.7)
*l(-S-)'+(-S-),- + ^-S-l+o—o. ой*
Предположим, что все характеристики турбулентности
можно представить как функции от характерного размера
турбулентных пульсаций — масштаба турбулентности / — и
кинетической энергии турбулентности Ь\
k = Fx{lt 6), e = F2(', b)y
где
\k\=L*T-\ \l\=Ly [b]=L2r-\ [e]=L2T-\
В таком случае с помощью П-теоремы получаем выражения для
коэффициента турбулентности k и диссипации е:
k = CxlVF или k=*lxVb, (11.1.3)
где
£ = С2-Ц^ или s = C-^-f (11.1.4)
где C = CoCi — постоянная, определяемая из эмпирического
материала.
Если теперь поток кинетической энергии турбулентности
выразить как турбулентный поток любой субстанции в форме
db
dz '
Fb = abk
где a,b = kb/k, а диффузию энергии турбулентности представить
как дивергенцию потока
Dd и db
= а/ь -з— « -з— ,
0 dz dz '
20*
308
Глава 11
то уравнение (11.1.2) можно записать в виде
(11.1.5)
Теперь в уравнениях (11.1.1), (11.1.3) и (11.1.5) содержится
шесть неизвестных (uf v, ky I, b, 0). Для определения
потенциальной температуры 0 используем уравнение притока тепла (см.
п. 7.8)
—— zTk —z -—= 0, (11.1.6)
dz т dz ■ рср dz ' v 7
где сумма радиационного и фазового притока тепла.
Этот член в принципе можно выразить через другие искомые
величины 0 и q (удельная влажность), однако это привело бы
к значительному усложнению задачи. Запишем пока уравнение
притока тепла в наиболее общем виде:
ат«—т- = -1— у (11.1.7)
т dz ?Ср
где
P(z) г 1 d<&
-j
dz.
?ср J ?ср dz
Аналогично уравнение притока влаги (для определения q)
-=-^-S-+t-S-0' (11Л-8)
1 dF А
где ; фазовый приток влаги, можно записать в форме
р dz
«.*-£—^7*". (1U9)
где
р J р dz
Для определения h (в дальнейшем будем обозначать эту
величину как /) воспользуемся выражением, обобщающим
формулу Кармана на случай двумерного стратифицированного
потока:
'«-«^£г. 01.1.Ю)
d<l>
~dz
Пограничный слой атмосферы
309
где
x=2x£?V\
*=Ьг)+Ы-)-а*-г^г- (11ЛЛ1)
Полученная система уравнений (11.1.1), (11.1.3), (11.1.5),
(11.1.7), (11.1.9) и (11.1.10) является замкнутой и позволяет
определить все искомые величины (и, v, kt /, 6, Э, q) при
заданных граничных условиях, характер которых будет зависеть
от конкретной специфики задачи.
Исследование решения выписанной системы показывает, что
основные трудности задачи заключаются в определении
характеристик турбулентности, и в частности коэффициента
турбулентности, которые связаны с вертикальными профилями
метеорологических элементов сложными нелинейными зависимостями.
Прежде чем искать решение задачи в выписанном виде,
рассмотрим случаи, когда удается упростить систему и за счет
этого получить обозримые аналитические решения. Это
оказывается возможным при рассмотрении малых высот или при
использовании некоторых априорных гипотез относительно
профиля коэффициента турбулентности в пограничном слое.
11.2. Распределение метеорологических элементов
и характеристик турбулентности вблизи поверхности земли
Слой вблизи поверхности земли (толщиной около 10—100 м)
часто называется приземным слоем (или подслоем). Здесь, как
правило, наблюдаются максимальные градиенты
метеорологических элементов. Важной особенностью приземного слоя, в
значительной мере оправдывающей выделение его в рамках
пограничного слоя, является относительное постоянство по высоте
турбулентных потоков. Хотя процессы в этом слое тесно связаны
с процессами во всем пограничном слое, часто для решения ряда
важных задач достаточно установить внутренние связи между
метеорологическими элементами и характеристиками
турбулентности в одном только приземном слое.
Получим систему уравнений для приземного слоя.
Проинтегрируем от го (уровень шероховатости) до г
уравнения (11.1.1):
cgs\n cL)dz = 0f
cgcosz)dz=0, (11.2.1)
du
~dz~
и da
kz dz
kjlv\kdv
dz \z dz
г +J2o)z(^-
z
— 2о)г (и —
Ко x
310
Глава 11
где а — угол между направлением геострофического ветра и
осью ох. Если ось ох направить вдоль вектора приземного
ветра, то нетрудно показать, что она будет совпадать и с
направлением касательного напряжения т у поверхности земли.
Действительно, если в общем случае а'—угол между
направлением приземного ветра и осью ох, а а"— угол между
направлением касательного напряжения и осью ох, то
dv/dz
► о da/dz '
ь и
В таком случае
, „ ту dvjdz
zx \z^o du/dz
dz \zQ ' dz
_*___ 2
(11.2.2)
где v* имеет размерность скорости и называется динамической
скоростью (или скоростью трения).
Используя (11.2.2) и переходя в правой части (11.2.1) к
безразмерным переменным (un = u/cgl vn = v/cg, zn = z/h, где h —
высота приземного слоя), получим:
. da
dz
= 1 +
5—(vn — sma)znt
dv
~dz
—\Un— ZQSCL)Zn
(черта сверху означает осреднение по высоте). Так как
безразмерные величины имеют порядок единицы и, кроме того, cosa =
= 0(1), sin a<gl (по наблюдениям a= 10-И50), то
, da
dz
1 +
2v>zCgh
0(1).
dv
~dz
—fJ-[0(1)-0(1)).
V
Из первого уравнения можно оценить высоту приземного
слоя А, которая должна удовлетворять условию
2u>zcgh
«1.
(11.2.3)
Пограничный слой атмосферы
311
Если 2(о2=Ю-4, cg= 10 м/с, ^ = 10-* м2/с2, тогда А<100 м.
Таким образом, в пределах приземного слоя —<С1, т. е.
направление ветра практически не изменяется, и для
определения скорости ветра можно использовать следующее уравнение:
и da 2
k4T = v*>
(11.2.4)
полагая, что ось ох совпадает с направлением ветра. Уравнение
(11.2.4) означает, что при z<h можно не учитывать силу Ко-
риолиса и движение воздуха рассматривать как одномерное.
Проинтегрируем теперь от го до г уравнение притока тепла
(11.1.6):
, dS
^k4z~
т dz
Ф (г) — Ф (0)
Если обозначить через Л> турбулентный поток тепла в
приземном слое (или у поверхности земли), т. е.
Л)=— рСр*тк
dQ
dz
то
OLTk
dS
dz
Для малых г (г<С
Ро'?сР
Ро
дФ/dzU
-=-1
1 дФ
Ро dz
Z.
(11.2.5)
] формула (11.2.5) примет вид
dz ?ср
(11.2.6)
Уравнение (11.2.6) означает, что в пределах приземного слоя
можно пренебречь радиационным и фазовым притоком тепла.
В морских условиях лучистый приток тепла играет важную роль
в формировании распределения температуры в приземном
(приводном) слое.
По аналогии с (11.2.6) можно получить из (11.1.8)
уравнение для определения удельной влажности:
Р '
*<** dz
(11.2.7)
где £0—скорость испарения. Уравнение (11.2.7) основано на
предположении о возможности пренебречь в приземном слое
притоком влаги за счет фазовых переходов.
312
Глава 11
С учетом выражений (11.2.4) и (11.2.6) уравнения (11.1.3),
(11.1.5) и (11.1.10) можно записать в виде:
„4
^M-f-gr+c-i-=0. (11-2-8)
k = l\/T, (11.2.9)
'—"infer- <1,-2Л°)
где
И
£ ^о
*"" £2 + г pcpk #
При выводе (11.2.8) считалось, что поскольку при z = zo
турбулентный поток кинетической энергии турбулентности равен
нулю (нет потока через поверхность), то для малых z
диффузией можно пренебречь. О некоторых эффектах, связанных
с влиянием диффузии, будет сказано в конце данного
параграфа.
Полученная система уравнений (11.2.4), (11.2.6) — (11.2.10)
позволяет определить все интересующие нас характеристики
приземного слоя. Постоянные интегрирования должны
определяться из граничных условий:
г = 2о, и = 0, 6 = 0(0), q = q(0), k = k(0). (11.2.11)
Параметры v*> Л>, £о предполагаются известными. Они могут
быть также определены после интегрирования уравнений, если
известны и, 0, q на какой-либо высоте (например, из
градиентных наблюдений). Прежде чем непосредственно решать
выписанную систему уравнений, рассмотрим подход, основанный на
использовании анализа размерностей.
I. Анализ выписанной системы показывает, что искомое
значение коэффициента турбулентности в приземном слое должно
а
зависеть от следующих параметров: о#, -|г, Ро/рСр, z (если
считать влажность пассивной субстанцией). В таком случае
*-/(«.. 4-•-£•*)• <П-2Л2>
где
[-f ]=z.r-*e->, [-g-)=zr->e, \z\=l.
Пограничный слой атмосферы
313
Для определения вида зависимости (11.2.12) используем
П-теорему. Так как в данном случае ищется связь пяти
физических величин, из которых только три имеют независимую
размерность (v#y г, g/T)y то соотношение (11.2.12) можно
раскрыть только с точностью до функции от безразмерного
аргумента:
g Ро
k J T 9cp
va*z*
Приравнивая показатели степени при основных размерностях,
определяем ai, с*2, pi, 02 и получаем
k = v*zF\ ^^ |. (11.2.13)
Т ?сР
Если обозначить через L комбинацию, имеющую размерность
длины, т. е.
(L — масштаб Монина—Обухова), получим выражение для
коэффициента турбулентности в виде
A = Ti,*F(-f). (11.2.15)
В (11.2.14) постоянная Кармана х введена для удобства
некоторых последующих выкладок, а знак выбран так, чтобы L>0
при устойчивой стратификации.
Установим связь между z/L и используемым обычно для
описания устойчивости числом Ричардсона, которое
характеризует отношение энергии турбулентности, возникающей за счет
силы плавучести, к продукции энергии турбулентности за счет
среднего движения. Воспользуемся выражением числа
Ричардсона через потоки:
Rf =
g Ро
du
Z4F
с учетом
2 du v2
zF
(-9
314
Глава 11
получим
R!4-ff(r)' (Н.2.16)
Из (11.2.16) видно, что z/L однозначно связано с числом
Ричардсона. Знак и числовое значение введенного масштаба L
характеризуют состояние устойчивости: L = oo при
безразличном равновесии, L>0 при устойчивой стратификации и L<0
при неустойчивой стратификации. Однако все характеристики
приземного слоя зависят не от L, а от z/L. Это означает, что
для малых высот все величины ведут себя так, как будто L = oo,
т. е. в области малых z все величины практически не зависят
от стратификации. Более глубокий анализ показывает, что
упомянутое обстоятельство является следствием преобладающего
влияния динамических факторов на режим турбулентного
потока вблизи стенки.
Соотношение (11.2.15) позволяет замкнуть систему
уравнений (11.2.4), (11.2.6) и (11.2.7), если известен вид функции
F(z/L).
Рассмотрим некоторые частные случаи, при которых удается
получить явный вид функции F(z/L).
Безразличная стратификация
Так как при этом Яо = 0, то L = oo и z/L=0. Измерения
в аэродинамических трубах и приземном слое показывают, что
F(0)^k (х~0,4). В таком случае из (11.2.15) для z^zo
получаем
k = *v*z. (11.2.17)
Если подставить (11.2.17) в (11.2.4) и (11.2.7) и
проинтегрировать их при условии (11.2.11) от zo до z, то получим:
Я-Я(0)^--^-\п4-, (П.2.18)
или при наличии данных градиентных измерении:
u = Ui г°
*0
Пограничный слой атмосферы
315
?-<7(0) = (?2-<7i)
ln-
*о
In
г-г
(11.2.19)
Итак, в случае безразличной стратификации
коэффициент турбулентности является линейной, а профили
метеорологических элементов — логарифмическими функциями высоты
4 и м/с
Рис. 11.2. Профиль
скорости ветра при
безразличной стратификации.
q2/K2
Рис. 11.3. Профиль
удельной влажности при
безразличной стратификации.
(рис. 11.2 и 11.3). Из (11.2.19) и (11.2.18) нетрудно получить
выражения для турбулентных потоков т и £0, пригодные для
расчета соответствующих величин по градиентным
наблюдениям.
Стратификация, близкая к безразличной
Примем, что турбулентный поток мал (а значит, мало z/L).
В этом случае F(z/L) целесообразно разложить в ряд Макло-
рена. Ограничиваясь первыми двумя членами ряда (так как
316
Глава 11
z2/L2 — уже величина второго порядка малости) и вынося за
скобку F(0) = к, получим:
'(-гМ'-'тЬ
Inz
Z30\-
-1,15V-
-2,30
4 и м/с
Рис. 11.4. Профиль
скорости ветра при
стратификации, близкой к
безразличной.
/) Р0=»0,05 кал/(см2 • мин),
2) А>=0,0,
3) Ро=— 0,05 кал/(см2 • мин).
inz
2У30
1,15
п
-1,15
О 7П
-
/I /
- \
I I I I
I I I
285
290
ек
Рис. 11.5. Профиль температуры при
стратификации, близкой к
безразличной.
Усл. обозначения см рис. 11.4.
где
Р =
/40)
(по современным данным, р изменяется в широких пределах —
от 0,6 до 10).
В таком случае (11.2.15) примет вид
ft —xz>#z(l—р-£-].
(11.2.20)
Из (11.2.20) видно, что при неустойчивой стратификации
(L<0) коэффициент турбулентности больше, чем при
устойчивой (1>0).
Пограничный слой атмосферы 317
Выражения для профилей метеорологических элементов
можно получить, если подставить (11.2.20) в (11.2.4), (11.2.6),
(11.2.7), проинтегрировать их от го до г и ограничиться
главными членами:
—2-0-s-+i»-r).
e=e(0)+7;(in-^+P-r).
? = ?(0) + ?.(ln^+p^). (П.2.21)
где
Т — р° а = £°
Итак, при стратификации, близкой к безразличной,
получаются линейно-квадратические профили k и
линейно-логарифмические профили и, 0 и q. Очевидно, что при устойчивой
стратификации градиенты метеорологических элементов больше, чем
при неустойчивой (рис. 11.4 и 11.5).
Свободная конвекция
В случае свободной конвекции и*->-0 и L->0 (так как
турбулентность возникает только за счет силы плавучести).
Поскольку k не может быть равным нулю или оо, то v* не должно
входить в формулу (11.2.15). Этому условию отвечает
следующее выражение для F(z/L):
При этом
k = A2z'\ (11.2.22)»
где
a-aL* р° V*
A2-Ax\*^r-— j .
1 В сущности, это означает, что при состоянии, близком к свободной
конвекции, имеет место следующее разложение:
'Ш-*(Я"('+с4+«-§-+-)-
318
Глава 11
Профили в и q определяются следующими соотношениями:
в = в(0)+^ (г-,/,-г0-,/'),
q = q(P)+B2(z-4>-Zo43), (11.2.23)
где
о ЗРо о 3£q
*51==—л > D1 ==z—л •
А<2?Срат z AtfOLq
Итак, при свободной конвекции получаются степенные профили
k, в и q.
Предельно устойчивое состояние {инверсия)
При предельно устойчивой стратификации становится
невозможным существование крупных вихрей (существование таких
возмущений связано с очень большими затратами энергии на
работу против силы плавучести) и турбулентность может
существовать лишь в форме мелких вихрей. В таком случае
турбулентный обмен между различными слоями воздуха затруднен
и турбулентность приобретает локальный характер, близость
стенки перестает влиять на режим турбулентности и,
следовательно, коэффициент турбулентности не должен зависеть от г.
Это означает, что в предельно устойчивом (но все еще
турбулентном) потоке
f{-t)-dxut\
Тогда
k = Dx<v*L, (11.2.24)
где Di — коэффициент пропорциональности.
Нетрудно показать, что при этом получаются линейные
профили и, 0 и q:
9 = 9(0) -D2z,
q = q(0)-D3z, (11.2.25)
где
D =- P° D = £°
2 pcpaTDxv*L ' 3 paQDxv*L
Наряду с приведенными выше формулами для профилей
метеорологических элементов при некоторых предельных условиях
стратификации имеются и интерполяционные формулы для про-
Пограничный слой атмосферы
319
межуточных стратификации, которые, правда, имеют более
сложный вид.
На примере рассмотренного выше подхода хорошо видна
эффективность использования теории подобия и анализа
размерности при решении задач с небольшим числом параметров.
Обратим внимание на то, что при выводе (11.2.15) удельная влажность
считалась пассивной субстанцией. В действительности устойчивость зависит
не только от градиента потенциальной температуры, но и от градиента
удельной влажности, т. е. в общем случае от градиента плотности. Поэтому
коэффициент турбулентности следует считать функцией параметров и*, g/p, Fp/p,
z,1 т. е.
k = F[v„ -^.
44-
Здесь
'wM-ar + Tp)
есть поток плотности; у р — равновесный градиент плотности. Используя П-
теорему, получаем
k = v*zF(-^\, (11.2.26)
где
L
vi
X
it . (11.2.27)
g t9
Р Р
Знак минус поставлен для того, чтобы при устойчивой стратификации
плотности, т. е. при Fp <0, L было больше нуля.
С помощью третьего уравнения движения, уравнения статики и
уравнения состояния влажного воздуха можно получить два равноправных
соотношения для определения условий вертикальной устойчивости:
dw
dw
~dF
—fr(4r+'■+«*»»•-й-)-'-
-fl-frl-^0'605^)^]""'-
Здесь Тъ — виртуальная температура (практически ТВ^Т)\ у&— сухоадиаба-
тический градиент.
Так как при безразличной стратификации ускорение частицы равно нулю,
можно определить у р:
_ р
Тр - т Та-
1 Если турбулентные потоки тепла и влаги в приземном слое не зависят
от высоты, то в число параметров можно включить турбулентный поток
плотности у поверхности земли.
320
Глава 11
В таком случае поток плотности можно записать в виде
Установим теперь связь между масштабами L и L и оценим диапазон
условий, для которых различие между ними может быть существенным.
Воспользуемся выражением для L (11.2.27) и выражением для потока
плотности, в которое подставим для р выражение из уравнения состояния
влажного воздуха. В таком случае, если пренебрежем в пределах приземного
слоя dp/dz, а градиенты температуры и влажности выразим через
соответствующие потоки (считая ат = ад = ар), получим
i т v3 \ ?Ср р ;
Переходя к потоку скрытого тепла J?E0 и вынося за скобку Р0, получим
L
или с учетом (11.2.14)
где
Т
•^0+-Е-)
L= , (11.2.28)
1 + —
^ Во
Р ^ 0,07;
Во = о?°р отношение Боуэна, которое при условии подобия профилей
температуры и влажности вплоть до самой подстилающей поверхности можно
записать в форме
Bo=^^w- (,,Д29>
Для суши испарение обычно мало, а значит, велико Во и L — L. Для условий
океана Во изменяется от 0,1 вблизи экватора до 1,0 в умеренных широтах.
Таким образом, L может в 2 раза отличаться от L, и нетрудно проследить
влияние этого факта на профили метеорологических элементов и
коэффициента турбулентности. Так как для морских условий знаменатель в (11.2.29)
обычно меньше нуля, знак Во определяется характером термической
стратификации: при неустойчивой стратификации Во>0 и L<L, при устойчивой
стратификации Во<0 и L>L.
II. Выше при получении F(z/L) и профилей
метеорологических элементов мы использовали уравнения (11.2.8) — (11.2.10);
соображений размерности было достаточно для получения
искомых функций с точностью до некоторых множителей (В* и др.)-
Рассмотрим теперь всю систему уравнений. Поскольку она зам-
Пограничный слой атмосферы
321
кнута, результаты, разумеется, никаких неопределенных
множителей уже содержать не будут, искомые величины выразятся
через элементарные функции и в пределах рассматриваемой
модели, будут описывать режим приземного слоя при любой
стратификации.
Введем следующие масштабы:
и v* Ь , -1/, 2 в г\ Ро
£о •, -r-=*o = *«*^o, -^ = /o=*c,/4Z0; (11-2.30)
Lo = L есть масштаб Монина—Обухова [см. (11.2.14)].
С учетом (11.2.30) исходная система может быть записана
в виде:
Яп q° pw*
a<*kn dzn
dzn
-=o,
I __o kn(\-kn) dzn
ln~A 2-kn dkn
Если исключить из последних трех уравнений 1п и Ьп, то
dkn 2(\-kn)sl
(11.2.31)
dzn
2-kn
(11.2.32)
Интегрируя это уравнение при условии lim&„ = 0 (ранее было
показано, что для малых z k = xv*z), получаем
Zn v я У 3 '
(11.2.33)
где у — вспомогательная функция, связанная с zn соотношением
(11.2.33), а с kn соотношением
1-/ = £„. (11.2.34)
Другие характеристики определяются как
Ьп=у\
1п = -
(11.2.35)
(11.2.36)
21 Заказ М> 612
322
Глава 11
Если в уравнениях притока тепла и влаги перейти к
приведенным значениям температуры и влажности
в = |сста£0, q = $aQdq, (11.2.37)
то решения первых трех уравнений системы (11.2.31) совпадут
друг с другом и примут следующий вид:
ил = вл+С2=?л+Сз = ^-+2агс1еу+1п^^-+С1.
(11.2.38)
Произвольные постоянные (С*) могут быть определены на
основании граничных условий. Если воспользоваться известной из
наблюдений зависимостью aT = aT(z/L), то можно перейти от
0П и qn к ®п и qn, которые при условии aT = ag будут
совпадать. Таблицы универсальных функций ип и 0 п для разных Zn
и у приведены в монографии Д. Л. Лайхтмана «Физика
пограничного слоя атмосферы». На рис. 11.6 показана зависимость
от zn (для скорости ветра от \gzn) следующих безразмерных
функций: 6п, &п, у, Aun = un(zn)—an(0,5). Хорошо видно
различие в кривизне профилей ветра при устойчивой и
неустойчивой стратификации. При малых zn подтверждается полученная
ранее линейная зависимость kn от высоты. По виду кривых kn
и Ьп можно качественно оценить влияние диффузии на режим
приземного слоя. При устойчивой стратификации для zn>2
градиенты Ъп малы и притоком энергии турбулентности, вероятно,
можно пренебречь; при неустойчивой стратификации такое
пренебрежение может привести к заметным искажениям. Эти
выводы подтверждаются результатами численного интегрирования
системы (11.2.4), (11.2.6) — (11.2.10) для случая, когда в
уравнении (11.2.8) сохраняется диффузионный член. При этом
показано, что влияние диффузии существенно только при сильной
неустойчивости.
Рисунок 11.7 иллюстрирует зависимость от zn компонент
уравнения баланса энергии турбулентности (11.2.8), деленных
a pQ
на -~ . При этом l/kn представляет безразмерную продук-
1 рср
цию, b2Jkn — безразмерную диссипацию, а приток энергии
турбулентности за счет силы плавучести равен 1,0. В области
малых \zn\ вклад стратификации в энергетику турбулентности
мал, однако при \zn 1=0,8 влияние стратификации становится
равным влиянию остальных компонент. При устойчивой
стратификации потеря энергии за счет работы против силы
плавучести компенсируется продукцией энергии турбулентности за
счет среднего движения; при неустойчивой стратификации
Пограничный слой атмосферы
323
Рис. 11.7. Профили компонент
уравнения баланса энергии
турбулентности.
/ — поступление энергии
турбулентности за счет среднего движения; 2 —
поступление энергии турбулентности за
счет работы против силы плавучести;
3 — диссипация энергии
турбулентности.
юо и
Рис. 11.6. Зависимость универсальных
функций kn> Ьп, У ОТ Zn И Attn ОТ lg2n.
Штриховая прямая соответствует k^ ="Zn.
21*
324
Глава 11
поступление энергии за счет реализации запасов энергии
неустойчивости компенсируется диссипацией энергии турбулентности.
Выразим число Ричардсона через полученные универсальные
функции:
Ri=_L(_^L)-'=-i^-=A.. (11239)
а7 \ dzn / ат ат v '
Для устойчивой стратификации (Ri>0) у<\, при неустойчивой
стратификации (Ri<0) у>1, при приближении к безразличной
стратификации (Ri-^0) y-^lfi.
Приведенное выше аналитическое решение системы
позволяет получить как частный случай рассмотренные ранее
профили метеорологических элементов и коэффициента
турбулентности при некоторых предельных условиях стратификации.
Если на основании (11.2.33) и (11.2.34) разложить kn в ряд
Маклорена вблизи точки zn = 0 (у = 1,0), то после некоторых
преобразований получим
Л 3_ \
У*/С' I 8 ^п I '
--yLV±Z\
и=-^(1п^+-§-г")>
е=-
Ро
pCpXf»
Ео
При свободной конвекции (zn-*—оо, у^оо) на основании
(11.2.40)
(11.2.33) у можно разложить в ряд:
у=-(4**у/8(с°+
при этом подстановкой в (11.2.33)
С3=4/э. В таком случае
3 /3 я Ро V/«
+...).
k— 2 х( 2
рСр
можно найти, что Со = 1,
16 1_\ ]
9 гп )'
'/3(l +
в =
х<хт(оо) \ рср
Ш"(х^)^'"+с°-. I (П.«1)
. 1 /з *g р0 \ '/./,1 8 1 \
Пограничный слой атмосферы
325
Для ряда важных прикладных задач (трансформация и
диффузия), в которых фигурирует большое число параметров,
желательно иметь простое аналитическое выражение для
коэффициента турбулентности. Наблюдения и рассмотренные модели
приземного слоя показывают, что возрастание скорости ветра
с высотой довольно хорошо аппроксимируется степенной или
логарифмической формулой. Такое изменение ветра (и других
метеорологических элементов) можно получить, используя
степенную формулу для коэффициента турбулентности, например
kn(Zn) = Azln 6.
(11.2.42)
При этом удается получить простые, легко обозримые решения
ряда прикладных задач.
Если проинтегрировать первые четыре уравнения системы
(11.2.31) с учетом (11.2.42), то нетрудно получить степенные
формулы:
1_ 2п — z0n
®л — вл (г0п) —-j- J
dzn
z0n "т
Яп — ЯпЫ = ^- j —
(*пУ
dzn
"0/2
Ы*п
1-е
bn = V\-Az\~\
(11.2.43)
или для размерных величин:
и =
%ALl
в(г)-0(го) =
«ю-^н- * J_£^,
"On
Лгп)гп
b = c-xuv\V\-Az\-\
) (11.2.44)
326 Глава 11
Если считать, что из-за слабого влияния стратификации при
малых z величина dk/dz\ZQ = KV* для любой стратификации
(кроме случая L = 0), то
Л—пЫт-)'- (11-2-45)
Параметр е должен удовлетворять следующим условиям:
[ 0 при Z,-^oo,
е(2ол)= 1 при L-++0, (11.2.46)
I—7з при Z.—-0.
Параметр е легко определить по данным градиентных
наблюдении
, если построить график u(Zi)=Fl— ), подобрав
такое значение е, при котором точки наилучшим образом ложатся
на прямую. Из этого же графика определяется и параметр
шероховатости го.
Установим связь е с L. Из (11.2.43) следует, что
}*г"' =-(1-е).
d In zn v '
С учетом (11.2.33) и (11.2.38) получаем
1—« Г^5-- (И-2-47>
Из (11.2.47) видно, что 8 оказывается функцией высоты.
Можно, однако, определить среднее значение е в слое (zin>
Z2n)> которое более определенно характеризует состояние
атмосферы:
i-«-—-—Г-|*Ч-&..
zn —zn J 1 — у8 л*
или после интегрирования
}~Г згг -г ъ 1^(У2)-АГ(У.)1, (П.2.48)
где
N (у) = 2 In (1 +у) J/T+7" - 2 arctg у+-§- У8.
Переменные t/i и г/2 определяются формулой (11.2.33).
Пограничный слой атмосферы
327
11.3. Расчет турбулентных потоков тепла, влаги
и количества движения
Турбулентные потоки являются важной количественной
характеристикой взаимодействия воздушного потока с
подстилающей поверхностью. Непосредственное измерение потоков
•z = —pu'w'9 Яо = — pCpW'Q',
£"o = -P^V (11.3.1)
сопряжено с рядом больших трудностей. В связи с этим особое
значение имеют методы расчета потоков по стандартным или
градиентным'наблюдениям. В настоящее время таких методов
существует довольно много. В данном параграфе мы изложим
только методику, основанную на использовании решения
нелинейной системы (11.2.31), которая представляется физически
наиболее обоснованной.
Ранее уже отмечалось, что для реализации полученных
решений необходимо знать зависимость величин aT = kT/k и aq =
= kq/k от z/L. Определению этих величин посвящено большое
количество работ, однако отсутствие надежных
экспериментальных данных о комплексе метеорологических элементов при
установившихся условиях над однородной поверхностью
затрудняет точное определение ат и aq. Большинство исследователей
считает, что ат близко к единице при безразличной
стратификации, увеличивается до 3,0—3,5 с ростом неустойчивости и меньше
единицы при устойчивой стратификации. По предварительным
данным ат^а<2.
На основании нелинейной модели приземного слоя можно получить
формуле и dS ,
лы для определения ат. Если представить ат = к—z— и выразить я
из (11.2.34) и (11.2.30), то Р
Г Т (Ро?ср)* Т/з 1
— Ь—PlH 0-,.,-g-' <1т>
Величину Р0 можно получить из уравнения теплового баланса поверхности
или прямых измерений; dS/dz находится из градиентных наблюдений. Для
определения L на основании (11.2.30) запишем
Д«2(^4^з) д*4 eL '
Если считать T/g «28, то
да (JL. _£L\
328
Глава 11
Для фиксированных гг- можно построить зависимость функции Ф от L,
которая позволяет определить L в зависимости от Дв/Да2. В качестве примера
на рис. 11.8 показана такая зависимость для z2=zA=2$ м, Zi=z3=0,5 м.
Теперь соотношение (11.3.2) позволяет определить сет. Полученная таким
путем зависимость ат от z/L и была использована для перехода от Gn к 6П.
Для определения турбулентных потоков с учетом (11.2.30)
можно записать:
ig-** AuAQ=--f^AunAQnf
flu? Рсрх
AuAq = --^-AunAqn9
Au = ^Aunt
-/
откуда
п 9 Дм лв
Р0=-р*2сР ЛЦяА6п
0 1 2lgL
О 10 1001м 5?Е=-р5?-£ А А ,
Рис. 11.8. Зависимость мас-
штаба! от 0>(L)=-^. ^*=^' (1L3'4>
Для использования формул (11.3.4) нужно сперва по Аи и
AG рассчитать L из (11.3.3), затем найти znu а потом по
заранее составленным таблицам найти АиПу AGn, Aqn. Более
целесообразно построить номограммы, позволяющие определить Ро
и v# как функции AG и Аи. Допустим, что z2=z^ и 21=23.
Зададим для выбранных величин Poj ряд величин и*г\ Найдем Lu
z2/Lu Zi/Lu (иП2)и (uni)u (Gn2h, (Qni)i. Определим (Aun)i и
(AQn)i и с помощью (11.3.4) перейдем к Aui и Двг\ Построим
теперь изолинии Poj и v*i в системе координат Аи, AG. В
качестве примера такая зависимость для 22=24 = 2,0 м и 21=23 =
= 0,5 м показана на рис. 11.9. Обращает на себя внимание, что
v# слабо зависит от градиента температуры при градиенте
скорости больше 1,0 м/с.
Нетрудно показать, что изолинии Ро можно рассматривать
как изолинии J2>Eq, если считать, что AQ=^^A^. Это стано-
ср
вится очевидным, если приравнять правые части первых двух
уравнений (11.3.4).
Сравнение результатов расчета с данными прямых
измерений (рис. 11.10) свидетельствует об их удовлетворительном
согласии.
Пограничный слой атмосферы
329
Над водной поверхностью градиентные наблюдения производятся редко,
поэтому желательно уметь определять турбулентные потоки по результатам
гидрометеорологических наблюдений, которые включают измерение
температуры поверхности воды, а также скорости ветра, температуры и влажности
воздуха на уровне судовых измерений z = a (для современных судов а=6-н
н-30 м). В качестве нижнего уровня нужно брать уровень шероховатости
X
Ср ""> Рис. 11.9. Номограмма для определе-
ния турбулентного потока тепла Р0,
затрат тепла на испарение J^Eq и
динамической скорости v* как функций
Аи, Д9, Aq.
1) Р0 и JZ'Eq [кал/(см2 • мин)]; 2) i/# (м/с).
Рои
0,5 г
0,5
ОА
0,3
0,2
0,1
-
_
—
"~ 0
X
о
ххо£о °
х °л х х
о X х'
о уо
csc< °
оу/о °
<
_ 1 . J 1
°;^<
^ .
О
О
х /
о 2
1 1
0,/ 42 ^ 0,4 0,5 Р0р
Рис. 11.10. Сравнение наблюденных (Р0 н)
и рассчитанных (Р0 Р) значений
турбулентного потока тепла [кал/(см2 • мин)].
/ — Суинбэнк, 2 — Цимлянск, 1965 г.
z=Zjo. Для морской поверхности, однако, уровень z0 уже не является
внешним параметром, так как он связан с действием ветра, вызывающего
развитие волн. В среднем выполняется следующая зависимость:
ZQ = m-
g
(11.3.5)
Коэффициент m находится в пределах 0,02—0,08.
Наблюдения показывают, что при z=z0 температура воздуха стремится
к температуре подстилающей поверхности, а удельная влажность — к
насыщающей удельной влажности при температуре поверхности. Скорость ветра
при z~Zq равна скорости поверхностного течения, которая, однако, как
правило, составляет всего около 2% скорости ветра на z=а.
Таким образом, специфика расчета турбулентных потоков по стандартным
наблюдениям над морем состоит в том, что нижний уровень (z=z0) не
330
Глава 11
-0,25 о 6
-0,20 0J
и а м/с
Рис. 11.11. Номограмма для расчета турбулентного
потока тепла Р0, затрат тепла на испарение J£Eq и
динамической скорости v * как функций скорости ветра иа и
разности значений температуры и удельной влажности
на г=14 м и 2 = 0 м.
/) Р0 и J2>E0 [кал/(см2 • мин)], 2) v* (м/с).
-40 -20
Рои
60г
Ь0
20
-20
-ttO
X
X х
J_
_L
20 40
°9 Рис. 11.12. Сравнение
наблюденных (Рон) (по данным Хас-
се) и рассчитанных (Pop)
значений потока тепла.
Пограничный слой атмосферы
331
фиксирован, а находится в процессе расчета на основании (11.3.5). В качестве
лримера на рис. 11.11 помещена номограмма для расчета v*, Р0 и JZ'Eq по
наблюденным значениям иа, Д6=6а — в(0), Aq=qa — Я(0) для г=а=14 м.
Некоторые результаты сравнения рассчитанных и наблюденных значений
потока тепла Pq приведены на рис. 11.12.
11.4. Однопараметрическая модель пограничного слоя
атмосферы (k = const)
Вернемся к рассмотрению системы (11.1.1), (11.1.3), (11.1.5),
(11.1.7), (11.1.9) — (11.1.11). Ранее уже говорилось, что основные
трудности заключаются в определении характеристик
турбулентности, которые связаны с профилями метеорологических
элементов сложными нелинейными зависимостями. Вместе с тем
известно, что даже грубая аппроксимация коэффициента
турбулентности часто приводит к удовлетворительным результатам.
Например, модель Акерблома—Экмана, в которой коэффициент
турбулентности считается заданной и постоянной величиной,
довольно правильно отражает ряд следующих из наблюдений
фактов (правый поворот и увеличение скорости ветра с высотой
в пограничном слое). Модели с априорным заданием профиля
коэффициента турбулентности (закон с изломом, степенной
закон и др.) дают еще лучшее согласование с наблюдениями,
особенно в нижней части пограничного слоя. При этом решения,
однако, имеют сложный вид.
Хотя в моделях с априорным заданием значения или
профиля коэффициента турбулентности нарушается взаимосвязь
коэффициента турбулентности с профилями метеорологических
элементов, можно указать по крайней мере на две причины
удовлетворительного согласия этих моделей с наблюдениями. Во-
первых, несмотря на широкий диапазон изменений
коэффициента турбулентности, он всегда остается положительным. Во-
вторых, искомые функции — ветер, температура и влажность —
удовлетворяют точным граничным условиям.
Рассмотрим наиболее простую модель, которая приводит
к-обозримым формулам и позволяет понять механизм
формирования процессов в пограничном слое атмосферы.
Заменим коэффициент турбулентности средним по высоте
значением k. В таком случае уравнения движения (11.1.1)
примут вид:
А-Ц—2<М«-«,)=0. (И.4.1)
332
Глава 11
Для определения k используем интегральное уравнение баланса
энергии турбулентности, которое на основании (11.1.2) можно
записать в форме:
-S-[[(-S-),+(-^),-+--S-]*-
и н
—L- j edz—jL j Ddz = 0, (11.4.2)
где H — высота пограничного слоя атмосферы.
Так как диффузия представляет собой только
перераспределение энергии турбулентности и ею на границах можно
пренебречь,1 в интегральном уравнении баланса можно не
учитывать последний член.
Среднюю диссипацию иногда представляют как некоторую
долю от продукции энергии турбулентности за счет основного
движения либо за счет притока энергии турбулентности,
связанного с плавучестью. Оба эти подхода, однако, даже качественно
плохо согласуются с действительным положением дел. В первом
случае диссипация убывает до нуля при приближении к
свободной конвекции, во втором случае всегда положительная и не
равная нулю диссипация связывается с величиной, которая
может быть как положительной, так и отрицательной. Более
естественно предположить, что средняя по пограничному слою
диссипация является функцией двух параметров — среднего
коэффициента турбулентности и толщины пограничного слоя
атмосферы. Вид этой функции легко находится из анализа
размерности:
н _
JLJ *dz=f(k, Я) = С,-^-. (11.4.3)
О
Соотношение (11.4.3) можно получить также из (11.1.4) и
(11.1.3), если считать, что для среднего коэффициента
турбулентности характерным масштабом является не Z, а Я. С учетом
приведенных соображений уравнение (11.4.2) можно переписать
в виде
*f Ш+(-й-Г-+--£]*-*. -&--<>• <»•«>
Примем простой линейный закон изменения турбулентного
потока тепла и влаги с высотой, который правильно учитывает
1 Небольшой обмен энергией между пограничным слоем и свободной
атмосферой вряд ли играет существенную роль.
Пограничный слой атмосферы
333
известные из наблюдений факты: у поверхности земли, при 2 = 0,
P(z) =Ро, E(z) =Ео; на верхней границе пограничного слоя, при
г = Я, все турбулентные потоки должны стремиться к нулю, т.е.
Р(Н) =Е(Н) = 0. В таком случае уравнения (11.1.7) и (11.1.9)
примут вид:
(l—£-). (И.4.6)
««*-£*- = - —
Для замыкания системы уравнений необходимо
дополнительное соотношение для определения Я. Это соотношение можно
получить из ряда качественно равноценных предположений.
Высоту пограничного слоя можно определить: 1) как уровень, на
котором модуль скорости ветра впервые становится равным
модулю скорости геострофического ветра, т. е. (и2+v2) \2=н =
= u2+v2\ 2) как уровень, в окрестностях которого градиент
скорости ветра по высоте равен нулю, т. е. —т— Уu2+v2\z=h = 0\
3) как уровень, на котором ветер впервые совпадает с
геострофическим по направлению. Ограничимся третьим
предположением, как наиболее простым:
v
а
z = H
(11.4.7)
где ug, vg — проекции геострофического ветра на оси ох и оу
соответственно.
Воспользуемся следующими граничными условиями:
при 2=0 u=v=*0, (11.4.8)
при z = H u-*ugt v^vgt T=THi q = qH. (11.4.9)
Граничное условие (11.4.8) следовало бы ставить на z=Zo,
однако рассматриваемая простая модель заведомо искажает
профиль ветра вблизи поверхности земли, поэтому введение
дополнительного параметра z0 вряд ли целесообразно.
В дальнейшем будем считать, что k = kT = kq, или aT = <xq =
= 1,0.
Примем следующий алгоритм решения: сперва из (11.4.1)
определим профиль ветра, а из (11.4.5) и (11.4.6)—профили
температуры и удельной влажности; затем используем
полученные решения и найдем из (11.4.3), (11.4.4) и (11.4.7)
диссипацию, коэффициент турбулентности и высоту пограничного слоя.
334 Глава 11
Умножим второе уравнение (11.4.1) на i (f = V — 1) и сложим
с первым. Тогда
а2ф 2а2/Ф=0, (11.4.10)
dz*
где
Решение (11.4.10) имеет вид
Ф = С1еа{Х + *)*+С&-а{1 + 1)ж. (11.4.11)
Для определения Ci и С2 перепишем для Ф граничные
условия (11.4.8) и (11.4.9):
при Z=*0 Ф^—Ug — tVg,
при z = H Ф = 0. (11.4.12)
Подставляя (11.4.12) в (11.4.11), получим, что Ci = 0,
С2= —ug — ivg. В таком случае
u+iv = {ug+lvg)(l-e-{l + l)a*). (П.4.13)
Если выразить e~iaz в тригонометрической форме и
разделить в (11.4.13) действительные и мнимые части, то
и = ug — ё~ аг (ug cos az -f vg sin az)t
v=vg — e~az(vgcosaz — ugsmaz). (11.4.14)
Годограф ветра, описываемый соотношениями (11.4.14),
называется спиралью Экмана. Для частного случая, когда ось
ох совпадает с направлением геострофического ветра (1^ = 0,
Ug = cg)y формулы (11.4.14) принимают вид:
и = cg (1 — е" az cos az),
v=cge~azsinaz. (11.4.15)
На рис. 11.13 показан универсальный годограф ветра, по-
и v
строенный в системе координат ип= и vn= ; точки на
Cg cg
кривой соответствуют разным значениям zn = az. Вектор ветра
на высоте гп% равен вектору, имеющему начало в точке ип =
= уп = 0, а конец в точке с соответствующим значением zn- В
пограничном слое, как следует из рис. 11.13, имеет место правое
вращение ветра с высотой.
Из анализа (11.4.14) или (11.4.15) хорошо видно влияние
турбулентности на вертикальный профиль ветра: сильная турбу-
Пограничный слой атмосферы
335
лентность (большие значения k) вызывает медленное
увеличение ветра с высотой, а слабая — быстрое. Так как со2 = со sirup
(<р — широта), то увеличение широты соответствует
уменьшению коэффициента турбулентности, а уменьшение <р —
увеличению k.
Угол между вектором геострофического ветра и вектором
ветра на любой высоте определяется как
tg" = --=-
\-е~
(11.4.16)
ft* г
0,2
0,75
Ш
VOm
\- °у10л
0,5
цШ
W5
\2fi0
\2.25
\2J50
\2J5
Wfio"*
Рис. 11.13. Универсальная спираль Экмана.
При 2 = 0 в (11.4.16) получается неопределенность типа %,
раскрыв которую (по правилу Лапиталя), находим, что a|z=o =
= 45°, т. е. ветер у поверхности отклоняется влево от
геострофического на угол 45°. Полученное значение угла примерно
в 1,5—2,0 раза больше наблюдаемого (для средних условий),
что связано главным образом с предположением о среднем
коэффициенте турбулентности.
Рассмотрим теперь на простых примерах особенности, обусловленные
изменением коэффициента турбулентности и геострофического ветра с высотой.
Получим формулы, описывающие распределение ветра с высотой при
&i=-const в нижней части пограничного слоя (z^h) и k2=const в верхней
части (z>h), используя на границе раздела между ними условие
непрерывности скорости и потоков количества движения. Ось ох направим вдоль
вектора геострофического ветра (vg=0, ug = cg). В таком случае система (11.4.1)
примет вид:
ki
&и{
+ 2а>2^ = а
(11.4.17)
**-^-2*z(tti-c*)=0.
где i=l соответствует z^h, a i=2 соответствует z>h.
(11.4.18)
336
Глава 11
Решая эту систему аналогично случаю с k = const при следующих
граничных условиях:
при г = 0 tt1 = t/1 = 0, (11.4.19)
При 2—"СО щ = ug = cg, V2 = vg = 0, (11.4.20)
dti\ t duo
при Z = h U\=U2, 1/1=1/2» Pl^l . = P2*2
и считая, что pi~p2, получим:
И1 + /Vl = _LllL с,«. (1 + 0 (*-*> _ _?+1 с*-«. (1 + 0 <*-/», (Ц.4.22)
а2 + /t/2 = - се~аг (1 +г) (г-h) + cg, (11.4.23)
где
-/-Й-
с = -
ssti [Л1(1+1)Л] + ch [Л1(1 + /)Л] *
Если разделить действительные и мнимые члены, то компоненты скорости
будут определяться следующими соотношениями:
"1= g2 + p2 {-^-**(*-Л) [acosai(2r-A)+psine1(^-A)]-
- * + * *-*><г-л) [ocosai(2r —Л)-р sinai (2Г —Л)] \ + се,
"1 = а2 + р2 {-^-L^(z"/t)hslnaiU^A)^pcosai(2r-/z)] +
+ -1+-L *-*!<*-Л> [a sin ai (2Г - A)+pcosfli (г-Л)] |.
И2-- ^у Г81^"^ [aCOSfl2(2r-A)-Psine2(^-A)] + С^.
t/2= fl2^L *-*<«-*> [а8И1Л2(*-А)+рсовв2(*-Л)]. (11.4.24)
где
а = cos aiA (s sh aiA + ch aiA),
P = sin a\h (scha\h + shaiA).
На рис. 11.14 для сравнения приведены годографы ветра, рассчитанные
по модели с k=const и по модели со ступенчатым изменением k. За счет
уменьшения k у поверхности земли по сравнению с первой моделью умень-
Пограничный слой атмосферы
337
шается угол поворота ветра (до 32°) и увеличивается скорость ветра.
Нетрудно убедиться, что при фиксированном k2 увеличение h должно приводить
к увеличению k\t и наоборот. Полученные результаты подтверждают ранее
сделанный вывод о возможном влиянии введения среднего коэффициента
турбулентности в пограничном слое на угол между направлениями приземного
и геострофического ветра. _
Заметное отличие ветра, рассчитанного по модели с k, от наблюденного
может быть также обусловлено влиянием термического ветра. Покажем это
на простом примере.
5 i01000u^c
Рис. 11.14. Влияние профиля коэффициента турбулентности
на годограф ветра в пограничном слое атмосферы (cg =
= 10 м/с, ф = 60°).
/) Т=8,2 м2/с; 2) fc|-l м2/с при z< 100 м, fe2-9 м2/с при 2>100 м.
Допустим, что в пограничном слое атмосферы известны средние
горизонтальные градиенты температуры:
дТ
g
g дТ
= m = const,
2а>27,о дх
= л = const.
(11.4.25)
В таком случае в уравнениях (11.4.1) компоненты геострофического ветра
можно представить как:
vg = vg 0 + Д1,т» tig = ug о + ДИт,
где ug0, vg0 — компоненты геострофического ветра у поверхности земли; Аит,
AvT—компоненты термического ветра.
Если k—const и ось ох направлена по вектору наземного
геострофического ветра, уравнения (11.4.1) запишутся следующим образом:
— d2u . 0 0
*-S—2"* {U " С*о)=2<°*т* (11А26)
Решая эту систему аналогично (11.4.1), получим:
и = cg о (1 — ё~ аг cos az) — mz,
v = cg 0e"az sin az + nz. (11.4.27)
22 Заказ № 612
338
Глава 11
На рис. 11.15 представлены годографы ветра, построенные для разных
значений горизонтального градиента температуры; они сопоставляются с
годографом ветра при отсутствии термического ветра. Как и следовало ожидать,
на основании формул (11.4.27) при дТ/дх = дТ1ду=±\°С1100 км (характерные
значения горизонтального градиента температуры) влияние термического ветра
на годограф незначительно до высоты около 100 м. Выше этого уровня при
росте температуры вдоль направления геострофического ветра (дТ/дх>0)
увеличивается перпендикулярная к геострофическому ветру компонента скорости,
а при падении температуры (дТ/дх<0) она уменьшается. На основании
/000 □
Рис. 11.15. Влияние горизонтального градиента температуры на
годограф ветра в пограничном слое атмосферы (с*о=10 м/с, £=8,2 м2/с,
Ф=60°).
/) дТ/ds^O (см. рис. 11.14); 2) dT/dx=dT(dy=\°Ci№ км; 3) дТ/дх-*дТ/ду=
«=—1°С/100 км; 4) дТ/дх~1°С/№ км, дТ/ду 1°С/100 км; 5) дТ/дх=—1°С/100 км,
дТ/ду=1°С/№ км.
(11.4.27) нетрудно получить формулы для определения направления ветра на
большой высоте и у поверхности земли:
6 °° и \z-
*Ч-Ты
п
» m
acg о + п
(11.4.28)
(11.4.29)
aCg о — /л
Отсюда следует выражение для предельного угла между направлениями ветра
на большой высоте и у поверхности земли:
acg0 (n + m)
*8(",—о)~ aCgo{n-m) + in2+m2) • (11А30>
В частном случае, когда, допустим, т=0, формулы (11.4.29) и (11.4.30)
принимают вид:
acgo + п
tg<*o =
acgo
«("•-"о)1
acgo
acgo + п
Пограничный слой атмосферы
339
Соответствующие углы можно изобразить графически (рис. 11.16). Как видно
из рисунка, при адвекции тепла (п<0) по сравнению со случаем, когда нет
адвекции, увеличивается правый поворот ветра с высотой, а при адвекции
холода (п>0) происходит даже левый поворот ветра с высотой.
Другим не менее интересным вопросом является определение высоты
пограничного слоя атмосферы при наличии термического ветра. Если в качестве
условия существования пограничного слоя
взять
(11.4.31)
то, подставив (11.4.27), нетрудно получить
g \2 I дТ х2
Л
Ufc-n-s-f <-£-<*-' >•
При 7о=300 К, ю,= 1(Н, Ya — Y =
= 0,4°С/100 км оказывается, что
-^-<7°С/100 км. (11.4.32)
(п>0)
,с0'(п>0)
<С0 (71=0)
Со (жО)
-►л?
СдО
V^eo (п<0)
Рис. 11.16. Векторы ветра у
поверхности земли и на большой
высоте (для т=0 и разных
значений п). Северное
полушарие.
Итак, для существования пограничного слоя
конечной толщины, при наличии
термического ветра необходимо, чтобы
выполнялось условие (11.4.32). Это условие
выполняется почти всегда, за исключением
фронтальных зон.
Для определения высоты пограничного слоя атмосферы запишем (11.4.27)
в виде:
Аи = — cgQe~ az cos az%
At, = cg0e~az sin az. (11.4.33)
где Au=u— Cgo + mz, Av=v— nz есть отклонения ветра на данном уровне от
геострофического на этом же уровне.
На верхней границе пограничного слоя ветер становится близким к
геострофическому, т. е.
(Ац)2 + (Аг;)2
(cg0-mz)* + nW
г=И
= е<1.
(11.4.34)
где
(cg0-mz)2 + n2z2 = cl.
В таком случае, подставив выражения для Аи и Av и преобразовав выражение
(11.4.34), получаем
е~2х
е - = е, (11.4.35)
\ acg о )
+ ■
П2
2.2
-JC2
ас
gO
где х=аН.
Для того чтобы (11.4.35) согласовалось со случаем n=m=0, когда аН=
= я, следует принять
е =е~^^ 0.0019.
22*
340
Глава 11
Теперь, решая трансцендентное уравнение (11.4.35) относительно х, можно
определить высоту пограничного слоя атмосферы при наличии термического
ветра.
Выше были рассмотрены наиболее простые модели, позволяющие
проследить влияние изменения коэффициента турбулентности с высотой и
термического ветра. Полученные при этом выводы качественно справедливы и для
более близких к реальным условиям моделей; соответствующие решения имеют
довольно сложный вид и здесь не приводятся.
Если проинтегрировать (11.4.5) и (11.4.6) при условии
(11.4.9), то получим выражения для профилей температуры и
удельной влажности:
1000
z=H
тг=тн+Ъ{Н-г)+
Р0 (Я-г)2
2Н
?cpk
(П.4.36)
<Я-*)2
Р*
2Н
200 \-
Т=ТН
Рис. 11.17. Профиль темпера
туры в пограничном слое атмо
сферы (1=5 м2/с, #=1000 м)
Кривая ....
Ро кал/(см2 • мин)
12 3
0,2 0,0 -0,2
(11.4.37)
На рис. 11.17 в качестве примера
приведены профили температуры
в пограничном слое для
безразличной (Л) = 0), устойчивой (Р0<0) и
неустойчивой (Ро>0)
стратификации. При Ро<0 наблюдается
характерное инверсионное распределение
температуры.
Реальное вертикальное
распределение температуры и удельной
влажности в пограничном слое
атмосферы может заметно отличаться от
распределения, описываемого формулами (11.4.36) и (11.4.37),
из-за весьма обременительного предположения о линейном
изменении потоков с высотой и выбора k = k. В первом
случае не учитывается известный из наблюдений факт смены
знака градиента температуры (а значит, направления потока
тепла) в верхней части пограничного слоя. Во втором случае
профили искажаются вследствие завышения коэффициента
турбулентности в нижней части пограничного слоя и занижения его
в верхней части.
В полученные выражения для профилей скорости ветра,
температуры и влажности входят неизвестные пока величины —
высота пограничного слоя атмосферы и коэффициент
турбулентности. Для определения Н используем (11.4.7), которое с учетом
(11.4.14) дает
{u2g-\-v2g)sinaH=0
Пограничный слой атмосферы
341
или
аЯ=тг, tf=ic-i/"_i_ . (11.4.38).
Таким образом, высота пограничного слоя увеличивается
с ростом k и уменьшением со2 (следует помнить, что для
экватора неприменимы геострофические соотношения и полученные
выше формулы не могут быть использованы).
Средний коэффициент турбулентности найдем из уравнения
баланса энергии турбулентности (11.4.4). Для этого выразим
через (11.4.15) и (11.4.5) компоненты баланса
при е~2аН<1 и
н
Т j к dz ~~— Т 2 Рср
Тогда (11.4.4) примет вид
JLJ£_g_rf2 = _JL^L^L_
С'
,2 i/ГГТ I £ Л) я г & п
1 К М Н—т~ — §~ — ci-^r=0-
Подставив в это уравнение (11.4.38) и решив его относительно'
k, получим
I.m_ifl+_S_nrJ5_-^.V (И.4.39>
Константу m = n3/ci можно определить на основании
эмпирических данных. Из наблюдений известно, что при безразличной
стратификации для <р = 50° и cg = \0 м/с #«1000 м. В таком
случае из (11.4.38) и (11.4.39)
#Ч2
гп= 22 =3,15 • 10"6. (11.4.40)
nCg
Формула (11.4.39) отчетливо показывает влияние
динамического и термического факторов на интенсивность турбулентного
обмена. Для безразличного равновесия k~c2, при
неустойчивой стратификации &~с2 (1+Д2), а при устойчивой
стратификации k ~ с2• (1 — Д2). Здесь
g
Л2^ g * Р0
Т 2?cp<*z £
342
Глава 11
С определением k задача решена, и теперь можно
рассчитать профили метеорологических элементов, если известны cgi
С02, А), Тн и qH.
Если воспользоваться (11.4.3), то нетрудно получить
выражение и для средней по пограничному слою диссипации:
н
-jr\zdz=-*
Рис. 11.18. Зависимость среднего
коэффициента турбулентности k (/) и высоты
пограничного слоя Я (//) от Ро и Cg.
Кривая
Ро кал/(см2 • мин)
/
-0,2
2
0,0
3
0,2
ИЛИ
^
edz = m
mn
(11.4.41)
Обращает на себя внимание то, что формулы (11.4.39) и
(11.4.41) справедливы только для
g
2рс
ршг
>-1Д
(11.4.42)
Указанное ограничение отражает возможность исчезновения
турбулентности при сильной устойчивой стратификации,
справедливое в количественном отношении только в рамках
рассмотренной модели.
На рис. 11.\£ и 11.19 показана рассчитанная по
рассмотренной выше модели зависимость среднего коэффициента
турбулентности, высоты пограничного слоя и компонент уравнения
баланса энергии турбулентности от геострофического ветра и
турбулентного потока тепла у поверхности земли для ф = 50°.
Пограничный слой атмосферы
34а
Для сё= 10 м/с коэффициент турбулентности изменяется
примерно на 5 м2/с при изменении стратификации от безразличной-
к устойчивой или неустойчивой [Ро=±0,2 кал/(см2, мин)].
По сравнению с безразличной стратификацией высота
пограничного слоя сильнее уменьшается при устойчивой стратификации,
чем увеличивается при неустойчивой. Если при безразличной
60-10*г-
w V
20
о V
-20
-ьо
-60
-во
-100
1,2,3
У
///
I
I I
10 15 СдМ/С
Рис. 11.19. Зависимость компонент уравнения
баланса энергии турбулентности Е{ (/), Е2 (II)
и £3 (///) от Р0 и cg.
Кривая 1
Р0 кал/(см2 • мин) .... 0
Н
0,2 -0,2
+*-£*■
Н
I
0
стратификации продукция энергии турбулентности
уравновешивается целиком диссипацией, то при неустойчивой
стратификации потери энергии турбулентности за счет диссипации должны
компенсировать продукцию энергии турбулентности за счет
среднего движения и силы плавучести. При устойчивой
стратификации продукция энергии турбулентности за счет среднего
344
Глава 11
движения расходуется на диссипацию и преодоление силы
плавучести. Обращает на себя внимание тот факт, что средняя по
всему пограничному слою продукция не зависит от
стратификации и коэффициента турбулентности, а определяется только
геострофическим ветром.
Если воспользоваться формулой (11.4.36), то все
интегральные характеристики пограничного слоя можно выразить через
перепад температуры во всем пограничном слое атмосферы.
Действительно, из этой формулы следует, что
Р0 ^ 2МГ0-Гя-ТаЯ)
(11.4.43)
В таком случае формулы (11.4.39), (11.4.41) и (11.4.42) примут
следующий вид:
т
4
* = Ч * тн~' (П.4.44)
oJ 1-
*~g
g mn TQ—TH~ 1*И
, (11.4.45)
"A**
>-i,o
или с учетом (11.4.38)
4- Т*-Тн-Ч*И >- 1,0. (11.4.46)
Т aczg
Рассмотренная выше простая модель пограничного слоя,
несмотря на целый ряд допущений, обладает определенными
достоинствами. Во-первых, она позволяет получить обозримые
аналитические выражения для описания основных процессов
в пограничном слое. Во-вторых, она может быть использована
в численных прогнозах для приближенного учета влияния
пограничного слоя, так как при этом важны не детали
вертикальной структуры пограничного слоя, а интегральные эффекты,
которые определяются довольно неплохо.
Пограничный слой атмосферы
345
11.5. Нелинейная модель пограничного слоя атмосферы
Рассмотренные выше простые модели, основанные на
априорном задании профиля коэффициента турбулентности, не
годятся для описания тонкой структуры пограничного слоя. Для
этого нужно получить решение нелинейной системы уравнений
(11.1.1), (11.1.3), (11.1.5), (11.1.7), (11.1.9) —(11.1.11). Запишем
эту систему в потоках количества движения и тепла (позже
будет показано, что это позволяет упростить граничные условия).
Если продифференцировать (11.1.1) по z и ввести обозначения
yl = k-£r, c = k-£-, (11.5.1)
то получим:
*" и*. •_<>.
dZ2 -T"wz k
-5— ^-t-0. (11.5.2)
Уравнение баланса энергии турбулентности с учетом (11.1.7)
примет вид
Jtr^ + -^— C-*?-+a*k^ = 0. (11.5.3)
k Т рср k ' ° dz dz v r
На основании (11.1.10) и (11.1.11) получаем:
l~~ * dtydz '
ч? + о2 i g P
№ ' T ?cpk #
(11.5.4)
Наконец, получим выражения, определяющие характер
изменения турбулентных потоков тепла и влаги с высотой.
Воспользуемся асимптотическими формулами для градиента
потенциальной температуры и удельной влажности в пограничном
слое атмосферы:
Здесь Yp = 0»6°C/100 м есть градиент температуры в свободной
атмосфере; р0 — коэффициент с размерностью L-1,
определяемый из наблюдений.
346
Глава 11
Эти соотношения правильно учитывают асимптотику
градиентов вблизи поверхности земли и на верхней границе
пограничного слоя. Действительно, при г->0 основным является первый
член, и тогда, как следует из теории приземного слоя и
наблюдений,
rfO Р0 dg _ £р
При z-*H первый член становится малым и градиенты
стремятся к величинам d@/dz=y&— Yp и dq/dz=—$oq.
С учетом (11.5.5) и (11.5.6) уравнения (11.1.7) и (11.1.9)
можно записать в виде:
Для определения Я можно использовать условие
* \z = H
(ei — малая величина), которое означает, что на верхней
границе пограничного слоя касательное напряжение составляет
малую долю от касательного напряжения вблизи поверхности
земли.
Система уравнений (11.5.2) —(11.5.4), (11.5.7) —(11.5.9)
является замкнутой и позволяет определить величины г), a, k> b,
U Н, Р и £. Проинтегрировав (11.5.1), (11.5.7) и (11.5.8), можно
найти и, vt в и q.
Запишем граничные условия задачи для случая, когда ось
ох совпадает с направлением приземного ветра (см. п. 11.2):
при 2 — 0 r\ = vl a = 0, b-+c~4tv\% k-+ 0; (11.5.10)
при z-*oo т| —0, a-*0, 6 — 0. (11.5.11)
Об условиях (11.5.10) речь уже шла в п. 11.2,1 а условия
(11.5.11) непосредственно следуют из определения пограничного
слоя.
Так как турбулентные потоки вблизи поверхности остаются
почти постоянными по высоте, решение задачи в потоках
позволило вместо граничного условия на z=zo>0 использовать
условие при 2->-0, при этом один параметр (го) оказывается несу-
1 Граничное условие для Ъ получается из анализа уравнения баланса
энергии турбулентности при z—>0; в этой области можно пренебречь
диффузией и рассматривать только одну компоненту скорости.
Пограничный слой атмосферы 347
щественным до момента перехода от потоков к профилям
скорости.
Выписанная выше система уравнений является нелинейной
и может быть решена только численно. Вместе с тем в ней и
в граничных условиях содержится довольно много параметров,
от которых будет зависеть решение. Чтобы уменьшить число
параметров, целесообразно свести задачу к безразмерному виду.
Применяя ранее описанную процедуру «обезразмеривания»
уравнений, получим следующую систему алгебраических
уравнений для определения масштабов:
J*-—2..^*-, -*-_2-.JL, A6-4.V5T.
/0 = *c'/4Z,i, Po = k0 ° , ^о = *о-7^-,
b0 = c-1/ivl (11.5.12)
Исключая из первых двух уравнений Li, нетрудно показать, что-
i1o = cro (при условии &,=^оо). В таком случае после некоторых
преобразований получаем:
Я; = Р0, Ео = Е0, u0 = v0 = ^. (11.5.13>
Используя (11.5.13), перепишем исходную систему в
безразмерном виде:
nl + °l
а1П„ 1 "я __п
*2 + *п -U'
<* *•
.2
--h-p i n i в d t dbn
kn=inVK,
=0,
(11.5.14)
(11.5.15>
(11.5.16)
(11.5.17)
•348
Глава И
In + °п Ц P„
kl
К- 2 rV^ -, (11.5.18)
Уп-^п dZa -*n[ Zn + L т 2и>г [Hn ) j,
(11.5.19)
En = *qkn-^- = kn(-j--%Llqn), (11.5.20)
ъ[н» Тг)+°»(Я- -Ц-) = *>- (11-5.21)
Здесь L — масштаб Монина—Обухова,
Jsto получается из уравнений (11.5.5) и (11.5.6)]. Обозначим
Zi/L через juio:
N = _x2^_^. (И.5.22)
* *
Граничные условия запишутся в виде:
при zn-+ 0 т|Л=1, ал = 0, 6Л — 1, kn-+0; (11.5.23)
при2л-^оо 7]п-а„ = *л-0. (11.5.24)
Таким образом, замкнутая система (11.5.14) — (11.5.21)
содержит только один параметр Li/L=\xo. Показатель степени т
следует выбирать из эмпирических данных.
Численное решение задачи (при т = 0, аь = 0,73, ат = 1,0, С =
= 0,046, х = 0,4, (3=0,54) выполнялось итерациями по kn\ в
качестве начального значения принималось kn=Zw По известному
k\ из (11.5.14) и (11.5.15) находились величины х\х и Ои из
(11.5.16)—Ьи из (11.5.18)—U. Затем из (11.5.17) определялось
км, и повторялся весь цикл до тех пор, пока max|&*+i — ki\ не
становился достаточно малой величиной.
Результаты расчетов т)п, сгп, т]^> °'п и *п приведены в
упоминавшейся выше монографии Д. Л. Лайхтмана и в статье
И. М. Бобылевой (см. список литературы). В качестве примера
на рис. 11.20 и 11.21 показана зависимость г]п, an, kn, bn от zn
и |я0. С ростом неустойчивости стратификации поток количества
движения менее резко уменьшается с высотой и увеличивается
Пограничный слой атмосферы
349
высота пограничного слоя, увеличивается как значение
максимума коэффициента турбулентности, так и высота, на которой
он расположен. Прослеживаются интересные особенности
вертикального распределения Ьп: сперва наблюдается рост Ьп>
связанный с вкладом термического фактора, а затем — убывание
до нуля на верхней границе пограничного слоя. На рис. 11.22
приведены профили компонент баланса энергии турбулентности.
ЪЛ;к„;Ю
4
2Н
1Щ
-0,5
Рис. 11.20. Зависимость
безразмерных касательных напряжений
от Цо и zn.
1 Г\80
1 Л
\\ /
W /
1
1
1
V
К-/
^v80
\ \
\ \
\ \
\ \
\ \
\ \
\ \
\ \
1 V
__ ^ /
2
г-—i
0,2
Ofi
Рис. 11.21. Профили
коэффициента турбулентности ()) и
кинетической энергии
турбулентности (2) для разных
значений \i0.
Генерация энергии турбулентности за счет среднего движения
/ Л7 r\n + ol \ ( Ьп\
I N = I и диссипация I 2 =—— I играют основную роль
в нижней части пограничного слоя; термический фактор [|ы(гп)]
становится особенно существенным в верхней части
пограничного слоя. Диффузия энергии турбулентности Lf = —; \ knX
l azn \
X п ) I обусловливает перенос вихревой энергии снизу вверх
и имеет разные знаки в верхней и нижней частях пограничного
слоя.
Если определить высоту пограничного слоя из условия
I 1*+a*L =н =0,05,
I \ п п
то можно найти зависимость Нп от \хо (рис. 11.23).
350
Глава И
После того как определены потоки, можно рассчитать
компоненты скорости ветра, температуру и влажность по формулам:
«.-Afr*~?-««'-i-a~^«.
г0я
*0п
— = V
dzn v* и*
(11.5.25)
-50 N,Z/W
Рис. 11.22. Профили компонент баланса энергии
турбулентности, \х0=—1, ц0=—80.
/ — продукция, 2 — скорость диссипации, 3 — потеря
энергии турбулентности на работу против сил плавучести,
4 — диффузия.
Рис. 11.23. Зависимость высоты пограничного
слоя Нп от jio при 2o)z = l,26-10-4, z0 = 5-10-2 м. ^qq
/ —cg«=10 м/с, 2 — Cg-20 м/с.
0 20 W SO \l0
вп — вп (z0n) = J g £ dZn»
*0л
^я-^Л(20Я)= j -h-dz*>
J *qtcn
\
(11.5.26)
где б — угол между направлением приземного ветра и изобарой.
Пограничный слой атмосферы
351
Следует обратить внимание на то, что шероховатость теперь
фигурирует как существенный параметр:
__ 2а)г<гр __ 1
20л:
x2Rox
(11.5.27)
где
Ro=-
2ozZq
(11.5.28)
есть число Россби; х=-
геострофический коэффициент
KCg
трения.
На рис. 11.24 представлена зависимость г\' и о'п от logzn>
которая, согласно (11.5.25), характеризует вертикальный
профиль ветра. Отчетливо выделяется логарифмическая область,
где основная компонента скорости ип изображается прямой
линией (с ростом неустойчивости эта область распространяется
до больших высот). Другая компонента скорости в нижнем слое
почти не изменяется с высотой.
При расчете универсальных функций использовался параметр
\\o = Li/L, однако при решении прикладных задач обычно
известны внешние параметры cgy zo, Ро> 2coz, поэтому необходимо
указать способ перехода от внешних параметров к масштабам и
параметрам, принятым в расчетах.
Из (11.5.25) следует, что
dsn
dzn
куда
%С£" «n drin
— — LUo О, .
*п=*0„ V* dZ»
.. _ ** _[( "1»\2 , [L
*■- *cg \\.z„) 1 \t
zn~z0n
Un \21-V.
*n-*0n
(11.5.29)
tg8= — rfr,n-^^
dznldzn \zn = ;Qn-
С учетом (11.5.29) получаем трансцендентное уравнение
' 1\
L
Pog
2"z9cpTOcl
m-
Pog
2Mz?CpT0cg
X
wff dr,n N2 / dan \2| Ppg 1
(11.5.30)
352
Глава 11
которое связывает LJL с внешними параметрами:
м=—^
-8\-
^z^pT0c\
Ro
=^(таккакг°»=^Ы- (11-5-31)
м
о\-
0,01 \-
11<Г-в
-10
О^гп
Рис. 11.24. Отклонение компонент
скорости ветра от геострофической в
зависимости ОТ |Д,0 и \gzn.
в Igfto
Рис. 11.25. Номограмма
для определения
параметра |ы0 по заданным
значениям Ro и М'.
Результаты решения уравнения (11.5.30) приведены на
рис. 11.25, с помощью которого по данным синоптической карты
можно вычислять характеристики пограничного слоя атмосферы.
Необходимый для определения М турбулентный поток тепла
определяется или из уравнения теплового баланса, если исполь-
Пограничный слой атмосферы
353
зовать связь между облачностью и радиационным балансом,
а также отношение Боуэна, или по результатам наблюдений
в приземном слое.
Параметр шероховатости выбирается в зависимости от типа
подстилающей поверхности по эмпирическим данным.
X
о,з
о*
Г\°)
[ 1 J_ 1
■ /
Д 2
0 3
1 *
1 1
IgRo
Рис. 11.26. Зависимость геострофического коэффициента
трения х (а) и Угла полного поворота ветра в пограничном
слое а (б) от Ro и ц0.
а) 1 — Брукхавен, июль 1950 г., 2 — Брукхавен, 25 ноября 1950 г ,
*3 — Леттау, 4 — Хэнфорд, 1959 г; б) 1 — о. Симли (Леттау), 2 —
Шеппард и Омар, 3 — Упэвен (Добсон), 4 — Лейпциг (Леттау), 5 —
О'Нейл (безразличное равновесие), 6 — Северное море (Джеффрис),
7 — Брукхавен, 8 — Халтинер и Мартин (безразличное равновесие),
9 — США, Великие равнины (Бернштейн).
Приведенные на рис. 11.26 результаты сравнения расчета
с наблюдениями показывают, что такие важные характеристики
пограничного слоя, как геострофический коэффициент трения и
угол полного поворота ветра в пограничном слое атмосферы,
хорошо согласуются с наблюдениями (опытные данные
располагаются вблизи "соответствующей средним условиям изолинии
Цо = — 1).
11.6. Пограничный слой над морем (коэффициент
турбулентности не зависит от высоты)
Процессы в пограничном слое над морем характеризуются
рядом особенностей, связанных с существенным отличием
физических свойств воды от физических свойств суши. Большая
23 Заказ № 612
354
Глава 11
теплопроводность (особенно в верхнем слое, где развита
турбулентность) и теплоемкость воды способствуют тому, что море
может отдавать в атмосферу много тепла, а температура воды
при этом будет меняться несущественно, т. е. пограничный слой
над морем с большим основанием можно рассматривать в
стационарном приближении, чем пограничный слой над сушей.
С другой стороны, отсутствие свойственной для суши «пестроты»
подстилающей поверхности дает большие основания и для
рассмотрения горизонтально-однородного пограничного слоя
(исключение составляют гидрологические фронты и прибрежные
участки). Вследствие того что в море коротковолновая радиация
проникает до глубины 10—100 м (на суше она поглощается
в слое толщиной в доли миллиметра), радиационный баланс
поверхности определяется только притоками длинноволновой
радиации. За счет этого упрощается используемое в качестве
граничного условия уравнение теплового баланса поверхности
Я9ф=Ро+-№+Д. 01.6.1)
Здесь ЕЭф — эффективное излучение; Р0 и^Е0 — турбулентные
потоки явного и скрытого тепла; В — теплообмен поверхности
с нижележащими слоями.
Особенности динамических процессов в пограничном слое
над морем связаны с подвижностью поверхности. Рельеф
поверхности, ее шероховатость, скорость и направление движения
воды не только зависят от скорости ветра, но и в свою очередь
влияют на нее. Наличие таких обратных связей заставляет
рассматривать движение пограничных слоев атмосферы и моря как
движение сильно взаимодействующей системы, обе части
которой «связываются» турбулентным обменом.
Рассмотрим стационарный, однородный по горизонтали
поток. В рамках такой задачи будем считать заданными
градиенты давления в атмосфере и океане, которые формируются мак-
ромасштабными процессами. Коэффициент вертикального
турбулентного обмена будем считать постоянным по вертикали, но
разным для моря и атмосферы. Ограничимся рассмотрением
чисто динамической задачи и будем считать нейтральной
стратификацию пограничных слоев (dQ/dz = dp/dt, = 0). Волнистая
черта здесь и в дальнейшем показывает, что величина относится
к морю. Потребуем, чтобы записанные в потоках количества
движения уравнения движения, имеющие одинаковый вид для
атмосферы и моря:
-^ 2uz(ut-cglcosai) = 0 (11.6.2)
Пограничный слой атмосферы
355
(i — \ относится к атмосфере, a i = 2 — к морю, а —угол между
осью ох и направлением геострофического ветра или течения),
удовлетворяли следующим граничным условиям:
^Iz + ^-^lc-Co' а|г + г0=-а|с-<
й _, =и\
, . 1)\ =z<l)
С-►Co'
7]=7] = o=a=0 при Z—+oo, C-^oo
(11.6.3)
(11.6.4)
(11.6.5)
(£ отсчитывается вниз от поверхности). Первые- два
условия предполагают непрерывность потоков количества движения
и скоростей при стремлении к поверхности сверху и снизу.
Условие (11.6.5), как и ранее, предполагает, что на большом
расстоянии от поверхности турбулентность затухает и потоки
количества движения равны нулю.
Переходя к безразмерным переменным по формулам, рас-
п. 11.5 (;
смотренным в п. Н.Ь \ для моря и= ^- ип, v= ^~vn J » за~
пишем уравнения движения в виде:
, d
dzn
(vfn+i°n)+(Un+ivn)-
%Cg eU = Oi
< -Ж— fc+ *aя) + («я +toj+J^_e'r — 0. (11.6.6)
Если направить ось ox вдоль касательного напряжения
вблизи поверхности, то (11.6.3) примет вид
7l|z=o = P^=-'y)|c=o==P^l °|,=o=-a|c=o=°.
и в безразмерном виде граничные условия перепишутся в форме:
Ья+^я
2 =0 =
-Пп+^п С„ = 0=1,
(11.6.7)
\Un + ivn\zn = z0n = -V9lp \un+lvn
^n-^0n
(11.6.8)
hn+^/i
hn+^/
,=о.
(11.6.9)
23*
356 Глава 11
Продифференцировав (11.6.6) по z„ и £п, получим уравнения,
для решения которых достаточно граничных условий (11.6.7)
и (11.6.8):
Ш_г
у—— *•»
Ч»+£„ = е 2*" • (П.6.10)
Коэффициенты турбулентности можно определить из уравнения
баланса энергии турбулентности и гипотез теории подобия (см.
п. 11.4). Профили скорости находятся из (11.6.6) по заданным
касательным напряжениям (11.6.10).
Для определения четырех неизвестных параметров и*, v#t а
и а имеем из условия непрерывности касательных напряжений
v. = Vp/pv< (11.6.11)
и из условия непрерывности скоростей (11.6.8)
d -*.Cg ia
= M^rfe+^)|c„=o+^^ajl/"^r. (11.6.12)
Если р — угол между направлениями геострофического ветра и
геострофического течения, то
p_360° = a-a. (11.6.13)
d — — .
Подставив в (11.6.12) величины ——(Лп + fon) L ft и
azn itne0
(r\n + iQn)\z =0 и решив его с учетом (11.6.13), получим:
2
dzn
cs Q , \ се
cg \ cg
1 — 2 —=- cos В +
["'] [ч-VJft
1 — (cosp + sinp)
-tga= °4 . (11.6.14)
с
1 — (cosp — sinp)
Пограничный слой атмосферы 357
Таким образом, соотношения (11.6.11), (11.6.13) и (11.6.14)
определяют искомые параметры, и теперь из (11.6.6) нетрудно
получить выражения для скорости ветра над морем:
[(1 + 0/2 o>zz 1
>-*" *Л J.
u+iv=u0-\-lv0 y=^-cgl\-e *" J, (11.6.15)
Рис. 11.27. Система отсчета углов и годограф ветра
в пограничном слое над морем ( Cq = у а\ + х%).
где
«o = ^cos(p+a)-f
^o = ^sin(p+a)-
/tG + Kt/p )
/r(i + KT/p)
Из анализа формул (11.6.14) и (11.6.15) видно, что при
отсутствии - геострофического течения (cg = 0) направление течения
на поверхности совпадает с направлением геострофического
ветра. При более точном решении оказывается, что между
ними существует малый угол. Из этого следует аномальное
вращение ветра с высотой над морем: в самом нижнем слое
должно наблюдаться левое вращение, а выше — обычное
правое (рис. 11.27).
358
Глава 11
В монографии Д. Л. Лайхтмана (см. список литературы)
рассмотрены нелинейные системы уравнений для обоих
пограничных слоев (см. п. 11.5), показано, что полученное ранее решение
для пограничного слоя атмосферы (универсальные функции)
может быть использовано и для пограничного слоя моря.
11.7. Параметризация планетарного пограничного слоя
атмосферы
Проблема параметризации возникла в связи с численным
решением задач общей циркуляции атмосферы и океана. Дело
в том, что даже при использовании лучших ЭВМ шаг сетки,
на которой аппроксимируется система дифференциальных
уравнений, оказывается настолько большим,/что существенные
процессы, имеющие масштаб, меньший шага сетки, не могут быть
учтены явно. Эти «мелкомасштабные» явления приходится
учитывать косвенно, связывая их с параметрами, описывающими
свойства крупномасштабных полей, получаемых при расчетах
непосредственно. Достаточно надежная и конструктивная
параметризация требует глубокого понимания процессов и является
отнюдь не простым деЛом. В связи с ее актуальностью этой
проблеме в современных исследованиях уделяется много
внимания.
Параметризация "процессов в пограничном слое связана
с большим шагом по вертикали, который в лучших моделях
имеет порядок 1 км. Разумеется, при таком шаге невозможен
прямой расчет турбулентных потоков, отражающих
взаимодействие подстилающей поверхности и атмосферы и играющих
фундаментальную роль в эволюции крупномасштабных полей.
Ниже для описания характеристик пограничного слоя
атмосферы привлекаются методы анализа размерности.
Общепринятые приближения, являющиеся основой экмановского
пограничного слоя, — стационарность и однородность по горизонтали —
могут быть с известным приближением применены ко всему
земному шару, включая и большую часть тропической зоны;
исключением является экваториальная область шириной
около 5°.
При указанных упрощениях сравнительно небольшое число
внешних параметров определяет" основные свойства
пограничного слоя, в связи с чем естественно ожидать эффективных
результатов, применяя методы анализа размерностей. Разумеется,
информация в этом случае окажется менее конкретной, чем для
приземного слоя, в связи с увеличением количества размерных
параметров при переходе от слоя постоянных турбулентных по-
Пограничный слой атмосферы
359
токов ко всему пограничному слою. Тем не менее она является
полезной и необходимой для разработки рациональной
программы наблюдений и обработки экспериментальных
материалов.
Попытаемся прежде всего перечислить и в какой-то степени
обосновать выбор размерных величин, которые определяют
режим пограничного слоя.
1. Горизонтальный градиент давления т-—.\
р дп
Это основная сила, вызывающая движения. Его значение
и " направление обусловлены крупномасштабными
атмосферными процессами, и в теории планетарного пограничного слоя
горизонтальный градиент давления можно считать заданным
внешним параметром. В пределах пограничного слоя, как
правило, он мало меняется. Исключением являются ситуации,
связанные с фронтами; они требуют особого рассмотрения (вряд ли
в таких случаях целесообразно использовать методы анализа
размерностей).
2. Параметр Кориолиса / = 2cosin(p. Поскольку
имеются в виду процессы, характерный горизонтальный масштаб
которых достаточно велик, то естественно полагать, что влияние
вращения Земли должно быть эффективным, во всяком случае
в верхней части пограничного слоя. Здесь условия
приближаются к свободной атмосфере, где ускорение Кориолиса имеет
тот же порядок величины, что и горизонтальный градиент
давления.
3. Шероховатость подстилающей
поверхности г©. Она определяет характерный масштаб вихрей вблизи
деятельной-поверхности и интенсивность генерации вихревой
энергии в этой области. Параметр шероховатости в
значительной мере регулирует обмен между деятельной поверхностью и
атмосферой.
4. Стр атифика ция.-Она оказывает существенное
влияние на процессы в пограничном слое. При ее учете следует
рассматривать размерные величины, которые формируют
вертикальный температурный градиент на разных высотах. Для
вертикального градиента потенциальной температуры используем
ранее введенную интерполяционную формулу
-^-= НТа-То). (11.7.1)
Если это выражение проинтегрировать по всему пограничному
360
Глава 11
слою, то, исключив затем Ро из двух полученных уравнений, его
можно записать в следующем виде:
_g__ iW. + т," +Ta_v (11.7.2)
2\tl
В (11.7.1) и (11.7.2) приняты следующие обозначения: Ро—
турбулентный поток тепла; рср — объемная теплоемкость воздуха;
v* — динамическая скорость; Н — высота верхней границы
пограничного слоя или близкого к ней уровня; Г0 и Тн —
температура вблизи земной поверхности (на уровне zo) и на уровне Н
соответственно; у& =g/cp — сухоадиабатический градиент; ур —
стандартный градиент в нижней тропосфере; уа— Yp = 0>3-h
ч-0,5°С/100 м. Таким образом, в рамках предлагаемого
приближения стратификация в комплексе определяющих величин
должна быть отражена двумя параметрами:
т тн-то + 1*И < v
T=—Z 7Г-* И (Та-Тр).
In
На первый взгляд кажется достаточным принять перепад
температуры по всему пограничному слою как единственную
размерную величину, отражающую влияние стратификации на
режим пограничного слоя. Такое предположение является,
однако, ошибочным, если иметь в виду, что роль стратификации
в разных частях пограничного слоя существенно различна.
Известно (см. п. 11.2), что в нижней части пограничного слоя
стратификация сравнительно мало влияет на турбулентный обмен,
но она оказывается решающим фактором в верхней части слоя.
Поскольку фиксированный перепад может иметь место при
разном распределении температуры по высоте, то ясно, что одним
указанным параметром нельзя отразить влияние
стратификации.
5. Параметр Архимеда g/T. Его значение существенно
влияет на работу вихрей против силы плавучести.
Таким образом, любая физическая характеристика
пограничного слоя должна зависеть от следующего комплекса размерных
1 Дл
параметров: ——-, /, zo, 67\ уа— Yp> gIT* если Речь идет об
интегральных характеристиках для всего слоя. При отыскании
вида формул для профилей турбулентных потоков тепла,
количества движения и вертикальных градиентов соответствующих
величин или любой другой физической характеристики,
меняющейся с высотой, к указанным параметрам добавляется высота
z над поверхностью земли. Из шести параметров только три
Пограничный слой атмосферы 361
имеют независимую размерность. Используя П-теорему анализа
размерностей, получаем общее выражение для искомых
величин:
Fn=Fn(St Ro, Г, гл). (11.7.3)
Здесь Fn — искомая безразмерная характеристика пограничного
слоя; 5=—S интегральный параметр стратификации;
Tlcg
Ro=—■—■ число Россби;
Izo
g (Та-Тр)*4 _ "У
Т /2 /2 '
есть безразмерная частота Вяйсяла (cg — модуль
геострофического ветра); zn= безразмерная высота.
Для турбулентных потоков количества движения т, тепла Р,
скорости диссипации вихревой энергии в тепло во всем
пограничном слое е, угла а между касательным напряжением
у Земли и изобарой и высоты пограничного слоя Н получаем
следующие выражения:
Р
Р
-*-2?cpcgbT
= -Хт(5, Ro, Г), (11.7.5)
■ = Х.№ Ro, Г), (11.7.6)
'4
а = - sign а (5, Ro, Г), (11.7.7)
H=-^-Hn{Sy Ro, Г). (11.7.8)
Обратим внимание на то, что входящий в формулы параметр Г,
который в интервале широт 90—5° меняется более чем на два
порядка, может весьма существенно влиять на расчеты,
связанные с крупномасштабными процессами в атмосфере.
Нетрудно показать, что %и = %т- Профили метеорологических
элементов и коэффициента турбулентности представляются
следующими функциями высоты:
*<«>-*<*>> _lng,+»?-j-gn+lnRo, (Ц.7.9)
-»*—*,(Sf Ro, Г, z„), (11.7.10)
362
Глава 11
-£-=*»№ *°> г> **)■ (п.7.11)
Здесь t = l, 2; Ui = u\ u2 = v.
Контрольные вопросы
1. Что называется планетарным пограничным слоем
атмосферы?
2. Что является характерной особенностью приземного слоя
атмосферы? Какими параметрами и почему определяется
турбулентность в приземном слое?
3. Какие профили метеорологических элементов и
коэффициента турбулентности в приземном слое соответствуют
следующим условиям стратификации: безразличной, близкой к
безразличной стратификации, свободной конвекции и инверсии?
4. Как получить выражения для масштабов при сведении
к безразмерному виду системы уравнений в нелинейной модели
приземного слоя?
5. Каким параметром, помимо числа Ричардсона, можно
характеризовать стратификацию в приземном слое?
6. В чем состоят достоинства и недостатки моделей
пограничного слоя с априорным заданием профиля коэффициента
турбулентности?
7. В чем преимущество решения нелинейной модели
пограничного слоя в напряжениях?
8. Какие соотношения и почему можно использовать в
нелинейной модели вместо уравнения притока тепла и влаги?
9. В чем состоит специфика описания пограничного слоя
атмосферы над морем?
10. Какими внешними параметрами определяется строение
пограничного слоя атмосферы?
Глава 12. ПРОЦЕССЫ В НИЖНЕМ СЛОЕ АТМОСФЕРЫ
НАД НЕОДНОРОДНОЙ ПОДСТИЛАЮЩЕЙ
ПОВЕРХНОСТЬЮ
Общая постановка задачи. Трансформация полей температуры и
влажности. Трансформация динамических характеристик воздушного потока при
изменении шероховатости подстилающей поверхности. Некоторые приложения
результатов теории трансформации.
В предыдущей главе рассматривалось строение пограничного
слоя атмосферы при условии, что температура, влажность,
скорость и направление ветра являются функциями только
вертикальной координаты. Поскольку внутри пограничного слоя, как
правило, вертикальные градиенты названных элементов
значительно больше горизонтальных, при решении ряда проблем
такое приближение можно
считать удовлетворительным.
Однако известны явления, в
которых горизонтальная
неоднородность является существенной
особенностью; подчас само
возникновение таких явлений
вызвано горизонтальной
неоднородностью. Эти особые
случаи и рассмотрены в данной
главе. •
Поскольку поверхность
земли часто оказывается
неоднородной по своим физическим свойствам, различные ее участки
по-разному нагреваются, имеют разную увлажненность.
В процессе взаимодействия подстилающей поверхности и
расположенной над ней воздушной массы в последней
устанавливается определенное распределение метеорологических
элементов. Если в дальнейшем воздушная масса сместится на другую
поверхность (назовем ее новой) с существенно иными
свойствами, э результате турбулентного обмена теплом, влагой и
количеством движения между поверхностью и воздухом профили
температуры, влажности и скорости изменятся. С изменением
профилей температуры и ветра изменится и режим
турбулентности. Изменение свойств воздушной массы под влиянием
подстилающей поверхности называется трансформацией, а слой
воздуха z^h (рис. 12.1), в котором трансформировались
свойства,— внутренним пограничным слоем.
х=о
Рис. 12.1. Трансформация воздуха
при переходе его с суши на море.
364
Глава 12
В результате трансформации образуются или рассеиваются
туманы, происходит эволюция облачности, изменяется скорость
испарения и теплообмен поверхности с атмосферой и т. д.
Типичным примером трансформации является изменение
полей температуры и влажности в воздушной массе, которая
зимой переходит с суши на незамерзшее море. Сухой холодный
воздух, поступающий на поверхность моря, вследствие
вертикального турбулентного обмена между деятельной поверхностью
и воздушной массой увлажняется. На некотором расстоянии от
берега влажность воздуха может оказаться насыщающей, что
вызовет образование тумана. При дальнейшем продвижении
прогрев воздуха приведет к уменьшению относительной
влажности и рассеянию тумана.
Разработка теории таких явлений и развитие физических
основ их прогноза являются важной задачей теории
трансформации.
12.1. Общая постановка задачи
Рассмотрим трансформацию воздуха, который при своем
движении переходит с одной подстилающей поверхности на другую
с резко отличными свойствами (температурой, влажностью,
шероховатостью). При этом будем предполагать, что процесс
происходит довольно длительное время, так что в пределах
внутреннего пограничного слоя сформировались определенные профили
метеоэлементов и можно говорить о квазистационарном
состоянии. За ось ох выберем направление ветра.
В таком случае метеорологический режим пограничного слоя
атмосферы будет описываться следующей системой уравнений *:
и—$ \-^—^— = —з—k^ ^ V- ~* m, (12.1.1)
dx ' dz dz dz ' pcp dz ' cp v '
.-Й-+-Й—£-*-£-... 02Л.2)
«-£-+•-£—£-*-£-+-• («•'■»>
" ix +™ to ' [\ to I T to I c t + to * to ■
(12.1.5)
Подробно об этих уравнениях говорилось в п. 11.1.
Процессы над неоднородной подстилающей поверхностью 365
k = lVJ, (12.1.6)
/=_хс"/._*/* yj (12.1.7)
-£-+-£--<>. (12.1.8)
Здесь б — водность воздуха, т. е. количество жидкой воды в
единице массы влажного воздуха; m — скорость конденсации; .§*—
скрытая теплота парообразования.
Систему уравнений (12.1.1) — (12.1.8) можно считать
замкнутой, если рассматривать градиент давления и лучистый
приток тепла как заданные внешние параметры.
Чтобы сформулировать граничные условия, будем полагать
известными: 1) распределение метеоэлементов над старой
подстилающей поверхностью
S(x, z)\x=0=Sx(z)
(под 5 следует понимать 0, q, 6, и, k, б); 2) значения
температуры и влажности вблизи новой поверхности:
в(*. г)|г=г=е0(0),
Я{*> z)L=z=?0==/o<7max(eo),
лг>0
где fo — относительная влажность воздуха.
Поскольку капли воды адсорбируются поверхностью, то
Ь(х.г)\в=г=0.
| А* >0
Динамические характеристики, согласно модели приземного
слоя, описанной в п. 11.6, вблизи подстилающей поверхности
можно принять равными:
U(X, Z)\ : = г=™(Х> Z)\z = z=°>
k(x, z)
b(xt z)
z=2=*v*z0,
x > 0
x > 0
366
Глава 12
На больших высотах значения метеоэлементов не
трансформируются, поэтому
г -»-оо
х> О
дг > О
8С*. г)|^<»=8(00).
I х > О
| Jt >0
*(*. 2) 1,^ = 61 (00) = 0.
I х > О
Теперь задача сформулирована и может быть решена численно.
Пример численного алгоритма
1. По исходным (или полученным в предыдущем приближении)
значениям и, w и k определяются профили 6(х, г), ^(х, г), 6(х, г).
2. Из уравнения баланса энергии турбулентности по найденному в(#, г)
находится k(x, z), и решается «динамическая» часть задачи.
3. Вычисленные значения и, до, k используются для отыскания нового
приближения.
В связи с большим количеством параметров, от которых
зависит результат решения, последний весьма трудно
анализировать. Поэтому целесообразно получить для простейших случаев
аналитическое решение, которое сохранило бы качественные
особенности точного решения. Ниже приводятся примеры такого
решения.
Рассмотрим раздельно задачу о трансформации полей
температуры и влажности с априорными профилями коэффициента
турбулентности и скорости ветра без учета трансформации
последних, а затем — задачу о трансформации только ветра и
характеристик турбулентности.
12.2. Трансформация полей температуры и влажности
Будем исследовать изменение температуры и влажности
в нижнем слое атмосферы, где процесс трансформации выражен
наиболее четко, тем более что именно в этом слое формируются
такие важные «спутники» трансформации, как адвективные
туманы, заморозки и т. п. Такое ограничение позволяет пренебречь
лучистыми и фазовыми притоками тепла и упорядоченными вер-
Процессы над неоднородной подстилающей поверхностью 367
тикальными токами, поскольку их влияние в нижнем слое (за
исключением области, непосредственно примыкающей к
поверхности земли, где слабо развита турбулентность) существенно
меньше, чем влияние турбулентного обмена и адвективного
переноса.
В таком случае задача сводится к решению уравнения
■т§— т*-£-. <•«•'>
где S = Q или S = q в зависимости от того, о чем идет речь —
о трансформации температуры или влажности.
* Исходя из соображений, изложенных в п. 12.1, граничные
условия можно записать следующим образом:
S(x, z)\x=0 = Sl(z), (12.2.2)
S(x. *) 1,^,-5,(00). (12-2-3>
I дг>0
S(x, z)\z=Q=SQ(x). (12.2.4)
| x > 0
Заметим, что величина So(*)> вообще говоря, не является
известной функцией, поскольку она тоже подвергается
трансформации. Однако, если воздух переходит на поверхность водоема,
в силу сравнительной консервативности температуры водоема
величину So(x) можно считать известной.
Температура и влажность деятельного слоя почвы, в том
числе и ее поверхности, изменяются весьма существенно, и при
корректной постановке задачи следовало бы в качестве
граничного условия у поверхности привлечь условие баланса тепла,
а величину So{x) относить к числу искомых функций. В первом
приближении можно, однако, полагать So{x) заданной функцией,
а в дальнейшем по найденному распределению S(x, z) получить
выражения для компонент уравнения баланса тепла и из
решения этого уравнения (привлекая соответствующие уравнения
для почвы) найти более точное значение 5о(х).
В уравнениях (12.2.1) и и k есть функции обеих координат.
Однако профили и (г) и k(z) изменяются не в таких широких
пределах, как профили T(z) и q(z). Кроме того, как бы ни были
велики скорость ветра и турбулентный обмен, они уменьшаются
до нуля с приближением к поверхности и остаются неизменными
на границе внутреннего пограничного слоя. Поэтому при
решении задачи в той упрощенной постановке, которую мы приняли,
аппроксимация профилей u(z) и k(z) не играет большой роли
и может быть принята, например, степенной. Возникающие при
этом погрешности сравнительно невелики и не отражаются по
крайней мере на качественном анализе процесса. В принципе
368
Глава 12
уточнения могут быть даны в ходе последовательных
приближений. Исходя из этого, примем:
где ui и ki — соответственно значения скорости ветра и
коэффициента турбулентности на высоте Zi; е — параметр,
характеризующий термическую стратификацию атмосферы.1
При такой аппроксимации уравнение (12.2.1) приводится
к виду
«*-£—*-*'--£-. О2-2-5)
где
a? = ^-z\-2\ (12.2.6)
Уравнение (12.2.5) представляет собой линейное уравнение
второго порядка в частных производных. Чтобы привести его
к обыкновенному дифференциальному уравнению, введем новую
переменную
с=^^- (12-2-7)
Тогда
dS
дх
■*+-£-*--S-*-4?-(£«*+-§-4
Приравнивая коэффициенты при одинаковых приращениях и
учитывая (12.2.7), найдем:
dS 1 dS
дх — aV+2e * *
д i-« dS _ (1+2е)2 2 d*S . (1+2е) (1+3е) . dS
дг Z дг ~ •! + « ^ д& "+" ,i + « ^ дС *
1 Как показывают оценки, выполненные по экспериментальным данным,
величина е изменяется от 0,25 при инверсионных условиях до 0,10, при
сверхадиабатических градиентах.
Процессы над неоднородной подстилающей поверхностью 369
Подставляя эти выражения в (12.2.5), получим обыкновенное
линейное дифференциальное уравнение второго порядка:
<Ю | Г 1+3» 1 1 dS _0 /19 9Я\
rfC2 Т[ (1+2е)С (l+2e)2C2j rfC * и^.о;
Граничные условия при использовании переменной £
запишутся следующим образом:
5(С)|с=о=5ь (12.2.9)
*<С)|с^о-*о. (12.2.10)
Интегрирование (12.2.8) поддает
5(C) = С, j ^ СЧГ"Л, + С2,
оо
где Ci и С2 — постоянные интегрирования,
1+2е » Г— (1 +2е)2
Р
или, если ввести новую переменную Ф=-г—,
Р/с
5 = dj ^cpa-2rfcp+C2. (12.2.11)
Полученный интеграл — функция верхнего предела; он
называется неполной гамма-функцией:
j xa-le'xdx = T(at х).
Его значения затабулированы.
Постоянные d и Сг на основании граничных условий (12.2.9)
и (12.2.10) соответственно равны:
S\ — So __ S\ — Sq
Ci =
op Г(а-1) '
где Г (a— 1) —гамма-функция;
C2^=5o.
Следовательно, имея в виду (12.2.7), равенство (12.2.11)
можно записать так:
S(x, *)=S0+ г*~* r(a-l, ^2, + 2t). (12.2.12)
24 Заказ № 612
370
Глава 12
Как следует из (12.2.12), температура и влажность на высоте
z внутри трансформированного слоя отличаются от
соответствующих значений у поверхности на некоторую величину
"--п^?гг(-'. -£-*,+")-
Эта величина в каждой фиксированной точке тем больше, чем
больше различаются свойства подстилающих поверхностей.
Интенсивный турбулентный обмен способствует быстрой
«адаптации» воздуха к новой поверхности, а большая скорость
продвижения, напротив, замедляет процесс. Поэтому AS при прочих
равных условиях больше при малых значениях ki и больших
значениях и.\.
По мере продвижения над новой поверхностью (с
увеличением х) воздух все больше принимает свойства, характерные
для этой поверхности, и величина AS уменьшается.
На фиксированном х величина AS с удалением от
поверхности стремится к (Si — So), и на верхней границе
трансформированного слоя (z = h) выполняется соотношение
s~so 1 =1—V,
S\ — So \z = h
где v — малая величина.
Это соотношение позволяет получить формулу для оценки
высоты внутреннего пограничного слоя. Уравнение (12.2.12)
в таком случае можно записать следующим образом:
Г(а-1,ЛГ) «
Г(а-1) -1 '•
Здесь
N = ^^— • (12,2.13)
Следовательно,
Таблицы гамма-функций позволяют оценить значение N, при
котором v достаточно мало. Так, например, v = 0,05, если jV = 0,5
при устойчивом состоянии атмосферы и N близко к единице при
неустойчивой стратификации.
Процессы над неоднородной подстилающей поверхностью 371
12.3. Трансформация динамических характеристик
воздушного потока при изменении шероховатости
подстилающей поверхности
Ограничимся рассмотрением случая, когда стратификация
безразличная, а расстояния от границы раздела не очень
велики. При таких расстояниях можно считать, что внутренний
пограничный слой не выходит за пределы приземного слоя.
Будем по-прежнему считать, что ось ох совпадает с направлением
ветра, при х<0 шероховатость поверхности zrQ , а при х>0
шероховатость поверхности равна z^; ось оу направлена вдоль
границы раздела.
Для указанных условий система уравнений (12.1.1) — (12.1.8)
примет вид:
"£-+•-£—£-*-£-• <12-3-'>
-£-+-£--0, (12.3.2)
-*(£)'"< 4. 02-3.3)
дЬ . дЬ
*—**,,€^-$&-- О2-3-4)1
Если считать, что при х<0 существует установившийся
поток воздуха, т. е. можно использовать модель
горизонтально-однородного приземного слоя, а при х>0 на верхней границе
внутреннего пограничного слоя выполняется условие непрерывности
скоростей и потоков количества движения, то граничные
условия можно записать в виде (см. п. 11.2):
при х=0 и z^z'o
v
_»i
и=—^-1пг/2о, b = c~,tv,1 (12.3.5)
при z=Zo и л:>0
u = w = Ot k = *4vl(x)t k-^ = v'l{x), (12.3.6)
1 Выражение (12.3.4) получается из (12.1.6) и (12.1.7).
24*
372
Глава 12
При 2 = Л И Х>0
a=-f-lnA/2b, Л-^-=^2. (12.3.7)
Переопределенность граничных условий является кажущейся,
так как в число неизвестных ы, w> k, b входит еще и высота
внутреннего пограничного слоя А.
и w
Введем безразмерные величины ип= , wn= , kn =
и* ay*
k _ х z _ b _
— ~~7 > %n—"~7~ , Zn=—T7, On—"
K , ~n L% ^ H , „w ^ .
Для определения масштабов используем соотношения,
которые следуют из исходной системы уравнений и граничных
условий, дополнив их выражением для до*, полученным из
физических соображений: w^=y,(v^ — v'£), где v%—характерная
величина v'^(x) на больших х. Действительно, можно ожидать,
что масштаб для вертикальной скорости должен быть связан
с дивергенцией воздушного потока и, следовательно, с разностью
динамических скоростей над исходной и новой подстилающими
поверхностями.
С учетом указанных выше соотношений получаем следующие
выражения для масштабов:
K = *v&. w* = %{v.-vX L=^r /iv" - (12.3.8)
В таком случае систему уравнений можно записать через
безразмерные величины в виде:
«(«.-&-+•--&-)—£-*•-&-. (12-3-9>
дип L^evL = 0( (12.3.10)
Зг-(«.-&+-.-5Н-Ч-&-)ЧЬ <123">
К VK d^f" , (12.3.12)
Процессы над неоднородной подстилающей поверхностью 373
а граничные условия — следующим образом:
при хп=0 и zn > 1
яЛ = 1п2„, 6П = 1, (12.3.13)
при zn = m и хл >0
un = wn=0, kn=mp, kn-^-=p\ (12.3.14)
при zn = hn u хп>0
un = \nhn, kn-^=\, (12.3.15)
где
а= » , ♦ _!!_ = #
с
/2
т = -?-, /?= V . (12.3.16)
Если считать а малым параметром (небольшие изменения
параметра шероховатости), можно искать решение задачи в виде
разложения в ряд по а, ограничиваясь членами, содержащими
а в первой степени:
ип = ип0-\-липи wn = wa0-\-awnU
kn = kn0-\-cLknU bn = bn0-^abnl. (12.3.17)
Подставим (12.3.17) в систему (12.3.9) — (12.3.15), упростим
запись, отбросив индекс п, и выделим системы функций для
нулевого и первого приближения, приравняв коэффициенты при а
в нулевой и первой степенях. Начнем с рассмотрения первой
системы.
Решение системы в нулевом приближении
В этом приближении система уравнений имеет вид:
*k0-*g- = 0, (12>3.18)
дг и дг
дар . да0
дх "Т~ дг
\2
=0, (12.3.19)
*5(-*U-)2-6S. (12.3.20)
374
Глава 12
г граничные условия:
при z = m и х>0
Uo = Wo=Ot ko = mpt u0-^-=p2t (12.3.22)
при z = h и х>0
u0 = \nh. (12.3.23)
Проинтегрировав (12.3.18) по г, получим &o-r-^- = const или
с учетом (12.3.22) ko—:р-=р2, откуда на основании (12.3.20)
Ь0=р2. (12.3.24)
Перепишем (12.3.18) в виде
д&о дир , и д2ир _п
и используем (12.3.21). Тогда
Проинтегрировав полученное выражение с учетом (12.3.22),
получим
k0=pz. (12.3.25)
Подставив k0 в соотношение fa——= р2, найдем с учетом
{12.3.22) выражение для профиля ветра:
tf0=/?ln-J-. (12.3.26)
Из уравнения неразрывности (12.3.19) и граничного условия
(12.3.22) определима^:
wo—-g-(«ln«J~«+m). (12.3.27)
Наконец, используем граничное условие (12.3.23) для
определения р и dp/dx:
р= Ы\ , (12.3.28)
In —
т
dp I dh In т
dx h dx , о h
(12.3.29)
ln2-
m
Из (12.3.19) —(12.3.23) видно, что полученное решение
системы для нулевого приближения характеризует существенные
особенности строения квазиоднородного приземного слоя над
Процессы над неоднородной подстилающей поверхностью 375
новой подстилающей поверхностью. В этом нетрудно убедиться,
если записать, допустим, выражения для скорости и
коэффициента турбулентности в размерном виде:
V (х) 2
Яо = —h In ——,
т. е. зависимость от х учитывается только параметрически через
изменение динамической скорости. Для каждого значения л:>0
в этом приближении считаются справедливыми соотношения,
записанные для горизонтально-однородного приземного слоя.
Вертикальная скорость непосредственно связана с изменением
динамической скорости как функции х. Полученное в нулевом
приближении решение содержит неизвестную величину — высоту
внутреннего пограничного слоя /г, которая может быть
определена из граничного условия (12.3.15) только после решения
системы в первом приближении.
Решение системы в первом приближении
Для этого случая система уравнений примет вид:
"•-Йа-+«ь-т?--4-[*>-ё-+*ь-ё-]. <12-3-30>
т+т=°- <12-3-31>
«(*-8-+«*-Й-)-Ч-&-Г+
+2*-|гт- н!г+*> ^р (12-3-32>
ъ д2ир | . д^и\ __ лгт- ди\ 1 Ъ\ ди0 /i9qqo\
ki-d?T-lko-S2ir--Vbo -дГ-^Г^п=--дГ> (12.3.33)
2 Vh дг
граничные условия:
при z=m и х>0
ux = wx = 0, kx=0t V^ + *i^g- = 0, (12.3.34)
при z = h и х>0
«.-0. *о^+А, -*J—Ц£- • (12.3.35)
376 Глава 12
Подставив в (12.3.30) — (12.3.35) выражения для ko, 6о, Wo
и шо, после некоторых преобразований получим решения для
ku bu ии которые учитывают влияние горизонтальной адвекции
и вертикального движения воздуха:
kx=zF (г)-%--*-?!£-, (12.3.36)
b>=P-E-[F&-azln-tr}' (12-3'37>
".=т^-{гф.(г)-^(-)-4^|-х
Х[ЛФ,(Л)-даФ2(Л)]}, (12.3.38)
где
F(z)=z ln2-J— (Зг+да) In -£-+4 (г-да).
Ф1(г)=1п'-^-(6-а)1пп£-+(12-4«).
Ф1(а)в1„2_£.+ 61„^_ + (12_4-а),
Ф,(А) = Ф,(г)|г=й> Ф2(А) = Ф2(г)|г=А. (12.3.39)
Определим теперь h=h(x), для чего используем граничное
условие (12.3.35), которое с учетом (12.3.28) и (12.3.39)
примет вид
In —
1 dh lam F(A)=SJ !!« Л ^"V (12.3.40)
A d* in2_5_ W a 1пЛ 1„2_Л
m \ m
где
F(h) = F(z)\,=k.
Чтобы исключить в дальнейшем параметр а, вернемся к
обозначению безразмерных переменных индексом п и введем новую
безразмерную переменную хп:
Хп=^г-> хп = *хпу?. (12.3.41)
Процессы над неоднородной подстилающей поверхностью 377
Тогда (12.3.40) примет вид
^- = /?(А„),
где
1П2_^_ + 1„А-1пАя
m m а
R (hn) - ч2Ля in hnF (Ля)
и, следовательно,
А„
W-*&>-• <12-3-42>
Таким образом, для определения hn = hn(xn) нужно рассчитать
интеграл для разных значений m и АЛ.
После того как получена зависимость ЛЛ от m и *п, можно
рассчитать все искомые величины для нулевого и первого
приближений и затем воспользоваться (12.3.17), чтобы найти сперва
безразмерные, а потом с учетом (12.3.8) и размерные величины.
Найдем связь а с параметром m=z/0//z^J чтобы оценить, до
каких значений m можно использовать приближенные формулы
(12.3.17):
« v'' In m
Если при z = h
то
Ш» 1 -
V
*_
V
*
1 h
-In—г
т =
\
hn
V
*_
%
а
-1
In-**-
т
1 Л
- ln^r-
(12.3.43)
На рис. 12.2 показана зависимость hn от хп для разных
значений т (от 0,1 до 10). При малых хп (хп = 5- 102) наклон
поверхности раздела составляет Ун для т = 0,1 и */5 для т=10.
Для больших Хп (*п = 3-104) наклон уменьшается до V24 при
т = 0,1 и Vi3 при т = 10. На рис. 12.3 показана зависимость
v'£2(x)lv'£ от Хп', ее можно ислользовать для определения
значений а, соответствующих т = 10 и т = 0,1. Если принять для
378 Глава 12
лг = 10 предельное отношение v^/v^ =1,25, а длят=0,1 v'^/v'^ =
= 0,85, то в первом случае а =—0,25, а во втором а = 0,15. Итак,
полученные приближенные формулы могут быть использованы
при различии шероховатостей подстилающих поверхностей более
чем в 10 раз.
Рисунок 12.4 иллюстрирует изменение скорости ветра как
функции высоты при разных значениях хп. Штриховая линия
I 1 1 1 I
п1 ю2 ю3 ю* ЦХъ
Рис. 12.2. Зависимость безразмерной высоты hn от хп для разных
значений т.
соответствует логарифмическому профилю ветра над исходной
поверхностью. Для v^ =30 см/с, х = 0,4, 2^=2,5 см при переходе
с менее шероховатой на более шероховатую поверхность (т =
= 10, z^ = 20 см) на 2=0,5 м скорость ветра на расстоянии 1 км
уменьшается на 1,5 м/с, тогда как в обратном случае, при
переходе с более шероховатой на менее шероховатую поверхность
{т = 0,1, 2^ = 0,2 см), скорость на 2 = 0,5 м увеличивается на
0,7 м/с. Нулевое приближение отличается от первого не более
чем на 10%.
Вертикальное распределение кинетической энергии
турбулентности заметно зависит от хп. При m = 10 Ьп растет с
высотой, а потом падает до 1,0, тогда как при т = 0,1 слабое
изменение Ьп с высотой сменяется резким ростом до 1,0. Высота слоя
со слабым изменением Ьп увеличивается с ростом хп. При т =
= 10 первое приближение отличается от нулевого на 30%, тогда
как при т = 0,1 различие достигает 100%.
Процессы над неоднородной подстилающей поверхностью 379
7Г
1
0,5
J_
_L
J,
10z ю3 ю*
Рис. 12.3. Зависимость отношения касательных напряжений
от хп для разных значений т.
Ъдхп,
v (х)
5 10 0 5 tin
Рис. 12.4. Изменение с высотой zn безразмерной скорости
у. ~
и-а — —г и для разных значений хп и т.
* v
*
Значениях^:/) 1,78.10s, 2) 2,49 • 103, 3) 6,63 • 103, 4) 4,12.104
5) 8,63 • 102, 6) 6,73 • 103, 7) 1,48 • 10\ 8) 7,53 • 104.
380
Глава 12
Коэффициент турбулентности линейно увеличивается с
высотой до некоего уровня, выше которого начинается переход к
зависимости kn=zn, т. е. к профилю над исходной поверхностью.
Различие нулевого и первого приближения достигает 50—100%.
Ввиду большой сложности формул для первого
приближения вертикальной скорости ограничимся рассмотрением только
Won=wo/Kv'^ как функции zn. Если при m = 0,l won линейно
увеличивается с ростом 2п, то при т = 10 линейный рост начинается
только с некоторой высоты. Оценим два характерных значения
wo: при и^=50 см/с, z'0 = 2 см, х = 0,40 для 2=10 м, х= 132,6 м
получаем в случае т = 10 о>о = 2,2 см/с, для х = 297,3 м в случае
/п = 0,1 доо=0,71 см/с. Несмотря на приближенный характер этих
оценок, можно ожидать, что возникающие за счет
неоднородности шероховатости подстилающей поверхности упорядоченные
вертикальные движения могут играть заметную роль в
формировании режима приземного слоя.
В целом полученные результаты приближенного решения
удовлетворительно согласуются с результатами численных
расчетов и позволяют проанализировать процесс трансформации
воздушного потока за счет изменения шероховатости
подстилающей поверхности.
В заключение данной главы рассмотрим некоторые важные
процессы, связанные с неоднородностью подстилающей
поверхности.
12.4. Некоторые приложения результатов теории трансформации
1. Адвективный туман возникает в том случае, когда в
результате трансформации воздуха его фактическое влагосодержа-
ние становится больше максимальной удельной влажности.
Такая ситуация может быть следствием как увеличения влагосо-
держания воздуха при переходе его на более увлажненную
поверхность, так и понижения его температуры при переходе
на более холодную подстилающую поверхность.
Действительно, из определения относительной влажности
следует, что
df de dE
f ~~ e E
n coo e dE J£ dT
или, поскольку q ~ 0,622 — и -g- = jjrj, -y- ,
/ q RnT T \1*ЛЛ)
Процессы над неоднородной подстилающей поверхностью 381
Формула (12.2.12) позволяет оценить оба слагаемых в (12.4.1),
а следовательно, возможное изменение относительной
влажности и вероятность образования тумана.
Поскольку изменение свойств воздуха зависит от расстояния,
которое прошел воздух над новой подстилающей поверхностью,
вероятность образования тумана на разных расстояниях
различна. Можно оценить границы области, в которой образуется
туман, исходя из того, что на этих границах должно
выполняться равенство
q(x,z) = qm&x\T(x,z)\, (12.4.2)
Если представить qma-n(T) в виде разложения
^ax(7,) = <7,„ax(7'1)+^f^|r=ri(7'-7'1)+. . .
и ввиду того, что (Т—Т\)<^Т, ограничиться двумя первыми
членами разложения, то на основании (12.2.12) равенство
(12.4.2) можно записать следующим образом:
-y-»(7'i)+^|r = ri[(7'o-7',)-(7'o-7'l) r(;(~!l^m) 1 • (12.4.3)
В этом равенстве, согласно (12.2.13), Nm — функция zm и хШу
представляющих границы области тумана. Ее можно
определить, если по известным значениям q и Т на обеих
подстилающих поверхностях вычислить функцию Г(а—1, Nm)y поскольку
из (12.4.3) следует, что
Г/ 1 кг \ [?0 ~ 9шах (ТХ)) Г (а - 1) + (Тх - 7р) dqmfdT
1 (а— 1, IWm)= j- j .
(П-то)-^-\т=гГ^-до)
По вычисленному значению Г(а—1, Nm) нетрудно найти с
помощью таблиц этих функций значение Nmy а следовательно, и
границы области тумана, если известны скорость ветра и
коэффициент турбулентности на высоте 1 м.
2. Другая важная задача, которая может быть решена на
основании теории трансформации, состоит в определении
турбулентного потока тепла и скорости испарения с подстилающей
поверхности. Этот вопрос представляет интерес в связи с
оценкой влияния мелиорации на изменение микроклимата, с оценкой
изменения уровня небольших водоемов и пр.
Теплоотдачу П (или испарение) с поверхности а можно
записать следующим образом:
n=j*P0rfa,
382
Глава 12
где Pq — турбулентный поток тепла с единичной поверхности,
определяемый, как известно, выражением
Яо = — kpcp
дТ
dz
2 = 0'
если —r— »Ya (что в большинстве случаев в нижних слоях
атмосферы и наблюдается).
Применяя к (12.2.12) правило дифференцирования
определенных интегралов с переменными пределами, получим
Я д2 RyZ
Л l+2s )
А1+2»
(l+2t)»jr
I
dz
.(<rY-2)dcp +
Al+2e
~ (1+2.)»лг Г ДУ+»' >-Д а Г д2;
+ ^ L (1 +2в)2д; J d2 [(1 +
V+2i
2е)2дг.
После некоторых преобразований это выражение приводится
к следующему виду:
дТ
dz
_ (П-Уо)
2 = 0
'( 1+2е )
(1+2е)
1+2е
(*)"
+ 2*
А, 1+2Е
Таким образом, значение потока тепла с единичной
поверхности может быть вычислено по формуле
Ро = -?ср(Тх-Т0)-
(1+2е) 1+2е
1-Й
1+2е
Величина Pq тем больше, чем больше температура
поступающего воздуха отличается от температуры подстилающей
поверхности; Ро увеличивается с ростом скорости ветра и
интенсивности турбулентного обмена. С удалением от границы раздела
турбулентный поток с единичной площадки уменьшается,
поскольку температура воздуха по мере его продвижения над
новой поверхностью все больше приближается к температуре этой
поверхности.
Процессы над неоднородной подстилающей поверхностью 383
Теплоотдача с полосы шириной d и длиной L при ветре,
дующем вдоль полосы, согласно (12.3.2), определяется
выражением
d L
П„ = | j Рййхс1у = -?ср(Тх-Т0)Х
4^ / i+' \ 1+2е
X (1+2/>Т v(*~**) *
В общем случае при интегрировании по поверхности не
следует забывать, что х — расстояние вдоль линии, направление
которой совпадает с направлением ветра. Таким образом,
значение полного потока тепла с поверхности Па при прочих равных
условиях зависит от направления ветра, и при оценке,
например, потерь тепла или количества воды, испаряющейся с
поверхности водоема за длительное время, следует учитывать
повторяемость ветров различных направлений.
3. Одним из важных следствий трансформации воздуха
в приземном слое является изменение характеристик нижней
облачности, в частности высоты ее границ, вертикальной
мощности, запасов жидкой воды и водяного пара. Поэтому
полученные в п. 12.2 формулы могут быть использованы для анализа
эволюции нижней облачности.
Свойства облака в большой мере определяются термо- и вла-
гообменом с окружающей средой, которые зависят от
распределения температуры и влажности как внутри самого облака,
так и вне его.
Мы уже видели, что при переходе воздуха на подстилающую
поверхность, свойства которой существенно отличаются от
свойств той поверхности, над которой воздух находился
первоначально* профили температуры и влажности в нем изменятся.
Следовательно, изменятся турбулентные потоки тепла и влаги,
что повлечет за собой и изменение свойств облака.
Так, если воздух перейдет на более теплую сухую
подстилающую поверхность, распределение температуры в
подоблачном слое изменится таким образом, что облако будет получать
тепла больше, чем над старой поверхностью. Может начаться
испарение капель воды, содержащихся в облаке. Кроме того,
при такой ситуации, очевидно, усилится турбулентность
(увеличится термическая неустойчивость), что увеличит потери
облаком жидкой и газообразной воды вследствие диффузии.
Перечисленные эффекты могут привести к «поднятию» нижней
границы облака, к уменьшению в нем содержания жидкой
384
Глава 12
воды и водяного пара, к их перераспределению внутри
облака.
Рассмотренный пример показывает, что эволюция облака
зависит от комплекса процессов, обусловленных распределением
температуры и влажности вне облака и внутри его.
В простейшей модели, когда заданы коэффициент
турбулентности и скорость ветра и не учитывается лучистый приток тепла,
как уже говорилось в п. 12.2, распределение температуры и
влажности подчиняется уравнениям:
-£—£-* (тГ+1.)- 02.4.4)
«-Й-- -£-*-£■ <•*«»
В облачном слое воздух насыщен водяным паром. Поэтому здесь
существенную роль играют фазовые превращения воды, и
соответствующие уравнения (если для простоты полагать, что
твердая фаза отсутствует) запишутся следующим образом:
•-£—b-*(-S-+i-)+^-- <|2-4-в>
»-й—4-*(тМ-«• <12-4-7>
«-Я^—E-*(-S-P)+»- <12'4-8»
Здесь т — количество жидкой воды, образующейся в единицу
времени в результате конденсации: Р=—^-(Ya—
Ува)—изменение удельной влажности вертикально перемещающейся частицы,
если она насыщена водяным паром; б —водность, т. е.
количество жидкой воды в единице массы облачного воздуха. Пока
капли ведут себя как пассивная примесь, изменение водности
подчиняется такому же уравнению, как изменение водяного
пара, но источник имеет противоположный знак. На основании
этих соображений и записано уравнение (12.4.8).
На границе между облачным и внеоблачным слоями
градиенты температуры и влажности терпят разрыв. Поэтому при
решении системы уравнений (12.4.4) — (12.4.5) и (12.4.6) — (12.4.8)
отдельно для каждого слоя возникают определенные трудности
при «склейке» полученных результатов. Этих трудностей можно
избежать, если ввести новые характеристики: эквивалентную
температуру
Tm = T+^2-q. (12.4.9)
Процессы над неоднородной подстилающей поверхностью 385
и общее влагосодержание воздуха
Q = q+K (12.4.10)
градиенты которых на границе облака не терпят разрыва.
Умножим уравнения (12.4.5) и (12.4.7) на -=- и сложим
ср
первое из них с (12.4.4), а второе с (12.4.6). В обоих случаях
получим
дТ'экв д l ( дТ3
и
—агМт+т.). <12-4Л1>
дх
Сложив (12.4.7) и (12.4.8), получим
-g—в-*-ё- <»■*•«»
Уравнения (12.4.11) и (12.4.12) выполняются в обоих
рассматриваемых слоях.
Если считать известными свойства новой подстилающей
поверхности, а также распределение температуры и влажности
в воздушной массе в момент ее перехода на эту поверхность
и иметь в виду ограниченность по высоте влияния
подстилающей поверхности, то сформулированная задача будет подобна
той, которая рассмотрена в п. 12.2. Поэтому ее решение может
быть записано в форме (12.2.8). Оно позволяет рассчитать
профили Тэкв(г) и Q(z) на фиксированных значениях х,
сформировавшиеся под воздействием новой подстилающей поверхности.
По значениям Тэкв(г) рассчитывается профиль ^max(z).1
Если нанести на один график кривую изменения полного
влагосодержания с высотой Q(z) и соответственно Тэкв(г)
кривую максимальной удельной влажности ^тах(^), то пересечение
этих кривых покажет границы облака (рис. 12.5).
Действительно, вне облака удельная влажность меньше
максимальной, г сконденсированная вода практически отсутствует,
поэтому Q<?max. В облаке полное влагосодержание
складывается из водяного пара, достигающего здесь насыщения, и
капель, поэтому в облаке Q>^max. На границах облака 6=0, q =
= ?max = Q. Оценки, выполненные для разных значений х>
позволяют проследить, как изменяются границы (а следовательно,
и мощность) 'облака по мере его продвижения над новой
подстилающей поверхностью. Такие оценки показывают, что
наибольшие изменения претерпевает нижняя граница облака.
1 Для этого можно, например, задавая значения Т\ вычислить ГЭКв = 7',-|-
+ -—(7тах(7'/) и построить график ^тах(7'/) =/(ГЭкв),из которого в дальней-
ср
шем можно получать qm&x по известным значениям Тэкв.
25 Заказ № 612
386
Глава 12
Напомним, что в рассмотренной задаче не учитывалось
влияние лучистого притока тепла. Между тем если вне облачной
среды он играет сравнительно малую роль в тепловом балансе,
то поглощение и излучение радиации облаками могут весьма
существенно изменить температурный режим внутри облака.
Поэтому для более строгого решения задачи в исходных
уравнениях нельзя отбрасывать слагаемое, учитывающее лучистый
приток тепла. При этом, поскольку радиационный баланс
претерпевает существенные изменения на границах облака, а внутри
Рис. 12.5. Определение границ облака по
профилям максимальной удельной влажности qm&x (1)
и полного влагосодержания Q (2).
его практически остается постоянным по высоте, лучистый
приток можно аппроксимировать, например, двумя б-функциями1,
принимая
^-^- = Axl{z-h{)+A2b(z-h2),
где А\ и А2 — соответственно приток радиации вблизи нижней
hi и верхней кг границ облака.
В связи с ограниченным объемом учебного пособия мы не
можем останавливаться на решении задачи в такой постановке.
Укажем лишь, что учет лучистого притока тепла дает заметный
эффект.
Контрольные вопросы
1. Что понимается под трансформацией?
2. Сформулировать задачу об изменении температуры и
О свойствах 6-функции см. в главе 16.
Процессы над неоднородной подстилающей поверхностью 387
влажности воздуха при переходе его с одной подстилающей
поверхности на другую.
3. Привести уравнения в частных производных,
описывающие трансформацию, к обыкновенным дифференциальным
уравнениям и решить их.
4. Получить выражение для потока трансформирующейся
субстанции вблизи подстилающей поверхности. Каков его
физический смысл?
5. Как применить выводы теории трансформации к прогнозу
адвективных туманов и оценке влияния мелиоративных
мероприятий?
6. Как можно оценить изменения характеристик облачности
в результате трансформации?
7. Какой параметр и почему можно рассматривать как
малый в задаче о трансформации при изменении шероховатости?
8. Каков физический смысл нулевого и первого
приближения в указанной выше задаче?
Глава 13. СУТОЧНЫЙ ХОД МЕТЕОРОЛОГИЧЕСКИХ
ЭЛЕМЕНТОВ
Формулировка задачи о суточном ходе метеоэлементов. Некоторые результаты
численного решения. Суточный ход температуры при постоянном
коэффициенте турбулентности. Ночное понижение температуры.
Метеорологические элементы в нижнем слое атмосферы
претерпевают колебания с суточным периодом. Эти колебания
связаны с временным режимом поступления солнечной радиации.
Как известно, солнечная радиация является основной
компонентой баланса лучистой энергии. Поглощенная деятельным
слоем почвы лучистая энергия превращается в тепло и приводит
к соответствующим изменениям температуры поверхности.
Поэтому колебания поступающего к поверхности земли потока
лучистой энергии обусловливают колебательный режим
температуры поверхности.
Посредством теплопроводности тепловая волна
распространяется в атмосферу и в нижележащий слой почвы. С удалением
от поверхности по мере поглощения тепла амплитуда волны
затухает.
Под влиянием суточных колебаний температуры
поверхности изменяется не только температура воздуха, но и ее
вертикальный градиент. Поскольку от градиента температуры
существенно зависит интенсивность турбулентности, его изменения
сказываются на режиме турбулентного перемешивания, а
следовательно, на распределении всех метеоэлементов, профили
которых формируются под влиянием вертикального турбулентного
обмена.
Таким образом, изменение потока лучистой энергии в
течение суток вызывает суточные колебания полей температуры,
влажности, скорости ветра и интенсивности турбулентного
обмена. Взаимосвязь суточных колебаний всех метеоэлементов
является важной особенностью процесса.
13.1. Формулировка задачи о суточном ходе метеоэлементов.
Некоторые результаты численного решения
Чтобы исследовать закономерности суточных колебаний
метеоэлементов, учитывая взаимодействие полей, необходимо
рассматривать совместно временной ход всех метеорологических
характеристик пограничного слоя атмосферы.
Суточный ход метеорологических элементов
389
Рассмотрим случай, когда подстилающая поверхность
однородна по горизонтали, так что адвективные члены в уравнениях
малы. Будем полагать достаточно малыми и слагаемые,
связанные с лучистым притоком тепла в воздухе, фазовыми
превращениями воды и вертикальными движениями. Тогда система
основных уравнений, подлежащая решению, запишется следующим
образом:
1-т|-'"+Т»-|. 03-1-2)
-8—'"В-*"!-- <'3.1.3)
-й—.-г**- <13,-4>
-»-*Ф+..4-*Т5—■ "3.1.5)
-4?—"-Т7-- <13|-6>
Для замыкания системы (она содержит восемь
неизвестных— и, v, 6, Т, q, k, b, е) можно привлечь дополнительные
соотношения, как это уже делалось в п. 11.2:
k = lVI, (13.1.7)
s= b^f , (13.1.8)
Выше приняты следующие обозначения: Ti(£>)—температура
почвы на глубине £, отсчитываемой от поверхности вниз; а —
коэффициент температуропроводности почвы. Остальные
обозначения указаны в предыдущих главах.
Для решения системы (13.1.1) — (13.1.9) необходимо задать
граничные условия.
Поскольку из физического смысла поставленной задачи ясно,
что решение должно быть периодическим 1с периодом 1,
390
Глава 13
начальные условия можно не задавать, полагая, что
рассматривается установившийся периодический режим.
В качестве граничных условий на 2 = 0 воспользуемся
условием прилипания, из которого следует, что
»i*)\^o = v(*)\^o=0, (13.1.11)
и отсутствием разрыва температуры на поверхности:
вИ|^о=Л(^|^о = ео. (13.1.12)
В качестве второго условия на деятельной поверхности
используем уравнение баланса тепла
— кРср-лг\. ^Lk?
р dz
дд
z -* о v dz
с^0 = Яо. (13.1.13)
где Ro — радиационный баланс у поверхности1; piCi — объемная
теплоемкость почвы.
Граничное условие для влажности запишем,
воспользовавшись зависимостью влажности от температуры:
<7(*)Uo=/o<W(0o), (13.1.14)
где /о — относительная влажность у поверхности, которая
определяется увлажнением почвы и может считаться постоянной
в течение суток.
Кроме того, используем условие отсутствия потока энергии
турбулентности через поверхность, а именно
db ' =0. (13.1.15)
dz
z-+0
Условия на другой границе могут быть записаны на
основании следующих соображений.
Поскольку суточные колебания передаются от поверхности
в воздух благодаря турбулентному обмену, с удалением от
подстилающей поверхности они должны затухать, и на большой
высоте значения искомых характеристик можно считать
постоянными и получать их из решения соответствующих
стационарных задач. Таким образом,
"Uoo = \. «|,^,-«f. 03.1.16)
e(*)|,W-e„. ЪЩ^-Ъ. (13.1.17)
<7(z)Uoo=0. (13.1.18)
*(*)|,w=0. (13.1.19)
1 Напомним, что радиационный баланс R0 складывается из
коротковолнового излучения Солнца и длинноволнового излучения Земли и атмосферы.
Суточный ход метеорологических элементов
391
Решение сформулированной задачи может быть выполнено
только численно.
В качестве примера приведем некоторые результаты
численного решения, полученного при заданном суточном ходе
температуры поверхности.
На рис. 13.1 представлены кривые суточного хода
температуры воздуха и скорости ветра на высоте около 2 м. Из рисунка
Рис. 13.1. Суточный ход температуры воздуха
(/) и скорости ветра (2) на высоте около 2 м.
видно, что колебания температуры и скорости ветра хорошо
согласуются: время, когда отмечаются экстремальные значения,
почти совпадает.
По мере удаления от поверхности суточный ход
претерпевает существенные изменения (рис. 13.2 и 13.3). Так, амплитуда
суточных колебаний температуры на высоте около 240 м
убывает в 5 раз, а наступление максимума запаздывает на
несколько часов по сравнению с его наступлением на высоте 2 м.
Изменение суточного хода модуля скорости ветра с высотой
имеет более сложный характер. Если у поверхности (см.
рис. 13.3) скорость ветра максимальна в 15—18 ч, то на высоте
240 м наибольшие значения скорости приходятся на 3 ч. Такая
специфика суточного хода скорости ветра объясняется тем, что
в дневное время, когда имеет место интенсивный турбулентный
обмен, в нижние слои воздуха поступает большое количество
кинетической энергии из верхней части пограничного слоя, что
и обеспечивает максимальные скорости у земли. Этим же
вызвано уменьшение скорости ветра днем в верхней части
пограничного слоя.
392
Глава 13
Понятно, что существует переходная зона, в которой
суточный ход выражен слабо. Эта зона расположена на высоте около
Г
т
0,8 г
18Ьч
Рис. 13.2. Кривые суточного хода температуры
на разных высотах.
100 м и, очевидно, смещается в зависимости от интенсивности
турбулентного обмена.
18 21
12 15 18 Ьч
Рис. 13.3. Кривые суточного хода
модуля скорости ветра на разных высотах.
На рис. 13.4 показано, как изменяется в течение суток
направление ветра у земли. В ночные часы при слабо развитой
турбулентности направление ветра может отклоняться от изо-
Суточный ход метеорологических элементов
393
бары на 30—40°. Днем профиль ветра за счет интенсивного
турбулентного обмена сглаживается и угол отклонения ветра от
геострофического уменьшается. Как видно из рисунка,
результаты численного расчета хорошо согласуются с
экспериментальными данными.
Численное решение позволяет исследовать и суточный ход
таких характеристик, как геострофический коэффициент трения
V Рс\
—!£-, турбулентный поток тепла (рис. 13.5), коэффициент
Рис. 13.4. Суточный ход угла между
направлением ветра у поверхности земли
и направлением геострофического ветра.
/ — расчет, 2 — данные наблюдений
0,038 г
0fl3b\-
0,030'k
0,026}-
Рис. 13.5. Суточный ход
геострофического коэффициента трения vj G
(/) и вертикального турбулентного 0,0221
потока тепла Ро/рср (2).
H-V
18 21
12 15 Ьч
турбулентности и т. п. Однако, как отмечалось выше, по
результатам численного решения трудно представить в обозримой
форме влияние довольно большого количества факторов,
определяющих рассматриваемый процесс. С этой точки зрения более
удобным является аналитическое решение, даже если оно
получено при больших упрощениях.
Ниже рассматривается весьма простая модель суточных
колебаний, которая, однако, качественно хорошо описывает
реальный процесс.
13.2. Суточный ход температуры при постоянном
коэффициенте турбулентности
Рассмотрим суточный ход температуры, полагая, что
коэффициент турбулентности — постоянная величина. Можно считать,
что в рассматриваемой модели он заменен средней величиной.
Такой подход позволяет выяснить ряд важных особенностей
процесса и, кроме того, дает возможность получить связь между
394
Глава 13
коэффициентом турбулентности и характеристиками суточного
хода, например амплитудой, скоростью затухания ее с высотой
и т. п.
Полученные решения можно использовать для оценки
интенсивности турбулентного обмена по измерениям температуры,
т. е., по существу, для рассмотрения обратных задач.
Колебания радиационного баланса будем аппроксимировать
простой косинусоидой (хотя в действительности они имеют
более сложный характер):
#(*) = ^4-#iCOS<
где R — среднее суточное значение радиационного баланса у
поверхности; /?i — амплитуда его суточных колебаний; со=2я/24 —
частота колебаний.
Будем считать пренебрежимо малым испарение с
поверхности, что позволит не учитывать распределение влажности в
уравнении баланса тепла. Очевидно, это пренебрежение вполне
справедливо при исследовании суточного хода в засушливых
районах. При других условиях оно дает заметную ошибку.
В дальнейшем будет приведена формула, позволяющая оценить
этот эффект.
С учетом перечисленных допущений задача сводится к
решению уравнений:
-£-«*-g-. 03.2.1)
»ri.e«*gL (13.2.2)
dt dC2
при граничных условиях:
в (t, 2)U=o=7\(*. С)|с__.о, (13.2.3)
в(*. 2)|^оо = е„, (13.2.4)
Т^Л)\^ж = Тп, (13.2.5)
- k?cP "И" | ,=о_ ap,Cl ~Ж~ I ;=o=^+/?1 cos "*' (13-2>6>
Искомые величины в(/, z) и Ti(t, £) могут быть
представлены в виде суммы
Ф(г, *) = Ф(*)+Ф'(*. t),
где Ф(г, t) —искомая функция; Ф(г) —ее среднее суточное
значение; Ф'(г, t) —отклонение от среднего суточного.
Распределение средней суточной температуры по высоте
может быть получено из решения стационарной задачи [например.
Суточный ход метеорологических элементов
395
оно может быть рассчитано по формуле (11.4.36)]. Поэтому
поставленную задачу целесообразно решать, отыскивая только
отклонения температуры от среднего суточного значения.
Если иметь в виду, что ~тт~"=0> то уравнения для
отклонений на основании (13.2.1) и (13.2.2) можно записать так:
-$--*,-£-. 03.2.7)
J
где / = 1 для воздуха, / = 2 для почвы. Следовательно, k\ = ky
Zi=z, kz=ay z2=£.
Граничные условия для решения (13.2.7) следующие:
— kpcp
.Учитывая, что решение имеет волновой характер, можно
искать его в виде
Ф){г)9 t) = Cjeiil>i+t3zJ+Bje-i(iit+*4zJt (13.2.11)
где Cj и Bj — постоянные интегрирования.
Подставив (13.2.11) в (13.2.7), найдем:
ь-±1/й-Г-±(|+1)у^р.
к_±]/Г7^Г_±(,-1)у^Г'.
Теперь решение (13.2.11) может быть записано в виде
*'/ ^ ^ *-<± (I + D/-£-., -,e,±(,_i>^ • *,
Фу(*;, *) = С,е > +Яуе > .
Знаки в. показателях степени выберем таким образом, чтобы
удовлетворилось условие (13.2.10). Тогда
дФ[
дг
$lU = 0 = $2|C =
дФ'2
— а?\С\ —лг-
г = 0 °ь
Ф-1 =(
J\zJ = oo
= 0,
= /?lCOS0)^,
э.
(13.2.8)
(13.2.9)
(13.2.10)
(13.2.12)
396
Глава 13
На основании условий (13.2.8) и (13.2.9) определим постоянные
Cj и Bj. Так, из (13.2.8) следует, что
С\ = С2,
ВХ = В2. (13.2.13)
Условие (13.2.9) на основании (13.2.12) с учетом (13.2.13)
запишется так:
= /?i cos at = R{ -^ .
+
Из последнего уравнения можно получить выражения для С\
и Ви приравняв коэффициенты при еш и е~ш.
После несложных выкладок выражение для отклонений
температуры от ее среднего суточного значения записывается в
следующем виде:
о Г 2*7 ZJ ( г \
Ф)(г, t)= г*'е ,_ J __sin(^-+a>/— y-£-Zj).
М ' V<* l?cpVb+?\CiVa\ \ 4 ' Y 2kJ Jl
(13.2.14)
I / я
Поскольку Ф^(г, t) имеет максимальное значение при sin( —
+ (о/— ]/~~obZ ) i ^ амплитУДа суточных колебаний
температуры воздуха будет определяться формулой
A(z) = A(0)e j , (13.2.15)
где
A(0) = A(z)\z=0= g —- (13.2.16)
1 У" (pcp Уk +9\C\Va)
есть амплитуда колебаний температуры поверхности.
Как следует из (13.2.16), амплитуда суточных колебаний
температуры поверхности прямо пропорциональна амплитуде
колебаний радиационного баланса и тем меньше, чем больше
коэффициент турбулентности и теплопроводность почвы. Это
легко понять. При сильно развитой турбулентности тепло быстро
распространяется по вертикали, благодаря чему амплитуда
суточных колебаний температуры поверхности оказывается
сравнительно малой. И наоборот, при фиксированных колебаниях
радиационного баланса и слабой турбулентности амплитуда ко-
Суточный ход метеорологических элементов
397
лебаний температуры поверхности сравнительно велика; при
этом толщина слоя, в котором имеют место суточные
колебания, оказывается небольшой.
Существенное влияние на суточный ход температуры
поверхности оказывают теплофизические свойства почвы. Если почва
обладает хорошей теплопроводностью, то днем значительная
доля тепла уходит в нижележащие слои. Соответственно доля
тепла, идущая на теплообмен с воздухом (согласно уравнению
баланса тепла), уменьшается и максимум температуры в ее
суточном ходе оказывается сравнительно низким. Ночью поток
тепла в «почве направлен к поверхностному слою и частично
компенсирует потери тепла поверхностью на излучение, что
несколько повышает минимальную температуру.
Суточный ход температуры над хорошо проводящей почвой
оказывается более сглаженным, чем над почвой с малой
теплопроводностью.
С удалением от поверхности суточные колебания затухают.
'Как видно из формулы (13.2.15), амплитуда колебаний
убывает тем быстрее, чем меньше интенсивность турбулентного
(в воздухе) или молекулярного (в почве) теплообмена.
Из формулы (13.2.14) видно, что с высотой не только
изменяется амплитуда колебаний, но и происходит сдвиг фазы.
Поскольку для фиксированной фазы колебаний синус
должен быть величиной постоянной и, следовательно,
-^--f а)/— ]/ -^-z=const,
то
dt __ 1
или
'»-''~-Й5Г-' (13-2Л7)
где U и /Г—время, когда данная фаза наблюдается
соответственно на высотах zo и zi.
Из (13.2.17) следует, что наступление заданной фазы на
высоте гг запаздывает относительно ее наступления на высоте z\
и это запаздывание будет тем больше, чем меньше
интенсивность теплообмена.
Затухание суточных колебаний с высотой позволяет оценить
высоту температурного пограничного слоя атмосферы. Если
определить высоту пограничного слоя Н как уровень, до которого
распространяется влияние подстилающей поверхности, то на этом
уровне не будут отмечаться суточные колебания температуры.
398
Глава 13
Практически можно принять, что суточные колебания
отсутствуют, если их амплитуда уменьшилась по сравнению с
амплитудой у земли, например, в 50 раз. Тогда
Л(*) _ -K-ST* про
А(0) е — u,uz,
откуда
»-УЧ
2k In 0,02.
Напомним, что в рассмотренной задаче не учитывалось влияние
притоков тепла, поступающих в атмосферу при испарении с
поверхности. Между тем они входят в общий баланс тепла и могут
определенным образом изменить полученную картину.
Для того чтобы учесть этот процесс или по крайней мере
оценить возможные эффекты, надо в исходную систему
уравнений и граничных условий добавить уравнение диффузии
водяного пара (13.1.4), считая, например, что турбулентный поток
водяного пара определяется тем же коэффициентом
турбулентного обмена, что и поток тепла (ад = ат = 1), и ввести
соответствующее слагаемое в уравнение баланса тепла у поверхности
( — «S^p-р _ ). Тогда формула для отклонения температуры
воздуха от среднего суточного значения записывается в виде
Т'Ь *)= ^г _/ **—^zn 7ZTX
V^ [Vk (fcp + JF9 -fe£_) + Plci Va]
Xsin (^ + u>* - Y^L- z) . (13.2.18)
Как видно из (13.2.18), испарение приводит к уменьшению
амплитуды суточных колебаний.
На рис. 13.6 приведен пример суточного хода температуры на
высотах 1, 50 и 200 м, рассчитанного по формуле (13.2.14).
Хорошо видно, что амплитуда суточных колебаний затухает с
высотой и наблюдается сдвиг фазы колебаний во времени.
Сравнение величин, рассчитанных по формуле (13.2.14),
с экспериментальными данными (рис. 13.7) показывает, что
расчеты довольно правильно отражают характер процесса при
правильном подборе коэффициента турбулентности.
Суточный ход метеорологических элементов
ГС
2Ьг-
20\-
16
12
8
4
3 6 9 12 15 18 21 2Мч
Рис. 13.7. Суточный ход температуры
воздуха на высоте 2 м.
/ — рассчитанный по формуле (13.2 14),
2 —полученный по данным наблюдений.
1 Ум
/ 1
/ 1
г / /
/ /
/ /
г / /
1 / I
1 1 |_
_|
"—**%
\ \
ч\
J L
\\
\\
\\
1*
I I
12 15 18 21 24t4
Рис. 13.6. Суточный ход температуры
воздуха на разных высотах,
рассчитанный по аналитической формуле (13.2.14),
400
Глава 13
13.3. Ночное понижение температуры
Ночное понижение температуры в самом нижнем слое
атмосферы, хотя оно и является частью суточного хода,
целесообразнее рассматривать как самостоятельный процесс.
С одной стороны, это связано с тем, что учет ночного
выхолаживания весьма существен при решении важных
практических проблем. В результате ночного выхолаживания возникают
радиационные туманы и заморозки, которые могут принести
огромный ущерб народному хозяйству, если их заранее не
предсказать. При этом требуется довольно точный расчет
температуры, поскольку в таком случае оказывается важным правильно
указать время перехода температуры через 0°С или температуру
точки росы. Формула (13.2.14) необходимой точности не
обеспечивает.
С другой стороны, процесс ночного выхолаживания имеет ряд
специфических особенностей, позволяющих решить задачу более
точно, чем задачу о суточных колебаниях вообще. Главные из
этих особенностей состоят в следующем:
1) основной причиной ночного выхолаживания является
эффективное излучение, которое при неизменном облачном
покрове может считаться постоянным в течение ночи;
2) турбулентный обмен, интенсивность которого в п. 13.2
считалась постоянной, а в действительности довольно существенно
изменяется, в ночное время слабо развит и играет небольшую
роль;
3) значительно более важную роль в формировании поля
температуры ночью играет теплообмен в почве, для оценки
которого в настоящее время имеются достаточно надежные
методы;
4) в некоторых случаях может оказаться весьма
существенным выделение тепла при конденсации пара.
Для оценки ночного понижения можно привлечь
дополнительную информацию — распределение температуры в вечерние
часы To(z)—и решать задачу, отыскивая отклонение
температуры Т''(г, t) от этого начального распределения. Тогда задача
сводится к решению системы уравнений:
ри
начальных
дТ"
dt
дт'[
dt
условиях
T'(t,
г) к
/7
—" #2
:0=T\(t,
*
С) к
=о = 0
(13.3.1)
(13.3.2)
Суточный ход метеорологических элементов 401
и граничных условиях, аналогичных тем, что использовались
в п. 13.2 [см. условия (13.2.3) —(13.2.5)1.
Здесь Т" и Т" — соответственно отклонения температур
воздуха и почвы от их значений в начальный момент. Чтобы
избежать громоздких математических выкладок, связанных с
решением названной системы уравнений, применим несколько
упрощенный подход.
Во-первых, ограничимся исследованием ночного понижения
температуры деятельной поверхности, поскольку именно оно
представляет наибольший интерес для практики.
Во-вторых, поскольку главную роль в понижении
температуры ночью играет эффективное излучение и теплообмен с
почвой, а влияние турбулентного теплообмена сравнительно мало,
представим искомую величину в виде суммы
T'i(t, 0) = т0+ть (13.3.3)
где то — понижение температуры, связанное с первыми двумя
процессами; ti — изменение температуры поверхности за счет
теплообмена ее с воздухом.
Выражение для то может быть получено на основании
анализа размерностей. Согласно определению,
*о=/(ЕэФ, a, Plcl9 t), (13.3.4)
где £Эф — эффективное излучение, имеющее, как известно,
размерность kL~2T~l\ а — коэффициент температуропроводности
лочвы, размерность L2T~iw9 piCi — ее объемная теплоемкость,
размерность &L~30_1 (&, в, L, Т — размерности соответственно
тепла, температуры, длины и времени).
Как следует из П-теоремы анализа размерностей,
зависимость (13.3.4) имеет вид степенного одночлена:
т0 = С1£,эфа:з(р1£1)т t\
где d — безразмерная универсальная постоянная.
Тогда, поскольку размерности обеих частей уравнения
одинаковы, Должно быть:
Следовательно,
т0 = С1 ^ Еэф. (13.3.5)
?\с\ У а
Формула (13.3.5) впервые была получена Брентом. Она
может быть использована для грубой оценки понижения
температуры. Но не следует забывать, что эта формула не учитывает
26 Заказ № 612
402 Глава 13
турбулентного теплообмена и влияния конденсации, а потому
дает заниженные значения температуры.
Для отыскания ti получим сначала выражение для профиля
температуры воздуха T"(z, t), используя (13.3.5) в качестве
одного из граничных условий. Найдем решение первого из
уравнений (13.3.1)
дТ" __, №
dt dz*
при условиях
Г|,=о = т0 = С,Е,ф—*уТ,
имея в виду (13.3.2).
Перейдем к безразмерным переменным, принимая
Т"=Т'0Т"п, t = t0tn, z=Hzn, (13.3.6)
где величины с индексом п есть безразмерные переменные,-
a T'q, to и Н — соответственно характерные масштабы
температуры, времени и высоты. Последние выберем таким образом,
чтобы выполнялись равенства:
1 _ k т* — Г Р
77 — Т/Г» *о—чя9ф-
Vh
В таком случае задача сводится к решению уравнения
дК_ д*т"п
при граничных условиях
т"п\ 0=VTn, т'„\ _=о.
Решение такой задачи можно записать в виде
Tn=f(Zn> tn)
или, если вернуться к первоначальным переменным, имея в виду
Поскольку Н не входило в число определяющих аргументов
в первоначальной постановке задачи, функция ![~П'>*~Ш~)
Суточный ход метеорологических элементов
403
должна иметь такой вид, при котором Н в уравнении (13.3.7)
•сократилось бы. Это требование будет удовлетворяться, если
f\H* H2)-V tf2/i( YYt)'
Тогда
T"(z, () = Еэф—^
Pici У
тНувУ
(13.3.8)
Выражение (13.3.8) описывает профиль температуры воздуха
и позволяет определить турбулентный поток тепла у
поверхности и связанное с ним изменение температуры поверхности xi.
Чтобы найти xi, следует решить уравнение
дх\ __ <Э2Х1
dt
сУС2
(13.3.9)
при условиях
дТ"
Поскольку на основании (13.3.8)
дТ
(13.3.10)
дг
=А £эф
г = 0 ° уТр^ Уа '
где Aq — постоянный множитель, то соотношение (13.3.10)
можно переписать следующим образом:
dt\
;=о * (?\С\)2ауа
Если теперь снова перейти к безразмерным переменным,
приняв, что соответствующие характерные масштабы равны
, "2 т л р *^yj__ „
а (?\С\)2аУа
то исходная система уравнений запишется так:
di\n д*тХп
dtn
д^п
<
с„=о
= 1.
Решение ее будет иметь вид
26*
404
Глава 13
Проделав выкладки, аналогичные тем, которые были
выполнены при отыскании Т"(z, /), получим
*х = АхЕ9ф (pici)2fl Yt.
Таким образом, ночное понижение температуры поверхности
почвы может быть рассчитано по формуле
?\С\ У а \ pici У a J
Постоянные С\ и А должны быть определены экспериментально
или на основании точного решения задачи. По физическому
смыслу рассматриваемых процессов должно быть Л>0, и,
следовательно, влияние атмосферы сводится к поправке, прямо
пропорциональной интенсивности турбулентного обмена.
Контрольные вопросы
1. Как формируется механизм суточных колебаний
метеоэлементов?
2. Сформулировать и решить задачу о суточных колебаниях
температуры при постоянном коэффициенте турбулентности.
3. Как изменяется суточный ход температуры с высотой?
4. Какие процессы определяют ночное понижение
температуры?
5. Как и почему изменяется в течение суток скорость и
направление ветра?
Глава 14. ФИЗИЧЕСКИЕ ОСНОВЫ ПРЕДВЫЧИСЛЕНИЯ
МЕТЕОРОЛОГИЧЕСКИХ ПОЛЕЙ НА КОРОТКИЙ СРОК
Общие положения. Уравнения гидротермодинамики в изобарической системе
координат. Численное решение уравнения гидротермодинамики для задач
краткосрочного прогноза (примитивная или исходная система). Численное
интегрирование прогностической системы уравнений. Квазигеострофическая
система уравнений. Прогноз для баротропной и бароклинной атмосферы в ква-
зигеострофическом приближении. Использование квазисоленоидальных
приближений. Предвычисление облачности. Влияние пограничного слоя на
эволюцию крупномасштабных процессов. О согласовании исходных полей.
Проблема предсказания погоды заключается в определении
будущего состояния атмосферы по заданному начальному
состоянию и по внешним воздействиям, приводящим к изменению
или перераспределению энергии, причем последние должны
задаваться на все время прогноза.
Простейший метод прогноза — синоптический — заключается^
по существу, в экстраполяции элементов крупномасштабной
структуры атмосферы, определяющих условия погоды,—
воздушных масс, фронтов и барических систем. Прогноз самих
метеорологических элементов (ветра, температуры и т. д.) имеет
полуэмпирические основания и носит преимущественно
качественный характер.
Другой метод — численный прогноз — приводит к решению
системы уравнений гидродинамики при заданных начальных и
граничных условиях.
Впервые он был предложен в 20-х годах XX в. Л. Ф.
Ричардсоном. Однако в связи с большим объемом вычислений и
недостаточной информацией о начальном состоянии (из-за редкой
сети метеорологических станций и полного отсутствия
аэрологических наблюдений) такой подход в то время не мог быть
эффективно реализован. Это направление приобрело
практическую ценность лишь после создания сравнительно густой
аэрометеорологической сети и появления совершенных ЭВМ. В
настоящее время оно является основной линией, по которой идет
совершенствование методов прогноза погоды. Численный
прогноз, являясь естественным методом решения проблемы,
становится важной частью современной «техники» прогнозов погоды.
14.1. Общие положения
Начальное состояние, при котором ищется решение системы
уравнений гидродинамики, определяется трехмерными полями
метеорологических элементов в начальный момент времени;
405
Глава 14
необходимую информацию содержат материалы наблюдений на
сети станций.
Что касается граничных условий, то они должны быть
заданы в форме потоков тепла, водяного пара и количества
движения или эквивалентных им величин на границах атмосферы.
Граничные условия отражают влияние внешней среды на
процессы в атмосфере.
Основное внешнее воздействие теплового характера
обусловлено колебаниями коротковолновой радиации, заданными как
•функции времени и координат на верхней границе атмосферы.
Поступление солнечной радиации — астрономический фактор, он
поддается точному математическому описанию.
Соответствующие граничные условия легко сформулировать.
На нижней границе атмосфера соприкасается с почвой или
океаном. Здесь имеет место постоянный обмен теплом, водяным
ттаром и количеством движения. Эти процессы и должны
учитываться граничными условиями на деятельной поверхности.
Для континентов формулировка граничных условий не вызывает
больших трудностей. Требования к полю скоростей тривиальны.
Теплообмен и влагообмен можно учесть, добавив к системе
уравнений для атмосферы уравнения теплопроводности и
распространения влаги в почве.
При склейке решений для атмосферы и почвы
удовлетворяются условия непрерывности искомых функций и законы
сохранения энергии и массы водяного пара. Возможны и
приближенные условия на деятельной поверхности, при этом уравнения
распространения тепла и влаги в почве можно не привлекать.1
Гораздо сложнее учитывать влияние океана на атмосферные
процессы, которое к тому же является весьма существенным.
По-видимому, нет возможности определить обмен различными
свойствами между океаном и атмосферой без достаточно
корректного учета всей совокупности процессов в океане. Строго
товоря, задача прогноза должна формулироваться для системы
атмосфера—океан. В таком случае границей области, для
которой интегрируется система, является дно океана. Условия на
дне очевидны и могут быть записаны без особого труда. В
такой постановке задача сильно усложняется.
Однако при прогнозах на короткий срок дело обстоит проще.
Это можно понять, анализируя уравнения для кинетической
энергии или притока тепла, которые в ясной форме отражают
«факторы, вызывающие эволюцию полей метеоэлементов. При
этом оказывается, что приращение кинетической энергии или
температуры за некоторое время V в фиксированной точке за-
1 Например, можно брать эти потоки из климатических данных или во-
юбще пренебрегать ими, учитывая их сравнительную малость.
Пред вычисление метеорологических полей на короткий срок 40Г
висит от начальной неоднородности полей, которой, в
частности, определяются эффекты адвекции, от трансформации
кинетической энергии упорядоченных движений в энергию
турбулентности и во внутреннюю энергию (если речь идет об изменении
скорости) или от притока тепла (если имеются в виду
изменения температуры). Вклад адвекции в каждый данный момент
времени (в полное изменение прогнозируемой величины)
относительно велик по абсолютной величине, но меняет свой знак во-
времени, тогда как скорость трансформации кинетической
энергии в пульсационную, будучи относительно малой, имеет всегда
один и тот же знак; как правило, длительное время сохраняется
также знак притока тепла в свободной атмосфере. В связи с этим
краткосрочные изменения метеорологических полей по крайней
мере в свободной атмосфере определяются в основном
неоднородностью начального состояния атмосферы, а внешними
источниками или стоками энергии можно пренебрегать. Однака
с удлинением срока прогноза влияние адвекции ослабевает из-за
взаимной компенсации положительных и отрицательных
вкладов,1 относительная роль притоков энергии извне непрерывна
растет.
Из приведенных соображений следует, что среднее по
многим реализациям значение функций
\Т (4Г\ I ^кин \* ~Т~ * ) ^кин (О I
™ 1 \1 ) = Г+г >
t
N2(t )-
r -2-dt
можно использовать как количественный критерий разделения
прогнозов на краткосрочные, малой заблаговременности и
долгосрочные. (В формулах £Кин — кинетическая энергия; г —
скорость трансформации кинетической энергии в энергию
турбулентности; Q — приток тепла.) Очевидно, прогноз на время f
следует называть краткосрочным, если Ni(t')^>\, малой
заблаговременности, если Ni(t') =0(1), и долгосрочным, если
Настоящая глава посвящена физическим основам
численных прогнозов погоды в свободной атмосфере на короткий срок.
В св'язи с изложенными соображениями допустимо
использовать условие адиабатичности и не учитывать эффекты
1 Суммарный эффект адвекции за длительный промежуток времени
сводится почти целиком к горизонтальному перемешиванию; исключением
являются районы квазистационарных течений.
403
Глава 14
турбулентности, в том числе и трансформацию энергии
упорядоченных движений в вихревую.
После этих предварительных замечаний перейдем к
непосредственному изложению проблемы.
14.2. Уравнения гидротермодинамики в изобарической
системе координат
В системе (7.8.34) — (7.8.40) искомыми являются величины
и, v, w, р, 7, р, а аргументами — х, у, г, t (геометрическая
система координат). Но более удобно использовать в качестве
независимых переменных xPi yPi р, tp (изобарическая система
координат) и считать неизвестными uf v,z —£-, Г, Я. Здесь Я—
at
высота изобарической поверхности, xv=x, уР = у> tp = t.
Подобная замена оправдана, во-первых, более простым
видом уравнения неразрывности, что достигается
соответствующими преобразованиями, во-вторых, более удобной для
численного интегрирования областью, поскольку, будучи
полубесконечной по вертикальной координате, она трансформируется в
конечную, и, в-третьих, чисто техническим обстоятельством: дело
в том, что в настоящее время информация, поставляемая сетью
станций, задается для определенных изобарических
поверхностей. Ее использование при прогнозе облегчается после
указанной замены переменных.
Найдем связь между производными в старых и новых
координатах. Все выкладки проделаем для общего случая, выбирая
Р — а t * ^
в качестве одной из независимых переменных с= (оооо-
5 — а
щенная изобарическая система), где a = const, s = s(t, х> у) —
известная функция горизонтальных координат и времени.
Соответственно обозначим остальные координаты: yz = y, Х£=х, ti = t.
Зависимыми переменными при этом будут и; v, —тг, Т и 2 =
= Я(^, хь уь £). В частном случае при а = 0, 5 = 1 общие
уравнения принимают форму, соответствующую изобарической
системе координат.
Пусть имеем две точки в пространстве координат и времени.
Приращение какого-либо свойства на отрезке, соединяющем эти
точки, разумеется, не может зависеть от выбранной системы
координат, и, следовательно, если <р — одна из искомых функций,
то
Пред вычисление метеорологических полей на короткий срок 409*
= ?(*+Л, x+dx, y-\-dy, z+dz)-<t(t, х, у, г), (14.2.1).
= <Р(<с"Н«с. A:+rfxc, yc+rfyc, C+dC)-<p(*t, *o yc. С), (14.2.2>
причем d<p = d^; это тождество используется для отыскания
связи между производными в обеих системах координат.
Из (14.2.2) получаем выражение для индивидуальной
производной в '^-системе координат:
-^=^+"^+^+#-^ = 4г- 04.2.3).
di^ dt^ ' дх^ ' dyc ' d>c dl dt v '
Величина —— скорость изменения ^-координаты для
движущейся частицы; в дальнейшем —— будем обозначать чеоез £
at
и называть ^-компонентой скорости. Все индивидуальные
производные в исходной системе запишутся на основании (14.2.3),
если подставить вместо <р соответственно и, v, w, р, Т.
В уравнении (14.2.1) частные производные по
пространственным координатам (д<р/дх, ду/ду) берутся на фиксированной
высоте, а в (14.2.2) (ду/дх^ ду/ду^) —на фиксированной
^-поверхности.1 Это различие и подчеркивается индексом £. Связь между
производными в новых и старых переменных легко найти,
подставив в (14.2.2)
-гЫ(т?--'-л-)*+(4£-'-&)**+
+(-£-'-£К+**]-
dt^=dtt dxt=dx, dy^ = dy,
\dz
f Угол наклона изобарической поверхности к горизонтали
dx
: = 10~4 рад, поэтому в обеих системах координат производные по
горизонтальным координатам близки
/ ду/дх — ду/дх \
410
Глава 14
'Приравняв после этого коэффициенты в (14.2.1) и (14.2.2) при
•одинаковых дифференциалах, имеем:
dt
д'г
д?
dx
дх.
1 ду ( dp ~ ds \
-а дС \ д* ^ dt ) '
(dp r ds \
\dx ^ dx ) '
1 dep
d'f dy
dy dy.
1 dy I dp ~ ds \
- о ~Ж\Иу~~^~5у~)
dy
P£
d?
(14.2.4)
Для того чтобы выразить составляющие градиента давления
:в новой системе координат, в соотношениях (14.2.4) будем
полагать <p=z. Так как z — независимая переменная в
геометрической системе координат, то dz/dt = dz/dx = dz/dy = 0, а в
обобщенной изобарической системе координат z = H (/;, х^ у& £) —
искомая функция. Воспользовавшись уравнением статики,
получаем:
dH 1 [_dp_r_d±_\ \
\ dt dt )'\
0 =
0 =
dt,
dH
?g
dx^
i
?g
^
(dp c ds \
\dx ^ dx ) '
1 / dp ~ ds \
~йГ\~д~У ^~5уГ
1 =
dH
s — a d£
?g
(14.2.5)
(14.2.6)
Уравнение (14.2.6) является эквивалентом уравнения
статики. Теперь на основании (14.2.3) и (14.2.5) легко записать
уравнения динамики и уравнение притока тепла:
da
dti
dt.
dxr
-v
du
dy.
.;-£-*-,■
dH
ds
dv
dv
dt.
dxr
+v
dv
dye
dT
* dv ,
RT
dx^
dH
dtr
cp [a + (s —д)С]
P dxz
: ds
'g dyz p dy:
d(s — a)^ ^q
dtr
(14.2.7)
(14.2.8)
(14.2.9)
Вывод уравнения неразрывности менее тривиален. Приведем
подробные выкладки. Полагая в последнем из уравнений (14.2.4)
<p = t, найдем
Пред вычисление метеорологических полей на короткий срок 411:
s — а д* I д (s — а) *
Р ~~ g dz ~~~ g dz ^'
Это выражение подставим в уравнение неразрывности. Тогда
имеем
d a(s-a)c | а(5-д)с/ a? ■ a^ . a^ \_0 n49lnv
"S as I as \dx"^ дУ "T" a* J-u- u^-1^
Заметим теперь, что
rf a? _ a dcp . a a? . a a? . a a? _
^ a* ~~ dt dz «"" a* a* "» ay а* """^ а* a*
j_^ ^ _a^ _a_ _a^ _a_ _acp__
а-г аг ^ dz u dx ^ dz u dy ■ dz ш dz
a<p du a-f a^ a? a^ ad? a? aa
ax а<г ay az dz dz dz dt dx dz
a<p dv dy dw
dy dz dz dz '
На этом основании (14.2.10) можно записать в виде
a d (s — а) с a (s — д) с a& a(s — а) с а^ .
а^ d£ dx dz dy dz *
Из (14.2.4) следует, что —— = -rz—, поэтому в (14.2.11 >
дифференцирование по z всюду можно заменить
дифференцированием по £. Кроме того, как уже указывалось [см. (14.2.3) ]„
——=—-— >= поэтому (14.2.11) можно записать в виде
at ut^
а Г/ \r_i_r d(s — a) 1 a (s — л) du d (s — д) av ,
"аГ[^—а^ ■"" 57 J dx ас ay 5Г +
+<—)1ж+-5-]-°-
Здесь исцользовано
В последнем уравнении заменим дифференцирование по
горизонтальным координатам соответственно формулам (14.2.4)
и воспользуемся тем, что
а > rf (s—- д) d(s — a) { ~ а Г d (s — a) 1 d (s ~ a) .
ac ^ dt^ — dtz ' ^ a; [ <«c J— dtz ">
J_r Г dtf a (s —- д) . at; д (s — a) 1
+Св ["ЭГ a*c ~г~ ac a^ J>
412
Глава 14
тогда получим
д (s — а) С | d (s — а) , г\ ди д (s — а) , dv д (s — а)
ас ' dt^
• к Г дд d (s — л) , а*/ ^ (s — а) 1
+ *" ["dt дх~<, *~~di ду[ J ~~
да Г d(5 —д)С , 1 aC (5 — д) f a/? r ds \]
ас [ а*с "г" 5 - а ас I а* ^ a* JJ
_а^_ г a (s — д) с , 1 a (s — д) с i dp «, а$ \] .
ас [ ду: "+" 5-д ас \ ay ^ ay j] ■
+«-«)[4+-пттг(#-'#)+-^+
;-&-<-£)]-°-
1 s — д ас
После сокращения и объединения слагаемых под знак общего
дифференцирования получим окончательное выражение:
а (5 — д) . ад (5 — д) . dv(s-a) . ас (5 — д) __q ,j^ 2 12)
а^с ""■ дх: * ду^ * ас * v • • /
Добавив уравнение Клапейрона
р = р/?Г=а+С(5-а) (14.2.13)
к уравнениям (14.2.6) — (14.2.9), (14.2.12), получим шесть
уравнений для шести неизвестных (и, v, £, Н, р, Т).
14.3. Процедура численного решения уравнений
гидротермодинамики применительно к задачам краткосрочного
прогноза (примитивная или исходная система)
В дальнейшем мы будем пользоваться изобарической
системой координат (исключения будут указаны специально), в связи
с чем индекс £, который необходим для того, чтобы различать
дифференциальные операции в геометрической и обобщенной
изобарической системах, больше не потребуется. Систему
уравнений для предвычисления метеорологических полей на короткий
срок на основании (14.2.6) —(14.2.9), (14.2.12), (14.2.13),
полагая s = l, а = 0, запишем в следующем виде:
да ди , , дФ /лло1\
in-==-uJ-dzr+lv—dr> <14-зл>
dv dv , дФ /1/1 о о\
дТ дГ . RT пл Q Q4
-т— = —U;—. hx , (14.3.3)
at J dXj ' cpp • v 7
Пред вычисление метеорологических полей на короткий срок 413
■£---5Р. (Н.3.4)
ди}
^- = 0. (14.3.5)
Здесь: а)./= 1, 2, 3, Ui = u, u,2 = v, Uz = i = dpldt, Xi = x, хг = у,
Хз = р; б) при помощи уравнения Клапейрона из системы
исключена плотность; в) высота изобарических поверхностей
измеряется в геопотенциальных декаметрах, так что Q>=gH.
Сформулируем теперь граничные условия. На верхней
границе естественно воспользоваться условием сохранения массы
атмосферы; это означает, что
РЧ-оо = 0- (14.3.6)
Поскольку, кроме того, p|z-*oo->-0 для любого момента времени
над любой точкой Земли, то
^р___др_ _ dp ~
dt дх ду и
Тогда применительно к изобарической системе координат
указанное условие запишется так:
* I*—-(-Т(г+" 15Г+" 1?-+w Щ = St" I—= °- <14-3J>
На нижней границе области интегрирования, которой в
рассматриваемом случае является верхняя граница пограничного
слоя (предполагаем, что верхняя граница пограничного слоя
параллельна рельефу), используем условие обтекания. В
геометрической системе координат оно имеет вид
I dF , dF
Z m 0
(14.3.8)1
Запишем (14.3.8) в новой системе переменных. Для этого
воспользуемся тем, что из выражения
dp dp , dp
т
dt dt *UJ dxj
1 Строго говоря, это условие должно выполняться на z=F(x, у) и в
указанном виде может быть использовано, если неровности Земли достаточно
малы, т. е.
/ dF dF \
/о
^ г д ( dF dF \ |
414
Глава 14
следует
•~й-(*+«-£+"-£-')-й"$?-+
Подставив w из (14.3.9) в (14.3.8), получим
i др \' > ( дН . дН \ I
-*L,+'[-s^L+-J%1L]U-
_f[-+.^»L+„^2.]^. (14.3,0)
Здесь Ф=£#, Q)=gF, pF— давление на нижней границе.
Система уравнений (14.3.1) —(14.3.5), (14.3.7), (14.3.10)
содержит первые производные по времени от четырех искомых
функций — и, v, 7\ Фр=Ф| P=pF . Соответственно для ее
решения необходимо задать начальные поля скорости ветра,
температуры и геопотенциал на нижней границе. Вместо температуры,
впрочем, можно задать поле Ф, поскольку уравнение (14.3.4)
позволяет перейти от одной функции к другой. Можно также
вместо ФР задавать pF — давление на нижней границе, поскольку
(14.3.4) позволяет вычислить Ф^, если дано pF. Таким образом,
система должна решаться при следующих начальных условиях:
и|*=о = и°(*. У> Р)> ^|/=о = ^°(^, У, Р),
T\t=0=To(Xi у, р), ФР\<=0 = Фо{х, у, р)\р = ру (14.3.11)
Необходимые условия на горизонтальных границах сводятся
к требованию периодичности всех функций по широте и долготе.
Укажем путь численного решения задачи, по крайней мере
в принципе. Для этого необходимо все производные по времени
и координатам заменить конечными разностями. В узлах сетки
в начальный момент времени to заданы и, v, Т как функции х,
у, р. По этим данным вычисляется начальное поле т при
помощи уравнения (14.3.5) и условия (14.3.7) начиная с уровня
р = 0. Уравнение статики (14.3.4) при заданных начальных
полях температуры используется для вычисления начального
поля Ф.2 Таким образом, диагностические уравнения (14.3.4) и
1 Здесь использовано (14.2.5).
2 За начало отсчета Ф принимается какая-либо изобарическая
поверхность р=Рст, например поверхность 1000 мб.
Пред вычисление метеорологических полей на короткий срок 415
(14.3.5) применяются для восстановления полей, не
содержащихся в исходной информации. Теперь обратимся к собственно
прогностическим уравнениям (14.3.1), (14,3.2) и (14.3.3) для
расчета компонент скорости ветра в момент t0+At. Для этого
каждое из упомянутых уравнений запишем в виде
<р(*о+Д*. х, у, p) = <?(t0, х, у, p)+D9(t0, х, у, p)\t. (14.3.12)
Здесь D<p — разностный оператор, аппроксимирующий правые
части уравнений. Поскольку поля Фит для t = U вычислены с
помощью диагностических уравнений, то в (14.3.12) вся правая
часть известна и оно дает значение <p(to + At, ху уу р). Наконец,
оставшееся уравнение (14.3.10) используется для вычисления
pF(t0+Aty х, y)=pF(t0y х, y)+DpF(t0, х, у). Расчеты
выполняются для всей области интегрирования. Этим завершается
вычисление для момента to+At. На рис. 14.1 приведена
указанная последовательность расчетов. Процедура повторяется
шагами по времени, в процессе вычислений находятся все поля
в моменты U+iAt (t = l, 2, 3, ..., п) на весь интервал
прогноза nAt.
Вместо изобарической системы координат можно ввести так
называемую ст-систему координат (a = p/pF). В этой системе
нижняя граница области интегрирования совпадает с
координатной поверхностью, что оказывается более удобным для
численного интегрирования. Полагая в уравнениях (14.2.6) —
(14.2.9) и (14.2.12) s = pF(ty х, у)у а = 0, t> = o = p/pFy получим
прогностическую систему уравнений в а-координатах.
-^—-«у-ЖГ-+'«—^—=-^. 04-ЗЛЗ)
-g-= dv__t ™_^ _££_ (Н.3.14)
dta > dx)f9 дуз р ду, ^
дРр диРр dvpF д\Рр (14.3.16)
~dt • дх "г ду ' до — и> v '
дФ
дх
Z
дФ
с дрР
Р дх^
а dpF
dT RT dPFa
dt c.Pc.0 dt
cpPf*
=0, (14.3.17)
pRT=apF.
(14.3.18)
416
Глава 14
и° (х. у, р)
I/O (х, у, р)
ГО (jr. у, р)
Ф^(*. У- Р)
^•'■'>--J(^+-?f)''
ФО(*.у. />) = -* f ^С*. у. /» rfp
Рис. 14.1. Последовательность операций при чи
Выведем граничные условия в а-системе. Поскольку а =
= p/pF, то
da • 1 / dp , dp , d/> . dp
rf^
/^ V dt
dz
pF\ dt ^ " dx ^u dy
(14.3.19)
Отсюда следует, что из-за р \ г =оо — О" | z=oo = 0 должно быть
= 0. (14.3.20)
а-* о
Условие на нижней границе получим, заменив в (14.3.19)
производные от давления выражениями (14.2.5). После
несложных выкладок найдем
gw--
дФ
дФ
дФ
Pf
dt
дх
*Ув
(14.3.21)
= i
Условие обтекания рельефа удовлетворяется, если подставить
значение w из (14.3.8) после перехода в нем к а-системе
координат.
Процедура численного интегрирования уравнений в
а-системе аналогична описанной выше процедуре для изобарической
системы.
Пред вычисление метеорологических полей на короткий срок 417
да
dt
dv
t = o
= _ао**+лю.
аФо
y~dx~f
dt
дТ
dt
t = o
.„о**-/во_
дх
дФО
vaJ
;
ду
/ = о J dxj срр
dt
= —ао
д(ф£-ф)
/=о дх
д(ф£-Ф)
— I/O-
ay
а(ДЛ дг, у, р)=аО + -^-| А^
1/(Д*. х, у, р)=^0 + 4т-| А^
v J dt \о
Т (ЛЛ л:, у. /7) = ГО +
Фр(М.х. у, P) = *°F +
дТ
dt
дФг
dt
М
М
1
и т. д.
сленном прогнозе для свободной атмосферы.
14.4. О численном интегрировании прогностической
системы уравнений
Реализация приведенного алгоритма численного прогноза
может встретить трудности. Кажущаяся простота и ясность
описанной процедуры создает иллюзию, как будто она всегда
приводит к цели. Первой жертвой такой иллюзии был Л. Ф.
Ричардсон (1922 г.), о смелой попытке которого реализовать эту
процедуру упоминалось в начале главы. В действительности
нахождение приемлемого для практической работы алгоритма
является нелегкой задачей и опирается на важные результаты
численного анализа. Усвоение их необходимо для четкого
понимания вычислительного аспекта современных методов
прогноза погоды, в связи с чем коротко остановимся на этих
методах.
Разностные методы
Замена подлежащей решению дифференциальной краевой
задачи соответствующей разностной задачей допустима только
в том случае, если при измельчении сеточной области, в
которой ищется численное решение £д> это решение в каком-то
смысле приближается к решению £ исходной дифференциальной
задачи. Отклонение £д от £ можно оценивать различными
способами, например по максимуму модуля, в среднем квадратиче-
ском смысле и пр. Если это отклонение стремится к нулю при
27 Заказ № 612
418
Глава 14
безграничном уменьшении пространственно-временных шагов
сетки, то говорят, что имеет место сходимость разностного
метода в смысле выбранной оценки разности £ — £д. По существу,
это указывает на характер приближения решения разностного
уравнения к решению соответствующего дифференциального
уравнения. Внимательный анализ выбранного разностного
метода, проводимый обычно для модельной линеаризованной
задачи, позволяет установить как существование сходимости
в принципе, так и конкретный вид условия, при котором она
имеет место.
В качестве такого модельного уравнения, имеющего
непосредственное отношение к физическим процессам, описываемым
системой прогностических уравнений, рассмотрим простое
одномерное уравнение адвекции
— оо<х<оо, t^O, £/ = const
с начальным условием
*(*, 0) = Ч(х). (14.4.2)
Решение будем искать на дискретном множестве точек сетки
с шагами Ах, At:
xm = mLx, т = 0, ±1, ±2, . . .,
tH = kM, k = 0, 1,2,.. ., TV, NAt = T.
Переход от дифференциальной задачи (14.4.1) и (14.4.2)
к разностной задаче может быть осуществлен не единственным
способом. Заменим, например, производную по времени
разностью вперед, а пространственную производную — односторонней
разностью. Обозначая lhm=t>(mAxf kAt), имеем совокупность
разностных уравнений — разностную схему:
yk -f 1 rk rk *k
m Af m +U- m+[x m =0, (14.4.3)
C = 9m. 04.4.4)
Обозначив буквами £ и £ решения дифференциального и
разностного уравнений соответственно, мы подчеркиваем, что,
вообще говоря, это две различные функции. В силу того что
функция | непрерывна в области, а £ задана лишь в узлах сетки,
изучение аппроксимации сводится к их сравнению в этих узлах.
Вычислительная процедура очевидна. Переход от значений
функции £ в момент времени kAt к ее значениям в момент
Пред вычисление метеорологических полей на короткий срок 419
(k+l) At для всех точек сеточной области задается формулой
а (14.4.4) обеспечивает начальный счет (k = Q)m Разлагая
значения l(xmy /fc+i), l{xm+u h) в ряд Тейлора в окрестности
некоторой точки (xm, th)y принадлежащей к рассматриваемой области,
и подставляя их в (14.4.1), имеем
(14.4.6)
m к
Разностные уравнения (14.4.3) и (14.4.6) совпадают. Это
значит, что исходное дифференциальное уравнение
аппроксимируется разностным с точностью порядка О (Ах, At). Заметим, что
степенью Ах, At в остаточном члене определяется порядок
аппроксимации.
Что же произойдет при стремлении к нулю параметров
сетки? Чтобы ответить на этот главный вопрос, заметим, что
решение задачи (14.4.3) и (14.4.4) можно представить
суперпозицией простых гармонических волн. Удобно рассмотреть
поведение решения разностной задачи на одной из гармоник,
соответствующей некоторому волновому числу 5 с амплитудой jx,
зависящей от времени:
rb и. \ ^sxM k Asm Длг /л л л т\
W = fM**)£ m = \^se . (14.4.7)
Подставляя это выражение в (14.4.5), получим
^'^(l + t/^-t/-^4*). 04.4.8)
Отсюда видно, что амплитуда цЛ элементарной гармоники в
момент времени (k+l) At приобретает множитель
0=1 + */-к-О -J*'*) 04.4.9)
и через N шагов амплитуда будет равна
rf+"e[l + tf-JI-O -eis")\\l (14.4.10)
Для того чтобы при Д/->-0 (N = 77A£->oo) не происходил
экспоненциальный рост амплитуды, множитель G должен
удовлетворять условию
|0|<1 (14.4.11)
27*
420
Глава 14
ИЛИ
l+2i/-tj(l + £/-^)(l-cos5A*Kl,
откуда следует
°<-(/4t<L (14.4.12)
Условие (14.4.12) называется условием устойчивости схемы
(14.4.1). Из него видно, что (14.4.12) может выполняться лишь
при f/^О. Нетрудно убедиться, воспроизведя вышеприведенный
анализ, что в случае U>0 следует видоизменить схему, записав
yk-\-\ yk yk yk
<•* ]ц <-m Чк-l =Q> (H.4.12')
At ' w Lx
Соответствующее условие устойчивости имеет вид
°<^-ST<1- (14.4.13)
Какое же отношение имеет условие устойчивости разностной
схемы к искомому решению дифференциального уравнения?
Ответ на этот вопрос дается фундаментальной теоремой: при
наличии аппроксимации устойчивость является необходимым и
достаточным условием сходимости (теорема П. Лакса).
Необходимость различного разностного представления
производных в зависимости от знака (/, использованного в (14.4.3)
и .(14.4.12'), ясна из чисто физических соображений.
По смыслу уравнения (14.4.1) любое возмущение
переносится соответственно величине и знаку U и, стало быть,
изменение искомой величины (в нашем случае £) в точке (хт, 4)
обусловлено разностью 1(хт> tk) —\{хт-и tk) при С/>0 и
соответственно разностью l(xm+u tk)— I (хт, tk) при U<0.
-Наряду с рассмотренными условно устойчивыми разностными
схемами могут существовать и принципиально неустойчивые
схемы.
Убедимся, что схеме
yk •{-1 yk yk yk
At +U A* =0' (14.4.14)
аппроксимирующей исходную задачу с точностью О (At, Ах2),
соответствует множитель G вида
G=l-2£/-^/sinsA;c, (14.4.15)
откуда
| О| = [ 1 + (2^7-^sins Ajc)2],/2. -(14.4.16)
Пред вычисление метеорологических полей на короткий срок 421
Для этой схемы условие (14.4.11), вообще говоря, не
выполняется. (Оно выполняется только для отдельных гармоник с
волновым числом, удовлетворяющим условию sAx = mt, п = 0, 1,
2, ...) В таком случае говорят, что схема неустойчива.
Счет rio неустойчивой схеме быстро превращается в
хаотическую последовательность стремительно растущих чисел, не
имеющих никакого смысла.
Итак, для решения конкретной задачи надо воспользоваться
некоторой разностной схемой, проверив ее устойчивость на
соответствующей модельной задаче подобно тому, как это
делалось выше. Условие, полученное в результате проверки,
разумеется, следует рассматривать лишь как обязательное для
сходимости численных решений.
Отметим, что существуют схемы, устойчивость которых не
связана никакими ограничениями (так называемые неявные
схемы), однако за это преимущество приходится расплачиваться
при их реализации большим дополнительным объемом
вычислительной работы.
Неравенства (14.4.12) или (14.4.13) налагают ограничения
на временной шаг: Д^ , т. е. чем больше U — скорость
и
перемещения рассматриваемого возмущения, тем меньше
должен быть выбран временной шаг для того, чтобы численное
решение задачи было устойчивым. Если, например, речь идет
о распространении звуковых волн, то [/ = 330 м/с, и при Дх =
= 330 км должно быть Д/^17 мин.
Выбор такого малого шага — задача, обременительная для
вычислительной техники. Поскольку, однако, звуковые волны
вызывают весьма малые по амплитуде возмущения
метеорологических полей, то естественно поэтому стремление выполнить
некоторое препарирование уравнений с тем, чтобы в
прогностической системе не содержались решения типа звуковых волн.
В современной литературе это называется фильтрацией звуковых
волн.
В главе 10 об этом говорилось довольно подробно. Для
фильтрации звуковых волн необходимо воспользоваться условиями
статики по вертикали и пренебречь слагаемыми, отражающими
сжимаемость в уравнении неразрывности. Соображения
относительно целесообразности фильтрации звуковых волн в такой же
мере касаются и быстрых гравитационных волн. В упомянутой
главе указаны пути фильтрации этих волн.
Интересные с практической точки зрения задачи прогноза
включают более чем одно пространственное измерение и
временную координату. Это ставит перед вычислителем еще один
весьма сложный вопрос — нахождение эффективного алгоритма
счета многомерных задач. Остановимся кратко на идее одного
422
Глава 14
из используемых при этом методе — методе расщепления,
ограничившись двумерным случаем.
Рассмотрим уравнение
^f = U^+V*L, (u.4.17)
где х, у изменяются в области D с границей Г, при условиях
а|/=о = я°,
и\т = ит. (14.4.18)
Решение будем искать на дискретном множестве точек хт =
= тДх, уп = пАу} tk = kAt\ т, n, k — целые числа из заданной
совокупности. Запишем уравнение (14.4.17) в виде
т,п m'!^ = Lltl+L2tlt (14.4.19)
где LiU и Liu, каким-то образом аппроксимируют соответственно
первое и второе слагаемые исходного уравнения.
Предположим теперь, что временной шаг At раздроблен; про-
межуточное по времени значение обозначим и и запишем
вместо одного двумерного уравнения (14.4.17) два одномерных:
ит,п-ит,п _^ц> (14.4.20)
-=4г = ^«- (14-4.21)
Эквивалентность этой системы исходному уравнению легко до-
казать исключением промежуточной функции и. Граничные
условия при этом должны быть согласованы со вторым из условий
(14.4.18). Аналогичный прием распространяется на решение
трехмерных задач.
Рассмотрим применение метода расщепления подробнее. Для сокращения
записи введем операторы:
Тогда для уравнения (14.4.17) можно воспользоваться, например, следующей
схемой расщепления:
[,—ёг'п.]''+'-[ч-фп,] "'"•"'• <,4AM)
где uh+l — некоторое промежуточное значение между uk и ик+1. Реализация
схемы (14.4.23) проста и сводится к решению двух одномерных аадач.
Пред вычисление метеорологических полей на короткий срок 423
Если исключить из схемы (14.4.23) промежуточное значение w*+1,
подбила „.
ствовав на первое уравнение оператором /+ j-т— VoVt а на второе — операто-
М т/а
ром / — тт— Voy, то получим схему
(14.4.24)
или в развернутом виде
ui+1-u*
~m, п m, п
= ^^>* + 1 +"*) +4тГ^М"* + 1 +"*) +
М 4Ьх *^ i/i 4Ду у
+ 16 ^Ду UVbxby(u"-a»^). (14.4.25)
Воспользовавшись разложением искомой функции в ряд Тейлора в
окрестности точки (mAx, лД#, kM) и соотношением utt = Uuxt + Vuvt1 которое
является следствием (14.4.17) (если U, V не зависят от t), нетрудно получить,
что схема (14.4.25) или, что то же, (14.4.23) аппроксимирует исходное
уравнение (14.4.17) с точностью О (Л/2, Ах2, А(/2), т. е. со вторым порядком
точности по всем переменным. Вместе с тем в «нерасщепленном» виде схема
(14.4.25) трудна для реализации, ибо каждое из разностных уравнений
содержит девять неизвестных на временном слое /г + 1.
Остается заметить только, что схема (14.4.23) абсолютно устойчива, т. е.
не предъявляет в счете никаких ограничений на соотношение пространственно-
временных шагов сетки. Ограничиваясь скалярным случаем, для решения
в виде элементарной гармоники
и* = ybei (sxm bx + stn ^y)t (14.4.26)
где Su s2 — соответственно волновые числа по осям координат, имеем:
~Л + 1 = 2£ ^0,,»
1 " 2Ау Vi sin S<1 Ау
^г=—^ ;г*+^о£*+1
1 pj-T— б^/sin 5Х Ах
2Ьх
jj.*+l = G1G2^. (14.4.27)
или
причем
|GiG2|=l.
Подробный анализ алгоритмов решения многомерных
метеорологических задач на основе принципа расщепления содержится в ряде
специальных исследований.
424
Глава 14
Спектральные методы
Для численного решения задач прогноза погоды, помимо
разностных методов, успешно применяются и такие методы, в
которых решение ищется в виде разложения по конечному числу
функций, а коэффициенты разложения находятся решением
краевых задач более простого вида, чем первоначальная. Эти
методы обычно называют спектральными. Они обладают, вообще
говоря, повышенной точностью по сравнению со стандартными
разностными методами в сопоставимых условиях, сохраняют
интегральные характеристики задачи и обладают другими
привлекательными чертами, которые во многих случаях оправдывают
их применение.
Основную идею спектрального метода проиллюстрируем на
примере интегрирования простого уравнения типа (14.4.17).
Уравнение сохранения относительного вихря
^г+"^г+^=0- (14А28>
в плоском бездивергентном потоке с функцией тока г|>(л:, у, t)
имеет вид
г(ф)^-^_С-У(ф, С) = 0, (14.4.29)
где
t=V2<l>, (14.4.30)
причем в области D с границей Г функция г|э удовлетворяет
некоторым условиям:
"Нг^Фг. (14.4.31)
Н=о = Ф°. (14.4.31')
Представим функцию тока г|> в виде линейной комбинации
конечного числа функций:
ф«ф(х. у, *) = 2 ?„(<)*«(*. у). (14.4.32)
Функции Фп(х, у), называемые базисными функциями, должны
удовлетворять на Г граничным условиям (14.4.31) и обладать
некоторым свойством, которое оправдывало бы представление
решения в таком виде.
Предвычисление метеорологических полей на короткий срок 425
Решение в виде (14.4.32) можно рассматривать как
спектральное разложение искомой функции по конечному базису;
каждое слагаемое представляет гармонику разложения с
амплитудой, зависящей только от времени.
Одним из распространенных численных методов нахождения
решения исходной задачи в виде (14.4.32) является метод Га-
леркина. В этом методе амплитуды определяются из
требования, чтобы при подстановке в (14.4.29) функции \|э вместо i|>
[с учетом (14.4.30)] левая часть уравнения, z(t>), стала
ортогональной ко всем функциям системы {Фп(х, */)}^=1г т. е.
И *(?)**(■*. y)dxdy = 0 при k=l9 2, . . ., TV (14.4.33)
D
ИЛИ
N N N
2«м^- <?* V) - 2 2 *«. n?n (t) <?m (0=0, (14.4.34)
л = 1 я =1 m = 1
где
an,k=\ f V2Onq>kdxdy,
V
D
(14.4.35)
Таким образом, задача свелась к решению системы N
обыкновенных дифференциальных уравнений (14.4.34) при
начальных условиях (14.4.31'), что является более простой задачей по
сравнению с (14.4.29) —(14.4.31).
Очевидно, желателен такой выбор базисных функций Фп,
при котором коэффициенты системы an,h, bhm п были бы
сравнительно простыми. В этом направлении и развиваются
специализированные приемы реализации метода Галеркина.
Сходимость метода, т. е. близость в определенном смысле г|?^ к гр при
TV—^оо, должна быть установлена каждый раз с учетом типа
краевой задачи и применяемой численной процедуры.
Остановимся на вопросе конкретного выбора базиса в
некоторых типичных случаях.
Для задач с периодическими граничными условиями удобны
экспоненты с комплексными показателями, образующие орто-
нормированную систему
П( 1, n = mt
D^^dxdy^lm,^{ (14.4.36)
426 Глава 14
В силу периодичности ф(х, у, t) ее можно аппроксимировать
конечным рядом Фурье:
(14.4.37)
Это равенство выражает дискретное преобразование Фурье на
сетке DA с шагом Д=—— функции -ф в комплексной области
с вещественными независимыми переменными ху у 6 А\. Явное
выражение для коэффициентов Фурье <p(k, t) [k=(&i&2)] легко
вычислить, пользуясь ортогональностью показательных функций.
Оно имеет вид
<Р(к> 0=4г 2 Их, у, /)ехр[-/(М+%)]. (14.4.38)
Отметим, что, хотя в силу ортогональности базиса коэффициенты
системы уравнений (14.4.34) в данном случае имеют простой
вид, численная реализация спектрального метода может
встретить трудности, если не считаться с тем обстоятельством, что
компоненты волнового ветра, кратные N=——, неразличимы на
сетке Da с точки зрения представления (14.4.37).
Для задач численного прогноза на сфере естественно
рассматривать разложение искомой функции в ряд по сферическим
гармоникам
Ут,п(К p) = eimXPn,mb). (14.4.39)
Здесь X — долгота; fi = sincp (ф — широта места); Рп,т —
присоединенные полиномы Лежандра; т — зональное волновое число;
п^\т\ — целое положительное число. Решение в соответствии
со сказанным выше ищется в виде конечного ряда
М \m\+J
?(*. М)= 2 2 ?«.«(') Г(*.Р). (14.4.40)
т= —М л = | т |
что приводит к системе уравнений типа (14.4.34).
В заключение остановимся на примере реализации
спектрального метода, когда базисные функции Фп(х, у)
удовлетворяют уравнению типа
у2Фя = -С>л. (14.4.41)
Таким свойством обладает, например, базис из сферических
функций
ч2Ут,п(К v)=- n(natX) У т. Л, V)-
Предвычисление метеорологических полей на короткий срок 427
Без ограничения общности можно считать, что Фп|г =0. Тогда
легко показать, что система функций {Фп}^в1 ортогональна
в D. Будем считать ее также ортонормированной:
U*-*-^rfy-8---{i:^«. <i4-4-42)
С учетом (14.4.41) и (14.4.42) уравнение (14.4.34) примет вид
n ;v
п =1 m = \ D
k=\, 2, . . ., N. (14.4.43)
После вычисления интеграла в правой части (14.4.43) и
определения собственных чисел С2т из (14.4.41) амплитуды
спектрального разложения могут быть определены из системы уравнений
(14.4.43). Суммирование в виде (14.4.32) дает аппроксимацию
искомого решения \|э(х, г/, t).
Настоящий параграф носит иллюстративный характер — он
вскрывает проблематику подхода, связанного с реализацией
численных процедур прогноза. Для подробного знакомства с
теорией конечноразностных аппроксимаций и ее приложениями
следует обратиться к специальной литературе.
14.5. Квазигеострофическая система уравнений
для численных прогнозов
Правильный выбор численного алгоритма для решения
дифференциальных уравнений обеспечивает корректное решение
задачи прогноза в чисто вычислительном аспекте. Однако качество
численных прогнозов на короткий срок сильно зависит от
начальных данных. В этой связи весьма важно попытаться свести
к возможному минимуму погрешности прогноза, вызванные
случайными ошибками в начальных данных. Большие трудности
в этом плане, как уже упоминалось выше, вызваны близостью
ветра к геострофическому, вследствие чего из примитивной
системы уравнений прогнозируемые величины, в частности
компоненты скорости ветра, вычисляются как малая разность больших
величин. Погрешности начальных полей ветра, получаемых из
довольно грубых сетевых наблюдений, будут весьма заметно
влиять на результаты в течение всего интервала времени, на
который дается прогноз.1 Разумеется, что и ошибки неосторож-
1 Это становится очевидным, если вспомнить численный алгоритм.
Ошибки начальных полей ветра приводят к ошибкам в ускорениях, по которым
вычисляется поле скорости на первом временном шаге; последние будут
причиной погрешностей ускорений, вычисляемых во втором цикле, и т. д.
428
Глава 14
ного округления от шага к шагу могут накапливаться и при
большом количестве шагов могут оказаться заметными при
расчетах. Ошибки предвычисления вектора скорости влекут за со-^
бой погрешности других искомых.величин.
В настоящее время развиты методы объективного анализа
начальных данных, которые позволяют уменьшить погрешности
наблюдений или по крайней мере исключить самые большие
ошибки. Типичная методика такого рода будет рассмотрена далее.
Вместе с тем представляется целесообразным так
преобразовать исходную систему уравнений, чтобы искомые
крупномасштабные поля метеорологических элементов были менее
чувствительны к погрешностям исходных данных. Если при этом
качество прогноза и не улучшается кардинально, то по крайней
мере результаты предвычисления оказываются сглаженными и
автоматически исключаются большие ошибки.
Для того чтобы лучше приспособить уравнения
гидродинамики для целей прогноза, попытаемся прежде всего
формализовать факт близости ветра к геострофическому.
При чисто геострофических условиях из (14.3.1), (14.3.2) и
(14.3.5) следует:
0=—/«-|—Ц-, } (14.5.1)
•ч ди , dv
дх * ду I
Близость ветра к геострофическому, стало быть, означает,
что в каждом из уравнений (14.3.1), (14.3.2) и (14.3.5) все
слагаемые, кроме тех, которые фигурируют в (14.5.1), относительно
малы. Как правило, они на порядок меньше каждого слагаемого
(14.5.1). Это естественно наводит на мысль об отыскании
решений полных уравнений в виде разложений по малому
параметру. Такой путь впервые был указан И. А. Кибелем в 1940 г.,
им же разработана на практике соответствующая схема
численных прогнозов. Эта идея эффективно использована для
преобразования уравнений, в результате которого прогнозируемые
величины имеют порядок остальных слагаемых.
В трех указанных уравнениях перейдем к безразмерным
переменным:
Пред вычисление метеорологических полей на короткий срок 429
Масштабы выберем таким образом, чтобы искомые функции и
их производные имели порядок единицы. Подстановка (14.5.2)
в уравнения (14.3.1) и (14.3.2) дает:
дип ! ио /„ дип , ^ дип \ L т0Ц) *"
"0 dl/„
'о д/я
-4(1+-*$•-)
I "о /
НоУп
4
Л /
/о
Яо^/Г
Ф0
Ро
дФп
дрп
Ц
-Vn
)■
дхп
Ч"0
Ро
дФп
дРп
дУп = j (14.5.3)]
ц0 / да„ , dvn \ ■ т0 дт„ =Q
/-о \ ^л ' дУп ) *" Ро <*/>„
Легко показать, что масштабы можно выбрать так, чтобы
искомые функции и их производные имели порядок единицы.
Действительно, поскольку
1) 0{u) = 0{v),
2) 0(т)-°(т).
з>°(£И(-^Ь°(£Н(-£).
«)°(^)-°('-S-)-
то пяти масштабов ^о, то, Фо, £о, /о достаточно, чтобы
выписанные пять групп величин, имеющих одинаковый порядок, в
безразмерных переменных имели порядок единицы. Шестой
масштаб ро выберем так, чтобы величина --г— в безразмерных
переменных также имела порядок единицы.
Поскольку основной вклад в изменения метеорологических
* ди ъ I ди \
полей вносит адвекция, то должно быть -г-- = 0[и——I и
^ . dt \ дх I
dv -t dv \ ^
—т— = 0 I и-—— I.~ Это значит, что
dt \ дх I
'о
(14.5.4)
1 Здесь использована линейная аппроксимация l=l0 + fiy (k — среднее
значение параметра Кориолиса в прогнозируемой области).
430
Глава 14
Из близости ветра к геострофическому следует
т. е.
(14.5.5)
Исключив из (14.5.3) /0 и Ф0 на основании (14.5.4) и (14.5.5)
и разделив первые два уравнения на /о^о, а последнее — на ыо//о,
получим:
дип
-tin
дап
дхп
&)+-■■
дФп
„ ( дип | „ dvn | „, _^\ , я.
дРп
ton
дРп
= [ (14.5.6)
«-«.(1 + Р^У.)-
аФл
^я
дг^
Здесь
дхл
дУп
5 =
то^о
"оРо
Близость ветра к геострофическому в этих уравнениях
означает малость безразмерных параметров а и б; при а=6->-0
уравнения (14.5.6) вырождаются в геострофические соотношения
(14.5.1). Безразмерные уравнения (14.5.6) в явном виде
отражают их главный недостаток как уравнений для предвычисле-
ния. При прогнозируемых величинах стоит малый параметр в
качестве множителя, вследствие чего малые ошибки в исходных
данных приводят к заметным погрешностям результатов
расчета. Аналогичные обстоятельства являются причиной того, что
определение т из уравнения неразрывности приводит к большим
погрешностям.
Приступим теперь к преобразованию полученных уравнений,
в результате которого указанный недостаток уравнений будет
в известной степени ликвидирован. Для этого из первых двух
уравнений (14.5.6) получим уравнения для вихря скорости Qn
и для дивергенции Dn:
дип
2п =
Dn =
dvn
дхп
дхп
дуп
дУп
дуп
(14.5.7)
Пред вычисление метеорологических полей на короткий срок 431
После дифференцирования обоих уравнений попеременно по хп
и уп и соответствующих
(14.5.6) получим:
«(
~Гип
алгебраических операций взамен
dQn Ьл/ дхп dvn
dtn
дхп
-vx
д*п dvn
дуп dfn
п ду^) + *Ь(дхп дРп
"* дРп)-
dQn
п дРп
dt„ дрп
д I dv.
и„
д^п
ду
7(^)1+'[»
дхп дрп
dvn
■Р-Й--
' дхп Vn дрп )
v" dp
dv
дхп
д2Ф„
дип . I ди„ \2 ,
дуп "*" \дх„) Т
агфл
(14.5.8)
(В уравнения для вихря и дивергенции скорости подставлено
значение Dn из уравнения неразрывности.). Приближенную
систему получим, если в каждом из трех уравнений оставим
только главные (подчеркнутые в уравнениях) члены, учитывая,
что р-^«1, 0(a) =0(6):
/о
■(-Й-+-
д2фп
м»
dQn
дх„ '
д*Фп
ду
П I
дхп
дРп
■*-%■-■
к
дип
дхп
^*=
дУп
dvn дип
дх„
= 0.
дУп
) (14.5.9)
Из двух последних уравнений видно, что
Vn =
дхп
ип= —
дУп
(14.5.10)
Таким образом, в рассматриваемом приближении скорость ветра
описывается геострофическими формулами, а в уравнении для
эволюции поля скорости (уравнение вихря) учитывается агео-
строфичность. Это является основанием для того, чтобы
указанное приближение называть квазигеострофич_шшм^
432
Глава 14
Возвращаясь к размерным переменным, выпишем теперь на
основании (14.5.9), (14.5.10), (14.3.1) —(14.3.5) новую систему
прогностических уравнений:
dt I - дДГ Т" ду -TV"— Jt Г" ^"
+-ifi£a~4-£-. 04-s.li)
~ ДФ
2-—■ (14.5.12)
— i-S-.-i-E- <'«-,8>
■£—ТГ- CI4.5.14)
-ЗГ+%-^-'-^- 0-1.2.3). (Н.5.15)
Уравнение неразрывности в рассматриваемом приближении
является следствием уравнений (14.5.13); оно не дополняет
выписанной системы, а является другой формой записи уравнений
(14.5.13) и, естественно, не должно здесь фигурировать.
Полученная система содержит пять уравнений для пяти неизвестных
{и, v, £2, Ф, Т) и является замкнутой.
В (14.5.11) £2 + 1 — вихрь скорости в абсолютной системе
координат, т. е. в системе координат, не скрепленной с Землей.
В этой связи Q + 1 часто называют абсолютным вихрем, a Q —
относительным вихрем.
' В преобразованной системе уравнений, в отличие от
исходной, производные по времени, представляющие главный интерес
в задачах прогноза, имеют тот же порядок, что и остальные
члены в уравнениях. Однако преобразованная система
уравнений менее точна из-за пренебрежения некоторыми слагаемыми
(как правило, последние достаточно малы).
Из полученных уравнений вытекает важное свойство
атмосферных процессов — сохранение потенциального вихря.
Запишем уравнение притока тепла в развернутой форме
дТ , дТ , дТ ( RT дТ \
, дТ , дТ (
dt ~" дх ~v ду ~~ \ срр др )
и заметим, что
RT дТ _ RT дТ dz = RT fa - 7 = &
срР dp ~ срр dz dp ~ Rp g/R Rp
Пред вычисление метеорологических полей на короткий срок 433
Величина cz=RT——-^-«8-10? м2/с2 (квадрат скорости звука,
умноженный на отношение вертикального градиента
потенциальной температуры к автоконвективному градиенту) меняется
мало; примем ее постоянной величиной, равной ее среднему
значению для тропосферы. Из упрощенного этим предположением
уравнения притока тепла
дТ i дТ | дТ т о /лл г- i/?\
u^+v^- = -e-c2 (14.5.16)
dt j дх ' ду Rp
и уравнения для вихря скорости исключим т. Тогда имеем
d(Q + z> , „ a(Q + p . a(Q + /) _ /р/г a v
dt ' " дх ' " <ty — с2 ар
ar , аг . аГ
X
И-5Н-£-+-$В- <14-517>
Правую часть (14.5.17) преобразуем, выполнив
дифференцирование:
д \ ( дТ , дТ , аГ \1 д ( дрТ , дрТ , а^Г \
— \ а/ар +" а* ар "» ^ ayap J"1""\ ар ад: "» др ду )'
Воспользовавшись формулами (14.5.13) и (14.5.14), легко
обнаружить, что в последнем уравнении вторая скобка справа
обращается в нуль, а именно:
ди^дТ_ ■ dv дТ = д / 1 дФ \ д / р дФ \
ар ад: '» ар ^ — ар \ /0 ay J ад: \ r dp )
а / 1 дФ \ а / р аФ \ р / а аФ а аФ
~~ар~\ /0 ад: J ay \я ар J я/0 \ ар ау ад: ар
а_ _аФ_ _а_ аФ \ = 0
ар ад: ду др )
Теперь уравнение (14.5.17) можно записать в виде
(т+«^+»ж)(2+'-Т^Н <14-5->8>
В этом уравнении величина
2+'-т^=ж <14-519>
называется потенциальным вихрем. Из уравнения (14.5.18)
следует, что потенциальный вихрь является консервативным свой-1
ством, перемещающимся со скоростью геострофического ветра. |
28 Заказ № 612
434
Глава 14
Выразим потенциальный вихрь через геопотенциал
изобарической поверхности, заменив Q и Т на Ф согласно формулам
(14.5.12) и (14.5.14):
М =
ДФ
/о
■Ч-
/о
S2 др
д ~2 <?ф
Р2
др
(14.5.20)
Если это выражение подставить в (14.5.18), то для определения
функции Ф получим следующее уравнение:
/0 dt
/о д
д*Ф
С* др
dpdt
= А
м-
Здесь
Ам = -и
дМ
дх
-V-
дМ
ду
(14.5.21)
(14.5.22)
есть адвекция потенциального вихря. Выразим Ам через
адвекцию вихря скорости Aq и адвекцию температуры Ат:
А^=—и
дх
a(Q + p _ 1 /
V ду /о I
дФ дьФ \
~~!х д^Г)
дТ
дТ
Ли 1 и 1
Р дФ
/о дх '
RTo ( дФ
дФ аДФ
ду дх
д дФ
др
(14.5.23)
дх ду 10р \ ду дх
_ _аФ_ _а_ _аФ_\
дх ду др )'
Подставим в (14.5.22) выражение М из (14.5.19). Тогда
Ам=-и
a(Q+Q
дх
-V
a(Q + p
/0/г
С2
(•
_д__дТр_
дх др
I а аГр \ л \ W ( д „ дТ > д „ дТ \
=л0
ду
др
а
с2 dp
rJ„ ^ L„, дТ \ l0R -(
р(и^х-+*пъг)—с*-Р[
дТ да
дТ dv
дх
dp ' ду dp )'
Выше мы уже выяснили, что последняя скобка справа равна
нулю. Воспользовавшись этим, найдем искомую связь:
Ам = Аг>
l°R д DA
(14.5.23')
Подставив (14.5.23) в (14.5.21), получим уравнение, широко
используемое в настоящее время для численных прогнозов:
A-g—W
«
с* др
Р(р
д дФ
dp dt
+ RATy (14.5.24>
Пред вычисление метеорологических полей на короткий срок 435
Следует, впрочем, заметить, что (14.5.24) может быть получено
из (14.5.11) и (14.5.15) непосредственно, если из этих
уравнений исключить т, a Q и Т заменить на Ф согласно (14.5.12) и
(14.5.14). Интегрированию уравнения (14.5.24) и анализу
полученных решений будет посвящена значительная часть
настоящей главы.
После определения Ф из уравнения (14.5.24)
горизонтальные компоненты скорости вычисляются на основании (14.5.13),
температура — из (14.5.14), а затем из (14.5.16) находится
р-компонента скорости.
Получим теперь граничные условия, которым должно
удовлетворять искомое решение. Они вытекают из тех же
физических соображений, на основании которых формулировались
граничные условия для примитивной системы уравнений,— из
постоянства массы земной атмосферы и из условия обтекания
воздушным потоком рельефа земной поверхности. В изобарической
системе координат соответствующие уравнения представлены
формулами (14.3.7) и (14.3.10). Теперь их нужно записать через
одну только функцию Ф. Для этого из (14.5.16) и (14.5.14)
выразим т через Ф:
'--ЗД-*)--*('-5-ТГ+*Ч <14-5'25>
Поскольку при р-+0 т->-0 на основании (14.3.7) и рАт\ р+о->-0,
так как Ат — конечная величина, то должно выполняться
следующее условие:
'"-Яг-тН-.-0- <14-5-26)
Подставив т из (14.5.25) в (14.3.10) и воспользовавшись
геострофическим приближением, при котором решается задача [см.
дФ дФ
формулу (14.5.13), из которой следует, что и и-т—Ьи-— = 0)],
получим
\ R л р2 д дФ ]_(j^_ дФ дФ
1~~& т ~&~~оУ~ЬТ— RT \dt U дх V ду /JP=Po
(14.5.27)
Если пренебречь влиянием рельефа, полагая, что земная
поверхность параллельна плоскости хоу, то в этом уравнении
<ЭФ дФ о
= =0 и условие на нижней границе приобретает про-
дх ду
стой вид:
28*
436
Глава 14
Проблема граничных условий по горизонтальным
координатам легко решается, если областью интегрирования является вся
атмосфера; они вытекают из существования периодичности.
Однако при прогнозах на короткий срок для небольшого района
нелогично решать систему уравнений для такой области.
Совершенно ясно, что крупномасштабные атмосферные возмущения
распространяются со скоростью, близкой к скорости ветра,
и заметно влияют на ситуацию данного района лишь те из них,
которые расположены от района, для которого дается прогноз,
на расстояниях порядка vo&t. При и0=Ю м/с и At = 24 ч это
расстояние равно примерно 900 км; таким и должен быть
характерный размер рационально выбранной области. До сих пор
не предложены какие-либо основательные соображения, из
которых можно было бы получить условия на границах такой
области. Можно думать, однако, что главный вклад в режим
погоды данного района вносит ближайшая окрестность; благодаря
этому даже весьма приближенный учет состояния атмосферы на
далеком расстоянии от точки, для которой дается прогноз,
будет мало влиять на результат.
Более подробно этот вопрос рассмотрен в следующем
параграфе.
Помимо граничных, необходимо задавать и начальные
условия. В рассматриваемом приближении, как следует из (14.5.21),
достаточно задать начальное поле функции Ф. Это не вызывает
трудностей.
14.6. Численный прогноз для баротропной атмосферы
в квазигеострофическом приближении
Дадим решение задачи прежде всего для наиболее простой
модели атмосферы. Допустим, что атмосфера баротропна, т. е.
р = р(р). Это равносильно предположению, что р = р(р).
Из уравнения состояния в таком случае следует, что Т = Т(р) =
= p/Rp(p). В изобарической системе координат /, х, у, р —
независимые переменные, но поскольку рассматривается модель
атмосферы, в которой Т зависит только от р, то
дТ дТ дТ ^ /1 л с л\^
1 Это означает, что на каждой изобарической поверхности температура
не меняется ни со временем, ни по координатам. Отсюда, разумеется, не
следует, что она вообще постоянна. В фиксированной точке температура может
меняться во времени соответственно изменению давления в этой точке. Она
также различна в разных точках пространства, не расположенных на одной и
той же изобарической поверхности.
Пред вычисление метеорологических полей на короткий срок 437
В таком случае из уравнения притока тепла (14.5.15) следует,
/ дТ RT \ . дТ RT Л
что т(— 1 =0, а так как — =^0, то должно
\ др сРр / др сРр
быть т=0.
В рассматриваемом случае, следовательно, подлежащая
решению задача сводится к интегрированию уравнения
Д^- = /<И2> (14.6.2)
которое получается из (14.5.24) и (14.5.25) при т = 0.
По найденному полю Ф вычисляются компоненты скорости
ветра на основании формул (14.5.13).
Рассматриваемый частный случай может быть
интерпретирован и совершенно иначе. Предположим, что поле скорости
ветра аппроксимировано формулами
«уС. х, у, p) = A(p)uj(t, х, у),
где ui = uy Uo = v, Uj — средняя по всей атмосфере компонента
скорости. Это означает, что направление скорости ветра не
изменяется с высотой, так как
д v (t, х, у, р) д v (Л х, у) ^
др и (Л х, у, р) др и (/, х% у)
В таком случае
^('. х, у, p)=A(p)Q(t, х, у),
а уравнение для вихря скорости можно записать следующим
образом:
A(p)<*+A4p)(u^+v^)^p)v = l0^.
Если полученное уравнение проинтегрировать по р от нуля до
/?о (наземное давление, близкое к стандартному значению) и
принять x(t, х, у, p)|o0=const =0, полагая отсутствие потока
массы на обеих границах атмосферы, то получим:
dQ
■*(i#+;-£)+*-o.
dt
Перейдя здесь к первоначальным переменным, имеем
dQ , А? ( dQ . dQ \ , 0 п Са \\
438
Глава 14
На некотором уровне р=р* А2=А(р); для этого уровня
получаем уравнение
совпадающее с (14.6.2) после выражения Q*, v^ и* через Ф*.
Этот уровень носит название эквивалентно баротропного, и
соответственно модель атмосферы называется эквивалентно баро-
тропной. Анализ эмпирического материала показал, что в
атмосфере имеются два эквивалентно баротропных уровня: р(£~
-200 мбар, р™«600 мбар.
Уравнение (14.6.2), если вспомнить выражение для Aq [см.
{14.5.23)], есть нелинейное уравнение третьего порядка. Его
интегрирование численными методами в принципе возможно,
однако такой прямой подход представляется довольно серьезной
вычислительной проблемой. Разумеется, не может быть и речи
о получении его решения в виде какой-либо более или менее
простой формулы. Задача кардинально меняется, если считать
дФ
неизвестной величиной не Ф, а Ф=—гт-. Такая постановка, бу-
ot
дучи удовлетворительной для прогноза, позволяет легко
получить решение аналитически.
В уравнении (14.6.2) для Ф теперь отсутствуют производные
по р, в связи с чем отпадает необходимость в удовлетворении
граничным условиям по вертикальной координате. Это
обстоятельство по физическому смыслу связано с отсутствием
вертикального взаимодействия между слоями; соответствующий
механизм полностью исключен, поскольку в уравнениях, к
которым сведена задача, отсутствует р-компонента скорости,
посредством которой оно осуществляется. Все изменения во времени
вызваны существованием начальной горизонтальной неоднород-
/ дФ дФ \
ности (Лй^=0, —-г-^О, —-—ф0 I и ее последующим
перераспределением в соответствии с полем скоростей, которое также
меняется в результате функционирующей обратной связи.
Что касается граничных условий по горизонтальным
координатам, то, разумеется, они необходимы. Обычно при этом
используются следующие соображения: если вокруг точки, для
которой ищется Ф, провести окружность достаточно большого
радиуса /?, то можно думать, что на разных участках указанной
окружности Ф имеет разные знаки, а в среднем по всей окруж-
Пред вычисление метеорологических полей на короткий срок
439*
ности искомая величина (Ф) близка к нулю. Исходя из этого,.
(14.6.2) будем решать при граничных условиях
^-j Ф(г, 6)с/8|г=Л = Ф(/?) = 0. (14.6.4>
О
Второе граничное условие (уравнение второго порядка,
соответственно требуются два граничных условия) вытекает из
требования конечности Ф во всей области, включая начало
координат, которое следует из физического смысла рассматриваемой
величины. После получения общего решения уравнения этому
условию можно легко удовлетворить.
Для получения решения удобно преобразовать уравнение к
полярным координатам. Воспользуемся выражением для
лапласиана
#2Ф £2Ф . 1 дФ , 1 <Э2Ф
а^ дх* ^
ду2
дг2
дг
Г2 д62
(14.6.5>
Подставим его в (14.6.2) и проинтегрируем уравнение по
окружности некоторого радиуса г (О^г^Я), Тогда
Здесь
_^2ф 1 йФ , j- . ч_ 1 дФ
2те
342(r) = 4rj А, (г, 8)rf8,
е=2л
=0. (14.6.6)
дФ
дЬ
в=2те
9 = 0
дФ
дЬ
0 = 2ic
дФ
дб
= 0.
8=0
Интегрирование однородного уравнения (14.6.6) выполняется
элементарно. Приводим соответствующее решение:
Ф0 = С\ In г+С2.
(14.6.7)
Методом вариации произвольных постоянных нетрудно
получить решение неоднородного уравнения
г
6 = С? In г 4-С2° /0 |Л2(0 In -£-rfr'. (14.6.8)
Здесь С°х, С£— произвольные постоянные. Поскольку
1пг|->—оо, то для того, чтобы решение всюду было конечным,
г-»0
440
Глава 14
нужно принять С°{=0. На основании условия (14.6.4) найдем:
С2°=-/0 j Ая(г')г'In-£-dr'9
после чего получим окончательное выражение
г R
Ф(г) = /
IЛ2 (г') г' In -jrdr'-l А3 (г') г' In |- rfr'
(14.6.9)
Если в (14.6.9) г->-0, то Ф(г) ->Ф, и в пределе получим
R
Ф(0) = Ф(г)|_0=-/0|л2(г')г'1п^-^'. (14.6.10)
о
Формула (14.6.10) позволяет вычислить значение тенденции
геопотенциала в некоторой точке, которую мы принимаем за
начало координат, на основании поля AQ в круге радиусом R
вокруг рассматриваемой точки. Подставив значение Aq и
обозначив элемент площади в полярных координатах г' dr' dbr
через ds, можно записать (14.6.10) в следующей форме:
2* R
Ф(г)|г=0=—^f \Aa(r', b')\n-£-ds. (14.6.11)
6 О
Легко дать простую интерпретацию полученной формуле:
изменение геопотенциала в точке изобарической поверхности
вызвано адвекцией вихря из некоторой области, окружающей
рассматриваемую точку. Адвекция вихря из каждого элемента
площади дает вклад в суммарное изменение геопотенциала,
пропорциональный логарифму отношения радиуса всей области к
расстоянию элементарной площадки от точки, в которой ищется
изменение геопотенциала. Таким образом, чем дальше элемент
площади от рассматриваемой точки, тем меньше он влияет на
изменение геопотенциала. В связи с этим вес, с которым входит
вклад от единичной площадки, расположенной на расстоянии г
от расчетной точки, в искомое изменение геопотенциала,
называется функцией влияния.
В рассматриваемой модели функция влияния
°(т)=^1пт>0- (14-6Л2>
Расчетная формула в таком случае имеет вид
2* R
Ф (0) = -/о J j А2 (г', &') G [С) ds. (14.6.13)
0 0 х '
Пред вычисление метеорологических полей на короткий срок 44 Г
Поскольку во всей области функция влияния сохраняет свой
знак, то вклад каждой площадки определяется знаком А& на
этой площадке.
Если по формуле (14.6.13) выполнить вычисления по всему
полю (передвигая начало координат), то мы получим поле
тенденции; прибавив значения ФД^ к исходному полю Ф = Ф(0,
найдем поле Ф в момент t+^dt, которое принимается исходным
для следующего временного шага.
Рис. 14.2. Средние месячные
значения коэффициента
корреляции (/), средних квадратиче-
ских ошибок геопотенциала
АТ5оо (2)у средних
квадрэтических ошибок вектора скорости
ветра (3) 24-часовых прогнозов
по баротропной модели за
10 месяцев 1967—1968 гг.
Несмотря на значительную схематизацию, связанную с
использованием баротропных моделей, последние улавливают
основные физические процессы, которые определяют изменение
поля геопотенциала в средней тропосфере. Подтверждением
этого являются приведенные на рис. 14.2 средние месячные квад-
ратические ошибки 24-часовых прогнозов поля геопотенциала
а(ДФ), поля вектора скорости ветра o(Av) и коэффициента
корреляции R между прогнозируемыми и фактическими
изменениями геопотенциала. Можно предполагать, что на основе
рассмотренной модели плохо предсказывается возникновение новых
крупномасштабных особенностей, обусловленных внешними
притоками энергии или кардинальными преобразованиями
начальных запасов, связанных обычно с упорядоченными
вертикальными движениями.
14.7. Численный прогноз для бароклинной атмосферы
в квазигеострофическом приближении
В случае бароклинной атмосферы, как уже говорилось,
р-компонента скорости исключается из уравнений для вихря ско-
рости и притока тепла. После этого для Ф получено
эллиптическое уравнение [см. (14.5.24)]
^&+4A*4^-*-&-'^ (14>7Л)
о(дФ) б(ди;
дом м/с
VII IX
3 J 0,6
442 Глава 14
На основании (14.5.26) и (14.5.28) запишем краевые условия
для Ф:
=0, (14.7.2)
>>%
/7 = 0
дР
Здесь
Я (Та-f)
/>-^-+аФ = -ЯЛг. (14.7.3)
а=-
g
Граничные условия по горизонтальным координатам в дан-
лом случае основываются на соображениях, которые
использованы для баротропной модели:
*L„=0. (14.7.4)
По начальному полю Ф находится правая часть уравнения
(14.7.1). После решения (14.7.1) по формуле
Ф(*0-{-Д*, х, у, /?) = Ф(/0, х, у, /?) + Ф(/0, х, у, р)М
вычисляется Ф для момента t0 + Aty затем вычисления
повторяются. Шагами по времени, таким образом, находится поле Ф
на все время прогноза, а затем по формулам (14.5.14), (14.5.13),
(14.5.15) вычисляются поля Г, и, v, т.
Линейное уравнение (14.7.1) будем решать методом
интегральных преобразований. Оператор Лапласа запишем в
полярной системе координат, после чего проинтегрируем уравнения
и граничные условия по окружности переменного радиуса г
с центром в точке, для которой дается прогноз. Такая операция
выполняется элементарно; уравнения задачи после этого
приобретают следующий вид:
~dfP ^Г+72- — -дГг-дГ=— Ab-R-Sp-рАт. 04.7.5)
"'£-
р=0
p^-+a<b = RAT. (14.7.7)
Напомним, что здесь
7(Р. O—srJ/G». г, в)М. (14.7.8)
2тс
Пред вычисление метеорологических полей на короткий срок
443
Введем новые независимые переменные:
С—£-. b=r-L9
Ро с '
(14.7.9)
где ро — среднее давление у земной поверхности, так что 0^£^
^1. После чего умножим (14.7.5) на б/(Л,, 6)d6 и
проинтегрируем по б от нуля до оо (здесь параметр Х>0). Тогда,
поскольку
'А5£/(Х, »)*_/»*.
а/
дЬ
Ф
+
о
получим
оо ~7- оо оо
£e£W<b. »>*<*9*ч^-£-!-*-£-*| +
00
(14.7.11)
о
Выберем теперь функцию / так, чтобы
rf5
/*8/(>-. 8),
= 0,
(14.7.12)
(14.7.13)
(14.7.14)
|8 = 0
Два линейно независимых решения уравнения (14.7.12)—/0(?w,
б) и No{h, б) —являются функциями Бесселя 1-го и 2-го рода,
нулевого порядка. Функция No(K б) имеет логарифмическую
особенность в нуле и не может быть использована в качестве
подходящего решения по условию (14.7.14); функция J0(k, б)
удовлетворяет обоим граничным условиям, в связи с чем
примем
/(К Ъ)=МК *). (14.7.15)
Все интегральные члены в (14.7.11) равны нулю. Это следует
из того, что:
а) 8/0(Х, S)U=0=0, 8 ^^
db
1 = 0
=о,
444
Глава 14
-^z- и Ф — конечные величины по физическому смыслу;
б) ЬЧь-
=^оо, 8ф|5 = оо^оо,
тогда как Jo(k, 6) U-юо и m-jTm\^t,00 стремится к нулю. В таком
случае (14.7.11) можно записать в виде
dBTt:
<если
<7(С X)=(V0(X, 8)Ф(8, С) Л,
6
оо
о
оо
Вр-Х> = /?f Лг(§', С)8'Л(Х, 8')<й\
(14.7.16)
(14.7.17)
(14.7.18)
Уравнение (14.7.16) на основании (14.7.6) и (14.7.7) должно
решаться при краевых условиях:
Г2 дд
с=о
=0,
(.-^+*4=ВТ
;=i
(14.7.19)
(14.7.20)
После того как найдено q, решение исходной задачи, т. е.
определение Ф(6, £), сводится к обращению интеграла (14.7.17).
Соответствующая формула обращения известна: это так
называемая формула Ханкеля, согласно которой, если
то
f*(u) = $yf(y)Jo(uy)dy,
f(У) = .f«/*(«) Jo {ay) da.
Пред вычисление метеорологических полей на короткий срок 445
На этом основании окончательное решение задачи выражается
через вспомогательную функцию следующим образом:
Ф(8. Q = jW, >0>Л(>. 8) Л.
(14.7.21)
Остается найти функцию #(£, К) на основании (14.7.16),
(14.7.19), (14.7.20). Неоднородное уравнение (14.7.16) решается
методом вариации произвольных постоянных. Решение
соответствующего однородного уравнения легко находится: ему
удовлетворяет степенная функция £п, если только п2 = Х2 — п, т. е.
Л1,2=-4-±"|/^-+Х2=-^-±!А-
Таким образом, функцию q можно искать в виде
?(С х)=с,(дс"+с2(С)с"1.
(14.7.22)
Подставив (14.7.22) в (14.7.16) и следуя далее традиционным
путем, найдем общий интеграл:
?(С >о=ск
(V 2 +* . п^г 2 ^
+ С£
+
+irj[Be(C„x,+^i^]x
о
(14.7.23)
Для того чтобы удовлетворялось условие (14.7.19), необходимо
положить С£=0, так как
•оо,
ибо [i>V2. Другая постоянная на основании (14.7.20) равна
1
С?=-
в
Пс = 1
1
"2" + И 2|xfo — -Y+A о
5а(С, X)-f
ДС|ВГ(С1, X)
«1
X
X
К2""(—4-+i*)-^2 (а--г-^J*
(14.7.24)
446
Глава 14
Подставив найденную теперь функцию
1
♦ с. «--С^Ц.,-.^ j[*,(c. х)+ "■'ff- >> ]х
Х[> Ci 2 -С 2 С, 2 J Л, (14.7.25)
в (14.7.21), получим решение задачи. После некоторых
преобразований найденное решение для 5 = 0 можно привести к виду
6(0, С) = Ф(0, t) = f f f Лв(Сь s', »)02(С, С, 5f)5frfs'^id»-h
0 0 0
2тс оо 1
+ 1 ИЛ^ь 5'> &)Ог(Сь С, s')dCis'<fe'rf». (14.7.26)
0 0 0
В таком виде решение приобретает отчетливый физический
смысл. Изменение геопотенциала в точке М(0> £) обусловлена
всем полем адвекции вихря и адвекции температуры. Вклад
каждого элемента объема dV = s' ds'dbxd'b с центром в точке
(Sit s'> в) в полное изменение геопотенциала различен и
определяется двумя функциями влияния: Gq(£i, £, s) для адвекции
вихря и Gt(£i» £, 5) для адвекции температуры. Заметим, что-
функции влияния различны для разных уровней. На рис. 14.3<
приведены обе функции влияния для £ = 0,5 и £ = 1,0.
Из вида функций влияния выясняются следующие важные
особенности:
1. Абсолютная величина обеих функций влияния убывает
с удалением от точки, для которой дается прогноз, причем
функция влияния для вихря убывает значительно медленнее.
2. Функция влияния для вихря во всей области отрицательна.
Это значит, что знак изменения геопотенциала всегда
определяется знаком адвекции вихря. Адвекция отрицательного вихря
в любую точку (Ло<0) приводит в таком случае к уменьшению'
высоты изобарических поверхностей и соответственно к
понижению давления. И наоборот, адвекция положительного вихря
приводит к росту Ф и, стало быть, к повышению давления.
Пред вычисление метеорологических полей на короткий срок 447
3. Функция влияния для температуры отрицательна для
точек, расположенных вблизи земной поверхности (£«1); для
других изобарических поверхностей она имеет разные знаки: выше
поверхности, для которой дается прогноз (£i>£), она
отрицательна, а для нижележащих уровней положительна. Таким
образом, при Ат>0 в области, расположенной выше уровня, для
1,0\
0,8
0,6
ОЛ
0,2
О
ОЯ
ОЛ
(O&luS)
GqWZuSJ
-0,5
J
-0J5
cQ№Zi;s)
Рис. 14.3. Функции влияния для температуры GT и
вихря GQ .
которого дается прогноз (£i>£), или при Лг<0 в нижележащей
области (£i<£) высота изобарической поверхности
уменьшается. В обратном случае, разумеется, изменения высот
изобарических поверхностей будут иметь противоположный
знак.
4. Относительно уровня £ = 0,5 функция влияния для
температуры симметрична и имеет противоположные знаки, в связи
с чем на этом уровне полностью или частично компенсируется
влияние термических факторов на изменение высоты
поверхности 500 мбар, если температурные адвекции выше и ниже этой
поверхности имеют одинаковый знак. В этом случае изменение |
поля Ф определяется только динамическими факторами и, стало
быть, допустима гипотеза бездивергентности.
448
Глава 14
14.8. Использование квазисоленоидальных приближений
для численного прогноза
Квазигеострофическое приближение, как это следует из двух
предыдущих параграфов, основано на геострофических
формулах для компонент скорости. К сожалению, наиболее
критические ситуации в атмосфере, при которых происходят
кардинальные изменения в режиме погоды, представляющие главный
интерес для прогнозиста, по-видимому, хуже всего описываются
геострофическими соотношениями, не говоря уж о безусловной
неприменимости рассмотренного приближения в экваториальной
зоне.
В связи с этим естественна попытка использовать более
точные соотношения для расчета вектора скорости. Одна из
такого рода возможностей обнаруживается при анализе уравнения
(14.5.8) для дивергенции скорости. Дело в том, что в этом
уравнении содержатся члены 0(1) (которые только и сохраняются
в квазигеострофическом приближении), группа слагаемых 0(a)
и слагаемые 0(аб). Если в уравнении (14.5.8) отбросить только
самые малые слагаемые — порядка (аб), то второе уравнение
(14.5.9) следует записать в виде
dvn дип
„ \( дип \2 , 0 dvn дип , / dvn \2] _
а [\~д^) ~^А дхп ^7 + 1 дуп)\ —
д*Фп
дхп ду
dxi
*У%
_4_р _,, !^о_
-f- Ъ4п — Un —г— .
(14.8.1)
Тогда вместо системы уравнений (14.5.11) — (14.5.15) имеем
другую систему:
d(Q + Q , d(Q + l)
dt
дх
d(Q + l) , дх
~V dj =l«lfr>
»-«+(l)'+4t+(|)'+^
da
dv
я* "» dy '
RT
dx
дФ
~др
дТ
dt
; дх^
RT
cPP
\ (14.8.2)
Второе уравнение этой системы обычно называют уравнением
баланса.
! В рассматриваемом случае геострофические формулы для
скорости ветра непригодны, поскольку они не удовлетворяют
уравнению баланса. Но из уравнения неразрывности в принятом
Предвычисление метеорологических полей на короткий срок 449
приближении следует существование функции тока \|), так что
«--S-. »—-8-. <14-8-3>
2--Ё--£-А*- (14-8-4>
Прогностическую систему уравнений (14.8.2), в принципе
более точную, чем квазигеострофическая, после введения функции
тока согласно (14.8.3) и выражения для вихря (14.8.4) запишем
в следующем виде:
уравнение вихря
dt ду дх ' дх ду dp г дх ' v '
уравнение статики
г-чНЬ (14-8-6>
уравнение баланса
*[(&-£)-hSfefl+f-3-+"»-*»- <14-8-7'
уравнение притока тепла
дТ д^ дТ +_ д*< дт _ с* (и*л\
Мы имеем для четырех функций (г|\ т, Т, Ф) четыре уравнения;
компоненты скорости вычисляются по формулам (14.8.3).
Рассматриваемая модель атмосферы называется квазисоле-
ноидальной. Употребление такого термина в данном случа~ё~свя-~
"зано~~с~тежгчто уравнение неразрывности используется в форме,
соответствующей бездивергентным или соленоидальным
(трубчатым) течениям. Однако при выводе уравнения для вихря
скорости дивергенция скорости считается отличной от нуля, т. е.
частично учитывается несоленоидальный эффект.
При помощи уравнения статики из записанной системы
уравнений исключается температура; оставшиеся три уравнения
содержат неизвестные г|), Ф, т. В квазисоленоидальном
приближении задача легко решается для среднего уровня I—— = 0) . При
таком условии система расщепляется. Из (14.8.5) находится
функция тока, при этом полностью применим аппарат,
использованный для баротропной квазигеострофической задачи.
29 Заказ № 612
450
Глава 14
д<\> (г, О
dt
На основании формулы (14.6.11) для бездивергентного уровня
имеем
2* /?
I _, 1 Г Г г а» д (дф + о а* а(Дф + р 11п /г ,
|r = o 2r. J J I йк dy <ty 5^ J [n~aS-
о 0
(14.8.9)
По рассчитанному на каждом временном шаге полю
Н+л/=П+-эНа' (Н.8.10)
Ф находится из решения уравнения баланса (14.8.7), которое
при известном поле яр представляет собой уравнение Пуассона
для Ф. Для первого временного шага поле г|) вычисляется по
начальному, взятому из наблюдений полю Ф. Для расчетов также
используется уравнение баланса, однако для функции г|) оно
уже является уравнением Монжа—Ампера.
Гораздо более сложной является трехмерная задача. Она
оказывается значительно труднее аналогичного случая в квазигео-
строфическом приближении. Это связано с тем, что в квазисо-
леноидальном приближении уравнение притока тепла содержит
<ЭФ д\Ь
—г—, а уравнение для вихря ^-, тогда как в квазигеостро-
фическом приближении в обоих уравнениях содержится —тт--
Для упрощения задачи иногда в уравнении притока тепла
геопотенциал заменяется /яр. В этом случае решение задачи
выполняется так же, как это сделано в предыдущем параграфе для
трехмерной модели.
Итерационные методы решения задачи, в которых не
используется указанное упрощение уравнения притока тепла,
оказываются весьма громоздкими. Фактически в настоящее время не
существует удовлетворительного вычислительного алгоритма
для решения системы уравнений (14.8.5) — (14.8.8).
14.9. Предвычисление облачности
Проблема прогноза облачности сводится к предвычислению
полей температуры и влажности. В этих полях облачность
выделяется как зона, в каждой точке которой удельное влагосодер-
жание (масса водяного пара и продуктов конденсации в единице
массы воздуха) больше или равно максимальной при данной
температуре и давлении удельной влажности.
Знак «больше» относится к внутренним точкам, а знак
«равно» — к границам облаков. Разработка методов предвычис-
Предвычисление метеорологических полей на короткий срок 451
ления параметров облачности — одна из наиболее трудных
проблем теории. Это связано, в частности, с весьма жесткими
требованиями к предвычислению полей температуры и влажности.
Для иллюстрации этого обстоятельства ниже приведено
количество водяного пара pw, которое конденсируется в
насыщенном воздухе при понижении температуры на 1°С в разных
интервалах температуры при атмосферном давлении 1000 мбар:
Т°С . . -20, -19 -15, -14 -10, -9 -5, -4 0, 1 5, 6 10, 11 15, 16
?w г'мз 0,09 0,13 0,19 0,25 0,35 0,46 0,61 0,81
Как следует из этих данных, в характерном для нижней
атмосферы интервале температур при понижении температуры на
ГС в 1 м3 насыщенного воздуха конденсируется от 0,1 до 0,8 г
водяного пара. Вместе с тем из эмпирических данных известно,
что водность облаков составляет 0,1—0,2 г/м3.
Таким образом, погрешность в температуре на ГС (или во
влажности на 0,2 г/м3) при критическом состоянии
(относительная влажность близка к 100%) приводит к ошибкам в
водности, близким к значению средней водности в облаках, т. е.
такая погрешность может приводить к качественно неверным
результатам. Эти обстоятельства усугубляются еще и тем, что
образование и эволюция облачности вследствие реализации
скрытой теплоты и влияния облачности на радиационный баланс
атмосферы заметно усложняют механизм, формирующий
температурное поле, а стало быть, и задачу о прогнозе в целом. В связи
с этим предвычисление параметров облачности в настоящее
время может выполняться лишь с большими ошибками. Тем не
менее совершенствование численных методов — единственный
реальный путь удовлетворительного решения проблемы.
Использование корреляционных связей между параметрами облачности
и некоторыми метеорологическими элементами, которые можно
прогнозировать более надежно, не улучшает ситуации.
Принципиально задача о предвычислении облачности может
быть легко сформулирована математически. Исследование и
решение соответствующей системы уравнений важны по крайней
мере как основа для выполнения численных экспериментов,
которые позволят выяснить влияние внешних условий на процесс
формирования облачности и в конечном счете приведут к
существенным для прогностической практики результатам.
При формулировке задачи следует учитывать, что облачность
по своим свойствам поглощать и излучать длинноволновую
радиацию близка к черному телу, вследствие чего лучистый
теплообмен играет значительную роль в эволюции
облачности. На нижней границе, как правило, радиационный баланс
положительный (облачность получает лучистую энергию),
29*
452
Глава 14
на верхней — отрицательный. Кроме того, с облачными слоями
часто связано заметное усиление турбулентности (вероятно, как
следствие неустойчивой стратификации вблизи нижней границы).
Возникающий при этом обмен теплом, водяным паром и
продуктами конденсации играет немаловажную роль в процессах
образования и рассеяния облаков. Учитывая «чувствительность»
процесса фазовых переходов к малейшим колебаниям температуры,
можно определенно утверждать, что теория облачности должна
основываться на весьма корректном учете эффектов радиации и
турбулентности.
Разумеется, облачность тесно связана с динамикой
атмосферы (в частности, с вертикальными движениями) и является
частью сложного процесса, в результате которого формируется
погода. Здесь будет рассматриваться, однако, чисто
термодинамическая часть, поскольку наличие облачности не приводит
к каким-либо изменениям вида уравнений динамики. Будем
полагать, что они заданы в одной из форм, рассмотренных в
предыдущих параграфах. Существенно иначе запишется уравнение
притока тепла. В нем даже в рамках краткосрочного прогноза
нельзя пренебрегать притоками тепла. Кроме уравнения притока
тепла в измененной форме, к системе уравнений необходимо
добавить уравнения распространения водяного пара и жидкой
воды. Таким образом, чисто динамическая система должна быть
дополнена следующими уравнениями:
дТ . дТ . дТ . /дТ RT \
-^ТГ^(*-*т.«). (И.9.1)
СР?
&+«£+^+^--«.«f ^-«-^ (14-9-3)
Здесь q — удельная влажность; qm^— максимальная
удельная влажность; б —удельная водность; гт — притоки тепла,
обусловленные турбулентностью и радиацией; eq и ее—
турбулентные притоки водяного пара и продуктов конденсации соответст-
венно; т= z——р — скорость конденсации водяного пара,
at
отнесенная к единице объема, размерность m=ML2T~i\
ступенчатая функция
, (0 При <7<<7тах,
U(q-qm)-{x при q^{
-Я
max*
Пред вычисление метеорологических полей на короткий срок 453
Выражения для ет, ед, еа мы не будем выписывать здесь
в явном виде. В соответствующих главах эти вопросы уже
обсуждались. Достаточно сейчас иметь в виду, что уравнения, из
которых они определяются, не содержат новых функций, кроме
тех, которые уже фигурируют в (14.9.1) и (14.9.2).
Уравнения движения и статики замыкают систему (14.9.1)
и (14.9.2) для области, где отсутствует облачность (т = 0, 6 =
= 0). Для облачных слоев m = m(x, у, р) есть новая,
подлежащая определению неизвестная функция; здесь для замыкания
системы можно использовать связь между температурой и
максимальной упругостью водяного пара, т. е. Е(Т)У в насыщенном
воздухе:
<7 = <7тах=0,623 ALD.. (14.9.4)
Остается сформулировать граничные условия для q и б
[граничные условия, связанные с интегрированием уравнения
(14.9.1), обсуждались ранее]. Если s(ty х, у, р) =0 есть
уравнение границы облачности, то должно быть
8|*=о = 80. (И.9.5)
где бо — минимальная водность, характерная для границ облака
(определяется эмпирически).
Что касается удельной влажности, то она должна
удовлетворять следующим условиям:
?L-o=o. О4-9-6)
q\ =0,623г £(Го) . (14.9.7)
Здесь г — относительная влажность на деятельной поверхности,
причем 0<г^1 в зависимости от влажности почвы.
Решение подобной задачи можно разделить на две части:
гидродинамическую (например, в квазигеострофическом
приближении) и термодинамическую.
Гидродинамическая часть включает:
уравнение вихря скорости
A-F-M»+p"|- (14-9-8)
уравнение притока тепла
dp dt "+" р r_t~ р \ dp р dp ср др ) "•"
сР?Р
•Uifl-q^) (Н.9.9)
1 Здесь использовано уравнение статики ЗФ/дР=—RT/p.
454
Глава 14
и геострофические соотношения
U\ = u, u2 = v, Х\=х, х2=у. (14.9.10)
Термодинамическую часть можно записать в следующем
виде:
■£*+'(-£-£)-•,+£«.. (МАП)
(*/—-&—£)•
Здесь О — эквивалентная температура; Q — полное влагосодер-
жание. Они равны
Ср (14.9.13)
Уравнения (14.9.11) и (14.9.12) получаются из (14.9.1) —
(14.9.3) простым сложением. Такое преобразование удобно,
потому что уравнения для О и Q имеют совершенно одинаковый
вид как для облачной, так и для безоблачной части атмосферы.
Для определения скорости фазовых переходов т получим
диагностическое уравнение. Воспользуемся тем, что в облачных
слоях выполняется уравнение (14.9.4), из которого следует
dt — Е dT dt p x' Vt.v.iv
Подставим сюда значение dq/dt из (14.9.2), а затем из
полученного уравнения и из уравнения (14.9.1) исключим dT/dt.
После элементарных выкладок найдем:
_ JL_f^L_ q IRT \ dE А
т *< *Т Z dT ^ р\ср Е dT )
Р ~~ & 0,623 dE ' К1*-*-™)
ср р dT +
Укажем теперь путь, которым задача может быть решена.
Динамическая часть задачи при условии, что т — известная
функция, принципиально не отличается от предвычисления
полей для бароклинной модели атмосферы в квазигеострофическом
приближении. Полагая в первом приближении т = 0, можем
воспользоваться готовыми формулами (см. п. 14.7).
Пред вычисление метеорологических полей на короткий срок 455
Остановимся на схеме решения термодинамической части
задачи. Допустим, что в уравнениях (14.9.11) и (14.9.12)
компоненты вектора скорости {и, v, т) известны из решения
динамической задачи и требуется определить только д и Q. Для этих
функций можно получить граничные условия на основании
соответствующих условий для исходных функций. После того как
для О и Q сформулированы граничные условия, линейные
уравнения (Г4.9.11) и (14.9.12) интегрируются. По найденным
значениям О и Q можно найти границы облачности и скорость
фазовых переходов т. Воспользуемся тем, что на границе
облачности б = 6о, значит,
« (14.9.16)
T=b-^-(Q-b0).\
Соотношения (14.9.16) подставим в условие (14.9.4), которое
также выполняется на искомой границе. Тогда
Q_80==^if(»-^Q+^50). (14.9.17)
Поскольку Q = Q(ty х, у, р) и '&=#(;£, у, t, р) —теперь
известные функции, то (14.9.17) представляет собой трансцендентное
уравнение, из которого определяется геометрическое место
точек, образующих поверхность облачности.
После того как на основании (14.9.17) определена область,
занятая облачностью, вычисляется температура и влажность.
Внутри облака температура находится из следующего
трансцендентного уравнения:
Г+0,623 ^Е{Т) =b(t, х, у, р). (14.9.18)
срР
По найденному Т вычисляется удельная влажность
q = ^(T-%) (14.9.19)
и, наконец, водность
Вне облака
b^(Q-q). (14.9.20)
q = Q(t, х, у, р),
T=b-^-Q(t, х, у, р),
Ср
&=0.
(14.9.21)
Наконец, по найденным полям q и Т при помощи
диагностического уравнения (14.9.15) рассчитывается скорость
456
Глава 14
конденсации га/р, которая и подставляется в уравнение (14.9.9)
при решении динамической части задачи. Задача в целом
решается итерациями, которые начинаются решением
динамической системы, причем т/р на первой итерации полагается
равным нулю.
14.10. Влияние пограничного слоя на эволюцию
крупномасштабных процессов
В предыдущих параграфах проблема предвычисления
метеорологических полей рассматривалась в адиабатическом
приближении, эффекты турбулентности считались пренебрежимо
малыми. Эти упрощения, как правило, допустимы для свободной
i t ,
i t ,
^-х4-Ч~к*—'-b4-t-rT-T-r
"•»~|"ГТ"1Т ! MP"
О, n
^_
r 1000 km
Рис. 14.4. Схема связи между пограничным слоем и свободной атмосферой.
атмосферы. Однако при формулировке краевых условий
предполагалось, что нижняя граница параллельна рельефу, и из
условий обтекания находилась вертикальная скорость. В такой
постановке удается лишь грубо учитывать чисто кинематическое
влияние земной поверхности. Для более адекватной
формулировки граничных условий необходимо рассмотреть механизм
взаимодействия пограничного слоя и свободной атмосферы.
Соответствующая схема представлена на рис. 14.4. На рисунке
показана серия чередующихся барических образований.
Упорядоченные восходящие движения в циклонах и нисходящие
движения в антициклонах показаны двойными стрелками.
В результате нисходящих движений воздух попадает в
пограничный слой (точка А на рис. 14.4). Здесь он находится
длительное время (точки Л, В, С) и вследствие турбулентного
перемешивания (одинарными стрелками показаны вихревые
движения внутри пограничного слоя) трансформируется. Его
температура и влажность меняются соответственно разности тем-
Пред вычисление метеорологических полей на короткий срок 457
ператур и влажности между воздухом и деятельным слоем
почвы. В конечном счете в результате восходящих движений
циклонической области трансформированный воздух попадает
в свободную атмосферу (на схеме точка D). Таким образом,
турбулентность и упорядоченные вертикальные движения
осуществляют обмен различными свойствами между свободной
атмосферой, с одной стороны, пограничным слоем и деятельной
поверхностью— с другой. Из вышесказанного становятся
очевидными два обстоятельства:
1) для того чтобы корректно учитывать непрерывно
существующий обмен свойствами между пограничным слоем и
свободной атмосферой, в уравнениях необходимо сохранять слагаемые,
отражающие перенос различных субстанций упорядоченными
вертикальными движениями; в свободной атмосфере это
основной механизм связи между слоями, расположенными на разных
уровнях;
2) при решении задач об эволюции полей во времени
необходимо систему уравнений для свободной атмосферы решать
совместно с уравнениями для пограничного слоя.
Так, например, даже при прогнозе на 10 ч при вертикальной
скорости 1 см/с частица воздуха, находившаяся вначале где-то
в средней части пограничного слоя, переместится по вертикали
на 360 м и успеет выйти в свободную атмосферу. Из этого
следует, что крупномасштабная горизонтальная неоднородность
деятельной поверхности уже за 10—12 ч приводит к заметным
эффектам в свободной атмосфере.
Рассмотренной в предыдущем параграфе квазигеострофиче-
ской моделью прогноза на нескольких уровнях не учитывается
непосредственная передача количества движения от слоя к слою,
а транспорт тепла вследствие замены фактического
вертикального градиента температуры средним значением сглаживает
реальные процессы. Каким же должен быть путь более
корректного учета эффектов пограничного слоя в задачах
краткосрочного прогноза?
Остановимся на учете наиболее важного процесса —
теплообмена между пограничным слоем и свободной
атмосферой.
Система уравнений (14.4.11) — (14.4.15), удовлетворительная
как первое приближение для свободной атмосферы, должна
быть дополнена уравнениями для пограничного слоя. При этом
уравнения динамики можно записывать в экмановском
приближении с параметрическим учетом горизонтальной
неоднородности и нестационарности. Уравнение притока тепла следует
записывать точно, поскольку в нем все слагаемые имеют
одинаковый порядок величины (можно допустить лишь приближенный
учет лучистого притока тепла).
458
Глава 14
Краевые условия для уравнений пограничного слоя
формулируются на основе решения системы уравнений для свободной
атмосферы с отброшенными эффектами пограничного слоя. Из
этого решения в качестве приближенных условий на верхней
границе пограничного слоя используются поля скорости ветра
и температуры (в общей задаче — и влажности). На
деятельной поверхности используются условия прилипания и уравнение
теплового баланса. Из решения уравнений для пограничного
слоя в этом приближении находятся поля вертикальной
скорости [w(H)\ и градиента потенциальной температуры на верхней
Г dQ I / ч 1
границе пограничного слоя I—— =Ya — Ун(х, у) .
L clz \ц J
Указанные поля в первом приближении будут отражать
условия в пограничном слое и на деятельной поверхности. Они
теперь используются для корректировки условия (14.3.10).
Если прогноз дается в квазигеострофическом приближении,
то на основании (14.5.25) и (14.3.10) искомое условие имеет
следующий вид:
(14.10.1)1
Остановимся более подробно на расчете вертикальной
скорости на верхней границе пограничного слоя. Выше отмечалась
исключительная роль упорядоченных вертикальных движений во
взаимодействии свободной атмосферы и пограничного слоя.
Правильный расчет вертикальных скоростей здесь является важным
звеном. Ниже мы будем пользоваться геометрической системой
координат. Соображения, по которым вводится изобарическая
система, в задачах пограничного слоя теряют свое значение.
Наиболее простой и естественный способ расчета вертикальной
скорости основан на использовании уравнения неразрывности.
Затруднения, возникающие при соответствующих вычислениях
для свободной атмосферы из-за близости ветра к
геострофическому, в рассматриваемом случае отпадают.
Интегрируя уравнение неразрывности по всему пограничному
слою (zo, Я), получаем
н
W
<">—!(-£-+-£-)*■ (14Л0-2)
1 Подчеркнем, что здесь уп(х, у) будет различным над теплой и
холодной подстилающей поверхностью и таким путем будет учитываться вклад
неоднородности деятельной поверхности в эволюцию процессов в свободной
атмосфере.
Пред вычисление метеорологических полей на короткий срок 459
Компоненты скорости ветра, необходимые для расчетов ш(Я),
можно определить, пользуясь уравнениями динамики в
следующем виде:
*»-■с—b-^h-S-. <14-">-3>
*~TJ-+-B-T-S-- (,4-10-4)
Из (14.10.3) и (14.10.4) найдем дивергенцию скорости:
/ ( дц | ^ \ | о д ( д zy д tx \
\дх*ду / ' Рг,~ ^ [ ^ Р ^У Р /
д I dv . dvu , dt/t; , dvze/ \ ,
дх\~дГ*~~dJT^~~oY~ ""~~3*~j"*~
, d / da , daa , dav , daw \
+ "5>Г\"аГ ' dF"1 5y~ "I dz~)'
Подставим выражение для дивергенции в (14.10.2) и выполним
интегрирование. Тогда найдем
*-(») —[(■E-:?~yf)L+(-E-'—5-»)L-] +
''-5-(V+-S-+tt)1*- (,4-'°-5)
Полученное уравнение отражает влияние главных факторов на
поле вертикальных скоростей. В формуле (14.10.5)
T-(-C-^-5-^)L—<"> <И-,а6>
— вклад турбулентности; он представляет собой вертикальную
скорость, обусловленную дивергенцией трения;
н
Jj-$vdz = w2(H) (14.10.7)
— вклад в поле вертикальных скоростей, связанный с
изменением параметра Кориолиса ф-эффект);
( "
1 I / д д \\ . f Г <* / <k> , dvu i dvv \
460
Глава 14
— приращение вертикальной скорости в пограничном слое,
вызванное инерцией.
В пределах пограничного слоя первое слагаемое, как
правило, много больше остальных, в связи с чем остальными
слагаемыми можно пренебречь или учитывать их во втором
приближении.
Вычислим главную часть — wiy пользуясь теорией экманов-
ского пограничного слоя. В тех случаях, когда интерес
представляет интегральный эффект пограничного слоя, допустимо
основываться на однопараметрической модели погранслоя (k =
= const). (В таких задачах гораздо важнее учитывать
горизонтальную неоднородность турбулентности, чем ее изменение
по вертикали.) При этом можно принять zo = 0.
Воспользовавшись соотношением (11.4.13) для комплексной
скорости
u+lv = uH+iv„—(uH+lvH)e-a*ix + l\ (14.10.9)
найдем вертикальную компоненту вихря касательного
напряжения:
\J-l2l.) д-Ы)}\ -\J_(kj!L) d-(k-^)]\ -
I дх \ 9 I ду \ р ^J U = o L дх \К дг ) ду Г дг /JUo-
-*[T5-"-SiTffa—5-R«-U!!ia-]L- (,4-,010)
Из (14.10.9) следует
HatzV) |,=0 = («//+^)а(1+0 = аК«//-^)+'(«я+^)].
(14.10.11)
Подставив (14.10.11) в (14.10.10), получим
дх \ р / ду \ р /
_KKi[^±^--^pLJ. (Н..0..2)
Если воспользоваться выражениями для геострофической
скорости, то из (14.10.12) следует
Ограничиваясь в (14.10.5) только главными слагаемыми,
получим применяющуюся в настоящее время формулу для расчета
вертикальных скоростей:
w(H) = wx <//) = -£■ V£r2 Аф"' (14.Ю.14)
Пред вычисление метеорологических полей на короткий срок 461
На основании полученного ранее выражения для
коэффициента турбулентности [см. (11.4.39) ]
ъ *3 О2 (х , «* А) \
^ 107 o>z V^r 2Г0 ?g<»zG2)
и геострофической формулы для модуля ветра
уравнение (14.10.14) можно записать в следующем виде:
w{ )= Ц V 1+2^7^7^Р
(14.10.15)
Здесь, имея в виду соотношение Боуэна Во = -~г-, удобно
ввести вместо турбулентного потока тепла радиационный
баланс, который можно определить по сетевым данным:
Po = TJ^R~0,09R. (14.10.16)
В экмановском приближении легко получить формулу для
расчета ш2(Я). Воспользовавшись (14.10.9), после простых
выкладок найдем
н
_w.,0-^(4--^). <".«*">
Приведем, наконец, формулу для оценки вклада
инерционных слагаемых в поле вертикальных скоростей. Полагая, что
в (14.10.8) внеинтегральный член является главным, найдем
после несложных выкладок:
(W).^(^.e.,_^.,1^).e.,o-.i£b^+
[тг ~ш <4Ф« v ф»> + тг 4т <4Ф» v ф«>] •
^3
, 1,55-10-4
(14.10.18)
Более точный способ расчета крупномасштабных
вертикальных движений в пограничном слое в экмановском приближении
основан на использовании замкнутой системы уравнений,
включающей в качестве неизвестной функции высоты коэффициент
462 Глава 14
турбулентности (см. главу 9). Из указанного решения находится
геострофический коэффициент трения
Z(Ro, ^--д———
и угол между касательным напряжением у земли и
геострофическим ветром a(Ro, juo). Поскольку задача решается только
численно, то х и a задаются в форме таблиц. Обозначим угол ме-
У
С Рис. 14.5. Отсчет направления
касательного напряжения и
геострофического ветра в стан-
дартной системе координат.
жду направлением оси ох (направление параллели) и
касательной к изобаре через ао (рис. 14.5); тогда получим
^1(^)=^H^-X2G2cos(a + a0)-^rx2G2sin(a + ao)).
(14.10.19)
На рис. 14.5 показано положительное направление отсчета
углов. Поскольку G, Ro и \io меняются от точки к точке, то
достаточно рассчитать Ro и jio для трех точек, по ним с помощью
таблиц вычислить % и а, а затем по формуле (14.10.19) найти
wi(H).
Полученные результаты касались расчета вертикальной
компоненты скорости над ровной земной поверхностью. В условиях
сложного рельефа, например над горными массивами, когда
спектр неровностей содержит волны, размер которых сравним
с масштабом барических образований, возникают совершенно
новые обстоятельства, с которыми приходится считаться.
Мелкомасштабные неровности, достигающие здесь
значительной высоты, сильно меняют интенсивность турбулентного
обмена. По-видимому, для учета соответствующих эффектов
достаточно надлежащим образом увеличить в предыдущих
формулах коэффициент турбулентности. Гораздо труднее учитывать
совместное влияние крупномасштабной части спектра
неровностей и турбулентность. Они приводят к заметным изменениям
основного (сглаженного) поля скорости, в частности, возникает
вытеснение потока, натекающего на горный массив, вверх,
причем в зависимости от интенсивности турбулентности
существенно меняется чисто кинематическое влияние рельефа.
Предвычисление метеорологических полей на короткий срок 463
В настоящее время вертикальные движения, вызываемые
совместным влиянием обоих факторов, можно оценить лишь очень
грубо. Идею, лежащую в основе такого учета, можно
интерпретировать следующим образом.
Вернемся к уравнению (14.10.1), которое годится и для
условий сложного рельефа. В данном случае, однако, под 2о =
=Zo(x, у) следует понимать уравнение сглаженного рельефа,
Н = Н — высота пограничного слоя в условиях неровной земной
поверхности, форма которой сглажена в определенном смысле.
Введем новую систему координат (х, у, г), так что
х = х, у=у, z = z — z0(x, у).
В таком случае
да да ди dz$
дх дх д7 дх
dv dv dv dzo
(14.10.20)
Подставим (14.10.19) в (14.10.1) и выполним
интегрирование, учитывая, что u(z) |-_0 =0, v(z) |-_0 =0. Тогда получим
•*- Г [il+f]£-т'!г-"1-т'("-4
(14.10.21)
Последние два слагаемых учитывают вертикальную скорость,
связанную с обтеканием горного массива. Первое слагаемое
обычно вычисляется по формуле (14.10.15), при этом Я— zo = H
представляет собой высоту пограничного слоя над
рассматриваемой поверхностью и принимается постоянной величиной.
Следует указать, что в качестве исходных данных в
полученные формулы входит информация о поле геопотенциала в
свободной атмосфере, в связи с чем, как уже указывалось, задачу
в целом приходится решать итерациями, полагая на первой
итерации wH = 0.
14.11. О согласовании исходных полей
Используемые для прогноза начальные данные в силу
методики измерений содержат значительные погрешности. Кроме
того, в них включены локальные неоднородности полей, мало
464
Глава 14
влияющие на эволюцию крупномасштабных процессов, прогноз
которых имеется в виду. В связи с этим и возникает проблема
специальной обработки исходных данных, которая привела бы
к уменьшению как погрешности измерений, так и
мелкомасштабных возмущений, связанных с недостаточной
репрезентативностью метеорологических станций. В результате такой
процедуры отфильтровываются источники, порождающие фиктивные
нарушения временного режима — «шумы», не имеющие
отношения к реальной эволюции крупномасштабных процессов.
Идея такой обработки начальных данных достаточно ясна.
Дело в том, что исходные поля, полученные в результате
измерений, должны вместе с тем удовлетворять уравнениям
гидротермодинамики. Однако если попытаться провести
соответствующую проверку, то легко обнаружить, что это отнюдь не так.
И разумеется, это связано, с одной стороны, с указанными
недостатками исходной информации, а с другой, с неадекватностью
используемой системы уравнений. Любая практически
приемлемая система прогностических уравнений не может и не должна
отражать все мелкие детали метеорологических полей, влияние
которых объективно включено в исходный материал. Система
уравнений всегда основана на какой-либо упрощенной модели
реальных процессов. Но если полагать, что принятая модель
атмосферы дает практически приемлемую точность, то
целесообразно выполнить некую «подгонку» исходных данных, после
которой они с лучшим приближением удовлетворяли бы системе
уравнений. В процессе такой подгонки, которую обычно
называют согласованием исходных полей, погрешности начальных
данных могут быть заметно уменьшены. Процедура
эффективного препарирования исходной информации широко
используется в современной практике, однако возможности здесь далеко
не исчерпаны.
Остановимся кратко на некоторых способах согласования,
применяемых в настоящее время.
Согласование полей ветра, температуры и геопотенциала
на основе геострофических соотношений и уравнения статики
Поскольку в свободной атмосфере действительный ветер
близок к геострофическому, а уравнение статики выполняется
с большой точностью, то измеренные значения температуры и
компонент вектора скорости (7\ и, v) и значения, рассчитанные
по полю геопотенциала (Ф):
7 1 д® ^ I дФ Tf. 1 дФ /1/1 и п
и=—Г^-> v = -l*> Т= —/TThTTT' <14Л1Л>
Пред вычисление метеорологических полей на короткий срок 465
должны различаться на сравнительно малую величину /'.
(Здесь всюду /* — значения соответствующей величины после
корректирования.) Очевидно,
5-Ф+Ф-. «■_;-._-■-(*-+»)-,.
, ~ 1 / дФ' . дФ \
Г = Т-Т= J-(-*^_+**_)_ Г. (14.11.2)
/? \ д\пр ' <^In/7 / v '
Если прогноз дается для некоторой области V, то
естественно выбирать поле поправок таким образом, чтобы интеграл
1И[аНа'2+^2) + а2г2+азф'2]^^^1п/? = / (14.11.3)
V
был минимальным. Нетрудно понять, что введение таких
поправок приблизит измеренные значения функций к значениям,
задаваемым моделью, в данном случае формулами (14.11.1). В
соотношении (14.11.3) веса а\у а|, а?3 выбираются разными; это
позволяет учесть предполагаемую близость измеренных и
вычисленных по формулам (14.11.1) значений соответствующих
величин, а также отразить различие в ошибках измерений ветра
и температуры. Известно, что для минимума интеграла его
первая вариация б/ должна равняться нулю, т. е.
J И К (а' 8«Ч-«' Ъ*о') + л\Г 8Г + а2ф' 8Ф'] dxdyd\np=0.
v
(14.11.4)
По смыслу задачи в соотношении (14.11.2), которым
определяются значения f , функции Ф, и, v, Т заданы; выбирать и,
стало быть, варьировать можно только поле Ф'. На этом
основании
Ьи'=- -j- *¥-. bv'=-1 дЬФ'
I ду ' I дх '
8Г=_ 1 *™L, (14-11.5)
R д\пр v '
30 Заказ № 612
466
Глава 14
Подставляя (14.11.5) в (14.11.4) и выполняя интегрирование по
одной из переменных, получаем
дЬФ' ,
JHn(-f-5-»'+T-t»')-8-3? ш-,
V
+ а|Ф' l<b'\dxdyd\xvp=\ f—о^-у-йФ'
+ 1
f |а*-у-8Ф' | rfydlnp-j |а|-£-8Ф'
Рг
dxdy-\-
Х\ р\
+ШМ-£т-тх)+*те7Т+4»']»*'*с<у.11л,.
(14.11.6)
Здесь r/i(x, р), у2(х, р), Xi(y, р), x2(r/, р), pi(x, у), р2(х, у)—
уравнения поверхностей, выделяющих объем V.
Без существенных искажений можно полагать, что всюду на
поверхности, ограничивающей рассматриваемый объем, 6Ф' = 0.
Соответствующие погрешности по крайней мере не выходят за
пределы допущений, обусловленных исходной моделью. При
таком допущении двойные интегралы равны нулю. Поскольку,
кроме того, внутри рассматриваемого объема 6Ф' может
принимать разные значения, то подынтегральная функция в
тройном интеграле должна равняться нулю, т. е.
■?(-5-т--е-т-)+«-яЬ--*-+«5»'-<>- ('«•»•*>
Уравнение (14.11.7) совместно с тремя уравнениями (14.11.2)
составляет систему из четырех уравнений для четырех
функций: и', v'у Ф', Г'. Численное решение этой системы не
представляет трудностей.
Динамическое согласование
Изложенная выше процедура согласования основана на
геострофических соотношениях и уравнении статики. Естественным
обобщением рассмотренного подхода было бы использование
полных уравнений динамики вместо геострофического баланса.
Простейшей реализацией такой идеи является «челночный
прогноз». Он сводится к прогнозу метеорологических полей на один
шаг по времени вперед, а затем на один шаг назад, при этом
нелинейные слагаемые на возвратном временном шаге вычис-
Пред вычисление метеорологических полей на короткий срок 467
ляются не по начальным данным, а по результатам, полученным
на временном шаге вперед. Естественно, что пересчитанные
начальные поля будут при этом отличаться от исходных.
Многократное повторение такой процедуры приводит в конечном
счете к взаимному согласованию полей, которые
предписываются им системой уравнений, используемой для прогноза. Для
пояснения сказанного изложим применяемую в настоящее время
технику согласования на основании челночного прогноза.
Запишем общий вид уравнений динамики:
ж—*^-*-**- (14Л1-8>
Для интегрирования уравнения (14.11.8) по времени
используется метод Эйлера с пересчетом. Первый цикл корректировки
начальных данных сводится к следующему расчету:
первый шаг вперед
«I(AO = M0) + <MM0)]A*,
^1)(АО = ^(0) + ФЛ^(А/)]А/,
(14.11.9)
(14.11.10)
первый шаг назад
и] (0) = «i,) (М)-Ф1 [и\1) (АО] А/,
йГ)(0) = ^1)(^)-фЛ^(0)]А^.
После этого начинается второй цикл, для которого исходными
данными являются поля ^(О).
Указанная процедура должна выполняться на основе
замкнутой системы уравнений.
Контрольные вопросы
1. Каковы физические основания для различной
формулировки задач краткосрочного и долгосрочного прогнозов?
2. Как получить связь между производными в
геометрической и изобарической системах координат?
3. Указать последовательность вычислений
метеорологических полей при прогнозе на основе примитивной системы
уравнений.
4. На каких физических предпосылках строится модель
прогноза на среднем уровне?
5. В чем сущность квазигеострофической модели
краткосрочного прогноза?
6. Что такое функция влияния?
7. Что такое вычислительная неустойчивость?
30*
Глава 15. ОСНОВЫ ОБЩЕЙ ЦИРКУЛЯЦИИ АТМОСФЕРЫ
И НЕКОТОРЫЕ ВОПРОСЫ ЭНЕРГЕТИКИ АТМОСФЕРЫ
Уравнения гидродинамики для общей циркуляции атмосферы. Первые
гидродинамические модели. Двухуровенная модель Н. Филлипса. Девятиуровенная
модель Д. Смагоринского. Преобразование энергии в атмосфере.
15.1. Понятие «общая циркуляция атмосферы». Уравнения
гидродинамики, описывающие крупномасштабные движения
в атмосфере
Атмосферные движения в силу своей многомасштабности
имеют очень сложную структуру. Несмотря на то что основные
законы, которым подчиняется динамика атмосферы, известны
сейчас достаточно точно, при решении задач общей циркуляции
атмосферы (ОЦА) встречается
множество трудностей,
значительная часть которых до сих пор
не преодолена.
Само понятие «общая
циркуляция атмосферы» многогранно.
С одной стороны, ОЦА — это
некоторое осредненное по времени
состояние атмосферы, где
сохранены все особенности
локального характера. С другой стороны,
это глобальное состояние ат-
Рис. 15.1. Схема правосторонней мосферы в данный момент. Иног-
сферической системы координат, да ОЦА рассматривается как
построенной для точки М. набор различных синоптических
ситуаций, проявляющихся в
атмосфере постоянно или почти постоянно (внутритропическая
зона конвергенции, струйные течения, центры действия
атмосферы, муссонная циркуляция и т. д.). Наконец, под ОЦА
понимают комплекс некоторых статистических характеристик.
При решении большинства задач по теории общей
циркуляции атмосферы уравнения гидродинамики часто записывают
в сферической системе координат. Воспользуемся сферическими
координатами г, т> и К: г — радиальная координата,
направленная от центра Земли, О и X — широтная и долготная координаты
(f} = 90° — <р есть дополнение до широты <р), направленные
соответственно на юг и восток (рис. 15.1). В этом случае урав-
Общая циркуляция и энергетика атмосферы
469*
нения гидродинамики для единичной массы воздуха в
проекциях на криволинейные оси г, #, А записываются в виде:
уравнения движения
dt ^Vr dr
vb dvr
v.
dvr
дЪ
rsinu dl
vl + vt = 1 dp ,
Г p Лг I
ar
i
r* sin &
аг/Л
+2^81п*-*+^[^(*1Р^) +
a*
■vr-
0
va <4
r2sin2^
urV*
dr
db
rsinft dX
= -^^+2^cos*+t["
1
1
d
' r2Sin& a&
а*л dv.
(*2PSln»-^) +
1
r2 ar
a
*!РГ5
^ctg8 =
ar
V* <4
r2Sin2»
dv.
d\
vv
(**)].
(15.1.2>
a*
и&"х
ar
^
+-H-
1
r2 ar
prsin^ ax
i a
rsinft ax ' г ' r
- 2o)^r sin Ь — 2u>vb cos ft -f-
i a
ctg& =
at/,
db
(*2psin&-^x
■)+
~ r2Sm2^ ax
уравнения неразрывности
(**т)]'
(15.1.3)
ар , i a(pr2t;r)
i
dt
Г2
ar
rsinft
«йЦ^+^]_а (15.i.4>
уравнения притока тепла
з
2"
i = \
dT
.-1 Т
dt
dp
■vr
dT
dT
dT
(dp
\ dt
dr
dp
db
dp
rsinb ax
dp
v
dr
db
rsinu ax
(15.1.5)
В уравнениях (15.1.1) — (15.1.5) vr, v$, v%. — проекции
скорости на соответствующие криволинейной оси; р — давление; р —
плотность; g— ускорение свободного падения; о — угловая
скорость вращения Земли; ku k2 — коэффициенты турбулентности
соответственно для вертикального и горизонтального
турбулентного перемешивания; x = cP/cv — показатель адиабаты (ср и
470
Глава 15
cv — удельная теплоемкость при постоянном давлении и объеме
соответственно); г\ — приток тепла за счет излучения и
поглощения частицами воздуха длинноволновой и коротковолновой
радиации; гч—приток тепла вследствие турбулентного
перемешивания; ез — приток тепла за счет фазовых превращений воды
в атмосфере.
При заданных ег, а также при адиабатическом процессе,
з
когда 2]ег = 0, система уравнений (15.2.1) — (15.2.5) с привле-
г = 1
чением уравнения состояния
p = pRT (15.1.6)
является замкнутой.
При решении задач ОЦА, в которых часто интегрирование
системы (15.1.1) — (15.1.5) по времени выполняется вперед на
длительный период — порядка сотен суток, учет притоков тепла
е* является обязательным условием, поскольку пренебрежение
ими может привести к очень большим ошибкам.
Сложность системы уравнений гидродинамики, описывающей
ОЦА, и связанные с этим математические трудности приводят
к необходимости ее упрощения. Последнее требует тщательного
качественного анализа уравнений и привлечения значительного
объема эмпирических данных.
15.2. Первая гидродинамическая модель общей циркуляции
атмосферы Н. Е. Кочина
Основы гидродинамической теории общей циркуляции
атмосферы были разработаны Н. Е. Кочиным в 1933 г. Он указал,
что проблему общей циркуляции надо решать параллельно с
проблемой лучистого и турбулентного теплообмена в атмосфере.
Поскольку решить задачу в таком объеме в то время было
невозможно, в модели предусматривалось использование
некоторых упрощающих предположений. Так, процессы общей
циркуляции считались стационарными и зональными. Кроме того,
предполагались заданными поля температуры Т($у z) и
приземного давления /?о(Ф).
Задача моделирования ОЦА решалась в три этапа. На
первом рассчитывались поля давления с использованием
барометрической формулы. На втором этапе по уравнениям Экмана—
Акерблома вычислялись горизонтальные компоненты скорости
ветра. На третьем этапе с помощью уравнения неразрывности
были получены вертикальные скорости.
По найденным значениям градиента давления может быть
рассчитано поле геострофического ветра. Сравнение поля скоро-
Общая циркуляция и энергетика атмосферы
471
сти ветра, найденного из уравнений Экмана—Акерблома, с
полем геострофических скоростей позволило оценить роль
турбулентной вязкости (табл. 15.1).
Из табл. 15.1 следует, что турбулентная вязкость
существенно уменьшает скорость ветра в тропосфере, в связи с чем
скорость действительного ветра везде меньше скорости
градиентного ветра.
Таблица 15.1. Значения зональных составляющих скорости ветра (м/с),
вычисленные без учета и с учетом влияния турбулентного перемешивания
(зима, 2 = 6 км)
kx м2/с
0
2,67-103
9°
15
7,6
5,4
35
11,6
8,6
55
11,4
7,7
75
11,6
7,9
Достоинства модели ОЦА, предложенной Кочиным,
заключается в следующем:
1) модель впервые построена на гидродинамической основе;
2) в модели была выявлена роль атмосферной
турбулентности;
3) модель хорошо отражает зональную структуру ОЦА.
К основным недостаткам модели следует отнести:
1) необходимость принимать заданными поля температуры
и приземного давления, в то время как эти поля сами зависят
от внешних условий и являются существенными
характеристиками ОЦА;
2) пренебрежение эффектом макромасштабного
горизонтального турбулентного перемешивания.
15.3. Модель общей циркуляции атмосферы Е. Н. Блиновой
Одним из главных механизмов ОЦА являются обширные
квазистационарные области низкого и высокого давления,
называемые центрами действия атмосферы (ЦДА). Определение этих
ЦДА и было одной из основных задач при создании Е. Н.
Блиновой модели общей циркуляции атмосферы.
При построении модели центров действия атмосферы были
приняты следующие допущения:
1) все движения в атмосфере стационарны;
2) вертикальные части конвективных производных скорости
пренебрежимо малы;
472
Глава 15
3) силы турбулентного трения отсутствуют;
4) все характеристики движения f могут быть разделены на
чисто зональные компоненты f и малые отклонения от чисто
зональных компонент /'; отсюда следует, что
^х=^х(^ &)+*>!(*, Ъ, X), щ=<о'ъ(г9 Ь, X),
p = ~p(z, »)+/>'(*. О, X), Т=Т(г, ») + 7"(*. Ь9 X),
Р = р(г, Ъ) + ?'(г, 8, X), (15.3.1)
и, стало быть,
-§—£-£-•£-* см-*»
5) поле температуры Г (г, О, X) считается заданным.
Для решения поставленной задачи необходимо прежде всего
отыскать чисто зональные значения скорости v\, давления р,
температуры Т и плотности р. С этой целью предполагается,
что
^x = aasin&, (15.3.3)
где a = 6371 км — радиус Земли; a — так называемый индекс
циркуляции, имеющий смысл угловой скорости вращения
частицы вдоль круга широты с радиусом вращения R = asin-&.
Для получения чисто зонального значения давления р (z, Ф)
воспользуемся геострофическим приближением уравнений
динамики (15.1.2), считая, что это приближение описывает чисто
зональное движение. Привлекая к нему равенство (15.3.3),
получим
-^- = a2<oapsin2&. (15.3.4)
Пренебрегая изменением плотности по горизонтали,
проинтегрируем (15.3.4) по широте от ft до /& = 0, в результате чего
будем иметь
p(z, b)=>pQ+a?a<uisin2b, (15.3.5)
где /?о — давление на полюсе.
Используя уравнение состояния и равенство (15.3.5),
получим выражение и для расчета чисто зональных значений
температуры:
T(z, &)=T0-f Csin2», (15.3.6)
где
Общая циркуляция и энергетика атмосферы
473
В качестве исходного уравнения для решения задачи
использовалось уравнение вихря. Строилась одноуровенная модель,
причем в качестве рассматриваемого уровня был выбран
средний (бездивергентный) уровень. С учетом бездивергентности
уровня, а также трех первых допущений, о которых было
сказано выше, уравнение вихря скорости в сферической системе
координат можно записать в виде
0 =
-е-
dQ
д£
1
dp ар
дЬ
asinb дХ I р2д281п& \ дЬ дХ
где
2 =
1 rd(t/xsin$) dvb
asinb
дЪ
дХ
■]•
4f-S-)-*»
(15.3.7)
(15.3.8)
Для преобразования (15.3.7) воспользуемся условием квази-
соленоидальности, т. е. введем функцию тока if через
соотношения:
1 д<\> \
ч=-
vx=-
asinb дХ
1 dty
а дЬ
(15.3.9)
Имея в виду, что с применением (15.3.9)
в-риг[-1г(-«»эМ + -»г(-Ёг-Й-)]-"^
1 Лл /
а также заменяя в (15.3.7) — ~^7~ выражением (
1 др
1 дТ
р ds
р ds
)у где 5=Ф, Я, после небольших преобразований вме-
Т ds
сто (15.3.7) получим
1 г a^ а (у зф) аф а (у щ ] . 2о) a^
а2 sin» I а& > ах ах аа J "г л2 ах ~~
_ 1 ( др дТ др дТ\
~ а^тsinа\ а& ах ах а& г
(15.3.10)
Здесь V2—«горизонтальная» часть лапласиана.
Уравнение (15.3.10) является нелинейным. Для его
линеаризации искомые значения метеоэлементов представим как сумму
чисто зональных слагаемых и малых отклонений от зональных
величин. При этом, учитывая малость последних, их квадратами
474
Глава 15
и произведениями их производных будем пренебрегать. Выпол-
бив это, с учетом (15.3.1) и (15.3.2) получим
a2Sind L дЪ д\ дХ дЪ \*~ л2 дХ ~~
_ 1 ( др дТ' dp' df\ /1с о in
""o^sin* \дЬ дХ дХ дЬ ) ' {Ю.й.И)
Уравнение (15.3.11) можно упростить, если преобразовать
производные от чисто зональных характеристик по Ф с помощью
равенств (15.3.3), (15.3.4) и (15.3.9). Кроме того, в соответствии
с оценкой слагаемых в скобке правой части (15.3.11),
выполненной Блиновой на основании эмпирических данных, примем
дЪ дХ ^ дХ дЪ (10.6.1Z)
и в связи с этим будем пренебрегать последним слагаемым
в этой скобке. В результате вместо (15.3.11) можно записать
-^+^r('+^-^f^. 05.3.13)
Разложим в ряд по сферическим функциям незональные
отклонения функций тока
оо п
<|>'(&, X)—2 2 (AjrcoswX+Bj?sinjnX)/>J?(cos&) (15.3.14)
п = \ т~\
и известные на среднем уровне (из допущения 5) незональные
отклонения температуры
оо п
Т'(Ъ, Х)= 2 2 (*?, ncosтк+ъ, пsinm\)P%(cosЪ). (15.3.15)
Здесь п — степень; т — порядок присоединенных функций Ле-
жандра Р™ (cos #); Л™, В™, %™п , т™п —коэффициенты,
подлежащие отысканию. После подстановки правых частей (15.3.14)
и (15.3.15) в уравнение (15.3.13) с последующим его
преобразованием получаем искомые коэффициенты:
9пл2 [,/в п — т , ,т П + 1 -\-ТП\
А„ = —— — - , (15.3.16)
r[2(l+_)-„(„ + l)]
о, J /Тт п — т т п + 1 +т \
д.,М^-п^+^^+Н^ (15.3.17)
Г[2(1+^)-„(Я + 1,]
Общая циркуляция и энергетика атмосферы
475
Подставив (15.3.16) и (15.3.17) в правую часть (15.3.14),
вначале получим поле г|?г (О, А,), а затем с использованием
условий (15.3.9)—и поле составляющих скоростей ^(Ф, А,) =
= уф и уя, для чего к найденным значениям v'% (ft, X)
предварительно добавим известные из (15.3.3) значения vx($).
Для определения поля давления воспользуемся уравнением
движения (15.1.3). С учетом принятых в модели допущений это
уравнение запишется в виде
ft X I X X i ft X i (\
= W4f-4- (15.3.18)
p# sin & (M *> v '
Линеаризируем (15.3.18) по аналогии с линеаризацией
уравнения вихря (15.3.10) и после незначительных преобразований
с одновременным привлечением соотношений (15.3.3) и (15.3.9)
окончательно получим
.= _ap-sin&^_(^.)+2p(a+lo)cos»4r- (15-ЗЛ9>
Уравнение (15.3.19) позволяет получить по известному на
среднем уровне полю ^'(Ф, Я,) значения незональных отклонений
давления р'(р, X) на этом же уровне, а с использованием
(15.3.5) и значения р(Ф, X). Зная ро0&, X), по барометрической
формуле можно определить также и давление на уровне моря.
В изложенной модели ОЦА индекс циркуляции а был принят
зависящим только от широты О. В действительности, как
показали многие исследования, а меняется от сезона к сезону,
а также является функцией высоты г. Кроме того, при
дальнейшем развитии модели Блинова пришла к выводу, что можно
решить пространственную задачу отыскания полей давления и
скорости не только на среднем, но и на любом уровне,
принимая для этого условие приближенной соленоидальности
движения для всей атмосферы. В этом случае к уравнению вихря
(15.3.7) добавляется «дивергентный» член, после чего с
привлечением уравнения неразрывности, записанного для
стационарного случая в виде
d?vz
dz
-р£> = 0,
где «горизонтальная» дивергенция
d(t^sin&) dvx
flSlflfr L
дЬ ' dk
476
Глава 15
вместо (15.3.7) получим
v, дй
дО. 2(0 sin Ь
= \ (
а дЬ ' a sin ft дХ
др дТ др дТ
дЬ дХ
дХ дЪ
)+
2о) cos ft д (р*>г)
Р
д-гг
(15.3.20)
Линеаризация уравнения (15.3.20) по-прежнему выполняется
<: привлечением условий (15.3.1), (15.3.2) и (15.3.12), а также
равенств (15.3.3) и (15.3.9). В результате будем иметь
[■
д(уЦ') , 2(а + о>) д^
дХ
а*
дХ
'-}-
- '"L10" -gl+2.cos9 а(Г-' ■
7 дХ ' дг
(15.3.21)
Здесь функция тока я|/=г|/(Ф, А,, г), а индекс циркуляции а для
конкретного сезона года считается зависящим не только от
широты, но и от высоты г.
Интегрируя обе части (15.3.21) по z при граничных
условиях
получим соотношение
л<
2 (а + со) . д<|/'
ах
Д2
ах
pdz =
сю
2o)fl2cos» f дТ' -.
(15.3.22)
Используя (15.3.19) и барометрическую формулу в виде
/>(», У, z)=p0(b, Х)ехр
gdz
RT (*, X, г)
можно получить с помощью (15.3.22) уравнение для расчета
поля ро($, X).
В своих дальнейших исследованиях Блинова отказалась от
использования эмпирических данных для получения поля
температуры. Для полного решения задачи (построения замкнутой
теории ОЦА) рассмотренная выше система уравнений дополня-
.лась уравнением притока тепла, уравнениями переноса
радиации и уравнением теплопроводности для почвы.
Общая циркуляция и энергетика атмосферы
477
15.4. Численные эксперименты по общей циркуляции атмосферы.
Двухуровенная модель Н. Филлипса
В рассмотренных моделях ОЦА имели место значительные
ограничения. К главным ограничениям следует отнести
принятие условия бездивергентности движения, необходимость
линеаризации системы уравнений, необходимость предварительного
знания поля температуры. Все это обусловливалось как
недостаточностью знаний закономерностей атмосферных процессов, так
и невозможностью решения полной системы уравнений
гидродинамики без соответствующей вычислительной техники. И только
появление быстродействующих электронных вычислительных
машин дало наконец возможность реализации
гидродинамических моделей ОЦА.
Одной из первых работ в области моделирования ОЦА с
использованием полной системы уравнений является работа
Н. Филлипса «Общая циркуляция атмосферы. Численный
эксперимент», опубликованная в 1956 г. Настоящий параграф
посвящен изложению физических предпосылок и математического
аппарата, используемых в работе Филлипса.
Постановка задачи. Исходные уравнения
В упомянутой работе рассматривается двухуровенная
модель ОЦА в квазигеострофическом приближении. В этой
модели приближенно учитываются притоки тепла и турбулентное
трение.
При выводе уравнений гидродинамики для упрощения
выбранной модели используется квазипрямоугольная стандартная
(ось х направлена на восток, ось у — на север) изобарическая
система координат, в связи с чем кинематический эффект,
обусловленный кривизной земной поверхности, не учитывается.
Кроме того, вводится допущение о малости членов в уравнениях
движения, содержащих вертикальные составляющие скорости.
Таким образом, уравнения горизонтального движения запи-
ываются в виде (см. главу 14):
-tt-^+^^-to=-^r+*2V2tf-f£-eF, (15.4.1)
dt ' " дх~и ду *и— дх "^ v ~^6 др
dV *-*^+*&+l*--^+b^+g* (15.4.2)
dt ^" дх^и ду "Г"— ду -Г-2 v "-Г5 др
где Ф — геопотенциал. Два последних члена в обоих уравнениях
соответственно описывают макромасштабное горизонтальное и
ди
вертикальное турбулентное перемешивание; хх = —92gki—z— и
др
478 Глава 15
xv = —р^й1-т- есть компоненты напряжения турбулентного
трения вдоль осей х и у.
Уравнения движения замыкаются:
уравнением статики
£ — ■£. 05.4.3)
уравнением неразрывности
-£■+-£•+-£-«• ом-*)
где x = dp/dt — аналог вертикальной скорости,
уравнением притока тепла
%-(тг+-4г+*4г)т-7* <15-4-5>
где c2=RT (уа — y)/g — так называемый параметр устойчивости.
Модель атмосферы
В выбранной двухуровенной модели используются уровни
750 и 250 мбар для характеристики движений в нижней и
верхней половине атмосферы. К этим двум основным уровням вво-
Омбар дятся еи*е ТРИ
вспомогательных: 0, 500 и 1000 мбар. При
250 этом уровни 0, 250, 500, 750 и
1000 мбар и характеристики их
состояния обозначаются
соответственно индексами 0, 1, 2,
V//SW////////////////////////////////A
500
750
1000
Рис. 15.2. Модель атмосферы по
Н. Филлипсу.
3 и 4. На рис. 15.2 основные уровни показаны сплошными
линиями, вспомогательные уровни — штриховыми.
Преобразования уравнений движения. Учет вертикального
турбулентного перемешивания
Для преобразования уравнений движения
продифференцируем вначале уравнение (15.4.1) по у, а уравнение (15.4.2) по
х, после чего из второго уравнения почленно вычтем первое.
Общая циркуляция и энергетика атмосферы
479
В результате получим уравнение вихря в изобарической
системе координат:
=*,V°2+g^(£-^). 05.4.6)
Здесь Q = dv/dx — ди/ду — вертикальная составляющая вектора
вихря скорости; D = du/dx+dv/dy — горизонтальная часть
дивергенции скорости; р =д1]ду = 2со cos>cp/a— параметр Россби.
В уравнении вихря отброшено слагаемое QD вследствие
малости.
Для записи уравнения (15.4.6) применительно к основным
уррвням 1 и 3 введем граничные условия: на уровнях /?4 =
= 1000 мбар и /?о = 0 вертикальные скорости Т4=т0 = 0.
Из уравнения неразрывности (15.4.4) следует, что
D=—p-,
dp
откуда, переходя к конечным разностям, получим для третьего
и первого уровней:
D =—( — ] ~ ^2-^4 ^ ^2
3 \ dp h Р2 — Ра " Рч '
т0 — ^2 21_
Р0 — Р2 Р2
(15.4.7)
Рассмотрим теперь в уравнении (15.4.6) слагаемое,
характеризующее вертикальное турбулентное перемешивание.
На верхней границе атмосферы (тх)о= (т1/)о = 0. В свободной
атмосфере, в частности на уровне рг = 500 мбар, хх и ту
должны быть значительно меньше, чем у поверхности Земли.
В итоге получаем для уровня pi
а для уровня /?з
&[др \дх ду )\\ и'
gldp \дл
g
[[ дх ду h \ дх ду )а\ _ *g
дх ду
дх ду /4
Рч — Ра Ра
Согласно экспериментальным данным, вблизи поверхности
Земли турбулентное трение пропорционально квадрату
скорости ветра:
K| = WL (15.4.8)
480 Глава 15
где х — безразмерный коэффициент пропорциональности,
введенный Тейлором и в среднем равный 0,003; са — скорость ветра
на уровне анемометра. В рассматриваемом случае для простоты
считается, что напряжение Т4 направлено под постоянным углом
к скорости геострофического ветра и пропорционально
произведению этой скорости на ее характерное значение. Принимая
далее, что скорость ветра на уровне анемометра составляет
в среднем 70% геострофической скорости, т. е. что u = 0Jugy v =
= 0Jvg и скорость ca = 0,7cag, с учетом (15.4.8) получим:
Ыа= -0,49хр4и^, | (15.4.9)
(ту)4=-0,49хр4<гу^. J
Здесь cag — геострофическая скорость на уровне анемометра.
В результате, используя (15.4.9), на основании условия ква-
зигеострофичности получим
Г д (fay дххХ\ __ 0,98%gcag / dvg dag\
ё[ dp [ дх ду )\з~ RT4 \ дх ду /4
= -*(Q,)4«-*24. (15.4.10)
Положив cag=\0 м/с, а Г4 = 273 К, примем значение
коэффициента & = 4- 10~6 1/с.
С учетом (15.4.7) и (15.4.10), а также используя равенство
поскольку (v-v)/ = y-p =(3i>, получим уравнение вихря для
уровней 1 и 3:
(ж+у* • v)(^+0-^ = *2V22b (15.4.11)
(4~v3- v)^3+/) + /^—*2V22a-№4, (15.4.12)
где у —горизонтальный оператор Гамильтона (набла).
Дальнейшее упрощение задачи заключается в замене
параметра Кориолиса его осредненным по всему пространству
значением /*, а также в принятии допущения о неизменности
параметра Россби р. Тогда на основании выполнения введенного
выше условия квазигеострофичности и, следовательно, равенства
нулю дивергенции геострофического ветра можно записать:
1 a$ at 1 дФ дФ
откуда
(\|> — функция тока).
Ф = /*Ф (15.4.13)
Общая циркуляция и энергетика атмосферы 481
Учитывая также допущение р = const и используя линейную
зависимость, получим
/=Ру. (15.4.14)
Уравнение (15.4.12) содержит величину вихря Q4. Эту
величину целесообразно исключить с помощью формулы линейной
экстраполяции
Q4_-J-23_-1-2,. (15.4.15)
Привлекая равенства (15.4.14) и (15.4.15), перепишем
теперь уравнения (15.4.11) и (15.4.12) в окончательном виде:
(I- + V, • ^(д.+ру)-/,-^-*,^,, (15.4.16)
(^-+V3-v)(23+Py)+/*^-=^V223-^-(323-2i). (15.4.17)
Преобразование уравнения притока тепла. Учет радиационного
притока тепла и влияния горизонтальной турбулентной диффузии
Для преобразования уравнения притока тепла (15.4.5)
применительно к уровню 2 представим вначале температуру Т2 с
помощью уравнения статики (15.4.3) в виде
Т — Р2 ( дФ\ ^ Ф\ — Ф3
l2~~ R \ dph~ R
откуда с использованием (15.4.13) получим
7-a»f*<*'-■<*>. (15.4.18)
Уравнение (15.4.5) с учетом (15.4.18) теперь может быть
переписано следующим образом: ,
^Г"(ж+v» • v)i(t>-*s)-^. 05.4.19)
В уравнении (15.4.19) 2j6/p есть величина, равная скорости
притока тепла к единице массы на уровне 500 мбар.
В рассматриваемой модели учитываются только два вида
притоков тепла: приток тепла к единице массы в единицу
времени вследствие переноса лучистой энергии (ei/p) и приток тепла
вследствие горизонтальной турбулентной диффузии (е2/р).
Прежде чем определить значения притоков тепла,
необходимо задать область интегрирования рассматриваемой двухуро-
венной модели атмосферы. Выбирается простейший случай —
31 Заказ № 612
482
Глава 15
прямоугольная область, ограниченная «стенками» при y = ±wy
но открытая с западной и восточной стороны (х = 0, L), где
поставлено условие периодичности, при котором значения
искомых функций при х = 0 и х = Ь совпадают (рис. 15.3). Приток
тепла вследствие переноса лучистой энергии представляется
в виде линейной функции широты (координаты у):
р \ w ) '
(15.4.20)
где Е — среднее в промежутке от у =—w до у=0 количество
Рис. 15.3. Область интегрирования
в модели Н. Филлипса.
Рис. 15.4. Потоки тепла к северу
(по данным Е. Минца).
1 — зима, 2 — лето.
энергии, получаемое (или отдаваемое) единицей массы воздуха
в единицу времени за счет радиационного нагревания или
охлаждения. Для приближенной оценки величины Е учтем, что
при установившемся состоянии скорость переноса тепловой
энергии через линию у = 0 (<р. = 45°) от х=0 до x = L может быть
представлена выражением EwLpJg (кал/с). Через 1 м этой
линии скорость переноса будет составлять Ewpjg [кал/(м - с)].
Из эмпирических данных (рис. 15.4) известно, что вихревой
перенос тепла через круг широты <р = 45°, длина которого
2ла cos 45° = 2,84 • 107 м, приблизительно составляет
EwLp4lg = 6 • 1019 кал/сут = 2,9 • 1022 эрг/с.
Но это означает, что поток тепла через отрезок круга
широты ф = 45° длиной 1 м равен
Ewp4lg=\013 эрг/(см • с) = 105 кДж/(м • с),
что и позволит оценить величину £. Так, положив ш = 45°Х
Общая циркуляция и энергетика атмосферы 483
ХШ км = 5.103 км, # = 9,81 м/с2, р4=Ю3 мбар = 105 кг/(с2-м),
получим искомое
Ё=2 . 10"3 кДж/(т • с) =0,48 • 10~3 кал/(кг • с).
Определим теперь значение изменения температуры в сутки,
соответствующее найденному значению Е. Поскольку изменение
температуры вследствие переноса лучистой энергии определяется
равенством
\ dt /л ?ср '
то, следовательно, при y=w
Шл=-^=-4 • 10~6 К/с—0.35 К/сут.
Наблюдения показывают, что полученная оценка
радиационного изменения температуры близка к действительным
значениям.
Для определения притока тепла вследствие горизонтальной
макротурбулентной диффузии воспользуемся уравнением
^L = <y4TV27\
где Лт— коэффициент горизонтальной турбулентной диффузии
тепла, или с привлечением (15.4.18) для уровня 2
-y = cpAr±V*(b-b)- (15.4.21)
Теперь с учетом (15.4.20) и (15.4.21) уравнение притока
тепла (15.4.19) можно представить соотношением
(15.4.22)
где коэффициент
Х2 = -^- = const.
Для упрощения системы (15.4.16), (15.4.17) и (15.4.22) Фил-
липс предполагает, что оператор v2 - V = vi * V=v3 * V-
Последнее означает, что адвекция функции \|?i — г|?з ~ Тг на всех трех
уровнях одинакова. Учитывая это обстоятельство и используя
31*
484
Глава 15
тождество Q = V^, получим в результате объединения трех
упомянутых уравнений систему вида
# —(V, • V)p.+Py)+*« V»?,+X»^(-J-). (15.4.23)
—5-[з?з-?1-4).2(Ф1-Фз)]. (15.4.24)
где
?i = V2+!—Х2(ф, —^3). (15.4.25)
д3=Ч2Ь+^(Ь-Ь) (15.4.26)
есть вспомогательные функции, названные Филлипсом
относительными потенциальными вихрями для уровней 1 и 3.
В (15.4.23) и (15.4.24) Ат и кг приняты равными AT = k2 =
= 105м2/с.
Практическая реализация численного эксперимента
Реализация модели осуществлялась на прямоугольной сетке
с количеством узлов 16X17, так что Д*/ = 625 км (2ш =
= 10 000 км), а Дх = 375 км (L = 6000 км). В качестве
граничных условий для х=0, L использовались условия периодичности,
а для y = ±w — условие справедливости для любого момента
времени t равенств
f = Q'=0
и
Здесь черта сверху определяет чисто зональную часть
характеристики, а штрих — малое отклонение от чисто зональной части.
Уравнения (15.4.23) и (15.4.24) записывались в
конечно-разностной форме и интегрировались при условии, что в начальный
момент времени t=0 изотермическая атмосфера находится в
состоянии покоя (t|?i=i|)3 = 0). На первом этапе интегрировались
уравнения для среднего движения с шагом At=l сут на 130 сут
вперед. В результате образовался межширотный градиент
температуры от —30, ГС при y = w до 30, ГС при у = —w. Второй этап
интегрирования начинается с того, что на поле tj>i и я|)з
накладывались случайные возмущения t|/ и ty'3 • Шаг интегрирования
Общая циркуляция и энергетика атмосферы
485
постепенно уменьшался от At = 2 ч до А/= 0,5 ч, что позволило
свести к минимуму вычислительную неустойчивость решения.
Прогноз сложного движения удалось провести на 31 сут вперед.
В качестве иллюстрации результатов второго этапа численного
Рис. 15.5. Распределение высот поверхности 1000 мбар (/) и
температуры на поверхности 500 мбар (2) на втором этапе
численного эксперимента Н. Филлипсз.
а —на 11-й день, б — на 23-й день.
эксперимента на рис. 15.5 приведены карты распределения
высот поверхности 1000 мбар и температуры на поверхности
500 мбар на 11-е и 23-и сутки.
15.5. Численные эксперименты по общей циркуляции атмосферы.
Девятиуровенная модель Д. Смагоринского
В настоящем параграфе рассмотрим девятиуровенную
модель общей циркуляции атмосферы по полушарию,
предложенную Д. Смагоринским в 1965 г.
Эта модель является более совершенной в сравнении с
моделью Н. Филлипса. К ее достоинствам относятся: 1)
значительно большее разрешение метеоэлементов по вертикали; 2)
отказ от квазигеострофических условий; 3) более точный учет
притоков тепла, в частности притоков тепла вследствие радиационного
486
Глава 15
нагревания и фазовых переходов воды; 4) учет различия
свойств подстилающей поверхности и ее рельефа; 5) более
детализированный учет влияния турбулентности в пограничном и
приземном слоях на процессы ОЦА.
Учет рельефа и а-система координат
Учет рельефа в модели осуществлялся путем записи
уравнений гидродинамики в сигма-системе (а-система) координат,
отличающейся от изобарической системы вертикальной
координатой
где р — давление на данном уровне; Pf(x, у, t)—давление на
уровне подстилающей поверхности.
Основное преимущество этой системы состоит в совпадении
подстилающей поверхности с координатной поверхностью о =
= const.
Недостатком а-системы является необходимость
экстраполяции получаемых от метеосети данных о давлении к уровню
фактического расположения земной поверхности.
В главе 14 основные уравнения гидродинамики (14.3.13) —
(14.3.18) были представлены в а-системе координат.
Модель атмосферы
Для модели выбирается прямоугольная сетка точек на карте
стереографической проекции для северного полушария. Начало
координат помещено в точке Северного полюса, ось ох
направлена по Гринвичскому меридиану, ось оу — по меридиану 90°
в. д. Число N узловых точек между полюсом и экватором
однозначно определяет сетку. Схема реализовалась для N = 20, что
соответствовало расстоянию между узлами сетки около 320 км
на экваторе, 540 км на широте ф = 45° и 640 км вблизи полюса
(рис. 15.6). В качестве вертикальной координаты, как уже
говорилось выше, выбиралась переменная o = p/pF. Вся атмосфера
разбивалась на девять слоев. При этом расстояния между
соседними уровнями были неодинаковыми: они выбирались таким
образом, чтобы обеспечивалось максимальное разрешение по
давлению у верхней и нижней границ атмосферы (рис. 15.7).
В этом случае имеет смысл ввести новую переменную а',
связанную с переменной о соотношением
^ =оЛ (3 —2оЛ),
Общая циркуляция и энергетика атмосферы
оо>
cTcf
i
О)
S» S Р £2
Сь <Ъ lo о-)
^ <хГ Ч"Г о?
О) <о о ^
<й <vj о <о
§ О) Ч <о
00
<о ОО
ci4 сГсГ
I
t t t
CI
II
■aha 4:
£
t
r
ОЭ СУ>>»|СЧ(
H
2 Я
I*
8.8
о н
ccj
° 2
я S
ЕЙ
CO
n
to
«и
CO
" 4
a>
<u
CD
2 8
<D
О
s
488
Глава 15
где Oh=(2k—1)/18 (k = l, 2, ..., 9). Тогда давление на уровне
k определяется как Pk = o/pF. Ниже используется новая
вертикальная координата а', но штрих отброшен.
Исходные уравнения гидротермодинамики и граничные условия
Исходными уравнениями являлись уравнения движения,
уравнения статики и состояния, уравнение неразрывности и
уравнения притока тепла и притока влаги, записанные для карты
стереографической проекции в 0-системе координат и
преобразованные к так называемому дивергентному виду.
Покажем это преобразование на примере уравнения (14.3.13).
Имеем
да
да . да . • да дН , ga &Рр дН , 1 , г-
dt ~" дх ~v ду ~" да ~ 6 дх * рр
Умножим обе части на pF и преобразуем второе слагаемое
справа с помощью уравнения статики (14.3.15). Тогда получим
да х да . да , • да
PfST+PfU. -jjt+PfV -^+Pf^ -jt- =
—PFe^-RT^+pFlv-\-pFFx.
Представим теперь каждое слагаемое в левой части
последнего уравнения как разность двух слагаемых:
d(pFa) ^dpF д(рри*) ud(PFu) , d(PFuv)
dt dt ' дх дх ' ду
_„ 6(Pfv) , *(Рри*) „ д(Рр°) __
U ду * да U да —
= -PFg^-*T^f+pPlv+pPFx.
Группируя слагаемые левой части и используя уравнение
неразрывности (14.3.16), окончательно получим уравнение движения
в дивергентной форме, которое и будет являться первым
исходным уравнением рассматриваемой схемы. С учетом
масштабного множителя для карты стереографической проекции
1,8658
пг = -
1 +sin ср
Общая циркуляция и энергетика атмосферы 489
это уравнение представим в виде
dt
^=-»'Ш^)+^т]-*^+^-
-mp,g^—mRT^f-+pFF,. (15.5.1)
Остальные уравнения преобразуются аналогично. Второе
уравнение движения запишем следующим образом:
-*Р*Щ—"ЧгтЦ?-+ргР,. (15.5.2)
Для замыкания (15.5.1) и (15.5.2) используем уравнение
статики совместно с уравнением состояния
дН RT
уравнение неразрывности
(15.5.3)
итока тепла
Л д ( PF"T \>д( Рг"т )]
[ дх \ m /"> ду \ тп )\
а также уравнение притока тепла
4Pft) _ тЛ д ( pf*t \ , а / р^т
3
ё(*Т) ■ *~1 Т dP . t = l П5 . gv
и уравнение притока влаги
д(РрЧ) _ т2\ д (РР"Я \ д ( РрЩ )]
Ft —~т [ дх { т )~Г~дГ\ т )\
-РрЩ^+РрРо-РрМ. (15.5.6)
3
В уравнении (15.5.5) £ е*/р есть сумма притоков тепла кеди-
г-1
нице массы в единицу времени, причем
з
2"
1=1 _ £1 | е2 | £3
р • р i р
490
Глава 15
где 8i — приток тепла к единице объема воздуха вследствие
переноса коротко- и длинноволновой лучистой энергии; ег—
приток тепла за счет вертикального и горизонтального
турбулентного перемешивания; ез — приток тепла за счет конденсации
водяного пара.
В уравнении (15.5.6) q — удельная влажность; Fq—
турбулентный приток влаги; М — количество сконденсировавшейся
влаги.
Граничные условия при численном интегрировании уравнений
задавались следующим образом. На боковой границе (экваторе)
предполагается наличие стенки, вдоль которой происходит
скольжение. Следовательно, нормальная составляющая скорости к
экватору vn = 0. Потоки тепла, влаги и количества движения
через экватор также равны нулю.
На верхней и нижней границах атмосферы вертикальная
скорость равна нулю, т. е. o = do/dt = 0 при а = 0; 1. Также на
верхней границе атмосферы равно нулю и напряжение
турбулентного трения, т. е. та|а=о = 0.
При реализации модели Смагоринский болыцое внимание
уделил выбору схем для вычисления характеристик сил
турбулентного трения Fx и Fy из (15.5.1) и (15.5.2), а также
значений радиационных притоков тепла ei из (15.5.5). В частности,
для учета последних в модели использовалась схема Манабе и
Стриклера, изложенная в главе 6. Кроме того, достаточно
корректно рассчитывались притоки тепла за счет турбулентного
перемешивания (ег) и вследствие конденсации водяного пара (ез),
турбулентный приток влаги Fq из уравнения (15.5.6).
Начальные условия и интегрирование по времени
В начальный момент времени атмосфера принималась
неподвижной и изотермической при температуре 289 К. Для
экономии машинного времени интегрирование уравнений в течение
первых 50 дней выполнялось с помощью довольно грубой сетки
с Af = 5. В продолжение следующих 20 дней было принято
разрешение сетки TV =10. В дальнейшем интегрирование
выполнялось с использованием N = 20. При этом переход к более
густой сетке осуществлялся путем линейной интерполяции скорости
ветра, температуры и давления. Для интегрирования по времени
использовались центральные разности.
К концу первого этапа интегрирования уравнений (15.5.1) —
(15.5.6) при разреженной сетке с jV=10 в верхней части
атмосферы прослеживалось развитие циркумполярного
циклонического вихря, в нижней части — антициклонического вихря.
Разность температур на экваторе и полюсе достигла к концу срока
Общая циркуляция и энергетика атмосферы
491
45°С. В последующие дни при использовании более густой сетки
начиналось заметное развитие волн в приземном поле
давления, указывающее на появление бароклинной неустойчивости.
Примерно к 100-му дню имело место образование волн в
западном потоке и проникновение полярного антициклона в
субтропические широты с одновременным формированием нескольких
субтропических антициклонов. Западный перенос в средних
широтах достигает земной поверхности, появляется многоячеечная
меридиональная циркуляция. Наконец, примерно к 230-му дню
эксперимента было достигнуто термическое равновесие. Все это
говорит о близости модели ОЦА к реальным условиям ее
развития.
Некоторые недостатки модели Д. Смагоринского
1. Из результатов эксперимента выяснилось, что учет тепла
конденсации водяного пара приводит к уменьшению
характерных" масштабов движения. Поэтому выбранное в модели
разрешение N = 20 оказалось явно недостаточным. Результаты были
бы намного лучше при большем разрешении.
2. Наличие стенки на экваторе является очень грубым
приближением. Модель ОЦА намного бы улучшилась при
отсутствии этой стенки, т. е. при моделировании ОЦА по всему земному
шару.
3. В модели практически отсутствует учет влияния на ОЦА
асимметрии нижней границы атмосферы за счет горных хребтов
и распределения суши и моря. Этот недостаток приводит к
невозможности моделирования сезонных центров действия
атмосферы типа сибирского антициклона.
4. Модель исключает возможность изучения полного
взаимодействия между радиационными потоками, влагообменом,
распределением озона и крупномасштабными движениями,
поскольку при вычислении радиационных изменений температуры
использовались климатологические данные о распределении
водяного пара, облаков и озона. Было бы интереснее вычислять
радиационные потоки, используя распределение водяного пара
и озона, получаемое путем интегрирования прогностических
уравнений.
5. В модели не учитывается влияние взаимодействия океана
и атмосферы на эволюцию крупномасштабных процессов.
15.6. Преобразования энергии в атмосфере
Полная энергия системы атмосфера—океан—суша за
промежутки времени, представляющие интерес для метеорологии, в
частности для задач прогноза, практически остается неизменной.
492
Глава 15
Это достигается тем, что глобальные свойства атмосферы и
деятельной поверхности, определяющие способность поглощать
и излучать радиацию и поле температуры, обусловливают такую
интенсивность потерь энергии длинноволновым излучением в
мировое пространство, которая для Земли в целом компенсирует
приток энергии извне в форме коротковолновой радиации
Солнца. Таким образом, в чисто энергетическом смысле система
может рассматриваться замкнутой. Непрерывные движения в ней
поддерживаются неравномерным распределением в пространстве
и во времени поступающей лучистой энергии. Этим же
достигается генерация отрицательной энтропии, которая компенсирует
ее рост в результате необратимости атмосферных процессов.1
Сложной цепи происходящих в атмосфере процессов
соответствует замкнутый цикл превращений энергии, включающий
превращения энергии внутри атмосферы и обмен энергией между
атмосферой, океаном и сушей. Некоторые виды энергии,
содержащиеся в рассматриваемой системе, не играют существенной
роли в динамике атмосферы, например энергия электрического
и магнитного полей. Это значит, что в цикле превращений
энергии, характеризующем атмосферное движение, они практически
не участвуют. Более того, рассматривая энергетику какого-либо
конкретного процесса, который обычно представляет собой лишь
отдельное звено в общем цикле преобразований энергии, можно
заметить, что лишь отдельные виды энергии подвержены
преобразованиям, тогда как остальные не изменяются и мало влияют
на его механизм. Так, например, при термической конвекции
происходит превращение внутренней и потенциальной энергии в
кинетическую энергию вертикальных движений, тогда как
кинетическая энергия горизонтальных движений изменяется мало.
Термическая конвекция в рассматриваемом плане является
термодинамической машиной, в которой кинетическая энергия
вертикальных движений возникает за счет запасов потенциальной и
внутренней энергии. Таким образом, виды энергии,
подверженные преобразованию, характеризуют специфику процесса и
соответствующий анализ позволяет в простой и обозримой форме
отразить его существенные особенности. Наличие значительных
запасов определенного вида энергии в атмосфере может иногда
использоваться как прогностический критерий процесса.
Другое важное обстоятельство, в силу которого энергетика
представляет значительный интерес, связано с формулировкой
задач теоретической метеорологии. При рациональных упроще-
1 Имея в виду сказанное, следует интерпретировать приток солнечной
радиации не как источник энергии атмосферных движений (ибо атмосфера
отдает столько же лучистой энергии, сколько и получает), а как источник
отрицательной энтропии.
Общая циркуляция и энергетика атмосферы
493
ниях системы уравнении соответственно рассматриваемому
явлению следует проверять, удовлетворяет ли упрощенная система
уравнений закону сохранения энергии. Фиктивные источники,
возникающие при плохом упрощении уравнений, приводят к
неограниченному росту скорости ветра и к искажению других
метеорологических полей.
Уравнения для энергии
Наиболее важными для атмосферных процессов являются
следующие виды энергии: кинетическая энергия горизонтальных
движений Ек= (u2+v2)/2, потенциальная энергия Eu = gz,
внутренняя энергия EB = cvT, кинетическая энергия пульсаций
скорости Ь = (u/2 + v'2 + u/2)/2, энергия скрытой теплоты фазовых
переходов воды Ec = J?q. В выписанных выражениях все виды
энергии отнесены к единице массы. При выводе уравнений
баланса различных видов энергии удобно пользоваться
тождеством
df __ dp/ . дрц/ . d?vf ■ dywf dp/ d9ujf Л5 6 1)
р dt ~~~ dt "> дх "> ду ~т~ dz dt dxj '
которое легко может быть получено из выражения для
индивидуальной производной некоторой функции f и уравнения
неразрывности. Интегрируя (15.6.1) последовательно по столбу с
единичным поперечным сечением в пределах 0^2^Я(/, х> у) и
О^г^оо, получим:
О 1 о о
dt
+ Ря/я(^+*я-^-f *н-Щ—™н), 05.6.2)
оо оо оо
-5Г$ Р/Л-—^-1 P««/^+J P-S-. 05.6.3)
о 1 о о
Здесь и ниже /=1, 2, 3, t = l, 2, Ui = u, u2=v, u$=w\ по
повторяющемуся индексу выполняется суммирование.
Физический смысл полученных выражений очевиден. Левая
часть представляет собой локальную скорость изменения
запасов функции / (в нашем случае одного из видов энергии) в слое
(0, Н) или (0, оо). Слагаемые справа описывают
изменения указанной величины, вызванные чистым переносом
(адвекция) ( -— J puifdz) , и вклад, обусло
вленныи изменением
494
Глава 15
рассматриваемой величины f в движущейся массе при переходе из
Н, оо
точки (х, у) в точку (x+udty y + vdt) J p—~-dz\ именно это
о dt
слагаемое отражает фактические превращения энергии в
фиксированной массе воздуха. Третье слагаемое в уравнении
(15.6.2)—приращение энергии из-за возможного перемещения
границы Я рассматриваемого слоя и потока через границу
благодаря вертикальным движениям:
- / дИ . дН , дН \ s ( dH \
9HfH\-5rJrUH^r+vH—y *,„) = ?„/„(-% WH).
Если в (15.6.2) и (15.6.3) df/dt выразить явно через те
внешние факторы, вследствие которых меняется энергия движущейся
массы, то тем самым будут выявлены причины изменения с
течением времени запасов соответствующего вида энергии в
интересующей нас точке. Для этого естественно обратиться к
уравнениям гидротермодинамики, которыми, по существу,
описывается режим любого свойства в движущейся массе. Умножая
уравнения движения, записанные в рамках обычных упрощений,
на uy v, wy получим выражения для изменения кинетической
энергии отдельных компонент скорости:
(4)--T«*+4"+T-£-*-*--f-*(-£-)'•
(15.6.4)
/ i/2 \ 1 др / , , 1 д , д V* , / di/ \2
dt
d
dt
dt
(15.6.5)
I w2 \ 1 dp d (gz) /An a ti\
Здесь первые слагаемые справа — изменения кинетической
энергии, связанные с работой против силы барического градиента.
При перемещении массы воздуха от более высокого давления
/ dp dp dp А
к более низкому (и—^-ксО, v—т-*<0, w-~i<.\)\ кинетическая
энергия соответствующей компоненты увеличивается, и
наоборот, при движении в сторону более высокого давления
кинетическая энергия уменьшается. Из (15.6.4) и (15.6.5) видно, что
Общая циркуляция и энергетика атмосферы
495
ускорение Кориолиса не меняет полной кинетической энергии
частицы:
d l 1*2 + 1/2
dt
.(J^+HL)-/„„+(_ toe) в0.
но вызывает обмен энергией между х- и ^-компонентами
скорости. В (15.6.4) и (15.6.5) третье слагаемое — приток
кинетической энергии, обусловленный вертикальным турбулентным
обменом; в этих же уравнениях четвертое слагаемое —
трансформация кинетической энергии в энергию турбулентности
[см. ниже уравнение (15.6.12)]. Второе слагаемое в (15.6.6) —
изменение потенциальной энергии перемещающейся массы
воздуха.
Поскольку всегда в атмосфере \dw/dt\ <Cg, то
—(—+H=whr+£)~£W=—г*"* (15-67)
т. e, при вертикальных перемещениях работа против силы
барического градиента совершается в основном за счет
потенциальной энергии движущейся массы. Ниже будет показано, что при
этом приращения потенциальной энергии происходят за счет
внутренней энергии. На основании (15.6.7) можно записать
уравнение баланса потенциальной энергии
d (gz) w dp
Tt ~" p dz '
Воспользуемся теперь уравнением притока тепла
-г—г-4-*-г-+-?-?- <i5-6-8>
для вывода уравнения баланса внутренней энергии. Для этого
продифференцируем выражение для потенциальной
температуры и исключим из полученного соотношения давление при
помощи уравнения состояния. Тогда имеем'
с -^L = c -JLJ*-±JLJl- (1569)
Cv dt cp 6 dt ^ P2 dt • (ю.о.щ
d@
Подставив в (15.6.9) —— из (15.6.8), получим
dcvT сР т д f дв ■ Q ■ р d? (15.6.10)
dt p О dz *p dz ^^^ P2 dt ' v 7
Здесь Q — нетурбулентные притоки тепла. Они равны
496
Глава 15
где г — полный поток лучистой энергии (поток длинноволновой
и коротковолновой радиации), направление которого считается
положительным, если он направлен сверху вниз; ei — скорость
диссипации вихревой энергии в тепло; ег — приток внутренней
энергии, обусловленный фазовыми переходами воды.
Заметим теперь, что
Т д , <Э6 д , Т дв
, <Э6 д и Т дв , дв д ( т \
в dz
Воспользовавшись уравнением статики, нетрудно показать, что
д ( Т \_ д ( р \«/ср_ g_
dz \ в )~ dz \To66~J "" сре •
Стало быть,
Подставим это выражение в (15.6.10). Тогда получим
окончательный вид уравнения баланса внутренней энергии:
dcvT _ сР д_ъ _7^_ае . g h ае
Л ~~ р йг *р е а* "I" 6 к dz "Г
+ ^Г-Й- + -Е-Н-.+Ч. • 05.6.11)
Запишем, наконец, уравнение баланса энергии турбулентности:
db и\( да\2 i / dv \2I £ a ^e i аь д и дЬ
dt
"*ш+(£п--н-г--.,+-^*-£-.
(15.6.12)
Теперь легко понять физический смысл отдельных слагаемых
в уравнениях (15.6.11) и (15.6.12). Вначале заметим, что
приращение внутренней энергии, непосредственно связанное с
турбулентностью, происходит, во-первых, в процессе турбулентного
перемешивания слоев с разной удельной внутренней энергией,
во-вторых, вследствие перехода внутренней энергии в
кинетическую энергию вихрей при неустойчивой стратификации (dQ/dz<
<0) или кинетической энергии вихрей во внутреннюю при
устойчивой стратификации (dQ/dz>0). Оба эти процесса,
связанные с турбулентностью, отражены первыми двумя слагаемыми
в правой части (15.6.11). Взаимные превращения внутренней и
вихревой энергии, как следует из уравнений (15.6.11) и (15.6.12),
представлены слагаемым ~%.^—^— • В таком случае второе из
Общая циркуляция и энергетика атмосферы
497
с д Т
упомянутых слагаемых в (14.6.11), а именно —~~^~~ ^Р"й"*
дв
Х—д—, есть не что иное, как скорость притока внутренней
энергии за единицу времени к единице массы, обусловленного
турбулентным обменом между слоями с разной температурой.
Третье слагаемое в (15.6.11), т. е. \^Y~rr) —изменение внутрен-
\ [J (ЛЬ I
ней энергии, вызванное работой расширения.
Заметим, что
/ dcvT \ р dy р ( ди . dv . dw \
\ dt JP ~р2~ "5^~ 'f~\ дх *~~ду~ ' dz /
_ I ( дар ■ dvp dwp \ \ I dp , dp . dp \
— ? \ дх ^ ду ^ dz )^ 9 \U дх ^V ду ^^ dz J'
(15.6.13)
Отсюда следует, что изменение внутренней энергии при
расширении фиксированной воздушной массы, которая движется в
неравномерном поле давления, состоит из двух частей. Одна из
[1 / дир , dvp , dwp \1
(—г11—I—a —I—я/1 —приращение внутренней
энергии, обусловленное взаимодействием рассматриваемой
массы с окружающей средой в процессе выравнивания
давления; эта часть внутренней энергии переходит во внутреннюю и
потенциальную энергию среды. Понятно поэтому, что при
интегрировании по замкнутой воздушной массе соответствующий
интеграл обращается в нуль, т. е.
Ш(т£-+-ЗГ+-т?-К«'*-°-
(УМ) v 7 '
Смысл второй части —\ua~~^v~d ~*~ш я/ нетРУДН0 п0'
нять, если обратить внимание на то, что такие же слагаемые, но
с обратными знаками содержатся в уравнениях (15.6.4), (15.6.5),
(15.6.11). Это, следовательно, та часть внутренней энергии,
которая превращается в кинетическую энергию горизонтального
движения и в потенциальную энергию (точнее, в потенциальную
и кинетическую энергию вертикальных движений) самой
воздушной массы.
32 Заказ № 612
498
Глава 15
Покажем теперь, что потенциальная энергия и внутренняя
энергия всего атмосферного столба находятся в постоянном
соотношении. Действительно,
cvT+gz=cvT-^^=cvT—^£l
dz "v dz
т. е.
cvT+gz=cpT-
д(*Р)
dz
Если это соотношение проинтегрировать по z по всему столбу
(О^г^оо), то получим
сю оо сю
J Eb?dz+\ EaPdz=-^-\ EB?dz
ИЛИ
| £np dz
0
I Etfdz
о
Это значит, что изменения обоих видов энергии происходят
взаимосвязанно, поэтому целесообразно рассматривать их сумму,
а не каждый вид энергии в отдельности. Эта сумма (Ев + Еи =
= £а) называется полной потенциальной энергией. Для всего
столба полная потенциальная энергия в точности равна
энтальпии.
Подставив теперь (15.6.4), (15.6.5), (15.6.8), (15.6.11),
(15.6.12) в (15.6.2), получим систему уравнений, описывающих
баланс энергии в единичном столбе высотой H(t, х, у) (в
частности, под И можно подразумевать планетарный пограничный
слой атмосферы):
-hpHEK(H)(-^L-wH), (15.6.14)
Общая циркуляция и энергетика атмосферы
499
я я
dt 0
J E»?dz sH E^dx~i вд^г+
о 'о о
+Ря£п(Я)(-^— wH), (15.6.15)
0 i_^ о o_
я
+r(//)-r(9)+j e,prfg+p„f.(//)(-g--a„)4_
Я
+ js2ptfz, (15.6.16)
0
я я
<tt
J »p*—-&-J *•>*+! *Ш+(т)"]'л-
0
я я я
+р*Ц-^-- «я). (15.6.17)
Система уравнений (15.6.14) — (15.6.17) отражает механизм
изменения различных видов энергии в пространственно
фиксированном столбе единичного поперечного сечения, высотой Я.
Она интересна тем, что дает основание для интерпретации
изменения состояний атмосферы, получаемых из наблюдений
определенной аэрологической станции, если данные наблюдений
представить в терминах энергии. Эти изменения обусловлены
следующими факторами:
а) адвективным притоком соответствующего вида энергии
(подчеркнуто прямой линией);
б) превращениями энергии, происходящими внутри самой
воздушной массы. Это те слагаемые, которые встречаются
32*
500
Глава 15
в уравнениях дважды, но с разными знаками (подчеркнуто
волнистой линией). Естественно, что эти слагаемые не меняют
полной энергии и при суммировании всех видов энергии
сокращаются;
в) приращениями энергии из-за взаимодействия движущейся
массы воздуха с окружающей средой или вследствие
реализации скрытой теплоты. Взаимодействие осуществляется
посредством изменяющегося внешнего давления, турбулентностью,
лучистым теплообменом и фазовыми переходами воды
(подчеркнуто прямой и волнистой линиями).
Уравнения баланса энергии для всего столба получим из
(15.6.14) — (15.6.17), устремив Я к бесконечности, при этом
также
I г\ и д&
-0,
и М
-0.
Как уже указывалось, в данном случае удобно ввести полную
потенциальную энергию вместо потенциальной и внутренней.
В результате получаем следующее соотношение:
сю оо сю
-i-f CpTpdz^^-j EiPdz= '$СрщТРаг-
о о 1 о
сю оо
+ f elPrfz+ J wdz-kpcp-£- I -r(0)+r(tf). (15.6.18)
0 0 0
Выразим здесь приток энергии, обусловленный фазовыми
переходами, через характеристики поля влажности,
воспользовавшись уравнением баланса водяного пара для единичного столба:
сю сю сю
-^-f g?dz = 3L-Jlw<fe_Ap|lJ_-^.f t#dz. (15.6.19)
Исключим из (15.6.18) и (15.6.19) е2 и введем эквивалентную
температуру ТЭ = Т -\- -==— Я- Тогда получим
ср
оо оо оо
j c^dz^-^-j uiCpT,?dz-j ^dz+
dt 0
+1 Ui-^dZ+l -i-k^r?dz+l •Я'Ь-ШгЩ+гЮ.
(15.6.20)
Общая циркуляция и энергетика атмосферы 501
Здесь мы использовали уравнение теплового баланса деятельной
поверхности
-*Рср^1+*'Р'с'4Н--^Р-ё-|=г(°)' 05-6.21)
0 0 0
и дТ
где &ipiCi
поток тепла с деятельной поверхности снизу.
Л71 I
-_ -~г—м, в (15.6.20) г(оо) —kipiCi ——I есть количе-
о
ство тепла, которое столб получает через верхнюю и нижнюю
границы. Запишем также уравнения баланса кинетической и
вихревой энергии для # = оо:
оо оо оо
f Ек9 dz=- -A- f UiEk9 dz-\ щ -!£- dz -
оо
* .
0
dt
оо оо оо
оо оо
-\ ~i~k-^9dz-\ exPdz. (15.6.23)
6 6
На рис. 15.8 приведена основанная на уравнениях (15.6.20),
(15.6.22) и (15.6.23) схема баланса энергии для единичного
столба. Тонкими стрелками показаны переходы энергии, которые
могут менять свое направление, толстыми — только
односторонние переходы.
Суммированием из (15.6.21) — (15.6.23) получим уравнение
баланса полной энергии
оо оо
-^-J (£«+Н«,Г,)рА £—J (EK+b+cpTb)?dz-
0 ' 6
оо
-I -^«fe+rM-Up.c.-g-j. (15.6.24)
Отсюда следует, что полная энергия столба изменяется за счет
адвекции, вследствие обмена энергией с окружающей средой,
вызванного боковым сжатием или расширением столба, и за
счет потока энергии через нижнюю и верхнюю границы столба
(лучистый поток на верхней границе и поток тепла посредством
-±-$uiCpT9fdz^
дх
- J tt/£Kp dz *--
oo
dT I
/•>'* J-f-**-"*
dz
s
duip
С _£Ui£
J ~dX-l
dz
Рис. 15.8. Преобразования
энергии в единичном столбе.
Общая циркуляция и энергетика атмосферы
503
теплопроводности на нижней). Интегрируя уравнения (15.6.20),
(15.6.22) и (15.6.23) по горизонтальным координатам (—Х^х^Х,
—Y^y^Y) и полагая для любой функции F(—X)=F(X),
F(—Y)=F(Y), что эквивалентно интегрированию по всей
атмосфере, получим:
■ш-1 E-dM—i -St -г- i * -й-й-'*-
(15.6.25)
(Л) (Й) Xl г (Л)
lc,T,dM= lu*
dM
(M) (M)
dt
+ J -^-k-^-dM+ J eirfAf, (15.6.26)
(Л1) (Af) (/W) (M)
(15.6.27)
Здесь всюду M — масса атмосферы Земли, dM=pdxdy dz.
Атмосфера Земли в целом находится в тепловом равновесии,
на этом основании при получении уравнений (15.7.25) и (15.7.26)
полагалось
х у
J J [г(х, у, <x>)-klPlcl-¥r\z = o}dxdy=0. (15.6.28)
Анализируя уравнения (15.6.25) — (15.6.27), нетрудно понять
механизм, посредством которого может поддерживаться
постоянство основных видов энергии в атмосфере.
Непрерывная потеря кинетической энергии, связанная с ее
трансформацией в вихревую и равная — J*~^ ^—"М,
компенсируется превращением энтальпии и скрытой теплоты
парообразования в кинетическую энергию; соответствующая скорость
С dp dM и
генерации кинетической энергии равна — J ^%—^- • В свою
очередь потеря энтальпии и скрытой теплоты парообразования
восполняется за счет вихревой энергии в процессе вязкой
диссипации энергии вихрей в тепло и вследствие работы против силы
плавучести. Эти превращения энергии представлены слагаемыми
J (-тг^—н—\-Bi)dM. Постоянство энергии турбулентности при
(м)
наличии непрерывных потерь кинетической энергии вихрей
504
Глава 15
поддерживается поступлением вихревой энергии за счет
кинетической энергии основного потока. Скорость превращения
кинетической энергии в вихревую равна )k—г-^—-^—dM. На рис. 15.9
схематически изображен цикл преобразований энергии. По
эмпирическим оценкам, средняя скорость компенсирующих
переходов равна 2,3 Вт/м2 = 2,3- 1,43- 10"3 кал/(см2- мин).
fut^dM
тш)
Рис. 15.9. Основной цикл преобразований энергии
в атмосфере.
Если атмосферу рассматривать как некоторое рабочее тело,
производящее кинетическую энергию, а солнечную радиацию
рассматривать как тепло, поступающее от нагретого резервуара,
то нетрудно вычислить коэффициент полезного действия г\
соответствующей термодинамической машины (цикл глобальных
атмосферных процессов можно интерпретировать как
термодинамическую машину);
к
dz dz
?dz
2,3 . 1.43 • 10-3
= 0,01,
0,485 . 0,7
альбедо земной поверхности,
ч— /о/4(1_Л)
где /о =1,94 кал/(см2-мин), А
равное 0,3.
При оценке числовых значений основных видов энергии
обращает на себя внимание различный порядок величин энтальпии
и кинетической энергии. Действительно, первая из них имеет
порядок срТМ~с2М (с2 — квадрат скорости звука), тогда как вто-
Общая циркуляция и энергетика атмосферы
505
рая примерно равна (u2+v2)M\ их отношение — — «103.
u2+vz
Поскольку энтальпия является источником кинетической
энергии, то при характерном для атмосферы порядке величин двух
указанных видов энергии лишь очень незначительная часть
энтальпии переходит в кинетическую энергию.
При оценке взаимных превращений кинетической энергии и
энтальпии приходится, следовательно, определять малую
разность двух больших величин, представляющую собой разность
энтальпий начального и конечного состояния. Получить
достаточно надежное значение этой величины из эмпирического
материала невозможно. В связи с этим вводится более удобная
величина, так называемая доступная потенциальная энергия;
обозначим ее через £д. Под доступной потенциальной энергией
подразумевается часть энтальпии, которая при заданном
состоянии может перейти в кинетическую энергию.
Принято считать доступной потенциальной энергией £д
разность между полной потенциальной энергией (энтальпией)
заданного состояния и полной потенциальной энергией некоторого
условного состояния, полученного из первоначального состояния
в результате такого адиабатического перемещения масс воздуха,
при котором изобарические поверхности и поверхности равной
потенциальной температуры (изэнтропические поверхности)
совпадают. Определенное таким образом конечное состояние
характеризуется тем, что средняя температура между любыми
изобарическими поверхностями не зависит от горизонтальных
координат. Поэтому температурное поле не может давать вклад
в горизонтальный градиент давления, так как
1 д,р Т 1 дрр , Tgz дТ _ 1 дрр
dxt То ро dxi ' т2 dxi Ро d*i
(15.6.29)
В таком случае скорость превращения энтальпии в кинетиче-
Ui dp Ui дро'
скую энергию ^—= г минимальна или равна
р dxi ро dxi
нулю, если =0. Таким образом, можно говорить, что раз-
ох%
ность энтальпий исходного и конечного состояния, т. е.
доступная потенциальная энергия, равна или почти равна максимально
возможному приращению кинетической энергии за счет запасов
энтальпии. Легко понять, что £д и £к — величины одного
порядка.
На рис. 15.10 схематически показаны перемещения масс при
конструировании состояния, соответствующего нулевым запасам
£д. При предлагаемом перераспределении масса воздуха над
любой изэнтропической поверхностью остается неизменной. Это
506
Глава 15
значит, что и среднее давление столба над каждой изэнтропиче-
ской поверхностью не изменяется. В таком случае, если в
начальном состоянии
оо 0
(Еп+Ев)н= \dxdy\cpT?dz = - \dxdy \cfi[-l£)^ =
(S)
(S)
Ро
6 V ^ ' (S) о
™=п=п
4 4 4 4
Р*=Е
Т~ГГТ,
в,
Рис. 15.10. К схеме расчета доступной потенциальной энергии.
то в конечном итоге
(яп+£в)*=^^Пр-+1(е)й(е
6 v ^ ' (S) о
(для удобства начало отсчета температуры смещается так,
чтобы в(/?о) =0). На этом основании
Еп=-
сРРоох
^5— J dxdy\ (p*+l-p-*+l)d9. (15.6.30)
(5) 0
При получении выражения для £д не учитывалось влияние
скрытой теплоты парообразования. В принципе соответствующие
эффекты нетрудно учесть, вводя притоки тепла, связанные со
скрытой теплотой парообразования, если при перемещении масс воз-
Общая циркуляция и энергетика атмосферы
507
духа в процессе перехода к конечному состоянию достигается
насыщение.
Контрольные вопросы
1. Что подразумевается под термином «общая циркуляция
атмосферы»?
2. Каков физический смысл индекса циркуляции Е. Н.
Блиновой? Сформулируйте его свойства.
3. Какие идеи использованы в целях линеаризации
уравнений динамики в модели ОЦА Е. Н. Блиновой?
4. Каковы недостатки модели ОЦА в численном эксперименте
Н. Филлипса?
5. В чем различие физических предпосылок, положенных
в основу моделей ОЦА Н. Филлипса и Д. Смагоринского?
6. Назвать основные виды энергии в атмосфере. Вывести их
выражения.
-7. Каково соотношение между потенциальной й внутренней
энергией единичного столба воздуха?
8. Что такое доступная потенциальная энергия?
9. Каков основной цикл преобразования энергии в системе
ОЦА?
Глава 16. ТУРБУЛЕНТНОСТЬ В СВОБОДНОЙ АТМОСФЕРЕ
Общая постановка задачи. Турбулентность вблизи поверхности раздела.
Турбулентность в струйных течениях.
При рассмотрении вопросов динамики свободной атмосферы
в главе 8 мы принимали, что турбулентный обмен мал. Однако
и в свободной атмосфере нередко встречаются отдельные слои,
в которых развивается весьма интенсивная турбулентность,
играющая не менее важную роль, чем турбулентность в
пограничном слое. Так, исследования показали, что почти половина
энергии основного движения, которая трансформируется в энергию
турбулентности, приходится на турбулентность в свободной
атмосфере. С ней связаны существенные изменения
энергетического баланса крупномасштабных атмосферных движений, в том
числе и общей циркуляции атмосферы.
Турбулентный обмен приводит к отклонению ветра от
геострофического, что влечет за собой развитие вертикальных
движений.
Порывистость ветра, связанная с наличием в потоке вихрей,
может вызывать болтанку самолетов. Содержание водяного пара
на уровнях, где развивается турбулентность, нередко
оказывается недостаточным для образования облаков,1 что делает
такие зоны особенно опасными, поскольку их не удается
обнаружить визуально.
В связи с упомянутым выше изучение турбулентности в
свободной атмосфере становится важной проблемой.
Ниже рассмотрены теоретические модели наиболее типичных
случаев турбулентности в свободной атмосфере при некоторых
упрощающих предположениях.
16.1. Общая постановка задачи
Основным источником турбулентной энергии, как уже
говорилось, является кинетическая энергия среднего движения.
Турбулентность развивается там, где имеют место большие
вертикальные градиенты скорости ветра. Поэтому в пограничном слое,
где вследствие прилипания потока к подстилающей поверхности
1 Поэтому турбулентность в свободной атмосфере часто называют
турбулентностью ясного неба (ТЯН).
Турбулентность в свободной атмосфере
509
скорость ветра возрастает с высотой и градиенты достаточно
велики, практически всегда существует турбулентный обмен.
В свободной атмосфере турбулентность имеет в определенном
смысле случайный характер. Она развивается в слоях, где
вертикальные градиенты скорости велики из-за большой
неоднородности горизонтального поля температуры (большой термический
ветер). Типичными профилями ветра, при которых в свободной
атмосфере развивается турбулентный обмен, являются профили,
характерные для струйного течения, или «сдвиг» скорости
в сравнительно тонком слое, связанный обычно с фронтальной
зоной. Применяя подход, аналогичный тому, который был
использован в главе 11, можно получить выражения, позволяющие
оценить средние характеристики турбулентности в свободной
атмосфере, выяснить, какие величины определяют ее
интенсивность, толщину турбулизированного слоя и т. п.
Пусть в некотором слое имеет место установившийся
турбулентный обмен, энергетический баланс которого определяется
уравнением
—Н —Н —И
(16.1.1)1
Здесь Н — граница турбулизированного слоя.
Понятно, что величина Н зависит от интенсивности
турбулентного обмена. В дальнейшем она будет определяться как
высота, на которой ветер, отличавшийся внутри слоя от
геострофического, становится достаточно близким к нему.
Поскольку в уравнении (16.1.1) содержится три
характеристики турбулентности (k, е, Я), воспользуемся дополнительными
соотношениями, связывающими эти величины между собой (см.
п. 11.2):
k^CiHVF/ (16.1.2)
е = С2-Ц^. (16.1.3)
Будем считать градиент потенциальной температуры dQ/dz
заданным.
Скорость и направление ветра в пределах
турбулизированного слоя весьма существенно зависят от турбулентного обмена
и будут определяться из решения рассматриваемой задачи.
1 Предполагается, что основной запас турбулентной энергии содержится
в слое z=±H и диффузия ее на границах слоя пренебрежимо мала.
510
Глава 16
Поэтому к записанной системе уравнений необходимо добавить
уравнения движения:
(и, v, ugi vg — компоненты фактического и геострофического
ветра), которые можно привести к виду
-^ / . 2а2Ф-Н • 2а2а = 0. (16.1.4)
Здесь
a = ug+ivg,
а
2 .
Заметим, что в данной задаче горизонтальный барический
градиент не может считаться постоянным и, следовательно, а =
= /(2).
Рассмотрим два частных случая: турбулентность связана
с поверхностью раздела и с наличием струйного течения.
16.2. Турбулентность вблизи поверхности раздела
Известно, что на поверхности раздела барический градиент
резко изменяется. Поэтому здесь происходит интенсивная
генерация кинетической энергии основного движения в энергию
турбулентности и возникает турбулизированный слой.
Представим схематично поверхность раздела как
горизонтальную поверхность1, на которой геострофический ветер
меняется скачком (рис. 16.1). Выше или ниже поверхности раздела
барический градиент не изменяется с высотой, а его
направление остается постоянным и при переходе через поверхность.
Учитывая, что турбулентность приводит к отклонению ветра от
геострофического, можно предположить, что профиль фактического
ветра С (г) будет такой, какой изображен на рис. 16.1 штрих-
пунктирной линией.
1 Поверхность раздела в данном случае можно считать горизонтальной,
так как ее наклон не влияет на микротурбулентность.
Турбулентность в свободной атмосфере
511
Будем отсчитывать z от поверхности раздела и полагать, что
распределение ветра по обе стороны от поверхности раздела
(z ^ 0) симметрично. Тогда в уравнении (16.1.14), если записать
его для каждого из слоев z^O и 2^0, функция о будет
постоянной в пределах слоя, и уравнение может быть записано в виде
<*2ф.
</*2
■/ . 2а2Фу=0,
(16.2.1)
где
Qj^Uj+iVj—Oj;
z=H
/
У
'с®
/=1, 2 соответственно для z^O и
2^0.
Граничные условия, необходи- z=o\
мые для решения уравнения (16.2.1)
можно записать, исходя из
соображений непрерывности скорости z=-//(.
и потоков количества движения на
поверхности раздела:
Рис. 16.1. Модель профиля
J2 ^1=- "^ ветра вблизи поверхности раз-
G(z)
^i-^2U=±o = 02-G1 = -AG
(16.2.2)
дела.
йФх I
dz I z=+ о
= ko
d$2
dz
z = -0
или, если принять в силу симметричности профилей скорости
d<t>i
dz |*=+o"
dФ2
dz
(16.2.3)
Поскольку на большом удалении от поверхности раздела ветер
становится геострофическим, то
ф|г=±оо=0.
(16.2.4)
Решение уравнения (16.2.1) при граничных условиях
(16.2.2) — (16.2.4) имеет следующий вид:
<$. = #y-|_2^_Gj= + —£-eTazIcos az + isin az).
Здесь верхний знак берется при / = 1, а нижний — при у =2.
512 Глава 16
Приравнивая вещественные и мнимые части последнего
равенства, получим выражения для компонент ветра в турбулизи-
рованном слое:
Uj = GjT-^-eTazcosaz,
Vj=-^-eTaz sin az. (16.2.5)
Как и следовало ожидать, профиль ветра определяется скачком
барического градиента и интенсивностью турбулентного обмена.
Теперь выполним интегрирование уравнения (16.1.1).
Градиент потенциальной температуры примем равным
dz ~~ 2Н ~~ 2Н *
Поскольку в данной модели рассматривается случай
симметричного относительно 2 = 0 распределения, интегрирование по
слою ±# можно заменить интегрированием от нуля до Я. Тогда
уравнение (16.1.1) с учетом (16.2.5) может быть записано в виде
^e^dz-(+^k+.)jdz~0
или, если выполнить интегрирование, имея в виду, что е_2аН<С1,
и выразить среднюю по слою диссипацию е на основании
(16.1.2) и (16.1.3) через А: и Я,
Определим границу турбулизированного слоя из условия
vx=-^-e-aHsmaH=0.
Отсюда следует, что
а у
z
Подставив это выражение в (16.2.6) и решив его
относительно &, получим
*-S~^-(/H^SP-.-»-). 06.2.7)
где
Турбулентность в свободной атмосфере
513
Величина т = 10~5 оценивалась в главе 11. Нет оснований
полагать, что она будет иметь другое значение в данном случае.
Формула (16.2.7) показывает, что интенсивность
турбулентного обмена зависит в первую очередь от изменения (скачка)
барического градиента при переходе через поверхность раздела
и будет тем больше, чем больше это изменение. Влияние скачка
температуры сравнительно невелико и уменьшается с
увеличением AG.
Используя соотношения (16.1.2) и (16.1.3), нетрудно
получить выражения для оценки порывистости ветра в турбулизи-
рованном слое
УТ= V*> Vk (16.2.8)
С
I'll скорости диссипации энергии турбулентности в тепло
е = ——k. (16.2.9)
Формулы (16.2.7) — (16.2.9) позволяют оценить средние
характеристики турбулентности вблизи поверхности раздела по
данным стандартных аэрологических наблюдений.
Такие оценки, выполненные по данным температурно-ветро-
вого зондирования в нескольких пунктах СССР, показывают, что
интенсивность турбулентности, развивающейся вблизи
поверхности раздела, сравнительно невелика. Средние значения
коэффициента турбулентности редко превышают 10 м2/с Однако
такой интенсивности оказывается достаточно, чтобы в
результате отклонения ветра от геострофического развились
вертикальные движения, скорость которых может составлять
несколько сантиметров в секунду. Как известно, такие скорости
весьма существенно влияют на эволюцию облачных систем.
16.3. Турбулентность в струйных течениях
Струйное течение — это узкий поток с большой (до 200 км/ч)
максимальной скоростью в центре, весьма быстро убывающей
к периферии. Наблюдается струйное течение чаще всего в
верхней тропосфере или нижней стратосфере и обусловливается
сильной горизонтальной неоднородностью поля температуры
(дТ/dni около 2,5°С/100 км).
На рис. 16.2 схематически представлен профиль ветра при
наличии струйного течения. В узком интервале высот
наблюдается резкое изменение барического градиента, а
следовательно, и геострофического ветра G(z)y в то время как выше
и ниже этого интервала геострофический ветер имеет одинаковое
33 Заказ № 612
514
Глава 16
значение Gi, и остается постоянным по высоте (сплошная
кривая на рис. 16.2). Скорость Gi в дальнейшем будем
называть скоростью невозмущенного потока. Чтобы упростить
математическую часть задачи, полагаем, что изменяется только
модуль геострофического ветра, а направление его сохраняется
и совпадает с направлением оси ох.
Поскольку изменение барического градиента
(геострофического ветра) происходит в узкой зоне и резко выражено,
функцию а (г) в уравнении (16.1.4)
можно аппроксимировать б-функ-
z=H
z=0
цией
\
'Ч® а(г) = ро(г), (16.3.1)
где р — некоторый постоянный
множитель, имеющий размер-
' s^~ ность L2T~l.
У Напомним, что б-функцией на-
зывается функция б (х),
которая обладает следующими свой-
Рис 16.2. Модель распределения ствами: 1) она равна нулю при
ветра в струйном течении. всех х>фО и стремится к
бесконечности при х = 0\ 2) интеграл
от б-функции, взятый в пределах от —оо до +оо, равен единице,
так что
j 4x)f(x)dx=f(0).
— оо
Тогда уравнение (16.1.4) представляет собой линейное
неоднородное уравнение второго порядка. Решение его может быть
выполнено методом вариации произвольных постоянных.
Найдем сначала решение однородной части
^2ф0
2/а2Ф0=0.
dz*
Оно будет иметь вид
Ф0 = Схеа У21 z +С2е~аУ21 z. (16.3.2)
Решение неоднородной части будем искать в такой же форме,
но будем считать, что коэффициенты d и С2 зависят от высоты.
Для их определения надо подставить (16.3.2) в (16.1.4). При
этом, поскольку С\ и Сг — произвольные функции высоты,
потребуем, чтобы выполнялось равенство
aY2izJCx_ , e-*V&*Jb=Q9 (16.3.3)
dz ' dz v '
Турбулентность в свободной атмосфере 515
Решая уравнение (16.1.4) с учетом (16.3.2) и (16.3.3), получим:
оо
Z
z
Здесь Coi и Со2—постоянные интегрирования, которые
определяются из условия приближения скорости С (z) к скорости
невозмущенного потока d на достаточно большом удалении от
струи (z-+±oo). Чтобы это условие удовлетворялось, должно
быть
0)1 = C(J2 = 0.
Тогда решение уравнения (16.1.4) будет иметь вид
Ф(г)=а Y^\eaVTu Jo(Qe-aVT*d(,-
е-аУш f „£)<,«*»: <£
(16.3.4)
Если теперь в это равенство вместо о(£) подставить (16.3.1),
то при 2>0 первый интеграл в квадратных скобках обращается
в нуль, так как в интервале от 2 до оо <т(£) =0. При г<0 по
той же причине обращается в нуль второй интеграл. Поэтому
окончательное решение запишется в виде
Ф
= a?Y-re~+aV¥i2>
где знак минус в показателе степени берется при г>0, а знак
плюс — при 2<0.
Теперь, подставив значение Ф(г) и полагая y2t = t+l,
получим:
u-Gl=^-eTaz(cosaz±sinaz), (16.3.5)
^ = -4р е+ az (cos az + sin az). (16.3.6)
Здесь верхний знак относится к г>0.
Коэффициент р можно выразить через скорость ветра. Для
этого найдем отклонение скорости на оси струи Со от скорости,
невозмущенного потока G\.
33*
516
Глава 16
На основании (16.3.5) и (16.3.6) эта величина будет равн^
С0— G\ =АСп
*Р
откуда
1/0 АС0. (16.3.7)
Формулы (16.3.5) и (16.3.6) показывают, что скорость
струйного течения, имея максимальное значение в центре,
убывает с удалением от него, причем скорость убывания зависит
[с учетом (16.3.7)] от значения ДСо и интенсивности
турбулентного обмена.
Теперь, используя формулы (16.3.5) и (16.3.6), выполним
интегрирование (16.1.1). При этом будем полагать, что
вертикальный градиент температуры в струйном течении мало
изменяется с высотой.
В силу симметричности рассматриваемой модели
относительно оси струи (z = 0) интегрирование, как и в предыдущем
параграфе, будем производить от нуля до Я. За высоту Я
примем уровень, на котором ветер по направлению совпадает с
геострофическим Gu т. е. уровень, на котором v = 0. На основании
(16.3.6) этот уровень будет определяться из выражения
следовательно,
Н= пУ* . (16.3.8)
4)/<л2
В результате интегрирования получим, учитывая (16.3.7),
ДС0а£ |LJg_£tf-stf=0
или, если выразить Н и е через &, используя (16.1.2), (16.1.3)
и (16.3.8),
Полученное уравнение нетрудно решить относительно k:
*=™ ДС» .... (16.3.9)
' + и\ т dz 1
Турбулентность в свободной атмосфере
517
Интенсивность турбулентности в струйном течении зависит
главным образом от того, насколько резко выражена струя, т.е.
насколько сильно отличается максимальная скорость на оси
струи от скорости невозмущенного потока. Если оценить мно-
dS
житель при ——, нетрудно убедиться, что влияние
вертикального градиента температуры на величину k несущественно.
Средние значения порывистости ^Ь и диссипации е, как и
в случае турбулентности, связанной с поверхностью раздела,
определяются по известному значению k.
Оценки, выполненные по формуле (16.3.9) на основании
эмпирического материала, позволяют сделать вывод, что
турбулентность в струйных течениях имеет значительно большую
интенсивность, чем в турбулентных зонах вблизи поверхности
раздела, так как в них имеет место более сильное изменение
геострофического ветра. Значения k здесь имеют порядок 101—
102 м2/с Такая сильная турбулентность приводит к большой
порывистости ветра (средние значения пульсаций скорости
составляют несколько метров в секунду), весьма опасной для
авиации. Поскольку струйные течения наблюдаются на высотах
8—10 км, то, вероятно, именно с ними связана турбулентность
ясного неба.
Диссипация энергии турбулентности в тепло в струйных
течениях составляет (2,2-^2,8) • 10~3 м2/с3. Заметим, что, по
оценкам Брента, в пограничном слое она равна 2,8- 10~3 м2/с3.
Хотя полученные в этой главе формулы позволяют сделать
лишь весьма грубые оценки, они представляют существенный
интерес, так как дают возможность оценить интенсивность
турбулентного обмена по данным стандартных аэрологических
наблюдений.
Контрольные вопросы
1. Чем обусловлена турбулентность в свободной атмосфере?
2. Какие уравнения используются для определения средних
характеристик турбулентности в свободной атмосфере?
3. Сформулировать задачу (записать исходные уравнения и
граничные условия) о распределении фактического ветра:
а) вблизи поверхности раздела, б) в струйном течении.
4. Где больше и почему интенсивность турбулентного
обмена— вблизи поверхности раздела или в струйном течении?
5. Что такое ТЯН? С чем связан такой термин?
Глава 17. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ТУРБУЛЕНТНОГО ПОТОКА
Пространственный корреляционный тензор поля скорости. Баланс
различных компонент энергии турбулентности. Профили компонент энергии
турбулентности и интенсивности температурных пульсаций в пограничном слое
атмосферы. Спектральные характеристики турбулентного поля скорости.
Спектральная плотность энергии турбулентности. Спектр энергии в однородном
турбулентном поле. Гипотеза о статистическом равновесии. Гипотезы
Колмогорова о турбулентном режиме мелкомасштабных компонент турбулентности.
Модель Гейзенберга переноса энергии турбулентности по спектру.
Спектральные характеристики температурного поля. Влияние стратификации на
спектральные характеристики полей скорости и температуры.
С каждым годом возрастает интерес к изучению различных
характеристик турбулентности в связи с расширением сферы их
практического использования. В главе 11 была описана модель
строения пограничного слоя атмосферы, позволяющая по
некоторым заданным внешним параметрам определить не только
профили средних значений метеорологических элементов, но и
такие характеристики, как коэффициент вертикального
турбулентного обмена, энергия турбулентности и скорость ее
диссипации в тепло.
Однако для многих важных прикладных проблем (например,
загрязнение окружающей среды, распространение
электромагнитных и звуковых волн в атмосфере, определение нагрузок на
высотные сооружения, линии электропередачи и летательные
аппараты и др.) нужно знать не только перечисленные выше, но
и многие другие характеристики турбулентного потока, такие,
как отдельные компоненты энергии турбулентности и'*/2, u^J2r
#3/2/2, интенсивность температурных пульсаций Т/2/2 и т. д. При
этом часто интерес представляют не только интегральные
величины, характеризующие средние свойства всего потока, но и
спектральные характеристики, связанные с турбулентными
движениями разных масштабов.
В этой главе получены уравнения для определения
перечисленных выше характеристик турбулентности и описаны
основные закономерности их поведения.
Статистические характеристики турбулентного потока 519
17.1. Вывод и анализ уравнения для пространственного
корреляционного тензора поля скорости
Интересующие нас статистические характеристики поля
скорости могут быть получены из уравнения для пространственного
корреляционного тензора поля скорости Яц(хА, хБ, t), которым
называется среднее произведение двух компонент пульсаций
скорости в двух различных точках пространства:
Rlj(*A> хБ, 0=*Чхд, t)Uj(XB, t), (17.1.1)
где хА и хБ — радиусы-векторы точек А и Б.
Из определения следует, что корреляционный тензор
является тензором второго ранга; он называется также вторым
двухточечным моментом поля скорости.
Уравнение для /?г;(хА, хБ, t) можно получить из уравнения
движения, записанного в форме Навье—Стокса, которое при
предположении о квазинесжимаемости воздуха можно
представить в виде
dai i д 1 др , d2ui *> /i7 1 о\
Т+^Г "<"*=- — 1)it+"-^—gb"- (17Л-2)
В соответствии с подходом, подробно описанным в главе 7,
подставим в (17.1.2) вместо мгновенных значений компонент
скорости, давления и плотности сумму средних и пульсационных
величин:
Р=Р+Р'>
(17.1.3)
При этом, учитывая малость пульсаций плотности воздуха по
сравнению с ее средней величиной, можно использовать
линейное приближение
1 1 /i Р
-и
р +р' р \ р
Тогда (17.1.2) запишется так:
-^- (й, -\-и\) +-^- (Ui + Ui) (uk+u'k) =
1 /1 р' \ ( dp , dp9 \ , d*ui , д% .
(17.1.4)
520
Глава 17
Осреднив (17.1.4), используя сформулированные в главе 7
правила осреднения, получим уравнение для средней скорости
или первого момента поля скорости, которое в турбулентном
режиме может рассматриваться как случайное поле:
duj , duiuk ]^ouiuk _ J_ dp , дЩ
9
T^-£r+-iz----r-er+'i3--*°- <l7l-5>'
Уравнение для корреляционного тензора Rij(xA, хБ, /)
выводится следующим образом. В результате вычитания из (17.1.4)
осредненного уравнения (17.1.5) получается уравнение для
компоненты пульсационной скорости и'. , которое записывается для
точки А (хл). Аналогичное уравнение можно написать для и'.
в точке Б (хБ). Если умножить уравнение для u'iA на и'.Б,
а уравнение для и'.Б на и'.А , сложить оба полученных
уравнения и осреднить результат, то после несложных преобразований
можно получить следующее уравнение:
д1*и(*А-хБ-*) - dRij - dR
ij
di '— ~ UkA —The UkB dx
от oxkA oxkB
du. ^ujb д ~~' '' ~
— Rki —jHT Rki —yz ZTZ UiAUkAUjB —
oxkA UXkB UXkA
-fa UiAUkBtljB = fa— UjbPa -
kB 9 л iA
1 д ^^ , *jB?A dPA
~ dx— UiA Рб " =2 dx—
9Б 0X'JB 9 A 0XiA
^2— ~di И UjB —-2 \-UiA —~i
? Б °*JB V dxkA dxkB
JS
-^^—+v \»>B-rf^+ulA—£- . (17.1.6)
При выводе уравнения (17.1.6) было учтено, что пульсация
величины <р в одной точке не зависит от координат другой точки,
т. е. dy'JdXiA = 0. Из (17.1.6) видно, что изменение
пространственного тензора корреляции со временем происходит под
влиянием следующих факторов: среднего движения (первые четыре
члена в правой части), сил инерции (третьи моменты пульсаций
скорости — 5-й и 6-й члены), пульсаций давления (7-й и 8-й
1 др'
1 При получении (17.1.5) пренебрегают членом -=^ р' -5—. выражающим
корреляцию между пульсациями плотности и градиентом пульсаций давления;
этот член обычно предполагается малым. Членами такого типа будем
пренебрегать и при дальнейших преобразованиях.
Статистические характеристики турбулентного потока 521
члены), стратификации (9-й и 10-й члены, содержащие
пульсации плотности) и молекулярной вязкости (последние два члена
в правой части). Существенно при этом отметить, что в
уравнение для первого момента поля скорости (17.1.5) вошли вторые
моменты и'м'., а в уравнение для второго момента — третьи
моменты. Легко сообразить, что если с помощью описанной выше
процедуры получить из уравнения Навье—Стокса уравнение для
третьих моментов поля скорости, то в них войдут четвертые
моменты, и т. д. Это свидетельствует о принципиальной
незамкнутости системы осредненных уравнений: всегда в уравнениях для
n-ных моментов появятся п+1 моменты. Следовательно, для
замыкания системы уравнений должны быть заданы независимо
от этих уравнений дополнительные соотношения между
искомыми функциями. Проблема замыкания является
фундаментальной проблемой теории турбулентности. В зависимости от
поставленной задачи гипотезы формулируются для тех или иных
характеристик турбулентного движения.
Из уравнения (17.1.6) могут быть получены уравнения для
различных компонент энергии турбулентности, а также для
полной энергии турбулентности. Прежде чем это сделать, исследуем
более детально физический смысл некоторых слагаемых,
входящих в уравнение (17.1.6). Для этого удобно рассмотреть
сначала случай однородного турбулентного поля. Случайное поле
называется однородным, если его одноточечные моменты
(средние значения величин и их дисперсии) постоянны в
пространстве, а двухточечные моменты (корреляционные тензоры, третьи
моменты и т. д.) зависят от вектора к\ = хА — хБ, но не зависят
от координат каждой из точек.
Изучение свойств однородного турбулентного поля
оказывается чрезвычайно важным. Несмотря на то что реальные
турбулентные поля являются неоднородными, во многих случаях
можно использовать предположение о локальной однородности или
однородности течения в определенной плоскости или в каком-
либо направлении.
Чтобы получить уравнение для тензора корреляций скорости
в однородном поле, удобно перейти к новым переменным
^i = xiA-\-xiB. (17.1.7)
Из (17.1.7) следует:
Глава 17
<Э2 <J2
<)2 02
+2-^
1 дфи
-2 д2 4
<?2
(17.1.8)
Учитывая соотношения (17.1.8) и определение однородного
поля, получим из (17.1.6) уравнение для тензора корреляций
в однородном турбулентном поле:
Л тти(П. 0+Лу(Ч. 0 = 2v '-^Н-. (17.1.9)
Из этого уравнения видно, что изменение со временем
пространственного тензора корреляций в однородном турбулентном поле
происходит под влиянием молекулярной вязкости, сил инерции
и пульсаций давления. Вклад последних описывается тензорами
второго ранга, равными соответственно
Ti)(% t) = —^—{UiAUkAUjB--UiAUkBtljB)1 (17.1.10)
Рц(Ъ 0—-f -^rW^P~A-u'lAps). (17.1.11)
Рассмотрим, в чем состоит роль сил давления и инерции.
Из (17.1.11)
Рц{% t)=- ±-*-(u'iaP'a-UuPb) • (17.1.12)
Покажем, что Рц(г\, t) = 0.
Запишем условие несжимаемости, заменив в нем и{ = щ + и'л
дщ . ди\
—tl I _^- = 0
dxi ' dxi
Поскольку при осреднении этого уравнения получаем dui/dxi =
= 0, то очевидно, что условие несжимаемости может
удовлетворяться только, если du'ldxi = Q. Напишем последнее соотношение
для точек А и Б:
da'iA п du'iB
— 0, -з^-О.
dxiA ■ дх.Б
Умножим первое из них на р'Б , второе на р'А, сложим почленно
Статистические характеристики турбулентного потока 523
оба уравнения и осредним. Учитывая, что пульсации в одной
точке не зависят от координат другой точки, получим
ди1АРБ , ди1БРА ^q
дх1А дХ1Б
Для однородного турбулентного поля, используя (17.1.8),
запишем
ди1АрБ ди\БрА ^Q
Отсюда следует, что
/>«(Ч, 0 = 0. (17.1.13)1
Для случая, когда точки А и Б совпадают,
р„(0, 0 = 0. (17.1.14)
Но при /=/ и т] = 0 уравнение (17.1.9) для пространственного
корреляционного тензора поля скорости переходит в уравнение
баланса энергии турбулентности, так как Ru(Q> t) =26.
Следовательно, из соотношений (17.1.13) и (17.1.14) следует, что в
однородном турбулентном поле тензор давлений не вносит вклада
ни в суммарную корреляцию одинаковых компонент пульсаций
скорости, ни в полную энергию турбулентности, т. е. этот член
не может быть ни источником, ни стоком энергии
турбулентности. Можно считать поэтому, что тензор давлений описывает
перенос энергии турбулентности. Поскольку пульсации давления
вносят вклад в энергию различных компонент пульсаций
скорости, ибо
/МО, 0^0, Р22(0, 0^0, Я3з(0, 0^0,
но не меняют полной энергии турбулентности, то очевидно, что
их роль состоит в переносе энергии от одних компонент
пульсаций скорости к другим. Естественно предположить, что перенос
осуществляется от компонент с большей энергией к
компонентам с меньшей энергией, так что в конце концов силы давления
должны приводить к изотропности поля скорости.
Рассмотрим теперь, какова роль сил инерции. Из (17.1.10)
следует, что Тц(ц, t) ф0, но
Г„(0, 0 = 0. (17.1.15)
Следовательно, силы инерции также не вносят вклада в полную
энергию турбулентности, т. е. их роль может состоять лишь
1 Напомним, что здесь, как и раньше, подразумевается суммирование по
повторяющимся индексам, так что
Рц (Ч. О = ри (Ч. 0+^22 (Ч. О +^зз (Ч. О-
524
Глава 17
в перераспределении энергии. Пока у нас нет возможности
более детально исследовать роль сил инерции; мы вернемся к этому
вопросу немного позже.
17.2. Анализ уравнений баланса различных компонент
энергии турбулентности
Получим из общего уравнения (17.1.6) для
пространственного корреляционного тензора /?1;(хА, хБ, t) уравнения баланса
энергии турбулентности и ее различных компонент. Рассмотрим
типичные для многих задач условия — однородный по
горизонтали турбулентный поток, средние характеристики которого
зависят только от высоты; учтем также малость вертикальной
составляющей средней скорости ветра по сравнению с
горизонтальными. При этих допущениях, положив в (17.1.6) т) = 0 и
соответственно / = /, / = /=!, / = / = 2, i = / = 3, получим:
db ' ' ди\ / ' ди2
= — UzU:-^ иги2—^ 7rz—UiUiUz —
dt - "**1 дхъ "*** дхъ dxz
-i- -^p+ 1 i;p'-^+v*;4^-, (17.2.1)
J dx2 ""ГТ J2 "* дхъ "Г— dxl
1 d*\ -r—? dux д
= — U3U1 —^ -r— UiUiUs —
dt — ~6"1 дхъ дх3
1 ' dp' . ' &a
Т"ЪГ+Ш,-ЯГ- (17'2'2)
1 д**2 ~!~! du2
= — и3и2^г 7г—и2и2иг —
dt - ""*' дхъ дхъ
--г *-£-+*-&• (17-2-з)
ди3 а ' ' ' 1 ' др' ,
— и3и3из — и3 ■ L
dt - дхз ~^J"J J "* дх-
и'з?' др , / д2":
Яг+ъ-вг- (|7-2'4)
Уравнение баланса энергии турбулентности (17.2.1) было
выведено другим методом в главе 7. Вследствие широкого
использования уравнений (17.2.1) — (17.2.4) в исследованиях по
Статистические характеристики турбулентного потока 525
физике атмосферы, целесообразно детально проанализировать
физический смысл различных членов этих уравнений. Во всех
уравнениях члены с градиентом скорости среднего движения
содержат в качестве множителя турбулентные потоки количества
движения. Для мелкомасштабной турбулентности направление
этих потоков, как отмечалось в главах 7 и И, противоположно
направлению градиента средней скорости,1 поэтому
рассматриваемые чледы в уравнениях баланса (17.2.1) — (17.2.4) всегда
положительны и являются источниками энергии турбулентности.
Они характеризуют генерацию энергии турбулентности средним
потоком. Важно отметить, что генерационный член отсутствует
в уравнении (17.2.4) для вертикальной компоненты энергии
турбулентности.
Член с пульсациями плотности, характеризующий влияние
стратификации, при рассмотрении атмосферных процессов
целесообразно преобразовать, перейдя от пульсаций плотности
к пульсациям температуры. Из уравнения состояния при
пренебрежении относительными пульсациями атмосферного давления
следует р'/р~—Т'IT. Это позволяет выразить вертикальный
турбулентный поток плотности и'р' через турбулентный поток тепла
и'Т'
а именно
"зр'
72
дР
дх3
и,Т
Цг(-к) = -2гЪТ-. (17.2.5)
При нейтральной стратификации турбулентный поток тепла
равен нулю и стратификация не влияет на баланс энергии
турбулентности; при неустойчивости и'3Т'>0 и стратификационный
член является источником энергии турбулентности, а при
устойчивости и'3Т' <0 и этот член является стоком энергии
турбулентности. Отметим, что в рассматриваемом случае горизонтально
однородного турбулентного потока стратификационный член
входит только в уравнения (17.2.1) и (17.2.4).
Член, содержащий молекулярную кинематическую вязкость,
с помощью тождества
dui с д • Щ с dai \\ с ' dui
дх\ d*k dxk \ dxk ^ дх*
1 Для потоков различных субстанций, обусловленных крупномасштабной
турбулентностью, наблюдаются ситуации, когда их направление совпадает
с направлением градиентов средних полей. При использовании градиентной
гипотезы эти случаи соответствуют наличию отрицательной турбулентной
вязкости.
526
Глава 17
можно преобразовать следующим образом:
Ш1
д2а1 1 да1 I dat у фь I да
Н
дх\ 2 дх\ \ dxk ) дл2 \ dxk ) '
(17.2.6)
Первый член в (17.2.6) можно объединить с входящими
в (17.2.1) под знаком производной по высоте членами,
характеризующими влияние сил инерции и давления:
д
дх3
\uWiU,+4^uzp' -^-^) = Ш1Ь. (17.2.7)
Этот член, обусловленный вертикальной неоднородностью
турбулентности атмосферы, описывает перенос энергии
турбулентности в пространстве — диффузию энергии турбулентности.
Выражение в скобках в (17.2.7) представляет собой плотность
потока энергии турбулентности, связанного с переносом энергии
турбулентным движением (инерционный член), силами
давления и молекулярным движением. Два последних члена в (17.2.7)
обычно малы по сравнению с первым. Отметим, однако, что
возможность пренебрежения переносом энергии силами
давления нуждается в экспериментальной проверке.
Второй член в (17.2.6)
£ = V
dut
d*k
называется скоростью диссипации энергии турбулентности; он
описывает превращения энергии турбулентности в тепло под
действием молекулярной вязкости и является стоком энергии
турбулентности.
Таким образом, в соответствии с общим уравнением баланса
какой-либо субстанции а [см. уравнение (1.2.1)],
обсуждавшимся в главе 1, в уравнении баланса энергии турбулентности
члены, описывающие генерацию, диссипацию и влияние
стратификации, представляют собой источник энергии турбулентности
ди\ ' / ди-2
а члены, входящие в (17.2.7) под знаком производной,
, ' > > , 1 —*—*■ дЬ
Jb = tliUill2>-\—^и3р — v~^-
характеризуют вертикальный поток энергии турбулентности.
Отметим, что в рассмотренном нами приближении горизонтально
однородного турбулентного потока в этом уравнении отсутствует
Статистические характеристики турбулентного потока 527
конвективный поток энергии турбулентности. Аналогично могут
быть преобразованы и интерпретированы члены в уравнениях
(17.2.2) — (17.2.4). Члены этих уравнений, содержащие
пульсации давления, описывают, как следует из предыдущего
рассмотрения, перенос энергии соответствующей компоненты пульсаций
скорости как в пространстве, так и от одной компоненты к
другой. Эффектом переноса энергии различных компонент в
пространстве силами давления и молекулярным движением будем
пренебрегать по сравнению с их переносом турбулентным
движением.
Учитывая вышесказанное и вводя обозначения
•2
,2
м1
2
,2
2 и2
, *» = —2~ ,
°и/=="
,2
2
Diff3u^-^-«;a;«3,
Dif4^^r«2"2K3>
Diff,
-щ-UMui
Z\ / i Г
Diff*«-^- tittle,
du
dxk
2
t2 = ^
du2
dxk
2
du
e3 = ^^-J.< 07.2.8)
перепишем уравнения (17.2.1) —(17.2.4):
2
db ' ' ди\ ' ' duo r^.rr i g ' rr,'
(17.2.9)
d*l
= -uk[-$£— Diff. ^«i-^ *„ (17.2.10)
<tt ~л"' дх3 ^""« Г "' длг!
.2
^—d«4—r^=i:+^*F-^ <17-2Л2>
528
Глава 17
Экспериментальные данные и некоторые теоретические
исследования (см. главу 11) указывают на сравнительную малость
диффузионного слагаемого в балансе энергии турбулентности,
по крайней мере в пределах приземного слоя атмосферы. Если
в (17.2.9) пренебречь диффузией энергии, а также для простоты
не учитывать изменения направления ветра с высотой, то
уравнение баланса энергии турбулентности можно записать в виде
dt дх3
где
db =_tf3tfi-^-(l-Rf)_e, (17.2.13)
Rf = p ^= (17.2.14)
tt,tt3—г-1—
1 3 <?*3
есгь безразмерное число, называемое динамическим (или
потоковым) числом Ричардсона. Если использовать градиентную
гипотезу Буссинеска—Шмидта для вертикальных турбулентных
потоков тепла и количества движения, то (17.2.14) можно
переписать в виде
дВ
Rf = P^ / Р Х2 =**RU (17.2.15)
V дх3 )
где
*^-^1Ш' <,7-2-,6>
есть обычное (или градиентное) число Ричардсона; aT=kT/k —
обратное турбулентное число Прандтля. Очевидно, что число
Ричардсона характеризует относительную роль термических и
динамических факторов в балансе энергии турбулентности.
Как уже отмечалось, для мелкомасштабной турбулентности
— dui
и[и'г——<0 и Rf<0 при неустойчивой стратификации, Rf = 0
при равновесных условиях и Rf>0 при устойчивой
стратификации. Из уравнения (17.2.13) видно, что при устойчивой
стратификации стационарная (незатухающая) турбулентность
возможна лишь при
Rf<l. (17.2.17)
Это условие эквивалентно критерию возникновения
турбулентности в устойчиво стратифицированной среде, полученному
в главе 7 с помощью энергетического анализа эволюции
возмущения данного размера. Видно, однако, что критерий (17.2.17)
Статистические характеристики турбулентного потока 529
характеризует не столько условия возникновения, сколько
условия поддержания турбулентного режима. Безусловно, критерий,
полученный из энергетических соображений, является довольно
грубым: можно лишь утверждать, что стационарный
турбулентный режим будет существовать только при Rf<RfKp, причем
ясно, что RfKp<l.
Определение числового значения критического числа
Ричардсона представляет большой интерес. Однако к настоящему
времени оно известно еще не достаточно надежно. По имеющимся
теоретическим оценкам и экспериментальным данным можно
принять, что числовое значение Rf^0,25.
17.3. Профили различных компонент энергии турбулентности
в пограничном слое атмосферы
Несмотря на важность определения профилей компонент
энергии турбулентности как в чисто теоретическом плане, так
и для различных прикладных задач, они к настоящему времени
изучены недостаточно хорошо. Трудность теоретического
исследования этих характеристик связана с незамкнутостью
уравнений (17.2.10) — (17.2.12). Действительно, в этих уравнениях,
кроме искомых характеристик a2u, a2 , o2w, содержится ряд
неизвестных функций: |^, -g-, £3, DiffaM, Diff^, D№aw, u[-£^-,
> dp' > dp'
ii2-§—> Ui~if~ > £ь £2> ез> Для определения которых нужно
использовать другие уравнения и формулировать гипотезы
замыкания. Возможны различные подходы к рассматриваемой задаче.
В настоящее время предложено несколько моделей строения
пограничного слоя атмосферы, позволяющих определить профили
различных компонент энергии турбулентности. Эти модели
отличаются друг от друга различными способами замыкания
уравнений. Получаемые в рамках этих моделей характеристики
турбулентности значительно различаются. Что касается
экспериментальной проверки различных моделей, то, к сожалению, нужно
констатировать, что в настоящее время еще отсутствуют
надежные экспериментальные данные о профилях различных
характеристик турбулентности в пограничном слое атмосферы.
Результаты измерений разных авторов обнаруживают значительное
расхождение. Детальный анализ имеющихся экспериментальных
данных и рассмотрение всех моделей строения пограничного слоя
выходит за рамки настоящего учебного пособия.
Здесь будет описан лишь один из возможных подходов к
рассматриваемой проблеме. Он фактически состоит в том, что
34 Заказ № 612
530
Глава 17
к модели пограничного слоя атмосферы, изложенной в главе 11,
добавляются уравнения (17.2.10) — (17.2.12) .* В рамках этой
модели получены профили скорости ветра, коэффициента,
масштаба и энергии турбулентности и скорости ее диссипации
в тепло. Для остальных неизвестных функций, входящих в
уравнения для компонент энергии турбулентности, формулируются
гипотезы замыкания; некоторые из них являются естественными
в рамках рассматриваемой модели пограничного слоя. В
частности, для диффузионных членов, описывающих турбулентный
перенос по вертикали соответствующих компонент энергии
турбулентности, используются следующие соотношения:
d , d°l
Dlff. =
и
Diffa =
V
Diff, =
W
-a
— a
-a
■*:
dx3 J dxz
К
<txz * dx3
л . dol,
(17.3.1)
dxz 6 dxz
Для турбулентных потоков количества движения u'zu[ и u'zu'2
используется принятая в модели пограничного слоя градиентная
гипотеза Буссинеска—Шмидта.
Как будет показано ниже, диссипация энергии
турбулентности в тепло обусловлена главным образом наиболее мелкими
турбулентными образованиями, которые являются приближенно
изотропными. Вследствие этого можно предположить, что
ej « е2 « е3 « -g- е. (17.3.2)
Теперь для замыкания системы уравнений осталось сделать
предположение о членах, содержащих пульсации давления, роль
которых, как было показано, состоит в перекачке энергии от
одних компонент к другим.2 К сожалению, физический механизм
1 Поскольку о2и + a^ -f °w~b и уравнение баланса Ь включено в систему
уравнений пограничного слоя, то в действительности нужно использовать
только два уравнения из системы (17.2.10) —(17.2.12) или какую-либо их
комбинацию. Удобно взять разность уравнений для горизонтальных компонент и
уравнение для вертикальной компоненты.
2 Вблизи подстилающей поверхности энергия горизонтальных компонент
энергии турбулентности больше, чем энергия вертикальной компоненты. Из
уравнений (17.2.10) — (17.2.12) видно, что генерационные члены, содержащие
градиенты средней скорости, входят в уравнения для горизонтальных
компонент (при равновесных и устойчивых условиях только в этих уравнениях
имеются источники). Поэтому в приземном слое атмосферы перенос энергии
пульсациями давления осуществляется главным образом от горизонтальных
компонент энергии турбулентности к вертикальной.
Статистические характеристики турбулентного потока 531
этого процесса до сих пор детально не выяснен, что затрудняет
формулировку соответствующих гипотез. Предложено несколько
полуэмпирических соотношений, несущественно отличающихся
друг от друга; в их основе лежат некоторые качественные
соображения. Такие соотношения, в частности, могут быть получены
из соображений размерности. Можно предположить, что
переход энергии данной компоненты в энергию другой компоненты
зависит от энергии данной компоненты и характеристик,
определяющих интенсивность турбулентного обмена,— энергии и
масштаба турбулентности, т. е. определяющими параметрами явля-
о
ются и'. , Ь} I. В соответствии с этим предположением
' — / —Тг \
F^-Lp'-g^^vytn, &(/) = -^_cp^-J-J. (17.3.3)'
Необходимо иметь в виду, что в (17.3.3) не подразумевается
суммирование по повторяющимся индексам.
В линейном приближении можно записать
/?, = -*!£-(С|+В,-^-). (17.3.4)
3
Из условия 2] Fi = 0 можно найти
i=i
В{ = В2 = В3=-±- 2 С,. (17.3.5)
Следовательно,
Ft = - -^ А [J%-+Dt) , (17.3.6)
где
з
л=42сьА=-4-- (17-3-7)
1 Члены с пульсациями давления в (17.2.10) — (17.2.12) можно
преобразовать к виду
р l dxt 9 у dxi у dxt J
(по i здесь не суммируется!). Первым членом, описывающим перенос энергии,
как уже отмечалось, можно пренебречь.
34*
532
Глава 17
Для однородного по горизонтали турбулентного потока
Dl = D2 = Df (17.3.8)1
з
и так как Д]£>г=—2, то
ZV—2(1+D). (17.3.9)
С учетом гипотез (17.3.1), (17.3.2), (17.3.6) и соотношений
(17.3.7) —(17.3.9) разность уравнений (17.2.10) и (17.2.11) и
уравнение (17.2.12) для стационарных условий запишутся
следующим образом:
(17.3.10)
2АЪ*
1
1г , 2
— ч
АЬЪ^
1
Ь
-ov) — k3
7 dux V ( dut у
\ dxz ) \ dx3 ) _
—
йхъ *3 dxz -U'
-2(l+D)]-.^A,-g—
+ ^т
7--н°-
(17.3.11)
Коэффициенты А и D удобно выразить через значения
компонент энергии турбулентности вблизи земли. Из (17.3.10) и
(17.3.11) находим при хз-> го:
А= __„Л — = ^Л-, (17.3.12)
-2(1+D) =
1_
1
2°lo
C^'V
ЗЛ
2
(17.3.13)
1 При этом условии сделанное здесь предположение (17.3.6) о члене,
содержащем пульсации давления, совпадает с гипотезой Давыдова, согласно
которой
> dp' < dp'
dxt
dxj
ukak I / 1 \
где Bu B2 — некоторые размерные положительные коэффициенты, зависящие
только от энергии турбулентности Ь и масштаба /. Они равны:
ЬЧ— - п _1_
B<i = CL2
I
= Д2£-
Здесь аь а2 — безразмерные постоянные.
Статистические характеристики турбулентного потока 533
При получении (17.3.12) и (17.3.13) использованы соотношения
b(x3)\X3^z=C-'i'vl
к3-ф-\ =0,
3 dx3 \Х9-*г0
следующие из модели пограничного слоя (см. главу 11), и
обозначения
2 С*'2 /2 2 \
3Л0 = —о~ Va«o — ^г/0;,
tr
*
2 att<)C !г
Gwn 0 — о
*
для соответствующих характеристик на уровне шероховатости.
При этом нужно иметь в виду, что в соответствии с теорией
подобия, изложенной в главе 11, безразмерные компоненты
энергии турбулентности
2
2
2
Gun
2
Own
I
С
- Ju
v2
*
'/'о2
V
c'h<
v2
*
i
в приземном слое являются универсальными функциями
параметра z/L. При z/L-+0 они принимают постоянные значения,
которые можно взять из наблюдений.
Поскольку описанная в главе 11 модель строения
пограничного слоя позволяет найти профили скорости ветра,
коэффициента и энергии турбулентности, а также скорости диссипации, то
из (17.3.10) и (17.3.11) можно с учетом соотношений (17.3.12)
и (17,3.13) определить профили компонент энергии
турбулентности при разных значениях внешних параметров jli0 и Ro.
При численной реализации систему уравнений удобно
привести к безразмерному виду. Подставив (17.3.12) и (17.3.13)
в (17.3.10) и (17.3.11), получим:
* 2 4* Г/ ащп \2 / ай2п \2]
°"-ап0^[[-1й^) "ГЗ^ J-
_a;oJ^*^ * Лзя4^=0, (17.3.14)
2C/f bn dxZn 6п dxZn v '
534
Глава 17
2 h
2 2 , °л(ГЗл ср
awn — ownQUn 7 qs п —
°n
где
2 C,/8 /2 2\
Зл = о- Va" — °f/>
IT
2 _ c qw
З^л — 2 »
V
"зе 0 £
&*n=— X2B ^-д- В—£-
"з1
Уравнения (17.3.14) и (17.3.15) были решены численно при
следующих граничных условиях:
2 I 2
°я г -** = ал0>
Г3л *л0
2
rte*»-°. (17.3.16)
2 1 2
\x3n^zn0
2
-i*te—"°- (17-ЗЛ7)
На основании экспериментальных данных о2п0 и а^0 при
расчете были приняты равными 0,07 и 0,39 соответственно,
абХ2/2С,/2 = 0,27. Следует, однако, иметь в виду, что точность
экспериментального определения этих величин в настоящее
время еще не достаточно велика, поэтому приведенные
числовые значения могут быть уточнены при получении новых
экспериментальных данных.
На рис. 17.1 для разных типов стратификации атмосферы
при фиксированном числе Россби (Ro = 106) приведены профили
различных компонент энергии турбулентности, полученные в
результате численной реализации уравнений (17.3.14) и (17.3.15)
с граничными условиями (17.3.6) и (17.3.17). Видна сильная
зависимость значений компонент энергии турбулентности и
характера их изменения с высотой от стратификации атмосферы.
Из рисунка следует, что при всех типах стратификации
энергии горизонтальных компонент близки по величине. Значение
же вертикальной компоненты энергии турбулентности, несмотря
на поступление энергии от горизонтальных компонент благодаря
члену с пульсациями давления, остается все время меньше
горизонтальных. В качестве примера на рис. 17.2 сопоставлены тео-
Статистические характеристики турбулентного потока
If I
•
L_ 1 1 1
1 1
I
1
Is
* ^сх
1» S
О. К
"-*■ н £
'2= м £
I
►О
II Е
Si
а?
15
536
Глава 17
ретические профили горизонтальной компоненты энергии
турбулентности с экспериментальными данными, полученными на
300-метровой метеорологической мачте в Обнинске. Видно, что,
за исключением области вблизи подстилающей поверхности,
наблюдается удовлетворительное согласие между результатами
расчета и измеренными значениями о2 .
17.4. Профили интенсивности температурных пульсаций
в пограничном слое атмосферы
Уравнение для пространственной корреляционной функции
температурного поля
Яв(хд. х*> 0 = в'(хА) Ов'(х£, t) (17.4.1)
может быть получено из уравнения теплопроводности в
движущейся среде
с помощью процедуры осреднения, описанной в п. 17.1:
™в
(*л-
dt
хв,
u'ib
•0
;вд
— //
дХ1Б
+ Хв£
iA d*iA
~ tliA ©£
Э2*А ,
дх2 '
+ "iS
двА
дХ1А
V-Ф'л '
дх1Б
— UlB^A
дх],'
UjA&B
двБ
дх1Б '
#* Л
дх1А
(17
Здесь х — коэффициент молекулярной температуропроводности.
Из уравнения (17.4.3) видно, что изменение со временем
пространственной корреляционной функции температурного поля
происходит под влиянием следующих факторов: переноса
температурных пульсаций средним движением (1-й и 2-й члены
в правой части уравнения), поля средней температуры (3-й и
4-й члены), конвективного переноса температурных пульсаций
турбулентным полем скорости — смешанные третьи моменты
(5-й и 6-й члены) — и молекулярной теплопроводности (два
последних члена).
Уравнение для интенсивности температурных пульсаций G =
= 0/2/2 можно получить из (17.4.3), положив хЛ — хБ = 0.
Напишем его для однородного по горизонтали потока, средние
характеристики которого изменяются только с высотой, и учтем
Статистические характеристики турбулентного потока 537
малость вертикальной компоненты средней скорости по
сравнению с горизонтальными:
Последнее уравнение — это уравнение баланса интенсивности
температурных пульсаций.
Члены (17.4.4) имеют смысл, аналогичный смыслу
соответствующих членов уравнения баланса энергии турбулентности.
Перед градиентом средней температуры стоит член w3'0',
представляющий собой вертикальный турбулентный поток тепла.
Для рассматриваемой здесь мелкомасштабной турбулентности
направление турбулентного потока тепла противоположно
направлению градиента средней температуры, следовательно,
первый член в правой части (17.4.4) всегда положителен и является
источником интенсивности температурных пульсаций. Он
описывает генерацию пульсаций температуры средним температурным
полем. Второй член в правой части связан с пространственной
неоднородностью пульсационного поля температуры и описывает
диффузию интенсивности температурных пульсаций,
осуществляемую турбулентным движением:
^«;e'2 = Diff^. (17.4.5)
Наконец, последний член в (17.4.4) может быть представлен
в виде
где
Первый член в (17.4.6) характеризует диффузионный перенос
пульсаций температуры, осуществляемый молекулярным
движением; этот член пренебрежимо мал по сравнению с (17.4.5).
Второй член в (17.4.6) описывает уменьшение G вследствие
молекулярной теплопроводности и называется скоростью
выравнивания температурных неоднородностей.
В уравнении (17.4.4), кроме искомой величины G,
содержатся еще следующие неизвестные функции: w'36', Diff-— N.
Если это уравнение подключить к описанной в главе И модели
строения пограничного слоя атмосферы, то для турбулентных
538
Глава 17
потоков тепла и интенсивности температурных пульсаций
естественно использовать градиентную гипотезу:
de
из® — *зн ахъ '
2
u<d'2=-k— ^—. (17.4.8)
3 за'2 dx3 v '
Предположим также, что скорость выравнивания
температурных неоднородностей полностью определяется
интенсивностью температурных пульсаций и характеристиками,
описывающими турбулентный режим поля скорости, т. е. энергией и
масштабом турбулентности. Из соображений размерности тогда
получим следующее соотношение для N:
N==d^^-t (17.4.9)
где d — безразмерная постоянная.
С учетом (17.4.5) — (17.4.9) уравнение баланса интенсивности
температурных пульсаций для стационарных условий запишется
в виде
где d*=d/aT. Предполагается, что k = £_ = aTk3. Гранич-
зв'2 зе
ные условия задаются на высоте пограничного слоя Н:
G(*3)U=//=0 (17.4.11)
и на подстилающей поверхности. Граничное условие на уровне
шероховатости находится аналитически из (17.4.10) при
пренебрежении диффузионным членом
k
G{x*)\Xz+z=—aW
(dxj
(17.4.12)
x3-*z0
Используя результаты численной реализации описанной ранее
de
модели пограничного слоя атмосферы, т. е. считая kz, bt ——
известными функциями высоты и внешних параметров, можно
численно решить уравнение (17.4.10) с граничными условиями
(17.4.11) и (17.4.12) и получить профили интенсивности
температурных пульсаций и всех членов (17.4.10) при разных
метеорологических условиях.
Статистические характеристики турбулентного потока
539
На рис. 17.3 приведены профили G (хз) для устойчивых (|io =
= 50), нейтральных (|io = 0) и неустойчивых (|я0 = —50) условий;
число Россби фиксировано (Ro = 106). Видно сильное влияние
стратификации на величину G и ее зависимость от высоты.
Рис. 17.3. Профили дисперсии пульсаций
температуры при разных типах
стратификации атмосферы.
■5lgr,lg/?.lg/V
Рис. 17.4. Профили различных
членов уравнения баланса
интенсивности температурных
пульсаций при |Ло=0, 6= 10 м/с.
Г — генерация, D — диффузия, N —
диссипация.
В качестве примера на рис. 17.4 приведены профили
различных членов уравнения баланса интенсивности температурных
пульсаций для нейтральных условий. Из этого рисунка видно,
что на всех высотах генерационный член практически
балансируется со скоростью выравнивания температурных неоднородно-
стей; аналогичное соотношение между генерацией и величиной N
наблюдается и при устойчивых условиях. Отметим, что
диффузионный член оказывается важным лишь при неустойчивых
условиях, особенно на высотах, где d@/dx3 близко к нулю и,
следовательно, очень мал генерационный член.
На рис. 17.5 в качестве примера сопоставлены теоретические
профили G(z) с измеренными на метеорологической мачте
540
Глава 17
в Обнинске; можно считать, что полученные теоретические
результаты не противоречат экспериментальным данным.
Следует, однако, указать, что приведенный здесь метод не
является единственным методом определения интенсивности
температурных пульсаций.
В предыдущем
параграфе уже говорилось о том,
что в настоящее время
предложено несколько
численных моделей
строения пограничного слоя;
в рамках некоторых из них
вычисляются и профили
G(z).
В заключение
приведем уравнение для
пространственной
корреляционной функции
температурного поля в случае,
когда турбулентные поля
скорости и температуры
являются однородными.
Это уравнение
понадобится нам в дальнейшем. Из
(17.4.3) для однородного
турбулентного поля
получим
Рис. 17.5. Сравнение теоретического
профиля дисперсий пульсаций температуры
с экспериментальными данными.
/ — теоретическая кривая, соответствующая ц,0=
= —30, 6=5 м/с; 2 — осредненные
экспериментальные данные ИЭМ для умеренно неустойчивых
условий
dt
■ = ^«(ч, 0+
+ %«5#iL. „7.4.13)
dti
где член
W»to' *) = ^(и'*БвАвБ-и1Ав'АвБ) (17.4.14)
описывает конвективный перенос температурных пульсаций
турбулентным полем скорости. Из (17.4.14) следует, что
ф(0, 0=о,
(17.4.15)
т. е. конвективный член не вносит вклада в интенсивность
температурных пульсаций.
Статистические характеристики турбулентного потока 541
17.5. Спектральные характеристики турбулентного
поля скорости
Для многих важных задач интерес представляют не только
интегральные характеристики турбулентного потока,
рассмотренные в предыдущих параграфах, но и характеристики, более
детально описывающие структуру турбулентных полей. В
частности, при изучении болтанки самолетов наиболее важным
является определение энергии турбулентных вихрей, размер которых
сопоставим с размерами самолета. Такими более тонкими
характеристиками турбулентного потока являются спектральные
величины, связанные с турбулентными вихрями разных
размеров.
Уже указывалось на сложную структуру турбулентного
движения, проявляющуюся в наличии разных периодов (или
частот) флуктуации метеорологических элементов. Это позволяет
представить турбулентное движение как суперпозицию движений
вихрей разных масштабов. Для вычисления распределения
энергии по вихрям разных размеров нужно найти метод разложения
движения на составляющие, которое имеет вполне
определенный физический смысл — сумма энергий различных
составляющих должна равняться полной энергии турбулентности Ъ.
Таким методом является представление поля скорости в виде
интеграла Фурье по волновым векторам х, обратно
пропорциональным масштабу вихрей, который может быть разным в
разных направлениях. Представим пульсацию скорости в точке А
в виде интеграла Фурье:
а;.(хд, *) = JA(*. t)eixXAd%, (17.5.1)
где
А>(*> 0--srj »i(xA, t)e~i%XAdxA (17.5.2)
есть Фурье-компонента скорости, характеризующая вклад
в пульсацию скорости и'.(хА, t) составляющей движения с
волновым вектором х.
Составим пространственный корреляционный тензор поля
скорости:
Rlj(*A> ХБ, t)=tti(XAt t)Uj(XB, t) =
= |л;.(х, t)Aj(*'t t)ei%XAeU'XBdxAdxs. (17.5.3)
В однородном турбулентном поле корреляционный тензор
может зависеть лишь от разности ц=хА — хБ; это будет иметь
место, если
Д.(х, t)Aj(%'9 t) = OtJ(%9 t)l (% — *').
542
Глава 17
Подставив это соотношение в (17.5.3), получим
Rij{% 0 = J<M*, t)eiXfid%% (17.5.4)
где 0{j(m, t)—коэффициент Фурье-преобразования
пространственного корреляционного тензора, называемый спектральным
корреляционным тензором.
Положив в (17.5.4) т] = 0 и / = /, получим
/?«(О, 0 = 2* = J®«(x, t)d%. (17.5.5)
Тензор Ф«(х, 0» описывающий вклад вихрей с волновым
вектором х в энергию турбулентности, называется спектральным
тензором энергии.
Поскольку удобнее исследовать функции, зависящие от
скаляра, то обычно в рассмотрение вводится спектральная
плотность энергии турбулентности £(х, t), равная интегралу от
Фгг(х, t) по поверхности do сферы радиусом х = Ух2+х*+х23:
Я(х, 0 = 4" ФФ ф»(*> *№• (17.5.6)
х ,х. =х2
Из (17.5.5) тогда следует:
ос со
= 4"Jdx ( §§ ф"(х» 0^ = J£(*> *)<**• (17.5.7)
О \х^ =х« У О
Спектральная плотность энергии £(х, 0 характеризует вклад
в полную энергию турбулентности компонент движения с
волновым числом х безотносительно к направлению волнового
вектора.
Наиболее простым для исследования является случай
изотропного турбулентного поля, т. е. поля, в котором все
направления равноправны. Все осредненные скалярные функции,
описывающие статистическую структуру такого поля, остаются
неизменными при вращениях или зеркальных отображениях
системы координат. Так, например, спектр Фц (х, t) однородного
изотропного поля может быть функцией только длины вектора
х, так как это единственная инвариантная по отношению к
вращениям величина. Для изотропного поля из (17.5.7), переходя
к сферической системе координат, найдем связь между £(х, t)
и Ф„ (х, t) в виде
£(х, 0 = 4*х2Фи(х, t). (17.5.8)
Статистические характеристики турбулентного потока 543
Формулы (17.5.5) и (17.5.7) показывают, что условие равенства
суммы энергий всех компонент движения полной энергии
турбулентности выполняется при использовании
Фурье-преобразования поля скорости.
Можно на примере очень простой модели показать, что
волновое число обратно пропорционально размеру вихря.
Если рассмотреть корреляцию скорости внутри вихря
размером /, то можно предположить, что корреляция постоянна
внутри вихря и отсутствует вне вихря, т. е.
Тогда
(Ro при г</,
V ' v ' v ' ' \ О при г >/.
оо
Ф(*) = 4г I R(r)e-Urdr =
— оо
/
1 о Г -1аг л R°^ sinx/
ъ1
-I
^ sinx/
Функция — имеет максимум при х/ = 0 и обращается в нуль
х/
при х/=±я; таким образом, основной вклад в Ф(х) дают
волновые числа х = 2я//.
17.6. Вывод и анализ уравнения для спектральной плотности
энергии турбулентности
Рассмотрим однородное турбулентное поле. Уравнение для
пространственного корреляционного тензора поля скорости в этом
случае, как было показано в п. 17.1, имеет вид
-ft = ^у(Ч. 0+Лу(Ч, 0+2v —^ • (17.6.1)
Тензоры Tij(r\, t) и Рц(ц, t), характеризующие влияние сил
инерции и давления, определяются соотношениями (17.1.10) и
(17.1.11).
Подставив в (17.6.1) вместо Rij(r\, t) его выражение через
спектральный тензор Фг;(х, t), т. е. соотношение (17.5.4), и
аналогично введенные соответствующие спектральные тензоры
инерции и давления
7у(Ч, *) = Jsiy(x, t)ei%*d*t (17.6.2)
Ptj(% 0 = jX(*> *)Л*> (17.6.3)
544
Глава 17
получим
dt
= 5,;(х, t)+P4{*9 /)-2™'Ф„(х, t). (17.6.4)
Положив в (17.6.4) i = j, получим уравнение для спектрального
тензора энергии:
дФц£, 0=5,.(Х) t)_2*?*u(*. t). (17.6.5)
При этом спектральный тензор давления в силу соотношений
(17.1.13) и (17.6.3) обращается в нуль.
Если проинтегрировать (17.6.5) по всем х, то получим
уравнение баланса полной энергии в однородном турбулентном поле.
При этом инерционный тензор обратится в нуль, так как
вследствие (17.1.15)
оо
j Su(*. t)d* = Tu{0, 0=0.
— ос
Таким образом, становится ясным физический смысл
влияния сил инерции: они не вносят вклада в полную энергию
турбулентности, но меняют энергию, связанную с фиксированным
волновым вектором. Следовательно, силы инерции переносят
энергию в волновом пространстве от одних турбулентных вихрей
к другим.
Направление переноса энергии в волновом пространстве
можно выяснить из следующих физических соображений. Влияние
инерционных сил проявляется в распространении энергии по все
более широкой области волновых чисел и, следовательно, в
переносе (в статистическом смысле) энергии в те части
пространства, где она является наименьшей. Крупные вихри (малые х)
получают энергию от среднего движения и создаются в первую
очередь. Из (17.6.5) видно, что влияние диссипации тем больше,
чем больше х, т. е. мелкие вихри очень быстро теряют свою
энергию на работу против молекулярного трения. Из этих
рассуждений следует, что инерционный перенос происходит в
направлении от малых х к большим, т. е. мелкие турбулентные
вихри получают энергию от крупных.
Проинтегрировав (17.6.5) по всем направлениям волнового
вектора х, т. е. по поверхности do сферы радиусом х, получим
уравнение для спектральной плотности энергии:
дЕ(ъ, t) =т^ /)_2v*2£(x, t), (17.6.6)
Статистические характеристики турбулентного потока 545
где
Г(х, t)= j>j> Sif(x, t)do. (17.6.7)
Для изотропной турбулентности из (17.6.7) следует
Г(х, /) = 2icx2SH(x, 0- (17.6.8)
17.7. Общий вид спектра энергии в однородном турбулентном
поле. Гипотеза о статистическом равновесии
Спектральное уравнение баланса энергии турбулентности
(17.6.6) является незамкнутым, так как в него входит
неизвестная функция Г(х, /), характеризующая перенос энергии
турбулентности по спектру. Можно, однако, сделать некоторые
выводы о поведении £(х), не зная конкретного вида Т(х).
Рассмотрим сначала малые к. Разложим спектральный
тензор Фн(и, 0 в ряд в окрестности точки х = 0:
Фи(х, 0 = Q;. + x/Ciy/+x/xmQ;./m + 0(x3), (17.7.1)
причем тензорные коэффициенты Cij, Сг-#, Cijim зависят лишь
от t. Условие несжимаемости, которое в спектральной форме
имеет вид
с учетом -(17.7.1) можно записать так-
^Cij + KjKlCljl + KjWmCijtm + O (х4) =0. (17.7.3)
Это уравнение при любых х может выполняться лишь при
Таким образом,
Фч (х, O-xAyi+^mC^-bO (х3). (17.7.4)1
Подставив Фг;(х, t) в (17.5.6) и выполнив интегрирование
по doy получим
Я(х, /) = ^LCx4+0(x6). (17.7.5)
Из (17.7.5) следует, что спектральная плотность,
характеризующая вклад в энергию турбулентности от разных волновых
1 Можно показать, что из свойств, которым должен удовлетворять
спектральный тензор Oij(*i 0» следует, что Сщ = 0. Мы не приводим этого
доказательства, так как для нас наибольший интерес представляет поведение
функции £(х), а член Сщ в ней исчезает при интегрировании по сфере da.
35 Заказ № 612
546
Глава 17
чисел, быстро (пропорционально х4) стремится к нулю при
приближении к началу координат в волновом пространстве.
Кроме того, можно показать, что в области х->0 Г(х, t)
гоже стремится к нулю, как х4. Следовательно, из (17.6.6)
с учетом (17.7.5) следует, что
d£(xf t)
dt
ч-Я)
О, т. е. в
окрестности х—^0 спектральная плотность практически не меняется со
*-х
Рис. 17.6. Схематическое изображение спектров
различных членов спектрального уравнения баланса
энергии турбулентности.
/ — спектр энергии турбулентности Е{у.), 2 — спектр
диссипации х2£(к), 3 — спектр функции переноса Т(х.)\ 1 —
интервал энергии, // — интервал диссипации (вязкая подобласть).
временем. Это свидетельствует о неизменности крупных вихрей,
свойства которых определяются начальными условиями.
Распределение энергии по направлениям в крупных вихрях также
остается неизменным, поэтому если первоначально турбулентность
не является изотропной, то крупные вихри будут оставаться
анизотропными.
Рассмотрим теперь другой предельный случай, когда х-*оо.
Из (17.6.6) видно, что роль диссипативного члена тем больше,
чем больше х, т. е. мелкие турбулентные вихри быстро теряют
свою энергию на работу против сил молекулярного трения.
В простейшем случае, когда инерционным переносом можно
пренебречь, из (17.6.6) находим
£(х, t) = E(%, t0)e
-2vx2 (/-/„)
(17.7.6)
Видно, что спектр определен для произвольного момента,
если известна его начальная форма; при этом энергия, связанная
с вихрем, имеющим волновое число х, убывает со временем,
причем скорость убывания существенно увеличивается с ростом х.
Период, начиная с которого можно пренебречь инерционным
Статистические характеристики турбулентного потока 547
переносом энергии по сравнению с диссипацией, называется
конечным периодом вырождения.1
Таким образом, анализ предельных случаев позволяет
сделать вывод о следующем поведении спектральной плотности в
зависимости от волнового числа: сначала Е(к) увеличивается
с ростом х, достигает при некотором значении х = хэ
максимальной величины, а затем постепенно убывает, стремясь к нулю
при х->-оо (рис. 17.6). Масштаб /э = 2я/хэ, характеризующий
размер вихрей, на который приходится максимум энергии
турбулентности, называется внешним масштабом турбулентности.
Интервалы на оси волновых чисел, в которых сосредоточена
основная дол-я (например, 80 или 90%) полной энергии турбулентно-
оо оо
сти b= j£(x)dx и полной диссипации e=2v J x2£(x)dx назы-
о о
ваются соответственно интервалами энергии и диссипации.
На рис. 17.6 схематически указано расположение этих спектров;
на этом же рисунке представлен спектр Г(х), который должен
быть отрицательным при малых и положительным при
больших х, так как из интуитивных представлений следует, что
перенос энергии происходит от крупномасштабных компонент
к мелкомасштабным. Масштаб /д = 2л/хд, характеризующий
размер вихрей, дающих основной вклад в спектр диссипации,
называется внутренним масштабом турбулентности или
микромасштабом Колмогорова.
Изучению детальной структуры энергетического спектра
посвящено большое число теоретических и экспериментальных
исследований. Основная трудность теоретического исследования
энергетического спектра связана с тем, что в уравнение (17.6.6),
кроме искомой функции £(х, /), входит неизвестная функция
Г(х, /), характеризующая перенос энергии турбулентности по
спектру. Поэтому для определения Е (х, t) из (17.6.6) нужно
сделать предположение о механизме переноса энергии по
спектру и определить функциональную св#зь Г(х, t) с £(х, /) и х.2
Наиболее простым является случай установившегося
стационарного турбулентного потока. Этот случай представляет и
большой практический интерес. Ясно, что для однородной
турбулентности нельзя говорить о стационарности полной энергии
турбулентности. Возникает, однако, вопрос, могут ли отдельные
участки спектра находиться в равновесии и не изменяться
в течение достаточно большого промежутка времени. Чтобы
1 Напомним, что речь идет об однородной турбулентности, когда в
уравнениях баланса отсутствуют источники энергии турбулентности.
2 Очевидно, что для замыкания (17.6.6) необходимо предположить, что
Т(х, t) может зависеть только от £(х, t) и х.
35*
548
Глава 17
выяснить этот вопрос, нужно сравнить время изменения
(вырождения) полной энергии с характерным периодом турбулентных
вихрей данного размера. Полная энергия турбулентности
убывает со временем со скоростью, равной скорости диссипации
db/dt = —б, поэтому характерный период вырождения (или
характерное «время релаксации») турбулентности То= тгттг~
do/at
~—. Естественно считать, что характерный период
вырождения Го будет совпадать по порядку величины с характерным
периодом энергосодержащих вихрей
К i 1
dt
Здесь 6хэ—доля турбулентной энергии, заключенная в
энергосодержащих вихрях; для оценок можно принять Ькэ~Ь.
Условие Го~тэ приводит к соотношению
e = A4-f (17.7.7)
подтверждающемуся экспериментально; коэффициент
пропорциональности А порядка единицы. Таким образом, энергосодер-
жащие вихри вырождаются, т. е. область максимума спектра
далека от равновесия. Можно, однако, предположить, что
характерный период турбулентных вихрей тч~/к/ак убывает по
мере уменьшения их размеров (это весьма правдоподобное
предположение, которое подтверждается экспериментальными
данными). Тогда допустимо считать, что при некоторых условиях
(в первую очередь при больших числах Рейнольдса) будет
иметься область спектра с характерным периодом тх, для
которой процесс вырождения турбулентности является очень
медленным. Турбулентные вихри, принадлежащие этой области,
быстро приходят в состояние статистического равновесия, не
зависящего от условий порождения турбулентности и от времени.
Предположение о стационарности области турбулентных
вихрей, размер которых меньше масштаба энергосодержащих
вихрей, называется гипотезой о статистическом равновесии.
17.8. Гипотезы Колмогорова о турбулентном режиме
мелкомасштабных компонент турбулентности
Первое теоретическое исследование формы спектра в
интервале равновесия было выполнено Колмогоровым в 1941 г.
Естественно, что исследование этого интервала представляет инте-
Статистические характеристики турбулентного потока 549
рес лишь в том случае, если он охватывает широкую область
волновых чисел, т. е. когда интервалы энергосодержащих
вихрей и диссипации далеко отстоят друг от друга (хэ<^хд). Как
будет ниже показано, это имеет место при достаточно больших
числах Рейнольдса.
В интервале равновесия (17.6.6) принимает вид
r(y.)=2vx2£», (17.8.1)
т. е. турбулентные вихри находятся в равновесии под влиянием
сил инерции и молекулярной вязкости. Удобно записать это
уравнение для некоторого спектрального интервала х, оо;
ОО оо
5 (х) = j Т (у.,) rfx, = 2v J %\Е (х,) rfx, =
X X
X
= e-2vjx?£(xf)dxlf (17.8.2)
о
где e=2v Jx2£(x)<ix— полная скорость диссипации энергии тур-
о
булентности в тепло.
Из уравнения (17.8.2) нельзя определить функцию £(х),так
как в него входит дополнительная неизвестная функция 5(х).
Однако, даже не зная механизма переноса энергии по спектру,
т. е. не зная вида функции S (х), можно получить важную
информацию о поведении спектральной плотности £(х) в
интервале равновесия. Из уравнения (17.8.2) видно, что спектральная
плотность энергии турбулентности зависит от двух внешних
параметров— скорости диссипации энергии турбулентности в тепло
г и кинематической вязкости v. Эти же параметры определяют
и другие статистические характеристики поля скорости в
интервале равновесия. Проведенный анализ поясняет физическую
основу теории универсального равновесия, которую Колмогоров,
создатель этой теории, сформулировал в виде двух гипотез.
Первая гипотеза Колмогорова: «При достаточно
больших числах Рейнольдса существует область волновых
чисел х^>хэ, в которой турбулентность находится в статистическом
равновесии и однозначно определяется двумя внешними
параметрами— скоростью диссипации е и кинематической вязкостью
v». Это состояние равновесия является универсальным.
В соответствии с этой гипотезой
£,(х)=/7(х, в, v).
(17.8.3)
550
Глава 17
Из соображений размерности следует
где
'.-£)"••
Длина /д определяет характерный масштаб турбулентных
вихрей, для которых существен эффект диссипации; она
называется внутренним масштабом турбулентности. Из измерений
следует, что в нижнем 100-метровом слое атмосферы /д~1 мм.
Хотя первая гипотеза не позволяет получить явную
зависимость спектральной плотности £(х) от волнового числа, она
указывает, что спектр, вычерченный в координатах £(x)/(v5e),/4>
х/д, должен иметь универсальный вид для всех турбулентных
течений— в атмосфере, океане, в трубах и т. п.; это
обстоятельство имеет большое практическое значение. В настоящее время
наличие универсальной мелкомасштабной области в спектрах
различных турбулентных течений подтверждено
экспериментально.
Из (17.8.5) следует, что, чем меньше v, а следовательно, чем
больше число Рейнольдса, тем меньше размер турбулентных
вихрей, для которых влияние вязкости является существенным.
Можно поэтому предположить, что при очень больших Re в
равновесном интервале имеется подобласть турбулентных вихрей,
размер которых больше /д и которые не подвержены влиянию
молекулярной вязкости. Для этих турбулентных вихрей в (17.8.2)
можно пренебречь членом, содержащим v, и записать
S(x) = s. (17.8.6)
Из (17.8.6) следует, что в этой области турбулентный режим
определяется только инерционным потоком энергии по спектру,
который является постоянным и равен скорости диссипации е.
Величина е является теперь единственным внешним параметром.
В этом смысл второй гипотезы Колмогорова.
Вторая гипотеза Колмогорова: «Движение,
связанное с областью волновых чисел хэ<х<хд (или /д<С/<^/эЬ
называемой инерционной подобластью спектра, полностью
определяется одним внешним параметром — скоростью диссипации
энергии турбулентности в тепло е».
Из этой гипотезы следует
E(x)=F(*t e) = Cev,x-"7\ (17.8.7)
т. е. в инерционной подобласти спектральная плотность
уменьшается с ростом волнового числа по «закону 5/з». Этот закон
(17.8.4)
(17.8.5)
Статистические характеристики турбулентного потока 551
получил название закона Колмогорова—Обухова.1 Он
подтвержден экспериментально многочисленными наблюдениями,
проведенными как в атмосфере, морях, океанах, так и в различных
лабораторных установках. Безразмерная универсальная
постоянная С, входящая в (17.8.7), на основании экспериментальных
данных может быть принята равной 1,22.
Уже отмечалось, что для наличия широкой области
универсального равновесия и значительного инерционного интервала
число Рейнольдса для турбулентного потока должно быть
достаточно большим. Покажем это и остановимся подробнее на
качественной картине формирования развитого турбулентного
потока.Ж инерционному интервалу принадлежат турбулентные
вихри с размерами, удовлетворяющими неравенству /Д<С/<С/Э,
из которого следует, что для наличия широкой инерционной
области масштаб диссипирующих вихрей /д должен быть
существенно меньше масштаба энергосодержащих вихрей /э, т. е.
/д«4. (17.8.8)
Подставив (17.8.8) вместо /д в формулу (17.8.5) и использовав
соотношение (17.7.7), получим
fub*u
^—»1. (17.8.9)
Поскольку можно считать, что порядок b совпадает с порядком
квадрата характерной скорости потока, то (17.8.9) перепишется
так:
-^l = Re33"»l. (17.8.10)
Какие именно числовые значения Re удовлетворяют условию
(17.8.10), можно определить лишь на основании эксперимента.
В атмосфере это соотношение всегда выполняется.
На основе исследования общих свойств спектра энергии
турбулентности с учетом теории Колмогорова, а также механизма
возникновения турбулентности по Ландау, изложенного в главе 7,
можно представить следующую картину образования
развитого турбулентного движения в нестратифицированном потоке.
Движение становится турбулентным, когда число Рейнольдса
Re = uL/v достигает значения, превышающего критическое ReKp.
Однако возмущения разных масштабов появляются в потоке не
одновременно. Вначале возникают наиболее крупномасштабные
1 Этот закон был разными способами одновременно получен
Колмогоровым и Обуховым. Позднее, но независимо он был установлен также Гейзен-
бергом, Вейцзеккером и Онзагером.
552
Глава 17
пульсации, имеющие размер /i, сравнимый по порядку величины
с характерным масштабом L течения в целом. Свою энергию
наиболее крупные вихри получают непосредственно из осреднен-
ного движения, и их свойства зависят от условий образования:
режим этих крупномасштабных пульсаций является
неоднородным и неизотропным в той же степени, в какой это присуще
среднему потоку.
Наряду с числом Рейнольдса, определяющим свойства потока
в целом, можно ввести число Re* = a^/v для пульсаций разных
масштабов /. При больших Re возникающие в потоке самые
крупные вихри являются неустойчивыми, так как для них Re^>
>ReKp; они распадаются, порождая турбулентные движения
меньшего масштаба k<U. Когда Re*2 становится больше
критического, то неустойчивыми будут и эти вихри, которые
распадаются на еще более мелкие вихри масштаба /з, и т. д. В процессе
такого распада энергия переходит от крупного распавшегося
вихря к более мелким. Процесс распада продолжается до тех
пор, пока не возникнут столь малые вихри, что для них Re*n<
<ReKp. Такие вихри устойчивы и не распадаются на более
мелкие. Чем больше число Re для всего потока, тем более мелкие
вихри могут в нем возникнуть. Процесс дробления не может,
однако, продолжаться бесконечно долго. Как было показано,
для мелких вихрей существен эффект диссипации, поэтому очень
мелкие вихри не могут существовать в потоке: расходуя свою
энергию на преодоление сил молекулярного трения, они
смешиваются с окружающей средой, а кинетическая энергия этих
вихрей превращается в тепло.
В развитом турбулентном потоке максимальной энергией
обладают не самые крупные вихри, размер которых порядка iwac-
штаба неоднородностей среднего движения L, а вихри
промежуточного размера /Д</Э<А. Вследствие хаотичности процесса
передачи энергии начальные условия мало влияют на режим
пульсаций мелких масштабов /</э, который можно считать
стационарным и изотропным. В этой области турбулентность
является универсальной, и в ней существует инерционный интервал>
где имеет место «закон 5/з».
Необходимо отметить, что экспериментально определяется
одномерный временной спектр, например спектр продольной
оо
компоненты энергии турбулентности £1(0)) (w"/2 = J Ei(oy)d(o>
о
о) — частота). Переход от временного спектра к
пространственному осуществляется с помощью гипотезы Тейлора, согласно
которой турбулентные вихри перемещаются вдоль потока со
средней скоростью без искажений, оставаясь как бы заморо-
Статистические характеристики турбулентного потока 553
женными. В силу этой гипотезы, называемой гипотезой
замороженной турбулентности, возмущение с масштабом I (волновое
число х = 2л//), распространяющееся со скоростью и, вызывает
в точке х0 = х—ut квазиколебание с периодом х = 1/и и частотой
(д = и/1 = ки. Поэтому временной и пространственный одномерные
спектры связаны соотношением
^1(о))=^£'1(х=^). (17.8.11)
U \ U J
Аналогичные соотношения справедливы для спектров других
компонент.
Что касается перехода от одномерных спектров,
определяемых экспериментально, к теоретическому трехмерному спектру
£(х), то для изотропного турбулентного поля можно получить
следующие выражения:
где xt — компонента волнового вектора на ось х\. Легко видеть,
что в инерционном интервале одномерные спектры также
подчиняются «закону 5/з».
17.9. Модель Гейзенберга переноса энергии турбулентности
по спектру
Рассмотренная в предыдущем параграфе теория
Колмогорова позволила получить много сведений о поведении спектра
и даже явный вид этого спектра в инерционном интервале
только из соображений подобия. Другие методы определения
формы спектра основаны на решении спектрального уравнения
(17.8.2), дополненного гипотезой замыкания о переносе энергии.
Предложено несколько гипотез о виде функции переноса 5(х),
основанных либо на соображениях размерности, либо на
некоторых интуитивных представлениях о механизме передачи
энергии от крупных вихрей к мелким. Наиболее широкое
применение получила гипотеза Гейзенберга, предложенная в 1948 г.
Спектральное уравнение в равновесном интервале имеет вид
X
S(x) —2vjx?£ (y.,)rfxi-e=0. (17.9.1)
554
Глава 17
Напомним, что S(x) характеризует перенос энергии в область
малых вихрей x^xi^oo из области больших вихрей О^х^х.
Гейзенберг предположил, что механизм передачи энергии от
крупных вихрей к мелким качественно подобен процессу вязкой
диссипации, при котором крупные вихри теряют свою энергию
на работу против сил трения, создаваемых мелкими
турбулентными вихрями. Процесс вязкой диссипации на спектральном
языке описывается вторым членом левой части (17.9.1),
представляющим собой произведение коэффициента молекулярной
вязкости v на завихренность поля скорости, выраженную в
спектральной форме. Гейзенберг предположил, что трение,
создаваемое мелкими вихрями, можно формально описать введением
спектрального коэффициента турбулентной вязкости /С(х) и
поток энергии 5(х) представить в виде
X
5(х) = 2/Г(х) \%]E(%l)d%l. (17.9.2)
6
Выражение для К(х) Гейзенберг строит по аналогии с
формулой для коэффициента вязкости v, получаемой в
статистической физике: v~vTl (vT — тепловая скорость, / — длина
свободного пробега). Проводя аналогию между молекулярным и
турбулентным движением, длину свободного пробега можно
заменить масштабом турбулентного вихря, т. е. /~1/х, а тепловую
скорость — корнем из средней квадратической пульсации
скорости, т. е. ат->- у и'2, или на спектральном языке y^Z?(x)/x.
Поскольку /С(х) характеризует трение, создаваемое всеми
вихрями, меньшими данного, то
с»
КЫ^УЩ^^й^. (17.9.3)
х
Таким образом,
С» X,
S(x)=2Tjl/A^-rfx, j\|£(*2)rf*2, (17.9.4)
х V %1 о
где у— безразмерная постоянная.
После подстановки (17.9.4) в (17.9.1) спектральное
уравнение запишется так:
СЮ Х( X
e = 2TJl/-^^-rfx, J^(xj)dx2+2v fx^(x2)rfx2. (17.9.5)
х ' %i о о
Статистические характеристики турбулентного потока 555
Решение этого уравнения, которое легко получить с помощью
к
введения функции #(х) = J x^£,(x2)dx2, имеет вид
о
ZT(*) = ^V^[l + ^-U<]-';\ (17.9.6)
Из (17.9.6) следует, что в области волновых чисел,
удовлетворяющих неравенству
.<(Зта"--,ж-£, (17.9.7)
спектральная плотность меняется по «закону 5/з»:
£(x) = Cs2/Vv\ (17.9.8)
где
^> 4 «/з
3 /з
Таким образом, для инерционной области спектра из теории
Гейзенберга следует колмогоровский «закон 5/з», при этом для
масштаба вихрей, принадлежащих инерционному интервалу,
получено такое же неравенство, какое было указано
Колмогоровым.1 Для этой области из (17.9.3) с учетом (17.9.8) следует
^(x) = as,/3x-4/a (17.9.9)
или
АГ(х) = а*/4/з^ (17.9.10)
где а* = (2я)~4/зае,/з.
Нужно отметить, что этот важный закон, устанавливающий
зависимость коэффициента турбулентности от масштаба, был
эмпирически получен Ричардсоном еще в 1928 г.; он называется
«законом 4/з» или законом Ричардсона.
В другом предельном случае, когда х<^Схд, т. е. когда
рассматривается область вихрей, для которых существен эффект
диссипации, из (17.9.6) следует
£(х) = С,4 х-'. (17.9.11)
1 Напомним, что речь идет о равновесном интервале, поэтому
рассматривается х>ха.
553
Глава 17
Хотя, как и следовало ожидать из физических соображений,
модель Гейзенберга приводит к более сильному убыванию
спектральной плотности в диссипативной области по сравнению
с инерционной, она не согласуется с экспериментальными
данными, которые указывают на гораздо более сильное убывание
спектральной плотности энергии Е(к) с ростом х, чем это
следует из (17.9.11).
Таким образом, можно заключить, что физическая модель
переноса энергии по спектру, предложенная Гейзенбергом,
приемлема только в инерционном интервале.1 Это, видимо, связано
с тем, что введение понятия спектральной турбулентной
вязкости оправдано лишь в том случае, когда мелкие вихри,
создающие эту вязкость, статистически независимы от крупных; оно
вряд ли пригодно для описания совокупного действия вихрей,
имеющих размеры одного порядка.
Кроме модели Гейзенберга, было предложено несколько
других моделей переноса энергии турбулентности по спектру. Все
эти модели дают в инерционной области «закон —5/з»; одни из
них приводят к противоречивым результатам в вязкой
подобласти, другие — к лучшему совпадению с экспериментальными
данными, чем модель Гейзенберга. Подробный анализ
различных моделей переноса энергии по спектру выходит за рамки
настоящей книги. Читатель может познакомиться с ними в
специальной литературе.
Кратко рассмотрим лишь еще одну модель переноса энергии,
предложенную Пао, которая неплохо согласуется с измерениями
в вязкой области спектра. В этой модели процесс переноса
считается каскадным процессом, при котором спектральные
элементы непрерывно перемещаются в область больших волновых
чисел. Если скорость перемещения спектрального элемента равна
а(х) = dyt/dt, то поток энергии S(x) = а(х)£(х). Далее делается
предположение, что каскадная скорость перемещения
спектрального элемента сг(х) зависит только от 8 и х. Тогда из
соображений размерности следует
a(*)=:C-W/3 (17.9.12)
и
S(x) = C-V/3xV8£(x). (17.9.13)
Подставив (17.9.13) в (17.9.1) и решив полученное
уравнение, находим
£(x) = Cs4.-'/3exp(- ^-а>,е-,/8х/з). (17.9.14)
1 Имеются указания на то, что модель Гейзенберга переноса энергии по
спектру не противоречит экспериментальным данным и для области более
крупных вихрей, размер которых выходит за границы инерционного
интервала.
Статистические характеристики турбулентного потока 557
Полученная формула для спектральной плотности энергии £(х)
имеет смысл для всей равновесной области х^>хэ или /<^/э.
В инерционной области, т. е. для хэСхСхд=(е^3)'\ из
модели Пао следует «закон — 5/з». В вязкой области формула
(17.9.14) дает гораздо более быстрое убывание энергии £(х)
с ростом х, чем формула (17.9.11), что неплохо согласуется
с экспериментальными данными.
17.10. Спектральные характеристики температурного поля
и спектральное уравнение баланса интенсивности
температурных пульсаций
Использовав преобразование Фурье для пульсаций
температуры аналогично тому, как это было сделано для пульсаций
скорости, можно получить для пространственной корреляционной
функции пульсаций температуры в однородном турбулентном
поле соотношение
#Т(Ч, /) = ]>(*, t)ei%nd*, (17.10.1)
представляющее Фурье-трансформацию корреляционной
функции. Из (17.10.1) следует
/?т(0, 0 = 2O=J/7(x, t)d%. (17.10.2)
Таким образом, функция F(xJ) описывает вклад в
интенсивность температурных пульсаций G турбулентных вихрей с
волновым вектором х; она называется спектральной функцией
интенсивности температурных пульсаций (ИТП).
Проинтегрировав (17.10.2) по направлениям вектора х, т. е.
по поверхности do сферы радиусом х, получим спектральную
плотность ИТП
0(х, 0 = 2 <$<§> F(x, t)do, (17.10.3)
Х,Х2 =: X2
характеризующую вклад в G вихрей с волновым числом х:
с»
G = JG(x, t)d%. (17.10.4)
о
Для случая изотропного поля из (17.10.3) следует
G(x, 0 = 4**2^(|*|. ')• (17.10.5)
Уравнение для G (х, t) в однородном турбулентном поле,
которое получается из (17.4.3) при использовании Фурье-
трансформации пространственной корреляционной функции
558
Глава 17
температурного поля /?т(ть /) и функции Ч'ггОП' О, описывающей
конвективный перенос температурных пульсаций, имеет вид
*?(%. О +/?(х> /) = _хх20(х> ^ (17.10.6)
Функция /?(х, 0 связана с коэффициентом Фурье функции
переноса
соотношением
/?(*, 0 = 2 j j »F(x, /)<*».
которое для случая изотропного турбулентного поля дает
/?(х, 0 = 41сх2Т(|х|, О-
оо
Из условия (17.4.15) следует, что J У? (х, t)d>i = Oy т. е. функция
о
/?(х, /) не вносит вклада в полную величину ИТП, но меняет
значение G(x, /), связанное с движением данного масштаба.
Следовательно, функция /?(х, t) описывает конвективный
перенос по спектру ИТП.
Можно показать, что спектр ИТП имеет форму, аналогичную
форме спектра энергии турбулентности, т. е. G(x, /) сначала
увеличивается с ростом х, достигает при x = xG максимального
значения, а затем убывает при дальнейшем увеличении х. Вихри
с х>хс находятся в статистическом равновесии. Для
равновесной области спектральное уравнение записывается в виде
Ж*)=-х*20(*).
Напишем это уравнение для области волновых чисел от х до оо:
СЮ X
|/?(х,)Л, = Я(х) = ЛГ-х f 4G(*2)d4, (17.10.7)
X 6
где
оо
N = x fx2(7(x)rfx
6
есть скорость выравнивания температурных неоднородностей.
На основе уравнения (17.10.7) могут быть сформулированы
гипотезы Обухова о функции G(x) в равновесном интервале,
являющиеся обобщением гипотез Колмогорова на случай
температурного поля. При этом нужно иметь в виду, что вследствие
того, что функция Р(х), характеризующая перенос ИТП по
Статистические характеристики турбулентного потока 559
спектру, связана с пульсационным полем скорости, функция
G (к) должна также зависеть от внешних параметров, которые
определяют энергию турбулентности в этом спектральном
интервале. Поэтому первая гипотеза Обухова
формулируется следующим образом: в равновесном интервале
спектральная плотность ИТП зависит от четырех внешних параметров —
скорости диссипации е, скорости выравнивания температурных
неоднородностей N, кинематической вязкости v и молекулярной
температуропроводности х, т. е.
G(x) = <P(s, N, v, ъ х). (17.10.8)
Используя П-теорему теории размерности, (17.10.8) можно
написать в виде
0(х) = ^-5/^<ф^_л_> ^_у (17109)
Масштаб /*=xvVeV4 характеризует размер турбулентных вихрей,
вносящих основной вклад в спектр диссипации ИТП x2G(x); он
называется внутренним масштабом температурного поля.
Внутренние масштабы полей скорости и температуры связаны
соотношением
/, = /д(Рг)-1/4. (17.10.10)
где Pr = v/x — молекулярное число Прандтля.
Вследствие того, что влияние молекулярной
теплопроводности уменьшается при уменьшении волнового числа, можно
предположить, что в области XG<x<x5ic = e,'4x~3/4 спектральная
плотность не должна зависеть от характеристик молекулярного
движения. Интервал волновых чисел х0<х<х* называется
инерционно-конвективным интервалом. Для этого интервала
формулируется вторая гипотеза Обухова: в
инерционно-конвективной подобласти спектральная плотность ИТП
определяется двумя внешними параметрами — е и N. Из (17.10.9) для
инерционно-конвективного интервала легко получить формулу
для спектральной плотности ИТП:
G(x) = a/V£-Vsx-"/3, (17.10.11)
т. е. зависимость G(x) от волнового числа является такой же,
как и зависимость от х спектральной плотности энергии
турбулентности.
Формула (17.10.11) получена только из соображений
размерности, без каких-либо предположений о функции Р(х). Можно
показать, что использование для механизма конвективного
переноса ИТП по спектру модели Гейзенберга приводит к
формуле (17.10.11) в инерционном интервале и к закону G(x)~x-7
560
Глава 17
в вязкой области. Модель Пао дает для спектра ИТП в
равновесной области формулу
0(x) = a.Ve-,/\-5/3exp( ^аХе-,/зх4/з), (17.10.12)
которая не противоречит экспериментальным данным.
17.1 К Влияние стратификации на спектральные характеристики
полей скорости и температуры
Рассмотренные выше данные о спектральных
характеристиках энергии турбулентности и интенсивности температурных
пульсаций были получены без учета термического расслоения
атмосферы, проявляющегося в возникновении силы плавучести.
Как отмечалось при анализе уравнения баланса энергии
турбулентности, член, отражающий влияние силы плавучести, при
неустойчивой стратификации является источником, а при
устойчивой стратификации — стоком энергии турбулентности. В
термически расслоенной атмосфере вертикальное направление
оказывается выделенным; в этом случае можно предположить, что
турбулентность является локально-осесимметричной
относительно вертикали. Наличие силы плавучести приводит к тому,
что в стратифицированной атмосфере нельзя исследовать спектр
энергии турбулентности независимо от спектра ИТП.
Впервые соображения о влиянии стратификации на тонкую
структуру турбулентного потока были высказаны в 1959 г.
Обуховым, который предположил, что в термически
стратифицированной атмосфере статистические характеристики компонент
турбулентности с масштабом из инерционно-конвективного
интервала определяются тремя внешними параметрами — е, N\ р =
=g/T:
E(*) = F(*t TV, р, x)=Ce2/»x-,/MF(xZ#),
G(x) = (D(e, N, P, x)=rfe",/Wx~s/l4TT(xZ#). (17.11.1)
Видно, что в этом случае появляется новый масштаб длины
который был назван масштабом длины Обухова.
При р=0, т. е. в нестратифицированном потоке, L*—>-оо,
*¥ (xL*) =1 и 4rT(xL#)=l. Обухов предположил, что при (3^0,
но xL#3>l, т. е. для компонент турбулентности, масштаб
которых меньше L*, стратификация не оказывает влияния, т. е.
4я(xL*) и 4rT(xL^) стремятся к своим асимптотическим
значениям. Для турбулентных вихрей, размер которых I сопоставим
Статистические характеристики турбулентного потока 561
с L* и больше его (эта область спектра называется интервалом
плавучести), учет влияния стратификации необходим. Обухов,
однако, не установил конкретного вида функций ^(xL*) и
^T(xLJ.
Аналогичный подход был использован Болджиано (1962 г.),
который сделал добавочное предположение: в интервале
плавучести в устойчиво стратифицированной атмосфере величину е
можно исключить из числа значимых параметров, так как в этом
случае энергия, получаемая от более крупных вихрей,
практически полностью расходуется на работу против силы плавучести.
При этом предположении из (17.11.1) следует:
£(x)~?4/W2/V-n/5, (17.11.3)
G(x)«p3/W4/5x-7/s, (17.11.4)
т. е. в устойчиво стратифицированной атмосфере в интервале
плавучести имеет место «закон — и/б» для спектральной
плотности энергии и «закон — 7/5» для спектра ИТП.
Другой подход был предложен Ламли и Шуром. Этот подход
является по существу обобщением теории Колмогорова на
случай стратифицированной атмосферы. Напомним, что в теории
Колмогорова для инерционного интервала спектра содержатся
два предположения:
1) турбулентный режим в волновом пространстве полностью
•определяется спектральным потоком энергии турбулентности по
•спектру 5 (х);
2) спектральный поток в инерционном интервале постоянен
и равен е.
В теории Ламли—Шура делается допущение, что в
устойчиво стратифицированной атмосфере можно отказаться от
второго предположения, сохранив первое. Турбулентность,
удовлетворяющая этому условию, называется локально-инерционной,
т. е. при каждом волновом числе спектральная плотность
энергии определяется только спектральным потоком 5(х), но этот
поток теперь не постоянен, а зависит от х.
Можно показать, что при учете влияния стратификации
спектральное уравнение баланса в области статистического
равновесия запишется в виде
с»
5(x) = e-pjA/(x,)rfx1 = 8(x). (17.11.5)
Здесь второй член в правой части является спектральным
аналогом члена $и'3&', входящего в уравнение баланса для полной
энергии турбулентности, записанным для области волновых
36 Заказ № G12
562
Глава 17
чисел от х до оо; #(х)—спектр вертикального турбулентного
потока тепла:
и6Т'=\ Я(х)Л. (17.11.6)
6
По аналогии с гипотезой Колмогорова в теории Ламли—
Шура предполагается
Я(х) = /7(е(х), x) = C(e(x))2/3x~Vs. (17.11.7)
Функция е(х) может быть определена из уравнения (17.11.5);
для этого необходимо сделать предположения о спектре
турбулентного потока тепла #(х). В теории Ламли—Шура делается
предположение, что #(х) зависит от вертикального градиента
потенциальной температуры и от тех же характеристик, от
которых зависит спектр энергии турбулентности, т. е. от е (х) и х.
Из этого предположения следует, что
/Д*) = -а-Ц-(е(*)),/'х-''\ (17.11.8)
Подставив (17.11.8) в (17.11.5), нетрудно получить
s(x)=e2'"[l4-(^P], (17.11.9)
где
/ Л'З \-34
(17.11.10)
Подставив (17.11.9) в (17.11.7), находим
£(x) = Cb2/8Ji + (^)~4/8]x-";3. (17.11.11)
Из этого соотношения следует, что при (х/хр)~4/з<^ 1 имеет
место «закон — 5/з», а при (х/хр)~4/з^>1
Е^~$[1ГгУ3- (17.11.12)
Таким образом, из теории Ламли—Шура следует, что в
интервале плавучести, который определяется условием />1/хр
(причем масштаб длины Lp=l/xp отличен от масштаба длины
Обухова), спектр энергии турбулентности убывает с ростом
волнового числа по «закону —3».
Хотя на основании двух рассмотренных подходов получены
разные формы спектра энергии в интервале плавучести («закон
—п/ь» Болджиано и «закон —3» Ламли—Шура), вырисовыва-
Статистические характеристики турбулентного потока 563
ются и некоторые общие закономерности в поведении спектра
при наличии эффекта плавучести (существование инерционного
интервала с «законом —5/з», независимость энергии в интервале
плавучести от е).
Были предложены и другие подходы, позволяющие учесть
влияние стратификации на спектральные характеристики
турбулентности. Они главным образом основаны на решении системы
спектральных уравнений для энергии и ИТП, записанных с
учетом эффектов плавучести и порождения энергии и ИТП
средними полями скорости и температуры. При таком подходе
необходимо использовать предположения о механизмах переноса
энергии и пульсаций температуры по спектру, а также гипотезы
замыкания для спектральных турбулентных потоков тепла и
количества движения. Некоторые из этих подходов приводят
в интервале плавучести при устойчивых условиях к «закону
—п/ъ»у другие — к «закону —3»; имеются теории, в которых
в зависимости от значимости внешних параметров получается
либо «закон —п1ъ», либо «закон —3».
К сожалению, имеющихся экспериментальных данных о
спектральных характеристиках энергии и ИТП недостаточно для
надежного определения формы спектров в интервале плавучести.
Во многих случаях измерения указывают на наличие участка
спектра Е(к) с наклоном —3, часто обнаруживается также и
наклон —п1ъ-
Контрольные вопросы
1. Из каких соображений следует, что в однородном
турбулентном поле члены, содержащие пульсации давления,
характеризуют перенос энергии турбулентности от одних компонент
к другим?
2. Получите формулы (17.3.5) и (17.3.6).
3. В чем состоит физический смысл тензора инерции в
однородном турбулентном поле?
4. В чем смысл гипотезы о статистическом равновесии?
5. Какие области можно выделить в спектре энергии
турбулентности в термически стратифицированном турбулентном
потоке?
36*
Глава 18. ТУРБУЛЕНТНАЯ ДИФФУЗИЯ ПРИМЕСЕЙ
И ЗАГРЯЗНЕНИЕ АТМОСФЕРЫ
Формулировка задачи о распространении примесей в атмосфере.
Качественный анализ условий распространения примесей. Поперечное рассеяние частиц
от непрерывного точечного источника. Распределение примесей при разных
метеорологических условиях и разных параметрах выброса. Расчет
многолетних средних значений концентрации. Выбор высоты трубы при
проектировании промышленных объектов.
Изучение закономерностей распространения примесей,
поступающих в атмосферу из источников различного типа, является
одной из наиболее важных прикладных задач физики
атмосферы. Значение этой задачи определяется прежде всего тем,
что она тесно связана с проблемой охраны окружающей среды.
Загрязнение воздуха вредными веществами стало в последние
годы серьезной проблемой для большинства промышленно
развитых стран. С ростом числа и мощности промышленных
предприятий, вводом в действие новых электростанций (как
тепловых, так и атомных) возрастает опасность, что концентрация
примесей, поступающих в нижние слои атмосферы, может
превысить предельно допустимые величины. Совершенно очевидно,
что степень загрязнения нижних слоев атмосферы вредными
примесями зависит не только от технологических и
конструктивных параметров промышленных объектов (таких, как мощность
выброса, высота и диаметр труб, скорость переноса и
температура выбрасываемых в воздух веществ и т. п.), но и от тех
факторов, которые определяют процесс распространения
примесей в атмосфере. Этими факторами являются скорость ветра,
стратификация атмосферы, орография местности и характер
подстилающей поверхности. Они обусловливают скорость
переноса примеси вдоль направления среднего ветра и
интенсивность турбулентного перемешивания. При определении средних
значений концентрации за большие промежутки времени
упомянутый комплекс характеристик необходимо дополнить
информацией о повторяемости направлений ветра.
Первоочередная задача состоит в развитии теории
распространения примесей в атмосфере, которая позволила бы
получить информацию о загрязнении воздуха при разных
метеорологических условиях и разных параметрах источника. На основе
такой информации должны быть разработаны методы учета
метеорологических условий при проектировании и эксплуатации
Турбулентная диффузия примесей и загрязнение атмосферы 565
предприятий (выбор высоты трубы и мощности выброса,
рациональное размещение жилых массивов) с целью обеспечения
безопасного уровня загрязнения воздуха.
Приступая непосредственно к рассмотрению процессов
распространения примеси, следует иметь в виду, что в
подавляющем большинстве интересующих нас случаев они протекают
в пределах пограничного слоя атмосферы. Поэтому
представления о структуре последнего, в частности о механизме
турбулентного обмена, развитые в соответствующих главах,
естественно лежат в основе излагаемых ниже положений.
18.1. Математическая формулировка задачи о распространении
примесей в атмосфере
В главе 1 было получено уравнение баланса массы для
любой субстанции, взвешенной в воздухе, которое может быть
использовано и для описания рассеяния примесей, поступающих
в атмосферу. Это уравнение можно записать в виде
-5Г+^=--^-ф+/с(*ь '>• (18ЛЛ)'
Здесь С — объемная концентрация примеси, \C]=ML~3\ vi —
t'-тая компонента скорости ветра; /гДиф = —D— есть диффу-
знойный поток частиц примеси в r-том направлении,
обусловленный молекулярным движением; D — коэффициент молекулярной
диффузии; 1С — функция, описывающая источники и стоки
примеси.
Вид функции, описывающей поступление примеси, зависит
от конкретного типа источника — непрерывный или мгновенный,
точечный, линейный или объемный кч. п. В тех случаях, когда
источник сконцентрирован в точке или на плоскости, его удобно
учитывать с помощью краевых условий, исключая
соответствующее слагаемое из уравнения. Поскольку в дальнейшем будет
рассматриваться точечный источник, его наличие будет записано
в виде краевого условия. Стоками примеси могут быть
следующие факторы: радиоактивный распад (если в воздух поступает
радиоактивная примесь), захват частиц каплями дождя или
тумана. Для этих ситуаций функция 1С может быть записана
1 Уравнение (18.1.1) записано для частиц примеси, гравитационным
оседанием которых можно пренебречь. Если необходимо учесть гравитационное
оседание, происходящее с постоянной скоростью ш, то в левую часть (18.1.1)
следует добавить слагаемое —wdC/дхз. Отметим, что все излагаемые ниже
результаты при этом не изменятся.
-5G6
Глава 18
в виде /с=—С/т, где т — коэффициент, характеризующий
уменьшение концентрации примеси за единицу времени по указанным
выше причинам. Величина х имеет размерность времени и
может быть названа временем жизни частиц. В случае
радиоактивного распада т = Г/1п2, где Т — период полураспада. Если
же время жизни т характеризует захват частиц примеси
каплями дождя или тумана, то оно зависит от спектра капель
дождя (или тумана), интенсивности дождя (водности тумана),
а также от размера и физико-химических свойств частиц
примеси. Эта важная характеристика может быть определена либо
из теории процессов взаимодействия капель и частиц примеси,
либо на основании специально проведенных экспериментов.
С учетом сделанных замечаний, а также квазинесжимаемости
воздуха перепишем (18.1.1) в виде
-^+JLViC=D-^r—-. (18.1.2)
Вследствие турбулентного характера атмосферных движений
концентрация примесей, так же как и остальные характеристики
турбулентного потока, будет нерегулярно изменяться в
пространстве и во времени. Поэтому необходимо осреднить уравнение
(18.1.2). Заменив в нем С = С + С\ Vi = vi + v'. и использовав
•сформулированные в главе 7 правила осреднения, получим
дС , — дС д ГрГГ , п д2С С /ю 1 о\
-5r+,"dJ7=—3S7V'C +D-^-—• (18Л-3)
В (18.1.3) член v'.C описывает турбулентный поток примеси
в г-том направлении. Вследствие того что турбулентные потоки
примеси на несколько порядков превышают молекулярные
потоки Iv'C'^D—-—1, в (18.1.3) можно пренебречь вторым
членом в правой части по сравнению с первым. Тогда (18.1.3)
запишется следующим образом:
В дальнейшем мы будем интересоваться вопросом рассеяния
примесей, поступающих из непрерывного точечного источника,
и рассматривать установившееся распределение примеси, прене-
1 Имея в виду, что в (18.1.4) входят осредненные за интервал 7^30 мин
значения v\ и Сь в дальнейшем не будем ставить знак осреднения (черта
сверху) над этими величинами.
Турбулентная диффузия примесей и загрязнение атмосферы 567
брегая членом dC/dty описывающим изменение концентрации со
временем. Поскольку остальные члены (18.1.4) могут изменяться
со временем (в частности, вследствие суточного хода
метеоэлементов), величина С может параметрически зависеть от
времени; в этом смысле уравнение (18.1.4) дает возможность
определить изменение С в течение суток. Определение поля
концентрации примеси, возникающего вследствие наличия
непрерывного точечного источника, представляет наибольший интерес для
практики.
Если ось xi направить вдоль ветра, то можно пренебречь
членом, описывающим турбулентный перенос примеси в
направлении ветра I——и^С), по сравнению с ее переносом вет-
Vi—ц—) . Тогда уравнение (18.1.4) перепишется в виде
Уравнение для среднего значения концентрации является
незамкнутым, так как в него, кроме С, входят неизвестные члены
v'2C, v'3C , описывающие турбулентные потоки примеси.
Необходимо сформулировать гипотезы замыкания, основываясь на
некоторой модели турбулентного переноса примесей. Кроме того,
из (18.1.4) видно, что условия распространения примеси зависят
от поля ветра в пограничном слое атмосферы.
Обращаясь к вопросу о турбулентной диффузии примеси,
необходимо учесть важную специфику явления. Дело в том, что
в рассеянии облака примеси принимают участие турбулентные
вихри, размер которых меньше размера диффундирующего
облака. Более крупные турбулентные вихри вызывают смещение
облака примеси как целого, создавая faK называемую
извилистость струи. По мере роста размеров диффундирующего облака
с удалением от источника растет также характерный масштаб
турбулентных вихрей, обусловливающих рассеяние примеси.
Вследствие наличия подстилающей поверхности имеются
различия в характере турбулентного переноса примесей в
горизонтальном и вертикальном направлении. Если примеси
распространяются в нижнем слое атмосферы, то с ростом облака
непрерывно растет масштаб горизонтальных пульсаций,
принимающих участие в рассеянии. Что касается вертикальных пульсаций,
то их размер лимитируется расстоянием от земной поверхности,
1 В (18.1.5) также пренебрегают изменением направления ветра с высотой.
568
Глава 18
вследствие чего можно не учитывать рост масштаба вихрей,
приводящих к рассеянию по вертикали, по мере роста облака.
Поэтому для определения вертикального турбулентного потока
частиц примеси можно использовать соображения, аналогичные
тем, которые применялись для описания вертикальных
турбулентных потоков тепла и количества движения, а именно
предположить, что
дС
V3C =-k,(x3)^r. (18.1.6)
В то же время неясна принципиальная возможность
введения коэффициента турбулентности для описания
горизонтального турбулентного переноса примеси; в лучшем случае это
может привести к большим погрешностям. Трудность, связанная
с необходимостью учета зависимости от расстояния Xi
интенсивности горизонтального рассеяния, может быть обойдена
следующим образом. Экспериментальные данные указывают, что
рассеяние примеси в горизонтальном направлении х2
удовлетворительно описывается формулой Гаусса. В соответствии с этим
будем искать концентрацию примеси С(х\, х2> Хз) в следующем
виде:
_А
С{хи л-2> Хг) = -*-£=-S(xu х3), (18.1.7)
У 2тса2
где а2 — горизонтальная дисперсия частиц примеси; очевидно,
что о характеризует среднюю ширину облака частиц в
перпендикулярном среднему ветру направлении. В соответствии с
изложенными выше соображениями горизонтальная дисперсия а2
должна зависеть от расстояния от источника. Вопрос об
определении о будет рассматриваться ниже.
Подставив (18.1.6) и (18.1.7) в (18.1.5) и выполнив
интегрирование по хг от —оо до +оо, получим двумерное уравнение
турбулентной диффузии для определения функции S(xi, х3):
dS д 1 dS S /1о 1 о\
"•-згг—агг*»-ЕГ--- (18л,8)
Функция S(xu Хз) представляет собой полное количество
примеси в ориентированном перпендикулярно направлению ветра
параллелепипеде бесконечной длины с единичным поперечным
сечением. Эту величину будем называть плоской концентрацией,
[S]=ML~2.
Турбулентная диффузия примесей и загрязнение атмосферы 569
Для непрерывного точечного источника, находящегося на
высоте Л, решение уравнения (18.1.7) должно удовлетворять
следующим граничным условиям:
М
дхъ
ps)
X3 — Zq
=0,
S=(x\9 -*з) I*,-►оо = 0.
^
, dS
(18.1.9)1
Здесь М — мощность источника, т. е. количество примеси,
поступающей из источника за единицу времени. Величина р
характеризует поглощение примеси подстилающей поверхностью:
если подстилающая поверхность оказывается непроницаемой
для примеси, то р=0 (условие полного отражения); условию
полного поглощения соответствует р = оо, а значения 0<р<оо
соответствуют случаю частичного поглощения и частичного
отражения примеси на границе. В (18.1.9) б (х3 — h)—дельта-
функция;
(0 при Хз-^А,
о(х3 — п) = \
v ' { оо при лг3 = А-
Для решения уравнения турбулентной диффузии (18.1.8)
необходимо задать профили ветра и коэффициента
турбулентности. Используем для этой цели результаты численной
реализации модели пограничного слоя, описанной в главе 11. Поскольку
при решении системы уравнений пограничного слоя получены
универсальные зависимости в безразмерном виде2 un(zn> м-о,
Ro), kn{Zn, [Ло), то целесообразно уравнение (18.1.8) и
граничные условия (18.1.9) привести к безразмерному виду, используя
для г, u(z) и k(z) такие же масштабы, как и в главе 11. Это
даст возможность непосредственно 'реализовать полученные
результаты для ип и kn при решении уравнения диффузии.
В безразмерном виде уравнение и граничные условия
записываются так:
ип ^ — л* кп ■
дхп
дгп
дхп
(18.1.10>
1 С учетом гравитационного оседания второе краевое условие запишется
(*-35Г-«*-!*)
= 0.
x3 = z0
2 Здесь и далее un = vln, кгп = кПу Хщ=хП1 x3n=zn. Эти же
обозначения относятся и к размерным величинам.
570
Глава 18
С (у * \\ п _ ьп (*п — hn)
k ^
№п
^п \Хп > Zn)
= 0,
Здесь
"0п
= 0.
(18.1.11)
(18.1.12)
(18.1.13)
S„ =
Sv^L\
АН
*п = -
%Х
X,
Zn = -r =
\z
Ik
'^Л\
2 2
Рл =
j (18.1.14)
Разумеется, возможно только численное решение
сформулированной задачи, ибо ип и kn представлены в затабулирован-
ном виде. Отметим, что при численном решении граничное
условие при хп = 0 заменяется аппроксимацией Sn вблизи
источника какой-либо функцией, имеющей острый экстремум при
zn = hn, например аналитическим решением этой задачи при
un(zn) =un(hn) = const и kn(zn) =kn(hn) = const. Погрешности,
являющиеся следствием такой аппроксимации, быстро
сглаживаются с увеличением хп. Результаты численного решения
представляются в форме таблиц, описывающих зависимость Sn =
= Sn(xn, zn, An, jlxo, Ro). На практике наибольший интерес
представляют значения концентрации вблизи земной поверхности
гп~0, т. е. приблизительно на уровне дыхания.
Вследствие того что решение задачи может быть выполнено
только численно, представляется целесообразным выполнить
сначала качественный анализ зависимости Sn от основных
влияющих факторов.
18.2. Качественный анализ поля концентрации примеси
Как следует из уравнения (18.1.10) и граничных условий
(18.1.11) — (18.1.13), плоская безразмерная концентрация
определяется зависимостью
Sn = Sn(xn, zn, иП) kny hni ря, z0n). (18.2.1)
В свою очередь в теории пограничного слоя установлено, что
kn = kn(zn, jxo, Ro), (18.2.2)
*п = ия(гЯ9 {х<ь Ro). (18.2.3)
Турбулентная диффузия примесей и загрязнение атмосферы 571
Поэтому, используя (18.2.2) и (18.2.3), можно (18.2.1)
переписать в виде
Р„, l/l^o, 1/Ro). (18.2.4)
Обратимся к качественному анализу этой зависимости,
полагая в целях наглядности f3n = 0, что соответствует условиям
полного отражения примеси от земной поверхности. Вспоминая
явный вид |я0 и Ro и подставляя выражения для масштабов,
можем вместо (18.2.4) записать выражение
5^^-ф/А, JL9 P»S ^Р_, _^М (18.2.5)
Постоянную x мы везде опускаем, ибо вид функциональной
зависимости от этого не меняется.
Если учесть, что величина Xzo/v# весьма мала и на процесс
диффузии влияет слабо, то, очевидно, этот параметр,
отражающий влияние шероховатости, можно из рассмотрения исключить
(Xzo/v^~0)} Для наземных концентраций (г-*0, Xz/v*~0)
выражение (18.2.5) упрощается еще больше. И наконец, полагая,
что атмосфера стратифицирована нейтрально (Ро~0, Pog/pcpX
ХвоЯ^—0), вместо (18.2.5) получим
Рассмотрим ряд для 5 при малых и больших х. В первом
случае (x^vJX) справедливо разложение
5 = ^ГФ,(0, tt) + J* *>!<?■ «)+^*М0.«>
1 v ' ' v* дг • 2v2 ^2
,.2
где a = hk/v*. Величина Oi(0, а) =0, ибо при х-^0 S->0.
Поэтому из предыдущего выражения следует
S-«^*(l + 6-£+...), (18.2.7)
где
дФ\ (0, а)
а= а(а) =
дг
0—0\*)— 2 -^ j ^
1 Предполагается, что при A,z0A>*—> 0 функция остается конечной.
572
Глава 18
Если ограничиться двумя первыми членами разложения, то на
основе (18.2.7) можно сделать вывод, что при малых х
величина S меняется приблизительно по параболическому закону,
возрастая вместе с координатой.
При больших х (x^v^/K) разложение следует вести по
параметру vjx\. В итоге, рассуждая аналогично предыдущему и
учитывая, что при х->оо S-^О, получим
S=d\
М
('+». *+•••)•
(18.2.8)
Здесь
ах = ах (а) = т ,
дг
Ьх = Ъх (а) =-д- / ^
Г\=-
Хх
Из (18.2.8) видно, что при больших х концентрация убывает
приблизительно обратно пропорционально расстоянию от
источника.
Поскольку 5 = 0 при х^О и а;^-оо, а по физическому
смыслу 5^0, то внутри этого интервала величина 5 должна иметь
максимум.
Точку максимальной наземной концентрации хтах находим
= 0, используя (18.2.6). Это приводит
из условия
дх
к соотношению
дх 1ФЧ V* ' V* )]
= 0.
Отсюда получаем
-Ч-£)
(18.2.9)
Подставив (18.2.9) в (18.2.6), находим значение максимальной
наземной концентрации Smax:
с М ( h\ \
(18.2.10)
Турбулентная диффузия примесей и загрязнение атмосферы 573
При малых hX/v* (что на самом деле имеет место, ибо обычно
/z^lOO м, Я~10~4 с-1, а*~0,1 м/с) справедливы разложения:
хш* = а2н{\+Ь2^-+...), (18.2.11)
Smax = a3^L(l+*3-£-). (18.2.12)
Таким образом, в первом приближении можно считать, что
положение точки максимума меняется прямо пропорционально
высоте источника, а значение максимальной концентрации ему
обратно пропорционально.
Если бы мы рассматривали не высотный, а наземный
источник, то все предыдущие рассуждения полностью сохранили
бы силу; конкретные же результаты могут быть получены из
приведенных выше формул при Л = 0. При этом из (18.2.9) и
(18.2.10) следует, что xmax \ h^o -> 0, a Smax I л-м>->- оо.
Кстати заметим, что под высотой источника мы везде
понимаем сумму геометрической высоты трубы h и некоторой
добавочной высоты Ah. Последняя определяется подъемом облака
примеси над срезом трубы, который обусловлен наличием
первоначального количества движения в струе выходящих из трубы
газов и их перегревом по отношению к атмосферному воздуху.
Определение этой величины представляет собой специальную
и весьма сложную задачу, рассмотрение которой выходит за
рамки настоящего учебного пособия.
В заключение рассмотрим процесс распространения примеси
в условиях термической конвекции, когда влияние динамического
фактора, отражаемого величиной и*, является весьма малым
(v*-+Q) и решающее значение приобретает Ро. Как и ранее,
будем рассматривать плоскую концентрацию примеси от наземного
источника (Xh/v*=0) на уровне земной поверхности (Xz/v* = 0),
исключая влияние шероховатости (kzo/v#=0). При этих
условиях из (18.2.5) получим
5=^ф2/^, p°g 2 \. (18.2.13)
Формулу (18.2.13) можно переписать еще в виде
(18.2.14)
Если рассматривается наземный источник, то процесс диффузии
в основном имеет место в приземном слое, где влияние силы
Кориолиса является весьма малым. В силу этого комплекс,1
574
[лава 18
содержащий Л, можно исключить из рассмотрения. Так как в
данном случае v*—>-0, то соответствующий комплекс также
стремится к нулю. Поэтому вместо (18.2.14) получим
S=a4M у ^-х~ч\ (18.2.15)
где а4 = Ф2(0, 0).
Из (18.2.15) следует, что приземная концентрация убывает
обратно пропорционально расстоянию от источника в степени 4/з-
18.3. Поперечное рассеяние частиц, поступающих
из непрерывного точечного источника, в турбулентном потоке
В п. 18.1 было показано, что рассеяние частиц в
перпендикулярном среднему ветру направлении можно описать законом
Гаусса, единственным параметром которого является дисперсия
частиц а2. Эта величина характеризует среднее квадратическое
смещение частиц примеси, поступающих в атмосферу из
непрерывного точечного источника (или среднее квадратическое
расширение струи дыма).
Настоящий параграф посвящен определению а2. Для этого
необходимо рассмотреть движение частиц в турбулентном
потоке. Удобным оказывается лагранжев метод описания, когда
рассматривается движение фиксированной частицы, которое
в турбулентном потоке является случайным. Предположим, что
примесь «пассивна» (т. е. не влияет на движение среды) и
перемещается в потоке со скоростью, практически совпадающей со
скоростью течения в соответствующей точке.
Рассмотрим движение частиц примеси в поле однородной
стационарной турбулентности. Нас будет интересовать
перемещение частиц в перпендикулярном среднему ветру направлении у.
Поскольку компонента средней скорости в этом направлении
равна нулю, то перемещение частиц происходит под влиянием
пульсаций скорости, так что
-% = v'(t). (18.3.1)
Частица, находившаяся в начальный момент времени U в
начале системы координат, через время t (в момент V = to+t)
будет находиться в точке
с t
y = j^'(i;)#=jV (!;)#. (18.3.2)
/о 6
Турбулентная диффузия примесей и загрязнение атмосферы 575
Из (18.3.1) и (18.3.2) находим
и, следовательно,
t г t г
У2 (/) = 2 jV(i;)^ lv'(\x)d\x = 2ldl jV (l) v'(b)db. (18.3.3)
0 0 0 0
Осреднив (18.3.3) по времени, получим среднее квадратиче-
ское смещение частицы в турбулентной среде, называемое также
поперечной дисперсией:
о2 (/)=7(0 = 2 $d^v'(t)v' &) d\x. (18.3.4)
Черта сверху, как и раньше, означает осреднение по времени.
Согласно принятой в теории турбулентности эргодической
гипотезе, осреднение по времени эквивалентно осреднению по
большому числу частиц, которые последовательно начинают свое
движение из фиксированной точки — источника (осреднение по
статистическому ансамблю).
В отличие от хаотичного движения молекул, движения
частиц примеси в турбулентном потоке в разные моменты времени
§ и £t не являются независимыми, а в большей или меньшей
степени коррелированы. Введем в рассмотрение лагранжев
коэффициент корреляции
^(^«^ШВ.. (18.3.5)
Положим | — 5i = t. Тогда (18.3.4) преобразуется следующим
образом:
t о t s
o*(0 = 2Jd5 [v'(\)v'(\+%)d% = 2\dllv'(\)v'(\-x)d* =
0 -; 0 0
/ i
= 2v'2 \d\ )RL{i)dx. (18.3.6)
о 0
Формула (18.3.6) впервые была получена Тейлором в 1921 г. и
обычно называется его именем.
576
Глава 18
Выполним в (18.3.6) интегрирование по частям:
t i S t t
0 0 0 0 0
о 0
Тогда формулу (18.3.6) можно переписать в следующем виде:
/
o2(t)=2v'2$(t-x)RL(z)dx. (18.3.7)
о
В таком виде формула для дисперсии частиц в турбулентном
потоке была получена Кампе де Ферье в 1939 г.
Из (18.3.7) видно, что для определения o2(t) нужно знать
дисперсию пульсаций скорости v'2 в направлении у и лагранжев
коэффициент корреляции #ь(т). К сожалению, вследствие
больших трудностей, связанных с изучением лагранжевых
характеристик, функция /?ь(т) мало исследована как экспериментально,
так и теоретически. Однако известны некоторые свойства
коэффициента корреляции, а именно: /?L(0)=1, /?l(t) |t-k» = 0,
Rl(x)—симметричная относительно т функция, которые
позволяют определить зависимость от времени дисперсии частиц
o2(t) в двух предельных случаях — при малых и больших t.
Рассмотрим сначала малые t. Разложим Rl{^) в ряд:
#(0 = 1—233-. (18'3'8>
1 d2R I
где —гт- = г-5- • Величина К называется лагранжевым
№ ахЛ 1т=о
временным микромасштабом.
Подставив (18.3.8) в (18.3.7) и выполнив интегрирование,
получим
1 t2 f
что для ———< 1 дает
6 А2
#{1) = ч)'гр. (18.3.9)
Отсюда следует, что для малых промежутков времени
дисперсия частиц прямо пропорциональна квадрату времени
диффузии.
Турбулентная диффузия примесей и загрязнение атмосферы 577
Рассмотрим теперь случай, когда интервал времени t велик
по сравнению с лагранжевым интегральным временным
масштабом
со
TL=lRLW-z, (18.3.10)
О
характеризующим интервал времени, в течение которого
существует заметная корреляция между скоростями частицы в
турбулентном потоке (т. е. для t>rL, Rl(i) ->0). В этом случае при
интегрировании в (18.3.7) верхний предел можно устремить коо
и получить
оо
i2(t) = 2^:TL(t)-2^ ^ %RL(>z)d'z = 2v;TTLt+consL
о
Для больших / постоянная пренебрежимо мала по сравнению
с первым членом, следовательно,
о*У) = 2^Т^, (18.3.11)
т. е. при больших / дисперсия прямо пропорциональна времени
диффузии.
Изменение o2(t) со временем между рассмотренными двумя
предельными случаями зависит от формы корреляционной
кривой /?i,(t). Поскольку точная зависимость /?ь(т) от времени для
всех значений т неизвестна, то в настоящее время 'для
определения поперечной дисперсии a2(t) используются аппроксимацион-
ные формулы либо для #ь(т), либо непосредственно для o2(t).
В частности, можно использовать простейшую
интерполяционную формулу
о2(0== »''*-, (18.3.12)
удовлетворяющую предельным соотношениям (18.3.9) и
(18.3.11). При применении (18.3.11) к вычислению дисперсии
частиц на фиксированном расстоянии х от непрерывно
действующего источника нужно заменить t=x/u, где и — средняя
скорость ветра. Тогда получим
3 W= — ' ■
1+^—
2uTL
37 Заказ Хо 612
578 Глава 18
Для расчета поперечной дисперсии а2 (х) по (18.3.12) нужна
информация о TL, v'\ и. Профили дисперсий поперечных
пульсаций скорости ветра v'2(z) и средней скорости ветра и (г) при
разных внешних условиях можно получить в результате
численной реализации модели пограничного слоя, описанной в главе И,
дополненной системой уравнений для дисперсии пульсаций
различных компонент скорости (см. главу 17). Что касается лаг-
ранжева масштаба корреляции TL> то в рамках
рассматриваемой модели естественно связать его с характеристиками
турбулентности пограничного слоя. Предположим, что TL полностью
определяется значением соответствующей компоненты энергии
турбулентности и скоростью ее диссипации в тепло, т. е.
TL=f {/,*).
Из соображений размерности тогда следует
TL = a^=a^, (18.3.13)
где а — безразмерная постоянная величина. При получении
(18.3.13) учтено, что диссипация определяется
мелкомасштабными компонентами движения, являющимися приближенно
изотропными, так что скорость диссипации поперечной компоненты
энергии турбулентности в тепло равна е/3. Кроме того,
использовано соотношение e = b2/kz.
Подставив (18.3.13) в (18.3.12), получим
-С*
^n"j. • <18-ЗЛ4>
Для непосредственного использования результатов численной
реализации модели пограничного слоя атмосферы удобно
привести (18.3.14) к безразмерному виду. Введя масштабы
L, %и
k0=r.v*L, ^0=^2", £=—£*-,
Ио-^. ~<=§Г,' *о="|Ь ^ = C-ll'L\ (18.3.15)
перепишем (18.3.14) в безразмерном виде:
ul п
°%= я-т?-' <18-ЗЛ6>
1 + ** ^ "
v'2nunkn
Турбулентная диффузия примесей и загрязнение атмосферы 579
где
Входящие в (18.3.16) величины ип, v'n\ bn, kn являются
функциями безразмерной высоты гп, числа Россби Ro и
параметра стратификации \х0. Однако в расчетную формулу (18.1.7)
Рис. 18.1. Зависимость поперечной
дисперсии оу от расстояния при
разных типах стратификации атмосферы
(/i=100 м, G = 10 м/с, Ro=106).
Ю^хм
Рис. 18.2. Зависимость
поперечной дисперсии Оу от расстояния
при разных скоростях ветра
(ц0=0, /i=100 м).
входит осредненная по высоте дисперсия, поэтому значения ип,
v'*, йп, kn осреднялись по высоте в слое 0 — hn (hn —
безразмерная высота источника) и по формуле (18.3.16)
рассчитывалось оу(хПу Лп, цо, Ro).
Наибольший практический интерес представляют размерные
значения поперечной дисперсии оу{х, /г, ц0, Ro), которые легко
могут быть получены умножением безразмерных величин на
соответствующие масштабы, определяемые формулами (18.3.15).
На рис. 18.1 приведены значения поперечной дисперсии оу(х)
на разных расстояниях от источника при разных типах
стратификации атмосферы. Как уже отмечалось при анализе формулы
для Оу, дисперсия увеличивается при удалении от источника.
На всех расстояниях дисперсия увеличивается с ростом
неустойчивости. Такая зависимость оу от jlxo является естественной,
37*
580
Глава 18
поскольку с ростом неустойчивости усиливается интенсивность
турбулентного обмена, что приводит к увеличению рассеяния
частиц. На рис. 18.2 представлена зависимость дисперсии от
расстояния для равновесной стратификации при разных скоростях
геострофического ветра. Дисперсия увеличивается с ростом
скорости ветра вследствие усиления интенсивности турбулентного
обмена; видно, что влияние ветра особенно существенно на
небольших расстояниях от источника.
Отметим, что в Советском Союзе и за рубежом проводится
большое число экспериментов для определения дисперсий на
разных расстояниях при различных метеорологических
условиях.
Как следует из вышесказанного, значения дисперсий должны
зависеть от местных условий (широты места и шероховатости
подстилающей поверхности). В этом смысле наибольший
интерес представляли бы экспериментальные данные о безразмерных
величинах оп(хп, \io, Ro), которые можно было бы
непосредственно сопоставить с результатами теоретического расчета.
К сожалению, в настоящее время такого рода данные
отсутствуют. Кроме того, при проведении наблюдений используются
разные характеристики для определения типа стратификации,
что затрудняет как сопоставление различных наблюдений
между собой, так и сравнение их с результатами расчета.
Вследствие этого фактически можно провести лишь качественное
сопоставление результатов расчета с экспериментальными
данными. Из наблюдений, так же как из теории, следует, что
дисперсия растет с увеличением расстояния от источника и на
всех расстояниях она больше при неустойчивой стратификации,
чем при устойчивой.
18.4. Распределение в атмосфере примесей при разных
метеорологических условиях и разных параметрах выброса
Рассмотрим сначала поведение безразмерной плоской
концентрации Sn(xni zn> Цо> Ro), значения которой были получены
в результате численной реализации двумерного уравнения
диффузии (18.1.10) с граничными условиями (18.1.11) — (18.1.13)
при использовании модели строения пограничного слоя,
описанной в главе И. На рис. 18.3 приведены кривые распределения
вдоль оси хп наземной плоской концентрации Sn(*n, 0) при
разных типах стратификации атмосферы: jio = —50 (сильная
неустойчивость), |ы0 = 0 (равновесие), pio = 20 (умеренная
устойчивость). При всех типах стратификации кривые имеют
характерную форму: концентрация сначала растет при увеличении хп,
на некотором расстоянии хп max достигает максимального зна-
Турбулентная диффузия примесей и загрязнение атмосферы 581
чения Snmax, а затем убывает с удалением от источника. С
ростом неустойчивости увеличивается значение максимальной
концентрации и точка максимума приближается к источнику.
Отметим, что для рассмотренных параметров при устойчивой
стратификации (|ь10 = 20, см. рис. 18.3) точка максимума еще не
достигнута. Полученная зависимость распределения наземной
концентрации от стратификации объясняется тем, что из высотного
источника примесь может достигнуть поверхности земли только
Рис. 18.3. Зависимость безразмерной наземной плоской
концентрации Sn(*n, 0) от расстояния хп при разных
типах стратификации атмосферы (/in = 0,10, Ro=106).
за счет переноса ее турбулентными вихрями. Чем больше
интенсивность турбулентного обмена (а при прочих равных
условиях интенсивность турбулентного обмена увеличивается с
усилением неустойчивости), тем больше примеси поступает в
нижние слои атмосферы и тем ближе к источнику дымовая струя
достигает подстилающей поверхности.
Таким образом, при функционировании высотных источников
наиболее неблагоприятными (с точки зрения возникновения
наибольших максимальных концентраций вблизи земли) являются
случаи с неустойчивой стратификацией атмосферы. Отметим,
что для низких источников, включая и наземные, зависимость
распределения примесей от стратификации противоположна:
в этом случае наибольшее загрязнение нижних слоев атмосферы
создается при устойчивой стратификации.
На рис. 18.4 представлены кривые распределения
безразмерной плоской концентрации при равновесных условиях и
фиксированном числе Россби для трех эффективных высот источника.
582
Глава 18
Как следует из рассмотрения соответствующих кривых,
величина Sn max уменьшается приблизительно обратно
пропорционально Л, а точка хп max удаляется от источника прямо
пропорционально А. Этот же вывод следует из формул (18.2.11) и
(18.2.12). Физически такой результат тоже вполне очевиден,
ибо, чем выше труба, тем большее время требуется для
достижения примесью земной поверхности. В силу этого она успевает
рассеяться в большей степени, причем поступающее из
источника облако относится ветром на большее расстояние.
Sn(x^O)
Рис. 18.4. Зависимость от расстояния хп плоской
концентрации для разных эффективных высот источника h (|х0=0,
Ro=106).
Перейдем теперь к анализу распределения в атмосфере
наиболее важной для практики характеристики — объемной
концентрации вблизи земли на оси струи С(х, О, О, Л, pio, Ro). Эта
величина определяется по формуле (18.1.7). Размерные
значения плоской концентрации S(x, г, А, (я0, Rd) получаются путем
умножения безразмерных величин на масштабы, которые
рассчитываются по формулам (18.1.14). Необходимые для
определения объемной концентрации значения дисперсии оу берутся
с рис. 18.1 и 18.2.
На рис. 18.5 и 18.6 приведены кривые распределения
объемной концентрации соответственно при разных типах
стратификации (высота трубы и скорость ветра фиксированы) и при
разных высотах источника (при равновесных условиях и
скорости ветра G = 10 м/с). Из этих рисунков видно, что общие
закономерности, характеризующие поведение безразмерной плоской
концентрации при разных типах стратификации и разных
высотах труб, остаются в силе и для объемной концентрации. При
Турбулентная диффузия примесей и загрязнение атмосферы
583
фиксированной высоте источника Стах увеличивается с ростом
неустойчивости, а точка максимума xmax при этом приближается
м
Рис. 18.5. Распределение вдоль оси х объемной концентрации,
отнесенной к мощности выброса, С(ху 0,0) /М при разных типах
стратификации (/i=200 м, G = 10 м/с).
8г
Рис. 18.6. Зависимость от расстояния х объемной
концентрации, отнесенной к мощности выброса, С(х, 0,0)/М для
разных высот источника Л.
к источнику. При данной стратификации Cmax уменьшается с
увеличением высоты источника, а точка максимума удаляется от
трубы. Физическая интерпретация упомянутых
закономерностей аналогична приведенной выше для объяснения поведения
S(xn,0).
584
Глава 18
£-107с/м3
м
7.5,
5,0
Gm/c
10
На рис. 18.7 приведены кривые распределения примесей для
двух скоростей ветра при равновесной стратификации (ц0 = 0)
и фиксированной высоте источника Л = 100 м. Видно, что Стах
меняется приблизительно обратно
пропорционально скорости ветра,
а точка максимума хтАХ при
увеличении скорости ветра удаляется
от трубы.
Значения максимальной
концентрации Стах и расстояния, на
котором она достигается,
являются важными характеристиками
загрязнения воздуха. На рис. 18.8
приведены зависимости Стах и
*тах ОТ ВЫСОТЫ Трубы При раз-
ных стратификациях атмосферы.
Сравнивая ход кривых S(x) и
С(х), можно отметить, что при
одинаковых условиях, т. е. при
разных значениях \хо и А,
кривые С(х) лежат ниже кривых
5 (х). Последнее объясняется
тем, что объемная концентрация зависит от эффекта
поперечного рассеяния, учет которого естественно приводит к
уменьшению количества примеси, достигающей нижних слоев атмо-
15Y-
J_
2 4 6 в 10 хкм
Рис. 18.7. Распределение
объемной концентрации С/М при
равновесной стратификации
для двух скоростей ветра.
^Ш.Ю6с/м3
1$г Ф
\i0=50
~50 100 150
Рис. 18.8. Зависимость Стах/Л1 (а) и хтах (б) от
высоты трубы h для двух типов стратификации.
сферы. Увеличение интенсивности поперечного рассеяния с
удалением от источника приводит к тому, что при заданных
внешних параметрах максимум объемной концентрации всегда
расположен ближе к источнику, чем максимум плоской
концентрации.
Турбулентная диффузия примесей и загрязнение атмосферы 585
Контрольные вопросы
1. В чем состоит основное отличие в условиях рассеяния
примесей в вертикальном и горизонтальном (перпендикулярном
направлению среднего ветра) направлении?
2. Что характеризует горизонтальная дисперсия частиц
примеси? Как она зависит от стратификации и скорости ветра?
3. Как зависит значение наземной концентрации примеси,
поступающей из точечного высотного источника, от расстояния?
4. Как зависит значение максимальной концентрации и
расстояние, где она достигается, от стратификации атмосферы и
скорости ветра?
5. Какая метеорологическая информация необходима для
определения многолетних средних значений наземной
концентрации примеси?
ПРИЛОЖЕНИЕ
Цилиндрическая система координат
Сферическая система координат
Выражения для уравнений движения и неразрывности
1. Цилиндрическая система координат
dvr i *, dVr -U V* dvr Л. т dVr V*
dt ^Vr dr ~^~r~db"^~Vz~di ~r
— F 1 dP
dt
p dr
' \ Ur Г2 Г2 дЬ )
Г2 дЪ
Приложение
587
dt ^Vr dz^ r db ^Vz dz Гг p dz n~va^»
d? , d?vr ■ jgr_ ■ 1 ^ , aPt/z _n
a* "r dr "» г "Г r d& "Г д2 —и-
2. Сферическая система координат
dt/r I ^г , vb dvr , fx dvr v\+v{
dt ~T~Ur dr "г г а& "Г г sin й а\ г
~Г' р (?Г^Л Г Г2 г* ГХ%* r2stn& дХ Г2 д&
<Ч , .. <Ч , "a <Ч , «\ <Ч , V* ^ct8*
.^г 2 I !£_ &LJ X ft i r_!L
a* l r dr ] r a& ^rsinu dX r г г
» pr a» ^ \ » r2Sin2^ r2Sin2^ ax "^ r2 a& t
dvX i ,. <4 , *» <4 , ^X <4 , Ух | Vxctg»
dt ~7~Vr dr "" г a& "г" rsinft ax • r "T" г
A prsin
l_J^+ЛДг,х !^_ ■ 2cos» dvb
2 di/r
r2sin^ ax
aP ■ d9vr . 29vr . 1 dyvb \ d?vx ррд ctg %
dt~i~dr~rr\r db ' rsinft ax "Г" г
Выражения для градиента скалярной функции, ротора, дивергенции
и лапласиана
1. Цилиндрическая система координат
gradr«j>=-^-, grad^-Jr-^, grad,«|»=-g-,
. 1 dvz dv& . dvr dvz
. 1 a / v 1 dvr
a- 1 д , ч , 1 dv» , dv,
A a^ \ di/ . \ дц . щ
V дГ* "T" Г дГ "Т" Г2 a»2 1" ^2 *
588 Приложение
2. Сферическая система координат
grad,'j> = ^, grad><|> = —-JL, gradx ф = 7^^г
Г04^ = 7^[-Ж(81п*^)--Ж-]'
rot
1 Г 1 dvr д , ч1
"•.-rl-F^-S1-]-
^2ф
СПИСОК ЛИТЕРАТУРЫ
Основная литература
Гуди Р. М. Атмосферная радиация М., «Мир», 1966. 522 с.
Зилитинкевич С. С. Динамика пограничного слоя атмосферы. Л.,
Гидрометеоиздат, 1970. 290 с.
К и б е л ь И. А. Введение в гидродинамические методы краткосрочного
прогноза погоды. М., Гостехиздат, 1957. 375 с.
Кондратьев К. Я. Актинометрия. Л., Гидрометеоиздат, 1965. 691 с.
Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая
гидромеханика. Ч. 1 и 2. М., Физматгиз, 1963, ч. 1—583 с, ч. 2—727 с.
Лайхтман Д. Л. Физика пограничного слоя атмосферы. Л.,
Гидрометеоиздат, 1970. 341 с.
М а р ч у к Г. И. Численные методы в прогнозе погоды. Л ,
Гидрометеоиздат, 1967. 356 с.
Матвеев Л. Т. Основы общей метеорологии. Физика атмосферы.
Гидрометеоиздат, Л., 1965. 876 с.
М о н и н А. С. Прогноз погоды как задача физики. М., Гидрометеоиздат,
1972. 183 с.
Монин А. С, Я г л о м А. М. Статистическая гидромеханика. Ч. I. М.,
«Наука», 1965. 639 с.
Халтинер Дж., Мартин Ф. Динамическая и физическая
метеорология. М., Изд-во иностр. лит., 1960. 435 с.
Гандин Л. С, Лайхтман Д. Л., Матвеев Л. Т., Юдин М. И.
Основы динамической метеорологии. Л., Гидрометеоиздат, 1955. 647 с.
К главе 1
Гленсдорф П., Пригожий И. Термодинамическая теория
структуры устойчивости и флуктуации. М., «Мир», 1973. 280 с.
Гроот де С, Мазур П. Неравновесная термодинамика. М., «Мир»,
1964. 456 с.
К главе 2
Митра Ф. К. Верхняя атмосфера. М., Изд-во иностр. лит., 1955 639 с.
Физика верхней атмосферы. Под ред. Дж. Ратклиффа. М., Физматгиз,
1963. 504 с.
Ф л и г л ь Р., Б у з и н г е р Д ж. Введение в физику атмосферы. Гл. 2. М.,
«Мир», 1965. 431 с.
Хргиан А. X. Физика атмосферы. Гл. 1. Л., Гидрометеоиздат, 1969.
636 с.
К главам 3—5
Доронин Ю. П. Основы термодинамики атмосферы и океана
(конспект лекций). Л., Изд. ЛГМИ, 1973. 89 с.
Качурин Л. Г., Морачевский В. Г. Кинетика фазовых переходов
воды в атмосфере. Л., Изд-во ЛГУ, 1965. 136 с.
590
Список литературы
Качурин Л. Г. Физические основы воздействия на атмосферные
процессы. Л., Гидрометеоиздат, 1973. 366 с.
Кры станов Л. Избранные труды по физике атмосферы. Л.,
Гидрометеоиздат, 1968. 212 с.
Ландау Л. Д., Л и ф ш и ц Е. М. Статистическая физика. М., «Наука»,
1964. 567 с.
Р у м е р Ю. Б., Рыбкин М. Ш. Термодинамика и статистическая физика
и кинетика. М., «Наука», 1972. 399 с.
Флигль Р., Бузингер Дж. Введение в физику атмосферы. Гл. 2
и 3. М, «Мир», 1965. 431 с.
К главе 6
Градус Л. М., Нийлиск X. Ю., Фейгельсон Е. М. Интегральная
функция пропускания для облачных условий.— «Изв. АН СССР. Физика
атмосферы и океана», 1968, т. 4, № 4, с. 397—413.
Евсеева М. Г., Подольская Э. Л. Интегральная функция
пропускания в близкой инфракрасной области спектра.— «Тр. ЛГМИ», 1974, вып. 49,
с. 124—128.
Ковалева Е. Д., Шехтер Ф. Н. Влияние стратификации атмосферы
на радиационный приток тепла.— «Тр. ГГО», 1966, вып. 187, с. 104—114.
Кондратьев К. Я., Борисенков Е. П., Морозкин А. А.
Практическое использование метеорологических спутников. Л., Гидрометеоиздат,
1966, с. 74—104.
Королев Ф. А. Теоретическая оптика. М., «Высшая школа», 1966. 555 с.
Краснокутская Л. Д., Фейгельсон Е. М. Расчет потоков ИК
солнечного излучения в облачной атмосфере.— «Изв. АН СССР. Физика
атмосферы и океана», 1973, т. 9, № 10, с. 1003—1013.
Манабе С, Стриклер Р. Ф. Термическое равновесие с учетом
конвекции.— В кн.: Теория климата. Л., Гидрометеоиздат, 1967, с. 61—104.
Соболев В. В. Рассеяние света в атмосферах планет. М., «Наука»,
1972. 335 с.
Радиационные характеристики атмосферы и земной поверхности. Под ред.
К. Я. Кондратьева. Л., Гидрометеоиздат, 1969. 564 с.
Фейгельсон Е. М. Лучистый теплообмен и облака. Л.,
Гидрометеоиздат, 1970. 230 с.
Шифрин К. С. Рассеивание света в мутной среде. М.—Л., Гостехиздат,
1951. 288 с.
М 6 11 е г F. Der Strahlungsgleichgewicht in der Nahe der Erdoberf lache.—
„Meteorologische Rundschau14, 1960, Bd. 13, H. 5, S. 134—139.
Rodgers С D. The radiative heat Budget of the troposphere and lower
stratosphere. Mass. Inst, of Technology, Planetary Circulation Project, Rep.
N A2, 1967, 99 p.
К главе 7
Л а м л и Д ж. Л., П а н о в с к и й Г. А. Структура атмосферной
турбулентности. М., «Мир», 1966. 264 с.
Ландау Л. Д., Л и ф ш и ц Е. М. Механика сплошных сред. М.,
Гостехиздат, 1953. 795 с.
М о н и н А. С. Динамическая турбулентность в атмосфере.— «Изв. АН
СССР, сер. геофиз.», 1950, т. 14, № 3, с. 232—255.
М о н и н А. С. О свойствах симметрии турбулентности в приземном слое
воздуха.— «Изв. АН СССР. Физика атмосферы и океана», 1965, т. 1, № 1,
с. 45—55.
Обухов А. М. Турбулентность в температурно-неоднородной
атмосфере.— «Тр. Ин-та теор. геофизики АН СССР», 1946, вып. 1, с. 95—115.
Список литературы
591
Седов Л. И. Методы подобия и размерности в механике. М., «Наука»,
1965. 428 с.
X и н ц е И. О. Турбулентность. М, Физматгиз, 1963. 680 с.
К главе 8
Б р е н т Д. Физическая и динамическая метеорология. Л.—М., Гидроме-
теоиздат, 1938. 398 с.
К главе 9
Бай Ш и И. Введение в теорию течения сжимаемой жидкости. М., Изд-во
иностр. лит., 1962. 410 с.
Кочин Н. Е. Собрание сочинений. Т. 1. М — Л., Изд-во АН СССР, 1949.
613 с.
К главе 10
Бреховских Л. М. Волны в слоистых средах. М., Изд-во АН СССР,
1957.
Дикий Л. А. Теория колебаний земной атмосферы. Л., Гидрометеоиз-
дат, 1969. 195 с.
Извеков Б. И., Кочин Н. Е. Динамическая метеорология. Ч. 1 и 2.
Л , Гидрометеоиздат, 1935.
Каменкович В. М. Основы динамики океана. Л., Гидрометеоиздат,
1973. 240 с.
Мандельштам Л. И. Лекции по колебаниям. М., Изд-во АН СССР,
1955.
О г у р а Ю., Ч а р н и Д ж. Численная модель термической конвекции в
атмосфере.— В кн.: Труды Токийского симпозиума по численным методам
прогноза погоды. Л., Гидрометеоиздат, 1967, с. 232—264.
Э к к а р т К. Гидродинамика океана и атмосферы. М., Изд-во иностр.
лит., 1963.
К главе 11
Бобылева И. М. Расчеты характеристик турбулентности в
планетарном пограничном слое атмосферы — «Тр. ЛГМИ», 1970, № 40, с. 3—63.
Зилитинкевич С. С, Лайхтман Д. Л. Турбулентный режим в
приземном слое атмосферы.— «Изв АН СССР. Физика атмосферы и океана»,
1965, т. 1, Я° 2, с. 150—156.
Каган Б. А. О влиянии характера распределения коэффициента
турбулентности в море и атмосфере на профиль скорости дрейфовых течений и ветра
над морем.—«Тр. ЛГМИ», 1964, вып. 17, с. 128—149.
Казанский А. Б., Монин А. С. Турбулентность в приземных
инверсиях.—«Изв. АН СССР, сер. геофиз.,» 1956, № 1, с. 79—86.
Казанский А. Б., Монин А. С. О турбулентном режиме в приземном
слое воздуха при неустойчивой стратификации.— «Изв. АН СССР, сер.
геофиз.», 1958, № 6, с. 741—751.
Китайгородский С. А. Физика взаимодействия атмосферы и океана.
Л., Гидрометеоиздат, 1970. 284 с.
Лам л и Д ж., Л., Пановский Г. А. Структура атмосферной
турбулентности. М., «Мир», 1966. 264 с.
Монин А. С, Обухов А. М. Основные закономерности турбулентного
перемешивания в приземном слое атмосферы.— «Тр. Геофиз. ин-та АН СССР»,
1954, вып. 24 (151), с. 163—187.
592
Список литературы
Попов А. М. Расчетные профили метеорологических характеристик
в планетарном пограничном слое атмосферы. Л., изд. ЛГМИ, 1975. 97 с.
Пристли С. X. Б. Турбулентный перенос в приземном слое атмосферы.
Л., Гидрометеоиздат, 1964. 122 с.
Ролль Г. У. Физика атмосферных процессов над морем. Л.,
Гидрометеоиздат, 1968, с. 398.
Busch N. Е., Tennekes Н., Panofsky Н. A. Turbulence structure
in the planetary boundary layer.— "Boundary Layer Meteorology", 1973, vol. 4,
p. 211—264.
К u о H. L. Planetary boundary layer flow of a stable atmosphere over
the globe.—"J. Atmospheric Science", 1973, vol. 30, N 1, p. 53—65.
Wippermann F. A mixing-length hypothesis for the planetary layer
flow in the atmosphere.— "Beitr. Phys. Atmosph.", 1971, Bd 44, H. 4, S.
215—226.
К главе 12
Лайхтман Д. Л. Трансформация воздушной массы под влиянием
подстилающей поверхности.— «Метеорология и гидрология», 1947, № 1, с. 17—21.
Лайхтман Д. Л., Юдин М. И. Трансформация нижнего слоя
воздуха под влиянием подстилающей поверхности.— «Докл. АН СССР», 1953,
т. 93, № 2, с. 249—252.
Лайхтман Д. Л., Надежина Е. Д., Симонов В. В. Влияние
изменения внешних условий на трансформацию нижней облачности.— «Тр. ГГО»,
1965, вып. 167, с .67—72.
Лайхтман Д. Л., Тимофеев М. П. О методике расчета испарения
с поверхности ограниченных водоемов.— «Метеорология и гидрология», 1956,
№ 4, с. 19—23.
Надежина Е. Д. К вопросу о влиянии скачка шероховатости
подстилающей поверхности на режим турбулентного пограничного слоя.— «Тр. ГГО»,
1970, вып. 257, с. 109—116.
Радикевич В. М. Трансформация динамических характеристик
воздушного потока под влиянием изменения шероховатости подстилающей
поверхности.— «Изв. АН СССР. Физика атмосферы и океана», 1971, т. 7, № 12,
с. 1241 — 1250.
К главе 13
Дородницын А. А. К теории суточного хода температуры в слое
перемешивания.—«Докл. АН СССР», 1941, т. 30, № 5, с. 410—413.
Вагер Б. Г., Зилитинкевич С. С. Теоретическая модель суточных
колебаний метеорологических полей.— «Метеорология и гидрология», 1968,
№ 7, с. 3—18.
Лайхтман Д. Л. Предвычисление суточных колебаний температуры
в приземном слое атмосферы.— «Тр. ГГО», 1950, вып. 22, с. 3—14.
Лайхтман Д. Л. О введении температурной поправки на конденсацию
при радиационном выхолаживании приземного слоя атмосферы.— «Тр. ГГО»,
1951, вып. 27, с. 89—97.
Тимофеев М. П. О суточной изменчивости турбулентного обмена.—
«Тр. ГГО», 1950, вып. 22, с. 15—25.
Огнева Т. А. Некоторые особенности теплового баланса деятельной
поверхности. Л., Гидрометеоиздат, 1955. 120 с.
К главе 14
Белов П. Н. Практические методы численного прогноза погоды. Л.,
Гидрометеоиздат, 1967, с. 334.
Список литературы
593
Блинова Е. Н. Гидродинамическая теория волн давления,
температурных волн и центров действия атмосферы.— «Докл. АН СССР», 1943, т. 39,
№ 7, с. 85—89.
Г а н д и н Л. С, Д у б о в А. С. Численные методы краткосрочного
прогноза погоды. Л., Гидрометеоиздат, 1968. 426 с.
Томпсон Ф. Анализ и предсказание погоды численными методами. М.,
Изд-во иностр. лит., 1962. 239 с.
Труды Токийского симпозиума по численным методам прогноза погоды.
Л., Гидрометеоиздат, 1967. 360 с.
Юдин М. И. Новые методы и проблемы краткосрочного прогноза
погоды. Л., Гидрометеоиздат, 1963. 403 с.
К главе 15
Блинова Е. Н. Гидродинамическая теория волн давления,
температурных волн и центров действия атмосферы.— «Докл. АН СССР», 1943, т. 39,
№ 7, с. 85-89.
Блинова Е. Н. К вопросу об определении давления на уровне моря.—
«Докл. АН СССР», 1953, т. 92, № 3.
Блинова Е. Н. Общая циркуляция атмосферы и гидродинамический
долгосрочный прогноз погоды.— «Тр. Гидрометцентра СССР», 1967, вып. 15,
с. 3—36.
Кочин Н. Е. Об упрощении уравнений гидромеханики для случая
общей циркуляции.—Собр. соч. Т. 1. М.—Л., Изд-во АН СССР, 1949. 615 с.
Кочин Н. Е. Построение модели зональной циркуляции атмосферы.—
Собр. соч. Т. 1. М.—Л., Изд-во АН СССР, 1949. 615 с.
Лоренц Э. Н. Природа и теория общей циркуляции атмосферы. Л.,
Гидрометеоиздат, 1970. 259 с.
Манабе С, Смагоринский Д., Стриклер Р. Численное
моделирование средней картины общей циркуляции с учетом процессов влагообме-
на.— В кн.: Теория климата. Л., Гидрометеоиздат, 1967, с. 185—229.
Смагоринский Д., Манабе С, Холлоуэй Д. Результаты
численных опытов с девятиуровенной моделью общей циркуляции атмосферы.—
В кн.: Теория климата. Л., Гидрометеоиздат, 1967, с. 117—184.
Ф и л л и п с Н. Общая циркуляция атмосферы. Численный эксперимент.—
В кн.: Теория климата. Л., Гидрометеоиздат, 1967, с. 6—60.
К главе 16
Дюбюк А. Ф. Вертикальные скорости, возникающие за счет трения
в области фронта.—«Тр. ЦИП», 1951, вып. 26(53), с. 11—18.
Лайхтман Д. Л., Альтер-Залик Ю. А. Об использовании
аэрологических данных для определения болтанки самолета в свободной
атмосфере.— «Изв. АН СССР. Физика атмосферы и океана», 1965, т. 2, № 5,
с. 534—536.
Лайхтман Д. Л., Бютнер Э. К. К вопросу о турбулентности в
свободной атмосфере.—«Тр. ГГО», 1962, вып. 127, с. 122—126.
Лайхтман Д. Л., Ш н а й д м а н В. А. Ветер и турбулентный обмен
вблизи фронтальных поверхностей.— «Тр. ГГО», 1965, вып. 167, с. 205—210.
Турбулентность в свободной атмосфере. Л., Гидрометеоиздат, 1968. 336 с.
Авторы: Н. К- Винниченко, Н. 3. Пинус, С. М. Шметер, Г. Н. Шур.
'Шнайдман В. А. О турбулентности в области поверхности раздела.—
«Тр. ГГО», 1961, вып. 107, с. 151 — 154.
38 Заказ ЛЬ 612
594
Список литературы
К главе 17
Бэтчелор. Теория однородной турбулентности. М., Изд-во иностр. лит.,
1955. 188 с.
Колмогоров А. Н. Локальная структура турбулентности в
несжимаемой вязкой жидкости при очень больших числах Реннольдса.— «Докл. АН
СССР», 1941, т. 30, № 4, с. 299—303.
Ламли Дж. Л., ПановскийГ. А. Структура атмосферной
турбулентности. М., «Мир», 1966. 264 с.
Обухов А. М. О влиянии архимедовых сил на структуру
температурного поля в турбулентном потоке.— «Докл. АН СССР», 1959, т. 125, № 6,
с. 1246—1248.
П а н ч е в С. Случайные функции и турбулентность. Л., Гидрометеоиздат,
1967. 437 с.
Турбулентность в свободной атмосфере. Л., Гидрометеоиздат, 1968. 336 с.
Авторы: Н. К. Винниченко, Н. 3. Пинус, С. М. Шметер, Г. Н. Шур.
Хинце И. О. Турбулентность, ее механизм и теория. М., Физматгиз,
1963. 680 с.
К главе 18
Атмосферная диффузия и загрязнение воздуха. Под ред. А. С. Монина.
М., Изд-во иностр. лит., 1962. 507 с.
Вызова Н. Л. Рассеяние примеси в пограничном слое атмосферы. М.,
Гидрометеоиздат, 1974. 183 с.
Бютнер Э. К., Лайхтман Д. Л. О рассеянии пассивных частиц от
точечного источника в неоднородной атмосфере.— «Тр. ЛГМИ», 1963, вып. 15,
с. 130—136.
Лайхтман Д. Л., Г и с и н а Ф. А., К а п л а н С. Н. Принцип учета
метеорологических условий при проектировании промышленных предприятий.—
«Тр. ЛГМИ», 1963, вып. 15, с. 37—46.
Лайхтман Д. Л., Г и с и н а Ф. А., Крамер Н. И. Учет особенностей
атмосферной турбулентности при расчете мощности и высоты труб
промышленных предприятий.— «Изв. АН СССР. Физика атмосферы и океана», 1965,
т. 1, № И, с. 1205—1208.
Метеорология и атомная энергия. Л., Гидрометеоиздат, 1971. 636 с.
УКАЗАТЕЛЬ
А В
Абсолютно белое тело 131
— черное тело 121
Авогадро закон 17
Агеострофическое отклонение 244,
246, 301
Адаптация полей 301
Адвекция 407, 493
— вихря 434, 440, 446
Акерблома — Экмана модель 331, 470
Альбедо 130
— интегральное 131
— облаков 132
— спектральное 131
Анализ размерности 222
Архимеда параметр 360
Атмосфера бароклинная 441
— баротропная 436
— вертикальная протяженность 19
— верхняя граница 41
— газовый состав 19, 20
— загрязнение 564
— излучение 139
— неустойчивое состояние 75, 304
— однородная 21
— равновесное состояние 50, 75, 93
— стандартная 40
— структура 39
— циркуляция 468
— энергетика 491
Б
Безразмерная величина 210, 214, 216
Безразмерный комплекс 223
Блиновой модель 470, 471
Бойля—Мариотта закон 16
Болджиано метод 561
Больцмана формула 23
Боуэна отношение 320, 461
Брента формула 401
Бриз 220
Буссинеска—Шмидта гипотеза 528,
530
Бэта-эффект 281
Ван-дер-Ваальса уравнение 68
Ван-дер-Ховена измерения 195
Вертикальные движения 244, 457,
513
на границе пограничного слоя
458
над сложным рельефом 462
у поверхности раздела 257
Ветер, вертикальный профиль 351
— геострофический 219, 231, 235
— годограф 334, 337
— градиентный 229
— отклонение незональное 473
— отклонение от геострофического
242, 244
— поворот с высотой 335, 338, 357
— порывистость 508, 513, 517
— термический 235, 237, 337
Вина закон 123
Вихревой перенос тепла 482
Вихрь 191, 200, 271, 481
— адвекция 434, 440, 446
— масштаб 550, 551, 554, 559
— относительный 432, 484
— потенциальный 433, 484
— скорости 432
— турбулентный 191, 200
Влагосодержание 385, 454
Влажность абсолютная 65
— относительная 65
— удельная 65
Водность 90, 365, 455
Волновой вектор 265
Волны 261, 264, 273, 282, 301
— гравитационные 285, 288
— граничные условия 275
— длина 267
— звуковые 284, 292
— параметры 265, 281, 284, 302
— Россби 287
— теория 265, 281
— ударные 253
— эволюция 296
Временной шаг 421
Вторые моменты пульсаций 214, 521
Вязкость динамическая 115
— кинематическая 115
38*
596
Указатель
— молекулярная кинематическая 525
Вяйсяла частота 286, 361
Г
Газ идеальный 16
— насыщенный 70
— равновесное распределение 27
Газовая постоянная водяного пара
65
воздуха 65
универсальная 17
Галеркина метод 425
Гармонический ряд 267
Гауссово распределение 98, 568
Гейзенберга гипотеза 553, 556
Гей-Люссака закон 16
Геоид 12
Гессельберга—Фридмана таблица
210
Гетеросфера 27
Гиббса соотношение 78
Гипотеза Буссинеска—Шмидта 528,
530
— Гейзенберга 553, 556
— градиентная 538
— Давыдова 532
— сплошности 5, 6
— Тейлора 552
—эргодическая 194, 575
Гипотезы Колмогорова 549—553
— Обухова 558, 559
Гомосфера 27
Градиент автоконвективный 433
— влажноадиабатический 88
— давления горизонтальный 359
—плотности равновесный 319
— сухоадиабатический 48
— температуры 345
— удельной влажности 345
д
Давление газа парциальное 20, 24
—пара равновесное 104
Давыдова гипотеза 532
Дальтона закон 17
Двухточечные моменты 521
Джоуля опыты 43
Дивергенция 271, 475
Дилюции фактор 141
— эффект 140
Динамические условия на
поверхности 278
Диссипация газов 19, 28, 31, 35, 36,
41
— энергии 307, 322, 332, 342, 513, 517,
526, 530, 544, 546, 549, 552, 554
Диффузия молекулярная ИЗ
—внутренней энергии 15
— примеси 567
— турбулентная горизонтальная 483
— энергии турбулентности 307, 322,
332, 349, 526, 528
Длина свободного пробега 33, 554
3
Загрязнение атмосферы 564
Закон Авогадро 17
— Бойля—Мариотта 16
— Вина 123
— Гей-Люссака 16
— Дальтона 17
— Колмогорова—Обухова 551
— Ламберта—Буге 120, 125, 138
— «минус одиннадцати пятых» 561,
563
— «минус пяти третей» 556, 557, 562
— «минус семи пятых» 561
— «минус трех» 562
— «пяти третей» 550, 552, 553, 555
— сохранения количества движения
6, 18
массы 6, 18
энергии 6, 18
— Стефана—Больцмана 124
— тяготения 11
— Фикка 111
— Фурье 111
— «четырех третей» 555
Зародыш новой фазы 104, 105, 108,
ПО
Зональное значение давления 472
И
Излучательная способность 130
Излучение 132
— абсолютно черного тела 122
— атмосферы 139
— равновесное тепловое 122
— Солнца 138, 157, 172
Индекс циркуляции 472, 475
Индивидуальная производная 9, 409
Инерционный интервал 550, 551
Интенсивность излучения 118
— линии поглощения 135
— температурных пульсаций 557, 558
Испарение 64, 381
Источник 9
Указатель
597
— импульса 11
— наземный 573
— примеси 565, 569
К
Кампе де Ферье формула 576
Квазинесжимаемость воздуха 13
Квазистатичность 44
Кибеля число 219
Кинематические условия на
поверхности 276
Классификация атмосферных
движений 217
Клаузиуса—Клапейрона уравнение 80
Количество субстанции 7
Колмогорова гипотезы 549—553
— микромасштаб 547
Колмогорова—Обухова закон 551
Конвекция свободная 317, 324
— термическая 53, 54, 492
Конденсация спонтанная 108
Конечный период вырождения 547
Консервативные характеристики 202
Концентрация наземная 572, 574
— плоская 568, 570, 580
Кориолиса параметр 246, 272, 281,
359, 459
— сила 13, 219, 495
Кочина модель 470
Коэффициент безразмерный 215, 218
— вириальный 71
— вовлечения воздуха 58
— динамической вязкости 115
— излучения 121, 122
— корреляции лагранжев 575, 576
— молекулярной диффузии 26, 115
— ослабления 120, 127
— отражения 131
— поглощения 135, 137, 145
— полезного действия атмосферы 504
— рассеяния 126, 128, 158, 159
— серости 130
— трения геострофический 351, 353
— турбулентной вязкости 201
— турбулентной вязкости
спектральный 554
— турбулентной диффузии 201
— турбулентности 25, 201, 260, 307,
3(2, 317, 319, 325, 327, 341
Кривая стратификации 56
Критерии 215, 216, 219
Критеоий Рейнольдса 187
— турбулентности 187, 528
— устойчивости 52, 67, 76, 319
Критическая точка 70
Куртиса—Годсона приближение 137
Л
Лагранжев временной масштаб 576,
578
— коэффициент корреляции 575, 576
— микромасштаб 576
Лакса теорема 420
Ламберта—Буге закон 120, 125, 138
Ламли—Шура теория 561—563
Ландау схема турбулентности 188—
192, 551
Лорентцово поглощение 137
Лучистое равновесие 176
температурные профили 179, 182
Лучистый приток тепла 386, 482, 492
М
Максвелла формула 29, 33
Малые возмущения 269, 301
вертикальная компонента вихря
271
градиенты давления 270
дивергенция скорости 271
кинетическая энергия 279
энергетика 278
Манабе и Стриклера схема 490
Масштаб вихрей 551, 554, 559
— длины Обухова 560
— Монина—Обухова 313, 321, 348
Метод Болджиано 561
— Галеркина 425
— интегральных преобразований 442
— расщепления 422
— Ричардсона 405
— энергетический 192
Методы осреднения 194—198
— разностные 417
Микросостояние 93
Модель Акерблома—Экмана 331, 470
— Блиновой 470, 471
— Кочина 470
— облачности 452
— Пао 556, 560
— пограничного слоя атмосферы
нелинейная 345
однопараметрическая 331
— Смагоринского 485
— Филлипса 477
Монжа—Ампера уравнение 450
Монина—Обухова масштаб 313, 321,
348
Н
Натяжение поверхностное 102
Нормальное распределение 98
598
Указатель
О
Облака 221, 383
— альбедо 132
— волнистые 295
— границы 385
Обухова гипотезы 558, 559
— масштаб длины 560
— метод 560
Общая циркуляция атмосферы 468
Однородное турбулентное поле
521, 557
Одноточечные моменты 521
Оптическая толщина 158
Ортонормированная система 425
Осреднение 194, 195, 197, 566
— уравнений гидротермодинамики
198, 204, 205
Отношение Боуэна 320, 461
— смеси 65
П
Пао модель 556, 560
Параметр Архимеда 360
— Кориолиса 246, 272, 281, 359, 459
— плавучести 57
— Россби 361, 479, 528, 529
— стратификации 326, 361
— устойчивости 52, 478
— шероховатости 351
Параметры внешние 351
— внутренние 43
— волн 265, 281, 284, 302
— выбросов 564, 580
— колебания 264
Пересыщение 70, 104
— предельное 104
Периодичность 391
Планка функция 123
Плотность 20, 24
— локальное изменение 246
— спектральная 555, 559
энергии турбулентности 542,
544—547, 549, 550, 557
Поверхность изобарическая 409
— изэнтропическая 505
— раздела 102, 249, 510
вертикальные движения 257
граничные условия 511
динамические условия 254, 278
кинематические условия 254, 276
наклон 255, 256
стационарные волны 293
уравнения динамики 251
Поглощательная способность 131
Поглощающая масса 145
Поглощение 132
— коэффициент 135, 137, 145
— линия 136
—лорентцово 137
— полоса 135, 138, 139
— примеси поверхностью 569, 571
— спектр 135
Погосяна линейка 233
Пограничный слой атмосферы 219,
305, 307
взаимодействие со свободной
атмосферой 456
внутренний 363, 370
высота 333, 339, 341, 343, 346,
349, 397
над морем 353
параметризация 358
Подвижность 23
Подобные явления 215, 216
Показатель адиабаты 469
— политропы 45
Поток влаги 537
— импульса 11, 327
— плотности 319
— примеси диффузионный 565
— радиации 119
восходящей 148, 151
длинноволновой 172
нисходящей 154
— субстанции 8
молекулярный 111, 113, 114
турбулентный 25, 199, 202, 327,
568
— тепла 320, 482, 537
— частиц гравитационный 22
— энергии 554
турбулентности 307
Прандтля схема турбулентности 199
— число молекулярное 559
турбулентное 528
Приближение квазигеострофическое
427, 429, 431, 436, 441
— квазисоленоидальное 449, 473
—Куртиса—Годсона 137
Приземный слой 219, 309
высота 310
система уравнений 309, 321
Приток тепла 481
лучистый 386, 482, 492
турбулентный 203
Прогноз 405
— долгосрочный 407
— краткосрочный 407
— облачности 450
— «челночный» 466
— численный 405, 412, 416, 441
Указатель
599
Профиль линейно-квадратический 317
— линейно-логарифмический 317
— линейный 318
— степенной 317, 325
Процесс адиабатический 46, 48
— изобарический 44
— изохорический 44
— квазистатический 43
— квазистационарный 195
— колебательный 262
— необратимый 72
— обратимый 72
— политропический 45, 49
Пуассона уравнение 47, 109
Пульсация 519, 520, 552
— давления 523, 527, 531
— плотности 525
— скорости 541
— температуры 537, 538
интенсивность 536, 538
Путь смешения 200, 201
Р
Работа касательных напряжений 207
— силы градиента 494
плавучести 56, 208
Равновесие статистическое 95, 222,
548, 558, 561
— термическое 181, 182
— термодинамическое 95
локальное 124, 134, 143
полное 122
— универсальное 549
— фаз 78, 102
Радиационная диаграмма 173
Радиационный баланс 174, 451
— приток 169, 174, 386
Радиация 117
— восходящая 142
— в облаках 46, 156. 168
— длинноволновая 144, 162
— коротковолновая 154, 155, 157, 172
— нисходящая 144, 162
—рассеянная 160, 172
— уравнение переноса 141, 145, 155
Разделение газов 22, 27
Рассеяние света 125, 133, 139, 143
индикатриса 125, 129, 161
комбинационное 134
многократное 155
молекулярное 126
средневзвешенное 161
Рейнольдса критерий 187
— число 187, 551
Релаксации время 95, 134, 548
Рельеф 486
Ричардсона метод 405
— число 193, 313, 324, 528
Россби волны 287
— параметр 361, 479, 528, 529
С
Серое тело 130
Сжимаемость воздуха 272
Сила внешняя 11
— давления 522, 526
— инерции 525, 526, 544
— Кориолиса 13, 219, 495
—плавучести 51, 56
— тяжести 13
— центробежная 12
Сильный разрыв 250
Система координат геометрическая
И, 408, 588
изобарическая 408, 447
сигма 415, 486
сферическая 468, 587
цилиндрическая 586, 587
Скорость вертикальных движений 244
— выравнивания температурных не-
однородностей 537, 538, 558
— геострофического ветра 232
— групповая 267, 288
— динамическая 310
— компенсирующих переходов 504
— конденсации 455—456
— локальная 493
— наиболее вероятная 30
— тепловая 30, 554
— трения 310
— убывания плотности с высотой 26
— ускользания 29
— фазовая 266, 274, 285, 286, 288,
294
— фазовых переходов 454
Скрытая теплота переходов 80
Смагоринского модель 485
Согласование полей 463, 466
Содержание в атмосфере гелия 38
водяного пара 42
Солнечная постоянная 141
Соотношение Гиббса 78
— дисперсионное 267, 288, 292, 294,
295, 296, 303
Соотношения геострофические 300,
428, 454
Состояние макроскопическое 93
— метастабильное 70, 82, 101
— предельно устойчивое 318
— равновесное 50, 75, 93
— устойчивое 50, 75
Сохранение массы 413
600
Указатель
Спектр потока тепла 562
— скорости ветра 196
Спираль Экмана 334
Стефана—Больцмана закон 124
Стирлинга формула 94
Сток 9
Стратификация 50, 76, 314, 315, 322,
359
Струйные течения 509, 513
Субстанция 7, 8
Суточный ход 388, 394
геострофического коэффициента
трения 393
направления ветра 392
прогностическая система
уравнений 415
радиационного баланса 394
скорости ветра 391
температуры 391, 393, 396
турбулентного потока тепла 393
фаза 397
Схема Манабе и Стриклера 490
— неявная 421
— разностная 418, 420, 479
— турбулентности Ландау 188—192,
551
Прандтля 199
Т
Таблица Гессельберга—Фридмана
210
Тейлора гипотеза 552
— формула 575
Температура барометрическая 20
— виртуальная 67
— зональное значение 472
— изменения с высотой 483
— инверсия 248, 318
— локальное изменение 241
— ночное понижение 400
— отклонение 396, 398, 401
— потенциальная 46, 49
— профиль 403
— радиационное изменение 175
— эквивалентная 384, 454, 500
Тензор давлений 523
— корреляционный 519—521
— напряжений 13
Теорема Лакса 420
— пи 223, 307, 313, 319, 401
Теория волн 265, 281
— Ламли—Шура 561—563
— подобия 209
— разделения газов 20
Теплоемкость влажного воздуха 68
— политропическая 45
— удельная 114
Теплопроводность молекулярная 114
Термик 58, 61, 63
Термодинамики первое начало 16, 43,
47, 67
— второе начало 72
Термодинамическая вероятность 94,
97
Термодинамический потенциал 106
Трансформация 363, 408
— влажности 366
— динамических характеристик 371
— температуры 366
Тройная точка 82
Турбопауза 27
Турбулентное перемешивание 477, 479
— трение 478
Турбулентность 184, 185, 187, 317,
318, 505, 508, 518, 525, 528
— внутренний масштаб 547, 550, 559
— замороженная 553
— изотропность 542, 557, 558
— на поверхности раздела 260, 304,
510
— свободной атмосферы 508
— спектральные характеристики 541,
560
— характерный период вырождения
548
— ясного неба 508
У
Упрощение уравнений 209
движения 217
Упругость водяного пара 65
— насыщения 81, 83
Уравнение баланса 448
массы 27, 565, 566
теплового 354, 501
энергии внутренней 16
лучистой 15
механической 14
полной 14, 500
потенциальной 495
турбулентности 206, 209, 307,
332, 345, 406, 496, 509, 512, 524, 528
фазовых переходов 15
энтропии 72, 493
— Ван-дер-Ваальса 68
— вириальное 71
— вихря 424, 430, 433, 437, 449, 453,
479, 480, 481
— гидротермодинамики 223
Указатель
601
— движения 10, 13
в изобарической системе
координат 410
свободной атмосферы 225, 228
— дивергенции 430
— диффузии 6, 204, 568
—Клапейрона 412
— Клаузиуса—Клапейрона 80
— краткосрочного прогноза погоды
220
— Монжа—Ампера 450
— неразрывности 6, 10
в изобарической системе
координат 411, 489
— притока влаги 308, 489
тепла 6, 44, 308, 406, 410, 495,
432, 449, 453, 481, 489
— Пуассона 47, 109
— состояния 16, 65, 66
— спектральное 553, 558
— статики 21, 221
— субстанции 8, 9
— тензора корреляции 520, 522, 544
Уравнения критериальные 215
Уровень бездивергентный 449, 473
— выравнивания температуры 54, 60
— конвекции 61
— конденсации 85
— обращения 239
— шероховатости 329
— эквивалентно-баротропный 438
Условие несжимаемости 522, 545
Устойчивость движения 188, 190, 191
Ф
Фаза 265
Фазовая плоскость 265
Фазовые переходы 64, 69, 78, 101, 452
Физическое масштабирование 210
Фикка закон 111
Филлипса модель 477
Фильтрация звуковых волн 421
Флуктуация 5, 6, 92, 98
— вероятность 98
—плотности 101, 105
Форбса эффект 137, 157, 170
Формула Больцмана 23
— Брента 401
— Кампе де Ферье 576
— Максвелла 29, 33
— Стирлинга 94
— Тейлора 575
— Ханкеля 444
— Эпштейна 97
Фронт 249, 256
Функции базисные 424
Функция влияния 440, 446
— гамма 369
— дельта 514, 569
— источника 121, 143
— Планка 123
— пропускания 147
интегральная 149, 153, 163
длинноволновой радиации 164
коротковолновой радиации
159, 160, 166
— пространственная корреляционная
пульсаций температуры 557
— распределения 29
— состояния 72
Фурье закон 111
— компонента скорости 541
— преобразование 426
X
Ханкеля формула 444
Характерный масштаб 5, 211, 214, 403
высоты 21
турбулентных вихрей 550
Химический потенциал 78, 106
Ч
Частота 267, 290
— Вяйсяла 286, 361
— круговая 267
— суточных колебаний 394
Число волновое 265, 543, 555
— Кибеля 219
— Прандтля молекулярное 559
турбулентное 528
— Рейнольдса 187, 551
— Ричардсона 193, 313, 324, 528
потоковое 528
— столкновений молекул 32, 33
Ш
Шероховатость 351, 359
Э
Экзосфера 41
Экмана спираль 334
Эмаграмма 56
Эмдена решение 177
602
Указатель
Энергия 491, 498
— баланс 498, 501
— внутренняя 14, 43, 497
молекул 133
— доступная потенциальная 505
— кинетическая 14, 207, 494, 503, 504
пульсационных составляющих
скорости 206, 322, 349, 378, 524,
531, 533, 534
термика 61
—лучистая 14, 118
— магнитная 14
— неустойчивости 55
— потенциальная 14
— преобразование 492, 502
— термобарическая 280
— упругости 280
— фазовых переходов 14, 500
— химическая 14
— электрическая 14
Энтальпия 503—505
Энтропия 72, 93, 96, 492
Эпштейна формула 97
Эффективная масса 145
Ядро конденсации 109
ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Общие принципы 5
1.1. Атмосфера как сплошная среда —
1.2. Общая формулировка уравнения баланса 6
1.3. Уравнение баланса массы 9
1.4. Уравнение движения. Баланс импульса 10
1.5. Закон сохранения энергии. Уравнение баланса внутренней энергии 14
1.6. Уравнение состояния сухого воздуха 16
1.7. Сводные результаты 18
Глава 2. Газовый состав атмосферы 19
2.1. Газовый состав атмосферы на разных высотах (теория
диффузионно-гравитационного разделения газов) 20
2.2. Распределение плотности газа по высоте при наличии
турбулентного перемешивания 24
2.3. Время установления диффузионно-гравитационного разделения
газов 25
2.4. Диссипация газов из атмосферы 28
2.5. Уровень диссипации газов 31
2.6. Интенсивность и время диссипации газа из атмосферы 36
Глава 3. Термодинамические процессы в сухом воздухе 42
3.1. Уравнение первого начала термодинамики для идеальных газов 43
3.2. Связь между термодинамическими характеристиками при
заданном притоке тепла 45
3 3. Изменение температуры перемещающейся по вертикали массы
сухого воздуха 47
3.4. Условия статической устойчивости атмосферы 50
3.5. Уровень термической конвекции ' 53
3.6. Энергия неустойчивости 55
3.7. Влияние вовлечения воздуха на свойства перемещающейся по
вертикали воздушной массы 57
Глава 4. Термодинамические процессы во влажном воздухе .... 64
4.1. Основные характеристики влажного воздуха и соотношения между
ними 65
4.2. Уравнение состояния реальных газов и фазовые переходы .... 68
4.3. Второе начало термодинамики 72
4.4. Второе начало термодинамики и условия устойчивости атмосферы 75
4.5. Условия равновесия фаз. Уравнение Клаузиуса—Клапейрона ... 77
4.6. Изменение характеристик перемещающейся по вертикали массы
влажного воздуха 83
604
Оглавление
Глава 5. Некоторые приложения теории термодинамических
флуктуации к атмосферным процессам 92
5.1. Термодинамические флуктуации. Статистический смысл энтропии —
5.2. Вывод формулы для вероятности термодинамических флуктуации 96
5.3. Вычисление флуктуации термодинамических величин 98
5.4. Условия образования новой фазы 101
5.5. Вероятность образования зародышей новой фазы 105
5.6. Вычисление потоков различных субстанций 111
Глава 6. Лучистая энергия 117
6.1. Основные понятия. Законы взаимодействия радиации с веществом 118
6.2. Уравнения переноса радиации. Их упрощение и интегрирование в
разных спектральных областях 141
6.3. Радиационный баланс системы Земля—атмосфера.
Метеорологические приложения • 171
Глава 7. Система уравнений гидротермодинамики для турбулентной
атмосферы 184
7.1. Понятие о турбулентности —
7.2. Возникновение турбулентности 186
7.3. Методы осреднения 194
7.4. Вывод уравнения для осредненных величин 198
7.5. Связь турбулентных потоков с осредненными полями 199
7.6. Осредненные уравнения гидротермодинамики атмосферы 204
7.7. Баланс кинетической энергии турбулентных пульсаций 206
7.8. Упрощение уравнений динамики атмосферы. Классификация
атмосферных движений 209
Глава 8. Динамика свободной атмосферы 225
8.1. Уравнения движения в поле изобар, близких к окружностям ... —
8.2. Движение при чисто круговых изобарах 228
8.3. Геострофический ветер 231
8.4. Изменение геострофического ветра с высотой 234
8.5. Отклонение ветра от геострофического 242
Глава 9. Поверхности раздела в атмосфере 248
9.1. Общие свойства поверхностей раздела (сильный разрыв) 250
9.2. Наклон поверхности раздела двух воздушных масс 254
9.3. Упорядоченные вертикальные движения, обусловленные
поверхностью раздела 257
Глава 10. Волновые движения в атмосфере (линейная теория) . . . 261
10.1. Простейшие примеры образования волновых движений в
атмосфере —
10 2. Параметры волн 265
10.3. Вывод уравнений для малых возмущений относительно
состояния покоя 269
Оглавление
605
10 4. Краевые условия в задачах теории волн 275
10.5. Энергетика малых возмущений 278
10.6. Связь параметров волн с характеристиками основного состояния 281
10.7. Некоторые краевые задачи 292
10.8. О волнах в движущейся атмосфере 301
Глава П. Пограничный слой атмосферы 305
11.1. Система уравнений, описывающих строение пограничного слоя
атмосферы 306
11.2. Распределение метеорологических элементов и характеристик
турбулентности вблизи поверхности земли 309
11.3. Расчет турбулентных потоков тепла, влаги и количества движения 327
11.4. Однопараметрическая модель пограничного слоя атмосферы
(fc = const) 331
11.5. Нелинейная модель пограничного слоя атмосферы 345
11.6. Пограничный слой над морем (коэффициент турбулентности не
зависит от высоты) 353
11.7. Параметризация планетарного пограничного слоя атмосферы . . 358
Глава 12. Процессы в нижнем слое атмосферы над неоднородной
подстилающей поверхностью 363
12.1. Общая постановка задачи 364
12.2. Трансформация полей температуры и влажности 366
12.3. Трансформация динамических характеристик воздушного потока
при изменении шероховатости подстилающей поверхности 371
12.4. Некоторые приложения результатов теории трансформации . . . 380
Глава 13. Суточный ход метеорологических элементов 388
13.1. Формулировка задачи о суточном ходе метеоэлементов.
Некоторые результаты численного решения —
13.2. Суточный ход температуры при постоянном коэффициенте
турбулентности 393
13.3. Ночное понижение температуры 400
Глава 14. Физические основы предвычисления метеорологических
полей на короткий срок 405
14.1. Общие положения —
14.2. Уравнения гидротермодинамики в изобарической системе
координат 408
14.3. Процедура численного решения уравнений гидротермодинамики
применительно к задачам краткосрочного прогноза (примитивная или
исходная система) 412
14.4. О численном интегрировании прогностической системы уравнений 417
14.5. Квазигеострофическая система уравнений для численных
прогнозов 427
14.6. Численный прогноз для баротропной атмосферы в квазигеостро-
фическом приближении 436
14.7. Численный прогноз для бароклинной атмосферы в квазигеостро-
фическом приближении 441
606
Оглавление
14.8. Использование квазисоленоидальных приближений для
численного прогноза 448
14.9. Предвычисление облачности 450
14.10. Влияние пограничного слоя на эволюцию крупномасштабных
процессов 456
14.11. О согласовании исходных полей 463
Глава 15. Основы общей циркуляции атмосферы и некоторые
вопросы энергетики атмосферы 468
15.1. Понятие «общая циркуляция атмосферы». Уравнения
гидродинамики, описывающие крупномасштабные движения в атмосфере .... —
15.2. Первая гидродинамическая модель общей циркуляции атмосферы
Н. Е. Кочина 470
15.3. Модель общей циркуляции атмосферы Е. Н. Блиновой 471
15.4. Численные эксперименты по общей циркуляции атмосферы. Двух-
уровенная модель Н. Филлипса 477
15.5. Численные эксперименты по общей циркуляции атмосферы. Де-
вятиуровенная модель Д. Смагоринского 485
15 6. Преобразования энергии в атмосфере 491
Глава 16. Турбулентность в свободной атмосфере 508
16.1. Общая постановка задачи —
16.2. Турбулентность вблизи поверхности раздела 510
16 3. Турбулентность в струйных течениях 513
Глава 17. Статистические характеристики турбулентного потока . . 518
17.1. Вывод и анализ уравнения для пространственного
корреляционного тензора поля скорости 519
17.2. Анализ уравнений баланса различных компонент энергии
турбулентности 524
17.3. Профили различных компонент энергии турбулентности в
пограничном слое атмосферы 529
17.4. Профили интенсивности температурных пульсаций в пограничном
слое атмосферы 536
17.5. Спектральные характеристики турбулентного поля скорости . . . 541
17.6. Вывод и анализ уравнения для спектральной плотности энергии
турбулентности 543
17.7. Общий вид спектра энергии в однородном турбулентном поле.
Гипотеза о статистическом равновесии 545
17.8. Гипотезы Колмогорова о турбулентном режиме мелкомасштабных
компонент турбулентности 548
17.9. Модель Гейзенберга переноса энергии турбулентности по спектру 553
17.10. Спектральные характеристики температурного поля и
спектральное уравнение баланса интенсивности температурных пульсаций . . . 557
17.11. Влияние стратификации на спектральные характеристики полей
скорости и температуры 560
Оглавление
607
Глава 18. Турбулентная диффузия примесей и загрязнение
атмосферы 564
18.1. Математическая формулировка задачи о распространении
примесей в атмосфере 565
18.2. Качественный анализ поля концентрации примеси 570
18.3. Поперечное рассеяние частиц, поступающих из непрерывного
точечного источника, в турбулентном потоке 574
18.4. Распределение в атмосфере примесей при разных
метеорологических условиях и разных параметрах выброса 580
Приложение 586
Список литературы 589
Указатель 595
ГИСИНА ФРАДА АБРАМОВНА, ЛАИХТМАН ДАВИД ЛЬВОВИЧ,
МЕЛЬНИКОВА И Я ИЛЛАРИОНОВНА, ПАЛАГИН ЭРАСТ ГРИГОРЬЕВИЧ,
ПОДОЛЬСКАЯ ЭЛЬГА ЛАЗАРЕВНА, РАДИКЕВИЧ ВИТАЛИИ МИХАИЛОВИЧ,
ЮРГЕНСОН АЛЕКСАНДР ПАВЛОВИЧ
ДИНАМИЧЕСКАЯ
МЕТЕОРОЛОГИЯ
Редактор Г. Я- Русакова. Художественный редактор В. А. Баканов
Художник В. Г. Бахтин. Техн. редактор Л. М. Шишкова. Корректор Т. Н. Черненко
Сдано в набор 12/XII 1975 г Подписано к печати 2/VI 1976 г М-19730. Формат 60X90'/ie.
бумага тип. № 1. Печ. л. 38,0 Уч -изд. л 37,51. Тираж 3500 экз. Индекс МЛ-32. Заказ Мгб12.
Цена 1 руб. 55 коп. Гидрометеоиздат. 199053. Ленинград, 2-я линия, д. 23.
Ленинградская типография № 8 Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств, полиграфии и книжной торговли.
190000, Ленинград, Прачечный пер , 6.
Для законов сохранения массы, импульса и тепла
справедлива унифицированная запись
Jj*.-. div(Pva+Jir)+/.
Ускорение свободного падения и ускорение Корио-
лиса играют определяющую роль в формировании
полей метеорологических элементов:
К =-2 (wxv).
В атмосфере с большой точностью выполняется
уравнение статики
др
В свободной атмосфере сила Кориолиса
уравновешивается горизонтальным градиентом давления:
ю-1 др
р дп
Горизонтальная температурная неоднородность
обусловливает изменения ветра с высотой:
^т /r0 дп
Интегральные характеристики пограничного слоя
функционально связаны с геострофическим ветром и
параметром Кориолиса:
ь °2 и G
Вблизи земной поверхности скорость ветра
изменяется по закону
*0
Режим радиации связан с излучательными и погло-
щательными свойствами атмосферы:
<fe ~~ cos* v х х'#
Солнечная постоянная
/о =1381,644 Дж/(м2- с).
Закон пяти третей отражает спектральное
распределение пульсационной энергии:
г(«)-ЛЛ
Скрытая теплота парообразования
-2»=24,995 • 105 Дж/кг.
Сухоадиабатический градиент
Та = 0,0098°С/м.
Постоянная Стефана—Больцмана
«=5,669 • Ю"8 Вт/(м2 • К4).
Постоянная Планка
А = 6.625 • Ю-34 Дж • с.
Угловая скорость вращения Земли
(0=7,292- 10~5 рад/с.
Радиус экватора
Я = 6,378 • 10« м.
Ускорение свободного падения на широте 45°
£=9,806 м/с2.
Относительная молекулярная масса сухого воздуха
*а и водяного пара л, равны:
IS=28,97, (*„= 18,00.
Газовая постоянная сухого воздуха /?в и водяногс
пара Rn равны:
#„=286,8 ДжДкг • К),
/?„=460,0 ДжДкг • К).
Удельная теплоемкость воздуха при постоянном
давлении ср и при постоянном объеме cv равны:
ср= 1,007 ДжДкг- К),
^=0,720 Дж/(кг • К).