ИССЛЕДОВАНИЯХ

Е. В. Гу б л ер, А. А. Генкин
ПРИМЕНЕНИЕ
НЕПАРАМЕТРИЧЕСКИХ
КРИТЕРИЕВ
СТАТИСТИКИ
В МЕДИКО-БИОЛОГИЧЕСКИХ
ИССЛЕДОВАНИЯХ
ЛЕНИНГРАД. «МЕДИЦИН А»
ЛЕНИНГРАДСКОЕ ОТДЕЛЕНИЕ 1973

УДК 61 :519.24
Гу б л ер Е. В., Генкин А. А., Применение непараметрических
критериев статистики в медико-биологических исследованиях,
1973.
Отличием непараметрических критериев статистики, большин¬
ство из которых предложены в последние 25 лет, от традицион¬
ных для биологии и медицины параметрических критериев яв¬
ляется: а) меньшая трудоемкость вычислений; б) эффективность
при любых формах распределений, что делает целесообразным их
применение в тех случаях, когда форма распределения неиз¬
вестна. В последние 10 лет непараметрические критерии кратко
упоминаются почти в каждом руководстве по статистике для
биологов и медиков. Однако эта книга представляет собой пер¬
вый опыт статистического пособия для медиков и биологов, цели¬
ком посвященного непараметрическим методам. Ее первое изда¬
ние в виде краткой брошюры вышло в 1969 г. Настоящее издание
значительно расширено.
В книге рассмотрены различные непараметрические критерии,
приведены многочисленные примеры, отражающие опыт авторов
в их применении, и описана методика выбора наиболее адекват¬
ного критерия в каждом случае.
В приложении даны статистические таблицы, позволяющие
применять непараметрические критерии при разном объеме вы¬
борок — от 2—5 до 60 наблюдений и более.
Книга предназначена для широких кругов исследователей во
всех областях медицины и биологии.
Книга содержит 32 табл., библ. — 31 назв.
8-1
290-73

ПРЕДИСЛОВИЕ
К ПЕРВОМУ ИЗДАНИЮ
Говоря о внедрении математики в современную ме¬
дицину, часто имеют в виду сложные методы диагно¬
стики заболеваний или создание математических мо¬
делей патологических процессов. Между тем далеко
не всегда еще в медицинских, особенно клинических,
научных исследованиях применяются относительно
простые и известные способы статистической провер¬
ки достоверности делаемых выводов. Одной из причин
этого является относительно высокая трудоемкость
применяемых чаще всего для этой цели в биологии
и медицине параметрических статистических крите¬
риев.
В последние 15—20 лет разработаны непараметри¬
ческие статистические критерии, значительно менее
трудоемкие, а при распределениях, далеких от нор¬
мального, и более эффективные, чем параметрические.
Авторами настоящего краткого руководства рассмот¬
рены б различных критериев и 8 типовых случаев их
применения. Это позволяет при наиболее частых ва¬
риантах обработки экспериментальных и клинических
данных выбрать наиболее подходящий критерий для
проверки достоверности вывода о различиях между
сравниваемыми группами наблюдений. Часть мето¬
дов, изложенных в кратком руководстве Е.В. Гублера
и А. А. Генкина, описаны и в других пособиях по био¬
логической и медицинской статистике на русском язы¬
ке, однако их изложение в настоящем руководстве со¬
провождается примерами и пояснениями, отражающи¬
ми многолетний опыт авторов. Часть критериев ранее
не была описана в отечественных пособиях по приме¬
нению статистики в медико-биологических исследова¬
ниях.
Можно выразить уверенность в том, что настоящее
краткое пособие поможет многим медицинским работ¬
никам шире применять статистические методы обра¬
ботки экспериментальных и клинических наблюдений.
I*
3

ПРЕДИСЛОВИЕ
КО ВТОРОМУ ИЗДАНИЮ
В последние годы в статистике получают все боль¬
шее распространение непараметрические методы
оценки различий двух групп наблюдений, оценки
связи (корреляции) между двумя рядами наблюде¬
ний и отнесения наблюдений к одному из двух клас¬
сов. Авторам в последние 10 лет приходилось систе¬
матически применять эти методы, в той или иной
мере разрабатывать способы их применения, давать
консультации по этим вопросам, выступать по этому
поводу в различных медицинских аудиториях и в пе¬
чати. Это и привело в конце концов к созданию на¬
стоящего краткого пособия.
Основания для рассмотрения в отдельном пособии
методов применения непараметрических критериев
статистики в медико-биологических исследованиях
вкратце сводятся к следующему.
Сейчас уже ясно, что совершенно недостаточно
владеть одним из методов статистической оценки раз¬
личий двух групп наблюдений. В каждом случае
необходимо выбирать подходящий критерий. Это по¬
зволяет не только повысить эффективность статисти¬
ческой обработки, но и, как будет ясно из дальнейше¬
го, снизить ее трудоемкость. В большинстве меди¬
цинских исследований наиболее подходящим оказы¬
вается один из непараметрических критериев разли¬
чий, которые в настоящее время в медицине приме¬
няются относительно редко. Краткое рассмотрение
некоторых из этих критериев можно найти во многих
руководствах по медицинской и биологической стати¬
стике последних лет. Более подробное рассмотрение
их в отдельном пособии, возможно, будет способство¬
вать более широкому внедрению этих прогрессивных
методов в практику научных и клинико-диагностиче¬
ских исследований.
Сказанное относится и к непараметрическому ме¬
тоду оценки связи (корреляции) между рядами на¬
блюдений. Этот метод обладает аналогичными пре¬
имуществами перед классическим параметрическим
методом оценки связи: универсальностью и малой
трудоемкостью. Между тем сейчас статистическая ха¬
4

рактеристика связи между группами наблюдений
вообще редко применяется в медико-биологических
исследованиях, возможно именно из-за высокой тру¬
доемкости расчетов и малой информативности пара¬
метрического критерия связи при распределениях, да¬
леких от нормального.
Еще реже применяются в исследовательских рабо¬
тах и клинической практике статистические методы
диагностики и прогнозирования. Рассматриваемый в
этой книге метод составления диагностических и
прогностических таблиц по своей простоте (он не тре¬
бует применения вычислительной техники), относи¬
тельной универсальности и некоторым другим свой¬
ствам близок к непараметрическим. Как и они, он
имеет и существенные ограничения (универсальные
диагностические методы в принципе не могут быть
очень простыми).
Первоначально эта работа вышла в виде лекции
для врачей и слушателей Военно-медицинской акаде¬
мии им. С. М. Кирова (1966), а затем была издана
в виде небольшой брошюры [12] издательством «Ме¬
дицина» (1969). Тираж издания был очень невелик,
и брошюра быстро разошлась. Настоящее второе
издание значительно переработано и расширено по
сравнению с предыдущим (почти в 4 раза). В частно¬
сти, таблицы максимального числа инверсий по кри¬
терию U вычислены для числа наблюдений 60 в каж¬
дой выборке (а не 20, как в других известных авторам
руководствах); добавлены главы, посвященные об¬
щим статистическим понятиям (глава 1), оценке
связи между двумя рядами наблюдений (глава 3),
отнесению наблюдений к одному из двух возможных
классов (глава 4). Необходимо отметить, что глава 4
по стилю изложения несколько отличается от осталь¬
ных. В связи с новизной рекомендуемых в ней ме¬
тодов и приемов дано более подробное обоснование
некоторых из них.
Для удобства внутренних ссылок номера парагра¬
фов, формул, таблиц и рисунков в этом издании даны
в виде двух чисел, разделенных точкой. Первое из
чисел обозначает номер главы, второе — номер соот¬
ветствующего параграфа, формулы, таблицы или ри¬
сунка в данной главе.
5

Ссылки на литературные источники даются в
квадратных скобках в виде их номеров в указателе
литературы.
Для удобства пользования пособием оно снабже¬
но перечнем условных обозначений (стр. 7) и пред¬
метным указателем (стр. 135).
Следует отметить, что применение непараметри¬
ческих критериев статистики в медицине и биологии,
несомненно, заслуживает значительно более фунда¬
ментального изложения, чем в предлагаемом издании.
Представляет интерес более подробное изложение
общих принципов непараметрической статистики, рас¬
смотрение ряда непараметрических критериев разли¬
чий) критерия Колмогорова — Смирнова, критерия
Ван дер Вардена'и др.), более подробное рассмотре¬
ние последовательной статистической процедуры, ана¬
лиз методов и подходов к составлению машинных
алгоритмов и программ, использующих принципы не¬
параметрической статистики, и т. д. Однако авторы
ограничились минимумом наиболее простых непара¬
метрических методов, учитывая большую потребность
в кратком практическом пособии по непараметриче¬
ским критериям статистики для биологов и медиков.
Поэтому они сочли возможным издать эту небольшую
монографию в ее настоящем виде и будут благодарны
за все замечания о ее содержании.
Добавленные в этом издании главы 1 и 3 напи¬
саны А. А. Генкиным, глава 4 — Е. В. Гублером.
В подготовке таблиц «Приложения» принимал участие
М. Р. Питкин. Им предложен способ'расширения таб¬
лиц критерия U для численности выборок ^21 и про¬
ведены соответствующие расчеты (табл. III). Авторы
выражают глубокую признательность научному ре¬
дактору этой книги профессору Н. А. Толоконцеву.
И. Ф. Уткиной и А. Д. Мельцер авторы искренне
благодарны за полезные замечания и помощь в под¬
готовке рукописи к печати.

УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
ДК (*j) — диагностический коэффициент
i-ro диапазона (градации) /-го
признака.
КЗ — критерий знаков.
ТМФ — точный метод Фишера для
четырехпольной таблицы.
/(^ — информативность признака Xj.
F — критерий Фишера для срав¬
нения дисперсий.
М — средняя арифметическая ге¬
неральной совокупности.
п — число наблюдений (объем вы¬
борки) или число признаков.
N — общее число наблюдений.
Р — вероятность «нулевой гипоте¬
зы» (отсутствия различий).
Р(xjjЛ) или	— частость (вероятность) t-ro
диапазона (градации) /-го
признака соответственно для
заболеваний (состояний) А
и В.
Q — сумма «хвостов» по критерию
Q.
г — число серий по критерию г.
г{ — ранговый номер при ранговой
корреляции.
R — нормальный коэффициент кор¬
реляции (Пирсона).
s2 — дисперсия выборки.
7

Sx — среднеквадратичная ошибка
средней арифметической.
Т — сумма ранговых номеров по
критерию Т.
t — величина t по одноименному
критерию (Фишера — Стью-
дента).
U — число инверсий по критерию
U.
х — средняя арифметическая вы¬
борки.
х, у — разные значения признаков X
и У.
х\ — i-и диапазон (градация) при¬
знака X}.
а, Р — вероятности ошибок диффе¬
ренциальной диагностики.
сг2 — дисперсия генеральной сово¬
купности.
р — коэффициент корреляции ран¬
гов.
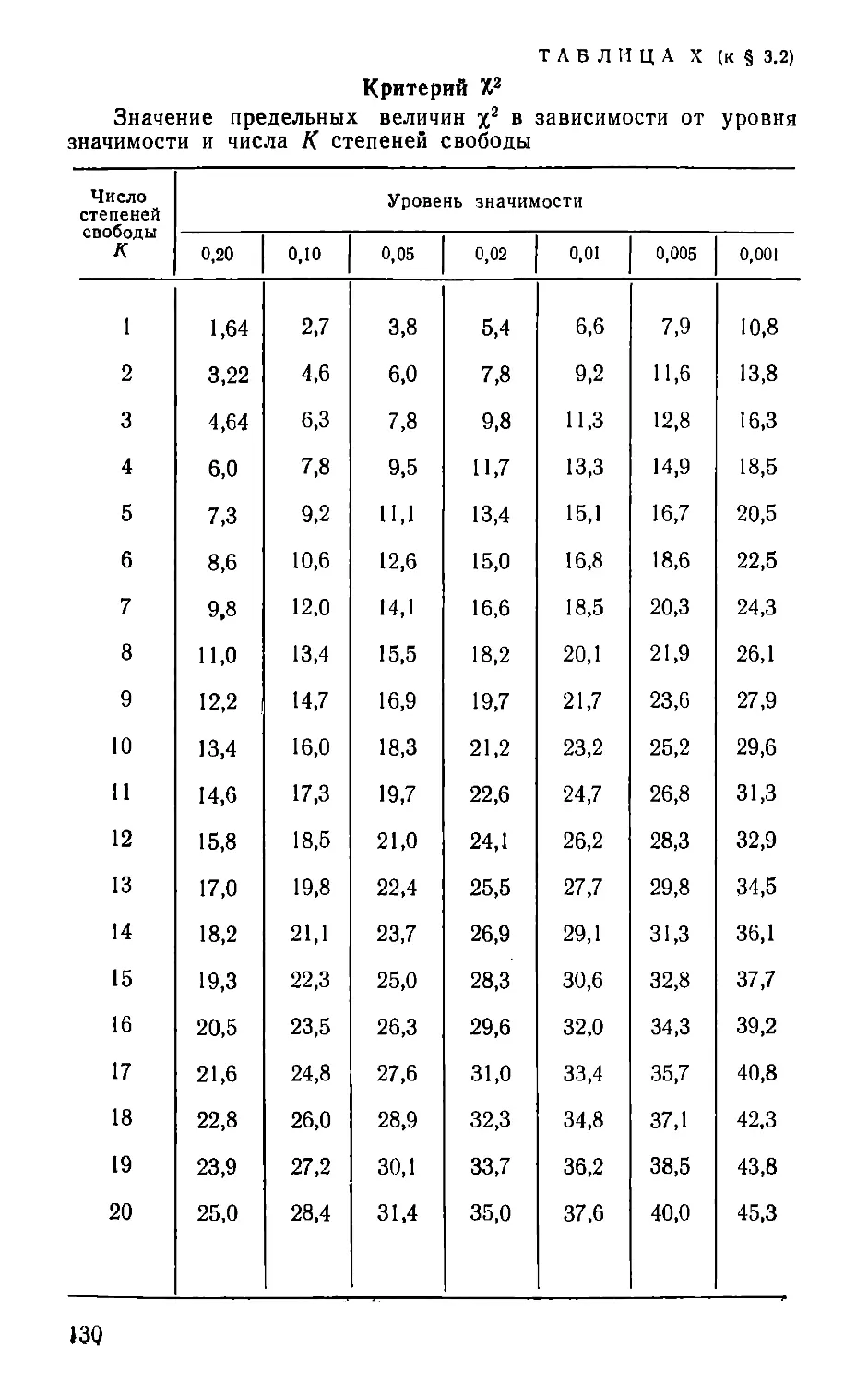
X2 —величина х2 по одноименному
критерию.

Глава 1
НЕКОТОРЫЕ ОБЩИЕ ПОНЯТИЯ
§ 1.1. ПРИРОДА СТАТИСТИЧЕСКИХ ВЫВОДОВ
Применение количественных методов в медико¬
биологических исследованиях предполагает прежде
всего, что объекты (явления), подлежащие изучению,
охарактеризованы каким-то образом с помощью со¬
вокупности признаков, имеющих количественную ме¬
ру. Нас не будет интересовать происхождение этих
чисел, алгоритмы вычисления и способы их измерения.
Отметим лишь, что они могут иметь самую различную
природу; среди них могут быть закодированы и каче¬
ственные особенности исследуемых объектов (явлений).
Многие задачи, возникающие в научно-исследова¬
тельской и практической работе врача и биолога,
связаны с необходимостью сравнивать между собой
две или несколько групп наблюдений, полученных при
разных условиях, а также с необходимостью класси¬
фицировать наблюдения (относить их к одному из
двух или нескольких классов). Решение подобных
задач может быть возможным только в том случае,
когда будет определено, что следует понимать под
различием (или тождественностью) групп наблюде¬
ний. Когда сравниваемые множества чисел настолько
различны, что не пересекаются, у исследователя
обычно не возникают сомнения, что он имеет дело
с разными множествами. Трудности начинаются, ког¬
да множества пересекаются. Необходимо иметь по¬
этому какие-то формальные правила, которые позво¬
ляли бы делать выводы о том, что сравниваемые со¬
вокупности различны.
Мы в настоящей книге будем рассматривать, как
решается эта задача для двух совокупностей. Это
наиболее важный и часто встречающийся случай.
Предполагается, что читатель знаком с основными
статистическими понятиями и имеет некоторый опыт
В лрименении таких распространенных критериев, как
9

t для сравнений средних арифметических или х2 Для
сравнения частот.
Первая попытка формализовать понятие различия
между двумя информационными совокупностями была
осуществлена Р. Фишером. В основе его модели ле¬
жит представление о бесконечном опыте, причем та¬
ком, что результаты наблюдений имеют одни и те же
статистические свойства. Такое бесконечное множе¬
ство чисел было названо генеральной совокупностью.
Из генеральной совокупности можно бесчисленным
числом вариантов брать конечные наборы чисел
(эмпирические выборки). Если эти конечные наборы
чисел являются выборками из одной и той же гене¬
ральной совокупности, то такие выборки, естественно,
считают неразличимыми. Если же они относятся к
разным генеральным совокупностям, то наблюдаемые
совокупности будут считаться различными. Определив
таким образом равенство (или различие) сравнивае¬
мых совокупностей или, как их обычно называют,
эмпирических выборок, Фишер разработал несколько
критериев, позволяющих по статистическим свойствам
совокупностей эмпирических наблюдений (выборок)
делать выводы о том, относятся ли они к одной гене¬
ральной совокупности или же они являются выбор¬
ками из различных совокупностей.
Когда эмпирическая выборка содержит группу
наблюдений, то для того, чтобы ее представить в
более компактной форме, вычисляются некоторые па¬
раметры, характеризующие в обобщенном виде вхо¬
дящие в нее результаты наблюдений. Для этой цели
вычисляют, например, среднее арифметическое (*),
дисперсию (s2) и ряд других характеристик, которые
обычно называют статистиками. Одни из них лучше
представляют свойства группы наблюдений, другие
хуже. Как правило, в любой статистике потеряна
часть информации по сравнению с той информацией,
которая содержится в исходной совокупности. Однако
при некоторых условиях можно найти такие стати¬
стики, которые сохраняют информацию о результатах
наблюдений без существенных потерь. Такие пара¬
метры называются достаточными статистиками.
Генеральная совокупность, состоящая из беско¬
нечного числа наблюдений, подчиняющихся нормаль¬
10

ному закону распределения, может быть исчерпываю¬
щим образом охарактеризована только двумя пара¬
метрами — средней арифметической и дисперсией
(М и а2)1. Это обстоятельство лежит в основе одного
из методов сравнения выборок между собой. Для
того чтобы убедиться, будут ли две конечные эмпи¬
рические выборки принадлежать к одной и той же ге¬
неральной совокупности, строятся некоторые вели¬
чины, которые характеризуют различия между их
средними и дисперсиями. В качестве одной из таких
величин обычно рассматривается величина t для
сравнения средних значений
t = K -fjJIiLr	(1.1)
V4.+4,
и величина F для сравнения дисперсий s2 и 52г
Г	5	(1-2)
(В формуле 1.1 К — число, зависящее от количества
наблюдений в сравниваемых выборках).
Из одной и той же генеральной совокупности
можно, вообще говоря, различными способами выби¬
рать конечные наборы чисел (эмпирические выбор¬
ки). Как правило, их средние и дисперсии будут отли¬
чаться от среднего и дисперсии генеральной совокуп¬
ности, к которой они относятся.
Поэтому даже в том случае, если сравниваемые
эмпирические выборки принадлежат к одной и той же
генеральной совокупности, величины t и F будут из¬
меняться в некотором диапазоне значений, причем
удается найти распределения величин t и F при усло¬
вии, что они характеризуют выборки, принадлежащие
к одной и той же генеральной совокупности.
Если найдены такие распределения, то для любых
двух параметров х\ и х,ч (или s2 и s2) можно опреде¬
лить вероятность того, что сравниваемые эмпириче¬
ские выборки взяты из одной и той же генеральной
1 Среднюю арифметическую и дисперсию выборки, в отличие
от аналогичных величин генеральной совокупности, обозначают
иначе: например, х и s2 (см. выше).
11

совокупности. Когда эта вероятность мала, допу¬
скают, что мы имеем дело с эмпирическими выборка¬
ми, которые принадлежат к генеральным совокупно¬
стям с разными статистиками (свойствами).
Вероятность Р того, что параметры сопоставляе¬
мых выборок характеризуют одну и ту же генераль¬
ную совокупность, принято называть уровнем значи¬
мости (существенности) различий.
Сказанное иногда формулируют иначе, вводя по¬
нятие нулевой гипотезы, хотя сам Фишер избегал
этого понятия. Нулевой гипотезой называют гипоте¬
зу, согласно которой две сравниваемые эмпирические
выборки принадлежат к одной и той же генеральной
совокупности. Если вероятность нулевой гипотезы
мала, то следует отклонить эту гипотезу. Это озна¬
чает, что сравниваемые выборки принадлежат к раз¬
ным генеральным совокупностям.
Принято считать достаточным такие различия,
при которых вероятность нулевой гипотезы не превы¬
шает 0,05. Впрочем, все определяется конкретной си¬
туацией. Для некоторых выводов такая вероятность
нулевой гипотезы может оказаться завышенной.
Здесь необходимо отметить одно обстоятельство,
которое не всегда учитывается экспериментатором.
Если вероятность нулевой гипотезы недостаточно
мала (скажем, Р>0,05), это еще не дает основа¬
ний принять нулевую гипотезу, так как тот факт,
что мы не обнаружили различий, может быть обуслов¬
лен не тем, что таких различий действительно нет, а
недостаточностью числа наблюдений или неправиль¬
ным выбором критерия различий (см. дальше, §2.10).
Поэтому, если вероятность нулевой гипотезы оказа¬
лась значительной (например, 0,10), следует сделать
осторожный вывод: «статистически значимых разли¬
чий выявить не удалось».
Если мы отвергли нулевую гипотезу, логически
можно представить себе три возможности: 1) первая
выборка по какому-то параметру больше второй;
2) вторая выборка по этому параметру больше пер¬
вой; 3) первая выборка отлична от второй, но мы не
знаем, в какую сторону она отличается. Поскольку
в последнем случае ошибка более вероятна, чем .в
первых двух, вероятность принятия нулевой гипотезы
12

в последнем случае должна быть в 2 раза меньше,
чем в первом и во втором, для того, чтобы мы могли
признать различия между выборками значимыми.
Поэтому для последнего случая Р должна быть не
больше 0,025, а для первых двух — не больше 0,05.
При оценке различий в средних тенденциях рас¬
пределения мы всегда знаем, какая из выборок боль¬
ше (если они вообще различаются), т. е. имеем дело
с первым и вторым случаями, когда достаточно, чтобы
вероятность нулевой гипотезы была равна или была
меньше 0,05. Лишь при оценке различий в форме рас¬
пределений мы можем иметь дело с третьим случаем,
при котором эта вероятность должна быть не бо¬
лее 0,025.
§ 1.2. ПОНЯТИЕ О НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЯХ
В основе модели Фишера лежит представление о
генеральной совокупности, элементы которой обла¬
дают одними и теми же статистическими свойствами.
Сразу же отметим, что это понятие отражает реаль¬
ность лишь для ограниченного числа количественных
признаков. В основном это такие признаки, которые
в наблюдаемый период времени имеют отчетливую
стационарность (отсутствует заметная эволюция).
Примером таких признаков могут быть антропологи¬
ческие переменные, признаки сельскохозяйственных
растений или размеры анатомических объектов. Фи¬
зиологические переменные даже в течение одного
опыта не всегда оказываются стационарными, так что
для них трудно обосновать гипотетическое существо¬
вание генеральной совокупности. Вообще для при¬
знаков, характеризующих динамику явлений, когда
отчетливо имеется эволюция, представление о ста¬
бильности вида распределений, а следовательно, и о
генеральной совокупности, неадекватно. Отсюда сле¬
дует, что будущее развитие статистики будет связано
с представлением о процессе, когда наблюдаемые
значения характеризуются не одним распределением,
а системой распределений, параметры которых зави¬
сят от номера наблюдений. Отмечая ограниченность
понятия о генеральной совокупности в том виде, в
каком оно было сформулировано Фишером, необхо¬
13

димо отметить исключительную роль этого понятия
в развитии статистического мышления и ту роль, кото¬
рую оно еще долго будет играть в решении различных
теоретических и прикладных задач. Но эксперимента¬
тор всегда должен помнить, что при динамических
ситуациях, там, где налицо эволюция, пользоваться
критериями существенности различий нельзя.
Другое ограничение методов, развитых Фишером,
связано с тем, что практически получить распределе¬
ние статистик (1.1) и (1.2) оказывается возможным
в основном тогда, когда средние и дисперсия являют¬
ся параметрами гауссовского (нормального) распре¬
деления или во всяком случае, когда они являются
параметрами вполне определенных распределений.
В реальном же опыте не всегда известен вид распре¬
делений, к которым принадлежат сравниваемые вы¬
борки. Это особенно существенно для медико-био¬
логического эксперимента. Поэтому использование
распределений статистик (1.1) и (1.2) без предвари¬
тельной проверки вида распределений, к которым
принадлежат сравниваемые выборки, может приво¬
дить к ошибкам при статистических выводах.
На преодоление указанных ограничений потрачено
много усилий, однако результаты пока еще доста¬
точно скромны. Наиболее разработанными оказались
методы, в которых не ставились специальные условия,
касающиеся формы распределений. Такие тесты иног¬
да называют не зависящими от формы распределе¬
ния (free-distribution test). Их называют еще и не¬
параметрическими. Последнее название связано с
тем, что при сравнении двух выборок так же, как и
в параметрическом случае, ищется распределение не¬
которой статистики типа (1.1), но такой, в которой
отсутствуют в явном виде параметры распределений
(средние арифметические, дисперсии), а используются
иные особенности, характеризующие ряды наблюдений.
В качестве таковых применяются обычно некоторые
относительные характеристики — ранги (см. § 3.1), ин¬
версии (§ 2.4), серии (§ 2.9). Именно поэтому методы
сравнения наблюдений, которые не зависят от вида
распределения, иногда называют ранговыми.
В последние 10—15 лет такие критерии получают
все большее распространение [1, 3, 5, 12, 15, 19, 20,23,
И

26]. Есть все основания считать, что их примене¬
ние в медико-биологических исследованиях более
оправдано, чем применение параметрических крите¬
риев. Во-первых, при распределениях, далеких от нор¬
мального, непараметрические критерии позволяют
обнаружить существенные различия тогда, когда, на¬
пример, критерий t их не выявляет. Так, в 6 из И
приведенных ниже примеров с помощью критерия t
обнаружить существенные различия не удалось, в то
время как непараметрические критерии их выявили.
Во-вторых, при распределениях, близких к нормаль¬
ному, непараметрические критерии также дают хоро¬
ший результат, почти не уступающий критерию /.
В третьих, привлекательной особенностью этих
критериев является их низкая трудоемкость. В част¬
ности, они не требуют вычисления средних арифмети¬
ческих (я), среднеквадратичных отклонений (s), оши¬
бок средних (s*), что необходимо при использовании
критерия t.
К сожалению, для многомерных совокупностей
(когда каждое наблюдение — многомерное) не разра¬
ботаны ранговые критерии. В этом случае неясно, как
ранжировать наблюдения; это можно сделать только
для таких наблюдений, когда все компоненты одного
вектора больше или меньше соответствующих компо¬
нент другого. Мы при оценке сравнения многомерных
совокупностей рекомендуем определять оценку суще¬
ственности различий для каждого признака в отдель¬
ности, используя один из непараметрических крите¬
риев, изложенных ниже (глава 2). При таком сопо¬
ставлении возможна потеря информации, которая
содержится во взаимосвязях между признаками. Од¬
нако оценку взаимосвязи можно проводить отдельно,
используя для этого более адекватные методы, чем
вычисление линейного коэффициента корреляции
Пирсона. При таком подходе мере взаимосвязи не
отводится подсобная роль, как это имеет место при
применении коэффициентов корреляции в критерии
Т2 — Хотеллинга, дискриминантном анализе и других
процедурах. В главе 3 приводятся некоторые из не¬
параметрических оценок взаимосвязи между призна¬
ками и даются практические иллюстрации высказан¬
ных положений,

Глава 2
КРИТЕРИИ РАЗЛИЧИЙ ДВУХ ВЫБОРОК
§ 2.1. ОБЩИЕ ЗАМЕЧАНИЯ
В этой главе мы последовательно рассматриваем
шесть непараметрических критериев, рассчитанных
для 6 различных случаев сравнения двух групп на¬
блюдений. При изложении мы исходим из того, что
читатель имеет известный навык в применении ши¬
роко распространенного критерия t (Фишера —
Стьюдента), а также критерия %2 («хи-квадрат»),
описываемых во всех современных руководствах по
медицинской и биологической статистике.
Предлагаемые 6 критериев могут быть отнесены
к трем раличным группам.
Статистической проверке подвергается чаще всего
вывод о том, что члены одной выборки по своей ве¬
личине больше членов другой выборки. С математи¬
ческой точки зрения это значит, что две сравниваемые
выборки (распределения) различаются по своим сред¬
ним тенденциям (характеристикой средней тенденции
может служить средняя арифметическая, медиана и
т. д.). Для оценки различий в средних тенденциях
служат 4 из 6 рассматриваемых критериев: критерий
знаков, критерий Т (парный критерий Вилкоксона),
критерий U (Вилкоксона — Манна — Уитни), критерий
Q (Розенбаума). Первые два из них — критерий зна¬
ков и Т — рассчитаны для связанных (парных) вы¬
борок, вторые два — для независимых.
Пятый и шестой критерии позволяют выявить как
различия в средних тенденциях, так и иные различия
между выборками. Бывают случаи, когда в опыте
наблюдается два противоположных типа реакций, на¬
пример в части опытов повышение, а в другой ча¬
сти— понижение артериального давления. Средние
значения в опыте и в контроле в этом случае могут
оказаться близкими, но распределения все же будут
16

различаться. Для выявления любых различий в рас¬
пределениях и предназначены эти два критерия. Если
распределения состоят только из двух градаций (на¬
пример, выжившие и умершие животные в двух се¬
риях опытов; лица с артериальным давлением выше
и ниже 140 мм рт. ст. среди двух групп обследован¬
ных людей и т. д.), целесообразно применить точный
метод Фишера для четырехпольной таблицы (ТМФ).
Если же градаций несколько или имеются просто
две несгруппированные выборки, то для выявления
любых различий в распределениях целесообразно
применить серийный критерий г (Вальда — Вольфо-
вица). Он позволяет статистически оценить достовер¬
ность вывода о существенных различиях между дву¬
мя группами наблюдений, но в чем именно эти раз¬
личия состоят, остается неизвестным. Решение этого
вопроса требует отдельного анализа.
При использовании шести непараметрических кри¬
териев исследователь испытывает трудность, которая
была ему незнакома, пока он пользовался одним кри¬
терием t: необходимо выбрать подходящий критерий.
Для того, чтобы облегчить эту задачу, в конце на¬
стоящей главы введен раздел «Выбор критерия раз¬
личий» (§ 2.10). Наиболее экономным, с точки
зрения времени, оказывается последовательное ис¬
пользование нескольких критериев в каждом случае
оценки значимости различий. Выгоднее начинать
оценку с наименее трудоемкого критерия и лишь, ес¬
ли он не выявил различий, применять более трудоем¬
кий и, как правило, более мощный критерий. Реко¬
мендуемый порядок применения критериев приведен
в табл. 2.6, помещенной в указанном выше парагра¬
фе. Ею желательно пользоваться на первых порах,
пока рекомендуемый порядок применения критериев
не стал привычным.
Рассмотрим последовательно все упомянутые кри¬
терии различий двух выборок и примеры их приме¬
нения.
В приведенных численных примерах наряду с
соответствующим непараметрическим критерием с
целью сравнения был применен и критерий /. Его
использование всегда было более трудоемким. Сле¬
дует подчеркнуть, что далеко не во всех случаях, в
17

которых различия обнаруживались с помощью непа¬
раметрических критериев, их можно было выявить
с помощью критерия t.
СЛУЧАЙ СВЯЗАННЫХ ВЫБОРОК
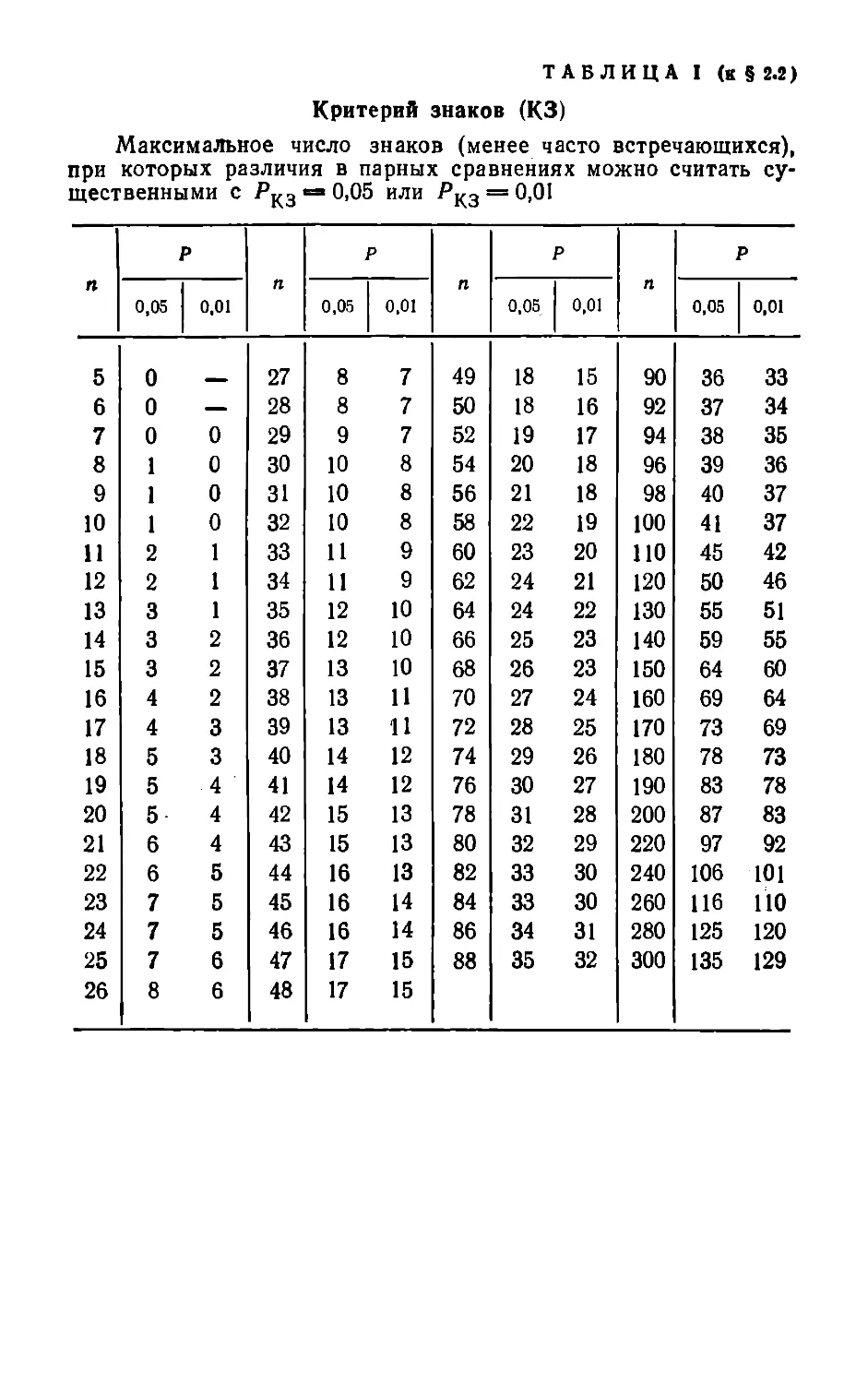
§ 2.2. КРИТЕРИЙ ЗНАКОВ (КЗ)
При сравнении двух связанных (парных) выборок
очень удобен критерий знаков [1, 3, 5, 12, 15, 19, 20,
21]. Напомним, что связанными называют такие вы¬
борки, в которых каждому наблюдению в опыте соот¬
ветствует свой контроль, так как он связан с опытом
единством каких-либо условий эксперимента. Чаще
всего это — исходный уровень измеряемого параметра
у того же животного. Иногда это—измеряемая ве¬
личина у контрольного животного близкого веса или
животного, помещенного в те же условия. Иногда
связь обусловлена временем: контрольный экспери¬
мент производят в то же время, когда и основной
опыт, и т. д.
При большом числе пар критерий знаков весьма
эффективен, хотя он учитывает не степень различий
в каждой паре, а лишь их направленность (знак).
Таблица I приложения позволяет применять крите¬
рий знаков при численности сравниваемых выборок
до 300. Если число наблюдений не очень велико (не
более 20), и критерий знаков не выявил различий,
целесообразно применить критерий Т (парный кри¬
терий Вилкоксона) —см. § 2.3.
Критерий знаков основан на подсчете числа одно¬
направленных эффектов в парных сравнениях. Рас¬
смотрим его применение на примере.
Пример 2.1. Через 2 суток после ожога у 6 из 8 собак со¬
держание гемоглобина в крови снизилось по сравнению с уров¬
нем, зарегистрированным через сутки после ожога, но у 2 собак
повысилось. Необходимо установить, является ли уменьшение сте¬
пени гемоконцентрации через 2 суток после ожога достоверным
или наблюдаемые изменения можно объяснить случайными коле¬
баниями содержания гемоглобина. В табл. I (см. приложение)
находим максимальное число менее часто встречающихся зна¬
ков, при котором еще можно считать обнаруженные различия су¬
щественными (при Ркз = 0,05). Таким максимальным числом яв¬
ляется 1 (при общем числе опытов 8). Следовательно, по крите¬
рию знаков снижение степени гемоконцентрации через 2 суток
после ожога не является существенным,
18

Более полное использование информации, в част¬
ности оценка степени различий в каждой паре срав¬
ниваемых величин, может позволить выявить сущест¬
венность различий в подобных случаях. Оценка сте¬
пени отклонения в парных сравнениях обеспечивается
критерием Т.
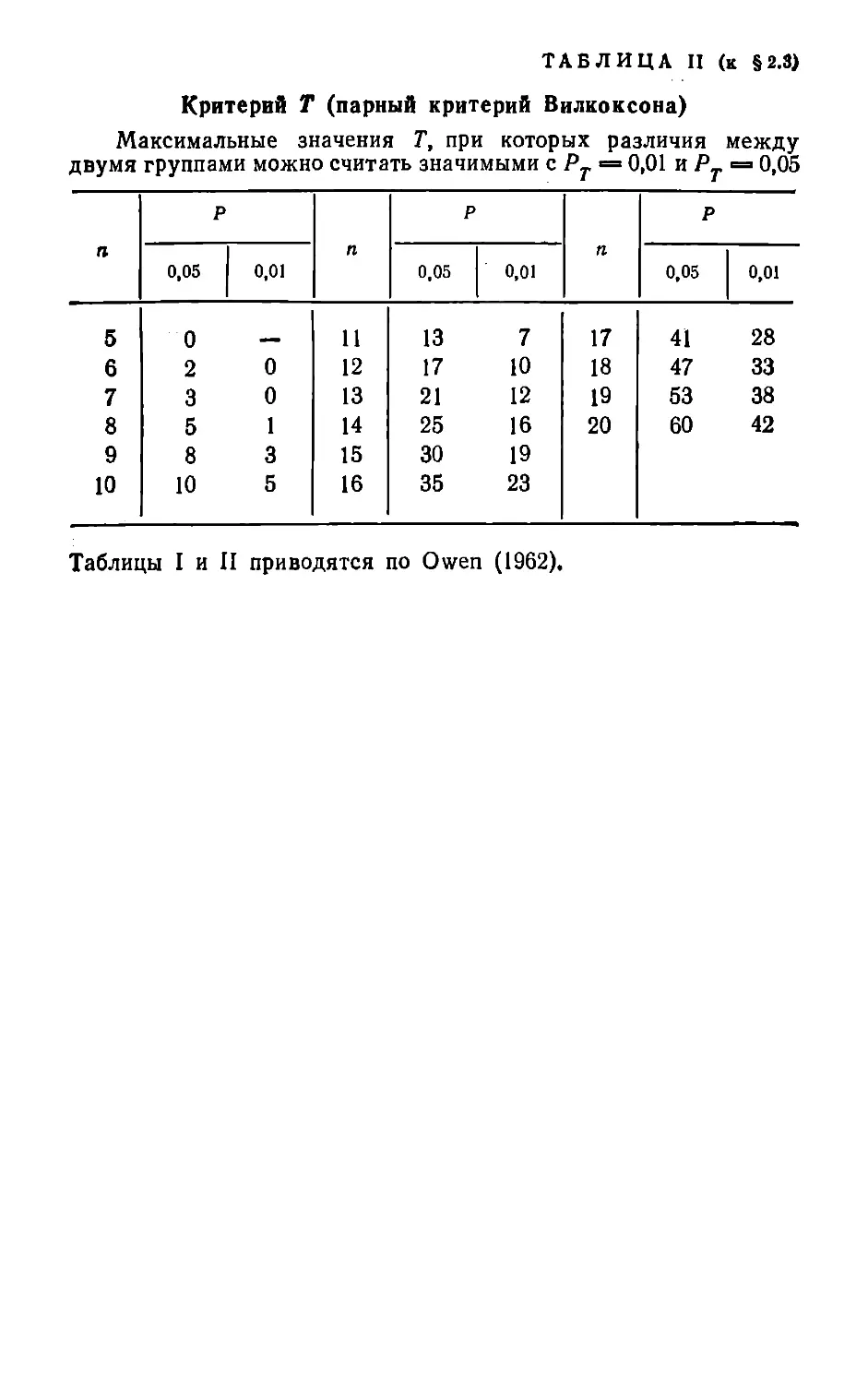
§ 2.3. КРИТЕРИЙ Т
(ПАРНЫЙ КРИТЕРИЙ ВИЛКОКСОНА)
Критерий Т [3, 5, 12, 15, 19, 20, 21, 27] так же, как
и критерий знаков, предназначен для оценки разли¬
чий в связанных выборках. Он является более мощ¬
ным критерием, чем критерий знаков, но имеющиеся
таблицы ограничивают его применение числом пар
не более 20. При большем числе пар он становится
довольно трудоемким. Кроме того, критерий знаков
в этом случае немногим уступает по мощности кри¬
терию Т.
Критерий Т основан на следующем приеме. Вы¬
численным разностям между связанными парами на¬
блюдений дают ранговые номера в порядке возра¬
стания абсолютных значений разности (без учета ее
знака). Совпадающим наблюдениям дают ранговые
номера, равные средним из их порядковых значений.
Например, одинаковые разности, стоящие на 3-м и
4-м местах, получают ранг 3,5. Далее вычисляется
величина Г, равная сумме ранговых номеров раз¬
ностей, имеющих отрицательное значение (т. е раз¬
ностей, противоположных наблюдаемым в большин¬
стве опытов).
В табл. II (см. приложение) для числа парных
наблюдений от 5 до 20 приводятся максимальные
значения Т, при которых различия можно считать
значимыми (существенными).
Пример 2.2. Рассмотрим в качестве примера те же данные,
которые рассматривались в связи с критерием знаков, однако ис¬
пользуем теперь их абсолютные значения (табл. 2.1). Разности
с отрицательным знаком (т. е. разности, говорящие о нарастании
гемоконцентрации вместо ее снижения, наблюдаемого в большин¬
стве опытов) имели ранговые номера 1 и 3. Следовательно,
Т *= 1 + 3 = 4. Это меньше 5 — критической величины Т при
п = 8 (при Рт = 0,05). Следовательно, критерий Т позволяет
установить, что снижение гемоконцентрации через 2 суток после
ожога можно считать существенным (значимым). Критерий t в
этом случае также выявил значимые различия (Р<<0,05).
19

ТАБЛИЦА 2.1
Пример применения критерия Т
(парного критерия Вилкоксона)
Содержание гемоглобина в крови собак
после ожога через
Ранговый номер
разности
сутки
2 суток
разность
107
88
19
6,5
93
74
19
6,5
121
92
29
8
85
72
13
4
89
90
- 1
1
110
108
2
2
81
67
14
5
102
110
-8
3
Если все же возникнет необходимость применить критерий Т,
когда число пар больше 20, можно воспользоваться свойствами
распределения Т при большом числе пар (20, 27). В этом случае
величина Т при справедливости нулевой гипотезы распределена
нормально со средней
j п{п+ 1)
4
и дисперсией
_2 п(л+1)(2д+1)
®г-		24
Таким образом, для того чтобы решить вопрос о справедли¬
вости нулевой гипотезы, вычисляется величина Т
Т — п {п + 1)
у__ Т-Т	4
°т Л Г п{п + 0(2п+ 1)
V	24
где Т — сумма рангов, полученная в опыте (см. пример 2.2).
Эта величина распределена нормально с нулевой средней и
единичной дисперсией:
F—0; ст~ 1.
т
Поэтому исходя из свойств нормального распределения, если
7 > 1,96, то можно с уровнем значимости Р < 0,05 считать нуле¬
20

вую гипотезу неверной, т. е. сравниваемые выборки различающи'
мися.
Если Т > 2,56, то вывод о различии выборок делают с уров¬
нем значимости Р < 0,01.
СЛУЧАЙ НЕЗАВИСИМЫХ ВЫБОРОК
§ 2.4. КРИТЕРИЙ U
(ВИЛКОКСОНА — МАННА — УИТНИ)
Критерий U [5, 23, 26, 27] применяют при незави¬
симых выборках. Он особенно удобен, когда число
наблюдений невелико (Пи П2^.20). Однако вычис¬
ленные для настоящего издания таблицы (табл. III
приложения) позволяют применять критерий U при
пи п2 ^ 60.
Рассмотрим методику применения критерия U на
примере.
Пример 2.3. Пусть в контроле (без лечения) и в опыте (с ле¬
чением) обнаружены следующие сроки гибели животных (в мину¬
тах) после введения токсического вещества:
без лечения — 39, 38, 44, б, 25, 25, 30;
с лечением — 46, 8, 68, 45, 32, 41, 41, 30, 100.
Необходимо упорядочить (расположить в порядке возраста¬
ния) первый и второй ряды в виде одного, так называемого об¬
щего упорядоченного ряда (табл. 2.2). Для того, чтобы можно
было различить числа, относящиеся к основной и контрольной
сериям, контрольные опыты располагают левее, а основные —
правее некоторой вертикальной черты (если общий упорядочен¬
ный ряд расположен вертикально).
В первом и втором рядах примера 2.3 есть пара
неразличающихся наблюдений (30 и 30). Их может
быть и больше. Вопрос о порядке их расположения
в упорядоченном ряду можно решить с помощью сле¬
дующего приема. Если неразличающихся чисел всего
два, их расположение в общем упорядоченном ряду
должно быть случайным Поэтому какое из них рас¬
полагать раньше, можно определить подбрасыванием
монеты или обращением к таблице случайных чисел
[13, 17, 19, 20]. Если есть два других неразличающих¬
ся числа в левой и правой части упорядоченного ряда,
их надо расположить в обратном порядке. Если
21

неразличающихся чисел 3, их располагают так:
30	30
30
или
30
30
30
Если четыре:
30
30
зо зо
зо или зо
30
30
и т. д. Принцип расположения состоит в том, чтобы
по возможности не давать приоритета ни левой, ни
правой половинам общего упорядоченного ряда. Оди¬
наковые числа левого и правого рядов должны быть
как можно более равномерно перемешаны.
Иногда рекомендуют исключать пары неразличаю¬
щихся наблюдений, соответственно уменьшая число
членов выборок. Однако это может привести к иска¬
жениям (к завышению существенности различий). Все
сказанное не относится к одинаковым наблюдениям
в пределах одного ряда. Порядок их расположения,
естественно, не имеет значения.
В табл. 2.2 результаты расположены в порядке
их возрастания, причем на каждой строке помещен
только один результат, полученный либо в контроле,
либо в опыте. Для критерия U существенны не сами
значения результатов наблюдения, а порядок их рас¬
положения. Обозначим результаты первой группы
наблюдений (группы X) через х, а второй группы
(группы Y) — через у. Тогда наш упорядоченный ряд
можно изобразить так: хухххууххуухуууу. Будем
считать идеальным такое расположение чисел, когда
после упорядочения располагаются сначала все числа
первого ряда (в табл. 2.2 — первого столбца), а потом
второго: хххххххууууууууу. Дальнейший анализ за¬
ключается в подсчете нарушений расположения чисел
по сравнению с их идеальным расположением. Одним
нарушением (инверсией) считают такое расположе¬
ние, когда перед некоторым числом первого столбца
стоит одно число второго столбца. Если перед неко¬
торым числом первого столбца стоят два числа вто¬
рого столбца, это считают за две инверсии и т. д
Число инверсий обозначают через U.
22

ТАБЛИЦА 2.2
Пример применения критерия U
(Вилкоксона—Манна—Уитни)
Срок наступления гибели в минутах
(общий упорядоченный ряд)
Число
X
без лечения
Y
с лечением
инверсий
6
8
0
25
1
25
1
30
30
32
1
38
3
39
41
41
3
44
45
46
68
100
5
Всего ...
14
Подсчитаем число инверсий в нашем примере. Числа 25, 25
и 30 первого столбца имеют перед собой по одному числу вто¬
рого столбца — 8, т. е. имеют по одной инверсии. Числа 38 и 39
первого столбца имеют перед собой по 3 числа второго столб¬
ца — 8, 30 и 32, т. е. имеют по 3 инверсии. Последнее число пер¬
вого столбца 44 имеет перед собой 5 чисел второго столбца. Об¬
щее число инверсий, таким образом, составляет:
67=1 + 1 + 1+ 3 + 3 + 5=14.
Обращаемся к таблице III (приложения), где для числа на¬
блюдений 7 и 9 находим максимальное значение U, при котором
еще можно делать вывод о существенном различии выборок. Оно
равно 15 при Ри = 0,05 и 9 при Ри = 0,01. Следовательно, при
14 инверсиях в этом случае можно утверждать, что различия ме¬
жду двумя взятыми рядами чисел существенны, причем 0,01 <<
< Рц < 0,05. Интересно отметить, что критерий t в рассмотрен¬
ном случае не выявил значимой разницы между сравниваемыми
группами наблюдений (Pt > 0,1).
В любом общем упорядоченном ряду инверсии
Можно подсчитывать двумя способами — относительно
23

группы X и относительно группы У. Следует выбрать
тот способ, который дает наименьшую сумму инвер¬
сий.
Подсчет инверсий в случае, когда п > 20, стано¬
вится довольно трудоемким. Для облегчения сумми¬
рования целесообразно воспользоваться каким-либо
суммирующим устройством. Простейшим из таких
устройств, совершенно достаточным, чтобы сделать
необременительным подсчет числа инверсий при
/г <1 100, является металлическая арифметическая
линейка «Ленинград».
После того, как мы рассмотрели понятие «инверсия», уяснили
методику подсчета числа инверсий U и последующей оценки зна¬
чимости различий Ри по величине U и числу наблюдений в ка¬
ждой выборке п 1 и п2 (с помощью таблицы III), необходимо
кратко пояснить методику вычисления максимального числа ин¬
версий U в таблице III при тех значениях п\ и «2 (>20), для
которых мы не нашли соответствующих данных в опубликован¬
ных таблицах [5, 23, 26].
При составлении той части таблицы III, которая касается вы¬
борок относительно большого объема («1,^2 >20), использова¬
лось следующее свойство статистики U (Ван дер Варден, 1960).
При значениях Пи п2 ^ 4 и П\ + щ > 20 распределение вели¬
чины U близко к нормальному со средним
*и = ~2 п1п2
и дисперсией
Su = iyniM,Il+n2+1)-
Из этого следует, что при справедливости нулевой гипотезы,
т. е. при отсутствии различий между выборками, величина
V--^n,n2 + l
t (2.1)
— njrt2 (я, +П2+ 1)
имеет нормальное распределение со средней, равной нулю
и дисперсией, равной 1
На основании формулы (2.1) и таблиц нормального распределе¬
ния с помощью ЭВМ были найдены такие значения U, которые
соответствуют уровню значимости Ру = 0,05; 0,01; 0,005; 0,001,
U
V
24.

t. e. при 0 = —1,6448; —2,3263; —2,5758; —3,0902. Они и пред¬
ставлены в табл. Ill для пи П2 > 20.
При расчете по формуле (2.1) выяснились некоторые интерес¬
ные особенности распределения U. Оказалось, что максимальное
число инверсий и, получаемое при расчете по формуле (2.1),
когда «1, п2 < 20, практически не отличалось от соответствующих
более точных значений U, которые удалось найти в опубликован¬
ных таблицах [5, 23, 26]. Точнее, из 190 значений U для Pv =
= 0,05 и Пи п2 ^ 20, имеющихся в опубликованных таблицах,
лишь 17 отличались от вычисленных приближенных значений U,
причем величина расхождений нигде не превышала 1. Эти расхо¬
ждения не нарастали с увеличением п\ и п2.
При Ри = 0,01 расхождения между вычисленными нами и
табличными величинами U наблюдались в большинстве случаев,
но их величина также никогда не превышала 1, причем вычислен¬
ные нами величины U отличались всегда в меньшую сторону,
т. е. в сторону более осторожной оценки значимости различий.
При высоких уровнях значимости Ри = 0,005 и Ри = 0,001
аналогичные расхождения становились более значительными, так
что пользоваться формулой (2.1) при ni,n2^20 практически
было невозможно. Например, при Ри — 0,001 расхождения до¬
стигали 4.
Поскольку в таблице III величина U при п\, я2 ^ 20 приве¬
дена по опубликованным таблицам, а при П\, п2 > 20 рассчитана
по формуле (2.1), указанные расхождения приводили к своеобраз¬
ному «краевому эффекту», который состоял в следующем. Зна¬
чения и, вычисленные по формуле (2.1), всегда были меньше
табличных, полученных на основании точного распределения U.
Поэтому при переходе к расчету U по формуле (2.1) в тех частях
таблицы, которые касаются высоких уровней значимости (Ри =
= 0,001 и Ри = 0,005), наблюдалось скачкообразное уменьшение
величин в столбцах таблицы вместо их обычного плавного нара¬
стания. Например, значения U, когда П\ = 21, а п2 < 10 при
Pv *s= 0,001, оказывались меньше на 1—3 единицы, чем вышерас-
положенные числа, находящиеся в этом же столбце, но заимство¬
ванные из опубликованных таблиц. Мы не сочли нужным исклю¬
чать эти «пограничные» значения U, так как они приводили лишь
к повышению осторожности вывода о различиях между выбор¬
ками с высоким уровнем значимости (Ри ~ 0,005 и Ри = 0,001).
При меньших уровнях значимости (Ри — 0,01 и Ри = 0,05) «крае¬
вой эффект» в таблице III не наблюдался.
§ 2.5. КРИТЕРИЙ U
(ПРОДОЛЖЕНИЕ)
Критерий U позволяет, если различия между опы¬
том и контролем при сравнении их по одному пока¬
зателю недостоверны, привлечь несколько показате¬
лей. Рассмотрим соответствующий пример.
Пример 2.4. При шоке различия в числе животных, живших
более. 3 суток, т. е. вышедших из шока, в сериях с лечением и без
лечения оказались недостоверными (по критерию х2)>
25

Попытаемся учесть также продолжительность жизни погиб¬
ших животных и артериальное давление через час пс^ле травмы.
Эти признаки также несут информацию о различии в тяжести
течения процесса в опыте и контроле. Расположим все наблюде¬
ния в порядке возрастающей тяжести состояния животных
(табл. 2.3): сначала (вверху) поместим всех выживших живот¬
ных, а среди последних — раньше тех, у которых было выше ар¬
териальное давление через час после травмы; далее — животных,
ТАБЛИЦА 2.3
Пример применения критерия U
с учетом двух показателей
Продолжительность
жизни
Артериальн
в мм рт.
один час по
(общий упоря
X
без лечения
эе давление
ст. через
еле травмы
доченный ряд)
Y
с лечением
Число
инверсий
и
Выжили
106
102
96
93
90
90
2
86
2
85
2
82
78
78
4
77
4
67
4
Погибли в первую
100
4
ночь
88
4
87
81
66
6
58
57
1 час 30 минут
Не измерялось
0 час 15 минут
» »
Всего ...
32
26

погибших ночью, также с учетом величины артериального давле¬
ния через час после травмы, и, наконец, животных, погибших в
день опыта с учетом продолжительности их жизни.
Расположение наблюдений было бы лишено инверсий, если
бы все леченые животные расположились в верхней половине
таблицы, а все контрольные — в нижней. Подсчитаем число ин¬
версий U. Оно оказалось равным 32. По табл. III (приложения)
определяем, что для числа наблюдений 12 и 10 максимальное
значение V, при котором различия еще достоверны, равно 24 при
Ри = 0,01 и 34 при Ри = 0,05. Следовательно, в обсуждаемом
случае различия достоверны с 0,01 < Ри С 0,05.
Критерий U в некоторых случаях целесообразно
использовать при связанных выборках, рассматривая
при этом их как независимые. Дело в том, что связи
между парами опыт — контроль могут оказаться сла¬
быми, а различия между ними — сильными. Тогда,
рассматривая выборки как независимые, мы можем
обнаружить различия, не выявляемые критериями для
связанных выборок. Это замечание особенно важно
для очень малых выборок, так как критерий знаков
и критерий Т можно применять при выборках, вклю¬
чающих не менее 5 пар, а критерий U применим уже
при П\ = п2 = 3.
В качестве примера рассмотрим результаты первых трех
опытов из табл. 2.1. (§ 2.3). Обозначив числа первого столбца
через у, а второго — через х и расположив их в общем упорядо¬
ченном ряду, получим следующую запись: хххууу. Число инвер¬
сий U = 0. По табл. III (приложения) определяем, что разли¬
чия в этом случае являются значимыми с Ри = 0,05.
С помощью критерия t в этом случае значимые различия
выявить не удается (Р« > 0,05).
§ 2.6. КРИТЕРИЙ U
(ОКОНЧАНИЕ)
Имеющиеся в настоящем пособии таблицы кри¬
терия U рассчитаны на число членов выборок
Яь ^2 ^ 60. Если число членов хотя бы одной из вы¬
борок превышает 60, то вместо имеющихся таблиц
используют формулу (2.1), где U — число инверсий,
п\, п2 — число наблюдений в дифференцируемых вы¬
борках.
Если полученная величина U равна или меньше —
1,65, то различия значимы с Ри ^ 0,05, если она
равна или меньше —2,05, то Ри ^ 0,02, если равна
27

или меньше — 2,32, то Ри ^ 0,01, если она равна или
меньше — 2,88, то Ри ^ 0,002.
Нередко различия между распределениями при¬
знака при дифференцируемых состояниях не сводятся
к различиям в средних тенденциях, а являются раз¬
личиями в форме распределений, например одно рас¬
пределение является двухвершинным, а другое —
одновершинным, причем различия в их средних не¬
значительны. Могут быть и оба распределения двух¬
вершинными, причем средние этих распределений
смещены одна относительно другой, так что против
вершины одного распределения приходится «впадина»
другого, но различия в средних все же невелики и
не являются статистически значимыми.
В этом случае можно воспользоваться критерия¬
ми для оценки различий в форме распределений
(§ 2.8, 2.9). Однако в некоторых ситуациях, в частно¬
сти при выборе наиболее информативных признаков
для вычислительной диагностики (см. главу 4), це¬
лесообразно все же пользоваться критерием U (ко¬
торый является весьма мощным при выявлении
различий в средних тенденциях), но двухвершинные
распределения рассматривать как два независимых
распределения, т. е. разбивать общий упорядоченный
ряд на 2 части и вычислять U для каждой из частей
отдельно. Граница разбиения общего упорядочевного
ряда подбирается при этом так, чтобы различия меж¬
ду сравниваемыми распределениями в каждой поло¬
вине общего упорядоченного ряда были по критерию
U наибольшими. Рассмотрим два примера.
Пример 2.5. Величины минимального артериального давления
в двух сравниваемых группах больных образовали следующий
общий упорядоченный ряд (табл. 2.4).
В группе X наибольшая плотность расположения членов вы¬
борки приходится на середину общего упорядоченного ряда, в
группе /—на его края. Это значит, что для группы У харак¬
терно либо более высокое, либо более низкое артериальное дав¬
ление, чем в большинстве наблюдений группы X. Выделив пар¬
тии больных с минимальным артериальным давлением не ниже
85 мм рт. ст. (I партия) и ниже этой величины (II партия), убе¬
ждаемся, что в каждой партии имеются статистически значимые
различия между группами X и У по критерию U (Ри < 0,05),
который выявляет различия в средних тенденциях. Отметим, что
эти средние тенденции в первой и второй партиях различаются
в разные стороны.
28

ТАБЛИЦА .4
Первый пример применения критерия U
после разделения общего упорядоченного ряда
на две части
Минимальное артериальное давление
Общий упорядоченный
ряд
Продолжение ряда
Окончание ряда
группа X
группа У
группа X
группа У
группа X
группа У
110
80
70
110
80
70
110
80
70
105
80
70
100
80
70
100
80
70
100
80
70
95
80
70
90
80
70
90
80
70
90
80
70
90
75
70
90
75
65
90
75
65
90
75
65
85
75
65
85
75
65
85
75
60
85
75
60
85
75
60
85
70
60
85
70
60
70
60
70
60
70
70
60
70
50
50
45
80
80
80
80
80
29

Пример 2.6. В этих же группах больных процент палочко¬
ядерных нейтрофилов в лейкоцитарной формуле образовал сле¬
дующий общий упорядоченный ряд (табл. 2.5).
Т А Б Л И Ц А 2.5
Второй пример применения критерия U
после разделения общего упорядоченного ряда на 2 части
Процент палочкоядерных нейтрофилов
Общий упорядоченный ряд
Продолжение ряда
группа X
группа Y
группа X
группа Y
65
16
54
15
46
15
45
15
44
14
43
14
40
13
36
12
35
12
35
12
35
11
34
11
32
11
32
10
29
10
28
10
28
9
28
9
27
9
21
8
21
8
8
20
7
20
6
20
6
19
6
19
5
19
5
18
3
18
3
17
2
17
2
17
17
Здесь плотность расположения членов выборки чередуется
сверху вниз так: в верхней части ряда преобладает группа X, по¬
том группа Y, потом снова группа X, потом опять группа Y.
30

По-видимому, этот упорядоченный ряд образован двумя двух¬
вершинными распределениями, смещенными друг относительно
друга. Разделив общий упорядоченный ряд на две части, как это
показано в табл. 2.5 двойной чертой, обнаруживаем статистиче¬
ски значимые различия между группами X и Y в обеих частях
ряда по критерию U (Ри < 0,01). В рассматриваемом случае
средние тенденции в каждой части ряда различаются в одну
и ту же сторону.
С увеличением числа наблюдений трудоемкость
критерия U возрастает. В этих случаях целесообраз¬
но сначала использовать критерий Q (Розенбаума).
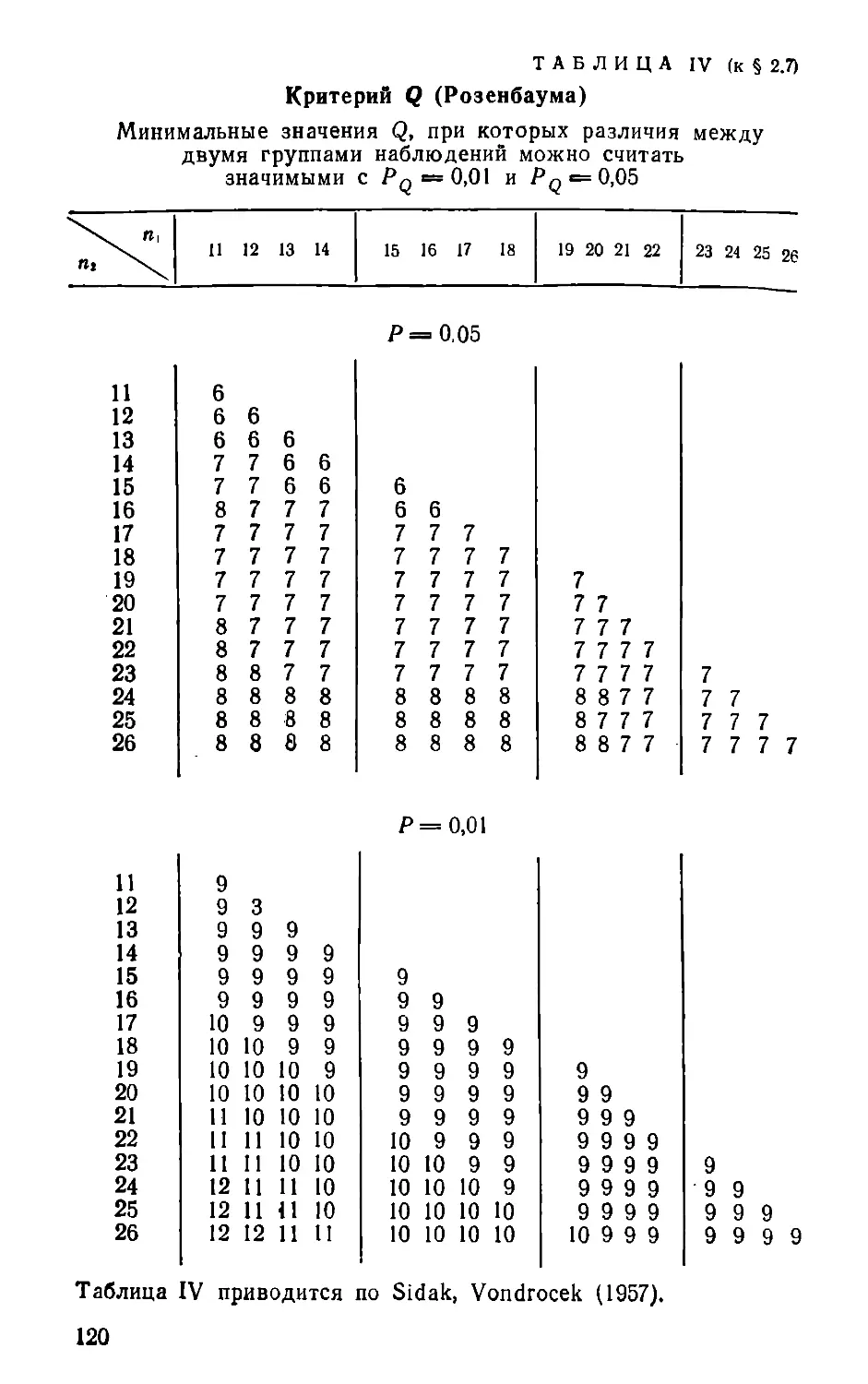
§ 2.7. КРИТЕРИЙ Q
(РОЗЕНБАУМА)
Критерий Q [23, 24] основан на сравнении двух
упорядоченных рядов наблюдений. Первым рядом
считается тот, где максимальная и минимальная ве¬
личины больше, чем в другом ряду. Подсчитываются
число 5 — количество наблюдений первого ряда, ко¬
торые больше максимальной величины второго ряда,
и число Т — количество наблюдений второго ряда, ко¬
торые меньше минимальной величины первого ряда.
Величины 5 и Г образно называют «хвостами» рас¬
пределений, а критерий Q — «критерием хвостов».
Когда сумма Q = 5 + Т достаточно велика, можно
считать различия сравниваемых выборок значимыми.
Критическое значение Q для количества наблюдений
11—26 в каждой выборке приводится в табл. IV (при¬
ложения). Если число наблюдений меньше 11, крите¬
рий Q применять нельзя. Зато при числе наблюдений
более 26 в каждой из сравниваемых выборок он не
имеет верхнего предела численности наблюдений,
причем справочные таблицы в этом случае уже не
нужны. При любом числе наблюдений больше 26 ми¬
нимальная величина Q, когда различия можно счи¬
тать существенными с Pq = 0,05, равна 8, а с
PQ = 0,01 — равна 10. Необходимо оговориться, что
эти минимальные значения Q при пь п2 > 26 справед¬
ливы при условиях, когда пi приблизительно равно пг.
Так, когда объем выборок не превышает 50, допусти¬
мы различия между П\ и п2 на 10, при /гь п2 от 51 до
100 допустимы различия на 15—20, при ri\, п2 > 100
допустимы различия между выборками в Р/г—2 раза.
31

Пример 2.7. Пульс у больных с площадью глубокого ожога
22—38% поверхности тела (верхний ряд) и 6—20% поверхности
тела (нижний ряд) составил:
196; 100; 104; 104; 120; 120; 120; 120; I 126; 130; 134
96; 100; 102; 104; 110; 118; 120 |
В этом случае 5 = 3, Т = 5, Q = S + 7' = 3 + 5 = 8. По
табл. IV (приложения) определяем, что при пх =11, п2 = 12 ми¬
нимальное значение Q, при котором различия между группами
существенны, при Pq = 0,05 равно 7, а при Pq = 0,01 равно 9.
Следовательно, в рассматриваемом случае различия существенны
с 0,01 < Pq С 0,05. Критерий t в этом случае также позволяет
выявить существенные различия (Pt < 0,01).
Критерий Q менее трудоемок, чем критерий U,
и поэтому сравнение двух независимых выборок, каж¬
дая из которых имеет больше 10 членов, целесооб¬
разно начинать с него. Однако критерий Q является
менее мощным, чем критерий U. Поэтому при отсут¬
ствии существенных различий между выборками по
критерию Q следует применить критерий U. Рассмот¬
рим пример последовательного применения этих двух
критериев.
Пример 2.8. У больных, рассмотренных в примере 2.7, про¬
цент нейтрофилов в лейкоцитарной формуле составлял соответ¬
ственно (верхний ряд — больные с менее обширным ожогом):
170,5; 85; 87; 88,5; 89; 89; 89; 90; 91,5; 92; 194; 96
74,5; 77,5; 79; 83; 83; 83; 83; 85, 87; 87; 90; 91; 93; 93; |
В этом случае оказалось: S = 2; Т — 1; Q = 2 + 1 = 3. Следо¬
вательно, по критерию Q различия нельзя считать значимыми.
Воспользуемся критерием U. Общий упорядоченный ряд в
нашем случае выглядит так (числа над буквами обозначают ко¬
личество инверсий):
11111111 2 3	8 8 10 10
ухуууууууухухухххххууххуухх
Сумма инверсий равна:
17=1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 2 + 3+8 + 8+ 10 + 10 = 49.
По табл. III (приложения) определяем, что при П\ = 12,
П2 — 15 различия значимы с Ри <0,05, если число инверсий не
превышает 55, и с Ри < 0,01, если инверсий не больше 42. Следо¬
вательно, в нашем примере по критерию U различия можно счи¬
тать существенными с уровнем значимости < 0,05. Вместе с тем
по критерию t различия не являются существенными (Pt > 0,05).
32

СЛУЧАЙ РАЗЛИЧИЙ
В ФОРМЕ РАСПРЕДЕЛЕНИЙ
§ 2.8. ТОЧНЫЙ МЕТОД ФИШЕРА (ТМФ)
ДЛЯ ЧЕТЫРЕХПОЛЬНОЙ ТАБЛИЦЫ
Простейшее альтернативное распределение, со¬
стоящее из двух градаций, часто встречается в экспе¬
риментальных исследованиях при оценке качествен¬
ных эффектов: распределение выживших и погибших
животных, распределение числа опытов, в которых
наблюдался и не наблюдался какой-либо качествен¬
ный эффект (например, приступ судорог) или количе¬
ственный эффект, достигший определенного предела
(например, падение артериального давления ниже
80 мм рт. ст.). Два альтернативных распределения с
двумя градациями размещаются в таблице из 4 кле¬
ток. Она называется четырехпольной таблицей. Для
оценки различия в четырехпольной таблице можно
использовать критерий %2. Однако его не рекомен¬
дуется применять, если число опытов в каждом из
сравниваемых распределений меньше 10. Точный ме¬
тод Фишера для четырехпольной таблицы (ТМФ) ли¬
шен этого ограничения, однако он требует довольно
громоздких вычислений. Для того чтобы их избежать,
В. С. Генес [8] разработал таблицы, которые в значи¬
тельно сокращенном и несколько модифицированном
виде представлены в табл. V (приложения). В ней
приведены числа наблюдений, в которых проявился
некоторый эффект (например, гибель животного) в
первом и втором распределении. В таблице показаны
те минимальные различия в числе однонаправленных
эффектов, которые позволяют считать различия меж¬
ду распределениями значимыми (с Р = 0,02s)1. Об¬
щее число наблюдений (п) в первом распределении
может колебаться от 2 до 20, во втором — от 2 до 16.
Пример 2.9. В первой серии опытов (основной) погибли все
3	животных, в контроле из 10 животных ни одно не погибло.
В табл. V (приложения) находим, что при rti = 3, Пг = 10 раз¬
1 При выявлении различий в форме распределений статисти¬
чески значимыми считают различия с 0,025, а не 0,05
(см. § 2.1).
2	Е. В. Гублер, А. А. Генкин
33

личия между опытом и контролем достоверны (Pjmф < 0,025).
По критерию t они тоже достоверны (Р < 0,05).
Точный метод Фишера, если учесть его малую
трудоемкость (при использовании таблиц), можно по¬
пытаться применять для оценки различий в любых
двух независимых выборках. Для этого необходимо
составить общий упорядоченный ряд из членов обеих
выборок и найти его середину, по обе стороны от ко¬
торой будет находиться одинаковое число членов. При
четном числе членов середина будет находиться меж¬
ду двумя числами, при нечетном она придется на
одно из чисел. Тогда путем подбрасывания монеты
или с помощью таблицы случайных чисел нужно от¬
нести это число к одной из половин упорядоченного
ряда. Далее следует в каждой половине определить
число членов, относящихся к первой и ко второй вы¬
боркам. Если по табл. V (приложения) эти соотноше¬
ния окажутся существенно различными, можно де¬
лать вывод о различиях между взятыми выборками
в их средних тенденциях. Если существенные разли¬
чия не будут выявлены, с этой же целью необходимо
применить критерий U.
Пример 2.10. У 4 больных на 2-й день после получения глу¬
боких ожогов на площади 6—15% поверхности тела пульс со¬
ставлял 82, 84, 88, 100 ударов в минуту, а у 6 больных с более
обширными глубокими ожогами (22—38% поверхности тела)
пульс был равен 96, 104, 120, 126 и 134 ударам в минуту. Воз¬
никает вопрос, можно ли по такому небольшому числу наблюде¬
ний делать вывод о существенных различиях в частоте пульса у
этих двух групп больных. Составим общий упорядоченный ряд:
82, 84, 88, 100,1
96, | 104, 120, 120, 126, 134
Найдем середину ряда (она отмечена вертикаль¬
ной чертой). В первой выборке ни один член не попал
в правую половину упорядоченного ряда, в которой
находятся 5 из 6 членов, входящих во вторую вы¬
борку. По табл. V (приложения) определяем, что эти
различия значимы (РТ1Лф = 0,025). Следовательно,
различия в частоте пульса у этих групп больных мо¬
жно считать существенными. По критерию t эти раз¬
личия также удается обнаружить (Р*<0,01), но вы¬
числение t занимает во много раз больше времени.
34

Точный метод Фишера можно также применить с
целью выявления различий в двух связанных выбор¬
ках, рассматривая их как независимые и действуя
так, как указано выше (пример 2.10). Это особенно
целесообразно делать при 4 парах, когда критерий Т
неприменим. Если различия в парах велики, а связь
относительно слаба, точный метод Фишера может вы¬
явить различия, не выявляемые критериями для пар¬
ных выборок. Еще более эффективным может ока¬
заться для этой цели критерий U (см. § 2.5).
Эффективность точного метода Фишера при оцен¬
ке различий двух выборок можно существенно повы¬
сить, изменив характер нулевой гипотезы и оценивая
не различия в средних тенденциях, а разницу в ча¬
стоте появлений некоторой величины изучаемого по¬
казателя, превышающей определенный предел.
Пример 2.11. При достаточно глубокой искусственной гипо¬
термии (ректальная температура 26°) в условиях морфино-эфир-
ного наркоза с кислородом у собак небольшая кровопотеря вы¬
зывала тахикардию. Такой реакции на кровопотерю, как правило,
не было при несколько более высокой температуре тела (27—
27,5°). Исходная частота пульса в обоих случаях была одинако¬
вой — в среднем 84 удара в минуту. Степень тахикардии измеря¬
лась по приросту числа ударов пульса через минуту после конца
кровопотери. Спрашивается, существенны ли различия в степени
тахикардии в обоих случаях. Составим общий упорядоченный ряд
(вверху расположены данные об изменении частоты пульса после
кровопотери, полученные при менее глубокой гипотермии):
-9, -8, -4, +10
+ 13,
+ 12, +12, +15, +15, +19
Границу между правой и левой половиной упорядоченного
ряда проведем не в его середине, а в произвольном месте, вы¬
бранном с таким расчетом, чтобы разница между рядами выяв¬
лялась наиболее отчетливо. Соответственно сформулируем цель
сравнения: будем проверять существенность различий в частоте
появления тахикардии, превышающей +10 ударов пульса.
В первом случае (при менее глубокой гипотермии) такая
тахикардия наблюдалась у одной собаки из 5, во втором слу¬
чае — у всех 5 животных. По табл. V (приложения) определяем,
что эти различия можно считать значимыми (£*тмф = 0,025).
Критерий t в этом случае также позволяет выявить различия
(Pt < 0,02), но после значительно более трудоемких расчетов.
С помощью точного метода Фишера иногда можно
выявить различия в форме распределений при отсут¬
ствии различий в средних тенденциях.
8*
85

Пример 2.12. При регистрации на электрокардиограмме
12 сердечных циклов подряд через 2 дня после ожога у собак
обнаружены следующие длительности интервалов R — R (в со¬
тых секунды):
86, 68, 56, 40, 38, 51, 78, 80, 71, 57, 51, 46.
Через 4 дня после ожога колебания длительности циклов (арит¬
мия пульса) были меньше:
50, 58, 59, 56, 50, 52, 54, 60, 62, 63, 64,
хотя средняя их длительность была почти одинаковой в первом
(60,2) и во втором случае (57,1 сотая секунды). Попытаемся вы¬
яснить, есть ли существенные различия между этими выборками
и в чем они состоят. Составим общий упорядоченный ряд:
38, 40, 46,	51, 61,	56, 57,	68, 71, 78, 80, 86
50, 50,	62, 54, 56,	58, 50, 60, 62, 63, 64,
Видно, что наиболее существенные различия между выбор¬
ками состоят в ширине распределений: во второй выборке ни
один из 11 ее членов не выходит за пределы, ограниченные чис¬
лами 50 и 64, а в первой выборке 8 из 12 ее членов находятся
вне этих пределов.
По табл. V (приложения) определяем, что такие различия
значимы (ЯТМФ < 0,025). Следовательно, через 4 дня после
ожога величина интервалов R — R колебалась меньше (т. е.
пульс был ритмичнее), чем через 2 дня после травмы.
Дальнейший анализ показывает, что в 5 из 12 случаев ин¬
тервал R — R в первой выборке превышал наибольшую вели¬
чину этого интервала во второй выборке. Эти различия также
значимы (РТМФ = 0,025). Следовательно, через 2 дня после
ожога аритмия пульса была связана с его периодическим уре-
жением (удлинением интервала R — R).
§ 2.9. СЕРИЙНЫЙ КРИТЕРИЙ г
(ВАЛЬДА — ВОЛЬФОВИЦА)
Критерий г [5, 13, 19, 21, 23] удобен тогда, когда
число наблюдений слишком невелико, чтобы приме¬
нять критерий х2 с многими степенями свободы, а
также критерий Колмогорова — Смирнова [5, 21]. Се¬
рийный критерий выявляет различия в распределе¬
ниях, не показывая, в чем они состоят.
Будем называть серией в общем упорядоченном
ряду, составленном из членов двух групп наблюдений,
такую последовательность наблюдений, которая при¬
надлежит к одной из групп. Например, в упорядочен¬
ном ряду:
хххх уууууу
1 2
36

—	две серии, в ряду
ххх уууу х у хххх у
1 2 У 4 ~~5~Т
—	6 серий.
Критерий г основан на том, что нулевая гипотеза
(предположение о принадлежности двух сравнивае¬
мых групп наблюдений к одной генеральной совокуп¬
ности) должна отбрасываться, если число серий до¬
статочно мало. Действительно, небольшое количество
серий будет в том случае, если группы «плохо пере¬
мешаны» и, следовательно, обладают различными
свойствами (принадлежат к различающимся по фор¬
ме распределениям). В табл. VI (приложения) для
объемов выборок nit пъ в пределах от 2 до 20 при¬
ведены максимальные значения числа серий (при
^ 0,025), при которых различия двух групп наблюде¬
ний можно еще считать значимыми.
Применим серийный критерий в случае, рассмот¬
ренном в примере 2.12.
Упорядочим два ряда интервалов R — R в виде одного ряда,
обозначив числа первого через х, а второго — через у:
XXX у у XX ууу хх уууууу ххххх
1 ~2 3 4 5 6 7
В упорядоченном ряду оказалось 7 серий. В табл. VI для
«1 = 12 и л2 = 11 находим критическое значение г, равное 7, от¬
куда делаем вывод, что различия между сравниваемыми распре¬
делениями интервалов R — R были значимы, хотя средние интер¬
валы R — R практически не различались. В чем состоят различия
этих распределений, мы уже выяснили выше (см. пример 2.12).
§ 2.10. ВЫБОР КРИТЕРИЯ РАЗЛИЧИЙ
Подытожим все, что было сказано выше о выборе
критерия в каждом случае сравнения двух выборок.
Разделим все возможные случаи на 9 групп в за¬
висимости от характера нулевой гипотезы, связанности
выборок и числа членов каждой выборки (табл. 2.6).
Прежде чем кратко рассмотреть каждый из слу¬
чаев, необходимо сделать три общих замечания.
1.	Для каждого из случаев в табл. 2.6 приведено
несколько критериев, расположенных в порядке воз¬
растающей трудоемкости. Если первый из них
37

ТАБ ЛИЦА 2.в
Выбор критерия
Рекомендуется применять критерии в порядке их перечис¬
ления. Каждый следующий критерий применяется,
если предыдущий не выявил различий
Номер
случая
В чем состоит
нулевая гипотеза
Связанность
выборок
Число
членов
каждой
выборки
Критерии
1
Нет различий
в центральных
тенденциях рас*
Связанные
(парные)
6-25
КЗ, Т, ТМФ, и, (0
2
пределений
То же
26-300
КЗ, (0
3
» »
2-5
ТМФ, и, (t)
4
Незави¬
2-10
тмф. и, (о
5
симые
11-20
Q, ТМФ, U, it)
6
То же
21-60
Q, U, (0
7
» »
>60
Q. (0
8
Нет различий
Незави¬
2-20
г
У
в распределениях
симые
>20
и
10
Нет различий
в частоте появ¬
ления некоторой
величины ана¬
лизируемого по¬
казателя, пре¬
вышающей оп¬
ределенный пре¬
дел (различий в
частоте одной из
альтернатив)
Незави¬
симые
2-20
ТМФ
выявил различия, этот ответ можно считать оконча¬
тельным. Если значимые различия с помощью первого
критерия выявить не удалось, необходимо применить
следующий критерий. Более трудоемкие критерии,
вообще говоря, обычно являются и более мощными.
Они могут выявить различия, не обнаруженные пре¬
дыдущим критерием.
2.	Обычно начинают с критериев, оценивающих
различия в средних тенденциях распределений. Если
они не выявили различий, целесообразно применить
38

критерий г, выявляющий любые различия в распреде¬
лениях. Если выявлены какие-то различия в распре¬
делениях при отсутствии значимой разницы в их сред^
них тенденциях, можно с целью дальнейшего анализа
использовать ТМФ для оценки различий в , частоте
появления некоторой величины анализируемого пока¬
зателя, превышающей определенный предел.
3.	Рассмотренные в настоящей главе критерии для
независимых выборок являются порядковыми. Они
требуют расположения всех наблюдений в общем
упорядоченном ряду (см. пример 2.3). Это позволяет
последовательно применить, не переписывая ряды, все
рассмотренные критерии для независимых выборок.
Рассмотрим последовательно каждый из 10 слу¬
чаев, выделенных в табл. 2.6.
Случай 1. Расположив пары наблюдений в поряд¬
ке возрастания разностей, применяем критерий зна¬
ков, а если он не выявляет различий, — критерий Т.
Если оба эти критерия не выявили различий, мо¬
жно попытаться рассматривать выборки как незави¬
симые и применить критерий U или ТМФ. Они могут
дать результат, если связь между парами выражена
слабо, а различия значительны.
Пример 2.13. Артериальное давление у собак в условиях мор-
фино-эфирно-кислородного наркоза по мере развития гипотермии
в большинстве случаев снижалось (табл. 2.7).
ТАБЛИЦА 2.7
Пример выбора критерия
Номера
опытов
1
2
3
4
5
6
7
8
9
10
Артериальное давление в мм рт.
ст.
При ректальной
температуре 30—32°
При ректальной
температуре 27—28°
140
122
148
180
121
96
116
92
78
95
98
100
119
92
111
87
112
86
134
106
Разности
-18
+32
-25
-24
+ 17
+2
-27
-24
-26
-28
Ранговые номера
разностей
3
10
6
4,5
2
1
8
4,5
7
9
39

Если считать выборки связанными, то оказывается, что при¬
менив критерий знаков и критерий Т, мы не можем обнаружить
существенного (значимого) снижения артериального давления. Не
выявляет его в этом случае и критерий t (Pt > 0,1).
Попробуем считать выборки независимыми. Составим общий
упорядоченный ряд:
78,	98,	111, 112, 116, 110, 121, 134, 140, 148,
8в, 87, 02, 02, 05, 0в, 100, 106,	122,	180
Сумма инверсий U здесь равна 27 (критическое значение U
для Ри = 0,05 равно 27). Следовательно, по критерию U разли¬
чия значимы с уровнем значимости 0,05.
Различия можно выявить также с помощью ТМФ: артериаль¬
ное давление ниже 110 мм рт. ст. наблюдалось в первой выборке
в 2 опытах из 10, а во второй — в 8 опытах из 10, эти различия
значимы (Ятмф = 0,025; см. табл. V приложения). Критерий t и
в этом варианте сравнения рассматриваемых выборок не выяв¬
ляет различий (Pi > 0,05).
Случай 2. Критерий знаков при больших выборках
является весьма эффективным. Применение критерия
t при больших выборках возможно, но чрезвычайно
трудоемко.
Случай 3. Применение критерия знаков и крите¬
рия Т возможно при числе пар не менее 5. Однако
если выборки связаны слабо, то можно, рассматривая
их как независимые, применить при числе пар не ме¬
нее 3 критерий U, а при числе пар не менее 4 — точ¬
ный метод Фишера (ТМФ).
Случай 4. Составив общий упорядоченный ряд, це¬
лесообразно начать с применения ТМФ (считая за
критический предел середину упорядоченного ряда).
Если это не даст результатов, следует поискать такой
предел, который позволит выявить различия. При этом
цель сравнения необходимо сформулировать по-но¬
вому (см. пример 2.11). Одновременно можно приме¬
нить критерий г, который также малотрудоемок, осо¬
бенно при наличии общего упорядоченного ряда.
Применение основного в этом случае критерия U
несколько более трудоемко, но и оно облегчается при
наличии общего упорядоченного ряда.
Случай 5. Обрабатывается, как и случай 4. Од¬
нако, составив общий упорядоченный ряд, в этом слу¬
чае целесообразно начать с применения критерия Q.
40

Случай 6. Применяются те же критерии, что в слу¬
чае 5, кроме ТМФ.
Случай 7. Применимы только критерии Q или t.
Случай 8. Критерий г легко применить, если иметь
общий упорядоченный ряд, во всех перечисленных
выше случаях. С него следует начинать, если речь
может идти о различиях в форме распределений при
отсутствии существенной разницы в их средних тен¬
денциях.
Случай 9. Можно попытаться применить критерий
U, разделив общий упорядоченный ряд на 2 части
(см. § 2.6). При этом могут выявиться часто встре¬
чающиеся различия в форме распределений, когда
хотя бы одно из них является двухвершинным.
Случай 10. Особенно характерен для оценки разли¬
чий в смертности, заболеваемости и в других альтер¬
нативных распределениях. Однако к этому случаю
могут быть сведены все перечисленные выше случаи,
если «1^20, п2 ^ 16 (см. примеры 2.10, 2.11, 2.12).
В заключение несколько слов о применении крите¬
рия t. В 5 из 11 рассмотренных примеров он позволил
выявить различия, причем в 2 случаях несколько бо¬
лее значимые, чем различия, обнаруженные с по¬
мощью непараметрических критериев. При распреде¬
лениях, близких к нормальному, этот критерий очень
чувствителен. Однако из-за высокой трудоемкости его
целесообразно применять лишь в том случае, если ни
один из непараметрических критериев не выявил зна¬
чимых различий, а на глаз они все же представляются
значительными.
§ 2.11. ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ
ОЦЕНКИ ЗНАЧИМОСТИ РАЗЛИЧИЙ
Поскольку непараметрические критерии не тре¬
буют вычисления среднеквадратичных отклонений (s)
и ошибок средних (s*), при оформлении результатов
опытов можно не приводить эти величины, тем более
что при распределениях, далеких от нормального, они
дадут искаженное представление о выборке. В таб¬
лице результатов опытов должны быть приведены:
количество наблюдений в каждой из групп, средние
арифметические (либо моды или медианы), пределы
колебаний, существенность различий (Р) и указан
41

критерий, по которому она определялась. Приводим
один из возможных вариантов таблицы результатов
(табл. 2.8).
T А Б Л И Ц А 2.8
Пример формы таблицы
Изменение содержания гемоглобина в крови собак
через сутки после ожогов разной глубины
Серия
Число
опытов
Средние арифме¬
тические и пре¬
делы колебаний
(в % к исходному)
Р (при со¬
поставле¬
нии с кон¬
тролем)
Кри¬
терий
Контроль (6-часовая
фиксация без ожога)
6
104 (88—120)
Поверхностный ожог
10% поверхности тела
5
110 (94—120)
>0,05
и
Глубокий ожог 10%
поверхности тела
5
118 (96—142)
<0,05
и
При подобном представлении результатов отсутст¬
вует такая прочно укоренившаяся в современной ме¬
дико-биологической литературе характеристика сте¬
пени колебаний, как среднеквадратичное отклонение
и ошибка средней. Несмотря на их несовершенство,
современная статистика не предлагает других подоб¬
ных им величин, которые, однако, не зависели бы от
формы распределений. Поэтому эти характеристики
так прочно удерживаются в научной литературе, во
многих случаях во вред делу. В силу своей трудоем¬
кости и неуниверсальности они ограничивают возмо¬
жности перекрестной оценки различий разных серий
опытов между собой. Такую оценку заменяют субъек¬
тивной «прикидкой» на основе сравнений различий
средних величин и ошибок средних.
На основе малотрудоемких непараметрических
критериев можно с целью перекрестного сравнения
всех серий со всеми рекомендовать составление мат¬
рицы следующего типа (табл. 2.9).
Попарное сравнение между собой четырех серий
требует составления 6 упорядоченных рядов, пяти
серий—10 рядов, шести серий—15 рядов, семи се¬
рий^— 21 ряда и т. д. Проверка различий по несколь-
42

ТАБЛИЦА 2.0
Матрица оценки статистической значимости различий
Сравнение содержания гемоглобина в крови собак
через сутки после ожогов разноI глубины
Серии
Серии
I
II
III
Р
Крите¬
рий
р
Крите¬
рий
р
Крите¬
рий
I
—
—
II
>0,05
и
—
—
III
<0,05
и
<0,05
и
—
—
IV
<0,01
и
<0,05
и
>0,05
и
ким критериям не требует переписывания упорядочен¬
ного ряда, и подобное сравнение почти всегда менее
трудоемко, чем вычисление в каждой серии средних
арифметических (х), среднеквадратичных отклонений
(s) и ошибок средних (s*).

Глава 3
ОЦЕНКА СВЯЗИ
МЕЖДУ ДВУМЯ РЯДАМИ НАБЛЮДЕНИЙ
§ 3.1. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ РАНГОВ
(СПИРМЕНА)
Наряду с анализом различий в средних тенден¬
циях или в форме распределений не менее важным
для понимания результатов опыта часто оказывается
оценка статистической связи (корреляции) между
двумя сравниваемыми рядами наблюдений. Ситуации,
когда появляется необходимость оценивать корреля¬
цию, могут быть самыми разнообразными. Часто воз¬
никает необходимость оценивать наличие связи между
интенсивностью или вообще разными градациями раз¬
дражителя и исследуемыми переменными. Кроме того,
надо иметь в виду, что в организме наблюдаемые пе¬
ременные обычно имеют определенный уровень связи
и этот уровень может изменяться при различных экс¬
периментальных условиях. Оценка статистической
связи позволяет понять взаимное влияние исследуе¬
мых факторов и различать между собой такие экспе¬
риментальные ситуации, когда оценка средних значе¬
ний или формы распределений может не выявить
различий.
Для решения таких задач в качестве меры взаимо¬
связи используется коэффициент линейной корреля¬
ции Пирсона [5, 13, 22].
Этот коэффициент с успехом применяют при ана¬
лизе различных экспериментальных данных в тече¬
ние многих десятилетий.
Эффективность оценки связи между переменными
при помощи этого коэффициента зависит, как и во¬
обще любая статистическая характеристика, от опре¬
деленных особенностей сопоставляемых совокупно¬
стей. Линейный коэффициент корреляции оказывает¬
44

ся наилучшей оценкой связи, если х и у являются
нормальными переменными, т. е. их распределение
является нормальным с устойчивыми средними значе¬
ниями X и у.
Если это не так, то обычный коэффициент корре¬
ляции может служить лишь приближенной характе¬
ристикой меры связи, и это приближение тем хуже,
чем больше отличаются от нормального распределе¬
ния наблюдаемые выборки. Если проанализировать
эту закономерность более точно, то решающим здесь
окажется не столько вид распределения, сколько фор¬
ма связи (так называемая форма уравнения регрес¬
сии) между сопоставляемыми величинами.
Когда сопоставляемые переменные являются нор¬
мальными, форма регрессии всегда линейна: при уве¬
личении одной из переменных другая в среднем ли¬
нейно возрастает. Вообще же говоря, не исключается
такой случай, когда переменные не являются нор¬
мальными, а форма регрессии остается линейной.
В этом случае коэффициент корреляции хотя и не бу¬
дет столь же адекватным, как и для нормальных вы¬
борок, но его использование для оценки связи будет
достаточно эффективным. В случае же значительного
отклонения от линейности линии регрессии использо¬
вание линейного коэффициента корреляции может
вообще ничего не давать.
При определенных условиях, а именно, когда
имеет место монотонное, но не обязательно линейное
изменение линии регрессии, оценку коэффициента
корреляции можно получить, вычисляя коэффициенты
корреляции не для самих значений х и у, а для их
рангов.
Для этого каждую выборку надо предварительно
проранжировать, т. е. приписать каждому х и у их
порядковые номера, соответствующие месту, которое
они занимают в ряду всех рассматриваемых значений
данной выборки. Эти порядковые номера—целые чи¬
сла от 1 до п, где п — объем выборки, — и называются
рангами. Обычно ранжируют в порядке убывания ве¬
личины значений признака. Тогда самому большому
значению будет соответствовать число 1, следующему
по величине — 2 и т. д., самому маленькому значе¬
нию — число п, где п — число значений выборки
45

(объем выборки). Так, ряду наблюдений
5,2 7,4 6,3 1,2 10,8
будут после ранжирования соответствовать числа
(ранги):
4	2 3 5 1
Возможность измерять корреляцию не между са¬
мими значениями, а между их относительными оцен¬
ками— рангами, позволяет оценивать связь и между
качественными признаками, когда точное количест¬
венное измерение признака по тем или другим причи¬
нам оказывается невозможным. Так, измеряют корре¬
ляцию между успеваемостью обучающегося по раз¬
ным предметам: здесь рангами являются обычные
оценки — баллы.
Если ранги оказываются полностью одинаковыми
для двух сравниваемых выборок, т. е. самому боль¬
шому числу в одной совокупности соответствует самое
большое в другой, второму по величине значению со¬
ответствует второе по величине в другой выборке и
так до минимального значения, то разность рангов
будет равна нулю. Это говорит о наличии однотип¬
ности, синхронности изменений, сравниваемых рядов.
При этом имеет место строгая положительная корре¬
ляция, и коэффициент корреляции будет равняться 1.
В общем случае величина коэффициента корреляции
должна зависеть от разности рангов di = ri — r*i, где
rt — ранг наблюдения в одной выборке, а г* — ранг
соответствующего наблюдения в другой.
Коэффициент корреляции рангов р вычисляется
по формуле
Р->--.-(£пГ1Г	(3.1)
п	п
где 2^=2 (г,-г!)2-сумма квадратов разностей
i=1 /=1 4 '
соответствующих рангов сопоставляемых выборок, а
п — число пар.
Пример 3.1. Исследовалась связь между средним периодом
ЭЭГ и критической частотой световых мельканий (К.ЧСМ). Для
восьми испытуемых были получены следующие данные (табл. 3.1).
46

Т А Б Л И Ц А 3.1
Первый пример вычисления корреляции рангов
по формуле 3.1
Связь между средним периодом ЭЭГ (СП ЭЭГ) и
критической частотой световых мельканий (КЧСМ)
Испытуе¬
мые
Средний
период
ЭЭГ
(уел. ед.)
КЧСМ
(гц)
Ранги
СП ЭЭГ
Ранги
КЧСМ
(ri~r*lY
1
3,54
41,9
8
5
9
2
4,02
42,0
2
4
4
3
3,71
44,8
6
1
25
4
3,98
42.7
3
3
0
5
3,57
43,1
7
2
25
6
4,32
38,0
1
8
49
7
3,86
38,3
5
7
4
8
3,90
41,0
4
6
4
Сумма квадратов разностей рангов (сумма последнего столб¬
ца) равна 120. По формуле (3.1) находим:
6-120 , 720
Р — 7 • 8 • 9	504 “ ’
Отрицательность коэффициента корреляции озна¬
чает, что при увеличении одной из переменных дру¬
гая, вообще говоря, уменьшается. Но последний, вы¬
вод можно будет сделать, если установить, что значе¬
ние коэффициента корреляции достаточно отличается
от нуля. Иначе говоря, необходимо оценить статисти¬
ческую значимость связи между СП ЭЭГ и КЧСМ: не
является ли значение коэффициента корреляции, вы¬
явленное в опыте, случайным отклонением, когда на
самом деле корреляция равна 0.
Действительно, полученное значение коэффициен¬
та корреляции, особенно если учесть, что при его вы¬
числении использовалось только 8 пар значений, еще
не позволяет достоверно установить наличие связи.
Необходим другой объективный критерий для решения
вопроса о том, зависимы ли анализируемые величины
(т. е., что р не равно 0). Как и при других статисти¬
ческих выводах, этот вывод можно сделать лишь при
определенном уровне надежности.
47

Мы приводим таблицы (табл. VII и VIII приложе¬
ния), в которых для выбранного уровня значимости
даны минимальные значения р, так что если получен¬
ное значение корреляции в опыте равно или больше
по абсолютной величине этого значения, то с выбран¬
ным уровнем надежности нулевая гипотеза отвер¬
гается, и можно делать вывод о наличии связи между
переменными.
Одной из этих таблиц (табл. VII) следует пользо¬
ваться, когда число пар составляет от 4 до 10. Когда
число пар больше 10, пользуются таблицей граничных
значений коэффициента обычной линейной корреля¬
ции (табл. VIII).
Обращаясь к нашему примеру, находим, что корреляция
0,420 не значима даже при уровне значимости 0,05. Когда
п = 8, минимальной значимой корреляцией должна быть вели¬
чина не менее 0,620 (по абсолютной величине) для того, чтобы
можно было предполагать зависимость анализируемых перемен¬
ных.
Для сопоставления двух коэффициентов корреля¬
ции, а не только для выяснения того, насколько дан¬
ный коэффициент корреляции отличается от нуля,
требуются более трудоемкие вычисления.
Пример 3.2. При продолжении изучения зависимости между
средним периодом ЭЭГ и КЧСМ в одной из групп были полу¬
чены следующие данные (табл. 3.2).
ТАБЛИЦА 3.2
Второй пример вычисления корреляции рангов
по формуле (3.1)
Испытуе¬
мые
СП ЭЭГ
(уел. ед.)
КЧСМ
(гц)
Ранги
СП ЭЭГ
Ранги
кчсм
1
3,93
43,3
3
5
4
2
3,65
43,4
8
4
16
3
4,33
43,5
1
3
4
4
3,90
43,0
5
6
1
5
3,95
44,8
2
2
0
6
3,92
46,1
4
1
9
7
3,78
42,7
6
7
1
8
3,70
42,5
7
8
1
36
4$

Вычисляя коэффициент корреляции по формуле
3.1, получаем его значение, равное 0,572. Это значе¬
ние корреляции, как следует из табл. VII приложе¬
ния, не является достаточным, чтобы делать вывод о
наличии связи между СП ЭЭГ и КЧСМ, так же как
в примере 3.1. Однако в первом случае корреляция
между критической частотой световых мельканий и
СП ЭЭГ была отрицательной, а во втором — положи¬
тельной. Весьма возможно, что наблюдаемые значе¬
ния есть просто случайные флуктуации р около нуле¬
вого уровня. Ведь ни в одном случае мы не доказали
с минимальным уровнем надежности 0,05, что сопо¬
ставляемые величины вообще зависимы.
Если бы мы располагали процедурой сравнения
разных коэффициентов корреляции и установили бы,
что они существенно различны (с определенным уров¬
нем надежности), то можно было бы предполагать,
что мы имеем дело с разными законами зависимости
и думать о причинах, которые обусловили эти различ¬
ные зависимости.
Методы сравнения двух коэффициентов корреля¬
ции разработаны для нормальной корреляции, но нет
каких-либо серьезных причин, которые препятство¬
вали бы распространению этих методов на сравнение
коэффициентов ранговой корреляции, вычисляемых
по формуле (3.1). Основой этих методов является
преобразование Фишера, которое позволяет исполь¬
зовать для сравнения коэффициентов корреляции
критерий Стьюдента. Оказывается, что если вместо
коэффициента корреляции р рассмотреть величину
то величина эта будет распределена приблизительно
нормально с известной средней z и дисперсией
которая не зависит от значения коэффициента корре¬
ляции,
49

Таким образом, если мы хотим сравнить два коэф¬
фициента корреляции pi и рг, следует в первую оче¬
редь найти
1	In ' +Pi тт ^	1 . 1 + Рг
*1 = Т ln I	— И z2 = тг In
2	1 - р, 2 1 - ps *
Для этого с помощью табл. IX приложения по извест¬
ному р находят z, не производя каких-либо вычисле¬
ний.
Затем вычисляют величину t по формуле:
' = —I г‘~г* I—>	(з-2)
			1
ti j 3 . — 3
которая имеет широко известное распределение t с
ti\ + п2 — 3 степенями свободы.
Проиллюстрируем сравнение двух коэффициентов
корреляции, используя данные примеров 3.1 и 3.2.
Пример 3.3. В первом случае pi = — 0,420, s\ = - ■ =
1 о — о
= 0,200, во втором случае р2 = 0,572,	^^ = 0,200.
По таблицам преобразования Фишера находим:
= — 0,447 г2 = 0,647.
по формуле (3.2):
_ — 0,447 — 0,650 — 1,097
0,200 + 0,200 — 0,400 — ’
По таблице распределения статистики t [3, 5, 11, 13, 19, 21]
находим, что такое t соответствует отрицанию нулевой гипотезы
с уровнем значимости 0,05.
Таким образом, с достаточно большим уровнем
надежности мы показали различие коэффициентов
корреляции рангов в сопоставляемых группах. Ответ
на вопрос, чем обусловливаются эти различия, орга¬
низацией ли экспериментальной ситуации, или, быть
может, индивидуальными различиями самих испытуе¬
мых, требует привлечения других сведений, которые
в приведенных примерах не рассматривались.
В рассмотренных примерах аналогичные резуль¬
таты могли бы быть получены и путем вычисления
линейного коэффициента корреляции. Однако приме¬
50

нение формулы (3.1) значительно облегчило вычисли¬
тельную работу. Еще раз подчеркнем, что в экспери¬
ментальной работе встречаются такие случаи (напри¬
мер, при полуколичественном выражении перемен¬
ных), когда наличие зависимости между переменными
можно установить только при вычислении ранговой
корреляции.
При вычислении ранговой корреляции приходится
сталкиваться с такими же трудностями, которые
встречаются при использовании непараметрических
критериев. Речь идет о наличии одинаковых значений
признаков. Неясно, какие ранги в таких случаях им
приписывать.
Целесообразно дать различные рекомендации пре¬
одоления этого затруднения в зависимости от харак¬
тера решаемых задач. Если приходится вычислять
много однотипных коэффициентов корреляции, то мо¬
жно. рекомендовать правило приписывать меньший
ранг (среди одинаковых значений признаков) тому
значению, которое встретилось в выборке раньше.
Если всегда придерживаться этого правила, то можно
гарантировать, что при массовых вычислениях точ¬
ность оценки корреляции будет достаточна для прак¬
тических целей.
Более точное ранжирование при наличии связей
заключается в том, что одним и тем же значениям
признака приписывают один и тот же ранг, равный
среднему арифметическому рангов,, которые назна¬
чаются с помощью предыдущего приема. Так, напри¬
мер, последовательность
3,5 8,1 7,3 6,0 3,5 4,0 7,3 3,5
первоначально имеет следующее ранжирование
6 1 2 4 7 5 3 8
Так как второе и третье значения одинаковы, при
уточнении им приписывается один и тот же ранг
а шестому, седьмому и восьмому один и тот же ранг
6	+ 7 + 8
3
61

В результате ранжирование вышенаписанного ряда
будет иметь следующий вид:
7	1 2,5 4 7 5 2,5 7
§ 3.2. ОЦЕНКА СВЯЗИ
МЕЖДУ КАЧЕСТВЕННЫМИ ПРИЗНАКАМИ
Ранговая корреляция Спирмена, рассмотренная
выше, в определенном смысле может рассматриваться
как мера зависимости не только между количествен¬
ными, но и между качественными признаками. Дейст¬
вительно, как мы видели, при измерении ранговой
корреляции абстрагируются от самих значений, а рас¬
сматривают только их отношение (больше — мень¬
ше). Но измерение связи с помощью коэффициента
ранговой корреляции Спирмена все же удобно лишь
тогда, когда первоначально сопоставляемые величины
имели количественное выражение.
В медико-биологических исследованиях довольно
часто приходится сталкиваться с такой ситуацией, ко¬
гда получить точное измерение признаков трудно или
невозможно. Так, например, в психофизиологии мож¬
но говорить лишь об увеличении или уменьшении
ощущения, вызываемого определенными раздражите¬
лями, не имея возможности точно измерить величину
самого ощущения; при исследовании генетических за¬
кономерностей имеют дело с такими признаками, как
цвет или форма плодов, исчерпывающее измерение
которых также вызывает трудности. В медицине часто
бывает необходимо узнать, существует ли связь (кор¬
реляция) между такими качественными признаками,
как возникновение заболевания, его исход, примене¬
ние данного вида лечения и т. д. Выявление взаимо¬
связи таких признаков между собой или с другими
факторами представляет не менее важную задачу,
чем исследование взаимосвязи количественных пере¬
менных.
Рассмотренный в § 2.8 точный метод Фишера мо¬
жет рассматриваться как один из способов оценки
взаимосвязи между некоторыми качественными при¬
знаками (см. Пример 2.9 на стр. 33). Но точный ме¬
тод Фишера ограничен небольшим числом наблюде¬
ний, в то время как обычно исследование взаимосвязи
52

качественных признаков требует большого статисти¬
ческого материала.
Пример 3.4. Требовалось узнать, имеется ли связь между
противохолерными прививками и таким качественным признаком,
как невосприимчивость к заболеванию. Данные Гринвуда и Юла
(1919), сведенные в четырехпольную таблицу, показали следую¬
щее (табл. 3.3).
таблица з.з
Незаболевшие
Заболевшие
Всего
С прививками
276
3
279
Без прививок
473
86
559
Итого ...
749
89
838
Если между заболеванием и прививкой нет зависимости, то
доля незаболевших из числа сделавших и не сделавших при¬
вивку должна быть одинаковой; соответственно и доля заболев¬
ших из числа сделавших и не сделавших прививку также дол¬
жна быть одинакова. В данном примере процент заболевших из
числа сделавших прививку—1,07%. Процент заболевших из
числа не сделавших прививку—15,4%. Чем больше отличие этих
частот от равенства, тем больше должна быть роль прививки
в предотвращении заболевания.
Если обозначить через *[, х\ градации одного
качественного признака, а через х\ — градации
другого, то различные экспериментальные случаи сво¬
дятся к четырехпольной таблице, аналогичной рас¬
смотренной выше (табл. 3.4).
В результате несложных вычислений можно пока¬
зать (см., например, Ван дер Варден, 1960), что оцен¬
ка различий соответствующих частот обеспечивается
критерием:
2 	(Пц « п22 — «12 • п21)2 • N	 g.
= («11 + «2l) («12 + «22) («11 + «12) («21 + «22)
Вероятность x2 при одной степени свободы (табл. X
приложения) может служить некоторой количествен¬
ной характеристикой величины этой зависимости. Во
всяком случае, когда Р <С 0,05, мы утверждаем, что
эта зависимость не равна нулю.
53

ТАБЛИЦА 3.4
Градации другого
признака
Градации одного
признака
Сумма по строкам
х'
х\
«5
частоты
х1
х2
«и
"21
"11 +"21
х\
"12
"22
"12 + ^22
Сумма по столб¬
цам
«11 + «12
«21 4" «22
N — «11 + «21 +«12 + «22
Возвращаясь к примеру 3.4, находим:
(276 X 86 — 473 X З)2 • 838
1	279 X 559 X 749 X 89
Полученное значение %2 позволяет сделать вывод
(см. табл. X приложения) о том, что между привив¬
кой и заболеванием холерой имеется статистическая
зависимость.
Читателя может удивить, что зависимость между
признаками оценивалась с помощью критерия %2, ко¬
торый ассоциируется обычно с оценкой различий ме¬
жду частотами. Здесь необходимо напомнить, что
один и тот же математический метод решает самые
различные задачи, на первый взгляд очень далекие.
В данном случае метод %2 позволяет оценивать связи
между качественными признаками потому, что эта
задача логически была увязана с необходимостью
оценки различий между некоторыми частотами.
Но применение %2 для измерения корреляции все-
таки связано с некоторыми трудностями и неудобст¬
вами.
Во-первых, х2 зависит от числа наблюдений N, а
не только от соотношений между частотами. Во-вто¬
рых, на основании формулы (3.3) получаются только
положительные числа, и значит, сведения о знаке кор¬
реляции не могут быть получены.
54

Чтобы исключить зависимость меры корреляции
от N, достаточно пользоваться величиной
Эта статистика для качественных признаков,
имеющих две градации, совпадает с коэффициентом
корреляции А. А. Чупрова (см. § 3.3).
Для получения информации не только о величине,
но и о знаке корреляции следует пользоваться фор¬
мулой
Величина К, так же как и коэффициент корреля¬
ции рангов Спирмена, изменяется в пределах от —1
до 1. Величина К имеет простую связь с х2-
На основании критерия (3.3) выше было установлено, что
корреляция между вакцинацией противохолерной сывороткой и
заболеваемостью холерой не равна нулю. Но этого еще недо¬
статочно, чтобы делать вывод о том, что применяемая сыворотка
эффективна.
Когда число наблюдений велико, наличие статистической свя-
зи между переменными обнаруживается и при низком уровне
этой связи.
Подсчитаем коэффициент корреляции по формуле (3.4) для
данных примера 3.4:
Эти вычисления показывают, что в рассматриваемом случае
эффективность противохолерной сыворотки следует признать
весьма низкой. Даже при значении коэффициента корреляции
0,3—0,4 будет еще слишком много случаев, когда прием лекар¬
ства не предохраняет от заболевания и, наоборот, много случаев,
когда заболевание отсутствует и без получения сыворотки.
С помощью подобных вычислений коэффициент
корреляции К может быть использован при срав¬
нительной оценке различных фармакологических
средств. Аналогично он используется и при оценке
токсичности различных факторов, если результаты
(«Ц ♦ «22 — ^12 * П2\)2
(«и + П2\) («12 + П22) (Лц + П\2) (Я21 + tl22)
К =
^11 * ^22 ^12 * ^21
(3.4)
У(пп + П2\) {п12 + n2i) (П\ \ + n\i) (^21 + ^22)
276 • 86 — 3 • 473
65

опыта могут быть сведены в четырехпольную таблицу.
Но особенно важны его применения при формирова¬
нии новых информативных признаков для дифферен¬
циальной диагностики (что такое информативность
признаков — см. § 4.2). Информативность коэффи¬
циента корреляции может быть значительно выше,
чем информативность каждого из коррелируемых
признаков.
§ 3.3. ОЦЕНКА СВЯЗИ
МЕЖДУ КАЧЕСТВЕННЫМИ ПРИЗНАКАМИ
(ПРОДОЛЖЕНИЕ)
В предыдущем параграфе мы рассмотрели случай
оценки взаимосвязи, когда признаки имели по две
градации. Наличие и отсутствие признака рассматри¬
вались как разные градации. Но возможны ситуации,
когда особенности качественного признака меняются
более градуально (сильная боль, умеренная боль,
слабые боли, отсутствие боли) или исследуются свя¬
зи таких качественных признаков, которые по своей
природе имеют больше чем две градации (например,
качественный признак «цвет глаз» имеет градации:
голубые, карие, серые и т. п.)
В этом случае мера взаимосвязи определяется
принципиально так же, как это было сделано для
признаков, имеющих две градации, но требует боль¬
ше вычислений.
Пусть N наблюдений классифицируется по двум
признакам Xi и х2, один из которых имеет k града¬
ций:*}, х\, ..., х\, а другой т градаций х\у х% ..
Результаты этой классификации могут быть пред¬
ставлены в таблице, подобной табл. 3.5.
В каждой клетке этой таблицы находится число,
показывающее число наблюдений, которые относятся
к соответствующим градациям признаков Х\ и х2. На-
иример, «12. Это число наблюдений, которые имеют
свойства х\ и х\. Вообще в клетке, расположенной
на пересечении i-того столбца и /-той строки, по¬
мещается tiij — число наблюдений, одновременно от¬
носящихся к градациям х\ и х]2 (или, другими слова¬
ми, имеющие свойства х\ и х£).
т

ТАБЛИЦА 8.5
Градации
признака
Хг
Градации признака х,
Сумма no
строкам
х1
Х1
х2
Х1
xk
Xl
частоты
*2
"II
"12
П1к
"10=£= l"“
х\
"21
"22
n2k
k
П20~ ^1П21
•
*
*
•
*
*2Ш
"ml
"m2
"mft
Пто= {^zlnmi
Сумма по
столбцам
т
i,n/>
т
"02 = yIj"/2
m
n° k=jlinJk
N
Если допустить, что признаки Xi и Хг независимы,
то на основании теоретических соображений можно
подсчитать, какими должны быть эти частоты. Коли¬
чественная мера, оценивающая различия между ча¬
стотами, наблюдаемыми в опыте (табл. 3.5) и теоре¬
тически рассчитанными, и будет мерой, оценивающей
зависимость признаков. В качестве такой меры ис¬
пользуется %2[22] или более современные информа¬
ционные статистики [14].
Оценим вначале различия между частотами пер¬
вого столбца табл. 3.5,
П\\, «21. • • •» ЛШ1
и частотами, теоретически полученными при предпо¬
ложении, что признаки х\ и х% независимы:
п ю * "01 д20 • "01 "то * "01	/о к\
N • N 	 N	^ }
Вычисление теоретических частот следует из простых
соображений теории вероятностей [5, 22].
67

Если оценивать различия экспериментально полу-
шых
лучаем:
чаемых и теоретических частот с помощью %2, то по-
(«11
%\=
«10 *«01 \2 „ «20 • «01
«10 • «01 «20 • «01
N	N
(„	«то * «01 V
[ Г”1 N~")
«то * «01
N
Проделав то же самое с частотами второго столбца,
получаем:
(„ «10 • «02 \2 [.. «20 • «02 \2
2	д, .)	{"*	—)
^	«ю *«02	«20 * «02
N	N
(..	«шо-«оз\2
] \ т2 ~ N )
«то * «02
N
Продолжая аналогично для других столбцов, мы по¬
лучаем для градации х\
( n10*n0fe\ ( n20'n0k\2
\nlk	—) [n2k	—)
%k
«10*«0fe	«20 * «Ofe
N	N
12
I..	«mo ‘ «ofe \2
\nmk— N )
' (3.6)
«m0 * «ofe
N
Общая мера зависимости получается суммированием
по всем градациям:
%2 = X? + + • • • +х1	(3>7)
Когда имеет место нулевая гипотеза (независи¬
мость Х\ и х2), величина %2 распределена как х2 с
/ = (k — 1) (m — 1) степенями свободы. В таблице X
для полученного значения х2 11 степеней свободы f
68

находим вероятность справедливости нулевой гипо¬
тезы. Когда Р <. 0,05, нулевая гипотеза отклоняется
и считается что Х\ и Хг зависимы.
В тех случаях, когда признаки оказываются зави¬
симыми, часто возникает необходимость определять
величину (уровень) этой зависимости. Непосред¬
ственно пользоваться величиной х2 для этой цели
нельзя. Это связано с тем, что при увеличении числа
наблюдений величина х2 будет увеличиваться и в та¬
ких случаях, когда соотношение между частотами
не меняется (например, все частоты увеличены в од¬
но и то же число раз). Увеличение х2 в этом случае
вполне закономерно, так как сам факт зависимости
или независимости гарантируется теперь большим
числом наблюдений и надежность вывода возрастает.
Но величина корреляции между признаками при этом
не должна изменяться. Чтобы исключить влияние чи¬
сла наблюдений на величину уровня связи между
признаками, пользуются коэффициентом
Ф = “дГ	(3.8)
где N — общее число наблюдений. Чтобы еще допол¬
нительно исключить влияние на величину корреляции
числа степеней свободы (k и т), пользуются коэф¬
фициентом
^	X2
NV(k- 1) (т- 1)
(3.9)
Последний коэффициент называется коэффициентом
корреляции А. А. Чупрова.
Пример 3.6. 725 учащихся обследовались с помощью различ¬
ных психологических тестов. На основании суммарного коэффи¬
циента, объединяющего информацию о результатах различных
психологических испытаний, весь обследованный контингент был
разделен на три группы. В I группу вошли учащиеся с наиболее
низкими средними психологическими оценками, во II группу —
учащиеся со средними оценками и в III группу — с наиболее вы¬
сокими психологическими средними баллами. С другой стороны,
пользуясь отзывами педагогического персонала, эти учащиеся
были разделены также на три группы: 1) с успешностью обуче¬
ния ниже средней; 2) со средней успешностью и 3) с успеш¬
ностью выше средней. Подробности психологического тестирова¬
ния и разбиения на градации в рассматриваемом примере пред¬
ставлены в книге проф. А. П. Нечаева «Ум и труд» (1926).
69

Результаты сравнения педагогической и психологической оценки
учащихся приведены в табл. 3.6.
ТАБЛИЦА 3.6
Сравнение педагогической и психологической оценки
учащихся
Педагогическая оценка
(номера групп)
Психологическая оценка
(номера групп)
Сумма по
строкам
1
2
3
число учащихся
1
53
92
25
170
2
91
253
91
435
3
18
52
50
120
Сумма по столбцам
162
397
166
725
Для оценки степени соответствия между психологи¬
ческими и педагогическими оценками воспользуемся
формулами, которые приводятся выше.
Теоретические частоты для первого столбца в слу¬
чае независимости должны быть (формула 3.5):
162-170 чо. 162-435 ^ 162.120
38« 		= 97*5> 		*= 26-8-
725 ’ 725 ’ ’	725
для второго (формула 3.5):
397-170 397-435	397-120
~725	92А 725 238,	~725	 65Д
для третьего (формула 3.5):
‘«•1ТО_МА l6VJj=99,5;	J66,-!20 = 27.4.
725	’ ’ 725	’ ’ 725
Находим последовательно (формула 3.6):
2 (53 - 38)2 (91 — 97,5)2 (18-26.8)2
Х1	38 + 97,5 + 26,8
—	5,92 + 0,44 + 2,89 = 9,25.
2	(92-92,8)2 (253 -238)2 (52 - 65,8)2
92,6 + 238 + 65,8 “
36
2	(25-38.9)2 (91 — 99,5)2 (50 - 27,4)2
Хз	23,4 + 99,5 + 27,4
= 0,006 + 0,95 + 2,81 = 3,77.
0 — 27,4)2
27,4
8,24 + 0,73 + 18,60 = 27,57.
60

Таким образом (формула 3.7):
X2 = 9,25 + 3,77 + 27,57 = 40,59.
Обращаясь к таблице X, устанавливаем, что для
4 степеней свободы 40,59 соответствует высокому
уровню значимости {Р <. 0,001). Значит, мы с высо¬
кой существенностью можем гарантировать наличие
связи между психологическими и педагогическими
оценками.
Но величина этой связи оказывается крайне не¬
значительной. Это мы устанавливаем, вычисляя ко-
эффциент Чупрова (формула 3.9):
40,59 40,59

Глава 4
ОТНЕСЕНИЕ НАБЛЮДЕНИЙ К ОДНОМУ
ИЗ ДВУХ ВОЗМОЖНЫХ КЛАССОВ
(ДИАГНОСТИКА И ПРОГНОЗИРОВАНИЕ)
§ 4.1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДА
Врачу часто приходится решать альтернативные
диагностические задачи, т. е. выбирать одну из двух
(а не из многих) диагностических гипотез, например
определять, является опухоль злокачественной или
доброкачественной; выявлять наличие или отсутствие
подчерепного кровоизлияния при закрытой травме че¬
репа; решать, не привело ли острое нарушение коро¬
нарного кровообращения к инфаркту миокарда; оп¬
ределять, чем вызвана желтуха — инфекционным ге¬
патитом или новообразованием, и т. д. Альтернатив¬
ными являются задачи определения прогноза заболе¬
вания и выявления угрожающего состояния при не¬
прерывном контроле за тяжелым или послеопераци¬
онным больным, а также при контроле за здоровым
человеком, находящимся в экстремальных условиях.
Для решения подобных задач могут быть исполь¬
зованы различные вычислительные методы распозна¬
вания [6, 7, 11, 16, 18]. В настоящем разделе мы рас¬
сматриваем один из таких методов — так называемую
последовательную диагностическую процедуру, кото¬
рая не требует применения вычислительной техники,
как на стадии составления диагностических таблиц
(хотя вычислительная техника сокращает эту рабо¬
ту), так и на стадии их применения для диагностики
и прогнозирования. Эта процедура, так же как опи¬
санные в главах 2 и 3 непараметрические критерии
различий и связи, может быть применена при раз¬
личном характере распределения признаков в рас¬
сматриваемых группах наблюдений (классах). Она
соответственно не требует вычисления таких пара¬
метров, как средние арифметические, дисперсии,
62

ошибки средних. Последовательная процедура рас¬
познавания, как и рассмотренные в главе 2 непара¬
метрические критерии, основана на рассмотрении
упорядоченных рядов признаков в сравниваемых
группах наблюдений и на последовательном анализе
построенных на их основе пар распределений.
В основе последовательной диагностической про¬
цедуры лежит метод последовательного (секвенци¬
ального) анализа, разработанный А. Вальдом (1947,
1960) и получивший распространение в ряде областей
техники, а также биологии и медицины [2, 17, 19, 20,
21]. Обоснование применимости последовательного
статистического анализа для диагностики и соответ¬
ствующие методические приемы его использования с
этой целью были даны А. А. Генкиным (1962) Весь
комплекс основных методических вопросов, связан¬
ных с диагностическим применением этого алгорит¬
ма, был впервые рассмотрен в совместной работе
авторов [10], а в дальнейшем в монографии одного
из них [11]. Принцип этого метода может быть пояс¬
нен на следующем примере.
Пример 4.1. Представим себе, что врачу необходимо осуще¬
ствить дифференциальную диагностику между инфекционным ге¬
патитом и холангитом. Известно, что пульс не более 70 ударов в
минуту встречается в 4 раза чаще при инфекционном гепатите,
чем при холангите, а пульс 76 ударов и более, наоборот, в 8 раз
чаще при холангите, чем при инфекционном гепатите *.
Допустим, у поступившего больного пульс составляет менее
70 ударов в минуту. Очевидно, вероятность диагноза «инфекцион¬
ный гепатит» в этом случае превышает вероятность диагноза «хо-
лангит» в 4 раза. (Сразу следует оговориться, что это верно лишь
в том случае, если частота гепатита и холангита среди больных,
обращающихся в данное лечебное учреждение, существенно не
различается).
Представим себе далее, что установлено также следующее:
пониженное число лейкоцитов в крови (4000—4500 в 1 мм3)
встречается в 5 раз чаще при гепатите, чем при холангите. Следо¬
вательно, если у поступившего больного 4000 лейкоцитов, диаг¬
ноз «инфекционный гепатит» у него еще в 5 раз вероятнее, чем
диагноз «холангит». В сочетании с предыдущим признаком это
1 Для установления подобных фактов при создании вычис¬
лительной системы распознавания подбирают группу наблюдений,
которую называют «группой обучения» (имеется в виду «обуче¬
ние» системы), включающую больных обоими дифференцируе¬
мыми заболеваниями А и В. На этой группе устанавливают ча
стоты различных симптомов при сравниваемых заболеваниях.
Иногда для этого частично используют данные литературы.
63

дает превышение вероятности первого диагноза над вероятностью
второго в 4 X 5 = 20 раз (здесь вновь необходимо заметить, что
этот расчет правилен лишь при том условии, если первый и вто¬
рой признаки достаточно независимы). Очевидно, если мы в та¬
кой ситуации каждый раз будем ставить первый диагноз, то это
в среднем будет правильным в 20 случаях из 21.
Набор признаков можно продолжать до достижения заранее
намеченной степени превышения вероятности одного из диагно¬
зов над вероятностью второго.
Рассмотренный в этом примере подход к диффе¬
ренциальной диагностике может быть выражен так:
Р(х\1а) Р(хЦа) P(xUa)	л
порог в<т(М-тт---тт<порог А (4л)
Поясним смысл этого неравенства.
— отношение вероятности (частости) Р, об-
р(х\1л)
Р(хЦв)
наруженной у больного первой градации первого
признака х\ (в рассмотренном примере — частоты
пульса менее 70 ударов в минуту) при заболевании
А — гепатите — к вероятности (частости) этой же
градации того же признака при заболевании В — хо-
лангите. Подобные отношения вероятностей называют
отношениями правдоподобия. В рассмотренном при¬
мере первое отношение правдоподобия равно:
Р(*!/Л) 4
Р(х\/в) Г
Второе отношение правдоподобия для обнаружен¬
ной у больного третьей градации второго признака
(число лейкоцитов в крови от 4000 до 4500) равно:
р{41Л) 5
Р(хЦв) 1 '
Их произведение равно:
Р(хЦА) р(хЦа) 4 5 20
Р(хЦв) * Р(хЦв) “7*1 1 ’
Р(х*1А)
где ^ — отношение правдоподобия для обнару¬
женной у больного i-й градации /-го признака при
64

заболевании А к вероятности этой же градации того
же признака при заболевании В.
Мы должны заранее решить, какое итоговое пре¬
вышение вероятности заболевания А над вероят¬
ностью заболевания В (и, наоборот, вероятности
заболевания В над вероятностью заболевания А) до¬
статочно для принятия соответствующей диагности¬
ческой гипотезы. Отношения вероятностей, достаточ¬
ные для принятия гипотез А или В, и называют по¬
рогами. Таким образом, сбор диагностической ин¬
формации и перемножение отношений вероятностей
найденных симптомов продолжают до тех пор, пока
правильно неравенство (4.1), т. е. пока не достигнут
«порог А» или торог В». Когда неравенство (4.1)
становится неверным, т. е. когда один из порогов до¬
стигнут или превышен, последовательную процедуру
распознавания прерывают и «выносят решение», т. е.
выбирают одну из; диагностических гипотез. Если до¬
стигнут порог А, ставят диагноз: «Заболевание А»,
если достигнут порог В — диагноз: «Заболевание В».
Если использована вся имеющаяся в нашем распоря¬
жении диагностическая информация, но ни один из
порогов ни разу не достигнут, то принимают решение
«имеющейся информации недостаточно для принятия
решения с намеченным уровнем ошибок» (так назы¬
ваемый «неопределенный ответ»).
Если априорные вероятности заболеваний А и В
Р(АУ, Р(В),
т. е. частоты болезней А и В среди больных, обра¬
щающихся в данное лечебное учреждение, различны,
и отношение
Р(А)
Р(В)
сильно отличается от единицы, это отношение априор¬
ных вероятностей включают в формулу (4.1), ставя
его, как правило, на первое место:
_ Р(А) P(xjA) Р(хУА)
порог В<	7-тгт‘ ) 1/ ч •••
Р{В) Р(х\В) Р(х\в)
р(хЧа)	л
... ; у, /- <порог А (4.2)
Р(х‘1в)
3	Е. В. Гублер, А. А. Генкин
65

Алгоритм, лежащий в основе последовательной
диагностической процедуры, вытекает из основных
теорем теории вероятностей и, в частности, из осно¬
ванной на них формулы Байеса, часто применяемой
при вычислительной диагностике [18]. При введении
определенных ограничений диагностической задачи и
начальных условий формула Байеса принимает вид
более простой формулы (4.1) принятия решения при
последовательной диагностической процедуре [11].
Пример 4.2. Рассмотрим случай, когда отношения вероятно¬
стей нескольких первых симптомов достаточно сильно отли-
1 1 1 -г
чаются от единицы, например, равны -g-,	. Тогда умно¬
жение отношений вероятностей первых симптомов даст превы¬
шение вероятности одного из возможных заболеваний над вероят¬
ностью другого в большое число раз.
L -L JL 1 = 1
8	* 4 * 2 * 2 128 *
Заранее решаем, что превышение вероятности одного из за¬
болеваний над вероятностью другого в 100 раз достаточно для
принятия решения: «Заболевание В», если достигнута пороговая
величина	или «Заболевание А», если достигнута пороговая
100 _
величина —j— • Тогда в рассматриваемом случае после использо¬
вания первых четырех симптомов достигается требуемый порог
Yqq-» Этого достаточно для принятия решения: «Заболевание В».
В математической статистике подобный подход,
когда последовательное накопление информации про¬
должается только до момента достижения порога,
предложен А. Вальдом. Он является отличительной
особенностью последовательного статистического
анализа. А. Вальд показал, что при таком подходе
требуется в среднем вдвое меньше информации для
принятия решения с определенным уровнем надеж¬
ности, чем при обычном «классическом».
В случае несимметричных порогов (например,
1: 100 и 50: 1) их вычисление несколько усложняется.
В общем случае величины порогов для принятия ре¬
шения с требуемым уровнем надежности по Вальду
66

определяют по следующей формуле:
порог А = 1 ~ а ;
а	(43)
порог B =
где а и р — ошибки первого и второго рода. Под
ошибкой первого рода а понимают ложную диагно¬
стику заболевания В, когда в действительности у
больного заболевание А. Ошибкой второго рода р
называют просмотр заболевания В и ошибочное
установление диагноза А, когда в действительности
у больного заболевание В.
Вывод формул (4.3) логически достаточно прост
[4, И], но за недостатком места мы его здесь не при*
водим.
Пример 4.3. Примем допустимый уровень гипердиагностики
заболевания В (т. е. ошибки первого рода а) равным 0,1 (10%),
а допустимый уровень просмотра заболевания В (ошибка второго
рода Р) равным 0,05 (5%). Произведем вычисление порогов.
а = 0,1; Э = 0,05.
А 1 -а 1-0,1 0,9
Р	Р “ 0,05 0,05
о а	0,1	0,1
Р	1 -р “ 1 -0,05 = "0^5
Таким образом, при последовательной процедуре
распознавания для выбора диагностической гипотезы
мы используем только ту часть диагностической ин¬
формации (в виде произведения отношений правдо¬
подобия), которая нужна для достижения определен¬
ного порога. Величина последнего определяется ве¬
личинами допустимых ошибок первого и второго рода.
Из соображений удобства вычислений целесооб¬
разно умножение отношений правдоподобия заменить
соответствующим ему сложением логарифмов этих
величин. Для того, чтобы эти логарифмы представ¬
ляли собой целые числа, их умножают на 10 и округ¬
ляют с точностью до единицы. Величину, которую
при этом получают, называют диагностическим коэф¬
фициентом. Диагностический коэффициент градации i
= 18:1
— 1:9,5
3*
67

признака Xj равен:
(4.4)
Соответственно и диагностические пороги:
порог А = —~-а; порог В = . а _
р 1 —р
должны быть заменены их логарифмами, умножен¬
ными на коэффициент 10:
«Логарифмические» пороги обозначают словом
«Порог» с большой буквы.
Пример 4.4. Произведем расчет логарифмических порогов в
примере 4.2:
Порог А = 10 lg (18: 1) = 10 • 1,2553 = 12,553 « + 13.
Порог В — 10 lg (1:9,5) * 10 lg 0,1052 =
Порог А представляет собой положительную вели¬
чину. По его достижении принимают гипотезу А. По¬
рог В является отрицательной величиной. По его до¬
стижении принимают гипотезу В.
Вместо вычисления порогов можно после принятия
допустимого уровня ошибок первого и второго рода
аир определить их с помощью табл. XII приложе¬
ния.
После замены отношений правдоподобия в фор¬
муле (4.1) диагностическими коэффициентами, а по¬
рогов А и В — их логарифмами, формула принятия
решения при последовательной диагностической про¬
цедуре приобретает вид неравенства (4.7):
Порог А = ю lg —
(4.5)
(4.6)
= 10 (- 0,978) = - 9,78 ~ - 10.
а

где хи х2, ..., Xj — обнаруженные у больного града¬
ции одноименных признаков (верхние индексы, обо¬
значающие номера градаций, здесь и ниже для про¬
стоты опущены).
Фактически то же неравенство можно изобразить
иначе, поскольку его слагаемые представляют собой
диагностические коэффициенты соответствующих диа¬
пазонов соответствующих признаков:
flip < ЯК (*0 + ЯК (х2) +...+ ДК(х,) < 10 lg (4.8)
10
Последовательную процедуру определения вели¬
чины диагностических признаков, отыскания соответ¬
ствующих им диагностических коэффициентов и их
суммирования продолжают, пока правильно неравен¬
ство (4.8), а когда оно становится неверным (т. е. ко¬
гда достигнут или превышен один из порогов), после¬
довательную процедуру распознавания прерывают и
выносят то или иное решение, в зависимости от того,
какой из порогов достигнут. Если при последователь¬
ном использовании всей имеющейся диагностической
информации неравенство (4.8) остается все время
правильным (т. е. ни разу не достигается ни один из
порогов), то выносят решение; «имеющейся инфор*
мации недостаточно для принятия решения с наме¬
ченным уровнем ошибок» (неопределенный ответ).
Все это называют правилом принятия решения
при последовательной процедуре распознавания.
Для сравниваемой пары заболеваний или состоя¬
ний заранее рассчитывают сначала величину
р(х\1а)
i° 'е п)
Р(хЦв)
называя ее диагностическим коэффициентом первого
диапазона первого признака:
/ .4	pix\U)
Дк^=тетт
Пример 4.5. Предположим, что из 100 больных с заболева¬
нием А пульс реже 80 ударов в минуту имели 20 человек (или
0,2 всех больных), а из 100 больных с заболеванием В такой же

пульс имели только 5 человек (или 0,05 всех больных). Тогда:
Величину 6,02 округляют с точностью до единицы. Получают:
Диагностические коэффициенты вычисляют и для
всех других диапазонов первого и остальных призна¬
ков, записывая их в виде диагностической таблицы
(см. табл. 4.6 на стр. 84) строго в порядке убываю¬
щей информативности. При использовании таблицы
допустимы пропуски в обследовании данного боль¬
ного и, следовательно, в списке признаков, применяе¬
мых для диагностики имеющегося у него заболева¬
ния, однако принцип, согласно которому раньше при¬
меняются более информативные признаки, должен
быть соблюден.
Как явствует из сказанного выше, при использо¬
вании последовательной диагностической процедуры
существенным является порядок расположения при¬
знаков в диагностической таблице, который опреде¬
ляет последовательность их использования при диаг¬
ностике.
Признаки в таблице размещают в порядке убы¬
вающей информативности, так как это минимизирует
среднее число шагов последовательной процедуры
(т. е. число признаков, используемых в рекомендуе¬
мой последовательности, до достижения определен¬
ного ответа) и число ошибок.
Под дифференциальной информативностью при¬
знака понимают степень различий его распределений
при дифференцируемых состояниях А и В. Чем силь¬
нее различаются эти распределения, тем больше ин¬
формации, позволяющей различить состояния А и В,
несет рассматриваемый признак. Если его распреде¬
ления при состояниях А и В вообще не пересекаются,
его информативность бесконечно велика; он во всех
0,2
10 lg	= ю lg 4 = 10.0,602 — 6,02.
0,05
ДК(х j) = 6.
§ 4.2. ВЫЧИСЛЕНИЕ ИНФОРМАТИВНОСТИ
ПРИЗНАКОВ
7Q

случаях позволяет однозначно определить, относится
рассматриваемый объект к классу А или В.
При использовании последовательной диагности¬
ческой процедуры удобной мерой для оценки инфор¬
мативности признаков является мера Кульбака [14].
В отличие от критерия х2 и других критериев стати¬
стической значимости различий, мера Кульбака по¬
зволяет оценить не достоверность различий ме¬
жду распределениями, а степень этих различий.
Сначала вычисляют информативность градаций
диапазонов признака Xj.
Согласно формуле Кульбака величина информа¬
тивности / диапазона i признака / равна:
I	(*') = ДК (*') 4- [Р (*}/ А) - Р (дг'/в)]	(4.9)
В описанную Кульбаком (1967) формулу здесь
введен коэффициент у, так как можно предполагать,
что именно на получаемую при этом величину /(•*/)
соответствующий диапазон i признака Xj в среднем
приближает сумму диагностических коэффициентов
к намеченному порогу у некоего среднего боль¬
ного [11].
Однако для определения порядка использования
признаков в диагностической таблице необходимо вы¬
числить информативность не одного диапазона при¬
знака, а всего признака. Информативность всего при¬
знака Xj равна сумме информативностей его диапа¬
зонов:
'(*/)-2'(*}) <4|0>
1
Этой величиной и руководствуются, располагая при¬
знаки в таблице в порядке убывающей информатив¬
ности.
Пример 4.6. Вычислим информативность первого диапазона
первого признака, рассмотренного в примере 4.5.
Д/t (*|)~ 6; Р(х\/А) = 0,2; Р{х\/в) -0,05;
/ (*!) - ДК(*|) • i [р (х\1 А) - Р W/в)) -
«= 6 • J (0,2 - 0,05) «= 3.0,15 — 0,45.
71

Вместо вычисления информативности диапазона
признака ее .можно определить по табл. XI приложе¬
ния. В этой таблице определение информативности
производится по заданному диагностическому коэф¬
фициенту и сумме частостей Р(х1{/А) +	так
как в некоторых случаях сумму частостей вычис¬
лить легче, чем разность1, а в остальных случаях она
не менее удобна, чем последняя.
Зная величину диагностического коэффициента Д/С(*}) и
сумму вероятностей (в %) попадания в этот диапазон наблюде¬
ний групп А и В:
Р (хЦА) + Р (хЦв) = 20 + 5 = 25%,
определяем по табл. XI, что информативность диапазона
/(*}) равна 0,45.
Предположим, что информативность других диапазонов этого
же признака равна 0,75 и 0,80. Тогда информативность всего при¬
знака х\ равна
/(*,)“/(*!) + / (*?) +1 (*?) = 0,45 + 0,75 + 0,80 = 2,0.
Это значит, что обращение к признаку Х\ при дифферен¬
циальной диагностике заболеваний А и В в среднем приблизит
среднего больного к диагностическому порогу (разумеется, пра¬
вильному, потому что средний больной будет приближаться
только к правильному порогу) на величину 2,0.
Информативность диагностической таблицы в це¬
лом, которую обозначим через /т, равна сумме инфор¬
мативностей всех признаков
/т=2/(*/)	(4.И)
/
Эта величина может быть использована для срав¬
нительной оценки разных таблиц.
1 Такими случаями, например, являются ситуации, в кото¬
рых диагностические коэффициенты после их вычисления подвер¬
гаются «сглаживанию» путем вычисления взвешенной скользя¬
щей средней (см. ниже), замене значащими числами, если они
оказываются равны нулю или бесконечности, и другой коррек¬
ции (см. [11]), а также случаи, когда в состав одного из призна¬
ков входят априорные вероятности дифференцируемых состояний
А и В: Р(А) и Р(В). Во всех этих ситуациях вероятности при¬
знаков Р(л^/л) и Р(х*/в) либо сильнее меняются, чем их сум¬
ма, либо труднее вычисляются, чем последняя.
72

§ 4.3. ПОДГОТОВКА ДИАГНОСТИЧЕСКОЙ
ТАБЛИЦЫ
При составлении диагностической таблицы пер¬
вой задачей, которую приходится решать, является
задача отбора наиболее информативных признаков из
числа доступных при диагностическом обследовании
больного. Признаки с низкой информативностью не¬
целесообразно включать в диагностическую таблицу,
так как они при наличии даже небольшой зависимо¬
сти между признаками, которую исключить невозмо¬
жно, легко становятся «шумом», мешающим выявле¬
нию полезного диагностического «сигнала».
Оказалось, что информативность признака, вычисленная опи¬
санным выше способом после разбивки шкалы признака на диа¬
пазоны, неудобна и недостаточна для отбора информативных при¬
знаков.
Во-первых, формула Кульбака оценивает степень различий
распределений признака, а не их достоверность (различия могут
быть и случайными). Применяя только эту формулу, мы рискуем
включить в диагностическую таблицу признаки, в действительно¬
сти не различающиеся при заболеваниях А и В.
Во-вторых, вычисление информативности по Кульбаку слиш¬
ком трудоемко, чтобы его использовать для отбора информатив¬
ных признаков, которых обычно оказывается меньше половины
среди первоначально взятых.
В-третьих, информативность признаков в большой мере за¬
висит от способа разбиения шкалы признаков на диапазоны. За
счет подчеркивания различий между распределениями Л и В при
произвольном выделении диапазонов информативность признака
может быть значительно преувеличена по сравнению с истинной.
Это приведет к ухудшению результатов диагностики в провероч¬
ной группе наблюдений и при эксплуатации таблицы.
Ранее одним из нас [И] были предложены эмпирические пра¬
вила для разделения шкалы признака на диапазоны. Однако вы¬
деление диапазонов в соответствии с этими правилами является
достаточно произвольным. Вместе с тем любой общий упорядо¬
ченный ряд, включающий члены двух выборок, расположенные
в порядке возрастания их численных значений, можно за счет
подчеркивания случайных различий разбить на диапазоны таким
способом, при котором информативность каждого диапазона бу¬
дет равна бесконечности. Для этого достаточно выделить такие
диапазоны, в каждом из которых содержатся наблюдения, отно¬
сящиеся только к одной из двух сравниваемых выборок. В этом
случае логарифм отношения вероятностей, т. е. диагностический
коэффициент в этом диапазоне, будет равен +оо или —оо, а ин-
(4.9)	равна эо. При использовании первого же такого признака
мы получим окончательный определенный ответ, который в зна¬
чительной части случаев будет ошибочным.
формативность диапазона
при расчете ее по формуле

Такое предельное подчеркивание различий при разбиении на
диапазоны, естественно, не практикуется. Однако даже более
слабая степень подчеркивания различий между распределениями
А а В может существенно завышать информативность признаков
и ухудшать результаты диагностики.
Для того, чтобы избежать этой опасности, мы применили сле¬
дующую систему мер.
Во-первых, предварительный отбор информативных признаков
мы производим с помощью непараметрического критерия разли¬
чий, не требующего предварительной разбивки шкалы признака
на диапазоны.
Во-вторых, при разбивке шкалы признака на диапазоны, что
рано или поздно необходимо сделать, мы руководствуемся фор¬
мальными критериями, не учитывая при этом степень различий
частот признаков в каждом диапазоне.
В-третьих, после разбивки шкалы признака на диапазоны мы
вычисляем не только вероятности (частости) признака в каждом
диапазоне, но и средневзвешенные («сглаженные») его частости,
при вычислении которых учитывают процент наблюдений, попав¬
ших как в данный, так и в соседние диапазоны. Это сглаживает
случайные колебания частостей в диапазонах, а также колебания,
которые могли быть вызваны сохранившимися элементами про¬
извола при разбивке шкалы на диапазоны.
~	частостям признака в каждом
логарифм, т. е. средневзвешенный диагностический коэффициент
Рассмотрим более подробно методику отбора при¬
знаков, разбиения шкалы признака на диапазоны и
вычисления средневзвешенных частостей признака в
каждом диапазоне.
Целесообразно различать предварительный и
окончательный отбор признаков по информативности.
Окончательный отбор признаков проводится после
вычисления информативности по Кульбаку предвари¬
тельно отобранных признаков. Вопрос о пороге ин¬
формативности для окончательного отбора остается
нерешенным. Мы считаем минимальной информатив¬
ностью для включения признака в диагностическую
таблицу / (xj) = 0,5.
Мы неоднократно пытались при недостатке информативных
признаков включать в диагностическую таблицу признаки с мень¬
шим уровнем информативности. Однако при проверке и использо¬
вании таблицы оказывалось, что такие признаки практически не
увеличивали число правильных определенных ответов, а иногда и
вычисляем их отношение и его
ДК:
(4.12)
74

уменьшали его, часто изменяя сумму диагностических коэффи¬
циентов в направлении «ошибочного» диагностического порога.
Что касается предварительного отбора информа¬
тивных признаков для дальнейшей работы, то его мо¬
жно проводить с помощью любого критерия различий.
Удобен для этого непараметрический критерий U
(Вилкоксона — Манна — Уитни). Использование это¬
го критерия не требует разбивки признака на диапа¬
зоны, как это необходимо, например, при использова¬
нии критерия х2 или при вычислении информативно¬
сти по Кульбаку. Методика использования критерия
U рассмотрена в § 2.4 и 2.6. Признаки, различия ме¬
жду которыми в группах А и В не являются статисти¬
чески значимыми, целесообразно исключить из даль¬
нейшей работы. Однако эта рекомендация не может
быть стандартной для всех случаев. Если информа¬
тивных признаков мало, а возможности для трудо¬
емкой обработки многих признаков имеются, оказы¬
вается целесообразным оставить для дальнейшей
работы и те признаки, у которых различия между
группами А и В недостаточно значимы (Р>*0,05).
Окончательный вывод об информативности всего на¬
бора признаков можно сделать только после проверки
составленной диагностической таблицы на достаточно
большой проверочной группе наблюдений. Если число
ошибок окажется велико, можно в дальнейшем ис¬
ключить наименее информативные признаки. При
этом, как правило, число ошибок уменьшается, но
число неопределенных ответов возрастает.
Если численность наблюдений велика, а разница
между их числом в группах А и В достаточно мала,
можно применить для предварительного отбора ин¬
формативных признаков критерий Q (Розенбаума),
описанный в § 2.7. Этот критерий менее трудоемок,
особенно при большом числе наблюдений, чем крите¬
рий U. Однако он является и менее мощным, чем кри¬
терий U. Поэтому если критерий Q не выявил разли¬
чий, а на глаз они имеются, можно применить крите¬
рий U.
Этот последний критерий рассчитан на выявление
различий в средних тенденциях. Однако мы рекомен¬
дуем его применять для предварительного отбора
признаков и в том случае, когда значимых различий
75

в средних тенденциях нет, но есть основания предпо¬
лагать различия между группами Л и В в форме рас¬
пределений. Способ применения критерия U в этом
варианте описан в § 2.6.
Выбрав с помощью критерия U значимо разли¬
чающиеся признаки, необходимо разбить шкалу ото¬
бранных признаков на 8—12 диапазонов. Важно вы¬
бирать границы диапазонов по какому-то формаль¬
ному критерию без учета степени различий частостей
в выбранных диапазонах. В качестве такого критерия
можно избрать следующий: границами между диапа¬
зонами считать круглые числа, удобные для после¬
дующего использования таблицы.
Если число диапазонов составляет менее 8, происходит
слишком большая потеря информации при вычислении средне¬
взвешенных частостей (см. ниже), и информативность признака
существенно снижается; при числе диапазонов более 12, наоборот,
вычисление средневзвешенных частотей нередко не дает необхо¬
димого «сглаживания», т. е. устранения случайных колебаний ча¬
стостей в диапазонах, приводящих к завышению диагностических
коэффициентов. Более жестко ограничить рекомендуемое число
диапазонов также не представляется возможным, так как тогда
становится невыполнимой рекомендация выбирать в качестве их
границы круглое число. Вообще говоря, возможности выделения
большого числа диапазонов увеличиваются с увеличением числа
наблюдений в выборке, однако более 10—12 диапазонов выде¬
лять нецелесообразно, так как это делает громоздкой диагности¬
ческую таблицу и усложняет ее использование.
Для того, чтобы свести к минимуму влияние вы¬
бора границ диапазонов на результаты диагностики,
после вычисления частостей Р (х*/Л) и Pfxj/B) в каж¬
дом диапазоне определяют «средневзвешенные»
(сглаженные) частости методом вычисления взвешен¬
ной скользящей средней [21, 7]. При этом учитывают
частости данного признака в 4 соседних диапазонах.
Вычисление взвешенной скользящей средней можно
осуществлять по следующей формуле [20, 21]:
Уъ = {У\ +202 + 4г/з + 2г/4 + Уб):1О	, ig.
У4 = (У2 + %Уз + 404 + 2^6 + Уа) 110
И т. д.,
где yi—член выборки, ближайший к любому ее краю;
yz — второй от края член выборки; г/з — третий от
края и т. д.; у3 и уь — «средневзвешенный» или «сгла¬
женный» член выборки.
76

Иногда приведенную формулу для краткости на¬
зывают формулой «14-2 + 44-2+1», имея в виду,
что при вычислении взвешенной скользящей средней
частость в рассматриваемом диапазоне помножают на
коэффициент 4, в соседних диапазонах — на коэффи¬
циент 2, а в диапазонах через один от рассматривае¬
мого— на коэффициент 1. Полученные величины сум¬
мируют и делят на сумму использованных коэффи¬
циентов, равную 10.
Для вычисления в крайних диапазонах взвешен¬
ной скользящей средней у2 и у\ В. Ю. Урбах рекомен¬
дует пользоваться другими формулами:
У\ = $У\ + — Уг — Уь): 10	(4.14)
У2 = (Зг/1 + 5у2 + Уз + у4): 10	(4.15)
Однако мы убедились, что лучший результат дает
применение для вычисления средневзвешенных часто¬
стей в крайних диапазонах той же формулы (4.13).
Это становится возможным, если предположить, что
существуют диапазоны и за пределами крайних. Обо¬
значим их номерами 0, —1, —2, —3 и т. д. Поскольку
в них не попало ни одного наблюдения, частости в
этих диапазонах равны нулю:
У0 = г/_1 = г/_2 = 1/-з== ••• “О*
Тогда средневзвешенные частости уг и pi при вычи¬
слении их по формуле (4.13) равны:
Уч. — (0 4- 2г/, + 4t/2 4- 2г/3 + У а) • Ю	(4.16)
р1 = (0 + 0 + 4г/1 +2у2 + у3): 10	(4.17)
При использовании этого приема появляется необ¬
ходимость также вычислить средневзвешенные часто¬
сти уо и у-1 в диапазонах, расположенных за преде¬
лами крайних:
Уо = (0 + о + 0 + 2у{ 4- Уг) • 10	(4.18)
= (0 4- о + 0 + 0 + ух): 10	(4.19)
Если эти диапазоны не лишены смысла, следует
считать, что при увеличении числа наблюдений в них
действительно попало бы некоторое число членов вы-
оорки, Если же они реально невозможны (например,
77

если крайний диапазон представляет собой часовой
диурез, равный нулю, то диурез меньше нуля, т. е. вы¬
деление мочи с отрицательным знаком, иначе говоря,
ее обратное поступление в уретру, в природе не встре¬
чается), то средневзвешенные величины уи уо и у~i
следует суммировать, и полученную сумму yi-\-yo-\-
'+ У-i считать средневзвешенной частостью у\ дан¬
ного признака в крайнем диапазоне.
§ 4.4. ПРИМЕР ВЫЧИСЛЕНИЙ
Рассмотрим в качестве примера вычисление диаг¬
ностических коэффициентов и информативности при¬
знака при дифференциальной диагностике 2 форм
ожогов, одна из которых (форма А) является более
тяжелой (глубокий ожог более 20% поверхности
тела), другая — менее тяжелой (глубокий ожог не бо¬
лее 20% поверхности тела); общая площадь ожога в
обоих случаях одинакова. Произведем вычисления
для одного признака. В качестве признака исполь¬
зуем «Коэффициент пульс-температура» (/(пт), кото¬
рый характеризует превышение частоты пульса над
нормой, характерной для данной температуры, и вы¬
числяется по формуле:
/Спт = /7 — 10 (Г — 30),	(4.20)
где П — число ударов пульса в минуту, Т — темпера¬
тура тела в градусах. Согласно этой формуле за
норму условно считают для температуры тела 36°
пульс 60 ударов в минуту, для температуры 37° —
пульс 70 ударов и т. д.
Ниже представлен общий упорядоченный ряд это¬
го признака (табл. 4.3).
Оценим существенность различий распределений
А и В по критерию U. Число инверсий U представ¬
лено в табл. 4.3. Инверсия вычислялась для ряда В.
По табл. III приложения определяем, что при
Па = 33, пв = 29 сумма инверсий 306 позволяет счи¬
тать, что распределения А и В различаются с уровнем
существенности <; 0,01. Важно отметить, что в
этом примере наблюдаются различия в средних тен¬
денциях распределений.
78

ТАБЛИЦА 4.3
Общий упорядоченный ряд признака «Коэффициент
пульс — температура» в 900 3-го дня болезни
Продолжение ряда
Форма А
Форма В
форма А
форма В
—14
7
10
16
25
26
30
30
32
34
37
38
—5
10
13
16
17
17
22
23
25
25
26
27
30
30
33
34
34
36
37
10
10
11
11
11
38
38
40
42
46
47
50
52
52
52
52
53
53
54
55
56
60
73
80
88
п» = 33
38
40
43
43
45
45
50
63
72
пв = 29
14
15
17
17
17
17
20
30
30
2 = 306
В соответствии с описанной выше методикой для
рСгьективизации разбиения общего упорядоченного
79

ряда на диапазоны выбираем такие равные между со¬
бой диапазоны, правыми (нижними) границами кото¬
рых служат круглые числа с таким расчетом, чтобы
количество диапазонов составляло 8—12. Их гра¬
ницы видны в табл. 4.4 В табл. 4.3 границы этих же
диапазонов показаны пунктирными линиями.
ТАБЛИЦА 4.4
Пример вычисления диагностических коэффициентов
и информативности диапазонов
Распределение признака «Коэффициент пульс — температура»
в 900 3-го дня болезни
Диапазоны
Частоты
(число
наблю¬
дений)
Частости
(веро¬
ятности)
в %
Сглажен¬
ные
частости
в %
Отношение
сглаженных
частостей
(вероятн.)
Диагностиче¬
ские коэффи¬
циенты ДК
Информатив¬
ность I
номера
границы
А
в
А
В
А
В
— 1
1
со
со
1
1
со
о
0
0
0
0
0,3
0 ,

_
0
—29	20
0
0
0
0
0,6
0,3
2,0
+з
0
1
—19	10
1
0
3
0
2,1
1,3
1,6
+2
0,01
2
—9— 0
0
1
0
3
2,7
4,0
1 : 1,5
—2
0,02
3
1—10
3
2
9
7
6
9
1 : 1,5
—2
0,03
4
11—20
1
4
3
14
7
15
1 :2,1
-3
0,11
5
21—30
4
8
12
28
12
21
1 : 1,75
—2
0,07
6
31—40
7
7
21
24
16
20
1 : 1.25
— 1
0,02
7
41—50
4
5
12
17
16
15
1,1
0
—
8
51—60
10
0
30
0
18
7
2,6
+4
0,21
9
61—70
0
1
2
3
10
3,5
2,9
+5
0,17
10
71—80
2
1
6
3
6
1,8
3,3
+5
0,10
И
81—90
1
0
3
0
2,6
0,9
2,9
+5
0,05
12
91—100
0
0
0
0
1,2
0,3
4,0
+6
0,03
13
101-110
0
0
0
0
0,3
0
—
—
—
Всего. . .
33
29
101
99
100,9
99,1
0,82
В табл. 4.4 приведен пример дальнейших расче¬
тов, проводимых в соответствии с § 4.1, 4.2 и 4.3.
Сначала (см. табл. 4.3) подсчитывают число наб¬
людений из групп А к В, попавших в данный диапа¬
зон. Это — частоты данного признака (см. табл. 4.4).
Затем вычисляют относительные частости в процен-
80

тах, принимая за 100% сумму частостей А во всех
диапазонах и такую же сумму частостей В. Напри¬
мер, в диапазон № 3 попало 3 наблюдения группы А.
Это составляет 9% от общего числа наблюдений в
этой группе (их всего 33). В этот же диапазон попало
2	наблюдения группы В. Это составляет 7% всех наб¬
людений группы В (29). Далее вычисляют сглажен¬
ные (средневзвешенные) частости для большинства
диапазонов — по формуле (4.13), для крайних диапа¬
зонов № 1, 2, 10 и 11—по формулам (4.16) и (4.17)
и для диапазонов № 0, —1, 12 и 13, расположенных
за пределами крайних,— по формулам (4.18) и (4.19).
Фактически же вычисление всех сглаженных часто¬
стей ведется по формуле (4.13), но часть слагаемых
многочлена оказывается равной нулю (см. § 4.3).
Для упрощения дальнейших вычислений средне¬
взвешенные частости в процентах округляют с точ¬
ностью до 1, кроме частостей, величина которых мень¬
ше 5%. В этих случаях округляют с точностью до
первого знака после запятой.
Например, для диапазонов № —1, 0, 1, 2, 3 груп¬
пы А сглаженные (средневзвешенные) частости рав¬
ны (соответственно по формулам 4.19, 4.18, 4.17, 4.16,
4.13):
t/_, = (0 + 0 +0 + 0 +у,): 10 = 3:10 = 0,3
Уо = (0 + о + 0 + 2У1 + у2): Ю = (2. з + 0): 10 = 0,6
У\ = (0 + 0 + 4|/i + 2у2 + уз): 10 = (4 • 3 + 2 • 0 + 9): 10 = 2,1
Уг = (0 + 2ух + 4у2 + 2г/3 + У*) • Ю =
= (2 • 3 + 4 • 0 + 2 • 9 + 3): 10 = 2,7
Уз = (У1 + 2у2 + 4уз + 2 г/4 + Уъ): 10 =
= (3 + 2 • 0 + 4 • 9 + 2 • 3 + 12): 10 » 6.
Следующим этапом является вычисление отноше¬
ний сглаженных частостей Л и В в каждом диапазоне
(см. табл. 4.4) и сглаженных диагностических коэф¬
фициентов по формуле (4.12). Все полученные вели¬
чины диагностических коэффициентов округляют с
точностью до единицы. Вычисление отношений сгла¬
женных частостей и их логарифмов (диагностических
коэффициентов) удобно вести с помощью логарифми¬
ческой линейки, на которой нанесены мантиссы
81

логарифмов. Для облегчения этих вычислений можно
также предложить следующую таблицу (табл. 4.5).
ТАБЛИЦА 4.5
Диагностические коэффициенты при различной величине
отношения вероятностей
Величина отношения
вероятностей 1
У
Диагностический
коэффициент
(10 lg у)
У
ДК
(10 lg у)
1—1,12
0
8,92—11,2
10
1,13—1,41
1
11,3—14,1
11
1,42—1,77
2
14,2—17,7
12
1,78—2,23
3
17,8—22,3
13
2,24—2,81
4
22,4—28,1
14
2,82—3,54
5
28,2—35,4
15
3,55—4,46
6
35,5—44,6
16
4,47—5,61
7
44,7—56,1
17
5,62—7,07
8
56,2—70,7
18
7,08—8,91
9
70,8—89,1
19
89,2—112
20
1 При вычислении отношения вероятностей следует всегда
делить большее на меньшее. В таблице приведены данные для
случая, когда числитель больше знаменателя. Если знаменатель
больше числителя, то отношение вероятностей следует записать
в виде единицы, деленной на полученный результат, а соответ¬
ствующий этому результату диагностический коэффициент,
найденный по таблице, снабдить знаком «—». Например, если
отношение вероятностей равно 2, то ДК=3; если отношение
вероятностей равно 1:2, то ДК ■* — 3.
Информативность каждого диапазона находят по
сумме сглаженных вероятностей А и В в данном диа¬
пазоне и абсолютной величине диагностического ко¬
эффициента, используя табл. XI приложения. Она из¬
бавляет от каких-либо вычислений при нахождении
информативности диапазона. Информативность при¬
знака равна сумме информативностей его диапазонов.
Например, информативность диапазона № 4
(табл. 4.4) находим следующим образом. Сумма
сглаженных вероятностей (частостей) в этом диапа¬
зоне равна:
р(*;/л)+р(*;/в)-7+is-гг
гг

Диагностический коэффициент в этом диапазоне
равен
дк(*}) = _3.
Соответственно информативность рассматривае¬
мого диапазона по табл. XI (приложения) равна
/(*})■-0,11.
Информативность признака в целом, равная сумме
информативностей диапазонов
'(*i)-'W+'W)+'(*i)+ +'W2).
приведена в строке «Всего» табл. 4.4.
В итоговой диагностической таблице приводят
только границы диапазонов и величины диагностиче¬
ских коэффициентов. Полезно также указать инфор¬
мативность признаков. Признаки в таблице распола¬
гают в порядке убывающей информативности.
В качестве примера приводим фрагмент таблицы
для выявления глубокого ожога на площади более
20% поверхности тела на 2—3-й дни болезни
(табл. 4.6). Под таблицей указан способ ее примене¬
ния, описание которого соответствует формуле (4.8)
принятия решения при последовательной диагности¬
ческой процедуре.
Пример использования таблицы. Предположим, поступил
больной, у которого:
общая площадь ожога = 50% (ДК = +3),
процент палочкоядерных на 3-й день = 30% (ДК = 0),
артериальное давление максимальное на 2-й день = 80 мм
(ДК= + 6),
остаточный азот крови на 2-й день = 65 мг % (ДК — +6),
коэффициент пульс-температура на 3-й день = —10 (ДК = +2).
В качестве ошибки первого рода а, которую будем считать
допустимой у больных с заболеванием А, изберем 5%, в качестве
ошибки второго рода Р, допустимой у больных группы В, избе¬
рем 2%. По табл. XII приложения определяем:
Порог Л = + 17; Порог В = — 13.
При этих порогах среди диагнозов А должно быть не более
2% ошибочных, среди диагнозов В ошибок должно быть не бо¬
лее 5%.
83

ТАБЛИЦА 4.0
Выявление глубокого ожога на площади более 20%
поверхности тела на 2—3-й дни после ожога пламенем
(возраст больных 16—50 лет) 1
№
приз¬
нака
Признак
Величина
признака
Сглаженные
диагностиче¬
ские
коэффици¬
енты
Информа¬
тивность
1
Общая площадь
21—25
-10
1 о я
ожога в % поверх¬
26—30
—7
1 ~>°
ности тела
31—40
-4
0.28
41-50
+3
0,18
51—60
+9
0,67
61—70
+ 11
0,55
>70
+ 14
2,03
6,56
2
Процент палочко¬
0-5
-9
0,63
ядерных нейтрофи¬
6—10
-4
0,33
лов в лейкоформуле
11 — 15
— 1
0,02
на 3-й день
16—20
0
0
21-25
— 1
0
26-30
-3
0,08
31—35
0
0
36—40
+4
0,07
41—45
+7
0 26
>45
+9
0,39
1,78
3
Артериальное
<70
+8
0,46
давление макси¬
71—80
+6
0,23
мальное в мм рт. ст.
81—90
+3
0,10
в 900 на 2-й день
91 — 100
+ 1
0,02
101-110
—2
0,17
111-120
-5
0,36
>120
-7
0,30
1,64
4
Остаточный азот
21-30
—2
0,02
крови в мг % на
31—40
-3
0,26
2-й день
41—50
— 1
0,02
51—60
0
0
61-70
+6
0,38
>70
+9
0,84
1,52
1 Таблица приведена не полностью.
84

Продолжение
№
приз¬
нака
Признак
Величина
признака
Сглаженные
диагности¬
ческие
коэффици¬
енты
Информа¬
тивность
5
Изменение числа
-20	18
-6
0,20
лейкоцитов в тыс.
-17	15
—4
0,14
в 1 мм3 на 3-й день
-14	12
0
0
по сравнению со
-11	9
+3
0,09
вторым
—8	6
+4
031
-5	3
+2
0,08
-2-0
-1
0,02
1—3
—2
0,02
4-6
-2
0,02
0,88
6
/Спт ~ коэффици¬
—29	20
+3
0
ент пульс — темпе¬
— 19	10
+2
0,01
ратура (превышение
-9-+10
-2
0,05
числа ударов пульса
11 — 12
—3
0,11
над нормой для
21-30
—2
0 07
данной темпера¬
31-40
— 1
0,02
туры) в 900 на 3-й
41-50
0
0
день
51—60
+4
0,21
61—90
+5
0,32
91—100
+6
0,03
0,82
Способ применения таблицы'. Найти диагностические коэф¬
фициенты, соответствующие обнаруженным у больного величи¬
нам признаков, и суммировать их до получения итоговых сумм:
+ 10 (ответ: глубокий ожог больше 20% поверхности тела);
—	10 (ответ: глубокий ожог не больше 20% поверхности тела).
Если после суммирования диагностических коэффициентов всех
найденных признаков ни один из порогов не достигнут — ответ
неопределенный (имеющейся информации недостаточно для
дифференциальной диагностики с вероятностью ошибки не выше
10%).
85

Применим диагностическую таблицу 4.6 у поступившего боль*
ного. Сумма диагностических коэффициентов у него равна
3	+ 0 + 6 + 6 + 2=+17.
Порог +17 для принятия решения «Заболевание А-» достигнут.
Дальнейшее обследование больного для решения поставленного
вопроса с намеченным уровнем надежности можно не проводить.
Следует обратить внимание, что в обследовании признаков были
пропуски. Это не мешает применению таблицы, хотя увеличивает
возможность неопределенного ответа.
Для проверки (опробования) диагностической таб¬
лицы сначала используют тот материал, на котором
она была составлена, считая каждого больного за
вновь поступившего. Однако желательно также осу¬
ществить проверку на специальной проверочной груп¬
пе больных. По окончании проверки составляют таб¬
лицу результатов проверки (табл. 4.7).
T АБЛ И ЦА 4.7
Результаты проверки диагностической таблицы
Проверка с диагностическими порогами: Порог А = +10;
Порог В = —10 (а = Р=10%)
Группы
Число
больных
Ответы (в X)
правильные
ошибочные
неопределен¬
ные
Проверочная
59
81
12
7
Основная
68
81
7
12
Обе вместе
127
81
95
9,5
Различные варианты способов составления диаг¬
ностических таблиц, а также более подробные сведе¬
ния о методике их проверки представлены в ранее
опубликованной монографии Е. В. Гублера [11].

ПРИЛОЖЕНИЕ
(справочные таблицы)

ТАБЛИЦА I (к § 2.2)
Критерий знаков (КЗ)
Максимальное число знаков (менее часто встречающихся),
при которых различия в парных сравнениях можно считать су¬
щественными с Ркз = 0,05 или Якз = 0,01
п
Р
п
р
п
р
п
Р
0,05
0,01
0,05
0,01
0,05
0,01
0,05
0,01
5
0
27
8
7
49
18
15
90
36
33
6
0
—
28
8
7
50
18
16
92
37
34
7
0
0
29
9
7
52
19
17
94
38
35
8
1
0
30
10
8
54
20
18
96
39
36
9
1
0
31
10
8
56
21
18
98
40
37
10
1
0
32
10
8
58
22
19
100
41
37
11
2
1
33
11
9
60
23
20
110
45
42
12
2
1
34
11
9
62
24
21
120
50
46
13
3
1
35
12
10
64
24
22
130
55
51
14
3
2
36
12
10
66
25
23
140
59
55
15
3
2
37
13
10
68
26
23
150
64
60
16
4
2
38
13
11
70
27
24
160
69
64
17
4
3
39
13
И
72
28
25
170
73
69
18
5
3
40
14
12
74
29
26
180
78
73
19
5
4
41
14
12
76
30
27
190
83
78
20
5
4
42
15
13
78
31
28
200
87
83
21
6
4
43
15
13
80
32
29
220
97
92
22
6
5
44
16
13
82
33
30
240
106
101
23
7
5
45
16
14
84
33
30
260
116
110
24
7
5
46
16
14
86
34
31
280
125
120
25
7
6
47
17
15
88
35
32
300
135
129
26
8
6
48
17
15

ТАБЛИЦА II (к §2.3)
Критерий Т (парный критерий Вилкоксона)
Максимальные значения Т, при которых различия между
двумя группами можно считать значимыми с Рт = 0,01 и Рт = 0,05
п
Р
п
Р
п
Р
0,05
0,01
0,05
0,01
0,05
0,01
5
0
. _
11
13
7
17
41
28
6
2
0
12
17
10
18
47
33
7
3
0
13
21
12
19
53
38
8
5
1
14
25
16
20
60
42
9
8
3
15
30
19
10
10
5
16
35
23
Таблицы I и II приводятся по Owen (1962).

ТАБЛИЦА 111 (к § 2.4)
Критерий V (Вилкоксона — Манна — Уитни)
Максимальное число инверсий U, при котором различия
между группами наблюдений можно считать значимыми
с Рц = 0,05, Ри =0,01, Ри =0,005 и Ри =0,001.
Лист 1
Значения U для пи п2^20 (выше двойной черты) приведены
по Owen (1962).
90

Лист 1 (продолжение)
Таблица III (продолжение)
91

Л ист 2
Таблица III (продолжение)
92

Лист 2 (продолжение)
Таблица III (продолжение)
93

JI и с т 3
Таблица III (продолжение)
94

Лист 3 (продолжение)	Таблица III (продолжение)
95

Лист 4
Таблица III (продолжение)
96

Лист 4 (продолжение)	Таблица III (продолжение)
4 Е. В. Гублер, А. А. Генкин
97

Лист 5 (продолжение)
Таблица III (продолжение)
п,
Пг
13
н
15
16
17
18
19
20
21
22
23
24
Р = 0,05
25
108
118
128
137
147
157
167
177
187
197
207
217
26
ИЗ
123
133
143
154
164
174
185
195
206
216
226
27
118
128
139
150
160
171
182
193
203
214
225
236
28
122
133
144
156
167
178
189
200
212
223
234
245
29
127
139
150
162
173
185
196
208
220
232
243
255
30
132
144
156
168
180
192
204
216
228
240
252
265
31
137
149
161
174
186
199
211
224
236
249
261
274
32
141
154
167
180
193
206
219
232
245
258
271
284
33
146
159
173
186
199
213
226
239
253
266
280
293
34
151
164
178
192
206
219
233
247
261
275
289
303
35
156
170
184
198
212
226
241
255
269
284
298
312
36
160
175
189
204
219
233
248
263
278
292
307
322
II
о
о
25
86
95
103
112
121
130
138
147
156
165
174
183
26
90
99
108
117
126
136
145
154
163
173
182
191
27
94
103
113
122
132
142
151
161
171
180
190
200
28
98
108
118
128
138
148
158
168
178
188
198
208
29
102
112
123
133
143
154
164
175
185
196
206
217
30
106
117
127
138
149
160
171
182
192
203
214
225
31
110
121
132
143
155
166
177
188
200
211
223
234
32
114
126
137
149
160
172
184
195
207
219
231
242
33
118
130
142
154
166
178
190
202
214
227
239
251
34
122
134
147
159
172
184
197
209
222
234
247
260
35
126
139
152
164
177
190
203
216
229
242
255
268
36
130
143
156
170
183
196
210
223
236
250
263
277
98

Лист 5 (продолжение)
Таблица III (продолжение)
N. П,
Пг N.
13
14
15
16
17
18
19
20
21
22
23
25
78
86
94
103
Р =
111
3,005
119
128
136
145
153
162
26
82
90
99
108
116
125
134
143
152
161
169
27
85
94
103
112
122
131
140
149
159
168
177
28
89
98
108
117
127
137
146
156
166
175
185
29
93
103
112
122
132
142
152
162
172
183
193
30
97
107
117
127
138
148
158
169
179
190
200
31
100
111
122
132
143
-154
165
175
186
197
208
32
104
115
126
137
148
160
171
182
193
205
216
33
108
119
131
142
154
165
177
189
200
212
224
34
112
123
135
147
159
171
183
195
207
219
232
35
115
128
140
152
164
177
189
202
214
227
239
36
119
132
144
157
170
183
195
208
221
234
247
25
61
68
76
83
0 = С
91
),001
98
106
114
121
129
137
26
64
72
80
88
96
104
112
120
128
136
144
27
67
76
84
92
100
109
117
125
134
142
151
28
71
79
88
96
105
114
122
131
140
149
158
29
74
83
92
101
110
119
128
137
146
156
165
30
77
86
96
105
114
124
133
143
153
162
172
31
80
90
100
109
119
129
139
149
159
169
179
32
84
94
104
114
124
134
144
155
165
175
186
33
87
97
108
118
129
139
150
161
171
182
193
34
90
101
112
122
133
144
155
166
178
189
200
35
93
104
116
127
138
149
161
172
184
195
207
36
97
108
120
131
143
155
166
178
190
202
214
24
170
178
187
195
203
211
219
227
236
244
252
260
144
152
159
167
174
181
189
196
204
211
219
226
4*
99

Лист б
Таблица III (продолжение)
100

Лист б (продолжение)	Таблица III (продолжение)
101

Лист 7
Таблица III (продолжение)
Nv П.
п2
4
5
6
7
8
9
10
11
12
37
36
49
63
Р =
77
= 0,05
92
106
121
135
150
38
37
51
65
79
94
109
124
139
155
39
38
52
67
82
97
112
128
143
159
40
39
53
69
84
100
115
131
147
163
41
40
55
70
86
102
118
135
151
168
42
41
56
72
88
105
121
138
155
172
43
42
58
74
91
107
124
142
159
176
44
43
59
76
93
110
128
145
163
181
45
44
61
78
95
113
131
149
167
185
46
45
62
80
97
115
134
152
171
189
47
46
64
81
100
118
137
156
175
194
48
47
65
83
102
121
140
159
178
198
37
20
32
44
Р =
56
= 0,01
69
81
95
108
121
38
21
33
45
58
71
84
97
111
125
39
21
34
46
59
73
86
100
114
128
40
22
35
48
61
75
89
103
117
132
41
23
36
49
63
77
91
106
121
136
42
23
37
50
65
79
94
109
124
139
43
24
38
52
66
81
96
112
127
143
44
25
39
53
68
83
99
115
130
146
45
25
40
54
70
85
101
117
134
150
46
26
41
56
71
87
104
120
137
154
47
27
42
57
73
90
106
123
140
157
48
27
43
58
75
92
109
126
143
161
102

Л и с т 7 (продолжение)	Таблица III (продолжение)
103

Лист 8
Таблица III (продолжение)
Ns\w'
Пг
13
14
15
16
17
18
19
20
21
22
23
24
37
165
180
195
210
Р =
225
0,05
240
255
271
286
301
316
332
38
170
185
201
216
232
247
263
278
294
310
325
341
39
175
190
206
222
238
254
270
286
302
318
335
351
40
179
196
212
228
245
261
278
294
311
327
344
360
41
184
201
218
234
251
268
285
302
319
336
353
370
42
189
206
223
240
258
275
292
310
327
345
362
380
43
194
211
229
247
264
282
300
318
335
353
371
389
44
199
216
235
253
271
289
307
325
344
362
380
399
45
203
222
240
259
277
296
315
333
352
371
390
408
46
208
227
246
265
284
303
322
341
360
380
399
418
47
213
232
251
271
290
310
329
349
369
388
408
428
48
218
237
257
277
297
317
337
357
377
397
417
437
37
134
148
161
175
Р =
189
3,01
202
216
230
244
258
271
285
38
138
152
166
180
194
208
223
237
251
265
280
294
39
142
157
171
185
200
214
229
244
258
273
288
303
40
146
161
176
191
206
221
236
251
266
281
296
311
41
151
166
181
196
211
227
242
258
273
289
304
320
42
155
170
186
201
217
233
249
265
280
296
312
328
43
159
175
190
207
223
239
255
271
288
304
321
337
44
;бз
179
195
212
228
245
262
278
295
312
329
346
45
167
183
200
217
234
251
268
285
303
320
337
354
46
171
188
205
222
240
257
275
292
310
328
345
363
47
175
192
210
228
245
263
281
299
317
335
353
372
48
179
197
215
233
251
269
288
306
325
343
362
380
104

Лист 8 (продолжение)	Таблица III (продолжение)
«1
Пг N.
13
14
15
16
17
18
19
20
21
22
23
24
37
123
136
149
162
Р =
175
0,005
188
202
215
228
242
255
269
38
127
140
154
167
181
194
208
222
235
249
263
277
39
131
144
158
172
186
200
214
228
242
257
271
285
40
134
149
163
177
191
206
220
235
249
264
279
293
41
138
153
167
182
197
212
226
241
256
271
286
302
42
142
157
172
187
202
217
233
248
263
279
294
310
43
146
161
176
192
207
223
239
255
270
286
302
318
44
150
165
181
197
213
229
245
261
277
294
310
326
45
153
169
186
202
218
235
251
268
284
301
318
335
46
157
174
190
207
224
240
257
274
291
309
326
343
47
161
178
195
212
229
246
264
281
298
316
334
351
48
165
182
199
217
234
252
270
288
305
323
341
359
37
100
112
124
136
Р =
148
3,001
160
172
184
197
209
221
234
38
103
115
127
140
152
165
177
190
203
216
228
241
39
106
119
131
144
157
170
183
196
209
222
235
249
40
110
122
135
149
162
175
189
202
215
229
243
256
41
113
126
139
153
167
180
194
208
222
236
250
264
42
116
130
143
157
171
185
200
214
228
242
257
271
43
119
133
147
162
176
191
205
220
234
249
264
279
44
123
137
151
166
181
196
211
226
241
256
271
286
45
126
141
155
171
186
201
216
232
247
263
278
294
46
129
144
159
175
190
206
222
238
253
269
285
301
47
132
148
163
179
195
211
227
243
260
276
292
309
48
136
151
168
184
200
216
233
249
266
283
299
316
105

Лист 9
Таблица III (продолжение)
п,
пг
25
26
27
28
29
30
31
32
33
34
35
Р = 0,05
37
347
362
378
393
408
424
439
454
470
485
501
38
357
373
388
404
420
436
452
467
483
499
515
39
367
383
399
416
432
448
464
481
497
513
530
40
377
394
410
427
444
460
477
494
511
527
544
41
387
404
421
438
456
473
490
507
524
541
559
42
397
415
432
450
467
485
503
520
538
556
573
43
407
425
443
461
479
497
515
533
552
570
588
44
417
436
454
473
491
510
528
547
565
584
602
45
427
446
465
484
503
522
541
560
579
598
617
46
437
457
476
495
515
534
554
573
593
612
631
47
447
467
487
507
527
547
566
586
606
626
646
48
458
478
498
518
539
559
579
600
620
640
661
Р = 0,01
37
299
313
327
341
355
370
384
398
412
426
440
38
308
323
337
352
366
381
395
410
424
439
453
39
317
332
347
362
377
392
407
422
437
452
467
40
326
342
357
372
388
403
418
434
449
465
480
41
336
351
367
383
398
414
430
446
462
477
493
42
345
361
377
393
409
425
442
458
474
490
507
43
354
370
387
403
420
437
453
470
487
503
520
44
363
380
397
414
431
448
465
482
499
516
533
45
372
389
407
424
441
459
476
494
511
529
547
46
381
399
416
434
452
470
488
506
524
542
560
47
390
408
426
445
463
481
500
518
536
555
573
48
399
418
436
455
474
492
511
530
549
568
587
36
516
53!
546
561
576
591
606
621
636
651
666
681
454
468
482
495
509
523
537
550
564
578
592
606
106

Лист 9 (продолжение)	Таблица ИГ (продолжение)
N. П,
п,
25
26
27
28
29
30
31
32
33
34
35
36
37
282
295
309
323
Р =
336
0,005
350
363
377
391
404
418
432
38
291
305
319
332
346
360
374
389
403
417
431
445
39
299
314
328
342
357
371
386
400
415
429
444
458
40
308
323
337
352
367
382
397
412
427
442
456
471
41
317
332
347
362
377
393
408
423
439
454
469
485
42
325
341
357
372
388
403
419
435
451
466
482
498
43
334
350
366
382
398
414
430
447
463
479
495
511
44
343
359
376
392
409
425
442
458
475
491
508
525
45
351
368
385
402
419
436
453
470
487
504
521
538
46
360
377
395
412
429
447
464
481
499
516
534
551
47
369
386
404
422
440
457
475
493
511
529
547
565
48
377
396
414
432
450
468
486
505
523
541
560
578
37
246
259
271
284
Р = (
296
),001
309
322
334
347
360
372
385
38
254
267
280
293
306
319
332
345
358
371
384
397
39
262
275
289
302
315
329
342
356
369
383
396
410
40
270
284
297
311
325
339
352
366
380
394
408
422
41
278
292
306
320
334
349
363
377
391
406
420
434
42
286
300
315
329
344
358
373
388
402
417
432
447
43
294
308
323
338
353
368
383
399
414
429
444
459
44
301
317
332
347
363
378
394
409
425
440
456
471
45
309
325
341
357
372
388
404
420
436
452
468
484
46
317
333
350
366
382
398
414
431
447
463
480
496
47-
325
342
358
375
392
408
425
442
458
475
492
509
48
333
350
367
384
401
418
435
452
470
487
504
521
107

Лист 10
Таблица III (продолжение)
108

Лист 10 (продолжение)	Таблица III (продолжение)
109

Лист 11
Т а б л и ц а III (продолжение)
'\чп,
Пг
4
5
6
7
8
9
ю
п
12
49
48
66
85
Р =
104
= 0,05
123
143
163
182
202
50
49
68
87
106
126
146
166
186
207
51
50
69
89
109
129
149
170
190
211
52
51
71
91
111
131
152
173
194
215
53
52
72
92
113
134
155
177
198
220
54
53
74
94
115
137
158
180
202
224
55
54
75
96
118
139
161
184
206
228
56
55
76
98
120
142
164
187
210
233
57
57
78
100
122
145
167
191
214
237
58
58
79
102
124
147
171
194
218
241
59
59
81
103
127
150
174
198
222
246
60
60
82
105
129
153
177
201
225
250
49
28
44
60
Р
77
= 0,01
94
111
129
147
165
50
29
45
61
78
96
114
132
150
168
51
29
46
63
80
98
116
135
153
172
52
30
47
64
82
100
119
137
157
176
53
31
48
65
83
102
121
140
160
179
54
31
49
67
85
104
114
143
163
183
55
32
50
68
87
106
126
146
166
187
56
33
51
69
89
108
129
149
177
190
57
33
52
71
90
110
131
152
173
194
58
34
53
72
92
113
133
155
176
198
59
34
54
73
94
115
136
158
179
201
60
35
55
75
96
117
138
160
183
205
110

Лист 11 (продолжение)
Таблица III (продолжение)
111

Лист 12
Таблица III (продолжение)
til
Пг
13
14
15
16
17
18
19
20
21
22
23
24
Р =
0,05
49
222
243
263
283
303
324
344
365
385
406
426
447
50
227
248
268
289
310
331
352
372
393
414
435
457
51
232
253
274
295
316
338
359
380
402
423
445
466
52
237
258
280
301
323
345
366
388
410
432
454
476
53
241
263
285
377
329
352
374
396
418
441
463
485
54
246
269
291
313
336
359
381
404
427
449
472
495
55
251
274
297
319
342
365
389
412
435
458
481
505
56
256
279
302
326
349
372
396
420
443
467
491
514
57
261
284
308
332
355
379
403
427
451
476
500
524
58
265
289
314
338
362
386
411
435
460
484
509
534
59
270
295
319
344
369
393
418
443
468
493
518
543
60
275
300
325
350
375
Р =
400
0,01
426
451
476
502
527
553
49
183
201
220
238
257
276
294
313
332
351
370
389
50
187
206
225
244
263
282
301
320
339
359
378
398
51
191
210
229
249
268
288
307
327
347
366
386
406
52
195
215
234
254
274
294
314
334
354
374
395
415
53
199
219
239
259
280
300
320
341
361
382
403
423
54
203
224
244
265
285
306
327
348
369
390
411
432
55
207
228
249
270
291
312
333
355
376
398
419
441
56
211
233
254
275
297
318
340
362
384
405
427
449
57
215
237
259
281
302
324
347
369
391
413
436
458
58
220
242
264
286
308
331
353
376
398
421
444
467
59
224
246
268
291
314
337
360
383
406
429
452
475
60
228
250
273
296
320
343
366
390
413
437
460
484
112

Лист 12 (продолжение)
Таблица III (продолжение)
Nv «1
Я*\ч
13
14
15
16
17
18
19
20
21
22
23
24
49
169
186
204
222
Р =
240
0,005
258
276
294
313
331
349
368
50
172
190
209
227
245
264
282
301
320
338
357
376
51
176
195
213
232
251
270
288
307
327
346
365
384
52
180
199
218
237
256
275
295
314
334
353
373
392
53
184
203
222
242
261
281
301
321
341
361
381
401
54
188
207
227
247
267
287
307
327
348
368
389
409
55
191
211
232
252
272
293
313
334
355
376
396
417
56
195
216
236
257
278
299
320
341
362
383
404
426
57
199
220
241
262
283
304
326
347
369
390
412
434
58
203
224
245
267
288
310
332
354
376
398
420
442
59
207
228
250
272
294
316
338
361
383
405
428
451
60
210
232
255
277
299
322
344
367
390
413
436
459
49
139
155
172
188
Р = (
205
3,001
222
238
255
272
289
307
324
50
142
159
176
192
210
227
244
261
279
296
314
331
51
145
162
180
197
214
232
250
267
285
303
321
339
52
149
166
184
201
219
237
255
273
291
310
328
346
53
152
170
188
206
224
242
261
279
298
316
335
354
54
155
173
192
210
229
247
266
285
304
323
342
362
55
158
177
196
214
233
253
272
291
310
330
349
369
56
162
181
200
219
238
258
277
297
317
337
357
377
57
165
184
204
223
243
263
283
303
323
343
364
384
58
168
188
208
228
248
268
288
309
330
350
371
392
59
171
191
212
232
253
273
294
315
336
357
378
399
60
175
195
216
236
257
278
300
321
342
364
385
407
5 Е. В. Гублер, А. А, Генкин
113

Лист 13
Таблица III (продолжение)
tl\
пг
25
26
27
28
29
30
31
32
33
34
35
49
468
488
509
530
§ II
3,05
571
592
613
634
654
675
Е0
478
499
520
541
562
583
605
626
647
669
690
51
488
509
531
553
574
596
618
639
661
683
704
52
498
520
542
564
586
608
630
652
675
697
719
53
508
530
553
575
598
620
643
666
688
711
734
54
518
541
564
587
610
633
656
679
702
725
748
55
528
551
575
598
622
645
669
692
716
739
763
56
538
562
586
610
634
657
681
705
729
753
777
57
548
572
597
621
645
670
694
719
743
768
792
58
558
583
608
633
657
682
707
732
757
782
807
59
568
594
619
644
669
694
720
745
770
796
821
60
578
604
630
655
681
707
733
758
784
810
836
49
408
427
446
465
° = (
484
),01
504
523
542
561
581
600
50
417
437
456
476
495
515
535
554
574
594
613
51
426
446
466
486
506
526
546
566
587
607
627
52
435
456
476
496
517
537
558
578
599
620
640
53
444
465
48В
507
528
549
570
591
612
633
654
54
453
475
496
517
538
560
581
603
624
646
667
55
462
484
506
527
549
571
593
615
637
659
680
56
471
494
516
538
560
582
605
627
649
671
694
57
481
503
526
548
571
593
616
639
662
684
707
58
490
513
536
559
582
605
628
651
674
697
721
59
499
522
545
569
592
616
640
663
687
710
734
60
508
532
555
579
603
627
651
675
699
723
747
36
С98
711
726
741
756
771
786
801
816
832
847
862
619
633
647
661
675
689
702
716
730
744
758
772
114

Лист 13 (продолжение)	Таблица III (продолжение)
N. Л,
П2 N.
25
26
27
28
29
30
31
•42
33
34
35
36
49
386
405
423
442
Р =
460
0,005
479
498
516
535
554
573
591
50
395
414
433
452
471
490
509
528
547
566
586
605
51
404
423
442
462
481
501
520
540
559
579
598
618
52
412
432
452
472
492
511
531
551
571
591
611
631
53
421
441
461
482
502
522
543
563
583
604
624
645
54
430
450
471
492
512
533
554
575
596
616
637
658
55
438
459
480
502
523
544
565
585
608
629
650
672
56
447
469
490
512
533
555
576
598
620
641
663
685
57
456
478
500
522
544
566
588
610
632
654
676
698
58
464
487
509
532
554
576
599
621
644
667
689
712
59
473
496
519
541
564
587
610
633
656
679
702
725
60
482
505
528
551
575
598
621
645
668
692
715
739
49
341
358
376
393
° = (
411
),001
428
446
463
481
498
516
534
50
349
367
385
402
420
438
456
474
492
510
528
546
51
357
375
393
411
430
448
466
485
503
522
540
558
52
365
383
402
421
439
458
477
496
514
533
552
571
53
373
392
411
430
449
468
487
506
526
545
564
583
54
381
400
420
439
458
478
498
517
537
556
576
596
55
389
409
428
448
468
488
508
528
548
588
588
608
56
397
417
437
457
478
498
518
539
559
580
600
621
57
405
425
446
467
487
508
629
550
570
591
612
633
58
413
434
455
476
497
518
539
560
582
603
624
646
59
421
442
463
485
506
528
550
571
593
615
635
658
60
429
450
472
494
516
538
560
582
604
626
648
671
б*
115

Лист 14
Таблица III (продолжение)
'Ч4. «1
Пг \
37
38
39
40
41
42
43
44
45
46
47
48
Р =
0,05
49
717
738
759
780
800
821
842
863
884
905
926
947
50
732
754
775
796
818
839
861
882
903
925
946
968
51
748
770
791
813
835
857
879
901
922
944
966
988
52
763
786
808
830
852
875
897
919
942
964
986
1009
53
779
802
824
847
870
893
915
938
961
934
1006
1029
54
794
818
841
864
887
910
934
957
980
1003
1026
1050
55
810
834
857
881
904
928
952
975
999
1023
1046
1070
$6
825
850
874
898
922
946
970
994
1018
1042
1067
1091
57
841
865
890
915
939
964
988
1013
1037
1062
1087
1111
58
856
881
906
931
956
981
1007
1032
1057
1082
1107
1132
59
872
897
923
948
974
999
1025
1050
1076
1101
1127
1152
60
888
913
939
965
991
1017
1043
1069
1095
1121
1147
1173
Р =
0,01
49
639
658
678
697
716
736
755
775
794
814
833
853
50
653
673
693
713
732
752
772
792
812
832
852
872
51
667
688
708
728
748
769
789
809
830
850
870
891
52
682
702
723
744
764
785
806
827
847
868
889
910
53
696
717
738
759
780
802
823
844
865
886
908
929
54
710
732
753
775
796
818
840
861
883
905
926
948
55
724
746
768
790
812
834
857
879
901
923
945
967
56
739
761
784
806
828
851
873
896
919
941
964
£86
57
753
776
799
822
844
867
890
913
936
959
982
1005
58
767
790
814
837
861
884
907
931
954
978
1001
1024
59
781
805
829
853
877
900
924
948
972
996
1020
1044
60
796
820
844
868
893
917
941
965
990
1014
1038
юзз
116

Лист 14 (продолжение)
Таблица ИГ (продолжение)
N. га,
rtj \
37
38
39
40
41
42
43
44
45
46
47
Р = 0,005
49
610
629
648
667
686
704
723
742
761
780
799
50
624
643
662
682
701
720
740
759
778
798
817
51
638
657
677
697
717
736
756
776
796
815
835
52
652
672
692
712
732
752
772
793
813
833
853
53
665
686
706
727
748
768
789
810
830
851
872
54
679
700
721
742
763
784
805
826
847
869
890
55
693
714
736
757
779
800
822
843
865
886
908
56
707
729
751
772
794
816
838
860
882
904
926
57
721
743
765
788
810
832
855
877
899
922
944
58
735
757
780
803
825
848
871
894
917
939
962
59
748
771
795
818
841
864
887
911
934
957
980
60
762
786
809
833
857
880
904
928
951
975
999
Р =
3,001
49
551
569
587
604
622
640
658
675
693
711
729
50
564
582
600
618
637
655
673
691
709
728
746
51
577
595
6Н
633
651
670
688
707
726
744
763
52
590
609
628
647
666
685
704
723
742
761
780
53
603
622
641
661
680
700
719
739
758
778
797
54
616
635
655
675
695
715
734
754
774
794
814
55
628
649
669
689
709
730
750
770
790
811
831
56
641
662
683
703
724
745
765
786
807
827
848
57
654
675
696
717
738
760
781
802
823
844
865
58
667
689
710
731
753
775
796
818
839
861
882
59
680
702
724
746
768
790
811
833
855
878
900
60
693
715
737
760
782
805
827
849
872
894
917
48
818
837
855
874
892
911
929
948
967
985
1004
1022
747
764
782
799
817
834
852
869
887
904
922
939
117

Лист 15
Таблица III (продолжение)
118

Лист 15 (продолжение)
Таблица III (продолжение)
119

ТАБЛИЦА IV (к § 2.7)
Критерий Q (Розенбаума)
Минимальные значения Q, при которых различия между
двумя группами наблюдений можно считать
значимыми с Pq = 0,01 и Pq = 0,05
П|
nt
11 12 13 14
15 16 17 18
19 20 21 22
23 24 25 26
Р = 0,05
11
6
12
6
6
13
6
6
6
14
7
7
6
6
15
7
7
6
6
6
16
8
7
7
7
6
6
17
7
7
7
7
7
7
7
18
7
7
7
7
7
7
7
7
19
7
7
7
7
7
7
7
7
7
20
7
7
7
7
7
7
7
7
7 7
21
8
7
7
7
7
7
7
7
7 7 7
22
8
7
7
7
7
7
7
7
7 7 7 7
23
8
8
7
7
7
7
7
7
7 7 7 7
24
8
8
8
8
8
8
8
8
8 8 7 7
25
8
8
8
8
8
8
8
8
8 7 7 7
26
8
8
8
8
8
8
8
8
8 8 7 7
Я = 0,01
11
9
12
9
3
13
9
9
9
14
9
9
9
9
15
9
9
9
9
9
16
9
9
9
9
9
9
17
10
9
9
9
9
9
9
18
10
10
9
9
9
9
9
9
19
10
10
10
9
9
9
9
9
9
20
10
10
10
10
9
9
9
9
9 9
21
11
10
10
10
9
9
9
9
9 9 9
22
11
11
10
10
10
9
9
9
9 9 9 9
23
11
11
10
10
10
10
9
9
9 9 9 9
9
24
12
11
11
10
10
10
10
9
9 9 9 9
9
25
12
11
11
10
10
10
10
10
9 9 9 9
9
26
12
12
11
11
10
10
10
10
10 9 9 9
9
Таблица IV приводится по Sidak, Vondrocek (1957).
120

ТАБЛИЦА V (к § 2.11)
Точный метол Фишера (ТМФ)
Число однонаправленных эффектов (признаков) в первой
и второй выборках, при котором различия между ними можно
считать существенными
Способ применения. В таблице приведены лишь минималь¬
ные существенные различия в числе однонаправленных эффектов
(при Ртмф = 0,025). При более значительных различиях — Ртмф
меньше 0,025.
ni — общее число наблюдений в первой группе; п2 — число
наблюдений во второй (контрольной) группе. На основном поле
таблицы — число наблюдений, где есть ожидаемый эффект в пер¬
вой (основной) группе. Слева в графе К — число наблюдений,
где есть тот же эффект во второй (контрольной) группе.
Таблица V представляет собой модификацию таблиц В. С.
Генеса (1964), основанных на точном методе Фишера для че¬
тырехпольной таблицы
121

Продолжение табл. V
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
6
0
—
—
4
4
5
5
6
6
7 7 7
7
8
9
9
10
10
11
11
1
—
—
4
5
6
6
7
8
8 9 10
10
11
12
12
13
14
14
15
2
7
8
9
10 И 11
12
13
14
15
15
16
17
18
3
	12
13
14
15
16
17
18
19 20
7
0
—
3
3
4
4
5
5
6
6 7 7
7
7
8
9
9
9
10
10
1
—
—
4
5
5
6
7
7
8 8 9
10
10
11
11
12
13
13
14
2
—
—
—
—
6
7
8
8
9 10 11
11
11
13
14
14
15
16
16
3
9
10 11 12
13
13
14
15
16
17
18
18
4
14
15
16
17
18
19 20
8
0
2
3
3
4
4
5
5
5
6 6 6
7
7
8
8
8
9
9
9
1
—
3
4
5
5
6
6
7
7 8 8
9
9
10
11
11
12
12
13
2
—
—
—
5
6
7
7
8
9 9 10
11
11
12
13
13
14
15
15
3
-
—
—
—
—
7
8
9
10 10 И
12
12
13
14
15
16
17
17
4
10 11 12
13
13
15
16
16
17
18
19
5
17
18
19 20
9
0
2
3
3
3
4
4
5
5
5 6 6
6
7
7
7
8
8
8
9
1
-
3
4
4
5
5
6
6
7 7 8
8
9
9
10
10
11
11
12
2
—
—
4
5
6
6
7
8
8 9 9
10
11
11
12
13
13
14
14
3
—
—
—
-
6
7
8
8
9 10 11
11
12
13
14
14
15
16
16
4
8
9
10 11 12
12
13
14
15
16
16
17
18
5
	12
13
14
15
16
17
18
19
19
6
20
10
0
2
3
3
3
4
4
4
5
5 5 6
6
6
7
7
7
8
8
8
1
—
3
4
4
5
5
6
6
7 7 8
8
8
9
9
10
10
11
11
122

Продолжение табл. V
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2
1
—
4
5
5
6
7
7
8 8 9
10
10
11
11
12
12
13
14
10
3
—
—
—
5
6
7
7
8
9 9 10
11
11
12
13
13
14
15
15
4
—
—
—
—
—
7
8
9
10 Ю 11
12
13
13
14
15
16
16
17
5
9
10 11 12
13
14
14
15
16
17
18
19
6
13
14
15
16
17
18
19
20
11
0
2
3
3
3
4
4
4
5
5 5 5
6
6
6
7
7
7
7
8
1
—
3
4
4
5
5
5
6
6 7 7
8
8
8
9
9
10
10
11
2
—
—
4
5
5
6
6
7
7 8 9
9
10
10
11
11
12
12
13
3
—
—
—
5
6
6
7
8
8 9 10.
10
11
12
12
13
13
14
15
4
—
—
—
—
6
7
7
8
9 10 11
11
12
13
13
14
15
16
16
5
—
—
—
—
—
—
—
9
10 11 11
12
13
14
15
15
16
17
18
6
—
—
—
—
—
—
—
—
10 11 12
13
14
15
16
16
17
18
19
7
15
16
17
18
19 20
12
0
2
3
3
3
3
4
4
4
5 5 5
5
6
6
6
7
7
7
7
1
—
3
4
4
4
5
5
6
6 6 7
7
8
8
8
9
9
10
10
2
—
3
4
5
5
6
6
7
7 8 8
9
9
10
10
11
11
12
12
3
—
—
4
5
6
6
7
7
8 9 9
10
10
11
12
12
13
13
14
4
—
-
—
5
6
7
7
8
9 10 10
11
12
12
13
14
14
15
16
5
—
—
-
—
6
7
8
9
10 10 11
12
13
13
14
15
15
16
17
6
—
—
-
—
—
—
8
9
10 11 12
13
13
14
15
16
17
17
18
7
13
14
15
16
17
18
18
19
8
16
17
18
19
20
13
0
2
2
3
3
3
4
4
4
4 5 5
5
5
6
6
6
7
7
7
1
—
3
3
4
4
5
5
5
6 6 7
7
7
8
8
8
9
9
10
2
—
3
4
4
5
5
6
6
7 7 8
8
9
9
10
10
11
11
12
123

Продолжение табл. V
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
3
—
—
4
5
5
6
7
7
8
8
9
9
10
11
11
12
12
13
13
4
—
—
—
5
6
7
7
8
9
9 10
10
11
12
12
13
14
14
15
5
—
—
—
—
6
7
8
8
9 10 И
11
12
13
13
14
15
16
16
6
—
—
—
—
6
7
8
9
10 11 11
12
13
14
14
15
16
17
17
7
9
10 11 12
13
14
14
15
16
17
18
19
8
12
13
14
15
16
17
18
19
19
9
18
19 20
0
2 2
3
3
3
4
4
4
4
5
5
5
5
6
6
6
6
6
7
1
2
3
3
4
4
4
5
5
6
6
6
7
7
7
8
8
8
9
9
2
—
3
4
4
5
5
6
6
7
7
8
8
8
9
9
10
10
11
11
3
—
—
4
5
5
6
6
7
7
8
9
9
10
10
11
11
12
12
13
4
—
—
—
5
6
6
7
8
8
9
9
10
11
11
12
13
13
14
14
5
—
—
—
5
6
7
8
8
9 10 Ю
11
12
12
13
14
14
15
16
6
—
—
-
—
6
7
8
9
9 10 11
12
12
13
14
15
15
16
17
7
—
—
—
—
—
—
8
9
10 11 12
12
13
14
15
16
16
17
18
8
10 11 12
13
14
15
16
16
17
18
19
9
13
14
15
16
17
18
19 20
10
19 20
0
2
2
3
3
3
3
4
4
4
4
5
5
5
5
6
6
6
6
6
1
2
3
3
4
4
4
5
5
5
6
6
6
7
7
7
8
8
8
9
2
—
3
4
4
5
5
5
6
6
7
7
8
8
8
9
9
10
10
11
3
—
3
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
4
—
—
4
5
6
6
7
7
8
9
9
10
10
11
11
12
13
13
14
5
—
—
—
5
6
7
7
8
9
9 10
11
11
12
12
13
14
14
15
6
—
—
—
—
6
7
8
8
9 10 11
11
12
13
13
14
15
15
16
124

Продолжение табл. V
2 3 4 5 6 7 8 9 10 И 12 13 14 15 16 17 18 19 20
7
7
8
9
10 10 И
12
13
13
14
15
16
16
1Г
8
9
10 11 12
13
13
14
15
16
17
17
18
9
11 12
13
14
15
16
17
17
18
19
10
15
16
17
18
19 20
0
2
2
3
3
3
3
4
4
4
4 4
5
5
5
5
6
6
6
6
1
2
3'
3
4
4
4
5
5
5
6 6
6
7
7
7
7
8
8
8
2
—
3
4
4
5
5
5
6
6
7 7
7
8
8
9
9
9
10
10
3
—
3
4
4
5
6
6
7
7
7 8
8
9
9
10
10
11
11
12
4
—
—
4
5
5
6
7
7
8
8 9
9
10
10
11
12
12
13
13
5
—
—
—
5
6
6
7
8
8
9 10
10
11
11
12
13
13
14
14
6
—
—
—
5
6
7
8
8
9 10 10
11
12
12
13
14
14
15
16
7
—
—
—
—
6
7
8
9
9 10 11
12
12
13
14
15
15
16
17
8
—
—
—
—
—
—
8
9
10 11 11
12
13
14
15
15
16
17
18
9
—
—
—
—
—
—
—
9
10 11 12
13
14
14
15
16
17
18
19
10
- 12
13
14
15
16
17
18
18
19
11
16
17
18
19 20
125

ТАБЛИЦА VI (к § 2.9)
Серийный критерий г (Вальда — Вольфовица)
Максимальные значения г (для серийного критерия Валь¬
да — Вольфовица), при которых различия в форме распределе¬
ний существенны (Рг ^ 0,025)
Таблица VI приводится по Siegel (1956).
ТАБЛИЦА VII (к § 3.1)
Ранговая корреляция
Минимальные значения коэффициентов ранговой корреляции,
при которых связь между двумя рядами наблюдений можно
считать значимой с надежностью Р, когда 4 ^ п ^ 10; п — число
пар сравниваемых наблюдений
р
п
0,05
0,025
0,01
0,005
0,001
4
1,000
5
0,900
1,000
1,000
1,000
6
0,771
0,828
0,886
0,942
1,000
7
0,678
0,768
0,836
0,893
0,964
8
0,643
0,714
0,786
0,857
0,928
9
0,633
0,700
0,767
0,833
0,900
10
0,564
0,685
0,746
0,806
0,867
Примечание: Эта таблица вычислена на основании таблиц
Л. Н. Большева и Н. В. Смирнова (1965).
Если число пар больше 10, критические значения коэффициента ранго¬
вой корреляции б\дут совпадать с вполне приемлемой точностью с крити¬
ческими значениями обычной нормальной корреляции (см. табл. VIII),
126

ТАБЛИЦА VIII (к § 3.1)
Нормальная корреляция
Минимальные значения коэффициентов нормальной корре¬
ляции, при которых связь между двумя рядами наблюдений
можно считать значимой с уровнем надежности Р\ п — число
пар сравниваемых наблюдений
р
п \
0,05
0,025
0,01
0,005
0,0025
0,0003
4
0,729
0,811
0,882
0,917
0,941
0,974
5
0,669
0,754
0,833
0,875
0,905
0,950
6
0,621
0,707
0,789
0,834
0,870
0,924
7
0,582
0,666
0,750
0,798
0,836
0,898
8
0,549
0,632
0,715
0,765
0,805
0,872
9
0,521
0,602
0,685
0,735
0,776
0,847
10
0,497
0,576
0,658
0,708
0,750
0,823
11
0,476
0,553
0,634
0,684
0,726
0,801
12
0,457
0,532
0,612
0,661
0,703
0,780
13
0,441
0,514
0,592
0,641
0,683
0,760
14
0,426
0,497
0,574
0,623
0,664
0,742
15
0,412
0,482
0,558
0,606
0,647
0,725
16
0,400
0,468
0,543
0,590
0,631
0,708
117
0,389
0,456
0,529
0,575
0,616
0,693
118
0,378
0,444
0,516
0,561
0,602
0,679
19
0,369
0,433
0,503
0,549
0,589
0,665
20
0,360
0,423
0,492
0,537
0,576
0,652
25
0,323
0,381
0,445
0,487
0,524
0,597
30
0,296
0,349
0,409
0,449
0,484
0,554
35
0,275
0,325
0,381
0,418
0,452
0,519
40
0,257
0,304
0,358
0,393
0,425
0,490
45
0,243
0,288
0,338
0,372
0,403
0,465
50
0,231
0,273
0,322
0,354
0,384
0,443
60
0,211
0,250
0,295
0,325
0,352
0,408
70
0,195
0,232
0,274
0,302
0,327
0,380
80
0,183
0,217
0,257
0,283
0,307
0,357
90
0,173
0,205
0,242
0,267
0,290
0,338
100
0,164
0,195
0,230
0,254
0,276
0,321
Таблицы VIII, IX и X
и Н. В. Смирнову (1965).
приводятся по Л. Н. Большеву
127

1
2
3
4
05
6
7
8
9
,10
1
2
3
4
Д5
6
7
8
9
Преобразование Фишера
(на поле таблицы — величина г)
ТАБЛИЦА
ООО
002
004
006
008
000
002
004
006
008
,000
,002
,004
,006
,008
,549
,552
,554
,557
,560
,010
,012
,014
,016
,018
,562
,565
,568
,570
,573
,020
,022
,024
,026
,028
,576
,579
,581
,584
,587
,030
,032
,034
,036
,038
,590
,592
,597
,598
,601
,040
,042
,044
,046
,048
,604
,607
,609
,612
,615
,050
,052
,054
,056
,058
,618
,621
,624
,627
,629
,060
,062
,064
,066
,068
,632
,635
,638
,641
,644
,070
,072
,074
,076
,078
,647
,650
,653
,656
,659
,080
,082
,084
,086
,088
,662
,665
,668
,671
,674
,090
,092
,094
,096
,097
,677
,680
,683
,686
,690
,100
,102
,104
,106
,108
,693
,696
,699
,702
,705
,110
,112
,114
,116
,118
,708
,712
,715
,718
,721
,120
,122
,124
,126
,128
,725
,728
,731
,734
,738
,130
,132
,134
,136
,138
,741
,744
,748
,751
,754
,140
,143
,145
,147
,149
,758
,761
,765
,768
,771
,151
,153
,155
,157
,159
,775
,778
,782
,785
,789
,161
,163
,165
,167
,169
,792
,796
,799
,803
,807
,171
,173
,175
,177
,179
,810
,814
,818
,821
,825
,182
,184
,186
,188
,190
,829
,832
,836
,840
,844
,192
,194
196
,198
,200
,848
,851
,855
,859
,863

.20
,202
,204
,206
,209
,211
1
,213
,215
,217
,219
,221
2
,223
,225
.227
,230
,232
3
,234
,236
,238
,240
,242
4
,244
,246
,249
,251
,253
,25
,255
,257
,259
,261
,264
6
,266
,268
,270
,272
,274
7
,276
,279
,281
,283
,285
8
.287
,289
,292
,294
,296
9
,298
,300
,302
,305
,307
,30
,309
,311
,313
,316
,318
1
,320
,322
,325
,327
,329
2
,331
,333
,336
,338
,340
3
,342
,345
347
,349
,351
4
,354
,356
,358
,360
,363
,35
,365
,367
,370
,372
,374
6
,376
,379
,381
,383
,386
7
,388
,390
,393
,395
,397
8
,400
,402
,404
,407
,409
9
,401
,414
,416
,418
,421
,40
,423
,426
,428
,430
,433
1
,435
,438
,440
,442
,445
2
,447
,450
,452
,455
,457
3
,459
,462
,464
,467
,469
4
,472
,474
,477
,479
,482
,45
,484
,487
,487
,492
,494
6
,497
,499
,502
,504
,507
7
,510
,512
515
,517
,520
8
,523
,525
,528
,530
,533
9
,536
,538
,541
,544
,546
to
4£>
,867
,871
,875
,879
,883
,887
,891
,895
,899
,903
,907
,911
,916
,920
,924
,928
,933
,933
,941
,946
,9505
,9549
,9594
,9639
,9684
0,973
0,978
0,982
0,987
0,991
0,996
1,001
1,006
1,011
1,015
1,020
1,025
1,030
1,035
1,040
1,045
1,050
1,056
1,061
1,066
1,071
1,077
1,082
1,088
1,093
1,099
1,104
1,110
1,116
1,121
1,127
1,133
1,139
1,145
1,151
1,157
1,163
1,169
1,175
1,182
1,188
1,195
1,201
1,208
1,214
1,221
1,228
1,235
1,242
1,249
1,256
1,263
1,271
1,278
1,286
1,293
1,301
1,309
1,317
1,325
1,333
1,341
1,350
1,358
1,367
1,376
1,385
1,394
1,403
1,412
1,422
1,432
1,442
1,452
1,462
1,472
1,483
1,494
1,505
1,516
1,528
1,539
1,551
1,564
1,576
1,589
1,602
1,616
1,630
1,644
1,658
1,673
1,689
1,705
1,721
1,738
1,756
1,774
1,792
1,812
1,832
1,853
1,874
1,897
1,921
1,946
1,972
2,000
2,029
2,060
2,092
2,127
2,165
2,205
2,249
2,298
2,351
2,410
2,477
2,555
2,647
2,759
2,903
3,106
3,453
,70
1
2
3
4
,75
6
7
8
9
,80
1
2
3
4
,85
6
7
8
9
,90
1
2.
3
4
,95
6
7
8
9

ТАБЛИЦА X (к§ 3.2)
Критерий X2
Значение предельных величин %2 в зависимости от уровня
значимости и числа К. степеней свободы
Число
степеней
свободы
К
Уровень значимости
0,20
0,10
0,05
0,02
0,01
0,005
0,001
1
1,64
2,7
3,8
5,4
6,6
7,9
10,8
2
3,22
4,6
6,0
7,8
9,2
11,6
13,8
3
4,64
6,3
7,8
9,8
11,3
12,8
16,3
4
6,0
7,8
9,5
11,7
13,3
14,9
18,5
5
7,3
9,2
11,1
13,4
15,1
16,7
20,5
6
8,6
10,6
12,6
15,0
16,8
18,6
22,5
7
9,8
12,0
14,1
16,6
18,5
20,3
24,3
8
11,0
13,4
15,5
18,2
20,1
21,9
26,1
9
12,2
14,7
16,9
19,7
21,7
23,6
27,9
10
13,4
16,0
18,3
21,2
23,2
25,2
29,6
11
14,6
17,3
19,7
22,6
24,7
26,8
31,3
12
15,8
18,5
21,0
24,1
26,2
28,3
32,9
13
17,0
19,8
22,4
25,5
27,7
29,8
34,5
14
18,2
21,1
23,7
26,9
29,1
31,3
36,1
15
19,3
22,3
25,0
28,3
30,6
32,8
37,7
16
20,5
23,5
26,3
29,6
32,0
34,3
39,2
17
21,6
24,8
27,6
31,0
33,4
35,7
40,8
18
22,8
26,0
28,9
32,3
34,8
37,1
42,3
19
23,9
27,2
30,1
33,7
36,2
38,5
43,8
20
25,0
28,4
31,4
35,0
37,6
40,0
45,3
130

ТАБЛИЦА XI (к § 4.2)
Информативность диапазонов признаков
Значение информативности диапазона при известных сумме
частостей и диагностическом коэффициенте.
Информативность приведена в сотых; полученную величину
необходимо разделить на 100
Сумма
частостей
(в %)
Диагностические коэффициенты
1
2
3
4
5
6
7
8
9
информативность
1
0
0
0
1
1
2
2
3
3
2
0
0
1
2
3
4
5
6
7
3
0
1
2
3
4
5
7
9
10
4
0
1
2
4
5
7
9
12
14
5
0
1
2
4
9
12
15
17
6
0
1
3
5
8
11
14
17
21
7
0
2
3
6
9
13
16
20
24
8
0
2
4
7
10
14
19
23
28
9
1
2
5
8
12
16
21
26
31
10
1
2
5
8
13
18
23
29
35
11
1
2
5
9
14
20
26
32
38
12
1
3
6
10
16
22
28
35
42
13
1
3
6
11
17
23
30
38
45
14
1
3
7
12
18
25
33
41
49
15
1
3
7
13
19
27
35
44
52
16
1
4
8
14
21
29
37
47
56
17
1
4
8
15
22
31
40
49
59
18
1
4
9
16
23
32
42
52
63
19
1
4
9
16
25
34
44
55
66
20
1
5
10
17
26
36
47
58
70
21
1
5
10
18
27
38
49
61
73
22
1
5
11
19
29
40
51
64
77
23
1
5
11
20
30
41
54
67
80
24
1
5
12
20
31
43
56
70
84
25
1
6
12
21
32
45
58
73
87
26
1
6
13
22
34
47
61
76
91
131

Таблица XI (продолжение)
Диагностические коэффициенты
Сумма
частостей
(в %)
1
2
3
4
5
6
7
8
9
информативность
27
2
6
13
23
35
49
63
79
94
28
2
6
14
24
36
50
65
82
98
29
2
7
14
25
38
52
68
84
101
30
2
7
15
26
39
54
70
87
105
31
2
7
15
27
40
56
72
90
108
32
2
7
16
28
41
58
75
93
112
33
2
7
16
28
43
59
77
96
115
34
2
8
17
29
44
61
79
99
119
35
2
8
17
30
45
63
82
102
122
36
2
8
18
31
47
65
84
105
126
37
2
8
18
32
48
67
86
107
129
38
2
9
19
33
49
68
89
110
133
39
2
9
19
34
51
70
91
113
136
40
2
9
20
34
52
72
93
116
140
41
2
9
20
35
53
74
96
119
143
42
2
9
21
36
54
75
98
122
147
43
2
10
21
37
56
77
100
125
150
44
3
10
22
38
57
79
103
128
154
45
3
10
22
39
58
81
105
130
157
46
3
10
23
40
60
83
107
133
161
47
3
11
23
40
61
84
110
137
164
48
3
11
24
41
62
86
112
139
168
49
3
И
24
42
64
88
114
142
171
50
3
11
25
43
65
90
117
145
175
51
3
12
25
44
66
92
119
148
178
52
3
12
26
45
67
93
121
150
182
53
3
12
26
46
69
95
124
153
185
54
3
12
27
46
70
97
126
157
188
55
3
12
27
47
71
99
128
160
192
56
3
13
28
48
73
100
131
163
195
57
3
13
28
49
74
102
133
166
199
58
3
13
29
50
75
104
135
169
202
59
3
13
29
51
76
106
138
171
206
132

Таблица XI (окончание)
Диагностические коэффициенты
Сумма
частостей
(в %)
1
2
3
4
5
6
7
8
9
информативность
60
3
14
30
52
78
108
140
174
209
61
4
14
30
52
79
109
142
177
213
62
4
14
31
53
80
111
145
180
216
63
4
14
31
54
82
113
147
183
220
64
4
14
32
55
83
115
149
186
223
65
4
15
32
56
84
117
152
189
227
66
4
15
33
57
85
118
154
192
230
67
4
15
33
58
87
120
156
195
234
68
4
15
34
58
88
122
159
198
238
69
4
16
34
59
89
124
161
201
241
70
4
16
35
60
91
126
163
203
244
Примечание. Для вычисления табл. XI на основе формул (4.6)
и (4.8) была выведена формула:
I (*у)=К [Р (х1А) + Р (х/В)],
где	(*}) “ 1+100,1Д/(}
При диагностических коэффициентах I, 2 ... 9 К принимает
одно из 9 значений:
ДК
1
2
3
4
5
6
7
8
9
К
0,0575
0,226
0,498
0,860
1,295
1,795
2,335
2,905
3,490
133

ТАБЛИЦА XII
Пороговые суммы диагностических коэффициентов
Величины пороговых сумм диагностических коэффициентов
при разном допустимом проценте ошибок первого и второго ряда
(по формуле А. Вальда для последовательного статистического
анализа).
При достижении порога со знаком «+» выносится решение
«заболевание Л», при достижении порога со знаком «—» выно¬
сится решение «заболевание В».
а
20%
10%
5%
2%
1%
0,5%
0,2%
0,1%
20%
+6
-6
+6,5
-9
+7
-12
+7
— 16
+7
-19
+7
—22
+7
-26
+7
-29
ю%
+9
-6,5
+9,5
-9,5
+ 10
-12,5
+ ю
— 16,5
+ 10
-19,5
+ 10
—22,5
+ 10
-26,5
+ 10
—29,5
5%
+ 12
—7
+ 12,5
-10
+ 13
-13
+ 13
-17
+ 13
-20
+ 13
—23
+ 13
-27
+ 13
-30
2%
+ 16
—7
+ 16,5
— 10
+ 17
-13
+ 17
-17
+ 17
-20
+ 17
-23
+ 17
-27
+ 17
-30
1%
+ 19
—7
+ 19,5
-10
+20
-13
+20
-17
+20
—20
+20
-23
+ 20
-27
+20
-30
0,5%
+22
-7
+22,5
-10
+23
-13
+23
— 17
+23
-20
+23
-23
+23
—27
+23
—30
0,2%
+26
—7
+26,5
-10
+27
-13
+27
-17
+27
-20
+27
-23
+27
-27
+27
-30
0,1%
+29
-7
+29,5
-10
+30
-13
+30
-17
+30
—20
+30
-23
+30
-27
+30
-30
Примечание, а —допустимый процент ошибок первого рода
(просмотр заболевания А, когда его принимают за заболевание В). 0 — до¬
пустимый процент ошибок второго рода (ложная диагностика заболевания
А, когда в действительности у больного заболевание В). Формула для
расчета первого порога (для вынесения решения «заболевание Л»):
т-r	л .п 1 100 —а
Порог А= 10 lg	5	.
Р
Формула для расчета второго порога (для вынесения решения «заболи
вание В>):
Порог В=Ю lg
134

ЛИТЕРАТУРА
1 Ашмарин И. В., Воробьев А. А. Статистические ме¬
тоды в микробиологических исследованиях. Л., 1962.
2.	Башаринов А. Е. и Флейшман Б. С. Методы стати¬
стического последовательного анализа и их приложения. М.,
1962.
3.	Б о л ь ш е в J1. Н. и Смирнов Н. В. Таблицы математи¬
ческой статистики. М., 1965.
4.	В а л ь д А. Последовательный анализ. Пер. с англ. М., 1960.
5.	Ван дер Варден. Математическая статистика. М., 1960.
6.	Вишневский А. А., А р т о б о л е в с к и й И. И., Б ы х о в-
с к и й М. Л. Машинная диагностика и информационный по¬
иск в медицине. М., 1969.
7.	Г е н е с B.C. Некоторые простые методы кибернетической
обработки данных диагностических и физиологических иссле¬
дований. М., 1967.
8.	Генес В. С. Таблицы достоверных различий между груп¬
пами наблюдений по качественным показателям. М., 1964.
9.	Генкин А. А. В сб.: Биологические аспекты кибернетики.
М., 1962.
10.	Генкин А. А., Г у б л е р Е. В. Применение последователь¬
ного статистического анализа для дифференциальной диаг¬
ностики и использование этого метода для различения двух
форм ожоговой болезни. В кн.: Применение математических
методов в биологии, в. 3. Л., 1964.
11.	Гу б л ер Е. В. Вычислительные методы распознавания па¬
тологических процессов. Л., 1970.
12.	Гу б л ер Е. В., Генкин А. А. Применение критериев не¬
параметрической статистики для оценки различий двух групп
наблюдений в медико-биологических исследованиях. М., 1969.
13.	К а м и н с к и й Л. С. Статистическая обработка лаборатор¬
ных и клинических данных. Л., 1964.
14.	Куль бак С. Теория информации и статистика. Пер. с англ.
М., 1967.
15.	Л а ш к о в К. В., П о л я к о в Л. Е. Непараметрические ме¬
тоды медикостатистических исследований. В кн.: Методологи¬
ческие вопросы санитарной статистики, 1965.
16.	М и с ю к Н. С., Г у р л е н я А. М., Лозовик В. В. Диаг¬
ностические алгоритмы. Минск, 1970.
17.	Митропольский А. К. Техника статистических вычисле¬
ний. М., 1971.
18.	П а р и н В. В., Баевский Р. М. Введение в медицинскую
кибернетику. Москва — Прага, 1970.
19.	С е п е т л и е в Д. Статистические методы в научных медицин¬
ских исследованиях. Пер. с болг. М., 1968.
20.	У р б а х В. Ю. Математическая статистика для биологов и
медиков. М., 1963.
135

21.	У р бах В. Ю. Биометрические методы. М., 1964.
22.	Юл Д. Э., Кендал М. Д. Теория статистики. М., 1960.
23.	Owen. Handbook of statistical tables, 1962.
24.	Rosenbaum S. Tables for a nonparametric test of location.
Ann. Math. Statist., 1954, 25, № 1, 146.
25.	S i d a k Z. J., Vondrocek, Simple nonparametric test. App-
lic. math., 1957, 2, № 3.
26.	S i e g e 1 S. Nonparametric statistics in behavior science. N. J.,
1956.
27.	Wilcocson F. Probability tables for individual compari¬
sons by ranking methods. Biometrie, 1947, 3, 119—122.
Дополнительная литература1
28.	Б p а й н e с С. М. (ред.). Биологическая и медицинская кибер¬
нетика (некоторые актуальные проблемы). М., 1971.
29.	Б ы х о в с к и й М. Л. и Вишневский А. А. Кибернетиче¬
ские системы в медицине. М., 1971.
30.	Введение в теорию порядковых статистик. Пер. с англ. под
ред. А. Я. Боярского. М., 1970.
31.	Гаек Я., Шидак 3. Теория ранговых критериев. Пер. с
англ. М., 1971.
32.	Ластед Л. Введение в проблему принятия решения в ме¬
дицине. Пер. с англ. М., 1971.
33.	Медицинская информационная система. Под общей редакцией
Н. М. Амосова. Киев, 1971.
1 Под номерами 28—33 приведена дополнительная справоч¬
ная литература, вышедшая после сдачи книги в печать.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ1
Байеса формула 66
Вероятность априорная, заболе¬
ваний 65
—	диагноза (прогноза), заболе¬
вания 65
—	нулевой гипотезы 12
Взвешенная скользящая сред¬
няя 76 (4.13)
Выбор критерия различий 3, 4,
17
Выборка (эмпирическая) 10
Выборки независимые 16, 21
—	связанные 16, 18
Вычислительные методы рас¬
познавания 62
Генеральная совокупность 10
Градация (см. также диапазон)
17, 54, 56, 64
Диагностическая гипотеза 65
—	таблица 70 (табл. 4.6)
Диагностический коэффициент
67	(4.4)
—	порог, см. порог диагности¬
ческий
Диапазон признака 64
	 крайний 77
Дисперсия 11
Значимость различий, ее уро¬
вень 12
Инверсия 22
Инверсии, их максимальное до¬
пустимое число 22 (III)
	—	его вычисление 24
(2.1)
Информативность диагностиче¬
ской таблицы 72 (4.11)
—	диапазона признака по Куль-
баку 71 (4.9) (XI)
—	признака 71 (4.10)
1 Числами без скобок показаны страницы: арабскими цифра¬
ми в скобках — номера формул и таблиц в тексте (последние —
после слова «табл.»); римскими цифрами показаны номера таблиц
приложения; указание «см.» означает, что термин, выделенный
курсивом, отдельно упомянут в предметном указателе.
Буквенные обозначения понятий представлены в разделе
«Условные обозначения» (стр. 7).
137

Корреляция нормальная (ли¬
нейная) 44
—	ранговая 45
Коэффициент диагностический
(см. диагностический коэффи¬
циент)
—	корреляции линейный 44
—	— — его значимость 48
(VIII)
—	— ранговый (Спирмена) 46
(3.1)
	—	его значимость 48
(VII)
	Чупрова 55, 159, 161 (3.9)
Коэффициенты корреляции, зна¬
чимость их различий 49
(3.2)	(IX)
Критерии, их мощность 3, 14
—	непараметрические 3, 13, 14,
16
—	параметрические 3, 15
Критерий знаков 18(1)
—	серийный г (Вальда—Воль¬
фовица) 36 (VI)
—	ТМФ (точный метод Фише¬
ра) 33 (V)
—	F (отношения дисперсий) 11
(1.2)
—	Q (Розенбаума) 31 (IV)
—	t (Фишера—Стьюдента) 16,
17,	41
—	Т (парный критерий Вил-
коксона) 19 (II)
—	U (Вилкоксона—Манна—
Уитни) 21 (2.1) (III)
	 сравнение по нескольким
признакам 25 (табл. 2.3)
		— при различиях в фор¬
ме распределений 28 (табл.
2.4, 2.5)
—	X2 16 (X)
	 при оценке зависимости
качественных признаков 53,
55, 57, 58
Неопределенный ответ, см. от¬
вет неопределенный
Нулевая гипотеза 12
Общий упорядоченный ряд 21
(табл. 2.2)
	расположение нераз-
личающихся наблюдений 21
Ответ неопределенный 65
Отношение априорных вероят¬
ностей 65
—	вероятностей (частостей) 64
—	правдоподобия 64
Оформление результатов оцен¬
ки значимости различий 41
(табл. 2.8)
Ошибки первого и второго рода
67
Порог диагностический 65, 66,
68	(4.3, 4.5, 4.6) (XII)
Последовательная диагностиче¬
ская процедура 62
Принятие решения при после¬
довательной процедуре рас¬
познавания 66, 69 (4.8)
Ранги (ранговые номера), ран¬
жирование 19, 45, 46
138

Распределение альтернативное
33
—	двухвершинное 28
—	его форма 28, 33
—	нормальное (гауссовское)
14,	15
—	различия в средних тенден¬
циях 13, 16, 28
—	— в его форме 13, 16, 28, 33
Серии см. критерий серийный
Статистики 10
Условные буквенные обозначе¬
ния 7
Частости признака 64
	средневзвешенные 76
Формула Байеса см. Байеса
формула
—	принятия решения при по¬
следовательной процедуре
распознавания (см.)

СОДЕРЖАНИЕ
Предисловие к первому изданию
Предисловие ко второму изданию
Условные обозначения ...
Глава 1. Некоторые общие понятия
§ 1.1. Природа статистических выводов
§ 1.2. Понятие о непараметрических критериях . .
Глава 2. Критерии различий двух выборок
§ 2.1. Общие замечания
Случай связанных выборок
§ 2.2. Критерий знаков (КЗ)
§ 2.3. Критерий Т (парный критерий Вилкоксона) .
Случай независимых выборок
§ 2.4. Критерий U (Вилкоксона — Манна — Уитни)
§ 2.5. Критерий U (продолжение)
§ 2.6. Критерий U (окончание) ........
§ 2.7. Критерий Q (Розенбаума)
Случай различий в форме распределений
§ 2.8. Точный метод Фишера (ТМФ) для четырех¬
польной таблицы
§ 2.$. Серийный критерий г (Вальда — Вольфовица)
§ 2.10. Выбор критерия различий .
§ 2.11. Оформление результатов оценки значимости
различий
Глава 3. Оценка связи между двумя рядами наблюдений .
§ 3.1. Коэффициент корреляции рангов (Спирмена)
§ 3.2. Оценка связи между качественными призна¬
ками
§ 3.3. Оценка связи между качественными призна¬
ками (продолжение)
Глава 4. Отнесение наблюдений к одному из двух возмож¬
ных классов (диагностика и прогнозирование) .
§ 4.1. Общая характеристика метода
§ 4.2. Вычисление информативности признаков . .
§ 4.3. Подготовка диагностической таблицы . . .
§ 4.4. Пример вычислений
3
4
7
9
13
16
18
19
21
25
27
31
33
36
37
41
44
52
56
62
70
73
78
140

Приложение (справочные таблицы)
Таблица I. Критерий знаков
Таблица	II. Критерий Т (парный критерий Вилкоксона)
Таблица	III. Критерий U (Вилкоксона—Манна—Уитни)
Таблица IV. Критерий Q (Розенбаума)
Таблица V. Точный метод Фишера
Таблица	VI. Серийный критерий г (Вальда—Вольфовица)
Таблица VII. Ранговая корреляция
Таблица VIII. Нормальная корреляция
Таблица IX. Преобразование Фишера
Таблица X. Критерий %2
Таблица	XI. Информативность диапазонов признаков .
Таблица XII. Пороговые суммы диагностических коэф¬
фициентов
Литература
87
88
89
90
120
121
126
127
128
130
131
134
135
Предметный указатель
137

ЕВГЕНИЙ ВИКТОРОВИЧ ГУВЛЕР
АЛЕКСАНДР АРОНОВИЧ ГЕНКИН
Применение
непараметрических критериев
статистики
в медико-биологических
исследованиях
Редактор Н. А. Толоконцев
Обложка художника В. К. Пахрицина
Художественный редактор А. И. Приймак
Технический редактор Г. Т. Лебедева
Корректор А. Ф. Лукичева
идано в набор 8/VI 1972 г.	Подписано к печати 24/1 1973 г.
Формат бумаги 84X108y32. Печ. л. 4,5. Бум. л. 2,25. Уел. л. 7,56
Уч.-изд. л. 8,07 JIH-73. М-12578. Тираж 5000 экз. Цена 81 коп. Заказ № 206
Бумага типографская № 2
Ленинград, «Медицина», Ленинградское отделение.
192104, Ленинград, ул. Некрасова, д. 10
Ордена Трудового Красного Знамени
Ленинградская типография имени Евгении Соколовой
«Союзполиграфпрома» при Государственном комитете
Совета Министров СССР по делам издательств, полиграфии
и книжной торговли
г. Ленинград, Л-52, Измайловский проспект, 29

Выйдет в свет в 1973 г.
Вожжова А. И. Методики изучения функций анализаторов при
физиолого-гигиенических исследованиях. Л., «Медицина», 15 л.
В книге дается описание основных методических приемов ис¬
следования различных функций анализаторов—слухового, вести¬
булярного, двигательного, кожного, зрительного и обонятельного,
а также их комплекса.
Приводятся фотоснимки общего вида и электрические схемы
приборов для физиологических исследований анализаторов, из ко¬
торых большая часть конструкции автора.
Даются пределы физиологических колебаний показателей
каждой функции, полученные на большом статистическом мате¬
риале при исследовании данными приборами.
Книга содержит примеры (с графическим изображением) ре¬
зультатов исследования различных функций анализаторов и их
изменений под влиянием условий внешней среды. Динамические
наблюдения в данных случаях позволяют дать гигиеническую
оценку изучаемым факторам внешней среды.
Книга представляет интерес для физиологов и гигиенистов
труда, научных работников и врачей, занимающихся вопросами
функциональной диагностики и исследованием влияния различных
факторов внешней среды на организм.

ВЫЙДЕТ В СВЕТ В 1973 г.
Мен и цк ий Д. Н., Трубачев В. В. Теория информации и
проблемы высшей нервной деятельности. JI., «Медицина», 10 л.
В монографии рассматриваются важнейшие направления ис¬
пользования идей, методов и средств теории информации и нейро¬
кибернетики в изучении высшей нервной деятельности человека и
животных. Обсуждаются особенности условных рефлексов при
вероятностном подкреплении, позволяющие по-новому определить
сигнальное значение раздражителей как отражение их статисти¬
ческой связи. Обобщаются новые результаты изучения и модели¬
рования процессов принятия решения человеком в ситуации вы¬
бора в зависимости от функционального состояния, а также от
количества и значимости перерабатываемой информации.
Издание рассчитано на широкий круг специалистов-физиоло-
гов, невропатологов и психиатров, психологов, а также работников
некоторых инженерных специальностей.