Текст
57(077)
P66
УДК 57(075.8)
Рокицкий П. Ф.
Р66 Биологическая статистика. Изд. 3-е, испр. Минск,
«Вышэйш. школа», 1973.
320 стр. с илл.
Учебное пособие для биологических факультетов университетов по одно-
именному курсу.
В книге подробно н последовательно изложены необходимые для биоло-
гических исследований статистические методы: группировка материала, со-
ставление вариационных рядов, вычисление важнейших статистических по-
казателей, .характеризующих совокупности, измерение корреляции и регрес-
сий, дисперсионный анализ, применение критерия соответствия. .Особое вни-
’ мание уделено понятиям вероятности и достоверности и их значению для
анализа биологических данных. Каждая глава содержит проверочные вопро-
сы и задачи (на материале ботаники, зоологии, животноводства, физиологии,
генетики, медицины и др.).
Табл.: 85, библиограф.: 2 с.
2102-010 57(077)
"М 304(05)73
ПРЕДИСЛОВИЕ
В биологий, медицине, сельском хозяйстве все чаще и чаще
используются математические и математико-статистические
методы. Возникает необходимость в создании ряда пособий
и руководств разной степени сложности по этим вопросам.
Настоящая книга представляет собой элементарное пособие
для студентрв и начинающих научных работников биологиче-
ского профиля. Она написана на основе вышедшей, в 1961 г.
книги «Основы вариационной статистики для биологов», одна-
ко в ее текст внесены значительные изменения и дополнения
в соответствии с замечаниями преподавателей вузов и Научных
работников.
Мы сочли целесообразным отказаться от термина «вариацион-
ная статистика». В свое время он был очень распространенным,
но сейчас употребляется довольно редко, так как содержит эле-
менты тавтологии (статистический метод обязательно предусмат-
ривает й изучение вариации). С другой стороны, применение ста-
тистических методов в биологии приобрело такие особенности^
что можно с полным правом говорить о биологической стдтисти-
ке как самостоятельной области статистики. Это и явилось осно-
ванием назвать книгу «Биологической статистикой». - Й
В работе подробно и последовательно изложены необходимые
для биологических исследований статистические методы: группи-
ровка материала, составление вариационных рядов, вычисление
важнейших статистических показателей,’характеризующих сово-
купности, измерение корреляции и регрессии, дисперсионный
анализ, применение критерия соответствия. Большое внимание
уделено понятиям вероятности и достоверности и их значению
для анализа биологических данных.
Изложенный в книге материал иллюстрируется конкретными
примерами из различных областей биологии. Каждая глава cq-
держит проверочные вопросы И задачи на материале ботаники,
зоологии, животноводства, растениеводства, физиологии, генети-
ку В приложении дается перечень огатистических показателей и
3
их формул и 11 статистических таблиц, необходимых для оценки
ряда показателей и проверки результатов.
Отзывы о книге, критические замечания и указания автор
просит направлять по адресу: г. Минск, Академическая, 27, Ин-
ститут генетики и цитологии АН БССР, академику П. Ф. Рокиц-
кому.
ВВЕДЕНИЕ
РОЛЬ МАТЕМАТИЧЕСКИХ
И МАТЕМАТИКО-СТАТИСТИЧЕСКИХ МЕТОДОВ
В БИОЛОГИИ
Современное естествознание развивается исключительно бы-
стрыми темпами. За немногие десятилетия совершенно измени-
лась физическая картина мира. Большой прогресс достигнут и в
области биологии, которая сейчас охватывает явления жизни на
самых различных уровнях, начиная от молекулярного и кончая
популяциями и экосистемами — сложными совокупностями мно-
гих видов животных и растений, населяющих территорию нашей
планеты.
Одним из важных факторов, стимулирующих дальнейшее раз-
витие различных областей естественных наук, является внедре-
ние в них математики. Еще К. Маркс отмечал, что использование
математики — это показатель зрелости науки. В настоящее вре-
мя стремление к математическому выражению соответствующих
закономерностей распространилось на все области знания, в том
числе на экономику и даже лингвистику.
В биологии использование математики началось значительно
позже, нежели в физике и'химии. Биология очень долго развивав
лаоь на основе только качественного анализа явлений. Правда,
еще в начале XVIII века Реомюр пытался найти математические
законы строения ячеек пчелиных сотов, а за 30 лет до него Ббрел-
ли делал математические расчеты движения животных. Однако
необходимость количественного анализа явлений жизни с ис-
пользованием ряда математических приемов и методов стала
яснб осознанной только в конце XIX века. Гальтон (1899)
разработал основы новой науки, названной им биометрией (или
биометрикой). Биометрия рассматривалась как наука о примене-
нии математических методов для изучения живых существ.
Для внедрения математики в биологию в конце XIX и начале
XX века имелись очень серьезные основайпя: "Одним из них'Был
перёходот описательного метода изучения явлений жизни к эк-
спериментальному. Хотя и при описательном подходе возможно
5
установление математических закономерностей (примё^^К§]*ут
быть законы движения небесных тел), однако преобладаЙШкгом
случае качественная оценка. Эксперимент ж " f“- ет
количественной опенки яддениГ и nnon^ffljg jaiHwr
гиН--№нетикИГраДио&иологииидругих эксДментя^ьных Об-пя.
стеи биологии повлекло зТсобой разработку многочислей’Йй)Гма-
тематических приемов и методу исследования. Большую роль
сыграли и чисто практические причйны.“Тйк, 'развитие агрономии
потребовало разработки: 1) схем опытов для выяснения влияния
на урожайность сельскохозяйственных культур различных факто-
.ров (удобр'енйй, способов .обработки почвы, различий в сортах и
пр.); .2) методов математического анализа результатов опытов;
3) способов доказательства достоверности влияния того или ино-
го фактора. При изучении действия различных препаратов, ве-
ществ или лекарственных средств на человека и животных также
понадобились математические методы, с помощью которых мож-
но было доказывать эффективность (или, наоборот, неэффектив-
ность) применения тех или иных веществ. В дальнейшем разрабо-
танные методы стали широко применяться в зоологии, ботанике
и других областях биологии.
Наконец, важнейшим обстоятельством, определившим приме-
нение математических и, в частности, математико-статистических
методов, явилось установление кардинального факта, что миощм
биологическим явлениям свойственны статистические яякономер-
_ности. обнаруживаеммр при изучении совокупностей но непри-
ложимые к отдельным единицам этих совокупностей.
Когда физики перешли от изучения поведения отдельных фи-
зических тел к изучению поведения множеств молекул, электро-
нов, они вступили в область действия статистических законов. На
этой основе создалась особая область физики — статистическая
физика, изучающая свойства и поведение систем, состоящих из-
огромного количества отдельных частиц. В оснбве многих физи-
ческих явлений, таких, как радиоактивный распад, термодинами-
ческие явления и некоторые другие, лежат статистические зако-
номерности. С их открытием закономерности, установленные эм-
пирически, например законы термодинамики, получили более
глубокое обоснование и были выведены из статистических, ве-
роятностных законов.
Примерно такое же положение наблюдается сейчас и в ряде
областей, биологии. Когда зоологи, ботаники. перешли,от', изуче-
ния отдельных «типичных» представителей вида к изучению мно-
гих особей одного вида, они обнаружили массовые явления
статистичеагой'ТфйрбщЗГТЫбЫГ РЗГСКИ; моллюсКй, Сбсны, колов-
раткигводброслй, инфузории и другйежй'вбТйые и растения ха-
рактеризуются изменчивостью, вариацией по самым разнообраз-
ным признакам. Такой же вариацией обладают н организмы,;
культивируемые Человеком: коровы различаются удоями за
тацию, живым весом, процентом жира в молоке; овцы — найд^
6
гами, длиной и тониной шерсти, весом; колосья пшеницы—ко-
личеством зерен в колосе, весом отдельных зерен и т. д. Пои
изучении : биологических - совокупностей, являющихся тиото?
целесообразным применить методы
сМЛЯ' _.
^ Tfo« для приложения статистических методов в биологии
очень значительно, так как многие экологические, генетические,
цитологические, микробиологические, радиобиологические явле-
ния — массовые по своей природе. В них участвуют не одна особь
'или клетка, не одна а-частица, не одна бактерия или вирусная
частица, а множества, т. е. совокупности, клеток, а-частиц, бакте-
рий, особей вида, семей и т. д. Осуществление событий в таких
совокупностях может быть оценено вероятностями, а анализ их
требует применения статистических методов.
Статистические методы существенно необходимы и при поста-
новке экспериментов, так как только с их помощью можно уста-
новить, зависит ли наблюдаемое различие между опытными и
контрольными делянками или группами животных от влияния
изучаемого фактора или же оно чисто случайно, т. е. определяет-
ся многими другими, не контролируемыми и не поддающимися
учету факторами. Понимание и учет статистических закономерно-
стей помогают экспериментатору составить методически обосно-
ванный план опытов, правильно их провести и, наконец, сделать
из них объективные выводы. При этом надо помнить, что никакая
математическая и статистическая обработка' не поможет, если
опыты были проведены неправильно или данные собраны не-
брежно.
Роль математики w математической статистики в бипппгик
особенно возросла в связи С развитием тяприи информации и ки-
0Щ>И1?Н11кй " nwu " пйлеягтрй матама.
ТИЮГ, Среди КОТОРЫХ главное место занимают теппий иеппятности.
математическая.статистика и мятемятическяя лпгикя,
. Использование математики в современной биологии не. огра-,
ничивается только статистическими методами. Поэтому биомет-
рия (или биоматематика, как ее -иногда называют) шире, нежели
биологическая статистика. Ойа использует также приемы и ме-
тоды из других областей математики: дифференциального и ин-
тегрального исчислений, теории чисел, матричной алгебры
и т. д.
Внедрение математики в биологию первоначально выража-
.лось в использовании отдельных математических и математико-
статистических методов для изучения тех ил/i иных биологиче-
ских вопросов и обработки данных, полученных из природы или
в лаборатории. Такие вопросы, хак изменчивость морфологиче-
ских, физиологических и экологических признаков животных и
растений и установление влияния на них внешних и внутренних
факторов, количественный учет и процессы, происходящие в по-
7
пуляциях, сходство и различия между видами, подвидами и ины-
ми систематическими категориями, рост.индивидуальный и рост
популяций, могут изучаться лишь с помощью математических и
математико-статистических методов. Более того, в различных об-
ластях биологии (генетика, эволюционное учение, селекция, фи-
зиология) уже ставится задача выразить соответствующие биоло-
гические процессы или явления в математической форме, дать им
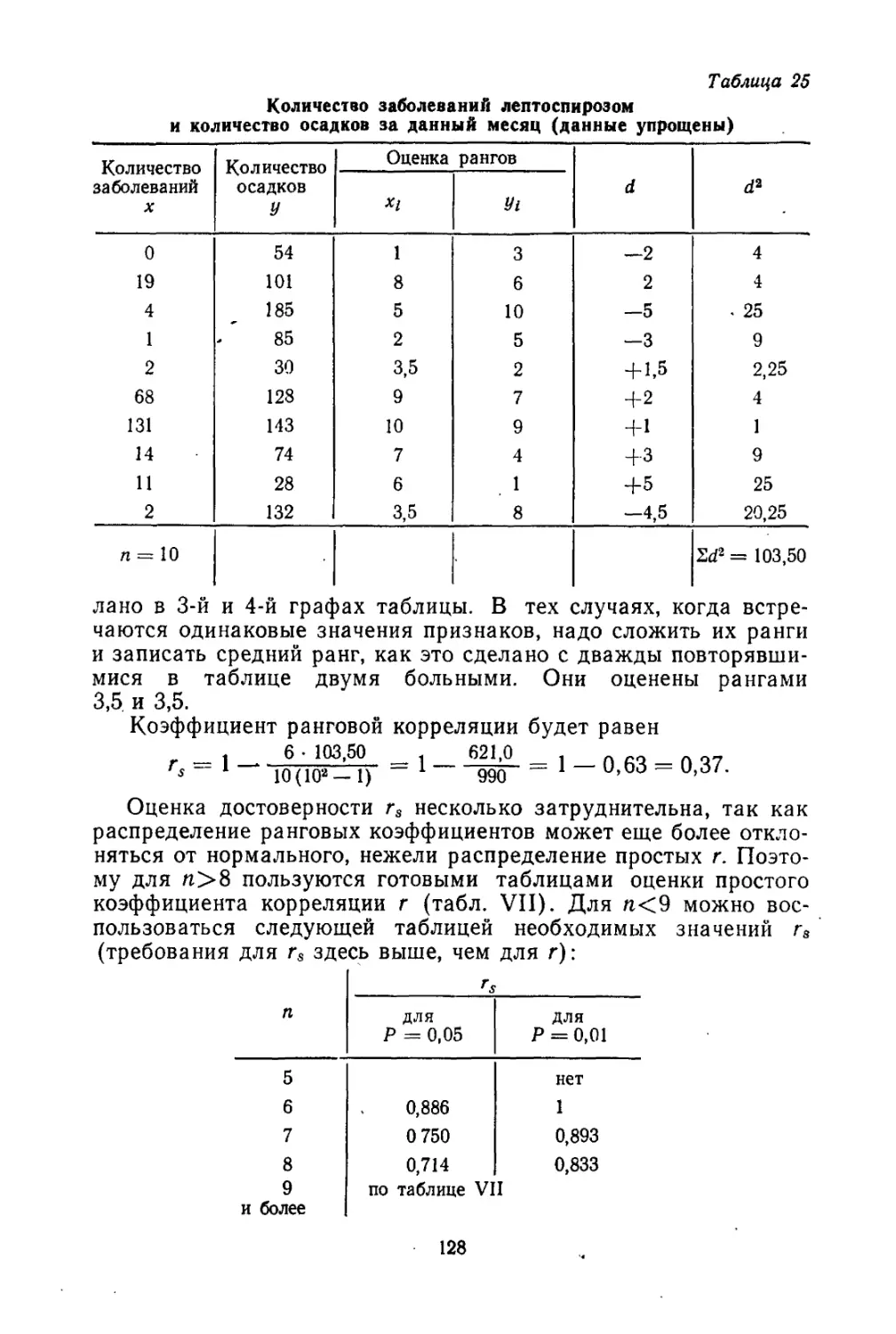
строго математическое выражение. Сбывается то, что более полу-'
века тому назад гениально предвидел И. П. Павлов. В своей речи
«Естествознание и мозг» в 1909 г. он сказал; «...Вся жизнь от про-
простейших* до сложнейших организмов, включая, конечно, и че-
ловека, есть длинный ряд все усложняющихся до высочайшей,
степени уравновешиваний внешней среды. Придет время, пусть
отдаленное, когда математический анализ, опираясь на естествен-
нонаучный, охватит величественными формулами уравнений все
эти уравновешивания, включая в них, наконец, и самого себя».*
В этой' книге изложены элементарные основы ^биологической,
или вариационной, статистики в объеме, предусмотренном учеб-
ными планами биологических, факультетов университетов. Одна-
ко книга написана таким образом, чтобы с важнейшими стати-
стическими методами могли познакомиться и начинающие
научные работники — биологи, зоологи, ботаники, агрономы, зоо-
техники, не проходившие специальной подготовки в вузе. Све-
дения о более сложных статистических приемах и методах чита-
тель найдет в специальных руководствах, которые указаны в за-
ключительной части книги.
• Павлов И. П. Собр. соч., т. III, кн. I. М., 192S, стр. 124.
ГЛАВА 1
ГРУППИРОВКА ДАННЫХ, СОВОКУПНОСТЬ
И ВАРИАЦИОННЫЙ РЯД
акт
Характеристика совокупности. Всякое множество отдельных.
отличающихся друг отдругаи вто же“в^^Усх~лпны'х"‘пawwl
ём^юТ^^^^^ЖДЕйВЗк^юстпГявляютсяпопуляции рыжих
пблевок^РогоилТгТшого района, стадо коров данного хозяйства,
потомство определенного быка, заготовляемые в области или
крае беличьи шкурки, растения на опытных делянках, группа
цыплят, на которых ставится* опыт по применению антибиотиков,
мальки окуня в озере и т. д. Понятие совокупности применимо не
только к животным и растениям. Такими же совокупностями яв-
ляются, например, дети, родившиеся в стране в течение какого-то
года или месяца, молекулы газа в том или другом объеме. В сб-
егав совокупности входят различные члены, или единицы: для по-
пуляции животных — каждое отдельное животное, для стада
коров единицей является каждая корова, для совокупности шку-
рок — каждая шкурка, для потомства быка — каждый теленок,
от него полученный, для совокупности зерен гречихи — каждое
отдельное зерно.
АПИИНП совокупности начывяютпб^мом..сдадд-
ЙУКВОЙ-И Минина совокуп-
ности может характеризоваться определенными признаками, на-
пример: коровы — удоями за лактацию, весом, мастью; молекулы
газа — скоростями их движения и т. д. Каждый изучаемый при-
знак принимает разные значения у разЖ’ГЯЯГТдаИПГТЯ^^
ности, онТОЯЯВТСя в сво£^'значеЖ!иот7МГЭТ'ёЯМИМЦЦ''ССТ№уПИ!Т;*
стТПг другрр.._^то различие между единицамиL'сЗвок^пнОВТЯ
называется еариаццей или дисперсией (т. е. рассеянием) .Мы
говорим’— «НрйЭйаК варьирует», ото означает, что он принимает
различные значения у разных членов совокупности, например, у
коров данной породы, мышей опытной группы, поросят одного
помета и т. д. Значение, или меру признака, для той или иной
9
называют ^щ^чШ8-»;обоэйача1от опреде-
леннди буквой. Раньшеварйантыообэначали буквой о, теперь
. чаще обозначают буквой х. В таком случае ряд вариант в сово-
лупности следует обозначать как хи х2, х2, .... х», Общее Же
обозначение любой варианты Х{. Значок^^- порядковый, номер
варианты. Саму же варьирующую величину, т. е. величину, изме-
няющуюся под влиянием многих случайных причин и могущую
принимать разные значения, называют случайной переменной х.
Варианты являются ее числовыми значениями.
В то же время, несмотря на различия между вариантами,
входящими в совокупность, она обладает внутренней однород-
ностью. Члены совокупности сходны по ряду важных признаков.
Беличьи шкурки неодинаковы по размерам, качеству меха, ок-
раске, но все они — шкурки особей одного и того же вида — бел-
ки обыкновенной. Зерна пшеницы отличаются друг от друга по
весу и другим химическим и физическим признакам, но все они —
зерна пшеницы, а не ячменя, могли быть выращены на одном
пдле и т. д.
Чаще всего в состав совокупностей входят отдельные особи.
Так, например, при характеристике стада коров по весу во взрос-
лом состоянии (на 1 января определенного года) за единицу сово-
купности следует взять каждую корову. Однако единицей сово-
купности может быть не каждое животное в отдельности, а только
какая-то его характеристика. Так, изучая вариацию коров стада
по молочной продуктивности, можно* взять единицей удой за
.каждую лактацию. Тогда при общем количестве коров в стаде,
например 100 голов, количество изучаемых за несколько лет удо-
ев может быть 500 или 600. Отдельными вариантами будут вели-
чины удоев за каждую лактацию. Можно изучать вариацию того
или иного признака во'врёменй даже на одном животном. Как
известно, жирность молока изменяется не только по дням лакта-
ции, но и по отдельным дойкам того же дня. Варьирующие дан-
ные о проценте жира в молоке определенной коровы,'полученные
путем измерения жирности з,а ряд доек и дней лактации, также
составляют совокупность, которую можно изучить статистически-
ми методами. Такой же совокупностью, очевидно, является ряд
показателей состава крови у одной морскрй свинки в течение ка-
кого-то времени.
Таким образом, сумма наблюдений или измерений есть тоже
совокупность. Каждое отдельное наблюдение, при котором уста-
навливается значение случайной переменной, является единицей
ЭТОЙ совокупности. .
Совокупность может состоять из других, более частных сово-
купностей. Так, совокупность из всех животных -данной породы
распадается на частные совокупности — стада отдельных хо-
зяйств, колхозов или совхозов. В пределах стада одного хозяй-
ства можно выделить еще более частные совокупности, например
потомство определенных быков. При постановке опытов по изуг
.10,
чёнию влияния каких-либо антибиотиков-на рост крыс '.внутри
совокупности, охватывающей всех опытных и контрольных жи-
вотных, каждую группу, подвергавшуюся воздействию опреде-
ленных факторов, можно рассматривать- как самостоятельную,
более частную совокупность. Во всех случаях мы сталкиваемся с
постоянными различиями как внутри отдельных частных сово-
купностей, так и между ними.
Наиболее Общую совокупность называют, генеральной. Это —
теоретически бесконечно большая или во всяком случае'ПриОли-
жающаяся к бесконечности совокупность всех единиц или членов,
которые могут быть к ней отнесены. Так, если бьГ можно было
изучить всех особей данного вида, например всех коров или всех
больших синиц, то они составили бы генеральную совокупность.
Генеральная совокупность может состоять из такого большого
количества единиц, что изучить их всех нет возможности. Поэто-
му ПрЯКТИЧАГКН притппмтл.п ИМРТЬ дело СО СРаВНИТРЛКНП Hf>6n.nb,
щими, выборочными совокупностями. Тяк. ялплпг. изучающий
в природе тот или другой вид, отлавливает несколько сотен эк-
земпляров'и по ним стремится сделать вывод о всех особях вида.
Вопрос о том, в какой степени по выборочной совокупности
можно судить о генеральной, принадлежит к числу важнейших
теоретических и практических вопросов в биологической ста-
тистике. Он изложен в гл. 4.
Задачей изучения ВСЯКОЙ совокупности является получение
статистических Тили, как иногда говорят, биометрических) харак-
теристик,, или показателей, которые почноляют судить о данной
совокупности в пеломг о различиях внутри нее и об отличии ее ОТ
других, сходных с ней или близких к ней совокупностей. Сово-
купность становится статистической именно тогда, когда в ее
описание вносится количественный метод. Применение количест-
венного метода изучения совокупности и позволяет получать для
нее ряд статистических показателей. С их помощью мы получаем
основную информацию о совокупности.
Варьирующие признаки и их учет. При изучении единиц сово-
купности по тем- или другим признакам необходимо записать по-
лученные данные. Лучше всего производить такого рода записи
на карточках, так как их можно затем группировать любым об-
разом. При большом колйчестве карточек обработка записей
может производиться счетной машиной. В этом случае карточки
должны быть перфорированными, т. е. в определенных местах на
них должны быть пробиты дырочки или сделаны вырезы в соот-
ветствии с записанными цифрами. Машина сама производит не-
обходимые подсчеты но этим, дырочкам или вырезам. Наконец, в
особо сложных случаях все полученные при опытах или наблю-
дениях данные переводятся на условный код. Кодированные дан-
ные записываются в соответствующих частях электронно-счетных
машин. Такие машины в Дальнейшем могут обработать получен*
нЫе данные, при этом с большой скоростью.
11
Способы обработки данных: сильно зависят от того, каков ха-
рактер вариации изучаемых признаков. Различия между вариан-
тами^МОРГГ-ВГтяжяткг» r кяких.тп J Ь» ^тгагпию
совокупность животных характери-
зуют по масти, тогда каждая варианта должна получить качест-
венную характеристику в соответствии с заранее принятыми обо-
значениями: черная, рыжая, черно-пестрая, черно-рыжая и т. д.
В этом простейшем случае подсчет числа особей в каждой из вы-
деленных групп дает представление о составе популяции в целом.
В других случаях различия между няпидгитями будут количсс-
твётЫми. ^Ко'личёственная-вар'иация может' брлть лнух типов:
Ц Й первом глупя» разли-
чия между вариантами, отдельными значениями случайной пере-
менной, выражаются целыми числами, между которыми нет и не
может быть переходов. Например, количество детенышей в по-
мете (поросят у свиноматок, щенков у серебристо-черных лисиц),
число сосков у свиноматок, число лучей в плавниках рыб, коли-
чество лепестков в цветке, число позвонков у птиц и т. д. Для
изучения подобного варьирования надо сосчитать у каждой еди-
ницы совокупности число изучаемых элементов и записать его на
соответствующую карточку. При непрерывной вариации значения
вариант не обязательно выражаются только целыми числами.
Все зависит от того, какая степень точности принимается для ха-
рактеристики данного количественного признака. Так, например,
при изучении веса крупного рогатого скота можно ограничиться
значениями вариант, выраженными в килограммах, отбросив
граммы, но совершенно недостаточно округлять до килограммов
веса рыб, так как грамм здесь имеет большое значение. В опы-
тах же по изучению влияния гормонов на рост гребня у цыплят
вес гребня придется измерять в миллиграммах. Молочную про-
дуктивность за лактацию обычно' выражают в килограммах, но
общая картина удоев не изменится, если округлять ее до десятков
килограммов. Оценка же жирности молока в процентах, выра-
женных целыми числами, явно недостаточна, ее надо давать с
учетом десятых и даже сотых-долей процента. Однако во всех
этих и. им подобных случаях существует непрерывная вариация,
выражающаяся в том, что между вариантами возможны все пе-
реходы. При изучении непрерывной вариации надо все единицы
совокупности характеризовать количественно с той степенью точ-
ности, которая заранее намечена и больше всего подходит в дан-
ном конкретном случае. - >
Группировка данных при качественной вариации. Чтобы про-
анализировать ту или иную совокупность, необходимо Сгруппиро-
вать полученные отдельные варианты и 'затем представить эту
группировку в виде таблицы или ряда. При упорядочении полу-
ченных данных легко обработать их математически и вывести
статистические показатели; которые будут исчерпывающе харак-
теризовать изучаемую совокупность. Проблема группировки
12
занимает большое место в статистике вообще (особенно в эконо-
мической), так как ошибочная группировка данных может при-
вести к неправильным выводам о существе изучаемого явления.
Наиболее проста группировка при качественной вариации.
Так, если норки различаются по окраске, то их распределение
может быть выражено в количестве животных каждой окраски и
в процентах, которые составляют норки каждой окраски от обще-
го количества животных, как это показано в табл. 1.
Таблица 1 -
Распределение 500 норок по окраске_____
Типы норок Количество животных Процент от общего количества
Стандартные коричневые . . . 120 24
Серебристо-голубые ..... 160 32
Сапфировые 180 36
Черные скандинавские . . . . 40 8
Всего'.... 500 100
Частным случаем качественной [ вариации является альтерна-
тивная, когда в совокупности можно выделить только две группы.
У членов одной группы присутствует определенное качество (или
признак), у членов другой группы его нет. Так, при проверке
на туберкулез животные распадаются на 2 группы — с положи-
тельной реакцией и с отрицательной. Одни коровы в данном ста-
де рогатые, другие — комолые и т. д.
) Группировка данных Яри количественной дискретной вари-
аций. При количественной вариации необходимопредва'ри'/ёльно
наметить- для таблицы классы, охватывающие все полученные
количественные данные от минимальных до максимальных. Это'
легко сделать пои прерывной /дискретной) количественной из-
менчивости.
Допустим, что была изучена плодовитость 80 самок серебрис-
то-черных лисиц, т. е. число родившихся у каждой самки щенков.
Варианты Xi, Хз, х3,.... Хво этой совокупности выражены цифрами,
представленными в табл. 2.
1 Количество щенков у 80 самок серебристо-черных Таблица 2 лисиц
4 5 3 4 6 7 8 3 1 4
6 4 4 * 3 2 5 3 4 5 4
5 3 4 5 у 4 х 4 4 6 5 7
6 4 5 4 4 4 4 2 3 4
5 5 4 5 4 4 6 4 4 4
4 8 7 5 4 9 4 3 4 4
5 4 6 4 4 3 4 4 4 2
4 4 5 4 6 4 - 3 3 4 2
13
Отсюда естественно VCT»wrmwtR 9 уларов;_С » птиудм л V 3
итгХ—и распределить все варианты по этим 9 классам. Наибо-
лее простым способом разнесения вариант по классам является сле-
дующий. Составляется «таблица с намеченными 9 классами ив со-
ответствующие горизонтальные строчки разносятся все варианты,
начиная, от первой. Обозначаются они так: первые четыре вариан-
ты данного класса — точками, а последующие—черточками, соеди-
няющими четыре точки. Число 10 будет в таком случае фигурой |х( .
Пример разноски первых 20 вариант, записанных в двух верх-
них строчка^ табл. 2, дан в табл. 3.
Таблица 3 Таблица 4
Разноска 20 вариант по классам Распределение 80 самок серебристо-черных лисиц по количеству щенков в помете
Классы (число щенков в помете каждой самки) Частоты (количе- ство самок в каждом классе)
Классы Частоты
1 . 1 1 1
2 • 1 4
3 : : 4 * 3 10
4 39
4 —*7 5 13
5 : . 3 6 7
7 3
•6 : 2 8 2
7 • 1 9 1
-б • 1 п = 80
- После разноски по классам всех 80 вариант может быть со-
ставлена сводная таблица о 2 графами—«классы» и «частоты»
(табл. 4). В этих графах не обязательно писать полностью, что
под классами понимается число'щенков в помете каждой самки,
а под частотами — количество вариант в .каждом классе. Это
должно быть ясно из самого существа подобных таблиц.
Вторичная группировка данных при количественной дискрет-
ной вариации. В разобранном выще примере классов намечено
столько, сколько было в изученной совокупности'различных, зна-
чений вариант (от 1 до 9 щенков). Однако такой способ будет
Нецелесообразным при очень большой, вариаций дискретного
признака.
И
Так, например, у змей ЬЖ£гё|ре»Ш§ getulus «ЗДЙ^твЬ
товых щитков варьировало от 40 до 58 (табл. 5).
> Таблица 5
Количество хвостовых щитков у ВО экземпляров змеи
Lampropeltls getulus
42 - -‘58J 44 54 41 50 46 46 54 48 , 43 49
50 48 46 46 45 ' 53 48 48 53 53 48 41
46 40 50 43 , 49 51 52 46 42 44 48 45
47 46 43 50 47 45 48 40 44 42 48 45
54 50 56 48 45 45 51 42 44 47 46 45
Если классы намечать по значениям каждой варианты, т. е.
40, 41 и т. д., то получится 19 классов, ряд окажется растянутым,
труднообозримым, с перерывами в некоторых классах. Лучше
наметить классы, охватывающие несколько значений вариант,
.например: 40—41, 42—43 и т. д. или 40—42, 43—45 и т. д.
В первом случае вариационный ряд будет состоять из 10 классов,
во втором — из 7. Приняв второй вариант, получим вариацион-
ный ряд, представленный в табл. 6.
Классовый промежуток (обычно обозначается буквой i) в
данном случае равен'3.
Вариационный ряд и его графическое изображение. Таким об-
разом, после распределения всех вариант по классам получают-
ся^яды. в,которых показано. как часто встречаются варианты
"каждого класса и как варьируют признаки от_мини»$адьной вели-
чины до мякурмя.пкнпй _TaifWA ряды были названы вариационны-
(о вари у дяд'^иожносудить не толькоо границах
колеблемост i
раишя. hapMMHMi,. В первом
примере максимальной часто-
той обладал класс «4 пленка», '
за ним следовали ' классы
«3 щенка» и «5 щенков». Наи-
f» tf 11 t* (4*» li ? 15 (•)Й1ЖиТГ
более редкими по частоте ока-
зались крайние классы «1 ще-
нок» и «9 щенков». В вариаци-
онном ряду числа хвостовых
щитков наибольшей частотой
характеризовался класс «45—
48 щитков».
Класс, обладающий на-
иболь^ёТ^ЧЯТлЯ^Д^^лЯя^ип
название модального. значения
же крайних классов называют
Лимитами или пределами.
более точно все же считать ли-
Таблица 6
Распределение 60 змей Lampropeltls
getulus no числу хвостовых щитков
Классы Частоты
40-42 8 ,
43—45 14
46—48 20 '
49—51 9
52-54 ~ 7 • .
55—57 Л
58-60* Л
| п=60
15
Рис. 1. Полигон распределения 80 самок
серебристо-черных лисиц по числу щен-
, ков в помете.
мятами не значения самих
классов, а минимальные и
максимальные значения ва-
риант.
Всякий вариационный
ряд можно изобразить гра-
фически. Графическое изоб-
ражение вяпиарион^дрз—ья^
да в общем_лидДВл|ци1до
ЛКР[ия или йммыдшА
кривщ^-
~~ Существуют два способа
графического изображения
конкретных варияциоиныт
рядов. -Первый из них, при-,
меняющийся при дискретной
вариации, но 'вЛЬм случаёТ
если классы намечены пд^тпрл^ным значениям вариант, носит
название-яблмгона распределения. /На оси абсцисс нанесены
классы, на оси ординат — частотьГвысота каждого класса, про-
порциональная частоте класса, отмечаетстгкружкомГ Соединение
кружков, которШГй нанесены частддь^ 'дает'-ломанукгдднию, как
это показано на рйсТЛТ ‘
При построениИ-Полигонон нужно всегда доводить их справа
и слева до нулевых классов-^, е. тех еоеедпнх классов.- в которых
уже нет ни одной^варианты. В нашем примере ими являются
классы «О щенков* и-«Ю-щеПк~ов».
Но изображение с помощью полигона не годится для вариа-
ционного ряда числа щитков у змей. Так как классы объединяют
3 значения вариант (40—41—42, 43—44—45 и т. д.), их частоту
надо выражать не перпендику-
ляром, а СТ™»ЛиУРМ; енинмиш
ем которого ЯВЛЯЮТСЯ a ->mup-
ния класса, а высота пропор-
циональна численности класса
(рис. —Такой ступенчатый
график носит название гисто-
граммы. Из гистограммы лег-
ко получить и полигон распре-
деления, соединив линиями се-
редины верхних сторон всех
столбиков. Началом и концом
полигонов тогда будут середи-
ны соседних нулевых классов.
Однако правильнее в данном
случае пользоваться тольк'о-тн-
стограммами. '" -
40 43 46 43 52 55 58 6f
Классы по числу щитков
Рис. 2. Гистограмма распределения
60 змей Lampropeltis по числу хвосто-
вых щитков.
16
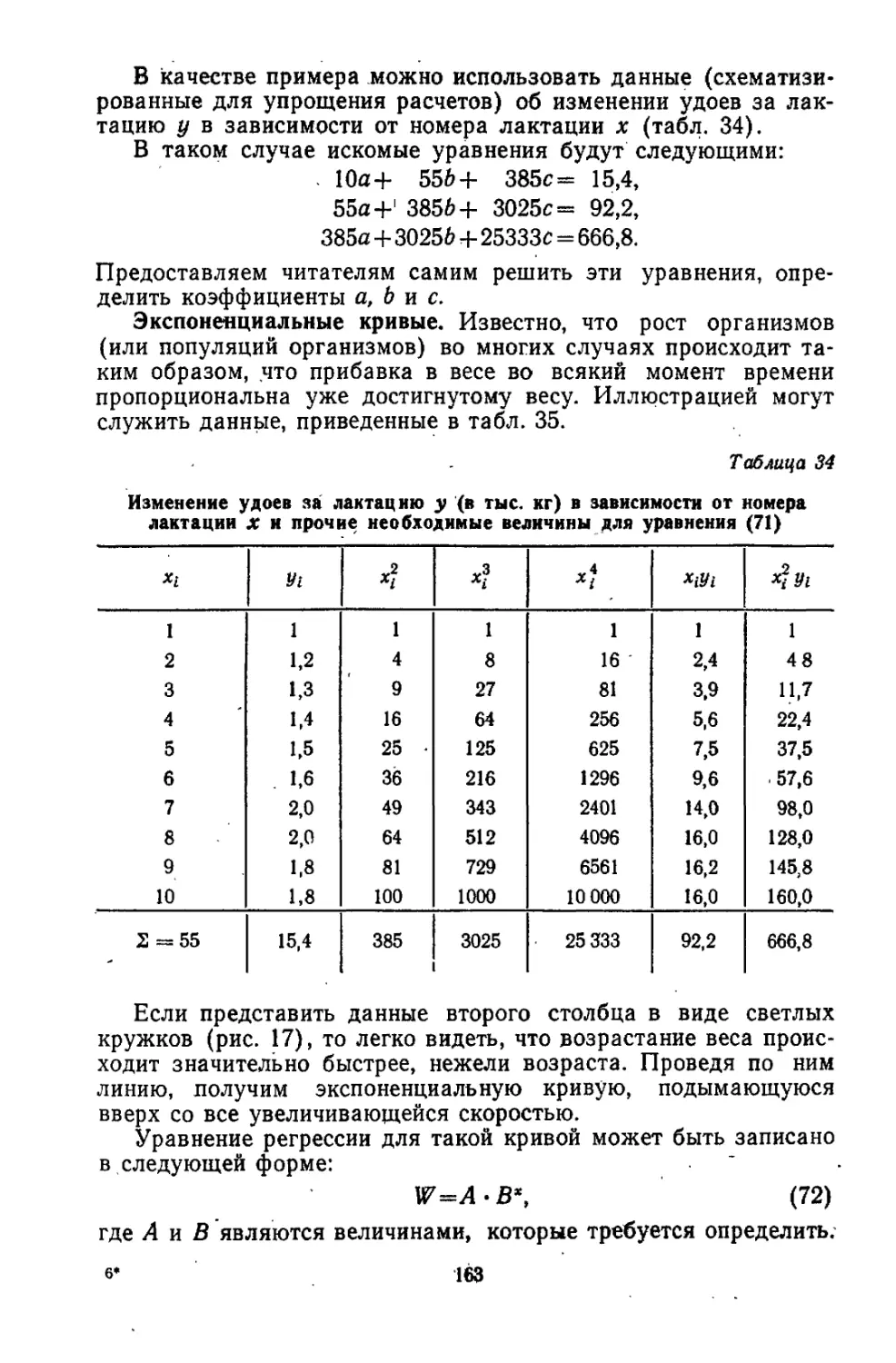
Оба разобранных вариа- ционных ряда имели по одному модальному классу. Однако возможный-случаи, когда Тва7 риационном ряду обнадеживав Таблица 7 Веса 2$ кроликов (в кг) (для боль» шей наглядности взяты кролики различных пород)
3,2 4,5 5,2 5,6 6,0
ется —яеукилько модальных
кЖГСЙУГй тШда полигон явлФ-11 1 3,8 4,7 5,2 5,7 6,3
ется многовершинным, наиоо- 4,1 4,9 5,3 5,8 6,4
Лес приний цриАЯюй" итого- 4,3 5,0 5,3 -5,8 6,7
вершинности, особенно. , при 4,3 5,1 5,4 5,9 7,3
очень растянутых рядах, явля- ется недостаточное Количество
вариант~Ь' 'И^чёННОй~Тбвбкупности.л При ма^дм_щисдц_особей
в некоторых классах вариационного ряда может вообще не быть
ниодцц^дщщащщ. Вариационный ряд окажется с перерывами,
ГТарЯЯционная кривая — разорванной на части. Однако, если
и при большом числе особей в изучаемой совокупности наблю-
дается дву- или многовершинность, причину этого надо искать
в самом биологическом материале. Последний, по-видимому,
представляет собой смешение двух качественно различных сово-
купностей, которые или находились в резко отличных условиях
внешней среды, или принадлежат к разным типам, морфам. Так
как многие виды в природе являются полиморфными или ди-
морфными, то соединение в одном ряду особей разных морф
может дать внешнюю картину дву- или многовершинности.
Известно, например, что платиновые лисицы отличаются по чис-
лу щенков от, серебристо-черных, поэтому было бы неправильно
помещать в один вариационный ряд по этому признаку и плати-
новых, и серебристо-черных лисиц. Наконец, возможны случаи,
когда дву- или многовершинность определяется свойствами
самих изучаемых признаков и поэтому характеризует вполне од-
нородный материал.
Группировка данных при количественной непрерывной вари-
ации. Группировка данных в этом случае является наиболее
трудной. Допустим, что в результате взвешивания 25 кроликов
различных пород были получены варианты, представленные в
табл. 7, при этом они^ расположены в так называемом ранжиро-
ааиид^ QfffltyT е. от меньших.величин к большим. 7
Здесь нет тех естественных классов,' с которыми мы встреча-
лись при анализе прерывной, дискретной вариаций. Их необхо-
димо наметить произвольно. Разница, между наибольшим и наи-
меньшим значением вариант в нашем примере 7,3—3,2=4,1 кг.
Весь этот интервал надо разбить на определенное количество
классов. Если принять за желательное количество классов 8 или
9, размеры их должны быть 0,5 кг. В таком случае можно наме-
тить следующие классы: 3,0—3,4 кг; 3,5—3,9; 4,0—4,4; 4,5—4,9;
5,0—5,4; 5,5—5,9; 6,0—М кг и~т; д. .
Начало первого класса не обязательно должно совпадать со
17
ЗйаЧениемминимальной варианты/Л^йё.чтобы-онобылоболте
^круглённым числом. В примере с^йдотами минимальная вари-
анта 3,2 кг, за начало же класса взято 3,0.
На правильное построение шкалы для классов надо обращать
очень большое внимание. Во-первых, необходимо, чтобы величи-
на классового промежутка бняю воргда-оДной и тсПГже^Выло бы
неправильно, если бы в начале ряда был взят к-лассовый~проме-
жуток 0,5 кг, как внашём примере, а в конце ряда — 1,0 кс Во-
вторык,. граййцй кЛИШЖ ДОЛЖНЫ бы'гь намичиНьГтйКИМ ооравфи,
чтобы одна и та же цифра нё пЬвТбРйлась в двух классах. Если
первый класс Заканчивается величиной 3,4, Т(Гвторой клас£л<?л-
жен начинаться со "следующей ни пирядкуТЦПрры— ЗД'Тгсли бы
классы были намечены "следующим образом. 4,0—4,5; 4,5—5,,0;
5,0—5,5 и т. д., то всегда было бы сомнение, к какому классу
отнести особь со значением 4,5 или 5,0. Если же один класс будет
охватывать значения вариант от 4,0 до 4,4 включительно, а дру-
гой — от 4,5 до 4,9 включительно, разноска вариант по намечен-
ным классам не вызовет затруднений. Ее можнб проводить тем
же методом, который использован при составлении табл. 3 и 4.
В 'левой части табл. 8 представлен вариационный ряд распре-
деления 25 кроликов по весу при разбивке на классы с i=0,5 кг.
Ряд получился несколько растянутым — 9 классов. Его можно
сделать более сжатым, приняв i—1,0 кг, как это сделано в правой
части таблицы.
Таблица 8
Распределение 25 кроликов по весу (в кг)
Классы Частоты Классы Частоты
3,0—3,4 1 3,0—3,9 2
3 5—3,9 1 4,0-4,9 6
4,0—^4,4 3 5,0-5,9 12
4,5—4,9 3 6,0—6,9 4
5,0—5,4 7 7,0—7,9 1
5,5—5,9 5
6,0—6,4 3
6,5—6,9 1
7,0—7,4 1 -
. i = 0,5 п = 25 i = 1,0 п = 25
При выборе числа классов надо одновременно иметь в виду
размеры классового промежутка. Они должны быть! или целымй
числами, или округленными дробями. Лучше, Чтобы ( было равно
0,5; 1; 5; 16, а не 0,45; 1,1; 6; 11, если даже количество классов
18
прйэтом будет несколько меньшим или ббльшим указанвсгр
выше. , -• ' '' .'. '
Возника ет вопрос: сколько же классов надо намечать при
стятигтицр;ской лЛпаоотке материала? Это зависит от объема
совокупности, т. е. га. На практике моййо руководствоваться при -
мерно следующими правилами:
Количество вариант > Число классов
25—40 - 5—6
40—60 . - 6—8
60—100 7—10Г
100—200 8-12
более 200 10—15
Вариационный ряд при непрерывной изменчивости также мо-
жет быть изображен на. графике. В этом случае нужно строить
гистограмму, т. е. ступенчатую диаграмму, аналогичную изобра-
женной на рис. 2. Классы в данном случае имеют значения 3,0—
3,9; 4,0—4,9 и т. д., но на ось абсцисс достаточно нанести только
начальные значения классов (рис. 3).
Характер распределения вариант в вариационном ряду.
Изучая распределение вариант в вариационных рядах, представ-
ленных в табл. 4,6 и 8 и выраженных в виде графиков на рис. I—
3, легко заметить некоторые общие закономерности, я именно:
1) большинство вариант располагается в средней части вариа-
ционного ряда или около середины вярияпипннай-тгрмапй,
наблюдается максимум вариант, как бы их сгущение: 2) распре-
деление вариНгг-в-ббе стороны от.зтого макСпмУмДболее или
менее симметрично; 3) частота вариант ппгтяпаннд. убыяярт «•
краям вариационного ряда.
Эти закономерности в той или иной степени присущи любому
вариационному ряду,- В дальнейшем мы увидим, что закономер-
ности вариационного ряда основываются на закономерностях
случайной вариации, изучаемы? тдлргёа порпятчпстр^
Классы по весу
Рис} 3.
ВОПРОС ы
Г. Что такое совокупность? При-
меры различных совокупностей.
2. Че# отличается выборочная со-
вокупность от генеральной?
* 3. Что такое варианта? Случайная
переменная?
4. Какими могут быть различия-
между отдельными вариантами?
5. Каковы принципы группировки
данных при качественной изменчивости?
При количественной дискретной? При
количественной непрерывной изменчи-
вости?
& На сколько классов надоразби-
вать фактические данные при количе- 25 кроликов по'весу.
19
етвенной изменчивости? Целесообразно ли замечать 10—15 классов, когда\
л<100?
7. Что такое вариационный ряд? Особенности распределения вариант в ва-
риационном ряду.
8. В чем разница между гистограммой и полигоном распределения?
9. Каковы возможные причины многовершинности вариационных кривых?
ЗАДАЧИ
1. Было подсчитано число лучей в хвостовых плавниках камбалы:
53 51 52 55 56 49 51 52' 54 56
54 53 52 53 51 55 53 55 53 54
'51 , 51 56 54 54 53 54 54 55 53
52 55 53 53 56 53 52 56 52 52
56 55 50 54 49 54 54 55 54 55
52 51 55 52 55 54 51 54 53 54
54 56 54 55 53 53 56 55 54 53
55 52 53 52 51 55 53 54 51 50
53 54 55 52 55 52 53 50 53 52
58 57 . 57 58 56 57 56 58 57 57
Составьте вариационный ряд и начертите полигон распределения.
2. В 400 к вадратах гемоцитометра было подсчитано число дрожжевых
клеток. Представьте эти фически: данные в виде вариационного ряда, а также гра-
2 2 4 4 4 5 2 4 7 7 4 7 5 2 8 67344
3 3 2 4 2 5 4 2 8 6 3 6 6 10 8 3 5 6 4 4
7 9 5 2 7 ~ 4 4 2 4 4 4 3 5 6 5 4 14 2 6
4 1 4 7 3 2 3 5 8 2 9 5 3 9 5 5 2 4 3 4
4 1 5 9 3 4 4 6 6 5 4 6 5 5 4 3 5 9 6 4
4 1 5 10 4 4 4 6 6 5 4 6 5 5 4 3 5 9 6 4
.3 7 4 5 1 8 5 7 9 5 8 9 5 6 6 4 3 7 4 4
7 5 6 3 6 7 4 5 8 6 3 3 4 3 7 4 4 4 5 3
8 10 6 3 3 6 5 2 5 3 11 3 7 4 7 3 5 5 3 4
1 3 7 2 5 5 5 3 3 4 6 5 6 1 6 4 4 4 6 4
4 2 5 4 8 6 3 4 6 5 2 6 6 1 2 2 2 5 2 2
5 9 3 5 6 4 6 5 7 1 3 6 5 4 2 8 9 4 5 3
2 2 11 4 6 6 4 6 2 5 3 5 7 2 6 5 5 12 7
5 12 5 8 2 4 2 16 4 5 12 9 1 3 4 7 3 6
5 6 5 4 4 5 2 7 6 2 7 3 5 4 4 5 4 7 5 4
8 4 6 6 5 3 3 5 7 4 5 5 5 6 10 2 3 8 3 5
6 6 4 2 6 6 7 5 4 5 8 6 7 6 4 2 6 114
7 2.5 7 4 6 4 5 1 5 10 8 7 5 4 6 4 4 7 5
4 3 1 6 2 5 3 3 3 7 4 3 7 8 4 73144 .
7 6 7 2 4 5 1 3 12 4 2 2 8 7 6 7 6 3 5 4
20
Можно обработать данные по каждым 100 квадратам отдельно и сравнить
полученные четыре вариационных ряда.
3. У 60 валахских овец была измерена длина правого уха (в см):
12* КУ 14 И 13 12 12 12 15 13
Н 12 12 14 12 И 13 12 13 14
11 13 14 12 13 12 12 14 12 14
13 13 12 13 12 13 12 11 И 12
13 14 12 14 13 14 13 12 14 15
10 11 10 11 15 И 16 11 11 11
Составьте вариационный ряд и постройте полигон распределения.
4. Количество птенцов в гнездах лесной ласточки Iridoprocne bicolor было
следующим:
4 5 4 5 5 4 5 4 3 5 4 5
6 1 6 4 4 4 5 5 3 5 5 4
6 4 6 2 3 ' 4 5 5 5 5 5 5
4 5 5 6 4 6 2 5 5 3 5 5
5 4 6 4 5 5 5 5 5 5 5 5
5' 5 4 6 7 6 3 5 5 6 5 5
5 4 4 2 4 4 6 2 6 5 4 5
5 5 5 5 4- 5 4 6 5 4 7 5
5 5 6 6 4 4 4 6 5 4 3 5
5 7 5 5 5 5 4 3 7 6 4 4
Составьте вариационный ряд. Постройте полигон распределения.
5. Представьте в виде вариационного ряда и графически данные о длине
Листьев садовой земляники (в см):
8,2 9,7 5,6 7,4 8,0 6,4 6,6 6,8 8,4 7,1
9,0 6,0 7,6 8,1 11,8 5,8 9,3 7,3 8,2 7,2
7,2 6,4 7,7 9,0 8,1 7,1 7,1 8,8 7,5 9,2
7,5 6,8 7,0 6,4 7,4 8,2 6,3 7,0 8,1 10,0
7,0 7,1 8,7 6,3 8,6 7,7 7,3 8,0 8,4 9,3
7,3 6,0 7,7 6,1 9,6 7,4 7,2 7,2 8,7 7,5
9,1 6,4 8,3 6,5 8,2 7,2 6,9 -6,9 8,2 9,0
7,4 8,0 8,4 7,0 7,1 7,4 6,6 6,4 8,3 7,9
8,3 7,2 7,2 6,6 6,6 7,7 8,7 5,6 7,5 5,7
6,9 7,4 7,2 6,2 6,9 6,8 9,2 9,2 7,1 6,5
5,2 8,0 7,1 8,4 8,1 6,8 6,1 6,8 7,9 8,0
5,6 7,8 7,2 8,8 6,6 6,6 5,6 8,1 9,0. 8,4
7,1 7,4 8,7 8,9 7,8 7,3 8,6 8,7 8,2 8,9
6,4 8,6 7,8 5,7 8,5 10,4 8,6 7,7 8,1 8,2
8,5 7,8 7,9 7,5 6,7 7,0 7,9 7,5 8,7 6,8
8,1 7,8 7,8 8,2 7,2 7,9 9,5 7,6 7.0 7,0
7,7 8,1 7,3 7,0 7,4 7,6 8,4 7,3 5,9 9,4
7,8 7,0 7,6 6,6 7,5 9,3 8,1 7,4 ‘ 8,6 8,2
8,0 7,0 7,0 10,2 6,3 9,6 8,4 8,4 8,0 7,4
8,0 6,2 6,8 10,3 8,5 7,0 7,8 8,1 7,0 7,2
Можно взять для обработки не 200 вариант, а только 100.
21
WWnH»*»'•iiiBBrt-ittocwi (в мм i> у оленьихмыш ей Peromyscus manicu-
latus в возрастё одного 58' 57< года: 64 61 56 65 63 58 63
60 59 61 54 58 66 67 63 63
61 60 58- 57. • 65 61 60 68 ' 64
63 56': 59 64 61 64 57 ч 60 63
58 > 52 60 59 57. 61 54 58 64
62 59 60 63 60 60 64 59. 63
63 59 62 63 61 65 61 64 57,
59 ' 54 .64 63 57. 59 59 . 58 63
63 62 62 60 62 57 56 60
. бз 57 63. 61 59 61 59 ‘ 60
- Составьте вариационный ряд. Постройте график. Обратите внимание на
количество необходимых классов и размеры классового промежутка.
7. Изучен живой вес 63 телят холмогорских помесей при рождении (в кг):
27 32 32 31 32 28 37 35 26 28
32 39 34 30 37 26 27 40 35 37
28 43 26 - 35 . 45 26 35 32 32 35
35 28 32 36 32 36 37 ' !|3 28 ' 31
36 33 33 28 23 26 34 32 36 27
32 39 30 30 36 38 24 32 30 31
28 36 36
Составьте вариационный ряд и изобразите его взять величину классового промежутка? 8. Обхват тела (в мм) у густеры оз. Швакшта числами (л s= 80): на графике, выражался Какую надо следующими
80 -75 78 85 78 85 80 77 83 85
88 94 95 86 80 73 78 90. 95 90 • . /
80 75 83 7Q 78 83 75 78 86 81
62 7.7 75 73 80 80 74 73 82 72
80 .90 80 78 60 65 75 72 64 67
74 80 68 75 76 65 70 78. 75 83
85 70 88 73 56 75 70 73 68 66
65 66 Я 78 63 68 6? ’ 70 60 56
Составьте вариационный ряд и начертите гистограмму.
9. Длина тела у 77 экземпляров плотвы оз. Швакшта была следующей
в мм):
143 157 148 153 . 150 142 164 139. ф 140
143 120 144 130 138 124 127 137 139 129
128 119 120 138 130 114 126 138 ' 117 132
130 145 140 153 137 142 145 137 141 125
148 138 140 I# 135 139 125 13> 131 120
127 118 120 124 134 111 132 133 100 132
143 134 138 “ 130 135 133 134 151 . 107 ПО
94 95 142 148 136 165, 172 ,
Составьте вариационный ряд и, начертите гистограмму.
„10’ 11№на верхнего ау&г'у тающего Acropitbecua rlgldus была следующей (в мм): ископаемого млекойи-
6,8 6.2 6,3 6,1 6,1 5,7
6,5 6,0 6,1 5,8 6,3 ^2
6,2 5,4Ч 5,9 6,0 5,7 5,9
6,1 6,7 6,2 6,5 6,2 6,1
6,2 5,7 6,1 5,7 5,9 6,0
5,7 5,9 6,1 5,9 6,0 6,1
Составьте вариационный ряд и начертите гистограмму. Какие размеры клас-
сового промежутка следует выбрать при составлении данного ряда?
11. Составьте вариационный ряд и изобразите его графически для следую-
щих данных об удоях коров за 300 дней лактации (в кг):
3586 2761 2825 . 3807 3858 3904 3530 1951 2362 2729
3453 2635 3752 2666 3331 923 2948 3428 2574 2581
3165 2361 4055 2440 2763 2838 2893 2461 791 4011
2148 2144 2856 2293 3246 2955 3920 3205 2949 2559
2358 2766 2849 3420 2833 3528 3250 1474 2632 2108
2580 3468 903 3027 3177 3666 3242 2715 2730 2748
3115 2330 3339 2033 1850 2093 3642 3736 3847 4080
3847 2934 3676 4155 3306 3734 2199 2468 2448 3293
3465 2540 4288 3685 4708 3758 2735 3363 3306 3511
4052 3380 3154 4571 1426 2981 3224 1480' 1586 1953
2340 2520 2855 2600 3711 3073 3708 4167 4526 1600
1360 2192 2690 3390 3350 3009 3940 '3510 3658 2326
3445 3170 2271 2007 2107 4901 3002 2934 3007 1687
3458 4915 3090 1917 3382 4773 2331 1420 3656 1966
3651 4174. 1274 2247 3859 1548 2620 3564 4507. 2562
4659 4985 2132 3047 4582 2815 2973 4305 2340 3043
3021 4194 2654 3001 5190 2665 3230 5235 3936 4980
3148 3015 1785 2088 2026 2390 2064 4207 2540 4853
1450 2118 2936 4510 4216 " 3315 2821 3431 3354 4106
1501 2454 3287 4580 1965 1563 3559 3401- 2728 3491
ГЛАВА 2
' СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ
ДЛЯ ХАРАКТЕРИСТИКИ СОВОКУПНОСТИ ч
Размах вариационного ряда и лимиты. В предыдущей главе
раскрыты способы сведения данных, составляющих статистиче-
ские совокупности, в вариационные ряды. Каждый вариационный
ряд и его графическое изображение — это как бы «сгущение»
исходного фактического материала, превращение его в нагляд-
ную форму. Однако этого недостаточно; Очень важно получить
характеристики для совокупности, которые были бы выражены
цифровыми показателями. С их помощью можно было бы сравни-
вать разные ряды. Одним из простейших способов количествен-
ной характеристики вариационного ряда является указание на
его размах, т. е. на верхнюю и нижнюю его границы, которые
обычно называют лимитами. Если, например, известно, что вари-
ационный ряд по молочной продуктивности одного стада коров
имеет размах от 2000 до 4000 кг, а другого — от 2500 до 6800 кг,
то, казалось бы, можно сделать вывод о более высоком качестве
второго стада. Однако лимиты не указывают на то, как распреде-
ляются По изученному признаку отдельные члены совокупности.
Вот почему для характеристики совокупности нужны такие по-
казатели, которые отражали бы свойства всех ее членов.
Две группы показателей для характеристики вариационных
рядов. Вариационные ряды могут различаться: я) по тому зна-
чению признака? вокруг которого конпентпируётся большинство
вариант, Эта..внадинце признака отражает как .бы уровень раз-
вития признака в данной совокупности, дли., иначе, центральную
тенденци^Ояда»степени вариации
вариант вокруг уровня, пр степенц..отклонения „от. центральной
тенденции ряда, ~ " -
Соответственно этому статистические показатели разделяются
на две группы: показатели, которые характеризуют центральную
тенденцию, или уровень ряда, й показатели, измеряющие степень
вариации.
К первой группе относятся различные средние величины: мо-
да, медиана, средняя арифметическая греттмяпгеометрическая
КО второй — варияпипнный пазмя^прпнее абсолютное отклоне-
24
ние, среднее квадратическое отклонение^варианса^ (дисперсия),
коэффициенты асимметрии и вариации. Существуют еще и дру-
гие показатели, но их мы не будем рассматривать, так как они
редко применяются в биологической статистике. .
Мода и медиана. При изучении распределения самок лисиц
по числу щенков в помете обнаружилось, что 39 самок из общего
числа 80 имели по 4 щенка, т. е. класс «4 щенка» обладал наи-
большей частотой. Такой класс был назван модальным. Значение
же модального класса называют модой. Мода обозначается сим-
волом Мо. Величина моды является как бы типичной для всей
совокупности. Действительно, в нашем примере почти половина
самок из 80 имела в помете именно 4 щенка.
Для ряда распределения змей по числу хвостовых щитков
(табл. 6) модальным является класс «46—48 щитков». А так как
класс здесь охватывает несколько значений вариант, то для его ха-
рактеристики надо вычислить среднее значение класса. Оно равно
46~^~48 = 47. В таком случае Мо = 47 щиткам. Точно так же
для ряда распределения кроликов по весу (табл. 8, левая часть)
среднее значение модального класса = 5,2. Мо = 5,2 кг.
К числу средних величин относится также медиана. Медиа-
на — это значение варианты, находящейся точно в середине ряда
(обозначается Me).
. Чтобы найти такую варианту, надо сначала расположить все
варианты по порядку от минимальных их значений до максималь-
ных. Такое расположение вариант называют ранжировкой.
В табл. 7 веса 25 кроликов представлены в ранжированном виде.
13-я по счету варианта разделяет ряд из 25 вариант точно попо-
лам. Её значение — 5,3 кг. Это число и является медианой данно-
го ряда.
Чтобы определить Me при четном числе вариант, надо взять
значения двух соседних срединных вариант, например при п=80
значения вариант с порядковыми номерами 40 и 41, и разделить
их сумму на 2. В примере, представленном в табл. 4, обе эти
варианты будут иметь значения «4 щенка», следовательно, Me
данного ряда — 4,0. . <
Медиана И мода дают известное представление о совокупно-
сти в целом. Они .характеризуют своего рода типичное в данной
совокупности (конечно, речь идет только о каком-то определен-
ном признаке).
Использование моды и медианы в-биологии в настоящее вре-
мя довольно ограничено, но в некоторых случаях без них очень
трудно обойтись, в частности, если полученные данные не явля-
ются чисто количественными, а поэтому не могут быть представ-
лены в виде точного вариационного ряда. Так, например, тя-
жесть заболевания подопытных животных или их упитанность
можно условно оценивать степенями: слабая, удовлетворитель-
25
•— или ЙДЙО д т. д. Тогда мода
нлймедиана могут достаточно хорошо характеризовать типичное
В совокупности.
' Обычно же, когда изучаемая совокупность достаточно., одно-
родна и вариация внутри нее чисто количественная, выгоднее
, пользоваться другимих:редними величинами.
Средняя арифметическая и ее свойства. Нахождение средней
арифметической—это в сущности замена индивидуальных варьи-
рующих значений признаков отдельных членов совокупности неко-
торой уравненной величиной при сохранении основных свойств всех
членов совокупности. Этому условию в наибольшей степени удов-
летворяет так называемая средняя арифметическая, обозначаемая х
(ранее обозначали М).
Представим себе, что ряд членов совокупности, т. е. ряд зна-
чений случайной переменной хъ х„ ..., х„, заменим таким же ря-
дом из одинаковых величин х>т. е.
7, х, х, .. .,х (п раз).
Тогда сумма всех ^вариант совокупности^ xt + х2 + хя + .. ,-f- ха
будет равна х + х + х + ... + х(л раз), т. е. пх. Сумму всех ва-
риант совокупности можно сокращенно обозначить £хг (xz—обоз-
начает значение любой варианты; греческая буква S—большая сиг-
ма-—обозначает суммирование; конкретные суммы часто обознача-
ют также латинской буквой S). Тогда S xi — пх, откуда
' т- <«)
Иногда пишут также
(la)
В математической статистике суммирование обозначают бо-
лее сложным способом, а именно: вверху над знаком суммы 2
записывают количество суммируемых единиц (в данном слу-
чае п), а внизу символ ряда i=l. Это значит, что ряд охватывает
варианты от первой до n-й. Прй таком обозначении формула (1а)
для средней арифметической может быть записана и так:
Мы получили наиболее общую и в то же время наиболее
простую формулу средней арифметической. Для того чтобы вы-
* При вычислении средней арифметической можно было бы обозначать
— ' t
варианты просто е. Тогда х» —. Однако в некоторых случаях, как это будет
видно в последующих главах, лучше обозначать любуй варианту более точно»
f символом I, т. е> х<.
26 .
кайлить срёДНю»о ариФметичясвую доетяточно сложить значения
Йех пяри^нт (ня <шетя*/илй яр^фмпметр<>) и сумму разделить
на общее'число вариант. В простейших случаях так и-делают.
Приведенные в табл. 7 веса 25 кроликов в сумме Составляют
131,8 кг. Тогда-
7 = 4г-= 5,27 кг.
Очевидно, в таких случаях можно пользоваться данными, по-
лученными непосредственно при анализе членов совокупности,
не прибегая к группировке вариант.
Однако при большом количестве вариант этот прямой способ
определения средней арифметической по указанным формулам
оказывается не столь удобным, как кажется (если только, конеч-
но, нет арифмометра). Кроме того, при его применении нет воз-
можности вычислить некоторые другие биометрические показате-
ли. Поэтому на практике часто пользуются окольными методами
вычисления средней арифметической на основе уже сгруппиро-
ванных данных. Эти методы будут разобраны позднее.
Окольные методы вычисления средней арифметической, а
также возможности оперирования средними арифметическими
основаны на определенных математических свойствах средних
арифметических^ которые можно изложить в простой форме без
специального доказательства следующим образом.
1. Если каждую из вариант совокупности, для которой' вычис-
ляется средняя арифметическая, увеличить или уменьшить на одну
и ту же величину, то и средняя арифметическая соответственно
увеличится или уменьшится на столько же. В алгебраическом вы-
ражении это означает, что если совокупность хь х*, х3, .... х„,
.имеющая среднюю арифметическую-х, будет заменена совокупнос-
тью (xt— а), (х2 —а), (х8—а)....(х„—а), то средняя арифмети-
ческая для новой совокупности будет равна' х—а.
2. Алгебраическая, сумма отклонений отдельных вариант от сред-
ней арифметической (т. е. разностей между каждым конкретным
значением признака и средней арифметической) равняется нулю:
' (Х1— 7) + (х2—7) + (х3—х) + ... 4* (хя —х)"= О
или
E(xz—х) = 0.
Это положение очень важно для понимания сущности - средней
арифметической как своего рода равнодействующей для всех варь-
ирующих величин совокупности. В то же время оно даёт возмож-
ность проверить правильность вычисления средней арифметической.
3. Сумма* квадратов отклонений от средней арифметической
меньше суммы квадратов отклонений от любой другой величины* Л,
Не равной х, т. е. S (xz-— х)* < S(xz —А)*, если А не равно х. _
, .Два последних положения позволяют применить непрямой -
27
способ вычисления средней арифметической и других биометри-
ческих показателей с (помощью условной средней Л.
Значение средней арифметической и ее сущность. Средняя
арифметическая, как и некоторые другие средние, известна из-
давна. Она имеет очень большое значение в науке и технике. Нет
буквально ни одной биологической работы, в которой не встре-
чались бы в той или другой форме средние арифметические.
Средняя арифметическая является обобщающей величиной,
которая как бы впитывает в себя все особенности'да иной сово-
купности или ряда распределений. Она отражает уровень всей
совокупности в целом, дает сводную, обобщенную Характеристи-
ку данного* изучаемого признака.
Цифровое значение средней арифметической как таковое мо-
жет не встретиться ни в одном конкретном случае в совокупности.
Может оказаться, что ни одна варианта не будет ей равной. Если
среднее число щенков у серебристо-черных лисиц рдвно 4,7, то,
очевидно, фактическое число щенков никак не может быть дроб-
ным. В этом смысле средняя арифметическая является абстрак-
тной величиной. Но в то же время она и конкретна. Она выража-
ется в тех же единицах измерения, что и варианты ряда. При
определении средней арифметической взаимопогашаются, отме-
таются случайные колебания, отклонения от центральной
тенденции, от уровня вариационного ряда и выступает общий
закон явления. Вскрывается типичное для всей совокупности
в целом.
В то же время нужно предостеречь от возможных ошибок в
понимании средней арифметической. Средняя арифметическая харак-
теризует всю совокупность в целом, а не отдельные члены совокуп-
ности. Среднее число щенков в помете лисиц 4,7 относится толь-
ко ко всей группе, каждая же отдельная лисица характеризуется
своим числом щенков в помете—от 1 до 9. Далее, средняя имеет
смысл только по отношению к качественно однородной совокуп-
ности. Так, нельзя .вычислять средний вес животных для группы,
включающей и молодняк разных возрастов и взрослых животных.
Надо взять каждую возрастную группу отдельно и для них вы-
числить х. Поскольку средняя арифметическая относится к данной’
совокупности, перенесение ее на явления, выходящие за. ее рамки,
рискованно без специального анализа вопроса о правомерности та-
кого перенесения. В дальнейшем мы увидим, что особое место в
вариационной статистике занимает вопрос о том, каким образом
на основе данных о той или иной частной совокупности можно
делать выводы о других совокупностях подобного же, рода.
Наконец, средняя относится лишь к отдельным изучаемым
признакам и не может быть автоматически перенесена на их
сумму.
Измерение вариации. Вариационный размах и средние откло-
нения. Средняя арифметическая указывает на то, какое значение
признака наиболее характерно для данной совокупности. Но са-
29
ма по себе она еще-недостаточна для характеристики совокупно-
сти, так как главной особенностью совокупности является нали-
чие разнообразия между ее членами, т. е. вариации. Если бы не
было вариации, то информацию о совокупности можно было бы
получить по одному члену совокупности. При наличии же вариа-
ции эта информация должна быть основана на учете характера
и степени вариации.
Учет вариации того или другого признака в совокупности
имеет очень большое значение для биолога, так как всякая вариа-
ция в популяции животных или растений в конечном счете отра-
жает различия между организмами — в их наследственной при-
роде и в тех условиях, при которых они выращивались. Приемы
работы с животными должны меняться в зависймости от харак-
тера их вариации. Без оценки вариации невозможно и сравнение
двух совокупностей.
Два стада коров могут иметь очень близкие средние удои,
но в одном величины удоев сильно различаются, в другом же ко-
ровы представляют собой довольно однородную группу с неболь-
шим размахом колебаний,
Определение вариационного размаха, т. е. разницы между
максимальным и минимальным значениями вариант, может в
известной степени указывать на степень вариации, но оно недо-
статочно. Во-первых, крайние величины в рядах не очень устой-
чивы, и при изменении количества изучаемых особей они легко
сдвигаются. Во-вторых, при одних и тех же пределах вариации-
распределение отдельных вариант в рядах может быть различ-
ным. ,
Иллюстрацией сказанного является распределение частот по
классам в трех вариационных рядах, представленных в табл. 9.
Ряды 1 и 2 имеют одинаковые значения крайних классов,- но рас-
пределение частот в них различно. Ряд 3 близок по характеру
распределения частот к ряду 1, однако он более растянут и охва-
тывает-болыпе классов.
Вот почему для характеристики различий между отдельными
значениями случайной переменной х, иначе говоря, вариации меж-
ду членами совокупности нужен такой показатель, который обоб-
щал бы колеблемость всех вариант. Для этого надо сравнивать
варианты или друг с другом, или с какой-то одной постоянной
величиной. В 'качестве последней лучше всего взять среднюю
арифметическую. Мы уже видели, что каждое значение хх, х2, хя,
х4, ..., хп в какой-то степени отличается от х, т. е. отклоняется
от средней арифметической в сторону плюса или минуса. Каза-
лось бы, наиболее простым способом .характеристики вариации в
совокупности было бы сложить все значения (х,—х), т.е. получить
сумму (xt—х) и разделить ее на_и. Но, согласно второму свойству
средней арифметической, S (xt—х) = 0. Поэтому для получения по-
казателя, носящего название среднего отклонения Или среднего
29
Таблица 9
Распределение частот по классам
в 3 вариационных рядах
'Частоты
Классы
ряд 1
ряд 2
ряд 3
1
' 2
' 3
4
5
'б
7
8
9
10
11
1
6
14
6
1
3
6
10
6
3 х
1
1
3
9
20
40
20
9
3
1
I
п = 28
п = 28 п =т 108
абсолютного отклонения, брали сумму отклонений вариант от
х, т. е. разницу между значением каждой варианты и х, без уче-
та знаков и делили ее на л, т. е. долучали величину
2|хг-7|*
ч п
Раньше этим показателем Довольно широко пользовались/
Однако оказалось, что среднее отклоненйе не улавливает истин-
ной закономерности вариации,^. е. рассеяния вариант в совокуп-
ности или вариационном ряду вокруг средней арифметической.
Варианса и среднее квадратическое' отклонение. Более совер-.
шенными показателями, характеризующими вариацию, являются
средний квадрат отклонений вариант отсредней арифметической,
иначе называемый вариансой** и среднее квадратическое откло-
* Скобки в виде прямых, вертикальных линий указывают на то, iro зна-
чения в скобках надо брать без учета знаков, поэтому разница всегда поло-
жительная.
*♦ В литературе (советской и зарубежной) существует разнобой в тер-
минах. Так, в нашей литературе средний квадрат отклонений нередко назы-
-вают дисперсией, иногда же девиатой. Однако на различных языках мира его
называют вариансой (англ, variance, нем. Variant, фр. variance, польск. wa-
riancja), поэтому и по-русски, на наш взгляд, правильнее употреблять термин
варианса. Словом же дисперсия мы будем обозначать самый факт варьирова-
ния, т. е. разброса, рассеяния переменных величин.
39
Вариансу обраначШУ
tr2 (греческая буква ,сигма) или s* {латинская буква эс), а сред-
нее квадратическое отклонение — о, или s. В специальной Литера-
туре греческие и латинские обозначения относятся к различным
типам совокупностей, в' частности в применении к конкретным
выборкам часто пишут s2 и s. Но так как в советской литературе
является привычным обознанение среднего квадратического от-
клонения через а, мы> решили сохранить это обозначение и для
выборочной совокупности, хотя, как это будет видно из дальней-
шего изложения, значения этого показателя для генеральной и
выборочной совокупностей, о которых говорилось на стр. И, не
совсем одинаковы., • —
По самому смыслу варианса и среднее квадратическое от-
клонение должны определяться следующим образом:
°8 = -------- и а = у .
Это можно сформулировать так: варианса — это сумма квад-
ратов отклонений отдельных значений вариант от вредней ариф-
метической, деленная на общее количество вариант, а среднее
квадратическое отклонение — корень квадратный из этого част-
ного. Хотя после'извлечения корня квадратного получаются зна-
чения со знаками плюс и минус, обычно берут только положи-
тельное значение.
Однако приведенные формулы были бы верны, если бы сред-
нее квадратическое отклЬнение вычислялось для генеральной сово-
купности, т. е. в этом случае брали бы отклонения от средней
арифметической генеральной совокупности (обозначаемой [*), п бы-
ло бы объемом генеральной совокупности. Фактически же вычис-
ления можно проводить только по данным о выборочной совокуп-
ности, для которой и известны хил. Оказывается, что Сели
вычислять s и а* по указанным выше формулам, то получится за-
ниженная, или, как говорят в'статистике, смещенная (щенка ва-
риации в совокупности*.
Именно поэтому во многих руководствах их значения для вы-
борочных совокупностей обозначают иными символами: а и А
Чтобы устранить получающуюся неточность и получить несме-
щенные значения вариансы и среднего квадратического отклоне-
ния, следует применить следующие формулы:
, =
п — 1
или
(2)
л * Подробнее об этом см. б кн. Юл и Кендэлл. Теория статистики, стр. 541—
Урбах В. Ю. Биометрические методы, стр. 104—106.
31
и •
О)
Степени свободы. Величина п — 1 получила особое назва-
ние — число степеней свободы (точнее, число степеней свободы
вариации). Мы будем обозначать ее буквами df. Так как во
многих разделах статистики приходится пользоваться числом
степеней свободы, то следует объяснить его значение.
Выше уже указывалось, что если известен ряд от Xi до хп,
состоящий ‘на п членов или наблюдений, то для него общей
характеристикой является средняя арифметическая. Возникает
вопрос, как может быть определено каждое отдельное значение
ряда. Очевидно, его всегда можно узнать,.если известны средняя
арифметическая и остальные наблюдения, т. е. п-— 1. Иначе го-
воря, определение одного значения в данной совокупности зави-
сит от остальных значений. Так, напрцмер, если известно, что
2 кролика в сумме весят 6 кг, а один из них весит 2,5 кг, то вес
второго уже точно определен весом первого, т. е. имеется лишь 1
степень свободы (2—1 = 1). Если 3 кролика весят 5 кг,' то вес
одного всегда точно определяется весом двух других, между ко-
торыми уже возможна вариация, т. е. в этом случае имеются
2 степени свободы (3—1=2) и т. д.
В общем виде при численности членов совокупности п число
степеней свободы df = n — 1. Вот почему точнее вычислять о® и о,
пользуясь знаменателем п — 1. При большом п разница между п
нп — 1 настолько невелика, что она мало отразится на значении
вариансы (и сигмы). Но при малом п разница будет значительна.
Так, если п = 6, а сумма квадратов отклонений равна 60, то сред-
ний квадрат отклонений от средней арифметической будет равен
не -у- = 10,0, а == 12,0. Поэтому надо разделить сумму квад-
ратов отклонений на число степеней свободы, т. е. на n — 1 = 5.
В некоторых случаях, как это будет видно в дальнейшем, чис-
ло степеней свободы вычисляется более сложно.
Таким образом, исходным началом для вычисления вариансы
и среднего квадратического отклонения является сумма квадратов
отклонений от х, или просто <сумма квадратов». Сумма квадратов
и средний квадрат — это две важнейшие величины, широко исполь-
зуемые во многих вычислениях.
На сумме же квадратов построены ойень многие формулы,
применяемые в различных разделах биологической статистики.
Как будет показано в дальнейшем, из этих общих формул (2) и
(3) были выведены различные рабочие формулы, более удобные
для вычислений, хотя некоторые из них менее точные, чем общие
(2) и О).
Вычисление статистических показателей для данных, не сгруп-
пированных в вариационный ряд. Если, отдельные варианты сово-
32
купности не сгруппированы в вариационный ряд (а иногда и нет
смысла это делать, например, при малой численности изучаемых
животных или малом числе наблюдений), то можно вычислить х,
о2 и с с помощью формул (2) и (3). Тогда целесообразно составить
подсобную табличку, в которую должны быть записаны значения
всех вариант, как это показано в табл. 10.
Таблица 10
Процент жира в молоке 10 опытных коров
Процент жира х^ *1 — Х (*г-*)*
4Д 0,4 0,16
3,8 0,1 . 0,01
3,5 “0,2 0,04
4,0 о,з 0,09
, 3,9 0,2 0,04
3,8 1 0,1 0,01
3,7 0 0
3,6 “0,1 0,01
3,2 —0,5 0,25
3,4 —0,3 0,09
Sxj = 37,0 2 = 0,70
.
х = 3,7
По формуле (1) определяем среднюю арифметическую:
“ 37,0 о *7 л/
. х = = 3,7% жира.
После определения х могут быть заполнены вторая и третья
графы таблиц. Подсчитывать 2 (х, — х) не обязательно, так как она
должна быть равна нулю (согласно указанному выше второму
свойству средней арифметической). Но все же полезно это сделать
для проверки, не допущена ли ошибка в вычислении^ л
По формулам (2) и (3) определяем:
_ 0J0 = 0 0777; G = Y QffnT = 0,28% жира.
Если в качестве знаменателя взято п, а не л— 1, 'то значений
вариансы и среднего квадратического отклонения окажутся нес-
колько заниженными:
а2 = = 0,0700; о = |/0Х)70б = 0,27% жира.
Прямой способ вычисления статистических показателей для
данных, сгруппированных в вариационный ряд. Если все вариан-
• 2 П. Ф. Рок и цк ий z 33
ты разнесены по классам, каждый из которых характеризуется
определенным значением вариант и частотой, то среднюю арифме-
тическую можно вычислить по формуле
где f — частота класса, X — значение класса и п — общее коли-
чество вариант. _
Вычисление S(xz— х)2 при большом числе вариант довольно
трудоемко, особенно если отклонения выражаются дробями. Но
так как
S (xz — х)2 = S xf — = ZfXi —
fl fl
то можно обойтись без вычисления отклонений вариант от сред-
ней арифметической.
Рабочие формулы для вычисления о2 и ст тогда будут следую-
щими:
. °2 = -п-г” ; (5)
• (б)
Эти формулы отличаются от формул (2) и (3) числителем.
В качестве примера используем вариационный ряд, приведен-
ный в табл. 4, прибавив в табл. 11 дополнительные графы, нуж-
ные для вычислений по формулам (5) и (6).
Таблица 11
Вычисление х и а для ряда распределения 80 самок серебристо-черных
лисиц по количеству щенков в помете (X)
^Значение класса X . Частота f fx /Х2
1 1 1 1
2 4 8 16
3 10 30 90
4 39 156 624
5 13 65 х325
6 7 42 252
7 3 21 147
8 2 16 128
9 1 9 81
• п = 80 2 = 348 2 = 1664
34
В таком случае
х = -gg- = 4,35 щенка;
1/1664-W 1/1“ ,__
о = у ----79---= V 79 = }/1,9 = 1,38 щенка;
оа=1,9.
В указанном примере X является единственным значением
класса и выражается целым числом (вариация является дискрет-
ной). В тех же случаях, когда класс охватывает несколько значе-
ний вариант, как в табл. 6 (змеи) или в табл. 8 (кролики), надо в
качестве величины X взять среднее значение класса, сложив на-
чальные и конечные цифры класса и разделив сумму пополам.
Например, в табл. 6 (первая строка) среднее значение класса бу-
дет равно 4042 = 41, в табл. 8 (правая сторона) 3-°+.3,9. 3,45«
Такой способ вычисления средних значений классов иногда
вызывает сомнения и неясности. Но дело в том, что любое коли-
чественное значение варианты включает в себя и близкие к нему
значения. Так, если мы округленно записываем вес кролика 3,0,
то это значит, что такой цифрой будут характеризоваться также
кролики с точным весом 2,950 кг, 2,960, 2,970 и т. д., а также
3,010 кг, 3,020, 3,025, 3,040, кончая 3,049 кг. Кролик с весом
3,05 кг попадает, очевидно, в группу кроликов с округленным ве-
сом 3,1 кг. Точно так же и вес 3,9 кг включает веса от 3,850 до
3,949 кг.
Таким образом, если фактический класс записывается, как
3,0—3,9, то подлинный класс охватывает более широкий интервал
от 2,950 до 3,945 кг. Тогда легко рассчитать, что середина этого
„ .с 3.0 + 3.9
интервала приходится на величину 3,45, т. е. она равна —j-
Для вариационного ряда числа щитков у змеи вычисления бу-
дут довольно легкими, так как средние значения классов X выра-
жаются целыми числами. Для вариационного же ряда весов кро-
ликов значения X будут дробными, и поэтому прямой способ вы-
числений по указанным формулам (5) и (6) потребует громоздких
подсчетов. В таком случае выгоднее применить иной, непрямой
способ вычислений х и о с помощью условной средней.
Непрямой способ вычисления статистических показателей.
В качестве условной средней А можно взять любую величину, од-
нако выгоднее всего для большей простоты вычислений выбрать
такое значение fl, которое было бы близко к средней, о чем мож-
но судить по расположению частот в вариационном ряду. Практи-
чески это значит, что УСЛОВНЕЙ средней Л vcwMo-gMHTim- чт е-
ние того класса, в котором располагается наибольшее количество
вариант или который находится примерно в середине ряда. Кроме
2* 35
того, А должно быть целым числом. Это упростит все расчеты.
В дальнейшем вместо вычисления отклонений всех' вариант сово-
купности от средней арифметической х берут их отклонения от
принятой условной средней А. Часть из этих отклонений будет
иметь знак плюс, другая же часть —минус.
... Если сумма положительных и отрицательных отклонений от А
окажется равной нулю, то условная средняя А полностью совпа-
дает с . истинной средней арифметической х, как это вытекает из
второго свойства средней, арифметической. Если сумма всех откло-
нений окажется величиной положительной, значит, принятая услов-
ная средняя меньше истинной. Если же сумма всех отклонений
будет величиной отрицательной, принятая условная средняя боль-
ше истинной. В обоих случаях для того, чтобы перейти от услов-
ной средней А к средней арифметической х? надо внести в приня-
тую величину А поправку b с тем или иным знаком.
Таким образом, х — А + Ь. Поправка b равна сумме всех поло-
жительных и- отпипательных -отклонений вариант совокупности от
Л, деленной на общее число вариант^ Практически удобнее откло-
нения вычислять не в фактических их значениях, а в условных
(обозначаемых через а), равных 1, 2, 3 или —1, —2, —3 и т. д.,
как это сделано в табл. 12, а в дальнейшем полученную сумму
условных отклонений, деленную на п умножить на величи-
ну классового промежутка i. Тогда
, .2 fa
b —-1-1—.
п
Окончательная же рабочая формула для вычисления средней
арифметической будет следующей:
х = А + Ь = А + №. (7)
Если отклонения с самого начала выражаются в фактических
величинах, тогда, очевидно, сумму отклонений умножать на i не
нужно. Однако предпочтительнее во всех случаях вычисления про-
изводить в условных отклонениях и лишь позднее учитывать ве-
личину I. __
Средняя арифметическая х часто выражается числом £ десятич-
ной дробью, имеющей несколько знаков. Отклонения от х <уг^лъ-
ных вариант, т. е. (х{—х), будут также дробными величинами,
возведение которых в квадрат усложняет вычисления.
Среди свойств средней арифметической было одно, имеющее
прямое отношение к непрямому способу вычисления а и о2, а
именно: сумма квадратов отклонений от средней арифметической
меньше суммы квадратов отклонений от любой другой величины А,
не равной х
36
Значит, сумма квадратов отклонений от условной величины А
всегда больше суммы квадратов отклонений от х, при этом на
определенную величину, а именно: на величину (х— А)г, умно-
женную на п, т. е. _ _
2 (xz — Л)2 = 2 (xt — х)2 + п (х — Л)2.
Отсюда
2 (х(- — х)2 = 2 (х2 — Л)2 — п (х —Л)2.
Замена суммы квадратов отклонений от средней арифметиче-
ской суммой квадратов отклонений от условной средней Л с вне-
сением соответствующей поправки дает возможность составить и ра-
бочие формулы для вариансы и среднего квадратического откло-
нения: _
8 = S(xt-Af-n(x~A)\
п — 1 ’ ' '
а = S(xj —Я)а —п(х —Л)» ф)
В случае, если варианты сгруппированы в вариационный ряд
с частотами /(точнее /(), можно воспользоваться следующими
упрощенными формулами:
О* = — (i - Л)!;
Выше мы указывали, что условное отклонение каждой вариан-
ты от Л можно обозначить через а, тогда истинное отклонение
(х; — Л) = ai. Разница между х и Л, как видно из указанной вы-
ше формулы (7), равна i Подставив эти величины в предыду-
щие формулы, получим окончательные рабочие формулы для а’ио:
= (10)
' (П)
Применим эти формулы к одному из вариационных рядов, ра-
зобранных в предыдущей главе, например к ряду распределения
25 кроликов по весу. Построение табл. 12 является стандартным
для вычисления х и а с помощью условной средней.
В качестве условной средней возьмем среднее значение класса
5,0 — 5,4, т. е. 5,2.* Сумма отклонений от условной средней в
условных же единицах равна + 2. Тогда
* Практически совсем не обязательно заполнять всю вторую графу
табл. 12. Достаточно-только вычислить по указанному выше способу среднее
значение класса, выбранное в качестве А.
37
Таблица 12
Распределение 25 кроликов по весу (в кг)
Классы .Средние значения классов Частоты / Условные отклоне- ния а /в М2
3,0-3,4 3,2 1 —4 —4 16
3,5—3,9^ 3,7 1 —3 —3 9
4,0—4,4 * 4,2 3 —2 —& 12
4,5—4,9 4,7 3 —1 —3 3
5,0-5,4 5,2 7 '• 0 0 0
5,5—5,9 5,7 5 1 5 5
6,0-6,4 6,2 3 2 6 12
6,5—6,9 6,7 1 3 3 9
7,0—7,4 7,2 1 4 4 16
/ = 0,5 кг п = 25 2 — 16 + + 18 =+ 2 2 =82
6 _ = 0,5 • А = 0,04 КГ.
Отсюда
х = А + = 5,2'+ 0,04 = 5,24 кг.
Для вычисления а по формуле (11) надо взять из таблицы
значение 2 fa2 и использовать уже полученную величину
Тогда
а = 0,5 V— 0,082 = 0,5 У 3,2736 = 0,5 • 1,81 = 0,90 кг.
Вариансу в данном случае выгоднее вычислить не по форму-
ле (10), а обратным путем, т. е. возведением в квадрат вычислен-
ного среднего квадратического отклонения. Тогда
а2=0,902 = 0,81.
В разобранном примере i ~ 0,5. Очевидно, что в тех случаях,
когда 1=1 (пример в табл. 4), вычисления х и а будут проще.
Желательно, чтобы средняя арифметическая и среднее ква-
дратическое отклонение вычислялись с точностью по крайней ме-
ре на один десятичный знак большей, нежели значения отдель-
ных вариант. Кроликов взвешивали с точностью до 0,1 кг, сред-
няя же арифметическая и среднее квадратическое отклонение
(5,24 и 0,90 кг) вычислены с точностью до 0,01 кг. Поэтому под
корнем надо было иметь числа с 4 десятичными знаками.
38
Вычисление статистических показателей с помощью условной
средней для данных, не сведенных в вариационный ряд. В неко-
торых случаях целесообразно и для данных, не сгруппированных
в вариационный ряд, применять непрямой способ вычислений х и
ст с помощью условной средней. Отклонения каждой варианты от А,
как обычно, а. В таком случае
S(x»-A).
п
В табл. 13. приведены 20 значений живого веса при'рождении
морских свинок (из пометов с 2 детенышами) и значения (xi— Л)
и (xz — Л)2. Тогда .(*
2(xz — Л) = 5;
Таблица 13
Вычисление хи? для данных о весе (в г)
при рождении 20 морских свинок
Веса при рождении х/ Отклонения от А Х[—А Квадраты отклонений (х/-Л)2
30 0 0
30 0 0
26 —4 ► 16
32 +2 4
30 0 0
23 —7 49
29 -1 1
31 + 1 1
36 +6 36
30 0 0
25 —5 25
34 +4 16
32 +2 4
29 —1 1
28 —2 * 4
27 -3 9
38 +8 64
31 + 1 1
34 +4 16
30 0 0
А =30 2 = 4-5 2 = 247
39
<- = ^ = 0,25;
1 = A + b = 30,0 + 0,25 = 30,25 г.
Среднее квадратическое отклонение по формуле (9).
а = l/2(xi-A)2-n(x-Af‘ 1/ 247-20(0,25)» =
г л —1 У 19
= У 2^- = /1793 = 3,60 г;
ст2 = 12,93.
Взвешенные средние арифметические и средние квадратичен
ские отклонения. Если анализируется сложная совокупность, со-
стоящая из нескольких частных, для каждой из которых уже из-
вестна средняя арифметическая, можно вычислить так называе-
мую взвешенную среднюю арифметическую для сложной сово-
купности по фррмуле
- ^l'll+x^lt+x^l3+•+xknk ....
nl + «2 4" n3 + • • • + nk ’
где xj, х2, х3, ... х* — средние арифметические отдельных частных
совокупностей, a nlt пг, ns, ... ,пк — число членов в каждой част-
ной совокупности (их называют также весами частных совокуп-
ностей).
Всего совокупностей k. Сумма ni + n2+n3+...-{-nk=n.
Можно также определить взвешенную вариансу (и среднее
квадратическое отклонение) для объединенной совокупности по
формуле
02 („!-!) +,2 (П2_1) + ... + фп4-1)
о2 = -----------. (13)
Это будет средняя арифметическая варианс частных совокуп-
ностей.
Возьмем следующий схематический пример. Для трех групп
(частных совокупностей)
«i = 6 Xi = 10 о? = 4
«2 =10 х2 = 12 ст2 = 3
п3=18 х3 = 9 <г- = 2
Тогда
- _ 40-6+12- 10 + 9-18 _ .. ,.
Авзв — 34 ' — *v, 1,
<т8 _4-5 + 3-9 + 2- 17 ...
и взв — 34__з —
овзв= 1 7ёГ= 1,6.
40
Существенно, что знаменатель представляет собой сумму чи-
сел степеней свободы трех отдельных групп, которая в данном
случае равняется п—3.
Различные модификации формул для суммы квадратов, варианс
и средних квадратических отклонений. Как уже указывалось, в
некоторых случаях варианса (и среднее квадратическое откло-
нение) может быть вычислена не по общим формулам (2), (3), а по
рабочим. Среди последних были формулы (5), (6), (8). Все они ос-
нованы на том, что сумма квадратов отклонений вариант от сред-
ней арифметической, т. е. 2(х;— х)2, может быть преобразована
различным образом. Так, например, если принять А равным нулю,
то формула (8) для а2 принимает такой вид:
Иначе говоря, можно получить значение вариансы, вычтя
из суммы квадратов вариант квадрат средней арифметической,
умноженный на п, и разделив эту разность на число степеней
свободы. Таким же образом вариансу можно вычислить и на
основе данных табл. 10. Для этого понадобится лишь графа х2.
Ее легко получить с помощью таблицы квадратов или арифмо-
метра.
Учитывая, что п = 8, для вычисления а2 (и соответствен-
но а) знаменателем надо взять число степеней свободы л—1=7.
Дальнейшее преобразование формулы (14) позволяет еще более
упростить схему вычислений, сделав ее очень удобной, в частнос-
ти, для машинных вычислений. Так как пх — Ех;, то
S х'1 — S х,х
(15)
п — 1
S хI — 2 х,х
И — 1
.(15а)
В этом случае для определения вариансы нужны только: сум-
ма всех вариант (Zx,), сумма квадратов всех вариант (2х?), сред-
няя арифметическая (х) и число вариант или наблюдений (п).
'т' S X/ ,
Так как х — то, подставив значение х в предыдущие фор-
мулы, получим:
(16)
(16а)
Эта формула еще более удобна, особенно для машинных вы-
числений. Приведенная выше формула (5)
является модификацией для случая, когда данные сгруппирова-
ны в вариационный ряд и для каждого класса известны среднее
значение класса X и частота f.
В зависимости от того, какие данные следует обработать и
какие технические возможности имеются для проведения вычис-
лений, можно'применять любую из этих формул. Так, например,
данные табл. 13 о весе при рождении морских свинок могут быть
обработаны с помощью счетной машины на основе следующих
исходных данных:
Тогда
о2
п = 20; X xt == 6Q5; 2 х? = 18547.
х = = = 3°.25 г.
2 xf — xi)2 18547________ 6Q53
_1________= 20 = 245,75
п — 1 19 19 —
В числителе для о2 получено по этой формуле то же число
245,75, как и при применении формулы (9). С помощью различ-
ных формул вычисляется в конечном счете одна и та же величина
в числителе для о2, а именно. S (х, — х)2, т. е. сумма квадратов
отклонений вариант от средней арифметической. Так как сумма
квадратов отклонений представляет собой важнейшую величину
в целом ряде разделов биологической статистики, небесполезно дать
сводку различных ее значений, вытекающих из указанных выше
формул: _
2(х, —х)2
1. &
п ’
2. 2/Х2——^)2;
3. 2х2—пх2;
4. 2 х? — 2 х(х;
5. 2(х(. — Л)2 — п(х —Л)2;
6. 2fa2i2 —ш2/-^2.
' \ п I
Сумму квадратов отклонений от средней арифметической
2(xz — х)2 часто называют сокращенно суммой квадратов. Мы бу-
дем в дальнейшем обозначать ее буквами ss. Из этого списка ра-
42
бочие формулы 1, 3 и 4, как и общая формула 2(xt—х)*, не тре-
буют группировки исходных данных в вариационный ряд.
Вычисление суммы квадратов может быть сильно облегчено
приемом, который носит название кодирования. Он заключается
в том, что фактические варианты уменьшают на какую-либо ве-
личину, с новыми их значениями проводят все необходимые дей-
ствия, а в окончательный результат вносят поправку.
Допустим, что изучают 10 телят, веса которых (в кг): 106, 117,
124, 127, 128, 131, 136, 141, 145 и 158. Из этих значений вариант
можно вычесть по 100 кг и к оставшимся величинам применить
первую формулу для суммы квадратов. Тогда
2Xi = 6+ 17+24 + ...+58 = 313;
2х;2=62 + 172+...-Ь582= 11741;
2(xz — х)2 = Ц741—1944,1.
Такой же была бы сумма квадратов и в том случае, если бы
были взяты подлинные веса: 124, 127, ..., 158 кг. Чтобы полу-
чить х, надо будет пр ибавить к то число, которое было ра-
нее отнято, т. е. 100:
х = ^+100= 131,3 кг.
При работе с данными, выражающимися десятичными дробя-
ми, удобно их превращать в целые числа, умножая на соответ-
ствующий множитель (10, 100, 1000 и т. д.) и внося в дальнейшем
необходимые исправления в результат.
Из всего сказанного видно, что для определения статистиче-
ских показателей требуется довольно большая вычислительная
работа, но объем ее может быть сокращен правильным выбором
метода, наиболее подходящего для обработки данного материа-
ла, и применением имеющихся технических средств для вычисле-
ний (простые счеты, логарифмические линейки, таблицы квадра-
тов, арифмометры). При наличии счетных машин лучше всего
пользоваться прямым способом вычислений, так как он дает наи-
более точные результаты. Непрямому же способу в силу искус-
ственной разбивки материала на классы всегда сопутствует из-
вестная неточность. Впрочем, она невелика. Поэтому в практиче-
ской работе биологу, не имеющему в руках солидной вычисли-
тельной техники, часто выгодно применить непрямой способ,
даже при некоторой его неточности. Но непременным условием
на всех этапах определения статистических показателей, начиная
со сбора исходных цифр и проведения измерений и кончая вычис-
лениями, является безошибочность расчетов и данных. Малейшая
неточность хотя бы в одной строке таблицы при .возведении в
квадрат или умножении приведет к серьезной ошибке в оконча-
тельном результате.
43
Поэтому для контроля необходимо выполнять повторно все
действия, только в другом порядке, например, складывать числа
второй раз не сверху, а снизу. Кроме того, необходимо строго
выполнять правила приближенных вычислений, обязательно
определяя и следующий знак в десятичной дроби, чтобы правиль-
но округлить предыдущий.
Закон сложения вариации. Выше мы разбирали вычисление
взвешенных средней арифметической и среднего квадратического
отклонения в том случае, когда изучаемые совокупности состоят
из нескольким частных совокупностей или групп, полученных в
результате проведения отдельных опытов или наблюдений в при-
роде. Для частных совокупностей известны их объемы tii,
«2» • • nk, средние арифметические хх, х2......хА, вариансы
о’, of, ..., о| и ’ средние квадратические отклонения Oi,o2.oft.
Однако в общую вариацию объединенной совокупности наряду
с вариацией, измеряемой частными^вариансами of, о|, ..., из
которых может быть получена средневзвешенная варианса по фор-
муле (13), входит также вариация чдртных средних хх, х2, ..., хк
вокруг общей средней х. Поэтому общая дисперсия сложной сово-
купности может быть выражена следующим образом:
О20 = О2А +O2i
где о’ —общая варианса, о/ — варианса, измеряющая вариацию груп-
повых средних вокруг общей средней, и о2 — средняя взвешенная
варианса, получаемая из варианс отдельных групп, т. е. средняя
характеристика внутригрупповой вариации.
Этот общий закон сложения вариации имеет большое значе-
ние, так как он лежит в основе особого метода, носящего назва-
ние дисперсионного или вариансного анализа. Он рассматрива-
ется в гл. 8.
Средняя геометрическая. Средняя арифметическая — наибо-
лее часто применяемый статистический Показатель, в том числе
в биологии. Однако в некоторых случаях; (например, при изуче-
нии темпов роста организмов или роста целых популяций) при-
ходится пользоваться другой средней величиной — средней гео-
метрической. \
Формула для ее вычисления следующая: \
= • х2 • х3... х„ = А (17)
Очевидно, что при ее определении надо исключать варианты,
выражающиеся нулем или отрицательным числом.
* Знак П. является знаком произведения.
44
На практике вычисление средней геометрической производится
с помощью логарифмов по следующей рабочей формуле:
logXg. = -(logXi+logXa+logXa + + logx„), (17а)
т. е. логарифм средней геометрической равен арифметической сред-
ней суммы логарифмов отдельных значений х. По значению logXg.
затем определяется величина xg.
Основным критерием, для применения средней геометрической
является возрастание данного признака путем не арифметическо-
го прибавления к первоначальному значению какой-то величины,
а умножением пропорционально степени.
При таком характере возрастания значений х арифметическая
средняя дает очень неточные результаты, и лучше пользоваться
геометрической средней. Это значит, что надо заменить арифмети-
ческие значения признака ик логарифмами и оперировать в даль-
нейшем уже ими. Так, например, если в пробах планктона были
получены показатели от 4285 до 43 300, то их следует перевести в
логарифмы (log 428 = 2,63; Ipg 43 300 = 4,64 и т. д.), сложить все
логарифмы и разделить на п. Полученное значение logxr потенциру-
ется, и таким образом получается значение средней геометричес-
кой, выраженное в конкретных значениях изучаемого признака.
Коэффициент асимметрии. В некоторых случаях вариационные
ряды могут быть асимметричными, или, как еще говорят, скошен-
ными. Асимметричность рядов отражает важные их особенности.
Асимметрию оценивают разными способами, например, берут раз-
ницу между х и Мо и делят на среднее квадратическое отклоне-
ние. Существует также особый показатель — коэффициент, или
критерий, асимметрии. Будем обозначать его gi (значок 1 ставится
потому, что есть еще один показатель g2 — коэффициент крутизны
распределения, который мы не будем рассматривать).
Формула для вычисления gY следующая:
- п — п 2 (х‘ ~
ё1 ~ (л-])(«-2) KW
или в несколько упрощенной форме
Z(z,-7y •
па3
Использование этой формулы можно продемонстрировать на
данных табл. 10. Нужно только ввести еще одну графу (х, —х)#.
В данном случае S (xt — х)3 будет равна — 0,060. Тогда
_ —0,060 _ ообо _ П97
gl Ю-0,283 0,220
Таким образом, если данные табл. 10 изобразить в виде ва-
риационного ряда, он окажется асимметричным. Знак минус при
(18)
(18а)
45
коэффициенте асимметрии указывает на направление асиммет-
рии. Перевес наблюдений — в правой части ряда, хвост же кри-
вой распределения вытянут влево (левосторонняя асимметрия),
в чем можно легко убедиться, построив полигон но данным
табл. 10. При положительной асимметрии, наоборот, хвост’кри-
вой будет вытянут вправо (правосторонняя асимметрия). Впро-
чем, асимметрия не всегда хорошо выявляется в форме графика,
так как последний сильно зависит от способа разбивки ряда на
классы.
Коэффициент же асимметрии дает вполне объективную меру
асимметрии. Если, он равен нулю, ряд симметричен. При боль-
шой асимметрии он может быть и больше 1.
Коэффициент вариации. Среднее квадратическое отклонение (о)
выражается в тех же единицах, что и х, например: при измерении
веса кроликов —в килограммах и граммах, при измерении глубины
груди крупного рогатого скота — в сантиметрах. Сравнивать вариа-
цию разных групп животных можно только в отношении одного, и того
же признака. Если же одна сигма выражена в сантиметрах, а другая —
в килограммах, судить о том, в каком случае вариация больше, а в ка-
ком меньше, нет возможности. Для сравнения вариации различных
признаков (а также степени изменчивости групп животных разных
видов) применяют так называемый коэффициент вариации (обозна-
чается^и, с.о. или С).
Коэффициент вариации представляет собой отношение ст к х>
выраженное в процентах, иначе говоря, он показывает, какой про-
цент от х составляет ст:
а = °-Л (19)
Для примера применим эту. формулу к вариационным рядам
распределения по различным признакам, а именно: кроликов —
по живому весу, крупного рогатого скота — по промерам груди, ’
коров —по жирности молока.
Для первого из них х = 5,24 кг; о = 0,90 кг;
V= 0’95 24100 =
Для второго х = 73,85 см; о = 2,45 см;
2.45-100 ооп/
v==-73^5-=3’3%<
Для третьего х = 3,8% жира; ст = 0,18% жира;
о = —U100- = 4,7%.
0,0
Наименьший коэффициент вариации характеризует данные по
промерам груди. Очень высокий коэффициент вариации для дан-
46
ных по весу 25 кроликов, что неудивительно, так как в этой
группе были взяты кролики разных пород. Чем более однороден
изучаемый материал (по происхождению, условиям выращивания
и т. д.), тем меньшими окажутся коэффициенты вариации. Одна-
ко даже при достаточной однородности материала степень измен-
чивости различных признаков может быть различной, что зависит
от особенностей самих признаков. Известно, например, что жирность
молока — признак значительно менее изменчивый, нежели удой за лак-
тацию. Если в стаде коров показатели по удою за лактацию х =
= 3000 кг, а ст = 400 кг, жирности же молока х = 3,8 % и о =
= 0,24%, то соответствующие коэффициенты вариации будут
следующими:
по удою 40^0°° = 13,3%;
по жирности молока °’2з810° =6,3%.
В однородном биологическом материале коэффициенты ва-
риации чаще всего бывают порядка 5—10%.
Таким образом, коэффициент вариации дает возможность
сравнивать изменчивость признаков, выражающихся в различ-
ных единицах измерения, и устанавливать различия в степени
изменчивости. Для биолога, животновода, растениевода очень
важно знать, насколько изучаемый ими материал выравнен или,
наоборот, разнороден, в какой степени устойчивы взятые для
сравнения признаки.
Учет изменчивости с помощью коэффициента вариации очень
важен при планировании опытов, устаНовл'ении величины необ-
ходимых опытных групп, а также при оценке результатов опытов.
Так, если ранее было установлено, что изменчивость изучаемых
признаков колеблется в пределах 10—15%, а в опыте были по-
лучены данные, выходящие за эти пределы, то искать допущен-
ную ошибку нужно или в самой постановке опытов, или в вычис-
лениях, или, наконец, предположить, что какое-то непредвиден-
ное обстоятельство повлияло на степень точности опытов.
Известно, что средняя арифметическая и среднее квадратичес-
кое отклонение некоторых признаков изменяются более или менее
параллельно в зависимости от возраста, сезона года и других
причин.-Величина а также может иногда увеличиваться и в связи
с увеличением самой х. В таких случаях удобно пользоваться
коэффициентом вариации, так как он оказывается более устойч и-
вой величиной. Как указано, v определяется на основе уже извест-
ных х и ст. Но, зная v и х, можно определить о.
Однако одного коэффициента вариации явно недостаточно для
характеристики совокупности. Он является лишь дополнительным
показателем, полезным при наличии ~х и о (или о®). Показателями
же, действительно характеризующими всякую совокупность, явля-
47
ются Xi сг и а’. Они дают возможность, не имея самой совокуп-
ности, как бы построить ее, так как х указывает на наиболее ти-
пичное значение х, около которого сосредоточивается большинство
вариант, а о измеряет вариацию. Поэтому их можно назвать на
математическом языке параметрами совокупности.
ВОПРОСЫ
1. Как характеризовать структуру совокупности при качественных разли-
чиях между вариантами?
2. Что такое вариационный размах и лимиты?
3. Какие две группы показателей позволяют характеризовать вариационные
ряды?
4. Что такое медиана, мода?
5. Основная формула средней арифметической.
6. Могут ли совпасть значения х, ТИо и Л1е? .
7. Свойства средней арифметической.
8. В чем заключается прямой способ вычисления х?
9. Среднее квадратическое отклонение как мерило изменчивости совокуп-
ности. Общая формула для него.
10. Что такое варианса?
11. Методы вычисления суммы квадратов отклонений с помощью различ-
ных формул.
12. Степени свободы. Значение этого показателя при вычислении а2 и з.
При каких значениях п более точным является использование числа степеней
свободы, а не количества вариант (наблюдений)?
13. Можно ли приравнять условную среднюю А к нулю? Какой вид тогда
примут формулы для вычисления х и а2?
14. Формулы для вычисления статистических показателей, если данные не
сгруппированы в вариационный ряд.
15. В чем заключается прямой способ вычисления х и а для данных, сгруп-
пированных в вариационный ряд?
16. Какие формулы применяются при непрямом способе вычисления стати-
стических показателей?
17. Можно ли применить условную среднюю для обработки данных, не
сгруппированных в вариационный ряд? .
18. Как вычисляются взвешенные х и а2? Определение числа степеней
свободы для объединенной совокупности.
19. -В каких случаях целесообразно пользоваться средней геометрической?
Формула средней геометрической и ее преобразование с помощью логарифмов.
20. В чем заключается закон сложения вариации?
21. Какая разница между а и о? В каких случаях важно использование у?
22. Почему х и а являются основными - характеристиками вариационного
ряда?
ЗАДАЧИ*
12. Вычислите х, з2 и а для вариационного ряда задачи 1. Обдумайте,
какой из изложенных способов вычисления выгоднее применять в каждом кон-
кретном случае. _ •
13. То же для задачи 2.
* 14. То же для задачи 3. . ,
* Для удобства пользования задачами им дана сплошная нумерация, не-
зависимо от глав, где они помещены.
48
15. То же для-задачи 4.
16. То же для задачи 5.
17. То же для задачи 6.
18. То же для задачи 7.
19. То же для задачи 10.
20. На телятах холмогорских помесей были получены следующие средне-
суточные привесы (в г): 700; 667; 765; 733; 857; 423; 633; 566; 706; 518;
766; 520.
Вычислите х и а. Надо ли для данного материала составлять вариацион-
ный ряд?
21. Былб сделано 5 определений содержания кальция в крови (в усл. еди-
ницах): 11, 27; 11, 36; 11, 09; И, 16; 11, 47. Вычислите х, а2 и о.
22. Живой вес при рождении 11 поросят был следующий (в кг): 1,2; 1,1;
1,3; 0,9; 1,4; 1,0; 1,5; 1,3; 1,2; 1,4; 1,0. Вычислите х, а2 и а. Какую формулу
для вычисления среднего квадрата удобнее применить?
23. Обработайте следующие данные о длине третьего верхнего предкорен-
ного зуба у 21 экземпляра ископаемого млекопитающего Ptilodus montanus
(в мм):
3,2 2,8 2,9 3,0 3,1 3,3 2,9
3,1 2,7 3,4 2,9 3,0 2,9 2,8
2,6 3,0 2,8 3,0 3,1 2,9 3,0
Вычислите х и а.
24. Имеются мужчин: следующие данные о росте (длине тела) (в см) взрослых
162 151 161 170 167 164 166 164 173 172
165 153 164 169 170 154 163 159 161 167
168 164 170 166 176 157 159 158 160 161
167 155 166 167 173 165 175 165 174 167
170 169 159 159 160 156 161 162 161 181
159 169 160 169 161 161 166 164 170 180
158 167 169 165 166 172 168 171 178 178
171 165 161 162 182 164 171 169 176 ' 177
170 169 171 160 165 165 179 161 178 173
168 171 163 165 166 166 166 169 167 166
167 172 169 171 168 162 165 168 171 174
165 168 167 170 170
Определите х и а. Постройте гистограмму.
25. У 10 свиноматок было по следующему количеству поросят в помете:
12, 10, 5, 8, 9, 10, 9, 7, 10, 11. ‘
Можно ли вычислить х и с прямым способом?
26. Вес цыплят белых леггорнов (в г) за 2 месяца был следующим: 1-я
неделя —62,7; 2-я—121,4; 3-я — 193,0; 4-я —380,0; 5-я —481,0; 6-я —504,0;
7-я —719,0 и 8-я неделя — 759,0. Определите, на сколько увеличивался вес по.
неделям, и после этого вычислите средний привес по формуле средней геоме-
трической.
49
27. У 1060 студентов исследовали биение пульса. Колебания были от 43
до 108 ударов в минуту. Данные были сгруппированы в следующий вариа-
ционный ряд (I = 4):
Классы 43—46 Чаете 1
47—50 2
51-54 6
55—58 22
59—62 52
63—66 79
67-70 118
71-74 165
75—78 186
79—82 165
83-86 103
87-90 82
91—94 45
95—98 19
99—102 11
103-106 3
107—110 1
,1060
Вычислите х и а методом условной средней. Постройте гистограмму. Умень-
шите число классов вдвое, приняв i = 8, и вычислите х и а. На сколько из-
менились результаты при увеличении размеров классов?
28. В 1932 г. в г. Москве вес мальчиков при рождении составил следу-
ющий ряд:
Вес при рождении Относительная
(в г) численность (в %)
1000—1499 0,84
1500—1999 2,05
2000—2499 5,02
2500—2999 17,23
3000—3499 37,52
3500—3999 27,47
4000—4499 8,52
4500—4999 1,24
5000—5499 0,11
100,0
Определите средний вес мальчиков при рождении и среднее квадратичес-
кое отклонение. Какими формулами придется пользоваться? _
О т в е т: х==3309 г; <т=596 г.
50
29. Промеры длины хвоста (в см) валахских овцематок в возрасте 4х/2 года
и старше распределились в следующий ряд:
Длина хвоста Частота Длина хвоста Частота
27—28 1 I < 43—44 70
29—30 0 45—46 80
31—32 2 47—48 60
33—34 5 49—50 27
35—36 12 51-52 18
37—38 33 53-54 4
39—40 64 55-56 5
41—42 64 1 57-58 1
Вычислите xt <з и v. _
Ответ: л = 43,0 см; а — 45 см; v= 10,3%.
30. Распределение по степени жирности хвоста 775 промеренных валахских
овцематок в возрасте 4 и старше лет было следующее:
Обхват хвоста (в см) Число маток Обхват хвоста (в см) Число маток
13—14 1 33—34 101
15-16 1 35-36 71
17-18 2 37—38 33
19—20 4 39—40 29
21—22. 24 41—42 8
23—24 60 43—44 6
25-26 84 45—46 5
27—28 116 47—48 2
29-30 123 49-50 1
31—32 104
Вычислите х, а и v. _
Ответ: х — 30,4 см;а == 5,1 см; о = 16,7%.
31. Определите среднюю взвешенную длины хвоста по следующим трем
выборкам оленьих мышей Peromyscus maniculatus, взятых из разных мест США:
Местность Размеры выборки Средняя длина хвоста (х) в мм
Энн Арбор 106 57,20
Александер 86 60,43
Грэфтон 78 66,13
32. Были получены следующие средние арифметические для пяти _групп
телок: х= 262 кг (л = 10);~г2 = 238 кг (л = 3); х8 = 260,5 кг (л — 7); =
= 275 кг (л = 15) и =± 255,4 кг (л » 5).
51
Вычислите взвешенную среднюю арифметическую. На сколько взвешенная
Сбудет отличаться от х, полученной без учета весов отдельных групп телят?
33. В течение 10 месяцев лактации каждый месяц определяли у коровы
Астра жирность молока. Были получены следующие помесячные показатели
процента жира в молоке: 3,4; 3,0; 3,0; 3,2; 3,2; 3,4; 3,5; 3,7; 4,0; 4,3. Удои
по месяцам были следующими (в кг): 400, 600, 520, 360, 300, 260, 200, 150,
90, 50.
Определите средний процент жира в молоке за всю лактацию двумя спо-
собами: а) сложением помесячных процентов жира и делением суммы на 10;
б) вычислением средней взвешенной с учетом количества молока за каждый
месяц лактации. Какой способ точнее?
34. Разные культуры засевались в совхозе на разных площадях и имели
следующую урожайность:
Культура Урожайность (в ц/га) Площадь (в га)
Пшеница озимая 15,2 170
Пшеница яровая 9,4 450
Кукуруза 16,0 600
Овес 9,5 150
Какова средняя урожайность в совхозе?
35. В культурах, полученных на поверхности агара в чашках Петри, оп-
ределяли количество микробных клеток. Были получены следующие средние
количества в разных опытах (в млрд, на 1 мл): опыт 1—1,5 (ni = 6); опыт 2—2,6
(п2 — Ю); опыт 3—0,8 (п3 = 15); опыт 4—1,1 (п4 = 5).
Определите среднее количество микробных клеток для всего материала в
целом.
36. Были установлены следующие показатели высоты в холке (в см):
X а
для телят 60
для молодых коров 100
Отличаются ли они по степени изменчивости?
37. Применили три разных метода определения хлорофилла на выборках
из 12 листьев растений, при этом получили следующие статистические пока-
затели (в мг):
Xi = 61,4 Oj = 5,22
х2 ~ 337 о2 = 31,2
х3 - 13,71
а3- 1,2
Сравните коэффициенты вариации при разных методах и сделайте выводы.
38. .При изучении роста лабораторны х крыс коэффициент вариации веса
крыс (56—84-дневного возраста) был примерно 13%, а х = 200 г. Чему равны
среднее квадратическое отклонение и варианса веса крыс?
39. Было установлено, что в полевых опытах с пшеницей коэффициент
вариации урожая с гектара около 5%. Будет ли неожиданным, если при сред-
нем урожае 25 ц/га среднее квадратическое отклонение окажется около 0,5 ц?
40. Было установлено, что в группе свиней средняя скорость роста со-
ставляла 560 г в день. Определите а, если известно, что и — 10%.
52
ГЛАВА 3
ЗАКОНОМЕРНОСТИ СЛУЧАЙНОЙ ВАРИАЦИИ
Вероятность и ее исчисление. Основной особенностью биоло-
гической статистики является то, что она имеет дело не с еди-
ничными явлениями или объектами, а с их совокупностями.
Отдельные члены совокупности, как правило, в той или другой
степени отличаются друг от друга, варьируют. Каждый из них
представляет собой как бы отдельный случай, который осуще-
ствляется под влиянием многих определяющих причин. Однако
этих причин может быть так много, что обнаружение их для
каждого отдельного случая становится невозможным.
Каждое отдельное явление, взятое само по себе, представ-
ляется случайным, но, взятые в массе, они обнаруживают опре-
деленные, так называемые статистические закономерности. Вот
почему можно предсказать результаты для массового явления
в целом. В отношении же каждого единичного явления, каждого
отдельного члена совокупности приходится говорить только об
известной возможности, или вероятности, значения, которое
они приобретают. Для зоотехника, работающего с крупным ро-
гатым скотом холмогорской породы и знающего, что средняя
жирность молока коров этой породы около 3,5%, ясно, что воз-
можность, или вероятность, найти корову-холмогорку с жир-
ностью молока 3,5% очень велика, но встретить корову с жир-
ностью 4,5% — маловероятно. В этом примере, оценка вероятно-
сти как возможности кажется очень ясной -и понятной. Но так
бывает далеко не всегда.
Возьмем такой пример. Ветеринарный врач зверосовхоза
применил для лечения заболевших какой-то болезнью лисиц
новое лекарство. Выяснилось, что из лисиц, получивших лекар-
ство, погибло только 4%, а среди не получавших лекарства
отход был равен 13%. От чего же зависит разница в проценте
отхода? От того ли, что в опытной группе применили новое ле-
карство, или, может быть, лекарство никакой роли не сыграло?
Когда нет точной уверенности в правильности того или другого
суждения, часто употребляют слово «вероятно». Прибавкой к
нему слов «очень» или «мало» выражают степень уверенности.
53
Сторонник применения лекарства может сказать: «Очень веро-
ятно, что именно благодаря применению лекарства отход в опыт-
ной группе был меньше». Но человек, настроенный скептически,
будет утверждать обратное: «Если бы и не давали лекарства, все
равно в одной группе лисиц отход был бы больше, а в другой
меньше в силу других причин, создавших разницу между груп-
пами».
Этот пример показывает, что биологу в его практике прихо-
дится очень часто встречаться с вероятностями, большими или
малыми, и что ответить на многие вопросы можно, только зная
некоторые, хотя бы самые элементарные положения теории ста-
тистики и лежащей в ее основе теории вероятности.
Что же такое вероятность? Это возможность осуществления
определенного события в некотором количестве случаев из об-
щего числа возможных, или, иначе говоря, степень уверенности
в том, что событие произойдет.
Исходным в понятии вероятности является понятие равно-
возможности, на основе которого можно отделить необходимые
явления от случайных. Так, если при осуществлении события А
возможно только событие В, то налицо необходимая связь явле-
ний. Если же при А равновозможны и В и С, мы имеем дело
с проявлением возможности в виде случайного. Случайное —
это такое же объективное явление, как и необходимое, и оно
так же обусловлено различными причинами, как и необходимое,
только характер причинности здесь иной, а именно: возможен
не один, а два результата или более. Эти возможности (и явля-
ются вероятностями. Процесс осуществления явления на основе
известной его возможности, или вероятности, называется веро-
ятностным или стохастическим. Теория вероятности изучает ма-
тематические законы таких процессов.
Вероятность можно выразить математически по следующей
формуле:
(20)
где пг — число благоприятных случаев, а п — число всех воз-
можных, или, правильнее, равновозможных, случаев.
Так, если на каждой из сторон кубика написаны цифры 1, 2,
3, 4, 5, 6, то вероятность того, что наверху будет цифра 4, рав-
на -g-, ибо всех возможных положений кубика может быть
шесть, и лишь один случай благоприятный. Значительно слож-
нее рассчитать вероятность того, что при одновременном выбра-
сывании двух кубиков сумма цифр наверху равна 6. Для этого
следует рассчитать все возможные случаи сочетания цифр в двух
кубиках:
1 + 1 2+1 3+1 4+1 5+1 6+1
1+2 3+2 3+2 4+2 5+2 6+2
54
1+3 2+3 3+3 4 + 3 5+3 6 + 3
1+4 2+4 3+4 4+4 5+4 6+4
1 + 5 2+5 3 + 5 4+5 5 + 5 6 + 5
1+6 2+6 3+6 4 + 6 5+6 6 + 6
Таким образом, возможно 36 случаев (п — 36). Благоприятных
же случаев, когда цифры двух кубиков дают в сумме число 6, бу-
дет только 5 (они подчеркнуты). Значит, вероятность выбрасыва-
ния 2 кубиков с суммой цифрг наверху, равной 6, может быть вы-
ражена по формуле р = —:
5
р~ 36 •
Эти примеры являются теоретическими. На подобных при-
мерах, или моделях, решаются многие задачи по теории вероят-
ностей. Можно привести немало и биологических примеров осу-
ществления событий на основе той или иной вероятности.
Выше уже указывалось, что особи мужского и женского пола
у очень многих видов животных рождаются примерно в равном
количестве. Это значит, что на каждые 100 потомков в среднем
должно родиться 50 самок и 50 самцов, отсюда вероятность рож-
50
дения от коровы телочки или бычка равна Р = [до = 0,5 (или
50%).
Другой биологический пример. Чтобы оценить вероятность рож-
дения комолого теленка, надо знать количество рождавшихся ра-
нее в данном стаде или породе комолых и рогатых животных.
Так, если в данной породе за несколько последних лет обнаруже-
но 110 комолых телят из общего количества 55000 родившихся,
то вероятность рождения от коровы данной породы комолого те-
ленка равна р = 55qq0 = 0,002. Это значит, что в среднем на каж-
дую 1000 случаев приходится только 2 случая рождения комолых
телят. На этом же примере легко понять и другую вероятность,
как бы обратную величине р, что родится не комолый, а рогатый
теленок. Последняя вероятность обозначается буквой q. Она выра-
жается в данном случае величиной, равной 0,998. Алгебраическая
сумма величин р и q равна 1, т. е. сумма вероятностей противо-
положных событий равйа единице.
Из этих примеров вытекает важный теоретический вывод:
количественной характеристикой вероятности того или иного
явления, т. е. объективным мерилом, по которому можно судить
о возможности возникновения явления в будущем, может быть
относительная частота явления, установленная эмпирически на
достаточно значительном фактическом материале.
Если некоторое явление имеет вероятность р, то относитель-
ная частота его, обнаруживаемая в опыте или при наблюдении,
55
будет близка к р, при этом она будет тем ближе к р, чем больше
было проведено опытов или наблюдений. Если заранее дается
определенная вероятность, то по ней можно найти ожидаемую
частоту явления, которая будет получена при проведении опы-
тов. И наоборот, зная относительную частоту, можно найти при-
ближенное значение вероятности, которое может служить для
характеристики частоты данного явления в последующих опы-
тах или наблюдениях. Но вероятность проявляется только при
большом числе наблюдений или опытов.
Приведенные примеры показывают, что вероятности р и со-
ответствующие им q могут иметь самые разные значения — от
величин, близких к нулю или равных ему, до величин, близких
к единице или равных ей. В нашем примере вероятность рож-
дения комолого теленка очень мала. Однако существует немало
событий, обладающих еще меньшей вероятностью. Наконец,
если р = 0, то на свершение данного события вообще нельзя рас-
считывать.
Но могут быть события, вероятность которых, хотя и очень
близка к нулю, но все же нулю не равняется. Практически мож-
но утверждать, что вероятность обнаружения в стаде холмогор-
ской породы коровы с жирностью молока 6,5% равна нулю, но
возможен все же какой-то исключительный случай, когда в силу
. своеобразных физиологических условий холмогорская корова
может дать молоко исключительно высокой жирности. Очевидно,
вероятность подобного события будет выражена очень малой
дробью.
Однако и события, обладающие очень малой вероятностью,
осуществляются вполне закономерно, хотя они могут казаться
невозможными. Маловероятные события при многократном пов-
торении явления приобретают вполне устойчивую и определен-
ную вероятность их осуществления, хотя бы такое событие про-
исходило в одном случае из многих миллионов. Так, с точки зре-
ния вероятности возникновение жизни на Земле представляется
необычайно редким событием. Но каким бы невероятным ни ка-
залось возникновение жизни или тех этапов, из которых скла-
дывалось возникновение жизни на Земле, времени для этого
было достаточно, поэтому оно наверняка могло произойти хотя
бы один раз, чего было уже достаточно для дальнейшего разви-
тия жизни.
По мере приближения величины р к единице событие стано-
вится все более достоверным. Если р=1, то событие бесспорно
наступит. Оно вполне достоверно.
Наоборот, то, что обладает малой вероятностью, мало досто-
верно. В жйзни мы всегда считаемся, сознательно или бессозна-
тельно, с эмпирическими вероятностями, оцениваем вероятности
и действуем согласно этим оценкам. При этом мы, как правило,
не придаем значения явлениям, обладающим малой вероят-
ностью.
56
Оценка того, насколько мала должна быть вероятность, что-
бы с ней можно было не считаться, в значительной мере зависит
от степени важности события, о котором идет речь. Так, если
вероятность воздействия нового удобрения на понижение уро-
жая равна 0,05, это не должно помешать его применению, так
как в 0,95 случая оно окажется полезным. Совсем другое дело,
если оказывается, что новое лекарственное средство может с ве-
роятностью, равной 0,05, принести не пользу, а вред организму
больного. В этом случае его применение не может быть допу-
щено.
Эти примеры мы приводим для того, чтобы подвести изуча-
ющего биологическую статистику к принципу, широко применя-
емому сейчас в опытах и наблюдениях, когда заранее намечают
приемлемую величину (или уровень) вероятности и считают ее
достаточной для доказательства получения того или иного эф-
фекта.
Теоремы сложения и умножения вероятностей. Для понима-
ния закономерностей случайной вариации важны две теоремы.
Первая из них — теорема сложения вероятностей — относится
к таким независимым друг от друга событиям, которые несов-
местимы; вторая — теорема умножения вероятностей — также
к независимым событиям, но совместимым друг с другом или
следующим друг за другом. Эти теоремы можно проиллюстри-
ровать следующими элементарными примерами.
На клумбе растут 20 красных, 30 синих и 40 белых астр.
Какова вероятность сорвать в темноте окрашенную астру? Она
равна сумме вероятностей сорвать красную, или синюю астру,
т. е.
= 20 -, зо _ 50
Р ~ 90 90 ~ 90
Второй пример несколько сложнее. Какова вероятность, что
при выбрасывании двух кубиков, на гранях которых написаны
цифры от 1 до 6, наверху будет сумма не менее 10? Эта вероят-
ность составляется из суммы трех вероятностей: получить сумму цифр
10, сумму 11 и сумму 12. Первая вероятность, как легко рассчитать из
Данных выше сочетаний двух цифр, р10= А, вторая —ри=
1 fit
и третья —р12 = Сумма их составит-^-, или -j~.
Для умножения вероятностей необходимо, чтобы второе собы-
тие Е2 осуществлялось только при осуществлении события Еи
при этом осуществлении Е± не4 влияет на вероятность осуществ-
ления Е2, т. е. Ег и £2 независимы. .
Какова вероятность наличия цифры 4 наверху двух выброшен-
ных одновременно кубиков? При выбрасывании одного кубика ве-
роятность появления цифры 4 равна При выбрасывании второ-
57
го кубика вероятность та же----Общая вероятность р =
_ 1 J____1_
— 6 6 36
Второй пример. Какова вероятность прохождения по лабирин-
ту с шестью развилками и шестью тупиками? Очевидно, что на
каждом развилке вероятности попасть или в тупик, или к следу-
ющему развилку одинаковы — по Тогда при наличии шести
развилков общая вероятность будет равна
-1 1 1 1 1 111
* 2 ' 2 ’ 2 * 2 ‘ 2 ‘ 2 2" — 64'
Эмпирические и теоретические вероятности. В приведенных
выше примерах исчислялись так называемые эмпирические ве-
роятности. Они приложимы только к тем конкретным совокупно-
стям, для которых они вычислены. Вероятность появления
комолых телят относится к определенной изученной группе
скота. Для породы, в которой очень много комолых животных,
вероятность появления комолых телят окажется во много раз
выше вычисленной. Для практики же очень важно судить не
только об отдельных конкретных случаях, но и о всех возмож-
ных случаях этого рода.
Математическая теория, имея дело с отдельными, частными
наблюдениями, выработала методы, позволяющие по результа-
там наблюдений судить о тех результатах, которые имели бы
место, если бы изучалась не только данная совокупность осу-
ществившихся случаев, но и теоретически мыслимая совокуп-
ность всех возможных случаев этого рода. Иначе говоря, по
эмпирическим, опытным вероятностям, основанным на учете
конкретных относительных частот тех или других явлений,
можно судить о теоретических, или так называемых априорных,
вероятностях, т. е. таких, которые можно брать заранее, до про-
ведения опыта.
В предыдущих главах приведено несколько вариационных
рядов. Каждый из них являлся результатом изучения некоторо-
го, сравнительно небольшого числа животных. Так, суждение
о плодовитости серебристо-черных лисиц, ее средней величине
и изменчивости было сделано по 80 экземплярам. Но можно бы-
ло бы изучить не эту маленькую группу лисиц, а всех лисиц,
разводимых в СССР. Такая совокупность всех конкретных объ-
ектов, которую можно было бы изучить, называется, как уже
сказано выше, генеральной. Иногда ее называют также популя-
цией. * Изученная же небольшая группа представляет собой как
* Надо отличать популяцию в статистическом смысле, как генеральную '
совокупность, от популяции в экологическом и генетическом смысле, как группы
животных, населяющих определенную территорию. Однако зоолог или ботаник
постоянно имеет дело с выборками из конкретных популяций.
68
бы выборку из генеральной совокупности, поэтому ее называют
выборочной. Наконец, можно себе представить и теоретически
мыслимую совокупность, т. е. совокупность всех возможных на-
блюдений, в том числе и таких, которые практически не были
осуществлены. Такую совокупность называют стохастической.
Теория вероятностей как раз дает возможность построить
абстрактные совокупности, представляющие собой отображение
реальных совокупностей. В таких абстрактных стохастических
совокупностях, доступных точному математическому анализу,
вероятности становятся теоретическими. Очевидно, в жизни мы
встречаемся, как правило, с выборочными совокупностями, но
по ним мы стремимся судить о генеральной или стохастической
совокупности. Так, для изучения окуня данного озера нет надоб-
ности изучать всю его популяцию, т. е. генеральную совокуп-
ность, а достаточно взять выборочную совокупность в количестве
100, 200 или 1000 особей. По капле крови больного можно де-
лать выводы о состоянии всей крови, данные об изменчивости
.нескольких десятков леммингов позволяют судить о всей попу-
ляции леммингов и т. д.
Если бы все особи популяции были сходны, то уже по одной
особи можно было бы получить полную информацию о всей гене-
ральной совокупности, всей популяции. Но в действительности
существует очень большое разнообразие как среди самих особей
популяции, так и в отношении условий внешней среды, в кото-
рой они живут и развиваются. Поэтому и проводимые много-
кратно выборки из генеральной совокупности никогда не будут
одинаковыми.
Естественно, возникает вопрос: каковы же закономерности
вариации внутри каждой совокупности и каково 'взаимоотноше-
ние между разными типами совокупностей? Это дает возмож-
ность подойти и к другому важному вопросу, можно ли по ста-
тистическим показателям, полученным на основании изучения
одной совокупности, например выборочной, судить о статисти-
ческих показателях других
видов совокупности, напри-
мер генеральной. Иначе го-
воря, это вопрос о том,
насколько достоверны стати-
стические показатели, полу-
ченные по выборочной
совокупности, чтобы можно
было судить по ним о гене-
ральной совокупности.
Распределение вероятно-
стей — основа вариации, Об-
ратимся опять к вариацион-
ному ряду. Выше было разо-
брано несколько эмпириче-
Количество курочек
Рис. 4. Полигон распределения случаев
с разным количеством курочек среди 10
цыплят (общее число случаев — 1024).
59
ских вариационных рядов и показано, что для всех них характер-
но Определенное распределение вариант, а именно: чем ближе
значения вариант к средней арифметической, тем выше их часто-
та; чем дальше — тем реже они встречаются. В конечном счете
это распределение вариант основано на теоретической закономер-
ности уменьшения вероятности встречаемости той или иной вари-
анты по мере ее удаления от средней.
Для иллюстрации того, что вариационный ряд действительно
основан на вероятности, покажем, как распределяются вероят-
ности появления курочек среди 10 цыплят. Начнем со случая,
когда среди'них нет ни одной курочки (0), далее 1 курочка из
10 цыплят, 2 курочки, 3 курочки и т. д. и, наконец, когда все
цыплята — курочки (табл. 14).
Таблица 14
Распределение вероятностей появления
разного количества курочек среди 10 цыплят
Количество
курочек 0 1 ' 2 3 4 5 6 7 8-9 10
Количество
случаев 1 10 45 120 210 252 210 120 45 10 1
Вероятности 0,001 0,010 0,044 0,117 0,205 0,246 0,205 0,117 0,044 0,010 0,001
Если графически выразить данные табл. 14, то будет полу-
чена изображенная на рис. 4 вариационная кривая (полигон)
распределения случаев с разным количеством курочек среди
10 цыплят. Это так называемая биномиальная кривая распреде-
ления, соответствующая разложению бинома Ньютона. Бино-
миальность кривой распределения можно уяснить на следующем
примере.
Представим себе, что мы подбрасываем одновременно 2 мо-
неты. Будем считать выпадение герба (Г) благоприятным слу-
чаем, а выпадение решетки (Р) неблагоприятным. Возможны
4 случая выпадения герба и решетки.
В первом случае обе монеты выпадут гербами-вверх (ГГ).
Во втором на первой монете вверху герб, на второй — решетка
(ГР). В третьем случае на первой монете вверху решетка, а на
второй — герб (РГ). Второй и третий случаи совпадают по ре-
зультату. Каждый из них является комбинацией одного благо-
приятного (Г) и одного неблагоприятного (Р) случаев. Нако-
нец, в четвертом случае обе монеты выпадут решетками вверх
(РР). Какова же вероятность каждого результата?
Вероятность выпадения герба обозначим буквой р, а вероят-
ность выпадения решетки — q. В данном случае p — q = Тог-
да вероятность выпадения двух монет одновременно гербами вверх
равна произведению вероятностей, т. е. р • р = р1. Вероятность вы-
падения одной монеты гербом вверх и другой — решеткой вверх
60
равна р • q. Так как таких случаев с разным т/^ядком наступле-
ния благоприятного и неблагоприятного результатов два, то их ве-
роятности суммируются: pq + pq — 2pq. Наконец, вероятность со-
четания двух неблагоприятных случаев, т. е. выпадение решетки,
равна q • q —q2. Таким образом, для простейшего примера из 2 со-
бытий мы имеем следующее их распределение:
(/7 + /7)2=р2+2/?<7+<72.
Такое же рассуждение можно применить к сочетанию 3, 4 и т. д.
событий.
Во всех случаях получение вероятности различных сочета-
ний независимых событий основывается на том, что вероятности
нескольких комбинаций выражаются членами разложения бино-
ма (p+q)k, где k — число независимых случайных событий,
р и q — соответствующие вероятности благоприятных и неблаго-
приятных событий. Чтобы получить не отдельные вероятности,
а вероятные численности разных результатов при данном общем
числе п, надо умножить их на это общее число случаев, т. е. ис-
пытаний. В приведенном выше примере число сочетаний разного
количества курочек и петушков равно 10, т. е. мы имеем дело
с биномом (р+<7)10. Его разложение в виде конкретного количе-
ства .случаев каждого сочетания дано во второй строчке табл. 14
(п=1024), а вероятности отдельных случаев — в третьей строч-
ке. Сумма вероятностей должна быть равна 1.
В середине XIX в. бельгийский статистик Кетле построил
вариационную кривую, изучив распределение по росту 26000
солдат американской армии. Кетле пришел к выводу, что рас-
пределение особей в вариационном ряду следует коэффициентам
разложения двучлена, возведенного в известную степень. Вспом-
ним, какими будут коэффициенты при отдельных членах разло-
жения бинома Ньютона а+Ь при возведении его в разные степени:
(а+ЬУ=а+Ь,
(a+b)2=a2+2ab±b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a + b)4 = a4+4a3b + 6a2b2+4ab3+b4 и т. д.
Эти коэффициенты легко получить с помощью треугольника
Паскаля, в котором цифры каждого .последующего ряда по-
лучаются путем сложения двух цифр ряда, расположенного над
ним:
1
1 1
12 1
13 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
61
\Ч пчтсеп
Рис. 5. Аппарат Гальтона.
Распределение вариант в виде
вариационного ряда, частоты в
котором следуют коэффициентам
разложения бинома Ньютона, как
следствие совместного влияния
многих независимых факторов
может быть наглядно показано с
помощью доски, или аппарата,
Гальтона (рис. 5).
Этот аппарат представляет
собой коробку, в верхней части
которой расположен ящичек с
выходным отверстием посредине.
В средней части коробки воткну-
ты булавки, причем булавки
каждого последующего ряда
расположены против середин про-
межутков предыдущего ряда.
В нижней части коробка разделе-
на перегородками на ряд отделе-
ний. Коробка ставится наклонно,
примерно под углом 30° к
поверхности пола или стола. В
верхний ящичек насыпается
дробь. Отдельные дробинки, падая через отверстие ящичка, встре-
чают на своем пути булавки, при столкновении с ними отклоня-
ются вправо или влево и, наконец, падают в отделения нижней
части аппарата.
Оказывается, что накопление дробинок в этих отделениях
образует фигуру, аналогичную гистограмме или полигону рас-
пределения вариационного ряда, с характерной концентрацией
большинства вариант в средней части и рассеянием их вправо
и влево. Расположение дробинок в отделениях аппарата явля-
ется результатом встреч дробинок со многими булавками, при
которых дробинки могли многократно отклоняться в сторону от
прямого пути. Чаще всего происходило взаимное погашение этих
отклонений: дробинка, первый раз отклонившись вправо, второй
раз отклонялась влево и т. д. и в конечном счете попадала в од-
но из средних отделений. В других, более редких случаях откло-
нения в одном и том же направлении вправо или влево совпада-
ли, и дробинка попадала в одно из крайних правых или левых
отделений. Но максимальные отклонения являются самыми
редкими, т. е. обладают очень малой вероятностью.
Подобно этому положение вариант в вариационном ряду
является результатом суммирования многих случайных факто-
ров, вызывающих отклонения вариант от средней в разных на-
правлениях, причем каждое сочетание факторов осуществля-
ется с определенной вероятностью.
62
Таким образом, вариационный ряд с характерным для него
расположением большинства вариант вблизи его центральной
части и рассеиванием к краям ряда является в то же время и
распределением вероятностей. Это значит, что в вариационном
ряду случайная переменная х принимает разные значения:
*1, Х2, Хз.Хп —
под влиянием большого количества самых разнообразных при-
чин, независимых, как правило, друг от друга. Поэтому вариа-
цию величины х можно рассматривать как случайную. Отдель-
ным значениям х t можно придать соответствующие вероятности
Pi- Pi> Р2> Рз> •••, Рп- Совокупность значений xz и соответствую-
лцих им вероятностей р{ и называется распределением.
Биномиальное распределение. Если вероятности появления
отдельных значений xt выражаются величинами, .соответствую-
щими коэффициентам разложения бинома Ньютона, как это
было показано выше, распределение называется биномиальным.
Биномиальное распределение относится к признакам, варьи-
рующим дискретно, прерывисто. В табл. 4 был приведен эмпи-
рический ряд распределения самок серебристо-черных лисиц по
числу щенков, в помете. Именно ряды такого типа относятся
к биномиальному распределению. Частоты отдельных классов
тогда пропорциональны коэффициентам разложения бинома
Ньютона (p+q)h, где р — вероятность появления данного собы-
тия (или признака), q— вероятность непоявления, a k — число
классов, отличающихся по наступлению данного события (или
появлению признака).
При биномиальном распределении возможны различные зна-
чения р и q, например: р=0,7 и р = 0,3 или р=0,9 и ?=0»1 и т. д.
При этом меняется и форма лолигона. По мере увеличения раз-
личий между р и q полигон становится все более скошенным,
асимметричным. Однако по мере увеличения п даже при значи-
тельном различии между р и q степень симметрии полигона
.вновь усиливается.
Как и для других распределений, параметрами для биноми-
ального распределения являются средняя арифметическая
и среднее квадратическое отклонение, которые можно опредё5
лить с помощью приведенных выше формул для любого конкрет-
ного эмпирического ряда.
Теоретически их значения определяются значениями вероят-
ностей р и q, а также значением k; т. е. числа независимых собы-
тий, распределение которых изучается.
Средняя арифметическая при биномиальном распределении
x — kp (21)
и среднее квадратическое отклонение
<г = (22)
63
Эти формулы дают возможность связать определенные х и <т,
вычисленные на основе данного конкретного материала, с вероят-
ностями -р к q.
Возьмем следующий пример, схематизированный для упрощения
подсчетов. В 96 группах цыплят, подвергавшихся эксперименталь-
ному воздействию, определяли количество погибших цыплят (табл. 15).
Таблица 15
Распределение погибших цыплят в 96 группах
Количество погибших цыплят X Частота /
0 6 0 0
1 24 24 24
2 36 72 144
3 24 72 216
4 6 24 96
л = 96 S = 192 2 = 480
Для количества погибших цыплят х можно вычислить по фор-
муле (4) и о —по формуле (6):
- 2/Х 192 о
х -- =дб—2 цыпленка на группу,
_________- — 1/ ----------= 1 цыпленок.
п — 1 ' 95
С другой стороны, при биномиальном распределении можно
определить х и <т через величины k, р и q,' а именно:
х = kp = 4 • 0,5 = 2;
о = V kpq — 4 • 0,5 • 0,5 -- 1.
В данном случае принято, что р — q = как точно установ-
ленные теоретические вероятности. Но возможны и другие значе-
ния вероятностей р и q.
Так, например, было получено следующее. фактическое распре-
деление самок в 103 пометах с 4 мышками в каждом помете:
Количество самок 0 12 3 4
Число пометов 8 32 34 24 5
_ - 8 - 0+ 1-32 + 2 - 34 + 3-24 + 4.5 , ЯЛЛ
Тогда х =------------103 -------—J-----= 1,864.
Но так как х = kp, k — 4, то р = = 0,47.
. 64
Это вероятность появления самок. Вероятность же появления
самцов <7 = 0,53.
Исходя из формулы cs2=kpq, можно вычислить
ст2=4- 0,47 -0,53= 1,0.
Так как данный ряд является рядом разложения бинома
(0,54 + 0,47)4 при п=103, то легко вычислить, сколько особей
следует ожидать в каждом классе. Получатся следующие цифры
для частот каждого класса:
Количество самок 0 12 3 4
Ожидаемое число пометов 8 29 38 23 5
Уже на глаз видно большое совпадение фактически получен-
ных величин с ожидаемыми.
В гл. 9 будет показано,
ствия фактических опытных
как определяется степень соответ-
данных ожидаемым с помощью ме-
>• “тода хи-квадрат.
Распределение Пуассона. Распределение Пуассона, или пуас-
соново распределение, подобно биномиальному, относится к дискрет-
ной, или прерывистой, изменчивости. Оно имеет самостоятельное
значение, хотя его можно рассматривать и как предельный случай
биномиального. При биномиальном распределении значения р и q
могут быть близки друг к другу, при пуассоновом же р очень ма-
ло, Т. е. события псушесталяитгся очень редко, а <? ‘приплижяется'"'
к единицеШоэтому физики применяют закономерности пуассонова
распределения к таким явлениям, как испускание радиоактивны-
ми веществами а-частиц, где число а-частиц очень мало по сравне-
нию с общим числом атомов. В биологии пуассонову распределе-
нию удовлетворяют редко наблюдаемые явления, например явление
полиэмбрионии в семенах растений, частота рождения троен и четверен
у человека, количество сорных растений на делянках посевов или чис-
ло вредных насекомых, попадающих в ловушки, частота островков
Лангерганса в тканях поджелудочной железы и др. Многие расчеты
в современной радиобиологии основываются на анализе пуассонова
распределения, так как и здесь приходится встречаться с очень
редкими событиями. Если, например, происходит облучение груп-
пы клеток или бактерий 7-лучами, то число облучаемых объектов,
т. е. наблюдаемых событий (n = k), очевидно, очень велико, на-
блюдаемые же изменения (смерть отдельных бактерий, цитологичес-
кие изменения в клетках) являются редкими событиями т, веро-
ятность которых (р = выражается очень малым числом.
Распределение отдельных наблюдений является при этом чаще
всего асимметричным, но симметрия возрастает с увеличением х.
При увеличении р распределение приближается к биномиаль-
ному. Пуассоново распределение характеризуется в сущности толь-
ко одним параметром — средней арифметической х, так как о8 в
этом случае обычно равна х или близка ей по значению. Именно по это- -
3 П. Ф. Рокицкий
65
му равенству я и а* легче всего определить, что данное распреде-
ление является пуассоновым.
Средняя арифметическая для пуассонова распределения (обыч-
но она обозначается не х, а греческой буквой лямбда—к) равна пр,
где р—вероятность обнаружения данного признака, а п — количе-
ство фактически проведенных наблюдений:
х = X = пр = о2. (21а)
Величина р может быть очень малой.
Частоты распределения Пуассона представляют собой следу-
ющий ряд:
п , ' «, х пХ пХа пХ® пХ*
"т- (нулевой член); -г-; —---------г? --------г* и т. д.
v 7 ' ек 2ек (2)(3)ек (2)(3)(4)ек
Здесь п — общее число вариант, е — основание натуральных
логарифмов и X, — средняя арифметическая.
Способы расчета теоретических частот для такого ряда изло-
жены в гл. 9.
Конкретные пуассоновы ряды являются конечными в силу
ограниченности количества наблюдений. Но теоретически они мо-
гут продолжаться до бесконечности.
Пример пуассонова распределения — распределение остров-
ков Лангерганса в поджелудочной железе обезьяны макаки
резус. Гистологические срезы проецировались на экран, учиты-
валось количество квадратов и нахождение на них островков
Лангерганса. Всего было просмотрено 900 квадратов. Вероят-
ность нахождения островка Лангерганса на любом квадрате
одинакова и в общем невелика. Но распределение островков по
отдельным квадратам, показанное в табл. 16, неравномерно.
Можно предположить, что оно соответствует распределению Пу-
ассона.
Таблица 16
Распределение островков Лангерганса по отдельным квадратам
________ткани поджелудочной железы макаки резус_________
Количество островков в квадратах X Количество квадратов f fX
0 327 0 0
1 340 340 340
2 160 320 640
3 53 159 477
4 16 64 256
5 3 15 75
6 1 6 35
п = 900 2=904 2 = 1824
66
Воспользовавшись формулами (4) и (6), можно вычислить
х_л_ —= __= 1,о,
2/х»_ет
(J2 = ____«_
п — 1
1824-221’
10 900 = 923 _
899 — 899 ~
1,03.
Близость значений х и о2 служит доказательством, что рас-
пределение островков Лангерганса является пуассоновым.
Вероятность появления островков Лангерганса может быть
определена по формуле
Она очень мала. Именно поэтому распределение и следует за-
кону Пуассона.
А Нормальное распределение и его характеристика с помощью
Нормированного отклонения. Если при7?иномиалыкм£'распдеде-
лении значение показателя бйнШга~~(р+^)^ является конечным,
то при приближении k ‘ к ‘бесконечности распределение стано-
вится непрерывным.
Полигон же распределения превращается в симметричную
плавную кривую, так как верхние границы ломаной линии по-
лигона сольются в гладкую кривую линию. Она получила назва-
ние нормальной вариаЦШУнной-КРивей (рис. 6). Само же распре-
деление называется в такую же плавную кривую
превращается и гистограмма, если размеры классов последова-
тельно уменьшать в 2, 4, 8 и т. д. раз.
Нормальное распределение занимает важнейшее-местов-ета-
тистике вообще и в биологической статистике в частности, так
как очень многие эмпирические..-распределения биологических
признаков, характеризующиеея-ненрерывной вариацией, прибли-
жаются к нормальному, следуют ему.
Теоретическая же основа вариации та же, и при бино-
миальном распределении: вариация в совокупности — результат
совместного действия мйогих раянбй'аправленных~и независимых
друг от друга факторов; Со-
гласно же теореме А. М. Ля-
пунова, если случайная ве-
личина является суммой
большого числа независи-
мых слагаемых, то она с до-
статочной степенью точности
будет распределяться по
нормальному закону.
Rot почему закон нор- ~36 гв ~,в х +1в *29 +Э6
« Нормальная ааря^са. яря,.я.
ОДИН из ОСНОВНЫЕ—ЗАКОНОВ Отклонения вариант вправо и влево от х
статист и веских явлении. охватывают несколько больше
67
. Для изучения закономерностей вариации^ при нормальном
распределении в настоящее время широко' пользуютея-так на-
зываемым нормированным отклонением, которое бук-
вой t* Нормированное откдонение~41ред€тав-ляет-сибой откло-
- нение той или другой варианты-^или-труптгБгвариант) от средней
арифметической., выраженное-в- сигмах, т.-ст.
= (23)
Отсюда х(—'x—to.—
В дальнейшем будет показано, что t имеет несколько более ши-
рокий смысл и что оно может выражаться не только в сигмах.
Каждая варианта характеризуется определенным значением . t,
указывающим ее положение в вариационном ряду или на кривой
распределения. Так, если варианта № 26 имеет значение t= 4-1,5,
это значит, _что она располагается в правой части кривой на рас-
стоянии от х в 1,5 о. Если варианта № 38 имеет значение t —
== — 2,6, она расположена в левой части кривой на расстоянии от
х в 2,6 0 и т. д.
Размещение вариант в вариационном ряду при нормальном
распределении характеризуется определенными закономерно-
стями. Дело в том, что в нормальной кривой отклонения от сред-
ней арифметической практически охватывают приблизительно
6 сигм: 3 сигмы вправо от средней и 3 сигмы влево, как это вид-
но на нормальной вариационной кривой рис. 6.
Зная вариационную кривую распределения вариант по тому или
иному признаку и предполагая, что распределение является нор-
мальным, можно заранее предсказать, какой процент изученных
особей (или вариант) укладывается в пределах + 1 ст, в пределах
± 2 ст, в пределах + 3 о. Так, в пределах + 1 ст располагается
68,3% всех вариант данного ряда, в пределах ±2ст — 95,5% и в
пределах + 3ст— 99,7% всех вариант. В таком случае значения t
для отдельных вариант колеблются в пределах примерно 4 3. Раз-
личные значения t ограничивают определенные части вариационно-
го ряда. В то же время распределение t указывает на закономер-
ность уменьшения количества вариант по мере отдаления от сред-
ней арифметической, что основано на закономерности распределе-
ния вероятностей.
Вероятность любого отклонения от средней есть функция
нормированного отклонения. Эта функция выражается довольно
сложной формулой, которую мы здесь приводить не будем, но
на ее основе была составлена готовая таблица так называемого
* В литературе встречаются самые различные обозначения нормирован-
ного отклонения — и, Т, d и т. д., обозначение же t часто относят только к вы-
раженным в сигмах отклонениям выборочной средней от генеральной. Однако,
чтобы не затруднять читателя, мы ограничились одним обозначением норми-
рованного отклонения.
68
нормального интеграла вероятностей. Так как к ней придется не
раз обращаться в связи с разбором материала самых различных
частей нашего курса, она дана в приложении (табл. I), а не в
тексте.*
В табл. I первая колонка слева дает значения t с одним де-
сятичным знаком, второй десятичный знак t представлен 10 стол-
бцами, на которых вверху стоят цифры от 0 до 9. Тогда /=0,11
соответствует значение вероятности 0876 (в таблице 2-я стро-
ка, 2-я цифра), значению t= 1,00—6827 (11-я строка, 1-я циф-
ра) и т. д.
В целях упрощения для вероятностей даны лишь десятич-
ные знаки, поэтому слева надо к ним присоединять ноль и запя-
тую, т. е. число 0876 надо записать как 0,0876, число 6827— как
0,6827 и т. д.
Геометрически величины, находящиеся в табл. I, являются
долями площади нормальной кривой в границах от—t до +/.
Эти доли выражают в то же время и вероятность.
С помощью табл. I можно определить вероятность нахождения
вариант в данных границах величины ±/, т. е. отклонения от сред-
ней арифметической, выраженного в сигмах.
Так, вероятность того, что взятая наугад особь из части вариа-
ционного ряда, ограниченной справа и слева от средней одной сиг-
мой, т. е. +1/ (/ = ± 1 о), равна 0,6827; двумя сигмами, т. е.
± 2/, — 0,9545; тремя сигмами, т. е. в пределах + 3/, —0,9973
и т. д.
Закономерности нормального распределения дают возможность
по двум параметрам, х и о, построить весь вариационный ряд. Так,
если известно, что х = 40 см, а = 3 см, п — 500, то размах вариа-
ции всего ряда должен быть от 31 до 49 см. 68% особей, т. е.
340 из 500, будут иметь значение признака от 37 до 43 см. Если,
наоборот, мы знаем только максимум и минимум вариационного
ряда, то можно приближенно, без вычислений, определить и сред-
нее квадратическое отклонение, разделив вариационный размах на 6.
Однако надо иметь в виду то обстоятельство, что изучаемая сово-
купность, являющаяся только выборкой из генеральной совокуп-
ности, обычно имеет ограниченный объем. Чем меньше п изучае-
мой совокупности, тем менее точно фактический вариационный
ряд с его минимумом и максимумом отображает теоретический
вариационный ряд, который можно было бы построить на основе
изучения генеральной совокупности и который должен охваты-
вать 6 о. Поэтому для определения о по размаху вариации при п.
около 30 величину размаха надо делить не на 6, а только на 4;
при п = 50 — на 4,5; при п= 100 — на 5 и т. д.
Вот почему лучше определять среднее квадратическое откло-
* Эта и другие таблицы, помещенные в приложении, будут обозначаться
римскими цифрами.
69
нение более точными методами, по формулам, приведенным
в гл. 2.
Доверительные вероятности. Существенно важны две вероятнос-
ти, которые постоянно упоминаются в биологических, зоотехниче-
ских и агрономических работах с использованием методов биомет-
рии. Их обычно выражают величинами 0,95 и 0,99. Из табл. 1
можно установить, что с вероятностью 0,95 любая случайно взятая
особь будет отклоняться от х не более чем на 1,96 о, или, иначе,
с вероятностью 0,05 она будет за пределами 1,96 а. С веро-
ятностью же< равной 0,99, она будет отклоняться от *х не бо-
лее чем на* 2,58о. Вероятность выхода за пределы ±2,58 о
равна 0,01.
Если же взять в качестве границы За, то вероятность откло-
нения от х больше чем на За(/> ± 3) очень мала — всего 0,0027.
Это очень важное правило часто называют правилом трех сигм.
Три сигмы как бы ограничивают пределы случайного рассеяния
внутри вариационного ряда. То, что находится в пределах За, от-
носится к данному ряду; то, что за пределами За, вероятнее все-
го, к этому ряду уже не относится. Но для достижения вероят-
ности 0,9900 достаточно взять границы только + 2,58 а.
Вероятность, выражающаяся величиной 0,99, достаточно
велика, и в тех случаях, когда достигнута такая вероятность,
можно с очень большой степенью уверенности делать вывод
по поводу отнесения особи к той или иной группе, относительно
результатов опыта и т. д. Но нередко можно остановиться и на
более низком уровне вероятности, например 0,95. В этом случае
отклонения от ожидаемого будут уже в 5% случаев (вероят-
ность 0,05). Вероятности 0,95 и 0,99, или 95% и 99%, полу-
чили название доверительных вероятностей, т. е. таких, значе-
ниям которых можно достаточно доверять или которыми можно
уверенно пользоваться.
Понятие доверительной вероятности, в настоящее время ши-
роко используемое в статистике, было введено английским био-
логом и статистиком Р. Фишером.
Вероятности, принятые как доверительные, в свою очередь
определяют доверительные границы и доверительный интервал
между ними. На них можно основывать оценку той или иной
величины и те границы, в которых она может находиться при
разных вероятностях.
Для различных вероятностей доверительные интервалы будут
следующими:
Вероятности Интервалы
0,95 —1,96а ...+1,96а
0,99 —2,58а ... +2,58а
0,999 —3,03а ... + 3,03а
ТО
Вероятности можно обозначать как в долях единицы, так
и в процентах, поэтому'в последующем мы будем употреблять
параллельно оба обозначения.
3 Уровни значимости. Определенным" значениям вероятностей
ютветствуют так называемые уровни значимости. Вероятности
0,95 (95%) соответствует уровень значимости 0,05 (5%). По
отношению к закономерностям нормального распределения* это
означает, что выход за пределы принятых границ возможен в
порядке случайности с вероятностью 0,05, т. е. в 5% случаев ри-
скуют ошибиться в своих выводах.
. При вероятности 0,99 уровень значимости 0,01 (1 %). Слу-
чайное отклонение возможно лишь с вероятностью 0,01, т. е. риск
ошибиться в оценках составляет только 1% (1 случай на 100).
Таким образом, уровень значимости обозначает вероятность
получения случайного отклонения от установленных с опреде-
ленной вероятностью результатов. С помощью уровня значи-
мости можно установить, в каком проценте случаев (или с ка-
кой вероятностью) все же возможна ошибка в результатах, в тех
выводах, которые делаются на основе опыта, в оценке достовер-
ности показателей или различий между какими-то величинами,
полученными в опытах или при наблюдениях.
При научном исследовании надо не только получить те или
другие результаты, но и сделать выводы, поэтому очень важно,
чтобы получаемые выводы имели достаточно высокую достовер-
ность (употребляют также термины значимость, существен-
ность). Например, 5%-ный уровень значимости (0,05) указывает,
что возможна в силу случайности ошибка в 5°/о случаев. В не-
которых случаях можно удовлетвориться и таким результатом.
Но если нужна большая доказательность результатов, то уро-
вень значимости должен быть повышен до 1°/о (0,01). Чем цифра
меньше, тем уровень значимости, а следовательно, и достовер-
ность результатов выше. При уровне значимости 0,01 (1%)
вывод не обоснован только в одном случае из 100. Такую значи-
мость считают уже высокой и широко ею пользуются. Но быва-
ют случаи, когда уровень значимости может быть еще выше —
0,001. Тогда вывод не обоснован только в одном случае из 1000.
Выше указывалось, что в каждом конкретном случае, исходя
из важности события, устанавливается граница той вероятности,
с которой считаются в жизни, и той, с которой не считаются. Уро-
вень значимости в таком случае — это та вероятность, которой
решено пренебрегать в данном исследовании или явлении.
Односторонние и двусторонние оценки. На рис. 7 представ-
лена нормальная вариационная кривая, на которой нанесен до-
верительный интервал при вероятности 0,95. Выход за пределы
этого интервала измеряется общей величиной 0,05, которая распре-
деляется на две стороны кривой, по 0,025 с каждой стороны. Гео-
метрически— это доли площади под нормальной кривой распреде-
ления. Те же доли площади под нормальной кривой в пределах от
71
Рис. 7. Нормальная кривая с довери-
тельным интервалом (при р=0,95) от
х— 1,96<т до х+Г,96о, Двусторонний
выход за пределы доверительного ин-
тервала по 0,025 на каждую сторону.
Рис. 8. Граница доверительного ин-
тервала при р=0,95 внутри интер-
вала и р=0,05 за его пределами
при односторонней оценке (/=1,64).
х — to до x-\-to даны и в табл. I. Чтобы установить долю пло-
щади, остающуюся за этими ..пределами, надо из 1 вычесть указан-
ную в таблице величину для данного t. Эта доля, очевидно, рас-
пределяется по обе стороны кривой. Учет отклонений в обе стороны
от средней арифметической наиболее част в биологических яв-
лениях. Но бывают случаи, когда надо учесть только односторон-
нее отклонение. Так, если при отборе надо оставить для последу-
ющего разведения 5% лучших животных, то установить значение /,
отсекающее 5% с правой стороны кривой распределения, непосред-
ственно по табл. I уже нельзя. Очевидно, надо будет сделать пе-
ресчет, а именно: 5 помножить на 2 и взять такое значение t, при
котором внутри х + to останется доля вариант 0,90. t будет рав-
на 1,64. Доверительный интервал отсекается границей x-f-l,64o.
Это показано на рис. 8.
Существуют готовые таблицы, где даны площади под нор-
мальной кривой, отсекаемые определенными значениями t только
справа или только слева от средней (табл. XII—XIV):*
Уравнение нормальной кривой распределения. Кривая нор-
мального распределения может быть охарактеризована матема-
тически с помощью определенного уравнения. Это уравнение но-
сит следующую форму:
(х, — X)2
1 Г?3
и — — /— е
аУ2л
В него входят все уже известные величины, а именно х — сред-
няя арифметическая,** о и о2 — среднее квадратическое отклоне-
* См. книгу Weber Е. Grundriss der biologischen Statistik.
»» В дальнейшем мы увидим, что в уравнение входит средняя арифметиче-
ская генеральной совокупности, которая обозначается греческой буквой ц, а не
средняя арифметическая выборки х.
72
ние и варианса, характеризующие степень колеблемости вокруг
средней. Эти две величины являются параметрами нормального рас-
пределения. Число л (читается пи) равно 3,14159, а е — основание
натуральных логарифмов — равно 2,71828. В показателе степени ве-
личины е находится возведенное в квадрат нормированное отклоне-
ние t = Xl~x . При нормальном распределении большая часть пло-
щади кривой укладывается в пределах + 3/ (или в пределах ± 3 о,
так как t выражено в сигмах). Точки перегиба нормальной кривой
приходятся на + 1 о и — 1 о.
В средней части нормальная кривая выпукла, по краям она
вогнута. _
Если принять а = 1 и заменить значение Xi~~ величиной t, то
уравнение кривой нормального распределения примет следующую
более простую форму:
1 - —
у = __е 2.
* /2 л
Высчитанные для разных значений t величины у и дадут ор-
динаты нормальной кривой.
В табл. 17 даны значения ординат, выраженные в долях
единицы, для разных t. Иногда приводят значения ординат к
стандартному п=10 000. Тогда они будут выражены целыми
числами.
Из этой таблицы видно, что в случае нормального распределе-
ния при t = 3,0 кривая практически сливается с осью абсцисс.
Продолжение кривой за пределами + 3 о можно заметить только
при очень большом числе изучаемых особей.
При п = 10000 только 2 варианты (с каждой стороны кривой)
будут иметь t = 3,9 и одна — t — 4,0.
Сопоставление конкретных частот с ординатами нормального
распределения. Чтобы привести в соответствие частоты любого
конкретного распределения с приведенными теоретическими орди-
натами, достаточно только знать а данного ряда и п. Тогда мож-
но определить постоянный множитель для перехода от теоретиче-
ских ординат к ординатам конкретного ряда. Этот множитель ра-
вен —. Так, если д = 168, а о = 2,45, то
а ’
Л 168 СО Е
Т = = 68’5-
Ордината, соответствующая средней арифметической, имею-
щая ^=0, будет равна 68,5X0,3989=27,X Для всех остальных
классов ряда определяются соответствующие иМ нормированные
отклонения t и по ним табличные координаты. Умножение их на
множитель дает искомые ординаты. По ним строится конкретная
73
Таблица 17
Значения ординат (в долях единицы)
для разных t
t Ординаты t Ординаты
0,0 0,3989 1,6 0,1109
0,1 0,3970 1,7 0,0940
0,2, 0,3910 1,8 0,0790
о,з 0,3814 1,9 0,0656
0,4 0,3683 2,0 0,0540
0,5 0,3521 2,1 0,0440
0,6 0,3332 2,2 0,0355
0,7 0,3123 2,3 0,0?83
0,8 ' 0,2897 2,4 0,0224
0,9 0,2661 2,5 0,0175
1,0 0,2420 2,6 0,0136
1,1 0,2179 2,7 0,0104
1,2 0,1942 2,8 0,0079
1,3 0,1714 2,9 0,0060
1,4 0,1497 3,0 0,0044
1,5 0,1295 3,9 0,0002
4,0 0,0001
кривая распределения, которую можно сравнивать с нормальной
кривой.
Эмпирические ряды распределения и их отклонение от теорети-
ческих. Конечным результатом изучения той или иной совокупнос-
ти по определенным признакам является составление эмпирическо-
го вариационного ряда, его графическое изображение в виде поли-
гона или гистограммы и вычисление основных статистических по-
казателей (х и о или о2). Очень большое количество биологических
признаков варьирует в соответствии с закономерностями нормаль-
ного распределения. Однако возможны случаи, когда фактические
распределения в той или иной степени отклоняются от теорети-
ческих. Это может проявиться как в форме кривой распределения,
так и в особенностях полученных статистических показателей.
В гл. 1 уже упоминалось о дву- или многовершинности кривых
распределения, могущих быть результатом объединения в-одну со-
вокупность двух или нескольких групп, в действительности отли-
чающихся друг от друга. Очевидно, что в таких структурно неод-
нородных рядах и нельзя ожидать проявления закономерностей
нормального распределения.
74
Перед биологом будет стоять задача расчленения исходного ма-
териала на более однородные группы, с тем чтобы каждую из них
обработать самостоятельно, выразить ее в виде кривой распределе-
ния и вычислить статистические показатели.
Одновершинная кривая распределения может быть не вполне
симметричной. Полезно вычислить показатель асимметрии, который
дает объективную оценку степени асимметрии, трудно уловимую на
глаз при рассмотрении графиков. Неполная симметрия (скошенность)
иногда есть результат неполноты материала, т. е. недостаточного
количества изученных вариант. Если асимметрия значительна, сле-
дует проверить, не является ли полученное распределение пуассо-
новым. Критерием его, как указано выше,, служит примерное ра-
венство х и о2. Однако асимметрия ряда может зависеть и от при-
роды изучаемого признака, по каким-либо причинам легче варьиру-
ющего в одном направлении и труднее — в другом.
Соответствие фактического распределения нормальному дает воз-
можность судить и о том, в какой степени изучаемый эмпири-
ческий материал действительно однороден, нет ли в нем отдельных
вариант, которые по тем или иным причинам резко выделяются
из изучаемой совокупности. При проведении опытов иногда полу-
чают так называемые «выскакивающие» результаты, которые явно
не укладываются в общую картину вариации полученных данных.
При изучении материала, взятого из природы или хозяйства, так-
же бывают случаи, когда одна или несколько вариант отклоняются от
средней арифметической значительно больше, чем на 3 а. Так, например,
если при_ изучении веса при рождении большой группы телят по-
лучены х = 32 кг и а = 3 кг, то теленок с весом 17 кг окажет-
ся далеко за _пределами изменчивости этой группы телят. Его от-
клонение от х будет равно 5 о.
В практике экспериментальной работы нередко такие «выскаки-
вающие» значения исключают из анализируемого материала, считая
их результатом не замеченной при проведении опыта или наблю-
дения неточности, ошибки или каких-либо частных «патологичес-
ких» обстоятельств, нарушающих общую картину.
Однако это можно делать лишь в тех случаях, когда весь
остальной материал действительно укладывается в очень четкий и
симметричный вариационный ряд. При асимметричном же распре-
делении некоторые варианты могут отклоняться от ~х значительно
больше чем на Зет в силу самой закономерности вариации. Поэто-
му исключение подобных вариант из рассматриваемого материала
будет неправильным.
Выше уже указывалось, что, хотя теоретический ряд распре-
деления должен охватывать (если он нормальный) примерно 6
значений среднего квадратического отклонения,, в конкретном
эмпирическом вариационном ряду это будет наблюдаться в об-
щем довольно редко. При малых п соответствующий нормально-
му эмпирический ряд может охватывать не 6, а 5 или 4<т.
7S
Возможно также большее сгущение вариант вблизи .средней
арифметической при недостатке их в боковых частях распреде-
ления («крутизна») и, наоборот, ненормально малая частота ва-
риант в классах, близких к средней арифметической («плоско-
вершинность»). При «крутизне» значения а малы по сравнению
с теми же параметрами нормального ряда, при плосковершин-
ности, наоборот, велики. Это легко проверить, если, сохраняя х,
уменьшать или увеличивать значение а. Вариационная кривая
при этом будет делаться или более острой, или более плоской.
Таким образом, биолог должен очень вдумчиво анализиро-
вать получерные эмпирические ряды распределения и, оценивая
их математически, не забывать об их биологической природе,
отнюдь не* стремясь подогнать их к тому или иному виду теоре-
тических кривых.
Методы сравнения эмпирических рядов с теоретическими с по-
мощью критерия хи-квадрат изложены в гл. 9.
ВОПРОСЫ
1. Что такое вероятность? По какой формуле вычисляется вероятность?
2. Какие процессы называются вероятностными или стохастическими?
3. Приведите примеры некоторых биологических явлений, осуществление
которых может быть оценено известной вероятностью.
4. Можно ли не считаться с возможностью событий, обладающих малой
вероятностью?
5. Какое значение имеет р для очень достоверных событий?
6. Какая связь существует между частотой определенного явления и веро-
ятностью?
7. Чему равна сумма р + д?
8. Какая разница между эмпирической и теоретической вероятностью?
9. Дайте определения теорем сложения и умножения вероятностей. Проил-
люстрируйте их примерами.
10. Если бы все особи популяции были одинаковы, по какому количеству
особей можно было бы получить информацию о популяции?
11. Какая связь существует между вариацией в пределах вариационного ря-
да и распределением вероятностей?
12. Что иллюстрирует аппарат Гальтона?
13. Что такое биномиальная кривая распределения? Какая общая формула
является основой для биномиального распределения?
14. Что такое k в биноме (р + ?)А?
15. Какими параметрами характеризуется биномиальное распределение? Явля-
ется ли оно дискретным или непрерывным?
16. Как можно связать значения х и а2 при биномиальном распределении со
значениями р, q и &?
17. Чем отличается распределение Пуассона от биномиального? _
18. Можно ли заметить распределение Пуассона по значениям х и а2?
19. Какими параметрами характеризуется распределение Пуассона?
20. Какой ряд выражает частоты распределения Пуассона?
21. Что такое нормальное распределение и как оно связано с биномиаль-
ным?
22. Почему нормальное распределение является непрерывным?
23. Что такое нормированное отклонение? Сколько t охватывает вариацион-
ный ряд при нормальном распределении?
24. Что показывает таблица нормального интеграла вероятностей?
25. Какой процент особей укладывается в пределах ± 1 и, ± 2 а, ± 3 в?
76
26. Какие вероятности считаются доверительными?
27, Дайте определение терминов «доверительные границы» и «доверитель-
ный интервал».
- 28. Каков доверительный интервал при нормальном распределении с веро-
ятностью 0,95; 0,99?
29. Что такое уровень значимости? Какая связь между уровнем значимос-
ти и вероятностью? Можно ли выражать уровень значимости в процентах? На
что указывает процентная величина уровня значимости?
30. Каков характер распределения при малых значениях и?
31. В каком случае для достижения одной и той же вероятности значения t
должны быть бдльшими — при малом п или при большом?
32. Чем могут отличаться эмпирические ряды распределения от теоретических?
33. Всегда ли кривые распределения симметричны?
34. Обязательно ли эмпирический ряд распределения должен охватывать
± 3 а? Что такое «выскакивающие значения»?
ЗАДАЧИ
41. Какова вероятность, что в семье из 6 детей: а) все 6 будут девочками;
б) все дети будут одного пола; в) что первые 5 детей будут девочками, а 6-й
мальчиком?
ЛЧ 11.1
Ответ: 64> 32’ 64-
42. Какова вероятность, что в семье из 7 детей: а) первые 3 будут девоч-
ками, а остальные 4 — мальчиками; б) что будет по крайней мере одна девочка?
Л 1 1 127
Ответ: i2g; 1 — 128 — 128’
43. Какова вероятность, что при обратном скрещивании гороха, гетерози-
готного по зеленой окраске горошин, выборка из 12 горошин будет: а) состо-
ять только из зеленых горошин; б) только из желтых; в) содержать по край-
ней мере 1 желтую; г) содержать по крайней мере 1 зеленую?
1 1 4095 4095
Ответ: 4096 : 4096 : 4096 : 4096'
44. В табуне лошадей гнедых было 250, а вороных —150. Какова вероят-
ность того, что одна из пойманных наудачу лошадей будет гнедой, вороной?
Чему равна сумма этих двух вероятностей?
45. Какова вероятность, что в семье, имеющей 3 детей: а) первый будет
мальчик, а остальные 2 —девочки; б) что последний будет мальчиком, а пер-
вые 2 — девочками; в) что будут 1 мальчик и 2 девочки; г) что будут 2 маль-
чика и 1 девочка?
1 1 . 3 . 3 .
Ответ: 8 : 8 : 8> 8
1
46. Предполагая, что частота рождения мальчиков -тр определите процент
однояйцовых двоен по следующим объединенным для числа пар двоен данным:
235 615 пар было с 2 мальчиками, 220 335 — с 2 девочками; 265 291 пара состо-
яла из 1 мальчика и 1 девочки.
Ответ: 26,4%.
47. При спаривании черных гетерозиготных по рыжей окраске коров с ры-
жим быком ожидается расщепление в потомстве 1:1. Какова вероятность, что
все 6 телят от коров будут черными? Какова вероятность рождения двух чер-
ных телят? Ответ: 0,016; 0,25.
48. За период 6 лет было учтено 154 444 пары двоен. Из них было разно-
полых 58 382, только с мальчиками 49425 и только с девочками 46637. Рас-
77
считайте, какое количество пар двоен было однояйцовых. Для простоты расчета
примите, что соотношение полов точно 1:1.
Какова вероятность рождения однояйцовых и двуяйцовых двоен?
« Ответ: 0,24 и 0,76.
49. По данным переписи населения в СССР в 1926 г. было 71 043 357 муж-
чин и 75 984 558 женщин.
Какова вероятность рождения особей мужского пола в населении?
50. 1-06 опоросов по 8 поросят в каждом распределились по числу самцов
следующим образом:
- Число самцов 1 2 3 4 5 6 7 8
Количество опоросов 5 9 22 25 26 14 4 1
Приняв, что в данном случае имеется биномиальное распределение, вычис-
лите х и а. С помощью х определите р и q. Попробуйте вычислить отдельные
значения количества опоросов, развернув формулу (р + <?)8» при л = 106.
Ответ: р » 0,52; q = 0,48.
51. На 10000 семей с 4 детьми было: все девочки — в 641 семье, 3 девоч-
ки и 1 мальчик — в 2625 семьях, 2 девочки и 2 мальчика — в 3748 семьях,
1 девочка и 3 мальчика — в 2420, все мальчики—в 566 семьях. Исходя из пред-
положения о биномиальности распределения, вычислите вероятность рождения
мальчиков и девочек.
52. Среди 402 опоросов свиней дюрок-джерзейской породы, в каждом из
которых было 8 поросят, пометы распределялись следующим образом:
Количество самцов в. помете 0123 45678
Количество опоросов 1 8 37 81 162 77 30 5 1
Определите х и а обычным методом и по величине х определите р и q. ,
53. Вероятность наступления некоторого события р = 0,30. Производится
2000 испытаний. В каком количестве случаев будет наблюдаться данное собы-
тие и каково его среднее квадратическое отклонение?
Ответ: в 600 случаях; а = 20.
54. В 100 пробах, в каждой из которых находилось по 1200 зерен ржи,
проверяли наличие двойных зародышей. Оказалось, что в некоторых пробах на-
ходили от 1 до 6 таких зародышей. Распределение найденных зерен с 2 заро-
дышами по пробам было следующим:
Количество зерен с двумя зародышами 0 1 2 3 -4 Ъ 6
. Число проб 6 24 32 18 9 6 5
Вычислите обычным путем среднюю арифметическую количества зерен с
2 зародышами на пробу, а также вариансу данного ряда. К какому типу рас-
пределения следует отнести этот ряд? Какова вероятность нахождения зерен с
2 зародышами в общей популяции зерен ржи? *
55. В опыте Резерфорда и его сотрудников было изучено распределение
2608 промежутков времени (в каждом было 0,125 минуты) по количеству рас-
павшихся за каждый промежуток атомов:
Количество атомов» распав-
шихся за 1 промежуток времени 0 1 2 3 4 5 6 У 8 9 10 11 12 13 14
Количество промежутков 57 203 383 525 532 408 273 139 45 27 10 4 0 .1 2
Проверьте, является ли это распределение пуассоновым.
\ 56. В 1000 выборок семян клевера определенного веса были найдены семена
повилики, которые распределялись по выборкам следующим образом:
гЧисло семян повилики в одной выборке 0 12 3
Количество выборок * 599/ 315 74 12
78
Докажите, что этот ряд является пуассоновым.
Какова вероятность появления семян повилики в пробах семян клевера?
Ответ: X = 0t499; с9 = 0,469; р = 0,0005.
57. В горизонтальных слоях было найдено на каждом квадратном метре по-
верхности следующее количество экземпляров ископаемого млекопитающего
Litolestes notissimus:
Количество экземпляров на квадрат 0 1 2 3 4 5 и больше
Количество квадратов 16 9 3 1 1 О
Определите х, а и а2. К какому типу относится данное распределение?
58. Пользуясь таблицей нормального интеграла вероятности, рассчитайте
какая доля^ вариант находится в вариационной кривой: а) между — 1,5а и + 1,0а;
б) между х и 4-2,6 а; в) между хи — 1,8 а; г) между 4- Ь и 2,8 а; д) в интер-
вале х±1,65а; е) в интервале х±0,68а; ж) за пределами 4-2,2 а; з) за преде-
лами ± 2.4 а.
Ответ; 0 77; 0,495; 0,46; 0,838; 0,90; 0,50; 0 0139; 0,0164.
59. При каком значении ± t 50% вариант находится в пределах данного
значения tt а другие 50% — за его пределами?
60. Какому уровню значимости соответствует t =» 2,6 (при п = 1000, при
п = 6, п — 15)?
61. На 1000 мальчиков 13-летнего возраста было установлено, что 390 из
них отклоняются от средней арифметической по росту (высоте тела) не более
чем иа 1,4 дюйма (х = 57,3 дюйма). Можно ли по этим данным определить
примерную величину а, если предусматривается нормальное распределение?
Ответ: 2,7 д.
62. Какое значение*/ нужно взять, чтобы оно ограничивало 95% площади ва-
риационной кривой при разных значениях л, а именно: если л = 4;л=12;
л = 20?
Ответ: 3,2; 2,2; 2,1;
63. Если совокупность очень большая, при каком значении t возможны
случайные отклонения за его пределами в сторону плюса в 2,5% случаев, в
5,0% случаев?
64. Известно, что группа коров, охватывающая 10 тысяч голов, имеет по
удою за лактацию х = 3200 кг и а = 300 кг. Сколько в группе может быть
коров, удои которых за лактацию превышают 4100 кг? В каких пределах
колеблются удои преобладающей части группы (70%) коров?
Ответ: 13—14 коров; 2900—3500 кг.
65. Выловленная в пруду рыба имела по весу х = 375 г и а = 25 г. Ка-
кова вероятность, что вес пойманных рыб будет: а) в пределах от 325 до 425 г;
б) не более 400 г; в) не более 425 г; г) не менее 375 г; д) не менее 350 г?
Ответ: 0,95; 0,84; 098; 0 50; 0.84.
ГЛАВА 4
ОЦЕНКА ДОСТОВЕРНОСТИ СТАТИСТИЧЕСКИХ
ПОКАЗАТЕЛЕЙ
Проблема достоверности в статистике. Приемы и методы, из-
ложенные в предыдущих главах, дают возможность исчерпыва-
юще охарактеризовать биологические совокупности. Каждая со-
вокупность может быть представлена в виде ряда распределения.
Для ряда распределения можно определить статистические по-
казатели, указывающие на наиболее типичный уровень развития
изучаемого в совокупности признака и на степень вариации от-
дельных единиц совокупности вокруг этого уровня.
Большинство из них — именованные величины (средняя ариф-
метическая, мода, медиана, среднее квадратическое отклонение),
некоторые выражаются в процентах (коэффициент вариации)
или, наконец, являются неименованными числами (варианса, ко-
эффициент асимметрии). Но так как все они — статистические
величины, то есть основаны на изучении массовых явлений, воз-
никает очень важный теоретически и практически вопрос о том,
насколько они достоверны.
Проблема достоверности занимает видное место в статистиче-
ской теории.
Выборочные и генеральные совокупности. Изложенные в пре-
дыдущей главе общие закономерности случайной вариации дают
возможность подойти к вопросу об оценке достоверности статис-
тических показателей. Но для этого надо вновь вернуться к двум
типам совокупностей — генеральной и выборочной. В гл. 1 уже
говорилось о различиях между ними.
Напомним, что генеральная совокупность — это вся подлежа-
щая изучению совокупность данных объектов. В пределе она
рассматривается как состоящая из бесконечно большого коли-
чества отдельных единиц. Та часть объектов, которая подверга-
ется исследованию, называется выборочной совокупностью или
просто выборкой.
Оба типа совокупностей в общем характеризуются одинаковыми
закономерностями случайной вариации. Для их характеристики мо-
гут быть вычислены статистические показатели: средняя арифме-
80
тическая и среднее квадратическое отклонение. Среднюю арифме-
тическую мы обозначали ранее символом х. Условимся теперь, что
х обозначает среднюю арифметическую выборочной совокупности.
Среднюю арифметическую генеральной совокупности будем обозна-
чать р. (греческая буква мю, или мй). Каково же соотношение меж-
ду хи ц?
Допустим, что для совокупности, состоящей из 168 коров сим-
ментальской породы, была получена средняя арифметическая глу-
бины груди 73,8 см. 168 коров представляют собой выборку из ге-
неральной совокупности, охватывающей популяцию всех коров сим-
ментальской породы. Если бы мы взяли ряд выборок из популя-
ции симментальской породы, то обнаружилось бы, что х этих вы-
борок будут различными. Одни из х будут несколько больше чем
73,8 см, другие — меньше.
Очень важно, что распределение выборочных средних при до-
статочном их количестве близко к нормальному, поэтому к нему
относятся указанные в предыдущей главе закономерности. Оказы-
вается, что отдельные значения средних арифметических выборок
(х) варьируют вокруг средней арифметической генеральной совокуп-
ности р>. Вариация же выборочных средних вокруг р- может быть
измерена своим средним квадратическим отклонением, своей сигмой.
Эта сигма получила название средней ошибки или средней квадрати-
ческой ошибки. Иногда ее называют также стандартной ошибкой.
Именно она указывает на степень близости х и р..
Формула для средней ошибки. Средняя ошибка для х может
быть вычислена по формуле
(24)
Р Л»
В прежних руководствах по статистике ее обозначали буквой
т. Ее можно было бы изобразить и как ст-, так как она является
не чем иным, как средним квадратическим отклонением вариаци-
онного ряда, составленного из значений отдельных х, т. е. выбо-
рочных средних. Обычно же среднее квадратическое отклонение,
обозначавшееся выше знаком о, относится к вариационному ряду,
составленному из вариант, т. е. xt. Так как средние арифметичес-
кие выборочных совокупностей варьируют вокруг |д, то в формуле
ошибки надо было бы взять среднее квадратическое отклонение (ст)
генеральной совокупности/Чтобы получить его значение, пришлось
бы изучить всю генеральную совокупность, что невозможно. Кро-
ме того, тогда не было бы и надобности определять среднюю
ошибку выборки.
Оказалось, что вместо среднего квадратического отклонения
генеральной совокупности можно без большой погрешности взять
для формулы (24) значение среднего квадратического отклонения
выборочной совокупности. Разница между ними невелика, и при
81
достаточно большом количестве наблюдений (практически не-
сколько десятков) они будут равны друг другу. Именно поэтому
мы употребляем знак о и для среднего квадратического отклоне-
ния выборки. В специальной же литературе знак о относят толь-
ко к генеральной совокупности, а среднее квадратическое откло-
нение выборки обозначают через s.
В знаменателе формулы (24) под корнем п — объем выбороч-
ной совокупности. Это значит, что величина средней ошибки
обратно пропорциональна численности выборочной совокупности.
В примере с глубиной груди у симментальских коров п = 168
и о = 2,45. Отсюда средняя ошибка для средней арифметической
глубины груди изученных 168 симментальских коров
2,45 Л 1*7
s- — '— = 0,17 см.
х /168
Средняя ошибка — ошибка выборочности. Термин «ошибка»
часто вводит в заблуждение начинающих, которые предполага-
ют, что она является результатом недостаточной аккуратности
в работе. Это не так. Средняя ошибка — это статистическая
ошибка. Она не имеет ничего общего с ошибкой точности. Само
собою разумеется, что все измерения (веса и промеров рыб, удо-
ев коров и жирности их молока, настригов шерсти овец и ее дли-
ны) надо делать точно и добросовестно. Но статистические пока-
затели для выборочной совокупности всегда имеют так называе-
мые ошибки выборочности (их также называют ошибками репре-
зентативности), которые представляют собой среднюю величину
расхождения между средними значениями изучаемых признаков
в выборках и генеральной совокупности. .
Так как s— = —р=~» то очевидно, что размер определяемой
средней ошибки зависит от сигмы выборочной популяции и от ее
объема. Чем лучше взята выборка и чем больше ее размеры, тем
меньше и средняя ошибка, тем меньше расхождение между зна-
чениями признаков в выборочных и генеральной совокупностях.
Биолог почти всегда имеет дело с выборками — и при прове-
дении опытов с животными или растениями, и при изучении ма-
териала, взятого из природы,— генеральные же совокупности
остаются неизвестными. Поэтому он должен постоянно помнить
о том риске, который сопутствует его выводам. Часто эти выводы
основываются на изучении небольшого материала, поэтому полу-
ченные в опытах или наблюдениях статистические показатели
могут иметь значительные статистические ошибки. Легко видеть,
что в силу колеблемости выборочных средних вокруг средней ге-
неральной совокупности один какой-либо опыт может дать ре-
зультат, отклоняющийся от истинного на 2 или Даже 3 ошибки.
Но при значительном количестве опытов их результаты будут
группироваться близко к центру распределения генеральной со-
82
вокупности, т. е. к р, что дает возможность уверенно сделать
- правильный вывод.
Закон больших чисел. В связи между статистическими пока-
зателями выборочных и генеральных совокупностей выражается так
называемый закон больших чисел. В наиболее общем виде этот за-
кон заключается в том, что чем больше число п некоторых слу-
чайных величин, тем их средняя арифметическая ближе к средней
арифметической генеральной совокупности, тем меньше разница
между х и [л. По мере увеличения п вероятность осуществления
приближения х к р- становится все большей, стремясь при п — со
к единице, т. е. к полной достоверности.
В этом заключается теорема одного из основоположников ма-
тематической статистики русского математика П. Л. Чебышева.
Так как всякое явление, как правило, складывается из массы
единичных, случайных явлений, то закон больших чисел выступа-
ет как реальный закон объективной действительности. Именно он
лежит в основе нормального распределения вариант в вариационном
ряду, т. е. распределения значений случайной переменной х вокруг х,
- а также в основе распределения выборочных х вокруг р.
Выборочные средние, для которых вычисляются средние
ошибки, являются такими же случайными величинами, как и зна-
чения вариант в обычном вариационном ряду. С возрастанием
объемов выборок их вариация вокруг генеральной средней < ста-
новится все меньше. Средняя же арифметическая из всех выбо-
рочных средних должна быть равна средней арифметической
генеральной совокупности, т. е. р.
Таким образом, основное содержание закона больших чисел
состоит в том, что при увеличении п отдельных выборок происхо-
дит взаимное погашение индивидуальных отклонений от неко-
торого уровня, характерного для всей совокупности в целом.
Именно тогда проявляется закономерность, лежащая в основе
биологического процесса. Закон больших чисел — одно из выра-
жений диалектической связи между случайностью и необходи-
мостью. __
Распределение х малых выборок. Когда выборки являются до-
статочно большими по объему, распределение их средних арифме-
тических является нормальным. Однако если выборки малы
(л<30), то возникает большое сомнение в возможности суждения
по таким выборкам о генеральной совокупности. В значение f мо-
жет вкрасться значительная неточность.
В биологических исследованиях нередко приходится встре-
чаться с выборочными совокупностями, состоящими из очень
ограниченного количества вариант или наблюдений.
Возникает вопрос о том, каковы в этих случаях закономерно-
сти распределения выборочных средних арифметических.
' Ответ на него практически дал английский математик Госсет,
который писал под псевдонимом Стьюдент. Поэтому изученное
83
Ьм распределение вероятностей получило название /-распределе-
ния по Стыоденту.
Теоретическое обоснование закона распределения.-открытого
Стьюдентом, было дано Фишером".’Существенно то, что оно мо-
жет быть использовано'и при очень малых количествах.вариант.
Критерий t по Стыоденту — Фишеру представляет собой следу-
ющее:
/=•£=£. (23а)
57 1
Легко видеть, что эта формула принципиально сходна с фор-
мулой (23). Ее отличие в том, что в знаменателе находится не сг,
a s-. Величина же s- вычисляется по формуле (24) — как частное
от деления среднего квадратического отклонения выборочной сово-
купности на корень квадратный из численности той же совокуп-
ности. Оказалось, что распределение значений t отличается от нор-
мального, при этом тем сильнее, чем меньше п. Поэтому и веро-
ятности нахождения выборочных средних в пределах определенных
значений + t значительно снижаются по сравнению с нормальным
распределением, как это видно из табл. II приложения. Иначе го-
воря, для достижения тех же вероятностей нужно взять значитель-
но большие интервалы x±t$^. Так, при п = 5 вероятность 0,95
достигается лишь при t = ± 2,8, а вероятность 0,99 — при t = +4,6.
На рис. 9 представлены для сравнения две кривые: для нор-
мального распределения при п = оо и для /-распределения при
п = 5. У нижней кривой края более растянуты вправо и влево.
По 2,5% выборочных средних справа и слева отсекаются: в верх-
ней кривой при / = 1,96, в нижней — при / = 2,78. В обоих случа-
ях вероятность — 0,95, а уровень значимости — 0,05.
В практической работе надо исходить из определенных уров-
ней значимости, поэтому были составлены рабочие таблицы, по
которым можно определять минимальное значение /, обязательно
требующееся для данной вероятности (табл. III).
Табл. III построена на основе заранее принятых необходимых
доверительных вероятностей и соответствующих им уровней зна-
чимости. Для упрощения в ней даны только 4 уровня значимости
(0,1; 0,05; 0,02 и 0,01), в полных таблицах обычно приводят и
иные уровни значимости. Если, например, выборка включает
только 10 наблюдений (число степеней свободы 9), а требуется
по условиям опыта уровень значимости 0,01 (и доверительная
вероятность 0,99), то величина / должна быть не менее 3,25.
Уровню значимости 0,05 (и доверительной вероятности 0,95)
удовлетворяет при п — 9 величина / =• 2,62.
По мере увеличения п /-распределение приближается к нор-
мальному. При п>30 разница между ними практически исчезает.
Нижняя строка табл. III, где п = оо, связывает значения / по
Стьюденту со значениями /, приведенными в табл. I для нормаль-
84
Рис. 9. Разные значения t, отсекающие по 2,5% площади справа и сле-
ва: а — под кривой нормального распределения (n=oo; /=1,96); б —
под кривой /-распределения по Стьюденту (п=5; /=2,78).
ного интеграла вероятностей. Для более точных расче/ов вероят-
ности надо пользоваться таблицами Стьюдента 'при малом
п(п<20) и таблицами нормального интеграла вероятности при
больших л(п>20). Следует иметь в виду, что указанные в верх-
ней части табл. III значения Р являются двусторонними крите-
риями. Односторонние же критерии вдвое меньше. Надо будет
применять тот же метод пересчета, о котором говорилось в гл. 3.
Например, для Р = 0,05 при одностороннем критерии надо брать
цифры той колонки табл. III, где Р = 0,10, а для Р =>0,01 —из
колонки, где Р =<0,02.
Исследования Стьюдента сыграли громадную роль, так как
дали возможность работать с малыми выборочными совокупно-
стями так же, как и с большими. При этом надо только учиты-
вать различия в вероятностях для t в зависимости от размеров
выборок.
,s- как мерило колеблемости вариационного ряда, составлен-
ного из х. Распределение выборочных средних подчиняется закону
нормального распределения.
85
Из генеральной совокупности может быть получено громадное
количество различных выборочных совокупностей, несколько отли-
чающихся друг от друга составом входящих в них единиц. При
этих условиях получить все возможные величины выборочных сред-
них, очевидно, нет возможности. Но в этом и нет надобности,
так как согласно закону нормального распределения, известен про-
цент значений х, находящихся в пределах отклонений на + 1s-,
± 2s—, + 3s- от средней генеральной совокупности, аналогично
тому, как это было установлено для распределения вариант в
обычном вариационном ряду (в пределах + la, ± 2s, + За). Таким
образом, в -пределах ± 1s- находится 68,3% всех выборочных
средних, в пределах ± 2s-— 95,5 % всех выборочных средних,
в пределах ± 3s- —99,7% всех выборочных средних.
.Это дает возможность использовать выборочную среднюю для
оценки генеральной средней. Нужно только знать среднюю ошибку.
Так как точное значение н неизвестно, можно использовать вмес-
то ji среднюю арифметическую выборки х и, зная s-, с опреде-
ленной степенью вероятности судить о пределах, в которых за-
ключены возможные величины выборочных средних.
Определение доверительного интервала для «. Так как выбо-
рочные средние х колеблются вокруг средней арифметической ге-
неральной совокупности (*, то по ним можно с некоторой вероят-
ностью судить о р.. Для оценки р надо будет воспользоваться ве-
личиной ошибки и нормированным отклонением t.
Вероятность появления данной величины средней арифмети-
ческой для выборки из генеральной совокупности является функ-
цией того же нормированного отклонения, с помощью которого
была дана выше характеристика нормального распределения.
Поэтому можно установить с определенной вероятностью те
границы, в которых находится^ средняя арифметическая генераль-
ной совокупности, с помощью х, s— и t из формулы (23а), а именно:
х — ts— < р х + /Sj, (25)
или, иначе,
х —+
У п у п
Эти границы получили название доверительных', интервал, т. е.
разница между максимумом и минимумом, также называется дове-
рительным.
Естественно, что <т в данном случае — среднее квадратическое
отклонение не генеральной, а конкретной выборочной совокуп-
ности.
Обычно заранее устанавливают ту или иную доверительйую
вероятность, с которой желают установить доверительные грани-
цы для р., например /7=0,95; р—0,99; р=0,999, что соответст-
вует уровням значимости 0,05; 0,01; 0,001. Чтобы указать, какой
86
уровень значимости или вероятности принимается в данном слу-
чае, при букве t записывают показатель уровня значимости, на-
пример: /os или /оь Кроме того, необходимо обращать внимание
на п. При большом п значение t можно взять из таблицы нор-
мального интеграла вероятностей (табл. 1), при малом п — из
таблицы Стьюдента (табл. II).
В примере с глубиной груди симментальского скота п = 168.
Величина tOs (т. е. вероятность 0,95, а уровень значимости 0,05)
по табл. I будет 1,96. Так как s-=0,17 см, то доверительный
интервал, в котором находится значение при уровне значимости
0,05, будет от 73,8 — 1,96 • 0,17 = 73,5 до 73,8 + 1,96 • 0,17 = 74,2.
Этот вывод можно формулировать и так: 0,95 — это вероятность
того, что данный интервал 73,5 — 74,2 содержит р.
Для иллюстрации определения доверительного интервала для
(1 при малом п возьмем такой пример. Определяли концентрацию
витамина С в томатном соке (в мг/100 г сока). При этом х =
= 20 (мг/100 г), sr = 0,965 (мг/100 г), п = 17.
Надо определить интервал с доверительной вероятностью
0,95 (Р = 0,05). Так как п меньше 20, надо воспользоваться
табл. II для /-распределения по Стьюденту.
Так как в табл. II нет графы п = 17, надо взять циф-
ры вероятностей средние между п = 16 и п — 18. Для веро-
ятности 0,95 значение / будет между 2,1 и 2,2 примерно 2,12.
Тогда /08 • s- = 2,12 • 0,965 = 2,05 (мг/100 г), а доверительные гра-
ницы будут 20 — 2,05— 17,95 и 20 4-2,05 = 22,05 (мг/100 г).
Еще проще воспользоваться для установления / табл. III. При
п= 17 количество степеней свободы равно 16. В пересечении гра-
фы для уровня значимости 0,05 и строки df = 16 находим / =
= 2,12. На эту величину умножаем
Учет доли выборки при вычислении средней ошибки. Указан-
ная выше формула средней ошибки (24) достаточно точна в тех
случаях, когда численность выборочной совокупности (и) очень ма-
ла по сравнению с численностью генеральной совокупности (N).
Отношение-^- носит название доли выборки. Если генеральная со-
вокупность численно не очень велика (теоретически, как указыва-
лось выше, ее принимают бесконечно большой, разные генераль-
ные совокупности могут быть и ограниченных объемов), выборка
же достаточно большая по количеству и особи ее не возвращают-
ся обратно в генеральную совокупность, то это может сказаться
на величине средней ошибки. Обычно при вычислении ее по фор-
муле (24) она оказывается завышенной. Для получения более точ-
ного значения средней ошибки в нее следует ввести поправку/
учитывающую соотношение а именно
87
Тогда
(24а)
п 1/1 Л
S- = -7=- V 1---лГ-
х /п r N
Если доля выборки мала, подкоренное выражение и сама
поправка близки к единице. Средняя ошибка почти не изменится.
Если же доля выборки более или менее велика, поправка повлия-
ет на величину ошибки. Можно составить следующую табличку
величин поправок при различных долях выборки:
Доля выборка 0,1 0,25 0,3 0,5 0,6 0,7 0,8
Поправки (]/1— о,95 0,87 0,84 0,71 0,63 0,55 0,45
Отсюда ясно, что поправку целесообразно применять лишь
в тех случаях, когда численность выборки составляет не менее
20—25% численности генеральной совокупности.
В зоологических и ботанических исследованиях такие случаи,
очевидно, редки, и тогда можно вычислять ошибку по обычной
формуле (24).
Определение необходимого объема выборочной совокупности.
Ъ практике биологических исследований часто возникает вопрос о
том, сколько животных (или растений) данного вида надо взять,
чтобы получить достаточно правильное представление о популяции
вида (по изучаемому признаку). Вообще говоря, следует стремить-
ся к большему числу наблюдений, однако очевидно, что числен-
ность выборки не может возрастать бесконечно. Она должна иметь
какие-то рациональные границы, которые будут зависеть прежде
всего от желаемой точности наблюдения, т. е. допустимого расхож-
дения между средней арифметической (по данному признаку) вы-
борки и средней арифметической генеральной совокупности, а так-
же от заданной вероятности и от степени однородности популя-
ции. Желаемая точность (обозначим ее А) — это возможное при
принятой вероятности отклонение х от р., т. е.
А = ts-^
А так как s— = —4=-, то Д = t —^=. Отсюда
/2аа
П = - Д2-. (26)
Значение t определяется ожидаемой вероятностью результа-
та выборочного обследования. При р = 0,997 t должно быть рав-
но 3. При р=О,95 можно ограничиться t=2. Величина Д берет-
ся заранее. Так, например, изучая вес зайцев, можно принять,
что желаемая точность должна быть в пределах 0,2 кг,
т. е. Д= 0,2 кг.
Несколько труднее решить вопрос о величине среднего квад-
88
ратического отклонения изучаемой популяции вида, заранее не-
известной. В качестве ее приблизительной оценки можно взять
сигму по данным проводившихся ранее исследований или попы-
таться вычислить ее по максимальным и минимальным значени-
ям изучаемого признака, имея в виду, что вариационный размах
должен охватывать примерно шесть средних квадратических
отклонений.
Выборочный метод. Некоторая погрешность органически
присуща, результатам всякого наблюдения, проведенного на
основе выборки. Эту погрешность и измеряет средняя ошибка,
которая поэтому и называется ошибкой выморочности (или, ина-
че, ошибкой репрезентативности). Вместе с тем совершенно не-
обходимо, чтобы выборочная совокупность достаточно хорошо
отображала генеральную совокупность, иначе суждение о гене-
ральной совокупности по выборке будет неправильным, несмотря
на правильность статистических вычислений.
Добиться правильного отображения генеральной совокупно-
сти можно при одном непременном условии — отборе вариант
для выборки на основе случайности. Чем в большей степени
этот отбор будет случайным, тем более правильными будут вы-
воды, делаемые на основе выборочной совокупности. Именно
тогда можно полагаться на результаты выборочного наблюдения.
Наиболее простой способ получения случайных выборок —
отбирать экземпляры с помощью таблицы случайных чисел.
На принципе случайности основываются различные схемы отбора
вариант для выборки: случайная бесповторная выборка, когда
взятые для выборки варианты уже не возвращаются обратно
в генеральную совокупность, случайная повторная выборка
с возвратом взятых для выборки вариант обратно в генеральную
совокупность и т. д. Все они подробно рассматриваются в спе-
циальных пособиях (см. список литературы в конце книги).
Необходимо поэтому предостеречь ботаников и зоологов от
отбора для выборок так называемых типичных образцов. При та-
ком способе создания выборочных совокупностей очень трудно
избежать субъективизма, тенденциозности.
Средние ошибки для о и v. В некоторых случаях могут по-
надобиться средние ошибки для других биометрических показа-
телей. Они вычисляются по следующим формулам:
(28>
s для я «, -
V
5 для *s* = ТйГ
Эти формулы можно применять только при- большом числе на-
блюдений. При малом п применяются другие, более сложные ме-
тоды.
Средняя ошибка и здесь дает возможность по такому же прин-
ципу, как для х, определить доверительные границы для оно.
(27>
89
Допустим, что о = 3,5, п = 200. Тогда sa = = 0,175. При
уровне значимости 0,01/ = 2,58.
Доверительные границы для а будут:
и 3,5 — 2,58.0,175 = 3,05
3,5 4-2,58 0,175 = 3,95.
Это значит, что среднее квадратическое отклонение при уров-
не значимости 0,01 находится между 3,05 и 3,95.
Таким образом, с помощью средней ошибки можно устано-
вить, приняв' определенную вероятность, возможные границы
для колебаний средней арифметической, среднего квадратическо-
го отклонения и любых иных статистических показателей. Это
дает возможность предсказать по выборочной совокупности свой-
ства генеральной совокупности.
Впрочем, о2 выборочной совокупности очень близка к ст2 ге-
неральной совокупности.
’ Оценка достоверности статистических показателей с помощью
средней ошибки. Оценка достоверности х? Роль средней, или
статистической, ошибки в статистическом анализе очень велика.
С одной стороны, как было показано выше, она позволяет опреде-
лить границы для показателей генеральной совокупности, например,
для |J-, а с другой стороны, дает возможность оценить степень до-
стоверности самих статистических показателей, в частности сред-
ней арифметической данной выборочной совокупности.
Что же следует понимать под достоверностью средней ариф-
метической? Фактическая средняя арифметическая всегда явля-
ется выборочной. Поэтому для суждения о ее достоверности надо
сравнить ее со средней арифметической генеральной совокупно-
сти. Мерилом достоверности явится нормированное отклонение,
для вычисления которого можно использовать приведенную выше
формулу (23а).
Возникает вопрос о том, откуда же взять величину [*? Возмож-
ны два случая. В первом у. представляет собой определенную, от-
личающуюся от нуля, величину, значение которой можно
примерно предположить по другим данным. Допустим, что
изучали жирность молока 10 коров. Были получены следующие
показатели: х = 3,7%; а — 0,28%; %- = 0,09%. Если при этом ра-
нее изучали жирность молока в других выборках и получали
различные значения выборочных средних, то можно вычислить
среднюю из этих средних. Допустим, что она оказалась равна 4,0%.
Можно принять ее за р. Тогда -
3,7 — 4,0 _0,30 _ по
1 — 0,09 — 0,09 ~
При малом п( = 8) следует проверить достоверность по
табл. II. Вероятность достоверности (р = 0,987) вполне доста-
точная.
90
Однако возможен и второй, более редкий случай при анализе
экспериментальных данных, когда действие.изучаемого фактора
может быть и положительным, и отрицательным. Тогда р. следует
приравнять нулю. В этом случае
(29)
__ "К
В общем можно сказать, что х, вычисленные для большинства
биологических показателей даже на сравнительно малых по раз-
мерам выборочных совокупностях, чаще всего будут достаточно
достоверными, если только ряд не слишком растянут. Однако ме-
жет получиться иначе, если приходится оперировать эксперимен-
тальными данными, в которых фигурируют какие-либо условные
или относительные величины, часть последних может иметь и от-
рицательный знак. Тогда установление достоверности ~х совершен-
х но необходимо.
t V7 Нулевая гипотеза. Метод средней ошибки позволяет сравни-
вать между собой любые две группы животных или растений,
например: две выборочные совокупности, взятые из природной,
неизученной популяции; выборку из какой-то уже известной
группы и группу, из которой эта выборка взята; опытную и конт-
рольную группы при постановке опытов — и установить, насколь-
ко достоверны различия между их статистическими показателями
(средними арифметическими, вариансами и др.).
Общие принципы сравнения -основываются .на анализе так
называемой нулевой гипотезы. Согласно этой гипотезе, первона-
чально принимается, что между--данными показателями (или
группами, на основе которых они получены) достоверного разли-
чия нет, т. е. что обе группы вместе составляют один и тот же
однородный материал, одну совокупность. Статистический ана-
лиз должен привести или к отклонению нулевой, гипотезы, если
доказана достоверность полученных различий, или к ее сохра-
нению, если достоверность различий не доказана, т. е. различия
признаны случайными. Но так как все статистические показатели
и различия между ними характеризуются определенными уров-
нями значимости, то отбрасывание нулевой гипотезы должно
быть связано с принятием определенного уровня значимости.
Так, если признан необходимым уровень значимости 0,01 и если
вероятность достоверности данного статистического показателя
или разницы между показателями не удовлетворяет этому усло-
вию, т. е. она ниже 0,99 (например, 0,97, 0,91, 0,88), то нет осно-
ваний для отбрасывания нулевой гипотезы. Ее надо считать пра-
вильной по крайней мере до тех пор, пока новые данные не дадут
возможности ее опровергнуть, доказав, что существующие разли-
чия не являются чисто случайными.
Конечно, и в том случае, когда нулевая гипотеза считается
опровергнутой, какой-то шанс, что она в действительности верна,
остается. При уровне значимости 0,01 этот шанс составляет
91
1 на 100, т. е. в 1 % случаев отбрасывание нулевой гипотезы было
ошибкой. Если достигнут уровень значимости не 0,01, а 0,001,
то уверенность в том, что нулевая гипотеза действительно отвер-
гнута правильно, резко возрастает (лишь 1 шанс на 1000 случа-
ев, что она все же верна). При Р = 0,05 уверенность в правильно-
сти вывода составляет лишь 95 случаев из 100, а в 5 возможен
неправильный вывод.
Таким образом, если полученные данные характеризуются
уровнем значимости Р>0,05, то нет оснований отклонять нулевую
гипотезу. Если Р<0,01, то для отбрасывания нулевой гипотезы
основания достаточные.
Но значительно неопределеннее положение вещей, если ре-
зультаты анализа или сравнения удовлетворяют уровню значи-
мости 0,05, но не удовлетворяют уровню значимости 0,01. Надеж-
ное суждени^оказывается невозможным. Очевидно, что в таких
случаях должны быть проведены дополнительные опыты, чтобы
решить, следует ли отбрасывать нулевую гипотезу. Вообще надо
иметь в виду, что сохранение нулевой гипотезы еще не означает
ее правильности. Может оказаться все же, что она неправильна.
Сохранение же нулевой гипотезы оставляет вопрос открытым.
Приведенная выше оценка достоверности средней арифметиче-
ской выборочной совокупности также являлась проверкой нулевой
гипотезы. Согласно нулевой гипотезе, х = 0. Надо было до-
казать, что х достоверно отличается от нуля. При достаточном
доказательстве, удовлетворяющем принятому уровню значимости,
нулевая гипотеза отбрасывается, т. е. признается достовер-
ность х. Если это не удается сделать, остается правильной нуле-
вая гипотеза (недостоверность х) впредь до новых опытов.
Оценка достоверности разницы между средними арифметиче-
скими двух выборочных совокупностей. Если была получена раз-
ница между средними арифметическими двух генеральных сово-
купностей, то, очевидно, не может стоять вопрос о статистической
ошибке этой разницы. Эта разница всегда достоверна, даже если
она и очень мала. Иное дело, если сравниваются две выборочные
совокупности, например: две группы морских свинок, подвергав-
шихся воздействию химических веществ или физических факто-
ров, две группы коров, сравниваемые по удою и взятые из одной
породы,хозяйства и т. д. В этих случаях разница между средни-
ми имеет свою статистическую ошибку, с которой ее можно срав-
нить и установить, достоверна эта разница или нет. Нулевая
гипотеза в данном случае будет сводиться к тому, что две изуча-
емые выборочные совокупности происходят из одной и той же ге-
неральной совокупности и что разница между их средними ариф-
метическими случайна, т. е. лежит в пределах ошибки выбороч-
ности.
Чтобы иметь право отвергнуть нулевую гипотезу, надо дока-
зать, что разница между средними арифметическими достоверна,
т. е. удовлетворяет требуемому уровню значимости.
92
Для установления достоверности разницы между средними
арифметическими надо воспользоваться нормированным откло-
нением £* Нормированное отклонение примет следующую форму:
t = .AZA.. (31)
S(X1 — х2)
На самом деле формула для t должна быть несколько слож-
нее, а именно:
s(7 — 72)
Но так как надо исходить из нулевой гипотезы о том, что
две выборочные средние арифметические взяты из одной генераль-
ной’ совокупности, то |*1 = [х2 и правая часть числителя обращается
в нуль.
Числителем является разница между средними арифметически-
ми двух групп (знак разницы не имеет значения). Ее можно обо-
значить сокращенно буквой d. В знаменателе же — средняя ошибка
этой разницы, т. е. sfo-Tj или более сокращенно sd. Тогда
t = {- . (31а)
Существует два способа определения средней ошибки разницы.
Первый из них применяется, КОГДА обе сравниваемые группы обла-
дают достаточно большой численностью,“большей чем по 30 осо-
бей в каждой. Средняя ошибка разницы определяется тогда по
формуле
^ = /<44- (32)
Допустим, что мы хотим сравнить по удою 2 группы коров.
В одной группе = 50._ В другой п2 = 40. Средние удои и ошиб-
ка для первой группы: ± s- = 2100 ± 120 кг; для второй груп-
пы: xt’± s— = 2635 ±140 кг. Разница между средними удоями
2 групп 2
d = хг — Хх = 2635 — 2100 = 535 кг.
Ошибка разницы
sd = у s^ — s^ = ]/1402+ 1202 = 184 кг.
Таким образом, d ± sd = 535 ± 184 кг, a t — = 2,91.
По таблице нормального интеграла вероятности (табл. I) на-
♦ В некоторых руководствах по статистике при больших значениях п пи-
шут вместо буквы t букву и или Tt относя обозначение t только к малы1( вы-
боркам. Но чтобы не усложнять формул, мы для всех случаев нормированных
отклонений и при оценке достоверности будем употреблять то же обозначение t.
93
ходим, что в этом случае вероятность достоверности очень вели-
ка — 0,9963.
При отсутствии таблиц можно исходить из правила трех сигм:
если разница превышает свою ошибку почти в три раза, она до-
стоверна с вероятностью не менее 0,99. Но из сказанного выше
видно, что в таком высоком значении t нет надобности. Если
п>30, то /=2,58 гарантирует достоверность разницы с вероят-
ностью 0,99.
При сравнении двух групп с малыми п, особенно с неодинако-
выми п, ошибка разницы определяется по формуле:
„ 1 /~я — *i)a + s (х2 —~х2у ( пг + п2 \
“ V + \ П.-П, / .
Смысл этой формулы заключается в том, что нельзя пользо-
ваться просто готовыми средними ошибками, вычисленными зара-
нее для двух сравниваемых групп, как это было при применении
формулы (32), а нужно сначала сложить суммы квадратов откло-
нений по' обеим группам, т. е. получить объединенную сумму
квадратов отклонений, затем определить вариансу объединенных
рядов (путем деления объединенной суммы квадратов на сумму
чисел степеней свободы обеих групп) и, наконец, после умножения
П1 + Ля
на п7'п8' и извлечения квадратного корня получить ошибку раз-
ницы.
Для иллюстрации сказанного возьмем следующий пример.
На двух группах крыс был поставлен опыт по сравнению влия-
ния разных рационов на рост. Крысы первой группы (п = 12)
получали рацион с высоким содержанием белка, крысы второй
(п = 7) — с низким. Привесы за 56 дней опыта для каждой кры-
сы составляли (в г): первая группа — 134, 146, 104, 119, 124, 161,
107, 83, 113, 129, 97, 123; вторая группа —70, 118, 101, 85, 107,
132, 94.
После обработки данных с помощью одной из формул для
сумм квадратов можно составить табл. 18.
d = Xi—х2 — 19 г.
Таблица 18
Сводные данные по сравнению 2 групп крыс, получавших разные рационы
Рационы Количество крыс Число сте- пеней сво- боды df Средний при- вес х (в г) Сумма квад- ратов откло- нений 2(Х/—Т)2
Высокобелковый . . 12 11 120 5032
Низцрбелковый . . . 7 6 101 2552
2=17 2=7584
94
Подставив все значения
в формулу (33), получим
ч -i/™4 (НТЪ
“ V ~17------15Т?—
= У 100,9262 = 10,04.
Отсюда
t = 19 = 1 89
1 10,04 *’ОУ
По табл. III находим,
что (при df—17 и уровне
значимости 0,05) / должно
быть не менее 2,11, полу-
ченное значение / ниже
табличного. Для уточнения
ж
L I jr "T' h-----------
X
В -----ssssafc
x
Ш -----BSSE^SS
120121122123124 125126127128129
Длина крыльев
Рис. 10. Графическое изображение со-
отношения показателей длины крыль-
ев (в мм) 3 видов скворцов (/ — St.
contra, II—St. ginginiamus, III —
St. fuscus)). Тонкие -линии — вариа-
ционные размахи; поперечные черточ-
ки— х; заштрихованы доверительные
границы.
вероятности достоверной разницы
воспользуемся табл. II. Из нее видно, что /=1,89 соответствует
вероятности только 0,92, т. е. уровень значимости равен 0,08. Та-
ким образом, можно считать, что разные рационы не привели к
разделению популяции крыс по привесам на две достоверно от-
личающиеся друг от друга популяции, иначе говоря, нулевая
гипотеза не может быть отвергнута. Конечно, опытные группы
были слишком малы. Возможно, что при их увеличении была бы
получена более достоверная разница между группами крыс, нахо-
, дившимися на разных рационах кормления.
' г Графический метод сравнения средних арифметических. Для
’-'сравнения средних арифметических можно также использовать
очень наглядный графический метод. В качестве иллюстрации
этого метода рассмотрим рис. 10.
Были получены следующие данные о длине крыльев ( в мм)
у 3 видов скворцов:
Вид n X a s X
Sturnus contra .... 11 123 ' 2,3 0,7
St. ginginiamus .... 13 127 2,0 0,6
St. fuscus 8 126 2,6 0,9
На рисунках нанесены: тонкими линиями — размах вариации
длинны крыльев для каждого вида скворцов; поперечной черточкой
—х; толстыми заштрихованными линиями—доверительные интер-
валы для х. Так как по каждому виду было изучено немного
особей, то для вычисления доверительных границ и интервалов
взято / = 3, что обеспечивает уровень значимости, близкий к 0,01
(для одного вида 0,02).
85
График наглядно показывает, что значение х длины крыльев
St. contra располагается за пределами доверительных интервалов
для средних St. ginginiamus и St. fuscus, значит, эта средняя ариф-
метическая достоверно отличается от средних двух других видов.
Между видами St. ginginiamus и St. fuscus различие по длине крыльев
недостоверно, так как их средние арифметические находятся в
пределах доверительных границ друг друга.
Следует отметить, что кривые распределения всех трех видов
налегают друг на друга. Это видно по значительному совпадению
линий вариадионных размахов. Но, несмотря на трансгрессию
между кривыми распределения St. contra и St. ginginiamus, раз-
личие между ними достоверно.
) Достоверность разницы между попарными данными. В неко-
торых случаях можно значительно упростить все расчеты по
проверке достоверности разницы, оперируя непосредственно зна-
чениями разниц между вариантами обеих групп. Для этого надо,
чтобы последние были сгруппированы попарно. Такой случай
как раз имеет место, если опытная и контрольная группы (или
две опытные группы) составлены из отдельных партнеров одно-
яйцовых двоен того вида, у которого бывают однояйцовые двой-
ни. Один член каждой пары двоен помещается в одну опытную
группу и подвергается воздействию фактора А, а другой — в дру-
гую группу и подвергается воздействию фактора В. Подобную же
парность данных можно получить, если, например, для изучения
влияния микроэлементов на число крольчат в помете эксперимен-
тировать с одними и теми же крольчихами, которые в период
одних окролов рассматриваются как контрольные, а в период
других — как опытные. При оценке быков-производителей по по-
томству сравнивают попарно удои коров-дочерей с удоями их
матерей. При изучении влияния на листья препаратов вируса
табачной мозаики на одну половину листа влияют одним препа-
ратом, а на вторую —другим, затем сравнивают половины листь-
ев и т. д. Такой попарный метод имеет ряд преимуществ перед
методом создания опытной и контрольной групп из случайно
взятых особей или методом аналогов.
Существенным условием парного метода является такой спо-
соб образования пар, чтобы различия внутри пар были меньши-
ми, чем между парами.
В качестве примера возьмем данные о весах самок и самцов
мышей (табл. 19) в возрасте 125 дней в 25 пометах (в каждом
помете были 1 самка и 1 самец). Данные последнего столбца —
d— можно обработать, как вариационный ряд.
Предоставляем каждому возможность сделать эту обработку
самостоятельно, применив для вычисления статистических пока-
зателей указанные выше формулы.
Приведем лишь готовые данные: d = 2,04; а8 =13,177; а =
= 3,63; sd = 0,73; t = 4~ = 2,81.
sd
96
Таблица 19
Попарное сравнение веса самок и самцов мышей (в г)
Номер поме- та Вес d Номер помета Вес d
9 d 9 с?
1 26 16,5 9,5 14 22,5 20,5 2
2 20 17 3 15 23,5 19,5 4
3 18 16 2 16 23,5 22,5 1
4 28,5 21 7,5 17 25 20 5
5 23,5 23 0,5 18 24,5 20,5 4
6 20 19,5 0,5 19 23,5 18 5,5
7 22,5 18 4,5 20 20,5 24,5 —4
8 24 18,5 5,5 21 20 22 -2
9 24 20 4 22 20,5 20 0,5
10 25 28 —3 23 25 20 5
11 22 27,5 -5,5 24 23,5 23 0,5
12 24 20,5 3,5 25 22 24 —2
13 22,5 23 -0,5
Число степеней свободы df — п — 1 =24.
Из табл. III видно, что при df = 24 для уровня значимости
0,01, т. е. вероятности р = 0,99 в пользу- вывода о достоверности
разницы, t должно быть 2,80. Полученное значение t = 2,81 как
раз лежит в границах требуемой достоверности, иными словами,
между средним весом $9 и мышей разница достоверна, или,
как еще говорят в статистике, значима, существенна. Таким
образом, нулевая гипотеза должна быть отвергнута.
Критерий знаков. Анализ результатов при попарном сравне-
нии может быть сделан и более простым способом, без вычисле-
ния разницы между средними арифметическими и ее ошибки.
Одним из таких способов является применение критерия знаков.
Допустим, что изучается влияние какого-то внешнего факто-
ра на физиологический или биологический признак. В некоторых
случаях этот фактор может давать сдвиг в изучаемом признаке
в сторону «плюс», в других — в сторону «минус». Обычно прини-
маемой нулевой гипотезой является отсутствие влияния данного
фактора. Тогда количество случаев «плюс» и «минус» будет более
или менее одинаковым. Так, при 20 опытах может быть 9 «+»
и 11 «—», или 11 « + » и 9 «—», или 10 «+» и 10 «—» и т. д. Одна-
ко возможно, что количество случаев « + » будет значительно
превышать количество случаев «—» (или наоборот). Тогда возни-
кает сомнение, насколько полученное отклонение от равного со-
отношения является случайным. По мере .увеличения разницы
4 П. Ф. Рокицкий
97
между количеством случаев <+» и количеством «—» вероятность
равного соотношения падает и, наконец, становится настолько
малой (например, ниже чем 0,05), что появляется основание от-
бросить первоначальную нулевую гипотезу и тем самым признать
с достаточной вероятностью, что изучаемый фактор действует.
В самом деле, если бы из 10 подопытных животных все 10
дали реакцию «плюс», то вероятность чисто случайного совпаде-
/ 1 V’ 1
ния равнялась бы /—I = у—. Это является достаточным осно-
ванием для утверждения, что полученный результат—10 случаев
положительной реакции на 10 животных —не случаен.
Так как'проведение расчетов на основе теории вероятности
в каждом конкретном случае было бы делом громоздким, прибе-
гают к готовым таблицам, где рассчитано минимальное количест-
во « + » или «—» случаев, превышение над которым при данном п
достаточно, чтобы считать разницу достоверной с уровнем значи-
мости 0,05 или 0,01.
В несколько упрощенном виде такая таблица приведена
в конце книги (табл. IV). ;
Применение критерия знаков может быть проиллюстрировано
приведенным выше примером попарного сравнения веса самок
и самцов мышей. Всего пар было 25. В 19 случаях вес самок был
больше веса самцов и в 6 случаях — меньше. Из табл. IV видно,
что при /1=25 граничные количества 17 и 19, т. е. достаточно
18 случаев «+», чтобы считать разницу достоверной с уровнем
значимости Р = 0,05, и 20 случаев «+», чтобы считать разницу
достоверной с уровнем значимости Р=0,01. Таким образом, про-
верка с помощью критерия знаков дала примерно те же резуль-
таты, что и сравнение разницы с ее ошибкой.
Критерий знаков выгодно применять в силу его простоты, осо-
бенно для первоначальной оценки результатов опытов. Однако
надо иметь в виду, что он недостаточно чувствителен и в некото-
рых случаях не дает возможности уловить фактически существу-
ющие различия, что может быть сделано более тонкими метода-
ми, в том числе обычным критерием достоверности разницы t.
Более сложный критерий Уилкоксона, в котором учитывается
не только знак разницы, но и ее абсолютное значение, описан
в специальной литературе. Там же говорится и о некоторых дру-
гих, так называемых непараметрических критериях, т. е. критери-
ях, не основанных на обычных параметрах, характеризующих
ряды распределения.*
Сравнение средних квадратических отклонений и варианс.
Если сравниваемые группы численно достаточно велики, сравне-
ние их изменчивости может быть проведено по тому же принци-
* См. Урбах В. Ю. Математическая статистика для биологов и медиков,
стр. 286; Weber Е. Grundriss der biologischen Statistik, гл. 61—71; Ван дер
Варден Б. Л. Математическая статистика, гл. 12.
98
пу, как и сравнение х, т. е. с помощью показателя t. В данном
случае
Д1 — СТЙ
/ =
(34)
В знаменателе — ошибка разницы между средними квадрати-
ческими отклонениями. Она вычисляется по формуле
/Й+ (35>
При t > 3 разницу между сигмами можно считать, как обыч-
но, достоверной, существенной.
Однако, в силу ряда теоретических соображений, изложение
которых выходит за рамки элементарного курса, значительно бо-
лее точным методом для сравнения вариации и установления
достоверности различий между сравниваемыми группами явля-
ется так называемый критерий F, -представляющий собой отно-
шение варианс (средних квадратов):
. (36)
Если обе вариансы а? и равны, тогда F = 1. Очевидно, что ну-
левой гипотезой является признание' равенства варианс. Если они
не равны, то нужно доказать, что это неравенство не случайно,
достоверно.
Значения F, являющиеся границами для признания достовер-
ности разницы между вариансами, приводятся в специальных
таблицах, где учитываются разные объемы сравниваемых групп
(вернее, разные числа степеней свободы этих групп) и принима-
ются различные уровни значимости. В несколько сокращенном
виде они представлены в табл. V (для уровня значимости 0,05)
и в табл. VI (для уровня значимости 0,01).
Обычно отношение варианс берут -таким образом, чтобы в чи-
слителе была большая варианса.
Если полученная величрна F больше табличного значения при
принятом уровне значимости, различие между вариансами при-
знается достоверным; если она меньше, то расхождение между
вариансами может считаться несущественным, случайным, т. е.
нулевая гипотеза остается неопровергнутой.
Практическое значение F очень велико в целом ряде специ-
альных разделов статистики, особенно в дисперсионном (или
вариансном) анализе, излагаемом далее, в гл. 8.
Если различия между вариансами групп в опытах, где ана-
лизируется влияние различных факторов (удобрения, корма, ле-
карства, химические вещества, наследственные свойства произ-
водителей и т. д.) на'растения или животных, могут быть призна-
ны достоверными, это позволяет устанавливать влияние тех или
иных факторов на изучаемые признаки или биологические свой-
99
ства (урожайность, молочность, устойчивость к заболеваниям
и т. д.).
'В этой главе мы ограничимся лишь общим представлением
о критерии F и использовании для оценки достоверности таб-
лиц V и VI.
В качестве примера проанализируем следующие данные опы-
тов по влиянию шести различных рационов кормления на яйце-
носкость кур.
Между средними групп с разным кормлением варианса оказа-
лась равной а* = 1074,5, при этом — 5.
Варианса'же внутри групп, получавших одинаковые рационы
кормления,'равна а* = 312,4, при этом dft — 114.
Таким образом, между группами кур с разным кормлением
разнообразие по яйценоскости больше, нежели внутри групп.
Чтобы доказать, достоверно ли это различие в вариации, обра-
тимся к критерию F-.
F - - 3 44
Р ~ 312,4 ~
По табл. VI в пересечении строки, где df2= 120 (так как нет
114), и столбца, где dfi=5 (вертикальные столбцы указывают
число степеней свободы для большей вариансы), находим чис-
ло 3,17. Полученное значение F превышает табличное. Значит,
различия по яйценоскости между группами кур с разными ра-
ционами кормления достоверны с вероятностью 0,99 (только
в 1 случае из 100 эта разница может быть следствием случай-
ности).
Можно привести и более простой пример использования кри-
терия F. Допустим, нужно сравнить изменчивость по высоте в
холке групп черно-пестрого и красно-пестрого скота. Для первого
«1 = 100 и aj = 16,32, для второго п2 = 42 и = 14,44.
Тогда
F = 1.13.
14,44 ’
В табл. V и VI в вертикальных столбцах .нет цифры 100.
Тогда надо взять df\ = оо. По горизонтали же можно взять
dfi = 40. Обратимся сначала к табл. VI. При уровне значимости
0,01 F должно быть больше 1,80. Этому уровню значимости по-
лученное значение F явно не удовлетворяет. В таком случае, мо-
жет быть, различие между вариансами af и а* удовлетворяет уров-
ню значимости 0,05. По табл. V F для dfi = оо и d/2 = 40 рав-
но 1,51. Фактическая величина F ниже и этой величины. Отсюда
можно сделать вывод, что хотя черно-пестрый и красно-пестрый
скот отличаются по масти, но их вариансы по высоте в холке
достоверно не отличаются друг от друга. Вероятность различия
между вариансами, как случайного, более 0,05. Нулевая гипотеза
о равенстве варианс сохраняет свое значение и остается неопро-
вергнутой.
100
ВОПРОС ы
1. Отличаются ли друг от друга по закономерностям случайной вариации
выборочная и генеральная совокупности?
2. В какой степени средняя арифметическая выборочной совокупности
характеризует среднюю_арифметическую генеральной совокупности?
3. Как колеблются х отдельных выборок вокруг средней арифметической
генеральной совокупности?
4. Что такое средняя ошибка? Какова ее формула?
5. В каких пределах по отношению к х выборочной совокупности может
находиться средняя арифметическая генеральной совокупности? С какой веро-
ятностью?
6. В чем заключается ошибка выборочное™?
7. Объясните, в чем заключается закон больших чисел?
8. Закон больших чисел как основа распределения вариант в вариационном
ряду, х отдельных выборок и ошибок.
9. Какова зависимость между значением средней ошибки и объемом сово-
купности?
10. Изменяются ли доверительные границы и доверительный интервал для
|л при разных величинах п? Когда надо пользоваться /-распределением Стьюдента?
И. В чем заключается поправка в формулу средней ошибки на учет доли
выборки?
12. По какой формуле можно определить необходимый объем выборочной
совокупности?
13. Кратко охарактеризуйте основные предпосылки выборочного метода.
14. Как вычисляются средние ошибки для а и и?
15. Как оценивается достоверность х ?
16. Объясните сущность нулевой гипотезы и дайте примеры.
17. Как оценивается достоверность разницы между средними арифметиче-
скими? Одинаковы ли способы оценки при малых и больших п?
18. Как получить объединенную сумму квадратов отклонений для двух
рядов?
19. Как формулируется нулевая гипотеза при сравнении двух средних
арифметических?
20. В чем преимущество попарного сравнения данных? Приведите примеры
из биологии. 4
21. Объясните графический метод сравнения средних арифметических.
22. В чем заключается критерий знаков? Как пользоваться табл. IV?
23. Можно ли установить достоверность разницы между средними квадра-
тическими отклонениями с помощью /?
24. Что такое критерий Г? Как пользоваться табл. V и VI?
25. В чем заключается нулевая гипотеза при сравнении варианс?
26. Можно ли считать достоверным различие между вариансами, если факти-
ческое значение F больше табличного? Если оно меньше табличного?
ЗАДАЧИ
66. Средний процент жира в молоке за лактацию коров холмогорских по-
месей был следующим: 3,4; 3,6; 3,2; 3,1; 2,9j_3,7; 3,2; 3,6; 4,0; 3,4; 4,1; 3,8;
3,4; 4,0; 3,3; 3,7; 3,5; 3,6; 3,4; 3,8. Определите л, а и s7 Установите довери-
тельные интервалы для х при вероятности 0,99; при вероятности 0,95.
67. На 400. растениях гибридной ржи первые цветки появились в среднем
на 70,5 дня после посева. Среднее квадратическое отклонение было 6,9 дня.
Определите среднюю ошибку для х и доверительные интервалы при Р = 0,05
и Р = 0,01.
~ 68. При изучении длины листьев садовой земляники были получены
х = 7,86 см; а = 1,32 см. Так как п = 502, то «7= ±0,06 см. Определите до-
верительные интервалы для средней арифметической генеральной совокупности
101
с уровнями значимости 0,01; 0,02 'и 0,05. Можно ли пользоваться в данном
случае таблицей нормального интеграла вероятности?
69. Было измерено 9 листочков земляники. Получены значения х — 5,0 см;
с — 1,5 см; = ±0,5 см. Каковы доверительные интервалы для х при уров-
нях значимости 0,05; 0,01?
70. При обследовании 150 взрослых мужчин средний рост был равен 167 см, а а — 6 см. В каких пределах находится средняя арифметическая генеральной совокупности с вероятностью 0,99? С вероятностью 0,95? 71. Были получены следующие данные о весе тушканчиков (Dipus aegyp- tins): i Самцы 186 190 165 182 182 182 180
173 157 179 164 146 173 144
156 156 165 160 160 161 144
153 152 151 173
Самки 162 163 190 188 147 146 145
157 162 186 175 147 145 145
155 174 180 148 175 145 144
153 165 141 164
Отличаются ли по весу самцы от самок?
72. Температура тела тушканчиков оказалась следующей:
У самцов 37,5 37,9 37,4 37,8 36,8 37,8 37,5
У самок 37,8 38,1 37,0 37,5 37,7 37,8 37,6
Отличаются ли самцы и самки по температуре тела?
73. У серебристо-черных лисиц подмосковных совхозов было подсчитано
количество желтых тел в яичниках:
В 1933—1935 гг. 5 3 8 4 6 4 5 9 5
5 4 3 5 5 5 5 7 4
- 5 7 5 3 3 5 4 5 4
В 1959-1962 гг. 6 7 4 5 5 6 7 5 6 8
7 7 5 6 4 , 5 7 5 6 4
5 7 6 5 5 5 6 6 6 5
6 8 7 7 6 6 6 7 7 6
5 9 8 8 5 8 5 6 7
Достоверно ли различие по числу желтых тел на самку за 2 периода
времени?
74. У баранов мериносовой породы были произведены промеры рогов (в см):
Годичный 47 53 50 56 49 52 51 58 55
возраст 50 48 51 51 48 60 51 57 57
51 54 52 58 50 51 51 58 53
52 49 59 61 50 52 51 63 62
54 53 54 68 54 63 64 57 57
60 57 60 69 57 56 54 54 55
61 59 57 70 58 57 55
Трехлетний 83 87 89 77 80 78 82 75 73
возраст 71 76 86 90 84 88 72 73 68
72 75 74 81 91 85 79 78 69
68 73 68 71 75 71 76 72 66
63 65 66 69 73 69 71 72 67
. 70 64 51 67 70 66 62 65
102
Различаются ли по длине рогов бараны годичного и трех летнего возраста?
75. 12 черно-пестрых коров покрыты джерсейским быком. Получены сле-
дующие данные о количестве молока за лактацию (в кг) и о жирности его у
матерей и дочерей:
Матери До че ри
количество молока % жира количество молока % жира
1983 3,25 3509 5,29
3674 3,81 3110 6,04
3976 2,96 3181 5,24
3391 3,24 2997 5,25
4344 2,82 2991 5,14
3784 2,83 3720 4,72
3628 2,79 3268 4,54
3957 3,08 3595 4,97
2185 3,01 2939 5,13
4980 3,23 3213 4,98
2709 3,68 3240 5,58
2807 2,96 3388 4,81
Сравните удои и жирность молока дочерей и матерей (попарным методом).
76. Для 7 коров известны следующие данные об их убойном весе (в кг) в
теплом состоянии х и после охлаждения у:
х 322,6 250,6 287,3 408,1 338,0 213,5 323,3
у 318,9 247,0 279,7 403,0 334,7 209,3 319,2
Определите достоверность разницы между средним убойным весом в теп-
лом состоянии и средним убойным весом после охлаждения двумя способами:
сравнением х обоих рядов и обработкой разниц между двумя убойными весами
каждой коровы.
77. На 10 парах крыс определяли биологическую ценность белков земля-
ного ореха—сырого Р и жареного /?. Пары данных (в услов. ед.) были следую-
щими: 61—55, 60-54 , 56—47, 63—59, 56—51, 63—61, 59—57, 56—54 , 44—63,
61—58. Достоверна ли разница? Какой метод можно применить для установ-
ления ошибки разницы? На сколько изменятся результаты, если исключить рез-
ко отличающуюся от остальных пару данных 44—63? Достаточны ли получен-
ные данные для того, чтобы можно было сделать какой-либо вывод?
78. Для определения pH применили 2 типа электродов. При первом пока-
зания pH: 5,78; 5,74; 5,84; 5,80; при втором—5,82; 5,87; 5,96; 5,89. Следует
ли отбросить нулевую гипотезу?
79. Пробы по 15 зерен кукурузы разных стадий зрелости проверяли на
устойчивость к раздавливанию. Первая проба дала следующие цифры (в едини-
цах давления): 42, 50, 36, 34, 45, 56, 42, 53, 25, 65, 33, 40, 39, 43, 42; вто-
рая — 43, 44, 51, 40, 29, 49, 39, 59, 43, 48, 67, 44, 46, 54, 64. Проверьте,
достоверно ли различие между двумя х?
80. Было изучено общее содержание азота в плазме крови крыс-альбиносов
в возрасте 37 и 180 дней. Результаты 'выражены в граммах на 100 куб. см
плазмы. В возрасте 37 дней 9 крыс\ имели: 0,98; 0,83; 0,99; 0,86; 0,90;
103
0,81; 0,94; 0,92 и 0,87. В возрасте 180 дней 8 крыс имели: 1,20; 1,18; 1,33; 1,21;
1,20; 1,07; 1,13 и 1,12. Установите доверительные интервалы для разницы с ве-
роятностью 0,95.
81. Для изучения влияния рационов с добавкой 10 мкг витамина Bj2 на
рост свиней было составлено попарно 16 групп, в каждой из которых было по
6 голов. Средние суточные привесы в фунтах (на 100 фунтов живого веса)
представлены в следующей таблице:
Рационы Пары групп
1 2 3 4 5 6 7 8
С В12 1*60 1,68 1,75 1,64 1,75 1,79 1,78 1,77
Без Вт 2 1,56 1,52_ 1,52 1,49 1,59 1,56 1,60 1,56
d 0,04 0,16 0,23 0,15 0,16 0,23 0,18 0,21
Какова достоверность разницы?
82. Имеются следующие данные об удоях 12 коров-матерей и их дочерей
по полновозрастным лактациям (в кг):
Удой
матерей 3770 3817 2450 3463 3500 5544 3112 3150 3118 3018 4291 3463
Удой
дочерей 2991 4593 3529 4274 3103 3947 3491 3559 2916 4580 4510 4144
Достоверна ли разница между, удоями матерей и дочерей? Какой метод
сравнения можно применить?
83. Был проведен опыт по подкормке 32 свиноматок препаратом афаромом,
содержавшим железо и медь, в целях уменьшения процента мертворожденных
поросят. От каждой матки получали 1 опорос, когда добавляли в корм
афаром, и 1 опорос контрольный, когда добавки препарата не было, Маток
покрывали всегда одними и теми же хряками. Получены следующие результаты:
Номера маток Мертворожденные, % Номера маток Мертворожденные, %
при афароме без афарома при афароме без афарома
1 0 8,3 12 ПЛ 0
2 0 12,5 13 11,1 0
3 0 9,1 14 0 25,0
4 18,2 22,2 15 0 9Д
5 0 10,0 16 0 14,3
6 25,0 33,3 17 0 35,7
7 10,0 0 18 0 63,6
8 ПЛ 0 19 0 9J
9 0 16,7 20 0 10,0
10 0 28,6 21 22,2 40,0
11 0 25,0 22—32 0 0
104
Установите, достоверна ли разница i в проценте мертворожденных опытной
и контрольной группы? Можно ли применить метод обработки значений d как
вариационного ряда? 84. Б1£л и по л учены с лед у ющие
Классы 1-я выборка 2-я выборка
(в мм) (из штата (и; 1 штата распределения по длине хвоста в 2
Айова) Сев. Дакота) выборках оленьих мышей. Peromyscus
52-53 0 maniciilatus, взятых из географически отдаленных мест (см. слева).
54—55 3 1 Достоверна ли разница между
56—57 11' 2 ними?
85. Для определения содержания
58—59 18 < 2 хлора в химическом соединении были
60-61 21 * 3 применены методы А и В. Результаты следующие (в %): при методе А—27,5;
62—63 20 * ’ 8 27,0; 27,3; 27,6; 27,8; при методе
64-65 9" 25 В —27,9; 26,5; 27,2; 26,3; 27,0; 27,4; 27,3; 26,8.
66—67 2 11 Примените критерий F для уста-
68-69 1 * 10 новления разницы между вариансами данных, полученных этими методами
70—71 0 5 (для упрощения вычислений можно от
72-73 0 7 всех отдельных значений х отнять 27,0%).
74^75 0 2 86. В опыте по откорму 15 баранов
76-7Л гих бкранов 0 примерно того 2 получали ежедневно в качестве под- кормки по 5 г фосфорной муки, 15 дру-
же возраста, веса и происхождения были контроль-
ными. Суточный привес был следующим (в г):
ОпЫТНЯЯ
группа 23 4 277 214 201 174 167 184 157 196 173 190 191 141 150 1 91
Контрольная
группа 183 154 175 159 157 189 198 165 176 124 173 182 204 151 147
Каким методом можно установить, достоверна ли разница между опыт-
ной и контрольной группами по суточному привесу? Определите эту разницу
и выясните, достоверна ли она. Выясните также, отличались ли опытная и кон-
трольная группы по вариансе и достоверно ли это различие.
87. Получены следующие данные о длине крыльев у представителей 3 ви-
дов скворцов Sturnus из Индии (в мм):
St contra 120, 120, 121, 122, 125, 126, 126, 125, 122, 123, 122.
St. ginginiamus 129, 123, 128, 125, 126, 127, 129, 125, 124, 129, 128, 127, 127.
St. fuscus 122, 127, 125, 128, 127, 122, 129, 127.
Достоверна ли разница между средними длин крыльев трех видов?
88. Для популяции мужчин возраста от 25 до 30 лет а длины тела 4,5 см.
Для выборочной группы 400 спортсменов а=3,5 см. Случайно ли отклонение
в величине а по длине тела у спортсменов от а популяции?
89. Сравнивали влияние мягкого и жесткого облучения на смертность яиц
дрозофилы, при этом вычисляли разности средних и отмечали их знак. Группы
яиц возраста 1—3 часа дали из общего числа 20 случаев 15 случаев «+» и
5 случаев «—» («-}-» — превышение смертности при мягком облучении над смерт-
ностью при жестком). А группы возраста 4—7 часов все 11 случаев — только
«+»• С помощью критерия ’знаков определите достоверность различий между
воздействием мягких и жестких лучей.
Ответ: на яйца старших возрастов
мягкие лучи действуют достоверно силь-
нее, чем жесткие.
105
90. Для проверки последовательного действия противоглистных препаратов
проверяли количество яиц гельминтов на грамм кала до и после дачи пре-
парата. Знаком «+> обозначались случаи снижения количества гельминтов
после дачи препарата, знаком «—» — увеличения или сохранения прежнего коли-
чества. В 9 пробах было 7 случаев «+» и 2 случая «—>. Можно ли считать
влияние препарата доказанным?
91. При изучении суточных привесов 30 баранчиков выяснилось, что они
происходят от 4 разных производителей. Данные о привесах потомков этих про-
изводителей были следующие;
Производитель А 124 151 196 141 174 201 147 157
» В 183 150 198 191 154 173 157 159
С 234 167 189 165 175 190 176
D 173 184 277 214 182 191 204
Определите х и а2 для привесов каждой группы баранчиков, общую вари-
ансу и вариансу между группами. Установите с помощью критерия F досто-
верность разницы между этими вариансами.
92. В отчете о проведении опыта по изучению роста телят сообщается, что
был получен среднесуточный привес 560 г при величине ошибки 8 г. Известно
также, что изменчивость телят по весу характеризуется коэффициентом вариа-
ции примерно в 10%. Можно ли на основе этих данных установить, сколько
телят было под опытом?
О т в е т.\ ~ 50.
93. Предполагается произвести выборочным методом определение среднего
веса зерен партии пшеницы. Сколько зерен должна содержать выборочная со-
вокупность, чтобы с вероятностью 0,95 отклонение полученного в выборке сред-
него веса зерен от среднего веса зерен во всей партии не превышало 0,001 г?
В предыдущих обследованиях а == 0,05 г.
Ответ: 9604.
ГЛАВА 5
ИЗМЕРЕНИЕ СВЯЗИ. КОРРЕЛЯЦИЯ
Понятие о корреляции. Изложенные в предыдущих главах
методы анализа дают возможность изучать вариацию животных
по каждому отдельному признаку — весу, промерам, плодовито-
сти и т. д. Однако в ряде случаев важно знать, какова зависи-
мость между вариацией двух или даже нескольких признаков,
изменяются ли два признака самостоятельно, независимо друг
от друга или, может быть, вариация одного признака в какой-то
степени связана с вариацией другого.
Существуют две категории связей, или зависимостей, между
признаками: функциональные и корреляционные, или статисти-
ческие. При функциональных зависимостях каждому значению
одной переменной величины соответствует одно вполне опреде-
ленное значение другой переменной. Такие зависимости наблю-
даются в математике и физике. Различные измерительные при-
боры основаны на функциональных зависимостях. Так, высота
ртутного столбика в термометре дает точный и однозначный от-
вет о- температуре воздуха или воды.
Между радиусом окружности R. и ее длиной С существует
функциональная зависимость по известной из элементарной гео-
метрии формуле С=2лЯ. Иначе говоря, каждому значению R
соответствует строго определенное значение С. Точно так же
накал нити в электрической лампочке определяется напряжени-
ем (конечно, при прочих равных условиях).
Наряду с функциональными существуют корреляционные, или
статистические, связи, при которых численному значению одной
переменной соответствует много значений другой переменной.
Например, между количеством внесенных на поле удобрений
и урожайностью пшеницы существует бесспорная зависимость, но
это не значит, что определенному количеству удобрений соответ-
ствует строго определенная величина урожая. В силу участия
в формировании урожая на данном участке поля, многих других
факторов (состава и структуры почвы, способа внесения удобре-
ний и разной их заделки, различий в методах посева пшеницы
107
и т.'д.) каждому количественному значению удобрений соответ-
ствует несколько значений урожаев, которые могут быть выра-
жены в виде ряда распределения.
Функциональная связь имеет место по отношению к каждому
отдельному наблюдению. Корреляционная же связь проявляется
лишь в среднем для всей совокупности наблюдений. В отноше-
нии же отдельных наблюдений она очень неполна и неточна.
Известно, например, что существует корреляция между весом
животного и его высотой. Это означает, что более высокие живот-
ные обычно тяжелее более низких. Но полного соответствия меж-
ду значениями этих признаков нет. В некоторых случаях более
низкое живбтное окажется более тяжелым и наоборот.
Если функциональную связь выразить математически, в виде
определенного уравнения, то изменению аргумента соответствует
вполне определенное приращение функции. При корреляции же
приходится иметь дело с сопряженной вариацией изучаемых при-
знаков. Это выражается в том, что отклонения от средних значе-
ний по обоим признакам идут в какой-то степени сопряженно,
параллельно. При этом они могут идти или в одном направлении
(с увеличением одного признака другой также увеличивается),
или в разных (с увеличением одного другой уменьшается).
Поэтому различают положительную и отрицательную кор-
реляции.
При положительной корреляции зависимость между призна-
ками прямая: при увеличении одного увеличивается и другой.
При отрицательной корреляции зависимость между признаками
обратная: увеличение одного признака соответственно связано
с уменьшением другого. В случае качественных признаков отри-
цательная корреляция будет обозначать, что присутствие одного
признака преимущественно совпадает с отсутствием другого,
а при положительной — присутствие одного преимущественно
совпадает с присутствием другого.
В органической природе наблюдается сложное пересечение
множества различных причин, взаимных влияний и их следствий,
поэтому так часты в ней именно корреляционные, а не функци-
ональные зависимости.
Корреляционные зависимости наблюдаются между очень
многими признаками организмов — морфологическими, физиоло-
гическими, а также между различными биологическими процес-
сами. Еще Кювье уделял большое внимание корреляциям между
отдельными органами и частями тела животных. Дарвин писал
о корреляционной изменчивости и о значении корреляций в эво-
люции. Известно множество корреляционных зависимостей, ко-
торые очень хорошо изучены. Так, с увеличением дозы ионизиру-
ющего облучения увеличивается количество мутаций. Чем боль-
ше детенышей в помете многоплодных животных, тем меньше
каждый из них весит (пример отрицательной корреляции). Есть
корреляция между пигментом волос и цветом глаз у человека
108
и т. д. В настоящее время изучение различных корреляций явля-
ется важным разделом многих биологических дисциплин.
Зачастую познание корреляционных зависимостей имеет
и большое практическое значение. Так, для животновода очень
важно знать, какова связь между общим удоем за лактацию
и процентом жира в молоке, иначе говоря, дают ли более высоко-
удойные коровы молоко с повышенным содержанием жира или,
наоборот, с пониженным и насколько часто встречаются исклю-
чения из той или другой зависимости. Оценку качеств коровы
обычно производят по полновозрастной, т. е. по третьей или чет-
вертой лактации. Но если бы была установлена положительная
корреляция между удоем за первую и удоем за третью лактацию,
тогда можно было бы предсказывать удой коровы за третью лак-
тацию по ее удою за первую лактацию. Степень уверенности, до-
стоверности подобного предсказания, очевидно, зависит от степе-
ни корреляции. Вот почему возникает потребность в количествен-
ном измерении корреляции. Для этого служит ряд методов,
наиболее распространенным из которых является вычисление так
называемого коэффициента корреляции.
Коэффициент корреляции и методы его вычисления. Смысл
корреляции заключается в сопряженности вариации признаков
(пока мы будем говорить о корреляции только двух признаков
и такую корреляцию условимся называть простой). Если мы хо-
тим установить наличие корреляционной зависимости и ее сте-
пень, нам надо узнать, насколько параллельно идет вариация
по двум признакам.
Наиболее простым и в то же время очень грубым способом
такого сравнения вариаций является построение графиков, на
которых была бы выражена кривыми вариация признаков у осо-
бей данной совокупности изучаемых животных. 11о~ тому, на-
сколько параллельно шли бы кривые изменения признаков, мож-
но было бы судить о корреляции. Однако этот изредка применя-
емый на практике способ не дает никакого мерила корреляцион-
ной зависимости, кроме чисто зрительного впечатления о колеба-
ниях линий на графике. Непосредственное сравнение вариации
двух признаков затрудняется и тем обстоятельством, что они, как
правило, выражены в разных измерениях. Вот почему при изуче-
нии корреляции прибегают к нормированному отклонению Л Л
Напомним, что нормированное отклонение t представляет
собой отклонение тех или других вариант от их средней арифме-
тической, выраженное в долях среднего квадратического откло-
нения. Выражая отклонения отдельных особей от средних ариф-
метических по обоим признакам .одновременно, можно сопостав-
лять вариацию по обоим признакам.
Допустим, например, что мы хотим выяснить, насколько свя-
занно варьируют у лисиц длина туловищачх и длина хвоста у.
Для этого сопоставим значения t по х и по у для некоторого ко-
личества лисиц: :
109
№ 1 № 2
tx + 2,0 + 0,8
ty +1,8 +0,9
№ 3 № 4 № 5
— 0,4 +1,2 +0,2
— 0Д +1,3 +0,3
№6 № 7
— 1,7 —2,7
— 1,4 —2,9 и т. д.
Ясно, что чем теснее связана вариация по этим двум призна-
кам, тем чаще совпадут значения t обоих признаков и по знаку,
и по количественному значению. Места, занимаемые ими в вари-
ационных кривых длины туловища и длины хвоста, будут пример-
но одинаковыми. Наоборот, при отсутствии корреляции совпаде-
ние величин t по обоим признакам будет чисто случайным.
Таким образом, зависимость между t обоих рядов, т. е. меж-
ду величинами tx = - и 1у = (или отношение между
ними), может быть мерилбй корреляционной связи.
Оказалось, что нормированные отклонения обладают рядом
ценных математических свойств. Приведем некоторые из них
в готовом виде без математического обоснования.
Первое свойство заключается в том, что среднее произве-
дение двух нормированных отклонений, т. е.
п ’
колеблется от 0 до 1.
Среднее произведение нормированных отклонений
п
можно записать и в иной форме, а именно: txty. Черта наверху,
охватывающая обе буквы, будет обозначать, что взята средняя.
При полном отсутствии связи между изучаемыми признаками
tjty = 0, а при полной, т. е. уже функциональной, связи между
признаками txty = 1.
Второе свойство среднего произведения t заключается в том,
что его знак будет разным в зависимости от типа связи: если
увеличивающемуся значению одного признака соответствует уве-
личивающееся значение второго — знакпипрс, если с увеличени-
ем значения одцого признака значение этороЬо уменьшается —
знак минус.
* Наконец, оказалось, что теми же свойствами характеризуется
не только среднее произведение tytx, но и их -среднее отношение
Г*у 1
LG Г
Квадратные скобки в данном случае означают, что отношение
также берется в среднем.
Вот почему обе эти величины были приняты как мерило тес-
ноты корреляционной связи двух признаков и получили название
коэффициента корреляции, который обозначается буквой г.
110
Таким образом,
Г tx’ty
или
Последнее выражение мы сейчас рассматривать не будем.
Укажем только, что оно приводит к так называемому основному
корреляционному уравнению, или уравнению регрессии ty=rtx,
преобразование которого дает обычное уравнение прямой
у = а + bx. С ним мы познакомимся в гл. 6, когда будем говорить
о регрессии.
Первое же выражение является общим видом формулы, при-
меняемой при вычислениях простого коэффициента корреляции
f —
п
Т ак как
. _ (х,—~х) . ,
°х ’ у~ ’у '
ТО
г = ^(х,—7)(у<—~у)
noyiy
(37)
(38)
В формуле (38) величина xt— х обозначает отклонение каж-
дой изучаемой особи от средней" х одного признака, распределён-
ного по ряду х, а величина ул — у — отклонение той же особи от
средней у другого признака, выражающегося рядом у. Таким об-
разом, для того чтобы получить числитель, надо учесть отклоне-
ния каждой особи от средних по обоим признакам, перемножить
их и затем просуммировать. В знаменателе же формулы уже из-
вестные величины: п — число особей, ах — среднее квадратическое
отклонение ряда по признаку х (или просто ряда х) и оу — сред-
нее квадратическое отклонение ряда по признаку у (ряду у).
Рабочие формулы для вычисления коэффициента корреляции.
Практически можно использовать как приведенную выше общую
формулу (38), так и ее видоизменения, которые легко получить
путем алгебраического преобразования числителя и знаменателя.
Существует довольно много различных рабочих формул для
вычисления г прямым способом, т. е. при непосредственном
использовании отдельных значений xt и соответствующих им
Одной из наиболее часто применяема* формул является следу-
ющая:
г = У) \ доч
Эта формула получена путем простого преобразования форму-
лы (38), где вместо огя и оу подставлены их.значения
111
~-1.. И
Коэффициент корреляции в данном случае выражен только
с помощью отклонений от средних, так что все вычисления стано-
вятся однотипными.
В качестве примера вычисления коэффициента корреляции
по формуле (39) используем данные о весе 10 петушков 15-днев-
ного возраста х и весе их гребешков у. Они обработаны в табл. 20
таким образом/ чтобы все нужные для формулы величины были
выражены в* отклонениях от средних арифметических. Тогда
2302 2302 . Л
/ 1 ЛО Q *7 -' | О , О f *
у 1000-6954 2637
* Таблица 20
Данные для вычисления коэффициента корреляции между весом тела
х (в г) 10 петушков 15-дневного возраста и весом их гребешков у (в мг)
Номер пар *i У1 X/ — X (Xi— х )2 ’г (Уг~ У )8 1ч|^ 1 1
1 83 56 0 0 —4 16 0
2 72 42 -11* 121 — 18 324 198
3 69 18 —14 196 —42 1764 588
4 90 84 7 49 24 576 168
5* 90 56 7 49 —4 16 —28
6 95 107 12 144 47 2309 564
7- 95 90 1 12 144 30 900 360
& 91 68 8 64 8 64 64
9 75 31 -Ь 64 —29 841 232
10 70 48 -13». 16^ —12 144 156
2 = 830 Т=83 2 = 60,0 ~у = 60 2—1000 2 —6954 2 = 2302
Отклонения вариант от средних иногда выражаются очень
большими числами, с десятичными дробями. Тогда можно приме-
нить другие формулы, например
г = (40)
У(2х?-П?)(2у?-ф)
112
Таблица 21
Данные для вычисления коэффициента корреляции между живым
весом бычков при рождении х (в кг) и средним суточным привесом у (в г)
У1 А У*
38,5 694 1482,25 481 636 26719,0
46,0 901 2116,00 811 801 41446,0
43,0 736 1849,00 541 696 31648,0
43,0 1005 1849,00 1 010 025 43215,0
40,5 841 1640,25 707 281 34060,5
44,0 743 1936,00 552 049 32692,0
38,0 896 1444,00 802 816 34048,0
35,0 863 1225,00 744 769 30205,0
40,5 855 1640,25 731 025 34627,5
54,0 830 2916,00 688 900 44820,0
2 = 422,5 2 = 8364 2 = 18097,75 2 = 7 071 998 2 = 353481,0
При замене х и у исходными для их вычисления величинами
IX; St/;
—- и — получим
п п J
(41)
Данные табл. 21 о связи живого веса бычков при рождении
х и среднего суточного привеса у обработаны таким образом, что
может быть применена одна из формул (40) или (41).
Так, для формулы (41) понадобятся следующие данные:
2t/z = 422,5 • 8364 = 3533790,
Xiq j 3 533 790 _______ 353379
n 10 ’
(2xi)2 = = 17850,6,
n 10
(Sy^ = 8W = 6995649 6
n 10 ’
В табл. 21 имеются следующие итоговые цифры:
= 353481,
2xz2 = 18097,75,
St/? = 7071998.
113
Подставив все эти величины в формулу (41), получим
г = 353481-353379 = 4- 0 023
V(18097,75 — 17850,6) (7071998 — 6995649,6) + ’
Мы приводим эти три модификации основной формулы коэф-
фициента корреляции (в действительности их значительно боль-
ше) потому, что в различных руководствах и работах можно
встретиться с неодинаковыми методами вычисления г. Кроме то-
го, и конкретные условия полученного фактического материала
могут побудить отдать предпочтение одной из перечисленных
формул в зависимости от того, какие показатели легче вычислите
и какими легче оперировать, надо ли группировать полученные
данные в классы или без этого можно обойтись, велико ли коли-
чество наблюдений или мало и т. д.
Особенно важно выбрать подходящую формулу в тех случа-
ях, когда для вычисления коэффициента корреляции можно при-
менить счетную технику.
В формулах (39), (40) и (41) применяется прямой способ вы-
числения г на основе использования вариант xt и у,, средних х
и у и отклонений от них.
Непрямой способ вычисления г. Формула Бравэ. При значи-
тельном числе особей в изучаемой' совокупности техника вычис-
ления может быть упрощена подобно тому, как это было сделано
в случае вычисления х и о, путем учета отклонений не от х или
у, а от условных средних Ах и Ау.
В этом случае применяется следующая рабочая формула для
коэффициента корреляции (формула Бравэ):
fajfly nbxby /лп\
г =------г--------- (42)
па^у
Эта формула отличается от общей формулы (38) только
структурой числителя. Она позволяет проделать все вычисления
как для получения сигмы каждого ряда, так и для вычисления г,
пользуясь одной и той же таблицей, которая называется корре-
ляционной решеткой. Все величины в формуле могут быть взяты
в условных значениях, т. е. без умножения на величины классо-
вых промежутков обоих вариационных рядов ix и iy. Так как обе
эти величины входят и в знаменатель, и в числитель, то они со-
кращаются.
Для составления корреляционной решетки и вычисления ко-
эффициента корреляциии используем данные об удоях по макси-
мальной лактации и средней жирности молока за эту же лакта-
цию 100 коров холмогоро-печорских помесей, взятых без всякого
выбора из группы учтенных нами в 1954—1957 гг. лучших коров
колхозов и совхозов Коми АССР. Нижним лимитом является
удой 4000 л, верхним — 8400 л (для упрощения удои округлены).
Жирность молока колебалась от 3,0 до 4,4%. Классы для вариа-
114
ционных рядов: по удою молока за лактацию (в л) —4000—4499,
4500—4999, 5000—5499, 5500—5999 и т. д.; по проценту жира—
2,9—3,0, 3,1—3,2, 3,3—3,4 и т. д.
Определив классы, следует построить корреляционную решет-
ку. На двух сторонах квадрата (вверху по горизонтали и слева
по вертикали) наносят значения классов обоих рядов. По гори-
зонтали классы записывают слева направо от меньших значений
к большим. По вертикали же это можно сделать двумя разными
способами. При одном значения классов записывают сверху вниз
от меньших к большим. При другом — наоборот, сверху вниз от
больших к меньшим. Первый способ кажется с первого взгляда
более простым, но он противоречит построению обычной системы
координат, на основе которой строятся линии регрессии (гл. 6).
Поэтому для достижения единообразия с материалом следующей
гл. 6 применим второй способ, как это и сделано в табл. 22. Сред-
ние значения классов для корреляционной решетки не требуются.
Таблица 22
Корреляционная решетка для удоев за лактацию х (в л)
и среднего процента жира у в молоке 100 коров холмогоро-печорских помесей
4,3—4,4
4,1—4,2
3,9-4,0
3,7-3,8
3,5-3,6
3.3-3,4
3,1— 3,2
2,9-3,0
f х -
№
/а2
2
1
1
5
3
15
45
1
4;=Т55-»'И'
~ О'№ "1Я
=1'Ж'
Примечание. Звездочками отмечены значения b и а, не умноженные на t
115
В макет корреляционой рёшетки надо разнести показатели
для всех 100 коров. Причем данные об изученных особях вно-
сятся в соответствующие клетки решетки одновременно по обоим
признакам. Так, например, если первые 3 коровы из списка име-
ли показатели удоя: корова № 1 — 4100 л и 3,0% жира; корова
№2 — 5700 л и 3,1 % жира и корова № 3 — 4900 л и 4,4% жира,
то корова Ко 1 должна быть, внесена в клетку на пересечении
класса в 4000—4499 л по удою и класса 2,9—3,0 по проценту
жира, т. е. в нижнюю левую клетку; корова № 2 — в клетку на
пересечении классов 5500—5999 и 3,1—3,2, т. е. в четвертую
клетку предпоследнего горизонтального ряда; корова № 3 — во
вторую клетку самого верхнего горизонтального ряда. При раз-
носке можно пользоваться тем же приемом, который был приме-
нен при построении вариационного ряда, а именно: обозначать
варианты точками и соединяющими их черточками.
В табл. 22 разноска 100 коров уже проведена. Цифры, стоя-
щие в каждой клетке, обозначают, таким образом, число коров,
имеющих удой и процент жира согласно классам. Суммы всех
особей в горизонтальных строках пишутся справа (ряд у по про-
центу жира), суммы всех особей в вертикальных столбцах
пишутся внизу (ряд х по удою). Справа внизу в угловой клетке
надо записать сумму всех особей (100). Она относится как
к ряду х, так и к ряду у.
С помощью корреляционной решетки можно получить все
величины, необходимые для вычисления коэффициента корре-
ляции. Величина и в нашем случае равна 100. Чтобы получить
Ьх и by, а также ох и ву, достаточно обработать 2 вариацион-
ных ряда: ряд х (по удою за лактацию) и ряд у (по проценту
жира в молоке), которые расположены в нижней и правой частях
таблицы. Если в ней нет места, можно выписать эти ряды на
отдельных листках. Однако предпочтительнее первое, как это
будет видно в дальнейшем. Поэтому в корреляционной решетке,
представленной в табл. 22, проделана и обработка вариацион-
ных рядов х и у.
Вновь обращаем внимание на то, что вычисленные для обоих
рядов значения b и а в данном случае неполные, как бы условные.
Они не умножены на величины классовых промежутков i, по-
этому отмечены звездочками. Для ряда х величина классового
промежутка равна 500 л, а для ряда у — 0,2% жира. Очевидно,
что для получения окончательных значений b и о (и х, если она
нужна) надо ввести поправки на i. Для вычисления же коэффи-
циента корреляции умножать на ix и соответственно на iy нет
необходимости только потому, что они все равно сЬкращаются,
находясь в числителе и в знаменателе формулы.
Осталось вычислить последнюю величину для включения
в формулу коэффициента корреляции — первый член числите-
ля Zfaxav.
116
Для этого можно воспользоваться той же корреляционной
решеткой табл. 22, но для лучшего уяснения всех действий сле-
дует переписать ее вновь без граф fa и fa2 (табл. 23).
Величина Zfaxay представляет собой сумму произведений от-
клонений каждого класса от условной средней по ряду х и от
условной средней по ряду у (ахау), умноженных на число особей
в данном классе f. В табл. 23 клетки тех классов, которые были
приняты за условные средние как по ряду х, так и по ряду у,
можно зачеркнуть или выделить жирными линиями, так как для
каждой такой клетки произведение ахау равно нулю. Для всех
остальных клеток корреляционной решетки надо получить произ-
ведения отклонений каждого класса по ряду х и по ряду у,
перемножить их и записать в углу каждой клетки, как это сдела-
но в таблице.
Разберем теперь, как вычисляются необходимые произведе-
ния отклонений. В клетке, расположенной в нижнем левом углу
решетки, помечена лишь одна особь (класс по удою 4000—4499 л
и по проценту жира 2,9—3,0). Чтобы получить для нее произве-
дение ахау, надо посмотреть на расположенные справа и внизу
вариационные ряды. Они показывают, что для данной особи от-
клонение ах=— 2, а отклонение ау=— 3. Отсюда произведение
ахау= ( — 2) • ( — 3) =6. Цифра 6 записана в верхнем правом
углу этой клетки. Можно взять для примера какую-либо другую
клетку, например в верхнем ряду третью справа, где помечены
две особи. Для данной клетки ахау=(+4) • (+4) = 16. Для по-
следней правой клетки третьего ряда снизу ахау— (—1) • ( + 6) =
= —6. Однако в'табл. 23 произведения отклонений даны без зна-
ка. Дело в том, что они будут иметь всегда определенный знак
в зависимости от того, в какой части корреляционной решетки
расположены соответствующие клетки. Решетка разделяется
нулевыми рядами (горизонтальным и вертикальным) на четыре
части, называемые обычно квадрантами. В левом верхнем квад-
ранте ау положительны, ах отрицательны, поэтому их произве-
дения всегда будут иметь знак минус. В нижнем-левом квадранте
и ах, и ау являются отрицательными величинами, их произведе-
ния — положительными. В правом верхнем квадранте все ах
имеют знак плюс и ау — знак плюс, поэтому их произведения —
величины положительные. В правом нижнем квадранте, наобо-
рот, ах имеет знак плюс, а ау — знак минус, их произведение
будет также величиной отрицательной. Вот почему писать в каж-
дой клетке знак плюс или минус нет необходимости, достаточно
запомнить знак для каждого квадранта решетки. Не нужно так-
же писать произведения ахау в тех клетках, где не было помече-
но ни одной особи.
После записи значений ахау в клетках корреляционной ре-
шетки надо помножить каждое произведение ахау на число
особей в классе и после этого просуммировать все произве-
дения.
117
Таблица 23
Корреляционная решетка для удоев за лактацию х
и среднего процента жира у в молоке 100 коров
холмогоро-печорских помесей
X. X у 4000—4499 4500—4999 I 5000—5499 5500—5999 । 6000—6499 1. 6500—6999 1 7000—7499 7500—7999 8000—8499 1 ау
4,3—4,4 в г 4 2 0 1 16 2 6 +4
4,1—4,2 6 3 3 5 8 +3
3,9—4,0 4 7 2 7 0 1 4 1 6 1 17 +2
3,7—3,8 2 7 1 6 0 6 1 5 24 + 1
3,5—3,6 0 3 0 2 0, 7 0 6 0 1 19 0
3,3—3,4 2 1 1 3 0 2 1 4 2 1 3 2 4 1 5 1 6 2 17 — 1
3,1-3,2 0 3 2 1 4 1 6 1 12 1 7 » —2
2,9—3,0 6 1 9 1 2 —3
/ X 23 25 20 16 4 5 3 1 3 100
—2 —1 1 0 1+! +2 +3 +4 +5 +6
Примечание. Эта таблица дана для вычисления произведений ахау\
они записаны в верхнем правом углу каждой клетки решетки, где имеются
особи.
118
Неплохо воспользоваться длй этого вспомогательной таблицей
(табл. 24).
Таблица 24
Произведения f ахау для всех клеток табл. 23
по квадрантам
1-й квадрант (знак—)
7-2= 14 7-2=14
7-4 = 28 5-3 = 15
3-6 = 18 2-4=8
1-8 = 8 —111
6-1=6
2-й квадрант (знак+)
5-1=5
1-4 = 4
2-16 = 32
1-6 = 6
+ 47
3-й квадрант (знак+)
1-6 = 6
1-2 = 2
3-1=3
+тг
4-й квадрант (знак —)
1-2 = 2
4-1 =4
1-4 = 4
1-2 = 2
1-9 = 9
1-6 = 6
2-3 = 6
1-4 = 4
1-5 = 5
1-12 = 12
2-6= 12
— 66
По данным табл. 24 можно получить значение %faxay. Оно
равно +11+47-111-66=+58-177=-119.
Теперь можно проставить все полученные значения в форму-
лу коэффициента корреляции:
_—119—100 • 0,03 • 0,69 _
Г ~~ 100 • 1,66 • 1,93 — и’'36.
Возможные значения коэффициента корреляции. Прежде все-
го необходимо обратить внимание на знак при коэффициенте
корреляции. При положительной корреляции г будет иметь знак
плюс, при отрицательной — минус. В нашем примере знак минус
указывает на отрицательную корреляцию между величиной
удоев за лактацию и процентом жира в молоке, т. е. на то, что
в изученной группе коров с увеличением удоев жирность молока
несколько снижается.
Коэффициенты корреляции могут колебаться от 0 до +1 при
положительной корреляции и от 0 до — 1 при Отрицательной,
корреляции. Если г = 0, то это означает, что вариация обоих
признаков происходит независимо. При значениях г ¥0 вариации
обоих признаков взаимосвязаны, т. е. с изменением одного при-
знака меняется и другой (в том же направлении—при положи-
тельной корреляции и в противоположном направлении — при от-
рицательной корреляции).
Предварительные выводы о характере связи можно сделать
из анализа расположения вариант в корреляционной решетке,
119
что видно из сравнения шести схем рис. 11. На них показано
возможное распределение вариант по отдельным клеткам корре-
ляционной решетки при корреляциях, отличающихся по знаку
и величине.
Если варианты расположены в решетке равномерно в овалег
с увеличением частот ближе к средним по ряду х и соответ-
ственно по ряду у, как это требуется по законам случайной
вариации (рис. И, а), то в этом случае можно говорить о неза-
висимом варьировании признаков х и у, т. е. об отсутствии
корреляции между ними (г = 0). Сгущение вариант ближе
к диагоналям указывает на наличие корреляции, при этом можно
судить о знаке корреляции по тому, к какой именно диагонали
происходит сгущение: если к диагонали, проходящей от верх-
него правого угла к нижнему левому (рис. 11, б, в, б),— то кор-
реляция положительная; если к диагонали, проходящей от верх-
него левого угла к нижнему правому (рис. fl, г, г),— корреляция
отрицательная. Наконец, по степени сгущения можно судить
о величине корреляции. При расположении вариант в широком
овале (рис. 11, б, г) г равно'примерно 0,5. Чем уже овал, тем
больше коэффициент корреляции (рис. 11, в\ г=0,8). Наконец,
если варианты расположены только по диагонали, г=1
(рис. И, д и е). В этом случае зависимость между х и у ста-
новится функциональной, т. е. каждому значению х соответству-
ет определенное значение у и наоборот.
Однако расположение вариант в корреляционной решетке
далеко не всегда бывает столь правильным. Нахождение одной
или нескольких вариант в стороне от овала может резко изме-
нить предполагаемое значение г. Поэтому для более точного
измерения степени связи в вариации двух признаков или двух
переменных величин необходимо вычисление коэффициента кор-
реляции.
Какие значения г можно считать большими, а какие сред-
ними и малыми? С первого взгляда может показаться, что вели-
чина ~г, близкая к 0,5, является достаточно высоким коэффициен-
том корреляции и что в этом совпадение вариации двух
признаков должно быть в 50% случаев. На самом деле это не
так. Даже при полном отсутствии корреляции будут случаи,
когда отклонения от средних по обоим признакам для данной
особи окажутся примерно одинаковыми, иначе говоря, когда по
обоим признакам особь будет находиться примерно в одном
и том же месте вариационного ряда. Так, из рис. 11, а видно, что
некоторые группы вариант расположены в одних и тех же поряд-
ковых классах общих рядов х и у. например в классах «3» и «3»,
«5» и «5» и т. д.
Таким образом, и при отсутствии корреляции будет наблю-
даться в силу закономерностей случайной вариации как случай-
ное совпадение в вариации двух признаков, так и случайное
несовпадение, примерно в равном соотношении. При наличии
120
Рис. 11, Распределение вариант в корреляционных решетках при
корреляциях, отличающихся по знаку и величине.
г
- о
о
о
о
о
о
- г—1,0 о
12 3 0 5 6 7
е
же корреляции какая-то доля изменчивости одного признака
будет вполне закономерно определяться изменчивостью другого
признака. Оказывается, что степень «связанности» в вариации
двух величин более точно измеряется квадратом коэффициента
корреляции, т. е. г2. Это значит, что при г = 0,5 25% вариации од-
ного признака объясняется вариацией другого признака, по ос-
тальной же части вариации соотношение между признаками
чисто случайное. При г=0,3 менее 10% изменчивости объясня-
121
ется таким же образом. При г=0,7 около 50% изменчивости
одного признака определяется изменчивостью другого призна-
ка. При таком же коэффициенте корреляции, как 0,9, 81 % ва-
риации одного признака закономерно связан с вариацией дру-
гого признака, в остальных же 19% случаев совпадение или
несовпадение вариаций двух признаков чисто случайно.
Таким образом, хотя коэффициент корреляции и указывает
на общность элементов в двух коррелированных рядах, но не вся
эта общность объясняется закономерной связью в вариации
двух признаков.
Из сказанного ясно, что о тесной корреляции можно говорить
только в тех' случаях, когда г не ниже 0,7. Коэффициенты корре-
ляции порядка 0,5—0,6 следует считать средними, коэффициен-
ты же ниже 0,5 указывают на слабую связь.
Выборочность коэффициента корреляции. Оценка его досто-
верности. Фактически полученный коэффициент корреляции г
всегда является выборочным, так как он вычисляется на основе
ограниченной совокупности, представляющей выборку из гене-
ральной. Поэтому он имеет свою ошибку — ошибку выморочно-
сти. Эта ошибка будет мерой расхождения между г и коэффици-
ентом корреляции для генеральной совокупности р (греческое
ро). Таким образом, определив среднюю ошибку, можно судить
о степени достоверности г. Согласно нулевой гипотезе, р=0,
т. е. признается, что в генеральной совокупности нет корреляции
между варьирующими признаками. Тогда
' = <43>
При значении t, удовлетворяющем определенной вероятности
(0,95 или 0,99), можно считать нулевую гипотезу отвергнутой,
т. е. признать данное значение г достоверным. ,
Таким образом, для оценки достоверности выборочного коэф-
фициента корреляции надо вычислить среднюю ошибку коэффи-
циента корреляции.
Однако по отношению к коэффициенту корреляции вопрос
о средней ошибке обстоит, значительно сложнее, чем по отно-
шению к средней арифметической. Выборочные средние, как
указано в гл. 4, распределяются вокруг средней арифметиче-
ской р. в соответствии с нормальным законом, и это было осно-
ванием для формулы ошибки средней арифметической.
Распределение же выборочных коэффициентов корреляции,
оказывается, далеко не всегда следует нормальному закону.
Поэтому вычисление средней ошибки для г связано с известными
трудностями, а иногда даже приходится пользоваться околь-
ным методом — переводом г в число z (о числе z см. ниже).
При больших выборках (в данном случае при п>100) и при
не очень высоком коэффициенте корреляции среднюю ошибку
для г можно вычислить по формуле
122
Тогда
s =1=^-
' /п •
(44)
u rVn
l~ 1 —г»-
(45)
Для вычисленного ранее коэффициента корреляции между
удоем коров за лактацию и процентом жира в молоке, равно-
го — 0,38,
sr = = 0,0856 да 0,09,
t — .2^8 =42
1 0,09
Очевидно, что коэффициент корреляции обладает высокой
достоверностью. Уровень значимости ниже чем 0,01. Нулевая
гипотеза, что р=0, опровергается.
Распределение г при малых выборках и при очень малых или
больших его значениях может значительно отличаться от нор-
мального, поэтому применение формулы (44) в таких случаях
может привести к неверной оценке достоверности коэффициента
корреляции. Оказались необходимыми более точные методы
оценки. Одним из них является следующая формула для sr:
Отсюда
' = ПЬ~^~2- <47>
Допустим, что при п = 11 был получен коэффициент корре-
ляции г — 0,56.
В таком случае
t =-- 0,56 — Т/ 11 9 — 0*56'3 _о ло
/Г^Ц56’ Г 11—2 0 83 - 2,03.
В табл. II ^-распределения по Стьюденту нет .колонки с п=11
и строки с Z=2,03. Поэтому надо взять цифры вероятности, сред-
ние между значениями п=10 и п=12 для значения /=2,0. Полу-
чаем вероятность 0,926, т. е. уровень значимости 0,07. Очевидно,
что такой коэффициент корреляции нельзя считать досто-
верным.
Чтобы не усложнять работу вычислением ошибки и последу-
ющим обращением к таблице распределения t, можно пользо-
ваться табл. VII, с помощью которой легко определить досто-
верность г при разных df. непосредственно по значению коэффи-
циента корреляции.
В табл. VII даны два уровня значимости: 0,05 и 0,01. В более
'Подробных таблицах приводятся и иные уровни значимости.
123
Чтобы можно было считать полученный коэффициент корреля-
ции достовер'ным, он должен превышать табличное значение при
данном df. Так, например, при уровне значимости 0,05 и df=9
коэффициент корреляции должен быть не менее 0,60. При df=9
и уровне значимости 0,01 г должен быть не менее 0,74. Получен-
ный выше коэффицент корреляции 0,56 при п=11 не удовлетво-
ряет обоим уровням значимости.
Из табл. VII видно, что значимость одного и того же коэф-
фициента корреляции может быть весьма различной в зависи-
мости от величины выборки,, по которой он вычислен. Так,
например, если г=0,70, то при n = 10 (df = 8) он может быть
признан достаточным только для уровня вероятности 0,95,
т. е. для уровня значимости 0,05. Если же принять уровень
значимости 0,01, то он не может считаться достоверным. Это
значит, что при уровне значимости 0,01 нулевая гипотеза не мо-
жет быть отброшена. Если же n=16 (cff=14), а г=0,70, то
нулевая гипотеза отвергается при обоих уровнях значимости.
При n = 8 (df = 6) г=0,70 является недостоверным, т. е. нулевая
гипотеза остается в силе при обоих уровнях значимости.
При больших п даже значительно меньшие коэффициенты
корреляции могут быть достоверными. Так, коэффициент корре-
ляции г= — 0,22 достоверен при п=150 с вероятностью 0,99,
т. е. при уровне значимости 0,01. При п=100 и г=— 0,22 нулевая
гипотеза не может быть отвергнута при уровне значимости 0,01.
Наконец, при п=70 коэффициент корреляции г=— 0,22 недосто-
верен. Нулевая гипотеза по-прежнему остается в силе.
Перевод г в число Z. В некоторых случаях даже улучшенный
метод определения ошибки коэффициента корреляции может
оказаться недостаточным в связи со значительным отклонением
распределения г от нормального (особенно при высоких значе-
ниях г). Вот почему Фишером было предложено заменять г дру-
гой величиной z. Преимуществом z является то, что распределе-
ние величин z значительно ближе к нормальному, чем распреде-
ление г. Преобразование г в z производится по определенной
формуле, давать которую здесь нет надобности, так как перевод
г в z и обратно можно сделать по готовой табл. VIII.
Средняя ошибка для z вычисляется по формуле
Оценка достоверности z может производиться, как обычно,
с помощью t, при этом
t = («)
sz
Допустим, что г=0,606 и п=10.
Определим z по табл. VIII. Он будет равен 0,7.
Ошибка для z
124
Тогда
/ = 1W = 1,851
Так как распределение z близко к нормальному, то, несмотря
на малое п, можно воспользоваться табл. I. Значение /=1,85
дает вероятность 0,93, т. е. уровень значимости 0,07. Очевидно,
корреляция не доказана. Нулевая гипотеза остается в силе.
Определение достоверности разницы между г. Значение чис-
ла z заключается еще и в том, что только с его помощью можно
определить достоверность или недостоверность разницы между
двумя коэффициентами корреляции или между фактически по-
лученным коэффициентом корреляции и теоретически ожидае-
мым, а также провести объединение данных по нескольким кор-
реляциям, вычисленным на основе малых выборок.
Так, например, при изучении корреляции между высотой
В холке и живым весом у крупного рогатого скота были полу-
чены следующие коэффициенты корреляции:
в группе черно-пестрого скота и = +0,675;
в группе рыже-пестрого скота г2= +0,761.
Количество пар наблюдений в каждой группе равно Ю0.
По табл. VIII переводим значения г в значения z. Тогда
Zi = +0,82 и Z2= + l,0.
Ошибка для разницы между Zi и z2 определяется по обычной
формуле ошибки разницы:-
Sd2 = Ksf+sl-
Здесь
1
$1 — $2 — —7= •
/97
Тогда
Sd2 ~~ ]/”'97 ^”97 = О’1^
Отсюда
t - _ -0.18 = 1,28.
s<t2 “0,14
Даже не обращаясь к таблицам, можно сказать, что разница
недостоверна. Если мы проверим вероятность по таблице нор-
мального интеграла вероятности (или по таблице Стьюдента при
п = оо), то увидим, что вероятность достоверности всего только
0,789. Это значит, что в 211 случаях из 1000 (или в 21 из 100)
разница между Zj и г2 может возникать по чисто случайным
причинам. Поэтому естественно, что такое различие между
125
' Zi и Zj статистически недостоверно. Это значит, что нулевая гипо-
теза об отсутствии различий между группами черно-пестрого
и рыже-пестрого скота в отношении корреляционной зависимо-
сти высоты в холке и живого веса не может быть отброшена.
Доверительные границы для р. Если достоверность выбороч-
ного коэффициента корреляции г доказана, то с помощью сред-
ней ошибки можно установить доверительные границы для
коэффициента корреляции р той генеральной совокупности, из
которой взята выборочная совокупность. В некоторых случаях
(когда п достаточно велико, а г близко к 0,5) это можно сделать
тем же способом, который применялся для установления дове-
рительных границ для у., т. е. путем вычитания или прибавления
2 (или 3) ошибок по общей формуле:
г — tsr < р < г + tsr. (50)
Так, при г=0,38 и sr=0,09 (п= 100) доверительные границы
для уровня значимости /*=0,05 будут:
0,38-2 • 0,09< р<0,38+2 • 0,09;
0,20<р<0,56.
Однако, учитывая, что распределение величины z более близ-
ко к нормальному, чем распределение г, лучше определять дове-
рительные границы с помощью z по формуле
z — tsz < z0 < z + tsz. (50а)
В дальнейшем z переводятся в г. Допустим, что при п=12 было
получено г=0,82. Тогда z=l,16.
Ошибка для
s. = -г 1-г-т = -JL = 2- = о>зз.
* /12 — 3 /9 3
При Р = 0,05 для доверительных границ достаточно взять
/=2.
Определяем доверительные границы для Zo генеральной сово-
купности по формуле (50а):
1,16-2-0,33<z0<l,16 + 2-0,33;
0,50<z0<l,82.
Теперь определяем граничные значения г по z в обратном
порядке и получаем доверительные границы для р:
0,46<р<0,95.
Границы для р очень велики. Кроме того, существенно, что
полученное для выборочной совокупности значение г (=0,82)
находится не посредине между максимумом и минимумом, а бли-
же к максимуму. Это значит, что распределение г асимметрич-
но. Определение доверительных границ непосредственно по г
дало бы очень неточные оезультаты.
126
Из всего сказанного следует очень важный для биолога вы-
вод, что даже достоверным значениям выборочных коэффициен-
тов корреляции нельзя придавать абсолютное значение и что
надо учитывать возможную их колеблемость по отдельным вы-
боркам.
Коэффициент ранговой корреляции. Для вычисления обычно-
го коэффициента корреляции необходимо, чтобы исходные дан-
ные были выражены достаточно точно. Однако это далеко не
всегда возможно. Существуют такие количественные признаки,
которые с трудом поддаются точной оценке. Кроме того, распре-
деление одного или обоих коррелирующих признаков может
быть очень неравномерным и неправильным.
Эти трудности можно обойти, если применить оценку вариант
по каждому признаку порядковыми номерами от меньших зна-
чений к большим (или наоборот). Порядковый номер по каж-
дому признаку является его рангом. Отсюда название этого
метода — определение коэффициента ранговой корреляции (или
коэффициента корреляции рангов). Существует 2 коэффициента
ранговой корреляции — Спирмэна и Кендэла. О коэффициенте
Кендэла можно найти данные в специальной литературе.* По-
этому ограничимся разбором коэффициента Спирмэна.
Для коэффициента ранговой корреляции Спирмэна примем
обозначение rs.
•Формула для его вычисления следующая:
_ , 62 (х, -у,-)»
s ~~ ‘ п(п» —1) ’
(51)
где Х{ и tji — ранги по первому и второму признаку,
п — число пар коррелируемых величин.
Разницу рангов можно обозначить буквой d.
Тогда
г =1_______6^-. .
s л(п2 —1) •
В качестве простейшего примера использования коэффициен-
та ранговой корреляции Спирмэна приведем следующий. В.одном
из районов Львовской области появились случаи заболевания
безжелтушным лептоспирозом (водной лихорадкой). Можно
было предположить, что повышенный процент заболеваний бы-
вает в месяцы с большим количеством осадков. Для установле-
ния этой связи следует сопоставить среднее количество осадков
в июле и августе (за несколько лет) и количество заболеваний
лептоспирозом в эти же месяцы данного года (табл. 25).
Казалось бы, по данным табл. 25 можно вычислить обычный
коэффициент корреляции. Однако оба признака очень неустой-
чивы. Поэтому лучше выразить их вариацию в рангах, что и сде-
• См. Ван дер Варден Б. Л. Математическая статистика; Юл Дж. Э„
Кендал М. Дж. Теория статистики.
127
Таблица 25
Количество заболеваний лептоспирозом и количество осадков за данный месяц (данные упрощены)
Количество заболеваний X Количество осадков У Оценка рангов d da
*1 У1
0 54 1 3 —2 4
19 101 8 6 2 4
4 185 5 10 —5 < 25
1 85 2 5 —3 9
2 30 3,5 2 + 1,5 2,25
68 128 9 7 +2 4
131 143 10 9 +1 1
14 74 7 4 +3 9
11 28 6 1 +5 25
2 132 3,5 8 —4,5 20,25
л = 10 2d2 = 103,50
лано в 3-й и 4-й графах таблицы. В тех случаях, когда встре-
чаются одинаковые значения признаков, надо сложить их ранги
и записать средний ранг, как это сделано с дважды повторявши-
мися в таблице двумя больными. Они оценены рангами
3,5 и 3,5.
Коэффициент ранговой корреляции будет равен
1 10(10а— 1) — 1 990 “ 1 0,63 — 0,37.
Оценка достоверности rs несколько затруднительна, так как
распределение ранговых коэффициентов может еще более откло-
няться от нормального, нежели распределение простых г. Поэто-
му для п>8 пользуются готовыми таблицами оценки простого
коэффициента корреляции г (табл. VII). Для п<9 можно вос-
пользоваться следующей таблицей необходимых значений гв
(требования для г3 здесь выше, чем для г) :
п
ДЛЯ Р = 0,05 для Р = 0,01
5 нет
6 0,886 1
7 0 750 0,893
8 0,714 0,833
9 и более по таблице VII
128
Очевидно, что коэффициент корреляции г«=0,37 недостове-
рен, так как необходимые значения га при n=10(df=8) 0,63
(при Р=0,05) или 0,77 (при Р=0,01). Впрочем, использованные
данные по лептоспирозу взяты только в качестве примера для
вычисления га. Возможно, что если бы п было больше, был бы
получен и достоверный, хотя и невысокий количественно, коэф-
фициент ранговой корреляции.
Первоначально коэффициент корреляции рангов Спирмэна
применялся в психологии, где оценки очень часто выражаются
в рангах (или баллах). В настоящее время им пользуются и в
биологии. Ранговый и простой коэффициенты корреляции до-
вольно близки друг к другу. Самое главное, что коэффициент
ранговой корреляции легко вычислять. Поэтому есть смысл
пользоваться им для первоначальной ориентировки, есть ли
связь между признаками, даже в тех случаях, когда они хорошо
определяются количественно. Для более точного установления
зависимости в дальнейшем можно провести вычисление г. Если
же оценка признаков в рангах единственно возможная, надо удо-
влетвориться вычислением га.
Корреляция и причинность. Если корреляция доказана, то
это значит, что существует сопряженность в вариации двух (или
нескольких — при более сложных корреляциях) признаков. Но
было бы неправильно делать из этого вывод о наличии причин-
ной зависимости между изучаемыми признаками. Так, при отри-
цательной корреляции между величиной удоя за лактацию
и средней жирностью молока было бы неправильно видеть при-
чину снижения жирности молока в самом факте повышения
удоев. В действительности здесь дело в сложном, характере
физиологических процессов, лежащих в основе молоко- и жиро-
образования, что приводит к сопряженной вариации обоих при-
знаков. Но обнаружение определенного рода зависимости между
удоем и процентом жира может быть полезным для понимания
соотношения этих процессов. По-видимому, молокообразование
и жирообразование — два различных процесса, протекающих
с неодинаковой скоростью. В определенных случаях возможно
отставание в процессе образования молочного жира по сравне-
нию с образованием молока, что и является причиной возникно-
вения отрицательной корреляции между количеством молока
и его жирностью. Однако соотношение этих процессов у различ-
ных коров неодинаково. В корреляционной решетке табл. 22
в верхнем правом квадрате представлены коровы, совмещающие
высокие удои (до 7500 л) с высокой жирностью молока
(до 4,4%). Очевидно, у таких коров соотношение процессов мо-
локо- и жирообразования несколько иное, чем у большинства
изученных коров, что и приводит к неполной сопряженности
вариации по молочной продуктивности и жирности молока.
Иногда корреляция между признаками может возникнуть
в силу чисто случайных причин, связанных с подбором исходного
5 П. Ф- Рокицкнй
129
материала для изучения. Известным примером такого рода
является случай установления в одном стаде крупного рогатого
скота корреляции между величиной удоя и наличием дополни-
тельных сосков, в то время как в других стадах она не была
обнаружена. Причиной корреляции оказалось то, что среди
оставляемых на племя телят часть происходила от хороших ко-
ров, имевших дополнительные соски. Поэтому при распределении
вариант в корреляционной решетке по признакам удоя и много-
сосковости получилось, что у группы коров более высокие удои
совпали с наличием дополнительных сосков, унаследованных
ими от коров-родоначальниц.
Можно* обнаружить корреляцию между признаками в силу
того, что один из взятых признаков является частью другого
признака или оба они являются частями какого-то третьего
признака. Так было бы, если бы мы стали вычислять корре-
ляцию между высотой лошадей и длиной их ног. В высоте
лошади важнейшую часть составляют размеры ее конечностей.
Таким образом, при корреляционном анализе необходимо
проводить и соответствующий биологический анализ, чтобы
установить причины той или иной связи между признаками или
явлениями. В некоторых случаях применение более сложных
методов корреляционного анализа позволяет наметить и причин-
ные зависимости, установить удельный вес отдельных факторов
в корреляционных связях между признаками.
Множественная и частная корреляция. Общеизвестно, что
в биологических явлениях обнаруживается действие многих
факторов, связи между которыми очень часто носят статистиче-
ский характер и потому могут быть изучены методами биологи-
ческой статистики. Так, например, урожай кукурузы на поле
может колебаться в зависимости от исходного материала (сорт,
линия, характер гибридности), от почвенных условий, внесенных
удобрений, влажности и температуры в период роста и развития
растений и т. д. Вариация любого признака животных также
связана с вариацией многих факторов (наследственности и внеш-
ней среды в широком смысле этого слова). Наконец, изменчи-
вость многих признаков у одних и тех же животных и растений
часто происходит сопряженно, связанно.
К числу приемов изучения связи между многими признаками
относится установление коэффициентов множественной и частной
корреляции. Под множественной корреляцией обычно понимают
зависимость изменения величины х от одновременного измене-
ния величин у, z и т. д. Однако ввиду того, что значение множе-
ственной корреляции в биологии невелико, в нашем кратком
курсе ее можно не рассматривать. Значительно более ценным
является метод частной корреляции. Допустим, что 3 изменчи-
вые величины или 3 признака х, у, г коррелируют друг с другом,
их коэффициенты простой корреляции гху, гхг и гуг. Связи между
признаками можно выразить графически. ’
130
Если существует довольно значи-
тельная корреляция между х и г и
между у и г, можно думать, что кор-
реляция между х и у создается за счет
одновременного влияния на них треть-
его фактора (признака) г. В таком
случае возникает задача изучить связь
между признаками х и у, выключив
влияние на эту связь третьего признака г, как бы элиминировав
его.
В биологии имеется достаточно много примеров такого рода.
Так, при изучении корреляции между разными промерами жи-
вотных и их живым весом можно предполагать, что зависимость
между определенными промерами создается за счет влияния
живого веса. Это обстоятельство маскирует настоящую зависи-
мость между промерами.
Во многих случаях изучение корреляции между признаками
животных затрудняется тем, что их вариация находится под
влиянием возраста. Почти невозможно подобрать группу живот-
ных одного возраста, даже если берется, казалось бы, очень
узкая возрастная группа. Поэтому часто бывает необходимо
элиминировать из корреляций между теми или иными морфоло-
гическими или биологическими показателями влияние возраста.
Для этой цели служит частный коэффициент корреляции (ко-
эффициент частной корреляции), формула которого следующая:
- ___ rxy rxz ’ ryz
*xy-z -- --------------------
(52)
Путем соответствующей перестановки букв можно получить
формулы для Гхг.у и гуг.х.
r*Z---Гху • ?zy
(52a)
f zy*x —
zy rzx * ryx
(526)
Для упрощения обозначений вместо букв х, у, z часто пишут
цифры 1, 2, 3. Тогда коэффициент частной корреляции обознача-
ется так: Г12-3-
Точка, стоящая между буквами или цифрами, обозначает в
данном случае не умножение, а выделение того третьего призна-
ка, влияние которого надо выключить из корреляционной зависи-
мости между первыми двумя. С помощью формулы (52) элимини-
руется
можно
ных и
одна из переменных изменчивых величин. Этот же метод
применить и для элиминации 2 величин при 4 перемен-
т. д. Тогда
. г12-4 г13-4 г23-4
/19.44 = .
rd—rj3.4)(l — Г3з,4)
(53)
6*
131
В качестве примера частной корреляции могут служить дан-
ные о корреляции между давлением крови (1), содержанием в
ней холестерина (2) и возрастом (3), полученные при изучении
142 женщин. Вычислялись следующие коэффициенты корре-
ляции:
г12=0,25; Г1з=0,33; г2з=0,51.
Так как высокое кровяное давление может быть связано с высо-
ким содержанием холестерина в стенках кровеносных сосудов,
целесообразно тщательно проанализировать коэффициент г12.
Но очевидно, что и давление крови, и концентрация холестерина
увеличиваются с возрастом. Поэтому возникает вопрос, создает-
ся ли корреляция между 1 и 2 за счет их общей связи с возра-
стом или же она реально существует для каждого возраста.
Эффект возраста может быть элиминирован по формуле (52).
Предоставляем каждому произвести необходимые вычисления
самостоятельно. В конечном счете Г12-з=0,12.
По табл. VII можно установить, что при п=150 (в таблице
нет строки п=142) для достоверности коэффициента корреляции
даже при уровне значимости 0,05 он должен быть не менее 0,16.
Полученный коэффициент корреляции, очевидно, недостоверен.
Следовательно, внутри отдельных возрастных групп между дав-
лением крови и содержанием холестерина корреляции нет. Это
суждение можно выразить и в несколько более осторожной
форме: взятая для изучения группа не дала возможности обна-
ружить связь между давлением крови и содержанием холесте-
рина, если такая связь и существует. Пока нет оснований отбра-
сывать нулевую гипотезу.
Применение и дальнейшее развитие корреляционного метода
в биологии. Корреляционный метод применяется очень широко
в самых различных науках, в том числе и в биологии. Зоолог
изучает многообразные связи между морфологическими призна-
ками животных, а ботаник — между различными признаками
растений. Зоотехник широко пользуется методом корреляций
для изучения связи между молочной продуктивностью и особен-
ностями экстерьера, между различными свойствами молока,
между удоями за разные лактации, между различными физиоло-
гическими признаками и скоростью роста и т. д. Немаловажное
значение имеет корреляция в генетике и селекции, где часто
используются корреляционные связи между признаками родите-
лей и потомков, матерей и дочерей. С помощью других, более
сложных методов корреляционного анализа удается выделить
фенотипические и генотипические корреляции. В рамках же
нашего курса мы даем представление лишь об элементарных
приемах корреляционного анализа.
Корреляционные плеяды. Метод корреляционных плеяд пред-
ложен П. В. Терентьевым (1928) и применен им при изучении
систематики земноводных и пресмыкающихся. Ему же принад-
132
лежит и самый термин корреляционные плеяды, под которым
понимается вся сложная сеть корреляционных связей между
многими признаками. Таким образом, метод корреляционных
плеяд представляет собой развитие корреляционного метода
в приложении к анализу связей между большим количеством
признаков. Так, если изучается одновременно 15 признаков, то
может быть получено 106 коэффициентов корреляции между
этими признаками, взятыми попарно. Так как, очевидно, значе-
ния коэффициентов корреляции могут быть различными (учиты-
ваются только достоверные коэффициенты), то возникает необ-
ходимость выявления коэффициентов на разных уровнях: от
г = 0,1 до г = 0,9. Для этого П. В. Терентьев разработал графиче-
ский метод корреляционного цилиндра, разрезаемого на различ-
ных уровнях. Хотя метод корреляционных плеяд требует доволь-
но большой вычислительной работы, он позволяет с большой
ясностью и точностью выделить наиболее существенные из
очень большого числа связей, обычно существующих в любом
изучаемом явлении. Конкретный же анализ этих связей должен
вскрыть их биологическую природу.
Ошибка разницы между средними арифметическими при на-
личии корреляции. После рассмотрения корреляционной связи
следует вновь вернуться к некоторым из разобранных в преды-
дущей главе вопросов. При сравнении совокупностей ошибка
разницы между средними арифметическими вычислялась по фор-
муле (32). При этом принималось, что между отдельными
значениями переменной величины в обеих совокупностях нет
корреляции. Однако приходится учитывать возможность неко-
торой сопряженности в их вариации, например, под влиянием
какой-то общей причины, фактора, действовавшего на отдельные
варианты обеих, совокупностей. Такие случаи возможны тогда,
когда изучаются две группы животных, живущих одновременно
и в сходных условиях внешней среды. Если доказано наличие
корреляционной связи между сравниваемыми выборочными
совокупностями 1 и 2, ошибка разницы должна вычисляться по
формуле
— 2s--s^-r12. (54)
Когда проводится попарное сравнение каких-либо показате-
лей, также необходимо проверить, нет ли между двумя сравни-
ваемыми группами корреляции, чтобы в этом случае внести необ-
ходимую поправку в расчет ошибки разницы.
При вычислениях необходимо учитывать знак коэффициента
корреляции. При положительной корреляции подкоренное выра-
жение уменьшается, а при отрицательной — увеличивается.
Возможные ошибки в применении метода корреляций. При
всем громадном значении этого метода необходимо учитывать,
что не всегда он дает точные результаты. Есть даже термин
«ложная корреляция». Он означает, что, несмотря на получение
133
достоверного коэффициента корреляции, на самом деле корре-
ляции нет. Причины ложной корреляции могут быть субъ-
ективными, зависящими от ошибок тех, кто проводит кор-
реляционный анализ, и объективными, определяемыми свой-
ствами изучаемой группы животных или растений. Оче-
видно, что, как и в других случаях статистического анализа,
должен быть исключен всякий произвол в сборе исход-
ного материала, недопустимы ошибки в проведении наблюде-
ний, измерений, взвешиваний и т. д. Значительно сложнее вопрос
об объективных причинах ошибочных результатов корреляцион-
ного анализа. Их нельзя вскрыть без тщательного разбора
исходного материала и, прежде всего, без анализа корреляцион-
ных решеток. Вот почему не следует ограничиваться лишь
вычислением коэффициентов корреляции (что легко сделать
прямым способом), а целесообразно построение корреляционных
решеток.
Одна из частых причин ложной корреляции — неоднород-
ность изучаемой совокупности, ее состав из двух или даже не-
скольких совокупностей, отличающихся, по средним арифметиче-
ским (а иногда и по средним квадратическим отклонениям). На
рис. 11 показано распределение точек (вариант) на корреляци-
онных решетках при различных значениях г. При однородности
изучаемого материала точки располагаются в овале, вытянутом
по одной из диагоналей решетки. Чем уже этот овал, тем больше
коэффициент корреляции. В случае же неоднородности материа-
ла точки располагаются неравномерно и дают два (или больше)
сгущения, соответствующие отличающимся друг от друга сово-
купностям, включенным в одну корреляционную решетку.
В результате может быть получен высокий общий коэффициент
корреляции (по всему материалу), а если разделить материал
на две совокупности, то в каждой из них корреляции может
не быть ровсе или же она окажется очень низкой. Приме-
ров неоднородности материала, включаемого в одну корреля-
ционную решетку, довольно много в литературе. Так, в одной
работе, посвященной изучению связи между плотностью всего
колоса пшеницы и плотностью его верхушки, уже по структуре
корреляционной решетки можно было сделать вывод, что в нее
включены две совокупности — плотноколосая, располагающаяся
в одном углу решетки, и неплотноколосая — в другом. По каж-
дой из них коэффициенты корреляции близки к нулю, а общий
коэффициент корреляции был равен +0,64±0,06. Значение
коэффициента корреляции может оказаться завышенным и в
тех случаях, когда он вычислен на материале, полученном
в разные годы, если только была общая тенденция изменения
обоих изучаемых признаков во времени, то есть наблюдается
возрастающий или уменьшающийся динамический ряд. То же
самое может наблюдаться и при объединении материала из
разных мест. Однако, можно освободиться от влияния третьего
134
фактора, искажающего значение коэффициента корреляции,
используя метод частной корреляции, задача которого как раз
и заключается в «очищении» простого коэффициента корреляции
от влияния других, объективно существующих факторов, одно-
временно влияющих на оба изучаемых признака.
В биологии часто прибегают к изучению корреляции между
различными относительными величинами: индексами, процент-
ными числами, а также суммарными величинами. Здесь всегда
есть опасность получения ложной или относительно неточной
оценки корреляционной зависимости, поэтому необходимо разо-
браться в существе анализируемых величин. Так, очевидно, что
если изучается корреляция между целым и частью, которая
в него входит, то возникает дополнительная положительная
корреляция. При изучении же корреляции между процентными
числами возникает отрицательная корреляция в силу того, что
сумма всех процентов должна равняться 100, а поэтому отдель-
ные части этой суммы находятся в обратной зависимости по
отношению друг к другу.
Иногда складывается такая ситуация, что при анализе одной
части материала обнаруживается корреляция между двумя при-
знаками, а в другой — нет. Тогда необходимо проверить, на-
сколько две эти части материала идентичны. Если, например,
они собраны в разные годы, то, возможно, в самом материале
произошли изменения в характере вариации — по одному при-
знаку она уменьшалась, а по другому осталась на прежнем
уровне или даже возросла. В результате может значительно
измениться и характер корреляционной связи.
По расположению вариант в корреляционной решетке мож-
но судить и о том, какова зависимость между признаками —
прямолинейная или криволинейная. В последнем случае обыч-
ный коэффициент корреляции становится неподходящим для
характеристики связи. Тогда лучше сразу прибегнуть к методу
регрессии или воспользоваться другими критериями, описывае-
мыми в специальной литературе.
ВОПРОСЫ
1. Что такое корреляция?
2. Какая разница между корреляционной и функциональной зависимостями?
3. Какая разница между положительной и отрицательной корреляциями?
4. Коэффициент корреляции как мерило сопряженности в вариации признаков.
Его определение с помощью двух нормированных отклонений.
5. В чем заключаются важнейшие свойства среднего произведения двух
нормированных отклонений?
6. Напишите общую формулу для вычисления коэффициента корреляции.
Какие изменения можно внести в ее числитель и знаменатель?
7. Напишите формулу коэффициента корреляции, в которую входили бы
только значения отклонений от средних; только одни средние показатели; толь-
ко значения вариант и их сумм.
8. В чем заключается рабочая формула коэффициента корреляции Бравэ?
В каких случаях выгоднее ее применять?
.135
9. Что такое, корреляционная, решетка? Объясните, как она строится.
Можно ли судить о характере корреляции по расположению данных в корре-
ляционной решетке?
10. Каковы возможные значения коэффициента корреляции? Какие значения
коэффициента корреляции следует считать высокими, средними и почему?
11. Всегда ли при г = 0 корреляционная связь отсутствует?
12. Чему равен коэффициент корреляции при полной корреляционной связи?
13. Чем отличается г от р?
14. Напишите обычную формулу средней ошибки коэффициента корреля-
ции. В каких случаях ее можно применять?
15. Как пользоваться таблицей VII?
16. В чем преимущество числа г перед коэффициентом корреляции г?
Можно ли переводить г в z и обратно?
17. Напишите формулу средней ошибки и значение t для z.
18. Как понимать нулевую гипотезу в применении к коэффициенту корре-
ляции, к разнице между двумя коэффициентами корреляции?
19. Как определить доверительные границы для р?
20. Что такое ранговая корреляция? Какова формула коэффициента ранго-
вой корреляции?
21. Является ли наличие корреляции доказательством причинной зависимости
между изучаемыми варьирующими признаками?
22. Что такое множественная корреляция?
23. Напишите формулу коэффициента частной корреляции и объясните ее
значение.
24. В чем сущность метода корреляционных плеяд?
25. Изменяется ли формула ошибки разницы средних арифметических при
наличии корреляции между двумя рядами распределения?
ЗАДАЧИ
94. Длины первого молярного х и второго молярного у зубов у ископае-
мого млекопитающего Phenacodus primaevus оказались следующими (в мм):
х 10,7 10,8 10,6 10,7 10,1 11,2 11,4 12,1 12,3 12,0 12,3 12,7 12,9
у 11,2 10,9 10,5 10,5 9,6 11,2 11,3 12,2 12,1 11,7 11,0 13,2 13,0
х 12,8 13,1 13,3 13,3 13,4 12,7 12,5 12,7 13,6 13,5 13,7 13,6 13,8
у 12,2 13,4 12,6 12,2 12,0 11,2 11,4 11,3 13,6 13,2 12,7 12,9 12,3
Определите коэффициент корреляции, оцените его достоверность и устано-
вите доверительные границы при Р == 0,05.
95. У окуня озера Баторино измерены длина головы х и длина грудного
плавника у:
х 66 61 67 73 51 59 48 47 58 44 41 54 52.47 51 45
у 38 31 36 43 29 33 28 25 36 26 21 30 28 27 28 26
Определите корреляцию между х и у.
96. Надо было установить, есть ли корреляция между высотой головы х
и длиной 3-го членика усика у у Drosophila funebris. Для этого с помощью
окуляр микрометра получены следующее данные по х и у (в делениях окуляр-
микрометра):
х 15 16 15 15 16 16 17 18 18 17 17 17 15 16 15 15 15 17
у 29 31 32 33 32 33 33 36 36 35 35 35 35 33 31 31 31 35
х 15 13 15 14 17 15 16 15 15 16 15- 16 15 16 18 17 14 15
. у 33 30 32 31 35 33 33 32 30 33 33 33 30 31 34 34 31 33
х 14 15 15 13 15 16 14 15 15 15 14 15 15 15 16 18 15 14
у 31 31 33 30 30 33 30 33 31 32 30.31 31 32 33 35 32 32
136
х 15 15 14 16 17 15 15 15 14 15 14 15 17 15 17 15 14 15
у 32 31 31 33 35 32 31 34 30 33 32 32 35 31 36 33 33 33
х 18 17 17 18 17 17 16 17 18 18 16 16 17 17 16 16 17 16
2/35 36 34 35 33 32 34 34 34 35 35 33 34 33 35 33 33 33
Вычислите коэффициент корреляции и определите его достоверность.
97. Между живым и убойным весом свиней на материале 533 голов был
получен г = 0,986. Каковы доверительные границы этого коэффициента корре-
ляции при вероятности 0,95?
98. Получены следующие данные о продолжительности беременности у кро-
ликов породы шиншилла при различных размерах помета (число крольчат в
помете х и длительность беременности в днях у):
х 1 8 3 5
у 33 30 31 31
х 6 5 7 8
у 32 32 31 32
х 6 8 6 5
у 31 31 32 32
7 8 4 8 3 4
31 32 31 31 32 33
10 6 7 6 7 6
31 31 30 31 31 32
8 7 6 5 9 5
31 30 32 31 31 31
4 8 8 5 7
32 31 31 31 31
5 10 7 8 8
31 30 32 32 31
3 4 7 8 9
32 32 31 31 31
6 6 5 6 6
30 31 32 32 31
6 5 6 5 4
31 31 32 30 31
5 6 2 2 4
31 31 32 33 33
Есть ли корреляция между длительностью плодоношения и размерами по-
мета?
99. Учитывали плодовитость самок серебристо-черных лисиц х в совхозе
«Белорусский» и плодовитость их дочерей у:
* 6 7 5 6 5 5 4 5 5 4 6 7 6 5 6 6 7 5 6 673674
2/4544623326697247568 10 45542
х 5 5 6 5 6 4 5 7 7 6 6 6 5 7 6 5 4 6 5 566568
2/5659364342573545 3 72 325374
х 5 6 6 5 6 6 5 5 7 6 6 5 6 6 5 7 5 5 5 445556
у 2 4 5 3 6 3 2 5 34 3 3 5 3 6 5 6 5 4 234627
х 6565656566687845677 775564
2/64,2 6412453274656345 373883
Есть ли корреляция между плодовитостью матерей и плодовитостью их
дочерей?
100. Были получены следующие данные о весе ягнят-баранчиков (одинцов)
у и весе баранов — их отцов — х (в кг).
х 76,6 72,2 67,0 66,5 63,3 65,4 63,9 63,1 63,0 62,5 62,2
у 4,56 4,79 4,49 4,32 4,59 4,32 4,67 4,29 4,57 4,20 4,12
х 61,0 60,2 60,0 59,6 59,5 58,9 58,0 57,8 57,6 57 0
у 4,13 4,70 3,80 4,23 3,76 4,08 4,61 4,37 4,30 4,0
х 56,8 55,4 55,0 53,8 53,7 52,0 51,4 51,0 50,9 48,5
у 3,82 4,12 4,19 4,16 4,09 4,12 4,02 4,31 4,06 4,03
Есть ли корреляция между весом баранчиков и весом их отцов?
101. При объединении ряда данных о корреляции между длиной крыла и
длиной хоботка у пчел г = 0,721 (п= 126 пчелам). Каковы его доверительные
границы при вероятности 99%?
102. У 100 серебристо-черных лисиц (совхоз «Белорусский») были измерены
(в см) длина туловища х и длина хвоста у:
X 70 65 66 65 71 68 64 57 66 65 67 62 67 62 63 57 64 66 69 58
у 40 40 40 40 40 42 39 38 41. 43 39 45 43 38 40 40 41 45 43 37
х 63 67 67 67 65 65 67 70 65 71*69 64 64 66 69 72 66 66 67 66
у 45 38 39 37 42 38 38 38 38 40 39 43 43 42 40 41 47 47 40 40
137
х 76 68 71 71 67 66 69 64 69 71 64 71 66 68 68 66 65 66 67 66
у 41 40 41 34 38 44 47 37 42 40 40 42 39 45 36 40 40 40 40 37
х 68 65 63 66 66 65 65 65 65 64 66 67 63 64 69 69 65 65 69 67
у 40 40 40 40 40 41 39 41 39 40 40 42 38 43 41 41 40 40 41 45
х 68 61 69 61 64 62 66 59 65 62 68 61 67 69 69 66 66 71 67 65
у 40 38 37 38 37 39 37 39 38 40 41 39 41 40 50 40 40 39 44 41
Есть ли корреляция между длиной туловища и длиной хвоста у лисиц?
Если коэффициент корреляции окажется достоверным, определите доверительные
границы для него при Р = 0,05,
103. Были получены следующие данные о весе х (в кг) и длине туловища у
(в см) 100 серебристо-черных лисиц (совхоз «Белорусский»):
х 4,7 4,6 5,2 5,1 5,3 5,3 4,6 4,8 5,8 5,7 4,5 5,7 5,0 4,8 4,7 5,2 4,6
у 70 65 69 70 66 68 65 71 69 68 57 73 65 67 71 62 69
х 5,5 5,5 4,8 4,7 6,0 5,1 5,2 4,5 5,0 5,0 4,9 5,5 5,2 5,6 5,2 5,7 5,3
у 62 63 67 64 64 66 68 69 58 63 67 74 67 67 70 65 71
х 5,4 5,3 4,6 5,6 5,1 4,9 5,2 5,3 5 0 5,3 5,6 5,0 5,1 5,5 5,6 5,2 5,0
у 63 64 64 66 63 69 62 72 66 66 67 67 66 63 67 62 71
х 5,5 5,6 5,0 6,7 4,7 5,3 5,0 5,1 5,0 5,1 4,8 5,0 6,0 5,5 4,6 4,5 4,5
у 67 66 66 69 64 69 70 62 68 68 72 68 67 66 69 65 65
х 5,4 5,0 4,9 5,0 5,7 5,9 5,6 5,1 5,1 4,6 4,9 6,2 5,6 5,2 5,1 4,5
у 65 65 64 66 66 67 62 63 64 69 69 68 65 69 67 68
х 4,8 5,5 6,0 5,3 4,8 5,3 5,1 5,4 4,7 5,0 5,9 5,0 5,2 5,6 5,2 5,1
у 61 64 62 66 59 65 62 68 61 67 69 69 66 66 67 70
Есть ли корреляция между весом и длиной туловища у лисиц?
104. Были получены следующие данные о весе х (в г) левой камеры сердца
и длине ядер у (в р.) в мышцах сердца:
х 207 221 256 262 273 289 291 292 304 328 372 397 460 632
у 16,6 18,0 15,9 20,7 19,4 19,8 11,7 21,0 23,0 13,6 19,6 22,9 19,4 28,4
Ввиду резко асимметричного распределения вариант по ряду х примените
для установления связи коэффициент ранговой корреляции.
105. Была определена корреляция между длиной хвоста и длиной всего те-
ла у 2 видов змей Lampropeltls polyzona (и — 19, г = 0,988) и L. ellapsoides
(и = 25, г — 0,899). Переведите г в z и определите достоверность разницы меж-
ду ними.
106. В двух группах свиней изучали корреляцию между привесом и коли-
чеством использованного корма. В первой нз них (п = 5) был получен г = 0,87,
во второй (п = 12) — г —0,56. Различаются ли эти коэффициенты корреляции?
Можно ли проводить сравнение г без перевода их в г?
107. В двух выборках изучали корреляцию между одними и теми же вели-
чинами х и у. Были получены коэффициенты корреляции гх = 0,85 (лА = 20) и
Г2 = 0,70 (л2 = 30). Достоверно ли различие между ними? Можно ли анализи-
ровать различие между i\ и г2 непосредственно или надо переводить г в г?
108. На 12 экземплярах солонгая (Mustela altaica) были получены следую-
щие данные о длине тела х (в мм), длине хвоста у (в мм) и весе г (в г):
х 172 175 163 165 161 174 159 154 163 172 164 172
у 81 90 74 78 70 86 80 70 79 81 77 81
z 83 110 72 84 86 130 116 80 122 83 94 83
138
Определите путем вычисления коэффициента ранговой корреляции, есть ли
связь между длиной тела и длиной хвоста и длиной тела и весом солонгаев.
Оцените степень достоверности полученных коэффициентов ранговой корреляции.
109. Были получены следующие данные о весе х (в кг) и размерах шкур-
ки — длина у и ширина z (в см) — бобров, добытых в октябре — декабре:
Самки х 8,90 13,30 14,35 19,00 29,6
у 76 92 85 104 105
z 37 49 48 54 44
Самцы х 5,40 6.45 7 00 11,10 12,0 12,05
У 69 71 83 85 84 83
z 35 35 42 42 42 44
х 14,65 17,15 17,25 19,05 19,55 29,9
у 87 93 97 92 92 102
z 44 49 46 48 50 50
Есть ли корреляция между этими признаками?
ПО. У 25 экземпляров днепровского ерша были изучены: длина’ тела х
(в см), вес у (в г) и вес гонад z (в г):
х 10,0 10,0 10,4 10,4 10,5 1Q5 10,6 10,7 10,7 10,7 10,8 10,8 10,9
у 19,0 20,0 28,0 35 27 26 28 28 30 27 29 27 31
z 2,2 2,1 3,1 4,4 3,5 2,9 3,8 3,2 2,1 2,6 3,4 2,8 3,2
х 11,0 11,0 11,0 11,0 11,1 11,2 11,3 11,3 11,5 12,5 12,6 13,6
у 27 31 30 28 32 45 31 35 37 49 54 56
z 3,2 3,3 4,0 34 2,6 3,2 2,8 4,6 3,8 6,7 7,0 8,7
Определите коэффициенты корреляции между этими признаками и значения
средних арифметических с их ошибками.
111. У 16 экземпляров щук были измерены длина тела х (в см), вес у (в г)
и вес икры z (в г):
х 33,4 31,8 38,0 33,4 42,5 90,0 38,0 67,0
у 456 375 484 456 788 7900 9581 3550
z 32 34 24 19 , 126 744 42 579
х 35,4 42,8 36,0 50,5 53,4 62,0 64,0 71,0
у 478 783 365 1300 1998 2320 3650 3450
z 49 138 22 ПО 287 149 461 202
Определите коэффициенты корреляции между всеми тремя признаками (об-
щие и частные).
112. При изучении максимальной длины (1), ширины (2) и высоты (3) коро-
нок последних верхних молярных зубов у 28 экземпляров ископаемого млеко-
питающего Acropithecus rigidus были получены следующие коэффициенты кор-
реляции: г12 = 0,355; г13 = 0,795 и г2з = — 0,046. Определите коэффициенты
частной корреляции г12.3, г13.2 и г23<1. Проверьте степень достоверности всех
этих коэффициентов корреляции.
113. По данным А. К. Митропольского для 500 человек в возрасте от 21
до 28 лет были получены следующие коэффициенты корреляции между ростом (1),
окружностью груди (2) и весом (3): г12 = 0,395; г13 = 0,692 и г2з = 0,646.
Определите частные коэффициенты корреляции г12.3 и r23il.
114. На однополых однояйцовых двойнях (32 пары) было проведено изуче-
ние связи между заболеванием туберкулезом х, наследственностью у и влияни-
ем внешней среды z. Коэффициенты корреляции были следующими: гху = 0,47;
rxz = 0,45; гуг = 0,07. Значение наследственного предрасположения к туберку-
лезу могло быть недостаточно выявлено в силу наличия влияния на туберкулез
.139
внешних условий. Проверьте это путем вычисления коэффициента частной кор-
реляции Установите, насколько он достоверен.
115. Коровы холмогорские помеси 2-го поколения по высоте в холке х,
глубине груди у и ширине в моклоках z были следующими:
X 125 126 133 130 126 132 130 130 122 133 131
У 69 69 70 71 68 73 72 72 66 76 70
Z 56 52 49 53 42 56 53 53 51 57 ;5о
X 131 138 132 127 125 122 123 128 126 126 124
У 57 73 71 71 68 67' 69 70 70 65 68
2 55. 50 54 53 50 50 49 52 52 51 52
X 13'1 123 131 132 129 133 124 124 126 123
У 69 70 70 72 67 70 60 68 64 [65
г 54 51 54 52 54 53 46 55 50 47
Вычислите r^y, rxzt ryzt гу2-х. Определите также х, z и s% для всех"; трех
признаков.
-116. В опытах по кормлению 30 крыс в течение 28 дней были получены
следующие данные (в г) (начальный вес хХ| количество скормленной пищи х2,
конечный вес у):
Xi 25,8 15,8 18,1 13,3 20,1 10,1 17,1 21,0 23,7 11,2
х2 98 116 104 99 153 98 103 112 133 80
у 14,8 9,7 11,3 26,0 44,7 21,0 25,2 13,7 38,5 5,8
хг 10,2 16,4 15,9 8,0 26,0 2,4 7,5' 15.9 10,7 6,4
х2 87 138 96 102 155 107 142 110 80 83
у 17,7 40,0 17,1 3,0 37,3 9,7 36,3 21,2 4,5 4,0
Xi 16,9 12,2 13,4 15,0 13,8 17,8 20,4 7,9 16,0 12,8
х2 105 96 90 24 153 82 88 66 118 135
у 20,2 20,5 18,9 26,4 25,4 9,4 21,2 9,2 41,1 31,3
Вычислите коэффициенты корреляции: 1) между хх и х^ 2) между Xi и у;
3) между х2 и у. Определите коэффициент частной корреляции г23.ь
117. В 36 анализах крови определяли: х—число эритроцитов (в миллионах),
у — содержание гемоглобина (в %) и г — оседание крови за 24 часа (в мм):
X 0,80 0,71 2,63 3,19 2,80 3,14 3,21 3,28 3,63 3,30 4,10 3,29
У 22 45 61 66 72 83 73 82 78 82 81 82
Z 8 18 24 26 28 29 30 30 30 30 32 32
X 3,46 3,32 з,п 3,28 3,66 3,90 4,33 3,80 3,82 3,81 4,20 4,47
У 77 80 82 79 84 75 82 79 87 87 87 90
Z 32 33 33 34 34 34 34 35 36 37 37 38
X 3,71 4,22 3,90 4,36 1,30 2,50 2,80 3,10 2,87 3,68 3,59 3,40
У 97 96 92 94 27 50 63 71 70 72 76 71
Z 40 40 40 44 12 20 26 28 29 30 30 30
Определите коэффициент корреляции гХу, тх2 и ту2 и коэффициенты частной
корреляции: гХ2.^ гху.г и гу2.х.
ГЛАВА б
ИЗМЕРЕНИЕ СВЯЗИ. РЕГРЕССИЯ
Многообразие методов изучения связи. Известно, что раз-
личные зависимости широко распространены как в органиче-
ской, так и в неорганической природе. Их изучение проводилось
уже давно и привело к разработке большого количества мето-
дов их математической характеристики.
Первым из них являлся р'азобранный в предыдущей главе
корреляционный метод, или метод корреляций.
Понятие о регрессии. Коэффициент корреляции указывает
лишь на степень связи в вариации двух переменных величин,
или, как иногда говорят, на меру тесноты этой связи, но не дает
возможности судить о том, как количественно меняется одна
величина по мере изменения другой. На этот последний вопрос
позволяет ответить другой метод определения связи между
варьирующими признаками, носящий название метода ре-
грессии.
В современной статистике, в том числе биологической, коэф-
фициентами корреляции пользуются реже, чем прежде. Метод
же регрессии приобретает все большее значение. Анализ взаи-
моотношения двух изменчивых величин с помощью метода
регрессии часто может дать очень ценные результаты, особенно
в практическом отношении. В некоторых случаях для освещения
различных сторон вопроса надо применять и корреляционный, и
регрессионный методы анализа.
При простой корреляции изучается зависимость между из-
менчивостью двух признаков х и у. С помощью регрессии ста-
вится дополнительно задача установить, как количественно ме-
няется одна величина при изменении другой на единицу. Так
как изменчивых величин две, то регрессия, очевидно, может быть
двусторонней: определение изменения у по изменению х и опре-
деление изменения х по изменению у. В этом заключается глав-
ное отличие метода регрессии от метода корреляции.*_
* О случае односторонней регрессии речь будет идти ниже.
141
Регрессия может быть выражена несколькими способами:
путем построения так называемых эмпирических линий регрес-
сии, путем составления уравнений регрессии и построения теоре-
тических линий регрессии и, наконец, с помощью вычисления
коэффициенту регрессии. Первые два способа позволяют выра-
зить регрессию графически.
Эмпирические линии регрессии. Для построения эмпириче-
ских линий регрессии можно воспользоваться обычной корреля-
ционной решеткой. Но в ней следует заменить границы классов
средними значениями классов. Общая схема решетки с теми
данными, которые нужны для построения эмпирических линий
регрессии, представлена в табл. 26.
Таблица 26
Схема корреляционной решетки для построения эмпирических линий
регрессии
В столбце справа выписаны средние значения признака х для
.классов ряда у, т. е. регрессия х по у. Шести значениям у (от г/i
до z/e) соответствуют шесть значений х (от xt до хв)- Важно, что
значения у являются в данном случае строго размеренными, т. е.
выраженными в классах ряда у, значения же х являются ,конк-
142
ретными средними по признаку х тех вариант, которые располо-
жены в каждой горизонтальной строке. Именно поэтому они обо-
значены знаками xlt и т. д. Внизу, в горизонтальной строке,
даны соответствующие значения у для классов ряда х, т. е.
регрессия у по х. В этом случае семи значениям х (от Xi до х7)
соответствуют семь значений у (от /л до у7). Таким образом, при
регрессии у по х точными значениями классов будут значения
Xi, х2, х3, .... х7; значения же у — это средние значения по дан-
ному признаку группы вариант, расположенных в вертикальных
столбцах.
В качестве конкретного примера в табл. 27 приведена не-
сколько упрощенная решетка живого веса х и обхвата груди у,
составленная по данным о 300 коровах симментальской породы.
Таблица 27
Корреляционная решетка живого веса х (в кг)
и обхвата груди у (в см) 300 коров симментальской породы
для построения эмпирических линий регрессии
Значения цифр в "графах х/у и соответственно у/х получаются
путем обработки данных каждой горизонтальной строки или вер-
тикального столбца как небольшого вариационного ряда. Так,
например, во второй снизу строке табл. 27 (по горизонтали) ука-
заны 4 варианты: две из них имеют веса по 225 кг, одна —
275 кг и одна — 325 кг. Средняя по 4 вариантам 263 кг. В ниж-
ней строке только одна варианта, вес которой 225 кг. Поэтому в
графе х/у записана цифра 225 кг.
143
225 275 325 375 425475 525575 X
Рис. 12. Эмпирические линии регрессии у по
х и х по у (х — живой вес (в кг), у — об-
хват груди (в см) коров симментальской
породы).
В третьей строке снизу
все особи, входящие по
обхвату груди в один
класс «155 см», составля-
ют по весу вариационный
ряд, охватывающий клас-
сы от 225 до 425 кг. В си-
лу полной симметрично-
сти ряда среднюю можно
определить без подсче-
та — на глаз. Она равна
325 кг. Для вариант, рас-
положенных в вертикаль-
ных столбцах, значения
классов надо брать из
графы у. Так, например,
в первом вертикальном
столбце 4 варианты име-
ют среднюю 145 см.
В предпоследнем вертикальном столбце приведены 9 вариант,
с обхватом груди 175 см и 15 — с обхватом груди 185 см. Сред-
няя арифметическая из 24 вариант будет равна
175 • 9 + 185 15
24
= 181 см.
Корреляция вычислена на основе изучения 300 особей (эта
цифра проставлена в пересечении граф fv и f* и представляет
собой Sf«=Sfv). Однако в регрессии х по у число пар значений
х и у равно только 7, т. е. п=7, а в регрессии у по х п=8. Это
объясняется тем, что варианты, находящиеся в каждом классе,
объединены в единые группы, и в дальнейшем все операции
проводятся со средними этих групп.
На основе показателей ~х/у и у/х табл. 27 можно построить на
одном графике обе линии регрессии, как это сделано на рис. 12. На
горизонтальной оси х отмечены средние значения классов х^На
вертикальной оси «/ — средние значения классов у. Значения X по
классам у нанесены темными кружками. Соединяющая их линия
представляет собой линию регрессии х по у. Таким же образом
построена и линия регрессии у по х (значения у нанесены светлы-
ми кружками).
Обозначать линии регрессии достаточно только символами х/у
и у/х, а не х/у и у/х, так как в некоторых случаях это будут не
средние горизонтальных строчек и вертикальных столбцов, а конк-
ретные значения х и у.
Дело в том, что методом регрессии можно пользоваться и
в тех случаях, когда данные Сводятся лишь к немногим единич-
ным наблюдениям величин у и соответствующих им значений х.
144
4
3-
О 5 10 15 20 25 30 X
Рис. 13. Корреляционное поле с нанесен-
ными на него значениями температур
внешней среды х (в град) и количества
поглощенного кислорода у (в мл/г веса)
у белых крыс.
Тогда на корреляционное по-
ле можно нанести эмпири-
ческие точки значений пар.х
и у и по расположению точек
судить о связи между х и у.
На рис. 13 представлено
корреляционное поле, на ко-
тором нанесены значения
Температуры внешней среды
и количества поглощенного
кислорода белыми крысами.
Точек всего 7, так что их
можно непосредственно со-
единить линией, как это и
сделано на рисунке, и полу-
чить эмпирическую линию
регрессии. Однако легко
видеть, что если бы точек было больше и, в частности, по
нескольку точек с близкими значениями х и у, то непосредствен-
но по точкам провести эмпирическую линию было бы уже нель-
зя. Пришлось бы сначала объединить их в группы, подобно тому,
как это сделано в табл. 27.
Выравнивание эмпирических линий регрессии. Уже один вид
эмпирической линии регрессии может подсказать, какая форма
связи имеет место в данном конкретном случае (прямолинейная,
параболическая или какая-либо иная). Дальнейшие способы
анализа регрессии зависят от той задачи, которую намечает ис-
следователь. Если предполагается установить общую законо-
мерность связи между двумя величинами, тогда надо будет по-
пытаться найти тип связи и в дальнейшем с помощью специаль-
ных методов составить соответствующие уравнения. Но может •
быть и более элементарная задача — в какой-то степени элими-
нировать случайные колебания эмпирической линии регрессии и
тем самым получить возможность более точно судить о том, как
меняется одна величина (у) вслед за изменением другой (х).
В таких случаях прибегают к приему, носящему название
выравнивания. Имеется в виду такое выравнивание, которое
достигается с помощью простейших приемов или даже на глаз.
Хорошим и технически очень легким приемом является ис-
пользование так называемой скользящей средней. Фактически
полученные значения у,., расположенные по фиксированным зна-
чениям х,, заменяют новыми, полученными путем сложения 3
или 5 рядом расположенных значений yi и деления суммы на 3
или на 5.
Для получения последующей величины у берут 3 или 5 зна-
чений уи сдвинутых на единицу. Это значит:
„ Vi + lfa + Уз „пи ,. _ «/1 + у»+уэ + у< + у5 .
У1 = ----з---- или уг------------§ ,
145
у* = У» + У» + У« или yt ^.У^ + Уз + Уз + ^ + У». ;
уъ = Уз + у^ + у» или у* = у» + у« + у»+.у» + Уг. и т. д.
Метод скользящей средней в обеих вариантах показан в
табл. 28, а графическое изображение линий регрессии — на
рис. 14.
Таблица 28
Средний вес яиц у в 15 поколениях кур, х, у' — скользящие средние
по 3 значениям у, у” — то же по 5 значениям у
Xi Vi у' У" Xi Vi У' у"
1 55,4 — — 9 58,0 57,7 57,4
2 54,0 54,1 — 10 59,2 58,9 58,4
3 53,0 53,4 54,3 11 59,6 59,3 59,0
4 54,1 54,1 53,9 12 59,2 59,2 59,2
5 55,1 54,1 53.9 13 58,8 59,0 59,2
6 53.2 54,2 54,5 14 59,0 59,0 —
7 54,3 54,5 55,3 15 59,3 —
8 56.0 56,3 56,1
При подсчете скользящих средних по 3 значениям теряются
2 точки на кривой — по одной справа и слева; при подсчете по
5 значениям теряются 4 точки — по две справа и слева. Поэтому
выгоднее всего применение этого метода при большом числе то-
чек. Впрочем, исчезающие точки, можно все же поставить путем
Рис. 14. Эмпирическая линия регрессии, показывающая изменение веса
куриных яиц (в г) за 15 поколений разведения линии. Штриховая
линия—выравненная методом скользящей средней по Зу<.
146
интерполяции от соседних точек или просто продолжением ли-
ний впррво и влево. Ряд, составленный из у”, еще более вырав-
нен, нежели ряд, составленный из у' (на рис. 14 он не нанесен,
чтобы не загромождать график).
Уравнение регрессии. Эмпирическая линия регрессии обычней
представляет собой более или менее ломаную линию. Она до-
статочно наглядно отображает характер связи между двумя
изменчивыми величинами х и у, но не дает возможности точно
определить любое значение х по заданному значению у или, на-
оборот, значение у по заданному значению х. Для этой цели мо-
гут служить уравнения регрессии.
Уравнение прямолинейной регрессии в общем виде можно
записать так:
у^у^Ь^—х). (55)
Оно выражает определенную зависимость, а именно: что
вслед за отклонением х от средней по ряду х происходит и от-
клонение у от средней по ряду у, причем показатель b является
коэффициентом пропорциональности, т. е. величиной, указываю-
щей на количественную связь в изменении у при изменении х.
При переносе у в правую часть равенства получим
У,- = ~У + b (xi —"*) (55а)
Если х приравнять нулю, то у будет первоначальным значе-
нием у, с которого надо начинать построение линии регрессии
при х — 0. Его можно обозначить через а. Уравнение регрессии
примет вид обычного уравнения прямой линии, известного из ана-
литической геометрии:
у = а + Ьх. (56)
Здесь у и х представляют собой коррелирующие в своей вариа-
ции величины, а — первоначальное значение у при х=0, Ь — ко-
эффициент пропорциональности, который показывает степень
зависимости х от у. Это уравнение предусматривает прямоли-
нейную зависимость между х и у, т. е. прямолинейную регрес-
сию. При наличии криволинейной зависимости применяются’ бо-
лее сложные уравнения.
Для того чтобы определить значения а и & в уравнении
у=а+Ьх, надо решить систему двух уравнений:
1. па + (2 xt) Ь = 2 уц
2. (2х,)а + (2х?)& = 2ед. (57)
Составление этих уравнений основано на так называемом ме-
тоде наименьших квадратов, т. е. с помощью их вычисляются та-
кие параметры для уравнений, при которых сумма квадратов
отклонений эмпирических значений у (ут теоретически вычислен-
ных окажется наименьшей.
147
Фактические данные о конкретных парах значений и yt
позволяют определить необходимые для решения системы урав-
няй величины: п; и
Уравнения регрессии можно рассматривать двояко: а) как
уравнения для оценки индивидуальных значений у по связан-
ным с ними значениям х (либо, наоборот, индивидуальных х по
связанным с ними у), б) как уравнения для оценки средней ве-
личины тех значений у, которые связаны с данными частными
значениями х (или, наоборот, средних для значений х, связанных
с данными частными значениями у).
Для иллюстрации первого случая можно использовать циф-
ровые данные о связи температуры внешней среды с количест-
вом поглощенного кислорода у крыс, представленные графиче-
ски на рис. 13. Необходимые величины для составления уравне-
ния регрессии у по х приведены в табл. 29. После подстановки
итоговых значений этой таблицы в уравнения 1 и 2(57) они при-
обретут следующий вид:
I. 7 а+105 b = 16,2;
2. 105 а+2275 Ь = 181.
Для решения их обычными алгебраическими методами надо
умножить коэффициенты уравнения 1 на 15 и вычесть уравнение
1 из уравнения 2:
105а + 22756 = 181
~ 105а + 15756 = 243
7006 = —62
Отсюда 6 = — 0,089 (^ — 0,09).
Таблица 29
Связь между температурой внешней среды х
(в град) и количеством поглощенного кислорода у
(в мл/г веса) у крыс и определение величин
для составления уравнения регрессии у по х
Xi У1 х?
0 3,8 oz 0
5 3,4 25 17
10 2,6 100 26
15 2,0 225 30
20 1,7 400 34
25 1,4 625 35
30 1,3 900 . 39
2х/ = 105 2У/=16,2 2xf =2275
х = 15 !/ = 2,3 л = 7 -
148
После подстановки значения Ь в уравнение 1 получим зна-
чение а:
7а^16,2+9,35 =25,55;
__ а=3,65.
В окончательном виде уравнение регрессии будет сле-
дующим:
у=3,65- 0,09 х.
Если подставить в уравнение регрессии различные значения
температур внешней среды, можно получить соответствующие
этим температурам количества поглощенного кислорода, как
это показано в графе 3, помещенной ниже табл. 33. По некоторым
температурам эмпирические и теоретические значения количе-
ства поглощенного кислорода довольно сильно отличаются друг
от друга.
Второй случай — составление уравнений регрессии для связи
средних значений одного признака с определенными значениями
второго признака — может быть показан на примере данных
табл.-27 о связи живого веса и обхвата груди у коров. Исполь-
зуем их для вычисления величин, нужных для определения ре-
грессии у по х (табл. 30).
Таблица 30
Данные о связи между живым весом х (в кг) и обхватом груди у (в см)
у коров и определение величин для составления регрессии у по х
*1 У1
225 145 50 625 32625
275 156 75625 42900
325 160 105625 52000
375 166 140 625 62 250
425 170 180 625 72 250
475 175 225625 83125
525 182 275625 95 550
575 182 330625 104 650
Sxt = 3200 lyi = 1336 = 1 385 000 1Х(У = 545 350
х^400; 167.
Первая графа таблицы — xt — среднее значение классов по
ряду х, вторая графа — yt — соответствующие каждому среднему
значению х частные средние арифметические у по ряду у. Третья
и четвертая графы получаются из первых двух. Надо иметь в ви-
149
ду, что п в данном случае не общее количество изученных живот-
ных, а число пар коррелированных значений xt и yt, т. е. п — 8.
После подстановки итоговых значений табл. 30 в уравнения
1 и 2(57) они приобретут следующий вид:
1. 8а + 32006 = 1338; .
2. 3200а 4- 1 385 0006 = 545 350.
Умножаем уравнение 1 на 400 и вычитаем его из уравнения 2:
_ 3200а + 1 385 0006 = 545 350
3200а + 1 280 0006 = 534 400
1050006= 10950
Отсюда 6 = 0,104.
Можно удовлетвориться степенью точности до второго знака
после запятой, т. е. принять, что 6=0,10. -
Путем подстановки значения 6 в уравнение 1 получим зна-
чение а:
8а= 1336 - 0,10-3200;
8а = 1016;
а=127.
Таким образом, в окончательном виде уравнение регрессии
будет следующим:
у= 127+0,10 х.
Подставляя в уравнение регрессии различные значения Xt —
225, 275, 325 и т. д., получим теоретические значения обхвата
груди, соответствующие данным значениям живого веса. Так,
для х, = 200 кг t/i будет равно 147 см; для %i = 500 кг у{=177 см
и т. д.
у Теоретическая линия per-
Рис, 15, Теоретическая линия регрес-
сии у по х\ у — обхват груди коров
(в см), х — живой вес (в кг). На гра-
4 фике нанесены также значения а(а=
= 127 см) и 506(506=5 см, или 6=
=0,1 см). Кружками обозначены эмпи-
рические значения у.
рессии. зная коэсрфиценты а
и Ь уравнения регрессии, мож-
но построить теоретическую ли-
нию регрессий. Для данных о
живом весе и обхвате груди ко-
ров она представлена на
рис. 15.
Величина а отсекает на оси
у от нуля тот отрезок, с кото-
рого начинается линия регрес-
сии. Величина же b определяет
угол подъема линии регрессии
над горизонталью. Это рас-
стояние по оси у между двумя
соседними теоретическими точ-
ками, т. е. увеличение у при
переходе от одного значения х
150
к другому. При увеличении веса коровы на 50 кг обхват груди
увеличивается на 5 см, что и показано на рисунке. Для приведе-
ния теоретической линии регрессии в сущности достаточно опре-
делить положение только двух точек, взяв любые два значения
для х (желательно не очень близкие друг к другу) и вычислив
соответствующие им значения у. Так, если для х мы возьмем
значения 300 кг и 500 кг, то у соответственно будут равны 157 и
177 см. На рис. 15 они отмечены крестиками. Кружочками обо-
значены эмпирические значения yt. При соединении их и получа-
ется эмпирическая линия регрессии. Очевидно, что разброс эмпи-
рических точек вокруг теоретической линии регрессии очень не-
большой.
Если бы мы нанесли на рис. 15 также теоретическую линию
регрессии х по у, то увидели бы, что две теоретические линии
пересекаются в точке, соответствующей средним значениям обо-
их признаков. При отсутствии корреляции теоретические линии
регрессии пересекутся под прямым углом друг к другу, а при
полной корреляции они полностью совпадут. Чем меньше угол
между линиями регрессии, тем выше корреляция между призна-
ками X и у.
Односторонняя регрессия. При определении регрессии"указы-
валось, что она является двусторонней, т. е. что можно рассмат-
ривать изменение х по у и изменение у по х. В разобранном вы-
ше примере рассматривалась регрессия обхвата груди по живо-
му весу коров, но можно было проанализировать и обратную
регрессию — живого веса по обхвату груди, так как оба призна-
ка обладают случайной вариацией.
Однако в биологических исследованиях возможны случаи,
когда из двух изучаемых признаков только один свободно варь-
ирует, значения же второго признака являются строго фиксиро-
ванными. Так, при изучении колебаний численности лесной мыши
у по годам х первый признак у может варьировать, второй же
признак х такой свободной вариацией не обладает, ибо годы точ-
но установлены. Поэтому можно ограничиться изучением регрес-
сии только у по х, а не х по у.
Коэффициент регрессии. Значительно легче составить уравне-
ние регрессии, если известно значение коэффициента Ь. Дело в
том, что b представляет собой не что иное, как коэффициент
регрессии, чаще всего обозначаемый R. Коэффициент регрессии
может использоваться и самостоятельно как количественная
мера регрессии. В силу двусторонности регрессии коэффициен-
тов может быть два: Rx/y и Ry;x- Обозначают их и так: Rx,y и
Ry.x. Для их вычисления можно применить следующие формулы:
Rxi» = r^ (58)
и
Ryix = r%-. (58а)
151
Сигмы можно заменить квадратными корнями из квадратов
отклонений (п — 1 взаимно сокращаются). Тогда
(«»
и
(59а)
Необходимо помнить, что в данном случае сигмы должны быть
выражены в их абсолютных значениях, т. е. вычислены с учетом
величин классовых промежутков. Эту оговорку приходится делать
потому, что при вычислении коэффициента корреляции, как ука-
зывалось выше, можно было пользоваться условными сигмами,
т. е. их значениями, не умноженными на величину классового
промежутка.
Таким образом, коэффициент регрессии может быть вычислен,
если известны сигмы обоих вариационных рядов по признакам х
и у и коэффициент корреляции между ними. Коэффициент рег-
рессии прямо пропорционален коэффициенту корреляции, однако
равны они только в том случае, если отношение — = 1, т. е.
когда сигмы обоих рядов одинаковы.
Коэффициент корреляции между живым весом поросят у и их
возрастом х равен 0,988; сту = 3,69; ах = 2,58. Тогда
Rx/9 = 0,988- =1,41;
Rv/X = 0,988 - jg = 0,69.
Значение R (= b) может быть вычислено и в том случае, если
нет готовых значений г ист, — с помощью средних отклонений и
средних квадратов отклонений от средней. Подстановка их вместо
ст и г в формулу для R дает возможность получить следующие
рабочие формулы для b(= R):
а) выраженные в отклонениях от средних арифметических:
OylX - > S (Xi — х)2 h Sfo—х)(уг —у) . x/y 2(У1-уГ ’ (60) (60а)
б) выраженные в конкретных значениях xt и yt: t
Ь,“~ ’ 1 п (61)
152
v,„ ... 2 XlZyi
<«">
Используем для вычисления b по формулам (60) и (60а) дан-
ные приведенной выше табл. 29. При этом понадобится подсоб-
ная табл. 31. В данном случае коэффициенты регрессии & (или/?)
равняются:
=-тбг = - °’089 ~ - о-09’
Ьх/У = = -10>67-
Таблица 31
Данные для вычисления b (R)
изменения количества поглощенного кислорода у крыс
в связи с изменением температуры внешней среды
Xi У1 X/— X (*; — *)2 У1 — У (У1— у)2 X + 1 i SJ X
0 3,8 —15 225 1Л 2,25 —22,5
5 3,4 —10 100 1,1 . 1,21 —11,0
10 2,6 -5 25 0,3 0,09 -1.5
Д5 2,0 0 0 —0,3 0,0 0
20 1,7 5 25 -0,6 0,36 -3,0
25 1,4 10 100 —0,9 0,81 —9,0
39 1,3 15 225 —1.0 1,00 —15,0
ZxL = 105 х = 15 2уг = 16,2 У = 2,3 S = 700 2=5,81 2 = — 62,0
Это значит, что с увеличением температуры на Г количество
поглощенного кислорода уменьшается на 0,09 мл/г веса. При
расчете же температуры по количеству поглощенного кислорода
наблюдается такая зависимость: увеличение поглощенного, кис-
лорода на 1 мл/г веса соответствует снижению температуры на
10,67°.
Так как х и у известны, то легко составить и уравнения рег-
рессии, для чего надо определить значение а по частной формуле
у = а + Ьх. Откуда а — у — 6хГ(В данном случае речь идет об ог)
Подставив в эту формулу имеющиеся данные, получим
а = 2,3—(—0,09) -15=2,3+1,35=3,65.
В окончательном виде получается уравнение
у=3,65 -0,09 х.
153
Таблица 32
Связь длины туловища * (в см) и веса тела у (в кг) у 20 взрослых людей
и закодированные данные для вычисления коэффициента регрессии R (=&)
XI У1 xf У’ х'у' (*')а
165 56 5 6 30 25
176 75 16 25 400 256
175 70 15 ’ 20 300 225
168 ' 61 8 11 88 64
167 61 7 11 77 49
172 63 12 13 156 144
175 72 15 22 330 225
180 80 20 30 600 400
179 76 19 26 494 361
173 68 13 18 234 169
166 57 6 7 42 36
178 76 18 26 468 324
169 60 9 10 90 81
169 64 9 14 126 81
170 63 10 13 130 100
176 71 16 21 336 256
180 78 20 28 560 400
169 62 9 12 108 81
177 75 17 25 425 289
176 71 16 21 336 256
• 2 = 260 7=13,0 2 = 359 ' 7= 17,95 2 = 5330 2 = 3822
Для второго уравнения надо будет вычислить а, пользуясь зна-
чением bx/у (а = х — by):
а = 15-(-10,67) •2,3=15+24,5=39,5.
Уравнение будет следующим:
х=39,5-10,67 у.
Применение формул (61) и (61 а) можно показать на итого-
вых данных табл. 29. Для лучшего усвоения метода возьмем при-
мер несколько более сложный, но типичный для случаев опреде-
ления регресии непосредственно по ряду коррелирующих значе-
ний х и у. У 20 взрослых людей изучали рост (длину туловища)
х (в см) и вес тела у (в кг). Так как числа отдельных измерений
довольно большие, для облегчения вычислений можно прибег-
154
нуть к приему, носящему название кодирования (о нем говори-
лось на стр. 45—46). Для этого уменьшим все значения х< на
160, а значения «/< на 50. Закодированные числа xf и у' записаны
в графах 3 и 4 табл. 32. С ними, очевидно, будет легче получить
данные последних двух граф таблицы, нужные для вычисления
коэффициента регрессии по формуле (61). Тогда
5330 — 260'359
д ___ 20 663 । г л
Ьу>Х ~ 3822“ 442 - 1’50-
20
Закодированные средние х' = 13 и у' = 17,95. Следовательно,
истинные средние равны:
х = 160 + 13 = 173 см; у = 50 + 17,95 = 67,35 кг.
Уравнение регрессии можно записать по общей формуле
(55а):
«/ = 67,95+1,50 (х—173).
Достоверность линии регрессии и коэффициента регрессии.
Подобно коэффициенту корреляции и ряду других статистиче-
ских показателей, коэффициент регрессии всегда определяется на
основе выборочной совокупности. Значит, он является выбороч-
ным показателем, само же конкретное уравнение регрессии так-
же может быть названо выборочным. Уравнение истинной линии
регрессии будет выглядеть следующим образом: «/ = а + 0х.
Параметры а и b выборочного уравнения регрессии служат
для оценки истинных значений а и 0, т. е. их значений в гене-
ральной совокупности.
Нулевой гипотезой является отсутствие связи, т. е. признание
того, что коэффициент регрессии не отличается от нуля. Для того
чтобы иметь право отбросить нулевую гипотезу, необходимо уста-
новить достаточную достоверность Ь, что может быть сделано
путем сопоставления b с его ошибкой sb (t = —У При достовер-
\ /
ности b можно по величине ошибки sb оценить и степень близости
Ь к 0.
Поскольку в определении линии регрессии участвуют два па-
раметра а и Ь, следует отдельно рассмотреть, как могут они
варьировать в выборочных совокупностях, взятых из одной и той
же генеральной совокупности.
Теоретическая линия регрессии обычно расположена под боль-
шим или меньшим углом по отношению к оси абсцисс. Этот
угол определяется величиной Ь. В геометрическом смысле b есть
тангенс угла между линией регрессии и осью абсцисс (или орди-
нат— если рассматривать вторую линию регрессии). При отсутст-
вии регрессии Ь = 0, и тогда линия регрессии у по х должна идти
горизонтально по отношению к оси абсцисс, а линия регрессии х
по у — вертикально. Место их пересечения соответствует средним
155
значениям обоих признаков. Таким образом, каждая линия регрес-
сии обязательно пройдет через точку К (рис. 16), координаты
которой х, у. Это важно для понимания возможной колеблемости
линии регрессии. Так как b имеет ошибку sb, то, очевидно, зна-
чения выборочных b могут находиться в границах, определяемых
этой ошибкой. Это значит, что угол наклона линии регрессии мо-
жет быть или большим, или меньшим. Как показано на рис. 16,
линия регрессии АВ пересекает точку К и имеет угол наклона
по отношению к горизонтали ВК.Кг. Но истинная линия регрессий
заключена внутри пары углов, образованных пересечением линий
/liBi и Л2В2. Если углы ВгК и В2К построены по верхней и ниж-
ней границам Ъ с учетом только одной ошибки, то вероятность
нахождения истинной линии регрессии в этих границах равна 0,68.
Однако уравнение регрессии имеет еще свободный член а. Он
определяет величину отрезка, отсекаемого на оси у линией регрес-
сии АВ. Величина а также имеет свои границы колеблемости, по-
этому линия регрессии при том же значении Ъ, т. е. при том же
угле наклона ее к оси абсцисс, может проходить или несколько
ниже линии АВ, или несколько выше. Так как надо учитывать
оба параметра уравнения регрессии, то установление доверительных
границ для линии регрессии не так просто. В общем можно
считать, что границы доверительного интервала представляют со-
бой Кривые линии типа гипербол (линии MN л ОР на рис. 16). Это
значит, что по мере отдаления от средней точки (х, у) они расши-
ряются. Крайние точки, по которым строится линия регрессии,
обладают большей ошибкой.
Однако при проведении специальных опытов можно добиться
достаточно больших п на всех частях интервала изменений х
166
(или соответственно у) и принять, что дисперсия отдельных зна-
чений у (или х) будет примерно одинаковой на всех частях ин-
тервала. В таком случае можно применять сравнительно про-
стые методы для оценки достоверности коэффициента и линии
регрессии.*
Основой для определения возможной вариации линии регрес-
сии является сумма квадратов отклонений фактических значений
yt от вычисленных теоретически yt по тем же значениям ряда х.
Так, если использовать приведенные выше данные о связи погло-
щенного кислорода с температурой внешней среды, то можно со-
ставить следующую таблицу для расчета квадратов отклонений
(табл. 33); Значения для третьего столбца были вычислены по
уравнению регрессии у = 3,65 — 0,09х.
Полученную сумму квадратов отклонений, т. е. S (yt — у^\ на-
до разделить на число степеней свободы, которое в данном слу-
чае равно п — 2, так как при вычислении отклонений использу-
ются две величины, а не одна.
Тогда
(62)
(63)
Величину (ifa — у() иногда обозначают для сокращения через dy.x.
Подставив в формулы (62) и (63) соответствующие значения
из табл. 33, получим а2х.у = 0,0630 и иу.х = 0,25 мл/г поглощен-
ного кислорода.
Эта величина <jy.x имеет такое же значение, как о в вариацион-
ном ряду. В пределах одной су.х распределяются отклонения от
теоретической линии регрессии вверх и вниз (направление вверх и
вниз надо считать по оси у) в 68% случаев. С вероятностью
0,997 можно утверждать, что эти отклонения от теоретической
линии регрессии расположатся в пределах ± 3<Tj,.x. В данном слу-
чае Зо = 0,75.
Значок у • х показывает, что рассматривается регрессия у по
х, т. е. изменение в величине у по точно установленным значе-
ниям ряда х. При рассмотрении регрессии х по у надо писать
х • у.^(У(—у{)а может быть получена и без специальной табл. 33,
из данных предыдущей табл. 31, для чего можно использовать
следующую рабочую формулу:
* Более полное изложение вопроса об оценке достоверности регрессии и о
ее доверительной зоне см. в кн.: Урбах В. Ю. Биометрические методы,
стр. 300—309; Снедекор Дж. .У. Статистические методы, стр. 135—144.
157
Таблица 33
Фактические (у,) и теоретические (yt) значения количества поглощенного
кислорода (в мл/г) веса) у крыс в зависимости от температуры
внешней среды (хг)
Xi A У1 Отклонение ОТ у? (У1— yb Квадраты от- клонений (У1 — yi?
0 < 3,8 3,65 0,15 0,0225
5 3,4 3,20 0,20 0,0400
10 2,6 2,75 ’ —0,15 0,0225
15 2,0 2,30 —0,30 0,0900
20 1,7 1,85 -0,15 0,0225
25 M 1,40 0 0
30 1,3 0,95 0,35 0,1175
2 = 0,3150
Тогда
^(yt — У^ = s (уI — у)*------
\И1 w w Ы Х(хг —х)г
s (у. _7)2 _ I2 — —
S (Xj — x)2
n — 2
(62а)
2 (х, — х)г '
п — 2
При подстановке соответствующих величин из табл,
лучим
(63а)
31 по-
Ошибка
или при
,/581
I/ °’81 700 _ ос
®ух — V 7 — 2 — 0,25.
коэффициента регрессии вычисляется по формуле
Gy-X
sb =___________-
V 2(х4 — х)а
замене ау.х ее значением в отклонениях
(64)
Зь —
(п— 2)2(хг —х)»
(64а)
158
Так как оу.х в разобранном примере уже вычислена (= 0,25),
нужно ее разделить на корень квадратный из —х)*, значение
которого можно взять из табл. 31.
В таком случае
sb = = 0,0096.
b /700
Степень достоверности устанавливается,‘как обычно, по вели-
чине t\
t = ~~- (65)
Ofc
При этом надо брать df = п — 2.
Коэффициент регрессии b = 0,09 или, точнее, 0,089, отсюда
По табл. III находим, что полученное значение t превышает
требующееся t при уровне значимости 0,01.
Нулевая гипотеза, предусматривающая, что Р = 0, должна быть
отброшена.
Если коэффициент регрессии был вычислен с помощью вели-
чин г, ах, оу, то средняя ошибка для него может быть получена
по следующей формуле:
Sby-X~~^ V
Соответственно
' <66а>
Сравнение коэффициентов .регрессии. Оно производится так же,
как и сравнение других статистических показателей. Разница
между ними делится на ошибку разницы, которая вычисляется
путем объединения сумм квадратов обеих выборочных совокуп-
ностей по следующей формуле:
, / $ si
- 1/ 2 (Xi )S + 2(Ха_-)а • (67)
При малых величинах совокупностей, на которых получены
коэффициенты регрессии, вносятся некоторые усложнения, подоб-
ные тем, с которыми приходилось встречаться при вычислении
ошибки разницы между средними арифметическими двух малых
выборок. Аналогично им за(Ь1-ьг) вычисляется по такой формуле:
/(nx-2)s? + (n8-2)sg /1 . 1 \
(«! - 2) + (па — 2) ^2 (Х1 _ 2 (х2 - ла)3 /
(67а)
159
Достоверность же определяется по значению
/ = (68)
Srf(Z>,-b,)
с помощью табл. II или III.
Связь между регрессией и корреляцией. В начале главы уже
указывалось на то, что основное корреляционное уравнение ty =
— rtx может быть преобразовано в обычное уравнение регрессии.
Вспомним, что t представляет Собой нормированное отклонение:
При замене ty и <х.в формуле ty = rtx их полными значениями
получим
У1~~У гх‘~\
Если помножить обе половины равенства на <гу, оно примет
следующий вид:
Так как г ~ — Ь, то
(У1 — y^b^t-x);
В данном случае Ьу,х,
Мы получили то самое уравнение регрессии, с которого нача-
ли рассмотрение вопроса о регрессии. Вот почему основное кор-
реляционное уравнение ty—rtx может быть названо и уравне-
нием регрессии. Прямая регрессии, построенная на основе
уравнения регрессии, представляет собой не что иное, как геомет-
рическое изображение линейной корреляционной связи.
Особенностью метода регрессии является то, что зависимость
между изменяющимися величинами может рассматриваться
как бы в двух разных направлениях, т. е. регрессия может быть
двусторонней — х по у и у по х. Отсюда существование двух
коэффициентов регрессии. Коэффициент же корреляции служит
общим мерилом сопряженной вариации двух признаков. Он бо-
лее искусствен, нежели регрессия. При регрессии один признак
выступает в качестве независимой переменной, а другой — в ка-
честве зависимой, и наоборот, причем эти зависимости имеют
чаще всего совершенно конкретный смысл. Математически коэф-
фициент корреляции представляет собой среднюю геометриче-
скую из двух коэффициентов регрессии.' •
В самом деле
Ьх-у ~ Г И Ьу.х = Г^.
160
Отсюда
Ьх-Ц ' bg -n Я= Г9
и
г = V Ьх.у Ьу.х. (69)
Поэтому как в формуле коэффициента корреляции, так и в
формулах коэффициентов регрессии центральное место занимает
сумма произведений отклонений по ряду х и по ряду у, т. е.
S (xt — x)(yt — у). Эта сумма является числителем как в общих
формулах коэффициенту корреляции (38), (39), так и в общей фор-
муле коэффициента регрессии (60) и в сущности служит настоя-
щим мерилом сопряженной вариации признаков х и у, или, иначе,
так называемой ковариации. Формула ковариации следующая:
rnv -
- Л _ 1 •
Ковариационный анализ составляет особый раздел современ-
ной вариационной статистики.* Здесь же коварнация упомина-
ется как связующее звено между корреляционным и регрессион-
ным методами анализа.
Криволинейные зависимости. Хотя прямолинейная зависи-
мость между х и у, которая рассматривалась в предыдущих раз-
делах главы, является наиболее простой формой связи, однако
она обнаруживается во многих биологических явлениях и может
быть очень Ёажной для их понимания. Так, например, известно,
что количество возникающих мутаций прямо пропорционально
дозе облучения. Установление этого положения имеет фундамен-
тальное значение. Оно показывает, что при любой самой малень-
кой дозе ионизирующих излучений возникают мутации.
С помощью уравнения прямолинейной регрессии можно опре-
делять значение одного признака по значению другого, что имеет
и практический смысл. Так, связь процента обезжиренного
остатка в молоке у с процентом жира х выражается уравне-
нием '
у = 8,09 4- 0,253 х.
Поэтому по х можно определить у и наоборот. '
Но нередки случаи, когда связи между х и у оказываются
более сложными ти регрессия ре может быть выражена прямой
линией. Так, известно, что с повышением возраста коров средние
удои за лактацию возрастают. Но эта положительная связь на-
блюдается примерно до 7—8 лактаций, в дальнейшем же, наобо-
рот, средние удои падают. Если выразить эти данные на графи-
ке, нанеся на ось абсцисс возраст коров, а на ось ординат —
средние удои, то получится куполообразная кривая, сначала
* С лим 'можно познакомиться по специальной литературе (см. Снеде-
кор Дж. У. Статистические методы, гл. 13 и 14). ' . \
6 п. Ф. РОКИЦКИЙ 161
подымающаяся вверх, а затем опускающаяся. Характер кривой,
таким образом, отображает реальное биологическое явление,
а именно: изменение лактационной способности коров в процессе
их индивидуальной жизни и развития.
Выражая с помощью регрессии изменение веса животного с
возрастом, обнаруживаем, что в одни периоды жизни линия
регрессии окажется прямой, в другие — постепенно затухающей
кривой. Подобные примеры можно привести из самых различных
областей биологии. Поэтому необходимо в каждом конкретном
случае выяснить характер связи и, если она оказывается не
прямолинейной, использовать для ее характеристики более
сложные методы, изложенные в специальных руководствах.*
В рамках же нашего элементарного курса ограничимся рассмот-
рением лишь некоторых простейших случаев.
Криволинейная регрессия может быть выражена разнообраз-
ными кривыми: параболическими и гиперболическими, экспонен-
циальными и асимптотическими, логистическими и др. Все они
отражают своеобразие определенных биологических процессов:
Разберем коротко только две из них.
Параболические кривые второго порядка. Выше был приве-
ден пример изменений удоев за лактацию с возрастом. На гра-
фике будет наблюдаться сначала подъем кривой до максимума,
приходящегося примерно на 8—9-ю лактацию, далее кривая
опускается вниз. Такие параболические кривые могут быть вы-
ражены уравнением
у—а + Ьх+сх2. (70)
Это уравнение параболы второго порядка.
Чтобы получить значения параметров а, b и с, надо составить
и решись следующую систему уравнений:
1. па + (2х{)Ь + (2х?)с= 2у£
2. (2x/)a + (2xi2)6 + (2x?)c = 2xiy/; (71)
3. (2 xZ) а + (2 х?) b + (2 х/) с = 2 xlyt.
• Необходимые величины для включения в эти уравнения нахо-
дят с помощью вспомогательной таблицы, в которой должны быть '
графы:' х(, у(, xf, xf, xt, xty( и х?у(. Четыре из них были при со-
ставлении уравнения прямой у = а Ьх.
В дальнейшем надо решить систему 3 уравнений обычным
применяемым в алгебре способом: сначала путем уравнения
коэффициентов при а освободиться от первого члена уравнения,
сведя 3 уравнения с 3 неизвестными к 2 с 2 неизвестными, и за-
тем тем же способом освободиться от второго неизвестного. При
некотором округлении значений у и х вычисления окажутся не
очень громоздкими.
* Пдохинский Й. А. Биометрия, гл. 6; Урбах В. Ю. Биометрические мето-
ды, гл. 8 й 9.
162
В качестве примера можно использовать данные (схематизи-
рованные для упрощения расчетов) об изменении удоев за лак-
тацию у в зависимости от номера лактации х (табл. 34).
В таком случае искомые уравнения будут следующими:
10а + 556+ 385с = 15,4,
55а+' 3856+ 3025с = 92,2,
385а + 30256 + 25333с = 666,8.
Предоставляем читателям самим решить эти уравнения, опре-
делить коэффициенты а, 6 и с.
Экспоненциальные кривые. Известно, что рост организмов
(или популяций организмов) во многих случаях происходит та-
ким образом, что прибавка в весе во всякий момент времени
пропорциональна уже достигнутому весу. Иллюстрацией могут
служить данные, приведенные в табл. 35.
Таблица 34
Изменение удоев за лактацию у (в тыс. кг) в зависимости от номера
лактации х и прочие необходимые величины для уравнения (71)
Xi У1 х2 Х1 X3 xi
1 1 1 1 1 1 1
2 1,2 4 8 16 2,4 48
3 1,3 9 27 81 3,9 11,7
4 1Л 16 64 256 5,6 22,4
5 1,5 25 • 125 625 7,5 37,5
6 1,6 36 216 1296 9,6 57,6
7 2,0 49 343 2401 14,0 98,0
8 2,0 64 512 4096 16,0 128,0
9 1,8 81 729 6561 16,2 145,8
10 1,8 100 1000 10 000 16,0 160,0
S =55 15,4 385 । 3025 i 25 333 92,2 666,8
Если представить данные второго столбца в виде светлых
кружков (рис. 17), то легко видеть, что возрастание веса проис-
ходит значительно быстрее, нежели возраста. Проведя по ним
линию, получим экспоненциальную кривую, подымающуюся
вверх со все увеличивающейся скоростью.
Уравнение регрессии для такой кривой может быть записано
в следующей форме:
W=A-B*, (72)
где А и В являются величинами, которые требуется определить;
в* 163
А
I °-
г*-
р °
______ 1>Р9°£---- -
О 5 10 ,15
возраст (Одних)
Рис, 17, Изменение, с возрастом сухого веса кури-
ных эмбрионов (светлые кружки) и логарифмы ве-
са (темные кружки).
Логарифмируя это уравнение, получим ‘
log 1Г=1оёЛ + (1о£В)х, (72а)
что соответствует обычному уравнению прямой у — а + Ьх (log W
соответствует у, log Л—a; log В—Ь).
В третьем столбце'табл. 35 даны логарифмы W. На рис. 17
они обозначены темными кружками, расположенными почти по
прямой. Таким образом, с помощью логарифмирования первона-
чальных данных произведено их . выравнивание. Практически
очень часто ограничиваются лишь графическим изображением
Таблиц а 35
Изменение сухого веса куриных эмбрионов W (в г)
от 6-дневного до 16-дневного возраста х
(в днях) и логарифмы этого веса
Возраст * Сухой вес Логарифм W
6 0,029 —1,538
7 0,052 —1,284
8'“ 0,079 —1,102
9 0,125 —0,903
10 0,181 —0,742
11 0,261 —0,583
12 0,425 —0,372
13 0,738 —0,132 •
14 1,130 4 0,053
15 1,882 0,275
16 2,812 > 0,445
кривых роста вй «собЬЙ Ь^^^ряфмйчёск^.З^геЛНа^в|й$
бумаге на одной из ординат нанесена логарифмическая шкала;
а на-другой — обыкновенна^. Тогда можно не составлять спе-
циальных уравнений регрессии. -
Определить же значения log Л и log В для уравнения прямой
log W=log А + (log В) х
можно по данным табл. 35, пользуясь теми же приемами, кото-
рые были даны выше при решении уравнения прямолинейной
регрессии.
Уравнение прямой будет таково:
у= -2,689 + 0,1959 х.
Здесь у выражен в логарифмах веса, х — в днях. 0,1959 —
это логарифм 1,57, а 2,689 — логарифм 488,65. Поэтому в нату-
ральном масштабе экспоненциальное уравнение будет иметь
следующий вид:
W = 1’57х
460,00
ИЛИ
' № = 0,002046-1,57*.
ВОПРОСЫ
1. Что такое'регрессия? ,
2. В чем преимущество регрессии по сравнению с корреляцией?
’ 3. Какими способами может быть выражена регрессия?
4. Изложите ход работы по построению эмпирической линии регрессии.
5. Под каким углом пересекаются эмпирические линии регрессии при слабой-
корреляции? При сильной корреляции?
6. Напишите уравнение регрессии в общем виде; в виде уравнения прямой.
7. Напишите систему двух уравнений для определения’ значений а и b
в уравнении у = а + Ьх,
8. Как строится теоретическая линия регрессии, если решено уравнение рег-
рессии?
9. Что выражает уравнение регрессии х по у и уравнение регрессии у по х?
10. В каком случае две теоретические линии регрессии пересекаются под
прямым углом друг к другу? Когда они совпадают?
11. Чему равен тангенс угла между линией регрессии и осью х?
12. Напишите формулы коэффициента регрессии.
13. Может ли коэффициент регрессии быть равным коэффициенту корре-
ляции? -
14. Каково взаимоотношение R и 6?
15< , Напишите формулы для Ъ (в отклонениях и в конкретных значениях
х и у). ч ,
16. В чем заключается физический смысл ошибки линии регрессии? Как
определяются доверительные границы линии регрессии?
17. Почему коэффициент регрессии надо называть выборочным?
18. Каково число степеней свободы при определении ошибки линии рег-
рессии?
19. Как формулируется нулевая гипотеза по отношению-к регрессии?
20. Напишите несколько формул для ошибки коэффициента регрессии.
21. Можно ли вычислить среднюю ошибку. для Коэффициента регрессии,
пользуясь сигмами и коэффициентом корреляции?
*166
22. Как проводится сравнение двух коэффициентов регрессии при больших
и малых п? ч
23. Преобразуйте корреляционное уравнение ty — rtx в уравнение рег-
рессии.
24. Какова связь коэффициента корреляции с двумя коэффициентами рег-
рессии?
25. Какая величина называется ковариацией?
26. В чем разница между прямолинейной и криволинейной зависимостями?
27. Как выровнять эмпирическую линию регрессии с помощью скользящей
средней?
28. Каково уравнение для параболической кривой второго порядка?
29. Что такое экспоненциальная кривая? Можно ли преобразовать ее"
в прямую?
ЗАДАЧИ*
118. У 20 взрослых мужчин были измерены высота (длина тела) х (в см)
и вес у (в кг):
X 165 176 175 168 167 172 175 180 179 173
У 56 75 70 61 61 63 72 80 76 68
X 166 178 169 169 170 176 .180 169 177 176
У 58 76 60 64 63, 71 78. 63 75 71
Составьте корреляционную решетку и вычислите г и $г. Эти же данные
используйте для определения регрессии у по х всеми методами.
119. Предполагается, что между количеством настриженной шерсти у и жи-
вым весом овец х имеется зависимость. Для 10 овец были получены следую-
щие данные (в кг):
х 50 55 60 50 65 60 50 55 50 65
у 4,0 4,2 4,1 4,2 4,5 4,3 4,1 4,4 4,0 4,2
Постройте линии регрессии у по х (теоретическую и эмпирическую). Опре-
делите коэффициент регрессии.
120. Были получены следующие данные о длине грудного х и брюшного
у плавника у окуня озера Баторино:
х 38 31 36 43 29 33 28 25 36 26 21 30
у 40 34 38 42 26 33 29 26 36 27 22 32
х 27 27 28 26 26 25 24 28 28 27 33 27
у 28 26 32 26 28 27 25 28 30 26 32 27
х 26 23 22 25 24 .29 25 25 30 2 3 24 32
у 29 23 24 30 26 30 27 28 32 23 24 32
х 24 25 30 25 26 30 29 22 29 28 26 28
у 25 27 33 27 27 32 28 24 31 32 27 30
х 25 31 25 32 27 31 28 29 26 32 27 31
у 25 34 26 32 29 30 29 29 26 35 26 33
х 28 28 26 33 30 27 21 28 26 30 23 27
у 29 31 29 33 31 31 23 30 27 29 24 28
Составьте корреляционную решетку и вычислите г и sr. Постройте эмпири-
ческую и теоретическую линии регрессии у по х и определите коэффициент
регрессии.
* Из задач, приведенных в конце гл. V многие могут быть использованы
также для построения линий регресии и вычисления коэффициентов регрессии,
например 94, 95, 96, 99, 102, 103, 115, 117 (в последних двух любые 2 пары
признаков).
166
121. Для 10 петушков леггорнов 15-дневного возраста были получены сле-
дующие данные о весе их тела х (в г) и весе гребня у (в мг):
' х 83 72 69 90 90 95 95 91 75 70
/ у 56 42 18 84 56 107 90 68 31 48
Нанесите эти данные на график и составьте уравнение регрессии у по х.
122. Путем еженедельного взятия проб с поля было изучено изменение
высоты растений сои у (в см) с возрастом х (в неделях):
л 1 2 3 4 5 6 7
у 5 13 16 23 33 38 40
Выразите эти > данные на графике и постройте эмцирическу ю линию регрес-
сии у по х. Составьте уравнение регрессии.
123. Для установления связи между содержанием фосфора в почве х и со-
держанием фосфора в злаковых*1 растениях у было проведено 9 анализов со
следующими результатами:
х 1 4 5 9 13 11 23 23 28
у 64 71 54 81 93 76 77 95 109
Составьте уравнение регрессии и установите достоверность 6.
124. Было проведено сравнение удоев первой лактации х с третьей у по
33 коровам холмогорской помеси (в л):
X 1522 239 1521 2700 1789 2496 1197 1105 1701 2218 1790
у 3693 4453 1446 2134 2940 4353 2066 2152 2396 2435 3140
X 2964 1287 1756 1406 1810 1299 2609 2519 1927 1655 1320
у 4700 2113 2513 3249 2553 2320 4612 3201 3173 3326 1639
X 2586 1928 3884 2968 2200 1753 1508 1803 1811 2300 1697
У 4562 3482 4257 3465 2448 3435 3747 2112 3061 2985 2721
Начертите эмпирические и теоретические линии регрессии и составьте ур;
нения регрессии.
125. На белых крысах была показана следующая зависимость между тем-
пературой внешней среды х (в град) и количеством поглощенного кислорода у
(5 мл/г веса):
х 0 5 10 15 20 25 28 29
у 3'83 3,35 2,60 2,02 1,69 1,42 1,39 1,38
х 30 31 32 33 34 35 40
у 1,29 1,39 1,39 ' 1,45 1,65 1,61 2,40
Постройте эмпирическую линию регрессии у по х, вычислите уравнение пря -
молинейной регрессии, определите достоверность Ь,
126. Вычислите коэффициент регрессии по следующему ряду данных (в мм)
о длине хвоста х и общей длине тела у у самок королевской змеи Lam propel -
tis polyzona:
X 37 49 50 51 53 54 68 86 93 106
У 284 375 353 366 418 408 510 627 683 820
X 130 137 142 142 146 149. 155 156 187
У 1056 986 1086 1086 1078 1122 1254 1202 1387
Составьте уравнение регрессии и определите достоверность Ь.
127. Между возрастом овцематок х (в годах) и длительностью плодоноше-
ния ягнят у (в днях) оказалась следующая зависимость:
х 2 3 4 5 6 7
у 149,5 149,3 150,0 150,9 150,5 151,4
Постройте эмпирическую и теоретическую линии регрессии и составьте
уравнение регрессии.
167
428? Следующее уравнение выразкаёт эавнбнмоегь между количеством
отелов коров л и удоем за лактацию у (в кг) в пределах первых 7 отелов: .
у = 1800 + 70л?.
Рассчитайте теоретические удои коров после отелов, начиная с первого и
кончая седьмым, и изобразите эту закономерность на графике. •
129. Фактическая урожайность зерновых культур (в ц/га) в одном совхозе
по годам была следующей:
Годы . 1953 1954 1955 1956 1957 J958 1959
Урожайность 7,8 7,7 8,5 10,0 8,4 11,3 10,5 '
Постройте эмпирическую и теоретическую линии изменений урожайности
по годам, Составьте уравнение регрессии.
130. У 10 телят по глубине груди х (в см) и живому весу у (в кг) были
получены следующие данные:
х 91 86 94 95 104 92 98 84 96 99
у 62 43 60 73 87 65 79 *52 65 68
Постройте эмпирические и теоретические линии регрессии х по у и у по х;
вычислите коэффициенты регрессии. Определите достоверность Ь.
131. Известны данные для 10 бычков о весе при рождении х (в кг) и су-
точном привесе у (в г):
х 38,5 46,0 43,0 43,0 40,5 44,0 38,0 35,0 40,5 54,0
у 694 901 736 1005 841 743 ' 896 863 855 830
Постройте линию регрессии (эмпирическую и теоретическую) у по х.
132. Были получены следующие данные о потреблении кислорода у пияв-
ками (в г на кг/час) в зависимости от температуры х (в град):
х 5,5 5,6 6,2 8,4 . 9,0 10,5 16,1
у 16.1 14,9 18,8 32,5 32,1 37,1 88,5
х 16,6 17,1 18,8 19,8 20,0 20,7 26,5
у 91,0 94,0 122,0 162,0 167,0 187,0 436,0
Постройте график, на который нанесите точками 14 пар значений х и у.
Убедитесь, что они расположены не по прямой, а по кривой линии. После этого
замените арифметические значения у их логарифмами и вновь постройте гра-
фик» где на одной из осей нанесите log//. Вычислите коэффициент регрессии
&log у.х и_ составьте по этим данным уравнение регрессии log у по х.
133. Под влиянием облучения рентгеновыми лучами наблюдалось следую-
щее замедление размножения вируса мозаики Аукуба у (в тыс.) в зависимости
от длительности облучения х (в мин):
х О 3 7,5 15 30 45 60
у 271 226 209 108 59 29 12
Составьте уравнение регрессии, приняв за у логарифм количества вирусов
и за х —минуты облучения. Постройте эмпирическую и теоретическую (ось
ординат — логарифмы) линии регрессии.
134. В табл. 34 приведены данные об изменении удоев за лактацию у с
возрастом х. Составьте уравнение криволинейной регрессии у по х и начертите
график.
135. Было учтено среднесуточное количество перевариваемых веществ кор-
ма х (в /Кг), съеденного коровой за 12 месяцев лактации:.
Месяц 1 2 3 4 5 6 7 8 9 10 11 12
х . 11,3 12,8 13,2 13,6 13,4 13,2 12,9 12,8 12,5 12,2 11,9 11,5
Предполагая, что зависимость выражается параболической кривой второго
порядка, составьте уравнение регрессии.
468
*
ГЛАВА 7
СТАТИСТИЧЕСКИЙ АНАЛИЗ ВАРИАЦИИ
ПО КАЧЕСТВЕННЫМ ПРИЗНАКАМ
Группирпнкя вариант, отличяюшиу-д- качественными призна-
ками. В предыдущих главах разобраны статистические методы,
применяемые для анализа количественной вариации. Нсьбиологу
довольно часто приходится иметь дело с различиями в совокуп-
ностях по качественным признакам, таким, как окраска медово-
го покрова живохяьне-гили цветков растений, наличие или отсут-
ствие различных морфологических признаков, реагирование или
нереагирование организмов на' определенное воздействие внеш-
ней среды и т. д; И здесь очень важно использование для анали-
за совокупностей математико-статистических методов. В табл. 1
(гл. 1) приведен пример распределения 500 норок по окраске».
Группировка сводилась к подсчету особей, относящихся к каж-
дой качественной группе, и ‘ к выражению количества особей
каждой группы в виде относительной доли или просто доли в
общем объеме совокупности. Эта доля может быть выражена
или в процентах, как это было сделано в табл. 1, или в долях
единицы.
Таким образом, при изучении качественных признаков мы
встречаемся со следующими величинами: а) абсолютные числен-
ности группы — их обозначают символами ро, р\, рг и т. д.;
б) их доли, выраженные или в долях единицы, или в процентах
•(обозначения: q, р, г, s и т. д.). Доли единицы в ряде случаев
предпочтительнее, чем проценты; перейти от одного обозначения
,к другому, очевидно, очень просто — путем умножения на 100.
С первого взгляда может казался, что эти величины резко
отличны от показателей, характеризующих количественные при-
знаки. Однако, как это- будет видно из содержания данной гла-
вы; качественные признаки и их вариация могут быть в такой
же степени подвергнуты статистическому анализу, как и коли-
чественные, и по отношению к ним возникают те же проблемы,
а именно: Нахождение наиболее типичного значения признака,
установление степени вариации вокруг, него, устайовление зави-
симости между качественными признаками или между качест-
16S
венными и количественными и, наконец, оценка достоверности
всех полученных при изучении качественных признаков показа-
телей. ,
Альтернативная вариация. Простейшим случаем качествен-
ной вариации является альтернативная, . когда совокупность
состоит только из 2 групп: одной, имеющей данный признак,
и другой — его не имеющей. Численность первой группы можно
обозначить через рь а численность второй — через ро. Тогда доля
особей, имеющих признак, будет
P-V’ ' <73>
а доля особей, не имеющих его,
? = -^. (73а)
Но так как p + q = 1, то вместо q можно написать 1 — р:
?=1-Р = *. (736)
В дальнейшем надо будет строго придерживаться этих обо-
значений.
Обозначения р и q сразу напоминают о вероятности. И дей-
ствительно, относительная доля в то же время измеряет вероят-
ность. Если доля членов совокупности, имеющих определенный'
признак, равна р (имеется в виду, конечно, очень большая, или
генеральная, совокупность), то при отборе наудачу какого-либо
члена совокупности вероятность того, что он будет как раз с рас-
сматриваемым признаком, также равна р.
Так как с альтернативной изменчивостью легче работать, то
в. ряде случаев целесообразно для анализа превращать несколько
качественных групп в две альтернативные. Например, если име-
ются кролики разной окраски, в том числе белые (альбиносы),
то можно разделить кроликов сначала только на 2 группы: окра-
шенных и белых.
Средняя арифметическая и среднее квадратическое отклоне-
ние при альтернативной вариации. Возникает вопрос, можно ли
при альтернативной вариации вычислять статистические пока-
затели, как это делалось ранее для вариационных рядов по ко-
личественным признакам. Для этого разберем, каким будет в
этом случае вариационный ряд.
В общем виде данные при альтернативной изменчивости мо-
гут быть представлены в виде двух классов: класса «О», охваты-
вающего варианты с отсутствием данного признака, и «1» —
с присутствием его. Сокращенный вариационный ряд, состоя-
щий только'из двух классов, можно обработать, подобно ряду
при количественной изменчивости (табл. 36).
170
Таблица 36
Общая схема обработки ряда при качественной изменчивости
Классы Частоты f ’Отклонения от условной средней а /а /а3
0 Ро 0 0 0
1 Pi 1 7Р1 Р1
i = 1 Ро + Pl = П S = рг 2 = Pi
Применив обычные формулы
x = A + b = A + i
П
и
’ а - f 1/ s fat Рfa V
г п< \ п ) '
получим
х = 0 + -^ = -^-.
‘пл
Так как это фактически доля определенного качественного класса,
в общей совокупности, то можно писать вместо х букву р, т. е.
х = Р = Х , (74)
Таким образом, относительная доля в совокупности особей,
имеющих данный признак, соответствует средней арифметической
при количественной вариации.
Среднее квадратическое отклонение будет выражаться вели-
чиной
„ _ 1 / Pi I Pi'2
p V nj ( л) :
Но так как n = p0 + pit то подкоренную величину можно пре-
образовать следующим образом:
а = = 1/(Ро + Р1)Р1-Р? = VpEpL, (75)
р Т П2 Г Па Г ,П2 4 7
. Отношение — = р, а отношение — = а.
П п 1
Тогда
<>P = Vpq, (76)
а поскольку 1 — p — q, то среднее квадратическое отклонение мо-
жет быть записано так:
171
(76а)
варианса
' o* = W = p(l-p). (77)
Применим указанные формулы к данным о 284 коровах, кото-
рые были подвергнуты туберкулинизации. Отрицательную реакцию
дала 201 корова, положительную — 83. Эти данные можно внести-,
в табл. 37.
Таблица 37
Распределение коров по реакции на туберкулез
Классы Частоты, а fa
0 201 0 0 0
1 83 1 83 83
- п = 284 2=83 2=83
В таком случае
83 п оп. 201 п
Р ~ 284 ~ ? —' 284 ~
Значение р и q можно выразить и в процентах —29 и 71.
а = ]/0,29 • 0,71 = F 0,2059 = 0,45 (или 45%).
Средняя ошибка. Как и 6 случае количественной изменчи-
вости, частота качественного признака, выраженная в долях
единицы или в процентах, имеет свою статистическую ошибку,
так как она определяется на основе изучения конкретной выбо-
рочной совокупности. Значения полученных долей, определенные
для ряда выборочных совокупностей, будут колебаться вокруг
доли генеральной совокупности по тем же законам,, которые
указаны выше, в гл., 4, для колебаний средних арифметических
выборочных совокупностей вокруг генеральной средней, т. е.
средней арифметической генеральной совокупности. Мерой этих
колебаний является средняя, или статистическая, ошибка. При-
менительно к качественной вариации она вычисляется по следу-
ющей формуле:
Если доля выражена в процентах, то
. sp= \/ Р^Р). ' (79)
Для приведенного выше примера с реакцией коров на тубер-
кулез
172
sp F 0.0007= 0,027.
Ошибка будет одна и та же как для доли реагировавших ко-
ров, так и для доли нереагировавших:
р ± sp = 0,29 ± 0,027;
q ± sg = 0,79 ± 0,027.
Доли и их ошибки могут быть выражены и в процентах:
29% ± 2,7%; 79% ±2,7%.
Так как величины р и q изменяются в обратном отношении,
друг к другу, то легко рассчитать, что Для каждого данного зна-
чения п средняя ошибка не может быть больше величины
' j/ 0,5-0,5 ' _ |/ 0,25
Это обстоятельство может быть полезно в тех случаях, когда
биолог почему-либо не уверен в точности полученного значе-
ния р. Тогда лучше цзять в качестве ошибки эту максимально
возможную величину.
Поправка на соотношение объемов выборочной и генераль-
ной совокупностей. Формула (78) применяется в тех случаях,
когда объем выборочной совокупности, по которой определена доля,
очень мал по сравнению с объемом генеральной совокупности.
Если же выборочная совокупность составляет довольно большую
часть генеральной совокупности (что возможно в зоологии при
изучении малочисленных видов или в медицине при изучении
сравнительно редких заболеваний), Следует аналогично формуле
(24а) ввести в подкоренное выражение множитель 1 — где
п—объем выборочной совокупности, a N — объем генеральной.
В таком случае формула ошибки для доли примет следую-
щий вид:
(№)
Для примера, приведенного в табл. 37, можно применить
формулу (78) без поправки, так как выборка, состоящая из
284 коров, очевидно, составляет очень маленькую часть гене-
ральной совокупности коров.
Иначе обстоит дело в следующем примере. Допустим, что в
вузе учится 6400 студентов-заочников. Из них взята выборка (по
принципу бесповторного отбора) в 1000 человек, среди которых
оказалось 200 участников Великой Отечественной войны. Доля
последних составляет
р = 0,20 (или 20%).
При расчете v ошибки доли надо учесть, что выборочная совокуп-
ность 1000 студентов довольно велика по сравнению с генераль- ;
173
ной, которойнадо считать общее количество студентов-заочников
вуза. Поправка 1 — -J- =1 — = 1 — 0,16 = 0,84. Тогда
SP = V ?,2?об~6,8° • = Ко,000134 = 0,012 (или 1,2%).
Доверительные границы для доли. Возможные границы, в
пределах которых находится значение доли для генеральной
совокупности (обозначим ее Ро), определяются по формуле
p-tsp<P0<p+tSp. (80)
Эта формула, очевидно, аналогична формуле (25). Приняв
определенное значение t, соответствующее доверительной вероят-
ности (0,95 или 0,99), можно определить доверительные границы
для генеральной, доли, т. е. доли генеральной совокупности.
Возьмем следующий пример. С помощью реакции Шика выясня-
ли иммунитет детей по отношению к дифтерии. У 10% проверен-
ных, (а всего было проверено 1600 детей), реакция была поло-
жительной. Спрашивается: в каких пределах колеблется процент
детей с положительной реакцией на дифтерию? - >
Ошибка для 10% равна
’,-/^=0.75.
Значения t для формулы (80) определяются принятым для
доверительных г.раниц уровнем значимости.
Для Р = 0,05 достаточно взять /=1,96, для Р=0,01 значение t
должно быть 2,56.' На практике/чтобы избежать лишних вычис*
лений, часто берут округленные значения t: 2; 2,5 и 3. Если взять
/=3 (а это обеспечивает уровень значимости более высокий, не-
жели 0,01, т. е. Р<0,01), то
10-3 • 0,75<Р0<10+3 • 0,75.
I
Доверительные границы для процента детей, дающих поло-
жительную реакцию на дифтерию: 7,75—12,25.
Отсюда вытекает важный практический вырод: нельзя при-
давать абсолютного значения получаемым в биологических ohbi-
тах или наблюдениях процентам*. Нередко ^биолог, стремясь к
большой точности, вычисляет проценты с десятыми и даже соты-
ми долями. Но из статистической природы доли должно быть
ясно, что значение доли или процента имеет свои границы ко-
леблемости, зависящие от величины ошибки и иногда выражаю-
щиеся несколькими процентами. Поэтому разница в несколько
процентов, а тем более десятых процента, чаще всего является
несущественной. Следует указать, что определение доверитель-
ных границ для доли указанным выше способом дает достаточно
точные результаты в тех случаях, когда р близко к 0,5. В тех же
случаях, когда оно близко к нулю или единице, ошибка, вычис-
174
ляемая по обычной формуле, довольно сильно искажается. В та-
ких случаях для получения бол^е точного значения ошибки
пользуются вспомогательной величиной <р (фи) (табл. XV): *
<Р = 2 arcsinj/p.
Определение ошибки для абсолютных численностей групп.
Иногда возникает необходимость оценить возможную колебле-
мость не доли (или процента), а конкретных количеств особей с
тем или другим признаком. Тогда в формуле ошибки надо заме-
нить значения долей р и q абсолютными численностями р\ и ро,
а величину ошибки для перевода долей в абсолютнее численно-
сти помножить на п. В конечном счете формулы ошибки для
абсолютных численностей рх и р0 будут следующими:
____ (81)
В приведенном выше примере количество коров, давших поло-
жительную реакцию на туберкулез, было 83 (из общего числа
284). Тогда
= 7,7^8.
Конкретные числа особей с их ошибками можно записать так:
Pi + sPt = 83 ± 8;
Ро ± sPt = 201 + 8.
, Вычисление ошибки при р=0. При учете качественной вариа-
ции возможен случай, когда в какой-то выборочной совокупно-
сти нет ни одного случая с признаком А, т. е. р^—О и, значит,
р=0, или же единиц с признаком А очень мало, так что р выра-
жается очень малым числом. Тогда вычисляют долю (в процен-
тах) и ее ошибку несколько окольным путем, носящим название
метода Ван-дер-Вардена.
При этом методе
(82)
(83)
Допустим, например, что среди 30 школьников класса не ока-
залось ни одного, проявившего положительную реакцию Шика
(на дифтерию). Так как Pi = 0, то
__________
*0 методе фи см. в кн.: Урбах В. Ю. Математическая статистика для
биологов и медиков, стр. 178—180; Плохинский Н. Д, Биометрия, стр. 144—146.
175
sp = Жюзо == 3,2%.
Таким образом, несмотря на отрицательный результат, по-
лученный на 30 школьниках, возможны случаи положительной,
реакции в других выборочных совокупностях с верхней грани-
цей до 9,6% случаев (при £=3,0).
Расчет необходимой численности выборочной совокупности. f
В гл. 4 есть раздел, посвященный установлению необходимого
размера выборочной совокупности для получения статистиче-
ских показателей количественных признаков с желательной точ-
ностью. Аналогично можно определить п в случае качественной
вариации.
Так как ошибка доли
Р I п
то желаемая точность
д = ц/ЖЕё1.
Отсюда
„ = 4 (84)
Для использования этой формулы надо знать величину р,
; которая может быть установлена только после предварительного
изучения выборочной совокупности. Если в распоряжении био-
лога уже имеются какие-то ориентировочные данные о возмож-
, ной в§личине доли, их можно использовать. Но если их нет, луч-
ше взять максимально возможную величину произведения
р(1 — р). Таким максимумом, как указывалось выше, является
0,25. В этом случае р—0,5. При всех других значениях р (боль-
ших или меньших 0,5) произведение р(1—р) будет меньше,
чем 0,25.
Допустим, например, что требуется определить размеры вы-
б.орки для установления доли в популяции вида особей женско-
го пола со степенью точности не менее чем 0,02 (или 2%) и с ве-
роятностью 0,95. Тогда £ = 2,0; р(р —1)=0,25; А=0,02. Отсюда
п — 22 0^2, j = о,ООО4 =
Определение достоверности разницы между выборочными до-
лями (или процентами). Из гл. 4 уже известно, что' для опреде-
лений достоверности разницы между двумя показателями надо
знать разницу d, ее ошибку sd и £ = —. Очевидно, что эти общие
положения относятся и к,, определению, достоверности разницы
между долями (или процентами). 1 - '
176
На следует разяЙчН» 2 'Йу^Й,' когДа 2 сравниваемые д<*Ли
определяются: а) на материале одной и той же выборочной сово-
купности; б) на материале разных выборок. " .
В‘первом случае можно воспользоваться обычными формулами
для определения разницы и ошибки разницы:
. . = Рх — Ру; «4 = V Spx + s3Py,
Допустим, что из 28 . обезьян макака резус 16 было заражено
вирусом А. и 12 — вирусом В. В первой группе заболели 4 обезья-
ны, а во, второй — 6. Случайна ли разница в степени заражения?
Р, = А = о,25;
Р, = 4 = 0,50; Spy=i/SJE_o,14.
Тогда
4 = |рх-ру | = 0,25*
и 'sd = У 0,112 + 0,14а = 1/^317 = 0,18;
t = °»2| = 1,4.
По табл. I или II (Сты^нта) устанавливаем, что
р=0,84 и Р=0,16.
Очевидно, разница в степени заражения недостоверна.
Второй случай, когда, доли определяются на разных совокуп-
ностях, более сложен. В этом случае сшибка' разницы вычисля-
ется по формуле
sd(Px-py).= ]/w(±. + ±.j, (85)
где пх и пу —численности двух совокупностей (или групп), на
которых определены доли рх и ру.
Но для применения этой формулы надо сначала определить р
как среднюю взвешенную из рх и ру по формуле
р = Р*'п* + Ру‘п* - (86)
пл+пу
или использованием непосредственно абсолютных численностей осо-
бей по каждой совокупности: ,
р = .. (86а)
П пу
* Прямые скобки показывают, чтб берется абсолютная розница без учета
знака* .
ITf ,
Для иллюстрации этого метода разберем следующие примеры.
Сравним 2 стада коров по реакции на туберкулез. В первом ста-
де состоявшем из 284 коров, реагировавших (Р1Л.) было 83, в дру-
гом, состоявшем из 50 коров, реагировавших (Ру1) было 6. В таком
случае рх = Ц = 0,29 и р? = | = 0,12:
d=|px-py|=O,17.
Полученные в двух группах данные надо сравнивать не друг
с другом, а с показателями теоретически мыслимой единой сово-
купности, из-которой взяты 2 выборки: одна —284 коровы, а дру-
гая — 50 коров.
Для такой совокупности р можно вычислить по формуле (86)
или (86а). В данном случае
_ 83+6 _ 0 „7
Р ~ 284 + 50 ~ °’27'
Поэтому и ошибку для средних двух групп следует вычислять,
исходя не из частных рх и ру, а из р генеральной совокупности.
Формула для ошибки разницы (85) была следующей:
Подставив в эту формулу конкретные значения, получим:
»» = |/°’27 ' ОЛЗ У, + +) - 0.068.
Отсюда
По таблице интеграла вероятности такое значение t дает ве-
роятность 0,9883 и уровень значимости 0,0117. Отсюда можно
сделать вывод о существенном различии в реакции на туберку-
линизацию двух групп коров, то есть нулевая гипотеза должна
быть отброшена.
Ввиду некоторой трудности изложенного материала и важ-
ности этих методов для биологических исследований приведем
еще один пример, на этот раз из генетики.
При воздействии гамма-лучами на самцов дрозофил было
получено 2% летальных, сцепленных с полом мутаций (на
450 хромосом); при той же дозе гамма-лучей в сочетании с воз-
действием на личинок вещества ионола — 7% мутаций (на
500 хромосом). Надо установить, влияет ли кормление личинок
ионолом на увеличение количества летальных мутаций, вызы-
ваемых гамма-лучами.
Ход расчетов будет следующим:-
d = |7-2| = 5(4);
178
п 2 - 450 + 7 - 500 .......
р =----------= 4,6(%);
*=«.в • М®+й)== м«);
<=JJ = 3,6.
Достоверность разницы доказывается с уровнем значимости
Р<0,01.
Следует отметить, что применение двух указанных методов
дает значительно отличающиеся результаты только в том слу-
чае, если численности изучаемых групп очень неодинаковы.
Если же пх и пу не очень отличаются друг от друга, можно с
успехом применять для определения sd простейшую формулу
Sd = Vs^ + s^py .
Достоверность разницы между долями выборочной и гене-
ральной совокупности. В биологических исследованиях возмож-
ны такие случаи, когда есть основание предполагать, какой
должна быть теоретическая доля, т. е. доля для генеральной
совокупности; с ней-то и надо сравнивать фактически получен-
ную долю; т. е. долю в выборочной совокупности. Например, рас-
щепление, фактически полученное в потомстве определенных
скрещиваний или в популяции, можно сравнить с теоретически
ожидаемым по законам Менделя или по определенным форму-
лам генетической структуры популяции.
Для определения достоверности разницы между фактически
полученной и теоретической долями надо сначала вычислить
ошибку этой разницы. Но в формуле ошибки разницы sd =
= + %, вторая ошибка должна быть ошибкой генеральной
доли , т. е. доли генеральной совокупности. Последняя, как и
средняя арифметическаягенеральной совокупности, ошибки не
имеет, поэтому sd = Далее, сама ошибка может быть вы-
числена не на основе эмпирических р и q, а на основе теорети-
ческих. В таком случае ошибка разницы
Приведем следующий пример. При скрещивании друг с другом
короткоухих овец (первое поколение от скрещивания длинноухих
с безухими) было получено 7 длинноухих, 9 короткоухих и 6 без-
ухих. Ожидается, что расщепление должно быть в соотношении
1:2:1. Надо определить, отличается ли от теоретически ожидае-
мого фактически полученное количество гетерозиготных’ форм
(т. е. короткоухих овец).
Тогда
179
р = J* = 0,41; Р = Q,50; d «0,09;
t = °’09- =09
1 о,ю и,а’
Очевидно, что нет расхождения между теоретически ожидае-
мой долей гетерозигот и фактически полученной.
Установление корреляционной связи при качественной вариа-
ции. Существует несколько способов установления зависимостей
при качественной вариации. Разберем' наиболее простой из
них — при альтернативной вариации.* В этом случае выясняет-
ся вопрос о том, встречается ли совпадение присутствия обоих
качественных признаков или, наоборот, отсутствия их чаще, чем
это должно быть по случайным причинам. Корреляционная ре-
шетка при этом значительно упрощается, как показано на
табл. 38.
Таблица 38
Схема корреляционной решетки при альтернативной
изменчивости
Классами нулевым (0) и первым (1) обозначаются или два.
качественных признака (например, голубая окраска, черная
окраска), или отсутствие и присутствие какого-либо одного при-
знака (например, безрогость, рогатость). В клетках указывает-
ся количество особей с тем или иным сочетанием признаков.
Суммы горизонтальных строчек пишутся справа, а вертикальных
столбцов — внизу, как и в корреляционной решетке при количе-
ственной изменчивости.. Коэффициент корреляции вычисляется
по следующей формуле:,
г _ orf be________ (87j
/(a+6)(c + d)(a + c)(& + d)‘ V '
В силу того, что группировка на классы является очень гру-
бой, значение г может оказаться несколько завышенным. Более
* Более полно .об изучении качественной вариации говорится в кн.: Юл
Дж. Э„ Кендэлл М. Дж. Терри» статистики, гл. 1, 2, 17; Урбах В. Ю. Матема-
тическая статистика для биологов и. медиков, некоторые параграфы, в гл. 4,
180
правильное значёииеполучйтСяпри внесении в 'формулу по-
правки ИейТса на размеры выборки: f
| ad — bc) — -^-
r' = ~— .. 2 (87a)
(Прямые скобки показывают, что надо взять абсолютное зна-
чение разности ad — be.)
Все сказанное в гл. 5 о свойствах коэффициента корреляции,
его количественной оценке и оценке его достоверности относится
и к коэффициенту корреляции при альтернативной изменчи-
вости.
В качестве примера приведем следующие данные о связи
между окраской шерсти и- цветом глаз у 100 особей кроликов
(табл. 39). ,
Таблица 3
Корреляционная решетка для окраски шерсти у и цвета глаз х у кролика
^Красные гАаза Некрас- ные глаза 2
Белая шерсть . . . 29 11 40
Окрашенная шерсть 1 59 , 60
2 30 70 100
При подстановке -всех значений сумм из таблицы в форму-
лу получим
+Q.76.
/30 • 70 • 40 60
Внесение поправки по формуле (87а) в данном случае очень
мало изменит результат, а именно: получится г’ = 0,73.
Так как количество наблюдений достаточно велико (100), то
ошибка для г’ может быть вычислена по простой формуле
s • - = = 0,047.
г /п У100
Достоверность г не вызывает никаких сомнений.
Решетку, состоящую из 2X2 пблей, можно применять для
анализа и более сложных случаев, если только они укладывают-
ся в сопоставимые Лары, например: болезнь— выздоровление,
применение лекарства А — применение лекарства В...
Так, при изучении действия препарата на уменьшение забо-
леваемости можно применить такую же решетку из четырех
полей. Тогда по горизонтали надо, написать: «не подвергавшиеся^
181
воздействию», «подвергавшиеся»; по вертикали — «невыздоро-
вевшие», «выздоровевшие». При наличии связи между примене-
нием препарата и выздоровлением численности а и d будут
больше, чем численности b и с. Если же связи нет, численности
а, Ь, с и d будут примерно одинаковыми.
Возможны случаи, когда в одном ряду рассматривается ва-
риация по качественному признаку, а в другом — по количест-
' Таблица 40
Корреляционная решетка для
установления зависимости
между состоянием по туберку-
лезу у и условиями жизни х
однополых двоен
венному, т. е. изучается корреляция
между количественным и качествен-
ным признаками. Тогда корреляци-
онная решетка будет иметь своеоб-
разный характер: по одному ряду,
например ряду х, будет несколько
классов, а по другому — у — только
2 класса. При вычислении коэффи-
циента корреляции применяется
обычная формула для количествен-
ной изменчивости. Но надо учесть,
что вместо 4 квадрантов обычной
корреляционной решетки будет
только 2 квадранта, так как 2 дру-
гих окажутся нулевыми.
Иногда по условиям анализа
нельзя удовлетвориться разбивкой
материала по каждому признаку
только на 2 альтернативные груп-
пы. Приведем пример. Изучалось 75 пар однополых близне-
цов, у которых по крайней мере один партнер был тубер-
кулезным. Ставилась задача — выяснить, существует ли корре-
ляция заболеваемости туберкулезом с условиями среды, в кото-
рой жили близнецы. Состояние каждой пары близнецов по отно-
шению к заболеванию туберкулезом могло быть следующим:
полностью сходные —'С; сходные, но слабо — с; несходные, но
в слабой степени —-d; резко отличавшиеся — D. Таким же обра-
зом и по отношению к условиям среды, в которых жили партнеры
каждой близнецовой пары, были выделены 4 группы: С — пол-
ностью сходные условия; с — сходные условия, но сходство до-
вольно слабое; d — несходные условия, однако несходство было
не очень резко выражено; D — условия резко различные. Корре-
ляционная решетка будет состоять не из 4, а из 16 полей. Она
представлена в табл. 40.
Ее можно обработать так же, как обычную корреляционную
таблицу для количественных признаков, приняв условно за ну-
левые классы третью строчку по горизонтали и третий верти-
кальный столбец.
Изучение взаимосвязи между качественными признаками мо-
жет также проводиться с помощью критерия соответствия, или
согласия (хи-квадрат), о чем будет сказано в гл. 9.
182
ВОПРОСЫ
1. С какими величинами приходится встречаться при изучении качествен-
ных признаков? '
2. Что такое относительная доля, или доля? Как может выражаться доля?
3. Почему обозначения доли те же, что и обозначения вероятности?
4. Какую вариацию называют альтернативной?
5. Как можно составить вариационный ряд при альтернативной вариации?
6. Какому показателю вариационного ряда при количественной вариации
соответствует доля?
7. Напишите формулу среднего квадратического отклонения для качествен-
ной вариации, формулу средней ошибки.
8. Каков смысл средней ошибки доли? -
9. Когда' надо вносить в формулу средней ошибки поправку на соотноше-
ние объемов выборочной и генеральной совокупностей?
10. Дайте пример определения доверительных границ для доли.
11. Как определить ошибку для абсолютной численности группы?
12. Можно ли вычислить ошибку при р = О?
13. Как сделать расчет необходимой численности выборочной совокупности?
14. Методы определения достоверности разницы между долями (или про-
центами).
15. Какова формула коэффициента корреляции при альтернативной вариа-
ции (без поправки и с поправкой на группировку)?
ЗАДАЧИ
136. У 48 коров холмогорских помесей соски были коническими, у 12 —
цилиндрическими. Определите р и s для числа цилиндрических сосков (в долях
единицы и в абсолютных величинах).
137. Из 253 детей школьного возраста, реиммунизированных скарлатинозным
токсином, у 6 наблюдалась кожная реакция на месте введения препарата с диа-
метром свыше 5 см. Каковы доверительные границы для процента реагирования
при Р — 0,05, при? — 0,01?
138. Из общего числа 2417 человек, которым привита поливакцина, силь-
ная реакция и реакция средней силы наблюдалась у 561 человека. Каковы до-
верительные границы для процента сильно- и среднереагировавших при р =
= 0,99, при р = 0,95?
139. На 18 000. больных зарегистрировано 72 больных диабетом. Опреде-
лите процент диабетиков в популяции и его ошибку. Установите доверительные
границы для процента диабетиков при вероятности 0,95.
' 140. За длительный период наблюдали случаи гастрической геморрагии, при
этом оказалось, чЗ'о за первые 4 года их было 40, 10 из них со смертным ис-
ходом, а за последующие 6 лет — 60 случаев, в том числе 5 смертных. Досто-
верна ли разница в проценте смертных случаев за первые 4 года и после-
дующие 6 лет?
141. Среди крыс Rattus norvegicus найдено 539 самцов и 570 самок. Како-
вы доверительные границы для доли самцов в популяции (с р = 0,95)? Соот-
ветствует ли полученное соотношение полов отношению 1:1?
142. Стадо ярославского скота состояло из 200 голов: 120 из них было
черно-пестрых, а 80 — нечерно-пестрых (рыжих и рыже-пестрых). Каковы доли
или проценты черно-пестрых и нечерно-пестрых в стаде? Достоверна ли разница
между процентами тех и других?
143. При облучении дозой в 300 р дрозофил, питавшихся обычным кормом,
на^805 культур F2 получено 80 сцепленных с полом мутаций. При облучении
той же дозой дрозофил, кормившихся кормом, содержавшим железо, на 2756
культур F2 получено 357 сцепленных с полом мутаций. Какой процент мутаций
получен в обоих опытах? Повлиял ли корм, содержавший железо, на процент
мутаций?
144. В нескольких йометах мышей получено 32 самца и 18 самок. Досто-
верна ли разница между количеством самок и количеством самцов? Каковы
доверительные границы для доли самок и доли самцов? 4
• 183
145? Под влиянием рентгеновского облучения $ двух линиях мышей по-
.являлись уродства: в резистентной 10 уродливых мышат и 90 нормальных и
в'не£езистентной90 уродливых и 60 нормальных. Достоверна ли разница в ко-
личестве уродств между резистентной и нерезистентной линиями'мышей?
Ответ: да.
146. Рассчитайте среднее квадратическое отклонение для числа рецёсси-
вов, равного 750 (при отношении 3:1 и при отношении 9:7).
Г47. Во втором поколении дрозофил получено расщепление: 483 — с крас-
ными (нормальными) глазами и 129 — с пурпурными. Рассчитайте теоретиче-
ское отношение численностей (при расщеплении 1:1) и сравните с ним факти-
чески полученное.
148. При обратном скрещивании получено 798 дрозофил с зачаточными
крыльями и 843.—с нормальными. Рассчитайте ожидаемое расщепление при
отношении 1: L и сравните фактически полученные результаты с ожидаемыми.
149. У дрозофилы обнаружены 3 мутации от доминантного аллеля white
к рецессивному (на 136 тыс. гамет) и 6 мутаций от рецеСсива к доминанту
(на 190 тыс. гамет). Есть ли разница между частотой мутирования в противо-
положных направлениях?
150. По окраске зерен у гороха получено расщепление: 6022 желтых и
2001 зеленых. Проверьте, достоверна ли разница между фактически получен-
ным и ожидаемым числом желтых зерен при моногибридном расщеплении
с 25% рецессивных форм.
151. Из 30 больных одной болезнью умерло 4 человека. По массовым же
статистическим данным частота смертей от этого заболевания была равна 0,133.
Достоверна ли разница между фактически наблюдавшейся частотой смертных
случаев и ожидаемой? Какими таблицами для определения достоверности t
надо пользоваться?
152. К 20 больным тифом применено новое лечебное средство С, к 20 дру-
гим — средство Е. В первой группе ни одного смертного случая не было, во
второй — умерло 10. Достоверна ли' разница между группами, т. е. можно лн
говорить о достоверном эффекте средства’С?
153. Сравните следующие данные о соотношении бычков и телочек за Яго-
да: в 1958 г. бычков родилось 783, телочек — 724; в 1959 г. бычков — 770,
телочек — 801.
154. При скрещивании ангорских длинношерстных кроликов с кроликами,
' имевшими. нормальную длину шерсти, в первом поколении получены нор-
мальношерстные кролики. От обратного скрещивания их с ангорскими получе-
но 62 крольчонка — 33 нормальношерстных и 29 длинношерстных. Соответству-
ет ли это отношению 1:1?
155. При обследовании 3 стад молочного скота одного хозяйства на тубер-
кулез были получены следующие данные: s
Численность стада 40 100 10
Коровы с положительной реакцией (в %) 5 2 60
Достоверно ли различие между стадами по количеству реагировавших?
Определите также средний процент реагировавших по хозяйству в целом.
156. При скрещивании черноглазых морских свинок, гетерозиготных по
красноглазию, с красноглазыми получено черноглазых 45 и красноглазых 38.
Соответствует ли это отношению 1:1?
' 157. В хозяйстве родилось 92 бычка и 100 телочек. Определите проценты
бычков и телочек и их статистические ошибки. Соответствует ли полученное
соотношение полов отношению 1:1?
158. Из 150, леченных методом А, умерло 15, а из 300, леченных по ме-
тоду Б, умерло 45. Случайна ли разница в смертности или полученное разли-
чие достоверно, т. е. является результатом различных способов лечения?
159. В двух детских садах было по 50 детей. В одном ч заболело гриппом
2 человека, в другом — 7 человек. Случайна ли эта разница или же заболевае-
мость в детских садах была различна?
164
;1М В опытах по вызыванию мутаций рентгеновыми лучайи. у дрозофилы
получены следующие данные: \
Группы Количество изу- ченных X-хромосом Количество леталь- ных мутаций
Контроль 32 140 63
Доза 1500 р 15 281 649
» 3000 р 11738 1027
» 6000 р 9116 1462 •
Достоверны ли различия между группами, получавшими разные дозы об-
лучения? Какова зависимость процента мутаций от дозы?
Г61. В потомстве облученных рентгеновыми лучами самцов дрозофилы изу-
чали (генетическими методами) появление инверсий, делений и транслокаций.
Получены следующие данные:
Группы Количество изу- ченных хромосом Количество хромо- сомных нарушений
Контроль 1447 0
Доза 1500 р : 1371 8
» 3000 р . . . . 982 21
» 6000 р ...... 734 54
Насколько достоверны различия между группами, получившими разные до-
зы облучения? Постройте график зависимости числа хромосомных нарушений
от дозы.
162. В одной и той же отаре овец наблюдались следующие различия в
проценте двоен. 1929 г.— ягнилось 1076 маток, из них двойневых 217 (20,2%);
1930 г. — ягнилось 1005 маток, из них двойневых 133 (13,2%). Достоверна ли
разница в проценте двойневых между 1929 и 1930 гг.?
163. Для установления связи между наличием завитка у ягнят и тониной
ости их матерей были изучены 1319 ягнят, данные о- которых представлены в
следующей таблице.
Тонина ости у матерей (по ка- тегориям) Наличие завитка у ягнят 2
0 1
I < II III 75 936 * 1011
IV V VI 27 281 . 308
• 2 102 1217 1319
Д85
Какова корреляция между наличием завитка у ягнят и тониной ости у их
матерей?
164. Данные о наличии сережек на шее и на ушах у 320 гиссарских овец
представлены в следующей четырехпольной таблице:
У X На ушах 2
0 1
шее 0 41 14 55
' та - К 1 214 . 41 265
2 265 55 320
Есть ли связь между наличием сережек на шее и на ушах?
Ответ: нет*
165. В 1939 г. были опубликованы следующие данные о распределении за-
болевших и не заболевших гриппом среди работников Центрального универма-
га в Москве» вдыхавших и не вдыхавших противогриппозную сыворотку:
Группы Незаболевшие Заболевшие Итого
Вдыхавшие сыворотку .... 497 4 501
Не вдыхавшие сыворотку . . . 1675 150 1825
Итого . . 2172 154 2326
Вычислите коэффициент корреляции между вдыханием противогриппозной
сыворотки и незаболеванием гриппом и определите, насколько он достоверен.
ГЛАВА 8
ДИСПЕРСИОННЫЙ АНАЛИЗ
Сложная обусловленность признаков животных и растений.
Анализируя биологические особенности животных и растений
в природе или при разведении их в культуре, легко убедиться
в их постоянной зависимости от многих внешних и внутренних
факторов. Так, мыши-полевки варьируют в своем росте и разви-
тии в зависимости от размеров их родителей, от времени рожде-
ния, от числа детенышей в пометах, в которых они родились, от
погодных условий, от количества получаемой ими пищи и т. д.
Вес телят при рождении и в последующие периоды их жизни
определяется наследственными особенностями их матерей и от-
цов, условиями эмбрионального развития, уровнем кормления
и содержания. Все это создает громадное разнообразие живот-
ных и растений по их морфологическим и физиологическим свой-
ствам не Только в условиях природы, но даже при разведении
их человеком в относительно однородных условиях.
Такая сложная обусловленность биологических свойств орга-
низмов привела к необходимости разработки соответствующих
математических методов, с помощью которых можно было бы
выделить влияние отдельных факторов и оценить их относитель-
ную роль в общей изменчивости этих свойств. К их числу отно-
сится излагаемый в данной главе дисперсионный анализ.
Сущность дисперсионного анализа. Дисперсионный, или ва-
риансный, анализ (analysis of variance) представляет собой
в настоящее время самостоятельную и очень важную главу
биологической статистики. Сущность его заключается в уста-
новлении роли Отдельных факторов в изменчивости того или
иного признака. .
Дело в том, что влияние тех или других факторов на изу-
чаемый признак (или признаки) никогда не может быть выде-
лено в чистом виде. Хотя при проведении опытов и стараются
сохранить условия максимально однородными, все же разлим-
ные опыты дают несколько неодинаковые результаты. Объяс-
няется это тем, что да них влияют многочисленные случайные
187
;4^е’гдятёл^Й'ва, многие другиё факторы, йескОлько мёйяющйёсЙ
от опыта к опыту и не поддающиеся контролю. Тем более велика
роль таких дополнительных неконтролируемых факторов при
проведении анализа не в экспериментальных условиях,, а непо-
средственно в природе.
Вот почему возникает важная задача разложения общей
изменчивости признака на составные части, с одной стороны
определяемые изучаемыми конкретными факторами, а с дру-
гой — вызываемые случайными, неконтролируемыми причинами.
Дисперсионный анализ позволяет оценивать значимость влия-
ния отдельных факторов, а также их Относительную роль
в общей изменчивости.
Методы дисперсионного анализа были разработаны англий-
ским математиком и биологом Р. Фишером и применялись пер-
воначально главным образом для анализа результатов опытов
в растениеводстве и в животноводстве. Для различных схем опы-
тов были разработаны соответствующие схемы дисперсионного
анализа. Однако в дальнейшем выявилась полная возможность
использования дисперсионного анализа как при изучении биоло-
гического материала, взятого из природы, так и любых экспери-
ментальных данных.
На русском языке изложение методов Фишера по диспер-
сионному анализу применительно к полевым- опытам впервые
было дано Н. Ф. Деревицким в приложении к книге В. Иоган-
сена «Элементы точного учения об „изменчивости и наследствен-
ности с основами биологической статистики» (М.— Л., 1933).
В настоящее время во всех руководствах по статистике вооб-
ще и по биологической статистике в частности имеются главы
и разделы, посвященные этому методу. В 1960 г. в Новосибирске
вышла книга Н. А. Плохинского «Дисперсионный анализ».
Общие предпосылки. Представим себе, что мы анализируем
отклонение особи (или группы особей) от средней арифметической
популяции (х или р.), причем предполагается, что это отклонение
в некоторой степени связано с действием на. данную особь како-
го-то определенного фактора, например географических условий
местности, принадлежности к породе и т. д.
Тогда
/
х — р = А + е,
где н — средняя арифметическая популяции; ,
х — конкретное значение переменной (варианта);
А — доля отклонения переменной, связанная с влиянием дан-
ного конкретного фактора; .
е — остаточная часть отклонения, не объяснимая влиянием
данного, фактора. Это смесь всех Неконтролируемых и не-
определенных факторов, иначе говоря, результат случай-
ных отклонений.
188
Оченъ ваЖно,-что в фактическйготклонении варианты (ЙН-
менйой) от средней фигУрируют-Йкомпонента: а) та часть откло*
нения, которая зависит именно от данногр фактора; б) остаточ-
ная часть, не зависящая от данного фактора. В таком случае
можно сравнить значения А н е. .
При достоверном влиянии' изучаемого фактора значение А
будет в достаточной степени превышать значение е. По степени
превышения А над е можно судить о том, насколько достоверно
влияние данного фактора.
Приведенную общую схему, относящуюся - к отдельному .от-
клонению, можно перенести на вариацию многих вариант,
т. е. выразить степень вариации в вариансах (дисперсиях):
ей = а2А + о», (88)
т. е. общая варианса равна сумме 2 варианс: вариансы, опреде-
ляемой вариацией фактора А, и вариансы, определяемой други-
ми, неконтролируемыми (случайными) причинами.
Более сложный случай — отклонение переменной х от сред-
ней арифметической популяции ц, под влиянием 2 причин/влия-
ния факторов А и В. Например, фактором А может быть геогра-
фическое влияние местности, а фактором В — сезон года/
Тогда
х— |а = Л + В + АВ + е.
Здесь А — доля отклонения, связанная с влиянием фактора А;
В — доля отклонения, связанная с влиянием фактора В;
АВ — доля отклонения, связанная с влиянием не отдельных
факторов Л и В, а их взаимодействия;
е— остаточная, случайная часть отклонения.
В значениях варианс общая вариация о* может быть пред-
ставлена как
= аН о2ав + о2е. (88а)
Очевидно, что схему можно усложнять и дальше. Так, при
3 факторах
х — = А 4* В 4* С 4* ЛВ 4" ВС 4" ЛС 4~ ЛВС 4~ е.
Л, В, С —главные факторы;
АВ,ВС и АС — взаимодействие первого порядка;
ЛВС — взаимодействие второго порядка.
Аналогично можно выразить изменчивость вариант в вариан-
сах (о2).’
Нетрудно заметить, что сказанное выше непосредственно свя-
зано с тем, что изложено в разделе о вариансе (гл. 2).
Градации факторов и их характер. Обычно каждый изучае-
мый в эксперименте фактор Л имеет не одно, а несколько зна-
чений, которые называют градациями или уровнями фактора А.
В пределах же каждого уровня отдельные переменные (вариан-
ты) принимает разные значения, т. е. наблюдается случайная
189
вариация. То же относится и к более сложным случаям, когда
в общей изменчивости участвует несколько факторор, каждый
‘из которых может иметь свои уровни. Проводя дисперсионный
анализ влияния различных факторов, следует иметь в виду раз-
личный характер уровней факторов.
В одних случаях эти уровни фактически точно установлены.
Например, изучая влияние сезонов года, выделяют зиму, весну,
лето, осень. Внешние условия этих сезонов года строго фикси-
рованы.
С другой стороны, могут быть такие факторы, уровни кото-
рых не являются точно фиксированными или которые имеют
вообще все'возможные случайные градации. Так, например, сре-
ди факторов, влияющих на размеры детенышей у многоплодных
животных, надо учитывать и такой, как число детенышей в по-
мете. Но ему свойственна случайная вариация в довольно ши-
роких пределах. Например, у серебристо-черных лисиц число
детенышей в помете может колебаться от 1 до 10, а иногда
и большему песцов — от 4 до 20. Такие факторы называют слу-
чайными, понимая под этим только то, что случайными могут
быть разные их уровни. Впрочем, надо иметь в виду, что случай-
ные уровни некоторых из них тоже можно сделать фиксиро-
ванными.
Отсюда следует, что возможны очень разные схемы, или
модели, для дисперсионного анализа. Они могут различаться по
числу анализируемых факторов (одно-, двух-, трехфакторные
и т. д.), по характеру градаций внутри факторов (с фиксирован-
ными факторами, со случайными, смешанные схемы).
Есть еще так называемые иерархические модели (широко
используемые в зоологии, генетике). В этом случае уровни одно-
го фактора не располагаются случайно среди уровней других
факторов, но связаны с ними иерархически (иерархические моде-
ли будут рассмотрены особо).
При наличии единых общих принципов конкретные методы
дисперсионного анализа будут зависеть от того, с какой схемой
расположения материала приходится'иметь дело.
Таким образом, весь изучаемый материал может быть разбит
на ряд групп, различающихся как по отдельным факторам, так
и по их градациям. Изучение методами дисперсионного анализа
вариации внутри этих групп, между группами и, наконец, вариа-
ции всего материала в целом дает возможность установить,
влияют ли данные факторы на изменчивость или нет и какие из
них имеют больший удельный вес в общей изменчивости. •
Нулевая гипотеза. Как и в других случаях статистического
анализа, при дисперсионном анализе следует исходить из перво-
начально принимаемой нулевой гипотезы, а именно: что данный
фактор А (или В, или С и т. д.) не влияет. Если правильна ну-
левая гипотеза, должна быть равна нулю (то же относится
к оЬ, ci и т. д.), т. е. вся вариация сводится только к случайной.
190
Для того чтобы отбросить нулевую гипотезу, нужно доказать,
что Ол достоверно (т. е. с вероятностью не меньшей, чем 0,95,
или с уровнем значимости 0,05) отличается от нуля. Достовер-
ность значения может быть установлена, как это обычно де-
лают по отношению к любому статистическому показателю, путем
деления его на ошибку, т. е. (а? в данном случае играет роль
ошибки).
, Простейшая схема варьирования при различии по одному
фактору. Для того чтобы понимать смысл расчетов при диспер-
сионном анализе, очень важно с самого начала ясно представ-
лять возможную вариацию в тех группах, на которые разбивает-
ся фактический материал.
Разберем простейшую схему, когда анализируется влияние
только одного фактора, могущего принимать разные градации,
или количественные уровни:
1, 2, ... , i, ... , а.
Отдельные наблюдения (варианты) разбиваются на группы
согласно этим градациям фактора, изучаемого в опыте или при
наблюдениях в природе. Важно, что изучаемый фактор только
один, например: сортность культуры, или принадлежность к раз-
ным видам, или влияние удобрения, или роль способов обработ-
ки почвы и т. д. При наличии двух или нескольких факторов
потребуются более сложные схемы.
Распределение вариант при различии по одному фактору
представлено в табл. 41.
Таблица 4]
Схема варьирования при различии групп по одному фактору
Группы по одно- Отдельные варианты (наблюдения)*^ Суммы по Средние по
му фак- тору 1 2 3 f п группам Ti группам Xi
1 *12 *13 хч xin 2х> = Тг *i
2 *21 *22 *23 X2j Х2П SXg = *2
i */1 *f2 */3 Xij xin 2*/ = Ti *г
а *а1 *д2. *аэ xaj хап = Ta *^
ZXiJ = Т X
191
Я&сло наблюдений (вариант) в каждой группе п, но равное
число в группах не обязательно. Прит неравном числе можно
исходить из среднего числа nf.
Групп, иначе уровней фактора А,— а. Количество всех ва-
риант 1
' N—an( — atii).
Обычно разные уровни принято обозначать буквой i, а от-
дельные варианты (наблюдения) — буквой j. Поэтому каждую
варианту, независимо от того, где она находится, можно обо-
значать в общем виде как xfi. В пределах каждого уровня (груп-
пы) отдельные варианты принимают случайные значения:
Х.1, Х.2, Х,3, ... , X.].х.„.
Суммы вариант по каждой группе (в графе «суммы по груп-
пам») обозначены буквами Ть Т2,..., Т),..., Та. В общем виде их мож-
но обозначать Т(. Общая же сумма всех вариант 2 ху = Т. В по-
следней графе даны средние по группам xlt х2, ... , xt , ... , ха.
В общем виде групповые средние можно обозначить через хь
Общую же среднюю для всех вариант всех групп — через ~х.
Разное варьирование вариант и его характеристика. После
введения этих обозначений можно приступить к разбору варьи-
рования данных, представленных в.табл. 41.
Можно выделить как бы 3 типа, или направления, варьи-
рования:
а) общее варьирование всех вариант (ху), независимо от того,
в какой группе они находятся, вокруг общей средней х;
б) варьирование групповых средних х;, или, иначе, средних
каждого уровня данного изучаемого фактора, вокруг общей сред-
ней х;
в) варьирование вариант х1} внутри каждой группы вокруг
каждой групповой средней
Для характеристики этих варьирований при проведении дис-
персионного анализа используются уже известные из общего
курса статистики величины:
а) суммы квадратов отклонений от средней арифметиче-
ской;
б) средние квадраты отклонений, т. е. суммы квадратов,
деленные на количество степеней свободы. Это вариансы о2.
Суммы квадратов. Для всех 3 типов варьирования можно
вычислить суммы квадратов (слово «отклонений» для краткости
будем отбрасывать). В общем виде они будут следующими:
1. Общая сумма квадратов _
2(х/;-х)2.
И
Значок ij около знака суммы обозначает, что суммирование
прозводится по всем вариантам всех групп.
J92
2. Сумма квадратов для групповых средних
Sn^xj —х)2.
Чтобы эта величина была того же порядка, что и первая, введен
множитель nt, т. е. среднее число вариант в каждой группе (если
число вариант во всех группах одинаково, то просто п).
3. Сумма квадратов отклонений вариант от групповых сред-
них внутри каждой группы, иначе говоря, для случайной вариа-
ции внутри групп
2[2(х„—^)2].
i i
Два знака сумм указывают, что суммация производится
дважды: внутри каждой группы, т. е. по отдельным / (от 1 до п),
а затем по всем уровням i (от 1 до а).
Степени свободы. Чтобы вычислить средние квадраты (ва-
риансы), надо разделить каждую сумму квадратов на соответ-
ствующие им числа степеней свободы, которые будут следую-
щими:
для общей дисперсии
df=N— 1 (N=an);
для дисперсии групповых средних
df=a— 1;
для случайной вариации вариант внутри групп
df= (n—\)a=na—a—N—а.
Нетрудно заметить, что сумма чисел степеней свободы для
групповых средних и для вариации внутри групп должна рав-
няться числу степеней свободы для общей дисперсии:
' (N—a) + (a—l)=N—l.
Общая схема дисперсионного анализа при одном факторе.
Общая схема дисперсионного анализа приведена в табл. 42. Из
нее видно, что общая вариация разлагается на 2 компонента:
один из них — это вариация групповых средних (по градациям
фактора А) вокруг общей средней х; другой — вариация отдельных
вариант внутри групп. Последнюю вариацию можно рассматривать
как случайную в том смысле, что она создается многими неконт-
ролируемыми факторами (кроме учитываемого фактора Л). При де-
лении сумм квадратов, обозначаемых ss, на число степеней сво-
боды получаются средние квадраты (вариансы)—ms, непосредст-
венно измеряющие суммарную вариацию (формула (89)), и 2 ее
компонента (формулы (90) и (91)).
В дальнейшем мы увидим, что' весь этот анализ понадобится
для того, чтобы сравнить 2 средних квадрата — второй и третий,
пользуясь критерием -г)* 0 КОТОР°М говорилось в гл. 4.
7 П. Ф. Рокицкий
Таблица 42
Схема дисперсионного анализа (анализа вариансы) при одном факторе
Источник варьирования Сумма квадратов SS Число степеней свободы df Средний квадрат ms Номер фор- мулы для ms
Общее (все ва- рианты) (89)
Групповые сред- ние (фактор Л) 2пг (xl—"х)« а~ 1 —1— 2лг(^-х)а а— 1 i (90)
Варианты внут- ри групп (слу- чайные откло- * нения) 2 [2 (ху- 7?] N-а •«-'и (91)
Рабочие формулы для вычисления сумм квадратов. Вычисле-
ние сумм квадратов отклонений непосредственно по исходным
данным вполне возможно, но требует много труда. Поэтому
лучше воспользоваться рабочими формулами, основанными на
одной из формул для суммы квадратов отклонений, приведен-
ных в гл. 2, а именно той, где сумма квадратов отклонений вы-
числяется по значениям вариант:
Второй член является как бы поправкой к первому (его
в литературе обозначают буквой С).
Если далее использовать приведенные выше обозначения Sx,
для каждой группы (уровня фактора А) через Г, (Ть Т2. , Т{,
... , Та), суммы всех вариант — Т, число наблюдений в каждой
группе обозначать tit, общее число вариант — N, то рабочие фор-
мулы будут выглядеть довольно просто:
общая сумма квадратов
сумма квадратов для групповых средних
Т».
7 лг ’
сумма квадратов для вариант внутри групп (т. е. для случай-
ных отклонений)
Практически совсем не обязательно вычислять все 3 суммы
квадратов, достаточно вычислить только 2, например, первую
194
и вторую. Третья может быть получена путем вычитания второй
из первой.
При делении сумм квадратов на числа степеней свободы по-
лучаются средние квадраты (вариансы); Таким образом,-рабочие
формулы для них будут следующими:
для общего варьирования
= (89а)
для групповых средних
ms = a*= (2-^-— (90а)
а— 1 \ i nt N Г ' ’
для случайных отклонений
’» = ’’ = (^5’ (91а>
Проиллюстрируем методы дисперсионного анализа на 2 при-
мерах — ботаническом и зоологическом. При этом в первом из
них численности вариант в группах будут одинаковыми, что
упростит расчеты.
Пример дисперсионного анализа при однофакторной схеме
и одинаковой численности вариант в группах. В лаборатории
определяли содержание каротиноидов в листьях канатника в раз-
ные часы суток. Полученные данные представлены в табл. 43.
Такое построение таблиц является стандартным при дисперсион-
ном анализе и очень удобно для дальнейших вычислений.
Таблица 43
Содержание каротиноидов (в мг/дм8) в листьях канатника (Abutilon)
в разные часы суток
Часы суток Определение Х/у rt «г *i Г2
1 2 3 4
15 1,41 0,95 1,00 0,93 4,29 4 1,07 18,4041
18 . 1,17 1,10 0 84 1,01 4,12 4 1,03 16,9744
21 1,38 1,38 0,91 1,36 5,03 4 1,26 25.3009
24 0,62 0,48 0,43 0,62 2,15 4 0,54 4,6225
6 0,74 0,41 0,41 0,43 1,96 4 0,50 3,9601
9 0,76 0,59 0,74 0,46 2,55 4 0,64 6 5025
12 0,64 1,02 1,04 0,98 3,68 4 0,92 13,5422
Т = 23,81 Г8 = 566,9161 AZ=28 27j=89,3069
7*
195
Графа xt показывает, что среднее содержание каротиноидов в
различные части суток неодинаково. Однако каждая средняя вы-
числена только на основании 4 вариант, т. е. 4 определений ка-
ротиноидов (в 4 листах). Поэтому вместо обычного приема
сравнения средних арифметических, описанного в гл. 4, лучше
применить дисперсионный анализ, который поможет вскрыть разли-
чия между группами в целом.
Так как в формулах имеется величина 2х?^, то полезно со-
ставить вспомогательную таблицу, в которой все значения Ху воз-
водятся в квадрат и после этого суммируются.
Чтобы не загромождать текст главы таблицами, приведем эту
сумму в окончательном виде: 2x^ = 22,7316.
Первый этап работы — вычисление суммы квадратов.
Общая сумма квадратов равна:
2x2 — Цр = 22,7316 — 56-^161 = 22,7316 — 20,2470 = 2,4846.
У Ч N 28
Для вычисления суммы квадратов отклонений от групповых
средних по формуле
т*
ini N
надо было бы каждое Т? разделить на соответствующее nt. Но так
как во все часы дня было по 4 определения, то вычисления упроща-
ются, а именно:
2
?^г--?г=4-2:7’* -^=4-‘89’3069-20-2470=
= 22,3267 — 20,2470 = 2,0797.
Сумма квадратов для случайных отклонений
р 2
2x2 — 2 — = 22,7316 — 22,3267 = 0,4049.
ij ч nt '
Степени свободы будут следующими:
для общей вариации df = N— 1 =28— 1 =27;
для групповых средних df—a — 1 =7— 1 =6;
для случайных отклонений df = N—а = 28 —7=21.
В результате деления сумм квадратов на числа степеней
свободы в соответствии с формулами (89а), (90а) и (91а) по-
лучим 3 средних квадрата (вариансы). После этого может быть
составлена сводная таблица дисперсионного анализа (табл. 44).
Заключительным этапом дисперсионного анализа является сравне-
ние 2 средних квадратов, т. е. о2. Один из них характеризует варьи-
рование групп по часам суток, т. е. влияние изучаемого фактора —
времени суток, а другой—случайное варьирование вариант, в дан-
ном примере отдельных определений, внутри каждой группы. Этот
196
Таблица 44
Дисперсионный анализ данных о содержании каротиноидов в листьях
канатника в разные часы суток
Источник варьирования Сумма квадратов SS Число степеней свободы df Средний квадрат ms * F факти- ческое F табличное
при Р=0,05 при Р=0,01
Общее 2,4846 27 —
Фактор А (вре- мя суток) 2,0797 6 0,3466 0,3466 0,0193 “ 2,57 3,81
Случайные от- 21 0,0193 = 18,0
клонения 0,4049
Примечание. В последующих таблицах графы «сумма квадратов»,
«число степеней свободы» и «средний квадрат» будут отмечаться только сим-
волами ss, df, ms (последний взамен о2).
последний средний квадрат можно обозначить ot Он является, та-
ким образом, мерилом случайной ошибки. Поэтому в некоторых
работах и книгах его называют просто ошибкой. Сравнение о2 мо-
жет быть сделано с помощью критерия
о котором говорилось в гл. 4.
При нулевой гипотезе of тогда F — 1. Чтобы отвергнуть
2 2
нулевую гипотезу, надо доказать, что неравенство О] и 02 не слу-
чайно, т. е. выходит за пределы случайной ошибки. Граничные
значения F приведены в табл. V и VI для 2 уровней значи-
мости: Р = 0,05 и Р = 0,01. Достоверным признается такое факти-
чески полученное значение F, которое превышает табличное. В на-
шем случае фактическое F= 18,0; табличные же — 2,57 и 3,81.
При дисперсионном анализе величина F указывает на влия-
ние изучаемого фактора А в общей изменчивости материала. Для
нашего конкретного примера это означает, что можно считать
доказанным влияние времени суток на содержание каротинои-
дов в листьях канатника с уровнем значимости Р<0,01, т. е. с ве-
роятностью р>0,99.
Первоначальная нулевая гипотеза об отсутствии влияния
времени суток отвергается.
Пример дисперсионного анализа при однофакторной схеме
и различной численности вариант в группах. Разберем следую-
щий пример из зоологии. Изучали длину крыльев у самцов
3 видов скворцов. Полученные данные сведены в табл. 45.
197
Таблица 45
Длина крыльев самцов (в мм) 3 видов скворцов
Виды Измерение отдельных ПТИЦ Xij Tt n. Xi
Sturnus contra 120 120 121 122 122 126 122 123 125 125 126 1352 11 122,9 1827 904
St. ginginia- mus 123 124 125 125 126 127 127 127 128 128 129 129 1518 12 126,5 2 304 324
St. fuscus 122 122 125 127 127 127 128 129 1007 8 125,9 1 014 049
T=3877 ^=31
Ех?, = 1202 + 120* + ... + 1282 + 1292 = 485 097; Т2 = 15 031 129.
Можно было бы оценить достоверность различий между по-
лученными средними арифметическими длины крыльев 3 видов
и обычными методами (гл. 4), но данный пр.имер также удобен
для дисперсионного анализа.
Общая сумма квадратов
—тег = 485 097 — 150^12^ = 485097 — 484875 = 222.
ij J N 31
Сумма квадратов для групповых средних вычисляется несколько
сложнее, чем в примере с содержанием каротиноидов. Так как
п групп неодинаковы, то нельзя использовать 2Т?, а надо частные
у 2
.—- вычислять для каждой группы отдельно:
Ъ
„ Т* Т» 13522 , 1518® , 1007® ,оло7е
f - -АГ “ -ГГ- + -12- + ~8~ - 484875 =
1827904 , 2304324 . 1014079 .о.о_е
= —11—+—12— +---------§----484875 =
= 484956 — 484875 = 81.
Сумма квадратов для случайных отклонений
2
2 —1- = 485097 — 484956 = 141.
ij ini
Числа степеней свободы будут соответственно 30, 2 и 28.
Общие итоги вносятся в сводную*табл. 46..
198
Таблица 46
Дисперсионный анализ данных о длине крыльев
у самцов 3 видов скворцов
Источник варьиро- вания F факти- ческое F табличное
«SS df ms при P=0,05 при P=0,01
Общее 222 30 — __
Фактор А (виды) 81 2 40,5 S* -ci 5,0 ~8>1 3,34 5,45
Случайные откло- нения 141 28 5,0
Влияние межвидовых различий на длину крыльев доказы-
вается с уровнем значимости Р<0,01, т. е. с вероятностью
р>0,99.
Вопрос об установлении различий между группами (в данном
случае между видами) при дисперсионном анализе будет рас-
смотрен в конце этой главы.
Параметры, оцениваемые средними квадратами. На первом
этапе дисперсионного анализа можно ограничиться только уста-
новлением достоверности или недостоверности влияния изучае-
мого фактора. Так обстоит дело в ряде конкретных исследова-
ний по агрономии, растениеводству, животноводству, зоологии,
ботанике. Анализ заканчивается определением значения F, т. е.
отношения среднего квадрата (вариансы) групповых средних
к среднему квадрату (вариансе) вариант внутри групп, т. е. слу-
чайной вариации, и сравнением полученного F с табличными.
Однако в ряде случаев, особенно в эволюционно-генетиче-
ских, селекционных, популяционных исследованиях, необходим
более глубокий анализ. Дело в том, что получаемые значения
средних квадратов позволяют оценивать некоторые существенно
важные параметры. В приведенных примерах дисперсионного
анализа была использована модель фиксированных факторов.
Так, средние показатели длины крыльев скворцов разных видов
являются строго фиксированными видовыми показателями, а не
результатами случайных выборок из популяции, в котордй были
бы смешаны все виды скворцов. Иное дело — вариация по длине
крыльев внутри групп скворцов, состоящих из особей одного
вида. В каждом случае она характеризует конкретную выборку
из популяции данного вида, в пределах которой происходит
случайная вариация.
Проведенный с помощью критерия F анализ указывает
только на то, что вариация средних длины крыльев отдельных
видов заведомо отличается от случайной вариации длины крыль-
ев внутри выборок.
199
Таблица 47 Параметры* оцениваемые средними квадратами табл. 44 и 46 Однако очень важно уяс- нить более глубокий смысл среднего квадрата групповых средних. Дело в том, что ва-
Источник варьиро- вания Оценива- емые парамет- ры риация групповых средних имеет сложную природу. Хотя групповые средние, как это было в примере со скворцами,
Фактор А Случайные откло- нения пх2 и являются фиксированными, но и они варьируют вокруг не- которой средней ц. Их откло- нения от ц определяются как
принадлежностью к опреде-
ленному виду скворцов, так и случайной вариацией того же по-
рядка, что и вариация отдельных особей внутри групп.
Вот почему средний квадрат вариации групповых средних
может быть разложен на 2 компонента: и х2 (греч. каппа).
В предыдущие таблицы дисперсионного анализа по одному фак-
тору А следует ввести еще одну графу под заглавием «ожидае-
мый средний квадрат» или «оцениваемые параметры» (табл. 47).
Коэффициент п поставлен перед х2 для того, чтобы привести
средний квадрат, измеряющий видовую принадлежность, к уров-
ню первичных наблюдений. Так как п для разных групп могут
быть неодинаковы, можно взять среднюю величину П{. Для при-
мера с 3 видами скворцов «1 = 10, и тогда х2 определяется так:
л 40,5 — 5,0 35,5 о ее
х =—По---------= —= 3>55-
сущности х2 оценивает роль различий между видами сквор-
В
цов. Позднее мы встретимся с ней вновь, поэтому ограничимся
сказанным. Следует лишь добавить, что выделение оцениваемых
параметров позволяет лучше понять значение критерия F при
дисперсионном анализе. Теперь видно, что F оценивает отно-
шение
0 2 + ПХ2
~7Г-
Если х2 = 0, тогда F равно или близко к единице и нулевая
гипотеза остается в силе. Это значит, что различия по длине
крыльев, обусловленные принадлежностью скворцов к разным
видам, или различия по содержанию каротиноидов в листьях,
обусловленные разными часами суток, не доказаны.
При достаточной величине х2 значение F будет превышать
табличное, т. е. выходить за пределы случайных отклонений, что
явится основанием для отбрасывания нулевой гипотезы, т. е. для
признания достоверного влияния фактора А.
В связи с этим необходимо сделать одно предупреждение. Для
уверенности в правильном применении критерия F надо, чтобрг
200
значение знаменателя, т. е. of, было установлено достаточно ос-
новательно, на числе степеней свободы не менее 10. Если же
случайные отклонения основываются на малом числе степеней сво-
боды, значение of ненадежно. Тогда потребуется увеличение ко-
личества опытов.
Если сложная вариация групповых средних по изучаемому
фактору является не результатом фиксированных градаций данного
фактора, а следствием случайной вариации, то расчеты при дис-
персионном анализе по одному фактору ничем не отличаются от
изложенных выше, но смысл оцениваемых параметров меняется.
Вариация по А будет тогда настоящей случайной вариацией, ко-
торая может быть оценена не условной величиной х2, а вариансой
ст2 со значком А, т. е. Стд.
Правая сторона табл. 47 может быть записана следующим
образом:
Источник варьирования Оцениваемые параметры
Фактор А af + «’ А
Случайные отклонения ’f
F в этом случае представляет собой частное
8 f +
При оа =0 F = 1, т. е. нулевая гипотеза сохраняется. Если F
достоверно, нулевая гипотеза отбрасывается. Чтобы получить точ-
ную величину ад, надо вычесть из вариансы групповых средних
вариансу случайных отклонений и разность разделить на п.
Из сказанного ясно, почему в формулах (89) и (89 а), (90) и
(90а). (91) и (91а) вариансы были обозначены только знаками ms.
Вариансу для случайных отклонений можно обозначить как of.
Варианса же групповых средних не может быть обзначена как од,
так как в действительности она включает и of и о а (или х2 при фик-
сированных градациях по фактору Я).
Варьирование при двухфакторной схеме. Выше уже указы-
валось, что при участии в общей вариации 2 факторов А и В
анализ осложняется наличием взаимодействия между этими
факторами. Поэтому общая сумма квадратов при двухфакторной
схеме разлагается на 4 компонента: а) вариация под влиянием
фактора А; б) вариация под влиянием фактора В; в) вариация
под совместным влиянием А и В, т. е. взаимодействия А и В,
и г) случайные отклонения.
Кроме того, надо помнить, что при двухфакторной схеме
каждый уровень одного фактора должен сочетаться с любым
201
уровнем второго фактора. Так, если изучаются какие-то данные
за 3 года о животных из 3 различных местообитаний, то необхо-
димо, чтобы по каждому месту были данные всех трех лет. Если
же этого нет, то нужно применять другую схему анализа.
- Распределение вариант при варьировании по 2 факторам пока-
зано в табл. 48. В графах «вар.» помещены варианты, в графах
«пок.» — показатели Тих.
Символом г обозначается количество групп (уровней) по
фактору А, т. е. количество горизонтальных рядов (1, 2, 3, ...,
I, ..., г); с — количество Трупп (уровней) по фактору В, т. е. ко-
личество вертикальных столбцов, или колонок (1, 2, 3..... /,
..., с); п — число наблюдений в каждой клетке таблицы. В дан-
ном случае п равно 3*, но не обязательно, чтобы оно было оди-
наковым во всех клетках. Все же для простоты расчетов
выгоднее последнее, тогда nrb = N, т. е., общему числу всех на-
блюдений.
- Каждая варианта (наблюдение) может быть обозначена в общем
виде как xljk, т. е. как Л-тое наблюдение в ряду i и в вертикаль-
ном столбце /. Конкретная же варианта х имеет 3 значка. Первый
обозначает номер группы по фактору А, т. е. номер горизонталь-
ной строчки, второй — номер группы по фактору В, т. е. номер
вертикального столбца, третий — номер в данной клетке. В каж-
дой клетке даны сводные показатели: сумма вариант клетки (Т..)
и средняя арифметическая их (х..). Значки при них указывают
номера горизонтальной строчки и вертикального столбца. В общем
виде показатели для каждой клеточки Tlf иху.
Показатели для горизонтальных строчек, то есть для градаций фак-
тора А, даны справа в вертикальных столбцах: Тх., Т2., ..., Tz., Тг. и
соответственно хх., х2. и т.д. В общем виде их будем обозначать
Tz. и xz. или просто Tz и xz.
Для вертикальных столбцов (градаций по фактору В) показате-
ли представлены в нижней^части табл. 48. Это суммы Т.ъ Т.2< ...,
T.j... Т.с и средние х.х, x.2jl ...,~x.jt .... х.с. В общем виде они бу-
дут обозначаться как Ти х.} или просто Tj и х}.
Общая сумма всех вариант всех клеточек обозначается Т, а
общая средняя арифметическая — х.
Вычисление сумм квадратов и средних квадратов. После
введения всех этих обозначений можно перейти к построению
общих формул сумм квадратов, необходимых для проведения
дисперсионного анализа при 2 факторах.
Они будут следующими:
* Так как варьирование групп по фактору Л и по фактору В всегда срав-
нивают со случайными отклонениями вариант в пределах каждой группы как
мерилом случайной вариации (<те* 2), то последняя должна быть измерена на
достаточном материале. Это значит, что в каждой клетке надо иметь не менее
2 наблюдений, а еще лучше, если их будет больше.
202
Таблица 48
Схема варьирования при различии групп по 2 факторам
Группы (уровни) по фактору А Группы (уровни) по фактору В и отдельные наблюде- ния xijft внутри них Сумма по группа» фактора A Средние по груп- пам фактора А X/
1 2 3 . . . j . . . c
, вар. i вар. 8 С ex 3 i * (X Я CQ ПОК. • ex 2 § c
1 *111 *112 *113 Тп *121 *122 *123 Л2 * 12 *131 *132 *183 w 1 W со *1/1 *1/2 *1/8 Ту Xij *1C1 *1/2 *1/3 Tlc ~X1C Tv Xv
2 *211 *212 *213 *21 *221 *222 *223 И 1 к а *231 *232 *233 J1 s'1 *2/1 *2/2 *2/3 Ti} Xlj *2/1 *2/2 *2/3 T^c X^c Tt- ~Xv
3 *311 *812 *313 T’si Tai *321 *322 *328 Тзг ~х» *331 *332 *333 «г3 8 8 *3/1 *3/2 *3/3 T3j ~X3j *3/1 *3/2 *3/3 Тзс ~Хзс Ta. ~Хз-
i */11 */12 */13 Тц */21 */22 */23 S’ е* |*Г *231 */32 */33 *1 CO bi *//l *//2 *//3 TU ~*U *//l *f/2 *//3 ^ic &1с Ti- ~X,
J
Г *Г11- *Г12 *Г13 Тп ~Хп */21 */22 */23 1 С1 СО Ю */31 */32 */33 m co 1* *//l *r/2 *Г/3 Trj ~*rj *//l *//2 *Г/3 Trc xrc Tr. ~xr.
Суммы по группам фактора BTj Т.г r.t Г.» T-J T.c T —
Средние по группам фактора Вх/ X» 1 ~х-з Л ~*-« - X-J ~X-c — ^x
203
Общая сумма квадратов
—*)2.
ijk
т. е. простая сумма квадратов отклонений всех наблюдений от
общей средней арифметической.
Сумма квадратов для варьирования по фактору Л
nc£](xz— х)2,
i
т. е. ^помноженная на пс сумма квадратов отклонений всех значе-
ний xt от общей средней арифметической.
Сумма квадратов для варьирования по фактору В
пг^^-х)2,
т. е. помноженная на пг сумма квадратов отклонений всех значе-
ний Ху от общей средней арифметической.
Сумма квадратов для взаимодействия А и В
п — fa——*12 =
ч
= пS[*И—— Xj 4-х]2.
»7
Наконец, сумма квадратов для случайных отклонений
X‘J
т. е. сумма квадратов отклонений вариант от средних Отдельных
клеток таблицы.
Числа степеней свободы df таковы: для общего варьирования
гсп — 1, для варьирования по фактору Аг — 1, для варьирования
по фактору Вс — 1, для взаимодействия А и В (г— 1) (с— 1), для
случайных отклонений rc(n— 1).
Общая схема разложения вариации при двухфакторной схеме
дисперсионного анализа представлена в табл. 49. В ней же даны
и общие формулы для средних факторов, которые получаются
путем деления сумм квадратов на число степеней свободы.
Рабочие формулы при двухфакторном анализе. Для упроще-
ния расчетов лучше применить рабочие формулы для сумм квад-
ратов, а именно:
для общего варьирования
для варьирования по фактору А
J_yT?г2
ПС 1 пгс>
для варьирования по фактору В
204
_LyT*_TL
nr LA nrc>
для варьирования, характеризующего взаимодействие А и В,
для варьирования случайных отклонений (внутри всех групп)
Ух?. _ -LVt-
Zr l)k па1ч-
tjk Ч
В этих формулах п — число вариант в каждой клеточке; с —
число вертикальных столбцов, т. е. групп по фактору В; г — чис-
ло горизонтальных строчек, т. е. групп по фактору А.
Величина означает уже фигурировавшую ранее сумму
квадратов всех вариант. Далее приходится иметь дело с различ-
ными суммами вариант:
Ту — сумма вариант по отдельным клеткам (как рядов, так
и столбцов);
Т, —сумма вариант для i-рядов, т. е. рядов по уровням (груп-
пам) фактора А;
Т] — сумма вариант для /-столбцов, т. е. колонок по уровням
(группам) фактора В;
Т — общая сумма всех вариант.
Применение этих формул для сумм квадратов дает возможность
пользоваться не средними, имеющимися в табл. 48, а только сум-
мами вариант, кроме только того, что понадобится сумма квадратов
всех вариант (2х?;й). Поэтому в схеме варьирования табл. 48 мож-
но не записывать средних в отдельных клетках.
/11 \
Коэффициенты при отдельных суммах — и т. д. I слу-
жат для приведения всех величин к одному порядку. Число сте-
пеней свободы для, всех сумм квадратов приведено в табл. 49.
Поэтому можно записать следующие рабочие формулы для сред-
них квадратов, получающиеся путем деления сумм квадратов на
соответствующие числа степеней свободы:
для общего варьирования
для варьирования по фактору А
для варьирования по фактору В
(92 а)
(93а)
(94 а)
205
Таблица 49
Схема дисперсионного анализа при 2 факторах
Источник варьирования Сумма квадра- тов SS Число сте- пеней сво- боды df Средний квадрат ms Номер фор- мулы ms
Общее ГСП — 1 1 у (92)
- \х ijk х Г ijk ГСП— \L^xijk~ Х¥
Фактор А (группо- вые средние по г — 1 пс Vi — - (93)
г — l'2j ( Л;— X )2
фактору Л) Фактор В (группо- ЛшЛ 1 V - — i с-i £<*/-*)* !
(94)
вые средние по фактору В) "r 2j (-Г/—X)’ / с-1
Взаимодействие А и В (*/>—*7- (r-D(c-l) {r—\)(c— 1)S<*V— ij
— ху-|-х)» -Xi — Xj-^xY (95)
Случайные откло- нения jk xi j)2 ГС (п — 1)
rc («-1)2/ ijk
— xijT (96)
для взаимодействия Л и В
- 1 / 1 V Т2 1_ уТ2 J_yT2 , Л \
7715 (г — 1)(с —1) \ ПС 1 пг^^гсп)
для случайных отклонений
W - гс(л- 1) ($*''* -4^ Т» )'
(95а)
(96а)
Примеры дисперсионного анализа при двухфакторной схеме.
Проводились опыты по удобрению карповых прудов известью
(600 гк]га негашеной извести), суперфосфатом (72,8 кг! га Р2О5)
и известью и суперфосфатом вместе (с трехкратной повтор-
ностью) . Четвертый пруд в каждом блоке не удобрялся. Оконча-
тельные данные о продуктивности прудов (в переводе на 300 рыб
в каждом пруду) представлены в табл? 50.
Таким образом, n=3, r=2, с=2, jV=12. Применение рабочих
формул позволит вычислить значения сумм квадратов.
Общая сумма квадратов
Sx\]tt= 582 + 84я + ... + 74s + 852-=
= 52312 — 49 923 = 2389.
206
Таблица 60
Продуктивность карповых прудов с применением удобрений
Группы по фактору'Л (кальциевые удобрения) Группы по фактору В (фосфорные удобрения} Ti *1
О Р
вари- анты xijk Tii вари- анты xijk тч
0 58 84 39 Ти = 181 72 72 * 64 Тц = 208 Tj. = 389 хР = 64,83
Са 49 55 48 Та1 = 152 74 74 85 Т№ = 233 Га. = 385 ^.-64,17
т} Та = 333 Т.г = 441 Т = 774
xi х.1 = 55,5 х?2 —73,5 x = 64,5
5^ = 52312
<7*
Сумма квадратов для варьирования по фактору А (кальций)
S = т (389* + 385г) ~49 923•= -^б546 —
— 49923 = 49924 — 49923 = 1.
Сумма квадратов для варьирования по фактору В (фосфор)
7F? Т/ ~ S = Т(333' + 44Р) — 49 923 = —У— “
— 49 923 = 50 895 — 49 923 = 972.
Сумма квадратов для взаимодействия А и В
4-Sn —;s-SТ? - yS7'? + £ = 4-(181- +208- + 152’ +
+ 233е) — 49 924 — 50 895 + 49 923 = 1533*18 —
207
— 49 924 — 50895 + 49 923 = 51 139 — 49 924 —
— 50895 + 49 923 = 243.
Сумма квадратов для случайных отклонений
SxL —= 52312 — 51 139 = 1173.
ijk ’ п ij 1
Сводка результатов дисперсионного анализа дана в табл. 51.
- Таблица 51
Дисперсионный анализ данных о влиянии удобрений Са, Р и Са + Р
на продуктивность карповых прудов
Источник варьи- рования SS df tns F фактическое F табличное
при Р = 0,05 при Р = 0,01
Общее 2389 11 — — — —
Са 1 1 1 +-W — —
Р 972 1 972 972 -66 147“ 6,6 5,32 11,26
Са + Р 243 1 243 241 = 17 147 ’ 5,32 11,26
Случайные отклоне- ния 1173 8 147 — — —
С помощью критерия F проверяется достоверность средних
квадратов для источников варьирования: Са, Р и Са + Р. Роль Са
оценивает Р=у1= 0,007, т. е. роль Са не доказана.
972
Для влияния Р F = =6,6. Табличные значения F при df = 1
и df = 8: для Р — 0,05 — 5,32 и для Р = 0,01 — 11,26. Таким об-
разом, эффект фосфора можно принять доказанным (нулевая ги-
потеза отвергается). Все же полученное значение F удовлетворяет
только уровню значимости Р = 0,05. При более жестких требова-
ниях следовало бы воздержаться от окончательного вывода до
проведения новых, более полных исследований. Дело в том, что
опыты были поставлены только на трех повторностях, поэтому
число степеней свободы для случайных колебаний (df = 8) ниже
минимально допустимого числа 10, о чем говорилось выше. F для
взаимодействия Са + Р очень мало (=1,7), поэтому в данном
случае влияние взаимодействия не доказано. Нулевая гипотеза ос-
тается в силе.
208
Второй пример более сложный. Здесь по каждому фактору
не 2 градации, как в предыдущем примере, а больше. Больше и
число степеней свободы.
На 5 самках дрозофилы поставлен опыт по изучению развития
мушек из оплодотворенных яиц при разных температурах (20, 25,
30°). От каждой самки при каждой температуре брали
по 40 яиц. Их разделяли на 2 группы по 20 яиц в каждой.
Таким образом, приведенные в табл. 52 данные о количестве
неразвившихся яиц относятся к каждой из 30 групп опыта, в ко-
торых первоначально было по 20 яиц.
Таблица 52
Количество неразвившихся яиц (включая и погибших личинок)
в каждой группе от 5 самок при разных температурах
Самки (фактор Л) Температуры (фактор В) Tt
20° 25° 30°
группы Тц группы Тц группы Тц
1 2 1 2 1 2
1 1 1 Тц~2 0 4 Т1г = 4 0 1 Лз=1 Tv = 7
11 9 Та = 20 5 5 = 10 10 14 Т23 = 24 Та. = 54
3 4 3 Тэт = 7 3 2 Таг = 5 1 1 Т33 = 2 Т3. = 14
4 10 7 Т41 = 17 8 6 Т« = 14 5 7 Т43 = 12 Т4. = 43
5 2 0 7.1 = 2 2 0 Ти = 2 2 4 Лз = 6 ть. = 10
Т] Т.х=48 Т.2 = 35 Т.8 = 45 Т= 128
Следовательно, п=2; г=5; с—3; N—3Q.
С помощью рабочих формул (92 а) — (96 а) можно вычислить
все средние квадраты. Начать надо опять с вычисления сумм
квадратов. Они будут следующими:
общая
^;-£. = (1’+1’+--- + 2’ + 4,)-ТГ =
= 958 — 546 = 412;
сумма квадратов для фактора А (индивидуальность самок)
iS Tl - £ = 4- (72 + 542 + 642 + 432 + 102) - -
= 852 — 546 = 306;
209
сумма квадратов для фактора В (влияние температуры)
-^, = -я(48’ + 35- + 45>)-^=
= 555 — 546 = 9;
сумма квадратов для взаимодействия А и В
+ —1^7? +£„-
= -у (22 +*202 + 7’ + ... + 122 + 62) —852 — 555 + 546 =
= 924 — 852 — 555 + 546 = 63;
сумма квадратов для случайных отклонений
У х2 _ ± J Т2, = 958 — 924 = 34.
ijk J п ij
Числа степеней свободы для разных сумм квадратов: общей
гсп—1=29; по фактору А г—1=4; по фактору В с—1=2; для
взаимодействия (г—1) (с—1) =8; для случайных отклонений
rc(n— 1) = 15.
Деление сумм, квадратов на число степеней свободы даст не-
обходимые средние квадраты (вариансы). Для общего варьиро-
вания средний квадрат не нужен.
В табл. 53 приведены окончательные результаты.
Таблица 53
Дисперсионный анализ данных о количестве неразвившихся яиц
дрозофилы при разных температурах
Источник варьи- рования S3 df ms F фактическое F табличное
при Р = 0,05 при Р=0,01
Общее Фактор А (индивиду- альность самок) 412 306 29 4 76,5 76,5 __333 2,3 ,3 3,06 4,89
Фактор В (разные тем- пературы) 9 2 4,5 -^1 = 19 2,3 3,68 6,36
Взаимодействие А и В 63 8 7,9 7,9 — з 4 2,3 ~3, 2,64 4,0
Случайные отклоне- ния 34 15 2,3
Достоверность средних квадратов, характеризующих вариа-
цию количества неразвившихся яиц в зависимости от температу-
ры во время развития и индивидуальности самок.а также взаи-
модействие между этими факторами проверяется обычным путем
210
с помощью критерия F. Можно считать, что влияние индиви-
дуальности самок доказано с уровнем значимости Р<0,01. Влия-
ние температуры не доказано. Влияние взаимодействия нельзя
считать окончательно доказанным, так как фактическое F превы-
шает табличное только при Р=0,05, однако на него необходимо
обратить внимание.
В связи с результатами данного опыта следует отметить,
что дисперсионный анализ, как и всякий иной математический
метод, не может заменить соответствующего биологического
анализа. В данном конкретном случае он дает лишь указание
на роль индивидуальности отдельных самок в изменчивости ко-
личества неразвившихся яиц и на недоказанность влияния темпе-
ратур 20—25—30°. Биолог же должен изучить причины этих явле-
ний. В частности, без биологического анализа нельзя понять,
почему все же взаимодействие между индивидуальностью самок
и температурой во время развития оказывает некоторое влияние
на количество неразвившихся яиц.
Оцениваемые параметры при двухфакторном дисперсионном
анализе. При двухфакторном дисперсионном анализе, как и при
анализе по одному фактору, значения средних квадратов оцени-
вают определенные параметры вариации: при фиксированных
уровнях факторов — условные, которые можно обозначить бук-
вой х2, и при случайных уровнях — отражающие действительную
случайную вариацию и поэтому обозначающиеся обычными о2.
Возможен и третий случай—смешанная модель, когда уровни
одного фактора, например А, фиксированные, а другого (В) —
случайные. Оцениваемые параметры для трех моделей следую-
щие:
Источник варьи- рования ms Оцениваемые параметры
I II ш
Фактор А 1 а1 + лсхл ’’ + па^в + пс°А °2+По?4в + лс*Д
Фактор В 2 + ПГ а3е + "а3Ав + пгвЯ ’5 + пп^
Взаимодействие А и В 3 "е + П^АВ °2 + ЛаЛВ
Случайные откло- нения 4 ве
В приведенных выше примерах двухфакторного анализа зна-
менателем при вычислении F был взят средний квадрат последней
строчки таблицы, то есть ms случайных отклонений. Сравнение
оцениваемых параметров по 3 моделям показывает, что значе-
ния F для оценки достоверности влияния факторов Л и В, а так-
же взаимодействия Л и В надо вычислять по-разному, в зависи-
мости от характера модели. В I модели (уровни по обоим факто-
211
рам фиксированы) во всех случаях знаменателем должен быть
ms4. Во II модели (уровни по обоим факторам случайные) mst
используется как знаменатель, только для оценки достоверности
взаимодействия. Для оценки же роли факторов Ли В — знамена-
тель ms3. Но если наличие взаимодействия не доказано, то можно
взять знаменателем ms4 и для вычисления Fa и Fb. Наконец, в
смешанной модели (III) F для оценки роли взаимодействия пред-
ставляет собой отношение ms3: ms4-, для оценки влияния А (фак-
тора с фиксированными уровнями) ms\: tns3 и для оценки влия-
ния В (фактора со случайными уровнями) msz : ms4.
Однако некоторые авторы считают возможным не придавать
значения Этим различиям и во всех Случаях знаменателем для
вычисления F брать средний квадрат случайных отклонений,
то есть ms4.
Дисперсионный анализ при трехфакторной схеме. При струк-
туре материала, различающегося по 3 факторам, применяется
принципиально та же схема анализа, что и при различиях по
2 факторам, но она более сложна и поэтому требует большого
внимания при расчетах.
Общая сумма квадратов разлагается на 8 компонентов:
1. Эффект фактора А.
2. Эффект фактора В.
3. Эффект фактора С.
4. Взаимодействие А и В.
5. Взаимодействие А и С.
6. Взаимодействие В и С.
7. Взаимодействие А, В и С вместе (взаимодействие второго
порядка).
8. Случайные отклонения.
Каждая отдельная варианта обозначается 4 значками, а имен-
но xysz. Соответствующие средние: х— средняя арифметическая
всех наблюдений; xt, xt п xk — средние для уровней по_ фактору
А, по фактору В и по фактору С отдельно; xtj, xik и сред-
ние для всех уровней по 2 факторам без учета третьего; xijk—
средние всех клеток решетки.
Чтобы не спутать буквы, можно обозначить число групп по
„факторам А, В и С одной буквой г со значками 1, 2, 3. Тогда
общая схема анализа может быть представлена в табл. 54.
Средний квадрат, как обычно, получают делением суммы
квадратов на число степеней свободы, поэтому для экономии
места его можно не включать в таблицу. Общая схема анализам
в сущности та же, которая была изложена выше для дисперсион-
ного анализа по 2 факторам. В частности, таков же расчет сумм
квадратов и степеней свободы для взаимодействия по двум фак-
торам. Наряду с учетом взаимодействия А и В добавляется учет
взаимодействия Л и С и В и С. Новым является учет взаимодей-
ствия всех 3 факторов Л, В и С.
212
Таблица 54
Схема дисперсионного анализа при 3 факторах
Источник
вариации
SS
Общее
Фактор А
Фактор В
Фактор С
Взаимодействие
А и В
Взаимодействие
В и С
Взаимодействие
А и С
Взаимодействие
А, В и С
Случайные от -
клонения
Stfyj» —*)2
ijkl
л/Уз S — *)2
i
«'i'sS (</ —х)2
/
n'l'zSfo —*)2
k
nr3 S'(хц —~Xi —~Xj 4-х)2
_ ‘i
«'1 S (xjk —~Xj -^Xk +~*)2
ik
nr2 S (xtk ~~~~Xi — x * 4- x)2
ik
— x'ij — xik — Xjk 4-7i + */ +
ijk
+ xk — x)2
S (xijhi — Хць)г
ijkl
nrlr2r» — 1
Г1— 1
'2—1
ra— 1
('1-1) ('2-0
('2-1) ('3-1)
('1-1) ('3-1)
('1-1)('2-1)X
X('3-l)
'1'2' (« — 1)
Пользование квадратами отклонений различных средних от
общей средней в случае анализа по 3 факторам еще более ослож-
нило бы технику расчетов, поэтому и здесь для подсчета сумм
квадратов целесообразно пользоваться рабочими формулами, J3
которых фигурируют квадраты вариант и суммы вариант по
группам.
Они будут следующими:
общая изменчивость
V 2 _ Т8 .
ijkl Xt )Ы «'1'2'3*
эффект А
«'2'3 i
ПГ1ГаГа
213
эффект В
——ZjT,--------—;
nV, j * nriWt
эффект С
«V» k «'Ws
взаимодействие А и В
1-У^2 1 У <р2 1 У V2 , 7» .
~ j---------- — Z-l i i-^‘i T" яг"г r~'
nr3 ij 3 nr2rS I nrlr3 / nrlr2r3
взаимодействие В и С
-~-Ит1 +
nri jk я nrirs / пг1гг k 'Wi
взаимодействие А и С
-LTiT2lk--^— Sr?—^StI+^t;
nr2 ik R ПГгГ9 i nrlr2 A ^Wl
взаимодействие А, В и С
+-^г
случайные отклонения •
Sx?,w-4-STU
цы ,ы п uk 1
рг
Во всех этих формулах поправка одна и та же —пг^"* т*е-
квадрат суммы всех вариант, деленный на общее их количество.
При вычислении первой части рабочих формул важно не спутать,
какие конкретно суммы надо возводить в квадрат. Чтобы не
загромождать текста, ограничимся только этими формулами для
сумм квадратов в буквенной символике без окончательных формул
для средних квадратов и без приведения конкретных примеров.
Оцениваемые средними квадратами параметры при 3 факторах
принципиально не отличаются от указанных выше для случая
двухфакторного дисперсионного анализа. Они приведены в табл. 55
для случая, когда уровни по всем факторам будут случайными;
Если же различия между уровнями по одному из факторов явля-
ются не случайными, а фиксированными (смешанная схема), соот-
ветствующий компонент вариации надо обозначать не о2, а
каким-либо иным значком, например х1, как указывалось при раз-
214
Таблица 55
Оцениваемые параметры при трехфакторном дисперсионном анализе
Источник варьирования ms Оцениваемые параметры
Фактор А
Фактор В
Фактор С
Взаимодействие А и В
Взаимодействие В и С
Взаимодействие А и С
Взаимодействие А, В и С
Случайные отклонения
1
2
3
4
5
6
7
8
°? + Па3АВС + '"’з’Дв + лга°Дс + пг^А
ае + ^АВС + ПГ^АВ + пг1а&С + nrlrS®b
+ ^АВС + «'УДс + nrl°^C +
°2e + ™ABc + nr^AB
°e + ”аЛВС + nrla%C
+ na3ABC + nr2°^C
°?
боре однофакторной схемы, или просто К со значком, обозначаю-
щим данный фактор А, В, С и т. д.
Разбор параметров, оцениваемых различными средними квад-
ратами, показывает, что в данном случае оценить с помощью
критерия F достоверность влияния отдельных факторов и их
взаимодействия значительно-сложнее, чем в предыдущих случаях
дисперсионного анализа. Поэтому мы ограничимся сказанным,
отослав читателя, которому понадобятся эти методы, к специаль-
ной литературе.*
Иерархическая схема дисперсионного анализа. Все предыду-
щие схемы были факторными. В них предусматривалось, что
уровни одного фактора сочетаются с любыми уровнями всех дру-
гих факторов. Таким образом создаются группы вариант, на ко-
торые действуют любые сочетания всех изучаемых факторов.
Обычные факторные схемы чаще всего применяются в опытах,
план которых строится экспериментатором заранее. Очевидно,
что такой план должен предусматривать наличие всех сочетаний
градаций разных факторов (или почти всех, что иногда возможно
при так Называемых «выпавших» группах опыта).
Однако при анализе материала, взятого из природы или из
хозяйства, обычные факторные схемы могут быть неосуществи-
мыми, так как внутри градаций (групп) фактора А возможны
различные, отличающиеся друг от друга градации (группы)
факторов В, С и т. д.
Так, например, при изучении данных об удоях коров-дочерей,
происходящих от разных родителей и относящихся к разным
породам, обнаружится определенная связь между группами
и влияющими на них факторами (рис. 18).
См. Снедекдр Дж. У. Статистические методы, гл. 12, стр. 336—342.
215
Факторы
Уровни
Рис, 18, Схема иерархических связей между факторами и их
уровнями. Уровни низшего порядка располагаются только
внутри определенных уровней высшего порядка. Факторы:
А — породы; В — быки; С — покрытые ими коровы; D — до-
чери; х — варианты, т. е. удои коров-дочерей по отдельным
лактациям.
К породе I относятся только быки А, В, С. Остальные быки
других пород (И и III). Бык А покрыл коров 1, 2, 3; бык В — ко-
ров 4, 5 и 6; бык С — опять иных коров 7, 8, 9, 10 и т. д. Корова 1
дала дочерей а и Ь\ корова 2 — дочь с; корова 3 — дочерей d, е nf
и т. д. Наконец, от каждой дочери было изучено по нескольку
лактаций li, lz и т. д.
Варьирующие по отдельным лактациям удои коров зависят
от 4 факторов: породы, быки, матери, дочери, но связь между
ними осуществляется по иерархической лестнице — от более об-
щих факторов к более частным, или от факторов высшего поряд-
ка к факторам низшего порядка. Поэтому такие схемы, или мо-
дели, получили название иерархических.
Подобным же образом может быть сгруппирован зоологиче-
ский или ботанический материал по факторам: виды, подвиды,
экотипы, места обитания, выборки, отдельные экземпляры. Для
иерархических схем характерно отсутствие свободных сочетаний
между градациями факторов А, В, С и т. д., в этом их отличие от
рассмотренных выше факторных схем. Так, коРовы-дочери могут
быть только от определенных матерей, а не от любых коров попу-
ляции. Одни коровы-матери покрыты одними быками, а другие —
другими. Определенные экотипы входят в состав одних подвидов,
другие — в состав других и т. д.
Иерархические лестницы могут быть короче или длиннее в за-
висимости от количества учитываемых факторов.
Очевидно, что варьирование при иерархической схеме будет
принципиально отличаться от варьирования при обычной фактор-
ной схеме. Для простейшего случая — двухфакторной иерархиче-
ской схемы — оно представлено в табл. 56.
216
Таблица 56
Варьирование при иерархической двухфакторной схеме
дисперсионного анализа
Группы (уровни) по фак- тору А Группы по фак- тору В Отдельные наблюдения (варианты) x^k Tl) xij Ti Xi
1 2 k ... с
1 1 2 / Ь хт *112 *и& хпс *121 *122 *12А *12С *1/1 *1/2 Xljk XLjC Х1Ы *Ш xlbk xlbc‘ Л1 ^12 Ti) Tlb *11 *12 *lb Tx Xl
2 1 2 / Ь *211 *212 *21ft *2U *221 *222 *22ft *22c *2/1 *2/2 *2/k X2jc *261 *2fr2 *2ftjfe X?bC Tn ^2b *2i *22 *2/ X2b Tt x2
i 1 2 i ь *111 */12 Xilk xiic */21 */22 */2A */2C Xljl Xlj2 Xijk XljC xibl xib2 xibk xlbc Ta Tlt Tu Tlb */i */2 xib Ti Xi
а 1 2 / b xail xai2 xaik xalc xa 21 *a22 *a2 ft * a2c xa Ji xa/2 xa j k xa jc xabi xab2 xabk xabc Tai T' a2 Tab *ai xa2 xaj xab Ta ~Xa
T X
217
Применяются следующие обозначения: а — число групп
(уровней) по фактору А (в таблице имеются группы, обозначен-
ные 1, 2, i, а); b — количество групп (уровней) по фак-
тору В. Во всех группах фактора А в приведенной схеме b одина-
ково (1, 2, .... /, Ь), но в конкретном материале такие случаи
обычно редки, поэтому b должно обозначать среднее-число групп
по фактору В внутри отдельных групп фактора А. Точно так же
и с должно обозначать среднее число вариант (или наблюдений)
в каждой группе фактора В (в схеме варианты обозначены 1,
2...k, ..., с), так как одинаковым оно практически никогда не
бывает.
Каждая варианта обозначается в общем виде как хцъ. Сим-
вол i указывает, что варьирование происходит по группам факто-
ра А, символ j — на варьирование групп по фактору В внутри
групп фактора А. Наконец, символ k относится к случайной ва-
риации вариант внутри групп фактора В (и тем самым внутри
групп фактора Л).
Обозначения средних: х—средняя арифметическая для всех
вариант, xi— средние для групп фактора А, х1} — средние для
групп по фактору В внутри групп фактора А.
Суммы вариант обозначаются буквами Т: — суммы вари-
ант каждой строчки, т. е. внутри каждой / — группы фактора —
и, значит, во всех i — группах фактора А; 7\ — суммы вариант
во всех группах фактора А; Т — общая сумма всех вариант.
По тйкому же принципу может быть построена схема и для
количества факторов больше 2. Тогда группы по фактору В
в свою очередь дробятся на группы по фактору С и т. д.
Общая схема двухфакторного дисперсионного анализа при
иерархической связи представлена в табл. 57. В ней указаны
Таблица 57
Общая таблица двухфакторного дисперсионного анализа
при иерархической схеме с указанием оцениваемых параметров
Источник варьирования SS df ms Оцениваемые параметры
Общее *)2 ijk abc — 1 ms
Фактор А be S (xL — x)2 i a — 1 msi + + ь^а
Фактор В C (хц ~~~ Xi) O' a(ft-l) ms2
Случайные от- клонения ab(c — 1) ms3 •J
218
формулы для сумм квадратов и для чисел степеней свободы,
а также оцениваемые параметры. Для средних квадратов, кото-
рые в табл. 57 отмечены только номерами, общие формулы, оче-
видно, будут следующими:
для общего варьирования
Li/*
для варьирования групповых средних по фактору А
bc£ (xt— х)2
для варьирования групповых средних по фактору В
для случайных отклонений
ч
ms3 — аЬ (с — 1) Xu {xi)k xij)
L</*
(97)
(98)
(99)
(100)
Рабочие формулы при иерархической схеме. При иерархи-
ческой схеме, как и в других случаях дисперсионного анализа,
для вычисления сумм квадратов и средних квадратов выгоднее
пользоваться рабочими формулами, при этом надо начинать
с верхней точки иерархической схемы.
Рабочие формулы для сумм квадратов будут-следующими:
для общего варьирования
i/*
для варьирования по фактору А
для варьирования по фактору В
для случайных отклонений
• *’/*
i/*
Следует обратить особое внимание на отличие рабочих формул
для суммы квадратов при иерархической двухфакторной схеме от
рабочих формул при обычной двухфакторной схеме. В последнем
случае поправка для всех сумм квадратов (кроме случайных от-
219
J’S
клонений) одна и та же —В первом же случае такая по-
правка пригодна для исчисления общей суммы квадратов и суммы
квадратов отклонений от групповых средних по фактору, располо-
женному как бы на вершине иерархической лестницы. Для полу-
чения же сумм квадратов для последующих звеньев этой лестницы
надо вычитать из первой части выражения основную часть суммы
квадратов предшествующего звена. Это позволяет дать общую
схему рабочих формул сумм квадратов для любого числа факто-
ров, расположенных по нисходящей лестнице. Например, для
сумм квадратов пяти факторов:
фактор А'
1 V т?_________1 т2,
bcdef Li 1 abcdef 1 ’
фактор В
1 У1 7’»_______1 У1 'г?.
cdef Li bcdef Li 1 ’
фактор С
и т. д.
ijk Ij
Наконец, сумма квадратов для случайных отклонений
' S Xijklmn у~ У Тцы
ijklmn ijklm
а для общего варьирования
^Xtjkimn— ~^def Т2.
ijklmn
Зная рабочие формулы для сумм квадратов при двухфакторной
иерархической схеме, можно легко получить значения средних
квадратов, разделив суммы квадратов на соответствующие им
числа степеней свободы (указанные в табл. 57). Тогда рабочие
формулы для средних квадратов будут иметь следующий вид:
для общего варьирования (вычисление необязательно)
ms
1
abc — 1
.«7*
у2 “
abc
для варьирования по фактору А
msi
а ~ 1
(97а)
(98а)
для варьирования по фактору В
22&
для случайных отклонений
ms3 —
_____1_
ab (с —
|Г ХЧ'Ь
к*
О I
Ч
(99а)
(100а)
В табл. 57 показаны параметры, оцениваемые средними квад-
ратами. Из их структуры видно, что для установления достовер-
ности влияния факторов А и В придется брать разные знамена-
тели:'для В — ns3, т. е. се, а для А — mss, т. е. +
р,— mh
А ms2'
Это очень важное отличие от обычной двухфакторной схемы.
Кроме того, здесь нет взаимодействия А и В. Исходя из парамет-
ров, можно вычислить точные значения и вычитанием вто-
рого среднего квадрата из первого или третьего из второго и деле-
нием на соответствующие коэффициенты (Ьс или с).
Примеры дисперсионного анализа при иерархической схеме.
Так как иерархическая схема очень слабо освещена в литера-
туре (как нашей, так и зарубежной, кроме книги Снедекора),
проиллюстрируем ее двумя отличающимися по материалу при-
мерами.
Первый из них — зоотехнический. Поросят забивали по
достижении ими веса 90 кг и измеряли их длину. От каждой
матки брали по 4 поросенка. Данные о длине 60 поросят,
происходящих от 3 хряков и 15 маток, представлены в табл. 58,
составленной в форме, удобной для дисперсионного анализа.
Здесь а=3; 6=5 и с=4; N = abc = 6Q. Степени свободы:
по фактору Л (хряки) а—1=2; по фактору В (матки) а{Ь —1) =
= 12 и для случайных отклонений (особи) ab(c—1)=45,
общая 60—1=59.
Для определения средних квадратов сначала вычислим суммы
квадратов:
общая
V*2 — = 521274,25 — 5596°0’52 = 521274,25 — 520894,84 =
ilk
= 379,42;
для фактора А (хряки)
4г У И - -?г = 4г (18442 + 1856® + 1890,52) — 520894,84 =
c/v uQC
i
== 520953,11 — 520894,84 = 58,27;
221
Таблица 58
Данные о длине поросят (в см), происходивших от 3 хряков
и 15 маток, весом в 90 кг
Хряки (фактор Л) Матки (фактор В) Длина отдельных поросят Ti} Ti
1 2 3 4
1 92,5 93,5 95,0 89,5 370,5
2 , 93,0 98,0 95,0 92,5 378,5
м 3 *94,0 91,0 93,0 92,0 370,0 1844,0
4 89,0 89,0 88,0 91,0 357,0
5 93,0 91,0 94,0 90,0 368,0
6 91,5 95,0 91,0 91,0 368,5
7 92,0 95,5 95,5 92,5 375,5
N 8 95,5 90,5 94,5 92,5 379,0 1856,0
9 88,5 91,0 91,5 96,5 367,5
10 93,5 94,0 91,0 93,0 371,0
11 96,0 95,0 89,0 95,0 375,0
12 94,0 96,0 93,5 97,0 380,5
0 13 94,5 100,0 95,0 96,0 385,5 1890,5
14 92,5 93,0 93,0 92,5 371,0
15 91,0 94,0 99,0 94,5 378,5
S x?Jk = 521274,25 Т = 5590,5
для фактора В (матки)
— У ГЛ — ^-Ут?=4-(370,52 + 378,88+ ... + 37Р + 378,5а) —
С шшЛ ОС
— 520953,11 = 521053,57 — 520953,11 = 100,46;
случайные отклонения
^xfjk —= 521274,25 — 521053,57 = 220,68.
4/Л
Зная суммы квадратов, можно вычислить средние квадраты
по формулам (98а), (99а) и (100а). Итоги дисперсионного ана-
лиза даны в табл. 59.
Влияние маток на длину поросят при забое не доказано. Ну-
левая гипотеза остается в силе. Что же касается роли хряков, то
222
Таблица 59
Дисперсионный анализ данных о длине поросят в зависимости
от хряков и маток
Примечание. Ввиду отсутствия в табл. V и VI строчки df — 45 взяты
табличные значения F для df = 40.
полученное F несколько превышает табличное при Р — 0,05, но
значительно ниже табличного при Р=0,01, поэтому и влияние
хряков нельзя считать доказанным.
Второй пример — зоологический. Сравнивали группы особей
Drosophila persimilis из трех разных местностей по количеству
стернальных щетинок. В каждой группе было по 4 выборки,
состоящих из 5 особей. Полученные данные сведены в табл. 60.
Из табл. 60 видно, что градации по местностям а = 3; число
выборок в каждой местности Ь~4; количество особей в каждой
выборке с —5.
Суммы квадратов следующие:
общая
Г *?/*---Ц- = 70607,0 — = 70607,0 — 69156,15 = 1450,85;
. Clue* ои
‘7*
для фактора А (местности)
ТгЕ77 - £ = i <5782 + 6734 + 7864) “ 69156,15 =
= 70240,45 — 69156,15= 1084,30;
. для фактора В (выборки)
~ -iST«? = 4'(1454 + 1434 + 15Р + +1932 +
“ + 193а) — 70240,45 = 70276,20 — 70240,45 = 35,75;
для случайных отклонений (особи)
Sx?/*----= 70607,0 — 70276,2 = 330,8.
223
Таблица 60
Число стернальных щетинок у Drosophila persimllis
из разных местностей Америки
Фактор А (местности) Фактор В (выборки) Данные по отдельным ОСОбЯМ Xqk ТИ Л
А 1 27 31 30 30 27 145
2 26 28 29 31 29 143 578
3 28 31 31 28 33 151
' 4 29 25 28 27 30 139
В 1 35 33 33 35 38 174
2 33 33 31 33 37 167
3 32 36 33 33 33 167 673
4 32 35 31 34 33 165
С 1 41 34 40 41 42 198
2 41 40 23 37 41 202 786
3 37 42 36 41 37 193
4 45 38 31 36 43 193
Т = 2037
2х/.а = 70 607
Окончательная сводка дана в табл. 61.
Таблица 61
Дисперсионный анализ данных о числе стернальных щетинок
у Drosophila persimllis из разных местностей
Источник варьи- рования SS df ms F фактическое F табличное
при Р = 0,05 при Р=0,01
Общее 1450,85 . 59 — — — —
Фактор А (мест- ности) 1084,3 2 542,15 542,15 ~W ’6 4,26 8,02
Фактор В (выбор- ки) 35,75 9 3,97 lg=0,58 0,00 2,12 2,89
Случайные откло- 330,8
нения 48 6,85 — — —
224
Выборки достоверно не отличаются друг от друга. Влияние
же местности бесспорно. Это значит, что популяции из разных
мест представляют собой географические расы.
Количественная оценка влияния отдельных факторов. Наряду
с доказательством влияния того или иного фактора на вариацию
признака в изучаемом материале, часто возникает необходимость
установления меры этого влияния и его доли в сумме влияния
всех факторов. В литературе одно время распространилось мне-
ние, что оценка долей влияния может быть сделана по проценту
суммы квадратов, приходящейся на каждый фактор, в общей
сумме квадратов. Но этот очень простой способ неправилен, так
как сумма квадратов не является мерилом вариации. О вариации
можно судить только по средним квадратам (ms), получающим-
ся в результате деления сумм квадратов на соответствующие им
числа степеней свободы.
Весь принцип дисперсионного анализа основывается, как пока-
зано выше, на использовании критерия F, который представляет
собой частное от деления одного среднего квадрата на другой
(variance ratio, по терминологии создателей дисперсионного анали-
за, то есть отношение варианс, а средние квадраты и представ-
ляют собой вариансы). Но очевидно, что абсолютная величина ms
не дает оснований для суждения о количественном действии фак-
тора А, В и т. _д., так как ms, как правило, имеет сложную
структуру и состоит из двух или более компонентов. Так, при
а®
однофакторном анализе F = ----. Числитель msi со-
стоит из двух компонентов. Он больше знаменателя на величину
па л. При достаточной величине этого компонента F будет значи-
тельно больше 1 и становится достоверным, чем и доказывается
влияние фактора А, то есть нулевая гипотеза, что фактор А не
влияет, может быть отброшена. Таким образом, влияние фактора А
определяется значением по а. Вот почему необходимо определить
абсолютное значение оД. В данном случае оД = . Уста-
новив значение аД, можно его сопоставить с суммой оД и о*, ко-
торая составляет всю вариацию, создающуюся за счет организо-
ванного фактора и остальных случайных факторов. Доля влияния
А будет равна _|_аг- Обозначим ее символом р£ .
В примере, приведенном в табл. 41, mst = 40,5; ms2 — 5,0;
n, = 10. Отсюда оД = 40»5~^° =3,55. (Для простоты написа-
ния пользуемся обозначением о вместо греческой буквы каппа, так
как это не влияет на конечные выводы.)
3 55
Тогда доля влияния р% = "355*4.50 = (или до'
лю же влияния случайных факторов приходится 0,59 (или 59%)
общей вариации.
8 П. Ф. Рокицкий
225
Анализ результатов двухфакторного дисперсионного комплекса
проводится по тому же принципу.
-Для модели со случайными уровнями по обоим факторам А
и'В:
. ms1—mst. я _ —ms3.
А ~~ rw ’ ° nr ’
о ms3 — ms4
.
Знаменателем для определения долей влияния каждого факто-
ра является сумма пД + + <г*АВ + а9,.
Но если роль какого-то фактора А или В или взаимодействия
между ними АВ не доказана, то этот компонент включать в расче-
ты не нужно. Так, например, по данным, приведенным в табл. 53,
mSi = 76,5; ms2 = 4,5; ms3 — 7,9; mst = 2,3;
n = 2; r — 5; c = 3.
Проверка по критерию F показала отсутствие достоверного,
влияния фактора В. В таком случае нет надобности вычислять
значение
Остаются о! = 76,5~2,3 = 12,4; а9АВ = 7^~-2,3- = 2,8; <т’ = 2,3;
оД + = 17,5.
Доля влиянияр‘£ = = 0,71 (или 71%);
» > Ряд = fTy = 0.16 (или 16%).
Случайные факторы ответственны за 0,13 (13%) всей вариации.
При установлении долей влияния в дисперсионном комплексе,
построенном по иерархической схеме, нужно помнить, что ms по-
следовательно вычитаются один из другого (см. табл. 57). Тогда
msi—msi. « mst — msa
be ’ =--------
Вычисление долей влияния проводится тем же способом, что
и при обычном двухфакторном анализе, за исключением того, что
при иерархической схеме нельзя выделить компонент взаимодей-
ствия. Поэтому знаменатель состоит только из трех компонентов:
если же действие одного из факторов не доказано,
то из двух. Из данных табл. 61 видно, что достоверно лишь влия-
ние места сбора дрозофил (фактор А). Поэтому оценивается роль
этого фактора:
2 msi — msi 542,15 — 3,97 ос п
°А =----~ =---------20----= 26’7-
Отсюда доля влияния различий в местности в общей вариации:
a^_j_os = 26,7 4 6,9 = (или 79%).
226
В обычных опытах часто ограничиваются доказательством с по-
мощью критерия F влияния (или невлияния) того или иного фак-
тора. Лишь изредка возникает потребность в установлении отно-
сительной доли влияния разных факторов.
В исследованиях же по генетике и селекции определение точ-
ных значений варианс (пл, а\в и т. д.) становится существен-
но необходимым, так как на них основан ряд важных генетичес-
ких параметров: коэффициентов наследуемости, генетической кор-
реляции и многих других.
Определение достоверности разницы между группами. Дис-
персионный анализ позволяет установить, существуют ли досто-
верные различия между отдельными градациями изучаемого
фактора (или факторов). Однако само по себе значение F не
указывает на то; насколько велики эти различия’ и тем более
не дает указаний, между какими градациями разницы достовер-
ны, а между какими — недостоверны. Поэтому в тех случаях, ког-
да методами дисперсионного анализа доказано влияние изучае-
мого фактора, следует выяснить достоверность различий между
отдельными опытными группами (градациями данного фактора).
В простейшем случае однофакторного анализа все различия меж-
ду средними групп (без учета знаков) могут быть сведены
в табл. 62.
Таблица 62
Разницы между средними арифметическими групп по фактору Л
Группы Х[
Х{ *з X»
1 хг—ха XL — Х1 х1~хз х1~ х2
2 х2 ^xt *2—*3 —
3 *3 Хз—'ха Xd—Xl — —
i xi х1 — ха — — —
а Ха - — — — —
Очевидно, что некоторые клетки нет надобности заполнять.
Так, абсолютные разницы x2—xi и х(— х2 равны друг другу.
Чтобы оценить достоверность каждой разницы между средни-
ми арифметическими, нужно сравнить ее с ошибкой. Последняя
может быть вычислена по значению aj. Тогда
Величина п в данном случае—число вариант в каждой группе.
8*
227
При оценке достоверности различий между средними ариф-
метическими, рассмотренной выше (гл. 4), принималось, что
отношение разницы d к ее ошибке sd, т. е. / = — , должно быть
таким, чтобы оно гарантировало вероятность достоверности не ме-
нее чем 0,95 (или Р = 0,05). При больших численностях изучае-
мых групп такой вероятности удовлетворяет t = 1,96, при малых
численностях значение t надо устанавливать по таблице Стьюдента
(табл. II).
При использовании метода дисперсионного анализа дело
обстоит несколько сложнее. Варианса ае2 является средним ме-
рилом случайных отклонений во всем изучаемом материале. Она
определяется путем деления суммы квадратов на число степеней
свободы, которое в свою очередь зависит как от количества ва-
риант в каждой группе, так и от числа групп. Поэтому восполь-
зоваться непосредственно табл. I или II для нахождения необхо-
димой величины t нет возможности.
Чтобы облегчить расчеты, были заранее вычислены значе-
ния отношений d: «а> превышение над которыми существенно
при уровне значимости 0,05. Расчеты сделаны для разного коли-
чества групп а и степеней свободы df (имеется в виду df случай-
ных отклонений). Сокращенная таблица для этих значений (их
обычно называют коэффициентами Q) дана в приложении
(табл.IX).
Можно пользоваться этой таблицей двумя способами: 1) раз-
делить разницу между сравниваемыми средними на ошибку. Если
полученное отношение больше табличного значения Q, разница
достоверна; 2) умножить ошибку на табличное значение при дан-
ных а и df. Тем самым определяется граничное значение разницы
Таблица 63
Разницы между средним содержанием каротиноидов X/
в листьях канатника в разные часы суток
Группы (часы суток) Xi разных часов суток Ч а сы и Xj
12 0,92 9 0,64 6 0,50 24 0,54 21 1,26 18 1,03
15 1,07 0,15 0,43* 1 0,57* 0,53* 0,19 0,04
18 1,03 0,11 0,39* 0,53* 0,49* 0,23 —
21 1,26 0,34* 0,62* 0,76* 0,72* — —
24 0,54 0,38* 0,10 0,04 — — ‘ —
6 0 50 0,42* 0,14 — — — —
9 0,64 0,28 1— — — — —
12 0,92 — — — — — —
228 "
с уровнем значимости 0,05. Все конкретные разницы, превышаю-
щие граничные значения, достоверны, непревышающие — недо-
стоверны.
Проанализируем достоверность различий между содержанивхМ
каротиноидов в листьях канатника в разные часы суток (см. в
табл. 43). Разницы между средними групп приведены в табл. 63.
Так как = 0,0193, а число вариант в каждой группе 4, то
s- = ]/ .Ц193 = / 0,0048 = 0,07.
При df=20 (ближайшее к df=21) и а = 7 табличное значение
Q = 4,6. В таком случае ошибку надо помножить на 4,6. Гранич-
ное значение для разницы, обеспечивающее Р=0,05, равно 0,07X
X 4,6 = 0,32.
Достоверными являются разницы, отмеченные в табл. 63
звездочками. В основном это различие в содержании каротинои-
дов между дневными и ночными часами.
ВОПРОСЫ
1. Из каких компонентов складывается фактическое отклонение варианты
от средней арифметической при 1, 2, 3 контролируемых факторах?
2. Что такое градации факторов? Какая разница между фиксированными
и случайными градациями факторов?
3. Напишите на бумаге схемы варьирования при одном факторе, при двух
и при иерархической схеме.
4. Каковы в общем виде формулы для сумм квадратов отклонений: общей,
групповых средних и случайной вариации внутри групп при однофакторной
схеме, при двухфакторной схеме? То же для числа степеней свободы?
5. Что такое средний квадрат (варианса)?
6. Напишите рабочие формулы, применяемые при однофакторной схеме дис-
персионного анализа, при двухфакторной схеме.
7. Как установить достоверность влияния изучаемого фактора?
8. С какими табличными значениями F надо сравнить F получаемое фак-
тически?
9. Какие параметры оценивают средние квадраты? В чем истинное значе-
ние показателя F при дисперсионном анализе?
10. Какое дополнительное влияние может быть учтено при двухфакторной
схеме дисперсионного анализа?
11. Как надо устанавливать значения варианс при двухфакторной схеме
для фактора Л, фактора В и взаимодействия А и В?
12. В чем заключается иерархическая схема дисперсионного анализа?
13. Чем отличаются рабочие формулы сумм квадратов при иерархической
схеме от рабочих формул при обычных моделях дисперсионного анализа?
14. Как вычисляются F при иерархической схеме?
15. Каковы методы определения достоверности разницы между средними
арифметическими отдельных групп при дисперсионном анализе?
16. Как вычисляется средняя ошибка для средних арифметических отдель-
ных групп? '
17. Как используются коэффициенты Q?
229
ЗАДАЧИ
166. Изучали продолжительность развития эмбрионов (в днях) кроликов
разных пород:
Породы Продолжительность развития отдельных крольчат
Альбиносы 30 36 31 30 34 32 34 32 33 32
35 32 31 33 33 35 31 33 32 33
Шиншилла 31 32 30 34 32 31 30 31 зо 31
30 32 31 32 30 31 33 32 32 33
Голландские 30 29 30 31 30 30 30 31 31 31
30 31 29 32 . 31 31 30 31 31 31
Польские 30 31 29 30 29 30 29 31 29 30
30 30 31 30 30 30 31 30 31 30
Влияет ли породность на продолжительность развития эмбрионов кро-
ликов?
167. У кубышки (Nymphea) 4 раза в сутки определяли содержание каро-
тиноидов:
Часы суток Определения
1 2 3 4 5 6 7 8 9 10
18 1,42 1,30 1,68 1,59 1,49 1,62 1,36 1,26 1,58 • 166
24 1,45 1,38 1,49 1,71 1,54 1.57 1,34 1,32 1,66 1,39
6 1,48 । 1,42 1,58 1,67 1,50 1,80 1,35 1,36 1,67 1.49
12 1,43 1,38 1,47 1,33 1,22 1,35 1,Ю 1,08 1,34 1.11
Влияет ли время суток на содержание каротиноидов в листьях кубышки?
Ответ: F = 4,03.
168. У сирени (Syringa Emodi) в разные часы суток изучали содержание
каротиноидов. Результаты были следующие:
Определения
Часы суток 1 2 3 4 5 6 7 8 9 10
18 0,60 0,64 0,69 0,52 0,65 0,52 0,58 0,63 0,69 0,48
24 0,61 0,72 0,72 0,58 0,46 0,52 0,72 0,59 0,71 0,79
6 0,58 0,59 0,66 0,46 0,47 0,56 0,70 0,60 0,60 0,64
12 0,70 0,57 0,67 0,87 0,52 0,66 — 0,59 0,65 0,66
Изменяется ли содержание каротиноидов в листьях сирени в 1 ечение суток?
Ответ: F » 1,54.
230
169. Получены следующие данные о содержании хлорофилла о (в мг/дм*)
в листьях канатника (Abutilon) в разное время суток:
Часы суток Определения
1 2 3 4
15 3,06 2,88 2,83 2,41
18 3,20 2,97 2,50 3,03'
21 1,82 1,73 . 1,33 2,25
24 1,67 1,26 1,52 1,36
6 2,76 - 1,26 J 46 1,32
9 2,78 2,70 2,49 1,66
12 2,41 3,22 1,90 2,00
Влияет ли время суток на содержание хлорофилла?
Ответ: F — 6,15.
170. Изучали живой вес ягнят-одинцов при рождении (в кг), ношенных
разное число дней:
Длительность беременности Живой вес ягнят
145 3,8 2,9 3,3 3,6 3,8 3,7 4,8 5,1 3,4 3,3
146 3,7 2,9 3,3 3,6 3,9 3,7 4,7 5,0 3,4 3,2
147 3,9 4,1 4,4 5,0 3,0 2,9 4,0 3,2 4,2 4 3
148 4,0 5,2 4,3 2,9 4,1 3,9 3,2 3,9 4,1 4,0
149 4,0 5,3 4,2 3,0 4,0 3,9 4,2 3,3 4,0 4,1
150 4,1 4,3 5,4 3,1 4,0 4,0 4,3 3,9 4,0 4,1
151 4,3 4,2 5,5 4,2 4,1 4,1 4,4 3,5 4,1 3,6
152 4,3 3,6 4,4 5,5 4,0 4,1 4,5 4,1 4,2 4,3
153 4,4 4,7 3,9 4,6 5,7 4,3 4,8 4 9 4,7 4,7
Примените метод дисперсионного анализа для выяснения влияния длитель-
ности плодоношения на живой вес ягнят.
171. Были получены следующие данные о содержании хлорофилла а в
листьях томата (в услов. ед.) в различные часы суток:
Определения
Часы суток 1 2 3 4 5 6 7 8 9 10
18 0 22 0,27 0,22 0,23 0,20 0,28 0,32 0,28 0,29 0,27
24 0,23 0,24 0,24 0,26 0,23 0,25 0,26 0,28 0,30 0,23
6 0,25 — 0,19 0,24 0,20 — 0,30 0,27 0,20 0.26
12 0,24 0,28 0,25 0,27 0,22 0,27 0,32 0,30 0,29 0,27
231
Определите методами дисперсионного анализа, оказывает ли влияние вре-
мя суток на содержание хлорофилла а в листьях томата.
Ответ: F — 1,5.
172. Были получены следующие данные о содержании хлорофилла b в лис-
тьях томата (в у слов, ед.) в различные часы суток:
Определения
Часы суток 1 2 3 4 5 6 7 8 9 10
18 0,087 0,106 0,091 0,097 0,077 0,103 0,118 0,104 0,099 0,108
24 0,086 0,092 0/095 0,100 0,086 0,096 0,101 0,113 0,113 0,092
6 0,093 — 0,091 0,089 0,081 —• 0,118 0,106 0,088 0,096
12 0,088 0^091 0,104 0,113 0,079 0,097 0,114 0,107 0,103 0,093
Определите методами дисперсионного анализа, оказывают ли влияние раз-
личные часы суток на содержание хлорофилла b в листьях томата.
Ответ: F = 2,17«
173. На Узбекской опытной рисовой станции проводились опыты по изуче-
нию влияния удобрений на урожай риса. В 1-й опытной J группе применяли
удобрение Р2О6 + N; во 2-й — то же удобрение, а также предпосевную обра-
ботку почвы. Получены следующие данные (в ц/га):
Группы Урожаи на делянках
Контрольная 35 33 31 37 42 35 40
Опытная 1 -я 43 48 54
Опытная 2-я 36 31 42 36
Проанализируйте полученные результаты.
174. В опытах по изучению влияния синэстрола в дозе 0,5 мг (инъекции
масляного раствора и кристаллов) на вес яйцеводов пятисуточных цыплят
получены следующие результаты (в мг):
Группы Вес отдельных яйцеводов
Масляный раствор Кристаллы Контроль 125 160 200 141 254 11& 23 40 130 122 44 120 5 6 7 9
Примените метод дисперсионного анализа для установления влияния синэ-
строла. Сравните средние арифметические отдельных групп, пользуясь величи-
ной статистической ошибки по данным дисперсионного анализа.
232
175. Получены следующие данные о плодовитости мышей при облучении
рентгеновыми лучами:
Группы 1 Число мышат от отдельных самок
Контроль 10 12 И 10
Доза 100 р 8 10' 7 9
Доза 200 р 7 9 6 4
плодовитость мышей?
Влияет ли облучение на
176. Годовые удои (в л) отдельных коров распределялись в зависимости от
количества отелов следующим образом:
Количество отелов Годовые удои отдельных коров
1 2115 2290 2230
2 2238 2364 2310
3 2462 2381 2236 2327
4 2381 2472 2415 .
5 2430 2375 2402 2405
6 2504 2471 2371 2400 2628
7 2439 2508 2439 2784
Влияет ли количество отелов на годовые удои коров?
177. Изучали живой вес ягнят-одинцов при рождении (в кг), ношенных
разное число дней:
Длительность беременности Живой вес отдельных ягнят
145 4 1 5,1 3,5 2,8 4,2 4,1 4,0 3,9 4,6 3 5
146 4,2 4,4 4,0 2,9 4,1 4,2 4,4 4,1 4,0 5,1
147 4,1 5,0 2,8 3,9 4,2 4,3* 4,4 4,1 4,1 5,1
148 4,4 5,7 3,9 4,5 4,4 4,3 3,8 4,1 4,5 4,4
149 4,3 5,6 3,0 3,9 4,1 4,2 4,3 4,7 4,5 4,4
150 4,5 5,0 5,2, 4,6 4,3 3,0 4,7 4,6 4,0 5,1
151 **4,6 5,3 5,5 4,4 4,3 3,2 4,0 4,5 5,0 5,2
152 4,6 5,4 6,1 4,8 4,4 3,2 4,8 4,7 4,0 4,2
153 4,8 5,5 5,2 4,9 4,5 3,4 4,9 4,4 5,1 5,3
Выясните влияние длительности плодоношения на
живой вес ягнят.
233
178. Получены следующие данные о продолжительности эмбрионального раз-
вития коз при рождении их одинцами, двойнями, тройнями:
Группы по ко- личеству коз- лят от одной самки Длительность эмбрионального развития отдельных козлят
Одинцы 148 151 153 150 151 150 154 152 151 151 149 150 152 152 151 150 152 149 148 151 152 152 152 151 151 150
Двойни 154 151 152 151 151 152 152 150 151 152 152 151 149 152 148 150 151 151 153 152 149 151 148 149 150 151
Тройни 150 152 149 153 151 148 150 148 149 149 147 148 150 149 152 149 148 149 149 148
Есть ли разница в продолжительности эмбрионального развития между
козлята ми-одинцам и, двойнями и тройнями1? Примените метод дисперсионного
анализа и обычное сравнение средних арифметических.
179. Определяли концентрацию кальция в 3 листах на 4 растениях турнеп-
са по 2 определениям на каждый лист. Получены следующие данные (в % к су-
хому веществу):
Растение Лист Определения
1 3,28 3,09
1 2 3,52 3,48
3 2,88 2,80
1 2,46 2,44
2 2 1,87 1,92
3 2,19 2,19
1 2,77 2,66
3 2 3,74 3,44
3 2,55 2,55
1 3,78 3,87
4 2 4,07 4,12
3 3,31 3,31
Примените дисперсионный анализ для установления роли индивидуальнос-
ти растений й различий между листьями в изменчивости содержания кальция.
180. Получены следующие данные о содержании хлорофилла b (в мг/дм2)
в листьях канатника (Abutilon) в разное время суток:
234
Часы суток Определения
1 1 2 1 3 1 4
15 1,24 1,32 0,98 0,95
18 0,92 0,84 0,69 0,81
21 0,47 030 0,28 0,41
24 0,34 0,82 0,99 0,69
6 0,94 0,82 0,95 0,94
9 1,15 1,30 0,76 0,93
12 1,03 1,17 0,88 0,85
Влияет ли время суток на содержание хлорофилла b в листьях канатника?
Ответ: F = 9,1.
181. Гибридные крысы вскармливались самками разных генотипов (четырех
линий Л, F, /, J). В таблице приведены средние веса крыс по каждому помету
на 28-й день вскармливания (в г):
Пометы из линий Крысы-кормилицы из линий
А F / J
62 55 53 42
68 42 62 54
Л1 64 60 50 61
65 53 48
60 40
60 51 57 51
52 65 59 41
N 49 62 47
48 64 53
62
37 56 40 50
36 70 46 44
О 68 67 61 55
55
56
59 60 45 45
58 53 57 52
Р 54 56 61 53
42
54
Какое влияние иа вес вскармливаемых крыс оказывали генотипические
различия между самка ми-кормилицами и пометами, из которых происходили
изучаемые крысята?
235
182. У 3 петухов леггорнов определяли количество сперматозоидов. Пробы
брали в течение 2 недель с интервалом 1—2 дня. Получены следующие дан-
ные (в млн./мм8):
Номера петухов Отдельные определения
1 2 13 4 5 6 7 8 9
1 V 3,5 4,1 3,6 47 4,4 — — —
2 1,9 1,3 1,6 1,6 Ы 2,0 2,2 1,1 1,1
3 - 3,7 3,2 2,2 3,4 3,8 2,5 35 4,2 4,1
Различаются ли петухи по густоте спермы?
183. Изучали процент гемоглобина в крови кур разных пород:
Породы Отдельные наблюдения
самцы самки
Итальянские 87 92 86 91 90 93 90 53 59 50 52 62 60
Куропатчатые 91 90 88 89 64 68 70 60
Минорки 85 82 85 86 89 84 59 62 65 70 65 63
Бентамы 82 82 85 65 68 72
Влияет ли породность и пол на процент гемоглобина?
184. При кормлении тушканчиков сухой и влажной пищей получены сле-
дующие данные о средних температурах тела самок и самцов тушканчиков:
Пол Отдельные наблюдения
сухая пища | влажная пища
Самки 36,9 36,8 37,0 36,6 37,3 36,8 37,3 37,1
Самцы ..... 36,7 36,7 36,8 36,6 36,7 37,0 37,0 36,9
Примените метод дисперсионного анализа для выяснения роли пола и корм-
ления сухими и влажными рационами в изменчивости температуры тела.
185. Подсчитывали количество желтых тел в яичниках серебристо-черных,
лисиц в течение ряда лет:
Годы | Количество желтых тел у отдельных самок
1933-1935 4 5 6 6 3 4 5 5 6 5
1936—1938 5 4 3 6 6 5 6 5 5 5
1943—1947 4 7 4 5 6 5 5 6 5 5
1948—1949 8 5 6 4 5 5 7 6 6 5
1950—1952 5 8 7 6 5 5 6 6 5 6
1953—1955 5 5 7 5 7 6 6 6 8 6
1959-1962 6 6 5 7 5 7 6 8 6 6
Изменилось ли количество желтых тел за 30 лет?
236
186. Получены следующие данные об удое коров за год (в тыс. л.), жи-
вом весе коров (в кг) и количестве израсходованных на каждую корову кон -
центратов (в тыс. кормовых ед.)
Номера коров Удой за год Живой вес Израсходовано концентратов Номера коров Удой за год Живой вес Израсходовано концентратов Номера коров Удой коров Живой вес Израсходовано концентратов
1 6,3 472 2,9 26 3,9 527 1,9 51 3,1 439 1,1
2 5,1 444 2,1 27 37 483 1,5 52 3,0 379 1,1
3 47 487 2,3 28 37 469 1,5 53 3,0 439 1,2
4 4,5 479 2,2 29 37 548 1,6 54 3,0 423 1,2
5 4,3 507 1,5 30 3,7 432 1,8 55 3,0 526 1,3
6 4,3 445 2,0 31 37 465 1,8 56 3,0 450 1,3
7 4,3 471 2,2 32 3,7 520 1,8 57 2,8 484 1,2
8 4,2 474 1,7 33 3,5 494 1,4 58 2,8 468 1,2
9 4,2 491 1 7 34 3,5 421 1,4 59 2,8 438 1,2
10 4,2 481 1,8 35 3,5 438 1,4 60 27 406 1,1
11 4,2 502 1,8 36 3,5 453 1,4 61 27 443 1,3
12 4,2 479 1,9 37 3,5 498 1,4 62 2,6 469 1,1
13 4,2 507 2,0 38 3,5 558 1,4 63 2,6 375 1,1
14 4,2 483 2,1 39 3,5 478 1,5 64 2,6 465 1,2
15 4,2 496 2,1 40 3,5 502 1,5 65 2,6 406 1,2
16 4,1 468 2,0 41 3,5 538 17 66 2,6 497 1,3
17 4,1 462 1,6 42 3,4 452 1,2 67 2,4 496 0,9
18 3,9 469 1,4 43 3,4 448 1,3 68 2,3 478 0,9
19 3,9 529 1,4 44 3,4 451 1,3 69 2,3 434 0,7
20 3,9 428 1,5 45 3,4 472 1,4 70 2,2 464 0,9
21 3,9 465 1,5 46 3,4 461 1,5 71 22 424 0,9
22 3,9 466 1,6 47 3,4 543 1,6 72 1,9 481 0,9
23 3,9 475 1,6 48 3,2 427 1,1 73 1,9 406 0,9
24 3,9 487 17 49 3,2 483 1,4 74 1,8 534 0,9
25 3,9 456 1,9 50 3,2 454 1,6 75 1,6 510 0,7
С помощью дисперсионного анализа установите, влияют ли живои вес и
количество использованных концентратов на удои коров за год.
187. Изучено количество водных насекомых в разные сезоны года в пробах
из 2 речек Северной Каролины (США):
237
Месяцы и годы Отдельные пробы
речка 1-я речка 2-я
Декабрь 1952 Март 1953 Июнь 1953 Сентябрь 1953 7 19 18 9 1 15 29 114 24 37 49 64 124 63 83 51 81 106 72 100 67 87 68 9 25 16 10 9 28 14 35 22 18 45 29 27 20 26 38 44 127 52 40 263 189 45 100 115
Примените дисперсионный анализ для установления влияния на количество
насекомых сезона года (фактор А) и места сбора насекомых (фактор В).
О т в е т: Рл = 9,60; Fs = 0,006; Рлв = 2,90.
188. Получены следующие данные о живом весе симментальских коров
совхоза «Тросцянец» (разной кровности и разного возраста):
Кровность Возраст
первотелки второго отела третьего отела и старше
Помеси 2-го поколения 580 562 571 589 612 531 542 682 554 571 601 665 690 682 662 691 640 651 647 682 632 673 670 668 690 712 664 645 68Q 629 684 640 670 675 664
Помеси 3-го поколения 599 602 660 620 634 584 -562 543 670 680 630 602 576 527 534 541 659 670 648 673 647 682 671 670 645 672 663 654 632 642 657 680 692 720 647 644 600 667 701 650 643 690 691 642 656
Помеси 4-го поколения 590 542 514 592 596 608 624 544 596 630 532 580 597 605 604 612 641 590 660 682 694 642 671 696 605 678 680 640 641 670 657 656 655 657 700 780 664 620 705 704. 694 696 706 705 695 697 704 705 707 718
Помеси 5-го поколения и чистопо- родные Влияют Л1 610 627 662 658 590 540 602 620 602 610 611 614 627 522 590 1 кровность и возраст 682 690 720 702 690 670 660 701 на живой вес симмент: 720 784 701 740 724 690 678 721 724 725 709 712 зльских коров?
ГЛАВА 9
ИЗУЧЕНИЕ СТЕПЕНИ СООТВЕТСТВИЯ
ФАКТИЧЕСКИХ ДАННЫХ ТЕОРЕТИЧЕСКИ ОЖИДАЕМЫМ
Фактические данные и научная гипотеза. Количественное изу-
чение биологических явлений обязательно требует создания ги-
потез, с помощью которых можно объяснить эти явления.
Чтобы проверить ту или другую гипотезу, нужно получить
посредством наблюдения или путем проведения специальных
опытов ряд фактических данных и сопоставить их с теоретически
ожидаемыми согласно данной гипотезе. Если фактически полу-
ченные данные совпадают с теоретически ожидаемыми, то это
может быть достаточным основанием для принятия данной ги-
потезы, для признания ее правильности. Если же фактические
данные недостаточно согласуются с теоретическими, не соответ-
ствуют им, возникает большое сомнение в правильности предло-
женной гипотезы. Степень несоответствия фактических наблюде-
ний теоретически ожидаемым результатам может быть различ-
ной. В одних случаях разница между ними очень невелика и
может оказаться чисто случайной, в других — она достаточно
значительна. Отсюда возникает задача статистической оценки
разницы между фактическими данными и теоретически ожидае-
мыми, установления того, в каких случаях и с какой степенью
вероятности можно считать эту разницу достоверной и, наоборот,
когда ее следует считать несущественной, незначимой, находя-
щейся в пределах случайности. В последнем случае сохраняется
гипотеза, на основе которой рассчитаны теоретически ожидаемые
данные или показатели.
Критерий соответствия хи-квадрат. Степень соответствия фак-
тических данных ожидаемым, иными словами, согласия факти-
ческих данных с предложенной гипотезой, может быть измерена
особым показателем, обозначаемым греческой буквой % в квадра-
те (х2)> отсюда его название критерий хи-квадрат. В советской
литературе его называют по-разному: критерий соответствия,
критерий согласия. Мы будем употреблять название критерий
соответствия хи-квадрат или просто хи-квадрат.
239
Наиболее общий вид формулы для критерия соответствия
<101)
где О — фактически наблюдаемое, а Е — теоретически ожидаемое
число, или показатель для данной группы.
Таким образом, хи-квадрат представляет собой меру отличия
наблюдаемых значений, или показателей, от тех значений, или
показателей, которые должны были бы получиться при правиль-
ности первоначально принятой (нулевой) гипотезы. Математиче-
ски же хи-'квадрат — это сумма частных от деления квадратов
отклонений фактически полученных чисел от ожидаемых на чис-
ло ожидаемых.
Закономерности распределения х2- Допустим, что при изуче-
нии расщепления у томатов по окраске плодов получено 310 крас-
ных плодов и 90 желтых. Ожидалось же при обычном моногиб-
ридном скрещивании отношение 3 : 1, т. е. 300 красных и 100 жел-
тых.
о _ (310 - 300)» , (90— 100)» _ , „о
Z 300 + 100
Возникает вопрос, что это за число и как по нему судить, до-
стоверно ли отличается полученное фактически расщепление от
теоретически ожидаемого?
Если бы фактически полученные теоретически ожидаемые
числа полностью совпадали, то х2 был бы равен нулю. По мере
увеличения разницы между фактическими числами и ожидаемы-
ми величина хи-квадрат будет возрастать. Так как отклонения
фактических чисел от ожидаемых возводятся в квадрат, то значе-
ния хи-квадрата могут быть только положительными. В этом его
отличие от других критериев (например, от t, которое может
иметь знаки плюс и минус).
Подобно тому как это сделано по отношению к распределе-
нию других показателей, изучено и распределение хи-квадрат.
Оказалось, что оно зависит от п, вернее, от числа степеней свобо-
ды тех данных, по которым производится сравнение фактических
и теоретических данных. Каждому же значению х2 соответствует
и определенная вероятность аг? попнленнп Распределение их
асимметрично. При изображении этого распределения на графи-
ке окажется, что малые значения х2 будут обладать наибольшей
частотой, с увеличением же значений х2 их частота будет падать.
Значения хи-квадратов могут возрастать от нуля до бесконеч-
ности. Соответственно этому вероятности их появления убывают
от 1 до 0. Отсюда вытекает возможность рассчитать, какова
вероятность появления х2 ниже или выше определенной величины.
Так как соотношение между хи-квадратом и вероятностью его
появления довольно сложное, то для практического применения
этого критерия пользуются готовыми таблицами. Одна из них да-
240
на в приложении (табл. X). В этой таблице в левом вертикальном
столбце даны степени свободы, а справа—предельные, или гра-
ничные, значения %2 при разных вероятностях и для различ-
ных df.
Понятия вероятности и значимости в применении к X2- На
практике не столь важно знать, какое точное значение вероят-
ности соответствует данному значению х2> а важно, в какой сте-
пени достоверно полученное значение х2-
Критерий х2 используется для проверки определенной гипоте-
зы, которая считается нулевой. Нулевая гипотеза обозначает, что
нет различия между фактически полученными и исчисленными
теоретическими данными. Значения х2» имеющиеся в табл. X,
указывают те границы, до которых полученные значения х2 оста-
ются с определенной вероятностью в рамках случайных отклоне-
ний, т. е. когда нет оснований сомневаться в принятой гипотезе.
Значения же х2> превышающие табличные значения, будут ука-
зывать на несостоятельность гипотезы, т. е. вынуждают отбросить
нулевую гипотезу.
Обычно принято считать допустимой границей вероятности
вероятность 0,05. Следовательно, если получено значение х2, близ-
кое или несколько превышающее значения х2 в графах с вероят-
ностью от 0,99 до 0,10, но не превышающее значение х2, находя-
щееся в графе с вероятностью *0,05, нет оснований отбрасывать
нулевую гипотезу. Ее можно считать по-прежнему правильной.
Если же получено значение х2> превышающее то, которое нахо-
дится в графе с вероятностью 0,05 (конечно, при данном числе
степеней свободы), есть основание отбросить нулевую гипотезу,
так как осталось только 0,05 (или 5%) шансов, что она правиль-
на. Тем больше оснований для отбрасывания нулевой гипотезы,
если фактически полученное значение х2 превышает табличное в
графе вероятности 0,01.
Отбрасывание нулевой гипотезы — это признание того, что
различие между фактическими и теоретически ожидаемыми ре-
зультатами является достоверным, значимым.
В примере с расщеплением по окраске плодов у томатов по-
лучено значение х2=1»33. Так как групп только 2, то df=l. По
данным первой строки табл. X видно, что такое значение х2 соот-
ветствует вероятности около 0,25 (среднее между 0,30 и 0,20).
Значит, совпадение между фактическими результатами и ожидае-
мыми достаточно велико. Принятая гипотеза о том, что имеется
расщепление 3 : 1, подтверждается. Но если бы при анализе рас-
щепления и при df= 1 х2 было бы равно, например, 6,4, то вероят-
ность правильности нулевой гипотезы (т. е. что здесь действи-
тельно имеется отношение 3:1) оказалась бы только около 0,01.
Это явилось бы достаточным основанием признать, что наблюда-
ется существенное отклонение от ожидаемого отношения, т. е. что
гипотеза о расщеплении в отношении 3: 1 должна быть отверг-
нута. При разборе отдельных конкретных примеров мы будем в
241
дальнейшем еще не раз обращаться к табл. X. Сейчас надо лишь
отметить, что с помощью критерия х? как бы взвешивают риск
ошибиться, сохраняя нулевую гипотезу или, наоборот, ее отбра-
сывая.
Если отбрасывание первоначальной нулевой гипотезы проис-
ходит при /7=0,05, то это означает, что, хотя нулевая гипотеза
отбрасывается, еще имеется 5% шансов (5 случаев на 100 или
1 случай на 20), что она правильна. Так что, отбрасывая нуле-
вую гипотезу, исследователь стоит перед возможностью, что он
все-таки ошибся. Если отбрасывание нулевой гипотезы произво-
дится при р = 0,01, то шанс на ошибку только 1 на 100.
Возьмем теперь противоположный случай. Полученное зна-
чение х2 несколько превышает табличное при значении р=0,95,
’ но ниже табличного при р=0,90. Мы имеем право говорить о зна-
чительном совпадении фактических и теоретически ожидаемых
данных, т. е. нулевая гипотеза сохраняется. Однако при этом име-
ется шанс на противоположную ошибку, что все-таки нулевая ги-
потеза неверна. Этот шанс, правда, очень невелик (5 случаев
из 100). Он явно недостаточен, чтобы отбросить первоначальную
нулевую гипотезу. Но такие переходные случаи обычно вызы-
вают наибольшие затруднения при анализе опытных данных.
Если вероятность наблюдаемых значений х2 находится между
0,5 и 0,6, то считается, что значение х2 не выходит из пределов
допустимого и достаточных оснований для отбрасывания нулевой
гипотезы нет. Но шансы на ошибочность этого мнения уже воз-
растают.
В биологических исследованиях принято отбрасывать нуле-
вую гипотезу (при df—1), когда хи-квадрат превышает 3,841 (со-
ответственно при df~2 превышает 6,000; при df=3 превышает
7,82 и т. д.). Значения хи-квадрат, превышающие эти величины,
составляют как бы область отбрасывания нулевой гипотезы. Они
достаточно значимы, достоверны, чтобы отбросить нулевую ги-
потезу. При этом вероятность того, что нулевая гипотеза все же
верна, как раз составляет 0,05.
Так как в понимании вероятности соответствия и несоответст-
вия имеются некоторые тонкости, следует обратить на них внима-
ние и разобрать вопрос подробнее. Когда в гл. 4 рассматривалась
оценка разницы между средними арифметическими, то указыва-
лось, что она должна быть достаточно высока, чтобы разница
считалась достоверной. При этом в качестве достоверных были
взяты вероятности 0,99 и 0,95. Уровни же значимости 0,01 и 0,05
являлись величинами, определяющими шансы на признание раз-
личия достоверным, в то время как оно на самом деле только слу-
чайно. В табл. X вероятности имеют как бы обратный смысл.
Так, в строке df=6 значение х2=5,35, что соответствует р=0,50.
Допустим, что при анализе получен х2=5,40 (при том же числе
степеней свободы). Это означает следующее. Если бы было взя-
то большое число выборок из нормальной совокупности, то боль-
242
ше 50% этих выборок имело
бы %2 той же величины, т. е.
больше чем 5,35. Поэтому наб-
людаемое в данном примере
отклонение фактических частот
от теоретически ожидаемых
(например, при нормальном
распределении вариационного
ряда или при любом другом
определенном теоретическом
отношении между группами)
случайно, т. е. эмпирическая
выборка имеет тот же харак-
тер, что и теоретическая сово-
купность.
Налицо соответствие, веро-
ятность которого 0,50. Однако
вероятности р соответствует
как бы дополнительная веро-
ятность q. В данном случае таб-
личной вероятности 0,50 соот-
ветствует дополнительная веро-
ятность, тоже 0,50. Это — веро-
ятность противоположного со-
бытия, а именно: что соответст-
вия нет и изучаемая выборка
распределена иначе, чем теоре-
тическая. Очевидно, что нет ос-
нований отбрасывать исходное
Рис. 19. Положения хи-квадрат при
р=0,50 (верхняя схема), р=0,05
(средняя) и при р=0,01 (нижняя схе-
ма) на кривой распределения хи-квад-
рат. df=f>. Заштрихованные участки —
доли площади под кривой, соответ-
ствующие шансам на случайное от-
клонение фактических значений хи-
квадрат от теоретически ожидаемых.
положение о соответствии, т. е. о том, что получившееся отклоне-
ние от ожидаемого, выражающееся %2=5,40, случайно.
Сказанное иллюстрируется верхней частью рис. 19. В средней
части рисунка показано, какая доля кривой распределения отсе-
кается при х2= 12,59. Если было получено "фактическое зна-
чение х2= 12,72, то это значит, что вероятность случайного от-
клонения фактически полученных величин от теоретически ожи-
даемых только 0,05. Основание для отбрасывания нулевой гипо-
тезы уже имеется. Еще больше оснований отбросить нулевую
гипотезу, если х2 выше 16,81 (нижняя часть рис. 19).
Для признания достоверности разницы между средними
арифметическими в гл. 4 указаны доверительные вероятности 0,95
и 0,99. По отношению к критерию соответствия можно считать
доверительными вероятностями для несоответствия 0,05 и 0,01.
Дополнительными вероятностями к ним и будут 0,95 и 0,99.
Рассматривавшиеся выше уровни значимости 0,05 и 0,01 ука-
зывали на шансы случайной разницы между изучаемыми стати-
стическими показателями, если разница признавалась достовер-
ной. Вероятности 0,05 и 0,01 при анализе соответствия указывают
243
на шансы наличия соответствия^, если признается достоверным
несоответствие, т. е. отбрасывается нулевая гипотеза.
Конечно, надо помнить, что биолог очень редко основывает
свои выводы только на проверке гипотезы методом хи-квадрат.
Всякий выборочный опыт доставляет лишь известные данные,
но не может служить окончательным доказательством гипотезы.
В процессе исследования новые доказательства прибавляются к
уже существующим. Таким образом, происходит как бы нараста-
ние информации о данном явлении. Если какой-то опыт имеет
большую ценность, то в результате его может быть создана и
новая гипотеза, которая должна проверяться или новыми опыта-
ми, или путем выяснения ее соответствия уже установленным
научным положениям. Одним вычислением хи-квадрата и уста-
новлением того факта, что он обеспечивает достоверность соот-
ветствия или несоответствия на каком-то уровне вероятности,
ограничиваться в научном исследовании нельзя. Чтобы быть
уверенным в выводах, нужно провести такое количество опытов
или наблюдений, при котором возможная ошибочность их была
бы максимально снижена.
Число степеней свободы при пользовании критерием хи-квад-
рат. Из табл. X видно, что распределение хи-квадрат очень силь-
но зависит от числа степеней свободы. Поэтому надо учитывать
именно число степеней свободы, а не просто число наблю-
дений или групп.
Число степеней свободы — это общее число величин, по кото-
рым вычисляются соответствующие показатели, минус число тех
условий, которые связывают эти величины, т. е. уменьшают воз-
можность вариации между ними. Ранее число степеней свободы
определялось как n—1 и п — 2. При пользовании критерием
хи-квадрат оно может вычисляться по-разному.
В простейших случаях при вычислении %2 число степеней сво-
боды будет равно числу классов, уменьшенному на единицу. Так,
если при расщеплении возникает 2 класса, то не связанным с на-
блюдаемой частотой является лишь первый класс, второй же уже
связан с первым. Тогда df= 1.
Если при расщеплении изучаются 4 класса (например, в про-
стейшем случае дигибридного наследования), df = 3. При провер-
ке соответствия частот по классам, распределенным в решетке с
числом полей 2x2, 2X3, 4X4 и т. д., обычно пользуются следую-
щей формулой для числа степеней свободы: (г— 1) (с— 1), (102),
где г — число горизонтальных рядов, с — число вертикальных
столбцов. В таком случае при расположении опытных данных в
таблице из 4 полей (2x2) число степеней свободы равно только
1, в таблице из 9 полей (3x3) df=4, в таблице из 6 полей (2x3)
d/ = 2 и т. д.
При проверке соответствия полученного распределения вариант
в вариационном ряду нормальному, биномиальному и другим ви-
244
дам распределения берется число фактических классов (несколько
классов, объединяемых при подсчете в один, считаются за один
класс) и из них вычитается 2 или 3, так как фактическое и те-
оретическое распределения могут совпадать по 2 элементам (на-
пример, п и’х) или по 3 (например, п, х и а).
Однако возможны и некоторые другие, более сложные слу-
чаи, когда установление числа степеней свободы требует тща-
тельного обдумывания: какие элементы данного изучаемого ком-
плекса могут принимать любые произвольные значения, а какие
их определяют, являются как бы фиксированными, выполненны-
ми, а поэтому совпадают у сравниваемых показателей.
Суммирование нескольких %2 и критерий разнородности. При
проведении нескольких опытов по одному и тому же вопросу
можно вычислять частные х2 для каждого отдельного опыта, а
затем получить значение х2 для суммы опытов путем простого
суммирования частных х2- Число степеней свободы также будет
равно сумме чисел степеней свободы складываемых х2- Так, на-
пример, если в каждом отдельном опыте df=\, а опытов было 5,
то число степеней свободы для общего х2 равно 5. Достоверность
полученного значения х2 можно проверить по той же табл. X.
С другой стороны, можно обработать весь материал в целом,
не считаясь с отдельными опытами, получить соответствующие
эмпирические значения, вычислить теоретически ожидаемые ве-
личины и получить х2- Сравнение значений х2, полученных двумя
разными способами объединения опытного материала, позволяет
судить о степени его однородности или неоднородности.
Для иллюстрации сказанного возьмем следующий пример. На
11 гетерозиготных растениях кукурузы наблюдали расщепление
по окраске проростков на зеленые и желтые. В некоторых случа-
ях оно точно соответствовало отношению 3 : 1 (например, 27 зе-
леных и,9 желтых проростков), в других несколько отклонялось в”
ту или другую сторону (например, ПО зеленых и 39 желтых,
98 зеленых и 24 желтых). Значения хи-квадратов по отдельным
растениям колебались от 0,00 до 2,00. При суммировании всех х2
было получено значение 6,54 (при Проверка по табл. X
показывает высокое соответствие эмпирических данных теорети-
чески ожидаемым (р около 0,80). Когда весь материал был объ-
единен в одну группу, расщепление оказалось следующим:
854 зеленых и 249 желтых проростков (при ожидаемых числах
827,25 и 275,25). Вычисленный по этим данным х2 равен 3,46;
df=l. При df=l границей является значение х2 = 3,84 (р = 0,05).
Таким образом, и по итоговым данным можно говорить о нали-
чии соответствия между эмпирическими и теоретическими чис-
лами, т. е. о том, что нулевая гипотеза правильна. Но между
значениями х2> вычисленными двумя способами, наблюдается
разница. Именно она и должна указывать на степень однород-
ности или неоднородности опытных данных. Записать это можно
следующим образом:
245
Степени свободы Хи-квадрат
Сумма 11 хм-квадратов 11 6,54
Хи-квадрат по объединенным данным . ; 1 3,46
Разница (разнородность) 10 ' 3,08
Проверка по табл. X показывает, что разнородность очень ма-
ла. Значение £ "Приблизительно 0,98. Такой результат бывает да-
леко не всегда. Надо считаться с возможностью значительной
разнородности данных от различных опытов или наблюдений.
Поэтому необходимо составлять таблицы для анализа с помощью
критерия хи-квадрат таким образом, чтобы каждая из них
охватывала относительно однородный материал. Лучше предва-
рительно проанализировать данные нескольких опытов отдельно,
чем сразу же, без проверки степени однородности соединять их
воедино, рискуя получить неверные результаты в силу сумми-
рования неоднородных материалов.
Вычисление теоретически ожидаемых чисел и определение хи-
квадратов при анализе расщепления. Формула для определения
X2 настолько проста, что ее применение чаще всего не вызывает
затруднений. Более сложным является в некоторых случаях
определение теоретически ожидаемых величин. Поэтому целесо-
образно разобрать несколько конкретных примеров, на которых
удастся продемонстрировать все приемы определения хи-квад-
рата.
Метод хи-квадрат очень часто применяется при генетических
исследованиях, когда нужно проверить соответствие частот
классов, получаемых при расщеплении, свободном комбиниро-
вании или сцеплении, частотам, ожидаемым при той или иной
генетической гипотезе. В этом случае для вычисления ожидае-
мых чисел надо помножить общее число изучаемых фактически
особей на соответствующую долю, теоретически ожидаемую при
данном типе исследования.
Наиболее простой пример расщепления при моногибридном
скрещивании представляют собой данные о результатах скрещи-
вания томатов, гетерозиготных по окраске плодов. Было получено
310 красных и 90 желтых плодов. Если ожидать расщепления
3 : 1, то каждая категория вычисляется, как доля от п: п и
-|-я. В данном случае красных плодов должно было быть
• 400 = 300, желтых — -L • 400 = 100.
Получено значение ’ха = 1,33. При df — 1 фактические резуль-
таты хорошо совпали с теоретически ожидаемыми.
Возможно применение и более простой формулы
246
= (103>
где а и b — фактические числа в каждом классе, а г—теорети-
ческое отношение соответствующих классов в популяции. Для
расщепления у томатов вычисление хи-квадрат по этой формуле
дает ту же величину:
а (310-3-90)* _
X 3 - 400 — bod.
Второй пример. При скрещивании короткоухих овец (являю-
щихся гетерозиготами, полученными от скрещивания нормаль-
ных и длинноухих овец с овцами, лишенными наружного уха)
получено 22 потомка, в том числе 7 овец с нормальными ушами,
9 короткоуких и 6 безухих. Так как гетерозиготы по фактору
длины ушей фенотипически, отличаются от гомозиготных форм,
ожидается в F2 расщепление 1 :2: 1. Для получения ожидаемых
категорий 22 умножим наи -^-Получим 5,5; 11,0 и 5,5. Со-
поставление фактических результатов с ожидаемыми произво-
дим с помощью табл. 64.
Х2=0,82 при df=3 — 1=2.
Таблица 64
Вычисление критерия хи-квадрат для данных о расщеплении
по длине ушей у овец
Частоты О — Е (О—Е)2 (О — Е)2 Е
О Е
7 5,5 1 5 2,25 0,410
9 11,0 — 2,0 4,00 0,364
6 5,5 0,5 0,25 0 045
2 = 22 2 = 22 - 1 - X2 = 0,819
По табл. X находим, что это значение хи-квадрат имеет веро-
ятность, среднюю между 0,75 и 0,50, примерно 0,67.
Таким образом, наблюдается довольно полное соответствие
между фактическими и теоретически ожидаемыми частотами.
Исходную нулевую гипотезу о том, что в данном случае полу-
чено расщепление в отношении 1:2:1, можно считать правиль-
ной.
По тому же принципу производится вычисление ожидаемых
чисел при более сложных типах расщепления, например
9 : 3 : 3: 1; 12 : 3 : 1 и т. д. Так, например, допустим, что наблю-
дается расщепление по фенотипу на 4 группы при обычном ди-
247
= 0,96;
= 5,79;
= 1,17.
гибридном скрещивании: АВ —117, АЬ —26, аВ—18 и^аЬ — 7.
Всего 168.
Тогда ожидаемые числа будут следующими:
ЛВ —4--168 = 94,5;
аВ и Ab — по-Дг • 160 = 31,5;
lb
ab — 4г 168 = 10,5.
lb
Для получения /2 надо вычислить следующие 4 величины:
(117 — 94,5)2
94,5
(26 — 31,5)2
31,5
(18 — 31,5)2
31,5
(7 — 10,5)2
10,5
Отсюда х2 = 13,28.
Так как групп —4, число степеней свободы — 3. Такое вы-
сокое значение /2 дает основание отвергнуть нулевую гипотезу
и считать, что существует достоверное отклонение от ожидаемо-
го отношения.
Применение критерия хи-квадрат к четырехпольным табли-
цам. Критерий хи-квадрат можно применить для анализа мно-
гих других опытных данных — физиологических, генетических,
медицинских, сельскохозяйственных, когда анализируется влия-
ние различных факторов на те или иные биологические процес-
сы и явления. Правда, для этих случаев современная биологиче-
ская статистика дает в распоряжение биолога также и другие
методы, например метод дисперсионного анализа, рассмотрен-
ный в гл. 8. Но анализ с помощью критерия хи-квадрат значи-
тельно проще. Данные опытов обычно можно сгруппировать в
таблицы, состоящие из нескольких полей (2x2, 2X3, 4X4
и т. д.). Исходной нулевой гипотезой, которая должна быть или
отвергнута после определения %2, или, наоборот, сохранена, яв-
ляется отсутствие влияния тех или других факторов.
Разберем несколько примеров из разных областей биологии.
Изучали частоту появления сцепленных с полом мутаций у дро-
зофилы при подкормке солями железа и без подкормки. В опы-
тах получено 2756 культур с применением подкормки, 805 куль-
тур без подкормки. Среди первых мутации получены в 357 куль-
турах, в 2399 культурах мутаций не было. Среди вторых
мутации были в 80 культурах, а в 725 культурах мутаций не на-
блюдалось.
248
Исходная нулевая гипотеза заключается в том, что число му-
таций не изменяется при наличии подкормки, т. е. что частота
мутаций как в группе получавших подкормку, так и в группе не
получавших одинакова. Исходя из такой гипотезы, можно рас-
считать ожидаемое число культур с мутациями и без мутаций в
каждой группе на основе итоговых цифр 3561,437 и 3124, т. е..
числа 2756 и 805 разбить пропорционально числам 437 и 3124:
2756 * 437 OOQ
3561 338 ’
2756 • 3124 _ O/11Q
3561 - 24 1 8.
Это теоретически ожидаемые численности культур с мутаци-
ями и без мутаций для культур с применением подкормки. Име-
ется в виду, что между числом культур, давших мутации и не
давших, в группе с подкормкой будет такое же соотношение,
как в опыте в целом. Таким же образом вычисляются теоретиче-
ски ожидаемые частоты и для культур без подкормки. Они бу-
дут следующими:
давшие мутации
805 • 437
3561 “ ’
не давшие мутации
805 • 3124 _ЛС
-3561— = 706’
Фактически полученные и записанные в скобках теоретически
ожидаемые частоты представлены в табл. 65.
Таблица 65
Проверка влияния подкормки солями железа
на частоту вызванных облучением мутаций
Группы Число культур F2 Всего
давшие мутации не давшие мутации
С подкормкой . . 357(338) 2399(2418) 2756
Без подкормки . . 80(99) 725(706) 805
Всего . . . 437 3124 3561
Дальнейшие расчеты сводятся к получению 4 отклонений
фактических чисел от теоретических, возведению каждого из
них в квадрат, делению каждого квадрата отклонений на теоре-
тическое число и, наконец, к суммированию, в результате чего
получается хи-квадрат.
249
Можно проделать эти вычисления без специальной таблицы.
Тогда
2 __ (357 — 338)* . (2399 — 2418)» , (80 — 99)» , (725 — 706)»
Z ~ 338 + 2418 • .99 "* 706 ~
_ 19» 19» , 19» , 19» _
” 338 ' 2418 ' 99 + 706 “
-19‘ (-33» + Я8+У + w) =361 0149 - 5>38-
Число степеней свободы при 4 полях равно 1. По табл. X
нужно просмотреть верхнюю строчку. Полученное значение х2
больше табличного при р==0,025, но меньше при р—0,01, т. е.
оно н'е удовлетворяет требуемому для точных генетических опы-
тов уровню значимости. Влияние подкормки на изменение коли-
чества мутаций нельзя считать полностью доказанным.
Второй пример возьмем из области применения лекарствен-
ных средств, где критерий хи-квадрат используется очень
часто. В стаде, состоявшем из 93 коров, был высокий процент
абортов. Для проверки препаратов против абортироцания был
поставлен опыт на 46 коровах, остальные 47 коров были конт-
рольными. В группе коров, получивших препарат, нормальный
отел был у 38 коров, а 8 абортировали. В контроле коров с нор-
мальным отелом было 33, абортировавших 14. Всего, таким об-
разом, было абортировавших 22 коровы и с нормальным отелом
71. Чтобы применить критерий х2> надо вычислить ожидаемые
численности, разбив числа 46 и 47 пропорционально итоговым
числам 22 и 71.
Таблица 66
Результаты опыта по применению противоабортного препарата
Группы коров Количество коров Всего
абортировавших с нормальным отелом
Получившие препарат . . . 8 (10,9) 38 (35,1) 46
Контрольные 14(11,1) 33(35,9) 47
Всего 22 71 93
В табл. 66 приведены результаты опыта. В скобках около
каждого фактически полученного числа записано теоретически
ожидаемое число коров при нулевой гипотезе о том, что препа-
рат не влияет на процент абортов.
Вычислить общий х2 можно так, как это было проделано вы-
ше на примере мутаций, но можно представить ход вычислений
в особой .табл. 67.
250
Таблица 67
Определение х2 по данным опыта
с влиянием противоабортного
препарата на отелы коров
Частоты (O-E)» (O-E)2
0 E
E
8 10,9 —2,9 8,41 GJT
38 35,1 2,9 8,41 0,24
14 11,1 2,9 8,41 0,76.
33 35,9 -2,9 8,41 0,23-
X» = 2,oa
Проверка по табл. X по-
казывает, что такое значе-
ние %2 недостаточно, чтобы
отвергнуть нулевую гипоте-
зу, т. е. считать действие
препарата доказанным. Ве-
роятность случайности от-
клонения еще очень велика
(между 0,25 и 0,10).
Сокращенная формула
для вычисления %2 и поправ-
ка на непрерывность Йейтса.
Можно вычислить значение
X2 для данных, внесенных в
четырехпольную таблицу, и
без определения разниц ме-
жду фактически полученны-
ми (О) и теоретически ожи-
даемыми (Е) частотами вариант по следующей формуле:
а _ (ad — be)* п
1 - (a+b)(c+d)(a+c)(b + dy
Здесь буквами а и b обозначены частоты для 2 верхних полей
таблицы, а буквами end — для 2 нижних. В знаменателе —
произведение сумм частот по горизонтальным строчкам (а+б)
и (c+d) и по вертикальным столбцам (a-t-c) и (b+d). Общая
сумма n=a+b+c+d.
Для данных табл. 66 по этой формуле
. (8 - 33 - 38- 14)»-93 _ 9ПП
* — 46 • 47 22 • 71 —
Распределение х2> как это* видно из табл. X, является непре-
рывным, распределение же групп в таблицах, подобных табл. 66,.
дискретно. Поэтому применение критерия х2 к случаям сопо-
ставления фактических и ожидаемых частот при дискретных
распределениях сопряжено с некоторой неточностью, особенно
если число наблюдений в группах мало. Одним из способов
уменьшения неточности является объединение малочисленных
групп, примеры чего будут даны ниже. Возможно также внесе-
ние поправки в числитель формулы (104), так называемой по-
правки на непрерывность Йейтса. Формула с поправкой будет
следующей:
11 ad — be | —g- n J • n
(104>
(a + b)(c + d)(a + c)(b + dy (Ю4а>
Прямые скобки, в которых находится ad — be, показывают,
что берутся только абсолютные, т. е. положительные, разности:
ad—be.
251
Значение х2 Для данных той же табл. 66 с учетом поправки
будет следующим:
| 8 33— 14 38 |
х2 =
46 47 • 22 71
I2
• 93
_f[268 —47]2 • 93 _ 4 540 213 __ < «к
“ 46 47 • 22 • 71 “ 3377044 ~
При больших количествах опытных животных или растений
поправка Йейтса мало изменит результаты, при малых же она
необходима,
вычисленное
не-
по-
Таблица 68
Определение у,2 с поправкой Йейтса
по данным опыта о влиянии противо-
абортного препарата на отелы коров
О' Е О'—Е (О'—Е)2 о су 1 О
8,5 10,9 — 2,4 5,76 0,53
37,5 35,1 2,4 5,76 0,16
13,5 11,1 2,4 5,76 0,52
33,5 35,9 — 2,4 5,76 0,16
Х2 = 1,37
совершенно
Значение х2>
без поправки, всегда
сколько преувеличено,
этому оно будет указывать
на большую значимость ре-
зультатов, чем это имеет ме-
сто на самом деле. Правда,
в данном конкретном случае
и завышенное значение х2 не
давало оснований отверг-
нуть нулевую гипотезу.
Поправка Йейтса может
быть использована и в тех
случаях, когда вычисление
X2 производится путем вычи-
тания теоретической часто-
ты из фактически получен-
ной. Для этого надо каждую разность уменьшить на 0,5, т. е. сде-
лать все фактические частоты на 0,5 ближе к средней.
Данные табл. 67 приведены в табл. 68 в исправленном виде.
Многопольные таблицы. Хотя работать с четырехпольными
таблицами легче всего, но в некоторых случаях фактические
данные можно представить только в виде таблиц с большим чис-
лом полей: 2x3, 3X3 и т. д. Тогда число степеней свободы вычи-
сляется по данной выше формуле (102). Само же вычисление х2
делается обычно прямым путем. Не применяется также и по-
правка Йейтса.
Приведем следующий пример. Надо было проверить, одина-
ково ли содержание дифтерийного антитоксина в крови детей
2 детских садов А и В. Фактическое распределение детей по со-
держанию антитоксина показано в табл. 69.
Исходить надо из нулевой гипотезы, что дети обоих детских
садов не отличаются по содержанию в их крови антитоксина.
В таком случае теоретически ожидаемые частоты должны быть
пропорциональны итоговым цифрам: 98, 70 и 42, т. е. для са-
да А — 43, 30 и 19 и для сада В — 55, 40 и 23.
252
Таблица 69
Распределение детей двух детских садов
по содержанию дифтерийного антитоксина в крови
Детские сады Содержание антитоксина Всего
до 0,1 ОД—0,5 0,6 и выше
А 46 28 18 92
В 52 42 24 118
Всего 98 70 42 210
Вычисление %2 дано в табл. 70. %2=0,69. df= (г—1) X (с— 1) =
= (2-1) (3-1) =2.
Таблица 70
Определение х2 для данных о содержании
дифтерийного антитоксина в крови детей
двух детских садов
О Е (О-Е) (О — Е)2 1 О
46 43 3 9 0,21
28 30 — 2 4 0,13
18 19 — 1 1 0,05
52 55 — 3 9 0.16
42 40 * 2 4 ОДО
24 23 1 1 .0,04
X2 = 0,69
Такое значение х2 соответствует вероятности ~0,7, т. е. нет
оснований отвергать нулевую гипотезу. Дети в детских садах А
и В не отличаются по содержанию дифтерийного антитоксина.
Использование х2 Для установления наличия сопряженности.
В предыдущих главах уже говорилось о различных методах изу-
чения связи между признаками, т. е. сопряженной вариации.
Для этой цели может быть использован и критерий хи-квадрат.
Нужно только составить соответствующие четырехпольные и
многопольные таблицы, аналогичные тем, которые рассматрива-
лись ранее. Только в них должно быть дано распределение осо-
бей по 2 признакам, сопряженность или связь между которыми
253
нужно будет установить. Такие таблицы называются таблицами
сопряженности. Расчеты хи-квадрата по этим таблицам ничем
не отличаются от изложенных выше для четырехпольных или
многопольных таблиц, поэтому на них можно не останавливаться.
В числе задач, помещеных в конце главы, есть несколько, в кото-
рых вычисление %2 требуется только для выяснения наличия со-
пряженности (№ 194, 195, 196, 197, 202, 210).
Существенно то, что таблицы сопряженности могут быть со-
ставлены как по качественным признакам, так и по количествен-
ным, но по таким, которые можно разбить на какие-то условные
группы, например: «высокий», «средний», «низкий». Для просто-
ты расчетов в некоторых случаях записывают все данные даже в
чет'ырехпольной решетке. Тогда фактический ряд вариации по
количественному признаку надо искусственно разделить на 2 ча-
сти с помощью средней арифметической или, еще лучше, ме-
дианы, или даже какой-то условной величины. Получатся 2 груп-
пы вариант ниже определенного значения А и выше. То же мож-
но сделать и по другому количественному признаку.
Так, при изучении связи между длиной последних нижних
малых коренных зубов и количеством зубцов на них у ископае-
мого млекопитающего Ptilodus получены данные, которые ока-
залось возможным представить в виде четырехпольной таблицы
(табл. 71).
Таблица 71
Таблица сопряженности длины последних нижних малых
коренных зубов (в мм) с количеством зубцов на них
у ископаемого млекопитающего Ptilodus
Длина зубов Количество зубцов
13 и меньше « 14 и больше Всего
8,0 и больше 0(4,1) 15(10,8) 15
7,9 и меньше 8(3,9) 6(10,1) 14
Всего 8 21 29
По длине зубов животные разделены только на 2 группы.
То же сделано и по числу зубцов на зубах. В скобках даны ожи-
даемые численности при нулевой гипотезе, предусматривающей
отсутствие связи. С помощью критерия хи-квадрат можно или
признать правильной нулевую гипотезу (т. е. что связь между
изучаемыми признаками отсутствует), или отвергнуть ее (т. е.
признать наличие связи). Иначе говоря, хи-квадрат указывает
только на отсутствие или наличие связи, но сам по себе не мо-
жет служить мерой связи.
254
Последнюю можно определить с помощью особого коэффи-
циента взаимной сопряженности, предложенного А. А, Чупро-
вым, в формулу которого входит %2.*
Вычисление ожидаемых частот для теоретических вариаци-
онных рядов и определение соответствия эмпирических рядов
теоретическим. После составления вариационного ряда и вычи-
сления характеризующих его статистических показателей —
средней арифметической и среднего квадратического отклоне-
ния — возникает необходимость установить, насколько фактиче-
ски полученное распределение соответствует одному из известных
теоретических распределений. В нашем курсе мы ограничились
только 3 распределениями: биномиальным, нормальным и пуас-
соновым. Разберем на простейших примерах применение мето-
да хи-квадрат для сравнения эмпирических распределений с
теоретическими.
В качестве примера биномиального распределения возьмем
распределение числа хрячков в пометах свиноматок, в каждом
из которых было по 6 поросят. Оно показано в первых двух
графах табл. 72.
Таблица 72
Сравнение эмпирического распределения числа хрячков в пометах
свиней с теоретически ожидаемым при биномиальном распределении
Количество хрячков в помете Фактическое число поме- тов О Теоретически ожидаемое Е О — Е (О —£)» О Ст> 1 3 м
0 3,45 ) — 5,15 26,5225 1,10
1 16)19 20,70 / 24,15
2 53 51,75 + 1,25 1,5625 0,03
3 78 69,00 + 9,00 81,0000 1,17
4 53 51,75 + 1,25 1,5625 0,03
5 10 118 20,70 1 24,15
6 8 ) 3,45 / — 6,15 37,8225 1,57
п = 221 п = 220,8 X2 = 3,90
(~ 221)
Так как в данном случае имеется дискретная, прерывистая
изменчивость, следует ожидать биномиального распределения, в
котором ряд получается на основе разложения бинома (р + q)k.
Приняв, что р = q = можно вычислить- ожидаемые частоты
каждого класса, установив величину k (напомним, что можно
* Об этом см. в кн.: Урбах В. Ю. Математическая статистика для биологов
и медиков, стр. 143.
255
воспользоваться для этой цели треугольником Паскаля). Так как
в данном ряду 7 классов, то k = 6. Тогда частоты классов будут
выражаться следующими цифрами:
221"СТ; 6-221 --Х; 15-221-А-; 20-221-А;
15 - 221 - 6 - 221 - 221 - А,
После выполнения арифметических вычислений получаем
теоретически ожидаемые частоты. Они записаны в третьей гра-
фе табл. 72., Одним из условий правильного применения крите-
рия соответствия является наличие в каждом из эмпирических
илй теоретических классов не менее 5 вариант. Поэтому следует
объединить 2 верхние строки (0 и 1) в один класс и то же проде-
лать с 2 нижними строками. Все дальнейшие вычисления, при-
веденные в табл. 40, само собой ясны. Число степеней свободы в
данном случае по формуле df=k —2. Тогда df = 5 —2 = 3.
Пользуясь табл. X, находим, что вычисленное значение х2
превышает табличное, находящееся в графе р = 0,50, но меньше
табличного графы р=0,25. Таким образом, обнаруживается хо-
рошее соответствие фактических частот вариационного ряда
ожидаемым при биномиальном распределении.
По тому же принципу проводится сравнение эмпирических
частот вариационного ряда с теоретическими и вычисление х2
при нормальном и пуассоновом распределениях. Но рассчитать
теоретические частоты при этих распределениях значительно
труднее.
Напомним, что пуассоново распределение в принципе является
тем же биномиальным, но относится к явлениям, обладающим
очень малой вероятностью. Поэтому оно асимметрично. Как ука-
зано в гл. 3, характерным признаком для пуассонова распределе-
ния является то, что средний квадрат отклонений и средняя
арифметическая (х или к) количественно почти равны. Именно
по этому признаку можно отличить пуассоново распределение от
других распределений. .
Теоретические частоты пуассонова распределения представляют
собой следующий ряд:
п , „ . ГпХ nX1 пХ* , пХ4 „ „ „
-т- (нулевой член); -у-; —т-; ----г-; --------г- и т- Д*
? У е* 2е\ (2) (3) (4) ех
Здесь п — общее количество вариант в вариационном ряду, е —
основание натуральных логарифмов (значение его приблизительно
равно 2,718, а его логарифм при основании 10 равен 0,43429...),
X — средняя арифметическая вариационного ряда при пуассоновом
распределении (х). Коэффициенты в знаменателе являются извест-
ными из математики факториалами, обозначаемыми знаком «!».
Факториал для первого члена 0! = 1, для второго 11 = 1, для
третьего 21 = 1 • 2, для четвертого 3! = 1 • 2 • 3 и т. д.
256
Поскольку в значение частот входит величина е, возведенная
в степень 1, расчеты надо вести с помощью логарифмов, позднее
же по логарифму определить данную частоту.
Для удобства расчетов ряд теоретических частот выгоднее
представить в'следующем виде:
п I п \ 1( п^ \ ( \ v / n^s \ ( ^ \
\ ; ит‘д‘
Достаточно вычислить первый член, и тогда все последующие
члены можно получить из предыдущих путем умножения на X,
-у и т. д. На конкретном примере ход вычислений
с применением логарифмов будет выглядеть следующим образом.
Допустим, что средняя арифметическая X = 3,0204. Средний квад-
рат отклонений, т. е. о?, также равен 3,0204. Отсюда можно сде-
лать вывод, что распределение пуассоново. Число вариант п = 98.
Первый член ряда равен
98
еЗ,0204 •
Логарифмируем его: log 98= 1,99123; log (а3-0204) =3,0204X
X log е = 3,0204 • 0,43295= 1,31175.
При логарифмировании дроби надо от логарифма числителя
отнять логарифм знаменателя:
1,99123-1,31175 = 0,67948.
Таков логарифм искомой частоты. По логарифму определяем
частоту, которая равна 4,78.
Зная первый член ряда, все последующие можно найти и без
помощи логарифмов. Так, для получения второго члена надо
умножить число 4,78 на значение X, т. е. на 3,0204. Получим час-
тоту 14,44. Для получения третьего члена надо умножить частоту
второго члена на -у- • 3,0204. Получим частоту 21,81 и т. д. Но
применение логарифмов для вычисления всех последующих членов
пуассонова ряда избавляет от производства кропотливых действий
умножения и деления.
Так, для получения второго члена, логарифм которого уже
известен и равен 0,67948, к величине 0,67948 надо прибавить
log 3,0204, т. е. 0,48007. Сумма двух логарифмов равна 1,15255,
отсюда частота —14,44. Для получения третьего члена к значе-
нию логарифма 1,15955 надо снова прибавить log 3,0204, т. е.
0,48004, и отнять log 2, который равен 0,30103. Получим 1,33859,
по которому определяем частоту третьего члена ряда, равную
21,81 и т. д. Все операции с помощью логарифмов можно прово-
дить на одной таблице, прибавляя и вычитая соответствующие
логарифмы: ' ' ,
После вычисления теоретических частот для всех классов
Распределения составляется таблица, аналогичная табл. 72.
9 П. Ф. Рокицкий
257
„ л (О—Е)»
Сумма величин последней графы g и дает искомое значение
Xя. Если количество вариант, в каком-либо из крайних классов
меньше 5, следует объединить его с 1—2 соседними. Объедине-
ние должно быть проведено одинаково как по фактическому ряду;
так и по теоретически ожидаемому.
Число степеней свободы устанавливается тем же путем, как
и при биномиальном распределении (df=k—2). Так как все
дальнейшие операции по вычислению х2 просты, мы не даем
специального примера на распределение Пуассона.
Последним из 3 рассмотренных распределений является нор-
мальное. При непрерывной количественной изменчивости очень
важно знать, в какой степени полученный фактически вариа-
ционный ряд следует нормальному распределению. Критерий
хи-квадрат позволяет достаточно легко установить степень тако-
го соответствия. И здесь более сложным и трудоемким является
установление теоретических численностей каждого класса ва-
риационного ряда при нормальном распределении. Необходи-
мые для этого вычисления можно показать на примере табл. 73.
Таблица 73
Фактический вариационный ряд распределения 300 початков
кукурузы по длине (в мм) и теоретически вычисленный ряд
в соответствии с нормальным распределением
Центральные значения классов Фактические частоты О Теоретически вы- численные час- тоты Е о (О — Е)2 (О-Ер Е
80 1 2,17 )
90 2 6,45 J 8’6 -5,6 31,36 3,646
. 100 17 15,3 1J 2,89 1,889
ПО 39 29,3 9,7 94,09 3,211
120 44 44,8, -0,8 0,64 0,014
130 66 55,0 и,о 121,00 2,200
140 42 54,2 — 12,2 148,84 2,746
150 34 43,0 -9,0 81,00 1,884
160 29 27,3 1,7 2,89 0,106
170 18 13,9 4,1 16,81 1,209
180 3 5,68
190 3 1,86 8,0 0,0 0 0,000
200 2 0,49
, \ г п = 300. п = 295,4 = ~ 300 х* = = 16,905
258
Статистические показатели для этого ряда следующие: х =
= 134,3 мм, а = 21,3 мм.
Задача вычисления теоретических частот сводится к тому,
чтобы отнести к уже имеющимся классам возможные значения
частот, если они распределены по законам нормального распре-
деления.
Как было показано в гл. 3, нормальное распределение очень
хорошо выражается в сигмах. На этом принципе построена
табл. I, с помощью которой можно определить, какая часть
вариант находится в пределах того или другого значения t, т. е.
нормированного отклонения, выраженного в сигмах. Необходи-
мо перевести имеющиеся классы, выраженные в миллиметрах, в
классы, выраженные в сигмах или долях сигмы, и после этого
установить, сколько вариант должно приходиться на каждый
данный отрезок нормальной кривой, ограниченный определен-
ными значениями сигмы. Вычисление частот нормальной кривой
может быть проделано разными способами. Мы разберем один
из них, наиболее простой.
Возьмем в качестве примера класс табл. 73 с центральным
значением «100». Границы этого класса 95,0 и 104,9. В значениях
сигмы они будут, следующими:
95,0—134,3 , Q.-. 104,9 — 134,3 , OQn
-2~17з “ -1>845° И - 2Тз- “ 1’380°'
Какая же доля из общего числа вариант при нормальном
распределении должна быть в интервале между —1,845 о и
-1,380 о?
Ответить на этот вопрос можно с помощью табл. I, но так как
это потребовало бы некоторого дополнительного перерасчета
цифр, то удобнее пользоваться табл. XI, в которой даны готовые
частоты для каждого отрезка нормальной кривой в так называе-
мом накопленном виде, т. е. последующие частоты прибавлены
к предыдущим. По этой таблице находим, что значению <т= 1,845
соответствует величина. 4673, а значению а= 1,380 — величина
4162. Это числа особей при общем числе 10 000. Их можно выра-
зить и как доли — в виде дробей 0,4673 и 0,4162. Тогда доля осо-
бей .в этом интервале м^жду двумя значениями накопленных
частот составит 0,4673 — 0,4162 =0,0511. Ожидаемая частота для
данного класса при п=300 будет 0,0511 -300 = 15,33.
Таким же методом можно вычислить теоретические частоты
для всех других классов. Они внесены, в табл. 73 в готовом
виде. Для определения хи-квадрата целесообразно, как это бы-
ло сделано в других рядах, присоединить классы с малым чис-
лом вариант к соседним. Минимальное число вариант, как и в
поле решетки, 5.
В окончательном виде значение %2 =16,905. Число степеней
свободы в данном случае 10—3=7, так как теоретический и эм-
пирический ряды имеют 3 общих элемента: общее количество
9* 259
вариант, среднее квадратическое отклонение и среднюю арифме-
тическую. ,
По табл. X обнаруживаем, что полученное значение %2 выше
табличного при р=0,05, но ниже табличного при р=0,01.
Сравнение двух эмпирических распределений. Наряду со
сравнением эмпирических распределений с теоретическими
иногда нужно сравнить 2 эмпирических распределения друг с
другом. Формула х2 в этих случаях несколько сложнее, а именно:
У 2 _ 1 У (/1Д2 /1 ле\
. ' nln2 « fl + fi ’
где ft и f2 — частоты классов первого и второго рядов, a nt и
п2 — число особей в каждом из них. В качестве примера можно
взять данные табл. 74. Так как количество вариант в некоторых
классах мало, произведено объединение первых двух классов и
последних четырех. В результате вместо 11 классов получи-
лось 7.
Таблица 74
Сравнение вариационных рядов промеров длины х яиц кукушки.
Для I ряда «1 = 76, для II — пг = 54, х = 0,5 мм
X /1 /2 ft** ftfh fin2 — fzni (Zl"2—/Л)2 (/1П8—М1)« fl + fi
40 1 1 Л 7 )
41 1)2 б)12 108 912 804 646416 46173
42 8 14 432 1064 632 399 424 18 156
43 3 8 162 608 446 198916 18 083
44 9 9 482 684 202 40 804 2 267
45 13 6 702 456 246 70 516 3711
46 20 3 1080 228 852 725 904 31 561
47 6 2 1134 152 982 964 324 41 057
48 и
21
49 2
50 2
• fi± =76 П2~ 54 1 = 161001
Отсюда число степеней свободы df = 7—1=6, так как един-
ственным общим элементом 2 рядов является одинаковое число
классов.*
Таким образом,
fi + ft
161001.
260
Коэффициент же
В результате
1 _ 1_______________1
Л1ПЯ 76,54 4104
х2 =
161001 _оп 1
4104
. Проверка по табл. X показывает высокую достоверность
различия между рядами (Р<0,01). Нулевая гипотеза, что оба
ряда взяты из одной популяции, должна быть отвергнута.
ВОПРОСЫ
1. Зачем нужно измерять соответствие фактических данных ожидаемым?
2. Что такое критерий соответствия хи-квадрат? Напишите общую фор-
мулу для его вычисления.
3. Каковы закономерности распределения хи-квадрат? В каком случае %2
должен быть равен нулю? Почему распределение %2 асимметрично?
4. При каких значениях х2 следует отвергать нулевую гипотезу?
5. В каких границах вероятности значения х2 указывают на соответствие
между фактическими и теоретически ожидаемыми данными?
6. Имеется ли шанс на правильность нулевой гипотезы, если она отбрасы-
вается? Каков этот шанс при вероятности 0,01; при вероятности 0,02?
7. Объясните, почему границей для соответствия признается 0,05. Какова
в этом случае вероятность того, что несоответствия действительно нет?
8. Что такое область отбрасывания нулевой гипотезы?
9. Проведите параллель между уровнями значимости 0,05 и 0,01 прн уста-
новлении достоверности разницы между статистическими показателями и веро-
ятностями 0,05 и 0,01 при анализе соответствия. Укажите также на различия.
10. Можно ли делать выводы о правильности научных гипотез только на
основе х2?
11. Как устанавливается число степеней свободы при пользовании критери-
ем хи-квадрат? Сколько степеней свободы при расщеплении 12:3:1; при
расщеплении 9:3:3: 1; при распределении данных в таблице с числом полей
4X4; при сравнении эмпирического вариационного ряда, состоящего из
10 классов, с нормальным?
12. Как производится суммирование нескольких х2?
13. Изложите способ определения степени однородности или разнородности
опытного материала.
14. Как рассчитать ожидаемые частоты при расщеплении 1:2:1; 1:1;
2: 1; 9:3; 3: 1?
15. Напишите рабочую формулу х2 для случая, когда известно теоретиче-
ское отношение классов в популяции.
16. Как рассчитать ожидаемые частоты в классах таблицы с 4 полями?
17. Напишите формулу критерия соответствия для таблицы с 4 полями.
18. В чем заключается поправка на непрерывность в формуле для х2?
19. Как вычислять хи-квадрат при многопольных таблицах?
20. Можно ли использовать критерий хи-квадрат для установления наличия
сопряженности? Измеряет ли х2 тесноту связи?
21. Как вычислить ожидаемые частоты при биномиальном распределении?
22. Как вычислить ожидаемые частоты при пуассоновом распределении?
Напишите формулу для первого (нулевого) члена пуассонова распределения.
23. Почему следует объединять эмпирические классы с малым числом ва-
риант?
24. Изложите методы вычисления теоретических частот прн нормальном
распределении с помощью табл. XI.
25. Почему при сравнении эмпирического ряда с нормальным число степе-
ней свободы меньше числа классов на 3, а не на 2?
261
26. Напишите формулу ха ПРИ сравнении 2 эмпирических вариационных
рядов.
27. Как устанавливается число степеней свободы при определении соответ-
ствия 2 эмпирических вариационных рядов?
ЗАДАЧИ
189. По окраске фасолин наблюдали следующее расщепление: сильно окра-
шенных 92, наполовину окрашенных 182 и имеющих только небольшую окра-
шенную зону 81. Проверьте соответствие полученных частот ожидаемым при
расщеплении 1 : 2 : 1.
190. Среди, 162 детей, наследовавших от одного из родителей фактор
группй крови М, а от другого фактор М9 оказалось 46 с группой крови М,
68 с группой крови ММ и 48 с группой крови М. Рассчитайте ожидаемые час-
тоты при отношении 1:2:1 между группами ЛГ, ММ и М и определите сте-
пень соответствия эмпирических данных теоретически ожидаемым с помощью х2-
191. При скрещивании особей, несущих лактоглобулины молока А и В, бы-
ло получено 14 коров, из которых 2 было с лактоглобулином А, 6 — с лакто-
глобулином В и 6 — с обоими лактоглобулинами А и В. Проверьте соответ-
ствие полученных данных ожидаемым при гипотезе, что расщепление идет по
формуле 1А : 2АВ : /В.
192. У рачков гаммарусов наблюдалось следующее расщепление по
окраске глаз:
Номера семей Количество особей Номера семей Количество особей
с черными глазами с красными глазами с черными глазами с красными глазами
1 79 14 5 139 57
2 120 31 6 24 9
3 81 27 7 19 8
4 95 29 8 45 11
Проверьте соответствие полученного расщепления теоретически ожидаемо-
. му 3:1 по отдельным семьям и по всему материалу в целом (2 способами).
193. В 4 сериях опытов получено в В2 следующее расщепление по окрас-
ке у кур:
Серия Темноокрашенные Белые
1 112 43
2 76. 22
3 146 12
4 143 44
Проверьте соответствие полученных данных ожидаемым при отношении
3: 1 до всему материалу в целом и по каждой серии отдельно. Однороден ли
опытный материал?
262
194, Каракульских ягнят классифицировали при рождении по размерам за-
витка. Они же потом оценивались по типу конституции. Получены следующие
данные о распределении ягнят по размерам завитка и типам конституции (в %):
Размер завитка Типы конституции
нежный крепкий грубый
Мелкий .... 41,1 56,1 2,8
Средний .... 0,6 86,5 12,9
Крупный . . . 0,2 17,4 82,4
Есть ли связь между размером завитка и типом конституции?
195. Оценивалась конституция 1506 каракульских овец при рождении и в
полуторалетнем возрасте:
Конституция при рождении Конституция в пол у тора летнем возрасте Всего
нежная крепкая грубая
Нежная 16 52 21 89
Крепкая 15 485 325 826
Грубая 28 190 374 592
Всего . . . . 59 727 721 1507
Есть ли зависимость между конституцией ягнят в полуторалетнем воз-
расте и цри рождении?
196. В опытном стаде овец учитывали количество сосков у маток и много-
плодие. Всего было учтено 2492 матки, которые распределились по количеству
сосков и рождению одинцов, двоен и троен следующим образом:
Матки С количеством сосков Всего
2 3 4 больше 4
С 1 ягненком .... 1084 251 854 28 2217
С 2 и 3 ягнятами . . . 122 30 119 4 275
Всего . . . . 1206' 281 973 32 2492
Проверьте с помощью критерия хи-квадрат, есть ли связь между количе-
ством сосков и многоплодием.
263
197. Определите методом хи-квадрат, есть ли связь между числом зубцов
на 4-м нижнем премолярном зубе и длиной зубов (в мм) у ископаемого млеко-
питающего Ptilodus montanus:
Длина зубов Число зубцов ' Всего
13 14 15
8,0 и больше .... 0 14 1 15
7,9 и меньше .... 8 5 1 14
Всего 8 19 2 29
198. При скрещивании черных кур, гетерозиготных по белой окраске, полу-
чено следующее расщепление: черных гомозиготных 18, черных гетерозиготных
42 и белых 26. Соответствует ли оно ожидаемому 1 : 2 : 1?
199. Во втором поколении у дрозофилы получено следующее расщепление:
134 нормальных, 43 с глазами цвета сепия, 40 с зачаточными крыльями, 12 с
глазами сепия и с зачаточными крыльями. Соответствуют ли полученные дан-
ные ожидаемому отношению 9 : 3 : 3 : 1?
200. Определите методом хи-квадрат, достоверна ли разница в соотноше-
нии полосатых и гладких форм между 2 популяциями улитки Сераеа nemo-
ralis:
Местность Количество улиток Всего
полоса- тых гладких
Эмеренвиль 32 2 34
Орсэ 120 13 133
Всего 152 15 167
201. От 4900 отелившихся коров родились 2361 телка и 2539 бычков. По-
лучено ли в данном случае достоверное отклонение от соотношения 1 : 1?
202. Определите с помощью хи-квадрат, есть ли связь между количеством
дорзальных и анальных лучей у летающей рыбы Exocoetus obtusirostris по
следующим данным:
* Анальных лучей Дорзальных лучей Всего
12—13 14-7-15
14 5 9 14
15 22 7 29
Всего 27 16 43
264
203. От одной пчеломатки, гетерозиготной по белой окраске глаз, полу-
чено белоглазых трутней 811 н черноглазых 806. Соответствует ли это расщеп-
ление отношению 1:1?
204. От одной пчеломатки, гетерозиготной по белой окраске глаз и искус-
ственно осемененной спермой белоглазого трутня, получено белоглазых самок
183, черноглазых 199; белоглазых трутней 8 и черноглазых 11. Насколько по-
лученное соотношение соответствует отношению 1:1 (отдельно по диплоидным
самкам и гаплоидным самцам)?
205. Определите методом хи-квадрат, достоверна ли разница в проценте
желтоокрашенных раковин между европейскими популяциями улитки Сераеа
nemoralis: •
Местность Количество форм Желтые (В %)
желтых 1 красных ! | всего
Дильбеек, Бельгия 22 24 46 47,8
Стокгольм, Швеция 23 33 56 41,1
Нидербронн, Франция 50 15 65 76,9
206. При полевых исследованиях найдено 522 рыжих хомяка и 172 черных.
Среди 6798 заготовленных шкурок черных было 1781. Соответствует ли фак-
тическое отношение рыжих и черных теоретическому отношению 3:1? Досто-
верны ли различия между данными полевых исследований и заготовок (про-
верьте по критерию разнородности и обычным методом достоверности разницы)?
207. Проверяли различия между количеством служебных собак, выдержи-
вающих и не выдерживающих сильного звукового раздражителя (трещотка) при
дрессировке их в трудных и легких условиях:
Отношение к трещотке Количество собак Всего
дрессированных в трудных ус- ловиях дрессированных в легких усло- виях
Легко выдерживавшие . . . 15 12 27
С трудом выдерживавшие . 0 7 7
Невыдерживавшие .... 1 4 5
Всего . . . 16 23 39
Есть ли разница между собаками, которых дрессировали в разных усло-
виях?
208. Проведена иммунизация детей против скарлатины очищенным адсорби-
рованным скарлатинозным токсином. Результаты среди привитых и непривитых
детей были следующими:
265
Группы Число детей Всего
заболевших незаболевших
С прививкой . . . 6 653 659
Без прививки . . 90 628 718
Всего . . . 96 1281 1377
На основе вычисления у3 сделайте выводы, эффективна ли иммунизация.
209. Морским свинкам вводили под кожу комплексную вакцину против
чумы. Получены следующие результаты:
Группы Количество. морских свинок Всего
выживших погибших
Вакцинированные . . 6 14. 20
Н ев акции и ров а иные . 0 7 7
Всего ... 6 21 27
Какие выводы можно сделать об эффективности подкожной вакцинации?
210. Получены следующие данные о связи длительности эмбрионального
развития (в днях) каракульских ягнят с размерами завитка:
Длительность эмбрионального развития Количество ягнят с завитками
мелкими средними крупными
140—146 50 130 22
147—153 660 2565' 540
154—160 185 893 184
Проверьте наличие связи.
211. Две группы найденных в геологически различных местах остатков
ископаемого млекопитающего рода Ptilodus отличались по числу зубцов на
последнем премолярном зубе:
266
Число зубцов I группа II группа
12 5 0
13 1 8
14 0 19
15 0 2
Определите, достоверна ли разница в числе зубцов между I и II группами.
212. От скрещивания коров чалой окраски, гетерозиготных по красной (ры-
жей) окраске, с красным (рыжим) быком было получено 5 чалых и 11 красных
телят. Рассчитайте, какое отношение должно было бы быть при расщеплении
1 : 1 и 3 : 1 и к какому из них ближе полученные результаты.
213. У 10 растений гороха наблюдали следующее количество круглых А
и морщинистых а бобов:
А 45 27 24 19 32 26 88 22 28 25
а 12 8 7 10 11 б 24 10 6 7
Проверьте с помощью критерия хи-квадрат соответствие полученных 'дан-
ных ожидаемому при расщеплении в отношении 3 : 1 сначала 'для каждого
отдельного растения, а затем для всех 10 растений вместе, получив сводное
значение х2- Обратите внимание на число степеней свободы сводного х2-
214. При обратном скрещивании томатов, гетерозиготных по зеленой лист-
ве, с томатами, имеющими желтую листву, получено 671 растение с зеленой
листвой и 569 — с желтой. Вычислите х2 и определите по табл. X его досто-
верность. Какое биологическое объяснение можно дать факту отставания коли-
чества рецессивных форм от ожидаемого?
215. В одной серии опытов по инъекции в яйца кур женских половых гор-
монов вылупилось на 21 особь только 2 нормальных самца, все остальные были
или нормальными самками или проявляли какие-то признаки женского пола.
Является ли такое отношение полов только крайним отклонением от нормаль-
ного отношения 1 : 1 или же оно достоверно от него отличается?
216. В стаде крупного рогатого скота за 7 лет зарегистрировано 6972 быч-
ка и 7126 телочек. Проверьте гипотезу,.что отношение полов у крупного рога-
того скота 1:1.
217. В Fa дигибридного скрещивания получено расщепление по фенотипу
82ЛВ, 12АЬ, ЗЗаВ и 8аЬ. Проверьте с помощью х2 его соответствие ожидаемо-
му отношению 9 : 3 : 3 : 1.
218. В опытах с анализом дигибридного расщепления в 2 группах получе-
ны значения х2, равные 13,28 и 9,82. При объединении данных в одну группу
Ха — 12,37. Вычислите степень неоднородности между 2 группами. Какое число
степеней свободы для суммы двух у2; для х2 объединенных данных?
219. Проверялось действие 2 концентраций (в %) одного и того же инсек-
тицида на тлей. Результаты оказались следующими:
Концентрация инсектицида Количество тлей
выжив- ших погибших
1 3 62
0,5 13 55
Определите х2 и сделайте выводы.
267
220. Во время эпидемии под наблюдением были 32 больных. К 18 из них
применили новое лечебное средство. В результате 15 человек выздоровело и 3
умерло. Из 14 человек, лечившихся прежними лекарствами, умерло 9 и выздо-
ровело 5. Вычислите х3 2 методами: по формуле (104) и по формуле (104а) —
и сделайте выводы относительно результативности нового лечебного средства.
221. Прививки против сыпного тифа 18 483 людям дали следующие резуль-
таты:
Группы Количество Всего
заболевших незаболевших
С прививкой . , , . 56 - 6 759 6815
Без прививки . . . 272 11 396 11668
Всего . . .* 328 18155 18 483
Примените критерий ха к анализу роли прививок против сыпного тифа и
сделайте выводы.
222. Проверьте соответствие фактического вариационного ряда, составлен-
ного по данным задачи 1, теоретическому при нормальном распределении.
223. Проанализируйте вариационный ряд, составленный по данным зада-
чи 2. К какому типу распределения ч он относится? Проверьте соответствие с
предполагаемым теоретически типом 'распределения.
224. Проверьте соответствие вариационного ряда, составленного по данным
задачи 5, теоретическому при нормальном распределении.
225. Проверьте соответствие вариационного ряда, представленного в табл. 4,
теоретическому, предполагая биномиальное распределение.
226. Проверьте соответствие вариационного ряда, представленного в табл. 6,
теоретическому при нормальном распределении; при пуассоновом распределении.
227. Примените х2 к данным табл. 37.
228. Соответствует ли нормальному распределению вариационный ряд за-
дачи 27?
ЗАКЛЮЧЕНИЕ
Тех, кто впервые встречается со статистическими методами,
обычно пугает обилие вычислительной работы. Однако надо
помнить, что глубокий анализ биологических вопросов не может
быть проведен без применения статистических методов, без вы-
числения необходимых статистических показателей и установле-
ния степени их достоверности.
Во введении мы уже указывали, что целый ряд биологиче-
ских явлений и процессов носит по существу статистический
характер. Поэтому только с помощью методов биологической
статистики можно вскрыть своеобразие этих процессов и явле-
ний и дать им количественную характеристику.
Простое вычисление средней арифметической представляет
собой анализ статистического процесса, так как главное при
этом заключается в установлении свойств не одного какого-либо
животного, а всей изучаемой группы, стада, породы. Промеры
50 коров во всех случаях дадут лучшее представление о породе,
нежели промеры одной коровы, но только применение статисти-
ческих методов позволит ответить на вопрос, достаточно ли 50 ко-
ров, чтобы судить о породе, и какова степень достоверности вы-
водов.
Известно, что животные, как правило, неодинаковы по своим
наследственным, природным качествам и в то же время находят-
ся под непрерывным воздействием многообразных факторов
внешней среды. Реакции различных организмов на условия
внешней среды, на кормление, содержание, воспитание также
неодинаковы. Ставя любой, самый простейший опыт с животны-
ми, необходимо считаться с рядом осложняющих условий, мно-
жеством чисто случайных и не поддающихся точному учету,
факторов, влияющих на опытных и контрольных животных
и изменяющих их биологические и хозяйственные признаки. Вот
почему статистические понятия и подходы сейчас нераздельно
входят в биологическую науку.
Однако, как ни важно умение пользоваться теми или иными
методами или приемами вычислений, главное заключается в по-
269
нимании их сути, в понимании значения математического и ста-
тистического подхода к биологическим явлениям. При любом
анализе — данных ли опыта или результатов наблюдений —
громадное значение имеют понятия вероятности, значимости,
достоверности. Объективно оценить полученные из опыта или
наблюдения данные — это значит суметь оценить их достовер-
ность. Наличие разницы между показателями 2 групп животных,
опытной и контрольной, само по себе не является доказатель-.
ством достоверного различия между ними, доказательством
влияния того или иного изучаемого фактора, если , при этом не
установлена достаточная статистическая достоверность этой
разницы. Но надо иметь в виду, что недостаточная достовер-
ность выводов еще не является основанием для того, чтобы
полностью отвергнуть возможность влияния того или иного
фактора. При недостаточной достоверности результатов необхо-
димо вновь повторить опыт или наблюдение, чтобы снизить
статистическую ошибку и окончательно убедиться в достоверно-
сти или, наоборот, в недостоверности выводов. Конечно, всякий
опыт должен быть правильно поставлен. Плохой опыт никогда
не может дать точных и достоверных результатов, как бы хоро-
шо ни обрабатывали его данные статистически.
Надо постоянно помнить, что математические методы при
ьсем их значении не могут заменить биологических методов. Био-
логическая статистика лишь помогает биологическому исследо-
ванию, делает его более точным. Установить причину тех или
иных биологических явлений или связей между ними можно
только с помощью биологического исследования.
Учитывая непрерывное расширение сферы применения мате-
матических и статистических методов в биологии и развитие
биологической статистики как самостоятельной научной дисцип-
лины, автору очень хотелось сделать данное руководство
возможно более полноценным и насыщенным современными
статистическими методами и подходами. Но в то же время
приходилось помнить, что оно должно служить прежде всего
учебным пособием по курсу вариационной статистики, для ко-
торого на биологических факультетах университетов и в других
вузах биологического профиля отводится ограниченное число
учебных часов. Поэтому в книге изложены, преимущественно эле-
ментарные основы биологической статистики. При изучении
студентами биологических факультетов основ вариационной
статистики надо использовать только часть материала книги,
а именно: введение и гл. 1, 2, 3, 4, 5 и 7. В некоторых главах
можно пропустить отдельные разделы, например о частной
корреляции и коэффициенте ранговой корреляции в гл. 5, о кри-
терии знаков в гл. 4 и некоторые другие. Остальные главы книги
могут быть основой для проведения спецкурсов. Так, в Белорус-
ском и других университетах для студентов-старшекурсников
читается курс сИзбранные главы биометрии», в котором более
270
полно по сравнению с общим курсом рассматривается корреля-
ционный анализ, а также разбираются вопросы регрессии, дис-
персионного анализа и применения критерия хи-квадрат. Иногда
дисперсионный анализ читается как самостоятельный курс для
веех желающих (студентов и научных работников).
Очевидно, что данная книга может быть использована и на-
чинающими научными работниками для изучения статистических
методов в биологии и как пособие при практической полевой или
экспериментальной работе.
Изучение курса статистики обязательно требует упражнений
и решения задач. Только в процессе практического освоения ста-
тистического материала вырабатывается правильное понимание
статистических подходов и методов. Но в то же время при
решении задач необходимо избегать чисто механического исполь-
зования статистических формул. Надо, чтобы решение задач
сопровождалось разбором основных теоретических положений
статистики.
Автором составлено по своим данным и по различным лите-
ратурным источникам свыше 200 задач и упражнений для всех
разделов курса. Однако желательно, чтобы в каждом вузе были
использованы для статистической обработки и собственные
экспериментальные материалы по своей специальности. Для не-
которых, преимущественно более трудных, задач даны ответы.
Для лучшего усвоения теоретического материала в конце
каждой главы приведены провецрчные вопросы.
В приложениях даны: а) указатель символов; б) перечень
статистических показателей и их формул и в) статистические
таблицы (I—XI). Последние взяты из различных источников,
главным образом основных монографий и пособий по матема-
тической и биологической статистике, но чаще всего несколько
упрощены и сокращены по сравнению с исходными таблицами.
Совершенно’необходимо, чтобы студенты привыкли пользоваться
статистическими таблицами, так как это не только облегчает
статистический анализ конкретного материала, но и значительно
углубляет понимание самих статистических закономерностей,
приучает к важнейшим статистическим понятиям, особенно та-
ким, как вероятность, достоверность, значимость, распределе-
ние и др*
Многие важные для биолога-исследователя вопросы, как-то:
методика постановки и планирования опытов, способы взятия
проб и выборок, различные более сложные методы анализа,—
естественно, не нашли отражения в данной книге. Кроме того,
в каждой области биологии подчас применяются специфические
приемы и методы статистического анализа. Поэтому желаю-
щим расширить свои знания необходимо познакомиться со спе-
циальными руководствами и пособиями, которых в настоящее
время много; их список по разделам дается ниже.
ЛИТЕРАТУРА
По математической статистике и теории вероятности
1. Юл. Дж. 3.t Кендэл М. Дж. Теория статистики. М., Госстатиздат, 1960.
(Основное, очень просто написанное пособие по статистике.)
2. Ван дер Варден Б. Л. Математическая статистика. М., Изд-во иностр,
лит., 1960.
3. Миллс Ф. Статистические методы. М., Госстатиздат, 1958.
4. Урланис Б. Ц. Общая теория статистики. М., Госстатиздат, 1962.
5. Гнеденко Б. В., Хинчин A. fl. Элементарное введение в теорию вероят-
ностей, 6-е изд. М., Изд-во «Наука», 1964.
6. Феллер В. Введение в теорию вероятностей и ее приложения. М., Изд-во
«Мир», 1964. (Значительное место уделено приложениям теории вероятности к
генетике и другим областям биологии.)
7. Мостеллер Ф., Рурке Р., Томас Дж. Вероятность. М., Изд-во «Мир»,
1969.
По биологической стати^ике и биометрии в целом
1. Снедекор Дж. У. Статистические методы в применении к исследованиям
в сельском хозяйстве и биологии. М., Сельхозгиз, 1961. (Основное, используе-
мое во всем мире пособие; подробно разработаны методы анализа эксперимен-
тальных данных.)
2. Плохинский Н. А. Биометрия. М., Изд-во Моск, ун-та, 1970. (Особенно
подробно изложены вопросы репрезентативности выборочных показателей и ана-
лиза криволинейных зависимостей.) /
3. Weber Е. Grundriss der biologischen Statistik, 4-e Auflage. Jena. G. Fi-
scher Verlag, 1961. (Наиболее полное и систематическое изложение теории и
практики биологической статистики.)
4. Урбах В. Ю. Биометрические методы. М., Изд-во «Наука», 1964. (Очень
полная сводка многих методов, включая и малоизвестные приемы непараметри-
ческой статистики.)
5. Бейли Н. Статистические методы в биологии. М., Изд-во иностр,
лит., 1962.
6. Меркурьева Е. К. Биометрия в селекции и генетике с.-х. животных. М.,
Изд-во «Колос», 1970. *
7. Mather К. Statistical analysis in biology^ London, Methuen, 1966.
8. Математические методы в биологии. М., ВИНИТИ, 1969.
9. Фишер Р. А. Статистические методы исследований. М., Госстатиздат,
1958. (Классическая работа Фишера явилась основной для целого направления
в современной статистике.)
10. Bancroft. Introduction to biostatistics. London, Cassell a. Co, 1957.
11. Lienert G. A. Verteilungsfreie Methoden in der Biostatistik. Meisenheim
am Gian, Verlag A. Hain, 1962. (Наиболее полное и очень просто написанное
изложение методов так называемой непараметрической статистики, в настоящее
время довольно широко применяемых в психологии, медицине и биологии.)
12. Otto Е. Biometrie. Halle, Deutscher Bauernverlag, 1958.
272
Специально по дисперсионному анализу
1. Поморский /О. Л, Новейшие методы вариационной статистики. Л.,
Изд-во Ин-та ОЗДиП, 1939. (Первая в СССР книга с популярным изложением
методов дисперсионного анализа.)
2. Плохинский Н. А. Дисперсионный анализ. Новосибирск, Изд-во Сиб. отд.
АН СССР, 1960. (Хорошее практическое руководство; материал этой книги во-
шел также в указанную выше книгу Н. А. Плохинского «Биометрия».)
3. Шеффе Г. Дисперсионный анализ. М., Физматгиз, 1963. (Специальная
монография, требующая от читателя математической подготовки.)
По планированию опытов и методике опытного дела
I953I* FiSCher design of experiments. Edinburg — London. Olivera. Boyd,
2. Cochran IF., Cox G. Experimental designs, 2-d ed. N.-Y. — London, J. Wi-
ley, 1957. (Книги Фишера и Кокрена и Кокса являются основными руководства-
ми по планированию опытов.)
3. Романовский В. И. Применение математической статистики в опытном
деле. М. — Л., Гостехиздат, 1947. (Одна из лучших книг по биологической
статистике в целом и по применению статистических методов в растениеводстве.)
4. Деревицкий Н. Ф. Опытное дело в растениеводстве. Кишинев, Изд-во
АН Молдавской ССР, 1962. (Наиболее полное современное руководство, напи-
санное на высоком теоретическом уровне.)
5. Финни Д. Применение статистики ,в опытном деле (сельское хозяйство),
М., Госстатиздат, 1957.
6. Уишарт Дж., Сандерс Г. Основы методики полевого опыта. М., Изд-во
иностр, лит., 1958.
7. Доспехов В. А. Методика полевого опыта. М., Изд-во «Колос», 1965.
По применению методов биологической статистики в различных
областях биологии
1. Kempthorne О. An introduction to genetic statistics. N.-Y.— London
J. Wiley, 1957. (Наиболее полный теоретический разбор статистических мето-
дов при анализе различных генетических и селекционных проблем.)
2. Falconer D. S. Introduction to quantitative genetics. Edinburgh — Lon-
don, Oliver a. Boyd, 1961. (Содержит изложение математических приемов, при-
меняемых в генетике, и их результатов.)
3. Simpson G. G., Roe A., Lewantin R. Quantitative zoology. N.-Y.—Bur-
lingame, Harcourt a. Co, 1960. (Статистические методы в зоологии, в частности
при полевых зоологических исследованиях.)
4. Бессмертный Б. С, Математическая статистика в клинической, профи-
лактической и экспериментальной медицине. М., Изд-во «Медицина», 1967.
5. Сепетлиев Д. Статистические методы в научных медицинских исследо-
ваниях. М., Изд-во «Медицина», 1968.
6. Weber Е. Mathematische Grundlagen der Genetik. Jena, veb. P. Fischer,
1967.
7. Ашмарин И. П., Воробьев А. А. Статистические методы ^микробиоло-
гических исследованиях. М., Медгиз, 1962.
8. Хилл А. Б. Основы медицинской статистики. М., Медгиз, 1958.
9. Черныш В, И., Напалков А. В. Математический аппарат биологической
кибернетики. М., Изд-во «Медицина», 1964.
Следует также указать 4 тома трудов всесоюзных конференций.
10. Применение математических методов в биологии. Л., Изд-во Ленингр.
ун-та, сб. 1, 1960; сб. 2, 1963; сб. 3, 1964; сб. 4, 1969.
273
ПРИЛОЖЕНИЯ
указатель символов
Л —условная средняя арифметическая.
А — константа при экспоненциальном росте.
а — условное отклонение от условной средней.
а — число вариант в поле 00 четырехпольной решетки.
а — количество групп по фактору А (при иерархической схеме
дисперсионного анализа).
ах — условное отклонение от условной средней по ряду х.
ау — условное отклонение от условной средней по ряду у.
а (греч. альфа) — свободный член в уравнении регрессии г/ = stрх для гене-
ральной совокупности.
В — константа при экспоненциальном росте.
b — поправка к условной средней арифметической.
b — число вариант в поле 01 четырехпольной решетки.
b — коэффициент при х в выборочном уравнении регрессии.
b — количество групп по фактору В (при иерархической схеме
дисперсионного анализа).
(Ьу.х) — коэффициент регрессии в выборочной совокупности.
₽ (греч. бета) — коэффициент при х в уравнении регрессии для генеральной
совокупности; коэффициент регрессии в генеральной совокуп-
ности.
с — количество групп (уровней) по фактору В (при дисперсионном
анализе) или вариант в группах.
с — число вариант в поле 10 четырехпольной решетки.
d — разница между любыми величинами, чаще всего между сред-
ними арифметическими.
d — число вариант в поле II четырехпольной решетки.
df — число степеней свободы.
£ — теоретически ожидаемая численность (частота).
F — критерий F (вариансное отношение).
* f — частота класса.
gi — коэффициент асимметрии.
i — обозначение градаций по фактору А (при дисперсионном ана-
лизе).
i — классовый промежуток.
/ — обозначение градаций по фактору В\ наблюдений внутри гра-
даций (прн дисперсионном анализе).
k — число классов.
х2 (греч. каппа) — условное обозначение вариансы для фактора с фиксированны -
ми градациями.
X(греч.лямбда) — средняя арифметическая при пуассоновом распределении.
274
m —число благоприятных случаев*
ms—-средний квадрат (варианса). '
р (греч. ми) — средняя арифметическая генеральной совокупности.
N — общее число. вариант во всех группах (при дисперсионном
анализе).
N — объем генеральной совокупности
п — число вариант в группе; число вариант в выборочной сово-
купности; общее число случаев.
«1 («•••) — численности Групп 1(2..'.).
til — среднее число вариант для нескольких групп.
пх— численность качественной группы х.
пу — численность качественной группы у.
О — фактически полученная численность (частота).
Р — уровень значимости.
р — вероятность (появления события).
р — доля особей с определенным качественным признаком.
Pi (о; 2...) — абсолютные численности качественных групп 1 (0; 2...).
—доля влияния факторов А, В... в общей вариации.
Ро —доля генеральной совокупности.
рх —г абсолютная численность качественного класса в группе х.
ру — абсолютная численность качественного класса в группе у.
Q — коэффициент для получения достоверных разниц между груп-
пами при дисперсионном анализе.
q — вероятность (непоявления события).
<71(0; 2...) — абсолютные численности качественных групп 1 (0; 2...).
/?х.у (Rrx) — коэффициент регрессии.
г — коэффициент корреляции выборочной совокупности.
г — теоретическое отношение численностей альтернативных клас-
сов.
г — количество групп (уровней) по фактору А (при дисперсионном
анализе).
rs — коэффициент ранговой корреляции (по Спирмэну).
р (греч. ро) — коэффициент корреляции для генеральной совокупности.
s—средняя ошибка; среднее квадратическое отклонение выбороч-
ной совокупности.
Gi— ftt) — средняя ошибка разницы между двумя коэффициентами ре-
грессии.
— средняя ошибка разницы между средними арифметическими.
sd(px—/>у) — средняя ошибка разницы между двумя долями.
Sp — средняя ошибка выборочной доли.
sr$ — средняя ошибка коэффициента ранговой корреляции.
sr — средняя ошибка выборочного коэффициента корреляции.
Sa — средняя ошибка среднего квадратиче.ского отклонения.
s(®t—a>) — средин ошибка разницы между двумя средними квадрати-
ческими отклонениями.
ss — сумма квадратов отклонений.
s-—средняя ошибка средней арифметической.
so — средняя ошибка коэффициента вариации,
средняя ошибка г-числа.
S (греч. сигма)—знак суммирования.
а (греч. сигма) — среднее квадратическое отклонение.
— среднее квадратическое отклонение для доли.
Gy.x — среднее квадратическое отклонение для. линии регрессии.
а2 — варианса (дисперсия).
— варианса по фактору Л.
“ варианса для взаимодействия Л и В.
—варианса по фактору В.
о2 — варианса случайных отклонений (при дисперсионном анализе).
275
а* —варианса доли,
Т — сумма всех вариант (при дисперсионном анализе).
Ti — сумма вариант по группам фактора А (при дисперсионном
анализе).
Тц— сумма вариант по группам фактора В внутри групп фактора
А (при дисперсионном анализе).
t — нормированное отклонение.
tx — нормированное отклонение по ряду х.
ty — нормированное отклонение по ряду у.
v — коэффициент вариации. ' *
U? — вес.
X — значение класса .в вариационном ряду.
х обозначение ряда х.
X}*— любая варианта в ряду (совокупности) х.
( Хц—-любая варианта в ряду х и одновременно в ряду у.
xijk — к-ая варианта в ряду х и одновременно в ряду у.
х — средняя арифметическая выборочной совокупности х.
Xi — средняя арифметическая для групп (градаций) по фактору А.
Jx; —средняя арифметическая для групп (градаций) по фактору В.
xt / — средняя арифметическая для подгрупп внутри градаций по А
__ и 5.
xg —- средняя геометрическая.
X2 (греч. хи) — хи-квадрат.
у— обозначение ряда (совокупности) у.
yj_— любая варианта в ряду (совокупности) у.
ч у — средняя арифметическая выборочной совокупности у.
У1 — теоретически вычисленная средняя арифметическая для группы
• (при регрессионном анализе).
z — число г; преобразованный коэффициент корреляции выбороч-
ной совокупности.
z0 — преобразованный коэффициент корреляции генеральной сово-
купности.
СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ И ФОРМУЛЫ
Ввиду разнообразия обозначений, которые применяются в ли-
тературе для одних и тех же показателей, в квадратных скобках
приведены разные наименования данного статистического показа-
теля и некоторые из встречающихся символов. В скобках справа
от формул указаны номера, под которыми они даны в тексте.
Некоторые из более общих формул приводились в тексте без
номеров.
Варианса [средний квадрат, дисперсия, девиата; а2 или s2; ms]
Общая формула
°2 = — -(nSiX)3- Xf (2)
или
= (2)
Рабочие формулы:
а) а2 = ; (8)
276
S xf— (Sxi?
б) ?2 _ ‘ П (16)
3 Л-1
' 2х? — • х
й2 — » (15)
° “ Л-1
rt Sxf— пх2
Г) а2 __ _ _ * . (14)
° “ л-1
д) ст2 — П • (5)
° “ Л-1
к 2 S fa2i2 .2 ( S fa \2 z -, 4
доли при альтернативной вариации
°2 = Р<7 = Р(1— Р)- (77).
При дисперсионном анализе (однофакторная схема) [ms]
Общие формулы:
а) общего варьирования
ms = J(хц — х)г’ (89)
б) варьирования групповых данных (по фактору Л)
ms 3 nt (xt — х)2; (90)
в) случайных отклонений
ms = ____а 2 ^2 (хгу xz)2J. (91)
Рабочие формулы:
а) общего варьирования
= (89а)
б) варьирования групповых средних (по фактору Л)
ms = —Ц-fs— — (90а)
а-1 I ( п/ ьN г v '
в) случайных отклонений
ms
N ~а \ ll 1 i nz I
(91a) ‘
При дисперсионном 'анализе (двухфакторная схема) [ms]
Общие формулы:
а) общего варьирования
277
= (92)
*/*
61 варьирования по фактору А .
ms = 7^rE(^~^; (93)
i
в) варьирования по фактору В .
= (94)
/
г) взаимодействия А и В
ms = (г-Щс-О {хч~'XJ~х,+ х?' (95)
и
д) случайных отклонений
ms rc(n —1) S ~~ Х‘^'
‘7*
Рабочие формулы:
а) общего варьирования
ms=-75^r(l>-£); <92а>
б) варьирования по фактору А
ms = _(93а)
r-1 I ис ‘ rcn г v 7
\ i I
в) варьирования по фактору,В
- = (94а)'
' / /
г) взаимодействия А и В
ms = ~.--... /±УТ4—-ly Tl— -У Т/+—У, (95а)
(г—-1)(с— 1) I П 1 пг J J ГСП г 7
\ И i ! ' !
д) случайных отклонений
<9ба>
\ Uk а /
* При дисперсионном ' анализе (двухфакторная иерархическая
схема) [ms]
Общие формулы:
а) общего варьирования
278
1
/ns = —--------
abc —
'ijk—*)a >
L ijk
б) варьирования по фактору A
bc^ & “ *>21’’
i
в) варьирования по фактору В
„ 1
msl=-^
L ii
г) случайных отклонений
ms»= ^<7znj[S(J
L ijk
'ijk— xij)* •
Рабочие формулы:
а) для общего варьирования
1
ms = —г----г
abc — 1
L ijk
б) для варьирования по фактору А
._______________ 1 Г 1 Т2
abc ’
^2
abc ’
"«1 = ^=4
в) для варьирования по фактору В
mS* = а (6-1) ~ S Т‘‘ ~ lx
ij i
г) для случайных отклонений
mSa== ab(c — \) S*''* с~•
L ilk Цк
Варианса взвешенная
. _ о? (rti — 1) + a£(»t — И + • • • + °к(Пк — О
n — k
Варианса линии регрессии
Я, _ .
-----------•
У, —У)]*
Qy-x —
(97)
(98)
(99)
(100)
(97а)
(98а)
(99а)
(100а)
(13)
(62)
(62а)
n — 2
279
Вариансы разложение
. в’=^ + 9’; • (88)
+ °Ь + ^ав-Ь • • • + ае- (88а)
Вариансное отношение [критерий значимости F]
F = (36)
Вероятность [р, но вероятность соответствия, а также уровень
значимости — PJ
Общая формула р — (20)
Вероятность дополнительная lq; Q]
q=\ —р.
Вероятностей сумма
р + ? = 1.
Вероятность при пуассоновом распределении
х
Доля [р; для генеральной совокупности Ро]
р = (73)
= (73а)
При р = 0 (по Ван
дер Вардену)
„ (Р1+1)-100
Р~ п + 2
(82)
Доля взвешенная
Рх ‘ пх + Ру ' пу
Р — Пх + Пу
использованием абсолютных численностей
Р1х + Ply
Р —----;—'
пх + пу
Доля генеральной совокупности [Ро1
Доверительные границы
р — tsp < Ро < р + tsp.
Корреляционное уравнение
ty — г • tx.
Коэффициент асимметрии
в nZ(xt — X)3.
Доля взвешенная с
(86)
(86а)
(80)
(18)
280
упрощенная формула
= —-^-пя/)8 • (18а)
Коэффициент вариации [коэффициент изменчивости; v; с. v.; С].
V = a^JOO (19)
Коэффициент простой корреляции [прямолинейной, обычной,
линейной; г]
Общая формула
б)
В)
Г)
Различные преобразования (рабочие формулы):
r== Sfo —х)(у< —У) .
пяхау
V 2(Х[-ХУ2(У1-^’
—пху
(Sx/—лх2) (2у’—п у*) ’
2х,у;-
|Д2х*_(2^(2у;_
(2У<Н ’
Л. /
Рабочая формула для корреляционной решетки
S fa^Oy — nbxby
Г Л°х°у ‘
При альтернативной изменчивости
__________________________ad — be____.
Г ~ f (a+b)(c + d)(a + c)(b + d) ’
(38)
(39)
(40)
(41)
(42)
(87)
с поправкой на группировку
\ad — bc\-
г = , - 2 (87а)
/(«+6)(c+d)(a + c)(b + d)
Коэффициент корреляции для генеральной совокупности [р; z0]
Доверительные границы
г — tsr<?^r + tsr’, (50)
z — tsz z0 < z + tsx. (50a)
Коэффициент частной корреляции (при 3 признаках)
Гху ГХ2 * Гуг
?xy z “77======»
(1 — Гхг)(1 —Гу г)
(52)
281
. (52а) У /0-^(1-^) = .. . (526) /0-^)0”^)
Коэффициент частной корреляции (при 4 признаках)
Г12.34 = ^12.4-^13.4^3.4 _ . (53) V (!-^3.4)0-'Ы
Коэффициент корреляции в значениях коэффициента регрессии
г — |/ Ьх.у • Ьу.х . (69)
Коэффициент корреляции рангов (коэффициент ранговой кор
реляции Спирмэна; г/, р]
г — 1 zgn G - 1 „(„i-i) • (ОМ
Коэффициент регрессии lRx.y = R х = Ьх.у; а также Ryx =
Т
= ^*1
1) Rx.y = r^, (58) Ryx = г (58а)
2) , Rx.y = гл/ 2 <*<-*)* , ' (59) Ryx = n / ; (59a) V S(x£-^2
3) h — /60) Ьух~ 2(^-^ ’ (60) . _ 2(хг-х)(уг— у). ffin '
4) bu x~ Гх- (SXf)a ’ (61) 1 n v« S X( X yi Stl^ - (61a)
Критерий соответствия хи-квалрат [критерий согласия; крите-
рий хи-квадрат; /2]
282
Общая формула
Z2 = S-^^-. (101)
При определенном теоретическом отношении (г) частот клас-
сов
(103>
для таблицы из 4 полей
== --------~ Ьс^ • п________• (104)
Х (a + 6)(c+d)(a + c)(6 + d) ’ 7
с поправкой на непрерывность
Г 1 Г
11 ad — be |-п • п
Х’ = (a+&)(c + d)(a + c)(& + d) ; <104а)
для сравнения двух эмпирических распределений
.,2 1 у (Zin« /ап1)2 /1лк\
д+7, • (10&)
Критерий г [число z; преобразованный коэффициент корре-
ляции]
Z = Ц- [loge (1+ Г) — loge (1 — Г)].
Нормированное отклонение [критерий значимости /; иногда
символ t применяют только для малых выборок: тогда нормиро-
ванное отклонение при больших п обозначают символами и,-Т,
d и др.]
В общем виде
t = t (23)
а также
/ = или t = (23а)
Для оценки достоверности х (при |* — 0)
t = (29)
Х 4 „
для оценки достоверности разницы между х± и х2
t = ; (31)
х,)
или сокращенно
t = 4:> <31a>
sd
283
для оценки разницы между сигмами
t = СТ1 — ♦ s(’l—*») (34)
для оценки достоверности коэффициента корреляции: а) общая
sr sr (43)
б) при больших п и средних значениях г
/ — г Г~п. 1 ” 1 -г2’ (45)
в) при малых п
t= ~==.уп — 2\ V 1— г® г (47)
для оценки достоверности числа г
t = —; 3Z (49)
для оценки достоверности коэффициента регрессии
Sb (65)
для оценки достоверности разницы между и Ь2
t = bi~b* ' S(bt-b,) (68)
Средняя арифметическая [х или М — для выборочной ности; х0 или р—для генеральной совокупности] Общая формула для несгруппированных данных сов оку п-
2х( Л “ п (1)
или
И 1 II а|- м II 3|- (1а)
при данных, сгруппированных в классы,
2/Х. п ' (4)
при использовании условной средней А
х = А + (7)
взвешенная
X “Ь + » » » + Xknk . (12)
П1 + л2 + • • • 4“ fljfe ’
2S£
при альтернативной изменчивости
* = (74)
при биномиальном распределении (в значениях вероятности)
x = fcp; (21)
при пуассоновом распределении [х обозначается знаком X]
X = x = np»o2. (21а)
Средняя арифметическая генеральной совокупности [х0; |а]
Доверительные границы
• х — x + /s-. (25)
Средняя геометрическая [g или л?]
xg = Xj • х2 • • • хп = }/ ГЦ ; (17)
log ~xg= (logxr + logx2 + ... + log xn). (17a)
Среднее квадратическое отклонение [стандартное отклонение;
стандарт; о или s]
Общая формула:
а = i / 2Ц-7)8 (3)
у л — 1
Рабочие формулы:
а) а = 1 f 2Ц—Л)8—я(х—Л)8 . (9)
у п— 1
б) 0 = ]/Г ; (16а)
*
В) ; (15а)
у п — 1 х '
г) (l4a)
Д) а==1Л2/Х2—<6)
е) —О»
в частотах или долях альтернативных классов:
»,= (75)
285
Op = Vpq ; (76)
op = V P(l-P) , (76a)
при биномиальном распределении (в значениях вероятностей)
а = y~kpq~; (22)
линии регрессии
Оух = ’ • (63)
2 (i/z _ ^)2 _
________________2 (*<-*)* (63а)
п —2 '
Средняя ошибка, (средняя квадратическая ошибка; стандартная
ошибка; $; т]
средней арифметической [s^; т^]
а
(24)
с учетом доли выборки
О
п .
7Г ’
среднего квадратического отклонения [sa; т<Д
а
So — ;
У2п
коэффициента вариации (sv; mv]
sv = — ;
v V2n
разницы между средними арифметическими хг и х2 [sd; md;
1/ si ; \ (32)
(24а)
(27)
(28)
sd —
разницы между средними арифметическими Xi и х^ при наличии
корреляции
* _ 1Л| + 2<г- • г • (54)
— F Xi 1 х3 ' 12» . ' '
разницы между средними арифметическими Xi и х2 при малых п
S/l = I Г S (X! — 7i)a + Z (Хд — ^)2 / )• (зз)
|/ . (П1-1) + (Д2-1) \ ш-л2 /’
разницы между средними квадратическими отклонениями [s^;
286
доли при альтернативной вариации
<78>
то же с учетом доли выборки
Sp=1/££(1_ « ); (78а)
доли при альтернативной вариации в процентах
s₽ = |/ Р<™-Р1.. ' (79)
доли при р = О (по Ван дер Вардену)
(®>
где #
p = !a±i№; (82)
конкретных чисел при альтернативной вариации
%=’,;= («К
разницы между долями
^-,>=/'«(77+^; (85)
коэффициента корреляции при больших п и средних г [sf; tnr]
1 -г2
s, = —т=-;
(44)
коэффициента корреляции при малых п
Sr
(46)
для z-числа
°г~ А
коэффициента регрессии [sd; ть]
(48)
в отклонениях sh„„ = —- - У*. —; (64)
V у. 2(хг-7)>
________________S(XL~X>* ; (64а)
287
в сигмах
(66)
и
<66а)
разницы между коэффициентами регрессии при больших п
1 / с2 с2
2,х ’ 7у, + 2/ж 7у» 1 <67)
при малых п
g - 1 /<"1-2)^+(п2-2)^ / 1 1 \ ,67 .
- |/ (Л1 _ 2) + (п2 - 2) + S(xs-£)«J- { )
Степени свободы [df или f;* иногда у]
В простейших случаях
df = п — 1.
При дисперсионном анализе (однофакторная схема):
для общего варьирования
df = N- 1 = ап — 1;
для варьирования групповых средних (фактора А)
df = а — 1;
для случайных отклонений
df — an—a = а(п— 1).
При дисперсионном анализе (обычная двухфакторная схема):
для общего варьирования
df = гсп — 1;
для варьирования по фактору А
df = г— 1;
для варьирования по фактору В
df = c—l;
для взаимодействия А и В
df = (r-l)(c-l);
для случайных отклонений
df = rc(n— 1).
При дисперсионном анализе (иерархическая двухфакторная
схема):
288
для общего варьирования
df — abc— 1;
для варьирования по фактору А
df — a — 1-,
для варьирования по фактору В
df=a(b—l)',
для случайных отклонений
df = ab(c— 1).
При сравнении эмпирических распределений с теоретическими
df — k — 2 (биномиальное);
df — k — 3 (нормальное).
В таблицах состава с r-рядами и с-столбцами
d/ = (r —1)(с—1). (102)
Сумма квадратов [дисперсия; ss]
Общая формула 2(х;— х)2.
Рабочие формулы при вычислении о и. о2:
а) 2х?—г) 2x?-2xz ~х,
б) 2 {xt-AY-n{x - Л)2; д) 2 /X2----;
в) 2 х? — лх2; е) 2 fa*i2 — ni2
При дисперсионном анализе (однофакторная схема) [ssj
Общие формулы:
для общего варьирования
2 (х0- - х)2;
о
для варьирования групповых средних (фактор А)
Sn/fa—x)*;
для случайных отклонений
2[2(ху — xz)2J.
Рабочие:
для-общего варьирования
10 П. Ф. Рокяцкий 289
для варьирования групповых средних (фактор Л)
у 21 _ 21-
I N •
для случайных отклонений
2х&-2^-.
ij i nl
При дисперсионном анализе (двухфакторная схема)
Общие формулы:
для общего-варьирования
? (Xijk
4k
для варьирования по фактору А
ncZ(xt — х)®;
для варьирования по фактору В
nr 2 (х, — х)®;
для взаимодействия А и В
nZ^u—Xt —~Xj +х)®;
для случайных отклонений
Рабочие формулы:
для общего варьирования
2x^-2!;
ijk ГСП
для варьирования по фактору А
ПС i ГСП
для варьирования по фактору В
— 2 Т? —
ПГ ; ' ГСП’
для взаимодействия Л и В
---Ls?? —2_£Т? = 22;
п Ц 4 ПС I ПГ ] ‘ ГСП'
для случайных отклонений
2х?д—Lsn.
у ‘1k П И
290
При дисперсионном анализе (трехфакторная схема)
Общие формулы см. по табл. 54;
рабочие в тексте гл. 8 (стр. 226).
При дисперсионном анализе (иерархическая двухфакторная
схема)
Общие формулы:
для общего варьирования
2 (*У*-*Л
l]k
для варьирования по фактору А
be 2 (х£ — х)2;
для варьирования по фактору В
c^(xtj xz)2;
у
для случайных отклонений
2 xij)2-
о®
Рабочие формулы:
для общего варьирования
V 2 Т2
iXiik °Ьс’
для варьирования по фактору А
be ( abc
для варьирования по фактору В
— 2ТЛ- -jJ-277;
для случайных отклонений
2 x^—LzT^.
ilk с ij
Уравнение кривой нормального распределения
(Х£—х)!
1 2^~
у = —
а/2я
или при о=1 и"введении величины t
Уравнение регрессии
«•
291
в общем виде
Vi — y = b(xt — х);_ (55)
преобразованное
У1 = У + Ь(х1 — х); (55а)
в виде уравнения прямой
у = а + Ьх. (56)
Системы уравнений для его решения:
1. па + (2 Xi) b = 2 yt-,
2. ^xl)a+(^xt)b='Zxlyi. (57)
Для параболической кривой 2-го порядка
у = а 4- Ьх + сх*. (70)
Системы уравнений для его решения
1. па 4- (2 xt) Ь (S xt) с = 2 yt;
2. (2 xt) a + (2x?)b + (2 xt) с = 2 ед; (71)
3. (^xt)a + (Zxl)b + (^xt)c = 2xtyl.
Для экспоненциальной кривой
W = А • Вх\ (72)
преобразованное в логарифмическую форму
log W = log А 4- (log В) х. {72$
Численность необходимая выборки
при количественной вариации
>» а*
« = -1Н (26)
при альтернативной вариации
п = (84)
292
СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
I. Таблица вероятностей при нормальном распределении. До-
ли площади под нормальной кривой в пределах от —I до -bi-
ll. Доли площади под кривой 1-распределения, по Стью денту
в пределах от — t до +1 для малого числа наблюдений п.
III. Значения t при различных уровнях значимости (Р).
IV. Количество «+» или «—» знаков, превышение над кото-
рым при данном п достаточно, чтобы считать разницу достовер-
ной с уровнями значимости Р = 0,05 и Р= 0,01.
V. Значения F при уровне значимости 0,05.
VI. Значения F при уровне значимости 0,01.
VII. Необходимые значения коэффициента корреляции при
различных уровнях значимости Р и разном числе степеней свобо-
ды (df = n — 2).
VIII. Значения г при разных z (от 0 до 2,99).
IX. Коэффициенты Q (округлены до одной десятой) для по-
лучения достоверных разниц между группами при дисперсионном
анализе Р = 0,05).
X. /’-распределение.
XI. Частоты (накопленные) нормального распределения. п =
= 10000.
XII. Доли площади под нормальной кривой, отсекаемые t
слета от средней.
XIII. Доли площади под нормальной кривой, отсекаемые t
справа от средней.
XIV. Доли площади под нормальной кривой, отсекаемые t
справа и слева от средней.
XV. Значения <р.
XVI. Случайные числа.
XVII. Значения F при уровне значимости 0,001.
298
Таблица I
Таблица вероятностей при нормальном распределении.
Доли площади под нормальной кривой в пределах от — f до -f-/
t Сотые доли t
0 1 2 3 4 5 6 7 8 9
0,0 0000 0080 0160 0239 0319 0399 0478 0558 0638 0717
0,1 - 0797 0876 0955 1034 1113 Т192" 1271 1350 1428 1507
0,2 1585 1663 1741 1819 1897 1974 2051 2128 2205 2282
о.з 2358 2434 2510 2586 2661 2737 2812 2886 2961 3035
0,4 3108 3182 3255 3328 3401 3473 3545 3616 3688 3759
0,5 3829 3899 3969 4039 4108 4177 4245 4313 4381 4448
0,6 4515 4581 4647 4713 4778 4843 4907 4971 5035 5098
0,7 5161 5223 5285 5346 5407 5467 5527 5587 5646 5705
0,8 5763 5821 5878 5935 5991 6047 6102 6157 6211 6265
0,9 6319 6372 6424 6476 6528 6579 6629 6680 6729 6778
1,0 6827 6875 6923 6970 7017 7063 7109 7154 7199 7243
1,1 7287^ -7330 7373 7415 7457 7499 7540 7580 7620 7660
1,2 7699" 7737 7775 7813 7850 7887 7923 7959 7995 8029
1,3 8064 8098 8132 8165 8198 8230 8262 8293 8324 8355
1,4 8385 8415 8444 8473 8501 8529 8557 8584 8611 8638
1,5 8664 8690 8715 8740 8764 8789 8812 8836 8859 8882
1,6 8904 8926 8948 8969 8990 901Г 9031 9051 9070 9090
1,7 9109 9127 9146 9164 9181 9199 9216 9233 9249 9265
1,8 9281 9297 9312 9327 9342 9357 93Л 9385 9399 9412
1,9 9426 9439 9451 9464 9476 9488 9500 . 9512 9523 9534
2,0 9545 9556 9566 9576 9586 9596 '980Й Ч93ТГ *9625 9634
2Д 9643 9651 9660 9668 9676 9684 9692 9700 9707 9715 ’
2,2 9722 9729 9736 9743 9749 9756 9762 9768 9774 9780
2,3 9786 9791 9797 9802 9807 9812 9817 9822 9827 9832
2,4 9836 9840 9845 9849 9853 9857 9861 9865 9869 9872
2,5 9876 9879 9883 9886 9889 9892 9895 9898 9901 9904
2,6 9907 9909 9912 9915 9917 9920 9922 9924 9926 9929
2,7 9931 9933 9935 9937 9939 9940 9942 9944 9946 9947
2,8 9949 9960 9952 9953 9955 9956 9958 9959 9960 9961
2,9 9963 9964 9965 9966 9967 99^ 9969 9970 9971 9972
3,0 9973 9981 9986 9990 9993 9995 9997 9998 9999 9999
294
Таблица II
Доли площади под кривой ^-распределения по Стьюденту в пределах
от — t до +1 для малого числа наблюдений п
2 3 4 5 6 7 8 I9 10 12 14 16 18 20 00
6,1 063 071 073 075 076 076 077 077 077 078 078 078 078 079 080
0,2 126 140 146 149 151 152 153 154 154 155 155 156 156 156 158
0,3 186 208 216 221 224 226 227 228 229 230 231 232 232 233 236
0,4 - 242 272 284 290 294 297 299 300 302 303 304 305 306 306 311
0,5 295 333 347 357 362 365 368 369 371 373 375 376 377 377 383
о,6 344 391 409 419 425 430 433 435 437 439 441 433 444 444 452
0,7 389 444 466 417 485 490 493 496 498 502 504 505 507 508 516
0,8 430 492 518 531 540 546 550 553 556 558 562 564 565 566 576
09 467 537 537 581 591 597 602 606 608 613 616 618 619 621 632
1,0 500 577 609 626 637 644 649 653 657 661 664 667 669 670 683
1,1 530 614 648 667 679 687 692 697 700 705 709 711 713 715 729
1,2 558 647 684 704 716 725 731 736 739 745 748 751 753 755 770
1,3 583 677 716 737 750 759 765 770 774 780 784 788 789 791 806
¥ 605 704 744 766 780 789 796 801 805 811 815 818 821 822 838
1,5 626 728 769 792 806 816 823 828 832 838 842 846 848 850 866
1,6 644 749 792 815 830 839 846 852 856 862 866 870 872 874 890
1,7 661 769 812 836 850 860 867 872 877 883 887 890 893 895 911
1,8 677 786 830 854 868 878 885 890* >89£ 901 905 908 910 912 928
1,9 692 802 846 870 884 894 901 906 910 916 920 923 925 927 943
го 705 816 861 884 898 908 914 919 923 929. 933 936 938" 940 954
2,1 717 829 873 896 910 920 926 931 935 940 944 947 949 951 964
22 728 841 885 907 921 930. 936 941 945 950 954 956 958 960 972
295
Продолжение таблицы
'V 2 3 4 5 6 7 8 9 10 12 "14 16 18 20 00
2,3 739 852 895 917 930 939 945 950 953 958 961 964 966 967 979
2,4- 749 862 904 .926 938 947 953 957 960 965 968 970; 972 973 984
2,5 758 870 912 933 946 953 959 963 966 970 973 975 977 978 988
2,6 766 878- 920 940 952 959 965 968 971 975 978 980 981 982 991
2,7 774 886 926 946 957 964 969 973 976 979 982 984 985 986 993
2,8 782 893 932 951 962 969 973 977 979 983 985 987 988 989 995
2,9 789 899 937 956 966 973. 977 980 982 986 988 989 990 991 996
3,0 795 905 942 960 970 976 980 983 985 988 990 991 992 993 997
3,1 801 910 947 964 973 979 983 985 987 990 992 993 994 994 998
3,2 807 915 951 967 976 981 985 987 989 992 993 994 995 . 995 999
3,3 813 919 954 970 979 984 987 989 991 993 994 995 996 996 999
3,4 818 923 958 973 981 986 989 991 992 994 995 996 997 997 999
3,5 823 927 961 975 983 987 990 992 993 995 996 997 997 998 1
3,6 828 931 963 977 984 989 991 ‘993 994 996 997 997 998 998
3,7 832 934 966 979 986 990 992 994 995 996 997 998 998 998
3,8 836 937 968 981 987 991 993 995 996 997 998 998 999 999
3,9 840 940 970 982 989 992 994 995 996 998 998 999 999 999
4,0 844 943 972 984 990 993 995 996 997 998 998 999 999 999
4,1 848 945 974 985 991 994 995 997 997 998 999 999 999 999
4,2 851 948 975 986 992 994 996 997 998 999 999 999 999 1
4,3 855 950 977 987 992 995 996 997 998 999 999 999 999
4,4 858 $52 978 988 993 995 997 998 998 999 999 999 1
4,5 861 954 980 989 994 996 997 998 999 999 999 1
4.6 864 956 981 990 994 996 998 998 999 999 1
4,7 867 958 982 991 995 997 998 998 999 999
4,8 869 959 983 991 995 997 998 999 999. -999
4,9 872 961 984 992 996 997 998 999 999 1
296
Таблица III
Значения t при различных уровнях значимости (Р)
Число сте- пеней сво- боды Уровень значимости Р
о,1 0,05 0,02 0,01 0,001
1 6,31 12,7 31,82 63,66 -
2 2,92 4,30 6,97 9,93 31,60
3 2,35 3,18 4,54 5,84 12,94
4 2,13 2,78 3,75 4,60 8,61
5 2,02 2,57 3,37 4,03 6,86
6 1,94 v 2,45 3,14 3,71 5,96
7 1,90 V‘2,37 3,00 3,50 5,41
8 1,86 2,31 2,90 3,36 5,04
9 1,83 2,26 2,82 3,25 4,78
10 1,81 2,23 2,76 3,17 4,59
И 1,80 2,20 2,72 3,11 4,44
12 1,78 ' 2,18 2,68 3,06 4,32
13 1,77 2,16 2,65 3,01 4,22
14 1,76 2,15 2,62 2,98 4,14
15 1,75 2,13 2,60 2,95 4,07
16 1,75 2,12 2,58 2,92 4,02
17 1,74 -2,11 2,57 2.9Q 3,97
18 1,73 2,10 2,55 2,88 3,92
19 1,73 2,09 2,54 2,86 3,88
20 1,73 2,09 2,53 2,85 3,85
21 1,72 2,08 2,52 2,83 3,82
22 1,72 2,07 2,51 2,82 3,79
23 1,71 2,07 2,50 2,81 3,77
24 1,71 2,06 2,49 2,80 3,75
25 1,71 2,06 2,49 2,79 3,73
26 1,71 2,OS' 2,48 2,78 3,71
27 1,70 2,05 2,47 2,77 3,69
28 1,70 2,05 2,47 2,76 3,67
29 1,70 2,05' 2,46 2,76 3,66
30 ' 1,70 2,04 2,46 2,75 .3,65
1,64 1,96 т’ 2,33 2,58 3,29 Lt
297
Таблица IV
Количество «+> или «—» знаков, превышение над которым при данном п
достаточно, чтобы считать разницу достоверной с уровнями значимости
Р = 0,05 или Р = 0,01
п Р Р п Р п Р
0,05 0,01 0,05 0,01 0,05 0,01 0,05 0,01
10 8 -9 34 23 24 58 36 39 82 50 53
11 9 10 35 23 25 59 37 39 83 50 53
12 9 10 36 24 26 60 38 40 84 51 54
13 10 И 37 24 26 61 38 40 85 52 54
14 И 12 38 25 27 62 39 41 86 52 55
15 ' И 12 39 26 27 63 39 42 87 53 55
16 12 13 40 26 28 64 40 42 88 53 56
17 12 13 41 27 29 65 40 43 89 54 57
18 13 14 42 27 29 66 41 43 90 54 57
19 14 15 43 28 30 67 41 44 91 55 58
20 14 16 44 28 30 68 42 45 92 55 58
21 15 16 45 29 31 69 43 45 93 56 59
22 16 17 46 30 32 70 ' 43 46 94 56 59
23 16 18 47 30 32 71 44 46 95* 57 60
24 17 18 48 31 33 72 44 47 96 58 61
25 17 19 49 31 33 73 45 47 97 58 61
26 18 19 50 32 34 74 45 48 98 59 62
27 19 20 51 32 35 75 46 49 99 59 62
28 19 21 52 33 35 76 47 49 100 60 63
29 20 21 53 34 36 77 47 50
30 20 22 54 34 36 78 48 50
31 21 23 55 35 37 79 48 51
32 22 23 56 35 38 80 49/ 51
33 22 24 57 36 38 81 49 52
298
Таблица V
Значения F при уровне значимости 0,05 (d/i — число степеней свободы для большей вариансы,
которая берется числителем)
df2 dh 1 2 3 4 5 6 7 8 9 10 12 15 20 30 QO
1 161 200 216 225 230 234 237 239 241 242 244 246 248 250 254
2 18,51 19,00 19,16 19,25 19,30 19,33 19,35 19,37 19,38 19,40 19,41 19,43 19,45 19,46 19,50
3 10,13 9,55 9,28 9,12 9,01 8,94 8,89 8,85 8,81 * 8,79 8,74 8,70 8,66 8,62 8,53
4 7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00 5,94 5,91 5,86 5,80 5,75 5,63
5 6,61 5,79 5,41 5,19 5,05 4,95 488 4,82 4,77 4,74 4,68 4,62 4,56 4,50 4,36
6 5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 4,00 3,94 4,87 3,81 3,67
7 5,59 4,74 4,35 4,12 3,97 3,87 3,79 3,73 3,68 3,64 3,57 3,51 3,44 3,38 3,23
8 5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3,35 3,28 3,22 3,15 3,08 2,93
9 5,12 4,26 3,86 3,63 3,48 3,37 3,29 3,23 3,18 3,14 3,07 3,01 2,94 2,86 2,71
10 4,96 4,10 3,71 3,48 3,33 3,22 3,14 3,07 ' 3,02 2,98 2,91 2,85 3,77 2,70 2,54
11 4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2.90 2,85 2,79 2,72 2,65 2,57 2,40
12 4,75 3,89 3,49 3,26 3,11 3,00 2,91 2,85 2,80 2,75 2,69 2,62 2,54 2,47 2,30
13 4,67 3,80 3,41 3,18 3,02 2,92 2,83 2,77 2,71 2,67 2,60 2,53 2,46 2,38 2,21
14 4,60 3,74 3,34 з.п 2,96 2,85 2,76 2,70 2,65 2,60 2,53 2,46 2,39 2,31 2,13
15 4,54 3,68 3,29 3,06 2,90 2,79 2,71 2,64 2,59 2,54 2,48 2,40 ’ 2,33 2,25 2,07
Продолжение таблицы V
dh *
«Л 1 2 3 4 5 6 7 8 9 10 12 15 20 30 do
16 4,49 3,63 3,24 3,01 2,85 2.74 2,66 2,59 2,54 2,49 2,42 2,35 2,28 2,19 2,01
17 4,45 3,59 3,20 2,96 2,81 2,70 2,61 2,55 2,49 2,45 2,38 2,31 2,23 2,15 1,96
18 4,41 3,55 3,16 2,93 2,77 2,66 2,58 2,51 2,46 2,41 2,34 2,27 2,19 2,И 1,92
19 4,38 3,52 3,13 2,90 2,74 2,63 2,54 2,48 2,42 2,38 2,31 2,23 2,16 2,07 1,88
20 4,35 3,49 3,10 2,87 2,71 2,60 2,51 2,45 2,39 2,35 2,28 2,20 2,12 2,04 1,84
21 4,32 3,47 3,07 2,84 2,68 2,57 2,49 2,42 2,37 2,32 2,25 2,18 2,10 2,01 1,81
22 4,30 3,44 3,05 2,82 2,66 2,55 2,46 2,40 2,34 2,30 2,23 2,15 2,07 1,98 1,78
23 4,28 3,42 3,03 2,80 2,64 2,53 2,44 2,37 2,32 2,27 2,20 2,13 2,05 1,96 1,76
24 4,26 3,40 3,01 2,78 2,62 2,51 2,42 2,36 2,30 2,25 2,18 2,П 2,03 1,94 1,73
25 4,24 3,39 2,99 2,76 2,60 2,49 2,40 2,34 2,28 2,24 2,16 2,09 2,01 1,92 1,71
26 4,22 3,37 2,98 2,74 2,59 2,47 2,39 2,32 2,27 2,22 2,15 2,07 1,99 1,90 1,69
27 4,21 3,35 2,96 2,73 2,57 2,46 2,37 2,31 2,25 2,20 2,13 2,06 1,97 1,88 1,67
28 4,20 3,34 2,95 2,71 2,56 2,45 2,36 2,29 2,24 2,19 2,12 2,04 1,96 1,87 1,65
29 4,18 3,33 2,93 2,70 2,55 2,43 2,35 2,28 2,22 2,18 2,10 2,03 1,94 1,85 1,64
30 4,17 3,32 2,92 2,69 2,53 2,42 2,33 2,27 2,21 2,16 2,09 2,01 1,93 1,84 1,62
40 4,08 3,23 2,84 2,61 2,45 2,34 2,25 2,18 2,12 2,08 2,00 1,92 1,84 1,74 1,51
60 4,00 3,15 2,76 2,53 2,37 2,25 2,17 2,10 2,04 1,99 1,92 1,84 1,75 1,65 1,39
120 3,92 3,07 2,68 2,45 2,29 2,17 2,09 2 02 1,96 1,91 1,83 1,75 1,66 1,55 1,25
ОО 3,84 3,00 2,60 2,37 2,21 2,10 2,01 1,94 1,88 1,83 1,75 1,67 1,57 1,46 1,00
Таблица VI
Значения F при уровне значимости 0,01 — число степеней свободы для большей вариансы
которая берется числителем)
dfi 1 2 3 4 5 i 6 7 8 9 10 12 15 20 30
1 4052 4999 5403 5625_ 5764 5859 5928 5982 6022 6056. 6106 6157 6209 6261 6366
2 98,50 99,00 99,17 99,25 99,30 99,33 99,36 99,37 99,39 99,40 99,42 99.43 99,45 99,47 99,50
3 34,12 30,82 29,46 28,71 28,42 27,91 27,67 27,49 27,35 27,23 27,05 26,87 26,69 26,50 26,13
4 21,20 18,00 16,69 15,98 15,52 15,21 14,98 14,80 14,66 14,55 14,37 14,20 14,02 13,84 13,46
5 * 16,26 13,27 12,06 11,39 10,97 10,67 10,46 10,29 10,16 10,05 9,89 9,72 9,55 9,38 9,02
6 13,75 10,92 9,78 9,15 8,75 8,47 8,26 8,10 7,98 7,87 7,72 7,56 7,40 7,23 6,88
7 12,25 9,55 8,47. 7,85 7,46 7,19 6,99 6,84 6,72 6,62 6,47 6,31 6,16 5,99 5,65
8 11,26 8,65 7,59 7,01 6,63 6,37 6,18 6,03 5,91 5,81 5,67 5,52 5,36 5,20 4,86
9 10,56 8,02 6,99 6,42 6,06 5,80 5,61 5,47 5,35 5,26 5,11 4,96 4,81 4,65 4,31
10 10,04 7,56 6,55 5,99 5,64 5,39 5,20 5,06 4,94 4,85 4,71 4,56 4,41 4,25 3,91
11 9,65 7,21 6,22 5,67 5,32 5,07 . 4,89 4,74 4,63 4,54 4,40 4,25 4,10 3,94 3,60
12 9,33 6,93 5,95 5,41 5,06' 4,82 4,64 4,50 4,39 4,30 4,16 4,01 3,86 3,70 3,36
13 9,07 6,70 5,74 5,21 4,86 4,62 4,44 4,30 4,19 4,10 3,96 3,82 3,66 3,51 3,16
14 -8,86 6,51 5,56 5,04 4,69 4,46 4,28 4,14 4,03 3,94 3,80 3,66 3,51 3,35 3,00
15 8,68 6,36 5,42 4,89 4,56 4,32 4,14 4,00 3,89 3,80 3,67 3,52 3,37 3,21 2,87
Продолжение таблицы VI
1 2 3 4 5 — 6 7 8 9 10 12 15 20 30 00
df,
16 8,53 6,23 5,29 4,77 4,44 4,20 4,03 3,89 3,78 3,69 3,55 3,41 3,26 3,10 2,75
17 8,40 6,11 5,18 4,67 4,34 4,10 3,93 3,79 3,68 3,59 3,46 3,31 3,16 3,00 2,65
18 8,29 6,01 5,09 4,58 4,25 4,01 3,84 3,71 3,60 3,51 3,37 3,23 3,08 2,92 2,57
19 8,18 5,93 5,01 4,50 4,17 3,94 3,77 3,61 3,52 3,43 3,30 3,15 3,00 2,84 2,49
20 8,10 5,85 4,94 4,43 4,10 3,87 3,70 3,56 3,46 3,37 3,23 3,09 2,94 2,78 2,42
21 8,02 5,78 4,87 4,37 4,04 3,81 3,64 . 3,51 3,40 3,31 3,17 3,03 2,88 2,72 2,36
22 7,95 5,72 4,82 4,31 3,99 3,76 3,59 3,45 3,35 3,26 3,12 2,98 2,83 2,67. 2,31
3 23 7,88 5,66 4,76 4,26 3,94 3,71 3,54 3,41 3,30 3,21 3,07 2,93 2,78 , 2,62 2,26
24 7,82 5,61 4,72 4,22 3,90 3,67 3,50 3,36 3,26 3,17 3,03 2,89 2,74 2,58 2,21
25 7,77 5,57 4,68 4,18 3,85 3,63 3,46 3,32 3,22 3,13 2,99 2,85 2,70 2,54 2,17
26 7,72 5,53 4,64 4,14 3,82 3,59 3,42 3,29 3,18 3,09 2,96 2,81 2,66 2,50 2,13
27 7,68 5,49 4,60 4,11 3,78 3,56 3,39 3,26 3,15 3,06 2,93 2,78 2,63 2,47 2,10
28 7,64 5,45 4,57 4,07 3,75 3,53 3,36 3,23 3,12 3,03 2,90 2,75 2,60 2,44 2,06
29 7,60 5,42 4,54 4,04 3,73 3,50 3,33 3,20 3,09 3,00 2,87 2,73 2,57 2,41 2,03
30 7,56 5,39 4,51 4,02 3,70 3,47 3,30 3,17 3,07 2,98 2,84 2,70 2,55 7,39 2,01
40 7,31 5,18 4,31 3,85 3,51 3,29 3,12 2,99 2,89 2,80 2,66 2,52 2,37 2,20 1,80
60 7,08 4,98 4,13 3,63 3,34 3,12 2,95 2,82 2,72 2,63 2,50 2,35 2,20 2,03 1,60
120 6,85 4,79 3,95 3,48 3,17 2,96 2,79 2,66 2,56 2,47 2,34 2,19 2,03 1,86 1,3 9
00 6,63 4,61 3,78 3,32 3,02 2,80 2,64 2,51 2,41 2,32 2,18 2,04 1,88 1,70 1,00
Таблица VII
Необходимые значения коэффициента корреляции г при различных уровнях
значимости Р и разном числе степеней свободы df(df—n—2)
df Р df Р
0,05 0,01 0,05 0,01
5 0,75 0,87 * 27 0,37 0,47
6 0,71 0,83 28 0,36 0,46
7 067 0,80 29 0,36 0,46
8 0,63 0,77 30 0,35 0,45
9 0,60 0,74 35 0,33 0,42
10 ОМ 0,71 40 0,30 0,39
11 0,55 0,68 45 0,29 0,37
12 0,53 0,66 50 0,27 0,35
13 0,51 0,64 60 0,25 0,33
14 0,50 *0,62 70 0,23 0,30
15 0,48 0,61 80 0,22J 0,28
16 0,47 0,59 . 90 0,21 j 0,27
. 17 0,46 0,58 100 0,20) 0,25
18 0,44 0,56 125 0,17 0,23
19 0,43 0,55 150 0,16 0,21
20 0,42 0,54 200 0,14 0,18
21 0,41 0,53 300 0,11 0,15
22 0,40 0,52 400 0,10 0,1?
23 0,40 0,51 500 0,09 0,12
24 0,39 0,50 700 0,07 0,10
25 0,38 0,49 900 0,06 0,09^
26 0,37 0,48 1000 0,06 0,09
303
Таблица VIП
Значения г при разных величинах z (от 0 до 2,99). Для краткости ноль
перед коэффициентом корреляции опущен, поэтому 0997 надо читать
как 0,0997
2 Сотые доли z
0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0000' 0100 0200 0300 0400 0500 0599 0699 0798 0898
0,1 0997 1096 1194 1293 1391 1489 1586 1684 1781 1877
0,2 1974 2070 2165 2260 2355 2449 2543 2636 2729 2821
0,3 2913 3004 3095 3185 3275 3364 3452 3540 3627 3714
0,4 3800 3885 3969 4053 4136 4219 4301 4382 4462 4542
0.5 4621 4699 4777 4854 4930 5005 5080 5154 5227 5299
0.6 5370 5441 5511 5580 5649 5717 5784 5850 5915 5980
0,7 6044 6107 6169 6231 6291 6351 6411 6469 6527 6584
0,8 6640 6696 6751 6805 6858 6911 6963 7014 7064 7114
0,9 7163 7211 7259 7306 7352 7398 7443 7487 7531 7574
1,0 7616 7658 7699 7739 7779 7818 7857 7895 7932 7969
1,1 8005 8041 8076 8110 8144 8178 8210 8243 8275 8306
1,2 8337 8367 8397 8426 8455 8483 8511 8538 8565 8591
1,3 8617 8643 8658 8692 8717 8741 8764 8787 8810 8832
1,4 8854 8875 8896 8917 8937 8957 8977 8996 9015 9033
1,5 9051 9069 9087 9104 9112 9138 9154 9170 9186 9201
1,5 9217 9232 9246 9261 9275 9289 9302 9316 9329 9341
1,7 9354 9366 9379 9391 9402 9414 9425 9436 9447 9458
1,8 9468 9478 9488 9498 9508 9517 9527 9536 9545 9554
1,9 9562 9571 9579 9587 9595 9603 9611 9618 9626 9633
2,0 9640 9647 9654 9661 9668 9674 9680 9687 9693 9699
2,1 9705 9710 9716 9721 9727 9732 9738 9743 9748 9753
2,2 9757 9762 9767 9771 9776 9780 9785 9789 9793 9797
2,3 9801 9805 9809 9812 9816 9820 ' 9823 9827 9830 9834
2,4 9837 9840 9843 9846 9849 9852 9855 9858 9861 9863
2,5 9866 9869 9871 9874 9876 9879 9881 9883 9886 9888
2,6 9890 9892 9894 9897 9899 9901 9903 9904 9906 9908
2,7 9910 9912 9914 9915 9917 9919 9920 9922 9923 9925
2,8 9926 9928 9929 9931 9932 9933 9935 9936 9937 9938
2,9 9940 9941 9942 9943 9944 9945 9946 9947 9948 9949
304
Таблица IX
Коэффициенты Q (округлены до одной десятой) для получения достоверных
разниц между группами при дисперсионном анализе (Р ~ 0,05)
Число степе- ней свобо- ды df Количество групп а
2 3 4 5 6 7 8 it 9 10 И 12
6 3,5 4.3 4,9 5,3 5.6 5,9 6,1 6,3 6,5 6,7 6,8
. 7 3,3 4,2 4,7 5,1 5.4 5,6 5,8 6,0 6,2 -6,3 6,4
8 3,3 4,0 4,5 4,9 5,2 5,4 5,6 5,8 5,9 6,1 6,2
9 3,2 4,0 4,4 •4.8 5,0 5,2 5,4 5,6 5,7 5,9 6,0
10 3,1 3,9 4,3 4,7 4,9 5,1 5,3 5,5 5,6 5,7 5,8
11 3,1 3,8 4,2 4,6 4,8 5,0 5,2 5,4 5,5 5,6 5,7
12 3,1 3,8 4,2 4,5 4,8 5,0 5,1 5,3 5,4 5,5 5,6
13 3,1 3,7 4,2 4,5 4,7 4,9 5,1 5,2 5,3 5,4 5,5
14 3,0 3,7 4,1 4,4 4,6 4,8 5,0 5,1 5,3 5,4 5,5
15 3,0 3,7 4,1 4,4 4,6 4,8 4,9 5,1 5,2 5,3 5,4
16 3,0 3,7 4,1 4,3 4,6 4,7 4,9 5,0 5,2 5,3 5,4
17 3,0 3,6 4,0 4,3 4,5 47 4,9 5,0 5,1 5,2 5,3
18 3,0 3,6 4,0 4,3 4,5 4,7 4,8 5,0 5,1 5,2 5,3
19 3,0 3,6 4,0 4,3 4,5 4,6 4,8 4,9 5,0 5,1 5,2
20 3,0 3,6 4,0 . 4,2 4,5 4,6 4,8 4,9 5,0 5,1 5,2
24 2,9 3,5 3,9 4,2 4,4 4,5 4,7 4,8 4,9 5,0 5,1
30 2,9 3,5 3,8 4,1 4,3 4,5 4,6 4,7 4,8 4,9 5,0
40 2,9 3,4 3,8 4,0 4,2 44 4,5 4,6 4,7 4,8 4,9
60 2,8 3,4 3,7 4,0 4,2 4,3 4,4 4,6 4,7 4,7 4,8
120 2,8 3,4 3,7 3,9 4,1 4,2 4,4 4,5 4,6 4,6 4,7
305
Таблица X
^-распределение
df Вероятности значения превышающего табличное
0.99 0,95 0,90 0,75. 0,50 0,25 0,10 0,05 0,025 0,01
1 • 0,02 0,10 0,45 1,32 2,71 3,84 5,02 6,63
2 0,02 0,10 0,21 0,58 1,39 2,77 4,61 5,99 7,38 9,21
3 0,11 0,35 0,58 1,21 2,37 4,11 6,25 7,81 9,35 11,34
4 о,зо 0,71 1,06 1,92 3,36 5,39 7,78 9,49 11,14 13,28
5 0,55 1,15 1,61 2,67 4,35 6,63 9,24 11,07 12,83 15,09
6 0,87 1,64 2,20 3,45 5,35 7,84 10,64 12,59 14,45 16,81
7 1,24 2,17 2,83 4,25 6,35 9,04 12,02 14,07 16,01 18,48
8 1,65 2,73 3,49 5,07 7,34 10,22 13,36 15,51 17,53 20,09
9 2,09 3,33 4,17 5,90 8,34 11,39 14,68 16,92 19,02 21,67
10 2,56 3,94 4,87 6,74 9,34 12,55 15,99 18,31 20,48 23,21
11 3,05 4,57 5,58 7,58 10,34 13,70 17,28 19,68 21,92 24,72
12 3,57 5,23 6,30 8,44 11,74 14,85 18,55 21,03 23,34 <26,22
13 ди 5,89 7,04 9,30 12,34 15,98 19,81 22,36 24,74 27,69
14 4,66 6,57 7.79 10,17 13,34 17,12 21,06 23,68 26,12 29,14
15 5,23 7,26 8,55 11,04 14,34 18,25 22,31 25,00 27,49 30,58
16 5,81 7,96 9,31 11,91 15,34 19,37 23,54 26,30 28,85 32,00
17 6,41 8,67 10,09 12,79 16,34 20,49 24,77 27,59 30,19 33,41
18 7,01 9,39 10,86 13*68 17,34 21,60 25,99 28,87 31,53 34,81
19 7,63 10,12 11,65 14,56 18,34 22,72 27,20 30,14 32,85 36,19
20 8,26 10,85 12,44 15,45 19,34 23,83 28,41 31,41 34,17 37,57
21 8,90 11,59 13,24 16,34 20,34 24,93 29,62 32,67 35,48 38,93
22 9,54 12,34 14,04 17,24 51,34 26,04 30,81 33,92 36,78 40,29
23 10,20 13,09 14,85 18,14 22,34 27,14 32,01 35,17 38,08 41,64
24 10,86 13,85 15,66 19,04 23,34 28,24 33,20 36,42 39,36 42,98
25 11,52 14,61 16,47 19,94 24,34 29,34 34,38 37,65 40,65: 44,31
26 12,20 15,38 17,29 20,84 25,34 30,43 35,56 38,89 41,92 45,64
27 12,88 16,15 18,11 21,75 26,34 31,53 36,74 40,11 43,19 46,96
28 13,56 16,93 18,94 22,66 27,34 32,62 37,92 41,34 44,46 48,28
29 14,26 17,71 19,77 .23,57 28,34; 33,71 39,09 . 42,56 45,72 49,59
30 14,95 18,49 20,60 24,48 29,34 34,80 40,26 43,77 46,98 50,89
40 22,16 26,51 29,05 33,66 39,34 45,62 51,80 55,76 59,34 63,69
50 29,71 34,76 37,69 42,94 49,33 56,33 63,17 67,50 71,42 76,15
60 37,48 43,19 46,46 52,29 59,33 66,98 74,40 79,08 83,30 88,38
70 45,44 51,74 55,33 61,70 69,33 77,58 85,53 90,53 95,02 100,42
80 53,54 60.39 64,28 71,14 79,33 88,13 96,58 101,88 106,63 112,33
90 61,75 69,13 73,29 80,62 89,33 98,64 107,56 113.14 118,14 124,12
100 70,06 77,93 82,36 90,13 99,33 109,14 118,50 124,34 129,56 135,81
306
Таблица XI
Частоты (накопленные) нормального распределения, п — 10 000
. а Сотые доли а
4,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0000 0040 0080 0120 0160 0199 0239 0279 0319 0359
ОД 0398 0438 0478 0517 0557 0596 0636 0675 0714 0753
0,2 0793 0832 0871 0910 0948 0987 1026 1064 1103 1141
0,3 1179 1217 1255 1293 1331 1368 1406 1443 1480 1517
0,4 1551 1591 1628 1664 1700 1736 1772 1808 1844 1879
0,5 1915 1950 1985 2019 2054 2088 2123 2157 2190 2224
0,6 2257 2291 2324 2357 2389 2422 2454 2486 2517 2549
0,7 2580 2611 2642 2673 2704 2734 2764 2794 2823 2252
0,8 2881 2910 2939 2967 2995 3023 3051 3078 3106 3133
0,9 3159 3186 3212 3238 3264 3289 3315 3340 3365 3389
1,0 3413 3438 3461 3485 3508 3531 3554 3577 3599 3621
1.1 3643 3665 3686 3708 3729 3749 3770 3790 3810 3830
1.2 3849 3869 3888 3907 3925 3944 3962 3980 3997 4015
1,3 4032 4049 4066 4082 4099 4115 4131 4147 4162 4177
1,4 4192 4207 4222 4236 4251 4265 4279 4292 4306 4319
1,5 4332 4345 4357 4370 4382 4394 4406 4418 4429 4441
1,6 4452 4463 4474 4484 4495 4505 4515 4525 4535 4545
1,7 4554 4564 4573 4582 4591 4599 4608 4616 4625 4633
1,8 4641 4649- 4656 4664 4671 4678 4686 4693 4699 4706
1,9 4713 4719 4726 4732 4738 4744 4750 4756 4761 4767
2,0 4772 4778 4783 4788 4793 4798 4803 4808 4812 4817
2,1 4821 4826 4830 4834 4838 4842 4846 4850 4854 4857
2,2 4861 4864 4868 4871 4875 4878 4881 4884 4887 4890
2,3 4893 4896 4898 4901 4904 4906 4909 4911 4913 4916
2,4 4918 4920 4922 4925 4927 4929 4931 4932 4934 4936
2,5 4938 4940 4941 4943 4945 4946 4948 4949 4951 4952
2,6 4953 4955 4956 4957 4959 4960 4961 4962 4963 4964
2,7 4965 4966 4967 4968 4969 4970 4971 4972 4973 4974
2,8 4974 4975 4976 4977 4977 4978 4979 4979 4980 4981
2,9 4981 4982 4982 4983 4984 4984 4985 4985 4986 4986
3,0 4987 4987 4987 4988 4988 4989 4989 4989 4990 4990
3,1 4990 4991 4991 4991 4992 4992 4992 4992 4993 4993
3,2 4993 4993 4994 4994 4994 4994 4994 4995 4995 4995
3,3 4995 4995 4995 4996 4996 4996 4996 4996 4996 4997
3,4 4997 4997 4997 4997 4997 4997 4997 4997 4997 4998
3,6 4998 4998 4999 4999 4999 4999 4999 4999 4999 4999
3,9 5000
307
Таблица XII
Доли площади под нормальной кривой» отсекаемые t слева от средней
t Сотые доли t
0 1 2 3 4 1 5 1 6 7 8 9
0,0 5000 4960 4920 4880 4840 4801 4761 4721 4681 4641
-од 4602 4562 4522 4483 4443 4403 4364 4325 4286 4246
—0,2 4207 4168 4129 4090 4052 4012 3974 3936 3897 3859
—0,3 3821 3783 3744 3707 3670 .3632 3594 3557 3520 3483
—0,4 3446 3409 3372 3336 3300 3270 3227 3192 3156 3121
—0,5 3085 3050 3015 2971 2946 2912 2877 2843 2809 2776
—0,6 2743 2709 2676 3643 2611 2578 2546 2514 2482 2451
—07 2420 2388 2358 2327 2296 2266 2236 2206 2177 2148
—0,8 2119 2089 2061 2033 2004 1977 1949 1921 1894 1867
—0,9 1841 1814 1788 1762 1736 1710 1685 1660 1635 1611
—1,0 1587 1562 1539 1515 1492 1468 1446 1423 1401 1378
—1,1 1357 1335 1313 1292 1271 1251 1230 1210 1190 1170
— 1,2 1151 1131 1112 1093 1075 1056 1038 1020 1003 0985
—1,3 0968 0951 0934 0917 0901 0885 0869 0853 0838 0823
—1,4 0808 0793 0778 0763 0749 0735 0721 0708 0694 0681
-1,5 0668 0655 0642 0630 0618 0606 0594 0582 0571 0559
—1,6 0548 0537 0526 0515 0505 0495 0486 0475 0465 0455
—17 0446 0436 0427 0418 0409 0401 0392 0384 0375 0367
—1,8 0359 0351 0344 0336 0329 0321 0314 0308 0300 0294
—1,9 0287 0281 0274 0268 0262 .0256 0250 0244' 0238 0233
-2,0 0228 0222 0217 0212 0207 0202 0197 0192 0188 0183
—2,1 0179 0174 0170 0166 0162 0158 0154 0150 0146 0143
—2,2 0139 0136 0132 0129 0125 0122 0119 0116 0113 ОНО
—2,3 0107 0104 0102 0099 0096 0094 0091 0088 0086 0084
—2,4 0081 0079 0078 0075 0073 0071 0069 0067 0066 0064
—2,5 0062 0060 0059 0057 0055 0054 0052 0051 0049 0046
-2,6 0047 0045 0044 0043 0041 0040 0039 0038 0037 0036
—2,7 0035 0034 0033 0032 0031 0030 0029 0028 0027 0026
—2,8 0026 0025 0024 0023 0022 0022 0021 0020 0020 0019
—2,9 0019 0018 0017 0017 0016 0016 0015 0015 0014 0014
—3,0 0014 0010 0007 0005 0003 0002 0002 0001 0001 0000
308
Таблица XI/1
Доли площади под нормальной кривой, отсекаемые t справа от средней
t . Сотые доли t
0 1 2 3 4 5 6 7 8 9
0,0 5000 5040 5020 5120 5159 5199 5239 5279 5319 5359
0.1 5398 5438 5478 5517 5557 5596 5636 5675 5714 5753.
0,2 5793 5832 5871 5909 5948 5987 6026 6064 6103 6141
0,3 6179 6217 6256 6293 6331 6368 6406 6443 6480 6517
0,4 6554 6591 6627 6664 6700 6736 6772 6808 6844 6879
0,5 6915 6950 6985 7029 7054 7088 7123 7157 7190 7224
0,6 7257 7291 7324 7356 7389 7421 7454 7486 7517 7549
0,7 7580 7611 7642 7673 7703 7734 7764 7793 7823 7852
0,8 7881 7910 7939 7667 7995 8023 8051 8078 8106 8133
0,9 8159 8186 8212 8238 8264 8289 8315 8340 8364 8389
1,0 8413 8437 8461 8485 8508 8531 8554 8577 8599 8621
1,1 8643 8665 8686 8708 8728 8749 8770 8790 8810 8830
1,2 8849 8869 8888 8906 8925 8943 8962 8979 8997 9015
1,3 9032 9049 9066 9082 9099 9115 9131 9146 9162 9177
1,4 9192 9207 9222 9236 9251 9265 9278 9292 9306 9319
1,5 9332 9345 9357 9369 9382 9394 9406 9418 9429 . 9441
1,6 9452 9463 9474 9484 9495 9505 9515 9525 9535 9545
1,7 9554 9564 9573 9582 9591 9599 9608 9616 9625 9633 "
1,8 9641 9648 9656 9664 9671 9678 9685 9692 9699 9706
1,9 9713 9719 9726 9733 9738 9744 9750 9756 9761 9767
2,0 9772 9778 9783 9788 9793 9798 9803 9808 9812 9817
2,1 9821 9826 9830 9834 9838 9842 9846 9850 9854 9857
2,2 9861 9864 9868 9871 9874 9878 9881 9884 9887 9890
2,3 9893 9895 9898 9901 9903 9906 9909 9911 9913 9916 .
2,4 9918 9920 9922 9924 9926 9928 9930 9932 9934 9936
2,5 9938 9940 9941 9943 0944 9946 9948 9949 9951 9952
2,6 9953 9955 9956 9957 9958 9960 9961 9962 9963 9964
2,7 9965 9966 9967 9968 9969 9970 9971 9972 9973 9974
2,8 9974 9975 9976 9977 9977 9978 9978 9979 9980 9981
2,9 9982 9981 9982 99$3 9984. 9984 9985 9985 9986 9986
3,0 9986 9990 9993 9995 9997 9998 9998 9999 9999 9999
309
Таблица XIV
Доли площади под нормальной кривой, отсекаемые t справа и слева
от средней
i Сотые доли t
0 1 2 3 4 5 6 7 8 9
0,0 1000 .9920 9840 9761 9681 9601 9521 9441 9362 9283
0,1 9203* 9124 9045 8966 8887 8808 8729 8650 8571 8493
0,2 8415 8337 8259 8181 8103 ’ 8026 7949 7872 7795 7718
0,3 7642 7566 7489 7414 7338 7263 7188 7114 7039 6965
0,4 6892 6818 6745 6672 6599 6527 6455 6383. 6312 6241
0,5 6171 6101 6031 5961 5892 5823 5755 5687 5619 5552
0,6 5485 5419 5353 5287 5222 5157 5092 5028 4965 4902
0,7 4839 4777 4715 4654 4593 4532 4472 4413 4354 4295
0,8 4237 4179 4122 4065 4009 3953 3898 3843 3789 3735
0,9 3681 3628 3576 3524 3472 3421 3370 3320 3271 3222
1,0 3173 3125 3077 3030 2983 2937 2891 2846 2801 2757
1,1 2713 2670 2627 2585 2543 2501 2460 2420 2360 2340
1,2 2301 2263 2225 2187 2158 2113 2077 2041 2025 1970
1,3 1936 1902 1868 1835 1802 1770 1738 1707 1676 1645
1,4 1615 1585 1556 1527 1499 1470 1442 1416 1389 1362
1,5 1336 1310 1285 1260 1236 1211 1188 1164 1141 1118
1,6 1095 1074 1052 1031 1010 0989 0969 0949 0930 0910
1,7 0891 0873 0854 0836 0819 0801 0784 0767 0751 0734
1,8 0719 0703 0688 0672 0658 0643 0628 0615 0601 0588
1,9 0574* 0561 0549 0536 0524 0512 0500 0488 0477 0466
2,0 0455 0444 0434 0423 0413 0404 0394 0384 0375 0366
2,1 0357 0349 0340 0332 0323 0315 0308 0300 0292 0285
2,2 0278 0271 0264 0258 0251 0244 0238 0232 0226 0220
2,3 0214 0209 0203 0198 0193 0188 0183 0178 0173 0168
2,4 0164 0159 0155 0151 0147 0142 0139 0135 0131 0128
2,5 0124 0121 0117 0114 0111 0108 0105 0102 0099 0096
2,6 0093 0091 0088 0085 0082 0080 0078 0076 0074 0071
2,7 0069 0067 0065 0063 0061 0060 0058 0056 0054 0053
2,8 0051 0049 0048 0046 0045 0044 0042 0041 0040 0038 ‘
2,9 0037 0036 0035 0034 0033 0032 0031 0030 0029 0028
3,0 0027 0019 0014 0010 0007 0005 0003 0002 0001 0001
310
Таблица XV
Значения <pf = 2агс sin Ур]
% 0 1 2 3 4 5 6 7 8 9
0.0 0,000 0,020 0,028 0,035 0,040 0,045 0,049 0,053 0,057 0,060
од 0,063 0,066 0,069 0,072 0,075 0,077 0,080 0,082 0,085 0,087
0,2 0,089 0,092 0,094 0,096 0,098 0,100 1,102 0,104 0,106 0,108
0,3 0,110 0,111 0,113 0,115 0,117 0,118 0,120 0,122 0,123 0,125
0,4 0,127 0,128 0,130 0,131 0,133 0,134 0,136 0,137 ОД 39 0,140
0,5 0,142 0,143 0,144 0,146 0,147 0,148 0,150 0,151 0,153 ОД 54
0,6 0,155 0,156 0,158 0,159 0,160 0,161 0,163 0,164 0,165 0,166
0,7 0,168 0,169 0,170 0,171 0,172 0,173 0,175 0,176 0,177 0,178
0,8 0,179 0,180 0,182 0,183 0,184 0,185 0,186 0,187 0,188 0,189
0,9 0,190 0,191 0,192 0,193 0,194 0,195 0,196 0,197 0,198 0,199
1 0,200 0,210 0,220 0,229 0,237 0,246 0,254 0,262 0,269 0,277
2 0,284 0,291 0,298 0,304 0,311 0,318 0,324 0,330 0,336 0,342
3 0,348 0,354 0 360 0,365 0,371 0,376 0,382 0,387 0,392 0,398
4 0,403 0,408 0,413 0,418 0,423 0,428 0,432 0,437 0,442 0,446
5 0,451 0,456 0,460 0,465 0,469 0,473 0,478 0,482 0,486 0,491
6 0,495 0,499 0,503 0,507 0,512 0,516 0,520 0,524 0,528 0,532
7 0,536 0,539 0,543 0,547 0,551 0,555 0,559 0,562 0,566 0,570
8 0,574 0,577 0,581 0,584 0,588’ 0,592 0.595 0,599 0,602 0,606
9 0,609 0,613 0,616 0,620 0,623 0,627 0,630 0,633 0,637 0,640
10 0,644 0,647 0,650 0,653 0,657 0,660 0,663 0,666 (У,670 0,673
11 0,676 0,679 0,682 0,686 0,689 0,692 0,695 0,698 0,701 0,704
12 0,707 0,711 0,714 0,717 0,720 0,723 0,726 0,729 0,732 0,735
13 0,738 0,741 0,744 0,747 0,750 0,752 0,755 0,758 0,761 0,764
14 0,767 0,770 0,773 0,776 0,778 0,781 0,784 0,787 0,790 0,793
15 0,795 0,798 0,801 0,804 0,807 0,809 0,812 0,815 0,818 0,820
16 0,823 0,826 0,828 0,831 0,834 0,837 0,839 0,842 0,845 0,847
17 0,850 0,853 0,855 0,858 0,861 0,863 0,866 0,868 0,871 0,874
18 0,876 0,879 0,881 0,884 0,887 0,889 0,892 0,894 0,897 0,900
19 0,902 0,905 0,907 0,910 0,912 0,915 0,917 0,920 0,922 0,925
20 0,927 0,930 0,932 0,935 0,937 0,940 0,942 0,945 0,947 0,950
21 0,952 0,955 0,957 0,959 0,962 0,964 0,967 0,969 0,972 0,974
22 0,976 0,979 0,981 0,984 0,986 0,988 0,991 0,993 0,996 0,998
23 1,000 1,003 1,005 1,007 1,010 1,012 1,015 1,017 1,019 1,022
24 1,024 1,026 1,029 1,031 1,033 1,036 1,038 1,040 1,043 1,045
25 1,047 1,050 1,052 1,054 1,056 1,059 1,061 1,063 1,066 1,068
26 1,070 1,072 1,075 1,077 1,079 1,082 1,084 1,086 1,088 1,091
27 1,093 1,095 1,097 1,100 1,102 1,104 1,106 1,109 1,111 1,113
28 1,115. 1,117 1,120 1,122 1,124 1,126 1,129 1,131 1,133 1,135
29 1,137 1,140 1,142 1,144 1,146 1,148 1,151 1Д53 1,155 1,157
30 1,159 1,161 1,164 1,166 1,168 1,170 1,172 1,174 1,177 1,179
311
Продолжение таблицы XV
% 0 1 2 3 4 5 6 7 8 9
31 1,182 1,183 1,185 1,187 1,190 1,192 1,194 1,196 1,198 1,200
32 1,203 1,205 1,207 1,209 1,211 1,213 1,215" 1,217 1,220 1,222
33 1,224 1,226 1,228 1,230 1,232 1,234 1,237 1,239 1,241 1,243
34 1,245 1,247 1,249 1,251 1,254 1,256 1,258 1,260 1,262 1,264
35 1,266 1,268 1,270 1.272 1,274 1,277 1,279 1,281 1,283 1,285
36 1,287 1,289 1,291 1,293 1,295 1,297 1,299 1,302 1,304 1,306
37 1,308 1,310 1,312 1,314 1,316 1,318 1,320 1,322 1,324 1,326
38 1,328 1,330 1,333 1,335 1,337 1,339 1,341 1,343 1,345 1,347
39 1,349 1,351 1,353 1,355 1,357 1,359 1,361 1,363 1,365 1,367
40 1,369 1,371 1,374 1,37б 1,378 1,380 1,382 1,384 1,386 1,388
41 1,390 1,392 1,394 1,396 1,398 1,400 1,402 1,404 1,406 1,408
42 1,410 1,412 1,414 1,416 1,418 1,420 1,422 1,424 1,426 1,428
43 1,430 1,432 1,434 1,436 1,438 1,440 1,442 1,444 1,446 1,448
44 1,451 1,453 1,455 1,457 1,459 1,461 1,463 1,465 1,467 1,469
45 1,471 1,473 1,475 1,477 1,479 1,481 1,483 1,485 1,487 1,489
46 1,491 1,493 1,495 1,497 1,499 1,501 1,503 1,505 1,507 1,509
47 1,511 1,513 1,515 1,517 1,519 1,521 1,523 1,525 1,527 1,529
48 1,531 1,533 1,535 1,537 1,539 1,541 1,543 1,545 1,547 1,549
49 1,551 1,553 1,555 1,557 1,559 1,561 1,563 1,565 1,567 1,569
50 1,571 1,573 1,575 1,577 1,579 1,581 1,583 1,585 1,587 1,589
51 „1,591 1,593 1,595 1,597 1,599 1,601 1,603 1,605 1,607 1,609
52 1,611 1,613 1,615 1,617 1,619 1,621 1,623 1,625 1,627 1,629
53 1,631 1;633 1,635 1,637 1,639 1,641 1,643 1,645 1,647 1,649
54 1,651 1,653 1,655 1,657 1,659 1,661 1,663 1,665 1.66Г 1,669
55 1,671 1,673 1,675 1,677 1,679 1,681 1,683 1,685 1,687 1,689
56 1,691 0,693 1,695 1,697 1,699 1,701 1,703 1,705 1,707 1,709
57 1,711 1,713 1,715 1,717 1,719 1,721 1,723 1,725 1,727 1,729
58 1,731 1,734 1,736 1,738 1,740 1,742 1,744 1,746 1,748 1,750
59 1,752 1,754 1,756 1,758 1,760 1,762 1,764 1,766 1,768 1,770
60 1,772 1,774 1,776 1,778 1,780 1,782 1,784 1,786 1,789 1,791
61 1,793 1,795 1,797 1,799 1,801 1,803 1,805 1,807 1,809 1,811
62 1,813 1,815 1,817 1,819 1,821 1,823 1,826 1,828 1,830 1,832
63 1,834 1,836 1,838 1,840 1,842 1,844 1,846 1,848 1,850 1,853
64 1,855 1,857 1,859 1,861 1,863 1,865 1 867 1,869 1,871 1,873
65 1,875 1,878 1,880 1,882 1,884 1,886 1,888 1,890 1,892 1,894
66 1,897 1,899 1,901 1,903 1,905 1,907 1,909 1,911 1,913 1,916
67 1,918 1,920 1,922 1,924 1,926 1,928 1,930 1,933 1,935 1,937
68 1,939 1,941 1,943 Ц946 1,948 1,950 1,952 1,954 1,956 1,958
69 1,961 1,963 1,965 1 967 1,969 1,971 1.974 1,976 1,978 1,980
70 1,982 1,984 1,987 1,989 1,991 1,993 1,995 1,998 2,000 2,002
71 2,004 2,006 2,009 2,011 2,013 2,015 2,018 2,020 2,022 2,024
312
Продолжение таблицы XV
% 0 1 2 3 4 5 6 7 8 9
72 2,026 2,029 2,031 2,033 2,035 2,038 2,040 2,042 2,044 2,047
73 2,049 2,051 2,053 2,056 2,058 2,060 2,062 2,065 2,067 2,069
74 2,071 2,074 2,076 2,078 2,081 2,083 2,085 2,087 2,090 2,092
75 2,094 2,097 2,099 2101 2,104 2,106 2,108 2,111 2,113 2,115
76 2,118 2,120 2,122 2,125 2,127 2,129 2,132 2,134 2,136 2,139
77 2,141 .2,144 2,146 2,148 2,151 2,153 2,156 2,158 2,160 2,163
78 2,165 2,168 2,170 2,172 2,175 2,177 2,180 2,182 2,185 2,187
79 2,190 2,192 2,194 2,197 2,199 2,202 2,204 2,207 2,209 2,212
80 2,214 2,217 2,219 2,222 2,224 2,227 2,229 £2,231 2,234 2,237
81 2,240 2,242 2,245 2,247 2,250 2,252 2,255 2,258 2,260 2,263
82 2,265 2,268 2,271 2,273 2,276 2,278 2,281 2,284 2,286 2,289
83 2,292 2,294 2,297 2,300 2,302 2,305 2,308 2,310 2,313 2,316
84 2,319 2,321 2,324 2,327 2,330 2,332 2,335 2,338 2,341 2,343
85 2,346 2,349 2,352 2,355 2,357 2,360 2,363 2,366 2,369 2,372
86 2,375 2,377 2,380 2,383 2,386 2,389 2,392 2,395 2,398 2,401
87 2,404 2,407 2,410 2,413 2,416 2,419 2,422 2,425 2,428 2,431
88 2,434 2,437 2,440 2,443 2,447 2,450 2,453 2,456 2,459 2,462
89 2,465 2,469 2,472 2,475 2,478 2,482 2,485 2,488 2,491 2,495
90 2,498 2,501 2,505 2,508 2,512 2,515 2,518 2,522 2,525 2,529
91 2,532 2,536 2,539 2,543 2,546 2,550 2,5§4 2,557 2,561 2,564
92 2,568 2,572 2,575 2,579 2,583 2,587 2,591 2,594 2,598 2,602
93 2,606 2,610 2,614 2,618 2,622 2,626 2,630 2,634 2,638 2,642
94 2,647 2,651 2,655 2,659 2,664 2,668 2,673 2,677 2,681 2,686
95 2,691 2,695 2,700 2,705 2,709 2,714 2,719 2,724 2,729 2,734
96 2,739 2,744 2,749 2,754 2,760 2,765 2,771 2,776 2,782 2,788
97 2,793 2,799 2,805 2,811 2,818 2,824 2,830 2,837 2,844 2,851
98 2,858 2,865 2,872 2,880 2,888 2,896 2,904 2,913 2,922 2,931
99,0 2,941 2,942 2,943 2,944 2,945 2,946 2,948 2,949 2,950 2,951
99,1 2,952 2,953 2,954 2,955 2,956 2,957 2,958 2,959 2,960 2,961
99,2' 2,963 2,964 2,965 2,966 2,967 2,968 2,969 2,971 2,972 2,973
99,3 2,974 2,975 2,976 2,978 2,979 2,980 2,981 3,983 2,984 2,985
99,4 2,987 2,988 2,989 2,990 2,992 2,993 2,995 2,996 2,997 2,999
99,5 3,000 3,002 3,003 3,004 3,006 3,007 3,009 3,010 3,012 3,0РЗ
99,6 3,015 3,017 3,018 3,020 3,022 3,023 3,025 3,027 3,028 3,030
99,7 3,032 3,034 3036 3,038 3,040 3,041 3,044 3,046 3,048 3,050
99,8 3,052 3,004 3,057 3,059 3,062 3,064 3,067 3,069 3,072 3,075
99,9 3,078 3,082 3,085 3,089 3,093 3,097 3,101 3,107 3,113 3,122
100 3,142
313
Таблица XVI
Случайные числа
5489 5583 3156 0835 1988 3912 0938 7460 0869 4420
3522 0935 7877 5665 7020 9555 7379 7124 7878 5544
7555 7579 2550 2487 9477 0864 2349 1012 8250 2633
5759 3554 5080 9074 7001 6249 3224 6368 9102 2672
6303 6895 3371 3196 7231 2918 7380 0438 7547 2644
7351 5634 - 5323 2623 7803 8374 2191 0464 0696 9529
7068 7803* 8832 5119 6350 0120 5026 3684 5657 0304
3613 1428 1796 8447 0503 5654 3254 7336 9536 1944
5148 4534 2105 0368 7890 2473 4240 8652 9435 1422
9815 5144 7649 8638 6137 8070 5345 4865 2456 5708
5780 1277 6316 1013 2867 9938 3930 3203 5696 1769
1187 0951 5991 5245 5700 5564 7352 0891 6249 6568
4184 2179 4554 9088 2254 2435 2965 5154 1209 7069
2916 2972 9885 0275 0144 8034 8122 3213 7666 0230
5524 1341 9860 6565 6981 9842 0171 2284 2707 3008
0146 5291 2354 5694 0377 5336 6460 9585 3415 2358
4920 2826 5238 5402 7937 1993 4332 2327 6875 5230
7978 1947 6380 3425 7267 7285 ИЗО 7722 0164 8573
7453 0653 3645 7497 5969 8682 4191 2976 0361 9334
1473 6938 4899 5348 1641 3652 0852 5296 4538 4456
8162 8797 8000 4707 1880 9660 8446 1883 9768 0881
5645 4219 0807 3301 4279 4168 4305 9937 3120 5547
2042 1192 1175 8851 6432 4635 5757 6656 1660 5389
5470 7702 6958 9080 5925 8519 0127 9233 2452 7341
4045 1730 6005 1704 0345 3275 4738 4862 2556 8333
5880 1257 6163 4439 7276 6353 6912 0731 9033 5294
9083 4260 5277 4998 4298 5204 3965 4028 8936 5148
1762 8713 1189 1090 8989 7273 3213 1935 9321 4820
2023 2589 1740 0424 8924 0005 1969 1636 7237 1227
7965 3855 4765 0703 1678 0841 7543 0308 9732 1289
7690 0480 8098 9629 4819 7219 7241 5128 3853- 1921
9292 0426 9573 4903 5916 6576 8368 3270 6641 0033
0867 1656 7016 4220 2533 6345 8227 1904 5138 2537
0505 2127 8255 5276 2233 3956 4118 8199 6380 6340
6295 9795 1112 $761 2575 6837 3336 9232 7403 8345
6323 2615 3410 3365 1117 2417 3176 2434 5240 5455
8672 8536 2966 5773 5412 8114 0930 4697 6919 4569
1422 5507 7596 0670 3013 1351 3886 3268 9469 2584
2653 1472 5113 5735 1469 9545 9331 5303 9914 6394
0438 4376 3328 8649 8327 ОНО 4549 7955 5275 2890
314
Таблица XVII
Значения F при уровне значимости 0,001 ( dfi — число степеней свободы
для большей вариансы, которая берется числителем)
1 2 । 3 4 5 6 12 24 00
1 405 284 500000 540 379 562500 576 405 > 585 937 '610 667 623 497 636 619
2 998,5 999,0 999,2 999,2 999,3 999,3 999,4 999,5 999,5
3 167,5 148,5 141,1 137,1 134,6 132,8 128,3 125,9 123,5
4 74,1 61,3 56,2 53,4 51,7 , 50,5 47,4 45,8 44,1
5 47,0 36,6 33,2 31,1 29,8 28,8 26,4 25,1 23,8
6 35,5 27,0 23,7 21,9 20,8 20,0 18,0 16,9 15,8
7 29,2 21,7 18,8 17,2 16,2 15,5 13,7 12,7 Н,7
8 25,4 18,5 15,8' 14,4 13,5 12,9 11,2 10,3 9,3
9 22,9 16,4 13,9 12,6 И,7 11,1 9,6 8,7 7,8
10 21,0 14,9 12,6 и,з 10,5 9,9 8,5 7,6 6,8
11 19,7 13, S 11,6 10,4 9,6 9,1 7,6 6,9 6,0
12 18,6 13,0 10,8 9,6 8,9 8,4 7,0 6,3 5,4
13 17,8 12,3 10,2 9,1 8,4 7,9 6,5 5,8 5,0
14 17,1 11,8 9,7 8,6 7,9 7,4 6,1 5,4 4,6
15 16,6 11,3 9,3 8,3 7,6 7,1 5,8 5,1 4,3
16 16,1 п,о 9,0 7,9 7,3 6,8 56 4,9 4,1
17 15,7 10,7 8,7 7,7 7,0 6,6 5,3 4,6 3,9
18 15,4 10,4 8,5 7,5 6,8 6,4 5,1 4.5 3,7
19 15,1 10,2 8,3 7,3 6,6 6,2 5,0 4,3 3.5
20 14,8 10,0 8,1 7,1 6,5 6,0 4,8 4,2 3,4
22 14,4 9,6 7,8 6,8 6,2 5,8 4,6 3,9 3,2
24 14,0 9,3 7,6 6,6 6,0 5,6 4,4 3,7 з,о
26 13,7 9,1 7,4 6,4 5,8 5,4 4,2 3,6 2,8
28 13,5 8,9 7,2 6,3 5,7 5,2 4,1 3,5 2,7
30 13,3 8,8 7,1 6,1 5,5 5,1 4,0 3,4 2,6
60 12,0 7,8 6,2 5,3 4,8 4,4 з,з 2,7 1,9
120 11,4 7,3 5,8 5,0 4,4 4,0 з,о 2,4 1,6
00 10,8 6,9 5,4 4,6 4,1 3,7 2,7 2,1 1,0
315
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аппарат Гальтона 62
Асимметрия 45, 75
коэффициент 45
при пуассоновом распределении 65,
75
Биномиальное распределение 63—65,
265
применение X2 266
частоты ожидаемые, вычисле-
ние 265
Биологическая статистика 3, 7, 8, 269
литература 272, 273
Биоматематика 7
Биометрия 5
Варианса 30
взвешенная 40
при дисперсионном анализе 199,
200, 225, 226
при пуассоновом распределении 67
разложение 44'
формулы 41—43, 276—280
Вариансное отношение см. Крите-
рий F
Вариансный анализ см. Дисперсион-
ный анализ
Варианта 10
Вариационная кривая 16
многовершинная 17—18, 74
нормальная 67
Вариационная статистика см. Биоло-
гическая статистика
Вариационный размах 24, 28
и среднее квадратическое отклоне-
ние 69, 79
Вариационный ряд 15
при альтернативной изменчивости
170—171
закономерности 19
и распределение вероятностей
59—63
эмпирический 74—75
Вариация 9
альтернативная 13, 170
закон сложения 45, 189
измерение 28
качественная 12, 13, 169
количественная непрерывная 12,
17—19
количественная прерывная 12, 14,
15
коэффициент 46, 281
Вероятность 7, 53
доверительная см. Доверительные
вероятности
малая 56, 66
общая формула 54
определение 54
в применении к х2 241—244
теоремы сложения и умножения
51-58
теоретическая (априорная) 58
эмпирическая 58
Взаимодействие факторов 189
оценка при дисперсионном анали-
зе 208, 211, 215, 225, 226
Выборочная совокупность 11, 59,
80—85, 122, 155
необходимый объем при количест-
венной вариации 88
при альтернативной вариации 176
распределение г 122
распределение х 83
Выборочный метод 89—91
Выравнивание линий регрессии 145—
146 •'
Выскакивающие значения 75
Гистограмма 16
Градации (уровни факторов) 189
случайные 190, 201, 211
фиксированные 190, 200, 211
Данные, группировка 13—19
Дискретный признак см. Вариация
качественная
Дисперсионный анализ 187—229
предпосылки теоретические 188—
189
схемы
однофакторная 193—200
двухфакторная 201—211
трехфакторная 212—214
иерархическая 215—224
Дисперсия см. Варианса
Доверительные вероятности 70
Доверительные границы и интервалы
70, 86—87, 90, 126
для доли 174
316
при малых п 86—87
Доля 169—171
при альтернативной вариации 170
и вероятность 170
выборки 87
Зависимость криволинейная 161—165
Закон больших чисел 83
Закономерности статистические 6, 7,
53
Значимость
при %2 241—244
См. также Уровни значимости
Изменчивость см. Вариация
Информации теория 7
Качественные признаки см. Вариация
качественная
Кибернетика 7
Классы 13
группировка в классы 13—15, 35
промежуток 15, 35
число в зависимости от п 19
Ковариационный анализ 161
Количественные признаки см. Вариа-
ция количественная
Корреляционная решётка 114—118
Корреляционное поле 121, 145
Корреляционные плеяды 132
Корреляция 107
при альтернативной вариации
180—181
квадрат коэффициента корреляции
121
коэффициент простой корреляции
409, 111—113, табл. VII
доверительные границы 126
множественная 130
и нормированное отклонение 109—
отрицательная 108
оценка достоверности 122, табл. VII
положительная 108
преобразование г в z 124, табл. VIII
и причинность 129—130
рангов 127
и регрессия 160
средняя ошибка коэффициента
корреляции 122—123
уравнение 111, 161
частная 130—131
формула Бравэ 114
Коэффициент Q 228, табл. IX
Коэффициент изменчивости см. Ва-
риация, коэффициент
Криволинейная зависимость 161—165
Кривые распределения 16, 59
многовершинные 17, 18
Критерий знаков 97, табл. IV
Критерий F 99, 197, табл. V, табл. VI
Критерий t см. Оценка достоверности.
Нормированное отклонение
Критерий разнородности 245
Критерий соответствия (х2) 239—261
при анализе расщепления 246, 247
при анализе многопольных таблиц
253
общая формула 240
поправка на непрерывность 251
при сравнении двух эмпирических
распределений 260
распределение %2 240, табл. X
и сопряженность 253
степени свободы 244
суммирование нескольких х2 245
формула для многопольной табли-
цы 251
эмпирических рядов теоретически
ожидаемым
при биномиальном распределе-
нии 255
при нормальном распределе-
нии 258
при пуассоновом распределе-
нии 256—258
Лимиты 16
Медиана 25
Многовершинность кривых распреде-
ления 17, 74
Мода 15, 25
Массовые явления 7, 53, 270
Математические методы в биологии
5, 6, 7, 270
Нормальная кривая распределения 67
накопленные частоты табл. XI
Нормальное распределение 67—69,
табл. I, табл. III, табл. XI
вычисление ожидаемых частот 255
ошибок 81
уравнений кривой 72—73
Нормальный интеграл вероятностей
табл. I
Нормированное отклонение 68, табл. I,
табл. II, табл. III
для коэффициента корреляции 109
для коэффициента регрессии 159
при малых выборках, распределе-
ние 83, табл. II
как мера корреляционной зависи-
мости ПО—111
при нормальном распределении 68
при оценке средней арифметиче-
ской 90—91
для разницы между средними 93
для разницы между сигмами 99
для разницы между z 125
и уравнение регрессии 155
и установление доверительных гра-
ниц 86
для числа z 124
Нулевая гипотеза 91, 197
- и данные опытов 241, 249
при %2 241
область отбрасываний 242«--243
317
Относительные числа 169—170
Оценка достоверности 80—100
коэффициента вариации 89
коэффициента простой корреля-
ции 122
коэффициента ранговой корреля-
ции 128
коэффициента регрессии 155
линии регрессии 155
разницы между вариансами
159—160
разницы между группами при ди-
сперсионном' анализе 227
разницы между долями выборок
176—177
разницы между долями в выбороч-
ной и генеральной совокупности
179—180
разницы между коэффициентами
регрессии 159
разницы между сигмами 99
разницы между средними арифме-
тическими 92—96
при альтернативной изменчиво-
сти 176
графическим методом 95—96
при попарных данных 96
разницы между числами z
122—125
среднего квадратического откло-
нения 89
средней арифметической 90
числа z 122
Оценки
двусторонние 71
генеральной совокупности по вы-
борочной 85, 90
односторонние 71
Параболические кривые 162
Параметры
вариационного ряда 48
оцениваемые при дисперсионном
анализе 200, 211, 215, 218, 225
Показатели статистические 24—48
степени вариации 24
тенденции (уровня) 24
Полигоны распределения 16
Популяция см. Совокупность гене-
ральная
Признаки варьирующие 11
качественные 12, 169
количественные непрерывные 12
количественные прерывные 12
учет 11, 12, 169
Пуассоново распределение 65—67
вычисление теоретических частот
256-257
Ранжировка 17
Регрессия 141
вариация линии регрессии 155
и корреляция 161
коэффициент 151—155
односторонняя 151 *
оценка достоверности 155
теоретическая линия регрессии 150
уравнение 147—148
эмпирическая линия регрессии
142—143
Скользящая средняя, метод 145
Случайная переменная, значение см.
Варианта
Случайность и необходимость 54
Совокупность 9, 10
выборочная (см. также -Выбороч-
ная совокупность) 11, 59, 82
генеральная 11, 82
единицы 9
закономерности случайной вариа-
ции 59
объем 9
параметры 48
стохастическая 59
* структура 10
частная 11
Среднее квадратическое отклонение 30
при альтернативной вариации
171—172
при биномиальном распределении
63
доверительные границы 90
вычисление 31—41
Среднее отклонение 30
Средний квадрат см. Варианса
Средняя арифметическая 26
при альтернативной вариации 171
при биномиальном распределении
63
взвешенная 40
” ныбирочНбТГ совокупности 81
вычисление 26, 28,. 34, Д8_.
генеральной совокупности 81
доверительные границы 86—87
значение 28
ошибки в понимании 28
при пуассоновом распределении
66—67 ’
свойства 26
условная 35—36
Средняя геометрическая 24, 44
Средняя ошибка 81, 89
абсолютных численностей альтер-
нативных групп 175
доли 172—173
при р=о 175
при дисперсионном анализе 197
значение 82—85
коэффициента вариации 89
коэффициента корреляции 122
коэффициента регрессии 158
разницы между долями 176
разницы между средними арифме-
тическими 92—96
318
при наличии корреляции 133
разницы между средними квадра-
тическими отклонениями 99
разницы между z 125
средней арифметической 81
при альтернативной изменчиво-
сти 172
среднего квадратического отклоне-
ния 89
при учете доли выборки 88
числа z 124
Стандартное отклонение см. Среднее
квадратическое отклонение
Статистики см. Показатели статисти-
ческие
Степени свободы 32, 193, 244
при биномиальном распределе-
нии 256
для вариансы 32
в многопольной решетке 244
при нормальном распределении 259
при пользовании хи-квадратом 244
при пуассоновом распределении
258
Сумма квадратов 41—43
формулы
при дисперсионном анализе 192,
194, 202, 213, 219, 220
общие 42
Теоретически ожидаемые величины,
.вычисление
при данных, сгруппированных в
многопольные таблицы 248, 251
< для биномиального распределения
255, 256
для нормального распределения
68, 69, 259
для пуассонового распределения
256, 257
при расщеплении 246
Точность, степень 12, 38
Треугольник Паскаля 61
/-Распределение по Стьюденту 83—85,
табл. II
Уровни значимости, 71, табл. III
Функциональная зависимость
107—108
Число z 124
оценка достоверности 124
преобразование в г 124—126,
табл. VIII
Эксперимент 7
Экспериментальный метод 6
Экспоненциальная кривая 163—165
• уравнение 163
ОГЛАВЛЕНИЕ
Предисловие ... ...............................
Введение. Роль математических и математико-статистических ме-
тодов в биологии .........................................
Глава 1. Группировка данных, совокупность и вариационный ряд
Глава 2J Статистические показатели для характеристики совокуп-
ности '...................................................
Глава 3. Закономерности случайной вариации................
Глава 41 Оценка достоверности статистических показателей
Глава 5. Измерение связи. Корреляция ........
Глава 6. Измерение связи. Регрессия.......................
Глава 7. Статистический анализ вариации по качественным при-
знакам ...................................................
Глава 8. Дисперсионный анализ.............................
Глава 9. Изучение степени соответствия фактических данных тео-
ретически ожидаемым...................................
Заключение ...............................................
Литература ...............................................
Приложения ......................................
Предметный указатель .....................................
3
5
9
24
53
80
107
141
169
187
239
269
272
274
316
Рокицкай Петр Фомич
БИОЛОГИЧЕСКАЯ СТАТИСТИКА
Редактор А, Шалковская
Обложка Г. Важнова
Ху дож. редактор И. Беленькая
Техн, редактор П. Фрайман
Корректор С. Вернова
АТ 17007. Сдано в набор 3/VUI 1972 г. Подписано к пе-
чати 26/1 1973 г. Бумага 60 X 90'/ie типогр. № 3. Печ. л. 20.
Уч.-изд. л. 20,65. Изд. № 71-81. Зак. 1451. Тираж 7000 экз.
Цена 74 коп.
Издательство «Вышэйшая школа» Государственного
комитета совета Министров БССР по делам издательств,
полиграфии и книжной торговли. Редакция литературы
по естествознанию и математике. Минск, 220600, ул. Ки-
рова, 24.
Полиграфический комбинат нм. Якуба Коласа Государ-
ственного комитета Совета Министров БССР по делам
издательств, полиграфии и книжной торговли. Минск,
ул. Красная, 23.