Автоматика и регулирование воздушно-реактивных двигателей - Черкасов Б.А.

Автор: Черкасов Б.А.

Теги: техника средств транспорта автоматика реактивные двигатели

Год: 1965

Похожие

Теория, расчет и проектирование авиационных двигателей и энергетических установок

Теория и расчет воздушно-реактивных двигателей

Теория авиационных газотурбинных двигателей. Часть 2

Конструкция и прочность авиационных газотурбинных двигателей

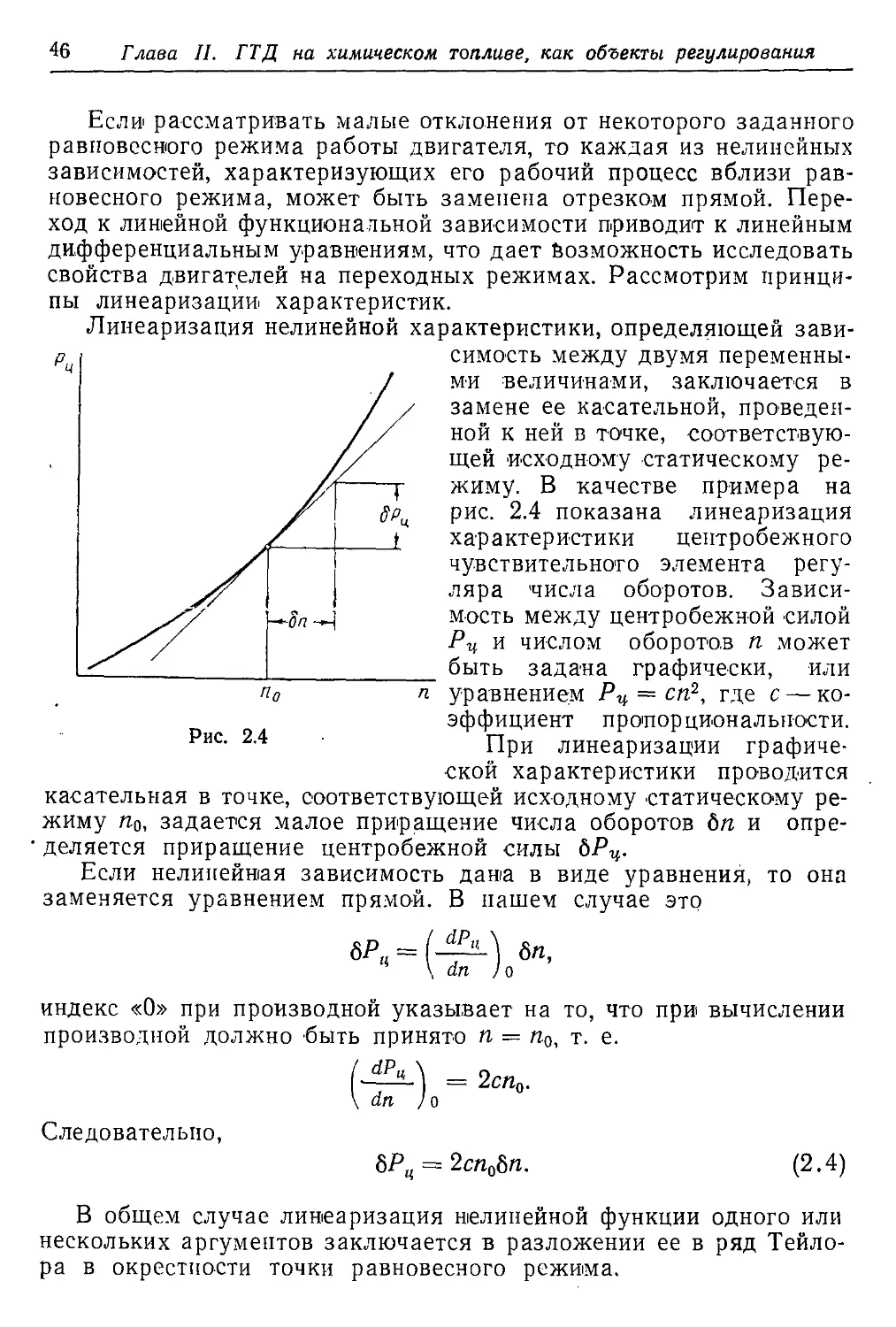
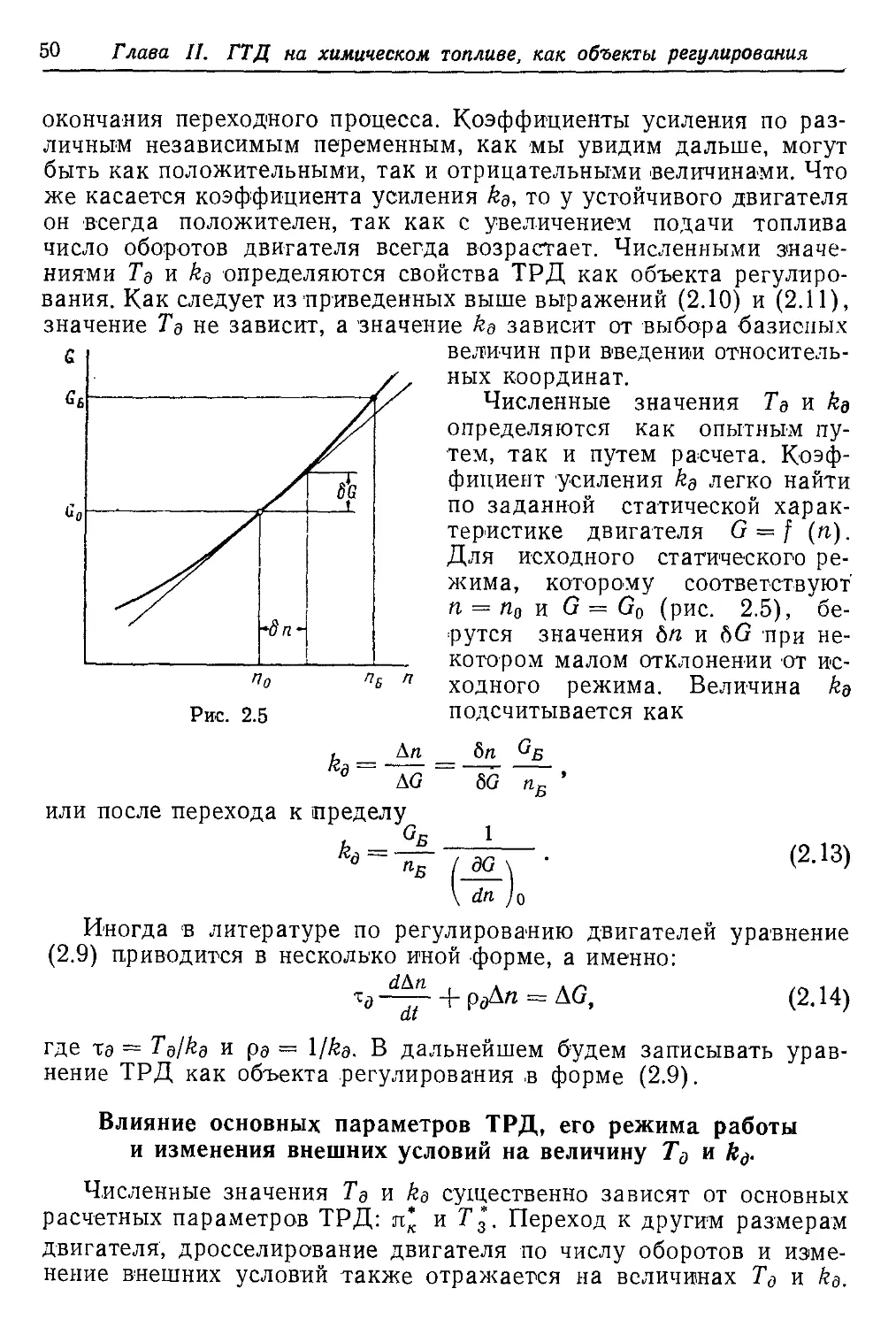
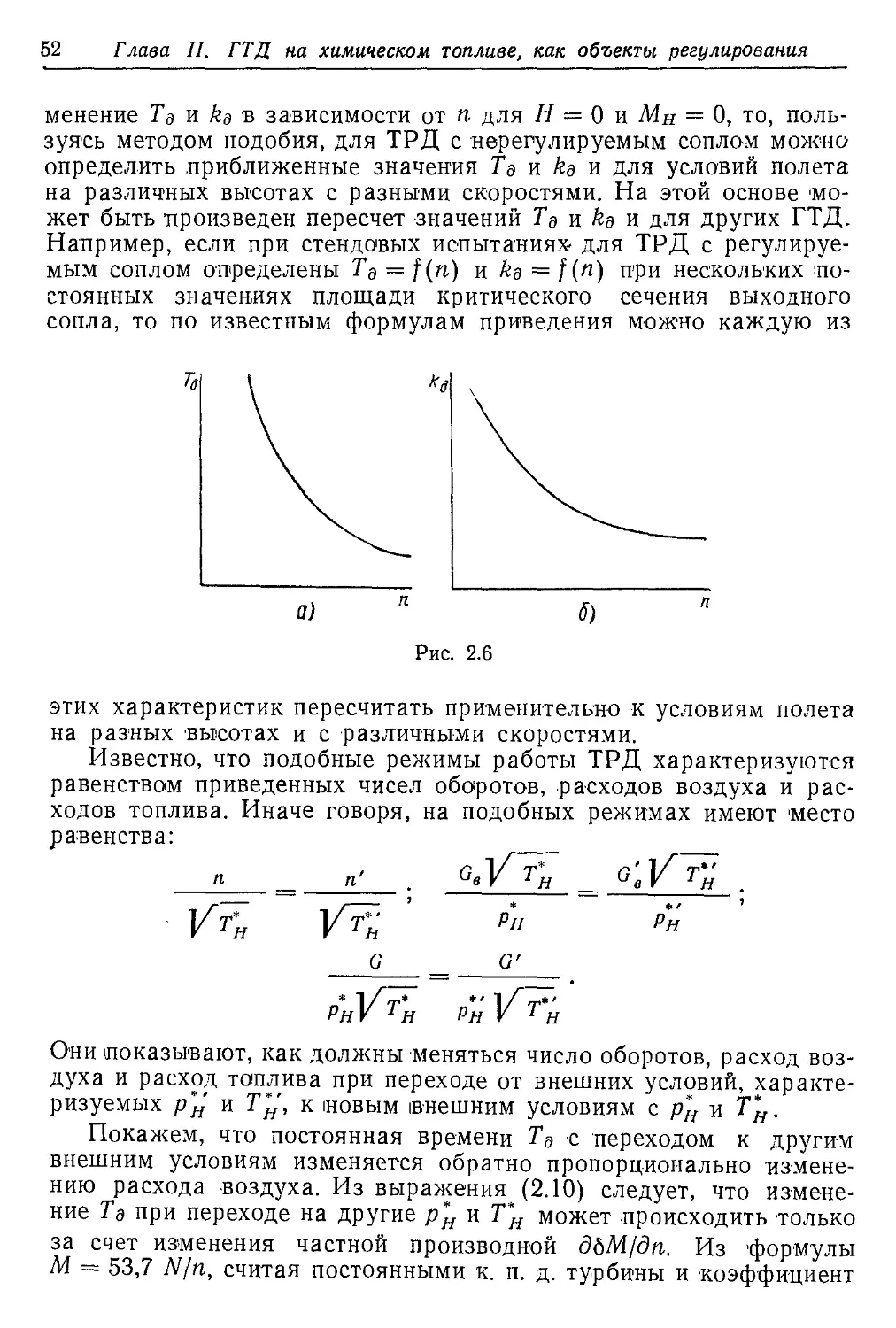
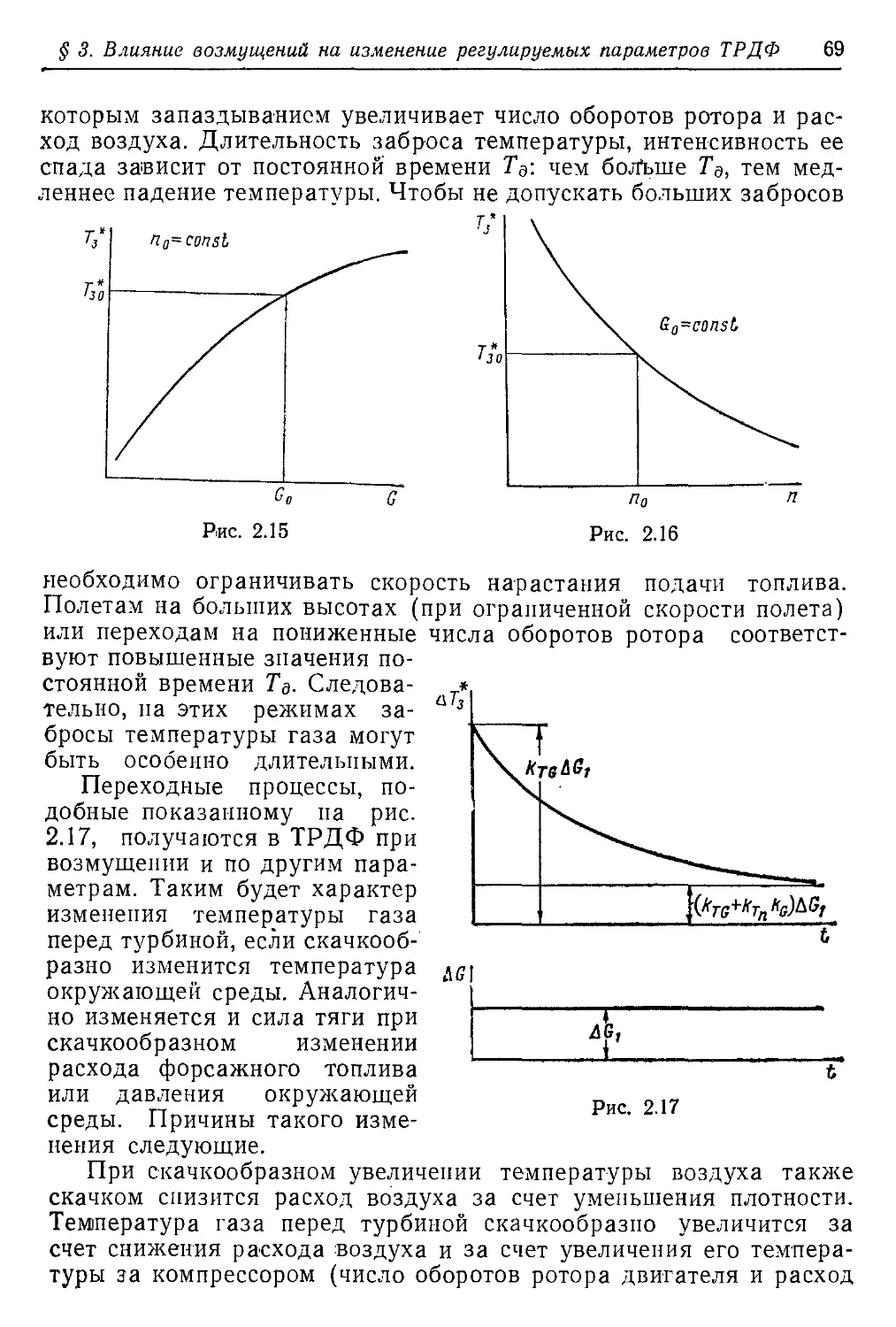
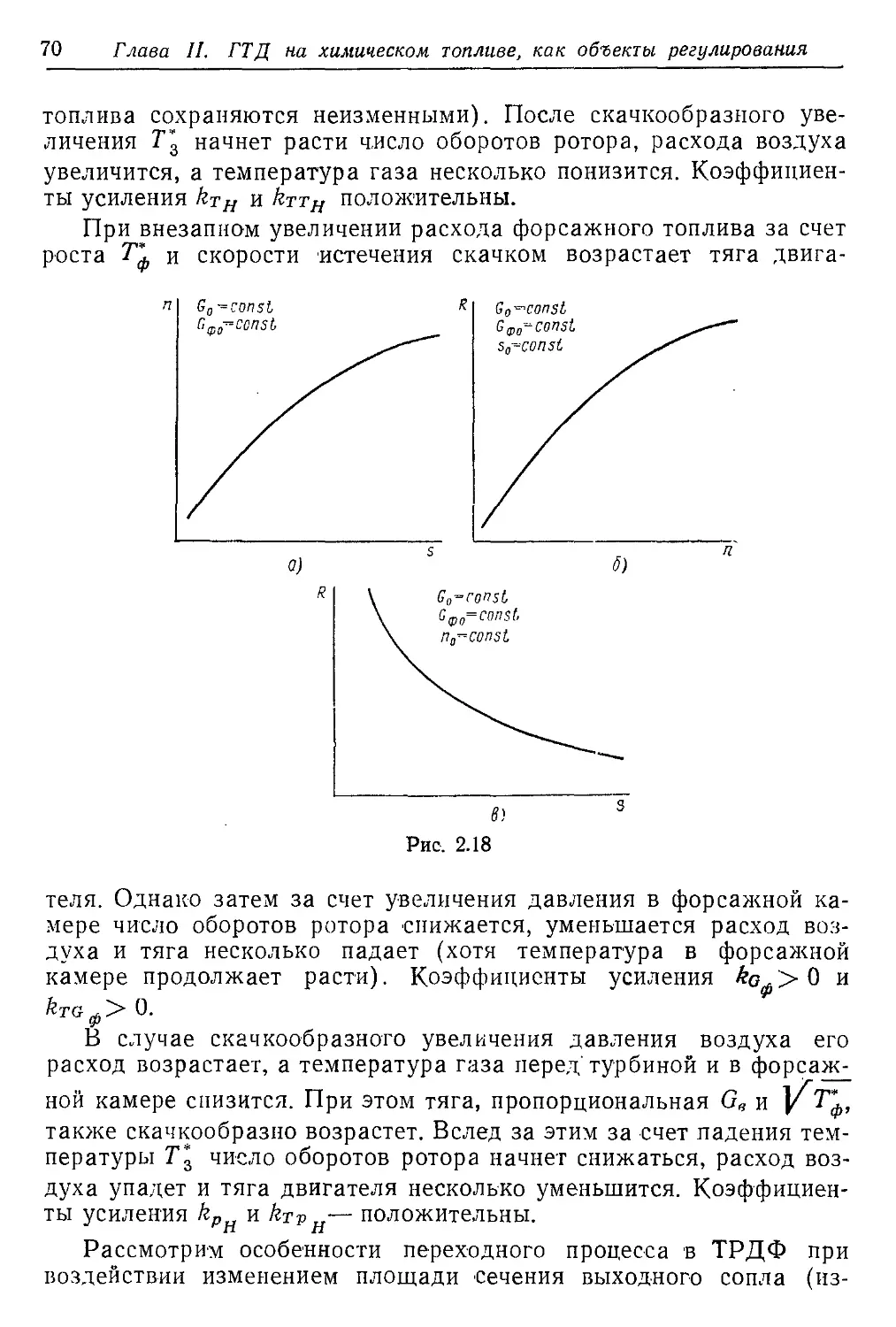
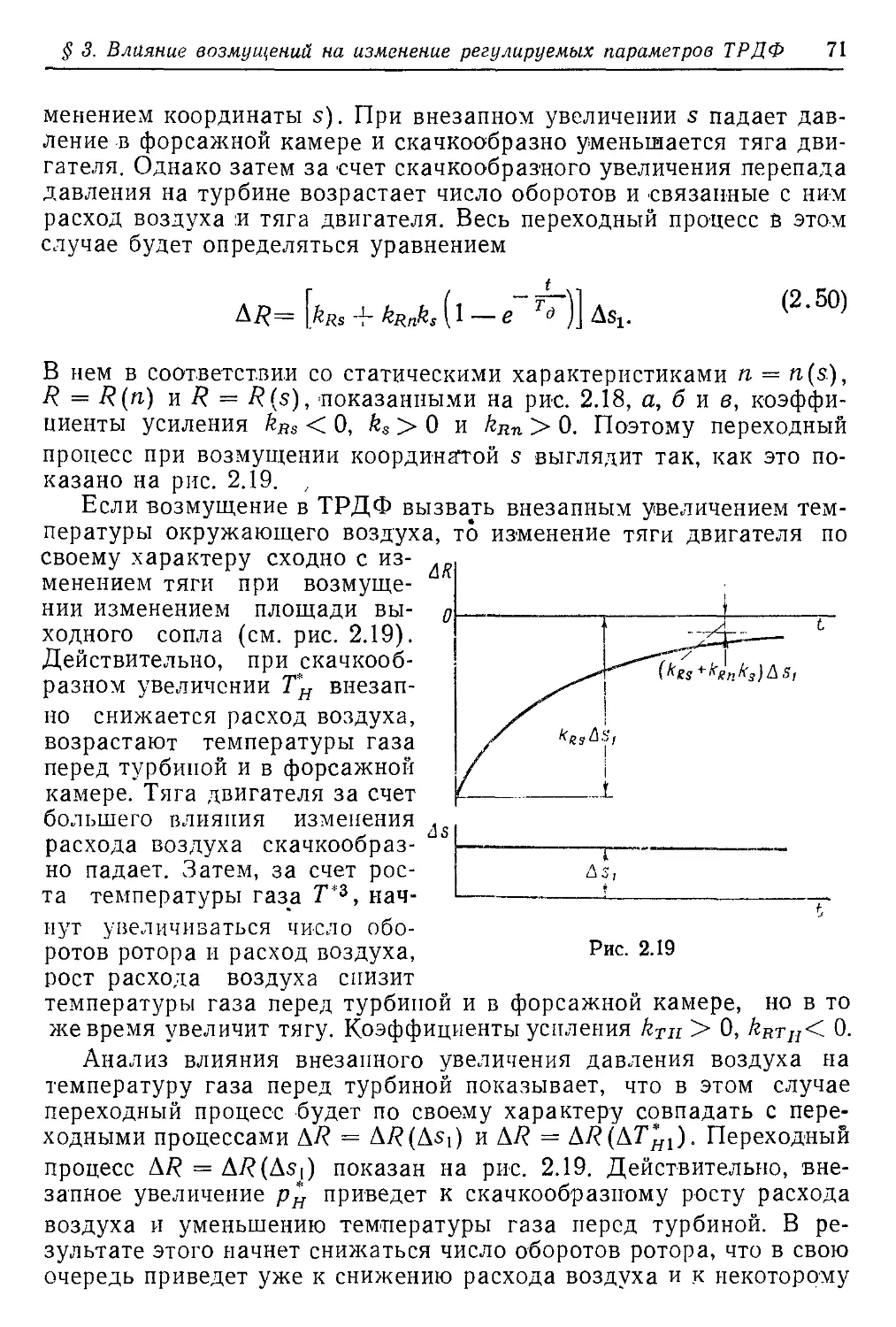
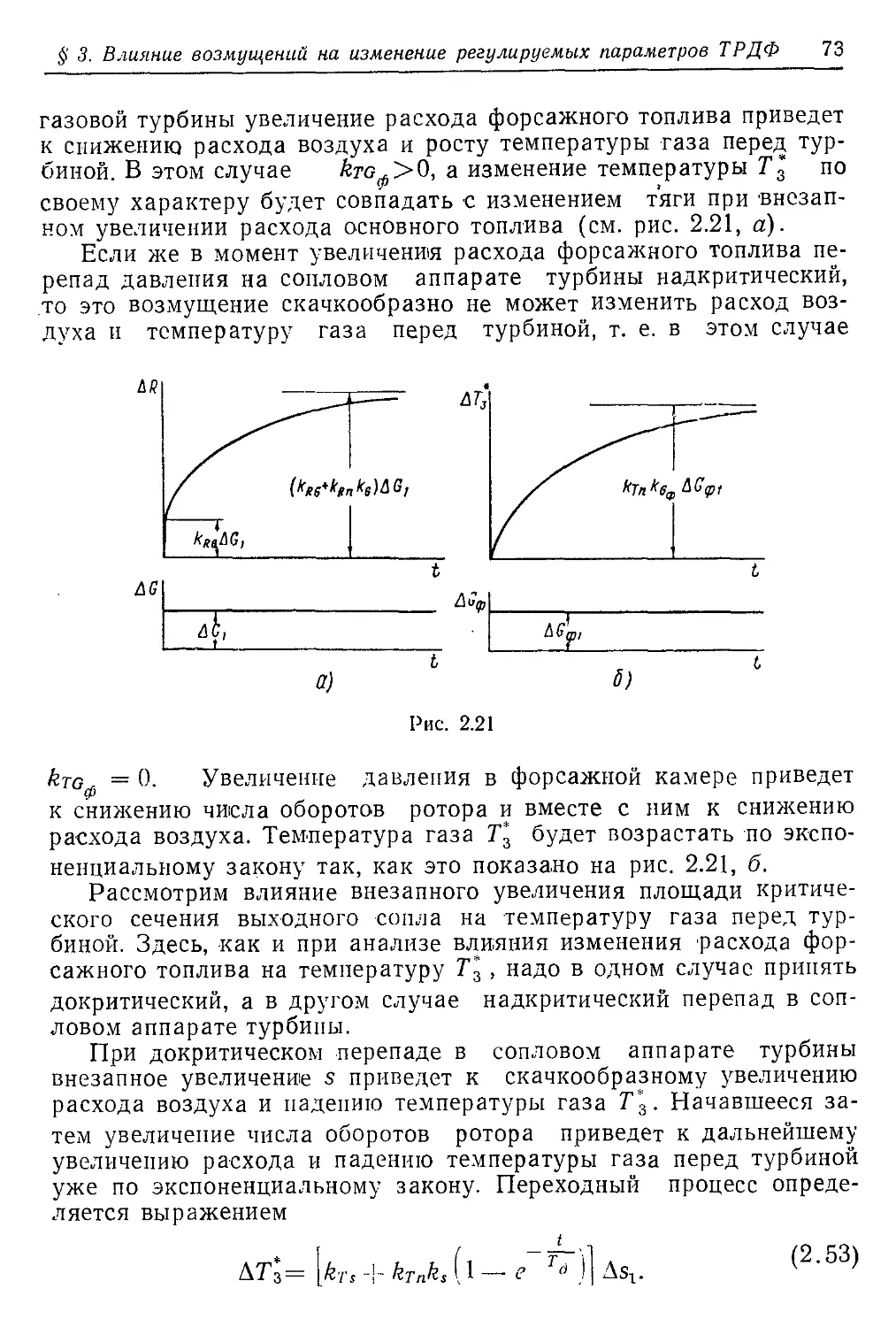
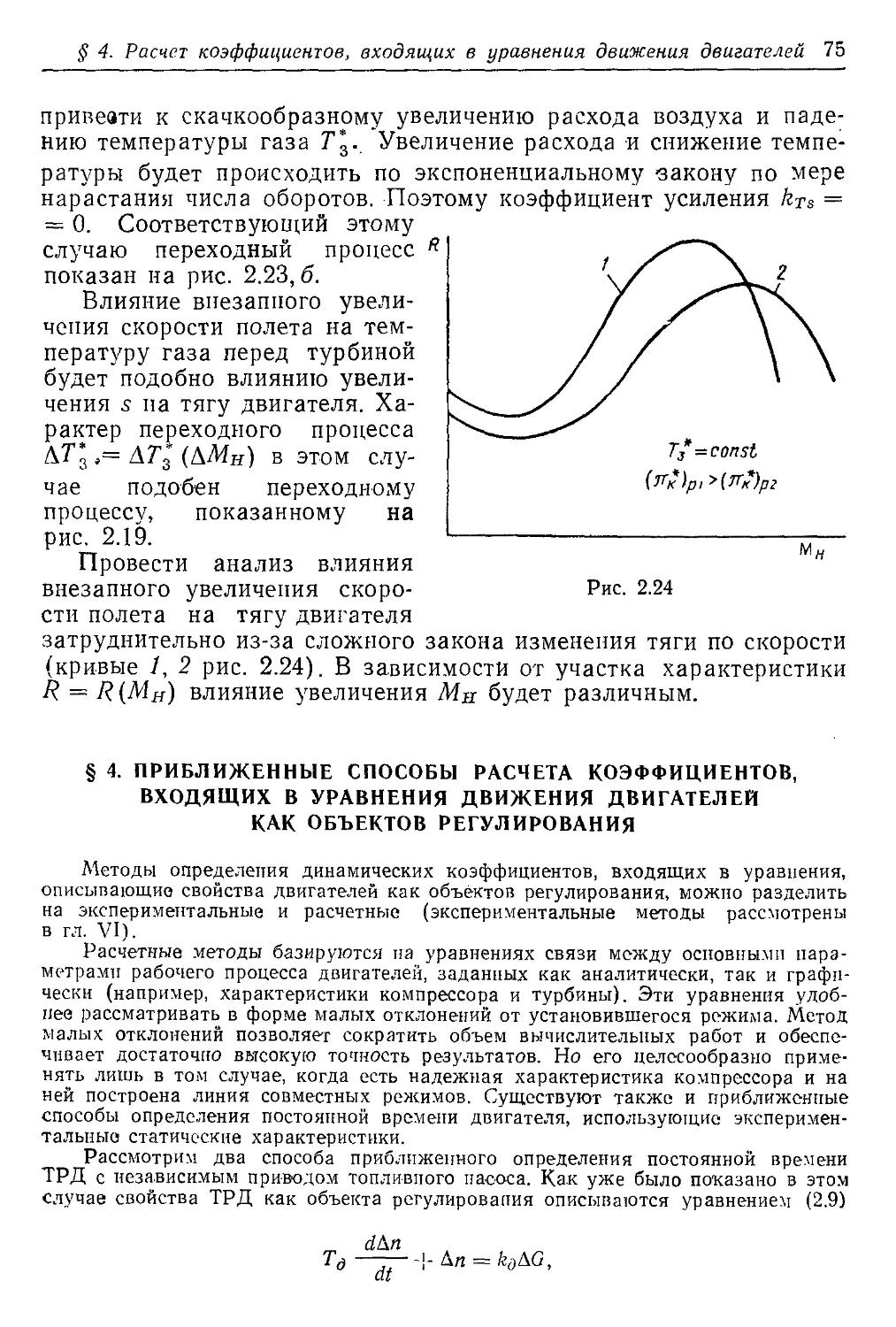
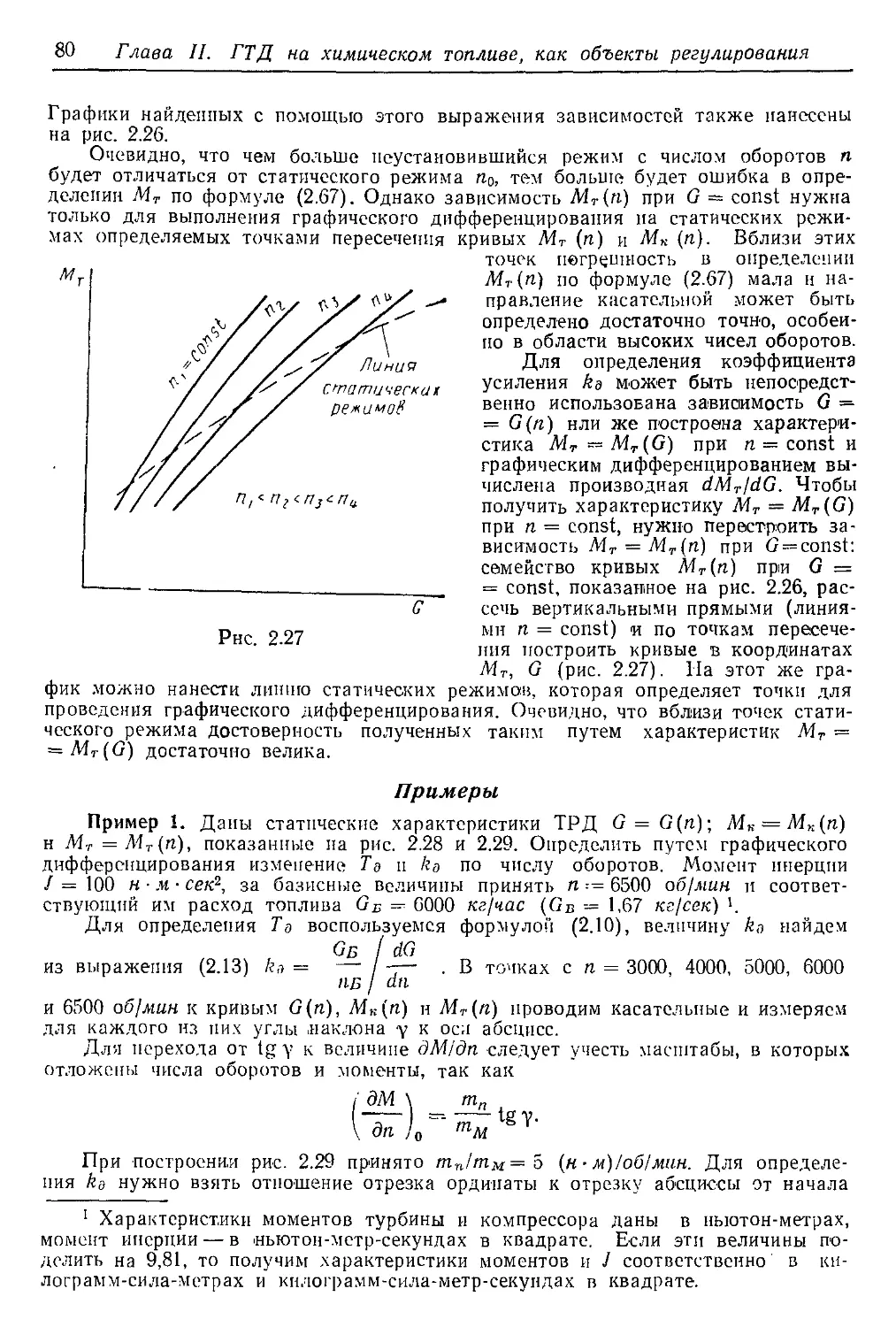
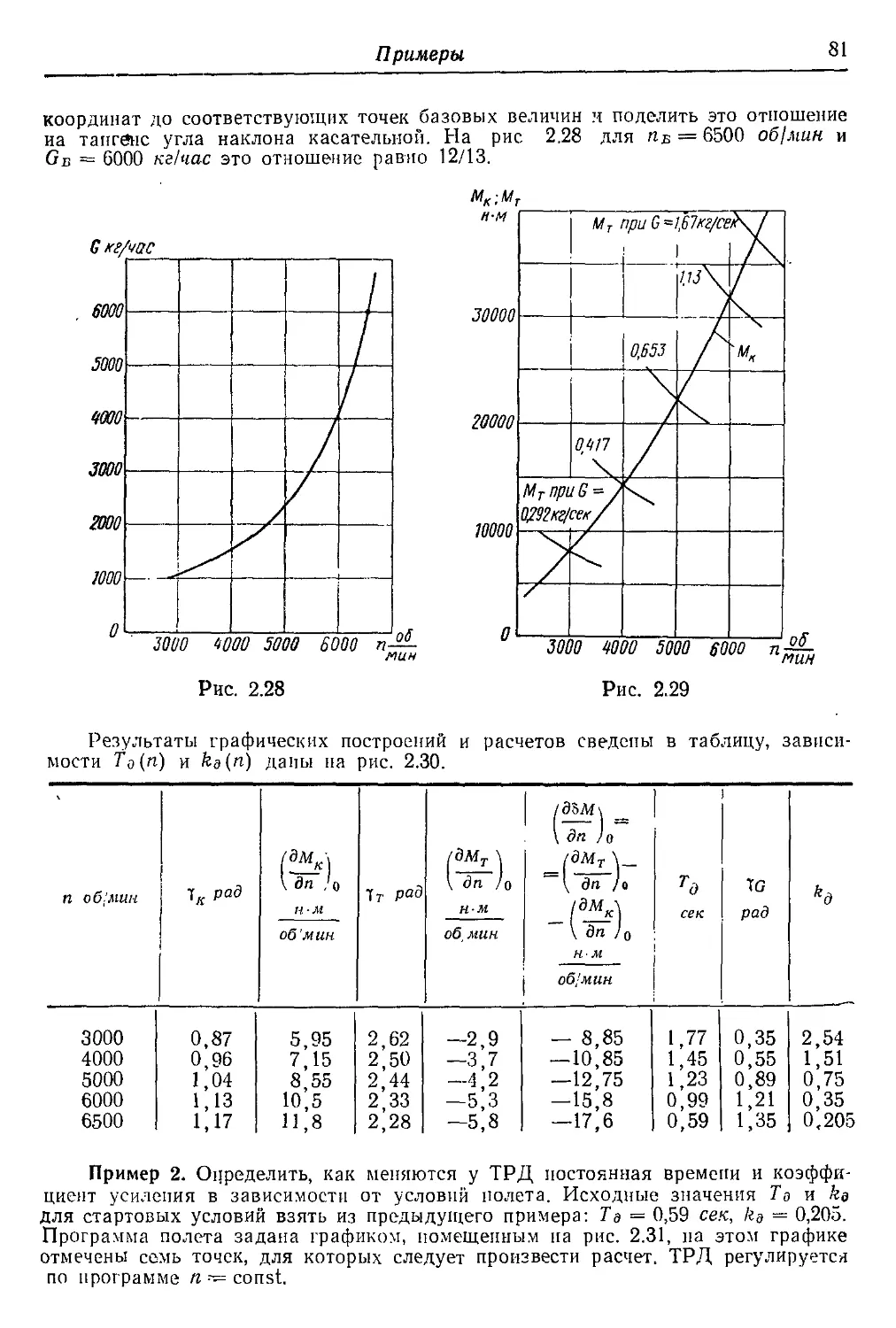
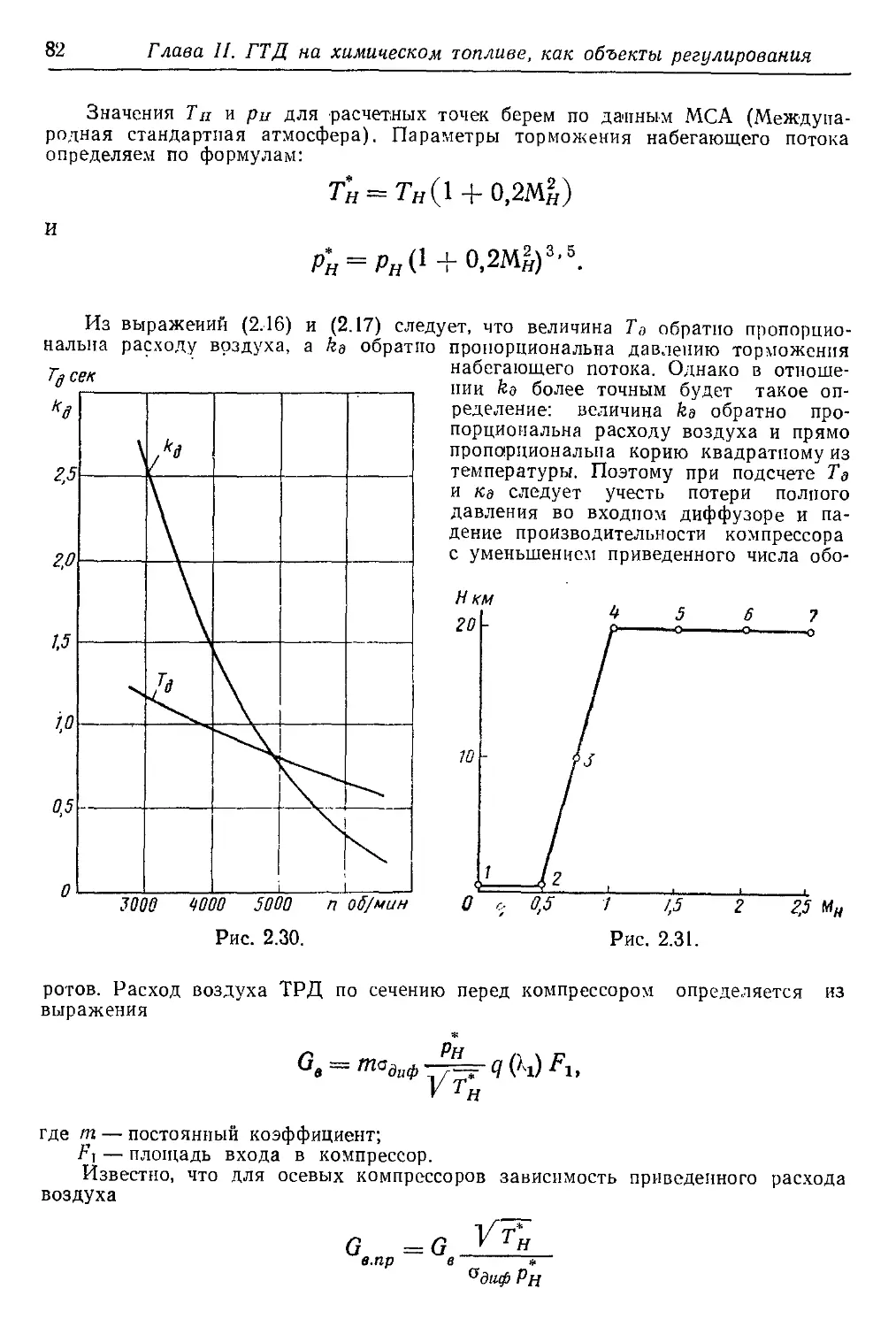
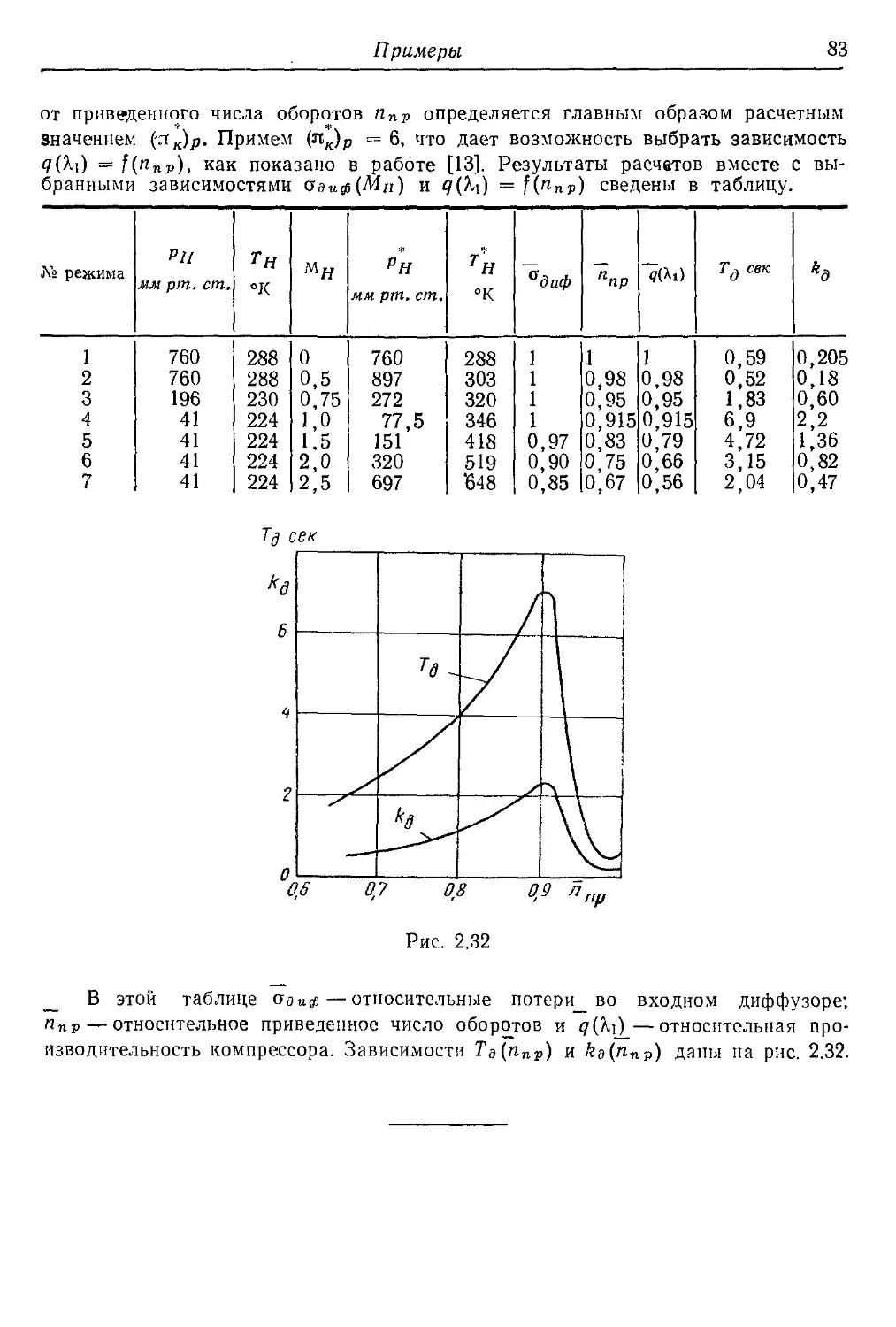
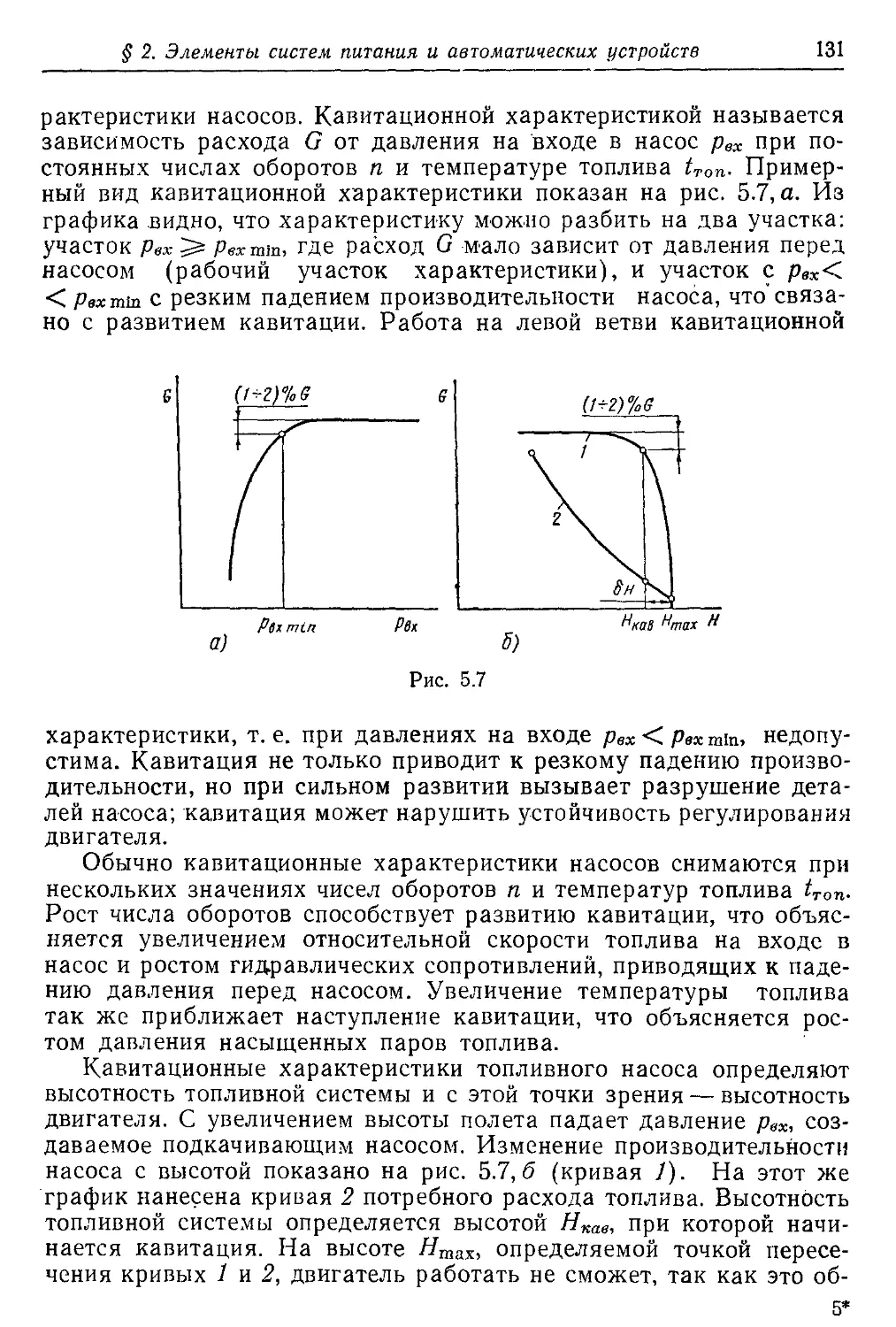
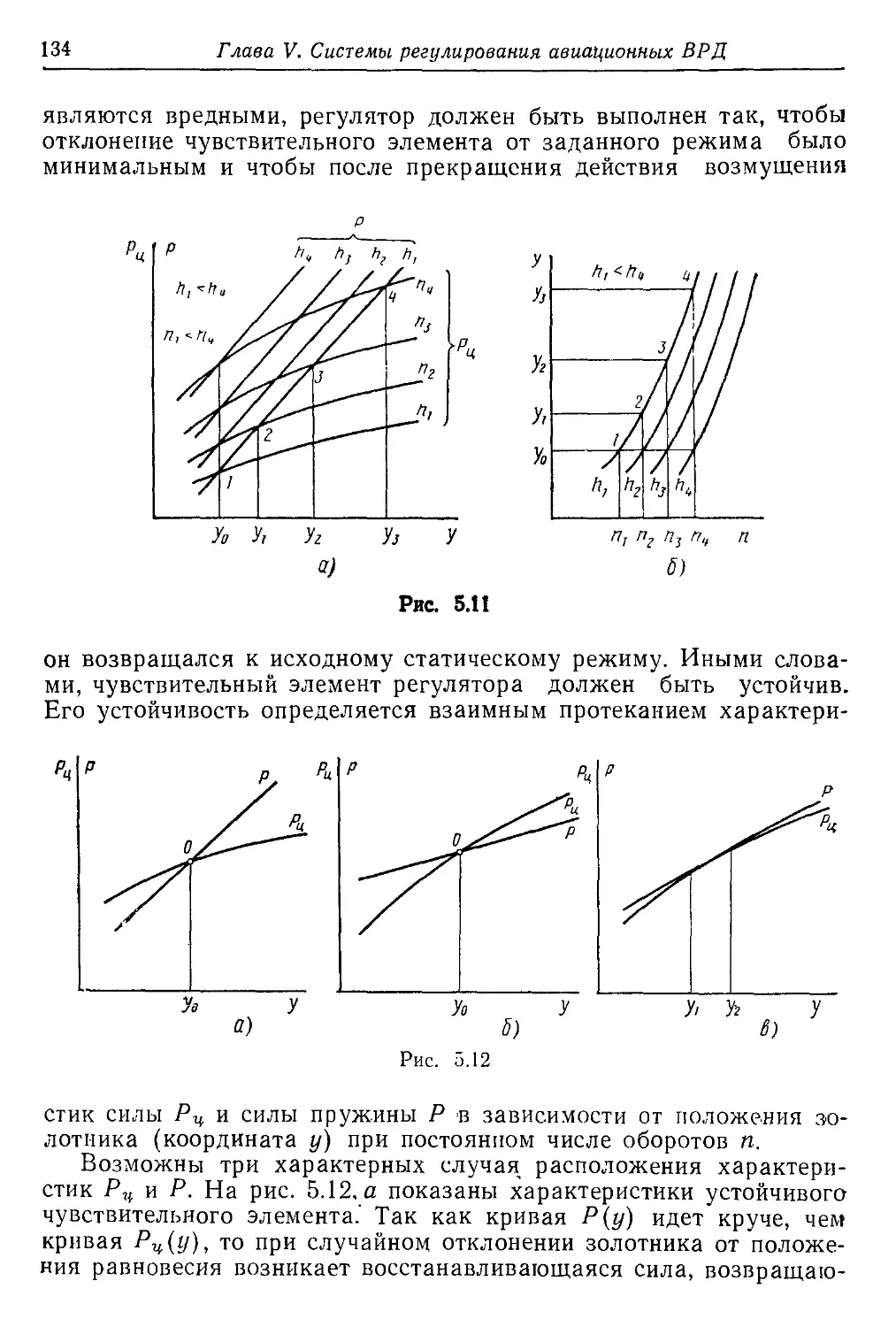
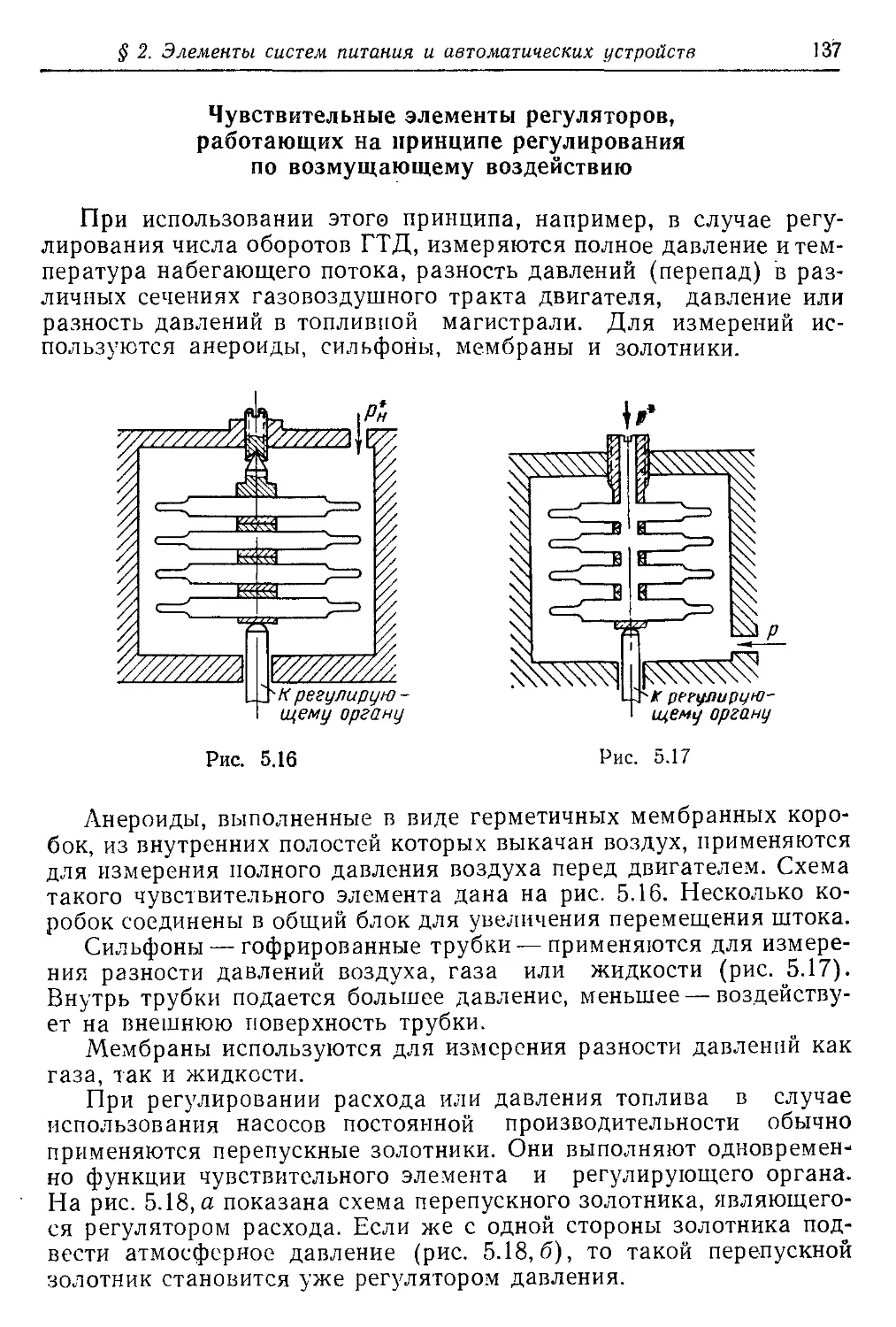
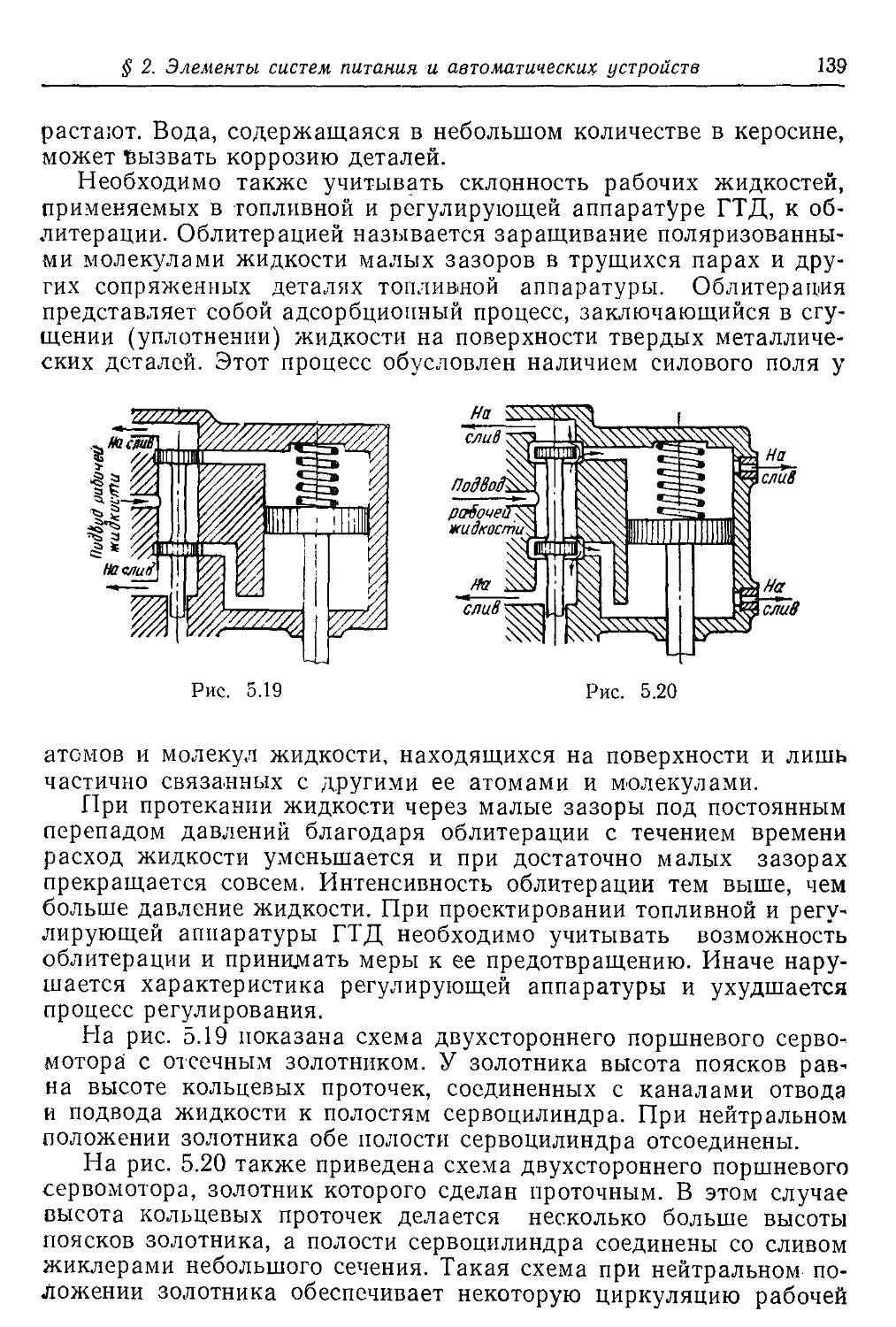
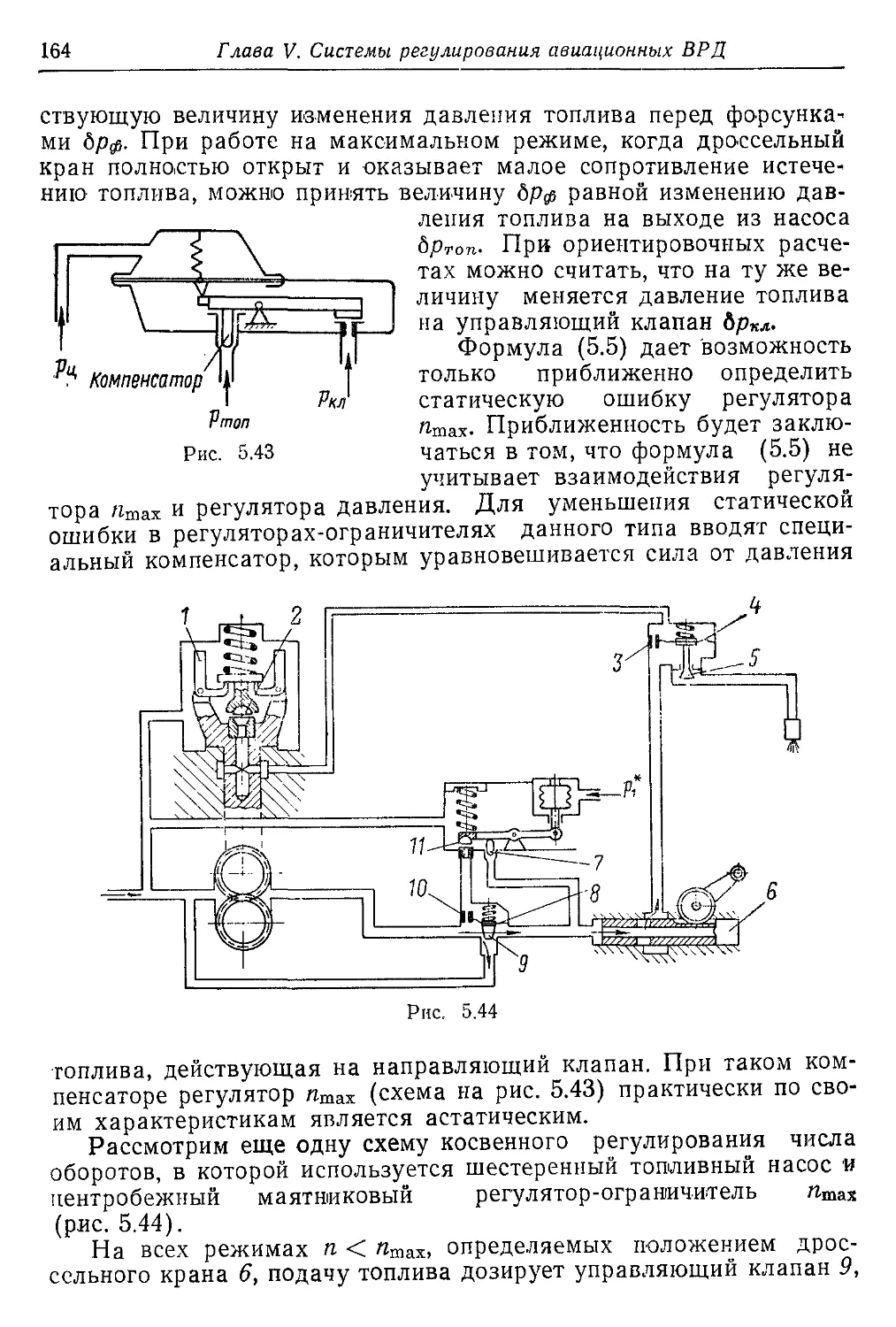
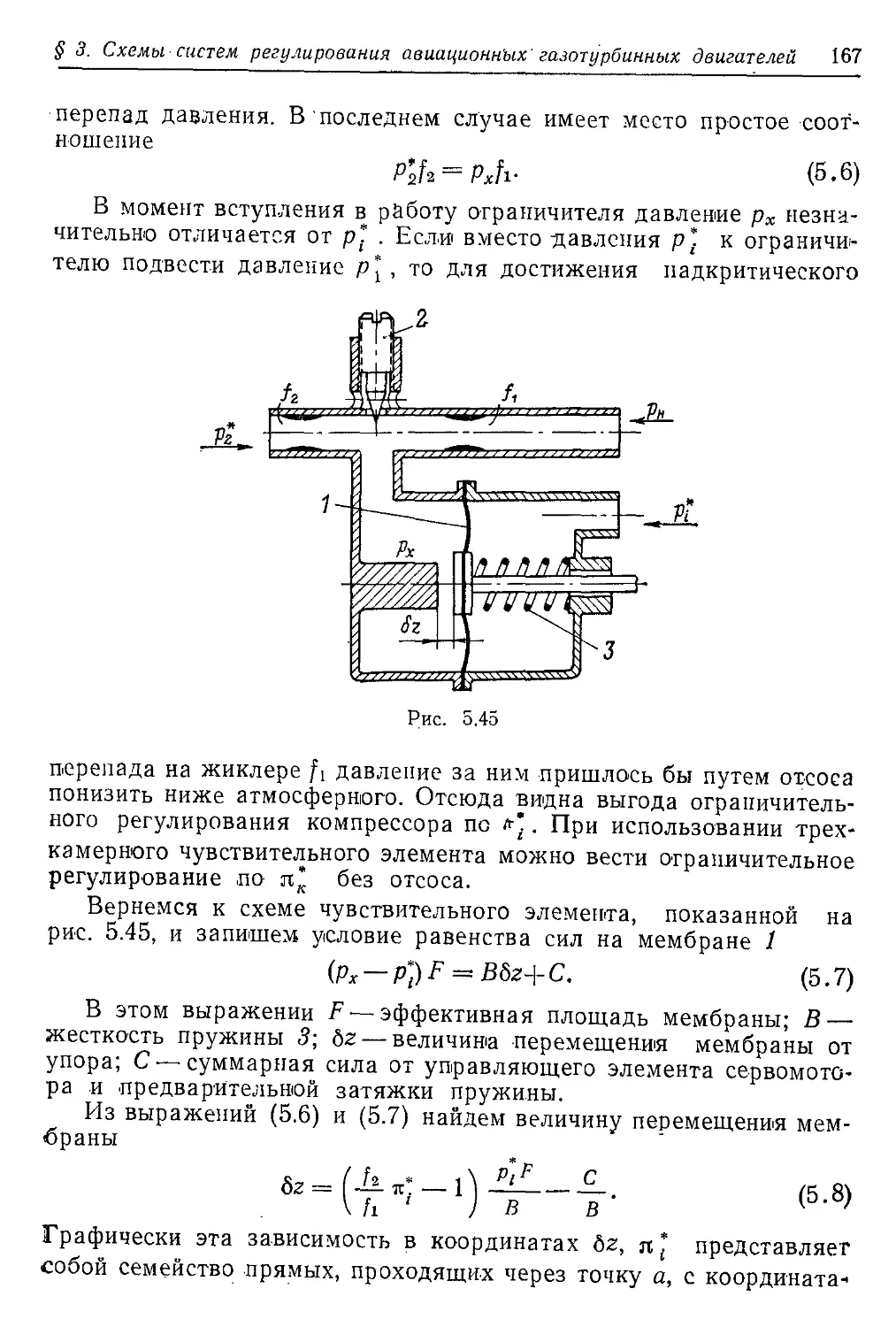
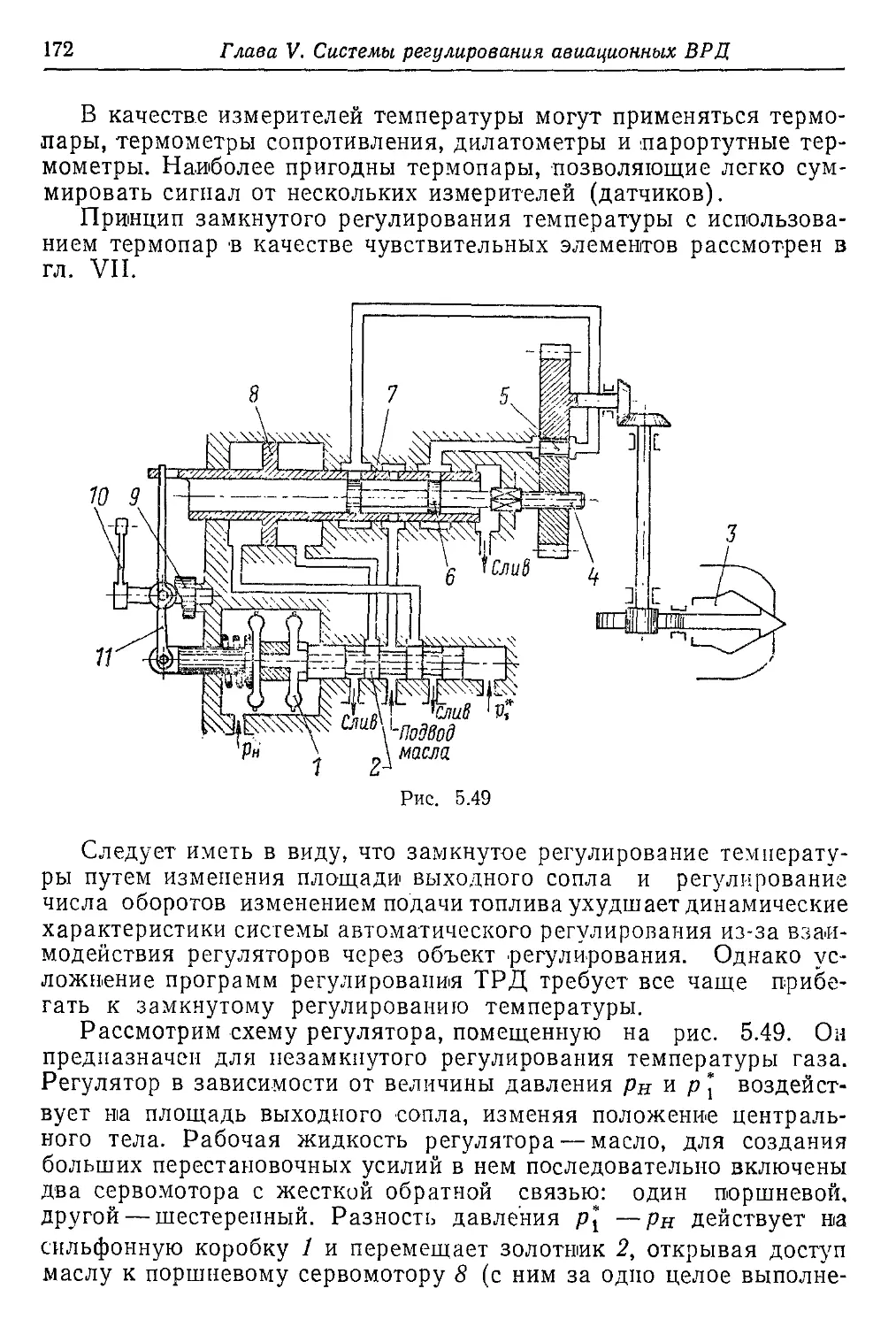
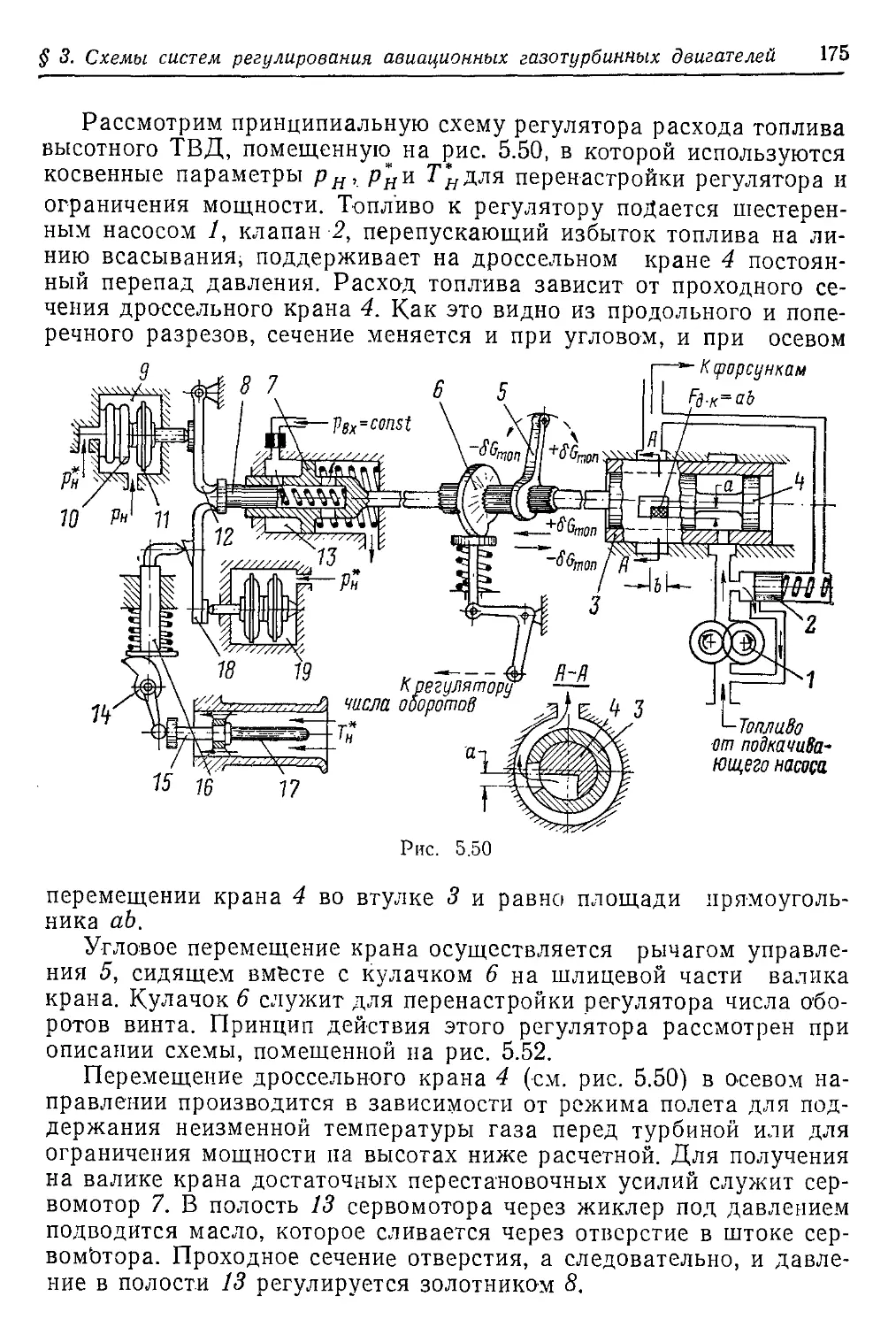
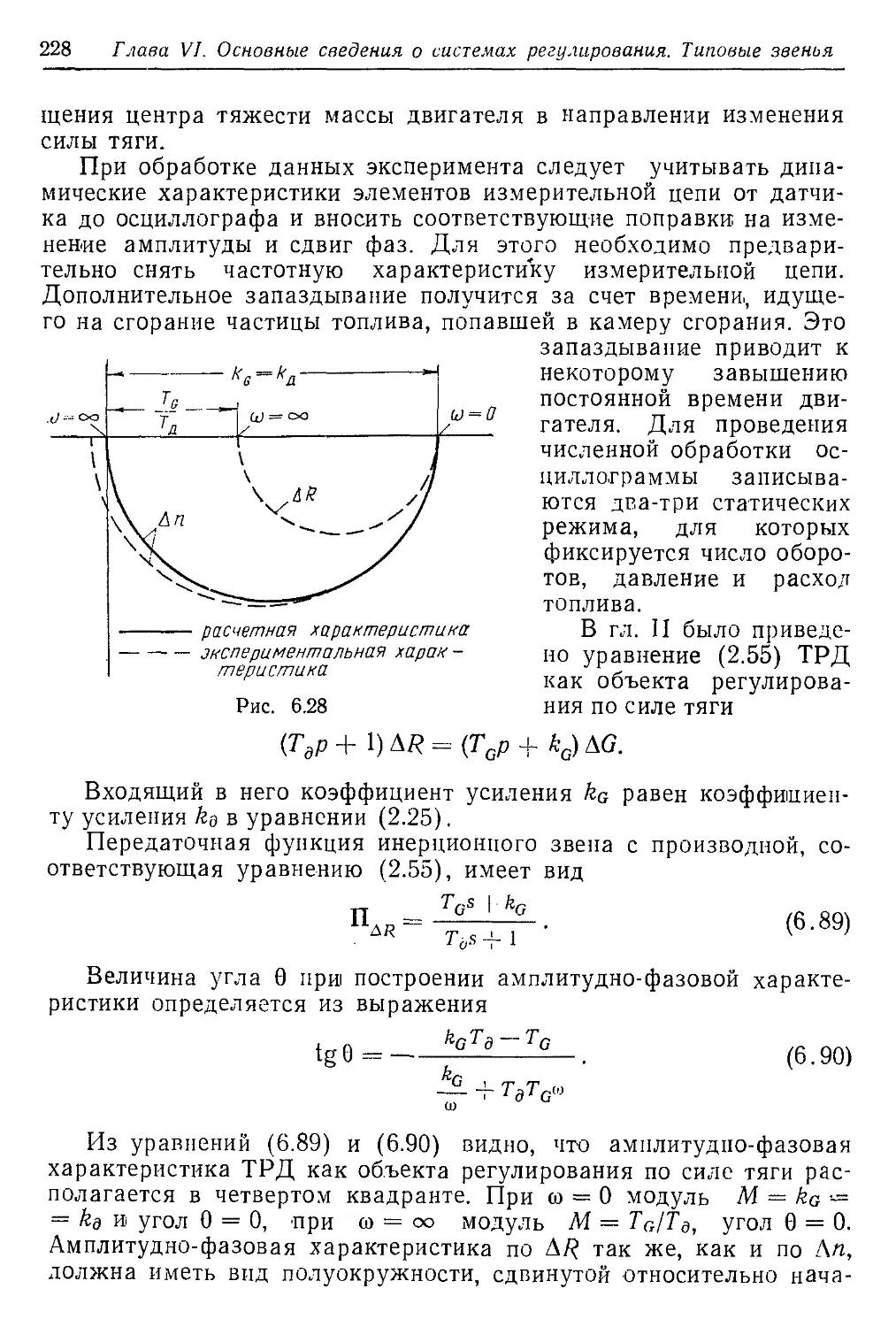
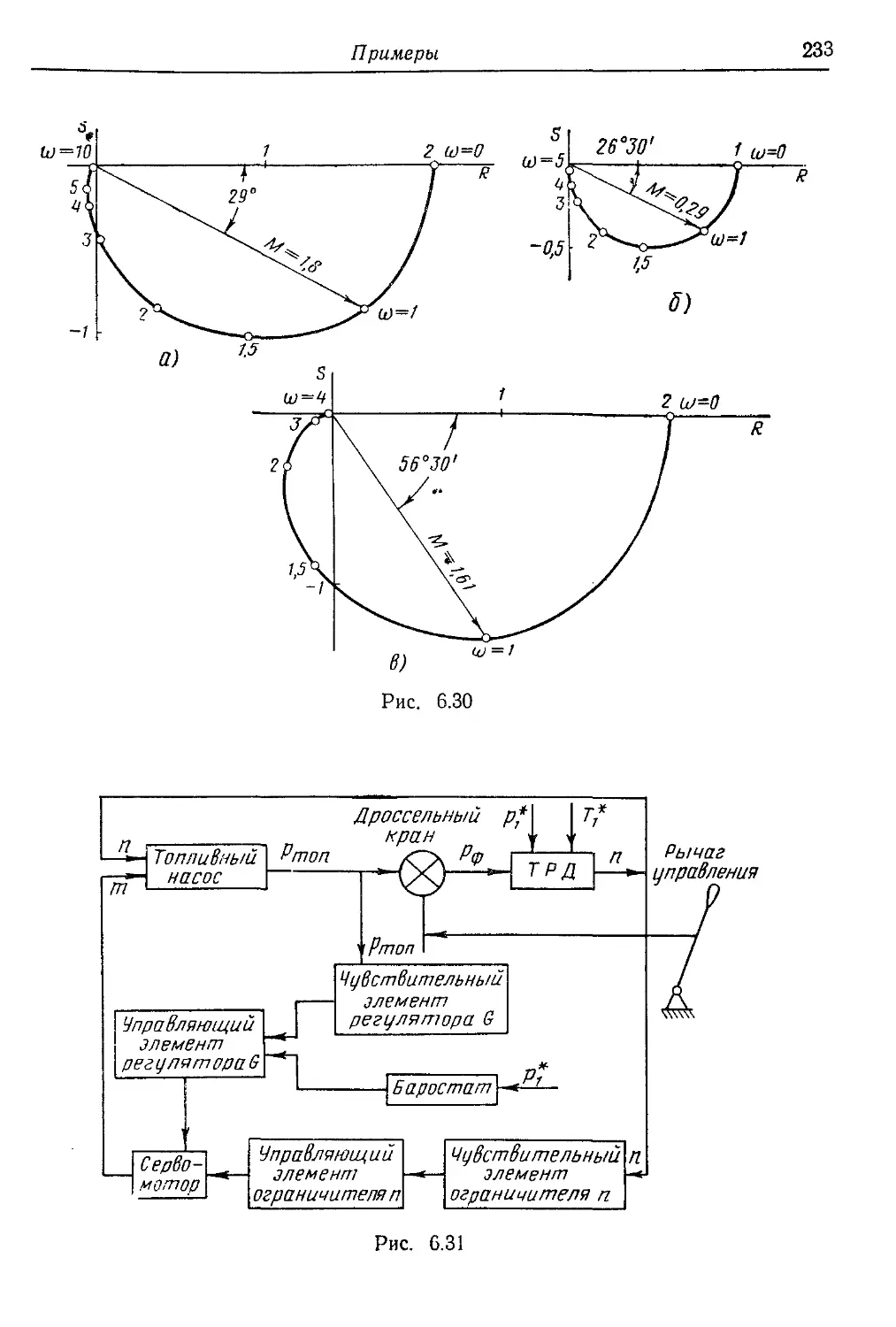
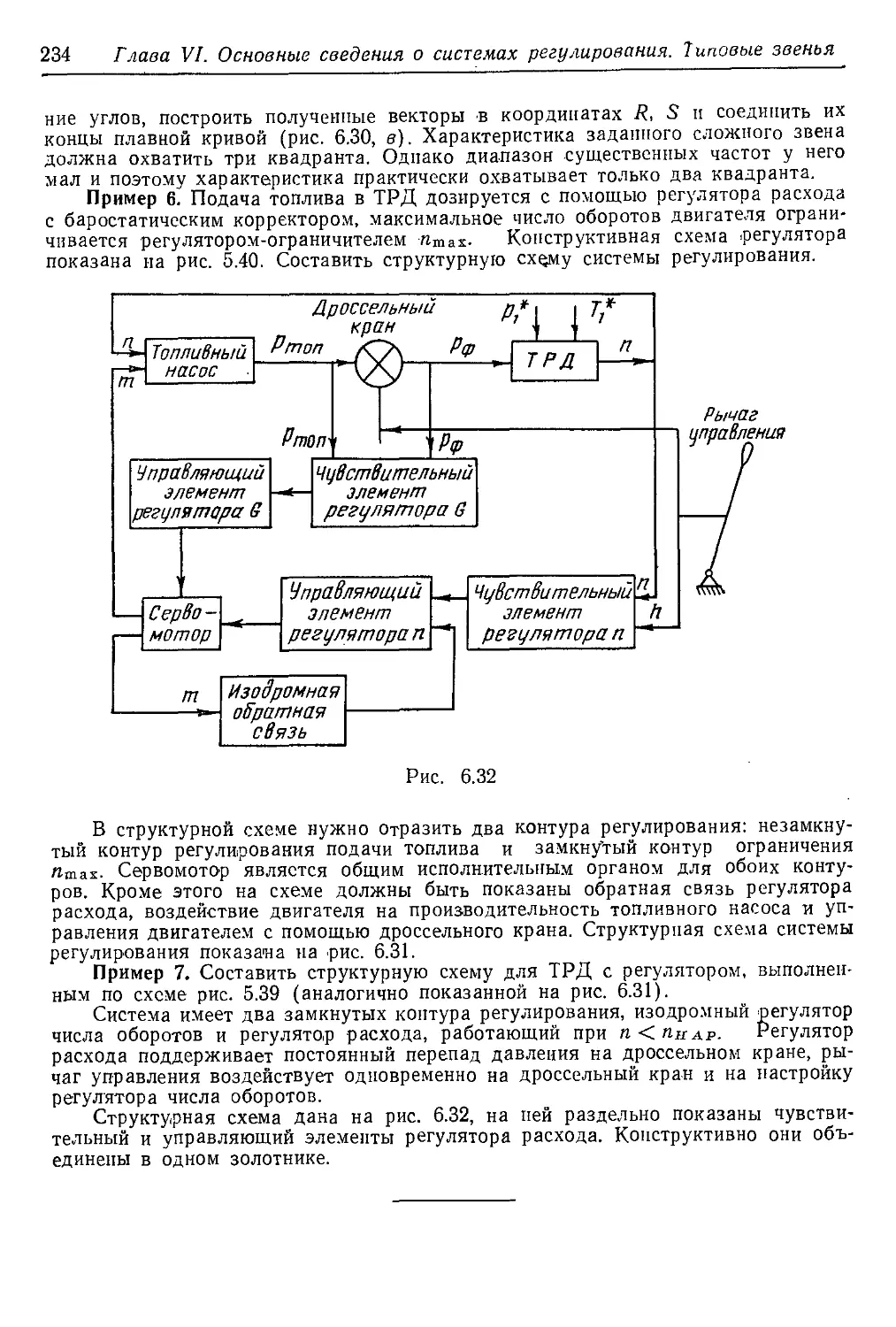
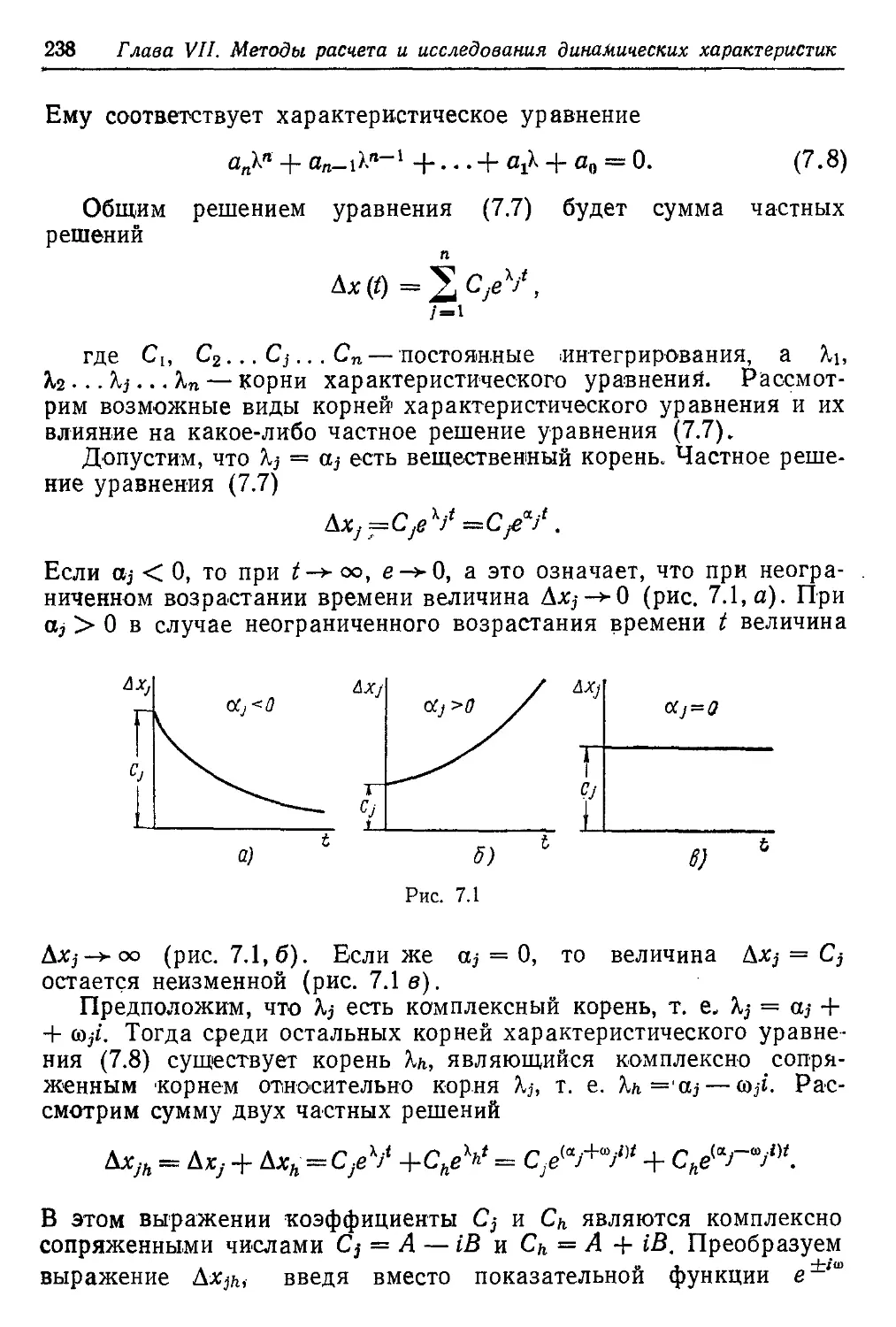
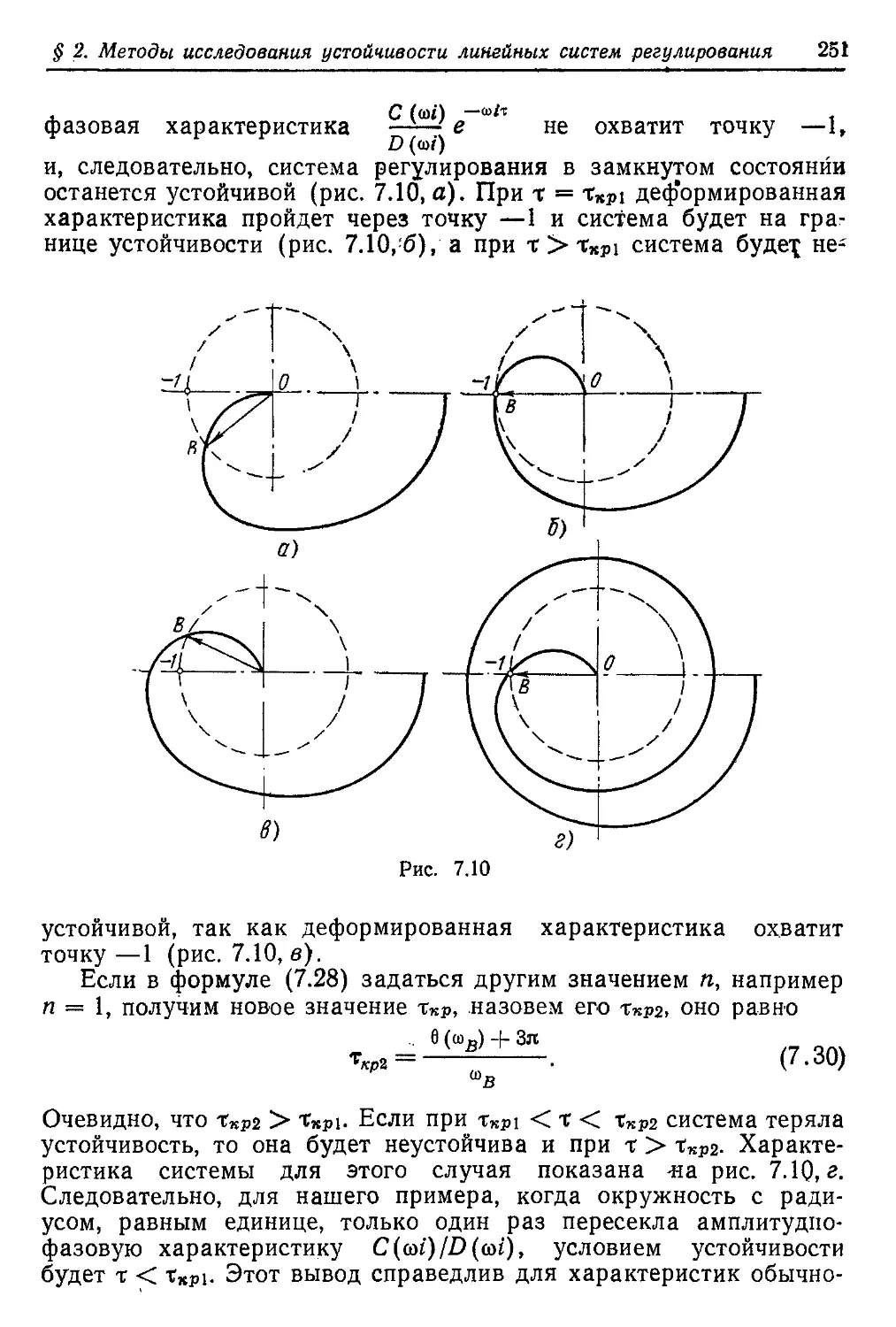
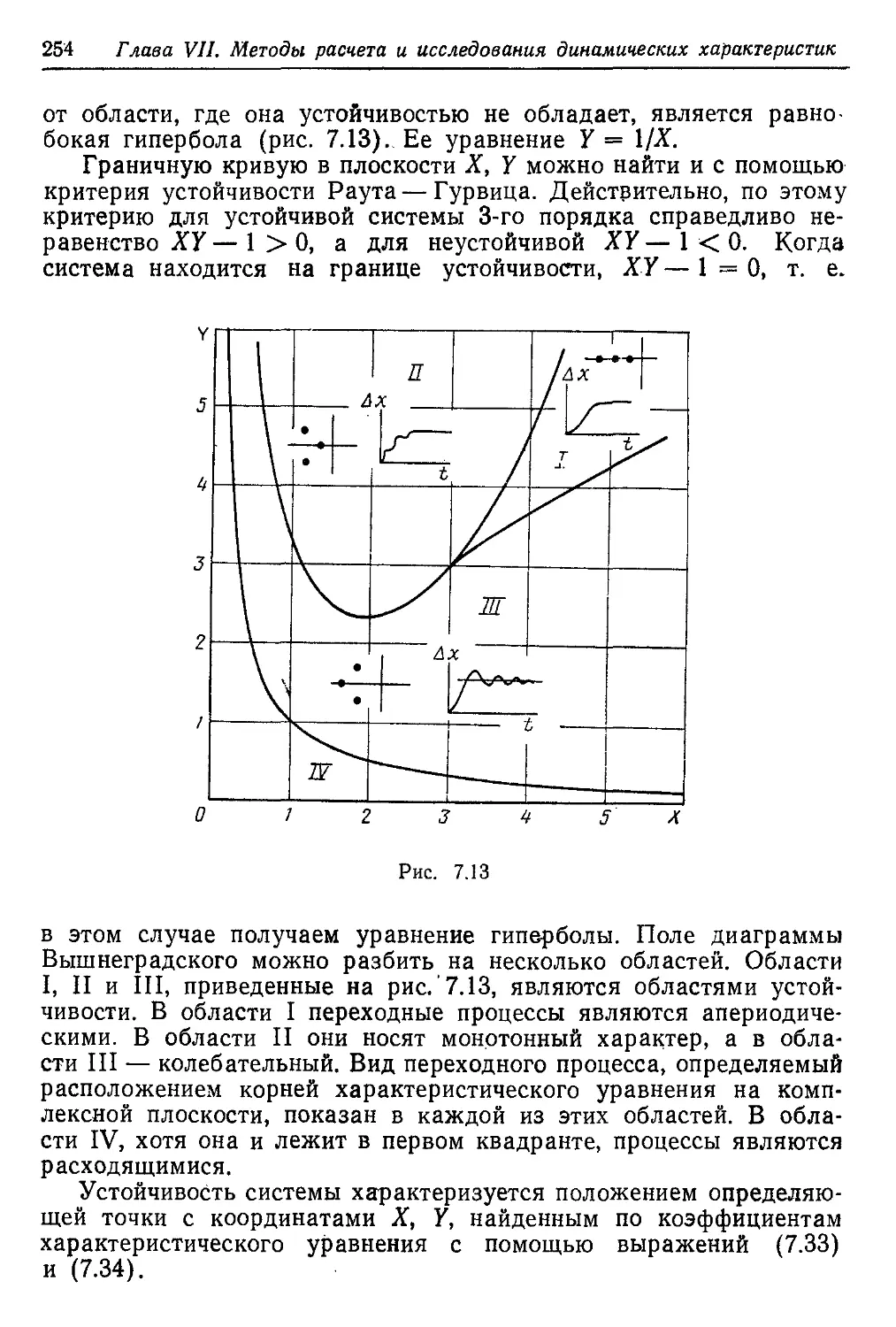
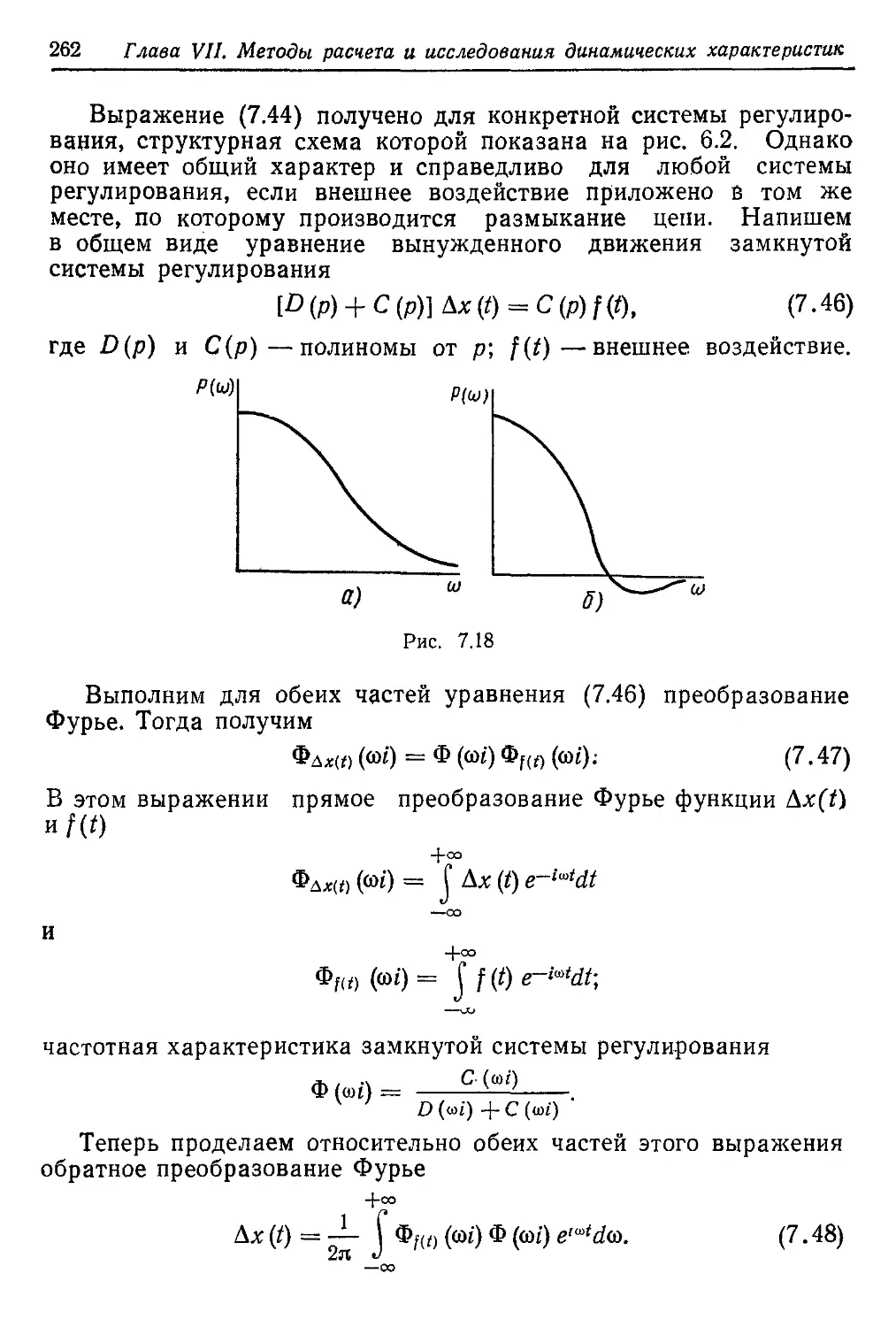
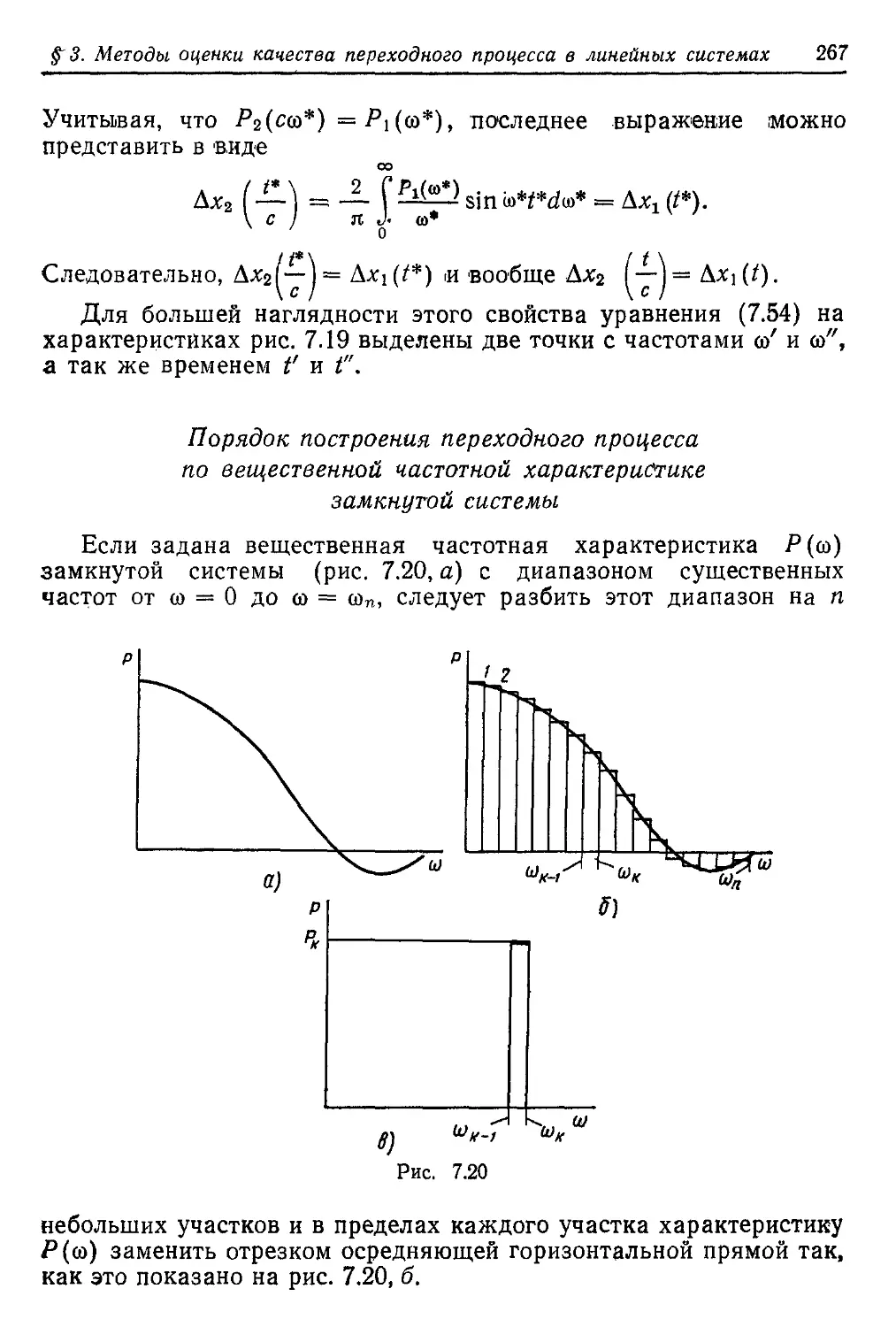
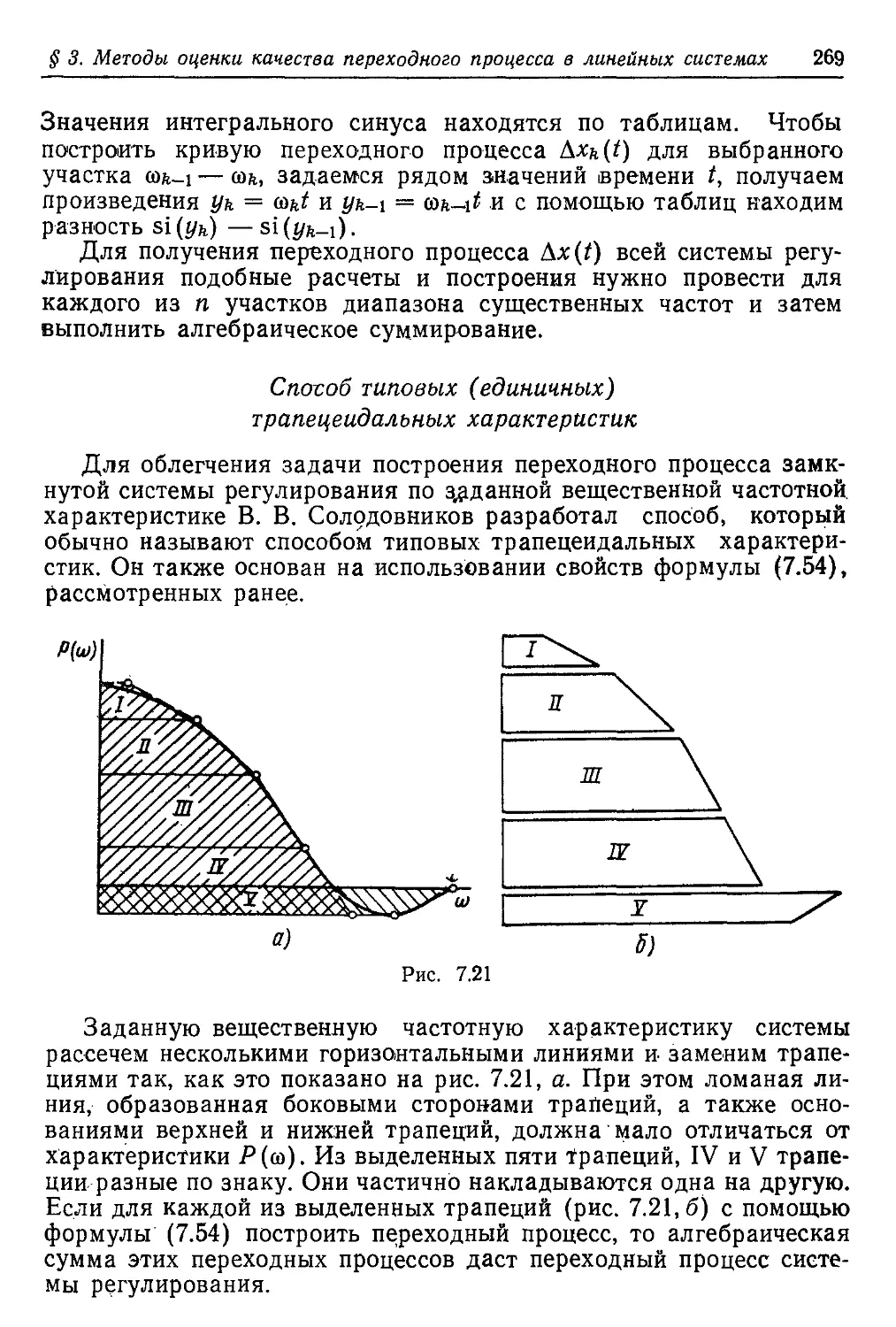
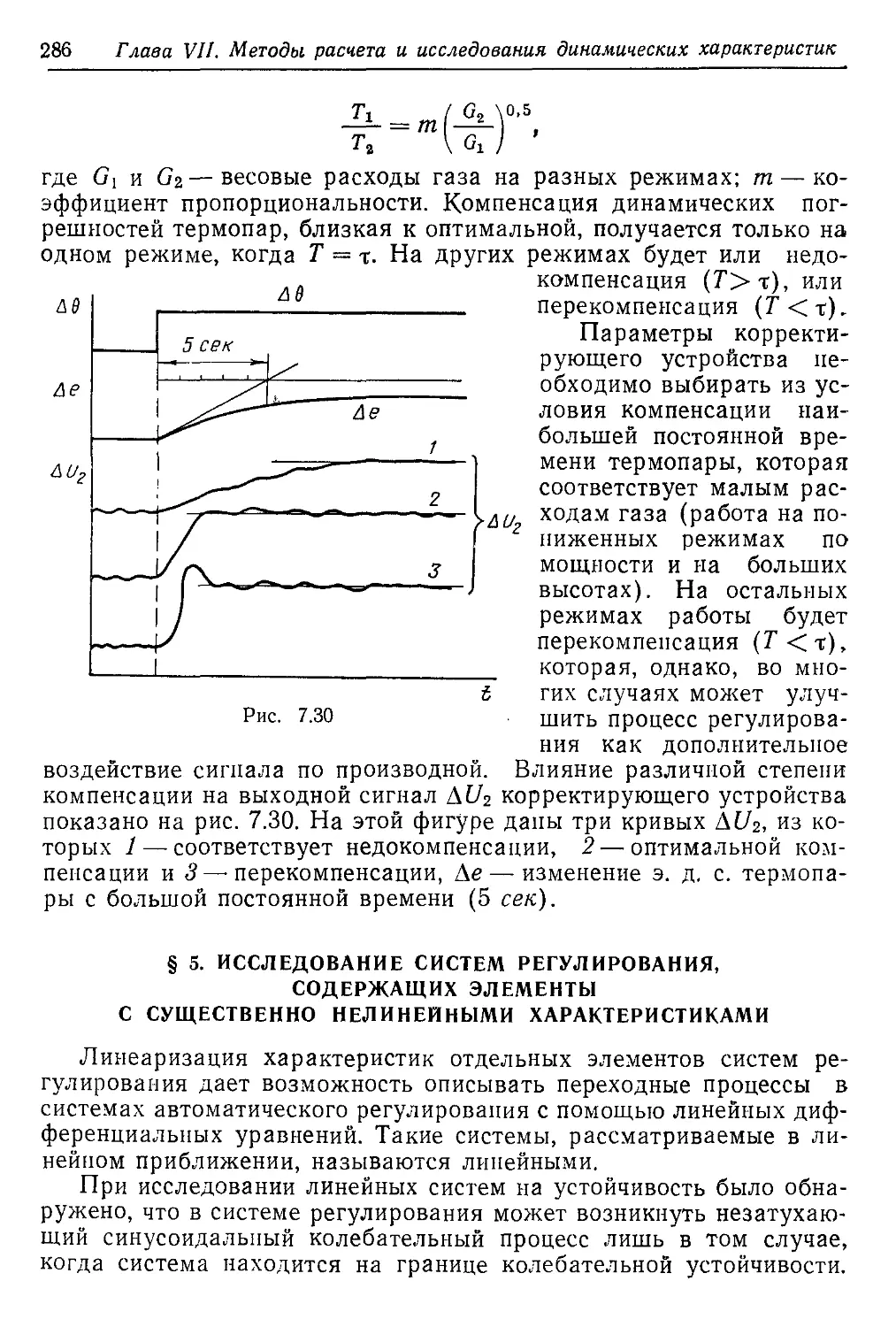
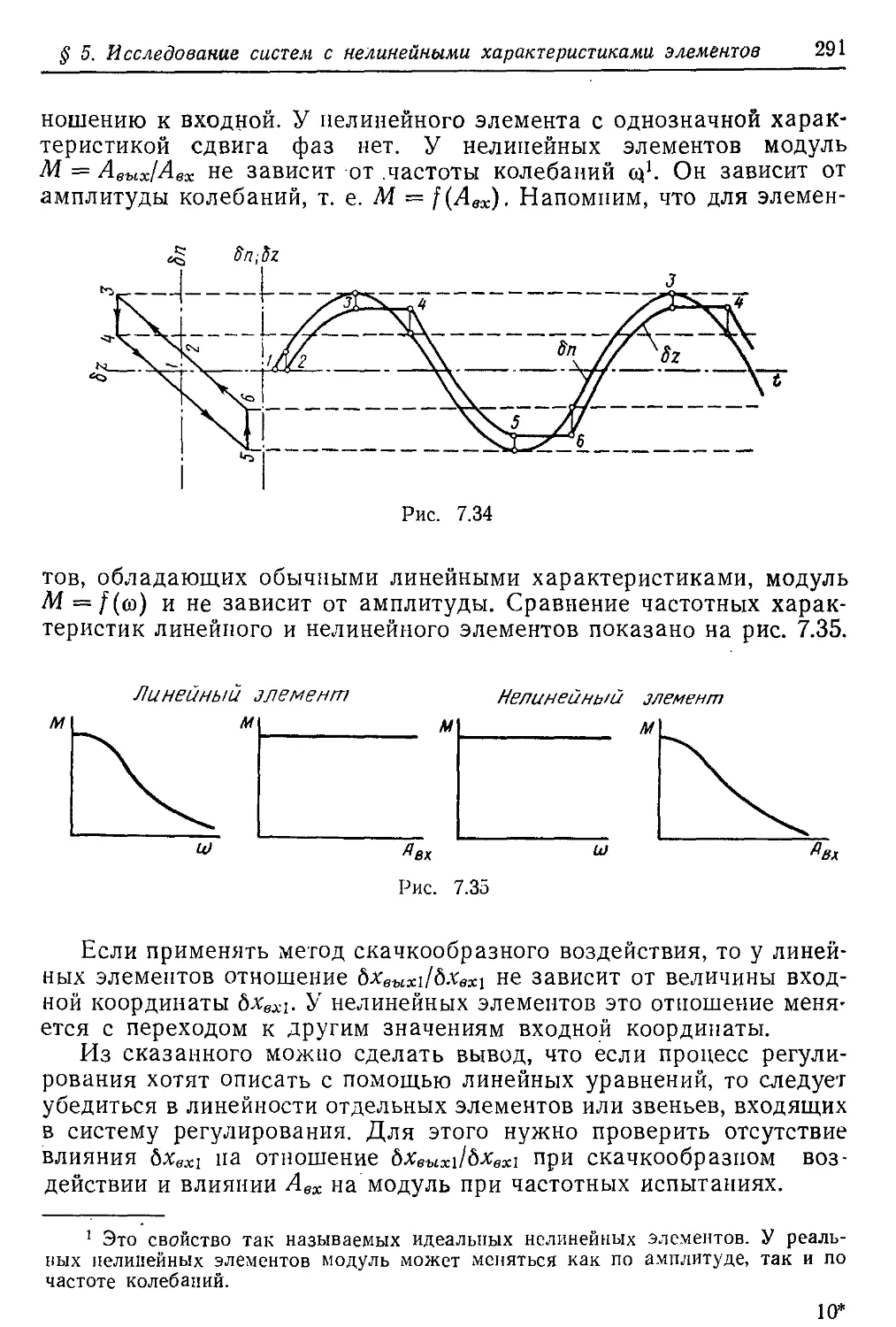
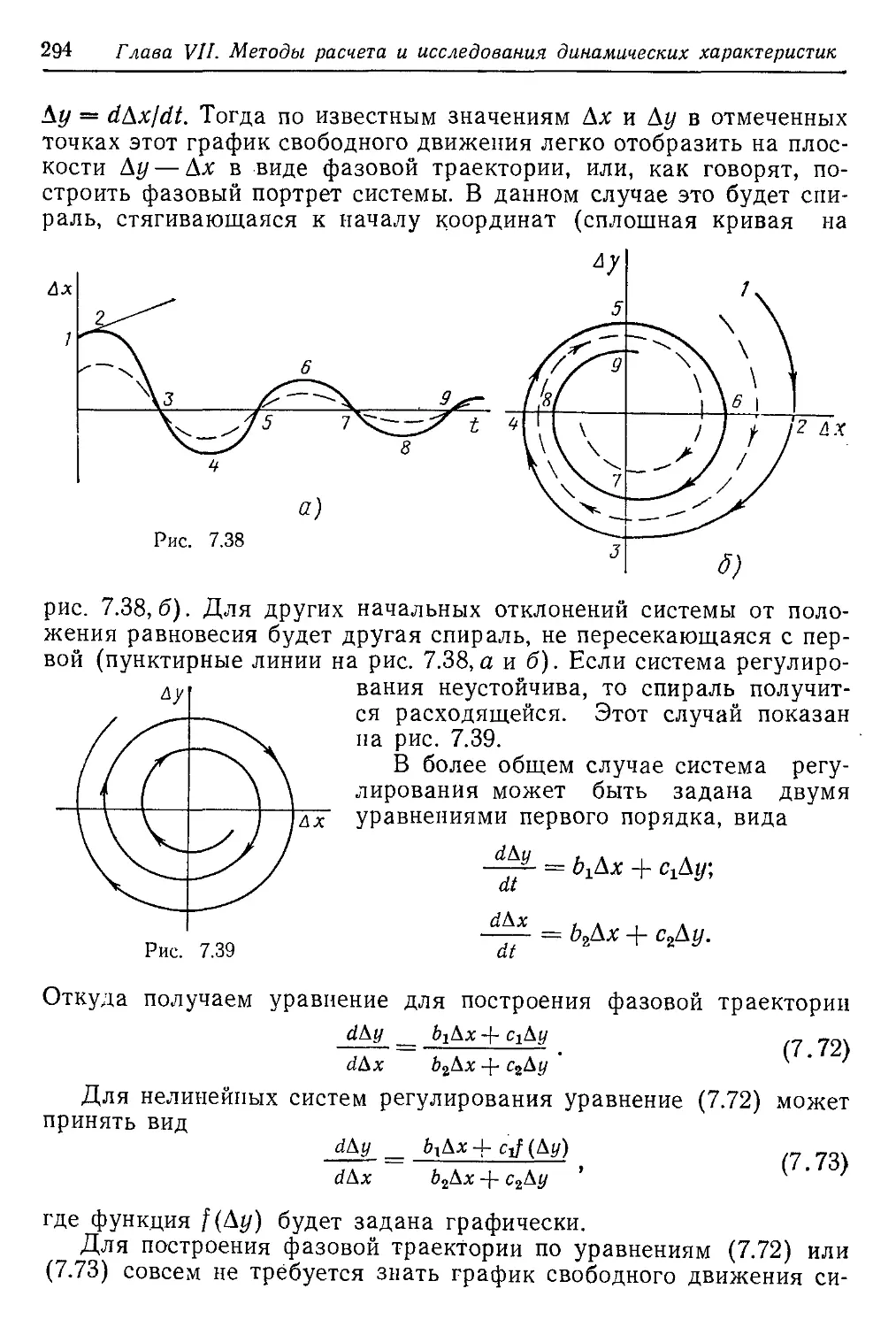
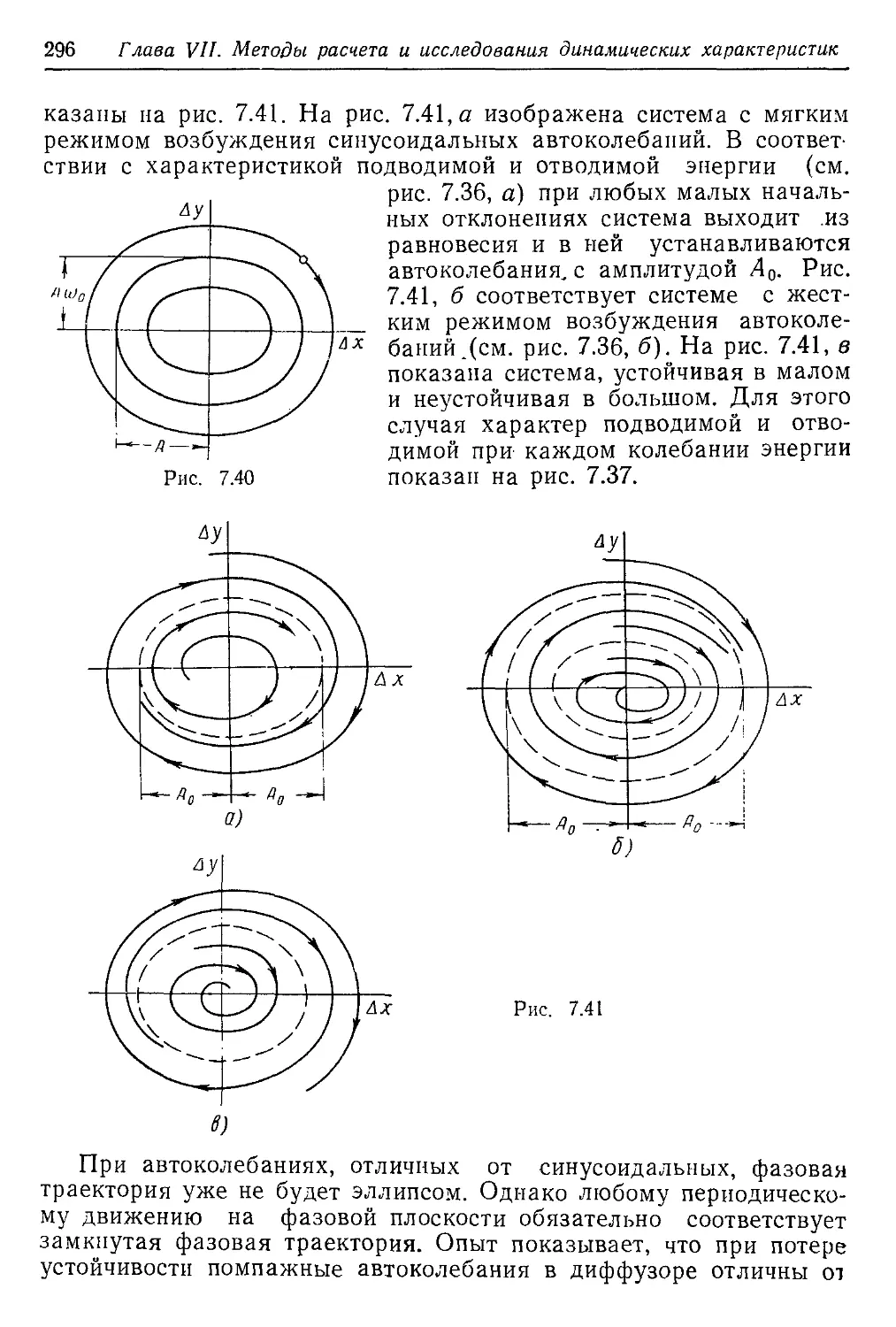
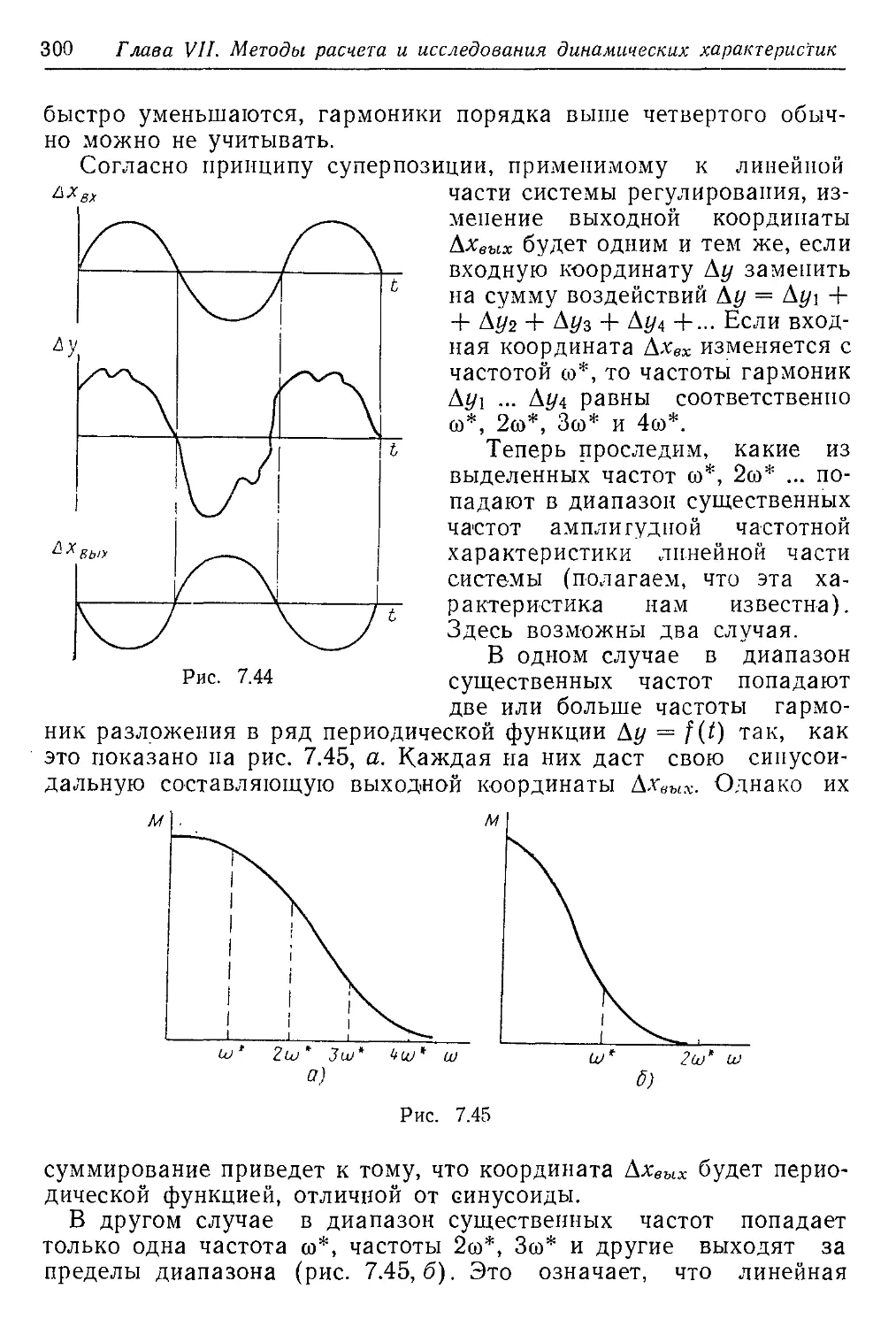
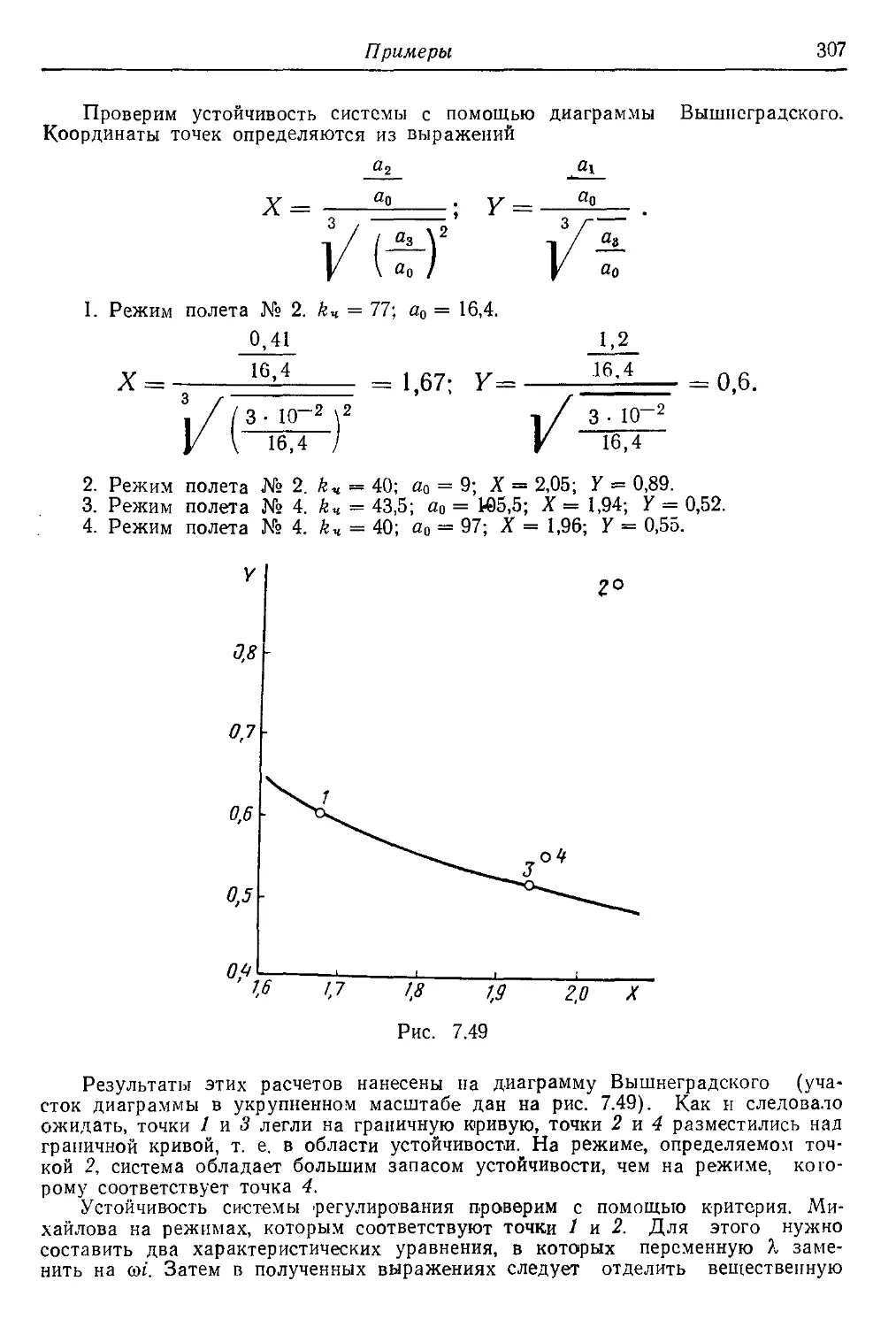
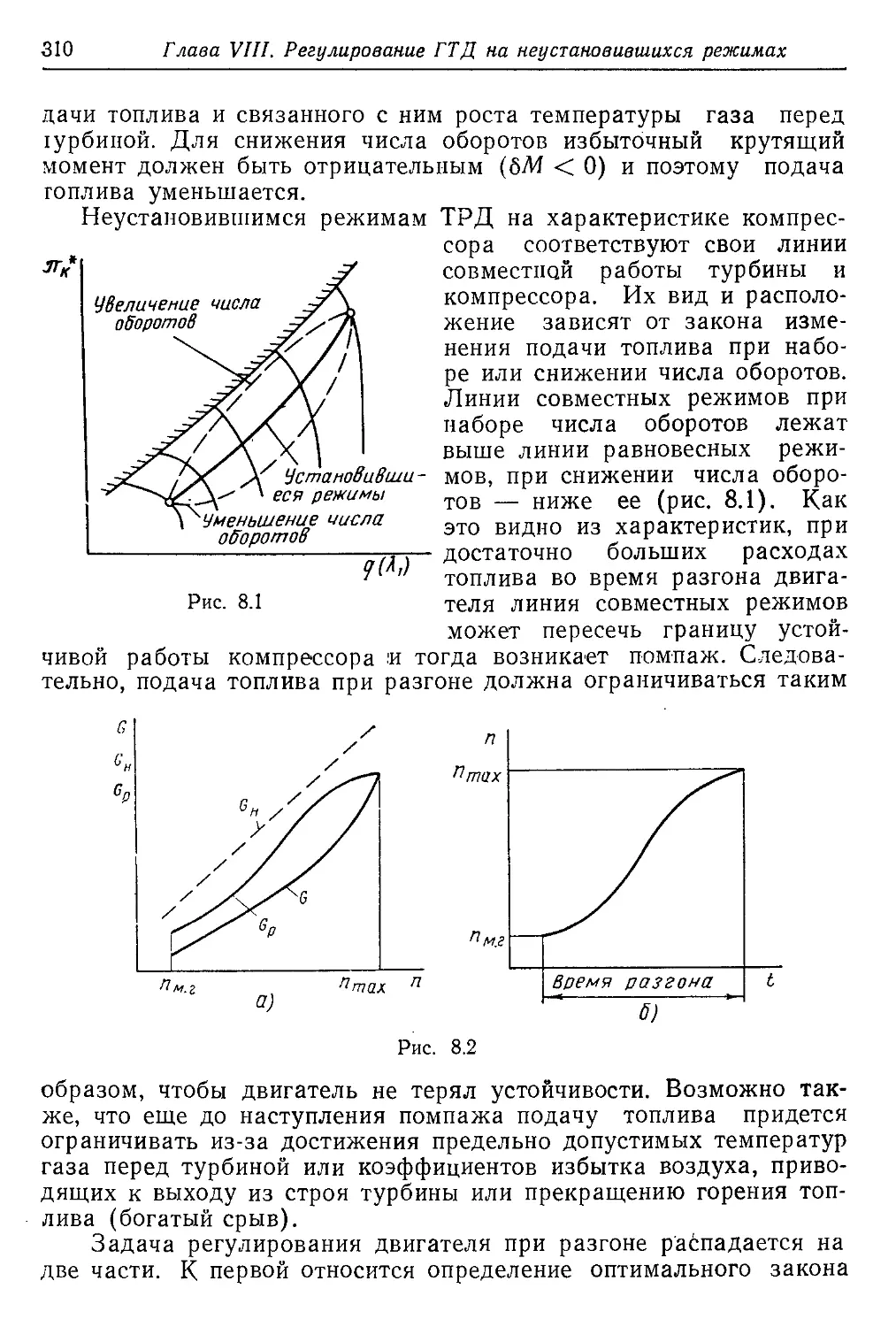
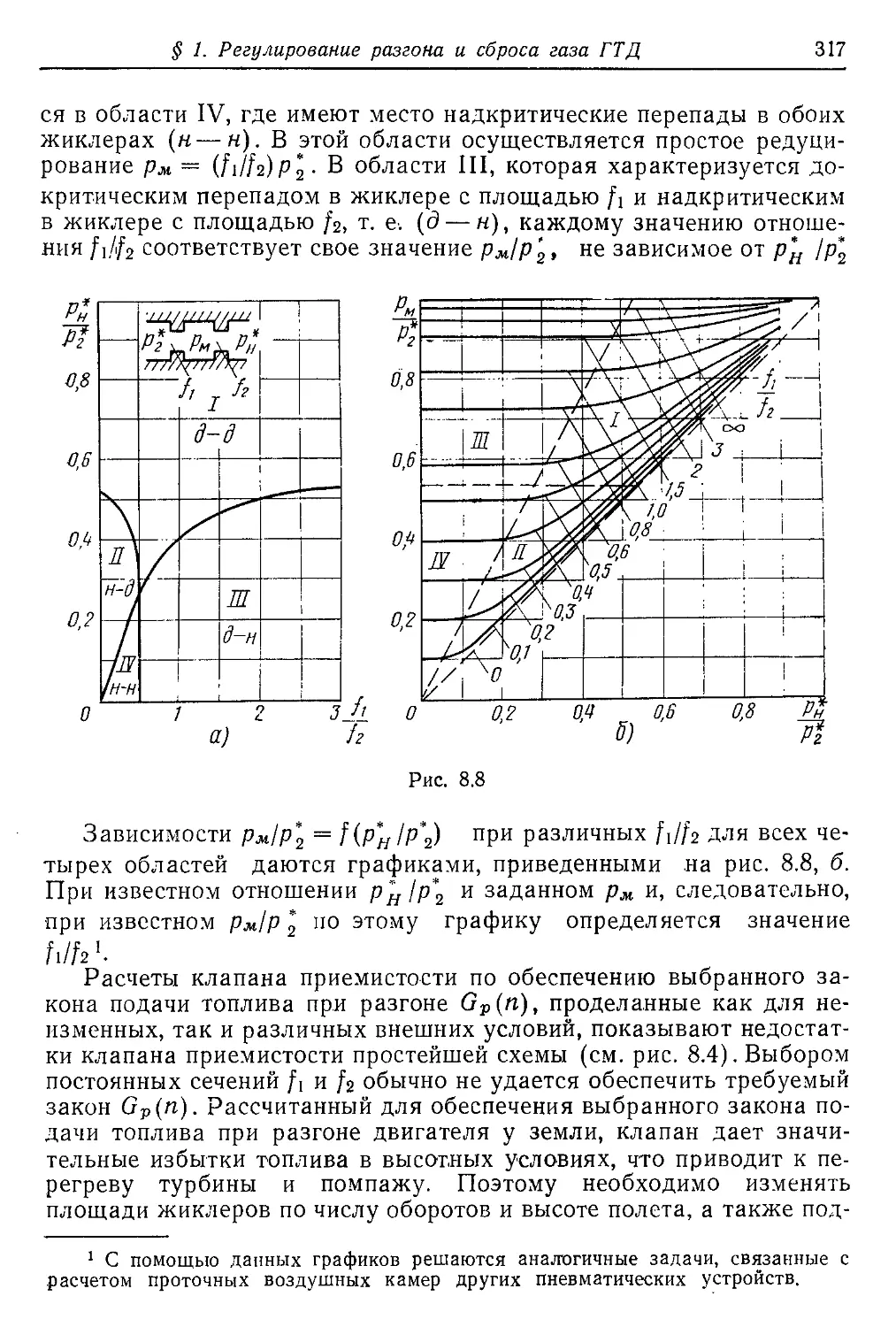
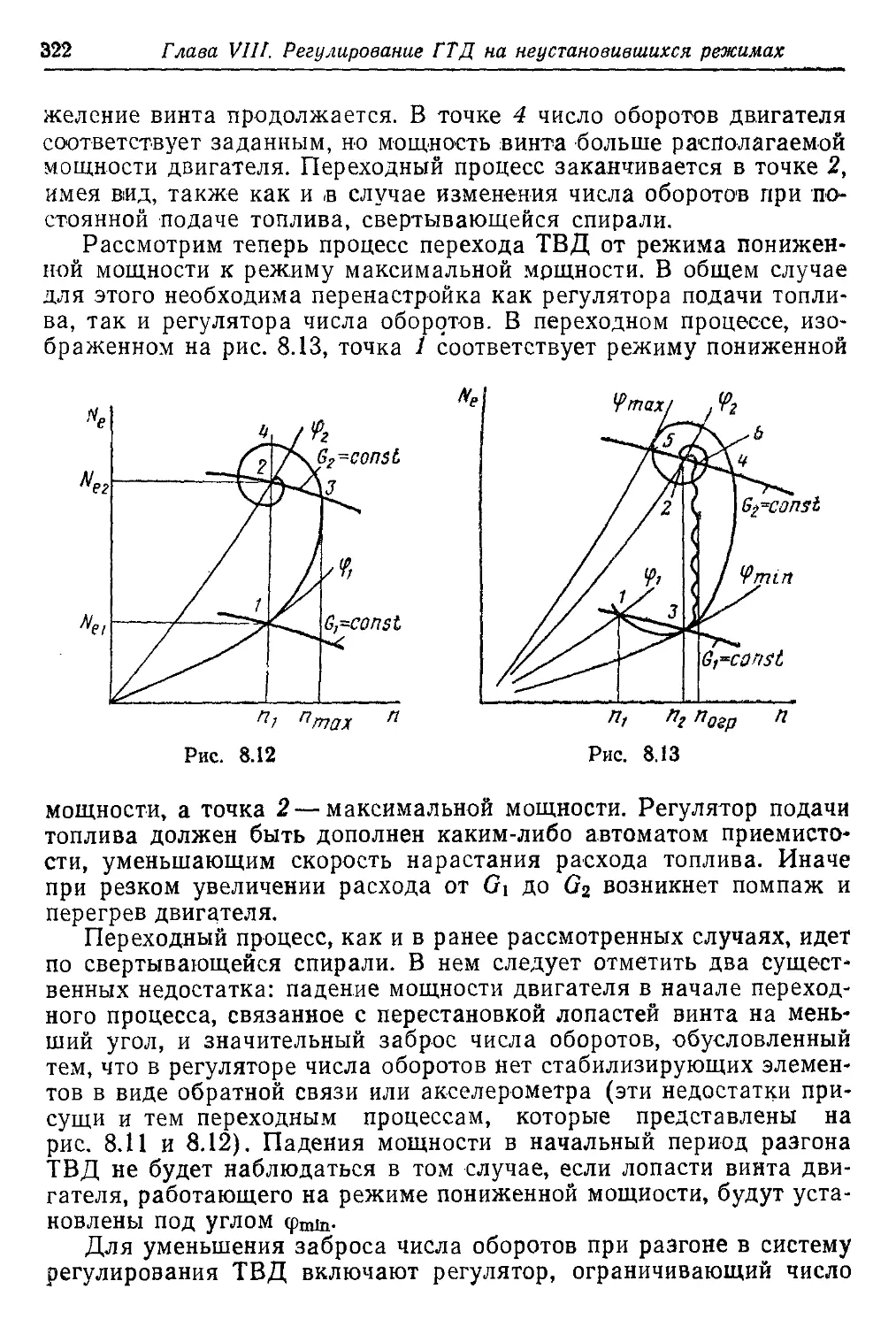
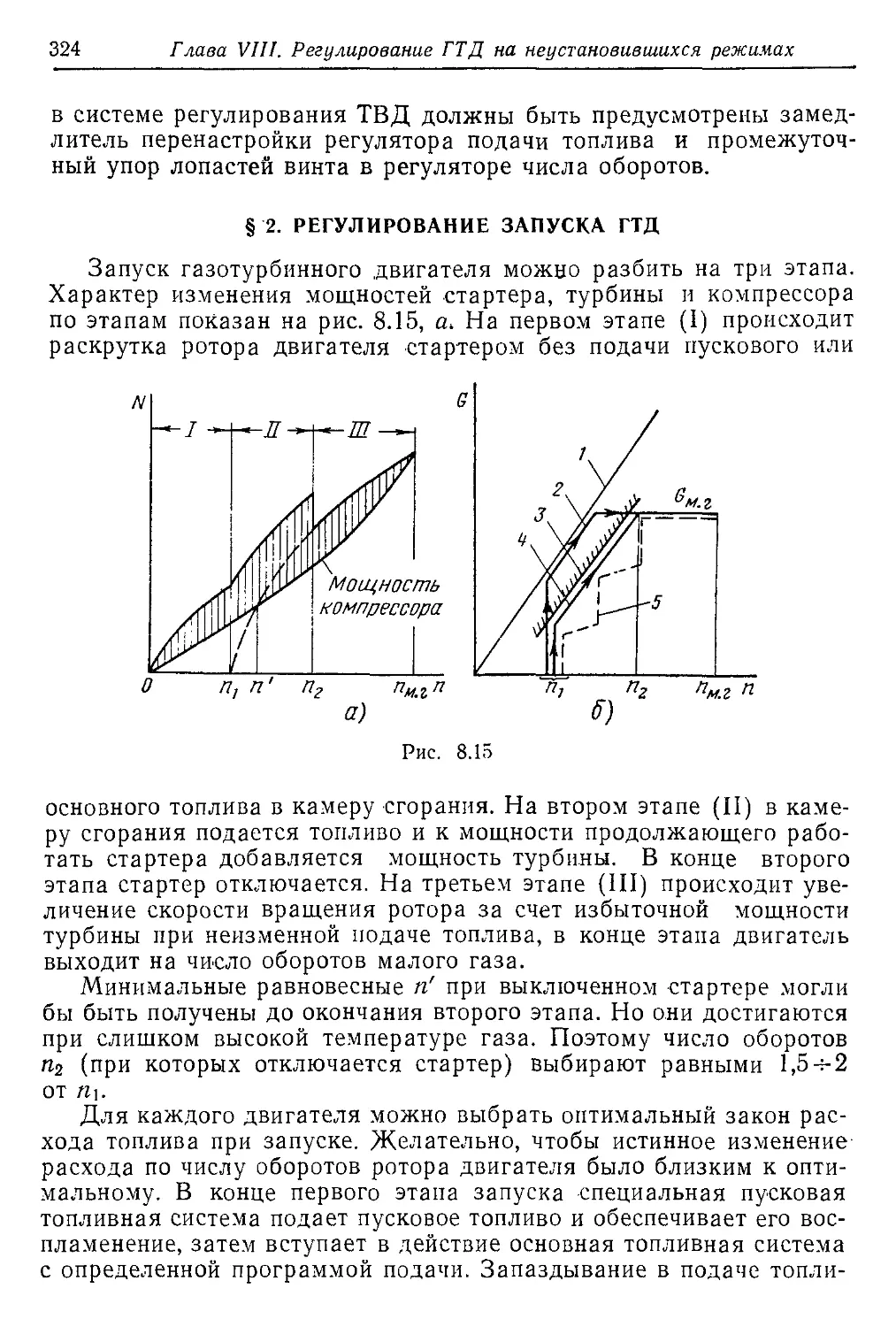
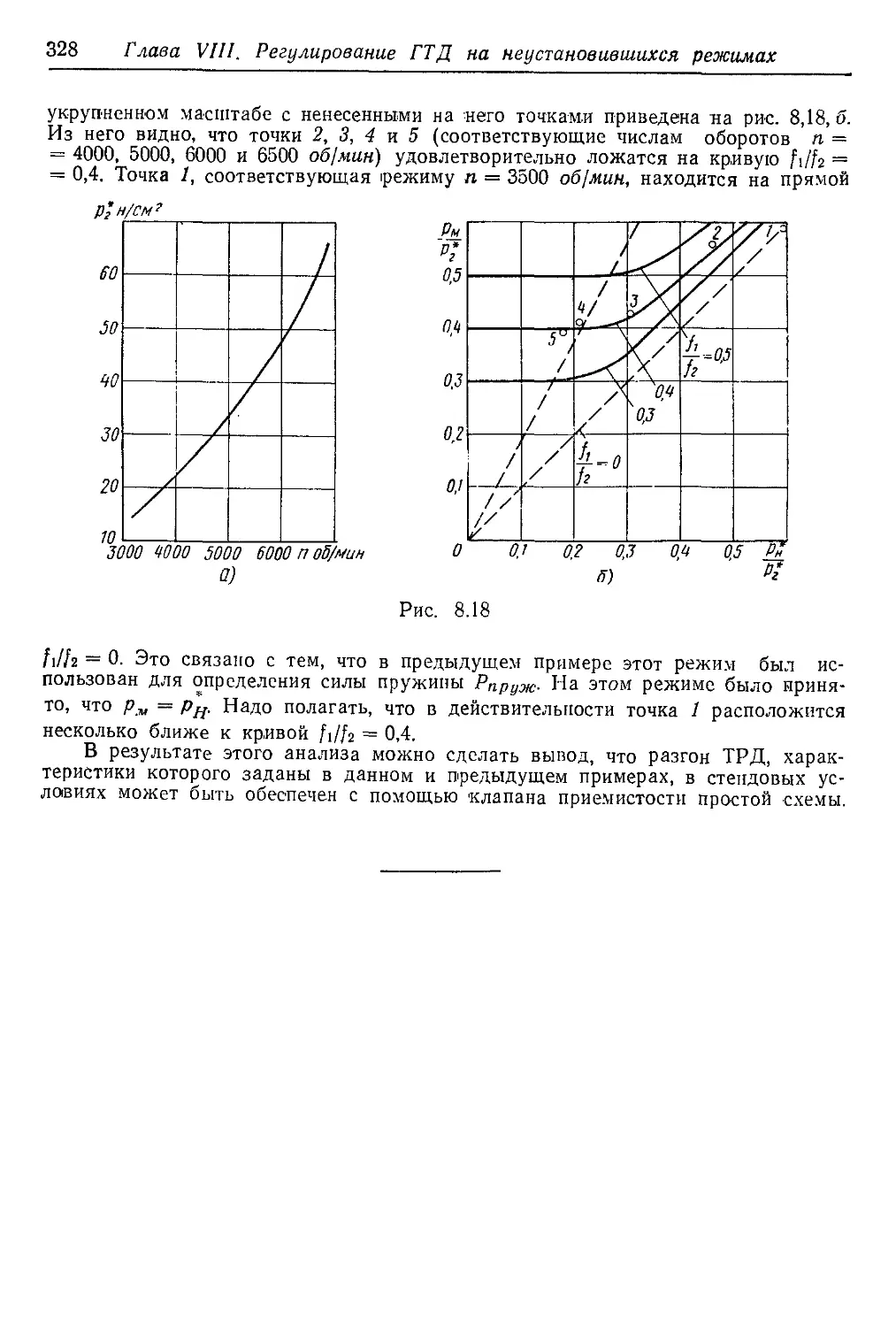
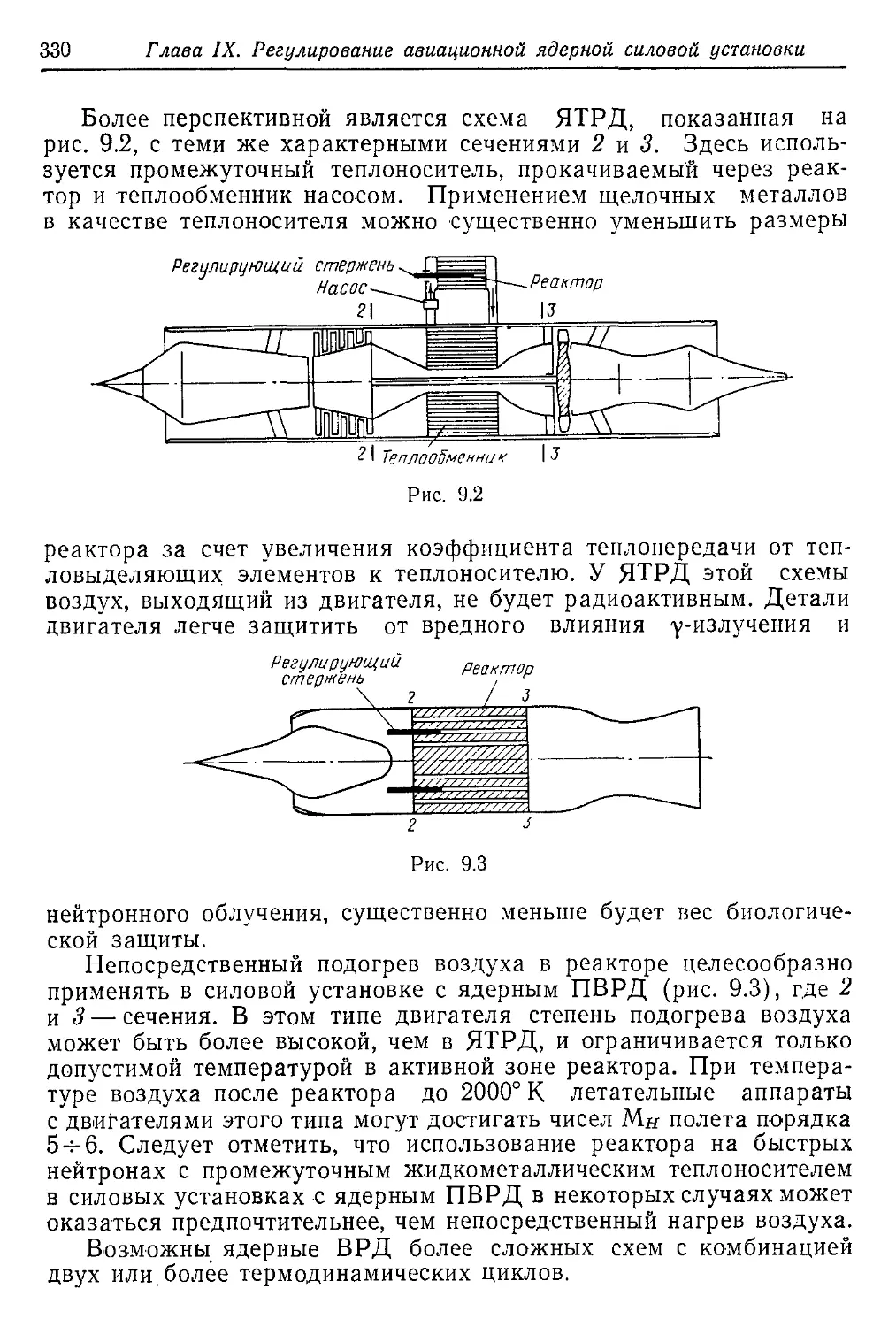
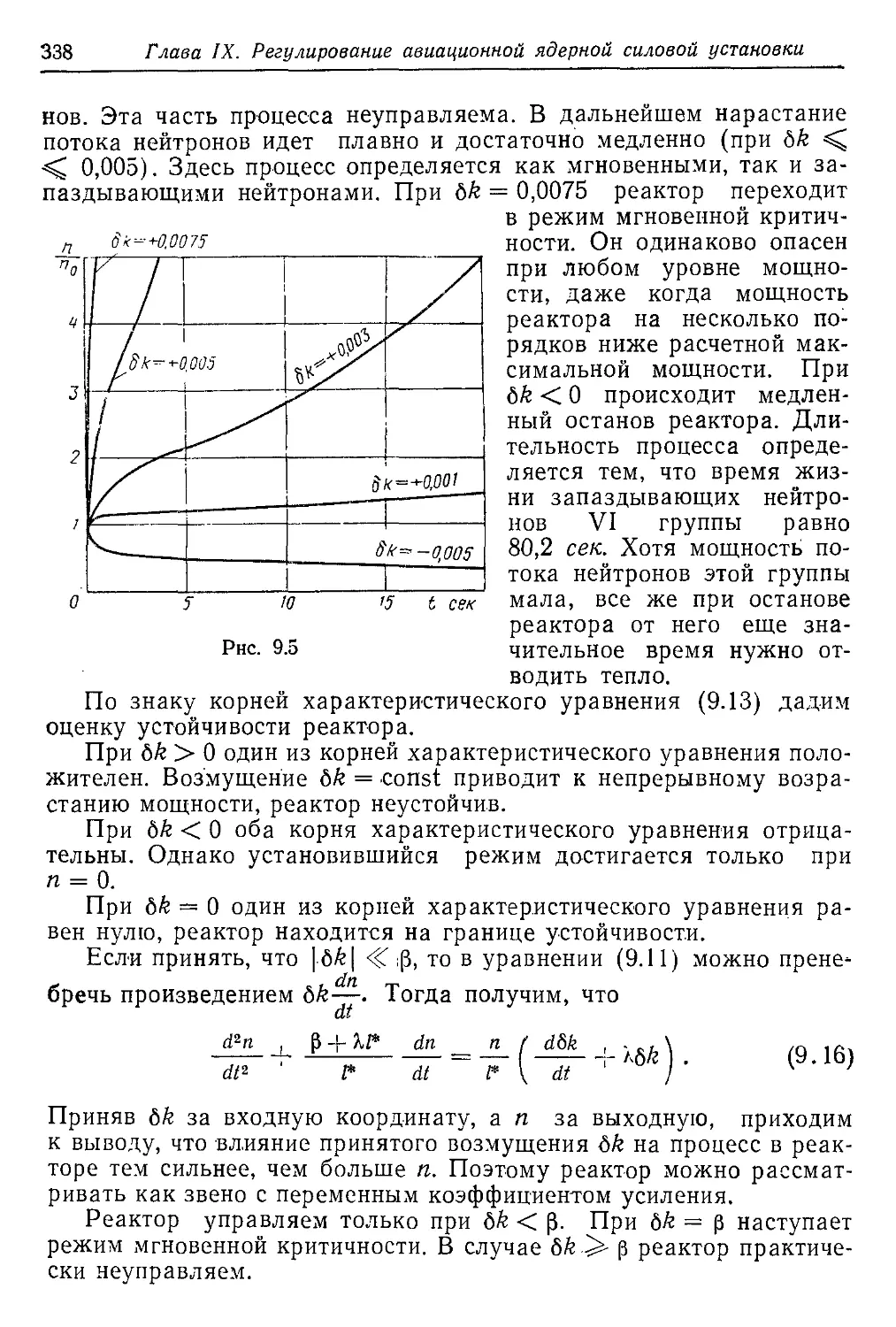
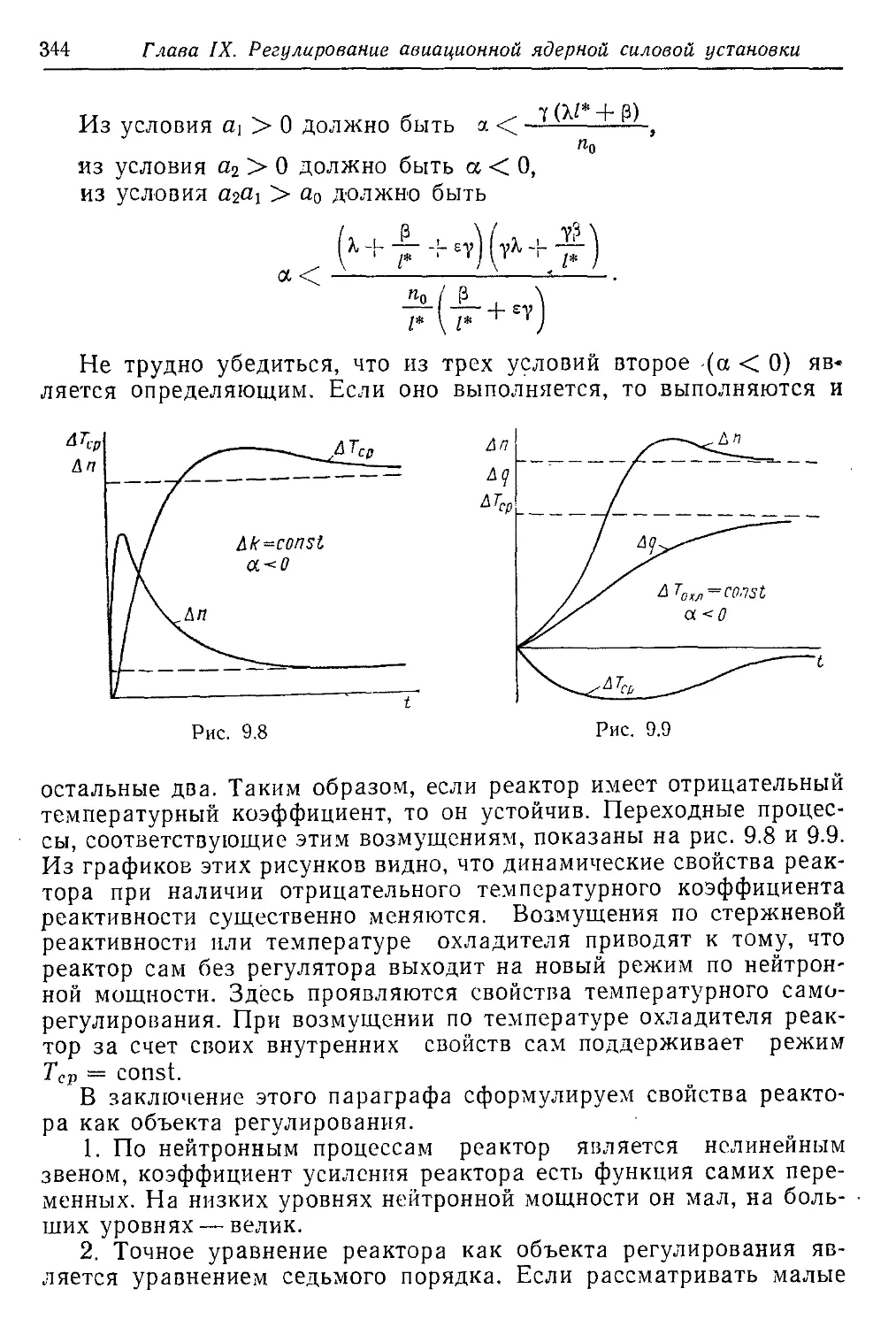
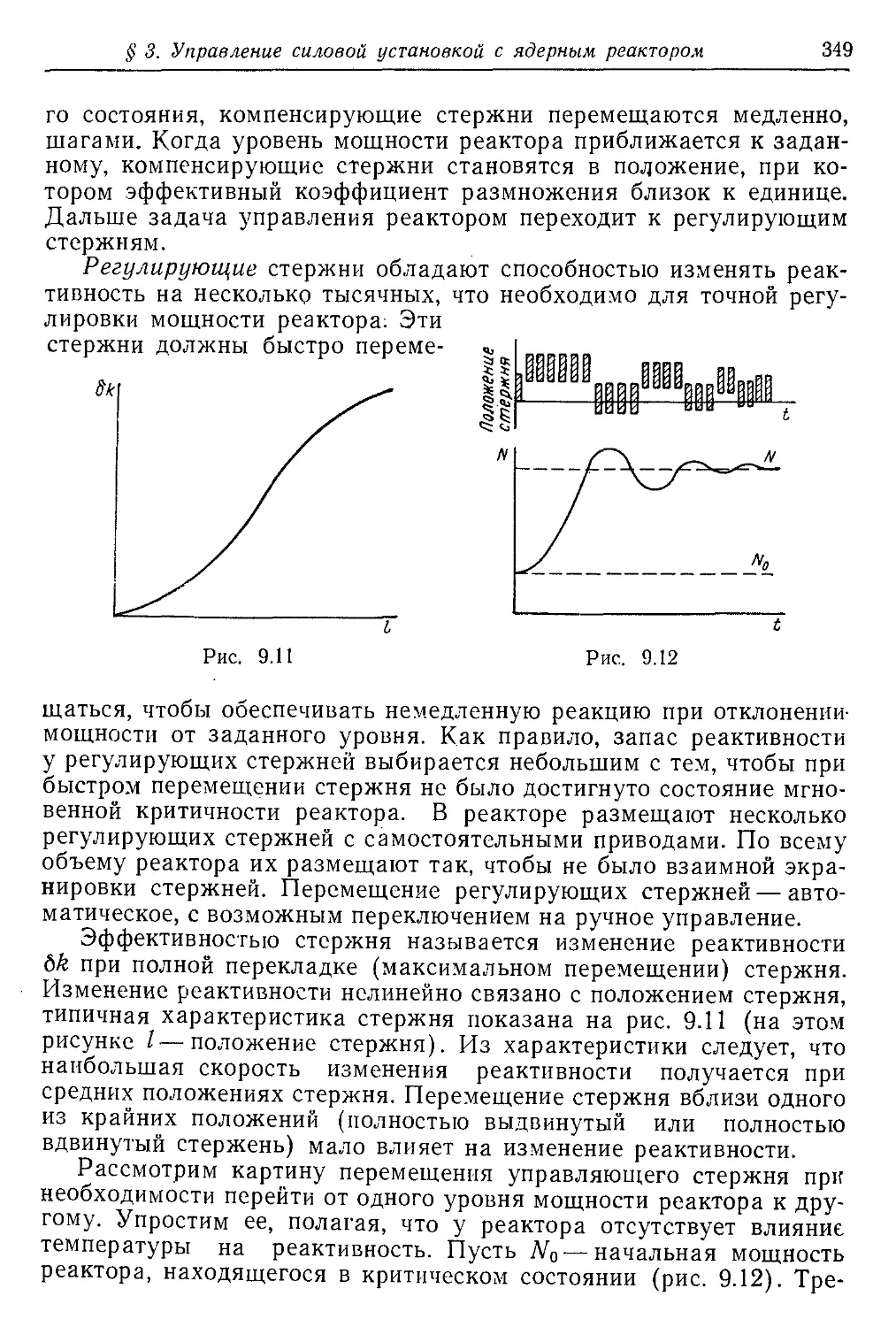
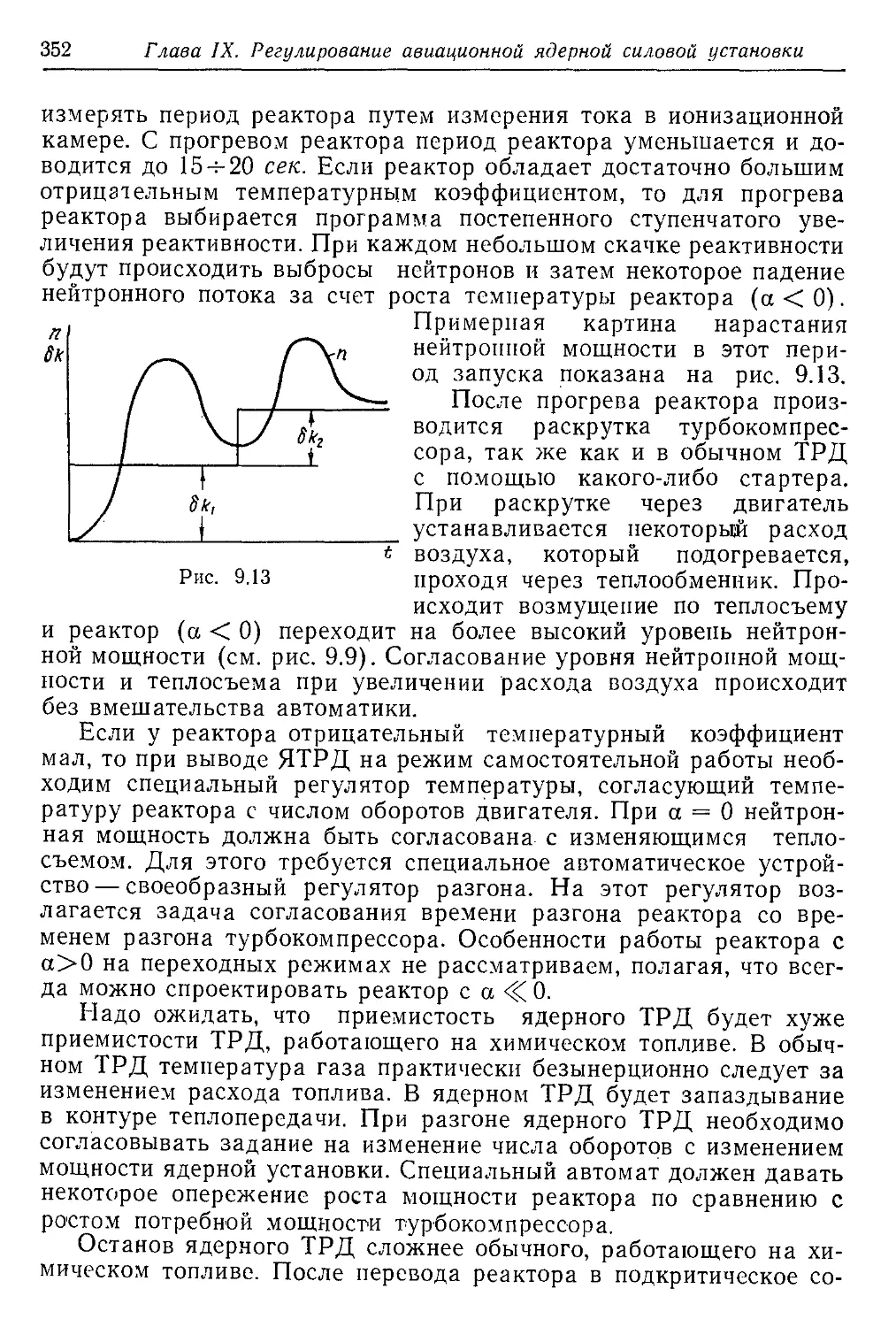
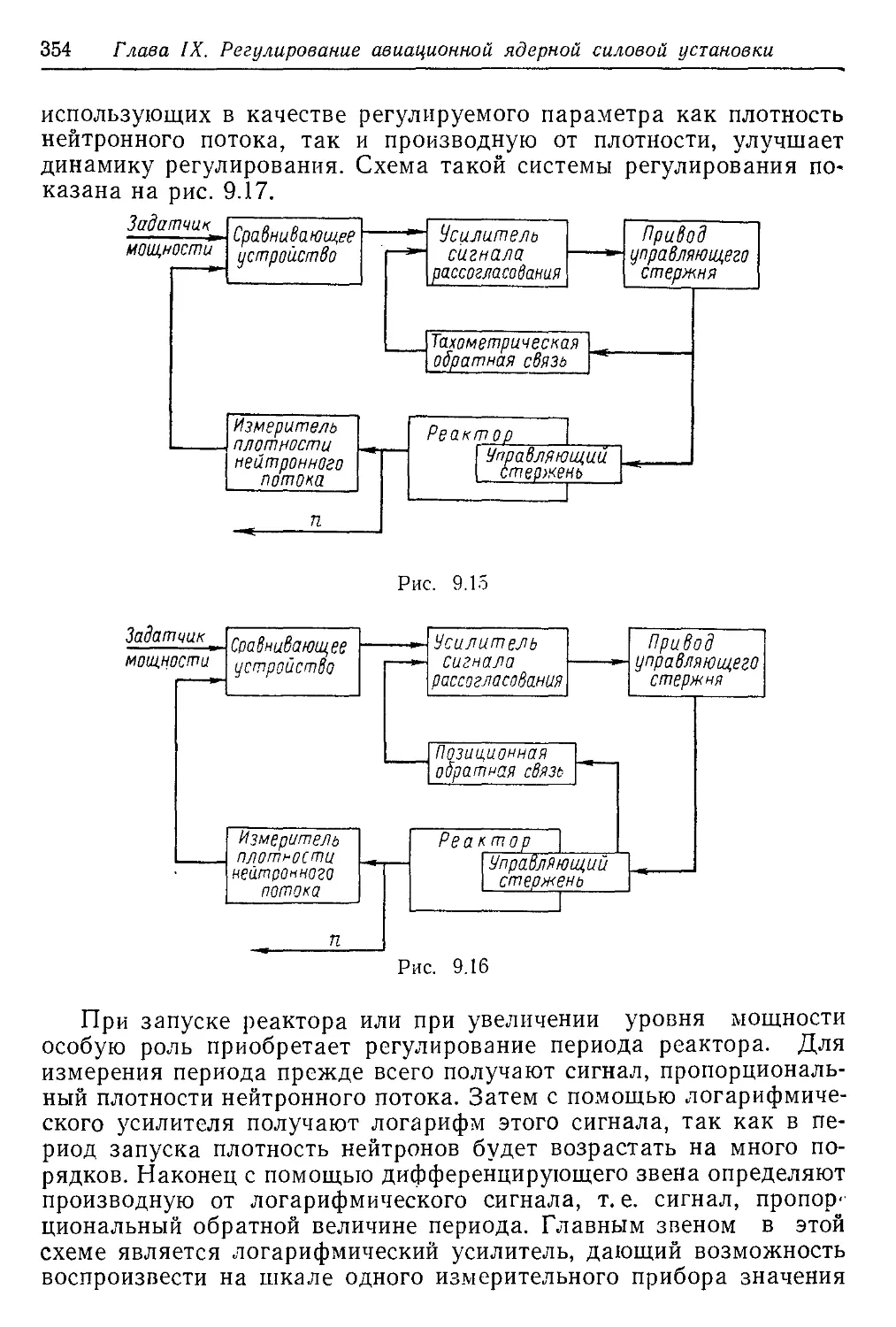
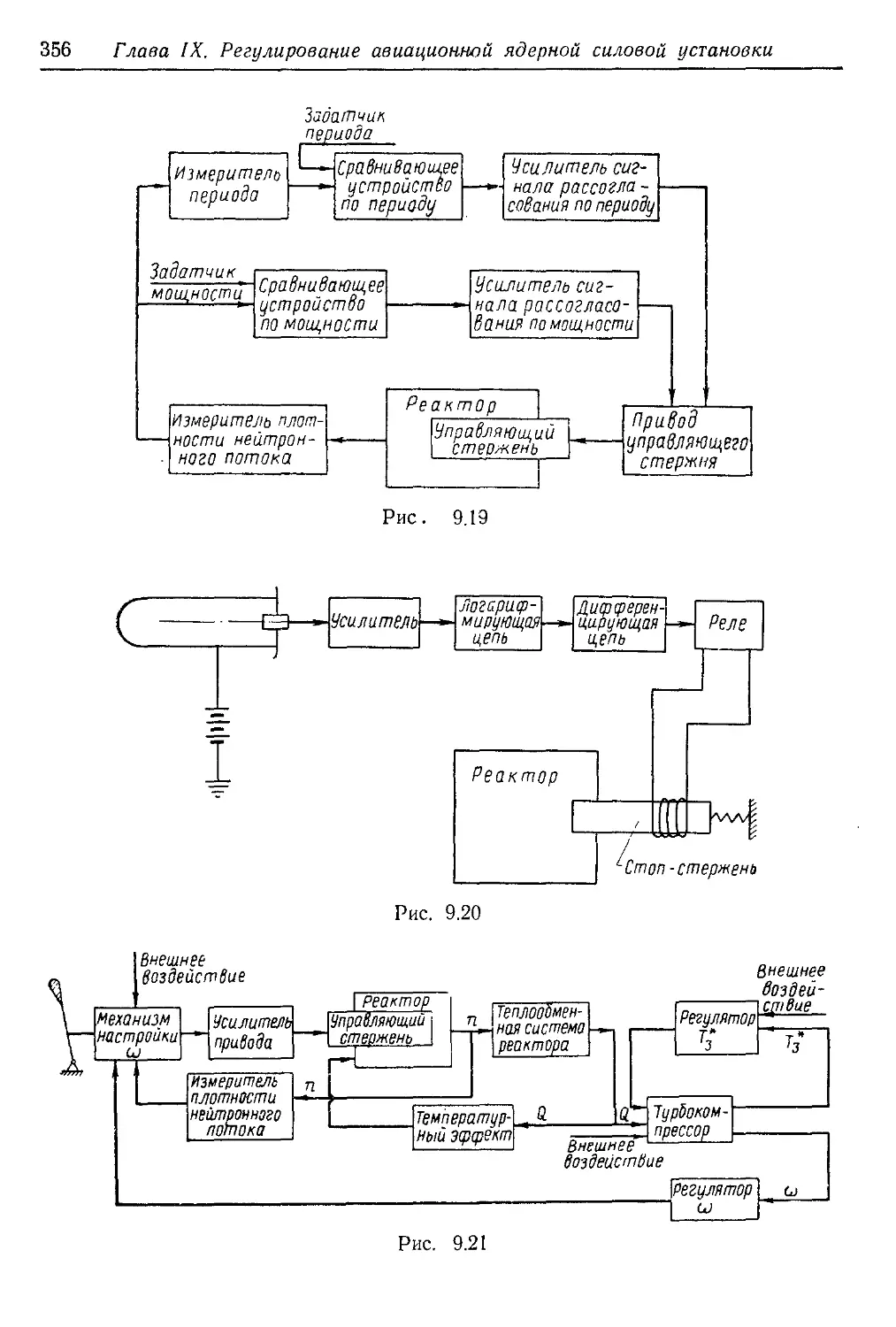
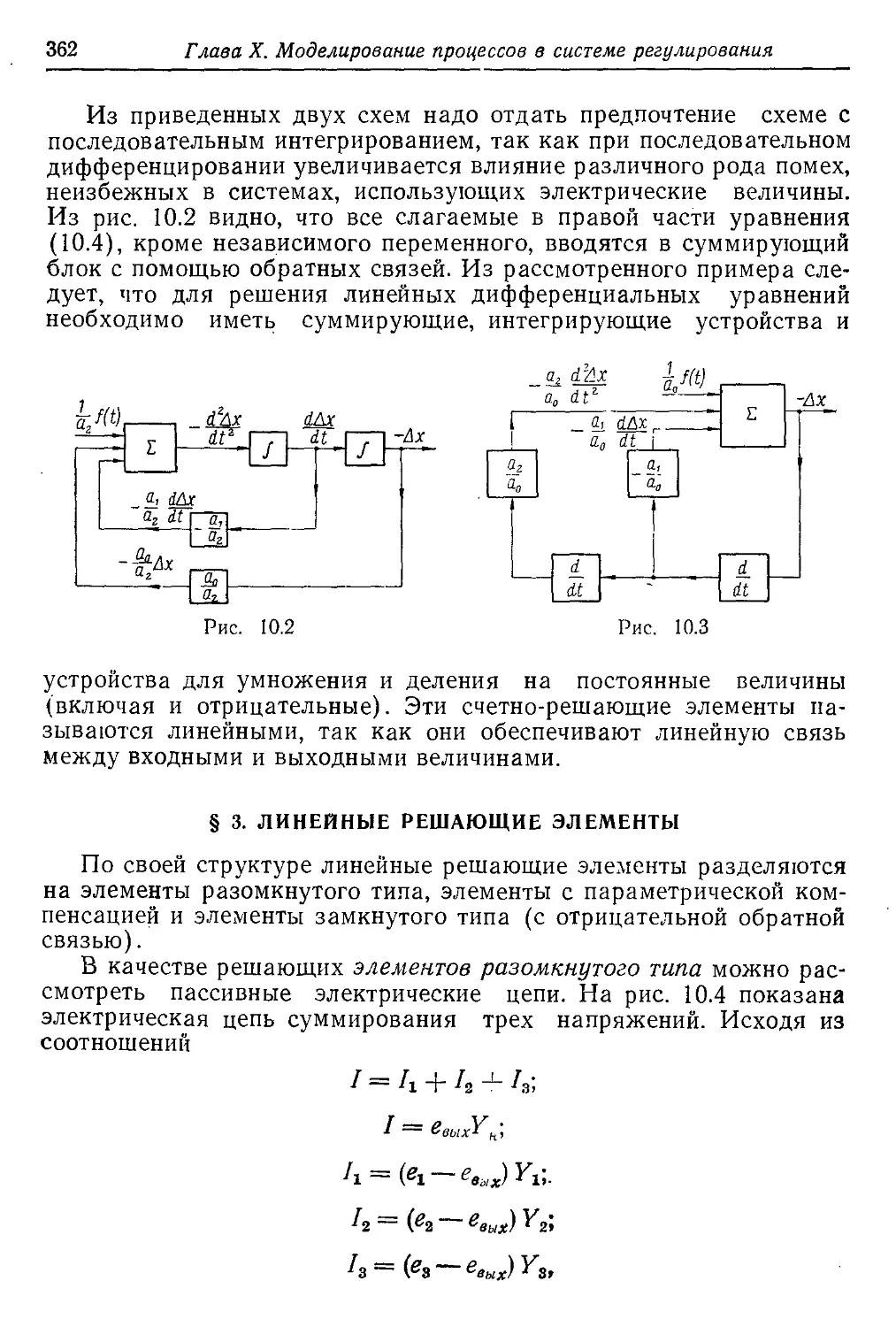
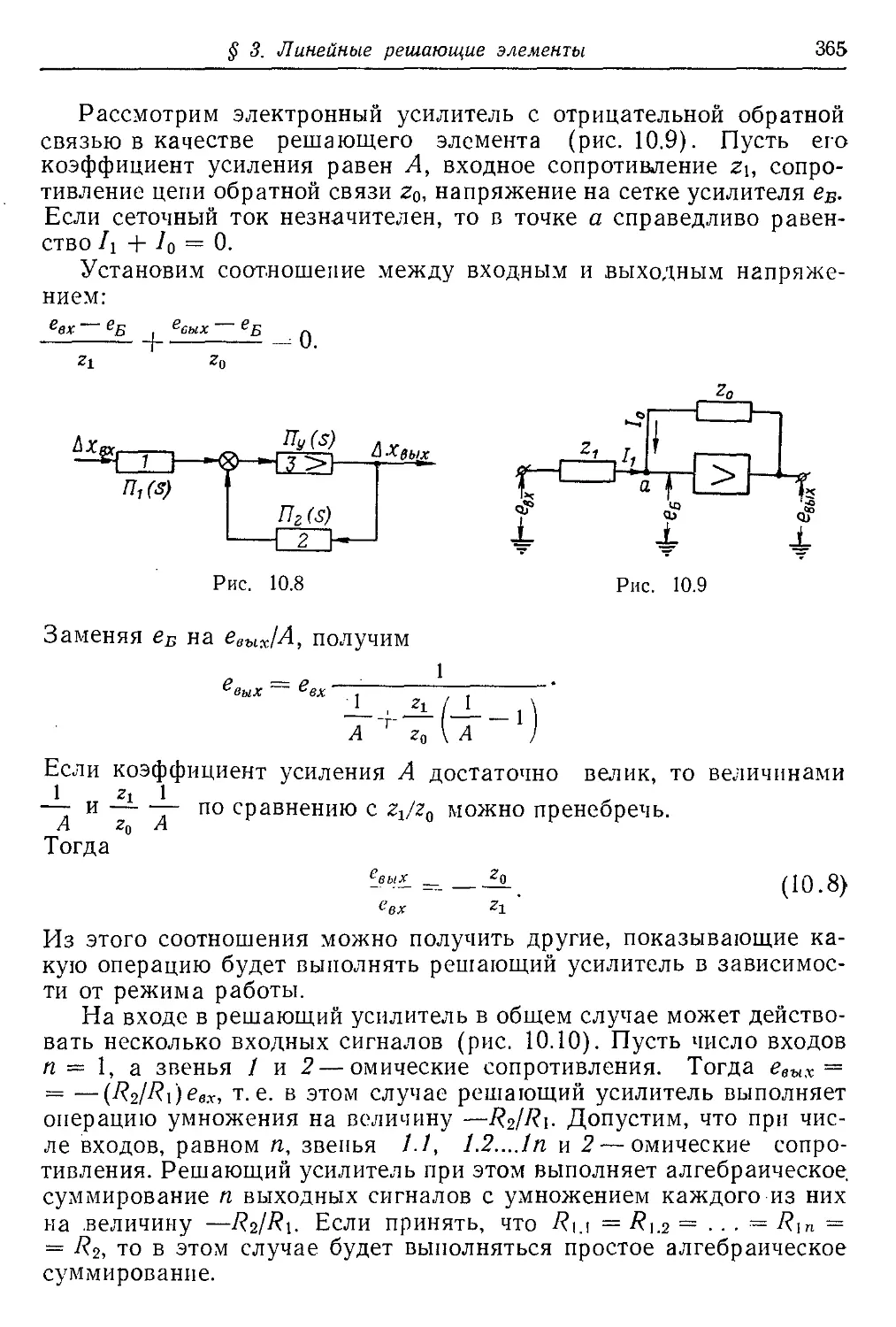
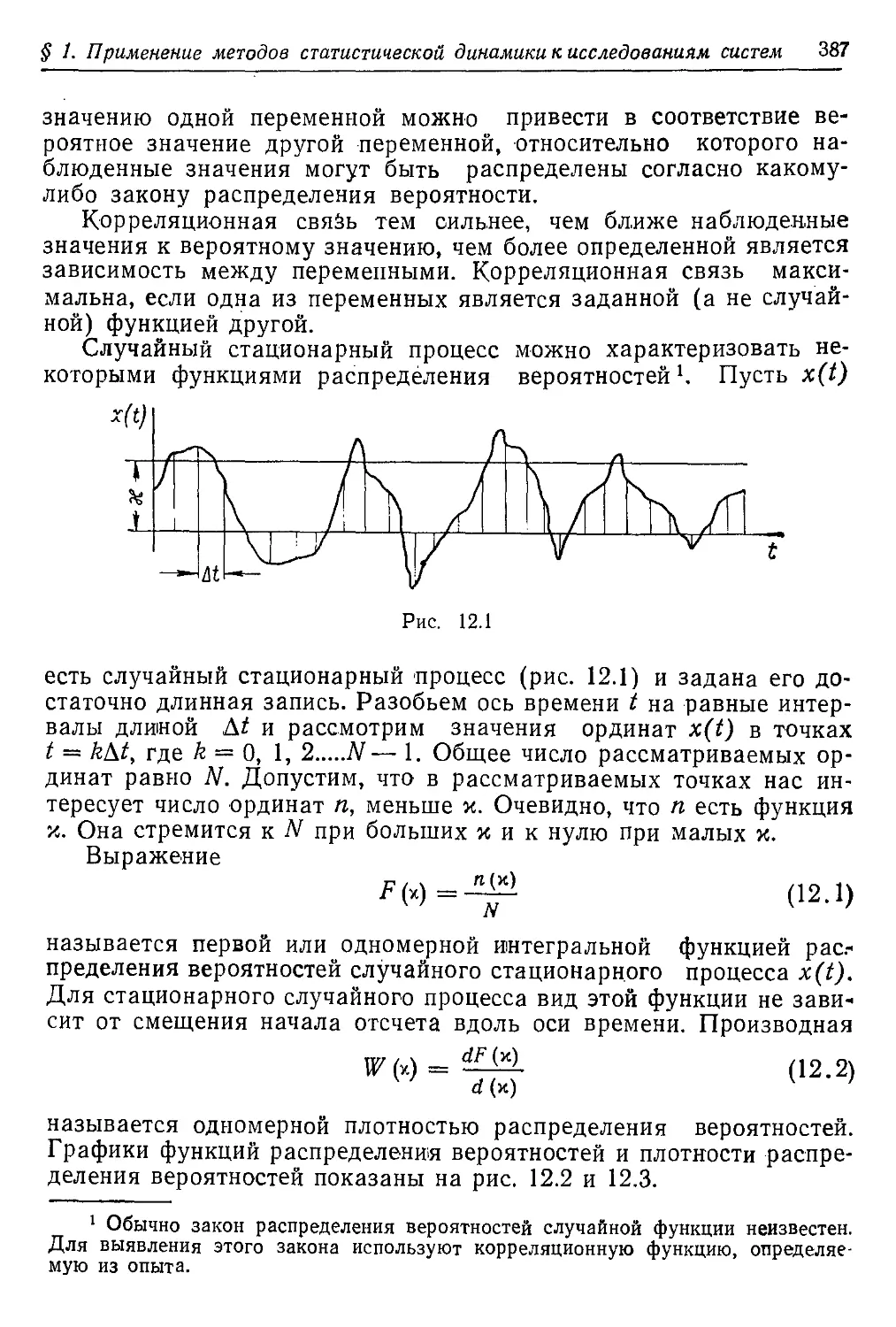
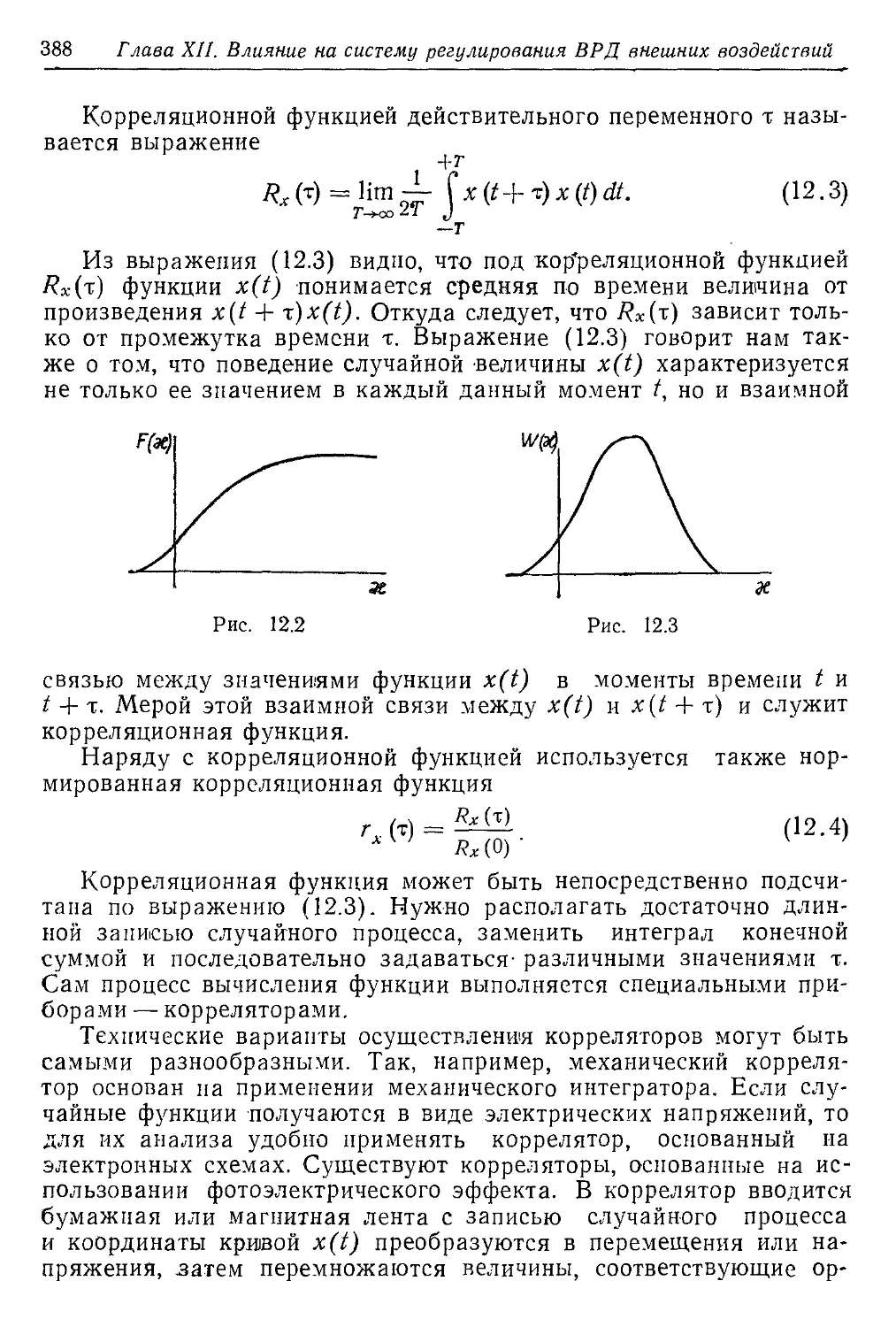
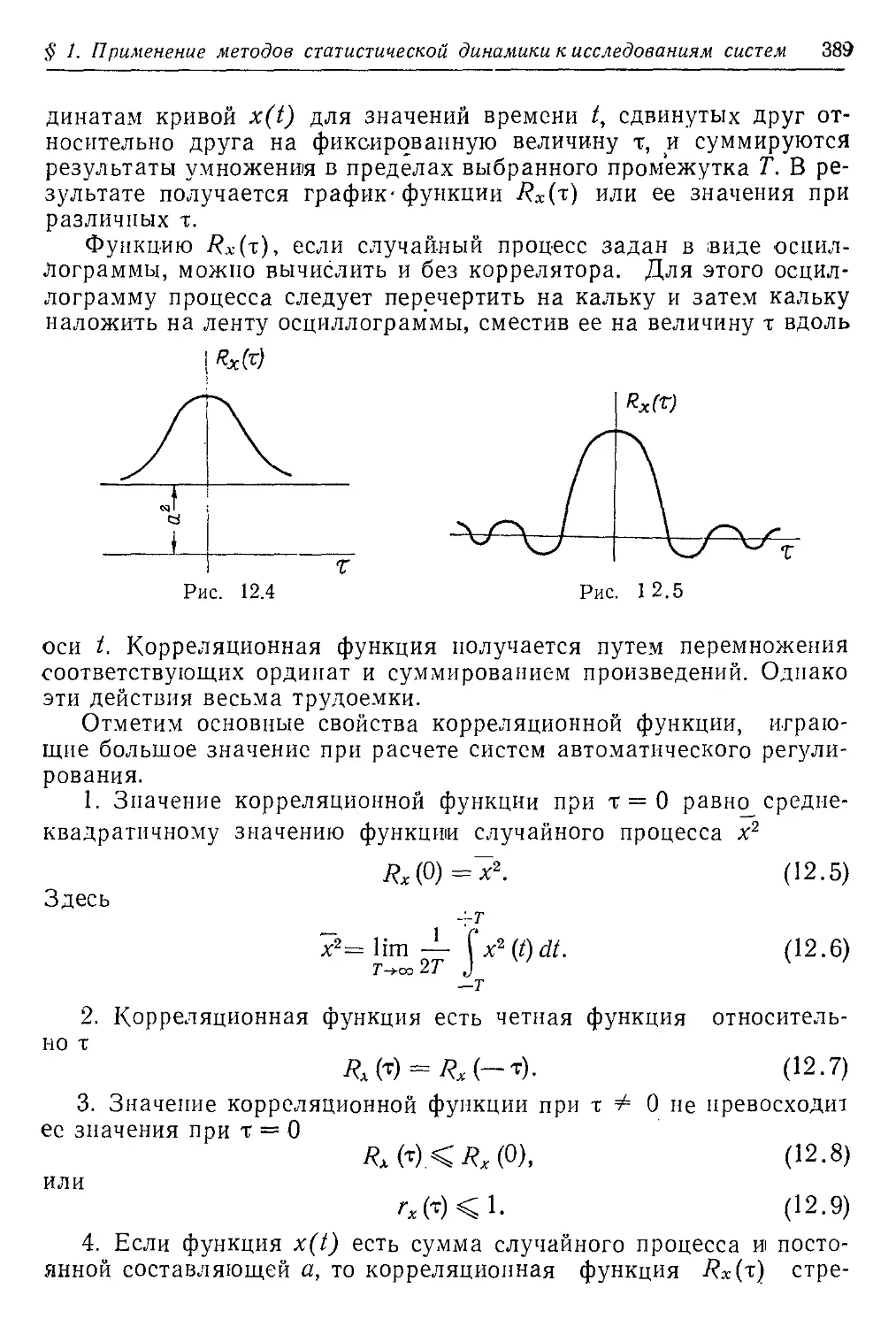
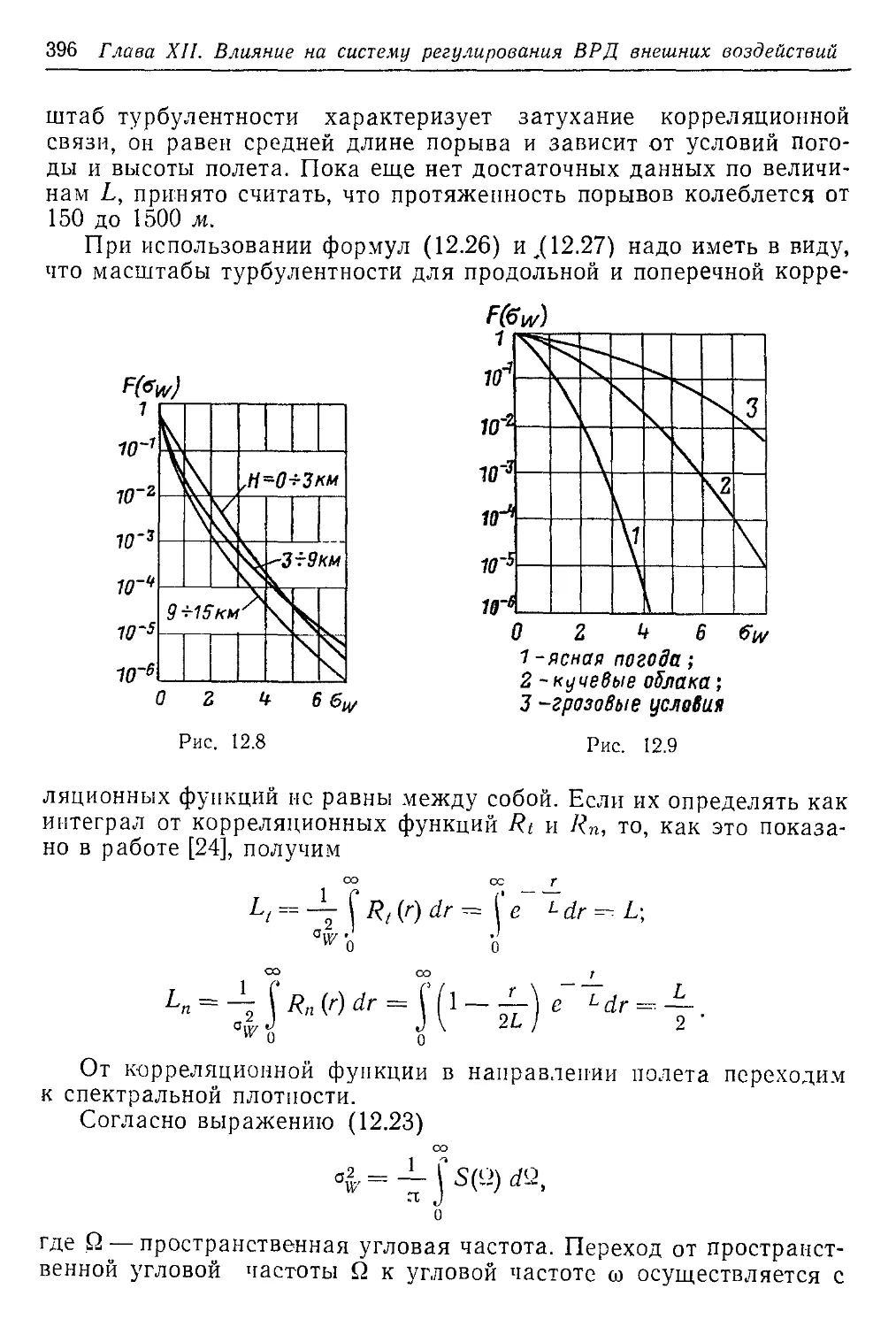
Текст

Автоматика
и регулирование
воздушно-
реактивных
двигателей
Б. А. ЧЕРКАСОВ
АВТОМАТИКА
И РЕГУЛИРОВАНИЕ
ВОЗДУШНО-РЕАКТИВНЫХ
ДВИГАТЕЛЕЙ
Допущено
Министерством высшего и среднего
специального образования РСФСР
в качестве учебника
для авиационных вузов и факультетов
ИЗДАТЕЛЬСТВО
«МАШИНОСТРОЕНИЕ»
Москва 1965
УДК 629.13 : 621.454.001.1
В книге излагаются принципы регулирования авиационных
газотурбинных и прямоточных воздушно-реактивных двигате-
лей. Главное внимание уделяется тем особенностям рабочего
процесса различных типов ВРД н их элементов, которые
существенно влияют па работу всей системы регулирования.
Рассматриваются методы аналитического и эксперименталь-
ного исследования систем регулирования и расчета регули-
рующей аппаратуры. Дается общее представление о регули-
ровании ядерных ВРД, о принципах экстремального регули-
рования авиационной силовой установки и о применении ста-
тистических методов расчета, позволяющих учитывать влияние
случайных воздействий на системы управления.
Книга является учебником для студентов авиационных
втузов, по курсу «Автоматика и регулирование воздушно-реак-
тивных двигателей». Она может быть полезной инженерам и
научным сотрудникам, работающим в области автоматическо-
го регулирования авиационных двигателей.
Рецензенты чл.-корр. АН СССР А. М. Люлька и кафедра «Теории двигате-
лей» летательных аппаратов Казанского авиационного института
Редактор капд. техн, наук А. Н. Добрынин
ПРЕДИСЛОВИЕ
В связи с непрерывным ростом скоростей и высот полета все
более и более усложняются задачи регулирования авиационных
двигателей.
В предлагаемой книге автор стремился отразить современный
уровень знаний по вопросам теории и практики автоматического
регулирования авиационных двигателей. В ней приведены необхо-
димые для практической работы сведения из теории автоматичес-
кого регулирования. Для чтения книги требуется предварительная
подготовка в области теории лопаточных машин, воздушно-реактив-
ных двигателей и ядерной энергетики.
В книге разобраны особенности рабочего процесса различных
типов ВРД и их элементов, которые существенно влияют на работу
всей системы регулирования. Подробно рассмотрены свойства раз-
личных ВРД как объектов регулирования.
Поскольку основным регулирующим фактором в системе регу-
лирования авиационного двигателя является изменение расхода
топлива, существует тесная связь, в работе устройств системы ре-
гулирования и топливной системы. Во многих случаях выбор си-
стемы регулирования двигателя предопределяется условиями рабо-
ты топливой системы и наоборот. Поэтому в книге уделено внима-
ние характеристикам отдельных элементов топливных систем.
Гл. IX книги посвящена вопросам регулирования ядерных авиа-
ционных двигателей и главным образом ядерному реактору как
объекту регулирования.
При анализе динамики регулирования ВРД весьма широко ис-
пользуются методы физического и математического моделирования.
Эффективность этих методов проявляется особенно сильно при изу-
чении нелинейных систем. Поэтому в книге излагаются основные
принципы моделирования процессов автоматического регулиро-
вания.
Если раньше системы автоматического регулирования ВРД в
основном лишь поддерживали заданный режим, то сейчас становят-
ся реальностью системы автоматического управления, осуществляю-
щие поиск наивыгоднейшего режима, в частности, системы экстре-
мального регулирования. Разработка подобных систем регулирова-
ния относится к одному из новых разделов теории автоматического
управления, базирующейся на аппарате математической логики.
4
Предисловие
В книге дается общее представление о принципах построения
самонастраивающихся систем автоматического управления. Фор-
мулируется задача экстремального регулирования авиационного
двигателя.
Сейчас во всех областях автоматики широко применяются ста-
тистические методы расчета, которые позволяют учитывать не толь-
ко строгр заданные, но и разного рода случайные воздействия на
системы управления. В книге излагается методика обработки ха-
рактеристик случайных воздействий, получаемых опытным путем,
и представления их в такой форме, при которой они могут исполь-
зоваться для расчета регулирующей аппаратуры ВРД.
Автор весьма признателен рецензентам чл.-корр. АН СССР
А. М. Люльке и коллективу кафедры «Теории двигателей летатель-
ных аппаратов» КАИ за их труд. Автор приносит глубокую благо-
дарность проф. А. В. Штоде, просмотревшему рукопись всей книги,
д-ру техн, наук Б. С. Воронкову, д-ру техн, наук Ю. Н. Нечаеву и
канд. техн, наук И. И. Хайдукову, которые читали ее отдельные
главы. Они сделали ряд ценных замечаний, учтенных при оконча-
тельном редактировании книги.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
п— число оборотов; плотность потока нейтронов.
Т — абсолютная температура потока в различных сечениях газовоздушного
тракта двигателя; постоянная времени.
л — степень повышения или понижения, давления.
а — коэффициент избытка воздуха; температурный коэффициент реактивности;
угол выхода потока из соплового аппарата.
G — расход топлива; расход воздуха.
р — давление потока в различных сечениях газовоздушного тракта двигателя;
оператор дифференцирования.
о — коэффициент восстановления полного давления.
X — относительная скорость потока; переменная и корни в характеристичес-
ком уравнении.
q(X) — газодинамическая функция.
m— постоянный коэффициент в уравнении расхода; масса; координата регу-
лирующего органа; коэффициент пропорциональности.
k — коэффициент усиления; показатель адиабаты; коэффициент запаса устой-
чивости.
g — ускорение силы тяжести.
R — тяга двигателя; газовая постоянная.
v — показатель политропы; коэффициент, характеризующий устойчивость
двигателя.
т] — коэффициент полезного действия.
М — число Маха потока.
М — крутящий момент.
с — скорость потока; коэффициент пропорциональности.
а — скорость звука.
7 — удельный вес.
Н — высота полета; работа сжатия или расширения.
8 — абсолютное приращение.
Д — относительное приращение.
6
Основные обозначения
и — окружная скорость.
N — мощность.
v — скорость полета.
<р — угол установки лопастей винта; функциональная зависимость.
у — коэффициент распределения расхода воздуха между контурами ТРДД.
г — коэффициент распределения эффективной работы между контурами
ТРДД.
f — функциональная зависимость.
9 — угол; относительная температура.
Р — сила.
F — функциональная зависимость; площадь.
J — момент инерции.
и — угловая скорость; угловая частота.
t — время.
т — постоянная времени; время.
р — плотность; величина, обратная коэффициенту усиления.
s— координата; переменная в преобразовании Лапласа; переменная в пере-
даточной функции.
i — передаточное число редуктора.
Т-о — количество воздуха, необходимое для сгорания 1 кг топлива.
ср — теплоемкость при постоянном давлении.
е — основание натуральных логарифмов.
Ни — низшая теплотворная способность топлива.
|х — коэффициент расхода; переменная.
Q—• объемный расход; тепловая энергия.
х — координата.
А — амплитуда колебаний.
С —• емкость конденсатора; постоянная интегрирования.
U — напряжение в цепи.
II — передаточная функция.
Индексы
Верхние индексы
* — параметры заторможенного потока.
' — параметры внешней среды и двигателя, выделенные из текущих парамет-
ров; параметры первого контура ТРДД.
" — параметры, второго контура ТРДД.
Основные обозначения
7
Нижние индексы
Н — в невозмущенном -потоке перед двигателем,
/, 2, 3, 4 и 5 — характерные сечения воздушного и газового тракта ТРД: пе-
ред компрессором, за компрессором, перед турбиной, за тур-
биной, на срезе выходного сопла.
к — компрессор.
т — турбина.
кр — критическое сеченне соплового аппарата турбины или выход-
ного сопла; критический перепад; крутящий момент.
пр — приведенное значение параметра.
в — воздух; высоконапориый каскад ротора компрессора; винт
воздушный.
ф — форсажный; форсунка.
с.а — сечение соплового аппарата турбины.
р — расчетное значение.
г — газ; горло.
к.с — камера сгорания.
а — осевая составляющая скорости.
г — последняя ступень компрессора.
ст — ступень.
потр — потребный.
расп — располагаемый.
помп — помпажный режим.
у — устойчивость.
S — суммарное значение.
н — низконапорный каскад ротора компрессора; насос.
т.к — турбина компрессора.
т.в — турбина винта.
п — передний винт.
з — задний винт.
е — эффективный.
с — сопло; сервомотор.
же — эквивалентный.
О — заданный режим; установившийся режим; исходный статичес-
кий режим;
ц — центробежный.
д — двигатель.
дн — двигатель с насосом.
8 Основные обозначения
Б — базисный.
диф — диффузор; дифференцирующее звено.
ср — среднее.
ск — скачок.
опт — оптимальный.
топ — топливо.
кав — кавитация.
зол — золотник.
пор — поршень.
раб — рабочая жидкость
сл — слив.
к ат — катаракт.
вх — вход.
вЫХ—'ВЫХОД.
Глава 1
АВИАЦИОННЫЕ ГАЗОТУРБИННЫЕ ДВИГАТЕЛИ.
ОСОБЕННОСТИ РАБОЧЕГО ПРОЦЕССА
И ВОЗМОЖНЫЕ ПРОГРАММЫ РЕГУЛИРОВАНИЯ
§ 1. ОДНОКАСКАДНЫЕ ТУРБОРЕАКТИВНЫЕ ДВИГАТЕЛИ
Регулируемые параметры и регулирующие факторы
Задача регулирования двигателей заключается в реализации
присущих им статических характеристик, к которым в первую оче-
редь относятся зависимости тяги и удельного расхода топлива от
числа оборотов, скорости и высоты полета. Без автоматического ре-
гулирования не может быть эффективного использования современ-
ного ГТД. Автоматическое регулирование осуществляется по опре-
деленной программе, в значительной степени обусловленной аэро
динамическими свойствами летательного аппарата.
Программой или законом регулирования называется зависи-
мость изменения регулируемых параметров от условий полета. Как
правило, программа регулирования на максимальном режиме пре-
дусматривает наиболее полное использование двигателей по тем-
пературе газа перед турбиной и числу оборотов ротора при одно-
временном обеспечении надежной работы по условиям тепловой и
динамической напряженности деталей.
Основным типом’ двигателя в современной авиации является
однокаскадный турбореактивный двигатель (ТРД), обычно форси-
рованный по тяге за счет ввода дополнительного топлива в газо-
вый тракт за турбиной (ТРДФ). Схема однокаскадного ТРДФ с
обозначением характерных сечений (/, 2, 3, 4, 5) воздушно-газово-
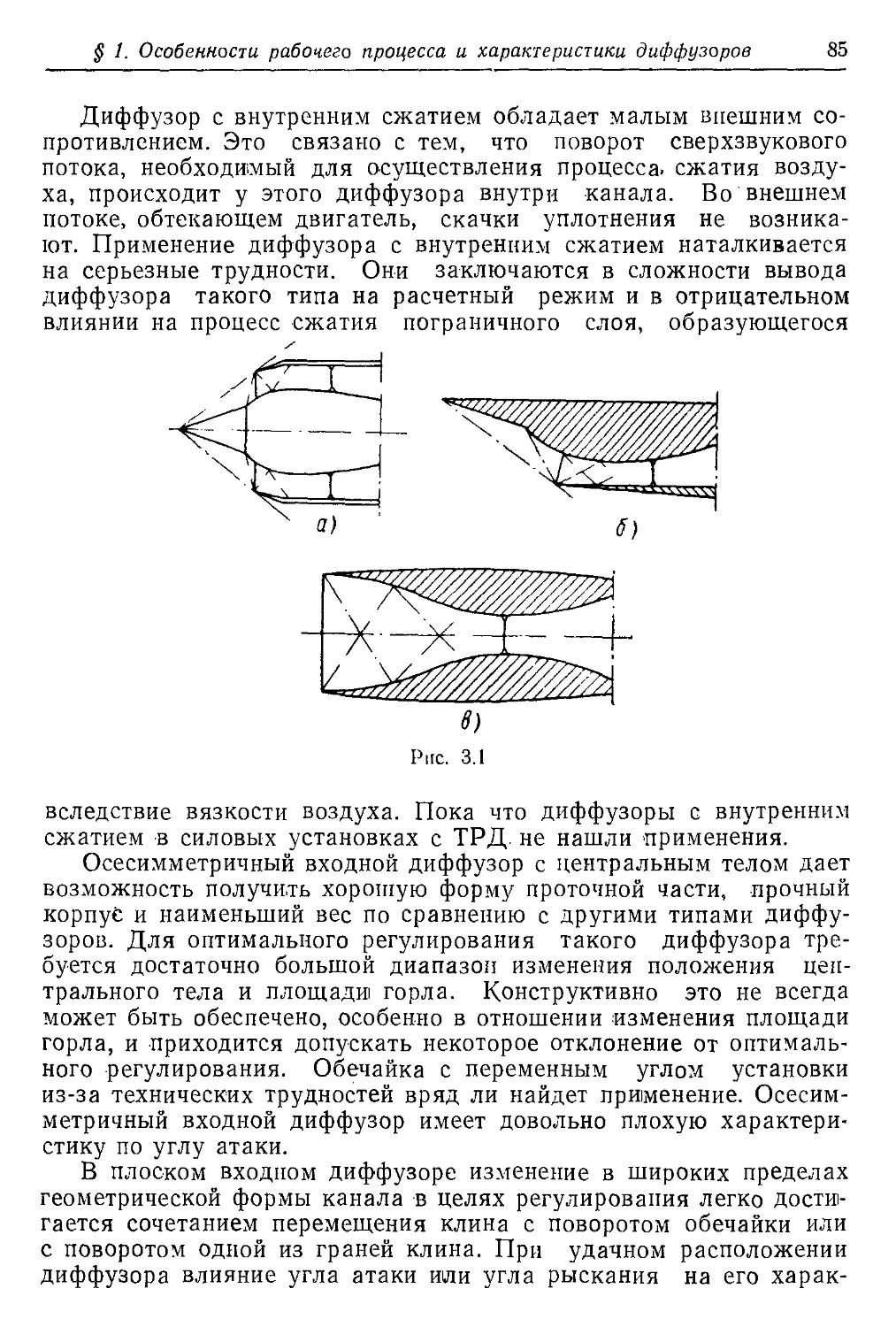
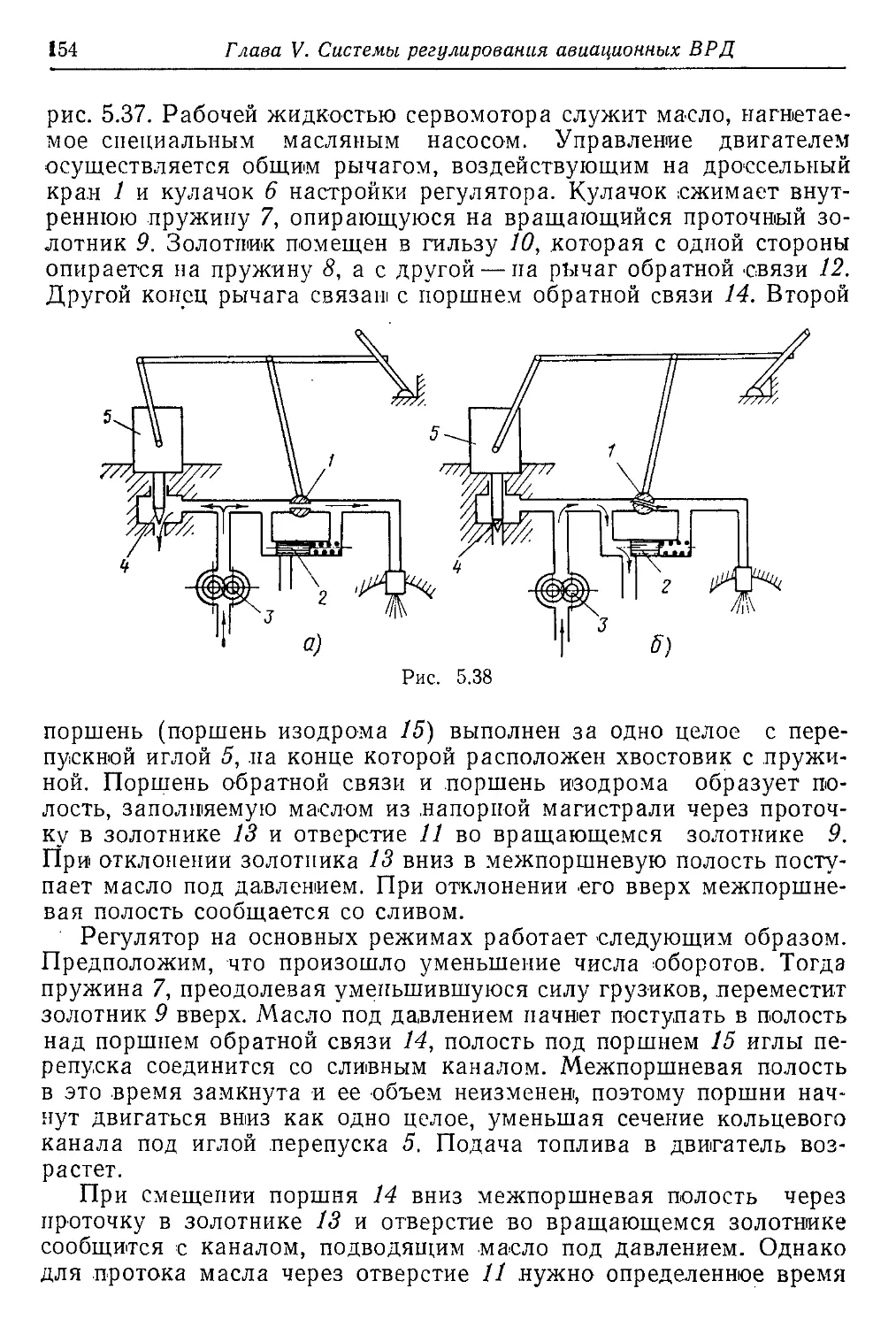
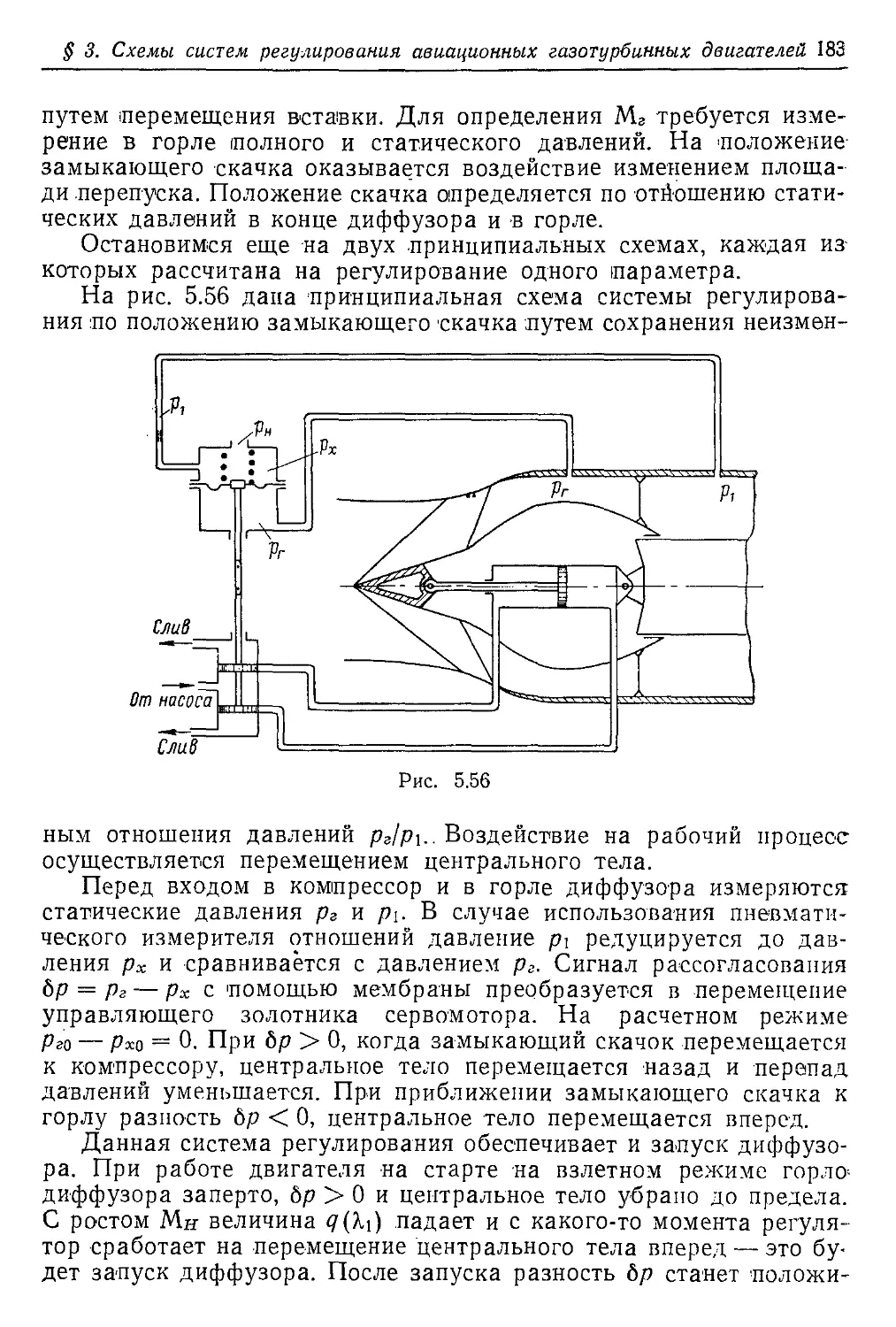
го тракта показана на рис. 1.1.
Для ТРД наиболее важными параметрами рабочего процесса,
определяющими его характеристики, являются степень повышения
давления компрессора л* и температура газа перед турбиной Т*3
От них зависят удельная тяга и удельный расход топлива двига-
теля.
Для ТРДФ появляется третий определяющий параметр — темпе-
ратура газа в форсажной камере Т*5, или суммарный коэффициент
избытка воздуха as .
10 Глава 1. Авиационные ГТД. Рабочие процессы и программы регулирования
Обычно основные параметры рабочего процесса являются регу-
лируемыми параметрами. Воздействуя на основные параметры, сох-
раняя их постоянными или меняя по определенному, заранее выб-
ранному закону, получают нужные статические характеристики
двигателя. Однако для газотурбинных двигателей принимать сте-
пень повышения давления за регулируемый параметр не всегда
удобно. Это связано с тем, что с изменением высоты и скорости по-
лета л* существенно меняется. Вместо л* за один из регулируе-
мых параметров принимают истинное число оборотов ротора дви-
гателя п. Число оборотов ротора двигателя при данных условиях
Н 12 3 4 5
Рис. 1.1
полета определяет не только тягу и удельный расход топлива, но
и допустимость того или иного режима по условиям прочности де-
талей двигателя. В некоторых случаях регулируемым параметром
/ 288 т.
~v~, где г ^емпера-
тура заторможенного потока воздуха перед компрессором. В даль-
нейшем для упрощения записей за приведенное число оборотов
примем пропорциональную ему величину п] /Л .При неизменных
геометрических размерах двигателя и надкритическом перепаде в
выходном сопле регулирование по ппр равносильно регулированию
по л’.
Значение регулируемых параметров контролируется с помощью
регулирующих факторов. Для ТРД и ТРДФ к ним относятся изме-
нение расхода основного и форсажного топлива, изменение некото-
рых геометрических размеров двигателя (площади критического се-
чения выходного сопла, углов установки сопловых лопаток турбины,
направляющих лопаток компрессора и др.). На каждый регулируе-
мый параметр нужен свой регулирующий фактор и соответственно
свой регулятор.
Если регулирующих факторов меньше, чем основных парамет-
ров рабочего процесса, то пе все они могут быть приняты за регу-
лируемые параметры. Так, например, для ТРД с изменяемой пло-
щадью сечения выходного сопла регулируемыми параметрами мо-
гут быть число оборотов ротора двигателя п и температура газа
§ 1. Однокаскадные турбореактивные двигатели
11
Т* а,регулирующими факторами — изменение расхода топлива и
площади сечения выходного сопла. Для ТРДФ с двухпозиционным
нерегулируемым выходным соплом на три параметра рабочего про-
цесса приходятся только два регулирующих фактора: расход ос-
новного и форсажного топлива. Поэтому один из параметров ра-
бочего процесса, допустим, температура газа Т* , не регулируется.
В том случае, когда регулирующих факторов меньше, чем ос-
новных параметров рабочего процесса, может быть введено огра-
ничительное регулирование. Если в упомянутом выше ТРДФ с двух-
позиционным нерегулируемым выходным соплом будет чрезмерно
расти температура газа перед турбиной, изменение расхода основ-
ного топлива может быть использовано для поддержания макси-
мально допустимого значения температуры Т3. С момента исполь-
зования изменения расхода топлива для ограничительного регули-
рования температуры газа число 'оборотов ротора двигателя уже
перестанет быть регулируемым параметром.
Влияние регулирующих факторрв на регулируемые параметры
осуществляется через соответствующие регуляторы. Так, например,
для двух регулируемых параметров п и Т3 необходимы два регу-
лятора, которые взаимодействуют между собой. Рассмотрим упро-
щенную картину работы этих регуляторов, приняв, что они дей-
ствуют последовательно один за другим.
При увеличении но какой-либо причине числа оборотов ротора
двигателя по сравнению с заданным значением регулятор числа
оборотов уменьшит подачу топлива, число оборотов снизится, но
вместе с этим упадет и температура газа Т *. Тогда вступит в дей-
ствие регулятор температуры. Он уменьшит площадь сечения вы-
ходного сопла, перепад на турбине л* упадет, что приведет к даль-
нейшему снижению (ниже заданного значения) числа оборотов ро-
тора. Поэтому опять вступит в действие регулятор п, который
теперь увеличит подачу топлива и приведет число оборотов ротора
к заданному значению при расчетной величине температуры газа.
В действительности работа упомянутых двух регуляторов будет
проходить не последовательно, а одновременно, что отразится на ра-
боте регуляторов и па переходном процессе в системе регулиро-
вания.
Возможные программы регулирования основных режимов
Рассмотрим возможные программы регулирования основных ре-
жимов, под которыми будем понимать максимальные режимы ТРД
или максимальные нефорсажные режимы ТРДФ.
За один из регулируемых параметров примем п или л/]/"Т\ , за
другой, если у двигателя регулируемое сечение выходного сопла.—
12 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
температуру газа Т^. Принято на величину п или Т\ воздейст-
вовать изменением расхода топлива (G—>-n; G-^-n/j/V,), а на ве-
личину температуры газа Т* — изменением площади сечения вы-
ходного сопла Тогда можно наметить четыре основные
программы регулирования1:
1. п = const, Тз = const;
2. п — const;
3. —-— = const, Т\ = const;
Л
4. —— = const.
Vt\
При использовании первой и второй программ регулирования
работа двигателя в условиях различных высот и скоростей полета
приводит к изменению величины п/ . Использование второй и
четвертой программ, для которых FKp = const, связано с изменени-
ем Тд и необходимо производить численную оценку изменения тем-
пературы.
С увеличением скорости полета приведенное число оборотов ро-
тора двигателя п/]/~Т^падает (программы регулирования первая и
вторая) и режим работы компрессора изменяется. Падение приве-
денного числа оборотов сопровождается уменьшением л* и приве-
денного расхода воздуха Gg.rep, изменяется и к. п. д. компрессора.
Значительное снижение n/j/V*обычно приводит к возникновению
неустойчивой работы компрессора и к помпажу двигателя2. Пом-
паж может также возникнуть и при n/jZ(п/j/ Т* )р. Для того,
чтобы заранее знать, будет ли двигатель устойчиво работать во всем
диапазоне изменения высот и скоростей полета, на характеристику
компрессора нужно нанести линию совместных режимов турбины
и компрессора.
• Кроме основных программ, возможны комбинированные программы регу-
лирования. Они рассмотрены ниже.
2 В данном случае под неустойчивой работой компрессора или двигателя в
целом понимается такой режим работы, когда вследствие интенсивного срыва
потока с лопаток компрессора в отдельных ступенях возникают пульсации
потока, предшествующие помпажу. В дальнейшем понятие устойчивости движе-
ния будет дано более строго.
§ 1. Однокаскадные турбореактивные двигатели
13
Построение линий совместных режимов
Для построения линий совместных режимов используют урав-
нения расхода газа и работы турбины и компрессора. Напишем
уравнение расхода, для двух сечений двигателя: для сечения.на вхо-
де в компрессор Fr и для критического сечения соплового аппарата
турбины (Fc.a)Kp- Изменением расхода за счет отбора части возду-
ха на охлаждение и за счет ввода топлива пренебрегаем. Тогда
-7= q (хх) ргтв = q (kcJ (Рс.а)крсС'Отг.
т/ Т* л/ Т*
У 1 1 Г 2 3
Здесь
1 1
q GO = (k ~ 1 — 7+~1 ,'2) k‘~ 1 — газодинамическая функция;
ос.а—коэффициент восстановления полного давления в сопло-
вом аппарате турбины.
Для основных режимов работы двигателя q(kc.a)~ 1.
Применим составленное уравнение расхода к программе регули-
рования п = const и Т*3 = const. После преобразования получим
? (Х1) П _ П с-а}кртг°К'С°с-а (1
< Vt*i Fxmey Т3
где еГк.с—коэффициент восстановления полного давления в каме-
Л + 1 /----
( 2 \2(k— 1) , / kg
ре сгорания, пг = ------ ' 1/ — ; для воздуха
\fe + 1/ |/ R
шв = 0,396; для Таза можно принять пгг — 0,388.
Коэффициенты сгк. с и сгс.а, входящие в правую часть выражения
(1.1), с переходом от одного режима работы двигателя к другому
изменяются незначительно. Остальные величины правой части не-
изменны, поэтому-можно записать
-^-nDp = const1. (1.2)
Уравнение (1.2) решается подбором. Величину его правой части
находят по значениям параметров расчетного режима двигателя.
Для заданных высоты, скорости полета и числа оборотов ротора оп-
ределяют ппр. После этого на найденной кривой ппр = const харак-
теристики компрессора выбирают несколько точек; для каждой из
них по известным значениям л* и <?(%i) определяют величину ле-
вой части уравнения (1.2), сравнивают ее с величиной правой части
и решают, какая из выбранных точек удовлетворяет условию (1.2).
Совокупность найденных точек для различных ппр дает линию сов-
местных режимов.
14 Г лава /. Авиационные ГТД. Рабочие процессы и программы регулирования
Для осуществления программы регулирования п = const. Т3 =
= const требуется изменять площадь критического сечения выход-
ного сопла. Необходимое изменение FKP можно определить, исполь-
зуя уравнение расхода, составленное для критических сечений соп-
лового аппарата (Fc.n)KJ> турбины и выходного сопла FKP:
OQ'c-a) {^с.а)кр ^г^с.а Я Q'Kp) кр^г^кр
и уравнение политропы
V
* / \ V— 1
Р.З _ I 'з \
* I 'Г* I
Ра \ Та )
Примем, что для основных режимов работы двигателя q{kKp) ~
~ 1. Исключив из уравнения расхода с помощью уравнения поли-
тропы отношение температур Tg/T*, после преобразования по-
лучим
•у-— 1
р — (F 1 -• 2» (1-3)
1 кр V с.а)кр 'т
акр
В этом уравнении
п*т — степень расширения газа в турбине;.
v — показатель политропы расширения в турбине, который
можно Припять равным 1,3;
crKJJ — коэффициент восстановления полного давления в дозву-
ковой части выходного сопла.
Степень расширения газа определяется из условия равенст-
ва работы турбины и компрессора
А-1
л — 1 \ / 1 ' '
При решении этого уравнения можно пренебречь изменением
к. п. д. турбины и для разных режимов работы двигателя принять
его постоянным.
При использовании программы регулирования п = const для
построения линии совместных режимов иа характеристике компрес-
сора также составляется уравнение расхода, которое приводится к
виду:
i^l/ —= const,. (1.4)
* » т*
1
§ 1. Однокаскадные турбореактивные двигатели
15
Из уравнения (1.4) нужно исключить температуру Т*3 . Для это-
го вернемся к уравнению (1.3). Из него следует, что при неизмен-
ной площади и надкритическом перепаде и выходном сопле степень
расширения газа в турбине л* остается постоянной, не зависящей
от изменения условий полета. Постоянство л* дает возможность
упростить уравнение работы и привести его к виду
й-1
Г*3 < k -1
—~ ~ 2-------;----const3. (1,5)
Г1 Чк
Уравнение (1.5) является расчетным для определения темпера-
туры газа Т*ъ. Оно показывает, что изменение температуры газа
перед турбиной пропорционально изменению полной работы сжа-
тия воздуха в компрессоре (при'Т]“ = const).
Окончательное выражение для построения линии совместных ре-
жимов при использовании программы регулирования п = const по-
лучается в следующем виде:
/ \
k -1
----------------------= const,.
* * О 4
^КПК
(1-6)
Это уравнение, подобно уравнению (1.2), также решается под-
бором точек на характеристике компрессора.
Сравнение различных программ регулирования
Рассмотрим особенности намеченных нами первой (п = const,
Уз = const) и второй (п = const) программ регулирования ТРД.
При использовании первой программы, когда Т* = const, дви-
гатель более полно используется по температуре, так как во всем
диапазоне рабочих режимов температура газа будет иметь макси-
мальное значение. При применении второй программы регулиро-
вания величина температуры газа зависит от изменения полной
работы сжатия воздуха Н*. В свою очередь для заданной харак-
теристики компрессора величина Н"к определяется расположением
линии совместных режимов. При использовании первой программы
регулирования полная работа сжатия тоже зависит от расположе-
ния линии совместных режимов, но температура Т*3 остается по-
стоянной, так как изменение Н* компенсируется изменением сте-
пени расширения газа л* .
Расположение линий совместных режимов на характеристике
компрессора, кроме особенностей программы регулирования, в зна-
16 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
чительной степени обусловлено расчетным значением л*. Величи-
на л* влияет так же на крутизну границы устойчивой работы ком-
прессора: с ростом л* крутизна несколько увеличивается.
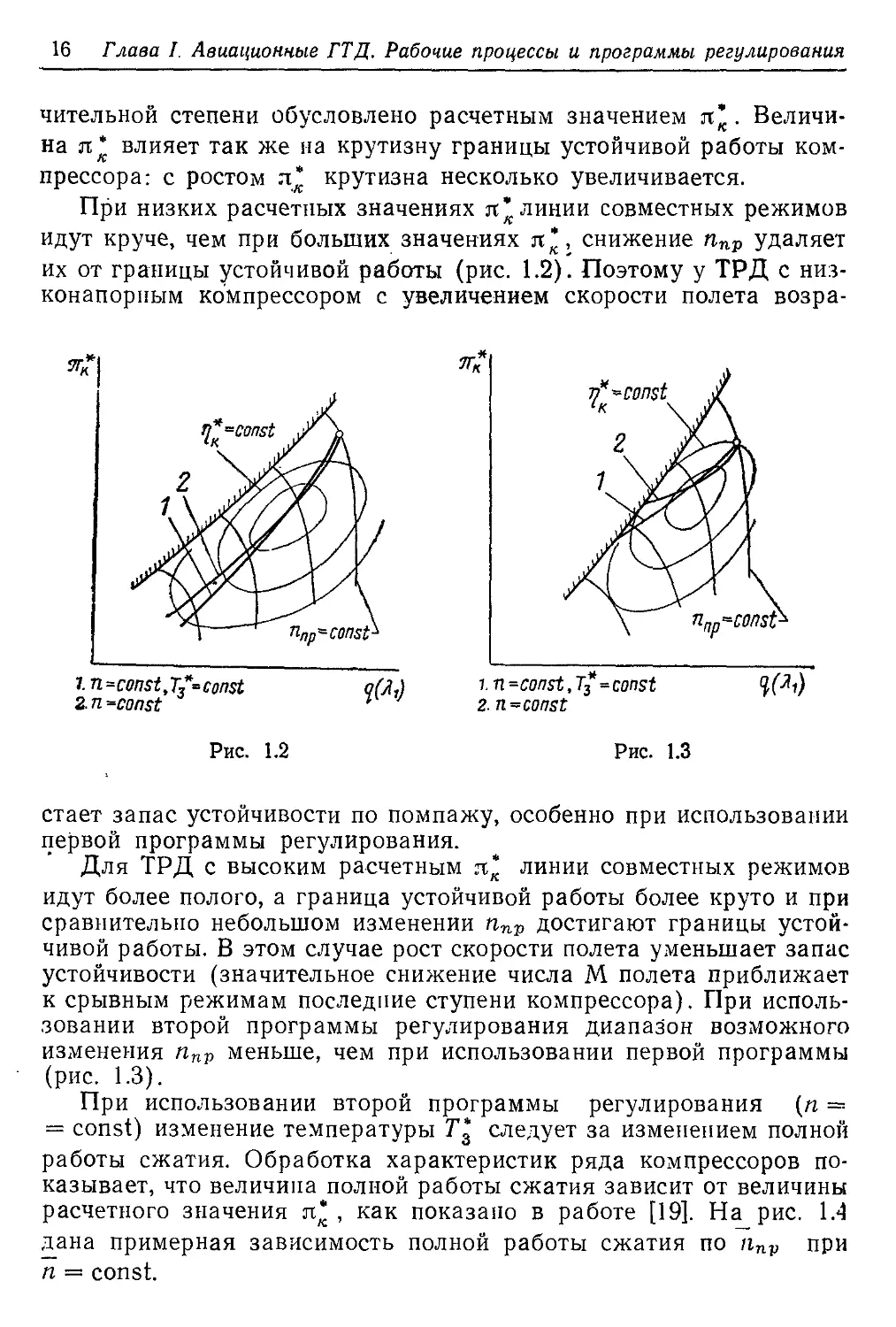
При низких расчетных значениях л* линии совместных режимов
идут круче, чем при больших значениях л*, снижение ппр удаляет
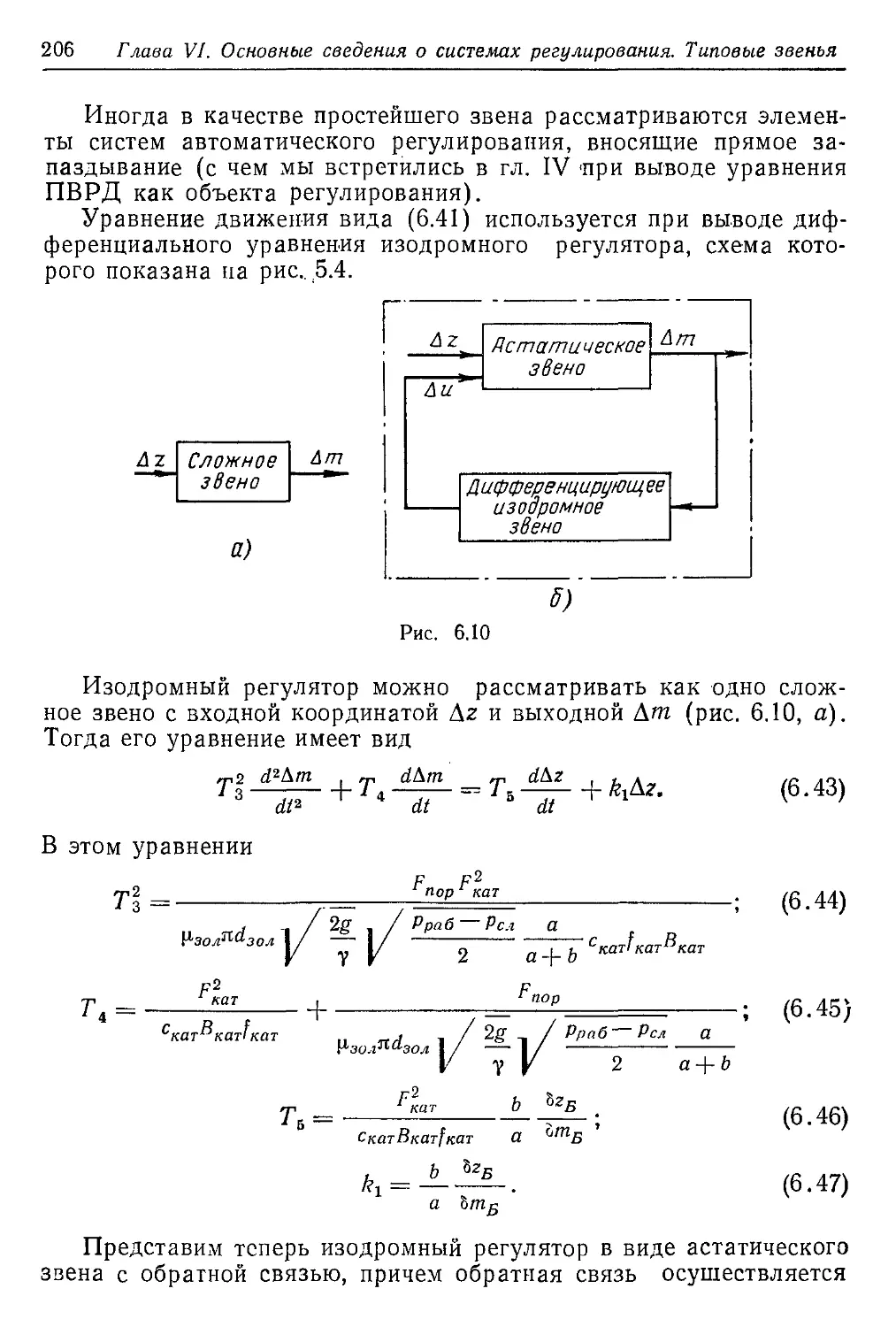
их от границы устойчивой работы (рис. 1.2). Поэтому у ТРД с низ-
конапорным компрессором с увеличением скорости полета возра-
Рис. 1.3
стает запас устойчивости по помпажу, особенно при использовании
первой программы регулирования.
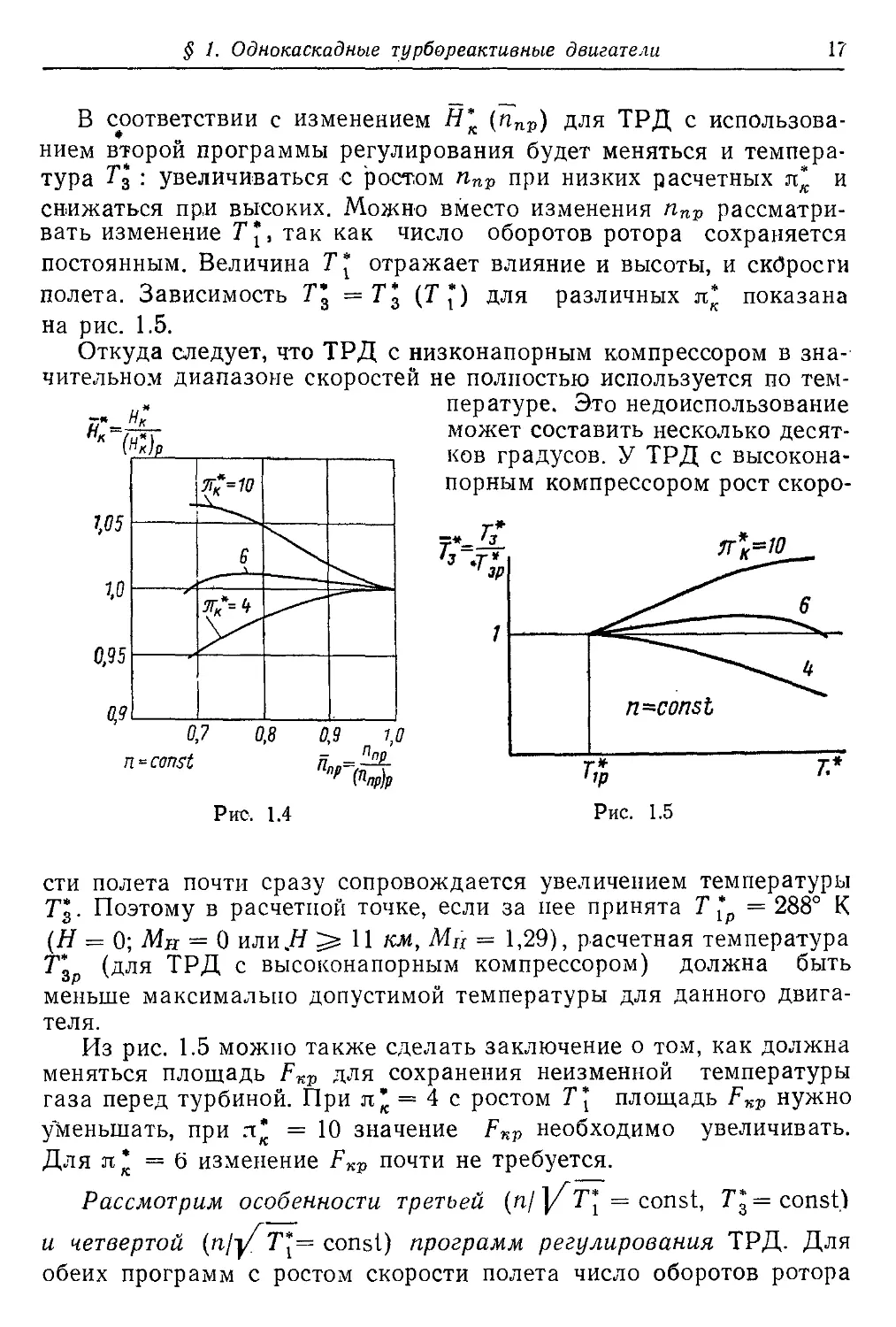
Для ТРД с высоким расчетным л* линии совместных режимов
идут более полого, а граница устойчивой работы более круто и при
сравнительно небольшом изменении ппр достигают границы устой-
чивой работы. В этом случае рост скорости полета уменьшает запас
устойчивости (значительное снижение числа М полета приближает
к срывным режимам последние ступени компрессора). При исполь-
зовании второй программы регулирования диапазон возможного
изменения ппр меньше, чем при использовании первой программы
(рис. 1.3).
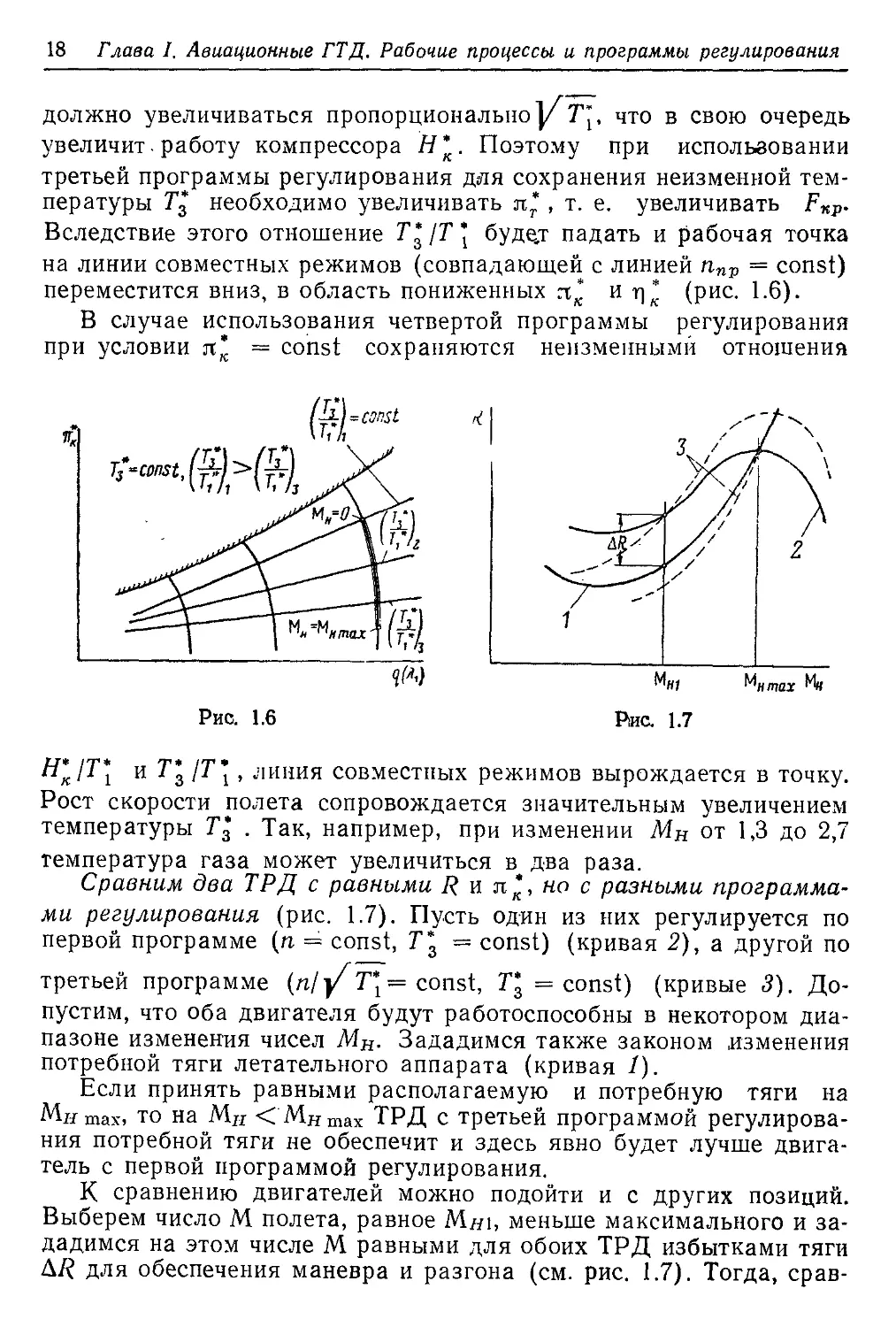
При использовании второй программы регулирования (м =
= const) изменение температуры Т* следует за изменением полной
работы сжатия. Обработка характеристик ряда компрессоров по-
казывает, что величина полной работы сжатия зависит от величины
расчетного значения л* , как показано в работе [19]. На рис. 1.1
дана примерная зависимость полной работы сжатия по iinv при
п = const.
§ 1. Однокаскадные турбореактивные двигатели
17
В соответствии с изменением Н*к (ппр) для ТРД с использова-
нием второй программы регулирования будет меняться и темпера-
тура : увеличиваться с ростом ппр при низких расчетных л* и
снижаться при высоких. Можно вместо изменения ппр рассматри-
вать изменение Т*, так как число оборотов ротора сохраняется
постоянным. Величина Т* отражает влияние и высоты, и скОросги
полета. Зависимость Т3 = Т3 (Т*) для различных л* показана
на рис. 1.5.
Откуда следует, что ТРД с низконапорным компрессором в зна-
чительном диапазоне скоростей не полностью используется по тем-
сти полета почти сразу сопровождается увеличением температуры
T*z. Поэтому в расчетной точке, если за нее принята Т * = 288° К
(Н = 0; = 0 или./7 11 км, Мн = 1,29), расчетная температура
Т*3р (для ТРД с высоконапорным компрессором) должна быть
меньше максимально допустимой температуры для данного двига-
теля.
Из рис. 1.5 можно также сделать заключение о том, как должна
меняться площадь FKp для сохранения неизменной температуры
газа перед турбиной. При л* = 4 с ростом Т\ площадь FKP нужно
уменьшать, при л* = 10 значение FKP необходимо увеличивать.
Для л* = 6 изменение FKp почти не требуется.
Рассмотрим особенности третьей (п/ ]/"Т* = const, Т3 = const)
и четвертой Т\= const) программ регулирования ТРД. Для
обеих программ с ростом скорости полета число оборотов ротора
18 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
должно увеличиваться пропорционально)/ Т’, что в свою очередь
увеличитработу компрессора Н*. Поэтому при использовании
третьей программы регулирования для сохранения неизменной тем-
пературы Тз необходимо увеличивать л*, т. е. увеличивать FKP.
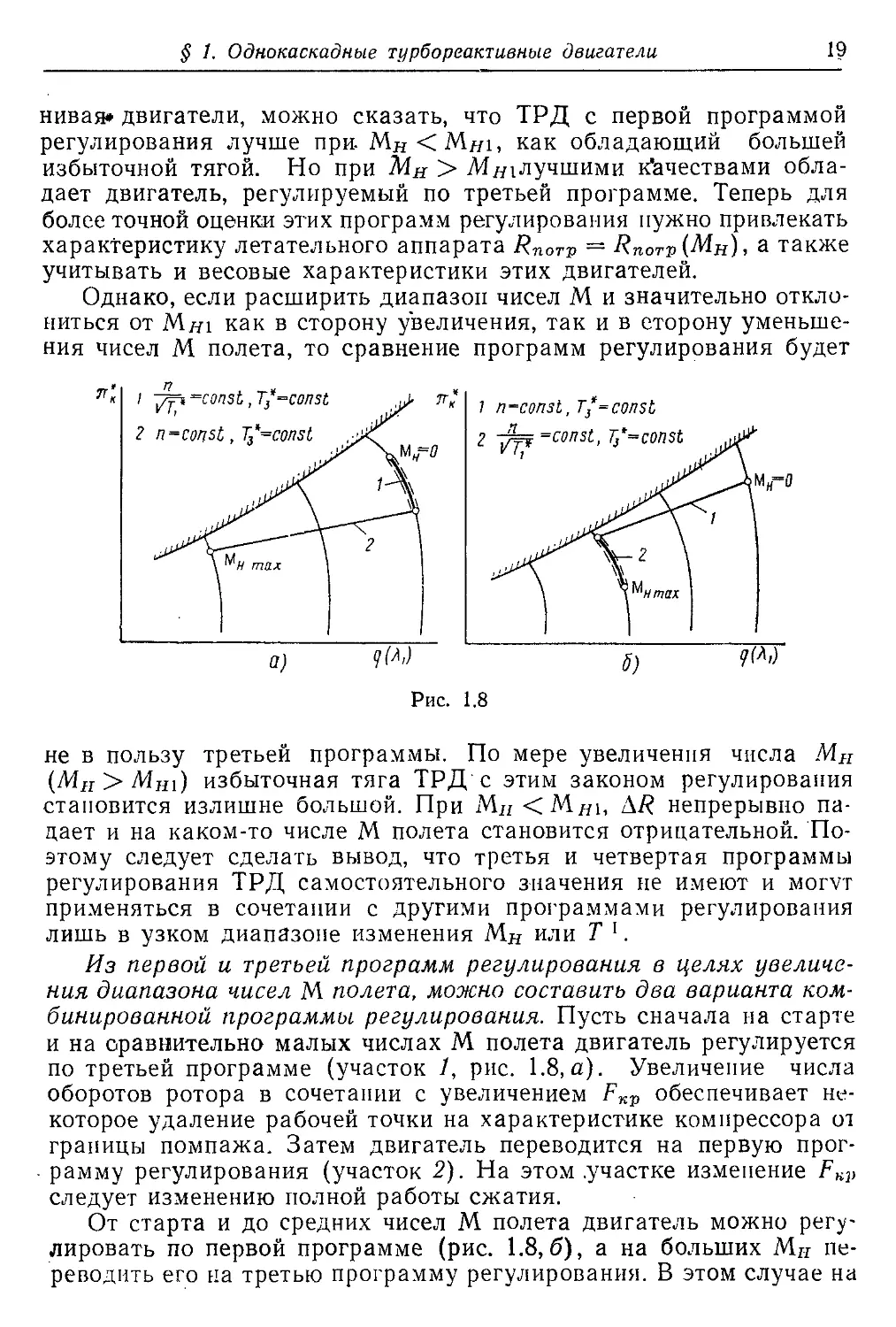
Вследствие этого отношение Т*/Т\ будет падать и рабочая точка
на линии совместных режимов (совпадающей с линией ппр = const)
переместится вниз, в область пониженных л* и ц* (рис. 1.6).
В случае использования четвертой программы регулирования
при условии л* = const сохраняются неизменными отношения
Н'* IT* и Т*3 /Т\ , линия совместных режимов вырождается в точку.
Рост скорости полета сопровождается значительным увеличением
температуры Т3 . Так, например, при изменении Мн от 1,3 до 2,7
температура газа может увеличиться в два раза.
Сравним два ТРД с равными R и л’, но с разными программа-
ми регулирования (рис. 1.7). Пусть один из них регулируется по
первой программе (n = const, Т*3 = const) (кривая 2), а другой по
третьей программе (n/у/ Т* = const, Т3 = const) (кривые 3). До-
пустим, что оба двигателя будут работоспособны в некотором диа-
пазоне изменения чисел Мн. Зададимся также законом изменения
потребной тяги летательного аппарата (кривая 7).
Если принять равными располагаемую и потребную тяги на
Мншах, то на Мн < МНтах ТРД с третьей программой регулирова-
ния потребной тяги не обеспечит и здесь явно будет лучше двига-
тель с первой программой регулирования.
К сравнению двигателей можно подойти и с других позиций.
Выберем число М полета, равное Mhi, меньше максимального и за-
дадимся на этом числе М равными для обоих ТРД избытками тяги
Д/? для обеспечения маневра и разгона (см. рис. 1.7). Тогда, срав-
§ 1. Однокаскадные турбореактивные двигатели
19
нивая» двигатели, можно сказать, что ТРД с первой программой
регулирования лучше при- Мн < Мш, как обладающий большей
избыточной тягой. Но при Мн > Мшлучшими качествами обла-
дает двигатель, регулируемый по третьей программе. Теперь для
более точной оценки этих программ регулирования нужно привлекать
характеристику летательного аппарата Rnorp — Rnorp (Мн), а также
учитывать и весовые характеристики этих двигателей.
Однако, если расширить диапазон чисел М и значительно откло-
ниться от Mhi как в сторону увеличения, так и в сторону уменьше-
ния чисел М полета, то сравнение программ регулирования будет
а) §) 7^,)
Рис. 1.8
не в пользу третьей программы. По мере увеличения числа MfI
избыточная тяга ТРД с этим законом регулирования
становится излишне большой. При Мн<М.ц\, AR непрерывно па-
дает и на каком-то числе М полета становится отрицательной. По-
этому следует сделать вывод, что третья и четвертая программы
регулирования ТРД самостоятельного значения не имеют и могут
применяться в сочетании с другими программами регулирования
лишь в узком диапазоне изменения Мн или Т 1.
Из первой и третьей программ регулирования в целях увеличе-
ния диапазона чисел М полета, можно составить два варианта ком-
бинированной программы регулирования. Пусть сначала на старте
и на сравнительно малых числах М. полета двигатель регулируется
по третьей программе (участок 1, рис. 1.8, а). Увеличение числа
оборотов ротора в сочетании с увеличением FKV обеспечивает не-
которое удаление рабочей точки на характеристике компрессора от
границы помпажа. Затем двигатель переводится на первую прог-
рамму регулирования (участок 2). На этом .участке изменение FKP
следует изменению полной работы сжатия.
От старта и до средних чисел М полета двигатель можно регу-
лировать по первой программе (рис. 1.8,6), а на больших Мн пе-
реводить его на третью программу регулирования. В этом случае на
20 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
участке 1 изменение FKp будет определяться изменением работы
сжатия Н*, а на участке 2 с ростом скорости полета Fnp должно
увеличиваться.
Если в любой последовательности сочетать вторую и четвертую
программы регулирования, то участки кривых 1 на рис. 1.8, а и 2
на рис. 1.8,6 стягиваются в точки.
Применение рассмотренных комбинированных программ регули-
рования не полностью решает задачу обеспечения устойчивой рабо-
ты компрессора ТРД во всем диапазоне изменения чисел М полета
от старта до Мнтах. Для расширения диапазона устойчивой работы
необходимо вводить дополнительное регулирование. Оно заключа-
ется в изменении установочных углов лопаточных аппаратов ком-
прессора, турбины и в использовании перепуска воздуха или газа.
Способы расширения диапазона устойчивой работы компрессора
Расширение диапазона устойчивой работы компрессора может
быть достигнуто двумя способами: 1) перемещением рабочей точ-
ки на характеристике компрессора в область больших приведенных
расходов или фиксацией ее по отношению к неизменной границе
устойчивой работы; 2) смещением границы устойчивой работы ком-
прессора в область меньших приведенных расходов.
В первом случае нужный эффект достигается за счет снижения
сопротивления сети, на которую работает компрессор. (Для ком-
прессора ТРД сетью является весь воздушно-газовый тракт двига-
теля после компрессора). Во втором случае нужно воздействовать
на характеристику сети.
Снижение сопротивления сети достигается или перепуском ча-
сти газа в газовый тракт, параллельный основному, минуя турбину,
или поворотом сопловых лопаток турбины на больший угол выхо-
да cti. Технически проще осуществить перепуск газа, тем более, что
такой способ регулирования почти не отражается на экономичности
двигателя. Выполнить вращающиеся сопловые лопатки труднее из-
за специфических условий работы турбины. Однако больших ре-
зультатов этими средствами достигнуть нельзя.
При регулировании ТРД по программам п = const, Т3 = const
или п = const и при достижении больших скоростей полета, соот-
ветствующих Мн 2, приведенный расход по сравнению с расхо-
дом в стартовых условиях снижается на несколько десятков про-
центов. Осевая скорость перед первой ступенью сильно падает, а
последние ступени компрессора работают на режимах, близких к
запиранию. Поэтому снижение сопротивления сети лишь немного
увеличит производительность компрессора и приведет к запиранию
последних ступеней.
§ 1. Однокаскадные турбореактивные двигатели
21
Сопловой аппарат турбины с поворотными лопатками может
оказаться полезным при регулировании двигателя по программе
п/ j/^T* = const, Т з = const. С ростом скорости полета для поддер-
жания неизменной температуры газа нужно увеличивать FKV выход-
ного сопла, но при этом падает л* и т]* (см. участок 1 рис. 1.8. а).
Чтобы поднять л* и т]* компрессора необходимо уменьшить сече-
ние соплового аппарата турбины, т. е. повернуть сопловые лопатки
на меньший угол щ.
Для современных ТРД с высокими л* характерным является ис-
пользование на низких ппр промежуточного перепуска воздуха в
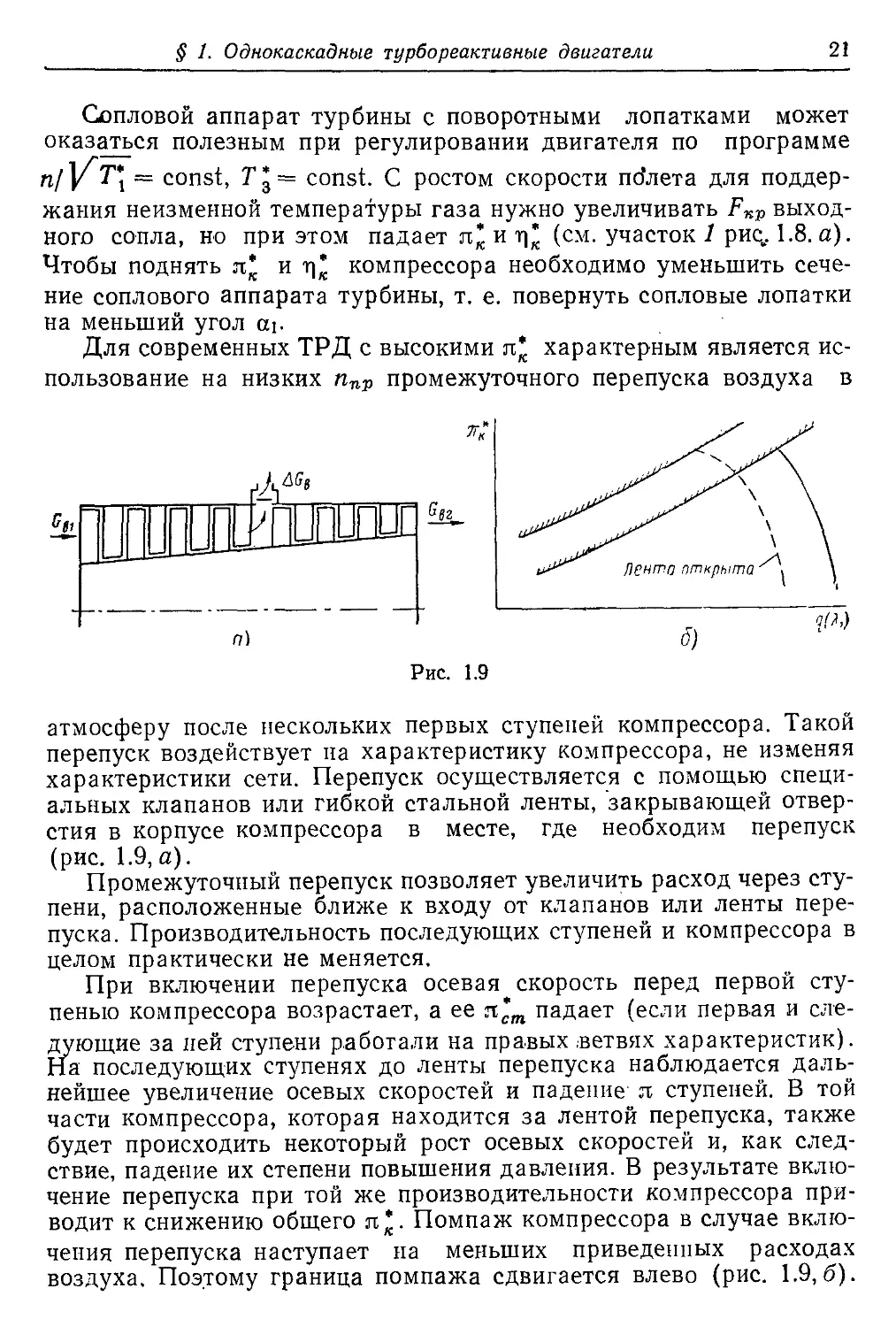
Рис. 1.9
атмосферу после нескольких первых ступеней компрессора. Такой
перепуск воздействует па характеристику компрессора, не изменяя
характеристики сети. Перепуск осуществляется с помощью специ-
альных клапанов или гибкой стальной ленты, 'закрывающей отвер-
стия в корпусе компрессора в месте, где необходим перепуск
(рис. 1.9, а).
Промежуточный перепуск позволяет увеличить расход через сту-
пени, расположенные ближе к входу от клапанов или ленты пере-
пуска. Производительность последующих ступеней и компрессора в
целом практически не меняется.
При включении перепуска осевая скорость перед первой сту-
пенью компрессора возрастает, а ее л *ст падает (если первая и сле-
дующие за пей ступени работали на правых .ветвях характеристик).
На последующих ступенях до ленты перепуска наблюдается даль-
нейшее увеличение осевых скоростей и падение л ступеней. В той
части компрессора, которая находится за лентой перепуска, также
будет происходить некоторый рост осевых скоростей и, как след-
ствие, падение их степени повышения давления. В результате вклю-
чение перепуска при той же производительности компрессора при-
водит к снижению общего л*. Помпаж компрессора в случае вклю-
чения перепуска наступает на меньших приведенных расходах
воздуха. Поэтому граница помпажа сдвигается влево (рис. 1.9,6).
22 Глава I. Авиационные ГТ Д. Рабочие процессы и программы регулирования
При промежуточном перепуске в атмосферу выбрасывается воз-
дух, прошедший сжатие лишь в части ступеней компрессора. От-
сюда мощность, затраченная на его сжатие, сравнительно не-
велика.
На компрессорах некоторых ТРД приходится устанавливать не
одну, а несколько лент перепуска после различных ступеней. Опре-
деление числа лент и последовательность их включения произво-
дится опытным путем.
Одним из эффективных средств расширения диапазона устойчи-
вой работы компрессора является
установка спрямляющих и направ-
jr/| л ляющих аппаратов с поворотными
I / у лопатками. Поворот лопаток произ-
УС У водится с таким расчетом, чтобы
лт при данном приведенном расходе
/ у было обеспечено уменьшение угла
У \ атаки на входе в решетки профилей
7 \ рабочих колес.
\ При таком изменении устано-
/ ' ' вочных углов лопаток большие углы
--------------------- атаки, соответствующие развитому
?И>) срыву со спинки профиля, достига-
рис j 10-------------ются на меньших приведенных рас-
‘ ’ ходах. Это отодвигает влево грани-
цу помпажа.
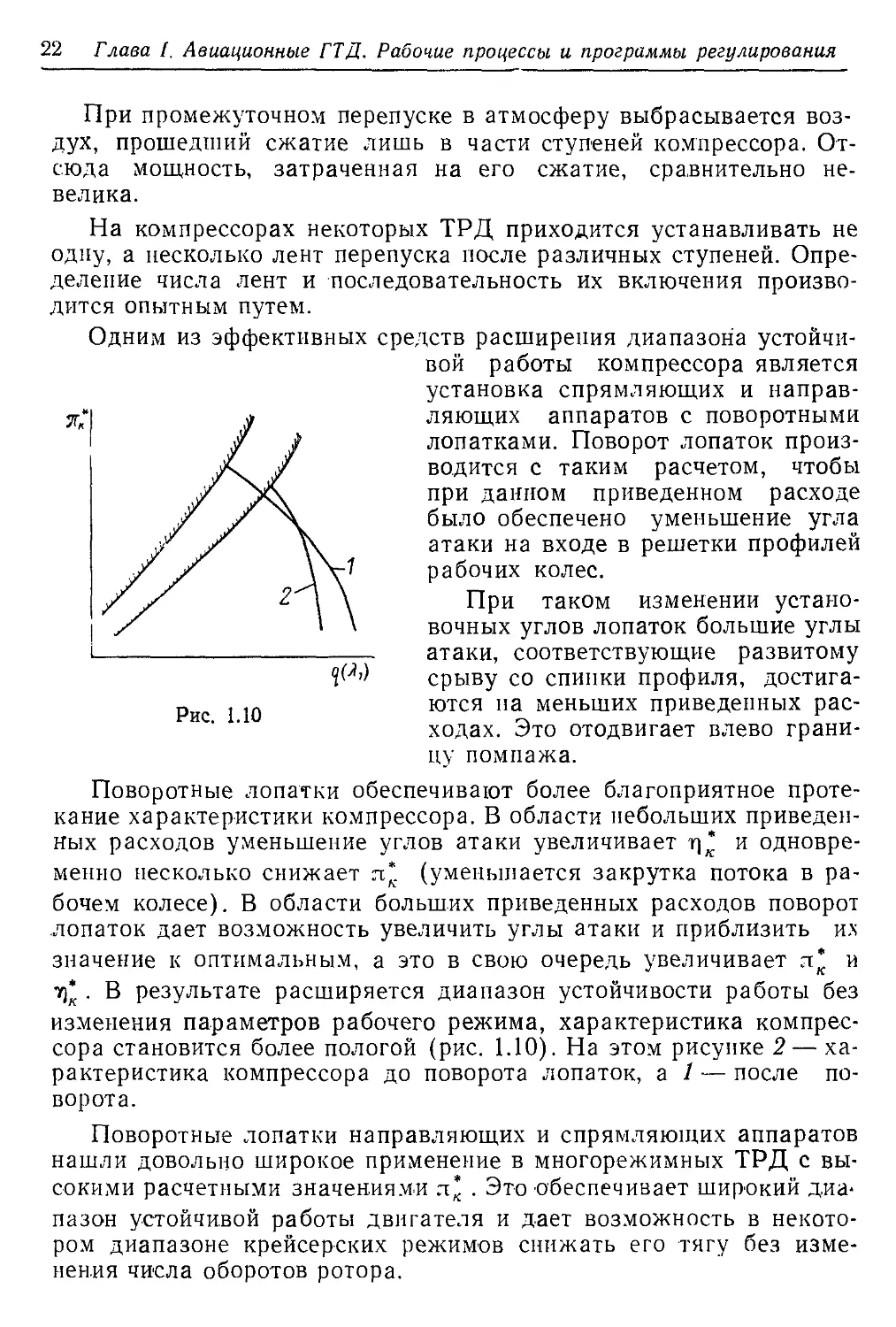
Поворотные лопатки обеспечивают более благоприятное проте-
кание характеристики компрессора. В области небольших приведен-
ных расходов уменьшение углов атаки увеличивает т)‘ и одновре-
менно несколько снижает я* (уменьшается закрутка потока в ра-
бочем колесе). В области больших приведенных расходов поворот
лопаток дает возможность увеличить углы атаки и приблизить их
значение к оптимальным, а это в свою очередь увеличивает л* и
т)‘ . В результате расширяется диапазон устойчивости работы без
изменения параметров рабочего режима, характеристика компрес-
сора становится более пологой (рис. 1.10). На этом рисунке 2 — ха-
рактеристика компрессора до поворота лопаток, а 1 — после по-
ворота.
Поворотные лопатки направляющих и спрямляющих аппаратов
нашли довольно широкое применение в многорежимных ТРД с вы-
сокими расчетными значениями л* . Это обеспечивает широкий диа-
пазон устойчивой работы двигателя и дает возможность в некото-
ром диапазоне крейсерских режимов снижать его тягу без изме-
нения числа оборотов ротора.
§ 1. Однокаскадные турбореактивные двигатели
23
Регулирование основных режимов современного ТРД
При регулировании современного ТРД с расчетным я* ^>6
обычно используется комбинированная программа регулирования в
сочетании с регулированием компрессора (как правило, это проме-
жуточный перепуск воздуха). Без этих мероприятий невозможно
обеспечить большой диапазон высот и скоростей летательного ап-
парата (Н = 0 -4- 25 км, М-н = 1,2 н- 3 для больших высот и Мн «С 1,5
для малых высот).
В зависимости от типа и назначения летательного аппарата, а
также с учетом характеристики компрессора выбирается расчетное
значение температуры Т\ . Для Т* > Т*}р принимается программа
регулирования п = const (или п = const, Т”3 = const), а при Т*
Т*1р осуществляется переход, на программу регулирования
Ппр = (пПр)р = const (или пПр = const, = const).
Расчетное значение л’ для (пПр)р выбирается с 7 4- 10 процент-
ным запасом устойчивости компрессора по помпажу, который опре-
деляется из выражения
/ * \ / * \
I 1 _ I Пк I
k /ПОМП \ @в-пр /р j QQ (17)
( \
' @в-пр / Р
——| —отношение параметров компрессора, при кото-
рых наступает помпаж на ппр — (ппр)р.
На крутых участках характеристики компрессора (Ge.np)noMn ~
= (.Ge. пр) р^ поэтому
* / * \
_ 10()
(<)р
Для пологих участков характеристики л*кпомп « (л’)р, откуда
£ (^а.пр)р (6в-пр)помп. Jqq
{6в-пр)помп
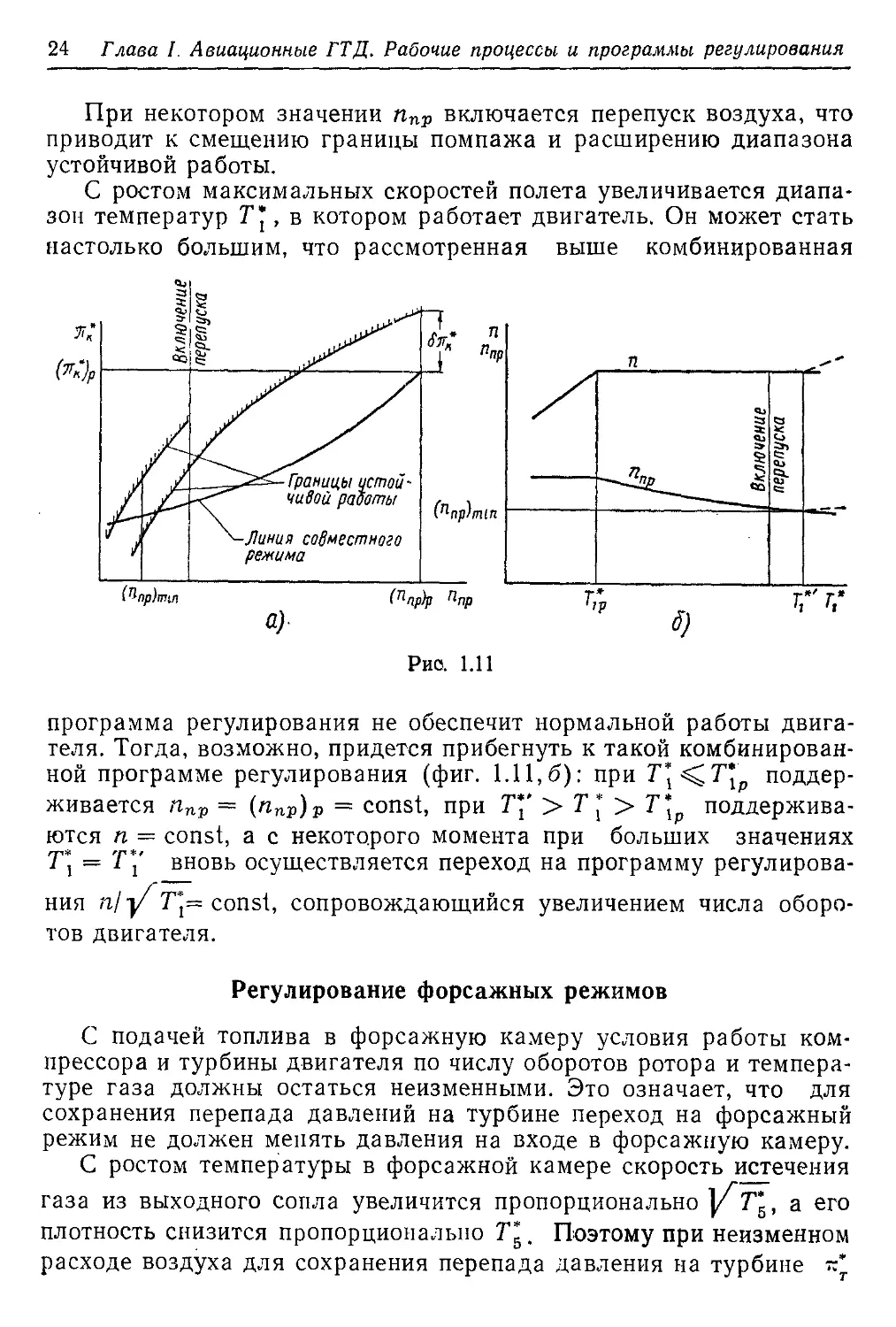
Комбинированная программа регулирования, дополненная прог-
раммой регулирования компрессора, показанная на рис. 1.11, а.
Регулирование по (ппр)р = const при осуществляет-
ся сохранением л* = (л’)р за счет уменьшения подачи топлива и
снижения числа оборотов ротора. Такое регулирование обеспечива-
ет противопомпажный запас 6л *.
24 Глава I. Авиационные ГТД,. Рабочие процессы и программы регулирования
При некотором значении пПр включается перепуск воздуха, что
приводит к смещению границы помпажа и расширению диапазона
устойчивой работы.
С ростом максимальных скоростей полета увеличивается диапа-
зон температур Т*, в котором работает двигатель. Он может стать
настолько большим, что рассмотренная выше комбинированная
программа регулирования не обеспечит нормальной работы двига-
теля. Тогда, возможно, придется прибегнуть к такой комбинирован-
ной программе регулирования (фиг. 1.11,6): при поддер-
живается ппр = (nnp)p = const, при Т*' > Т * > Т*1р поддержива-
ются п = const, а с некоторого момента при больших значениях
Т\ = Т\' вновь осуществляется переход на программу регулирова-
ния п/ Т\= const, сопровождающийся увеличением числа оборо-
тов двигателя.
Регулирование форсажных режимов
С подачей топлива в форсажную камеру условия работы ком-
прессора и турбины двигателя по числу оборотов ротора и темпера-
туре газа должны остаться неизменными. Это означает, что для
сохранения перепада давлений на турбине переход на форсажный
режим не должен менять давления на входе в форсажную камеру.
С ростом температуры в форсажной камере скорость истечения
газа из выходного сопла увеличится пропорционально а его
плотность снизится пропорционально Т*5. Поэтому при неизменном
расходе воздуха для сохранения перепада давления на турбине -*
£ 1. Однокаскадные турбореактивные двигатели
25
площадь критического сечения выходного сопла FKV должна увели-
читься пропорционально Т*5.
Во время работы на форсажном режиме у ТРДФ три парамет-
ра рабочего режима являются регулируемыми параметрами. Это п
или Т*, Г* и . Вместо температуры газа в форсажной каме-
ре за регулируемый параметр можно принять суммарный коэффи-
циент избытка воздуха as . Регулирующими факторами будут G,
Оф а F-кр.
У многих ТРДФ выходное сопло сделано двухпозиционным, т. е.
створки сопла, определяющие его площадь, могут занимать только
два положения. Уменьшенному сечению сопла соответствует рабо-
та двигателя па нефорсажных режимах, а переход на форсажный
режим сопровождается увеличением сечения сопла. Такой двига-
тель нужно рассматривать как двигатель с нерегулируемым сече-
нием сопла.
В противоположность этому типу двигателей есть двигатели, у
которых створки могут занимать’любое положение и тем самым
изменять площадь критического сечения сопла от минимального
до максимального значения. В зависимости от той или иной кон-
струкции выходного сопла можно наметить различные программы
регулирования форсажных режимов или программы регулирования
основных и форсажных режимов.
ТРДФ с многопозициопныМ—Соплом может регулироваться по
программе п — const или п/]/Т, = const; Т* = const, Т*5 = const
или a а = const. В этом случае управлять регулируемыми парамет-
рами целесообразно в следующем порядке: G-+n или G-+nl\^T\-,
или FKV-+T*3.
Программы регулирования ТРДФ с двухпозиционным соплом
Основной контур (турбокомпрессор) регулируется по програм-
ме п = const или п/]/~Т\ = const.
Форсажный контур регулируется по одной из следующих про-
грамм:
1. —j- = const;
Pi
2. —£• = const;
Pz
3. it* = const;
т >
26 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
4. Т* = const или аа = const;
5. Т*3 const.
Могут применяться и другие программы регулирования.
На ранней стадии развития реактивной авиации двигатели име-
ли низкие расчетные значения л*. Поэтому на дозвуковых скоро-
стях полета в выходном сопле такого двигателя устанавливался
докритический перепад давления, а турбина работала на перемен-
ной степени расширения л'. Отсюда следует, что в тех условиях
параметр л* не рационально было выбирать за регулируемый па-
раметр. Таким образом, возникли первая и вторая программы
(Gos/p* = const, G$lp*2 = const). При использовании этих программ
регулирования форсажного контура в общем случае не выдержива-
ется условие сохранения неизменным режима работы основного
контура, влияние подачи форсажного топлива на л * не контроли-
руется, что (Может привести к значительному отклонению Т*3 от рас-
четного значения.
Регулирование форсажного контура по третьей программе
(л* = const) сейчас получило наибольшее распространение, так как
турбины современных ТРД на основных режимах работают на пос-
тоянных перепадах давления.
Как уже было показано, при регулировании основного контура
ТРДФ по программе п — const температура газа Г* не остается
постоянной и в своем изменении следует за изменением полной ра-
боты сжатия Н’ . В свою очередь температура газа в форсажной
камере Т'5 в своем изменении следует за изменением температуры
У -1
Т3, так как при данном расходе газа Т* зависит от Т* = /л*т '
и от Gos. Если на каких-либо режимах полета температура газа Т3
падает, т. е. ТРД недоиспользуется по температуре перед турбиной,
то на этих режимах он недоиспользуется и по температуре в фор-
сажной камере.
Условие Г* = const в двигателях с двухпозиционным соплом
может быть выполнено путем корректирования величины л’ с изме-
нением внешних условий, т, е. за счет применения программы
г.т = лг (/ J.
Стремление повысить степень форсирования ТРДФ приводит к
тому, что суммарный коэффициент избытка воздуха становится
очень низким. ТРДФ с большой степенью форсирования работают
при as = 1,14-1,12, что создает существенные трудности в исполь-
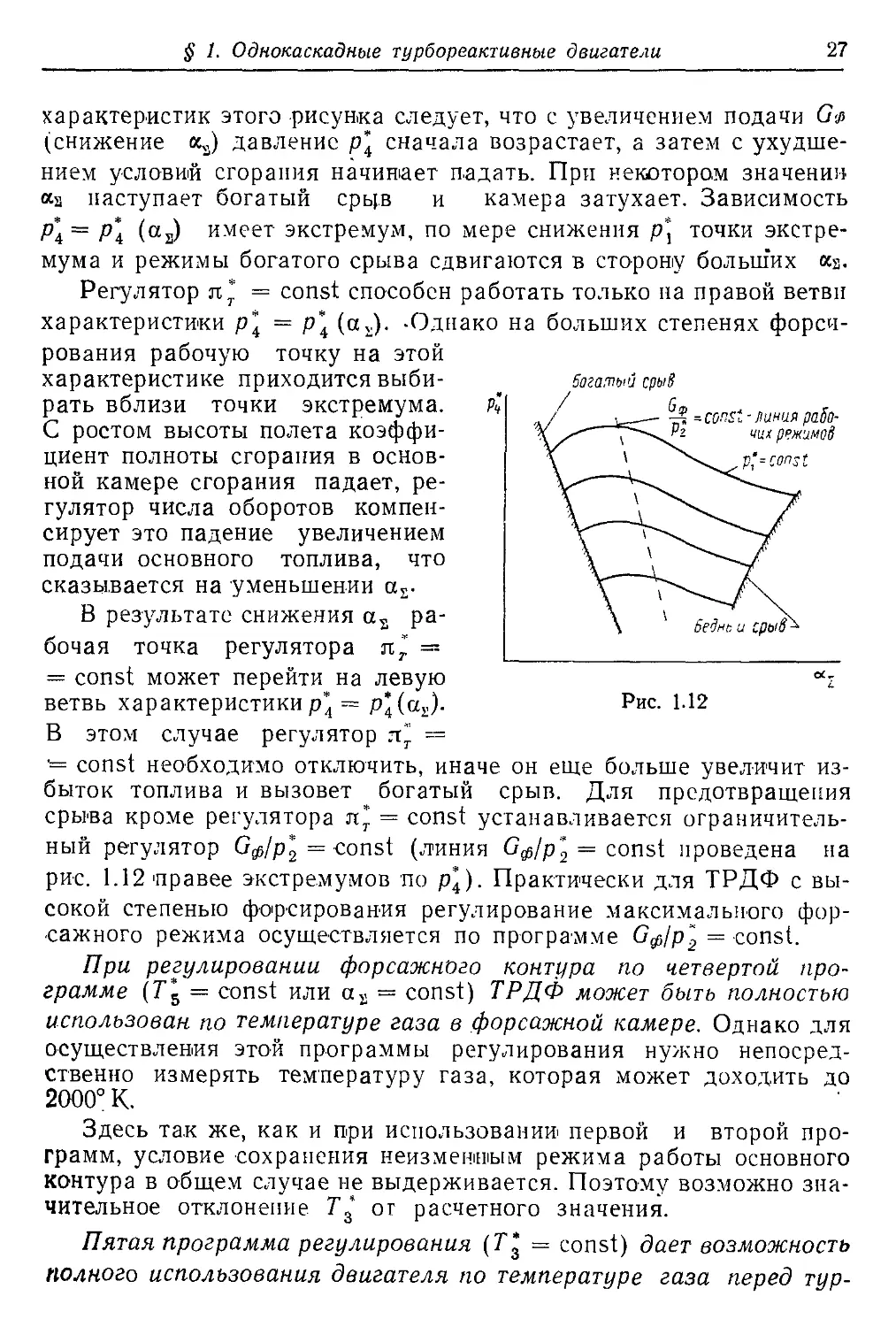
зовании программы регулирования л* = const. На рис. 1.12 показа-
на зависимость давления в форсажной камере р* от суммарного
коэффициента избытка воздуха as для различных значений р[. Из
§ 1. Однокаскадные турбореактивные двигатели
27
характеристик этого рисунка следует, что с увеличением подачи G<j>
(снижение cQ давление р\ сначала возрастает, а затем с ухудше-
нием условий сгорания начинает падать. При некотором значении
аа наступает богатый срцв и камера затухает. Зависимость
р\ = р\ (as) имеет экстремум, по мере снижения р\ точки экстре-
мума и режимы богатого срыва сдвигаются в сторону больших as.
Регулятор it* = const способен работать только на правой ветви
характеристики р\ = р\ (си). -Однако на больших степенях форси-
рования рабочую точку на этой
характеристике приходится выби-
рать вблизи точки экстремума. р»
С ростом высоты полета коэффи-
циент полноты сгорания в основ-
ной камере сгорания падает, ре-
гулятор числа оборотов компен-
сирует это падение увеличением
подачи основного топлива, что
сказывается на уменьшении as.
В результате снижения as ра-
бочая точка регулятора л’ —
— const может перейти на левую
ветвь характеристикир’= р\(аД. Рис. 1.12
В этом случае регулятор л* =
— const необходимо отключить, иначе он еще больше увеличит из-
быток топлива и вызовет богатый срыв. Для предотвращения
срыва кроме регулятора л* = const устанавливается ограничитель-
ный регулятор G$lp*2 = const (линия Ggs/p’= const проведена на
рис. 1.12 правее экстремумов по р*Д. Практически для ТРДФ с вы-
сокой степенью форсирования регулирование максимального фор-
сажного режима осуществляется по программе Сф1р“2 = const.
При регулировании форсажного контура по четвертой про-
грамме = const или as = const) ТРДФ может быть полностью
использован по температуре газа в форсажной камере. Однако для
осуществления этой программы регулирования нужно непосред-
ственно измерять температуру газа, которая может доходить до
2000° К.
Здесь так же, как и при использовании! первой и второй про-
грамм, условие сохранения неизменным режима работы основного
контура в общем случае не выдерживается. Поэтому возможно зна-
чительное отклонение от расчетного значения.
Пятая программа регулирования (Т* = const) дает возможность
полного использования двигателя по температуре газа перед тур-
28 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
биной. В этом случае изменение работы сжатия Н* компенсируется
изменением л*, что достигается за счет различной подачи форсаж-
ного топлива. Температура Т*5 или аа будут менять свое значение.
Поэтому регулятор Т*3 = const следует дополнить ограничительным
регулятором —= const.
Рг
При использовании программы регулирования п = const, Т*ъ =
= const требуется измерять температуру газа перед или за турби-
ной. В настоящее время регуляторы температуры уже начали при-
меняться в эксплуатации.
Представляет интерес частичный форсаж двигателя. В ТРДФ с
двухпозиционным соплом он нецелесообразен, так как уменьшение
расхода форсажного топлива приведет к снижению температуры
газа перед турбиной (при п = const). Известно, что выгоднее под-
водить тепло к воздуху там, где есть наибольшее давление, т. е. в
основную камеру сгорания. Здесь же получается, что частичный
форсаж достигается уменвшением подвода тепла и в основную и в
форсажную камеры сгорания.
Для экономичного частичного форсажа нужно иметь многопо-
зиционное выходное сопло, или сопло, у которого створки, кроме
двух крайних, могут занимать любое промежуточное положение.
Частичный форсаж, так же как и полный, может регулироваться по
программе л* = const (или Т*3 — const). Для уменьшения степени
форсирования достаточно уменьшить площадь критического сече:
ния выходного сопла. В соответствии с этим регулятор л’ = const
уменьшит подачу 6ф.
§ 2. ДВУХКАСКАДНЫЕ ТРДФ
Особенности рабочего процесса
С отклонением от расчетного режима у высоконапорного комп-
рессора ТРД крайние ступени компрессора в первую очередь попа-
дают в нерасчетные условия. Так, с уменьшением ппр первые сту-
пени начинают работать на больших углах атаки и на левых ветвях
характеристик, а последние ступени — на малых (или отрицатель-
ных) углах атаки и на крайних участках правых ветвей своих ха-
рактеристик. Эта особенность работы отдельных ступеней ком.прес'-
сора на ппр < (лпр)р может быть выражена в виде отклонения па-
раметра са/ик от расчетного значения:
первые ступени са/ик < (са/ик) р;
средние ступени са/ик ~ (со/ик) Р,
последние ступени cajuK > {cajuK)v.
£ 2. Двухкаскадные ТРДФ
29
Где ик — окружная скорость на внешнем диаметре рабочего колеса
ступени.
Как на первых, так и на- последних ступенях к. п. д. на нерасчет-
ных режимах заметно снижается. В целом т|* уже при небольшом
снижении ппр быстро падает. Изменение са/ик получается тем более
резкое, чем выше л* расчетное.
Предположим, что у такого двигателя, работающего на
ппр < (п.пр)р без регулятора, ротор компрессора будет разделен на
две части с приводом каждой из них от своей турбины. Тогда
произойдет самопроизвольное изменение числа оборотов первого и
второго роторов но сравнению с теми числами оборотов, на которых
двигатель работал до разделения ротора.
Число оборотов ротора первой части компрессора (будем назы-
вать ее низконапорным каскадом и обозначать индексом «н») упа-
дет. Число оборотов ротора второй части компрессора (соответ-
ственно .высоконапорный каскад с обозначением индексом «в») воз-
растет.'Оба каскада по своим изменившимся параметрам са/ик при-
близятся к расчетному режиму, диапазон устойчивой работы комп-
рессора возрастает.
Причины, заставляющие каскады самопроизвольно изменять
свои числа оборотов, следующие. Переход первых ступеней на левые
ветви характеристик сопровождается увеличением их крутящего
момента, поэтому Мкр.н > (Мкр) р. Для вращения последних ступе-
ней, работающих на правых ветвях характеристик, нужен меньший
крутящий момент, т. е. Мкр_в < (Мкр)р. Если у двигателя с двухсту-
пенчатой турбиной до условного разделения ротора был надкрити-
ческий перепад в выходном сопле, то после разделения ротора на
две части с переходом на пРР < (ппр) р перепады давлений теперь
уже на обеих турбинах не изменятся, что приведет к условию
Нт.н!НТ'в = const. Отсюда следует, что число оборотов ротора низ-
конапорного каскада должно упасть, а высоконапорного — воз-
расти.
Если же до условного разделения ротора перепад в выходном
сопле по каким-либо причинам снизился и стал докритическим, то
падение перепада в первую очередь скажется на второй турбине —
турбине низконапорного каскада. Тогда Нт,н1Нт_в < (Нт.н1Нт.в') р.
Это обстоятельство еще больше усилит эффект снижения пн после
условного разделения ротора на две части.
При сравнении однокаскадного и двухкаскадного ТРДФ мы го-
ворили об условном разделении ротора компрессора на две части.
Теперь, выявив принципиальные особенности двухкаскадного ТРДФ,
об этой условности можно больше не упоминать. Двухкаскадные
ТРДФ нашли применение в авиации как многоцелевые двигатели
с достаточно высокой экономичностью. Их способность изменять
соотношение чисел оборотов роторов обеспечивает значительно
больший диапазон устойчивой работы по сравнению с однокаскад-
30 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
ным ТРДФ, имеющим то же значение л*. Схема двухкаскадного
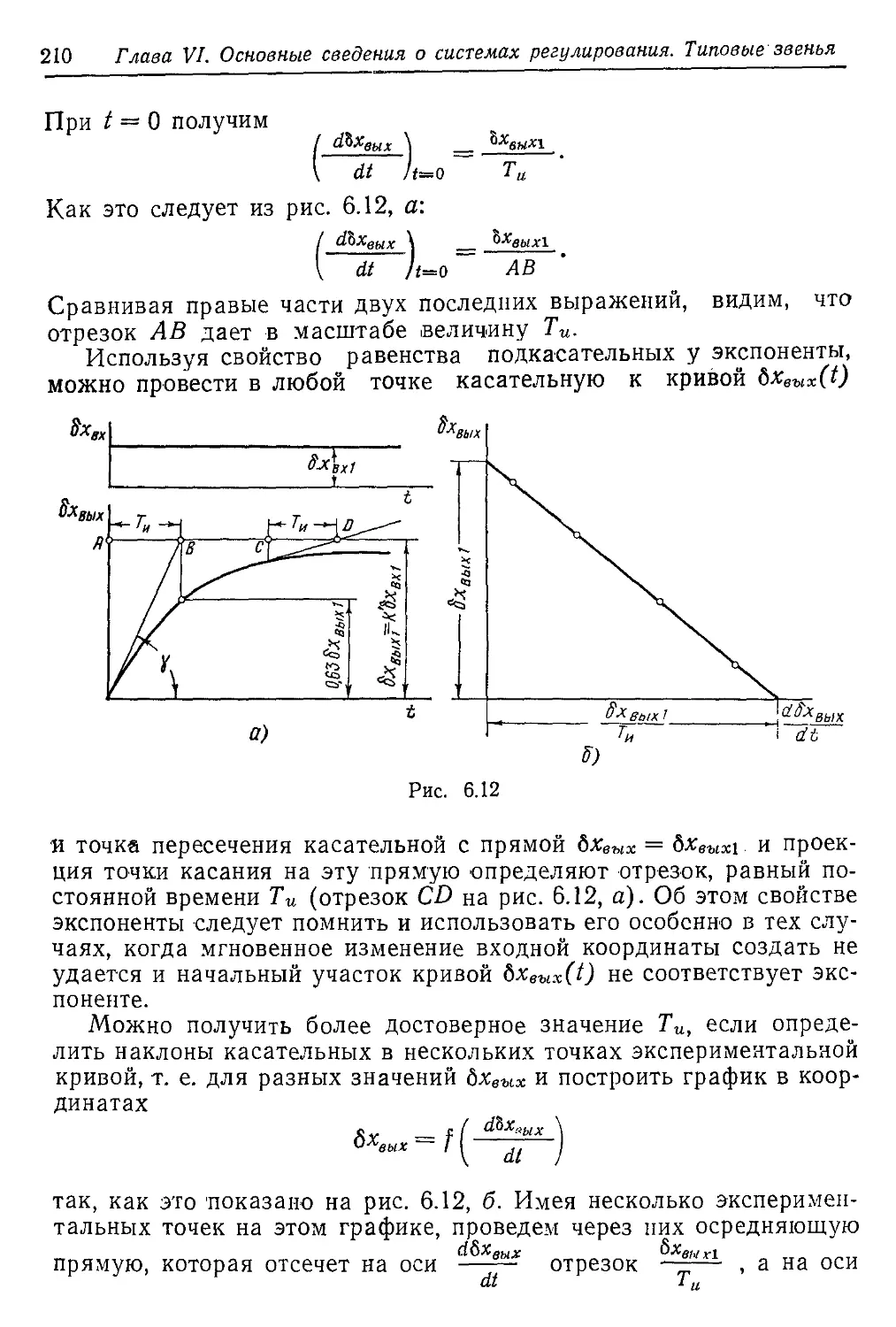
ТРДФ показана на рис. 1.13.
Изменение соотношения между числами оборотов ротора обоих
каскадов при разных внешних условиях является основным свойст-
вом двухкаскадного ТРДФ. Это свойство принято называть сколь-
жением роторов. Остановимся на нем несколько подробнее.
Рис. 1.13
Допустим, дто двухкаскадный ТРДФ работает без регулятора
числа оборотов, ио подача топлива в камеру сгорания основного
контура осуществляется таким образом, что для различных Т\
температура газа перед турбиной остается неизменной. Тогда с
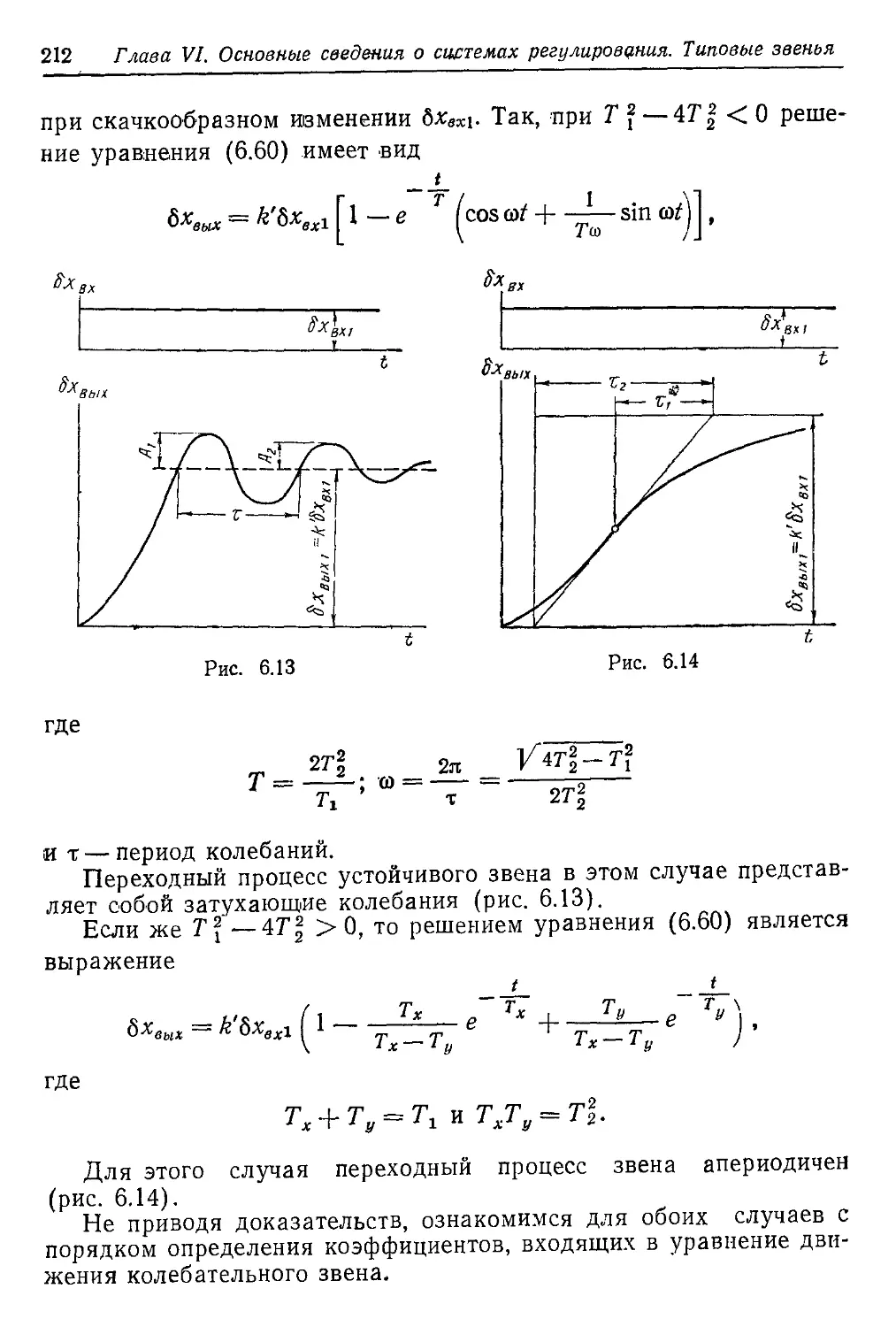
ростом Т\ число оборотов пн будет падать, а пв—возрастать
п»
Рис. 1.14
(рис. 1.14). На расчетном режиме (для Т\р) часто принимают
«в ~ «н, откуда скольжение ив/пк~1.
Более удобно характер скольжения роторов двухкаскадного
ТРДФ пв!пн представить в виде зависимости от приведенных чисел
оборотов низконапорного каскада (пк)тар так, как это показано
на рис. 1.15. При построении графика рис. 1.15 можно не связывать
себя условием постоянства Т* или работы двигателя без регуля-
тора. Подобная зависимость будет характерна для двухкаскадного
ТРДФ и в том случае, если двигатель работает с регулятором и
для него, например, принята программа регулирования пн = const.
Рассмотрим еще некоторые особенности рабочего процесса
двухкаскадного ТРДФ. На расчетном режиме двухкаскадный
§ 2. Двухкаскадные ТРДФ
31
ТРДФ имеет высокие n‘s, но работй сжатия и л* каждого кас-
када невелики. Поэтому следует ожидать, что линия совместных
режимов турбины и компрессора у каждого каскада будет идти
достаточно круто, так, как это наблюдается у ТР'ДФ с низкими
значениями лк*. Однако расход воздуха через весь компрессор оп-
ределяется главным образом высоконапорным каскадом, который
может в одних случаях быть как бы дросселем для пизконапорного
каскада, а в других случаях просасывать через него воздух. Отсю-
да следует, что характеристики высоконапориого каскада отража
ются на протекании линии совмест-
ных режимов низконапорного кас-
када. тз
Возьмем двухкаскадный ТРДФ,
у которого число оборотов ротора
высоконапорного каскада поддер-
живается постоянным (ne= const).
С ростом скорости полета при до-
критическом истечении из выход*-
ного сопла перепад на турбине низ-
конапорного каскада возрастает и
пн увеличивается. Объемный расход
воздуха через компрессор по причи-
не того, что пв = const возрастает Рис. 1.16
в меньшей степени по сравнению
с ростом пн. Поэтому отношение (са/ик)п падает, углы атаки на ло-
патках рабочих колес первых ступеней растут, а режим работы
компрессора приближается к границе помпажа.
Напомним, что в противоположность этому, у однокаскадного
ТРДФ с невысоким л’ с ростом скорости полета линия совмест-
ных -режимов удаляется от границы помпажа.
Изменение площади критического сечения выходного сопла у
двухкаскадного ТРДФ сказывается главным образом на приведен-
ной работе HtIT*z турбины низко-напорного каскада (рис.. 1.16).
Поэтому даже значительное изменение FKP почти не влияет на по-
ложение линии' совместных режимов высоконап-орного каскада, а
при пв = const изменение FKp слабо сказывается на Т^. Когда же
при FKP < (FKp)p приведенная работа турбины Нт.в1Т3 начинает
падать, то запас устойчивости компрессора снижается так же, как
И у однокаскадного ТРДФ.
Влияние изменения FKP на низконапорный каскад велико. Если
при пв= const уменьшить FKp, то снизится HT.n'iT*3 и пн. Расход
Воздуха в области больших пн уменьшится незначительно, так как
ПО условию пв = const.
Вследствие слабого изменения расхода воздуха параметр
32 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
(Са/ик) н первых ступеней возрастет, углы атаки на лопатках рабо-
чих колес уменьшатся. Увеличение FKp даст обратный эффект.
Таким образом, в противоположность однокаскадному ТРДФ
уменьшение FKP у двухкаскадного ТРДФ приводит к увеличению
запаса устойчивости компрессора.
Эту особенность двухкаскадногоТРДФ, у которого пв — const,
необходимо учитывать при переходе на форсажный режим. Подача
форсажного топлива и включение зажигания в форсажной камере
должны сопровождаться увеличением FKP. Однако, если произойдет
запаздывание в воспламенении топлива в форсажной камере и па-
дение в ней давления, число оборотов ротора низконапорного ком-
прессора пн увеличится. В этом случае, как уже было выяснено,
запас устойчивости компрессора уменьшится и может возникнуть
помпаж.
Возможные программы регулирования
У двухкаскадного ТРДФ по сравнению с однокаскадпым на
один регулируемый параметр больше. Регулирующие факторы
остаются те же: изменение расхода основного и форсажного топли-
ва. Изменение FKp часто предпочитают использовать не для регули-
рования температуры газа Т$, а для организации частичного фор-
сажа или комбинации частичного и двухступенчатого форсажа.
Тогда могут быть приняты две программы регулирования:
1. пн = const, те* const;
2. пе — const, I?* = const.
Использование регулирующих факторов в первом случае G->
->п„, 6о5->-л*, а во втором G->ne,
Из двух нерегулируемых в каждой программе параметров один
(число оборотов пв или пн) следует ограничивать. Тогда при над-
критическом перепаде давления в выходнО1М сопле изменение
температуры газа Г’ будет пропорционально изменению полной
работы сжатия компрессора высоконапорного каскада.
Отметим, однако, что у некоторых двухкаскадных двигателей
величина нерегулируемых параметров не ограничивается.
Ограничение чисел оборотов пв или пн осуществляется уменьше-
нием подачи основного топлива. Поэтому с момента ограничения
числа оборотов одного каскада число оборотов другого уже не бу-
дет постоянным.
Отсюда следует, что кроме двух упомянутых программ регули-
рования могут быть намечены комбинированные программы, кото-
рые и применяются на практике.
Рассмотрим особенности обеих программ регулирования. Счи-
тают удобным за расчетный режим для газотурбинных двигателей
§ 2. Двухкаскадные ТРДФ
33
выбирать скорость полета, соответствующую Мц„ = 1,29 и высоту
полета > 11 км (в этом случае Т\р = 288° К). Покажем, что
при таком (Выборе расчетного-режима для Мц > Мрр по изменению
силы тяги двухкаскадного ТРДФ выгоднее применять первую про-
грамму регулирования (nH = const, л* = const), а для М1С <
< Мир — вторую программу (ne = const, л* = const).
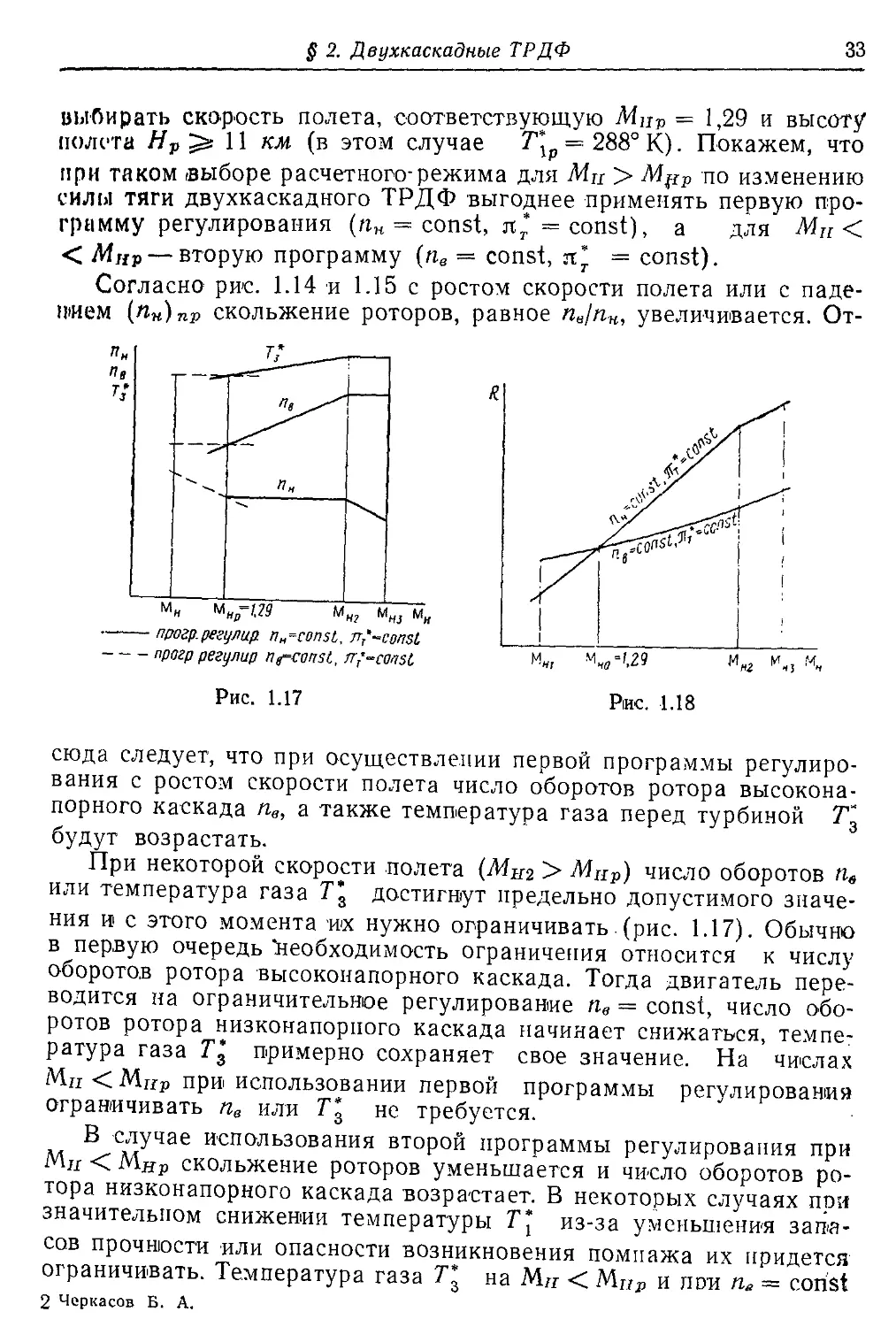
Согласно рис. 1.14 и 1.15 с ростом скорости полета или с паде-
нием (п«)пР скольжение роторов, равное пв1пн, увеличивается. От-
------прогр-регулир n „-const, л '-const
------прогр регулир n/-const, л'-const
Рис. 1.17
сюда следует, что при осуществлении первой программы регулиро-
вания с ростом скорости полета число оборотов ротора высокона-
порного каскада пв, а также температура газа перед турбиной 7“
будут возрастать.
При некоторой скорости полета (Миг > МНр) число оборотов п»
или температура газа Т\ достигнут предельно допустимого значе-
ния и с этого момента их нужно ограничивать (рис. 1.17). Обычно
в первую очередь ^необходимость ограничения относится к числу
оборотов ротора высоконапорного каскада. Тогда двигатель пере-
водится на ограничительное регулирование пв = const, число обо-
ротов ротора низконапорпого каскада начинает снижаться, темпе-
ратура газа примерно сохраняет свое значение. На числах
Мп < Мир при использовании первой программы регулирования
ограничивать пв или Т*а не требуется.
В случае использования второй программы регулирования при
Мп < Мир скольжение роторов уменьшается и число оборотов ро-
тора низконапорного каскада возрастает. В некоторых случаях при
значительном снижении температуры Т*г из-за уменьшения запа-
сов прочности или опасности возникновения помпажа их придется
ограничивать. Температура газа 7* на Ми < МПр и пои ne = const
2 Черкасов Б. А.
34 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
меняется незначительно. При Мн > МнР никаких ограничений на
параметры регулирования накладывать не нужно.
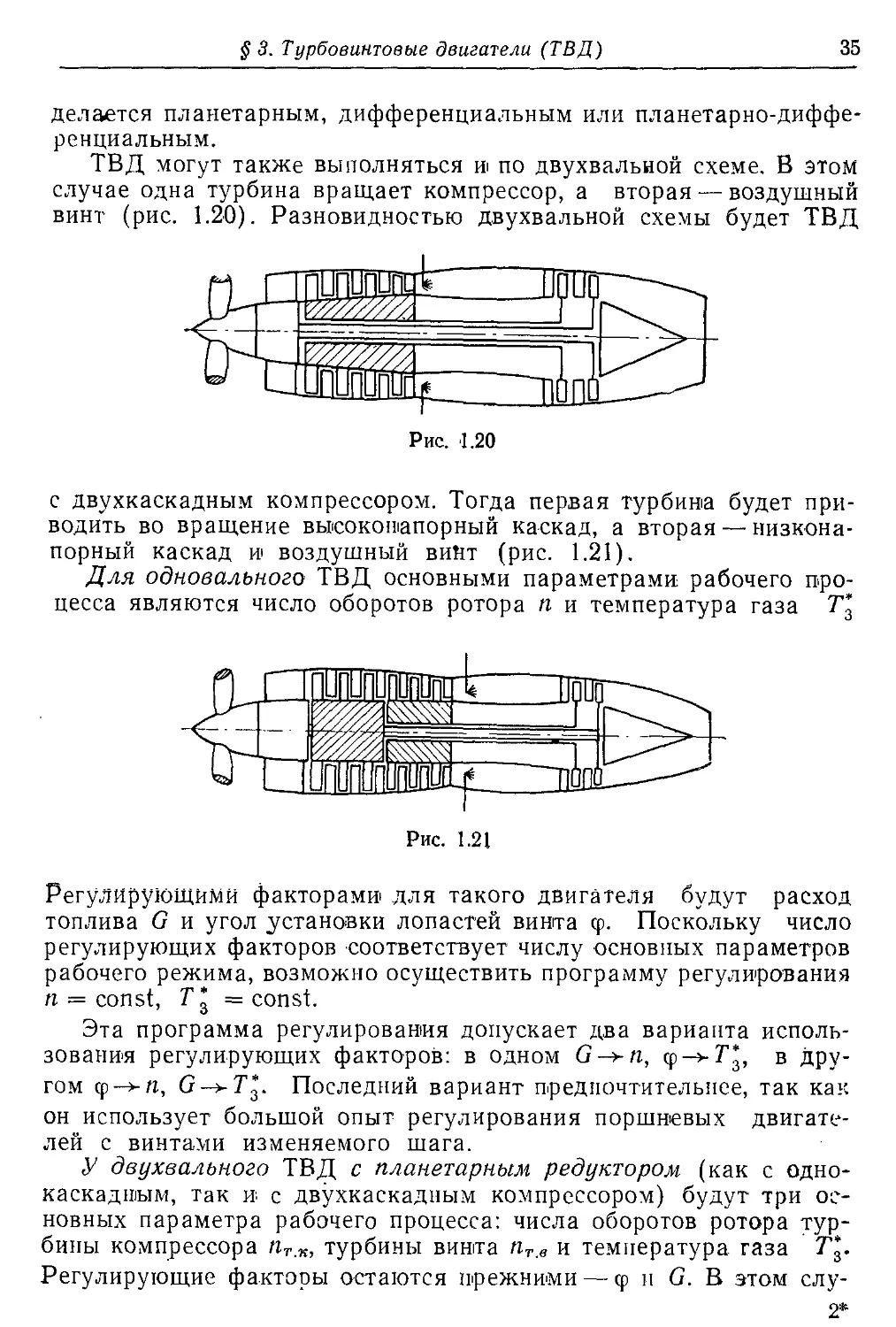
Рассмотрим изменение тяги двухкаскадного ТРДФ в некотором
диапазоне чисел М, МН1 < М11р < Мнз. Примем, что на МНр = 1,29
тяга двигателя не зависит от выбора программы регулирования.
Расчеты показывают, что в случае использования первой про-
граммы регулирования за счет роста пв расход воздуха с увеличе-
нием Мн возрастет быстрее, чем при регулировании двигателя во
второй программе. Поэтому кривая R = Д (Мн) для пн — const идет
круче, чем при пв = const (рис. 1.18). Отсюда следует, что програм-
му регулирования пн = const, л* = const выгоднее применять на
больших скоростях полета, а программу пв = const, л* = const на
малых.
§ 3. ТУРБОВИНТОВЫЕ ДВИГАТЕЛИ (ТВД)
Программы регулирования основных режимов
Летательные аппараты с ТВД предназначены для сравнитель-
но небольших скоростей полета (Мн^ 1). Оптимум в распределе-
нии свободной энергии между воздушным винтом и выходным соп-
лом мало меняется по числу М полета в пределах от Мн = 0 до
Мятах < 1. Для его достижения расширение газа в турбине долж-
но происходить до атмосферного давления или до давления, не-
сколько меньше атмосферного. Поэтому газовый тракт двигателя
Рис. 1.19
за турбиной выполняется или как канал постоянного сечения, или
в виде диффузора. Регулирующий фактор в виде выходного сопла
переменного сечения в данном типе газотурбинного двигателя от-
падает.
Для достижения высокой экономичности в ТВД приняты высо-
кие значения л’. В целях расширения диапазона устойчивой рабо-
ты в компрессорах ТВД обычно применяется перепуск воздуха.
Часто ТВД выполняются по одновальной схеме, когда турбина
приводит во вращение и компрессор, и воздушный винт (рис. 1.19).
Редуктор двигателя для передачи мощности на два соосных винта
§ 3. Турбовинтовые двигатели (ТВД)
35
делается планетарным, дифференциальным или планетарно-диффе-
ренциальным.
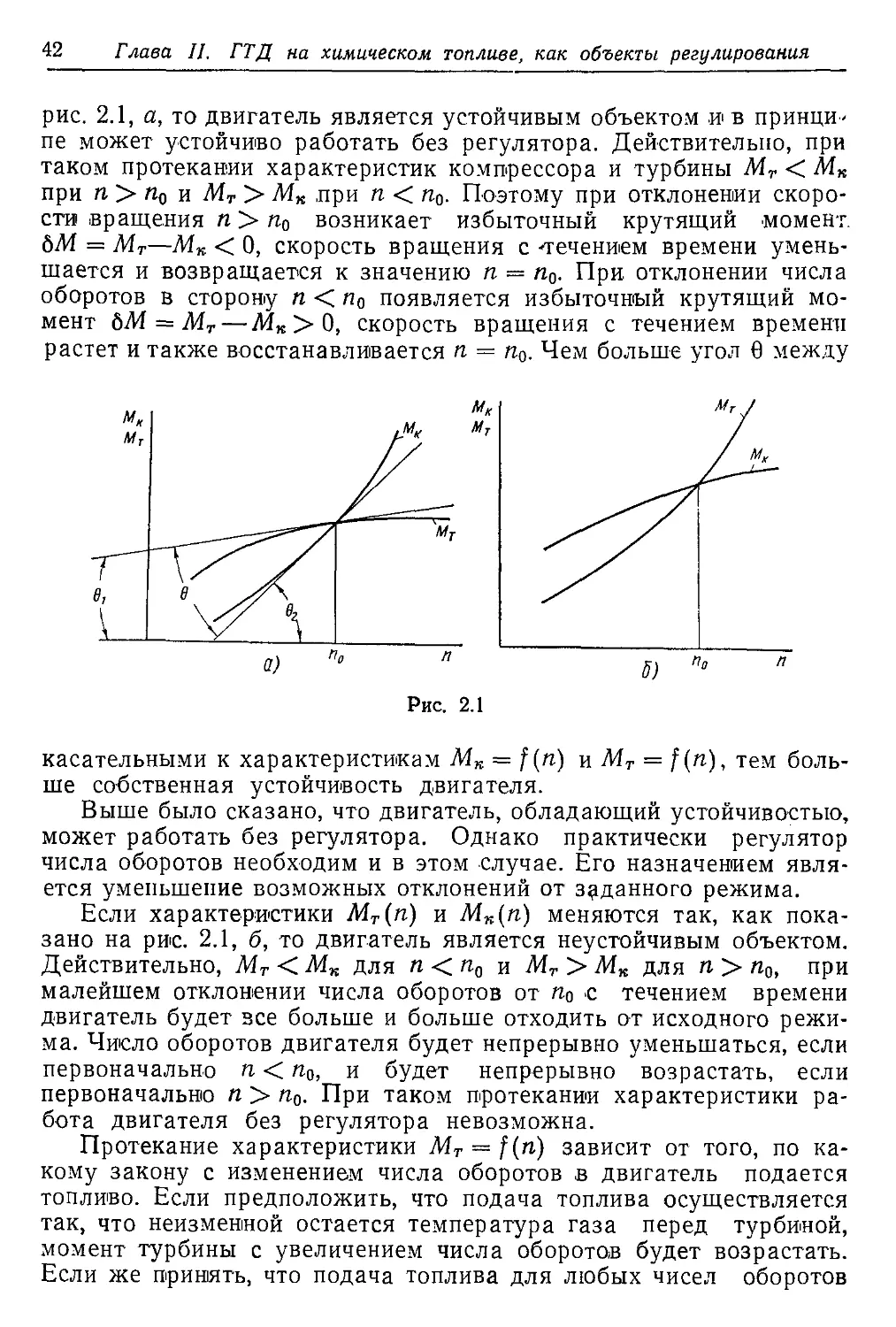
ТВД могут также выполняться и по двухвальной схеме. В этом
случае одна турбина вращает компрессор, а вторая — воздушный
винт (рис. 1.20). Разновидностью двухвальной схемы будет ТВД
Рис. 1.20
го
ЕлЙ
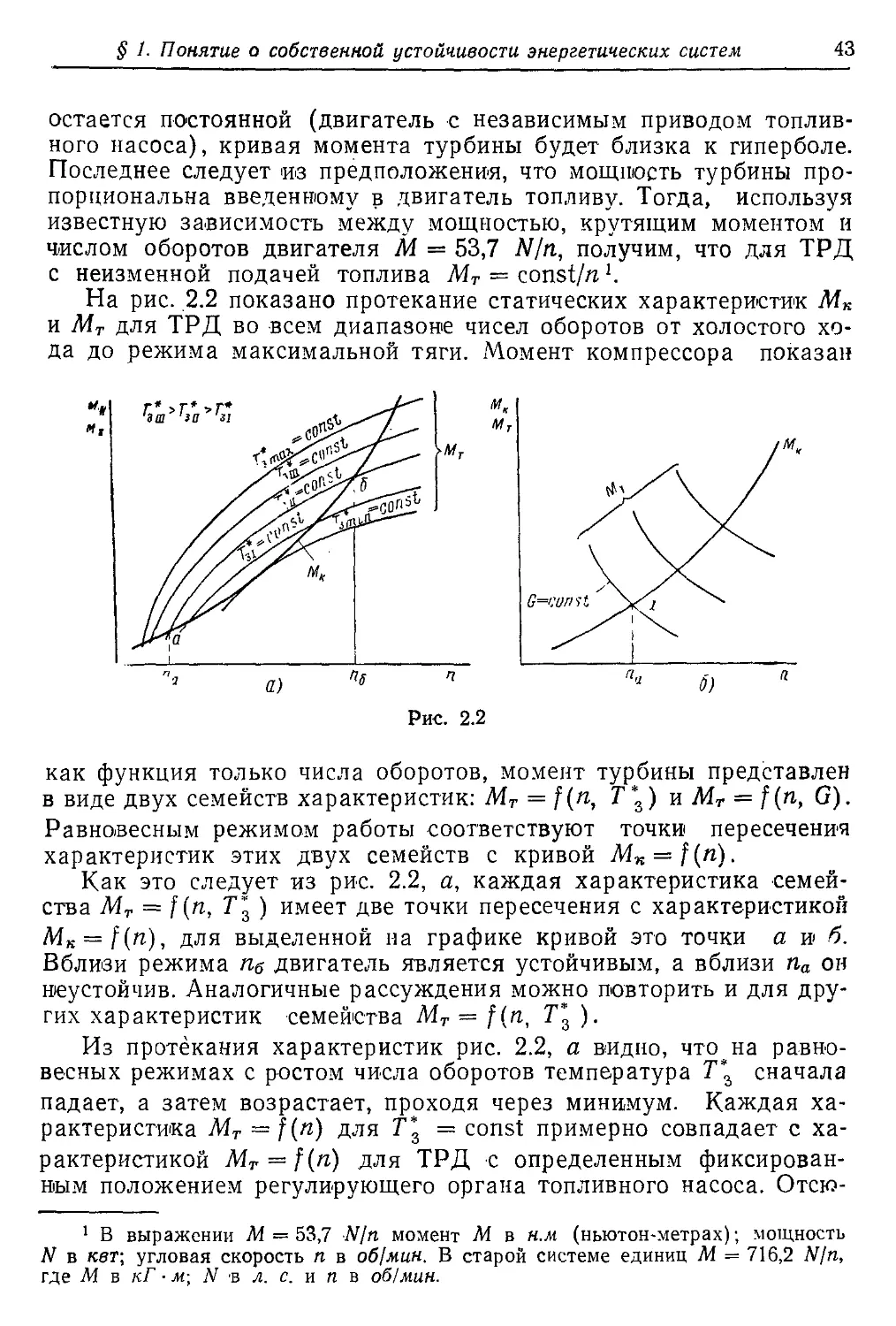
с двухкаскадным компрессором. Тогда первая турбина будет при-
водить во вращение высоконапорный каскад, а вторая — низкона-
порный каскад и воздушный винт (рис. 1.21).
Для одновального ТВД основными параметрами рабочего про-
цесса являются число оборотов ротора п и температура газа Г*
Рис. 1.21
Регулирующими факторами для такого двигателя будут расход
топлива G и угол установки лопастей винта ср. Поскольку число
регулирующих факторов соответствует числу основных параметров
рабочего режима, возможно осуществить программу регулирования
п = const, Г* = const.
Эта программа регулирования допускает два варианта исполь-
зования регулирующих факторов: в одном G->-n, ср->Г*, в дру-
гом ср --> п, G-+T*. Последний вариант предпочтительнее, так как
он использует большой опыт регулирования поршневых двигате-
лей с винтами изменяемого шага.
У двухзального ТВД с планетарным редуктором (как с одно-
каскадным, так и с двухкаскадным компрессором) будут три ос-
новных параметра рабочего процесса: числа оборотов ротора тур-
бины компрессора пт.к, турбины винта птв и температура газа Т*3.
Регулирующие факторы остаются прежними — ср и G. В этом слу-
2*.
36 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
чае возможны несколько вариантов программ регулирования, из
них нужно отдать преимущество такому: пт.в = const, пт.к = const.
В этом варианте целесообразно поддерживать числа оборотов так:
G-+nTK, ср->птв. В отношении температуры газа нужно преду-
смотреть ограничительное регулирование так, чтобы ^з^-^зтах-
Дифференциальный редуктор обладает-двумя степенями свобо-
ды. Это означает, что для этого редуктора числа оборотов двух ва-
лов могут быть выбраны и они определяют число оборотов третьего
вала.
Здесь три основных параметра рабочего процесса. Одним из них
будет температура газа T*z, двумя другими — любая пара из чи-
сел оборотов: ротора турбины п, переднего винта па и заднего вин-
та п3. Регулирующими факторами будут подача топлива G, углы
установки лопастей винтов — переднего <рп и заднего <р3.
Возможны следующие программы регулирования:
1. п = const, пп = const, 7* = const;
2. п — const, п3 = const, Тз = const;
3. па = const, п3 = const, Тз = const.
На поддержание параметров целесообразно использовать 6->
->7’*, ф3-фп->«п ИЛИ фп->«, фз-*-«з или фп->«п, фз->«з-
В динамическом отношении большим преимуществом обладает
программа регулирования п = const; п3 = const; Т* = const с ис-
пользованием регулирующих факторов в следующем порядке: фп~*
Фз->«з;
В случае отклонения числа оборотов ротора одного из винтов
от заданного значения появляется заметная вибрация винтов и па-
дает к. п. д. всей соосной винтовой установки. Чтобы точнее под-
держать равенство чисел оборотов винтов в систему регулирования
включается синхронизатор, выполненный в виде дифференциала.
При отклонении числа оборотов одного из винтов от заданного зна-
чения дифференциал воздействует на соответствующий регулятор
числа оборотов.
Остановимся на вопросе регулирования мощности двигателя на
высотах ниже расчетной. С увеличением высоты при неизменной
скорости полета за счет изменения расхода воздуха мощность ТВД
непрерывно падает. Если некоторая высота полета принята за рас-
четную высоту Нр, то на мощность двигателя Nep, соответствую-
щую высоте Нр, производится расчет основных деталей двигателя
на прочность. Для высот Н < Нр мощность ТВД Ne > Nep. Поэтому
для сохранения расчетных значений запасов прочности на этих вы-
сотах мощность двигателя необходимо ограничивать.
§ 3. Турбовинтовые двигатели (ТВД)
37
Снижение мощности возможно различными путями. Ее можно
снизить, уменьшив расход воздуха (уменьшив п) и сохранив тем-
пературу газа Г*, можно снизить температуру газа Т*. сохранив
число оборотов ротора п. Наконец, мощность может быть снижена
как за счет уменьшения числа оборотов п, так и за счет температу-
ры газа Т*3. На практике часто предпочитают снижать темпера-
туру газа Т3, сохраняя п = const (рис. 1.22).
На участке ограничения мощности от Н = 0 до Н = Нр удель-
ный расход топлива несколько уменьшается с ростом высоты по-
лета. Снижение удельного расхода
топлива объясняется падением тем-
пературы воздуха, ростом за счет
этого л* и экономичности двигателя
(полагая, что Н км).
Ограничение мощности при со-
хранении скорости вращения рото-
ра удобно тем, что в этом случае
крутящий момент Мкр на валу вин-
та будет пропорционален мощности
Ne. Крутящий момент на валу мо-
жет быть непосредственно измерен.
Особенно легко это сделать, когда в
ТВД 'используется планетарный ре-
дуктор. В этом случае нужно измерить окружное усилие, переда-
ваемое неподвижной шестерней на корпус двигателя. Устройства,
служащие для этой цели, называются измерителями крутящего мо-
мента (ИКМ).
Регулирование ТВД по величине Мкр является ограничитель-
ным регулированием. При достижении Мкр предельно допустимого
значения сигнал от ИКМ вызывает уменьшение подачи топлива.
Регулирование ТВД на крейсерских режимах
Для ТВД большое значение имеет работа на крейсерских режи-
мах, т. е. на таких режимах, когда Ne< Иеном, и регулирование
двигателя »а этих режимах. Одна и та же крейсерская мощность
может быть получена при различных сочетаниях чисел оборотов
ротора п и температуры газа Т*. Программа регулирования долж-
на обеспечить минимально возможный удельный расход топлива
при любом значении мощности двигателя и гарантировать доста-
точный запас устойчивости компрессора.
Расчеты показывают, что различные программы регулирования
крейсерских режимов почти не отличаются по экономичности. Это
дает основание упрощать систему регулирования ТВД на крейсер-
ских режимах и не требовать от нее высокой точности соблюдения
38 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
выбранной программы. Однако выбранная программа регулирова-
ния крейсерских режимов должна обеспечить безопасную и устой-
чивую работу двигателя при любых условиях полета. С этой целью
рассмотрим дроссельную характеристику ТВД (рис. 1.23).
На этом рисунке показана зависимость эффективной мощности
N, от числа оборотов ротора п при различных расходах топлива О.
На этом же графике Ne(n, G) нанесены характеристики Ne(n, <р).
показывающие изменение мощности воздушного винта в зависимо-
сти от числа оборотов ротора и угла установки лопастей. Область
возможного изменения
мощности двигателя на
этом рисунке ограничена
рядом линий. Они пока-
зывают наступление пом-
пажа, достижение пре-
дельно допустимых тем-
ператур газа и чисел обо-
ротов ротора, область ав-
торотации и границу ус-
тойчивого горения в каме-
ре сгорания.
Из характеристик сле-
дует, что с уменьшением
расхода топлива для пе-
рехода к заданному уров-
ню крейсерской мощно-
сти необходимо выбрать
программу изменения
’ср и п. Очевидно, что для получения достаточно глубоких крейсер-
ских режимов программа <р = const не годится, так как в этом слу-
чае при снижении п довольно быстро наступит помпаж. Наиболее
удобной и часто употребляемой является программа регулирования
п = const, которой сопутствует наибольшее по сравнению с други-
ми программами снижение температуры газа. При ее осуществле-
нии настройка регулятора числа оборотов ротора остается неиз-
менной и снижение подачи топлива сопровождается только умень-
шением угла установки лопастей винта.
Программа регулирования крейсерских режимов п = const не
обеспечивает перехода к уровню мощности малого газа. В этом
случае после достижения <р = фпцп дальнейшее уменьшение мощ-
ности сопровождается .снижением числа оборотов ротора.
§ 4. ДВУХКОНТУРНЫЕ ТРД (ТРДД)
Существует несколько различных схем ТРДД: однокаскадные
и двухкаскадные, с форсированием путем ввода дополнительного
топлива за турбиной или во второй контур и без форсирования, со
§ 4. Двухконтурные ТРД (ТРДД)
39
смешением и без смешения потоков, с отбором и без отбора газов.
Будем рассматривать только однокаскадный нефорсированный
ТРДД, его схема показана та рис. 1.24. Этот тип двигателя нашел
применение в гражданской авиации. По своим характеристикам он
занимает промежуточное место между ТРД и ТВД.
К основным параметрам рабочего процесса этого типа двига-
теля, кроме числа оборотов ротора п и температуры газа Т*,
нужно отнести коэффициенты распределения между контурами
расхода воздуха у и эффективной работы г. Однако параметрами
у и z трудно управлять и их нецелесообразно относить к парамет-
рам регулирования. Таким образом, за параметры регулирования
Рис. 1.24
примем только п и Т* , а за регулирующие факторы изменение
расхода топлива G и изменение площадей критического сечения
выходных сопел первого контура F'Kp и второго контура F“p.
Рассмотрим следующие программы регулирования:
1. п = const,
2. п = const;
3. п = const.
= const
т*з = const
Во всех программах целесообразно регулировать число оборо-
тов ротора двигателя изменением расхода топлива G, а температу-
ру газа — изменением F ' или F"Kp.
При работе двигателя на режиме п = const изменение высоты
и скорости полета существенно отражаются на значениях у и г.
С ростом Мн степень двухконтурности у возрастает, а доля эффек-
тивной работы первого контура z уменьшается. С ростом высоты
полета (Н 11 км) у снижается, a z возрастает.
На величине температуры газа Г* будет сказываться главным
образом изменение у и z. Кроме того, Т*3 будет зависеть от изме-
нения полной работы сжатия компрессоров первого и второго кон-
туров.
При регулировании ТРДД по первой программе, учитывая толь-
ко влияние у и z, при поддержании Т* = const с ростом Мн для
получения большого значения л* сечение сопла F'K необходимо
40 Глава I. Авиационные ГТД. Рабочие процессы и программы регулирования
увеличивать. Из тех же соображений с ростом высоты полета до
Н = И км нужно F'Kp уменьшать.
При регулировании ТРДД по второй программе изменение ко-
эффициентов у и z для поддержания = const необходимо ком-
пенсировать изменением F"Kp. На характер изменения F"p сущест-
венное влияние оказывает вид характеристики компрессора второ-
го контура.
Рассмотрим два предельных случая. Пусть в одном случае на
характеристике компрессора второго контура в координатах к* =
= (п«р > G'iJ линии п"пр = const представляют собой гори-
зонтальные прямые. Тогда с ростом Мн для снижения коэффициен-
та у нужно уменьшать F’ , а с возрастанием Н — увеличи-
вать F"Kp.
Пусть во втором случае п"пр = const—-вертикальные линии, что
будет соответствовать у = const. С ростом Мн для увеличения z за
счет снижения Н"к необходимо увеличивать F"p, ас возрастанием
высоты полета — уменьшать F’ .
Из анализа этих двух предельных случаев видно, что реализа-
ция второй программы регулирования ТРДД встречает существен-
ные трудности. Реальная характеристика компрессора второго кон-
тура может иметь такой вид, что в зависимости от значения п"пр
нужно по-разному компенсировать влияние высоты и скорости по-
лета изменением F' .
КР
При регулировании двигателя по третьей программе (полагая,
что л * = const) с ростом Мп температура газа Т*3 увеличивается,
а с ростом высоты полета — падает. Следовательно, эта програм-
ма регулирования может быть использована в сравнительно не-
большом диапазоне изменения Мн.
Для всех трех программ регулирования необходимо непосред-
ственное измерение температуры газа. В третьей программе оно ис-
пользуется для введения ограничительного регулирования Т*.
Для ТРДД можно применять также программы регулирования
п/У'т\ = const; Т3 = const или = const (F*р = const).
Но в случае значительного изменения Ми двигатели, регулируемые
но этим программам, будут иметь слишком низкие стартовые тя-
ги. Поэтому данные программы регулирования самостоятельного
значения не имеют, а могут применяться лишь в комбинации с
программами п = const; Т* = const или п = const (F' = const).
Глава II
ГАЗОТУРБИННЫЕ ДВИГАТЕЛИ, РАБОТАЮЩИЕ
НА ХИМИЧЕСКОМ ТОПЛИВЕ,
КАК ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
§ 1. ПОНЯТИЕ О СОБСТВЕННОЙ УСТОЙЧИВОСТИ
ЭНЕРГЕТИЧЕСКИХ СИСТЕМ
Одним ив важных свойств ГТД как объекта регулирования яв-
ляется его собственная устойчивость. Под устойчивостью энергети-
ческой системы вообще, в том числе и газотурбинного двигателя,
понимается способность системы работать на заданном режиме при
отсоединенном регуляторе, т. е. при неизменном положении регу-
лирующего органа.
Для определения собственной устойчивости энергетической си-
стемы существенным является вид ее статической характеристики.
Так, устойчивость нагнетающей воздушной системы определяется
взаимным расположением характеристик компрессора и потреб-
ляющей сети, т. е. изменением располагаемого и потребного напора
по расходу воздуха. Устойчивость летательного аппарата по ско-
рости полета определяется изменением со скоростью потребных и
располагаемых тяг. Устойчивость авиационного двигателя по числу
оборотов характеризуется изменением потребного и располагаемо-
го крутящего момента по скорости вращения вала двигателя.
Способность устойчивой энергетической системы после снятия
возмущений возвращаться к прежнему статическому режиму назы-
вается самовыравниванием.
Собственная устойчивость ГТД
Для ГТД существенным является протекание статических ха-
рактеристик изменения момента сопротивления компрессора Мк и
движущего момента турбины Мт, построенных в функции от числа
оборотов.
Рассмотрим особенности собственной устойчивости ТРД с нере-
гулируемым соплом. Если вблизи заданного числа оборотов п0, со-
ответствующего равновесному режиму работы двигателя (Мк =
= Л4Г), эти характеристики протекают так, как это показано на
42 Глава II. ГТД на химическом топливе, как объекты регулирования
рис. 2.1, а, то двигатель является устойчивым объектом ив принци-
пе может устойчиво работать без регулятора. Действительно, при
таком протекании характеристик компрессора и турбины Мт < Мк
при п > п0 и Мт > Мк при п < п0. Поэтому при отклонении скоро-
сти вращения п > п0 возникает избыточный крутящий момент.
дМ = Мт—Мк < 0, скорость вращения с -течением времени умень-
шается и возвращается к значению п — п0. При отклонении числа
оборотов в сторону п < п0 появляется избыточный крутящий мо-
мент бМ = Мт— Мк > 0, скорость вращения с течением времени
растет и также восстанавливается п = п0. Чем больше угол 6 между
касательными к характеристикам Мк = f(n) и Мт = f (п), тем боль-
ше собственная устойчивость двигателя.
Выше было сказано, что двигатель, обладающий устойчивостью,
может работать без регулятора. Однако практически регулятор
числа оборотов необходим и в этом случае. Его назначением явля-
ется уменьшение возможных отклонений от заданного режима.
Если характеристики Мт(п) и Мк(п) меняются так, как пока-
зано на рис. 2.1, б, то двигатель является неустойчивым объектом.
Действительно, Мт < Мк для п < п0 и Мг > Мк для п > п0, при
малейшем отклонении числа оборотов от п0 с течением времени
двигатель будет все больше и больше отходить от исходного режи-
ма. Число оборотов двигателя будет непрерывно уменьшаться, если
первоначально п < п0, и будет непрерывно возрастать, если
первоначально п > п0. При таком протекании характеристики ра-
бота двигателя без регулятора невозможна.
Протекание характеристики Мт = f(n) зависит от того, по ка-
кому закону с изменением числа оборотов в двигатель подается
топливо. Если предположить, что подача топлива осуществляется
так, что неизменной остается температура газа перед турбиной,
момент турбины с увеличением числа оборотов будет возрастать.
Если же принять, что подача топлива для любых чисел оборотов
§ 1. Понятие о собственной устойчивости энергетических систем
43
остается постоянной (двигатель с независимым приводом топлив-
ного насоса), кривая момента турбины будет близка к гиперболе.
Последнее следует ив предположения, что мощность турбины про-
порциональна введенному в двигатель топливу. Тогда, используя
известную зависимость между мощностью, крутящим моментом и
числом оборотов двигателя М = 53,7 N/n, получим, что для ТРД
с неизменной подачей топлива Мт = const/л
На рис. 2.2 показано протекание статических характеристик Мк
и Мт для ТРД во всем диапазоне чисел оборотов от холостого хо-
да до режима максимальной тяги. Момент компрессора показан
как функция только числа оборотов, момент турбины представлен
в виде двух семейств характеристик: Мт = f(n, Т*3) и Мт = f(n, G).
Равновесным режимом работы соответствуют точки пересечения
характеристик этих двух семейств с кривой MK = f(n).
Как это следует из рис. 2.2, а, каждая характеристика семей-
ства Мг = /(л, Г’ ) имеет две точки пересечения с характеристикой
Мк = /(л), для выделенной на графике кривой это точки а и б.
Вблизи режима пб двигатель является устойчивым, а вблизи па он
неустойчив. Аналогичные рассуждения можно повторить и для дру-
гих характеристик семейства Мт = f(rt, Т*3).
Из протекания характеристик рис. 2.2, а видно, что на равно-
весных режимах с ростом числа оборотов температура Т\ сначала
падает, а затем возрастает, проходя через минимум. Каждая ха-
рактеристика Мт = f(n) для Г* = const примерно совпадает с ха-
рактеристикой Mr = f(n) для ТРД с определенным фиксирован-
ным положением регулирующего органа топливного насоса. Отсю-
1 В выражении М = 53,7 N/n момент М в н.м (ньютон-метрах); мощность
N в кет; угловая скорость п в об/мин. В старой системе единиц М = 716,2 N/n,
где М в кГ м; N в л. с. и п в об/мин.
44
Глава II. ГТД на химическом топливе, как объекты регулирования
да следует, что при работе в области малых чисел оборотов дви-
гатель вместе с топливным насосом оказывается малоустойчивым
или даже неустойчивым объектом.
Если бы подача топлива в двигателе не зависела от изменения
числа оборотов и поддерживалась постоянной для данного режима
специальным регулятором расхода топлива, то характеристика
Mr = f(n) имела бы вблизи точки а такой вид, как это показано
на рис. 2.2, б. Двигатель при его работе на режиме, соответствую-
щем точке а, был бы устойчивым.
Сказанное выше об устойчивости ТРД с нерегулируемым соп-
лом в равной мере относится к ТРД с регулируемым соплом, к
ТВД и другим ГТД при условии, что в переходном процессе не из-
меняются площадь сечения выходного сопла, угол установки ло-
пастей винта и др. Анализ собственной устойчивости ТВД показы-
вает, что за счет особенностей протекания характеристик Мт и Мк
область устойчивой работы по числу оборотов у ТВД меньше, чем
У ТРД.
О собственной устойчивости ГТД можно судить не только по
взаимному расположению кривых движущего момента турбины и
момента сопротивления компрессора. Эти две характеристики мо-
гут быть заменены одной характеристикой избыточного момента
t>M (п) — Мт (п) — Мк (п).
Перестроенные таким путем характеристики ТРД, ранее пока-
занные на рис. 2.2, а, приведены теперь на рис. 2.3, б. Каждая кри-
вая этого семейства характеристик имеет две точки пересечения с
осью абсцисс, за исключением одной при Тзт1п , имеющей точку
касания па. Точки пересечения или точка касания определяют рав-
новесные статические режимы.
Статический режим устойчив в том случае, если избыточный
момент двигателя отрицателен при отклонении числа оборотов в
сторону увеличения, и положителен при отклонении п в сторону
уменьшения. Как это следует из особенностей протекания харак-
§ 2. Уравнения движения различных ГТД
45
теристик дМ(п), статические режимы, соответствующие п0 > па —
устойчивы, а для па<па-—неустойчивы. Этот вывод, очевидно,
совпадает с выводом об устойчивости ТРД, сделанным при анали-
зе характеристик рис. 2.2, а.
На рис. 2.3, а показано протекание характеристик избыточного
момента, соответствующих характеристикам рис. 2.2, б. Вид ха-
рактеристик подтверждает вывод, что в этом случае все статичес-
кие режимы устойчивы.
Будем оценивать собственную устойчивость двигателя с по-
мощью коэффициента v = tg0i — tg02 (см. рис. 2,1, а). Заменим
тангенсы углов 0i и 02 через частные производные движущего мо-
мента и момента сопротивления по числу оборотов, учтя, что кру-
тящие моменты зависят от нескольких переменных *. Получим
йМд
виж ___ dMc(inp
дп дп
(2-1)
или для ТРД
В случае использования характеристики избыточного момента
эти выражения примут вид
Двигатель устойчив, если v < 0. Он неустойчив при v > 0 и ней-
трален (находится на границе устойчивости) при v = 0.
§ 2. УРАВНЕНИЯ ДВИЖЕНИЯ РАЗЛИЧНЫХ ГТД
Линеаризация характеристик
Функциональные зависимости между различными параметрами
авиационных двигателей, как правило, нелинейны. Их использова-
ние при выводе уравнений движения двигателей, т. е. уравнений,
описывающих переходные процессы в двигателях при действии
на них каких-либо возмущений, приводит к тому, что уравнения
движения получаются нелинейными дифференциальными уравне-
ниями. Современный математический аппарат не дает возможности
решать нелинейные дифференциальные уравнения общего типа
аналитическим путем.
1 Выше мы принимали, что момент компрессора зависит только от числа
оборотов двигателя. Будет точнее считать его функцией числа оборотов и тем-
пературы газа перед турбиной (или расхода топлива). С ростом температуры
объемный расход газа через сопловой аппарат турбины возрастает. Это требует
от компрессора, при заданных числах оборотов увеличения напора, сопровож-
дающегося ростом крутящего момента.
46 Глава II. ГТД на химическом топливе, как объекты регулирования
Если рассматривать малые отклонения от некоторого заданного
равновесного режима работы двигателя, то каждая из нелинейных
зависимостей, характеризующих его рабочий процесс вблизи рав-
новесного режима, может быть заменена отрезком прямой. Пере-
ход к линейной функциональной зависимости приводит к линейным
дифференциальным уравнениям, что дает Возможность исследовать
свойства двигателей на переходных режимах. Рассмотрим принци-
пы линеаризации характеристик.
Линеаризация нелинейной характеристики, определяющей зави-
Рис. 2.4
симость между двумя переменны-
ми величинами, заключается в
замене ее касательной, проведен-
ной к ней в точке, соответствую-
щей исходному статическому ре-
жиму. В качестве примера на
рис. 2.4 показана линеаризация
характеристики центробежного
чувствительного элемента регу-
ляра числа оборотов. Зависи-
мость между центробежной силой
Рц и числом оборотов п может
быть задана графически, или
уравнением Рч = сп2, где с — ко-
эффициент пропорциональности.
При линеаризации графиче-
ской характеристики проводится
касательная в точке, соответствующей исходному статическому ре-
жиму п0, задается малое приращение числа оборотов би и опре-
деляется приращение центробежной силы 6РЧ.
Если нелинейная зависимость дана в виде уравнения, то она
заменяется уравнением прямой. В нашем случае это
индекс «О» при производной указывает на то, что при вычислении
производной должно быть принято п = и0, т. е.
= 2сп0.
\ an Jo
Следовательно,
ЬРЦ = 2cn0fri.
(2.4)
В общем случае линеаризация нелинейной функции одного или
нескольких аргументов заключается в разложении ее в ряд Тейло-
ра в окрестности точки равновесного режима.
§ 2. Уравнения движения различных ГТД
47
Приращение функции определяется при малом приращении
аргументов только по линейной части ряда, нелинейные члены от-
брасываются. Пусть имеется функция F(x, у, z)'=0, для которой
х0, Уо, zo— исходные значения аргументов. Требуется найти при-
ращение функции в окрестности рассматриваемой точки при пере-
ходе к новым значениям аргументов х = х0 + бх; у = Уо + бу; z —
= z0 + бг. Тогда
F(x, у, z)^F(x0, у0, z0) + (~'\ 6х+ (-¥-'} 8у + (~\ 8z,
\ дх Jq \ ду /о \ oz /о
или
8F (х, у, 8х + (-^\ бу + (-^| Sz- (2-5)
\ дх /о \ ду /о \ dz /о
Индекс «О» при частных производных, как и раньше, указывает,
что производные берутся при исходных значениях аргументов.
Линеаризация нелинейных характеристик допустима только в
тех случаях, когда рассматриваются малые отклонения. Будем
считать малыми такие отклонений, при котовых в рассматриваемой
характеристике еще нет ощутимых расхождений между данной
кривой и касательной к ней. Это определение малых отклонений,
для которых допустима линеаризация, не является строгим. Вели-
чина отклонений зависит от характера задачи, при решении кото-
рой используются линеаризованные статические характеристики, и
от требуемой точности решения.
Если линеаризуется функция от нескольких параметров, то сле-
дует аналогично решить вопрос о законности линеаризации, рас-
сматривая в отдельности характеристики, построенные по каждому
из параметров, и касательные к ним в точках, соответствующих
исходному статическому режиму. Если характеристики заданы
уравнениями, то исследование расхождений между кривой и каса-
тельной к ней может быть проведено также и аналитическим путем.
Для одной и той же характеристики наклоны линеаризующих пря-
мых различны в зависимости от того, для какой из исходных точек
характеристики проводится линеаризация.
Рассматривая двигатели как объекты регулирования, будем
предполагать, что при малых отклонениях указанным выше спосо-
бом можно линеаризовать любую из статических характеристик
двигателя. Следует иметь в виду, что рассмотренный способ линеа-
ризации не является единственным. Возможны и другие способы
линеаризации, при которых кривая заменяется не касательной к
ней в заданной ее точке, а секущей.
Уравнение ТРД как объекта регулирования
При выдаче задания на проектирование регулирующей аппара-
туры наряду с оценкой устойчивости двигателя существенно также
знание количественных показателей, которыми определялось бы
48
Глава II. ГТД на химическом топливе, как объекты регулирования
поведение двигателя при его работе без регулятора. Такими пока-
зателями являются величины коэффициентов в дифференциальном
уравнении двигателя как объекта регулирования, которое исполь-
зуется при исследовании процессов регулирования.
Газотурбинный двигатель на переходных режимах может в от-
дельные моменты времени накапливать или расходовать рабочее
тело, тепловую и механическую энергию. Однако, учитывая неболь-
шой объем газовоздушного тракта двигателя, обычно упрощают
исследование переходных процессов и пренебрегают аккумулирую-
щими способностями двигателя в отношении рабочего тела и теп-
ловой энергии. Тогда поведение двигателя на переходных режимах
описывается только одним известным уравнением динамики
J = 8М, (2.6)
dt
где ЬМ = Мт — Мк — избыточный крутящий момент;
J — момент инерции вращающихся частей двигателя;
со — угловая скорость вращения ротора двигателя, равная
~ рад/сек-,
t — время.
Полагая расход топлива G независимым от числа оборотов дви-
гателя, установим функциональную зависимость
8М = МТ — MK~f(n, G).
Рассмотрим малые отклонения от некоторого заданного режима
работы. Примем для малых приращений п и G при отклонениях
от исходного статического режима обозначения б/г = п — п0 и
.6G = G — Go. Соответственно с этим будем считать би > 0, когда
п > п0 и 6G > 0, когда G > Go.
Проведя линеаризацию зависимости бМ = f(n, G) и учтя, что
бсИ0 = 0 (так как Мто = Мк0), получим
= + 6G. (2.7)
\ дп /о п \ dG )о v ’
Укажем также, что
rfu> ________________ л dn л d8n
dt ~ 30 dt ~ 30 dt ’
так как би = п — п0 и dna[dt = 0. Подставляя в уравнение (2.6)
это значение dtoldt и используя выражение (2.7), получим
6О. (2.8)
30 dt \ дп /о \ dG /о V
Введем относительные координаты Ап = Ьп1пБ и AG — 6G/GB,
пользование которыми удобнее, чем пользование абсолютными
§ 2. Уравнения движения различных ГТД
49
координатами бп и 6G. Величины., к которым относят абсолютные
значения отклонений параметров, называют базисными величинами
и обозначают с индексом «Б». В качестве базисных могут быть
взяты различные постоянные величины. При выводе уравнения ТРД
как объекта регулирования удобно принять за базисные величины
максимальное число оборотов и соответствующий им расход топ-
лива в стартовых условиях.
Умножим и разделим правую часть выражения (2.8) на йБ,
, / дЪМ \ „
разделим его обе части на —I——10 . 1огда получим следующее
уравнение ТРД как объекта регулирования:
Та—+ A« = MG. (2.9)
Уравнение (2.9) является линейным дифференциальным урав-
нением с постоянными коэффициентами и с правой частью.
В нем
= —дхд-; (2-10)
доМ\
дп )о
(2.И)
Коэффициент Тд имеет размерность времени и называется по-
стоянной времени двигателя. Постоянная времени характеризует
инерционное запаздывание в изменении числа оборотов двигателя
при изменении подачи топлива. По физическому смыслу любая по-
стоянная времени— величина положительная. В выражении (2.10)
Та > 0 в том случае, если рассматривается устойчивый двигатель,
у которого
v = <о.
\ дп /о
Если же двигатель неустойчив, то для сохранения условия
Тэ>0 уравнению (2.9) придают вид
Td^--\n = kdKG. (2.12)
at
Безразмерный коэффициент kg носит название коэффициента
усиления двигателя. Он характеризует чувствительность двигателя
к изменению подачи топлива. В отличие от постоянной времени Та
коэффициент усиления характеризует не только величину Ап в пе-
реходном процессе, но и устанавливает связь между подачей топ
лива и числом оборотов для нового статического режима после
50
Глава II. ГТД на химическом топливе, как объекты регулирования
окончания переходного процесса. Коэффициенты усиления по раз-
личным независимым переменным, как мы увидим дальше, могут
быть как положительными, так и отрицательными величинами. Что
же касается коэффициента усиления kg, то у устойчивого двигателя
он всегда положителен, так как с увеличением подачи топлива
число оборотов двигателя всегда возрастает. Численными значе-
ниями Тд и kg определяются свойства ТРД как объекта регулиро-
вания. Как следует из приведенных выше выражений (2.10) и (2.11),
значение Тд не зависит, а значение ka зависит от выбора базисных
величин при введении относитель-
ных координат.
Численные значения Тд и kg
определяются как опытным пу-
тем, так и путем расчета. Коэф-
фициент усиления kg легко найти
по заданной статической харак-
теристике двигателя G = f (ц).
Для исходного статического ре-
жима, которому соответствуют’
п = п0 и G = Go (рис. 2.5), бе-
рутся значения бп и 6G при не-
котором малом отклонении от ис-
ходного режима. Величина kg
подсчитывается как
, Лп 8п Gs
КА------------ ---
ДО &G nR ’
О
или после перехода к пределу
—--------------------------------------
6 пБ / ао х •
\ dn )о
(2.13)
Иногда в литературе по регулированию двигателей уравнение
(2.9) приводится в несколько иной форме, а именно:
^-^ + P(,A«==AG, (2.14)
где тд = Tgjkg и рэ = \/kg. В дальнейшем будем записывать урав-
нение ТРД как объекта регулирования в форме (2.9).
Влияние основных параметров ТРД, его режима работы
и изменения внешних условий на величину Тд и kg.
Численные значения Тд и kg существенно зависят от основных
расчетных параметров ТРД: л* и Т$. Переход к другим размерам
двигателя, дросселирование двигателя по числу оборотов и изме-
нение внешних условий также отражается на величинах Тд и kg.
§ 2. Уравнения движения различных ГТД
51
Рассмотрим зависимость динамических коэффициентов ТРД от
его диаметральных размеров. Для этого сравним два геометриче-
ски подобных двигателя с равными л’, Т*3, скоростями воздуха
на входе в компрессор и окружными скоростями на 'внешних диа-
метрах компрессоров. Значение производной дбМ/дп, 'стоящей в
знаменателе выражения (2.10), овязано с величиной избыточного
момента, который увеличивается с ростом расхода воздуха.
Момент инерции ротора с учетом толщины дисков пропорциона-
лен пятой степени диаметра -двигателя, а расход воздуха только
его квадрату. Поэтому с увеличением диаметральных размеров
числитель в выражении (2.10) будет расти быстрее знаменателя.
Следовательно, с увеличением поперечных размеров ТРД его по-
стоянная (времени возрастает.
Увеличение диаметральных размеров ТРД приводит к сниже-
нию kg. Это следует из статических характеристик G = f(n) срав-
ниваемых двигателей. На режимах с равными окружными скоро-
стями кривая G = f(n) пойдет более круто у двигателя больших
размеров, как имеющего большие* расходы воздуха. Следователь-
но, kg снижается (при условии равенства Gb/пб).
Увеличение расчетного значения л* при неизменном числе обо-
ротов и поперечных размерах двигателя приводит к росту произ-
водной и к снижению производной ddM/dG. В результате
и Tg, и kg уменьшаются.
Рост степени подогрева воздуха 0 = Т*3/Т2 приводит к увели-
чению дЬМ/дп и к снижению Tg. Коэффициент усиления kg оста-
нется почти неизменным, так как уменьшение Ьп/bG из статической
характеристики двигателя с большим 0 будет компенсироваться
РОСТОМ Gjs.
Увеличение числа оборотов двигателя сопровождается ростом
д^М/дп и падением Tg (рис. 2.6, а). Как это следует из статической
характеристики (см. рис. 2.5) и выражения (2.13), приращение
расхода топлива 6G приводит к росту числа оборотов двигателя.
С ростом скорости вращения расход воздуха увеличивается, что
сопровождается падением kg (рис. 2.6,6).
Производная дбМ/дп зависит от величины к. п. д. компрессора.
У ТРД с высоконапорными компрессорами т]*на максимальном
числе оборотов ниже, чем на крейсерском режиме. Учитывая изме-
нение Ge и ц* по числу оборотов, следует ожидать, что максимум
д^М/дп будет близок к крейсерскому режиму. В этом случае с ро-
стом числа оборотов Tg будет сначала падать, а затем, пройдя через
минимум, несколько возрастать.
Разработка регулирующей аппаратуры чаще всего ведется одно*
временно с доводкой двигателя, поэтому в (начальной стадии до-
водочных работ оказывается возможным получить опытным путем
значения Tg и kg лишь для стендовых условий. Если известно из-
52
Глава II. ГТД на химическом топливе, как объекты регулирования
менение Тд и kg в зависимости от п для Н = 0 и Мн = 0, то, поль-
зуясь методом подобия, для ТРД с нерегулируемым соплом можно
определить приближенные значения Тд и kg и для условий полета
на различных высотах с разными скоростями. На этой основе мо-
жет быть 'произведен пересчет значений Тд и kg и для других ГТД.
Например, если при стендовых испытаниях для ТРД с регулируе-
мым соплом определены Тд = f(n) и kg = f (п) при нескольких по-
стоянных значениях площади критического сечения выходного
сопла, то по известным формулам приведения можно каждую из
Рис. 2.6
этих характеристик пересчитать применительно к условиям полета
на разных высотах и с различными скоростями.
Известно, что подобные режимы работы ТРД характеризуются
равенством приведенных чисел оборотов, расходов воздуха и рас-
ходов топлива. Иначе говоря, на подобных режимах имеют место
равенства: ____ __________
п = п' . г; = .
1/Е уТг ’ рн р*н
G _ G'
РнУГ'гн Рн^Т н
Они показывают, как должны меняться число оборотов, расход воз-
духа и расход топлива при переходе от внешних условий, характе-
ризуемых р*н и Т*н', к новым внешним условиям с рИ и Т*н.
Покажем, что постоянная времени Тд с переходом к другим
внешним условиям изменяется обратно пропорционально измене-
нию расхода воздуха. Из выражения (2.10) следует, что измене-
ние Тд при переходе на другие р*И и Т*н может происходить только
за счет изменения частной производной <ЭбМ/<Эн, Из 'формулы
М = 53,7 N[n, считая постоянными к. п. д. турбины и коэффициент
§ 2. Уравнения движения различных ГТД
53
выделения тепла в камере сгорания и принимая, что мощность
пропорциональна расходу топлива, находим, что бМ = 53,7 6(&G/fi).
Используя связь между числом оборотов и расходом топлива на
подобных режимах, получим
8М = 8М' ,
* Г '
Рн
(2.15)
где 6Л4'— избыточный момент при условиях и Т^;
бМ — избыточный момент при условиях р*н и Т*н.
Применяя еще раз формулы подобия, получим
Откуда следует, что значение постоянной времени двигателя при
новых р*н и Тн равно
Тд=Т'д
* f
Рн
*
Рн
или
Тд = Т’д-^,
Ge
(2.16)
где Т’д —значение постоянной времени при р'^ и . Из выраже-
ния (2.16) следует, что при равных приведенных числах оборотов-
двигателя постоянная времени уменьшается с ростом скорости и
возрастает с увеличением высоты полета.
Хотя коэффициент усиления kg — величина безразмерная, с пе-
реходом к другим внешним условиям он также претерпевает изме-
нения, так как принятые при его определении базисные величи-
ны пБ и Ge следует считать неизменными. Применение формул
приведения к производной дбМ/dG показывает, что она изменяется
пропорционально Т*н/Т*н > т- е-
д&М
dG
1 / Т'н дШ'
V Г’ дй’ •
Г1
54
Глава II. ГТД на химическом топливе, как объекты регулирования
а производная dbMfdn, как уже было выяснено, изменяется про-
порционально
Рн
Рн
Т
В результате получаем, что для других внешних условий коэффи-
циент усиления
о о *
Рн
(2.17)
Из выражения (2.17) видно, что при равных приведенных чис-
лах оборотов kg уменьшается с ростом скорости и увеличивается
с высотой полета. Выражения (2.16) и (2.17) не являются расчет-
ными. Из выражения (2.16) видна только зависимость Тд от рас-
хода воздуха. В выражение (2.17) в явном виде расход воздуха
не входит, но его изменение оказывает существенное влияние на kg.
Согласно выражению (2.11) величина kg зависит от производных
/ дъм \ / дъм \ гт
—-— и —— . Первая из них пропорциональна расходу воз-
\ дп / \ ди /
духа, а вторая — обратно пропорциональна корню квадратному из
температуры торможения воздуха. В результате получается зави-
симость kg от давления торможения воздуха перед двигателем.
При подсчете Tg и kg для различных условий полета следует
знать, как в действительности меняется расход воздуха. Для этого
следует учитывать потери полного давления во входном диффузоре
двигателя и уменьшение производительности компрессора при сни-
жении приведенного числа оборотов. Полученные зависимости
Т9(п, Мн, Н) и kg(n, М-н, Н) строятся по приведенному числу обо-
ротов двигателя. Определение Тд и kg для различных внешних усло-
вий облегчается тем, что для предварительного динамического рас-
чета системы регулирования обычно важно знать лишь приблизи-
тельное их значение. Погрешность на 20 4- 30% при таких расчетах
можно считать допустимой. Пример расчета Тд и kg приведен в кон-
це главы.
Уравнение ТРД, рассматриваемого как объект регулирования
совместно с топливным насосом
Производительность топливного насоса зависит от скорости вра-
щения его вала и от положения регулирующего органа насоса.
В плунжерных насосах таким регулирующим органом является
поршень сервомотора, изменяющий наклон шайбы, в системах пи-
J 2. Уравнения движения различных ГТД
55
тания двигателя с шестеренным насосом регулирующим органом
служит игла для 'перепуска топлива
Примем в общем виде, что производительности насоса опреде-
ляется выражением G = G(n, т), где п — число оборотов двига-
теля (число оборотов вала насоса пропорционально числу оборотов
двигателя); т — координата, характеризующая положение регули-
рующего органа. При малых отклонениях от исходного режима
приращение 'производительности равно
/ dG \ . [ dG \ „
6G ~ ---- б»+ ----- бт.
\ dn /о \ dm /о
Перейдя к относительным координатам AG = dG/GB; Ан- =
= Ъп/пБ и Am = btnftnE, где GB, пБ и тБ — базисные значения про-
изводительности насоса, числа оборотов и координаты регулирую-
щего органа, получим уравнение Насоса в виде
AG = kn\n (2.18)
где
, ( dG \ пБ , I dG \ тБ
k„ = ---- ---- и кт= [------ -----.
\ dn /о Ge т \ dm /о GB
С помощью уравнения (2.18) исключим из уравнения (2.9) от-
носительное приращение расхода топлива AG и после преобразо-
вания получим дифференциальное уравнение ТРД, рассматривае-
мого как объект регулирования совместно с топливным насосом:
Td.B^ + An = ^.BAm. (2.19)
at
В этом уравнении
4, _ (2 211

1 — kdkn
Используем выражение (2.13) для преобразования (2.20). По-
лучим ^.« = —Д-— (2-22) \ dn /но / dG \ \ dn ]до
1 Схемы регулирования подачи топлива рассмотрены в гл. V.
56
Глава II. ГТД на химическом топливе, как объекты регулирования
На рис. 2.7, а совмещены характеристики потребного и распола-
гаемых расходов топлива. Каждой кривой располагаемого расхода
соответствует некоторое значение т. Возможные режимы работы
двигателя с насосом определяются точками 1, 2, 3, 4, 5 пересечения
кривых, один из таких режимов выбран за общий базисный для
двигателя и насоса.
Из анализа выражений (2.22) и взаимного расположения харак-
теристик располагаемого и потребного расходов топлива следует,
что Тд.н>Та. Величина Та.„ тем больше, чем меньше потребный
расход топлива при данном числе оборотов, или чем ниже число
X и ГТ I / dG \
оборотов при неизменных Мн- и п. При i—— / Hr- , 'Стремя-
’ дп !но/ \ дп ,'до
щемся к единице, величина Тд_н стремится к оо.
Влияние режима работы на kg.H удобнее проследить с помощью
выражения (2.21) и характеристик на рис. 2.7, а. Числитель выра-
жения (2.21) состоит из произведения kdkm. Коэффициент kt
с уменьшением потребного расхода топлива растет, а коэффи-
циент km падает со снижением потребного расхода при фиксиро-
ванном числе оборотов двигателя и растет при снижении потреб-
§ 2. Уравнения движения различных ГТД
57
ного расхода за счет падения скорости вращения. Однако в своем
изменении произведение k;)km остается конечной величиной. По-
скольку знаменатели в выражениях (2.20) и (2.21) одинаковы, при
I dG \ // дО \ ,
—— / -т— , стремящемся к единице, величина «эн стре-
\ дп /но/ \ дп /до
мится к оо так же, как и 7эн- При / ---- >1 коэф-
\ дп 1нО/ \ дп /до
фициенты Тд.н и ka.H становятся отрицательными. Разрыв функций
Тэ.н = f(n) и kg.H — f(n) говорит о том, что ТРД с топливным насо-
сом как объект регулирования потерял устойчивость. В этом случае
уравнение (2.19) приводится к виду
Т \n = kd H\m,
о.н dt о.н >
(2.24)
где
Возможная потеря устойчивости видна также из характеристики
(рис. 2.7, б), где показана зависимость между положением регу-
лирующего органа насоса и числом оборотов ТРД. При п < пт,
когда имеет место «обратное» действие регулирующего органа,
меньшим числам оборотов соответствуют большие значения коор-
динаты т — двигатель неустойчив. При отклонении числа оборотов
в сторону увеличения располагаемая подача топлива при т = const
будет больше потребной и двигатель начнет разгоняться до нового
устойчивого состояния равновесия. При отклонении числа оборотов
в сторону уменьшения потребная подача будет больше распола-
гаемой, двигатель начнет уменьшать число оборотов вплоть до
полной остановки. Этот вывод о связи устойчивости ТРД с избы-
точным расходом топлива полностью соответствует зависимости
устойчивости от избыточного момента (см. рис. 2.2, а).
58
Глава II. ГТД на химическом топливе, как объекты регулирования
По заданным величинам Тэ, kg и характеристикам располагае-
мых и потребных расходов топлива с помощью выражений (2.22)
и (2.23) могут быть вычислены Тд.н и kg.H, их примерный вид пока-
зан на рис. 2.8, а и б.
Уравнения других типов одновальных ГТД
Для ТРДФ с регулируемым соплом вывод уравнения двигателя
как объекта регулирования отличается от вывода уравнения (2.9)
лишь тем, что момент турбины Мт, а следовательно, и избыточный
момент 6М является функцией не только числа оборотов п и по-
дачи топлива в основную камеру сгорания. На величину Мт будут
также оказывать влияние подача топлива в форсажную камеру бф
и площадь критического сечения выходного сопла, т. е. бМ =
= f(n, G, G^, s). Здесь s — координата, определяющая положение
элемента, которым регулируется площадь критического сечения
выходного сопла.
Для исходного статического режима
6Л1О = fo (п, G, бф, s) = °,
Считая, что двигатель является устойчивым, и повторяя те же
выкладки, что и при выводе уравнения (2.9), получим
Тд + Дп = kd\G + kd + kds\s. (2.25)
at
В этом уравнении Тд и kg определяются теми же выражениями, что
и для уравнения (2.9), т. е. выражениями (2.10) и (2.11):
/ д&М \
\дбф /° Офв
Если при увеличении s площадь критического сечения сопла
возрастает, то kgs > 0. Коэффициент kg# < 0, так как с увеличе-
§ 2. Уравнения движения различных ГТД
59
нием подачи топлива в форсажную камеру давление в ней растет
и число оборотов двигателя падает.
Рассмотрим ТРДФ с приводными насосами подачи топлива в
основную и форсажную камеры сгорания. Примем, что производи-
тельность насосов определяется выражениями G= G(n, tri) и
°Ф = °ф (п, тф), (2.26)
а после линеаризации
AG = / dG > к К — АпД ' dG \ тБ
Io Ge ' dm 1 о Gs
AG. = ( дСф- к П R 1 — \п + ' dG \ тБ
ф \ дп /о ов дтф /0
Аиг,
А/Иф
(Gs, пБ и тБ приняты общими для обоих насосов), или по фор-
муле (2.18)
Исключая
и AGgg, после
Тд.н
dt
В этом уравнении
AG = &nAn + ktnkm,
AG^ = ^пфДп + ^тфА/Пф. (2.27)
из (2.25) с помощью двух последних выражений AG
преобразования получим
d^n + An = kdltAm + кд.Н'ф&тф + kSHbs.
(2.28)
'р ___T'g
1 kd^n '^д-ф^пф
Как уже было сказано /гд > 0, a kd.$ < 0. Потеря устойчивости
наступает при 1 — kpkn — кэ.фкпф 0. Откуда следует, что основ-
ной насос уменьшает собственную устойчивость ТРДФ (также, как
и у нефорсажного ТРД), а форсажный насос увеличивает. Таким
образом, пёреход на форсажный режим увеличивает область чисел
оборотов, в которой ТРДФ может устойчиво работать без регуля-
тора.
Для одновального ТВД дМ = f(ti, G, <р), где <р — угол установки
лопастей винта. Избыточный момент ЬМ = МТ— Мк— Мв, где
Мд—момент воздушного винта, приведенный к валу двигателя.
Соответственно уравнение ТВД как объекта регулирования
имеет вид
+ An = kd\G +
at
в этом уравнении kd!9 < 0.
Приведенные выше уравнения относятся к случаю регулирова-
ния числа оборотов. Так же могут быть выведены и дифференци-
альные уравнения, которыми определяется при малых отклонениях
от заданного режима изменение температуры перед турбиной Т\
(2.29)
(2.30)
60
Глава II. ГТД на химическом топливе, как объекты регулирования
или тяги двигателя R. Часто более удобной является запись диф-
ференциальных уравнений в операторной форме. Так, например,
в операторной форме записи уравнение (2.30) примет вид
(Tdp + 1) An = k<AG + ^А?> (2.31)
где р = d[dt — оператор дифференцирований. В дальнейшем будут
использоваться обе формы записи дифференциальных уравнений.
ТРДФ как объект регулирования по силе тяги
В настоящее время большое значение приобрела задача регу-
лирования двигателя совместно с летательным аппаратом. Такое
регулирование дает возможность более полно использовать как
двигатель, так и летательный аппарат. С этой точки зрения важно
знать динамические свойства ТРДФ, рассматривая в качестве регу-
лируемого параметра непосредственно его тягу. Для этой цели
необходимо составить уравнения связи между отдельными пара-
метрами двигателя и дополнить их уравнением движения ротора на
неустановившемся режиме работы двигателя.
В переходном процессе принимаются постоянными теплоемко-
сти воздуха и газа, потери полного давления по проточной части
двигателя, коэффициенты избытка воздуха и выделения тепла. При
малых отклонениях от стационарного режима переходные процес-
сы рассматриваются как квазистационарные.
Линеаризация исходной системы уравнений рабочего процесса
двигателя и исключение промежуточных. параметров приводит
уравнение ТРДФ как объекта регулирования по силе тяги к виду 1
(Тдр + 1) АД = {Тар + kG) AG + (Тофр + koj №ф + (Tsp + ks) As +
+ \НР + + (ТР{1р + kpH) dpH (Ттнр + kTfp) АТн +
+ (Тар + ka) кадиф. (2.32)
В случае ТРД без форсажа для неизменных внешних условий
уравнение (2.32) значительно упрощается и принимает вид
(Тдр + 1) АД = (Top + ka) AG. (2.33)
Громоздкость исходной системы уравнений и ее решения не
дают возможности привести здесь вывод уравнений (2.32) и выра-
жений, для входящих в него постоянных времени и коэффициентов
усиления.
1 Это уравнение получено В. И. Новиковым. Им также проведено экспери-
ментальное исследование ТРД как объекта регулирования по силе тяги, изло-
женное в работах [14], [15].
§ 2. Уравнения движения различных ГТД
61
Следует отметить, что на переходный процесс ТРД по силе тяги
оказывает влияние не только величина независимых переменных
Л<7, AGje, Д2.н, Дрн и ДТн, но и скорость их изменения.
Двухкаскадный ТРДФ как объект регулирования
Рассмотрим двухкаскадный ТРДФ, предположив независимый
от вала двигателя привод основного и 'форсажного топливных насо-
сов. Ранее приведенное уравнение динамики (2.6)
= 82И
dt
справедливо для обоих роторов. Между компрессорами и турбина-
ми обоих каскадов есть газодинамическая связь, изменение числа
оборотов одного каскада вызывает изменение моментов и числа
оборотов другого. Поэтому для каждого каскада примем функцио-
нальную зависимость
= пв, Gt 6ф, s). (2.34)
Проведя линеаризацию, зависимостей (2.34), после преобразо-
ваний уравнения (2.6) получим:
для низконапорного каскада
+ An„ = k&AG + кОфН AG0 + kn Ьпв + kSHbs, (2.35)
для высоконапорного каскада
Тв ——— 4* Д«в == ^oeAG 4* kc в &Оф-]~ kn Апн 4- &seAs. (2.36)
dt ф н
Постоянные времени и коэффициенты усиления в уравнении
(2.35) определяют из выражений:
л / д6Ми \
„ 30 " , _ \ dG ) 0 ° Б .
“ / дЬМн \ / двМн \ пнБ
\ дпн )о \ дпн /о
/о
62
Глава II. ГТД на химическом топливе, как объекты регулирования
Для уравнения (2.36) постоянная времени и коэффициенты
усиления могут быть записаны аналогично с соответствующей за-
меной индексов. Следовательно, для вычисления коэффициентов,,
входящих в уравнения (2.35) и (2.36), нужно иметь десять харак-
теристик моментов в таком виде, как это показано на рис. 2.9—
2.12 >.
Рассмотрим знаки этих коэффициентов. Они будут определяться
знаком производной, стоящей в числителе, так как для двигателей,,
к - дЪМн. п дЪМв
обладающих устойчивостью, --------- < 0 и ------ < 0. Оба коэф-
опн дпв
фициента усиления по основному топливу kGK и kGe положительны,
так как с ростом расхода топлива температура газа увеличивается
и избыточные моменты растут.
Коэффициент ka^H < 0 потому, что с ростом расхода форсаж-
ного топлива увеличивается давление в форсажной камере и умень-
шается избыточный момент низконапорного каскада.
Влияние увеличения G# на избыточный момент высоконапор-
ного каскада скажется только в том случае, если сопловой аппарат
1 Из десяти потребных характеристик на этих фигурах показаны только-
шесть. Зависимости dM(n), fiM(G), SM(G^) и 6A4(s) однотипны для обоих,
каскадов.
§ 2. Уравнения движения различных ГТД
63
низконапорного каскада, работает на докритическом перепаде дав-
ления, Поэтому кафв 0.
Если положить, что увеличение координаты s соответствует уве-
личению FKp, то с ростом s перепад давления на турбине низко-
папорного каскада возрастает, избыточные моменты увеличива-
ются, поэтому ksH > 0. Влияние изменения s на высоконапорный
каскад, также как и при воздействии Оф, имеет место только при
докритическом перепаде в сопловом аппарате турбины низконапор-
ного каскада. Следовательно, kse 0.
Если увеличить число оборотов высоконапорного каскада при
неизменном числе оборотов низконапорного каскада и расходе
топлива, то расход воздуха возрастет, л* компрессора низконапор-
ного каскада уменьшится и снизится потребный крутящий момент,
поэтому избыточный момент на низконапорном каскаде будет воз-
растать, хотя увеличение расхода воздуха сопровождается паде-
нием температуры газа перед турбиной. Таким образом, йП(;>0.
При увеличении числа оборотов низконапорного каскада за счет
роста п* увеличится л* всего компрессора. Это, обстоятельство
приведет к возрастанию Мк.в. Изменение Мт в почти не произойдет,
так как увеличение степени расширения скажется главным обра-
зом па турбине низконапорного каскада. Следовательно, рост пн
сопровождается падением бМв, отсюда kne < 0.
Уравнения (2.35) и (2.36), описывающие динамические свой-
ства двухкаскадного ТРД, можно решить как относительно Дпи,
так и Дп8. Проделаем это перейдя для упрощения к ТРД без фор-
сажа с постоянными размерами сопла (^0^ = 0 и Д$ = 0). Соот-
ветственно получим
+ (Т«+ +(1 - ЧЧ> +
+ (^вн 4-W%) ДО; (2.37)
64 Глава J1. ГТД на химическом топливе, как объекты регулирования
тнте. + (Тн + Тв) + (1 - knkn^ne = kGeTH +
+ (kGe -р kGHknj &G. (2.38)
Коэффициент при Дпн или Дп9 в уравнениях (2.37) и (2.38),
равный 1—k пн^пв , всегда положителен, так как произведение
knHkne < 0. Отсюда следует, что двухкаскадный ТРД с независи-
мым приводом топливного насоса как объект регулирования устой-
чив.
Перейдем к двухкаскадному ТРД, у которого топливный насос
приводится от вала двигателя. Возьмем уравнение насоса (2.18)
в виде
ДО = km\m + kn\n.
Примем, что топливный насос приводится от ротора высоконапор-
ного каскада и рассмотрим совместно уравнения (2.38) и (2.18).
Исключив переменную ДО, получим
г- + (Тн + Te-kGeknTH) + (1 -knknH-kGekn~
— kGHkn kn) \пв = kmkGeT„ + km (kGe + kGHkn ) Д/П. (2.39)
H at H
Очевидно, что топливный насос можно было связать с ротором
низконапорного каскада и рассматривать уравнение (2.18) совмест-
но с (2.37).
Коэффициенты усиления kGe, kGH и kng — положительны. Коэф-
фициент усиления knH < 0. Отсюда видно, что в левой части урав-
нения (2.39) коэффициенты при переменной Апв и ее производных
при некотором соотношении входящих в уравнение (2.39) постоян-
ных времени и коэффициентов усиления могут стать отрицатель-
ными. Подобная картина получится и в том случае, если топливный
насос будет приводиться от ротора низконапорного каскада.
Следует сделать вывод, что двухкаскадный ТРД, работающий
совместно с топливным насосом, подобно однокаскадному, с умень-
шением числа оборотов с некоторого момента может стать соб-
ственно неустойчивым. Соотношение между областями устойчивой
и неустойчивой работы по числу оборотов связано с индивидуаль-
ными свойствами конкретного двухкаскадного ТРД. Это соотноше-
ние также зависит от места привода топливного насоса.
§ 3. ВЛИЯНИЕ РАЗЛИЧНОГО РОДА ВОЗМУЩЕНИЙ
НА ИЗМЕНЕНИЕ РЕГУЛИРУЕМЫХ ПАРАМЕТРОВ ТРДФ
Рассмотрим поведение ТРДФ при воздействии на него различ-
ного рода возмущений. Под возмущающими воздействиями будем
понимать изменение расхода основного и форсажного топлива, пло-
§ 3. Влияние возмущений на изменение регулируемых параметров ТРДФ 65
щади сечения реактивного сопла, изменение внешних условий —
давления и температуры окружающей среды, скорости полета. За
регулируемые параметры примем числа оборотов, температуру газа
перед турбиной и тягу двигателя. Примем также, что приводы
основного и форсажного топливных насосов не связаны с ротором
двигателя.
Влияния возмущений на изменение числа оборотов двигателя
Рассматривая вначале в качестве регулируемого параметра
число оборотов двигателя, запишем
(Тдр 4* 1) Дм = kg\G 4- Ло ДСф 4- ksAs 4- kp крн 4- kp &Тн + ЫАн.
ф н п н н
(2.40)
Независимые переменные ДО, ДО$, As и т. д., расположенные
в правой части уравнения (2.40), могут изменяться произвольно.
Однако представляет интерес их изменение или по гармоническому
закону (это будет рассмотрено в гл. VI), или же в виде ступенча-
той, скачкообразной функции. В последнем случае воздействие
изменением, например, расхода форсажного топлива будет иметь
вид: при t < 0 относительное приращение Дбф = 0, при t > 0 вели-
чина Дбф = Абф! = const. Часто ступенчатую функцию берут в
виде единичной функции, т. е. для нашего случая AG,/ = AG,/,! = 1.
Проанализируем последовательно влияние отдельных видов воз-
мущений на число оборотов двигателя. Положим, что ДС = Дбр
Тогда
(Тдр+ 1)Дп = ^оДО1. (2.41)
Выражения
Дн = ^(1—е~^)ДО1> (2,42)
Д/г — Дпю(1—е Тд ) (2.43)
будут являться решением уравнения (2.41). В последнем выраже-
нии Д«ю = kG — относительное отклонение оборотов от исход-
ного статического режима в конце переходного процесса. Очевидно,
что при других возможных видах скачкообразного, воздействия,
предусмотренных в правой части уравнения (2.40), переходный про-
цесс по числу оборотов сохранит свой экспоненциальный характер.
Коэффициент усиления в уравнении (2.41)
/ д&м \
kG =-----
/ дШ \ «б
\ дп /о
3 Черкасов Б. А.
66 Глава II. ГТД на химическом топливе, как объекты регулирования
Для устойчивого двигателя дЪМ/дп < 0. Поэтому знак kG, а так-
же и остальных коэффициентов усиления уравнения (2.40) зависит
от знака числителя. С увеличением расхода основного топлива из-
быточный момент возрастает, так как растет температура газа пе-
ред турбиной. Поэтому kG > 0. Отсюда вид переходного процесса
в ТРД по числу оборотов при возмущении'в виде скачкообразного
изменения подачи топлива в основную камеру сгорания будет та-
ким, как это показано на рис. 2.13.
Такой же качественный характер переходного процесса по чис-
лу оборотов получится в случае воздействия изменением координа-
Рис. 2.13
Рис. 2.14
ты s и при изменении температуры окружающей среды. При увели-
чении s площадь критического сечения сопла возрастает, перепад
давления на турбине увеличивается, откуда dbMfds >0 и ks > 0.
В случае увеличения температуры окружающего воздуха возра-
стает температура за компрессором и снизится расход воздуха. За
счет этого поднимется температура газа перед турбиной (G=const)
и число оборотов двигателя начнет возрастать. Следовательно
дЬМ/дТ* > 0 и kT >0.
При увеличении расхода форсажного топлива перепад давле-
ния на турбине падает, избыточный момент уменьшается, производ-
ная ddM/dG^ < 0, откуда kG < 0. Переходный процесс, соответст-
вующий этому возмущению, показан на рис. 2.14. Этот характер
переходного процесса сохранится в случае возмущения увеличением
давления окружающего воздуха или скорости полета. Действитель-
но, оба вида возмущения за счет роста рн и за счет роста Мн при-
водят к увеличению расхода воздуха. При неизменном расходе
§ 3. Влияние возмущений на изменение регулируемых параметров ТРДФ 67
основного топлива температура газа перед турбиной падает, что
и приводит к снижению избыточного момента. Таким образом,
кр н 0 и k Мн 0.
Влияние возмущений на температуру газа перед турбиной
Выведем уравнение движения ТРДФ по температуре газа перед
турбиной. Примем в общем виде функциональную зависимость
Тз = Т'з(п, G, Оф, s, рн, Тн, тЛ.н).
Относительное приращение температуры газа АТ] при
приращениях независимых переменных равно
ДТз = kTnAn Д kioAG Д kTo Авф д kTsAs Д kTpApH Д
ф н
+ ктт АТн + ^тм ДМ/;,
п п 11
где
/ дТ„ \ пК
&гл=1——I —kro=
V дп /о ТЗБ
дТа \ ОБ
----- ------- и т. д.
•sc /о т’:Б
Решим выражение (2.45) относительно Ап и исключим
уравнения (2.40). После подстановки получим
малых
(2.45)
Ап из
№
(Тдр -(- 1) (АТз — kroAG — кта^АСтф — kr.As — ктР^Рц —
— ктт„АТн — кт:л^АА\н) = krn (koAG -ф ко^АОф -р ksAs +
+ kP[ Ар], + kT, АТ» д ймяДМя). (2.46)
После преобразований выражения (2.46) уравнение движения
ТРДФ по температуре газа будет иметь следующий вид:
(Тдр + 1) АТ] = [коктп 4~ kpo (Тдр + 1)1 &G [kc ктп + кто^ X
X (Тдр + 1)] Дбф Д [kskTn + Pts (Тдр + 1)1 Дз Д (kpHkin +
-^ктР[1(ТдР-У 1)] Др^ + + кттн(Тдр+ 1)]Д7Д Д
+ [&м ,,ктп + &тм„ (ТдР + 1)] ДМ//. (2.47)
п а
Следует отметить, что в левой части уравнения (2.47) осталась
та же постоянная времени Та, что и ,в уравнении (2.40). Это не слу-
чайно и объясняется следующим.
3*
68
Глава II. ГТД на химическом топливе, как объекты регулирования
При равных температурах воздуха за компрессором температу-
ра газа перед турбиной определяется соотношением между расхо-
дами воздуха и топливом. В принятую зависимость (2.44) расход
воздуха явно не входит, он зависит от числа оборотов ротора. От-
сюда следует, что как изменение п, так и изменение температуры
газа перед турбиной определяется постоянной времени Тр.
В этой же главе было составлено уравнение движения ТРДФ
по силе тяги (2.32). В исходные уравнения рабочего процесса ТРДФ
не вошло уравнение топливного насоса, т. е. рассматривался
ТРДФ с независимым приводом топливного насоса. Из уравнения
расхода газа видно, что расход газа связан сл*,а через л’ с чис-
лом оборотов ротора двигателя. Изменение числа оборотов в свою
очередь подчиняется уравнению динамики.
Поэтому изменение тяги в уравнении (2.32) определяется той
же постоянной времени Тр, что и изменение числа оборотов ротора
и температуры газа перед турбиной в уравнениях (2.40) и (2.47).
Разница в уравнениях (2.32), (2.40) и (2.47) заключается в их пра-
вых частях: в других значениях коэффициентов усилений и в том,
что на характере изменения ATJ и А/? сказывается не только вели-
чина независимых переменных, но и скорость их изменения.
Возьмем частный случай уравнения (2.47), используя воздей-
ствие только за счет скачкообразного изменения расхода основного
топлива
(Тдр+ 1)АТ; = [Ытп + ^С(Тдр+ 1)] АСЪ (2.48)
его решением будет выражение
дт; = [^о + kTnkG\\-e ^)]aGx. (2.49)
Определим знаки входящих в уравнение (2.48) коэффициентов
усиления kTG и kTn. Знак 'kTG совпадает со знаком производной
dT^/dG, а знак kTn совпадает со знаком призводной дТ\ /дп. С уве-
личением расхода топлива и при неизменном числе оборотов ро-
тора температура газа перед турбиной возрастает (рис. 2.15), отку-
да следует, что коэффициент усиления kTe > 0. Увеличение числа
оборотов при неизменном расходе основного топлива приводи”
к падению температуры газа перед турбиной за счет роста расхода
воздуха (рис. 2.16). Это означает, что kTn < 0. Как уже было опре-
делено раньше, kG > 0.
Учитывая знаки коэффициентов усиления, определяем характер
переходного процесса по температуре газа перед турбиной при
скачкообразном увеличении расхода основного топлива (рис. 2.17).
Из графика этого рисунка следует, что при скачкообразном увели-
чении расхода топлива получается заброс температуры газа, про-
порциональный kjG. Причина заброса температуры заключается в
том, что при изменении расхода топлива двигатель не сразу, а с не-
§ 3. Влияние возмущений на изменение регулируемых параметров ТРДФ 69
которым запаздыванием увеличивает число оборотов ротора и рас-
ход воздуха. Длительность заброса температуры, интенсивность ее
спада зависит от постоянной времени Тэ: чем больше Тд, тем мед-
леннее падение температуры. Чтобы не допускать больших забросов
необходимо ограничивать скорость нарастания подачи топлива
Полетам на больших высотах (при ограниченной скорости полета)
или переходам на пониженные числа оборотов ротора соответст-
вуют повышенные значения по-
стоянной времени Tg. Следова-
тельно, па этих режимах за-
бросы температуры газа могут
быть особенно длительными.
Переходные процессы, по-
добные показанному па рис.
2.17, получаются в ТРДФ при
возмущении и по другим пара-
метрам. Таким будет характер
изменения температуры газа
перед турбиной, если скачкооб-
разно изменится температура
окружающей среды. Аналогич-
но изменяется и сила тяги при
скачкообразном изменении
расхода форсажного топлива
или давления окружающей
среды. Причины такого изме-
4GI
4G,
t
Рис. 2.17
нения следующие.
При скачкообразном увеличении температуры воздуха также
скачком снизится расход воздуха за счет уменьшения плотности.
Температура газа перед турбиной скачкообразно увеличится за
счет снижения расхода воздуха и за счет увеличения его темпера-
туры за компрессором (число оборотов ротора двигателя и расход
70
Глава II. ГТД на химическом топливе, как объекты регулирования
топлива сохраняются неизменными). После скачкообразного уве-
личения Т'з начнет расти число оборотов ротора, расхода воздуха
увеличится, а температура газа несколько понизится. Коэффициен-
ты усиления kTfi и Ьттн положительны.
При внезапном увеличении расхода форсажного топлива за счет
роста Тф и скорости истечения скачком возрастает тяга двига-
Рис. 2.18
теля. Однако затем за счет увеличения давления в форсажной ка-
мере число оборотов ротора снижается, уменьшается расход воз-
духа и тяга несколько падает (хотя температура в форсажной
камере продолжает расти). Коэффициенты усиления £о^>0 и
к™Ф> 0.
В случае скачкообразного увеличения давления воздуха его
расход возрастает, а температура газа перед турбиной и в форсаж-
ной камере снизится. При этом тяга, пропорциональная Ge и у Т*ф,
также скачкообразно возрастет. Вслед за этим за счет падения тем-
пературы Tj число оборотов ротора начнет снижаться, расход воз-
духа упадет и тяга двигателя несколько уменьшится. Коэффициен-
ты усиления kpH и krP — положительны.
Рассмотрим особенности переходного процесса в ТРДФ при
воздействии изменением площади сечения выходного сопла (из-
§ 3. Влияние возмущений на изменение регулируемых параметров ТРДФ 71
менением координаты s). При внезапном увеличении s падает дав-
ление в форсажной камере и скачкообразно уменьшается тяга дви-
гателя. Однако затем за счет скачкообразного увеличения перепада
давления на турбине возрастает число оборотов и связанные с ним
расход воздуха и тяга двигателя. Весь переходный процесс в этом
случае будет определяться уравнением
А#= [kits 4- kRnks [ 1 — е Го )] Asx.
(2.50)
Рис. 2.19
В нем в соответствии со статическими характеристиками п = n(s),
R = R(n) и R = -ft(s), показанными на рис. 2.18, а, б и в, коэффи-
циенты усиления йдз <0, ks > 0 и kRn > 0. Поэтому переходный
процесс при возмущении координатой s выглядит так, как это по-
казано на рис. 2.19. ,
Если возмущение в ТРДФ вызвать внезапным увеличением тем-
пературы окружающего воздуха, то изменение тяги двигателя по
своему характеру сходно с из-
менением тяги при возмуще-
нии изменением площади вы-
ходного сопла (см. рис. 2.19).
Действительно, при скачкооб-
разном увеличении Тн внезап-
но снижается расход воздуха,
возрастают температуры газа
перед турбиной и в форсажной
камере. Тяга двигателя за счет
большего влияния изменения
расхода воздуха скачкообраз-
но падает. Затем, за счет рос-
та температуры газа Т*3, нач-
нут увеличиваться число обо-
ротов ротора и расход воздуха,
рост расхода воздуха снизит
температуры газа перед турбиной и в форсажной камере, но в то
же время увеличит тягу. Коэффициенты усиления kTII > 0, kRT}]< 0.
Анализ влияния внезапного увеличения давления воздуха на
температуру газа перед турбиной показывает, что в этом случае
переходный процесс будет по своему характеру совпадать с пере-
ходными процессами ДА* = и ДА? = Д/?(Д7’^1). Переходный
процесс ДА? = Д/?(Д5() показан на рис. 2.19. Действительно, вне-
запное увеличение приведет к скачкообразному росту расхода
воздуха и уменьшению температуры газа перед турбиной. В ре-
зультате этого начнет снижаться число оборотов ротора, что в свою
очередь приведет уже к снижению расхода воздуха и к некоторому
72 Глава II. ГТД на химическом, топливе, как объекты регулирования
увеличению температуры Т*3. Коэффициенты усиления kPH и kTpH
отрицательны.
Рассмотрим влияние на изменение тяги двигателя внезапного
увеличения расхода основного топлива. В этом случае скачкооб-
разно возрастут температуры газа перед турбиной и в форсажной
камере, скорость истечения газа из выходного сопла и тяга дви-
гателя. Вследствие увеличения температуры Т*3 начнется раскрут-
ка двигателя, что приведет к росту расхода воздуха и к дальней'
шему увеличению тяги. Переходный процесс определяется урав-
нением t
^R== + — в Т& )] AG15
знаки коэффициентов усиления, входящих в это уравнение, выяв-
ляются с помощью статических характеристик R = R(G) и п =
= n(G), которые даны на рис. 2.20, а и б. Из этих характеристик
следует, что &rg и knn положительны (как уже было определено
раньше, feG > 0). Вид переходного процесса показан на рис. 2.21, а.
Выявим характер изменения температуры газа перед турбиной
при внезапном увеличении расхода форсажного топлива. Переход-
ный процесс в этом случае определяется уравнением
АТз— Ч~ ктпксф{ 1 — е Т,> )] ,(2.52)
Входящие в него коэффициенты усиления krn и отрицательны,
так как с ростом расхода форсажного топлива число оборотов ро-
тора падает, а с падением п растет температура Т"3 из-за умень-
шения расхода воздуха.
Что же касается значения коэффициента усиления Ьтвф, то
здесь могут быть два случая.
При докритическом перепаде давления в сопловом аппарате
§ 3. Влияние возмущений на изменение регулируемых параметров ТРДФ 73
газовой турбины увеличение расхода форсажного топлива приведет
к снижению расхода воздуха и росту температуры газа перед тур-
биной. В этом случае &то^>0, а изменение температуры Т*й по
своему характеру будет совпадать с изменением тяги при внезап-
ном увеличении расхода основного топлива (см. рис. 2.21, а).
Если же в момент увеличения расхода форсажного топлива пе-
репад давления на сопловом аппарате турбины надкритический,
то это возмущение скачкообразно не может изменить расход воз-
духа и температуру газа перед турбиной, т. е. в этом случае
Рис. 2.21
ктвф = 0. Увеличение давления в форсажной камере приведет
к снижению числа оборотов ротора и вместе с ним к снижению
расхода воздуха. Температура газа Т*3 будет возрастать по экспо-
ненциальному закону так, как это показано на рис. 2.21, б.
Рассмотрим влияние внезапного увеличения площади критиче-
ского сечения выходного сопла на температуру газа перед тур-
биной. Здесь, как и при анализе влияния изменения расхода фор-
сажного топлива на температуру Т3 , надо в одном случае принять
докритический, а в другом случае надкритический перепад в соп-
ловом аппарате турбины.
При докритическом перепаде в сопловом аппарате турбины
внезапное увеличение s приведет к скачкообразному увеличению
расхода воздуха и падению температуры газа Т3. Начавшееся за-
тем увеличение числа оборотов ротора приведет к дальнейшему
увеличению расхода и падению температуры газа перед турбиной
уже по экспоненциальному закону. Переходный процесс опреде-
ляется выражением
ЛТз = \kTs -|- kmks (1 —• "ТГ'П Л (2.53) е d )|As1. v ’
74 Глава II. ГТД на химическом топливе, как объекты регулирования
Из статических характеристик Т‘3 = T*z (s), Т”3 = Т‘ (п) и
п = n(s), показанных на рис. 2.22, а, б и в, следует, что kTs < О,
ктп<0 и fes>0.
Переходный процесс для этого случая показан на рис. 2.23, а.
Если же принять, что в сопловом аппарате газовой турбины
установился надкритический перепад давления, то внезапное уве-
личение s и снижение давления в форсажной камере не может
§ 4. Расчет коэффициентов, входящих в уравнения движения двигателей 75
Рис. 2.24
привезти к скачкообразному увеличению расхода воздуха и паде-
нию температуры газа T*z. Увеличение расхода и снижение темпе-
ратуры будет происходить по экспоненциальному закону по мере
нарастания числа оборотов. Поэтому коэффициент усиления kTs =
= 0. Соответствующий этому
случаю переходный процесс
показан на рис. 2.23,6.
Влияние внезапного увели-
чения скорости полета на тем-
пературу газа перед турбиной
будет подобно влиянию увели-
чения s па тягу двигателя. Ха-
рактер переходного процесса
,= ДГ* (ДЛ4н) в этом слу-
чае подобен переходному
процессу, показанному на
рис. 2.19.
Провести анализ влияния
внезапного увеличения скоро-
сти полета на тягу двигателя
затруднительно из-за сложного
(кривые 1, 2 рис. 2.24). В зависимости от участка характеристики
R = влияние увеличения Мн будет различным.
закона изменения тяги по
§ 4. ПРИБЛИЖЕННЫЕ СПОСОБЫ РАСЧЕТА КОЭФФИЦИЕНТОВ,
ВХОДЯЩИХ В УРАВНЕНИЯ ДВИЖЕНИЯ ДВИГАТЕЛЕЙ
КАК ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
Методы определения динамических коэффициентов, входящих в уравнения,
описывающие свойства двигателей как объектов регулирования, можно разделить
на экспериментальные и расчетные (экспериментальные методы рассмотрены
в гл. VI).
Расчетные методы базируются на уравнениях связи между основными пара-
метрами рабочего процесса двигателей, заданных как аналитически, так и графи-
чески (например, характеристики компрессора и турбины). Эти уравнения удоб-
нее рассматривать в форме малых отклонений от установившегося режима. Метод
малых отклонений позволяет сократить объем вычислительных работ и обеспе-
чивает достаточно высокую точность результатов. Но его целесообразно приме-
нять лишь в том случае, когда есть надежная характеристика компрессора и на
ней построена линия совместных режимов. Существуют также и приближенные
способы определения постоянной времени двигателя, использующие эксперимен-
тальные статические характеристики.
Рассмотрим два способа приближенного определения постоянной времени
ТРД с независимым приводом топливного насоса. Как уже было показано в этом
случае свойства ТРД как объекта регулирования описываются уравнением (2.9)
„ dAn
Тд ~РГ~ -|- Ап = ^()AG,
at
76
Глава II. ГТД на химическом топливе, как объекты регулирования
здесь так же, как и в выражениях (2.10) и (2.11):
Тд J зо / абм \ ’
\ дп Jo
I дШ \
. _ у dG '° 5
д / дШ \
------------ ПБ
\ дп /о
Для определения производной ддМ/дп, стоящей в знаменателе выраже-
ния (2.10), можно использовать статическую характеристику ТРД G = G(n) и
таким путем определить Та. Этот способ расчета постоянной времени предложен
А. В. Штодой.
Определение постоянной времени Та с помощью
статических характеристик ТРД.
Из уравнения (2.9) следует, что на установившемся режиме, когда dAn!dt = Q,
kd^ AG
ний (2.11) и (2.54), после сокращения
_ / ддМ \ /
\ дп /о \
дп
8G пк
Откуда, переходя к пределу, получим
GB
kd = -^—. (2.54)
И
\ rfn/O
Выбрав на статической характери-
стике G = G(n) произвольные базисные
величины GB и пБ и выполнив графиче-
ское дифференцирование для исследуе-
мого статического режима п0 (рис. 2.25),
/Л? \
найдем производную “— и числен-
\dn /0
ное значение коэффициента усиления
Кд.
Приравняем правые части выраже-
получим
ддМ. \ I dG \
dG Jo \ dn /о '
Подставим полученное в выражение (2.10) и будем иметь новую
для определения Т8
формулу
Тд =
— J
30
(2.55)
§ 4. Расчет коэффициентов, входящих в уравнения движения двигателей 77
Преобразуем входящую в формулу (2.55) производную ddM/dG. Избыточ-
ный момент дМ = Мт— Мп, момент турбины и момент компрессора можно пред-
ставить в виде
Мк
30 GSHK
л п.
где Н*к и Нт—эффективные работы сжатия и расширения. Как и раньше, при-
мем, что Gz = Ge. Тогда для данного статического режима можно записать
д „ ,
или
36М \
3G /о
ЗбМ \
. dG Jo
30
лп0
/ ЗЯ*
ЗЯ* \ '
3G /о.
*
Для установившегося режима
(я;-я;)о=я;о-я;о=о.
Учитывая слабую зависимость работы сжатия от изменения расхода топлива или
температуры газа перед турбиной примем, что дНк jdG = 0. Тогда
! 36М \ 30 „ ( дН*\
НН =—• <2-56)
\ 3G /о л/г0 \ dG /о
Представим частную производную ЗЯТ /3G в виде произведения двух част-
ных производных
= (2.57)
3G дТ* dG
и определим их.
Запишем выражение для определения эффективной работы турбины
1
* и примем, что параметры турбины лт и ж т]г не зависят от температуры ж газа Т3.
Тогда
V1
дН* k „Г, L = —Я 1 * кг \ * — Лт J т]т>
37* кг— 1 '
ИЛИ
ЗЯ* я;
зт; ' 1 3 (2.58)
78
Глава II. ГТД на химическом топливе, как объекты регулирования
Температуру газа перед турбиной определим из выражения
т*___т* л. ^к-с^и^
3~ 2 (cp)cpGe ’
тогда
дТ3 ъ\к.сНи
9G (Гр)сР Gg
(2.59)
Подставим в выражение (2.57) найденные значения частных производ-
ных (2.58) и (2.59). Получим / дН*т ' \ dG ) ) Ят0 Чк-сНи (2 60) 0 Т* (Cp)CpG до О U
Исключим с помощью последнего выражения частную производную дНт /dG
ИЗ уравнения (2.56). Найдем, что (_д8М\ _ 30 \ 3G /о л (ср)Ср nQT^0
откуда
или
30 т!К,сЦи Н"т0 / dG \
л (СрЪр „о7*о \ dn 'о
т_ ( л \2 (cp)cpJ потзо
* 1 30 J . ( dG\
(2.62)
Вместо производной (dG!dn)0 в выражение для вычисления Та можно вклю-
чать коэффициент усиления ko. Тогда формула для определения 7а примет вид
л V (cp)cpJ пв пеТзо
30/ т1К,сни Ge h*q
(2.63)
Из выражений (2.62) и (2.63) следует, что для вычисления Тд нужно рас-
полагать статическими характеристиками G=G(n), л*=л*(тг) и Т^ — Т\{п).
Зависимость лг = лг (п) требуется для вычисления работы турбины. Опа может
быть заменена зависимостью лк = лк (и) и т]* = г]” («)•
Необходимость использования зависимости Т 3 = Т$(п) в данном способе опре-
деления Тд вносит некоторые трудности, так как для определения среднемассо-
вой температуры газа перед турбиной нужно иметь 6—10 датчиков температуры.
Ниже изложен второй приближенный способ определения постоянной времени Тд,
который не требует знания характеристики Т^=Т3(п).
§ 4. Расчет коэффициентов, входящих в уравнения движения двигателей 79
Приближенное построение характеристик
крутящих моментов ТРД по данным стендовых испытаний
Для определения Та по формуле (2.10) нужно знать производную
ддМ дМт дМ д
дп дп дп дп
(2.64)
Примем функциональные зависимости Мк = Мк(п) и Мт = Мт(п, G). Зави-
симость Мк — Мк(п) может быть легко вычислена по стендовым характеристи-
кам, для этого нужно знать расход воздуха и полную работу сжатия, так как
30 GX
л п
Полная работа сжатия определяется до перепаду температур в компрессоре
^ = 7—
(2.65)
Следовательно, для определения Нк нужно измерять температуру воздуха за
компрессором и знать температуру окружающей среды.
Расход воздуха или газа может измеряться в различных сечениях двигателя.
Если нет мерного насадка на входе, то
расход газа можно мерить в критичес-
ком сечении выходного сопла. Он бу-
дет равен
*
г
G, — —т=-
У75
(2.66)
здесь рс — коэффициент расхода
сопла. Кроме того, снимается зависи-
мость расхода топлива от числа оборо-
тов G = G(n).
Из формулы (2.66) следует, что
нужно измерять температуру газа Т5.
Однако измерения в выходном сопле
проще, чем измерения в камере сгора-
ния. Если же на входе в двигатель ус-
тановлен мерный насадок, то необходи-
мость в измерении температуры газового
потока отпадает. Таким образом, по данным стендовых испытаний строится ха-
рактеристика Мк = Мк(п) и для каэкдой точки этой кривой известен расход
топлива (рис. 2.26).
Перейдем к определению зависимости Мт = Мт(п) при G = const.
На статических режимах HTf = НКа. Сделаем предположение, что на неуста-
новившихся режимах в полезную работу на валу турбины превращается та же
доля введенной вместо с топливом тепловой энергии, что и па статических режи-
мах. Тогда для заданного расхода топлива
Л#(М,
Мт
п
(2.67)
80 Глава II. ГТД на химическом топливе, как объекты регулирования
Графики найденных с помощью этого выражения зависимостей также нанесены
на рис. 2.26.
Очевидно, что чем больше пеустановившийся режим с числом оборотов п
будет отличаться от статического режима п0, тем больше будет ошибка в опре-
делении Мт по формуле (2.67). Однако зависимость Мт(п) при G ~ const нужна
только для выполнения графического дифференцирования на статических режи-
мах определяемых точками пересечения кривых Мт (п) и Мк (га). Вблизи этих
точек погрешность в определении
Л4т(га) по формуле (2.67) мала и на-
правление касательной может быть
определено достаточно точно, особен-
но в области высоких чисел оборотов.
Для определения коэффициента
усиления kd может быть непосредст-
венно использована зависимость G =
= G(n) нли же построена характери-
стика Мт — MT(G) при п = const и
графическим дифференцированием вы-
числена производная dMT/dG. Чтобы
получить характеристику Мт — MT(G)
при га = const, нужно перестроить за-
висимость Мт = Мт(п) при G — const:
семейство кривых Мт(п) при G =
= const, показанное на рис. 2.26, рас-
сечь вертикальными прямыми (линия-
Рнс 2 27 ми п = const) и По точкам пересече-
' ’ пня построить кривые в координатах
Мт, G (рис. 2.27). На этот же гра-
фик можно нанести линию статических режимов, которая определяет точки для
проведения графического дифференцирования. Очевидно, что вблизи точек стати-
ческого режима достоверность полученных таким путем характеристик Мт =
= MT(G) достаточно велика.
Примеры
Пример 1. Даны статические характеристики ТРД G = G(n); Мк = Мк(п)
н Мт = Мт(п), показанные па рис. 2.28 и 2.29. Определить путем графического
дифференцирования изменение То и kg по числу оборотов. Момент инерции
I = 100 н • м • сек2, за базисные величины принять га == 6500 об/мин и соответ-
ствующий им расход топлива йБ — 0000 кг/час (GE = 1,67 кг/сек) '.
Для определения То воспользуемся формулой (2.10), величину ka найдем
Gs / dG
из выражения (2.13) ka = —- / -— . В точках с га = 3000, 4000, 5000, 6000
пб / dn
и 6500 об/мин к кривым G(n), Мк(п) и Мг(п) проводим касательные и измеряем
для каждого из них углы наклона у к оси абсцисс.
Для перехода от tgy к величине дМ/дп следует учесть масштабы, в которых
отложены числа оборотов и моменты, так как
/ 6А4 \ шп
При построении рис. 2.29 принято mn/mM= о (н м)/об/мин. Для определе-
ния kg нужно взять отношение отрезка ординаты к отрезку абсциссы от начала
1 Характеристики моментов турбины и компрессора даны в ньютон-метрах,
момент инерции — в ньютон-метр-секундах в квадрате. Если эти величины по-
делить на 9,81, то получим .характеристики моментов и J соответственно в кн-
лограмм-сила-метрах и килограмм-сила-метр-секундах в квадрате.
Примеры
81
координат до соответствующих точек базовых величин ч поделить это отношение
иа тангенс угла наклона касательной. На рис 2.28 для Пв = 6500 об/мин и
GB ~ 6000 кг/час это отношение равно 12/13.
Рис. 2.28
Рис. 2.29
Результаты графических построений и
мости Та(п) и ka(n) даны па рис. 2.30.
расчетов сведены в таблицу, завпси-
п об мин Д рад \ дп /о н-м 7 т Рад /дМт \ \ дп /о Н-М /Э5Л1\ \ дп /о /дМт \ дп /о \ дп )0 Н-М об-мин тд сек TG рад kd
об 'мин об, мин
3000 0,87 5,95 2,62 —2,9 — 8,85 1,77 0,35 2,54
4000 0 96 7,15 2 50 —3,7 —10,85 1,45 0,55 1,51
5000 1,04 8,55 2,44 —4,2 —12,75 1,23 0,89 0,75
6000 1,13 10,5 2 33 —5,3 —15,8 0,99 1,21 0 35
6500 1,17 П,8 2,28 —5,8 —17,6 0,59 1,35 0,205
Пример 2. Определить, как меняются у ТРД постоянная времени и коэффи-
циент усиления в зависимости от условий полета. Исходные значения То и ka
для стартовых условий взять из предыдущего примера: Тд = 0,59 сек, ka = 0,205.
Программа полета задана графиком, помещенным иа рис. 2.31, на этом графике
отмечены семь точек, для которых следует произвести расчет. ТРД регулируется
по программе п — const.
82 Глава И. ГТД на химическом топливе, как объекты регулирования
Значения Тп и ри для расчетных точек берем по данным MCA (Междуна-
родная стандартная атмосфера). Параметры торможения набегающего потока
определяем по формулам:
Т*н = Тн(\ + 0,2М2н)
и
Рн = Рн(1 + °>2Мн)3’5.
Из выражений (2.16) и (2.17) следует, что величина Та обратно пропорцио-
нальна расходу воздуха, a kg обратно пропорциональна давлению торможения
Рис. 2.30.
набегающего потока. Однако в отноше-
нии fea более точным будет такое оп-
ределение: величина fee обратно про-
порциональна расходу воздуха и прямо
пропорциональна корню квадратному из
температуры. Поэтому при подсчете Тд
и кя следует учесть потери полного
давления во входном диффузоре и па-
дение производительности компрессора
с уменьшением приведенного числа обо-
ротов. Расход воздуха ТРД по сечению перед компрессором определяется из
выражения
¥
V тн
где m — постоянный коэффициент;
Л — площадь входа в компрессор.
Известно, что для осевых компрессоров зависимость приведенного расхода
воздуха
G = G ........у
в.пр в »
адиф Рц
П римеры
83
от приведенного числа оборотов ппр определяется главным образом расчетным
значением (лк)р. Примем (лк)р = 6, что дает возможность выбрать зависимость
<7(Xi) = f(renj>), как показано в работе [13]. Результаты расчетов вместе с вы-
бранными зависимостями Одиф(Мц) и = Цппр) сведены в таблицу.
№ режима Рн мм рт. ст. Тн °К МН рн мм рт. ст. 1 о ** а; •' °диф "пр Т() сек kd
1 760 288 0 760 288 1 1 1 0,59 0,205
2 760 288 0,5 897 303 1 0,98 0,98 0,52 0,18
3 196 230 0,75 272 320 1 0,95 0,95 1,83 0,60
4 41 224 1,0 77,5 346 1 0,915 0,915 6,9 2,2
5 41 224 1.5 151 418 0,97 0,83 0,79 4,72 1,36
6 41 224 2,0 320 519 0,90 0 75 0,66 3,15 0,82
7 41 224 2,5 697 648 0,85 0,67 0 56 2,04 0,47
_ В этой таблице ооиа—относительные потери_ во входном диффузоре;
ппр — относительное приведенное число оборотов и <y(A.i)—относительная про-
изводительность компрессора. Зависимости Ts(nnp) и ks(nnp) даны па рис. 2.32.
Глава III
РЕГУЛИРОВАНИЕ СВЕРХЗВУКОВЫХ ВХОДНЫХ
УСТРОЙСТВ
§ 1. ОСОБЕННОСТИ РАБОЧЕГО ПРОЦЕССА И ХАРАКТЕРИСТИКИ
ВХОДНЫХ ДИФФУЗОРОВ
Типы входных диффузоров
Входное устройство воздушно-реактивного двигателя предна-
значено для преобразования кинетической энергии набегающего
потока в работу сжатия воздуха и для подвода воздуха в количе-
ствах, необходимых для работы двигателя. Оно должно обладать
малым внешним сопротивлением и устойчиво работать в широком
диапазоне изменения высоты, скорости полета и режима работы
двигателя. Качество входного устройства следует оценивать вели-
чиной эффективной тяги силовой установки.
При неизменных геометрических формах устойчивая работа
входного устройства возможна лишь в узком диапазоне изменения
условий полета и режима работы двигателя. Расширение диапазо-
на устойчивой работы нерегулируемого входного устройства неиз-
бежно связано с уменьшением эффективной тяги в расчетных
условиях. В силу этого эффективная тяга двигателя на его расчет-
ном режиме становится тем ниже, чем шире задается диапазон
изменения внешних условий и режимов работы двигателя. Поэто-
му нерегулируемые входные устройства целесообразно применять
на однорежимных летательных аппаратах с ТРД или ПВРД. Усло-
вия работы нерегулируемого входного устройства могут быть
улучшены подбором соответствующей программы регулирования
двигателя.
Входные устройства представляют собой диффузорные кана-
лы. Свойства входных устройств определяются характеристиками
используемых в них диффузоров.
По способу торможения воздушного потока входные устройст-
ва разделяются па входные устройства с диффузорами с внешним
сжатием, смешанным сжатием и с полностью внутренним сжатием.
Первые два из них выполняются в виде осесимметричных каналов
с выступающим центральным телом (рис. 3.1, а) или в виде плос-
ких каналов с односторонним клином (рис. 3.1, б). Диффузор с
полностью внутренним сжатием представляет собой суживающе-
расширяющийся канал (рис. 3.1, в).
§ 1. Особенности рабочего процесса и характеристики диффузоров
85
Диффузор с внутренним сжатием обладает малым внешним со-
противлением. Это связано с тем, что поворот сверхзвукового
потока, необходимый для осуществления процесса, сжатия возду-
ха, происходит у этого диффузора внутри канала. Во внешнем
потоке, обтекающем двигатель, скачки уплотнения не возника-
ют. Применение диффузора с внутренним сжатием наталкивается
на серьезные трудности. Они заключаются в сложности вывода
диффузора такого типа на расчетный режим и в отрицательном
влиянии на процесс сжатия пограничного слоя, образующегося
вследствие вязкости воздуха. Пока что диффузоры с внутренним
сжатием в силовых установках с ТРД. не нашли применения.
Осесимметричный входной диффузор с центральным телом дает
возможность получить хорошую форму проточной части, прочный
корпус и наименьший вес по сравнению с другими типами диффу-
зоров. Для оптимального регулирования такого диффузора тре-
буется достаточно большой диапазон изменения положения цен-
трального тела и площади горла. Конструктивно это не всегда
может быть обеспечено, особенно в отношении изменения площади
горла, и приходится допускать некоторое отклонение от оптималь-
ного регулирования. Обечайка с переменным углом установки
из-за технических трудностей вряд ли найдет применение. Осесим-
метричный входной диффузор имеет довольно плохую характери-
стику по углу атаки.
В плоском входном диффузоре изменение в широких пределах
геометрической формы канала в целях регулирования легко Дости-
гается сочетанием перемещения клина с поворотом обечайки или
с поворотом одной из граней клина. При удачном расположении
диффузора влияние угла атаки или угла рыскания на его харак-
86
Глава III. Регулирование сверхзвуковых входных устройств
теристики невелико. Разновидностью плоского диффузора являет-
ся диффузор так называемого совкового типа.
Во входных устройствах сверхзвуковых летательных аппара-
тов используются диффузоры внешнего или смешанного сжатия.
У летательных аппаратов с одним или двумя ТРД в фюзеляже
обычно делаются плоские регулируемые диффузоры, расположен-
ные по бокам фюзеляжа, реже используется носовая часть фюзе-
ляжа для размещения в ней осесимметричного регулируемого
диффузора. При боковом расположении диффузоры иногда выпол-
няются полукруглыми.
Плоские входные диффузоры применяются также па летатель-
ных аппаратах с двумя или четырьмя двигателями, заключенны-
ми в крыльях. Если же двигатели размещаются на пилонах под
крыльями, то используются осесимметричные диффузоры.
В этой главе рассматриваются характеристики входных диффу-
зоров с внешним и смешанным сжатием, которые необходимо
учитывать при разработке системы регулирования силовой уста-
новки.
Характеристики нерегулируемого входного диффузора
Работа диффузора определяется коэффициентами восстанов-
ления полного давления oaugs = Pi 1рц, расхода ф = Fn/Fex и
внешнего сопротивления сХвн = xeH/qFM, где Fh — площадь воз-
душной струи в невозмущенном потоке, входящей в диффузор;
Fex и FM — площади входа и миделя диффузора или двигательной
гондолы; q — скоростной напор; хвн— сила внешнего сопротивле-
ния, состоящая из сопротивления обечайки, гондолы и дополни-
тельного сопротивления.
В сверхзвуковом диффузоре с внешним сжатием для сравни-
тельно небольших сверхзвуковых скоростей полета, схема кото-
рого показана на рис. 3.2, а, самое узкое сечение — горло — прак-
тически совпадает с плоскостью входа. Система скачков на входе
заканчивается прямым скачком, и перед горлом диффузора поток
дозвуковой. После прямого скачка поток опять разгоняется до
сверхзвуковой скорости и в конце диффузора скачкообразно снова
§ 1. Особенности, рабочего процесса и характеристики диффузоров
87
переходит в дозвуковой. Замыкающий скачок препятствует рас-
пространению вверх по потоку колебаний давления перед двига-
телем, которые могли бы привести к неустойчивой работе диффу-
зора. Запас устойчивости диффузора тем больше, чем дальше по
потоку расположен замыкающий скачок уплотнения, т. е. чем
больше его интенсивность. Однако с ростом интенсивности замы-
кающего скачка снижается величина oaugs-
Следует отметить, что в диффузорах этого типа течение внутри
канала может остаться дозвуковым. Но тогда с ростом противо-
давления в конце диффузора замыкающий прямой скачок на входе
в диффузор перемещается вверх по потоку и переходит в голов-
ную волну. Внешнее сопротивление диффузора возрастает.
Чтобы отодвинуть момент образования головной волны, в не-
расчетных условиях для больших сверхзвуковых скоростей полета
применяется диффузор другой схемы торможения (см.
рис. 3.2, б). Здесь осуществляется смешанное торможение потока:
частично внешнее, частично внутреннее. На входе в канал диф-
фузора поток обладает некоторой сверхзвуковой скоростью, кото-
рая продолжает снижаться в сужающемся канале. В целях обес-
печения запуска диффузора его горло должно быть перерасшире-
но. Вследствие перерасширения на расчетном режиме поток в
горле будет сверхзвуковым и в расширяющейся части канала
продолжает разгоняться пока в замыкающем скачке не перейдет в
дозвуковой. Диффузор со смешанным сжатием, кроме замедлен-
ного роста внешнего сопротивления в нерасчетных условиях, дает
также возможность избежать образования головной волны при
спутных порывах ветра.
Величина противодавления зависит от режима работы двигате-
ля и условий полета. С ростом противодавления замыкающий
скачок в канале диффузора перемещается вверх по потоку и про-
тяженность сверхзвуковой зоны течения уменьшается. Замыкаю-
щий скачок устойчив только в расширяющейся части канала. Если
рост противодавления заставит его переместиться вверх по потоку
за горло диффузора, то скачок сразу превратится в выбитую го-
ловную волну, что может привести к помпажу силовой установки.
Падение противодавления приводит к перемещению замыкаю-
щего скачка вниз по потоку и к росту его интенсивности. За скач-
ком поле скоростей и давлений потока неравномерно, что в случае
использования диффузора в силовой установке газотурбинного
двигателя вызывает вибрацию лопаток компрессора и может при-
вести к их поломке. Внешним признаком слишком сильного при-
ближения замыкающего скачка к компрессору и его большой
интенсивности является появление «зуда».
В зависимости от величины противодавления при расчетном
для системы скачков на входе числе Мн полета может установить-
88
Глава III. Регулирование сверхзвуковых входных устройств
ся один из трех характерных режимов работы диффузора: закри-
тмческий, критический и докритический.
Закритический режим характеризуется наличием сверхзвуко-
вой зоны за горлом диффузора. Рост противодавления при сохра-
нении сверхзвуковой зоны не изменяет условий течения потока
на входе в диффузор, сохранятся неизменными величина коэффи-
циента расхода и величина внешнего сопротивления (при ф = 1
дополнительное внешнее сопротивление отсутствует).
Рис. 3.4
Критический режим характеризуется положением замыкающе-
го скачка в горле диффузора и отсутствием сверхзвукового тече-
ния в расширяющейся части канала. Дальнейший рост противо-
давления приводит к возникновению головной волны и переходу
диффузора на докритический режим. Чем сильнее противодав-
ление, тем дальше отходит головная волна от плоскости входа и
тем сильнее растет внешнее сопротивление диффузора. При
каком-то достаточно большом противодавлении наступает потеря
устойчивости диффузора.
Характеристики диффузоров строятся в двух видах. В одном
случае это графическая зависимость oaugs, Ф и сХвн от приведен
пого расхода воздуха Gnv (рис. 3.3). В другом случае графиче-
ская зависимость oaugs и cXg/i от коэффициента расхода ф
(рис. 3.4). Так как Gnp = GB}/Т'н/р*н, то между коэффициентом
расхода ф и приведенным расходом воздуха существует связь
Gnp = <fGe.p_^__, (3.1)
Рц ®диф
где GB.P— расход воздуха через диффузор при такой скорости
полета, когда ф = 1.
§ 1. Особенности рабочего процесса и характеристики диффузоров
89
Положение рабочей точки на характеристике диффузора зави-
сит от внешних условий и режима работы двигателя и опреде-
ляется из уравнения расхода, составленного для двух сечений: в
невозмущенпом потоке перед диффузором и па входе в двигатель.
Его преобразование приводит к выражению
<z(W
----—
q (М)Л
адиф
(3-2)
где д(ля) и — приведенные плотности тока соответственно
на входе в диффузор и в двигатель;
Fx = Ei/FeA — относительная площадь входа в двигатель.
Выражение (3.2) в координатах соиф— <р есть уравнение пря-
мой, проходящей через начало координат (рис. 3.5). Величина ее
углового коэффициента зависит от внешних ус-
ловий, режима работы двигателя и соотноше-
ния геометрических размеров диффузора.
На характеристиках q>(GnJ>), Ъдиф(СпР),
сх (^ад) и оэ«сб(ф), показанных на рис. 3.3
и 3.4, закритическим режимам соответствуют
участки характеристик с неизменным значе-
нием ср и сильно изменяющейся величиной
ввиф (правые ветви характеристик). На до-
критических режимах (левые ветви характе-
ристик) величина вд-иф почти не меняется, а ср
изменяется сильно. Некоторое снижение овиф
Рис. 3.5
объясняется разрушением головной волной
системы косых скачков. Критическому режиму соответствует точка
перехода с одной ветви характеристики па другую.
У диффузоров, рассчитанных на сравнительно небольшую
сверхзвуковую скорость полета возможен достаточно плавный пе-
реход от докритического режима к закритическому. В этом слу-
чае на докритическом режиме зависимость вдиф(Спр} или
О9и$(ср) может иметь слабо выраженный максимум. Разновид-
ность такой характеристики показана пунктиром на рис. 3.3 и 3.4
(для Ми = Мн, ).
Следует отметить, что на числах Мн полета, меньших расчет-
ного, при работе диффузора на закритическом режиме из-за недо-
статочной площади горла все же будет образовываться головная
волна. Однако в этом случае потеря устойчивости не наступает.
Влияние изменения внешних условий и режима двигателя
на работу нерегулируемого входного диффузора
Рассмотрим сначала влияние изменения числа Мн полета при
программе регулирования ТРД п — const. Число Мн полета прежде
всего влияет на углы наклона косых скачков уплотнения. Затем
90
Глава III. Регулирование сверхзвуковых входных устройств
следует иметь в виду, что с изменением Мн меняется величина
приведенного числа оборотов компрессора, что отражается на его
производительности и величине противодавления на выходе из
диффузора.
Предположим, что диффузор работает на расчетном числе по-
лета МНр на закритическом режиме: косые скачки фокусируются
на кромке обечайки (ср = 1), в расширяющейся части канала диф-
фузора имеется сверхзвуковая область течения. При снижении
Мн угол наклона косых скачков увеличивается, их пропускная
способность снижается, что приводит к падению коэффициента
расхода (ср < 1). Пропускная способность горла диффузора па-
дает быстрее, чем пропускная способность косых скачков, что
объясняется падением скоростного напора. Если площадь горла
выбрана большей, чем необходимо для пропуска воздуха на рас-
четном режим'е, то при некотором снижении Мн диффузор будет
работать без головной волны. Снижение Мн приведет к увеличе-
нию ппр и росту производительности компрессора, что увеличит
область сверхзвукового течения в расширяющемся канале и при-
близит замыкающий скачок уплотнения к компрессору. При даль-
нейшем снижении Мп пропускная способность горла диффузора
станет недостаточной, оно запрется, а перед входом в диффузор
возникнет головная волна. Производительность компрессора еще
больше возрастет, замыкающий скачок может настолько прибли-
зиться к компрессору, что возникнет «зуд».
При числе Мн полета, больше расчетного, при сохранении за-
критического режима коэффициент расхода остается равным еди-
нице, хотя косые скачки уплотнения падают на внутреннюю по-
верхность обечайки. Производительность компрессора уменьшает-
ся, противодавление растет и замыкающий скачок перемещается
вверх по потоку, приближаясь к горлу диффузора. При дальней-
шем увеличении! Мп диффузор перейдет на докритический режим с
образованием головной волны на входе, коэффициент расхода не-
сколько уменьшится. Отсутствие сверхзвуковой зоны в расширя-
ющейся части канала может привести к потере устойчивости.
В качестве примера, иллюстрирующего приведенные рассужде-
ния, на рис. 3.6, а и б даны характеристики нерегулируемого диф-
фузора с нанесенной на них линией рабочих режимов (при со-
вместной работе с ТРД, который регулируется по закону п =
= const). Как видно из характеристик, кривые для коэффициента
вдиф располагаются тем выше, чем меньше Мп. Увеличение оаи$
связано со снижением потерь в системе скачков уплотнения.
С уменьшением Ми падает коэффициент расхода ф, что вызывает
увеличение дополнительного сопротивления и рост коэффициента
схвн, особенно с момента запирания горла. Линия критических ре-
жимов в области запирания горла располагается вертикально, по-
§ 1. Особенности рабочего процесса и характеристики диффузоров
91
скольку на этих режимах число М потока в горле остается по-
стоянным, равным единице.
Влияние высоты полета на работу входного диффузора сказы-
вается через изменения температуры и давления окружающего
воздуха. Если с увеличением высоты происходит падение темпера-
туры, то приведенное число оборотов двигателя возрастает, произ-
водительность компрессора увеличивается (Мп = const, п =
= const). В соответствии с увеличением производительности ком-
прессора замыкающий скачок уплотнения смещается вниз по по-
Рис. 3.6
""""ттгк—
I---:-----к-»— м ,
РиОичая
линия ys
б)
@пр
МИ, < МНр<^НЗ

току и становится более интенсивным. Если до изменения темпе-
ратуры диффузор работал на' докритическом режиме, то с ее
уменьшением может наступить закритический режим. Если же
закритический режим уже имел место, то значительное снижение
температуры может вызвать «зуд».
Рост высоты, независимо от изменения температуры окружаю-
щего воздуха, из-за падения плотности для поддержания Мл =
— const приводит к увеличению угла атаки самолета. Полет при
некотором угле атаки создает косой обдув диффузора, рост угла
атаки усиливает его. При косом обдуве течение воздуха становит-
ся несимметричным, снижаются коэффициенты расхода q> и давле-
ния воиф. Косой обдув приводит к значительной неравномерно-
сти статического давления в поперечных сечениях канала диффу-
зора. Это вызывает перетекание воздуха, набухание и отрыв
пограничного слоя и преждевременное появление неустойчивой
работы.
Изменение режима работы двигателя (за счет п — var, Т*3—
var или Th —var) сказывается на производительности компрессо-
ра и противодавлении за диффузором. Рост п и падение 7”3 или Тн
92
Глава III. Регулирование сверхзвуковых входных устройств
снижает противодавление и может вызывать появление «зуда» при
работе на закритическом режиме. В случае снижения п и увеличе-
ния Т*3 или Тн возможен переход на докритический режим (если
до этого он был закритическим) и появление неустойчивой работы.
Из сказанного следует, что для получения наилучших данных
двигательной установки и обеспечения устойчивой работы нере-
гулируемого диффузора в некотором диапазоне изменения числа
оборотов двигателя и числа Мн полета, на максимальной скорости
полета режим работы диффузора должен быть закритическим.
Для отдаления образования головной волны и связанного с ней
резкого увеличения дополнительного сопротивления при снижении
Мн целесообразно на расчетном значении Мир иметь несколько
переразмеренное горло диффузора. На расчетной скорости полета
перерасшнрение горла приведет к некоторому снижению тяги си-
ловой установки, но на это нужно идти, если летательный аппа-
рат рассчитан на достаточно большой диапазон скоростей.
§ 2. ВЛИЯНИЕ СПОСОБА РЕГУЛИРОВАНИЯ НА ХАРАКТЕРИСТИКИ
ВХОДНОГО ДИФФУЗОРА
Возможные способы регулирования входного диффузора
Регулирование входного диффузора производится для получе-
ния высоких значений коэффициента оаи«б, снижения его внешнего
сопротивления на нерасчетных режимах и обеспечения устойчивой
работы. Регулирование заключается в согласовании пропускных
способностей системы скачков, горла диффузора и двигателя.
У регулируемого диффузора степень перерасширения горла
выбирается минимальной, значительно меньшей, чем у нерегули-
руемого. Небольшое перерасшнрение должно компенсировать
спутные порывы ветра, а также вероятностные колебания давле-
ния на установившихся и переходных режимах. Регулирование
улучшает характеристики диффузора на режимах взлета и малых
скоростей полета и обеспечивает его «запуск».
Для снижения внешнего сопротивления желательно, чтобы в
нерасчетных условиях течение на входе в диффузор было сверх-
звуковым, без головной волны. В этом случае расход воздуха,
пропускаемый системой косых скачков, можно назвать располагае-
мым расходом, ему соответствует располагаемый коэффициент
расхода
Gpacn Урасп 1 /-^exQ О'н) •
V тн
Располагаемый расход должен быть пропущен горлом диффузора.
Если пропускная способность горла мала, то появится головная
волна, течение иа входе в диффузор станет дозвуковым, а дейстйи-
§ 2. Влияние способа регулирования на характеристики диффузора
93
тельный коэффициент расхода будет меньше располагаемого, оп-
ределенного из условия сверхзвукового течения на входе. Излишне
большая пропускная способность горла приведет к значительному
падению овиф.
Производительность компрессора двигателя определяет потреб-
ный расход воздуха и соответствующий ему потребный коэффи-
циент расхода. Если оценить для каждого режима возможные зна-
чения <5диф, то фпотр можно определить из выражения (3.2)
_ <7 (^1) ~р
<?М1ПР -^дифд^)11
Регулирование диффузора заключается в согласовании! коэф-
фициентов расхода фрасп и срп огр*
При еррасп = Фпотр диффузор работает на критическом режи-
ме. При фрасп < ф?ютр режим становится закритическим. В случае,
если фрасп > фпотр, то для сохранения сверхзвукового течения на
входе следует организовать перепуск воздуха в атмосферу из до-
звуковой части диффузора.
При фрасп > Фпотр диффузор без перепуска переходит на до-
критический режим с образованием головной волны. Известны
самолеты, параметры входных устройств которых выбраны так,
что расчетным режимом диффузора внешнего сжатия является
докритический режим. При этом, полагают, что высокое значение
сейф и соответствующее увеличение внутренней тяги двигателя
компенсирует рост внешнего сопротивления. При работе па докри-
тическом режиме следует учитывать возможность потери устойчи-
вости.
Рассмотрим регулирование диффузора, обеспечивающее в не-
котором диапазоне изменения скоростей полета сверхзвуковое те-
чение на входе. Можно наметить несколько способов регулирова-
ния диффузора или несколько способов компенсации несогласо-
ванности! расходов воздухозаборника и двигателя.
1. Перепуск воздуха. Если располагаемый расход воздуха
через диффузор на высоких скоростях полета больше потребного
расхода через двигатель, то излишек воздуха может быть выпу-
щен через регулируемые створки, расположенные на боковой по-
верхности диффузора между горлом и двигателем, или через спе-
циальную обводную систему с суживающимся-расширяющимся
регулируемым соплом в донной части двигательной гондолы или
летательного аппарата (рис. 3.7, а). Выпуск сжатого воздуха,
обладающего большой энергией, нужно рассматривать как недо-
статок данного способа. К тому же, вытекающие через боковые
створки воздушные струи увеличивают внешнее сопротивление
диффузора и снижают эффективную тягу силовой установки.
Чтобы рост сопротивления не был слишком большим, открытие
створок должно быть невелико. Перепуск воздуха через регули-
94
Глава III. Регулирование сверхзвуковых входных устройств
руемые сопла в донной части фюзеляжа дает значительно мень-
шее увеличение сопротивления по сравнению с перепуском через
створки.
При взлете на острых кромках диффузора образуется срыв
потока, а при низких скоростях полета динамическое сжатие воз-
духа мало и его плотность не намного отличается от плотности
атмосферы. В этих условиях пропускная способность горла диф-
фузора недостаточна и располагаемый расход через диффузор
меньше потребного расхода двигателя. Использование створок на
Рис. 3.7
боковой поверхности диффузора дает возможность уравнять рас-
ходы, через створки воздух будет из внешнего пространства посту-
пать в двигатель (см. рис. 3.7, б).
2. Изменение геометрической формы диффузора. Этот способ
нашел широкое применение и ниже рассматривается более под-
робно.
3. Изменение режима работы двигателя. Для силовой установ-
ки с ТРД этот способ заключается в изменении числа оборотов
двигателя, а с ПВРД — в изменении температуры газа или площа-
ди критического сечения выходного сопла.
Трудности регулирования ТРД на больших скоростях полета в
настоящее время заставляют отказаться от этого способа. Целе-
сообразно приспосабливать диффузор к работе двигателя, а не на-
оборот. Однако, возможно, что задача оптимального регулирова-
ния силовой установки, например, регулирование на минимальный
километровый расход топлива, потребует изменения режима рабо-
ты и двигателя, и диффузора.
Регулирование входного диффузора путем изменения
его геометрической формы
Изменение расхода воздуха через диффузор достигается откло-
нением части сверхзвукового потока, набегающего па диффузор,
на внешнее обтекание. Это отклонение может быть получено за
§ 2. Влияние способа регулирования на характеристики диффузора
95
счет изменения положения клина или центрального тела относи-
тельно обечайки, или за счет изменения площади входа с помощью
поворотной обечайки (без изменения положения клина). Возмож-
но сочетание обоих путей. Одновременно с отклонением части
сверхзвукового потока должна изменяться и площадь горла.
Осесимметричные и плоские диффузоры следует рассматри-
вать раздельно. У них разные возможности в отношении изменения
геометрических форм и должен быть принципиально разным под-
ход к их регулированию.
Рис. 3.8
Рис. 3.9
Под изменением геометрической формы осесимметричного диф-
фузора понимается изменение относительного положения цен-
трального тела 1К — /к/^ктах, где 1К—расстояние от вершины кону-
са, образующего центральное тело, до плоскости входа в диффу-
зор. В таком диффузоре изменение формы центрального тела
практически невозможно. Технически сложно и выполнение обе-
чайки с переменным углом наклона. На обечайке возникают боль-
шие аэродинамические силы, плавность ее обводов должна обес-
печить безотрывное обтекание как внешней, так и внутренней
поверхностей. Поэтому у осесимметричных входных диффузоров де-
лают неподвижные обечайки.
С изменением внешних условий путем перемещения централь-
ного тела может быть восстановлено сверхзвуковое течение, без
головной волны, на входе в диффузор и получена нужная пло-
щадь горла. Площадь горла диффузора зависит от угла наклона
обечайки |30б, положения центрального тела и его диаметра в том
сечении, где образуется критическое сечение диффузора. При
Роб = const с выдвижением центрального тела, т. е. с ростом 1К
площадь горла диффузора уменьшается.
Поскольку осесимметричные диффузоры выполняются с обе-
чайками, имеющими постоянный угол наклона, отклонение части
сверхзвукового потока достигается при неизменной площади вхо-
да. Схема течения применительно к такому способу регулирования
показана на рис. 3.8.
Различные геометрические формы плоского диффузора могут
быть получены как изменением 1К или роб, так и обоих этих геоме-
трических параметров. Схема течения при отклонении части сверх-
звукового потока изменением площади входа диффузора с помо-
щью поворотной обечайки показана на рис. 3.9,
96
Глава III. Регулирование сверхзвуковых входных устройств
На рис. 3.10, а показана схема плоского диффузора с подвиж-
ным ступенчатым клином. Горло диффузора в этой схеме обра-
зуется между клином и специальной профилированной вставкой.
Для регулирования площади горла перемещается профилирован-
ная вставка. Предусматривается отсос пограничного слоя. Этот
способ регулированйя горла может быть применен и в осесиммет-
ричном диффузоре. Но в плоском диффузоре его выполнить легче.
Рис. 3.10
На рис. 3.10, о дана схема плоского диффузора, у которого
площадь горла регулируется с помощью подвижной рампы. Сверх-
звуковой поток сначала отклоняется неподвижным клином 1, а
затем — подвижным клипом 2. Подвижные элементы 3, 4 и 5 пока-
заны в двух крайних положениях, с неподвижными элементами
они скреплены шарнирами 6. В диффузоре предусмотрен отсос
пограничного слоя.
На рис. 3.11 показана в плане схема силовой установки одного
из зарубежных самолетов. Подвод воздуха к двигателю обеспе-
чивается плоскими диффузорами, расположенными по бокам фю-
зеляжа. Диффузоры регулируются перемещением клина и от-
крытием створок перепуска. Перед диффузорами с фюзеляжа от-
сасывается пограничный слой.
Перечисленные три способа компенсации несогласованности
воздухозаборника и двигателя не равноценны по увеличению ло-
бового сопротивления при переходе к нерасчетным условиям
полета. Наибольший прирост лобового сопротивления дает регу-
лирование диффузора путем перемещения центрального тела или
§ 3. Выбор программы регулирования входного диффузора
97
клин^. Несколько меньший прирост получается при изменении
площади входа с помощью поворотной обечайки. Перепуск возду-
ха дает наименьший прирост лобового сопротивления. Преимуще-
ства перепуска существенно сни-
жаются, если перепуск осуществ-
ляется с помощью створок на бо-
ковой поверхности диффузора. Знанья
Возможно сочетание нескольких
методов компенсации.
§ 3. ВЫБОР ПРОГРАММЫ
РЕГУЛИРОВАНИЯ ВХОДНОГО
ДИФФУЗОРА
Фюзеляж
Прямой
В предшествующем парагра- ’
фе бЫЛИ разобраны СПОСОбЫ КОМ- Створки
пенсации коэффициентов расхода
диффузора и двигателя как прин-
цип регулирования диффузора. !
Однако непосредственное измере-
ние коэффициентов расхода за-
труднительно и использование по-
добного параметра в качестве па-
Двигатель
раметра регулирования нецеле- Рис. 3.11
сообразно. Программа регулиро-
вания в значительной степени определяется типом входного устрой-
ства. Поэтому рассмотрим раздельно программы регулирования
диффузоров внешнего сжатия и смешанного сжатия.
Диффузор внешнего сжатия
Этот тип диффузора целесообразно использовать при скоростях
полета, соответствующих Мн =С2. Примем, что на докритическом
режиме работы его характеристика подобна показанной пункти-
ром на рис. 3.3 и 3.4. В этом случае, пренебрегая некоторым ро-
стом внешнего сопротивления, регулирование целесообразно ве-
сти на (о0иеб)тах- Для различных значений Мн величина (оди^тах
меняется, но положение головной волны можно считать неизмен-
ным. Таким образом, за параметр регулирования берем коорди-
нату Хек, определяющую положение головной волны относительно
плоскости диффузора (рис. 3.12), а программой регулирования
будет (хск)опт = const. Оптимальному положению скачка соответ-
ствует наибольшее значение свиф.
За регулирующие факторы могут быть приняты подвижное
центральное тело (клин) или перепуск. Возможно в некоторой
последовательности воздействие обоих факторов. Регулируемый
4 Черкасов Б. А.
98
Глава III. Регулирование сверхзвуковых входных устройств
перепуск, как уже было сказано, лучше делать в донной части
двигательной гондолы.
Перемещение центрального тела или клина в диффузорах
внешнего сжатия мало отражается
на площади горла. Оно меняет
главным образом величину
слива сверхзвукового потока
па внешнее обтекание.
Положение головной волны
перед входом в диффузор (ко-
ордината Хек) зависит от внеш-
них условий и от режима ра-
боты двигателя. Примем, что
влияние внешних условий про-
является только при изменении
Мн. Двигатель воздействует
на диффузор изменением про-
изводительности компрессора,
что сказывается на величине
давления в конце диффузора.
Производительность компрес-
сора характеризуется величи-
ной приведенного расхода
На установившихся ре-
жимах работы двигателя при
надкритическом перепаде в выходном сопле и неизменных геомет-
рических размерах производительность компрессора может быть
также определена через ппр или л*.
Влияние 1К на положение скачка при неизменных Ми и g(Xi)
показано на рис. 3.13. При движении центрального тела или кли-
на назад головная волна уходит от входа диффузора вперед и мо-
жет возникнуть помпаж. Движение центрального тела вперед при-
водит -к тому, что замыкающий скачок входит внутрь канала. При
значительном его перемещении вниз по потоку может возникнуть
§ 3. Выбор программы регулирования входного диффузора
99
«зуд». На этом же графике отмечено желательное положение го-
ловной волны (хск)опт, при котором получается (аэиаз)тах.
Располагая характеристиками компрессора и диффузора, мож-
но рассчитать зависимость /ДМп, <?(Xi)] для условия (хск)0Пт —
= const. Ее примерный вид показан на рис. 3.14. Характер изме-
нения /к, показанный на этом рисунке, сохранится, если вместо
координаты использовать пПр
что при работе компрессора сов-
местно с турбиной с ростом про-
изводительности увеличиваются
ппР и л*.
Как уже было сказано, вместо
1К за регулирующий фактор мо-
жет быть принят перепуск возду-
ха. Влияние перепуска, характе-
ризуемое площадью Fnep, на по-
ложение головной волны показа-
но на рис. 3.15. На больших ско-
ростях полета горло диффузора
будет переризмерено, воздуха
поступит больше, чем требуется,
и его излишки выпускаются в атмосферу. Что же касается старта
и малых скоростей полета, то на этих режимах при запертом горле
давление перед двигателем р\ будет меньше атмосферного рн-
В этом случае для обеспечения тяги к двигателю нужно подво-
дить воздух через регулируемые отверстия на боковой поверхности
диффузора между горлом и двигателем.
Диффузор смешанного сжатия
Для входного устройства с диффузором такого типа коэффи-
циент <5диф можно представить в виде произведения
сдиф ~ Статраз.ск-
В этом произведении ат — коэффициент восстановления дав-
ления в системе косых скачков при отклонении сверхзвукового
потока центральным телом или клином. При неизменной конфи-
гурации центрального тела величина ат является функцией Мн
и положения центрального тела (координаты /к).
Коэффициент втр определяет потери на трение внутри канала
диффузора, величина втр мало зависит от регулирования диффу-
зора. Можно считать, что с;тр = const.
Коэффициент Оз.ск характеризует интенсивность замыкающего
скачка в расширяющейся части канала диффузора. Его величина
зависит от согласования пропускной способности горла и произ-
4*
100
Глава Iff. Регулирование сверхзвуковых входных устройств
водительности компрессора. Рост площади горла увеличивает ин-
тенсивность замыкающего скачка и смещает его ближе к ком-
прессору, величина о3. си падает. Дросселирование двигателя
(сниженйе производительности компрессора) приводит к росту
Ста. си и перемещению замыкающего скачка ближе к горлу диффу-
зора. Для обеспечения устойчивой работы режим диффузора дол-
жен быть закритическим с замыкающим скачком, расположенным
несколько за горлом. При этом для снижения внешнего сопротив-
ления необходимо, чтобы диффузор работал без головной волны.
Таким образом, с одной стороны, выбором площади горла нужно
обеспечить пропускную способность системы косых скачков без
головной волны. С другой стороны, в выборе площади горла сле-
дует исходить из обеспечения определенного положения замы-
кающего скачка. В общем случае удовлетворить оба эти требова-
ния нельзя. Поэтому несогласованность пропускной способности
горла и двигателя нужно компенсировать путем перепуска.
Для оптимального регулирования диффузора смешанного сжа-
тия нужно использовать три параметра регулирования. Программа
регулирования может быть такой.
1. Пересечение линии первого косого скачка с кромкой обечай-
ки. 2. Отсутствие головной волны при минимальной степени пере-
расширения горла. 3. Стабильное положение замыкающего скачка
(Л-з.си ~ Const).
Регулирование по первому параметру обеспечит оптимальное
восстановление давления в системе косых скачков, регулирование
по второму параметру гарантирует от возникновения головной
волны. Третий параметр дает высокое значение а3. ск при доста-
точном запасе устойчивости.
Соответственно для этих трех параметров регулирующими
факторами являются перемещение центрального тела или клина,
поворот обечайки или перемещение вставки, изменяющей пло-
щадь горла, изменение площади окон или сопел перепуска. Раз-
дельное регулирование системы скачков и пропускной способности
горла может быть осуществлено по схеме, приведенной на
рис. 3.10, а.
Раздельное регулирование по трем параметрам достаточно
сложно. Для его осуществления необходимы три регулятора, ко-
торые будут между собой взаимодействовать. Однако задачу регу-
лирования диффузора смешанного сжатия можно упростить.
На регулирование диффузора большое влияние оказывает вы-
бор расчетного значения (л*)р компрессора, от которого зависит
величина приведенного расхода воздуха на различных режимах
работы двигателя и в различных внешних условиях. При доста-
точно больших (л*)р для двигателя, регулируемого по программе
п = const, с уменьшением скорости полета требуется вдвигать
§ 3. Выбор программы регулирования входного диффузора 101
центральное тело (клин) для получения высокого ат и увеличи-
вать площадь горла для работы на закритическом режиме без го-
ловной волны.
Площадь горла осесимметричного диффузора при регулирова-
нии перемещением центрального тела зависит от угла наклона
обечайки, формы и размеров центрального тела и его положения
относительно обечайки. Поэтому при соответствующем выборе
Роб с изменением 1К, для достижения наибольших от, можно полу-
чить и необходимое для работы без головной волны Fs. Стабили-
зация положения замыкающего скачка будет обеспечена регули-
рованием перепуска.
Эффективность геометрического воздействия на расход плоско-
го диффузора существенно зависит от начального угла обечайки.
Чем меньше ее начальный угол, тем сильнее изменение расхода
отклонением обечайки и, наоборот, тем слабее влияет на расход
движение клина. При небольших начальных углах обечайки уве-
личение рОб слабо влияет на рост сх и поэтому изменение расхода
с помощью поворотной обечайки выгоднее, чем изменением поло-
жения клина. Однако со снижением скорости полета эти преиму-
щества регулируемой обечайки уменьшаются. При возможности
использования в плоском диффузоре передвижного клина и пово-
ротной обечайки для окончательного выбора способа воздействия
на характеристики диффузора необходимо учитывать характери-
стику компрессора и степень необходимого изменения расхода
воздуха по высоте и скорости полета.
Можно еще в большей степени упростить регулирование вход-
ного устройства с диффузором смешанного типа, оставляя только
один воздействующий фактор. Так, при использовании только
подвижных центрального тела или клина за регулируемый пара-
метр следует выбрать положение замыкающего скачка. Такое ре-
гулирование может привести к снижению ат и па некоторых ре-
жимах полета к появлению головной волны.
В некоторых случаях применяется ступенчатое регулирование
диффузора, при котором центральное тело или клин имеют не-
сколько фиксированных положений. Переход из одного положения
в другое происходит при достижении определенного значения чис-
ла Мп полета или ппр.
Схема замены непрерывного перемещения центрального тела
ступенчатым для диффузора внешнего сжатия показана на
рис. 3.16, а. При взлете конус полностью вдвинут, этому его поло-
жению соответствует 1Ко. При достижении числа Мя полета, равно-
го Мн,, конус выдвигается и занимает положение, характеризуемое
величиной 1К1- Это положение конуса сохраняется до числа Мн
полета равного Мн, и т. д. Число перестановок конуса, а также ве-
личины его потребного перемещения определяются диапазоном чи-
сел Мп полета, а также взаимным расположением границ неустой-
102
Глава Ш. Регулирование сверхзвуковых входных устройств
чивой работы диффузора (границ наступления помпажа и «зуда»).
Пунктирная линия на рис. 3.16, а определяет закон оптимально-
го перемещения конуса по величине оди8б. Эта линия проходит до-
вольно близко от границы помпажа. Ее положение определяется
характером изменения вди# по положению конуса 1К, показанного
Рис. 3.1(5
на рис. 3.16,6. В связи с ростом максимальных скоростей полета,
а следовательно, и диапазона скоростей полета, следует отдать
предпочтение регулированию диффузора с непрерывным изменени-
ем положения конуса.
§ 4. ОСОБЕННОСТИ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ДИФФУЗОРОВ
Входной диффузор смешанного сжатия, работающий на закри-
тическом режиме, условно можно считать состоящим из двух ча-
стей: сверхзвуковой и дозвуковой. Их разделяет замыкающий ска-
чок уплотнения. На расчетных режимах интенсивность замыкаю-
щего скачка невелика, на нерасчетных режимах нерегулируемого
диффузора при падении противодавления она значительно возра-
стает.
На диффузор действуют возмущения, идущие как со стороны
двигателя, так и извне. Если возмущения идут извне, то они прак-
тически мгновенно охватывают всю сверхзвуковую часть и време-
нем переходных процессов в ней можно пренебречь. Возмущения,
идущие со стороны двигателя, на сверхзвуковую часть не распро-
страняются, но они могут изменить положение замыкающего скач-
ка. При движении в сторону горла и достижении замыкающим скач-
ком определенного положения он выходит из канала диффузора и
превращается в головную волну. Система скачков на входе разру-
§ 4. Особенности динамических характеристик диффузоров
103
шается и картина обтекания диффузора изменяется практически
мгновенно.
При скачкообразном изменении внешних условий,режим обтека-
ния сверхзвуковой части диффузора меняется так же мгновенно.
Отсюда следует, что динамические характеристики диффузора в ос-
новном связаны с характеристиками его дозвуковой части.
В дозвуковой части диффузора имеет место запаздывание в пе-
редаче возмущений по тракту и вызываемый ими сложный переход-
ный процесс. Допустим, что за счет увеличения числа оборотов дви-
гателя или включения системы перепуска расход воздуха на выходе
из диффузора увеличился. Тогда давление на выходе упадет и про-
тив потока пойдет волна разряжения, перепад давления па замы-
кающем скачке изменится и перестанет удовлетворять условию его
равновесия.
Для восстановления нужного перепада скачок начнет переме-
щаться, что в свою очередь также вызовет возмущение в виде вол-
ны сжатия, идущей по потоку. Отражение волны разряжения и сжа-
тия от замыкающего скачка и компрессора еще более осложнит
картину неустановившегося течения. После некоторого колебатель-
ного процесса (за счет инерции столба воздуха) через компрессор
или систему перепуска установится новый режим с новым расходом.
В дозвуковой части диффузора всегда есть некоторые колеба-
ния давления, связанные с колебаниями внешнего потока и коле-
баниями режима работы двигателя, сказывающиеся на положении
замыкающего скачка. Однако эти колебания являются слабыми
(акустическими), они не отражаются на устойчивости течения в
диффузоре и пе учитываются при проектировании регулирующей
аппаратуры. При регулировании по замыкающему скачку следует
иметь в виду, что замыкающий скачок очень чувствителен к изме-
нению внешних условий и положению регулирующих органов. При
появлении возмущения в первый момент времени замыкающий
скачок основную часть пути перемещается с большой скоростью, а
затем медленно приближается к своему новому положению. Эта
особенность усложняет задачу регулирования диффузора по поло-
жению замыкающего скачка.
Глава IV
РЕГУЛИРОВАНИЕ СВЕРХЗВУКОВЫХ ПРЯМОТОЧНЫХ
ВОЗДУШНО-РЕАКТИВНЫХ ДВИГАТЕЛЕЙ (СПВРД)
§ 1. ОСОБЕННОСТИ РАБОЧЕГО ПРОЦЕССА
В этой главе рассматриваются только маршевые сверхзвуковые
прямоточные ВРД (в дальнейшем просто ПВРД). Такие ПВРД
являются двигателями однорежимными, рассчитанными на опреде-
ленное число Мп полета. Они обладают достаточно высокой эконо-
мичностью и предназначены для летательных аппаратов большой
дальности.
В целях упрощения конструкции и управления рабочим процес-
сом ПВРД принято делать с нерегулируемым выходным соплом.
Однако для большего представления о характеристиках ПВРД в
некоторых случаях будем отходить от этого положения и допускать
возможность изменения площади критического сечения выходного
сопла. Схема ПВРД с характерными сечениями I, т, 2, 3, пр дана
на рис. 4.1.
Летательный аппарат с ПВРД невыгодно разгонять вспомога-
тельными двигателями до расчетной величины Мн = МНр. При не-
котором значении Мн < МПр вспомогательные двигатели отклю-
чаются и дальнейший разгон летательного аппарата продолжается
основным двигателем — ПВРД. Поэтому каждый маршевый ПВРД
в некотором небольшом диапазоне скоростей работает на разгон-
ном режиме, что необходимо учитывать при разработке системы ре-
гулирования.
Для выбора в дальнейшем программы регулирования рассмот-
рим зависимость коэффициента эффективной тяги Сц3ф и удельно-
го расхода топлива суэ от изменения расхода топлива G и числа
Мл полета (сЛОф равен коэффициенту внутренней тяги за вычетом
коэффициента внешнего сопротивления). Тяга двигателя, а следо-
вательно, и коэффициент внутренней тяги зависит от степени рас-
ширения газа в сопле. В расчетах по выбору программы регулиро-
вания для определения тяги можно считать, что двигатель имеет
сопло Лаваля с площадью выходного сечения, равной площади ка-
меры. Расчет ведется для ряда значений чисел Мн полета. Одно из
них — МНр и соответствующее ему число М2 потока в конце диф-
§ J. Особенности рабочего процесса
105
фузора -принимаются за расчетные. Для общности рассуждений за
независимую переменную принимают приведенный расход топлива
Gnp, под которым понимают эффективный расход отнесен-
ный к давлению окружающей среды и площади поперечного сече-
ния двигателя
Влияние числа Мгг полета на сПэ$ и суЭ рассматривается при
сравнительно небольших отклонениях Мн от расчетного значения.
Рис. 4.1
Предположим, что при данных Мн и Gnp диффузор работает
па критическом режиме (замыкающий скачок уплотнения располо-
жен в горле диффузора). При снижении расхода топлива диффузор
перейдет на закритический режим. За горлом диффузора возникнет
система внутренних интенсивных скачков уплотнения, уменьшится
коэффициент восстановления полного давления и степень повыше-
ния давления диффузора. В результате снижения расхода топлива
коэффициент эффективной тяги сГ!3ф начнет резко падать.
При подаче топлива в двигатель больше, чем это необходимо
для поддержания критического режима, диффузор переходит на
докритический режим с возникновением выбитой ударной волны и
возрастанием внешнего сопротивления. Коэффициент восстановле-
ния полного давления и степень повышения давления диффузора
остаются почти неизменными. Коэффициент эффективной тяги СцЭф
хотя и увеличивается, но значительно меньше, чем при возрастании
расхода топлива в закритической области. Это связано с увеличени-
ем внешнего сопротивления. Пределом увеличения расхода топли-
ва будет возникновение неустойчивой работы диффузора. Подобные
характеристики ПВРД в некотором диапазоне изменения Мя пока-
заны на рис. 4.2.
Минимальный удельный расход топлива получается при работе
диффузора ПВРД на критическом режиме. Для Мя = const в слу-
чае отклонения в ту или другую сторону приведенного расхода топ-
лива от значения, соответствующего критическому режиму, удель-
106
Глава IV. Регулирование СПВРД
ный расход топлива возрастает. Особенно резкое увеличение суа
получается при переходе на докритический режим (рис. 4.3).
Графики, представленные на рис. 4.2 и 4.3, дают возможность
исключить параметр Gnp и получить зависимость с,,э от коэффи-
циента эффективной тяги слэдВ (рис. 4.4). Из графика рис. 4.4 сле-
дует, что при Мн = const рост тяги (увеличение cR3$) при работе
диффузора ПВРД на докритичес-
ком режиме достигается ценой зна-
чительного увеличения cyg. В случае
необходимости некоторое снижение
тяги с переходом на закритический
режим может быть получено при
небольшом росте cyg.
Если у ПВРД сделать регули-
руемое сопло, то такой двигатель
сможет работать на режимах, су-
щественно отличающихся от рас-
четного, с незначительный увеличе-
нием удельного расхода топлива.
ПВРД с регулируемым соплом об-
ладает большим диапазоном тяг и обеспечивает избыточную тягу
для разгона и маневрирования летательного аппарата. Это дости-
гается одновременным увеличением расхода топлива и площади
критического сечения сопла.
§ 2. ВЫБОР ПРОГРАММЫ РЕГУЛИРОВАНИЯ
Основными параметрами рабочего процесса ПВРД являются
’'а = Pi IP11 (степень повышения давления диффузора) или Ма
(число М потока на выходе из диффузора) и температура газа в
§ 2. Выбор программы регулирования
107
конце камеры сгорания Т* Вместо температуры газа за основной
параметр рассматривают также коэффициент избытка воздуха а.
Эти параметры рабочего процесса могут быть приняты за парамет-
ры регулирования. Регулирующими факторами являются измене-
ние расхода топлива и площади критического сечения сопла, а для
двигателя с неизменным сечением сопла — только изменение рас-
хода топлива.
Сначала рассмотрим ПВРД с Fnp = const. В этом случае изме-
нение расхода топлива G должно быть направлено на регулирова-
----принято для Критич
расчета
----действительное
протекание
проиесса
Закритич
режимы
режимы
До критич
режимы
6 пр
Рис. 4.6
ние или М2. Прежде чем наметить возможные программы регу-
лирования маршевого ПВРД, рассмотрим влияние параметров ре-
гулирования р2/рн и М2 на коэффициент эффективной тяги сЛэбб,
а также зависимость параметров регулирования от изменения чис-
ла Мл полета и приведенного расхода топлива Gnp.
С увеличением скорости полета величина р\/рн возрастает.
В свою очередь рост р*2 /рн приводит к увеличению коэффициента
эффективной тяги сЯэ$ так, как это показано на рис. 4.5. Из гра-
фиков этого рисунка, а также рис. 4.3 и 4.4 следует, что если под-
держивать критический режим течения воздуха в диффузоре, го
ПВРД будет развивать тягу, близкую к максимальной, при мини-
мальных удельных расходах топлива.
На рис. 4.6 показано влияние приведенного расхода топлива на
величину степени повышения давления в диффузоре ПВРД. В за-
критической области работы диффузора увеличение расхода топли-
1 Наряду с М2 можно использовать равноценный ему параметр регулиро-
вания — коэффициент скорости ?.21 что и сделано в этой главе при выводе урав-
нения движения ПВРД.
108
Глава IV. Регулирование СПВРД
ва приводит к росту р2* 1ри- При переходе в докритическую область
в зависимости от свойств конкретного диффузора дальнейшее уве-
личение расхода топлива или не отразится на величине р*2 !ри, или
приведет к некоторому ее падению. Это означает, что регулятор,
рассчитанный на увеличение подачи топлива при работе диффузо-
ра в закритической области, не выполнит- своего назначения, если
режим работы диффузора будет соответствовать докритической об-
ласти, и нормальная работа ПВРД нарушится. Чтобы избежать
этого необходимо соответствующим путем задать программу изме-
нения р2 1ри по числу Ми полета: для каждого значения Мн за-
данная величина р*2 /ра должна быть меньше, чем р* /Рн при кри-
тическом режиме работы диффузора. Если же программное изме-
нение отношения р*2 /рн по Мн будет совпадать с его значением при
критическом режиме, то необходимо предусмотреть ограничение в
максимальной подаче топлива.
На рис. 4.7 показана зависимость коэффициента эффективной
тяги ПВРД от числа М2 потока на выходе из диффузора. Из гра-
фика этого рисунка следует, что в рассмотренном диапазоне чи-
сел Мн величина М2 на линии критических режимов меняется не
сильно. На докритических режимах работы диффузора число М2
влияет на коэффициент эффективной тяги cRa$ сравнительно мало.
На закритнческих режимах это влияние велико. Отсюда следует,
что если задаться программой изменения М2 по числу Мн полета,
соответствующей критическим режимам диффузора, то можно обес-
печить тягу ПВРД, близкую к максимальной, при наименьших рас-
ходах топлива.
Зависимость М2 от приведенного расхода топлива Gnp представ-
ляет собой монотонную функцию (рис. 4.8), что говорит о более
§ 2. Выбор программы регулирования
109
Критич.
режимы
йокритич~~
режимы
Сопротивление
летательного
аппарата
Рис. 4.9
Крейсерский,
режим
Закритич.
режимы
^np5>^npi
snp5
^прч
йпрз
пр г
Gnpi
и число Ми полета
неизмен-

удобном использовании параметра Мг в программном регулирова-
нии по числу Мя по сравнению с параметром р\ /ра.
Программа изменения По Мн, также как ир!2 /рн по Мн, мо-
жет быть выбрана в закритической области работы диффузора
ПВРД. И это оказывается необходимым для обеспечения устойчи-
вости летательного аппарата по скорости полета.
На рис. 4.9 дана зависимость сЯЭф от Мн для различных приве-
денных расходов топлива Gnp. На этот же график нанесена кривая
коэффициента сопротивле-
ния летательного аппарата
по скорости полета. Точка г
пересечения кривой коэффи-
циента сопротивления с ли-
нией Сндф при выбранном
приведенном расходе топли-
ва Gnp определяет устано-
вившийся режим полета.
Если эта точка пересечения
лежит на линии критических
режимов работы диффузора,
то летательный аппарат бу-
дет устойчив только тогда,
когда какое-либо внешнее
возмущение приведет к уве-
личению Мн. В этом случае
при Мц > МНр располагае-
мая тяга будет меньше потребной
ном приведенном расходе Gnp снизится до расчетного значения.
Когда внешнее возмущение приводит к снижению Мн, то распо-
лагаемая тяга становится меньше потребной. Скорость полета про-
должает падать, а диффузор переходит на докритичсский режим
работы. В этом случае для восстановления скорости полета до рас-
четной необходимо увеличить расход топлива, но роет расхода мо-
жет вызвать неустойчивый режим диффузора.
Отсюда следует, что для обеспечения крейсерской скорости ле-
тательного аппарата диффузор ПВРД должен работать в закрити-
ческой области. Тогда летательный аппарат будет устойчив в не-
котором диапазоне скоростей как меньших, так и больших расчет-
ной, а двигатель будет располагать некоторым избытком тяги для
разгона и стабилизации скорости.
ПВРД с регулируемым выходным соплом имеет большее преи-
мущество по сравнению с двигателем с FKP = const в отношении
регулирования скорости полета. Такой двигатель также должен
иметь программное изменение Мо по Мн. При увеличении FKP с не-
изменным расходом топлива давление в камере сгорания снижает-
по
Глава IV. Регулирование СПВРД
ся, а число М2 потока в конце диффузора возрастает. Рост М2 вы-
зовет увеличение расхода топлива, давление в камере сгорания
опять возрастет и тяга двигателя повысится, что будет равноцен-
но переводу двигателя на форсажный режим. Таким образом,
ПВРД с регулируемым выходным соплом на крейсерской скорости
полета обеспечивает потребную тягу с наименьшим удельным рас-
ходом топлива и в то же время обладает большой избыточной тя-
гой при переходе на форсажный режим. Эта избыточная тяга соз-
дается без опасности перехода диффузора на докритический режим
работы. Поскольку регулируемое сопло используется только для
форсирования ПВРД, оно может быть выполнено, как и в ТРД,
двухпозиционным.
Рассмотренные в этом параграфе характеристики ПВРД дают
возможность выбрать программу регулирования маршевого ПВРД,
обеспечивающую высокую экономичность и устойчивую работу диф-
фузора в небольшом диапазоне изменения чисел Мд- полета. Могут
быть использованы программы р%1рн = /(Мн) или М2 = /2(Мн).
Обе программы регулирования должны обеспечить работу диффу-
зора ПВРД в закритической области с заданным запасом устойчи-
вости. Как уже было показано, предпочтение следует отдать вто-
рой из них, а именно программе регулирования М2 = /2(МЛ).
При достижении летательным аппаратом расчетной скорости
полета ПВРД переводится на программу регулирования М.11р
= const.
При использовании любой программы регулирующим фактором
остается изменение расхода топлива. На участке разгона влияние
регулирующего фактора может быть усилено переводом ПВРД на
форсажный режим, если выходное сопло двигателя выполнено двух-
позиционным.
Расчетная маршевая скорость может поддерживаться только за
счет собственной устойчивости летательного аппарата с ПВРД.
Однако регулятор способствует более быстрому восстановлению
скорости при внешних возмущениях, действующих на двигатель и
летательный аппарат. В случае больших внешних возмущений и
значительного снижения скорости полета, по сравнению с расчет-
ной, ПВРД может быть переведен на форсированный режим, если
предусмотрено двухпозиционное выходное сопло.
§ 3. ОБЛАСТЬ ВОЗМОЖНЫХ РЕЖИМОВ РАБОТЫ МАРШЕВОГО ПВРД
В рассмотренных ранее характеристиках увеличение расхода
топлива на разгонном участке ограничивалось появлением выби-
той ударной волны и потерей устойчивости диффузора. Другим ог-
раничением в увеличении расхода является устойчивость горения
топлива. На участке разгона коэффициент избытка воздуха может
стать ниже допустимого, что повлечет за собой срыв пламени. Для
§ 3. Область возможных режимов работы, маршевого ПВРД
111
предотвращения срыва нужно ввести ограничительное регулирова-
ние по а. Ограничительное регулирование по устойчивости процес-
са сжатия в диффузоре, дополненное ограничительным регулирова-
нием по устойчивости горения, определит область возможных режи-
мов работы маршевого ПВРД на разгонном участке.
На рис. 4.10 показаны располагаемые тяги маршевого ПВРД
и потребная тяга летательного аппарата в некотором диапазоне из-
менения Мн. Располагаемые тяги даны в виде зависимостей
Rpacn = RpacnfM-u) при G = const и при а = const, потребная тяга
в этом диапазоне скоростей представлена параболической зависи-
мостью. Область возможных режимов ПВРД определяется гранич-
ными кривыми: слева расположена граница устойчивой работы
диффузора, справа проходит вертикальная прямая Мишах, положе-
ние которой связано с прочностью двигателя. За верхнюю гранич-
ную кривую примем-линию сыип = const, ее положение определяет-
ся условием надежного горения богатой смеси. Нижняя граница
обусловлена или надежностью распыла топлива (Gmln = const),
или устойчивостью горения бедной смеси (аШах = const).
Вспомогательные двигатели разгоняют летательный аппарат до
скорости (Ми) нач. На этом режиме тяга маршевого двигателя /?0
равна потребной тяге летательного аппарата и соответствует точке
О на кривой потребной тяги.
На расчетном режиме Мп = Мдр тяга двигателя равна /?]
(точка / на кривой потребной тяги). Разность бМн = Мир—
— (44п)иач определяет протяженность разгонного участка. Набор
скорости от (Мн) нач до Мнр обеспечивается созданием избыточной
тяги маршевого двигателя путем повышения температуры газа
в камере сгорания выше температуры установившегося режима.
112
Глава IV. Регулирование СПВРД
Пренебрегая временем, необходимым для совершения тепловых
и газодинамических процессов, полагаем, что изменение расхода
топлива мгновенно отражается на силе тяги (участок Оа характе-
ристики на рис. 4.10). Нарастание расхода топлива на участке ab
ограничивается возможностью потери устойчивости. Поэтому на
начальном этапе участка разгона летательного аппарата нужно ре-
гулировать рабочий процесс диффузора. За параметр регулирова-
ния можно принять положение замыкающего скачка уплотнения,
фиксируя его между двумя сечениями I и т (см. рис. 4.1) в расши-
ряющейся части канала за горлом диффузора, в которых измеряет-
ся статическое давление. Регулирующим фактором остается изме-
нение расхода топлива. Подача топлива должна увеличиваться,
если замыкающий скачок перемещается за сечение т по потоку.
Подача топлива должна уменьшаться при перемещении против по-
тока и расположения его перед сечением I.
Следующий, второй этап участка разгона летательного аппарата
характеризуется достижением в камере сгорания коэффициента из-
бытка воздуха и = «min- Ограничительное регулирование в подаче
топлива на этом этапе проводится с целью не допустить богатый
срыв пламени. Второй этап заканчивается при числе Мп полета,
равном Мдр, или несколько меньшим. Коэффициент избытка воз-
духа а при регулировании па amm = const непосредственно не из-
меряется, а определяется путем сравнения расхода топлива и воз-
духа. Такой метод определения а не обладает большой точностью,
так как при его использовании не учитывается изменение полноты
сгорания топлива.
При достижении летательным аппаратом заданной скорости по-
лета двигатель переводится на программу регулирования Мир =
= const с непосредственным измерением Мн (участок cld характе-
ристики на рис. 4.10). Для достижения достаточно высокой эконо-
мичности на маршевом режиме заданную скорость полета
требуется поддерживать с высокой точностью, допустимое отклоне-
ние бМп = ± 0,05 -т- 0,1.
В случае, если скорость летательного аппарата превысит задан-
ную (Мн > МНр), регулятор Мпр = const уменьшит подачу топли-
ва. При значительном снижении расхода топлива в камере сгорания
может возникнуть бедный срыв. Чтобы избежать этого, в системе
регулирования должен быть еще один ограничительный регулятор,
обеспечивающий при Мп > Мнр, amax = const.
Расположение границы устойчивой работы диффузора в поле
статических характеристик двигателя существенно зависит от сте-
пени перерасширения горла диффузора и от угла атаки, на котором
работает диффузор (угол атаки летательного аппарата). Увеличе-
ние угла атаки сдвигает границу устойчивой работы диффузора
вправо и уменьшает область возможных режимов работы двига-
теля.
§ 4. ПВРД как объект регулирования
ИЗ
При пулевом угле атаки и при достаточно перерасширенном
горле граница устойчивой работы диффузора может настолько
сдвинуться влево, что потери устойчивости при разгоне угрожать
не будут. В этом случае можно обойтись без ограничительного ре-
гулятора по положению замыкающего скачка.
§ 4. ПВРД КАК ОБЪЕКТ РЕГУЛИРОВАНИЯ
Для определения свойств ПВРД как объекта регулирования не-
обходимо учитывать его способность в отдельные моменты времени
на неустановившихся режимах накапливать или расходовать рабо-
чее тело и тепловую энергию. Следует напомнить, что в гл. II, рас-
сматривая свойства ТРД как объекта регулирования, этими осо-
бенностями ТРД мы пренебрегали и учитывали только аккумули-
рование механической энергии.
Для ПВРД следует также принять во внимание запаздывание в
передаче воздействий по газовоздушному тракту от камеры сгора-
ния к диффузору. Это запаздывание определяется некоторым про-
межутком времени от момента изменения расхода топлива до мо-
мента изменения параметров потока в диффузоре. В связи с отно-
сительно длинными коммуникациями изменение внешних условий
передается на чувствительные элементы регуляторов также с неко-
торым запаздыванием. Его необходимо учитывать, когда двигатель
рассматривается совместно с регулятором.
Аккумулирующие свойства ПВРД относительно рабочего тела
могут быть выражены с помощью уравнения
GH + GT —G (4.1)
Н Топ кр dt
В этом уравнении расход воздуха через диффузор ПВРД
Gh = Gh (Рн’ (4.2)
расход газа через критическое сечение сопла
GKP = GKp (Рн’ ТН> (4.3)
аккумулированное рабочее тело
G = G (рн, Тн, lH, I., т ,); (4.4)
расход топлива
Gt on ~~ Gtип о + ^>GTcn. (4.5)
В уравнениях (4.2) — (4.4) 7,н и 7,2 — коэффициенты скорости не-
возмущенного потока и потока в конце диффузора; тПоЭ = Т‘ъ /Т*н —
степень подогрева газа.
114
Глава IV. Регулирование СПВРД
Уравнения (4.2) — (4.5) — нелинейны. Учтя, что на установив-
шемся режиме
G п 4-G —G =0, (4.6)
НО 1 monQ крО 9 ' z
запишем уравнение (4.1) в малых приращениях. В его левую часть
поместим величины, содержащие Хг и тпоэ. Перейдем от абсолютных
приращений к относительным, взяв за базисные величины парамет-
ры исходного установившегося режима. Тогда после преобразова-
ний получим в операторной форме дифференциальное уравнение
(S1Z? + Р1) ДД -г (s2p + р2) Дт„пд = vAGffl0„ (s8p + р3) Арн ф-
+ (ДР + Pi) &Т н + (s5p + р5) Д).я. (4-7)
В этом уравнении
Запишем уравнение, отражающее способность ПВРД аккумули-
ровать тепловую энергию:
+ = (4.8)
dt
В уравнении (4.8) Qe=Qe(pn, Тп, \п)—тепло, внесенное в дви-
гатель с воздухом*, Qron == Qtoh(T/f,G7*071.) “Тепло, вне-
сенное топливом (теплотворная способность топлива в скрытой ви-
де входит в Тпоэ); Qa = Qa = (рн, Тн, Тн, 1,2, Тпод)— тепло, уносимое
из двигателя струей газа; Q = Q (pH, Тн, Хн, 1-2, ттаоэ)—запасенное
в двигателе тепло.
С уравнением (4.8) проделаем преобразования, подобные тем,
которые были проделаны в отношении уравнения (4.1). После пре-
образования получим
(ДР + Pi) Д}*2 + (ЧъР +‘32) ^под -= (ЯзР + Зз) ДРН +
+ (ДР + 31) Д^н + (ДР + Зз) д^н + РД(Д1оп- (4 • 9)
§ 4. ПВРД как объект регулирования
115
Выражения для коэффициентов, входящих в уравнение (4.9),
аналогичны выражениям для коэффициентов уравнения (4.7).
Из уравнений (4.7) и (4.9} исключим степень прдогрева Tnos и
получим одно уравнение с пятью неизвестными. Оно приводится к
виду
Сф2 + т2р + 1) АХ, = (т3р -|- /гг) AGmOT 4 (т2р2 4- т3р 4- /г2) Арн +
+ СФ2 + ЪР + &з) ^Тн + (т2р2 + т9р + /г4) ДХн, (4.10)
где т — постоянные времени, a k — коэффициенты усиления.
При выводе уравнений (4.7) и (4.9), а следовательно, и (4.10)
нами не учитывалось запаздывание в передаче воздействий по трак-
ту и коммуникациям двигателя, о котором говорилось в начале это-
го параграфа. Учет запаздывания необходим в том случае, если
время запаздывания соизмеримо с. величинами коэффициентов,
входящих в уравнение (4.10).
Сам по себе процесс запаздывания сложен. Поэтому будем его
аппроксимировать прямым запаздыванием, т. е. простым измене-
нием аргумента t на величину запаздывания. Положим, что пре-
вращение жидкого топлива в газообразные продукты сгорания
происходит за время t\. В свою очередь образование продуктов
сгорания при изменении расхода топлива вызовет изменение пара-
метров воздуха в диффузоре не мгновенно, а через время t2. Отсю-
да изменение регулируемого параметра AZ2 отстает от изменения
расхода топлива на время to = t\ + t2. Тогда можно написать
AGmo„(0=AGmo„(/-Q. (4.11)
Дифференциальное уравнение (4.10) записано нами в оператор-
ной форме. Поэтому уравнение (4.11), учитывающее прямое запаз-
дывание, также нужно представить в операторной форме, а именно
AGmo„ = e~pt°\Gmon.
Теперь в уравнение (4.10) вместо координаты AGTon нужно ввести
AG^on. Поэтому уравнение (4.10) примет вид
(т!р2 + т2р + 1) АХ, = (т3р + kJ e~pt°t\Gmon + (т?р2 4- т3р 4-
+ kJ Лрн + (т2р2 + ър+ kJ \ТН + (т2р2+т9р + kJ . (4.12)
В качестве регулируемого параметра удобнее использовать не
%2, а оР = Рг/р*И1>- Здесь р2 — статическое давление в конце диффу-
зора. Оно мало отличается от полного давления р*2 , но поле стати-
ческого давления более равномерно, чем поле полного давления;
р*{ —полное давление за прямым скачком. Следовательно, ор—
легко измеряемая величина.
116
§ 4. ПВРД как объект регулирования
Параметр аР является функцией Хн и Х2- Эту функцию можно
линеаризовать
Д3р = (— АХЯ + (Л>-2. (4.13)
\ /0 °ро \ ^2 /0 °ро
С помощью уравнения (4.13) из уравнения (4.12) исключим ве-
личину ЛХ2 и после преобразования получим уравнение ПВРД как
объекта регулирования в окончательном виде (это уравнение вы-
ведено и исследовано И. И. Хайдуковым):
(Tip2 + Т2р + 1) Дар = (Т3р + ^) e~pt°bGTm + (Tip2 +
-1- Т Д) А2) Дря + (Г2р2 Т,р -I- kJ ЛТН +
+ (Т2р2 + 79р-;-А4)ДХн. (4.14)
При выводе уравнения (4.14) учтены сжимаемость воздуха и
тепловая инерция двигателя. Учтено также запаздывание в переда-
чей импульса давления из камеры сгорания в диффузор.
Численное определение коэффициентов, входящих в уравнение
(4.14), можно сделать только для конкретного двигателя, если бу-
дут известны в явном виде зависимости (4.7) — (4.13) и подобные
им другие.
Для определения таких зависимостей принято весь объем ПВРД
делить на три части (диффузор, камеру сгорания и выходное соп-
ло) и по каждому объему, например, для определения количества
рабочего тела, найти численные значения интегралов:
J ydv = J -;dv = tnK CvK jk c-,
°диф vk.c
frdv = mcvcyKP.
°C
При их вычислении полагают, что на неустаповившихся режимах
характер распределения давления и температуры по длине двига-
теля такой же, как и на установившихся режимах. В пределах каж-
дого объема коэффициенты т при малых отклонениях от устано-
вившегося режима считаются постоянными.
Глава V
СИСТЕМЫ РЕГУЛИРОВАНИЯ
АВИАЦИОННЫХ ВОЗДУШНО-РЕАКТИВНЫХ ДВИГАТЕЛЕЙ
§ 1. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СИСТЕМ РЕГУЛИРОВАНИЯ
Назначение регулятора и требования к системам регулирования
При регулировании какого-либо параметра, определяющего ра-
бочий режим двигателя, от регулятора требуется, чтобы он устой-
чиво поддерживал заданное значение регулируемого параметра.
Регулятор должен быстро, без больших колебаний восстанавливать
это значение в случаях, когда произошло отклонение от установив-
шегося режима работы.
Регулятором называется устройство, измеряющее отклонение
регулируемой величины и вырабатывающее воздействие, величина
которого зависит от измеренного отклонения. Регулятор имеет из-
мерительный (чувствительный) элемент, регулирующий оргап и
связывающее их промежуточное передаточное устройство. Перечис-
лим элементы, из которых в принципе состоит любой регулятор.
Чувствительные элементы. Они измеряют величину регулируе-
мого параметра или возмущающего воздействия. Мощность их
больше мощности чувствительных органов измерительных прибо-
ров, так как обычно они приводят в действие последующий элемент
регулятора. Особенно мощными должны быть чувствительные эле-
менты рассмотренных ниже регуляторов прямого действия.
Задающие элементы. Изменяют настройку регулятора, задавая
значение регулируемого параметра.
Сравнивающие устройства. Служат для выявления разности
двух величии, из которых одна может задаваться механизмом наст-
ройки, а другая определяется положением регулирующего органа.
Преобразовательные элементы. Ими принято называть специ-
альные элементы, предназначенные для преобразования одной фи-
зической величины в другую без сообщения дополнительной энер-
гии. Например, в емкостном преобразователе угол поворота пласти-
ны преобразуется в емкость между пластинами.
Преобразование происходит и в чувствительном элементе. Одна-
ко, если выработанная им физическая величина неудобна по каким-
118
Глава V. Системы регулирования авиационных ВРД
либо причинам для дальнейшего использования, то в регулятор вво-
дят преобразователь.
Усилительные устройства. Сигнал сравнения, равный разности
измеренной и заданной величин, воздействует на управляющий эле-
мент усилителя. В результате этого воздействия на выходе из уси-
лителя происходит усиление сигнала. В гидромеханических регуля-
торах усилителями мощности обычно являются гидравлические сер-
вомоторы, ,в электрических регуляторах — электромоторы. Они
дают перемещение силового элемента.
Регулирующие органы. Силовой элемент усилителя перемещает
регулирующий орган и изменяет энергетическое состояние объекта
регулирования. В результате величина регулируемого параметра
приближается к заданному значению.
Стабилизирующие устройства. В гидромеханических регулято-
рах стабилизирующие устройства часто выполняются в виде успо-
коителей и в виде жестких и изодромных обратных связей с целью
улучшения процесса регулирования. Жидкостные успокоители спо-
собствуют гашению колебаний тех звеньев, которые обладают зна-
чительной массой. Обратные связи между регулирующим органом
или силовым элементом усилителя и его управляющим элементом
приводят к «предварительному отключению» сервомотора, что спо-
собствует затуханию колебаний регулируемой величины в процессе
регулирования.
Регулирование может вестись или только по величине парамет-
ра рабочего процесса двигателя, или по величине параметра и по
величине ее производной по времени. В этом случае в регуляторе
должен быть второй чувствительный элемент, который измеряет
скорость изменения параметра.
Отдельные элементы регулятора, например, чувствительный
элемент, задающее и сравнивающее устройства в регуляторе числа
оборотов, конструктивно могут быть объединены в одно целое.
В регуляторах некоторых типов могут отсутствовать усилители или
стабилизирующие элементы.
Система регулирования силовой установки с ГТД должна быть
построена так, чтобы все функции управления двигателем были
полностью автоматизированы. Это требование определяется как
свойствами самих ГТД, так и условиями эксплуатации скоростных
летательных аппаратов. Во время полета па большой скорости не-
обходимо, чтобы летчик был предельно разгружен от любых функ-
ций управления, кроме тех, которые прямо относятся к управлению
полетом.
Система регулирования должна обеспечивать нормальное про-
текание рабочего процесса двигателя. Ни при каких условиях не
должны возникать помпаж или срыв пламени в камерах сгорания,
необходимо иметь возможность быстро увеличивать число оборотов
или мощность двигателя.
§ 1. Общие принципы построения систем регулирования
119
Большое значение имеет эксплуатационная надежность системы
регулирования, которая во многом предопределяется выбором
принципиальной схемы регулирования и питания топливом ГТД.
Работа регулирующей аппаратуры не должна нарушаться при
инерционных перегрузках, возникающих на некоторых режимах по-
лета. Уже при выборе принципиальной схемы регулирования ГТД
нужно помнить, что недостатки в работе регулирующей аппаратуры
приводят к неполному использованию возможностей двигателя, а
иногда могут служить и причиной аварии летательного аппарата.
При разработке регуляторов ГТД используются общие принци-
пы теории и техники автоматического регулирования, которые нача-
ли успешно разрабатываться еще во второй половине прошлого сто-
летия и нашли применение в самых различных отраслях техники.
Однако регуляторы ГТД обладают рядом специфических особен-
ностей, обусловленных как особыми требованиями, предъявляемы-
ми к характеристикам процесса регулирования ГТД, так и кон-
структивным объединением этих регуляторов в одних агрегатах
с топливными насосами.
Существуют два основных принципа регулирования: по отклоне-
нию регулируемого параметра от заданного значения и по возму-
щающему воздействию.
При регулировании по отклонению чувствительный элемент ре-
гулятора измеряет величину регулируемого параметра и сравнивает
ее с заданной. В случае возникшего отклонения чувствительный
элемент непосредственно или с помощью какого-либо усилителя
производит перемещение регулирующего органа таким образом, что-
бы возникшее отклонение было устранено. В конце процесса регу-
лирования указанное отклонение может быть получено каким угод-
но малым, поэтому принцип регулирования по отклонению нашел
широкое применение.
При использовании этого принципа регулирование идет по замк-
нутому циклу: объект регулирования воздействует на чувствитель-
ный элемент регулятора, а затем регулятор воздействует на объект.
Поэтому регулирование с использованием принципа отклонения на-
зывают также замкнутым регулированием.
При регулировании по возмущающему воздействию регулятор
реагирует на внешние возмущения. Его чувствительный элемент
измеряет величину возмущения и перемещает регулирующий орган
так, чтобы скомпенсировать действие этого возмущения на регу-
лируемый параметр. В этом случае регулирование ведется по не-
замкнутому циклу: регулятор воздействует на объект регулирова-
ния, но обратного воздействия объекта па регулятор нет. Принцип
регулирования по возмущающему воздействию называют также
принципом компенсаций или незамкнутым регулированием. При его
использовании точность регулирования получается меньше, чем при
замкнутом регулировании. Возможна комбинация обоих принципов.
120
Глава V. Системы регулирования авиационных ВРД
Для ТРД с неизменяемой площадью проходных сечений газо-
воздушного тракта число оборотов обычно выбирается за регулиру-
емый параметр. Регулирование числа оборотов производится из-
менением расхода топлива. Воспользуемся принципом отклонений
и применим его для регулирования числа оборотов. В этом случае
регулятор будет иметь чувствительный элемент, который измеряет
число оборотов. При отклонении числа оборотов от заданного зна-
чения чувствительный элемент перемещением регулирующего ор-
гана изменяет подачу топлива так, чтобы восстановилось заданное
число оборотов. На примерах схем регуляторов числа оборотов
рассмотрим кратко общие принципы построения систем регулиро-
вания. Следует отметить, что свойства, присущие этим схемам, со-
хранят свою силу и в случае регулирования любых других пара-
метров.
Статический регулятор прямого действия
Регулятором прямого действия называется регулятор, у кото-
рого чувствительный элемент непосредственно связан с регулирую-
щим органом. Перемещение регулирующего органа происходит за
счет энергии самого чувствительного элемента.
На рис. 5. 1, а дана одна из возможных схем регулятора числа
оборотов прямого действия. Из схемы видно, что чувствительный
элемент регулятора состоит из шарнирно закрепленных грузиков 1,
муфты 2 и пружины 3 При вращении грузиков развивается цент-
робежная сила, осевая составляющая которой перемещает муфту
и связанную с ней через рычаг дозирующую топливную иглу 5 (ре-
гулирующий орган). Положение муфты и дозирующей иглы опре-
деляется равенством осевой составляющей центробежной силы ч
1 Чувствительный элемент такого типа называется центробежным маятни-
ковым чувствительным элементом. Его характеристики рассмотрены в § 2 этой
главы.
§ 1. Общие принципы построения систем регулирования
121
силы сжатия пружины. Для настройки регулятора па другое число
оборотов перемещается упор пружины 4.
При переходе к новой высоте или скорости полета меняется
момент сопротивления на компрессоре двигателя или, иначе, меня-
ется нагрузка двигателя. Новой величине нагрузки должен соот-
ветствовать другой расход топлива, т. е. другое положение дозирую-
щей иглы 5. Не трудно убедиться, что регулятор, выполненный по
этой схеме, при изменении нагрузки не может точно поддерживать
заданное число оборотов (полагаем, что упор 4 пружины чувстви-
тельного элемента не меняет своего положения). Действительно,
если у земли при расходе топлива Go двигатель работал с числом
оборотов п0, го с переходом на высоту Н{ (считаем число Мн полета
неизменным) дозирующая игла должна быть несколько опущена,
что уменьшит проходное сечение и обеспечит расход топлива
Gi < Go. Перемещение иглы вниз повлечет за собой перемещение
муфты 2 вверх и некоторое увеличение сжатия пружины 3. Однако
дополнительное сжатие пружины может произойти только за счет
роста осевой составляющей центробежной силы — за счет увеличе-
ния числа оборотов двигателя до П[.
Соответствующая приведенному рассуждению характеристика
G = f(n) показана на рис. 5. 1,6. На этой характеристике линии /
и 2— потребные расходы топлива соответственно у земли и на вы-
соте Т/i; линия 3—расход топлива, поддерживаемый регулятором.
Величина ди = П\—п0 — статическая ошибка регулирования, отку-
да регулятор называется статическим. Статический регулятор пря-
мого действия прост по своему устройству и это является его до-
стоинством. К недостаткам регуляторов этого типа относятся, во-
первых, необходимость увеличивать массу грузиков, и следователь-
но, размеры регулятора для получения достаточно больших пере-
становочных усилий на регулирующем органе и, во-вторых, стати-
ческая ошибка регулирования. Она возрастает тем сильнее, чем
больше изменяется нагрузка на двигатель. Поэтому статические
регуляторы прямого действия называются еще пропорциональными.
Астатический регулятор непрямого действия
Регулятором непрямого действия называется регулятор, у кото-
рого связь между чувствительным элементом и исполнительным
органом'осуществляется через промежуточный элемент. Исполни-
тельный орган перемещается за счет энергии какого-либо посторон-
него источника.
Схема астатического регулятора числа оборотов непрямого дей-
ствия показана на рис. 5.2, а. Чувствительный элемент регулято-
ра связан с золотником 1 гидравлического поршневого сервомотора.
На схеме золотник находится в нейтральном положении, которое
соответствует равновесному числу оборотов двигателя. Поршень
122
Глава V. Системы регулирования авиационных ВРД
сервомотора 2 с чувствительным элементом жестко не связан и при
данном положении муфты чувствительного элемента 3 может зани-
мать любое положение. Это означает, что регулятор, выполненный
по этой схеме, способен поддерживать заданное число оборотов
при различных нагрузках двигателя. Его расходная характеристика
G = f(n) показана на рис. ,5.2,5. Кривые 1 и 2 — потребные рас-
ходы топлива у земли и на высоте Яг, линия 3 — расход топлива,
поддерживаемый регулятором.
При отклонении числа оборотов от заданной величины избыточ-
ная центробежная сила грузиков смещает золотник. Для этого
больших перестановочных усилий не требуется, так как золотник
уравновешен. К золотнику под давлением подводится рабочая жид-
кость (масло или керосин). При смещении золотника она попадает
в одну из полостей цилиндра сервомотора, передвигает поршень и
связанную с ним дозирующую иглу. В это же время рабочая жид-
кость из другой полости цилиндра сервомотора свободно вытекает.
У астатического регулятора непрямого действия нет недостат-
ков, присущих регулятору, изображенному на рис. 5.1, а: отсутст-
вует статическая ошибка регулирования, большие перестановочные
усилия на дозирующей игле могут быть получены при небольших
размерах чувствительного элемента и всего регулятора. Однако от-
сутствие непосредственной связи между чувствительным элементом
и дозирующей иглой затрудняет достижение удовлетворительного
процесса регулирования.
Обычно процесс регулирования при изменении настройки регу-
лятора или нагрузки двигателя носит медленно затухающий коле-
бательный характер. Это связано с тем, что вследствие инерцион-
ности маховых масс турбины и компрессора изменение числа обо-
ротов ротора двигателя отстает от изменения расхода топлива, от-
рицательно сказываются также и силы сухого трения в элементах
регулятора. Так, например, при отклонении числа оборотов в сторо-
ну увеличения от заданного значения произойдет смещение золот-
ника и начнется движение дозирующей иглы, уменьшающее подачу
§ 1. Общие принципы, построения систем регулирования
123
топлива. Переход золотника в нейтральное положение еще не будет
означать окончания процесса регулирования, так как он произой-
дет не в тот момент, когда расход топлива будет соответствовать
заданному числу оборотов при изменившейся нагрузке двигателя, а
позже. Поэтому в своем изменении число оборотов не стабилизиру-
ется на заданном значении и будет продолжать уменьшаться.
Затем регулятор начнет увеличивать подачу топлива, вслед за уве-
личением подачи будет возрастать число оборотов ротора[ двига-
теля и это определит медленно затухающий колебательный процесс.
Регулирование собственно неустойчивых объектов, таких как
ТРД с топливным насосом на пониженных числах оборотов, с по-
мощью астатического регулятора непрямого действия невозможно.
Для улучшения процесса регулирования в регуляторах непря-
мого действия нужно связать поршень сервомотора с золотником и
контролировать движение дозирующей топливной иглы, как это
сделано в регуляторе с жесткой обратной связью.
Статический регулятор» непрямого действия
(регулятор с жесткой обратной связью)
Схема этого регулятора числа оборотов показана на рис. 5.3, а,
она является дальнейшим развитием схемы астатического регуля-
тора непрямого действия. При отклонении режима работы двига-
теля от равновесного, например, в сторону увеличения числа обо-
ротов, под действием избыточной силы муфта чувствительного эле-
мента, перемещаясь вверх, поворачивает рычаг АС относительно
точки С. Сместившийся вверх золотник открывает доступ рабочей
жидкости в верхнюю полость сервоцилиндра, сервопоршепь и дози-
рующая топливная игла начинают движение вниз, подача топлива
уменьшается и число оборотов двигателя падает. Однако в этом
случае движение поршня сервомотора не остается бесконтрольным.
Шток поршня увлекает за собой рычаг АС, который теперь вра-
124
Глава V. Системы регулирования авиационных ВРД
щается уже около точки А. Золотник, связанный с рычагом А С,
уменьшает сечение щели подвода рабочей жидкости, приближаясь
к нейтральному положению. Процесс регулирования быстро закан-
чивается.
Мы упростили действие регулятора, рассматривая сначала пе-
ремещение муфты чувствительного элемента под действием избы-
точной центробежной силы и вращение рычага АС вокруг точки С,
а затем — движение поршня сервомотора и вращение рычага АС
около точки А. В действительности одновременно может происхо-
дить и отклонение муфты, и перемещение поршня сермотора. Рычаг
АС будет находиться в более сложном движении.
Не трудно убедиться, что улучшение динамических характерис-
тик двигателя с регулятором данной схемы достигается ценой ста-
тической ошибки регулирования. Для доказательства этого пред-
ставим себе расположение деталей регулятора при фиксированном
упоре пружины для двух режимов работы двигателя: у земли с
большим расходом топлива и на высоте — с малым.
Когда заканчивается процесс регулирования, золотник занимает
нейтральное положение, перекрывая своими поясками оба канала,
связывающие полости цилиндра сервомотора с каналом подвода
рабочей жидкости. Следовательно, на различных установившихся
режимах работы двигателя точка В рычага АС занимает одно и то
же положение. С увеличением высоты полета для уменьшения пода-
чи топлива дозирующая игла должна опуститься, опустится и точ-
ка С рычага АС. При неизменном положении точки В точка А
рычага АС поднимется, вместе с рычагом переместится вверх и
муфта чувствительного элемента, сильнее сжимая пружину.
Такое перемещение дозирующей иглы, рычага и муфты может
произойти только в том случае, если число оборотов двигателя
несколько увеличится и появится избыточная центробежная сила,
сжимающая пружину. Следовательно, при неизменной настройке
регулятора с жесткой обратной связью рост высоты полета (умень-
шение нагрузки двигателя) приводит к увеличению числа оборотов
ротора двигателя. Очевидно, что рост скорости полета при неизмен-
ной высоте (увеличение нагрузки двигателя) снизит число оборо-
тов ротора. Соответствующая этим рассуждениям расходная ха-
рактеристика G == f(n) приведена на рис. 5.3,6.
Здесь линии / и 2 — потребные расходы топлива соответственно
у земли и на высоте ВЦ; линия 3—расход топлива, поддерживае-
мый регулятором; бп = —П\ — статическая ошибка регулирова-
ния.
Если изменить соотношение плеч рычага АС, то это отразится
и на статических, и на динамических характеристиках регулятора.
Так, если при неизменной длине рычага АС уменьшать плечо АВ, то
статическая ошибка регулирования снизится (кривая 4 на рис.
5.3,5). Вместе с этим процесс регулирования будет более продол-
§ 1. Общие принципы построения систем регулирования
125
жительным и может принять колебательный характер. Регулятор
по своим характеристикам будет приближаться к астатическому
регулятору. При увеличении плеча АВ (длина рычага АС остается
неизменной) статическая ошибка растет. Этому Случаю соответ-
ствует кривая 5 на рис. 5. 3, б. Вместе с тем процесс регулирования
будет быстро заканчиваться и иметь апериодический характер.
Выведем приближенную зависимость для оценки статической
ошибки регулирования. Обозначив через бт — перемещение дози-
рующей топливной иглы и через 6z— перемещение муфты чувстви-
тельного элемента, составим соотношение между ними для различ-
ных статических режимов
6z == 8т —.
ь
Здесь а и b плечи рычага АВ (см. рис. 5.3,а). Примем квадратич-
ную зависимость осевой составляедцей центробежной силы от чис-
ла оборотов Рц = сп2, где с — коэффициент пропорциональности.
Тогда приращение центробежной силы б/\ = 2 спобп, где п0—
число оборотов исходного статического режима, а бп—приращение
числа оборотов. Приращение центробежной силы на новом статиче-
ском режиме уравновесится приращением силы сжатия пружины
Вбг = бРч — 2 спобп, где В — характеристика пружины. Исполь-
зуя последнее выражение и уравнение связи между бг и бт, по-
лучим
В-—'
6га = —— Ът. (5.1)
2cn0 v ’
Для определения статической ошибки на каком-либо режиме по
отношению к исходному режиму с числом оборотов п0 кроме ве-
личин, характеризующих регулятор, нужно располагать проливоч-
ной характеристикой дозирующей топливной иглы G = f(m). Оп-
ределив по этой характеристике величину dm для рассматриваемого
нового режима, подсчитываем статическую ошибку регулирования.
Рассматриваемая следующая схема регулятора числа оборотов
является дальнейшим развитием схемы регулятора с жесткой об-
ратной связью. Она сочетает в себе достоинства астатического ре-
гулятора и регулятора с жесткой обратной связью: отсутствие ста-
тической ошибки регулирования, хорошие динамические характе-
ристики при удачно выбранных параметрах регулятора.
Изодромный регулятор
Схема изодромного регулятора приведена на рис. 5.4 Из схемы
следует, что в изодромном регуляторе жесткой обратной связи меж-
ду поршнем сервомотора и золотником нет. Поршень сервомотора
соединен с рычагом АС не непосредственно, а через специальное
126
Глава V. Системы регулирования авиационных ВРД
устройство, носящее название катаракт. В данной схеме катаракт
состоит из поршня 2, связанного с рычагом АС, цилиндра 1, соеди-
ненного с поршнем сервомотора, и пружины 4, которая работает
как на сжатие, так и На растяжение. Цилиндр катаракта заполнен
вязкой жидкостью (например, маслом), его полости по обе сторо-
ны поршня 2 соединены между собой каналом с жиклером 3.
В начале процесса регулирования изодромный регулятор ведет
себя как С1атпческий регулятор. При отклонении двигателя от рав-
новесного режима, например, в сторону увеличения числа оборо-
тов, золотник сместится вверх и откроет доступ рабочей жидкости
в верхнюю полость цилиндра серво-
мотора. Поршень сервомотора нач-
нет перемещаться вниз и \ влечет за
собой рычаг АС так же, как и в ре-
гуляторе с жесткой обратной свя-
зью. Золотник будет приближаться
к нейтральному положению.
Однако на этом процесс регули-
рования не закончится. При движе-
нии точки С рычага ЛС.вниз растя-
нется пружина 4 и на поршне 2 воз-
никнет перепад давлений. Под дей-
ствием этого перепада жидкость че-
рез жиклер 3 будет перетекать из
нижнюю. Растянутая пружина 4, сжи-
верхней полости цилиндра в
маясь, несколько приподнимет рычаг и золотник, в результате чего
поршень сервомотора и дозирующая топливная игла переместятся
еще немного вниз. Подобные рассуждения можно продолжить и
дальше, двигатель постепенно будет приближаться к равновесному
режиму работы. Поршень сервомотора и связанная с ним дозирую-
щая игла в процессе регулирования при изменении нагрузки сна-
чала большую часть своего пути проходят быстро. Остаток пути
при приближении к новому равновесному режиму проходится срав-
нительно медленно.
Не трудно убедиться, что по окончании процесса регулирования
статическая ошибка будет полностью снята. При изменении нагруз-
ки на новом равновесном режиме двигателя золотник и пружина
катаракта займут нейтральное положение, поршень сервомотора
и дозирующая игла сместятся, положение поршня катаракта от-
носительно его цилиндра изменится. Рассматривая последователь-
но смещение золотника сначала за счет избыточной силы, развива-
емой грузиками, и движения поршня сервомотора, а затем за счет
натяжения пружины 4, мы, конечно, упростили картину работы ре-
гулятора. В действительности перемещение золотника в процессе
регулирования происходит одновременно под действием всех трех
факторов.
§ 1. Общие принципы построения систем регулирования
127
Динамические характеристики изодромного регулятора можно
приблизить как к характеристикам статического, так и астатичес-
кого регуляторов. Если уменьшать сечение жиклера 3, увеличивая
сопротивление для перетекания жидкости в цилиндре катаракта,
или снижать жесткость пружины 4, то изодромный регулятор будет
приближаться к статическому. Время, необходимое для снятия ста-
тической ошибки регулирования, будет увеличиваться. В пределе,
заглушив жиклер 3 и сняв пружину 4, получим статический регу-
лятор с жесткой обратной связью.
При уменьшении сопротивления перетеканию жидкости в ци-
линдре катаракта и увеличении жесткости пружины 4 регулятор
по своим свойствам приближается к астатическому. Он становится
астатическим при закреплении точки С рычага АС и удалении ка-
таракта.
Говоря о динамических характеристиках регуляторов различных
схем, мы предполагали, что действия регулятора каждый раз на-
правлены на устранение влияния внешних возмущений и изменив-
шейся нагрузки и приводят регулируемый параметр объекта к
заданной величине. В действительности так бывает не всегда. Не-
удачно выбранные параметры регулятора или неучтенное влияние
сил сухого и вязкого трения может привести к медленно затухаю-
щим колебаниям регулируемого параметра или даже к колебаниям
с нарастающей амплитудой. Об этом подробнее говорится в гл. VI
и VII.
Регулятор непрямого действия с регулированием
по скорости вращения и угловому ускорению
(регулирование с предварением)
В ранее рассмотренных схемах эффективное вмешательство ре-
гулятора в работу двигателя начинается лишь тогда, когда за счет
избыточной силы, развиваемой грузиками, преодолеваются силы
трения в механизме регулятора и чувствительный элемент переме-
щается на некоторую величину от положения равновесия.
Существуют регуляторы, которые реагируют как на отклонение
параметра, так и на скорость его изменения. Применительно к ре-
гулированию числа оборотов такой регулятор изменяет подачу
топлива при отклонении угловой скорости и появлении углового
ускорения. Это даст возможность уменьшить отклонение регулиру-
емого параметра в начале процесса регулирования.
Поясним сказанное с помощью характеристик, показанных на
рис. 5.5, а. Допустим, что у двигателя, работающего без регулято-
ра, наблюдаются колебания угловой скорости по синусоиде относи-
тельно заданного статического режима (кривая бп). Регулятор
должен гасить эти колебания, но чтобы он вступил в действие тре-
буется некоторое начальное отклонение числа оборотов (пусть это
128
Глава V. Системы регулирования авиационных ВРД
будет 6«i). При отклонении числа оборотов по синусоиде возникает
угловое ускорение, изменяющееся по косинусоиде (кривая dnldt).
Оно будет наибольшим в начальный момент, когда бп = 0.
Если в регуляторе сделать два параллельных чувствительных
элемента, реагирующих на бп и dnjdt, то для эффективного дейст-
вия регулятора потребуется меньшее начальное отклонение числа
оборотов (б«2<бП1). Чувствительные элементы, реагирующие на
угловое ускорение, называются акселерометрами.
Регулирование числа оборотов или какого-либо другого пара-
метра рабочего процесса по отклонению и по производной легче
осуществить при использовании электрических регуляторов. Одна-
ко могут быть применены и гидромеханические устройства. Одна
из возможных схем такого регулятора числа оборотов дана на
рис. 5.5, б.
В корпусе акселерометра 1, приводимого во вращение от вала
двигателя, размещен маховичок 2. Его вращение осуществляется
через пружины кручения 3. На оси корпуса акселерометра распо-
ложен винт 4, входящий в резьбовое отверстие маховичка 2.
На равновесном режиме корпус 1 и маховичок 2 вращаются как
одно целое. При изменении скорости вращения ротора двигателя
возникнет угловое ускорение. ^Маховичок, скручивая пружины 3,
начнет перемещаться по винту 4, воздействуя на рычаг АС и золот-
ник регулятора. После того, как вновь установится статический
режим, пружины 3 раскрутятся и вернут маховичок на прежнее
место.
Допустим, что число оборотов двигателя изменяется так, как
это показано на рис. 5.5, а (кривая б«). Тогда при появлении поло-
жительной величины dnfdt число оборотов корпуса 1 станет больше
числа оборотов маховичка 2 и он начнет перемещаться по винту 4
вниз, увлекая за собой конец рычага АС (точка А). Рычаг, вра-
щаясь около точки В, сместит золотник вверх, в результате чего
поршень сервомотора и дозирующая игла пойдут вниз, подача топ-
§ 2. Элементы систем питания и автоматических устройств
129
лива уменьшится. Эффект описанного действия усилится за счет
того, что под влиянием избыточной силы, развиваемой грузиками,
муфта чувствительного элемента при достижении некоторого от-
клонения бге станет перемещаться вверх и ускорит движение золот-
ника. В конце процесса регулирования, когда появятся отрица-
тельные ускорения (при положительной величине бге), акселерометр
будет ускорять движение золотника к нейтральному положению.
Дополнительное воздействие по; производной с тем же эффектом
улучшения динамических характеристик регулирования можно за-
менить регулированием по нагрузке. Для ГТД нагрузка определяется
величиной крутящего момента на валу ротора. Следует отметить,
что регулирование числа оборотов двигателя только по величине
нагрузки или по угловому ускорению невозможно. Это объясняется
тем, что одно и то же угловое ускорение может наблюдаться при
различных числах оборотов, а одной и той же нагрузке (одному
и тому же крутящему моменту) прдт изменении скоростей и высот
полета будут соответствовать разные числа оборотов двигателя.
В системах регулирования чисел оборотов авиационных двига-
телей с использованием гидромеханических регуляторов точность
регулирования на максимальном режиме достигает 0,Зч-0,5%.
В заключение анализа схем регуляторов числа оборотов еще раз
отметим, что выявленные свойства механических или гидромеха-
нических регуляторов отдельных типов сохраняют свое значение при
регулировании других параметров рабочего процесса и при перехо-
де к пневматическим или электрическим системам регулирования.
§ 2. ЭЛЕМЕНТЫ СИСТЕМ ПИТАНИЯ И АВТОМАТИЧЕСКИХ УСТРОЙСТВ
Топливные насосы
Для подачи топлива в ГТД применяются плунжерные, шесте-
ренные и центробежные насосы. Каждый из этих типов насосов
имеет свои особенности, определяющие возможные области их при-
менения.
Плунжерные насосы получили широкое распространение в ка-
честве насосов в системах топливопитания основного контура. Они
обеспечивают высокие давления (до 15- 106 н/м2) и дают возмож-
ность регулировать расход топлива при постоянном числе оборотов
ротора насоса путем изменения положения наклонной шайбы.
Шестеренные насосы также нашли большое применение. Они
просты по своей конструкции и надежны в эксплуатации. Шесте-
ренные насосы используются в системах питания с давлением до
5-Ю6—8-106н/л12. При равных габаритах производительность
шестеренного насоса в 1,5—2 раза больше, чем у плунжерного.,
Основным недостатком шестеренных насосов является постоянная
производительность при неизменном числе оборотов насоса. Для
5 Черкасов Б. А.
130
Глава V. Системы регулирования авиационных ЁРД
использования в системах питания ГТД шестеренные насосы снаб-
жаются устройствами для перепуска топлива. Поэтому часть топ-
лива при прохождении через насос перепускается обратно в бак
или в магистраль перед насосом. На больших высотах полета доля
перепускаемого топлива становится настолько большой, что это
обстоятельство может заметно повысить температуру топлива в
баке. Кроме того, затрачивается лишняя энергия на привод насоса.
Центробежные насосы характеризуются способностью обеспе-
чивать большие расходы топлива и простотой регулирования рас-
хода. Центробежные насосы целесообразно применять в тех слу-
Рис. 5.6
чаях, когда расходы топлива превышают 20. 000 л)час при давле-
нии 5- 106—7 • 106 h-Im2. Недостатком насосов этого типа является
то, что при снижении числа оборотов насоса давление за ним па-
дает примерно пропорционально квадрату числа оборотов. Это за-
трудняет использование центробежных насосов в качестве насосов
в системах питания основного контура ГТД при запуске и на по-
ниженном числе оборотов. Перспективным является использование
турбонасосных агрегатов — применение специальных воздушных
или газовых турбин для привода центробежных насосов.
Остановимся на основных характеристиках топливных насосов.
К ним относятся зависимости изменения расхода G по числу обо-
ротов насоса п при заданных давлениях топлива за насосом ртоп
и зависимость изменения давления топлива рТоп по расходу при
постоянном числе оборотов насоса. Эти характеристики наиболее
существенны для процессов регулирования ГТД. Для плунжерных
и шестеренных насосов они показаны на рис. 5.6, а и 5.6,6. Для
центробежного насоса характерно сравнительно небольшое изме-
нение давления в широком диапазоне изменения расхода при за-
данном числе оборотов насоса. Примерная характеристика центро-
бежного насоса дана на рис. 5.6, в.
Кроме характеристик, показанных на рис. 5.6, для работы си-
стемы топливопитания большое значение имеют кавитационные ха-
§ 2. Элементы систем питания и автоматических устройств
131
рактеристики насосов. Кавитационной характеристикой называется
зависимость расхода G от давления на входе в насос рвх при по-
стоянных числах оборотов п и температуре топлива tTon. Пример-
ный вид кавитационной характеристики показан на рис. 5.7, а. Из
графика видно, что характеристику можно разбить на два участка:
участок рех Рвх min, где расход G мало зависит от давления перед
насосом (рабочий участок характеристики), и участок с рвх<
< Рвхmm с резким падением производительности насоса, что'связа-
но с развитием кавитации. Работа на левой ветви кавитационной
характеристики, т. е. при давлениях на входе рвх< pexmin, недопу-
стима. Кавитация не только приводит к резкому падению произво-
дительности, но при сильном развитии вызывает разрушение дета-
лей насоса; кавитация может нарушить устойчивость регулирования
двигателя.
Обычно кавитационные характеристики насосов снимаются при
нескольких значениях чисел оборотов п и температур топлива tTon.
Рост числа оборотов способствует развитию кавитации, что объяс-
няется увеличением относительной скорости топлива на входе в
насос и ростом гидравлических сопротивлений, приводящих к паде-
нию давления перед насосом. Увеличение температуры топлива
так же приближает наступление кавитации, что объясняется рос-
том давления насыщенных паров топлива.
Кавитационные характеристики топливного насоса определяют
высотность топливной системы и с этой точки зрения — высотность
двигателя. С увеличением высоты полета падает давление рвх, соз-
даваемое подкачивающим насосом. Изменение производительности
насоса с высотой показано на рис. 5.7,6 (кривая 1). На этот же
график нанесена кривая 2 потребного расхода топлива. Высотность
топливной системы определяется высотой Нкав, при которой начи-
нается кавитация. На высоте //max, определяемой точкой пересе-
чения кривых 1 и 2, двигатель работать не сможет, так как это Ge-
s’
132
Глава V. Системы регулирования авиационных ВРД
ласть сильно развитой кавитации. Чем раньше наступает кавита-
ция, тем ниже высотность топливной системы.
Если кавитационная характеристика, приведенная на рис. 5.7,6
(кривая /), принадлежит шестеренному наоосу, а по кривой 2 изме-
няется потребный расход топлива, то при работе двигателя по
программе п = const насос обладает избыточной производитель-
ностью. Избыток топлива, определяемый отрезками ординат меж-
ду кривыми 1 и 2, перепускается в топливной бак или в топливную
..магистраль перед насосом. Перепуск больших масс топлива и свя-
занный с ним подогрев топлива неблагоприятно сказывается на
жавитационных характеристиках насоса, так как вызывает местные
.возмущения потока в магистралях и рост давления насыщенных
ларов топлива.
На процессе регулирования ГТД может отразиться неравномер-
ность подачи топлива насосом, особенно при запуске двигателя
и при его работе на пониженных режимах. Неравномерность пода-
,чи топлива связана с чередованием в работе плунжеров у много-
плунжерного насоса, зубьев шестеренного насоса и лопастей колеса
центробежного насоса. При некоторых условиях в топливных маги-
стралях за насосом могут возникнуть резонансные колебания дав-
ления. Для работы регулирующей аппаратуры имеют также значе-
ния характеристики сил трения в деталях насоса, величина усилий,
передающихся от наклонной шайбы насоса на поршень сервомото-
ра и ряд других.
Чувствительные элементы регуляторов числа оборотов
При регулировании скорости вращения ротора ГТД применяют-
ся центробежные маятниковые, гидроцентробежные и электриче-
ские чувствительные элементы. Наибольшее распространение из
перечисленных типов получили первые два. Рассмотрим их основ-
ные свойства и характеристики.
На рис. 5.8 дана конструктивная схема центробежного маятни-
кового чувствительного элемента. Его отличие от чувствительных
элементов, показанных на рис. 5.2, 5.3 и 5.4, заключается в том.
что здесь муфта чувствительного элемента непосредственно связа-
на с золотником, а не через рычаг, как это было показано раньше.
Такая непосредственная связь дает возможность выполнить золот-
ник вращающимся и тем самым значительно снизить силы трения.
На равновесном числе оборотов осевая составляющая центробеж-
ной силы равна силе сжатия пружины. Осевая составляющая цент-
робежной силы Рч при данных передаточном числе от двигателя
к регулятору, размерах и массах деталей чувствительного элемента
зависит от числа оборотов двигателя и положения грузиков, свя-
занного с координатой у.
Примерная зависимость силы Рч от числа оборотов п и коорди-
наты у показана на рис. 5.9, а. Сила Р сжатия пружины (см. рис-
§ 2. Элементы систем питания и автоматических устройств
133
5.8) определяется ее жесткостью В, положением золотника (коор-
динатой у) и положением упора пружины h, с помощью которого
производится настройка регулятора на
заданное число оборотов. Зайисимость
Р = /(У, h) показана на рис. 5.10. При-
мем за положительное направление
координаты у перемещение золотника
вверх и координаты h — перемещение
упора пружины вниз (см. рис. 5.8).
Располагая зависимостями Рч =
= f(n, у) и Р = f(y, h), можно постро-
ить статическую характеристику цен-
тробежного маятникового чувствитель-
ного элемента. Для этого нужно гра-
фики рис. 5.9, б и 5.10 совместить так,
как это показано па рис. 5.11, а. Течки
1, 2, 3, 4 пересечения двух семейств
кривых дают возможность перейти к
статической характеристике чувстви-
тельного элемента у = / (/г, ге); которая
показана на рис. 5.11, б. Статическая
характеристика может быть получена
как расчетным, так и эксперименталь-
ным путем.
Во время работы двигателя чувст-
вительный элемент подвержен различ-
Рис. 5.8
ного рода возмущениям, которые вы-
зывают некоторые перемещения золотника регулятора, не связан-
ные с изменением скорости вращения ротора. К таким возмущениям
Рис. 5.10
Рис. 5.9
относятся вибрации двигателя, различного рода маневры, произво-
димые летательным аппаратом и т. п. Поскольку эти возмущения
134
Глава V. Системы регулирования авиационных ВРД
являются вредными, регулятор должен быть выполнен так, чтобы
отклонение чувствительного элемента от заданного режима было
минимальным и чтобы после прекращения действия возмущения
Рис. 5.11
б)
он возвращался к исходному статическому режиму. Иными слова-
ми, чувствительный элемент регулятора должен быть устойчив.
Его устойчивость определяется взаимным протеканием характери-
Рис. 5.12
стик силы Рч и силы пружины Р в зависимости от положения зо-
лотника (координата у) при постоянном числе оборотов п.
Возможны три характерных случая расположения характери-
стик Рч и Р. На рис. 5.12, а показаны характеристики устойчивого
чувствительного элемента.' Так как кривая Р(у) идет круче, чем
кривая Рч(у), то при случайном отклонении золотника от положе-
ния равновесия возникает восстанавливающаяся сила, возвращаю-
$ 2. Элементы систем питания и автоматических устройств
135
щая его в исходное положение, которая тем больше, чем больше
разность
/ ЭР \ / дРн \
\ ду Jo \ ду J о
На рис. 5.12,6 показаны характеристики, которыми обладает не-
устойчивый чувствительный элемент, а на рис. 5.12, в — характери-
стики чувствительного элемента с безразличным равновесием (ас-
татический чувствительный элемент на участке от г/i до г/г)-
В регуляторах числа оборотов ГТД могут применяться лишь
устойчивые чувствительные элементы. Устойчивость должна сохра-
няться не только при случайных возмущениях, но и при отклоне-
нии числа оборотов от заданного значения или при перенастройке
регулятора.
Центробежный чувствительный элемент более устойчив на по-
ниженных числах оборотов, с ростом скорости вращения его устой-
чивость уменьшается. Это связано с тем, что статическая характе-
ристика центробежного маятникового чувствительного элемента
(см. рис. 5.11,6) нелинейна. При одних и тех же приращениях чис-
ла оборотов изменение координаты у в области малых чисел обо-
ротов меньше, чем в области больших. В свою очередь нелиней-
ность статической характеристики объясняется тем, что сила Рч,
пропорциональна ге2, в то время как сила сжатия пружины зависит
линейно от се деформации, т. е. от координаты у.
В реально выполненных конструкциях чувствительных элемен-
тов не удается полностью избежать сил сухого трения. При откло-
нении двигателя от равновесного ре-
жима и появления избыточной силы
перемещения муфты чувствитель- рч
ного элемента и золотника регулятора
не будет до тех пор, пока величи-
на ЬРи не превысит силы сухого тре-
ния Ртр. Отсюда появляется нечувст-
вительность регулятора к небольшим
изменениям числа оборотов, характе-
ризуемая зоной нечувствительности.
При неизменной силе трения ширина
зоны нечувствительности меняется по
числу оборотов, она растет с перехо-
дом к малым числам оборотов и умень-
шается с переходом к большим.
Из характеристики, приведенной на рис. 5.13, видно, что при-
ращение скорости вращения, необходимое для преодоления силы
трения, с уменьшением числа оборотов возрастает (бгг, < б«г). Из-
менение ширины зоны нечувствительности объясняется квадратич-
ной зависимостью центробежной силы от числа оборотов. Хотя си-
136
Глава V. Системы регулирования авиационных ВРД
лы сухого трения невелики (приведенными к золотнику, силы тре-
ния удается довести до 0,1-4-0,15 н), с ними приходится считаться
и для уменьшения их влияния ограничивать диапазон работы ре-
гулятора числа оборотов. Величина сил трения зависит от рода
рабочей жидкости регулятора. Применение в качестве таковой ке-
росина может повысить силы сухого трения. Однако использование
Рис. 5.14
масла, хотя и желательно, усложняет
конструкцию регулятора.
Остановимся на основных свойствах гидроцентробежного чувст-
вительного элемента, схема которого показана на рис. 5.14. На
конце валика, кинематически связанного с ротором двигателя, си-
дит крыльчатка 1. К крыльчатке подводится рабочая жидкость,
давление рабочей жидкости на выходе из крыльчатки пропорцио-
нально плотности жидкости и квадрату числа оборотов. Сила дав-
ления Рч с сильфона 2 передается на золотник 3 и на равновесных
режимах уравновешивается силой Р пружины 4.
По сравнению с маятниковым центробежным гидроцентробеж-
ный чувствительный элемент обладает тем недостатком, что его
равновесное число оборотов при неизменном положении упора 5
пружины 4 изменяется вместе с 'изменением весовой плотности ра-
бочей жидкости. Снижение плотности на 1% приводит к увеличе-
нию равновесного числа оборотов примерно на 0,5%. Поэтому ре-
гулятор с гидроцентробежным чувствительным элементом требует
перенастройки в зависимости от времени года.
Однако у гидроцентробежного’ чувствительного элемента есть
и свои преимущества. Сила давления жидкости на сильфон не
связана с положением золотника (с координатой у). Поэтому устой-
чивость гидроцентробежного чувствительного элемента не зависи"
от числа оборотов, во всем диапазоне изменения которых наклон
линий Р больше наклона линий Рц (рис. 5.15). Силы трения у него
меньше, что объясняется отсутствием центробежных грузиков.
§ 2. Элементы систем питания и автоматических устройств
137
Чувствительные элементы регуляторов,
работающих на принципе регулирования
по возмущающему воздействию
При использовании этого принципа, например, в случае регу-
лирования числа оборотов ГТД, измеряются полное давление и тем-
пература набегающего потока, разность давлений (перепад) в раз-
личных сечениях газовоздушного тракта двигателя, давление или
разность давлений в топливной магистрали. Для измерений ис-
пользуются анероиды, сильфоны, мембраны и золотники.
Рис. 5.16
Рис. 5.17
Анероиды, выполненные в виде герметичных мембранных коро-
бок, из внутренних полостей которых выкачан воздух, применяются
для измерения полного давления воздуха перед двигателем. Схема
такого чувствительного элемента дана на рис. 5.16. Несколько ко-
робок соединены в общий блок для увеличения перемещения штока.
Сильфоны — гофрированные трубки — применяются для измере-
ния разности давлений воздуха, газа или жидкости (рис. 5.17).
Внутрь трубки подается большее давление, меньшее — воздейству-
ет на внешнюю поверхность трубки.
Мембраны используются для измерения разности давлений как
газа, так и жидкости.
При регулировании расхода или давления топлива в случае
использования насосов постоянной производительности обычно
применяются перепускные золотники. Они выполняют одновремен-
но функции чувствительного элемента и регулирующего органа.
На рис. 5.18, а показана схема перепускного золотника, являющего-
ся регулятором расхода. Если же с одной стороны золотника под-
вести атмосферное давление (рис. 5.18,6), то такой перепускной
золотник становится уже регулятором давления.
138
Глава V. Системы регулирования авиационных ВРД
Регуляторы расхода и давления, схемы которых даны на
рис. 5.18, являются статическими регуляторами. Статическая ошиб-
ка регулирования зависит в обеих схемах от жесткости пружины, от
характеристики изменения площади проходного сечения перепуск-
ных отверстий по ходу золотника, от площади золотника, на кото-
рую действует давление жидкости, а также от характеристик пото-
ка жидкости. В регуляторах расхода и давления функции чувстви-
тельного элемента и регулирующего органа могут быть разделены,
например при использовании мембраны и перепускной дозирую-
щей иглы.
Гидравлические сервомоторы
В системах регулирования авиационных ГТД гидравлические
сервомоторы нашли широкое применение. Они используются или
как гидравлические усилители, когда перестановочные усилия на
регулирующем органе велики, или как программные замедлители
при перенастройке регулятора с одного числа оборотов на другое
(см. о гидрозамедлителях в гл. VIII).
Сервомотор состоит из управляющего элемента и исполнитель-
ного органа. В качестве управляющих элементов используются
отсечные или проточные золотники или управляющие клапаны.
Исполнительные органы выполняются обычно в виде поршней, пе-
ремещающихся за счет давления рабочей жидкости. Перемещение
управляющего элемента происходит при изменении положения
чувствительного элемента регулятора. Поршень сервомотора свя-
зан с регулирующим органом или элементом настройки регулятора.
В качестве рабочей жидкости используются масло или керосин.
Применение масла почти полностью устраняет силы сухого трения
и предохраняет детали регулятора от коррозии. Однако в этом
случае нужен дополнительный насос, чтобы создать необходимое
давление перед сервомотором. Применение керосина дополнитель-
ного насоса не требует, так как основной насос дает достаточно вы-
сокое давление. Керосин обладает плохой смазывающей способ-
ностью и поэтому силы сухого трения в элементах регулятора воз-
§ 2. Элементы систем питания и автоматических устройств
139
растают. Вода, содержащаяся в небольшом количестве в керосине,
может вызвать коррозию деталей.
Необходимо также учитывать склонность рабочих жидкостей,
применяемых в топливной и регулирующей аппаратуре ГТД, к об-
литерации. Облитерацией называется заращивание поляризованны-
ми молекулами жидкости малых зазоров в трущихся парах и дру-
гих сопряженных деталях топливной аппаратуры. Облитерация
представляет собой адсорбционный процесс, заключающийся в сгу-
щении (уплотнении) жидкости на поверхности твердых металличе-
ских деталей. Этот процесс обусловлен наличием силового поля у
Рис. 5.19
атомов и молекул жидкости, находящихся на поверхности и лишь
частично связанных с другими ее атомами и молекулами.
При протекании жидкости через малые зазоры под постоянным
перепадом давлений благодаря облитерации с течением времени
расход жидкости уменьшается и при достаточно малых зазорах
прекращается совсем. Интенсивность облитерации тем выше, чем
больше давление жидкости. При проектировании топливной и регу-
лирующей аппаратуры ГТД необходимо учитывать возможность
облитерации и принимать меры к ее предотвращению. Иначе нару-
шается характеристика регулирующей аппаратуры и ухудшается
процесс регулирования.
На рис. 5.19 показана схема двухстороннего поршневого серво-
мотора с отсечным золотником. У золотника высота поясков рав-
на высоте кольцевых проточек, соединенных с каналами отвода
и подвода жидкости к полостям сервоцилиндра. При нейтральном
положении золотника обе полости сервоцилиндра отсоединены.
На рис. 5.20 также приведена схема двухстороннего поршневого
сервомотора, золотник которого сделан проточным. В этом случае
высота кольцевых проточек делается несколько больше высоты
поясков золотника, а полости сервоцилиндра соединены со сливом
жиклерами небольшого сечения. Такая схема при нейтральном по-
ложении золотника обеспечивает некоторую циркуляцию рабочей
140
Глава V. Системы регулирования авиационных ВРД
жидкости через полости сервомотора, что улучшает чувствитель-
ность регулятора. В условиях эксплуатации двигателя при низких
температурах окружающей среды достаточно длительная работа
двигателя на равновесном режиме может привести к загустеванию
масла в замкнутых полостях сервоцилиндра. Циркуляция масла
предотвращает загустевание. При .использовании керосина в каче-
стве рабочей жидкости циркуляция не обязательна, однако, цир-
куляция дает возможность удалить из полостей сервомеханизма
воздух.
Большое значение для динамики регулирования имеет быстро-
действие сервомотора, т. е. величина перемещения сервопоршня в
единицу времени. Быстродействие тем больше, чем меньше пло-
щадь поршня сервомотора, чем больше время-сечение открытия
окон золотника, чем выше давление рабочей жидкости перед золот-
ником. Снижение площади поршня с целью увеличения быстродей-
ствия сервомотора имеет свои границы. Вместе с уменьшением
площади перестановочные усилия становятся меньше.
Наличие в одной из полостей цилиндра сервомотора пружины
и в другой полости штока, связывающего поршень с регулирующим
органом, делает сервомотор с проточным золотником статическим.
Это означает, что каждому положению сервопоршня соответствует
свое определенное положение золотника вблизи его нейтрального
положения. Действительно, чем выше, например, будет расположен
поршень (см. рис. 5.20), тем сильнее сожмется пружина. Для удер-
жания поршня в этом положении давление рабочей жидкости под
поршнем необходимо иметь больше давления над ним. Для этого
проточный золотник должен занять такое положение, чтобы зазор,
по которому жидкость поступает в полость цилиндра под поршнем,
был бы больше зазора подвода жидкости в полость над поршнем.
Статическая ошибка, вносимая сервомотором с проточным золот-
ником, отражается на точности регулирования. Понятие нейтраль-
ного положения золотника становится несколько условным.
Наряду с разобранными типами гидравлических сервомоторов
с цилиндрическими золотниками большое распространение полу-
чили сервомоторы с клапанными управляющими элементами. На
рис. 5.21 показана одна из схем такого сервомотора с односторон-
ним плоским управляющим клапаном. Остановимся на особеннос-
тях его работы.
В нижнюю полость цилиндра сервомотора подводится давление
топлива, равное давлению за насосом. В другой, верхней полости
цилиндра давление топлива будет ниже, так как, с одной стороны,
эта полость соединена с магистралью за насосом через жиклер 1,
а с другой стороны, через плоский клапан 2 она соединена с давле-
нием слива. Если плоский клапан полностью закрыт, то давление
в верхней полости станет равным давлению за насосом и поршень
§ 2. Элементы систем питания и автоматических устройств
141
переместится вниз. Если плоский клапан полностью открыть, то
давление в верхней полости будет близко к сливному и поршень
переместится вверх. В положении равновесия силы,'действующие на
обе стороны поршня, равны между собой. Количество топлива, при-
текающего через жиклер 1,
равно количеству топлива, вы-
текающего через жиклер пло-
ского клапана 2. При движе-
нии сервопоршня равенство
расходов нарушается.
Если плоский клапан при-
поднять (увеличить координа-
ту у), то расход через жиклер
плоского клапана увеличится,
давление в полости цилиндра
над поршнем упадет, перепад
на нем увеличится и поршень
начнет перемещаться вверх,
сжимая пружину. Перепад дав-
ления на поршне равен пере-
паду давления на жиклере 1.
Поэтому одновременно с движением поршня вверх расход через
жиклер 1 возрастет. Движение поршня прекратится, когда сумма
всех действующих на поршень сил (сила от перепада давлений
топлива, сила пружины и усилие от регулирующего органа) будет
равна нулю. В новом положении равновесия поршня расходы через
жиклер 1 и жиклер плоского клапана сравняются. Поскольку каж-
дому определенному положению плоского клапана 2 всегда соот-
ветствует определенное положение поршня, сервомотор с управля-
ющим клапаном является статическим. Его статическая характери-
стика у = f(m), показанная на рис. 5.22, б, может быть получена
из сравнения расходов Q! и Q2 (см. рис. 5.22, а). Здесь Q1 — расход
142
Глава V. Системы регулирования авиационных ВРД
через жиклер 1, a Q2 — через плоский клапан (см. рис. 5.21). На
рис. 5.22, а каждому положению равновесия, определяемому точка-
ми пересечения кривых, соответст-
вует определенное давление над
поршнем при неизменном давлении
перед сервомотором.
В этом типе сервомотора силы
сухого трения меньше, чем в серво-
моторе с управляющим золотником.
К его недостаткам надо отнести
влияние силы струи топлива, выте-
кающего из-под клапана, на клапан-
ный управляющий элемент.
На рис. 5.23 дана схема сервомо-
тора с двухсторонним клапанным
Рис- 5.23 управляющим элементом. От поло-
жения клапана, связанного с чувст-
вительным элементом, а также, возможно, и с механизмом обрат-
ной связи, зависит распределение давления в полостях цилиндра и
положение поршня.
Клапан минимального давления топлива
Рис. 5.24
С ростом высоты полета потребный расход топлива ТРД при
неизменном числе оборотов падает. Снижение расхода достигается
уменьшением давления топлива перед форсунками. Для каждого
двигателя существует минимально
допустимое давление рфт\м, опреде-
ляемое условиями хорошего распы-
ла топлива и устойчивого горения.
При работе двигателя на малом га-
зе в высотных условиях, а также
при резкой уборке рычага управле-
ния давление топлива перед фор-
сунками может стать ниже допусти-
мого (рф < рфты), что приведет к
срыву пламени и самопроизвольно-
му выключению двигателя. Для
предотвращения срыва в систему
питания вводятся специальные ав-
томатические устройства, ограничи-
вающие минимальное давление, выполняемые в виде клапанов
прямого или непрямого действия. При достижении некоторой высо-
ты полета эти клапаны включаются автоматически.
Схема клапана прямого действия показана на рис. 5.24. Клапан
этого типа используется обычно в системах незамкнутого регулиро-
§ 2. Элементы, систем питания и автоматических устройств
143
вания числа оборотов. Клапан 1 связан штоком с мембраной 2, на
которую действует пружина 3. Сила пружины, регулируемая вин-
том 4, определяет то минимальное давление Рдзпнп.за дроссельным
краном, при котором клапан вступает в действие. В полости над
клапаном давление топлива’ ртоп равно давлению перед дроссель-
ным краном, давление за клапаном над мембраной близко к давле-
нию за дроссельным краном рф. Давление под мембраной равно
давлению на входе в топливный насос. Когда давление Рф достига-
ет той величины, на которую отрегулирован клапан (рф = Pgsmin),
под действием пружины 3 клапан 1 приподнимается и открывает
дополнительное сечение параллельно дроссельному крану для про-
хода топлива. Высоту полета, на которой включается клапан, назо-
вем высотой включения Нвкл.
Клапан является статическим. После его включения и дальней-
шего падения ртоп с ростом высоты, полота давление топлива на ма_
лом газе рфМ.г, а следовательно, и расход GM г не остаются постоян-
ными. Покажем это. Составим уравнение равновесия сил, действую-
щих на клапан в его рабочем положении:
{Ртоп рф.м.) /кл “Ь (рф.м.г Р в>) fM Рпр о
В этом уравнении fM — эффективная площадь мембраны; —
площадь клапана; Рпр о — сила пружины клапана в его закрытом
положении; 6/г — перемещение мембраны (клапана); В —характе-
ристика пружины.
Перемещение клапана б/г обычно невелико, па некоторых выпол-
ненных конструкциях оно равно 0,5ч-0,7 мм. Поэтому при неболь-
шой жесткости пружины В величиной Вб/i можно пренебречь. Если
же принять неизменным давление рвх, уравнение равновесия сил
примет вид
Ртоп ГКЛ + Рф.м.0 (fM - f J = Рпр 0 + Рвх fM = COnst <5 • 2)
Из уравнения (5.2) следует, что с увеличением высоты полета (е
уменьшением ртоп) минимальное давление перед форсунками р#.м.е,
ограничиваемое клапаном, возрастает.
При неизменном положении рычага управления двигателем на
упоре малого газа (аМг — const) из-за снижения потребного расхо-
да топлива и роста давления рф.м.г на высотах Н > Нвкл число обо-
ротов малого газа возрастает. Высота полета, на которой они срав-
няются с максимальным числом оборотов, будет максимальной вы-
сотой— потолком двигателя (Н = Нпот). Примерное изменение
давления топлива и числа оборотов малого газа по высоте полета
показано на рис. 5.25.
При полете на высоте, больше высоты включения клапана, в ры-
чаге управления появляется «мертвый ход» — перемещение рычага
управления, не приводящее к изменению числа оборотов двигателя.
144
Глава V. Системы регулирования авиационных ВРД
Чем больше высота .полета, тем больше «мертвый ход» рычага. На*
личие «мертвого хода» (или площадки высотного малого газа)'
объясняется тем, что с перемещением рычага и увеличением сече-
ния дроссельного крана открытие клапана несколько уменьшается.
В результате давление топлива и его расход в некотором диапазо-
не угла поворота рычага не изменяются. Примерная зависимость
числа оборотов от положения рычага управления показана на
рис. 5.26.
Рис. 5.27
Клапаны минимального давления непрямого действия нашли
применение в центробежных регуляторах числа оборотов. В таких
системах клапан,, схема которого показана на рис. 5.27, воздейству-
ет на сервомотор регулирующего органа. Клапан состоит из золот-
ника 1, мембраны 2, являющейся чувствительным элементом, и
пружины 3. Сила затяжки пружины, определяющая величину рфташ,
$ 2. Элементы систем питания и автоматических устройств
145
регулируется винтом 4. Пока давление за дроссельным краном боль-
ше мияимального давления, на которое рассчитан клапан {рф >
> Рфты), мембрана 2 прогнута вниз, пружина 3 сжата и золотник /
находится в нижнем положении на упоре. Доступа ‘топливу из ма-
гистрали перед дроссельным краном к сервомотору регулирующего
органа нет. С ростом высоты полета давление рф падает, перепад
давления на мембране уменьшается. При рф = pgsmin золотник при-
открывает отверстие, ведущее к сервомотору регулирующего органа
С дальнейшим ростом высоты полета регулирующий орган переме-
щается таким образом, что
Давления ртоп и рф — рф mln
остаются неизменными (с
точностью до величины ста-
тической ошибки клапана).
При регулировании чис-
ла оборотов нелинейность
статической характеристики
центробежного чувствитель-
ного элемента и различное
влияние сил сухого трения
на ее отдельных участках —
одна из причин сужения
диапазона автоматической
работы регулятора по ско-
рости вращения двигателя. Регулятор вступает в действие не с чис-
ла оборотов малого газа пм_г, ,а с так называемого числа оборотов
начала автоматической работы (число оборотов НАР) пиЛр>пм.г.
В диапазоне чисел оборотов от пм,г до пНАР подача топлива до-
зируется регулятором расхода, обеспечивающим постоянный расход
при неизменном положении дроссельного крана. Поэтому при пос-
тановке у земли дроссельного крана на упор малого газа с ростом
высоты полета число оборотов малого газа будет расти до тех пор,
пока не вступит в действие центробежный регулятор числа оборотов
(при пмг = пНЛР). С’ дальнейшим увеличением высоты полета ре-
гулятор поддерживает пНАР = const, а давление рф падает. При дос-
тижении рф = Pgsmin включается клапан минимального давления,
поддерживающий рф т\п = const, число оборотов малого газа воз-
растает. Пределом увеличения высоты полета является достижение
Пм.г = ^тах-
Примерное изменение Рф.м.г и пм г по высоте полета показано на
рис. 5.28. После включения клапана минимального давления в рабо-
ту его влияние на положение регулирующего органа противопо-
ложно влиянию чувствительного элемента регулятора числа оборо-
тов, стремящегося поддержать пНАР — const. Однако влияние кла-
пана сильнее и рост высоты приводит к увеличению числа оборотов.
При использовании клапана минимального давления непрямого дей-
146
Глава V. Системы регулирования авиационных ВРД
ствия, так же как и клапана прямого действия, на больших высотах
начало перемещения рычага управления от упора малого газа
сопровождается появлением «мертвого хода» и площадки высотно-
го малого газа.
Дроссельные устройства изодромных регуляторов числа оборотов
На рис. 5.4 была показана принципиальная схема изодромного
регулятора числа оборотов с катарактом. Одним из элементов ка-
таракта является дроссельное устройство, выполненное в этой схе-
ме в виде жиклера 3. От величины его гидравлического сопротив-
ления существенно зависит характеристика изодромного регулятора.
Гидравлическое сопротивление катаракта должно быть достаточно
большим. Однако сделать его, например, просто в виде отверстия
небольшого диаметра нельзя, так как отверстие легко может засо-
риться и работа регулятора нарушится.
Рис. 5.29
Ниже приведены примеры конструктивного выполнения некото-
рых дроссельных устройств. На рис. 5.29, а показано дроссельное
устройство изодромного регулятора числа оборотов одного из дви-
гателей, выполненное в виде отверстия на вращающемся золотни-
ке 1. Отверстия на втулке обратной связи 2 и лыски на золотнике /
сделаны таким образом, что за один оборот золотника входное и
выходное отверстия дросселя оказываются сообщенными друг с
другом на протяжении примерно 13° поворота золотника. По вели-
чине расхода отверстие во вращающемся золотнике диаметром
1,5 мм эквивалентно отверстию диаметром в 0,1 мм.
Показанное на рис. 5.29, б дроссельное устройство выполнено в
§ 2. Элементы систем питания, и автоматических устройств
147
виде вирта. Входной и выходной каналы сообщаются между собой
посредством резьбовой канавки 1 винта 2. Сопротивление такого
дросселя удобно регулировать, изменяя длину I рабочего участка
резьбы. Широкое применение нашли дроссельные сопротивления,
составленные в виде пакетов из ряда плоских жиклеров 1
(рис. 5.29, в) с калиброванными отверстиями, разделенными проме-
жуточными шайбами 2. Для увеличения гидравлического сопротив-
ления отверстия смежных плоских жиклеров смещены относительно
друг друга. Регулировка гидравлического сопротивления пакета
производится путем изменения числа плоских жиклеров или измене-
нием взаимного расположения их отверстий.
Центробежные форсунки (типы и характеристики)
В современных авиационных ГТД применяются главным обра-
зом центробежные форсунки, двигатели с испарительными или
струйными форсунками встречаются редко. Поэтому в дальнейшем
остановимся па схемах и характеристиках только центробежных
форсунок.
Форсунка должна работать в широком диапазоне изменения рас-
ходов топлива. Изменение расхода через форсунку проще всего
достигнуть путем увеличения давления топлива. Однако с увеличе-
нием давления возрастает в эксплуатации количество дефектов в
топливной системе и растут трудности изготовления деталей топлив-
ной системы. Поэтому нежелательно, чтобы давление топлива перед
форсунками превышало 4-106ч-5-10в н[м2.
К форсункам предъявляются жесткие требования по тонкости
распиливания и по углу факела распыленного топлива. Правиль-
ным сочетанием формы факела, тонкости распиливания и организа-
ции воздушного потока можно получить устойчивое горение, макси-
мально возможную полноту сгорания и падежный запуск двигателя.
Рассмотрим схемы различных типов центробежных форсунок и их
характеристики.
Одноканалъная центробежная форсунка. Ее схема показана на
рис. 5.30, а, а расходная характеристика — па рис. 5.30, б. Форсун*
ка имеет один топливоподводящий канал 1 и от трех до шести тан-
генциальных отверстий 2, создающих закрутку потока в вихревой
камере 3. Существенным недостатком одноканальной форсунки яв-
ляется резкое изменение давления топлива на входе в форсунку при
изменении расхода топлива. Это видно из уравнения расхода
<2ф = с ~ &Рф, (5.3)
где брф = рф — ръ — перепад давления на форсунке; ц— коэффи-
циент расхода; Fc — площадь выходного сопла; у — удельный вес
топлива.'
148
Глава V. Системы регулирования, авиационных ВРД
При работе одноканальной форсунки на одном и том же топливе
и при постоянной температуре коэффициент расхода ц практически
не изменяется. Поэтому расход топлива через форсунку определя-
ется величиной перепада давления брф и главным образом давле-
нием рФ.
Предположим, что у двигателя расход топлива должен изме-
ниться в 20 раз. Тогда при использовании одноканальных форсунок,
перепад давления на форсунке необходимо изменить в 400 раз. Ес-
ли в этом случае выбрать приемлемое по соображениям прочности
элементов системы питания давление перед форсункой рф при мак-
симальном расходе топлива, то при значительном снижении расхода
давление рф будет настолько мало, что не обеспечит качественного
распыла топлива. Если же на минимальном расходе выбрать давле-
ние, обеспечивающее требуемый распыл топлива, то на больших
расходах топливная система выйдет из строя из-за чрезмерно вы-
соких значений рф. Значительный диапазон изменения давления рф
не позволяет использовать одноканальную форсунку в качестве ос-
новной рабочей форсунки современных ГТД. Она может применять-
ся только для вспомогательных целей, в частности, как пусковая
форсунка.
Двухканалъная центробежная форсунка (рис. 5.31). Форсунки
этого типа выполняются однокамерными (рис. 5.31, а), двухкамер-
§ 2. Элементы, систем питания и автоматических устройств
149
ними (рис. 5.31, б) и двухсопловыми' (рис. 5.31, в). Применение
двухканальных форсунок дает возможность увеличить крутизну рас-
ходной характеристики форсунки и получить требуемое изменение
расхода топлива в меньшем диапазоне давлений на форсунке.
У двухканальных форсунок имеется два подводящих канала. Один
канал 1, основной, предназначен для подачи больших количеств,
топлива, обеспечивающих основные режимы работы двигателя.
Другой канал 2, вспомогательный, служит для подачи топлива на
режимах малых расходов.
На режиме запуска основной канал закрыт клапаном-распреде-
лителем 3 и топливо подается в форсунку только по вспомогатель-
ному каналу1.
По мере увеличения давления во вспомогательном канале с не-
которого момента начнет приоткрываться клапаы-распределитель.
Изменение его степени открытия вызовет изменение коэффициента
расхода р. При закрытом клапане коэффициент расхода мал и тре-
буемые малые количества топлива поступают в форсунку с доста-
точно высоким давлением. Открытие клапана-распределителя при-
водит к увеличению коэффициента расхода.
В начальный момент открытия клапана-распределителя за счет
дросселирования им топливного потока давление в основном канале
значительно меньше, чем во вспомога-
тельном. Это обстоятельство приводит к
ухудшению тонкости распыливания топ-
лива. Ухудшение распыливания тем силь-
нее, чем меньше давление, при котором
включается клапан-распределитель.
Примерная расходная характеристи-
ка двухканальной форсунки дана на
рис. 5.32. На этой характеристике кри-
вая 1 (ее сплошная и пунктирная части)
определяет расход только через вспомо-
гательный канал, а кривая 2 показывает,
какой был бы расход при подводе топлива к форсунке через оба
канала. Действительное изменение расхода следует кривой Oabc, ее-
участок ab соответствует постепенному перемещению распредели-
тельного клапана.
Однокамерные двухканальные форсунки могут давать большую-
неравномерность расхода в момент включения основных каналов.
Это связано с неравномерностью сопротивления вспомогательных
тангенциальных каналов. Так, если в одной из форсунок, связанной
1 В схемы двухканальных центробежных форсунок, а также помещенных
далее перепускных форсунок условно включены перепускные клапаны. В дейст-
вительности перепускные клапаны выполняются отдельно от форсунок и явля-
ются самостоятельными элементами систем питания. Они называются автома-
тами распределения топлива (APT) или распределительными клапанами (РК).
150
Глава V. Системы регулирования авиационных ВРД
с общим коллектором, сопротивление вспомогательных тангенци-
альных каналов больше, чем у других, то давление в вихревой ка"
мере этой форсунки ниже, чем в остальных. Тогда при включении
в работу основного канала расход через эту форсунку возрастает
за счет пониженного противодавления в .вихревой камере.
В двухкамерной ищи двухсопловой форсунке с двумя подводя-
щими каналами распыливание топлива, идущего через основной ка-
нал, несколько ухудшается. Однако вместе с тем существенно сни-
жается влияние давления во вспомогательной вихревой камере на
расход топлива при включении клапана-распределителя. Это объ-
ясняется тем, что топливо из .вспомогательной вихревой камеры по-
дается в центральную часть основной вихревой камеры и ее сопла,
где давление значительно ниже.
Все виды двухканальных центробежных форсунок обеспечивают
25ч-30-кратный диапазон изменения расхода топлива при макси-
мальном давлении на входе .в форсунку, не превышающем 5- 108нЛи2.
Дальнейшее увеличение диапазона изменения расхода топлива в
форсунках этого типа связано с заметным ухудшением качества
распиливания на режимах пониженного расхода. Вследствие этого
в системы питания двигателей включают клапаны минимального
давления топлива, что приводит к росту числа оборотов малого газа
в высотных условиях. Значительное расширение диапазона расхода
топлива при приемлемых значениях давления на входе и при хоро-
шем качестве распыливания требует перехода к перепускным или
комбинированным перепускным форсункам.
Перепускная центробежная форсунка. Если при заданном мини-
мальном расходе топлива добиться увеличения скорости топлива на
входе в вихревую камеру 1 (рис. 5.33), то это увеличит радиус воз-
душного вихря и благоприятно скажется на распыливании топлива.
Поэтому целесообразно увеличить-скорость во входном канале 2 по
сравнению со скоростью потребного на данном режиме расхода топ-
§ 2. Элементы систем питания автоматических устройств
151
лива. Излишек топлива, поступившего в вихревую камеру этой фор-
сунки, по кольцевому отверстию 3 и перепускному каналу 4 возвра-
щается в топливную систему.
Расход топлива через перепускную форсунку практически зави-
сит лишь от давления на входе в форсунку и количества перепус-
каемого топлива. Последнее определяется давлением в перепуск-
ном канале и профилированием перепускного клапана 5. Характе-
ристика перепускной форсунки дана на рис. 5.34, где QK — произ-
водительность насоса; Q# — ра.сход топлива через форсунку; Qnep —
объем перепускаемого топлива.
В перепускной форсунке на режиме малых расходов потери на-
пора в тангенциальных отверстиях и вихревой камере значительно-
меньше, чем в двухкаыальной форсунке. Это объясняется большим
размером тангенциальных отверстий и большим объемным расходом
вихревой камеры. Поэтому диапазон допустимого изменения расхо-
да топлива у перепускной форсунки в 2-?3 раза больше, чем у двух-
канальной. В этом отношении перепускная форсунка не ограничи-
вает дальнейшего развития газотурбинных двигателей.
Перепускная форсунка не свободна от недостатков. Наиболее
серьезный из них заключается в том, что подача топлива к фор-
сункам на всех режимах рабо-
ты двигателя почти неизменна.
В связи с этим производитель-
ность топливного насоса на по-
ниженных режимах значитель-
но завышена, чем в случае при-
менения других форсунок.
Этот недостаток существенно
снижается с переходом к ком-
бинированным перепускным
форсункам.
Комбинированная перепу-
скная форсунка (КПФ). Схе-
ма возможного варианта КПФ
показана на рис. 5.35. Рассмот-
рим принцип действия КПФ на режимах пониженных расходов.
Топливо от насоса под давлением, которое в частном случае может
поддерживаться постоянным, по вспомогательному каналу 1 через;
тангенциальные отверстия 2 поступает в вихревую камеру. Часть
топлива через сопло форсунки поступает в камеру сгорания двига-
теля, остальная часть топлива через другие тангенциальные отвер-
стия 3 поступает в основной канал 4 и, пройдя клапан-распредели-
тель 5, попадает во всасывающую магистраль перед насосом.
По мере увеличения давления топлива во вспомогательном ка-
нале клапан-распределитель, перемещаясь, уменьшает перепуск
топлива, поступление топлива в камеру сгорания увеличивается.
152
Глава V. Системы регулирования авиационных ВРД
Следовательно, на режимах пониженных расходов КПФ работает
как простая перепускная форсунка. При дальнейшем увеличении
давления топлива во вспомогательном канале клапан-распредели-
тель займет такое положение, при котором перепуск топлива во
всасывающую магистраль полностью прекратится. Топливо в вих-
ревую камеру начнет поступать и через вспомогательный, и через
основной каналы. На этих режимах КПФ
Pecn~const з, работает как двухканальная центробеж-
4 ная форсунка.
---/ Возможны два способа регулирова-
иия КПФ. По первому из них поддержи-
/ вается постоянное давление во вспомога-
/ тельном канале (рвсп — const) достаточно
1/ высокое для хорошего распыливания топ-
___________L—_______ лива на всех режимах работы двигателя.
Росн Рос По второму способу поддерживается по-
стоянным перепад давления на форсунке
Рн‘с- 5-36 (дрф = const). Второй способ регулиро-
вания хотя несколько и усложняет схему
топливопитания, однако на больших высотах полета не допускает
возникновения в системе излишне высокого давления топлива.
На рис. 5.36 показана расходная характеристика КПФ, постро-
енная при постоянном давлении во вспомогательном канале peen.
За независимую переменную взято давление в основном канале
Росн. На этой характеристике лйния 1—2 соответствует расходу
топлива через форсунку на режиме перепуска, линия 2—3— расхо-
ду топлива через форсунку после прекращения перепуска, линия
4—2—3 характеризует подачу топлива к форсунке. В точке 2 при
давлении топлива в основном канале р'осн прекращается перепуск
топлива во всасывающую магистраль и начинается подача топлива
в вихревую камеру через оба канала.
§ 3. СХЕМЫ СИСТЕМ РЕГУЛИРОВАНИЯ ГТД
Регуляторы газотурбинных двигателей имеют самое разнообраз-
ное конструктивное оформление. В них используются различные
типы чувствительных элементов и усилителей, применяются разно-
образные способы стабилизации процесса регулирования. Поэтому
при изучении систем регулирования различных типов двигателей,
находящихся в эксплуатации, в первую очередь следует обращать
внимание на принципы их построения и на особенности, отличающие
одну систему от другой.
Замкнутое регулирование измеренного числа оборотов ТРД
На рис. 5.37 приведена схема изодромного регулятора числа
оборотов ТРД с шестеренным насосом постоянной производитель-
ности, имеющего регулируемое выходное сопло. Этот регулятор
£ 3. Схемы систем регулирования авиационных газотурбинных двигателей 153
числа оборотов выполнен вместе с регулятором расхода топлива,
который вступает в работу на пониженных режимах. Взаимодейст-
вие регулятора числа оборотов и регулятора расхода легче понять
с помощью принципиальной схемы, приведенной на plic. 5.38. Рабо-
та системы регулирования на максимальных и крейсерских режи-
мах двигателя показана на рис. 5.38, а. На этих режимах сечение
Рис. 5.37
дроссельного крана 1 велико, а перепад давления на нем мал.
Поэтому золотник регулятора расхода 2 перекрывает перепускное
отверстие и регулятор расхода те работает. Дозирование расхода
топлива, поступающего из шестеренного насоса 3, осуществляется
с помощью изодромного регулятора 5 и его перепускной иглы 4.
С переходом на пониженные режимы (рис. 5.38, б) изодромный
регулятор 5 выключается (на схеме его перепускная игла 4 дове-
дена до упора). Сечение дроссельного крана 1 уменьшено и за счет
создавшегося на нем перепада давления в работу вступает регуля-
тор расхода 2. Золотник регулятора расхода песет функции и чув-
ствительного элемента, и регулирующего органа. Однако в регуля-
торе (см. рис. 5.37) они разделены: золотник 2 является только
чувствительным элементом, а регулирующим органом служит пере-
пускная игла 5. Вернемся к схеме изодромного регулятора на
154
Глава V. Системы регулирования авиационных ВРД
рис. 5.37. Рабочей жидкостью сервомотора служит масло, нагнетае-
мое специальным масляным насосом. Управление двигателем
осуществляется общим рычагом, воздействующим на дроссельный
кран 1 и кулачок 6 настройки регулятора. Кулачок сжимает внут-
реннюю пружину 7, опирающуюся на вращающийся проточный зо-
лотник 9. Золотник помещен в гильзу 10, которая с одной стороны
опирается на пружину 8, а с другой — па рычаг обратной связи 12.
Другой конец рычага связан с поршнем обратной связи 14. Второй
Рис. 5.38
поршень (поршень изодрома 15) выполнен за одно целое с пере-
пускной иглой 5, на конце которой расположен хвостовик с пружи-
ной. Поршень обратной связи и поршень изодрома образует по-
лость, заполняемую маслом из напорной магистрали через проточ-
ку в золотнике 13 и отверстие И во вращающемся золотнике 9.
При отклонении золотника 13 вниз в межпоршневую полость посту-
пает масло под давлением. При отклонении его вверх межпоршне-
вая полость сообщается со сливом.
Регулятор на основных режимах работает следующим образом.
Предположим, что произошло уменьшение числа оборотов. Тогда
пружина 7, преодолевая уменьшившуюся силу грузиков, переместит
золотник 9 вверх. Масло под давлением начнет поступать в полость
над поршнем обратной связи 14, полость под поршнем 15 иглы пе-
репуска соединится со сливным каналом. Межпоршневая полость
в это время замкнута и ее объем неизменен, поэтому поршни нач-
нут двигаться вниз как одно целое, уменьшая сечение кольцевого
канала под иглой перепуска 5. Подача топлива в двигатель воз-
растет.
При смещении поршня 14 вниз межпоршневая полость через
проточку в золотнике 13 и отверстие во вращающемся золотнике
сообщится с каналом, подводящим масло под давлением. Однако
для протока масла через отверстие 11 нужно определенное время
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 155
и поэтому в начале процесса регулирования поршни 14 и 15 дви-
жутся„как одно целое, а регулятор работает подобно регулятору с
жесткой обратной связью.
При движении поршня обратной связи 14 вниз1 гильза 10 сле-
дует за золотником 9 и догоняет его. Хотя окна гильзы располо-
жатся против поясков золотника, регулятор еще не будет находить-
ся в положении равновесия. Поступление масла в межпоршйевую
полость продолжается, поршень 14 пойдет вверх, смещая гиль-
зу 10 вниз, а поршень 15 последует вниз, уменьшая количество
перепускаемого топлива. Перемещение поршня 14 вверх продол-
жится до тех пор, пока золотник 13 не перекроет канал ’подвода
масла в межпоршневую полость. Увеличение подачи топлива, свя-
занное с движением иглы перепуска вниз,, вызовет рост числа
оборотов двигателя. Последующее перемещение золотника 9 вниз
под действием возросших центробежных сил грузиков приведет его
в положение равновесия.
В действительности процесс регулирования сложнее, чем это
следует из приведенного описания. Движение поршней 14 и 15 и
изменение объема межпоршневой пЪлости происходит одновремен-
но. Однако главное заключается в том, что в начале процесса ре-
гулирования изодромный регулятор ведет себя как регулятор с
жесткой обратной связью и по своим характеристикам близок к
статическому регулятору. В конце процесса статическая ошибка ре-
гулирования снимается и для разных внешних условий число обо-
ротов двигателя, поддерживаемое регулятором на статических ре-
жимах, остается неизменным.
Рассмотрим работу регулятора в диапазоне оборотов от пмг до
Пнар, когда подача топлива дозируется регулятором расхода. При
установке рычага управления в положение, соответствующее пони-
женным режимам, перепад давления на дроссельном кране 1 воз-
растает. Этот перепад измеряется и поддерживается постоянным с
точностью до величины статической ошибки золотником 2. Золот-
ник, таким образом, выполняет роль чувствительного элемента, а
подача топлива определяется только проходным сечением дрос-
сельного крана.
Так как излишек топлива перепускается с помощью той же иг-
лы 5, изодромный регулятор отключается. Для этого полость меж-
ду поршнями 14 и 15 и полость под поршнем 15 сообщаются меж-
ду собой с помощью каналов 16 и 17 и паза в валике дроссельного
крана 1. Кроме того, канал 16 через проточку в золотнике 2 сооб-
щается со сливом.
Работа регулятора расхода начинается в тот момент, когда зо-
лотник 2 сообщает полость 4 с магистралью высокого давления
топлива. В этом случае игла 5 поднимается, увеличивая перепуск
топлива. При большом повышении давления в магистрали за топ-
ливным насосом золотник 2 выполняет роль предохранительного
156
Глава V. Системы, регулирования авиационных ВРД
клапана, сообщая дополнительно напорную топливную магистраль
с перепуском через канал 3. Переход двигателя с основных режи-
мов на пониженные происходит плавно, так как в обоих случаях
для дозировки топлива используется перепускная игла 5.
Рассмотрим еще одну схему (рис. 5.39) изодромного регулятора
числа оборотов, в котором сервомотор является общим силовым
органом регулятора подачи топлива и регулятора числа оборотов.
Регулятор выполнен как одно целое вместе с плунжерным насосом
переменной производительности. Производительность насоса изме-
няется поворотом наклонной шайбы, от угла установки которой за-
висит ход плунжеров. В качестве рабочей жидкости в силовых
элементах регулятора используется топливо, отбираемое от ма-
гистрали высокого давления за насосом. Поршень сервомотора свя-
зан с наклонной шайбой насоса.
Центробежный маятниковый чувствительный элемент 2 приво-
дится во вращение от ротора плунжерного насоса 1. Перед золот-
ником чувствительного элемента установлен клапан постоянного
давления 3. Он снижает величину давления топлива, подводимого
к золотнику и сервомотору, и тем самым снижается сила трения.
Подвод топлива в межпоршневую полость сервомотора происходит
через пакет 12, составленный из шайб с небольшими отверстиями.
При перемещении рычага 8 управления на режиме п > пНАР
одновременно происходит перенастройка регулятора и перемеще-
ние дроссельного крапа 5. На режиме п = пНАР колпачок И, на-
детый на пружину чувствительного элемента, доходит до упора и
при дальнейшем перемещении рычага 8 в сторону уменьшения чис-
ла оборотов остается в неизменном положении. Тем самым регуля-
тор числа оборотов выключается из работы.
На режимах от п = пНар до п = пм_г дозирование подачи топ-
лива происходит с помощью регулятора расхода. Его чувствитель-
ный элемент — золотник 7, а регулирующий орган — поршень 13
сервомотора. Золотник 7 на числе оборотов п = Пиар и ниже под-
держивает постоянный перепад на дроссельном кране. Топливо в
полость над золотником 7 попадает через жиклер 6, что сделано с
целью использовать золотник 7 для регулирования подачи топлива
при наборе числа оборотов (см. гл. VIII).
Пружина золотника 7 отрегулирована па определенный пере-
пад давления. Если перепад на дроссельном крапе возрастет, то
золотник, поднимаясь вверх, с помощью каналов 9, 4 и 10 сооб-
щает межпоршневую полость со сливом, а полость левее поршня 13
сервомотора — с напорной магистралью. При этом поршень 13 пе-
редвигается вправо и насос переходит на меньшую производи-
тельность.
Рассмотренные в качестве примера две схемы (см. рис. 5.37 и
5.39) систем регулирования гидромеханического типа не исчерпы-
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 157
Л регулятору
При ем и гтости
12 От подначивающего
---> насоса
158
Глава V. Системы регулирования авиационных ВРД
вают Bicex возможностей прямого регулирования числа оборотов.
Находят применение также и электрические или электрогидрав-
лические регуляторы числа оборотов.
Незамкнутое регулирование измеренного числа оборотов ТРД
В системах незамкнутого регулирования числа оборотов чув-
ствительные элементы регулятора измеряют давление и темпера-
туру полного торможения воздуха на входе в двигатель. В соот-
ветствии с изменением этих параметров подача топлива
корректируется таким образом, чтобы число оборотов ротора не
отклонялось от заданного значения.
Для упрощения системы регулирования часто ограничиваются
измерением одного только давления полного торможения, что при-
водит к некоторому изменению числа оборотов при постоянном по-
ложении дроссельного крана. Поэтому во избежание недопустимой
раскрутки ротора двигателя регулятор расхода топлива дополняют
регулятором максимального числа оборотов.
Корректировка подачи топлива может производиться двумя спо-
собами. В одном из них чувствительный элемент через сервомотор
воздействует на положение дроссельного крана, сохраняя на нем
постоянный перепад давления. В другом — положение дроссельно-
го крана остается неизменным, но перед ним меняется давление
топлива.
На рис. 5.40 приведена конструктивная схема статического ре-
гулятора расхода ТРД, дополненного регулятором максимального
числа оборотов. Рассмотрим работу системы регулирования на
всех числах оборотов двигателя, кроме максимальных. К плунжер-
ному насосу 1 топливо поступает от подкачивающего насоса. Во
всем диапазоне чисел оборотов регулирующим органом является
поршень 2 сервомотора, шток которого связан с наклонной шайбой
насоса. От насоса по каналу высокого давления 14 топливо посту-
пает к дроссельному крану 4 и далее к форсункам, от этого же
канала питается топливом и сервомотор. В одном узле с дроссель-
ным краном находится игла 5, дозирующая подачу топлива к фор-
сункам на режиме малого газа, когда кран 4 находится на упоре
малого газа. В этот же узел включен клапан минимального давле-
ния топлива перед форсунками 6, схема действия которого была
рассмотрена ранее (см. рис. 5.24).
В полости цилиндра сервомотора левее поршня 2 (см. рис. 5.40)
давление топлива всегда такое же, как и в канале высокого дав-
ления 14. Полость цилиндра сервомотора правее поршня 2 соеди-
нена с каналом 14 калиброванным отверстием 15. Если слива топ-
лива из этой полости нет (когда канал 12 перекрыт), то давление
топлива по обе стороны поршня сервомотора одинаково. В этом
случае силой пружины 13 и давлением топлива в полости цилиндра
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 159
К APT форсунок
160
Глава V. Системы регулирования авиационных ВРД
сервомотора правее поршня, действующим на площадь, равную
сечению штока поршня, поршень 2 удерживается в крайнем левом
положении. Наклонная шайба расположена под наибольшим углом
и насос дает при каждом данном числе оборотов наибольшую пода-
чу. При сообщении полости правее сервомотора со сливом давле-
ние топлива в ней упадет и поршень 2 под действием давления в
полости слева от него переместится вправо, поворачивая наклон-
ную шайбу в направлении уменьшения подачи топлива. Меняя пло-
щадь проходного сечения на выходе из канала 12, можно устанав-
ливать поршень 2 в любые положения: от положения максималь-
ной подачи топлива до положения, при котором производитель-
ность топливного насоса равна нулю.
Регулирование слива из канала 12 производится с помощью
баростатического корректора (или короче, баростата). Чувстви-
тельным элементом баростата, реагирующим на изменение высоты
и скорости полета, служит анероидная коробка 9, к которой подво-
дится давление полного торможения воздуха на входе в двигатель.
С изменением давления изменяются сила анероида 9, передавае-
мая на рычаг 10, и положение управляющего клапана И. Зазор
между сливным жиклером 7 и управляющим клапаном 11 опреде-
ляет площадь проходного сечения на выходе из канала 12. С пере-
ходом от одного режима работы двигателя к другому он меняется
незначительно. Для различных давлений р*н (изменение высоты
или скорости полета) сила, с которой анероид действует на ры-
чаг 10, меняется. Это заставляет рычаг повернуться и изменить за-
зор между жиклером и управляющим клапаном. Увеличение или
уменьшение зазора влечет за собой изменение давления в полости
правее поршня сервомотора, перемещение поршня и переход насо-
са на другую производительность. Вследствие этого меняется дав-
ление перед дроссельным краном 4 и изменяется сила на штоке 8,
действующая на рычаг 10. В результате управляющий клапан зай-
мет примерно такое положение, которое он занимал до изменения
внешнего давления р*н. Его новое положение будет отличаться от
старого только за счет того, что сервомотор является статическим.
Изменение положения дроссельного крана 4 отражается на ве-
личине давления топлива перед ним и на величине силы штока 8,
действующей на рычаг 10. Последнее обстоятельство вызовет пе-
ремещение рычага и изменение положения управляющего клапана.
Вследствие этого изменяется давление в полости! правее поршня
сервомотора и насос перейдет на другую производительность. Дав-
ление топлива перед дроссельным краном примет свое прежнее зна-
чение, старое положение займет управляющий клапан (некоторое
отличие будет только за счет статической ошибки, вносимой серво-
мотором).
Шток 8 является элементом обратной связи баростата. На
участке подвода к нему давления от напорной магистрали включе-
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 161
oilcan st
Мц-const
Ht Нг Н
Рис. 5.41
но сопротивление 3, выполненное в виде пакета из шайб с неболь-
шими отверстиями. Это сопротивление демпфирует колебания дав-
лений в соединительном топливном канале, которые могут расстро-
ить работу системы регулирования давления топлива баростатом.
Различают потребную и располагаемую характеристики баро-
стата ртоп = f (р*н ), где ртоп—давление топлива за насосом.. По-
требная характеристика баростата для заданного числа оборотов
и скорости полета определяется величиной необходимого расхода
топлива, характеристиками форсунок и дроссельного крана. По-
требная характеристика в общем случае не-
линейна.
Располагаемая характеристика бароста-
та имеет линейный характер. Ее вид зави-
сит от эффективных площадей анероида 9 и
штока 8, от соотношения плеч рычага 10, на
который действуют силы анероида, сила
давления топлива на шток и сила пружины.
Несовпадение потребной и располагаемой
характеристик рТОп = f{P//) приводит к из-
менению числа оборотов двигателя по высоте полета. Примерная
зависимость п = f (Н) показана на рис. 5.41. Из рисунка следует,
что только для двух высот Нх и Н2 число оборотов двигателя будет
равно заданному. В диапазоне высот от Hi до Н2 при неизменном
положении дроссельного крана число оборотов двигателя будет
превышать заданное.
Потребную характеристику Pron~f(p*H) можно несколько
спрямить и приблизить к линейной располагаемой характеристике.
Для этого используют соответствующее профилирование распреде-
лительного клапана (при двухканальных форсунках), вводят спе-
циальные программные редукционные клапаны (при одноканаль-
ных форсунках) и температурные корректоры. Все это усложняет
систему питания и не дает достаточной гарантии совпадения по-
требной и располагаемой характеристик баростата. Поэтому при
использовании незамкнутых систем регулирования числа оборотов
приходится мириться с некоторым их изменением. Регулятором-
ограничителем максимальной скорости вращения ротора предотв-
ращается повышение числа оборотов свыше максимально допусти-
мого значения.
Максимальное число оборотов регулируется (ограничивается)
статическим регулятором с гидроцентробежным чувствительным
элементом и управляющим клапаном. На скоростях вращения ни-
же скоростей начала включения ограничителя в работу полушарй-
ковый клапан 17 (см. рис. 5.40) закрывает жиклер 16, что обеспе-
чивается натяжением пружин 18 и 19 и зазором 20 между рычагом
клапана и упором эластичной мембраны 21. Мембрана 21 — чувст-
6 Черкасов Б. А.
162
Глава V. Системы регулирования авиационных ВРД
вительный элемент. Снизу на нее действует давление топлива на
входе в насос, сверху — давление, создаваемое в полости качающе-
го узла действием центробежных сил при прохождении топлива
через наклонные отверстия 22 в роторе насоса. Следовательно, си-
ла давления топлива на мембрану зависит от квадрата угловой
скорости вращения ротора. При достижении максимального’ числа
оборотов мембрана прогибается, преодолевая силы пружин 18 и 19,
поворачивает рычаг с управляющим клапаном и открывает жик-
лер 16. Топливо через жиклер сливается из полости правее поршня
сервомотора, давление в пей па-
дает и поршень 2 переводит насос
на меньшую подачу.
В некотором диапазоне изме-
нения числа оборотов на подачу
насоса одновременно воздейству-
ют баростат и ограничитель ^шах*
Совместная работа регуляторов
в случае открытия дроссельного
крана характеризуется изменени-
ем скорости вращения, давлением
топлива за насосом и дроссель-
ным крапом в зависимости от его
положения так, как это показано
на рис. 5.42. При изменении по-
ложения дроссельного крана от
угла ам.г до- щ баростат поддер-
живает постоянное давление топлива за насосом ртоп, давление
топлива перед форсунками рф растет, насос переходит на большую
подачу, число оборотов двигателя возрастает, приближаясь к мак-
симальным. Иначе говоря, диапазон 6cti есть зона работы баро-
стата.
Если бы не было регулятора-ограничителя, то ю дальнейшим
увеличением угла поворота дроссельного крана число оборотов ро-
тора, достигнув максимального значения (угол аг и соответствую-
щая ему точка 2), продолжали бы увеличиваться (пунктирная кри-
вая). Регулятор-ограничитель вступает в действие при установке
дроссельного крана на угол <ц, когда число оборотов п еще меньше
Птах (точка 1). При дальнейшем открытии дроссельного крана (в
диапазоне углов щ -j- аз) на подачу насоса воздействуют баростат
и регулятор-ограничитель. Баростат стремится поддерживать дав-
ление за насосом, его управляющий клапан уменьшает слив топли-
ва через жиклер 7 (см. рис. 5.40). Регулятор-ограничитель увели-
чивает слив топлива через жиклер 16 и его действие здесь противо-
положно действию баростата. Диапазон углов баг есть зона
совместной работы баростата и ограничителя nmax.
В результате взаимодействия обоих регуляторов при повороте
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 163
дроссельного крана на угол аз число оборотов ротора двигателя
не будет превышать максимально допустимого значения. В точке 3
жиклер баростата будет полностью закрыт. При дальнейшем от-
крытии дроссельного крана (от угла аз до атах) регулятор-ограни-
читель поддерживает максимальное число оборотов ротора, уве-
личивая слив топлива через жиклер 16 и снижая давление за на-
сосом. Диапазон углов баз есть зона работы ограничителя Птах-
Регулятор-ограничитель максимального числа оборотов, выпол-
ненный так, как это показано на рис. 5.40, является статическим
регулятором. С увеличением высоты полета уменьшаются давление
топлива на управляющий клапан и сила, способствующая поворо-
ту рычага. Уменьшение этой силы может быть компенсировано
только увеличением силы давления на мембрану, что требует роста
давления топлива за счет действия центробежных сил ротора и»
следовательно, увеличения числа оборотов. В результате этого с
увеличением высоты полета максимальное число оборотов двига-
теля возрастает, а с ростом скорости полета — падает.
Статическая ошибка регулятора-ограничителя бп как функция
изменения давления топлива на управляющий клапан бркл может
быть определена из следующих соображений. В начальный момент
открытия жиклера 16 рычаг регулятора находится в состоянии
равновесия под действием моментов сил пружин 18 и 19, перепада
давлений топлива на мембрану 21 и давления топлива на управ-
ляющий клапан 17. Момент от сил пружин 18 и 19 стремится
удержать клапан в закрытом положении, его величина не зависит
от режима работы двигателя.
Записав уравнения моментов для двух высот полета (напри-
мер для Н = 0 и для Яшах) и вычтя из одного уравнения другое,
получим
+ fxh8pKjI = 0. (5.4)
В этом выражении FM — эффективная площадь мембраны 21; —
площадь жиклера 16г, 8рч и 6ркл— приращение давления топлива
соответственно на мембрану и на управляющий клапан; Ц и /2 —
плечи рычага регулятора, на которые действуют силы давления топ-
лива на мембрану и управляющий клапан. Приняв квадратичную
зависимость между давлением топлива па мембрану и числом
оборотов (Рц = сп2, где с — коэффициент пропорциональности),
получим, что 6рц = 2сп06п. С учетом последнего выражения урав-
нение (5.4) примет вид
б/г=-^2 8pKt.
2cnaFMh Икл
Если для заданного максимального числа оборотов двигателя у
земли По известно изменение расхода топлива при изменении вы-
соты полета, то по характеристике форсунок можно найти соответ-
6*
(5-5)
164
Глава V. Системы регулирования авиационных ВРД
ствующую величину изменения давления топлива перед форсунка-
ми Ърф. При работе на максимальном режиме, когда дроссельный
кран полностью открыт и оказывает малое сопротивление истече-
нию топлива, можно принять величину равной изменению дав-
ления топлива на выходе из насоса
Spron. При ориентировочных расче-
тах можно считать, что на ту же ве-
личину меняется давление топлива
на управляющий клапан Ьркл.
Формула (5.5) дает возможность
только приближенно определить
статическую ошибку регулятора
^тах. Приближенность будет заклю-
чаться в том, что формула (5.5) не
учитывает взаимодействия регуля-
тора Птах и регулятора давления. Для уменьшения статической
ошибки в регуляторах-ограничителях данного типа вводят специ-
альный компенсатор, которым уравновешивается сила от давления
Рис, 5.44
топлива, действующая на направляющий клапан. При таком ком-
пенсаторе регулятор nmax (схема на рис. 5.43) практически по сво-
им характеристикам является астатическим.
Рассмотрим еще одну схему косвенного регулирования числа
оборотов, в которой используется шестеренный топливный насос и
центробежный маятниковый регулятор-ограничитель Птах
(рис. 5.44).
На всех режимах п < птах, определяемых положением дрос-
сельного крана 6, подачу топлива дозирует управляющий клапан 9,
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 165
связанный с мембраной 8. Камера над мембраной 8 сообщается
через отверстие 10 с линией высокого давления и через отверстие
под клапаном И баростата со всасывающей линией насоса. На
этих режимах клапан 2 закрывает сливное отверстие и давление
топлива в камере над мембраной 4 равно давлению за дроссель-
ным краном. Клапан 5 не препятствует доступу топлива к фор-
сункам.
Во время работы на максимальном режиме при увеличении чис-
ла оборотов ротора грузики 1 поднимают клапан 2, что приводит к
падению давления в камере над мембраной 4, связанной с напор-
ной магистралью через отверстие 3. С падением давления над мем-
браной перемещается клапан 5, дросселирующий топливо, подво-
димое к форсункам. Это приводит к увеличению давления на
выходе из насоса и в свою очередь через плунжер 7 вызывает ре-
акцию баростата. В результате давление над мембраной 8 умень-
шается и управляющий клапан 9 увеличивает перепуск топлива в
магистраль перед насосом.
Регулирование приведенного числа оборотов ТРД
В гл. I при анализе возможных программ регулирования основ-
ного контура ТРД было показано, что современные ТРД, предна-
значенные для работы в большом диапазоне высот и скоростей по-
лета, регулируются по смешанной программе. Смешанная програм-
ма предусматривает наряду с регулированием по закону п = const
в некотором диапазоне изменения температуры Т\ регулирование
по закону п/ Т* = const.
Регулирование по постоянству приведенного числа оборотов
может осуществляться как путем поддержания п/у^Т\ = const, так
и путем сохранения неизменной величины л* . В первом случае
необходимо непосредственное и раздельное измерение п и Т\ . Во
втором случае для поддержания /г/]/~Т* = const, как это следует
из характеристик (см. рис. 1.14), достаточно измерять и поддержи-
вать неизменным л', что значительно проще.
Ограничение степени повышения давления воздуха
в компрессоре
Регулирование приведенного числа оборотов с раздельным из-
мерением оД не обладает достаточной точностью. Температура
термопатрона, измеряющего величину Т* ( зависит не только от
температуры воздуха. На нее влияет тепловой поток, идущий от
двигателя, и теплообмен между воздухом и стенками капала, по
которому воздух подводится к термопатрону. В зависимости
166
Глава V. Системы регулирования авиационных ВРД
от степени влияния этих факторов температура воздуха, омываю-
щего термопатрон, может быть выше или ниже Т\ . Термопатрон
обладает большой инерцией. При быстром снижении Т[ за счет
динамического запаздывания в перенастройке регулятора числа
оборотов текущее значение приведенного числа оборотов может
значительно превысить допустимую величину и привести к неустой-
чивой работе компрессора. Поэтому большое значение приобретает
регулирование приведенного числа оборотов по л,. При не-
изменных геометрических размерах проточной части двигателя при
надкритических перепадах в выходном сопле величина ппр одно-
значно определяется значением лк*. Для ограничения ппр^ (ппр)р
достаточно ввести ограничительное регулирование (л* )Р
(см. рис. 1.11).
Измерение я’ может быть осуществлено практически безынер-
ционно и с небольшой статической ошибкой. Регулятор должен
иметь чувствительный элемент, реагирующий на изменение л* в
сторону увеличения от заданного предельного значения (л* )пРеэ-
Он может воздействовать или на настройку регулятора числа обо-
ротов, или на управляющий клапан сервомотора.
Чувствительные элементы применяются двух- или трехкамерно-
го типа (с одной или двумя мембранами) с пневматическим ре-
дуктором. В случае использования двухкамерного чувствительного,
элемента удобнее измерять и ограничивать не величину л, всего»
компрессора, а степень повышения давления нескольких последних
ступеней л^ = р*2 /р^, где р*{ —давление за i-ступенью. При зна-
чении ппр max ограничение величины л) равноценно ограниче-
нию л* .
Принципиальная схема двухкамерного чувствительного элемен-
та с пневматическим редуктором приведена на рис. 5.45. Воздух с
давлением /?’ подводится к редуктору, имеющему два жиклера с
площадями fi и fz, в полость правее мембраны 1 подводится дав-
ление р*Г Для настройки редуктора на требуемую величину
(л - )Преэ служит регулировочный винт 2, стравливадощий воздух
после жиклера f2- Для увеличения (л, )пРеэ регулировочный винт 2
следует вывертывать, стравливая воздух и уменьшая давление рх.
Под площадью жиклера fi можно понимать общее проходное се-
чение собственно жиклера ft и канала под регулировочным .винтом.
Чувствительный элемент воздействует на регулятор числа обо-
ротов только в том случае, если рх>р*.. При рх <^Р( мембрана
доходит до упора. Соотношение площадей жиклеров выбирается
таким, чтобы на всех режимах работы чувствительного элемента в.
выходном или в обоих жиклерах обеспечивался надкритический
§ 3. Схемы систем регулирования авиационных' газотурбинных двигателей 167
перепад давления. В последнем случае имеет место простое соот-
ношение
РУг = РхЬ- (5-6)
В момент вступления в работу ограничителя давление рх незна-
чительно отличается от р* . Если вместо -давления pt к ограничи-
телю подвести давление р[ , то для достижения надкритического
Рис. 5.45
перепада на жиклере fi давление за ним пришлось бы путем отсоса
понизить ниже атмосферного. Отсюда видна выгода ограничитель-
ного регулирования компрессора по л*. При использовании трех-
камерного чувствительного элемента можно вести ограничительное
регулирование по л* без отсоса.
Вернемся к схеме чувствительного элемента, показанной на
рис. 5.45, и запишем условие равенства сил на мембране 1
(px-p^F=,B8z+C. (5.7)
В этом выражении F-—эффективная площадь мембраны; В —
жесткость пружины 3; бг— величина перемещения мембраны от
упора; С —суммарная сила от управляющего элемента сервомото-
ра и предварительной затяжки пружины.
Из выражений (5.6) и (5.7) найдем величину перемещения мем-
браны
с_. (5.8)
\ fi ‘ j в в v ’
Графически эта зависимость в координатах бг, л? представляет
собой семейство прямых, проходящих через точку а, с координата-
168
Глава V. Системы регулирования авиационных ВРД
ми л*а — fi/f2 и i>za = —С/В (рис. 5.46). Предположим, что ограни-
читель вступает в действие в момент схода мембраны с упора, т. е.
при 6z = 0. Тогда начальные значения nJ , которые будет поддер-
живать ограничитель, равны
(5.9)
Графически на рис. 5.46 они определяются как точки пересече-
ния семейства прямых с осью абсцисс при различных р". и харак-
теризуют статическую ошибку ограничителя. Для снижения ста-
тической ошибки следует уменьшать суммарное усилие С. При
С л; 0 давление левее мембраны, при котором ограничитель вступа-
ет в действие, рхо — р]- Откуда
Регулирование форсажного режима ТРДФ
В ТРДФ форсаж включается при работе двигателя на макси-
мальном числе оборотов. Постоянство числа оборотов поддержива-
ется регулятором, воздействующим на подачу топлива в основную
камеру сгорания. Регулированием подачи топлива в форсажную
камеру режим работы турбины и компрессора сохраняется таким
же, как и та нефорсажном режиме.
Режим работы форсажной камеры ТРДФ определяется двумя
параметрами Т*ф и nJ . Для ТРДФ с двухпозиционными створка-
ми выходного сопла лишь один из них может быть принят за регу-
лируемый параметр. В случае использования методов косвенного
регулирования, когда подача топлива в форсажную камеру осу-
ществляется в соответствии с параметрами окружающей среды, не-
посредственных измерений регулируемого параметра не произво-
дится. В случае прямого регулирования за регулируемый параметр»
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 169
целесообразно выбрать л* как величину легко измеряемую. Из пе-
речисленных в гл. I возможных программ регулирования форсаж-
ного контура остановимся на двух программах Оф!р\ = const и
л* = const. Первая из них является программой косвенного регу-
лирования форсажного режима, вторая — программой прямого ре-
гулирования.
Для сохранения неизменным режима работы турбокомпрессора
подача форсажного топлива G,fi должна соответствовать давлению
Рис. 5.47
р\ и температуре . Между р\ и G# существует прямая зави-
симость, влияние Т*н более сложно. Для упрощения системы регу-
лирования при косвенном регулировании применяют регуляторы,
дозирующие подачу топлива в форсажную камеру сгорания в за-
висимости только от величины р\ . Влияние температуры Т"н учи-
тывается путем выбора наиболее вероятной скорости полета при
работе двигателя на форсажном режиме. При отклонении действи»
тельной скорости полета от расчетной или при несоответствии пара-
метров окружающей среды их стандартным значениям величина л’2
на форсажном и нефорсажном режимах будет различной. Это раз-
личие приведет к изменению температуры Т* , поскольку регулятор
основного контура будет поддерживать постоянное число оборотов
ротора двигателя.
Рассмотрим некоторые принципиальные схемы систем косвен-
ного и прямого регулирования форсажного режима ТРДФ.
На рис. 5.47 дана схема регулирования подачи топлива по р\
Этот регулятор является программным регулятором, он автомати-
чески перенастраивается при изменении р '{ . Регулятор в принципе
работает так же, как и регулятор, схема которого показана на
рис. 5.40. Отличие заключается только в обратной связи. Здесь она
170
Глава К Системы регулирования авиационных ВРД
механическая. На рис. 5.47 показано: 1 — топливный форсажный
насос; 2— кулачок обратной связи; 3— амероид, реагирующий на
изменение р\ . Поскольку топливный насос от ротора двигателя не
отключается, на нефорсажных режимах ТРДФ необходимо обеспе-
чить некоторую прокачку топлива для охлаждения насоса. Это
достигается с помощью дополнительного крана 4, сблокированного
с отсечным краном 6. При установке кранов 4 и 6 в положение,
Рис. 5.48
показанное в правой части рис. 5.47 (нефорсажный режим), по-
лость правее поршня сервомотора сообщается со сливом через
жиклер 5, что обеспечивает некоторую небольшую производитель-
ность насоса. Напорная магистраль через капал 7 соединяется с
линией всасывания основного топливного насоса. В систему пита-
ния включен дроссельный клапан (па схеме не показан). Он слу-
жит для повышения давления па выходе из насоса 1 до значений,
необходимых для обеспечения работы сервомотора при полете па
больших высотах.
На рис. 5.48 приведена схема прямого регулирования подачи
топлива в форсажную камеру. Чувствительным элементом в регу-
ляторе этой схемы служит мембрана 1. В камеру под мембраной
подводится давление за турбиной р*4 . Для разгрузки мембраны ка-
мера над ней сделана проточной: через жиклер 2 она соединена с
давлением за компрессором р*2, а через жиклер <3 — с давлением
окружающей среды рц. Подбором жиклеров 2 и 3 давление в про-
точной камере рх может быть получено близким к р* .
J 3. Схемы систем регулирования авиационных газотурбинных двигателей 171
При надкритическом перепаде в выходном сопле величина л’
ие зависит от режима полета. Эту величину будет поддерживать
регулятор. При изменении давления р\ мембрана 1 прогибается и
через рычаг 4 перемещает управляющий клапан 5. Перемещение
управляющего клапана вызывает изменение давления в пружинной
полости сервомотора 6, связанного с дозирующей иглой 7. Подача
топлива в форсажную камеру определяется положением дозирую-
щей иглы, клапан 10 поддерживает на ней постоянный перепад
давления. Выключение подачи форсажного топлива производится
поворотом сблокированных кранов 8 и 11. При этом все топливо,
подаваемое насосом 9, перепускается в бак или на линию всасыва-
ния насоса основного контура, кран 11 сообщает пружинную по-
лость сервомотора также с линией всасывания.
Регулятор данного типа позволяет осуществлять частичный фор-
саж. Для этого нужно створки выходного сопла поставить в поло-
жение, соответствующее меньшему сечению, по сравнению с сече-
нием выходного сопла полного форсажа.
В гл. I при анализе возможных программ регулирования фор-
сажных режимов ТРДФ была приведена характеристика р', =
= /(as ) для различных р\ (см. рис. 1.12), из которой следовало,
что регулятор л* = const может работать только на правой ветви
такой характеристики. Для предотвращения возможного перехода
рабочей точки на левую ветвь этой характеристики регулятор
л* = const нужно дополнять ограничительным регулятором
G$lp*2. — const. Одна из возможных схем ограничительного регуля-
тора включена в схему системы регулирования форсажного конту-
ра на рис. 5.48. Ограничительный регулятор состоит из рычага 14
с управляющим клапаном 12. К рычагу 14 с одной стороны прило-
жена сила от анероида 15, на внешнюю поверхность которого дей-
ствует давление р2 , а с другой стороны — сила плунжера 13, свя-
занного через напорную магистраль с давлением р$. Следует от-
метить, что такой ограничительный регулятор не может точно под-
держивать йф/р * = const, так как расход топлива G$ нелинейно
связан с давлением р$.
Регулирование температуры газов ТРД
Для регулирования температуры газов используются системы
замкнутого или незамкнутого регулирования. При замкнутом регу-
лировании чувствительным элементом регулятора служит измери-
тель температуры газа. При незамкнутом регулировании темпера-
туры измеряются параметры рабочего процесса или окружающей
среды, от которых температура газа двигателя зависит лишь кос-
венно. К таким параметрам относятся давление р\ , температура
Т и число оборотов ротора двигателя п.
172
Глава V. Системы регулирования авиационных ВРЦ
В качестве измерителей температуры могут применяться термо-
пары, термометры сопротивления, дилатометры и парортутные тер-
мометры. Наиболее пригодны термопары, позволяющие легко сум-
мировать сигнал от нескольких измерителей (датчиков).
Принцип замкнутого регулирования температуры с использова-
нием термопар в качестве чувствительных элементов рассмотрен в
гл. VII.
Следует иметь в виду, что замкнутое регулирование температу-
ры путем изменения площади выходного сопла и регулирование
числа оборотов изменением подачи топлива ухудшает динамические
характеристики системы автоматического регулирования из-за взаи-
модействия регуляторов через объект регулирования. Однако ус-
ложнение программ регулирования ТРД требует все чаще прибе-
гать к замкнутому регулированию температуры.
Рассмотрим схему регулятора, помещенную на рис. 5.49. Он
предназначен для незамкнутого регулирования температуры газа.
Регулятор в зависимости от величины давления рн и р, воздейст-
вует на площадь выходного сопла, изменяя положение централь-
ного тела. Рабочая жидкость регулятора — масло, для создания
больших перестановочных усилий в нем последовательно включены
два сервомотора с жесткой обратной связью: один поршневой,
другой — шестеренный. Разность давления р\ —рн действует на
сильфонную коробку 1 и перемещает золотник 2, открывая доступ
маслу к поршневому сервомотору 8 (с ним за одно целое выполне-
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 173
на гильза 7). Обратная связь осуществляется рычагом 11. Серво-
мотор 8 перемещает гильзу 7 золотника 6 с большими проходными
сечениями и обеспечивает доступ маслу к шестеренному сервомото-
ру 5. Сервомотор через систему зубчатых передач перемещает
центральное тело 3 выходного сопла. Для обеспечения обратной
связи от сервомотора 5 к золотнику 6 на золотнике сделан резьбо-
вой хвостовик 4, а на одной из шестерен сервомотора — резьбовое
отверстие. Хвостовик ввернут в это отверстие. Так как золотник 6
вращаться не может, то во время действия сервомотора 5 он пере-
мещается в осевом направлении.
При запуске двигателя и на режимах от пм.г до крейсерских
режимов центральное тело 3 вдвинуто внутрь сопла, что обеспечи-
вает наибольший перепад давлений на турбине. С наступлением
крейсерских режимов центральное тело занимает свое рабочее по-
ложение. Это достигается с помощью рычага 10, связанного с ры-
чагом настройки регулятора числ.а оборотов, и профилированного
кулачка 9, меняющего положение опоры рычага обратной связи 11.
Системы регулирования ТВД
В настоящее время наибольшее распространение получили ТВД
с общей турбиной для привода компрессора и винта (одновальные
ТВД). Поэтому остановимся на особенностях регулирования ТВД
этой схемы.
Для одновального ТВД регулирующими факторами являются
изменение подачи топлива G и угла установки лопастей воздушно-
го винта ср. Им соответствуют два регулируемых параметра: число
оборотов ротора двигателя п (или число оборотов винта) и темпе-
ратура газа перед турбиной Т*3. Опыт показывает, что в системах
регулирования целесообразно на число оборотов ротора п воздей-
ствовать изменением угла установки лопастей винта ф, а на тем-
пературу газа перед турбиной — изменением подачи топлива.
Возможные программы регулирования ТВД были рассмотрены
в гл. I. В соответствии с этими программами системы регулирова-
ния турбовинтовых двигателей, предназначенных для больших вы-
сот полета, на максимальных режимах и на высотах полета боль-
ше расчетной (Я Нр) регулируются по программе п = const,
Т*3 - const. На высотах полета Н < Нр изменением температуры Т
обеспечивается Ne = const и п = const.
Переход на крейсерские режимы достигается одновременным
снижением расхода топлива и переходом к меньшим установочным
углам лопастей винта ф. В некотором диапазоне изменения мощно-
сти число оборотов ротора двигателя может сохраняться неизмен-
ным. Для перехода на глубокие крейсерские режимы (вплоть до
мощности малого газа) вместе с уменьшением подачи топлива не-
174
Глава V. Системы регулирования авиационных ВРД
обходимо снижать число оборотов ротора. При этом температура
газа перед турбиной сначала падает, а затем при приближении к
мощности малого газа несколько возрастает.
Два параметра регулирования требуют включения в систему
регулирования двух регуляторов. Один из них — регулятор числа
оборотов. Второй — обычно регулятор расхода, автоматически пе-
ренастраивающийся по рд(или р\), рн и , с помощью которого
производится косвенное регулирование Т$. При переходе от мак-
симального к крейсерским режимам двигателя необходимо строго
согласовывать перенастройки регулятора числа оборотов и регуля-
тора расхода топлива. Для этого в системе регулирования двига-
теля предусмотрен так называемый агрегат объединенного управ-
ления, координирующий перенастройку обоих регуляторов от еди-
ного сектора управления. Необходимость агрегата объединенного
управления усложняет систему регулирования. Она упрощается,
когда переход на крейсерские режимы осуществляется перена-
стройкой только регулятора расхода при сохранении п = const.
В этом случае перенастройка обоих регуляторов необходима лишь
в узком диапазоне числа оборотов при переходе на глубокие крей-
серские режимы.
Регулирование расхода топлива по рн, р*н и Т*н (использование
внешних параметров) приводит к погрешности в подаче топлива
до ±50 кг/час. Для двигателей мощностью Ne = 50004-6000 л. с.
у земли при полете на высоте 8-4-10 км эта погрешность составит
ошибку по расходу топлива ±10% и может дать нежелательное
повышение температуры газа.
Для большей точности следует регулятор расхода перенастраи-
вать по параметрам рабочего процесса двигателя р*2, Т*2. Непо-
средственное регулирование температуры с помощью быстродейст-
вующих регуляторов дает возможность точно поддерживать темпе-
ратуру газа перед турбиной на основных режимах и избежать за-
броса температуры на переходных режимах. По сравнению с не-
замкнутым регулированием так же прогрессивным является вве-
дение ограничительного регулирования температуры газа перед или
за турбиной.
В системе регулирования высотных ТВД должно быть преду-
смотрено ограничение мощности двигателя на высотах ниже рас-
четной. Ограничение может производиться путем замкнутого или
незамкнутого регулирования. При замкнутом регулировании на
числе оборотов ротора п = nmax измеряется крутящий момент на
валу винта и при достижении предельно допустимого значения
Мкр вступает в действие ограничитель, уменьшающий подачу топ
лива. Незамкнутое регулирование по ограничению мощности про-
изводится по величине скоростного напора, для чего измеряется
разность давлений р*н— рн.
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 175
Рассмотрим принципиальную схему регулятора расхода топлива
высотного ТВД, помещенную на рис. 5.50, в которой используются
косвенные параметры рн, р^м. Т^для перенастройки регулятора и
ограничения мощности. Топливо к регулятору подается шестерен-
ным насосом 1, клапан 2, перепускающий избыток топлива на ли-
нию всасывания, поддерживает на дроссельном кране 4 постоян-
ный перепад давления. Расход топлива зависит от проходного се-
чения дроссельного крана 4. Как это видно из продольного и попе-
речного разрезов, сечение меняется и при угловом, и при осевом
Рис. 5.50
перемещении крана 4 во втулке 3 и равно площади прямоуголь-
ника ab.
Угловое перемещение крана осуществляется рычагом управле-
ния 5, сидящем вместе с кулачком 6 на шлицевой части валика
крана. Кулачок 6 служит для перенастройки регулятора числа обо-
ротов винта. Принцип действия этого регулятора рассмотрен при
описании схемы, помешенной на рис. 5.52.
Перемещение дроссельного крана 4 (см. рис. 5.50) в осевом на-
правлении производится в зависимости от режима полета для под-
держания неизменной температуры газа перед турбиной или для
ограничения мощности на высотах ниже расчетной. Для получения
на валике крана достаточных перестановочных усилий служит сер-
вомотор 7. В полость 13 сервомотора через жиклер под давлением
подводится масло, которое сливается через отверстие в штоке сер-
вомЬтора. Проходное сечение отверстия, а следовательно, и давле-
ние в полости 13 регулируется золотником 8.
176
Глава V. Системы регулирования авиационных ВРД
Коррекция подачи топлива по р*И и Т*н осуществляется рычагом
18. Положение рычага 18 зависит от величины давления р*н, под-
веденного в полость 19, где расположен анероид, и от положения
штока 16, определяемого температурой Т*н. С ростом давления р*н
стержень анероида укорачивается и рычаг 18 поворачивается про-
тив часовой стрелки, золотник 8 перемещается влево, увеличивая
сечение отверстия, через которое сливается масло из полости 13.
В результате падения давления в этой полости поршень сервомо-
тора 7 переместится влево, а проходное сечение дроссельного крапа
возрастет за счет размера Ь.
С ростом температуры Т*н увеличение давления паров жидкости,
заполняющей термопатрон 17, сместит стержень 15 влево, что при-
ведет к повороту кулачка 14 по часовой стрелке. Шток 16 сме-
стится вверх, вместе с ним сместится и опора рычага 18. Золотник
8 переместится вправо, проходное сечение дроссельного крана
уменьшится.
Ограничение мощности на высотах ниже расчетной достигается
перемещением рычага 12. В полости 9, куда подводится давление
Рн, размещены сильфон 10 и анероид И, воздействующие на общий
шток. В сильфон 10 подводится давление р^. Ограничитель мощ-
ности работает так, что с ростом рн и падением скоростного напора
рычаг 12 поворачивается влево и расход топлива увеличивается, а
с ростом скоростного напора и падением рн рычаг 12 поворачи-
вается вправо и расход топлива уменьшается. Во время действия
ограничителя в направлении уменьшения мощности между рыча-
гом 18 и золотником 8 образуется зазор.
Регулирование скорости вращения винта в ТВД имеет ряд спе-
цифических особенностей. Регуляторы числа оборотов применяются
электромеханического и гидравлического типов. Наибольшее рас-
пространение получили гидравлические регуляторы, в которых ис-
пользуются поршневые или шестеренные сервомоторы для пере-
становки лопастей винта. Поскольку золотник чувствительного эле-
мента регулятора числа оборотов расположен на корпусе двига-
теля, а гидравлический сервомотор во вращающейся втулке, между
ними трудно установить жесткую обратную связь. Поэтому регу-
ляторы числа оборотов винта выполняются астатическими, что от-
рицательно отражается на их динамических характеристиках.
Акселерометры в этих регуляторах для дополнительного воздейст-
вия по производной от регулируемого параметра еще не нашли
применения из-за трудностей создания высокочувствительных и
малоинерционных конструкций.
В астатических регуляторах числа оборотов винта рост скоро-
сти полета усиливает влияние изменения угла установки лопасти
винта ср на изменение п. Поэтому с ростом скорости полета в си-
стеме регулирования могут возникнуть незатухающие колебания
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей177
числа оборотов винта. В целях борьбы с этим явлением можно бы-
ло бы уменьшить быстродействие регулятора. Однако идти на
уменьшение быстродействия нельзя, так как в этом случае медлен-
нее ликвидируются отклонения числа оборотов от заданного зна-
чения и ухудшается приемистость двигателя.
Сервомоторы регуляторов числа оборотов применяются двух-
стороннего действия, т. е. перевод лопасти винта с малого устано-
вочного угла ср на большой и с большого на малый происходит
путем подвода масла под давлением то по одну, то по другую сто-
рону поршня сервомотора. Переводу лопасти на меньшие ф способ-
ствуют аэродинамические силы, действующие на лопасть. Поэтому
для увеличения угла установки лопасти требуется большее давле-
ние масла, чем для уменьшения ф. С этой целью в системе регули-
рования предусматриваются специальные устройства, повышаю-
щие в нужный момент давление масла.
Каждому режиму полета должны соответствовать свои устано-
вочные углы лопасти. Так например, на режиме малого газа ври
скорости полета v = 0 угол фт1п~ 5°. В этом случае лопасть рабо-
тает при некотором положительном угле атаки и создает неболь-
шую положительную тягу. Если же зафиксировать этот минималь-
ный угол ф при v > 0, то лопасти будут работать с отрицательными
углами атаки и винт даст отрица-
тельную тягу. Чтобы винт гаран-
тированно давал положительную
тягу на любой скорости полета,
минимальный установочный угол
Ф нужно повысить примерно до
25°.
Для охвата всего диапазона
мощностей ТВД на различных
скоростях и высотах полета уста-
новочный угол ф должен менять-
ся в пределах примерно от 5 до
60°, т. е. рабочий диапазон изме-
нения угла установки составит
бфраб ~ 55°. Однако этими значе-
ниями не исчерпывается потреб- Рис. 5.51
ность в изменении угла установ-
ки. Для уменьшения длины пробега самолета при посадке лопасти
винта устанавливают под углом ф < 0 и получают отрицательную
тягу винта (реверс тяги). В случае необходимости выключения
двигателя в полете и прекращения вращения винта его лопасти
устанавливаются во флюгерное положение — по потоку под углом
Фсбл — 90°. Характерные положения лопастей винта показаны на
рис. 5.51. В этих положениях лопасти фиксируются с помощью упо-
ров во втулке винта. Обозначениям на рис. 5.51 соответствуют:
178
Глава V. Системы регулирования авиационных ВРД
ф — упор флюгирования; р — упор реверса; м— упор минимально-
го угла установки при работе двигателя на месте; п — односторон-
ний промежуточный упор, определяющий минимальный установоч-
ный угол в полете и не препятствующий лопасти проходить его при
увеличении угла ср (на посадочной скорости на этом упоре винт
дает небольшую положительную или отрицательную тягу и потреб-
ляет минимальную мощность).
Для безопасности полета необходимо исключить возможность
возникновения в полете отрицательной тяги воздушного винта. Зна-
чительная отрицательная тяга может привести к потере устойчи-
вости самолета. Отрицательная тяга может возникнуть в трех
основных случаях: 1) при повреждении двигателя или неисправно-
сти регулятора подачи топлива, 2) при падении давления в масло-
системе воздушного винта и 3) при резком уменьшении подачи
топлива при нормально действующих двигателе и системе регу-
лирования.
В первом случае снижение мощности и самопроизвольное вы-
ключение двигателя, вызванное его повреждением или неисправ-
ностью регулятора подачи топлива, приведет к падению числа обо-
ротов. Регулятор для восстановления числа оборотов уменьшит
угол установки лопастей винта, в результате чего винт начнет по-
треблять энергию от набегающего потока воздуха, т. е. перейдет
на режим авторотации. При этом винт начнет развивать отрица-
тельную тягу, значительно превышающую положительную тягу на
крейсерской скорости полета. Угол установки лопастей <р на режиме
авторотации зависит от величины момента сопротивления враще-
нию ротора неисправного двигателя. Чем сопротивление больше,
тем на меньший угол <р переведет лопасти регулятор числа оборо-
тов, тем больше отрицательная тяга.
Во втором случае при неисправности маслосистемы воздушного
винта и падения в ней давления лопасти винта под действием аэро-
динамических сил перейдут на меньший установочный угол. В ре-
зультате возникнет отрицательная тяга.
В третьем случае резкое снижение подачи топлива при исправ-
ном двигателе и нормально действующей системе регулирования
вызывает большое уменьшение угла установки лопастей. В полете
это может привести к отрицательным углам атаки потока, набе-
гающего на лопасти, и к возникновению отрицательной тяги.
Наиболее эффективным средством борьбы с отрицательной тя-
гой является флюгирование воздушного винта. Перевод лопастей
винта во флюгерное положение с одновременным выключением дви-
гателя обеспечивает безопасность полета самолета с ТВД и пре-
дохраняет детали двигателя от разрушения. Для предотвращения
авторотации скорость перестановки лопастей во флюгерное поло-
жение должна быть достаточно большой.
Для улучшения маневренности самолета на земле система регу-
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 179
лирования ТВД предусматривает преднамеренное создание отри-
цательной тяги. Для этого лопасти винта устанавливаются на от-
рицательные углы ср. Такое положение лопастей винта называется
реверсированием винта, а режим работы винта — реверсированием
тяги. На рис. 5.51 лопасть винта на режиме реверса находится на
упоре р.
Реверсирование тяги винта дает возможность сократить пробег
самолета после посадки и облегчает разворот многомоторных са-
Рис. 5.52
молетов при рулежке. Чтобы предотвратить раскрутку ротора, ско-
рость перестановки лопастей винта в положение реверса должна
быть достаточно большой.
Ознакомимся с одной из возможных принципиальных схем ре-
гулятора скорости вращения винта, помещенной на рис. 5.52. Эта
схема отвечает всем перечисленным выше требованиям, предъяв-
ляемым к данным системам, за исключением одного: она не дает
возможности реверсировать тягу.
Поршневой сервомотор регулятора выполнен двухсторонним.
При подводе масла в полости А или Б поршень 4 перемещается и
с помощью механизма 6 поворачивает лопасти винта 7.
При отклонении числа оборотов от заданного значения центро-
бежный чувствительный элемент 20 смещает из положения равно-
весия золотник 21 и открывает доступ маслу от насоса 12 через
обратный клапан 13 к сервомотору. При отклонении числа оборо-
180
Глава V. Системы регулирования авиационных ВРД
тов в сторону увеличения золотник 21 смещается вверх и масло
по каналу большого шага (БШ) поступает в полость А, лопасти
поворачиваются на больший угол ср и устанавливается заданное
число оборотов, полость Б в это время через канал малого шага
(МШ) соединена со сливом. В случае отклонения числа оборотов
в сторону уменьшения масло под давлением поступает в полость Б
по каналу МШ, полость А соединена со сливом.
Как уже говорилось выше, повороту лопастей на меньший
угол ср способствуют аэродинамические силы. Поэтому, чтобы пере-
становка лопастей в сторону увеличения углов ф и в сторону их
уменьшения происходила с одинаковой скоростью, в полость А сер-
вомотора масло подводится под большим давлением. Для этой цели
служат клапаны 14 и 17. Клапан 14 отрегулирован на 4-Ю6 h/jh2
и поддерживает это давление в канале БШ. Клапан 17 отрегулиро-
ван на 0,8-10® н!м2, это давление поддерживается в канале МШ.
Движение сервопоршня во втулке винта ограничивается тремя
упорами: упором 3 определяется минимальный установочный угол
фт1п при работе двигателя на земле на месте, упор 5 обеспечивает
флюгирование винта, упор 2 — промежуточный, он определяет про-
межуточный угол српром в полете. В полете упор 2 находится в
верхнем положении и ограничивает перемещение поршня 4 в сто-
рону уменьшения установочных углов ф. Механизм управления упо-
ром 2 состоит из клапана 19 и поршня 1, выключение упора 2 про-
исходит автоматически. Когда при посадке самолета появляется
нагрузка на шасси, автоматически замыкается цепь соленоида кла-
пана 15, который открывает доступ маслу под давлением 4-10® m/jh2
к опорному поршню 16 пружины клапана 17. В результате этого
давление масла в канале МШ увеличивается до 4-10® н!м2, кла-
пан 19 сдвигается влево и обеспечивает подвод масла под давле-
нием к поршню 1. Промежуточный упор 2 убирается, а поршень 4
сервомотора перемещается влево до упора 3 минимального шага
винта.
Для перевода винта во флюгерное положение служит насос 11.
Его электромотор включается при закрытии стоп-крана. Одновре-
менно с закрытием стоп-крана рычагом .9 золотник 21 поднимается
вверх и открывает доступ маслу в полость А. После того как пор-
шень 4 дойдет до упора 5 и давление масла в полости А повысится,
гидравлический выключатель 18 отключает флюгерный насос 11.
Для вывода винта из флюгерного положения открывается стоп-
кран и рычаг 9 дает возможность золотнику 21 под действием пру-
жины опуститься в нижнее положение. Одновременно с открытием
стоп-крана включается флюгерный насос 11 и открывается кла-
пан 15. Масло от флюгерного насоса под большим давлением по-
ступает по каналу МШ в полость сервомотора.
При аварийном падении мощности двигателя происходит авто-
матическое флюгирование винта. Сигналом к флюгированию слу-
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 181
жит появление на валу двигателя отрицательного крутящего мо-
мента. В этом случае предусмотренный в конструкции редуктора
манометр замыкает соленоид клапана 10, одновременно включается
электромотор флюгерного насоса 11, масло от нгГсоса поступает
под поршень 8, золотник 21 поднимается вверх и открывает доступ
маслу в полость А.
Системы регулирования входного диффузора
При регулировании входного диффузора может использоваться
как замкнутое, так и незамкнутое регулирование. В случае замкну-
того регулирования регулятор непосредственно измеряет какой-
либо параметр рабочего процесса и изменяет в нужном направле-
нии положение регулирующего органа. При незамкнутом регулиро-
вании регистрируются изменения внешних условий или режим
работы двигателя и в соответствии с ними по заранее выбранной
программе меняется положение регулирующих органов диффузора.
Системы косвенного регулирования по Gduip дают точность при-
мерно 6%, чему соответствует изменение тяги примерно 9%. Си-
стемы прямого регулирования обеспечивают большую точность.
Рис. 5.53
При регулировании по трем параметрам точность по оэидз полу-
чается до 1%. Аппаратура систем прямого регулирования полу-
чается проще, чем систем косвенного регулирования, но взаимо-
действие нескольких регуляторов сужает область устойчивой рабо-
ты входного диффузора. Большая точность прямого регулирования
объясняется тем, что принятая программа косвенного регулирова-
ния не может учесть всех факторов, влияющих на рабочий процесс
входного диффузора.
Остановимся на некоторых возможных схемах прямого регули-
рования. В них всегда для определения величины выбранного пара-
метра регулирования измеряется отношение статических или пол-
ных давлений в двух фиксированных сечениях диффузора.
На рис. 5.53 приведена схема измерения статических давлений
для определения положения головной волны во входном диффузоре
182
Глава V. Системы регулирования авиационных ВРЦ
Хп
X
Х3
Ха
хск
хо (хСк)опт
Рис. 5.54
внешнего сжатия. На схеме кружками отмечены места датчиков
давлений, положение переднего датчика совпадает с оптимальным
положением головной волны (координата х0).
Обозначим через х отношение статических давлений: % = р\1рхо-
Если головная волна займет положение левее первого датчика
(хск > Хо), то величина % будет близка к единице, так как в этом
случае pi несколько меньше рхо за
счет гидравлических* потерь. В случае
перемещения головной волны правее
первого датчика (хск < Хо). отношение
статических давлений возрастет, %> 1.
Примерное изменение % по координа-
те хск показано на рис. 5.54.
Сигнал рассогласования по % уси-
ливается и используется для переме-
щения регулирующего органа. Если
это подвижное центральное тело или
клин, то при х > 1 (Хек < хо) централь-
(увеличивается координата /к). При переме-
Хо) центральное тело вдвига-
ное тело выдвигается
щении головной волны вперед (хек
•ется. Таким образом, система регулирования по положению голов-
ной волны выполняется как система по стабилизации отношения
давлений pi/px0.
Оптимальное регулирование входного устройства с диффузором
смешанного сжатия, как уже об этом говорилось в гл. III, требует
регулирования по трем параметрам с использованием трех воздей-
ствующих факторов. Для фиксации на кромке обечайки первого
косого скачка с помощью передвижного клина можно использовать
измерение полных давлений двумя датчиками. Эти датчики распо-
ложены перед обечайкой и несколько смещены друг относительно
друга. На схеме измерений, показанной на рис. 5.55, датчики отме-
чены кружками.
Работа входного устройства без головной волны достигается
стабилизацией числа М потока в горле диффузора (Мг = const)
§ 3. Схемы систем регулирования авиационных газотурбинных двигателей 183
путем перемещения вставки. Для определения М3 требуется изме-
рение в горле полного и статического давлений. На положение
замыкающего скачка оказывается воздействие изменением площа-
ди перепуска. Положение скачка определяется по отношению стати-
ческих давлений в конце диффузора и в горле.
Остановимся еще на двух принципиальных схемах, каждая не-
которых рассчитана на регулирование одного параметра.
На рис. 5.56 дана принципиальная схема системы регулирова-
ния по положению замыкающего скачка путем сохранения неизмен-
ным отношения давлений ps/pi.. Воздействие на рабочий процесс
осуществляется перемещением центрального тела.
Перед входом в компрессор и в горле диффузора измеряются
статические давления рг и pi. В случае использования пневмати-
ческого измерителя отношений давление pi редуцируется до дав-
ления рх и сравнивается с давлением рг. Сигнал рассогласования
Нр = рг— рх с помощью мембраны преобразуется в перемещение
управляющего золотника сервомотора. На расчетном режиме
рго — рхо = 0. При бр > 0, когда замыкающий скачок перемещается
к компрессору, центральное тело перемещается назад и перепад
давлений уменьшается. При приближении замыкающего скачка к
горлу разность Ир < 0, центральное тело перемещается вперед.
Данная система регулирования обеспечивает и запуск диффузо-
ра. При работе двигателя на старте на взлетном режиме горло*
диффузора заперто, Ир > 0 и центральное тело убрано до предела.
С ростом Ми величина <7 (Л-i) падает и с какого-то момента регуля-
тор сработает на перемещение центрального тела вперед — это бу-
дет запуск диффузора. После запуска разность Ир станет положи-
184
Глава V. Системы регулирования авиационных ВРД
тельной, центральное тело будет несколько убрано назад и займет
нужное положение для стабилизации замыкающего скачка, соот-
ветствующее режиму полета.
На рис. 5.57 приведена принципиальная схема регулирования
горла диффузора. Она может быть использована при раздельном
регулировании системы скачков на входе перемещением клина и
скорости потока в горле изменением положения вставки. Програм-
ма регулирования М3 — const обеспечивает работу входного устрой-
ства без головной волны. Для измерения рг/р* в данной схеме
Рис. 5.57
применен пневматический рычажный измеритель отношения давле-
ний, точнее — измеритель величины рг/ап.гр^ > так как перед насад-
ком полного давления образуется прямой скачок. Влияние коэффи-
циента вп.г легко учесть, так как при М = const и коэффициент
ап.г = const. Величина рг — рг!<зп.гр*г сравнивается с заданной ве-
личиной рго, определяемой предварительным натяжением анерои-
дов и выбором плеч рычага. Сигнал рассогласования используется
для перемещения золотника сервомотора. На малых дозвуковых
скоростях полета регулятор будет удерживать вставку в заднем
положении, обеспечивая Ляпах. Такое положение вставки облегчает
в дальнейшем с ростом скорости запуск диффузора.
§ 4. ПОВЫШЕНИЕ НАДЕЖНОСТИ ТРД и ТВД С ПОМОЩЬЮ
СРЕДСТВ АВТОМАТИКИ
В связи с быстрым развитием транспортной реактивной авиации
задача повышения надежности двигателей и значительного увели-
чения их ресурса стала весьма актуальной. С позиции автоматиче-
ского регулирования эту задачу можно разбить на две части.
§ 4. Повышение надежности ТРД и ТВД с помощью средств автоматики 185
К одной из них относится повышение надежности ТРД и ТВД с по-
мощью средств автоматики. Другая часть задачи состоит в повы-
шении надежности самих автоматических устройств.
Для современных ТРД характерны программы регулирования
с большим диапазоном изменения ппр. К системам регулирования,
которые должны обеспечить их реализацию, следует предъявить
требования повышения точности регулирования числа оборотов,
введения всережимного или ограничительного регулирования тем-
пературы газа с помощью быстродействующих регуляторов темпе-
ратуры, улучшения систем регулирования компрессора на пони-
женных ппр.
Все эти требования в равной мере относятся и к системам регу-
лирования ТВД. Специфичным для ТВД является целесообразность
использования замкнутого регулирования прямых параметров дви-
гателя и необходимость дальнейшего улучшения систем, предот-
вращающих возникновение отрицательной тяги и повышающих
безопасность полета. Остановимся на некоторых вопросах, связан-
ных с повышением надежности автоматических устройств.
Для нормальной работы системы регулирования большое зна-
чение имеет чистота топлива. Необходима тщательная очистка топ-
лива до его поступления в систему топливоподачи. Желательно,
чтобы содержание механических примесей в топливе было не боль-
ше 0,0001%, а максимальный размер частиц не превышал 54-7 мк.
Требуемая степень очистки может быть получена с помощью цен-
тробежных фильтров, но они слишком громоздки. По своим филь-
трующим качествам хороши компактные бумажные фильтры. Одна-
ко фильтрующие элементы бумажных фильтров уже через несколь-
ко часов работы требуют замены.
Обычно ресурс системы топливопитания и регулирования лими-
тирует качающий узел. При полете с числом Ми = 3 и продолжи-
тельностью до 2,5 час топливо в баках нагревается на 220-4-250° С.
Дальнейший подогрев топлива на 20-4- 30° С происходит в топливо-
масляных радиаторах, которые в системах питания ряда двигате-
лей устанавливаются перед топливным насосом. При таких высо-
ких температурах нельзя рассчитывать на надежную работу топ-
ливных плунжерных и шестеренных насосов. Затруднено также
использование топлива в качестве рабочей жидкости в силовых
цилиндрах автоматики створок выходного сопла.
Для освоения еще больших скоростей полета лучше переходить
на центробежные насосы с установкой топливо-масляных радиа-
торов на линии высокого давления. Для управления створками вы-
ходного сопла использовать сжатый воздух. Переход к системам
питания с центробежными насосами (? механическим или турбо-
приводом) затруднит запуск двигателя. Возможно, что для обес-
печения запуска потребуется своя система питания с насосом дру-
гого типа.
486
Глава V. Системы регулирования авиационных ВРД
Задача повышения надежности находится в тесной связи с не-
обходимостью дальнейшего повышения точности регулирования.
Расчеты показывают, что на числах Мл 2,5 одновременное сни-
жение числа оборотов п и степени расширения газа в турбине л*
на 1% приводит к падению температуры газа перед турбиной на
40° С и тяги двигателя до 8%. В свою очередь это обстоятельство
влечет увеличение расхода топлива и снижает дальность полета
на 5 4-10%. Увеличение числа оборотов и связанное с ним повы-
шение Т g сильно снижает ресурс двигателя.
С точки зрения приведенных данных гидромеханические регу-
ляторы обладают недостаточной точностью регулирования. Они
обеспечивают точность .регулирования числа оборотов ±0,3 4- 0,5%,
степени расширения газа ±3% и приведенного расхода форсаж-
ного топлива G$Ip*2 ±5%. Гидромеханические регуляторы содер-
жат много плунжерных пар, клапанов, мембран, пружин, силь-
фонов. Все эти элементы должны сохранять работоспособность
и точность характеристик в очень трудных условиях. С ростом вы-
соты ,и скорости полета число элементов регуляторов все возра-
стает, а условия их работы ухудшаются. Регуляторы работают в
условиях длительного воздействия высоких температур топлива
и воздуха. Детали регуляторов подвергаются инерционным и виб-
рационным нагрузкам и претерпевают температурные деформации.
Поверхности трущихся частей изнашиваются, меняются характери-
стики чувствительных и дроссельных элементов. Отсюда малый ре-
сурс систем топливопитания и регулирования двигателей.
Дублирование и резервирование отдельных узлов и элементов
гидромеханических регуляторов практически невозможно. Невоз-
можен и полный предполетный контроль системы регулирования.
Гидромеханические регуляторы выполняются в виде крупных моно-
блоков и размещаются на коробках приводов двигателей. Двига-
тель весь закрыт агрегатами и трубопроводами, доступ к регулиро-
вочным элементам систем затруднен, замена агрегатов сложна.
Выполнение всех регулировок требует остановки двигателя, часто
следует слив топлива, затем заполнение системы, проливка, про-
крутка и многократные запуски с целью удаления воздуха. Все это
сокращает ресурс двигателя.
Изложенные выше специфические условия работы гидромеха-
нических регуляторов приводят к выводу, что для увеличения на-
дежности и ресурса целесообразно сочетать точную автоматиче-
скую систему регулирования с узким диапазоном работы и простое
надежное ручное управление. Но это не решает всех задач управ-
ления силовой установкой.
С ростом высоты и скорости полета силовая установка лета-
тельного аппарата усложняется. Управление воздухозаборником,
основным и форсажным контурами, створками выходного сопла,
§ 4. Повышение надежности ТРД и ТВД с помощью средств автоматики 187
средствами механизации компрессора, уборки и выпуска шасси
произввдится различными системами, недостаточно связанными
между собой. Они требуют неоднократного применения ручных
переключателей, контролируются многочисленными’ приборами и
сигнальными лампами.
Необходимо объединение систем и автоматическое управление
всей силовой установкой по оптимальной программе. Гидромехани-
ческие регуляторы плохо приспособлены к такому объединению,
В этом отношении перспективным является применение пневмати-
ческих и особенно электрических регуляторов.
Особенности электрических систем регулирования
Электрические регуляторы, как и гидромеханические, состоят
из чувствительных элементов, элементов сравнения, усилителей и
исполнительных органов. В чувствительном элементе измеренный
параметр двигателя (скорость врайХения, давление, температура)
преобразуется в электрической сигнал, который затем сравнивается
с заданной величиной в элементе сравнения. Сигнал сравнения
поступает в усилитель (их может быть несколько) и оттуда в ис-
полнительный орган (электромотор, электромагнит). Последний
связан с каким-либо органом, воздействующим на рабочий процесс
двигателя (элементы, дозирующие топливо, механизм, перемещаю-
щий створки выходного сопла и т. п.). Детальный анализ работы
систем регулирования, использующих электроавтоматику, не вхо-
дит в нашу задачу. Здесь мы ограничимся только перечислением
общих свойств электрических систем регулирования и их сравне-
нием с гидромеханическими системами.
Непосредственно на двигателе размещаются только первичные
датчики электрических сигналов (чувствительные элементы) и ис-
полнительные органы. Остальные элементы системы располагаются
в специальных отсеках летательного аппарата, где к ним может
быть обеспечен легкий доступ. То же самое можно сказать и отно-
сительно электрических систем регулирования других элементов,
силовой установки, например, воздухозаборника.
Точность регулирования электрических систем выше, чем гид-
ромеханических. На работу электрического регулятора числа обо-
ротов не влияют изменение вязкости топлива, его загрязнение,
коксование, попадание воздуха и др. Можно ожидать, что электри-
ческие системы регулирования обеспечат точность регулирования
числа оборотов ±0,2% и температуры перед турбиной ±Зч-5°С
(сюда не входит ошибка, связанная с определением среднемассо-
вой температуры газа). Регулирование двигателя на разгоне осу-
ществляется с отклонением от программы до 5%.
Электрические системы дают возможность широкого дублиро-
вания элементов и резервирования узлов. Облегчается предполет-
ный контроль и может проводиться непрерывный контроль в полете
188
Глава V. Системы регулирования авиационных ВРД
с автоматическим переключением в случае необходимости на ре-
зервную систему. Для двухдвигательного самолета при выходе из
строя системы регулирования одного двигателя резервной может
явиться система регулирования второго двигателя, которая в этом
случае управляет обоими двигателями.
Электрические системы дают возможность реализовать програм-
му регулирования любой сложности. С их применением можно ста-
вить задачу оптимизации управления силовой установкой.
Размещение в приборном отсеке элементов систем регулирова-
ния воздухозаборника и двигателя, выполненных из однотипных
узлов, дает возможность обмена сигналами для согласования режи-
мов, не прибегая к сложным передачам. Включение в общую си-
стему регулирования блоков управления рулями высоты, уборкой
и выпуском шасси, кислородной системой и других позволит раз-
работать типовые программы взлета, набора высоты, маршевого
полета на режимах наибольшей экономичности, посадки и т. п. Эти
программы будут выполняться автоматически. На пилота в этом
случае лишь возлагается задача включения нужной программы, но
и эта операция при необходимости может осуществляться с назем-
ных станций.
Электрические системы регулирования легче, чем гидромехани-
ческие. поддаются расчету и моделированию. Их доводку и иссле-
дование можно проводить до начала полетных испытаний. Дли-
тельность полетных испытаний резко сокращается, так как измене-
ние настройки регуляторов не требует остановки двигателя и за
один полет можно испытать десятки настроек блоков.
Перечисление особенностей электрических систем регулирования
не должно привести к неверному представлению о легкости созда-
ния таких систем. К их отрицательным сторонам относится еще
недостаточная надежность в условиях работы авиационной сило-
вой установки. Нормальная работа ряда элементов электрических
систем регулирования, например, усилителей, возможна только в
сравнительно небольшом диапазоне изменения температуры. Не-
обходима также строгая стабилизация питания. Наиболее трудной
задачей, по-видимому, будет создание надежных датчиков первич-
ной автоматики, преобразующих изменение параметров рабочего
процесса двигателя в электрические сигналы. Много усилий потре-
бует создание комплектов типовых узлов. По-прежнему остаются
тяжелые условия работы топливных насосов. Для повышения на-
дежности плунжерных насосов их нужно делать менее нагружен-
ными по числу оборотов и давлению топлива, хотя снижение на-
грузки противоречит требованию уменьшения веса.
Примеры
Пример 1. Определить статическую ошибку в случае изменения высоты по-
лета от Н = 0 до Wmax при замкнутом регулировании числа оборотов по про-
Примеры
189
грамме n = const с помощью регулятора с жесткой обратной связью
(см. рис 5.3, а).
Исходные данные: п0 = 10.000 об/мин, характеристика пружины В = 14н/с.и;
отношение плеч рычага а/Ь = 0,2;' перемещение дозирующей углы с изменением
высоты Н = 0 до //щах 6т = 1 см. Известно также, что осевая составляющая
центробежной силы, развиваемой грузиками регулятора, на режиме п0 =
= 10.000 об/мин равна 70 «.
Статическую ошибку регулирования определим по формуле (5.1), для этого
следует сначала найти коэффициент пропорциональности с.
с = —4-= 7 10 1 н-сек2,
п0
затем
а
В —
8п = —— 8т =----------14-°Л—т-1 = 200 об/мин.
2сп0 2-7. 10~7104
При регулировании авиационного двигателя такая ошибка недопустимо
велика.
Пример 2. Определить статическую ошибку регулирования при использова-
нии регулятора-ограничителя максимальных оборотов системы незамкнутого
регулирования числа оборотов (см. рис. 5.40) при изменении высоты полета
ОТ Н = 0 ДО Н = //щах-
Исходные данные для расчета по формуле (5.5): иОшах = 10.000 об/мин-,
соотношение плеч рычага Л Дг = 1; площадь жиклера управляющего клапана
= 1,78 • 10~2 см2 (с/ж = 1,5 мм); площадь мембраны F м = 40 см2. Давление
топлива перед форсункой с увеличением высоты от Н = 0 до Ятах снижается
на 600 н/см2. На режиме иОтах = 10.000 об/мин перепад давления на мембране
равен 7,4 н/м2.
Статическая ошибка в регулировании nmax определяется снижением давле-
ния топлива на управляющий клапан. Изменение давления на управляющий
клапан принимаем равным 600 н/см2.
Определяем коэффициент с, имея в виду что перепад давления на мембране
пропорционален квадрату числа оборотов:
Тогда
Рца __ 7,4 _ у , ip--8 н-сек2
«Отах 108 ~ ’ СМ* '
-Ы^ЪРкл = 1-78-10~2600 = 180 об/мин.
2сп0ЕЛ/1 2 • 7,4 • 10“810440
Такая ошибка в изменении итах для авиационного двигателя слишком ве-
лика. Ее можно уменьшить, подведя к рычагу со стороны мембраны давление
топлива за насосом (см. рис. 5.43).
Глава VI
ОСНОВНЫЕ СВЕДЕНИЯ О СИСТЕМАХ РЕГУЛИРОВАНИЯ
ТИПОВЫЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
§ 1. ПОНЯТИЕ О СИСТЕМЕ РЕГУЛИРОВАНИЯ. ОБЪЕКТ РЕГУЛИРОВАНИЯ
И РЕГУЛЯТОР КАК ЗАМКНУТАЯ СИСТЕМА РЕГУЛИРОВАНИЯ
Выделение звеньев в системе регулирования
Изучению динамики автоматического регулирования авиацион-
ного двигателя должно предшествовать ознакомление с основными
методами, которыми пользуются при исследовании процессов ре-
гулирования. К ним относятся выделение в системах регулирова-
ния типовых звеньев, составление дифференциальных уравнений
и определение коэффициентов, входящих в эти уравнения. Большое
значение играют так называемые частотные характеристики типо-
вых звеньев, которые используются в дальнейшем при анализе ди-
намики регулирования.
В авиационной силовой установке объектом регулирования яв-
ляется двигатель. Вместе с регулятором он образует замкнутую
систему регулирования. Если в силовой установке используется
газотурбинный двигатель, у которого регулируется скорость вра-
щения ротора, то при отклонении числа оборотов от заданного зна-
чения приходит в движение механизм регулятора. Новое положение
деталей регулятора приводит к тому, что изменяется подача топ-
лива. В результате отклонение скорости вращения уменьшается и
число оборотов ротора приближается к заданному значению.
Замкнутую систему регулирования можно представить в виде
схемы, которую будем называть структурной схемой системы регу-
лирования. Такая структурная схема показана на рис. 6.1, а. На
ней стрелками показано воздействие двигателя на регулятор изме-
нением числа оборотов и регулятора на двигатель изменением по-
дачи топлива.
Пусть скорость вращения ГТД поддерживается с помощью ста-
тического регулятора непрямого действия с жесткой обратной
связью. Схема такого регулятора дана на рис. 6.1, б. На ней стрел-
ками показаны подача топлива от насоса к дозирующей игле, ра-
бочей жидкости к золотнику и вращение приводного валика. При
§ 1. Понятие о системе регулирования
191
исследовании системы регулирования регулятор целесообразно
рассматривать не как одно целое, а разбить па несколько элемен-
тов -— звеньев. Имеет смысл выделить два звена, чувствительный
элемент и сервомотор с жесткой обратной связью, и представить
систему регулирования в виде замкнутой цепи из трех последова-
тельно расположенных звеньев: двигателя, чувствительного эле-
мента и сервомотора регулятора. Структурная схема такой системы
регулирования показана на рис. 6.1, в.
а)
в)
Рис. 6.1
В системе регулирования от одного звена к другому происходит
передача воздействий. Направление воздействий на стуктурной схе-
ме системы показано стрелками. Выбор направления воздействий
не произволен. Изменение положения муфты чувствительного эле-
мента происходит только за счет отклонения числа оборотов дви-
гателя от заданного значения. Перемещение поршня сервомотора
может быть только в результате движения муфты чувствительного
элемента. Изменение числа оборотов двигателя происходит при из-
менении положения поршня сервомотора и связанной с ним дози-
рующей топливной иглы.
В связи с направленностью воздействий от одного звена к дру-
гому у каждого звена в системе регулирования есть входной и вы-
ходной параметры или входная и выходная координаты. В нашем
примере для муфты чувствительного элемента как звена системы
регулирования входной координатой будет изменение числа обо-
ротов приводного валика регулятора, а выходной — изменение по-
ложения муфты чувствительного элемента. Для сервомотора вход-
192 Глава VI. Основные сведения о системах регулирования. Типовые ввенья
ной координатной будет перемещение муфты, а выходной — пере-
мещение дозирующей иглы. Наконец для двигателя изменение по-
ложения дозирующей иглы является входной координатой и вы-
ходной— изменение числа оборотов валика привода регулятора.
Из этого перечисления следует, что одна и та же координата
является выходной для предшествующего звена и входной для по-
следующего звена.
В соответствии с положением линеаризованной теории автома-
тического регулирования поведение системы регулирования изуча-
ется при малых отклонениях ее от исходного статического режима.
Обозначим текущие значения положения муфты чувствительного
элемента, сервомотора регулятора и число оборотов ротора двига-
теля через z, m и п. Соответственно через г0, т0 и п0 обозначим
значения этих параметров на исходном статическом режиме. При-
ращение координаты звена при отклонении системы от положения
равновесия определится как разность между текущим значением
координаты и ее значением на исходном статическом режиме:
oz = z — Zt,; 8т = т— тр\ 8п = п— п0.
Как уже было показано в гл. II удобнее рассматривать не аб-
солютные, а относительные изменения координат. Для этого нуж-
но ввести базисные величины и относить к ним приращения коор-
динат. Приращение регулируемого параметра 8п целесообразно от-
нести к значению этого параметра на исходном статическом режиме
(в рассматриваемой системе регулирования это будет п0) пли к
максимальному числу оборотов Птах. Для других входных и выход-
ных координат за базисные величины можно принять максималь-
ные приращения координат:
8гк = 8г ; 6пгк = 8т
Ь max* max
Тогда относительные координаты будут представлять собой отно-
шения:
л 8п д 6z Л 8m
Дп =-----; Дг = -т— ; Д/п = -т—.
п0 ^Б 1тБ
Переход к относительным координатам при соответствующем
выборе базисных величин дает возможность сравнивать между со-
бой характеристики отдельных двигателей как объектов регулиро-
вания и их регуляторов. Поэтому в дальнейшем будем пользовать-
ся относительными координатами и в общем случае входную коор-
динату обозначать Дхвх, а выходную Дхвмх. Следует установить
правило знаков координат отдельных звеньев. Целесообразно увя-
зывать знаки отдельных координат с направлениями, в которых
передаются воздействия в системе регулирования, приняв, что
действие сил инерции и трения не проявляется.
Для чувствительного элемента входную координату Дп будем
§ 1. Понятие о системе регулирования
193
считать положительной, если величина входного параметра воз-
растает, т. е. если 6п = п — п0 > 0. Тогда в соответствии с возрас-
танием числа оборотов применительно к рассматриваемой схеме
системы регулирования, показанной на рис. 6.1, о, будем считать
положительными Аг и Ат тогда, когда муфта чувствительного эле-
мента перемещается вверх, а поршень сервомотора вниз.
Отклонение системы регулирования от исходного статического
режима происходит под влиянием внешних воздействий. Если при
регулировании числа оборотов ТРД регулирующим фактором, с
помощью которого устанавливается заданный равновесный режим,
является изменение расхода основного топлива, то к внешним воз-
действиям будут относиться изменение высоты и скорости полета,
Рис. 6.2
изменение настройки регулятора числа оборотов, расхода форсаж-
ного топлива, площади критического сечения сопла и др. Внешнее
воздействие в виде изменения настройки регулятора (управляю-
щее воздействие) приложено к чувствительному элементу как зве-
ну системы регулирования. Поэтому в цепи воздействий его следу-
ет указать отдельной стрелкой на входе в это звено и рассматри-
вать как вторую входную координату. Изменения внешних условий,
расхода форсажного топлива и площади критического сечения вы-
ходного сопла (возмущающие воздействия) оказывают воздействие
непосредственно на двигатель и должны быть отражены в виде до-
полнительных входных координат на звене, соответствующему
двигателю на структурной схеме системы регулирования (рис. 6.2).
Внешние воздействия в общем случае являются некоторыми задан-
ными функциями времени. Они могут действовать непрерывно в
течение всего процесса регулирования или только в некоторой его
части.
Разомкнутая система регулирования.
Переход от разомкнутой к замкнутой цепи воздействий
При изучении процессов регулирования в замкнутых системах
удобнее предварительно эти процессы рассмотреть в разомкнутой
цепи воздействий. Укажем, что имеется в виду под размыканием
системы регулирования и в чем будет заключаться последующий
переход опять к замкнутой системе регулирования.
7 Черкасов Б. А.
194 Г лава VI. Основные сведения о системах регулирования. Типовые звенья
Сущность размыкания системы регулирования поясним на при-
мере системы, показанной на рис. 6.1, б. Предположим, что валик,
связывающий двигатель с регулятором и приводящий во вращение
центробежные грузики, имеет участок с — d, который может быть
удален. Предположим, так же, что при удалении этого участка ва-
.лика вращение регулятора осуществляется от электромотора экс-
периментальной установки (рис. 6.3). Если двигатель работает на
числе оборотов п0 и от него приводится во вращение регулятор, то
оба участка валика с — с и d— d так же вращаются с тем же чис-
лом оборотов (полагаем, что передаточное число между ротором
Рис. 6.3
двигателя и валиком привода регулятора равно единице). Измене-
ние числа оборотов двигателя с nQ до п вызовет такое же измене-
ние числа оборотов обоих участков валика с — d от п0 до п.
При числе оборотов ротора двигателя п0 удалим участок вали-
ка с — d, одновременно переведя привод регулятора на электромо-
тор. Число оборотов электромотора подбираем таким, чтобы ре-
гулятор и участок валика с — с вращались с тем же числом оборо-
тов По- Если двигатель устойчив и на систему не передаются внеш-
ние воздействия, то при таких условиях система регулирования «не
заметит» разрыва валика привода регулятора, т. е. размыкания
цепи воздействий. Теперь, сохраняя систему регулирования разом-
кнутой, увеличим число оборотов электромотора и станем вращать
регулятор и участок валика с — с с числом оборотов п > п0. Тогда
под действием возросших центробежных сил грузиков муфта чув-
ствительного элемента переместится вверх, сдвинет золотник и ра-
бочая жидкость регулятора начнет поступать в верхнюю полость
цилиндра сервомотора, перемещая дозирующую иглу вниз на
уменьшение подачи топлива. В результате число оборотов ротора
двигателя снизится до какого-то значения п' < п0. Следовательно,
в разомкнутой системе регулирования при правильно выполнен-
ном регуляторе изменение скорости вращения участка с — с валика
§ 2. Типовые звенья систем регулирования ВРД
195
в одном направлении приводит к изменению скорости вращения
участка d—d валика в противоположном направлении. Величина
изменения числа оборотов- ротора двигателя и участка валика d—d
может быть самой различной. Она зависит от характера нараста-
ния центробежной силы грузиков по числу оборотов, от жесткости
пружины, профиля дозирующей иглы, характеристик компрессора
и турбины двигателя и др.
Всю разомкнутую систему регулирования будем рассматривать
как некоторое сложное звено. За входную координату этого звена
Дхвх примем относительное изменение числа оборотов участка ва-
лика с — с. Следовательно, Дхвх = Лпвх. Выходной координатой
звена Ахвых будет относительное изменение числа оборотов участка
валика d — d.
Поэтому ДХвых = Дивых. По принятому ранее правилу знаков
величина Дивж является положительной, когда число оборотов
участка валика с — с возрастает."В этом случае число оборотов-
участка валика d — d падает. Откуда следует, что за положитель-
ное значение Аивых следует взять значение ДивЬ(Ж, связанное с
уменьшением числа оборотов участка валика d — d.
Перейдем теперь опять к нормальной работе системы регулиро»
вания по замкнутой схеме, но сохраним отмеченные участки вали-
ка привода регулятора с —с и d — d (см. рис. 6.1, б). Теперь из-
менение Дхвх = Д«вх во времени (относительное изменение числа
оборотов участка валика с — с) определяется изменением скорости
вращения ротора двигателя АхеЬ1Х = ДивЬ1Х (относительное измене-
ние числа оборотов участка валика d — d) и равно по абсолютной
величине Апвх, так как валик представляет собою единое целое. Од-
нако Д«вх и Дивых противоположны 'По знаку, потому что мы приня-
ли за положительное значение выходной координаты ее изменение,
связанное с уменьшением ДивЬ1х в случае увеличения Дивх от исход-
ного значения и0.
Приведенные рассуждения дают основание сделать вывод, что
для перехода от разомкнутой к замкнутой цепи воздействий, за
входную координату системы регулирования следует принять ее
выходную координату, взятую с обратным знаком, т. е.
= ^Хвых' (6.1)
Этот вывод будет нами использован в дальнейшем при иссле-
довании дифференциальных уравнений движения систем регули-
рования.
§ 2. ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ РЕГУЛИРОВАНИЯ ВРД
В начале этой главы уже было сказано, что любая система ре-
гулирования, в том числе и система регулирования ВРД, может
быть представлена в виде совокупности отдельных звеньев, опре-
деленным образом связанных между собой. Для того чтобы отве-
7*
196 Глава VI. Основные сведения о системах регулирования. Типовые звенья
тить на вопрос, как протекают процессы регулирования во всей си-
стеме, необходимо предварительно изучить характеристики ее от-
дельных звеньев. Эти характеристики связывают между собой
выходную координату звена кхвЫх, входную \хвх и время.
Чтобы ввести однообразие при разбивке систем регулирования
на отдельные звенья, А. В. Михайловым в 1938 г. было предложе-
но понятие типового звена. Тип звена определяется видом переход-
ного процесса, происходящего в звене. Если в разных звеньях ди-
намические процессы при малых отклонениях описываются одним
и тем же по виду дифференциальным уравнением, то эти звенья
•однотипны, несмотря на различное конструктивное оформление и
на различие в физических процессах, протекающих в этих звеньях.
Типовых звеньев совсем немного (рассматриваются только устойчи-
вые звенья). Дадим им названия: астатическое, инерционное, коле-
бательное, дифференцирующее и усилительное. Следует отметить,
что астатическое и дифференцирующее звенья можно считать ус-
тойчивыми только условно. Рассмотрим виды типовых звеньев.
Астатическое звено
Астатическим звеном называется звено, движение которого опи-
сывается уравнением 1
т = д (6.2)
U ft <зЛ \ '
at
Рассмотрим динамические свойства гидравлического сервомо-
тора применительно к схеме астатического регулятора скорости
вращения непрямого действия (рис. 6.4, а) и составим для него
уравнение движения. Получив уравнение движения, убедимся, что
гидравлический сервомотор (без обратной связи, т. е. без механиче-
ской связи между поршнем сервомотора и золотником) по своим
динамическим свойствам является астатическим звеном. Исполь-
зуем уравнение расхода. Примем, что при смещении золотника на
величину f>y (рис. 6.4, б) объемный расход жидкости, поступающей
через оплошную кольцевую щель в одну из полостей цилиндра,
будет равен _
Q = l/ у Vppao — Pi, (6.3)
где рзол — коэффициент расхода через золотник; d30Jl — диаметр
золотника; ррав и у — давление рабочей жидкости и ее удельный
вес; pi — давление в полости цилиндра сервомотора, сообщенного
с каналом подвода рабочей жидкости.
1 В литературе по теории автоматического регулирования астатическое зве-
но называется также интегрирующим или нейтральным звеном.
§ 2. Типовые звенья систем регулирования ВРД
197
Другая полость цилиндра сервомотора в это время сообщена со
сливом. Если скорость движения поршня сервомотора такова, что
не происходит разрыва струи рабочей жидкости и отрыва поршня
от нее, то такое же количество рабочей жидкости пройдет из ци-
линдра через кольцевую щель около второго пояска золотника на
слив
Q = ^d30J>y 2|УРг~Рсл, (6.4)
5)
где р2 — давление рабочей жидкости в полости цилиндра сервомо-
тора, сообщенной со сливом; рсл — давление слива.
Разность давления на поршне сервомотора вызывает его движе-
ние и определяет перестановочную силу
R = Fnop (Р1 — Р2),
где Fnop — площадь поршня.
Из выражений (6.3) и (6.4) следует, что
(6.5)
Р1 +Pi = РрОб+ Рсл- (6.6)
Если дозирующая игла, которой оканчивается шток сервомо-
тора (см. рис. 5.2), хорошо уравновешена от действующих на нее
сил давления топлива, то перестановочная сила R будет мала.
В этом случае можно пренебречь разницей в давлении р} и р2 и
принять, что ру = р2 = р. Тогда из равенства (6.6) следует
р = . (6.7)
Секундный объем, описываемый поршнем сервомотора, можно
представить как произведение площади поршня па скорость его
передвижения
(6-8)
198 Глава VI. Основные сведения о системах регулирования. Типовые звенья
где f>m — приращение координаты, определяющей положение
поршня. Этот объем будет равен расходу жидкости через золот-
ник.
Приравняем правые части выражений (6.3) и (6.8) и учтем
равенство (6.7). Тогда ___ ___________
г, dim , /2g /~ Реаб Рсл .
пор Р-зол'^зол 1/ 1/ 2
Примем за входную координату перемещение муфты чувстви-
тельного элемента 6г. Координата 6г связана с бу зависимостью
где а и b — плечи рычага сервомотора (см. рис. 6.4, а).
Введем базисные величины ЫпБ и бгя. Тогда с учетом
ния (6.10) уравнение (6.9) примет окончательный вид
т d^Hl .
Та-----= Дг.
dt
В уравнении (6.11)
j, a -J- b Fnop &тБ
& U Ttd 1 / 2g 1 /”Рпаб Рсл ^гБ
\1зол‘шэол I / -- I / --------
k V V 2
есть постоянная времени гидравлического сервомотора и
время — постоянная времени астатического звена, поскольку урав-
нение (Ь.Н) совпадает по форме с уравнением астатического звена
(6.2). Относительные координаты Дг и Дт являются соответствен-
но входной и выходной координатами гидравлического сервомо-
тора.
выраже-
(6.11}
(6-12)
в то же
Инерционное звено
Если движение звена описывается уравнением
Ta-^f^ + \Xeux = kAXex, (6.13)
at
то такое звено называется инерционным *. В гл. V были рассмот-
рены свойства регулятора скорости вращения с жесткой обратной
связью (см. рис. 5.3). Сервомотор регулятора этого типа по своим
динамическим характеристикам является инерционным звеном.
Чтобы доказать это, следует воспользоваться уравнением расхода
так, как это было сделано при выводе уравнения движения серво-
мотора астатического регулятора скорости вращения.
1 В литературе по теории автоматического регулирования инерционное зве-
но называется также апериодическим или одноемкостным звеном.
§ 2. Типовые звенья систем регулирования ВРД
199
Для сервомотора, схема которого показана на рис. 6.5, справед-
ливы ранее полученные соотношения (6.3) — (6.9). Что же касает-
ся перемещения золотника ду, то его следует рассматривать как
результирующее, определяемое перемещениями л!уфты чувстви-
гёльного элемента регулятор-а dz и поршня сервомотора dm. Если
полагать, что правый конец рычага АВ неподвижен, то связь ме-
жду ду' и dz определяется соотношением
где а и в — плечи рычага АВ-, ду' — перемещение золотника только
за счет смещения муфты чувствительного элемента. Приняв не-
подвижным левый конец рычага АВ, найдем связь между ду" л
дт(ду" — перемещение золотника только за счет смещения порш-
ня сервомотора):
ду" = —(6.15)
аД-Ь
Истинное перемещение золотника ду определится как разность
ду'—ду", так как перемещение муфты чувствительного элемента и
поршня сервомотора при нарушении равновесия регулятора проис-
ходит в противоположном направлении. Поэтому
ду = —b— dz-~8т. (6.16)
а о а + о
С помощью последнего выражения из уравнения (6.9) исклю-
чим перемещение золотника ду. Тогда
р dbm . 1 f2g f Рраб — Рсл
пор dt v |/ 2
х(-4т6г--4-6т\ (6.17)
\ а + Ь а + о )
200 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Введя базисные величины' и преобразовав это выражение, по-
лучим уравнение движения гидравлического сервомотора с жесткой
обратной связью как инерционного звена
где
Тс — + = kc\z,
dt с
постоянная времени сервомотора и
а ЪтБ
(6.18)
(6.19)
(6.20)
коэффициент усиления сервомотора.
Следует отметить, что уравнения вида (6.13) были получены
в гл. II, когда рассматривался ТРД как объект регулирования по
числу оборотов. Следовательно, ТРД является инерционным зве-
ном, если учитывать его способность аккумулирования только од-
ной механической энергии.
Колебательное звено
Колебательным звеном называется звено, движение которого
описывается уравнением 1
+ Л + дХвыА = kbxex. (6.21)
til III
Примером колебательного звена может служить чувствитель-
ный элемент центробежного регулятора. Он состоит из шарнирно
подвешенных грузиков, муфты и пружины (см. рис. 5.1); в ряде
случаев колебательное звено может иметь конструктивно оформ-
ленный демпфер колебаний. Для чувствительного элемента вход-
ной координатой будет являться приращение числа оборотов бп, а
выходной — изменение положения муфты бг.
На переходных режимах при числе оборотов ротора п осевая
составляющая центробежной силы грузиков Рч уравновешивается
силами пружины Рпр, инерции Ри и вязкого трения Ртр. Поэтому
Рц = Рпр + Ри + РтР. (6.22)
На установившемся режиме при числе оборотов п = п0; Ри0 = 0
и Ртро = 0. Откуда Рц0 = Рпр0.
1 В литературе по теории автоматического регулирования колебательное
звено иногда называют апериодическим или статическим звеном второго по-
рядка.
§ 2. Типовые звенья систем регулирования ВРД,
201
Запишем силы, входящие в уравнение (6.22), в виде приращений.
ОчеВИДНО, ЧТО ЬРц = Рц" Рц0> ЬРпр = Рпр— Рпро> &Ри ” Ри',
&Р тр — Р ТР’
8Р^ЬРпр + Ри + Ртр. (6.23)
При малых отклонениях от установившегося режима, пренебре-
гая изменением радиуса инерции, можно считать, что сила Рч про-
порциональна квадрату числа оборотов, т. е. Рц = см2. Тогда най-
дем приращение центробежной силы в виде 8РЦ = 2сп08п. Прира-
щение силы пружины 8РпР = B8z, где В — характеристика пружи-
ны; —приращение координаты, характеризующей положение
муфты чувствительного элемента.
Сила вязкого трения пропорциональна скорости перемещения
муфты. Поэтому РТр = ₽------, где р — константа демпфирования
di
, - dz dSz , . .
колебании, а —--— = —— , так как z, = z0 + 6z >.
dt dt
Сила инерции Pu пропорциональна ускорению муфты, т. е.
Р и = М ,
“ dt* ’
где М — масса, приведенная к муфте. Теперь уравнение (6.23) при-
мет вид
М + ? ТГ"+ B8z 2сп°8п- (6 • 24>
Приняв за базисные величины п0 и 8zs, приведем уравнение
(6.24) к форме (6.21).
Т2Ф^£_ + Т х —+ \z = k ч\п, (6.25)
dt* 1 dt 4 ' v
rr\ 2
где Т 2
М_. т = _р_
в ’ 1 ~ в
_ 2сп2
коэффициент усиления чув-
ствительного элемента.
Как уже отмечалось раньше, входных координат звена может
быть несколько. Применительно к муфте чувствительного элемента
как колебательному звену второй входной координатой, кроме ко-
ординаты 6z, будет перемещение упора пружины с целью измене-
ния настройки регулятора. Рассматривая это перемещение как
какую-то функцию времени f (/), запишем приращение силы пру-
жины в виде
8Рпр~ B[8z—f(t)].
1 В общем случае константа демпфирования колебаний Р называется коэф-
фициентом вязкого трепня.
202 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Тогда уравнение (6.25) примет вид
?2 + Ti d£ + Дг = k^n + k*f (0> (6.26)
at at
1
где kH = ~т~ — коэффициент усиления по настройке.
Дифференцирующее звено
Дифференцирующим звеном называется звено, движение кото-
рого описывается уравнением вида 1
\хвых = Тдиф^. (6.27)
at
Рассмотрим движение поршня катаракта относительно его ци-
линдра (или относительно поршня сервомотора) как пример диф-
ференцирующего звена (рис. 6.6). За входную координату примем
би —перемещение поршня катаракта относительно его цилиндра,
за выходную координа-
ту примем би — абсо-
лютное перемещение
поршня катаракта.
Между этими пере-
мещениями существует
связь
6u = 6m — 6ц,
где 6m — перемещение
поршня гидравлическо-
го сервомотора.
Из уравнения рас-
хода через жиклер ка-
таракта следует, что
, (6.28)
где wKaT — скорость течения жидкости через жиклер катаракта:
fvar — площадь жиклера катаракта; FKaT — площадь поршня ката-
ракта.
Примем, что при ламинарном течении жидкости скорость тече-
ния через жиклер пропорциональна перепаду давления на поршне
катаракта, т. е.
&кат — Гкат^>Ркат, (6.29)
1 В литературе по теории автоматического регулирования дифференцирую-
щее звено называют также скоростной связью между звеньями.
§ 2. Типовые звенья систем регулирования ВРД
223
где сКат — коэффициент пропорциональности. В свою очередь пе-
репад давления ЪрКат образуется за счет деформации пружины ка-
таракта. Поэтому
ЬРкатВ кат = ВкатЬи, (6.30)
где Вкат — характеристика пружины катаракта.
На исходном статическом режиме (брКат)о = 0 и (щКат)о = О-
СлеДОВателЬНО, "ССкат ^^кат
Используя выражения (6.29) и (6.30), преобразуем уравнение
(6.28). Оно примет вид
Вкатки - _~ р clttv oi\
Скат ~ ]кат— "кат “7“ • (O.O1J
г кат [at
Вводя базисные величины bvE и ЬиБ и переходя к относитель-
ным координатам, окончательно получим
Аи = Ткат^, (6.32)
at
где
fr2 X?»
T^-=—-B—f\UR (6-33)
ькат °кат I кат
постоянная времени катаракта как дифференцирующего звена.
Усилительное звено
Если в уравнениях инерционного или колебательного звеньев
постоянные времени достаточно малы, то влиянием производных в
переходном процессе звена можно пренебречь. В таком звене вы-
ходная координата без всяких искажений и запаздываний воспро-
изводит входную координату. Их соотношение определяется коэф-
фициентом усиления звена. Уравнение усилительного звена имеет
вид
Ахй.,, = k\xM. (6.34)
В качестве усилительных звеньев могут рассматриваться, на-
пример, короткий трубопровод, заполненный жидкостью, и дрос-
сельный кран.
Статическая связь между звеньями
Передача воздействий от одного звена к другому осуществляется
с помощью связей между звеньями. Эти простые или статические
связи определяют постоянные, независящие от времени соотноше-
ния между двумя или несколькими координатами. Примером такой
связи может служить рычажная передача (рис. 6.7). В частном
случае входная координата последующего звена может быть рав-
204 Глава VI. Основные сведения о системах регулирования. Типовые звенья
на выходной координате предыдущего звена, что соответствует или
прямому соединению звеньев, или, например, для показанной на
рис. 6.7 рычажной передачи, отношению плеч а/b = 1.
Использование элементарных электрических цепей
для получения типовых звеньев
Рассмотренные типовые звенья легко могут быть получены в
элементарных электрических цепях, включающих в различных ком-
бинациях омические, емкостные и индуктивные сопротивления.
Так, астатическое звено может быть представлено электричес-
кой цепью, показанной на рис. 6.8, а, где Uex и ивых— входное и
выходное напряжение; 7? — омическое сопротивление; С — емкость
конденсатора; i — сила тока в цепи. Согласно законам электротех-
ники имеем
вых + iR = UвХ> (6 • 35)
= с ли«ых . (6.36)
dt
Если омическое сопротивление цепи выбрать много больше ем-
костного, то можно принять без большой погрешности, что I «
~ UexIR. Тогда получим, что
RC^-^ = Uex (6.37)
Если же омическое сопротивление будет сравнимо с емкостным,
то та же цепь станет уже инерционным звеном. Действительно, ис-
ключая из уравнения (6.35) с помощью (6.36) силу тока I, получим
+ = (6.38)
Электрическая цепь, показанная на рис. 6.8, б, где L — участок
с индуктивным сопротивлением, может рассматриваться как ко-
§ 2. Типовые звенья систем регулирования ВРД
205
лебательное звено. Потеря напряжения на участке индуктивного
сопротивления равна
Ul = L-^, (6.39)
а связь между Uex и ивых может быть записана в виде
ивых + ^~ + iR = Uex.
at
Тогда с учетом выражений (6.35) и (6.39) найдем
LC + RC + и°^ = и«- (6-39а)
Рис. 6.9
На рис. 6.9 показана электрическая цепь, которую при малом
сопротивлении R можно рассматривать как дифференцирующее
звено. Для этой цепи Uebix + Uc = Uex, где Uc —падение напряже-
ния на участке емкостного сопротивления. Если сопротивление R
мало, то ивых Uс, и тогда Uc ~ Uex или i = С _
at
Учитывая, что ивых = iR, получим
usux-RC^-. (6.40)
at
Элементарные электрические цепи удобны для демонстрации и
изучения переходных процессов в типовых звеньях.
Некоторые другие виды простейших звеньев
В некоторых случаях наряду с разобранными выше типовыми
звеньями рассматриваются дифференцирующее статическое изо-
дромное звено и дифференцирующее изодромное звено, переход-
ные процессы в которых описываются уравнениями
Т\ + k\xeblx = Т2-^ + Дхвх (6.41)
и
Л (6.42)
at at
206 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Иногда в качестве простейшего звена рассматриваются элемен-
ты систем автоматического регулирования, вносящие прямое за-
паздывание (с чем мы встретились в гл. IV при выводе уравнения
ПВРД как объекта регулирования).
Уравнение движения вида (6.41) используется при выводе диф-
ференциального уравнения изодромного регулятора, схема кото-
рого показана на рис., ,5.4.
б)
Рис. 6.10
Изодромный регулятор можно рассматривать как одно слож-
ное звено с входной координатой Az и выходной Ат (рис. 6.10, а).
Тогда его уравнение имеет вид
d2km . гр d&m ?р d^z . , * zc,-io\
Т3——-+т4—— = (6.43)
dt2 dt dt
В этом уравнении
гр ___ кат Ь ^гБ
СкатВкат$кат а
. b 8гн
kl =---------
а ЪтБ
(6.44)
(6.45)
(6.46)
(6Л7)
Представим теперь изодромный регулятор в виде астатического
звена с обратной связью, причем обратная связь осуществляется
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 207
через дифференцирующее изодромное звено так, как это показано
на рис. 6.10, б. Тогда уравнения этих двух звеньев будут иметь вид
Те
Тт
dbm_ __
dt 2 3
d\u । А._ zp d&m
——— -4— (\Ц -— i «-
dt dt
В этих уравнениях
Тв =
р
* пор
Рраб — Рсл
т.
Ts =
2
, Ь ^гБ
Kn ' ” " |
a + b ЪтБ
д' ЪиБ
a + & ЪтБ ’
F2 ’
кат .
1 ,
скат^кат^кат
____^кат ^тБ_____
скат fкат ^кат ^иБ
(6,48)
(6.49)
(6.50)
(6.51)
(6.52)
(6.53)
(6.54)
Рзол^^зол
&3 —
Если из уравнений (6.48) и (6.49) исключить координату Ды, то
опять придем к изодромному регулятору как к сложному звену
с уравнением (6.43).’Отметим также, что дифференцирующее изо-
дромное звено, движение которого описывается уравнением (6.42),
может быть получено как сложное звено при последовательном сое-
динении инерционного и дифференцирующего звеньев.
§ 3. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
КОЭФФИЦИЕНТОВ, ВХОДЯЩИХ В УРАВНЕНИЯ ТИПОВЫХ ЗВЕНЬЕВ
Для исследования динамики систем регулирования нужно не
только уметь выделять типовые звенья в системе регулирования и
составлять их уравнения. Необходимо знать численные значения
входящих в них постоянных времени и коэффициентов усиления.
При определении коэффициентов возможны два пути: расчетный
и экспериментальный. В случае использования расчетного пути фор-
мулы для определения коэффициентов какого-либо звена получают-
ся в процессе вывода уравнения движения этого звена. Так, напри-
мер, формула (6.19) есть расчетная формула для определения по-
стоянной времени гидравлического сервомотора с жесткой обратной
связью, являющегося инерционным звеном. Расчетный путь опреде-
ления коэффициентов уравнений не обладает большой точностью.
208 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Допущения при выводе основных уравнений, отсутствие достовер-
ных данных по коэффициентам истечений, вязкости и другим могут
привести к существенным ошибкам. К расчетам приходится прибе-
гать главным образом в тех случаях, когда регулятор или его эле-
менты еще только проектируются или находятся в стадии произ-
водства. Если только есть возможность, следует использовать экспе-
риментальный путь определения динамических коэффициентов,
входящих в уравнения движения типовых звеньев, из которых со-
стоит исследуемая система регулирования.
Экспериментальное исследование системы регулирования в це-
лом (обычно в разомкнутом состоянии), ее отдельных элементов
и типовых звеньев заключается в определении закона изменения
выходной координаты Ахвых при выбранном законе изменения
входной координаты Дхет.'-На практике используют два закона изме-
нения Ахвзс, определяющие два способа экспериментального исследо-
вания систем регулирования и их звеньев.
При использовании первого способа задают постоянное значение
входной координаты: при /<0 Ахвх(/) = 0, при / О Axex(t) =
— Ахвж1 — const. Этот способ называется способом скачкообразного
воздействия, при его использовании характер изменения выходной
координаты существенно зависит от типа звена.
Второй способ основан на том, что входная координата изме-
няется по синусоиде: Ахвж = Ахв sin at, где Авх — амплитуда колеба-
ний*. В соответствии с этим выходная координата будет так же из-
меняться по синусоиде с некоторым сдвигом по фазе и с различным
соотношением аплитуд на разных угловых частотах со изменения
входной координаты. Этот способ называется частотным способом.
Рассмотрим оба способа применительно к типовым звеньям систем
регулирования с целью определения входящих в уравнения их
движения динамических коэффициентов.
Способ скачкообразного воздействия
Астатическое звено. В уравнении астатического звена
dt вх
положим Ах0Х = Axexi = const и решим его относительно бхвмх, пе-
рейдя от относительных координат к абсолютным. Последнее свя-
зано с тем, что при эксперименте на ленте осциллографа или како-
го-нибудь другого самопишущего прибора будут фиксироваться из-
менения абсолютных координат.
1 Здесь начальная фаза Дхвж принята равной пулю (90 = 0). В общем слу-
чае следует записать Дхвх = Аех sin (wt + (Jo).
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 209
Получим
8хвых = ^^- — 1.
вЫЛ гр
хвхБ 1 а
(6.55)
где = const — абсолютное значение входной координаты;
%вх Б И Хв-ых Б — базисные величины входной и выходной коор
динат.
Из уравнения (6.55) следует, что при скачкообразном воздейст
вии выходная координата астатического звена есть прямая, прохо
дящая через начало координат
(рис. 6.11).
Постоянная времени Та опре-
деляется из выражения
Та = (6.56)
хвхБ
где у — угол наклона прямой.
Инерционное звено. Возьмем
уравнение инерционного звена
Т dAxe.„lx Д _ £Д „
1 и J. г ЧХвнх — К1ЛЛвХ,
at
перейдем от относительных координат к абсолютным и примем
8хвх = 8хвх1 — const.
Тогда
Ти + 6хвых = Л'бх^. (6 • 57)
at
где k' — коэффициент передачи или крутизны характеристики1.
Решая уравнение (6.57) относительно 6хвЪ1Х, получим
8xet/ix^k'8xexl (1 — е = 6хвыЛ(1 — е г«). (6.58)
График изменения 8хвЪ1Х при = const показан на рис. 6.12, а.
Продифференцируем 8хвых по времени
__t
-^- = 8хеых1-^е \ (6.59)
ги
1 Термин «коэффициент усиления» применяется для выражений в безраз-
мерных координатах. В размерных выражениях коэффициент k' называют коэф-
фициентом передачи (если он сам безразмерен) или крутизной характеристики
(если он имеет размерность).
210 Глава VI. Основные сведения о системах регулирования. Типовые звенья
При t — 0 получим
/ сЯХдыл \ _
\ dt Jt=Q Ти
Как это следует из рис. 6.12, а:
/ <1$>Хвых \ _
\ dt /i=o А В
Сравнивая правые части двух последних выражений, видим, что
отрезок АВ дает в масштабе величину Ти.
Используя свойство равенства подкасательных у экспоненты,
можно провести в любой точке касательную к кривой 8хвых(()
и точка пересечения касательной с прямой бхвыж = бХвиэл и проек-
ция точки касания на эту прямую определяют отрезок, равный по-
стоянной времени Ти (отрезок CD на рис. 6.12, а). Об этом свойстве
экспоненты следует помнить и использовать его особенно в тех слу-
чаях, когда мгновенное изменение входной координаты создать не
удается и начальный участок кривой бХвыхбО не соответствует экс-
поненте.
Можно получить более достоверное значение Ти, если опреде-
лить наклоны касательных в нескольких точках экспериментальной
кривой, т. е. для разных значений 6хвЪ1х и построить график в коор-
динатах
так, как это показано на рис. 6.12, б. Имея несколько эксперимен-
тальных точек на этом графике, проведем через них осредняющую
прямую, которая отсечет на оси d—отрезок ~выг-- , а на оси
dt Ти
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 211
бХвыж отрезок бХвыжь После этого, зная 6xewX/, определяем Ти- Осно-
ванием к такому определению является то, что из уравнения (6.57)
'г ,_ §Хвых
dt
при t = О
бхвых = О
и
J1 ~
/ ^Хдых \
\ dt Jt=o
Вернемся еще раз к выражению (6.58)
6хвк* = 6хвых1‘(1— е г«)
и найдем чему будет равно значение бхвыа: при t = Ти. Приняв
t ~ Т'и, ПОЛуЧИМ 6Xgbtx = dXg^jxi ИЛИ дХдых 0,63бХвих1
(см. рис. 6.12, а). Эту зависимость можно использовать для опре-
деления постоянной времени инерционного звена Ти без проведе-
ния касательной к экспоненте.
Коэффициент усиления инерционного звена k' определяется
из отношения k' = (см. рис. 6,12, а). Это следует из урав-
0*8X1
нения (6.57), в котором при t стремящейся к °о, —=0. Для
dt
перехода к коэффициенту усиления k, входящему в уравне-
ние (6.13), следует использовать принятые базисные величины. По-
лучим
хвыхБ
Колебательное звено. Возьмем уравнение колебательного звена
Т22 + Tt + дх = kKxex
dt* dt вых
и перейдем от относительных координат к абсолютным. Примем
<5хет = 6xexi = const. Уравнение звена примет вид
Т1 + 8х^ = k'8x^- (6-60)
dt* dt
Здесь k' — коэффициент передачи или крутизны характеристики.
В зависимости от соотношения постоянных времени колеба-
тельного звена Ti и Тг будет различие в переходном процессе
212 Глава VI. Основные сведения о системах регулирования. Типовые звенья
при скачкообразном изменении бХвяь Так, при Т f — 4Т j < 0 реше-
ние уравнения (6.60) имеет вид
Г т / 1 V
&хвыХ — k'&xexi 1 — е I cos at + sin atj ,
Рис. 6.13
где
2Tl 2„ V-H-f-r?
Г = —;» = _ = 2-,_
и т — период колебаний.
Переходный процесс устойчивого звена в этом случае представ-
ляет собой затухающие колебания (рис. 6.13).
Если же Tf — 4Tf >0, то решением уравнения (6.60) является
выражение
___t_ ____t
\ 1 х — 1 у 1 х — 1 у /
где
ТХ + ТУ = ТХ и тхту = т22.
Для этого случая переходный процесс звена апериодичен
(рис. 6.14).
Не приводя доказательств, ознакомимся для обоих случаев с
порядком определения коэффициентов, входящих в уравнение дви-
жения колебательного звена.
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 213
В первом случае, когда Zf —4Tj <0, по осциллограмме пере-
ходного процесса (см. рис. 6.13) необходимо определить период ко-
лебаний т и измерить амплитуды двух смежных колебаний Ai и Аг-
Постоянные времени Тг и определяются по формулам:
Т — - •
2 /5,3 (1g Д)г + 39,4 ’
т 4’6^А)Г*
1 т *
(6.61)
(6.62)
где А есть отношение амплитуд А — Аг/Ар Коэффициент усиления,
как и для инерционного звена, определяется из отношения
Во втором случае, когда Т‘ —>0, нужно провести каса-
тельную к кривой переходного процесса в точке ее перегиба (см.
рис. 6.14). Проекция этой касательной на прямую дхеыХ1 = const
определит два отрезка: ti и т2. Далее для 'Нахождения постоянных
времени Тг и следует воспользоваться вспомогательным графи-
ком, показанным на рис. 6.15. Зная величину Ti/t2, выбираем соот-
ветствующую этому отношению секущую и находим значения
Ту/хг и Тх/хг, а затем Ту и Тх. После этого определяем интересую-
щие нас величины
Т2 = Утхть-
(6.63)
214 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Т\ = Тх + Ту. (6.64)
Появление вспомогательных постоянных времени Тх и Ту объяс-
няется тем, что апериодический переходный процесс получается
при последовательном соединении двух инерционных звеньев с по-
стоянными времени Тх и Ти (рис. 6.16). Если рассматривать эти
два звена как одно сложное звено, то цго уравнение по форме бу-
дет совпадать с уравнением колеба-
тельного звена (6.21), у которого по- ох
стоянные времени Т2 и Л связаны
с постоянными времени инерцион-
ных звеньев соотношениями (6.63)
и (6.64).
Ь
Рис. 6.17
Рис. 6.16
Методом скачкообразного воздействия трудно воспользоваться
в том случае, когда Т f — 4Т^ < 0, но по абсолютному значению
эта разность близка к нулю. Для такого сочетания постоянных
времени Т2 и Т\ переходный процесс может иметь вид, подобный
показанному на рис. 6.17.
Дифференцирующее звено. Запишем уравнение дифференци-
рующего звена
л „ -- Т dkxex
^Хвых * диф
Если задать Ахвж = Axexi = const, то в момент времени t = О
производная - - = оо, а при t > 0 она равна нулю. Следова-
тельно, скачкообразное изменение входной координаты дифферен-
цирующего звена должно было бы привести к мгновенному бес-
конечно большой интенсивности всплеску в значении выходной
координаты. В действительности этого не получается, так как
реальные дифференцирующие звенья всегда имеют некоторое
инерционное запаздывание. Определить постоянную времени Tgu$
в уравнении (6.27) методом скачкообразного воздействия невоз-
можшо.
Если же принять, что дифференцирующее звено имеет некото-
рое инерционное запаздывание, то ему соответствует уравнение1
Ти^^- + бхвыг = Тдиф^-. (6.65)
at at
1 Это уравнение дифференцирующего изодромного звена. См. уравнение
(6.42).
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 215
Решая уравнение (6.65) относительно бХвих при бхвж = бхвж1 —
= const, получим
_______________________________________t
8хвых = ~^-8хм1е Т“ (6.66)
•* и
а при t = 0 5хех
^>хвых\=0 = 6хм1. (6.67) SXex’\
“ вх , ‘
График переходного процесса
дифференцирующего звена с запаз- I \
дыванием при скачкообразном воз- j \
действии показан на рис. 6.18. Из
графика следует, что касательная &
к экспоненте, проведенная через ^1^ \
точку при t = 0, дает возможность |_______\
определить Ти. Затем по величине ’ . г । | Г
первоначального всплеска выходной "
координаты определяется Тдиф. Рис. 6.18
Частотный способ
При использовании частотного способа определения динамиче-
ских коэффициентов типовых звеньев входная координата изме-
няется по гармоническому закону 6хвх = Xexsin at, или 8х0Х =
= Двжсоз(о^, где Авх — амплитуда, а со — частота колебаний. Уст-
ройства, с помощью которых достигается гармоническое измене-
ние бхвх, называемые датчиками колебаний, могут быть самыми
разнообразными и зависят главным образом от конструктивного*
оформления исследуемого звена. На рис. 6.19 показана схема
датчика колебаний при исследовании гидравлического сервомото-
ра с жесткой обратной связью. На этой схеме от электромотора /
вращается кулачок 2. Профиль кулачка подобран так, чтобы план-
ка 3, а с нею и рычаг исследуемого сервомотора колебались по
синусоиде. Изменение частоты колебаний со достигается измене-
нием скорости вращения электромотора. Изменение амплитуды Аех
обеспечивается путем перемещения кулачка 2 вдоль планки 3.
При изменении входной координаты по гармоническому закону
по такому же закону будет изменяться и выходная координата, но
только с некоторым сдвигом фазы колебаний на угол 0. На
рис. 6.20 дан примерный вид осциллограммы при частотных испы-
таниях. По ней непосредственно можно узнать период колебаний
т и сдвиг колебаний по времени te (на осциллограмме есть отмет-
ка времени), измерить амплитуды колебаний Авх и Авых. По этим
216 Глава VI. Основные сведения о системах регулирования. Типовые звенья
величинам определяем частоту колебаний ю = 2л/т рад/сек, угол
сдвига фазы колебаний 6 = (о/е= 2л -у рад и отношение амплитуд
Л4 = Авых/Авх.
Для каждого типового звена есть свои соотношения, с помощью
которых по известным М и 6 определяются постоянные времени и
коэффициенты усиления. Приведем эти соотношения.
Рис. 6.19 Рис. 6.20
Астатическое звено
М = ——; (6.68)
Таш
0 = —у. (6.69)
Инерционное звено М = ; V l+T’^2 tg 0 = — Тиа. (6.70) (6.71)
Колебательное звено k
М — (6.72)
У (1 —+ Ы0-
(6.73)
1 — Г2
Дифференцирующее звено (без инерционного запаздывания)
М = ТдифЫ)’, (6-74)
® =+т- (6.75)
§ 3. Экспериментальное определение коэффициентов уравнений звеньев 217
Рассмотрим вывод приведенных формул на примере вывода
формул (6.70) и (6.71) для инерционного звена. Исходное уравне-
ние инерционного звена (6.13)
т д = м
U 1 вил о Л
В этом уравнении следует положить \хвх = Arasin at или
Дхвх = Aexcos at и решить его относительно Дхвых. Примем такой
путь решения: входную координату будем изменять по закону
Лхад = Авхеimt , тогда, очевидно, выходная координата будет
комплексной величиной. Воспользуемся формулой Эйлера, дающей
связь между показательной и тригонометрическими функциями.
Имеем
Авд.е“и/ = Авх cos at 4- iAex sin at. (6.76)
Согласно принципу суперпозиции, если на линейную систему
регулирования действуют несколько возмущений, то переходный
процесс, вызванный этими возмущениями, равен алгебраической
сумме переходных процессов от отдельных возмущений. В нашем
случае возмущение по формуле (6.76) состоит из двух частей: из
вещественной и мнимой. Переходный процесс, вызванный ими,
также будет состоять из вещественной и мнимой частей. Тогда
можно сделать вывод, что вещественная часть решения уравнения
+ Ахвых = kAex e':mi (6.77)
at
явится решением исходного уравнения
Т„ + дх = kAex cos at. (6.78)
Ищем решение уравнения (6.77) в виде
bxe„x = W(ai)AexeM, (6.79)
где IF(cof)—комплексное число. Для его определения продиффе-
ренцируем уравнение (6.79) и сделаем подстановку в уравнение
(6.77).
Получим
iTaaWAexeimt + WAex ei,nt = kAex еы,
откуда
Освободясь от мнимости в знаменателе, найдем, что
W = R + iS, (6.81)
'218 Глава VI. Основные сведения о системах регулирования. Типовые звенья
где
р _ & .
1 + 7>з ’
(6.82)
kTu<s>
1 н- Л>2
(6.83)
5 =
Комплексное число W мож-
но представить в виде вектора
на комплексной плоскости
(рис. 6.21). Тогда
W = R + iS = М cos 0 +
+ iM sin 0 = М (cos 0 + i sin 6),
или
Г = Л1е!'е, (6.84)
где М = У R2 + S2— модуль комплексного числа W;
0 — его аргумент (tgQ = S/R).
Вернемся к выражению (6.79). Теперь
&хвых = AsxMe‘6e‘mt = АвхМУ"*+\
или
АхвыХ = АехЛ4 [cos (cof + 0) + i sin (cof -j- 0)]. (6.85)
Найденное значение Ахвых соответствует входному воздействию
. Поэтому вещественная часть правой части уравнения
(6.85) является решением уравнения (6.78). Следовательно, при
AXqx = AexCOS cof
Ахеых = АвхМcos (со/ 4- 0). (6.86)
Произведение АвхМ есть амплитуда колебаний выходной ко-
ординаты Авых. Откуда
М = ^-. (6.87)
АдХ
Зная, что М = У R2 + S2, а также учитывая (6.82) и (6.83), полу-
чим первую формулу для инерционного звена (6.70)
У1 + Т2^ ’
Из выражения (6.86) следует, что 0 есть сдвиг фазы колеба-
ний выходной координаты. Как это видно из рис. 6.21, tg 0 = S/R.
§ 4. Частотные характеристики типовых звеньев
219
Тогда, снова используя (6.82) и (6.83), получим вторую формулу
для инерционного звена (6.71)
tgO;=-7>.
Соответствующие зависимости для других типовых звеньев по-
лучаются аналогично.
§ 4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ
Как это следует из формул (6.68) — (6.75), для определения
коэффициентов, входящих в уравнение движения звена, нужно за-
дать изменение его входной координаты по гармоническому зако-
ну с какой-либо частотой и по найденным из эксперимента значе-
ниям М. и 0 найти искомые коэффициенты. В уравнение движения
колебательного звена входят три коэффициента: Т2, Т\ и k. Для их
определения необходимо провести эксперимент уже на двух раз-
личных частотах. В практике исследования элементов систем ав-
томатического регулирования может возникнуть и такая задача:
определить к какому типовому звену относится тот или иной эле-
мент системы и определить присущие ему коэффициенты. В этом
случае частотные испытания элемента должны быть проведены не
на одном или двух значениях, а для ряда значений частот измене-
ния входной координаты.
Вообще для получения удовлетворительной точности испыта-
ния любого элемента системы регулирования необходимо прово-
дить на ряде частот.
Можно поставить и обратную задачу: определить, как будут
меняться М и 0 звена данного типа, динамические коэффициенты
которого известны, при изменении частоты входной координаты
звена со. Здесь мы уже подходим к понятию частотных характе-
ристик типовых звеньев, которые наиболее полно отражают их
свойства.
Частотные методы исследования систем автоматического регу-
лирования разработаны очень подробно и нашли широкое приме-
нение в инженерной практике. В этой главе ниже рассмотрены
частотные характеристики типовых звеньев и построение частот-
ных характеристик системы регулирования по характеристикам
отдельных звеньев. Использованию частотных характеристик для
исследования устойчивости систем регулирования и определения
качества их переходного процесса посвящена значительная часть
гл. VII.
Будем рассматривать следующие частотные характеристики:
амплитудную, фазовую и амплитудно-фазовую. Находят примене-
ние также вещественные и мнимые частотные характеристики.
Амплитудной частотной характеристикой звена называется
характеристика М = /(со).
220 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Для астатического звена согласно формуле (6.68) это будет
гипербола (рис. 6.22, а). Для инерционного звена, как это следует
из формулы (6.70), при со = 0 величина М = k. Для достаточно
больших значений со, когда Г*со2 » 1, характеристика М = /(со)
близка к гиперболе (рис. 6.22, б).
Вид характеристики М = /(со) колебательного звена существен-
но зависит от соотношения постоянных времени Т\ и Т2.
В случае, если » Т2, характеристика М = f (со) колебатель-
ного звена напоминает по виду характеристику инерционного зве-
на: при со = 0 величина М = k, с увеличением со значение М не-
прерывно уменьшается. Однако, если увеличивать постоянную
времени Т2 или уменьшать 7\, характеристика колебательного
звена приобретает другой вид: с ростом со модуль М = /(со) снача-
ла возрастет, а затем при дальнейшем увеличении со, пройдя через
максимум, начинает быстро падать (рис. 6.22, в). Частота со =’
= соРез, при которой М = f (со) имеет максимум, называется резо-
нансной частотой. При некоторых значениях а> = апроп величины
М = /(со) астатического, инерционного и колебательного звеньев
становятся столь малыми, что ими можно пренебречь. Диапазон от
со = 0 до со = (Опроп, в котором изменение частоты заметно сказы-
вается на изменении М, называют диапазоном существенных ча-
стот, или диапазоном пропускаемых частот. Амплитудной частот-
ной характеристикой дифференцирующего звена является прямая,
проходящая через начало координат (рис. 6.22, г). Это следует из
формулы (6.74).
Фазовой частотной характеристикой звена называется харак-
теристика 0 = / (со).
У астатического звена выходная координата отстает по фазе от
входной координаты на угол 0 = —л/2 рад. Этот угол не зависит
от частоты со (рис. 6.23, а).
У инерционного звена, как это следует из формулы (6.71),
выходная координата отстает по фазе от входной координаты. Это
отставание возрастает с увеличением частоты со. При изменении
со от 0 до оо величина tg 0 изменяется от 0 до —оо. Следовательно,
угол 0 меняется от 0 до —л/2 (рис. 6.23, б).
§ 4. Частотные характеристики типовых звеньев
221
Для колебательного звена сдвиг фазы выходной координаты по
отношению к входной координате определяется формулой (6.73).
Из этой формулы следует, что с ростом со от 0 до оо величина
tg 0 изменяется сначала от 0 до —о° и затем от +°о до 0. Откуда
видно, что выходная координата по фазе отстает от входной и
угол 0 с ростом со меняется от 0 до —л (см. рис. 6.23, в).
У дифференцирующего звена выходная координата по фазе
опережает входную на угол +л/2. Это следует из формулы (6.75)
и показано на рис. 6.23, г.
Амплитудно-фазовой частотной характеристикой называется
характеристика Л1 = )(0). Для ее построения можно использовать
характеристики М — f(co) и 0 = f(co). Для какой-либо частоты
со величина М в виде вектора в полярных координатах отклады-
вается так, чтобы направление М с положительным направлением
оси абсцисс составляло угол 0, соответствующий данной частоте.
Концы векторов М, построенные таким путем для различных со,
соединяются между собой. Обычно на характеристике M =
указывается, каким значениям со соответствуют отдельные точки
кривой. Не трудно убедиться, что амплитудно-фазовая характери-
стика М = f (0) • есть годограф комплексного числа W, которое как
это видно из выражения (6.79), связывает выходную координату
звена с входной координатой, если на входе в звено осуществляется
воздействие вида Авхе ‘mt. Это комплексное число согласно уравне-
нию (6.84) и рис. 6.21 может быть представлено на комплексной
плоскости в виде вектора с модулем М, образующего с положи-
тельным направлением вещественной оси угол 0.
Выражение (6.79) носит общий характер и может быть приме-
нено к любому типовому или сложному звену.
222 Глава VI. Основные сведения о системах регулирования. Типовые звенья
У астатического звена амплитудно-фазовая частотная характе-
ристика (в дальнейшем ее будем называть амплитудно-фазовой
характеристикой) располагается на отрицательной части мнимой
оси комплексной плоскости так, как это показано на рис. 6.24, а.
Амплитудно-фазовая характеристика инерционного звена охва-
тывает четвертый квадрант комплексной плоскости и является
правильной полуокружностью (рис. 6.24, <б). В этом легко убе-
диться, проверив, что вектор есть среднее пропорциональное
между диаметром полуокружности, равным k, и проекцией векто-
ра All, на диаметр, равный AliCOsOi.
Амплитудно-фазовая характеристика колебательного звена
охватывает четвертый и третий квадранты комплексной плоскости
(рис. 6.24, в). При со = 0 годограф вектора М лежит на вещест-
венной оси, модуль вектора равен k. При со, стремящейся к <х>,
модуль вектора стремится к нулю, годограф заканчивается в на-
чале координат.
У дифференцирующего звена амплитудно-фазовая характери-
стика располагается на положительной части мнимой оси
(рис. 6.24, г). При со = 0 величина А! = 0, а при со, стремящейся к
оо, значение М также стремится к оо.
Вещественной частотной характеристикой называется характе-
ристика /? = /(со). Она может быть получена как расчетным пу-
тем, так и путем перестроения экспериментальной амплитудно-фа-
зовой характеристики М — f(0). При расчетном построении харак-
теристики R = /(со) для каждого типового звена может быть полу-
чена расчетная формула. Так, например, для инерционного звена»
такой формулой является формула (6.82)
_ k
R== 1 + '
Если имеется экспериментальная амплитудно-фазовая характе-
ристика звена, то на ней нужно взять ряд точек, для которых от-
мечены значения со. Проведя в эти точки характеристики векторы
4. Частотные характеристики типовых звеньев
223
из начала координат и проектируя их на вещественную ось,
строим характеристику R = f(a).
Мнимой частотной характеристикой называется характеристика
5 =/(со). Она строится аналогично вещественной’ частотной ха-
рактеристике. Так, для инерционного звена расчетной формулой
будет формула (6.83)
е kT„U>
При использовании экспериментальной амплитудно-фазовой
характеристики векторы, проведенные из начала координат, про-
ектируются на мнимую ось.
Передаточная функция
Введем понятие передаточной функции. Передаточной функ-
цией звена называется отношение изображения по Лапласу вы-
ходной координаты к изображению входной координаты. При со-
ставлении передаточных функций изображения производных бе-
рут для нулевых или естественных начальных условий. Поэтому
передаточная функция легко может быть получена из уравнения
движения звена и наоборот. Так, например, если уравнение инер-
ционного звена в операторной форме имеет вид
(7> + 1) АхвыЛ = k\xex,
то его передаточной функцией будет
П (s) = -^вых - =-----, (6.88)
Ахзл. Тus 4- 1
где Ахвж и Ахвыж —изображения входной и выходной координат.
Передаточные функции составляются не только для отдельных
звеньев, но и для групп звеньев и для системы регулирования в
целом. Передаточную функцию можно рассматривать как форму
описания соотношения между выходным и входным сигналом.
Если переменную s в выражении для передаточной функции зве-
на заменить на сос, то полученное новое выражение будет соот-
ветствовать амплитудно-фазовой характеристике звена. В этом
не трудно убедиться на примере того же инерционного звена. При
замене в уравнении (6.88) переменной s на coi получим выраже-
ние (6.80)
W = ----------.
г«(“0 + 1
Как мы уже выяснили, годограф комплексного числа W при из-
менении со от 0 до оо является амплитудно-фазовой характери-
стикой звена.
224 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Частотная характеристика разомкнутой системы регулирования
Возьмем два последовательно расположенных звена (рис. 6.25)
•и на первое из них окажем воздействие вида Дхвх1 =Лвхе1Ш< . На
выходе из первого звена получим
^euxl = AexWie^;
Рис. 6.25
где Выходная координата первого звена одновре-
менно является входной координатой второго звена. Поэтому вы-
ходная координата второго звена
&хвых2 ^AexWxW2eimt,
где
W2 = М2е'\
Предположим теперь, что звенья 1 и 2 образуют одно сложное
звено, обведенное на рис. 6.25 пунктирной линией. Если входная
координата сложного звена Дхвж = Авхем , то его выходная
координата
Ахвых = A,xWeint.
Очевидно, что комплексное число
W = WtW2 = °2).
Комплексные числа и представленные в виде годогра-
фов на комплексных плоскостях, являются частотными характери-
стиками звеньев. Их произведение, равное W, будет частотной ха-
рактеристикой сложного звена.
Чтобы найти произведение двух комплексных чисел, их модули
М следует перемножить, а аргументы 0 сложить. Если заданы ча-
стотные характеристики двух звеньев, то для построения характе-
ристики сложного звена на характеристиках звеньев следует взять
ряд точек с равными значениями со, найти соответствующие им
М и 0 и произвести умножение. Затем по найденным значениям
М = MiM2 и 0 = 01 + 02 отложить на плоскости векторы и пост-
роить по концам этих векторов годограф. На рис. 6.26, в показана
§ 5. Экспериментальное определение коэффициентов уравнений двигателей 225
характеристика сложного звена, построенная по характеристикам
входящих в него инерционного (рис. 6.26, а) и колебательного
(рис. 6.26, б) звеньев. Характеристика этого сложного звена охва-
тывает три квадранта.
Очевидно, что сложное звено может состоять не из двух, а
из любого количества звеньев. Порядок построения частотной ха-
рактеристики останется тем же. Поэтому, если разомкнутая систе-
ма регулирования задана в виде цепочки последовательно распо-
ложенных звеньев, амплитудно-фазовая характеристика всей
разомкнутой системы регулирования определится как произведе-
ние амплитудно-фазовых характеристик входящих в нее звеньев..
В заключение этого раздела отметим, что свойства типовых
звеньев и составленных из них разомкнутых систем регулирования
существенно зависят от частоты изменения входной координаты и
не зависят от изменения ее амплитуды. Эта особенность является
принадлежностью только линейных систем автоматического регу-
лирования.
§ 5. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ,
ВХОДЯЩИХ В УРАВНЕНИЯ ДВИЖЕНИЯ ДВИГАТЕЛЕЙ,
КАК ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
Определение динамических свойств ТРД представляет доста-
точно сложную техническую задачу. Рассматривая ТРД как ли-
нейное звено, целесообразно исследовать его по числу оборотов и
8 Черкасов Б. А.
226 Глава VI. Основные сведения о системах регулирования. Типовые звенья
по силе тяги, используя в качестве регулирующего фактора изме-
нение расхода топлива.
Для проведения подобных экспериментов на полноразмерном
.двигателе его удобно оборудовать автономной системой питания,
.действующей параллельно основнойНа рис. 6.27 показана по-
добная система питания с плунжерным насосом, приводимым во
вращение от электромотора, с помощью которой исследовался на-
турный ТРД с центробежным компрессором.
Снабженный дополнительной системой питания, двигатель за-
пускается обычным путем, работает на своей собственной системе
питания и выводится на нужный режим. Затем включается насос
автономной системы питания, но топливо в ней с помощью пере-
крывного крана 3 закольцовывается и в двигатель не поступает.
Для перевода двигателя на автономную систему питания необхо-
димо перевести в другое положение стоп-кран 1 и связанный с ним
перекрывной кран. До переключения в автономной системе пита-
ния нужно установить расход и давление, соответствующее вы-
бранному режиму работы двигателя. Давление топлива регули-
1 Если основная система питания двигателя включает регулятор расхода
топлива, то можно обойтись без создания автономной системы питания.
§ 5. Экспериментальное определение коэффициентов уравнений двигателей W
руется краном 2, расход топлива—изменением наклона шайбы
насоса 8, связанной через шток сервопоршня и рычаг с электромо-
тором 4. При правильном подборе давления и расхода топлива
перевод двигателя на автономную систему питания происходит
достаточно плавно. Перед выключением двигатель опять перево-
дится на основную систему питания.
При работе двигателя на автономной системе питания можно
изменять расход топлива. Скачкообразное изменение расхода дос-
тигается резким изменением положения наклонной шайбы соле-
ноидом 7. Расход топлива по гармоническому закону изменяется
кулачком 6 и электромотором 5. Изменением скорости вращения и
положения кулачка создаются переменные расходы с различными
частотами и амплитудами. ТРД обладает сравнительно небольшим
диапазоном пропускаемых частот. Поэтому верхний предел часто-
ты возмущающих гармонических колебаний в системе топливопи-
тания может не превышать 8 ч-10 рад/сек. Желательно, чтобы
были достижимы наименьшие частоты порядка 0,15-4-0,2 рад!сек.
Запись на больших частотах малых значений амплитуд ис-
следуемого параметра представляет большую трудность. Однако
нельзя рекомендовать идти на увеличение амплитуд входа по мере
повышения частоты колебаний. ТРД является нелинейным объек-
том и всякое увеличение амплитуды уменьшает точность получен-
ных динамических коэффициентов. В связи с этим следует отме-
тить особенность автономной системы питания, показанной на
рис. 6.27. При неизменной скорости вращения ротора насоса 8
амплитуда входных возмущений с увеличением частоты не толь-
ко не возрастает, но даже немного уменьшается вследствие
влияния изменения амплитудной характеристики топливной аппа-
ратуры.
Величина расхода топлива определяется по значению давления
в топливный магистрали перед форсунками. Можно считать, что
при малом изменении расхода, когда амплитуда колебаний не пре-
вышает 8-4-10% от-установившегося режима, вполне допустимо
линейное представление зависимости расхода топлива от давле-
ния. Возможность такой линеаризации подтверждается расчетом
и экспериментом.
Измерение силы тяги при частотных испытаниях ТРД имеет
некоторую специфику. Для измерения необходимо, чтобы какой-
либо элемент конструкции в силовой установке под действием
силы тяги мог перемещаться или деформироваться. В случае ис-
пользования деформации элементов конструкции (например,
стальных колец, обладающих линейной деформацией) в качестве
датчика силы тяги удобно применять проволочные преобразова-
тели (тензодатчики). Нельзя допускать, чтобы составляющая силы
от вибрации центра тяжести массы двигателя во время его работы
проходила через тензодатчик. Нельзя также допускать переме-
8*
228 Глава VI. Основные сведения о системах, регулирования. Типовые звенья
щения центра тяжести массы двигателя в направлении изменения
силы тяги.
При обработке данных эксперимента следует учитывать дина-
мические характеристики элементов измерительной цепи от датчи-
ка до осциллографа и вносить соответствующие поправки на изме-
нение амплитуды и сдвиг фаз. Для этого необходимо предвари-
тельно снять частотную характеристику измерительной цепи.
Дополнительное запаздывание получится за счет времени, идуще-
го на сгорание частицы топлива, попавшей в камеру сгорания. Это
запаздывание приводит к
некоторому завышению
постоянной времени дви-
гателя. Для проведения
численной обработки ос-
циллограммы записыва-
ются два-три статических
режима, для которых
фиксируется число оборо-
тов, давление и расход
топлива.
В гл. II было приведе-
но уравнение (2.55) ТРД
как объекта регулирова-
ния по силе тяги
(Tgp+l)\R = (TGp + kG)bG.
Входящий в него коэффициент усиления kG равен коэффициен-
ту усиления kg в уравнении (2.25).
Передаточная функция инерционного звена с производной, со-
ответствующая уравнению (2.55), имеет вид
П, - IgiJ. feg
дк Tas -ъ 1
(6.89)
Величина угла 0 при построении амплитудно-фазовой характе-
ристики определяется из выражения
tg 0 ------------£_. (6.90)
| Гр гр
Из уравнений (6.89) и (6.90) видно, что амплитудно-фазовая
характеристика ТРД как объекта регулирования по силе тяги рас-
полагается в четвертом квадранте. При со = 0 модуль М = kG •-=
= kg и угол 0 = 0, при со = оо модуль М. = TGITd, угол 0 = 0.
Амплитудно-фазовая характеристика по ЛА1 так же, как и по Л/г,
должна иметь вид полуокружности, сдвинутой относительно нача-
Примеры
229
ла координат. Исследования двигателя ВК-1А, проведенные
В. И. Новиковым [14], это хорошо подтвердили. Они также пока-
зали, что при больших частотах амплитудно-фазовая характери-
стика ТРД по Дм захватывает третий квадрант, т. ё. отставание по
фазе выходной координаты больше л/2 (рис. 6.28). Для двигателя
ВК-1А на режиме п = 10000 об/мин были найдены значения Та =
= 0,99 сек; TG — 0,37 сек и kG = ka = 1,19.
Немонотонное запаздывание выходной координаты Д/?, прохо-
дящее через максимум, объясняется тем, что изменение тяги, дви-
гателя зависит от изменения температуры газа и расхода воздуха,
т. е. числа оборотов ротора. Изменение температуры газа можно
считать безынерционным. Поэтому, когда при достаточно боль-
ших частотах изменения расхода топлива амплитуда изменения
числа оборотов ротора становится малой, изменение тяги зависит
главным образом от изменения температуры. В конце диапазона
пропускаемых частот инерционного запаздывания тяги двигателя
по расходу топлива уже не наблюдается.
ную
камеру
От компрессора | Из
Рпор'пор
В
• • •
От клапана
постоянного
даВления
Рис. 6.29
Примеры
Пример 1. На рис. 6.29 показана принципиальная схема регулятора подачи
форсажного топлива в ТРД. Регулятор состоит из чувствительного элемента /,
выполненного в виде мембраны с рычагом
и плоским клапаном 3, и гидравлического
сервомотора 5. С одной стороны мембраны
подводится регулируемое давление р4, а
с другой — давление рх (часть давления
р2 ) При перемещении задатчика 2 дав-
ление Рх изменяется. В одну из полостей
цилиндра сервомотора подводится давле-
ние топлива рф, поступающего в форсаж-
ную камеру. Его величина пропорциональ-
на расходу форсажного топлива (р$ =
= k}G$, где й]—коэффициент пропорцио-
нальности). В другой полости сервомотора
давление топлива будет ниже, так как с од-
ной стороны эта полость соединена с напор-
ной топливной магистралью через жиклер
4, а с другой стороны через плоский кла-
пан 3 рычага чувствительного элемента I
она соединена с давлением слива, которое
условно принимается равным нулю. Требу-
ется вывести уравнение движения поршня
гидравлического сервомотора.
Вывод уравнения движения начнем с
выбора направления отсчета координат.
Примем за положительные значения коор-
динат изменение параметров регулятора,
*
вызванное увеличением р4, т. е. перемеще-
ние мембраны вниз, плоского клапана вверх, сервопоршпя влево. За положитель-
ное направление изменения давлений топлива в различных полостях и каналах
и расхода топлива примем их увеличение. Обозначим перемещение мембраны
6Л, плоского клапана бг, сервопоршпя бу.

230 Глава VI. Основные сведения о системах регулирования. Типовые звенья
При выводе уравнения пренебрежем массой сервопоршня, поскольку силы,
действующие в гидравлическом сервомоторе, обычно значительно больше сил
инерции. Тогда условие равенства всех сил, действующих на поршень, будет
FnotPnof + Р — Fipa — O. В этом уравнении Fnop площадь сервопоршня;
Рпор—давление топлива в полости сервопоршня; Р— сила пружины сервопорш-
ня; Fi — площадь сервопоршня со стороны дозирующей иглы; р$ — давление
топлива за дозирующей иглой.
Условие равенства сил можно записать в приращениях. Тогда оно будет
иметь вид *
Fnop^Pnop Р}Ър$ = 0,
где В — жесткость пружины.
Приращение брпор найдем, рассмотрев условие неразрывности жидкости
в полости сервомотора. В положении равновесия сервопоршень находится в не-
подвижном состоянии и количество топлива Qx, притекающего через жиклер 4,
равно количеству топлива Qn.n, вытекающего через плоский клапан 3. Поэтому
QwcO ” Qn-кО-
При движении сервопоршня уравнение расхода будет иное, так как изме-
няется объем полостей цилиндра сервомотора. В силу неразрывности количество
топлива Q, соответствующее этому изменению, должно добавиться в зависимо-
сти от направления движения сервопоршия либо к Q&, либо к Qn.n.
Расход топлива Q, связанный с движением сервопоршня, определится как
произведение площади сервопоршня на скорость его перемещения. При движе-
нии поршня в сторону увеличения координаты у это топливо, как и все топливо,
притекающее через жиклер 4, должно пройти через плоский клапан 3. Уравнение
неразрывности будет иметь вид
doy
О.ж + Fnop = Qn.K,
где 0ж и Qn-к могут быть определены по формулам истечения
Qw: ~ afx V Рф Рпор
Qn.K ~ afn.K VРпор.
Здесь а — коэффициент пропорциональности;
}ж — площадь проходного сечения жиклера;
1п.к — площадь проходного сечения плоского клапана.
При записи уравнения расхода через плоский клапан давление слива принято
равным нулю.
РаСХОДЫ Q^. И Qn.K ЯВЛЯЮТСЯ НеЛИНеЙНЫМИ ФУНКЦИЯМИ От Рпор, Р<Д И fn.K,
поэтому необходимо произвести их линеаризацию:
QjiC — Qq/co “Г 1 f dQw: \ _д0ж_\ □ 1 “Ap+I -4 1 *PnOp> \ дрф V дрпор . о
Qn.K = Qn.K<) + ( dQn.K \ / dQn.K \ do Wnop+ 1 d, \ °Pnop / 0 \ °ln.K /0
Частные производные
дОж \ . / dQw \ , / dQn.K \ . / dQn к \
дрф /о \ дрпор / о \ дРпор / о \ dfn.K I
Примеры
231
найдем из формул истечения:
/ ___________af ж_______ ___
1 дрф (Рф Рпор}й
дЧж \ ______________а1ж_________
дРпор / 0 2 ~}F (рф Рпор)о
/ ^Чп.к \ п.к О
\ дРпор / о V Рпорр
dQn.K \ г-----------
дг I — а V Pnopo'—kt,
а1п.к /0
где k2, k3, k4 — сокращенное обозначение соответствующих производных. Так
как dfn-к пропорционально бг, следовательно, и б/i (бг и б/i связаны между со-
бой через отношение плеч рычага), то можно написать 6fn.* = k^&h, где k3 —
коэффициент пропорциональности.
Подставив линеаризованные выражения Q-ж и QnK в уравнение неразрывно-
сти и учтя, что Q-,.o = Qn-ко, найдем
к26рф— (k2 + k3) 8рпор + Fnop
Решив это уравнение совместно с уравнением равновесия сервопоршня (ис-
ключив координату брпор) и используя связь между р$ и GgfSp# — k^G#), по-
лучим уравнение гидравлического сервомотора
Fnop d8y
kt-~k3 dt
4- В&у = Fnop 8h + lF ~r— +klFl ) Мф,
K2 + «3 \ K2 + «3 /
пли в безразмерных координатах
Fnop dby ktk5 FnophB
—Д и — j-.
B(k2-\-k3) dt ' У k2 + k3 ВуБ
fei
В
' k2FnOp \
----- ~7,—
k2+kj Уб ф
Следует отметить, что поршень сервомотора в данной схеме регулятора яв-
ляется инерционным звеном, хотя жесткой обратной связи между ним и управ-
ляющим элементом нет. Это свойство поршня обусловлено пружиной, помещен-
ной в цилиндре сервомотора.
Пример 2. Осциллограмма частотного испытания элемента регулятора на
одной частоте показала, что выходная координата сдвинута по фазе по отно-
шению к входной координате на угол — л/2. Можно ли отсюда сделать вывод,
что испытуемый элемент регулятора по своим динамическим характеристикам
относится к астатическому звену?
Чтобы ответить на поставленный вопрос необходимо снять хотя бы еще одну
характеристику элемента регулятора на частоте, отличной от частоты первого
испытания. Если сдвиг фаз вновь будет равен — л/2, то испытуемый элемент
относится к астатическому звену.
Пример 3. Были проведены частотные испытания поршневого гидравличес-
кого сервомотора, выполненного по схеме рис. 6.5. Осциллограмма показала, что
при периоде колебаний, равном 5 сек, выходная координата отстает по фазе на
0,5 сек. Отношение амплитуд выходной координаты к входной равно 0,8. Опре-
делить постоянную времени и коэффициент усиления сервомотора.
232 Глава VI. Основные сведения о системах регулирования. Типовые звенья
Испытуемый сервомотор согласно схеме рис. 6.5 имеет жесткую обратную
связь. Поэтому относим его к инерционному звену и применяем для подсчета
постоянной времени и коэффициента усиления формулы (6.70) и (6.71).
Определяем частоту колебаний
2л
ш =-----
т
—- — 1,26 рад/сек
5
и угол сдвига фаз
/й 0,5
О = 2л — = 2л —= 0,628 рад.
т 5
По формуле (6.71) находим постоянную времени
Используем формулу (6.70) для вычисления коэффициента усиления
k = м\/~ 1 + ГцШ2 = 0,8 V 1 4- 0,7252 = 0,99.
Пример 4. Построить амплитудно-фазовые частотные характеристики коле-
бательного и инерционного звеньев, заданных уравнениями
(0,01р2 4- 0,5р 4- 1) Дхеыл. = 2Дхвл-
И
(0,5р т 1) Дхвыл' — ^Хвх-
Для колебательного звена выражением частотной характеристики является
0,01 (шг)2 4-0,5ш1 4~ 1 ’
Представляя комплексное число W в виде суммы вещественного и мнимого
чисел W = R + iS, найдем, что
________2 (1 — 0,01о>2) __ 2 0,5о>_
(1—0,01 <1)2)2 4- 0,25(1)2 Н (1 —0,01(1)2)2 -(-0,25<1)2 ’
Задаемся рядом значений о) и определяем для каждого из них R и S. Например,
для ю = 1 величины R = 1,61 и 5 = —0,81. Затем на графике с координатами
R, S отмечаем точки, соответствующие различным ы, и соединяем их между
собой. Характеристика колебательного звена показана на рис. 6.30, а.
Выражением частотной характеристики для инерционного звена является
1
№ = п к . , . , откуда
0,5ш1 4- 1
1 0,5ш
Д =-------------- и S = —-------1.
1 4-0,25«)2 1 + 0,25о)2
Построенная по этим расчетным формулам характеристика показана па
рис. 6.30, б.
Пример 5. Два звена, колебательное п инерционное, частотные характеристи-
ки которых приведены на рис. 6.30, а и б, соединены последовательно. Построить
графоаналитическим путем частотную характеристику совокупности этих двух
звеньев как одного сложного звена.
На заданных характеристиках звеньев нужно взять точки с разными часто-
тами, из начала координат провести в эти точки векторы и измерить их модули
и углы наклона к вещественной оси. Произведя перемножение модулей и сложе-
Примеры
233
Рис. 6.31
234 Глава VI. Основные сведения о системах регулирования. Типовые звенья
ние углов, построить полученные векторы в координатах R, S и соединить их
концы плавной кривой (рис. 6.30, в). Характеристика заданного сложного звена
должна охватить три квадранта. Однако диапазон существенных частот у него
мал и поэтому характеристика практически охватывает только два квадранта.
Пример 6. Подача топлива в ТРД дозируется с помощью регулятора расхода
с баростатическим корректором, максимальное число оборотов двигателя ограни-
чивается регулятором-ограничителем лтах. Конструктивная схема регулятора
показана на рис. 5.40. Составить структурную сх^му системы регулирования.
Рис. 6.32
В структурной схеме нужно отразить два контура регулирования: незамкну-
тый контур регулирования подачи топлива и замкнутый контур ограничения
«шах. Сервомотор является общим исполнительным органом для обоих конту-
ров. Кроме этого на схеме должны быть показаны обратная связь регулятора
расхода, воздействие двигателя на производительность топливного насоса и уп-
равления двигателем с помощью дроссельного крана. Структурная схема системы
регулирования показана на рис. 6.31.
Пример 7. Составить структурную схему для ТРД с регулятором, выполнен-
ным по схеме рис. 5.39 (аналогично показанной на рис. 6.31).
Система имеет два замкнутых контура регулирования, изодромный регулятор
числа оборотов и регулятор расхода, работающий при п<.Пнлр. Регулятор
расхода поддерживает постоянный перепад давления на дроссельном кране, ры-
чаг управления воздействует одновременно на дроссельный кран и на настройку
регулятора числа оборотов.
Структурная схема дана на рис. 6.32, на пей раздельно показаны чувстви-
тельный и управляющий элементы регулятора расхода. Конструктивно они объ-
единены в одном золотнике.
Глава VII
МЕТОДЫ РАСЧЕТА И ИССЛЕДОВАНИЯ
ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В ЛИНЕЙНОЙ СИСТЕМЕ РЕГУЛИРОВАНИЯ
По заданным уравнениям движения типовых звеньев состав-
ляется уравнение системы регулирования: сначала для разомк-
нутой системы, а затем для замкнутой системы. Рассмотрим поря-
док составления дифференциального уравнения разомкнутой си-
стемы регулирования на частном примере, используя для этой
цели систему, структурная схема которой показана на рис. 6.2.
Она состоит из двигателя, чувствительного элемента и гидравли-
ческого сервомотора. Для этой системы характерно расположе-
ние входящих в нее звеньев цепочкой. За выходную координату
примем Апвыж, за входную — Апвж. Второй входной координатой
будет изменение положения упора пружины муфты чувствитель-
ного элемента, с помощью которого изменяется настройка регу-
лятора (считаем, что внешних воздействий на двигатель нет). Бу-
дем полагать, что положение упора пружины есть некоторая
функция времени f(t).
Координаты Az и Ат, входящие в уравнения движения чувст-
вительного элемента и гидравлического сервомотора, являются
промежуточными и их следует исключить. В соответствии с выво-
дами, сделанными в гл. II и VI, выпишем уравнения (2.19), (6.18)
и (6.25):
(Тд,нр + 1) \пвыХ =
(Т ср + 1) Am = &cAz;
(Т2р2 + Тгр + 1) Az = k41\nex + k42f(t).
Для исключения промежуточных координат Az и Ат достаточ-
но перемножить соответственно левые и правые части этих трех
уравнений, после чего промежуточные координаты сокращаются.
Получим {Т2р2 + Tip + 1} {Т'Р + {Тднр + 1}
— k4lkckd.H^flex -|- k^kgkd.nf (f) (J • 1)
236 Глава VII. Методы расчета и исследования динамических характеристик
или
(а4р4 + а3р3 4- а2р2 + агр 4- а0) \пвых = ЬйЛпвх + cof (t), (7.2)
где
а4 = TlTcTd.H- а3 = Т22 (Тс + Т8.н) + TJJa.^
~ Т2 4~ Т1Тс 4* Т-jT-fe- Т СТа.к;
а1 = + Тс 4~ Тд.н, «о—!»
&о = k41kJia.H, Cq == k43kck8,n.
Уравнение (7.2) есть уравнение вынужденного движения
разомкнутой системы регулирования, показанной на рис. 6.2, по-
скольку изменение во времени координаты \пвых зависит от зако-
нов изменения входных координат Лпвх и f(i).
Для перехода к уравнению замкнутой системы регулирования,
как это было показано в гл. VI, следует приравнять \пвх =
= —Дпвых. Тогда получим уравнение вынужденного движения
замкнутой системы регулирования (индекс при координате Дп от-
брасываем)
[(Tip2 + т1Р +1) (Тср + 1) (Тд.нр + 1) + (7-3)
или
(а4р4 + азР3 4- йгР3'+ «хР 4- «о) \п = cof (t). (7.4)
Сравнивая между собой левые части уравнений (7.1) -4- (7.4),
убеждаемся, что переход от разомкнутой к замкнутой системе ре-
гулирования не изменяет коэффициенты при производных. Ме-
няется только коэффициент при регулируемой координате.
В нашем примере для разомкнутой системы регулирования аораз =
= 1, а для замкнутой системы аОзам = 1 + k4ikcka.H.
Удобнее рассматривать не вынужденное, а свободное движение
системы регулирования. Под свободным движением системы по-
нимается такое движение, когда на систему регулирования ни-
какие внешние силы воздействия не оказывают. Эти силы, выводя-
щие систему регулирования из состояния равновесия, действуют
раньше, а к началу отсчета времени их действие прекращается
и движение системы происходит только под действием внутренних
сил. Число видов вынужденного движения системы регулирования
не ограничено, так как любому закону изменения входной коорди-
наты будет соответствовать свой вид вынужденного движения.
Закон свободного движения для каждой системы регулирования
только один.
Отсутствие внешних воздействий при свободном движении
математически означает, что правая часть уравнения движения
системы равна нулю. Поэтому для нашего примера уравнение
§ 2. Методы исследования устойчивости линейных систем регулирования 237
свободного движения разомкнутой системы регулирования будет
иметь вид
(Т22р2 + Т1Р - 1) (Тср Ч- 1) (Тд.нр + 1) Апвых = 0 (7.5)
и для замкнутой системы регулирования
[{Tip2 + Т1Р + 1) (Г ср + 1) (Тд.нр + 1) + k41kckd.H\ Ап = 0. (7.6)
Как это следует из уравнений (7.5) и (7.6), форма уравнения
свободного движения разомкнутой или замкнутой системы регули-
рования не изменится, если его составлять относительно других
координат. При вынужденном движении вид правых частей диф-
ференциальных уравнений зависит от того, в каком месте размы-
кается система регулирования и какие внешние воздействия при-
ложены в месте размыкания. Особенности уравнений движения
разомкнутой и замкнутой систем регулирования, находящихся
в свободном или вынужденном движении, показаны на примере
конкретной системы регулирования. Аналогично могут -быть со-
ставлены уравнения для систем регулирования с любым числом
звеньев, расположенных цепочкой.
§ 2. МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
ЛИНЕЙНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
Понятие устойчивости системы регулирования
Изменение высоты или скорости полета вызывает нарушение
равновесного режима работы двигателя. За этим нарушением
следует восстанавливающее действие регулятора и в системе регу-
лирования возникает переходный процесс или процесс регулиро-
вания.
Процесс регулирования считают устойчивым, если система
регулирования, будучи выведена из состояния равновесия, после
устранения внешних воздействий возвращается (после неограни-
ченного промежутка времени) к исходному положению равновесия
и остается в этом положении. Устойчивость системы, является
обязательным требованием, предъявляемым к системе автоматиче-
ского- регулирования. Собственная устойчивость двигателя и дру-
гих звеньев, входящих в систему регулирования, устойчивость
системы в разомкнутом состоянии еще не достаточны для устой-
чивости системы регулирования в замкнутом состоянии.
Как это следует из определения, данного в начале этого пара-
графа, при анализе устойчивости рассматривается свободное
движение системы. За исходное уравнение свободного движения
-примем уравнение вида
„ dn\x , dn~xkx , , d&x , * n /-7
an + an— i----:—H •.. + #!—-—F a0Ax —- 0. (7.7)
dtn dtn~x dt
238 Глава VII. Методы расчета и исследования динамических характеристик
Ему соответствует характеристическое уравнение
ап№ + ап-\кп~1 4-...+ аЛ + ао = 0. (7.8)
Общим решением уравнения (7.7) будет сумма частных
решений
п
Ах (0 = С1е^ >
i=\
где Ci, C2...Cj...Cn—постоянные интегрирования, а Хь
Х.2... Kj... Хп — корни характеристического уравнения. Рассмот-
рим возможные виды корней характеристического уравнения и их
влияние на какое-либо частное решение уравнения (7.7).
Допустим, что Xj = ctj есть вещественный корень. Частное реше-
ние уравнения (7.7)
Дху =Cje У —С^А.
Если а3 < 0, то при t-+<x>, е->0, а это означает, что при неогра-
ниченном возрастании времени величина Дх3->0 (рис. 7.1, а). При
а, > 0 в случае неограниченного возрастания времени t величина
Дх3-—> оо (рис. 7.1,6). Если же а3 = О, то величина Дх3 = С,
остается неизменной (рис. 7.1 в).
Предположим, что А.3 есть комплексный корень, т. е. Х3 = а3 +
+ (»ji. Тогда среди остальных корней характеристического уравне-
ния (7.8) существует корень Хл, являющийся комплексно сопря-
женным корнем относительно корня Х3, т. е. Хл='а3— ®3i. Рас-
смотрим сумму двух частных решений
Дхл = Дху + ДхЛ = +Cke^ = С^+ш^ + Cfte(a>~“/K.
В этом выражении коэффициенты С3 и Ch являются комплексно
сопряженными числами Cj = А — IB и Ch. = А + iB. Преобразуем
выражение Дх^, введя вместо показательной функции е±,ш
§ 2. Методы исследования устойчивости линейных систем регулирования
239
тригонометрическую cos со ± i sin со. После преобразования полу-
чим
\xjh = 2 /Л2 + В2еа/ sin (9 + со/), (7.9)
д
где 9 = arctg —.
В
Вид функции Axjh(f) зависит от знака а,. При а, < 0 это будут
затухающие колебания (рис. 7.2, а), так как с увеличением време-
ни t амплитуда 2 ]/а2 + В2 непрерывно уменьшается. В слу-
чае, если aj > 0, это будут расходящиеся колебания с непрерывно
возрастающей амплитудой (рис. 7,2, б). При щ = 0 будут незату-
хающие колебания с амплитудой 2 V А2 + В2 (рис. 7.2, в).
Вернемся снова к общему решению уравнения (7.7)
Дх/)= Е С,ех'‘.
/='
Проделанный анализ говорит о том, что Дх(/) при неограничен-
ном воэрастании времени t только в том случае будет стремиться
к нулю, если к нему будет стремиться каждое частное решение
уравнения (7.7). Последнее возможно лишь при условии, что все
вещественные корни и вещественные части комплексно сопряжен-
ных корней будут отрицательны. Если хоть один из вещественных
корней будет равен нулю, то величина Дх(0 с течением времени
2'40 Глава VII. Методы расчета и исследования динамических характеристик
будет стремиться к постоянному значению, отличному от нуля.
В этом случае система регулирования будет находиться на границе
апериодической устойчивости. Если же хоть у одной пары ком-
плексно сопряженных корней .вещественные части будут равны ну-
лю, т. е. корни будут чисто мнимыми, величина &x(t) по мере уве-
личения I будет стремиться к колебаниям с постоянной амплиту-
дой. В этом случае система регулирования будет находиться на
границе колебательной устойчивости.
Таким образом, для устойчивости системы регулирования не-
обходимо и достаточно, чтобы все вещественные корни и вещест-
венные части комплексно сопряженных корней характеристическо-
го уравнения были отрицательны.
"Эти выводы справедливы для линеаризованных уравнений,
полученных в результате разложения нелинейных характеристик
в ряд Тейлора и отбрасывания всех членов разложения, содержа-
щих отклонения координат в степенях, выше первой. Можно ли
выводы об устойчивости линеаризованных систем распространить
на реальные системы? Общее определение устойчивости движения
было дано в 1892 г. А. М. Ляпуновым в его работе «Общая задача
об устойчивости движения». Пользуясь теорией Ляпунова, можно
строго обосновать законность линеаризации дифференциальных
уравнений движения и решить ряд нелинейных задач, возникаю-
щих в области регулирования. Однако по линеаризованным урав-
нениям нельзя судить о том, что происходит на границе устойчи-
вости системы или вблизи ее. Поэтому в практических задачах
нельзя допускать, чтобы характеристические уравнения, кроме
корней с отрицательной, вещественной частью, имели нулевые или
чисто мнимые корни.
Критерии устойчивости
Прямой путь определения устойчивости системы заключается
в решении характеристического уравнения и в определении знаков
вещественных частей его корней. Но это легко сделать только
в том случае, если степень характеристического уравнения не пре-
вышает третью. Решения характеристических уравнений более
высоких степеней вызывает затруднения. Поэтому надо искать
пути, дающие возможность определить устойчивость системы регу-
лирования без решения ее характеристического уравнения.
Можно отметить некоторые необходимые, но еще недостаточ-
ные признаки устойчивости системы регулирования по виду харак-
теристического уравнения. Так, в характеристическом уравнении
n-й степени все коэффициенты до а0 должны быть отличны от
нуля. Если, например, коэффициент а0 = 0, то один, из корней
характеристического уравнения равен нулю и система регулирова-
ния будет находиться на границе апериодической устойчивости.
§ 2. Методы исследования устойчивости линейных систем регулирования 241
Необходимо также, чтобы все коэффициенты характеристического
уравнения были одного знака. Этого второго признака вместе
с первым достаточно для- устойчивости систем регулирования,
описываемых дифференциальными уравнениями второго порядка,
но недостаточно для систем/движение которых определяется урав-
нениями более высоких порядков.
Существуют способы, дающие возможность определять знаки
вещественных частей корней характеристических уравнений
любой степени без их решения и тем самым определять устойчи-
вость систем регулирования. Условия, при которых все корни
характеристического уравнения имеют отрицательную веществен-
ную часть, в теории автоматического регулирования называются
критериями устойчивости.
Критерий Раута — Гурвица
В 1877 г. Раут предложил, метод исследования систем на устой-
чивость, описываемых линейными дифференциальными уравнения-
ми с постоянными коэффициентами. Критерий Раута был дан
в форме алгоритма, т. е. в виде правила, определяющего последо-
вательность математических действий, необходимых для решения
задачи.
Условия устойчивости, вытекающие из критерия Раута, можно
представить в виде неравенств, содержащих коэффициенты харак-
теристического уравнения (даются без доказательств).
Для системы, имеющей характеристическое уравнение
а2Х2 4- ахХ 4- а0 = О,
необходимые и достаточные условия устойчивости имеют вид
а2 > 0; <?0>0- (7.10)
Для системы с характеристическим уравнением
+ а,/2 + ах\ + а0 = 0
необходимые и достаточные условия устойчивости записываются
в виде
а3 > 0; а, > 0; а-, >0; ап > 0; )
\ ’ (7.11)
a2a1 — a3a0>0. J
Для системы, имеющей характеристическое уравнение
а?-4 + а3>-3 + а2).2 + ах\ + а0 = 0,
необходимые и достаточные условия устойчивости приобретают
вид
а4>0; а3>0; <?2>0; ах>0; а0 > 0;1 _
(а2ах — а3а0)а3 — а4а2 > 0. J ;
242 Глава Vff. Методы расчета и исследования динамических характеристик
Аналогичные неравенства, определяющие условия устойчивости
систем с характеристическими уравнениями более высоких степе-
ней, будут усложняться по мере повышения степени характери-
стического уравнения.
В 1895 г. швейцарский математик Гурвиц установил условия,
при соблюдении которых все вещественные части корней уравне-
ния отрицательны. Критерий Гурвица отличается от критерия
Раута только по форме.
В общем случае уравнения n-й степени (7.8)
ап\п + + ап_2Х'’-2 +... + + а0 = О
вещественные части его корней будут отрицательны, если при по-
ложительных коэффициентах уравнения ап, an_x,... аь а0 будут
также положительны определитель А и его п — 1
нальныё миноры Дь Д2,... Дп-ь
Определитель
art_ian_3>i ап_5 ' | О
। । 1 ।
&п &п—2 ! &п—4 1 • • • • • • - О
-------д ( 1 ;
О ап—1 ап—з [ । >
I 1 !
Д =
......................а21 а0 J О
----------------------------1 ।
......................а3 «1 i О
------------------------------------1
главные диаго-
(7.13)
О....................а4 а2 а0
составляется в следующем порядке. Сначала заполняется главная
диагональ от верхнего левого угла, начиная с коэффициента ап-ь
до нижнего правого угла с коэффициентом а0. Затем заполняются
столбцы определителя: вниз от коэффициентов главной диагонали
идут коэффициенты с увеличивающимся индексом, а вверх —
с уменьшающимся индексом. Свободные места в- столбцах после
коэффициентов ап и а0 заполняются нулями. Главные миноры Дь
Д2 •.. Дп-1 внутри определителя Д выделены штриховыми линиями.
Критерий Михайлова
В 1938 г. А. В. Михайлов предложил критерий устойчивости,
нашедший широкое применение. Рассмотрим доказательство этого
критерия. Пусть уравнение (7.8) является характеристическим
уравнением системы. При подстановке в него вместо X любого из
корней Xi, Х2... левая часть уравнения обращается в нуль.
Если же значения X не будут совпадать с корнями характеристи-
§ 2. Методы исследования устойчивости линейных систем регулирования
243
ческого уравнения, то левая часть уравнения будет отлична от
нуля. Поэтому для общности обозначим через ДХ) многочлен,
составляющий левую часть уравнения (7.8)
f (X) = ап\п + + ап_2Х"-2 +... + + а* (7.14)
Этот же многочлен можно написать в другой форме
f(k) = an(k-X1)(k-k2)...(k-kn_1)(k-k„). (7.15)
Рассмотрим свойства многочлена ДХ), придав чисто мнимые
значения переменной X, т. е. приняв, что X = сои'.
Тогда
f (cw) = ап (<м)п + а„_1 (со/)"-1 +... + аг (coi) + а0, (7.16)
или
(<oz) = ап (<£ri — Хх) (coi — Х2)... (<вг — Ху). .. (coz — Х„_!) (<в г — Х„). (7.17)
Предположим, что нам известны корни характеристического
уравнения (7.8) Xi, Хг,... Xj... Хп- Для общности рассуждений
примем, что корень Х> является комплексным числом. Тогда раз-
ность см — Х3- может быть представлена как разность двух векто-
ров на комплексной плоскости. В случае отрицательной вещест-
венной части корня Х3-(а3- < 0) эта разность показана на рис. 7.3, а,
в случае положительной (Х3- >0) — на рис. 7.3, в.
Пройдем всю мнимую числовую ось, задаваясь значениями со
от —оо до + оо. При этом обнаружим, что вектор, соответствую-
щий разности сог — Xj, в пределе повернется по абсолютному зна-
чению на угол л: в положительном направлении (против часовой
стрелки), если корень Х, имеет отрицательную вещественную часть
Глава VIf. Методы расчета и исследования динамических характеристик
(рис. 7.3,6) и в отрицательном направлении (по часовой стрелке),
если вещественная часть корня Xj — положительна (рис. 7.3,г).
В соответствии с выражением (7.17) комплексное число f(o>i)
может быть представлено на комплексной плоскости как произве-
дение п векторов. Известно, что для получения произведения
комплексных чисел их модули перемножаются, а аргументы сум-
мируются. Если все п корней характеристического . уравнения
имеют отрицательную вещественную часть (устойчивая система
регулирования), то каждый из п векторов coi— Х3- при измене-
нии о от —оо до + оо повернется на угод +л. Тогда вектор,
соответствующий комплексному числу повернется в поло-
жительном направлении на угол + пл. Если же хоть один из
корней характеристического уравнения имеет положительную
вещественную часть или же корень будет чисто мнимым, угол
поворота вектора f(coi) при изменении со от —оо до +оо будет
меньше пл.
Для определения положения вектора / (<oi) на комплексной
плоскости удобнее воспользоваться выражением (7.16), отделив
в нем вещественную часть от мнимой. Тогда можно записать
f (coi) = А -|- iB. (7.18)
В выражении (7.18) А есть функция четных степеней со, а В —
нечетных. В силу этого А (со) = А (—со).
Вместо совокупности векторов удобнее воспользоваться годо-
графом вектора f(coi), который будет симметричен относительно
вещественной оси. Поэтому можно рассматривать диапазон со
только от 0 до +оо.
При изменении со от 0 до оо у устойчивой системы регулирова-
ния вектор f(a>i) повернется на угол +п
л
Т
а его годограф, на-
зываемый годографом Михайлова, беря свое начало на веществен-
ной оси (при со = 0 f(<ai) = aa), последовательно охватит такое
количество квадрантов, каков порядок дифференциального урав-
нения.
Если же система регулирования неустойчива (не все корни
характеристического уравнения имеют отрицательную веществен-
ную часть), последовательность охвата годографом квадрантов
комплексной плоскости нарушается.
В качестве примера на рис. 7.4, а показано протекание годо-
графа вектора f(coj) для характеристического уравнения 4-й степе-
ни устойчивой системы регулирования (даны обе ветви годогра-
фа). На рис. 7.4,6 показан один из возможных видов годографа
для характеристического уравнения той же степени, когда система
регулирования неустойчива.
Дадим теперь формулировку критерия Михайлова. Система
регулирования будет устойчива в том случае, если годограф век-
§ 2. Методы исследования устойчивости линейных систем регулирования 245
тора полученный путем замены переменной X в характери-
стическом уравнении системы на <oi, беря свое начало при <о = О
на положительной вещественной оси, при изменении со от 0 до +оо
последовательно пройдет в положительном наиравлении, т. е.
против часовой стрелки, т^кое количество квадрантов, какова
степень характеристического уравнения.
У устойчивой системы регулирования годограф вектора f(©i)
последовательно пересекает вещественную и мнимую оси комплек-
сной плоскости. Эту последовательность легко проследить, если
построить зависимость от <о вещественной части А (со) и мнимой
части В (и) комплексного числа f(coi) согласно уравнению (7.18).
Нарушение в последовательности пересечения осей является при-
знаком неустойчивой системы.
На рис. 7.5 дано изменение А (и) и В (со) для устойчивой
(рис. 7.5, а) и неустойчивой (рис. 7.5, б) систем регулирования
,4-го порядка, годографы которых были ранее показаны на
рис. 7.4, а и 7.4, б. Критерий Михайлова применим как для разом-
кнутых, так и для замкнутых систем регулирования.
Амплитудно-фазовый критерий устойчивости
По виду амплитудно-фазовой характеристики разомкнутой си-
стемы регулирования можно судить об ее устойчивости в замкну-
том состоянии. Метод, дающий возможность проводить подобные
246 Глава VII. Методы расчета и исследования динамических характеристик
суждения, был предложен в 1932 г. Найквистом применительно
к радиотехническим системам при исследовании усилителей
с обратной связью. В 1938 г. А. В. Михайлов показал возможность
применения метода Найквиста для исследования систем автомати-
ческого регулирования.
Амплитудно-фазовый критерий устойчивости формулируется
следующим образом: для того чтобы система регулирования, устой-
чивая в разомкнутом состоянии, была устойчивой и в замкнутом
состоянии, необходимо и достаточно, чтобы годограф вектора
амплитудно-фазовой частотной характеристики разомкнутой систе-
мы W (cot) не охватывал бы точку с координатбй—1 (см.
рис. 7.6, а) на вещественной оси. Этот критерий устойчивости
легко доказать, если исходить из доказанного выше критерия
устойчивости Михайлова.
Уравнение движения системы в разомкнутом состоянии может
быть записано в виде
D (р) ^Хеых = С (р) Дхм, (7.19)
где D(p) и С(р) —полиномы от р. В реальных системах степень С
не превышает степени D.
Запишем также уравнение свободного движения разомкнутой
системы
^(Р)Л-^ = О (7.20)
и характеристическое уравнение
Д(А)=0. (7.21)
Для исследования разомкнутой системы на устойчивость с по-
мощью критерия Михайлова переменную А, нужно заменить на
fpaM-DM- (7-22)
Перейдем теперь к замкнутой системе регулирования для чего
в уравнении (7.19) приравняем Лхвых = —Дхвж. Тогда получим
уравнение свободного движения замкнутой системы
[Р(р) + С(р)]Дх = 0 (7.23)
и соответствующее ему характеристическое уравнение
D (А).+С (X) = 0. (7.24)
Для построения годографа Михайлова замкнутой системы так-
же заменим в уравнении (7.24) переменную А, на cot
+ (7.25)
Разделим уравнение (7.25) на уравнение (7.22)
fsQM (<oi) _ Р(<ог) + С (tot) _ j j С (tot)
fpaa^i) D (tot) D (tot) ’
§ 2. Методы исследования устойчивости линейных систем регулирования 247
отношение есть амплитудно-фазовая характери-
D (юг)
стика разомкнутой системы регулирования, которую считаем за-
данной графически.
Поэтому
b™ (t0Q. = I + w (coi). (7.26)
fpa.3 (®0
Для некоторого значения со = <о3' величина W (atji) представ-
ляется вектором на комплексной плоскости, который нужно сло-
жить с вектором +1 (рис. 7.6, а). Такое сложение вектора +1
с рядом векторов W(ai) для различных значений со приведет
к параллельному сдвигу на +1 годографа амплитудно-фазовой
характеристики. Однако годограф вектора ?зам можно получить
f раз
более простым путем, не проводя дополнительных построений. Для
этого достаточно на графике амплитудно-фазовой характеристики
перенести-начало координат в точку —1 так, как это показано на
рис. 7.6, б.
248 Глава VII. Методы расчета и исследования динамических характеристик
Из формулировки критерия Михайлова следует, что век-
тор fpas(wt) системы регулирования, устойчивой в разомкнутом
состоянии, при изменении со от 0 до +оо повернется на угол +«-у-
При замыкании системы степень характеристического уравнения
осталась неизменной, так как было принято, что степень полино-
ма С(р) не превышает степени полинома' D(p). Поэтому, если
система регулирования остается устойчивой и в замкнутом состоя-
нии, вектор при изменении со от 0 до +оо также повер-
нется на угол +птр При делении комплексных чисел-аргументы
вычитаются, отсюда результирующий угол поворота вектора
= 1 + W (cot)
fpas (“О
при изменении со от 0 до +оо равен нулю, как это показано на
рис. 7.6, в. Действительно, при изменении со от со = 0 до со = coi
этот вектор повернется на угол —а, при изменении со от coi до соз
на угол +а, при изменении со от соа до со3 на угол +р и при изме-
нении со от со3 до со = оо на угол —р. Результирующий угол равен
—а + а+ р — р = 0. Такой результат будет получаться во всех
случаях, когда амплитудно-фазовая характеристика системы не
охватывает точку —1 на вещественной оси.
На рис. 7.6, г показана амплитудно-фазовая характеристика
системы, устойчивой в разомкнутом состоянии, охватывающая
точку —1 на вещественной оси. Не трудно убедиться, что в этом
случае результирующий угол вектора f3aM(coi)/fpa3(coi) при изме-
нении со от 0 до +оо не будет равен нулю. Это означает, что при
замыкании система регулирования теряет устойчивость. Когда
-амплитудно-фазовая характеристика разомкнутой системы про-
ходит через точку —1, это означает, что при замыкании система
находится на границе устойчивости.
Влияние прямого запаздывания на устойчивость
В гл. IV при выводе уравнения ПВРД как объекта регулирова-
ния было введено понятие прямого запаздывания. Как уже было
сказано, его влияние на характер переходного процесса сказывает-
ся в том, что изменение выходной координаты начинается лишь
спустя время т после изменения входной координаты. Переходная
функция смещается в этом случае на величину т по оси времени
передаточная функция имеет вид Пзап = е-" . Фазовый угол, соот-
ветствующий прямому запаздыванию, отрицателен и равен 0 =
= —тсо. Амплитудно-фазовой характеристикой звена, содержащего
только прямое запаздывание, является окружность, на ней в отри-
цательном направлении отмечаются частоты, определяемые равен-
§ 2. Методы исследования устойчивости линейных систем регулирования 249
ством 0 ~ —т<о. Каждая точка этой окружности соответствует бес-
конечному множеству значений частот (рис. 7.7), однако в реаль-
ных системах регулирования обычно играют роль только частоты,
соответствующие первому обходу окружности. Звенья, содержащие
только прямое запаздывание, практически встречаются редко.
Чаще звенья с прямым запаздыванием встречаются в сочетании со
звеньями, вносящими в переходный процесс отставание или опере-
жение по фазе.
Если система регулирования состоит из последовательного со-
единения звеньев, вносящих отставание или опережение по фазе,
со звеном прямого запаздывания, то передаточная функция такой
системы будет иметь вид
П = (7.27)
Р(з)
где C(s) и £>(s) —полиномы от $. Амплитудно-фазовая характе-
ристика такой разомкнутой системы как бы деформируется и пре-
вращается в спираль, охватывающую начало координат: векторы
характеристики С(<ог)/У? (сог), не изменяя своего модуля, повора-
чиваются по часовой стрелке на углы сот, пропорциональные со.
Деформированная характеристика дана на рис. 7.8. На этом
рисунке, так же как на рис. 7.9 и 7.10, она условно показана
охватывающей конечное число квадрантов. В действительности
деформированная характеристика — бесконечная спираль, стяги-
вающаяся к началу координат.
Как показал Я. 3. Цыпкин, амплитудно-фазовый критерий
устойчивости может быть распространен и на системы с прямым
запаздыванием. При некотором значении времени запаздывания т
амплитудно-фазовая характеристика С (ai)/D (cot) может деформи-
роваться настолько, что новая кривая, соответствующая характе-
ром) —.
ристике ——-в , пройдет через точку —1, т. е. система регу-
D(o)z')
лирования окажется на границе устойчивости. При деформации
250 Глава VII. Методы расчета и исследования динамических характеристик
характеристики С (cot)/.О (cot) модули векторов не изменяются. По-
этому в точку —1 на вещественной оси может попасть лишь тот
вектор, у которого до поворота модуль был равен единице. Чтобы
определить, какие векторы могут попасть в точку —1, следует про-
вести окружность радиусом, равным единице, с центром в начале
координат. Точки пересечения этой окружности с амплитудно-
фазовой характеристикой С(<вг)/£)(<вг) покажут те векторы, кото-
рые после поворота могут
попасть в точку —1.
Рассмотрим случай, ког-
да окружность с радиусом,
равным единице, только
один раз пересекает ампли-
тудно-фазовую характери-
стику (см. рис. 7.9). Пусть в
точке пересечения В часто-
та равна сов, а аргумент век-
тора ОВ равен 0(<вв)- Оче-
видно, что если система в
результате влияния прямого
запаздывания будет нахо-
диться на границе устойчи-
вости, то это произойдет
при частоте <»в- Поэтому на-
Рис. 7.9
зовем ее критической частотой сокр = <»в- Определим, каково долж-
но быть время прямого запаздывания т = ткр, чтобы при частоте
<акр ~ а>в система регулирования находилась на границе устойчи-
вости. Если при деформации аМплитудно-фазовой характеристики
вектор О В совпадает с вещественной осью и будет равен —1, то
аргумент этого вектора может быть равен —л, —Зя ... —л(1 + 2га).
Тогда,, учитывая, что фазовый угол прямого запаздывания отрица-
телен, можно записать
0 (®w) — ТКр°\р = — л (1 + 2га),
откуда
0 (юкр) + л U+ 2ft) по,
т,_ ------------------(7. zo)
кр ®кр
Здесь п = 0; 1; 2 ...
Приравнивая <вкР = сов и полагая п — 0, по формуле (7.28)
находим наименьшее время прямого запаздывания ткР1, при кото-
ром система будет находиться на границе устойчивости:
0.(?в) "Ь51
'крт. ~
“в
(7.29)
Полученное значение ткР1 следует сравнить с т звена прямого
запаздывания. Если т < ткрь то после деформации амплитудно-
§ 2. Методы исследования устойчивости линейных систем регулирования 251
. С (coi) —,
фазовая характеристика ........е не охватит точку —1,
D (coi)
и, следовательно, система регулирования в замкнутом состоянии
останется устойчивой (рис. 7.10, а). При т = тхР1 деформированная
характеристика пройдет через точку —1 и система будет на гра-
нице устойчивости (рис. 7.10,-б), а при т > rxpi система буде^ не-
устойчивой, так как деформированная характеристика охватит
точку —1 (рис. 7.10, в).
Если в формуле (7.28) задаться другим значением п, например
п — 1, получим новое значение хкр, назовем его хкрг, оно равно
в (“в) + 3я
Т«р2 —
ШВ
(7.30)
Очевидно, что тхР2 > тхрь Если при тхР1 < т < тхР2 система теряла
устойчивость, то она будет неустойчива и при т > тхрг. Характе-
ристика системы для этого случая показана -на рис. 7.1Q, г.
Следовательно, для нашего примера, когда окружность с ради-
усом, равным единице, только один раз пересекла амплитудно-
фазовую характеристику C(a>i)/D(a>i), условием устойчивости
будет т < тхРь Этот вывод справедлив для характеристик обычно-
252 Глава VII. Методы расчета и исследования динамических характеристик
л С(0) ,
го типа, у которых при «в = 0 отношение > 1, а при <в->оо
С (<ог) п
отношение —— -+ 0.
D (ы
Мы рассмотрели влияние прямого запаздывания на устойчи-
вость достаточно простой системы, у которой амплитудно-фазовая
характеристика охватывает всего два квадранта. Интересно от-
метить, - > ? с~рм'1ат“тьное влияние на устойчивость прямого
запаздывания может проявляться в еще более простой системе,
состоящей из одного инерционного звена и звена прел;сто запазды-
вания. Если инерционное звено будет иметь большой коэффициент
усиления, то для потери устойчивости достаточно небольшого
времени запаздывания.
Могут встретиться более сложные случаи, когда окружность
с радиусов, равным единице, дважды пересекает амплитудно-
фазовую характеристику (рис. 7.11). В этом случае с ростом вре-
мени запаздывания т получится чередован-, -а по ткр полос устойчи-
вости и неустойчивости (рис. 7.12). Оно прекратится" только при
достаточно большом значении т, когда система окончательно
станет неустойчивой.
Определение областей устойчивости
При разработке систем регулирования может получиться так,
что для анализа устойчивости будут составлены уравнения
звеньев, входящих в систему, но не для всех звеньев могут быть
найдены точные значения коэффициентов. Так, например, на
практике встречаются трудности при определении постоянной
времени двигателя или коэффициента вязкого трения и чувстви-
тельном элементе.
Возникает вопрос, в каком диапазоне можно допустить изме-
нение того или иного коэффициента без потери устойчивости
$ 2. Методы исследования устойчивости линейных системы ре':,.' -53
системы регулирования? Иногда появляется необходимость внести
некоторые конструктивные изменения в регулятор, например, из-
менить соотношение плеч рычага обратной связи или жесткость
пружины сервомотора и т. п. Сохранится ли при этом устойчи-
вость системы? Ответы на эти* вопросы в ряде случаев могут быть
получены путем определения областей устойчивости системы.при
изменении одного или двух параметров, входящих в коэффициен-
ты дифференциального уравнения системь! регулирования.
Диаграмма Вышнеградского
Впервые задача построения области устойчивости по парамет-
рам, зависящим от коэффициентов дифференциального уравнения,
была поставлена и решена И. А. Вышнеградским в 1874 г. Его
исследования относятся к системам регулирования, движение
которых описывается дифференциальными уравнениями 3-го по-
рядка. Возьмем характеристическое уравнение 3-й степени
а3к8 + а2Х2 ф- аг~к *{- а0 = 0, (7.31)
у которого as > 0; а2 > 0; ах > 0 и а0 > 0.
Преобразуем это уравнение так, чтобы вместо четырех коэф-
фициентов, в общем случае могущих принимать различные значе-
ния, остались только два. Для этого разделим все члены уравнения
на а0 и введем новую переменную
V Оо
После преобразования получим
?з + Х<р2 + у?+ 1 = о, (7.32)
где
X = °2 1 •
i/лЦ2’ (7-33)
V \ав J
у = ai 1
а° ,7"^ ’ (7.34)
V а0
Приняв X и У за переменные, Вышнеградский нашел граничные
значения этих переменных, при которых вещественная часть кор-
ней уравнения (7.32) еще является отрицательной. В плоскости
X, У граничной кривой, отделяющей область устойчивости системы
254 Глава VII. Методы расчета и исследования динамических характеристик
от области, где она устойчивостью не обладает, является равно-
бокая гипербола (рис. 7.13). Ее уравнение У = 1/Х.
Граничную кривую в плоскости X, У можно найти и с помощью
критерия устойчивости Раута — Гурвица. Действительно, по этому
критерию для устойчивой системы 3-го порядка справедливо не-
равенство XY — 1 > 0, а для неустойчивой XY — 1 < 0. Когда
система находится на границе устойчивости, XY —1=0, т. е.
в этом случае получаем уравнение гиперболы. Поле диаграммы
Вышнеградского можно разбить на несколько областей. Области
I, II и III, приведенные на рис.'7.13, являются областями устой-
чивости. В области I переходные процессы являются апериодиче-
скими. В области II они носят монотонный характер, а в обла-
сти III — колебательный. Вид переходного процесса, определяемый
расположением корней характеристического уравнения на комп-
лексной плоскости, показан в каждой из этих областей. В обла-
сти IV, хотя она и лежит в первом квадранте, процессы являются
расходящимися.
Устойчивость системы характеризуется положением определяю-
щей точки с координатами X, У, найденным по коэффициентам
характеристического уравнения с помощью выражений (7.33)
и (7.34).
§ 2. Метода исследования устойчивости линейных систем регулирования 255
Метод D-разбиения
Общий метод построения областей устойчивости для систем
регулирования, движение которых описывается дифференциальны-
ми уравнениями любых порядков, разработали А. А. Соколов
и Ю. И. Неймарк. Он получил название метода .О-разбиения.
Этот метод дает возможность выделить области устойчивости
по одному или двум параметрам. Этими параметрами могут быть
коэффициенты дифференциального уравнения процесса' регулиро-
вания, постоянные времени или коэффициенты усиления отдель-
ных звеньев, входящие в уравнение линейно. Рассмотрим сущность
метода .D-разбиения по одному параметру и покажем его. практи-
ческое применение.
Допустим, что дано характеристическое уравнение системы
регулирования
апкл4- ап_\Кп—х + • • • 4~ • - • -{- <2i/1-|-ao=O,
(7.35)
все коэффициенты которого, кроме коэффициента а-„ известны.
Требуется определить область значений а,, при которых система
будет устойчива.
Предположим, что мы можем решить характеристическое
уравнение (7.35). Тогда, задавшись каким-либо значением коэф-
фициента aj, найдем корни уравнения и (расположим их на ком-
плексной плоскости. Пусть корни разместятся справа и слева от
мнимой оси (рис. 7.14, а), что будет являться признаком неустой-
чивости системы.
Задаваясь подобным образом самыми разнообразными значе-
ниями коэффициента aj и решая характеристическое уравнение,
убедимся, что его корни будут перемещаться по комплексной
плоскости. Интересен момент, когда какая-нибудь пара комплекс-
но-сопряженных корней или какой-либо вещественный корень
будут находиться на мнимой оси. В этом моменту комплексно-
сопряженные корни будут чисто мнимыми корнями, а веществен-
ный корень будет равен нулю (рис. 7.14,6).
256 Глава VII. Методы расчета-и исследования динамических характеристик
При незначительном изменении коэффициента а,- в ту или
другую сторону эти корни перейдут в левую или правую полу-
плоскость. Переход их в левую полуплоскость приблизит систему
к состоянию устойчивости.
Если рассматриваемая система обладает устойчивостью, то при
некотором значении коэффициента aj все корни уравнения, за ис-
ключением одной пары корней или за исключением одного корня,
расположатся в левой полуплоскости, а оставшаяся пара или один
корень будут находиться на мнимой оси (рис. 7-. 14, в). Этот случай
наиболее интересен, система находится на границе устойчивости,
малейшее изменение в определенном направлении значения коэф-
фициента aj может сделать ее устойчивой. Приведенное рассужде-
ние позволяет отметить важность момента перехода корней урав-
нения из правой полуплоскости в левую.
Поставим теперь иную задачу. Рассмотрим, как будет меняться
коэффициент характеристического уравнения aj, если его корни
будут чисто мнимыми. Для этого решим уравнение (7.35) относи-
тельно aj и положим X = <вг:
aj~ (ы) ' ( ?
Правую часть выражения (7.36) можно освободить от мнимо-
сти в знаменателе и представить ее в виде обычного комплексного
числа
aj = Л (со) + IB (а). (7.37)
Пробежим всю мнимую числовую ось, задаваясь различными
значениями со от —оо до + оо. Получим ряд значений числа aj.
Это число можно представить в виде годографа на комплексной
плоскости. Этот годограф, симметричный относительно веществен-
ной оси, будет являться отображением мнимой оси плоскости
корней на плоскость aj.
Выше была отмечена • важность перехода корней из правой
полуплоскости в левую. Чтобы удобнее было за этим следить,
с левой стороны мнимой оси сделаем штриховку (рис. 7.15,а).
Подобную штриховку сделаем и на годографе в плоскости aj.
Левая сторона здесь будет определяться направлением течения
годографа при изменении со от со = —оо к со = +оо (рис. 7.15,6).
Годограф, проведенный в плоскости aj, разбивает эту плоскость
на несколько областей. На рис. 7.15,6 они обозначены I, II; III
и IV. Внутри каждой области изменение коэффициента aj не при-
водит к переходу корня из одной полуплоскости в другую. Это
значит, что каждой такой области соответствуют определенные
количества корней слева и справа от мнимой оси.
Будем рассуждать так: пусть в области I будет находиться m
корней характеристического уравнения (7.35) с отрицательной
§ 2. Методы исследования устойчивости линейных системы регулирования 257
Вещественной частью, тогда их число в других областях опреде-
лится особенностями пересечения годографа при переходе из
одной области в другую. Так, в соответствии с рис. 7.15, б, в обла-
стях II и IV число корней с отрицательной вещественной частью
должно быть на один корень больше, чем в области I, т. е. m + 1.
Это следует из того, что при переходе из области I в область II
или в область IV происходит переход с незаштрихованной сторо-
ны годографа в заштрихованную. На том же основании можно
Рис. 7.15
сказать, что в области III число корней с отрицательной вещест-
венной частью будет меньше на один корень по сравнению
с числом корней в области I, т. е. m— 1.
Таким образом, в областях II и IV находится наибольшее
число корней характеристического уравнения с отрицательной
вещественной частью. Эти области претендуют на то', чтобы быть
областями устойчивости, уж если при каких-то значениях систе-
ма будет устойчива, то эти значения щ лежат в областях II и IV.
Коэффициенты уравнений движения систем регулирования есть
вещественные числа. Поэтому в областях II и IV, претендующих
на устойчивость, нужно выделить отрезки вещественной оси, т. е.
из всей совокупности значений а, выделить их вещественные зна-
чения. В дальнейшем следует взять какие-либо значения коэффи-
циента aj в пределах выделенных отрезков вещественной оси
области II и области IV, подставить их в. характеристическое
уравнение (7.35) и с помощью любого критерия устойчивости
убедиться, что области II и IV действительно являются областями
устойчивости.
При построении годографа в плоскости a-j важно определить
точки пересечения его с вещественной осью. Для этого использует-
ся уравнение (7.37), в котором многочлен В (со) приравнивается
нулю. Решением уравнения В (<в) = 0 находятся значения <о, при
которых происходит пересечение годографа с вещественной осью.
9 Черкасов Б. А.
258 Глава VII. Методы расчета и исследования динамических характеристик
Для этих же значений «в определяются граничные значения =
= Д(<в), отделяющие одну область в плоскости годографа а, от
другой. Далее рассматриваются только области, претендующие на
устойчивость. Если проверка с помощью критериев устойчивости
покажет, что в точках пересечения годографа с вещественной осью
на границах областей система регулирования находится на грани-
це устойчивости, то внутри этих областей она устойчива.
§ 3. МЕТОДЫ ОЦЕНКИ КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА
В ЛИНЕЙНЫХ СИСТЕМАХ РЕГУЛИРОВАНИЯ
Общие соображения по оценке качества переходного процесса
Нельзя ограничиться только определением устойчивости систе-
мы регулирования. Важно знать, какой характер переходного
процесса вызывает в ней внешние воздействия, или, как говорят,
каково качество регулирования. Качество регулирования иссле-
дуется только у устойчивых систем регулирования.
Вид переходного процесса зависит от характера внешних воз-
действий и от места их приложения. Для системы автоматического
регулирования ТРД следует рассматривать влияние возмущающе-
го воздействия, приложенного к двигателю, и управляющего воз-
действия, приложенного к регулятору. Если задано уравнение
движения замкнутой системы регулирования
(апрп + an^ipn~l +... + alP + au)I\x = f(t), (7.38)
то за внешнее воздействие f(t) при исследовании системы регули-
рования принимают единичную ступенчатую функцию: при t < О
функция f(t) = 0 и при функция f(t) = 1 (рис. 7.1'6, а).
Тогда уравнение (7.38) примет вид
(апрп + an-ipn'~l + ... + а1р + а0)Дх = Дхт (7.39)
Внешнее воздействие Д%1 = 1 вызовет в системе регулирования
переходный процесс, являющийся переходом от старого (Дх = 0
при I — 0) к новому статическому режиму, характеризуемому
величиной Дх(оо). В общем виде он показан на рис. 7.16, б. Строго
говоря, переход к новому статическому режиму совершается за
бесконечно большое время. Поэтому устанавливают некоторый
допуск б на величину Дх(оо) и считают временем регулирова-
ния tp такое время переходного процесса, в течение которого
текущее значение регулируемого параметра Дх(£) настолько при:
ближается к Дх(оо), что разница между ними с этого момента
и в дальнейшем не превышает (б).
Качество регулирования определяется временем tp, величиной
перерегулирования и числом колебаний за время tp. Оно тем
лучше, чем быстрее устанавливается заданный статический режим,-
т. е. чем меньше время регулирования tp. Связь между време-
§ 3. Методы оценки качества переходного процесса в линейных системах
259
нем tv и допуском 5 на величину Дх(оо) определяется соотноше-
нием
(7.40)
Дх(оо) 1 "
где 6 берется в процентах от Ах(оо), обычно принимают S =
= ±3%.
Качество регулирования тем лучше, чем меньше отклонение
текущего значения регулируемого параметра Дх(() от заданной
величины Дх(оо). Это отклонение называется забросом регулируе-
мого параметра и определяется выражением
ДХтах Дх (ос)
Дх(оо)
На участке регулирования tp желательно также иметь наименьшее
число колебаний параметра Дх(/), которое определяется как число
экстремумов выше линии Дх(оо).
Исследование качества регулирования удобнее вести не по
параметру Дх(/), определяемому уравнением вынужденного дви-
жения (7.39), а по параметру Аг (7). Связь между параметрами
Дг(() и Дх(() видна из рис. 7.17, а и устанавливается выражением
Дг(() = Дх(ос) —Дх((). (7.41)
Вид переходного процесса Дг(() показан на рис. 7.17,6. Он со-
ответствует уравнению свободного движения
(,апРП + ап—1рп~1 ~Г . • ~г <hP + Qo) — О,
9*
260 Глава VII. Методы расчета, и исследования динамических характеристик
которое получается в том случае, если считать, что возмущение
в системе регулирования было вызвано единичной функцией до
дачцла отсчета времени, т. е. при t < 0 возмущение Д%1 = I, а при
t 0 .возмущение Д%1 = 0.
Полное представление о качестве переходного процесса полу-
чается путем решения дифференциального уравнения движения
системы и построения графика переходного процесса. Это просто
сделать для системы регулирования, переходный процесс которой
описывается уравнением второго порядка. Если переходный про-
цесс в системе регулирования описывается уравнением третьего
Рис. 7.17
порядка, то основные параметры переходного процесса можно
определить без решения дифференциального уравнения. Для этого
надо воспользоваться графиком, построенным Г. Г. Калишем
и В. И. Крутовым в поле диаграммы Вышнеградского и приве-
денном в работе [8].
Качество регулирования систем, описываемых дифференциаль-
ными уравнениями более высоких порядков, может быть оценено
прямыми или косвенными методами. К прямым относятся частот-
ный метод построения переходного процесса, рассмотренный
в этой главе, и метод моделирования, которому посвящена гл. X.
К косвенным методам относятся интегральные оценки качества,
основы которых также изложены в гл. VII.
Частотный метод построения переходного процесса
Связь переходного процесса с вещественной частью
частотной характеристики замкнутой системы регулирования
Для построения переходного процесса в линейной системе
регулирования можно воспользоваться частотным методом. Этот
метод не требует решения характеристического уравнения системы
и поэтому применим к системам регулирования, свойства которых
описываются дифференциальными уравнениями любых порядков.
§ 3. Методы оценки качества переходного процесса в линейных системах ’261
В предыдущей главе мы познакомились со способом построе-
ния частотной характеристики разомкнутой системы регулирова-
ния по характеристикам ее отдельных .звеньев. Теперь рассмотрим
порядок перехода от частотной характеристики разомкнутой си-
стемы регулирования к частотной характеристике замкнутой
системы. Для этой цели воспользуемся уже знакомой нам систе-
мой регулирования, состоящей из турбореактивного двигателя
с насосом, центробежного чувствительного элемента и гидравли-
ческого поршневого сервомотора. Структурная схема этой системы
регулирования показана на рис. .6.2.
Выражение частотной характеристики этой системы регулиро-
вания в разомкнутом состоянии имеет вид
ь ъ ъ.
W (ai) = 5--------2-^-----------------• (7.42)
[Т22 (a>/)2+ 1](7>+ 1)(V+1)
Если принять, что единичное внешнее воздействие приложено
в месте размыкания цепи, то при переходе от разомкнутой
к замкнутой системе регулирования выражение частотной харак-
теристики системы примет вид
ф(йм-)= —---------------------------------------. (7 43)
[Т22 (<dz)2+ 7>г-+1] (Тсы +1)(Га.>+ \) + kkckd.H
Не трудно установить связь между выражениями (7.42)
и (7.43). Для этого нужно числитель и знаменатель правой части
выражения (7.43) поделить на произведение
[Тг (coi)2 + T^i 4- 1] (7\cot + 1) + 1).
Проделав это, получим
_ W (<£><)
Ф (Ш1) = 1 + г (<*>/) • ‘
Частотная характеристика замкнутой системы Ф(со£) приводит-
ся к обычной форме комплексного числа
Ф (cot) = /’(со) + iQ (со), (7.45)
где /’(со) —вещественная часть частотной характеристики замкну-
той системы регулирования, a Q(co) —ее мнимая часть.
Вид Ф(соО, а следовательно, и ее составляющих Р(со) и Q(co)
зависит от места приложения воздействия в системе, а также от
того, относительно какой координаты решается система исходных
дифференциальных уравнений.
Вещественная частотная характеристика замкнутой системы
регулирования /’(со) может иметь вид, подобно показанному на
рис. 7.18, а или 7.18, б.
262 Глава VII. Методы расчета и исследования динамических характеристик
Выражение (7.44) получено для конкретной системы регулиро-
вания, структурная схема которой показана на рис. 6.2. Однако
оно имеет общий характер и справедливо для любой системы
регулирования, если внешнее воздействие приложено в том же
месте, по которому производится размыкание цепи. Напишем
в общем виде уравнение вынужденного движения замкнутой
системы регулирования
[D(p) + C(p)]Ax(0 = C(p)f(0, (7.46)
где £>(р) и С(р)—полиномы от р; f(t)—внешнее, воздействие.
Выполним для обеих частей уравнения (7.46) преобразование
Фурье. Тогда получим
Фдх(П (®0 = Ф (<м) Фщ) (со/).' (7.47)
В этом выражении прямое преобразование Фурье функции \x(t}
и/(О
+°°
Фдх(0 (coi) = J Дх (0 e~imidt
—СО
и
-1-00
фЩ) (“0 = J f (0 e-iatdt;
частотная характеристика замкнутой системы регулирования
Ф (cui) =
С (coz)
D (<oz) + С (сое)
Теперь проделаем относительно обеих частей этого выражения
обратное преобразование Фурье
4-СО
Дх (0 = — f Ф/(<) (coi) Ф (coi) elmid(£>. (7.48)
2л v
—со
§ 3. Методы оценки качества переходного процесса в линейных системах 263
Уравнение (7.48) устанавливает связь переходной функции
Дх(/) с частотной характеристикой замкнутой системы Ф(со/)
в зависимости от вида внешнего воздействия f(t). В такой форме
для непосредственного использования ено не удобно и требует
преобразования.
Как это делалось и раньше, внешнее воздействие f(t) примем
в виде единичной функции, т. е. при t < 0 функция f(t) = 0 и при
t 0 функция f(/) = 1. Но преобразование Фурье можно сделать
только для абсолютно интегрируемой функции, т. е. для такой,
+°°
когда/ [/(/)]d/ < оо. В нашем случае функция f(/) не абсолютно
—оо 4-°о
интегрируемая, так как при />0 f(t) = 1 и J [f(t)]dt-+oo. Чтобы
выполнить преобразование Фурье, заменим ее другой функцией:
при t < 0 функция f(t) = 0;
при t 0 функция f(t)= e~ct.
При достаточно малых положительных значениях с функция
/(/) близка к 1. Выполним для нее прямое преобразование Фурье,
а затем положим с -> 0 и получим в пределе преобразование
Фурье для /(/) = 1, которое используем для подстановки в урав-
нение (7.48)
-|-СО -|-О0 -J-CO
Фк<)(со/) = f e-cte~ijtdt = f е-(с+^)1 dt =----—I •
J J c 4- coz I
Учтем, что при t < 0 функция /(/) = 0. Поэтому
СО
фКл (шВ =------!—е—(с+ш»)/1 ——!—.
с + со/ С + И»
Теперь, полагая, что с -> 0, получим
Фцо (<-»') . (7-49)
0)4
а уравнение (7.48) примет вид
-|-со
Дх (t) = — J elmtdw. (7.50)
—оо
В выражение (7.50) введем вместо показательной функции e‘“f
тригонометрическую cos со/“+ i sin со/, а также воспользуемся вы-
ражением Ф(со/) = Р(со) + i'Q (со). Тогда
4-0°
Дх(/) = — Р (cos со/ -{- t sin со/) rfco. (7.51)
2л а со/
—00
264 Глава VII. Методы расчета и исследования динамических характеристик
Освободимся в правой части выражения (7.51) от мнимости
в знаменателе и отделим вещественную часть от мнимой. После
преобразования пблучим
ДХ(/) = — f ^(a>)sinco/ + Q(co)coSo>/
v 2л J <о
-|-оо
i f Р (со) cos mt — Q (со) sin a>t
2л J co
—co
(7.52)
Известно, что Р(о) —функция четных степеней со, a Q(co) —
функция нечетных степеней со. Иначе говоря, Р(со) = Р(—со) —
четная функция, Q(co) =—Q(—со) — нечетная функция. Отметим
также, что cos со/ является четной функцией, т. е. cos со/ =
= cos (—со/), sin со/ — нечетной функцией, т. е. sin со/ = —sin (—со/).
Проводя подобные рассуждения относительно подынтегральных
функций правой части выражения (7.52), придем к выводу, что
Р (со) sin mt + Q («о) COS o>t , P (co) COS co/— Q (co) sine»/
——--------------------четная функция, ——---------------------
Ш (0
нечетная функция. Поэтому у первого интеграла в правой части
выражения (7.52) вместо пределов интегрирования от —со до +°о
можно взять пределы от 0 до +°°, удвоив его, а второй интеграл
следует отбросить, так как он равен 0. Следовательно,
СО
Дх (/) = -L f (7.53)
л J со
о
Теперь рассмотрим два момента времени +/ и —/, помня, что
при / < 0 f(t) =0. Используя еще раз свойство четности триго-
нометрических функций, запишем
для +/
ОО
Дх(/) = _L ( £H^l+^Hcos^
Л J
для —/
СО
Q _ 1 С —Р(со) sin со/4-Q (со) cos со/
ли со
о
Вычитая из верхнего выражения нижнее, найдем, что
СО
дх(/) = 2_Р,(“)sin
Л е 0)
О
(7.54)
§ 3. Методы оценки качества переходного процесса в линейных системах 265
Основные свойства уравнения (7.54)
Рассмотрим три свойства уравнения (7.54) в пределах диапа-
зона существенных частот характеристики Р(со).
Первое свойство называется свойством линейности, оно заклю-
чается в следующем. Допустим, что вещественной частотной хараю
теристике Ру (со) соответствует переходный процесс ДхД/), а ха-
рактеристике Р2(®) — переходный процесс Дх2(/). Если же имеет-
ся частотная характеристика Р(со) = РДсо) + Р2(со), то ей
соответствует переходный процесс Дх(/) = kxy(t) + &х2(1). Дей-
ствительно,
Л ,,, 2 f Р (со) sin mt , 2 f Pi(®)+P2 (co) . , ,
Дх (/) =-- -----------du =----- I sin wt du =
л J co nJ co
— — f sin ut d«>4- — f sin ut du = Axx (t) + Дх2 (0-
П J co л J co
о 0
Это свойство остается справедливым, когда рассматривается
сумма, не двух, а большего числа вещественных частотных харак-
теристик. В случае, если частотная характеристика Р(со) =
= Pi(co)—Р2(со) и ей соответствует переходный процесс Дх(/),
а характеристикам Ру (со) и Р2(со) соответствуют переходные про-
цессы Дхх (t) и Дх2 (/), то
Дх (() = Дхх (/) — Дх2 (/).
Второе свойство носит название свойства пропорциональности.
Суть его такова. Допустим, что имеются вещественные частотные
характеристики Pi (со) и Р2(со) и им соответствуют переходные
процессы ДхД/) и Дх2((). Если между ординатами частотных
характеристик есть связь через постоянный множители с так, что
Р2(со) = сРДсо), то ординаты соответствующих им переходных
процессов также будут связаны с помощью множителя с, т. е.
Дх2(/) = сДхДО- Д«я доказательства этого положения напишем
Л 2 fp. (со) . , , 2 СсР1(ш) . , ,
Дх2 (/) = — I - sin со/ du = — I -- 7 sin со/ du=
Jt J О) л J 0)
о 0
2c f Pi (co) . , ,
—---- —t-У > sin co/ dco.
Tt J <0
0
Откуда следует, что Дх2 (/) = сДХ[ (/). Очевидно, что второе свой-
ство формулы (7.54) может быть получено из первого, если число
слагаемых характеристик Р(со) положить равным с и все их
приравнять между собой.
266 Глава VII. Методы расчета и исследования динамических характеристик
Третье свойство обычно называют теоремой масштабов. Форму-
лировка теоремы масштабов такова: при изменении для характе-
ристики Р(ч>) масштаба по оси и в каком-либо направлении
(например, в сторону увеличения) масштаб по оси t соответ-
ствующей характеристики Дх(^) меняется во столько же раз
в противоположном направлении (для взятого примера — в сторо-
ну уменьшения).
На рис. 7.19, а показаны характеристики Pi (со) и /э2(«>), при-
чем характеристика Р2(со) получается из характеристики Рх (со)
изменением масштаба по оси со в с раз. Таким образом, для
любого значения со РДсо) = Р2(ссо). На рис. 7.19, б характеристика
ДХ1(0 соответствует характеристике Pi (со). Можно показать, что
для любого значения t характеристика Дх2(() = ДХ1(—). Для
\ с /
этого рассмотрим выражение
со
Дх2 (/) = — ( Рг sin ш/с/ю
nJ СО
о
и введем новые переменные со* и t* так, чтобы со = ссо* и t = t*(c.
Тогда
СО
л / t* \ 2 i‘ Р2 (ссо*) . Л t* , ф
Дх2 — = — I ———- sin сш* — асы* =
\ с I л J ссо* с
4 ' о
со
_ JL [ Р* {са). ) sin (,)*/* (/ш*.
nJ со*
о
§ 3. Методы оценки качества переходного процесса в линейных системах 267
Учитывая, что Р2(ссо*) = Л (со*), последнее выражение можно
представить в виде
СО
Дх2 (-—') = ~ Г ) sin w*t*dw* = Дхх (/*).
\ с I л Л со*
1 о
Следовательно, Дх2| —) = ДхД/*) и вообще Дх2 ~)= Д*1(0-
\ С / \ с )
Для большей наглядности этого свойства уравнения (7.54) на
характеристиках рис. 7.19 выделены две точки с частотами со' и со",
а так же временем t' и t".
Порядок построения переходного процесса
по вещественной частотной характеристике
замкнутой системы
Если задана вещественная частотная характеристика Р(со)
замкнутой системы (рис. 7.20, а) с диапазоном существенных
частот от со = 0 до со = соп, следует разбить этот диапазон на п
Рис. 7.20
небольших участков и в пределах каждого участка характеристику
Р(со) заменить отрезком осредняющей горизонтальной прямой так,
как это показано на рис. 7.20, б.
268 Глава VII. Методы расчета и исследования динамических характеристик
Осреднение вещественной частотной характеристики в преде-
лах каждого из п участков дает возможность построить переход-
ные процессы по участкам.
После этого, используя первое свойство формулы (7.54), все
ординаты переходных процессов алгебраически суммируются
п
^x(t) = Y.^xk(f).
ft=l
Рассмотрим построение переходного процесса для одного из п
участков вещественной частотной характеристики от coft-i до ад
(рис. 7.20, в). Для этого участка Р(со) = 0 при со < ад-i и со > ад.
Величина Р (со) = Ph = const при ад-i со ад. Этому участку
вещественной частотной характеристики соответствует переходный
процесс
ОО
(/) = — f ^^sin co/dw=
Л V О)
о
“ft “ft
2 f Pk . , 2 n f sin mt ,
= — I — Sin<o/d<o=-—Pk I ----------aco =
Л v CO Л J CO
“ft-1 “ft—1
(“ft “ft-1 \
J co J co /
о 0
Преобразуем последнее выражение, введя время t в дифференциал
и знаменатель подынтегральной функции, а также в пределы ин-
тегрирования. Тогда
“ft—i “ft-i'
fsin wt , Г sin co/ . , f sin co/ , i’ sin co/ , ,
------dco = I -----aw; I -------a co = I -----aw.
co J co/ J co J co/
ooo о
Обозначив <£>ht — Уъ. и ад-Д = yh~^ получим
/"ft yk-\ \
Л \J у J У J
чо 0
У .
fsin У j
Выражение I----«У обозначается через si (у) и называется инте-
о
тральным синусом. Таким образом,
А** (0 = ~pk Isi (t/ft) — si (t/ft-i)]• (7•55)
л
§ 3. Методы оценки качества переходного процесса в линейных системах 269
Значения интегрального синуса находятся по таблицам. Чтобы
построить кривую переходного процесса Axk(t) для выбранного
участка i — <о&, задаемся рядом значений времени t, получаем
произведения ук = <i>ht и уь-\ = соь-ч/ и с помощью таблиц находим
разность si(yfe) — si(t/ft_i).
Для получения переходного процесса \x(t) всей системы регу-
лирования подобные расчеты и построения нужно провести для
каждого из п участков диапазона существенных частот и затем
выполнить алгебраическое суммирование.
Способ типовых (единичных)
трапецеидальных характеристик
Для облегчения задачи построения переходного процесса замк-
нутой системы регулирования по заданной вещественной частотной,
характеристике В. В. Солсщовников разработал способ, который
обычно называют способом типовых трапецеидальных характери-
стик. Он также основан на использовании свойств формулы (7.54),
рассмотренных ранее.
Заданную вещественную частотную характеристику системы
рассечем несколькими горизонтальными линиями и заменим трапе-
циями так, как это показано на рис. 7.21, а. При этом ломаная ли-
ния, образованная боковыми сторонами трапеций, а также осно-
ваниями верхней и нижней трапеций, должна мало отличаться от
характеристики Р(<о). Из выделенных пяти Трапеций, IV и V трапе-
ции разные по знаку. Они частично накладываются одна на другую.
Если для каждой из выделенных трапеций (рис. 7.21,6) с помощью
формулы (7.54) построить переходный процесс, то алгебраическая
сумма этих переходных процессов даст переходный процесс систе-
мы регулирования.
Значения
0,00 0,05 0. 10 0. 15 0.20 0.25 0.30 0,35 0.40
0 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,5 0,158 0,166 0,175 0,176 0,190 0,197 0,205 0,213 0,191
1,0 0,310 0,325 0,341 0,356 0,371 0,387. 0,402 0,417 0,432
1,5 0,449 0,471 0,493 0,515 0,537 0,559 0,580 0,601 0,627
2,0 0,571 0,600 0,628 0,655 0,682 0,709 0,733 0,761 0,785
2,5 0,673 0,706 0,739 0,771 0,802 0,832 0,861 0,889 0,916
3,0 0,755 0,792 0,828 0,863 0,895 0,928 0,958 0,986 1,013
3,5 0,814 0,854 0,892 0,929 0,963 0,995 1,024 1,051 1,076
4,0 0,856 0,898 0,937 0,974. 1,008 1,038 1,066 1,090 1,110
4,5 0,882 0,924 0,964 1,000 1,032 1,061 1,084 1,104 1,120
5,0 0,895 0,939 0,977 1,012 1,042 1,067 1,087 1,102 1,112
5,5 0,901 0,944 0,982 1,015 1,042 1,063 1,079 1,088 1,092
6,0 0,903 0,945 0,981 1,013 1,037 1,054 1,065 1,069 1,068
6,5 0,903 0,945 0,979 1,009 1,030 1,044 1,050 1,050 1,044
7,0 0,904 0,945 0,978 1,006 1,024 1,034 1,037 1,033 1,023
7,5 0,906 0,948 0,979 1,005 1,021 1,027 1,027 1,020 1,007
8,0 0,911 0,951 0,983 1,007 1,020 1,024 1,021 1,011 0,998
8,5 0,917 0,959 0,989 1,011 1,022 1,024 1,018 1,007 0,993
9,0 0,925 0,966 0,996 1,016 1,025 1,025 1,017 1,006 0,992
9,5 0,932 0,973 1,003 1,021 1,028 1,026 1,018 1,006 0,993
10,0 0,939 0,980 1,009 1,025 1,030 1,027 1,018 1,005 0,994
10,5 0,944 0,985 1,013 1,028 1,031 1,026 1,016 1,005 0,994
и,о 0,947 0,988 1,015 1,028 1,030 1,024 1,013 1,002 0,993
11,5 0,949 0,989 1,015 1,027 1,028 1,020 1,009 0,998 0,992
12,0 0,950 0,990 1,015 1,025 1,024 1,015 1,004 0,994 0,989
12,5 0,950 0,990 1,013 1,022 1,019 1,009 0,998 0,989 0,986
13,0 0,950 0,989 1,012 1,019 1,015 1,004 0,993 0,986 0,984
13,5 0,950 0,989 1,011 1,016 1,011 1,000 0,990 0,984 0,984
14,0 0,951 0,990 1,010 1,015 1,008 0,997 0,987 0,983 0,985
14,5 0,953 0,991 1,011 1,014 1,006 0,995 0,987 0,984 0,987
15,0 0,956 0,993 1,012 1,014 1,006 0,995 0,987 0,986 0,991
15,5 0,958 0,996 1,013 1,014 1,006 0,995 0,989 0,989 0,995
16,0. 0,961 0,998 1,015 1,014 1,006 0,995 0,990 0,992 0,999
16,5 0,963 1,000 1,015 1,015 1,005 0,996 0,992 0,995 1,002
17,0 0,965 1,001 1,016 1,014 1,005 0,996 0,993 0,998 1,006
17,5 0,966 1,002 1,016 1,013 1,003 0,995 0,994 0,999 1,007
18,0 0,966 1,002 1,015 1,012 1,002 0,994 0,994 1,000 1,007
18,5 0,966 1,002 1,014 1,010 1,000 0,993 0,994 1,001 1,007
19,0 0,966 1,002 1,013 1,008 0,998 0,992 0,994 1,001 1,006
19,5 0,967 1,001 1,012 1,006 0,996 0,991 0,994 1,001 1,005
20,0 0,967 1,001 1,011 1,004 0,995 0,991 0,994 1,001 1,004
20,5 0,967 1,002 1,010 1,003 0,994 0,991 0,995 1,001 1,003
21,0 0,968 1,002 1,010 1,003 0,994 0,991 0,996 1,002 1,003
21,5 0,970 1,003 1,010 1,002 0,994 0,993 0,998 1,004 1,003
22,0 0,971 1,004 1,011 ’1,002 0,994 0,994 1,000 1,005 1,004
22,5 0,972 1,005 1,011 1,002 0,995 0,996 1,002 1,006 1,004
23,0 0,973 1,006 1,011 1,002 0,995 0,997 1,003 1,006 1,004
23,5 0,974 1,006 1,011 1,002 0,995 0,998 1,004 1,006 1,003
24,0 0,975 1,006 1,010 1,001 0,995 0,998 1,005 1,006 1,002
24,5 0,975 1,006 1,009 1,000 0,995 0,999 1,005 1,005 1,000
25,0 0,975 1,006 1,008 0,999 0,995 0,999 1,004 1,004 0,999
25,5 0,975 1,006 1,007 0,998 0,994 0,999 1,004 1,002 0,997
26,0 0,975 1,005 1,006 0,997 0,994 0,999 1,003 1,001 0,996
Т а б л и ц а
Лх-функцнй
0.45 0.50 0.55 0.60 0. 65 0.70 0.75 0. 80 0.85 0. 90 0.95 1.00
0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000 0,000
0,229 0,186 0,244 0,252 0,255 0,265 0,275 0,283 0,294 0.299 0,305 0,313
0,447 0,461 0,476 0,491 0,505 0,519 0,534 0,548 0,561 0,575 0,590 0,602
0,642 0,662 0,682 0,701 0,720 0,741 0,757 0,775 0,791 0,810 0,827 0,842
0,810 0,831 0,856 0,878 0,899 0,919 0,938 0,957 0,974 0,991 1,008 1,022
0,941 0,963 0,988 1,010 1,030 1,048 1,066 1,082 1,096 1,109 1,121 1,131
1,038 1,061 1,081 1,100 1,116 1,131 1,143 1,154 1,162 1,169 1,174 1,177
1,097 1,116 1,133 1,147 1,157 1,165 1,171 1,174 1,175 1,174 1,171 1,166
1,127 1,141 1,151 1,158 1,162 1,163 1,161 1,156 1,150 1,141 1,132 1,119
1,131 1,138 1,141 1,141 1,138 1,131 1,122 1,111 1,098 1,083 1,069 1,053
1,117 1,117 1,114 1,107 1,097 1,084 1,069 1,053 1,036 1,019 1,003 0,987
1,091 1,086 1,076 1,064 1,048 1,031 1,014 0,996 0,978 0,963 0,948 0,931
1,062 1,051 1,036 1,020 1,001 0,984 0,966 0,949 0,934 0,922 0,914 0,907
1,030 1,018 1,001 0,983 0,965 0,933 0,948 0,920 0,911 0,905 0,905 0,906
1,009 0,992 0,975 0,957 0,941 0,927 0,917 0,911 0,909 0,911 0,917 0,926
0,991 0,975 0,958 0,943 0,931 0,923’ 0,919 0,920 0,926 0,935 0,946 0,962
0,982 0,966 0,952 0,941 0,934 0,932 0,936 0,944 0,955 0,970 0,987 1,002
0,978 0,964 0,954 0,948 0,947 0,952 0,961 0,975 0,991 1,008 1,024 1,037
0,978 0,968 0,962 0,961 0,967 0,976 0,990 1,006 1,023 1,038 1,051 1,060
0,982 0,975 0,973 0,977 0,987 1,000 1,016 1,032 1,047 1,058 1,065 1,066
0,985 0,982 0,984 0,993 1,006 1,020 1,036 1,049 1,059 1,063 1.062 1,056
0,988 0,988 0,994 1,005 1,019 1,033 1,046 1,054 1,057 1,054 1,046 1,033
0,990 0,993 1,001 1,014 1,027 1 039 1,047 1,048 1,044 1,034 1,021 1,005
0,991 0,996 1,006 1,018 1,029 1,036 1,038- 1,034 1,024 1,010 0,994 0,978
0,990 0,997 1,007 1,018 1,026 1,029 1,025 1,015 1,000 0,985 0,970 0,958
0,989 0,997 1,007 1,015 1,020 1,017 1,009 0,996 0,979 0,965 0,955 0,950
0,989 0,997 1,006 1,012 1,012 1,005 0,993 0,979 0,965 0,955 0,952 0,955
0,989 0,998 1,005 1,008 1,004 0,994 0,982 0,968 0,958 0,955 0,960 0,970
0,991 0,999 1,005 1,005 0,998 0,987 0,975 0,965 0,961 0,965 0,976 0,991
0,994 1,002 1,005 1,002 0,995 0,983 0,974 0,969 0,972 0,988 0,997 1,013
0,998 1,005 1,006 1,002 0,993 0,983 0,977 0,978 0,987 1,001 1,018 1.032
1,003 1,008 1,007 1,001 0,992 0,985 0,984 0,990 1,003 1,019 1,032 1,033
1,007 1,010 1,008 1,001 0,994 0,990 0,993 1,003 1,018 1,031 1,040 1,039
1,010 1,012 1,008 1,001 0,996 0,995 1,001 1,014 1,027 1,035 1,037 1,028
1,011 1,012 1,007 1,000 0,996 0,999 1,008 1,021 1,030 1,032 1,026 1,012
1,011 1.010 1,004 0,998 0,997 1,002 1,013 1,022 1,027 1,023 1,011 0,994
1,010 1,008 1,001 0,997 0,997 1,004 1,014 1,020 1,019 1,008 0,993 0,978
1,008 1,004 0,998 (У, 994 0,997 1,005 1,012 1,014 1,008 0,094 0,979 0,969
1,006 1,001 0,995 0,993 0,997 1,004 1,009 1,006 0,995 0,981 0,970 0,967
1,003 0,997 0,992 0,992 0,997 1,003 1,005 0,998 0,985 0,974 0,969 0,973
1,001 0,995 0,991 0,992 0,998 1,003 1,001 0,991 0,980 0,972 0,975 0,986
1,000 0,994 0,991 0,994 1,000 1,002 0,998 0,987 0,978 0,977 0,988 1,001
0,999 0,993 0,992 0,996 1,001 1,002 0,996 0,986 0,982 0,987 1,001 1,015
0,998 0,994 0,994 0,999 1,004 1,002 0,995 0,988 0,988 0,998 1,014 1,025
0,998 0,995 0,997 1,002 1,005 1,002 0,995, 0,992 0,997 1,010 1,024 1,029
0,998 0,996 1,000 1,005 1,007 1,002 0,996 0,996 1,005 1,019 1,028 1,028
0,998 0,997 1,002 1,007 1,007 1,002 0,997 1,001 1,011 1,022 1,025 1,016
0,998 0,999 1,003 1,008 1,006 1,001 0,999 1,005 1,015 1,021 1,016 1,003
0,998 0,999 1,004 1,007 1,004 0,999 0,999 1,007 1,015 1,016 1,006 0,990
0,997 0,999 1,004 1,006 1,002 0,997 0,999 1,007 1,012 1,007 0,993 0,980
0,996 1,000 1,004 1,004 0,999 0,996 1,000 1,007 1 ;008 0,998 0,984 0,975
0,996 1,000 1,003 1.001 0,997 0,995 1,000 1,005 1,001 0,989 0,978 0,976
0,996 1,000 1,002 0,999 0,995 0,995 1,000 1,002 0,996 0,984 0,978 0,984
272 Глава VII. Методы расчета и исследования динамических характеристик
Рассмотрим одну из выделенных трапецеидальных характери-
стик (рис. 7.22,а). Эта характеристика как геометрическая фигура
определяется ординатой Р(<о)ш = о = Т’(О) и частотами сос и со^ или
частотой <0d и отношением х = (oc/(£>d- Этими же величинами опреде-
ляется и соответствующий выделенной трапецеидальной характе-
ристике переходный процесс. Возьмем теперь какую-либо трапе-
цеидальную характеристику = 1 и <0d = 1, т. е. так называе-
мую единичную трапецеидальную характеристику (рис. 7.22,6).
Ее будет определять лишь одна величина х = сос/<о<г- Значение х
может изменяться от 0 до 1. При х = 1 трапеция превращается в
квадрат (рис.,,7.22,в), а при х = 0 — в треугольник (рис. 7.22,г).
Для типовых единичных трапецеидальных характеристик с раз-
личными х раз и навсегда построены переходные процессы, пред-
ставленные в виде таблиц -функций. В этих таблицах указано
время t* и для данного значения х приведены ординаты переход-
ного процесса Ах (О, обозначенные Лх.
Для построения переходного процесса Ахь(^), соответствующе-
го выделенной'трапецеидальной характеристике, например, пока-
занной на рис. 7.22, а, нужно определить значение х и выписать из
таблицы Л» -функций для ряда значений t* отвечающие им при дан-
ном х значения Л %. Затем для перехода от единичной трапецеи-
дальной характеристики к Axh(t) необходимо умножить /гх на Р(0)
и разделить t* на <0d- Полезно составить следующую таблицу.
§ 3. Методы, оценки качества переходного процесса в линейных системах 273
/* к t —
Таким же образом определяются переходные процессы, соответ-
ствующие остальным выделенным трапецеидальным характеристи-
кам, строются их графики и алгебраически суммируются. Такое
построение Ах(0 показано на рис. 7.23. Переходные процесс^! здесь
соответствуют трапецеидальным характеристикам, показанным на
рис. 7.21,6. Переходный процесс замкнутой системы регулирова-
ния
Ах (/) = Axi + Ахц + Ахщ + Axiv + Axv.
Приближенная оценка качества
переходного процесса по виду
вещественной частотной характеристики
Основываясь на свойствах формулы (7.54), некоторое заключе-
ние о качестве переходного процесса можно сделать исходя лишь
из вида вещественной частотной характеристики замкнутой систе-
мы регулирования.
Так, например, если в двух системах характеристики Р(со) ма-
ло отличаются друг от друга, то малое различие будет и в переход
ных процессах этих систем.
Если характеристики Р(а>) двух систем регулирования отличны
одна от другой, то чем выше значения <о, при которых есть отли-
чие, тем при .меньших значениях t будут расхождения в переход-
ных процессах и'тем меньше, эти расхождения по абсолютной вели-
чине. Поэтому можно пренебречь различием в характеристиках при
274 Глава VII. Методы расчета и исследования динамических характеристик
си > соп, если
Р(“>п)
Р(0)
0,1-ь 0,2
и сравнивать их между собой в диапазоне со от 0 до ип.
Если для всех со в диапазоне от и = 0 до и = соп характеристи-
ка Р (to) > 0 и при этом dP(to)/d(to) 0, то максимальная величина
перерегулирования
Ахтах —Ах (°о) i00 is о/о.
Дх (оо)
Желательно, чтобы характеристика Р (и) изменялась плавно,
так как экстремумы и пики приводят к медленно затухающему пе-
реходному процессу. Если характеристика Р(со) терпит разрыв, т. е.
при со = Ий. P(toft) оо, система находится на границе устойчи-
вости.
Начальное значение переходной функции Дх(0) равно конечно-
му значенйю /’(оо) вещественной частотной характеристики, т. е.
Дх(0) = /’(оо). Конечное значение Дх(оо) переходной функции
равно начальному значению Р(0) вещественной частотной харак-
теристики, т. е. Дх(оо) = Р(0).
Интегральные оценки качества переходного процесса
Общие соображения
Этот способ оценки качества регулирования относится к кос-
венным способам оценки. Он не требует решения характеристичес-
кого уравнения системы и построения кривой переходного процес-
са и может быть применен как к линейным, так и к нелинейным си-
стемам автоматического регулирования.
Допустим, что движение замкнутой системы регулирования
описывается уравнением
(апРп + ... + щр + а0) bz = 0.
Предположим, что можно определить величину какого-либо из
интегралов, в подынтегральную функцию которых будет входить
переменная Дг:
/0 == J |Дг|бй; (7.56)
о
оо
Ix^^zdt-, (7.57)
о
оо
/a = jAzat#. (7.58)
о
3. Методы оценки качества переходного процесса в линейных системах 275
Примем без доказательств положение, что качество регулирова-
ния системы тем выше, чем меньше величина одного из перечислен-
ных интегралов. Достоинства интегральной оценки определяются
тем, насколько она отражает качества переходного процесса и ка-
кие трудности встают на пути ее определения. Наиболее просто
Рис. 7.24
определяется интеграл Ц. Применим преобразование Лапласа к
уравнению движения системы.
Так как
СО
L [Аг (0] = J e~stkz (0 dt.
о
то
со
Д = jAz(0^ = L[Az(0]
О
(7.59)
при s = 0. Очевидно, что при преобразовании производных, входя-
щих в уравнение движения, нельзя принимать нулевые начальные
условия.
Интеграл Z2 вычисляется с помощью вещественной частртной ха-
рактеристики замкнутой системы и интеграла Фурье. Интеграл 1о
276 Глава VII. Методы расчета и исследования динамических характеристик
вычислить довольно трудно и он не нашел применения. Следует ска-
зать, что по величине интегралов 10, Ц и Z2 нельзя высказать какие-
либо строгие суждения о характере переходного процесса. Так,
например, из двух переходных процессов, показанных на
рис. 7.24, а и б предпочтение следует отдать апериодическому пере-
ходному процессу (см. рис. 7.24, а). Однако величина интеграла /1
для колебательного процесса (см. рис. 7.24, б) будет меньше, чем
для апериодического, так как составляющие площади под кривой
процесса суммируются алгебраически, с учетом знака.
Этого недостатка, присущего интегральной оценке с помощью
интеграла Ц, нет у интегральной оценки с использованием интег-
рала Z2. Но и при ее использовании не всегда получается объектив-
ная оценка качества. Так, расчеты показывают, что /гтш получает-
ся при изменении Дг по закону
Дз(0 = Дг(0)^-, (7.60)
u>t
который характеризует медленно затухающий колебательный про-
цесс. Соответствующая этой переходной функции подынтегральная
функция Дг2 показана на рис. 7.24, в сплошной линией. Пунктир-
ной линией на этом же рисунке показано желательное изменение
подынтегральной функции Дг2. И хотя величина Z2 для колебатель-
ного процесса будет меньше, чем для апериодического (пунктирная
линия на рис. 7.24, в) предпочтение нужно отдать апериодическому
переходному процессу.
Обобщенная интегральная оценка
Более объективную картину дают те интегральные оценки, ко-
торые учитывают не только изменение функции Де, но и ее произ-
водных. Если отразить влияние только первой производной на ка-
чество регулирования, то интегральная оценка (назовем ее обоб-
щенной интегральной оценкой) примет вид
СО
Iv = + (7.61)
b L
Значение интеграла Z® будет мало в том случае, если не будет
длительных отклонений параметра Дг и не будет длительного су-
ществования больших значений производных dAzjdt. Коэффициен-
том т следует задаться. Он определяет влияние производных в ве-
личине интеграла Z®.
Рассмотрим, как определяется, интеграл 7®, когда задано урав-
нение движения системы. Обозначим в выражении (7.61) подын-
тегральную функцию через V.
§ 4. Способы улучшения динамических характеристик систем. Синтез систем 277
Тогда
СО
I^Vdt.
о
Чтобы выполнить интегрирование, выберем другую квадратич-
ную функцию U из условия dUldt = —V или Vdt = —dU.
Откуда
Iv = JVdt = -]dU = - <7°| = U (0),
bo о
так как для устойчивой системы U(oo) — 0.
Таким образом, вычисление интеграла Iv сводится к определе-
нию функции U.
§ 4. СПОСОБЫ УЛУЧШЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ.
ПОНЯТИЕ О СИНТЕЗЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Динамические характеристики систем автоматического регули-
рования могут быть улучшены введением специальных корректи-
рующих устройств. Корректирующие устройства бывают парал-
лельными и последовательными. Параллельные корректирующие
устройства называются внутренними обратными связями *.
Внутренние обратные связи
Во всякой замкнутой системе регулирования существует обрат-
ная связь, образующаяся за счет воздействия объекта регулиро-
вания на регулятор. Эта обратная связь является внешней. Вместе
со связью за счет воздействия регулятора на объект регулирова-
ния образуется замкнутый контур (см. рис. 6.1) или одноконтурная
система регулирования.
Для изменения свойств звена или группы звеньев внутри основ-
ного контура регулирования введением внутренних обратных свя-
зей можно образовать дополнительные параллельные контуры регу-
лирования. Для этого выходную координату звена (или группы
звеньев) Ахвых можно связать с входом звена (или группой звень-
ев), свойства которого следует изменить. Предварительно выход-
ная координата Axewx преобразуется в звене обратной связи в коор-
динату Ахо.с (рис. 7.25). В частном случае такое преобразование
может не производиться.
Если при подаче сигнала Ахвх + Ах0. с на входе в звено, окру-
женное внутренней обратной связью, выходной сигнал возрастает.
1 Встречаются параллельные корректирующие устройства, которые затрудни-
тельно классифицировать как обратную связь.
278 Глава VII. Методы расчета и исследования динамических характеристик
Рис. 7.25
то это является признаком положительной обратной связи. В этом
случае вместе с ростом коэффициента усиления увеличивается и
постоянная времени звена, при больших коэффициентах усиления
может наступить потеря устойчивости. Поэтому в системах автома-
тического регулирования положительные обратные связи самостоя-
тельного значения не имеют. В дальнейшем мы будем рассматри-
вать только отрицательные обратные связи. Обычно звенья обрат-
ной связи выполняются стати-
ческими или дифференцирую-
щими, они делятся на простые
и инерционные.
Простая статическая обрат-
ная связь определяется уравне-
нием
^Хо.с = Ьц.<АХвыХ’ (7.62)
Для инерционной статиче-
ской обратной связи уравнение
примет вид
Р d^x0.c Д _ , д
1 л ./> dt Г ^ЛО.С -- по,с
(7.63)
о.с
Дифференцирующей простой обратной связи соответствует урав-
нение
(7-64)
(7.65)
д ,„ т1 4Дх8Ы,г
1ЛЛо.с 1 диф л ’
at
а дифференцирующей .инерционной
гр dkx0.c । д _____________________гр d&xeblX
°-с dt °-с ~ диф dt
В уравнениях (7.62) — (7.65) Т0.с и Тдиф — постоянные времени,
а&о.с — коэффициенты усиления звеньев обратной связи. Могут
быть и более сложные преобразования координат Ахвыж в звеньях
обратной связи.
Рассмотрим, как меняются свойства типовых звеньев с введени-
ем различных дополнительных обратных связей. Допустим, что про-
стая статическая обратная связь введена в астатическом звене.
Тогда уравнение звена (6.1) примет вид
т dAxebllc д — Ах
at
Учитывая уравнение (7.62), после преобразования получим
Т\_ dAxsv + АХ = _дх
о.с dt tZo-C
(7.66)
о. с
§ 4. Способы улучшения динамических характеристик систем. Синтез систем 279
Уравнение (7.66) по форме совпадает с уравнением инерцион-
ного звена. Но при достаточно больших коэффициентах усиления
Ло. с.звена обратной связи постоянная времения Talk0.c будет мала
и производной в левой части можно пренебречь. .Тогда получим
^Хвых ~ & &хвх> (7 ®7)
где k' = —-— .
hoc
Предположим, что простой статической обратной связью окру-
жено колебательное звено
Т22 + Л + Ьхвых = k (Дхвх - /г0.сДхвых).
at* at
После несложных преобразований получим
(Г')2-^^ + Л^^+Дхвых = ^Дхвх, (7.68)
где
/р2 гп
(Т2)2 ----2-— ; Т[ = —; k' =----------------•
1 + kk0.c 1 + kk0.c 1 + kk0.c
Из уравнения (7.68) следует, что охват колебательного звена этим
видом обратной связи не меняет его типа, инерционность звена па-
дает, но вместе с тем падает и коэффициент усиления. Снижение
инерционности звена (уменьшение постоянных времени при первой
и второй производных) может привести к изменению вида переход-
ного процесса звена. Покажем это на примере. Пусть у колебатель-
ного звена 7\ = 1 сек и Т2 = 0,4 сек (Т2 = 0,16 сек2). Следователь-
но, Т\ > 2Т2, что определяет апериодический переходный процесс.
Предположим, что после введения обратной связи 1 + kk0.c = 2.
Тогда Т\ = 0,5 сек, (Т'2)2 = 0,08 сек2 (Т2 ~ 0,283 сек). При этом
Т\ <2Т ', откуда следует, что переходный процесс будет уже ко-
лебательным.
При достаточно больших значениях k0.c новые постоянные вре-
мени Т2 и Т[ станут настолько малыми, что влиянием первой и
второй производных на переходный процесс можно будет пренеб-
речь. Тогда уравнение (7.68) превратится в алгебраическое урав-
нение.
В некоторых случаях обратная связь не только не улучшает ха-
рактеристики звена, но даже ухудшает их. Это можно показать на
примере инерционного или астатического звеньев, окруженных диф-
ференцирующей простой обратной связью.
В этом случае для астатического звена можно написать
Т й&хвых _ __». —Av ____Т й&хвых
2 а ,, &хсх ‘ХХо.с ‘ХХвх 2 диф ,, »
280 Глава VII. Методы расчета и исследования динамических характеристик
откуда получаем
(Та + Тдаф)^^- = ^вх.
Из последнего выражения следует, что тип звена не изменился, а
постоянная времени возросла.
Не трудно убедиться, что дифференцирующая простая обратная
связь не изменит и типа инерционного звена и приведет лишь к уве-
личению постоянной времени. Действительно,
Ти + &хвых = k (Дх„ - Тдиф
at at
ИЛИ
(Ти + кТдаф) + Ьхвых = Ых9Х.
Если же дифференцирующую простую обратную связь исполь-
зовать для колебательного звена, то это приведет к увеличению по-
стоянной времени 7\ при тех же значениях Т2 и k. Рост ?i означает,
демпфирование колебаний и в ряде случаев может оказаться вы-
годным.
Проведенный анализ показывает, что правильным выбором ти-
пов дополнительных обратных связей можно улучшить характери-
стики отдельных звеньев и системы регулирования в целом. Введе-
ние дополнительных обратных связей превращает одноконтурную
систему регулирования в многоконтурную. Поясним, как в этом
случае доставлять уравнение движения системы регулирования.
Предположим, что в систему регулирования введены две допол-
нительные обратные связи и она стала трехконтурной (рис. 7.26,а).
Полагаем, что уравнения основных звеньев и звеньев обратной свя-
зи заданы. Выделим вначале контур, состоящий из звена I и перво-
го звена обратной связи (рис. 7.26,6). Для него обычным порядком
составляется уравнение разомкнутой системы, а затем производйтся
ее замыкание. Координаты Дх3 и Дх0.с2 для этого выделенного кон-
тура являются внешними воздействиями. В результате вместо трех-
контурной системы регулирования получим двухконтурную, в кото-
рую входит сложное звено I; ОС1 (рис. 7.26, в). Далее выделим еще
один замкнутый контур со сложным звеном I; ОС1 и звеньями II
и ОС2 (рис. 7.26, г). Для него координата Дх3 будет внешним воз-
действием. Составив уравнение второго выделенного контура, по-
лучим одноконтурную систему регулирования, в которую будет вхо-
дить сложное звено I; ОС1; II; ОС2 (рис. 7.26,6).
В системах регулирования авиационных двигателей встречают-
ся и более сложные схемы, чем рассмотренная, у которых связи
между отдельными звеньями перекрещиваются. В этом случае по-
рядок составления уравнения системы регулирования сохраняется,
хотя весь процесс составления уравнения становится более гро-
§ 4. Способы улучшения динамических характеристик систем. Синтез систем 281
Рис. 7.26
моздким. Имея дифференциальные уравнения всех звеньев, нужно
учесть уравнения связей и исключить все координаты кроме той, по
которой произведено размыкание цепи. Затем по общим правилам
следует перейти к уравнениям замкнутой системы.
282 Глава VII. Методы расчета и исследования динамических характеристик
Последовательные корректирующие устройства.
Принцип построения быстродействующего регулятора
температуры газа
Последовательные корректирующие устройства служат обычно
для преобразования сигнала ошибки (производные или интегралы
от сигнала) и включаются последовательно е объектом регулирова-
ния. Введение производных в закон регулирования дает возмож-
ность улучшить качество системы регулирования. Введением интег-
ралов можно добиться уничтожения статической ошибки в системе
регулирования. Ниже мы остановимся только на особенностях вве-
дения производных.
Наличие производной от регулируемой величины в системе ре-
гулирования ускоряет действие рёгулятора на участке возрастания
отклонения регулируемой величины и тормозит действие регулято-
ра на участке ее уменьшения. Следовательно, введение производной
от регулируемой величины компенсирует инерционное запаздыва-
ние. В этом случае регулятор работает как бы с опережением, учи-
тывает тенденцию последующего развития процесса изменения ре-
гулируемой величины и тем самым улучшает качество регулирова-
ния. Однако вести регулирование только по производной от
отклонения регулируемого параметра нельзя. Ее надо использовать
вместе с самим отклонением регулируемого параметра. Поэтому
обычно применяются комбинированные дифференцирующие устрой-
ства, на выходе из которых получается суммарный сигнал. Состав-
ляющие этого сигнала пропорциональны отклонению регулируемо-
го параметра и производной по времени от этого отклонения.
Рассмотрим схему быстродействующего регулятора температу-
ры газа в качестве примера использования последовательного кор-
ректирующего устройства. Применение регулятора температуры
газа дает возможность наиболее полно использовать возможности
газотурбинного двигателя. Следует иметь в виду, что тонкие кром-
ки лопаток газовых турбин прогреваются в течение 3 ч- 4 сек.
Поэтому всякие забросы температуры газа в двигателе нужно бы-
стро ликвидировать с помощью регулятора температуры, который
должен быть практически безынерционным.
Как всякий регулятор, замкнутый регулятор температуры дол
жен иметь чувствительный элемент, измеряющий температуру.
В качестве таких чувствительных элементов наиболее удобно ис-
пользовать термопары, они обладают наименьшей, но все же
заметной тепловой инерцией по сравнению с другими чувствитель
ными элементами и позволяют легко суммировать несколько сигна-
лов от разных датчиков, расположенных в различных точках тем-
пературного поля. С изменением теплового режима двигателя тер-
мопара требует некоторого времени для прогрева и подачи сигнала
в систему регулирования. Поэтому безынерционное измерение тем-
§ 4. Способы улучшения динамических характеристик систем. Синтез систем 283
пературы при прямом использовании термопары в качестве чувстви-
тельного элемента невозможно. Тепловая инерция требует опреде-
ленного времени, в течение которого регулятор восстановит задан-
ную температуру. Это время будет тем больше, чем больше тепловая
инерция измерителя температуры.
Температура, измеренная термопарой, не совпадает с истинной
температурой газа. Измеренная температура характеризует» уста-
новившееся состояние, при котором количество тепла, подведенное
к спаю термопары от газа путем конвекции равно количеству тепла,
отдаваемого спаем за счет радиации и теплопроводности. Экрани-
рование термопар уменьшает разницу между измеренной и истин-
ной температурами, но в то же время ухудшает их динамические
свойства, т. е. увеличивает запаздывание в передаче сигнала.
Динамические свойства термопар характеризуются постоянной
времени
Т = -^ сек,
aS
где с — удельная теплоемкость термопары; у — удельный вес ма-
териала спая; J7 — объем спая; а — коэффициент теплопередачи от
газа к спаю; S — поверхность спая. Коэффициент теплопередачи а
зависит от весового расхода воздуха, проходящего через двигатель.
С увеличением высоты полета весовой расход падает, вместе с ним
падает и а, постоянная времени термопары растет. Для обычных
экранированных термопар с протоком газа, которые могут быть
установлены на двигателе, постоянная времени будет изменяться
в пределах 3 4-6 сек.
Изменение термоэлектродвижущей силы термопары по времени
в зависимости от изменения температуры газа описывается диффе-
ренциальным уравнением
(Тр+ 1)Де = М9,
где Де — изменение э. д. с. термопары; k — коэффициент усиления,
характеризующий чувствительность термопары; Д0 — изменение
температуры.
По виду переходного процесса термопара относится к инерцион-
ному звену. Это означает, что переходный процесс в таком звене
заканчивается за время /пер.пр ~ ЗТ. Регулятор температуры с тер-
мопарами, имеющими постоянные времени в несколько секунд, обес-
печит хорошее регулйрование только очень медленных тепловых
процессов. Для газотурбинных двигателей могли бы подойти тер-
мочувствительные элементы с постоянными времени в несколько до-
лей секунды. Снижение тепловой инерции путем уменьшения раз-
меров термопар понижает их прочность. Следовательно, прямое ис-
пользование термопар не может служить базой для создания
безынерционных регуляторов температуры.
284 Глава VII. Методы расчета и исследования динамических характеристик
Введем в цепь регулирования после термопар комбинированное
последовательное корректирующее устройство с тем, чтобы на вы-
ходе из него сигнал содержал .составляющие, пропорциональные из-
менению э. д. с. термопар и производной от изменения э. д. с.
Корректирующее устройство будем подбирать с такой характери-
стикой, чтобы оно обеспечило безынерционное действие регулятора.
Создание системы регулирования или ее отдельных элементов с
заранее заданными характеристиками называется синтезом систе-
мы. Поставленная здесь задача подбора корректирующего устрой-
ства является примером достаточно простой задачи синтеза.
Предположим, что в регуляторе температуры только одно зве-
но — чувствительный элемент (термопары) — обладает инерцион-
ностью. Его передаточную функцию обозначим П(з). В то же вре-
мя передаточная функция безынерционного регулятора должна
иметь вид По(-х) = k. Присоединим к чувствительному элементу с
передаточной функцией П(з) корректирующее устройство с пере-
даточной функцией П1 (з), которую выберем из условия По(з) ==
= П(з)П1 (з). Отсюда находим П1(з) = По(з)/П(з).
Передаточная функция термопары в качестве чувствительного
элемента имеет вид П(з) = k]{Ts +1), где Т — постоянная вре-
мени термопары.
Предположим, что передаточная функция корректирующего ус-
тройства П1(з) = тз + 1, где т— постоянная времени.
Тогда передаточная функция регулятора
П0(з) = П(з)П1(з) = /г^±1_.
Если удовлетворить условие т = Т, то получим безынерционную
передачу сигнала или безынерционное измерение температуры, ди-
намические погрешности термопары будут скомпенсированы. Пере-
даточную функцию П1 (з) = тз + 1 получить практически невозмож-
но, но есть устройства, передаточные функции которых могут быть
приближены к функции П1(з) = тз + 1. Одним из таких устройств
является пассивный дифференцирующий четырехполюсник типа RC
(сопротивление — емкость), схема которого показана на рис. 7.27.
Для этой схемы зависимость напряжения на выходе U2 от напря-
жения на входе Ui определяется выражением
U2 = k Tp+1 Ult
ktp+ 1
где т = RC и k = ——— .
Ri + Rh
С уменьшением k передаточная функция пассивного дифференци-
рующего четырехполюсника будет приближаться к виду ts + 1, но
§ 4. Способы улучшения динамических характеристик систем. Синтез систем 285
при этом величина выходного сигнала уменьшается и требуются до-
полнительные усилители. На практике обычно выбирают k =
= 0,02 ч- 0,01.
Корректирующее устройство действует следующим образом.
При скачкообразном увеличении температуры в камере ДО э. д. с.
Рис. 7.27
Рис. 7.28
термопар и напряжение ДС^ на входе в корректирующее устройст-
во начнут увеличиваться по экспоненциальному закону. В связи с
этим изменится сила тока Дй через сопротивление Ri (рис. 7.28) и
. . „ d&U ,
ток Д?2 = С потечет через конденсатор, где Дс/ — падение нап-
ряжения на участке сопротивления Rv Полная компенсация дина-
мической погрешности термопар
получится в том случае, если уве-
личение силы тока Дгн = Дй +
+ Дй через нагрузочное сопро-
тивление RH будет постоянно по
времени (что и показано на рис.
7.28). Тогда напряжение ДП2 воз-
растет скачкообразно.
Принципиальная структурная
схема регулятора температуры
Рис. 7.29
газа с коррекцией динамических
погрешностей термопар показана на рис. 7.29. На этой схеме 1 —
термопара, 2 — предварительный усилитель, 3 — корректирующее
устройство, 4 — основной усилитель, 5 — исполнительный меха-
низм, дозирующий подачу топлива. Де — изменение э. д. с. термо-
пары, Д1/ — изменение напряжения за основным усилителем,
Дб/ — изменение координаты регулирующего органа. Схема замы-
кается через камеру сгорания двигателя, в которой изменяется
температура газа Д0 за счет изменения подачи топлива.
При изменении расхода газа через двигатель постоянная време-
ни термопары меняется по закону
286 Глава VII. Методы расчета и исследования динамических характеристик
Ti
—— — Ш
Tt
G2 \0,5
где Gi и Gz—весовые расходы газа на разных режимах; m — ко-
эффициент пропорциональности. Компенсация динамических пог-
решностей термопар, близкая к оптимальной, получается только на
одном режиме, когда Т — т. На других режимах будет или недо-
Рис. 7.30
компенсация (7’>т), или
перекомпенсация (Г<т),
Параметры корректи-
рующего устройства не-
обходимо выбирать из ус-
ловия компенсации наи-
большей постоянной вре-
мени термопары, которая
соответствует малым рас-
ходам газа (работа на по-
ниженных режимах по
мощности и на больших
высотах). На остальных
режимах работы будет
перекомпенсация (Г <т),
которая, однако, во мно-
гих случаях может улуч-
шить процесс регулирова-
ния как дополнительное
воздействие сигнала по производной. Влияние различной степени
компенсации на выходной сигнал Д[/2 корректирующего устройства
показано на рис. 7.30. На этой фигуре даны три кривых kU2, из ко-
торых 1 — соответствует недокомпенсации, 2 — оптимальной ком-
пенсации и 3—• перекомпенсации, Де — изменение э. д. с. термопа-
ры с большой постоянной времени (5 сек.).
§ 5. ИССЛЕДОВАНИЕ СИСТЕМ РЕГУЛИРОВАНИЯ,
СОДЕРЖАЩИХ ЭЛЕМЕНТЫ
С СУЩЕСТВЕННО НЕЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ
Линеаризация характеристик отдельных элементов систем ре-
гулирования дает возможность описывать переходные процессы в
системах автоматического регулирования с помощью линейных диф-
ференциальных уравнений. Такие системы, рассматриваемые в ли-
нейном приближении, называются линейными.
При исследовании линейных систем на устойчивость было обна-
ружено, что в системе регулирования может возникнуть незатухаю-
щий синусоидальный колебательный процесс лишь в том случае,
когда система находится на границе колебательной устойчивости.
$ 5. Исследование систем с нелинейными характеристиками элементов
287
Для этого необходимо, чтобы два корня характеристического урав-
нения были мнимыми-сопряженными, а у остальных корней вещест-
венная часть была отрицательной.
Очевидно, что незначительное изменение какого-либо параметра
системы регулирования должно привести к нарушению этого усло-
вия и колебания станут затухающими или расходящимися. Поэто-
му возможность возникновения незатухающих колебаний в линей-
ной системе регулирования можно рассматривать лишь теоре-
тически.
Однако практика показывает, что в системах регулирования,
устойчивых в линейном приближении, возникают незатухающие
колебания синусоидальной или более сложной формы. Такие коле-
бания зачастую наблюдаются и в системах регулирования авиаци-
онных двигателей. Незатухающие колебания, возбужденные каким-
либо внешним источником, выводят систему из состояния равнове-
сия. В дальнейшем возникшие колебания не нуждаются во внешнем
возмущении и целиком определяются свойствами данной системы
регулирования. Такие незатухающие колебания носят название ав
токолебаний.
При линеаризации характеристик в некоторых случаях теряют-
ся их существенные особенности и эти особенности невозможно об-
наружить в линеаризованных дифференциальных уравнениях. Как
результат этих потерь •— возникновение непредвиденных ранее ав-
токолебаний. Изучение автоколебаний и разработка мер по их пре-
дотвращению имеют большое значение для инженерной практики.
Изучение процессов регулирования в нелинейных системах за-
труднено тем, что эти процессы описываются нелинейными диффе-
ренциальными уравнениями. Современный математический аппарат
не дает возможности решать нелинейные дифференциальные урав-
нения общего типа аналитическим путем. Поэтому наиболее эффек-
тивным способом изучения динамики нелинейных систем автомати-
ческого регулирования является математическое моделирование, с
которым мы познакомимся в гл. X. В теории автоматического регу-
лирования разработаны методы, позволяющие в некоторых случа-
ях обходить возникающие при исследовании нелинейных систем
математические трудности. К таким методам относится, например,
рассматриваемый ниже метод гармонического баланса, примени-
мый к изучению автоколебаний, когда опи близки к синусоидаль-
ным.
Элементы с существенно нелинейными характеристиками
Рассмотренный в гл. II принцип линеаризации характеристик
предусматривал, что монотонная нелинейная зависимость одной ве-
личины от другой может быть линеаризована. При небольших от-
клонениях аргумента от его исходного значения приращение функ-
288 Глава VII. Методы расчета и исследования динамических характеристик
ции определяется как приращение аргумента, умноженное на тан-
генс угла наклона касательной к кривой в точке, соответствующей
исходному значению аргумента. Однако существуют характеристи-
ки, у которых отсутствует упомянутая монотонность и в отношении
которых подобная линеаризация проведена быть не может. Такие
характеристики будем называть существенно нелинейными.
В качестве примера элементов систем регулирования, обладаю-
щих существенно нелинейными характеристиками, рассмотрим зо-
Рис. 7.31
лотник с перекрытием каналов и чувствительный элемент центро-
бежного регулятора с сухим трением. На рис. 7.31, а показан
элемент золотника с цилиндрической канавкой, причем высота ка-
навки выполняется равной или несколько больше высоты пояска
золотника. Такой золотник при малых перемещениях обладает ли-
нейной зависимостью изменения объемного расхода 6Q от переме-
щения золотника dz. Золотнику с перекрытием, схема которого да-
на на рис. 7.31, б, присуща существенно нелинейная характеристи-
ка. Она показана на рис. 7.31, в. Крутизна наклонных участков
этой характеристики зависит от величины гидравлического сопро-
тивления окон золотника и трубопроводов. В предельном случае-
наклонные участки характеристики становятся вертикальными от-
резками (рис. 7.31, г).
Рассмотрим характеристики чувствительного элемента центро-
бежного регулятора с сухим трением. Его схема показана на
§ 5. Исследование систем, с нелинейными характеристиками элементов
289
рис. 7.32, а, а приближенная зависимость силы сухого трения по
скорости перемещения муфты чувствительного элемента — на
рис. 7.32, б. Для простоты пренебрежем силами вязкого трения и
инерции. Будем полагать, что на муфту действует сила, развивае-
мая грузиками, силы сухого’ трения и пружины. Если в исходном
положении равновесия регулятора (6z = 0) дать некоторое прира-
щение центробежной силы 6РЧ < а, то муфта чувствительного эле-
мента и золотник сервомотора не изменят своего положения. При
дальнейшем увеличении центробежной силы (а < 6РЦ < бРч1а;1Х)
муфта чувствительного элемента начнет перемещаться и ее движе-
ние, определяемое наклоном характеристики на рис. 7.32, в, будет
зависеть от жесткости пружины. Для того чтобы задержать муфту
чувствительного элемента на каком-либо уровне, сила, развиваемая
грузиками, должна быть уменьшена на величину силы трения а, а
для движения муфты в обратном направлении согласно рис. 7.32, б
ее следует еще уменьшить на величину а.
При периодическом изменении приращения центробежной силы
&Рц от + 6РЧ max до —&РЧ max при принятых допущениях перемеще-
ние муфты чувствительного элемента или золотника сервомотора
будет происходить по петлевой характеристике (см. рис. 7.32, в).
Эта характеристика не только существенно нелинейна, по и иеод-
10 Черкасов Б. А.
290 Г лава VII. Методы расчета и исследования динамических характеристик
нозначна. Сила, развиваемая грузиками, связана с числом оборо-
тов зависимостью Рч = сп2 или в приращениях
8РЦ = 2сп08п = с'8п.
Следовательно, петлевая характеристика присуща не только зави-
симости 8z = 1(8Рц), но и зависимости 8z = f(8n). Если шарнирные
соединения механизма регулятора выполнены с люфтами (зазора-
ми), то это также приводит к петлевой характеристике. Представ-
ляет интерес золотник с перекрытием и чувствительный элемент
центробежного регулятора с сухим трением подвергнуть частотным
испытаниям. Приняв характеристики этих элементов такими, ка-
кими они показаны на рис. 7.31, г и 7.32,8, можно представить,
каким будет изменение выходных координат (объемного расхода
через золотник 8Q и положения муфты чувствительного элемента
8z) при изменении по гармоническому закону положения золотни-
ка в первом случае и числа оборотов ротора двигателя во втором.
Такие частотные характеристики даны на рис. 7.33 и 7.34. Там же
показаны и способы их построения. Для удобства построения исход-
ные характеристики нелинейных элементов, показанные на
рис. 7.31, г и 7.32, в, повернуты на 90°.
Характеристики, подобные характеристикам, показанным на
рис. 7.33 и 7.34, можно получить и экспериментально, осциллогра-
фируя изменения входных и выходных координат нелинейных эле-
ментов при частотных испытаниях. Вид частотных характеристик
нелинейных элементов говорит о том, что в случае изменения вход-
ной координаты по синусоиде колебания выходной координаты по-
лучаются отличными от синусоидальных.
Если нелинейный элемент обладает неоднозначной (петлевой)
характеристикой, то выходная координата сдвинута по фазе по от-
§ 5. Исследование систем с нелинейными характеристиками элементов
291
ношению к входной. У нелинейного элемента с однозначной харак-
теристикой сдвига фаз нет. У нелинейных элементов модуль
М = Авых/Авх не зависит от частоты колебаний ад1. Он зависит от
амплитуды колебаний, т. е. М — f(Aex). Напомним, что для элемен-
тов, обладающих обычными линейными характеристиками, модуль
М = /(со) и не зависит от амплитуды. Сравнение частотных харак-
теристик линейного и нелинейного элементов показано на рис. 7.35.
Рис. 7.35
Если применять метод скачкообразного воздействия, то у линей-
ных элементов отношение bxeuxi/bxexl не зависит от величины вход-
ной координаты бХвхь У нелинейных элементов это отношение меня-
ется с переходом к другим значениям входной координаты.
Из сказанного можно сделать вывод, что если процесс регули-
рования хотят описать с помощью линейных уравнений, то следует
убедиться в линейности отдельных элементов или звеньев, входящих
в систему регулирования. Для этого нужно проверить отсутствие
влияния 6хвх1 па отношение ЬхвЫх116xexi при скачкообразном воз-
действии и влиянии Авх на модуль при частотных испытаниях.
1 Это свойство так называемых идеальных нелинейных элементов. У реаль-
ных нелинейных элементов модуль может меняться как по амплитуде, так и по
частоте колебаний.
10’
292 Глава VII. Методы расчета и исследования динамических характеристик
Виды автоколебаний. Исследование динамики нелинейных систем
с помощью фазовой плоскости
Автоколебательный режим является свободным движением си-
стемы. При каждом полном колебании в систему регулирования
подводится определенное количество энергии, идущей на компенса-
цию неизбежных потерь на трение в механизме регулятора и на
Другие потери энергии в системе. Для устойчивости цикла автоко-
лебаний должно быть выдержано условие равенства подвода и от-
вода энергии за каждый цикл. Кроме того, должно быть определен-
ное взаимное расположение характеристик подводимой и отводи-
мой энергии.
Автоколебания могут иметь мягкий или жесткий режим возбуж-
дения. При мягком режиме возбуждения любое малое отклонение
системы от положения равновесия приводит к колебаниям с воз-
растающей амплитудой. Когда амплитуда достигнет определенной
величины, устанавливаются автоколебания. Изменение подводимой
( + е) и отводимой (—е) энергии по величине амплитуды для этого
случая показано на рис. 7.36, а. Из него следует, что автоколебания
устанавливаются при значении амплитуды, равной Ао- Если же на-
чальное отклонение регулируемого параметра системы будет боль-
ше Ао, то в дальнейшем при свободном движении системы ампли-
туда колебаний убывает и в тот момент, когда она достигнет зна-
чения Ао> установится автоколебательный режим.
На рис. 7.36,6 показано изменение подводимой ( + е) и отводи-
мой (—е) энергии в зависимости от амплитуды в системе с жест-
ким режимом возбуждения автоколебаний. Из этого рисунка сле-
дует, что если начальные отклонения от положения равновесия не
превысят А[, в системе регулирования возникнут затухающие коле-
бания и через некоторое время она вернется к положению равно-
весия. При начальных отклонениях А1<А<А0 возникнут коле-
§ 5. Исследование систем с нелинейными характеристиками элементов
293
При небольших начальных от-
Рис. 7.37
бания с возрастающей амплитудой, которые перейдут в автоколеба-
ния с амплитудой Ло- Если же начальные отклонения превысят Ло,
то амплитуда колебаний будет уменьшаться и при достижении
А = Ао возникнут автоколебания.
Взаимное расположение подводимой и отводимой энергии в сис-
теме может быть таким, как это показано на рис. 7.37. В этом слу-
чае автоколебаний не наблюдается. “
клонепиях А < Ак колебания в си-
стеме затухают и она приходит в
состояние равновесия (как говорят,
система устойчива в малом). При
начальных отклонениях А > Ак ам-
плитуда колебаний непрерывно воз-
растает, к состоянию равновесия
система не вернется (принято гово-
рить, система неустойчива в боль-
шом).
Если система регулирования (ли-
нейная или нелинейная) описывает-
ся дифференциальным уравнением
второго порядка, то присущие ей
быть изображены на фазовой плоскости. Метод фазовой плоскости
поясним на примере линейной системы регулирования второго по-
рядка, уравнение которой имеет вид
„ сРДх , d\x , д „
dt* dt 0
динамические процессы могут
(7.69)
Заменим уравнение (7.69) двумя уравнениями первого порядка:
aokx -j- аМу
dky ______
dt
d\x .
— = Ду-
dt
(7.70)
Поделив в системе (7.70) одно уравнение на другое, получим
d&y _ а0Дх + aj&y
d&x a^txy
(7.71)
С помощью уравнения (7.71) на плоскости Ау— Дх, называемой
фазовой плоскостью, можно отобразить свободное движение систе-
мы регулирования, описываемой уравнением (7.69).
Рассмотрим, как это делается. Допустим, что система регулиро-
вания устойчива и ее переходный процесс в свободном движении
показан на рис. 7.38,а (сплошная линия). Пронумеруем характер-
ные точки этой кривой и представим, что в каждой из них, напри-
мер, в точке 1, проведена касательная и определена величина
294 Глава VII. Методы расчета и исследования динамических характеристик
\у = dAxjdt. Тогда по известным значениям Дх и Ду в отмеченных
точках этот график свободного движения легко отобразить на плос-
кости Ду — Дх в виде фазовой траектории, или, как говорят, по-
строить фазовый портрет системы. В данном случае это будет спи-
раль, стягивающаяся к началу координат (сплошная кривая на
рис. 7.38,6). Для других начальных отклонений системы от поло-
жения равновесия будет другая спираль, не пересекающаяся с пер-
вой (пунктирные линии на рис. 7.38,а и б). Если система регулиро-
вания неустойчива, то спираль получит-
ся расходящейся. Этот случай показан
на рис. 7.39.
В более общем случае система регу-
лирования может быть задана двумя
уравнениями первого порядка, вида
= b^x + ^Ду;
dt J
— = bzbx + с2Ду.
Откуда получаем уравнение для построения фазовой траектории
dky _ ciAy ,7 72у
dAx 62Ax + CjAy ' ’ 7
Для нелинейных систем регулирования уравнение (7.72) может
принять вид
dky = М* + Cif (Ay)
dAx 62Ax 4- c2Ay ’
где функция f(&y) будет задана графически.
Для построения фазовой траектории по уравнениям (7.72) или
(7.73) совсем не требуется знать график свободного движения си-
§ 5. Исследование систем с нелинейными характеристиками элементов
295
стемы регулирования. График свободного движения, показанный на
рис. 7.38, а, был использован нами только для того, чтобы показать
связь переходного процесса системы регулирования с ее фазовой
траекторией.
Для построения фазовой, траектории системы следует на фазо-
вой плоскости Ау — Ах выбрать произвольную точку и значения Ду
и Дх, соответствующие этой точке, подставить в уравнение (7.72)
или (7.73). Получив величину производной dAy/dAx для выбран-
ной точки, тем самым находим для нее направление касательной к
фазовой траектории. Вторая точка выбирается вблизи первой. Она
должна лежать на найденной касательной к фазовой траектории,
проходящей через первую точку. Затем определяется направление
касательной, проходящей через вторую точку и т. д. Вид фазовой
траектории зависит от значения коэффициентов bly b2, Ci и с2. Если
фазовая траектория стягивается к началу координат, то система ре-
гулирования устойчива.
Если в уравнении (7.69) положить сн = 0, то система регулиро-
вания будет находиться на границе колебательной устойчивости
^^+<в2Дх = 0, (7.74)
d/а 0
где

а2
Интегрирование уравнения (7.74) дает
Дх = A sin ю0/, (7.75)
где А — амплитуда колебаний.
Из (7.75) получим, что
Ду = Дю0 cos ю0Л (7.76)
Используя уравнения (7.75) и (7.76), находим, что sin aot =
= Дх/Д и cos aot = Ay!Аю0- Откуда следует
_^_+ АУ2 = 1. (7.77)
А2 (Ао>0)2
Уравнение (7.77) есть уравнение эллипса с полуосями А и Д(По-
следовательно, фазовая траектория гармонического движения име-
ет вид эллипса. Изображающая точка перемещается по эллипсу в
направлении по часовой стрелке. При различных амплитудах ко-
лебаний эллипсы, соответствующие различным фазовым траекто-
риям, имеют разные размеры (рис. 7.40).
Таким образом, синусоидальные незатухающие колебания ото-
бражаются на фазовой плоскости движением изображающей точки
по эллиптическим фазовым траекториям. Некоторые фазовые ди-
аграммы, характерные для нелинейных систем регулирования, по-
296 Глава VII. Методы расчета и исследования динамических характеристик
казаны на рис. 7.41. На рис. 7.41, а изображена система с мягким
режимом возбуждения синусоидальных автоколебаний. В соответ-
ствии с характеристикой подводимой и отводимой энергии (см.
рис. 7.36, а) при любых малых началь-
ных отклонениях система выходит из
равновесия и в ней устанавливаются
автоколебания, с амплитудой До- Рис.
7.41, б соответствует системе с жест-
ким режимом возбуждения автоколе-
баний.(см. рис. 7.36, б). На рис. 7.41, в
показана система, устойчивая в малом
и неустойчивая в большом. Для этого
случая характер подводимой и отво-
димой при каждом колебании энергии
показан на рис. 7.37.
При автоколебаниях, отличных от синусоидальных, фазовая
траектория уже не будет эллипсом. Однако любому периодическо-
му движению на фазовой плоскости обязательно соответствует
замкнутая фазовая траектория. Опыт показывает, что при потере
устойчивости помпажные автоколебания в диффузоре отличны от
$ 5. Исследование систем с нелинейными характеристиками элементов
297
синусоидальных. Изменение давления по времени в дозвуковой ча-
сти диффузора (на входе в двигатель) может быть описано диффе-
ренциальным уравнением второго порядка
К + Np = S, (7.78)
d/2 dt
где К, N и S — коэффициенты уравнения, зависящие от геометри-
ческих размеров и коэффициента расхода диффузора, скорости по-
тока перед двигателем, внешних условий и числа Мя полета.
Положим у = dp/dt, тогда уравнение (7.78) можно привести к
виду
y-^-^Ky^-Np + S. (7.79)
dp
Это нелинейное уравнение удобно исследовать с помощью фа-
зовой плоскости. Результаты такого исследования приведены
на рис. 7.42, а и б’.Случай а (см. рис. 7.42, а) соответствует устой-
чивому режиму диффузора, приток воздуха в диффузор и расход
через компрессор равны между собой. Движение изображающей
точки по любой фазовой траектории всегда направлено к равно-
весной точке А. Случай б (см. рис. 7.42,6) показывает, что в рабо-
чем диапазоне давлений нет равновесного режима. Изображаю-
щая точка из любого положения переходит на замкнутую траек-
торию, что говорит об устойчивом автоколебательном процессе.
В заключение этого раздела отметим, что построением фазовой
траектории в фазовом пространстве можно исследовать системы
регулирования, описываемые уравнениями третьего порядка.
1 Уравнение (7.79) получено и исследовано с помощью фазовой траектории
С. А. Гаевским.
298 I лава VII. Методы расчета и исследования динамических характеристик
Метод гармонического баланса
Как уже отмечалось ранее, в системах регулирования ГТД,
устойчивых в линейном приближении, иногда возникают автоко-
лебания. Это говорит о том, что некоторые элементы таких систем
обладают существенно нелинейными характеристиками.
Исходя из того, что автоколебания в авиационных силовых ус-
тановках недопустимы, можно сформулировать задачу их иссле-
дования:
1) при проектировании регулятора, располагая частотными
характеристиками линейных и нелинейных элементов, убедиться,
что в системе регулирования автоколебания не возникнут;
2) при возникновении автоколебаний в системе регулирования
исследовать их причины и найти способ их устранения.
В отношении автоколебаний,. форма которых близка к сину-
соидальной, поставленная задача может быть решена с помощью
метода гармонического баланса. Этот метод был разработан в
1937 г. Н. М. Крыловым и Н. Н. Боголюбовым применительно к
задачам радиотехники и позднее был использован Л. С. Гольд-
фарбом для решения некоторых нелинейных задач автоматическо-
го регулирования. Ниже изложены основы метода гармонического
баланса в форме, предложенной Л. С. Гольдфарбом.
Прежде всего следует уяснить, при каких условиях в системе,
имеющей элементы с нелинейными характеристиками, могут воз-
никнуть автоколебания синусоидальной формы. Будем рассмат-
ривать только такие нелинейные элементы, для которых выходная
координата зависит от входной координаты и не зависят от ее
производных по времени. Считаем, что в системе регулирования
имеется только один нелинейный элемент. Чтобы конкретизиро-
вать задачу, примем, что система регулирования состоит из трех
звеньев: чувствительного элемента центробежного регулятора
числа оборотов, гидравлического сервомотора и двигателя. Струк-
турная схема такой системы регулирования показана на рис. 6.1, в.
Пусть нелинейным элементом является чувствительный эле-
мент, в котором будем учитывать силы сухого трения и пренебре-
гать силами вязкого трения и силами инерции. Его характеристи-
ка будет подобна показанной на рис. 7.32, в. Остальные звенья
системы регулирования обладают линейными характеристиками.
Структурная схема такой системы регулирования дана на
рис. 7.43, а, в ней линейные звенья объединены в линейную часть.
Эта структурная схема будет являться частным случаем структур-
ной схемы, показанной на рис. 7.43, б и состоящей из нелинейного
элемента и присоединенной к нему линейной части.
Исследуем свойства системы регулирования, структурная
схема которой приведена на рис. 7.43,6, сначала в разомкнутом
состоянии. Если из эксперимента известны частота и амплитуда
§ 5. Исследование систем с нелинейными характеристиками элементов
299
синусоидальных автоколебаний, возникающих в замкнутой систе-
ме регулирования, то при размыкании системы входную коорди-
нату Дхвж нужно изменять по синусоидальному закону с той же
частотой и амплитудой. Пусть это будет Дхвх = 4exsino>*t
Согласно правилу перехода от замкнутой к разомкнутой цепи
воздействий выходная координата по абсолютной величине равна
входной координате и противоположна ей по знаку. Следователь-
но, в нашем случае выходная координата Дхвых также меняется
по синусоиде с частотой со* и амплитудой Авх, но имеет сдвиг по
Нелинейный Линейная часть
а)
Линейная
часть
5)
& -X вь/х
* !
I
_____________I
Рис. 7.43
фазе на угол л, т. е. находится в противофазе по отношению к
входной координате.
Известно так же, что если входную координату нелинейного
элемента изменять по синусоиде, то его выходная координата бу-
дет изменяться по сложному периодическому закону, отличному
от синусоидального, с частотой, равной частоте изменения вход-
ной координаты. Таким образом, в нашей разомкнутой системе
получается: входная координата Дхвх нелинейного элемента изме-
няется по синусоидальному закону, его выходная координата
Дг/, являющаяся входной координатой линейной части, изменяется
по сложному периодическому закону, выходная координата си-
стемы Дхвыж снова изменяется по синусоиде, находясь в противо-
фазе к входной координате. Это изменение координат Дхвх, Ду и
&хвых показано на рис. 7.44. Координата Ду изменяется по слож-
ному периодическому закону, но линейная часть системы преоб-
разует ее в выходную координату.— синусоиду Дхвых. Это преоб-
разование объясняется следующим. Любую периодическую функ-
цию Ду = /(/) можно разложить в ряд Фурье и получить Ду =
= Ayi + Ду2 + Д«/з + Ду4-, где Дуь Ду2, Ду3 и Ду4 — 1, 2, 3 и 4-я
гармоники ряда Фурье. С ростом порядка гармоник их амплитуды
300 Глава VII. Методы расчета и исследования динамических характеристик
быстро уменьшаются, гармоники порядка выше четвертого обыч-
но можно не учитывать.
Согласно принципу суперпозиции, применимому к линейной
части системы регулирования, из-
менение выходной координаты
АхвЫх будет одним и тем же, если
входную координату \у заменить
на сумму воздействий \у = Az/i +
+ Ду2 + Az/з + Az/4 + ... Если вход-
ная координата Дхвх изменяется с
частотой со*, то частоты гармоник
Az/i ... Az/4 равны соответственно
со*, 2ш*, Зсо* и 4со*.
Теперь проследим, какие из
выделенных частот со*, 2со* ... по-
падают в диапазон существенных
частот амплитудной частотной
характеристики линейной части
системы (полагаем, что эта ха-
рактеристика нам известна).
Здесь возможны два случая.
В одном случае в диапазон
существенных частот попадают
две или больше частоты гармо-
ник разложения в ряд периодической функции Ду = /(/) так, как
это показано па рис. 7.45, а. Каждая на них даст свою синусои-
дальную составляющую выходной координаты \хвых. Однако их
суммирование приведет к тому, что координата Дхвых будет перио-
дической функцией, отличной от синусоиды.
В другом случае в диапазон существенных частот попадает
только одна частота а>*, частоты 2(о*, Зы* и другие выходят за
пределы диапазона (рис. 7.45,6). Это означает, что линейная
§ 5. Исследование систем с нелинейными характеристиками элементов
301
часть системы гасит все гармоники, выше 1-й. На выходе из ли-
нейной части координата АхвЫх будет изменяться по синусоиде с
частотой со*. Этот случай и представляет для нас интерес.
Следовательно, автоколебания синусоидальной формы в си-
стеме регулирования с нелинейным элементом могут возникнуть
только в том случае, если линейная часть системы будет гасить
все гармоники, кроме первой. Поэтому можно принять, что Ау —
— Ау\. Зададим на входе в разомкнутую систему регулирования
(см. рис. 7.43, б) синусоидальное изменение входной координаты
Дхв1- = .4вж sin at. На выходе из нелинейной части примем во вни-
мание только 1-ю гармонику, полагая, что линейная часть гасит
все остальные гармоники. Тогда
Az/i = sin (at + 9Н),
где Ai — амплитуда 1-й гармоники; 0„ — сдвиг фазы колебаний в
нелинейном элементе системы регулирования.
Величина Ау\, являясь входной координатой для линейной ча-
сти системы, вызовет изменение выходной координаты Дхвыж по
закону
&хвых = Авых sin (at 4- 9„ 4- 9J,
где 0л — сдвиг фазы колебаний в линейной части системы регули-
рования.
В уравнении процесса регулирования переход от разомкнутой
к замкнутой цепи воздействий выражается в том, что за входную
координату принимается выходная координата, взятая со знаком
минус, т. е. Ахвх = —Дхвыж. В нашем случае это означает, что если
в замкнутой системе регулирования возникли автоколебания, то
при размыкании системы имеют место соотношения Авх — Авых и
0« + 0л = —л.
Остановимся на задаче определения 1-й гармоники Ayi разло-
жения в ряд Фурье функции Ay = f(Aexsin at). Известно, что лю-
бая периодическая ограниченная вещественная функция f(x),
имеющая конечное число разрывов и экстремумов за период, мо-
жет быть разложена в ряд
со со
f (х) = а0 4- ак sin kx 4- cos ^А’> (7 • 80)
kA
где
2т.
ао = 4- t W dx-
2л v
0
2к
ак = — I f (х) sin kxdx\
Я J
о
302 Глава VII. Методы расчета и исследования динамических характеристик
2т.
1
bK = “ f (%) cos kxdx.
b
Если за период колебаний среднее значение функции f(x) равно
нулю, то нулевой член разложения ряда а0 отсутствует.
Обозначим для сокращения записи Авх = А и at = <р. Тогда
Az/ = f (A sin ср). 1-я гармоника ряда Az/i определяется из выра-
жения
Ау1 = ai sin ? + bi cos ср, (7.81)
где
2л 2-
й!= — f f(A sin <р) sin cp-dcp; H^sin?)cos<p-z/<p.
о 0
Следует иметь в виду, что при однозначной характеристике
нелинейного элемента (например, характеристика золотника с пе-
рекрытием, показанная на рис. 7.31, в и г) коэффициент bi = 0.
Отметим так же, что коэффициенты и Ь\ не зависят от ф и яв-
ляются функциями только амплитуды А, так как интегрирование
ведется по ф в пределах от 0 до 2л. Поэтому можно записать,
что й! = f\ (Л); bi = /’ (Л). Удобнее использовать функции, не-
сколько отличающиеся от (Л) и /”2(Л), а именно /1(Л) =
= f\ (Л)/Л и /г(Л) = f*2 (А)/А. Тогда можно написать, что а\ —
= Л/1(Л) и bi = Л/2(Л) или, упрощая запись, ai — Afi v.b\ =
= Af2. Отметим, что Д и f2 есть функции амплитуды Л колебаний
Ахвх.
Вернемся к выражению (7.81). Его теперь можно представить
в виде
Az/i = Af± sin <р + Af2 cos <p. (7.82)
Умножим и разделим правую часть выражения (7.82) на ве-
личину j/ff + f2. Тогда получим
Az/i = А У fl + (sin <р cos 6К + cos <р sin 0Н),
или _______
+/2Sin('? + 0*)> (7-83)
f
где 0„ = arctg ——сдвиг фазы колебаний в нелинейном элемен-
h ______
те; множитель аУ fl + f2 —амплитуда Ах
колебаний Az/h откуда следует, что модуль
нелинейного элемента Мн — AJA определяет-
ся из выражения
§ 5. Исследование систем с нелинейными характеристиками элементов
303
< = //?+ П- (7-84)
Итак, в результате разложения периодической .функции в ряд
Фурье и некоторых преобразований мы выяснили, что отношение
амплитуд Мн и сдвиг фазы колебаний 0Н в нелинейном элементе
зависят только от амплитуды входа Л и не зависят от частоты со.
Что же касается преобразования колебаний
= АМН sin (<? + 9J
в колебания
A^e«* = ^sin(<{> + e4 + 0J,
то оно полностью определяется амплитудно-фазовой характери-
стикой линейной части системы.
Амплитудно-фазовую характеристику линейной части можно
представить в виде комплексного числа
№Л=МЛЛ. (7.85)
По аналогии для нелинейного элемента также можно напи-
сать выражение
WH = МНЛ. (7.86)
Годограф комплексного числа WH называют амплитудной ха-
рактеристикой нелинейного элемента. Этот годограф показывает
изменение Мн и 0И при различных значениях амплитуды А.
Для всей системы регулирования можно написать
WIV t = МНМлецон+°А , (7.87)
Очевидно, что у замкнутой системы регулирования, находящейся
в режиме автоколебаний, МНМЛ = 1 и 0Н + 0л = 0. Откуда 'следует,
что = 1.
Переход к разомкнутой системе регулирования (Ахвх = —Ахвых
дает WHWjt = —1, или WM — —l/WH. Введя обозначение —1/1Г„ =
= zH, получим
W.t = zH. (7.88)
Уравнение (7.88) является комплексным. Его решение опреде-
ляет амплитуду и частоту синусоидальных колебаний системы
регулирования, находящейся в режиме автоколебаний.
Для решения уравнения (7.88) нужно располагать данными
частотных испытаний нелинейного элемента и линейной части си-
стемы, представленных в виде годографов комплексных чисел
WH и №л. Их примерный вид показан на рис. 7.46, а и б. Годо-
граф WH необходимо перестроить в годограф 2„ =---------. Для
304 Глава VII. Методы расчета и исследования динамических характеристик
этого для каждого значения амплитуды А из графика WH берутся
значения Ц и f2, а комплексное число zH записывается в форме
zH приводится к обычной форме комплексного числа и представ-
ляется точкой па плоскости zH. Совокупность таких точек для раз-
личных А дает годограф zH.
Графическое решение
уравнения (7,88) дается точ-
ками пересечения кривых
и zH, построенных па од-
ном графике так, как это
показано па рис. 7.47. Если
же кривые №л и zH нигде не
пересекаются, то в системе
регулирования автоколеба-
ния синусоидальной формы
возникнуть не могут. Если
же кривые №л и zH пересе-
Рис. 7.47
каются, то точки пересече-
ния определяют величину амплитуды А по отметкам на кривой zH
и частоты со по отметкам па кривой при которых могут возник-
нуть автоколебания синусоидальной формы.
Для того чтобы автоколебания действительно возникли, необ-
ходимо, чтобы цикл автоколебаний, определяемый точками пере-
сечения кривых №л и zH, был устойчив. Однако правильно решить
вопрос об устойчивости цикла колебаний не всегда удается.
Поэтому метод гармонического баланса надо использовать сле-
дующим путем. Если при проектировании регулятора расчеты по-
казывают, что кривые №л и zn пересекаются в- одной или несколь-
ких точках, то следует так изменить конструктивные параметры
регулятора, чтобы этого пересечения кривых не происходило.
Примеры
305
В том случае, когда автоколебания, близкие к синусоидаль-
ным, возникли уже в выполненной системе регулирования, то,
применив метод гармонического баланса, можно найти точку пе-
ресечения характеристик WJl и zH и определить соответствующие
этой точке амплитуду и частоту. Затем следует выявить влияние
конструктивных параметров на положение характеристики и
и дать рекомендации по устранению автоколебаний.
Примеры
Пример 1. Дано характеристическое уравнение системы X3 + X2 -i- К + щ = 0.
Определить методом .D-разбиения область значений коэффициента а0, при кото-
рых система будет устойчивой.
Решаем характеристическое уравнение относительно а0, заменяем перемен-
ную X на сог: а0 = ы2 + (со3—со)г. Для построения годографа в плоскости а0 за-
даемся несколькими значениями со и находим составляющие векторов а0: вещест-
венная часть Л = со2, мнимая часть В = со3—со. Состав-
ляем таблицу.
U)
А
В
1,5
2,25
1,87
0,5
0,25
0,375
Строим годограф, дополняя его симметричной
ветвью для отрицательных значений со. Отмечаем на
годографе штриховкой слева направление обхода
(рис. 7.48). Получаем, что область устойчивости мо-
жет лежать только внутри петли годографа. Система
может быть устойчивая при 0 -С ао =£ 1.
Производим проверку. Для этого решаем харак-
теристическое уравнение и определяем значение кор-
ней при а0 = 0 и при ао = 1. Если система устойчива, то на границах найденной
области по а0 она должна находиться на границе устойчивости.
1)й0 = 0; X3 + X2 + X = 0; X (V + X + 1) = 0;
= 0;
^2,3 — ~
4 2 2
1
1
0
Один из корней уравнения равен нулю. Система на границе апериодической
устойчивости.
2) а0=1; Xs-I -Х2 + Х+1 = О; (X2 + 1) (X -|- 1) = 0; Хх == — 1; Х2>3 = +/.
Пара корней имеют чисто мнимое значение. Система на границе колебательной
устойчивости.
Следует отметить, что данная задача проще решается с помощью критерия
устойчивости Раута—Гурвица. По этому критерию устойчивость системы, описы-
ваемой уравнением третьего порядка, определяется неравенством а2а\—а3а0>0.
В нашем случае я3 = а2 = щ = 1, поэтому 1 — а0 > 0. Откуда для устойчивости
необходимо aQ < 1. Поскольку коэффициенты уравнения величины положитель-
ные, а0 лежит в пределах от 0 до 1.
Пример 2. Система регулирования состоит из ТРД, чувствительного эле-
мента и сервомотора, ее структурная схема показана на рис. 6.1, в. Для ТРД в
зависимости от условий полета принято: при Н — 0 и Мн = 0,5 — Та.н = 0,6 сек
306 Глава VII. Методы расчета и исследования динамических характеристик
и ka.u = 0,2; при II = 20 км и Мн = I — Те.и = 8,0 сек и ka.n = 2,4 (програм-
ма полета взята такой же, как и в примере 2 гл. II, полагаем, что Та.п и ka.n с
изменением внешних условий меняются так же, как и Та и ka). Для сервомото-
ра дано Те = 0,1 сек, kc = 1. В чувствительном элементе регулятора пренебре-
жем влиянием массы, приведенной к муфте чувствительного элемента, что дает
возможность принять Та = 0. Задана постоянная времени чувствительного эле-
мента Ti = 0,5 сек.
Определить величину коэффициента усиления чувствительного элемента k4,
при которой обеспечивается устойчивость системы регулирования для любого
режима полета, предусмотренного программой примера 2 гл. II. При анализе
устойчивости системы использовать критерии устойчивости Раута—Гурвица,
Михайлова и диаграмму Вышнеградского.
Составим уравнение разомкнутой системы регулирования. ТРД и сервомотор
представляют собой инерционные звенья; чувствительный элемент, с учетом то-
го, что Т2 = 0, рассматриваем так же, как инерционное звено. В операторной
форме уравнение разомкнутой системы имеет вид
(Tip-р 1) IX д-нР 4" 1) — k4kck(),HI^nex-
Приравниваем Ап8Х =—&пвых и переходим к уравнению замкнутой системы
iP + 1) (Тср + 1) (Тд.нр 4- 1) Д- k4kckd.H] Ап = 0
Или
(ЯзР3 + а2рг + Й1Р + а0) Ап = 0,
где
аз — ТтТсТд.н* я2 == 7'1Т'С 4- Т\Тд.н 4- ТсТд'Н;
а1 = Ti + Тс 4- Тд.н- а0 — 1 4- k4kcko.H.
Из примера 2 гл. П было «видно, что постоянная времени и коэффициент
усиления двигателя могут изменяться в широких пределах. Для принятой в
этом примере программы полета наименьшие значения Та и ka получаются для
режима полета № 2, а наибольшие для режима полета № 4 *. Нами было при-
нято, что эти режимы определяют также максимальный диапазон изменения
Та.п и ka.u. Поэтому, если будет подобрано значение k4, при котором система
регулирования будет устойчива на режимах полета № 2 и 4, то она будет
устойчива на любом режиме заданной программы.
Определяем значения коэффициентов, входящих в уравнение движения
замкнутой системы.
Режим полета № 2.
п3= 0,5 • 0,1 • 0,6 = 3 • 10~2;
а2-= 0,5 • 0,1 4- 0,5 • 0,6 4-0,1 • 0,6 = 0,41;
а1 = 0,5 4-0,14-0,6= 1,2;
По = 14" 0,2/гч,
Согласно критерию Раута—Гурвица система устойчива при a2a;— а3а0 > 0,
или 0,41 • 1,2 — 3 • 10-2 а0 >0, а0 < 16,4.
Откуда k4 < 45,4/0,2, или k4 < 77.
Режим полета № 4. а3 = 0,4; а2 = 4,85; а{ = 8,6.
Применяя критерий Раута—Гурвица, получим 4,85 • 8,6—О,4по > 0; а0 < 105,5;
. 104,5
k » < = 43,5.
2,4
Из двух значений k4 следует выбрать меньшее, но при k4 = 43,5 система
будет устойчива на режиме полета № 2 и находится на границе устойчивости
на режиме полета № 4. Поэтому для дальнейших расчетов примем k4 = 40.
\ Точнее, в заданной программе полета есть такой режим, близкий к режи-
му 4, на котором значения Та и ka несколько больше.
Примеры
307
Проверим устойчивость системы с помощью
Координаты точек определяются из выражений
диаграммы Вышпеградского.
1. Режим полета № 2. k4 = 77; а0 = 16,4.
0,41 1,2
2. Режим полета № 2. k4 = 40; а0 = 9; X = 2,05; У — 0,89.
3. Режим полета № 4. k4 — 43,5; а0 = W5,5; X = 1,94; У = 0,52.
4. Режим полета № 4. k4 — 40; а0 = 97; X = 1,96; У — 0,55.
Результаты этих расчетов нанесены на диаграмму Вышнеградского (уча-
сток диаграммы в укрупненном масштабе дан на рис. 7.49). Как н следовало
ожидать, точки 1 и 3 легли на граничную кривую, точки 2 и 4 разместились над
граничной кривой, т. е. в области устойчивости. На режиме, определяемом точ-
кой 2, система обладает большим запасом устойчивости, чем на режиме, кото-
рому соответствует точка 4.
Устойчивость системы регулирования проверим с помощью критерия. Ми-
хайлова на режимах, которым соответствуют точки 1 я 2. Для этого нужно
составить два характеристических уравнения, в которых переменную X заме-
нить на mi. Затем в полученных выражениях следует отделить вещественную
308 Г лава VII. Методы расчета и исследования динамических характеристик
часть от мнимой, задаваясь рядом положительных значений т, построить годо-
графы. Для нашего примера они приведены на рис. 7.50. Расположение годо-
графов показывает, что на режиме, определяемом точкой 1 (см. фиг. 7.49), сис-
тема находится на границе устойчивости. На другом режиме (точка 2) система
устойчива. Так как характеристические уравнения отличаются только значения-
ми а0, один годограф может быть получен из другого сдвигом начала коорди-
нат вдоль вещественной оси на величину 16,4—9 = 7,4.
Глава VIII
РЕГУЛИРОВАНИЕ ГТД НА НЕУСТАНОВИВШИХСЯ
РЕЖИМАХ
§ 1. РЕГУЛИРОВАНИЕ РАЗГОНА И СБРОСА ГАЗА ГТД
Неустановившиеся режимы ГТД
Авиационный двигатель должен обладать способностью при
увеличении подачи топлива за короткое время переходить от
наименьшей тяги к наибольшей (ТРД) или от наименьшей к
наибольшей мощности (ТВД). Эта способность двигателя назы-
вается приемистостью.
Для ТРД увеличение тяги обычно связано с возрастанием
числа оборотов Набор мощности у ТВД в зависимости от способа
регулирования пониженных режимов может сопровождаться или
только увеличением угла установки лопастей винта (затяжелени-
ем винта), или ростом числа оборотов и затяжелением винта.
Если рассматривать ТРД, у которого рост тяги сопровождается
увеличением числа оборотов, то его приемистость определяется
временем набора числа оборотов от минимальных до максималь-
ных, или временем разгона. Время разгона существенно зависит
от параметров рабочего режима двигателя, его размеров, от внеш-
них условий и закона подачи топлива при разгоне.
В предшествующих главах мы использовали характеристику
компрессора, с нанесенной на ней линией совместных режимов
работы турбины и компрессора. Следует отметить, что эта линия
соответствует равновесным режимам, определяемым равенством
крутящих моментов турбины и компрессора. Переход от одного
числа оборотов к другому вдоль линии равновесных режимов тре-
бует медленного изменения подачи топлива. Для быстрого набора
числа оборотов необходимо увеличить крутящий момент турбины
и создать положительный избыточный момент на валу турбоком-
прессора (Мт— Мк = 8М>0). При неизменной площади крити-
ческого сечения выходного сопла это достигается увеличением по-
1 Как уже было показано в гл. I, у ТРД с несколькими поворотными на-
правляющими аппаратами осевого компрессора возможно некоторое изменение
тяги при постоянном числе оборотов.
310
Глава VIII. Регулирование ГТД на неустановившихся режимах
Увеличение числа
оборотов
Рис. 8.1
еся режимы
Уменьшение числа
оборотов
дачи топлива и связанного с ним роста температуры газа перед
Iурбиной. Для снижения числа оборотов избыточный крутящий
момент должен быть отрицательным (6М < 0) и поэтому подача
топлива уменьшается.
Неустановившимся режимам ТРД на характеристике компрес-
сора соответствуют свои линии
совместной работы турбины и
компрессора. Их вид и располо-
жение зависят от закона изме-
нения подачи топлива при набо-
ре или снижении числа оборотов.
Линии совместных режимов при
наборе числа оборотов лежат
выше линии равновесных режи-
- мов, при снижении числа оборо-
тов — ниже ее (рис. 8.1). Как
это видно из характеристик, при
—уз-:— достаточно больших расходах
' топлива во время разгона двига-
теля линия совместных режимов
может пересечь границу устой-
чивой работы компрессора и тогда возникает помпаж. Следова-
тельно, подача топлива при разгоне должна ограничиваться таким
образом, чтобы двигатель не терял устойчивости. Возможно так-
же, что еще до наступления помпажа подачу топлива придется
ограничивать из-за достижения предельно допустимых температур
газа перед турбиной или коэффициентов избытка воздуха, приво-
дящих к выходу из строя турбины или прекращению горения топ-
лива (богатый срыв).
Задача регулирования двигателя при разгоне распадается на
две части. К первой относится определение оптимального закона
§ 1. Регулирование разгона и сброса газа ГТД
311
подачи топлива Gp(n), обеспечивающего наилучшую приеми-
стость двигателя при сохранении достаточного запаса по помпа-
жу и при допустимых температурах газа перед турбиной. Для
разных внешних условий эти законы будут различными. Они опре-
деляются обычно экспериментально при испытании двигателя на
стенде и в полете на летающей лаборатории. Вторая часть задачи,
возлагаемая на топливо-регулирующую аппаратуру, -заключается
в обеспечении выбранного закона подачи топлива при разгоне.
На рис. 8.2, а показаны характеристики потребных и располагае-
мых расходов топлива для неизменных внешних условий: G — по-
требный расход топлива на установившихся режимах; Gv — по-
требный расход топлива при разгоне; 6И—количество топлива,
подаваемое насосом. На рис. 8,2, б дана типичная кривая изме-
нения числа оборотов ТРД по времени при разгоне.
Снижение подачи топлива при сбросе газа также необходимо
регулировать. Если не ограничивать скорость уменьшения расхо-
да топлива, то топливо-воздушная смесь может настолько обед-
няться, что самопроизвольно прекратится горение.
Работа регулятора числа оборотов ТРД на режиме разгона
В предшествующих главах рассматривалось действие различ-
ного типа регуляторов при малых отклонениях числа оборотов,
как регулируемого параметра, от его значения на установившемся
режиме. Проанализируем теперь работу регулятора при больших
отклонениях числа оборотов от заданного значения, примером
чему является разгон двигателя. Предположим, что на двигателе
установлен изодромный регулятор числа оборотов, схема которого
приведена на рис. 5.37, и изменение режима происходит от числа
оборотов малого газа до максимального числа оборотов. При раз-
гоне регулятор перемещением рычага управления и поворотом ку-
лачка 6 (см. рис. 5.37) перенастраивается от пм.г до nmax. Темп
перенастройки зависит от скорости перемещения рычага. Наиболее
трудные условия для работы регулятора создаются при его мгно-
венном перемещении.
В результате перестановки рычага и перенастройки регулятора
дроссельный кран 1 полностью открывается, перепад давления на
нем падает, что заставляет золотник 2 закрыться и занять поло-
жение, показанное на схеме. Кулачок 6, сжимая пружину 7, за-
ставляет золотник 9 переместиться вверх, что сообщает полость
над поршнем 14 с напорной масляной магистралью и полость под
поршнем 15 со сливом. Оба поршня начинают быстро переме-
щаться вниз, уменьшая перепуск топлива. После того, как золот-
ник 13 дойдет до упора и поршень 14 остановится, движение порш-
ня 15 и иглы перепуска 5 замедлится и будет продолжаться толь-
ко за счет поступления масла в межпоршневую полость через
312
Глава VIII. Регулирование ГТД на неустановившихся режимах
дроссельное отверстие 11. При достаточно малом отверстии 11
в принципе может быть получено любое замедленное движение иг-’
лы 5 и соответственно замедленное нарастание подачи топлива
к форсункам в конце разгона. Из описанного здесь действия ре-
гулятора, казалось бы, можно сделать вывод, что в разобранной
схеме регулятор числа оборотов способен не только поддержи-
вать заданные стационарные режимы^ но и обеспечивать нужную
дозировку топлива при разгоне. Однако это не так.
Основное перемещение поршня 15 происходит по характеристи-
ке, близкой к линейной. Поэтому возникают трудности в обеспе-
чении оптимальной характеристики Gp (см. рис. 8.2, а). Возмож-
но, что в процессе разгона дозирующая игла 5 (см. рис. 5.37)
полностью перекроет сливное отверстие. Тогда подача топлива
к форсункам будет равна производительности насоса GM, значи-
тельно превышая потребный расход оптимальной характеристики.
Если уменьшить ход поршня 14 и сделать достаточно малым
дроссельное отверстие 11, то характеристику располагаемой пода-
чи топлива при разгоне можно приблизить к потребной характе-
ристике Gp. Но тогда при работе двигателя на установившихся ре-
жимах регулятор будет слишком медленно восстанавливать число
оборотов в случае их отклонения от заданного значения. Допу-
стим, что при выбранном ходе поршня 14 будут получены удовлет-
ворительные характеристики разгона у земли. Но в этом случае
при регулировании разгона в высотных условиях получатся боль-
шие избытки топлива, что приведет к помпажу или перегреву тур-
бины.
В случае использования регулятора расхода, схема которого
приведена на рис. 5.40, как для регулирования основных режимов,
гак и для регулирования разгона, будет получен тот же результат,
что и при использовании изодромного регулятора числа оборотов.
Поршень сервомотора обладает примерно прямолинейной харак-
теристикой и с его помощью трудно изменять подачу топлива при
разгоне по оптимальному закону. При резком открытии дроссель-
ного крана насос может перейти на максимальную производи-
тельность. Снижение быстродействия регулятора расхода путем
уменьшения площади калиброванного отверстия 15, необходимое
для регулирования разгона, ухудшит характеристики регулятора
при работе двигателя на стационарных режимах
Поскольку регулятором числа оборотов не обеспечивается нор-
мальная приемистость двигателя при любых условиях полета,
в ГТД применяются дополнительные регулирующие устройства,
не работающие при малых отклонениях от установившихся режи-
1 С некоторыми допущениями в отношении оптимальных по времени харак-
теристик разгона при работе во всех условиях может быть сделан регулятор,
позволяющий с помощью одного механизма и точно поддерживать заданный
режим, и обеспечивать разгон.
§ 1: Регулирование разгона и сброса газа ГТД
313
мов и вступающие в действие только при разгоне двигателя. Эти
дополнительные регулирующие устройства называются автомата-
ми приемистости. Они бывают незамкнутого и замкнутого типов
и работают по определенной программе. В незамкнутых автоматах
приемистости программирование ведется по времени. В замкну-
тых — по одному или нескольким параметрам, зависящим от про-
цессов, протекающих в двигателе. К незамкнутым автоматам
приемистости относятся гидрозамедлители и ограничители нара-
стания давления топлива (ОНД).
В гидрозамедлителе, схема которого показана на рис. 8.3, при
любой скорости движения рычага 1 скорость сервопоршня 3 по-
Рис. 8.3
стоянна и замедленна. Величина скорости определяется сечением
жиклеров 2. Рычаг 4 гидрозамедлителя может воздействовать или
на затяжку пружины центробежного регулятора числа оборотов,
или на дроссельный кран регулятора расхода топлива. Следует
иметь в виду, что без усложнения схемы гидрозамедлителя нель-
зя получить оптимальную характеристику расхода топлива Gp =
= f(n) для различных внешний условий, так как движение серво-
поршня 3 происходит с постоянной скоростью независимо от вы-
соты полета.
В одной из схем ОНД давление топлива перед форсункой дей-
ствует на золотник, который является одновременно и управляю-
щим элементом сервомотора регулятора. При резком перемещении
рычага управления происходит сильное нарастание давления топ-
лива, золотник смещается и сообщает полость цилиндра сервомо-
тора со сливом, что замедляет скорость нарастания давления.
Золотник ОНД нагружен пружиной. Она опирается на поршень,
который при вступлении в действие ОНД за счет роста под ним
давления топлива начинает перемещаться, усиливая затяжку
пружины. От скорости перемещения поршня зависит временная
характеристика ОНД. Подбор временной характеристики дости-
гается изменением сопротивления дроссельного пакета, через ко-
торый топливо подводится в полость под поршень ОНД. При ис-
314
Глава VIII. Регулирование ГТД на неустановивишхся режимах
пользовании ОНД также нельзя избежать коррекции на измене-
ние внешних условий. Все неточности коррекции приведут или
к недоиспользованию возможностей двигателя, или к забросам
температуры газа и появлению помпажа. К достоинствам програм-
мных по. времени ограничителей относится отсутствие колебаний
в изменении параметров рабочего процесса двигателя.
К замкнутым автоматам относятся пневматические автоматы
приемистости и автоматы, обеспечивающие заданную программу
изменения подачи топлива по числу оборотов. Большое распро-
странение получили пневматические автоматы, регулирующие дав-
ление топлива перед форсунками (так называемые клапаны прие-
мистости) .
Клапаны приемистости
Действие автоматов этого типа связано с величиной разности
давлений р*2 —р*н, причем имеет место своего рода положитель-
ная обратная связь: чем больше разность р*2 — р*н, тем больше
давление перед форсунками р$ и расход топлива.
Принципиальная схема клапана приемистости показана на
рис. 8.4. Упругая мембрана 3 отделяет верхнюю проточную камеру
от нижней непроточной. Давление в верхней камере рм в зависи-
мости от соотношения площадей жиклеров 2 и 5 может изменяться
в пределах от р* до р*н. На золотник 6 действует сила, пропор-
циональная разности давлений рм — р*н , сила пружины 4 и сила,
пропорциональная давлению топлива р$. В зависимости от соотно-
шения этих сил золотник 6 занимает разное положение, изменяя
сечение перепуска. Чем больше рф и меньше рм — Р*н при выбран-
ной силе затяжки пружины 4, тем больше сечение перепуска и тем
больше топлива перепускается на линию всасывания. При малых
значениях Рф и большой разности рм — р*н золотник 6 занимает
нижнее положение, закрывая перепуск. Наибольшие перемещения
золотника вверх будут получаться при резкой перенастройке ре-
гулятора с числа оборотов малого газа на максимальный режим.
В этом случае при разгоне дозирующая игла 1 может полностью
закрыть перепуск.
На схеме рис. 8.4 клапан приемистости установлен параллель-
но регулятору числа оборотов. Однако на практике клапан приеми-
стости обычно используется для воздействия на регулирующий ор-
ган регулятора числа оборотов. Так, если в системе регулирования
подача топлива обеспечивается плунжерным насосом, то клапан
или автомат приемистости воздействует на изменение давления
в полости цилиндра сервомотора и тем самым на положение порш-
ня сервомотора и производительность насоса.
При работе клапана приемистости возможен колебательный
процесс в подаче топлива, который придает колебательный харак-
§ 1. Регулирование разгона и сброса газа ГТД
315
тер изменению числа оборотов и температуры газа. Колебатель-
ный процесс может быть вызван начальным возмущением (сраба-
тывание в начале разгона механизма регулятора числа оборотов,
закрытие клапанов перепуска воздуха из компрессора, изменение
площади сечения выходного сопла и др.). При возмущении кла-
пан приемистости должен возвратить процесс к заданной харак-
Регулятор
числа
о5оротов
Рис. 8.4
теристике подачи топлива. На
рис. 8.5 сплошной линией по-
казано изменение потребного
расхода топлива при разгоне
ТРД, а пунктирной линией —
действительный расход топли-
ва, определяемый клапаном
приемистости при наличии ко-
лебательного процесса.
Рис. 8.5
Расчет пневматического клапана приемистости заключается
в установлении нужной зависимости давления в проточной камере
рм как функции давления р* ив подборе площадей fi и f2 жикле-
ров 2 и 5 (см. рис. 8.4). Полагаем заданными характеристики по-
требной при разгоне подачи топлива Gp = f(n) и давления за
компрессором p"'2 = f(n), а также характеристику форсунок G =
= f(p$). Эти характеристики показаны на рис. 8.6, а, б и в. Зада-
ваясь различными значениями р*2, исключаем переменные G и п
и находим зависимость р$ = f(p’), показанную на рис. 8.7, а.
Составим уравнение равновесия золотника клапана приемисто-
сти (см. рис. 8.4)
(Рф Рм) Г ЗОЛ = Р пруж 4~ (Рм Pfj) (РМ F зол). (8.1)
В этом уравнении F30jl— площадь золотника 6; FM — эффек-
тивная площадь мембраны 3; Рпруж — сила пружины 4.
316
Глава VIII. Регулирование ГТД на неу становившихся режимах
Упростим выражение (8.1), пренебрегая величиной Р30Л, малой
по сравнению с FM, и величиной рм, малой по сравнению с р$.
Решая упрощенное уравнение относительно давления рм, получим
Поскольку перемещения золотника невелики, можно принять,
что Рпруж = const. Тогда, задаваясь различными значениями р*фг
найдем зависимость pM = f(p$). Учитывая уже ранее упомянутую
характеристику р$ = f (р*2), получим потребную зависимость рм =
— /(РгЬ показанную на рис. 8.7, б.
В дальнейшем нужно так выбрать площади жиклеров Д и f2 и
отношение fi/f2, чтобы обеспечить нужную зависимость рм = f(p2)-
В этих жиклерах могут установиться надкритические («) или до-
критические (д) перепады давлений и в зависимости от сочетания
перепадов в пневматической проточной камере установится один из
четырех возможных режимов истечения. Возможные режимы в ко-
ординатах Рн!р2 = показаны на рис. 8.8, а, каждому ре-
жиму соответствует своя область, отмеченная римской цифрой.
Наиболее простая зависимость между рм =f(p*2) и fi/fz получает-
§ 1. Регулирование разгона и сброса газа ГТД
317
ся в области IV, где имеют место надкритические перепады в обоих
жиклерах («— н). В этой области осуществляется простое редуци-
рование рм — В области III, которая характеризуется до-
критическим перепадом в жиклере с площадью и надкритическим
в жиклере с площадью /2, т. е. (д — н), каждому значению отноше-
ния f}lf2 соответствует свое значение рм1р2, не зависимое от р*н /р*2
Зависимости рм/р2 = f(p*NIP*2) при различных f}/f2 для всех че-
тырех областей даются графиками, приведенными на рис. 8.8, б.
При известном отношении р’н1р*2 и заданном рм и, следовательно,
при известном рм/р 2 по этому графику определяется значение
fdfz1.
Расчеты клапана приемистости по обеспечению выбранного за-
кона подачи топлива при разгоне Gp(n), проделанные как для не-
изменных, так и различных внешних условий, показывают недостат-
ки клапана приемистости простейшей схемы (см. рис. 8.4). Выбором
постоянных сечений и f2 обычно не удается обеспечить требуемый
закон Gp(n). рассчитанный для обеспечения выбранного закона по-
дачи топлива при разгоне двигателя у земли, клапан дает значи-
тельные избытки топлива в высотных условиях, что приводит к пе-
регреву турбины и помпажу. Поэтому необходимо изменять
площади жиклеров по числу оборотов и высоте полета, а также под-
1 С помощью данных графиков решаются аналогичные задачи, связанные с
расчетом проточных воздушных камер других пневматических устройств.
318
Глава VIII. Регулирование ГТД на неустановившихся режимах
Рис. 8.9
к сербамотору
9
Рис. 8.10
§ 1. Регулирование разгона и сброса газа ГТД
319
бирать характеристику распределительного клапана (РК). Пнев-
матический расчет клапана для различных условий дает возмож-
ность определить закон изменения f\ и f2 Для перехода к клапану
усложненной схемы. Принципиальная схема такого клапана прие-
мистости показана на рис. 8/9.
Рассмотрим еще одну схему пневматического автомата разгона,
дозирующего подачу топлива по давлению р*2 с коррекцией на ве-
личину В этом автомате (рис. 8.10) на линии подачи топлива
от насоса к форсункам установлена дозирующая игла <3. На ней
поддерживается постоянный перепад давления с помощью клапа-
на 1, воздействующего на производительность насоса. Положение
дозирующей иглы определяется величиной давления рх (редуциро-
ванное давление р2), подводимого в камеру анероида 10. Усилие
от анероида 10 передается на рычаг 5, который уравновешен пру-
жиной 4. С ростом р* при увеличении числа оборотов двигателя
условие равновесия на рычаге 5 нарушается, эффективное сечение
жиклера 6 уменьшается, давление на сервопоршне 2 дозирующей
иглы падает. В результате дозируЬэщая игла перемещается вверх,
увеличивая площадь для прохода топлива. Пружина 4 осуществ-
ляет обратную связь между дозирующей иглой и рычагом 5.
Коррекция по л* дает возможность увеличить интенсивность
подачи топлива на заключительном этапе разгона, где есть доста-
точный запас по помпажу. Давление, пропорциональное л*, полу-
чается с помощью анероида 8 и сильфона 9, находящегося под дав-
лением р\ . Анероид и сильфон помещены в камеру, находящуюся
под давлением р*2. При увеличении л* сильфон перемещает кла-
пан 7 вправо, давление рх возрастает. Если клапан полностью за-
крыт, то давление рх, действующее на анероид 10, равно р2. Следо-
вательно, давление рх, а также и расход топлива на режиме разгона
являются функциями р*2 и л*к .
Особенности построения характеристик разгона ТРД
Остановимся на вопросе построения характеристик разгона
ТРД. Здесь возникают трудности, связанные с нелинейностью ха-
рактеристик отдельных звеньев системы регулирования, а также
с изменением в процессе разгона ее структуры. Для ТРД, рассмат-
риваемого как инерционное звено, движение описывается линейным
дифференциальным уравнением
Тд— + Дп = йаДС.
dt
При разгоне число оборотов меняется в широких пределах, по-
этому коэффициенты уравнения Тр и kg уже не являются постоян-
320
Глава VIII. Регулирование ГТД на неустановившихся режимах
ними величинами, а зависят от выходного параметра — от числа
оборотов. Кроме того, Та и ka меняются с изменением высоты по-
лета.
Изменение структуры системы регулирования связано с тем, что
в процессе разгона вступают в работу или выключаются из работы
некоторые регулирующие устройства. В начальный период разгона
совместно работают регулятор числа оборотов и автомат приеми-
стости, причем первый из них стремится увеличить, а второй — огра-
ничить подачу топлива в двигатель. В основной стадии разгона ра-
ботает только автомат приемистости. В конце процесса разгона при
достижении заданной скорости вращения снова вступает в действие
регулятор числа оборотов, а клапан приемистости автоматически
выключается из работы. На каждом из этих участков процесс раз-
гона описывается различными дифференциальными уравнениями,
которые из-за нелинейности аналитическим путем решить сложно.
Поэтому построение характеристик разгона должно быть проведено
с помощью какого-либо из приближенных методов. Можно, напри-
мер, разбить процесс на отдельные участки, для каждого из кото-
рых допустима линейная аппроксимация, и вести построение от уча-
стка к участку, принимая за начальные значения координат для
каждого из участков конечные их значения на предшествующем
участке. Чаще, однако, характеристики разгона получают методом
математического моделирования с помощью электронных модели-
рующих установок. Этому вопросу посвящена гл. X.
Особенности процесса разгона и набора мощности ТВД
Приемистость ТВД следует раздельно оценить по числу оборо-
тов и по мощности.
Приемистость по числу оборотов характеризуется временем пе-
рехода двигателя от пм.г до «шах- Этот переход у современных ТВД
составляет всего 2ч-4 сек, так как при разгоне могут быть получены
большие избыточные мощности, а число оборотов малого газа всего
лишь на 20-г-30% отличаются от максимальных.
Приемистость по мощности характеризуется временем измене-
ния мощности двигателя от минимальной до максимально возмож-
ной. Для современных ТВД это время составляет 15 ч-20 сек и опре-
деляется главным образом скоростью перестановки лопастей воз-
душного винта.
Прежде чем разобрать общий случай перехода с режима мало-
го газа на режим максимальной мощности, связанный с перена-
стройкой регуляторов подачи топлива и числа оборотов, остановим-
ся на двух частных случаях. На рис. 8.11, а изображен процесс
перехода ТВД с на п2 при неизменной подаче топлива. Если бы
перенастройка регулятора числа оборотов происходила медленно,
в каждый момент времени располагаемая мощность двигателя рав-
§ 1. Регулирование разгона и сброса газа ГТД
321
нялась потребной мощности винта. Процесс перехода шел бы по
линии 1—2. При быстрой перенастройке регулятора с на п2 сер-
вомотор регулятора с достаточно большой скоростью начнет пере-
ставлять лопасти на винте на меньшие углы <р, возникшая на винте
избыточная мощность приведет к большому ускорению ротора.
Обычно регулятор числа оборотов винта не имеет стабилизирую-
щих средств, с помощью которых обеспечивалось бы предварение
перекрытия золотника регулятора. Поэтому при достижении задан-
ного значения п2 лопасти винта могут находиться на установочном
угле, близком к минимальному углу (pmin .(точка 4), и избыточная
мощность на винте приведет к дальнейшему росту числа оборотов.
При п > п2 регулятор начнет затяжелять винт, в точке 5 распола-
гаемая и потребные мощности сравняются, но число оборотов будет
больше заданных. При дальнейшем затяжелении винта потребная
мощность станет больше располагаемой, что приведет к снижению
числа оборотов. Процесс пойдет по свертывающейся спирали и по-
степенно подойдет к точке 2, являющейся точкой равновесного ре-
жима п2.
На рис. 8.11, б тсхт же процесс набора числа оборотов ТВД пока-
зан во времени. Здесь чередованию положительной и отрицательной
избыточной мощности соответствует затухающий колебательный
процесс (точки на рис. 8.11, б соответствуют точкам рис. 8.11, а).
На рис. 8.12 показан переходный процесс при перенастройке
регулятора подачи топлива ТВД: от мощности Ne\, соответствую-
щей расходу топлива Gi (точка 1), к мощности Ne2, соответствую-
щей расходу G2 (точка 2). При этом настройка регулятора числа
оборотов остается неизменной. В случае быстрого увеличения рас-
хода топлива от G] до G2 рост располагаемой мощности происходит
практически безынерционно. Появление избыточной мощности вы-
зывает раскрутку ротора двигателя, в результате чего регулятор
числа оборотов затяжеляет винт. В точке <3 потребная и располагае-
мая мощности равны, но число оборотов больше заданных и затя-
И Черкасов Б. А.
322
Глава УШ. Регулирование ГТД на неустановившихся режимах
желение винта продолжается. В точке 4 число оборотов двигателя
соответствует заданным, но мощность винта больше располагаемой
мощности двигателя. Переходный процесс заканчивается в точке 2,
имея вид, также как и ,в случае изменения числа оборотов при по-
стоянной подаче топлива, свертывающейся спирали.
Рассмотрим теперь процесс перехода ТВД от режима понижен-
ной мощности к режиму максимальной мощности. В общем случае
для этого необходима перенастройка как регулятора подачи топли-
ва, так и регулятора числа оборотов. В переходном процессе, изо-
браженном на рис. 8.13, точка 1 соответствует режиму пониженной
G^const
G,=const
nt пг nogp n
Рис. 8.13
/77 nmax n
Рис. 8.12

мощности, а точка 2 — максимальной мощности. Регулятор подачи
топлива должен быть дополнен каким-либо автоматом приемисто-
сти, уменьшающим скорость нарастания расхода топлива. Иначе
при резком увеличении расхода от G\ до О2 возникнет помпаж и
перегрев двигателя.
Переходный процесс, как и в ранее рассмотренных случаях, идет
по свертывающейся спирали. В нем следует отметить два сущест-
венных недостатка: падение мощности двигателя в начале переход-
ного процесса, связанное с перестановкой лопастей винта на мень-
ший угол, и значительный заброс числа оборотов, обусловленный
тем, что в регуляторе числа оборотов нет стабилизирующих элемен-
тов в виде обратной связи или акселерометра (эти недостатки при-
сущи и тем переходным процессам, которые представлены на
рис. 8.11 и 8.12). Падения мощности в начальный период разгона
ТВД не будет наблюдаться в том случае, если лопасти винта дви-
гателя, работающего на режиме пониженной мощности, будут уста-
новлены ПОД УГЛОМ фщщ.
Для уменьшения заброса числа оборотов при разгоне в систему
регулирования ТВД включают регулятор, ограничивающий число
§ 1. Регулирование разгона и сброса газа ГТД
323
оборотов. Он воздействует на подачу топлива и может быть выпол-
нен в виде однорежимного регулятора числа оборотов, подобно то-
му, которым дополнен регулятор расхода, показанный на рис. 5.43.
Без регулятора, ограничивающего число оборотов, переходный про-
цесс (см. рис. 8.13) идет по кривой 1—3—4—5—2. В случае включе-
ния в систему этого регулятора переходному процессу соответствует
кривая 1—3—6—2.
В начале этой главы было сказано, что у ТРД скорость сниже-
ния подачи топлива при сбросе газа необходимо регулировать. Эта
необходимость обусловливается силь-
ным обеднением топливо-воздушной
смеси, могущим привести к самопро-
извольному прекращению горения.
Против переобеднения смеси исполь-
зуют обычно гидрозамедлители, .сни-
жающие скорость перенастройки ре-
гулятора числа оборотов или переста-
новки дроссельного крана. Включение
в систему регулирования клапана ми-
нимального давления, принцип дейст-
вия которого был рассмотрен в гл. V,
также способствует стабилизации го-
рения при сбросе газа.
В ТВД уменьшение мощности в по-
лете путем резкого снижения подачи
топлива (при неизменной настройке
регулятора числа оборотов) также
приводит к значительному обеднению
смеси и затрудняет процесс горения.
Рис. 8.14
Но, кроме того, резкое уменьшение
подачи топлива в полете может вызвать значительную отрицатель-
ную тягу винта. На рис. 8.14 показан переходный процесс ТВД
при снижении расхода топлива, например, при посадке, от G[ до
G2. В начале переходного процесса число оборотов падает, так
как располагаемая мощность двигателя меньше потребной мощ-
ности винта. Регулятор числа оборотов начнет облегчать винт,
и если установочный угол лопастей будет приближаться к cpmin, то
возникнет большая отрицательная тяга. Переходный процесс пой-
дет по кривой 1—3—4—5—6—7—2 (при включении в систему
регулятора, ограничивающего число оборотов). Для уменьшения
отрицательной тяги служит промежуточный упор, определяющий
минимальный установочный угол лопастей винта в полете српром-
При установке лопастей на промежуточный упор переходному
процессу соответствует кривая 1—3—4—8—7—2. Таким образом,
для обеспечения надежной работы двигателя и для предотвраще-
ния возникновения большой отрицательной тяги при сбросе газа
Ц* Черкасов Б. А.
324
Глава VIII. Регулирование ГТД на неустановившихся режимах
в системе регулирования ТВД должны быть предусмотрены замед-
литель перенастройки регулятора подачи топлива и промежуточ-
ный упор лопастей винта в регуляторе числа оборотов.
§2. РЕГУЛИРОВАНИЕ ЗАПУСКА ГТД
Запуск газотурбинного двигателя можно разбить на три этапа.
Характер изменения мощностей стартера, турбины и компрессора
по этапам показан на рис. 8.15, а. На первом этапе (I) происходит
раскрутка ротора двигателя стартером без подачи пускового или
основного топлива в камеру сгорания. На втором этапе (II) в каме-
ру сгорания подается топливо и к мощности продолжающего рабо-
тать стартера добавляется мощность турбины. В конце второго
этапа стартер отключается. На третьем этапе (III) происходит уве-
личение скорости вращения ротора за счет избыточной мощности
турбины при неизменной подаче топлива, в конце этапа двигатель
выходит на число оборотов малого газа.
Минимальные равновесные п' при выключенном стартере могли
бы быть получены до окончания второго этапа. Но они достигаются
при слишком высокой температуре газа. Поэтому число оборотов
П2 (при которых отключается стартер) выбирают равными 1,5н-2
ОТ П\.
Для каждого двигателя можно выбрать оптимальный закон рас-
хода топлива при запуске. Желательно, чтобы истинное изменение
расхода по числу оборотов ротора двигателя было близким к опти-
мальному. В конце первого этапа запуска специальная пусковая
топливная система подает пусковое топливо и обеспечивает его вос-
пламенение, затем вступает в действие основная топливная система
с определенной программой подачи. Запаздывание в подаче топли-
§ 2. Регулирование запуска ГТД
325
ва затягивает весь цикл запуска, увеличивает время работы стар-
тера. Слишком ранняя подача топлива приводит к перегреву тур-
бины и может вызвать помпаж.
На рис. 8.15, б показаны располагаемые и потребные расходы
топлива при запуске. Линия <3 соответствует предельно допустимым
расходам топлива из условия отсутствия помпажа и приемлемой
температуры перед турбиной. Производительность топливного на-
соса (линия 1) больше, чем величина потребного расхода топлива.
Если попытаться запустить двигатель без средств автоматики, вруч-
ную, и на числе оборотов щ перевести дроссельный кран или рычаг
управления из положения «стоп» в положение «малый газ», то рас-
ход топлива будет нарастать до величины йм.г (линия 2). В неко-
тором диапазоне числа оборотов при неавтоматическом запуске
располагаемый расход будет равен производительности насоса и
значительно превысит предельно допустимый расход. Чтобы при не-
автоматическом запуске расход не превышал предельно допусти-
мый, дроссельный кран из положения «стоп» в положение «малый
газ» должен перемещаться замедленно в течение перехода от обо-
ротов п} к оборотам п2- Очевидно, такой способ запуска нельзя счи-
тать удовлетворительным. Наилучшие условия для запуска созда-
ются в том случае, когда подача топлива по числу оборотов изме-
няется по линии 4, близко расположенной к линии предельно
допустимых расходов <3. Для этого запуск должен быть автомати-
зирован. (О регулировании подачи топлива по линии 5 говорится
в конце этого параграфа.)
В применяемых топливных автоматах запуска регулирование по-
дачи топлива при запуске производится одним из трех способов.
1. По сигналу разности давления р’2 —р* излишек топлива, по-
даваемого насосом, перепускается специальным клапаном в маги-
страль перед насосом.
2. С помощью гидравлического замедлителя, включенного в топ-
ливную систему, по мере нарастания давления топлива уменьшает-
ся перепуск, увеличивается подача к форсункам.
3. В топливную Магистраль вводится несколько параллельно
расположенных клапанов. По мере роста числа оборотов они после-
довательно открываются, увеличивая подачу топлива к форсункам.
Излишек топлива перепускается, для этой цели может быть исполь-
зован автомат приемистости.
Рассмотрим схему и принцип действия топливного автомата за-
пуска последнего типа (рис. 8.16). Автомат содержит три электро-
магнитных клапана 2, 3 и 5. Перед запуском к ним подводится
напряжение, удерживающее их в закрытом положении до числа обо-
ротов П[ (по обозначениям рис. 8.15). Чувствительный элемент ав-
томата таходинамо 1 (см. рис. 8.16), подавая напряжение, пропор-
циональное числу оборотов двигателя, последовательно прекращает
подачу тока к электромагнитам клапанов. При прекращении деист-
826 Глава VIII. Регулирование ГТД, на неустановившихся режимах
вия электромагнитов клапаны под действием пружин открываются,
расход топлива, поступающий к форсункам, регулируется сечения-
ми жиклеров 4. Таким путем осуществляется ступенчатое регулиро-
вание подачи топлива по числу оборотов (линия 5 на рис. 8.15, б).
Такое регулирование хотя и приводит к некоторому проигрышу во
времени запуска по сравнению со временем при оптимальной пода-
че топлива (линия 4), однако отличается простотой и надежностью.
Во время запуска с помощью этого автомата дроссельный кран 7
(см. рис. 8.16) стоит в положении «малый газ». Все топливо, пода-
ваемое насосом при перепускается автоматом приемисто-
сти 6 на линию всасывания.
Примеры
Пример 1. Заданы характеристика потребного расхода топлива при разгоне
ТРД в стендовых условиях Gp(n), характеристика комплекта форсунок G(Po5).
Они показаны на рис. 8.17, а и б.
Требуется определить характеристику давления воздуха над мембраной
р.-л(п) клапана приемистости, при которой обеспечивается выбранный закон по-
дачи топлива во время разгона двигателя. Схема клапана приемистости приве-
дена на рис. 8.4, заданы его размеры: полезная площадь мембраны FM. = 30 см2,
диаметр золотника <130Л — 1 см. Клапан должен вступать в действие при дав-
лении топлива перед форсунками Рф =100 н[см2, при этом в связи с низкими
давлениями пониженных режимах можно пренебречь разностью давлений
рм—р*н> действующей на мембрану, и принять ее равной нулю.
Для определения давления рм используем зависимость (8.2). Эта же зави-
симость дает возможность найти силу пружины Рпруж при Р^ — Ррт^® и
р'ф = 100 н[см2, тогда
Р —F ol ——~ 100=78,6 н.
Г пруж зол^ф 4
Примеры
327
Полагая Рпочж = const, задаемся на характеристике Gp(n) рядом значе-
ний п (см. рис. 8.17, а), находим для каждого из них Gp и соответствующие им
значения рф (см. рис. 8.17, б). Так, например, для п = 5000 об/мин Gp = G =
= 3600 кг/час, откуда р$ = 255 н/смг.
в)
Рис. 8.17
Расчет ведется для стендовых условий, следовательно, Р н~ 10,12 н/см2.
Для рф = 255 н/см2 получим
Рм= Ю.12 -р
255 0,786 — 78,6
30
= 14,18 н/см2.
Найденная зависимость рм (п) приведена на рис. 8.17, в.
Пример 2. Задана характеристика р2(п), показанная на рис. 8.18, а. Тре-
буется определить отношение fj/г проходных сечений жиклеров клапана прие-
мистости (см. рис. 8.4), обеспечивающее найденную в предыдущем примере за-
висимость рм(п). Эта зависимость показана на рис. 8.17, в.
Как и в предыдущем примере, задаемся несколькими значениями чисел
оборотов п: 3500, 4000, 5000, 6000 и 6500 об/мин. Для каждого значения п по
графикам рис. 8.17, в и 8.18, а находим соответствующие им рм и р2. Затем
определяем отношения рм/р*2 и Рн1Р*2, приняв р‘н= 10,12 н/см2. Полученные
отношения рм/р2 и Рц/Р2 P-ля каждого числа оборотов являются координата-
ми точек, которые следует нанести на график рис. 8.8, б. Часть этого графика в
328 Г лава VIII. Регулирование ГТД на неустановившихся режимах
укрупненном масштабе с ненесенными на него точками приведена на рис. 8,18,6.
Из него видно, что точки 2, 3, 4 и 5 (соответствующие числам оборотов п =
= 4000, 5000, 6000 и 6500 об/мин) удовлетворительно ложатся на кривую fi/fj =
= 0,4. Точка 1, соответствующая режиму п = 3500 об/мин, находится на прямой
f\l!i = 0. Это связано с тем, что в предыдущем примере этот режим был ис-
пользован для определения силы пружины Рпруж- На этом режиме было приня-
то, что рм = Рц. Надо полагать, что в действительности точка 1 расположится
несколько ближе к кривой fi/fa = 0,4.
В результате этого анализа можно сделать вывод, что разгон ТРД, харак-
теристики которого заданы в данном и предыдущем примерах, в стендовых ус-
ловиях может быть обеспечен с помощью клапана приемистости простой схемы.
Глава IX
РЕГУЛИРОВАНИЕ
АВИАЦИОННОЙ ЯДЕРНОЙ СИЛОВОЙ УСТАНОВКИ
§ 1. СХЕМЫ ЯДЕРНЫХ ВРД
В предшествующих главах в качестве объекта регулирования
рассматривались авиационные силовые установки, источником
энергии которых является химическая энергия топлива. Развитие
ядерной энергетики открыло широкие перспективы использования
энергии ядерного распада в транспортных силовых установках и
в первую очередь в силовых установках морских судов. Блестящим
подтверждением возможностей нового вида энергетики явилась по-
стройка мощного ледокола «Ленин» с атомным реактором—источни-
ком тепловой мощности. Изучаются возможности применения ядер-
ной энергии в авиационных силовых установках.
Ядерный воздушно-реактивный двигатель отличается от обыч-
ного воздушно-реактивного двигателя только способом нагрева воз-
духа. Нагрев воздуха в ЯВ.РД происходит непосредственно в реак-
торе или в теплообменнике, к которому тепло переносится от реак-
тора промежуточным теплоносителем.
На рис. 9.1 дана схема наиболее простого ядерного ТРД (с ха-
рактерными сечениями 2 и 3), у которого воздух нагревается непо-
средственно в ядерном реакторе. Однако эта схема имеет сущест-
венный недостаток: воздух после реактора будет радиоактивен.
Кроме того, при создании двигателя по этой схеме возникает про-
блема охлаждения и изоляции вала турбокомпрессора от у-излуче-
ния и нейтронного облучения.
330
Глава IX. Регулирование авиационной ядерной силовой установки
Более перспективной является схема ЯТРД, показанная на
рис. 9.2, с теми же характерными сечениями 2 и 3. Здесь исполь-
зуется промежуточный теплоноситель, прокачиваемый через реак-
тор и теплообменник насосом. Применением щелочных металлов
в качестве теплоносителя можно существенно уменьшить размеры
реактора за счет увеличения коэффициента теплопередачи от теп-
ловыделяющих элементов к теплоносителю. У ЯТРД этой схемы
воздух, выходящий из двигателя, не будет радиоактивным. Детали
двигателя легче защитить от вредного влияния у-излучения и
нейтронного облучения, существенно меньше будет вес биологиче-
ской защиты.
Непосредственный подогрев воздуха в реакторе целесообразно
применять в силовой установке с ядерным ПВРД (рис. 9.3), где 2
и 3 — сечения. В этом типе двигателя степень подогрева воздуха
может быть более высокой, чем в ЯТРД, и ограничивается только
допустимой температурой в активной зоне реактора. При темпера-
туре воздуха после реактора до 2000° К летательные аппараты
с двигателями этого типа могут достигать чисел Мн полета порядка
5 ч-6. Следует отметить, что использование реактора на быстрых
нейтронах с промежуточным жидкометаллическим теплоносителем
в силовых установках с ядерным ПВРД в некоторых случаях может
оказаться предпочтительнее, чем непосредственный нагрев воздуха.
Возможны ядерные ВРД более сложных схем с комбинацией
двух или. более термодинамических циклов.
§ 2. Реактор как объект регулирования
331
За регулируемые параметры ЯТРД следует выбрать число обо-
ротов турбокомпрессора и температуру воздуха перед турбиной.
Регулирующими факторами будут плотность нейтронного потока
в реакторе и площадь критического сечения выходного сопла. Изме-
нением потока нейтронов целесообразно воздействовать на число
оборотов турбокомпрессора, а изменением площади выходного соп-
ла— на температуру воздуха перед турбиной. Выделяемое реакто-
ром тепло пропорционально плотности нейтронного потока, поэтому
ее можно рассматривать как величину, аналогичную расходу топли-
ва в обычных ТРД.
Программа регулирования ЯТРД может быть выбрана сходной
с программой регулирования ТРД, работающего на химическом
топливе. Это может быть, например, постоянство числа оборотов
турбокомпрессора и температуры воздуха перед турбиной. Если ле-
тательный аппарат с ЯТРД рассчитан на широкий диапазон скоро-
стей полета и в том числе на большие сверхзвуковые скорости, то
приведенное число оборотов компрессора будет сильно меняться.
В этих условиях может возникнуть необходимость специального ре-
гулирования компрессора, так же как и у обычного ТРД, для рас-
ширения диапазона устойчивой работы.
Кроме этой основной программы регулирования должно осуще-
ствляться ограничительное регулирование по величине и скорости
нарастания нейтронного потока. С этой точки зрения реактор сле-
дует рассмотреть как самостоятельный объект регулирования.
Поэтому в этой главе основное внимание обращено на свойства
реактора как объекта регулирования. Разобраны также вопросы
управления и контроля за процессом в реакторе, приведены неко-
торые возможные структурные схемы регулирования реактора и
всего ЯТРД. При чтении этой главы необходимо знакомство с осно-
вами ядерной физики и процессами, происходящими в энергетиче-
ских ядерных реакторах.
§ 2. РЕАКТОР КАК ОБЪЕКТ РЕГУЛИРОВАНИЯ
В системе регулирования ЯТРД реактор есть лишь одно из зве-
ньев системы. Однако специфические особенности реактора требуют
тщательного исследования его динамических свойств. Входной ко-
ординатой реактора является реактивность, выходной — мощность
реактора, определяемая средней плотностью нейтронного потока.
Следует различать стержневую реактивность, задаваемую внеш-
ними регулирующими органами, и истинную реактивность, завися-
щую от процесса в реакторе. В понятие изменение стержневой
реактивности будем включать любой преднамеренный способ изме-
нения реактивности. У реакторов на тепловых нейтронах основной
способ изменения реактивности заключается в перемещении стерж-
ней в активной зоне реактора, выполненных из материала, погло-
332
Глава IX. Регулирование авиационной ядерной силовой установки
щающего тепловые нейтроны. Реактивность реакторов на быстрых
нейтронах изменяется перемещением в активной зоне части ядерно-
го горючего или изменение относительного расположения горючего
и отражателя. На величину истинной реактивности влияет темпера-
тура нагреваемого в реакторе теплоносителя, отравление и выгора-
ние горючего. Эти влияния надо рассматривать как обратные связи
реактора, из которых вторая сказывается,только при длительной
работе реактора. Структурная схема реактора как звена в системе
Рис. 9.4
регулирования с обратными
связями показана на рис. 9.4.
Влияние отравления и вы-
горания есть отрицательная
обратная связь. Влияние тем-
пературы теплоносителя на вы-
ходе из реактора (она пропор-
циональна мощности реактора
при неизменной температуре
теплоносителя на входе) мо-
жет явиться как отрицатель-
ной, так и положительной об-
ратной связью. Однако реак-
тор стараются спроектировать
гак, чтобы имел место отрица-
тельный температурный эф-
фект реактивности, что будет равносильно отрицательной обратной
•связи. В дальнейшем будем рассматривать динамические свойства
реактора как без обратных связей (температурный коэффициент
реактивности равен нулю, истинная реактивность совпадает со
стержневой реактивностью), так и с отрицательной обратной связью
по температуре теплоносителя. При охлаждении реактора газовым
теплоносителем на реактивность, кроме температуры, в некоторой
степени влияет также давление газа — барометрический эффект ре-
активности. Влиянием обратной связи по барометрическому эффек-
ту, отравлению и выгоранию в дальнейшем пренебрегаем.
Период реактора
При изучении динамики реактора важным понятием является
понятие периода реактора.
Способность реактора увеличивать мощность за счет избыточ-
ной реактивности характеризуется периодом реактора, т. е. време-
нем, в течение которого мощность реактора меняется в е раз.
Рассмотрим разгон реактора за счет возмущения по коэффи-
циенту размножения k. В стационарном режиме при t = 0 величины
п0 = const, k = 1. При возмущении избыточной реактивностью k —
= I + &k (поскольку k » 1, с достаточной для практики точностью
§ 2. Реактор как объект регулирования
333
можно принять стержневую реактивность р = 6&). Здесь и дальше
примем обозначения:
п0—-число нейтронов в исходном поколении в единице
объема реактора;
«о(1+ 6&)—число нейтронрв в следующем за исходным поко-
лении;
По(1 + 6&)2— число нейтронов во втором поколении;
п0(1 + 6k)m—число нейтронов в m-м поколении.
Показатель степени m зависит от рассматриваемого интервала
времени разгона \t и периода жизни одного поколения нейтронов I*.
Таким образом, tn = Поэтому плотность потока нейтронов
в любой момент времени определяется выражением
At
n = n0(l + 6k)1" ,
или
In 2L = _^Lin(i+б/г). (9.1)
«о i
Для упрощения выражения (9.1} разложим множитель 1п(1 +
+ 6k) в ряд
/1 I СМ si, Sk2 , 6k3 ,
1П (1 + 6k) = 6k--— -г —-------— H-----
Поскольку величина 6k мала, можно отбросить все члены разложе-
ния, кроме первого, как имеющие более высокие порядки малости.
Тогда получим, что
In — = — Ыг,
п0 I*
ИЛИ
At «ь
— =ez* . (9.2)
па
ГТ
Исходя из определения периода реактора нужно положить — 6k =
= 1, интервал времени А/ в этом случае равен периоду реактора
Т = АЛ
Откуда
т = —
6k
(9.3)
Если не учитывать влияния доли запаздывающих нейтронов, то
время жизни одного поколения нейтронов определяется временем
диффузии теплового нейтрона. Оно равно 10-3 сек'.
Примем избыток коэффициента размножения над единицей 6k =
— 0,005 и определим насколько быстро будет нарастать в таком
1 Время 10~3 сек свойственно только тепловым нейтронам. Для реакторов
на промежуточных и быстрых нейтронах оно составит 10-4 + 10~7 сек.
334
Глава IX. Регулирование авиационной ядерной силовой установки
реакторе (без учета запаздывающих нейтронов) поток нейтронов.
В этом случае период реактора Т = 0,2 и
а
— = е~ = е5^.
па
Зададимся различными значениями Д/ и определим отношение
п/п0: М = 0,5 сек, п/п0 ~ 12; Ы = 1 сек' п/п0 ~ 148; Д/ = 2 сек,
п/по ~ 220. Из полученного результата следует сделать вывод, что
поток нейтронов нарастает чрезвычайно быстро, реакция практиче-
ски не управляема, так как быстродействия системы автоматиче-
ского регулирования будет недостаточно. Однако учет запаздываю-
щих нейтронов совершенно меняет картину.
Запаздывающие нейтроны в случае использования урана-235
испускаются шестью группами с временем задержки от 0,07 сек до
80,2 сек. Доля запаздывающих нейтронов невелика и составляет
всего лишь 0,75%, но с их учетом средневзвешенное время жизни
нейтрона /* повышается до 0,1 сек.
Примем опять избыток коэффициента размножения 8k = 0,005.
Тогда период реактора возрастает до 20 сек и управление реакто-
ром становится вполне возможным. Следует отметить, что при
8k < 0,005 период реактора будет еще больше. Такой большой пе-
риод еще не говорит о том, что приемистость ядерного ТРД будет
хуже приемистости ТРД, работающего на химическом топливе.
Период реактора можно снизить за счет увеличения 8k. Но скорость
увеличения числа оборотов двигателя будет ограничиваться про-
цессами передачи тепла от реактора или теплоносителя к воздуху.
Уравнение движения реактора по нейтронной мощности
(без учета температурного эффекта реактивности)
Если в период существования исходного поколения нейтронов
дать приращение реактивности 8k = k— 1, то в последующем поко-
лении нейтронов появится приращение 8п, состоящее из прираще-
ния мгновенных нейтронов 8пм и запаздывающих 8п3. Таким обра-
зом, 8п = 8пм + 8п3. Если бы все нейтроны были мгновенными, то
количество нейтронов последующего поколения определилось из
выражения п = n0(l + 8k). Однако p-я доля нейтронов тратится на
создание ядер-предшественников запаздывающих нейтронов. Для
данного поколения они пропадают и поэтому можно записать
«о(1 + 8k) (1 — р) n0(l + 8k—р), отбрасывая произведение бйр,
как величину второго порядка малости.
Тогда за период времени Af количество мгновенных нейтронов
будет равно
At
п = nQ (18k — $)!* . (9>4)
§ 2. Реактор как объект регулирования
335
В этом выражении доля запаздывающих нейтронов [3 опреде-
ляется как сумма долей запаздывающих нейтронов каждой из ше-
6
сти групп: р = Pi-
Прологарифмируем выражение (9.4), разложим логарифм сум-
мы в ряд и отбросим величины высших порядков малости
1пп= 1пи0+-у-1п(1 +6k — Р)ж lnn0+-у-(б£ — р).
Откуда
Используем разложение в ряд показательной функции
1 .. 2! 3!
и отбросим все члены ряда, кроме первых двух. Тогда предшест-
вующее выражение примет вид
(- , 6k — р ЛД
п — п01 1 -)--— I ,
\ " j
что дает возможность найти приращение мгновенных нейтронов
6ПЛ1 = ПОА=ГДЛ (9.5)
Перейдем к определению запаздывающих нейтронов 6п3. Введем
обозначения:
Ci — плотность i-й группы источника запаздывающих нейтронов;
i Xi— постоянная распада; величина, обратная периоду, за кото-
рый плотность с; меняется в е раз (cj0/ci = еприЛ/ = l/?„f).
Тогда можно записать
или
6сг-= с;о(1 — е~х*д/). (9.6)
Каждое ядро-предшественник при своем распаде испускает один
запаздывающий нейтрон. Тогда 6n3i = &Ct, или, используя выраже-
ние (9.6):
6nJi = cI-o(1 — е-Х/Л*).
Разлагая последнее выражение в ряд, после упрощения получим
6«31 = c/0W (9.7)
Уравнение (9.7) показывает, что рост числа запаздывающих
нейтронов происходит за счет распада ядер-предшественников: ко-
личество ядер-предшественников уменьшается на такое же число,
на сколько увеличивается количество запаздывающих нейтронов.
336
Глава IX. Регулирование авиационной ядерной силовой установки
Но в то же время из каждого поколения нейтронов образуются но-
вые ядра-предшественники прг. Следовательно, приращение плот-
ности источника запаздывающих нейтронов может быть представ-
лено в виде
бС/==ф.-^-_ (9-8)
I*
Для перехода от одной группы ко всему количеству запаздываю-
щих нейтронов проводим суммирование и осреднение:
6 6
бп3 = = с<№-,
z=i i=i
Для урана-235 1ср = 12,24 сек, = 0,082 —5—. После сум-
IС р СвК
мирования и осреднения переходим к пределу txt-^dt, п0-^п, с0-^-
->с. Переход к пределу дает возможность па базе уравнений (9.5) и
(9.8) получить дифференциальные уравнения реактора по нейтрон-
ной мощности в двухгрупповом приближении 1
— == AzzL п + (9.9)
dt I*
J^JLn — кс. (9.10)
dt I*
Для исследования динамических характеристик реактора сле-
дует исключить переменную с — осредненную плотность запазды-
вающих нейтронов. Для этого продифференцируем по времени
уравнение (9.9) и с помощью уравнения (9.10) исключим производ-
ную dc/dt. Предварительно из уравнения (9.10) исключим перемен-
ную с, используя для этого уравнение (9.9).
Получим
d2n _
de _ р
dt ~ I*
d2n _ n d8k
dt2 ~ Z* dt
n — p dn de
Z* dt I* dt + ' dt ’
,8k — P dn __ 8k dn .
Z* dt I* dt
8k — p dn . . 8k , dn
--------------L- A---fl — К-----
/* dt I* dt
(9.П)
1 Точное уравнение реактора как объекта регулирования без осреднения по
Р является уравнением седьмого порядка.
§ 2. Реактор как объект регулирования
337
Окончательно получим
fl —dfe'- Z*X dn--1_ /_dS£ ? Д п = 0. (9.12)
d/2 Z* dt Z* \ dt I v ’
Динамические Характеристики реактора 1
Уравнение (9.12) нелинейно, так как в него входят произведе-
ния 6kn и б&—. Оно решается в общем виде при скачкообразном
dt
изменении реактивности ^бй = const, Это дает возмож-
ность определить динамические характеристики реактора, у кото-
рого температурный коэффициент реактивности по нарастанию
нейтронной мощности равен нулю.
От дифференциального уравнения (9.12) переходим к соответ-
ствующему ему характеристическому уравнению и определяем его
корни. Получим
s,, =_ р + -»+1/. + A6fe. (9.13)
2Z* — |/ 4Z*2 Z* v
Решением уравнения (9.12) будет
п = cteSit + c2es^, (9.14)
где ci и С2 — постоянные интегрирования. Для их определения ис-
пользуем начальные условия. При t — 0 поток нейтронов п = п0—
стационарный режим реактора. При t < 0 возмущение 6k = 0,
dnldt = 0 и, как это следует из уравнения (9.9), (р//*)«0 =/_с0.
Последнее равенство сохраняется и в первый момент после введе-
ния возмущения 6k. Тогда при t = 0 из уравнения (9.9) получаем,
что
! dn\ Ь/г
— =—«о-
\ dt ]t=Q I*
Начальные условия дают два уравнения для определения по-
стоянных интегрирования:
С1 сг — п0,
__ 6k (9.15)
S]C1 4“ — № П0'
Z*
Найдя их, можно рассчитать переходный процесс реактора по ней-
тронной мощности для различных возмущений 3 k. Его график по-
казан на рис. 9.5.
Начало переходного процесса характеризуется резким нараста-
нием потока нейтронов, связанным с выбросом мгновенных нейтро-
1 Этот и последующие разделы § 2 написаны по материалам статьи
Б. С. Воронкова [4].
338
Глава IX. Регулирование авиационной ядерной силовой установки
нов. Эта часть процесса неуправляема. В дальнейшем нарастание
потока нейтронов идет плавно и достаточно медленно (при «С
0,005). Здесь процесс определяется как мгновенными, так и за-
паздывающими нейтронами. При 6k = 0,0075 реактор переходит
в режим мгновенной критич-
реактора от него еще зна-
Рнс. 9.5 чительное время нужно от-
водить тепло.
По знаку корней характеристического уравнения (9.13) дадим
оценку устойчивости реактора.
При 6k > 0 один из корней характеристического уравнения поло-
жителен. Возмущение 6k = const приводит к непрерывному возра-
станию мощности, реактор неустойчив.
При 6k < 0 оба корня характеристического уравнения отрица-
тельны. Однако установившийся режим достигается только при
п = 0.
При 6k = 0 один из корней характеристического уравнения ра-
вен нулю, реактор находится на границе устойчивости.
Если принять, что | б£| < ;0, то в уравнении (9.11) можно прене-
бречь произведением 6k—. Тогда получим, что
d2n , р Ц- /./* dn
dt2 ' /* ~dT
п I d6k
( dt
(9.16)
Приняв 6k за входную координату, a n за выходную, приходим
к выводу, что влияние принятого возмущения 6k на процесс в реак-
торе тем сильнее, чем больше п. Поэтому реактор можно рассмат-
ривать как звено с переменным коэффициентом усиления.
Реактор управляем только при 6k < 0. При 6k = р наступает
режим мгновенной критичности. В случае 6k р реактор практиче-
ски неуправляем.
$ 2. Реактор как объект регулирования
339
Линеаризация уравнений (9.9) и (9.10)
и частотная характеристика реактора
Для перехода от переменных к их приращениям примем п =®
= п0 + бп, с — со + 6с. Тогда уравнение (9.9) примет вид
~ А=± („0 + б „) + х (св 4- 6с).
at I*
Пренебрегая произведением 6пб& и учитывая, что— п0 = Лс0, по-
<*
лучим
— J&L + 5п = — 8k + — 6с.
р dt ' р Р
Введем базисные величины пБ, сБ, 8kB и перейдем к относи»
тельным приращениям. Тогда найдем, что
А^ + д„=_^До_д& + .2^_^дс. (9.17)
Р dt Р пв Р Яд
Проведя линеаризацию уравнения (9.10), придем к его новому
виду
дс= Л_2*_дп. (9.18)
1 Л Ы* сБ
Исключим из уравнений (9.17) и (9.18) переменную Дс и полу-
чим линеаризованное уравнение реактора по нейтронной мощности
. ...i - A ш \ (9.19)
1*1+ Р dt* dt пБ /*1 + Р\ dt )'
Рассмотрим частотную характеристику реактора. Его передаточ-
ная функция в соответствии с уравнением (9.19) имеет вид
п (s') = -А” п° ................S + V
U Afe " f*X + p /..........Г \
\!*X + P + Г
(9.20)
Целесообразно строить приведенную частотную характеристику
так, чтобы она не зависела от уровня мощности Пр и базисных вели-
чин Пв и 8kB. Введем коэффициент х = — и запишем выраже-
пБ
ние для построения приведенной частотной характеристики
= =; _L......юг~+х----Ф
340
Глава IX. Регулирование авиационной ядерной силовой установки
Ее вещественная и мнимая части определяются из равенства
Ц7(ш)^Р(ш) + 1<2(ш),
где Р(ш) = £ ; (9.21) /«<о»+(У"+р)» Q(») _ - .'У + МУ+.Р) (9.22) ' ’ <Op*2<02+(M*+p)2]- '
Для построения частотной характеристики удобно ввести без-
размерную частоту £2 = Z*<o. Если в уравнениях (9.21) и (9.22) пре-
небречь произведением А/*, стоящим в круглых скобках, по сравне-
нию с р, то выражения для приведенных вещественной и мнимой
частей частотной характеристики принимают вид:
Р(ш) =-----; (9.23)
' ' аг + '
Q(„) , (9.24)
Построенная по этим формулам для
/* = IO-3 сек, р = 0,0075 и Л, = 0,082
амплитудно-фазовая частотная характе-
ристика реактора показана на рис. 9.6.
Характеристика как бы распадается на
две части. Вертикальный участок харак-
теристики, соответствующий низким ча-
стотам, определяется запаздывающими
нейтронами. Другой участок, близкий
к полуокружности (подобный характе-
ристике инерционного звена), соответствует высоким частотам и
определяется временем жизни мгновенных нейтронов. Из рис. 9.6
следует, что полоса пропускания частот реактора прямо зависит
от времени жизни мгновенных нейтронов.
Температурный коэффициент реактивности и его влияние
на устойчивость реактора
Изменение реактивности при изменении температуры на 1° назы-
вается температурным коэффициентом реактивности и обозначает-
ся а. Если температурный коэффициент отрицателен, то реактор
находится в устойчивом состоянии (образуется отрицательная об-
ратная связь). Если у такого реактора произойдет случайное возму-
щение по стержневой реактивности (бй > 0), то по мере роста тем-
пературы реактора избыток истинной реактивности будет умень-
шаться и дойдет до нуля. Реактор перейдет на новый устойчивый
§ 2. Реактор как объект регулирования
341
режим, уровень мощности повысится. Изменение реактивности с ро-
стом температуры объясняется различными причинами. Часть из
них связана с изменением ядерных свойств материала реактора.
Так, например, с увеличением температуры возрастает паразитный
резонансный захват нейтронов ураном-238, увеличивается скорость
и длина диффузии тепловых нейтронов, что увеличивает вероят-
ность их утечки. Тепловое расширение реактора увеличивает его
размеры, изменяет соотношение поверхности и объема ядерного
горючего и также увеличивает утечку нейтронов. Численные значе-
ния а у различных реакторов лежат в достаточно широких пре-
делах.
Температурный коэффициент реактивности особенно велик
у гомогенных реакторов, содержащих гомогенную смесь урана с за-
медлителем. Он значительно ниже у гетерогенных реакторов. Так,
например, у гомогенного реактора Лос-Аламосской лаборатории
(сфера диаметром 30,5 см) а'=—30-10-51/°С. У гетерогенного
уран-графитового реактора кубической формы со стороной, равной
8 м, работающего на природном уране, а = —2,9 * 10-51/°С. Послед-
няя величина приведена только для сравнения. Вообще-то авиаци-
онный реактор будет работать только на обогащенном уране. Воз-
можно применение уран-бериллиевых или уран-окисебериллиевых
реакторов.
С учетом влияния температуры реактора на величину реактив-
ности истинную реактивность гетерогенного реактора можно оце-
нивать с помощью выражения
п
8k + S ^8Tit
i=l
где Ti и ai — температура отдельных элементов реактора и прису-
щие этим элементам коэффициенты аъ В случае гомогенного реак-
тора небольших геометрических размеров можно оперировать сред-
ней температурой и поэтому записать
8k + а.8Тср.
С учетом последнего выражения уравнение (9.9) примет вид
dn 8k -J- а8Тер — p
— -_fl
dt-----------------I*
ле.
(9.25)
Величина средней температуры реактора Тср зависит от уровня
нейтронной мощности и количества отводимого от реактора тепла,
являющихся функцией времени t.
Составим баланс тепла
ст8Тср ~ /. [п (/) — q (/)] А/,
]2 Черкасов Б. А.
342
Глава IX. Регулирование авиационной ядерной силовой установки
откуда после перехода к пределу получим
^L = 8[n(0-7(01-
at
Здесь с — удельная теплоемкость; m — масса реактора; q—-тепло,
отводимое от реактора; % и е = к/епг — коэффициенты пропорцио-
нальности.
Преобразуем уравнение (9.26). Используя вместо переменных
Тср, п и q их приращения, можно написать
d8TCp
~^-=^(^-8q).
Теплосъем q зависит от температуры тепловыделяющих элемен-
тов и от температуры охладителя или для гомогенного реактора —
от температуры реактора и охладителя. Поэтому
7 = У (Тер— ТохТ
(9.26)
или
8q = у (8Тср — 8Техл),
где у — средний коэффициент теплопередачи.
Тогда
(9.27)
=Е(г>п — у8Тср + у8Т 0Х1)-
d8TCD
+ гу8Тср = воп 4- ву8Тихл.
Введем базисные величины и получим в окончательном виде за-
висимость относительного приращения средней температуры реак-
тора от относительного приращения нейтронной мощности и темпе-
ратуры охладителя
± + дТср = ±Дп + ЬТОХЛ.
dt СР У ТсрБ ТсрБ
Чтобы связать изменение /ХТср с возмущением по реактивности,
вернемся к уравнению (9.25) и проведем его линеаризацию. После
преобразований получим
TLd±L + \n — ТсрБ&Тср + — —Дс. (9.28)
0 dt ' 0 пБ ' р пБ Р ср р пБ
Рассматривая уравнение (9.28) совместно с уравнением (9.18),
исключим переменную Дс. Будем иметь
I* d2&n d&n _ «0 / dbk , I “ По
Z*A,+ p dt2 + dt ~ пБ1*Х+^\ dt Z*A,+p пБ
X Тс рБ
(9.29)
§ 2. Реактор как объект регулирования
343
Уравнения (9.27) и (9.29) дают возможность определить влия-
ние ДР и ДТохл на изменение нейтронной мощности и температурно-
го режима реактора при а 0. Величина &ТОХЛ условно рассматри-
вается как внешний фактор, не зависящий от режима работы реак-
тора. Это соответствует как бы разомкнутой системе охлаждения
реактора, а реактор является источником тепловой мощности
(рис. 9.7).
Уравнения (9.27) и (9.29) можно решить совместно как относи-
тельно Дп, так и ДТср. Проделав это, получим в операторной форме
Приращение Дк
Рис. 9.7
записи два уравнения:
(р3 + агР2 -г ЩР - г «о) = кБ (р2 -|- Ь{р 4- b0) Др +
-k^AP +с) ДТ0Х1; (9.30)
(р3 + а2р~ 4- ахр -4 а0) \Тср = k'B (р 4- с) ДР 4- /г'охл (р + d) Р^ТЬХЛ. (9.31)
В этих уравнениях приняты следующие обозначения:
= а —— 4~ ^у; d = а 4- *,
2 Z* r Z*
I , , У? ио \
«1 = е ул — <х-А ; Р£ = —--------------
Z*
п.й.
ао = — « ~
Z* / Z*«fi
е6/г£«0
1*Т к ’
ерь
апо^УТохлБ
Рв
охл
ьо = Аеу; /гохл=--
1*пБ
Т с
/ охлБ
' ТсрБ
с =-- К.
Рассмотрим устойчивость реактора в свободном движении. Вос-
пользуемся для этой цели критерием устойчивости Раута — Гурвица.
Согласно этому критерию для устойчивости необходимо выполнить
условия: а2 > 0; «I > 0; «о > 0 и a2«i > «о. Все величины, входящие
в коэффициенты уравнений (9.30) и (9.31), кроме температурного
коэффициента реактивности а, существенно положительны.
344
Глава IX. Регулирование авиационной ядерной силовой установки
у| В)
Из условия а1 > 0 должно быть я < ———,
из условия а2 > О должно быть а < О,
ИЗ условия tZ2«l > О-о должно быть

Не трудно убедиться, что
ляется определяющим. Если
из трех условий второе (а < 0) яв-
оно выполняется, то выполняются и
остальные два. Таким образом, если реактор имеет отрицательный
температурный коэффициент, то он устойчив. Переходные процес-
сы, соответствующие этим возмущениям, показаны на рис. 9.8 и 9.9.
Из графиков этих рисунков видно, что динамические свойства реак-
тора при наличии отрицательного температурного коэффициента
реактивности существенно меняются. Возмущения по стержневой
реактивности или температуре охладителя приводят к тому, что
реактор сам без регулятора выходит на новый режим по нейтрон-
ной мощности. Здесь проявляются свойства температурного само-
регулирования. При возмущении по температуре охладителя реак-
тор за счет своих внутренних свойств сам поддерживает режим
ТСр — const.
В заключение этого параграфа сформулируем свойства реакто-
ра как объекта регулирования.
1. По нейтронным процессам реактор является нелинейным
звеном, коэффициент усиления реактора есть функция самих пере-
менных. На низких уровнях нейтронной мощности он мал, на боль-
ших уровнях — велик.
2. Точное уравнение реактора как объекта регулирования яв-
ляется уравнением седьмого порядка. Если рассматривать малые
§ 3. Управление силовой установкой с ядерным. реактором
345
отклонения от установившегося режима работы реактора, то допус-
тимо шесть групп запаздывающих нейтронов свести к одной группе,
обладающей «эффективным» временем запаздывания. В этом слу-
чае реактор приближенно описывается уравнением1 второго порядка.
При малых отклонениях возможна линеаризация исходных урав-
нений.
3. При наличии отрицательного температурного коэффициента
реактор приобретает свойства температурного саморегулирования.
Возмущения по bk и теплосъему уже не приводят к неограничен-
ному возрастанию или спаду нейтронной мощности.
§ 3. УПРАВЛЕНИЕ СИЛОВОЙ УСТАНОВКОЙ С ЯДЕРНЫМ РЕАКТОРОМ
Измерение мощности реактора
Ядсрный реактор, являющийся источником энергии в авиацион-
ной силовой установке, должен быть связан с системой управления
для регулирования и ограничения уровня его мощности и обеспе-
чения правильного режима его работы. Остановимся в первую оче-
редь на измерении мощности реактора.
В принципе об уровне мощности реактора можно судить по ве-
личине тепловой энергии силовой установки, для чего было бы
достаточно измерять расход и изменение температуры теплоноси-
теля при прохождении его через реактор. Однако для обеспечения
безопасности работы ядерной силовой установки следует иметь
аппаратуру,,фиксирующую мгновенные изменения режима реак-
тора.
Полная тепловая мощность реактора есть результат тепловыде-
лений различных ядерных процессов, происходящих в активной
зоне. Но уровень мощности реактора принято считать пропорцио-
нальным плотности нейтронного потока, так как непосредственно
от деления ядер выделяется более 90% энергии и менее 10%—от
0- и у-излучений. Однако дело не только в количестве энергии. Из-
мерения интенсивности |3- или у-излучений не могут дать правиль-
ного представления об уровне мощности, присутствие долгоживу-
щих продуктов распада приводит к тому, что изменение интенсив-
ности р- или у-излучений отстает от изменения мгновенной мощнос-
ти реактора. Так, например, уже при выключенном реакторе
имеется сильное у-излучение.
Для обнаружения различных излучений используется главным
образом их способность ионизировать газы. Задача измерения из-
лучения сводится к наблюдению ионизационных эффектов. По-
скольку нейтроны не обладают способностью прямой ионизации
газов, внутри датчика нейтронного потока нужно создать условия
для ядерного взаимодействия, в результате которого возникнут за-
ряженные частицы.
346
Глава IX. Регулирование авиационной ядерной силовой установки
В качестве датчиков нейтронного потока могут быть исполь-
зованы ионизационные камеры. Известны ионизационные камеры
нескольких типов, но все они основаны на увеличении проводимо-
сти газа под воздействием нейтронного потока. Простейшая иони-
зационная камера (рис. 9.10) представляет собой герметический
сосуд с двумя электродами, к которым приложена разность потен-
циалов V. Сосуд заполняется газом и помещается вблизи активной
зоны реактора. Задача сводится к измерению ионизационного то-
ка I. Между обкладками электродов всегда существует сопротивле-
ние утечки Ry, через него течет ток утечки Iv. Поэтому на внешних
зажимах камеры получается ток 1в = I — Iv = I---—• Обычно ве-
личина тока 1в лежит в интервале 1СН4-н1СН а, и нет камер для ис-
пользования в таком широком диапазоне.
Для измерения потока быстрых нейтронов ионизационную ка-
меру обычно заполняют водородом или метаном под высоким дав-
лением. При измерении потока медленных нейтронов камера запол-
няется трехфтористым бором. В этом случае под воздействием по-
тока нейтронов в ионизационной камере идет ядерная реакция
В10 + и'->Не4 + Li7.
Образующиеся ядра гелия и лития летят с большой скоростью
н ионизируют заполняющий камеру газ. Между корпусом камеры
и центральной нитью проходят импульсы тока, причем количество
импульсов в единицу времени равно количеству нейтронов, попав-
ших в камеру. Следовательно, количество импульсов пропорцио-
нально плотности потока нейтронов.
Широкое применение стали находить ионизационные камеры
несколько другого типа, так называемые камеры с твердым покры-
тием. В этих камерах один или оба электрода покрываются тонким
слоем детектирующего вещества (карбид бора, уран-235). Иониза-
ционная камера такого типа может быть значительно прочнее ка-
$ 3. Управление силовой установкой с ядерным реактором
347
меры, заполненной трехфтористым бором, и требует для работы
в несколько раз меньшего напряжения источника тока.
Для использования ионизационной камеры в широком диапа-
зоне изменения мощности реактора можно менять ее положение в
реакторе. С увеличением плотности нейтронного потока камеру по-
степенно выдвигают из активной зоны с тем, чтобы количество ней-
тронов, попадающих в камеру в единицу времени, не было слишком
большим.
Для измерения нейтронного потока большой плотности приме-
няются ионизационные камеры, измеряющие не число импульсов
в единицу времени, а силу ионизационного тока. Такая камера
в качестве ионизатора имеет набор графитовых дисков, покрытых
с обеих сторон бором.
Для измерения интенсивных потоков нейтронов и, следователь-
но, для измерения уровня мощности реактора можно применять
термопарные датчики, горячий спай которых покрывают бором.
Возникающая э.д. с. прямо пропорциональна плотности потока ней-
тронов.
Для увеличения э.д.с. обычно в одном компактном датчике
(их называют термостолбиками) последовательно соединяют не-
сколько десятков термопар. Термостолбики, как это и свойственно
термопарам, обладают большой инерцией. Их постоянная времени
лежит в пределах 3 -г- 10 сек. Это затрудняет их применение в сис-
теме регулирования ядерной силовой установки.
Отдельный датчик нейтронов, выполненный в виде ионизацион-
ной камеры или термостолбика, еще не дает возможности судить
об уровне мощности реактора. Помещенный в какой-либо точке
реактора, он дает представление о нейтронном потоке вблизи этой
точки. В других местах реактора нейтронные потоки могут сильно
отличаться. Полное представление о мощности реактора можно
получить, определяя средний поток нейтронов во всем его объеме.
Для этого нужно несколько датчиков разместить в различных точ-
ках реактора и затем осреднить их показания. При этом удобнее
использовать термостолбики, так как ионизационные камеры имеют
довольно большой объем. Однако большая постоянная времени
термостолбиков может потребовать введения в систему регулиро-
вания последовательных корректирующих устройств для снижения
их динамической погрешности.
Средства управления реактором
Постоянное присутствие в реакторе управляющих стержней,
поглощающих нейтроны, искажает поток нейтронов в соседних со
стержнем участках реактора и приводит к неравномерному выго-
ранию ядерного горючего, а также вызывает лишний расход ней-
тронов. Последнее не столь существенно для больших реакторов,
31В
Глава IX. Регулирование авиационной ядерной силовой установки
имеющих невысокую избыточную реактивность и при большой на-
грузке работающих с почти полностью выведенными стержнями.
Но для небольших реакторов на обогащенном горючем с довольно
мощными потоками нейтронов необходимо располагать значитель-
ными резервами реактивности. Для этих реакторов снижение поте-
ри нейтронов достигают конструктивными мероприятиями, комби-
нируя перемещение горючего или замедлителя с перемещением
поглотителя.
Управляющие стержни — это общее название стержней, пред-
назначенных для грубой и тонкой регулировки реактора и для пред-
охранения силовой установки от разрушения и обеспечения без-
опасности экипажа летательного аппарата. В зависимости от наз-
начения управляющие стержни разделяются на компенсирующие,
регулирующие и аварийные.
Компенсирующие или пусковые стержни предназначены для
грубой регулировки реактора и при своем перемещении очень эф-
фективно влияют на реактивность. Компенсирующие стержни при-
меняются для приведения реактора при его запуске в состояние,
близкое к заданному уровню мощности. Они также служат для
компенсации изменения реактивности, которое возникает в ходе
эксплуатации реактора. Речь идет о компенсации изменения реак-
тивности, вызываемой температурным эффектом, выгоранием горю-
чего и отравлением.
В § 2 этой главы было показано, что температура, при кото-
рой работает реактор, существенно влияет на реактивность. При
отрицательном температурном коэффициенте реактивности реак-
тор, будучи критическим в холодном состоянии, становится под-
критическим при разогреве. Поэтому, чтобы прогреть реактор,
нужно компенсировать отрицательный температурный коэффици-
ент, т. е. обеспечить дополнительную реактивность.
Как известно, отравление заключается в возникновении продук-
тов деления, обладающих высоким эффективным сечением погло-
щения тепловых нейтронов. Это приводит к значительным и отно-
сительно быстрым изменениям реактивности. Одним из самых вы-
соких эффективных сечений поглощения обладают осколки деления
Хе135. В реакторах, предназначенных для работы с высокими ней-
тронными потоками, эффект отравления ксеноном затрудняет реше-
ние проблемы управления: выключение реактора приводит к вре-
менному возрастанию концентрации ксенона. Поэтому компенси-
рующие стержни реактора, установленного в силовой установке
летательного аппарата или морского судна, должны иметь резерв
реактивности для компенсации максимального отравления, чтобы
обеспечить быстрый повторный запуск реактора.
Компенсирующие стержни при полном перемещении могут соз-
дать реактивность, в несколько раз превосходящую значение мгно-
венной критичности. Поэтому, чтобы реактор не достиг критическо-
§ 3. Управление силовой установкой с ядерным реактором
349
го состояния, компенсирующие стержни перемещаются медленно,
шагами. Когда уровень мощности реактора приближается к задан-
ному, компенсирующие стержни становятся в положение, при ко-
тором эффективный коэффициент размножения близок к единице.
Дальше задача управления реактором переходит к регулирующим
стержням.
Регулирующие стержни обладают способностью изменять реак-
тивность на несколько тысячных, что необходимо для точной регу-
лировки мощности реактора; Эти
стержни должны быстро переме-
щаться, чтобы обеспечивать немедленную реакцию при отклонении-
мощности от заданного уровня. Как правило, запас реактивности
у регулирующих стержней выбирается небольшим с тем, чтобы при
быстром перемещении стержня не было достигнуто состояние мгно-
венной критичности реактора. В реакторе размещают несколько
регулирующих стержней с самостоятельными приводами. По всему
объему реактора их размещают так, чтобы не было взаимной экра-
нировки стержней. Перемещение регулирующих стержней — авто-
матическое, с возможным переключением на ручное управление.
Эффективностью стержня называется изменение реактивности
при полной перекладке (максимальном перемещении) стержня.
Изменение реактивности нелинейно связано с положением стержня,
типичная характеристика стержня показана на рис. 9.11 (на этом
рисунке I—положение стержня). Из характеристики следует, что
наибольшая скорость изменения реактивности получается при
средних положениях стержня. Перемещение стержня вблизи одного
из крайних положений (полностью выдвинутый или полностью
вдвинутый стержень) мало влияет на изменение реактивности.
Рассмотрим картину перемещения управляющего стержня при
необходимости перейти от одного уровня мощности реактора к дру-
гому. Упростим ее, полагая, что у реактора отсутствует влияние
температуры на реактивность. Пусть No-—начальная мощность
реактора, находящегося в критическом состоянии (рис. 9.12). Тре-
350
Глава IX. Регулирование авиационной ядерной силовой установки
буется увеличить его мощность до N. Сначала управляющий стер-
жень должен быть несколько выдвинут, чтобы создать избыточную
реактивность. Тогда мощность реактора начнет возрастать. Если
система управления реактором обладает опережающим действием,
то еще до достижения заданного уровня мощности управляющий
стержень должен быть глубже введен в реактор и обеспечить нуле-
вую избыточную реактивность при подходе к новому уровню мощ-
ности. Если же опережающего действия у системы нет, то перевод
стержня на нулевую избыточную реактивность в момент, когда
реактор достигнет заданного уровня мощности, в дальнейшем при-
ведет к некоторому забросу мощности. Чтобы его погасить, стер-
жень нужно будет вдвинуть еще глубже и создать отрицательную
избыточную реактивность. В результате получится затухающий
переходный процесс, управляющий стержень некоторое время бу-
дет колебаться около положения, соответствующего критическому
состоянию реактора. Этот случай и показан на рис. 9.12.
Аварийные стержни (или стоп-стержни) предназначены для
останова реактора в случае возникновения аварийных условий.
В принципе реактор может быть выведен из строя в результате
интенсивного разогрева при чрезмерном увеличении мощности или
же при скачкообразном изменении температуры (например, при
отказе системы охлаждения).
Сигналы, от которых должна срабатывать аварийная система,
можно разбить на две группы. К первой, более важной из них,
отнесем слишком высокий поток нейтронов, очень малый период
реактора и прекращение подачи электрического тока. Ко второй
группе сигналов можно отнести слишком высокие температуры
теплоносителя на выходе из активной зоны реактора или на входе
в реактор, слишком высокую радиоактивность теплоносителя или
слишком высокую радиоактивность около реактора, снижение рас-
хода теплоносителя, повреждения в цепях измерения. Количество
аварийных сигналов надо по возможности ограничивать, а систему
аварийной защиты упрощать. Сложная система защиты с большим
числом аварийных сигналов приведет к ее частому включению.
Следует искать компромиссное решение между абсолютно безопас-
ной системой контроля реактора и возможностью его эксплуатации
в авиационной силовой установке. Представляется целесообразным,
чтобы аварийная система автоматически выключала реактор в слу-
чае появления аварийных сигналов первой группы. При возникнове-
нии аварийных сигналов второй группы решение о выключении
реактора должно приниматься экипажем летательного аппарата.
Реактор на быстрых нейтронах может аварийно выключаться
удалением части горючего из активной части или же удалением
отражателя. Для выключения реактора на тепловых нейтронах в
него вводят стержни из материала, сильно поглощающего нейтроны.
Надо полагать, что реактор ядерной авиационной силовой уста-
§ 3. Управление силовой установкой с ядерным реактором
351
новки будет обладать небольшой теплоемкостью. Поэтому датчик
нейтронного потока или скорости нарастания нейтронного потока,
а также датчик температуры реактора, связанные с аварийными
стержнями, должны быть 'практически безынерционными. Аварий-
ные стержни снабжаются быстродействующим приводом, который
должен срабатывать даже при отказе источника питания. Это мо-
жет быть пружинный привод или электромагнит, отпускающий
стержень при выключении питания.
Особенности запуска, приемистости и останова ядерного ТРД
Последовательность запуска ядерного ТРД заключается .снача-
ла в физическом запуске реактора и выводе его в критическое со-
стояние при нулевой мощности, затем в прогреве реактора до рабо-
чей температуры холостого хода двигателя и, наконец, в раскрутке
турбокомпрессора и переводе двигателя на самостоятельную ра-
боту. Различают первый запуск реактора и запуск ранее работав-
шего реактора.
Первый запуск реактора с новым ядерным горючим занимает
много времени и является опасным. В реактор помещают источник
нейтронов с таким расчетом, чтобы нейтроны на пути от источника
к счетчику проходили через ядерное горючее. Система блокировки
не позволяет выдвинуть компенсирующие стержни до тех пор, пока
не будут зарегистрированы несколько нейтронов. После этого
стержни начинают медленно выдвигать. Программа движения
стержней должна обеспечить желательный закон изменения мощ-
ности.
В начале периода запуска реактора плотность нейтронного
потока очень мала (порядка 10~6 от максимальной плотности), по-
ток плохо подчиняется статистическим законам и испытывает
сильные флуктуации. Поэтому показания счетчика нейтронов мо-
гут искаженно отражать действительное состояние реактора. А это
означает, что приборы не укажут своевременно на переход реакто-
ра в мгновенно-критическое состояние. При недостаточно быстром
срабатывании аварийной защиты реактор выйдет из строя.
Повторный запуск реактора несколько менее опасен, так как
исходная плотность нейтронного потока сравнительно велика.
Источниками нейтронов в ранее работавшем реакторе являются
различного рода ядерные реакции с участием продуктов распада
ядерного горючего. Продукты распада могут испускать нейтроны
и непосредственно.
Прогрев реактора до рабочих температур двигателя происходит
за 15 — 20 мин. Для этого необходимо дальнейшее удаление ком-
пенсирующих стержней, и за счет возмущения по dk реактор выво-
дится из состояния холодной надкритичности. В этот период пуска
плотность нейтронного потока возрастает настолько, что можно
352
Глава IX. Регулирование авиационной ядерной силовой установки
измерять период реактора путем измерения тока в ионизационной
камере. С прогревом реактора период реактора уменьшается и до-
водится до 15-4-20 сек. Если реактор обладает достаточно большим
отрицательным температурным коэффициентом, то для прогрева
реактора выбирается программа постепенного ступенчатого уве-
личения реактивности. При каждом небольшом скачке реактивности
будут происходить выбросы нейтронов и затем некоторое падение
нейтронного потока за счет роста температуры реактора (а<0).
Примерная картина нарастания
нейтронной мощности в этот пери-
од запуска показана на рис. 9.13.
После прогрева реактора произ-
водится раскрутка турбокомпрес-
сора, так же как и в обычном ТРД
с помощью какого-либо стартера.
При раскрутке через двигатель
устанавливается некоторый расход
воздуха, который подогревается,
проходя через теплообменник. Про-
исходит возмущение по теплосъему
и реактор (а < 0) переходит на более высокий уровень нейтрон-
ной мощности (см. рис. 9.9). Согласование уровня нейтронной мощ-
ности и теплосъема при увеличении расхода воздуха происходит
без вмешательства автоматики.
Если у реактора отрицательный температурный коэффициент
мал, то при выводе ЯТРД на режим самостоятельной работы необ-
ходим специальный регулятор температуры, согласующий темпе-
ратуру реактора с числом оборотов двигателя. При а = 0 нейтрон-
ная мощность должна быть согласована с изменяющимся тепло-
съемом. Для этого требуется специальное автоматическое устрой-
ство— своеобразный регулятор разгона. На этот регулятор воз-
лагается задача согласования времени разгона реактора со вре-
менем разгона турбокомпрессора. Особенности работы реактора с
а>0 на переходных режимах не рассматриваем, полагая, что всег-
да можно спроектировать реактор с а «0.
Надо ожидать, что приемистость ядерного ТРД будет хуже
приемистости ТРД, работающего на химическом топливе. В обыч-
ном ТРД температура газа практически безынерционно следует за
изменением расхода топлива. В ядерном ТРД будет запаздывание
в контуре теплопередачи. При разгоне ядерного ТРД необходимо
согласовывать задание на изменение числа оборотов с изменением
мощности ядерной установки. Специальный автомат должен давать
некоторое опережение роста мощности реактора по сравнению с
ростом потребной мощности турбокомпрессора.
Останов ядерного ТРД сложнее обычного, работающего на хи-
мическом топливе. После перевода реактора в подкритическое со-
§ 4. Системы автоматического регулирования ядерного ТРД
353
стояние спад нейтронного потока за счет запаздывающих нейтро-
нов идет довольно медленно. Турбокомпрессор уже остановится,
а выделение тепла еще будет продолжаться в количестве большем,
чем может быть отведено путем естественного рассеивания. Потре-
буется специальное продувочное устройство для охлаждения
реактора.
§ 4. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯДЕРНОГО ТРД
Регулирование нейтронной мощности реактора, как правило,
осуществляется по замкнутой схеме. Регулируемым параметром в
этом случае будет сила тока ионизационной камеры или термостол-
бика, которая сравнивается с силой тока задатчика мощности. Ток
рассогласования слишком мал и не может быть непосредственно
использован для привода управляющего стержня. Поэтому ток
рассогласования проходит предварительно усилитель. Простейшая
блок-схема автоматического регулирования нейтронной мощности
реактора показана на фиг. 9.14.
В системах регулирования ядерных силовых установок могут
применяться различного рода усилители и в первую очередь элек-
трические. В зависимости от назначения они могут быть магнит-
Рис. 9.14
ными, электронными, релейными и электромашипными. Электро-
двигатели, используемые как силовые элементы для привода управ-
ляющих стержней, могут быть постоянного тока (сериесные двига-
тели и двигатели с независимым возбуждением) и двухфазные
асинхронные двигатели переменного тока.
Система регулирования (см. рис. 9.14) обеспечит точность регу-
лирования мощности не более ±0,5%. Для повышения точности
регулирования мощности применяются системы с дополнительными
обратными связями: тахометрической (рис. 9.15) или позиционной1
(рис. 9.16). Применение систем регулирования мощности реактора,
1 Позиционная обратная связь является статической. Ее применение неиз-
бежно связано с некоторой статической ошибкой регулирования.
354 Глава IX. Регулирование авиационной ядерной силовой установки
использующих в качестве регулируемого параметра как плотность
нейтронного потока, так и производную от плотности, улучшает
динамику регулирования. Схема такой системы регулирования по-
казана на рис. 9.17.
Рис. 9.15
Рис. 9.16
При запуске реактора или при увеличении уровня мощности
особую роль приобретает регулирование периода реактора. Для
измерения периода прежде всего получают сигнал, пропорциональ-
ный плотности нейтронного потока. Затем с помощью логарифмиче-
ского усилителя получают логарифм этого сигнала, так как в пе-
риод запуска плотность нейтронов будет возрастать на много по-
рядков. Наконец с помощью дифференцирующего звена определяют
производную от логарифмического сигнала, т. е. сигнал, пропор-
циональный обратной величине периода. Главным звеном в этой
схеме является логарифмический усилитель, дающий возможность
воспроизвести на шкале одного измерительного прибора значения
§ 4. Системы автоматического регулирования ядерного ТРД,
355
мощности, изменяющиеся в широком диапазоне. Схема системы
регулирования периода показана на рис. 9.18.
Для практических целей желательно, чтобы автоматическое
регулирование уровня мрщности реактора на стационарных режи-
мах и регулирование периода реактора на нестационарных режимах
Рис. 9.17
Рис. 9.18
осуществлялось в одной системе регулирования. Схема такой си-
стемы регулирования дана на рис. 9.19.
Важное место в системе регулирования реактора занимают
устройства для его аварийного выключения. Аварийное выключение
реактора производится как при превышении допустимого уровня
мощности вследствие отказа основной системы регулирования
уровня мощности реактора, так и при превышении допустимой ско-
рости нарастания мощности вследствие отказа системы регулирова-
ния периода реактора. Скорость нарастания мощности ограничи-
вается по двум причинам. Во-первых, она характеризует прибли-
жение реактора к мгновенно-критическому состоянию. Во-вторых,
если при большой скорости нарастания мощности ограничитель
уровня мощности начнет выключать реактор в момент достижения
356 Глава IX. Регулирование авиационной ядерной силовой установки
Задатчик
Рис. 9.19
Рис. 9.20
Рис. 9.21
§ 4. Системы автоматического регулирования ядерного ТРД
357
им максимальной расчетной мощности, то получится заброс мощ-
ности, значительно превышающий допустимый уровень.
Схема системы аварийного выключения реактора при превыше-
нии допустимой скорости нарастания мощности приведена на
рис. 9.20. Сочетание логарифмирующей и дифференцирующей це-
пей даст возможность измерить относительную скорость нараста-
ния мощности, независимо от уровня мощности, на котором реак-
тор находится в данный момент. Следует помнить, что переход
реактора в мгновенно-критическое состояние одинаково опасен при
любом уровне мощности, даже когда мощность реактора на не-
сколько порядков ниже расчетной максимальной мощности.
В заключение на рис. 9.21 приведена схема системы регулиро-
вания ЯТРД, у которого параметрами регулирования является ско-
рость вращения, ротора турбокомпрессора о> и температура газа
перед турбиной Г* . Регулирующим фактором для скорости враще-
ния ротора будет изменение тепловой мощности реактора. Измене-
ние площади критического сечения выходного сопла, как и обычно,
является регулирующим фактором для параметра .регулирования
Т*3. Реактор в этой схеме разбит на две части: реактор как источник
нейтронной мощности и как источник тепла. Схема системы регу-
лирования упрощена, в ней нет регулирования периода реактора
и его аварийного выключения.
Глава X
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
§ 1. СПОСОБЫ МОДЕЛИРОВАНИЯ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Аналитическое исследование и численное решение задач в от-
ношении сравнительно простых систем автоматического регулиро-
вания авиационных силовых установок, описываемых линейными
дифференциальными уравнениями, представляет значительные
трудности и требует много времени. Эти трудности возрастают при
усложнении рабочего процесса двигателей и структурных схем
систем регулирования, при учете изменения параметров системы,
прямого запаздывания в передаче сигналов и др. Многие системы
автоматического регулирования описываются нелинейными диф-
ференциальными уравнениями высоких порядков, для которых еще
не разработаны методы решения. Однако сроки исследования и до-
водки систем регулирования авиационных силовых установок могут
быть значительно сокращены при использовании методов модели-
рования.
Сущность моделирования заключается в замене всей системы
автоматического регулирования или ее некоторых частей моделью,
динамические характеристики которой близки к характеристикам
замененной части исходной системы автоматического регулирова-
ния. Очевидно, что при такой замене переходные процессы в моде-
ли будут аналогичны переходным процессам в исходной системе
автоматического регулирования. Их можно наблюдать и регистри-
ровать, сравнивать с результатами аналитических расчетов и на
этой основе делать заключение о качестве системы.
Моделирование может быть физическим, математическим и
смешанным.
При физическом моделировании процессы, происходящие в мо-
делях, имеют общую физическую природу с оригиналом. К физи-
ческому моделированию прибегают в тех случаях, когда математи-
ческое описание процессов нельзя признать достаточно надежным.
В авиационной технике и, в частности, двигателестроении физиче-
ское моделирование широко используется при исследовании рабо-
чих процессов компрессоров, турбин, диффузоров и других элемен-
§ 1. Способы, моделирования физических процессов
359
тов двигателей. Физическое моделирование элементов авиационных
двигателей позволяет углубить знания о явлениях, в них происхо-
дящих, и уточнить математическое описание этих .явлений. Однако
изготовление моделей и сами эксперименты обычно требуют боль-
ших затрат и создания сложных установок. Изменение параметров
объекта требует переделки модели или ее замены.
При физическом моделировании свойства систем автоматиче-
ского регулирования воспроизводятся полнее, чем при математи-
ческом моделировании. В некоторых случаях, например, при ис-
следовании пневматических устройств, без физического моделиро-
вания обойтись практически нельзя.
Применение электронных моделирующих устройств получило
название математического моделирования. Методы математическо-
го моделирования основаны на идентичности дифференциальных
уравнений, описывающих происхддящие явления в оригинале и в
модели. Электронные моделирующие устройства обладают тем не-
оспоримым качеством, что с их помощью можно вычислить непре-
рывную зависимость функции от определяющих ее параметров.
Как уже было показано, любую систему регулирования можно
разбить на типовые звенья. Тип звена определяется видом переход-
ного процесса и ему соответствует определенное дифференциаль-
ное уравнение. Используя различные элементы электрических
цепей, из них составляют типовые звенья и систему в целом, соот-
ветствующую исследуемой системе регулирования. По осциллограм-
ме переходного процесса в такой системе делают заключение о пе-
реходном процессе в исходной системе регулирования. Таким путем
моделируют и делают заключение о сложных динамических систе-
мах автоматического регулирования как по звеньям, так и в целом.
При математическом моделировании оригиналом является ма-
тематическое описание процесса в исходной системе. Поэтому точ-
ность результатов моделирования зависит от того, насколько до-
стоверно математически описываются свойства отдельных элемен-
тов и исходная система регулирования в целом.
Наряду с физическим и математическим моделированием широ-
ко применяется смешанное моделирование, позволяющее совмес-
тить преимущества обоих методов. Так, например, целесообразно
исследовать реальную аппаратуру системы регулирования на мо-
делях объектов регулирования, используя в качестве динамической
модели объекта любую из промышленных электронных модели-
рующих установок. Такое моделирование позволяет достаточно лег-
ко воспроизвести динамику сложных систем регулирования. Для
подключения к электронной моделирующей установке регулирую-
щей аппаратуры, как правило, нужны специальные устройства —
преобразователи. Они различаются на входные и выходные, их наз-
начение— преобразовывать сигналы давления, угловой скорости,
температуры, линейных и угловых перемещений в электрические
360
Глава X. Моделирование процессов в системе регулирования
сигналы и наоборот. Схема подключения регулятора к модели по-
казана на рис. 10.1. На этой схеме 1 — входной преобразователь;
2— моделирующая установка, заменяющая объект регулирования;
3— выходной преобразователь; 4 — регулятор.
Авиационные двигатели как объекты регулирования сравнитель-
но малоинерционны. Поэтому для проведения моделирования с за-
данной точностью сами преобразователи должны обладать высоки-
ми динамическими качествами. Следует отметить, что в некоторых
случаях, когда объекты регулиро-
вания сравнительно .просты (од-
новальные ТРД и ТВД, у которых
регулируется только один пара-
метр), могут быть использованы
физические аналоги двигателей.
Рис. 10.1 Тогда регулирующая аппаратура
может присоединяться к физиче-
ской модели двигателя без преобразователей. При моделировании
более сложных двигателей целесообразно применять электронные
моделирующие установки.
§ 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
За последние годы математическое моделирование стало исполь-
зоваться очень широко. Поэтому остановимся на нем более под-
робно.
Математическое моделирование невозможно без аналитического
исследования системы, которое требует знания дифференциальных
уравнений, описывающих поведение системы регулирования.
Математические вычислительные машины, используемые в ка-
честве моделирующих устройств, дают возможность, избегая трудо-
емких численных расчетов, определить влияние отдельных пара-
метров системы регулирования на ее .устойчивость и качество пере-
ходного процесса.
Математическое моделирование можно рассматривать как осо-
бый метод численного интегрирования. Используемые для модели-
рования математические машины непрерывного действия не тре-
буют специального программирования и обладают большим быст-
родействием. С их помощью можно моделировать системы с раз-
личного рода нелинейностями и различными функциональными
зависимостями между переменными, возможно введение перемен-
ных параметров, различных начальных условий, систематических
и случайных процессов.
На математических моделях обычно решается прямая задача,
т. е. отыскивается закон движения системы по заданным дифферен-
циальным уравнениям, начальным условиям и возмущениям. Од-
нако возможно решение и простейших обратных задач: определение
§ 2. Математическое моделирование
361
возмущений, вызывающих заданный закон движения. Математиче-
ские машины непрерывного действия обладают меньшей точностью,
чем цифровые машины. Однако этот недостаток не, так уже суще-
ственен, так как точность исходных величин обычно меньше, чем
точность работы моделирующей машины.
Дифференциальные уравнения движения системы регулирова-
ния задаются в различных видах. Так, например, это может быть
одно уравнение типа
rf«Ax
6Ц ---------------
П dtn
dn~xSx
an-\ -------
dtn~x
rfAx
dt
, * z. dmf (t) , , dm~XW) , , , df(t) . , ,,,,
4- a0Ax — bm + bm_\ m_i-----------b- • • + bt — (- bof (/), (10.1)
или система дифференциальных уравнений первого порядка типа
п
а‘ S + (10-2)
dt Z!
(где Qi, bik — коэффициенты системы уравнений; Дхь Лх2....
Дхг,...Дхп — координаты системы; Fi(t)—возмущающие воз-
действия), или уравнения движения звеньев, из которых состоит
система. Все эти формы уравнений могут быть использованы для
набора на моделирующих установках. Их воспроизведение осуще-
ствляется или путем понижения порядка производной, или путем
ее повышения.
Для примера рассмотрим систему, движение которой описыва-
ется уравнением второго порядка
^-rr+ai—+ а0Дх= f(t). 10.3)
cu2 at
Для набора на моделирующей установке методом понижения по-
рядка производной уравнения (10.3) его решают относительно вто-
рой производной
=----— — -2°-Дх + (Ю.4)
dt2 аг dt а2 а«
В этом случае схема набора решающих элементов должна дать
возможность осуществить последовательное интегрирование и сум-
мирование величин с учетом знака (рис. 10.2). На вход в первый
блок поступают величины после каждого интегрирования, умножен-
ные на постоянные коэффициенты с помощью блоков умножения.
На рис. 10.3 дана структурная схема набора решающих элемен-
тов для того же уравнения (10.3) методом повышения порядка
производной.
362
Глава X. Моделирование процессов в системе регулирования
Из приведенных двух схем надо отдать предпочтение схеме с
последовательным интегрированием, так как при последовательном
дифференцировании увеличивается влияние различного рода помех,
неизбежных в системах, использующих электрические величины.
Из рис. 10.2 видно, что все слагаемые в правой части уравнения
(10.4), кроме независимого переменного, вводятся в суммирующий
блок с помощью обратных связей. Из рассмотренного примера сле-
дует, что для решения линейных дифференциальных уравнений
необходимо иметь суммирующие, интегрирующие устройства и
Рис. 10.2 Рис. 10.3
устройства для умножения и деления на постоянные величины
(включая и отрицательные). Эти счетно-решающие элементы на-
зываются линейными, так как они обеспечивают линейную связь
между входными и выходными величинами.
§ 3. ЛИНЕЙНЫЕ РЕШАЮЩИЕ ЭЛЕМЕНТЫ
По своей структуре линейные решающие элементы разделяются
на элементы разомкнутого типа, элементы с параметрической ком-
пенсацией и элементы замкнутого типа (с отрицательной обратной
связью).
В качестве решающих элементов разомкнутого типа можно рас-
смотреть пассивные электрические цепи. На рис. 10.4 показана
электрическая цепь суммирования трех напряжений. Исходя из
соотношений
/ = Л + /2^/3;
I= eSblxY н;
A = (ei евыз^ У11.
^2 = (^2 ^2»
Л = (*3 ^вых) ^3»
§ 3. Линейные решающие элементы
363
получим, что
3
(10.5)
Здесь Уи, Уь Y2 и Y3 — значе-
ния проводимостей по участкам.
Из выражения (10.5) следует, что
результат суммирования зависит
от числа слагаемых и от величи-
ны нагрузочного сопротивления
RH. При 7?н->0 зависимость ре-
зультата суммы от величины на-
грузки и числа слагаемых умень-
шается, но при этом резко падает
величина выходного напряжения.
• На рис. 10,5, а показана пас-
сивная электрическая цепь для
'построения интегрирующего уст-
ройства, а на рис. 10.5, б—для
построения дифференцирующего устройства. В этих цепях исполь-
зуется свойство конденсатора накапливать заряд, когда к его об-
кладкам приложена разность потенциалов. Через конденсатор по-
течет ток 1С = C(de]dt), сила тока может служить мерой производ-
ной от приложенной к его обкладкам разности потенциалов. В это
Рис. 10.5
же время разность потенциалов на обкладках конденсатора, вклю-
ченного в электрическую цепь, является мерой интеграла по време-
ни от прг гекающего через пего тока.
Как и в случае суммирования, точность выполнения пассивны-
ми электрическими цепями операций дифференцирования и интег-
рировав 1я тем выше, чем меньше величина напряжения на выходе
цепи. Э о затрудняет их использование в линейных решающих эле-
ментах Для увеличения выходного напряжения в пассивную элек-
трическую цепь можно включить электронный усилитель (рис. 10.6).
С помощью электронного усилителя можно компенсировать погреш-
364
Глава X. Моделирование процессов в системе регулирования
ность, вносимую пассивной электрической цепью, для этого в уси-
литель вводится положительная обратная связь. Решающие эле-
менты, построенные на этом принципе, называются элементами с
параметрической компенсацией (рис. 10.7). Данный способ построе-
ния решающих элементов по сравнению с ранее рассмотренным
имеет то преимущество, что здесь не требуются усилители с боль-
шим коэффициентом усиления ky и нет необходимости в специаль-
ном подборе параметров цепи. Однако нужно строго стабилизиро-
вать коэффициент усиления, иначе меняются собственные динами-
ческие характеристики решающего элемента. Нельзя также до-
стигнуть полной компенсации погрешности цепи, так как это может
Рис. 10.7
привести к неустойчивой работе решающего элемента даже при
небольших изменениях параметров.
При построении решающих элементов замкнутого типа (с отри-
цательной обратной связью) используются принципы, положенные
в основу замкнутых систем автоматического- регулирования. На
рис. 10.8 показана схема простейшей системы автоматического
регулирования с отрицательной обратной связью. При большом
коэффициенте усиления основного звена 3 зависимость выходной
координаты ДХвых от входной координаты &хвх с достаточной сте-
пенью точности может быть представлена в виде
(10.6)
оыл тг , . «Х» \ /
П2 («)
где ПДз) и II2(s) —передаточные функции'звеньев 1 и 2.
Из выражения (10.6) следует, что связь между величинами \хвых
и Дхвж определяется только параметрами цепи обратной связи и
входной цепи. Это означает, что такая система автоматического ре-
гулирования в зависимости от вида передаточных функций Пг
и П2 может выполнять различные математические преобразования
входной величины. Иначе говоря, рассмотренная система регули-
рования при большом коэффициенте усиления [передаточная функ-
ция усилителя /7у(з)] пригодна для решения дифференциальных
уравнений вида
ГГ2 (S) Дхеых 11^ (®) Д^ох*
(Ю.7)
§ 3. Линейные решающие элементы
365
Рассмотрим электронный усилитель с отрицательной обратной
связью в качестве решающего элемента (рис. 10.9). Пусть его
коэффициент усиления равен А, входное сопротивление Z\, сопро-
тивление цепи обратной связи z0, напряжение на сетке усилителя ев.
Если сеточный ток незначителен, то в точке а справедливо равен-
ство Л + 70 = 0.
Установим соотношение между входным и выходным напряже-
нием:
евг еБ j ебых еБ q
zi г0
Лг^. Пу (Л л V.
n,(s)
nz(s)
Рис. 10.8
Рис. 10.9
Заменяя ев на евых/А, получим
е * 1
A Zg \ А /
Если коэффициент усиления А достаточно велик, то величинами
1 Zj 1
— и-------— по сравнению с Z}/z0 можно пренеоречь.
Д Zq /1
Тогда
.A. (Ю.8)
СвХ Z1
Из этого соотношения можно получить другие, показывающие ка-
кую операцию будет выполнять решающий усилитель в зависимос-
ти от режима работы.
На входе в решающий усилитель в общем случае может действо-
вать несколько входных сигналов (рис. 10.10). Пусть число входов
п — 1, а звенья 1 и 2— омические сопротивления. Тогда ееых —
= —(7?2/7?1)ев.т, т. е. в этом случае решающий усилитель выполняет
операцию умножения на величину —R.zlR\- Допустим, что при чис-
ле входов, равном п, звенья /./, 1.2....1п и 2— омические сопро-
тивления. Решающий усилитель при этом выполняет алгебраическое
суммирование п выходных сигналов с умножением каждого из них
на .величину —7?2/7?i. Если принять, что 7?и = T?i,2 = .. . = Дщ =
= Т?2, то в этом случае будет выполняться простое алгебраическое
суммирование.
366
Глава X. Моделирование процессов в системе регулирования
Возьмем п = 1 и включим во входную цепь омическое сопротив-
ление /?1, а в цепь обратной связи емкость Сг. Тогда получим, что
t
eaM = ~-^\eexdt, (10.9)
Рис. 10.10
т.' е. в этом случае решаю-
щий усилитель выполняет
операции интегрирования по
времени входной величины
(при п входных слагаемых
выполняется операция инте-
грирования суммы входных
сигналов). Если же в цепь
обратной связи включено
омическое сопротивление Д2,
а во входную цепь емкость
Сь то решающий усилитель
работает в режиме диффе-
ренциатора и евых опреде-
ляется из выражения
р _____ ___D Г ^-евл
евЫХ~~ ,, .
dt
(10.10)
Решающие элементы замкнутого типа (с отрицательной обрат-
ной связью) обладают наилучшими качествами по сравнению с
решающими элементами разомкнутого типа и элементами с пара-
метрической компенсацией. Поэтому за последнее время они нашли
широкое применение при математическом моделировании.
§ 4. МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ РЕГУЛИРОВАНИЯ
С НЕЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ И С ПРЯМЫМ
ЗАПАЗДЫВАНИЕМ В ПЕРЕДАЧЕ СИГНАЛА
С помощью электронных моделей наряду с линейными исследу-
ют также и нелинейные системы автоматического регулирования.
Для этого в моделирующие устройства вводят функциональные пре-
образователи, воспроизводящие заданные нелинейные функции
одного или нескольких аргументов.
Функциональные преобразователи могут быть разомкнутого и
компенсационного типа. У первых сигналы проходят непосредствен-
но с входа на выход, а у компенсационных — только при охвате
отрицательной обратной связью. В последнем случае уменьшается
влияние возмущений и колебаний параметров на точность работы
преобразователя. Функциональные преобразователи выполняются
§ 4. Моделирование элементов систем с нелинейными характеристиками 367
на электронных лампах, электронных лучевых трубках в виде
электромеханических следящих систем с функциональными потен-
циометрами или специально профилированными, кулачками. Наи-
большее развитие получили функциональные преобразователи, по-
строенные на диодах и электронных лучевых трубках. Диодные
функциональные преобразователи выполняются обычно в виде па-
раметрических устройств, использующих линейнокусочную аппрок-
симацию заданной функции. Они могут быть универсальными и
специализированными.
Универсальные функциональные преобразователи дают возмож-
ность путем перестройки вос-
производить различные функ-
циональные зависимости. Они
сложны по своему устройству
и требуют большого числа ре-
гулировочных операций при
настройке на заданную нели-
нейность. При их использова-
нии встречаются затруднения
при воспроизведении немоно-
тонных функций (например, с
двумя экстремумами), налага-
ются ограничения в крутизне
воспроизводимых функций.
Специализированные диодные функциональные преобразовате-
ли предназначены для воспроизведения элементарных нелинейных
функций, часто встречающихся в системах автоматического регули-
рования. Такое специализированное устройство может быть рассчи-
тано на воспроизведение определенной нелинейности, например,
квадратной параболы или синусоиды. Из структурной схемы такого
преобразователя (рис. 10.11) следует, что оно выполняется в виде
решающих усилителей, снабженных нелинейными преобразователя-
ми выходного и входного напряжений в соответствующие токи.
Как уже указывалось выше, при исследовании переходных про-
цессов систем регулирования авиационных силовых установок в
некоторых случаях необходимо учитывать прямое запаздывание в
передаче сигналов. При построении математических моделей таких
систем прямое запаздывание воспроизводится при помощи специ-
альных блоков, называемых блоками запаздывания.
В системе регулирования элемент, дающий прямое запаздыва-
ние, имеет передаточную функцию вида
Пт (s) = е-«. (10.11)
Если передаточная функция блока запаздывания будет такой
же, то воспроизведение характеристик запаздывания будет идеаль-
ным. Однако полного совпадения передаточных функций добиться
368
Глава X. Моделирование процессов в системе регулирования
не удается и блоки запаздывания вносят в математическую модель
системы регулирования некоторую погрешность.
По конструктивному выполнению блоки запаздывания можно
разбить на две группы. Блоками первой группы амплитудная час-
тотная характеристика элемента с прямым запаздыванием воспро-
изводится точно, а фазовая характеристика приближенно. К таким
блокам относятся системы из активных и йассивных четырехполюс-
ников, имитирующих длинные электрические линии, и системы с
решающими усилителями. На рис. 10.12 приведена схема бло-
ка запаздывания, составленная из двух пассивных RC четырехпо-
люсников, с разделительными усилителями между ними. Блоки за-
паздывания, построенные на пассивных цепочках, ограничены по
Рис. 10.12
величине времени запаздывания и не позволяют в процессе моде-
лирования непрерывно его менять. Применение активных цепей по
сравнению с пассивными дает заметное преимущество. Наибольший
интерес в этой группе представляют блоки запаздывания, исполь-
зующие решающие усилители.
Блоки запаздывания второй группы точно воспроизводят фазо-
вую частотную характеристику, а амплитудную — приближенно.
Они основаны на использовании магнитной ленты в качестве запо-
минающего устройства.
При малых временах запаздывания целесообразно применять
блоки запаздывания с решающими усилителями, а при больших —
блоки с магнитной записью.
Пример
Пример. В исследовании ядерпо-энергетических систем широко используют-
ся электронно-моделирующие устройства. Рассмотрим принципы их моделирова-
ния на одном частном примере.
Наиболее просто применить моделирующую установку для моделирования
одного только реактора с учетом одной группы запаздывающих нейтронов и
температурного эффекта реактивности. Воспользуемся для этого случая линеа-
ризованной системой уравнений динамики реактора в абсолютных прираще-
ниях:
= лбе 6N -f-—'Ok, (10.12)
at----------------------------------------I* I*
d8c p
— = —6N — T8c, (10.13)
dt I* '
Пример
369
d8Tcg 8N 8Тса
с± = (10.14)
dt_________ypcv т
8k = 8kcm — | a | 8Tcp. (10.15)
В этих уравнениях приняты следующие обозначения (в дополнение к обоз-
начениям, использованным в гл. IX): W— тепловая мощность реактора; 6АСГ—
стержневая избыточная реактивность; 8k — истинная избыточная реактивность;
Yp—плотность материала реактора; с — теплоемкость материала реактора;
т — среднее время теплоотвода от реактора.
Вывод уравнений (10.12) — (10.15) здесь не приводится, так как в § 2 гл.
IX с необходимой подробностью рассмотрена динамика реактора.
Для нашего примера можно составить достаточно простую структурную
схему, моделирующую систему уравнений (10.12) — (10.15). Для каждого из
трех дифференциальных Уравнений выделяем по одному решающему усилителю,
работающему в режиме .интегратора. Для алгебраического уравнения (10.15)
выделяем решающий усилитель, работающий в режиме сумматора
Чтобы получить напряжение ступенчатого возмущения Vo, так же необходимо
выделить один решающий усилитель. Возмущение Vo снимается с выхода этого
усилителя, работающего в режиме сумматора. На его вход подается через
входное сопротивление напряжение от гнезда «возмущение». Для линейного ха-
рактера изменения возмущения этот усилитель должен работать в режиме ин-
тегратора. Число входных сопротивлений решающего усилителя равно числу
членов в правой части уравнения, для которого он выделен. Соединение решаю-
щих усилителей в общую схему определяется видом уравнений, входящих в
систему (10.12) — (10.15). Общая структурная схема для моделирования этой
системы уравнений показана на рис. 10.13. Эта схема требует небольшого коли-
чества оборудования, а моделирующая установка, собранная по ней, способна
решать разнообразные задачи динамики одного реактора. Схема может нара-
щиваться вплоть до схемы установки, моделирующей всю совокупность процес-
сов в ядерпю-эпергетических системах.
О 50 WO 150 WO teen
В)
*)
Рис. 10.14
Пример
371
На рис. 10.14 показаны графики переходных процессов, описываемые сис-
темой уравнений (40.12) — (10.15): изменение мощности реактора ДМ и темпе-
ратурного режима ДТср для исходного значения температурного коэффициента
а (см. рис. 10.14, а), изменение* мощности реактора ДМ (см. рис. 10.14,6) и из-
менение температурного режима ДТср (см. рис. 10.14, в) для трех значений
температурного коэффициента а. Во всех случаях возмущение создавалось из-
менением реактивности. Моделирование проведено на машине ЭМУ-8 для сле-
дующих значений коэффициентов уравнений системы:
(3 = 0,00755; I* = 2-10-3 сек; % = 0,0817 сек-1;
т = 50 сек; ура> = 100 кет-сек!0С; па = 1000 кет.
Возмущение по реактивности принято 6ACT = 4-10-4. Для определения за-
висимости протекания переходных процессов в реакторе от температурного
коэффициента реактивности задавалось три значения а: —10~s 1/°С; —0,67-Ю-5
1/°С и —2'10~5 1/°С. Для перехода от одного значения а к другому требуется
только изменить величину сопротивления 4.1 (см. рис. 10ЛЗ).
При создании электронпо-моделирующих установок для моделирования
ядерно-энергетическях систем возникают ряд трудностей, связанных главным
образом с особенностями процессов, происходящих в этих системах. Остановим-
ся на основных из них.
Прежде всего следует отметить большой диапазон изменения одной из ос-
новных характеристик состояния реактора — мощности. В режиме разгона она
может меняться в 1010 раз, причем это изменение происходит примерно за
30 сек.
Второй особенностью является необходимость в отдельных, но очень важ-
ных случаях, длительного исследования процессов в ядерно-эпергетической сис-
теме. Это, например, относится к спаду мощности при останове реактора и осо-
бенно к процессам отравления. Необходимая длительность исследования этих
процессов достигает 30 час.
К третьей особенности ядерно-энергетических систем нужно отнести само-
регулирование. По соображениям безопасности все они проектируются так,
чтобы работали в области устойчивости. Но область устойчивой работы реакто-
ра ограничена- и ее границы очень важно знать в стадии проектирования и эк-
сплуатации реакторных систем.
Все перечисленные особенности ведут к усложнению схем электропно-моде-
лирующих установок. Первая особенность требует большого масштабного коэф-
фициента, вторая — дополнительного оборудования, обеспечивающего примене-
ние метода фиксации результатов, третья — широкого диапазона изменения па-
раметров.
Глава XI
ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
§ 1. ОСНОВНЫЕ понятия
Для современного уровня развития техники весьма актуаль-
ным является создание самонастраивающихся систем автоматиче-
ского управления. Самонастраивающаяся автоматическая система
осуществляет поиск оптимального состояния и в некотором смыс-
ле обладает способностью наилучшим образом приспосабливаться
к изменяющимся окружающим условиям, воздействующим на
объект регулирования.
На обычные системы автоматического регулирования возлага-
ются задачи поддерживать постоянство регулируемых величин
или обеспечивать заданный закон их изменения. Что же касается
самонастраивающихся систем, то в их задачу входит обеспечение
оптимального значения регулируемой величины. Как правило,
оптимальному режиму управляемой системы соответствует экст-
ремум (максимум или минимум) какого-либо параметра, характе-
ризующего ее эффективность. Регулирование на экстремум яв-
ляется наиболее простым вариантом самонастраивающейся систе-
мы. Однако для экстремального регулирования необходимо, что-
бы объект регулирования обладал характеристикой с оптимальной
точкой, характеристикой с экстремумом.
С изменением внешних условий значение экстремума и его по-
ложение могут меняться, но это не скажется на точности системы
экстремального регулирования. Она находит и фиксирует новое
положение экстремума и, таким образом, корректирует изменение
внешних условий.
У любого объекта регулирования существуют независимые
физические величины, их можно для краткости назвать входами
объекта. В определенной функциональной зависимости к ним на-
ходятся другие физические величины, называемые выходами
объекта. Входные величины (входы) подразделяются на основ-
ные и вспомогательные.
Авиационный двигатель является сложным объектом регули-
рования. Задача его экстремального регулирования осложняется
тем, что выход объекта обычно зависит от большого числа основ-
§ 2. Типы автоматов оптимизации
373
ных и вспомогательных входов,
будут величина расхода топлива
ского сечения выходного сопла,
Для ТРД основными входами
и величина площади критиче-
т. е. параметра, которые мы
раньше называли регулирующими факторами. За выход можно
принять удельный расход топлива. В качестве вспомогательного
входа можно рассматривать поворотный направляющий аппарат
компрессора, так как назначение вспомогательных входов
чается в том, чтобы изменять соотношения, связывающие
ные входы и выходы.
заклю-
основ-
Для вывода системы регулирования на оптимальный режим
применяются автоматы оптимизации, являющиеся замкнутыми
системами с обратной связью. Они получают преобразованные
сигналы с выхода системы, формируют управляющий сигнал и ав-
томатически заставляют систему настраиваться на оптимальный
режим. Автоматы оптимизации должны обеспечивать наилучшие
режимы работы даже в том случае, если неизвестны точные ха-
рактеристики объекта регулирования и работа его протекает при
сильных возмущающих воздействиях. Для автомата оптимизации
не важна форма и количественная оценка связи между входом и
выходом объекта регулирования. Необходимо только существо-
вание экстремальной характеристики. Это существенно отличает
экстремальные системы регулирования от обычных систем, в кото-
рых предполагается, что объект регулирования сохраняет свои
характеристики, принятые в расчет при проектировании регуля-
тора.
§ 2. ТИПЫ АВТОМАТОВ ОПТИМИЗАЦИИ
Автоматы оптимизации разделяются на два класса. К одному
из них относятся автоматы, реагирующие на чувствительность, под
которой понимается скорость изменения выхода. К другому клас-
су относятся автоматы с запоминанием экстремума.
В свою очередь автоматы оптимизации, реагирующие на чувст-
вительность, могут быть трех видов: с прямым использованием
сигнала по чувствительности, с непрерывным поисковым сигналом
(обычно рассматривается синусоидальный поисковый сигнал), с
дискретными сигналами скорости изменения выхода (автоматы
шагового типа). Во всех трех случаях объект регулирования ис-
пользуется для получения сигнала, пропорционального чувстви-
тельности!; отклонение этого сигнала от нуля используется для
создания входного управляющего сигнала. В автоматах с запо-
минанием экстремума входной управляющий сигнал получается
в виде разности между оптимальным сигналом на выходе и теку-
щим значением выходного сигнала.
13 Черкасов Б. А.
374
Глава XI. Экстремальное регулирование
Экстремальное регулирование с прямым использованием
сигнала по чувствительности
В этом случае поисковое воздействие осуществляется в виде
простой пилообразной функции; она изменяется по времени с пос-
тоянной скоростью и может менять свой знак.
В системе регулирования имеем нелинейное звено, которое ха-
рактеризует оптимальный режим. Пусть это звено обладает одним
входом и одним выходом. Вначале пренебрегаем влиянием всяких
запаздываний в системе регу-
лирования и полагаем, что вы-
ход определяется только мгно-
венной величиной входа. При
небольших изменениях входа
можно принять, что в окрест-
ностях точки оптимума связь
между выходом и входом осу-
ществляется по параболичес-
кому закону. Расположив для удобства начало координат в точ-
ке оптимума (рис. 11.1), эту связь можно представить в виде
y = —kx2, (11.1)
где х — вход звена; у — выход звена.
Начинаем поиск при отрицательных значениях входа (х< 0)
и увеличиваем х с постоянной скоростью. Выход сначала увеличи-
вается, достигает наибольшего значения и затем начинает умень-
шаться. Для параболической зависимости по уравнению (11.1) про-
изводная dyldt, являющаяся сигналом чувствительности, умень-
шается по линейному закону и изменяет знак, проходя через нуль
(рис. 11.2). При определенном значении производной dyldt (назо-
вем его критическим значением) под действием сигнала чувстви-
тельности Происходит реверс направления изменения входа, про-
изводная dy/dt скачкообразно увеличивается, а затем опять умень-
шается по линейному закону вплоть до нового реверса. Поиск про-
должается, система рыскает около оптимального режима. В ре-
зультате рыскания средний уровень выхода будет ниже значения
§ 2. Типы автоматов оптимизации
375
выхода в точке оптимума. Если обозначить амплитуду выхода че-
рез А, то для принятого параболического закона у(х) средний
уровень выхода снизится на величину Л/3. Это будет потеря поис-
ка. Обозначим период поиска т и определим критическую величи-
ну сигнала чувствительности — сигнала реверса. Используя выра-
жение (11.1), получим
У- = — 2kx ~
dt dt •
В момент реверса х = УA/k , а производная dx/dt равна
/Т _____________
dx у k 2 f А
dt т т |/ k
V
Откуда
(^У.\ (11.2)
\ dt ) кр т
Для снижения потерь поиска амплитуду выхода А желательно
уменьшать. Но тогда, как это следует из выражения (11.2), умень-
шается величина критического значения сигнала реверса, что уве-
личивает опасность случайных реверсов. При уменьшении т возни-
кает трудность отделения из-
менений выхода, вызванных
поиском, от изменений, вы-
званных случайными причина-
ми — различного рода помеха-
ми. Во всякой физической си-
стеме помехи неизбежны. Они
могут быть низкочастотными и
высокочастотными. Область
5
5S
§
5:
Область
шумов
Частоты
Область Воз-
можных час-
тот экстре-
Ппппгп iMQJlbHOZO
3fftpa^e^°ea-
низкочастотных помех, назы- Рис. 11.3
ваемая полосой дрейфа, вызы-
вается медленными изменениями внешних или внутренних условий
в системе. Область высокочастотных помех называется областью
шумов (рис. 11.3). Автоматическая оптимизация системы в значи-
тельной степени зависит от того, есть ли между областью дрейфа и
областью шумов полоса частот в достаточной мере свободная от
помех. В этой полосе можно уменьшать амплитуду выхода А без
боязни потерять сигнал выхода среди помех. Полоса частот, сво-
бодная от помех, определяет также и величину периода поиска т.
Очевидно, что частота поисковых колебаний должна быть больше
частоты дрейфа и меньше частоты шумов.
Однако этим не исчерпываются трудности при использовании
пилообразной функции в качестве управляющего сигнала. Если
13й
376
Глава XI. Экстремальное регулирование
выход все же содержит случайные помехи, то при дифференциро-
вании по времени для образования сигнала реверса влияние амп-
литуд высокочастотных составляющих помех возрастает. Действи-
тельно, если составляющими сигнала выхода будут функции
by = a sin at, являющиеся результатом помех в системе, то в сигнал
реверса они войдут в виде dbyldt = аа cosyyt. Откуда видно, что при
равных амплитудах чем больше частота помех, тем больше вред-
ная, случайная составляющая сигнала реверса, тем больше воз-
можностей появления случайных реверсов.
Экстремальное регулирование с непрерывным поисковым
сигналом
Положение системы вблизи точки экстремума с линейным из-
менением входа может быть обеспечено путем создания в системе
режима непрерывных вынужденных колебаний сравнительно не-
большой амплитуды. Эти колебания могут быть синусоидальными
или в виде прямоугольных импульсов, для их возбуждения в сис-
тему вводится специальный генератор колебаний. Частотная со-
ставляющая сигнала на выходе, полученная в результате воздейст-
вия входного сигнала, выделяется с помощью частотного фильтра
и сравнивается с входным поисковым сигналом. Покажем, что
знак или фаза выходного поискового сигнала зависят от измене-
ния положения системы относительно точки экстремума. Если меж-
ду входом и выходом системы имеется зависимость y = f(x), то
при отсутствии в такой системе инерционного запаздывания вы-
ходной сигнал пропорционален входному by = kcbx. Коэффициен-
том пропорциональности является коэффициент усиления kc =
= (dy/dx'jo. На участке линейной зависимости у = j(x) коэффици-
ент усиления — величина постоянная.
Рассмотрим реакцию объекта регулирования, имеющего экстре-
мальную характеристику, при воздействии на входе синусоидаль-
ного возмущения. Пусть участки 1 и 3 этой характеристики, распо-
ложенные левее и правее точки экстремума, являются линейными,
а участок 2 — параболическим (рис. 11.4). В пределах линейной
части характеристики (участки 1 и 3) выход равен произведению
входа на коэффициент усиления, знак которого определяется зна-
ком производной выхода по входу. Поэтому, если на участке 1
вход системы изменять по синусоиде, то выход также станет изме-
няться по синусоиде. Амплитуда выхода равна амплитуде входа,
помноженной на коэффициент усиления, который в пределах участ-
ка 1 является положительной и постоянной величиной. Следова-
тельно, на этом участке фазы выхода и входа совпадают. Проводя
аналогичные рассуждения относительно, участка 3, приходим к вы-
воду, что- фаза выхода противоположна фазе входа, так как коэф-
фициент усиления на участке 3 отрицателен.
§ 2. Типы автоматов оптимизации
377
Разберем теперь влияние изменения входа по синусоиде на па-
раболическом участке 2 характеристики, для которого у = —kx2.
Если система находится в экстремальной точке, то изменение вхо-
да по синусоиде с некоторой небольшой амплитудой А дает
у = —kA2 sin2 at, или
/гЛ2 /1 п л
у =--------(1 — cos 2wZ),
откуда видно, что амплитуда- выхода пропорциональна квадрату
амплитуды входа, а частота — вдвое больше частоты входа. При
теристики, на выходе получается сложный гармонический сигнал.
Он может быть разложен на две составляющих, из которых одна
будет иметь частоту входного -поискового сигнала, а другая — удво-
енную частоту.
При произвольной форме характеристики объекта регулирова-
ния в случае изменения входа по синусоиде на выходе, кроме со-
ставляющей с частотой входа, будут высокочастотные синусоидаль-
ные составляющие. Их частота возрастет с увеличением кривизны
характеристики объекта. Действительно, любой криволинейный
участок характеристики объекта регулирования можно представить
в виде комбинации прямолинейного участка (касательная к кривой)
и дополнительного криволинейного (рис. П.5). Откуда следует,
что независимо от формы характеристики выходной сигнал всегда
содержит основную составляющую, частота которой равна частоте
синусоиды входа. Эта основная составляющая совпадает по фазе
с входным сигналом, если режим работы системы лежит левее точ-
ки максимума, и находится в противофазе к входному сигналу,
когда режим системы сдвигается правее точки максимума.
Совместный эффект линейного изменения входа и синусоидаль-
ного поискового сигнала при той же зависимости у = —kx2 показан
378
Глава XI. Экстремальное регулирование
на рис. 11.6. К выходному сигналу и сигналу чувствительности от
линейного входа добавлены только основные составляющие поис-
кового сигнала. При переходе системы через точку оптимального
режима изменяется фаза суммарных выходного сигнала и сигнала
чувствительности. Изменение фазы используется в качестве управ-
ляющего сигнала. Он изменяет управляемый вход, приближая со-
стояние системы к оптимальному режиму работы.
Рис. 11.7
Рис. 11.8
Рис. 11.6
Экстремальная система регулирования с непрерывным поиско-
вым сигналом может быть выполнена д виде системы с использо-
ванием резонансного фильтра или синхронного детектора (демоду-
лятора). На рис. 11.7 показана структурная схема экстремальной
системы регулирования с резонансным фильтром. На вход объекта
регулирования 1 от внешнего генератора колебаний 5 (модулято-
ра) непрерывно поступают синусоидальные колебания. Из объек-
та регулирования выходной сигнал поступает на резонансный
фильтр 2, где выделяется его основная составляющая, поступающая
затем в усилитель 3. Усиленный Сигнал попадает в фазочувстви-
тельный двигатель 4, который связан с исполнительным органом,
изменяющим режим работы системы регулирования. Выбор часто-
ты входного поискового сигнала зависит от инерционности объекта
§ 2. Типы автоматов оптимизации
379
регулирования. Чем больше инерционность, тем ниже должна быть
частота поиска, так как высокие частоты объект регулирования не
пропустит. Однако создать резонансный фильтр на .низкие частоты
практически невозможно. Поэтому экстремальная система с резо-
нансным фильтром может быть использована только для малоинер-
ционных объектов регулирования. От этого недостатка свободны
системы экстремального регулирования с синхронным детектором
(рис. 11.8). Из объекта регулирования 1, а также из генератора
колебаний 3 сигналы поступают в синхронный детектор 2. Резуль-
тирующий сигнал из синхронного детектора направляется в
фильтр 4, а затем в усилитель 5 и исполнительный орган 6. Из ге-
нератора колебаний 3 поисковые сигналы идут также и па вход
в объект регулирования.
Система экстремального регулирования с непрерывным поиско-
вым сигналом имеет большое преимущество по сравнению с систе-
мой, где используется прямой сигнал чувствительности. В пей
уменьшается влияние высокочастотных помех на управляющий
сигнал. Возможность применения системы экстремального регули-
рования с непрерывным поисковым сигналом определяется также
полосой частот системы, свободной от помех (см. рис. 11.3). Ча-
стота поиска должна лежать в этой полосе, и если объект регули-
рования управляется несколькими экстремальными регуляторами
с различными частотами поиска, то полоса частот, свободная от по-
мех, должна быть достаточно большой.
Экстремальное регулирование с использованием
дискретных сигналов скорости изменения выхода
При использовании этого способа, так же как и в ранее разоб-
ранных, скорость изменения входа задана и постоянна по величине.
Управляющий сигнал для осуществления реверса, пропорциональ-
ный скорости изменения выхода, получается путем сравнения от-
дельных значений усредненных выходных сигналов, взятых через
равные промежутки времени, называемые шагами. Применение
автоматов оптимизации шагового типа для получения сигнала чув-
ствительности выгодно в том случае, когда выход системы содер-
жит много помех. Влияние этих помех можно значительно осла-
бить правильным выбором шага. Шаг должен быть достаточно ко-
ротким, чтобы исключить влияние низкочастотных помех (дрейфа).
Он должен быть достаточно большим, чтобы избежать вредное
влияние высокочастотных помех и не допустить ложных реверсов.
Чтобы уменьшить возможность случайных реверсов, в систему ре-
гулирования вводят так называемую зону стабилизации, которая
устанавливает величину необходимой разности средних значений
выхода двух соседних шагов. Пока эта разность не достигнута ре-
верс не произойдет. Чем шире зона стабилизации, тем больше поте-
ри поиска.
380
Глава XI. Экстремальное регулирование
§ 3. ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ РЕЖИМА
АВИАЦИОННОГО ДВИГАТЕЛЯ
ТРД как объект экстремального регулирования
Рассмотрим турбореактивный двигатель как самостоятельный
объект экстремального регулирования. Наиболее простым объек-
том будет ТРД с постоянным сечением выходного сопла. Его ти-
пичная дроссельная характеристика показана на рис. 11.9. Нали-
чие экстремума по суэ дает возможность осуществлять экстремаль-
ное регулирование, но только на крейсерском режиме. Такое
Рис. 11.9
Рис. 11.10
изменение удельного расхода топлива двигателя объясняется глав-
ным образом специфическими особенностями характеристики ком-
прессора. Минимум по Cyd = f(n* , т]') получается в тех случаях,
когда в целях снижения удельного веса двигателя идут на повыше-
ние напорности ступеней компрессора, что и приводит к некоторому
снижению к. п. д. компрессора на максимальном числе оборотов.
При регулировании на (cyd)min входом экстремальной системы ре-
гулирования двигателя будет абсолютный расход топлива, а выхо-
дом— удельный расход. Упрощенная структурная схема такой
системы регулирования приведена на рис. 11.10.
Поскольку наличие экстремума на кривой суэ определяется
только особенностями характеристики компрессора, то это означа-
ет, что для поддержания двигателя па оптимальном режиме необ-
ходимо фиксировать рабочую точку на линии совместных режимов
турбины и компрессора. Иначе говоря, нужно перейти на програм-
му регулирования ппр = const. Но тогда с увеличением скорости
полета измеренное число оборотов двигателя должно возрастать,
а с увеличением высоты полета — падать. В первом случае число
оборотов двигателя и температура газа перед турбиной могут пре-
высить допустимые значения по запасу прочности деталей двига-
теля. Во втором случае может быть значительное падение тяги.
§ 3. Экстремальное регулирование режима авиационного двигателя
381
Экстремальное регулирование ТРДФ
совместно с летательным аппаратом
Рассмотренный выше способ экстремального регулирования
ТРД с Fnp = const .не представляет большого практического инте-
реса. Его можно применить только к однорежимному двигателю
летательного аппарата большой дальности, для которого будет ха-
рактерной работа на режиме минимального удельного расхода.
Правильнее двигатель рассматривать не автономно, а совместно
с летательным аппаратом. Тогда, например, в отношении транс-
портного самолета, можно поставить задачу отыскания такого ре-
жима работы двигателя, который обеспечил бы минимальный ки-
лометровый расход топлива.
Усложним несколько условия и рассмотрим ТРДФ с перемен-
ной конфигурацией газрвоздушного тракта, например, с изменяемы-
ми площадью критического сечения сопла, конфигурацией входного
диффузора, поворотными лопатками компрессора. Такой двига-
тель как объект регулирования будет иметь несколько входов и у
него больше возможностей для экстремального регулирования.
Действительно, заданная тяга ТРДФ может быть получена при раз-
личном числе оборотов, температуре газа перед турбиной или
в форсажной камере. Изменение тяги по требуемому закону дости-
гается при сохранении прежним числа оборотов двигателя, воздей-
ствием только на температуру газа перед турбиной и в форсажной
камере. Или, не меняя температурного режима, того же результата
достигают воздействием на положение регулирующего органа
входного диффузора и на число оборотов двигателя.
Тягу двигателя или скорость полета надо подобрать так, чтобы
километровый расход топлива ск был минимальным. Если двига-
тель имеет несколько основных входов, то поиск минимального ки-
лометрового расхода топлива может осуществляться двумя спо-
собами.
По первому из них система регулирования должна иметь столь-
ко самостоятельных экстремальных регуляторов, сколько основных
входов имеет двигатель, например, экстремальный регулятор по по-
даче топлива в основной контур, в форсажный контур, по площади
критического сечения выходного сопла, по положению регулирую-
щего органа входного диффузора. Действие каждого экстремаль-
ного регулятора направляется на поиск минимального километро-
вого расхода. Структурная схема такой системы экстремального
рггулирования показана на рис. 11.11.
По второму способу система регулирования содержит только
один экстремальный регулятор, который последовательно связы-
вается с различными регулирующими органами, т. е. последова-
тельно производит поиск частных экстремумов по различным основ-
ным входам, постепенно подводя систему к минимально возмож-
382
Глава XI. Экстремальное регулирование
ному километровому расходу. Структурная схема системы
регулирования для этого способа дана на рис. 11.12. Чтобы пока-
зать, что регулирование ведется по двум входам, на ней условно
показано два экстремальных регулятора.
Предпочтение, видимо, нужно отдать этому способу, так как
в первом случае будет взаимное влияние экстремальных регулято-
ров друг на друга через летательный аппарат, что создаст трудно-
сти в отработке такой системы регулирования. При использовании
как первого, так и второго способов в систему регулирования
должны быть включены также ограничительные регуляторы числа
Рис. 11.11
Рис. 11.12
оборотов, температуры газа и положения замыкающего скачка
уплотнения во входном диффузоре.
Отметим попутно, что изменение рабочего процесса в диффузоре
отражается на величине эффективной тяги, которую трудно изме-
рить и затем использовать в качестве регулируемого параметра.
Поэтому применение экстремального регулирования к входному
диффузору с отысканием экстремума по километровому расходу
топлива дает возможность наилучшим образом использовать его
характеристики.
Рассматривая ТРДФ совместно с летательным аппаратом и воз-
действие ТРДФ на летательный аппарат через тягу двигателя,
нужно иметь в виду следующее. Изменение положения регулирую-
щих органов двигателя вызывает изменение тяги сравнительно с
небольшим запаздыванием. Что же касается изменения скорости
за счет изменения тяги, то здесь наблюдается большое запаздыва-
ние в связи с большой массой летательного аппарата. В свою оче-
редь это изменение скорости опять вызывает изменения тяги. От-
меченные особенности усложнят работу экстремальных регуляторов
§ 3. Экстремальное регулирование режима авиационного двигателя
383
и могут привести к нежелательным переходным процессам в систе-
ме регулирования. Поэтому целесообразно периодически отключать
экстремальные регуляторы, -фиксируя положение регулирующих
органов двигателя. В это время изменение тяги будет происходить
только за счет изменения скорости летательного аппарата, работа
силовой установки приблизится к работе на статическом режиме,
система будет успокаиваться.
Изменение тяги в процессе поиска экстремума может нару-
шить горизонтальный полет летательного аппарата. Чтобы его со-
хранить, необходимо изменение тяги согласовывать с изменением
положения руля высоты, что может быть сделано непосредственно
или с помощью автопилота.
Возможности применения экстремального регулирования
для достижения заданного качества переходного процесса
в авиационной силовой установке
Авиационные газотурбинные двигатели работают в условиях
широкого изменения скоростей и высот полета, что приводит к из-
менению динамических параметров двигателей как объектов регу-
лирования. А это означает, что параметры регуляторов, выбранные
в качестве оптимальных для одних условий полета, с их изменени-
ем могут оказаться неудовлетворительными и приведут к нежела-
тельным переходным процессам или к потере устойчивости системы
регулирования.
Поставим задачу достижения определенного качества переход-
ного процесса авиационной силовой установки. Допустим, что
нормальная работа ТРДФ обеспечивается регуляторами числа обо-
ротов и температуры газа перед турбиной, снабженными корректи-
рующими устройствами для компенсации динамических погрешно-
стей. Расчеты и моделирование показывают, что для достижения
заданного качества- регулирования при изменении внешних усло-
вий или при переходе на другой режим необходимо менять по-
стоянную времени в корректирующем устройстве регулятора тем-
пературы и коэффициент усиления в корректирующем устройстве
регулятора числа оборотов (подробнее см. работу [3]).
Допустим, что изменение параметров корректирующих устройств
осуществляется с помощью замкнутой самонастраивающейся сис-
темы. Необходимо выбрать критерий качества процесса регулиро-
вания, который и должна обеспечить система экстремального регу-
лирования. Поскольку среди параметров рабочего процесса двига-
теля нет подходящих экстремальных характеристик для оценки
качества, такую характеристику следует создать искусственно. Ка-
чество процесса регулирования можно оценить по характеристикам
типа интегральных оценок, рассмотренных в гл. VII.
384
Г лава XI. Экстремальное регулирование
Предположим, что в регуляторе числа оборотов двигателя осу-
ществляется поиск по какому-либо параметру корректирующего
устройства, меняющего коэффициент усиления регулятора. Одно-
временно поисковый сигнал вводится в электронную счетную
машину, являющуюся математической моделью системы регулиро-
вания. Она позволяет получить квадрат переменной величины,
суммировать переменные и производить операции интегрирования.
Устройство для оценки качества переходного процесса, состоящее из
двух квадратов, одного сумматора, четырех операционных усили-
телей и одного интегратора, произведет вычисление интеграла
t
^IdAn\2]dt (Ц.З)
\ dt ) J
О
за заданный промежуток времени для единичного возмущения.
Переменная в выражении (11.3) Дп—приращение числа оборотов.
При сравнении полученного значения I с заданным значением
13 определяется величина А/ = I —13, используемая как сигнал ре-
верса поиска. Предварительно следует выяснить имеет ли функция
Д/ экстремум по степени коррекции, оставаясь положительной,
или же она меняется монотонно^ проходя через пуль. Поисковое уст-
ройство должно фиксировать систему коррекции вблизи такого зна-
чения коэффициента усиления, при котором Д/ = Д/min или
Д/ = 0. Несмотря на сравнительную простоту данного способа, он
вряд ли найдет практическое применение. В некоторых случаях та-
кой критерий качества дает колебательный переходный процесс.
Несколько перспективных разновидностей систем с экстре-
мальной настройкой корректирующих устройств предложено
А. А. Красовским [11]. Анализ этих систем здесь производить не
целесообразно, так как подобные автоматические устройства яв-
ляются предметом изучения других специальных курсов. Следует
только подчеркнуть, что выбор оптимальных значений параметров
корректирующих устройств регуляторов можно осуществить с по-
мощью специальных схем самонастройки. Эти схемы включают
элементы образования экстремальных характеристик, элементы
поиска и реализации экстремума.
Глава XII
ВЛИЯНИЕ НА СИСТЕМУ РЕГУЛИРОВАНИЯ
АВИАЦИОННОГО ВОЗДУШНО РЕАКТИВНОГО ДВИГАТЕЛЯ
СЛУЧАЙНЫХ ВНЕШНИХ ВОЗДЕЙСТВИЙ
§ 1. ПРИМЕНЕНИЕ МЕТОДОВ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
К ИССЛЕДОВАНИЯМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
В предшествующих главах книги были рассмотрены методы
анализа устойчивости и качества линейных систем автоматическо-
го регулирования в случае воздействий, являющихся заданными
функциями времени. Под этим понимается, что значение воздейст-
вующей функции в любой будущий момент времени t однозначно
определяется ее значением в некоторый исходный момент време-
ни t = 0.
В качестве заданной функции времени обычно используется
единичная ступенчатая функция. Такое типовое или пробное воз-
действие создает неблагоприятные, по реально возможные условия
работы системы.
В действительности воздействия, приложенные к системам ав-
томатического регулирования, в реальных условиях обычно яв-
ляются не заданными, а случайными, непрерывно изменяющимися
функциями времени. Для случайной функции нельзя заранее
с полной определенностью установить ее зависимость от времени.
В качестве примера, иллюстрирующего это положение, можно
взять систему регулирования, состоящую из самолета и автопилота.
Хаотическое движение масс воздуха, колебания плотности и тем-»
пературы действуют на самолет, вызывают изменение подъемной
силы и лобового сопротивления и в виде случайных сигналов по-
ступают на автопилот.
Однако случайные воздействия иногда можно рассматривать
как заданные. Допустим, что возмущение представляет собой от-
дельные импульсы, возникающие случайно, но разделенные доста-
точными промежутками времени, в течение которых система регу-
лирования успевает приходить в установившееся состояние. Воз-
можно, что случайные воздействия будут иметь такой вид, что их
можно разбить па участки, аппроксимировать по участкам типовы-
386 Глава XII. Влияние на систему регулирования ВРД внешних воздействий
ми функциями и рассматривать состояние системы регулирования
в конце каждого участка.
Если же воздействия имеют вид непрерывно, хаотическим об-
разом колеблющихся функций, то поведение системы регулирования
нельзя рассматривать как ряд следующих друг за другом перехо-
дов из одного установившегося состояния в другое. Разработан-
ные применительно к этим случаям методы анализа систем авто-
матического регулирования представляют большой интерес. Один
из них основан на введении статистических характеристик воздей-
ствия. Такими характеристиками обычно являются корреляцион-
ные функции или спектральные плотности. Теория корреляции
есть часть теории стационарных случайных процессов, разработан-
ная А. Н. Колмогоровым и А. Я. Хинчиным.
Статистическая динамика является в настоящее время одним
из наиболее важных и перспективных разделов теории автомати-
ческого регулирования. Методы расчета систем автоматического
регулирования с использованием приемов математической стати-
стики для обработки сигналов на входе или выходе какой-либо
системы расширяют наши возможности в отношении более полно-
го учета реальных условий работы автоматических систем.
Любая система автоматического регулирования всегда нахо-
дится под действием случайных возмущений. Поэтому во многих
задачах практики возникает необходимость учета влияния случай-
ных процессов на работу систем автоматического регулирования.
В задачи статистической динамики входят вопросы анализа и син-
теза систем регулирования, находящихся под действием случайных
Возмущений.
Задача анализа данной системы заключается в определении ха-
рактеристик ее точности по заданным вероятностным характери-
стикам, действующих на нее случайных возмущений.
Задача синтеза состоит в определении передаточной функции
системы таким образом, чтобы при известных вероятностных ха-
рактеристиках, действующих на нее случайных возмущений, обес-
печивалась наивысшая точность воспроизведения заданного зако-
на преобразования управляющего воздействия.
В данной главе рассматриваются некоторые вопросы примени-
тельно только к задаче анализа.
Функция распределения и корреляционная функция
Случайным процессом будем называть случайную величину, не-
прерывно зависящую от времени. Случайный процесс может быть
стационарным. Тогда он не имеет тенденции к нарастанию или за-
туханию, статистические характеристики его отдельных достаточно
продолжительных участков должны быть одинаковыми.
Между переменными в случайном процессе (стационарном или
нестационарном) существует корреляционная связь, если каждому
§ 1. Применение методов статистической динамики к исследованиям систем 387
значению одной переменной можно привести в соответствие ве-
роятное значение другой переменной, относительно которого на-
блюденные значения могут быть распределены согласно какому-
либо закону распределения вероятности.
Корреляционная свяйь тем сильнее, чем ближе наблюденные
значения к вероятному значению, чем более определенной является
зависимость между переменными. Корреляционная связь макси-
мальна, если одна из переменных является заданной (а не случай-
ной) функцией другой.
Случайный стационарный процесс можно характеризовать не-
которыми функциями распределения вероятностей *. Пусть x(t)
Рис. 12.1
есть случайный стационарный процесс (рис. 12.1) и задана его до-
статочно длинная запись. Разобьем ось времени t на равные интер-
валы длиной At и рассмотрим значения ординат x(t) в точках
t — kAt, где k = 0, 1, 2.N— 1. Общее число рассматриваемых ор-
динат равно N. Допустим, что в рассматриваемых точках нас ин-
тересует число ординат п, меньше к. Очевидно, что п есть функция
х. Она стремится к N при больших я и к нулю при малых х.
Выражение
(12.1)
называется первой или одномерной интегральной функцией рас-
пределения вероятностей случайного стационарного процесса x(t).
Для стационарного случайного процесса вид этой функции не зави-
сит от смещения начала отсчета вдоль оси времени. Производная
П7(Х)=^М. (12.2)
называется одномерной плотностью распределения вероятностей.
Графики функций распределения вероятностей и плотности распре-
деления вероятностей показаны на рис. 12.2 и 12.3.
1 Обычно закон распределения вероятностей случайной функции неизвестен.
Для выявления этого закона используют корреляционную функцию, определяе-
мую из опыта.
388 Глава XII. Влияние на систему регулирования ВРД внешних воздействий
Корреляционной функцией действительного переменного т назы-
вается выражение
Я, (т) = Пт ~ С х (t + т) х (/) dt. (12.3)
Г->со J
—Т
Из выражения (12.3) видно, что под корреляционной функцией
7?х(т) функции x(t) понимается средняя по времени величина от
произведения x(t + x)x(t). Откуда следует, что Ях(т) зависит толь-
ко от промежутка времени т. Выражение (12.3) говорит нам так-
же о том, что поведение случайной величины x(t) характеризуется
не только ее значением в каждый данный момент t, но и взаимной
Рис. 12.3
(12.4)
связью между значениями функции x(t) в моменты времени t и
t + т. Мерой этой взаимной связи между x(t) и x(t + т) и служит
корреляционная функция.
Наряду с корреляционной функцией используется также нор-
мированная корреляционная функция
г (Т) =
А /?И0)
Корреляционная функция может быть непосредственно подсчи-
тана по выражению (12.3). Нужно располагать достаточно длин-
ной записью случайного процесса, заменить интеграл конечной
суммой и последовательно задаваться- различными значениями т.
Сам процесс вычисления функции выполняется специальными при-
борами — корреляторами.
Технические варианты осуществления корреляторов могут быть
самыми разнообразными. Так, например, механический корреля-
тор основан на применении механического интегратора. Если слу-
чайные функции получаются в виде электрических напряжений, то
для их анализа удобно применять коррелятор, основанный на
электронных схемах. Существуют корреляторы, основанные на ис-
пользовании фотоэлектрического эффекта. В коррелятор вводится
бумажная или магнитная лента с записью случайного процесса
и координаты кривой x(t) преобразуются в перемещения или на-
пряжения, затем перемножаются величины, соответствующие ор-
$ 1. Применение методов статистической динамики к исследованиям систем 389
динатам кривой x(t) для значений времени t, сдвинутых друг от-
носительно друга на фиксированную величину т, и суммируются
результаты умножения в пределах выбранного пром’ежутка Т. В ре-
зультате получается график'функции 7?ж(т) или ее значения при
различных т.
Функцию /?х(т), если случайный процесс задан в виде осцил-
лограммы, можно вычислить и без коррелятора. Для этого осцил-
лограмму процесса следует перечертить на кальку и затем кальку
наложить на ленту осциллограммы, сместив ее на величину т вдоль
оси I. Корреляционная функция получается путем перемножения
соответствующих ординат и суммированием произведений. Однако
эти действия весьма трудоемки.
Отметим основные свойства корреляционной функции, играю-
щие большое значение при расчете систем автоматического регули-
рования.
1. Значение корреляционной функции при т = 0 равно_ средне-
квадратичному значению функции случайного процесса х2
(12.5)
Здесь
--T
х2= lim — {x2(t)dt. (12.6)
т^2Т J V '
—т
2. Корреляционная функция есть четная функция относитель-
но т
^) = ^(-О- (12.7)
3. Значение корреляционной функции при т ¥= 0 не превосходит
ее значения при т = О
^W<^(0), (12.8)
или
МШ (12.9)
4. Если функция x(t) есть сумма случайного процесса и посто-
янной составляющей а, то корреляционная функция 7?ж(т) стре-
390 Глава XII, Влияние на систему регулирования ВРД внешних воздействий
мится к а2 при т-> ±оо (рис. 12.4). Если же рассматриваемый про-
цесс не содержит неслучайной составляющей, то
Rx (т) 0 ПРИ т -> ± ОО.
5. Если рассматриваемый процесс есть сумма случайного и за-
данного периодического процесса, то в пределе при т->±оо корре-
ляционная функция Rx{x) превращается в периодическую функцию
той же частоты (рис. 12.5). Построение корреляционной функции
суммарного процесса легко позволяет выделить неслучайную со-
ставляющую, которую можно отбросить и получить корреляцион-
ную функцию только для случайного процесса.
Использование преобразования Фурье
В теории автоматического регулирования важную роль играет
преобразование Фурье. В обычных затухающих переходных про-
цессах переходная функция и соответствующая ей частотная ха-
рактеристика (комплексный частотный спектр) являются преобра-
зованием Фурье друг для друга. В стационарных случайных про-
цессах преобразование Фурье связывает корреляционную функцию
и спектральную плотность.
Случайная стационарная функция x(t) при Z->oo не стягивает-
ся к нулю. Поэтому для нее не существует преобразования Фурье.
Можно использовать другую функцию —Xr(t), которая совпадает
с x(t) при —Т равна нулю при всех остальных зна-
чениях времени t (рис. 12.6). Функция Xr(t) — ограничена, стяги-
вается к нулю при t-*-oo и для нее существует преобразование
Фурье
флг (М = У Хт (0 e-iatdt. (12.10)
—г
Для случайного процесса x(t) выражение
Ф4М = Пш -i-Ф (г<о) (12.Н)
Г->со 2/ Т
можно рассматривать как условное преобразование Фурье.
1. Применение методов статистической динамики к исследованиям систем 391
Спектральной плотностью случайного процесса x(t) называется
квадрат модуля функции Ф*(йо)
5(ф)=[Фх(Н12. (12.12)
Для x(t) корреляционная функция имеет вид
+Т
Кт (т) = ~ J Хт (О XT (t +x)dt (12.13)
—г
при —Т <t < +Т.
Так как при t<—Т и t> +Т функция /?т(т) = 0, то корреля-
ционная функция для x(t) равна
7?(т) = limTfrfr), (12.14)
Г-*-со
Функция 7?т(т) имеет преобразование Фурье
+со
Фдг (г<0) = J 7?т (т)е-/шгй?т,
или с учетом выражения (12.13)
ФЛг (i«>) =
Г+Г
J хт (0 Хт (t + т) dt
-—т
e~imXdx.
(12.15)
Подынтегральная функция интеграла, стоящего в скобках, рав-
на нулю при t < —Т и t > + Т. Поэтому для него пределы интегри-
рования могут быть расширены до —оо и +оо без изменения ре-
зультатов интегрирования. Тогда, введя в качестве сомножителей
eimi и е~м, получим выражение
ФКг(й>) = — ^XT(t)elatdt f Хт (t + т) dt. (12.16)
Во втором интеграле выражения (12.16) интегрирование ведет-
ся по т. Полагая t = const, введем новую переменную б = t + т.
Тогда
,-f-CO +00
Фдг (го>) = ^7 J Хт (0 eij>tdt у хт(р)е1ш<Чо,
—СО —со
ИЛИ
Фдг(М=-^Фхг(МФ.т(-^)= -^[Ф^®)12. (12.17)
392 Глава XII. Влияние на систему регулирования ВРД внешних воздействий
Из выражения (12.17) видно, что Ф^.г (гео) есть функция дей-
ствительная, а не комплексная, так как произведение двух комп-
лексно-сопряженных чисел дает действительное число.
Если устремить оо и перейти к пределу, то
ПтФЯг(й) = Нт-^-ДФ (гео)]2. (12.18)
Т~>со Т->со 21 1
Левая часть выражения (12.18) есть условное преобразование
Фурье корреляционной функции /?т(т). Если случайный процесс
x(t) таков, что корреляционная функция /?(т) стягивается к ну-
лю, тогда нет необходимости вводить условное преобразование.
Поэтому в дальнейшем будем просто рассматривать преобразова-
ние Фурье корреляционной функции /?(т).
Правая часть выражения (12.18), куда входит квадрат модуля
функции Ф* (ico), по определению равна спектральной плотно-
сти S(co).
Тогда
-П°О
Фл (и) = J R (т) e-^di = S (со) (12.19)
(12.20)
Далее учтем, что спектральная плотность S(co) —функция дей-
ствительная, а корреляционная функция /?(т) —четная. Поэтому
можно отбросить равные нулю мнимые части и перейти к преде-
лам интегрирования от 0 до +о°. Соответственно получим
СО
S (со) = 2 J 7^(т)созтсоб/т; (12.21)
о
со
(т) = — f S (со) cosтюda. (12.22)
Л J
о
Из выражения (12.21) и (12.22) следует, что корреляционная
функция и спектральная плотность являются косипус-преобразова-
ниями Фурье друг для друга. Формула (12.21) дает возможность
вычислить шТектральпую плотность по заданной корреляционной
функции. Интегрирование ведется по участкам, на которых кривая
Л(т) заменяется отрезками прямых или экспонентами (рис. 12.7).
§ 1. П рименение методов статистической динамики к исследованиям систем 393
Установим связь между среднеквадратичным значением случай-
ной величины и спектральной плотностью. Учитывая выраже-
ние (12.5), для т = 0 получим
СО
X2 — — f S (со) с/со.
л J
о
Если на входе в линейную си-
стему действует внешнее возму-
щение хвж(/), являющееся слу-
чайным стационарным процессом,
то выходная координата системы
%вых (/) будет также иметь харак-
тер случайного стационарного
процесса. Между спектральными
плотностями входной и выходной’
’(12.23)
Рис. 12.7
координат есть связь. Покажем ее.
Допустим, что функции входа ц выхода системы являются огра-
ниченными. Это означает, что на входе в систему xTex(t) = xex(t)
при —Т < t < +Т и хТвх = 0 при t < —Т и t > +Т. Соответствен-
но для выхода системы Хтвых = хвых(Г) при —7’</<+Г и
Хтвых(1) = 0 при t<—Т и t> + Т. Тогда для функции xTex(t)
и Хтв-ых(1) существует преобразование Фурье
фг = ф фО’ю).
1вых хТвх
(12.24)
Здесь Ф(гсо) —-амплитудно-фазовая частотная характеристика зам-
кнутой системы от входа к выходу. Если обе части выраже-
ния (12.24) поделить на 2Т и перейти к пределу при Т-+<х>, то по-
лучим условное преобразование Фурье. Возведя обе части равенст-
ва в квадрат, находим связь между спектральными плотностями
(со) = (со) [Ф (гео)]2. (12.25)
Из выражения (12.25) видно, что спектральная плотность на выхо-
де из линейной системы равна спектральной плотности внешнего
возмущения на входе, умноженной на'квадрат модуля амплитудно-
фазовой частотной характеристики этой системы.
Последовательность расчета системы регулирования
Изложим последовательность расчета системы автоматического
регулирования, когда возмущение вызвано стационарным случай-
ным процессом. В первую очередь с помощью коррелятора или не-
посредственным подсчетом (в этом случае интеграл заменяется
конечной суммой) обрабатывается запись возмущающего воздейст-
394 Глава XII. Влияние на систему регулирования ВРД внешних воздействий
вия. В результате обработки определяется корреляционная функ-
ция возмущения. Если найденная корреляционная функция при
т->оо не стягивается к нулю, а стремится к /?(т) = а2, то среднее
значение возмущения равно а. В этом случае начало отсчета воз-
мущений переносится па величину а, а начало отсчета корреляци-
онной функции на а2. Тогда при т->оо в новых координатах сред-
нее значение возмущения и корреляциойная функция равны нулю.
По найденной корреляционной функции строится кривая спект-
ральной плотности. Для этого корреляционная кривая заменяется
ломаной линией и вычисляется интеграл (12.21) по участкам. Вме-
сто замены кривой па ломаную линию возможно использование
какой-либо иной кусочной аппроксимации. После этого строится
график квадрата модуля амплитудно-фазовой характеристики как
функции частоты. Ординаты этого графика множатся на значения
спектральной плотности возмущения при одинаковых частотах.
В результате получается согласно соотношению (12.25) спектраль-
ная плотность случайного процесса на выходе системы. Строится
кривая спектральной плотности выхода SXgux (со), планиметрирует-
ся в соответствии с 'соотношением (12.23) и находится среднеквад-
ратичное значение выходной координаты системы регулирования
при заданном стационарном случайном процессе.
§ 2. МАТЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ТУРБУЛЕНТНОЙ АТМОСФЕРЫ
ТРДФ или ПВРД, находящиеся в условиях сверхзвукового по-
лета, будут непрерывно подвергаться возмущающим воздействиям
различной интенсивности, вызываемым турбулентной атмосферой.
Скорость любой частицы воздуха может быть представлена
в виде суммы двух составляющих: постоянной, общей для всего по-
тока воздуха рассматриваемой области, и переменной, носящей слу-
чайный характер, которая будет случайной функцией времени и ко-
ординат данной частицы воздуха.
На основные параметры рабочего процесса двигателя (напри-
мер, на число оборотов и температуру газа для ТРДФ) турбулент-
ные порывы воздуха большого влияния оказать не могут и ими
можно пренебречь. Но они будут вызывать дисперсию углов атаки
и скольжения и их влияние на течение воздуха в диффузоре может
оказаться существенным и нарушить нормальную работу системы
регулирования диффузора (систему перепуска воздуха или систе-
му, управляющую положением центрального тела диффузора).
Атмосферную турбулентность на ограниченных участках пути
самолета считают изотропной и однородной. Это предполагает, что
на какой-либо высоте в значительном по размерам слое частицы
воздуха обладают одинаковыми свойствами, а поле скоростей тур-
булентного движения однородно (стационарно). Исчерпывающие
§ 2. Математические характеристики турбулентной атмосферы
395
сведения о количественных характеристиках турбулентной атмос-
феры могут появиться только после проведения широко поставлен-
ных экспериментов. Однако те опытные данные, которые уже на-
коплены у нас и за рубежом, подтверждают возможность считать
атмосферную турбулентность в некоторой области в слое данной
высоты изотропной и однородной.
Вид корреляционных функций турбулентной атмосферы уста-
навливается экспериментальным путем. На основе экспериментов
в теории изотропной турбулентности даются приближенные анали-
тические выражения соответственно продольной и поперечной нор-
мированных корреляционных функций для поля скоростей в двух
точках, разделенных произвольным вектором г:
Rn (г) = 4 (1 — )
(12.27)
е
В соответствии с выражением (12.26) корреляционная функция
проекции скорости порыва воздуха на направление полета (на
ось х) будет иметь вид
(12.28)
Здесь 4— среднее значение квадрата (дисперсия) любой компо-
ненты скорости турбулентного движения; х = х— х' — приращение
координаты х, пропорциональное приращению времени при неиз-
менной скорости полета; А —масштаб турбулентности.
Таким образом, состояние турбулентной атмосферы определяет-
ся дисперсией скорости и масштабом турбулентности.
Дисперсия скорости Ow определяется как среднеквадратичное
значение скорости ветра. Она характеризует интенсивность поры-
вов, зависящих от условий погоды и высоты полета. При продол-
жительном полете как условия погоды, так и высота полета могут
изменяться, будет нарушаться стационарность случайных порывов
воздуха. Дисперсию порывов можно определить по вероятностным
экспериментальным характеристикам, показанным в работе [7].
На рис. 12.8 и 12.9 показано влияние высоты и условий погоды на
функцию распределения вероятности F(ow) среднеквадратичного
значения случайного порыва ветра. Выбрав величину Gw, по этим
графикам весьма приближенно можно предсказать вероятность
пребывания летательного аппарата в атмосфере с этим значе-
нием Отт-
Масштаб турбулентности L характеризует линейные размеры
области, в которой соответствующие составляющие скорости поры-
вов ветра коррелированы заметным образом. Иначе говоря, мас-
396 Глава XII. Влияние на систему регулирования ВРД внешних воздействий
штаб турбулентности характеризует затухание корреляционной
связи, он равен средней длине порыва и зависит от условий пого-
ды и высоты полета. Пока еще нет достаточных данных по величи-
нам L, принято считать, что протяженность порывов колеблется от
150 до 1500 м.
При использовании формул (12.26) и /12.27) надо иметь в виду,
что масштабы турбулентности для продольной и поперечной корре-
1 -ясная погода;
2 -кдчевые одяака;
3 -грозовые условия
Рис. 12.9
ляционных функций не равны между собой. Если их определять как
интеграл от корреляционных функций Rt и Rn, то, как это показа-
но в работе [24], получим
V'o
- Mr =- L-
О
Ln = ~~ I Rn (/•) dr = (
M 0
От корреляционной функции
к спектральной плотности.
Согласно выражению (12.23)
1
<j2
“Тл L
е Ldr — —
2 ’
в направлении полета переходим
о
где Q— пространственная угловая частота. Переход от пространст-
венной угловой частоты Q к угловой частоте и осуществляется с
§ 2. Математические характеристики турбулентной атмосферы
397
помощью соотношений fix = at и х = vt. Откуда fi = a/v, здесь
о — скорость полета.
После подстановки и интегрирования получим
= — _24т.
л 1 + tW
(12.29)
где т = L/v — средняя продол-
жительность порыва ветра.
S(fi) отражает только стати-
стические свойства турбулент-
ной атмосферы. S(co) помимо
этих свойств содержит данные ДО
о скорости полета летательно-
го аппарата. Увеличение скоро- дг
сти полета уменьшает долю
энергии случайных порывов
воздуха в области низких час- д
тот. Это повышает возмож-
ность системы регулирования
по фильтрации помех турбу-
лентной атмосферы на больших скоростях полета.
На рис. 12.10 показано влияние частоты, скорости полета и мас-
штаба турбулентности на значение спектральной плотности.
ЛИТЕРАТУРА
1. Айзерман М. А., Лекции по теории автоматического регулирования,
Фпзматгиз, 1958.
2. Б о д и е р В. А., Автоматика авиационных двигателей, Оборонгиз, 1956.
3. Боднер В. А., Рязанов Ю. А., К вопросу синтеза структурных схем
самонастраивающихся систем регулирования ТРДФ, Сб. «Автоматическое регули-
рование авиадвигателей», № 3, Оборонгиз, 1961.
4. В о р о н к о в Б. С., Ядерный реактор как объект регулирования, Сб. «Авто-
матическое регулирование авиадвигателей», № 2, Оборонгиз, 1960.
5. Гози М., Ках ан Т., Управление ядерными реакторами, Атомиздат, 1960.
6. Д р е й п е р Ч. С., Ли И. Т., Принципы автоматической оптимизации,
Сб. «Автоматическая оптимизация управляемых систем», ИЛ, 1960.
7. Доброленский Ю. Н., Турбулентность атмосферы как источник воз-
мущений для систем автоматического управления самолетом, Известия АН СССР,
«Энергетика и автоматика», № 5, 1961.
8. 3 а л м а п з о н Л. А., Черкасов Б. А., Регулирование газотурбинных и
прямоточных воздушно-реактивных двигателей, Оборонгиз, 1956.
9. Иващенко Н. Н., Автоматическое регулирование, Машгиз, 1962.
10. Коган Б. Я., Электронные моделирующие устройства и их применение
для исследования систем автоматического регулирования, физматгиз, 1959.
11. Красовский А. А., Поспелов Г. С., Основы автоматики и техни-
ческой кибернетики, Госэнергоиздат, 1962.
12. Кунцевич В. М., Системы экстремального управления, Гостехиздат
УССР, 1961.
13. Нечаев Ю. Н., Входные устройства сверхзвуковых самолетов, Воен-
издат, 1963.
14. Новиков В. И., Экспериментальное определение динамических свойств
ТРД как звена в системе автоматического управления полетом, Сб. «Автоматиче-
ское регулирование авиадвигателей», № 3, Оборонгиз, 1961.
15. Новиков В. И., ТРД и ТРДФ как звено в системах автоматического
управления самолётом, Сб. «Автоматическое регулирование авиадвигателей», № 3,
Оборонгиз, 1961.
16. Основы автоматического регулирования, под ред. В. В. Солодовникова,
Машгиз, 1954.
17. Реактивные двигатели, под ред. Ланкастера О. Е, Воениздат, 1962.
18. Солодовников В. В., Введение в статистическую динамику систем
автоматического управления, Техтеориздат, 1952.
19. С т е ч к и н Б. С., К а з а н д ж а н П. К., Алексеев Л. П., Гово-
ров А. Н., Коновалов Н. Е., Нечаев Ю. Н., Федоров Р. М., Теория
реактивных двигателей, Оборонгиз, 1958.
Литература 399
20. Фельдбаум А. А., Электрические системы автоматического регулиро-
вания, Обороигиз, 1954.
21. Шевяков А. А., Автоматика авиационных силовых установок, Оборон-
гиз, 1960.
22. Ш т о д а А. В., А л е щ е.н к о С. П., И в а и о в А. Я., К р а с а в ц е в В. С.,
Морозов Ф. Н., С е к и с т о в В. А., Шнуков А. Т., Конструкция авиацион-
ных газотурбинных двигателей, Воеииздат, 1961.
23. Шульц М., Регулирование энергетических ядерных реакторов, ИЛ, 1957.
24. Press Н., Meadows М. Т., Hadlock J. A., Reevaluation of data on
atmospheric turbulence and airplane gust loads for application in Spectral calcula-
tions, NACA Report, No. 1272, 1956.
25. Жир ер д И., Моделирование динамики ядерного реактора, «Лаборато-
рия», № 16, 1956.
26. Камерон Р., Остин Д., Электронная модель реактора, «Ядерная
энергия», т. 2, № 12, 1957.
ОГЛАВЛЕНИЕ
Стр.
Предисловие ........................................................ 3
Основные обозначения ................................................. 5
Г лава I. Авиационные газотурбинные двигатели. Особенности рабочего про-
цесса и возможные программы регулирования ............................ 9
§ 1. Однокаскадные турбореактивные двигатели..................... 9
§ 2. Двухкаскадные ТРДФ ......................................... 28
§ 3. Турбовинтовые двигатели (ТВД) .............................. 34
§ 4. Двухконтурные ТРД (ТРДД) ................................... 38
Глава II. Газотурбинные двигатели, работающие на химическом топливе,
как объекты регулирования ........................................... 41
§ 1. Понятие о собственной устойчивости энергетических систем ... 41
§ 2. Уравнения движения различных ГТД ........................... 45
§ 3. Влияние различного рода возмущений на изменение регулируемых
параметров ТРДФ .................................................. G4
§ 4. Приближенные способы расчета коэффициентов, входящих в урав-
нения движения двигателей как объектов регулирования ............. 75
Примеры .................................................... 80
Глава III. Регулирование сверхзвуковых входных устройств ............ 84
§ 1. Особенности рабочего процесса н характеристики входных диф-
фузоров .......................................................... 84
§ 2. Влияние способа регулирования на характеристики входного диф-
фузора ....................................................... 92
§ 3. Выбор программы регулирования входного диффузора .......... 97
§ 4. Особенности динамических характеристик диффузоров ........ 102
Глава- IV. Регулирование сверхзвуковых прямоточных воздушно-реактив-
ных двигателей (СПВРД) ............................................. 101
§ 1. Особенности рабочего процесса ............................. 104
§ 2. Выбор программы регулирования ............................. 106
§ 3. Область возможных режимов работы маршевого ПВРД ........... 110
§ 4. ПВРД как объект регулирования ............................. 113
Глава V. Системы регулирования авиационных воздушно-реактивных дви-
гателей ............................................................ 117
§ 1. Общие принципы построения систем регулирования ............ 117
§ 2. Элементы систем питания и автоматических устройств ........ 129
Оглавление
401
§ 3. Схемы систем регулирования ГТД ........................... 152
§ 4. Повышение надежности ТРД и ТВД с помощью средств автоматики 184
Примеры ................-.................................. 188
Глава VI. Основные сведения о системах регулирования. Типовые звенья
и их характеристики ................................................ 190
§ I. Понятие о системе регулирования. Объект регулирования и регу-
лятор как замкнутая система регулирования ...................... 190
§ 2. Типовые звенья систем регулирования ВРД .................. 195
§ 3. Экспериментальные методы определения коэффициентов, входящих
в уравнения типовых звеньев .................................... 207
§ 4. Частотные характеристики типовых звеньев ................. 219
§ 5. Экспериментальное определение коэффициентов, входящих в урав-
нения движения двигателей, как объектов регулирования .......... 225
Примеры ................................................... 229
Глава VII. Методы расчета и исследования динамических характеристик
систем автоматического регулирования ............................... 235
§ I. Дифференциальные уравнения переходных процессов в линейной
система регулирования .......................................... 235
§ 2. Методы исследования устойчивости линейных систем регулирова-
ния ............................................................ 237
§ 3. Методы оценки качества переходного процесса в линейных сис-
темах регулирования ............................................ 258
§ 4. Способы улучшения динамических характеристик систем автома-
тического регулирования. Понятие о синтезе систем автоматиче-
ского регулирования ............................................ 277
§ 5. Исследование систем регулирования, содержащих элементы с су-
щественно нелинейными характеристиками ......................... 286
Примеры ................................................... 305
Глава VIII. Регулирование ГТД на неустановившихся режимах ......... 309
§ 1. Регулирование разгона и сброса газа ГТД ................... 309
§ 2. Регулирование запуска ГТД ................................. 324
Примеры ................................................ 326
Глава IX. Регулирование авиационной ядериой силовой установки ..... 329
§ 1. Схемы ядерных ВРД ......................................... 329
§ 2. Реактор как объект регулирования .......................... 331
§ 3. Управление силовой установкой с ядерным реактором ........ 345
§ 4. Системы автоматического регулирования ядерного ТРД ....... 353
Глава X. Моделирование процессов в системе автоматического регулиро-
вания .............................................................. 358
§ 1. Способы моделирования физических процессов ............... 358
§ 2. Математическое моделирование ........................... 360
§ 3. Линейные решающие элементы ............................... 362
§ 4. Моделирование элементов систем регулирования с нелинейными
характеристиками и с прямым запаздыванием в передаче сигнала 366
Пример ......................................................... 368
402
Оглавление
Глава XI. Экстремальное регулирование ............................. 372
§ 1. Основные понятия ......................................... 372
§ 2. Типы автоматов оптимизации ............................... 373
§ 3. Экстремальное регулирование режима авиационного двигателя 380
Глава XII. Влияние на систему регулирования авиационного воздушно-ре-
активного двигателя случайных внешних воздействий .................. 385
§ 1. Применение методов статистической динамики к исследованиям
систем автоматического регулирования ........................ 385
§ 2. Математические характеристики турбулентной атмосферы ..... 394
Литература ........................................................ 398
Борис Александрович Черкасов
АВТОМАТИКА И РЕГУЛИРОВАНИЕ ВОЗДУШНО-РЕАКТИВНЫХ
ДВИГАТЕЛЕЙ
Переплет художника Л. А. Витте
Издательский редактор Г. А. Бубнов Техн, редактор А. Я. Новик
Г—27214 Подписано в печать 1/IX 1965 г. Учетпо-изд. л. 27,19
Формат бумаги 60 X 9О‘/1б = 12,63 бум. л.—25,25 печ. л.
Цена 1 р. 10 к. Тираж 5500 экз. Заказ 1945/1281
Сводный план 1965 г. № 684
Экспериментальная типография ВНИИПП
Государственного комитета Совета Министров СССР по печати
Москва И-51, Цветной бульвар, 30
Замеченные опечатки
Стр. Строка Напечатано Должно быть
13 10 сверху (Т) (Т)
49 9 сверху /_66Л1\ \ дп J 0п ь . <?6Л4 \ & )л
114 8 снизу Q? - Qe = (РИ, Q-г = Q-г (Рц’
115 7 снизу (t§p2 + tiP-I fe3) (тер2 + т7р.:-й3)
184 14 снизу М = const Мг const
206 5 сверху (6.41) (6.42)
233 Рис. 6.30, а 29° 27°
233 Рис. 6.30, б М = 0,29 М = 0,8У
233 Рис. 6.30, в 56°30' 53° 30'
238 13 сверху е -> 0 а/ л
243 12 сверху (wz) = f (u>i)
255 15 сверху ап— Л/1— 1 . п—1 а Л п-1
285 5 снизу Ad Да
305 Таблица 0,375 —0,375
311 16 сверху а = —30-10~SI/°C а^—30-10~51/°С
311 18 сверху а = —2,9-10~51/°C а = —2,9-10~51/°С
369 Рис. 10.13 Звено 1 5zz 6/V
384 9 сверху квадратов квадраторов
Заказ 1S45.1281