Текст
A. 3. ФР АДИН, Е. В. РЫЖКОВ
ИЗМЕРЕНИЕ ПАРАМЕТРОВ
АНТЕННО-ФИДЕРНЫХ
УСТРОЙСТВ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ
ПО ВОПРОСАМ СВЯЗИ И РАДИО
МОСКВА 1962
ПРЕДИСЛОВИЕ
Развитие антенной техники за последние годы характери-
зуется, во-первых, разработкой и внедрением в практику боль-
шого числа новых типов антенн, во-вторых, внесением разнооб-
разных усовершенствований в конструкции и схемы ранее при-
менявшихся типов антенн. Новые разработки часто проводятся
теоретически. При этом почти всегда математический анализ
делается для идеализированных условий, а расчёты проводятся
по приближённым формулам, в связи с чем результаты теоре-
тического решения нуждаются в экспериментальной проверке,
в основе которой лежит измерение параметров антенн. Многие
же задачи антенной техники, по которым теория недостаточно
развита, решаются целиком экспериментально. Таким образом,
эксперимент играет важнейшую роль при разработке новых ан-
тенн и служит как средством проверки выводов теории, так и
самостоятельным методом исследования.
Измерение параметров антенн необходимо ещё по следую-
щим причинам.
1) Антенны всех диапазонов от еверхдли’нных до миллимет-
ровых волн, находящиеся в эксплуатации на радиостанциях
различного назначения, с течением времени подвергаются де-
формациям, которые приводят к изменению их параметров. По-
этому правилами эксплуатации предусматривается проведение
периодических контрольных измерений параметров антенн, их
регулировка и настройка соответственно результатам измерений.
2) На заводах при массовом выпуске антенн требуется из-
мерение их параметров.
3) Применение методов автоматического управления аппа-
ратурой радиостанций требует, в частности, установки приборов
постоянного контроля и регулировки параметров антенн.
В условиях, когда антенные измерения призваны решать
столь широкий круг задач, естественно, возникает необходи-
мость в пособии, в котором достаточно полно и систематизиро-
вание освещались бы эти вопросы. Между тем, до настоящего
времени изложение вопросов антенных измерений встречается
либо в периодической литературе в виде статей, посвящённых
отдельным частным схемам и измерительным приборам, либо в
3
учебниках по общим курсам антенных устройств или радиоиз-
мерений, в которых вопросы антенных измерений являются ча-
стными и освещаются весьма.ограниченно.
Предлагаемая вниманию читателей книга является попыт-
кой восполнить указанный пробел.
Книга предназначается для инженеров и техников, которым
в своей практической работе приходится производить измерение
параметров антенн, и может быть использована также в качестве
учебного пособия при изучении курса антенн.
Наряду с описанием методов измерений и измерительных
приборов, проверенных многолетним опытом и получивших ши-
рокое распространение на практике, в книге содержатся сведе-
ния о получивших известность в периодической литературе но-
вых разработках и идеях, могущих служить основой для даль-
нейших усовершенствований измерительной техники в области
антенных измерений. Поэтому книга будет полезна также спе-
циалистам, разрабатывающим новую аппаратуру для измере-
ния параметров антенн.
Книга, естественно, не может претендовать на исчерпываю-
ще полное изложение всего теоретического и экспериментально-
го материала по измерению параметров антенн, накопленного к
настоящему времени. Приводимая библиография должна по-
мочь читателю найти, в случае надобности, дополнительные
сведения по излагаемым вопросам.
Считаем своим приятным долгом выразить глубокую'благо-
дарность доктору технических наук Я. Н. Фельду за ценные за-
мечания, сделанные при рецензировании, и доктору технических
наук Б. В. Брауде, взявшему на себя труд редактирования книги.
Отзывы и замечания по книге следует направлять в Связь-
издат (Москва-центр, Чистопрудный бульвар, 2).
Авторы
1. ПАРАМЕТРЫ АНТЕННО-ФИДЕРНЫХ
УСТРОЙСТВ
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Классификация параметров антенн
Антенна представляет собой преобразователь энергии.
Передающая антенна преобразовывает поступающую от выход-
ного контура передатчика энергию переменных токов высокой
частоты в энергию электро-магнитного излучения, т. е. в энергию
пространственной электромагнитной волны, Приёмная антенна,
наоборот, преобразовывает энергию приходящей электромагнит-
ной волны в энергию переменных токов высокой частоты, пере-
даваемую во входной контур приёмника.
Таким образом, работа антенны всегда связана с двумя ви-
дами энергии. В соответствии с этим параметры, характеризую-
щие антенну, разделяются на две группы. К первой относятся
параметры, связанные с энергией переменных токов высокой
частоты: входное сопротивление, резонансные частоты, частотная
характеристика, полоса пропускания и т. п. Ко второй группе
относятся параметры, связанные с энергией в виде электромаг-
нитного излучения. Они образуют группу так называемых харак-
теристик излучения. К ним относятся: диаграмма направленно-
сти, ширина главного лепестка, относительный уровень побоч-
ных максимумов, коэффициент усиления, коэффициент направ-
ленного действия, эффективная площадь, действующая высота
и т. п.
Обе группы параметров характеризуют работу в равной ме-
ре как передающих, так и приёмных антенн. Согласно теореме
взаимности и её следствиям параметры антенны имеют опреде-
лённую величину независимо от того, используется ли антенна
в качестве передающей или приёмной. Поэтому исследование
антенн производится в зависимости от удобства при том или
ином виде работы.
Определить некоторые параметры при экспериментальном
исследовании можно лишь путём непосредственных измерений.
Эти параметры будем называть первичными экспериментальны-
5
ми параметрами или просто первичными. Остальные параметры,
которые будем называть вторичными экспериментальными или
просто вторичными, могут быть найдены графически или расчёт-
ным путём по известным первичным. В первой группе парамет-
ров первичным является входное сопротивление. По известным
значениям входного сопротивления в диапазоне частот могут
быть найдены резонансные частоты, частотная характеристика,
полоса пропускания. Во второй группе первичными параметра-
ми являются диаграмма направленности и коэффициент уси-
ления. По известной диаграмме направленности можно найти
ширину главного лепестка, относительный уровень боковых мак-
симумов, а также получить представление о коэффициенте на-
правленного действия. По известному значению коэффициента
усиления можно найти эффективную площадь и действующую
высоту антенны.
Первичные экспериментальные параметры антенн
Входное сопротивление 1)
Если подключить к антенне источник электродвижущей
силы (эдс), то в ней возникнет ток. Амплитуда и фаза тока будут
различны в разных точках антенны. Точки, между которыми
подключается источник эдс, называются входом антенны.
Отношение напряжения источника эдс на входе антенны к
входному току называется входным сопротивлением антенны и
обозначается через ZA. Его активная и реактивная составляю-
щие обозначаются через RA и ХА.
Диаграмма направленности
Как известно [Л1], поле излучения антенны в полярных
координатах выражается следующим образом:
—imr в
Е=\2^Н = А~~Е(Ъ,^),— , (1.1)
где Е — напряжённость электрического поля;
Н — напряжённость магнитного поля;
г, О, <р — полярные координаты с началом в средней точке
антенны (рис. 1.1);
, , . . 2к
m — коэффициент фазы, равный — ;
А, — длина волны;
*) В приводимых определениях считаем антенну передающей.
A — множитель» пропорциональный амплитуде тока (у
проволочных антенн) или напряжённости поля в
раскрыве {у дифракционных антенн) и являющийся
функцией размеров антенн;
F (ft, ф) —нормированная функция угловых координат ft и
ф, т. е. такая функция, максимальное значение ко-
торой, соответствующее углам fto, фо, равно 1.
2
Рис. 1,1, Полярная систе-
ма координат г О ф, сё
связь с прямоугольной
системой xyz и направ-
ление векторов: распро-
странения Р, электриче^
скего Е и магнитного Н
полей
Из ф-лы (L1) видно, что при постоянном г значение £ и Я за
висят от координат О и ф/ Функция F (ft, ф), выражающая эту
зависимость, представляет собой диаграмму направленности ан-
тенны. Таким образом, наличие у антенны определённой диаграм-
мы направленности указывает на то, что интенсивность её излу-
чения [) различна в разных направлениях при разных ft и ф.
Направление ft—fto, ф — фо, при котором F (ft, ф) равно 1, на-
зывается направлением главного максимума диаграммы направо
ленности.
Коэффициент усиления
Под коэффициентом усиления антенны G понимают от-
ношение интенсивности излучения антенны в направлении глав-
ного максимума (при ft=fto, ф = фо) диаграммы иаправленности
]) Под интенсивностью излучения понимают мощность излучения, прихо-
дящуюся на единицу площади фронта волны.
7
к среднему значению интенсивности излучения, соответствующе-
му коэффициенту полезного действия т) = 100%. Таким образом»
G = —= -ЛаксГ- , (1.2)
Р ЗОР 7
4яг»
где Емахс — значение Е, соответствующее
<р—<ро— определённое при том же расстоянии г, на котором
определяется среднее значение интенсивности поля;
Р — мощность, поступающая в антенну.
Фидерные линии. Их параметры и характеристики
Большинство современных антенн питается по фидерным
линиям (фидерам). Под фидерной линией понимают соединитель-
ную линию между антенной и передатчиком или между антенной
и приёмником, представляющую собой два параллельных прово-
да, коаксиальный кабель, полый волновод и т. п.
Схематически фидерную линию будем обозначать в виде
двухпроводной линии (рис. 1,2), к которой присоединён с одного
конца источник эдс, а с другого — нагрузка, например антенна,
входное сопротивление которой равно Z А , Параметрами фидерных
линий являются: волно-
вое сопротивление р, коэф-
фициент затухания 0 1)
и коэффициент скорости п,
равный отношению ско-
рости света в вакууме?)
к фазовой скорости в фи-
дере. Эти параметры
зависят от типа линии
(двухпроводная, коаксиальная» волноводная и т. п.), от ее раз-
меров, типа (порядка) волны, частоты колебаний и от материа-
ла, из которого сделана линия.
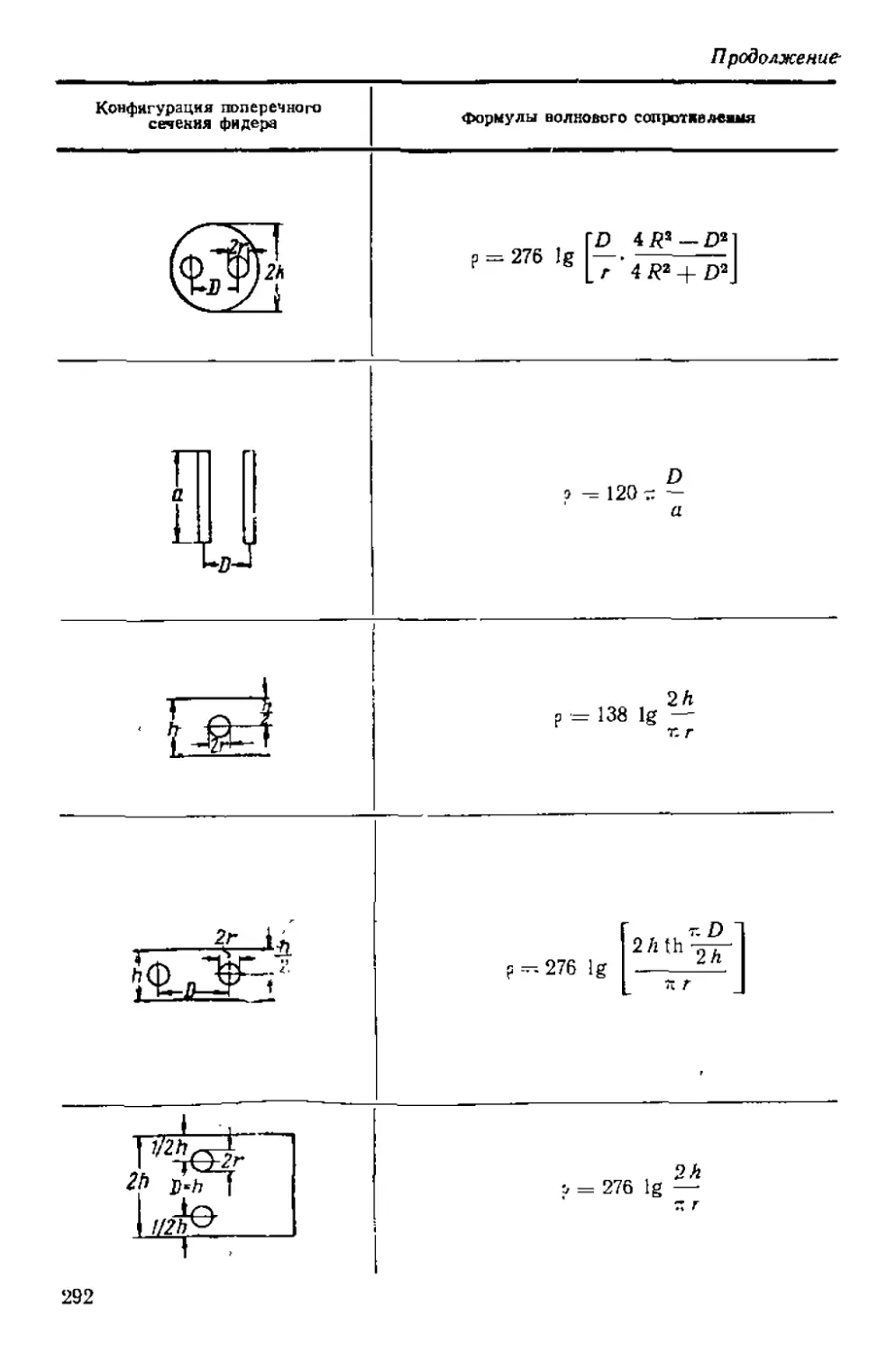
Формулы для расчёта параметров некоторых из фидерных
линий даны в приложении 3.
Под влиянием приложенной эдс на фидерной линии возникает электро-
магнитная волна, которая движется в сторону нагрузки ZA. Обозначим ток и
напряжение этой волны в сечении х соответственно через U™d и • а на-
пряжение и ток в сечении ж=0 (в месте подключения нагрузки — через * 2
’) Согласно ГОСТ 1494—61 с I июля 1962 г. вводится обозначение ко-
эффициента затухания а, коэффициента фазы
2) В гибких коаксиальных фидерных линиях п>1 и называется коэффи-
циентом укорочения, ® волноводах д<1.
8
ХЮ
Рис. 12. Схематическое изображение фи-
дерной линии
Utf3 и Напряжения и соответствующие им токи связаны между собой
соотношениями:
7 ?пад _ мад 0
~ 1х. г
7 гпйд __ jftdd _
U0 — Iq Р
(1.3)
Как правило, фидерная линия имеет очень малое затухание. Поэтому бу-
дем считать её идеальной — не имеющей затухания. Рассматривая х как те-
кущую координату линии, можно записать:
U"a3 = U^eimx
упад
тпад__ тпад Лтх ° _ _ J/nx 1)
‘к 70 е = е
Р
(1.4)
В сечении х—0 падающая волна частично поглощается нагрузкой, ча-
стично отражается обратно к источнику эд с. Обозначим напряжение и ток
отражённой волны в сечении х=0 соответственно через У^тр и 1^тр f а в точ-
ке х — через U°mp и 1пхтр.
Между напряжениями и токами отражённой волны имеют место соотно-
шения, аналогичные соотношениям между напряжениями и токами падающей
волны:
Отношения
истр = 1атр^
уптр уыпр g4—\тх
]отр fomp imx
U°m?
Uo jjnad
и0
J6mp
Г h tnad
/0
(1.5)
(16)
иосят название коэффициентов отражения соответственно по напряжению и
току. Эти коэффициенты определяются через сопротивление нагрузки ZA и
волновое сопротивление р следующим образом:
U> za + ?
г'. = ~ги,
где р — модуль, а ф — фаза коэффициента отражения.
(Г7>
>) При наличии заметного затухания волны на фидере и при фазовой
скорости v ффс в ф-лах (1.4) и следующих нужно заменить im на у=р+1т'г
2?ш
где Р — коэффициент затухания, т'= —— .
Поскольку и Г/ отличаются лишь по фазе на постоянную величину
л, то нет надобности вводить в рассмотрение оба коэффициента; Будем в даль-
нейшем под коэффициентом отражения понимать Гу .
Напряжение Ux и ток 1Х в каждом сечении линии равны сумме соответ-
ственных значений падающей и отражённой волн:
Ux = + UTP - е*тх (* + ре~*т*+'г )
упад ► .
/ж lnQd = —-— eimx(l — р 6-2^+^
Л х р
Если выразить Г’ц через ZA и р согласно (1.7), a через
2Z-
Уо « U^ad -ф U™? = iff*-------— ,
ZA
получим/
U
cos тх -ф- i sin tnx
А р V)
Ix = ~ sin /пх + ‘ cos тх}
Минимальные значения напряжения и тока Umuh)
равны:
1^1
I ^мик 1 — (1 р)
р
а их максимальные значения (U макс) и (1Маке) равны:
1^е| = Щ^|о+Р)
I ^макс I — (1 + Р)
Р
(1.12)
Коэффициент бегущей волны (кбв) * 2) к равен
Umuk ___
^макс
(1.8)
419)
(1Л0)
(Ml)
(1.13
I __ 1___P
11макс I 1 + P
к
*) При учёте затухания па липин тригонометрические функции в (1.10)
заменяются соответствующими гиперболическими функциями.
2) В литературе часто пользуются понятием коэффициента стоячей вол-
ны (ксв), который равен ---
10
Легко видеть из (1.8), что во всех случаях координата минимума на-
пряжения, которую обозначим через х0, совпадает с координатой максимума
тока, а координата максимума напряжения, которую обозначим через хмахс
— с координатой минимума тока, причём:
2_ . ?
2т 4 2m
*«==
(1.14)
х -
Хмакс~2т
(1.15)
Поскольку точки минимума и максимума напряжения смещены друг от-
носительно друга на постоянную величину то можно ограничиться рас-
смотрением только одной из них. Будем рассматривать точку хо.
Отношение ~ представляет собой сопротивление фидера в, сечении х.
Обозначим это сопротивление через Согласно (L7) и (L8)
1 + Г„ e_amjt 1 + V
Zx = R 4-1 X => р----------------- = Р-----Г-1
Л-Ги_
(1.16)
где — коэффициент отражения я сечении лг, равный -----г*.
х U*
Сопротивление Zx может быть выражено также через коэффициент бе-
гущей волны к, если вести отсчёт координаты х от сечения xdx&. Действ ителк-
но, введём новую координату
X — X — хл.
(1.17)
Подставив значение х из (1.17) в (1.8) и произведя соответствующие пре-
образования, получаем
] 4- ре-J — ре"211”*'
1 — ре 2imx'+Ic j pg 2lmx‘
Освободившись от мнпъюстн в знаменателе выражения (JJ8)
Р через к согласно (IJ3), получаем
кЧ* 0,5i (1 — к1) sin 2тхг
cos3 тх' 4- к1 $ша тх
(1.18)
я вырази»
(1.19)
Таким образом, сопротивление фидера в любом сечении про-
порционально волновому сопротивлению фидера р и является
функцией двух величин: либо комплексного коэффициента отра-
жения Г их (см. (1.16)], т. е. его модуля р и фазы ф, либо коэффи-
циента бегущей волны к и координаты х', отсчитываемой от сече-
ния фидера, в котором имеется минимум напряжения [см. (1.19)],
в сторону передатчика.
11
Прямоугольная диаграмма сопротивлении
Измерение входного сопротивления антенн производится обычно не
на одной, а на нескольких частотах, лежащих в пределах некотором полосы
частот^ По данным измерений строится график зависимости входного сопро-
тивления от частоты. Поскольку входное сопротивление является комплексной
величиной! то требуется, вообще говоря, строить два графика: один для ве-
щественной, другой для мнимой составляющих сопротивления.
Если применить метод изображения, показанный на рис. 1.3, то можно
Представить зависимость входного сопротивления от частоты при помощи од-
ной кривой. Сущность этого метода заключается в следующем.
Плоскость чертежа рассматривается как комплексная плоскость, на кото-
рой ось абсцисс является вещественной осью, ось ординат—мнимой, а ком-
плексные величины изображаются точками. Вдоль вещественной оси откла-
дываются в выбранном масштабе значения — > а вдоль мнимой оси — зна-
Р
X
чеямя —, где р — волновое сопротивление фидера, питающего антенну. Из-
Р
меренные на различных частотах величины входного сопротивления изобра-
жаются на графике в виде точек, а частоты, на которых производилось из-
мерение, обозначаются цифрами около Этих точек.
„ . Я Я
Легко показать, что на комплексной плоскости ~, геометрическое
место точек одинаковых значений коэффициента бегущей волны к. есть ок-
ружность.
Рис. 1.3. Изображение зависимости входного сопротивления от частоты
в виде кривой на прямоугольной диаграмме сопротивлений
12
Действительно, согласно (L13) и (1.7)
(1-20)
Для освобождения от иррациональности в выражении (1.20) восполь-
зуемся алгебраическим тождеством
а — & а 4* b А as
----- к _ = 2---------3—— '
а — b а2 — &
(1.21
Так как выражение (1.20) имеет вид ----- , то
а 4- b
Р
Равенство (1.22), в свою очередь, приводится к виду
Я
Уравнение (1.23) в координатной системе —
?
X
является уравнением
Р
окружности радиуса, равного
центром
в точке
с
Экстремальные значения —
о
\ I
имеют место При
X
— — 0 и равны
Р
х Р /макс К \ Р Zмин
На рис. 1.3 нанесено семейство окружностей, удовлетворяющих ур-нию
(1.23) при разных значениях к. Все точки одной и той же окружности соот-
ветсгвугот одному и тому же значению к, в то время как значения И""р~
различны для различных точек окружности.
Заметим, что на фидерной линии (однородной) коэффициент бегущей вол-
13
ны одинаков для всех сечений, в то время как сопротивление Zx меняется от
сечения к сечению по ф-ле (1.19). При этом величины
_____________к__________
Р cos1 тх' 4- к1 si п* тх?
(1 24)
0,5 (1 — к1) sin 2/ихг
X__________,
р cos1 тхг 4- яс1 sin1 тхг
(1.25>
р
част>
RA
определяемые по ф-ле (1.19), связаны между собой так же, как — и
Р
ур-нием (1.23). Это легко доказать, подставив (L24) и (1.25) в левую
(1.23),
Далее функция Z Л от х' является периодической с периодом ~~, причём в
R X
пределах одного периода —, как видно из (1.24), меняется от к при х'=л
р 2
1 X •
до — при х'=«(2п+1) —, т. е. меняется в тех же пределах, в которых
D
меняется—-согласно ф-ле (1.23). Следовательно, отдельные точки окружности
Р
к»’const на рис. ЬЗ.дают величины сопротивлений, соответствующие при за-
данном к отдельным сечениям фидера, характеризуемым координатой х',
R X
Найдём связь между величинами сопротивлений •— ,-----и
Р Р
сечения л/. Для этого разделим (1.25) на (1.24):
координатой
откуда
sin 2тх',
(1.26)
X
Р
1
sin2mx'
(L27)
1
Подставив в (1.23) значение к^~~^ из
и отбросив индексы Аг получим
(1.22), 0,5 Л— -кЛиз (1.27)
(1.28)
и
X
Р
R
Р
Левая часть (1.28) преобразовывается к виду
Подставив (1.29) » (1.28), получим:
4
ctg^Smx',
(L30)
а из (1.30)
+ (-у-— cig 2mx'^ = со$ес»2тх'. (1-31)
Р
Зная коэффициент бегущей волны к на фидере и координату сечения х',
можно, подставив к и х' в (1.23) и (1.31)» получить систему уравнений для
R X п R X
определения *— и —. Для графического определения — я — по известным
Р Р Р Р
значениям к и / на графике рис. 1.3 к окружностям к=const добавляются кри-
вые тх'^const. Из (131) видно, что кривые mx'=const являются дугами
R Л X
окружностей радиуса, равного cosec 2mx/ в с центром в точке — = U, — =
Р Р
—cig 2тх\
Так как cosec’o—ctg2a~l, то все эти окружности пройдут через точку
р р
R X
Прямоугольная координатная система —,— с нанесёнными на ней ок-
Р Р
ружностями к—const и кривыми mx «const носит название прямоугольной
диаграммы сопротивлений.
Полярная диаграмма сопротивлении
В основе построения полярной диаграммы сопротивлений лежит
двухмерная полярная система координат, у которой радиальной координатой
является модуль коэффициента отражения р. а угловой координатой — фаза
Ф коэффициента отражения, которая меняется по длине фидера согласно фор-
муле ср=2тх' (рис. 1.4а).
Так как каждому значению р соответствует вполне определённое значе-
ние коэффициента бегущей волны к, то можно па радиальной оси указывать
не р, а соответствующее ему значение к. Вместо угловой координаты 2тх'
удобнее указывать величину tux'. При этом исходная система координат при-
нимает вид, показанный на рис. 1.46 или 1.4е.
Заметим, что поскольку р меняется от 0 до 1, то вся диаграмма занимает
ограниченную часть плоскости, заключённую внутри круга радиуса, равного
единице. Каждой точке внутри этого круга соответствует определенное зна-
чение к и определённое значение тх'. Но, как отмечалось выше, каждому зна-
чению к и тх' соответствует вполне определённое значение . Чтобы найти
Р
Zx R
величину —г необходимо нанести на диаграмме семейства кривых =const
и const. Для нахождения формы этих кривых обратимся к ур-нию (1.18).
Р
Рис, 1Л. К пояснению принципа построения полярной диа-
граммы сопротивлений:
й) основная сетка координатных линий р, 2/пх'; б) соот-
ветствующая рис, а сетка координатных линий к, 2/пх';
в) соответствующая рис. а сетка координатных линий л, znx'
Освободившись от мнимости в знаменателе, получаем соответственно
шественной и мнимой частей:
Я_ = I-P*
р I + р2 +- 2р cos 2тхг
X 2р sin 2тх‘
р 1 4- р2 _|_ 2р cos 2тх'
Уравнения (1.24а) преобразовываются к виду:
Р2
2
R -г р
pCQs2tnx' 4-
R Y _ _ _?!________
р + я/ (Я-1-р)1
р
р* + 2р cos 2mxf — 2 — р sin 2тх' + 1 4-
для вс-
(1.24а)
(L25a)
(L26a)
2 -292
17
р
Уравнение (1,25а) является уравнением окружности радиуса —— с цент-
К+р
/ R \ р
в точке I , тс ); а ур-ние (1.26а) — окружности радиуса ~~ с цеит-
\ К-у-р / X
ром
ром
в точке
При обозначении координат цент-
ров пользуемся системой полярных координат, причём на первом месте ука-
зана радиальная координата, а на втором—угловая, отсчитываемая от па-
правления 27Пх'~0.
На рис. 1.5 показана сетка координатных линий--—const и— —const.
Полярная диаграмма сопротивлений с обеими системами координатных линий
/ R X \
(к, /пх') и ( — । '— приведена в приложении 1. .
\ Р ₽ '
Рис. L5. Сетка координатных линий—,—закладываемая на сетку
Р Р
рис. 1,4в и образующая совместно с последней полярную
диаграмму сопротивлений
U
Вторичные параметры первой группы. Частотная
характеристика, резонансные частоты, полоса пропускания
Как уже говорилось, измеренные на различных частотах
величины входного сопротивления удобно наносить на диаграмме
сопротивлений в виде точек (рис. 1.3). Кривая, соединяющая экс-
периментальные точки, представляет собой частотную характери-
стику антенны. Точки пересечения частотной характеристики с
прямой _~ 0 являются резонансными точками, а соответст-
р
вующие им частоты f 0 и — резонансными частотами.
При проектировании антенн и фидерных линий стремятся так
подобрать их параметры, чтобы получить на фидерных линиях
режим бегущей волны. Так как в чистом виде получить такой ре-
жим практически трудно, обычно задаются определённым допу-
ском на коэффициент бегущей волны.
Полоса пропускания антенны определяется как полоса частот,
в пределах которой коэффициент бегущей волны удовлетворяет
заданному допуску 9* Полоса пропускания легко может быть
определена при помощи диаграммы сопротивлений. Для этого
па ней проводится окружность к = const, соответствующая допу-
ску на коэффициент бегущей волны (например, окружность, со-
ответствующая к = 0,5 на рис. 1.3). Все точки частотной /Характе-
ристики, лежащие внутри окружности, удовлетворяют допуску
к > 0,5. Частоты и f2, при которых частотная характеристика
пересекается с окружностью, являются крайними частотами по-
лосы пропускания. Разность —fi определяет ширину поло-
сы пропускания антенны.
В ряде случаев, особенно па длинных и средних волнах, ча-
стотную характеристику определяют как кривую зависимости
мощности в антенне от частоты при условии, что на всех частотах
к антенне приложено одинаковое напряжение U. Кроме того,
предполагается, что при этом на рабочей частоте реактивная
часть входного сопротивления антенны скомпенсирована после-
довательно приключенной реактивностью Л\. При указанных ус-
ловиях входное сопротивление антенны и элемента настройки рав-
но Zaq — /?ло *на рабочей частоте и ZA = /?л + 1 (Хл + на
остальных частотах, а частотная характеристика определяется
формулой
ц,’ Ягл+(Хл + Х,у '
______ Као
’) Имеется в виду, что в указанной полосе частот по характеристикам
излучения антенна заведомо удовлетворяет предъявляемым требованиям
2‘ 19
Ее графическое изображение дано на рис. 1.6. Сплошная кри-
вая построена для рабочей частоты fpagt соответствующей часто
те а пунктирная — для рабочей частоты fpaj , соответствую-
щей частоте ^(см. рис., 1.3). Так как при ' рабочая ча-
стота совпадает с резонансной, то зцесъ в расчёте принято Х'н =
—0. При fpa6—f* положено X* — 0,2р.
Pwc. 2.6. Кривая зависимости мощности в антенне от частоты при одинаковой
на всех частотах амплитуде напряжения на зажимах антенны, соответствую-
щая кривой рис 1.3
В обоих случаях частотный интервал между двумя экспери-
ментальными точками на рис. 1.3 принят равным 0,01
По частотной характеристике рис. 1,6 ширина полосы пропу-
скания Д/л определяется длиной хорды, соединяющей точки х =
= — где *макс~ максимальное значение х (/).
В некоторых случаях частотная характеристика получается
несимметричной относительно рабочей частоты, как при f рлС .
Симметрирование характеристики осуществляется включением
дополнительных реактивностей.
Графическое изображение диаграммы направленности
• 1
Одним из наиболее распространениях способов графиче-
скою изображения диаграмм направленности антенн является
вычерчивание так называемых полярных диаграмм направлен-
ности.
20
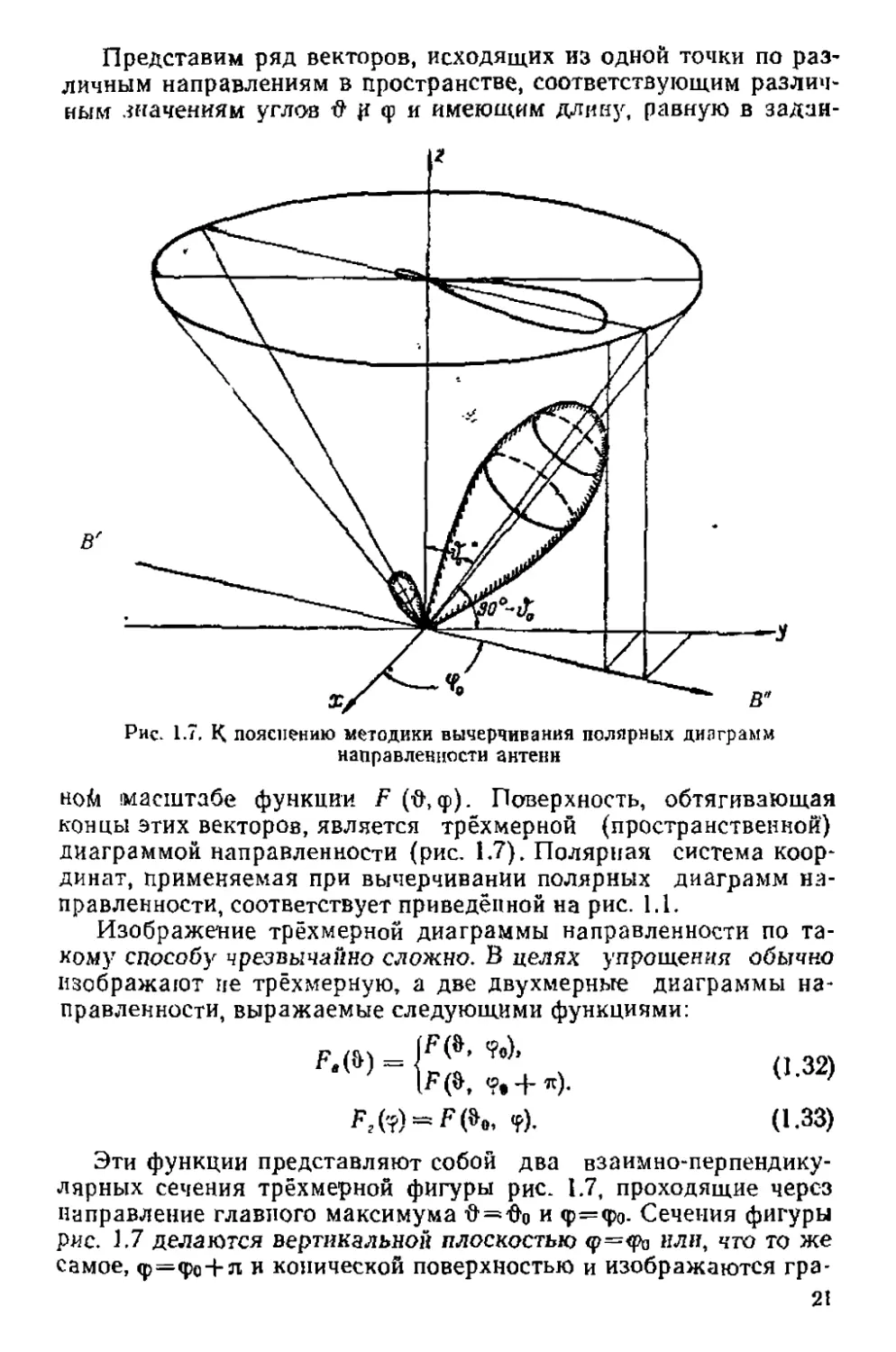
Представим ряд векторов, исходящих из одной точки по раз-
личным направлениям в пространстве, соответствующим различ-
ным значениям углов # р ф и имеющим длину, равную в задан-
Рис 1.7, К пояснению методики вычерчивания полярных диаграмм
направленности антенн
ноМ 'масштабе функции F (О, ф). Поверхность, обтягивающая
концы этих векторов, является трёхмерной (пространственной)
диаграммой направленности (рис. 1.7). Полярная система коор-
динат, применяемая при вычерчивании полярных диаграмм на-
правленности, соответствует приведённой на рис. 1.1.
Изображение трёхмерной диаграммы направленности по та-
ком}- способу чрезвычайно сложно. В целях упрощения обычно
изображают не трёхмерную, а две двухмерные диаграммы на-
правленности, выражаемые следующими функциями:
Fe(&) = /j 22)
<?). (1.33)
Эти функции представляют собой два взаимно-перпендику-
лярных сечения трёхмерной фигуры рис. 1.7, проходящие через
направление главного максимума ft-do и ф—фо- Сечения фигуры
рис. 1.7 делаются вертикальной плоскостью <р=<ра или, что то же
самое, ф=фо + л и конической поверхностью и изображаются гра-
21
фически в виде двух плоских кривых (рис. 1.8). Кривая рис,
1,86 представляет собой проекцию на горизонтальную плоскость
Рис. 1.8. Полярные диаграммы направленности, соответствующие трех-
мерной диаграмме рис. 17:
$) в вертикальной плоскоегл, &) в горизонтальной плоскости
пространственной кривой сечения конуса и трёхмерной диаграм-
мы направленности.
Функция Fe (fl1) и соответствующая ей кривая рис, 1.8а иосит
название диаграммы направленности в вертикальной плоскости,
а функция F2 (ф) и соответствующая ей кривая рис. L86 — диа-
граммы направленности в горизонтальной плоскости.
Во многих случаях как трёхмерная диаграмма направленно-
сти, так и двухмерные в вертикальной и горизонтальной плоско-
стях состоят из многих лепестков (рис. 1.9).
Рис. 1.9, Много лепестковые полярные диаграммы направленности, харак-
терные для низкорасполпженных остронаправленных антенн с учётом
влияния земли:
а) в вертикальной ^плоскости, 6J в горизонтальной плоскости
22
Диаграммы направленности рис. L9 характерны для низко-
расположенных остронаправленных антенн с учётом влияния
земли. Для остропаправленпых антенн, расположенных высоко
над поверхностью земли, трёхмерная диаграмма направленности
имеет вид, показанный на рис. 1.10л. Для получения двухмерных
диаграмм направленности трёхмерную диаграмму пересекают
двумя взаимно-перпендикулярными плоскостями, проходящими
через направление главного максимума, причём, как правило, бе-
рут плоскости, параллельные электрическому Е и магнитному Н
векторам поля излучения. Эти двухмерные диаграммы называют
диаграммами направленности соответственно в Е- и //-плоско-
стях (рис. 1J0б и в). По виду они подобны диаграмме направ-
ленности рис. 1.9 б.
Горизонтальная и вертикальная плоскости, или Е- и //-пло-
скости, проходящие через направление главного максимума, на-
зываются главными плоскостями.
Полярные диаграммы направленности наглядны. По ним
легко представить, каково распределение излучения по различ-
ным направлениям в пространстве. Однако они неудобны при оп-
Рис. 1.10. Диаграмма направленности антенны, рассчитанная для свободного
пространства:
а) трёхмерная диаграмма и характерные Е- и //-плоскости; 6) диа-
грамма в //-плоскости; в) диаграмма в £-плоскости
23
ределении вторичных параметров антенн, так как не позволяют с
достаточной точностью определить малые углы и совершенно
непригодны для определения уровня поля вне главных плоско-
стей.
Чтобы облегчить точное определение вторичных параметров,
часто вычерчивают двухмерные диаграммы направленности, вы-
ражаемые функциями (1.32) или (1.33) в прямоугольных коорди-
натах (рис. 1,11),
В последние годы стал применяться новый метод изображе-
ния диаграмм направленности, который будем называть карто-
графическим. Сущность его заключается в следующем,
Так как напряжённость поля является функцией двух коорди-
нат fl и ф, то можно строить плоскую сетку этих координат в ка-
кой-либо координатной системе подобно сетке параллелей и ме-
ридианов на географических картах, а на этой сетке изобразить в
виде замкнутых кривых линии одинакового значения напряжён-
ности поля. При этом могут применяться координатные системы:
прямоугольная (рис. М2), прямоугольно-параболическая
(рис. 1.13) полярная (рис. 1.14) и другие. Числа у кривых указы-
вают уровень поля по отношению к уровню главного максимума
(относительный уровень) соответственно в относительных значе-
ниях, процентах или децибелах. Точками внутри отдельных групп
замкнутых кривых отмечены направления главного и боковых
максимумов. При таком построении диаграмма отображает сфе-
24
Рис. I.И. Диаграмма направленности в прямоугольных координатах
с применением по оси ординат масштабов:
л) линейного, 6) квадратичного, в) логарифмического
25
ру, каждая точка которой соответствует определённому направле-
нию О, ср, а уровни поля — векторы, перпендикулярные к поверх-
ности сферы и имеющие длину, равную F (Ф, ср). Поверхность, об-
Рис. 1J2. Картографическая диаграмма направленности, построенная
в прямоугольных координатах
Рис. 1.13. Картографическая диаграмма направленности, построенная в пря-
моугольно-параболических координатах
тягивающая концы векторов, образует ряд холмов, соответствую-
щих боковым лепесткам, ив ысокую гору, соответствующую
главному лепестку.
26
По картографической диаграмме можно построить прямо-
угольные двухмерные диаграммы направленности вида рис. 1.11
в различных плоскостях. Например, двухмерную диаграмму на-
правленности в вертикальной плоскости можно построить по диа-
грамме рис. 1.12, если вдоль прямой ср = 90° в точках ее пересече-
ния с линиями равного уровня восстановить перпендикуляры дли-
ной, равной уровню поля в этих точках, и соединить концы пер-
пендикуляров огибающей кривой. Аналогично могут быть по-
строены двухмерные диаграммы направленности с помощью кар-
тографических диаграмм рис. 1ЛЗ и 1.14.
Вторичные параметры антенн, связанные с диаграммой
направленности: относительный уровень боковых
максимумов, ширина главного лепестка, коэффициент
направленного действия
Из диаграммы направленное™ легко определить ширину
главного лепестка и относительный уровень боковых макси-
мумов.
Относительный уровень боковых максимумов есть отношение
напряженности поля или интенсивности излучения в направле-
нии боковых максимумов к напряжённости поля или интенсив-
ности излучения в направлении главного максимума. Так как
при вычерчивании диаграммы направленности напряжённость
поля или интенсивность излучения в направлении главного мак-
симума принимается за единицу, то относительный уровень бо-
ковых максимумов виден непосредственно из диаграммы направ-
ленности.
Ширина главного лепестка 20 по полярным диаграммам
рис. 1.9 и 1 ДО определяется углом между направлениями, соот-
ветствующими уровню 0,707, отдельно для каждой из двухмер-
ных диаграмм направленности.
Ширина главного лепестка 20 по прямоугольным диаграм-
мам направленности рис. 1,11 определяется длиной (в градус-
ном или радианном выражении) хорды, соединяющей
главного лепестка, соответствующие уровню -yL- — 0,707
точки
(при
линейном масштабе), 0,5 (при квадратичном) и —3 дб (при ло-
гарифмическом).
По картографическим диаграммам направленности ширина
главного лепестка 20 определяется следующим образом. На
диаграмме наносится линия уровня 0,707 (70,7% или 3 дб). За-
тем проводится хорда этой линии, проходящая через точку глав-
ного максимума. Длина этой хорды, выраженная в градусах, и
есть ширина главного лепестка. Очевидно, что таких хорд мож-
28
0-34)
но провести бесчисленное множество, причём каждая будет от-
носиться к двухмерной диаграмме направленности в плоскости,
проходящей через данную хорду и центр отображаемой на диа-
грамме сферы.
Коэффициент направленного действия (кнд) антенны связан
с диаграммой направленности сложной зависимостью.
Под коэффициентом направленного действия антенны D по-
нимают отношение интенсивности её излучения в направлении
главного максимума к среднему значению интенсивности её из-
лучения по всем направлениям, т. е.
£2
^макс
D_____________ 120х__________
2it к
----— f d ф ( ——— г2 sin В d &
4nr«J rJ 120х
о о
Подставив в (1 >34) значение Е из (1.1) и учитывая, что в на-
правлении главного максимума Fj^KC(^t ф) — F(f>o, ф0) = 1» по-*
лучим
D ------------—------------, (1.35)
2я it
J d? J/’(«. ?)sin8d&
О о
Из (L35) видно, что для расчёта D нужно знать ср), т. е.,
вообще говоря, трёхмерную диаграмму направленности. В ряде
случаев трёхмерная диаграмма направленности является фигу-
рой вращения относительно оси & = 0. При этом
9
D =--------------. (1.36)
О
Знаменатель выражения (1.36) может быть найден графиче-
ски как площадь фигуры, ограниченной в прямоугольных коор-
динатах осью абсцисс и кривой F2 (fl) sin fl, а в полярных коор-
динатах — кривой F (fl) К sin# и отрезками векторов F (0)
и F (л).
Формулы (L35) и (1,36) дают точные значения кпд, если из-
вестно точное выражение для F{fl, ф). Однако найти F(fl, ф) до-
статочно точно экспериментальным путём трудно. Поэтому огра-
ничиваются, особенно для остронаправленных антенн, прибли-
жёнными методами определения кпд через ширину главного ле-
пестка диаграммы направленности 20 в двух главных плоско-
29
стях. Связь между кнд и 20 можно найти, руководствуясь сле-
дующими соображениями»
Как известно [Л2], у плоскостных синфазных антенн:
D = (1.37)
20, —
«1
28г = х2 —
Oj /
(1.38)
где 3 — площадь антенны;
а — линейный размер антепны (длина, ширина, диа-
метр и т. д J;
v и х — коэффициенты пропорциональности; индексы 1 и 2
указывают на принадлежность величин одной или
другой главной плоскости, в которой определяет-
ся двухмерная диаграмма направленности.
Углы 01 и 02 выражены в радианах. Величины S и о связаны
между собой простыми соотношениями:
в случае круглой площадки
5= ЛГ
4 ’
в случае прямоугольной площадки
5 ==
Исключая из (1.37) и (1.38) S и а, получим:
для круглой площадки
v ___________
для прямоугольной площадки
D = 4irv
(1.39>
(1.40>
(1.41>
(1.42>
*1*2
20^02
Подставляя в ф-лы (1.41) и (1.42) значения v, Xj и x2l полу-
ченные в [ЛЗ] для прямоугольных и круглых синфазных пло-
скостных антенн при разном законе изменения амплитуд, и вы-
ражая 20J и 202 в градусах, приходим к следующей приближён-
ной формуле:
34 000
20*202
(143)
зо
Для диаграммы направленности в виде фигуры вращения
20(=202
D =34000 (1.43а)
(20)» г
Вторичные параметры антенн, связанные с коэффициентом
усиления: коэффициент полезного действия, эффективная
площадь» действующая высота
Измерив величину коэффициента усиления G антенны и
определив но ф-ле (1,43) значение D, можно вычислить коэффи-
циент полезного действия антенны:
т( = -£-, (1.44>
Эффективная площадь антенны S зфф связана с G соотноше-
нием
/па
= (С45>
Действующую высоту антенны hd можно определить через G
следующим образом.
В случае проволочных антенн коэффициент А в ф-ле (1,1)
можно выразить через входной ток IА и действующую высо-
ту hd\
A = WmIAhd. (L46>
Величина Р в ф-ле (1.2) равна
Подставив в (1.2) Ем получим откуда Ло Р = /^л. (1.47) из (1.1), А из (1.46) и Р из (1.47)„ 30т«Л? G= d , (1.48) (L49> 3t
Исследование антенн на моделях
При разработке новых типов антенн часто прибегают к
этх экспериментальному исследованию на моделях,1) Для этой
цели изготовляют антенну, подобную разрабатываемой, по все
линейные размеры которой уменьшены или увеличины в неко-
торое число /о раз. В такое же число /о раз уменьшают или уве-
личивают по сравнению с волной, на которую рассчитана иссле-
дуемая антенна, длину волны электромагнитных колебаний, воз-
буждающих модель. Предполагается, что модель антенны на
яолне, в /0 раз меньшей чем рабочая волна, имеет те же электри-
ческие параметры и характеристики, что и исследуемая антен-
на на рабочей волне. Измерив параметры модели, получают
представление о параметрах исследуемой антенны.
Дадим вкратце теоретическое обоснование этого метода.
Электромагнитное поле антенны удовлетворяет уравнениям
электродинамики:
rot Е + и — = О
r di
T0Ch—g^^.!}e=q
dt
(i.50)
Дифференциальные ур-ния (1.50) являются общими для всех
электромагнитных явлений и характеризуют соотношение меж-
ду векторами поля Е и Н в каждой отдельной точке простран-
ства.
Для заданного конкретного электромагнитного процесса мож-
но получить картину поля, г е. аналитическую зависимость от-
дельных составляющих поля от пространственных координат,
решив ур-ния (1.50) и определив постоянные интегрирования из
граничных условий. Очевидно, одинаковые граничные условия
приведут к одинаковому решению, а разные — к разным реше-
ниям. Например, две одинаковые антенны, питаемые от одина-
ковых генераторов, создадут вокруг себя одинаковые поля, а две
разные антенны во всех случаях создадут разные поля. Нельзя
рассчитывать получить от модели такое же поле, как от искомой
антенны, так как различны их размеры, а также длины волн
электромагнитных колебаний. Однако в виду геометрического по-
добия модели и исследуемой антенны и пропорционального из-
менения длины волны можно рассчитывать па подобие полей
антенны и се модели. Это подобие выражается в следующем.
’) Практические указания по исследованию антенн на моделях били впер-
вые сформулированы М. С. Нейманом в 1934 г. [Л4[
32
В ур-ниях (1.50) векторы поля Е и И, параметры среды е, ц,
а, координаты х, у, г и время t выражены в практической рацио-
нализированной системе единиц МКС. Выбор этой системы еди-
ниц объясняется практической целесообразностью. Принци-
пиально можно пользоваться любой системой единиц.
Введём в общем виде новую систему единиц, в которой век-
торы поля и Hh параметры среды p,i и координаты xit
У\, и время /1 связаны с аналогичными выражениями в прак-
тической системе единиц соотношением
Е = eElt Н = hH^ г = е0£п у, = а
X = /охь у — 1пУъ г = /oZlf t = ’
где е, Л, et, оф, /0, tQ— переводные множители из одной
системы единиц в другую.
Подставив (1.51) в (1.50) и учитывая линейность оператора
rot, получим:
—
rot Ег — !- = е.
*♦< <3*1
rot Hi------et -------------------в, /, — Oj £\ = 0
tji ot1 * h 1 1
Чтобы привести ур-ния (1.52) к виду (1.50), а именно:
rot^ + jij^i =0
rot^-e,-^----aiEi= 0
oh
требуется выполнение следующих условий:
Но М «0 „ I е __ 1
------ -----“ Сл 1л-------------1 .
(1-52)
(1.53)
(1-54)
Уравнения (1.53) ничем, кроме обозначений, не отличаются
От ур-пий (1.50). Следовательно, в любой системе единиц, но при
соблюдении условий (1,54), уравнения Максвелла можно выра-
зить так же, как в практических единицах.
Положим, имеются две разные антенны, питаемые от двух
разных источников эдс. Размеры одной антенны, параметры её
источника эдс и среды будем выражать в практических едини-
цах, а размеры другой антенны, параметры её источника эдс и
3-292 33
среды — в повой системе единиц. Чтобы найти электромагнит-
ное поле, воспользуемся для одной антенны ур-ниями (1.50), а
для другой — ур-ниями (1.53). Так как ур-ния (1.53) идентичны
ур-ниям (1-50), то можно в обоих случаях получить для состав-
ляющих поля одинаковые функции от координат и указанных
параметров, если в обоих случаях будут одинаковые граничные
условия. Это характеризует подобие полей антенны и её модели.
Одинаковые граничные условия означают в данном случае,
что размеры первой антенны, выраженные в практических еди-
ницах, численно равны размерам второй антенны, выраженным
в новой системе единиц или, иначе, все линейные размеры вто-
рой антенны отличаются в /о раз от линейных размеров первой
—* —>
антенны. Аналогично величины Е, Н, е, ц, о\ относящиеся к пер-
вой антенне, должны отличаться соответственно в е, Л, /0, во, Ио,
Со раз от величин £1э Hi, bj, сц, относящихся ко второй ан-
тенне. При этом переводные* множители должны быть связаны
между собой ур-ниями (1.54).
Обычно средой антенны, так же как и модели, является воз-
дух. Поэтому.
Ео ~ 1 - (1-55)
Векторы поля также выразим в обоих случаях в одинаковых
единицах, т. е. положим
(1.56)
При выполнении условий (1.55) и (1.56) ур-ния (1.54) перехо-
дят в уравнения:
y--l-,f0 = l0t (1.57)
*0
з<Л-= г, «о---. (1.58)
*0
Из (1.57) и (1.58) видно, что при уменьшении размеров ан-
тенны в /о раз для сохранения подобия полей антенны и модели
требуется, во-первых, уменьшение единиц отсчёта времени в /о
раз, во-вторых, увеличение удельной проводимости проводов мо-
дели в /о раз. Поскольку возбуждающие антенну колебания гар-
монические, уменьшение единиц отсчёта времени в /о раз соот-
ветствует уменьшению периода колебаний в /о раз, т. е. умень-
шению длины волны или увеличению частоты колебаний. Как
сказано выше, при исследовании на моделях длина волны дейст-
вительно укорачивается пропорционально уменьшению линей-
ных размеров антенны. Удельная проводимость же при умень-
шении линейных размеров проводов антенны хотя и увеличи-
34
взется благодаря поверхностному эффекту, но значительно мед-
леннее, чем требуется (примерно пропорционально V/0)*
Активное сопротивление антенн состоит из двух слагаемых—
сопротивления излучения и сопротивления потерь, характери-
зующих соответственно энергию излучения и энергию потерь.
Так как проводимость проводов определяет лишь потери энер-
гии, то в том случае, когда потери малы по сравнению с энер-
гией излучения, изменение проводимости практически несуще-
ственно с точки зрения подобия.
Следовательно, при пропорциональном изменении линейных
размеров антенны и длины волны модель создаёт поля, подоб-
ные полю исследуемой антенны лишь в случае, если у модели и
антенны сопротивление потерь пренебрежимо мало по сравнению
с сопротивлением излучения.
В заключение необходимо сделать следующие замечания.
1) Из условия (1,54) вытекает, что при уменьшении размеров
антенны, подобие полей может быть сохранено за счёт измене-
ния диэлектрической и магнитной проницаемостей среды при со-
хранении периода колебаний, но не может быть сохранено за
счёт изменения размерности векторов поля, поскольку в ур-ниях
е h
(1,54) Zq умножается в одном случае на-—, в другом на — *
Л е
2) Одинаковые математические выражения для векторов
поля у антенны и модели при означают, что отношение
электрического вектора к магнитному будет в обоих случаях
одинаковым, а следовательно, обе антенны будут иметь равные
входные сопротивления.
3) Уменьшение или увеличение единиц измерения длины в
/о раз в выражении для векторов поля у модели означает изме-
нение картины поля в радиальных направлениях от модели, со-
ответствующее укорочению длийы волны. Но зависимость от по-
лярных углов, поскольку углы являются безразмерными величи-
нами, сохранится одинаковой у антенны и модели. Следователь-
но, диаграмма направленности и связанные с пей параметры, а
также коэффициент усиления (в связи с тем, что сопротивление
потерь мало и коэффициент полезного действия равен почти
единице) одинаковы у модели и антенны.
Итак, метод моделирования заключается в исследовании мо-
дели антенны, линейные размеры которой уменьшены или уве-
ЛШ1ИПЫ в п раз по сравнению с ра/мерами исследуемой аитеппы,
на волне соответственно короче или длиннее рабочей волны так-
же в п раз при условии, что сопротивление излучения как иссле-
дуемой антенны, так и модели во много раз превосходит сопро-
тивление потерь. Исследование модели позволяет определить
входное сопротивление, диаграмму направленности, коэффициент
усиления и связанные с ними параметры исследуемой антенны*
3* 35
Краткие сведения из теории приёма радиоволн
При расчёте приёмных антенн часто используется экви-
валентная схема рис. 1.15, на которой ZA — входное сопротивле-
ние антенны; Zпр — входное сопротивление приёмника; е —элек-
тродвижущая сила, возбуждаемая приходящей* электромагнит-
ной волной на выходе антенны, равная
e — EhdF($y (1.59)
Здесь Е — напряжённость поля приходящей волны,
А а— действующая высота антенны,
F(&, <jp) — нормированная диаграмма направленности ан-
тенны.
Согласно схеме рис. 1.15 напряжение на входе приёмника
Рис. 1.15. Эквивалентная
схема приёмной антенны
О-60)
г ^пр УГ & л г
а мощность, выделяющаяся во вход-
ной цепи приёмника,
(1.61)
Наибольшая мощность выделяется при так называемом оп-
тимальном режиме, определяемом следующими условиями:
1) <р) = 1, т. е. волна приходит с направления главного
максимума диаграммы направленности;
2) =2Л, т. е. входные сопротивления антенны и приёмни-
ка—комплексно сопряжённые величины.
Таким образом, при оптимальном режиме мощность, выде-
ляющаяся во входной цепи приёмника, равна
Р
пр опт »
(И62)
а напряжение на входе приёмника
г j __
u пр опт 2
(1.63$
J
36
Мощность в оптимальном режиме может быть выражена так-
же через эффективную площадь антенны или через её коэффл
цнент усиления:
Р _ с __
пропт 120л 480л* ’
(1.64)
Согласно (1.61) н (1.62) Р„р и Рпропт связаны между собой
соотношением
4R R
Pnp = PnponmF\^ ^?А-2- (1.65)
\L*P -г А )
С учётом (1.64)
р E*WG„pF*(b,<f)4RARn/,
480л* (Zfif + % А )2
(1.66)
Сравнивая (1.64) и (1.62), получаем
(1.67)
В соответствии с введённой выше классификацией действую-
щую высоту hd будем считать вторичным параметром антенны.
Если антенна присоединяется к приёмнику через фидерную
линию длиной / с волновым сопротивлением р и затуханием |J
то напряжение па входе приёмника
ипр = ^,у) z;p (ch71-----------р- sh7 Л , (1.68)
где . н
р
ch 71 4*--sh 7 /
Z-ap = Р--------, (1.69)
—ch 714- sh 71
Z-np
Т = im. (1.70)
При наличии согласования фидерной линии как с антенной,
так и с приёмником (ZA =2пр=*р) из ф-л (1.68) — (1,70) полу-
чается следующее выражение для модуля С7лр:
„ EhdF_(\<f) -₽г (] 71)
яр 2 f
37
При согласовании фидерной линии лишь с одной стороны, со
стороны антенны или со стороны приёмника, остаются справед-
ливыми ф-лы (1.60), (1.61), (1.64) и (L65) при добавлении в
правой части множителя е или е соответственно для напря-
жения или мощностей. Заметим, что, поскольку коэффициент ог-
Оражения на фидере Г с того конца, который
не согласован, определяется по ф-ле (1.7),
напряжение на входе приёмника можно вы-
разить следующим образом:
EhaFeT9t , (1.72)
причём знак минус соответствует согласова-
♦ нию со стороны приёмника, а знак плюс —
согласованию со стороны антенны.
В ряде случаев в качестве приёмной ан-
На teod приемника теНны применяется рамка, шунтированная
Рис. 1.16. Рамка, шуИ. ёмкостью (рис. 1.16), служащей для наст-,
тированная ёмкостью ройки системы в резонанс.
В этих случаях напряжение на входе
приёмника
т. EWmSsinO
UnPc-~i-^с " RA<*C ’
где S — площадь рамки,
•ft — угол между направлением прихода волны и нормалью
к плоскости рамки,
— число витков рамки,
С — ёмкость конденсатора настройки,
— активная часть входного сопротивления рамки.
Уравнение (173) справедливо, если активное сопротивление
приёмника, внесённое в контур рамки, значительно меньше R А.
2. РЕЗОНАНСНЫЕ МЕТОДЫ ИЗМЕРЕНИЯ
ВХОДНОГО СОПРОТИВЛЕНИЯ
Общие положения
Измерение входного сопротивления антенн резонансным
методом основано на использовании свойства колебательных
контуров <резко изменять вблизи резонанса ток или напряжение
при незначительном изменении сопротивления. Измеряемое со-
противление включается в измерительный колебательный контур,
состоящий из сосредоточенных постоянных, как один из его эле-
ментов. В ряде случаев (на метровых и дециметровых волнах'к
контуры составляют из отрезков линий с распределёнными по-
стоянными.
Применение находят различные резонансные методы^ Одни
из них основаны на сравнении измеряемого сопротивления с
эталонным, другие1 — на измерении характеристик резонансных
контуров: собственной (резонансной) частоты колебаний, доб-
ротности и т. д. Отдельные методы встречаются в различных ва-
риантах, отличающихся друг от друга схемой индикатора и ме-
стом его включения.
Метод добавочного сопротивления
Схема измерительной установки, применяемой в методе
добавочного сопротивления, показана на рис. 2.L Она состоит из
генератора высокой частоты, измерительной цепи и трансформа-
/Ънера-
торвч
Трансформатор связи Измерительная цель
Рис. 2.1. Скелетная схема измерительной установки, применяемой
в методе добавочного сопротивления
39
тора связи между генератором и измерительной цепью. Измери-
тельная цепь состоит из сопротивлений: эталонного переменного
реактивного X „ эталонного переменного активного R, и изме-
ряемого Z^. Схема содержит также приборы, измеряющие токи
как в цепи генератора, так и в измерительной цепи. Активное со-
противление R3 может быть замкнуто накоротко, т. е, электри-
чески исключено из цепи, переключателем П.
Порядок измерений по этой схеме следующий. Подключается
измеряемое сопротивление ZA и одновременно замыкается нако-
ротко эталонное сопротивление R3t после чего измерительная'
цепь настраивается в резонанс при помощи эталонного реактив-
ного сопротивления X О резонансе можно судить по максиму-
му тока / 2 в измерительной цепи (по максимальным показа-
ниям прибора А2). Значение максимального тока и величина
реактивного сопротивления Х\ записываются. Затем включает-
ся эталонное активное сопротивление Rs> проверяется резонанс
контура и записывается повое значение тока . При необходи-
мости контур подстраивается в резонанс изменением реактив-
ного сопротивления Х3.
По данным измерений Г2 и Г2 можно вычислить активную
составляющую RA измеряемого сопротивления ZA по формуле
Ял = Л,(2.1)
Для определения реактивной составляющей Ха измеряемое
сопротивление закорачивают (Z»=0) и, добиваясь резонан-
са, получают новое значение эталонного реактивного сопротив-
ления X’. Искомая реактивная составляющая Хл определяет-
ся по формуле
= (2.2)
Выражение (2.1) справедливо, если напряжение lh на вто-
ричной катушке L2 трансформатора связи одинаково при вклю-
ченном и выключенном сопротивлении R3. При слабой связи
между катушками и L2 трансформатора связи постоянство
U2 будет иметь место при постоянстве U\ или 1\ и может быть
проконтролировано по постоянству показаний амперметра А1.
Так как измеряемое сопротивление может иметь реактивную
составляющую как ёмкостного, так и индуктивного характера,,
эталонная реактивность должна представлять либо градуирован*
ный переменный конденсатор, либо градуированный вариометр-
На основе рассмотренного метода создано [Л5] несколько,
приборов для измерений входного сопротивления антенн.
40
Метод добавочного сопротивления характеризуется просто-
той схемы и простым непосредственным отсчётом измеряемого
сопротивления. Однако он не лишён недостатков. Основными из
них являются:
1) сравнительно большая погрешность измерений, особенно
при близких значениях токов Г2 и /*, что соответствует боль-
шим величинам сопротивления /?
2) пониженная чувствительность прибора при больших вели-
чинах так как в этом случае для заметного изменения тока
/2 приходится включать весьма высокоомное добавочное со-
противление R„ приводящее к малой величине тока /2;
3) для поддержания постоянства напряжения U2 необходима
работать с очень малыми величинами связи между катушками
Li и L2, что снижает чувствительность и помехоустойчивость
прибора (от внешних источников эдс);
4) в величину RA входят активные сопротивления ампермет-
ра А2, катушки связи L2 и переменной эталонной реактивности
Сумма указанных сопротивлений должна быть заранее извест-
на для любой частоты, поскольку её нужно вычесть из измеряе-
мой величины R А.
Практические схемы измерений входного сопротивления ан-
тенн методом добавочного сопротивления приведены па рис. 2.2
Рис. 2.2. Принципиальная схема измерительной установки, применяемой
в методе добавочного сопротивления при использовании рабочего пере-
датчика
и 2.3. Эти схемы находят применение при настройке длинновол-
новых и средневолновых антенн. При использовании схемы
рис. 2.2 измерительная цепь подключается к тому же передатчи-
ку, который питает исследуемую антенну; при использовании же
схемы рис. 2.3 в качестве источника высокой частоты исполь-
зуется измерительный генератор (генератор стандартных сиг-
налов).
Процесс измерений следующий.
41
1) При закороченном сопротивлении R3 антенну А связываю?
с передатчиком или измерительным генератором, настроенным
на рабочую частоту радиостанции, н настраивают в резонанс
при помощи вариометра L„, индуктивности LA или ёмкости СА.
Связь между катушками L св и LA должна быть минимальной.
Записывают показания: амперметра A# (ток 1Ф ), включённого в
фидерную линию (рис. 2.2), или Аг (ток 1Г ), включённого в цепь
измерительного генератора (рис. 2.3), антенного амперметра Ал
Рис 2,3* Принципиальная схема измерительной установки, приме-
няемой в методе добавочного сопротивления при использовании
специального измерительного генератора (ГСС)
(ток /л), величины ёмкости настройки СА или индуктивности ка-
тушки La и вариометра LB.
2) При введённом сопротивлении R3. увеличивая связь меж-
ду катушками Lca и LA , устанавливают прежнюю величину тока
или / ги записывают величину полученного антенного тока 1А1.
По данным этих измерений определяют активное сопротив-
ление антенны и всех элементов измерительной цепи по формуле
___R
! А
fAt
(2-3)
3) Повторяют указанные выше измерения при закороченной
антенне и отмечают новые значения токов ГА, ГА и величины
ёмкости С'А или индуктивности L'A и вариометра Lei . Опреде-
ляют вносимое сопротивление Reit измерительной цепи по фор-
муле
. (2.4)
1А
42
Когда активная составляющая входного сопротивления ан-
тенны мала, следует учитывать также и сопротивление гА, вклю-
чённое в измерительную цепь прибора Ал. В этом случае
; ------гА. (2.5)
^-1
‘а
Активная составляющая входного сопротивления антенны,
таким образом, определяется по формуле
= М
Реактивная составляющая входного сопротивления антенны
ХА определяется по данным измерений ёмкости Сл и С’А или шь
дуктивностей Ьд и Ь'д по формулам:
X^530X.zJ--------Ц, ом, (2.7)
сл /
• о* М
где СА— емкость при включённой антенне, пф,
Сд — ёмкость при закороченной антенне, пф,
La— индуктивность при включённой антенне, мкгн,
L'A— индуктивность при закороченной антенне, мкгн,
> — длина волны, м.
Метод вольтметра и амперметра
Схемы измерений по методу вольтметра и амперметра
.таны на рис. 2.4 и 2.5. Схема рис, 2.4 применяется при питании
Рис. 2.4. Схема измерительной установки, применяемой в методе
вольтметра и амперметра при использовании рабочего передатчика
43
измерительной цепи от передатчика, а схема рис. 2.5—при пи-
тании, этой цепи от специального измерительного генератора.
Измерения проводятся в следующей последовательности.
Антенну А подключают к передатчику или измерительному
генератору при помощи трансформатора связи, состоящего из
Язнсритемж!* цепь
Рис. 2.5. Схема измерительной установки, применяемой в ме-
тоде вольтметра и амперметра при использовании специаль-
ного измерительного генератора
слабо связанных индуктивностей и £л. На зажимы катушки
индуктивности La включают высокоомный ламповый вольтметр
Л В. Настройку в резонанс измерительной цепи производят при
помощи вариометра £,или ёмкости СА и подбором LA. Условию
резонанса соответствует максимальное отношение измеряемых
величин UА и IА.
Искомые величины активной и реактивной составляющих
входного сопротивления измеряемой антенны определяют по
формулам:
Я = —, (2.9)
1 а
. __ 530k 1880 г .
л - ~С^ “ {la +
(2.10)
где Сд— ёмкость, пф;
La и La — индуктивность, мкгн,
У.— длина волны, м.
Для выяснения наличия, а затем исключения ошибок, обуслов-
ленных возможными паразитными связями ёмкостного или индук-
тивного характера между передатчиком или измерительным гене-
ратором, с одной стороны, и измерительной цепью, с другой сто-
роны, рекомендуется повторить измерения при повороте катуш-5
ки Lfe или катушки £л на 180°. При отсутствии паразитных свя-j
зей показания вольтметра UA и амперметра IА не должны изме-;
няться с поворотом катушки. Если же показания меняются, TGj
значение UA доводят до прежней величины и фиксируют новый
44 1
показания I а амперметра, В этом случае активная составляю-
тая входного сопротивления определяется по формуле
Можно, наоборот, сохригить во втором измерении величину
тока /А в измерительной цели и произвести два измерения напря-
жения (Д7Х и U2) на La> до и после поворота катушки, тогда
(2-12>
Учёт сопротивления амперметра производится способом, ана-
логичным указанному выше.
Метод куметра
Для измерения входного сопротивления антенн и фидеров
на сравнительно низких радиочастотах применяют куметры.
Принцип измерения в этом случае основывается на том, *1то
в последовательном резонансном контуре, состоящем из ёмкости
С и индуктивности Lt напряжение на ёмкости в Q раз больше
приложенной к зажимам контура эдс. Q — добротность контура,
равная
Q = (2.13)
к
где L — индуктивность катушки,
7? — активное сопротивление катушки и подводящих провод-
ников.
Конденсатор полагается идеальным, т. е. не имеющим потерь.
Определив добротность исследуемого контура Q, зная ёмкость
конденсатора С и частоту резонанса можно определить актив-
ную и реактивную составляющие сопротивления элементов, вклю-
чённых в контур, по формулам:
L = , (2.14)
<О0 С
(2.15)
Схема измерительной установки по Методу куметра приведе-
на на рис. 2.6. Она состоит из генератора высокой частоты, тран-
46
сформатора связи и измерительной цепи. В свою очередь, изме-
рительная цепь содержит сопротивление гп и резонансный кон-
тур, к зажимам 1 и 2 которого присоединяется исследуемое со-
противление.
Принцип работы данной схемы следующий.
Ток высокой частоты /0 от генератора, проходя по активному
сопротивлению г0> которое является сопротивлением куметра
(оно берётся порядка 0,01 <-0,1 cwt), вызывает на нём падение на-
пряжения U. Это напряжение приложено к контуру, состояще-
Измерительная цепь
Транарарматар
сдязц
Рис. 2.6. Схема измерительной установки по методу
куметра
му из конденсатора С с малыми потерями и исследуемого со-
противления ZA (например, антенны), подключаемого к зажи~
мам 1—2. Измерив напряжение U ср на конденсаторе1 С в момент
резонанса при помощи лампового вольтметра, находим доброт-
ность контура по формуле
(2-16)
Зная Q и С, по ф-лам (2.14) и (2.15) определяем L и /?.
Куметр позволяет определить реактивные и активные состав-
ляющие исследуемых сопротивлений также и в случае реактив’
ности отрицательного знака, что особенно важно при измерениях
на длинных и сверхдлинных волнах. Порядок измерений следую-
щий.
К зажимам 1—2 куметра (рис. 2.6) приключают сначала эта-
лонную индуктивность такой величины, чтобы можно было на
требуемой частоте определить добротность контура, состоящего
из этой индуктивности и ёмкости куметра С. Пусть эта доброт-
ность составляет Qh а ёмкость на резонансной частоте оказа-
лась равной С\. Далее подключают исследуемое сопротивление
либо последовательно с эталонной индуктивностью Li
46
(рис. 27), либо параллельно конденсатору С (рис. 2.8) !). За-
тем вновь производят настройку всего контура в резонанс с
частотой генератора и определяют добротность всего контура
Q2 и ёмкость конденсатора С2.
ZA
г0
И тралсформтпору
связи
Рис. 2.7. Схема присоединения измеряемого сопротиз-
лсния последовательно с эталонной индуктивностью
По полученным данным можно рассчитать активную и
реактивную составляющие исследуемого сопротивления Za .
Для схемы рис. 2.7:
В случае С|>С2 реактивное сопротивление ХА будет иметь,
индуктивный характер, сели Ci<C2, то реактивное сопротивле-
ние ХА имеет емкостный характер. Из (2.17) может быть опре-
делена соответственно индуктивность L А или ёмкость СА иссле-
дуемого сопротивления Z А,
Для схемы рис. 2.8, когда Z А состоит из ёмкости С Аи парал-
лельно включённого сопротивления R А,
(2.18 а)
Qi — Q? Ci
(2.186)
Часто измерения входного сопротивления антенн при помо-
щи куметра выполняют по схеме рис. 2.9. Она отличается от пре-
дыдущих схем наличием эталонных сопротивлений /?о, £о, Со и
переключателя 11, имеющего постоянный 1 и переменные О' и 2
контакты. Переключатель П позволяет включать в схему либо
антенну, либо эталонные сопротивления.
’) Применяется в основном схе'ма рис. 2,8. Это объясняется тем, что из-
мерения входного сопротивления при помощи ку метра проводят обычно толь-
ко для несимметричных антепн и фидеров.
47
Измерения по схеме рис. 2.9 проводят в следующем порядке:
переключатель П ставят в положение 0 и, подключив таким об-
разом исследуемую аптенну А параллельно конденсатору С ку-
Рис. 2.8. Схема присоединения измеряемого сопротивления
параллельно переменному конденсатору
метра, настраивают контур куметра в резонанс на исследуемой
частоте и определяют добротность Qb Одновременно фиксируют
напряжение U ток /о- Далее переключатель П ставят в поло-
к трансформа-
тору
Рис. 2.9. Схема измеряемой установки, применяемой в методе ку-
метра при наличии в пей эталонных сопротивлений: активного
индуктивного £0 и ёмкостного Со
жепие 2, отключая тем самым исследуемую антенну и подключая
вместо неё эталонные сопротивления /?0, Со или Со (в зависимо-
сти от знака исследуемой реактивности). Величины последних
подбирают таким образом, чтобы получить при том же значе-
нии тока /о добротность контура Qr и напряжение на конденса-
торе U сР.
Входное сопротивление антенн определяют через получен-
ные величины /?о, Со или Со. В случае ёмкостного Характера его
реактивной составляющей
(2.19),
В случае индуктивного характера реактивной составляющей]
входного сопротивления 1
ZA =r/?t+io>f L. (2.2М
В настоящее время отечественная промышленность вы-j
пускает куметры на частоты от самых низких частот диапазона
48 1
сверхдлинных волн до частот порядка 300 Мгц. Однако на часто-
тах свыше 3—5 Л4гц точность измерений получается малой.
Объясняется это тем, что 1) начинает существенно сказываться
влияние соединительных проводов, подключаемых между ку-
метром и антенной, 2) снижается точность эталонных сопротив-
лений и 3) в диапазоне высоких частот возрастает активное со-
противление антенн и соответственно уменьшается реактивное
сопротивление, что приводит, в свою очередь, к снижению доб-
ротности антенн. Поэтому обычно применение куметров для из-
мерения сопротивлений антенн ограничивается только диапазо-
ном длинных и средних волн.
Существенный недостаток куметров в случае их применения
для антенных измерений заключается в том, что в них, как пра-
вило, применяются генераторы малой мощности и высокочувст-
вительные неизбирательные индикаторы (ламповые вольтмет-
ры). При этом даже небольшие паводки от посторонних источни-
ков вызывают большие погрешности измерений. Большой уро-
вень наводок, имеющий место при исследовании антенн боль-
ших размеров, может повредить прибор. Поэтому куметры при-
меняют для исследования антенн небольших размеров, напри-
мер антенн переносных радиостанций, рамочных антенн, антенн
приёмных радиостанций и т. п.
При помощи куметров сравнительно просто измерить низко-
омные и высокоомные активные сопротивления. Добротность
контура со срелпеомными сопротивлениями настолько пони-
жается, что измерение их при помощи куметра становится за-
труднительным или даже практически невозможным.
При измерениях с куметром, так же как и с другими измери-
тельными приборами, заземление должно быть выполнено весь-
ма тщательно. В случае измерений несимметричных антенн ку-
метр должен быть обязательно подключён к заземлению (или
противовесу) исследуемой антенной системы.
Метод замещения
Одна из схем, основанная на методе замещения, показа-
на на рис. 2.10. Измерения проводят в следующем порядке.
Переключатель /7Г ставят в положение 1 (в схему включает-
ся антенна) и схему настраивают в резонанс, например, при по-
мощи ёмкости С. Момент настройки определяют по максимуму
тока 1а в антенне. Затем переключатель П\ переводят в положе-
ние 2. В схему включается измерительная цепь и отключается ан-
тенна. Измерительная цепь состоит из ёмкости С э и сопротивле-
ния R а в случае1, когда антенна возбуждается па волне длиннее
собственной, или индуктивности L, и сопротивление Rs, когда
антенна возбуждается на волне короче собственной. Вновь об-
4—292 49
разованный контур настраивают в резонанс ёмкостью С э или
индуктивностью L эи изменением сопротивления 7?, доводят ток
в цепи до той величины, которую он имел при включённой аптен-
Гснс ро-
тор 6ч
।_____;
Трансформатор
Иоморитыи нан цепь
Рис. 2Л0. Схема измерительной установки по методу замещения, в ко-
торой антенна и цепь эталонных сопротивлений включается поочерёдно
не. Тогда активная составляющая входного сопротивления ан-
тенны может быть определена по формуле
или
(2.21)
<2-22)
где гС9 или г — сопротивление потерь соответственно конден-
сатора С,или катушки индуктивности L 9 .
Номера терьная цепь
Рис. 2.11. Схема измерительной установки по методу замещения,
в которой антенна закорачивается .
Реактивная составляющая входного сопротивления антенны^
равна включённой в цепь при резонансе эталонной ёмкости CJ
или эталонной индуктивности L,. |
Применение находит также схема, показанная на рис. 2.11.1
Измерения при помощи этой схемы производят следующими
образом. Закоротив вход антенны переключателем Z7j, настраиЛ
вают эквивалентной ёмкостью С 3 или индуктивностью Ls измеЦ
рительную цепь в резонанс (по максимуму тока /г) и замечают
50 I
величины эталонных сопротивлений R' и X', а также тока Д>.
Затем, размыкая переключатель /7Ь включают антенну в изме-
рительную цепь, вновь настраивают её в резонанс при помощи
реактивностей Са и L3 и добиваются получения в контуре преж-
ней величины тока Л изменением активного сопротивления
Теперь резонанс будет иметь место при других значениях эта-
лонных сопротивлений. Обозначим их через /?* и X'. Значе-
ния RA и ХА— составляющих измеряемого сопротивления—
равны:
Ra=LR,=R's-R;, (2.23)
Хл=АХа = Х;-Х;. (2.24)
При пользовании схемами рис. 2,10 и 2.11 следует обращать
особое внимание на контроль за постоянством тока Ц или на-
пряжения Ui на протяжении всего опыта.
Схема рис. 2.11 имеет меньшее число измерительных элемен-
тов по сравнению со схемой рис. 2.10 и более удобна при изме-
рениях.
Существует сравнительно большое число вариантов схем из-
мерения по методу резонанса и замещения. Они отличаются
друг от друга главным образом по виду индикатора и способу
его включения в схему. Встречаются схемы [Л6], в которых ан-
тенная и соответственно эквивалентная цепи включаются в коп-
тур, находящийся в анодной цепи измерительного генератора.
Индикатором в этом случае1 служит гальванометр в цепи сетки
лампы генератора, который регистрирует изменение тока сетки
при измерениях. В других схемах [Л7] антенная, а также эквива-
лентная измерительная цепи присоединяются параллельно кон-
Рис. 2.12. Схема измери-
тельной установки по
методу замещения, в ко-
торой антенна включает-
ся параллельно колеба-
тельному контуру
туру в цени сетки измерительного генератора, а индикатором
служит миллиамперметр в анодной цепи, регистрирующий из-
менение анодного тока (постоянной составляющей) при изме-
рениях.
На рис. 2.12 приведена схема измерений, которую сравни-
тельно легко осуществить в лабораторных условиях* При изме-
рениях антенну подключают параллельно анодному контуру
LKCK измерительного генератора, измеряют частоту колебаний
этого генератора и фиксируют величину тока в одной из его це-
пей (постоянные составляющие в цепи сетки или анода). Отклю-
чив затем антенну, подключают параллельно анодному контуру
эквивалентную замещающую цепь, составленную из элементов
Ся и 7?, или L , и %9 (в зависимости от характера реактивного
сопротивления), и подбирают их величины так. чтобы восстано-
вить прежний режим измерительного генератора и частоту гене-
рируемых колебаний. По данным Сэ и L3 определяют вход-
ное сопротивление антенны.
Антенные и фидерные омметры
При измерениях входного сопротивления антенн прихо-
дится считаться с тем, что под влиянием приходящих радиоволн
и электромагнитных волн от случайных индустриальных и атмо-
сферных электрических разрядов па входе антенны возбуж-
даются электродвижущие силы самых различных частот и уров-
ней. Эти посторонние эдс мешают измерениям, вносят ошибки,
снижающие их точность, а при большом уровне могут повредить
прибор. Для ослабления действия посторонних эдс в ряде изме-
рительных схем, основанных на методе резонанса, применяются
измерительный генератор повышенной мощности и рассчитан-
ные на большую мощность приборы. При этом действие мешаю-
щих напряжений может быть практически исключено. Исполь-
зуя этот принцип, А. А. Пистолькорс [Л8] разработал приборы,
получившие название антенных и фидерных омметров: первые —
для антенных измерений в диапазоне средних, вторые — Корот-
ких волн.
Принципиальная схема фидерного омметра приведена на
рис. 2.13. Измерительный генератор состоит из задающего гене-
ратора и усилителя мощности. Измерительный контур, содержа-
щий ёмкость С¥1 основную индуктивность и две одинаковые
добавочные катушки Дт, включается в анодную цепь лНхМп уси-
лителя. В положении 1 переключателя П\ концы добавочных ка-
тушек замыкаются между собой непосредственно, в положении
2—через сопротивление 0,5 ом. Это положение переключателя ис-
пользуется при измерении малых активных сопротивлений мето-
дом замещения. В положениях 3, 4 и 5 концы катушек сое-
диняются через разные сопротивления других величии.
Конденсаторы Cj служат для симметрирования схемы. Пере-
ключатель /72 даёт возможность привести схему в состояние,
годное для измерении как несимметричных, так и симметричных
антенн с фидерными линиями,
Индикатором прибора служит миллиамперметр в цепи ано-
да ламп усилительной ступени.
52
Для измерения активного сопротивления к одной паре кон*
тактов переключателя Пу (например, в положении 3) присоеди-
няют измеряемое сопротивление гх, а к другой паре (например,
4) — эталонное г3.
Ставя переключатель П\ в положение 3, конденсатором Ск
производят настройку анодного контура усилительной ступени..
।-----------------------1----------------------J__________________1
Задающий генератор Усилитель Измеригпетмя цель
Рис. 2.13. Принципиальная схема фидерного омметра
Резонансу соответствует максимум анодного тока, величину ко-
торого фиксируют. Затем переключатель ставят в положение 4
и подбирают сопротивление г# так, чтобы получить прежнее по-
казание прибора при минимуме анодного тока.
Постоянная составляющая анодного тока усилительной сту-
пени обратно пропорциональна эквивалентному сопротивлению
R^K9 анодного контура, определяемого формулой
Кеке —
г
(2.25)
где г — присоединяемое к анодному контуру активное сопро-
тивление, равное в первом случае искомому сопротив-
лению г а во втором — г9.
Равенство постоянных составляющих анодного тока в обоих
случаях определяет равенство и сопротивлений. Таким образом,
искомое активное сопротивление находится непосредственно из
измерений;
(2.26)
Для измерения положительных реактивностей (имеющих на
измеряемой частоте сопротивления порядка 200—1000 ом) ис-
53
пользуется метод последовательного резонанса с градуирован-
ными конденсаторами Со (рис. 2.14). Переключатель ставят
сначала в положение соответствующее, короткозамкнутым за-
жимам /—/, и настраивают анодный контур в резонанс. Затем
переключатель ставят в положение
Рис. 2.14. Схема из мерите ль пай цепи
фидерного омметра с применением
последовательного резонанса
2 и при помощи конденсато-
ров Со систему снова на-
страивают в резонанс (по
минимуму анодного тока),
причём ёмкость С* должна
остаться постоянной. По из-
вестной ёмкости Сэ конден-
саторов Со значение индук-
тивного сопротивления опре-
делится по формуле
XL = 477 —. (2.27)
При измерении положительных реактивных сопротивлений,
имеющих величину меньше 200 ол, можно воспользоваться мето-
дом параллельного резонанса. Схема измерения для этого слу-
чая приведена на рис. 2Л5. Измеряемое сопротивление Lx под-
ключают вместе с параллельно присоединённым к нему гра-
дуированным конденсатором С3 к зажимам фидерного омметра.
Рис. 2Д5. Схема измери-
тельной цепи фидерного
омметра с применением
параллельного резонанса
катушки L\ замыкают накоротко. Изменением ёмкости конден-
сатора Ск настраивают систему в резонанс при разомкнутых за-
жимах переключателя Яь Затем переключатель ставят в поло-
жение, при котором измеряемый контур С3 и Lr подключается
параллельно анодному контуру усилителя, и снова добиваются
резонанса изменением ёмкости конденсатора С3.
При резонансе
X ,= Хс = 477 — .
L с,
(2.28)
Отрицательные реактивные сопротивления величиной
50-^—1000 ом измеряются по методу сравнения с эталонным
конденсатором.
54
В случае измерения нагрузок с очень малыми отрицатель-
ными реактивностями удобно воспользоваться методом парал-
лельного резонанса с короткозамкнутой двухпроводной линией
известной длины. Измеряемое сопротивление С * с параллель-
но присоединённой к нему двухпроводной линией подключают к
Рис. 2.16. Схема измерительной цепи фидерного омметра с при-
менением короткозамкнутой двухпроводной линии
зажимам фидерного омметра (рис. 2.16). Двухпроводная линия
снабжена подвижным короткозамкнутым мостиком, при по-
мощи которого и добиваются резонанса. Метод измерения ана-
логичен описанному при измерении положительных реактивных
сопротивлений, меньших 200 ом. Отрицательное реактивное соп-
ротивление находится по формуле
xc=ptg^, (2.29)
Л
где р —волновое сопротивление двухпроводной линии,
1 — длина линии.
Идея создания специальных измерительных приборов для
антенных измерений типа фидерных и антенных омметров и в
настоящее время не потеряла своего значения. Можно отметить
появление новых разработок приборов такого типа, более совер-
шенных и более удобных в эксплуатации. Так, например, для
измерения входных сопротивлений антенно-фидерных систем, в
диапазоне длинных и средних волн может найти применение из-
мерительный прибор разработки Ленинградского электротехни-
ческого института связи [Л9]. Принципиальная схема этого при-
бора приведена на рис. 2.17.
Генераторная цепь прибора имеет маломощный генератор с
самовозбуждением и индуктивной обратной связью, собранный
на лампе 6КЗ. Катушки индуктивности контура этого генератора
намотаны на замкнутых карбонильных сердечниках. Имеется
три переключаемых с помощью переключателя П катушки, со-
ответствующие различным поддиапазонам, охватывающим сов-
местно диапазон частот 0,15 ч- 1,5 Мгц. Плавное изменение ча-
стоты в пределах поддиапазона осуществляется ёмкостью С.
55
Колебания маломощного генератора усиливаются дополнитель-
ной ступенью, собранной по апериодической схеме на лампе
6Н5С, используемой в качестве катодного повторителя с парал-
лельным питанием. На выходе усилителя может быть получено
напряжение до 50#, Мощность, отдаваемая в измерительную цепь
Рис. 2.17. Принципиальная схема фидерного омметра, разработанного
в Ленинградском электротехническом институте связи
при активной составляющей измеряемого сопротивления в
360 ом, доходит до 2,5 вт.
Сравнительно большое напряжение на выходе прибора обес-
печивает его хорошую помехоустойчивость внешним эдс, наво-
димым в измеряемой антенне.
Измерительная цепь прибора соединяется с усилителем
мощности при помощи высокочастотного трансформатора, соб-
ранного па замкнутом сердечнике. Вторичная обмотка этого
трансформатора секционирована. Та или иная секция трансфор-
матора выбирается в зависимости от порядка величины измеряе-
мого сопротивления. Работа прибора основана на методе резо-
нанса и замещения. При этом используется схема рис, 2.11,
56
Основным источником погрешности измерения при исполь-
зовании метода резонанса и замещения является влияние пара-
зитных ёмкостей измерительной цепи. Для уменьшения паразит-
ных ёмкостей обмоток вмсокочаснп него трансформатора, так
же как и ёмкостей между обмотками, сердечник делается торо-
идальной формы небольшого диаметра (внутренний — 10 мм,
наружный — 20 жле), а в качестве материала сердечника берёт-
ся оксифер, обладающий большой магнитной проницаемостью.
Для установки желаемого уровня напряжения на первичной
обмотке трансформатора служит потенциометр, включённый в;
цепь экранной сетки лампы генератора. Величина этого напря-
жения контролируется при помощи индикатора уровня кото-
рый представляет собой вольтметр на кристаллическом диоде.
Измерительная цепь прибора состоит из магазина эталонных
сопротивлений, переменного эталонного конденсатора, магазина
эталонных ёмкостей и набора добавочных индуктивностей.
Эталонные активные сопротивления выполнены частично из
высокоомного провода (единицы и десятки ом) со специальной
намоткой для уменьшения индуктивности, частично же (сотни
ом) — из непроволочных сопротивлений.
Переменный эталонный конденсатор обеспечивает перекры-
тие от 36 до 1080 пф. Магазин эталонных ёмкостей составлен из
конденсаторов типа КСО. Добавочные индуктивности измери-
тельной цепи выполнены в виде четырёх катушек с отводами на
замкнутых тороидальных сердечниках из оксифера. Ток измери-
тельной цепи контролируется при помощи индикатора настрой-
ки U2, который представляет собой вольтметр на кристалличе-
ском диоде. Чувствительность как индикатора настройки, так и
индикатора уровня в широких пределах регулируется измене-
нием сопротивления, включённого последовательно с измери-
тельным прибором.
Измерительный прибор питается от сети переменного тока1
напряжением 127 или 220 в. Он обеспечивает измерение активной
составляющей сопротивления в пределах /^=10—^ 1000 ом, а
реактивной составляющей в пределах ±104-1000 ом. По-
грешность измерений составляет примерно 5% и лишь на краяХ-
диапазопа она увеличивается до 10% (для реактивной состав-
ляющей) .
По своей схеме прибор рассчитан на измерение несимметрич-
ных антенн. Общий вид прибора показан на рис. 2.18.
Порядок измерений следующий. При подключённом изме-
ряемом сопротивлении 7.х устанавливают требуемую частоту
колебаний по волномеру (внешнему) и необходимый уровень
напряжения по индикатору уровня. Затем производят настрой-
ку измерительной цепи в резонанс при включённом измеряемом
сопротивлении и при нулевых положениях магазина активных
сопротивлений. Настройку осуществляют при помощи перемен-
57
кого эталонного конденсатора (могут быть также включены ма-
газины эталонных ёмкостей и добавочные индуктивности).
Для повышения точности измерений при настройке рекомен-
дуется использовать большие значения ёмкостей, однако такие,
чтобы резонанс получился еще достаточно острым.
После настройки измерительной цепи в резонанс фиксируют
-значение эталлоппой ёмкости и показание индикатора настрой-
Рис 2Л8, Передняя панель фидерного оммегра, разработанного е Ленин-
градском электротехническом институте связи
ки. Затем вводят активное сопротивление, равное (по порядку
величины) ожидаемому активному сопротивлению измеряемой
антенны, закорачивают входные зажимы прибора (закорачи-
вают Zx ) и вновь настраивают измерительную цепь в резонанс
по максимальному показанию индикатора настройки. При этом
фиксируют новое положение эталонной ёмкости и добиваются
зафиксированного в процессе первой настройки (при незакоро-
чеином Zx ) показания индикатора, варьируя величину актив-
ного сопротивления.
Активную и реактивную составляющие сопротивлений опре-
деляют на основе данных измерений по ф-лам (2.23) и (2.24).
Метод разветвления токов ’
Для измерения входного сопротивления антенны можно
использовать метод, основывающийся на применении второго
закона Кирхгофа. По этому методу, который будем называть
методом разветвления токов, применяются схемы, состоящие из
• ф?: - ••••--
измеряемого и эталонного сопротивлений, включённых парал-
лельно, и измеряются токи отдельно в каждой из параллельных
ветвей.
Рассмотрим схему рис. 2,19. Опа состоит из генератора вы-
сокой частоты, измерительной цепи и элемента связи (перемен-
ной). Измерительная цепь содержит две параллельные ветви, в
Рис. 2.19. Схема измерительной установки по ме-
тоду разветвления токов, рассчитанная на изме-
рение модуля комплексного сопротивления
одну из которых включено измеряемое сопротивление ZA (ан-
тенна), а в другую — переменное эталонное сопротивление
Каждая из ветвей снабжена индикатором тока. Регулируя
до полного совпадения величин токов в ветвях (/х = /_), по-
лучим равенство модулей измеряемого и эталонного сопротив-
лений
IZA | = R3. (2.30)
Основным недостатком схемы рис. 2,19 является то, что она
позволяет измерить лишь модуль комплексного сопротивления.
Чтобы измерить и фазу комплексного сопротивления, схему из-
мерений нужно усложнить. Для этой цели, в частности, может
Рис. 2.20. Схема трёх амперметров
быть применена схема рис. 2.20, получившая название схемы
трех амперметров, согласно которой измеряются не только токи
в ветвях, ио и общий ток.
Если измерить величины токов /ь 1$, то модуль полного
измеряемого сопротивления \ZA | равен
' |<.|=?с^ <231>
59
а фаза
’=arcsl”T-H‘ + (гМгГ|- <2-32>
Предложен ряд приборов для антенных измерений, исполь-
зующих метод разветвления токов [ЛЮ], В некоторых из них ис-
пользуются как данный метод в чистом виде, так и в сочетании
Рис, 2.2 L Принципиальная схема прибора, основанного на
сочетании методов разветвления токов и замещения
с методами резонанса и замещения [ЛИ], Принципиальная схе-
ма прибора, основанного на методе разветвления токов в соче-
тании с методами резонанса и замещения, приведена на рис. 2.2L
Измерения в этом случае производятся следующим образом.
Сначала при подключённой антенне изменением X 9 (со-
стоит из последовательно соединённой ёмкости С, и индуктив-
ности L, ) добиваются резонанса на заданной частоте в измери-
тельной цепи и фиксируют значение ёмкости конденсатора С'„
Затем изменением эталонного сопротивления добиваются
одинаковых показаний /1 и 72. Обозначим эталонное сопротивле-
ние, соответствующее равенству токов /j и /2, через R* ; оно ука-
жет измеряемое активное сопротивление антенны с учётом по-
терь в эталонных реактивностях (ёмкости С3 и катушки индук-
тивности £, ). Далее закорачивают вход антенны при помощи
переключателя Пх и цепь, состоящую теперь только из эталон-
ной ёмкости и индуктивности, вновь настраивают в резонанс
изменением только ёмкости С3 . Новое значение эталонной ём-
кости С* фиксируют. При этом регулируют сопротивление
до получения одинаковых токов Ц и /2. Полученное значение
будет равно сумме сопротивлений потерь в катушке индуктив-
ности 1Э и конденсатора Ct . Таким образом, активное сопро-
тивление антенны будет равно
(2.33)
60
Реактивное сопротивление антенны
= ---------^= Хх — X < .
А iu>C3 1<иСэ сз сз
(2.34)
Следует отметить, что метод разветвления токов может най-
ти применение главным образом для измерения входного сопро-
тивления антенн длинных и средних волн, поскольку в этих диа-
пазонах токи в разветвлённых цепях могут быть измерены до-
статочно точно.
Методы автоматического измерения входного
с оп ротнвле имя
Весь комплекс измерения входного сопротивления ан-
тенны методами, описанными выше, представляет собой весьма
продолжительную и утомительную работу. Ускоряют и облег-
чают процесс измерений методы автоматического измерения.
. мггкльный
ера тор
Рис. 2.22. Блок-схема прибора автоматического измерения
входного сопротивления
На рис. 2.22 изображена блок-схема одного из приборов ав-
томатического измерения входного сопротивления, используе-
мого в диапазоне длинных, средних и коротких волн. Она со-
стоит из четырёх частей; измерительного генератора, широкопо-
лосного усилителя, измерительной цепи и индикаторной части.
Измерительный генератор рассчитан на плавную автомати-
ческую перестройку частот в широком диапазоне. Он содержит
два генератора, из которых один настроен на фиксированную
частоту /о, а у другого частота плавно меняется «в пределах
h^f2 вращением (при помощи двигателя) ротора конденсатора
колебательного контура. Оба генератора работают в диапазоне
метровых волн. Напряжение, даваемое ими, поступает на смеси-
тель, в котором выделяются разностные частоты/^—
Другие частоты преобразования подавляются фильтром, вклю-
чённым на выходе смесителя.
61
После фильтра напряжение поступает на вход широкополос-
ного усилителя, от которого мощные колебания подаются в из-
мерительную цепь. Усилитель имеет на выходе очень большое
сопротивление , модуль которого примерно в десять раз боль-
ше модуля максимально
возможного сопротивления антенны.
Это обеспечивает практически по-
стоянную величину тока на выходе
усилителя, независимую от сопро-
тивления измерительной цепи.
Измерительная цепь состоит из
двух ёмкостей С и детектора Д.
К измерительной цепи подключает*
ся исследуемая антенпа.
Напряжение с детектора подаёт-
ся на индикаторную часть прибора,
состоящего из усилителя постоянно-
го тока и самописца, вращение
рабана которого синхронизировано с вращением двигателя,
Рис. 2,23. Упрощённая схема
прибора автоматического изме-
рения входного сопротивления
ба-
ИЗ-
меняющего частоту измерительного генератора»
Для анализа представим схему прибора упрощённо, как по-
казано на рис. 2.23, т. е. в виде источника эдс Е постоянного то-
ка с внутренним сопротивлением Ry , нагруженного на две па-
раллельные цепи, из которых одна представляет собой последо-
вательно соединённые сопротивления R с и а вторая — со-
противление Ra. Сопротивления и Равны соответ-
ственно сопротивлениям выхода усилителя, ёмкости, измеритель-
ной цепи, детектора и антенны.
Так как сопротивление Ry во много раз больше сопротивле-
ния цепей нагрузки, можно принять, что ток 1 не зависит от ве-
личины искомого сопротивления RA . Как видно из рис. 2.23,
соотношение токов /ь /2 и / определяется следующим равенст-
вом:
1 2ЯС + Кд
RA
Л _ h __ 1
Л+ I . . #А
1+^с+*д
(2.35>
(2.36)
а напряжение Уд на детекторе равно
= /2/?д = (/ - Л) Rz }Rn - . (2.37)
Поскольку I и /?д — величины постоянные, то напряжение
ид является функцией тока /ь который, в свою очередь, зависит
62
от Ra. При RA'^>2RC + /?д ток 11 -»• 0 и ид -> / 7?д, а при RA <
<^2ЯС+ЯД согласно (2.36)
—Y
2??с +₽д /
(2.38)
U„ = - *Л.*Д
2RC + /?д
(2.39)
Таким образом, во втором случае С/д пропорционально
Отсюда следует, что в схеме рис. 2.23 следует применять ёмкост^
ные сопротивления большой величины, т. е. включать малые ём-
кости, порядка нескольких пикофарад.
Схема рис. 2.23 анализировалась в предположении, что она
питается постоянным током и имеет в цепях активные сопротив-
ления. Сказанное целиком обобщается на случай переменных
токов и комплексных сопротивлений. Следует только иметь в ви-
ду, что в этом случае схема позволяет измерять лишь модуль
искомого сопротивления, В тех случаях, когда заведомо преоб-
ладает активная или реактивная составляющая, знание модуля
даёт представление об этой преобладающей части. По кривой
изменения модуля входного сопротивления можно также полу-
чить представление о собственных (резонансных) частотах,
Формула (2,39) является приближённой, и поэтому прибор
должен быть предварительно проградуирован по известным
сопротивлениям. Градуировка даёт зависимость уровня показа-
ний самописца от модуля сопротивлений. При больших ёмкостях
(малом сопротивлении ёмкостей) уровень показаний самописца
будет пропорционален \ZA\, так как будет иметь место соотноше-
ние
(2.40)
3. ИЗМЕРЕНИЕ ВХОДНОГО СОПРОТИВЛЕНИЯ
АНТЕНН МОСТОВЫМИ МЕТОДАМИ
Введение
Для определения входного сопротивления антенн на ча-
стотах от самых низких до десятков тысяч мегагерц широко ис-
пользуются мостовые схемы, по которым изготавливается спе-
циальная аппаратура (мосты).
Следует различать мосты, составленные из элементов в виде
сосредоточенных сопротивлений и из отрезков длинных линий
(фидеров). Первые применяются в настоящее время на волнах
от самых длинных до метровых. В диапазонах метровых и деци-
метровых волн находят применение коаксиальные мосты, а в
диапазоне сантиметровых и миллиметровых волн — волновод-
ные мосты.
Мостовые методы измерения входного сопротивления обес-
печивают более высокую точность измерений, а в ряде случаев
они более просты и более удобны, чем другие методы измерений.
Симметричный мост для длинных, средних
и коротких волн
На рис. 3.1 приведена принципиальная схема высокоча-
стотного моста типа ТМЕ-20, позволяющего измерять входные
сопротивления симметричных и несимметричных антенн в диа-
пазоне частот от 100 кгц до 20 Мгц.
Мост содержит декадный магазин активных сопротивлений
/?з и переменный конденсатор с параллельно подключённым
декадным магазином ёмкостей
Питание прибора осуществляется при помощи широкодиапа-
зонного высокочастотного генератора. В качестве индикатора
баланса используется специальная ламповая схема, имеющая на
выходе обычный телефон.
Ч На рис. 3.1 декадные магазины ёмкостей и сопротивлений отдельно
не показаны, чтобы не усложнять схему.
64
Мост рис. 3.1 имеет схему обычного моста переменного тока.
Он может быть включён как по симметричной, так и по несим-
метричной схеме. Если зажимы аа замкнуть на землю переклю-
чателем /7Ь то схема моста становится несимметричной и мож-
но измерять входные сопротивления несимметричных антенн.
Рис. 3.1. Принципиальная схема моста ТМЕ-20
При этом в зависимости от предполагаемого характера входно-
го сопротивления антенны (положительная реактивность иля
отрицательная) ёмкость С3 подключается переключателем /73 к
контактам либо вв, либо бб. Если антенна симметрична, то для
измерения её входного сопротивления переключатель выклю-
чается и схема моста становится электрически симметричной
относительно земли.
Максимальная ёмкость, которую дают конденсатор С$ и де-
кадный магазин ёмкостей, составляет 11 100 пф.
Величина сопротивлений, которую даёт магазин сопротивле-
ний, составляет 11111 ом. Практически удобнее при работе с
данным мостом оперировать проводимостями, поэтому градуи-
ровка магазина сопротивлений выполнена в единицах проводи-
мости.
Конструктивно мост оформлен в виде блока в металлическом
кожухе (рис. 3.2).
Генератор высокой частоты и индикатор расположены в от-
дельном блоке в металлическом кожухе. Мост связывается с ни-
ми двумя коаксиальными кабелями. На выходе индикатора
включены телефоны, по минимуму звука которых определяется
баланс моста. Блок-схема установки для измерения входного
сопротивления изображена на рис. 3.3.
Процесс измерений следующий.
5-292 65
Сначала включают в сеть генератор и по прилагаемым к не-
му графикам устанавливают частоту измерения. Затем мост ба-
лансируют согласно рабочей инструкции, прилагаемой к прибо-
Рис. 3.2. Вид передней
панели моста ТМЕ-20
ру, подключают антенну и, оперируя ручками декадных магази-
нов и переменного конденсатора, вновь добиваются баланса
моста, нарушенного при подключении антенны. Отсчитывают
значения активной проводимости gMM0> ёмкости СПф магази-
на, ёмкости Сз в делениях шкалы и вычисляют сопротивления
RA и % а антенны на частоте f по следующим формулам:
Х^=^Ь-10’
(ЗЛ)
Рис. 3.3. Блок-схема установки для измерения входного
сопротивления с помощью моста ТМЕ-20
Здесь g — активная проводимость антенны, отсчитанная по
прибору, ММО;
b — реактивная проводимость антенны, ммо, опреде-
ляемая по формуле
6 = 2к/С-Ю-3, . (3.2)
66
где f~ частота, на которой производилось измерение, Мгц
(определяется по прилагаемым к прибору графикам);
С — полная измеренная ёмкость, равная сумме ёмкостей ма-
газина С и переменного конденсатора С& пф (С3 так-
же определяется по прилагаемым к прибору графикам).
Несимметричный мост
Кроме высокочастотных симметричных мостов в прак-
тике антенных измерений находят применение высокочастотные
несимметричные мосты (рис. 3.4). Они более просты конструк-
тивно и могут быть собраны в лабораторных условиях.
Сначала мост уравновешивают при короткозамкнутых зажи-
мах аа, затем к этим зажимам,
освобождённым от закорачива-
ющей перемычки, присоединя-
ют измеряемое сопротивление
и снова добиваются баланса
моста.
При замкнутых зажимах аа
условие баланса моста опреде-
ляется выражениями:
RP = R.-^> (3.3)
___L__— _____1 - (з
i«cpI ra i<*cN '
Рис. 3.4. Схема несимметричного
высокочастотного моста
При включённом неизвестном сопротивлении Zx = + i Хх
уравнения баланса будут иметь вид:
(3.5)
iXr +
1____=
i «> Сръ
(3.6)
____
i <0 Суу
Из ур-ний (3.5), (3.6) и (3.3), (3.4) видно, что неизвестные
сопротивления (активное Rx и реактивное Хж) связаны с пара-
метрами моста следующими простыми соотношениями:
5*
, 1\
“ \ ^7>2 /
(3.7)
(3.8)
67
Из этих уравнений следует, что активное сопротивление Rx
определяется пределами изменения ёмкости СА, а реактивное
сопротивление Хх— пределами изменения ёмкости С#.
Измерение коэффициента бегущей волны на фидере
при помощи моста
Если в трёх плечах моста иметь активные сопротивления,
равные волновому сопротивлению фидера, питающего антенну
(рис. 3.5), то такой мост можно использовать для приближённо-
го определения коэффициента бегущей волны на фидере.
Рис. 3.5. К пояснению
метода измерения кбп
на фидере с помощью
моста
Пользуясь методом разветвления токов для схемы рис. 3.5,
можно написать следующую систему уравнений:
-2? — i2p — is р = ut
— ii Р + it + 2p) ig Z„p — 0
— *i P — h^np + *s (? + + 2Л/) — 0
где Znp—сопротивление прибора.
Из (3.9) следует:
• Ui(ZA+2Znp-h?)
ц 2(2вд-ь(-)(2л + ?) + t(ZA -Р) ’
t __________-4- 2р)__________
l3-2(Z„p + P)(Z4+Р)-Ьр(2л-р) *
Ток через прибор равен:
, =__________ц»(гл-0__________.
+ р)(zA 4- р) + p(ZA — f)
(3.9)
(3.10)
(ЗЛ1)
(3.12);
Если взять достаточно большое сопротивление прибора, удов*
летворяющее неравенствам > р, | Znp | > [ ZA то при-
ближённо
Uj 2а ~р
‘а 13 2(^ + р) + Р '
(3.13)
т. е. ток через прибор пропорционален коэффициенту отражений-
на фидере.
2, л —Р
Чтобы найти величину ---------, выражение (3.13) нужно
ZA +₽
УТ
разделить на -----1— . Данную величину можно получить,
измерив ток при короткозамкнутом плече 4. Действительно,
замкнув накоротко плечо 4, в которое включено искомое сопро-
тивление ZAi получим для тока через прибор следующее выра-
жение:
2(*лР + р)-? ~ 2(Zv+p) ’
Таким образом,
(G — М _ ] — к
I h G La %А + Р 1 *
(ЗЛ5)
Итак, при помощи моста, собранного по схеме рис. 3.5, мож-
но определить коэффициент отражения и кбв в фидере, питаю-
щем антенну, по отношению тока в диагонали моста, измеренно-
му при включении фидера в плечо 4, к току, измеренному при
короткозамкнутом плече 4.
Коаксиальные и волноводные мосты
Для измерений на метровых волнах, а также в длинно-
волновой части дециметровых волн находят широкое примене-
ние кольцевые коаксиальные мосты прямоугольной (рис. З.бп)
или круглой (рис. 3.66) формы с четырьмя ответвлениями, рас-
положенными через промежутки в четверть волны. Ответвления
служат плечами моста.
Принцип действия кольцевого моста основывается на том,
что в точках, отстоящих друг от друга на расстояние в полвол-
ны, токи и напряжения на фидере имеют одинаковые амплиту-
ды и противоположные фазы, а входные сопротивления тождест-
венно равны.
69
У кольцевого моста ряс» 3.6а коаксиальная линия плеча 1 в
точке 0 разветвляется на две ветви; длина одной ветви до точки
включения плеча 3 на полволны короче длины другой ветви до
этой точки. Если к плечу 1 моста присоединить согласованный
источник эдс, а плечи 2 и 4 замкнуть на одинаковые нагрузки, то
Рис. 3.6. Схема коаксиального моста в виде замкнутого кольца:
«) прямоугольного, б) круглого
энергия источника эдс распределится поровну между плечами
2 и 4 и не поступит в плечо 3, так как напряжения на ветвях в
точке включения плеча 3 будут одинаковы по амплитуде и про-
тивоположны по фазе. Если же нагрузки плеч 2 и 4 различны,
то в зависимости от степени этого различия большая или мень>
шая часть энергии источника эдс поступит в плечо 3 и возбудит
ток в индикаторе, включённом в это плечо.
Таким образом, присоединив к плечу 1 источник эдс, к плечу
2~эталонные сопротивления, к плечу 4 — искомую нагрузку, а
к плечу 3 — согласованный индикатор, можно по показаниям
этого индикатора, варьируя эталонные нагрузки, добиться ба-
ланса моста. При балансе искомое сопротивление равно эталон-
ному.
Этот же результат получится, если присоединить источник
эдс к плечу 3, а согласованный индикатор к плечу /.
Нагрузки могут быть включены в плечи 1 и 3, а источник
эдс и индикатор — в плечи 2 и 4. Плечи 1 и 3 принята называть
развязанными между собой. Аналогично между собой развяза-
ны плечи 2x4.
Соотношение волновых сопротивлений кольца и плеч, равное
У* 2, обеспечивает согласование моста, т. е. отсутствие отра-
жённой волны в плече, к которому присоединён источник эдс.
Находят применение также квадратные (рис. 3.7) и коак-
сиально-щелевые (рис. 3,8) мосты. Развязанные между собой
70
пары плеч для них имеют те же обозначения: /, 3 и 2, 4. По
принципу действия они аналогичны мостам рис. 3,6.
На рис* 3,9 показан кольцевой волноводный мост, аналогич-
ный коаксиальному (рис* 3.6) как по схеме, так и по принципу
действия.
Рис. 3.7. Схема квадрат-
ного коаксиального мо-
ста
Кольцевые мосты рассчитаны на одну фиксированную волну
и поэтому могут применяться лишь в очень узкой полосе частот,
что является их недостатком, 2
Рис. 3.9. Схема кольцевого
моста
волноводного моста
Рис. 3.8. Схема коаксиальпо-щслевого
В коротковолновой части дециметрового диапазона, где в
качестве фидерных линий используются как волноводы, так и
коаксиальные кабели, применяются также волноводно-коак-
сиальные мосты (рис. 3.10).
В технике сантиметровых волн широкое применение имеет
Т-мост (рис. ЗЛ). Он получается при совмещении двух развет-
влений прямоугольного волновода. Так, плечи /, 2 и 4 представ-
ляют собой разветвление в плоскости магнитного вектора
(//-плоскости), а плечи 3, 2 и 4 — разветвление в плоскости элек-
трического вектора (S-плоскости).
71
При разветвлении волновода в Я-плоскости волна, входящая
в среднее плечо (//-плечо), разделяется поровну на две синфаз-
ные волны (рис. 3.12), направляющиеся в боковые плечи, а при
Рис, 3,10. Схема волповодно-коак-
сиальиого моста
Рис. 3.11. Схема Т-моста
разветвлении волновода в Е-плоскости волна, входящая в сред-
нее плечо (Е-плечо), разделяется на две противофазные волны,
направляющиеся в боковые плечи.
Рис. 3.12 Картина электрических силсвых линий:
а) в //-тройнике моста, б) в Е-тройняке моста
Если волны одинаковой амплитуды одновременно входят в
плечи 1 и 3, то при одинаковой фазе обе волны перейдут в пле-
чо 2, а при противоположной фазе — в плечо 4.
Чтобы волна, входящая в какое-либо из плеч Т-моста, ответ-
вилась в //-плечо или Е-плечо, необходимо, чтобы опа образова-
ла у места разветвления картину электрических силовых линий,
72
подобную рис. 3,12а или б. Из этого следует, что если в оба бокс
вых плеча входят волны одинаковой амплитуды и одинаково
фазы, то они перейдут в Я-плечо, если одинаковой амплитуды,.,
но противоположной фазы, то в £-плечо.
Плечи 1, 3 и 2, 4 моста взаимно развязаны. Развязка плеч Л 3
очевидна, поскольку волна, поступающая в Я-плечо, не обра-
адI
зует поля, подобного рис. 3.126, а волна, поступающая в Е-пле-
чо, не образует поля, подобного рис. 3.12д. Что развязаны плечи
2, 4, легко понять из следующих рассуждений. Предположим, что
в плечо 2 входит волна, имеющая напряжённость поля £, От-
сутствие волны в плече 4 сложно трактовать, как наличие в этом
плече двух волн с амплитудами — и противоположными фа-
2
Рис. 3.13. Способы согласования Т-моста
зами. Фаза одной из них такая же, как у волны плеча 2, а у
другой — противоположная. Складываясь с волной плеча 2, они
дадут две волны амплитуды £, переходящие соответственно в
плечи Я и £ Таким образом, волна, входящая в плечо 2, разде-
лится между плечами 1 и 3 и не поступит в плечо 4..
7а
Приведённые выше рассуждения справедливы при условии
«годного согласования моста, означающего, во-первых, замыка-
ние всех его плеч на согласованные нагрузки, во-вторых, отсут-
ствие отражений во всех плечах от точки разветвления. Такой
мост называется «магическим».
Полное согласование моста осуществляется при помощи
диафрагм, реактивных штырей, ступенчатых переходов и т. п.
(рис. 3.13).
На сантиметровых волнах применение находит также волно-
водно-щелевой мост. Он представляет собой два волновода, при-
мыкающих друг к другу узкими стенками и связанных щелью
^рис. 3.14) в этой стенке. Щель делается во всю ширину стенки.
Подбором длины I щели можно добиться развязки плеч 1, 3 и
2, 4 и разделения мощности полны, входящей в одно из плеч с
нечётным номером, поровну между двумя плечами с чётным но-
мером и наоборот. Так как длина / практически точно подобра-
на быть не может и так как она не регулируется, то мост снаб-
жается винтом настройки.
Понятие о матрице рассеяния
Коаксиальный и волноводный мосты, имеющие четыре пле-
’ча, каждое из которых, согласно теории цепей с сосредоточенны-
ми постоянными, является двухполюсником, представляют со-
бой восьмиполюсник. Электромагнитная волна, входящая в од-
но из плеч, разделяется в общем случае между остальными пле-
чами и частично в точке разветвления отражается обратно ко
входу этого плеча. Отношение напряжённости поля отражённой
волны к напряжённости поля входящей волны при замыкании
74
всех плеч моста на согласованные нагрузки называется коэффи-
циентом отражения и обозначается через ..Отношение нап-
ряжённости поля волны, прошедшей в плечо с номером tn, к на-
пряжённости поля волны, входящей в плечо с номером п, также
при замыкании всех плеч на согласованные нагрузки называет-
ся коэффициентом передачи из плеча п в плечо т и обозначает*
ся через 5лт . Таким образом, каждое плечо характеризуется
четырьмя параметрами: коэффициентом отражения и тремя ко-
эффициентами передачи, а весь восьмиполюсник характеризует-
ся 16 параметрами, образующими так называемую матрицу рас-
сеяния S
5ц *$21 S4i
•$12 *$22 •$32 •$42
S
•$13 •$23 •$33 •$43
•$14 *$24 ^34 •$44
(3.16)
Если все плечи моста имеют одинаковые волновые сопротив-
ления, то согласно теореме взаимности
• $12 = S2i
* $13 — *$31
• $u = S41
* $23 — S32
• $24 = S42
• $34 = *$43
и равенство (3.16) можно привести к виду
(3.17)
•$11 •$12 •$13 Su
•$12 •$22 •$23 •$24
s ~ •$13 *$23 s33 •$34 (3.18)
•$14 *$24 •$34 •$44
Если входящие в плечи моста волны имеют напряжённость
поля соответственно Е\\ Еа*> Е*х и Ев4х, то напряжённость пеля
выходящих волн Е™х определится из уравнений вида
£«« = Е" Sllt + Е« S2n + S3„ + £« Sin, (3.19)
где индекс п—номер плеча, для которого определяется выходя-
щая волна.
75
Параметры матрицы рассеяния мостов определяются^
как правило, путем измерений коэффициентов отражения в
передачи.
Анализ работы коаксиальных и волноводных мостов
В случае измерения сопротивлений при помощи моста к
одной паре развязанные плеч присоединяют источник эдс и ин-
дикатор, а к другой — эталонное и искомое сопротивления. При-
мем, что источник эдс подключён к плечу Л индикатор — к плех
чу 3, эталонная нагрузка — к плечу 4, а искомое сопротивле-
ние — к плечу 2. Примем также, что источник эдс и индикатор
согласованы с волновым сопротивлением плеч.
Обозначим коэффициент отражения от эталонной нагрузки
через Г, а коэффициент отражения от искомой нагрузки
рез Гаск . Тогда будут иметь место соотношения:
рвх — Fet>w Г
Е.. f-Г • (3,20)
Напряжённость поля волны, входящей в плечо 1 от источни-
ка эдс, примем за единицу
Е‘х=1. (3.21)
Очевидно, что
Е*х = 0. (3.22)
Подставив значения Евх в ур-ние (3.19), получим следую-
щую систему:
' £Г = $п + Е‘«* ГaCKS21 + £ГЛ.514 '
Efx= Sls + Е™ recitSM + Гля5м
ЕГ = S18 + ЕГГискЪз + ЕГ ГятЗи ' (3>23)
= S14 ч- ЕГ rucKStt + Е'“' Г,ж544
Из второго и четвёртого уравнений системы (3,23) находим:
£вых ________ ^12 (1 — (3 24)
О (1 — ГэтЗц) *$24^искрят
5|дЗ«4Гкгу ____ (3 2g)
(1 —Г исхГ ът
Подставив Егых и из (3,24) и (3.25) в третье уравнение
системы (3.23), получаем для напряжённости поля выходной
76
волны в плече 3, т. е. для напряжённости волны, поступающей в
индикатор, следующее выражение:
раык__ £ г иск О — 4- in (( — Г
^3 — ^18 + ~ ~---- “ ~ ~
(1 — Г1 ’ ^эт^лч) — ^24
(^14^24^8 Ч~ ^18^44^34}
О Гаск^ъъ) U Г >*1*^44} — $24 ГискХ»т
Учитывая, что плечи /, 3 развязаны, можно в (3.26)
+
(3.26)
поло
жить
51з — 0.
(3.27)
При идеальном согласовании эталонной нагрузки Гзт *=0 и
ур-ние (3.26) с учётом (3.27) переходит в следующее:
£5ых _ иск
3 I ’ Гмск$и
(3.28)
В хорошо согласованном месте:
Тогда
т?вых -— 1 Г
3 4 z кек*
(3.29)
т. е. напряжённость поля волны, поступающей в индикатор в хо-
роню согласованном мосте при идеально согласованной нагрузке,
пропорциональна коэффициенту отражения. ।
В описанных выше коаксиальных и волноводных мостах
коэффициенты передачи в неразвязанные плечи Su и 5м либо
5з2 и S34, как правило, связаны между собой соотношением:
либо
Sls — $м
5дз ^—$24
512 514
5SJ == S34
(3.30)
(3.31)
При выполнении условий (3.30) или (3.31), как легко видеть
из (3.26) и (3.27), Езвых =0 при Гис*=Гзт> т. е. при уравновешен-
ном мосте напряжённость поля в индикаторном плече равна
нулю.
5а* ~ “
5as 0.
77
Из изложенного следует, что при согласованной эталонной
нагрузке мост можно отрегулировать так, чтобы показания ин-
дикатора были пропорциональны коэффициенту отражения от
искомой нагрузки, т. е. чтобы мост измерял коэффициент отра-
жения. При переменных эталонных нагрузках равновесия моста
можно добиться их варьированием, что позволяет измерить
входное сопротивление.
Двухпроводный мост
На рис. 3.15 показан двухпроводный мост, выполненный
в виде отрезка экранированной двухпроводной линии. В качест-
ве проводов двухпроводной линии взяты две одинаковые пла-
стины длиной /, шириной d и толщиной Л, находящиеся на рас-
стоянии D друг от друга. Экран имеет цилиндрическую форму и
закрывает двухпроводную линию как с боков, так и с торцов. В
торцовых стенках экрана сделаны отверстия, к которым подхо-
дят отрезки коаксиальных линий и через которые края пластин
присоединяются к их внутренним проводам. Оболочки коак-
сиальных линий присоединяются к экрану.
Таким образом, устройство, показанное на рис. 3.15, пред-
ставляет собой восьмиполюсник, образованный двумя несиммет-
ричными связанными между собой линиями, из которых одну
линию образует одна из пластин с экраном, а другую — другая
пластина с экраном.
Л. Г. Дорфман [Л29], подробно исследовавший такой мост,
доказал, что его свойства зависят от перечисленных параметров
I, d, А и D, а также от волнового сопротивления ро коаксиальных
отрезков, Зависимость дифференцированно от отдельных пара-
метров d, А и D аналитически не получена. Установлена зависи-
мость от их обобщённых характеристик Z+ + и , являю-
78
щихся волновыми сопротивлениями двухпроводной экраниро-
ванной линии для волн соответственно несимметричной и сим-
метричной. Величины Z++ и Z+_ могут быть определены че-
рез погонные индуктивности, измеренные по схеме рис, 3,16, па
формулам:
Z+ + 30L++ (сл<) | (3 32'
Z^_ = 30L+- (с-и) Г V ?
Рис. 3.16, К измерению обобщённых характеристик Z + + hZ4
При 1= —, согласовании всех плеч и выполнении равенств
-A-z_-2(/2~l)
-^=^-(/2+ 1)
л+— 2
(3,33>
пары плеч 3 и 2, 4 развязаны, мощность, поступающая в плечо
1 или 3, делится между плечами 2 и 4 поровну, мост согласован.
4. ИЗМЕРЕНИЕ ВХОДНОГО СОПРОТИВЛЕНИЯ
АНТЕННЫ ПРИ ПОМОЩИ
ИЗМЕРИТЕЛЬНЫХ ЛИНИЙ
Введение
Отрезок фидера, снабжённый устройством, позволяю-
щим снять кривую распределения напряжения на нём будем на-
зывать измерительной линией, а измерительное устройство, пе-
ремещающееся по фидеру, индикаторной головкой.
При подключении антенны к измерительной линии по кривой
распределения напряжения на фидере определяют коэффициент
бегущей волны к, который равен отношению минимального на-
пряжения к максимальному, и местонахождение минимума на-
пряжения х0. По известным к и находят входное сопротивле-
ние антенны ZA.
Метод измерения ZА при помощи измерительных линий был
впервые применён В. В. Татариновым [JI12] в 1931 г. для изме-
рения входного сопротивления коротковолновых антенн. Им же
была разработана теория этого метода и даны ценные указания
по его практическому выполнению. Впоследствии этот метод по-
лучил широкое распространение на дециметровых и сантиметро-
вых волнах.
Распределение напряжений и токов на фидерной линии
Если для определения величины сопротивления нагрузки необходим
мо знать /си Хе. то х а р а к т е р её (активная, реактивная, комплексная, а яри
комплексной—знак реактивной составляющей) можно определить по общем*
виду кривой распределения напряжений на фидере, т. е. по тому, в какой чет
верти находится минимум напряжения и имеется ли на фидере чисто бегущая,
чисто стоячая или смешанная волна.
На рис. 4.1 даны кривые распределения напряжений (сплошные линии) и
токов (пунктирные линии), получающиеся при различных видах нагрузки.
^Рассмотрим каждый случай в отдельности.
а) Фидер разомкнут (рис. 4.1а):
, Г у, — 1, р = 1, чр = 0, № 0,
Ux^2U^dcosmx, (4.1)
и%ад
1Х =• 21--sin тх. (4.2)
F
< гл-~
/>-/
кбв-0
a)
-’д
ft
Рис. 4J. Кривые
распределения на-
пряжений (сплош-
ные ЛИНИИ) и токоп
(пунктирные ли-
пни) на фидере:
б)
кб8-~
Z/Fp
p-о
К б в-t
%A~~* wC
Cm o~t
f
р-Я+гогЩ-^
кбв-0
кбо-о
ZA~>wL
где V'ep
0<-кб8<-1
где i-jr
0<-x68^t
Z/C-0
p-!
о zA-d<j>
\\р-£2
У
Sf=P
X5S-Z
кбв-0
р-^.
р R+J>
у-о
7*1
С U W<f
°) __
(<) разомкну! ом, б) короткое а мкн\том, в) нагруженном на ёмкость, г) нагру-
женном на индуктивность, д) нагруженном па согласованную нагрузку, е) на-
груженном на активное сопротивление, меньшее волнового, лс) нагруженном
на активное сопротивление, большее волнового, ,з) нагруженном па комплекс-
ное сопротивление с емкое гнои реактивной составляющей» нагруженном на
комплексное сопротивление с индуюивной реактивной составляющей
г*-292 81
На фидере образуется стоячая волна с пучностью напряжения и узлом
тока в точке х=0.
6) Фидер кироткозамкнут (рис, 4Ле5):
= 0, Г — 1, р = 1, ? = тс, к = О
l/x—2i Uga^ sin тх, (4.3)
2О'™д
1Х =-------cos тх. (4.4)
Р
На фидере образуется стоячая полна с узлом напряжения и пучностью
тока в точке х-0.
в) Фидер нагружен на ёмкость (рис, 4.1 в):
1
1 ~ i«С ~~? ,1
/д = , ^,^[7= I » Р — 1 । = r~F ^агс tg . к -= 0r
Л (о) С ♦ 1 , W С ?
— " Т + Р
1 со G
г
iarettf— — х 1 \
ux 2i U*ad е ia,csin I mx-arctg-— ) , (4.5)
X р /
и^ад isrcte-1- , J ч
/А ^ 2----е ^ср cos I тх — arc tg ~ . (4.6)
р \ to С ? J
Fla фидере образуется стоячая полна, причем первые от нагрузки узел
напряжения и пучность тока находятся в точке х0 — ~ arc tg —— .Так кая
I тс 1 тс X
arc tg —- < —, то хв <------— . т. е. х < .
to С р 2 m2 4
г) Фидер нагружен на индуктивность (рис. 4.1г):
i w L — р Л
= Гп ------------------ > Р = ^, <р — тс— 2arctg— , к — О,
л I <» L + р р
. t»> L
-.arctg---
Ux — 2 i L’q e p sin ( mx -|- arc tg — J . (4-7):
-iarctg^ wi j
lx — 2—- e p cos +arc tg—J, (4.8Й
На фидере образуется стоячая волнат причём узел напряжения и иучпосгм
тока находятся в точке j
XI (о L (йДтс X Л:
х0 = — - — arc tg — . Так как arc tg — < — , то — < х0 < — . <
2 т р Р 2 4 2 ;
д) Фидер нагружен на активное сопротивление, равное волновому
(рис. 4.1^): '
= р,Г^—0>р=>0, к = 1, j
t/r-C/™5el'nx , (4.Я
упад
Гх^-~е'тх. (4.10
На фидере образуется чисто бегущая волна,
е) Фидер нагружен на активное сопротивление, меньше волнового
(рис. 4.1е):
R— р р —R R
(4-И>
яп ч ,_____________—i arc tg (—? tg mx I
Ux = V H- P4 — 2p cos 2mx e \1—p ) ’
i triad ♦ , /1—p >. \
Ц] ------------------- —t arc tg tg mx
lx =---- /1 + ps + 2pcos 2mx e UtP ! . (4.12)
?
На фидере образуется режим промежуточный между стоячей и бегущей
волной. При х=0 имеет место минимум пап ряжения и максимум тока,
ж) Фидер нагружен на активное сопротивление, больше волнового
(рис. 4.1ж):
Р —-о /? — р р
'„.-^7. <" = 777,о<р<1.=-о.к_- .
Л ,---------------- — iarc tg ['—- tgmx)
= L^o /1 + p2+2pcos2rnjte U+p . (4.13)
7 7ла^ r . /14-Р . \
, Uq r-------------------- — I are tg !- Jg mr|
Ix—----- K1+ P2 — 2p cos 2mx e H““P /. (4.14)
На фидере образуется режим промежуточный между стоячей и бегущей
волной. При х—0 имеет место максимум напряжения и минимум тока.
з) Фидер нагружен на комплексное сопротивление с ёмкостной реактивной
составляющей (рис. 4.1 а):
г RA~' ха~?
и‘ RA— [ хл + ?
ZA-RA~iXA
т/ (*Л-Р)8 + *Л
V (*л+Р)2+^
,0 < р < 1.
При R>p
Ха ХА ХА X
<f = — arc tg--+ arc tg -—— - 2л — arc tg----+ arc tg -—— .
RA~ ? ял+р RA~f Ra+p
При R < p
XA XA
<f = = + arctg—--+ arctg———
?~ra R + P
В обоих случаях можно получить <р=л+ср', где <р/<л. Следовательно.
яал 5 5" 1Л Y <р' \ iarc tg Р— ig (тх— }1
Ux = 1/J 5 е 2 у I + Р2 — 2р cos 2 (rnx — — J е U+p I 2'_Ь
(4.15)
6* 83
2 Р 1 / / ф' \ terc ttf I tg!mx— £ у 1 + p*+2p cos 2 frnx — ^2/e P 2 • (4 16)
На фидере образуется режим промежуточный между стоячей и бегущей
волнами. Первые от нагрузки минимум напряжения и максимум тока попадают
1 ф' г. X
в точку х0 =-----~~ . Так как — < —, то .
tfl & & Ч
Коэффициент бегущей волны
}Л*а + р)8 +хгА-^А~ Р)8 + хгА
V (Ял + 084-^4- \/ (Ял-Р)8+*Г
и) Фидер нагружен на комплексное сопротивление с индуктивной реак-
тивной составляющей (рис. 4.1 о)
2л=Ял + **л .
1/(*л-Р)г + *л
F (*л+?)а+Хл
Ял + i Хл — р
Яд + i ^л + Р
0< р < I.
При R>p
ХА ХА
? = arc lg —-— arc tg ——-—
Яд - P Ял 4- p
При fl<p
xa XA
<t == it — arc tg--— — arc tg ——;-< я.
P-Ял Ял+р
Следовательно,
2 1Л 1+p«+2pcos2^mx---X
(4.18)
(4.19)
На фидере образуется режим промежуточный между стоячей и бегущей
волнами. Первые от нагрузки минимум напряжения д максимум тока, пола-
1 ср X ? к А
дают в точку —---------~Так как—'’ < — . то х0 <— ,
/71 Л ‘I L ii 4t
Коэффициент бегущей волны определяется по ф-ле (4.17).
В последних четырех случаях периодичность изменения напряжения н
тока с изменением координаты как по амплитуде, так и по фазе равна
84
Схема измерительной линии
На рис. 4.2 приведена схема измерительной линии.
Кривую изменения напряжённости электрического поля
(идентичную кривой распределения напряжения) снимают, пе-
ремещая индикаторную головку И вдоль фидера Ф, По этой
кривой, как отмечалось выше, может быть вычислено искомое
входное сопротивление нагрузки Z& .
На выходе генератора Г обязательно включается поглоти-
тель (аттенюатор) /7, который создаёт постоянную согласован-
Рис. 4.2. Схема измерительной линии
ную нагрузку для генератора и исключает влияние измеряе-
мого сопротивления на режим работы генератора. При отсут-
ствии поглотителя может возникнуть паразитная генерация, ис-
кажающая ход кривой распределения напряжения на измеритель-
ной линии.
Индикаторная головка И имеет элементы связи с проводами
фидера—зонды 3, детектор Д и стрелочный или электронный
прибор Q, показания которого пропорциональны напряжённости
электромагнитного поля в линии, как правило, в первой или вто-
рой степени. На рис. 4.2 изображена также масштабная линей-
ка, показывающая местоположение индикаторной головки на
фидере измерительной' линии.
Устройство измерительных линий
Общие замечания
Измерительные линии отличаются друг от друга устрой-
ством отрезков фидеров (длинных линий), индикаторных голо-
вок и способом перемещения индикаторных головок (ручное или
автоматическое от электродвигателя). ’
Некоторые виды измерительных линий приведены на рис. 4.3;
основные характеристики наиболее распространённых измери-
тельных линий, выпускаемых отечественной промышленностью,
даны в приложении 2.
83
Рис. 4.3. Измерительные . типа ИВЛ-1
UW4-10' в) типа ли ’ 7
у) типа ИЛ-Д; б) типа ^а 33-И
Фидеры измерительных линий J
На рис, 4,4 изображены поперечные сечения фидеров, иа
пользуемых в измерительных линиях, картина электрически]
(сплошные линии) н магнитных (пунктирная линия) СИЛ.0ВЫ1
линий, а также расположение зондов индикаторных головок, i
У полосковых фидеров возможно двоякое расположение зон!
дов: параллельно экранирующим пластинам (рис. 4,4в) и nepl
пендикулярно (рис, 4.4г). Оба вида расположения зонда могу!
иметь место как при круглом, так и при прямоугольном (пла1
стинчатом) внутреннем проводе. j
В соответствии с типом фидера измерительная линия назы<
вается: двухпроводной, коаксиальной, полосковой, волноводной
Применение того или иного типа измерительной линии зависит
от типа рабочего фидера, питающего антенну. .
На сантиметровых волнах питание антенны, как правило^
осуществляется полыми волноводами и при измерениях исподы
зуются волноводные измерительные линии. В тех случаях, когда
применяются полосковые линии, измерения целесообразно про,
изводить при помощи полосковой измерительной линии.
На дециметровых волнах применяются преимуществен нс
коаксиальные фидеры и соответственно коаксиальные измери-
тельные линии. Находят применение также полосковые измери-
тельные линии, которые на краях имеют коаксиальные переходы
и приспособлены для присоединения к коаксиальному фидеру.
На более длинных дециметровых волнах при лабораторные
исследованиях могут найти применение и двухпроводные изме-
рительные линии.
На волнах коротковолнового и отчасти метрового диапазо-
нов специальные измерительные линии не применяются. Распре^
деление напряжения снимается непосредственно на питающем
антенну рабочем фидере.
На рис. 4.Б показана конструкция фидеров, используемых г
измерительных линиях.
У двухпроводной измерительной линии провода фидера or
крыты, и зонды индикаторной головки имеют свободный доступ
к полю в фидере. У коаксиальной и волноводной измерительны^
линий фидер окружён металлической поверхностью. Для доступ
па зонда индикаторной головки к полю и возможности его nepej
мещения вдоль фидера на коаксиальном кабеле и на волноводе^
а иногда на экранирующей полоске прорезают щел!
(рис. 4.56, в, д)> .!
Для того чтобы максимально ослабить излучение через эт}|
щель, её прорезают вдоль линии внутренних токов и делают
кой. В коаксиальном фидере все линии токов продольны. В пря^
моугольном же волноводе картина поля соответствует волн^
TEqi и токи имеют как продольные, так к поперечные состав^
88
ляющие. Лишь на средней линии широкой стенки токи имеют'
продольное направление. Поэтому на волноводе щель делается
только вдоль средней линии широкой стенки.
Полосковый фидер аналогичен коаксиальному. В нем токи1
также продольны. Щель для ввода зонда в промежуток между
Рис. 4.4. Поперечные сечения фидероь-.
двухпроводного (а), коаксиального (б), полоскового с круглым внут-
ренним проводом (в), палоскоаого с прямоугольным (пластинчатым)
внутренним проводом (г), полого волновода (д)
89’
полосками может быть прорезана в любом месте на наружной
полоске (на рис. 4.4г показан лишь один из вариантов конструк-
ции).
Электромагнитное поле как в коаксиальном, так и в поло-
♦сковом фидерах имеет в каждом данном сечении потенциальный
Рис. 4.5. Отрезки фидеров, используемых в измерительных линиях:
а) двухпроводной, б) коаксиальной, в) полосковой с прямоугольным
внутренним проводом, г) полосковой с круглым внутренним проводом,
д) волноводной
характер и аналогично статическому полю. Поэтому методами
конформного преобразования они могут быть преобразованы
одно в другое. Проведя такое преобразование, можно показать,
что полосковый фидер при зазоре d и ширине полосок D
г90
(рис. 4.5г) эквивалентен коаксиальному фидеру с двусторонни-
ми зазорами шириной а радиан, где
На рис. 4.6 показан график зависимости а от—-, из которого
d
видно, что уже при — >4, а<0,02. Значение а = 0,02 соответ-
d
ствует щели шириной 1 мм при диаметре наружной трубы экви-
валентного коаксиального фидера 50 мм. Излучение столь узкой
щели на коаксиальном фидере сравнительно большого сечения
ничтожно.
91
Отмеченная эквивалентность полоскового и коаксиального
фидеров по статическому полю в поперечном сечении в значи-
тельной степени относится также к излучению через продоль-
ный зазор. Полосковый фидер даже при сравнительно большом
расстоянии между пластинами, но при соответствующем отно-
D
шении —по излучению эквивалентен коаксиальному фидеру
с очень узкой щелью. В этом отношении полосковый фидер обла-
дает известным преимуществом перед другими видами экрани-
рованных фидеров.
Длина щели на фидере измерительной линии делается не
меньше 1,5-ь2 длин волны, так как для получения достаточной
точности измерений требуется, чтобы снятая кривая напряжения
имела несколько минимумов и максимумов. У краёв фидера из-
мерительной линии должны быть регулярные (без щели) участки
длиной (1-М,5)Л, которые необходимы для сформирования ос-
новного типа волны в фидере, поскольку в точках включения эдс
и нагрузки имеются неоднородности, которые могут вызвать зна-
чительные локальные искажения поля. Таким образом, общая
длина фидера измерительной линии получается равной
(5-f6)A,. На длинных дециметровых, а также метровых волнах
поперечное сечение фидера имеет малые размеры по сравнению
с длиной волны. Поэтому сформирование основного типа волны
происходит на более коротком расстоянии от неоднородности,
что позволяет применять на этих волнах более короткие фидеры
измерительных линий.
Индика торные головки измерительных линий
На рис. 4,7 показаны три схемы индикаторной головки
двухпроводной измерительной линии. Они состоят из зондов 33
(рис. 4.7а) или рамок Р (одной — рис. 4.76, либо двух —
рис, 4.7в), имеющих слабую ёмкостную (зонды) или индуктив-
ную (рамки) связь с фидером, детектора Д, блокировочных дрос-
селей L6 , блокировочной ёмкости С6, прибора постоянного то-
ка Q, указателя У положения индикаторной головки по мас-
штабной линейке Л1. Чтобы детектор Д не был короткозамкнут
по постоянному току, в рамку последовательно включается ём-
кость Са. Все указанные элементы монтируются на изоляцион-
ной плате.
Для того чтобы расстояние между зондами 33 или рамками
Р и проводами фидера оставалось постоянным, индикаторную го-
ловку подвешивают на провода при помощи специальных крюч-
ков или ушек с желобами, прикреплённых к плате (рис. 4.8),
При помощи измерительной головки рис. 4,7а измеряется
распределение напряжения, а при помощи измерительных голо-
вок рис. 4,76 и а — распределение тока.
92
Для измерений на двухпроводных коротковолновых фидерах
применяется предложенный Г» 3. Айзенбергом [Л 13] измери-
тельный шлейф, представляющий собой четвертьволновую двух-
проводную фидерную линяю, присоединяемую с одного конца
Рис. 4.7. Схема индикаторных го*
ловок двухпроводной измеритель-
ной липки:
а) с ёмкостной связью, б) с по-
мощью одной рамки, в) с по
мощью дв>х рамок
металлическим контактом к рабочему фидеру, а с другого конца
замкнутую на амперметр. Схема, конструкция и способ подклю-
чения к фидеру измерительного шлейфа показаны па рис. 4.9.
На рис. 4.10 изображена общая схема индикаторных головок,
применяемых в коаксиальных, волноводных и полосковых из-
93
мерительных линиях. Как видно, индикаторная головка имеет
две цепи: зонда и детектора. Первая состоит из зонда и элемен-
тов настройки в резонанс (индуктивности и ёмкости или объём-
ные резонаторы) и электрически слабо связана с фидером изме-
рительной линии-
а)
Рис. 4.8. Индикаторная головка (а) двухпроводной измерительной линии (б)
( для лабораторных измерений
Цепь детектора непосредственной связи с фидером измери-
тельной линии не имеет и возбуждается от цепи зонда, с кото-
рой связана кондуктивно, индуктивно или ёмкостной связью.
Цепь детектора состоит из элемента связи, детектора и индика-
тора, Индикатором может быть прибор постоянного тока
94 у ;
г 1 ’ : у •
(микроамперметр), осциллограф с предварительным усилите*
лем и т. п.
Часто цепь детектора также содержит элементы настройки з
резонанс» <
а) О 6)
Рис. 4.9. Измерительный шлейф:
а) схема шлейфа, 6) измерение напряжения на фидере, в) измерение потен-
циала па отдельных проводах, г) конструктивное оформление измерительного*
шлейфа, д) схема измерений на четырёхпроводном фидере с помощью нзме-
. рительного шлейфа _ _ > .
Цепь зонда полностью экранирована. В цепи детектора
экранирован элемент связи, детектор и элементы настройки.
Индикатор (прибор), как правило, применяется выносной. К не-
му идёт экранированный провод. Открытые зажимы прибора
шунтируются ёмкостью, для того чтобы через них 'не было на-
водки внешних высокочастотных -помех в цепь детектора.
На рис. 4.11 приведены некоторые конкретные схемы индика-
торных головок. В индикаторной головке рис. 4Л1а в цепи зон-
да имеется резонансный контур из сосредоточенных постоянных
L и С. Цепь детектора связана с цепью зонда кондуктцвно. Вся
система настраивается в резонанс конденсатором. Регулиров-
ка чувствительности производится потенциометром в цепи по-
стоянного тока.
'На рис. 4.116, в, г, д показаны схемы индикаторных головок,
(Основывающиеся на применении коаксиальных резонаторов. Во
всех этих схемах предусматриваются три настройки. В схемах
рис. 4.116, г цепи зонда и детектора образуют самостоятельные
коаксиальные резонаторы, настраиваемые плунжером, причём в
одном случае (6) цепь детектора связана с цепью зонда кондук-
тивно, а в другом (г) — индуктивно. При автотрансформаторной
/кондуктивной) связи регулировка чувствительности (третья на-
цель зонда
Цель детектора
'Стенка фидера
Рис. 4.10. Схема индикаторных головок коаксиальных, по-
лосковых и волноводных измерительных линий
«стройка) может производиться изменением глубины погружения
зонда, или включением потенциометра в цепь постоянного тока,
либо введением расстройки в одну из цепей. При индуктивной
.связи наиболее целесообразным является регулировка чувстви-
тельности изменением связи. Оптимальным положением для лег-
ли является место пучности тока. Поэтому, как правило, петлю в
схеме рис. 4.11 г устанавливают непосредственно у поршня, а пе-
ремещение поршня используют для изменения связи. В схемах
рис. 4.118, д имеется лишь один коаксиальный резонатор в цепи
зонда. Детектор в обоих случаях кондуктивно связан с цепью
зонда, резонансной настройки не имеет, но его положение в ре-
зонаторе относительно точки пучности напряжения можно из-
менять.
Схема рис. 4.11в отличается от схемы рис. 4.116 тем, что в
первом случае резонатор образует одну прямоугольную коак-
сиальную полость, а во втором он состоит из двух полостей, за-
ключенных одна внутри другой и являющихся по электрической
схеме последовательно включёнными. Регулировать чувстви-
тельность в схемах рис. 4.118, д можно указанными выше спо-
собами, характерными для кондуктивной связи детектора и зон-
да, а также изменением положения детектора относительно пуч-
ности напряжения в резонаторе.
46
Рис. 4.1к Схемы индикаторных головок:
а) с резонансным контуром в цепи зондя, состоящим из индуктивности я ёмкости; б) с ре-
зонансными контурами в виде коаксиального резонатора как в цепи зонда, так и в це-
пи детектора при автотрансформаторной связи между этими контурами; в) с резонансным
контуром н кндс коаксиального резонатора лишь в цепи зонда; г) то >кс\ что на рис. б,
но при индуктивной связи между контурами зоила и детектора; д) то же, что па рис. в,
но резонатор выполнен из двух полостей, заключённых одна внутри другой; е) с круглым
волноводом в цепи чоцля, сечение которого значительно меньше критического; ж) с торои-
дальным резонатором в цепи зонда При индуктивной связи резонатора с зондом; з) то жек
что на рис. ж при ёмкостной связи резонатора с зондом; и) с резонансным контуром в
ниде волной одной резонансной полости
Схема индикаторной головки рис, 4.1соответствует случаю
передачи большой мощности по фидеру. Индикаторная головка
представляет собой круглый волновод (предельный), попереч-
ные размеры которого значительно меньше критических для вол-
ны низшего порядка. Волновод возбуждается с одного конца зон-
дом, в другом его конце помешается петля связи детектора. Из-
менением расстояния между зондом и петлёй детектора меняет-
ся связь и чувствительность прибора.
На рис. 4.1 Irw, з показаны схемы индикаторных головок, ос-
новывающиеся на применении тороидального резонатора в це-
пи зонда, соответственно для индуктивной и ёмкостной связи
зонда с резонатором. Цепь детектора, которая должна быть
замкнутой по постоянному току, имеет индуктивную связь с резо-
натором. Регулировка чувствительности может производиться
изменением связи, изменением глубины погружения зонда и т. и.
В индикаторной головке (рис. 4.11ц) как цепь зонда, так и
цепь детектора образуют реактивные штыри в прямоугольном
полом резонаторе, в котором возбуждается волна ТЕ^п. Оба
штыря имеют кондуктивный контакт в середине одной из широ-
ких продольных стенок резонатора (зонд — в верхней, цепь де-
тектора — в пижпеп) и проходят через отверстие в середине
противоположной стенки. Система имеет две или три настройки.
При трёх настройках обе торцовые стенки выполнены в виде
плунжеров, перемещение которых позволяет менять положение
зонда и детекторной цепи относительно пучности поля в резона-
торе. При двух настройках торцовая стенка у зонда делается
глухой. Резонатор состоит из двух частой, входящих одна в дру-
гую. Перемещением одной из них относительно другой можно ме-
нять объём резонатора и настраивать его в резонанс. Регулиров-
ку чувствительности целесообразно производить изменением по-
ложения детекторной цепи относительно пучности поля.
Применение той или иной схемы индикаторной головки зави-
сит в значительной степени от диапазона волн. Резонансный кон-
тур из ёмкостей и индуктивностей, а также тороидальный резо-
натор применяются на более длинных дециметровых волнах.
Коаксиальный и волноводный (полый) резонаторы целесообраз-
но применять на более коротких дециметровых волнах и на вол-
нах сантиметрового диапазона.
Размеры элементов 'фидера измерительной линии, а также
прямолинейность образующих фидер цилиндров должны быть
соблюдены с высокой степенью точности. Особо тщательно долж-
на быть сделана щель на фидере.
Крепление индикаторной головки на фидере, а также её пере-
мещение вдоль фидера должно 6ыте> выполнено так, чтобы зонд
оставался всё время строго в середине щели и чтобы с очень
большой точностью оставалась постоянной глубина погружения
зонда в фидер.
98
При расположении зонда индикаторной головки по схеме
рис. 4.4в он оказывается в очень слабом поле. Поэтому допу-
скается его погружение на значительную глубину. В индикатор-
ных головках таких измерительных линий, как правило, предус-
матривается возможность регулировки глубины погружения зон-
да оператором в процессе измерений.
При расположении зонда индикаторной головки соответствен-
но схемам рис. 4.46, а, д он оказывается в очень сильном поле.
Для обеспечения в этих условиях слабой связи зонд вводится в
фидер на небольшую глубину (порядка 5% расстояния до проти-
воположной проводящей поверхности). Следует учесть, что срав-
нительно небольшое увеличение глубины погружения зонда по
сравнению с указанной, резко увеличивает степень связи зонда и
фидера измерительной линии и может являться источником до-
полнительных ошибок измерения» Поэтому требуемая глубина
погружения зонда в ряде измерительных линий определяется при
отладке измерительной линии на заводе-изготовителе. В этих
случаях оператору не разрешается регулировать глубину погру-
жения зонда. Вопрос об ошибках измерения, вносимых зондом,
а также о влиянии глубины погружения зонда количественно
анализируется ниже.
Измерительные линии рассчитываются на возможность их
использования в некотором диапазоне воли. Диапазошюсть из-
мерительной линии определяется главным образом диапазоном
волн, в пределах которого возможна настройка в резонанс цепей
зонда и детектора индикаторной головки.
Детекторы измерительных линий
В качестве детекторов в схемах индикаторных головок
измерительных линий применяются главным образом полупро-
водниковые диоды, устройство которых показано на рис. 4,12.
Основным элементом, осуществляющим детектирование, яв-
ляется контактная пара, т. е. точечный контакт между кристал-
лом 5 (германиевым или кремниевым) и острым концом воль-
фрамовой пружинки 3 (иногда пружинка делается платино-ири-
диевой). Поддерживаются кристалл и пружинка соответствен-
но металлическими головками 1 и 2, которые между собой
скреплены керамическим цилиндром 4. В конструкции рис. 4.12а
кристалл поддерживается не непосредственно головкой У, а
винтом 6, ввинчиваемым в эту головку. Аналогично в конструк-
циях рис. 4.126, в пружинка поддерживается винтим 6, ввинчи-
ваемым в головку 2. Вращая винты, можно менять место кон-
такта пружины с кристаллом и подбирать его оптимальным.
В конструкциях рис. 4.12а и б в керамическом цилиндре
имеется отверстие 7, через которое полость цилиндра заливает-
7* 99
ся изоляционной массой (например, воском), стабилизирующей
контакт и предохраняющей контактную пару от попадания
влаги*
Головки детектора в несимметричных конструкциях (рис.
4.12а и б) имеют разные размеры, а в симметричной (рис* 4* 12а)
— одинаковые* Симметричные детекторы, как правило, имеют
малые общие размеры*
Для цепи высокой часто-
ты контактная пара может
быть заменена схемой
рис* 4*13, где R и С соответ-
ственно сопротивление и ём-
кость выпрямляющего слоя,
г — сопротивление растека-
ния в толще полупроводни-
ка* В диапазоне метровых и
примыкающих к ним деци-
метровых воли эта схема мо-
жет быть принята за схему
детектора в целом* На бо-
лее коротких дециметровых
волнах необходимо учиты-
вать индуктивность пружин-
ки и ёмкость между голов-
ками. При этом эквивалент-
ная схема детектора приоб-
ретает вид рис. 4.14. Для
стандартных детекторов
LK =3.9 а Сп =0,25пф.
На волнах короче 10 см го-
ловки детектора и пружин-
ка выступают как системы
из распределённых постоян-
ных и полная эквивалент-
ная схема детектора имеет
вид, показанный на рис. 4*15,
т* е4 вид 1 -образного четы-
рёхполюсника с сопротивле-
нием параллельной ветви Zc
и последовательной ветви
ZL, замкнутого на сопротивление точечного контакта Z.
Полярность напряжения, соответствующая большей прово-
димости показана на рис* 4.16.
Следует отметить, что полупроводниковые детекторы весьма
чувствительны к перегрузкам* Поскольку площадь контакта
очень мала, то уже при мощности в несколько эрг/сек, а у веко-
100
Рис. 4.12. Устройство кристалличе*
ских диодов:
а) несимметричного, с кристаллом,
поддерживаемым винтом; б) несим-
метричного с пружинкой, поддержи*
ваемой винтом; а) симметричного
торых детекторов даже при десятых долях эрг/сек, кристалл пе-
регревается и обгорает.
Кроме того, из-за нелинейности и непостоянства вольтампер-
ной характеристики детектора необходимо при точных измере-
Рис. 4.13. Эквивалентная схема кри-
сталлического диода для волн мет-
рового и дециметрового диапазонов
Рис. 4.14. Эквивалентная схе-
ма кристаллического диода для
воли сантиметрового диапазона
ниях периодически градуировать их; градуировка должна обя-
зательно проводиться также при изменении схемы и параметров
цепи детектора, например, при
смене прибора, включении шун-
тов и г д.
Градуировать детектор удобно
при помощи измерительной ли-
ния. Для этого ее ставят в ре-
жим короткого замыкания и
снимают распределение напряже-
ния вдоль фидера. Далее вы-
черчивают в определенном мас-
штабе кривую Ux=f(x) (подоб-
Рис. 4.16. Полярность напря-
жения, соответствующая боль-
шей проводимости
Рис, 4.15. Полная эквивалентная
схема кристаллического диода с
учётом распределённых парамет-
ров головок и пружинки
по кривой а, рис. 4.J7), где Vx — показания прибора Q, ах —
положение индикаторной головки па фидере измерительной ли-
нии. На этом же графике вычерчивают в любом масштабе кри-
101
вую sin tnx где m= — 1 так, чтобы она совпала с кривой а в
точках узлов напряжения (рис. 4.17). За начало отчёта х (х —0)
берут точку узла напряжения. Точки обеих кривых- соответст-
вуют друг другу» По этим кривым строят характеристику иссле-
дуемого детектора. Для это-
го вычерчивается график за-
висимости показаний х при-
бора Q от значений sin тх.
Масштаб для Q и sin тх вы-
бирается произвольно.
Пользоваться градуиро-
вочной кривой (характери-
стикой) детектора необхо-
димо если требуется полу-
чить достаточно точные экс-
Рис. 4.17. К построению градуировочной перименталъные данное. Од-
кривой детектора на ко на практике приходит-
ся производить поверочные
измерения, которые не требуют высокой точности. В этих случаях
для упрощения расчётов градуировочную кривую можно аппрок-
симировать степенной функцией
Q = Л|£/[\
(4.21)
где Q — показания прибора индикаторной головки,
U — напряжение на линии.
Если обозначить максимальные показания прибора индика-
торной головки через QM&Kr , а координату точки максимума
напряжения через хмакс, то
Q = A | U Г = Q.MaKC cos” т (х — хжвкс). (4.22)
Показатель степени п можно определить по эксперименталь-
ной кривой рис. 4.17. Проведём на рис. 4.17 хорду, соединяю-
щую точки Q— . Обозначим длину хорды через Дх. Точки
пересечения хорды и кривой удовлетворяют уравнению
Л х
= Q-маКС •
(4.23)
Из ур-ния (4.23)
следует
lg2
п=----------
lg cos у
(4.24)
102
Ax v'
Зависимость л от — дана на рис, 4.18. Из изложенного вы-
X. f
текаст простой способ определения показателя степени п. При
короткозамкнутом фидере измерительной линии определяют
максимальные показания прибора и координаты точек, лежащих
по разные стороны от пучности напряжения, в которых показания
прибора равны половине максималь-
ного. Зная расстояния между точка-
ми половинных показаний и длину
волны, можно по графику рис. 4.18
найти п.
В случае малых напряжений, при
которых обычно работают измери-
тельные линии, кристаллические де-
текторы имеют характеристику,
близкую к квадратичной (и —2).
Электрончо^вакуумные приборы при
малых напряжениях также имеют
нелинейную характеристику. Если
её выразить степенной функцией, то
показатель степени п будет равен
примерно 3/2.
Рис. 4.18. Кривая зависимости
показателя степени п градуиро-
Ах
вочной функции от “Г"
Индикаторные приборы измерительных линий
Измерительные линии снабжаются, как правило, микро-
амперметрами типа М-95 или М-91. Шкалы этих приборов име-
ют 100 делений с максимальной чувствительностью 10 мка на
всю шкалу или 0,1 мка на одно деление шкалы. Включением
шунтов типа РЧ чувствительность прибора может быть умень-
шена соответственно в 5, 10, 50, 100, 500, 1000 раз.
Реже встречаются стрелочные приборы со шкалой в
100—150 делений и с чувствительностью 100 мка на всю шкалу.
Точность измерения тока этими приборами составляет
±(1-И,5)%.
В измерительных линиях с автоматическим перемещением
индикаторной головки, как правило, имеется переключение с ав-
томатического привода на ручной. При включении ручного при-
вода используются указанные выше микроамперметры. При
включении автоматического привода в качестве индикаторного
прибора может быть использован осциллограф.
Механизм перемещения индикаторной головки
К механизму перемещения индикаторной головки
предъявляются следующие основные требования.
103
Должна иметься возможность грубого и плавного перемеще-
ния индикаторной головки. При плавном перемещении механизм
должен позволять изменять положение индикаторной головки па
десятые доли миллиметра в дециметровом диапазоне и на сотые
доли миллиметра в сантиметровом диапазоне. Соответственно
точность определения положения зоила должна составлять де-
сятые и сотые доли миллиметра. Ручки управления перемещением
lie должны иметь люфта. Зонд индикаторной головки должен
проходить по середине щели фидера й иметь постоянную глуби-
ну погружения.
Для удовлетворения перечисленных требований индикатор-
ная головка, как правило, прочно закрепляется на специальной
каретке, движение которой производится по весьма точно вы-
полненным прямолинейным направляющим. В каретке прикреп-
лены ролики на шарикоподгпипниках, которыми при помощи
пружин опа прижимается к направляющим. Благодаря этому
обеспечивается мягкое скольжение каретки по направляющим и
точно прямолинейное ее движение.
У измерительной линии ИВЛ-1 (см. рис. 4.3), индикаторная
головка которой построена по схеме рис. 4.11, в механизме пере-
мещения каретка не применяется. Здесь индикаторная головка
крепится к стальной трубе, имеющей диаметр, равный диаметру
наружной трубы цепи детектора, и образующей её продолже-
ние. Эта труба вставляется в шариковые подшипники специаль-
ного кронштейна, играющего роль направляющей.
Плавное перемещение индикаторной головки производится в
одних случаях фрикционным механизмом с замедляющей пере-
дачей, в других случаях — гайкой, закреплённой па каретке, и
проходящим через гайку вращающимся ходовым винтом, распо-
ложенным параллельно направляющим и прикрепленным к об-
щей станине с последними. Грубое перемещение производится
либо фрикционным механизмом без замедляющей передачи, ли-
бо вручную при отключённом механизме плавного перемещения.
Для автоматического (от электродвигателя) перемещения
индикаторной головки применяется система тайка—ходовой винт,
причём последний через систему шестерён соединяется с двига-
телем. В схеме включения двигателя предусматривается систе-
ма реверсирования, при помощи которой направление переме-
щения меняется автоматически на обратное при достижении ка-
реткой упора.
Методика определения входного сопротивления при помощи
измерительных линий
Для определения входного сопротивления нагрузки (ан-
тенны) требуется, как указывалось выше, снять кривую распре-
104
деления напряжения вдоль фидера измерительной линии, опре-
делить по снятой кривой коэффициент бегущей волны к и коор-
динату точки минимума напряжения х0, а затем произвести рас-
чёт по ф-ле (1,19) или по диаграммам сопротивлений.
На рис. 4.19 показан примерный вид данных измерений, По
оси абсцисс отложены координаты х положения индикаторной
головки на фидере измерительной линии, отмечаемые по мас-
штабной линейке, а по оси ординат — показания Q прибора ин-
дикаторной головки. Точками отмечены экспериментальные дан-
ные, соответствующие движению индикаторной головки в одну
сторону, кружками — в другую сторону. По данным измерения
на рис. 4.19 вычерчена зависимость Q от X-
По кривой рис. 4.20 определяется коэффициент бегущей волны
К = U , (4.25}
Щмакс)
где U (QMat(C ) и U ) — относительные значения напря-
жения в точках максимума и минимума, определяемые по гра-
дуировочной кривой детектора измерительной линии.
Для того чтобы найти точку Xq минимума напряжения, сле-
дует на графике распределения напряжения в области миниму-
ма провести несколько хорд, параллельных оси абсцисс (см.
рис, 4.19). Средние точки хорд дают координату х0. Если раз-
ным хордам соответствуют разные значения *о, то их усредняют.
Разброс данных может служить критерием точности измерений.
10&
При сравнительно малом к (к<0,25) не удаётся достаточно
точно снять всю кривую распределения напряжения из-за квад-
ратичной характеристики детектора, так как при этом мало
отношение . Действительно, если при таком малом к в точ-
О,макс
ке максимума стрелка прибора отклоняется на всю шкалу
(100—150 делений), то в точке минимума прибор покажет всего
несколько делений, что даст большую относительную ошибку.
Если в целях увеличения точности измерений увеличить QMUH,
то одновременно пропорционально возрастет QMaKC и стрелка
прибора в точке максимума напряжения уйдёт за шкалу.
Достаточно точную величину к в этих условиях можно по-
лучить разными способами. Некоторые из них основываются на
том, что для определения к пе обязательно иметь всю кривую
распределения напряжения от минимума до максимума, а до-
статочно знать лишь её участок. Поэтому ограничиваются сня-
тием небольшого участка кривой в области минимума (рис, 4.20)
или максимума (рис. 4.21), Затем на графике проводят несколько
хорд, параллельных оси абсцисс, и по длине хорды dL. а также
по значению Q, (точнее по соответствующему ему значению
Ui), на уровне которого проведена хорда, вычисляют к (здесь i
—помер хорды). Расчёт производят по формулам
dj
sm m —
K-_—r- 2-
1/ » di
у T^~~cos
имип z
(4*26)
JO6
в зависимости От того, производятся ли измерения в области
минимума или в области максимума напряжения. Здесь UMaH,
U яакс — относительные величины напряжения (определяемые по
градуировочной кривой детектора) соответственно в точках ми-
нимума или максимума напряжения.
При квадратичной характеристике детектора можно восполь-
зоваться непосредственно показаниями прибора Qt, Q-макс
индикаторной головки и по ним определить к:
di
sin т —
(4.28)
к =
2
— CDS2 til
или
1/ Qi , di
\ 7------ — cos2 m ——
У 2
K--------d;
sin m —
(4.29)
107
В тех случаях, когда показания Q прибора в точке мини-
мума малы даже в режиме наибольшей чувствительности, мож-
но определить коэффициент бегущей волны к по двум точкам
на кривой распределения напряжения в области минимума или
максимума (рис. 4.22). Если обозначить через di и di координа-
ты точек кривой относительно точки минимума, а через £71 и
U2 — напряжения, соответствующие этим точкам, то к будет
равен
Для большей точности расчет может быть повторен для
некоторых других точек кривой. Как показывается ниже, ошиб-
ка измерений, вносимая зондом, значительно меньше в обла-
сти минимума напряжения. Поэтому предпочтительнее измере-
ние производить в области минимума напряжения.
При поверочных измерениях, не требующих большой точ-
ности, можно вместо ф-лы (4,28) пользоваться более простой
формулой
(4.31)
где X — длина волны на фидере измерительной линии;
— ширина хорды, при которой показания прибора
индикаторной головки в два раза превышают ми-
нимальные
Рис. 4.22. К определению коэф-
фициента бегущей волны по
двум точкам
показания.
Формулу (4.31) легко получить
из (4.28), если принять, что харак-
теристика детектора квадратична и
если одновременно ввести следую-
щие аппроксимации:
(-^-Y--=2, (4.32)
sin m -у пг , (4.33)
1 — cos2m у- 0. (4.34)
В диапазоне дециметровых и сантиметровых волн измери-
тельная линия весьма часто отделяется от нагрузки (антенны)
Длинным фидером, имеющим повороты, сочленения и другие
элементы, затрудняющие определение электрической длины фи-
дера. В этих случаях измерения дают входное сопротивление
108
«сей антенно-фидерной системы в целом» Представление о вход-
ном сопротивлении антенны без фидера можно полупить сле-
дующим образом. Отсоединив антенну, закорачивают фидер в
точке его прежнего соединения с антенной или включают в эту
точку фидера активное сопротивление, меньшее его волнового
-сопротивления. Затем снимают распределение напряжения на
измерительной линии.
Если фидер однороден и искажения поля, вносимые пово-
ротами, сочленениями и другими элементами невелики, то мож-
но считать, что точка минимума напряжения на измерительной
линии отстоит от точки соединения фидера и антенны на рас-
стоянии целого числа полуволн, т. е. эти точки минимума напря-
жения можно принять за точки присоединения нагрузки (ан-
тенны) к измерительной линии.
Установка для автоматическом записи кривом распределения
напряжения
Для автоматической записи кривой распределения на-
пряжения на фидере измерительной линии находят применение
различные схемы. В схеме рис» 4.23 применяется измеритель-
Рис. 4.23. Схема установки для автоматической записи
кривой распределения напряжения, в которой применяется
фидер, изогнутый в полукольцо, и зонд, вращающийся по
полукольцу
109
ная линия, у которой фидер изогнут в полукольцо. По щели
фидера, проходящей также по полукольцу, перемещается зонд,
вращаемый электродвигателем Дв. В качестве индикатора ис-
пользуется осциллограф, на вертикальные отклоняющие пла-
стины которого подаётся напряжение, снимаемое с детектора Д.
Рис. 4.24. Схема установки
для автоматической записи,
кривой распределения на-
пряжения,. в которой приме-
няется волновод, изогнутый
по полукольцу, и вращаю-
щийся эксцентричный ди-
электрический диск
Горизонтальная развёртка осциллографа синхронизирована с
вращательным движением зонда. Для этой цели потенциометр
П, с которого снимается отклоняющее напряжение на горизон-
тальные пластины, вращается тем же двигателем, что и зонд.
В качестве отклоняющего напряжения может быть также ис-
пользована сеть переменного тока, питающего осциллограф. В
этом случае скорость вращения оси двигателя должна быть так-
же синхронизирована с горизонтальной развёрткой осцилло-
графа.
При наличии синхронизации на экране осциллографа получа-
ется неподвижное изображение, которое соответствует распреде-
лению напряжения вдоль оси фидера.
Такие автоматические измерительные линии с вращающим-
ся по полукольцу зондом могут быть построены и для волновод-
ных фидеров.
На рис. 4.24 показана схема волноводной автоматической
измерительной линии, построенная по иной принципиальной
схеме. Здесь зонд 3 остаётся неподвижным, а его положение от-
носительно узлов и пучностей напряжения на линии меняется
путём изменения фазовой скорости распространения волны по
вал поводу и смещения этих характерных точек относительно
зонда. Для этого волновод изогнут по дуге и на внутренней его
стенке прорезана щель, в которую вводится па разные глубины
вращающийся диэлектрический диск, имеющий эксцентричес-
кую форму. Для диска берётся диэлектрик, обладающий малы-
ми потерями и сравнительно небольшой диэлектрической про-
ницаемостью, порядка 2,5. На краях диск заостряется с темг
110
чтобы в полости волновода он не создавал резкого перехода от
воздуха к диэлектрику и не вызывал отражений от границы
воздух—диэлектрик. Синхронизируя вращение диска с раз-
вёрткой, можно получить и в данном случае неподвижное изо-
бражение на экране осциллографа.
Рис. 4.25. Схема установки для автоматической записи кривой
распределения напряжения, в которой применяется сжимаю-
щийся волновод с продольной щелью
Изменение фазовой скорости в волноводе можно получить,
меняя размер широкой стенки волновода. Для этого вырезается
продольная щель по средней линии обеих широких стенок, и
волновод сжимается. По этому принципу устраивается сжимае-
мая измерительная линия с неподвижным зондом, схема кото-
рой показана на рис. 4.25.
Заметим, что в схемах 4.24 и 4.25 одновременно с изменени-
ем фазовой скорости изменяется волновое сопротивление де>
формирующего участка волновода, что вносит ошибку в резуль-
таты измерений. Поэтому такого рода автоматические измери-
тельные линии нуждаются в предварительной градуировке.
Ошибки измерений при методе измерительных линий
Общие сведения
Согласно ур-нию (1.19) искомое сопротивление являет-
ся функцией параметров л и *о, определяемых при помощи из-
мерительной линии (нагрузка имеет координату .r = 0, xf-=—х0)
ZA = Ra Н- i ХА ~ р . (4.35)
№ sin'2 -j- cos2
Если к и _г0 измерены не точно и погрешность измерений со-
ставляет соответственно Д/с и Дх0, то точность определения ZA
jJaBiia
dZ, dZA
лгл^-^лк^^АХо. (4.36)
L/fV IAVq
ш
Из ур-ний (4,35) и (4.36) после разделения вещественной и
мнимой частей получаем:
Д RA со$* я?х0 — № sin2 mxQ Д к 2тс (1 — к2) sin 2mx0 Д х0
Яд № sin2 тх^ 4- cos2 гпх0 к к* sin3 тх^ -f- cos2 /пх0 Л ’^-37)
Д ж- 2№ Д к
—-------------------------------------+
*л (1 — л2) (л2 sin2 тх^ -у- cos2 тл0) л
। 4к (cos* ягх0 — K*sin2/nx0) Д х0 gg.
sfn 2тх0 (к2 sin2 mx0 + cos2 mx0) X '
Заметим, что ~ обычно очень малая величина, состав-
ляющая доли процента. Д*л Дх В ф-ле (4.37) для —— множитель при равен
р (4.39
причём в сечении, определяемом уравнением tgmx0= —, этот
j_
множитель имеет максимальное значение, равное 2 тс-------.
к
Поэтому при к = 0,5 максимальная ошибка в определении #л
вносимая неточностью измерения координаты минимума на-
пряжения, не превышает 1%.
В ф-ле (4.38) множитель при — имеет бесконечно боль-
А
X Л
шую величину при х0=п~, где п — целое число. Однако в
этих точках Хл=0. Таким образом, при малых величинах реак-
тивной составляющей её не удаётся измерить достаточно точно.
При больших величинах ХА точность её измерения зависит глав-
ным образом от точности определения к.
На точность измерения к влияют следующие факторы:
а) неточность отсчёта показаний индикаторного прибора,
б) наличие отражений в переходных устройствах (у коакси-
альных линий — в переходных фишках, у волноводных — в сое-
динительных фланцах),
в) неоднородности линии,
г) наличие отражений от зонда индикаторной головки.
Если обозначить через ДкЛ,Дк^,Д«4 и Дкг соответствующие
ошибки, вызываемые этими факторами, то суммарная ошибка
(квадратичная) будет равна
Д к = V (Д к«)г + (Д кб)а + (Л к.)2 + (Д к/. (4.40)'.
112
Неточность отсчета показаний индикаторного прибора
При квадратичной характеристике детектора коэффици-
ент бегущей волны выражается через показания прибора либо
по формуле
Qmokc *
либо по ф-лам (4.28), (4.29).
Относительная погрешность равна соответственно:
* Кд _ К 1 1 2 ’ ( &Q п {Quuh Окакс / (4.41)
Дк' _ 1 AQ Qua* (4-42) (4.42a)
или К к 2 ! 1 2 г QmUH Qi &Q Фмакг Qi QmOKC cos’ m. — 2 + — Qt di ‘ cos2 m — 2
Формулы (4.41), (4.42а) позволяют определить в каждом
конкретном случае целесообразность применения того или ино-
го метода измерения к.
Наличие отражений в переходных устройствах
Отражение от переходных устройств вызывает ошибку
в определении коэффициента отражения от измеряемого сопро-
тивления. Эта ошибка Др равна коэффициенту отражения от
переходного устройства. Так как коэффициент бегущей волны к
связан с коэффициентом отражения р соотношением
то
. Др । Др 2Др ^4ЛЗ)
К 1 + Р 1 — Р 1 — р2
Коэффициент отражения от переходных устройств Др опре-
деляют экспериментально следующим образом.
К измерительной линии присоединяют без дополнительных
переходов контрольную линию, представляющую собой корот-
козамкнутый при помощи плунжера отрезок длинной линии с
8-292 ИЗ
волновым сопротивлением, равным волновому сопротивлению
фидера измерительной линии. Перемещая плунжер контрольной
линии при помощи индикаторной головки, наблюдают за пере-
мещением точки минимума напряжения на фидере измеритель-
ной линии. При отсутствии отражений от переходных устройств
и равенстве волновых сопротивлений измерительной и конт-
рольной линий перемещение точки минимума напряжения рав-
но перемещению плунжера. При наличии отражений от пере-
ходных устройств перемещения различны, и по разности пере-
мещений можно определить Др.
Примем, что неоднородность, вызванная переходными уст-
ройствами, эквивалентна некоторой шунтирующей реактивно-
сти Контрольная линия также является реактивной нагруз-
кой. Когда длина контрольной линии равна целому числу поло-
вин длины волны в фидере “у) » т0 проводимость равна
бесконечности и шунтирующее действие переходных устройств
не проявляется. Наибольшее влияние на распределение напря-
жения на фидере измерительной линии переходных устройств
будет тогда, когда длина контрольной линии равна нечётному
числу четвертей длины волны в фидере [ (2л 4- 1)3*1 в этом
I 4 J
случае проводимость контрольной линии равна нулю и пере-
ходное устройство вызовет смещение узла напряжения на от-
резок 1Смещ> определяемый из условия
- (4.44)
р
При малой величине В можно заменить тангенс в левой
части (4.44) его аргументом. Тогда получим
-Г'«.« = !« ««)
?
Если вместо контрольной линии замкнуть фидер измери-
тельной линии на согласованную нагрузку, то коэффициент
отражения будет равен
1 ( 1 . . Л 2г.
И-------ч=---------------• <4'46>
Формулы (4.43) и (4.46) позволяют определить ошибку из-
мерения к, вызванную отражением от переходных устройств,
через максимальную разницу 1емеи( между перемещением
плунжера контрольной линии и перемещением индикаторной
головки измерительной линии.
IU
Неоднородность линии
Неоднородность линии вызывает. неравномерное рас-
пределение напряжения на фидере измерительной линии, т. е.
разные уровни максимумов и минимумов в различных частях
фидера. Влияние неоднородности линии также определяют экс-
периментально. Для этого снимают кривую распределения на-
пряжения на фидере измерительной линии в режиме короткого
замыкания. Неравномерность кривой при квадратичной харак-
теристике детектора определяют по формуле
А = „ gi ~ ад /4 474
V 2 а «1 'ф а2
где ой и аз — максимальные показания, наиболее отличающие-
ся друг от друга.
Ошибка в определении к равна
л U
(4.48)
Наличие отражений от зонда индикаторной головки
Зонды 3 (см. рис. 4.2), связывающие индикаторную го-
ловку с фидером измерительной линии, вызывают отражение
волн. Эти отражения различны в разных положениях зондов
относительно узла напряжения на фидере. Поскольку зонды пе-
ремещаются вдоль фидера измерительной линии, то снятая ими
кривая распределения напряжения отличается от истинной кри-
вой.
Напряжение и ток на проводах измерительной линии
(рис. 4.2) определяются ур-ниями (1.8). При отсутствии зон-
дов входное сопротивление линии в точке х равно
_ Ur _ 1 + Гу 9 е~'2тх
Z*~ Ir = Р 1 - e~i2mx
Если в точке х в линию параллельно включено сопротивле-
ние зондов Z3, то общее сопротивление в этой точке будет
7.7
z = . (4.50)
2X + Za
Приняв, что напряжение падающей волны не зависит
от нагрузки (это обеспечивается включением аттенюаторов),
»• 115
. (4.52)
из (4.49),
(4.53)
получим следующее выражение для напряжения U.'x уточке х,
учитывающее сопротивление зондов Z3
Ux = Ua0,ae'mx(l + Г) ,
где
Г Z Р — ZXZ3— ? (Zx ~F~ ^з) __Zx____Z3
~ Z+p" ZxZ,+ p(Zx + Z3)
Подставив в (4.51) значение Г из (4.52), а затем Zx
получаем
Г.' _ J ,пад \тх е~^тх
U х — ь'О “ -------------------- —
= __________и*_________
1+^(1 + ^.^)
где С/х — напряжение® точке х при отсутствии зондов [см. ф-лу
Г Ut— коэффициент отражения от нагрузки, т. е. отискомо-
го сопротивления в точке х=0.
Анализ выражения (4,53) приводит к следующим выводам,
1) Расхождение кривых Уя и U х зависит от коэффициен-
та отражения и от величины вносимого зондами сопротив-
ления Z3.
2) При Гу =0, т. е. при чисто бегущей волне значения
И'х и Ux отличаются друг от друга постоянным (не завися-
щим от х) множителем 1-|------— . Поэтому кривые Ux и Ux
2Z3
при /^=0 совпадают независимо от Z3. При малых значени-
ях р~ | Гу<| расхождение кривых невелико.
3) Расхождение кривых U'x и Ux тем меньше, чем больше
Z3
Р 4) При активном сопротивлении Z3 кривые U'x и Ux имеют
одинаковые точки минимума и максимума. Отличаются кривые
по коэффициенту бегущей волны. Ошибки, вносимые зондами,
выражаются в увеличении уровня минимумов и уменьшении
уровня максимумов, т. е. в увеличении коэффициента бегущей
волны.
116
(4-51)
Если обозначить измеренный коэффициент бегущей ’йЬлны
через к7, а действительный через к, то между ними имеет место
соотношение:
к' = к при — со, к/ rz 1 при Z3 — О*
(4.54)
5) При реактивном или комплексном сопротивлении Z3 име-
ет место как смещение узла напряжения, так и изменение коэф-
фициента бегущей волны у кривой U* по сравнению с кри-
вой U
6) Искажение кривой напряжения, вызванное сопротивле-
нием Z3 неравномерно. Наибольшее искажение имеет место в
области максимума напряжения, наименьшее — в области ми-
нимума. При малых коэффициентах бегущей волны возможно
получение большой точности даже при сравнительной большой
связи (малом Z3 ), если производить измерения в области мини-
мума напряжения.
Сопротивление Z3 зонда может быть измерено при помощи
второй измерительной линии следующим образом. Измеритель-
ную линию, сопротивление зонда которой должно быть изме-
рено, закрывают поршнем, и её зондом снимают кривую напря-
жения на фидере линии. Затем зонд устанавливают посреди-
не между двумя узлами напряжения, т. е. в пучности напряжения,
и цепь зонда настраивают в резонанс. Отрезок фидера измери-
тельной линии от поршня до пучности напряжения, где установ-
лен зонд, имеет бесконечно большое сопротивление, поэтому ре-
жим фидера определяется сопротивлением зонда, которое изме-
ряют при помощи второй измерительной линии.
Представление о величине Z3 можно получить, рассматривая
цепь зонда как резонансный штырь с переменной связью в со-
гласованном волноводе. Согласно [Л 14] коэффициент отражения
от зонда в фидере равен
Здесь — сопротивление излучения резонансного штыря,
— его сопротивление потерь,
117
причём
(4.56)
а /?Е в случае прямоугольного волновода с волной ТЕ01 равно
(4.57)
где г — радиус зонда.
о — проводимость;
а — размер широкой стенки волновода,
Ъ — размер узкой стенки волновода;
ношения сопротивления зонда к
волновому сопротивлению от глу-
бины погружения
= — tg—
д 2я X 2
Г — глубина погружения зон-
да,
/" — полная длина зонда.
Сопротивление зонда в ф-ле
(4.55) считается активным, так
как цепь зонда настраивается в
резонанс.
Зная коэффициент отражения
|Г| , вызванный зондом, и рас-
сматривая зонд как шунтирую-
щее фидер активное сопротивле-
ние R3, можно найти для Zx—p
(фидер согласован с нагрузкой)
= (4-58)
Подставляя |г| из (4.55), а
/?2 и соответственно из (4.56)
и (4.57), получим
(4.59)
На рис. 4.26 показаны графики зависимости — от глубины
р
Z' погружения зонда, рассчитанные по ф-ле (4.59) при значения®
остальных параметров, входящих в эту формулу, равных указав^
ным в табл. 4.1. . . ,
118 i
Таблица 4.1
Н«мер пп. см К см т, см X. см Г. см мл 0, м
1 7,2 3,4 0,01 10 >1.0 5,57-10’
2 2,3 1,2 0,01 3,2 >0,5 5,57*107
Соотношение между I" и /' взято, исходя из того, что зонд
имеет радиус г, указанный в табл. 4.1, лишь внутри фидера изме-
рительной линии и в щели, а дальше — в резонаторе — его ра-
диус резко увеличивается и достигает нескольких миллиметров.
Сопротивление потерь участка зонда, имеющего сравнительно
большой радиус, невелико. Поэтому в выражении (4.56) и после-
дующих можно учитывать, только тонкий участок зонда, кото-
рый превышает /' приблизительна на указанную в табл. 4.1 ве-
личину.
Значение о=5,57.107 соответствует меди.
5. РЕФЛЕКТОМЕТРЫ
Блок-схема рефлектометра
В результате работ по исследованию связанных длинных
линий [Л 1] А. А. Пистолькорс в 1939 г. предложил индикатор
отражённой волны. Дальнейшее усовершенствование этого ин-
дикатора завершилось созданием рефлектометра, предложен-
ного А. А. Пистолькорсом и М. С. Нейманом [Л 15].
Рефлектометр представляет собой прибор, включаемый в фи-
дерную линию (двухпроводную, коаксиальную, полосковую,
волноводную) и измеряющий модуль коэффициента отражения в
ней. По известному значению модуля коэффициента отражения
легко вычислить, пользуясь ф-лой (1-13), коэффициент бегущей
волны в фидерной линии. Используется рефлектометр, как пра-
вило, в качестве контрольного прибора в передающих фидерных
линиях.
В практике рефлектометры применяются также в качестве
измерителя мощности, передаваемой по фидеру. Прибор тако-
го типа был предложен Б. Г. Страусовым [Л44].
Рис. 5.1. Блок-схема рефлекто-
метра
правлении к передатчику.
На рис. 5,1 показана блок-схе-
ма рефлектометра. Он состоит из
двух идентичных частей, каждая
из которых содержит так назы-
ваемый направленный ответви-
тель НО, детекторно-усилитель-
ную схему Д и индикатор И.
Направленный ответвитель
представляет собой отрезок фи-
дерной линки, слабо связанный с
питающим антенну фидером Ф и
обладающий свойством реагиро-
вать лишь на волну одного на-
правления в фидере Ф\ прямую, распространяющуюся от пере-
датчика к антенне, или обратную, отражённую от антенны в на-
J20
Электромагнитные колебания, возбуждаемые в направленном
ответвителе, детектируются и усиливаются схемой Д, собранной
на полупроводниковых или вакуумных электронных приборах*
Выделяемый схемой Д сигнал фиксируется индикатором, по-
казания которого можно проградуировать, сделав их пропорцио-
нальными напряжению соответственно падающей или отражён-
ной волны.
Если один из направленных ответвителей (рис. 5,1) реагирует
на волну одного направления в питающем фидере Ф, а вто-
рой — на волну противоположного направления, то отношение
уровней сигналов их индикаторных устройств при соответствую-
щей градуировке даст модуль коэффициента отражения на фи-
дере Ф*
Наряду с рефлектометрами, у которых цепи отдельных на-
правленных ответвителей полностью самостоятельны, применя-
ются такие, у которых отдельные элементы двух цепей совме-
щены, Например, два направленных ответвителя могут быть
совмещены в одном отрезке фидерной линии или использовать-
ся один индикатор для двух цепей, причём он может быть пе-
реключаемым из одной цепи в другую для поочерёдного изме-
рения уровней их сигналов, а может быть включённым постоян-
но и фиксирующим отношение уровней сигналов. В последнем
случае блок-схема содержит специальный элемент, формирую-
щий напряжение, пропорциональное отношению уровней сиг-
налов, получаемых -в двух направленных ответвителях.
Встречаются различные типы направленных ответвителей,
отличающихся друг от друга типом питающего фидера (двух-
проводный, коаксиальный, полосковый, волноводный) и типом
фидера направленного ответвителя, а также видом связи меж-
ду фидерами и направленными ответвителями.
Основные характеристики направленных ответвителей
На практике каждый направленный ответвитель реагиру-
ет не только на волну прямого направления, но в большей или
меньшей степени и на волну противоположного направления.
Отошение уровня сигнала, получаемого на индикаторе при реак-
ции направленного ответвителя на волну заданного направле-
ния, к уровню сигнала, получаемого при его реакции на волну
противоположного направления, называется коэффициентом
направленности. Чем выше требования к точности измерений,
тем больше должен быть у ответвителя его коэффициент на-
правленности.
Направленный ответвитель связан, хотя и слабо, с рабо-
чим фидером. В результате некоторая доля мощности перехо-
дит из рабочего фидера в направленный ответвитель. Сте-
121
лень связи направленного ответвителя и рабочего фидера -оп-
ределяется отношением мощности, поступающей в направлен-
ный ответвитель, к мощности, переносимой по рабочему фи-
дёру в режиме бегущей волны. Это отношение называется пе-
реходным затуханием. Знать величину переходного затухания
необходимо для определения поступающей в направленный от-
ветвитель мощности, что, в свою очередь, необходимо для рас-
чёта детекторно-усилительной схемы и индикатора.
Направленный ответвитель шунтирует рабочий фидер й
вносит расстройку в режим бегущей волны. Поэтому его ха-
рактеризуют также коэффициентом бегущей волны
на участке рабочего фидера, к которому присоединён направ-
ленный ответвитель, при замыкании этого участка на согласован-
ную нагрузку.
Итак, основными характеристиками направленных ответви-
телей являются: коэффициент направленности, переходное за-
тухание и коэффициент бегущей волны.
Двухпроводный направленный ответвитель
Двухпроводный направленный ответвитель (рис. 52)
представляет собой отрезок двухпроводной линии длиной / с
волновым сопротивлением рг, располагаемый параллельно двух-
проводному рабочему фидеру Ф. С одной стороны (у зажимов
аа) ответвитель замкнут на активное сопротивление /? = р2, с дру-
гой (у зажимов бб) к нему присоединяется детекторно-усили-
тельная схема Д,
При режиме бегущей волны па фидере Ф и распростране-
нии волны слева направо ток в схеме Д (между зажимами бб)
равен нулю. При появлении на фидере Ф обратной (отражён-
ной) волны в схеме Д возникает ток, пропорциональный ампли-
туде обратной волны.
Поменяв местами сопротивление R и схему Д, можно полу-
чить ответвитель, не реагирующий на обратную волну и дающий
показания, пропорциональные прямой волне.
Для пояснения принципа действия двухпроводного направ-
ленного ответвителя (рис, 5.2) рассмотрим картину поля на
двухпроводном фидере в режиме бегущей волны, изображён-
ную на рис, 5.3а и б. Сплошные линии соответствуют электри-
ческим силовым линиям, пунктирные — магнитным силовым ли-
ниям. Магнитные векторы полей (рис* 5.3а и б) направлены в
противоположные стороны (при одинаковом направлении элек-
трического вектора). Это вызвано противоположным направ-
лением распространения бегущей волны, В обоих этих случаях
электромагнитное поле есть поле' плоской волны, распростра-
няющейся параллельно проводам фидера. Электрический Е а
122
магнитный Н векторы поля лежат в плоскости, перпендикуляр-
ной направлению распространения, и направлены примерно по
линиям биполярной системы координат. Соотношение между
величинами электрического и магнитного векторов в практиче-
ской системе единиц равно во всех точках
-| = 120«. (5.1)
Рис. 5.2. Схема двухпроводного направленного ответвителя
Фазы Е и Н совпадают. Картина поля на фидере перио-
дически (период равен X) повторяется. На рис. 5.3а и б изобра-
жена картина поля для фиксированного момента времени. С
течением времени эта картина перемещается по фидеру (воз-
душному) со скоростью с=3.108 м/сек.
В режиме стоячей волны (рис. 5.3s) система электрических
силовых линий смещена относительно системы магнитных си-
ловых линий на четверть волны. Обшая картина электромаг-
нитного поля неподвижна. Точки максимума (пучностей) элек-
трического поля £ совпадают с точками нулевого значения (уз-
лами) магнитного поля Н и наоборот. Во всех точках фаза Е
отличается от фазы Н на ~ .
Таким образом, каждому режиму работы фидера соответ-
ствует определённая каотина электромагнитного поля.
Внесём в поле два дополнительных провода, параллельных
проводам фидера. Под влиянием электромагнитного поля фи-
дера на дополнительных проводах индуцируются заряды и то-
ки, которые имеют своё вторичное электромагнитное поле, ис-
кажающее первичное поле Фидера (рис. 5.4). Легко видеть, что
у вторичного поля электрические силовые линии направлены
также, а магнитные — противоположно силовым линиям
первичного поля.
123
\"
*****
X JQOOC X
лос
х >ооде х
хюо&
И
• ••• хххх
Направление распростра-
нения бегущей Волны
ххххх " v ...• .
И
х хххх х
Рис. 5.3. Картина электрических (сплош-
ные линии) и магнитных (пунктирные
линии) силовых линий у двухпроводного
фидера:
а) при распространении бегущей волны
слева направо; б) при распространении
бегущей волны справа налево; в) при
стоячей волне
124
Рис. 5.4. Картина электрических и магнитных силовых линий при
наличии около фидерной линии дополнительных проводов:
а) расположенных на одной линии с основными проводами; б) рас-
положенных под линией основных проводов
125
- При режиме бегущей волны на фидере все элементы допол-
нительных проводов находятся под одновременным влияни-
ем и электрического и магнитного полей фидера, имеющих в
каждой точке одинаковые фазы и амплитуды, определяемые
соотношением (5.1). В результате в каждом элементе допол-
нительных проводов также возбуждается бегущая волна, имею-
щая направление распространения, противоположное направ-
лению распространения волны на фидере.
При режиме стоячей волны на фидере различные элементы
дополнительных проводов возбуждаются по-разному, Одни эле-
менты (около пучностей напряжения на фидере) находятся под
влиянием только электрического поля, другие (около пучностей
тока на фидере) — под влиянием только магнитного поля, а
третьи — и электрического и магнитного полей, но при сдвиге
фаз между полями в 90° и при различных соотношениях между
Ё и Н. отличающихся от (5.1). В результате во вторичных прово-
дах возбуждается распределение зарядов и токов, соответствую-
щее стоячей волне.
Замкнув рассматриваемые два дополнительных провода у
одного конца на сопротивление /?, у другого — на схему Д, как
показано на рис. 5.2, получим направленный ответвитель. Если
на фидере Ф (рис. 5.2) имеется бегущая волна, распространяю-
щаяся слева направо, то в ответвителе НО возникнет бегущая
волна, распространяющаяся справа налево. При /?=р2 энергия
этой волны поглотится в нагрузке, и в схеме Д тока не будет.
При /? #= р2 у зажимов аа возникает отражённая волна, которая
вызывает ток в схеме Д даже и при чисто бегущей волне в фи-
дере Ф. Если на фидере Ф имеется бегущая волна, распростра-
няющаяся справа налево, то сопротивление R, и сопротивление
схемы Д поменяются ролями.
Амплитуда напряжения на зажимах аа при распространении
волны на фидере слева направо или амплитуда напряжения на
зажимах бб при распространении волны на фидере справа на-
лево зависит, помимо режима работы фидера Ф и величин со-
противлений /?, р2, /?д (сопротивление схемы Д), также от сте-
пени связи направленного ответвителя и фидера. Степень свя-
зи, в свою очередь, определяется длиной I, диаметром проводов,
расстояниями между проводами.
Зависимость связи от длины I имеет сложный характер.
При связь увеличивается с увеличением I, а при — < I < —
связь уменьшается с увеличением Л причем при 2= — она рав-
на пулю.
Объясняется это тем, что направленный ответвитель рис. 5.2
является цепью с распределёнными по длине проводов источ-
никами эдс. Когда все источники имеют почти одинако-
12$
вые фазы и разность хода волн от отдельных источников до
зажимов аа составляет небольшую долю длины волны. Поэто-
му, чем этих источников больше, т. е, чем больше /, тем больше
напряжение на зажимах аа. При—фазы источников
эде весьма значительно меняются по длине проводов направ-
ленного ответвителя, причём отставание фаз источников про-
исходит по направлению распространения волны на фидере Ф.
Так как на направленном ответвителе волны распространяются
в обратную сторону, то напряжения на зажимах аа, создавае-
мые более далеко отстоящими участками направленного ответ-
вителя, имеют двойное отставание фазы. Поэтому любые две
л
точки, находящиеся на расстоянии — друг от друга, создают
4
нулевое напряжение на зажимах аа. В частности, проявляется
следующая закономерность: напряжение, создаваемое на участ-
ке длиной 1<— равно напряжению на участке длиной /'=——L
4 4
Подробный математический анализ работы направленного
ответвителя был выполнен А. А» Пистолькорсом, получившим
следующие зависимости тока /лна зажимах бб и тока 1R на за-
жимах аа оттока I ф* на фидере Ф в сечении 0:
1 + Гу. “ \ . ,
—------------Isin т I
— ГУ. fit '________
1 rv. R \
—-------— 1 cos ml
1 ~ Ги. ?tt '
(Хд + /?)cos ml+ I > Pol ) sln
д 1
(Яд + Я) cos
------- . (5.2)
sin ml
sin ml-\-
— 1
g60— ~ ’
(Яд + R) cos
sinmZ
---------- sin ml. (5.3)
g ) sin ml
г1 ♦ Яд
V
< Pl
где Ги — коэффициент отражения в точке х— 0 на фидере Ф,
£>д — входное сопротивление детекторно-усилительной
схемы,
— волновое сопротивление фидера Ф при отсутствии
направленного ответвителя
f#1= 2761g?U
(5.4>
127
ра«
(5.5)
Pi
— волновое сопротивление направленного ответвителя при
отсутствии фидера Ф:
PaS=2761g^>;
“22
— волновое сопротивление фидера Ф с учётом влияния на-
правленного ответвителя:
1 1 ^22 г - ^12
Р1- 276
(5.6)
Р«
< ^22
и—
“22
— волновое сопротивление направленного ответвителя с
учётом влияния фидера Ф:
1 * ^22 1гт2^12
lg — 1g ~г~ — ig2^—
р2 = 276 —>
(5.7)
Р12
^11
— взаимное волновое сопротивление фидера Ф и
теля:
ответви-
♦ ^11 Т ^22 . 2 ^12
Ig— Ig — — Ig2 —
о12—276—-------------£11 ;
а12
— волновое сопротивление связи:
рс — 276 1g
а12
(5.8)
(5.9)
Из ф-л (5.4) — (5.9) следует
Рл1Р« _ Рд2Р1 __ j
Р1«Рг
Коэффициент направленности D ответвителя, вида
согласно данному выше определению равен
(5.10)
рис. 5.2.,
° = т-=
‘д
cos
sin ml
Pc Pal Л
Pl 2
При /<^Х можно принять sin ml ~0, cosm/^sl. Тогда
4 1 4> R-^- 1 -Ь —
£) ~ PfP12_ р2
1 - R-^-
РсР12
(5.П)
А
Ра
(5.12)
Р«
128
Если одновременно /? = рг, то
D = сю.
(5ЛЗ)
/2
'Д Pai
Р ~ 1* —
'фЗ?«2
Уравнение (5.13) соответствует идеальному направленному
ответвителю.
Коэффициент передачи р равен
i . 1 + Ги, R\ . { 1 + ГД. йд)
—--------cosm/4- [ ----------+ —I
— Р» > ' 1— rUt 9ч. Pi '
R. \ ~
(Яд + Я) cos Ml-\- 1 Кд + Pai j
sin ml
£ sin2 ml
sin ml
(5.14)
ПриГа =0 (бегущая волна на фидере Ф) и /?=/?л=р*=рд2
Р= (“У- (5J5)
Можно показать [Л 16], что при режиме бегущей волны на
фидере Ф под влиянием рефлектометра на нём возникает отра-
жённая волна с коэффициентом отражения
р — (Р] ?ги) COS (Pi Pai) cos ml /g j g \
2?ai eiml + (pi - pel) cos ml 2?elelm'
Из (5.16) следует, что коэффициент бегущей волны направ-
ленного ответвителя равен
1 _(Р1~ Pai)CQS Ml
<5J7>
Так как — обычно очень малая величина, то коэффи-
2pfli
циент бегущей волны направленного ответвителя можно считать
равным 1.
Коаксиальные иаправлеяные ответвителя
На рис. 5.5 изображен один из типов коаксиальных на-
правленных ответвителей. Он представляет собой отрезок про-
вода длиной I, проложенный внутри рабочего коаксиального фи-
дера Ф на небольшом расстоянии от оболочки и замкнутый на
9—292 129
оболочку с одной стороны (у зажима а) через сопротивление
а с другой (у зажима б) — через детекторно-усилительную схе-
му. Провод вместе с оболочкой кабеля образует отрезок электри-
ческой экранированной фидерной линии, имеющей слабую связь
с рабочим концентрическим (коаксиальным) фидером Ф, кото-
рым является центральный провод и оболочка.
Рис. 5.5. Коаксиальный направленный ответвитель в виде
провода, проложенного внутри коаксиального фидера
По принципу действия этот направленный ответвитель иден-
тичен двухпроводному направленному ответвителю. Для него
справедливы ф-лы (5.11) — (5.16). Волновые сопротивления коак-
сиального ответвителя, если сохранить для них обозначения, при-
нятые для двухпроводного ответвителя, определяются следую-
щими приближёнными (в предположении /?0 и r2<d) выра-
жениями:
ра1=138 Ig^-,
Ptt2=1381g^^-,
'Л
, , R.
lg — lg--— -lg’-T
ft| = 138--r-i---d
lg r2/?0
. «L, $~d’
p2- 138—n-g
lgt
1e/?0. ^~dt
lg —lg
P1,= 138—b—
(5.18)
(5.19)
(5.20)
(5.21)
(5.22)
(5.23)
1 Л”
lg2 —
а
В d
’8^
Рс= 1381g
130
Принцип работы коаксиального направленного ответвителя вида рис. 5<5
может быть поясней также при помощи схемы рис. 5.61) На -этом рисуаке
провода 1 и 2 соответствуют жиле и оболочке коаксиального фидера,
лровод 3 — wanpaiBданному ответвителю, который замкнут на оболочку черев
сопротивления Z, и Z2. Провод 3 с сопротивлениями ZT и Z2 образует прово-
лочный виток, находящийся в магнитном поле тока /. Это ноле возбуждает
в нитке электродвижущую силу и круговой ток 1т, величина которого равна
Im = -^М! , (5.24)
” 2, + z, v
где М — коэффициент взаимной над унции.
Одновременно, находясь в электрическом поле фидера, провод 3 при ма-
лых по сравнению с длиной волны размерах приобретает потенциал того места,
где он расположен. Под влиянием этого потенциала через сопротивления Zj и
Z2 потекут токи /с[ и Аз2°аного направления, равные:
U Z,
/c'^L л+z/ (5 25)
i (а С Z^^j-Z^
и zt
fC2 ~ -j-----ТТ~ Т~^ ' <52в>
_1_ _£1£г_ Zj+Z,
1 (i) С Zj^Zg
где С — ёмкость провода 3 относительно провода А
Рис. 5.6. Эквивалентная
схема коаксиального на-
правленного ответвителя
вида рис. 5.5
При слабой связи направленного ответвителя с фидером—"Г/»
[(ОС
Поэтому с достаточной точностью можно принять:
А
i О) C(7Z2
^1 + ^2
(5.27)
/б2 =
io>C(7ZL
+ ^2
(5,28)
]) Эквивалентная схема, аналогичная схеме рис. 5.6, может служить и для
пояснения принципа работы двухпроводного направленного ответвителя малой
длины L
Э* 131
Полные токи через сопротивления Zi и Z2 равны соответственно:
Гг = let + “ 7- +М1У (5.29)
“Г
/г = 1С2 - Гт = -у'гТ" ^CUZl ~ МГ>’ <5-30)
, I ^2
В соответствии с задачей направленного ответвителя ток должен рав-
няться нулю при наличии на фидере бегущей волны, распространяющейся
слева направо. В режиме бегущей волны во всех точках фидера удовлетво-
ряется соотношение
U
Тя=р’
(5.31)
поатому для удовлетворения условия /з^= О требуется следующее соотношение
между параметрами схемы:
М U
CZt ~ I ~9'
(5.32)
Из (5.29) и (5.32) следует
/1
Zi +
(5.33)
Таким образом, подбором сопротивления Z{ можно добиться отсутствия
тока в сопротивлении Z2 независимо от величины последнего при наличии на
фидере бегущей волны, распространяющейся слева направо. Очевидно, что
при бегущей волне на фидере, распространяющейся справа налево, можно
подбором сопротивления Z2 добиться равенства нулю тока в сопротивлении Zr.
На рис. 5.7 показан направленный ответвитель, представляю-
щий собой отрезок коаксиального фидера с волновым сопротив-
лением р2, связанный с рабочим фидером круглым отверстием и
замкнутый с одной стороны на согласованную нагрузку /? = р2,
а с другой — на детекторно-усилительную схему Д, Ось направ-
ленного ответвителя образует острый угол ф с осью рабочего
фидера.
На рис. 5.8 показана картина электрических и Л!агнитаьгх си
левых линий в фидере при режиме бегущей волны и в направлен-
ном ответвителе при возбуждении его через круглое отверстие.
Как видно, направление электрических силовых линий сохра-
няется в направленном ответвителе таким же, как в фидере, а
магнитных силовых линий—меняется на противоположное. По-
этому следует ожидать, что при бегущей волне на фидере в от-
ветвителе также возбудится бегущая волна, ио противополож-
ного направления. Однако связь через круглое- отверстие харак-
132
теризуется тем, что магнитные силовые линии проникают через
него интенсивнее, чем электрические, и степень связи получается
различной по электрическому и магнитному полям. Когда ось
Рис. 5.7, Коаксиальный
направленный ответви*
тель в виде отрезка ко-
аксиальной линии, свя-
занный с рабочим филе*
ром круглым отверстием
ответвителя параллельна оси фидера, магнитная связь сильнее
электрической.
Для того чтобы ослабить магнитную связь и выравнять ее
с электрической, ответвитель поворачивают на угол ср относи-
тельпо фидера. Возможность регулировки связи по магнитному
полю объясняется тем, что в коаксиальных линиях распростра-
няется поперечная электромагнитная волна ТЕМ, у которой элек-
трическое поле радиально, а магнитное направлено по концен-
трическим окружностям с центром по оси линии. При малом
диаметре отверстия, когда можно пренебречь разностью фаз
полей на его краях, электрическое поле симметрично относитель-
но центра ответвителя как в фидере, так и в ответвителе. Поэ-
тому связь по электрическому полю не зависит от угла <р. Сило-
вые линии магнитного поля фидера лежат в плоскости его по-
перечного сечения и поэтому находятся в ответвителе под углом
Ф к поперечному сечению. Так как волна ТЕМ возбуждается
лишь поперечной составляющей магнитного июля то степень
связи по магнитному полю пропорциональна cos ср и может
быть уменьшена до величины связи по электрическому полю.
133
а)
.Ответвитель
ИМИИНШУД—
11111ИМНИ1Ь||;1;|||||
иммаиив'иииа»
'Фидер
Рис 5.8. Картина электри-
ческих и магнитных сило-
вых линий в коаксиальном
фидере, связанном с нап-
равленным ответвителем
круглым отверстием:
а) в продольном сечении;
б) в поперечном сечении;
в) компенсация отражён-
ной волны, вызванная от-
верстием, с помощью вин-
тов
В работе [Л 17] Бете показал, что при диаметрах отверстия
d< — и при бесконечно малой толщине перегородки между ко-
8
аксиальными линиями оптимальным углом, при котором коэф-
фициент направленности теоретически равен бесконечности, яв-
Ри-с. 5-9. График зависимости переходного з ату ха
ния направленного ответвителя вида рис, 5.7 от от-
ношения диаметра d отверстия к длине волны.
Сплошная кривая соответствует скомпенсирован-
ному винтами ответвителю, пунктирная — леском-
пев-си ров айном у
ное затухание (—50 дб и меньше). Для того чтобы увеличить
переходное затухание, следует увеличить диаметр отверстия
связи,. Но при этом резко уменьшается коэффициент направлен-
ности, а угол ф, соответствующий максимальному значению ко-
эффициента направленности, становится отличным от 60°. Объя-
сняется это тем, что вблизи больших отверстий возникают вол-
ны высших порядков, которые эквивалентны индуктивностям,
включаемым последовательно в линии. Они могут быть скомпен-
сированы ёмкостными винтами, включёнными напротив отвер-
стия как в фидер, так и в ответвитель.
Рисунки 5.9—5,11 иллюстрируют работу направленного от-
ветвителя с большим отверстием связи и влияние настройки при
помощи ёмкостных винтов. При компенсации винтами одновре-
менно ослабляется влияние отверстия на коэффициент бегущей
волны в рабочем фидере. Измерения проводились с коаксиаль-
ным фидером, имеющим внутренний диаметр 22 мм и диаметр
отверстия 28 мм, Диаметр ёмкостных винтов 6,3 мм.
135
Рис. 5.10. Графики зависимости а} уг-
ла оптимальной направленности у опт
а 6} коэффициента направленности D
направленного ответвителя вида
рис. 5.7 от глубины погружения
согласующих винтов
Рис. 5.11. График зависимости а) уг-
ла максим альной направленности и
и б) коэффициента направленности D
направленного ответвителя вида
рис. 5.7 от длины волны
136
Полосковые направленные ответвители
Полосковый фидер, как указывалось в предыдущей гла-
ве, эквивалентен коаксиальному фидеру. Поэтому полосковый
направленный ответвитель может быть выполнен по схемам,
аналогичным схемам рис. 5.5 и 5.7,
Рис. 5.12. Полосковый направленный ответвитель
Однако наиболее удобным оказался так называемый шлейф-
ный ответвитель (рис. 5.12), представляющий собой отрезок по-
лосковой линии, связанный с рабочим фидером шунтирующими
ветвями (шлейфами). Шлейфы раслола!аюгся на расстоянии —
друг от друга, их длина, как правило, также делается равной
137
Изменением длины шлейфов и их волнового сопротивления
можно регулировать степень связи и переходное затухание.
Число шлейфов может быть разным, обычно два или три, и
ответвители называют соответственно двухшлейфными или
трёхшлейфными,
В многошлейфных ответвителях шлейфы имеют разное пере-
ходное затухание. Соотношение величин переходного затухания
таково, что амплитуды волн, возбуждаемых отдельными шлеп-
фами в ответвителе пропорциональны биноминальным коэффи-
циентам. У двухшлейфного ответвителя оба шлейфа одинаковы,
у трёхшлейфного амплитуды волн относятся как 1:2:1, у че-
тырёхшлейфного — как 1 : 3 : 3 : 1 и т. д,
Для объяснения принципа действия многошлейфного направ-
ленного ответвителя рассмотрим ответвитель, изображённый на
рис. 5.12.
Пусть шлейф 1 возбуждает в ответвителе волны
Е\ = Е„<Г}т* (5.34)
к
Через Е' и Е" здесь и в последующих формулах обозначены
волны, распространяющиеся соответственно в сторону положи-
тельных и отрицательных значений х.
Поля волн, возбуждаемых шлейфами 2 и 3 в ответвителе,
равны соответственно:
Е’2 = 2£0e,m(l-SHW
Е’ — Е
g* elm(x-2S)—2imS
(5.35)
где S — расстояние между двумя соседними шлейфами.
Суммарное поле, возбуждаемое всеми шлейфами, равно:
£' -Е\ + Е2 + £• = £в(1 + 2 +1) = £0(1 + 1)2е—imt,
£" = £;+£;+£; = е;( i + 2e-2I,ns + e-Hms) =
= £oebnx(l + e~2lmS )’•
(5.36
138
При S = -j-
a“21«S к _
e == e
E” =0
(5.37)
Аналогично легко показать, что если связь ответвителя с фи-
дером осуществляется n-шлейфами и если амплитуды волн, воз-
буждаемых шлейфами, пропорциональны биноминальным коэф-
фициентам, то поле в направлении, совпадающем с направлен
нием распространения волны на фидере, равно
Е'~ЕВ^1, (5.38)
а в противоположном направлении
Е" = Et (1 + e21mS, (5.39)
причём, при $= —,Е"=0.
4
Таким образом, при шлейфной связи в отличие от рассмот-
ренных выше видов связи, в ответвителе возбуждается волна,
распространяющаяся в том же направлении, что в фидере. Су-
щественное отличие шлейфной связи заключается в том, что она
зависит от длины волны. Поэтому характеристики направленно-
го ответвителя являются функцией частоты.
Коэффициент направленности ответвителя приближённо мо-
жет быть найден по формуле
(5.40)
где п — число шлейфов;
/о — расчётная частота, для которой S —
f— фактическая частота,
П - г А
Переходное затухание при шлейфах длиной < = — , равно
К Р /
(5.41)
где р^ —волновое сопротивление фидера,
р — волновое сопротивление среднего шлейфа.
Заметим, что шлейфный ответвитель по существу является
мостовым устройством с переменным переходным затуханием,
аналогичным типу рис. 3.7.
139
Волноводные направленные ответвители
В волноводных направленных ответвителях могут при-
меняться виды связи фидера с ответвителем, аналогичные
описанным для коаксиальных и полосковых линий. На рис. 5.13
Рис 5.13. Волноводный направленный ответвитель с круглый
отверстием связи на широкой стенке
показана связь волноводов через круглое отверстие, аналогич-
ная связи коаксиальных линий через круглое отверстие (рис. 5.7).
а на рис. 5.14 — шлейфная связь, аналогичная шлейфной связи
Фидер
Рис. 5.14. Волноводный направленный ответвитель с шлейф-
ной связью
полосковых линий (рис. 5.12). 1Иожет использоваться также на-
правленный ответвитель в виде петли (рис. 5.15), аналогичный
направленному ответвителю рис. 5.5.
У прямоугольного волновода связь через круглое отверстие
в широкой стенке отличается по своему характеру от связи че-
рез круглое отверстие в узкой стенке. В первом случае
140
(рис. 5.13) имеет место связь как по электрическому, так и по
магнитному полю, аналогичная изображённой на рис. 5.8. Во
втором случае (рис. 5.16) существует связь только по магнит -
Рис. 5Л 5. Направленный ответвитель в виде петли
в волноводе
ному полю, поскольку у узкой стенки волновода электрическое
поле равно нулю. Поэтому в первом случае требуется одно от-
верстие (при соответствующем повороте волноводов друг отно-
сительно друга) для получения в ответвителе волны одного на-
правления (обратного волне на фидере), во втором же случае
одно отверстие возбуждает в ответвителе две волны, распрост-
раняющиеся от ответвителя в противоположные стороны, и для
получения волны одного направления требуется два или боль-
шее число отверстий, расположенных друг от друга на расстоя-
-
нии четверти волны в волноводе —.
Принцип действия двухщелевого или многощелевого волно-
водного направленного ответвителя вида рис. 5.16 аналогичен
принципу действия шлейф-
ного направленного ответ-
вителя. Волны, возбуж-
даемые ответвителями в
направлении, совпадаю-
щем с направлением рас-
пространения волны в фи-
дёре, имеют одинаковые
фазы, и в этом направле-
нии их поля складывают-
ся, а волны обратного
Рис. 5.16. Волноводный направлен-
ный ответвитель с двумя круглыми
отверстиями связи на узкой стенке
направленйя имеют про-
тивоположные фазы, и их поля, интерферируя, ослабляются.
Если степень связи для отдельных отверстий сделать пропор-
циональной биноминальным коэффициентам, то обратная волна
будет отсутствовать, и ответвитель будет напра!вленньш.
Связь волноводного фильтра с направленным ответвителем
может осуществляться через узкие щели.
Одиночная узкая щель вызывает в ответвителе две волны,
распространяющиеся от щели в противоположные стороны. Для
получения в ответвителе волны одного направления требуется
141
Рис. 5.17, Волноводный
направленный ответви-
тель с двумя щелями
связи на узкой стенке
V
Рис, 5.18. Волноводный направ-
ленный ответвитель с двумя
щелями связи, расположенный
своей широкой стенкой на уз-
кой стенке фидера
две или большее число щелей (рис. 5.17 и 5.18) длиной пример-
но— , расположенных на расстоянии —— друг от друга, либо
4 4
одна длинная щель (рис. 5J9).
Волноводный направленный ответвитель может быть полу-
чен также при связи через две щели, расположенные на широ-
кой стенке под углом 90° друг к другу (рис. 5.20) и имеющие об-
щую среднюю точку. Каждая из щелей возбуждает в ответви-
теле, как отмечалось выше, две волны, распространяющиеся в
разные стороны от щели. Однако волны, возбуждаемые про-
Рис. 5.19. Волноводный направленный ответвитель с длинной щелью
связи
дольной щелью, имеют на одинаковом расстоянии от щели оди-
наковые фазы в то время, как волны, возбуждаемые поперечной
щелью, имеют противоположные фазы [Л18]. Поэтому, если
средние точки поперечной и продольной щелей совмещены, а ам-
плитуды излучаемых ими волн одинаковы, то эти волны в ответ-
вителе будут в одном направлении (совпадающем с направлс-
142
нием распространения волны в фидере) складываться, а в про-
тивоположном направлении уничтожаться, т. е. в ответвителе
возбудится волна одного направления, совпадающего с направ-
лением волны в фидере.
Чтобы амплитуды волн обеих щелей были одинаковыми, се-
редина щелей должна помещаться в точках, где продольная
и поперечная составляющие магнитного поля равны. Эти точки
находятся на линии, отстоящей от края волновода обычно на
о
расстоянии примерно —, где а — размер широкой стенки вол-
4
новода
Рис. 5.20. Схема волноводного
направленного ответвителя с
крестообразной щелью
Рис. 5,2]. Волноводный направлен-
ный ответвитель с двумя кресто-
образными щелями
Рассматриваемые волноводные направленные ответвители
изготовляются, как правило, в виде отдельных волноводных сек-
ций. Фидер и ответвитель удобно располагать перпендикулярно*
друг к другу, как показ ано на рис. 5.20 [Л .46], Направление волн
в фидере и ответвителе в этом случае показано стрелками,
Для увеличения направленности и широкополосности, часто
применяется связь через две пары щелей (рис. 5.21).
Характеристики направленных ответвителей рассчитываются1
по следующим формулам.
В случае связи через одиночное круглое отверстие на широ-
кой стенке волновода (рис, 5.13) равенство связи по магнитному
Точнее. — на расстоянии of, определяемом из уравнения
. л d
а
14$
и электрическому полям имеет место при угле 0 между осями вол-
новодов, определяемом из условия
cos0-— (1* 1- Fg(0 , (5.41)
2 U / FH (0 '
где Хф — длина волны в волноводе;
Л — длина волны в свободном пространстве;
Fe—ослабление связи по электрическому полю, вызывае-
мое толщиной стенки
FH— ослабление связи по магнитному полю, вызываемое
толщиной стенки t.
Причём:
1
1
При удовлетворении условия (5.41) переходное затухание
nr \2
-----COS 0 г„
н
(5.44)
а коэффициент направленности
2
cos 8 -+
(5.45)
cos 0 — —-
2
При связи через два круглых отверстия, расположенных на
расстоянии -Ь? (рис. 5.16), переходное затухание
4
ИТГП. (5.46)
Коэффициент направленности
(Д ml)2 *
(5.47)
где Л ml— отклонение расстояния между отверстиями от
4
При связи через две щели с совмещёнными средними точка-
ми, расположенные под углом 90% переходное затухание
где 2Z — длина щели,
2U7 — ширина щели.
Две взаимно-перпендикулярные щели с общей средней точкой
могут располагаться под острым углом к оси волновода. Харак-
теристики направленного ответвителя не зависят от угла пово-
рота щелей и определяются ф-лами (5,48 )и (5,49). На рис. 5.22
показано расположение щелей под углом 45Л
10—272
6. СМЕШАННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
ВХОДНОГО СОПРОТИВЛЕНИЯ
Введение
Измерение входного сопротивления при помощи измери-
тельных линий требует длительных операций; при помощи же
рефлектометров искомый параметр определяется непосредствен-
но по прибору. Кроме того, измерительные линии весьма гро-
моздки, особенно в диапазоне дециметровых'и метровых волн,
в то время как рефлектометры компактны независимо от дли-
ны волны, что позволяет включать их в фидер в качестве посто-
янного контрольного прибора. Однако измерительные линии
позволяют полнее характеризовать режим работы фидера.
Из-за недостатков этих методов на практике нашли примене-
ние другие методы измерений характеристик режима работы
фидера, не уступающие рефлектометрам по простоте устройст-
ва, компактности и оперативности, а измерительным линиям —
по полноте характеристики режима. Они в той или иной степе-
ни используют элементы первых двух методов и поэтому назы-
ваются смешанными.
Метод трёх зондов
При этом методе применяются неподвижные ответвители,
связанные с фидером зондами подобно индикаторным головкам
измерительных линий. Зонды могут располагаться на произволь-
ных расстояниях друг от друга. Однако наиболее целесообраз-
но помещать их через промежутки, равные л/8 (рис. 6.1). Для
однозначного определения входного сопротивления достаточно
иметь три ответвителя, четвёртый рекомендуется в качестве
контрольного. Применение четвёртого зонда позволяет не толь-
ко производить контрольное измерение, но одновременно спо-
собствует компенсации расстройки, вносимой зондами, посколь-
ку расстройки, вносимые двумя нагрузками, включёнными в фи-
дер через четверть волны, взаимно компенсируются.
146
Обозначим напряжения в точках А, В, С, D (рис. 6.1) соот-
ветственно через UB, Uc, Uо. Согласно (4.7) между эти-
ми напряжениями существуют соотношения:
А~~
cos 135°
V2a
2
2 о
(6.1)
где ZD=/?+iZ— сопротивление фидера в точке D.
Рис. 6.1. К методу трёх
зондов
Так как индикаторы ответвителей при их градуировке пока-
зывают модуль напряжения, то из (6.1) получаем:
КР ’
Up
_ V R2 + X*
Р
ил! _ у к*+(?-%*) . V2
UB\ р 2
(6-2)
Для однозначного определения R и X достаточно двух урав-
нений из системы (6.2), третье служит для контроля точности
измерений.
Ю* 147
Из (6.2) следует:
X
Р
7?
р
(6.3)
или
X
Р
2
Л
(6Л)
Величины— и — можно определить, пользуясь диаграм-
Р Р
мой рис. 1.2. Для этого на ней следует провести одну окружность
R X
радиуса kd с центром в точке — — 0, —= 0 и вторую окруж-
— р р х
ность радиуса У 2 кА с центром в точке — — 0, — =1. Точка
пересечения этих окружностей даст значение Z;j. Для контрола
можно провести ещё третью окружность радиуса у 2 кс с цент"
ром в точке— = 0,— ——1. Все три окружности должны пе-
Р р
ресечься в одной точке. Контрольное измерение диктуется необ-
ходимостью градуировки детектора. Если предположить, чго
характеристика детектора степенная, то показатель степени
можно определить из условия пересечения указанных трёх ок-
ружностей в одной точке.
Заметим, что две окружности, вообще говоря, пересекаются
в двух точках. Но поскольку в нашем случае отсутствуют отри-
цательные значения /?, то в действительности во всех случаях
вычерчивать требуется не полные окружности, а полуокружно-
сти, пересечение которых произойдёт лишь в одной точке, и ZD
определится однозначно.
На рис. 6.2 приведена прямоугольная диаграмма сопротив-
лений с нанесёнными на вей семействами кривых кбв^ const,
const и kd-const, которая позволяет сразу определять ко-
эффициент бегущей волны на фидере и находить сопротивления
любых других точек фидера.
148
X
Рис. 6.2, Номограмма для определения входного сопротивления по методу
трёх зондов
149
Если расстояние между ответвителями отличается от—» то
8
- X
расчетные формулы, связывающие искомые параметры—и —
Р Р
с умеренными напряжениями UA, Vв, Uc, U3 значительно
усложняются. Обозначив расстояние между двумя соседними от-
ветвителями через I, будем иметь в общем случае:
UА = UD (cos 3ml + i sin 3ml
U£ = Up (cos2mf 4- i sin 2m/
Uc = UD (cos ml + i —sin ml
U \
Из (6.5) получим
к| (R® 4- X2) = R2 cos®3 ml 4- (X cos 3m/ 4- p s in 3m/)4
«1 (R2 + X®) = R® cos4 2m/ 4- (X cos 2m/ 4- p sin 2m/)4
к, (R® 4- X4) — R2 cos® ml 4- (X cos ml 4- p sin ml)2
где:
«i~
Ks-
K3 —
(6.5)
(6.6)
(6.6a)
(6.66)
(6.6b)
Uc
«D
Ub
Uj
va
UD
Откуда
X sin® 2ml [ — cos43m/] — sin4 3m/ f — cos4 2tnl j
P sin 6m/ [ — cos4 2ml1 — sin 4m/ (ж® — cos® 3m/|
sin2 2m/ Ky — cos4 ml ]— sin4 ml [ «j — cos4 2m/]
sin 2m/ [ *2 — cos4 2m/j — sin 4т/(к® — cos2 m/]
(—V—---------J-------Г cos 3т/ 4- sin 3m/Y —
X P / —COS*3fttf L X P / ,
— к2 —1 =---------1----cos 2m/4-p sin 2т1\* — к2 =
3P’J — cos4 2mi L \ P / P1!
=----------f f— cos ml 4- s in ml V — к? — 1. (6.
к^— cos4 ml Lx P / P J
150
Если пользоваться прямоугольной диаграммой сопротивле-
ний (рис. 1.2), то и при /¥=-— для определения величин ~ и
X ?
---- нужно провести три окружности и найти точки их пересе-
р
чения. В данном случае радиусы окружностей равны
, sin iml
к?----------,
— cos2 iml
а координаты центров равны
R _ д и X _ sin 2t ml
Р Р 2 (к? — cos21ml |
где i — целое число, равное 1,2 или 3, одинаковое у величины к
и под знаком тригонометрической функции.
Зная сопротивление (его активную R и реактивную X со-
ставляющие) в сечении D, легко найти, пользуясь данными пер-
вой главы, сопротивления в любой другой точке фидера.
Таким образом, при помощи трёх (по принципу действия)
или четырёх (практически) неподвижных ответвителей, идентич-
ных зонду индикаторной головки измерительной линии, получа-
ется тот же результат, что и при помощи измерительной линии
с подвижным зондом.
Импедометр Парцена
Импедометр Парцена представляет собой рефлектометр,
дополненный двумя ответвителями с зондами, аналогичными ин-
дикаторной головке измерительной линии.
Рефлектометр состоит из двух направленных ответвителей,
из которых один позволяет измерять напряжение Unad падающей
волны, другой — напряжение Uomp отражённой волны. Дополним
систему из двух направленных ответвителей третьим, ненаправ-
ленным (зондом), измеряющим полное напряжение U на фидере.
Эти три напряжения позволяют составить следующие равенства:
(jwp
упад
jl +pe1Ti = yrl + pa+2pcostp]=:|-^
(6-9)
(6.10)
151
Решая совместно ур-ния (6.9) и (6.10), получаем
ф — arc cos
упад
уотр
упад
(б. 11)
Уравнение (6.9) определяет модуль коэффициента отражения
р, а ур-ние (6.11) —его фазу ф. Однако по ур-пию (6.11) можно
3otfB 1
[ненаправленный отВетЗитель}
Рис. 6.3. Схема импедо-
метра Парнена
U [2
ипа^ I
ЗОНдЬ
вычислить лишь величину фазы, знак её остаётся неизвестным.
Для определения знака фазы применяется второй зонд, располо-
женный на расстоянии I от первого (рис. 6.3). Обозначим через
U\ напряжение, измеряемое зондом /, через lh — напряжение,
измеряемое зондом 2, а через ф — фазу коэффициента отражения
у зонда А Тогда:
|1+ре”’| = К 1+ P2 + 2pcos<p |, (6.12)
= V\+f? + ZpcM(4-2mt) = | . (6.13)
Определив ф сначала из ур-ния (6.12) или, что то же самое, из
ур-ния (6,11) при замене в последнем V на Uit можно затем но
ур-нию (6.13) проконтролировать как величину, так и знак ф.
Можно определить знак фазы ф и иным способом. Располо-
жим зонды 1 и 2 в одном сечении фидера (рис. 6.4), причём для
зонда 2 обеспечим возможность изменения глубины его погруже-
ния в фидер. Порядок измерений следующий. Сначала зонд 2
выводят и измеряют Unad, Uomp и при помощи двух направ-
ленных ответвителей и зонда 1. Затем зонд 2 вводят и измеряют
U2. Так как зонд 2 находится в одном сечении с зондом Л то это
измерение является лишь контрольным. Однако введение в фи-
152
дер зонда 2 эквивалентно включению дополнительной шунти-
рующей ёмкости, что позволяет определить знак ф по характе-
ру изменения величины ф. Уменьшение величины ф будет ука-
зывать на положительный знак <р, а увеличение — на отрица-
тельный*
Рис. 6.4. Схема импедомет-
ра Парцсна с двумя зонда-
ми, находящимися в одним
сечении
Вращающийся направленный ответвитель
Усовершенствование метода, изложенного в предыдущем
параграфе, заключается в применении вращающегося направ-
ленного ответвителя в виде витка, эквивалентная схема которо-
го показана на рис* 5.6,
У такого направленного ответвителя ток I в сопротивлении
Zr есть сумма токов ёмкостного и индуктивного. При расположе-
нии провода 3 (см* рис. 5.6) параллельно оси фидера ток Ц оп-
ределяется ф-лой (5.29). Если повернуть провод 5 на угол а от-
носительно оси фидера, то
Л =----(Ct/Z2 + Мо! cos а), (6,14)
А + А
где /Ио — коэффициент взаимоиндукции при параллельном рас-
положении провода 3 относительно оси фидера;
U и / — соответственно напряжение и ток на фидере*
Преобразуем (6.14) к виду
Л = ^4 (С‘/_ + z?C°S“) = Л(Сг + mcosa)> (бл5>
где А, С и т— величины, не зависящие от угла а;
Z= + i X— искомое входное сопротивление фидера в том се-
чении, в котором находится направленный ответ-
витель*
153:
Чтобы ф-ла (6.15) могла служить для определения Z, необ-
ходимо знать С и М или их отношение. Находят их следующим
образом. Рабочий фидер нагружают на согласованную нагруз-
ку. Тогда сопротивление Z будет равно р. Элементы же направ-
ленного ответвителя С, Л4 и Z2 подбирают такими, чтобы мини-
мум Л (теоретически нулевое значение) имел место при каком-то
угле о, отличном как от 0, так и от 90°. Вращая направленный
ответвитель, находим этот угол ао. Для него справедливо ра-
венство
Со 4- mcosao = 0. (6.16)
Если почленно разделить (645) на величины Ср и /rccostxo,
равные согласно (6.16) друг другу, но противоположные по зна-
ку, то
= -----—Y (6.17)
\ р cos л0 /
Формула (6.17) удобна тем, что первое слагаемое в скобках
есть нормированное значение искомого сопротивления, а вто-
рое — известная вещественная величина.
Для определения р фидера требуется измерить /г при не-
скольких углах а.
Рекомендуется сначала найти угол аЛЙЯ, при котором ток
имеет минимальное значение. Минимум тока имеет место при
& __ C0S Д ЧЦП (g
р COS а0
И
Затем можно произвести измерение при <х=90°. Ток | Л U*
при этом равен
I 11900 131 р • (6.20)
Из ур-ний (6.18) — (6,20) следует
X_____j / ^мин /с о 1 х
р * COSa, V I, ~ % ‘ '
г ’ ° О “JtUK
Для контроля могут быть сделаны дополнительные измере-
ния, например, при a=ao и а=180°+ао. В этих точках токи со-
ответственно равны:
(6.22^
154
Отношение —L_L^—
| Л !180° + a.
о R X
жения. Значения — и —
р р
= р есть модуль коэффициента отра-
могут быть найдены по данным изме-
нений графически следующим построением (рис. 6.5).
Рис, 6.5. Графическое построение для определения
входного сопротивления при измерении методом вра-
щающегося направленного ответвителя
R X
На ординате прямоугольной системы координат —> —
Р Р
(рис. 1.3) откладывается отрезок ОЕ равный в определённом
масштабе току |Л|алик, и через точку Е проводится горизон-
тальная линия EF (показана иа рис. 6.5 пунктиром). Затем ра-
диусами, равными в том же масштабе |/1|90о» |Л|а И
проводятся дуги MN, M'N\ MnN" и через точки пересечения
луг с прямой EF проводятся из начала координат О прямые.
Очевидно, что отрезки ОЕ, EG, EG^ EG2 должны быть пропор-
X J? 7? 7?
циональны соответственно -—,----------f- 1, — —L Так как из
Л Р Р р Р
ф-лы (6.18) величина — известна, то откладываем на оси аб-
Р к
сцисс отрезок ОА, равный —, и из точки А проводим верти-
Р
кальную линию до пересечения с прямой ОР в точке В, Через
точку В проводим горизонтальную прямую. Отрезки этой пря-
мой СВ, CDf и CD равны соответственно — 1 и——1, а
X Р Р Р
отрезок ОС на оси ординат равен —. Отрезки BD и BDT долж-
Р
яы быть равны между собой.
Приведённые выше данные измерений, а также построение,
сделанное на рис. 6.5, не позволяют определить знак X. Для оп-
ределения знака X в фидер вводится ёмкостный зонд аналогично
155
тому, как это делается в импедометре Парцена. Если X имеет
отрицательный знак, то прямая DD} опустится вниз.
На рис. 6.6 показан вариант конструкции вращающегося на-
правленного ответвителя.
Рис. 6.6. Конструкция вращающегося направленного ответвителя
Достоинством вращающегося направленного ответвителя яв-
ляется использование одного детектора, что должно обеспечить
большую точность, недостатком — трудность измерения боль-
ших. —, так как при этом угол ао должен быть близок к 90°,
р
что, в свою очередь, обеспечивается большим значением или
малой величиной Z2.
р
При значениях—- <1 целесообразно настроить систему так»
чтобы ао^30°.
156
Тройниковый измерительный ответвитель
коак-
сопротивлением р. Одна
с ВОЛНОВЫМ
Рис> 6.7. Схема тройникового измери-
тельного ответвителя
ТройниковЪ1й ответвитель (рис» 6.7) состоит из трёх оди-
накового сечения взаимно-перпендикулярных отрезков
спальной фидерной линии
ветвь (/) тройника дли-
ной 19 замкнута на эта-
лонное сопротивление
другая (2) длиной 1а —
на искомое сопротивление
2а > а третья (3) произ-
вольной длины присоеди-
нена к источнику электро-
магнитных колебаний.
У точки 0 разветвле-
ния отрезков помещена
небольшая вращающаяся
петля, причём ось враще-
ния и ось симметрии пет-
ли совладают с осью вет-
ви 3, присоединённой к
эдс, а плоскость петли
.перпендикулярна плоско-
сти, образованной осями
ветвей / и 2. Под влия-
нием магнитного поля
около точки 0 токов и
в петле возбуждается электродвижущая сила е, которая фик-
сируется с помощью схемы, аналогичной цепи детектора в ин-
дикаторной головке измерительной линии. По аналогии будем
и в данном случае эту схему называть цепью детектора. При
строго симметричном расположении петли относительно оси вет-
ви 3 ток в последней не будет вызывать эдс в петле.
Если обозначить через а угол между осью ветви 1 и пло-
скостью петли, а через М коэффициент взаимоиндукции между
петлей и проводами-ответвителя, то эдс в петле будет равна
1аг текущих в ветвях тройника / и Z
е = i(oM (ZjCOsa + IА sin a).
Между токами и имеет место соотношение
!а _ Zsa
(6.23)
(6-24)
где Z^o и ZAo— входные сопротивления ветвей 1 и 2 в точке 0.
157
Величина Z & связана с заданными величинами Z, и 13, со-
гласно (1.16) и (1.7), соотношением
. । Z»— Р ~2ип1э
Z = = р 1 + Л е-2|от'э _ + Z.+ p =
*° '3 1-Гэе-2ЬЧ j 4.-Р €~г^э
Z»+ Р
__ Z9 cos mla Ц- j р sin ш/у 25V
P cos ml3 Ц- i Za sin ml3
где Ula и lэ — напряжение и ток в точке 0 разветвления в
ветви 1;
Гэ — коэффициент отражения в ветви / в точке под-
ключения нагрузки Z3.
Учитывая (6.24), приводим (6.23) к виду
е = i о Л/Л f cosasin а.А . (6.26>
\ Лзо /
Измерив е при нескольких углах а, можно по данным изме-
рений найти ZM, а затем ZA по формуле
„ ZM cos ml. — i Р sin ml.
Z. ~ p —------*----1---(6.27>
P cos mlA — i ZM s;n mlA
или по диаграмме сопротивлений.
Наиболее удобно на дециметровых волнах использовать из-
мерительный ответвитель при Z, = О (короткозамкнутая линия)
и 1Я = , где п—0, 1, 2, 3. При таких значениях Z3 и 1а
Za0=±io. (6.28>
Знак плюс соответствует чётным значениям п, а знак ми-
нус — нечётным.
Подставив (6.28) в (6.26), получаем
е — iw44/,^cosa+i-y-sina^. (6.29)
Из сравнения (6.29) с (1.10) видно, что зависимость е от a
аналогична зависимости U х от тх. При этом одному полному
повороту петли (изменению а от 0 до 360°) соответствует переме-
щение индикаторной головки вдоль длинной линии на отрезок,
равный длине волны.
2 л 1 -1
Таким образом, в случае Z^=0 и :— X сопротивление
ZAQ может быть определено по кривой зависимости е от а ана-
8
логично определению ZA при помощи измерительной линии по
кривым зависимости Ux или 1Х от тх.
Следует заметить, что, поскольку кривая зависимости е от се
снимается при вращении петли, тройниковый измерительный от-
ветвитель очень удобен для автоматической записи этой кривой
на экране электронной трубки.
По принципу работы длина 1Э ветви 1 должна равняться не-
чётному числу восьмых долей длины волны. Однако ввиду иска-
жения поля в точке 0 разветвления и около поршня, замыкаю-
щего ветвь, не представляется возможным достаточно точно оп-
ределить расчётным путём необходимое положение поршня. Эк-
спериментально требуемое положение поршня может быть най-
дено, если ветвь 2 замкнуть на согласованную нагрузку ZА=р, а
затем добиться, чтобы е не менялось с изменением угла а. Так
как положение поршня зависит от частоты колебаний, то для
возможности использования тройникового измерительного ответ-
вителя в диапазоне частот следует предусмотреть микрометри-
ческое перемещение поршня с точной шкалой отсчёта его поло-
жения. Экспериментальную регулировку положения поршня сле-
дует провести во всём диапазоне частот предполагаемой работы
измерительного ответвителя и по данным эксперимента соста-
вить градуировочную кривую.
На волнах метрового диапазона условие —-— Л может
привести к сравнительно большой длине ветви Л Поэтому в дан-
ном случае можно ограничиться отрезками небольшой длины,
замкнутыми на переменную ёмкость или индуктивность.
Градуировка ёмкости или индуктивности производится так
же, как градуировка положения поршня, по признаку независи-
мости е от а при согласованной нагрузке в ветви 2.
Электродвижущая сила в петле будет наводиться не только
магнитным полем, но и электрическим. Зависимость электро-
движущей силы, наводимой электрическим полем, от угла а оп-
ределяется функцией, отличной от (6.23). Чтобы исключить влия-
ние электрического поля, петля должна экранироваться, т. е. из-
готовляться по принципу экранированных рамочных антенн. На
рис. 6.8 показано схематически выполнение экранировки.
Косинусоидальная и синусоидальная зависимости е от а бу-
дут иметь место лишь при однородном магнитнОхМ поле у точки
разветвления. Однако из-за указанного выше искажения поля на-
рушается его однородность, что приводит к ошибкам. Компенса-
ция искажений может быть произведена введением дополнитель-
ной стационарной замкнутой петли, плоскость которой совпа-
дает с плоскостью осей ветвей 1 и 2 и средняя линия которой
проходит по биссектрисе угла между осями этих ветвей
(рис. 6.9). Следует предусмотреть возможность регулировки глу-
159
’бины погружения этой петли в ответвитель. Для определения оп-
тимальной глубины погружения стационарной петли, соответст-
вующей наибольшей компенсации ошибки, возникающей за счёт
искажения поля, проводится регулировка положения поршня в
ветви / при согласованной ветви 2. Компенсации ошибки соог-
Рис. 6.8. Экранировка петли трой-
никового направленного ответви-
теля
Рис. 6.9. Дополнительная пеня
для компенсации искажений,
вызываемых рабочей петлёй
ветствует получение независимости е от а. Дополнительная про-
верка компенсации ошибки может быть проведена после отрегу-
лирования глубины погружения поршня при короткозамкнутой
или разомкнутой ветви 2. Компенсации ошибки соответствует ко-
синусоидальная или синусоидальная зависимость е от а.
ТрЪйниковый измерительный ответвитель с короткозамкнутой
или замкнутой на реактивное сопротивление ветвью / обладает
тем недостатком, что нуждается в экспериментальной регули-
ровке положения поршня или величины реактивности, которая
должна производиться предварительно в широком диапазоне ча-
стот или в каждом отдельном случае на частоте измерения, по-
скольку как положение поршня, так и величина реактивности
являются функциями частоты. В этом отношении преимуществом
обладает измерительный ответвитель, нагруженнелй па согласо-
ванное сопротивление. Подставив в (6.26) Z^o — р, получим в
данном случае
е ~ i coAlZ^cos а sin а) . (5.30)
Для определения Z ло достаточно произвести измерения е при
трёх углах, например он = 45°, аг —90°, аз=135°. Получаемые при*
этом значения будут равны: ?
160’ -
_i«W9 (l + z^0)
Z^O
г|353 = 1 <ш/вКЦ-1 + -^)
Из (6.31) следует:
*45° _ У 2 yf (^ло + р)2 + Хдо
^90° 2 F рг
с135* _ ]/2~ , / (*ло Р)2 + *до
^90° 2 F р2
(6.31)
(6,32)
Выражение (6.32) представляет собой систему из двух урав-
нений с двумя неизвестными R Ао и Хло. Как видно, Хлоиз (6.32)
может быть найдено только по величине, но не по знаку. Это яв-
ляется недостатком измерительного ответвителя с активным
эталонным сопротивлением. Для определения знака требуется
нагрузить ветвь 2 на реактивное сопротивление или сделать её
короткозамкнутой в соответствии с изложенным выше. Следует,
однако, иметь в виду, что для определения знака реактивной со-
ставляющей сопротивления Z ло нет надобности точно отрегули-
ровать положение поршня или величины реактивности, замы-
кающей ветвь 1. Для этого достаточно лишь знать знак и
квадрант, в котором находится точка минимума кривой зависи-
мости е от а. По этим данным знак реактивной составляющей
Ило может быть определён в соответствии с изложенными в чет-
вёртой главе соображениями о зависимости положения узлов на-
пряжения и тока на длинной линии от знака реактивной состав-
ляющей сопротивления нагрузки.
Таким образом, целесообразным является следующий поря-
док измерений входного сопротивления нагрузки при помощи
тройникового измерительного ответвителя, замкнутого на согла-
сованное (активное) эталонное сопротивление. Сначала ветвь 1
замыкается на согласованное сопротивление и в результате трёх
измерений (возможны дополнительные контрольные измерения)
определяется /?ло и |ХЛ0| . Затем ветвь 1 размыкается или замы-
кается накоротко и определяется квадрант, в котором находится
минимум значения е. Знак реактивной составляющей находится
по табл. 6.L
11—292 161
Таблица 6J
Ветвь 1 короткозамкнута Ветвь 1 разомкнута
h < Л : 4 К ,<: 2 G < X 4 А T<f X
а < 90° 90°<я< <180° а < 90° а > 90° 3 < 0 з > 90° а < 90° а > 90°
4- При каждые длине в четверг етви 1, ( ь волны. 4“ большей При дл - i + 1 X —, знаки че] ине ветви, кратн + эедуютс? . X ои —, I i через эеактив-
ная составляющая равна нулю.
Измерительный ответвитель с согласованным эталонным со-
противлением может быть использован для определения коэффи-
циента отражения в ветви 2, т. е. в качестве рефлектометра. Из
(6.31) следует
*135° _ | ZAJ) ~~ р |
*45° I ZA0 + ? |
(6.33)
где р — модуль коэффициента отражения.
Использование измерительного ответвителя в качестве реф-
лектометра возможно в двух вариантах: с одиночной вращаю-
щейся петлёй и выполнением двух измерений при а = 45° и а=
— 135°; с двумя неподвижными петлями, расположенными под
углами 45° и 135° к ветви L
Недостатком рефлектометра, построенного на базе измери-
тельного ответвителя с согласованным эталонным сопротивле-
нием» является то, что он может быть установлен не в любом ме-
сте работающего фидера, а лишь на прямоугольном повороте,
причём он требует резкого поворота фидера, в то время как
обычно, в целях сохранения согласования, повороты фидеров
делаются плавными. Кроме того, применение активного эталон-
ного сопротивления является причиной потерь примерно поло*
вины мощности. Поэтому такой направленный ответвитель неце-
лесообразно иметь постоянно включённым в рабочий фидер.
Однако представляется целесообразным устройство разъёма на
прямоугольном повороте фидера с возможностью замены участ-
ка наружной оболочки фидера рефлектометром, построенным по
принципу измерительного ответвителя с активным эталонным со*
противлением для его кратковременного включения на период
измерений.
162
7. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ФИДЕРНЫХ
ЛИНИЙ
Измерение коэффициента укорочения коаксиального кабеля
В коаксиальных фидерных линиях применяются изоля-
торы, закрепляющие внутренний провод относительно наружно-
го так, чтобы оси этих проводов совпали, В связи с наличием
изоляторов фазовая скорость иф распространения волны в фи-
дере отличается от скорости в вакууме (г=3- 10fi м/сек). Про-
порционально изменению фазовой скорости изменяется длина
волны в кабеле. Отношение длины волны в вакууме к длине вол-
ны в кабеле называется коэффициентом укорочения. Обозначим
его буквой п.
Знать коэффициент укорочения фидера необходимо для пра-
вильного определения длин отрезков фидера сложной антенной
системы, обеспечивающих требуемую фазировку её элементов,
и отрезков фидера, служащих четвертьволновыми трансформа-
торами, симметрирующими элементами и т. п. Кроме того, для
вычисления других параметров фидера по данным измерений
также требуется знание коэффициента укорочения.
Во многих случаях коэффициент укорочения рассчитывает-
ся. Например, при сплошном заполнении пространства между
проводами фидера изоляционным материалом фазовая скорость
волны будет
= <7-1)
где s' — относительная диэлектрическая проницаемость изо-
ляции.
В этом случае коэффициент укорочения равен Vг'. Сложнее
рассчитать коэффициент укорочения для кабеля, имеющего ча-
стичное изоляционное заполнение, например, гибкого кабеля с
изоляцией в виде пластмассовых лент, навитых на жилу кабеля
спиралью с большим шагом для того, чтобы на больших участ-
ках оставался воздушный промежуток между жилой и оболоч-
кой. Приближённо коэффициент укорочения может быть вы-
числен, в данном случае, по степени заполнения. Более точно
И* 163
его величина может быть измерена резонансным методом. Блок-
схема измерительной установки приведена на рис. 7.1.
Эта установка представляет собой цепь из последовательно
соединённых коаксиальных элементов: измерителя кбв в вице
измерительной линии или рефлектометра, коаксиальной вставки
Согласо-
ванная
нагрузна
Рис. 7.1. Блок-схема измерительной установки для измерения коэффициен-
та укорочения кабеля
с гнездом для параллельного включения исследуемого кабеля,
согласованной нагрузки. Питание подаётся от ГСС через атте-
нюатор, благодаря чему указанная цепь оказывается согласо-
ванной с двух сторон. Исследуемый кабель с одной стороны пе-
ремычкой замкнут накоротко, с другой—слабо связан с указан-
ной цепью (его жила погружается на небольшую глубину в коак-
сиальную вставку). Поэтому на частотах, далёких от резонанс-
ной, цепь остаётся согласованной, что регистрируется измерите-
лем кбв.
Изменением частоты добиваются резонанса, что фиксируется
на измерителе кбв резким падением коэффициента бегущей вол-
ны. Если длина кабеля lt а частота резонанса /оь то между ними
существует соотношение
I = 2£ t (7.2)
4 /(И
где N — целое число, подлежащее определению.
Плавно увеличивая частоту, находят вторую точку резонан-
са fa2, которая связана с длиной кабеля / следующим образом:
I = 2V+1
Из (7,2) и (7.3) находим;
jy __ fot ~F /<1Э
2 (/оз — Ан)
~ (/о2 f 01),
Уф 2/(fo2—/ох)
164
(7.3)
(7Л)
(7.6J
Для уточнения результата рекомендуется найти несколько че-
редующихся резонансных частот в пределах интересующего диа-
пазона.
Измерение волнового сопротивления
Волновое сопротивление фидерных линий рассчитывает-
ся по формулам, приведённым в приложении 3. Оно является
функцией размеров и формы поперечного сечения фидера и ди-
электрической проницаемости среды. В приложении 3 формулы
соответствуют воздушной среде между проводами фидера. При
наличии изоляции между проводами волновое сопротивление
уменьшается в е'раз, где п — коэффициент укорочения. Та-
ким образом, зная коэффициент укорочения, можно вычислить
волновое сопротивление, и, наоборот, зная волновое сопротивле-
ние фидера и. размеры поперечного сечения, можно найти коэф-
фициент укорочения из формулы
Р=-Р“-, (7.7)
п
где р — волновое сопротивление фидера с учётом изоляции;
ро — волновое сопротивление при воздушной среде между
проводами.
Таким образом, описанным выше резонансным методом изме-
рения коэффициента укорочения можно измерять и волновое со-
противление.
Существуют и другие методы измерения волнового сопротив-
ления. Один из них — измерение электростатической ёмкости
отрезка кабеля на постоянном токе или на низких частотах.
Зная ёмкость, длину и размеры поперечного сечения, можно вы-
числить волновое сопротивление по формуле
Р = У-3333р0< , (7.8)
где С — измеренная ёмкость, пф:
I — длина отрезка кабеля, м;
Волновое сопротивление фидера может быть найдено, если
известна кривая частотной зависимости активной части его вход-
ного сопротивления.
На рис. 7.2 показана примерная кривая зависимости входно-
го сопротивления фидера, нагруженного на комплектную нагруз-
ку, от частоты. Зная максимальное RMaK< и минимальное Rvafi
значения входного сопротивления кабеля, можно найти волно-
вое сопротивление по формуле
Р — УRjtaKc' Rmuh • (7*9)
165
Таким образом, волновое сопротивление может быть изме-
рено следующим образом. Исследуемый фидер с одного конца
замыкается на любую комплексную нагрузку, а с другой — при-
соединяется к установке для измерения входного сопротивле-
ния. Снимается и вычерчивается кривая активной части вход-
Рис. 7.2. Вид кривой зависи-
мости активной составляющей
входного сопротивления фиде-
ра) нагруженного на комплекс-
ную нагрузку, от частоты
кого сопротивления в таком ин*
тервале частот, чтобы на ней бы-
ли точки минимума и максимума*
Результаты измерений будут
тем точнее, чем больше снято то-
чек минимума и максимума. На
основе полученной кривой вели-
чина р вычисляется по ф-ле (7.9).
Точность измерений возрастает
также с ростом значения RMUK .
Поэтому желательно применять
активные нагрузки, ориентировоч-
но близкие к ожидаемому значе-
нию волнового сопротивления.
Следует также иметь в виду, что ф-ла (7.9) не учитывает за-
тухания фидера. Чтобы это не приводило к заметным ошибкам,
рекомендуется производить измерения на фидерах сравнительно
небольшой длины (но такой, чтобы можно было в измеряемом
диапазоне получить не менее одного максимума и одного мини-
мума) и выбирать нагрузку, близкую к волновому сопротивле*
нию.
Можно не снимать всю кривую зависимости Rt г от f, а огра-
ничиться измерением Rtv на двух смежных резонансных часто-
тах методом, описанным на стр. 163, 164,
Для определения волнового сопротивления можно восполь-
зоваться также измерением реактивной части Хах входного со-
противления короткозамкнутого или разомкнутого фидера.
Поскольку для разомкнутого фидера
X,xxx = -Pct^nl,
А.
(7.Ю)
а для короткозамкнутого
X,^3 = ptg^n/( (7.10а)
где I — длина отрезка кабеля, то
Р = VXtxxx-Xt~Ka , (7.11)
Измерение коэффициента затухания фидера
При распространении волны по фидеру часть энергии
теряется на джоулево тепло в проводах фидера и на диэлектри-
ческие потери в изоляторах. Вследствие этих потерь амплитуда
волны не остаётся постоянной, а экспоненциально убывает в на-
правлении распространения, т. е. для короткозамкнутого или
разомкнутого фидера справедливы равенства:
I UnQd I = I U™d I 1
1 ' 1 1 ° 1 L (7.12)
[ и°тР |=| Uomf I е“^ -1 I е_₽а+ж> J
где р — коэффициент затухания — или —а также
М ХЛ
х дб дб
может быть выражен в — или — ;
м км
I— длина фидера;
— амплитуда падающей волны в точке пита-
ния фидера;
— амплитуда отражённой волны в точке присое-
динения нагрузки;
и — амплитуды соответственно падающей и отра-
жённой волн в точках с текущей координа-
той X.
Простейший метод измерения коэффициента затухания фи-
дера предложен В. В. Татариновым. По этому методу фидер с
одного конца замыкается накоротко, а на другом конце, к кото-
рому подводится питание от генератора, измеряется коэффи-
циент бегущей волны, равный
К“ + “ i + e-*
= th р Z^₽ L (7.13)
Измерив коэффициент бегущей волны к, можно
коэффициент затухания 0 по формуле
вычислить
? = Т‘ (7.14)
Недостатком метода Татаринова является то, что коэффи-
циент бегущей волны может быть измерен только непосредствен-
но на фидере, при условии однородности его на сравнительно
большой длине. Применяемые на практике фидерные линии не
удовлетворяют одновременно обоим требованиям.
Действительно, открытые двухпроводные и четырёхпровод-
ные фидерные линии удовлетворяют первому требованию, но не
167
удовлетворяют второму. Аналогично, если в воздушном коак-
сиальном фидере с изоляционными шайбами, волноводе, а так-
же полосковой линии предусмотреть 3—4 отверстия, расположен-
ные через промежутки — , то коэффициент бегущей волны не-
8
посредственно на них может быть измерен по методу трех
зондов.
Рис 7.3. Блок-схема измерительной установки для измерения
коэффициента затухания фидера резонансным методом
Однако эти фидерные линии не могут быть сделаны однород-
ными на большой длине из-за наличия в отдельных местах изо-
ляторов между противофазными проводами, фланцев или пере-
мычек, соединяющих между собой отдельные участки фиде-
ра, и т. п.
Гибкие коаксиальные и двухпроводные кабели марок РК и
РД являются однородными, но они не позволяют непосредствен-
но на них измерять кбв. Можно измерить кбв, присоединив эти
кабели к измерительной линии, но тогда искажения возникнут в
переходных фишках.
Нарушение того или другого из указанных требований являет-
ся причиной малой точности метода и ограничивает его приме-
нение.
Коэффициент затухания фидера может быть измерен резо-
нансным методом. Блок-схема измерительной установки приве-
дена на рис. 7.3.
Закороченный с обоих концов отрезок фидера связан (слабой
связью) с одной стороны с цепью питания, состоящей из ГСС с
волномером, аттенюатора, измерителя мощности, а с другой —
с индикаторной цепью, состоящей из детекторно-усилительной
схемы, и прибора. В качестве короткозамыкателей целесообразно
использовать специальные отрезки фидера с плунжерами. В этих
отрезках фидера могут быть предусмотрены элементы связи с
цепями питания и индикации. В качестве измерителей мощности
могут использоваться градуированные измерительные линии или
рефлектометры.
168
Порядок измерений следующий. После сборки схемы произ-
водят настройку фидера в резонанс перемещением закорачиваю-
щих поршней или подбором частоты колебаний генератора, На-
стройка производится по максимуму показаний прибора индика-
торной цепи. Зафиксировав резонансную длину волны Хот мощ-
ность Р, поступающую в фидер, и показания прибора индикатор-
ной цепи, аттенюатором увеличивают мощность в два раза. При
этом увеличивается показание прибора индикаторной цепи. За-
тем, плавно укорачивая и удлиняя волну, добиваются первона-
чальных показаний прибора индикаторной цепи при более корот-
кой волне —А и более длинной Х2 = -j- Д%.
Как известно, логарифмический декремент затухания fi, рав-
ный
8=^^ (7,15)
^0
связан с коэффициентом затухания следующей зависимостью:
S = (7.16)
откуда
А..,
? = у1. (7.17)
Ао
В случае волновода [Л 19] коэффициент затухания р равен
₽=я^(¥)’ (7Л8>
л0 х л ✓
где Кф— длина волны в волноводе.
Вместо изменения длины волны можно вносить расстройку в
фидер, меняя его длину перемещением поршней и добиваясь пер-
воначальных показаний прибора индикаторной цепи при укоро-
чении и удлинении фидера. Если обозначить резонансную длину
исследуемого фидера через /о, а разность наибольшей и наимень-
шей длин, соответствующих половинной мощности по сравнению
с мощностью резонанса, через А/, то
в = ^££. (7.19)
^ф
При большой длине фидера или большой величине коэффи-
циента затухания, когда общее затухание исследуемого отрезка
сравнительно велико, можно измерить коэффициент затухания
при помощи установки, собранной по схеме рис. 7,4.
Измерителем мощности 1 определяется мощность посту-
пающая в фидер, а измерителем мощности 2 — мощность Р2, вы-
169
ходящая из фидера. При хорошем согласовании фидера с на-
грузкой коэффициент затухания равен
p = J-ln£-. (7.20)
Измерение по этой схеме можно производить как при двух
измерителях мощности, так и при одном, переключаемом. Во
втором случае измеритель мощности первоначально включает-
ся между фидером* и аттенюатором, а затем между фидером и
согласованной нагрузкой. При помощи аттенюатора показания
измерителя мощности делаются одинаковыми при обоих поло-
жениях. Значение — отсчитывается непосредственно по шкале
аттенюатора.
Рис. 7.4. Схема измерительной установки для измерения коэффи-
циента затухания фидера путём сравнения мощностей на входе
и выходе
Отрезок фидера как линейный пассивный четырёхполюсник
характеризуется матрицей рассеяния
Su Sis
S2i
причём согласно теореме взаимности
S12
(7.21)
f
(7.22)
Зная элементы матрицы рассеяния SH, S22 и Su, легко найти
коэффициент затухания по формуле
2/ l-|Sn|«
(7.23)
Таким образом, задача измерения коэффициента затухания
решается методом измерения элементов матрицы рассеяния.
Наиболее совершенный метод измерения элементов матрицы
рассеяния четырёхполюсника предложен Дешаном [Л2(Ц Метод
Дешана заключается в следующем. Исследуемый фидер
(рис. 7.5) присоединяется с одной стороны к отрезку фидера с
передвижным короткозамыкающим поршнем, а с другой — к из-
мерительной линии. Измеряется коэффициент отражения на из-
170
мерительной линии при восьми положениях поршня, отстоящих
друг от друга на одинаковых расстояниях, равных —. После-
16
дующие перемещения привели бы к повторяющимся результатам.
/|И сел еду е -
генератора' Нзмери'
тельная
мыи.
фидер
2 Передвижной
.__короткозамыка •
<ё^—юищй.
т—* поршень
линия
Рис. 7.5. Схема измерительной установки по методу Дешана
Результаты измерений наносятся на полярную диаграмму сопро-
тивлений (рис. 7.6). Пусть это будут точки Гц Г8. Все точ»
Рис. 7.6. Графическое построение для определения элементов
матрицы рассеяния по методу Дешана
ки должны лежать на окружности. Пусть точка С — центр этой
окружности, а О — центр диаграммы сопротивлений. Хорды,
соединяющие попарно точки Л н Л» Л и Л й г. д., должны не-
171
ресекаться в одной точке. Пусть это будет точка С'. Точки С и
С' соединяются прямой и к ней в этих точках восстанавливаются
перпендикуляры. Точки А и В пересечения перпендикуляров с
указанной окружностью соединяются прямой. Обозначим точку
пересечения прямой АВ с прямой С' С через О' н восстановим из
неё перпендикуляр к прямой С С'. Пусть это будет линия О'Е. Эле-
менты матрицы рассеяния определяются следующим образом:
1 о 1 100я In! • (7-24)
|522| = ^-, (7-25)
IS 1- 10T1 (7.26)
где R — радиус диаграммы сопротивлений, аг — радиус окруж-
ности, построенной по измеренным точкам.
Достоинством метода Дешана является возможность кон-
троля точности измерений по двум критериям: располагаются
ли измеренные точки, нанесённые на диаграмму сопротивле-
ний, на окружности и пересекаются ли все четыре хорды в одной
точке. Если измеренные точки не располагаются на окружности,
а хорды не пересекаются в одной точке, то применяется усредне-
ние.
Измерение коэффициента асимметрии и скоса волны на
открытых фидерных линиях
Питание симметричных антенн часто осуществляется от-
крытыми симметричными двухпроводными, четырёхпроводными,
многопроводными- фидерными линиями. В четырёхпроводпых и
многрпроводных фидерах все провода делятся па две одинако-
вые группы и в каждой из групп они по всей длине трассы через
определённые промежутки соединяются между собой перемыч-
ками, выравнивающими их потенциалы. Это позволяет четырёх-
проводные и многопроводные фидеры трактовать как двухпро-
водные, у которых каждый провод является сложным, состоя-
щим из системы нескольких проводов, а вопрос об асимметрии и
о скосе волны рассматривать применительно лишь к двухпровод-
ной фидерной линии.
Приведённые ранее соотношения, характеризующие . ре-
жим работы фидерных линий, в случае открытых фидеров спра-
ведливы только тогда, когда они однородны и симметричны. Осо-
бенностью однородной симметричной линии при симметричной
схеме питания и симметричной нагрузке является равенство ам-
172
плитуд и противоположность фаз токов и потенциалов двух про-
водов в соответственных точках. Пользуясь схемой рис. 7.7 и
обозначив через /ц СЛ ток и потенциал первого провода, а че-
Истник
питания
Нагрузкй
Рис. 7.7. Обозначение токов и потенциалов на про-
водах двухпроводной фидерной линии
рез /2, — ток и потенциал второго провода, можно записать
для однородного симметричного фидера:
При наличии неоднородностей на фидерной линии справед-
ливость соотношений (7.27) сохраняется, если неоднородности
симметричны. Однако у двухпроводных фидерных линий труд-
но обеспечить симметричность неоднородностей. Например, при
поворотах фидера (рис. 7.8) приходится либо один провод де-
лать длиннее другого, либо выравнивать длину проводов с по-
мощью перемычек, разных у разных проводов. Трудно также
обеспечить симметричное расположение обоих проводов относи-
тельно опор и заземленных предметов. Несимметрия отдельных
элементов фидерных линий приводит к нарушению условий
(7.27). Такое нарушение вызывается также неепмметрией вы-
хода передатчика или несимметрией входа приёмника. Кроме
того, несимметрия может быть вызвана нагрузкой, т. ег ан-
тенной.
Рис. 7.8. Пример поворота X >
двухпроводной фидерной \ \
линии
Нарушение условий (7.27) может выражаться как в неравен-
стве амплитуд
I Л 1 I ^2 I 1
(7.28)
так и в отличии фаз на величину, не равную 180°,
I Л | I /а I
+ ~Уг
I 1/11 11/11
(7.29)
Рисунок 7.9 иллюстрирует эти два вида асимметрии. Первый
характеризуется коэффициентом асимметрии, равным
|<Л1 + 1<М '
(7.30)
Второй вид асимметрии характеризуется скосом волны, рав-
ным
(7-31)
Рис. 7.9. К определению понятий: коэффициент асим-
метрии, скос волны
Кривые напряжения, изображённые на рис* 7.9, можно рас-
сматривать как результат суперпозиции двух волн: одной, ха-
рактеризуемой условиями (7.27) и называемой противофазной
(по Татаринову—двухтактной), и другой, характеризуемой ус-
ловиями;
С/1= С73 f
и называемой синфазной (по Татаринову—однотактной).
174
Измерение асимметрии наиболее удобно производить при
помощи однополюсного индикаторного прибора, показанного
схематически на рис* 7,10а. Катушка индуктивности £, перемен-
ный конденсатор С и кристаллический детектор Д заключен в
металлическую коробку, из которой выходит присоединенный
к схеме из этих деталей зонд 3.
Рис. 7.10. Однополюсный
индикатор
На передней стороне коробки находится микроамперметр. Ко-
робка укреплена на изоляционной плате, которая крючком под-
вешивастся па один из проводов исследуемого фидера.
Перемещая индикаторный прибор сначала по одному из про-
водов фидера и записывая показания микроамперметра, а затем
по другому, вычерчивают кривые напряжения на проводах фиде-
ра и находят коэффициент асимметрии q и скос волны ф*
17S
Поскольку добиться идеальной симметрии фидерной линии
невозможно и поскольку измерения выполняются с определен-
ной погрешностью, то некоторая асимметрия допускается. По
существующим нормам донускается коэффициент асимметрии
10% и скос волны 5°. Если измерения показывают наличие бо-
лее высоких параметров асимметрии (?>10%, ф>5°), то необ-
ходимо исследовать причину асимметрии.
Как указывалось выше, асимметрия может быть вызвана
приёмником или передатчиком, фидером и антенной. Прежде
всего следует проверить симметрию выхода передатчика или
входа приёмника. Поскольку измерения проводятся при подклю-
чении антенно-фидерной системы к какому-либо генератору —
измерительному или рабочему, то задача сводится к определе-
нию симметрии выхода передатчика. Определение симметрии
входа приемника представляет собой самостоятельную задачу,
не связанную непосредственно с антенно-фидерными измере-
ниями. Однако для полноты освещения вопроса об измерении
асимметрии ниже приводятся краткие сведения о методике и
специфике измерения асимметрии входа приёхМиика.
Для проверки симметрии выхода передатчика фидерную ли-
нию отключают и передатчик нагружают на заведомо симмет-
ричный эквивалент антенны. При помощи индикатора (рис. 7.10)
можно проверить равенство амплитуд потенциалов на выходных
полюсах передатчика. Соотношение фаз потенциалов измеряет-
ся методами, описанными в следующей главе. Заметим, что при
измерении разности фаз в качестве опорного напряжения может
быть, в частности, использовано напряжение от предокоиечной
ступени передатчика. Выход передатчика симметричен, когда по-
тенциалы па полюсах равн-ы по амплитуде и отличаются по фа-
зе на 180°
При наличии асимметрии выхода передатчика, которая не
устраняется элементами выходной цепи, следует присоединить
к фидеру вблизи выхода передатчика четвертьволновый коротко-
замкнутый шлейф. Сопротивление такого шлейфа для противо-
фазной волны чрезвычайно велико, а для синфазной — очень
мало, что приводит к утечке энергии синфазной волны в зазем-
ление и к симметрированию выхода передатчика. Очевидно, что
такой метод симметрирования возможен при работе передатчика
на одной волне или в узком диапазоне волн. Кроме того, этот
метод связан с потерей энергии.
Убедившись в симметричности выхода передатчика, прове-
ряют симметрию фидера. Для этого фидер закорачивают в ме-
сте его присоединения к антенне и по всей его длине проводят
измерение напряжения на проводах при помощи прибора
(рис. 7.10). Следует учесть, что асимметрия, вызванная каким-либо
фактором в одном месте может скомпенсироваться асимметрия-
176
ми, вызванными другими факторами в других местах фидера, и
привести на отдельных участках к симметрии. Поэтому контроль’
ные измерения должны проводиться по всей длине фидера.
При наличии большой (больше нормы) асимметрии на фи-
дерной линии определяется её источник. Для этого короткозамьь
катель, включённый ранее вблизи антенны, перемещается в сто-
рону передатчика до исчезновения асимметрии на оставшемся
участке. Это позволяет выделить участок фидера, на котором воз-
никает асимметрия, и принять меры к её ликвидации.
После отсимметрироваиия фидерной линии снимается корот-
козамыкатель. В результате фидер оказывается нагруженным
на антенну, что позволяет проверить её влияние на симметрию
волн на фидерной линии. Причиной асимметрии здесь может
быть разная высота подвеса симметричных половин антенны от-
носительно земли, разное расстояние этих половин от опор, раз-
ная их длина и некоторые дефекты изготовления: плохая пайка,
неисправность изоляторов и т. п.
Измерение распределения потенциалов на проводах фидерной
линии с целью определения асимметрии и скоса волны можно
производить также двухзондовым индикаторным прибором, по-
казанным на рис. 4.7а, или измерительным шлейфом
(см. рис. 4.9а). Для этого прибор или шлейф подвешивают
одним концом к одному проводу фидера. Перемещая его по про-
воду, снимают кривую распределения потенциала. Затем этим
же концом подвешивают прибор или шлейф к другому проводу
фидера для снятия кривой потенциала на нём. При этих изме-
рениях второй зонд прибора или второй провод шлейфа остаётся
висеть свободным в стороне от проводов фидера.
Если вместо зондовых приборов пользоваться рамочными, го
удаётся разделить волны противофазную и синфазную, Инди-
каторами, изображёнными на рис. 4.76 и в, измеряется противо-
фазная волна. Если поместить рамки приборов, как показано
на рис. 7.106 и в, то будет производиться измерение синфазной
волны.
Измерение асимметрии входа приёмника
Исследование влияния асимметрии входа приёмника на
режим работы фидерной линии показало [Л21], что отношение
синфазного тока I с на фидере вблизи входа приёмника к про-
тивофазному /я в этих же точках равно
, =------Т---- - (7-33)
я т + --(1~АЕЛ7,')+^-
12 -292
177
где Az — коэффициент асимметрии по сопротивлениям;
— коэффициент асимметрии по электродвижущим си-
лам (эдс);
т — коэффициент утечки;
^афп— сопротивление антеннс-фидериой системы по про-
тивофазной волне;
2афе— сопротивление антенно-фидерной системы по син-
фазной волне;
Z*x— входное сопротивление приёмника.
Рис. 7.11. К пояснению смысла коэффициентов асиммет-
рии Ае и коэффициента утечки т
Для пояснения физического смысла указанных коэффициен-
тов обратимся к развёрнутой схеме рис. 7.11 входной цепи приём-
ника. Под понимается сопротивление между входными зажи-
мами приёмника, а под Z' и Z"— сопротивления утечки между
каждым входным зажимом и заземлённым шасси приёмника.
Коэффициенты Mt М' и М" характеризуют связь входного кон-
тура приёмника соответственно с фидерной катушкой и с боко-
выми ветвями трёхполюспика, На рис. 7.11 для примера показа-
на трансформаторная связь во всех цепях, хотя в каждой цепи
могут быть связи самых различных видов (ёмкостная, индуктив-
ная, кондуктивная, комбинированная и т. п.).
Коэффициент асимметрии по сопротивлениям равен
7' _ 7"
А7 - -----— . (7.34)
z Z' + Z" '
Коэффициент асимметрии по эдс равен
Р.35>
178
где Е' и Е" — электродвижущие силы, появляющиеся на вход-
ных зажимах приёмника, если к входному кон-
туру приложено напряжение Ut>.
Коэффициент утечки равен
2Z'Z"
т =-----------
ZK(Z’+Z")
(7-36)
Входное сопротивление равно
z ZH(Z‘ + Z")
вх
(7.37)
Коэффициенты Az и т могут быть измерены по методу трёх
схем, сущность которых сводится к следующему.
При помощи высокочастотного моста по схемам рис. 7.12 из-
меряют входные проводимости предварительно настроенного на
рабочую частоту приёмника. По этим значениям вычисляют
коэффициенты Az и т.
Обозначим значения проводимостей соответственно схемам
через Ya, Y6 и Гв. Согласно рис. 7,12 они связаны с основными
параметрами трёхполюсника, эквивалентного входу приёмника,
следующими зависимостями:
(7.38)
Так как Ya — Y6— ~, то ф-ла (7.34) приводится к
виду
, Az - Ya~Y6 . (7.39)
•9
12’
179
В свою очередь, согласно (7.38) ф-ла (7.36) может быть пред-
ставлена в следующем виде:
Уа + Гб~Г,
К,
(7.40)
При помощи высокочастотного моста можно измерить и
входное сопротивление приёмника Z6X в необходимом режиме,
пользуясь при этом, например, схемой рис. 7.12а без заземления
входного зажима приёмника.
Рис. 7Л2. К методу трёх
схем
Коэффициент асимметрии по эдс может быть измерен по ме-
тоду противофазно-синфазного включения эдс на вход приёмни-
ка. Согласно этому методу напряжение требуемой частоты от
некоторого высокочастотного генератора Г, имеющего симмет-
ричный выход, подаётся на вход настроенного приемника по
двум схемам (рис, 7.13). Схема рис, 7.13а обеспечивает проти-
вофазное питание входа приёмника, а схема рис. 7.136 — син-
фазное.
В процессе измерений для каждой схемы подбираются такие
значения напряжений на выходе генератора Г, при которых на-
пряжение па выходе приёмника оказывается одинаковым для.
обеих схем. :
Обозначим величину эдс на выходе генератора Г для схемы^
рис. 7.1 За через а для схемы рис. 7.136 — через Ес . Можна^
Ея ie
показать, что отношение —- равно отношению —» определяем
&С ‘п J
180 $
мому по ф-ле (7.33) при замене Z0$a на 27?О, a Za&. на /?о> где
Ro — добавочное сопротивление в схемах рис. 7.13.
Рис* 7.13. К методу про-
тивофазно-синфазного
включения эдс
Решая (7.33) относительно Ав, получая
Ае ~
Wo.En .
Z9X^2EcAz
(7.41)
Эта формула упрощается, если принять либо Ro—О, либо
•у-2 > т и одновременно А _ 1.
8. ИЗМЕРЕНИЕ НАПРЯЖЁННОСТИ ПОЛЯ
Введение
Для определения характеристик излучения антенн (диа-
грамм направленности, коэффициента усиления и др,) требует-
ся измерить напряжённость электромагнитного поля, электриче-
ский и магнитный векторы которого в воздухе связаны простым
соотношением
Е = 120к/Л (8Л)
В ф-ле (8.1) Е выражено в вольтах на метр а Я — в
амперах- на метр (—)* Часто Е выражают в дробных едини-
цах-----, -----. Практически при измерениях определяют всег-
да напряжённость электрического поля Е. Поэтому в дальней-
шем под «измерением напряжённости поля» подразумевается
измерение напряжённости электрического поля Е волны.
Напряжённость поля характеризуется не только величиной
(амплитудой), выражаемой в —, —,-------, но также фазой и по-
ляризацией.
Фаза поля в каждой точке непрерывно меняется с течением
времени, пройдя полный цикл за один период. Одпако соотноше-
ние фаз поля в различных точках сохраняется с течением време-
ни. Поэтому при измерениях определяют разность фаз или фазы
в различных точках по отношению к фазе в какой-то начальной
точке, принятой за нуль.
Поляризация поля указывает направление электрического
вектора Е. Различают линейную, эллиптическую, круговую по-
ляризации. При линейной поляризации вектор электрического
поля сохраняет своё направление вдоль определённой прямой.
При эллиптической и круговой поляризациях направление век-
182
тора Е непрерывно меняется (вектор вращается в плоскости,
перпендикулярной направлению распространения), причём, при
эллиптической поляризации электрический вектор одновременно
с поворотом меняет свою величину, при круговой же поляриза-
ции он сохраняет свою величину постоянной. При эллиптической
и круговой поляризациях измеряются две взаимно-перпендику-
лярные составляющие поля излучения.
В случае линейной поляризации различают поляризацию го-
ризонтальную и вертикальную в зависимости от ориентации
электрического вектора относительно поверхности земли.
Измерение напряжённости поля излучения антенн производят
как на расстояниях прямой оптической видимости от излучаю-
щих антенн, так и в области за горизонтом. На расстояниях
прямой видимости амплитуда поля в каждой точке имеет, как
правило, определённую величину. На больших расстояниях, за
пределами горизонта, амплитуда поля часто подвергается флук-
туациям (замираниям). Поэтому при измерениях в пределах
прямой видимости измерительные приборы фиксируют опреде-
лённую величину поля, в то время как за пределами горизонта
измерительный прибор отмечает динамику изменения амплиту-
ды поля со временем. Полученные данные подвергают затем ста-
тистической обработке, для облегчения которой часто примени-
ются так называемые анализаторы поля.
Измерение амплитуды поля производят при помощи какой-
либо схемы приёмного устройства, включающей приёмную ан-
тенну, фидер и приёмник. В основе расчётов напряжённости
поля лежит теория приёма радиоволн, изложенная в первой
главе.
При измерении коэффициента усиления антенн необходимо
знать абсолютное значение амплитуды поля, в то время как при
снятии диаграмм направленности достаточно знать соотношение
между амплитудами поля в различных пунктах измерения.
Для измерения абсолютной величины амплитуды поля приме-
няется специальная аппаратура, содержащая достаточно точно
отградуированные приёмники и тщательно подобранные антен-
но-фидерные устройства, обеспечивающие хорошее согласование
во всём тракте высокой частоты от источника эдс до нагрузки.
Эта аппаратура позволяет определять напряжённость поля Е
в —— или в более крупных единицах по напряжению или току
на выходе приёмника. Для измерения соотношения между ам-
плитудами поля в разных точках (относительной величины ам-
плитуды поля) может применяться более простая аппаратура,
от которой требуется лишь знание формы кривой зависимости
(или аналитической зависимости) выходного напряжения или
тока от напряжённости поля,
183
Направление прихода радиоволны
При измерениях напряжённости поля до амплитуде, фазе
или поляризации необходимо знать направление прихода волны.
В тех случаях, когда измерения напряжённости поля проводят-
ся на расстояниях прямой оптической видимости от передающей
антенны, например при лабораторных исследованиях, измере-
ниях на антенном поле радиоцентров или вблизи антенного поля,
самолётных и вертолётных измерениях, направление прихода
волны определяется по прямой, соединяющей передающую ан-
тенну с пунктом, где проводятся измерения напряженности поля.
Когда измерения напряженности поля проводятся в пунктах,
лежащих за горизонтом по отношению к передающей антенне,
направление прихода волны определяется по плоскости большого
круга, проходящего через пункты излучения и приёма. Имеющие
место в некоторых случаях небольшие отклонения траектории
волны от плоскости большого круга несущественны при измере-
нии напряжённости поля, так как ошибка, получающаяся от
неучёта этих отклонений, лежит в пределах погрешности изме-
рений, Направление прихода волны по углу места (наклон
траектории волны к горизонту) зависит от условий распростра-
нения радиоволн.
Если основным фактором, определяющим распространение
радиоволн за горизонтом, является дифракция, что характерно
для диапазонов длинных волн и ультракоротких волн короче
трех, четырёх метров, а также для средних и коротких волн па
расстояниях нескольких десятков километров от передающей
антенны, то угол места можно считать равным нулю. Аналогич-
но равным нулю можно считать угол места, если основным фак-
тором, определяющим распространение радиоволн за горизон-
том, является рассеяние от локальных или слоистых неоднород’
ностей тропосферы, что характерно для ультракоротких волн.
Если же основным фактором, определяющим распростране-
ние радиоволн за горизонтом, явчяется отражение от ионизиро-
ванных слоёв атмосферы, что характерно «на весьма больших
расстояниях от передающей антенны для коротких волн, длинно-
волновой части ультракоротковолнового диапазона, а также для
средних волн в ночное время, то угол места Ф может быть вычис-
лен
по формуле
ft^arctg etg -
(8.2)
sm —
2R
где
г — расстояние между пунктами излучения и приёма,
R — радиус Земли,
Н — высота отражающего слоя (рис. 8,1),
184
Учитывая, что
н «
получаем приближённо
(8.3>
(8.4>
Из (8.4) следует, что 0=0, при
(8.5>
Расстояние гмоке называется предельным расстоянием одного-
скачка.. При г>гмако также можно считать 0=0.
Направление прихода волны может быть измерено. Это может
оказаться целесообразным при измерениях напряжённости
поля на коротких волнах при 'расстояниях г < гавке, по-
скольку короткие волны отражаются от слоя F, высота которого-
меняется в очень больших пределах, что, в свою очередь, вызы-
вает значительное изменение угла прихода волны.
Рис. 8.1. К определению
угла прихода волны, от-
ражённой от регулярных
слоёв ионосферы
Измерение направления прихода волны — это задача радио-
пеленгации. Однако следует учесть, что в отличие от обычных
задач радиопеленгации, заключающихся в определении азиму-
тального угла, в данном случае речь идёт об определении угла
места.
Эта задача может быть решена при помощи двух горизон-
тальных симметричных вибраторов, подвешенных на общих опо-
рах на разной высоте. Диаграмма направленности в вертикаль-
ной плоскости горизонтального симметричного вибратора имеет
185
главный лепесток, ширина которого уменьшается с увеличением
высоты подвеса вибратора, причём одновременно снижается на-
правление главного максимума (рис. 8.2). Лепесток 1 соответ-
ствует меньшей высоте повеса, лепесток 2 — большей. Когда
Рис. 8.2. К пеленгова-
нию методом равно-
сигнальной зоны
волна приходит с направления равносигнальной зоны (Ф =<Ь), в
обоих вибраторах возбуждаются электродвижущие силы одина-
ковой амплитуды. Когда волна приходит с других направлений,
электродвижущие силы, возбуждаемые в вибраторах, имеют
разные амплитуды. При -0,>Оо большую величину имеет ампли-
туда эдс в первом вибраторе, а при •О’<-О*о — во втором. Каждому
углу О соответствует определённое соотношение эдс вибраторов.
Таким образом, сравнивая эдс этих двух вибраторов, можно по
их отношению определить направление прихода волны по углу
места.
Вместо разноса вибраторов по высоте можно разнести их
вдоль азимутальной линии (рис. 8.3), В этом случае диаграммы
Рис. 8.3. К пеленгованию
по разпости фаз сигна-
лов
направленности обеих антенн в вертикальной плоскости одина-
ковы. Поэтому эдс в обеих антеннах будут при всех направле-
ниях прихода волны одинаковыми по амплитуде, но разными по
фазе. Разность фаз
6==wdcos&. (8.6)
Подавая сигналы от обоих вибраторов на общий приёмник и
добиваясь выравнивания фаз при помощи градуированного фа-
зовращателя, можно по повороту фазы, даваемому фазовраща-
телем, определить угол th
186
Разнос вибраторов вдоль азимутальной линии можно исполь-
зовать и следующим образом.
Сигналы от обоих вибраторов усиливаются в идентичных ка-
налах и подаются на суммо разностный трансформатор. Обоз-
начив эдс, возбуждаемую на первом вибраторе, через
е
получим для эдс второго вибратора
, md
-1—С<
еа = еое
а для суммы и разности здс соответственно:
ех — еа = 2 i е0 sin
(8-7)
(8-8)
(8-9)
Суммарное и разностное напряжения на выходе трансфор-
матора пропорциональны соответственно ej + e* и
Если суммарное напряжение подать на горизонтальные пла-
стины электронно-лучевой трубки, а разностное — на вертикаль-
ные, то на экране получится прямая, угол наклона которой к го-
ризонтальной линии равен — cos#. Следовательно, по углу на-
клона прямой на электронно-лучевой трубке можно определить
угол места
Волны, отражённые от ионосферы, характеризуются много-
лучёвостью, означающей приход в точку приёма нескольких
волн под различными углами #, Применяя импульсную модуля-
цию с продолжительностью импульсов, меньшей времени, тре-
буемого на прохождение волной отрезка, равного разности хода
лучей к двум разнесённым вибраторам, получим на экране
электронно-лучевой трубки под разными углами несколько ли-
пин, соответствующих волнам, приходящим под разными угла-
ми #.
При исследованиях распространения радиоволн может пред-
ставить интерес измерение не только угла места #, но также уг-
ла ф отклонения (девиации) траектории волны от плоскости
большого круга. Небольшая девиация может быть измерена при
помощи четырёх одинаковых вибраторов, из которых два распо-
лагаются по азимутальной линии (рис. 8.3), а два — на таком
же расстоянии друг от друга по линии, перпендикулярной к ази-
мутальной, причём обе пары — симметрично относительно об-
187
щей точки О (рис, 8.4). При угле девиации <р эдс на вибраторах
раины:
i cos В cos <р
—i cos В cos 9
^2 — е
. md * .
i — cos В sin у
е
— cos В sin f
= е0 е
(8.10)
Рис. 8.4. К пеленгованию0
при помощи системы из
двух пар противофазных
вибраторов
Образуем следующие комбинации эдс:
е1+2 = е1 + = cos cos & cos ?
€12 ~ et — е» — 2» «о sin — cos ft cos <p
I 2
— es — et — 2i e0 sinR^ cos ft sin ?
Г(8.11)
'34 ,с12
cos ft cos <p H-i sin
I cosftsin<p]|
Если расстояние d между вибраторами сделать настолько
малым, чтобы удовлетворялось неравенство^-^ 1, можно при-
ближённо заменить:
®12 ~ 2«o,
r -i = 2«?p ^cos ft е|<р .
(8.12)
Подавая сигнал, пропорциональный е^2 на горизонта льно-
отклоняющие пластины электронно-лучевой трубки, а сигнал,
пропорциональный — на вертикально-отклоняющие пласти-
ны, получим на экране эллиптическую фигуру, по параметрам
которой можно определить как Ф, так и ф.
Можно установить в центральной точке 0 отдельный вибра-
тор и напряжение, пропорциональное эдс на нём, подать на го-
ризонтально-отклоняющие пластины вместо напряжения, про-
порционального
При измерениях на средних или длинных волнах следует
применять несимметричные вертикальные антенны вместо гори-
зонтального симметричного вибратора.
Измерение соотношения амплитуд поля
На длинных передних волнах относительные амплитуды
поля можно измерять при помощи схемы рис. 8.5. В качестве ан-
тенны используется рамка, шунтированная переменной ем-
костью С, служащей для настройки антенны. Ламповый вольт-
метр ЛВ измеряет напряжение на зажимах антенны. Для снятия
диаграммы направленности рамка должна
иметь поворотное устройство, позволяющее
чтобы направление прихода волны было
параллельно плоскости рамки.
Согласно (1.73)
Е = U =AU, (8.13)
т. е. напряжённость поля пропорциональ-
на напряжению, измеренному ламповым
вольтметром. Из ф-лы (8.13) видно, что
в процессе измерения на одной какой-
либо частоте ёмкость конденсатора долж-
на быть постоянной. Схема рис. 8.5 при-
быть переносной и
установить её так,
Рис. 8.5. Схема измери-
теля относительной ам-
плитуды поля с рамоч-
ной антенной
годна при больших напряжённостях поля,
т. е. на близких расстояниях от передаю-
щей антенны. При слабых полях необ-
ходимо в схему включить усилитель. Сле-
дует иметь в виду, что рамочные антенны
применяются при вертикально-поляризованном поле, которое
как раз характерно для диапазона длинных и средних волн.
На коротких волнах, а также на волнах метровых и деци-
метровых применяются схемы рис. 8.6 — 8.9. В этих схемах в
качестве антенны используется симметричный вибратор. В про-
стейшем случае (рис. 8.6) симметричный вибратор замкнут не-
189
посредственно на индикатор напряжения (ламповый вольтметр)
или тока (термоамперметр). В схемах рис. 8.7 и 8.8 к зажимам
вибратора присоединены элементы настройки L и С, в качестве
Рис. 8.6. Схема простейшего ин-
дикатора относительной амплиту-
ды поля с симметричным вибра-
тором
прибора используется стрелочный или зеркальный гальвано-
метр, а в качестве выпрямителей — полупроводниковый детек-
Рнс. 8.7> Схема вибратор-
ного индикатора относи-
тельной амплитуды поля
с элементами настройки
и термопарой
тор (рис. 8.8 и 8.9) либо термопара (рис. 8.7). Между прибором
и детектором могут включаться блокировочные элементы: дрос-
сель Др и конденсатор С (рис. 8,9.)
го индикатора относитель-
ной амплитуды поля с эле-
ментами настройки и полу-
проводниковым диодом
Рис. 8.9. Схема вибраторного инди-
катора относительной амплитуды по-
ля с блокировочными элементами и
полупроводниковым диодом
Показания лампового вольтметра пропорциональны первой
степени напряжённости поля, а показания гальванометра с тер-
мопарой или полупроводниковым детектором пропорциональны
второй степени напряжённости поля.
При измерениях вибратор должен быть установлен в соот-
ветствии с поляризацией поля параллельно электрическому-век-
тору.
190
На сверхвысоких частотах напряжённость поля измеряется
при помощи рупорных или зеркальных антенн (рис. 8.10 и 8.11).
В схеме рис. 8.10 рупорная антенна Р присоединяется к волново-
Рис. 8.10. Схема рупорного индикатора относительной
амплитуды поля
ду В, внутри которого расположен стержень С (параллельно
вектору электрического поля) и поршень IL Стержень С с де-
тектором Д и гальванометром И образует замкнутую цепь по-
стоянного тока. Поршень 77 служит для настройки.
Рис. 8.11. Схема зер-
кального индикатора от-
носительной амплитуды
поля
В схеме рис. 8.11 облучателем зеркала 3 является симмет-
ричный вибратор, который соединён с детектором, блокировоч-
ными элементами и гальванометром.
Все перечисленные схемы после соответствующей градуиров-
ки могут быть использованы для измерения абсолютной ампли-
туды поля.
Измерение абсолютной амплитуды поля
Общие сведения
При измерениях малых значений амплитуды поля
(меньше десятков —J возбуждаемая эдс в антенне не может
At
191
•быть непосредственно измерена приборами. В этом случае при-
ходится предварительно усиливать принятый антенной сигнал.
В качестве усилителей используются высокочувствительные
радиоприемники, снабжённые индикаторами выхода. Для гра-
дуировки таких радиоприёмников или калибровки всей измери-
тельной схемы часто применяются методы сравнения или заме-
щения. Измерение напряжённости поля методом сравнения или
замещения часто называют компарированием.
Приборы, построенные на принципе компарироваяия, полу-
чили название компараторов поля или радиокомпараторов. По-
мимо таких приборов, в последнее время часто используются
для измерения абсолютной амплитуды поля высокочастотные
микровольтметры. Эти приборы также содержат высокочувстви-
тельный радиоприёмник с индикатором на выходе и специаль-
.ним устройством для калибровки усиления приёмника. Они
•строятся главным образом для измерения полей радиопомех и
называются измерителями радиопомех. Эти приборы часто ис-
пользуются и для измерения напряжённости полей радиостанций.
Для измерения абсолютной амплитуды поля могут быть так-
:же использованы и высокочастотные микроваттметры — так на-
зываемые измерители малой мощности.
По способу градуировки аппаратуры для измерения напря-
жённости поля методы измерения можно разделить на две боль-
шие группы [Л36]:
а) методы, в которых используется эталонный сигнал, вво-
дшчый непосредственно в приёмную цепь измерительного уст-
ройства;
б) методы, в которых используется эталонное поле, дейст-
вующее на приёмную антенну измерительного устройства.
Методы первой группы применяются обычно для градуиров-
ки передвижных измерительных устройств, а второй, как пра-
вило, — для первичной градуировки при стационарных измере-
ниях.
Компарирование по генератору стандартных сигналов
Схема измерений абсолютной амплитуды поля методом ком-
парирования по генератору стандартных сигналов приведена на
рис. 8.12.
Схема состоит из измерительной антенны А, фидера Ф, при-
ёмного устройства /7, выход которого замкнут на индикатор И,
генератора стандартных сигналов ГСС и аттенюатора Ат.
При измерениях используются:
а) антенны — как специальные, так и профессиональные на
рабочих местах;
б) генераторы стандартных сигналов — заводского изготов-
ления;
в) приемники — высокочувствительные магистральные, а на
укв — также специальные измерительные;
i) индикаторные приборы — ламповые вольтметры или галь-
ванометры с детектирующим устройством.
Данный метод по существу является методом замещения.
Измерения проводятся следующим образом.
Рис. 8.12. Схема измере-
ний абсолютной ампли-
туды поля методом коад-
ларировапия по ГСС
Сначала к приёмному устройству П присоединяют фидер Ф
с антенной А, и приёмник настраивают на частоту исследуемой
радиостанции (применяется работа передатчика в режиме несу-
щей). Точную настройку на частоту исследуемой радиостанции
производят по пулевым биениям слышимого сигнала на выходе
приёмника. Поскольку, как правило, приёмное устройство вы-
полняется по супергетеродинной схеме, то при настройке должен
быть включён второй гетеродин приёмника. В этом случае сиг-
нал промежуточной частоты преобразуется при помощи второго
преобразователя и второго гетеродина в сигнал тональной ча-
стоты.
Получив нулевые биения, последний гетеродин приёмника
расстраивают до получения какой-либо определённой заданной
частоты, например 1000 гц. Для определения частоты расстрой’
ки приёмное устройство обычно снабжается градуировочной
шкалой. Далее регулировкой усиления приёмного устройства по
индикатору И устанавливают уровень сигнала, близкий к мак-
симальным показаниям прибора.
Необходимо при измерении обратить особое внимание на ли-
нейность амплитудной характеристики приёмного тракта в пре-
делах всего динамического диапазона выходного прибора. Если
прибор И включён на выходе усилителя промежуточной часто-
ты. то требование линейности предъявляется к тракту промежу-
точной частоты приёмного устройства, если на выходе приёмно-
го устройства, — то ко всему тракту, включая и усилитель низ*
кой частоты. Цепь авторегулировок в приёмнике при измерении
ноля по данному методу должна быть выключена.
Записав показания прибора И, выключают передатчик ис-
следуемой радиостанции и производят калибровку усиления
13—292 193
приёмного устройства по генератору стандартных сигналов ГСС,
Для этого фидер ф от приёмного устройства отключают, а вме-
сто него ко входу приёмника подают выход ГСС через аттенюа-
тор Ат,
Настройку генератора стандартных сигналов точно на часто-
ту исследуемой станции производят аналогично описанному вы-
ше, и регулировкой напряжения, подаваемого с ГСС, добивают-
ся прежних показаний индикатора И. В случае, когда выходное
сопротивление генератора стандартных сигналов на выходе ат-
тенюатора согласовано со входом приёмного устройства, напря-
жение на входе приёмного устройства хМожст быть определено
по формуле
у -VJC£ (8.14)
где Urcc—напряжение, подаваемое с генератора стандартных
сигналов;
Ат— коэффициент ослабления аттенюатора.
Эдс на выходе антенны, наводимую полем исследуемой радио-
станции, можно определить через известное напряжение, пода-
ваемое от ГСС при замещении сигнала.
При выполнении условий согласования фидера Ф и приём-
ною устройства эдс антенны еА может быть согласно (1.67),
(8,14) и (1.7) определена по формуле
е. = EhdF@, <0 - —-L- =
л ' 7 Ат 1- Г
игсс. (Ra + ?) JI (8. i 5)
Ат р
где |3 — затухание фидера, на единицу длины фидера, неп\
I — длила фидера;
Ra — активное сопротивление антенны в точке включения её
в фидер;
р — волновое сопротивление фидера.
Зная эдс на зажимах антенны, а также параметры антенны,
легко найти напряжённость ноля, пользуясь данными первой
главы.
Этот метод измерения амплитуды поля находит сравнитель-
но широкое применение при антенных измерениях. На этом
принципе измерений построены специальные приборы — радио-
компараторы.
Главный недостаток этого метода заключается в следующем.
Генератор стандартных сигналов трудно экранировать так, что-
бы отсутствовало непосредственное его воздействие на входные
цепи приёмника, которое очень существенно при измерении сла-
бых сигналов. Поэтому метод компарирования по генератору
194
П—
Рис. 8.13. Схема выходной ступени
измерительного приемника с непо-
средственным включением инди-
каторного прибора в цепь лампо-
вого детектора
стандартных сигналов применяется при измерении амплитуд ло-
мкв
лей не меньше нескольких десятков — .
м
Выходные устройства в схемах измерения напряжённости
поля выполняются различными методами [Л41]. Как уже ука-
зывалось, во всех схемах из-
мерения с компарированием ис-
пользуются приемные устройства,
снабжённые приборами-индикато-
рами.
На рис. 8.13 приведена схема
выходной ступени измерительного
приёмника с непосредственным
включением индикаторного при-
бора в цепь лампового детектора.
Такая схема позволяет при помо-
щи двойного диода и мостовой
схемы компенсировать началь-
ный ток, протекающий через ин-
дикатор И. Данная схема требует
высокочувствительного индикато-
ра. Компенсация производится
регулировкой переменного сопро-
тивления R.
При измерении напряжённости
поля в большом диапазоне амп-
литуд часто используется вы-
ходное устройство с лагарифмической шкалой. Такие устройства
обычно находят себе применение при записях уровня сигнала,
подверженных замираниям.
На рис. 8.14 приведена мостовая схема выходной ступени
приёмного устройства с автоматической регулировкой усиления
Рис. 8,14. Мостовая схема выходной ступени приемного устройства с ав-
томатической регулировкой усиления
13*
195
(АРУ), которая позволяет осуществить логарифмическую
шкалу.
Часто при исследовании условий распространения радиоволн
применяется непрерывная регистрация уровня принимаемых
сигналов. Для этой цели выходные устройства снабжаются са-
мопишущими приборами или шлейфными осциллографами
(рис. 8J5).
Рис. 8.15. Блок-схема выходного устройства с самопишущим
прибором
С выхода усилителя промежуточной частоты измерительного
приёмника сигнал разветвляется на два канала. В одном имеет-
ся дополнительный усилитель промежуточной частоты (ДУС),
детектор Д<1 и прибор-самописец. Дополнительный усилитель
даёт возможность расширить динамический диапазон измерений
амплитуд сигнала. Второй канал имеет детектор второй гете-
родин усилитель низкой частоты и телефон Г. Этот канал ис-
пользуется для контроля за сигналом, а также для настройки
измерительного приёмника на требуемую частоту.
Компарирование по эталонной напряжённости поля
Измерение абсолютной амплитуды поля в месте приёма
может быть произведено при помощи приёмного устройства,
градуированного по так называемому эталонному полю. Это по-
ле создаётся специальной аппаратурой, состоящей из антенны
Ас , питаемой генератором Гс (рис. 8.16). Поле от антенны Ас
в месте расположения приёмной антенны АП заранее рассчиты-
вается и эталонизируется по измеренной величине мощности,
подводимой к антенне Ас и по её действующей высоте. Посколь-
ку поле в месте расположения антенны А п известно, можно
градуировать приёмное устройство Пр, снабжённое индикато-
ром И, непосредственно в величинах напряжённости поля.
196
Измерить напряжённость неизвестного поля можно также
методом сравнения с эталонным полем, В этом случае предва-
рительная градуировка приёмного устройства не требуется. Из-
мерение производят следующим образом. Сначала принимают
сигнал от исследуемого источника, поле которого неизвестно, и
замеч<зют показания индикатора И приёмника. Затем включают
источник эталонного поля и точно настраивают его на частоту
Рис. 8.16. К измерению напряжённости поля методом
компарирования по эталонной напряжённости поля
исследуемого сигнала. Изменяя подводимую к антенне Ас мощ-
ность, добиваются прежних показаний индикатора И, По пара-
метрам аппаратуры эталонной напряжённости поля расчётным
путём определяют поле сигнала.
В зависимости от диапазона волн в схеме аппаратуры эта-
лонной напряжённости поля могут применяться антенны различ-
ных типов (рис. 8.17). Так, для диапазона длинных и средних
волн удобно использовать рамку или вертикальный штырь. Для
диапазона коротких волн, а также метровых и дециметровых
волн диапазона укв находят широкое применение горизонталь-
ные или вертикальные симметричные вибраторы (в зависимо-
сти от поляризации исследуемого поля). В диапазоне сантимет-
ровых волн чаще всего применяются рупорные антенны. В этом
случае при измерениях антенна Ап должна находиться в зоне
Фраунгоферовой дифракпии антенны Ас (см. следующую главу).
Очевидно, что в случае применения направленных антенн Ас по-
следние должны быть ориентированы главным максимумом из-
лучения в направлении главного максимума антенны Ля. Сама
антенна А ( должна размещаться на открытой площадке, свобод-
ной от построек, деревьев и т. д„ поскольку последние могут ис-
казить эталонное поле как в результате поглощения энергии, так
и в результате вторичного излучения.
Поскольку главный максимум приёмной антенны Ап должен
быть ориентирован по направлению прихода исследуемой вол-
ны, практически всегда приходится антенну Ас располагать на
некоторой высоте над поверхностью земли, обеспечивая тем са-
197
мым приём антенной А п прямого луча от антенны Ас и исклю-
чая в значительной степени луч, отражённый от поверхности
земли. Располагают антенну Лс на специальных, обычно, дере-
вянных, мачтах или башнях, высотой порядка 10—20 я.
Рис. 8.17. Типы антенн, применяемых в схеме эталон-
ной напряженности поля:
а) горизонтальный симметричный вибратор; б) вер-
тикальный симметричный вибратор; в) штыревая ан*
тенна; г) рупориая антенна; д) рамочная антенна
Напряжённость эталонного поля на расстоянии г от антенны
Лс в случае штыревой антенны небольшой высоты (А < А) или
рамочной антенны определяется по формуле
£ = 37,7-104—, — , (8.16)
г к м
где / — ток на зажимах антенны, а;
hd — действующая высота антенны, л», равная:
у штыревой антенны
у рамочной антенны
. 2r. NS
h‘=-r-
Здесь N — число витков рамки,
S — площадь одного витка.
(8Л7) .
-J
(8.18) !
198
В случае антенны из симметричных вибраторов или рупор-
ной антенны напряжённость эталонного поля равна
£ _ 173 ™ ( (8.19)
Г 1 м
где рс— мощность генератора Г с, кет,
Gc— коэффициент усиления антенны Ас,
— коэффициент полезного действия фидера,
г — расстояние между антеннами Ас и км.
Формула (8.16) соответствует антенне, находящейся на
идеально проводящей плоскости и излучающей поле вертикаль-
ной поляризации. Она справедлива на длинных и средних вол-
нах при наличии под антенной хорошего заземления.
Формула (8.19) позволяет получить достаточно точное зна-
чение напряжённости поля на коротких волнах при излучении
поля горизонтальной поляризации и определении коэффициента
усиления Gr в предположении, что антенна расположена над
идеально отражающей плоскостью.
На ультракоротких волнах, особенно на волнах дециметро-
вых и сантиметровых, не удаётся определить эталонное поле до-
ста точно точно расчетным путем из за трудности учёта влияния
земли. Подъем антенны па сравнительно большую высоту в
этом случае не всегда достигает цели. Этим можно в той или
иной мере ослабить интенсивность отраженной от земли волны
и её влияние на величину напряжённости поля, но исключить
полностью отражение от земли не удаётся, так как всякая ан-
тенна излучает по всем направлениям, хотя и с разной интен-
сивностью* Если, например, боковое излучение, попадающее на
область, существенную для отражения, имеет уровень — 14 дб
(0,2 по напряжённости поля), то в зависимости от cooiноше-
ния фаз прямой и отражённой волн поле в точке приёма мо-
жет меняться от 1,2 до 0,8 от уровня прямой волны, т. е. в
1,5 раза.
Для учёта влияния земли на поле в точке приёма А. Р. Водь-
перт [Л.32] предложил снять в области измерений кривую зависи-
мости напряжённости поля от высоты над поверхностью земли,
пройдя при этом через точки минимума и максимума поля. Рас-
сматривая максимальное поле как сумму, а минимальное как
разность полей прямой и отражённой волн, можно из экспери-
ментальных данных определить коэффициент отражения от по-
верхности земли и учесть его в ф-ле (8.19), вычислив коэффи-
циент усиления антенны Gc с учётом отражения от поверхности
земли.
Применять эталонное поле весьма удобно не только для из-
мерения напряжённости поля сигнала, но и для контроля ис-
199
правности тракта в месте приёма, Действительно, используя
эталонное поле, можно всегда проверить весь приёмный тракт
в целом: приёмную антенну Ап , фидер и приёмное устройст-
во Пр.
При этом антенну Ас не обязательно располагать на линии
главного максимума антенны Ап. Кроме того, антенна Ас может
находиться па расстояниях, меньших, чем это требуется из усло-
вия (9,3)). Контрольная аппаратура обычно состоит из вибра-
торной антенны Ас с плечами X, установленной на некото-
ром расстоянии от антенны Ап, и из генератора Гс>
В качестве генераторов Гс используются измерительные гене-
раторы стандартных сигналов^ с выходной мощностью до 1 вт
или специально сконструированные генераторы с питанием от
аккумуляторов и батарей.
Эталонное поле может быть также использовано для на-
стройки антенн, например, снабжённых рефлекторами.
Компа рирование по генератору шумового сигнала
Измерение амплитуды слабых полей порядка единиц или
v мкв
долей ---- методом компарирования по генератору стандарт-
ных сигналов практически невозможно из-за очень низкой точ-
ности. Ошибки измерений обусловлены трудностью получения
на выходе ГСС точно калиброванных слабых сигналов. Сильные
же сигналы от ГСС, достаточно точно откалиброванные, при-
мерно на 80-4100 дб выше необходимых для измерения слабого
поля, и в схему приходится включать градуировочный аттенюа-
тор на 804-100 дб. В этом случае на измерениях сказывается по-
грешность калибровки аттенюатора, которая может быть до-
вольно значительной. Кроме того, поскольку при сильных сиг-
налах от ГСС между генератором и измерительным приёмником
вводится элемент с большим затуханием, то даже незначитель-
ная утечка энергии высокой частоты из-за недостаточной экра-
нировки генератора и непосредственное влияние энергии утечки
на приёмник может дать большую ошибку в определении уров-
ня сигнала на выходе приёмника.
При измерении амплитуд поля в диапазоне укв вместо ГСС
удобно использовать так называемые генераторы шумового сиг-
нала (ГШС), даюшие без аттенюатора уровень сигнала, близ-
кий к измеряемому. Это исключает ошибки от просачивания
сигнала и делает ненужным применение тщательной экраниров-
ки и точно калиброванного аттенюатора.
Мощность некоторых ГШС может быть легко определена
расчётным путём. Такие ГШС не требуют калибровки по друго-
200
му генератору и могут быть также использованы в качестве пер-
вичного стандарта для калибровки ГСС.
ГШС весьма удобен как для измерения внутренних шумов,
приёмного устройства, так и для измерения внешних шумов-
(шумов антенны). В последнем случае сигнал ГШС имеет тако»
же характер, как и измеряемый шум. Поэтому реакция прибора,
измеряющего мощность на выходе, одинакова как на сигнал,
так и на собственный шум.
Основным элементом ГШС является источник шумового^
сигнала, чаще всего это шумовой диод. Источником шума в дио-
де является «дробовой эффект» — флуктуации количества элек-
тронов, попадающих на анод за единицу времени.
Спектральная плотность квадрата тока дробовых шумов:
диода, работающего в режиме насыщения, равна
d( Н
—= (8.20>
где е — заряд электрона, равный 1,6 • 10“19, к;
/ — постоянный ток диода, а.
Спектр дробовых шумов равномерен в широком диапазоне'
частот от единиц килогерц до сотен и даже тысяч мегагерц.
В указанном диапазоне средний квадрат шумового тока в
пределах эквивалентной полосы шумов Д/, (eq) определяется*
выражением
/^ = 2е/Д/,. (8.21>
Если шумовой ток диода, поставленного в режим насыще-
ния, проходит через активное сопротивление /?с, то на послед-
нем возникает так называемое шумовое напряжение £7Ш. Прене*
брегая влиянием внутреннего сопротивления диода, можно*
принять
Выходное напряжение шумов регулируется изменением
анодного тока, что, в свою очередь, достигается изменением на-
пряжения накала диода. Оно может быть подсчитано по фор^
муле
t/шг = 5,64 • 10“3 Rc VTTT, мкв, (8.22>
где / — ток диода, ма,
— ширина полосы пропускания, кгц.
Таким образом, выходное напряжение шумового генератора-
может быть легко отрегулировано до нужной величины по из-
вестному току диода.
201
Принципиальная схема ГШС для диапазона метровых волн
представлена на рис. 8.18» а для дециметрового — па рис. 8.19.
Генератор состоит из шумового диода Д, соединенного парал-
лельно с сопротивлением Рс, которое берётся равным выходно-
му сопротивлению истопника сигнала. Для нейтрализации соб-
ственной ёмкости схемы и
диода в схеме рис. 8.18 слу-
жит индуктивность L. Для
Рис. 8.18. Принципиальная схема ге-
нератора шумового сигнала для диа-
пазона Aferpoawx воли
этой же цели в схеме
рис. 8.19 применяется на-
стройка индуктивным шлей-
фом» представляющим собой
коаксиальный отрезок дли-
ной меньше — » закорочен-
4
ный на конце настроечным
поршнем П. Развязка по вы-
сокой частоте между диодом
и источником питания осу-
ществляется фильтром, со-
стоящим из дросселей Др и
блокировочных конденсато-
ров СБ>
Регулировка анодного
тока диода осуществляется
переменным сопротивлением
/?, включённым в цепь на-
кала диода. Анодный ток
контролируется по милли-
амперметру mA,
Измерение напряжённости поля с компарированием по гене-
ратору шумового сигнала производят по схеме рис, 8.20. Здесь
А — измерительная антенна, III г — генератор шумов, ИП —
измерительный приёмник, И — индикатор, Р — переключатель.
В этой схеме, как и при компарировании по ГСС, исполь-
зуется метод замещения. Калибровка усиления приёмника про-
изводится по напряжению, развиваемому шумовым генерато-
ром. которое подсчитывается по ф-ле (8.22).
При измерении полей сигналов с малым уровнем, когда, на-
пример, сигналы, принятые с антенны, сравнимы по величине
с внутренними шумами приёмника и шумами антенны, папря-
жение сигнала на входе приёмника может быть определено по
формуле
(8.23)
.202
где и(сГш) — суммарное напряжение сигнала и шумов (шумов
приёмника и антенны);
Uiu/]A — суммарное напряжение шумов (шумов приёмни-
ка, приведённое ко входу, и шумов антенны).
Рис, 8J9, Принципиальная схема генератора шумового
сигнала для диапазона дециметровых волн
Формула (8.23) получена в предположении, что полезный
сигнал и внутренние шумы приёмника складываются по мощно-
сти.
При использовании шумо-П7$
вого генератора в качестве ис- V
точника калибровочного на-
пряжения сравнительно легко
можно произвести измерение
шумов, вносимых антенной
(тепловые шумы антенны).
Такие измерения часто прово-
дятся в диапазоне укв, когда
с этими шумами приходится
считаться.
В ф-ле (8.23) суммарное
напряжение ЬШ[ТА шумов соз-
Рис 8.20. Влок-схема измерительной
установки для измерения напряжён-
ности поля методом компарирования
по генератору шумового сигнала
даётся шумами приёмного устройства Uutnp и шумами антенны
U . .те
тАнт » с»
7/2 _ (J2 1 JJ2
и шПА шПр ' шАл/п *
(8-24)
203
Отсюда шумы антенны определяются следующей формулой
U шАкт — ^шПА
(8.25)
Напряжение U ^па определяется по показаниям выходного
прибора приемника, когда антенна подключена ко входу приём-
ника, а сигнал отсутствует.
Следует иметь в виду, что напряжение ишАнгп, в свою оче-
редь, определяется шумами фидера и самой антенны.
Напряжённость поля Е по измеренному значению напряже-
ния сигнала (Д на входе приемника определяется через эдс, вы-
числяемую по ф-ле (8.15) при
Аппаратура для измерения абсолютной амплитуды поля
Ра д ио компа рато ры
Радиокомпаратор — прибор, служащий для измерения
абсолютной амплитуды поля ио методу компарировання. В ком-
Раночно*
\онтснно
тор .
опсм
par op
Г" Яриё'ммм устройство
/Wjfy I
I Генератор I
{стандартны^
^сигналов j
Рис. 8.21. Блок-схема
радиокомпаратора
плект прибора входит приёмное устройство, генератор стандарт-
ных сигналов и антенна, обычно рамка (рис. 8.21). В этой схеме
204
принято компарирование по генератору стандартных сигналов с
градуированным ослаблением по высокой частоте. Сигнал, при-
нятый рамочной антенной, подводится ко входу приёмного уст-
ройства, где он усиливается и детектируется. Рамка вращается
и устанавливается на максимум показаний выходного прибора
приёмника.
В описываемом компараторе приёмник собран по схеме пря-
мого усиления и работает в режиме генерации. Низкочастотный
сигнал усиливается и подаётся на телефон и ламповый вольт-
метр Лб. На частоту этого низкочастотного сигнала настраи-
вается генератор звуковой частоты ЗГ, напряжение с которого
поступает на телефон Т2. Для точной настройки используется
метод акустических биений слышимых сигналов с двух телефо-
нов.
Далее, повернув рамку на угол 90° относительно первона-
чального положения, соответствующего максимуму приема, уст-
раняют эдс, наводимую полем исследуемой радиостанции. Вклю-
чают генератор стандартных сигналов и производят его на-
стройку на частоту сигнала станции. Для этого опять исполь-
зуют акустические биения слышимых звуковых сигналов в теле-
фонах Т} и Г2. Произведя регулировку мощности генератора,
при помощи ослабителя добиваются прежних показаний лампо-
вого вольтметра.
Электродвижущая сила, возбуждаемая полем в рамке, равна
е - Eh*. (8.26)
Её величина определяется компарироваиием и равна напря-
жению U, приложенному к рамке от генератора стандартных
сигналов.
Таким образом, напряжённость поля может быть найдена по
формуле
. (8.27)
Данная схема компаратора не является совершенной. В ней
трудно исключить непосредственное влияние генератора стан-
дартных сигналов и ослабителя на входную часть приёмника,
включая и рамку. Требуется тщательная экранировка отдель-
ных частей приёмника и генератора стандартных сигналов, а
также автономное питание генератора. Для ослабления влияния
всякого рода паразитных наводок были предложены схемы ком-
параторов, в которых градуированный ослабитель включается
в пепь усилителя промежуточной частоты приёмного устройства
компаратора. Приёмное устройство собирается по супергетеро-
динной схеме. Ослабитель компаратора работает всегда на од-
ной и той же частоте, что облегчает его конструктивное выпол-
205
некие и градуировку. В компараторах этого типа эдс, поступаю-
щая с генератора стандартных сигналов в рамку, может быть
взята значительно большей, чем эдс, возбуждаемая в рамке ис-
следуемым полем. В этом случае паводка паразитных полей на
входную цепь приёмника почти не сказывается. Экранировка ге-
нератора стандартных сигналов также упрощается. Компарато-
ры с градуированным ослабителем в цепи усилителя промежу-
точной частоты предназначаются [Л22] в основном для измере-
ния напряжённости полей радиостанций длинных, средних и ко-
ротких волн. Погрешность измерений составляет 30—40% при
измерении поля незатухающих сигналов напряжённостью не ни-
же 10 МКв/м.
Селективные микровольтметры. Измерители помех
В качестве компараторов электрического поля радио-
станций, работающих незатухающими колебаниями, а также
как селективные микровольтметры, могут быть использованы
измерители помех, выпускаемые отечественной промышлен-
ностью (краткие технические характеристики некоторых типов
измерителей помех даны в приложении 4).
Измерители помех представляют собой супергетеродинные
приёмники с инерционным детектором и индикаторным прибо-
ром па выходе. Их можно рассматривать как высокочастотные
микровольтметры, шкала которых градуирована в микроволь-
тах БХО/ЦИОго напряжения. Градуировка измерителей помех
производится при заводских испытаниях по генератору стан-
дартных сигналов, а в условиях эксплуатации. — по собствен-
ным шумам, т. е. по напряжению шумов ламп и контуров. Блок-
схема одного из измерителей помех (типа ИП-14) показана на
рис. 8.22.
В качестве антенны А при измерении напряжённости поля
сигнала радиостанции используется полуволновой симметричный
вибратор, действующая высота которого, как известно, равна
hd = —. Плечи вибратора сделаны из трубок, вставленных одна
в Другую и раздвигаемых для изменения длины плеча.
206
Прежде чем приступить к измерениям, устанавливают длину
плеч вибратора по меткам, соответствующим той или иной дли-
не волны. Сигнал с антенны А поступает на декадный делитель,
дающий ослабление входного напряжения в 10, 100 и 1000 раз, а
затем на усилитель высокой частоты увч. В смесителе Пр ча-
стота сигнала преобразовывается в промежуточную частоту
12 Мгц. Усилитель промежуточной частоты состоит из трех сту-
пеней. Выпрямленное напряжение промежуточной частоты с де-
тектора Д] подаётся на ламповый вольтметр JlBt собранный по
мостовой схеме. В одну из диагоналей моста подаётся стабили-
зированное напряжение, а в другую — включён выходной инди-
каторный прибор. Уравновесив мост, можно по величине ста-
билизированного напряжения определить подаваемое на вольт-
метр напряжение.
Детектор Дг с усилителем низкой частоты УНЧ и телефоном
Т служат для акустического контроля.
Зная показания прибора лампового вольтметра и действую-
щую высоту симметричного вибратора, находим напряженность
поля по формуле
9/
Е - — , (8.28)
где I — показание прибора лампового вольтметра,
h д — действующая высота антенны.
Микро ватт метры (измерители малой мощности)
Для измерения абсолютной амплитуды поля могут быть
использованы микроваттметры—измерители малой мощноеги
(ИММ).
Измерение мощности в этих приборах производится чаще
всего при помощи термосопротивлепия. При прохождении тока
высокой частоты по сопротивлению оно нагревается и величина
его полного сопротивления меняется. По этому изменению мож-
но найти величину поглощения термосопротивлением мощности.
В измерителях малой мощности в качестве тсрмосопротивле-
ний используются главным образом термисторы (рис. 8.23а),
представляющие собой полупроводниковый шарик (бусинку) /
диаметром приблизительно ОД мм, помешенный в стеклянный бал-
лон 5. С внешними выводами 4, впаянными в стенки баллона,
шарик соединяется проводами 3 из тонкой платиновой проволо-
ки. Выводы присоединяются к соответствующим зажимам изме-
рительной схемы.
Термистор обладает отрицательным температурным коэффи-
циентом, т. е. его полное сопротивление уменьшается с ростом
температуры.
207
Термисторы позволяют измерять мощность от единиц микро-
ватт до десятков милливатт во всём диапазоне укв. Чувстви-
тельность термистора составляет 30—70 ом/мвт; иногда она до-
ходит до 100 ом/мвт. Термисторы обладают примерно в 10—20
раз большей чувствительностью, чем измерительные болометры.
К щсту
Я
Рис. 8.23. Схемы-
а) термистора; б) коаксиальной высокочастотной головки; в) волноводной
высокочастотной головки; г) принципиальная схема ваттметра
Термисторный микроваттметр состоит из высокочастотной го-
ловки и измерительного моста.
Высокочастотная головка выполняется из отрезка коаксиаль-
ной или волноводной линии, термистора и органов согласования.
На рис. 8.236 показан вариант коаксиальной высокочастотной го-
ловки. Термистор включён в разрыв внутреннего провода коак-
сиальной линии. Поршни К\ и Кг служат органами настройки.
На рис. 8.23в показана волноводная высокочастотная головка.
Термистор находится в коаксиальной части коаксиально-волно-
водного перехода. Для согласования термистора с коаксиальной
линией и волноводом служат поршни Kz и
208
Измерительные мосты термисторного ваттметра служат для
определения изменения полного сопротивления термистора при
поглощении мощности высокочастотных колебаний, а следова-
тельно, и величины мощности.
Для того чтобы исключить влияние окружающей температу-
ры на результат измерений, термистор предварительно подогре-
вают постоянным или переменным током, приводя его полное со-
противление к определённой величине.
На рис. 8.23г показана принципиальная схема ваттметра, со-
стоящего из волноводной высокочастотной головки и измери-
тельного моста постоянного тока. Измерительный мост состоит
из трех плеч с сопротивлениями /?, обычно одинаковой величины,
и четвёртого плеча, которым служит термистор.
Рабочая точка па характеристике термистора (на кривой за-
висимости полного сопротивления от температуры) обычно вы-
бирается так, чтобы исходное сопротивление термистора
было равно /?. В этом случае ваттметр будет иметь наибольшую
чувствительность. Через плечи моста, в том числе и термистор-
ное, протекает постоянный ток. Его величину можно изменять по-
тенциометром /? п >
Перед измерением мост балансируется так, чтобы ток IА в
диагонали отсутствовал. После балансировки в волновод вводит-
ся измеряемая мощность. Применяют два метода измерения мощ-
ности: разбалансированного моста и сбалансированного моста.
По первому мощность определяется по току в диагонали. Под
действием высокочастотных колебаний термистор дополнитель-
но разогревается и баланс моста нарушается. В диагонали моста
появляется ток, равный
где /ог— ток в термисторном плече до подачи высокочастот-
ных колебаний,
А/?г — изменение сопротивления термистора,
/?д — сопротивление в цепи диагонали моста.
Изменение сопротивления термистора зависит от мощности,
поглощаемой термистором, т. е. является функцией мощности
Д^Г = <Р(РЯ5). (8.296)
Отсюда
'я = т£ <8-29в>
Так как ток разбалансировки в диагонали моста зависит от
измеряемой мощности, шкалу прибора, измеряющего этот ток,
14—292 204
можно проградуировать непосредственно в единицах мощности,
например в милливаттах.
Метод сбалансированного моста заключается в следующем.
При подаче в волновод высокочастотных колебаний сопротив-
ление термистора уменьшается и баланс моста нарушается.
Однако прежнюю величину сопротивления термистора можно
восстановить, если уменьшить величину постоянного тока, про-
пускаемого через термистор. Для этой цели служит потенцио-
метр Rn.
Измеряемая мощность высокочастотных колебаний опреде-
ляется как разность мощностей постоянного тока, поглощаемых
термистором при первой и второй балансировках моста (когда
вч колебания отсутствуют и когда вч колебания подаются к ват-
тметру) :
Р„=/^г-/^7 = -/у.
(8.30)
где lai и /02 — постоянные токи в термисторе после первой и
и второй балансировок,
RT— сопротивление термистора при сбалансирован-
ном мосте.
Выпускаемые отечественной промышленностью измерители
малой мощности позволяют измерять мощность в весьма широ-
ком диапазоне частот, начиная с коротких волн и кончая сверх-
высокими частотами. Диапазон мощностей простирается от не-
скольких ватт до десятков микроватт. Для измерения амплитуды
поля эти приборы снабжаются измерительной антенной, тип и
размеры которой выбираются в зависимости От диапазона волн
исследуемого источника. Одна из схем всей измерительной уста-
новки в этом случае представлена на рис. 8.24.
Рис. 8.24, Схема измери-
тельной установки с
ИММ
Измерительная антенна А, которой служит симметричный
вибратор, через коаксиальный фидер подключается к измерите-
лям малой мощности. Поскольку вход ИММ построен обычно по
несимметричной схеме, то на ультракоротких волнах приходи!-
ся применять симметрирующее устройство типа (7-колена, а на
коротких волнах —симметрирующий трансформатор.
210
При равенстве входного сопротивления вибратора, волновод-
ного сопротивления фидерной линии и входного сопротивления
МММ напряжение UTi развиваемое на сопротивлении термисто-
ра, определяется следующим выражением (считается, что фи-
дер не вносит потерь энергии):
vt=^-Vpr^, (8.31)
где ел — эдс, возбуждаемая иа зажимах антенны.
Поскольку измеренная мощность Р известна, можно опре-
делить и напряжение UT, а также еА. Через известную вели-
чину еА Далее определяется напряжённость поля Е по формуле
Е=Ц±. (8.26а)
Л
Измерение фазы поля
Знание фазовой диаграммы поля, т. е. распределения фаз
поля вдоль какой-либо линии или поверхности, причём это от-
носится как к полю в дальней зоне излучения, так и к полю в
ближней и промежуточной зонах, представляет большой прак-
тический интерес.
Знание фазовой диаграммы антенны в дальней зоне требует-
ся при разработке систем фазового сканирования, а также при
анализе антенн со специальной формой диаграммы направлен-
ности и определении влияния отражения от поверхности земли.
Знание фазовой диаграммы антенны в ближней зоне, в част-
ности» в раскрыве СВЧ антенн необходимо, поскольку она опре-
деляет амплитудную диаграмму направленности.
Знание фазовой диаграммы в промежуточной зоне требу-
ется при анализе работы облучателей зеркал и линз. Как из-
вестно, принцип работы зеркальных и линзовых антенн осно-
вывается на том, что зеркало (или линза) должно облучаться
точечным (или линейным) облучателем, т. е. таким облучате-
лем» который создаёт у поверхности зеркала (или линзы) сфе-
рический (или цилиндрический) фронт волны. Так как облу-
чатель имеет определённую протяжённость и располагается
сравнительно близко от зеркала или линзы, то в действительно-
сти фронт волны в той или иной степени отличается от сфери-
ческого (или цилиндрического). Таким образом, представляет
интерес знание действительной формы фронта волны или фа-
зовой диаграммы облучателей зеркал и линз на сравнительно
близком расстоянии от них.
Н* 211
Фазовые диаграммы, как и другие характеристики антенны,
рассчитываются. Однако нередко прибегают и к измерению
их.
Методика снятия фазовой диаграммы заключается в срав-
нении искомых фаз поля в различных точках пространства с
фазой какого-либо источника эдс той же частоты, которая оста-
Сигнал л
ценимой
фазы
Рис. 8.25. Блок-схема из-
мерительной установки
для снятия фазовой дна
граммы с измерительной
линией
ётся постоянной в процессе измерений данной фазовой диаграм-
мы и принимается за нуль. Сигнал постоянной нулевой фазы,
поступающий от указанного источника эдс, называется опорным
сигналом. Обычно для питания антенны и цепи опорного сигна-
ла используется один и тот же генератор, энергия которого раз-
ветвляется по этим двум Цепям.
В настоящее время известно много различных схем для сня-
тия фазовой диаграммы.
На рис. 8.25 показана схема с применением измерительной
линии. Измерительная линия присоединяется через переменные
аттенюаторы Л| и Дг с одного конца к цепи опорного сигнала, а
с другого — к цепи сигнала искомой фазы. Аттенюаторы долж-
ны быть свободны от фазовых искажений и обеспечивать дву-
стороннее согласование измерительной линии, и с этих точек
зрения они должны быть проверены перед началом измерений.
Кроме того, в схеме рис. 8.25 аттенюаторы служат для вырав-
нивания амплитуд сигналов опорного и искомой фазы.
Так как сигналы вызывают в измерительной линии волны
противоположных направлений, то в ней образуется картина сто-
ячих волн, положение узлов которой меняется с изменением
фазы исследуемого сигнала. Перемещая индикаторную голов-
ку измерительной линии и определяя смещение Д/ узлов, мож-
но определить изменение фазы Дф по формуле
Дф = — Л /. (8.32)
где кф— длина волны в фидере измерительной линии.
Вместо подвижной индикаторной головки можно применить
схему рис. 8.25 с измерительной линией, но с неподвижной ин-
дикаторной головкой, включив между измерительной линией и
аттенюатором А2 градуированный фазовращатель и добиваясь
при каждом измерении нулевых показаний прибора индикатор-
212
ной головки при помощи фазовращателя. В такой схеме раз-
ность фаз показывает непосредственно фазовращатель.
Если у измерительной линии индикаторную головку сделать
неподвижной, то теряется смысл в применении измерительной
линии и она может быть заменена фидером со стационарным
ответвителем.
Рис. 8,26. Блок-схема из-
мерительной установки
для снятия фазовой диа-
граммы с Т-мостом
На рис. 8.26 показана схема, эквивалентная по принципу дей-
ствия схеме с измерительной линией и неподвижной индикатор-
ной головкой. Вместо измерительной линии использован Т-мост.
Сравниваемые сигналы подаются в боковые плечи. Когда их
амплитуды и фазы равны, оба сигнала поступают в плечо в
плече Ё они отсутствуют. Следовательно, по нулевым показа-
ниям индикатора, включаемого в плечо Е, можно определять
равенство фаз сигналов обеих цепей. Разность фаз в двух точ-
ках поля можно определять по фазовращателю, как и в схеме с
неподвижным зондом.
Схема рис. 8.26 имеет следующие преимущества перед схе-
мой рис. 8.25: 1) у Т-моста боковые плечи развязаны следо-
вательно, в этой схеме Т-моста развязаны цепи опорного
сигнала и сигнала искомой фазы, чего нельзя сказать о схеме
рис. 8.25; 2) в схеме рис. 8.26 используется вся мощность, по-
ступающая в Т-мост, в то время как в схеме рис. 8.25 в цепь зон-
да измерительной линии ответвляется лишь незначительная
часть мощности, поступающей в измерительную линию, вслед-
ствие чего схема рис. 8.26 обладает большей чувствительностью,
чем схема рис. 8.25.
В рассмотренных схемах рис. 8.25 и 8.26 сигнал искомой фа-
зы компенсируется опорным сигналом, почему эти схемы назы-
ваются компенсационными. Наряду с этими схемами возможны
схемы непосредственного измерения разности фаз опорного сиг-
нала и сигнала искомой фазы с использованием осциллографа и
определением разности фаз по фигурам на его экране либо с
использованием преобразования разности фаз в приращение то-
ка или напряжения с последующим измерениехМ этих величин
стрелочными приборами. Систему, которая служит для измере-
213
ния фазы: измерительная линия с подвижным зондом, Т-мост
с фазовращателем, осциллограф и т. п. — кратко именуют фа-
зометром.
На рис. 8.27 изображена одна из схем измерения фазовой
диаграммы поля в ближней зоне. Она идентична схеме рис. 8.26
Рис. 8,27. Блок-схема измерительной установки для сня-
тия фазовой диаграммы в ближней зоне
и отличается от неё лишь тем, что конкретизированы некото-
рые её элементы. В качестве антенны взята линза. В качестве
фазовращателя используется измерительная линия. Она же од-
новременно служит разветвителем мощности, поступающей от
ГСС. Основная часть мощности направляется в облучатель
линзы, небольшая её часть ответвляется через индикаторную
юловку непосредственно к Т-мосту и служит опорным сигна-
лом.
Фазовая диаграмма снимается при помощи зонда, представ-
ляющего собой приёмную антенну и перемещаемого по задан-
ной линии (в частности, параллельно раскрыву линзы). Зонд
представляет собой волновод, суживающийся к концу и окан-
чивающийся диэлектрическим стержнем небольшой длины и
малого диаметра (рис. 8.27). Такая конструкция зонда объяс-
няется тем, что, с одной стороны, желательно, чтобы зонд обла-
дал направленным приёмом и тем самым принимал бы главным
образом с фронта (с направления своего главного максимума)
и не был бы чувствителен к волнам, приходящим с боковых и
задних направлений. С другой стороны, желательно, чтобы он
имел минимальную площадь с фронта, и усреднение фазы, про-
изводимое зондом, происходило с меньшей площади раскрыва.
При снятии фазовой диаграммы может быть использован пас-
сивный отражающий зонд (рис. 8.28). В схеме используется
два направленных ответвителя, из которых один реагирует на
прямую волну, другой — на отражённую. Помещённый в рас-
крыве антенны зонд вызывает отражённую волну в антенне,
214
которая передаётся в волноводный тракт, а затем отводится на-
правленным Ответвителем к Т-мосту. Фаза отражённой зондом
волны зависит от фазы поля, в которой находится зонд. Сле-
Актынщ
Ь /Ьашйшй
Рис. 8.28. Блок-схема измерительной установки для снятия фа*
зовой диаграммы при помощи отражательного зонда
довательно, перемещая зонд по раскрыву и измеряя фазу отра-
жённой зондом волны, можно получить искомую фазовую диаг-
рамму.
Фазовая диаграмма может
быть снята при работе антен-
ны на приём по схемам
рис. 8.29 и 8.30. В схеме
рис. 8.29 исследуемая антен-
на — активная, а рис. 8.30 —
пассивная. У антенны рис. 8.30
фидер замкнут плунжером, ко-
торый предназначен для её на-
стройки на рабочую волну.
Измерение фазовой диаг-
раммы поля в дальней зоне
Рис. 8.29. Блок-схема измерительной
установки для снятия фазовой диа-
граммы при работе активной иссле-
дуемой антенны на приём
представляет собой более сложную задачу, чем измерение фаз
поля в раскрыве антенны. Строго говоря, для снятия фазовой диа-
Рис. 8.30. Блок-схема измерительной установки для снятия
фазовой диаграммы при пассивной исследуемой антенне,
работающей на приём
граммы в дальней зоне требуется обходить исследуемую антен-
ну с каким-либо зондом по заданной кривой, расположенной на
большом расстоянии от неё. Вполне очевидны неудобства и
215
другие недостатки таких измерений. В целях упрощения задачи
обычно ограничиваются лишь контролем сферичности фазового
Фронта, т. е. снятием фазовой диаграммы на сфере, окружающей
антенну, что позволяет оставить зонд неподвижным и произ-
водить измерения вращением исследуемой антенны вокруг
предполагаемого центра фазового фронта.
исмед. бспомошп.
антенна антенна
Рис. 8.31. Блок-схема измерительной установки для из-
мерения фазовой диаграммы в дальней зоне
Измерения в дальней зоне должны производиться на спе-
циальных открытых политопах, свободных от посторонних соо-
ружений, Антенны — исследуемая и вспомогательная — должны
помещаться на специальных вышках, чтобы отражения от зем-
ли не влияли на измерения. При исследованиях малых антенн в
помещении лаборатории стены должны быть снабжены погло-
щающим покрытием.
Простейшая схема измерений в дальней зоне показана на
рис. 8.31. Она аналогична приведённым выше схемам измере-
ний в ближней зоне, в которых исследуемая антенна работает
на передачу. Отличие заключается в том, что 1) вместо зонда
применяется вспомогательная антенна; 2) из-за большого ослаб-
ления сигнала, вызванного разнесением антенн, применяется
чувствительный приёмник; 3) для подачи опорного сигнала на
фазометр применяется фидер, протянутый от одной вышки к
Другой.
В схеме рис. 8.31 фазы сигналов сравниваются на входе при-
ёмника по высокой частоте. Преобразованию частоты в приём-
нике подвергается суммарный сигнал. Помимо большого затуха-
ния, вносимого длинным высокочастотным кабелем, недостат-
ком схемы является также то, что из-за большой длины кабеля
малейшее изменение режима на одном конце приводит к значи-
тельному изменению фазы на другом конце. В результате эта
схема не отличается высокой точностью измерений.
216
Лучше в этом отношении схема, изображённая на рис. 8.32.
В этой схеме аппаратура обеих вышек совершенно идентична, за
исключением фазометра, который находится лишь на одной из
них. Принцип действия схемы следующий. На каждой вышке
имеются ГССУ направленный ответвитель, антенна, приёмник,
Рис. 8.32. Блок-схема
измерительной уста-
новки для измерения
фазовой диаграммы в
дальней зоне при
идентичной аппарату-
ре на приёмной и пе-
редающей вышках
Лелонмм». Яссмй.
антъннд антенне
а на одной из них фазометр. Частоты колебаний обоих ГСС
близки и отличаются на величину принятой низкой частоты.
Сигнал-генераторы служат одновременно гетеродинами, каж-
дый для своего приёмника. Обе антенны излучают колебания
своего ГСС и одновременно принимают колебания ГСС другой
вышки. Это обеспечивает выделение в обоих приёмниках од-
ной и той же низкой частоты. Колебания низкой частоты срав-
ниваются в фазометре по фазе.
Схема рис. 8.32 сложнее схемы рис. 8.31, но обеспечивает
значительно большую устойчивость и точность измерений.
Заметим, что сравнение фаз по низкой частоте позволяет
производить измерение очень малой разности фаз, если приме-
нить в фазометре умножение фазы.
Статистические методы обработки данных измерений
напряжённости поля при наличии флуктуаций (замираний)
Характеристики излучения антенн, измеренные на рас-
стояниях прямой оптической видимости, не совпадают с харак-
теристиками, измеренными на больших расстояниях за гори-
зонтом. Известно, например, что эффективный коэффициент уси-
ления остронаправлепных антенн на линиях связи тропосферного
рассеяния получается меньше рассчитанного для свободного
пространства. Аналогичный эффект возникает на укв линиях
ионосферного рассеяния. У укв антенн линий связи, использую-
щих отражения от метеорных следов, имеет место своего рода
трансформация диаграммы направленности. Известные измене-
ния претерпевают также на больших расстояниях характеристи-
ки антенн коротковолновых магистральных линий связи. Отме-
217
ченные факты были обнаружены главным образом опытным пу-
тём. Теория этих явлений к настоящему времени разработана
ещё недостаточно. Разработка и всё более широкое внедрение в
практику радиосвязи, радиовещания и телевидения новых мето-
дов передачи сигналов на большие расстояния с использованием
Рис 8.33. Кривая зависимости уровня поля от времени
при подверженности поля непрерывным беспорядочным
изменениям
явлений рассеяния на неоднородностях в тропосфере и ионо-
сфере диктуют необходимость проведения во всё более широких
масштабах измерений напряжённости поля и характеристик ан-
тенн на больших расстояниях за пределами прямой видимости.
Напряжённость поля далеко за пределами прямой оптичес-
кой видимости нестабильна, опа непрерывно и беспорядочно
изменяется, причём пределы изменений весьма значительны.
На рис. 8.33 показан характерный ход напряжённости поля с
течением времени. Как видно, зависимость напряженности поля
от времени не может быть выражена аналитически, так как раз-
личные уровни поля хаотически следуют друг за другом без ка-
кой-либо заметной закономерности. Поэтому определить харак-
теристики излучения непосредственно по данным измерений не-
возможно. Для этого требуется обработка данных, которая поз-
волила бы выяснить закономерность, лежащую в основе про-
цесса, приводящегося к графику вида рис. 8.33.
Флуктуации напряжённости поля, в частности, имеют место
в том случае, когда оно образуется в результате интерференции
полей многих волн, приходящих с разных направлений и выз-
ванных независимыми друг от друга нестабильными возбудите-
лями. Независимость и нестабильность возбудителей волн обус*
ловливает возможность разнообразных соотношений амплитуд
и фаз этих полей в разные моменты времени, обусловливает слу-
чайность уровня поля в каждый данный момент времени. Одна-
ко, несмотря на то, что уровень поля в каждый данный момент
времени является случайной величиной, встречающиеся уровни
218
поля в течение более или менее длительного периода времени нс
могут быть совершенно произвольными. Они следуют закономер-
ностям математической статистики и теории вероятности. Оста-
новимся вкратце на основных положениях теории вероятности и
математической статистики.
Предметом теории вероятности является случайная величи-
на, могущая принимать бесчисленное количество дискретных
или непрерывных значений. Случайной величиной называется та-
кая величина, значение которой в точности предсказать невоз-
можно, можно лишь утверждать, что она с известной вероятно-
стью примет одно из возможных значений.
Случайные величины каждого физического процесса под-
чиняются определённому для данного процесса закону распреде-
ления, показывающему, с какой вероятностью случайная вели-
чина принимает одно из своих возможных значений. Математи-
чески закон распределения выражается определённой функци-
ей F(x), причём дифференциал этой функции
dF (х) = F' (х) dx - W (х) dx (8.33)
показывает, какова вероятность того, что случайная величина
будет иметь значение, лежащее между х и x+dx.
Функция W(x) называется дифференциальной функцией рас-
пределения вероятности или плотностью распределения вероят-
ности. Из приведённого определения очевидно, что величина
F (х9) - F (xj = j W (х )dx (8.34)
показывает вероятность того, что случайная величина лежит в
пределах от х1 до xt, а величина
F(x) = J W(x)dx (8.35)
l —оо
— вероятность того, что случайная величина имеет значение, не
меньшее, чем х.
Очевидно также, что
J K7(x)dx=l. (8.36)
— Оо
Зная плотность распределения вероятностей, можно найти
ожидаемое среднее значение случайной величины по формуле
J xW(x)dx. (8.36а)
219
и среднее квадратичное значение случайной величины по фор-
муле
_ + °°
х3- j xW(x)dx. (8.37)
— оо
Наряду со средним и среднеквадратичным значениями ши-
роко пользуются так называемым медианным значением слу-
чайной величины, которая определяется по формуле
F(xo,s)= J0,5lT(x)dx= 0,5 (8.38)
— ОО
и так называемой величиной дисперсии а или, иначе, квадратич-
ным отклонением от среднего значения, определяемого форму-
лой
О2 = рх — х)2Г (х) dx - X2 — ф2 . (8.39)
—'ао
Аналогично могут быть введены и другие величины х0„ х01<»
и т. п.
Зная плотность распределения вероятности и одну из ука-
занных величин х, х\ Хо,5> а и т. д., можно легко найти и ос-
тальные величины.
Случайной величиной для нас является напряжённость поля
£. Поэтому, пользуясь ф-лами (8.33) — (8.39), будем подстав-
лять в них Е вместо х.
В разных физических процессах случайные величины подчи-
няются различным функциям распределения. Известны, напри-
мер, следующие функции распределения:
1) распределение Рэлея, при котором
U7(£)=g.e & . (8.40)
2) распределение Гаусса или нормальный закон распреде-
ления, при котором
(E-Eq,5 )*
1Г(Е) = -2” ; (8.41)
У 2га
3) логарифмический нормальный закон распределения, при
котором
ш
= " <8Л2>
Известны также функция распределения скоростей молекул
идеального газа, функция распределения энергии электронов
электронного газа в металлах с учётом и без учёта квантова-
ния и т. д.
Замирания поля условно делятся на два вида: быстрые и
медленные. Быстрые — это такие замирания, при которых на-
пряжённость поля проходит полный цикл, включающий одно
минимальное и одно максимальное значения, не менее одного
раза в секунду. Медленные — это такие замирания, при кото-
рых такой же цикл продолжается несколько минут и более. Вся
картина рис. 8.33 представляет собой наложение обоих видов
замираний.
По современным взглядам быстрые замирания подчиняют-
ся распределению Рэлея, а медленные — логарифмическому нор-
мальному закону. Распределение Гаусса не может отражать
процесс замираний, поскольку оно допускает с равной вероят-
ностью как положительные, так и отрицательные значения на-
пряжённости поля, в то время, как напряжённость поля есть су-
щественно положительная величина.
Обработка данных измерений заключается в проверке спра-
ведливости того или иного распределения и в определении ха-
рактеристических величин распределения EQ5.<j, £2 и т.п. в за-
висимости от того, какая из этих величин берётся в основу рас-
чёта характеристик исследуемой антенны.
Методика обработки данных измерений показана на рис. 8.33.
На экспериментальной кривой хода напряжённости поля, на-
блюдаемого в течение промежутка времени Tt проводятся на
разных уровнях прямые, параллельные оси абсцисс. Участки
этих прямых, являющиеся хордами обрабатываемой кривой,
выделены жирными линиями. Для каждого выбранного уров-
ня измеряется сумма длин указанных хорд. Отношение суммы
длин хорд по всему периоду наблюдений Т рассматривается как
вероятность того, что напряжённость поля может иметь значе-
ние не меньше того уровня, на котором проведены хорды. Затем
строится график измеренной кривой распределения вероятности
F(E) (рис. 8.34), из которого могут быть найдены медианное
значение £0 5, значения £0 9, E0<#n т. д. Кроме того, эксперимен-
тальная кривая функции распределения, полученная путём ста-
тистической обработки данных измерений, может быть сравнена
с одной из известных теоретических функций распределения для
установления закономерности и последующего расчёта других
характеристических величин.
Заметим, что интеграл
^W(E)dE (8.43)
221
при подстановке IF(E) из (8.40) приводится к виду
A (8.44)
а при подстановке IF(E) из (8.42) к виду
Интеграл (8.45) известен как интеграл Лапласа. Для него
составлены таблицы. Легко видеть, что все характеристические
величины Е, Е2, о и т. д. выражаются либо через интеграл вида
(8.44), либо через интеграл вида (8.45). Следовательно, расчёт
характеристических величин не представляет большого труда.
Для того чтобы определить, в какой мере измеренные кривые
распределения соответствуют тому или иному теоретическому
закону, целесообразно теоретическое распределение привести
к линейному закону с тем, чтобы на графике изобразить его
прямой линией. Так, для распределения Рэлея вместо
F (Е > Ежвя) =-Д- J Ее dE — е (8.46)
будем пользоваться функцией
<?(^як) - VlnF(E^ = . (8.47)
222
Преобразованную функцию G, позволяющую представить
закон распределения в виде прямой, будем называть масштаб-
ной функцией.
Если воспользоваться ф-лон (8.40), легко получить для рас-
пределения Рэлея
^ = ^о.5 =0,83/Г2. (8.48)
Через медианные значения функция G выражается следую-
щим образом:
6 = 0,83 .
Следовательно, откладывая на графике по оси абсцисс квад-
ратный корень из модуля натурального логарифма плотности
вероятности, а по оси ординат отношение соответствующего
уровня сигнала к медианному значению, получим закон распре-
деления Рэлея, изображённый в виде прямой линии.
В табл. 8.1 приведены данные пересчёта от функции распре-
деления Рэлея F(E„tr„) к соответствующей масштабной функции
G(F) = У |ln f|.
Таблица 8. 1
F (Емии) 1 0,95 0.9 0,8 0.7 0,6 0,5 0,4 0,3 0.2
G = /|lnF[ 0 0,225 0,326 0,47 0,595 0,715 0,83 0,955 м I ,26
F (Е>ии) 0,1 0,05 0,02 0,01 0,005 0,002 0,001 0,0005 0.0001
G = /|inF| 1 ,52 1 ,77 1,97 2,12 2,3 2,5 2,63 2,75 3.03
Зависимость —— от величины масштабной функции G (Емин)
Еяед
приведена на рис. 8.35.
Аналогично можно построить масштабную функцию
G(Ej,ow)% для логарифмического нормального закона распре?
деления.
Однако в данном случае это построение приходится делать
графически, так как интеграл для F(EMU„)i\& выражается в яв-
ной форме, а, как отмечалось выше, приводится к интегралам
Лапласа.
Значения масштабной функции G(EMall) приведены в табл.
8.2. В згой таблице приведены значения F.(E MltH) % = 100
(F (Еман1) — F (EMtlt 2)] и соответствующие им значения
223
? (Еми*) % 95—90 90—80 80—70 70—60 60—50 50—40
Ged I .5 1,8 1 .3 1 >1 1 .0 1,0
2—1 ,0 1 ,0—0,5 0,5—0,2 0,2—0,1 0,1—0.05 0,05—0.01
Ged 1,2 0,85 1 ,45 1.3 0,4 0,8
Ged—G (£*u«i)— G(EMUHi), которые на графике откладываются по
оси абсцисс. По оси ординат в данном случае откладывается зна-
чение 201g . Кривые зависимости 201g — от й(Елан),
ЛС,5 £0.5
построенные по данным табл 8.2 для различных значений и, при-
ведены на рис, 8.36.
224
Рис. 8.36. Графики зависимости отношения от
масштабной функции G (Емин) для различных значений о
15-292
225
Аппаратура автоматической обработки данных измерений
напряжённости поля прн наличии флуктуаций
Общие сведения
Запись кривой изменения напряжённости поля при по-
мощи самописцев требует, как указывалось выше, последующей
обработки. Метод обработки, описанный в предыдущем параг-
рафе, который будем называть ручной обработкой, чрезвы-
чайно трудоемкий и не отличается высокой точностью. Поэто-
му находит применение обработка этих кривых при помощи
электронно-счётных машин, а также специальных приспособ-
лений, ускоряющих и облегчающих работу. Могут быть исполь-
зованы механические интеграторы, планиметры и т< п.
Наряду с этим применяются приборы, которые подключа-
ются к выходу приёмника вместо самописцев и непосредственно
показывают величину функции распределения для разных уров-
ней поля. Эти приборы будем называть анализаторами уровня
поля или анализаторами замираний. Рассмотрим некоторые из
схем анализаторов замираний.
Анализаторы с релейной схемой
В этих анализаторах (рис. 8.37) сигнал с выхода при-
ёмника поступает на усилитель постоянного тока (УПТ), а за-
тем на систему электромеханических реле Р2 . - - Каж-
Рис. 8.37. Блок-схема ана-
лизатора уровня с при-
менением электромеха-
нических реле
дое реле при срабатывании включает или выключает свои ча-
сы n j и счётчик Включение происходит, когда уровень сиг-
нала на выходе УПТ достигает некоторого значения а
выключение, когда уровень сигнала падает ниже Дл*
каждого реле устанавливается своё значение при помощи
потенциометров Rit R2, - > -, R*- Число реле, часов, счётчиков и
226
потенциометров равно числу градаций уровня, которое намече-
но фиксировать.
Таким образом, каждые из часов показывают время, в те-
чение которого сигнал на выходе У ПТ был выше соответствую-
щего этим часам уровня U а счётчики регистрируют чис-
ло включений часов. Так как уровень сигнала на выходе У ПТ
связан с уровнем напряжённости поля Е, то при соответ-
ствующей градуировке системы можно по отношению времени
включения часов И i к общему времени работы анализатора
(фиксируется часами Яо), найти значение функции распреде-
ления F(Ej)
F(Ei)=^W(x)dx, (8.49)
О
соответствующее уровню поля £\-.
Анализатор уровня с пересчетной схемой
Описанный выще анализатор уровня не может быть ис-
пользован при исследовании быстрых замираний поля, посколь-
ку обычные электромеханические реле весьма инерционны.
Для повышения разрешающей способности анализатора и
получения возможности фиксации быстрых замираний (до де-
сятков или сотен герц) применяются схемы с пересчётом. Наи-
более распространённая схема такого анализатора приведена
Рис. 8.38. Блок-схема анализатора уровня с применением
пересчёта
на рис. 8.38. Напряжение Uc положительной полярности с вы-
хода приёмного устройства поступает на сетку лампы дискри-
минатора которая находится в режиме ограничения (на анод
лампы подаётся небольшое анодное напряжение Па). Одновре-
менно в катод лампы подаются импульсы прямоугольной фор-
мы с частотой следования —1000 гц и амплитудой U#, выра-
батываемые мультивибратором.
15* ш
В'реме»ная диаграмма дискриминатора приведена на
рис. 8.39.
Напряжение U z на сетке лампы Л\ равно
Us^Uc + UM~Et. (8.50)
Согласно рис. 8.39 импульсы тока в цепи анода лампы будут
появляться лишь тогда, когда£Л,>^э .
Рис. 8.39- Временная диаграмма дискриминатора,
входящего в пересчётную схему рис, 8.38
Подбирая напряжение U3 в соответствии с заданными уров-
нями, можно построить ряд таких дискриминаторов, которые бу-
дут реагировать только на определённый уровень сигнала, по-
ступающего с приёмного устройства.
Таким образом, при определённом уровне сигнала на входе
приёмного устройства в цепи анода лампы появляются импуль-
сы анодного тока. В дальнейшем для определения времени на-
хождения или превышения сигнала определенного уровня в
схеме предусматривается подсчёт числа импульсов тока в цепи
анода лампы дискриминатора. Для этой цели обычные элек-
тромеханические счётчики непригодны. Поэтому в схеме ана-
лизатора предусмотрена пересчётная схема (см. рис. 8.38), за-
дачей которой является преобразование импульсов с опреде-
лённой частотой следования в частоту следования более низ-
кую, например, с частоты 1000 гц в частоту 100 гц и т. д. Такая
пересчётная схема может понизить частоту следования импуль-
сов до единиц герц и менее. В этом случае на выходе такой пе-
ресчётной схемы могут быть включены обычные электромеха-
нические реле, счётчики, а также и электрочасы. Последние бу-
дут указывать время нахождения сигнала на определённом уров-
не за период наблюдения. Пересчёт числа импульсов обычно
228
производится при помощи триггерных схем и пересчётных яче-
ек, Для этой цели применяются электронные лампы, полупровод-
ники, а в последнее время декатроны [Л23].
Интеграторы
Рис. 8.40. Простейшая
схема интегратора
В качестве автоматических анализаторов находят при-
менение различные схемы интеграторов, основанных на принци-
пе накопления сигналов, поступающих с выхода приёмного уст-
ройства.
Интеграторами называются устройст-
ва, при помощи которых осуществляется
интегрирование скалярных функций. Эти
устройства по принципу действия подраз-
деляются на механические, электромеха-
нические и электрические.
При анализе радиосигналов, подвер-
женных непрерывным флуктуациям, на-
ходят применение как механические, так
и электрические интеграторы. Механические интеграторы, на-
пример в виде планиметров, используются, как указывалось
выше, при обработке кривой, записанной самописцем. При авто-
матической обработке сигнала применяются главным образом
электрические интеграторы.
Простейшая схема электрического интегратора показана на
рис. 8.40. Это — схема зарядки конденсатора С через сопротив-
ление /?.
Как известно, напряжение и на обкладках конденсатора про-
порционально интегралу по времени от тока i, протекающего в
цепи, т. е.
t
U^-L^idt. (8.5 i)
О
В свою очередь, в каждый данный момент времени
i , (8.52)
где Е — напряжение на входе цепи (см. рис. 8.40).
Подставив (8.52) в (8.51), получаем
i t
и~ ^Edt---------\udt. (8.53)
&R J CR J
n 0
3) Написано на основе разработок Ю. В. Маркова.
229
t
j Edt, (8.54)
о
t
§udt (8.55)
о
i. (8.56)
Если вычертить кривую зависимости Е от то площадь огра-
ниченная этой кривой и осью абсцисс, выразится первым интег-
ралом правой части ур-ния (8.53). Деля этот интеграл ка пе-
риод Т, в течение которого включён прибор, получим среднее
значение F. Следовательно, для определения среднего значения
Е схема рис. 8.40 может быть использована лишь при условии
1
и —----
CR
т. е. при
t
^Edt^
о
или
£»i
Условие (8.56) не единственное. Кроме него, необходимо ещё,
чтобы увеличение и было пропорционально t в первой степени.
Для нахождения условия, при котором удовлетворяется второе
требование, обратимся к формуле, выражающей зависи-
мость и от /.
Как известно,
- _L
и=Е~(Е-ий)е *с, (8.57)
где Uo — начальное напряжение на конденсаторе.
Разлагая экспоненциальную функцию в ряд, получаем
+ ] (8'58’
Из (8.58) видно, что второе требование выполняется при ус-
ловии
где Т — период времени работы схемы.
Если потребовать, чтобы линейная зависимость от времени
выполнилась с заданной точностью е, получим
T^2zRC. (8.60)
Условие (8.60) совпадает с условием (8.56). Таким образом,
оба требования — малая величина и по сравнению с Е и линей-
ная зависимость и от t — выполняются при работе схемы в тече-
ние времени Т, определяемом ур-нием (8.60).
230
Величина ёмкости С должна быть не более нескольких микро-
фарад, a R — не более нескольких мегом.
При таких значениях С и R получается небольшая величина
для периода времени Т возможной работы схемы. Если учесть,
кроме того, что напряжение и,
снимаемое с конденсатора, зна-
чительно меньше подаваемого
напряжения Е и что нагрузкой
должно быть чрезвычайно вы-
сокоомное сопротивление, при-
ходим к заключению, что схема
рис. 8.40 не пригодна в каче-
стве точного интегрирующего
устройства.
Освободиться от ряда не-
достатков схемы рис. 840 мож-
Рис. 8.41. Схема интегратора с уси-
лителем
но, включив в эту схему уси-
литель (рис. 8.41).
Анализ схемы рис. 8.41 показывает, что для нее допустимое
время интегрирования
/'-2с/?С(К+ 1),
(8.61)
где К — коэффициент усиления, а напряжение на выходе дости-
гает величины
U = КЕ------
-2sK£.
(8.62)
Таким образом, схема рис. 8.41 увеличивает допустимое вре-
мя интегрирования в (К+1) раз и напряжение на выходе в К
раз.
Рис. 8.42. Принципи-
альная схема одно-
лампового интеграто-
ра на пентоде
На рис. 8.42 показана принципиальная схема однолампового
интегратора, которая позволяет довести время интегрирования
до одной минуты, а напряжение на выходе получать в диапазоне
30 300 в.
231
В качестве индикатора интегратора используются как стре-
лочные приборы, так и самописцы. В конце периода интегриро-
Рис. 8.43. Схема управления для авто-
вания производится автома-
тическое считывание величи-
ны напряжения I! и возвра-
щение схемы в исходное со-
стояние (ёмкость С разря-
жается).
Для автоматического счи-
тывания в интеграторе пре-
дусматривается схема уп-
равления (рис. 8.43), состоя-
щая из электрочасов с про-
граммным механизмом к
обычной релейной схемы,
которая за данное время
магического считывания в интеграторе подключает интегратор к
выходу приёмного устройств
ва и по истечении положенного времени Т подключает регистри-
рующий прибор и приводит интегратор в исходное положение.
Метод тока короткого замыкания антенны
Методом компарирования по ГСС или генератору шумов
измеряется напряжение па входе измерительного приёмника.
Искомая величина — напряжённость поля — определяется за-
тем путём ряда пересчётов. Одной из промежуточных расчёт-
ных величин является эдс на входе антенны, связанная с на-
пряжением на входе приёмника через параметры антенны, фи-
дерной линии и приёмника. Эти параметры часто недостаточно
точно известны. Очевидно, что точность измерений можно повы-
сить, если измерять непосредственно эдс на входе антенны. Ре-
шение этой задачи даёт новый метод измерений, предложенный
Ю. Д. Карпинским [Л30] и названный автором методом короткого
замыкания антенны.
Как указывалось в первой главе, приёмная антенна обычно
представляется в виде источника эдс е и внутреннего сопротив-
ления Z А. Под электродвижущей силой понимается напряжение
на зажимах антенны в режиме холостого хода. Ю. Д- Карпин-
ским предложено представлять приёмную антенну в виде воз-
буждающего тока /д (ток короткого замыкания антенны) и соб-
ственной проводимости источника тока Ул == ? Между 1А и е
существует соотношение
= <8’63)
232
Схема измерений по методу тока короткого замыкания антен-
ны изображена на рис. 8.44.
В точке О сходятся четыре фидерные линии, к которым под-
ключаются измерительный приёмник /7, генератор стандартных
сигналов ГСС, генератор опорного сигнала ОГ и антенна Л.
Рис. 8.44. Схема измерений
по метолу тока короткого
замыкания антенны
. В ветви приёмника П включены аттенюатор Ат и индика-
торное устройство И. Фидерные линии на рис. 8.44 изображены
в виде коаксиальных кабелей, хотя в зависимости от диапазона
волн могут применяться и другие виды фидерных линий.
Измерения проводятся в следующем порядке.
Предварительно определяют уровень сигнала, поступающего
от антенны. Для этого в схему включают только три элемента:
ОГ, П и А (ГСС исключён из схемы) и отмечают показание при:
бора И.
Затем в схему включают ГСС и по нему производят градуи-
ровку генератора опорного сигнала ОГ. Градуировку производят
на уровнях, значительно превышающих уровень сигнала, посту-
пающего от антенны. Аттенюатор на выходе ОГ позволяет регу-
лировать этот уровень.
Закончив градуировку Ort из схемы вновь исключают ГСС и
производят градуировку измерительного приёмника.
По описанному методу измерений генератор опорного сигна-
ла и антенна всё время присоединены ко входу приемника. Сиг-
нал от антенны непрерывно поступает на вход приёмника. Чтобы
этот сигнал не мешал при измерении сигнала, поступающего от
ОГ, сигнал от ОГ должен значительно превышать сигнал от ан-
тенны. При измерении уровня сигнала от антенны генерации О Г
прерывается. При помощи аттенюатора добиваются одинаковых
показаний индикаторного устройства при поступлении сигналов
от антенны и от ОГ.
Зная уровень сигнала ОГ, при котором показание индикатор-
ного устройства равно показанию при фиксации сигнала антен-
ны» а также изменение ослабления, определяемое по шкале атте-
нюатора Ат, можно определить уровень сигнала антенны.
233
Особенность схемы рис. 8.44 и метода измерений, базирующе-
гося на этой схеме, заключается в том, что при компарировании
сигналов не переключаются элементы схемы, не считая включе-
ния ГСС для калибровки ОГ и его отключения.
Применение двух генераторов (ГСС и О Г) связано с тем, что
непосредственная градуировка измерительного приёмника и ком-
парирование сигнала антенны по ГСС привело бы к тому, что
антенна оказывалась нагруженной на ГСС, а это увеличивает
уровень шумов. Применение специального генератора ОГ с ма-
лой выходной проводимостью или с реактивной (ёмкостной) про-
водимостью позволяет значительно уменьшить уровень шумов.
{На рис. 8.45 показана одна из возможных схем выходной цепи
опорного генератора.)
Важной особенностью схемы рис. 8.44 является также то, что
юна позволяет определять ток короткого замыкания антенны 1А
и через пего непосредственно электродвижущую силу, возбуж-
денную на входе антенны, в то время как обычно применяемые
схемы с переключением в процессе компарирования ГСС и ан-
тенны позволяют, как указывалось, определять лишь напряже-
ние на входе приёмника.
Рис. 8.46. Эквивалентная
схема измерительной уста-
новки вида рис. 8.44
Действительно, схема рис. 8.44 может быть заменена экви-
валентной схемой рис. 8.46. На этом рисунке ГСС, О Г и антенна
изображены в виде параллельно включённых проводимостей
234
Y гсс и ^ог 1 возбуждаемых токами IА, 1 гсс и 10Г и проводимости
приёмника Y л, также включённой с ними параллельно. Так как
при измерении проводимости остаются постоянно включёнными,
а возбуждающие токи включаются поочерёдно, то, очевидно, оди-
наковым показаниям индикаторного прибора приёмника соот-
ветствуют одинаковые возбуждающие токи. Следовательно, если
проградуировать ГССЛ а по нему ОГ в величинах возбуждающе-
го тока, понимая под этим ток короткого замыкания соответст-
венно ГСС или ОГ, то при компарировании по схеме рис. 8.44
получим величину 1 А> возбуждённую на входе антенны в режи-
ме короткого замыкания. Зная действующую высоту антенны
hd, нормированную диаграмму направленности F, (О, ф) и на-
правление прихода волны (О, ср) можно определить напряжен-
ность поля Е по формуле
'л
(8.64)
Е =.
f)
При наличии фидерной линии между антенной и приёмником
измерение по схеме рис. 8.44 даёт величину тока короткого за-
мыкания на фидере в точке его присоединения к измерительной
установке. Обозначим этот ток через 1ф< Между /фи эдс е на за-
жимах антенны существует соотношение
, f Tj ' 1
1/ cos* ml 4- cos ml 4- p sin miy*
где Ra — активная часть входного сопротивления антенны,
Х^ — реактивная часть входного сопротивления антенны,
о — волновое сопротивление фидера,
/ — длина фидера.
С другой стороны, активная часть проводимости всей антен-
но-фидерной системы Re (УЛФ) в точке присоединения фидера к
измерительной установке, равна
А?
^е( Лф) cos* (Ал cos/nf 4-р sin
Из (8.65) и (8.66) следует
*«(улф)
(8.67)
Сравнивая (8.67) и (1.62) и учитывая (1.64), получаем
/2
= 4Р„_РР. = ?). (8.68)
235
Так как
то при I — 0, когда
F(*, ?)
30ic
(Удф)
(8.69)
_ 30«Л*
•^эфф — Ra >
Ке(ГЛФ) =
Ra
Ка + хаГ
ур-ние (8.69) переходит в ур-ние (8.64).
Если приёмная антенна установлена так, что направление
главного максимума её диаграммы направленности совпадает с
направлением прихода волны, F (О, ср) равно единице и выраже-
ния (8.64) и (8.69) соответственно упрощаются.
Заметим, что выражение (8.65) имеет экстремум при
, Р
t82miL-'~^+^ .. В7О)
Кд -Г аА — р
Найдя из (8.70) значения sin ml исозт/ и подставив их в
(8.65), находим, что ток короткого замыкания антенно-фидерной
системы имеет следующие экстремальные значения:
Фмин г~ —-----------;—~—г—— ———--------- ’ '
У R\ + Р« + Х2А + + *А - Р4)2 + 4ХА р4
1ф яакс = _ У2е. - (8.72)
У R\ + р« qx Х2а - У (Я* + Х*А - р*у + 4Х2а р«
Произведение экстремальных значений тока короткого замы-
кания равно
^Ф мип 1ф макс Р (8.73)
Уравнение (8.73) позволяет выразить напряжённость поля
через произведение экстремальных значений токов короткого* 1
замыкания следующим образом:
£• -___! . 1 f 30г',ф (8.74)
f ?) V 5зфф
Из изложенного следует, что схему рис. 8.44 можно собирать,
в нескольких вариантах. Во всех вариантах антенна соединяется
236
с тгриемни-ком фидерной линией той или иной длины. ГСС и О Г
могут присоединяться своими фидерными линиями оба либо к
зажимам антенны, либо к зажимам приёмника. В первом слу-
чае напряжённость поля рассчитывается по ф-ле (8.64), во вто-
ром по ф-ле (8,69). До включения антенны в схему должно быть
предварительно измерено одним из описанных выше методов в
первом случае — входное сопротивление антенны ZA> во втором
— входное сопротивление антенно-фидерной системы/^.Долж-
ны быть также определены диаграммы направленности антенны
и направление прихода волны; ГСС и ОГ градуируются по току
короткого замыкания в точке фидера, в которой они присоеди-
няются к антенне или приёмнику.
Возможно также присоединение ГСС и ОГ скользящим кон-
тактом к какой-либо средней точке фидера, соединяющего ан-
тенну с приёмником. Перемещая точку контакта по фидеру, на-
ходят !фмин и /флшхс> а затем рассчитывают напряжённость по-
ля по ф-ле (8.74). В этом случае не требуется предварительное
измерение входного сопротивления антенны или антенно-фидер-
ной системы.
Следует учесть, что
/ - w*1
1Ф макс
где к — коэффициент бегущей волны на фидере со стороны ан-
тенны.
Поэтому
g IФ макс / ЗОд /с р Iф мин / ЗОт: р уд
Г (а, у m у) У к8эфф * 1 }
Таким образом, измерение по схеме рис. 8.44 возможно так-
же и в случае» если скользящий контакт останется в точке мак-
симума или минимума короткого замыкания, но при этом во вре-
мя генерации ГСС или ОГ нужно измерять рефлектометром кбв
на фидере.
Калнбродинный метод измерения напряжённости поля
Использование для измерений напряжённости поля в
схемах, описанных выше, измерительных приёмников, селектив-
ных микровольтметров и других приёмных устройств требует
частой повторной калибровки усиления по эталонному сигналу,
что является существенным недостатком этих методов.
Свободным от этого недостатка является так называемый ка-
либродипиый метод измерения, предложенный 10. Д. Карпин-
237
ским и разработанный в Институте радиотехники и электроники
Чехословацкой академии наук [Л31], Измерение напряжённости
поля сигнала по этому методу производится следующим обра-
зом.
Ко входу приёмника, помимо измеряемого сигнала под-
водится опорный (калибрующий) сигнал известной амплиту-
ды. Опорный сигнал имеет частоту, Отличную от частоты изме-
ряемого сигнала, по такую, чтобы обе частоты fx и /о лежали в
пределах полосы пропускания приёмника и имели практически
одинаковое усиление.
Из отношения амплитуды нч биений (с частотой fx —/о или
/о—f х ) и постоянной составляющей напряжения на детекторе
можно определить амплитуду измеряемого сигнала.
Обозначим амплитуду измеряемого сигнала через Ux, а ам-
плитуду опорного — через Uo (рис. 8.47), причём Ux < Uq. Ре-
зультирующее напряжение U—Ur модулировано по ампли-
туде и фазе. При условии, что —* мало, огибающая результи-
рующего напряжения практически синусоидальна.
liytTb оба напряжения Ux и в равной степени усиливают-
ся приёмником и детектируются линейным детектором с равны-
ми нагрузками как для постоянного, так и низкочастотного тока.
Тогда отношение переменной(7_л^„ и постоянной U= состав-
ляющих на выходе детектора равно отношению амплитуд изме-
ряемого сигнала и опорного сигнала, т. е.
_ ^х
По измеренным значениям Uопределяется U х.
Если усиление приёмника Кт на частоте fх для измеряемого
сигнала отличается от усиления Ко на частоте /о опорного сигна-
ла, и если коэффициент передачи модуляции не равен коэффи-
циенту передачи постоянной составляющей, то в этом общем
случае можно написать
(8,77)
(8.78)
238
где К определяется, с одной стороны, нелинейностью детектора,
с другой — значениями нагрузок для постоянного и низкоча-
стотного сигнала. Путём выбора режима детектора сравнитель-
но легко можно получить К, близкое к единице. В случае, когда
К не равно 1, его значение должно быть определено эксперимен-
тально.
Л А'г
Отношение —очевидно, можно определить по резонанс-
но
ной кривой приёмника.
Практически желательно применить достаточно плоскую ре-
зонансную кривую приёмника, а частоту биений —fa илн
fa—fx выбрать достаточно малой по сравнению с шириной поло-
сы приёмника. В этом случае отношение — будет близко к
Ко
единице независимо от настройки приёмника в пределах верх-
ней части резонансной кривой.
На вход приёмника подаются одновременно измеряемый сиг-
нал и опорный сигнал ГСС; величина последнего выбирается та-
кой, чтобы на выходе детектора было получено удобное отно-
.«мкс
шение --------.
Для определения величины К подаётся на вход приёмника
амплитудно-модулированный сигнал от ГСС с известной глуби-
ной модуляции и измеряется Uи U^Maxc.
В связи с тем, что ГСС и источник измеряемого сигнала по-
калибродинному методу включаются в схему параллельно, по-
лучаем в результате отношение токов короткого замыкания ис-
точников радиосигналов [ЛЗО].
Напряжение U _ на детекторе можно с достаточной точ-
ностью поддерживать постоянным при помощи автоматической
регулировки усиления (АРУ). Если t/0 также будет постоянно,
отношение — определяется одним лишь значением низкоча-
статного напряжения на выходе детектора.
Схема измерений в этом случае показана на рис. 8.48. По-
стоянная составляющая напряжения на детекторе сравнивается
с опорным напряжением и, воздействуя на усиление приём-
ника через цепь АРУ, в которую может быть включён усилитель,
компенсирует изменения параметров приёмника, обусловленные
нестабильностью источников питания, температуры и т. п.
Значение U= проверяется вольтметром В. Переменная со*
ставляющая напряжения на детекторе фильтруется и, если тре-
буется, усиливается УПЧ и далее измеряется или записывается
самописцем.
Калибродинный метод позволяет применять для точных из-
мерений и для записи радиосигналов приёмники с весьма неста-
239
бильиыми параметрами, например радиовещательные, которые
в обычных измерительных схемах непригодны.
Как видно, стабилизацией постоянной составляющей
обусловленной действием стабильного опорного напряжения /7©
на вход приёмника, производится фактически стабилизация уси-
ления приёмника не только для опорного, но и измеряемого сиг-
налов.
—ifiL г—i
- UWV |—
*1__lyw
Рис. 8,48, Блок-схема из-
мерительной установки
по калибродинному ме-
тоду
Измерительный и калибровочный процесс как бы совме-
щаются и приёмник при измерении автоматически калибруется.
Как показывает анализ, калибродинный метод существенно
повышает и чувствительность измерений без значительного ус-
ложнения приемного устройства. Кроме того, применение калиб-
родинного метода повышает надёжность работы измерительно-
го устройства, поскольку в этом случае на входе приёмника по-
стоянно действует опорный сигнал. Наличие постоянной состав-
ляющей напряжения U = на выходе детектора и ее стабильность
являются признаком нормальной работы приёмника и измери-
тельной схемы в целом. Таким образом, калибродинный метод
позволяет непрерывно следить за состоянием приёмника. Пос-
леднее очень важно при непрерывной регистрации сигналов, на-
пример при длительных измерениях на экспериментальных ли-
ниях радиосвязи.
Динамический диапазон измерений калибродинным методом
выше, чем у обычных измерительных схем. Он может быть срав-
нительно легко расширен, если к выходу детектора присоеди-
нить несколько низкочастотных усилителей с разными коэффи-
циентами усиления.
Измерение поляризации поля радиоволн
При измерении поляризации поля необходимо учестй
особенности распространения радиоволн. |
Во многих случаях практики поле в точке приёма образуется^
в результате совокупного действия многих волн, приходящих‘й
240 .1
разных направлений. Это явление известно под названием мно-
голучёвости и встречается на частотах всех диапазонах. Наибо-
лее отчётливо многолучёвость проявляется в диапазоне корот-
ких волн на больших расстояниях от передающей станции. Из-
вестно» например» применение на коротких волнах антенны с уп-
равляемой диаграммой направленности для выделения отдель-
ных лучей. На ультракоротких волнах [Л35] поле в области пря-
мой видимости создаётся в результате интерференции двух волн:
прямой и отражённой от поверхности земли, а в области тени
многолучёвость создаётся в результате рассеяния от неоднород-
ностей в тропосфере или ионосфере. На длинных и средних вол-
нах поле в точке приёма образуется земной и ионосферной вол-
нами.
Однако в ряде случаев может потребоваться измерение поля
одной врлны, например, при измерениях поля некоторых евч ан-
тенн (рупорных, линзовых) в раскрыве или на близком расстоя-
нии от раскрыва, при измерениях поля облучателей зеркал и
линз, при измерениях характеристик поляризационных решёток
и т. п. При исследовании антенн на моделях можно создать ус-
ловия, при которых допустимо пренебречь полем волны, отра-
жённой от поверхности земли. Как однолучевос можно рассмат-
ривать поле в упомянутом выше случае приёма на антенну с уп-
равляемой диаграммой направленности в вертикальной плоско-
сти.
Для измерения поляризации поля, создаваемого однолуче-
вым распространением применяется та же аппаратура и те же
схемы, что и для измерения амплитуды поля, К аппаратуре
предъявляются лишь дополнительное требование возможности
вращения антенны на 360° вокруг направления прихода волны
с фиксацией отдельных положений и, естественно, требование
наличия шкалы, отмечающей угол поворота антенны. Примене-
ние вращающейся антенны характерно главным образом для
ультракоротких волн.
В аппаратуре применяется какая-либо из аптвпп линейной
поляризации: симметричный вибратор, рамочная антенна, вол-
новодный или рупорный излучатель прямоугольного сечения
и т. п.
Антенны ориентируются относительно направления прихода
волны следующим образом: ось симметричного вибратора уста^
павливается перпендикулярно направлению прихода волны, пло-
скость рамки — параллельно, раскрыв волновода или рупора —
перпендикулярно. При вращении антенн вокруг направления при-
хода волны как оси, данная ориентация антенн сохраняется.
Измерения сводятся к снятию кривой зависимости эдс на за-
жимах антенны от угла ее поворота. По этой кривой определяет-
ся поляризация. Если кривая имеет точки нулевых значений
эдс, то исследуемое поле линейно поляризовано. При наличии
16—292 241
на кривой точек минимума эдс ненулевого значения, исследуе-
мое поле имеет эллиптическую поляризацию, причём полуоси
эллипса пропорциональны соответственно максимальной и ми-
нимальной эдс. Круговой поляризации соответствует постоянная
величина эдс независимо от угла поворота антенны.
Таким образом, измерение поляризации поля данным мето-
дом позволяет в общем случае определить эллипс поляризации.
Принято эллиптическую поляризацию характеризовать коэффи-
циентом равномерности в, равным отношению малой оси эллип-
са к большой оси, и углом ср поворота большой оси эллипса отно-
сительно выбранного характерного направления (например, от-
носительно вертикали). Знание е и ф позволяет определить со-
отношение амплитуд ~ и разность фаз ф(—фз составляющих
г2
поля в двух взаимно-перпендикулярных характерных направле-
ниях, например вертикальном и горизонтальном, по следующим
формулам:
£i _ -| Г+ Е* tg* ?
V + 1
tg('h-w=-—'—г,
(1 — e2)siu2?
(8.79)
(8.80)
где индекс 1 соответствует составляющей поля, повёрнутой на
угол ф относительно большой оси эллипса, а индекс 2 — другой
составляющей поля.
Заметим, что определение эллипса поляризации недостаточ-
но для нахождения знака разности фаз или направления враще-
ния вектора поля.
Рассмотрим методику измерения поляризации поля при мно-
голучевом распространении, имея в виду суммарное поле всех
лучей. Эта методика находит применение в диапазоне корот-
ких, средних и длинных волн.
Пусть в точку наблюдения А приходят три волны (рис. 8.49):
одна ионосферная, падающая под углом ф к поверхности земли
и имеющая эллиптическую поляризацию, вторая — отражённая
от поверхности земли, имеющая также эллиптическую поляри-
зацию и третья — земная волна, имеющая линейную вертикаль-
ную поляризацию.
Обозначим поле земной волны через £0, а составляющие по-
ля ионосферной падающей эллиптически поляризованной волны
через
Е, = Е, е“’ф‘
(8.81)
242
Тогда суммарное поле будет иметь следующие компоненты
поля по осям координат х, у, z:
/ — i — ЛГ
Ех = Ег sin <р е“‘ф* \ 1 — Rt е
/ Аг\
£, = £»е“’Цц-Яге Х )
/ -ieg-i -у- аг
Ег = £г cos <р e”"1** \ 1 + R, е
(8.82)
+ Е»
где Rt и Rt, Q, и 6,— соответственно модули и аргументы ко-
эффициентов отражения от поверхности
земли;
Дг—разность хода лучей, равная ОЛ—ЛВ
(рис. 8.49).
Рис. 8.49, Схема ото-
жения полей трёх волн:
падающей, отраженной,
земной
В том часто встречающемся случае, когда R,=R,~1, 0, — О,
0=180°;
—tyl—I——- Аг
Ех = 2i£jsinipsin-^- Д re
Еу = 2i Ег sin -у- Д г е
-1ф,—1JL аг
£, = 2£i costpcosД ге -|-£в
(8.83)
Очевидно, определение суммарного поля требует измерения
всех трёх составляющих поля Ех, Еу и Ег по модулю и фазе.
Особенность измерений на длинных, средних и коротких вол-
нах заключается в применении стационарных измерительных ан-
тенн. Поэтому в измерительной установке используются три ан-
16* 243
теины линейной поляризации, ориентированные по осям х, у, г.
Для определения эллипса поляризации наиболее удобно в дан-
ном случае использовать катодный осциллограф, к взаимно-
перпендикулярным пластинам которого подаются напряжения
от какой-либо пары взаимно-перпендикулярных антенн.
Рис, 8.50. Схема измери-
тельной установки для
определения эллипса по-
ляризации в плоскости
ху
На рис. 8.50 показана простейшая схема измерительной уста-
новки для определения эллипса поляризации поля в плоскости
ху. Здесь входы приемников / и П подключены к двум горизон-
тальным ।взаимно-перпендикулярным антеннам, ориентирован-
ным одна вдоль оси х, другая — вдоль оси у, а выходы приёмни-
ков подключены к разным парам пластин катодного осцилло-
графа. Найдя по фигуре Лиссажу на экране осциллографа эл-
липс поляризации в плоскости ху, отключаем антенну, ориенти-
рованную по оси у, и подключаем вход второго приёмника к
вертикальной антенне для определения этим же путём эллипса
поляризации в плоскости xz, Аналогично для контроля может
быть найден эллипс поляризации в плоскости у 2.
Схема рис. 8.50 обладает тем недостатком, что требует пол-
ной идентичности приёмников по усилению и фазовому сдвигу,
что осуществить чрезвычайно трудно. Эта схема может быть
улучшена, если на одну пару пластин осциллографа подать на-
пряжение стабилизированного опорного сигнала, а сравнение
сигналов от антенн производить поочерёдным их подключением
к одному и тому же приёмнику, выход которого подключён ко
второй паре пластин осциллографа. При этом опорный сигнал
градуируется по сигналу одной из измерительных антенн. Его
амплитуда и фаза регулируются так, чтобы получить на экране
осциллографа прямую линию под углом 45°. Это соответствует
равенству опорного сигнала и сигнала выбранной антенны по
амплитуде и фазе. Переключив затем приёмник на вторую изме-
рительную антенну, можно по получающейся при этом фигуре
Лиссажу определить соотношение амплитуд и разность фаз сиг-
налов этих двух антенн. Если опорный сигнал градуировался по
антенне, ориентированной по оси х, то по рис. 8.51 определяем:
(8.84)
Еу I Уъ
$44
sin(-h-<H) = ^=-^. (8.85)
Уч
Поскольку в измерительной установке предусмотрены три
антенны, то в качестве источника опорного сигнала может быть
Рис. 8.51. К определению состав-
ляющих поля в характерных на-
правлениях по фигуре Лиссажу
Рис. 8.52. Схема измери-
тельной установки для опре-
деления эллипса поляриза-
ции с использованием вер-
тикальной антенны в каче-
стве источника опорного
сигнала
взят сигнал одной из них. На рис. 8.52 показана схема измере-
ний в момент, когда в качестве источника опорного сигнала взя-
та вертикальная антенна. Сравнив между собой сигналы гори-
зонтальных антенн, меняем места включения вертикальной ан-
тенны и одной из горизонтальных антенн и проводим аналогич-
ным путём сравнение сигналов вертикальной антенны и второй
горизонтальной.
Метод измерений, основанный на применений источника
опорного сигнала и па переключении сравниваемых антенн,
предполагает, что за время наблюдения поле в точке приёма до-
статочно стабильно. При быстрых изменениях поля приходится
пользоваться измерительными установками (рис. 8.50) с двумя
усилителями.
Некоторое усовершенствование этой схемы можно получить,
если использовать общий гетеродин для двух приёмников I и II
и автоподстройку частоты (рис. 8.53). Последняя схема даёт
возможность поддерживать стабильное усиление приёмников и
стабильные фазовые сдвиги, вносимые ими.
При наличии многолучёвости и требовании исследования по-
ляризации одной из волн обычно применяется импульсный ме-
тод измерений. Рассмотрим один из вариантов этого метода.
Сигнал, имеющий импульсную модуляцию, принимается на
две взаимно-перпендикулярные рамки Р\ и Р% (рис. 8.54), под-
ключённые каждая к отдельному приёмнику I и IL Выходы
245
Рис. 8.53. Схема измери*
тельной установки с об-
щим гетеродином
Рис. 8.54, Схема измерении
по импульсному методу
приемников присоединяются к двум парам пластин катодного
осциллографа. Последний имеет временную развёртку, синхро-
низированную с частотой следования импульсов. Электронный
пучок трубки отпирается на короткий промежуток времени, рав-
ный примерно продолжительности излучаемого импульса.
Таким образом, в короткие промежутки времени, равные
продолжительности импульса, на экране трубки вычерчивается
фигура Лиссажу, которая позволяет определить соотношение
амплитуд и разность фаз сравниваемых полей. Выбор того или
иного импульса производится предварительно путём изменения
фазы напряжения, питающего развёртку.
Метод импульсных измерений находит применение в так на-
зываемых поляриметрах [Л37].
9. СНЯТИЕ ДИАГРАММЫ НАПРАВЛЕННОСТИ
АНТЕНН
Определение минимального расстояния между исследуемой
и вспомогательной антеннами
Диаграмма направленности антенны является характе-
ристикой, не зависящей от расстояния. Однако это справедливо
лишь на очень больших расстояниях от антенны (строго говоря,
на бесконечно больших). Для каждой антенны в зависимости от
типа, размеров, длины волны и требуемой точности измерений
существует минимальное расстояние rMUfit на котором слабо
проявляется зависимость от расстояния и на котором диаграм-
мы направленности получаются практически (с принятой точ-
ностью) такими же, как на бесконечно больших расстояниях. Из-
мерения на расстояниях, меньших rM(iH , могут привести к оши-
бочному результату. Ниже показывается, как следует в отдель-
ных случаях определять гмин.
Рассмотрим дифракционные антенны с плоским круглым или
прямоугольным раскрывом (например, рупорные, зеркальные,
линзовые). Полученные результаты полностью распространяют-
ся также на проволочные антенны (синфазные, ромбические
и т. п.).
Согласно [ЛЗ] поле излучения Е таких антенн определяется
выражением
Е—А (9.1)
где А — медленно меняющаяся функция угловых координат &
и ф (рис.. 9.1) вида
Е s — поле в раскрыве;
г, — расстояние от отдельных точек раскрыва антенны до
удалённой точки М, в которой производится измере-
ние поля излучения;
m ==— ~ коэффициент фазы.
347
Расстояние г5 согласно обозначениям рис. 9.1 равно
V(x “ XJ2 + (.У - ys)2 + (г - zj2,
Учитывая, что
х — г sin & cos®
y = rsin&sm<? .
2 — г cos ft
xs = p_sCOS<p.s ’
ts —0
(9-3)
(9.4)
(9.5)
Рис. 9.1. К расчёту поля апертуры: круглой (а), прямоугольной (б)
можно rs выразить следующим образом:
rs = у^г2 — 2xsr sin & cos <р — 2ys sin & sin <? + х» + у» =
= ]Лг2 — 2ps г sin ft cos(» — <pj 4- о2. (9.6)
Так как — то выражение (9.6) мож-
но разложить в следующие сходящиеся ряды по степеням — и
Г
— или — :
rs = гр —— sin 8 cos® —— sin & sin <p -j-
2 2
—(1 —sin2 ft cos2 4) 4- — (I—sin2 ft sin2 4) -j- .
2ra 2r«
(9.7)
или
G = — -^-sin&cosfo —?,) +
p2 }
+ ^U-sin*&cos*(¥-?J] + ...J. # (9.8)
Выражение (9.1) приводится к виду (1.1) при условии, что
rs в подынтегральном выражении (9.1) полагается равным:
в знаменателе
г,^г, (9.9)
а в показателе степени
rsmr—xssin ® cos<p — ^sin&sint? = г — p5sin&cos(?— os). (9.10)
Равенство (9.10) получается из рядов (97) и (9.8) t если пре-
небречь в них слагаемыми выше первого порядка, и свидетель-
ствует о том, что на рассматриваемом расстоянии г поле Е имеет
характер плоской волны.
Расстояния, на которых электромагнитное поле излучения
имеет характер плоской волны и может быть вычислено с доста-
точной точностью при аппроксимации (9.9) и (9.10), определяют
так -называемую область дифракции Фраунгофера. Более близ-
кие расстояния, на которых в показателе степени выражения
(9.1) требуется учитывать также квадратичные слагаемые
£ (1 — sin2 & cos2 ?) +(1 — sin2 & sin* ?), (9.11)
определяют так называемую область дифракции Френеля. Рас-
стояние гмин является условной границей этих областей.
При радиосвязи или других видах передачи и приёма радио-
сигналов путём излучения пункт приёма находится в области
Фраунгоферовой дифракции электромагнитного излучения
передающей антенны. Поэтому практический интерес имеют и,
как правило, определяются характеристики излучения для этой
области. Измерения же в области дифракции Френеля дают дру-
гие характеристики, отличающиеся от искомых. Наибольшее от-
личие измеренных характеристик от искомых будет иметь место
при наибольшем значении квадратичных слагаемых рядов (9.7)
и (9,8), которые имеют максимум при 0 = 0, т. е. в направлении,
перпендикулярном плоскости раскрыва антенны. У синфазных
антенн Ф=0 соответствует направлению главного максимума
диаграммы направленности.
Для определения расстояния г мин потребуем, чтобы напря-
жённость поля Et а также характеристики излучения, вычислен-
ные с учётом квадратичных слагаемых рядов (9.7) и (9.8) с за-
249
данной точностью совпали с таковыми, вычисленными при ап-
проксимации (9.10). При этом, очевидно, достаточно, чтобы сов-
падение имело место при 0=0.
В направлении 0=0 аппроксимация (9.10) даёт
(9.12)
При учёте же квадратичных слагаемых имеем
г‘~г+г+±=г+^- (9-|3>
Подстановка (9.9) в знаменатель подынтегрального выраже-
ния (9.1), а (9.12) или (9.13) в его показатель степени приводит
к следующим формулам для поля излучения в направлении
0-0:
в области дифракции Фраунгофера
(9.М)
в области дифракции Френеля
2 2 2
Ем= А~— j j^e 2r dS = X^—- J J E,e 2' dS.
(9.15)
Если измерения производить в области дифракции Френеля,
то относительная ошибка составит
2 2
-1m
Е'« И£'е 2' ds
При Еа = const получим
(9.16)
2. 2
-1m Х‘+^
2r dS
(9.17)
S
где S — площадь раскрыва.
В случае прямоугольного раскрыва
C(LT) — iS(U) С (о) — iS(o)
U v
(9.18)
где:
В случае
8«— *
t
J* sin
£>i
V “ У2гТ
круглого раскрыва
D 2
2% 2 —Im
^РЧе
о 0
1 . mD* I
— sin-—-
2r л i 8r
PSdPs = 1— j-------1
mD'
8r
(9.19)
(9,20)
(9.21)
(9.22)
(9.23)
cos —• Pdt,
2
и - -Д
a —
На рис. 9.2 показаны кривые зависимости е и в от
_____:, причем для ед приведено несколько кривых, соответ-
ствующих различным значениям —, где D — длина широкой
стороны раскрыва, а 1У — узкой. Условие — =0,0 соответ-
ствует линейному излучателю.
Коэффициент усиления антенн G определяется из соотноше-
ния мощностей, которые пропорциональны квадратам напря-
жённостей полей. Поэтому ошибку по коэффициенту усиления
следует определять по формулам:
C(U)^\S(U) C(u) — \S(v)
U
о
. . mD*
sm1 ——
1 8г
= 1 — ----— <
mD1
8г
, На рис. 9.3 приведены кривые зависимости
D
причем для есл дано несколько кривых,
D'
ствующих различным значениям —.
(9.24)
(9.25)
й еохот
соответ-
251
Из изложенного следует, что для получения достаточно
точных характеристик излучения необходимо, чтобы величина
а^= была не больше некоторой величины амаке, соответ-
Рис. 9,2. Кривые зависимости относительней ошибки еп
D
и по полю от параметра а—
ствующей малой ошибке, т. е. малой величине е или е<?. Если
принять, что ошибка в определении напряжённости поля не
должна превышать 1% (s < 1 %)> а в определении коэффи-
циента усиления — 2% (£<? <2%), то =0,4. Так как ве-
личина а обратно пропорциональна корню из г, то соответ-
ствует гмин.
252
Приняв указанные допуски на точность определения папря*
жённости поля и коэффициента усиления, приходим к неравен-
ству:
^=2= <««„-0,4.
D * _ О>
ГмаЯ >Ч^Д~0,32Х-
(9.26)
(9.27)
Если требуются допуски на точность, отличные от указан-
ных, то по графикам рис. 9.2 и 9.3 ф-ла (9.27) может быть про-
корректирована.
Очень часто при определении гмим исходят не из требований
точности определения напряжённости поля или усиления, а из
2ВЗ
требования минимального значения квадратичного слагаемого в
(9.13). Ставится, например, условие, чтобы
Р» <_Х_
^глин 16
(9.28)
Это означает, что квадратичные фазовые ошибки не должны
превышать — =22,5°.
Так как наибольшее значение р5 имеет место на границе
раскрыва, где
(9.29)
то получается
Рз лах» — 2 *
D1
Гмн ** 0,5k
или
(9.30)
(9.31)
Легко видеть, что гмин , определяемое по ф-ле (9,27), мало
отличается от rMUff> определяемого по ф-ле (9.31).
Графики рис. 9.2 и 9.3 получены в предположении, что фазы и
амплитуды поля в раскрыве антенны постоянны. В действитель-
ности часто имеет место амплитудное распределение, характе-
ризующееся максимумом в середине и плавным спаданием к.
краям раскрыва. В этом случае в заданных размерах раскрыва
D ошибки е и eG будут меньше указанных на графиках 9.2 и 9.3.
Действительная величина ошибок е и может быть найдена по
рис. 9.2 и 9.3, если заменить реальный размер D в направлении
координатной оси х антенны эффективным размером В9ф$ вы-
численным по формуле
2
О,фф = J Edxt (9.32)
где Eq — напряжённость поля в центре раскрыва (при х—0)t
Е— функция напряжённости поля от координаты х.
Аналогично может быть найден эффективный размер антенны
в направлении оси у.
Приведённые выше соображения по определению ошибок из-
мерений бие0,а также гмин справедливы при условии, что изме-
рение напряжённости поля производится при помощи слабона-
правленной или ненаправленной антенны. Они справедливы так-
же, когда линейный размер вспомогательной антенны D gcrt зна*
254
чительно меньше линейного размера исследуемой антенны
или наоборот, В таких случаях в ф-лу (9,27) или (9.31) подстав-
ляют наибольший из них.
Если же вспомогательная антенна имеет примерно одинако-
вые линейные размеры с исследуемой антенной то сле-
дует отдельно определять е и для обеих антенн и общая
ошибка будет равна сумме этих ошибок. При определении гмия
следует исходить из суммарной
ошибки.
Расчётная формула в этом
случае может быть приближённо
выведена из следующих сообра-
жений [Л 42].
На рис. 9.4 показана иссле-
дуемая антенна ЛВ (предпола-
гается линейная) и на расстоя-
нии г от неё вспомогательная
антенна А'В'. Угол, под кото-
рым видна антенна А'В' из
центра антенны АВ равен
p—J’iC’-. (д.33)
Рис. 9.4. К пояснению принципа
определения минимального рас-
стояния между вспомогательной и
исследуемой антеннами
Очевидно, этот угол должен быть значительно меньше шири-
ны главного лепестка диаграммы направленности 20о исслёдуе-
мои антенны, т. е. Р«20в. (9.34)
Если принять за максимально допустимое значение для ₽=О,2-20, = -^-, (9.35) Лиам
получим r - D™- - 5 . (9.36) ми* 0,2-20. 20. '
Но, как известно, у остронаправленных антенн
Подставив 2©.^-^-. (9.37) °иеел (9.37) в (9.36), получаем ^ = 5 (9.38)
Формула (9.38) пригодна, если получаемое по ней значение
гтн больше того значения, которое получается по ф-ле (9.31).
В противном случае расчёт ведётся по последней.
255
. Заметим, что измерения в области френелевой дифракции
приводят при снятии диаграмм направленности синфазных ан-
тенн к преуменьшенным значениям побочных максимумов, а при
исследовании антенн типа бегущей волны — к преувеличенным
значениям побочных максимумов.
Рассуждения, изложенные выше, исходят из условия, что ис-
следуемая или вспомогательная антенны, либо и та и другая,
являются остронаправленными. Если обе антенны слабонаправ-
ленные, то измерения следует проводить в волновой зоне антен-
ны. Практически это означает, что
при D < ~
г ми*—(9.39)
при
мин, --- 2/,
(9.40)
где I — наибольший линейный размер антенны, при D>X спра-
ведлива ф-ла (9.27) или (9.31).
Методика снятия диаграмм направленности
Снять диаграмму направленности антенны можно двумя
методами: методом неподвижной антенны или методом вращаю-
щейся антенны.
Когда исследуемая антенна работает на излучение, то при
первом методе она неподвижна и вокруг неё по кругу переме-
щается индикатор поля со вспомогательной антенной, показы-
вающий величину напряжённости поля в разных точках круга.
При втором методе исследуемая антенна вращается вокруг сво-
ей оси, а индикатор поля со вспомогательной антенной неподви-
жен и показывает величину напряжённости поля в зависимости
от угла поворота исследуемой антенны.
Когда исследуемая антенна работает на приём (обычно в
этом случае опа подключается к приёмнику, измеряющему эдс
на её зажимах), то при первом методе опа неподвижна и вокруг
неё по кругу перемещается хорошо стабилизированный генера-
тор со вспомогательной антенной. Прибор исследуемой антенны
в этом случае показывает зависимость величины эдс от положе-
ния излучателя на круге. При втором методе исследуемая ан-
тенна вращается вокруг своей оси, а излучатель со вспомога-
тельной антенной неподвижен. Прибор исследуемой антенны по-
казывает зависимость величины эдс от угла поворота антенны.
Метод неподвижной антенны применяется всегда при снятии
диаграмм направленности антенн радиоцентров, которые весь-
256
ма громоздки и неподвижны, например, коротковолновых ан-
тенн магистральных линий связи, передающих телевизионных
и радиовещательных антенн метрового диапазона, укв антенн на
линиях связи, использующих явления рассеяния в тропосфере и
ионосфере, передающих радиовещательных антенн средних и
длинных волн и т. п. Снять диаграмму направленности этих ан-
тенн можно как наземными измерениями, так и самолётными и
вертолётными.
Наземные измерения обычно ограничиваются лишь предела-
ми главного лепестка диаграммы направленности. Предвари-
тельно при помощи геодезических инструментов, например тео-
долита, намечают ряд азимутов в пределах предполагаемого
сектора измерений и на азимутальных направлениях производят
разметку пунктов измерений, которые располагаются на одина-
ковых расстояниях г от центра антенны, причём г удовлетворяет
условию г>гми^ Обходя исследуемую антенну по кругу, произ-
водят измерения в намеченных пунктах.
Наземные измерения стационарных антенн страдают следую-
щими существенными недостатками: 1) они весьма ограничены,
так как позволяют получать диаграммы направленности лишь
в одной плоскости, причём, как правило, не в наиболее харак-
терной, поскольку у большинства антенн главный лепесток при-
поднят над горизонтом; 2) отличаются малой точностью, так
как из-за неровностей рельефа местности, с одной стороны, труд-
но обеспечить расположение всех точек измерений в одной пло-
скости, с другой стороны, вблизи поверхности земли, где произ-
водятся измерения, создаются искривления фронта волны и свя-
занные с этим искажения поляризации и уровня поля.
При малой точности и ограниченной ценности наземные из-
мерения весьма трудоёмки и сложны. Они требуют большой
подготовительной работы по выбору трассы обхода и разметке
пунктов измерений. Сами измерения требуют много времени и
практически не допускают автоматизации. Из-за указанных не-
достатков наземным измерениям диаграммы направленности от-
водится роль контрольных или предварительных измерений.
Современный уровень развития авиации даёт возможность ши-
роко использовать самолёты и вертолёты для снятия диаграмм
направленности. Позволяя произвести измерения в различных
плоскостях, допуская автоматическую запись уровня поля, об-
ладая в этом смысле универсальностью, самолётные и верто-
лётные измерения являются основными при снятии диаграмм
направленности стацио-нарных антенн.
Метод вращающейся антенны применяется при изучении
антенн сверхвысоких частот, при макетировании в диапазоне
свч антенн более длинноволновых диапазонов, а также при изу-
чении простейших антенн метровых волн: симметричного вибра-
тора, антенны «волновой канал», рамочной антенны и т. п. Ме-
17—292 257
тод вращающейся антенны позволяет применить автоматическую
запись диаграммы направленности.
При снятии диаграмм направленности антенн очень важно,
как указывалось в предыдущем параграфе, расположить иссле-
дуемую и вспомогательную антенны на расстоянии, превышаю-
щем гмиН [см. ф-лу (9.27) или (9.31)]. Кроме того, важно пра-
вильно определить центр антенны, т. е. точку центра круга, по
которому производится облёт или обход антенны (при первом
методе измерений) или точку, через которую проходит ось вра-
щения антенны (при втором методе измерений). Это особенно
важно, когда расстояние, на котором производятся измерения,
близко к гмин.
Центром антенны является центр фазового фронта волны,
излучаемой антенной. Он расположен в средней точке излучаю-
щей части антенны, например, у линзовых, зеркальных и рупор-
ных антенн, примерно в центре раскрыва, у диэлектрических и
спиральных антенн, а также коротковолновых антенн бегущей
волны — в средней точке соответственно оси диэлектрического
стержня, оси спирали, собирательного фидера. При снятии диа-
граммы направленности в вертикальной плоскости с учётом
влияния земли центром антенны является проекция указанной
средней точки на поверхность земли.
Диаграммы направленности антенн, как правило, многоле-
пестковые. В пределах каждого лепестка измерения следует
производить не менее чем в 10—12 точках, причём особенно
тщательно должны быть исследованы области максимума и ми-
нимума. При измерениях необходимо уделить внимание ста-
бильности работы передатчика и градуировки приемника. В тех
случаях, когда требуется точно измерить уровень боковых мак-
симумов, следует пользоваться приёмником с линейной шкалой
либо включить в цепь приёмника переменный аттенюатор, при
помощи которого добиваются одинаковых показаний индикато-
ра выхода приёмника.
Использование линз при снятии диаграмм направленности
Исследуемую и вспомогательную антенны при снятии
диаграмм направленности нужно разносить на расстояние
определяемое ф-лами (9.27) или (9.31), вследствие того что вы-
полнять измерения необходимо в поле плоской волны.
В действительности поле излучения любой антенны на зна-
чительных расстояниях от неё имеет характер почти сфериче-
ской волпы. Однако небольшой участок сферической поверхно-
сти при большом радиусе кривизны может быть с достаточной
точностью принят за плоский. При удовлетворении условия
(9.31) участок сферического фронта волны той же протяжённо-
258
сти, что антенна, отклоняется от плоскости меньше, чем на Л/16.
На практике часто невозможно выполнить условие (9.27) или
(9.31). В этих случаях измерения проводят специальными мето^
дам и, позволяющими получить более или менее правильный ре-
зультат в пределах главного лепестка и даже некоторых бли-
дизлехтническая
Рис. 9.5. К использовЭ’
нию диэлектрической
линзы для снятия диа-
граммы направленности
антенн на близких рас-
стояниях
Линза
Исследуемая
антенна
жайших к нему побочных лепестков. При измерении одним из
них [Л39, 40] в качестве вспомогательной используют линзовую
антенну, исследуемую антенну помещают в непосредственной
близости от раскрыва линзы.
Линза рассчитывается так, чтобы в её раскрыве была плос-
кая волна, распространяющаяся перпендикулярно к раскрыву.
Линзы могут быть использованы как металлические (ускоряю-
щие), так и диэлектрические (замедляющие). Диэлектрические
линзы делаются плоско-выпуклыми (рис. 9.5) с гиперболиче-
ской криволинейной поверхностью, а металлические — плоско-
вогнутыми (рис. 9.6) с эллиптической криволинейной поверхно-
стью. В обоих случаях раскрыв
линзы должен быть значительно
больше раскрыва исследуемой
антенны (каждый из линейных
размеров примерно в 2 раза).
Линзы делаются с гладкой по-
верхностью. Наличие ступенек
(зон) у линзы является источни-
ком ошибок.
Линза металлическая
Ряс. 9.6. К использованию метал-
лических линз для снятия диа-
грамм направленности антенн нА
близких расстояниях
Диэлектрические линзы де-
лают длиннофокусными. В этом
случае они имеют малую толщи-
ну, а следовательно, и малый
вес. В качестве материала для
линз вместо дорогостоящего и
тяжёлого полистирола или тефлона можно использовать пено-
пласт — дешёвый и лёгкий материал. Хотя пенопласт имеет
сравнительно малый коэффициент преломления (порядка
1,03-=-1,05), даваемая им фокусировка лучей может оказаться
17* ’ 259
достаточной для снятия диаграмм направленности в условиях
ограниченных расстояний. Зависимость толщины линзы d от
фокусного расстояния коэффициента преломления п и ши-
рины раскрыва линзы определяется следующей формулой:
1___
л > 1
Из (9.41) следует, что при
Или при
f 8 (»-!)
Полагая, например,-у-= — п—1,6, получим
Л D 1 ,
а при —-—, п=1,05
f 5
d = D—2,05 ^0,5£>.
40-0.1
(9.41)
(9.42)
(9.43)
(9.44)
(9.45)
(9.46)
В обоих случаях (п= 1,6 и 1,05) получаются приемле-
мые значения толщины и веса линз.
Исследование параболических зеркальных антенн
на уменьшенных расстояниях
В области дифракции Френеля фазовые сдвиги между
полями отдельных элементов антенны содержат квадратичные
ошибки по сравнению с фазовыми сдвигам» в области дифрак-
ции Фраукгофера. Установленная условная граница между
этими областями rMUIt, определяемая ур-нием (9.31), исходит
из определённого допуска / — /на фазовую ошибку. Для парабо-
лических зеркальных антенн разработан метод компенсации
260
квадратичных ошибок, позволяющий получить достаточно пра-
вильные данные по диаграмме направленности в пределах глав-
ного лепестка и ближайшего к нему побочного лепестка, при из-
мерениях в области дифракции Френеля (при г < rMati\
[ЛЗЗ, 34].
Данный метод заключается в смещении облучателя зеркала?
из фокуса вдоль оси. Как известно, такое смещение облучателя^
вызывает квадратичные фазовые ошибки в поле в раскрыве. Ес-
ли эти ошибки сделать противоположного знака ошибкам в по-
ле излучения, то оба вида ошибок друг друга скомпенсируют.
Существует три метода расчёта необходимого смещения &
облучателя из фокуса, метод геометрической оптики, метод рас-
чёта распределения фазы в раскрыве и метод эллиптического
отражателя.
Рис. 9,7. К исследованию
диаграммы направленно-
сти параболических ан-
тенн на близких расстоя-
ниях
Для пояснения метода геометрической оптики обратимся к
рис. 9.7, на котором F — точка фокуса параболы, a F' — место
нахождения облучателя. Точку приёма Р поместим на оси зер-
кала. Потребуем, чтобы длина траектории среднего луча до
точки Р была равна длине траектории крайнего луча, т. е. по-
требуем удовлетворения равенства
Д + / + 00' + г - AF' + АР. $А1)
Из свойств параболы следует:
f 4.00r = AF, (9.48)
оа > (9Л9)
16/
Из (9.47), (9.48) и (9.49) получаем
4+1+'+W = •
(9,50)
261
Приняв
(9.51)
и освободившись от радикала в (9.50), получаем
А = Я—
D \_D-f
По методу расчёта распределения фаз в раскрыве анализи-
руется подынтегральное выражение (9.1). Подставив в (9.1)
значения г3 из (9.13), получаем
(9.53)
где Ер — поле излучения на оси параболоида в точке Р.
Обычно, когда облучатель помещён в фокусе зеркала, Е3
имеет постоянную фазу во всех точках раскрыва. При смеще-
нии облучателя из фокуса появятся квадратичные фазовые
ошибки, и для Е3 правильным будет следующее выражение:
2
-im2A ( I-— \
E, = E0F(p4,T,)e V ' . (9.54)
где F (р^) — функция зависимости амплитуды поля от коор-
динат и <pf точек раскрыва, нормированная по отношению к
полю Ео в центре раскрыва.
Если теперь подставить Es из (9.54) в (9.53), то получим
/ р* Л.
—imr—Im I ~2Д
J Г
(2f)’+p2 J
* 'dS. (9.55)
Из (9.55) видно, что полная компенсация квадратичных оши-
бок невозможна, так как во втором слагаемом в квадратичных
скобках имеется р| в знаменателе. Но если потребовать ком-
пенсации квадратичных ошибок в точке
D
то получим
2 •
(9.56)
262
Уравнение (9.56) приводится к (9.52) при Почти оди-
наковый результат получен в обоих методах потому, что они оба
основываются на компенсации квадратичных ошибок для край-
них точек раскрыва.
Метод эллиптического отражателя исходит из того, что в
пределах сравнительно небольшой дуги около вершины пара-
болическая кривая совпадает с эллиптической. Если облучатель
поместить в фокусе эллипса, ближайшем к вершине, то все лу-
чи сфокусируются в другом фокусе эллипса.
Уравнение эллипса следующее:
4--^-" 1, (9.57)
а* &
где а и b — соответственно большая и малая полуоси эллипса.
Из (9.57) следует
х=а—а
ПРИТ?Г^1:
ОС?
х= а~
2Ь2
, 262
Уг= ---х
а
(9.58)
(9.59)
(9.60)
Уравнение (9.60) есть уравнение параболы с фокусным рас-
стоянием
2а
(9.61)
Полуоси эллипса связаны с фокусными расстояниями fi и /г
соотношениями:
(9.62)
ь = у (9,63)
Так как облучатель помещён в фокусе эллипса, а не в фоку-
се параболы, т. е. на расстоянии а не f от вершины, то сме-
щение облучателя из фокуса параболы равно
Введя обозначение
f^~r (9.65)
и выразив fi через f и f2t получим
4=^ = ;>Я1 + т+£+Ч-
Метод эллиптического отражателя даёт наилучшее приб-
лижение для Д.
Устройство для автоматического снятия диаграмм
направленности *)
В устройствах для автоматического снятия диаграмм на-
правленности применяется метод вращающейся антенны (см.
выше). Рассматриваемое устройство состоит из двух стоек. На
одной находится исследуемая вращающаяся антенна на другой—
неподвижная вспомогательная антенна. Стойки могут переме-
щаться друг относительно друга, что позволяет расположить ис-
следуемую и вспомогательную антенны на расстоянии г >
Исследуемая антенна может работать как в режиме пере-
дачи, так и в режиме приёма. Ниже рассмотрена работа иссле-
дуемой антенны в режиме передачи. После соответствующей пе-
рестановки элементов приведённые схемы могут быть использо-
ваны и для случая работы исследуемой антенны в режиме приёма.
На рис. 9.8 показана схема устройства для автоматическо-
го снятия диаграмм направленности с применением самопис-
ца в качестве индикаторного прибора. В этой схеме мощность
сигнала, поступающая от генератора высокой частоты, направ-
ляется через переменный аттенюатор в исследуемую антенну.
Небольшая часть мощности сигнала ответвляется при помощи
направленного ответвителя по фидеру непосредственно к стой-
ке вспомогательной антенны. Этот сигнал сравнивается с сиг-
налом, принятым вспомогательной антенной. Разностный сиг-
нал поступает в сервомеханизм, управляющий переменным ат-
тенюатором и доводящий ослабление мощности, поступающей в
передающую антенну, до такого уровня, при котором в срав-
нивающем устройстве сигналы становятся равными. Поворот ат-
тенюатора передаётся на самописец. Блоком вращения и вы-
работки угла регулируется скорость протяжки ленты самописца
в соответствии со скоростью вращения исследуемой антенны. Та-
ким образом, на ленте самописца вычерчивается диаграмма
направленности исследуемой антенны.
9 Данный параграф написан Л. Р. Венгровичем.
264
В данной схеме предусматривается импульсная модуляция
высокой частоты и временной коммутатор, который подаёт я
тракт приёмника, детектора и сравнивающего устройства поо-
черёдно то сигнал, непосредственно поступающий от ГСС по
фидеру, то сигнал, принятый вспомогательной антенной.
исследуемая
Лспомо еа тельная
антенна
Рис. 9.8. Блок-схема устройства для автоматического снятия диаграмм на-
правленности с применением самописца
Достоинством этой схемы является то, что результаты изме-
рений не зависят от колебаний мощности генератора, коле-
баний чувствительности приёмника и от амплитудной характе-
ристики всей приёмной части. Применение переменного аттенюа-
тора обеспечивает большой динамический диапазон измерений.
На рис. 9.9 показана схема устройства для автоматического
снятия диаграмм направленности, в которой индикаторным при-
бором является электронно-лучевая трубка с большим послесве-
чением. В индикаторе применяется механическое вращение от-
клоняющей катушки вокруг колбы. Системой сельсинов вра-
щение катушки синхронизируется с вращением антенны. Сель-
син’трансформатор служит для сообщения сельсину, управляю-
щему вращением катушки, дополнительной фазы по усмотре-
нию оператора для поворота диаграммы направленности на
экране электронно-лучевой трубки. Диаграмма направленно-
сти на экране вычерчивается в полярных координатах. Для
устранения размытости очертаний диаграммы направленности
26Б
из-за переходных процессов в усилителе применяется форми-
рующее устройство, которое отпирает трубку в момент установ-
ления тока в отклоняющей катушке.
Ряс. 9.9. Блок-схема устройства для автоматического снятия диаграммы
направленности с применением электронно-лучевой трубки с послесвечением
Если в схемах рис. 9.8 и 9.9 в качестве вспомогательной при-
менять антенну линейной поляризации и вращать ее вокруг ли-
нии, соединяющей её с исследуемой антеной, причём число обо-
ротов сделать в несколько раз больше числа оборотов исследуе-
мой антенны, диаграмма направленности получится промодули-
рованной поляризационной характеристикой.
Снятие диаграмм направленности антенн при помощи
самолётов н вертолётов
Общие сведения
Снятие диаграмм направленности стационарных антенн
диапазонов коротких и ультракоротких волн производится, как
указывалось выше, главным образом с самолётов и вертолё-
тов 9* Это позволяет производить измерение в любых плоско-
стях, получать данные для построения картографических диа-
грамм направленности и, кроме того, — даёт возможность авто-
матически записывать диаграмму направленности, что исключает
’) Снимать диаграммы направленности лучше с вертолетов, так как, во-
первых, с самолёта трудно коррелировать отметку показаний приборов с егц
местоположением и, во-вторых, измерения с самолёта нужно производить па
больших расстояниях, а для антенн с поднятым главным лепестком — и на
большой высоте, что требует сложной системы радиолокационного наблюде-
ния.
266
индивидуальные ошибки наблюдения и обеспечивает полную
объективность и документальность результатов. Первая автома-
тическая запись диаграммы направленности при помощи самолё-
та была произведена в 1934 г. В. В. Татариновым [Л 12].
Аппаратура для снятия диаграмм направленности с само-
лётов и вертолётов должна состоять из передающего устрой-
ства, приёмного устройства, вспомогательной антенны и прибо-
ров слежения за летательным аппаратом.
Возможны два варианта размещения аппаратуры: непосред-
ственно на летательном аппарате или на буксире?
Передающее устройство
Для снятия направленности антенн действующих пе-
редающих радиоцентров целесообразно использовать исследуе-
мую антенну в качестве передающей, а в качестве генератора —
рабочий передатчик в режиме несущей.
Для исследования антенн приёмных радиоцентров или строя-
щихся передающих радиоцентров нужно иметь специальные из-
мерительные генераторы, которые можно располагать как на
самом летательном аппарате, так и на буксире. В первом случае
в качестве измерительного генератора можно использовать ГСС,
но обычно ГСС рассчитаны на питание током частоты 50 гц,
а бортовая сеть имеет повышенную частоту, поэтому приходится
применять преобразователь частоты или аккумуляторы с преоб-
разованием постоянного тока в переменный.
Генераторы, устанавливаемые на буксирах, должны иметь
Малый вес, быть компактными и герметизированными. Удобно
питать их от батарей. Мощность генераторов невелика — от до-
лей ватта до 1 вт. Они должны быть рассчитаны на ряд фикси-
рованных частот. Установка требуемой частоты производится
перед полётом. В специальных генераторах, бортовых и буксир-
ных должна быть кварцевая стабилизация частоты.
Исследуемую антенну целесообразно использовать в качест-
ве приёмной.
Приёмное устройство
При снятии диаграмм направленности антенн действую-
щих передающих радиоцентров приёмной аппаратурой могут слу-
жить профессиональные приёмники, измерители напряжённости
поля, измерители помех и т. п. АРУ должна быть выключена и
приёмники проградуированы.
Размещение приёмника на летательном аппарате требует
обеспечения его помехоустойчивости, тщательной амортизации
его и самопишущих приборов.
267
Задача обеспечения помехоустойчивости облегчается благо-
даря использованию рабочего передатчика радиоцентра, кото-
рый, как правило, имеет большую мощность и может создать
значительные поля в месте приёма. Улучшить помехоустойчи-
вость можно хорошей экранировкой приёмника и блокировкой
его по питающим цепям.
При использовании исследуемой антенны в качестве приём-
ной наиболее целесообразно применять профессиональные при-
ёмники, имеющие высокую чувствительность, поскольку на ле-
тающем аппарате приходится, как указывалось выше, ставить
маломощные генераторы.
Вспомогательные антенны
На самолётах и вертолётах, выделенных специально для
антенных измерений, вспомогательные антенны могут быть
размешены оптимальным образом.
В настоящее время, при использовании обычных рейсовых
летательных аппаратов, могут быть предложены следующие
варианты размещения вспомогательных антенн.
Рис. 9.10. Размещение проволочного го-
ризонтального симметричного вибратора
на самолёте:
а) над его корпусом, б) между крылом
и хвостовой частью
При горизонтальной поляризации поля излучения в качест-
ве вспомогательных антенн используются симметричные виб-
раторы. На рис. 9.10 показано два варианта размещения корот-
коволнового вибратора из тонкого медного провода или антен-
ного канатика: над корпусом самолёта и между крылом и хво-
стовой частью. Размещение аналогичной антенны на вертолёте
показано на рис. 9.11. Наряду с проволочными применяются а1ь
теины из медных трубок, прикреплённых к деревянному штоку
268
Рис. 9.13, Размещение антенн из медных трубок: а) под
самолётом, б) под вертолётом
(рис. 9.12). На этом же рисунке показано размещение антенны,
рассчитанной на вертикальную поляризацию.
Для размещения антенны под корпусом летательного аппа-
рата (рис. 9.13) необходимо сооружать дополнительные кон-
струкции: мачты, механизмы для убирания антенн и т. п. На
практике этот вопрос решается следующим образом. Вибратор
монтируют на тефлоновых стойках, крепящихся к деревянному
бруску. Брусок привязывают обычно резиновыми жгутами в об-
269
хват корпуса машины (рис. 9.14). Вибраторы желательно рас-
положить так, чтобы их оси совладали с направлением движе-
ния летательного аппарата.
Наряду с антенной вертикальной поляризации (рис. 9.12) на-
ходит применение гибкий штырь (антенна Куликова).
Рис. 9.14. Крепление сим-
метричного вибратора *
хвостовой части вертолёта
Устройство антенны в случае размещения измерительной ап-
паратуры на буксире показано на рис. 9.15. В этом случае антен-
на оказывается на значительном расстоянии от летательного ап*
парата и её диаграмма направленности не искажается им, как
при описанных выше способах размещения. У буксирных антенн
один конец крепят к коническому парашюту из нейлона, а дру-
гой — через капроновый канат к летательному аппарату.
Размеры вибратора выбирают соответственно длине волны,
на которой ведутся испытания, из расчета 2 -^-,где — дли-
на плеча вибратора. Если 2 то для увеличения дей-
ствующей высоты вибратора на его концах располагают полые
металлические шары.
В случае буксирной антенны вертикальной поляризации
(рис. 9.15) к нижнему её концу должен быть подвешен груз для
придания ей вертикального положения.
Передатчик ^Антенна
Капронидт Лапронодый
\ канат „ \ мкат
Яктенна
Передатчик
Антенна
Рис. 9.15. Устройство антенны в случае разме-
щения аппаратуры па буксире к вертолёту
270
Приборы слежения за летательным аппаратом
Система слежения за летательным аппаратом и корреляция
показаний приборов, отмечающих напряжённость поля, с коор-
динатами летательного аппарата представляют сложную зада-
чу, не получившую ещё окончательного решения. Рассмотрим
некоторые из них, применяющиеся па практике.
В качестве приборов, отмечающих координаты летательного
аппарата, применяются теодолит, установленный вблизи иссле-
дуемой антенны и служащий для определения азимутного уг-
ла и угла места, и высотомер летательного аппарата для оп-
ределения высоты полёта. Этими приборами удобно пользовать-
ся, когда исследуемая антенна является приёмной. Прибор, по-
казывающий напряжение на выходе приёмника, может быть по-
мещён вблизи теодолита, так что возможна одновременная за-
пись углов установки теодолита и напряжения на выходе при-
ёмника. Самолёт или вертолёт должен летать по кругу с цент-
ром в средней точке антенны и на постоянной высоте, контроли-
руемой по высотомеру. Кроме того, он должен оставаться всё
время в поле зрения теодолита.
При измерениях с самолёта, летающего с большой скоростью,
и при острой направленности исследуемой антенны наблюдение
должны вести три оператора. Один наблюдает через зритель-
ную трубу теодолита за самолётом, держа его постоянно на
перекрещении нитей объектива, второй наблюдает за угловы-
ми шкалами теодолита, третий — за прибором, показывающим
напряжение на выходе приёмника или за самописцем. По сиг-
налу второго оператора, записывающего углы, третий записы-
вает напряжение на приборе или делает метки на ленте само-
писца.
При сравнительно широком лепестке диаграммы направ-
ленности антенны и небольшой скорости полёта наблюдение
могут вести два или даже один оператор. В случае вертолётных
измерений запись углов и напряжений производится в момен-
ты кратковременного зависания вертолёта. Наблюдение может
вести один оператор.
Если теодолит заменить автоматической радиолокационной,
станцией с большой разрешающей способностью и синхронизо-
вать её работу с работой самописца, то снимать диаграммы на-
правленности можно будет автоматически.
Если исследуемая антенна работает на излучение, а приём’
ная аппаратура размещена на летательном аппарате, в качест-
ве прибора для слежения также можно использовать теодолит.
Но поскольку оператор, записывающий напряжение на выходе
приёмника, находится в этом случае на летательном аппарате,
271
связь между Землёй и летательным аппаратом должна быть
очень хорошей. Измерения производятся следующим образом.
На трассе полёта намечаются наземные ориентиры, угловые
координаты которых известны. Пролетая над этими ориенти-
рами, оператор записывает напряжения на выходе приёмника.
Если для записи использовать самописец, то достаточно иметь
два ориентира—начальный, по которому самописец включается, и
конечный, по которому он выключается. Скорость полёта само-
лёта в период записи должна быть при этом строго постоянной.
При исследовании передающих антенн также возможно при-
менение радиолокационных станций, следящих за полётом само-
лёта, по сигналам которых записываются напряжения, вклю-
чается или выключается самописец. Вместо самописца может
применяться шлейфный осциллограф.
Для того чтобы измерения при помощи летательных аппара-
тов прошли успешно, требуется их тщательная подготовка и в
том числе проведение предварительных поверочных измерений.
Об использовании космических источников излучения
для снятия диаграмм направленности антенн
Помимо описанных методов исследования стационар-
ных антенн и антенн сантиметровых и дециметровых волн, на-
ходят применение методы, использующие космические источ-
ники излучения для снятия диаграмм направленности антенн.
Прежде чем космическое излучение достигает поверхности
Земли, оно проходит земную атмосферу. При этом волны, длин-
нее 16—20 м, отражаются от ионосферы, а волны, короче 1.25 оч,
поглощаются в тропосфере. Таким образом, поверхности Земли
достигают волны, лежащие в пределах «1,25 слс<Л<20 я.
Во всём указанном диапазоне спектр космического излучения
непрерывный и носит характер «шума». Излучение же земных
источников на несущей частоте является монохроматическим.
Другая особенность внеземного радиоизлучения заключает-
ся в том, что оно имеет почти круговую поляризацию, земные
источники излучают, как правило, поле линейной поляризации.
Самым мощным источником космического радиоизлучения
является Солнце. Что касается Галактики в целом, то из обще-
го. почти равномерного фона, создаваемого её радиоизлуче-
нием, выделяются отдельные дискретные источники. Наиболее
мощные из них Лебедь А, Кассиопея А, Крабовидная туман-
ность в созвездии Тельца, Дева А и Центавр А.
В отличие от Солнца, угловой диаметр которого равен 30\
указанные источники Галактики имеют угловые размеры не бо-
лее 3'4-5' и могут рассматриваться как точечные. Поэтому Солн-
це используется для снятия диаграмм направленности с шириной
272
главного лепестка больше 3°. При исследовании антенн с боль-
шой разрешающей силой используется радиоизлучение Лебе-
дя А и Кассиопеи А.
Однако возможность использования космических источников
излучения для снятия диаграмм направленности стационарных
антенн весьма ограничена по следующим причинам: 1) оно воз-
можно лишь в тех плоскостях, через которые в момент измере-
ний проходят источники; 2) благодаря атмосферной рефракции
измерения при малых углах (Д<25-г-30°) над горизонтом весь-
ма неточны, в то время как практически именно малые углы
представляют наибольший практический интерес; 3) каждую
отдельную диаграмму направленности нужно снимать продолжи-
тельное время. Ввиду чрезвычайной простоты и малой трудо-
ёмкости этих измерений они целесообразны, но, как правило,
могут играть лишь второстепенную роль и служить для контроля.
Для снятия диаграмм направленности больших вращающихся
антенн сантиметрового и дециметрового диапазонов использо-
вание космических источников может оказаться весьма полез-
ным.
Космические источники широко применяются для измерения
характеристик антенн, используемых в радиоастрономии. Эти
измерения тесно сочетаются с общими радиоастрономическими
измерениями. Подробный обзор методов измерений характери-
стик антенн с использованием космических источников дан в ра-
боте [Л45].
Снятие диаграммы направленности ферритовых антенн в
однородном магнитном поле
Снятие диаграмм направленности антенн, как указыва-
лось выше, должно производиться па расстояниях, при кото-
рых исследуемая и вспомогательная антенны находятся в об-
ласти Фраунгоферовой дифракции. Это означает, что волна,
излучённая одной из участвующих в эксперименте антенн, долж-
на иметь (с заданной точностью) около Другой антенны в преде-
лах протяжённости последней плоский фронт, одинаковые ампли-
туды и одинаковую поляризацию поля.
Это требование существенно в случае антенн больших раз-
меров, когда при разных углах поворота одной антенны отно-
сительно направления на другую создаются разные соотношения
фаз поля около отдельных элементов антенн. В случае ан-
тенн очень малых размеров по сравнению с длиной волны, на-
пример ферритовых, фазы поля около всех их элементов поч-
ти одинаковы независимо от поворота антенны относительно
направления прихода волны, и поэтому требование плоского
фронта волны снимается. Требование же постоянства амплитуд
18-292 273
и поляризации поля в пределах протяжённости антенны сохра-
няет свою силу и в данном случае.
Из сказанного следует, что для снятия диаграмм направ-
ленности, а также для измерения других параметров антенн
малых размеров по сравнению с длиной волны не обязательно
создавать поля излучения и разносить антенны до области
Фраунгоферовой дифракции. Измерение можно производить
в однородном квазистатическом поле.
Для снятия диаграмм направленности ферритовых антенн
таким однородным квазистатическим магнитным полем может
служить так называемое поле Гельмгольца [Л27]. Это — поле
между двумя круглыми синфазными рамками радиуса < X,
расположенными на расстоянии A=R друг от друга (рис. 9.16).
На рис. 9.17а показана картина магнитных силовых линий
одного круглого витка тока. Поле имеет две составляющие Hz
и /7р (направление координат / и р показано на рис. 9.16). Мож-
но показать [Л28], что эти составляющие в практической системе
единиц равны:
Нг = — 7 к + (9.67)
2тг/(/? + Р)2 + 22 [ (Я —p)» + Z3J к '
Н =------------1........ - к, + к2
₽ 2ярУ(7?+р)3 + 72 [ W-pP + Z2
где I — ток в витке,
*1 и кз — полные эллиптические интегралы первого и
го рода, равные:
Рис. 9.16. К измерению
параметров ферритовых
антенн в киазистатиче-
ском магнитном поле
я.
2 _____________
= J 1 — oasin2a da,
о
Причём
4Кр
а — —--------— .
(Я + р)2+ Z1
На оси витка (р=0):
_________________’
— 2 у (/?2 н- Z2)3
второ-
(9.69}
(9.70)
(9.71)
(9.72)
Я =0
р
На рис. 9.176 и в показана картина магнитных силовых ли-
ний двух круглых витков (рамок) тока, причем на рис. 9.176
изображены парциальные поля, а на рис. 9.17в — суммарное
274
поле. На последнем рисунке пунктирной линией обведена об-
ласть, в пределах которой с точностью до 2% поле постоянно по
амплитуде и поляризации. Эта область ограничена цилиндри-
ческой поверхностью, у которой диаметр основания и высота
Рис. 9.17. Картина магнитных силовых линий:
а) рамки, б) парциального поля двух рамок, в) суммарного поля
двух рамок
равны между собой и равны 0,85/?. Ось цилиндра совпадает с
осью рамок, а центр области совпадает с центральной точкой си-
р=0, Z= — I .
Магнитное поле в выделенной области можно считать рав-
ным удвоенному значению поля одного витка в центральной
точке
Иг = 2 ——----------— - 0,716 — .
z 2 НЯ* + 0,25Я2)3 Я
Это магнитное поле эквивалентно электрическому полю
плоской электромагнитной волны в воздухе, равному
£„, = 1201гЯг=86к-<-- (9-74)
К
Поле Гельмгольца является одним из видов эталонного по-
ля. Оно может быть определено с большой точностью по ве-
личине тока /, текущему в рамках.
Очевидно, что максимальная эдс возбудится на входе ан-
тенн при совпадении оси феррита с осью рамок. Диаграмма
направленности является функцией эдс от угла поворота оси
феррита относительно оси рамок.
Заметим, что измерения в поле Гельмгольца могут произ-
водиться в закрытом помещении, так как влияние стен поме-
щения и посторонних предметов на это поле незначительно, в
то время как измерения в поле излучения должны произво-
диться на открытых площадках, поскольку в помещениях отра-
жения от стен и посторонних предметов образуют сложную си-
стему стоячих волн, могущих привести к неправильному резуль-
тату.
18* 275
10. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА
УСИЛЕНИЯ АНТЕНН
Измерение коэффициента усиления стационарных антенн
Под стационарными понимают антенны, установленные
на антенном поле радиоцентра, положение которых постоянно и
не может быть изменено в процессе измерений.
Для определения коэффициента усиления стационарных ан-
тенн первоначально должны быть сняты их диаграммы направ-
ленности в вертикальной и горизонтальной плоскостях и най-
дено направление главного максимума. При дальнейших из-
мерениях исследуемая антенна может быть использована либо
в качестве передающей, либо в качестве приёмной.
В первом случае антенна присоединяется к передатчику и из-
меряется мощность Р, поступающая в антенну, и абсолютная
величина напряжённости поля излучения Е в направлении
главного максимума. Коэффициент усиления G вычисляется
по ф-ле (1.2)
о = ^,
ЗОР
где г — расстояние между антенной и местом измерений на-
пряжённости поля.
При использовании исследуемой антенны в качестве приём-
ной, она присоединяется к градуированному приёмнику, а пе-
редатчик с какой-либо передающей антенной помещаются на
некотором расстоянии r> rMUff [см. (9.31)] на линии главного
максимума диаграммы направленности исследуемой антенны.
Измеряется напряжение на входе приёмника U, напряжённость
поля Е у приемной антенны каким-либо методом, описанным
ранее, и входное сопротивление антенны ZA. Если антенна сое-
динена с приёмником фидерной линией, то необходимо хорошо
согласовать высокочастотный тракт по крайней мере с одной
стороны — со стороны антенны или со стороны приёмника. При
двустороннем согласовании действующую высоту антенны
можно вычислить по формуле
= (10.1)
£
276
При согласовании лишь с одной стороны согласно (1.72)
получим
, 2£/
ft —---------
£(1±Г)
где Г — коэффициент отражения на фидере, возникший на
той стороне, где отсутствует согласование, причём знак плюс1
берётся при согласовании со стороны антенны, а знак минус —
при согласовании со стороны приёмника.
Зная и ZA, можно найти коэффициент усиления по фор-
муле
(10.2)
120л*й|
В общем случае, при отсутствии согласования как со сторо-
ны антенны,.так и со стороны приёмника, расчёты чрезвычай-
но усложняются и могут быть произведены на основе данных
первой главы.
Из изложенного видно, что коэффициент усиления антенн
проще измерять, используя исследуемую антенну в качестве
передающей.
(10.3)
Измерение коэффициента усиления переносных антенн
методом сравнения (замещения)
Метод сравнения применяется либо при лабораторных
измерениях антенн сверхвысоких частот, либо при измерениях
макетов антени других диапазонов, исследуемых па сверх-
высоких частотах. Он заключается в сравнении коэффициента
усиления исследуемой антенны с коэффициентом усиления эта-
лонной антенны.
В качестве эталонной антенны можно рекомендовать пи-
рамидальный рупор. Его коэффициент усиления легко рассчи-
тывается и, как показали экспериментальные исследования,
измеренные значения коэффициента усиления в пределах точ-
ности измерений хорошо совпадают с теоретическими. Если
параметры рупора обозначить, как показано на рис. 10.1, то его
коэффициент усиления рассчитывается по формуле
(10.4)
причём величины —GE и — GH определяются по графикам
Di
рис. 10.2 и 10.3.
Схема установки для измерения коэффициента усиления по
методу сравнения показана на рис. 10.4.
277
Исследуемая Аи и эталонная >1, антенны поочерёдно под-
ключаются через фидер Ф и измерительную линию ИЛ к гене-
ратору высокой частоты Г. На расстоянии г > rMUfl от них поме-
щается аппаратура ИП для измерения относительной величины
напряжённости поля, состоящая из приёмной антенны АПр, де-
тектора Д (как правило, полупроводникового) и чувствитель-
ного гальванометра /7.
Рис. 10.1. Обозначение
параметров рупора
На измерительной линии определяется коэффициент бегу-
щей волны к и максимальное значение напряжения ЙМакс> а при
помощи аппаратуры ИП — относительная величина напряжённо-
сти поля Е в точке приёма. Если величины, измеренные при
подключении к генератору исследуемой антенны, снабдить ин-
дексом 1, а величины, измеренные при подключении к генера-
тору Г эталонной антенны, снабдить индексом 2, то коэффици-
ент усиления исследуемой антенны можно рассчитать по фор-
муле
F2 к» №
г[ и2макс гх
. (J0.5)
UJ макс
Измерение коэффициента усиления антенны методом срав-
нения можно производить также при работе исследуемой и эта-
лонной антенн па приём. В этом случае установка для измере-
ний собирается по схеме рис. 10.5. Переключатель Пр подключа-
ет поочерёдно антенны Аа и А, к цепи детектора и гальвано-
метра, а к генератору Г подключается постоянно какая-либо пе-
редающая антенна
Обозначив показания гальванометра через g и сохранив
прежнее значение за индексами 1 и 2, получаем при квадратич-
ной характеристике детектора
g1 = £l g2.
St
(10.6)
278
Рис. 10.2. Графики
— при различных
Л.
X
зависимости $£ от
Яа
значениях ~ (обозна-
чения см. на рис. 10.1)
(обозначения см. на рис. 10.1)
При использовании исследуемой антенны в качестве приём-
ной трудно обеспечить хорошее согласование детектора со вхо-
дом антенн Аи иА9, Неполное согласование, а также неодина-
Ряс, ЮЛ. Блок-схема уста-
новки для измерения коэф-
фициента усиления антенн
по методу сравнения при
работе исследуемой и эта-
лонной антенн на передачу
ковая степень согласования антенн Аи
ком больших погрешностей измерения.
Рис. 10.5. Блок-схема установ-
ки для измерения коэффициен-
та усиления антенн по методу
сравнения при работе иссле-
дуемой и эталонной антенн на
приём
и А 9 является источни-
Поэтому прсдпочтитель-
нее измерять коэффициент усиления по методу сравнения при
работе исследуемой антенны на передачу.
В рассматриваемом методе обе сравниваемые антенны Ац
и Аэ должны находиться точно в одинаковых условиях излу-
чения или приёма и быть разнесены на достаточно большое рас-
стояние r> гMttK в соответствии с соотношением (9.31).
Измерение коэффициента усиления по методу двух
идентичных антенн. Обобщение метода на две
нендентичные антенны
Измерения по данному методу проводятся при помощи
двух совершенно идентичных антенн, которые располагаются на
расстоянии r>rMUH друг от друга и ориентируются таким об-
разом, чтобы главные максимумы их диаграмм направленности
были ориентированы по одной прямой навстречу друг другу.
Одна из антенн работает на передачу, другая — на приём. Схема
измерительной установки показана на рис. 10.6. Приёмная ан-
тенна, так же как приёмник, должна быть достаточно хорошо
согласована с фидерной линией. Специальным прибором (боло-
метром Б или измерителем малой мощности) измеряется мощ-
280
ность Рт, поступающая в передающую антенну, и мощность
улавливаемая приёмной антенной. Усиление исследуемой ан-
тенны равно
0 = ^-1/^-. (10.7>
к У Рт г
Рис. 10.6, Блок-схема уста-
новки для измерения коэф-
фициента усиления антенн
по методу двух идентичных
антенн
Действительно, мощность, улавливаемая приёмной антенной
в оптимальном режиме,
р —
R ~ 120ге ’
где Е — напряжённость поля в месте нахождения приёмной ан-
тенны,
эффективная площадь антенны.
Напряжённость поля Е выражается через мощность Рт излу-
чения и через коэффициент усиления следующим образом:
(10.8).
£ УЗОРrG
(10.9)
Подставив в (10.8) значение Е из (10.9) и значение на
(1.41), получим
р = **-р
R (4я г)1 т’
Из (10.10) легко получить (10.7).
В том случае, когда коэффициент усиления одной из антенн
О] отличается от коэффициента усиления другой антенны Gj,
можно Gi и вг измерить комбинированным методом, включаю-
щим как метод сравнения, так и метод двух идентичных антенн.
По методу сравнения находим
G,
а= —
G.
(10.10)
(10.11)
Используя в методе двух антенн в качестве передающей ту,
усиление которой равно G,, а в качестве приемной — вторую с
281
усилением G2, измерив мощность PR, поступающую в передаю-
щую антенну, и мощность Рт, улавливаемую приёмной антенной,
получаем р = _ £2 G«- (10 12) « 120* 480*’ ’
где е^У30^, (10J3)
Подставив значение Е из (10.13) в (10.12), находим
Рт \4п г }
Решая совместно (10.11) и (10.14), получаем:
G / А ,
X у а
02 = 4те у- Vab.
(10.14)
(10.15)
(10.16)
Измерение коэффициента усиления антенн по методу
плоского экрана
Метод плоского экрана заключается в следующем.
Исследуемая антенна Ац (рис. 10.7) подключается к генера-
тору Г через измерительную линию ИЛ и фидер Ф- При помо-
щи измерительной линии опреде-
Т’ис. 10.7. К измерению коэф-
фициента усиления антенн по
методу плоского экрана
Ляется степень согласования антен-
ны с фидером. Прежде всего произ-
водится тщательная настройка ан-
тенно-фидерной системы так, чтобы
коэффициент бегущей волны на из-
мерительной линии получился близ-
ким к единице. Затем перед антен-
ной на произвольном расстоянии г
устанавливается плоский металли-
ческий экран Э, плоскость которого
-перпендикулярна направлению главного максимума излучения
антенны, а размеры таковы, что из центра антенны экран виден
под телесным углом, не меньшим телесного угла, занимаемого
главным лепестком диаграммы направленности антенны. Экран
нарушает согласование. При помощи измерительной линии опре-
деляется коэффициент бегущей волны, получаемый после уста-
новки экрана. По расстройке согласования Дк=1—к можно вы-
числить коэффициент усиления антенны.
282
Формула для расчёта коэффициента усиления выводится на
-основе следующих соображений.
При отсутствии экрана входное сопротивление антенны рав-
но волновому сопротивлению измерительной линии
= р,
Нарушение согласования объясняется тем, что под влиянием
плоского экрана изменяется входное сопротивление передаю-
щей антенны из-за того, что к первоначальному сопротивле-
нию добавляется наведённое сопротивление от экрана, которое
равно наведённому сопротивлению от такой же антенны, как
исследуемая, но расположенной на расстоянии 2 г и имеющей
обратную фазу колебаний. Как известно [Л24, 25, 26], наведён-
ное сопротивление выражается следующей формулой:
где
у _____ * 60Х 2 —
• __ . ХС*А — !2тг
Таким образом,
(10.17)
(10.18)
(10.19)
Полное сопротивление антенны с учётом сопротивления, на-
ведённого от экрана, равно
- п , 7 п /, .XGe-i2mr\ /, Л6еГКтг\
(10.20)
Коэффициент отражения на линии
(10.21)
Используя обозначение
1 —к Д к,
получаем
Дк
2 —Дк
-i — e-12mf
4п г
2 — i e~l2mr
4к г
(10.22)
283
Из (10.22) непосредственно следует
Д к - — (10.23)
4л г
ИЛИ '
(10 24)
По ф-ле (10.19) можно определить коэффициент усиления
антенны, не прибегая к согласованию антенны и фидера. Со-
гласно (10.19)
G = — feL. (10.25)
> кА
Величины RA и ZKaa могут быть найдены непосредствен-
ным измерением входного сопротивления антенны с экраном и
без него.
Таким образом, метод плоского экрана даёт возможность
определить коэффициент усиления антенны либо по величине
расстройки коэффициента бегущей волны Дк, вызываемой экра-
ном, если антенна без экрана имеет высокую степень согласо-
вания с фидерной линией, либо по величине отношения наведён-
ного сопротивления, вызываемого экраном, к активной состав-
ляющей сопротивления антенны без экрана.
В Отношении измерения коэффициента усиления антенны по>
величине расстройки Ак необходимо сделать следующие заме-
чания.
Уравнение (10.23) можно переписать следующим образом:
1
—---------г.
Д к G К
Графическое построение функции f(r)=— согласно ф-ле
(10.26) должно дать прямую линию (прямая а на рис. 10.8), про-
(10.26)
Рис. ЮЛ к определению среднего
значения изменения кбв (Дк)
С
/
о
Рис. 10.9. К определению среднего
значения коэффициента усиления
антенны по методу плоского
экрана
284
ходящую через начало координат. В действительности при изме-
рении по этому методу зависимость f(r) графически пред-
ставляет кривую приблизительно синусоидальной формы (кри-
вая б рис. 10.8), проведённую относительно прямой, определяе-
мой ур-нием (10.26). Такая кривая имеет место, когда естест-
венный коэффициент бегущей волны на фидере значительно от-
личается от 1 и для его повышения применяются элементы на-
стройки в виде реактивностей. При этом амплитуда колебаний
синусоидальной кривой б относительно прямой а тем больше, чем
больше отличается естественный коэффициент бегущей волны
от 1. в связи с тем, что является функцией г, коэффициент
усиления антенны — параметр, не зависящий от расстояния, —
окажется также функцией от расстояния вида рис. 10.9 (сину-
соидальная кривая).
Указанное отклонение экспериментальной кривой
от прямой объясняется тем, что включаемые в фидер для согла-
сования реактивности подобраны соответственно входному со-
противлению антенны без экрана. Включение экрана, как гово-
рилось ранее, изменяет режим бегущей волны на фидере. Это
изменение определяется не только отношением —, а
собе те
также тем, что включаемые в фидер реактивности определённым
образом трансформируют это отношение сопротивлений. Оче-
видно, что трансформация зависит от знака реактивной состав-
ляющей Хнов наведённого сопротивления. Поскольку согласно
(10J9) знак Хнав периодически меняется с перемещением эк-
рана через каждую четверть волны, то отклонение функции
f(r) от прямой также принимает периодический характер.
Ошибка в измерении коэффициента усиления меняется с той
же периодичностью. Для того чтобы найти истинное значение
коэффициента усиления, на графике зависимости G от г вида
рис. 10.9 проводят прямую посредине между экспериментальны-
ми точками кривой.
Хороший результат получается также, если вести расчёт G
по ф-ле (10.24), подставляя в неё Ак, равное среднему ариф-
метическому от двух значений, полученных для двух положений
экрана, отстоящих на четверть волны друг от друга.
Итак, определить коэффициент усиления антенны, согласо-
ванной с фидерной линией при помощи реактивностей, вклю-
чённых в фидер, можно двумя путями:
1) измерением двух значений Лк для двух расстояний экра-
на от испытуемой антенны, которые отличаются друг от друга
285
на — , и подстановкой их среднего арифметического значения в<
ф-лу (10.24);
2) серией измерений к при различных расстояниях эк-
рана от антенны, вычислением О для каждого измерения в от-
дельности и нахождением истинного значения Gacrn по прямой,,
проходящей посредине между экстремальными точками кри-
вой.
Определить коэффициент усиления можно и без согласова-
ния путём измерения RA и ZHaa и последующего расчёта по
ф-ле (10.25),
О влиянии отражения от поверхности земли на результаты
измерений коэффициента усиления антенн
В изложенных выше методах измерения коэффициента
усиления антенны предполагалось, что испытуемые антенны на-
ходятся в свободном пространстве. Из-за наличия вблизи ан-
тенн поверхности земли связь между испытуемыми антеннами
осуществляется не только по прямой линии, соединяющей пере-
дающую и приёмную антенны, но и по ломаной линии, обра-
зованной направлением движения энергии, отражённой от по-
верхности земли (рис. 10.10). Дополнительная паразитная
Рис. 10.10. К измерению коэф-
фициента усиления антенн при
наличии отражённой волны
связь между антеннами за счёт этой отражённой от земли энер-
гии электромагнитных волн может дать существенную погреш-
ность при измерении коэффициента направленности антенн.
Для того чтобы исключить влияние земли на результаты из-
мерений, можно использовать предложенный А. Р. Воль пер том
метод, сущность которого изложена в первой главе. Применитель-
но к измерению коэффициента усиления антенн этот метод за-
ключается в том, что одна из антенн, например эталонный ру-
пор, устанавливается на различной высоте от земли, как это по-
казано на рис. 10.10. Построив зависимость показаний индикато-
ра эталонной антенны от высоты её установки над землёй, полу-
чаем периодическую кривую, с помощью которой можно исклю-
чить влияние земли из результатов измерения. Если обозначить
286
Приложение /
Л
искомое показание индикатора при отсутствии влияния земли
через Uq, а найденные из эксперимента показания в минимуме
и ближайшем к нему максимуме построенной периодической.
кривой соответственно через и то значение 17о оп-
ределяется по следующей простой формуле:
г/ Uмакс 4“ мин /1Л07\
Значения 170, 17макс и UMUfi должны быть выражены в еди-
ницах напряжения»
Другой способ исключения влияния земли заключается в
выборе такой высоты установки антенны (или расстояния меж-
ду ними), при которой направление отражённого от земли луча
совпадёт с направлением нулевого излучения хотя бы для одной
из антенн.
При измерении коэффициента усиления по методу плоского
экрана влияние земли менее существенно и его можно в первом
приближении не учитывать.
Приложение f2
885:
ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ЛИНИЙ
Тип (марка) Диапазон частот (Мгч) Тип фидера Волновое сопротивле- ние фидера Чувствительность при работе с незату- хающими колеба- ниями Максимальная допустимая мощность Погрешность Перемещение эон да
ил-д 350—675 Коаксиальный 75 ом 220 мот с полу- проводниковым детектором; 2-г-б СЮ с диод- ным детектором — Для кевн не пре- вышает 2±5°/о Ручное, автоматиче- ское
ЛИ-1 500-3000 » 75 аи 20 мет — * Ручное
ЛИ-3 150-ЮОО Полосковый Две секции 75 и 50 ом 20-i-40 мет для секции 75 ом^ 40 мет секции 50 ом 1— 5°/о
ЛИ-4 500-3000 » То же 20 мет для секции 75 ом, 40 мет для секции 50 ом 50 вт Для кевн не превы- шает 2+10-7-120/0
ИВЛ-1 2500- 4000 Волноводный 72X34 мм — 20 мет 250 вт в не- прерывном режиме ±&°/о
ИКЛ-10 2300—4300 Коаксиальный 75 ом 0,2 ет 100 вт в не- прерывном режиме Для кевн ие пре- вышает 2+5°/о
икл-ш 2500- 10 350 50 cw — —• Для кевн не пре- вышает 2+10о/о
19—292
Тип (марка} Диапазон частот, Мгц Тип фидера Вэлновое сопротивле- ние фидера
ИКЛ-112 1000-3750 Коаксиальный 50 ол!
33-И 8200-12500 Волноводный 22.9ХЮ»2 лсл —.
ИВЛУ- 140 Опр. разм. вол нов, Волноводный для 3 см 10X23 мм. Для других диа- пазонов по отдель- ному заказу
КСВ-60-И (иэм. ксв) 8500-11 900 Волноводный 22,9X10.2 л.и —
ИСЛ-1 100-150 Коаксиальный РК-6 52+3 см
53-И (автомат) 8500- 9500 Волноводный 10X23 мм —
ИПСК-2 (нам. ноли, сопр.) 30—1000 Коакс. направлен- ный ответвитель 75 ом
60-И (изм. ко- эффи- циента стоячей волны) 8500-9600 Волноводный 10,2X22.9 мм
Продолжение
Чувствительность- лри работе с незату- хающими колеба-* НИЯМИ Максимальная допустимая мощность Погрешность Перемещение зонда
— — Для ксвн не пре- вышает Ручное
1 MVH — Нс превышает Ю±57о >
1 мет — Для ксвн не более 2Н_5с/о
— 50 вт Для ксвн не пре- вышает 2±1Оц/о
.— 50 вт Для изм. кбв зтО.03-^0,1; для изм, актмп. сопр. ±15"/о
— — Для ксвн не более 2,5±1О7о Автомати- ческое
20 мвт^-10 от в зависимости от индикатора Для изм. сопр. +20°/о» при изм. ксв не более ±10-bI2°/o
50 вт При изм. ксв 1,14-2,0—не прев. 2^1’0°/0
Приложение 3
ВОЛНОВОЕ СОПРОТИВЛЕНИЕ ФИДЕРОВ ПРИ ВОЗДУШНОМ ЗАЗОРЕ
МЕЖДУ ПРОВОДАМИ
Конфигурация поперечного сечения фидера Формулы волнового сопротивления
Г*~27 —♦ ф ф , Уо 4-2г+ VD — 2г Р = 276 In — /£>4-2г—УД —2г D при — » 1 D о - 276 1g — Г
6 о1 Dy У Df + 1% Р 138 1g L l\r
290
П родолжение
Конфигурация поперечного сечения фидера Формулы волнового сопротивления
О— ° t <>—<4 р = 172 - ° - 1 75 г
р=138 lg —
го
• L-a-J
? = 138 1g
0,539 а
D----
₽ = 138 ig —
2*
291
Продолжение
Конфигурация поперечного сечения фидера Формулы волнового сап ротке леями
©5 ГД 4 7?’—Д21 Р = 276 g —» ? ё г 4/?2-hD2]
292
Продолжение
Конфигурация поперечного
сечения фидера
Формулы волнового сопротивления
Р= 138
при W < 0,35(6—0и 4- < 0,25,
ь
120 х
Приложение 4
ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЕЙ НАПРЯЖЕННОСТИ ПОЛЯ И НАПРЯЖЕНИЯ ПОМЕХ
Наимено- вание прибора Назначение Диапазон частот (Ateq). Пределы измерения напряжения поля (лскз/лс) Погрешность измерения Чувстви- тельность Антенна
ИП-12М: Измеритель напряжён- ности поля и напряжения помех 0,16-4-20 2-2J0S +50% I мы Штырь 1 М
ИП-14 То же 164-160 1—3000 на 28 Л!гц 1—Ю6 на 150 Мгц +50% 1 мке Диполь в две рамки
ИП-15 0,16-5-20 2—10Б +40% 1 мкв Штырь
ИП-18 1504-400 4—2 НО4 +50% 1 мкв Диполь
ИП-21 » 4004-1000 6,5—8000 на 400 Мгц 30— 2000 на WO0 Мгц — —
ИП-23-А 400-5-750 На 400 Мгц 40—106 — — »
ИП-23-Б » 7004-1000 На 1000 Мгц 100—105 — —
ИП-26-М 164-150 То же, что ИП-14 — Диполь и рамка
ИП-32 » 0,15^2 80-6Л0* — — Дйполь
ИП-33 2-5-30 40-2-106 »
295
На нм ено-’ ванне прибора Назначение Диапазон частот (Мац)
ип-д Индикатор поля 350-Н675
ИНГИ » 2500ч-3750
38-И 8200ч-12 500
ИП-6 Измерительный приёмник 1504-400
ИГЬ7 То же 4004-1800
ИП-8 » 1000ч-2300
ИП-9 23004-4000
ИНП-5 (ИП-5) Измеритель напряжён- ности поля 184-150
Продолжение
Пределы измерения напряжения поля {мкв/м} Погрешность измерения Чувстви- тельность Антенна
30 дб 0,25-0,6 дб 2 мет Диполь с реф- лектором
40 дб 0,25 дб 2 мет То же
30 дб 0,25—1 дб 5 мет (макс» мощи» на вх, рут) Рупор
Пределы измерения напряжений 5—10 мкв до 0,1 в ±30% — —
То же, 5ч-50лкв до 0,1 в ±50% — -—•
Пределы измерения мощности 10“13—10“ ±40% —
То же ±40% — *-*
J.5-100103 ±30% 0,5 мне Диполь рамки
-
П риложение 5
ИЗМЕРИТЕЛИ МОЩНОСТИ
Наименование прибора Диапазо н частот (Мг^) Пределы измерения мощности Входное сопротив- ление (Ojtf) Погрешность намеренна
Измеритель малых мощностей типа ИММ-6 1 20 <3000 1 0,1-5-1000 мет 75 Не более ±10%
Измеритель малых мощностей типа ВИМ-1 Опреде- ляется типом термистор- ной головки 2 мкет+6 мет 50—75 Не более 13%
(Измеритель сред- них мощностей типа ИСМ-2 ЗОч-юоо 0,25-5-15 ет при непрерывной гене- рации; 5<5000 ет при импульсной генерации 75 ±15% прн непрерывной генерации; ±20°/0 при импульсной генерации
[Измеритель боль- ших мощностей ИБМ-2 30-HQ00 0,5 кет при непрерывной генерации; 0 ,5-е-500 кет прн импульсной генерации 75 ±20%
Измеритель мощ- ности ИМ- 4 2500-i-4000 3700 <9600 5-5-2000 ет (сред- нее значение) ±70%
Приложение 6
ГЕНЕРАТОРЫ СТАНДАРТНЫХ СИГНАЛОВ И ГЕНЕРАТОРЫ СИГНАЛОВ
Наименование прибора | Диапазон частот (Мгц) Вых одное напряжение или мощность
Генераторы стандартных сиг- налов ГСС-бА 100 кгц+25 0,1 МКв—1 в
Гене ратор стандарт ных сиг- налов ГСС-17 16-5-128 0,5 мкв—0,1 в на нагрузке 75 ом
Генератор стандартных сиг- налов ГСС-7 20-5-180 0,1 мкв— 0,1 й на нагрузке 75 ojm
Генератор стандартных сиг- налов ГСС-30 125+250 0,5 Л4К6—0,1 в на нагрузке 75 ом
Генератор метровых волн Г МВ 20+400 4 лкв —50 мо на нагрузке 75 ом
Генератор стандартных сиг- налов ГСС-12 Генератор стандартных сиг- налов ГСС-15: 150-5-1000 1) 1 мкв—0,1 в на нагрузке 75 ojh 2) Мощный выход 0,1 мет— 1 era на нагрузке 75 ол
ГСС-15А 150-1000 1) До 1 вт для ГССЛ5А и
ГСС’15Б 1000-2000 0,5 ет для ГСС-15Б на наг- рузке 75 ом 2) 100 мот до Ю^8 мквт наг нагрузке 75 ом
Генератор стандартных сиг- налов ГСС-27 2000--3800 1) Милливаттный выход не менее 30 мет на нагрузке 50 ом 2) Микроваттный выход 100 мквт—10^8 мквт на наг- рузке 50 о,и
Генератор стандартных сиг- налов ГСС-28М 3750-5-7500 1) Милливаттный выход’не менее 100 мет на нагрузке 50 ом 2) Микроваттный выход 10 мквт—2- 1Q-8 мквт на наг- рузке 50 ом
Генератор стандартных сиг- налов 43-И 8600-5-9600 0,1 мкет^1 мет при согла^ сованной нагрузке. Выход- волновод прямоугольного сече- ния 10/23 лд 297
Продолжение
Наименованно прибора Диапазон частот (Л4г/О Выходное напряжение иля мощность
Генератор сигналов ГС-23 150 кгц—130 Мощный выход—0 Л—2,5 ет в диапазоне 0,15—27 Мгц на нагрузке 75 ом; 0,1—0,7 ет в диапазоне 27— 135 Мгц на нагрузке 75 ом. Микровольтный выход 1 мкв— 0,1 в на нагрузке 75 ом
Генератор сигналов комбини- рованный ГСК-2 100+375 1 мке—0,1 в на нагрузке 75 ом
Генератор сигналов ГС-6 150+700 1 мет—3 ет на нагрузке 75 ом
Генератор сигналов ГС-22 2000+3000 0,001-^0,6 вт на нагрузке 75 ом
Генератор сигналов 51-ГС 8500+9600 Максимальная мощность вы - ходкого сигнала не менее 7 мет
Генератор сигналов ГС-624 7500+10400 Уровень выходной калиброван- ной мощности Ю^^-гЮ-4 ет
Комбинированный испыта- тельный прибор (рода ртес тор): РТ-10 PT-1QA 2700+3100 3060+3390 Пределы изменения выходной мощности IO*-4 ет
Приложение 7
ВСПОМОГАТЕЛЬНОЕ ОБОРУДОВАНИЕ
Угольные эквиваленты антенны типа УЭА-5 и УЭА-100
Угольные эквиваленты антенны типа УЭА-5 и УЭА-100 представляют собой'
переносное вспомогательно-измерительное устройство, предназначенное для
использования в качестве нагрузки линий и генераторов высокой частоты при
испытаниях и регулировке ах с отключённой ре^>ной нагрузкой.
Основные технические характеристики:
1. Рабочий диапазон частот 350—675 Мгц (85—45 сл<).
2. Сопротивление входа 75 олг ± 3 ом.
3. Максимально допустимая мощность па входе (среднее значение) 5 вг
(УЭА-5) или ЮОат (УЭА-100),
4. Максимально допустимое напряжение на входе 1 кв (УЭА-5) или 2,6 к&-
(УЭА-100),
5. Максимальный кбв в линии, нагруженной оконечнкком, 0,82—0,84-
6. Вход коаксиальный под фидер с волновым сопротивлением 75 ом.
Эквивалент антенны УЭА-100 снабжается калиброванным ответвителем
на 30±2 дб.
Коаксиальная оконечная нагрузка типа ЭАК-112
Оконечная согласованная нагрузка типа ЭАК-112 представляет собой;
вспомогательно-измерительное устройство, предназначенное для создания ре-
жима бегущей волны в коаксиальных передающих линиях, и используется в
качестве эквивалента антенны при наладке и испытаниях высокочастотных
трактов различных радиоустройств.
Основные технические характеристики
I. Рабочий диапазон частот 1000—10 000 Мгц (30—3,0 см).
2. Входное сопротивление 50 ом.
3. Коэффициент стоячей волны в липин, нагруженной согласованной на-
грузкой, не превышает 1,15.
4. Допустимая средняя мощность не более 1 от.
Аттенюатор плавный типа А ГМ
Аттенюатор плавный типа ЛП-1 представляет собой переносное вспомога-
тельно-измерительное устройство, предназначенное для получения плавно
изменяющегося ослабления мощности высокочастотных сигналов, а также для:
измерения ослабления, вносимого различными радиоустройсгвами.
Основные технические характеристики
L Рабочий диапазон частот 100—1000 Л4гц.
2. Пределы ослабления 15—120 дб.
3. Входное и выходное сопротивления 75 оль
29^
4. Основная погрешность ослабления: по шкале индикатора ±1 дб (от
30 дб и выше); по шкале *дб» ±1,5 дб (от 30 дб и выше).
5. Определение разностного ослабления в пределах 10 дб в линейном уча-
стке от 45 дб и выше производится с погрешностью пе более ±0,2 дб,
6. Коэффициент стоячей волны со стороны входа, начиная с 45 дб ослаб-
ления и выше, не более 1,5. Коэффициент стоячей волны со стороны выхода
при любом значении ослабления не более 1,5 в диапазоне частот 1-50—1000/Иг^
В диапазоне частот 100—150 Мгц допускается увеличение ксв до 1,9.
7. Максимальная допустимая мощность на входе 10 от.
Предельные коаксиальные аттенюаторы
типов АП-2, АП-3 и АП-4
Предельные коаксиальные аттенюаторы типов АП-2, АП-3 и А П-4 пред-
ставляют собой вспомогатедкно-измеритсльныс устройства, предназначенные
для получения плавно измеЛЩицегося ослабления высокочастотной мощности
в диапазоне от 500 до 10 000, Мгц, Кроме того, аттенюаторы могут быть ис-
„ пользованы н качестве образцовых мер при измерениях ослабления различных
Радиоустройств.
Основные технические характеристики даны в таблице.
Таблица
Тип аттенюатора
Наименование характеристик АП-2 АП-3 АП-4
Диапазон частот, Мгц 500—3000 1000-3000 зооо—iocoo
Верхние пределы регулировки ос- лабления, дб до 120 до 120 до 120
Начальное ослабление, не более, •дб 30 25 20
Погрешность измерения, не бо- лее. дб ± (0.05+ -f 0,005) + (0,05+ +0.005) ± (0,05+ +0,005)
Входное и выходное сопротивле- ния, ом 75 50 50
ксв входа, не более 1 .2—1,35 1,2-1,3 1,3—1,4
ксв выхода, не более 1,2—1,3 1.3 1,4—1,5
Мощность на выходе, вт 1 и более 1 и бочее 1 и более
Аттенюаторы ступенчатые типа АС-1
Аттенюаторы ступенчатые типа АС-1 представляют собой переносные
вспомогательно-из мери тельные устройства, предназначенные для ослабления
мощности в коаксиаитьцых линиях с волновым сопротивлением 75 ом в диапа-
зоне частот от 100 до 3000 Мгц.
Основные технические характеристики
1. Аттенюаторы типа АС-1 по своему устройству представляют омические
делители напряжения, собранные по схеме Т-образного четырех полюс} гик а,
300
В качестве сопротивлении делителя использованы тонкоплёночные поверхност-
ные сопротивления,
2. Величина ослабления 10, 15, 20, 25 и 30 дб.
3, Погрешность величины ослабления ±2 дб.
4. Рабочие диапазоны частот 100—3000 Мгц.
5. Входное и выходное сопротивления 75 ом.
6, Коэффициент стоячей волны в линии с волновым сопротивлением 75 ом
при нагрузке ее любым из аттенюаторов, входящих в комплект, не превы-
шает 1,5.
Фиксированные аттенюаторы типов ФАД-5/20,
ФАД-5 /30 и Ф АД-5/80
Фиксированные аттенюаторы типов ФАД-5/20, ФАД-5/30 и ФАД-5/80 пред-
ставляют собой переносные вспомогательно-измерительные устройства, пред-
назначенные для ответвления фиксированной доли мощности вч колебаний,
проходящей по коаксиальной линии передачи при измерениях частоты и мощ-
ности, а также при испытаниях генераторов и передатчиков дпм диапазона
волн.
Основные технические характеристики даны в таблице-
Таблица
Наименование характеристик Тип аттенюатора
ФАД-5/20 ФАД-5/30 ФАД.5/80
Рабочий Диапазон частот, Мгц 350—675 350—675 350—675
Ослабление по мощности, дб 20 30 80
Погрешность калибровки по ослаблению ±1,5 ±2 ±5
Наибольшая допустимая мощ- ность на входе (среднее значе- ние), 6/П 5 5 5
Наименьший допустимый кбв 75-омной коаксиальной линии, питающей аттенюатор 0,77 0,77 0,77
Сопротивление входа и вы- хода, ом 75±3 75±3 75±3
Габариты, мм 200X100x110 200X100x110 —-
Фиксированным аттенюатор типа ФАД-100/30
Фиксированный аттенюатор типа ФАД-КЮ/30 представляет собой пере-
носное вспомогательно-измерительное устройство, предназначенное для ослаб-
ления мощности высокочастотных колебаний, подаваемой из коаксиальной
линии передачи на измерительный прибор при измерении мощности генера-
торов и передатчиков дециметрового диапазона.
Основные технические характеристики
I. Диапазоны рабочих частот 350—675 Мгц (85—45 сл).
2. Ослабление по мощности 30 дб.
20—292 301
3. Погрешность калибровки по ослаблению +2 дб.
4. Наибольшая допустимая мощность на входе 100 вт.
5. Наибольший допустимый ксв в линии, питающей аттенюатор, 0,77_
6, Сопротивление входа 75 ±3
7. Вход коаксиальный под фидер с волновым сопротивлением 75 ом.
Сопротивление нагрузочное типа СН-1
Сопротивление нагрузочное типа СН-1 представляет собой переносное
вспомогательное устройство, предназначенное для использования в качестве
эквивалента согласованной нагрузки в диапазоне частот от 30 до 100 Мгц.
Кроме того, оно может быть использовано как фиксированный аттенюатор
с ослаблением по мощности порядка 18—19 дб с хорошо согласованным вхо-
дом и выходом в указанном диапазоне частот.
Основные технические характеристики
1. Входное сопротивление 75 ол.
2. Измеренный непосредственно на входе ксв не более 1,15 в диапазоне
частот 30—150 Мгц и но более 1,2 в диапазоне частот 150—1000 Мгц.
3. Допустимая мощность на входе в режиме непрерывной генерапии не
более К) вт.
4. Допустимое импульсное напряжение на входе не более 300 в.
5. Ослабление сигнала на ответвителе составляет 18,5±5 дб на частоте
500 Мгц.
6. Изменение величины ослабления в диапазоне рабочих частот не более
2 дб.
7. Входное сопротивление ответвителя 75 олс.
8. Измеренный непосредственно на выходе сопротивления ксв не бо-
лее 1,2 в диапазоне частот 30—500 Мгц и не более 1,2 а диапазоне частот
от 500—1000 Мгц.
Эквивалентные нагрузочные сопротивления типа ЭНС-5 и ЭНС-100
Эквивалентные нагрузочные сопротивления типа ЭНС-5 и ЭНС-100 пред-
ставляет собой переносное вспомогательно^измерителыюе устройство, пред-
назначенное для использования в качестве нагрузки линий и генераторов вы-
сокой частоты при испытаниях и регулировке их с отключенной реальной па-
грузкой.
Основные технические характеристики
I. Рабочий диапазон частот 150—375 Мгц (2—0,8 .и).
2. Сопротивление входа 75 ом ± 5%,
3. Максимально допустимая мощность на входе (среднее значение) 5 ат
(для ЭНС-5) и 100 вт (для ЭНС-100).
4. Максимально допустимое напряжение на входе 750 в (для ЭНС-5) и
3 кв (для ЭНС-100).
5. Максимальный кбв в линии, нагруженной оконечпиком, 0,8.
6. Вход коаксиальный под фидер с волновым сопротивлением 75 ом.
Эквивалентное нагрузочное сопротивление типа ЭНС-100 снабжается от-
ветвителем на 30 ±2 дб.
302
Эталонные реактивные сопротивления типов ЭРСК-112 и ЭРСК-НЗ
Эталонные реактивные сопротивления типов ЭРСК-112 и ЭРСК-ИЗ пред-
ставляют собой вспомогательно-измерительные устройства, предназначенные
для создания нагрузки в коаксиальных линиях с любым реактивным сопро-
тивлением.
Основные технические характеристики
1. Эталонное реактивное сопротивление типа ЭРСК-112 присоединяется к
коаксиальным линиям с сечением 10X4,34 мм и волновым сопротивлением
50 ом.
2. Эталонное реактивное сопротивление типа Э РСК-113 присоединяется
к коаксиальным линиям с сечением 16 к«Хб,95 мм и волновым сопротивле-
нием 50 ом.
3. Сопротивление ЭРСК-112 оканчивается вилкой соединителя типа
С:29-В, ЭРСК-113 оканчивается вилкой соединителя кабеля РК-6.
4. Вход подвижного поршня ЭРСК-112 и ЭРСК-ПЗ составляет 160 лис
Положение подвижного поршня вдоль линий для ЭРСК-112 и ЭРСК-НЗ опре-
деляется по шкале и нониусу с ценой деления 0,05 мм.
Высокочастотные соединители и коаксиальные переходники
Высокочастотные соединители представляют собой вспомогательно-измери-
тельные устройства, предназначенные для соединения отрезков гибкого кабеля
типа РК-29 с жёсткой коаксиальной линией внутренними размерами
10 лслХ4,34 мм и волновым сопротивлением 50 ом.
Коаксиальные переходники предназначены для сочленения высокочастот-
ных элементов, оканчивающихся соединителями для кабелей РК-29 и РК-6.
Основные технические характеристики
1. Волновое сопротивление соединителей и коаксиальных переходов 50 ом.
2. Ксв, вносимый соединителем, не превышает 1,5 в рабочем диапазоне
частот.
3. Обусловливаемый коаксиальным переходом ксв не более 1,2 для волн
длиной не мецес 8 см.
2О4
Приложение 8
КОНСТРУКТИВНЫЕ И ЭЛЕКТРИЧЕСКИЕ ДАННЫЕ СТАНДАРТНЫХ
ПРЯМОУГОЛЬНЫХ ВОЛНОВОДОВ
Обозначение типа Полоса пропу- скания, см Внутренние размеры, мм Толщина стенок мм Предель- ная мощ- ность Мет Максимальное затухание при частоте, рав- ной 1.5-крат» ной предель- ной частоте, дб/м
МЭК-5 48,3 --73,2 457,2/228,6 3,18 - 0,00141
МЭК-6 40,0 4-61,2 381,0X190.6 3,18 —- 0,00186
МЭК-8 33,0 4-46,8 292,1/146,1 3,18 — 0,00278
МЭК-9 26,1 -ь39,5 247.65X123,8 3,18 — 0,00351
МЭК-12 20,5 4-31,2 195,58X97,79 3,18 —» 0,00506
МЭК-14 17,3 4-26,3 165,10X82.55 2,03 — 0,00653
МЭК-18 13,63 4-20,70 129,54X64,77 2,03 — 0,00936
МЭК-22 11,45 4-17,45 109,22X54,61 2,03 — 0,0121
МЭК-26 9,1 j 4-13,83 86,36X43.18 2,03 — 0,0173
МЭК-32 7,60 4-11,55 72,14X34,04 2,03 10,5 0,0236
МЭК-40 6,13 4- 9,32 58,17X29,083 1,63 0,0311
МЭК-48 5,01 4- 7,62 47,55X22.149 1,63 4,86 0,0443
МЭК-58 4,26 4- 6,47 40,39X20,193 1,63 — 0,0539
МЭК-70 3,67 4- 5,58 34,85X15.799 1,63 2,29 0,0720
МЭК-81 3,00 4- 4,56 28,499X12,624 1,63 1,77 0,0993
МЭК-100 2,50 4- 3,66 22,860X10,150 1,27 0,99 0,127
МЭК-120 2,00 4- 3,05 19,050X9,525 1,27 —- 0,166
МЭК-140 1,67 4- 2,52 15,799X7,899 1,02 — 0,220
МЭК-180 1,36 4- 2,07 12,954X6,477 1,02 —- 0,298
МЭК*220 1,25 4- 1,70 10,668X4,318 1,02 0,22 0,463
МЭК-260 0,91 4- 1,38 8,636X4.318 1 ,02 —- 0,544
МЭК-320 0,75 4- 1,135 7,112X3,556 1,02 —1 0,729
МЭК-400 0,60 4- 0,910 5,690x2,845 1,02 —- 1,02
МЭК-500 0,5034- 0,763 4,775X2,388 1,02 — 1,33
МЭК-620 . 0,4004- 0,610 3,759X1,180 1,02 <— 1,90
304
Продолжений
Обозначение типа Полоса пропускания, см Внутренние размеры, дим Толщина стенок мм Предель- ная мощ- ность мет Максимальное затухание прц. частоте, ран - ной 1.5-крат-- ной предель- ной частоте,- дб/м
МЭК-740 0,3264- 0,496 3,099x1,550 1,02 —. 2,54
МЭК-900 0,268ч- 0,417 2,540X1,270 1,02 — 3,43
МЭК-1200 0,214ч- 0,326 2,052X1,016 1,02 ”— 4,78
Примечание L Содержащееся в наименовании типа волновода число
выражает приблизительно среднюю частоту рекомендуемого рабочего диапа-
зона в сотнях мегагерц. Например, МЭК-100 означает прямоугольный волно-
вод на среднюю рабочую частоту 10 000 Мгц (Х=3 МЭК — сокращённое
название Международной электротехнической комиссии, разработавшей стан-
дарт.
2. Допуски на внутренние размеры пе должны превышать 1 :500 номи-
нальной ширины (размера а) с абсолютным максимом 0,4 мм и абсолютным
минимумом 0,02 мм.
ОСНОВНЫЕ ПАРАМЕТРЫ
Марка кабеля Внутренний проводник Изоляция Диаметр По запол- нению, лел< Тип внешнего про- водника пли экрана
Конструкция диаметр мм диаметр по изоляци и мм ТИП ИЗОЛЯ' ции
1. 50-омные коаксиальные
РК-З-49 1X3,0 бм 3.0 11,3 + 1,5 И-1 — МО
РК-6 7/0,85 2t55 9,210,5 И-1 — МО
РК-19 1X0,68 0,68 2,410,1 И-1 МО
РК-28 7X0.71 2J3 7,310,3 ИЧ мд
РК-29 1X1.37 1,37 4,8±0,2 И-1 — мд
РК-47 7X0.71 2,13 7,3±0,3 И-1 — МО
РК-48 7X1,03 3,09 10,5.10,5 И-1 —• МО
РК-55 1X0,81 0,81 2,95+0,15 И-4 —* лмо
РК-59 1X0,81 0,81 2,9510,15 И-4 — лмд
РК-61 7X1,51 4,53 14,910,75 И-1 — МО
РК-63 7X0,23 0,69 2,0±0,125 И-1 — лмо
РКВ 1X3,04-12X1,0 5,010,3 18,012,0 И-1 — МО
РКП-21200 19X1,3 6,510,5 22,0±2,0 И-1 — МО
РКМ50 1X5,0 5,010,15 18,011,5 и.| — МП
2. 60-омные коаксиальные
РКГ-5 1X3,0 3,0±0,3 13,2511,25 И-1 МО
ОКС-5 1X3,0 3,010,3 13,2511,25 ич —' МП
РКГ-10 19X1,0 5,010,5 22,511,5 И-1 — МО
РКС-10 1X5,0 5,010,5 22,5-11,5 ич — МП
PKC-J5 19X1.6 8,0+0,5 35+2 И-J 1— МО
РКС-15 19X1,6 8,010,5 3512 И-1 — МП
РКПГЧО 49X0,56 5,010,3 20,511,5 И-1 — лмо
РКПГ-12 49X0,72 6,510,5 25,5+1,5 И-1 — ЛМО
305
28S2S2g2
<OOoK3K3tO<OK3N3
’+ 4- И- H- Rr- 14- 14- H
K?K34^4^COWb0t>3
A3
ослоэос^ооо
O'UOOGOOO
H- H- H- H- H- .4- 1+ J-
WWWCCWWWOJ
СЛ СЛ O1 сл СЛ СЛ
— K> ~ ~ ~ 1— *- to
CD CO О 4ж КЗ O> СГЭ on
02 05 о SO © г*-* 05 о о о о о О к— О о
to со to ь*^ •
со сл 00 00 сл ^4^ GQ р со КЗ
* А W А кА << ж А
о о> о Фо сл СО 0о КЗ 4* СЛ
Л- Н- н- н- н- !Р СЛ Н- н- н- hh 14- 14- 1+
to ю со О О Н“ О JO р © О О о
W ч» О А ш кА
о о о 00 к—к СЮ 05 05 **4 W ос?
50 i 53 50 сл со а сл О 52 <л О 52 52 52
СП А А 4М * •А м сл ж А
о сл о сл О сл Сл сл сл СП СП сл СП
Н- 14- 14- 1+ 14- 1+ I+- н- 1-Ь н- н- i7 1-Ь Н-
со со со to КЗ /О № КЗ to JK3 со N3 КЗ
4А к* ЬА
О сл о сл сл Сл сл сл сл *сл сл сл
4 - . - -
О о р КЗ о р р о о о о S 2
СП СП сл сл к—* От Сл сл Сл сл о
. .
о о о L £ь 4U »и 4^ |-[^- СП
о о о J сл СЛ сл сл сл сл СЛ сл сл о
_ . 4 -
4^ со 1 4*. К> ю © <о оо © kJ
м 1 А А кА А
о сл сл СЛ О сл СЛ Сл О О
кэ со
сл сл сл оо сл Сл 03 Со S 5
307
4* tO tO КО ~
Q СЛ СЛ — СЛ W
8 S 8 8 8 8
S"4 ко 8 E 5
О О О о
• Приложение № 9 РАДИОЧАСТОТНЫХ КАБЕЛЕЙ
кабели тип Защитная оболочка 1
наружный диаметр или размер, мм
Волновое сопротив- ление, ом
Ёмкость не более мкф/м
частота Мгц Затухание неп/км
максим, доп. значение
^Испытательное напряжение 50'пе- риодным перем. током Кб
Средняя пропускная мощность при 100 Мац Гокружаю- щая температура п-50 С% на жиле + 85а С) вт
Продолжение
Марка кабеля Внутренний проводник Изоляция Диаметр по запол- нению, мм Тип внешнего про- водника иди экрана
конструкция диаметр, Ал диаметр по заполнению Л1М тип изоля- 1 ции
3. 75-омные коаксиальные
РК-1 1X0.68 0,68 4,6±0,2 И-1 —. МО
РК-3 1X1,37 1,37 9,0±0,4 И-1 —• МО
РК-4 1X1,37 1,37 9,0+0,4 И-1 — —
РК-8 1X2,73 2,73 18,0±0,9 И-1 — МО
РК’20 7X0,37 1,Н 7,2±0,3 И-1 — МО
РК49 7X0,26 0,87 42±0,2 И-1 — МО
РК-60 19X0.41 2,05 13,1±0,8 ил — МО
РК-62 1/2,24 2,24 14,9 + 0,75 И-1 МО
ТКМ-75 1X3.0 3,0 20 + 1,5 И-1 — мп
4. 90-омные
РК-2 1X0,68 0,68 6,8±0,3 И-1 — МО
5, Кабели с воздушно-
РК-50 1X0,3 0,30 6,2±0,3 И-3 — МО
PK-S6 1X0,64 бм 0,64 3,7±0,2 и-з лмд
РК-Т 3-150 1X0,71 0,71 13,5+1,5 И-3 МО
РК-64 1X1,03 1,03 7,3 + 0,3 и-з — МО
РКК-03/10 1X0,3 0,3 + 0,02 11,0 И-5 — МО
РКК-28/10 1X2,83 2,83 + 0,05 И,5 И-5 — МП
РКК-5/18 1X5 5 + 0,15 18,5 и-з — МП
6. Симметричные кабели со
РД-13 1X0,79 0,79 1.8+0,1 И-1 ' 1,1 + + 0,2 мд
РД-17 7X0,79 2,37 6,3±0,3 И-1 13,0 + ±0,3 МО
308
Продолжение
Защитная оболочка волновое сопротив- ление» ОЛ* 1 1 1- Емкость» не более мкф/м Затухание неп/км Испытательное напряжение 50^ пе- риодичным персы. ТОКОМ, Ktf Средняя пропускная мощность при 100 Меч (окружаю- щая температура Ч 50а С. на жиле +851* CJ, $т
а 4 к наружный диаметр или размер, мм частота Мгц " • • 1 максим, доп. значение
кабели
01 7,3 ±0,4 77,512,5 68 45 9,5 7 275
01 13,0±0,8 74,512,5 70 45 5,5 12 850
02 11,0+0,7 74,512,5 70 45 8,0 12 850
01 21,0^1,0 75,0±3 68 60 3,0 18 2000
01 10.410.6 77t0 + 2t0 68 45 7t0 3 550
01 6,8 + 0,4 70,0+3,0 76 45 10t0 3 315
01 16,9±2,0 75,013 68 45 5,0 8 1250
01 18,711,1 75,0 + 3 68 45 4t0 7,5 1500
02 25±2 75,0±4,5 — 100 4,0. — —
кабели
01 9,6±0,6 92,5±2t5 57 45 6t5 10 45»
пластмассовой изоляцией
01 8t8±0,5 — 27 45 8,5 — —
05 6,1±0,8 — 48 45 10,0 3,0 —'
04 19,7 ±20 145,0Ц,0 30 7,0 1,8 2,0
05 1O,3±O,6 95,015 50 1000 22 1,0
06 14,5±1,5 200 + 3% 22 10 5 2,0 ——
07 19 7015% — 600 9 2,0 —
07 27±2 7015% 2000 13 4,0
скрученными npoi зодниками
01 7,3±0,4 8616 65 45 14,0 3 —'
01 6,6±1,0 10015 53 45 6,0 10 —
зоа
Марка кабеля Внутреним! проводник Изоляция Диаметр по запол- нению, мм Тип внешнего про- водника или экрана
конструкция диаметр мм диаметр по изоляции мм тип изоля- ции
7. Симметричные кабели
РД-14 7X0,079 2,37 6,3+0,3 И-1 13± ±0,3 —-
РД-18 1X0,79 0,79 1,В±0,3 И-1 4,12± ±0,2 —
8. Двух коаксиальные сим-
РД-15 1X0,37 1,11 7.01+0,3 ил ♦— МИО
РД-16 7X0,68 0,68 6,8 ±0,3 И-1 —- мио
РД-26 1X0,68 0,68 6,7 ±0,3 И-1 — мио
Примечание. И-1 — изоляция из кабельного полиэтилена; И-3—
полиэтилена; И-5 — колпачковая изоляция; МО — оплётка медной проволо
тфоволоки и ленты; ЛМО — оплётка из лужёной медной проволоки; ЛМД
оплётка из медной проволоки каждой жилы и общая оплётка поверх обоих
01 — оболочка из полихлорвинилового пластика; 02 — оболочка из свинца;
05 — оболочка из пи г мети ров ан но го полиэтилена; 06 — оболочка из поли
резиненная лента и оплётка из стальных проволок.
310
Продолжение
Защитная оболочка волновое сопротив- ление, ом Емкость, не более мкф/м Затухание неп/км Испытательное напряжение 50-пе- риод ичным перем. током, кв .... , Средняя пропускная мощность при 100 Мец (окружаю- щая температура ч 50а Сг на жиле + 85° С), вт
с наружный диаметр или ра амер, частота Мгц . максим, доп, i значение
без экрана
01 15,8±1,0 — — —' — 10 •—
01 6,6±0,4 — — — 4 —-
метричные кабели
01 Ih0±0,7X Х18,8 + 1,1 147,5±5,5 36 45 7,0 10 —
01 10,8±0,7Х Xie.4-1-1,1 192,5 + 12,5 28 45 6,5 10 —
02 9,9±0,6Х Х17,4+1,0 92,5± 12,5 28 45 6,5 7 —
изоляция воздушно-пластмассовая; И-4 — изоляция из стабилизированного
кой; МД — двойная оплетка медной проволокой; МП — медные плоские
— двойная оплетка из луженых медных проволок; МИО — индивидуальная
жил; МИ — индивидуальная оплётка медной проволокой каждой жилы;
0,3 — оболочка из резины; 04 — оболочка из хлопчатобумажной пряжи;
этилена и оплётка из капроновых нитей; 07 — оболочка из полиэтилена, про-
311
ЛИТЕРАТУРА
1. А. А. Пистолькорс. Антенны. Связьиздат, ]947.
2. Г. 3. Айзенберг. Антенны ультракоротких волн. Связьиздат, 1957..
3, А. 3. Ф радии. Аптенпы сверхвысоких частот. Изд. «Советское ра^
дио», 1957.
4. М. С. Н е й м а н. Передающие антенны. Энергоиздат 1934.
5. Scott Helt. «Electronics», Febr. 1934.
6. L. Sturm er. Zeitschr. far HochfrequenztechniK. June 1927»
7. Clapp. «PIRE». April 1930»
8. А. А. П и с т о л ь к о р с. Приемные антенны. Связьиздат, 1937.
9. В. А. X а ц ке л е в и ч, Л. Н. Яковлев. «Вестник связи», № 6, 1960-
10. Инструкция по настройке средневолновых вещательных антенн. Связь-
издат, 1958.
И. Е. С. Анцелиович. Радиотехнические измерения. Госэпергоиздат,
1958. :
12. В. В. Татаринов. Коротковолновые направленные антенны, Связь-
издат, 1936.
13. Г. 3. Айзенберг. Антенны для магистральных радиосвязей. Связь-
издат, 1948.
14. КА. Смирнов. Сборник трудов ЛЭИС, вып. Ill (33), 1957.
15. А. А. П исто лькорс, М. С. Нейман. «Электросвязь», № 4, 1941.
16. А. А. П и с т о л ь к о р с. «Научно-технический сборник по электросвя-
зи», № 1, 1937.
17, В е t h е М. A. The Physical Review, 1944.
18. Антенны сантиметровых волн. Под редакцией Я. Н4 Фельда. Изд. «Со-
ветское радио», 1950, <
19. Barlow and Cullen Micro-Wave Measurlments.
Имеется русский перевод. Измерения на сверхвысоких частотах под редакцией
В. Б. Штейншлейгера. Изд. «Советское радио», 1952.
20» G. Deschamps J. Appl. Phys, 24, № 8, 1953.
2k A. 3. Ф p а д и ti, В. А. О лен дский. «Радиотехника», № 2, 1955.
22. Г. А. Ремез. Курс основных радиотехнических измерений. Связьиз-
дат, 1955.
23. И. Т. Петрович, А. В. Козырев. Генерирование и преобразова-
ние электрических импульсов. Изд. «Советское радио», 1954,
24, Г. Т. Марков. «Радиотехника», № 1, 1948.
25. А. 3. Ф р а д и и. Журнал технической физики. IX, вып. 4, 1939.
26. А, 3. Ф р а д и н, Е. В. Рыжков. Пособие к лабораторным работам
по курсу антенн. Изд. ЛЭИС, 1951-
27» М. Meyer, «Eigenschaften und Dimension!erung von Ferntantennen»
«Funk-Technik» («Fernsehen — Elektronik»), № 15, 1956»
28. Л. Д. Гольдштейн и H. В. Зернов. Электромагнитное поле и
волны. Изд. «Советское радио», 1956, стр, 189—193.
29. Л. Г. Дорфмап. «Новый малогабаритный мост». Труды ЦКБ, 1959,
вып. 10, стр. 63—78.
30. Ю. Д. Карпинский. «Радиотехника и электроника». Изд. Акаде-
мии наук, т. V, № 11, 1960, стр. 1797—1801.
31» Т. Karpinsky Kalibrodynova metoda mereni radiovijeh signal й»
Zprva rislavu radiolechmky a elektroniky» CSAVc», Z—56»
32. А. P. Вольперт. «Радиотехника», т. 4, № 2, 1949, стр. 25—36.
33. Н. А. Е с е пк ин а. Об одном методе измерения диаграмм направлен-
ности радиотелескопов с высокой разрешающей способностью. Доклады Ака-
демии наук СССР, т» 113, № I, 1957.
34. Д, Ченг. «Имитирование Фраунгоферовых диаграмм направленности
в зоне Френеля». «Вопросы радиолокационной техники». Изд. иностранной ли-
тературы, № 2 (38), 1957.
35. М. П. Долуханов. Распространение радиоволн. Связьиздат, I960.
312
36. Report № 49. Mithods of Measuring Fieldstrength. CCIR. Dokuments of
4he VIII th Plenary Assambly. Warsaw. 1956, v, I,
37. Я. Л. Ал ьперт, В. Л. Гинзбург, Е. Л. Ф е й п б е р г. Распростра-
нение радиоволн. Гос. изд-во технико-теоретической литературы, 1953.
38. Г. П. Шкур ин. Справочник по электроизмерительным и радиоизме-
рительным приборам, т. П — Радиоизмсрительные приборы. Воениздат, 1960.
39. Д. Р. М е н це р. Дифракция и рассеяние радиоволн^ Изд. «Советское
радио», 1958,
40. G. A. Woonton, R, В. Borts and J. Л. Corruthers. Jnd оо
Measurements of Microwave Antenna Radiation Pattens by Means of a Metal
Zense. J. of AppL Phys. v. 21. Maj 195Q.
41. P. А.Валитой, В. H.’ Сретенский. Радиоизмерения на сверхвы-
соких частотах. Воениздат, 1951.
42. С, С. Culler, А. Р. King W. Е. Kock. PIRE, December 1947»
43, А. П. Дорохов. Расчет и конструирование антенно-фидерных уст*
ройств. Изд. Харьковского университета, I960.
44. С. И. Н а д е н е н к о. Антенны. Связьиздат, 1959.
45. В. С, Троицкий, Н. М. Цейтлин. «Известия высших учебных за-
ведений». Серия «Радиофизика», т. IV, № 3, 1961.
46. У. Гора к. «Направленные ответвители со взаимно-перпендикуляр-
ными волноводами». «Зарубежная техника связи», выпуск 2, 1961. Изд. Мини-
стерства связи СССР.
47. А. Р. В о л ь п е р т. «Теоретическое и экспериментальное исследование
фидерного рефлектометра». «Радиотехника», № 2, 1947.
v v v v v v
48. J a n Vrba, Mereni па centrmetrovjch vlnAch. I Meric! pristoje a
sikladni mereni. SNTL, Praha, 1958.
ОГЛАВЛЕНИЕ
Стр~
Предисловие . „ < 3
1. Параметры антенно-фидерных устройств
Основные определения
Классификация параметров антенн............................... 5
Первичные экспериментальные параметры антенн 4 &
Фидерные линии. Их параметры и характеристики .... 8
Прямоугольная диаграмма сопротивлений.........................12
Полярная диаграмма сопротивлений..............................15
Вторичные параметры первой группы: частотная характеристика,
резонансные частоты, полоса пропускания ...... 19
Графическое изображение диаграммы направленности , 20
Вторичные параметры антенн, связанные с диаграммой направлен-
ности: относительный уровень боковых максимумов, ширина
главного лепестка, коэффициент направленного действия . . 28
Вторичные параметры антенн, связанные с коэффициентом усиле-
ния: коэффициент полезного действия, эффективная площадь,
действующая высота............................................31
Исследование антенн на моделях................................36
Краткие сведения иэ теории приёма радиоволн...................32
2. Резонансные методы измерения входного сопротивления
Общие положения.............................................. 39
Метод добавочного сопротивления.............................. 39
Метод вольтметра и амперметра................................ 43
Метод куметра................................................ 45
Метод замещения............................................ 49
Антенные и фидерные омметры.................................. 52
Метод разветвления токов..................................... 58
Методы автоматического измерения входного сопротивления 61
3. Измерение входного сопротивления антенн мостовыми методами
Введение................................................ . 64
Симметричный мост для длинных, средних и коротких волн . . 64
Несимметричный мост.................................... 67
Измерение коэффициента бегущей волны на фидере с помощью
моста...................................................... 68
Коаксиальные и волноводные мосты ........ 69
Понятие о матрице рассеяния.............................74
Анализ работы коаксиальных и волноводных мостов ... 76
Двухпроводпый мост......................................78
314
Стр.
4. Измерение входного сопротивления антенн при помощи измери-
тельных линий .... *.............................. 80
Введение............................,......................* 80
Распределение напряжений и токов на фидерной линии 80
Схема измерительной линии.....................................85
Устройство измерительных линий................................85
Методика определения входного сопротивления при помощи из-
мерительных линяй............................., 104
Установка для автоматической записи кривой распределения на-
пряжения . , . *.....................* 109
Ошибки измерений при помощи измерительных линий . , . Ill
5. Рефлектометры.
Блок-схема рефлектометра.....................................120
Основные характеристики направленных ответвителей . * . 121
Двухпроводный направленный ответвитель.......................122
Коаксиальные направленные ответвители , 129
Полосковые направленные ответвители . 137
Волноводные направленные ответвители . . ' . * _ 140
6. Смешанные методы определения входного сопротивления
Введение . . . .............. » * 146
Метод трёх зондов . . . . 146
Импедометр Парпсна.......................................... 151
Вращающийся направленный ответвитель . . 153
Тройниковый измерительный ответвитель * 157
7. Измерение параметров фидерных линий
Измерение коэффициента укорочения коаксиального кабеля * . 163
Измерение волнового сопротивления ......................... *165
Измерение коэффициента затухания фидера » *..................167
Измерение коэффициента асимметрии и скоса волны па открытых
фидерных линиях..............................................172
Измерение асимметрии входа приёмника.......................177
8. Измерение напряжённости поля
Введение.....................................................182
Направление прихода радиоволны...............................184
Измерение соотношения амплитуд поля..........................189
Измерение абсолютной амплитуды поля..........................191
Аппаратура для измерения абсолютной амплитуды поля . * 204
Измерение фазы поля......................................... 211
Статистические методы обработки данных измерений напряжён-
ности поля при наличии флуктуаций (замираний) 217
Аппаратура автоматической обработки данных измерений напря-
жённости поля при наличии флуктуапий.........................226
Метод тока короткого замыкания антенны.......................232
Калибродинный метод измерения напряжённости поля . . 237
Измерение поляризации поля радиоволн .................. * 240
9. Снятие диаграммы направленности антенн
Определение минимального расстояния между исследуемой и
вспомогательной антеннами 247
Методика снятия диаграмм направленности......................256
315
Стр.
Использование линз при снятии диаграмм направленности . 258
Исследование параболических зеркальных антенн на уменьшен-
ных расстояниях . .............’................260
.Устройство для автоматического снятия диаграмм направленности 264
Снятие диаграмм направленности антенн при помощи самолётов
и вертолётов.............................................. 266
Об использовании космических источников излучения для сня-
тия диаграмм направленности антенн . 272
Снятие диаграммы направленности ферритовых антенн в одно-
родном магнитном поле.......................................273
10. Измерение коэффициента усиления антенн
Измерение коэффициента усиления стационарных антенн . , „ 276
Измерение коэффициента усиления переносных антенн методом
сравнения (замещения) . .....................277
Измерение коэффициента усиления по методу двух идентичных
антенн. Обобщение метода на две неидентичные антенны . 280
Измерение коэффициента усиления антенн по методу плоского
экрана..................................................... 282
О влиянии земли на результаты измерений коэффициента усиле-
ния антенн..................................................286
Приложения................................................ 287
Литература . ..........................312
Афроин Зеликович Фрадия
Евгений Васильевич Рыжков
ИЗМЕРЕНИЕ ПАРАМЕТРОВ АНТЕННО-ФИДЕРНЫХ УСТРОЙСТВ
Отв. редактор Б. В. Брауде Техн, редактор К. Г. Маркоч
Редактор Е. С. Новикова Оф Корректор Г. А. Васильева
Слано в набор 6/IV 1962 г. Подписано в печ, 1/VI 1962 г.
Форм, бум, 60Х90/|« 20,50 печ, л. (включая 2 вкл,) 18,70 уч.-изд. л.
Т-06266 ’ Тираж 13 000 экз. Зак. изд, 8368 Цена i руб. 14 коп.
Связьиздат, Москва-центр. Чистопрудный бульвар, 2.
Типография Связьиздата. Москва-центр, ул. Кирова, 40. Зак. тип, 292
ОПЕЧАТКИ,
замеченные в книге А. 3. Фрадина, Е. В. Рыжкова
«Измерения параметров антенно-фидерных устройств»
Стр. Строка Напечатано Должно быть
154 2 сн. (числитель) /(/? I)2 X1 V<7?—1)яч-ха
221 22 св. , • * ^о(5 , а, £? . . .
251 ф-ла (9.25) (знаменатель) mD2 ~&г 1 niD2 V \ 8г )
262 ф-ла (9.52) , / D \2[ * U / J J * " Г rd *|с> I — 1 .и J | L-^-j й — + +
Зак. 292