Автор: Bolobas S. Fulton W. Katok A. Kirwan Sarnak P.
Теги: mathematics higher mathematics cambridge university press differential geometric
ISBN: 0-521-80267-9
Год: 2001
Текст
145 Isoperimetric Inequalities
This introduction treats the classical isoperimetric inequality in Euclidean space
and contrasting rough inequalities in noncompact Riemannian manifolds. In Eu-
Euclidean space the emphasis is on quantitative precision for very general domains,
and in Riemannian manifolds the emphasis is on qualitative features of the
inequality that provide insight into the coarse geometry at infinity of Riemannian
manifolds.
The treatment in Euclidean space features a number of proofs of the classical
inequality in increasing generality, providing in the process a transition from the
methods of classical differential geometry to those of modern geometric mea-
measure theory; and the treatment in Riemannian manifolds features discretization
techniques and applications to upper bounds of large time heat diffusion in
Riemannian manifolds.
The result is an introduction to the rich tapestry of ideas and techniques of
isoperimetric inequalities, a subject that has beginnings in classical antiquity
and that continues to inspire fresh ideas in geometry and analysis to this very
day - and beyond.
Isaac Chavel is Professor of Mathematics at the City College of The City
University of New York. He received his Ph.D. in mathematics from Yeshiva
University under the direction of Professor Harry E. Rauch. He has published
in international journals in the areas of differential geometry and partial dif-
differential equations, especially the Laplace and heat operators on Riemannian
manifolds. His other books include Eigenvalues in Riemannian Geometry and
Riemannian Geometry: A Modern Introduction.
He has been teaching at the City College of The City University of New York
since 1970, and he has been a member of the doctoral program of The City Uni-
University of New York since 1976. He is a member of the American Mathematical
Society.
CAMBRIDGE TRACTS IN MATHEMATICS
General Editors
B. BOLLOBAS, W. FULTON, A. KATOK, F. KIRWAN,
P. SARNAK
145 Isoperimetric Inequalities
Isaac Chavel
The City University of New York
Isoperimetric Inequalities
Differential Geometric and
Analytic Perspectives
Cambridge
UNIVERSITY PRESS
PUBLISHED BY THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE
The Pitt Building, Tmmpington Street, Cambridge, United Kingdom
CAMBRIDGE UNIVERSITY PRESS
The Edinburgh Building, Cambridge CB2 2RU. UK
40 West 20th Street, New York, NY 10011-4211, USA
10 Stamford Road, Oakleigh. VIC 3166, Australia
Ruiz de Alarcon 13, 28014 Madrid. Spain
Dock House, The Waterfront, Cape Town 8001, South Africa
http://www.cambridge.org
© Cambridge University Press 2001
This book is in copyright. Subject to statutory exception
and to the provisions of relevant collective licensing agreements,
no reproduction of any part may take place without
the written permission of Cambridge University Press.
First published 2001
Printed in the United Stales of America
Typeface Times 10/13 pt System UR&.2e [tb]
A catalog record for this book is available from the British Library.
Library of Congress Cataloging in Publication Data
Chavel, Isaac.
Isoperimetric inequalities : differential geometric and analytic perspectives / Isaac Chavel.
p. cm. - (Cambridge tracts in mathematics ; 145)
Includes bibliographical references and index.
ISBN 0-521-80267-9
1. Geometry, Differential. 2. Isoperimetric inequalities. 3. Riemannian manifolds.
I. Title. II. Series.
QA641.C45 2001
5I6.3'6-dc21 2001016177
ISBN 0 521 80267 9 hardback
Contents
Preface
I Introduction
1.1 The Isoperimetric Problem
1.2 The Isoperimetric Inequality in the Plane
1.3 Preliminaries
1.4 Bibliographic Notes
II Differential Geometric Methods
II. 1 The C2 Uniqueness Theory
11.2 The C1 Isoperimetric Inequality
11.3 Bibliographic Notes
III Minkowski Area and Perimeter
III. 1 The Hausdorff Metric on Compacta
111.2 Minkowski Area and Steiner Symmetrization
111.3 Application: The Faber-Krahn Inequality
111.4 Perimeter
111.5 Bibliographic Notes
IV Hausdorff Measure and Perimeter
IV. 1 Hausdorff Measure
IV.2 The Area Formula for Lipschitz Maps
IV.3 Bibliographic Notes
V Isoperimetric Constants
V.I Riemannian Geometric Preliminaries
V.2 Isoperimetric Constants
V.3 Discretizations and Isoperimetric Inequalities
V.4 Bibliographic Notes
page ix
1
1
4
13
28
30
30
44
51
52
53
58
78
81
99
100
100
110
116
117
118
127
139
155
vn
viii Contents
VI Analytic Isoperimetrk Inequalities
VI. 1 L2 Sobolev Inequalities
V1.2 The Compact Case
V1.3 Faber-Krahn Inequalities
VI.4 The Federer-Fleming Theorem: The Discrete Case
VI.5 Sobolev Inequalities and Discretizations
VI.6 Bibliographic Notes
VII Laplace and Heat Operators
VII. 1 Self-adjoint Operators and Their Semigroups
VII.2 TheLaplacian
VII.3 The Heat Equation and Its Kernels
VII.4 The Action of the Heat Semigroup
VII.5 Simplest Examples
VII.6 Bibliographic Notes
VIII Large Time Heat Diffusion
Vin.l The Main Problem
VIII.2 The Nash Approach
VIII.3 The Varopoulos Approach
VII1.4 Coulhon's Modified Sobolev Inequality
Vrn.5 The Denouement: Geometric Applications
Vm.6 Epilogue: The Faber-Krahn Method
Vin.7 Bibliographic Notes
Bibliography
Author Index
Subject Index
157
157
161
165
170
174
183
185
185
192
201
216
222
224
225
226
234
236
240
243
249
253
255
263
265
Preface
This book discusses two venues of the isoperimetric inequality: (i) the sharp
inequality in Euclidean space, with characterization of equality, and (ii) isoperi-
isoperimetric inequalities in Riemannian manifolds, where precise inequalities are un-
unavailable but rough inequalities nevertheless yield qualitative global geometric
information about the manifolds.
In Euclidean space, a variety of proofs are presented, each slightly more
ambitious in its application to domains with irregular boundaries. One could
easily go directly to the final definitive theorem and proof with little ado, but
then one would miss the extraordinary wealth of approaches that exist to study
the isoperimetric problem. An idea of the overwhelming variety of attack on this
problem can be quickly gleaned from the fundamental treatise of Burago and
Zalgaller A988); and I have attempted on the one hand to capture some of that
variety, and on the other hand to find a more leisurely studied approach that
covers less material but with more detail.
In Riemannian manifolds, the treatment is guided by two motifs: (a) the
dichotomy between the local Euclidean character of all Riemannian manifolds
and the global geometric properties of Riemannian manifolds, this dichotomy
pervading the study of nearly all differential geometry, and (b) the discretiza-
discretization of Riemannian manifolds possessing bounded geometry (some version of
local uniformity). The dichotomy between local and global is expressed, in our
context here, as the study of properties of Riemannian manifolds that remain
invariant under the replacement of a compact subset of the manifold with an-
another of different geometry and topology, as long as the new one fits smoothly
in the manifold across the boundary of the deletion of the original compact
subset. Thus, we do not seek fine results, in that we study coarse robust invari-
invariants that highlight the "geometry at infinity" of the manifold. Our choice of
isoperimetric constants will even be invariant with respect to the discretization
of the Riemannian manifold. The robust character of these new isoperimetric
IX
x Preface
constants will then allow us to use this discretization to show how the geometry
at infinity influences large time heat diffusion on Riemannian manifolds.
Regrettably, there is hardly any discussion of isoperimetric inequalities on
compact Riemannian manifolds. That would fill a book - quite different from
this one - all by itself.
A summary of the chapters goes as follows:
Chapter I starts with posing the isoperimetric problem in Euclidean space
and gives some elementary arguments toward its solution in the Euclidean plane.
These arguments are essentially a warm-up. They are followed by a summary
of background definitions and results to be used later in the book. Thus the
discussion of the isoperimetric problem, proper, begins in Chapter II.
Chapter II starts with uniqueness theory, under the assumption that the bound-
boundary of the solution domain is C2. We first show that, if a domain fi with C2
boundary is a solution to the isoperimetric problem for domains with C2 bound-
boundaries, S2 must be an open disk. Then we strengthen the result a bit - we show
that if a domain is but an extremal for isoperimetric problems, then it must be a
disk. Then we consider the existence of a solution to the isoperimetric problem
for domains with C1 boundaries. We give M. Gromov's argument that for such
domains the disk constitutes a solution to the isoperimetric problem. But only if
one restricts oneself to convex domains with C1 boundaries does his argument
imply that the disk is the unique solution.
Chapter III is the heart of the first half of the book. It expands the isoperimet-
isoperimetric problem in that it considers all compacta and assigns the Minkowski area
to each compact subset of Euclidean space to describe the size of the boundary.
In this setting, using the Blaschke selection theorem and Steiner symmetriza-
tion, one shows that the closed disk constitutes a solution to the isoperimetric
problem. Since the Minkowski area of a compact domain with C1 boundary is
the same as the differential geometric area of the boundary, the result extends
the solution of the isoperimetric problem from the C1 category to compacta.
Moreover, one can use the traditional calculations to show that the disk is the
unique solution to the isoperimetric problem in the C' category. But uniqueness
in the more general collection of compacta is too difficult for such elementary
arguments.
Then, in Chapter III, we recapture Steiner's original intuition that successive
symmetrizations could be applied to any compact set to ultimately have it con-
converge to a closed disk - in the topology of the Hausdorff metric on compact sets.
We use this last argument to prove the isoperimetric inequality for compacta
with finite perimeter. The perimeter, as a measure of the area of the boundary,
Preface
XI
seems to be an optimal general setting, since one can not only prove the isoperi-
isoperimetric inequality for compacta with finite perimeter, but can also characterize
the case of equality.
In Chapter IV we introduce Hausdorff measure for subsets of Euclidean
space and develop the story sufficiently far to prove that the perimeter of a
Lipschitz domain in n -dimensional Euclidean space equals the (n — Yy-
dimensional Hausdorff measure of its boundary. The proof involves the area
formula, for which we include a proof.
Chapter V begins a new view of isoperimetric inequalities, namely, rough
inequalities in a Riemannian manifold. The goal of Chapters V-VM is to show
how these geometric isoperimetric inequalities influence the qualitative rate of
decay, with respect to time, of heat diffusion in Riemannian manifolds.
In Chapter V we summarize the basic notions and results concerning isoperi-
isoperimetric inequalities in Riemannian manifolds, and in Chapter VI we give their
implications for analytic Sobolev inequalities on Riemannian manifolds. Chap-
Chapter V consists, almost entirely, of a summary of results from my Riemannian
Geometry: A Modem Introduction, and I have included just those proofs that
seemed to be important to the discussion here. The discussion of Sobolev in-
inequalities in Chapter VI has received extensive treatment in other books, but our
interest is restricted to those inequalities required for subsequent applications.
Moreover, we have also treated the relation of Sobolev inequalities on Rieman-
Riemannian manifolds and their discretizations, one to the other. To my knowledge,
this has yet to be treated systematically in book form.
Chapter VII introduces the Laplacian and the heat operator on Riemannian
manifolds and is devoted to setting the stage for the "main problem" in large
time heat diffusion; its formulation and solution are presented in Chapter VHI.
The book ends with an introduction to the new arguments of A.A. Grigor'yan,
the full possibilities of which have only begun to be realized.
I have attempted to strike the right balance between merely summarizing back-
background material (of which there is quite a bit) and developing preparatory argu-
arguments in the text. Also, although I have summarized the necessary basic defi-
definitions and results from Riemannian geometry at the beginning of Chapter V,
I occasionally require some of that material in earlier chapters, and I use it as
though the reader already knows it. This seems the lesser of two evils, the other
evil being to disrupt the flow of the arguments in the first half of the book for
an excursus that would have to be repeated in its proper context later. Most of
that material is quite elementary and standard, so it should not cause any major
problems.
Xll
Preface
In order to clarify somewhat the relation between material quoted and ma-
material presented with proofs, I have referred to every result that either is an
exercise or that relies on a treatment outside this book as a proposition, and
every result proven in the book as a theorem. This is admittedly quite artificial
and obviously gives rise to some strange effects, in that the titles proposition
and theorem are often (if not usually) used to indicate the relative significance
of the results discussed. That is not the case here.
There are bibliographic notes at the end of each chapter. They are intended
to give the reader some guidance to the background material, and to give but
an introduction to a definitive study of the literature.
It is a pleasure to thank the many people with whom I have been associated
in the study of geometry since I first came to the City College of CUNY in
1970: first and foremost, Edgar A. Feldman and the other geometers of the City
University of New York - J. Dodziuk, L. Karp, B. Randol, R. Sacksteder, and
J. Veiling. Also, I have benefited through the years from the friendship and
mathematics of I. Benjamini, M. van den Berg, P. Buser, E. B. Davies, J. Eels,
D. Elworthy, A. A. Grigor'yan, E. Hsu, W. S. Kendall, F. Morgan, R. Osserman,
M. Pinsky and D. Sullivan. But, as is well known, any mistakes herein are all
mine.
The isoperimetric problem has been a source of mathematical ideas and
techniques since its formulation in classical antiquity, and it is still alive and
well in its ability to both capture and nourish the mathematical imagination.
This book only covers a small portion of the subject; nonetheless, I hope the
presentation gives expression to some of its beauty and inspiration.
Introduction
In this chapter we introduce the subject. We describe the classical isoperimet-
isoperimetric problem in Euclidean space of all dimensions, and give some elementary
arguments that work in the plane. Only one approach will carry over to higher
dimensions, namely, the necessary condition established by classical calcu-
calculus of variations, that a domain with C2 boundary provides a solution to the
isoperimetric problem only if it is a disk. Then we give a recent proof of the
isoperimetric inequality in the plane by P. Topping (which does not include a
characterization of equality), and the classical argument of A. Hurwitz to prove
the isoperimetric inequality using Fourier series. This is followed by a symme-
symmetry and convexity argument in the plane for very general boundaries that proves
the isoperimetric inequality, //one assumes in advance that the isoperimetric
functional D >-*¦ L2(dD)/A(D) has a minimizer. (So this is a weak version -
if the isoperimetric problem has a solution, then the disk is also a solution.)
Finally, we present the background necessary for what follows later in our
general discussion, valid for all dimensions. The subsections of §1.3 include a
proof of H. Rademacher's theorem on the almost everywhere differentiability of
Lipschitz functions, and a proof of the general co-area formula for C' mappings
of Riemannian manifolds. We obtain the usual co-area formula, as well as an
easy consequence: Cauchy's formula for the area of the boundary of a convex
subset of R" with C1 boundary.
LI The Isoperimetric Problem
Given any bounded domain on the real line (that is, an open interval), the
discrete measure of its boundary (the endpoints of the interval) is 2. And given
any bounded open subset of the line, the discrete measure of its boundary is
greater than or equal to 2, with equality if and only if the open set consists of one
open interval. This is the statement of the isoperimetric inequality on the line.
2 Introduction
In the plane, one has three common formulations of the isoperimetric
problem:
1. Consider all bounded domains in R2 with fixed given perimeter, length of
the boundary (that is, all domains under consideration are isoperimetric).
Find the domain that contains the greatest area. The answer, of course, will
be the disk. Note that the specific value of the perimeter in question is of no
interest, because all domains of perimeter L\ are mapped by a similarity of
R2 to all domains with perimeter L2 for any given values of Lu L2, and the
image under the similarity of an area maximizer for L i is an area maximizer
for L2.
2. One insists on a common area of all bounded domains under consideration,
and asks how to minimize the perimeter.
3. Lastly, one expresses the problem as an analytic inequality, namely, since we
know exactly the values of the area of the disk and the length of its boundary,
the isoperimetric problem is then expressed as proving the isoperimetric
inequality
A.1.1) L2>4jr/t,
where A denotes the area of the domain under consideration, and L denotes
the length of its boundary. The inequality is extremely convenient, in that it
remains invariant under similarities of R2, and one has equality if the domain
is a disk. One wishes to show that the inequality is always true, with equality
if and only if the domain is a disk.
One can consider the above for any R", n > 2. The proposed analytic isoperi-
isoperimetric inequality then becomes
A.1.2)
where S2 is any bounded domain in R" and 3SI its boundary, V denotes n-
measure and A denotes (n - l)-measure, B" is the unit disk in R", and S"
the unit sphere in R". We let u>n denote the n-dimensional volume of B" and
cn_i the (n - l)-dimensional surface area of S". It is standard that
. 1.3)
C.-1
^-rin/l)' -- n '
where r(jt) denotes the classical gamma function; and A.1.2) now reads as
A.1.4)
I/n
/. 1 The Isoperimetric Problem 3
One wants to prove the inequality and to show that equality is achieved if and
only if n is an n-disk. Note that for n = 2 we took in A.1.4) the square root of
A.1.1).
Remark 1.1.1 Throughout the book, domain will refer to a connected open
set. In general, we consider the isoperimetric problem for relatively compact
domains when we are working in the differential geometric setting (Chapters I,
II, V-VIIIj. Therefore, the disks that realize the solution in R" are open. In
Chapters III and IV, where we work in a more general setting, the isoperimetric
problem is considered for compacta. In that setting the disks that realize the
solution in R" are closed.
Remark 1.1.2 We have restricted the isoperimetric problem to domains in R";
but if we could solve this problem, then the isoperimetric problem for open
sets consisting of finitely many bounded domains would easily follow from the
solution for single domains. Indeed, assume one has the inequality A.1.2) for
domains inR". If
n = n, u n2 u • • •,
where each ft; is a relatively compact domain in R" such that
(cl denotes the closure), then Minkowski's inequality implies
-Aon).
A.1.5)
So the inequality extends to the union of domains. Note that equality implies
that S2 is a domain.
Remark 1.13 Note that for any domain fi in R", its volume is the n-dimensional
Lebesgue measure, and if 3ft is C1 then the area of 3ft is given by the standard
differential geometric surface area of a smooth hypersurface in R". However, if
9ft is not smooth, then one must propose an area functional defined on a collec-
collection of domains such that the area functional will give a working definition of the
area of the boundaries of the domains. Besides a number of natural properties
[see the discussions in Burago and Zalgaller A988)], one requires that the new
definition agree with the differential geometric one when applied to a domain
with smooth boundary. Then, with this new collection of domains and definition
of the area of their boundaries, one wishes to prove the isoperimeric inequality.
Also, one wishes to characterize the case of equality in each of these settings.
4 Introduction
Remark 1.1.4 As soon as one expands the problem to the model spaces of
constant sectional curvature, that is, to spheres and hyperbolic spaces, one has
no self-similarities of the Riemannian spaces in question. And if the disks on
the right hand side of A.1.2) are to have radius r, then the right hand side of the
inequality in A.1.2) is no longer independent of the value of r. Nonetheless, one
still has the isoperimetric inequality in the sense that all domains in question
with the same n-volume have the (n — l)-area of their boundaries minimized
by disks. For n = 2, the analytic formulation reads as follows: If M — M2,
the model space with constant curvature k, then the isoperimetric inequality
becomes
A.1.6)
L2 >4jiA-kA2,
with equality if and only if the domain in question is a disk. Of course, one can
still consider the isoperimetric problem, whether or not it is to be expressed as
an inequality, in the first or second formulation above.
Similarly, one can extend the isoperimetric problem and associated inequali-
inequalities to surfaces, or, more generally, to Riemannian manifolds. We shall consider
such inequalities in Chapter V.
Remark 1.1.5 Finally, one can consider a Bonnesen inequality. In R2, such an
inequality is of the form
L2 -
> B > 0,
where B is a nonnegative geometric quantity associated with the domain that
vanishes if and only if the domain is a disk.
L2 The Isoperimetric Inequality in the Plane
For any C2 path a> : (a, 0) -* R2 in the plane, the velocity vector field of <a is
given by its derivative <a', and acceleration vector field by <a". We assume that
to is an immersion, that is, at never vanishes. The infinitesimal element of arc
length ds is given by
ds = \<o\t)\dt.
Given any to e (a, 0), the arc length function of <a based at t0 is given by
s(t)= [ \<a\x)\dx.
1.2 The Isoperimetric Inequality in the Plane
Let
denote the unit tangent vector field along <a,
i : R2 -> R2
the rotation of R2 by n/2 radians, and
the oriented unit normal vector field along <a. Then one defines the curvature k
ofo>by
— -
ds ~
(indeed, since T is a unit vector field, its derivative must be perpendicular to
itself). Then the formula for the curvature, relative to the original path, is given
by
A.2.1)
One can easily show that
A.2.2)
~ ds
ds
The equations A.2.1) and A.2.2) are referred to as the Frenet formulae.
One can prove, from A.2.1), that if the curvature k is constant, then o> is an arc
on a circle (if not the complete circle).
1.2.1 Uniqueness for Smooth Boundaries
As a warm-up, we give the argument from classical calculus of variations. Given
the area A, let D vary over relatively compact domains in the plane of area A,
with C boundary, and suppose the domain Q,dQ€C2, realizes the minimal
boundary length among all such domains D. We claim that ft is a disk.
Proof Since Q is relatively compact in R2, there exists a simply connected
domain &o such that
?2 = J20 \ {finite disjoint union of closed topological disks).
We claim that since ft is a minimizer, then fto = ft. If not, we may add the
topological disks to ft, which will increase the area of the domain and decrease
Introduction
the length of the boundary, and therefore ft will not be a minimizer. Thus
fto = ft, and is bounded by an imbedded circle.
Let F : S1 ->¦ R2 e C2 be the imbedding of the boundary of ft. We always
assume that the path F is oriented so that u = -N at all points of F, where u
is the unit normal exterior vector field along 9 ft.
One then considers a 1-parameter family F« : S1 -> R2 of imbeddings
v : (—Co, fo) xS'-> R2,
such that the variation function v(e, t) given by
v(e, t) = T((t) = F(f) + *(e, f)i/(r). *@, t) = 0,
is C1. First,
9v 9*
Also
which implies
at
Taylor's theorem implies, for
the expansion
which implies
<=o
a*
at
^(t)\ ""'¦
Therefore, the area element d A in the curvilinear coordinates (t, e) is given
by
dA =
dv dv
rfe ds.
1.2 The Isoperimetric Inequality in the Plane 7
For the domain S2( determined by F( we have, for sufficiently small e,
A(n«)-A(n)= f da I {<j> + o(l))ds.
Jo Jr
Therefore, if A(Sl() = A(Si) for all e, then
f <f>ds = O.
Jr
Now let L(e) denote the length of I\. Since T has the shortest length, we have
L'@) = 0. Therefore, because
dt=f \r'\{l+€K</>+o(€))dt= [ {l
Jsi Jr
we have
0 = L'@)= f K<pds, I
Jr Jr
<pds=0
for any such variation of F.
Similarly, given any <f> e C1 such that fr <f>ds = 0, there exists a variation
v of F such that A(ft<) = A(ft) for all e, and L'@) = /r <4>ds. Then, by
assumption, we have
k</> ds = 0 V0 e C
To show that this implies that k is constant, we argue as follows: Given any
ir :S' -> RinC'.set
4>=\lr- I ifrds I I ds .
Then fr <j>ds = 0, which implies
where L denotes the length of F. Since ^ is arbitrary C, a standard argument
then implies that
A.2.3)
--J- f Kds = 0,
L Jr
that is, the curvature k is constant. Then, as mentioned, A.2.1) implies that F
is a circle.
8 Introduction
1.2.2 Quick Proof Using Complex Variables
Theorem 1.2.1 (Isoperimetric Inequality in Rz) Let SI be a relatively com-
compact domain, with boundary 3 ?2 e C1 consisting of one component. Then
Proof We denote any element of the plane as the complex number
z = x + iy,
and the area measure as an oriented volume element; so
dA =dx Ady = -dz A dz.
Then
47M(?2)
= if lni
lnidzAdz
an C ~ z
/
an
=/
/
»a JdQ
- the second equality follows from the fact that the winding number of 3 ?2
about any point z e ?2 is 1; the last equality follows from Green's theorem -
which implies the claim. ¦
1.2.3 The Method of Fourier Series
Lemma 1.2.1 (Wirtinger's Inequality) If f is a C\ L-periodic function on
Kand
i:
f(t)dt=O,
then
[ \f'\\t)dt > ^L [ \f\\t)dt,
o L. Jo
with equality if and only if there exist constants a~\ anda\ such that
1.2 The Isoperimetric Inequality in the Plane 9
Proof This is an exercise from Fourier series. The function f(t) admits a
Fourier expansion
f(t)
e2"k"L [
ake2
with ak = y[ f(t)<r2"
Similarly, we have
fit)'** T he2*"""- with bk = - (L f\t)e-^ik"Ldt.
t^ L J
The continuity of / implies bo = 0, and the hypothesis implies ao = 0. Inte-
Integration by parts implies
Parseval's inequality then implies
lL\f?dt =
JO
= L^rTk2\ak\2
which implies the inequality. One has equality if and only if ak = 0 for all
|*| > 1. ¦
Theorem 1.12 (Isoperimetric Inequality in R2) If SI is a relatively compact
domain in R2, with C1 boundary consisting of one component, then
with equality if and only if Si is a disk.
Proof If necessary, we translate ?2 to guarantee
x ds = 0, x = (jc
Jda
Let x = jt'ei + *2e2 be the vector field on R2 with base point x = (xl, x2).
One now uses the 2-dimensional divergence theorem, namely, for any vector
field x »-> ?(x) e R2 with support containing cl ?2, one has
A.2.4)
10
Introduction
where v denotes the outward unit normal vector field along 3 ?2. One can obtain
the formula A.2.4) by converting the traditional Green's theorem
A.2.5) ff 1^.-^-1 dA= f Pdx + Qdy,
JJa \dx dy } Jia
by choosing
For the left hand side of (I.2.S) one has
3x dy dx1
For the right hand side of A.2.5) one has
Pdx + Qdy = -?2dxl
For our vector field x, we have div x = 2 on all ?2. Then the divergence
theorem implies
2/t(?2) = f divx<M = / x-uds,
Ja Jaa
which implies
2/t(?2) = / x.uds
= /
Ja
< /
Ja
1/2
= ?l/2C?2)f/ \xfds
[Jaa
1/2
- the first inequality is the vector Cauchy-Schwarz inequality, and the second
inequality is the integral Cauchy-Schwarz inequality.
Parametrize 3fi with respect to arc length. Note that
dx
ds
1.2 The lsoperimetric Inequality in the Plane
'
along 3fi; so Wirtinger's inequality, applied to each coordinate function j
x2(s), implies
( / \
[Jan
\x\2ds
1/2
1/2
which is the desired inequality. The case of equality follows easily.
1.2.4 A Symmetry-and-Convexity Argument
Theorem 1.23 Consider the isoperimetric problem for all relatively cornp^\
domains in R2 with piecewise C1 boundaries, and assume the isoperime!141
problem in R2 has at least one solution, that is, there is a domain ?2 realiz'^
the minimum of the isoperimetric functional
D
L2(dD)
A(D) "
Then the open 2-disk also minimizes the isoperimetric functional.
Remark 1.2.1 Thus, we are only proving a weak result, namely, the analy1"'
isoperimetric inequality A.1.1) is valid if the isoperimetric functional has
minimizer.
Although the arguments from complex variables and from Fourier
given above are also valid when the boundaries are only piecewise C\ here
proof requires that the variational problem be defined over the extended
of domains.
^
*
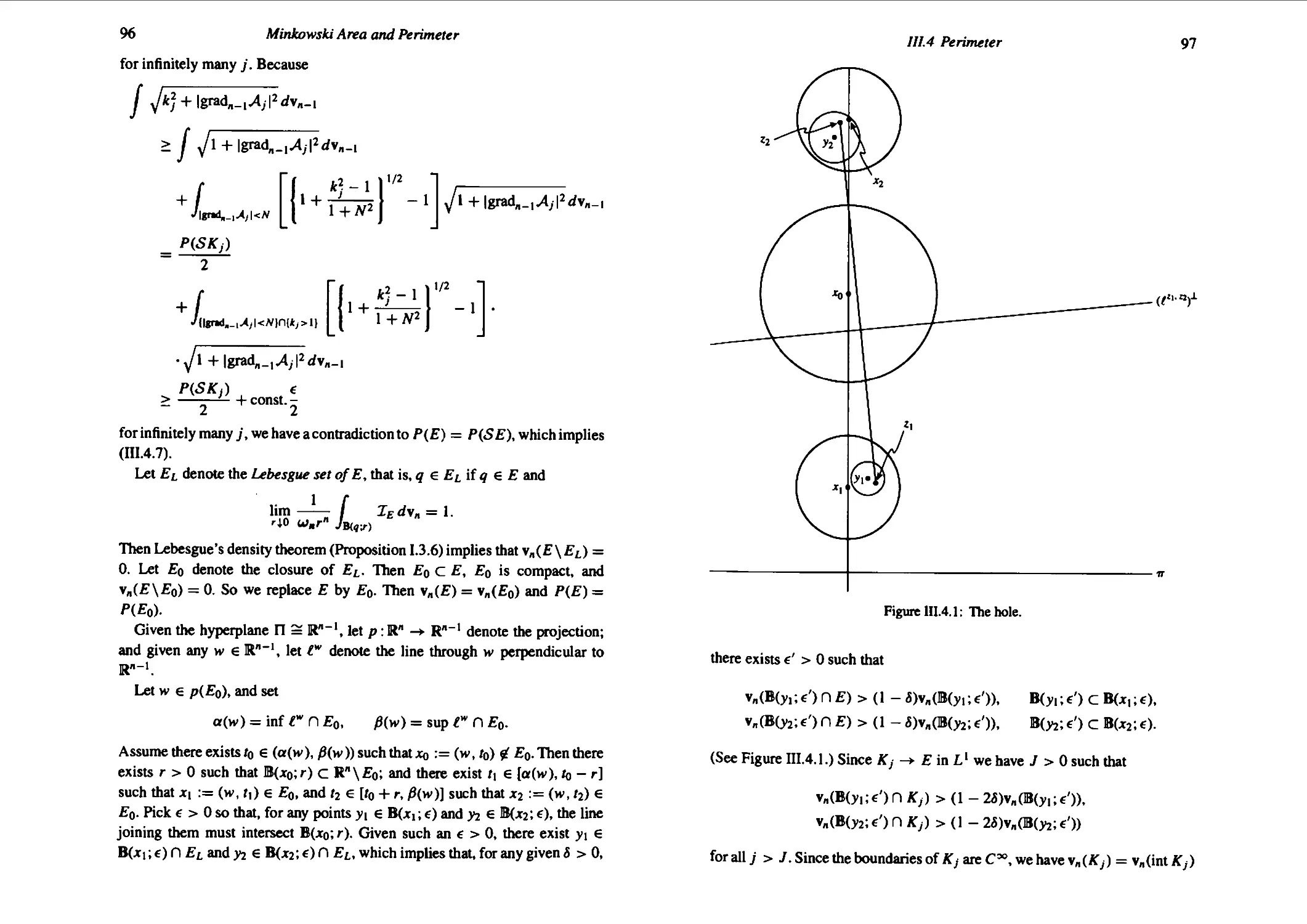
Proof Let ft be a minimizer. Pick a line II that divides ?2 into two open se
fi i, ^2 of equal area. Then
z.Cfi n ci no = z.C« n ci n2).
If not, and L(dSi n cl Si\) < Z.Cfi D cl n2). then one could replace 0 by P '
consisting of S2i union its reflection in n, which would imply that ?2 is no*
minimizer, which is a contradiction. So we may replace ?2 by a domain ?2* tn^
is symmetric with respect to the line n.
12
Introduction
Figure 1.2.1: The line through the origin intersecting dil.
By carrying out this argument successively, one may assume that there exists
a coordinate system in R2 such that ?2 is symmetric with respect to the two
coordinate axes. This implies that every line through the origin divides ?2 into
two open sets of equal area and, therefore (by the above argument), equal
bounding length.
Next, we may assume cl ?2 is convex. If not, we may replace it by its convex
hull, which increases the area and decreases the bounding length. Since the
origin is in ?2, we may think of d ?2 as the image of a piecwise C1 map defined
on the unit circle §' in R2.
Let w0 € d ?2 have a tangent line, not equal to the line from the origin through
w0. (See Figure 1.2.1.) We claim that the line from the origin to w0 must intersect
3 ?2 perpendicular to the tangent line at w0. If not, it will be possible to carry out
the construction ?2 i-+ ?2* described in the first paragraph above so that cl ?2*
is nonconvex, which is a contradiction.
Therefore, ?2 is convex with every point of differentiablity of 3 ?2 having its
tangent line orthogonal to the position vector. Let 6 denote the local coordinate
on S1, x the position vector on 3 ?2, and n the position vector on S1. Then
x= rn
at all points of differentiability of 3 ?2, which implies
3x 3r 3n
Because n is perpendicular to the tangent space, we conclude that r is differen-
tiable, with 3r/30 = 0, at all points of differentiability of 3?2, which implies r
is locally constant on the C1 arcs of 3?2. Thus 3 ?2 consists of a finite number of
1.3 Preliminaries
13
circular arcs connected by segments of lines that (the lines, not the segments)
pass through the origin. The convexity of ?2 implies 3 ?2 is a circle. ¦
Remark IJ*2 In higher dimensions one has to be careful about the convexity.
For example, it is not true that passing to the convex hull of a domain decreases
its isoperimetric quotient. Pick a standard imbedded solid torus in R\ where
the circle in the jry-plane has radius 1, and the rotated circle perpendicular to
the jy-plane has radius € <? 1. Then its isoperimetric quotient is asymptotic
to const.€"/3 as € j 0. On the other hand, the convex hull has isoperimetric
quotient asymptotic to const.€~2/3 as € i 0.
L3 Preliminaries
We describe here most of the background required for the rest of these notes.
The Riemannian geometric background is discussed in Chapter V.
Notation Let X be any space, A a subset of X. We let IA denote the indicator
(or characteristic) function of A, that is, Ia(jc) = 1 for x e A, and Ia(jc) = 0
for x e X \ A. The cardinality of A is denoted by card A.
Notation In any topological space X we let supp / denote the support of a
function / on X. We denote continuous functions of compact support by CC(X).
When the target is some vector space V, we write CC(X; V).
Notation Whenever discussing a measure space (X, 971, dp), we let || || p denote
the associated Lp norm. (In general, the a -algebra 971 is fixed, so we rarely
mention it.) If there is doubt as to which space or measure is intended, then
we also indicate our choice in the subscript: || ||p,x or || ||p,dM, as required. In
general we write || || = || ||2. We also indicate the L2 inner product by ( , ).
Unless otherwise indicated, these are spaces of real-valued functions.
Proposition 1.3.1 If the sequence (/)) converges to f in Lp(ji) for some p e
[1, +00], then (fj)has a subsequence that converges pointwise to f a.e.-[d(i].
Proposition 1.3.2 Let Xbea complete, separable metric space, Y a Hausdorff
space, f : X -*¦ Y a continuous map, and n a measure on Y such that every
closed subset of Y is ^-measurable. Then f(B) is ^-measurable for every Borel
subset B ofX.
14
Introduction
Figure 1.3.1: Equation A.3.1) when p = \, dfi(x) = dx.
Proposition 133 (Cavalieri's Principle) Let v be a measure on Borel sets in
[0, oo), 4> its indefinite integral, given by
4>(t) = v([0, f)) < +00 V t > 0,
(fi, E, fi) a measure space, and f a nonnegative ? -measurable function on
S2. Then
f 4>(f(x))dfi(x)= [ /*({/ > t))dv(t),
Ja Jo
or equivalently,
/ dfi(x) / dv(t)= / dv(t) / l{f>,)dpL.
Ja Jo Jo Ja
In particular, ifdv(t) = ptp~l dt, p > 0, then we have (see Figure 1.3.1)
f p f°° p-i f
Ja Jo Jq
Thus, if p = 1 and fi = Sx then
/(*)= [ I{f>t{x)dt.
Jo
Notation Let (X, d) be a metric space. For any subset A in X, let
int A denote the interior of A,
ext A = int(X \ A) denote the exterior of A,
cl A or the traditional A denote the closure of A,
1.3 Preliminaries 15
dA denote the boundary of A,
diam A denote the diameter of A,
[A]( = {x € X : d(x. A) < €} denote the €-thickening of A.
For any x e X and r > 0, let fl(.x; r) denote the open metric disk and D(jc; r)
the closed metric disk in X, with center x and radius r. We denote the metric
sphere bounding B(x; r) by S(x; r).
We consider n-dimensional Euclidean space R", n > 1, where we denote
arbitrary points by x = (xl,...,x"), y = (>>' ,y"),... e R". The inner
product is denoted by x, y i-+ x-y. The length of an element x is given by
|jc| = y/x-x, and the distance between x and y is given by d(x, y) = \x — y\.
In R", we write B"(jt;r) for B(x;r) and D"(jt;r) for D(;t;r). We omit the
superscript n when the context is sufficiently clear. We also write S"~'(*;/¦)
for S(x\ r), and drop the superscript when no problem will caused by doing so.
When x is the origin o we write
and
= B"(o;r),
B" = B"(o; 1),
= W(o;r),
= ny(o; I),
= S"-'(o; 1).
Definition Let (X, 971) be a measure space. Then an R*-valued measure A on
(X, 9Tt) is a map A : 9JI -*¦ R* such that
00
A(E) = ^2 A(?y) (which converges)
for all partitions {Ej} of ?, for all E e SER. (A partition {Ej} of ? is a countable
family of subsets in 971 that are pairwise disjoint, and whose union is E.)
If A is an Rl-valued measure on X, then its total variation measure, | A|, is
defined by
|A|(E) = sup ?] |A(E,)|,
where the supremum is taken over all partitions of E.
One knows that |X\(X) < +00.
Definition An Revalued measure A is said to be absolutely continuous with
respect to a positive measure fi on (X, 9JI), A «: fi, if A(E) = 0 whenever
ME) = 0.
16
Introduction
Proposition 1.3.4 (Radon-Nikodym Theorem) IfX<g.ti, then there exists
an R*-valuedfunction * in Ll(fi), that is, fx |*| dfi < +00, such that
-L
for all measurable E.
Also, there exists a measurable map v : X -*¦ S* such that
dX = i/d\X\.
Finally, let fibea positive measure, $ : X -> R* in Z-'(/x), and set
X(E) = f
Je
Then
•h
Definition Let X be a locally compact Hausdorff topological space, and fi a
positive Borel measure on X, that is, its a-algebra contains 33, all Borel subsets
of X. We say that fi is locally finite if fi(K) is finite for all compact K; a
measurable E is outer regular if
= inf{/x(V): E C V, V open};
a measurable E is inner regular if
fi(E) = sup{fi(K): K c ?, K compact};
the measure m is regular if every measurable ? is both inner and outer reg-
regular. The measure fi is a ftufon measure if it is locally finite and regular. An
Revalued measure A is an Revalued Radon measure if its total variation mea-
measure I A| is a Radon measure.
Proposition L3.5 (Riesz Representation Theorem) Let X be a locally com-
compact Hausdorff space, and&a bounded linear functional on CC(X; R*) (relative
to the sup norm). Then there exists a unique R* -valued Radon measure XonX
such that
*(*)
= f
Jx
for all $ : X -> Rk in CC(X;R*). Moreover,
11*11 = |A|(X).
1.3 Preliminaries
17
In R", we denote the standardLebesgue measure by dvn(x). When considering
a domain R in R" with C1 boundary 3fi, we denote the Lebesgue measure on
Q by dV, and the standard surface area measure on d?2 by dA. For the special
case of B" we denote the surface area measure on S"~' by d^in_x. Recall that
we use the notation
= / d\n, cn_i = / dnn_Y.
When n = 2, we replace <M by dL, and d V by rfyl.
When discussing an arbitrary fc-dimensional submanifold of an n -dimensional
Riemannian manifold, we use dVk to denote the fc-dimensional Riemannian
measure on the submanifold.
When discussing changes of coordinates on R", we refer to the new coordi-
coordinates as Euclidean coordinates if they are obtained from the standard coordinate
system by a Euclidean transformation.
Proposition 1.3.6 (Lebesgue Density Theorem) For f eL\W)we have
lim -L. f (/(,) - /(jto)| d\n(x) = 0
for almost all x<) € R".
In particular, for every measurable E in R" with positive measure, we have
va(?nB(jc;r))
hm = 1
for almost all x e E.
Notation A multi-index a is given by a = (ot\,.. .,an), where aJy j =
1,..., n, is a nonnegative integer, |a| = 01 H \-an. For the multi-index
a, D° denotes the differentiation
Definition We define a mollifier on R" to be a function j : R" -> [0, 00) €
C~(B") satisfying
We define, for all € in @, I),
Mx) = €-"j(x/€);
18 Introduction
and for any locally l} function / on R", that is, / e /-'„,., we define
a * /)(*) = f My - x)f(y)d\n(y) = f My)fix + y)dvn(y).
Proposition L3.7
(a) Ifu 6 L^., then supp/( * u = [suppu]<.
(b) Ifu 6 C°, then jt * u -*¦ u uniformly on compact subsets o/R" as€ I 0.
(c) Ifu e L^, then j(*u e C°°, and
(Da{j( * u)Xx) = (-1)"" f(Dajf)(y - x)u(y)dvn(y)
for any multi-index a. Moreover, ifu e Ck, then for all \a\ < k one has
DaU< * «) = U * (Dau),
by integration by parts.
(d) Ifu e L", then (i) j(*ue L", (ii) ||/€ *n||p < |u||p for all p e [1, oo],
and (hi) ||/( * u - u\\p -*¦ 0 for all p e [1, oo), as € ± 0.
Remark L3.1 If j(x) = j(-x) for all x e R", then
A.3.2) j{Jt * f)g dvn = j f(j< * g) dvn
for all /, g e /-'(R"). We shall henceforth assume the symmetry of all molli-
fiers, so A.3.2) will always apply.
Notation Let F : ?2 -> R* e C, where ?2 is open in R". For each x € ?2, we
denote the associated Jacobian linear transformation of F by Jf(x).
Definition Let F : ?2 -> R* € C1, where ?2 is open in R\ A point jc e ?2 is
called a critical point ofF if its associated Jacobian linear transformation Jf(x)
has rank < k.
A point y e R* is a critical value if there exists at least one point in its
preimage which is a critical point. The complement in R* of all critical values
of F consists of the regular values ofF. (This includes points not in the image
ofF.)
Proposition 1.3.8 (Sard's Theorem) Let F : ?2 -*¦ R* e Cl, where ?2 is open
in R", I > max{n — k, 0}. Let A denote the critical points of F. Then
n(F(A)) = 0.
1.3 Preliminaries
19
Remark 1-3.2 The cases where we invoke Sard's theorem usually have k = n,
in which case t > 1, or k = 1, in which case I > n.
Definition Consider the differential operator
—
defined on some domain D in R". We say that L is elliptic at x if there exists a
positive number fj.(x) such that
J2
j.k=\
for all p = (p\,..., pn) e R". We say L is elliptic on D if L is elliptic at every
point of D. We say L is uniformly elliptic on D if L is elliptic on D and there
is a positive constant /xo such that fi(x) > fio for all x e D.
Proposition 1-3.9 (Strong Maximum Principle) Let L be uniformly elliptic
on the domain D in R", with uniformly bounded coefficients ajk(x), bi(x), and
assume u : D -*¦ Re C2 satisfies the differential inequality
Lu>0
on all of D. Ifu attains a maximum at a point ofD, then u is constant on D.
Furthermore, assume (i) 3D e C1, (ii) u : D -> R e C2(D) n C°(D),
(iii) u < M on all of D, (iv) u = M at some point w e 3D, and (v) the ex-
exterior normal derivative du/dv is defined at w. Then
du A
— > 0
3
at w,
unless u = M on all of D.
We remind the reader that du/di/ at w is defined to be the limit of (grad u)(x)-v,
x e D, as x approaches w along the line through w with direction v.
1.3.1 Lipschitz Functions
Definition A Lipschitz function on the metric space (X, d) is a function u on
X for which there exists a nonnegative number K such that
A.3.3)
l«(zi) - «
, zi) V z,,
X.
20
Introduction
The Lipschitz constant Lip u is the smallest positive K for which A.3.3) is valid
forallzi,Z2 € X.
Theorem U.I Let (X,d) be a metric space, A C X.andf : A -> RLipschitz.
Then there exists g : X -*¦ R Lipschitz such that g\A — f.
Proof Let L = Lip /, the Lipschitz constant of /, and consider
g(x) = inf {/(>>) + Ld(x,y)).
yeA
For all x e X and y, z, e A we have
fit) - f(y) < Ld(z, y) < L{d(x, y) + d(x, z)h
which implies
f(z) - Ld(x, z) <f(y) + Ld(x,y),
which implies
f(z) - Ld(x, z) < g(x) < f(y) + Ld(x, y),
which implies g\A = f.
To show that g is Lipschitz, note
g(xi) - g(x2) = sup inf f(yi) + Ld(xx, yx) - f(j2) - Ld(x2, >^)
< sup L{d(xi, y2) - d(x2, >^)}
neA
<Ld(xux2). m
Theorem 132 (Rademacher Theorem) // / : R™ -* R" is Lipschitz. then
f is differentiable a.e.-[d\m].
Proof We may assume n = 1. We may also assume that we know the theorem
for m = 1 (since Lipschitz implies / is an absolutely continuous function of
one real variable).
Fix | e S", and let (D^f)(x) denote the directional derivative of / at
x e R" in the direction ? (should it exist). Also, let
B( = {x e R" : (D{/)(*) does not exist}.
Then \\(B( n {x +1$ : t e R}) = 0 for all x (we know the theorem forn = 1).
Therefore (by Fubini's theorem), \n(B() = 0 for every ? e S". In particular,
1.3 Preliminaries
21
by successively picking ? = e, eB (the natural basis of R"), the gradient
vector field grad / exists almost everywhere.
Next we wish to show that, for each ?,
A-3.4) @*/)« = Hgrad/)«
for almost every x. Indeed, given any <j> € Cf (R") we have (by change of
variables)
'-<fi(x)dvn(x)
-I
t J t
which implies (using dominated convergence)
¦f(x)dvn(x).
'iZ7)f
which implies A.3.4).
Finally, let {?,} be a countable dense set in S",
Aa = {x: grad/, D^ f exist &D^f = ?o-grad /},
a=l
Then vB(R"\/l) = 0. We now show that / is differentiable on A. For x € A,
y = x + t% e R\ we have
- fix) - (y - *).(grad /X*) = /(* +1$) - f(x) - f?-(grad f)(x)
= /(jr + tt-) - f(x + t$a) + f(x + r&)
which implies
-$a\\y-x\+ o(\y - x\).
which implies the theorem.
22
Introduction
Theorem 133 Let u be a Upschitz function on R" with compact support.
Subject u to mollification by j( as above. Then
\\j( *u- u\\p -*¦ 0, Hgrady, * u - gradi«||p -> 0
for all p e [1, oo) as € I 0.
Proof Since u is Lipschitz, the restriction of u to any line is absolutely con-
continuous; and thus all partial derivatives exist almost everywhere on R", and are
bounded with compact support. Thus, each partial derivative is an element of
Lp for all p € [1, oo]. Also, the absolute continuity along lines and the com-
compactness of the support of u imply the fundamental theorem of calculus for each
partial derivative, which implies
Jr. dxk
for ft = 1..... n. Then we may use the argument of Proposition I.3.7(c) to show
O >
One easily obtains the conclusion of the theorem. ¦
Example L3.1 Let K be & convex subset of R" with nonempty interior. (See
§1.3.3 below.) If K / R", then K is contained in a half-space H. Let n = 3//,
and p : R" -> n the orthogonal projection. Introduce Euclidean coordinates in
R" so that n = {*" = 0}. Define, for w = (jc1 jr") e p(K),
/(w) = inf{y: (w,y)eK).
Then the graph of jc" = /(>v) is the "lower" part of the bounding hypersurface
of K, and / is a convex function, that is,
f(ku + A - k)v) < kf(u) + A - k)f(v) V u, v e p{K), k € tO, 1].
Given u, v e int p(K), let luv denote the line in n through u, v, and set
Then one checks that
F(t) - F(x)
t - r
1.3 Preliminaries
23
is increasing with respect to both t and r, which implies the right and left hand
derivatives of /, F+ and F'_ respectively, exist everywhere, and
t — z
for all a < A < r < t < B < b, which implies F is locally Lipschitz on (a, b).
By Rademacher's theorem, the boundary of AT is a.e.-[Il, d\n-\] differentiable.
Remark 133 We recall for the reader the basic definition of Sobolev spaces.
Let ?2 be open in R". (The definitions that follow are also the ones that are used
when ?2 denotes an open subset of a Riemannian manifold.) By the Meyers-
Serrin theorem one has two equivalent characterizations of the Sobolev space
IV'•'(«).
First one considers the collection H of C°° functions / on ?2 for which both
/, grad / € Ll. Then one endows H with the pre-Banach norm
ll/lli.i =
llgrad/||,
and completes //.with respect to the norm || |h,i, to the Banach space W(n)
The second characterization goes as follows: We say that / e Z-'(fi) has a
weak Ll -derivative if there exists an L'(?2)- vector field ? such that
/ fdi\ijd\n = - I
Jn Ja
for all compactly supported C00 vector fields r\ on ?2. The vector field $, should
it exist, must be unique, and we denote it by ? = Grad /. Let Si be the Banach
space (it is indeed a Banach space) consisting of functions f e Ll possessing
weak L'-derivatives, with the norm || ||g given by
ll/lla = ll/lli + IIGrad/||,, / e fj.
Then, by the Meyers-Serrin theorem, Sj = W'^fi).
Clearly, all L'(?2) Lipschitz functions with L'(S2)-derivatives are elements
ofW'UO)
Notation We let fjc(n) denote the completion of Cf (O) in fj(fi).
1.3.2 Co-area Formula for Smooth Mappings
In this section, we use the method of moving frames. One can find treatments
of the method in the standard texts.
Let Mm, N" be C, r > 1, Riemannian manifolds, wj>«,and4>:Af->A^a
C1 map from M to N. We want to give an effective calculation of the volume
24 Introduction
disortion of the map, namely, of
= v/det ¦,oD»,)^l,
where 4>, denotes the associated Jacobian linear map of tangent spaces of M to
those of N, and ()** denotes the adjoint map. (When M and AT are Euclidean
spaces, we use the notation 7<& for <t>,.)
Let {eA), A = 1 wj, be an orthonormal moving frame on M with dual
co-frame {<oA}, and {?,}, y = 1,...,«, an orthonormal moving frame on N
with dual co-frame [&J). It is well known that the local volume forms on M
and N are given by a>x A--- AuT andfl1 A ••• Ad", respectively.
There exist functions o> a on M such that
where ** denotes the pullback of differential forms on N to M, associated
with the map *. If at some x e M we have dimker 4>,|x > m - n (that is, * is
a critical point of 4>), then
If at some x e M we have dim ker <1>,|X = m - n (that is, x is a regular point
of $), then * is a submersion on a neighborhood of x, and we may pick
en+i em to be tangent to the fibers of the local fibration about x associated
with the submersion, which implies e\,..., en is orthogonal to the fibration.
We therefore have
7 =
a—n
\ m,
which implies
which implies
<fr'@' a ¦•¦ A 6") = (det crJk)(ol A •¦• A(o".
One can easily check that
det (or-'*) = det *,|(ker Q,I.
Therefore, since
0, rank<J>. < n,
|det(«I>,|(ker<I>,)-L)|, rank*, = n
1.3 Preliminaries 25
(as one verifes rather easily), we have
A.3.5) J*@l A-ACif = ±<t>*(d1 A-- A6n) A (On+1 A--A(Om,
depending on whether deUo--'*) is positive or negative, which implies
Theorem 1.3.4 (Co-area Formula for Smooth Mappings) Let M, N be C
Riemannian manifolds, with m = dim M > dim N = n, r > m - n, and let
<t>: M -»¦ N e C. Then for any measurable function f : M -> R that is ev-
everywhere nonnegative or is in Ll(M), one has
A-3.6) [ fJ*dVn= [ dVn(y)[ (f\<t>-l[y])dVm.n
Proof We have, from A-3.5),
fJ*dVm
[
M
dVn
{y)f V\*-x
7*-'[y]
[y])dVm-,,,
where regval * denotes the set of regular values of $ in N. Since the map *
is Cr, the critical values of * constitute, at most, a set of measure 0 in AT (by
Sard's theorem - it is also valid for manifolds), which implies A.3.6). ¦
Corollary 13.1 (Co-area Formula for Smooth Functions) Let Mm be a
Cm Riemannian manifold, and let <P : M -*¦ R e Cm. Then for any measur-
measurable function f : M -*¦ R that is everywhere nonnegative or is in Ll(M), one
has
A.3.7) I f\gnd*\dV = f dvi(y) [
JM 7R 74>-l[y]
where grad * denotes the Riemannian gradient vector field of Q on M {see
§VIl
Corollary 132 Let A/* be a hypersurface in R* given by the graph of a C'
function 4>: G -> R, where G is open in R*; so M is given by
xk=4>(*1 **-'), (xl i»-')?C.
Then the surface area element on M, dA, is given by
where gradt_, denotes the gradient of functions on R*.
26
Introduction
Proof Let H be a hyperplane in R*, with normal vector i/; R* 'the hyperplane
{xk = 0} in R*, with normal vector ?; and p: H -> R*~' the projection. Then
A.3.9) JP = l«"?l-
Then apply A.3.6) with / = 1/ Jp, and calculate. ¦
Corollary 133 //fiCCR" w<J domain with C' boundary, v the exterior unit
normal vector field along dSi, and, for a given ? e S", p^ : dSl -> ?x is rte
projection, then
A.3.10)
/ |i/w
Jin
Proof Apply A.3.6), with / = 1. ¦
Corollary 13.4 If Si CC R" is a domain with C1 boundary, and for every
t e S", p^ : 3 ft -> ?L denotes the projection, then
A.3.11)
2u>n-l
Proof Integrate A.3.10) over ? e S". Then
/
in
an
= 2ACO)c.-2 / cose sin"Odd
Jo
n - 1
which implies the corollary.
Corollary 1.3.5 (Cauchy's Formula) If Si is convex, 30 e Cl. then
1.3 Preliminaries
Proof If Si is convex, then card (dSi n p4"'[>>]) = 2 for
all >> € P{CS2) = Pt(Si), ? e S", which implies the claim.
27
Corollary 13.6 If Si is convex, dSi e C1, and Qo is open containing Si.
C\ then
< ACfio)-
1.3.3 Some Geometric Preliminaries
Theorem L3.5 Suppose K is compact in R", with the property that, for any
? e S"~', K is symmetric with respect to some hyperplane perpendicular to ?.
Then the boundary ofK consists of a union of concentric (n — l)-spheres.
Proof Pick new Euclidean coordinates in R" so that K is symmetric with
respect to reflection in each of the coordinate planes. Then K is symmetric
with respect to the origin. Since any direction has an orthogonal hyperplane of
symmetry for K, and since K is already symmetric with respect to the origin,
then K must be symmetric with respect to any plane through the origin. Since
any half-line from the origin to 3 K can be taken to any other by a reflection in
a hyperplane through the origin, each connected component ofdK must be an
(n — l)-sphere centered at the origin. ¦
We recall just a few notions about convex sets in R".
Definition A set A in R" is convex ifx.yeA implies that Ajc + A - k)y e A
for all A. e @,1), that is, for any x and y in A the closed line segment [x, y] in
R" joining them is contained in A.
Definition A convex linear combination of elements xi,..., xt e R" is the
linear combination
where the coefficients satisfy
*
= 1, A.;>OVy.
One checks that if A is convex then any convex linear combination of elements
of A is a point in A.
28
Introduction
Definition Given AcR", define the convex hull of A, conv A, to be the smallest
convex set containing A.
Proposition 13.10 Given A, then conv A is given by the collection of all finite
convex linear combinations of elements of A.
If A is compact then conv A is compact.
If A is bounded, then conv A is bounded and diam conv A = diam A.
IfSis convex then S is convex.
IfSis convex compact then S = conv 35.
IfCis convex with nonempty interior, then int C is homeomorphic to R".
Definition Let A, B be subsets of R", and H a hyperplane. We say A and
B are separated by H if A and B lie in different closed half-spaces deter-
determined by H. If neither A nor B intersects H, we say H strictly separates A
and B.
Definition Let A be a subset of R", H a hyperplane, x € A. We say H is a
supporting hyperplane of A at x if x € H and H separates [x) and A. Note that
x g3A.
Proposition 13.11 Let A be closed, with nonempty interior. Then A is convex
if and only if every x e 3 A has a supporting hyperplane. Furthermore, if A is
closed convex, then A is the intersection of all closed half-spaces containing A.
L4 Bibliographic Notes
§1.1 For surveys of the isoperimetric inequality in Euclidean space, replete with his-
historical remarks and references, see Blaschke A9S6), Hadwiger A9S7), Osserman A978),
Talenti A993), and the more recent book by Burago and Zalgaller A988). For further
remarks, including some discussion of experimental proofs of the isoperimetric inequal-
inequality [one of which goes back to Courant and Robbins A941)], see Dierkes, Hildebrandt,
Kurster, and Wohlrab A992, pp. 42(M23).
On the issue of the proof of the isoperimetric inequality for general boundaries, the
following paragraph of Osserman A978, p. 1188) is worth repeating:
First, a general remark. If we start with a relatively smooth boundary, adding "wiggles"
to it will have very little effect on the volume enclosed, but will greatly increase the
surface area. Thus, one has the somewhat ironic situation that the more irregular the
boundary, the stronger will be the isoperimetric inequality, but the harder it is to prove.
The fact is, the isoperimetric inequality holds in the greatest generality imaginable, but
one needs suitable definitions even to state it.
1.4 Bibliographic Notes 29
The first unified solution of the isoperimetric problem in the model spaces of constant
sectional curvature (that is, Euclidean, spherical, and hyperbolic spaces) was given by
Schmidt A948, 1949). In Chavel A994) we gave separate proofs in each of the cases,
to highlight a variety of methods. The Euclidean argument given there will be given
in Theorem II.2.2 below. The isoperimetric argument for the sphere there is a new
Ricmannian theoretic argument by Gromov A986), and the hyperbolic space argu-
argument follows the symmetrization argument in Figiel, Lindenstrauss, and Milman A977).
Different symmetrization arguments will be developed here later.
The study of isoperimetric inequalities on surfaces is alive and well. See the discus-
discussions in Osserman A978,1979). More recent results can be found (just to give a sample)
in Adams and Morgan A999), Benjamini and Cao A996), Howards, Hutchings, and
Morgan A999), and Topping A997,1999). Extensive discussion of Bonnessen inequali-
inequalities can be found in Osserman A979).
§1.2 The complex variables proof follows Topping A997) (the proof was inspired by
F. Heiein). The Fourier series argument was first carried out by Hurwitz A901). The
name "Wirtinger's inequality" is apparently a misnomer. See the historical remarks in
the previous surveys.
Theorem 1.2.3 is from Howards, Hutchings, and Morgan A999). Blaschke A956,
p. 1), in discussing the idea, refers back to Steiner A881, p. 193ff).
The example of Remark 1.2.2 was supplied by an anonymous reader, to whom I extend
my thanks.
Another line of reasoning was initiated by M. Gage A984), wherein he proved that
if a convex curve in the Euclidean plane is deformed along its inward normal at a rate
proportional to its curvature at that point, then the isoperimetric ratio L2/A decreases to
the limit 4jt, and the convex curves become asymptotically circular - provided that the
shrinking curves do not develop singularities such as corners. The subject has developed
quite extensively since then (including the discussion whether the singularities exist),
both for surfaces and for higher dimensions, and one can find a partially updated bibli-
bibliography in Gage A991). Recent results, with applications to geometric inequalities, can
be found in Topping A998). Also, see Chou and Zho (scheduled to appear in 2001).
§13 For background in analysis, we generally follow Rudin A966). More recent
books that are helpful here are Licb and Loss A996) and Ziemer A989). Proposition
13.2 is from Federer A969, p. 69 ff.)
For treatments of Sard's theorem, see Hirsch A976) and Narasimhan A968). For the
strong maximum principle, see Gilbarg and Trudinger A977) and Protter and
Weinberger A984). For Sobolev spaces, see Adams A975) and Gilbarg and Trudinger
A977).
The general area and co-area formulae of geometric measure theory are discussed in
§3.2 of Federer's treatise A969). It seemed helpful to provide the general co-area formula
m the C1 category in order to see how much it contains, beyond the usual case of real-
valued functions. We present the area formula for Lipschitz mappings of R -*¦ R",
« < n, in §IV.2 below. The method of moving frames is discussed in Chavel A994).
One can find introductory material on convexity (including the Hahn-Banach theo-
*m and the Cauchy formula for areas of boundaries) in Berger's two-volume work on
Seometry A987, Chapters 11,12).
II
Differential Geometric Methods
In this chapter we present the differential geometric arguments. By their very
nature, they presuppose a certain smoothness of the boundary. Our method will
be to start with assuming that the boundary of the domain in which we are
interested is C2, and then weaken the assumption to just C1. We extend the
isoperimetric inequality to more general domains in the next chapter.
We use classical arguments to show that if a domain provides a solution to
the C2 isoperimetric problem, then the domain is a disk. Then we strengthen the
result a bit, to show that if the domain is just an extremal of the isoperimetric
functional, then it must be a disk (see the definitions below). More specifically,
we first introduce the standard local calculations of the differential geometry of
hypersurfaces in Euclidean space, and the first variations of volume and area of
domains and their boundaries under a 1-parameter family of diffeomorphisms.
Then we give Almgren's characterization of the solution to the isoperimetric
problem, followed by Alexandrov's characterization of an extremal for the
isoperimetric functional.
Thus, the C2 theory yields a characterization of the minimum (should it
exist) in its category. To prove the isoperimetric inequality for domains with C1
boundary, we present a proof based on Stokes's theorem, following M. Gromov.
The only drawback of the method is that, to characterize equality, one requires
that the domain be also assumed to be convex. We solve this latter problem with
Steiner symmetrization in the next chapter.
II.l The C2 Uniqueness Theory
II.l.l The Variation of Volume and Area
We first review the local calculations of classical differential geometry per-
pertaining to an (n — l)-dimensional regular hypersurface F in R". Although
we present the definitions of geometric quantities (such as the curvatures,
30
II.l The C2 Uniqueness Theory
31
Riemannian divergence, etc.) relative to specific choices of local coordinates,
standard arguments establish the invariance of these geometric quantities rela-
relative to changes of coordinates.
Assume F is given locally by the C1 mapping x : G -*¦ R" of everywhere
maximal rank, where G is an open subset of R". Sox = x(«); and the vectors
dx/du1 dx/du"'1
are linearly independent and span the tangent space to F at every x(u). We let
n(«) denote a choice of continuous normal unit vector field along F. When con-
considering a hypersurface F which is the boundary of a domain in R", the choice
for n will always be the exterior normal unit vector field - unless otherwise
indicated.
The Riemannian metric of F (that is, the first fundamental form) is given
locally by the positive definite matrix G(u), where
~(gjk), gjk - a||/gjf.
(II.l.l)
We also use the notation
G~l = (gjk), g = det G.
The associated surface area on F is given locally by
= 1 n-1.
Definition Let Q be a bounded domain in R", with C* boundary, k > 1. We
say that Q is a solution to the C* isoperimetric problem if, for any domain D
with C* boundary and volume equal to that of Q, we have A(dD) > A(dQ).
Let Q be a bounded domain in R", with C* boundary. We say that ft is a
Ck extremal of the isoperimetric functional if, for any 1-parameter family of
Ck diffeomorphisms *, : R" -> R" satisfying V(*,(?2)) = V(?2) for all t, we
have
d_
dt
= 0.
r=O
Assume that F is a C2 hypersurface in R" (so the Riemannian metric is C1)-
For any tangent vector field
dui
32 Differential Geometric Methods
along F, we have its Riemannian divergence (see §VII.2.1) given by
with an attendent intrinsic Riemannian divergence theorem for (n — 1)-
dimensional domains in F with Cl (n - 2)-dimensional boundaries; namely,
given an (n — l)-domain A CC F with C1 boundary 3A, and unit normal ex-
exterior (F-tangent) vector field u along 3 A, then
[
dA
The second fundamental form of F in R" is given locally by
32x
(II. 1.3)
Then
that is,
(II. 1.4)
bjk =
•n, j, k = 1, ...,n - 1.
32x _JL( dx\ dn dx - dn dx
Jk ~ dujduk'n~ duJ \n'duk) ~dul'~M ~ ~3^*3^*'
3x
If C — (Ljk) denotes the matrix of the G-self-adjoint linear transformation
associated with B, then
C = G~lB.
The mean curvature HofV in W is the trace of C, that is, the trace of B relative
to G, given by
and the Gauss-Kronecker curvature K of V in R" is the determinant of C, that
is, the determinant of B relative to G, given by
K = det G"'B.
We may think of n as a map that associates with every point x g F its normal
vector n g S" - commonly referred to as the Gauss map E : F -*¦ Sn~'. The
Jacobian linear transformation 0* of the Gauss map is then determined by
dx
dn
III The C2 Uniqueness Theory 33
Then (II. 1.4) implies that the matrix of E, is given by -C, which we write as
(II. 1.5) <d, = -G~lB.
Example IL1.1 If F is a relatively open subset of S"~'C). the (n - l>sphere
of radius r, then for the normal unit vector field along F exterior to B"(r), we
have
1
n = -x,
r
which implies [by (II. 1.4)]
therefore,
H = —
-1)
K =
rn-\
Theorem IL1.1 LetQ.be a bounded domain in R", with C2 boundary F. Given
anyC2 time-dependent vector field X :R"xR->R" onR", let *, : R" -*¦ R"
denote the 1 -parameter flow determined by X, that is, <t>, and X are related by
d_{
dt
Set
Then
(II. 1.6)
= / rj
ndA,
where n is chosen to be the exterior unit normal vector field along F, and
(II. 1.7) -A(*,(D)
at
= f {divr if - Hij-n}dA = - I Hrj-n dA.
where if denotes the tangential component ofi\.
Proof First,
= ff det U,(x)dyn(x),
34 Differential Geometric Methods
where 7<», denotes the Jacobian matrix of *,. Then
The formula for differentiating determinants states that for any differentiable
matrix function t k> A(t), where A(t) is nonsingular, one has
— det A = det A ¦ tr (A~l -- 1.
Therefore,
II
^ V(*,(«)) = ff (det 7*,) • tr
Now
so for/ = 0 we have, since *o = id,
3*,*
= \ n;
dxA
the Kronecker delta. Furthermore,
d . n c
— x &
f=0
3, 3**
3/
which implies, for r = 0,
r=0
which implies the first equality of (II. 1.6). The second equality follows from
the divergence theorem in R\
Assume the surface F is given locally by x = x(u), and set
For each fixed t we denote the Riemannian metric tensor on <D,(F) by
ay 3y . , ,
which implies
La(*,(D)= f ^¦
at Jr ot
H.I The C2 Uniqueness Theory
For the derivative of ^det (*_,-*), set H = (h)k), H~[ = (hjk)\ then
-VdetW= \
dt 2
w}~' det H ¦ (trW—
35
that is,
(II. 1.8)
3
m
3/
Set f = 0; then n(u) = (dy/dt)(u, 0). Write
v^ * 3x
along F. Then (II. 1.8) implies, for t = 0,
-%/detW
1=0
To calculate in more detail, one has
n-l
on x~~v I ( ox /OX i oq> on
—- = 2. 1 ~^—i + *? —:—7 I "•—^n + 0—^.
which implies, since n is perpendicular to 3x/3«* for all k = 1,..., n — 1,
a. 3x 3»)
;.*
3x
Ei* 91l v^ ,t / 9x 32x ^^ lk 3x 3n
gjKgki—-: + y g} n—• + y <t>gJ—•—
... duJ fr-J 3«* du(duJ *rr? duk duJ
;.*.< j.k.l j.k
,t 3x 3n
= divr rf - <pH.
36
Therefore,
Differential Geometric Methods
d_
di
= I (divr nT — Hn*n} dA.
Jr
Then the intrinsic Riemannian divergence theorem (II. 1.2) implies (since F is
closed, with no boundary) the second equality (II. 1.7). ¦
11.1.2 Uniqueness of a Solution to the C2 Isoperimetric Problem
Let SI be a bounded domain in R", with C2 boundary F. Recall that the nor-
normal unit vector along F is outward. Thus, if SI were convex, then the second
fundamental form B would be negative semidefinite.
Theorem II.1.2 Assume that SI is a solution to the C2 isoperimetric problem,
with volume of SI equal that of the unit n-disk in R". Then the mean curvature
H of T satisfies
-H <n-\
on all of V.
Proof Consider the isoperimetric functional
ACD)
where D varies over bounded domains in R" possessing C2 boundary. Let
4>, denote a 1-parameter family of diffeomorphisms of R", with associated
time-dependent vector field X = X(x, t) (as in the proof of Theorem II. 1.1),
?(*) = X(x, 0), 17 = ?|F. Then direct calculation implies, by (II.1.6), (II. 1.7),
and the fact that Si is an extremal of the isoperimetric functional,
°=JtH
va
which implies
( •¦ )
*/(?*))
1
1=0
f
Hrj-ndA
f rj-ndA
n-1
n
A(F)
A(F)
V(Sl)
(both integrals are over F). But since V(Sl) = u>n, and ?2 is a solution of the
//./ 77ie C2 Uniqueness Theory
isoperimetric problem, then A(F) < c,_i, which implies by A.1.3),
37
(H.1.10)
/ Hri-ndA
J rj-ndA
(both integrals are over F).
For any u>o e F, let 0 be a nonnegative C°° function compactly supported
on a neighborhood of wq in R", and choose
X(x, t) = 0(jc)na)o
(so this particular vector field is time-independent). Then by picking <p with
sufficiently small support about wo one obtains from (II. 1.10) that -H(wq) <
n — 1, which is the claim of the theorem. ¦
Remark II.1.1 The argument of the last paragraph, applied to (II. 1.9), implies
that H = const, namely H = (n - l)A(F)/n V(?2).
Theorem 11.13 Assume Q is a bounded domain in R", with C2 boundary F,
and n the exterior normal unit vector field along F. Assume the mean curvature
HofY satisfies
-H <n-\
along all of Y. Then
A(F) > c,,.!,
with equality if and only if SI is an n-disk.
Proof Start with Q = Q U F, and let C denote the convex hull of ?2, E = 3C
the boundary of C.
Letiu g E\(E n F), riasupportinghyperplaneofCatw.(SeeFigure0.1.1.)
Then there exists an x e Yl n (E n F) (if not, then C would not be the smallest
convex set containing SI), which implies (a) FT is the tangent hyperplane to F
at x, and (b) the line segment wx is contained in FI. These two imply that FT is
the unique supporting hyperplane to C at every point of vux, except possibly at
w. If n were not the unique supporting hyperplane of C at w, then E would
have a conical singularity at u\ which would imply that C is not the minimal
convex set containing Q. Therefore, every point of E has a unique supporting
hyperplane, that is, E is everywhere differentiable.
38
Differential Geometric Methods
Figure II. 1.1: The supporting hyperplane at x.
Since ? is convex, everywhere differentiable, then every point of ? has a
unique exterior unit normal vector, and the Gauss map
<3 : ? -> S"
that takes every point of w e ? to its exterior unit normal vector n(iu) is well
defined. The Gauss map is onto; furthermore, the Gauss map restricted to
?\(? fi F) adds no new points to the image in S"~' that are not already in
the image of ? n F, namely,
<&(?\(?nr))c<8(?nr).
Therefore, to calculate the image of the area of the Gauss map, that is, the area
of S", we restrict the integral to ? n F.
In a coordinate system on F, as described in the calculations above, the
Jacobian transformation of <8, <8,, is given in local coordinates by the linear
transformation described by —G~lB [see (II. 1.5)]. For points of ? n F we
have —B positive semidefinite, which implies, by the arithmetic-geometric
mean inequality,
_i = f
vnr
znr
-f
/snr
< A(?nF)
< A(F),
which implies the inequality.
If we have equality, then ? = F. Also, we have equality in the arithmetic-
geometric mean inequality, which implies all points are umbilics (that is, G~lB
11.1 The C2 Uniqueness Theory
39
is a scalar matrix at every point of F), which implies — G~' B is the identity.
Therefore (II. 1.4) implies there exists a constant vector b such that
n = x —b
on all of F. Thus
which implies F is a unit sphere.
11.1.3 Uniqueness of an Extremal of the C2 Isoperimetric Functional
Theorem II.1.4 Let SI be a bounded domain in R", with C2 boundary, that
is an extremal of the C2 isoperimetric functional. Then 3 ?2 has constant mean
curvature.
Proof Use the notation of Theorem II. 1.1, and set
4> =
If SI is an extremal for the isoperimetric functional then, for any choice of
vector field X for which
= const. Vf,
(such a flow is called incompressible) we have, by (II. 1.6),
/
Jr
and, by (II. 1.7),
/
Jr
<j>HdA = 0.
Thus,
/ 4>HdA=0 V0 such that [ 4>dA = 0.
Jr Jr
A standard argument [see the proof of A.2.3)] implies that H — const. ¦
We now write the equation for H as a second order elliptic quasilinear partial
differentia] operator of divergence form. We assume the hypersurface F is given
in nonparametric form, that is, the equation is described by
40 Differential Geometric Methods
over some domain in R"~'. So, in the parametric language,
xJ=uJ, ; = 1 n-l, JcB
Then
(where grad,,,, denotes the gradient in R"), from which one calculates the
metric tensor
30 30
which we write as
d<p
Note that
which implies
= |gradn_,|2A,
= /-
lgradB_,|2
Set
SJk =
Then for the second fundamental form we have
** ** ,c .
so B — <t>~lS. Then H = trG"'B implies
H = <D-'tr({/ - *
In what follows in this section (only), we substitute the notation V for gradn -1
Suppose we are given two fixed hypersurfaces
x" =
over some domain in R". Set
), IMC2,
and let //«,, H+ denote the mean curvatures associated with <p,ir, respectively
Similarly, we use the notations G* and G+, A$ and A+,S+ and 5^, to indicat
II.1 The C2 Uniqueness Theory
the quantities on each of the surfaces. Then direct calculation implies
41
-'t
-H+ = *-'tr(/ -
- *-')tr(/ -
Now
which implies
^
Also,
tr(A, -
>.*=!
where V@ + \fr) is written as a row vector.
Therefore there exist a vector field B on R" such that
where the operator .4 is given by
>lu) = *-'tr(/ -
We immediately have
Lemma II.l.l Considerthe hypersurfaces inR" determined by the functions
(f> and \fr, define A and B as above, and assume the two hypersurfaces have
identical mean curvature. Consider the second order linear elliptic differential
operator on R" given by
Luj = Aw +B-Vit).
Then the function w = <(> — \jr satisfies the second order linear equation
Lw = 0.
42
Differential Geometric Methods
Theorem n.1.5 Let Q be a bounded domain in R", with C2 boundary F, and
assume F has constant mean curvature. Then His an n-disk in R".
Proof settf = n
Fix any unit vector { g S", and pick Euclidean coordinates in R" so that
inf x" = 0
xeK
(where xn is the nth coordinate of x). Then there exists wo € F D {R" x {0}}
with tangent plane of F at wo equal to R" x {0}.
For each real a let no denote the hyperplane
na = R" x {a},
and set
Let
K~ = K n {xn <a], K+ = KH {xn > a],
r~ = rn[xn <a), r+ = rn[xn > a}.
rfl K~ = reflection of K~ in no,
rfl F~ = reflection of F~ in no.
(See Figure II. 1.2.) Then for sufficiently small a > 0, F~ has a nonparametric
representation over I~IO, and
Set
/3 = sup{a0 : rflK~ C AT+ Va < a0}
A x
R"
Figure II. 1.2: The reflection in na.
//./ The C2 Uniqueness Theory
43
Figure II. 1.3: Possibility (a).
Then one has two possibilities:
(a) There exists u>i g rfl FJ n F^", in which case rfl FJ and F^ are tangent at
u>,. (See Figure II. 1.3.)
(b) There exists w2 € F D FI^ such that the tangent hyperplane to F at w2 is
perpendicular to FI^. (See Figure II. 1.4.)
In either case (a) or (b) one may introduce Euclidean coordinates y =
(>',..., y") in R" about w - which is either wt or u>2 as the case may be -
so that r? and rfl F^ are described by
r,+ : yn=4>(y)\ TS_t, .,_K
rflr,
Figure II. 1.4: Possibility (b).
44
satisfying
Differential Geometric Methods
0(W) = Vr(W) = 0, V0(w) =
= 0.
[so w = (w, 0)]. Thus, the hyperplane v" = 0 is the tangent plane of the two
hypersurfaces at w. In case (a) we have if and \fr defined on some open set
U c R"-' about w, with
0 > V on U, 0(w) = Mw).
The strong maximum principle (Proposition 1.3.9), applied to Lemma II. 1.1,
then implies 0 = V on a neighborhood of w, and therefore on all of U. Thus
K is symmetric with respect to n^. Similarly, in case (b) we have 0 and V
defined on an open set U in R"~' with w g dU, and
> yjf onU,
where vu denotes the exterior normal (with respect to U) unit vector at w.
Again, the strong maximum principle implies <p = $ on all of U. Thus K is,
again, symmetric with respect to n^.
We conclude that given any { 6 S""', then K is symmetric with respect to
some hyperplane perpendicular to (. But then Theorem I.3.S implies 3 AT is a
finite union of concentric spheres. Since the mean curvature is constant on all
of f, one concludes that AT is a closed disk. ¦
IL2 The C1 Isoperimetric Inequality
We first establish the equivalence of the geometric isoperimetric inequality on
R" to an analytic Ll-Sobolev inequality.
Definition Define the isoperimetric constant 3 ofW by
3 = inf-
where ?2 varies over bounded domains in R" with C1 boundary.
Define the Sobolev constant 6 o/R" by
/ 11/11,
where / varies over C~(R").
11.2 TheCx Isoperimetric Inequality
45
Theorem IL2.1 (The Federer-Fkming Theorem) The isoperimetric and
Sobolev constants are equal, that is,
(II.2.1)
3 = 6.
Proof Let ?2 be any bounded domain in R" with C1 boundary. For sufficiently
small ( > 0 consider the function
II, Jte«,
\-(l/()d(x,dn), JceR"\n, d(x,dn)<€,
0, jceR"\f2, d(x,dn)>€.
Then f( is Lipschitz for every €, and (by Theorem 1.3.3) we may approximate
/, by functions <p(J e CfXR") for which
110*.; - /t|l<i/(«-i) -»¦ 0, ||grad0€,y - grad/€||i ^- 0
as j -*¦ oo. One has
llgrad/,11,
6 <
IIAII,
One checks that
lim
= V(Q).
Also,
which implies
lim /
Thus,
lgrad/<l =
, d(x,dSl)<(,
otherwise,
lim
for all such Q, from which we conclude
S<3.
It remains to prove the opposite inequality, that is,
(n.2.2)
forall/eC^R").
\f\n/("-l)dV
l-l/n
46 Differential Geometric Methods
Lemma IL2.1 Given any<p e C~(R"), then
(II.2.3) |grad |0| | = |grad0|
almost everywhere on R".
Proof On the open set {0 > 0} wehave|0| = 0, and on the open set {0 < 0}we
have |0| = -0, and (II.2.3) is certainly valid. Also, {0 = 0} n {grad0 9^ 0} is
an (n - l)-submanifoldof R", which implies yn([<p = 0} D {grad0 ^ 0}) = 0.
It remains to consider what happens when 0 = 0 and grad 0 = 0. Set, for
any e > 0,
Then0e -»¦ |0| ase 4,0, and grad 0€ -»¦ ±grad0ase 4,Owhen0 ^ 0(depend-
ing on whether 0 is positive or negative at the point in question). When 0 = 0,
then grad0c = 0; therefore grad0e -> grad 0 when 0 = 0 and grad0 = 0. In-
Integration by parts implies grad0e converges to the weak derivative of |0| in
Wu, which is grad |0|. ¦
Proof of (II.2.2) Given / g Cf(R"), let
n«) = {x : \f\(x) > t), V{t) =
Then the co-area formula (Corollary 1.3.1) implies
/ \gmdf\dV= HA(\f\-l[t])dt>3 f V(t)l-l/ndt,
JR> JO JO
and, by Cavalieri's principle (Proposition 1.3.3),
f |/r/c-D<fv= » rt
Jit- n — l Jo
So to prove (II.2.2) it suffices to show
01.2.4) f°°V(t)l-l/ndt > 1-5- /"OOri/c
Jo In - Wo
To establish (II.2.4) set
F(s) = T VC*I/" A, C(j) = (-?— I' t[/(n-l)V(t)dt
Jo I»— Wo
First,
F@) = G@);
//.2 r/i« C1 lsoperimetric Inequality
second, since V(s) is a decreasing function of j, we have
n — 1 f n I1/" f f
G'E) = l-il-5_l j r>/<-')
47
Then (II.2.4) follows immediately. ¦
Theorem 11.22 (lsoperimetric Inequality for C1 Surface Area) Let SI be a
bounded domain in R", with C1 boundary dQ. Then
(II.2.5)
Proof By the Federer-Fleming theorem (Theorem II.2.1), it suffices to show
that
A1.2.6)
j
Igrad/lrfV >
for all / € Ce°°(R").
Set C = [0, 1 ]", the unit n-cube in R". To prove (II.2.6) we first consider, for
any nonnegative function \i e C^R"), the maps uJ : R" -> [0, 00) defined by
uJ(x) = / d^ / fi(xl xJ-\ &. $'¦+»,....
J-00 JtL-l
7 = 1 n, and the function r\: R" -> C defined by
Then 17 = (^' rj") maps R" onto C, and
XJ), —'- =
[where we set un+\x) = fi(x)], which implies
det /„(*) = fj |^(,) = j j^ rtx) dx J
where 7, (jc) denotes the Jacobian linear transformation of rj at x.
48
Differential Geometric Methods
The best way to appreciate the mapping is to interpret it when ft is a bounded
domain in R" with C1 boundary, and fi = Xn, the indicator function of the
domain ft [despite the fact that, in this case, fi ? Cj(R")]. Then
«'(*) = vfl(ft)
:$¦<*¦})
and
vB(ft)
u2(x) = vfl_i(ft n {? € R" : *' = x1}),
2 _ Vn-l(ft n(|6B":?'= X\ I;2 < X2})
{X)
and, more generally,
= vB_,+1(ft n « :?' = *»,... ,
XJ])
(See Figure II.2.1.)
If Q is convex, then tj € C'(?2) n C°(?2), and ./tjC*) extends to a continuous
matrix function on ft. A special case is ft = B", in which case we denote tj
corresponding to Ib» by *. Then <t>\B" : B" -* C is & diffeomorphism, with
~l
det 7* = um~l.
We return to the general \i € CJ(R"), set
x2
length = v\x)n2(x)
Figure II.2.1: When fi = Z^j.
//.2 77ie C' Isoperimetric Inequality
49
and think of C as a vector field on R" with Kl < 1, as well as a mapping of R"
onto B". Then
umfi(x) = det
I ^ 1
by the arithmetic-geometric mean inequality.
To apply the above, given any nonnegative f e Cf, consider
Then (II.2.7) implies
= f(x)fi(x)l/n
which implies
A1.2.8)
lgrad/|<fV,
which implies (II.2.6) for / > 0.
Forarbitrary / e C(!,let(,/<)beamollifieronR'1 andsetF, = j, * \f\. Then
(II.2.8) implies
Let e 4,0; then, by Lemma II.2.1,
To consider the case of equality in (II.2.5), we consider, more closely, what
happens when fi = In, for the bounded domain ft with C' boundary. But we
must^assume that ft is convex to guarantee that the mapping { € C'(ft) n
C°(ft), and to guarantee that 7c(jc) extends to a continuous matrix function
on ft. First, we repeat the argument for the inequality. For all x € ft, (II.2.7)
implies
A1.2.9)
V(ftI/n
50 Differential Geometric Methods
which implies, by the standard divergence theorem,
f
/
which is the original version of the isoperimetric inequality.
If we have equality, then we have equality in (II.2.7) and (II.2.9) - which
implies
<niI1)
• >"' "•
on all of ?2; and we have equality in (II.2.10) - which implies
(II.2.12)
on all of 3?2. For convenience we assume V(Sl) = av. so wB/ V(?2) = 1.
From (II.2.11) we conclude, sinceC,J = t.J(xl,....x'), that
= XJ
for all j = 1 n (for / = 1, a' = const.)- On the boundary of ?2 we have
(since C|3?2 : 3 ?2 -> S")
From (II.2.12) we conclude that there exists a constant X (depending at most
on the point of the boundary of ?2) such that
for all j = 1 n. From the case j = n we have A. = 1 for all f" ^ 0, which
implies
N^ * 3«* ^
t—1 dxJ
for all points of 3 ?2 for which ?" ^ 0.
II. 3 Bibliographic Notes
51
Fix x',..., xn~2. Then
^r = °.
which implies that the locus {^r =const.r : t = 1, ...,n — 2}n3?2isacircle.
Thus the intersection of any 2-plane with dQ is a translate of a circle on the
sphere. Thus the intersection of Q with any 2-plane is a 2-disk of radius less
than or equal to 1.
Now the map < takes Si onto B". Therefore there must exist at least one 2-
plane for which its intersection with SI is a 2-disk of radius equal to 1. Pick two
antipodal points m \ and mi on the boundary of this 2-disk of radius equal to 1.
Then for any 2-plane through m \ and m2 the intersection of this new 2-plane
with ?2 is a 2-disk; since this new 2-disk contains m\ and m2, it must also have
radius equal to 1. We conclude that for every 2-plane through mi and tn2 the
intersection of the 2-plane with ?2 is a 2-disk with radius equal to 1. But then ?2
itself is an n-disk of radius equal to 1 and center at the midpoint of m \ and mi.
IIJ Bibliographic Notes
§11.1.1 The calculations of this section are classical, and one can find the necessary
background in the standard books. Nowadays, it is not fashionable to do the calculations
in local coordinates, but for a hypersurface in R" they are still extremely useful.
§11.1.2 The paper of F. Almgren A986), on which this section is based, is far more
ambitious than the result presented here. In fact, our formulation constitituted only
the heuristic for his results. Almgren starts with a (* - l>dimensional submanifold T
(not necessarily a hypersurface) of R\ * < n, and then seeks a * -submanifold Q with
boundary r that minimizes *-dimensional measure among all /fc-submanifolds bounded
by r. For the pair ($2, T), he then proves the *-dimensional isoperimetric inequality.
The first version of this theorem (the isoperimetric inequality for minimal surfaces) goes
back to Carleman A921). But Carleman's theorem assumes the existence of the minimal
surface, and that it is topologically a disk. Here, the existence must be proven as well.
Since it is known that one cannot expect (in sufficiently high dimensions) an everywhere
smooth area-minimizing submanifold $2 spanning T, one must broaden the competition
of submanifolds fi to more general geometric objects. But then one can include more
general r. We also note that methods are sufficiently powerful to yield characterization
of equality in the isoperimetric inequality, namely, it is realized if and only if T is a
(* - l)-sphere bounding a A-disk Cl.
§11.1.3 Our proof of Alexandra's theorem (Theorem II. 1.5) follows his original
A962). A subsequent analytic proof was given by Reilly A977). A more recent proof
was given in Ros A988); see the presentation in Oprea A997), Chapter 4. Earlier results
can be found in Liebmann A900) and Hopf A950).
§IL2 Federer-Fleming theorem was first proven independently in Federer and
Fleming A960) and Maz'ya A960); and the isoperimetric inequality for C1 surface
area is from Gromov A986), based on an idea of Knothe A957).
Ill
Minkowski Area and Perimeter
In this chapter, we take some first steps in geometric measure theory, namely, we
consider general compact sets, irrespective of the smoothness of their bound-
boundaries; and our prime method for proving the isoperimetric inequality for them
(after we give suitable definitions of the area of the boundary) is by Steiner
symmetrization. The symmetrization argument has great appeal to geometric
intuition (although its first presentation by Steiner was incomplete), so we work
with it in some detail. There are many other symmetrization schemes (see the
bibliographic notes at the end of the chapter); but Steiner symmetrization lends
itself, especially in the case of Minkowski area, to very simple arguments for
the isoperimetric inequality. Moreover, we are able, in the case of C' boundary,
to stay within the arguments of Minkowski area and Steiner symmetrization to
characterize the disk as the only case of equality. The argument of this last char-
characterization seems to be new, albeit unnecessary - because we shall characterize
equality in the more general setting of finite perimeter. However, it is a useful
preparation for the general argument Also, the C' isoperimetric inequality suf-
suffices to prove the Faber-Krahn inequality (§111.3 below) with characterization
of equality.
There are two types of possible definitions of areas of the boundary dK of
an arbitrary compact set K:
1. The area of 3 AT views 9 AT as a subset of R" without, necessarily, any reference
to K. Two examples are the (n — 1 )-dimensional Riemannian measure of a
C1 hypersurface of R", and the (n - 1 )-dimensional Hausdorff measure of
any arbitrary subset F of R" (to be considered below in Chapter IV). In each
example, the two definitions are simply applied to dK.
2. The second type of definition of area is a functional defined on the collection
of compact subsets of R", which assigns to each compact subset a num-
number meant to describe the area of its boundary. The examples we consider
52
///./ The Hausdorff Metric on Compacta
53
below are Minkowski area and perimeter. Our most general formulation
of the isoperimetric inequality for compact sets uses perimeter instead of
Minkowski area; and we are able, in the category of finite perimeter, to char-
characterize the case of equality. So, for us, this will be the optimal solution to
the isoperimetric problem.
Practical differences between Minkowski area and perimeter include the
following:
1. The perimeter functional is lower semicontinuous with respect to conver-
convergence of indicator functions in Ll, whereas no such semicontinuity exists,
in general, for the Minkowski area functional with respect to Hausdorff con-
convergence of compact sets. Nevertheless, one does have a restricted version
of lower semicontinuity for Minkowski area (see the end of the proof of
Theorem IH.2.8 below).
2. It is possible for a compact subset of R" to have n-dimensional Lebesgue
measure equal to 0 but its boundary to have positive Minkowski area, which
is not the case with perimeter.
3. Minkowski area has no natural localization for a relative neighborhood in the
boundary (but see a partial attempt in the proof of Theorem III.2.4), whereas
perimeter does.
4. Finally, the isoperimetric inequality for perimeter is sharper than the isoperi-
isoperimetric inequality for Minkowski area.
We note that a third example of the first type of area is the (n - \)-dimensional
integral geometric area IGA"~l(F) of a subset F of R", given by Corollary
1.3.4,
where pi denotes projection onto the hyperplane ^1. But we do not go into any
details here.
III.l The Hausdorff Metric on Compacta
Definition Let (X, d) be a metric space. For any compact subset K of X, define
the circumradius of K, r(K), by
r(K) = inf {p > 0: K c D(x; p) for some x e X).
Notation (Recall.) D(x;p) denotes the closed n-disk in R" of radius p, and
centered at x.
54
Minkowski Area and Perimeter
Notation (Recall.) Let (X, d) be a metric space. For any subset A in X, and
€ > 0, [A]f denotes the (-thickening of A, defined by
[A]( = {xeX:d(x,A)<€].
Remark UI.1.1 If A c [B]r and B c [C](, then A c [C]r+(. Also, if K is
compact, then
k = n [/a.
Definition Let X denote the collection of compact subsets of X. Given E and
F in X, define their Hausdorff distance, &(E, F), by
8(E, F) = inf {c > 0: ? C [F],, F C [?]<}.
One checks that (?, F) )-> 8(E, F) satisfies the axioms of a metric space.
Lemma III. 1.1 Let X be an arbitrary metric space. Then the junctions
K !-> r(K), K i-> diam K
are continuous on X.
Iffiisa positive measure on X that is finite on compact subsets, then
is upper semicontinuous on X, that is,
limsup fi(Ej)
for any convergent sequence (Ej) in X.
Proof If c > 0, and E, F e X satisfy S(E, F) < c, then, for any x e X and
R > 0 for which we have E c D(x; R), we must also have F c D(x; R + c).
This implies
r(F) </¦(?) + €.
By switching the roles of E and F, we obtain
which implies the claim for the circumradius.
Similarly, if E, F e X, and E c [F]«, then
< diam F + 2e.
diam E < diam
One easily has that 8(E, F) < c implies |diam E - diam F| < 2e.
1111 The Hausdorff Metric on Compact a
55
If Ej -*¦ E, then, given any c > 0, we have Ej C [E]( for sufficiently large
j, which implies fi(Ej) < fi([E]() for sufficiently large j, which implies
for all c > 0, which implies the claim. ¦
Theorem III.l.l (Blaschke Selection Theorem) Assume that (X, d) has the
property that closed and bounded subsets are compact. Then X, the space of
compact subsets of X, is complete. Furthermore, if X is compact then X is
compact.
Proof Let (?,) be a Cauchy sequence in X. Then consider
We claim that ?; converges to ? in the Hausdorff metric.
The Cauchy hypothesis implies that
is bounded for each j, which implies that
is compact for each j, which implies that E is nonempty compact.
Given e > 0, there exists N( > 0 such that
which implies
which implies
To prove that
Ec[Ej](
56 Minkowski Area and Perimeter
we argue as follows. If x € Ej, then x € [E& for all i > j, which implies
which implies that for each it > j there exists yk e Uo*?i suchthat<f(jt, >*) <
c. Since (y*) is a bounded sequence, it has a subsequence converging to some
point Jto- Since yt € (J,>* ?, for all I > k, we have xo € cl (J/>t ?, for all
* > j, which implies jc0 e ?, and <f (jc, x0) < €, which implies
Jc 6 [E](.
Therefore X is complete.
Assume X is compact. Let (Ej) be a sequence in X, all Ej pairwise distinct.
Given c > 0, there exists a cover of X by open metric disks B(x,;c), i =
1,..., M. Then there exists at least one subset
{*<, xit) ?{xi,...,
for which the cardinality
card \ES:ES c\J B(xit;e), Es D B(xit;() # 0 V ik
*=i
ik I = oo.
Then, for each such Es we have
Es C U «(*(,;«) C [?,]2<.
Set ?,,o = ?(, the original sequence. Assume one has the subsequence (Ei:N)
of (?(). Pick the subsequence (Ei;N+i) of (?<;*) by applying the above argument
,;*) with c = l/(N + 1). Set
In*,
GN+l =
*=i
Then
which implies
III. 1 The Hausdorff Metric on Compacta
57
which implies
N
for all i, j. Set FN = EN;N. Then
4
mm{^V, AT'}
which implies (/>) is a Cauchy sequence, which, by completeness, has a
limit. ¦
Let (X, d) be a metric space such that closed and bounded subsets of X are
compact. Then for each compact K c X there exists jc0 e X such that K c
D(xo; r(K)), where r(K) denotes the circumradius of K. We refer to this closed
metric disk as a circumdisk ofK, and denote it by DK. In Euclidean space R",
Dk is unique.
Lemma III.1.2 Assume also that n is a positive measure on X, and that
(X, d, fi) is homogeneous with respect to the metric and measure, that is, for
every x, y € X there exists a bisection <P '¦ X -*¦ X, preserving the distance d
and the measure fi, and taking x to y.
Given K € X, define
M{K) = {F 6 X:
Then there exists E e M(AT) such that
r(E) — min r(F).
FeMW
> 0}.
Similarly, given K e X, define
fi(K) = {F eX:n(.F)>n(K), diam F < diam K).
Then there exists E' e N(AT) such that
r(E')= min r(F).
N+l'
Proof Because we wish to minimize r(F) in both statements of the lemma,
it suffices to consider only those F e X for which r(F) < r(K). Furthermore,
because of the homogeneity of the metric and measure, it suffices to consider
only those F contained in DK, a circumdisk of K. Let
H = {FeX:FcZ>*}.
Then we already know that H is compact.
58 Minkowski Area and Perimeter
In the first statement of the lemma, we let
and
There exists a sequence (Fj) in Mo(/0 with r(Fj) -> a as ji -»• oo. Since
Mo(/ST) C H, there exists a convergent subsequence Ek -»¦?,? e H. By the
continuity of F h> r(F), we have r(E) = or. Therefore, it suffices to show
E € M(A").
Since fi(Ek) = fi(K) for all k, we have fi(K) < n(E). Given any € > 0,
there exists J > 0 such that 7 > 7 implies
o= inf r(F)= inf r(F).
FeM(JC) FeMo(K)
E C [?,]„
[?]* C
which implies
for all h > 0, which implies
Thus,
for all €, Ji > 0. First let c -> 0 and then h -* 0. One then has ? e M(/ST),
which implies the first claim.
In the second statement of the lemma, we let
and
Since H is compact, and N(K) is closed, we conclude that N0(AT) is compact,
and the second claim follows from the continuity of the functions F h> r(F)
and F -* diam F. ¦
III.2 Minkowski Area and Steiner Symmetrization
Definition Given a compact subset K of R", we define its Minkowski area
Mink (tf) by
Mink (K) = hm inf
A40
= inf r(F) = inf r(F)
fN(JC) F<EN(K)
III.2 Minkowski Area and Steiner Symmetrization 59
Remark III.2.1 Note that K t-> Mink (AT) is a functional defined on the col-
collection of compacts sets K - not on the boundary of K.
Remark IIL2.2 When n = 1, then
(III.2.1) Mink(tf) = 2 + 2(card {components of R \ K\ - 2).
In particular, the Minkowski area of a point x0 is 2, at the same time that
v({jc}) O
Remark III.2-3 When K is the closure of a domain SI in R", with C1 boundary
3Q, then it is a standard exercise in differential geometry that
where A denotes the standard Riemannian (n — l)-dimensional area.
Definition Let X = R\ X the collection of compact subsets of R" with
Hausdorff metric, and IT a hyperplane in R".
For every x € R", let I* denote the line in R" through x that is perpendicular
to IT. For every compact subset K of R" define the Steiner symmetrization of
K with respect to IT, stn K, by
stn K = (J {h-} x lw,
wen
where r denotes the closed interval in R,
lw = [-ow,aw], ow = ^v,(r n K).
So Vi(Iw) = y{(ew D K). (See Figure ffl.2.1.)
1 ¦ One verifies that stn K 's compact if K is compact.
2. Also, since
(HI.2.3)
we have
(III.2.4)
*n(K)
= f v,(r n
K)dyn_i(w),
vn(stn K) = yn(K)
for all K € X.
3- If t is a translation of R", then str(n) (tf) = t(stn (K)).
Lemma III.2.1 Let K € X, and assume K ^ ?>*, that is, K is not equal to
its circumdisk. Then there exist a finite number of Steiner symmetrizations in
60
Minkowski Area and Perimeter
n
slnK
Figure III.2.1: Steiner symmetrization.
hyperplanes U \,... Tlk such that
<r(K).
Proof The proof of the lemma rests on the following fact: Given a closed
n-disk D in R", with boundary (n — l)-sphere 5. Let o denote the center of D,
and n a hyperplane through o. For xeO, let {jci, JC2} = txC\S. Then given
c > 0, there exists 8 = 8(e, n) > 0 such that
D \stn (D
Bs(xl;8) U Bs{x2;8),
where Bs denotes the spherical cap in 5 with indicated center and radius. (See
Figure III.2.2.) That is, if we remove a disk in D of radius t. centered at jc,
then after we Steiner symmetrize we are missing spherical caps in S of radius
8 and centered at Jti and x2. If x € 5, then 8 can be chosen independent of the
plane PI.
Figure m.2.2: Steiner symmetrization for disk with hole.
111.2 Minkowski Area and Steiner Symmetrization 61
We now prove the lemma. We are given that K ^ DK. Let 5 denote the
boundary sphere of ?>*. We may assume that K C\S ^ S. For if not, there
exists a disk in the interior of DK, and in the complement of K. Then any
symmetrization st with respect to a plane through the origin o of DK will
produce spherical neighborhoods in 5 contained in Dk\ st K.
So we assume K n S ^ 5. Since DK \ K is relatively open, it suffices to
produce a finite number of planes FI i,.... FI* for which
(III.2.5) (stn, o-..ostn4tf)nS = 0.
Given x e S\K, there exists e > 0 such that the spherical cap Bs(x;e) c
S\K. Then the compactness of AT n S implies there exist a finite number
of points xi xic in K C\ S such that the (relatively) open spherical caps
{Bs(X)\e): j - 1 k) cover K D S, that is,
k
[J Bs(xj;e)DSnK.
For each j, consider the hyperplane FI; bisecting the chord xxj . Then this choice
of Fly, _/ = 1,..., k will satisfy (III.2.5), which implies the lemma. ¦
Theorem IIIJ5.1 (Isodiametric Inequality) For any K eXwe have
fdiam ATI"
2 J '
Thus, the disk minimizes the diameter of a compact set of given volume.
Proof We first show that given any F e X, we have
(III.2.6) diam stn F < diam F,
for any hyperplane FI in R".
Pick Euclidean coordinates in Rn where FI is identified by x" = 0, and write
R" as R"-1 x R with R" = n, and R = 1°, where o is the origin of R". Let
(w, a) and (v, /?) maximize distance in stn ^> that is,
d((w, a), (v, /?)) = diam stn F,
where w, v e R", a, /? e R. Because
d((w, a), (v, B)) = J\w-v\2+(a-B)>,
we must have both cases
a = — aw, B=av and a = aw, B = —av.
62
Let
Minkowski Area and Perimeter
= min (w D F, nw = max (w n F,
= min t D F, nv = max lv n F.
Then
which implies
so at least one of nw + fv or nv + ?w must be >|or| + |/J|, which implies
(III.2.6).
To finish the proof, given K, we consider the compact set E' in N(AT) that
minimizes the circumradius (Lemma III. 1.2). We claim that D?< = ?', that
is, ?' is a disk. If not, then Steiner symmetrizations preserve N(AT) [that is,
F e N(/O implies stn F e N(JO V n], and there exist a finite number of them
whose composition lowers the circumradius (Lemma III.2.1), which contradicts
the definition of E'. But 2r(E') < diam K, which implies
J" >
which implies the theorem.
III.2.1 The Isoperimetric Inequality for Minkowski Area
Theorem IIL2.2 (Brunn-Minkowski Inequality) Given K e X, let D de-
denote the closed n-disk of the same measure as K, that is, vn(Z>) = \n(K). Then
for all ( >0.
Proof First note that, by (III.2.1), the theorem is true if n = 1.
For general n > 1, we take the same approach as in the proof of the isodia-
metric inequality, namely, we first show that
(ffl.2.7) vB([stn F]f) <
for all F e X, c > 0, and all hyperplanes n in R".
111.2 Minkowski Area and Steiner Symmetrization 63
Pick Euclidean coordinates in R" so that n = R"~' x {0} - so we identify FI
with R", let o be the origin of R" , and V = R, as in the proof of Theo-
Theorem III.2.1. Let q : R" -*¦ R denote projection onto the jt"-axis= 1°. For any
well, let zw : R" -»¦ R" denote the translation by w. To help avoid confusion,
weletD(H';c) = ]Dn~1(H';c)denotetheclosed(n - l)-disk in U centered at w
and with radius e. Given wen, and F e X, then
(FH.2.8)
veD(w:t)
[We have written the formula in this manner to emphasize that we project
f C\F onto the x"-axis to obtain q(lv n F), carry out the 1-dimensional
v/e2 - |v — w|2-thickening in the x" -axis, and then translate out to the line lw.]
To prove (III.2.8) just note that (h>, a) € [F]^ if and only if there exists (v, /?) e
Fsuchthat|H' - v|2 + (P -aJ < c2,whichistrueifandonlyif<fRi(a,q(tv D
F)) < y/f2 — \w — v|2, which is the claim. Therefore
where /" is the 1-dimensional symmetrization ofivC\F (to pass from the
second to the third line we use the 1-dimensional isoperimetric inequality),
that is,
(IIF.2.9)
n [stn F]<) < v,(r n
Then (III.2.3) and (IU.2.9) imply (III.2.7).
To finish the proof, given K, we consider the compact set E in M( AT) which
minimizes the circumradius (Lemma III. 1.2). We claim that DE = E, that is,
? is a disk. If not, then Steiner symmetrizations preserve M(AT), and there
exist a finite number of them whose composition lowers the circumradius
(Lemma III.2.1), which contradicts the definition of E. ¦
Theorem 111.23 (Isoperimetric Inequality for Minkowski Area) If K is a
compact subset o/R", then Steiner symmetrization of K does not increase its
64 Minkowski Area and Perimeter
Minkowski area, that is,
A11.2.10) Mink (stn AT) < Mink (K)
for any hyperplane n.
Furthermore, if the closed n-disk D"(/?) has the same measure as K, then
A11.2.11) A(S"-'(/?)) = Mink(D"(K)) < Mink(iT).
If K is the closure of an open subset ?2 in R" with Cl boundary 3 ?2, then
(in.2.12) A($"-l(R))< AC?2),
which is expressed analytically as
(im.13) _A^]._>nu,V»
Proof Indeed, Theorem III.2.2 implies
+ h)) -
for all h > 0, which implies the claim. ¦
The problem with this approach is that while it quickly and elementarily gives
the isoperimetric inequality, it cannot characterize the case of equality - unless
one can sharpen the Brunn-Minkowski inequality to include an error term that
persists to the limit, as h -*¦ 0, and that vanishes if and only if AT is a disk. In
what follows, we shall give a variant of this argument.
Theorem IIL2.4 Assume SihasC1 boundary, K = ?2 compact. One has equal-
equality in (III.2.12) [equivalent^, (III.2.13)] if and only if SI isadisk.
Proof First note that we have the theorem for n = 1.
One might wish to apply Steiner symmerization directly to prove
ACstn ?2) < AC?2),
and then characterize the case of equality. But one does not know in advance that
if ?2 has C' boundary, Steiner symmetrization will preserve this smoothness.
(One can easily construct counterexamples. See Figure m.2.1.) Yet, there are
obvious examples where some smoothness is preserved. We show that this is
III.2 Minkowski Area and Steiner Symmetrization 65
always true, and the smoothness that is preserved has enough information to
provide the characterization of equality in (III.2.12) we are seeking.
Namely, we first give a local analogue of (m.2.7). Let n be a hyperplane in
R", and coordinatize R" as in the proof of Theorem ffl.2.1. For z e R" and
t > 0, let (as above) D(z; e) denote the closed (n - l)-disk in R" centered at
z with radius c, and let C(z;c) denote the solid n-cylinder in R" over D(z;c),
that is,
C(z;c) = D(z;c)xR.
For z e R"~', c > 0, and compact K in R", we have
V(ATnC(z;c))= f v,(r C\K)dyn.i(w)= V(stn AT nC(z;c)),
JD(z;t)
We define a "localized" Minkowski area Mink nu;( by
(See Figure m.2.3.) Then (HI.2.9) implies
(III.2.14) V ([stn K]h nC(z;c)) < V ([K]h nC(z;c)) ,
Figure m.2.3: {[*]»\*}nC(z;«).
66 Minkowski Area and Perimeter
which implies
(m.2.15) Mink n^;«(stn K) < Mink n^*"),
Return to K equal to the closure of Q with C1 boundary d&. Let
denote the projection map. Fix z e R"~' and c > 0, and assume that D(z;e)
consists of regular values of the projection of dQ, p\3Q. Let u denote the
exterior unit normal vector field along 3 ?2, and
Eh = [v
u, u e
t e
that is, Eh is the curved slab of thickness h determined by starting out at points
u € 3 ?2 sitting over D(z; c) and going out h units in the direction uu.
Lemma 111.2^ We have the differential geometric estimate
(m.2.16) wa[K]h \jr}nc(c«»- V([Eh])\ = O(h2)
ash 10. In particular,
Minkn.j;<(K) = AC?2 n C(z;c)).
Proof (See Figure III.2.4.) Let T = 3f2 n 3C(z;c). Then T is a compact C'
(n — 2)-dimensional submanifold of R", with fiber at w € F in the normal bun-
bundle of F, spanned by uw (the unit normal exterior vector field along dQ) and nw
[the unit normal exterior vector field along 3C(z; c)]. The linear independence
of vw and nw is guaranteed by the assumption that p is regular on all of D(z; t).
For each w e T, let
,, vw) e @,7r) and * = inf sin dw.
wer
For any r > 0, [F]r, the tubular neighborhood of F of radius r, satisfies
V([F]r) = O(r2)
as r 4, 0, since F has codimension 2. For any a > 1, an application of Taylor's
formula shows that the symmetric difference {[[K]h \K}n C(z;c)} A Eh of
{[K]h \K]D C(z;c) and Eh satisfies
\
A Eh C
as h i 0, which implies (III.2.16).
III.2 Minkowski Area and Steiner Symmetrization
67
Figure m.2.4: ?».
Lemma W.23 Assume that D(z; c) consists of regular values of the projection
of<M, p\dQ. Let
< < ak(w)
be C1 Junctions on D(z; c) such that
for all w € D(z; €). Define
Then
forallweD(z,€),and
(ni.2.17) AC(stn f2)nC(z;c)) < ACOnC(z;c))
with equality if and only ifk = 1, and SI D C(z;«) ij symmetric, up to transla-
translation, with respect to the hyperplane U.
n stn #: = [-
68 Minkowski Area and Perimeter
Proof Note that w »->• A(w) is C1, and
Mink n:z;((stn K) = A(8stn ft n C(z; c)),
by Lemma III.2.2. To compare the boundary areas, we have
A(8ftnC(z;O) = /"
where grad^cr, is the (n - l)-vector(8cr,78wi,... 8cr;/8wn_i), and the same
for gradn_,/3;, j = 1 k, and
A(8(stn
Two applications of the triangle inequality imply
;c)) = 2 f
|gradn_, - a,-|
(IH.2.18)
and
k
Therefore
(in.2.19) if Jk2 + |gradn_,,4|2 dvn_, < A(8« n C(z;OX
which implies A11.2.17). We have equality in (III.2.17) if and only if k = 1, and
the vectors (gradn_, -cri(w), l)and(gradn_,0i(w), 1) are linearly dependent.
Hence (since their last coordinate is equal),
= -Pi(w) + const.
on all of D(z; e), which implies ft D C(z; e) is symmetric, up to a translation,
with respect to the hyperplane n. ¦
Conclusion of the Proof of Theorem m.2.4. Sard's theorem (Proposition
1.3.8) implies that z is a regular value of p|8ft for almost all z e p(dft). Given
such a z e p(8ft), there exists e > 0 such that D(z;O consists only of regular
111.2 Minkowski Area and Steiner Symmetrization
69
values, for which (HI.2.17) follows, with its characterization of the case of
equality.
If we have equality in (III.2.12), then Steiner symmetrization does not strictly
decrease the Minkowski area of the boundary. In particular, we have equality in
(III.2.15) for any hyperplane n, z e n, and c > 0. Therefore, we have equality
in (HI.2.17) for all regular values of p\dQ. Therefore, by continuity, and by
applying the argument to every possible hyperplane I~I, we have that every line
in R" that intersects ft does so in a segment, that is, ft is convex. Furthermore,
ft is symmetric, up to a translation, with respect to any hyperplane FI. By the
convexity of ft and Theorem I.3.S, AT is a disk. ¦
III.2.2 Sequences of Steiner Symmetrizations
Our proof of the isoperimetric inequality used the fact that Steiner symmetriza-
symmetrization did not increase Minkowski area, while it preserved volume. The minimiz-
minimizing property of the disk then required an existence argument, using the Blaschke
theorem. A more intuitive approach to the minimizing property of the disk is
to expect that the more symmetric a compact set, the "closer" it should be to
realizing the minimum Minkowski area for fixed given volume. In this section
we begin carrying out this approach, namely, we show that starting with any
compact subset K of the plane, we may apply to it a sequence of rotations and
Steiner symmetrizations so that it will converge, in the Hausdorff metric, to a
closed disk. One can then use induction (on the dimension) to prove a similar
result for higher dimensions.
So we see the Minkowski area decreasing, hopefully, toward the area of the
disk. Note that Minkowski area is not necessarily lower semicontinuous, so we
cannot (on general principles) pass to the limit to conclude that the area of the
disk is less than or equal to all those in the sequence. But we shall be able to
prove this result for our particular sequence. We postpone the characterization
of equality to the discussion of perimeter.
Definition A Borel-measurable function /: R" -»• C vanishes at infinity if
f) < +oo V/>0.
Definition Let A be a Borel subset of R\ vn(A) < +00. We let A* denote the
Schwarz symmetrization of A, that is. A* is the open disk in R" with the same
volume as A.
Also, define the symmetric decreasing rearrangement of the function IA,J\,
by
70
Minkowski Area and Perimeter
-*• X
Figure III.2.5: Symmetric decreasing reaarangement.
For any Borel-measurable /: R" -*¦ C that vanishes at infinity, define the
symmetric decreasing rearrangement off, /*, by
= r
Jo
(See Figure III.2.5.)
Then we have the following facts (recall Cavalieri's principle (Theorem 1.3.3)):
1. /* > 0.
2. /* is spherically symmetric, that is, \x\ = \y\ implies /*(*) = f*(y).
3. /* is lower semicontinuous (since A* is open), which implies that /• is
measurable.
4. {/* > t] = (|/| > t}* for every t > 0; of course, the two sets have the same
volume.
5. If *: R+ -*¦ R+ is increasing, then
r = ¦<>/•.
6. One has
J' 4>o\f\diH = f<t>°fdvn
for any <j> = <pi —<fa. such that each <f>j, j = 1,2, is increasing and at least
one of <pio\f\ or <fao\f\ is in Ll(Rn).
7. We always have
ii/ii, = urn, v P > 1.
8. If/ <g then /•<«*•
Theorem 111.15 ///, g are nonnegative on R\ both vanishing at infinity, then
(III.2.20) j fgdvn<J f*g*dvn.
111.2 Minkowski Area and Steiner Symmetrization
71
If f = f* and strictly decreasing, then we have equality in (IH.2.20) if and
only ifg = g* a.e.
Proof By Cavalieri's principle (Theorem 1.3.3), we want to show
/ ds I dt I Ilf>l}I{g>s}d\n
Jo Jo JR"
/*OO /*OO f
< ds dt I,/>,}'Iu«}*</v»;
Jo Jo JR'
it suffices to show that
lAlBdvn< I Z*ArB,
for all A, B of finite volume. Assume vn(A) < vn(B). Then A* c B*, which
implies that the right hand side of (HI.2.21) is equal to vn(A*) = vB(A) >
vn(A n B), which is the left hand side of (III.2.21). This proves (III.2.20).
Now assume equality in (HI.2.20), f = f* strictly decreasing. Then
l{g>s)din = j fXlg->s)dvn
for almost all 5. It suffices to show that
j
which would then imply g = g*. Well, since / is spherically symmetric and
strictly decreasing, there exists a continuous function r = p(t) such that
B"(p(/)) = {/ >
V/>0,
which implies
:=/%„:
is continuous for any measurable C. For any given s, pick C = {g > s}. Then
Fc(t) < Fc-(t) for all t, by the original inequality (III.2.20), and / Fc(t)dt =
/ Fc-{t)dt, by assumption. This implies (by continuity) that Fc(t) = Fc(t)
for all t, which implies
v«({/ > /} n C) = vn({/ > t} n C*) = min (vB(/ > r). vn(C')}.
Butthisimplies,foreveryf,thatifC*contains{/ > t]thenCcontains{/ > t],
and if {/ > t) contains C* then {/ > t} contains C. Therefore C = C*. up to
measure zero, which implies [g > s} is a disk up to measure zero, for every s.
72 Minkowsla Area and Perimeter
Corollary III.2.1 For f and g in L2 we have
\\r-g*\\2<\\f-gh.
A generalization of Corollary III.2.1 goes as follows:
Theorem IIL2.6 Let J : R -> [0, oo) be convex, 7@) = 0; and let f,g be
nonnegative, vanishing at infinity. Then
(m.2.22)
f W - g*) dvn < J
Jo(f - g) dvn.
If J is strictly convex, f = f* strictly decreasing, then equality in (m.2.22)
implies g = g* a.e.
Proof Write J = J+ + /_, where
MO =
0, t < 0,
J(t), t > 0,
and
Then J+ and 7_ are convex.
Consider J+, and its right hand derivative; then
/+(»)- f J+'(*)ds,
Jo
which implies
i+o(/-«X*)= / J+'(f(*)-s)ds
Jgw
= /" 7+'(/(x) - iJJ,,^)^)^,
Jo
which implies
I J+o(f-g)Mdvn(x)= f ds f J+'(f(x)-s)Ilg<s](x)dvn(x)
Jtt." Jo Jttr
< f ds [ J+'(/*(x)-
Jo Jr«
111.2 Minkowsla Area and Steiner Symmetrization
73
(the second line follows from Theorem III.2.5). The same argument applies to
7_, which implies the inequality.
Now assume J is strictly convex, / = /' strictly decreasing, and equality
in (III.2.22). Then we have equality, separately, for J+ and 7_, which implies
J J+'(f ~ *)!(,<,) dvn = J J+'if - s)I{g.<s) dvn
2i.c.-[ds], which implies, by equality in (III.2.20), that g = g* a.e. ¦
Corollary m.2.2 For all p > 1 we have
(IH.2.23) \\r-g'\\p<\\f-g\\p.
Corollary m.23 Let S denote Steiner symmetrization with respect to some
hyperplane n in R", and Sf the Steiner symmetrization of any function f,
defined by
Then
(III.2.24)
for all fg eLp,p> 1.
,00
Sf(x)= / JS[\f\>t\(x)dt.
\\Sf-Sg\\p<\\f-g\\p
Proof Use the 1-dimensional Corollary III.2.2 with Fubini's theorem. ¦
Theorem IIL2.7 (Helly Selection Theorem) Given a uniformly bounded col-
collection <t> of increasing junctions on [a, b], there exists a sequence in 4> that
converges for every x e [a,b].
Proof Let ri, T2,... be an enumeration of the rationals in [a, b]. Then there
exists a sequence 01; in 4> such that the sequence ofnumbers0ij(r,)converges,
which, in turn, has a convergent subsequence fcjto), and so on. The sequence
<t>k,ic converges, as k -*¦ oo, for all rationals in [a, b] to a function <f> defined on
the rationals. Extend 0 to the irrationals by
= lim
where r varies over rationals < x. So <f> is continuous from the left, and
increasing.
74
Minkowski Area and Perimeter
< \4>k.k(Pz) - <t>k.kiP\)\ + \<t>k.k(p\) - <t>iPi)\
We show that <f>k.k(*o) -*¦ <t>(xo) for every xo at which <f> is continuous. Pick
p\ < xo < /t>2, Pj rational. Then
<1>k.k(xo) -
This implies
\<t>k.k(*o) -
from which one has the claim. So &,*(*) -*¦ <f>(x) at points of continuity of <f>.
Since <p is increasing, its points of discontinuity are countable. But one can
use the above diagonal argument to obtain the convergence on these points of
discontinuity of <p. ¦
Theorem IIL2? (Isoperimetrk Inequality for Minkowski Length in R2)
Let Fbea compact subset of the plane R2. Let stx denote Steiner symmetrization
with respect to the x-axis, sty Steiner symmetrization with respect to the y-axis,
a an irrational multiple of In, and Ra the rotation ofR2 by a radians. Finally,
set
Then a subsequence T'k FofT'F converges to the Schwarz symmetrization
ofF, F*. in the Hausdorff metric topology.
Also, T'F -*¦ F* in Lp, as j; -> oo, that is,
Finally,
(III.2.25)
||Jr; F - If.II, -*¦ 0 as j -+ oo, V p > I.
Mink(F')<Mink(F).
Proof Note that (HI.2.23) and (m.2.24) imply
(III.2.26) \\T-f-T-g\\p<\\f-g\\p.
Certainly, there is a closed disk Do such that F, and all T> ¦ F, are contained
in Do. By Blaschke's selection theorem, one has a subsequence T'k-F -*¦ D,
where D is a compact subset of Do. We want to show that D is a disk.
Set F)k = TikF. First note that, because styStjj, sixFjt = Fh for all jk, we
have
styst^D = D.
111.2 Minkowski Area and Steiner Symmetrization
75
(Although it is not obvious that Steiner symmetrization is continuous in the
Hausdorff metric - both Steiner and Schwarz symmetrization are continuous
in Lp - it is nevertheless true that if K; -*¦ K in the Hausdorff metric, and
Kj is Steiner-symmetric with respect to some line for all j, then K is Steiner-
symmetric with respect to that line.)
Next we show that
(III.2.27)
= D a.e.-[dv2].
Proof: Fix any quadrant Q of R2. Then Q C\ FJt is described by a graph satisfy-
satisfying the hypotheses of the Helly selection theorem (except that the functions are
decreasing), which implies there exists a subsequence - still denoted by jk -
for which the graph of Fjk converges to the graph of D. Lebesgue's dominated
convergence theorem then implies
(HI.2.28)
\\1f, -IdII,-»-0 as *-> oo,
for all p > 1. Let g be any spherically symmetric strictly decreasing function,
such as
g(x, y) =
(x, y) 6 R2.
Then TJ ¦ g = g and (III.2.26) imply \\g - ItifW I limit (we drop the sub-
subscript p for now). Since \\g -IfJI -*¦ \\g -loll, one has \\g-ITj.F\\ -*¦
\\g-XD\\.Aho,
\\T(g - ID)|| = \\g - IT.D\\ = lim \\g - lT.Flt II = ll« - IdII = \\g ~
(the last equality follows from the spherical symmetry of g), and
\\T(g - ID)|| = list, sty(Rag - I^D)|| = ||stx sty(g -
which implies
which implies, by equality in (III.2.22) (since g is spherically symmetric strictly
decreasing) that
sty stx RaD = RaD a.e. -[dv2 ].
In particular, RaD, in addition to D, is symmetric with respect to the x- and
y-axes. Let Hx denote reflection in the x-axis. Then
RaD = HxRaD =
which implies (III.2.27).
= R-aD,
76
Minkowski Area and Perimeter
Now set
then fiF) = 0 on a dense subset of [0,2n). We show that 6 i->- fiF) is contin-
continuous when p = 2. It suffices to show that
rF):=
is continuous. Pick a mollifier y(, c > 0; then
is continuous, and
\r(@) - r@)\ =
= f
j( * ID -
j( *lD)oR-e)d\n
<\\J(*Xd-Id\\\\Ir,d\\
= \\J(*Id-Id\\\\Id\\
-*¦ 0 uniformly in 6, as € I 0, which implies the claim.
Therefore ReD — D in L2 for all 0, which implies that D is a disk. Also,
since \\ITif - loll, I, we have [by (ffl.2.28)] ||Jr^ - ID\\P 4- 0.
It remains to show D = F* and (III.2.25). We certainly have (by Lemma
HI.1.1)
vn(F) = limsup \n(Fj) < vn(D).
Next, for every c > 0, we have vn([Fj\t) I. with respect to j. Since the subse-
subsequence Fjk -*¦ D in X, then for every c' < c there exists J such that
- C
V * > 7,
which implies
which implies
V k > J,
vn(D) <
We first conclude that vn(D) < vn(F), which implies the two volumes are
equal. Therefore D = F*. We also have
which implies (III.2.25).
77
111.2 Minkowski Area and Steiner Symmetrization
Theorem ITI.2.9 (Isoperimetric Inequality for Minkowski Area in R") Let
F be a compact subset ofR", n > 3. Then there exists a sequence Tj consisting
of rotations, Steiner symmetriziations, and (n — \)-dimensional Schwarz sym-
metrizations, such that Tj-F -*¦ F* in the Hausdorff metric topology, and in
Lpforallp> 1.
Finally,
(HI.2.29)
Mink(F*)<Mink(F).
Proof Let U denote the rotation of R" that takes en to en_i (and leaves the
orthogonal R" pointwise fixed), Fl = e^- = R", S\ = stn denote Steiner
symmetrization with respect to II, and Sz denote Schwarz symmetrization in FI;
set
T = SiSiH.
Then the argument of the proof of (III .2.28) implies that there exists a subse-
subsequence (kj),
Tj=Tk>,
such that Zjrf -*¦ ZD (in the various topologies) for some compact D, as
; -+ oo. We also have T> ¦ F ^ D in L'.
Since S\ and 52 commute, and TJ F -*¦ Din Lp, we have
S2T' ¦ F =
and
which implies
1 • F = Si
• F =
-* -F = T'F
D,
$20=0,
that is, D is rotationally symmetric with respect to the x"-axis. Also, given
g = e~W\ for example,
II* -Ziw,|| = IIK(« -Id)II = U -loll = H« -ZtdII = \\Si$2(g - 2kd)II.
that is.
which implies [by equality in (III.2.23)]
S2HD =
78 Minkowski Area and Perimeter
So both D and V.D are rotationally symmetric with respect to the x"-axis,
that is, D is rotationally symmetric with respect to both the x"-axis and the
x"~'-axis. Let j( be a mollifier, depending only on distance from the origin,
that is, spherically symmetric in W,
I( = jf *ID,
and let
p2 = (x1J + ...+(;c'-2J.
Then there exist functions / and g of two real variables, such that
Set x" = 0. Then
which implies
"-'J,0) =
2,0) =
= It{xl
that is, the function It(x) is radial in x, for every c, which implies XdOO is
radial in x, which implies D is a disk.
The proof of D = F* and (III.2.29) is the same as in the previous theorem.
IllJ Application: The Faber-Krahn Inequality
We present an application of symmetrization to analysis, more particularly, an
application of geometric isoperimetric inequalities to isoperimetric inequalities
for eigenvalues. The result goes as follows:
Definition Given any open set SI in R", one considers the functional
where <p ranges over C^°(Q), and the associated infimum
k*(Sl) = inf
0eC«(J
We refer to X*(tt) as the fundamental tone of SI.
It is well known that k*(Q) is the infimum of the spectrum of the Laplacian
-Aonfl, subject to vanishing Dirichlet boundary data (see the discussions in
§§VII.2 and VII.4 below). In addition, if Q is a domain with compact closure
III. 3 Application: The Faber-Krahn Inequality 79
and C°° boundary, then X*(S2) is an eigenvalue of the Laplacian on SI, that is,
there exists a solution <)> e C°°(Sl) to
(III.3.1)
moreover, <p\Sl # 0 and (d<p/dv)\dSl ^ 0, and the solution <p is unique up to a
multiplicative constant.
Theorem IIL3.1 Let SI be a bounded domain in R", and let B be the open
disk in W satisfying V(Q) = V(B). Then
If SI also has C°° boundary, then one has equality if and only if SI is isometric
toB.
Proof Fix a function / e C?(Sl), and set, for every t > 0,
n, = {\f\>t}, r, = an, c {|/| =»}.
We use the symmetric decreasing rearrangement (or Schwarz symmetrization)
of functions on SI, defined by
B, = n; = B"(p(»)), f\x) = f IB,(x)dt.
Jo
So B, is the disk of radius p(t) whose volume equals that of SI,, and /* is the
function that on the sphere S"~'(p(f)) has the value f. Then
So to prove the first claim of the theorem, it suffices to show that
(IH-3.2) llgrad/||2>||grad/'||2.
Set
Let (a, fi) be an interval consisting of regular values of /, and for t e (cr, /?) set
A(t) :=
Then 11->- V(t), p(t), A(t) are all C°° on (o, 0) with both V(t) and p(t) strictiy
decreasing. On (cr, 0) we have
dV n_xdp
dt ^ dt
-Z—
dr
,
dp/dt
80 Minkowski Area and Perimeter
where r denotes distance from the origin. On the other hand,
by the co-area formula (Corollary 1.3.1).
Finally, set
T = sup |/| and r0 =
To prove (III.3.2) we have, on the one hand,
fo ff
On the other hand we have, by the Cauchy-Schwarz inequality,
}{^ Igrad/r'rfA},
which implies
ff |grad/|2dV = f dtf |grad/|dA
JJa Jo Jr,
'Jo A2{t){l lgRld/'
= -f A2(tW(t)rl dt
Jo
> - r A2(sn
Jo
= -Cn-il —r<it
Jo P
-1
dt
(the last inequality is the isoperimetric), which implies (III.3.2).
To consider the case of equality, we assume that ft has a C°° boundary, in
which caseX*(ft)hasapositiveeigenfunction/ofXi($2). Of course,/|8ft = 0.
The eigenfunction equation (IH.3.1) implies
a2/
<0
111.4 Perimeter
81
for at least one of the j e {1,..., n}. Thus, by the implicit function theorem,
the set of points for which grad / = 0 is contained in an (n — l)-manifold. In
particular, for every f, V(V(t)) — 0, which implies V = V(t) is continuous with
respect to t.
Now one can argue as above. If X*(ft) = k*(B), then the argument shows that
A(dnt)= A(dB,) for all regular values of t. But then for every such t one has
Q, isometric to B,, and the strong maximum principle implies that ft = ft@)
is isometric to 5@) = B. ¦
III.4 Perimeter
III.4.1 Geometric Perimeter
Definition We say that a collection of measurable subsets (?,) of K" converges
to E in Ll if vn(?;- A E) -+ 0 as ; -> oo, that is, if IEj -*¦ 1e in L'(Rn):
lim f\lE)-
IE\dvn=0.
Definition The geometric perimeter geoper(?) of a measurable subset E of
R" is defined by
geoper(?) = inf (Iiminf A(dMj)},
where the infimum is taken over all sequences of open subsets Af, of K", with
Cx boundary, that converge to E in L1. One easily checks that if Ej -*¦ E in
Ll then
geoper(?) < Iiminf geoper(?;).
that is, ? h> geoper(?) is lower semicontinuous with respect to convergence
inL1.
Theorem IH.4.1 If K is compact, then K may be approximated in Ll by open
subsets with C°° boundary. Furthermore,
geoper(Ar)<Mink(Ar).
Proof Let f(x) = d(x, K), (j() a mollifier on Rn, and set
U = U * /•
Then sup |grad/,| = Lip/, < Lip/ = 1.
82 Minkowski Area and Perimeter
For any small h > 0, let a — h2. Then there exists c e @, a) such that
f(-l[(°,h-a)] CC [K]h\K,
and there exists a regular value t € (ct, A - ct ) of /(. By dominated convergence,
K may be approximated in L1 by /(~'[@, t)].
Furthermore, by the co-area formula (Corollary 1.3.1), we have
/ A(frl[t])dt = / |grad/,|dV < vn([K]h \ K),
Jo Jf.-<U<>.l>-o)\
which implies there exists a regular value t0 e (a,h — a) such that
(h - 2a)A(/r'[«o]) < VnilKl, \ K).
Also,
/r'fo] = 9ifrl[o, t0)), k c /r'[o, to] c vk\.
Given any p > 0, there exists hj -*¦ 0 such that
which implies, for €j e @, ay), ct; = li^, and associated /,,
j - 2ct,
(Mink (K) + p).
which implies the theorem.
HI.4.2 Functions of Bounded Variation
Definition Given an open set SI in R". The collection of functions on SI of
bounded variation, BV(ft), consists of those functions / e L'(&) for which
sup / fdi\i
< J
+oo,
where ? varies over C,!(Q) vector fields on Q satisfying |?| < 1 on all of SI. We
refer to these vector fields as admissible vector fields on SI.
If the function / e BV(ft), then the Riesz representation theorem (Proposition
I.3.S) implies that there exists a vector-valued Radon measure 6f on SI defined
by
J ftliv
1II.4 Perimeter 83
for all admissible vector fields ( on SI, and the total variation of 6f satisfies
|«/|(n) = sup f fdiv?dvn
where the supremum is taken over all admissible (.
Example IH.4.1 If / e Cl(Sl) n Z.'(fi), then / e BV(«) and
d6f(x) = -(grad f)(x)dvn(x).
Indeed, for any admissible ( we have
/ fdiv?d\n = - I grad/-^dvn
Ja Ja
Remark m.4.1 The same result (Example III.4.1) is valid in Wll(S2) (see
Remark 1.3.3 below).
Proposition HI.4.1 If SI' c Q then Ff)\sr = 6(f\Q').
Theorem HI.4.2 Let Si be open in R\ (fj) a sequence of functions in BV(fi)
such that fj^f in L^Q). Then f e BV(Q) and
\6f\(Sl) <liminf\6fj\(Sl).
y-.oo
Proof For any admissible ? on SI we have
f/div? =
= lim I /ydi
= lim f
< liminf \6fj\(Q)
- the second line follows from the compactness of the support of ?, / e L^,
and dominated convergence; and the last line uses |(| < 1 on all of SI. ¦
Corollary IH.4.1 Given the open set SI in R", endow the space BV(Sl) with
the norm
Then B\(Sl) is complete relative to the norm || ||bv-
84
Minkowski Area and Perimeter
Proof If (fj) is a Cauchy sequence in BV(fi), then (/)) is a Cauchy sequence
in Ll(Q), which implies there exists / 6 Ll(Q) such that /, -»¦ / as j -*¦ oo.
Then, by Theorem m.4.2, we have
\6(f - fj)\(Si) < liminf \6(fk - fj)\(Q) < liminf \\fk - /y
k~*OO K—+OQ
which implies the corollary. ¦
Remark IIIA2 Note that for arbitrary / e BV($2) we do not expect to ap-
approximate / by C°° functions, namely that there exist (fj) e C°°(n) such
*at Wfj ~ /Hi -*¦ 0 and \6(fj - /)h(J2) -*¦ 0, for this would imply that / 6
W '¦' (SI) - which is not necessarily the case (see the case of indicator functions
in Example III.4.2 below).
Theorem IIIA3 Given the open sets Q in R", A CC «, and f e BV(«),
satisfying
(III.4.1) |«/|(8A) = 0.
i^f G«) fc« a mollifier on Rn, f( = j( * f. Then
\6f\(A) = 1im\6f(\(A).
Proof One has f( -*¦ f in L'(Q), which implies
\6f\(A) < liminf \6f(\(A).
For $ admissible on A we have
j /(div? = j" (y( * /)div? = f /divO, ¦ C)-
Now supp(y» * $) C [supp^ c [Al, which implies
I ft*™*. < f /div(y( * O < \6f\([A]().
Ja J[aI
Therefore
\6f(\(A)<\6f\([A](),
which implies
limsup \6f(\(A) < \6f \(cl A) = \6f\(A)
by (III .4.1), which implies the theorem. ¦
111.4 Perimeter
Theorem IH.4.4 /// e BV(R"), (j() a mollifier on R", then
= lim \6f( \(Rn).
85
Proof The proof is similar to the proof of Theorem III.4.3.
Theorem III.4.5 Let Q be open in R\ Given any f e BV(fi), there exists a
sequence of C°° functions (fj) in h\(Q) such that
l-}™o f> = /•
Proof Given c> 0, there exists an open nocc« such that
Let «0 CC fii CC «2 CC • • ¦ be an exhaustion of Q, with
chose above, and set
Ai = «2.
^ = n<+i\clfi<_1, 1 = 2, 3
(&) a partition of unity of ft subordinate to (A*),
(j() a mollifier on R".
For each * = 1,2 pick €k in @, c) such that
the one we
S"PP ju * (ftk) C nk+2 \ cl Hk_2, «_, = 0,
f \M * (f<t>k) - f<t>k\ <€/2k,
I \U * (/grad^) - /grad&| < c/2*.
and set
^One easily sees that /, -> / in L'(O) as e | 0, which implies, by Theorem
|«/| < liminf |*/«|.
no
86 Minkowski Area and Perimeter
Given an admissible ( on ft, we have
= E [ /div<**0«.
* O) -
- the last equality uses the fact that (<?*) is a partition of unity. Now
f /div(*,a,*O)<l«/l(«);
•/a,
A* c ft \ cl Qo f°r aU * > 2, and every point in ft \ cl Qo is covered by at least
one of the collection (Ak) and at most two of the collection (At), which implies
T f /div (&(]« * O) < 2 f T /div (<fik(U * O)
<2|«/|(ft\clfto)<2e,
which implies
\6f(\(Q)<\6f\(Q) + 3€,
which implies the theorem. ¦
111.4.3 Caccioppoli Sets
We consider our most important example of functions of bounded variation -
indicator functions of Borel sets in R".
Notation For the indicator function of a set E for which Xe has bounded
variation, we always write
6E := 6XE.
111.4 Perimeter
87
Example II1.4.2 Given ft, let ? be a domain in K" with C1 boundary, and IE
its indicator function, with vn(E Dft) < +oo, that is, Jglft e Lx(Sl). Then it
is standard that Jf|ft ^ W1' '(ft). For any admissible ( on ft, we have
= f
JdEnn
where i/? is the exterior unit vector field along BE. If A(dE OQ) < +oo, then
Z?jfteBV(ft)and
= A(8E n Q).
Remark IIL4J For arbitrary measurable ? with Jf|ft e BV(ft), we always
have supp 6E C 3 ?. Indeed, if F is open in int (Q \ E), then I? | F = 0 implies
/ Jfdiv ^ = 0 for all admissible vector fields on F. If G is open in int (ft n ?),
then XE\G = 1 implies / J?div? = fG div? = 0 for all admissible vector
fields on G, which implies the claim.
We now extend Example III.4.2 to Lipschitz domains.
Definition A domain ?1 in K" is a Lipschitz domain if for each w e 8ft there
exist a neighborhood U = U(w) in R", Euclidean coordinates u, and a Lipschitz
function
4>:Un(W~l x {()})-> R
such that
9ft n {/ =
<t>(u\x) un-\x))).
For convenience, we shall write R"~' for R"~' x {0} and « = («',..., «""',
u") = (u,un),ueRn-1.
Example III.4J Let n be a Lipschitz domain, w e BQ, U, u, and <p as above,
and assume <p is differentiable at u(w). [By Rademacher's theorem (Theorem
I.I.3.2), <f> is differentiable a.e.-[dvn_i] on U nR".] Then 8ft has a tangent
hyperplane at w, with exterior unit vector v given by
v_ grad«/>-en
where e« denotes the unit vector in the positive direction of the «"-axis [the gra-
gradient here is(n - l)-dimensional]. Let (<?,) approximate^ in the Sobolev space
Wil(U n R"), 4>j e C°° for all ; (Theorem 1.3.3). Then <f>j -> <f> uniformly
88 Minkowski Area and Perimeter
on compacta. Let
Aj = {xeU:un(x)><f>j(u{x))),
Uj = exterior unit normal vector field along 3 A;.
Then
/ ZA,div? = f ^6Aj,
Ju Ju
where
&la(t) is the 1-dimensional delta function (of t) concentrated at a e R, and
Let j -*¦ oo. Then
f JA
Ju
f
Therefore, Jn|f/ e BV({/) and
which generalizes the classical formula A.3.8).
Definition We start with a Borel set E. For any open Si, we define the perimeter
ofE in Si, P(?; J2), to be \6E\(il) when finite, and otherwise +oo.
Remark III.4.4 ? Borel guarantees that E is |6?|-measurable.
Definition We also define
P(E) = P(E; R").
? is called a Caccioppoli subset of R" if P(?; Si) is finite for all bounded open
Si in R". A Caccioppoli set in R" is also referred to as a set with locally finite
perimeter.
Proposition IU.4.2 We always have:
(a) E CC Si CC Si, => P(?;Si) < />(?;Si,).
(b) P(E{ U ?2; Si) < />(?,; Si) + />(?2; Si), witfi ^Ma/ify ifd(Ex, ?2) > 0.
111.4 Perimeter 89
(cj vfl(?) = 0 => />(?) = 0.
^ vn(?, A ?2) = 0 => />(?,) = P(?2).
Remark III.4.5 Note that (c) in the above proposition differs markedly from
Minkowski area, where a set might have measure 0 but nonzero Minkowski
area (Remark III.2.2).
Remark III.4.6 We restate the definition of Caccioppoli set slightly differently.
A Borel set ? is a Caccioppoli set in R" if there exists a vector-valued Radon
measure /j on R" such that
j
div i dvn =
for all admissible ? on R". Indeed, for any bounded open Si in R" we have
/'(?;Si)<|/i|(Si)<+oo,
which implies ? is Caccioppoli. The measure ft must be unique; and since
fZ-dn= fZ-d6E
for all admissible ? on R", we have /j = 6E.
Theorem IH.4.6 Let E be a Borel set in R" such that IE e BV(R") (that is,
E has finite volume and perimeter), (j() a mollifier on R". Set <p = Xe and
(p( = i( * <p. Then
(III.4.3) \6E\(A) = lim\6<pt\(A)
for all A e R" with \6E\(A) = 0. Also,
(III.4.4)
Proof This is a direct application of Theorems m.4.3 and III.4.4. ¦
Theorem UI.4.7 (Co-area Formula for Perimeter) Given Si open in R",
/ e BV(Si), let F, denote the level domain
Then
(HI.4.5)
F, = {x € Si :/(*)
6F,dt, \6f\= P \6F,\dt.
J
90
Minkowski Area and Perimeter
Remark HI.4.7 Thus, when / is C00, the second equality in (III.4.5) reduces
(by Example m.4.1) to the co-area formula for smooth functions (Corollary
1.3.1).
Proof For any a e R, and
we have
Note that
r>0>
/.oo
a= / *«
J-oo
(t)dt.
|a-0|=
Then, for /(*), we have If,(x) = 2<-oo./(x))@. which implies that for any
admissible ? on Q we have
= J dt j {XFl - 1 }div S + j°°dtj Jf,di
= r dt f jf,di
J-oo J
= / i-6F,dt.
J-oo
\6f\< f \6F,\dt.
J
Therefore,
By Theorem III.4.5, there exists a sequence (/,) e C°° such that fj -»• / in
/.'(«) and |fi/;| -»• \6f\. Then
FA -XFl\dt = j dtj
I/; -
[where (Fj), denotes the level domain of /, associated with the value /], which
implies (Proposition 1.3.1) there exists a sequence (jk) such that ZiFh), -*¦ If,
III.4 Perimeter
in L\Q) for almost all /, as k -»• c». Therefore,
91
j \6F,\dt < j liminf \6(Fjt)r\dt
\6(Fjk),\dt
= lim inf \6fjt |
- the next to last equality follows from the co-area formula for C°° functions
(Corollary 1.3.1) - which implies the theorem. ¦
Lemma III.4.1 Let E be a Cacdoppoli set in R", (_/<) a mollifier on R", and
t e @, 1). Set <p = Ze and <p( = jf * <p, and
Then
I* -
Proof If jc e ?\(?€), then ^(x) = 1 and <p((x) < t, which implies
Similarly, if j: e (Ee), \ E then <p(x) = 0 and <p((x) > t, which implies
Therefore
J \<p(-<p\d\n> J tliEME + 0 ~
> min(/, 1 - /) J ^e,), - lE\dsn,
which implies the lemma. ¦
Theorem III.4.8 Let E be a Cacdoppoli set in R". Then there exists a sequence
of domains (Et) in R", with C°° boundary, such that
L1- lim IEl = Ie, Hm \6Et\ = \6E\.
i-+oo y-»oo
In particular, the perimeter of E is equal to its geometric perimeter.
92
Minkowski Area and Perimeter
Proof Start with <p = XE, the mollifier 0",) on R", <p, = je * tp, and (Ee), as
above. Then the co-area formula (Theorem III.4.7) implies
\6<pt\= / \6{E(),\dt.
Jo
For any bounded open SI, Lemma III.4.1 implies that XiE,), -*¦ 1E in LX(Q) as
€ I 0, for every / e @,1). Therefore, by Theorem III.4.2,
for all t, which implies,
\6E\ < liminf \6(E(),\
A0
\6E\= I \6E\dt
Jo
< f liminf \6(E(),\dt
Jo <l°
< liminf / \6(E(),\dt
= lim \6<pe\
= \6E\,
- the last equality follows from Theorem III.4.6 - which implies
|fi?| = liminf \6{E(),\
tiO
for almost all t €@, 1).
Now pick e* -*¦ 0 as k -*¦ oo. Then the same argument for E* = E(k shows
that
\6E\ = liminf \6{Ek),\
for almost all / e @, 1). Sard's theorem (Proposition 1.3.8) implies
v, l(Jcritval<0(J =0,
where, for any function H, critval H denotes the set of critical values of H. Let
/ be in the complement of |J* critval <pu in [0,1), that is, / is a regular value of
111.4 Perimeter 93
<p(t, for all k. Then there is a subsequence at = ?*, such that
\6E\ = lim \6(Eat),\.
t-*oo
Then the sequence (Eat), will do the job.
Thus geoper(?) < P(E). For any sequence Ee, dEt e C00, with Et-* E
in L1, we have
liminf A(8?<) = liminf />C?<) > P(E),
which implies P(?) < geoper (?), which implies the two are equal. ¦
Remark III.4.8 Note that the sets (Ea, )t converge to E in the Hausdorff metric
on compact sets.
111.4.4 The Isoperimetric Inequality for Perimeter
Remark III.4.9 Note that Theorem III.4.1 now implies that the isoperimetric
inequality (to be proved below) for perimeter is sharper than the isoperimetric
inequality for Minkowski area.
Theorem III.4.9 Steiner symmetrization does not increase perimeter.
Proof Let S denote Steiner symmetrization with respect to some fixed hy-
perplane, K a finite disjoint union of compact domains with C°° boundary.
Then
P(K) = A(8K) = Mink (K) > Mink (SK) > P(SK),
by Theorems III.2.3 and III.4.1. For arbitrary Borel E with finite perimeter, let
Kt -»• E in L\ P(Ke) -> P(E), as t -* oo , and 8Kt e C°° for all t. Then,
by Corollary III.2.3,
*,-2seIIi<P*,-IeIIi -^0,
which implies Isk, -*¦ Xse in Z.1, which implies
P(SE) < liminf P(SKt) < liminf P(Ke) = P(E),
which implies the claim.
94
Minkowski Area and Perimeter
Theorem ni.4.10 (Isoperimetric Inequality for Perimeter) Let E be com-
compact, and E* denote the Schwarz symmetrizjation ofE. Then
(III.4.6)
P(E') < />(?),
with equality if and only if E is an n-disk, except for (at most) a set of
d\n-measure equal to 0.
Proof (Geometric proof.) By Theorems III.2.8 and III.2.9, there exists a se-
sequence Tj consisting of Steiner symmetrizations, (n — l)-dimensional Schwarz
symmetrizations, and rotations such that Tj< • E -*¦ E* in V as j -> oo. Then
P(E') < liminf P(Tj • E) < P(E),
which implies the inequality.
(Analytic proof.) Given any / € BVC (where BVC denotes the compactly
supported functions in BV), we can approximate / by ft e C™ such that
11/* " /111 -> 0, llgrad/iH, = ||6/*||bv "> II«/IIbv,
as k -*¦ oo. We already have
Since /* -*¦ f in Z.1, then /*
Fatou's lemma.
/ pointwise a.e.-[dvn], which implies, by
" liminf \\fk\\n/{n-n< liminf ||*/*||bv = H*/Ibv-
t-»oo k-*oo
But this implies the isoperimetric inequality, by picking f = Xe-
We now characterize the case of equality in (III.4.6). The reader is referred
to the proof of Theorem III.2.4, where it is assumed that the boundary of the
minimizer is C1, since we will draw on that argument.
Fix E, compact, that satisfies equality in the isoperimetric inequality (III.4.6).
Then P(E) = P(SE) for every Steiner symmetrization.
Let AT; be a sequence of compact domains with C°° boundary such that
Kj -*¦ E, in the Hausdorff metric and in L1, and P(K}) -+ P(E). Fix a hyper-
plane n, and let S denote Steiner symmetrization with respect to fl.
Since K} -+ E in L\Rn), we have SKj -»• SE in L'(Rn), and, by passing
to subsequences if necessary, we may assume
\6Kj\ -»• |fi?|, 1*5^1 -»• \6SE\.
For each j, define the graph function A) on n associated with SKj, as in the
Hl.4 Perimeter
proof of Lemma IH.2.3. Then (HI.2.19) implies
95
= P(SKj).
which implies
P(E)>
>
II II
We claim that P(E) =
(III.4.7)
lim sup 2 / Jk* +
lim sup 2/ Jl + |;
lim P(SKj)
P(SE).
P(SE) implies
lim \n-i(kj >
j—*oo
lgradn_,Al2
gradn_,^|^
l) = 0.
Proof Assume there exists e > 0 such that
vn_i(A:; > 1) > e for infinitely many j.
Now
j) > 2 [ Jkj(w? + |gradn_lv4,|(H>J rfv
which implies that
,,.,^! > N) <
N
for sufficiently large j; so we may pick W sufficiently large so that
vn_1(|gradn_1.4;|>./V)<|
for sufficiently large j. Therefore
<N)O {kj > 1}) > 1,
% Minkowski Area and Perimeter
for infinitely many j. Because
-H |gradn_1v4/|2rfvn_,
J{\gnA,-[Ai\<N)r\[kj>\) II * "T iv
/2
P(SKj) e
> — + const. -
2 2
for infinitely many j, we have a contradiction to P(E) = P(SE), which implies
(ni.4.7).
Let EL denote the Lebesgue set ofE, that is, ? e EL if $ e ? and
lim~^ /
IEdvn = l.
Then Lebesgue's density theorem (Proposition 1.3.6) implies that vn(? \ EL) =
0. Let ?o denote the closure of El. Then Eq C ?, ?o is compact, and
vn(?\?0) = 0. So we replace E by Eo. Then vn(?) = vn(?0) and P(E) =
P(E0).
Given the hyperplane n = R"~', let p: R" -*¦ R" denote the projection;
and given any w e R", let ^^ denote the line through w perpendicular to
Rn-1
Let w e p(?o), and set
= inf er n ?0,
= sup r n ?0.
Assume there exists /o € (o(w), ^(w)) such that xo := (w, to) & ?o- Then there
exists r > 0 such that !(xo;r) C R"\?o; and there exist t\ e [a(w), to- r]
such that xi := (w, »i) e ?o, and r2 e I'o + r, 0(w)] such that X2 ¦= (w, t2) e
?0. Pick e > 0 so that, for any points y\ e B(;ri; e) and y2 e 1(j:2; c), the line
joining them must intersect B(*o;»"). Given such an e > 0, there exist yi e
B(jri; e) n ?t and n e B(j:2; e) n ?*,, which implies that, for any given 8 > 0,
.4 Perimeter
97
Figure 1II.4.1: The hole.
there exists e' > 0 such that
vn(B(y,;e')n?) > A -
(See Figure III.4.1.) Since ATy -»• ? in L1 we have J > 0 such that
; €'))
On^) > d -
vn(B(y2;O n Kj) > A -
> 7. Since the boundaries of Kj dieCx, wehavevn(ATy) = vn(int K})
98 Minkowski Area and Perimeter
for all j > J, which implies
vn(B(y,;e')flint*,) > A - 2S)vn(B(y,;€%
; «') n int *;) > A - 25)vn(B(y2; e'))
for all j > 7, which implies that for every j > J there exist points zi, z2 and
jO > 0 such that
C B(y,;<r')n
B(z2;p) c B(v2;e')n
Let llx -Z2 denote the line determined by z i and z2. Then for any line intersecting
B(zi; e'/2) and B(z2; e'/2) must intersect B(x0; r), which contradicts (III.4.7).
Therefore, C n Eo = l<x(w), p(w)].
Thus, equality in the isoperimetric inequality implies P(SEo) = P(E0) for
all symmetrizations S, which implies Eo must be convex. Then for any hyper-
hyperplane n, the corresponding functions a(w), -f}(w), w e pn(^o). are convex,
and hence locally Lipschitz. Set
A(w)= .
Since ?n is Lipschitz we have, by Example III.4.3,
\6E0\(w, y) = rfvn_i(w)
dy
(where S1 denotes the Dirac delta function on the line R1), which implies, by
(III.2.18),
P(E0) =
lgradn_, -a|2
> 2 j yi
= P(SE0),
with equality if and only if ?(w) + o(w) = const, for almost all w e
Continuity of the functions a(w) and 0(w) implies /3(w) + a(w) = const, for
all w e pn(^o)- Then ?0 is convex and is symmetric, up to a translation, with
respect to any hyperplane n, which implies Eo is a disk, by the convexity of
Eo and Theorem 1.3.5. ¦
U1.5 Bibliographic Notes
99
IIL5 Bibliographic Notes
The fundamental treatise on geometric measure theory is Federer's A969). An elemen-
elementary introduction is Morgan A988), and a more advanced treatment is Simon A984).
§111.1 The treatment of the Hausdorff metric on compact sets, including Blaschke's
theorem, follows BergerA987, Chapter 9).
§HL2 Steiner symmetrization can be found in Steiner A838). It initiated a whole
school of techniques with applications in geometry and analysis. See the geometric dis-
discussion in Burago and Zalgaller A988, Chapter 9), and analytic discussions in the classic
P61ya and Szegd A951), and the more recent Kawohl A985), and Baernstein A995).
Our use of the phrase Schwarz symmetrization is not universal. Except for Steiner
symmetrization, none of the nomenclature seems to be universal; so when reading any
presentation, caveat emptor applies.
The technique of using sequences of Steiner symmetrizations goes back, at least, to
(he important paper of Caratheodory and Study A909). The paper is one of the early -if
not the first - rigorous proofs of the isoperimetric inequality by Steiner symmetrization.
See the discussion in Blaschke A956, p. 43 ff.) Our treatment follows, rather closely,
Lieb and Loss A996, Chapter 3). Deeper results on approximations by sequences of
symmetrizations can be found in Almgren and Lieb A989) and Burchard A997).
§IIL3 Theorem III.3.1 answers in the affirmative a conjecture of Lord Rayleigh
A877, §210). It was first proven in Faber A923), Krahn A925).
The argument can be easily carried over to spheres and hyperbolic spaces; namely, as
soon as one has metric disks as the solution to the geometric isoperimetric problem in
these spaces, one automatically has the disks as solutions to the corresponding eigenvalue
isoperimetric problem. See Chavel A984, Chapter IV).
§111.4 The discussion of perimeter follows the exceptionally clear discussion of
Giusti A984, Chapter 1). Ziemer A989) was also very helpful.
The discussion of the isoperimetric inequality for the perimeter of compact sets was
influenced by Talenti A993). We did not follow his argument closely, since we were
able to use the previous arguments from Minkowski area.
IV
Hausdorff Measure and Perimeter
In this chapter we introduce the most general construction of measures in a
metric space, Hausdorff measure. As emphasized earlier, it provides a measure
on the boundary of any domain, in terms of that set itself (not as a boundary),
irrespective of regularity of the set.
We show that, in Euclidean space, Hausdorff measure in the top dimension
leads to the usual Lebesgue measure, and on smooth Riemannian manifolds
it leads to the usual Riemannian theoretic volume measure. Finally, we show
that if ft is a Lipschitz domain in R", then the (n — l)-dimensional Hausdorff
measure on the boundary of Q, 8Q, coincides with the perimeter measure of
Q. Our proof requires the area formula for Lipschitz maps, which we prove
here as well. It was tempting to include in this chapter the structure of the
boundary of domains with locally finite perimeter, and the relation of perimeter
to Hausdorff measure. But we would have had hardly anything to add to the
excellent treatment in Chapters 2-4 of Giusti A984); so we left the matter to
the reader to explore there.
IV.l Hausdorff Measure
Definition (Recall.) GivenasetX,aa-a/?e6nJ<SJnXisacollectionofsubsets
of X satisfying:
(i) <p,XeS;
(ii) ifAe<SthenX\/l€S;
(iii) if(Aj) e S then (J^ Aj e S for any countable sequence of subsets of X.
A measure on Sis a function ft: S -*¦ [0, +oo] satisfying:
(i) /i@) = 0,
(ii) (i is countably additive, that is, fi(\J} Aj) — Y.j MCA;) for countable pair-
wise disjoint (Aj) € «S.
100
IV.l Hausdorff Measure
101
Sometimes it is awkward to specify at the outset the a-algebra S. Instead,
using Carathe'odory's criterion,, one starts with an outer measure on the full
collection of subsets of X, 2X, aind creates the a-algebra and measure from the
outer measure. Namely,
Definition A function 4>: 2X ->* [0, +oo] is an outer measure if it satisfies:
for any
(i) #0) = 0;
(ii) <f> is monotone, that is, if A c B then <p(A) < 4>{B);
(iii) 4> is countably subadditiwe, that is, #((J, Aj) <
countable sequence of subsets of X.
One then calls a subset E of X ^-measurable if
<f>(A)=
for all A e 2X. The collection olf ^-measurable subsets of X, S+, is known to
be a ct-algebra, and the restriction n = <p\S,p of 4> to S$ is a measure.
Definition An outer measure (i iis called regular if to each Ac X there exists
a ^-measurable B D A such that n(B) = n{A). (Note that this definition of
regularity is for outer measures.;) Note that if fi is regular, then any sequence
(Aj) in X satisfying Aj C Aj+i,, for all j, also satisfies
If X is a topological space with oiuter measure ft, we say that fi is Borel regular
if for each Ac X there exists a Borel set B D A such that fi(B) = fi(A).
If (X, d) is a metric space withi an outer measure ft, we say that /a is a metric
outer measure if
d(A, B)>0
H(A UB) = fi(A) + fx(B).
Theorem IV.I.I (Carath^odory's Theorem) If ft is a metric outer measure
°n X, then all Borel sets are fi-mieasurable.
Proof It suffices to show
for all E c X satisfying fi(E) < +oo, and for all closed subsets C. Let
Cj = {x€X:: d(x, C) < \/j) = [C]Uj
102 Hausdorff Measure and Perimeter
for j = 1,2 Then E\C D E\Cj, which implies
fi(E) > ix((E\Cj) U (E n C)) = n(E\Cj) + m(? n C).
Let 7 -»• oo; we shall show that fi(E\Cj) -> (i(E\C). To this end, set
Then
E\C = (?\Ci) U |J /?; = (?\C*) U 0 Rj,
which implies
fi(E\Ck) < a(E\C) <
Now the series JV fi(Rj) converges; indeed,
;=*
7=1
Therefore ?/>*
0 as Jfc -»• c», which implies the theorem.
Definitioii Let X be a metric space, 7" a family of subsets of X, and (:P -*¦
[0, +oo]. A covering (?;) in J7 of a subset A in X is called a S-cover of A if
diam?j < S for all j.
Assume that (X, 7", ?) satisfy:
1. for every S > 0, X has a 5-cover;
2. for every S > 0, there exists ?ef such that f (?) < 5.
Define the S-Hausdorff (outer) measure fa on X by
where (?;) varies over all 5-covers of A by sets in J7, and the Hausdorff (outer)
measure rj/ on X by
= lim
IV.l Ham
Theorem IV.1.2 We have
(a) ^@) = 0;
(b) rjr(A) is well-defined, because fa
(c) A (-> ^f(A) is an outer measure.
Proof We only have to check subadd
is a 5-cover of B, then (Ej, F}) is a S
which implies
which implies
Theorem IV.l3 The Hausdorffmeas
fore, rjr is a Borel measure.
Proof Given A, B with d(A, B) > 0,
ofAUB. Then any given Ej car
which implies
U S) >
One now easily has
rJf(AUB)=:
Theorem IV.1.4 If the members ofT c
Proof GivenA c X,pickopen(l/*)-c
satisfying
Hausdorff Measure and Perimeter
104
and set
k=\ j=\
One checks that B is a Borel set containing A, and rj/(A) =
Definition Let X be a metric space, 0 < s < +oo, T = 2X all subsets of X,
and
f(E) = (diamf)',
with the conventions 0° = 1 and (diam 0Y = 0. The resulting S-Hausdorff and
Hausdorff measures are denoted by 7i's,7is, respectively, and referred to as the
standard S-Hausdorff and the standard Hausdorff measures on X. When no
explicit mention of T and f is made, we are always speaking of the standard
Hausdorff measures.
Note that W°(A) = card A.
Proposition IV.1.1 If X is a separable metric space, we obtain the same mea-
measure W if we pick
= {EcX:E closed}.
= Hn (because diam conv A = diam A for all A), we may add to the list:
= {E C X : E = convex}.
Proposition FV.1.2 Let X bea separable metric space. The following are equi-
equivalent:
(a) H'(A) = 0;
(b) H\(A) = 0 for some & > 0;
(c) given € > 0, there exists a cover (Ej) of A such that
< €.
Theorem IV.1.5 For 0 < s <t< +oo, A C X we have
(a) H'(A) < +oo =>¦ H'(A) = 0.
(b) H'{A) > 0 => H'(A) = +oo.
TV. 1 Hausdorff Measure
Proof Let (?,) be a 5-cover of A. Then
H'S(A) < ? (diam Ej)' < B'~s ? (diam Ej)',
which implies
which implies the theorem.
Definition The Hausdorff dimension of A in X is given by
dim A = sup {s: H'(A) > 0} = sup {s : K'(A) = +00}
= inf{/: 7i'(A) < +00} = inf {/: H'(A) = 0}.
Note that
Also,
ACB
dim A < dim B.
dim M Aj = sup dim Ay.
J
105
IV.1.1 Example. Euclidean Space
Remark IV.1.1 By Proposition IV. 1.2, if a Lebesgue-measurable set A in R"
has Lebesgue measure 0, then W(A) = 0.
Remark IV. 1.2 If X = R\ T a Euclidean transformation of R\ then
If A. >0then
= k"H'(A).
Lemma IV.1.1 Given any bounded open U C R\ and S > 0, there exists a
pairwise disjoint family of closed disks (D;) all contained in U such that
diam D, < S V ;, yn(U \UjDj) = 0.
|*roof Let U = \Jk Ck, where Ck are closed n-cubes with pairwise disjoint
interiors, and diam Ck < 8 for all k. Pick closed disks D; to satisfy
Dj c Cj, diamDy > -sideC, V j.
106 HausdorffMeasure and Perimeter
Then the radius r(Dj) of Dj satisfies
side Cj
r(Dj) >
4 '
vn(C,) > vn(D,) > -?i
and
which implies
Therefore there exists N\ > 0 such that
Now set
and find (in the same manner) pairwise disjoint DNl+l DNi c U\ satisfy-
satisfying
One continues in the same manner, to obtain the lemma.
Theorem IV.1.6 For all Lebesgue-measurable A C R" we have
Proof Let (?/) be a 5-cover of A. Then
IV.l Hausdorff Measure
by the isodiametric inequality (Theorem III.2.1), which impli
vn(A) < ^W(A).
107
es
For the opposite inequality: given any e > 0, there exists a sequence of open
/»-cubes Ij such that
diam/,• < S,
vn(A) <
(one first covers A with open U such that vn({/) < vn(i4) + e/3, then fills U
with closed n-cubes of diameter < S, and then thickens them slightly). Now to
each Ij we have pairwise disjoint closed disks (D,,*) with vn(/; \ U^ ";.*) = 0.
which implies, by Remark IV. 1.1,
Therefore
MJ
2" .
(the next to last inequality follows from the fact that each D,,* covers itself and
has diameter < 8), which implies the theorem. ¦
IV.1.2 Example. Riemannian Manifolds
Theorem IV.1.7 UtXbea separable, locally compact topological space that
admits an exhaustion by compact sets, and let (X,dx)and(X, d2) be two metric
structures on X, whose metric topologies coincide with the original topology,
and which satisfy
lim
m
>-«0 d\{x,y)
108
Hausdorff Measure and Perimeter
locally uniformly. Then Hausdorff measure is independent of the choice oj
metric.
Proof Let K be compact in X. Given e > 0, there exists p > 0 such that
d1(x,y)<p =» l-€<d^lll<l+€
di(x,y)
for all x, y e K. Then any 5-cover of K with respect to d\ is a A + eM-cover
of /if with respect to d2, from which we imply
(with obvious notation), which implies
Hs(K;d2)<H*(K;dt)
for all compact K. By switching the roles of d\ and di we obtain the opposite
inequality, which implies equality for all compact K. One easily obtains the
equality for general subsets of X. ¦
Theorem IV.1.8 Let M be a Riemannian manifold, with associated Rieman-
Riemannian measure dV. Let dH"'M denote the n-dimensional Hausdorff measure
associated with the Riemannian distance in M. Then
(IV. 1.1)
on all of M.
dV = -^
Proof (For the basic definitions and facts about Riemannian manifolds, see the
summary in § V. 1 below.) Let M be a Riemannian manifold, x: U -*¦ R" a chart
on M. Then the Riemannian measure on M is given in the chart by
dV = y/gdxl---dx",
where the local metric {, ) is given by the positive definite symmetric matrix
gij = <3/3x', d/dxj), g = det (gij).
On any compact subset of U, the Riemannian measure dV and the local
Euclidean measure dx = dx1 • • - dx" are equivalent, in the sense that each is
absolutely continuous with respect to the other.
Fix xo e U, and determine Riemann normal coordinates based at xq. Then
8'j(x) -*¦ &U' ti* Kronecker delta, as x -*¦ xo. In particular, y/~g(x) -*¦ 1 as
x -*¦ xo [(V.1.6) below]. Moreover, for any p > 0, there exists a sufficiently
small ro > 0 such that B(xo\ ro) C U and such that, for any vector ? in the
IV1 Hausdorff Measure 109
tangent bundle of B(xq; r0), the Riemannian length |?| of ? and the Euclidean
length 11A1 of ? induced by Riemann normal coordinates based at x0 satisfy
Furthermore, ro can be picked sufficiently small so that the geodesic path reali-
realizing the distance between two points of B(x0; ro) is completely contained i
B(xo; ro). Therefore,
in
, y)
(with obvious notation) for all x, y e B(xo; ro), which impli
lim
We first conclude
ies
c, y)
A + p)'sHsV < HsM < A 4-Y
on 5(jco; ro). Therefore, dHnM is equivalent to dHnK>, which is equivalent to
dV. Therefore there exists a positive function 0 on B(xo; ro) such that
dH"-M =
Since ^/g(x) -> 1 as x -*¦ xo, we have
2"
But xo is arbitrary in M, and d V and dHnM are independent of the choice of
any local coordinate system. We therefore have (IV. 1.1) on all of M. ¦
Corollary IV.1.1 Let X be a k-dimensional submanifold of the n-dimensional
Riemannian manifold Y. Then for any measurable A C X we have, by an
application of Theorems IV. 1.7 and IV. 1.8,
Vk(A) = ~
CX)= ~
c Y)
*vhere d Vj denotes the (k-dimensional) Riemannian measure of the Riemannian
Manifold X, endowed with its induced Riemannian metric.
110 Hausdorff Measure and Perimeter
IV.2 The Area Formula for Lipschitz Maps
Theorem FV.2.1 Let Xbea separable metric space, with family of subsets
containing all Borel sets, and monotone and countably subadditive $:!F
[0, oo]. Let \/f be the Hausdorff measure determined by ?. Then
= sup V {(«),
bTh
for all if/ -measurable A in X, where H varies over all partitions of A by Borel
sets.
Also, if H\, Hi,. ¦. is a sequence of partitions of A by Borel sets satisfying
lim sup diam B = 0,
then
lim V f(«) = 1r(A).
Proof Let S be a Borel set. If (Ej) is a <5-cover of S by Borel sets, then
< 5Z; <(?¦>). which implies t(S) < fo(S) for all 5 > 0, which implies
<(S) <
V Borel 5,
which implies
BeH
BeH
for all Borel partitions H of A (the equality is where we use the Vr-measurability
of A).
Set
Sj — sup diam B, Sj -> 0.
Given e > 0, there exists jo such that 7 > jo implies
by the very definition of the measure \foy. Therefore we also have
which implies the theorem.
IV.2 The A reea Formula for Lipschitz Maps 111
Theorem FV.2.2 Let X be a sseparable metric space, (Y, fi)a measure space,
and assume the map f: X -*¦ Y takes every Borel set B in X to a measurable
set in Y. Let ? be the collectioon of Borel sets in X, define the outer measure
= n{f{B))
on T, and let ty be the inducced Hausdorff measure on X. Then for any y(r-
measurable set A in X we havee
= [f aad(ADf-l[y])dn(y).
JYY
Proof Pick a sequence of Boreel partitions H\, H2,... of A such that
Sj = sup diam B, lim Si = 0,
and such that, for every j, each 1 Borel set in //, is the union of some subfamily
of Hj+\. Then for any y 6 Y wve have
as j —*¦ 00, which implies
+{A) = Unm
= linm
= linm
¦/~>00°
((B)
BeHj
/
= f icud(Anf-l[y])drty)-
Theorem IV12J Let X be a coomplete, separable metric space, Y a metric
space, and f: X -*¦ Y Lipschitz.; Then
nm(f(A)) < I card (A in f'^y}) dHm{y) < (Lip f)nHm(A)
for all Borel sets A in X.
Proof By Proposition 1.3.2, thee image of every Borel set B in X is Hm-
measurable in Y, We may then ddefine, as above,
112
Hausdorff Measure and Perimeter
for any Borel set B in X, and let V denote the induced Hausdorff measure on
X. Then for a sequence of Borel partitions Hi, H2,... of A such that Sj =
&upBeHj diam B, lim Sj = 0, and for every j, each Borel set in Hj is the union
of some subfamily of Hj+i, we have
= lim
j—>00
< (Lip/)m lim
= (Lip/)m?T(A),
that is,
+(A) < (Lip f)mHm(A)
for all Borel sets A, which implies
dHm(y) < f cud (A n /-
) ^K
for any Borel set A in X.
Proposition IV.2.1
(a) Assume L and a are linear transformations qfRm jucA f/wf
for all ?. Then
|deti-| < |dets|.
^ Any //near transformation T: Rm -»¦ R" may be factored as
T = hog, when geGLQC), h a O(Rm;R")
[where GUW) denotes the general linear group ofRm, and ?>(RW;R")
denotes the orthogonal linear mappings ofRm to R"].
Lemma IV.2.1 Given a continuous map f: Rm -> R", m < n, consider
Uj = {x: J/(x) exists and is univalent],
where J/(x) denotes the Jacobian linear transformation of f at x. Then, for
any real number k > \,Uf has a countable covering G by Borel sets such that,
for every Borel set E e G,
IV.2 The Area Formula for Upschitz Maps
(i) f\E is univalent,
(U) there exists a linear automorphism *: R« _» R-» such tha(
-') < A, LipCo(/|?)-i) <
< |det Jf(x)\ <
8
" to its image Jf(xXRm) in R".
Proof Pick f > 0 such that
A~'+e< 1 <A-e,
and fix a countable dense subset <S of GL(Rm)
Therefore, if x, , e Z(a, A)> |y _ x| <
- JO| -
1 ]S(y -
t0
Jf(x) = hog, where? « e GL^R), A
Then
e O(r;R")
= \8d)\
Since <S is dense in GL(R-"). we rmay pick
, e «S such that
y j 3
for this choice of a,, satisfies (i) above. Furthermore, by the existence of
114 Hausdorff Measure and Perimeter
J/(x), there exists a positive integer k such that
\f(y) - fix) - Jf(x)(y - x)\ < -4-1? - x\
II8 II
for all y e B(x; \/k), which implies
I/OO - fix) - Jf(x)(y - x)\ < e\8(y - x)\
for all y e B(x; l/k), which implies that x e Z(s; k). ¦
Theorem IV.2.4 (Area Formula) Let f: Rm -»• R" fee Lipschitz, m <n, and
A a Lebesgue measurable subset o/Rm. Then
(IV.2.1) /* |det //(*)! d\m = f card(/l n /"'
JA JK"
Proof If vm(i4) = 0 then, certainly, both integrals vanish (the right hand side
by Theorem IV.2.3).
First assume that A c Uj, and choose the covering G of A given by the
lemma. Pick a Borel partition H of A such that each B in H is contained in
some E in G. Then one has a map B i->- a e 5, for which
k-mHm(8(B)) = A-m|deta|vm(fl)
< / |detJf\d\m
JB
< Am|deta|vm(B)
that is.
We also have
which implies
\-7mnm{f{B)) < f \dtt Jf\d\m < A^W
JB
If we sum B over the Borel partition H, then Theorem IV.2.2 implies
A f card(Anf-l[y])dHm(y)< f \tetJf\d\m
Jtt" JA
^k2 f card(Anf-1[y])dnm(y).
Jtt"
Since k > 1 is arbitrary, we have (IV.2.1) when A c U/.
k-mHm(8(B))< f \detJf\d\m<kmHm(8(B)).
JB
< Hm{f{B)) < kmH(s(B)),
1V.2 The Area Formula for Lipschitz Maps
115
Now assume
A C [x: dimker Jf(x) > 0} = (x: det Jf(x) = 0).
For any e > 0 write
f = P°g,
where
p:R"xr^r, p(y,z) = y.
Then jc e /i implies
which implies that 5 and Jg(x) are univalent. Also, we have
II-WII < Lip/ +6.f
since ker J>(x) # {0}. Since /,,(*) is univalent, we have from the first half of
me proor that
= ? |det Jg\ dym < e(Lip/ +
Let e -> 0. Then
wm(/M)) < liim sup / [det 7, | </vm = 0
which implies the theorem.
^f P"*
the Lipschitz hypersiurface given by
on
Then
116 Hausdorff Measure and Perimeter
Proof One directly calculates .A* to be given by
3d>
The discussion of the perimeter measure of 3fi is found in Example II1.4.3.
IVJ Bibliographic Notes
There are many excellent treatments of Hausdorff measure, especially in dynamics.
However, our emphasis is toward its employment in geometric measure theory, for
which we have already referred the reader (in the previous chapter) to Federer A969),
Morgan A988), Simon A984).
§IVJ Our treatment follows Federer A969, pp. 241 -244).
Isoperimetric Constants
In this chapter we change our venue: we move from Euclidean space to the
broadercollection of Riemannian manifolds of bounded geometry. Thus we skip
over the intermediate levels of generalization, namely, the sphere and hyperbolic
space of all dimensions, symmetric spaces, and homogeneous spaces. Even
in these intermediate spaces, one gives away the abelian translation group of
isometries and the homotheties that play such an important role in Euclidean
space. Therefore one requires different methods from those we used earlier. In
the more general setting of this half of the book, we also have to change our
point of view with regard to the questions that we ask.
In a general Riemannian manifold, the chances of finding the domain of mini-
minimum boundary area, given the volume of the domain in advance, are essentially
nil except maybe in some very special cases. Furthermore, different choices of
the prescribed volume may change the whole character of the problem. Thus,
from the analytic perspective, we shall not be able to ask for the precise infimum
of the functional
D
A(dD)
(where n is the dimension of the manifold); nor is it obvious that this is the
correct analytic functional to study.
Rather, we shall ask the following: Find v e [ 1, oo] such that the isoperimet-
isoperimetric functional
D
A(8D)
)
is bounded away from 0. (For v = 1 the functional is D t-*- A(dD), and for
v = oo the functional is D t-*- A(dD)/V(D).] And it will suffice to let D vary
over relatively compact domains with smooth (that is, C°°) boundary.
117
118
Isoperimetric Constants
We shall have to adjust even this formulation of the problem to take ac-
account of the difference between the local Euclidean character of Riemannian
manifolds and their varied global behavior. This distinction will allow us to con-
consider discrete isoperimetric inequalties on graphs and, using the hypothesis of
bounded geometry, will allow us to compare global isoperimetric properties of a
Riemannian manifold with those of its discretizations (especially, Theorem
V.3.1).
In subsequent chapters, we shall continue this theme, employing it in the
study of large time heat diffusion in Riemamannian manifolds. But more of
that later.
In this chapter, we mostly present just a summary of the basic background,
nearly all of which is considered in Chavel A994). Detailed proofs are given
for results not covered there, or for results that are at the heart of the point of
view presented here.
V.I Riemannian Geometric Preliminaries
In this section we describe the universe we inhabit for the rest of the book-
Riemannian manifolds. The necessary definitions and results are given that
enable us to discuss the type of isoperimetric inequalities in which we are in-
interested.
Whenever we refer to a manifold, unless otherwise noted, we only have in mind
the interior. Also, unless otherwise noted, it is C°°, Hausdorff, with countable
base, and connected. The boundary, when it exists, is usually mentioned sep-
separately. (We do not assume that the boundary is connected.) Thus a compact
manifold has no boundary.
We are given an n-dimensional manifold M,n > 1. For any point p e M, we
denote the tangent space to M at p by Mp; and we denote the full tangent bundle
by TM, with natural projection n : TM -> M. If x: U -»¦ R" is a chart on M,
we denote the natural frame field associated with x by
01,..., 3n), dj = —j.
At each point p of U, the frame is the natural basis of Mp.
A Riemannian manifold is a manifold with an inner product on each of its
tangent spaces, denoted by {, >; the assignment of inner products, referred to
as a Riemannian metric on M, is C00 in the sense that if X, Y are C°° vector
fields on M, then the function {X, Y) is a C°° real-valued function on M. For
any f e TM the length of ?, |?|, is defined by |?| = <$, i
V.I Riemannian Geometric Preliminaries 119
Given Riemannian manifolds (M, g), (N, h), where g and h denote the re-
respective Riemannian metrics, one naturally considers the product Riemannian
structure on the product manifold M x N,as follows: For x e M, y e N the
tangent space (M x AO(x,y) is canonically isomorphic to MX(B Ny. For vectors
?, r) 6 Mx, f,ne Ny, we define the inner product of ? © ? and r\ © v by
, v).
© f, ij © v) =
Also, given a Riemannian manifold (A/, g) and an imbedded submanifold N in
M, then N carries a natural Riemannian metric g\N obtained by restricting the
inner product on tangent spaces of M to the tangent subspaces of W in M.
Let x: U -*¦ R" be a chart on the fixed Riemannian manifold M. Then for
each p e U, the matrix G(p) given by
(V.I.I)
= (gij(p)), gij(p) = <%,„ 3;,,),
is positive definite symmetric, and the functions gy :U -*¦ R, i, j = 1,..., n,
are C°° on U.
We also use the notation
(V.I.2)
= (g}k), g = det G.
Let Dl denote the continuous, piecewise C1 paths in M. For any path o>:
fa, P] -*¦ M e ?>', a>' denotes the velocity vector of a> at values oft where w
is C1, and the length of a>, l(a>), is defined by
/(»)=/ \<o'(t)\dt.
Ja
For M connected (our usual assumption), p,q e M, we define the distance
between p andq, d(p, q), by
d(p, q) = inf ?(a>),
where o> ranges over all paths (a:[a, fi] -*¦ M 6 ?>' satisfying <o(a) = p,
&{(i) = q. Then (/defines a distance metric on M. A path}/: (a, /?) -»¦ M e Dl,
\y'\ = const., is called a geodesic if for every t e (or, ft) there exists an e > 0
•such that
for all [oro, fio] C(t -e,t + e). That is, geodesies locally minimize distance.
It is known that any geodesic y must in fact be C°°. Furthermore, it is known
that given any ? 6 TM, there exists one and only one maximal geodesic y( :
(-or*, ft) -*¦ M, at, fr 6 @, +oo], satisfying ^@) = n{i-) and ^'@) = ?.
Of course, \y'\ = |?| on all of (-or*, fa). We write I( = (-af,fy).
120
lsoperimetric Constants
Let TM denote the subset of T M consisting of those ? e TM forwhich 1 e I(.
Define the exponential map, exp : TM -*¦ M, by
exp ? =
Then for every t e R, ? 6 TA/, for which f? e TM, we have
exp tl; =
Notation For every p e M we let expp = exp|(TA/ n A/,,). For every p e M
and r > 0, we let B(p;r) denote the open n-disk in Mp centered at the origin
of radius r. Recall that, for every p e M and r > 0, B(p; r) denotes the metric
disk in M centered at p of radius r.
For any p e M there exists an e > 0 such that expp is defined on B(p; 6) and is
a diffeomorphism of B(p; e) onto the metric disk B(p; e). Furthermore, if for
any r > 0 we have expp defined on all of B(p; r), then
exp, B(p;r) = B(p;r);
one just cannot guarantee that exp | B(p;r) is a diffeomorphism. The injectiv-
ity radius of p, inj p, is defined to be the supremum of all r > 0 for which
expp | B(p; r) is a diffeomorphism. By our first remark, inj p > 0 for every p.
The injectivity radius ofM, inj M, is defined to be the infimum of inj p, where
p varies over all of M.
The Riemannian metric also has a local convexity property, namely, given any
p e M, there exists ro e @, inj p] such that for any two points u,v € B(p\ro)
there is a unique length-minimizing geodesic in M joining u to v, and it is
completely contained in B(p; ro).
Let M be a Riemannian manifold. We say that M is geodesically complete
if for every ? e TM, the geodesic y$ is defined on all of R, that is, if exp is
defined on all of TM.
Proposition V. 1.1 If M is geodesically complete, then every closed and bound-
bounded subset is compact. As a consequence, M is a complete metric space. IfM
is a complete metric space, then M is geodesically complete. IfM is complete,
in either of the two meanings, then any two points of M can be joined by a
minimal geodesic.
V.I.I Connections and Curvature
We must first consider the Levi-Civita connection on M. Of course, differen-
differentiation of functions on a manifold is determined by the differentiable structure
V.I Riemannian Geometric Preliminaries 121
alone. But the differentiation of vector fields is not uniquely determined. A con-
connection is a rule for differentiating vector fields on a manifold. Let P°°(TM)
denote C°° vector fields on M, that is, the C°° sections in TM. Then a con-
connection on Mis a map V:TM x r°°(T M) -^ TM, which we write as V$Y
instead of V(?, Y), with the following properties: First we require that
be in the same tangent space as ?, and that for aJeR,p€^?-16
Y 6 r°°(TM),
Second, we require that for p 6 M,$ e MP,Y,YU Y2 6 r°°(TM)>f e C°°{M),
we shall have
v*(y, + y2) = vty, + vty2, vt(/y) = ($/)y,, + /0»)vty.
Finally we require that V be C°° in the following sense: if X, Y e r°°(rAf)
then Vxy e r°°(rA/).
A connection is a local operator in the following sense: Vt Y is uniquely deter-
determined by the values of Y in a neighborhood of p = n (?); in fact, it is determined
by the restriction of Y to a path in a neighborhood of p that passes through p
and which has velocity vector ? at p.
If M is a Riemannian manifold, then there exists a unique connection V
(henceforth called the Levi-Civita connection) for which
(V.I.3)
(VI.4)
for all differentiable vector fields X, Y,Z e T(TM). We shall always work with
this connection.
M is a Riemannian manifold with Levi-Civita connection V. The curvature
tensor, R, of M is defined by
R(X, Y)Z = VYVXZ -
- VlY.X]Z,
L *'/' Z'W e r(™)- One has that R(X, Y)Z at the point p depends
«nly on the values of X, Y, Z at „, and is trilinear on Mp. More generally, if
«(«*, WUZ) = a/?e*(X, y)z. Of course,
and(V 1.3) implies
R(Y, X)Z = 0;
R(X, Y)Z + R(Z, X)Y + R(Y, Z)X = 0.
122 Isoperimetric Constants
One also has
{R(X, Y)Z, W) - {R(Z, W)X, Y) = 0,
{R(X, Y)Z, W) + {R(X, Y)W, Z) = 0.
Since the curvature tensor vanishes identically for dim M = 1, all discussions
concerning the curvature tensor will assume dim M > 2.
To define the sectional curvature, one defines, for p e M, ?, r? e Mp,
f, if).
. if).
where
If |, r; are linearly independent tangent vectors in A/,,, then
is well defined and only depends on the 2-dimensional subspace determined
by ? and r}. We refer to /C(f, 77) as the sectional curvature of the 2-section
determined by ?, r?. We note that if G2 is the complete collection of all
2-dimensional spaces tangent to M, then G2 can be provided a C°° structure in
a natural manner, and K.: G2 -*¦ R will then be C°°.
For p e M, the Aicci tensor Ric: Afy, x Afy, -> R is defined by
Ric (?, if) = trace (f m
In particular, we have for any orthonormal basis of Mp, [e\,..., en}
Thus Ric is a symmetric bilinear form on Mp. To calculate its associated
quadratic form (referred to as Ricci curvature), pick [et,..., en} so that en =
So, for any unit vector ?, Ric (|, |)/(n - 1) is the average sectional curvature
of all 2-sections containing ?.
The Riemann and Ricci tensors measure how the Riemannian metric and
the Riemannian measure, respectively, of M differ at the infinitesimal level
from the Euclidean metric and measure (see §V.1.2 below). It is expressed as
V.I Riemannian Geometric Preliminaries
123
follows: Fix p e M and U = B(p; inj p), U = B(p; inj p). Then every choice of
orthonormal basis [e\ en} of Mp determines a chart n: U -*¦ R", referred
to as Riemann normal coordinates, given by
for q e U, that is, for v =
v e U we have
j e U we have n'(expv) = vJ. Then for
= SJk - \{R(v, ej)v, ek) + O{\v\\
(V.I.6) det^(exp v)) = 1 - |Ric(i>, v) + O(\v\3)
as u -»¦ 0.
If Af 1 and M2 are Riemannian manifolds, we say they are isometric if there
exists a diffeomorphism <p : M\ -*¦ M% such that
10.1 b = If li
for all I e TA/| (the subscripts indicate in which Riemannian manifold the
length is being evaluated), where <p* denotes the Jacobian map from TM\ to
TM2. The map <p is referred to as an isometry.
Let M be a Riemannian manifold of dimension > 2, AC the Riemann sectional
curvature of 2-dimensional spaces tangent to M. We say that M has constant
sectional curvature k,k € R,if JC(<r) = *• for all 2-sections <r. One has the three
standard model spaces of simply connected complete Riemannian manifolds
of constant sectional curvature. For k = 0 one has Euclidean space R", with
its standard Riemannian metric. Of course, the geodesies are the straight lines
in R". When k > 0, the n-sphere Sn(l/y/ic) in Rn+1 of radius \jyfic has con-
constant sectional curvature k. The geodesies ofSn(l/y/ic) are given by the "great
circles," the intersection with Sn(l/V*) of 2-planes in Rn+I that pass through
the center ofSn(l/y/ic). When k < 0, we have hyperbolic space given by the
ball model, namely, on the n-disk B"A /y/—ic) we define the Riemannian metric
2 _
~{
)
then the sectional curvature is constant equal to k < 0. One easily sees that,
in this model, the geodesies emanating from the origin are given by straight
lines emanating from origin, and their length to the boundary Sn~'(l/V-^)
is infinite. The rest of the geodesies consist of the intersection with B" A /^J^ic)
of those circles in R" that orthogonally intersect the boundary sphere
By the Hopf-Killing theorem, a complete simply connected Riemannian
manifold of constant sectional curvature k is uniquely determined up to
124
hoperimetric Constants
isometry. In particular such a space is isometric to the appropriate model among
those discussed above. We always refer to the model space as the model space
MK of constant sectional curvature k.
For convenience, we define the function
[
I
sin
k > 0,
k = 0,
k < 0.
Of course, <p(r) = SK(r) satisfies
0, <p@) = 0, <p'@) = 1.
Let M, be the model space of constant sectional curvature k. It is standard that
for any x e M, unit vector ? e Mx, and r > 0 (that is, when k < 0 - otherwise,
we have to restrict r e @, n/y/ic])y we have
(V.I.7)
ds2(exp r|) = dr2
where \di-\2 denotes the Riemannian metric on the (n — l)-dimensional unit
tangent sphere (henceforth denoted by) Sx in Mx.
V.I.2 Volumes of Disks and Areas of Spheres
We now consider the Riemannian measure dV on M. Let x: U -*¦ R" be a chart
on My with the Riemannian metric given in local coordinates by (V.I. 1) and
(V.1.2). Then the local measure
dV = V*°x~' dvn(\) = yfgdx1 ¦dx"
[where g is given by (V.1.2)] is well defined, that is, the integral
/(/;«/)= I (fVg)ox-1 dvn(x)
depends only on / and U - not on the particular choice of chart x. One then de-
defines a global Riemannian measure on M, also denoted by dV, using a partition
of unity.
i
Definition Given any x e M, we let Dx denote the largest starlike (relative to j
the origin) neighborhood of the origin of Mx on which exp is a diffeomorphism.'
For any ? e Sx, we let
e Dx V/e [0, r)}.
V.I Riemannian Geometric Preliminariy
es
So
125
For any x e M, r > 0> w ^ ^ ^ ^ ^
those elements « for which r« e D,. which ri *
we write as
wnte the Riemannian measure on Dx as
where rfMx($) denotes the Riemannian measure on S, induced by the Euclidean
Lebesgue measure on Mx. We also let V(x; r) denote the volume of B(x- r)
S(x-T^ M' ^ 1Ct ^^ den°te *" /OVVer are° «the
•Xjc, r), with center jc and radius r, that is,
and we let *(,; r) denote
;r):=/"
mefrfc jpAere S(jr; r)>
the (n - l)-dimensional Hausdorff measure of S(x;r).
Proposition V.I 2 One has
V(x;r)= ['nix;!
Jo
;t)dt
and
V(x;r+€)-V(X;r)
limsup __^ < %{x.r)<A(x;r)
for all r > 0.
Finally, A(x;r) = 2l(jc; r) for almost all r.
K/. J Curvature and Volume
Recall^ c^ denotes the („ - l^dimensional Riemannian measure of the
rim"/1 Unit SpherC S""'in R"- F«^ a real constant, and M the
TJi7z?rp]cX? Riemannian manifoid °f constant -«^ --
above, let rfy, = ^fr; I) rfrrf,.,«) denote the Riemannian
126
Isoperimetric Constants
measure on M» in geodesic spherical coordinates described above, and VK(r)
the volume of the metric disk in MK of radius r. Then
), VK(r) = c._, f SKn~
Jo
t)dt.
Bishop's comparison theorem states that if M is an n-dimensional Riemannian
manifold, x e M such that B(x; R) c TM [that is, the exponential map is
defined on all of B(x, R)], and
for all ? e A/,, q e B(x; R), then
(V.I.9)
v/•
which implies
(V.I.10) y/g(r,$)<SKn-l(r\
for all r e @, min {R, c(?)}), and
(V.I.I 1) V(*;r) < V,(r)
for all r e [0, R]. In particular, (V.I.9) implies that the function
that is, is nonincreasing with respect tor on@, min {R, c(?)}). Gromov's refine-
refinement of Bishop's comparison theorem states that, under the same hypotheses,
the function
(VI. 13) r»V(x;r)/VK(r)l,
that is, is nonincreasing with respect to r on [0, R].
V.I.4 LiouviUe's Theorem
On the unit tangent bundle of M, SAf, one has the geodesic flow, <t>t, defined
by
that is, <!>,? is the velocity vector of the geodesic y$@ = exp f? at the point
). Since y^'(t) has the same length as ?, <!>, indeed maps the unit tangent
V.2 Isoperimetric Constants 127
bundle to itself. The kinematic density is the measure dfi on SAf giv
/ Fdf*= f dV(x) f
JSM JM JS.
for functions F on SAf.
given by
Js,
U3 (Liouvffle's Theorem) Themeasure dponSAi is invariant
respect to the geodesic flow. sonant
V.2 Isoperimetric Constants
In this section we define the basic apparatus of isoperimetric constants that
we use in the sequel. We mention some of the most elementary examples that
guide the intuition, and we discuss the necessity of introducing a modified
apparatus of constants in order to deal with the dichotomy between local and
global considerations in the geometry of Riemannian manifolds. Probably the
most important result for our point of view here is Theorem V.2.4, which proves
the invariance of positivity of modified isoperimetric constants under compact
perturbations of a complete Riemannian manifold.
V.2.1 Definitions and Examples
Definition Let M be an n-dimensional Riemannian manifold, n > 2. Denote
by V its n-dimensional Riemannian measure, and by A the Riemannian measure
associated with (n - 1 )-dimensional submanifolds of Af. For each v > 1 define
the v-isoperimetric constant ofM, 3V(M), to be the infimum
where il varies over open submanifolds of M possessing compact closure and
C°° boundary.
For v = oo define Cheeger's constant, 3X(M)> by
above.
where n ranges over open submanifolds of M described
Remark V.2.1 If M is compact, then, by considering M\B(x;e) for small
« > 0, one can easily show that 3V(M) = 0 for all v. Therefore, we shall restrict
our interest to the case of noncompact manifolds. One can adjust the definitions
128
Isoperimetric Constants
of isoperimetric constants for the compact case and obtain a rich theory. See
our comments in § VI.2 below. Also, see the remarks in the Bibliographic Notes
to Chapter VI (§VI.6).
Definition Let <f>: M -*¦ N be a diffeomorphism between Riemannian mani-
manifolds M, N with respective metric tensors g, h. We say that ^ is a quasi-isometry
if there exists a constant c > 1 such that
for all ? e TM, the tangent bundle of M.
Two metric tensors g,h on a Riemannian manifold M are quasi-isometric
if the identity map \dM : (A/, g) -*¦ (M, h) is a quasi-isometry, that is, if there
exists a constant c > 1 such that
Remark V.2.2 The property 3V(M) > 0, v e [1, oo], is invariant under quasi-
isometry.
Example V.2.1 The first, R", n > 1, as discussed in previous chapters.
Example V.2.2 The hyperbolic spaces, M», k < 0. Then the Cheeger constant
3<»(M*) = (» — 1 )¦>/-*, where n = dirnM,. The proof goes as follows:
Let M be arbitrary Riemannian, x e A/, and r, ? geodesic spherical coordi-
coordinates on Dx. Let dr denote the radial vectorfield on Dx, given by
Then it is standard that the Riemannian divergence of dr (see §VII.2.1 below)
is given by
When M = M* then
div3r(exp r%) = ;L, _^ •
V.2 Isoperimetric Constants 129
When *: < 0, then c(?) = +00 V ^ 6 Sx - so D, = M,. Therefore any
relatively compact Q CC D,. Furthermore,
diva, >(n-
By the Riemannian divergence theorem,
A(dto) > / {dr, v)dA = if di\drdV > (n - l^/^
where v denotes the exterior unit normal vectorfield along 3 ?2. The lower bound
> (n -
is sharp, because one has
A(x;r)
(n -
^ic asr -*¦ +00.
As mentioned in Remark 1.1.4, if M = Mj, the simply connected Rieman-
Riemannian 2-manifold of constant Gauss curvature equal to k, then the isoperimetric
inequality is A.1.6):
L1 > An A - kA2,
where A denotes the 2-dimensional measure of the domain, and L the
1-dimensional measure of the boundary, with equality if and only if the do-
domain in question is a metric disk. When k < 0, the inequality A.1.6) is sharp in
two senses, because A.1.6) implies both the inequalities
L/Al/2 > y/4Jr, LI A > yf^ic.
The first is sharp for geodesic disks of radius r as r X 0, and the second is sharp
for geodesic disks of radius r asr ^ +00.
Thus, one has distinct isoperimetric behavior when discussing the local prop-
properties of the manifold versus the global ones. Indeed, one expects all local
isoperimetric behavior to be Euclidean in character [see (V. 1.5)], and the global
behavior to be quite diverse.
Remark \23 The inequality 3V(M) > 0 is only possible for n < v < 00.
Indeed, let v < n, and consider small geodesic disks B(x; e), with center x e M
and radius e > 0. Then for the isoperimetric quotient of B(x; e) we have
as e I 0; thus 3V(M) = 0 whenever v < n. So it seems at first glance that one
only has a discussion of isoperimetric constants for v > n = dim Af.
130
Isoperimetric Constants
Definition For each v > 1 and p > 0 define the v-modified isoperimetric con-
constant ofM, 3v,p(A/), by
= inf
where ft varies over open submanifolds of M possessing compact closure and
C °° boundary and inradius greater than p, that is, ?2 that contain a closed metric
disk of radius p.
Definition For v = 1 and p > 0 define the I-modified isoperimetric constant
ofM, 3,,P(A/), by
where ?2 varies over open submanifolds of M, described above, with inradius
greater than p.
For v = co and p > 0 define the modified Cheeger constant, 3<»,p(A/). by
. , A(dQ)
18f
where ?2 ranges over open submanifolds of M, described above, with inradius
greater than p.
Remark V.2.4 Given v e [1, co], then the existence of p > 0 for which
3v,p(A/) > 0 is invariant under quasi-isometry.
Example V.23 Consider the Riemannian product M = Mo xRk, where Mo
is an (n - &)-dimensional compact Riemannian manifold. Then h(M) = 0, as
noted in Remark V.2.3. Yet, for extremely large domains - for example, metric
disks of large radius - one expects the volume of these domains and the area of
their boundaries to reflect /^-dimensional space. We shall see (Example V.3.6
below) that 3V,P{M) > 0 for any p > 0 for all v e [1, *].
Example V.2.4 The 2-dimensional jungle gym JG2 is constructed by (a) con-
considering the integer lattice Z3 in R3, (b) connecting points, for which precisely
one of their coordinates differ by 1 and the other two coordinates are equal,
by a line segment parallel to the coordinate axis, (c) considering the surface
consisting of all points with distance from the 1-dimensional network to be
precisely equal to e, for some given small e > 0, and finally (d) smoothing out
V.2 Isoperimetric Constants
131
the corners in a bounded periodic (that is, Z3-invariant) fashion. We shall see
(Example V.3.7 below) that 33(JG2) > 0.
The verification of the positivity of the isoperimetric constants in the last two
examples requires discrete isoperimetric inequalities for graphs, which we con-
consider later.
V.2.2 Bask Results
Remark \2? It is an easy consequence of Minkowski's inequality that for
domains ft;, j = 1,..., Af, in M, and any * > 1, we have
From this Yau A975) has shown that in the definition of 3V(M), v e A, co], it
suffices to let ?2 range over open submanifolds of M that are connected.
Definition For each v > 1, define the Sobolev constant 6V(M) ofM by
where / varies over C~(A/).
For each p > 0, let C™p(M) consist of those compactly supported Lipschitz
functions 4>onM for which (a) there exists an x € M such that the preimage of
max |^|, n*, satisfies fy 2 D(x;p), and (b) $ \ M\fy e C°°. For each v > 1
and p > 0, define the modified Sobolev constant of M, 6V,P(M), by
(V-21) 6v.fi(M) = inf
where / ranges over CC°°O(A/).
Remark V.2.6 Even for GV(M) we may (by Theorem 1.3.3) allow / to vary
over compactly supported Lipschitz functions on M.
Theorem V.2.1 (The Federer-Fleming Theorem) The isoperimetric and
Sobolev constants are equal, that is.
(V.2.2)
MM) = 6V(M),
132
Isoperimetric Constants
and the modified isoperimetric and modified Sobolev constants are equal, thai
is.
(V.2.3)
3v.fi(M) = 6v,fi(M).
Proof The proof of (V.2.2) is the same as the proof of Theorem II.2.1, with the
substitution of v for n. The argument for (V.2.3) is a slight modification of the
proof of Theorem II.2.1. ¦
Theorem V.2.2 Suppose, for a given v e A, oo), we have 3V,P(M) > 0. Then
for the area and volume of metric spheres and disks we have
(V.2.4)
A(x;r)>3v,p(M)V(x;r)i-
for all x e M and r > p.
For the volume of metric disks we have
(V.2.3)
V'(x;r)>3v,p(M)V(x;rI-
(where the prime denotes differentiation with respect to r)for almost all r > p.
In particular,
(V.2.6)
liminf V(jc; r)r~v > 0.
rfoo
Proof The point, of course, is even when r > inj x.
Assume r > p. For e > 0 define the function rf: [0, oo) -> [0, 1] by
(a) t((s) = 1 when s e [0, r], (b) r((s) = (r + e- s)/e when s 6 [r, r + e],
and (c) x( (s) = 0 when s > r + e. Also define the Lipschitz function f(:M^>
Rby
My) = r((d(x, y)).
Then
Now let € I 0. Then
which implies the first claim.
V.2 Isoperimetric Constants
133
The second claim follows from the fact that A(x; r) = V'(x\r) for almost all
r. Now integrate (V.2.5) to obtain (V.2.6). ¦
A similar argument, using the corresponding Federer-Fleming theorem for
v = oo, shows
Theorem X23 Suppose 3OO(M) > 0. Then for the volume of metric disks we
have for all x e M
(V.2.7)
for almost all r > 0.
In particular,
(V.2.8)
V'(x;r)>300(M)V(x;r)
lim inf V(x;
rfoo
> 0.
Proposition VJ.1 If3v.fi(M) > Ofor some v 6 [1, oo), P > 0, then V(x; p +
6) is uniformly bounded from below for all x with d(x, dM) > p + e, for any
6 > 0. /Ifco, I^+^M) > 0 for all (x in [1, v).
Proposition V.2.2 Let SI be a domain in M with compact closure and C°°
boundary. Then 3OO(&) > 0.
Theorem V.2.4 Let D be a relatively compact domain in the Riemannian
complete M with C°° boundary V, and D' an n-dimensional Riemannian
manifold with compact closure and C°° boundary F, such that M' given by
M' = {M\D} U D' is C°° Riemannian. If3v,p(M) > Ofor given v e [1, oo)
and p>0, then there exists p' > 0 such that 3V^(M') > 0.
Proof (See Figure V.2.1.) Suppose we are given any a 6 @, oo). The number
« will be fixed throughout the argument, although its estimated value will be
determined as we go along.
Since 3ViP(M) > 0, there exists R > p such that
for all x e M. Let 8' denote the diameter of D'. We pick
p' = 2p + R + 8'.
Let E = M \ D, and suppose we are given ft' c m\ with compact closure
and C°° boundary, and J2' 2 B(y'; p').
134
Isoperimetric Constants
Figure V.2.1: The compact perturbation.
(i) We first assume that d{y\ D') < R. Then B(y'; p') 2 D', which implie
SO' c E. Set J2 = (O' \ D') U D. Then 3ft = 3ST, and J2 contains a disl
in M with inradius p, which implies
We obtain
' n
' n
that is,
(V.2.9) iP()
(ii) We now assume d(y', D') > R. Then B(y';«) c E, which implies
(V.2.10) V{Sl')x~xlv > V(y'; «)I-|/p > <M(r).
(ii-a) Assume first that V(Q' n ?) > i V(O'). Then
n ?)
' n ?)) - a(D
D
because /? > p. So
135
VT2 Isoperimetric Constants
Therefore we pick a at the very outset to also be greater than or equal
to 3,.p(A/)/22-'^. We obtain
(V.2.11) AidST) > pv.p(M)/22-l/v)V(n')l-l/v.
(ii-b) The final situation to consider is, therefore, d(y', D') > R and
V(n' C\iy)>{ V(SI') We still have (V210); then
, threfore, d(y
V(n' C\iy)>{ V(SI'). We still have (V.2.10); then
> A(da n d')
'WiSi1 HD')-- V(Q')l-l/v
a
^2 I
a
"I
-\/v
(the third inequality uses Proposition V.2.2). In addition to the above,
pick, at the outset, a sufficiently large so that
(V.2 1
Then (V.2.9HV2.12) will imply the theorem.
Example VJ.5 The proofs of Proposition V.2.1 and Theorem V.2.4 break down
when v — oo - unless we postulate the existence of po > 0 for which
(V.2.13)
v(x; po) > const. > 0
for all x (the constant independent of x). Moreover, one has a counterexample
for Proposition V.2.1. Consider the Riemannian metric on M = R1 x S1 given
by
Certainly there is no po > 0 for which (V.2.13) is satisfied for all at. At the same
time, one easily shows
3,,p(A/) = 0
for all v e [l,oo), p > 0.
136 Isoperimetric Constants
V.2.3 Bounded Geometry
Proposition X23
(a) (Croke's inequality) Let M bean arbitrary Riemannian manifold. Given
any o 6 M, p > 0, such that exp0 is defined on D(o\ p), then for
r < - min I inf inj x, p \
2 [xeB(o,fi) r\
we have
(V.2.14)
> const.
(where const.,, is a constant depending only on n = dim M) for all J2 c B(o;r),
which implies
(V.2.15)
V(o;r) >const.nr"
for all r < i min {infx€B(<,:p) injx, p\.
(b) (Buser's inequality) Let M be a complete n-dimensional Riemannian
manifold, with
(V.2.16)
*:<0,
foralll- 6 TM. Then there exists a positive constant c(n,K,r) depending on n,
k, andr, such that for any given x 6 M ,r > 0, and a dividing C°° hypersurface
T inB(x;r) withT imbeddedin D(x;r)andB(x\r) \ T = fti U ft2. where J2i,
J?2 on open in B(,x;r), we have
(V.2.17) min{V(ni), V(ft2)} < c(n,K,r)A(r).
Moreover, for any fixed r0 > 0 we have
(V.2.18) c(n,k, r) < c(n, *:, ro)r Vre@, ro].
Remark V.2.7 Croke's inequalities (V.2.14) and (V.2.1S) are statements that
the local isoperimetric behavior of an arbitrary Riemannian manifold is indeed
Euclidean.
Definition A Riemannian manifold M has bounded geometry if the Ricci cur-
curvature of M is bounded uniformly from below [as in (V.2.16)], and if the
injectivity radius of M is bounded uniformly away from 0 on all of M.
Theorem \2S If M is Riemannian complete with bounded geometry, then
> 0 for every p > 0.
Proof Set
V.2 Isoperimetric Constants
8 = min{/0, inj A/}.
137
Assume we are given Q as above, containing B(x; p) for some x e M. One
easily has the existence of z e M for which 3 J2 D B(z; 8/2) divides B(z; 8/2)
into two open subsets for which the smaller volume is greater than or equal to
V(z;8/2)/3. Then Buser's inequality (V.2.17) implies
A(dS2 n B(z;8/2)) > const.V(z' / \
and Croke's inequality (V.2.15) implies
V(z;8/2)>cn8\
which bounds A(dQ) away from 0. ¦
Here is an alternate characterization of modified isoperimetric constants.
Theorem V.2.6 Let M bea complete Riemannian manifold with bounded geo-
geometry. Then3Vifi(M) > Oforsomev > 1, p > 0 if andonly ifthere exists vq > 0
such that
(V.2.19) A(dii) > const.
for all domains ft with compact closure and C°° boundary.
Proof Assume that (V.2.19) is valid for all ft. Since M has bounded geometry,
then for any r0 > 0 there exists vo > 0 such that V(x; r0) > i>o for all x in M.
Then 3v,ro(M) > 0. ¦
To prove the converse, we first prove
Lemma V.2.1 Let M be Riemannian complete with bounded geometry, and set
R = j inj M. Then there exists a positive constant c such that for any domain
ft in M with compact closure and C°° boundary, satisfying
V(QnB(x;R))< l-V(x;R)
for all x in ft (so ft is uniformly thin), we have
138
Isoperimetric Constants
V.3 Discretizations and Isoperimetric Inequalities
Proof Given such an J2, then for each x e J2 there exists r{x) e @, R) such Proof There exists xo such that
that
139
V(x;r(*)). _
Let & _ J2 u B(x0; /?). Then J2' has inradius greater than or equal to R, which
Pick a finite collection [xt, r,}, r, = r(xt), such that {?(*,; r,)} are pairwise imphes
disjoint and {B(xf;3r,)} cover J2. Then Buser's inequality (V.2.18) and Croke's _ Am) > - ,Wom-i/,. > - wo,i-i/v
inequality (V.2.15)imply l J - J**K(") >-V*V(J2)' 1/v.
Also,
' ; R),
2const.
> const.r,"-',
which implies
'> R) < const./?" < const./i(aJ2 n B(x0; R)) < const.ACJ2)
(the second inequality follows from the same one in the proof of the previous
lemma), which implies
> const.
> const. J^ V(x,; r,I
< const.ACJ2),
which implies the lemma.
~l/"
> const,
;r.)
,_1/n
ConclusionoftheProofofTheorem V.2.6 We are assuming that 3, P(M) > 0
for sorae „ > { ^ p > Q ^ ^ = ^^ ^ R% R J ^ ^
Then V(J2> ^ "o implies the hypotheses of Lemma V.2.1, which implies
> const. \J2 V(x,;3r,)
> const. V(n)l-l/n
A(dV) > const.
Assume V(Q) >vo.Uv>n, then, by Theorem V.3.2 below,
[the second inequality is (V.I.I 1); the third line in Minkowski's inequality; anfl A®O) ~ C°nSt" V&)l~l/v
the fourth line follows from (V.I.13)]. [°r a" «• which implies the theorem in this case. Therefore assume v < n If
in tntSfiCS ** hyPOthCSeS Of Lemma V22' ^n we ¦« d«ne- Otherwise we are
Lemma V.2.2 L«/ M be Riemannian complete with bounded geometry, am Then C&SC ^ Le"lma V21> that n is ""°'formly *in" but has large volume.
assume 3v,fi(M) > Ofor some v > 1, p > 0. Let R = \inj M. There exists
positive constant d such that, ifQ is a domain in M with compact closure cam /1(an) > const.V(SlI-1'" > const V(m1~l/vvnl/''-l/m =
C°° boundary for which there exists x' eO satisfying wh . .
* Whlch ""Plies the theorem.
Here VJ Dlscretl2attons and Isoperimetric Inequalities
is no D^ti"^1106 diSCrete aPProximations t<> Riemannian manifolds. There
P^nse here to fine approximation; rather, we highlight what one might
J2 ii «o/ uniformly thin), then
MO) > • V(a)«-"-.
140
Isoperimetric Constants
V. 3 Discretizations and Isoperimetric Inequalities
141
refer to as the coarse geometry of the manifold. First we discuss graph structures
in their own right, and an apparatus of measures and isoperimetric constants
associated with graphs. And then we discuss them as discretizations of smooth
Riemannian manifolds. The most important result is Theorem V.3.1, which
allows one to verify the positivity of an isoperimetric constant in one category,
by checking in the other.
V.3.1 Volume Growth and Graphs
Definition Let X and Y be metric spaces with a bijection <(>: X -*¦ Y. We say
that # is a quasi-isometry if there exists a constant c > 1 such that
e-'dOc,,x2) < d(<t>{xx),<j>(x2)) < cd(xux2)
for all x\,X2 inX.
Let Q be a countable set such that for each ? e Q we have a finite nonempty
subset N(?) C5\{?|, of cardinality m(?), each element of which is referred to
as a neighbor oft-,v/'tih\he property that tj e N(?)ifandonlyif? e N(r?)forall
i-,T) 6 Q. Then one determines a graph structure G by postulating the existence
of precisely one oriented edge from any ? to each of its neighbors, the elements
of N(?). We refer to m(?) as the valence ofG at ?. We say that the graph G
has bounded geometry if the valence function m(?) is bounded uniformly from
above on all of Q. In such a case we let m = max {m(?): ? e Q).
A sequence of points (?o, ...,?*) is a combinatorial path of length k if ?; e
N(?;_ i) for all j = 1 *. The graph G is called connected if any two points
are connected by a combinatorial path. Note that m(?) > 1 for all ? if G is con-
connected. For any two vertices ? and rj in the connected graph G, one defines
their distance d(?, r?) to be the infimum of the length of all combinatorial paths
connecting ? to r}. We also refer to d as the combinatorial metric. We set the
notation for the respective metric "disks":
for any ? e Q.
Example VJ.1 Let F be a finitely generated group, with generator set A. Then
consider every element of F to be written as a word of minimum length in the
generators in A and their inverses. For the graph structure, given any y eF,
we let N(y) = y ¦ {AU A~x] be the neighbors of y. Then the combinatorial
metric of the graph structure may be realized by the word metric as follows:
Let A := (y\ yk] be a given set of generators of F. With every y e F we
associate the word norm ofy,\y\^, defined to be the minimum length of y as
a word in the given set of generators A and their inverses. Note that
IkU>0, with
\0y\a<\P\a
for all /J, y in F. The word metric on T is then given by
Thus the group theoretic word metric is equal to the graph theoretic combina-
combinatorial metric. It is common to refer to this graph as the Cayley graph of F.
Note that if we use a different set of generators B := {yj\ .... y*}, then we
have the metrics induced by A and B quasi-isometric to each other, namely,
Example VJ.2 Let M be a complete Riemannian manifold, and let F be any
finitely generated subgroup of isometries M acting freely and properly discon-
tinuously on M, such that M/ F is compact. For each x e M let || • \\x denote
the displacement norm on F, given by
\\Yh=d(x,yx)
for all y € F, where d denotes distance in M. Then again we have
IML>0, with
Wy\\x<
for all fi, y in F. Given a set of generators A of F, one has the existence of a
constants > 1 such that
oTx\y\a< WyWx <a\Y\A
for all yeP, which implies that the induced metrics are quasi-isometric.
Furthermore, the map ^: F -> M, given by
satisfies
,-i
, Y) <
, y)
forall p, Y in r - so * is a quasi-isometry (at the metric level) of r to its image
142
Isoperimetric Constants
Definition Let X and Y be metric spaces with map <f>: X -*¦ Y. We say that 0
is a rough isometry if there exist constants a > 1, b > 0, and e > 0 such that
<ad(xux2) + b
for all x\, x2 in X, and <j> is (-full, that is,
jreX
Note that the definition of rough isometry does not require that ^ be a bijection,
just a map; in fact, the map <j> need not be continuous.
Proposition VJ.1 If<j>:Xx -> X2 and \/r:X2^> X^are rough isometries, then
so is iff o<f>. If 4>\X -*Y is a rough isometry, then there exists <f>~ : Y -*¦ X
a rough isometry, for which both d(<(>~ o#(x), x)andd{$ o#~(y), y) are uni-
uniformly bounded on X and Y, respectively Any two spaces of finite diameter are
roughly isometric. If X and Y are roughly isometric, then X and Y x K are
roughly isometric, for any compact metric space K.
Return to the graph G. On the collection of vertices Q we have two natural
measures. The first is simply the counting measure di; thus, for any subset K.
of Q we have
t(AC) = card AC.
The second is what we call the volume measure dV on Q, defined by
Of course, when G has bounded geometry, the two measures are commensurate
in the sense that the Radon-Nikodym derivative of dM with respect to di is
uniformly bounded away from 0 and +oo. Because in what follows we generally
discuss graphs of bounded geometry, and we are only interested in qualitative
estimates on volumes, we shall work with the counting measure di - even when
we announce the results in terms of the volume measure d\l.
Now denote the collection of oriented edges of the connected graph G by Qe.
The oriented edge from ? to tj will be denoted by [?, r?]; and when we wish to
consider the unoriented edge connecting ? and rj, we denote it by [? ~ r?].
Any finite subset AC in Q determines a finite subgraph K of G, for which one
can describe a variety of suitable definitions for its boundary. Our definition
will be that the boundary ofK, 3K, will be the subset of Q, consisting of those
oriented edges that connect points of AC to the complement of AC in Q. We define
the area measure dA on Qe to be the counting measure for the oriented edges.
V.3 Discretizations and Isoperimetric Inequalities 143
Thus, for any finite subset of vertices, the area of its boundary will be equal to
the number of edges in the boundary.
Another definition of the boundary of a finite subgraph K of G is given by
Thus, by this definition, dK is a subset of vertices in the complement of K; its
area is defined to be its cardinality. When G has bounded geometry, the two
choices of area functions
K ¦-> ACK),
as functions on the collection of subgraphs K of G, are commensurate each
with respect to the other in the sense that the quotient of the two functions is
bounded uniformly away from 0 and oo.
Therefore, when G has bounded geometry, we will work with the counting
measure for the volume of K, and the second definition of dK as a subset of
G with counting measure for its area - despite the fact that the theorems are
formulated with respect to the original notions of volume, boundary, and area.
Definition We say that the Riemannian manifold M has exponential volume
growth if In V(x; r) > const.r for sufficiently large r; otherwise we say that M
has subexponential volume growth. Also, we say that M has polynomial volume
growth if there exists * > 0 such that V(x; r) < const./-* for sufficiently large
r 0
Similarly, we say that the graph G has exponential volume growth if
In V(?;r) > const.r for sufficiently larger; otherwise we say that Ghassubex-
ponential volume growth. Also, we say that G has polynomial volume growth
if there exists k > 0 such that V(?; r) < const.r* for sufficiently large r > 0.
Example X33 (Example V.3.1 continued.) When one is given a finitely gener-
generated group P with k generators A = [yi,... yK), then for the counting function
one has
where y is any element of F (because all elements of V have 2* elements in
each neighborhood). Moreover (Milnor, 1968), the limit of n^Wl/x, as A. -> oo,
exists.
144
Isoperimetric Constants
Furthermore, when M covers a compact Riemannian manifold with deck
transformation group f, then there exist constants a > 1, b > 0, and C > 1
such that c~lnA(a~lk - b) < V(x; k) < Cn^(aA + b) for every x e M.
Proposition V.3.2 Let G, F be connected, roughly isometric graphs, both with
bounded geometry. Then G has polynomial (has exponential) volume growth if
and only i/F has polynomial (has exponential) volume growth.
Definition For any v > 1 define the v-isoperimetric constant of G by
where K varies over finite subgraphs of G.
Proposition X33 // G, F are roughly isometric graphs, both with bounded
geometry, then \V(G) > 0 if and only if\v(F) > 0.
Example X3.4 (Example V.3.3 continued.) Considera finitely generated group
F, with fixed collection of generators A. We (henceforth) denote the combina-
combinatorial disk centered at the identity e of radius k by 0(k). On the graph associated
with F we work with the counting measure (and in this example we denote it
by V); so when discussing the volume of combinatorial disks, we are working
with the counting function. We define its "inverse" <t(A.), A. > 0, by
*(A.) = rain {k 6 Z+ : V(/t) > A.}.
That is, V(*(A.) - 1) < A. < V(*(A.)). Then for any finite subgraph K of F,
1 \/(K)
(V3 1) A,^wr^ ^ * "\"-/
The proof goes as follows:
Definition In any graph, not necessarily a group, given any function / on the
vertices, one defines the differential off, 2)/, on the edges by
»/([*, y]) = f(y) - fix),
and one integrates 2)/ relative to dA (see §VI.5 below).
For any function <f>: F -> R on the group F of finite support, and nonnegative
integer k, define the mean value function fa on F by
= J^ E
V.3 Discretizations and Isoperimetric Inequalities
145
So <f>k(x) is the mean value of 4> on the combinatorial disk centered at x with
radius k.
For k = \,y varies over AU A~\ which implies
which implies
E
* yeAKJA-[
For any* > 1, let y =
(set zo = e)
zt, I < k, where zj
\<f>(xy) - <f>(x)\ <
which implies
Next, for every k, the triangle inequality implies
{|*l > A-} C {|^ - ^| > k/2) U
which implies
V({|*| > A.}) < V({|^ - <f>k\ > k/2})
Also, one certainly has
so if we pick *o to be the smallest * for which
1. One has
< k/2, that is,
Isoperimetric Constants
146
that is,
Pick <j> = TK, and A. = 1. Then one obtains (V.3.1).
In particular,
(V.3.2) V(*) > const.*" V* => ACK) > const.V(K)'-V'
for all K of finite cardinality. So in the case of a group, a lower bound for volume
growth alone is equivalent to the corresponding isoperimetric inequality.
For v = oo the argument yields a slightly weaker result, namely,
const.V(K)
V(/t) > const.*00-* V *
for all K of finite cardinality.
ACK) >
const, log V(*) + const.
Example V33 If G is a Lie group with left-invariant Riemannian metric and
bi-invariant Riemannian (Haar) measure, then one can formulate and prove, in
similar manner, a corresponding result, that volume growth uniformly bounded
from below implies an isoperimetric inequality.
V.3.2 Discretizations
Definition Let M be a Riemannian manifold. A subset Q of M is said to be
(-separated, e > 0, if the distance between any two distinct points of Q is
greater than or equal to e.
Remark V.3.1 If Q is e-separated, then one always has only a finite number of
elements of Q in B{x;r) when the exponential map is defined on B(x;r + e/2)
[where, as above, B(x; p) denotes the disk of radius p centered at the origin of
the tangent space at x, Mx]. Indeed,
2 \J
B(x;r
where the union on the right hand side is disjoint union. Therefore
> card \Q n B(x; r)} inf V(r?;e/2).
egnB(xs)
But the compactness of B(x; r) implies inf,€j;n«(.r;r) ^(r?; e/2) > 0, which im-
implies an upper bound on card {Q D B(x; r)). So the real question is to obtain a
uniform upper bound for card Q n B(x; r) independent of x and Q.
V.3 Discretizations and Isoperimetric Inequalities
147
Lemma V.3.1 Let M be complete, with Ricci curvature bounded from below
as in (V.2.16) on all ofTM, and Q an (-separated subset ofM. Then
for allx 6 M and r > 0.
Proof Since card Q n B(x; r) is finite, there exists ^egfl B(x; r) such that
= inf
Therefore, the Bishop-Gromov volume comparison theorem (V.I. 13) implies
Definition Let M be a Riemannian manifold. A discretization ofM is a graph
G, determined by an €-separated subset Q of M, for which there exists p > 0
such that M = U*€ff &(%' P)- Then € is called the separation, and p the cov-
covering, radius of the discretization. The graph structure G is determined by the
collection of neighbors of $, N($) := \Q n fl($; 3/>)} \ \%\, for each ? e Q.
Remark \32 Note that card N(?) > 1, so G is connected.
Remark VJJ Lemma V.3.1 implies that when the Ricci curvature is bounded
from below as in (V.2.16), then for the graph G we have 1 + m(?) < VKFp +
*/2)/ VK((/2) := Nf,.p for all ? e G - so G has bounded geometry.
Proposition V3.4 Let M be Riemannian and G a discretization of M. Then
there exist a > 1 and b > Ofor which
(V3.3) a-'rf(*.,fc)<d(?i,&)<arf(*l,fc)+*>
for all ?,, ?2 in Q.Thus, M is roughly isometric to any of its discretizations, and
any two of its discretizations are roughly isometric.
Lemma V.3.2 Let Mbea complete Riemannian manifold, with Ricci curvature
bounded from below as in (V.2.16), and assume there exist positive constants
ro and Vq such that
V(x;ro)>Vo
148 Isoperimetric Constants
for all x G M. Then for any r > 0 one has a positive constant const., such that
V(x;r) > const.,
for all x e M.
Proof Ifr > r0, then simply use Vo. If r < r0, then simply note that the Bishop-
Gromov theorem (V. 1.13) implies
VK(r0)
which implies the claim.
Proposition V3.5 Let Mbea complete Riemannian manifold, with Ricci cur-
curvature bounded from below as in (V.2.16). Then for any discretization G ofM, G
has polynomial (has exponential) volume growth only if (if) M has polynomial
(has exponential) volume growth.
If, on the other hand, there exist positive constants r$ and Vo such that
V(jc;ro)> Vo
for all x e M, then for any discretization G of M, G has polynomial (has
exponential) volume growth if (only if) M has polynomial (has exponential)
volume growth.
V.3.3 Isoperimetry and Discretizations
This is the main theorem of the chapter.
Theorem V3.1 Let M be a complete Riemannian manifold with bounded ge-
geometry. Then for any v > 1 we have 2VtP(M) > 0 if and only if\v(G) > Ofor
any discretization G ofM.
Proof First, given 0ViP(M) > 0. By Proposition V.3.4, we may work with any
discretization. Therefore we consider a discretization G of M with separation
constant e > 0 and covering radius R = p. To show that IV(G) > 0, it suffices
to prove the existence of positive constants such that given any K. c Q we may
find ii c M of inradius > p for which
(V.3.4)
and
(V.3.5)
A(dQ)< const, card SIC,
V(Q) > const, card K.
V.3 Discretizations and Isoperimetric Inequalities
We proceed as follows: Given a finite subset K., set
Then
149
V(t-;R) <
where M^r is an upper bound (depending on e, R, and the lower bound of
the Ricci curvature) of the maximum number of (-separated points in a disk of
radius R (see Remark V.3.3). So for
VR := inf V(x; R) > 0
jreitf
[the positivity of Vr follows from Croke's inequality (V.2.15)], we have
which implies (V.3.5). For the upper bound of A(dSi) we note that
3QC (J S($;R).
Indeed, if x G dQ, then d(x, ?) > R for all ? € ?, and there exists ?0 G ?
such that x G S($o\ R). But there must exist ?' e Q such that d(x, ?') < R,
which implies ?' ^ K. Then d(?0, H') < 2/?. which implies |b e N(?')- So ?0 e
9(^ \ IC), which is the claim. Therefore,
A(d?l) < AK(R)cardd(g\K:) < mAK(R)caiddK:,
which implies (V.3.4). So we have the "only if claim of the theorem.
For the "if claim, we again note that we may work with any discretization.
Therefore assume that we are given the graph G, for which \V(G) > 0, with
covering radius R = p < inj M/2.
Suppose we are given ?2, with compact closure, C°° boundary, and inradius
greater than p. Set
fCo := {* € Q: V(Q n ««;/>)) > V($; p)/2),
Kx := {? € ^: 0 < V(fi n
So both ACq and ACi are contained in [il]p (ihe set of points with distance from
150 Isoperimetric Constants
Q less than or equal to p). Then for at least one of j = 0, 1 we have
(V.3.6)
<v(nn|J «(*;
V
If (V.3.6) is valid for j = 1, then we have directly from Buser's inequality
(V.2.18)
V(O)
n fi(?;p)) < const.M«,pAOQ)
< const.
[without any hypothesis on IV(G)], which implies
A(d?i) > const.V(Q) = const.V(Q)l/vV(QI-|/v > const.
since Si contains a disk of radius p, which, by Croke's inequality (V.2.1S), has
volume uniformly bounded from below. So we must consider the case when
(V.3.6) is valid only for j = 0.
First,
Therefore it suffices to give a lower bound of A(dSi) by a multiple of card
dfCo - the multiple independent of the choice of fCo. To this end, define
H c [Si]P by
H := {x e M: V(x;p)/2 = V(Q n B(x;p))).
For each % e 3ACo there exists t) G N(^), rj e ACo; we have, of course,
</(?, t)) < 3p.
By definition,
D B(r)\p)) > V(r)-p)/2, V(Q D
which implies the minimizing geodesic connecting ? to r) contains an element
? e H, which implies dfCo ^ [H\$p, which implies
V.3 Discretizations and Isoperimetric Inequalities
Let Q be a maximal 2p-separated subset of H. Thus
u
which implies
151
= 2M«,pconst. ? V(S2 n
D
- the third inequality uses the Bishop-Gromov comparison theorem (V.I. 13);
the following equality follows from the definition of H 3 Q; and the fourth
inequality uses Buser's inequality (V.2.18). ¦
Example V3.6 (Example V.2.3 continued.) Consider the Riemannian pro-
product M = Mo x R*. where Afo is an (« - t)-dimensional compact Riemannian
manifold. Then Proposition V.2.1 and Theorem V.3.1 imply that 3V,P(M) > 0
for any p > 0 for all v e [1, Jfc]. Indeed, both M and R* are discretized by Z*.
Since V(x;r) < const./-* for all r > 0, then Jfc is the maximum of all v for which
> 0 for some p > 0.
Theorem Y3J2 Let M have bounded geometry. Then, for any v >n,we have
3V{M) > 0 if and only i/lv(G) > Ofor any discretization G of M.
Proof The "only if is precisely as above.
So we assume that IV(G) > 0. Suppose we are given Q, with compact closure,
C°° boundary, and no assumption on the inradius. As above, we set
ACo := {? 6 Q: V(S2 n B(t-; p)) > Vtf;p)/2},
Ki := {? 6 G: 0 < V(€l n
Again, both ACq and /Ci are contained in [?2]p, and for at least one of j = 0, 1
152
we have (V.3.6):
Isoperimetric Constants
V(O)
< V
If (V.3.6) is valid for j = 0, then we may argue as above; for the only place
we invoked the hypothesis of the inradius uniformly bounded away from 0
was when (V.3.6) is valid only for j = 1. We therefore adjust the argument for
(V.3.6) valid only for j = 1. ¦
Lemma \33 There exists a constant jv > 0 such that
AtfSi D BQ;p)) > JvV(Si n BQ;p))l-l/v, p < ^
for all I-eld.
Conclusion of the Proof of Theorem VJ.2. Assume the lemma is valid. Then
A.1.5) implies
I\v/(v-l)
J2 V(QnBG;p))l-l'v\
Therefore, (V.3.6) and the lemma imply
V(O)
<v(an J BG-.
< const.AOO)|p/(l'-|),
which implies the theorem.
So it remains to prove the lemma.
Proof of Lemma \33. Let D = Si n B($;p); then
Therefore v > n implies
V3 Discretizations and Isoperimetric Inequalities
153
Figure V.3.1: C(.
so it suffices to prove
V(D)i-i/» < COnst.ACDn
Since p < inj A//2 we have, by Croke's inequality (V.2.14),
A(dD n
= const{A(dDC\
So we want to show
A(dD
n
Consider geodesic spherical coordinates centered at ?. Let
subset of S| for which
B($;p)}.
denote the
(See Figure V.3.1.) For each d e Cf, let
ct@) = sup{f > 0: exp td
Note that if oF) < p, then the geodesic segment from exp oFN to exp p6 is
contained in D. The Bishop-Gromov theorem (V.I. 13) implies
154
which implies
V(D) > ^^- f
AkKP) Jc
Isoperimetric Constants
which implies, by Buser's inequality (V.2.18),
A(dDnS(t-;p))<
< consl.A(dD D fl(?; p))
= const. A(dDr\B($;p)),
A(dD
which implies the claim. ¦
Example VJ.7 (Example V.2.4 continued.) Let JG2 denote the 2-dimensional
jungle gym in R3. Then Theorem V.3.2 implies that 33<JG2) > 0. Indeed, JG2
and R3 are simultaneously discretized by Z3.
Example V3.8 Given a noncompact M that covers of a compact Riemannian
manifold Mo, the deck transformation group F of the covering is a discretiza-
discretization (see Example V.3.2) of M. Then, by the proof of Proposition V.3.5 (see
Kanai, 1985), a volume growth of order > rk in M implies a volume growth in
F of order > ifc, which, by Example V.3.4, implies a ifc-isoperimetric inequality
in T, which implies a (modified) ifc-isoperimetric inequality in M.
V.3.4 Isoperimetric Inequalities on Products
For future reference we note:
Given the Riemannian manifolds Mj,j = 1,2, we consider the respective vol-
volume and area measures associated with the standard product metric on M, x M2.
Given the graphs GU), j = 1,2, we consider the graph GA) x GB) with
vertices
and oriented edges [(&, ?2). (m. %)] where either (a) ?, ~ $2 and ^1 = 172, or
0>) ?1 = Hi and fi ~ fa. with corresponding volume and area measures on the
vertices and edges.
Given the Riemannian manifolds Mj, j = 1,2, of bounded geometry,
with respective discretizations Gw, then the inclusion of the discretization
(GA) x GB))o in Mi x M2 is a rough isometry.
V4 Bibliographic Notes
155
Proposition VJ.6
(a) Let G0), j = 1,2, be two graphs, both with uniformly bounded valence
functions m.V\$), and assume IV/(GO)) > 0, Vj > I, j = l,2. Then
I,,+^(GA) x GB)) > 0.
(b) Let Mj, j = 1,2, be Riemannian manifolds of respective dimension nj. Let
vj > »j, j = 1,2, and assume that
Then
x M2) > 0.
(c) LetMj, j = 1, 2, be Riemannian manifolds as in (b). Letvj > 1 andp > 0,
and assume that
IVl,P(Mj)>0, y = 1,2.
Then
(V.3.7) Ivi+v2 ^(Mt x M2) > 0.
If, in addition, both Mi and M2 have bounded geometry, and
then
(V.3.8) IVl+vl(Mi x M2) > 0.
V.4 Bibliographic Notes
Nearly all the material of this chapter is detailed, with references, in Chavel A994). We
chose proofs from among the material there to emphasize our major themes, isoperime-
isoperimetric inequalities and discretizations. An very nice introductory survey is Burstall's article
in the 1998 Edinburgh Lectures (Davies and Safarov, 1999, pp. 1-29).
§V.l Proposition V.I .1 is known as the Hopf-Rinow theorem; see Hopf and Rinow
A931).
§ V.Z3 Propositions V.2.2 and V2.3(a) were first proved in Croke A980), and Proposi-
Proposition V2.3(b) in Buser A982). Theorem V.2.6 was communicated to me by A. Grigor'yan;
sec also his Grigor'yan A994b).
§VJ.l The proof in Example V.3.4 is from Coulhon and Saloff-Coste A993).
156
Isoperimetric Constants
§V3.2 Proposition V.3.4 was first proved in Kanai A985), with the hypothesis of Ricci
curvature bounded from below to obtain the upper bound. Subsequently, this hypothesis
was shown in Holopainen A994) to be unnecessary. Theorem V.3.2 was first proved in
Kanai A985).
§V3.4 An elegant proof of the product theorem. Proposition V.3.6, for the discrete
case is given in §3 of Varopoulos A985). (It is surely valid in the continuous case.) Also,
see Grigor'yan A985).
VI
Analytic Isoperimetric Inequalities
In this chapter we explore, in greater detail, the applications of isoperimet-
isoperimetric inequalities to Sobolev inequalities, a phenomenon only hinted at in the
Federer-Fleming theorem (Theorem II.2.1) and the Faber-Krahn inequality
(Theorem III.3.1). The application of isoperimetric inequalities to analysis is a
rich subject in its own right, although we only develop here what we need for
our particular study of the heat equation in later chapters. We also present the
analogue of these arguments in the discrete case, and discuss the equivalence of
Sobolev inequalities on Riemannian manifolds of bounded geometry, and the
corresponding Sobolev inequalities on their discretizations.
VI.l L2 Sobolev Inequalities
Let M be an n-dimensional Riemannian manifold.
Definition Let / be a C1 function on M. We define the gradient of f to be the
vector field on M satisfying
<grad /, ?) = df^) = $f Vt-eTM,
where df denotes the differential of / on M.
For C1 functions /, h on M we have
grad (/ + h) = grad / + grad/t,
grad fh = /grad h + /igrad /.
If x: U -* R" is a chart on M, then, with the usual notation
gij = (8,, dj), G = (jy). G~l = (gij),
157
158
we have
Analytic Isoperimetric Inequalities
d
j.k
dxJ
Note that the Riemannian metric on M naturally induces a metric on fibers
of TM*, namely, if a and p are covectors in the same fiber, then (a, 0) =
(9~l(u), d~l@)), where d: TM ->¦ TM * is the bundle isomorphism defined
by {0(?)}(»J) = (?> 1) for any ?. f e rw tot belong to the same fiber. One
verifies, rather easily, that for any differentiable function on M we have
= |grad/|
on all of M.
Lemma VL1.1 If the isoperimetric constant 3V(M) is positive for some given
v > 2, then
for any function <j> in Cf.
Proof Of course, we have 3V = 6V > 0, by the Federer-Fleming theorem.
Therefore,
Ilgrad/H, > 3J/L/(,-n
for all / e C~. Given any 0 e Cf\ let / = \<f>\p, p = 2(v - l)/(v - 2). Then
Igrad/| = pM"-1 Igrad |*| I = pW'1 |grad^|
(the last equality valid a.e.-dV - see Lemma II.2.1), which implies, by the
Cauchy-Schwarz inequality, that
L
|grad/|rfV <
which easily implies the claim. ¦
Remark VL1.1 We refer to (VI. 1.1) as the Nirenberg-Sobolev inequality.
Lemma VI.1.2 If3v(M) is positive for some given v > 2, then there exists a
positive const. „ such that
(VI.1.2)
forallfeC?.
VI. I L2 Sobolev Inequalities
159
Proof Start with the previous lemma for v > 2. The first step is to show that
&v > 0 for some v > 2 implies
f
d>2+4/vdV
Indeed, if v > 2, set / = \<f>\2, p = v/(v - 2), and g = \4>\*/v, q = v/2, and
use H6lder's inequality to obtain (VI.1.3) from (VI.1.1). On the other hand, if
v = 2, one has directly
II02||2 < const.||grad@2)||, < const.||4>||21|grad0||2.
Square both sides to obtain (VI. 1.3). To obtain (VI. 1.2), simply apply Holder
inequality to / = |^|4/(v+4), p = (v + 4)/4, and g = 2
(v + 4)/v.
s
q =
Remark VI.1.2 We refer to (VI.1.2) as the Nash-Sobolev inequality.
Theorem VI.1.1 The Nash-Sobolev inequality is equivalent to the Nirenberg-
NirenbergSobolev inequality.
Proof The proof of Lemma VI. 1.2 shows that the Nirenberg-Sobolev inequal-
inequality implies the Nash-Sobolev inequality. So it remains to consider the converse.
Suppose we are given a positive constant C such that
\\4>hl+Vv <
for all <f> e Cf, for some v > 2. Set
2v
Then
v + 2'
v + 2
Given any / e C» define, for every k e Z,
[0. / < 2*.
/* = min{(/ - 2*)+, 2*} = | / - 2*. 2* < / < 2*+1
I 2*. 2*+' < /
160
Analytic Isoperimetric Inequalities
V
A k .
Figure VI. 1.1: /*.
(see Figure VI. 1.1) and
Then
which implies
4/K
r , nl+2/x
= L-,A2]
1+2/v
that is.
Let
<C2{2*V(/>2*)}4/"/" lgrad/|2,
< C2{2*V(/ > 2*)}4/v / |grad/|
ak = 2k"V(f>2k), bk= t |grad/|2;
'ft
then (VI.1.4) implies
V/.2 T/i« Compact Case
161
which implies
JteZ
|2(l-«)
which implies the theorem. ¦
Theorem VI.1.2 (Cheeger's Inequality) If3x(M) > 0, then for any function
(f> in Cf we have
In particular, X(M) = inf spec - A (see §VII.l and §VII.2.2) satisfies
MM) > ]-3oo(MJ.
4
Proof The inequality for grad / is simply an adjustment of the argument for
(VI. 1.1) to the case v = oo. To obtain the Cheeger inequality for k(M) consider
thecase# = /2,forany/ e C™, and then use the Cauchy-Schwarz inequality,
followed by the characterization of eigenvalues (VII. 1.2) and (VII.2.4). ¦
Remark VI.13 When our manifold M is a relatively compact domain in some
larger Riemannian manifold, and M has C°° boundary, then our Sobolev con-
constant 6V, and the inequalities that follow from it, correspond to vanishing
Dirichlet data on the boundary dM. Therefore, in the Cheeger inequality in
Theorem VI.1.2, \{M) is the lowest Dirichlet eigenvalue of the Laplacian on
M. For vanishing Neumann boundary data, we use the definitions of the Sobolev
constants sv of the compact case (below), in which case A.((Af) is the lowest
nonvanishing Neumann eigenvalue of the Laplacian on M.
VI.2 The Compact Case
Here compact means compact without boundary, what was once called a closed
manifold.
Let M be compact Riemannian, n > 1 the dimension of M. Then, as men-
mentioned in Remark V.2.1, all isoperimetric constants vanish. Alternatively, by
162
Analytic Isoperimetric Inequalities
considering the function / = 1 on M one has that all the Sobolev constants
of M vanish. Nevertheless, one can adjust the definitions as follows (here one
only needs, for the geometry, the isoperimetric dimensions n and oo):
Definition Define the isoperimetric constant in(Af) by
in(M) = inf
where F varies over compact (n — l)-dimensional C°° submanifolds of M that
divide M into two disjoint open submanifolds Qi, Q2 of M.
Define Cheeger's constant ioo(Af) by
where F varies over compact (n — l)-submanifolds of M described above.
Remark VI.2.1 One has here, as in Remark V.2.5, that it suffices to assume
that the open submanifolds J2i and fi2 are connected.
Definition For v e A,00] define the Sobolev constant ofM, &V(M), by
(with the obvious interpretation for v = 00), where a varies over R, and / over
C°°. The analogue of the Federer-Fleming theorem (Theorem II.2.1) reads as
follows:
(VI.2.1) in(M) <
and Cheeger's inequality reads as
where ki(M) denotes the lowest nonzero eigenvalue of M.
Definition Given any function on M, we define its mean value fM by
'><¦¦=
Remark VI.2.2 For any s > 0, the ao that realizes infa || / - a \\,+i is charac-
characterized by
{sgn(/-ao)}l/-aol* = O.
VI.2 The Compact Case
163
Forv = ^wehavein^ \\f - a || 2 realized by the mean value fM of /over M.
For v = 00, we have infa \\f - a\\x realized by that a0 for which
ao}) =
Definition For M compact, we define the alternate Sobolev constant s'v(M) by
inf ^ . vetl.oo],
' 11/ — /mIIv/(v-1)
where / varies over C°°(Af).
Remark VL23 We comment on the relation between i^, Soo, s^. Clearly,
Suppose we are given a disconnection of M = Q, U Q2 U F, where Q,, Q2
are domains in Af and F is a compact (n - l)-submanifold of Af. Let F€,
e > 0, denote all points in Af whose distance from F is less than e, and assume
V(Q,) < V(Q2). Let /, be the function on M which is equal to 1 on J2, \ F,,
equal to -1 on J22 \ T(, and linear across F on F(. Then a standard argument
shows that
lim /
and
/« -a\dV > |1 -aUV(Q,)-const.a(} + |l +a\{V(Q2) -
> {|1 -o| + |l +a|}{V(Q1)-constA},
where St -* 0 as e I 0, which implies
»nf / \f(-a\dV > (
which implies ««, < A(V)/ V(Q,); so
Soo < ioo
Now given any function / e C°°(A/), pick the constant 0 so that, for
?2. = {/ > 0}, n2 = {/ < fi],
Analytic Isoperimetric Inequalities
164
we have
(see Remark VI.2.2 above); and let
D, = {q eQ
Then V(D,) < V(M)/2 for all f > 0, which implies, by the co-area formula
A.3.7) and Cavalieri's principle A.3.3),
/ |grad(/-0)|</V= / A(dD,)dt
n, Jo
V(D,)dt = ioo f \f-
Jn,
0\dV.
The same argument yields
which implies
n2
>\x f \f-
Jn2
0\dV,
/ |grad/|<fV = f \gml(f-P)\dV
n Jo
which implies s<x> > i<»; so
\f-a\dV,
On the other hand, if we work with fM instead of 0, then we are only
guaranteed that at least one of {/ — /«> 0}, {/ — /«< 0} has volume <
V(M)/2. The same argument then yields
In sum, we have
(VI.2.2)
*«> —
Remark VL2.4 If M is not closed, but has compact closure and C°° boundary,
then the above apparatus of isoperimetric and Sobolev constants is still well de-
defined, with the above inequalities. We only have to note that A.i (M) in Cheeger's
inequality is now replaced by fii(M), the first nonzero Neumann eigenvalue
of M.
VI.3 Faber-Krahn Inequalities 165
VL3 Faber-Krahn Inequalities
One may easily check that, for M = R", n > 1, one may express the Faber-
Krahn inequality, Theorem III.3.1, as the analytic inequality
for relatively compact SI in R" with C°° boundary, where CB depends only on the
dimension n, with equality if and only if Q is an n-disk in R" [in particular, CR =
k(B) V(BJ/n, where B denotes an n-disk in R"]. The bottom of the spectrum,
A.(?2), is discussed in VII. 1 and VII.2.2. For general Riemannian manifolds, we
do not even hope for precise geometric or eigenvalue inequalities. Nonetheless,
we can consider qualitative versions of the Faber-Krahn inequality, in the spirit
of the geometric isoperimetric inequality.
Lemma VI3.1 Let v > 2. Then
(a) The Nirenberg-Sobolev inequality
||gradM||2 > a\\uhvi(V-2h
for all u e Cf, implies the Faber-Krahn inequality
for relatively compact domains Si in M with C°° boundary,
(b) The NashSobolev inequality
llgrad«|h>0||«||21+2/lK||r2/\
for all u G C*. implies the Faber-Krahn inequality
HSi) > p2V(S2)-2/v
for relatively compact domains S2 in M with C°° boundary.
Proof Let u > 0 be an eigenfunction of k(Sl), || u \\ = 1 (see Proposition VII.4.1).
Then
Also,
which implies
' = f U2 < j f M2"A"-2)
(w—2)/v
2/k
which implies the claim.
166
Analytic Isoperimetric Inequalities
Again, u > 0 be an eigenfunction of k(Si), \\u\\ = 1. Then A. > 02||M||r4/\
and / m < \\u\\2V(SiI'2 = V(Q), which implies the claim. ¦
Remark VI3.1 We refer to the Faber-Krahn inequality of this lemma as a
Faber-Krahn inequality ofv-Euclidean type.
Theorem VI3.1 The Riemannian manifold M satisfies a Faber-Krahn in-
inequality ofv-Euclidean type, v > 2, if and only if it satisfies the corresponding
Nirenberg- and NashSobolev inequalities.
Proof We already know the "if part of the theorem, so we only consider "only
if." Let
2v
* ~ v-2'
and, for any relatively compact Si in M with smooth boundary, set
av(Si) = k(Si)V(SiJ/v, fiv(Si) = fof
It suffices to show that there exists const. > 0 such that
(VI.3.1) av(Si) < const.fiv(Si)
for all Si.
Proposition VI3.1 There exists a bounded u G C°°(Si) n f)c(Si) such that.
(i) u > 0, (ii) fQ uq dV = 1, (iii) A u = -/zv
Remark VI3.2 For the definition of f)c see Remark 1.3.3 and the discussion
in §VU.2.2.
Lemma VI3.2 Assume M satisfies the Faber-Krahn inequality ofv-Euclidean
type. Let u satisfy Proposition VI.3.1. Then there exists const.v, > 0 such that
V({u > ||m||oo -'}) > const., I — ,./,_,) v' e [0, llMlUinregval.,
where regval,, denotes the set of regular values ofu, av = av(Si), fiv = fiv(Si).
Proof Set
L =
Si, = {u > L-t).
Then
VI.3 Faber-Krahn Inequalities
167
> avV(Si,)-2'v,
and
K(Sit) <
fQi(u-L+t?
Now
[u - L + tf > j [u-L+t}2> (t/2JV(Sil/2),
which implies
which implies
Therefore,
which implies
1/2
'IV(Q,/2)J '
= V(O,)(lP+4V2lP.
( a»q [
*/»
at
Also,
= const.,.
168 Analytic lsoperimetric Inequalities
Next, fix o e Si that realizes Hgradulloo = max |gradu| := <5. Then
therefore.
which implies
as I -*¦ oo. Thus,
Sd(x,o)<— => xeSit/2>,
lim V (Sil/2,f«v+4»' = 1,
which implies the claim of the lemma. ¦
Conclusion of the Proof of Theorem VL3.1 Given u of Proposition VI.3.1,
then, by Cavalieri's principle (Proposition 1.3.3),
1 = f uqdV
= f
rL
= / qV(u >t)t"-ldt
Jo
fL
= / qV(u > L - t)(L - /)«"' dt
Jo
"/2
- -(«-l)v/2+v/2+4
= const. „
= const. „ I —
since -(q - \)v/2 + v/2 + q = 0.
Thus Faber-Krahn implies Nirenberg-Sobolev, which implies Nash-
Sobolev. ¦
All the analytic isoperimetric inequalities considered thus far require v > n
(check!), but a simple way to deal with v < n goes as follows:
Definition Let M be an arbitrary Riemannian manifold. Given a positive in-
increasing function g( v), v > 0. We say that a domain ?2 in M satisfies a geometric
VI.3 Faber-Krahn Inequalities 169
g-isoperimetric inequality if
A(dD) > g(V(D))
for all domains D CCSi.
Given a positive decreasing function A(v), v > 0. We say that a domain Si
in M satisfies an eigenvalue A-isoperimetric inequality if
X(D) > A(V(D))
for all D CC Si.
Remark VUJ Thus, A-isoperimetric inequalities are generalizations of
Faber-Krahn inequalities of Euclidean type.
Theorem VL3.2 Suppose Si satisfies a geometric g-isoperimetric inequal-
inequality, with g(v)/v a decreasing Junction ofv. Then Si satisfies an eigenvalue
K-isoperimetric inequality with
Proof This is the usual proof of Cheeger's inequality. For any u e C^°(D)
apply the co-area formula to u2. We define
we
and
Then
= {xeD:\u(x)\2>z],
V(t) = V(D(r)), A(z) =
2||«||2||grad«||2 > / |grad(«2)|rfV
JD
f°°
= / A(z)dz
Jo
g(V(z))dz
f0 V(T)
V(z)dz
V(z)dT
g(V(D))
V(D)
\\u\h\
170 Analytic lsoperimetric Inequalities
which implies, by (VII. 1.2) and (VII.2.4),
which implies the theorem.
4 V V(D) )
Example VI J.I Let M be a complete Riemannian manifold with bounded
geometry, and assume 3V,P(M) > 0 for some v > 1, p > 0. Then, by Theorem
V.2.6, M satisfies a geometric g-isoperimetric inequality, with g(y) given by
g(v) = const.
v < v0,
v > v0.
Then Theorem VI.3.2 implies that M satisfies a eigenvalue A-isoperimetric
inequality, where
!V~2/", V < Vn,
2/v
const.Vov~z/l\ v > v0.
Example V133, Similarly, let M be a complete Riemannian manifold with
bounded geometry and positive Cheeger constant, that is, 3oo(AO > 0. Then,
by the argument of Theorem V.2.6, M satisfies a geometric g-isoperimetric
inequality, with g(v) given by
= const.
v < v0,
Then Theorem VI.3.2 implies that M satisfies a eigenvalue A-isoperimetricj
inequality, where
fy-2/n v <; v
2/n
vo/", v > v0.
We shall consider a variant of the Nirenberg-Sobolev inequality in §Vm.4g
VI.4 The Federer-Fleming Theorem: The Discrete Case
We now formulate and prove the discrete Federer-Reming theorem. But firstj
Definition (Recall.) To every function / on a graph G we associate its di
ential, defined on Qe the oriented edges of G, by
VI.4 The Federer-Fleming Theorem: The Discrete Case 171
Theorem VI.4.1 (Discrete Co-area Formula) Let f: Q -* [0, +oo) have
finite support. Denote the collection of its values by f(Q) := {0 = fa < ft\ <
¦ ¦ • < PnY To each i'60,...,JV associate K, the subgraph ofG determined
by the vertices
by the vertices
Then
Proof First note mat 3K, = {tt. „]: m > A >
/(|?)}; so
and
1 ')¦
for any such [f, „] 6 aK, we have
which implies
E
? E E
E E
E
. f(n)<Pt
1=1
which is the claim.
172
Proof First,
Analytic Isoperimetric Inequalities
(jc -
x"-y" _Pxp
-l
px
p-\
so we may choose c-i = p. Next, fix any a > 1. If y < x < ay, then
y)P
~l ~
Ba)P~1'
(jc - y)(x + yy-1 ~
and if ay < jc.then
xp - yp > (I - a~p)xp, x-y<x, x + y <(l+a~l)x,
which implies
XP-yP l-Ct-p
(x - y)(x
So we may pick
= min i —
c\ = min
This proves the lemma. ¦
Lemma VI.4.2 Let a, be a decreasing sequence ofnonnegative numbers, and
Pj an increasing sequence of nonnegative numbers, with A) = 0. Then for any
p > 1 we have
IN \P N
Y.ttJllP<fii - ft-i)| ? const., ?>,(?/ - Pj-t")
7=1 I 7-1
for all N = 1,2
Proof UN -I, then both the right and left hand sides of (VI.4.1) are equal to
a\P\p. So (VI.4.1) is valid for N = \. For the induction step we have
.7=1
\N+l
N
l - fiN)
N+l
VI.4 The Federer-Fleming Theorem: The Discrete Case
173
i" - Pit")
Therefore, if for any N we have
then we also have
{N+\
(N
Eaj'/pwj-Pj-
y-i
1 E•>(/>/
1 •'*i
N+l
which is the claim.
U ** S°b0leV COnSUmt S
where /ranges over functions on Q with finite support, and the L> norms are
ST "d 'A on a "d a" ^^(We have
«¦
indicatOT fancti0° of «.
= 2A0K),
which implies8,@) < 2A(aK)/{V(K))(-i)/»fcrdl«chclioicesofK which
"nphes 8,@) < 2IV(G). Therefore, if SlP(G) > 0, then |r(G) > 0. To show 2
174 Analytic Isoperimetric Inequalities
opposite direction, we first note that
since \a — b\>\\a\ — \b\\ for all real a and b; therefore it suffices to consider the
case where / is nonnegative. Assume that I,,(G) > 0. Then for / nonnegative
we have
/ |D/| dA = 2 J2 AOK.-XA - ft-,)
JQ, ,=1
N
> 2IV(G)? MK,-)}0"-"/^/* - ft-i)
?
> const.lv(G)
\(v~l)/v
= const. I V(G) ||/1| „/(„_!)
- the third line follows from the argument of Lemma VI.4.2. Therefore,
I,,(G) > 0 implies SV(G) > 0. ¦
Remark VI.4.1 The results of §VI.l above all follow from the positivity of the
Ll Sobolev constant, and integral inequalities. Therefore, since the Federer-
Fleming theorem holds for graphs (as far as positivity of the isoperimetric and
Sobolev constants are concerned), we have the corresponding versions of the
above results for graphs.
VI.5 Sobolev Inequalities and Discretizations
Given a graph G with bounded geometry, let K be a finite subset of Q. Then for
any function / on Q, and any s > 0, we have
that is, the two expressions are equivalent in that their quotient is contained
in a compact subset of @, +oo), this subset independent of the choice of K
and /. For convenience define
In what follows, we will work with s = 2, so the notation will not get out of
hand. And whenever we write |3?/|(§) we mean v|3?/h(f )¦ One can then work
out the details for any other fixed value of s, for example s = 1.
Let X be a graph with bounded geometry, Y a metric space, and <p: X ->• Y a
rough isometry with rough isometry Constantsa > l,b > O.Thencard0~'[)']is
VI. 5 Sobolev Inequalities and Discretizations 175
uniformly bounded as y varies over Y. Indeed, if <j>(x\) = <f>(x2) then
a~ld(x\, x{) — b < 0, which implies that d(jtj, xi) is uniformly bounded, in-
independent of y. The bounded geometry hypothesis now implies the claim.
Similarly, if AT is a graph with bounded geometry, Y a metric space, and <p:
X -*¦ Y a rough isometry with isometry constants a > 1, b > 0, then for every
R > 0,y e F, the number of disks B(<p(x); /?)thatcoverjisboundeduniformly
from above independent of y. Indeed, if y e B{<p(x\); R) n B(<j>(x2); R) then
d@(jti), 0C*2)) < 2R, which again implies the claim by the rough isometry
hypothesis on <j> and the bounded geometry hypothesis on X.
Lemma VI.5.1 Let Xbea graph with bounded geometry, Y either a connected
graph or a complete Riemannian manifold, and <j>: X -*¦ Y a rough isometry.
Let f: X -* R andg: Y -*¦ R be nonnegative functions satisfying
(VI.5.1) f{x) < const. / g
JBWx);p)
for some p > 0, for all x € X, where & stands for /J or B depending on whether
Y is a graph or a Riemannian manifold. Then
(VI.5.2)
/ / < const. /
Jpu.R) yB(,
g-
Proof Recall that the constants a and b are from the definition of the rough
isometry.
Because <Pi0(x; R)) C. BD>ix);aR + b), we only have to count the number
of times any y in B@(jc); a R + b + p) contributes to the integral on the right in
(VI.5.2). Well, all multiple counting of<f>(x) comes from #"'[#(*)], which has
cardinality uniformly bounded from above. For the multiple contribution from
v within p of 4>(X), we only have to note that Biy; p) n <p(X) has cardinality
uniformly bounded from above for all y 6 Y. ¦
Notation When we have a map from 0: X -> Y, and a function f:Y-*R,
we denote by </>*/ the function defined on X by the usual <p*fix) = f(<p(x)).
Lemma VI.5.2 Suppose X and Y are graphs, X with bounded geometry,
<P ¦ X ~+ Y a rough isometry. Let f :Y -*¦ R. Then
I \4>*f\2 < const
JpU.R)
I l®@*/)l2 < const. /
Jfi(x:tt) J/H
for sufficiently large R, independent ofx.
176
Analytic hoperimetric Inequalities
VI.5 Sobolev Inequalities and Discretizations
Proof We only prove the second claim. We want to estimate |2>(^*/)l2 from
above, for each x e X. Namely,
x'eN(jr)
Set a + b := L. Then d(jc, jc') = 1 =>• d@(x), <f>(x')) < L, which implies
|2W'/)I2(*) < const. / |2>/|2.
Now use Lemma VI.5.1. ¦
Lemma VI.53 Let X be a graph with bounded geometry, and <t>: X -* X a
rough isometryfor which d(jc, 4>(jc)) is uniformly bounded from above. Then
[ \f -4>*f\2< const. [ |2>/|2
Jp(x.R) Jp(x\cona.R)
for sufficiently large R > 0, independent ofx.
Proof Because d(jc, <t>(x)) < K for some K > 0, for all x, we have
|/(jc) - f(<P(x))\2 < const, f |2>/|2,
which implies the claim.
Lemma VL5.4 Let$:X -*¦ Ybe a rough isometrybetween graphs ofbounded
geometry, and f:Y-+R a function on Y. Then, for sufficiently large R,
[ I/I2 < const, f |2)/|2 + const, f \4>*{f)\2,
Jpiy.R) J0(y;const.«) ./0(*(y);const.«)
where r/r denotes a rough inverse of<j>.
Proof Recall that every rough isometry <p has a "rough" inverse, that is, therft
exists a rough isometry ir : Y -*¦ X such that
are uniformly bounded on X and Y respectively. Now for any y e Y,v/e hav*
\f\\y) < const.H/ - D>oirr(f)\2 + |(^o^r(/)|2}(y)
< const. [ |2)/|2 + const.|@o^r(/)|2(y),
Jp(y.K)
177
which implies
/ I/I2 < const. / |2)/|2 + const, f |(^*o^'
< const.
which implies the proposition.
const.
|</>'(/)|2
Lemma Vlii (Kanai, 1985.) Let M be a complete Riemannian manifold
with Ricci curvature bounded uniformly from below. Then for any r > 0 there
exists a constant depending on r such that, for any u G C°°(D(o; r)).
JB(o
|gradM|rfV > const.r
|« - uB{or)\dV
for all o e M, where ub(O\t) denotes the mean value ofu over B(o; r).
Proof Write B for B(o; r). Assume uB = 0 and
V({x e B:u(x) > 0}) < V(B)/2.
For t > 0 set D, := {jc e B : u > t). Then, by Buser's inequality (Proposition
V.2.6(b)), we have for regular values of u
A(dD,)> const.r
which implies, by the co-area formula.
¦r
A(dD,)dt
> const., / V(D,)dt
Jo
= const.,
const
which is the claim.
UdV
- I \u\dV,
Jd
Given the complete Riemannian manifold M and a discretization G of M,
with bounded geometry, for which the separation radius is e and covering radius
s P, wlth e < p. Recall that t, g N(f) if rf(?, r,) < 3p. We now investigate the
178
Analytic Isoperimetric Inequalities
simultaneous validity of the various Sobolev inequalities on M and G. Of
course, we need maps between the function spaces on M and G.
VI.5.I The Discretization T> of Functions on M
Definition Given a smooth function F: M -*¦ R, its discretization f = VF':
G -+ R is defined by
>:i) Assume V(x;3p) > const. > Oforallx e M.Thenforanyp e [l,oo)
we have
1
< const
JBtf-Jp)
\F\"dV,
which implies (by Lemma VI.5.1)
f \VF\pdV < const. /
So one has ||Z>|| ,,_>,, < const, for all p e [1, oo].
:ii) Similarly, one has
< const
. /
JBiS.3
\F\dV < const. I \F\dV;
. I
JU
so HPIIi-k* < const.
(D:iii) Assume M has Ricci curvature bounded from below, and assume
V(jc; 3p) > const. > 0 for all x e A/. Then for i? e N(§) we have
JB$;
¦;3p)nB(r,;3p))
Since fl(?;3p)n B(i;;3p) 2 fi(midptf ,;p), which implies
3p) n B(j)\ 3p)) > const., we have
- (X>FXi?)|
< const. I [ \F(x) - (PF)(?)| dV(x)
U B(S;3pY\B(rr,}p)
+ f |F(jr)-(PFXij)|rfV(*)|
< const. I / |F(jc)-i
+ [ \F{x)-(VFKn)\dV(x)
JB(n;lp)
dV(x).
VI.5 Sobolev Inequalities and Discretizations 179
< const. I / |gradF\dV + f |gradF\dVI
< const. / |gradF|rfV,
JBdfip)
(we used Lemma VI.5.5 in the next to last inequality), that is,
\<PFYM) - (VFXn)\ < const. / |grad F\dV
JB(liAp)
for all ij ? N(f), for all ? e Q, which implies
|©(PF)|2(f) < const, f |grad F|2 rfV
for all ? 6 ?. Then Lemma VI.5.1 implies
/ \X)(VF)\2 dV < const. / Igrad F\2 dV
for all f e ?; letting /? -* +oo, we have
/ |S>(PF)|2</V< const. /" Igrad F\2dV.
JG JM
VI.5.2 The Smoothing S of Functions on Q
Definition Fix a function ^: [0, +oo) -* [0, 1 ] e Cf([0, 2p)) such that
\H@, p] = 1. With ? e ? associate the function ^ : M -* [0,1] defined by
and define
So the collection {^ }^6!; is a partition of unity on M subordinate to the locally
finite cover {fi(?; p))^eg of M. Then for each f:Q-*R define its smoothing
F = 5/: M -* R by
:i) Then
^cS 1 and
< 1.
180
Analytic Isoperimetric Inequalities
Also, assume the Ricci curvature is bounded from below. Then one has
from the Hdlder inequality that
s E
= E
(eg
which implies
I \Sf\»dV< f
JB(o;R) JB{o\R)
= E
< const.
< const.
JfH.ru, :conjt./?+const.)
[the third line follows from the Bishop comparison theorem (V.1.11)],
that is,
f \Sf\"dV < const. / \f\"tN,
where rjo is a vertex in Q within Riemannian distance p of o. In particular,
we also have
[ \Sf\"dV < const. / \f\pdV,
Jm Jg
that is, HSH^p < const, for all p > 1.
E:ii) Furthermore, assume V(x\p) > const. > 0 for all x G Af.If / > Othen
f
JM
(Sf)"dV
- E
[by the Bishop-Gromov theorem (V.I. 13)], that is,
for all/>0.
E:iii) Now consider
> const.
V1.5 Sobolev Inequalities and Discretizations
Given x, there exists ij, e Q D fi(jr; p), which implies
181
Therefore
KgradSf)\(x) < const.
which implies for any x e fi(/?; p),»? e Q,
Kgrad 5/)|2U) < const. ]T |/(f) - /(i?)|2 = const.|2)/|2(i7).
?efl(i);3p)
One now obtains, by the argument of Lemma VI.5.1,
/ |grad5/|2</V < const. / \T>f\2dV,
HgradS/lh < const.||2)/||2.
VI.S.3 First Smooth, Then Discretize: T>S
(VS:\) No assumption on M and G. We have
= E
(X>S:ii) Assume M has Ricci
fdV.
curvature bounded from below, and V{x\ p) >
et / b i f
rm below, and V{x\
const, for all x e M. Let / be a nonnegative function on G; then
BM/)(?) = —^—- / SfdV
> const. / SfdV> const. /(?),
which implies ||/||p < const.p||P5/||p for all p > 1.
182 Analytic hoperimetric Inequalities
VI.5.4 How Smoothing Followed by Discretization Differs
from the Identity: idg — VS
Note that
= ^^ f
V(S,3p)Jbu3P)
which implies
Since G has bounded geometry, we have
Therefore,
/ 1/ -
PS/I2 </V < const, f |2>/|2 </V
VI.5.5 How Discretization Followed by Smoothing Differs
from the Identity: idM — ST>
Again, we require both Ricci curvature bounded uniformly from below, and
V(x; p) > const, for all x e M. For a smooth function F: M -* R we have
{F(x) - F(y)} dV(y),
which implies
|F - SVF\(x) < const. [ |F(jr) - F(y)| dV(y).
JB<.x?p)
The Bishop comparison theorem (V.I. 10) implies
|F - SVF\(x) < const. / dpx(v) I Igrad F|(exp sv)ds,
Js. Jo
which implies
/ \F-SVF\2dV < const. / dp(v) I IgradF|2(exp sv)ds,
Jb(o;R) JSB&;R) Jo
Vl.6 Bibliographic Notes 183
where SB(o;R) denotes the unit tangent bundle over B{o\R) and dfj. the
Liouville measure on SB(o; R) (see V. 1.4). Therefore,
/ |F-«SPF|2</V < const. / dpL{v) I Igrad F|2(exp sv)ds
Jb(o;R) JSB(o-.R) Jo
= const. / ds I |grad F|2Gro4>,(v))^(v),
Jo JSB(o;R)
where 7r : SM -*¦ M denotes the natural projection, and <t>, the geodesic flow.
By Liouville's theorem on the invariance of the Liouville measure under the
action of the geodesic flow (Proposition V. 1.3), we have
f \F-SVF\2dV < const. / ds I Igrad F|2Gro4>,(v))^(v)
Jb(o:r) Jo Jsb(o,r)
= const. / ds I Igrad F\2(jz(v))dn(v)
Jo /¦I(S«(o;«))
< const. / Igrad F\2(n(v))dn(v)
JSB(o;R+Sp)
= const. / Igrad F\2dV.
JB(o;R+ip)
To summarize,
f \F-SVF\2dV < const. / |gradF|2rfV,
Jb(o;R) JB(o\R+ip)
f \F - SVF\2dV < const. / |gradF|2rfV.
M Jm
VI.6 Bibliographic Notes
Surveys of applications of isoperimetric inequalities in analysis can be found in Bandle
A980), Kawohl A985), Mossino A984), Payne A967), and the classic and Pdlya and
Szegfi A951). Also, see the recent survey (Hebey, 1999).
§VI.l The Nirenberg-Sobolev inequality can be found in Nirenberg A959, p. 14).
For Lemma VI. 1.2, see Moser A964. p. 116), Cheng and Li A981), and Nash A958).
For Theorem VI. 1.1 see Bakry, Coulhon. Ledoux, and Saloff-Coste A995).
One might wonder whether the Nirenberg- and Nash-Sobolev inequalities imply the
Federer-Fleming inequality, that is, whether the L2 Sobolev inequalities imply the the
L' Sobolev inequality. Counterexamples are presented in Coulhon and Ledoux A994).
Theorem VI. 1.2 is from Cheeger A970).
§VL2 Details for the analogue of the Federer-Fleming theorem (Federer and
Fleming, 1959) in the compact case can be found in Chavel A984, p. 111).
184
Analytic lsoperimetric Inequalities
A more delicate isoperimetric function for the compact case is inspired by
M. Gromov's proof of the isoperimetric inequality for spheres (Gromov, 1986). One
lets I(M, /?), 0 € @,1), denote the infimum of A(dSi) among all Si satisfying V(S1) =
PV(M). See the disucussion in B6rard A986, Chapter IV).
§VL3 As mentioned in V.4, one has a Faber-Krahn theorem in the model spaces
of constant sectional curvature. Similarly, one has generalizations of the Faber-Krahn
argument in Berard A986, Chapter IV).
Theorem VI.3.1 is from Canon A996). Proposition VI.3.1 is from Aubin A982,
p. 116 ff.). The general Faber-Krahn inequalities were first treated in Grigor'yan A994c).
§VL4 To my knowledge, the earliest proofs of the Federer-Fleming theorem for
graphs are in Varopoulos A985), where he considers the result there for Cayley graphs,
and in Dodziuk A984), where he considers the discrete Cheeger inequality.
One can consider both Riemannian manifolds and graphs with weight functions
associated to their measures. See the discussion in Chavel and Feldman A991) and
Coulhon and Saloff-Coste A995).
§VL5 The discussion of discretization and smoothing of functions follows the
treatments of Kanai A986a, 1986b) and Coulhon A992).
VII
Laplace and Heat Operators
Here, we introduce the Laplace operator on Riemannian manifolds and its asso-
associated heat diffusion, and prepare for the study of how geometric isoperimetric
inequalities on Riemannian manifolds are reflected in the properties of large
time diffusion. We present the necessary definitions and background results,
most of which can be found in Chavel A984). The ones we discuss in some
detail are either to correct an argument, or to fill in matters not discussed, there.
The manner in which the heat diffusion expresses the geometry of the manifold
will be presented in the next chapter.
VTI.l Self-adjoint Operators and Their Semigroups
Definition Let H be a Hilbert space with inner product (,). Recall that a linear
operator T: V(T) -> H on the subspace V(T) in H is an extension of the linear
operator of S: V(S) -> H ifV(S) c V(T) and T\D{S) = S. We write ScT.
The linear operator 7 : V(T) -y U is closed if every sequence (xk) in T>(T)
satisfying
x,
Txk
x,yeH,
must also satisfy
x G V{T), y = Tx.
A linear operator 7: V(T) -* H is dosable if it has a closed extension.
When 7 is dosable, then it has a minimal closed extension T, called its minimal
extension or, for short, its closure.
Definition Assume T : V(T) -*¦ H is a linear operator with dense domain, that
is, T>(T) = H. The domain of the adjoint 7* of T will consist of those x G H
185
186
Laplace and Heat Operators
for which there exists an element x* efi such that (jc, Ty) = (jc*, y) for all
y e TKT). For such jc we define T*x = x*.
The operator 7 is called symmetric if Gjc, y) = (jc, Ty) for all x,y e V(T).
In general, 7* is a closed operator. When 7 is symmetric, then T* is an extension
of 7, so 7 is closable. Then 7 is the smallest closed symmetric extension
of 7.
Definition We say that 7 is self-adjoint if 7 = T*. We say that 7 is essentially
self-adjoint if 7 has a unique self-adjoint extension, in which case 7 = 7*.
One knows that if 7,, 72 are self-adjoint, and X>G,) c V(T2), then 7, = 72.
Definition Let 7 be a symmetric operator on H with dense domain V(T), for
which there exists a real number e such that
(VH.1.1)
(*, Tx) > e(jc, x) VjceZ>G).
We then say that 7 is semibounded from below. We say 7 is nonnegative if
e >0.
Let 7 be semibounded from below, with e as given in (VII. 1.1); then the bilinear
form on Z>G) defined by
is positive definite, and hence defines an inner product. Complete V(T) to DT
relative to the inner product (, )r- Then it is known that DT may be realized as
a subspace of H, so T>(T) QDTC.H.
Definition Let 7 be semibounded from below and symmetric, with dense
domain. Define the Friedrichs extension JJr of 7 to be T*\Dt. That is, the
domain of JJr, 2)r, is given by
and 5r is given by
CTX,y) = (x,Ty) Vjc e QT,y G V(T).
Therefore, V{T) c3)rCDrcK, Also, 5r is self-adjoint, and
Er^,3') = U. Ty) VxeQT.yeDT.
The full result is:
VII. 1 Self-adjoint Operators and Their Semigroups 187
Proposition VII.1.1 Every semibounded from below symmetric operator with
dense domain has at least one self-adjoint extension, its Friedrichs exten-
extension. Moreover, 3> is the unique self-adjoint extension ofT whose domain is
contained in DT.
VII.1.1 The Spectrum of Self-adjoint Operators
Definition Let Ti be a Hilbert space with inner product (, ), 7: Z>G) ->«a
linear operator on H.
A complex number A. is in the resolvent set ofT if XI — T maps X>G) one
to one onto all of 7i, and if (A./ - 7)~' is bounded. In this case we refer to
(A./ - 7) as the resolvent ofT at k.
The spectrum ofT, spec 7, is the complement of the resolvent set of 7.
The spectrum is always a closed subset of the complex numbers. When 7
is self-adjoint (and this is the case we always study), spec 7 is contained in
the real axis. For 7 self-adjoint we have the spectral theorem, formulated as
follows:
Recall that an orthogonal projection is characterized as a self-adjoint trans-
transformation PofH for which P2 = P. In particular,
, <(>) = {P2<t>, <t>) = (P4>, P<t>) > 0
for all <j>. A spectral family is a family {?*: A. e R} of orthogonal projections
of Ji satisfying
1- ?ji<^ [that is, (Ex4>, <t>) < (E^, <f>) V^] when A. < fi;
2. Ea+o = Ex;
3. Ex -*¦ 0 as A. ->¦ -oo, and Ex -* I as A. ->¦ +oo (all convergence here is in
the operator norm).
Then the spectral theorem states that any self-adjoint transformation TofH
possesses a uniquely determined spectral family [Ex: A. e R} for which the
representation
f°
=
J-o
is valid. That is, for any 4> e V(J) we have
J—
188
Laplace and Heat Operators
where (dEx<f>, <t>) is now a Lebesgue-Stieljes measure (with respect to X) on
R, supported on spec T. The domain of T, TKT), consists of those 4> e 7i for
which
+00.
Furthermore, for any Borel function /(X), defined &.e.-[dEk] and finite, we
have
r
= r
J-
This last equation is a theorem if one takes the functional calculus of self-
adjoint operators as already well defined, and is a definition if one wishes to
first develop the functional calculus of self-adjoint operators from the spectral
family formulation of the spectral theorem.
In particular,
l|7>ll2 = (T24>, <f>) = (°° X2 {dEx<t>, <t>).
J—oo
Moreover, if / and g are two such functions satisfying
TKfiT)g{T)) = V(g(T)) n V(fg(T)),
then
f(.T)g(T)= f f(X)g(X)dEk.
J-oo
Definition Within spec T we distinguish a variety of subsets.
First, a number X is in the point spectrum if X is an eigenvalue of T, that is,
there exists a nontrivial element fofTi for which Tf = X/.
Next, assume T is self-adjoint. Then spec T c R. The discrete spectrum ofT
consists of those X € spec T for which there exists t > 0 such that
dim(?i+< - EX-t)(H) < oo.
So X is an eigenvalue of T of finite multiplicity, and is an isolated element of
spec 7".
We refer to the complement of the discrete spectrum as the essential spectrum.
Therefore, the essential spectrum consists of those X € spec T such that
for all € > 0.
VII. I Self-adjoint Operators and Their Semigroups 189
Thus X € spec T precisely when there exists a sequence [<f>n} Q T, \\4>n|| =
1 V n, such that (X — T)<pn -*¦ 0 as n -*¦ oo. And X is in the essential spectrum
precisely when the sequence can be chosen to be orthonormal. For any X 6
spec T, the sequence {4>n} is referred to as a sequence of normalized approximate
eigenfunctions ofX.
The spectral theorem implies that if Xo = inf spec T > —oo, then
> f
Therefore, T is semibounded from below, with best constant € > X<>. Con-
Conversely, if T is semibounded from below with constant t, X is an element of
spec T, and {<&,) is a sequence of normalized approximate eigenfunctions of X,
then
0 = lim ((X/ - Tyt>H, 4>H) = X - lim (T<f>n, <pH)<k- c,
so the spectrum is bounded from below, with € < Xo. We conclude that T is
semibounded from below if and only if the spectrum is bounded from below,
in which case we have
(VII. 1.2)
infspecT= inf
^ #*> II*II2
Note that the argument only involves those <t> € V(T), but the quadratic form
4> t-+ {T<(>, <t>) is defined on V((T - t)l/2), and the infimum, above, does not
change if we allow 4> to vary over V((T - Ol/2) 3 V(J -() = V(T).
VII.1.2 Quadratic Forms
In defining the Friedrichs extension, above, we started with a semibounded
symmetric operator 7 on a dense domain V(T), with which we associated a
quadratic form (, )r- We then used the quadratic form (, )r to define a self-
adjoint extension $T of the original T. Moreover, the domain of the quadratic
form is precisely V((T - Ol/2) [where e is given by (VII.1.1)]. Here we note
that one can start with the quadratic form as the fundamental object.
190 Laplace and Heat Operators
Definition Let V denote a dense domain in a Hilbert space H. Then a sesquilin-
earform Q' on V is a map Q':PxC->C such that
1 • G'C*. y) is linear in x,
2. Q'(x,y) = Q'(y,x).
We say Q' is semibounded from below if there exists (eR such that
(Vn.1.3) Q'(x,x) > c\\x\\2
for all x 6 T>. We say Q' is nonnegative if € > 0.
Given Q' semibounded from below, with t given by (VII. 1.3). Complete V
with respect to the inner product
= <2'(*. y) + (i - €X*. y)-
Assume the resulting space may be identified with a closed domain Dq 5 V
in %. Denote the new inner product on Dq by (, )q, and define on Dq the
quadratic form
Determine the Friedrichs operator $q by
sothedomainSgof^econsistsofthosejc € Dq for which there exists x* e H
such that (*•, y) = G(x, y) for all y e DQ. Then we define 5e* = x".
One knows that 5C is self-adjoint, and that Dq = TH^e'72)-
VI1.1.3 1-Parameter Semigroups
Definition Given a Banach space B, a family {T,:t> 0} of bounded linear op-
operators on B is said to be a C° 1 -parameter semigroup {.semigroup, for short) if:
2. if 0 < s, t < <x>, then T,TS = T,+s;
3. the map (t, /)>-»• T,f from [0, co) x B to B is jointly continuous.
We say that the semigroup T, is contractive if \T, || < 1 for all t > 0.
Given A) and B) in the definition of a semigroup, to verify C) of the definition
it suffices to verify that
UjnT,/-/
for all/eB.
VII. I Self-adjoint Operators and Their Semigroups 191
Definition With every semigroup T, we associate its (infinitesmal) generator,
Z, defined by
the domain of Z, D(Z), being those / 6 B for which the limit exists.
Proposition VII.13.
(a) T>(Z) is a dense linear subspace ofB, and 7",(D(Z)) c V(Z)forall t > 0.
Moreover,
T,Z = ZT,
on all ofV(Z), for all t > 0.
(b) Iff e V(Z), then F(t) =T,fis C1 on [0, +co)( and
F'(t) = ZF{t).
(c) Furthermore, Z isa closedlinearoperator, withV(Z) completewith respect
to the norm
Moreover, T, acts as a semigroup on V(Z)for this norm,
(d) Conversely to (b), if a path *(/) in V(Z) satisfies
on some interval [0, a), then
*(/) = 7,@@)) Vfe[0,a).
Thus, the infinitesmal generator uniquely determines the semigroup,
(e) A densely defined operator Z on the Banach space B is the infinitesmal
generator of a contractive semigroup if and only if all X > 0 lie in the
resolvent set of Z and
iiu - zr1 ii <x-'
for all X >0.
Proposition VII.13
(a) If B is a Hilbert space, and T, is a self-adjoint semigroup acting on B,
that is, T, is self-adjoint for each t > 0, then Z is also self-adjoint. IfZ is
192 Laplace and Heat Operators
nonnegative self-adjoint, then the spectral theorem implies that —Z is the
infinitesmal generator of a self-adjoint contraction semigroup,
(b) If Z is a symmetric operator with dense domain V in the Hilbert space B,
and for every f €V there exists € = €(/) > Osuch that the heat equation
(VII. 1.4) F'(t) = -ZF(t)
has a solution satisfying F@) = / and F(t) 6 V for all t € [0, «(/)], then
Z is essentially self-adjoint on V, and the solution to (VII. 1.4) subject to
the given conditions is unique.
VII.2 The Laplacian
VII.2.1 The Laplacian Acting on C2 Functions
Let M be an n-dimensional Riemannian manifold. If x :U -*¦ R" is a chart on
Af, then we have
g,, = C,,3;>. G = (*,-). G =(*"), g = detG>0.
Recall that, for any C function / on Af, we have
(grad /, |) = df{^) = |/ V | e TM.
For C functions /, h on Af we have
grad (/ + A) = grad / + grad h,
grad fh = f gradh + hgrad/.
If x:(/ -»• R" is a chart on Af, then
Definition For any C vector field X on Af we define the divergence ofX with
respect to the Riemannian metric, div X, by
(Recall, V denotes the Levi-Civita connection of the Riemannian metric.)
For the C1 function / and vector fields X, Y on M we have
div fX = (grad /, X> + /div X.
Vll.2 The Laplacian 193
If x: U -> R" is a chart on Af, and
then
Given x e M, and r € [0, c(|)), ^ eS, geodesic spherical coordinates on M
about x, with
the Riemannian measure in spherical coordinates (where d\ix denotes the
standard measure on S*), then for the radial vector field B/dr we have
9
One verifies that if X has compact support on M then we have the Riemannian
divergence theorem:
divXdV=0.
In particular, if / is a function and X is a C1 vector field on M, at least one of
which has compact support, then
(VII.2.1) f /div XdV = - j (grad /, X) dV.
Definition Let / be a C2 function on M. Then we define the Laplacian of /,
A/, by
A/ = div grad /.
Thus, in a chart x: U -»• R",
Furthermore, for C2 functions / and h on M we have
A) = A/ +AA,
div/gradA = f Ah + (grad f, gradh)
194 Laplace and Heat Operators
(this last formula only requires that f e Cl,h e C2), which implies
A /A = /AA + 2(grad /, grad A> + A A/.
One has Green's formulae: Let /: M ->• R 6 C2(M), A: Af ->• R e C'(Af),
with at least one of them compactly supported. Then
A A/ + (grad A, grad/>}dV = 0.
u
If both / and A are C2, then
f {AA/-/AA}</V = 0.
Ju
Let M be oriented, ft a domain in M with C°° boundary 3ft, and v the outward
unit vector field along 3ft that is pointwise orthogonal to 3ft (there is only one
such vector field). Then for any compactly supported C vector field X on M
we have
// divXdV= / (X, v)dA.
JJa Jaa
The corresponding Green's formulae are: Given M, ft, and v as just described,
and given / 6 C2(M), A e C\M), at least one of them compactly supported.
Then
(VII.2.2) ff {AA/ + (gradA, grad/)} dV = f A(v, grad/> dA.
JJa Jen
If both / and A are C2, then
(VH.2.3) ff [hAf-fAh}dV= f (A(v,grad/> - /(v, gradA)}<M.
J Ja Jsa
Notation We generally write 3//3v for (v, grad />.
VH.2.2 The Laplacian as an Operator on L1
Until now, we have only considered the pointwise action of the Laplacian on
functions which are C2. We now wish to view the Laplacian as an operator on j
the Hilbert space L2 = L2(M, dV). For any two functions /, g in L2 we have
the inner product and norm
(/.*)= / fgdV, \\ff= f fdV.
Ju Ju
VII.2 The Laplacian 195
We may also speak of L2 vector fields, and the associated inner product and
norm
norm
(X,Y)= f (X,Y)dV, \\X\\2= f lx\2dV.
JM Jm
Recall that, for any subset A of M, [A]r denotes the set of all points in M with
distance from A less than or equal to r.
We now consider the action of the Laplacian A on L2. Recall that Green's
formula states that if / € C2, h e C, one of which is compactly supported,
men
(VH.2.4)
(-A /, h) = (grad /, grad A).
Let Ac = A|C~. Then — Ac is a nonnegative symmetric operator on the dense
subspace Cf of I2, with associated quadratic form
Q'c = D[<p, yjr] := (grad <p, grad ^), 0, $ e Cc°°.
We refer to D[, ] as the Dirichlet energy integral. Complete Cf to Sjc relative
to the metric
on C?°, and define the Friedrichs extension $c — Ja, of Ac on the domain
©c = DAf. So Cf c T>c C f)c- Henceforth, unless otherwise noted, the self-
adjoint Laplacian on L2 will be the Friedrichs extension ffc. We will refer to $c
as the Friedrichs extension of the Laplacian on M.
The identification of Sjc goes as follows: Let H denote the collection of C°°
functions f on M for which both /, grad/ 6 L2. Endow H with the inner
product
(/, g)H = D[f, g) + (/, g), f,g€H,
and complete H, with respect to the inner product (,)//, to the Hilbert space fj.
Then Sjc is the closure of Cf in Sj.
For the elements of Sj themselves, we consider weak derivatives. Namely,
Definition We say that / e L2 has a weak derivative if there exists an L2
vector field X such that
(/, div Y) = -(X, Y)
for all compactly supported C°° vector fields Y on M. The vector field X, should
it exist, must be unique, and we denote it by X = Grad / [see (VII.2.1) above].
196
Laplace and Heat Operators
By the Meyers-Serrin theorem, f) is the Hilbert space consisting of functions
f e L2 possessing weak derivatives, with the inner product (, )fl given by
(/. g)r> = (Grad /, Grad g) + (/, g), f,gef).
Until now, M was an arbitrary Riemannian manifold. Assume, now, that M
has C°° boundary F and compact closure. Then we may consider the Laplacian
acting on functions with prescribed boundary conditions, chosen so that the
action is symmetric, from which we then determine the new Friednchs extension
for the domain of functions in question. The simplest is:
Definition (Vanishing Dirichlet Boundary Conditions) Let
Pdir = {/ e C°°(A7): f\r = 0}, p
Then —Adi, is nonnegative symmetric, and has associated quadratic form and
inner product given by
for all 0, \ff 6 Ddir. Complete the inner product (, )<«, to the subspace D&, and
thereby determine the Friedrichs extension $& of - Adu, on 33^, the Dirichlet
Laplacian on M.
Lemma VIL2.1 Let M have C°° boundary F and compact closure. Then given
any a, S > 0, there exists a Junction p e Cf(M) such that the support of p has
distance from F greater than S, that is, supp p C M \ [F]j, and
Proof Since M is compact, it has a constant c and a finite covering [U,:i =
1 ,...,€} by charts, for which the Riemannian metric in any of the charts satisfies
U J
for all I = (^ |"). Then mere exists a constant K such that for every
i = 1,..., I, and every C°° function F compactly supported on Ut we have
(VII.2.5) ||F||«2 + llgradFH*2 < *{||F||R.2 + HgradF||R.2},
where the subscripts R" and M refer to the respective L2 spaces. Fix the cover
14 = {U,:i = l,...,l], with subordinate partition of unity {<p,).
VI1.2 The Laplacian
Now consider the function q{ : M -» R defined by
197
I
= j d(q, D/& - 2, qe
Then
Subject each <p,es to mollification by j(t, as in §1.3; namely, for the index
« = («i €t), define
Pip) = Qi.eiP) = ^>2 (/«, *(<P,Qs)ox,-l)(x,(p))
i=i
i /.
= ? / A,(y. -x.(P))((*>«^)ox,-|)
i=i J
Then one can easily use Theorem 1.3.3 and (VII.2.5) to prove the lemma. ¦
Lemma VTL2.2 Let M have C00 boundary V and compact closure, and let
f:~M^>Rbe Lipschitz on ~M, with /|F = 0. Then, given any € > 0, there
exist S > 0 and a function <j> € C™(M) such that the support of<j> has distance
from F greater than h, that is, supp# C M \ [F]4, and
Corollary VIL2.1 The Dirichlet Laplacian gfa on M coincides with the
Friedrichs extension 3v of Ac on M. In particular, their associated quadratic
forms coincide, possessing the common domain f)c.
Proof of Lemma VII^-2. Let p: M -» [0, oo) 6 Cf satisfy the properties of
Lemma VII.2.1, and let <p = fp. Then
||/ - <f,\\2 = f f\\- pJ dV < consL/S,
by a standard calculation in Fermi coordinates based on F. Similarly,
grad(/ - <t>) = grad/(I - p) = A - p)grad/ + /grad(l - p).
198 Laplace and Heat Operators
which implies
lgrad(/ - <t>)\\p) < 2{|1 - p|2|grad/|2 + |/|2|gradp|2}(p)
< const.,
[the d(p, VJ in the numerator of the second term of the parentheses follows
from / vanishing on F]. But then calculation in Fermi coordinates, based on
f, implies
||grad/-grad0||2= f |grad/(l - p)\2dV < const/5,
which implies the proposition. ¦
Remark VIL2.1 We shall show in Theorem VII.4.2 below mat the Laplacian
with vanishing Dirichlet boundary condition is essentially self-adjoint.
Definition A function / e L2 on M has A/ acting as an L2 distribution on
M if mere exists g e L2 such that
*,*) = (/.A*)
We write A/ for g.
Theorem VII.2.1 If M is a complete Riemannian manifold, then Sjc = S).
Given any function f e C°° for which /, A / € L2, we also have grad / € L2
and
(VII.2.6)
(-A/,/) = (grad/, grad/).
Finally, Ac = A|C?° is essentially self-adjoint, so the Friedrichs extension &
of Ac is the unique self-adjoint extension of Ac.
Corollary VII.2.2 Let M be a complete Riemannian manifold. Then M has no
L2 nonconstant harmonic function, that is, any function f in L2(M) satisfying
A/ = 0 on all ofM must be constant. Moreover, given any X < 0, there is no
solution u 6 L2 to the equation
An + An = 0
except for u = 0 identically on M.
Proof of Theorem VII.2.1. Assume / e f){M) n C°°(Af). Fix o e M, and for
each €, R > 0, consider the function fR = ftf>R, where 4>r e Cf(B{o\ R + 3))
Vll.2 The Laplacian 199
satisfies
tpR\B(o;R)=l, 4>r, Igrad^l < 1+t;
such a function 4>R is constructed in Lemma VII.2.1. Then
11/ - Ml2 = / /2<1 - 4>kJ dV < const. / f2 dV -+ 0
as R -*¦ <x>, since / e L2. Similarly,
j
-4>R\2\gP>df\2}dV
lgrad/|2}dV
< if
f
M\B(o:K)
< const
. /
Jkr\B(<r,R)
asR -*¦ oo. Therefore/is aipproximatedinij by functions in fyc. Since Sj n C00
is dense in f) (by definition), we obtain fyc = fy.
Assume we are given the function / e C°° such that /, A / e L2. Then
which implies
^{Igrad/I2 + /A./} = -2J 4>Rf (grad**, grad />
< \ J 4>R2\&ad f\2 + 2 f f2\grad4>R\2,
which implies
5 /"
z JB
B(o;R)
lgrad/|2<^
< const. / /2 + |/A/|
< +00
200 Laplace and Heat Operators
for all R. This implies grad / 6 L2. But
f 0*2{|grad/|2 + /A/} = -2 j <t>Rf (grad**,grad/)
= -2 / ^/(grad^.grad/)
./i»(o:fl+3)\i»(o;fl)
< const. / I/Ilgrad/|,
./i»(o:fl+3)\i»(o:fl)
As /? -> oo we have
/" ^{Igrad/I2 + /A/} -> y |grad/|2 + /A /,
|/||grad/| -> 0,
which implies (VH.2.6).
For the essential self-adjointness of Ac we consider L2 to be a complex
Hilbert space with inner product
Ju
fgdV,
and with the Laplacian defined by operating on real and imaginary parts of a
complex-valued function. It is standard that Ac is essentially self-adjoint if and
only if
ker{Ac±j}* = 0,
that is, the subspace of functions / e L2 that satisfy
is trivial. So assume {Ac ± j }•/ = 0. Then (A ± /)/ = 0 as an L2 distribution.
Elliptic regularity then implies that / € C°°, and A / in the classical sense is
the L2-distributional Laplacian of /. Therefore
A / ± // = 0
on all of M. Multiply both sides of the equation by / and integrate over M.
Then
- I jAfdV= [ |grad/|2dV
Ju Ju
for all / e L2 n C°° for which A / 6 L2 [the purpose of this comment is to
VII. 3 The Heat Equation and Its Kernels 201
prove that (A/, /) is real]; therefore A / + if = 0 implies
if I/I2= f Igrad/I2,
Ju Ju
which implies / = 0. A similar argument applies to a solution of A / — if = 0,
and the theorem is proven. ¦
VIIJ The Heat Equation and Its Kernels
We are given a fixed Riemannian manifold M of dimension n > 1, with associ-
associated Laplacian A acting on C2 functions on M. The heat operator L associated
with the Laplacian acts on functions / = f(x, t) in C°(M x @, oo)), and is
given by
where / is C2 in the space variable x e M, and C in the time variable / e
@, oo). The homogeneous heat equation, or heat equation, is given by Lu = 0,
that is.
—,
dt
and the inhomogeneous heat equation is given by Lu
@, oo) ->¦ R € C°.
= — F, where F:Mx
The physical interpretation of the equation is given by considering the
Riemannian manifold as a homogeneous isotropic medium (with conveniently
normalized physical constants so that, for example, heat and temperature can
be considered one and the same), and u(x, t) is the temperature of x 6 M at
time /. Then the inhomogeneous heat equation describes the evolution of the
temperature distribution, with F(x, t) the instantaneous rate with respect to
time at which (by some external source) heat is supplied to, or withdrawn from,
x at time r. The argument is predicated on Newtonian heat conduction, namely,
given any domain n in M with compact closure and C°° boundary, the instan-
instantaneous change of the total temperature in fi with respect to time is equal to the
total change due to the supply of heat to, or withdrawal of heat from, ft, added
to the spatial rate of change of the heat distribution across the boundary of ft,
9ft. That is,
Jaa Sv
(w,t)dA(w).
202
Laplace and Heat Operators
By Green's formula we have
which implies
IL
for all such domains S2 in M. This then implies the inhomogeneous heat equation
on all of M.
Notation Henceforth, if there is no comment otherwise, given any function
/: M x @, +00) -> R, we denote the spatial component of the gradient of /
by grad /.
Definition A heat kernel is a continuous function p:MxMx@,oo) such
mat for every y e M the function u(x, t) = p(x, y, t) is a solution to the heat
equation with initial data
lim u(x, t) = &y(x),
no
the delta function concentrated at y, namely,
lim
no
f
for every bounded continuous 0: M -*¦ R.
Intuitively, p(, y,) is the solution of the heat equation resulting from an ini-
initial temperature distribution having total temperature equal to 1 concentrated at
y. We use the linearity of the heat equation (otherwise known as superposition
of solutions) as follows: If at time t = 0 the initial temperature distribution was
concentrated at y with total temperature a, then the solution to the heat equation
will be u = ap(, y,). If at time / = 0 the initial temperature distribution was
concentrated at the points y and z with total temperatures a and fi, respectively,
then the solution to the heat equation will be u = ap( ,y,) + fip(, z,). There-
Therefore if at time t = 0 we are given the temperature distribution /(>), then by
summing "spatially" the contribution of each point to the initial data, we obtain
with
no
u(x,t)= [ p(x,y,t)f(y)dV(y),
Jm
, t) = lim / p(x, y, t)f(y)dV(y) = f(x).
noJu
VII.3 The Heat Equation and Its Kernels
203
If, in addition, heat or refrigeration is supplied to M, as described by F(x, t)
above, then the contribution of f(, r), r e @, /), to the temperature distribution
at time / is given by
p(x,y,t-z)F(y,T)dV(y),
/
since we think of the function F(, r) as initial data for heat diffusion starting
at time r and lasting for t — t time units. So the total contribution to the
temperature distribution, at time /, by F is given by summing "temporally,"
namely,
[ dr [ p{x,y,t-T)F{y,x)dV(y).
o Ju
Therefore, we expect the solution to the inhomogeneous heat equation with
initial temperature distribution / and external source F to be given by
«(*,»)= f p(x,y,t)f(y)dV(y)+ f dr f p(x,y,t - r)F(y, r)dV(y).
Jm Jo Jm
Remark VIL3.1 Note that we have argued that p(x, y, t) is symmetric with
respect to Jt and y as 11 0, since p(x, ,t)-> Sx, intuitively, and p(, y, t) -*¦ Sy,
by hypothesis, as / ! 0. We shall see shortly that in all cases that we study,
have the symmetry p{x, y, t) = p(y, x, t) on all of M x M x @, +00).
y
we
VII.3.I The Heat Kernel of Euclidean Space
In order to calculate the heat kernel on R", we first derive a candidate, using
the Fourier transform. Then we check that our candidate is indeed legitimate.
Given a function/:R" -»• C in L'(R"), define its n-dimensional Fourier trans-
transform, /, by
tL"
-ixi dvH(x),
where
The basic properties of the Fourier transform are:
2. g(x) = f(x - y) => g(?) = «-'>•«?«); {*"-*/} (?) = ?» -
y).
204
Laplace and Heat Operators
3. {/(*x)f($) = A-?(|A); {/*gftf) = /(?)?(*),wheref*gdenotes
the convolution (normalized here to be)
(/ * gXx) = Bjt)-"
4. One also has the specific example
S. Consider the collection S of functions on R" that, with all their partial
derivatives of all orders, have rapid decrease on R". For functions / in 5 we
have
The Riemann-Lebesgue lemma implies, with these last two formulae, mat
the Fourier transforms maps S into S.
6. Finally, one has the Fourier inversion formula:
fix) = B*r"/2 f ?«y*-* <*Ў
Now, consider a solution u(x, t) to the heat equation on R", with initial data
4>(x). Since this is a formal calculation in search of a candidate solution, we
treat all functions as though they were in S, with respect to the space variable
for every t. Let v(%, t) be the Fourier transform of u(x, t) in the space variables,
that is.
f
JtL'
u(x,t)e-ix(dvn(x).
Then
jp
: [ Au(x,t)e-ix*dvH(x)
Jk>
,t)e-ixidvH(x)
that is,
W/. J 77» //ca/ Equation and Its Kernels
dv
205
For any fixed ?, view the equation as an ordinary differential equation in t, from
which one has
To evaluate c(?), let / = 0. Then one obtains c(?) = ^(?), the Fourier transform
of the initial data of 0. We conclude
If one now inverts the Fourier transform, to recapture u(x, t), one obtains
Our candidate, therefore, for the heat kernel on R" is
One can directly verify that E is C°° on R" x R" x @, oo) and is a solution
to the heat equation on R" in x and /. We now check that
lim E(x, y, t) = 8y(x).
First start with any nonnegative integrable function p: R" -*¦ R with
/p(x) dvH(x)=l, and set p((x) = €-"p(x/(). Then /pf (x)dvn(x) = 1, and
it is standard that for any bounded continuous function f(x) on R" we have
lim / p((x-yWx)dvn(x)=Ay)
<io J
[see Proposition l(b), where we have j( compactly supported on R"]. So, for
any fixed y,
Hm p((x -y) = Sy(x).
In our situation, we have
p(x) = 7i-»/2e-W\ E(x, y, t) = p1j(.x - y),
which implies the claim; so E is a heat kernel on R". Two important properties,
which we see repeatedly, are the symmetry and positivity of the heat kernel,
206 Laplace and Heat Operators
namely,
(VII.3.1) Eix,y,t) = Eiy,x,t)>0,
for all x, y e M and t > 0.
For a function fix) on R\ we have the following results for solutions to the
initial value problem for the homogeneous heat equation:
(VII.3.2)
Proposition VII.3.1
(a) If fix) is bounded continuous, then the function
(VII.3.3) uix,t)= f Eix,y,t)f(y)dvniy)
is a solution of (VII.3.2).
(b) We always have
(VH.3.4) / Wx,y,t)dvHiy)=\
for all (x, t) 6 R" x @, <x>). Iff is a function in L\ and u(x, t) is given
by (Vn.3.3), then
(VII.3.5)
uix,t)dvnix)= I fix)dyHix)
R- JV
for all t >0.
(c) If f e C° is supported on the compact set K, and uix, t) is given by
(VII.3.3), then
Wix,t)\ < (&n)-*l*e-***>KVM \j \fiy)\dvHiy)\ .
(d) If fix) is continuous on R", vanishing at infinity, that is,
lim fix) = 0,
|jr|-»oo
and uix, t) is given by (VII.3.3), then
lim uix,t) = 0, lim (gradii)(x, t) = 0.
|jf|->00 l*|->0O
(e) If fix) is bounded continuous on R", then from among all functions vix, t)
on R" x @, oo) satisfying
\vix, t)\ < const.,
VII. 3 The Heat Equation and Its Kernels
207
where the constant is independent of\x, t), thefunctionuix, t)givenbyiVU3.3)
is the unique solution to the initial value problem (VII.3.2).
For the initial-value problem for the inhomogeneous heat equation we have
Proposition VIL3.2 Given F: R" x [0, oo) -»• R e C1 such that supp F C
K x [0, oo) for some compact K in R", then the function
uix, t) = j^ Eix, y, t)fiy) dyHiy) + jf' dx ? ?(*, ,,, - T)F(y, x) dyn
satisfies
8u
(VII.3.6) Am - — = -Fix, t), \imuix, t) = fix),
at t\o
VII.3.2 Preliminary Principles
Proposition \U33 (DuhameTs Principle) Let M be a Riemannian manifold
with compact closure and C°° boundary ipossibly empty), and let u, v: M x
@, t) -*¦ R e C be C2 with respect to the space variable in M. Then for any
[a, 0] C @, t) we have
jj Wiz, t - 0)viz, P) -11B, / - a)viz, a))dViz)
= / dx f[ {Luiz, t - x)viz, x) - uiz, t - r)Lviz, x)} dViz)
dx / \—r-iw,t-x)viw,x)
dv 1
, t - x)-—(iy, r)} dAiw).
dvw I
Proposition VIL3.4 (Strong Maximum Principle) Let u be a bounded con-
continuous function on M x [0, T] that is C2 on M x @, T) and that satisfies
A—->0
on M x @, T). If there exists ix0, t0) in M x @, T] - note the half open
interval - such that
time
«(*o. 'o) = sup ii,
«x[0J|
208
then
Laplace and Heat Operators
u\M x [0, (ol = u(xo, t0).
Furthermore,ifMhasC°°boundary,u e C°(M x [0, T]),and(w, t\) e dM x
@, T] satisfies
then
u(w,t\)= sup u,
Mx[0,T]
du
—(u).
Remark VII3.2 If one is given An — du/dt < 0, then one has a correspond-
corresponding minimum principle. For solutions of the heat equation, both principles are
valid.
VII.3.3 Properties and Types of Heat Kernels
Definition Given a Riemannian manifold with heat kernel p(x, y, t), we say
that p(x, y, t) is symmetric if
p(x, y, t) = p(y,x,t)
on all of M x M x @, +oo). We say that p(x, y, t) is positive if
p(x, y,t)>0
on all of M x M x @, +oo).
We say that p(x, y, t) satisfies the conservation of heat property, or that
P(x, y, t) is stochastically complete, if
/ P(x,y,
Jm
t)dV(x)=l
for all (y, t) e M x @, +00).
For M noncompact, we say that p(x, y, t) satisfies the Feller property if
lim p(x,y,t) =
JT-KJO
for all (y, t) e M x @, +00).
Remark VII.3.3 If p is a heat kernel satisfying the symmetry property, then
. /) = (AypX*. y, t).
Definition Let M be a compact Riemannian manifold with no boundary, a
closed manifold. Then any heat kernel on such a manifold will be referred to
as a closed heat kernel.
VII.3 The Heat Equation and Its Kernels 209
Definition Let M be a Riemannian manifold with compact closure and C°°
(nonempty) boundary. Then a Dirichlet heat kernel q: M x M x @, 00) 6
C^ is^heat kernel on M that can be extended to a continuous function on
M x M x @, 00) such that
q(,y,t)\dM = 0
for all (y, t) e. M x @, 00). Thus the vanishing Dirichlet boundary data will
correspond to absolute refrigeration of the boundary.
Theorem VH3.1 Let p be either a closed or a Dirichlet heat kernel on a
Riemannian manifold M. Then p is symmetric in the two space variables in M.
One has uniqueness of heat kernels in both cases, that is, a closed Riemannian
manifold has at most one heat kernel, and a Riemannian manifold with compact
closure and C°° boundary has at most one Dirichlet heat kernel.
Proof Fix one of the two cases. Let p\, p2 be two kernels on M, set
u(z, r) = pi(z, x, r), v(z, r) = p^z, y, r),
and apply Duhamel's principle. Then the boundary integrals in Duhamel's prin-
principle (should the boundary be nonempty) vanish. Let a 4. 0, 0 f /. Then one
obtains
P2(x,y, 0 = pi(y,x,t).
If we apply the argument to any heat kernel p\ = P2 = p, then we have
P(x, y, t) = p(y, x, t)
for all x, y e M. So any heat kernel is symmetric in the space variables. But
given arbitrary heat kernels p\, pi, we may apply the symmetry to p\ and
thereby obtain p\ = pi. ¦
Theorem VII.3.2 Let pbea closed heat kernel on a Riemannian manifold M.
Then p satisfies the conservation of heat property.
Proof Simply note that
? [ p(x,y,t)dV(x)= [ ^p(x,y,t)dV(x)
ot Ju Jm °t
which implies the claim.
-L
, y, t)dV(x) = 0,
210 Laplace and Heat Operators
Given any Riemannian manifold M, set
We do not presume that ? will actually be a heat kernel on M, but it should be
some sort of approximate heat kernel. The question is in what sense, and with
what validity. The answer, for our purposes, goes as follows:
Proposition VII3.5 Assume M isa closed Riemannian manifold. Then M has
a closed heat kernel, which we know is unique.
Similarly, assume M is a Riemannian manifold with C°° boundary and com-
compact closure. Then M has a Dirichlet heat kernel, which we know is unique.
In either case, the heat kernel is locally Euclidean in the sense that, for any
compact K in M,
P(x, y, i
(VII.3.7)
lim
no ?(x,y,t)
uniformly for all x, y e K satisfying
= 1 + OK{d(x, y))
d{x, y) < mm
j
- j.
Theorem VII33 Assume p is a closed or Dirichlet heat kernel on a
Riemannian manifold M. Then p is always positive.
Proof From (VII.3.7) we know that the heat kernel p(x, y, t) assumes positive
values, and moreover is unbounded from above on M x M x @, T] for any
T >0.
If we are given the closed heat kernel p, and there exists (xo. yo, 'o) in
M x M x @, +oo) such that p(*o. yoi 'o) < 0, then, for fixed yo, u(x, t) =
P(x, yo, t) has a nonpositive minimum value on M x @, /0], which implies by
the strong minimum principle that there exist t\ e @, t0) and a nonpositive con-
constant S such that u(x, t) = S on all of M x @, t\ ], which implies a contradiction.
If we are given the Dirichlet heat kernel p, then for any fixed >o in M, the
function u(x, t) = p{x, yo, t) vanishes on the boundary 3M. Therefore, if u is
not positive everywhere on M, then there there exist (xo, t0) in M x @, +oo)
such that p{xo, yo, 'o) < 0. The argument is then the same as above. ¦
Remark VIIJ.4 Let p be a Dirichlet heat kernel on M. Since p(x, y, t) > 0,
then
dp
?(wyt)<0
V1I.3 The Heat Equation and Its Kernels 211
on all of 3 M x M x @, +oo). In particular,
? f p(x,y,t)dV(x)<0,
ot Ju
which implies
(VH.3.8) f p(x,y,t)dV(x)<l,
on all of M x @, +oo).
Definition Let M be an arbitrary noncompact Riemannian manifold. We say
that the positive heat kernel p is the minimal positive heat kernel if, for any
other positive heat kernel P(x, y, /) on M, we have p < P on all of M x M x
@, +oo).
Certainly, the minimal positive heat kernel is unique, by definition. For the
existence of the minimal positive heat kernel one starts with domains Ci in
M with compact closure and C°° boundary, and associates with each ?1 its
Dirichlet heat kernel qn- An application of the maximum principle implies that
for domains J2i cc Q2 we have
on ?2i x &! x @, +00).
The minimal positive heat kernel of M, p(x, y, t), is given by
P = sup qQ,
a
where we set qa to be identically equal to 0 on the complement of $2 x $2 x
@, +oo)inAf x M x @, +00). For any exhaustion $2, f M by relatively com-
compact subsets of M, we have the monotone convergence of qu, t P uniformly
on compact subsets of M as j -> 00. All derivatives of qu, converge to those
of p uniformly on compact subsets of M as j -> 00.
Then p is positive on all of M x M x @, +00), it is the minimal positive
heat kernel of M, it is symmetric, and it satisfies
(VII.3.9)
P(x,y,t)dV(x)<
for all (y, t) e M x @, +00). So, for 0 bounded continuous, the function u (x, t)
given by
«(*,»)= ? p(x,y,tL>(y)dV{y)
212 Laplace and Heat Operators
satisfies the heat equation, with
lim u(x, t) = <f>(x)
no
for all x e M.
Definition Given a Riemannian manifold M, we say that M satisfies the unique-
uniqueness property for the heat equation if for any bounded continuous function /
on M there is at most one bounded solution to the heat equation on M satisfying
lim u{x, t) = f(x).
Remark VII3.5 Of course, if M satisfies the uniqueness property, then M has
a unique heat kernel.
Remark VII3.6 Assume M satisfies the uniqueness property. Since for any
bounded continuous f(x) the function
(VH.3.10) u(x,t) = f p(x,y,t)f{y)dV(y)
Jm
is a solution to the initial value problem for initial data /, we conclude that every
solution to the initial value problem for the heat equation on M with bounded
continuous initial data / admits the representation (VII.3.10). In particular, the
solution u(x, t) = 1 admits the representation
1= I p(x,y,t)dV(y),
Jm
which implies M is stochastically complete.
Theorem VIL3.4 Let M be a compact Riemannian manifold. Then M satisfies
the uniqueness property.
Also, ifM has compact closure and C°° boundary, then given the boundary
data
u(w,t) = U(w,t) V(iy,/)e3Af x(O.oo)
for some function U(w, t), t > 0, M satisfies the uniqueness property.
Proof Let u(x, t) be a solution to the heat equation on M, in either of the two
cases.
VII.3 The Heat Equation and Its Kernels
Then
213
(uAu)(x,t)dV(x)
= - ff \gndu\2(x,t)dV(x)+ f (up-)(w,t)dA(w)
Therefore, if we have two solutions v\, V2 to the same initial-boundary value
problem, namely,
vj (x,0) = V2(x, 0) = 4>(x) VxzM
and (if there are nonempty boundary data)
v\(w,t) = vz(w,t) V(iy,/)e 8M x@,oo),
then the solution u = v\ — V2 has both vanishing initial and boundary data. But
its L2 integral does not increase with respect to time. So it stays constantly equal
to 0. So vi =V2. Therefore, solutions to the initial-boundary value problems
are unique. ¦
Remark VIL3.7 If M has C°° boundary and compact closure, then the
Dirichlet heat kernel of M is equal to the minimal positive heat kernel of M,
that is, p —qu-
Proposition VIL3.6 Assume M is Riemannian complete, with Ricci curva-
curvature bounded from below. Then M has the uniqueness property and the Feller
property.
curva-
curvaCorollary VDL33 Assume M is Riemannian complete, with Ricci curvature
bounded from below. Then M is stochastically complete.
Remark VIL3.8 If M does not satisfy the uniqueness property, then the coun-
counterexample to uniqueness cannot come from the minimal positive heat kernel
214
Laplace and Heat Operators
and solutions of the form (VII.3.10), because (VII.3.9) implies there is only one
solution of the initial value problem with initial data / of the form (VII.3.10).
Indeed, (VII.3.10) and (VII.3.9) imply
L
P(x,y,
So / = 0 implies u = 0, which is uniqueness.
Note the remark applies to any positive heat kernel P on M satisfying the
inequality (VII.3.9) for all (x, t) e M x @, oo).
On the other hand, if the minimal positive heat kernel p of M is stochastically
complete, then p is the unique heat kernel among all positive heat kernels on
M satisfying (VII.3.9). Indeed, if P is a positive heat kernel on M satisfying
(VII.3.9), then P > p on all of M x M x @, oo), which implies
1= I p{x,y,t)dV(y)< I P(x,y,t)dV(y)<l,
JM JM
which implies the claim.
Definition Let M be a Riemannian manifold that satisfies the uniqueness prop-
property for the heat equation. Then to every bounded continuous function 0 on M
one assigns the heat flow t v-* H,<f> of 0, defined by
= u(x, t),
where u(x, t) is the solution of the initial value problem with initial data <j>.
Theorem VII3.5 Let M be a Riemannian manifold that satisfies the unique-
uniqueness property for the heat equation. Then the heat flow H, is given by
= I p(x,y,t)<t>(y)dV(y),
Ju
where p is the unique heat kernel ofM. Furthermore, the heat flow H, satisfies
the semigroup property, namely,
+s = H,oH,
forallt,s > 0.
Proof Given a bounded continuous function /, both
u(x, t) = Ht+,f(x), v(x, r) = Hl0H,f(x)
are solutions to the heat equation. Both have the same initial values u(x, 0) =
v(x,0) = H,f(x), which is bounded continuous. The uniqueness then
VII.3 The Heat Equation and Its Kernels
impliesthat^, T, = v(x, r)foral](,; r) ? „ x (Q
215
Theorem VII3.6 Let M be a Riemannian manifold with compact closure and
C°° boundary, and let Q, denote the heat flow on M subject to the i
' constraint
that the solution vanishes ondM x @, oo). Then Q, is given by
(Q,4>)(x)= f q{x,y,tL>{y)dV(y),
JM
where q is the Dirichlet heat kernel ofM. Furthermore, the heat flow Q, satisfies
the semigroup property.
Proof The same as the previous theorem. ¦
Definition Given a Riemannian manifold M with heat kernel p. For any / > 0,
the heat kernel defines an integral operator P, by
(P,f)(x)= f p(x,y,t)f(y)dV(y)
JM
for any bounded continuous function / on M. Then
foralljce M.
Theorem VLL3.7 Let pbea closed, Dirichlet, or minimal positive heat kernel
on the Riemannian manifold M. Then p satisfies
.11) p(x,y,t+s)= f p(x,z,t)p(z,y,s)dV(z)
JM
for all x, y andt,s.
Proof In the first two cases, M satisfies the uniqueness property, which implies
the semigroup property.
For the minimal positive heat kernel, we first note that the Dirichlet heat kernel
q of a domain 12 in M satisfies (VII.3.11). Next, for an arbitrary noncompact
M, and an exhaustion $2y of M by domains with compact closure and C°°
boundary possessing Dirichlet heat kernels qjy one obtains (VII.3.11) for p by
passing to the limit of (VII.3.11) for qj. ¦
216 Laplace and Heat Operators
VII.4 The Action of the Heat Semigroup
Theorem VII.4.1 Let Mbea Riemannian manifold with minimal positive heat
kernel p (this includes closed and Dirichlet heat kernels). We denote by C the
space of functions Cf(M). Then for each positive k, the action of P, on C
extends to a contractive, continuous semigroup on Lk(M). Furthermore, P, is
positive self-adjoint on L2(M). Thus, any eigenvalue of P, must be positive,
with C°° eigenfunction.
Proof First, (VII.3.9) and the symmetry of p imply
(VH.4.1) f p(x,y,t)dV(y)<l
Jm
for all (x, t)e M x @, +00). For / e C we have
\\P,fh= f dV(x)\f p(x,y,t)f(y)dV(y)
Jm \Jm
< f dV(x)f P(x,y,t)\f(y)\dV(y)
Jm Jm
= I \f(y)\dV(y) [ p(x,y,t)dV(x)
JM JM
< / \f(y)\dV(y)
Jm
= ll/lli,
that is, HP,/Hi < ||/|h; in particular, ||/»,||i_»i < 1. Similarly, Haider's
inequality and (VII.4.1) imply
11^/11**= / 1/
JM \JM
p(x,y,t)f(y)dV(y)
dV(x)
< [ dV(x) f p(x,y,t)\f(y)\kdV(y)
Jm Jm
< I \f(y)\kdV(y),
Jm j
thatis,||P,/|U<||/||tforalU6[l,oo),/eC. ¦
Because the subspace C is dense in L\ for each k e [1, oo), we may extend
the bounded operator P,\C -* C°° to a bounded operator on Lk satisfying
< I
for all k e [1, oo] (the case k = oo is in Remark VII.3.8).
VII.4 The Action of the Heat Semigroup 217
Next, given k e [1, oo), we approximate / e Lk by <f> e C. Then
P,f ~f = P,{f -<t>) + P,4>-4> + 4>-f\
which implies
limsup \\P,f - f\\k < limsup {||P,{/ - ^}|U + \\P,4> -<t>h + 11^ - fh)
no no
= O(\\f-4>\\k)
as <p -»¦ / in Lk. Thus P,f -*¦ f in Lk for all k e [1, oo). Therefore P, is
continuous at / = 0.
The semigroup property
remains valid on Lk for all k.
Because P, is bounded, with symmetric kernel, P, is self-adjoint on L2.
Next, consider P, acting on L2, t fixed. Then
(P,f, f) = (Pt/2P,/2f, f) = (P,/2f, P,/2f) = \\P,/2ff > 0
(we mean L2 norm unless otherwise indicated). If there exists / such that
P,f = 0, then the above shows that P//2/ = 0. One uses the continuity of
the semigroup to show that this implies that / = 0. Therefore the quadratic
form associated with P, (as a self-adjoint operator) is positive definite, and all
eigenvalues of P, must be positive. Moreover, any eigenfunction of P, must
beC00. _
As discussed in §VII.1.3, the semigroup P,:Ll -*¦ Ll has generator A*
defined by
,/ lm,
uo /
with domain T>(K() consisting of functions for which the limit on the right hand
side exists in Ll. Then
T>(K() is dense in Ll, and T>(Et) is complete with respect to the norm
lfte = Wfh + IIA,/||,.
Notation We shall write A for A2.
Henceforth we shall fix P,: L2 -*¦ L2. Since P, is self-adjoint for all / > 0, we
have A is self-adjoint. It remains to identify A. We know that it is a self-adjoint
extension of Ar, the Laplacian acting on C™.
218 Laplace and Heat Operators
Theorem VII.4.2 Assume M has compact closure with C°° boundary, Q, the
heat semigroup associated with the Dirichlet heat kernel ofM. Then A is equal
to the Friedrichs extension 5c of Ac, the Laplacian acting on C™(M).
Proof Let Z>dir consist of those functions / 6 C°°(M), which satisfy f\dM =
0, so PdSr determines the Laplacian Adir associated with vanishing Dirichlet
boundary data, with Friedrichs extension 5dir = 5c (see Corollary VII.2.1).
Since Q,{V&1) 9 T>At for all / > 0, Proposition VII. 1.3 implies that A*, is
essentially self-adjoint. So, when M has compact closure and C°° boundary,
5C is the unique self-adjoint extension of A^r- In particular, the Friedrichs
extension 5c = A. ¦
Remark VII.4.1 It is worth noting that once we have the self-adjoint Dirichlet
Laplacian realized as the Friedrichs extension of the function space Cc3o(Af),
we have removed any mention of the boundary, its regularity, and the associated
boundary data from the characterization of the self-adjoint extension. There-
Therefore, for an arbitrary Riemannian manifold M one may refer to the Friedrichs
extension of C™(M) as the Dirichlet Laplacian. So one is always speaking of a
specific self-adjoint extension of the Laplacian. The issue of genuinely identi-
identifying the domain of the Dirichlet Laplacian is then a separate question, should
one be interested in it, or should one require the specific information. Then the
details of the geometry of M and its boundary would come to the fore.
Assume M is a complete Riemannian manifold. Then, by Theorem VII.2.1,
A is the unique self-adjoint extension of Ac. In particular, A agrees with the
Friedrichs extension 5c
Theorem VII.43 Let p denote the minimal postive heat kernel of an arbitrary
Riemannian manifold M, with associated semigroup P,. Then
(Vn.4.2) Hgrad Pt<p\\2 = -(ft*. A/>,0)
forall4>eC™,t > 0.
Proof (Here, A still denotes the pointwise Laplace operator.)
Start with an exhaustion of M, Dj f M, consisting of relatively compact
domains with C°° boundary, and their attendant Dirichlet heat kernels qj =
qD, t P- Associate with each qj its semigroup QJ. Then for any function <f> e
Cc°°(Af), we have
QJ,<t> -> P,<p, grad Q{<t> -*¦ grad
as j
VII.4 The Action of the Heat Semigroup
oo, uniformly on compact subsets of M. This implies
219
= -(Qi<t>, A<f>)
[the fourth line follows from qj f p, and the fifth line follows from Proposition
VII.1.2(a)]. For any compact K in M and e > 0 there exists j0 such that for all
j > jo we have
f
JK
< f
Ju
which implies
/ Igrad P,4>\2 dV < liminf / Igrad QJ4>\2 dV
In particular, letting e -J. 0 and K f M, we obtain
So grad P,4> e L2.
Therefore, given 4> e Cf, we have P,<p e Sj = I>(A1/2), the domain of the
quadratic form associated with A. Next, we note that the sequence QJcp is a
Cauchy sequence in f). Indeed, we certainly have QJ,4> a Cauchy sequence in
L2. As above, we also have
fgrad QJ,<p - grad Qfyf = -(QJ,4> -
= -(QJ,<t> -
^¦0
, AQj<t>
, QJ,A<t>
as j, k -*¦ oo. So Qjtfr is Cauchy in fy. Therefore, there exists * e fy such that
QJ,<p -* * in Sj as j -*¦ oo. Then * has an L2 weak derivative, that is, there
exists an L? vector field «C on M such that
(¦, X) = -(*, div X)
220
Laplace and Heat Operators
for all C°° vector fields X on M with compact support. But then for such a
vector field X we have
= lim -@/0,divX)
j-*oo '
= Urn (grad QJ,4>, X)
j-*oo
= lim (*. X),
j-*oo
which implies * = grad P,4>, which implies QJ,4> -*¦ P,<f> in Sj. Therefore
||grad/>,0||2 = lim^ ||grad QJ,4>f = -(/>,*, AP,4>),
which conludes the proof of the theorem. ¦
Theorem VII.4.4 Let M be an arbitrary Riemannian manifold, yc the
Friedrichs extension of Ac, and p the minimal positive heat kernel, with asso-
associated semigroup P, and infinitesmal generator A. Then
Proof Let T, be the 1-parameter semigroup generated by fo, tf> e Cf(M), and
set
Then v is a solution of the heat equation with vanishing initial data. We want
to show that v vanishes on all of M x @, oo).
The spectral theorem, Lebesgue's dominated convergence theorem, and the
estimate
< 2, 0 < x « 1,
combine to imply that we may differentiate / v2(x, t) dV(x), under the integral
sign, with respect to /. Then (see the proof of Theorem VII.3.4)
= f Av(x,t)v(x,t)dV(x).
By Theorem VII.4.3, for each / > 0, P,<f> is in the domain of &, and therefore
VII.4 The Action of the Heat Semigroup 221
v is in the domain of 3>, which implies
2diJ v2(x<*)dV(x)= I Av(x,t)v(x,t)dV(x)
= - j |gradt;|2(jt.O<*V(*)<0,
which implies the claim. ¦
Notation We henceforth write, when there is no confusion, A for A = $r.
Thus, if {Ex.: A. > 0) is a spectral family for A, then
f°°
A = -/ XdEk,
Jo
with associated quadratic form
D[f, f] = (-A/, /) = r\ (dExf, f)
Jo
possessing domain D((-AI/2) 2 2>(A); and
/•OO
P, = e~udEx.
Jo
Theorem VII.4.5 Let pbea closed or Dirichlet heat kernel on a Riemannian
manifold M. Then —A has discrete spectrum, and p(x, y, t) has the absolutely,
uniformly convergent Sturm—Liouville expansion
(VII.4.3)
p(x, y,t) =
oo
^2
7=1
where {0i, fa,...) is a complete orthonormal basis of L2(M) consisting of
eigenfunctions of—A, with the eigenvalue oftpj equal to X,. Also, <pj e C°°
for all j.
Proof Indeed, under these hypotheses, for every fixed /, p(x, y, t) is a Hilbert-
Schmidt kernel (that is, symmetric and square-integrable on M x M),
which implies the discreteness of the spectrum and the expansion (VII.4.3)
in L2(M x M). The stronger statement of convergence of (VII.4.3) follows
from Mercer's theorem (Riesz and Nagy, 1955, p. 245). ¦
Remark VII.4.2 Let p be the heat kernel of a compact Riemannian manifold
M. The constant functions clearly are annihilated by A, so \\ — 0. On the other
hand, if A<f> = 0, then 0 = (—A <j>, <p) = ||grad <f>\\2, which implies <p = const.
222 Laplace and Heat Operators
This implies X2 > O.ln particular,
1
which implies (using L2-L°° estimates of eigenfunctions, as in Li A980) for
example)
So the heat is evenly distributed throughout a compact manifold as / f +oo.
Notation For any Riemannian manifold M we let
= infspec - A.
Proposition VII.4.1 Assume X(M) has an L2 eigenfimction. Then the eigen-
function never vanishes, and the eigenspace of\(M) is I-dimensional.
Proposition VH.4.2 Given two domains ft) c JJ2 '" a Riemannian manifold
M, let —A] and — A2 denote their respective Laplacians; then A(S2i) > \(Sl2)-
When fli CC Sl2 then the inequality is strict. In particular, A.(?2) > \(M)for
any relatively compact ?2 in M.
VIL5 Simplest Examples
Example VIIJ.l If M = R", then
ds2 =
= dxi-dxn,
as discussed in §VII.3.1.
Example VIL5.2 Let M = H" = M_!, the n -dimensional hyperbolic space
of constant sectional curvature —1, and x e M. Then any point y e M is de-
determined by its distance r from x, together with the unit tangent vector ? at
x of the unique geodesic from x to y. So (r; ?) determine geodesic spherical
coordinates on all of M, relative to which
where |</?|2 denotes the Riemannian metric on Sz (the unit tangent sphere to
VII.5 Simplest Examples 223
M at x) with its standard metric. The volume element is given by
dV = sinki^
where d(ix(%) denotes the (n - l)-volume element of Sr. The Laplacian i
given by
is
;|) = i| + („ - i)coth r ^
to
where Af denotes the Laplacian on Sx, and fr denotes the restriction of / to
the metric sphere in M centered at x with radius r, viewed as a function on S,.
The simplest explicit formula for the heat kernel is when n = 3, namely, on H3
the heat kernel is given by
p(x y ,)=_L
p(x'y'l) D
2 Sinh d(x, y)
Example VIU3 If M = M\ x M2 is the Riemannian product of M\ and Mi,
then for any chart x = (x(, X2) on M, where xj is a chart on Mj,j = \, 2,
have for the matrix G* of the product Riemannian metric
we
C* =
where Gj denotes the matrix of the Riemannian metric on Mj. For F: M -* R
given by
M1 x M2,
we have
(with obvious notation). For the heat kernel we have
p((x]tx2), (y\,y2), t) = p\(xuy\,t)P2(x2, y2, t).
Example VIL5.4 If p is a closed or Dirichlet heat kernel on M, then by
Theorem VII.4.5, p(x, y, t) has the Sturm-Liouville eigenvalue-eigenfunction
expansion
(VII.5.1) p(x, y, t) = 2 e-x''*j(x»j(y).
where {Xi < k2 < • ¦ ¦ | +00} denotes the spectrum of—Aon M (it is discrete),
with eigenvalues repeated according to their multiplicity, and i<f>j :j = 1,...}
224
Laplace and Heat Operators
is a complete orthonormal basis of L2 such that <t>j is an eigenfunction of Xj
for each j.
Example VIL5.5 The 2-dimensional jungle gym JG2 as described in Example
V.2.4. We shall see that for sufficiently large time one has
P(x,y,t) <
VII.6 Bibliographic Notes
General references for the material in this chapter are Davies A980, 1989, 1995) and
Chavel A984,1994). [Formula C8) of Chavel A984, p. 150) is only valid when k < 0.]
See also the articles of Chavel, Davies, and Grigor'yan in the 1998 Edinburgh Lectures
(Davies and Safaro. pp. 30-94,14-225).
§VII.l Additional background for this section may be found in Yosida A978) and
Reed and Simon A975).
§VIL2 The Meyers-Serrin theorem is proved in Adams A975), Aubin A982), and
Gilbarg and Tnidinger A977). Theorem VII.2.1 was first proved in Gaffney A954); our
proof follows Karp A984). Corollary VII.2.2 is from Yau A976). Elliptic regularity is
treated in Gilbarg and Tnidinger A977, p. 176).
§VIIJ One can find a proof of the strong maximum principle in Plotter and
Weinberger A984, §111.3.4) for the case where M is diffeomeorphic to a domain in
Euclidean space. A standard continuation argument then extends the theorem to arbi-
arbitrary Riemannian manifolds.
The proof of Theorem VH.3.3 corrects an incorrect proof given in Chavel A984,
p. 139).
The uniqueness property and stochastic completeness for Ricci curvature bounded
from below (Proposition VII.3.6) was first proved in Dodziuk A983), and the Feller prop-
property in Yau A978). The last two results are valid in much greater generality; for stochastic
completeness, see Azencott A974), Davies A992), Gaffney A959), Grigor'yan A987),
Hasminkii A960), Ichihara A982, 1984, 1986), Karp and Li (unpublished), Oshima
A989), Pang A988,1996), Takeda A989,1991), Varopoulos A983). An extensive sur-
survey of these and other results can be found in Grigor'yan A999). For the Feller property,
see Azencott A974), Davies A992), Karp and Li (unpublished), Pang A988, 1996),
Gaffney A959). Hasminkii A960).
§VIL4 Theorem VII.4.4 is proved in Dodziuk A983). Proposition VII.4.1 is from
Sullivan A987).
§VIL5 Explicit calculations for the heat kernel on a hyperbolic space of any dimen-
dimension can be found in Davies and Mandouvalos A987) and Grigor'yan and Noguchi A998).
For the heat kernel on Lie groups, see the articles of Arede A985) and Fegan A976,
1983). For the heat kernel on homogeneous spaces, see Benabdallah A973). For the
special case of spheres, see Fischer, Jungster, and Williams A984) and Ndumu A986).
vra
Large Time Heat Diffusion
In this chapter we present the main result of this half of the book - Theorem
Vni.5.4 - that, in a complete Riemannian manifold of bounded geometry, a
positive modified isoperimetric constant 3V,P implies an upper bound for the
minimal positive heat kernel p of the type
P(x, y, t) < const./-y/2 V / > To > 0,
or, equivalently,
(Vm.0.1)
p
't+oo
for all x, y e M. So the result states that if M is "v-dimensional" in the sense
of isoperimetric inequalities, then it is at least "u-dimensional" in the sense of
heat diffusion. The method of proof is to pass from the geometric inequality
3vp > 0 to a modified Nirenberg-Sobolev inequality, which is then shown to
be equivalent to the large time upper bound (VIII.0.1).
The transition from 3V<P > 0 to the modified Nirenberg-Sobolev inequality is
achieved by shifting the problem to any discretization of the manifold (Theorem
VIII.5.2). A by-product of this argument is the invariance of (VIII.0.1) under
compact perturbations of M, of the type discussed in Theorem V.3.1.
The final section of the chapter closes the book with an alternate proof of
Theorem VUI.5.4 (see Example VI.3.1 and Example VIII.6.1 below) using
Grigor'yan's replacement of the Nirenberg-Sobolev inequalities with Faber-
Krahn isoperimetric inequalities as the primary tool for establishing upper
bounds on the heat kernel. The full possibilities of this method seem to go
well beyond the result presented here; so the best may be yet to come.
We assume, throughout this chapter, that M is a Riemannian manifold and p
its minimal positive heat kernel, with attendant semigroup P, acting on L2(M),
which is contractive, continuous, and self-adjoint. The infinitesimal generator
225
226
Large Time Heat Diffusion
of the semigroup is the Friedrichs extension of Ac, the Laplacian acting on
C™(M) considered as a dense subspace of L2(M).
The semigroup P, also has an action on Lk, k > 1, which is contractive
and continuous. Since Lk O L2 is dense in Lk, we shall be able to study the
norms of
P,: Lk n L2 -> Ll n L2
as though they were mappings from Lk to Le, with their associated norms
UP, «*,«.
VIII.l The Main Problem
Proposition VIII.1.1 Assume x e M such that the exponential map exp is
defined on the closed disk B(jc; R) in Mx. Then for
d(x, w) < R/2, 0 < r <
d(x, w)
we have
(VIII.1.1) p(x,w,s) < const.-^
s-n/2 + sr-(*+2)
,-{<Hx,w)-2rJ/4s
where 3n(B(z; p)) denotes the n-dimensional isoperimetric constant ofB(z\ p).
Recall that, for any Riemannian manifold M, we set
?(x, y, t) =
Theorem VIII.1.1 Assume M is a complete Riemannian manifold. Then for
every compact K CC M there exist positive constants {depending on K) such
that
(VIII. 1.2)
limsup
P(x, y, t)
?{x, y, t)
-1
< const.d(jt, y)
is valid for all x, y e K.
Proof We already know the result for M compact, so we assume that M is
complete and noncompact.
Given x and y in M, let Q be any domain in M, with C°° boundary and com-
compact closure, containing x, y, and let q denote the Dirichlet heat kernel of ?2.
Then p(x, y,t) > q(x, y, t) by the maximum principle, which implies by
VIII.l The Main Problem
227
Proposition VII.3.5 that
To prove
li™oUPf^-1+C°nSt^>)
we argue as follows: Let Si and q be as above. Then Duhamel's principle implies
P(x,y,t)-q(x,y,t)
da
= -/ ds I p(x,w,s)-^-(w,y,t-s)dA(w)
Jo Jan Bvw '
<| sup p(x,w,s)\ f ds f -~{w,y,t-s)dA(w
< sup p(x,w,s).
But one has, for any r e @, d(x, w)/2), the upper bound (VIII.1.1). Therefore
pick Si so that d(x, 3fi) is very large compared to d(x, y), fix r very small, and
let t i 0. Then one has, for some a e @,1),
.. P(x, y, t) q(x,y,t)
limsup -—-— < limsup
msup -—-—
no ?(x,y,t)
?(x,y,t)
+ lim sup
'10
?(x, y, t)
< 1 + const.d(jc, y),
which is the claim.
Remark VIII.1.1 One can see (VIII. 1.2) explicitly in both the example of H3
(Example VII.5.2) and the product metrics (Example VII.5.3), in the sense that
if one has this asymptotic behavior on each of the factors, then one also has it
on the product.
Remark VIII.1.2 The theorem remains valid even if M is not complete, but
one must formulate it differently. Namely, given any SI cc M, x e Si, the
inequality (VIII.1.2) will be valid for y sufficiently close to x.
228
Large Time Heat Diffusion
For large time considerations the behavior of the heat diffusion takes into ac-
account the large scale structure of the manifold, and then anything can happen.
Hyperbolic space displays an example of when the heat kernel decays expo-
exponentially with respect to time, and Euclidean space when the rate of decay with
respect to time is given by the dimension of the manifold. For M compact, one
has p(x, y, t) -> 1/ V(M) as t f +00. Therefore, for M = S""* x R*. the heat
kernel decays at the rate t~k/2, slower than that indicated by the dimension n of
M. Finally, we have examples of polynomial rate of decay that are faster than
that indicated by n, the dimension of M, namely, the jungle gym of Example
VH.5.5.
Main Problem Study the large time decay of the heat kernel, as a consequence
of geometric hypotheses on M.
Except for Theorem VIII. 1.4 (which is included for motivation), we shall restrict
ourselves to the study of upper bounds.
In general, upper bounds on the heat kernel are studied in two stages: The first
is referred to as on-diagonal upper bounds, namely, upper bounds for p(x,x,t).
By the semigroup property, the Cauchy-Schwarz inequality, and the symmetry
property we have
P(x,y,t)= [ P(x,z,t/2)p(z,y,t/2)dV(z)
Jm
Ul 1/2 I r 1 1/2
p\x,z,t/2)dV(z)\ \J P\z,y,tl2)dV{z)\
that is,
(Vm.1.3)
P(x, y, I) < y/p(x,x,t)y/p(y,y,t).
Therefore, as soon as we have any upper bound valid for p{x, x, t) for all x, we
automatically have an upper bound on p(x, y,t). But this upper bound could
not contain a Gaussian term of the form
Then the second stage is to produce new arguments to sharpen the upper bounds
based solely on the on-diagonal upper bounds. The introduction of the Gaussian
correction to the upper bounds is also referred to as the off-diagonal correction.
We shall not pursue this second stage here. It has recently been definitively
established that the correction in upper bounds does not depend on the specific
VIII. 1 The Main Problem 229
^T^l*!.?™™* "r. * **""*** of the heat equation that
kernel automatically imply off-diagonal
VHI.1.1 General Considerations
Theorem Vm.l2 For on-diagonal upper bounds have
(VUL1-4) 8UPJ>(*.*.0=llfi|||-oo.
Proof First, given / e L\ we have
\P,f\(x) - \J p(x, y, t)f{y)dV(y)
which implies
tPtf\{x) < sup p(x,y,
x.y
x.y
, jc, 1).
Therefore, || P, ||,_«, < sup, p(x, x, t). For the opposite inequality recall that
an approximate identity at x e M is a family of nonnegative functions 6h
h>0, satisfying Vht
L
4>hdv = 1
0, Hm f
<t>hdV =0
for all c > 0. Then 4>h -> Sxt the delta function concentrated at x, as h 1 0 For
such an approximate identity 0A at x we have
I
P(x, y, t)<ph(y)dV(y) = pl<t>h{x)
< IIP,IIl^oc||0*III
= II fill l-oo.
*• ™
Aat MM) demotes ihe inlimum of the specttum of the Lapteia, -a
230
Large Time Heat Diffusion
Theorem VIII.1J For all x e M we have that t \-+ ek(M)l p(x,x,t) is a
decreasing function oft.
Proof Let D be a relatively compact domain in M with C°° boundary and
Dirichlet heat kernel q. Then the Sturm-Liouville eigenvalue-eigenfunction
expansion of q, and X(D) > X(M) combine to imply e^U)lq(x, x, t) is a de-
decreasing function of t.
Now pick an exhaustion of M, Dtr f M as j f +00, by domains that are
relatively compact in M and that possess C°° boundary. Let qj denote the
Dirichlet heat kernel of Dr Since qj \ p, the lemma follows immediately.
Corollary VHI.1.1 The norm || P, || i-^x, decreases with respect to time.
Proposition VIII.1.2 Let X = X(M). For all x, y in M we have the existence
of the limit
(VIH.1.5)
for which we have the following alternative: Either T vanishes identically on
all of M x M, in which case k possesses no L2 eigenfunctions; or T is strictly
positive on all ofMxM, in which case X possesses a positive normalized L2
eigenfunction 4> (normalized in the sense that its L2 norm is equal to I) for
which
(VIII. 1.6) lim
/t+oo
locally uniformly on all ofMxM.
The simplest example of the case T = 0 is R", n > 1, discussed above —
just note that A. = 0, so e* p(x, y, t) = p(x, y, t) -*¦ 0 as t \ +oo. When M is
noncompact with compact closure and smooth boundary, then one always has
T strictly positive, and (Vm.1.6) follows from the Sturm-Liouville expansion
(VII.5.1)ofp.
We note some easy consequences of the proposition.
Corollary VIII.1.2 We always have
In p(x,y,t)
(VIII. 1.7)
lim
VIII. I The Main Problem 231
locally uniformly on M x M; and when M has finite volume V, we have
(VIII. 1.8)
locally uniformly on M x M.
Proof We wish to show
lim
If the limit function T is positive, then the result is obvious. So we are only
concerned with the situation where T is identically equal to 0. For any domain
Din M, let q& denote the Dirichlet heat kernel of D, and XD the lowest Dirichlet
eigenvalue of D. Then, of course, we have
eup(x, y, t)
We let t t +oo. Then
A - Xd < limmf
/t+oo f
Now let D t M. We conclude that
, Ine"p(x,y, t)
0 < liminf HK } .
t+ /
But since T — 0, we have In e*'p(x, y,t) < 0 for large r, which implies
(x,y,t)
lim sup
/t+oo
< 0,
which implies (VIII.1.7).
When M has finite volume then X = 0 with normalized L2-eigenfunction
= 1 I<JV(M} (for all x), which implies (VIII. 1.8). ¦
Corollary Vm.1.3 For any M we have
(Vni.1.9) lim p(x, y, t) = 0
/t+oo
if and only ifM has infinite volume.
Proof If M has finite volume, then (VIII. 1.8) implies that lim p, as t f +°o.
is nonzero. If, on the other hand, M has infinite volume, then (a) for X > 0
simply use (VIII. 1.5); and (b) for X = 0, if T were positive, we would have the
232
Large Time Heat Diffusion
existence of an L2 harmonic function on M, which is impossible by Corollary
vn.2.2. ¦
Corollary Vffl.1.4 Suppose M noncompact is a covering of a compact
Riemannian manifold. Then T is identically equal to zero. Consequently, if
the covering is nonamenable - by Brooks A981), X > 0 - then p tends to 0
faster than e~kl.
Proof If A. = 0, one uses the above corollary, because M has infinite volume.
If A. > 0 and T > 0, then, as mentioned above, the L2 eigenspace of X, which
is nontrivial, is 1-dimensional (by Proposition VII.4.1). But this is impossible,
by the invariance of the eigenspace under the action of the deck transformation
group. ¦
Remark VIU.l 3 A fundamental distinction emerges between the cases X = 0
and the cases X > 0. If one subjects the complete Riemannian manifold M to
a compact perturbation, then in the case of bounded geometry (that is, Ricci
curvature bounded from below and positive injectivity radius) X = 0 remains
invariant under the perturbation. Moreover (Theorem VIII.5.2 below) the rate
of polynomial decay of the heat kernel also remains invariant under the per-
perturbation. However, in the case X > 0 the value of X does not necessarily
remain invariant under the perturbation. Simply consider H", ^-dimensional
hyperbolic space of constant sectional curvature -1, with X = (n — 1 J/4, and
subject it to a compact perturbation in which it has a flat disk with lowest
Dirichlet eigenvalue strictly less than (n - lJ/4. Then the new Riemannian
metric has A. < (n - lJ/4 with appropriately slower heat kernel decay for large
time.
Our interest in what follows will usually involve polynomial decay with
respect to time. So we will be interested in the case X = 0.
VIII.1.2 Volume Growth Considerations
The most elementary geometric intuition is that, because the total amount of
heat in the space cannot increase with respect to time, the larger the space,
the quicker its heat kernel decays. Indeed, if M is compact, then \/V(M) is
the limit if the heat kernel as t \ +oo. In general, the intuition is valid, if not
sufficiently precise. Most, if not all, of our geometric results will aim toward a
deeper understanding of the effect of volume growth of a Riemmanian manifold
on heat kernel decay.
VIII. 1 The Main Problem
233
Theorem Vm.1.4 Giveno eMandfi> 0, for which one has the heat kernel
lower bound
(Vm.1.10) p(o, x, t) > con&l.rvl2e-dHo'x)'fi'
forallx eMandt>T>0, then one has the volume growth upper bound
(Vm.1.11) V(o;r)<comt.r"
for sufficiently large r > 0.
Proof The heat kernel lower bound implies
p(o,x, t)dV(x) >
which implies the volume upper bound.
y(o;>/?),
Remark VIIL1.4 There are results for a partial converse (Coulhon and
Gngor'yan, 1997): If (Vm.1.11) is valid for a given o € M and sufficiently
large r, then
(VIII.1.12)
p(o, o, t) > const.(f In t)~v/2
for large t. Examples exist to show the estimate is sharp. Also, one can improve
(VIII. 1.12) to
P(x,x,t) > const.r~v/2
assuming one is also given the upper bound
p(x,x,t) < const./~v/2
for large /. [See earlier versions in Benjamini, Chavel, and Feldman A996)].
Exampk Vffl.1.1 Does a volume growth lower bound imply a heat kernel
upper bound? No. Endow M = R2 with the Riemannian metric
ds2 = 4>{y){dx2 + dy2),
where
0 < 4>(-y) = Hy) e C°°,
= y-2 for
Then one easily sees that M has exponential volume growth. But general con-
considerations show, since the metric is conformal to the Euclidean plane (this is
234 Large Time Heat Diffusion
just for the 2-dimensional case), that
f<
p(x,x,t)dt = +00,
which precludes a rate of decay of the form / v/2, v > 2.
We shall need the following heat kernel upper bound in the sequel.
Proposition VIII. U Let M be complete with Ricci curvature bounded from
below by the constant -K, K > 0. Then for any a > 1, one has the upper
bound
(VIII. 1.13)
where the constant C(e) -> +oo as e -> 0.
Or
Remark VHL1.5 An application of Holder's inequality implies that for any
k, I and respective conjugates k', I' we have
II fill*-* = llfilr-*'.
Because P, is self-adjoint for all t, we have
We shall use this repeatedly throughout our arguments.
VfflJ The Nash Approach
Theorem VDL2.1 Assume there exists v > 0 such that the NashSobolev
inequality
(VIH.2.1) llgrad/lb > const.||/||2'+2/v||/||r2/v
is valid for all f e Cf. Then
(VIII.2.2) ||/»f||^00<const./-l'/2,
for all t >0.
Proof Set«(/) = || fi/||22. We then obtain
l-u\t) = (p,f, ytP,f\ = (P,f, AP,f) = -Hgrad
< -const.«(/I+2/"
u'(t)
VI11.2 The Nash Approach 235
by Theorem VII.4.3. Then
^«'(/) = -||gradP,/||22
that is,
which one integrates to obtain «(/) < const.||/||i2/~l>/2.
So ||fi||i_»2 < const./-v/4, which implies, by duality (Vm. 1.14), \\P,h-*oo <
const./-"/4, which implies (Vin.2.2). ¦
Remark VIII21 One can pass from «(/) < const-ll/lli2/-11/2 to (VIII.2.2)
without using duality (m.2.5). Namely, for any / € Cf we have
that is,
(w. y. t)fiy)dV{y)\ dV(w) < const.Il/H,2/-"/2,
constll/H,2/-"/2 > I \j p(w,y,t)f(y)dV(y)\ dV(w)
= j \j p(yv,y,t)f(y)dV(y)\
x j / p(w,z,t)f(z)dV(z)\ dV(w).
Given any x e M, let 4>h be an approximation of the identity concentrated at x,
and let f = 4>h- Then, letting h I 0, we obtain
const./-"/2 > / p(w, x,
which implies the theorem.
t)p(w,x, t)dV(w) = p(x,x,2t),
Theorem VIII.2.2 Conversely, assume (VIII.2.2) for all t > O.Then(VIll.2.l)
is valid on C*.
Proof Let 0 € C*. Then the spectral theorem impl
ies
-/Hgrad0||22,
Large Time Heal Diffusion
236
which implies
< r||grad0||22 + const.rl>/2||0||i2
for all / > 0. Now minimize the right hand side with respect to t. The minimum
is achieved at t0 = const.||0|li2/||grad0||22, which implies the Nash-Sobolev
inequality (VIH.2.1). ¦
Remark VTIL2.2 Here is a proof without using the spectral theorem. One
simply has
d
and
A ?
— ||grad/>,0||22 = --(P,<t>, A/>,0) = -2\\AP,if>\\2 < 0,
at at
which implies t >-*¦ ||grad Pt<Ph2 is nonincreasing, and
1Mb2 = \\P,<t>h2+ [ ||grad/>,0||2</r.
Jo
The Riesz-Thorin interpolation theorem (see Proposition Vm.3.1 immediately
below) implies, from (Vm.2.2), || P, || 1-2 < const./""/4 for all t > 0. Therefore
and we minimize as above.
VIU J The Varopoulos Approach
We first state some background results.
Proposition VIII J.I (Riesz-Thorin Interpolation Theorem) LetT.L2
L2 satisfy
where po, Qo, Pi,Qi € [0, 00]. Fork € @, 1), set
1 _ 1 - X X 1 _ 1 -X ±
Pa Po Pi' Qk <?o Qi
V11I.3 The Varopoulos Approach
237
Then
Proposition VIII J.2 (Maximal Theorem) Let Tt: L2 ^ L2 be a self-adjoint
contraction semigroup. To every function f e L2 associate the function
f*(x) = sup \T,f\(x).
Then
Wf'Hp < const.,11/11,
forallfeLPnL2,pe [1, +00].
Definition Let T, be a self-adjoint contraction semigroup with generator - A
(so A is nonnegative). We define
(where {Ek} is a spectral family for A) with domain consisting of those 4> e L2
for which
/
Jo
The definition is motivated by the fact that
/ e~*V-' dt =
Jo
for any given (i e @, 1).
Theorem VIII J.1 Let M be a Riemannian manifold, A = -A. Then
if and only ifM has infinite volume, if and only ifp(x, y, t) -* 0 as t f +oo.
Proof We have
i f°° r°°
"(M) Jo Jo
[°° -l
Jo ^ € dt
ro
= /
Jo*
dEk
= I -Eo,
238
Large Time Heat Diffusion
where ?o is the eigenspace of A. = 0, either the line of constant functions (Propo-
(Proposition V1I.4.1) or the origin in L2. If M has infinite volume, then L2 has no
nontrivial constant function. If M has finite volume, then the constant functions
are all in L2. ¦
Theorem VIII J.2 Let v > 2. Then (VIII.2.2) is valid for allt > 0 if and only
if
(Vm.3.1) ll/|l2v/(.-2) < const.||grad/||2
for all f 6 Cf, equivalently, if and only if
(Vm.3.2) ll(-A)-1/2/||2l)/(l)_2) < const.||/||2
forallfeV((-A)-1/2).
Proof Certainly, given (VITJ.3.1) on C* we have (VIII.2.1) by the proof
Lemma VI. 1.2, which implies (VIII.2.2) for all t > 0. For the converse, set
A = -A, and assume (VIII.2.2) on L2. By Theorem VIII.3.1 we have the
representation
A-u2f=_l n tw-iPifdt
Vn Jo
for all / e 2?((-A)-|/2), which implies, for any T > 0,
\A~l/2f\(x) < (sup |.
l/>0
1 f
j r^WP.h^d
Now use the Riesz-Thorin interpolation theorem, with
Po = 1, qo = oo. P\ — q\ - oo, A. = 1/2.
Then
Pi. =2, qx = oo,
which implies
llfllh-oo < Mn'^Afi* < const.r-"/4,
which implies
V7//.5 77j« Varopoulos Approach
27-1/2
y/Jt
239
Minimize the right hand side with respect to T. Then the minimum is
realized at
which implies
which implies
\A'll2f\{x) < cv\nl-2'v{x)\\fh2l
/
M
We therefore have (VIII.3.2). ¦
Remark Vm J.I We could have easily used Theorems VI. 1.1 and VIII.2.2 to
prove the above theorem. But the method is useful for other considerations, as
well. For example, the proof of the theorem also implies a short time result:
Theorem VfflJJ Let v > 2. Then (VIII.2.2) is valid for all t € @, 1] if and
only if
(Vm.3.3) ll/ll2v/(v-2) < const.{||grad/||2
for all f e Cf, equivalently, if and only if
(VIII.3.4) ||(-A)-I/2/||2v/A)_2) < const.{||/||2 +
forallfeV((-A)-l<2).
Proof Assume || P, || i^.^ < ct~v/2 for all t e @,1]. Consider the
semigroup
Then, by Theorem VIII. 1.1, ||/»,||i_»oo decreases with respect to time, which
implies T, satisfies || T, || i-oo < ct~v/2 for all t > 0. Now the infinitesimal gen-
generator of T, is A - /, which implies (VIII.3.3) by the previous theorem. The
converse is similar. ¦
240
Large Time Heat Diffusion
A direct consequence of the Li-Yau upper bounds (Proposition VIII. 1.3) and
Crake's inequality (V.2.15) is
Proposition VIIIJJ lfM is n-dimensional Riemannian complete with bound-
bounded geometry, then
< const./-n/2
for all t €@, 1].
In particular, when n>2,we have
(VIU.3.5)
forallf^Cf.
-2) < const.{||grad/||2
VDL4 Coulhon's Modified Sobolev Inequality
What if we are only given (Vm.2.2) for all t > 1?
Theorem VIU.4.1 If (VIII.2.2) is valid for all t > I, then for each
f e 2?((-A)-|/2) we have, instead of (Vm.3.2),
where g e L2 and h € L2v^v~2\ with
High < COnSt.il/H2, ||*||2v/(v-2) < COnSt.il/H2.
Proof First, set A = — A, and write
Certainly,
= r
Jo
which implies (using the proof of Theorem VIII.3.2),
\\PiA-1/2f\\2vnv-2)< COnSt.il/H2;
so we pick h = PiA~l/2 and g = (/ - Pi)A~l/2. Now
VIU.4 Coulhon 's Modified Sobolev Inequality 241
and
P,A*'2= f
This implies, for / e T>(P,Al/2),
\\P,Al/2ff < s-1 j (ks)e-2^ (dEkf, /) <
that is,
which implies
What about a converse? We first have
< const.
Theorem VHI.4.2 (Extrapolation Theorem) Given 1 < a < 0 < +00 f
which
ll^/lla-/} < const./ "*
for all t > 1. Then
ll/'/lli-oo < const./"',
where&=e{a-1-0-l}-i,forallt> 1.
Proof Fix 6 such that
or
Of
so 0, 1 - d e @, 1). First note that, for / > 2,
WPtfh = IIW//2/IU
< const./"'IIP;/2/||a
< const./"*||P,/2/||i
< const./"'\\f\U6\\Pl/2f\\0l-e
< const./"'||P,/2l|iV~9ll/lli
- the third line is Holder's inequality, applied to
, P=l/ad,
242 Large Tone Heat Diffusion
- which implies
II/>, II 1^0 < const./-«||/>;/21|, V"*,
which, in turn, yields
te/e IIP, IIi-*, < const. {(t/2Y"> ||P,l21|,_,}'-" .
So we wish to solve the inequality
a(t) < const{o(t/2))l-e, t > 2.
Well, we have
for all t > 1. Therefore, if we vary r e [1,2] and A = 0, 1,2,.... we obtain
o(t) < const., / > 1, which implies
P, || !_»A < const.
for all/ > 1.
Next, duality then implies
const./
</9
-</e
for all / > 1, where 0' = 0/@ - 1) denotes the conjugate of 0. Now duality
also implies
\\P,\\p'^a-< const./"'
for all / > 1. Then for 0 given by
0' a' '
we have (using Holder's inequality applied to \P,f\ = \P,f\e\P,f\l~e)
(VIII.4.3)
for all / > 2. So
for all / > 2. Set e' = eA - 0). Then the argument for (VIII.4.2) also implies
which implies
which implies the theorem.
const./-<'/e+<'/e),
VII1.5 The Denouement: Geometric Applications 243
Theorem VIII.4.3 Let M have infinite volume. Suppose we are given
(VUI.4.4) (-A)-|/2: L2 -* L2 + LlvKv~2\
is bounded inthe sense ofTheoremVlUAX and Pi: Ll -> L00 is also bounded.
Then (VIII.2.2) is valid for all / > 1.
Proof We first have by the Riesz-Thorin interpolation theorem [with a = 2,
and 0 = 2v/(v - 2)] that Pi: L2 ->• L2v/lv~2) is bounded, which implies
Pi(-A)-l/2: L2 -+ L2v/iv~2) is bounded, which implies
< const./~l/2
by (VUI.4.1), which implies, by the extrapolation theorem [with a = 2
0 = 2v/(v-2),e = l/2)],
II P,+i II i^oo < const./""/2
for all / > 0. _
VIII.5 The Denouement: Geometric Applications
Let G be a graph with vertices Q. Recall that for every ? € <7, we denote its
collection of neighbors by N(?), and its valence by m(?) = card N(^). The
collection of edges of G is denoted by ?,, with oriented edges denoted by [^, n]
where n € N(?). The measure of functions on ? is given by dV(lj) = m(%)di(%\
and of functions on Qe by </A([?, n]) = di([tf, n]), where di always denotes
counting measure.
Lemma VIIL5.1 For any function f ong we have
' K.nUG,
Proof We have
/«)- r m-\ E m+na.
which is the claim.
244
Large Time Heat Diffusion
Definition We define the Laplacian of the function f:Q-+R, denoted by
AG/.by
So Ac / is a function on Q.
Then for functions / and h we have
- f
/AG h d\ = -
K.I)]
{/(I?)-
= 1 / (Vf
2JQ.
iDh)dA,
that is,
- f
JQ
[
Q.
(X)f X>h)dk\
and
= 2 / /
We conclude
Theorem VIIL5.1 Ac »'* self-adjoint nonpositive bounded operator on
L2(Q, dV), with heat semigroup
P, = exp t AG,
wi/A associated heat kernel p(?, ^, r).
Remark VIII.5.1 Note that we are using two definitions of |D/|2. In §VI.5
we defined |S/|2 as a function on Q, the vertices of G, namely,
forthevertex^ e ^.HerelD/^isviewedasafunctionontheorientededges^,.
of G. But as noted at the very beginning of §VI.5, the definitions are equivalent.
VIII. 5 The Denouement: Geometric Applications
245
So for all arguments involving Sobolev inequalities, we may work with either
definition.
Example VIII.5.1 Consider the integer lattice Z* in R*. The graph structure
on Z* is given by: n € N(?) if and only if \n - ?| = 1 in R*. Then the heat
kernel p on the associated graph is given by
where Iv(z) = e~'v*/2Jv(iz) denotes the modified Bessel function.
Proof We only consider the case k = 1. The higher dimensional case is similar.
Let / = /(n), n € Z. The Laplacian here is given by
For u = u(n, t), where n ranges over the integers and t ranges over positive
time, consider the heat equation
3«
= —, t > 0,
at
(Vin.5.2)
with initial values given by
where <p(n) is a given function on the integers. Consider the function on the
circle, having time t as parameter,
then (VIII.5.2) becomes
which implies
u(n,t)eine;
W
—@,0 = {cos 8- l}f/@,O.
dt
U(8. t) = e-"-
One now uses the integral representation
4>(n)e
ine
Jn(z) = _L [
Large Time Heat Diffusion
246
to show
for the solution to the initial value problem, which implies the claim. Note that
1,@ = B^rr1/V{l - 0,A"')}, t t +00,
which implies, on Z*,
IIP/ IIi^x. ~ const./-*/2, t t +oo.
Remark VHI.5.2 The Varopoulos and Coulhon criteria apply as well to graphs
with heat diffusion with continuous time, and with "heat diffusion" with discrete
time, namely, random walks on graphs.
Theorem VHI.5.2 Let M be Riemannian complete with bounded geometry,
and let v > 1. Then (VIII.4.4) is satisfied on M if and only if the discrete
Nirenberg-Sobolev inequality (VIII.3.1) is valid on every discretization ofM.
In particular, the heat semigroup P, ofM satisfies
(VIII.5.3) IIP, II 1^00 =
if and only if
(VUI.5.4) IIP, II.^oc =
for the heat semigroup P, of any discretization G ofM.
Also, the estimate (Vm.5.3) remains invariant under compact perturbations
ofM.
Proof First, because M has bounded geometry, one knows, by Proposition
VIII.3.3, that Pi: L1 -> L°° is bounded.
Next, assume that v > 2. Let G be a discretization of M, and assume the
Nirenberg-Sobolev inequality (VIII.3.1) is valid on G. Consider the associated
discretization operator V and smoothing operator S on functions defined on M
and G, respectively.
Given any smooth function F: M -*¦ R, consider * = (- Am)~1/2F, and
write
= {<t>- SV<t>) + SV<t>.
Then (see §VI.5.5)
-SV<t>||2 <const.||grad<t>||2 = const.||F||2,
V1I1.5 The Denouement: Geometric Applications 247
and(byP:iiiof§VI.5.1)
ll<5P*||2i,/(v_2) < COnSt.||Z><t>||2v/(v-2)
< const.||X>T><t>\\2
< const.||grad*||2
= const. || F || 2.
Therefore, if one starts 'with the discrete Nirenberg-Sobolev inequality
(VIII.3.1) on G, one also has the inequality (Vin.4.4) on any discretization
ofM.
Conversely, assume (VHI.4.4) on M; and note that SV: Ll (M) -> L°°(M) is
bounded, which implies by Proposition VIII.3.1 (the Riesz-Thorin interpolation
theorem), that
ST>: L\M) -> L2v
is bounded, which implies [with (VIII.4.4)]
SV(-Am)-1'2 : L\M) -
is bounded. Therefore, given <f>: Q -*¦ [0, +oo) then [by E:ii) of §VI.5.2 and
(P5:ii)of§VI.5.3]
v-2) < const.\\SVS4>h*K»-2)
= const, llgrad S4>\h
< const. ||
which is the discrete Nirenberg-Sobolev inequality on G for nonnegative func-
functions. For arbitrary functions, one has
II XWI Ib <
and now can easily obtain the result for general <p.
By Theorem VIII.3.2 (applied to graphs) and Theorems VIII.4.1 and VTII.4.3,
we obtain the equivalence of the large time upper bounds on the heat semigroups
of M and G when v > 2.
Now assume 1 < v < 2, amd let Mi denote the Cartesian product of M with
R2. Then the upper bounds for the heat kernel and the Coulhon criteria are
to be considered for v, = v + 2, for which the theorem is valid. For (x, y) €
M x R2 := M\ (with obvious notations) we have
p(x, x, t) = const.r2/2pi((jc, y), (x, y), t)
248 Large Time Heat Diffusion
and for (?, n) e G x Z2 we also have
p(?, ?, r) ~ consU2/2Pl((?, 17), (?, 17),») as t1 +00.
So
P{x,x,t)<rv'2
One can now use the above argument for vj to obtain the result for v.
Finally, the estimate (VIII.5.3) remains valid under compact perturbation
of a manifold of bounded geometry since any discretization of M remains a
discretization under compact perturbation. ¦
Theorem VIIL53 Let M satisfy 3V(M) > 0 for some v > 1. Then (VIII.2.2)
is valid for all t > 0.
Proof Let v > 2. By Theorems VI. 1.1 and VI. 1.2, the hypothesis implies the
Nash-Sobolev inequality (VIII.2.1), which implies, by Theorem vm.2.1, the
upper bound (VIII.2.2) for all t > 0.
For v 6A,2), one argues as in the similar case of the above theorem. ¦
Corollary VIIL5.1 For the 2-dimensional jungle gym in R3 we have
WPth^co <const.r3/2 Vr>0.
For the 3-dimensional Heisenberg group with left-invariant Riemannian metric,
we have
I|/J,lli-O0<const.r4/2 Vr>0.
Proof Indeed, ZI3 is positive for the 2-dimensional jungle gym in R3, since one
has a simultaneous discretization of R3 and the jungle gym. Also, 34 is positive
for the 3-dimensional Heisenberg group (see Pansu A982)). ¦
Theorem VIII.5.4 If M is Riemannian complete with bounded geometry,
and 3ViP(M) > Ofor some v > 1 and p > 0, then we have the upper bound
(VIII.5.3).
In particular, for every complete Riemannian manifold with bounded geom-
geometry we have
(VIII.5.5) ||/J,lli^0O = O(r1/2), t
VIII.6 Epilogue: The Faber-Krahn Method 249
Proof First assume that v > 2. Then, by Theorem V.3.1, for any discretization
G of M we have IV(G) > 0, which implies (VIII.5.4) by the discrete version of
Theorem VIII.3.2. But this then implies (VIII.5.3).
If v < 2, then consider M\ = M x R2. This implies %+2.p(M\) > 0 by
Proposition V.3.6, which implies Iv+2(Gi) > 0 for the discretization Gi =
G x Z2 of Mx (where G is a discretization of M), which implies (VIII.5.4),
which implies (VIII.5.3) for A/,. But this then implies (VIII.5.3) for M. ¦
VIII.6 Epilogue: The Faber-Krahn Method
Recall (§VI.3) that, given a positive increasing function g(v), v > 0, we say that
a domain 12 in a Riemannian manifold M satisfies a geometric g-isoperimetric
inequality if
ACD) > g(V(D))
for all D CC 12.
Also, given a positive decreasing function A(v), v > 0, we say that a do-
domain 12 in a Riemannian manifold M satisfies an eigenvalue A-isoperimetric
inequality if
k(D) > A(V(D))
(where X denotes the lowest Dirichlet eigenvalue) for all D CC 12.
Proposition VI.3.2 stated that if 12 satisfies a geometric g-isoperimetric in-
inequality, with g(v)/v a decreasing function of v, then 12 satisfies an eigenvalue
A-isoperimetric inequality with
Definition Given a positive decreasing function A(v) on [0, +00), define the
function €(f) by
/«(') dv
vA(v)
So we must assume that v >-> {v A(v)} is integrable near v = 0. Equivalently,
?@ is defined as the solution to the initial value problem
€' = ?A(C), C@) = 0.
Lemma VIII.6.I Suppose ?2? satisfies the eigenvalue A-isoperimetric inequal-
inequality, u e Cf°°A2)( u > 0. Then Jor any 8 e @,1) we have
||grad«|||22 ^ n CXA /2||«||,2>
250 Large Time Heat Diffusion
Proof For any z > 0 we have
/ u2 -2zu+z2 = I (u-zJ
Ja Ja
-L+L
< f (u-zJ+ f z2
<f (u-zJ+fz2,
Ju>r Ja
which implies
which implies
' -2t\\u\U= f u2-2ru< [ (u-zJ,
Ja Ju>z
|grad«|2 > I |grad«|2
>X({u>z])f (u-zJ
> A(V({u > z})) f (u-zJ.
Now
which impbes
V({
U> Z})< - I U < - I U,
t Ju>x * Ja
- rJ > A(Rm|i/t) {||<f||22 -
Pickr = ^||«||22/2||M||i,andtheclaimfollows. ¦
Theorem VIII.6.1 If M satisfies the eigenvalue A-isoperimetric inequality,
then
const.
(VIII.6.2)
for all t >0.
fl 1-00 <
C(const.r)
Proof Fix y e M, and define
u(x,t) = p(x,y,t);
VIII.6 Epilogue: The Faber-Krahn Method
then fM u(x, t)dV(x) < 1. Define
3@= / u2(x,t)dV(x).
Ju
Then
3'(O = -2||grad«||22<-2(l-
by the previous lemma. Therefore,
" } da
<jAB/8o)
which impbes, letting t0 I 0,
da
<-2A - 8)(t - t0).
f
Jm
aAB/Sa)
Now substitute v = 2/Sa; then
> 2A - S)t.
r
which implies
which is the theorem.
'o vA(v)
3@ <
> 2A - S)t,
S<SB(l - S)t)'
251
Example VIII.6.1 (Example VI.3.1 continued.) Let M satisfy a geometric g-
isoperimetric inequality, with g(v) given by
where avol~u" = ^vo1^. Then Theorem VI.3.2 impbes that M satisfies a
eigenvalue A-isoperimetric inequality, where
v~2/\ v < vo,
V~2/v, V > Vo,
Therefore, one has the existence of to > 0 such that
't*<2, t>to,
252 Large Time Heat Diffusion
which implies, by Theorem VIII.6.1, that
f,-/l/2 t < tn
that is, we have an alternate proof of Theorem VIII.5.4 above.
Example VIII.6.2 (Example VI.3.2 continued.) Let M satisfy a geometric g-
isoperimetric inequality, with g(v) given by
v > v0>
where avo1'" = 0. Proposition VI.3.2 implies that M satisfies a eigenvalue
A-isoperimetric inequality, where
v<v0,
7] = 02/4, V > V0,
Therefore, one has the existence oft0>0 such that
or',"/', ,<*,
which implies, by Theorem VIII.6.1, that
which corresponds qualitatively to hyperbolic space [note that 17 is not neces-
necessarily k(M) — which is the sharp result, by Proposition VIII. 1.2].
Definition We say that a function /: @, ex?) -> @, 00) has at most polynomial
decay if there exists a > 0 such that for all / > 0,0 e [1, 2] we have
fifit) > af(t).
An example would be a function / satisfying f'(t)/f(t) > -N/t for all t.
Theorem VIII.6.2 Given M, consider the functions A(v) and C(r) related by
(VIII.6.1), and assume that ?'@/ ?(t)hasat most polynomial decay. If we are
also given that
for all t > 0, then
> const.A(V(n)/*)
VIII.7 Bibliographic Notes
253
for all k = 1, 2,..., where A.*(ft) denotes the k th Dirichlet eigenvalue ofth*
domain ft.
Proof Fix ft. From the Sturm-Liouville eigenvalue-eigenfiinction expansion
we have
where q is the Dirichlet heat kernel of ft, and {0i, fa,...} is a complete or.
thonormal basis of L2(ft) consisting of eigenfunctions of - A«ur with the eigen-
eigenvalue of 4>j equal to kj. This implies
*«-**'<
-k<'= [ q(x,x,t)dV(x)< f p(x,x,t)dV(x)<V(n)/<?(t),
,=, Jo Jo
which implies
tkk > In
for allt > 0. Pick t such that ?(t) = V(ft)/Jt, and pick t = 2t. Then
1 f rf 1
= - { — In <S(t)\
2 I at J,
forsome^ e @, 1)
f+e
2 <?(t)
which implies the theorem.
VIII.7 Bibliographic Notes
§VIII.l Proposition VIII. 1.1 is from Cheeger, Gromov. and Taylor A982); also see
Chavel A984, §VIII.4). Theorem VIII. 1.2 was first proved in Chavel and Karp A991),
and Corollary VIII. 1.2 was communicated privately by P. Li. (See also Li 1986a.)
Example VIII. 1.1 is from Varopoulos A989).
The arguments we use in subsequent sections all revolve around semigroup
theory, in one way or another, namely, the isoperimetric inequalities lead to Sobolev
254
Large Time Heat Diffusion
inequalities, which give upper bounds on \\P,\\ /.<_>/,*, for good choices of I and k.
The arguments can also yield off-diagonal corrections - see Davies A987, 1989),
Fabes and Stroock A986), and Carlen, Kusuoka, and Stroock A987). Davies's argu-
arguments A987,1989) emphasize log Sobolev inequalities, instead of the Sobolev inequal-
inequalities of the type considered here.
A different method, using parabolic Harnack principles for Riemannian manifolds,
also gives strong results, including lower bounds on the heat kernel. The early funda-
fundamental paper is Li and Yau A986b). In fact. Proposition VIII. 1.3 is from that paper, but
our use of the result gave no hint of its ultimate power. More recent fundamental papers
in parabolic Harnack inequalities are Grig or'yan A991) and Saloff-Coste A992), as
well as the very recent Yau A994,1995) and Bakry and Qian A999). For arguments not
relying on global uniformity of Harnack inequalities, see Davies A997).
Still another method for producing on-diagonal upper bounds is the use of the isoperi-
metric function of a manifold. It has been used to date on compact manifolds (see § V.4);
one can find a heat kernel comparison theorem, based on comparison of isoperimet-
ric functions, in Beiard and Gallot A983). See also the discussion in Berard A986,
Chapter V). The discussion there includes a Schwarz symmetrization argument for the
heat kernel, in the spirit of the original Faber-Krahn argument. See the original version
of this argument in Bandle A980, Chapter IV). Finally, see an abstract version of the
Schwarz symmetrization argument for the heat kernel, based on Kato's inequality, in
Besson's appendix to Berard A986).
§VIIL2 Theorem VIII.2.1 is from Nash A958), and Theorem VIII.2.2 from Carlen,
Kusuoka, and Stroock A987).
§Vm_3 Proposition VIII.3.1, the Riesz-Thorin interpolation theorem, can be found
in Reed and Simon A980, Vol. I); Proposition VIII.3.2, the maximal theorem, in Stein
A970). Theorem VIII.3.2 is from Varopoulos A986).
§VUI.4 Theorem Vm.4.2 is fromCoulhon A990).
§VIIL5 Lemma VIII.5.1 is from Dodziuk A984), and Theorem VHI.5.2 from
CoulhonA992).
Theorem VIII.5.4 was first proved in Chavel and Feldman A991), although we
preferred here to give the proof of Coulhon A992). The estimate (VIII.5.5) gives the
best rate of decay possible, for such generality. The first such result was proved by
Varopoulos, in Varopoulos A984), with exponent — j + € for any e > 0. Our result
confirms Varopoulos's conjecture, there, that one can sharpen the result to e = 0.
§VIII.6 This section is from Grigor'yan A994c). See also Grigor'yan's article in
the 1998 Edinburgh Lectures (Davies and Safarov, 1999). The methods of Grigor'yan
have been developed to give very strong results on off-diagonal corrections - strictly as
consequences of on-diagonal upper bounds alone (see Grigor'yan, 1994a).
All of our results on upper bounds were unobtainable as consequences of lower bounds
on volume growth alone (recall Example VIII. 1.1). More recently. Barlow, Coulhon, and
Grigor'yan B000) have shown that merely postulating V(x;r) > const.A* as r f +00
only implies a rate of decay given by p < /-*/<*+" as t f +00. Furthermore, the result
is sharp!
Bibliography
C. Adams & F. Morgan A999). Isoperimetric curves on hyperbolic surfaces. Proc.
Amer.Math. Soc. 129, 1347-1356.
R.A. ADAMS A975). Sobolev Spaces. New York: Academic Press.
A.D. ALEXANDROV A962). A characteristic property of spheres. Ann. Math. Pura
AppL 58,303-315.
F. ALMCREN A986). Optimal isoperimetric inequalities. Indiana Univ. Math. J. 35,
451-547.
F. ALMCREN & E.H. Lieb A989). Continuity and discontinuity of the spherically
decreasing rearrangement. J. Amer. Math. Soc. 2,683-773.
T. AREDE A985). Manifolds for which the heat kernel is given interms of geodesic
lengths. Lett. Math. Phys. 9,121-131.
T. AUBIN A982). Nonlinear Analysis on Manifolds. Monge-Ampire Equations.
New York: Springer-Veriag.
R. AZENCOTT A974). Behaviour of diffusion semigroups at infinity. Bull. Soc. Math.
France 102,193-240.
A. Baernstein A995). A unified approach to symmetrization. Symp. Mat. 35,
47-91.
D. Bakry, T. Coulhon, M. Ledoux, & L. Saloff-Coste A995). Sobolev
inequalities in disguise. Indiana Univ. Math. J. 44, 1033-1074.
D. Bakry & Z. Qian A999). Harnack inequalities on a manifold with positive or
negative Ricci curvature. Rev. Mat. Iberoamer. 15,143-179.
C. BANDLE A980). Isoperimetric Inequalities and Applications. Boston: Pitman.
M. Barlow, T. Coulhon, & A.A. Grigor'yan B000). Manifolds and graphs with
slow heat kernel decay. Preprint.
N. Benabdallah A973). Noyau de diffusion sur les espaces homogenes compacts.
Bull. Soc. Math. France 101,265-283.
I. Benjamimi & J. CaO A996). A new isoperimetric theorem for surfaces of variable
curvature. Duke Math. J. 85, 359-396.
I. Benjamini, I. Chavel, & E.A. Feldman A996). Heat kernel lower bounds on
Riemannian manifolds using the old ideas of Nash. Proc. London Math. Soc. 72,
215-240.
PH. Berard A986). Spectral Geometry: Direct and Inverse Problems, Lecture Notes
Math. 1207. Berlin: Springer-Veriag.
P.H. Berard & S. Gallot A983). Ine'galite's isope'rime'trique pour 1'equation de la
chaleur et application a 1'estimation de quelques invariants. Siminaire
Goulaouic-Meyer-Schwartz XV A983-1984).
M. BERGER A987). Geometry. Berlin: Springer-Veriag. 2 volumes.
W. Blaschke A956). Kreis und Kugel. Berlin: de Gruyter, 2nd edn.
255
256
Bibliography
R. Brooks A981). The fundamental group and the spectrum of the Laplacian.
Comment. Mat. Helv. 56, 581-598.
Yu.D. BURAGO & V.A. ZALGALLER A980). Geometric Inequalities. Berlin:
Springer-Verlag, 1988. Original Russian edition: Geometricheskie neravenstva,
Leningrad.
A. BURCHARD A997). Steiner symmetrization is continuous in W1- p. Geom. & Fcnl.
Anal. 7,823-860.
P. Buser A982). A note on the isopcrimetric constant. Ann. Sci. ?c. Norm. Sup., Paris
15,213-230.
C. CARATHEODORY & E. STUDY A909). Zwei Beweise des Satzes dass der Kreis
unter alle Figuren gleichen Umgangs den grOssten Inhalt hat. Math. Ann. 68,
133-144.
T. CARLEMAN A921). Zur theorie der Minimalflachen. Math. Z 9,154-160.
E.A. CARLEN, S. Kusuoka, & D.W. STROOCK A987). Upper bounds for symmetric
Markov transition densities. Ann. Inst. H. Poincari Prob. Stat. 23,245-287.
G. CARRON A996). In6galites isopenmetriques de Faber-Krahn et consequences. In
Actes de la table ronde de giomitrie dufffrentielle en I 'honneur de Marcel
Berber, Collection SMF S6 minaires et Congres 1,203-232.
I. Chavel A978). On A. Hurwitz' method in isopcrimetric inequalities. Proc. Amer.
Math. Soc. 71,275-279.
I. CHAVEL A984). Eigenvalues in Riemannian Geometry. New York: Academic Press.
I. Chavel A994). Riemannian Geometry: a modem introduction. Cambridge:
Cambridge Univ. Press.
I. Chavel & E.A. Feldman A991). Modified isoperimetric constants, and large time
heat diffusion in Riemannian manifolds. Duke Math. J. 64,473-499.
I. Chavel & L. Karp A991). Large time behavior of the heat kernel: the parabolic
A. -potential alternative. Comment. Math. Helv. 66,541-556.
J. CHEEGER A970). A lower bound for the smallest eigenvalue of the Laplacian. In
Problems in Analysis, R. Gunning ed., 195-199. Princeton Univ. Press.
J. CHEEGER, M. GROMOV, & M. Taylor A982). Finite propagation speed, kernel
estimates for functions of the Laplace operator, and the geometry of complete
Riemannian manifolds. J. Diff. Geom. 17,15-54.
S.Y. Cheng & P. Li A981). Heat kernel estimates and lower bounds of eigenvalues.
Comment. Mat. Helv. 56, 327-338.
K.S. Chou & X.P. Zhu B001). 77k Curve Shortening Problem. Chapman & Hall. To
appear.
T. COULHON A990). Dimension a l'infini d'un semigroup analytique. Bull. Soc. Math.
France 114,485-500.
T. COULHON A992). Noyau de chaleur et discretisation d'une varied riemanniene.
Israel J. Math. 80,289-300.
T. COULHON & A.A. Grigor'yan A997). On-diagonal lower bounds for heat kernels
on non-compact manifolds and Markov chains. Duke Math. J. 89,133—199.
T. COULHON & M. LEDOUX A994). Isoplrimftrie, decroisaance du noyau de la chaleur
et transformations de Riesz: un contra-example. Ark. Math. 32,63-77.
T. COULHON & L. Salopf-Coste A993). Isopenmettie pour les groupes et les
vari&es. Rev. Mat. Iberoamer. 9, 293-314.
T. COULHON & L. SalOFF-Coste A995). Varietes riemanniennes isoperimetriques a la
l'infini. Rev. Mat. Iberoamer. 3,687-726.
R. COURANT & H. ROBBINS A941). What« Mathematics? Oxford: Oxford Univ.
Press.
C.B. CrOKE A980). Some isoperimetric inequalities and eigenvalue estimates. Ann.
Sci. tc. Norm. Sup. Paris 13, 419-435.
Bibliography
257
E.B. Davies A980). One-Parameter Semigroups. London: Academic Press
E.B. Davies A987). Explicit constants for Gaussian upper bounds on heat kernels
Amer. J. Math. 109,319-334.
E.B. Davies A989). Heat Kernels and Spectral Theory. Cambridge: Cambridge Univ.
Press.
E.B. Davies A992). Heat kernel bounds, conservation of probability and the Feller
property. J. Analyse Math. 58,99-119.
E.B. Davies A995). Spectral Theory and Differential Operators. Cambridge-
Cambridge Univ. Press.
E.B. Davies A997). Non-gaussian aspects of heat kernels behaviour. J. London Math.
Soc. 55,105-125.
E.B. Davies & N. Mandouvalos A987). Heat kernel bounds on manifolds with
cusps. J. Fcnl. Anal 75, 311-322.
E.B. Davies & Y. Safarov, eds. A999). Spectral Theory and Geometry. Cambridge-
Cambridge Univ. Press.
U. DiERKES, S. HILDEBRANDT, A. KiJSTER, & O. Wohlrab A992). Minimal Surfaces.
Berlin: Springer-Verlag.
J. DODZIUK A983). Maximum principle for parabolic inequalities and heat on open
manifolds. Indiana Univ. Math. J. 32,703-716.
J. DODZIUK A984). Difference equations, isoperimetric inequality, and transience of
certain random walks. Trans. Amer. Math. Soc. 284, 787-794.
C. Faber A923). Beweiss, dass unter alien homogenen Membrane von gleicher
Flachc und gleicher Spannung die kreisfftrmige die tiefsten Grundton gibt.
Sitzungber. BayerAkad. Wiss., Matk-Phys., Munich, 169-172.
E.B. FABES & D.W. STROOCK A986). A new proof of Moser's parabolic inequality via
the old ideas of Nash. Arch. Rat. Meek Anal. 96, 327-338.
H. FEDERER A969). Geometric Measure Theory. New York: Springer-Verlag
H. FEDERER & W.H. FLEMING A960). Normal integral currents. Ann. Math. 72,
H.D. Fegan A976). The heat equation on a compact Lie group. Trans. Amer. Math.
Soc. 246,339-357.
H.D. Fegan A983). The fundamental solution of the heat equation on a compact Lie
group. J. Diff. Geom. 18,659-668.
T. FiGffiL, J. Undenstrauss, & V.D. Milman A977). The dimension of almost
spherical sections of convex bodies. Ada Math. 139, 53-94.
H.R. FISCHER, JJ. Jungster, & F.L. WILLIAMS A984). The heat kernel on the
2-sphere. Adv. in Math. 54, 226-232.
M.P. GAPFNEY A954). A special Stokes' theorem for complete Riemannian manifolds.
Ann. Math. 60, 140-145.
M.P. Gaffney A959). The conservation property of the heat equation on complete
Riemannian manifolds. Comm. PureAppl. Math. 12,1-11.
M. Gage A984). Curve shortening makes convex curves circular. Invent. Math. 76,
357-364.
M. Gage A991). References for geometric evolution equations. Dept. of Math Univ
of Rochester.
D. GlLBARG & N.S. TRUDINGER A977). Elliptic Partial Differential Equations of
Second Order. Berlin: Springer-Verlag.
E. Giusn A984). Minimal Surfaces and Functions of Bounded Variation Boston-
Birkh&user.
A.A. GRIGOR'YAN A985). Isoperimetric inequalities for Riemannian products
(in Russian). Mat. Zametki 38. Eng. Transl. Math. Notes 38, 849-854 MR:
87g53O62.
258
Bibliography
A.A. GRIGOR'YAN A986). On stochastically complete manifolds. Soviet Math. DokL
290. AMS TransL 34 A987), 310-313.
A.A. GRIGOR'YAN A991). The heat equation on noncompact Riemannian manifolds.
Mat. Sb. 182. AMS TransL 72 A992), 47-77.
A.A. GRIGOR'YAN A994a). Gaussian upper bounds for the heat kernel and for its
derivatives on a Riemannian manifold. In Classical and Modem Potential Theory
and Applications, K. GowriSankaran et al., eds., 237-2S2. Kluwer Academic.
A.A. GRIGOR'YAN A994b). Heat kernel on a manifold with a local Harnack inequality.
Comm. Anal. Geom. 2,111-138.
A.A. GRIGOR'YAN A994c). Heat kernel upper bounds on a non-compact manifold.
Rev. Mat. Iberoamer. 10, 395-452.
A.A. GRIGOR'YAN A999). Analytic and geometric background of recurrence and
non-explosion of the Brownian motion on Riemannian manifolds. Bull. Amer.
Math. Soc. 36, 135-249.
A.A. GRIGOR'YAN & M. NOGUCM A998). The heat kernel on hyperbolic space.
J. London Math. Soc. 30,643-650.
M. GROMOV A986). Isoperimetric inequalities in Riemannian manifolds. In
Asymptotic Theory of Finite Dimensional Normed Spaces, Lecture Notes Math.
1200, Appendix I, 114-129. Berlin: Springer-Veriag.
H. Hadwiger A957). Vorlesungen uberlnhalt, Oberfi&che, und Isoperimetrie. Berlin:
Springer-Veriag.
R.Z. Hasminkd A960). Ergodic properties of recurrent diffusion processes and
stabilisation of the solution of the Cauchy problem for parabolic equations. Theor.
Prob. Anal. 5, 179-196.
E. HEBEY A999). Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities.
Inst. Math. Sci. New York: Courant.
M.W. HlRSCH A976). Differential Topology. New York: Springer-Veriag.
I. HOLOPAINEN A994). Rough isometries and p -harmonic functions with finite
Dirichlet integral. Rev. Math. Iberoamer. 217,459-477.
H. HOPF A950). Cber Flachen mit einer Relation zwischen den Hauptkrummungen.
Mam. Nachr. 4, A950-1), 232-249.
H. HOPF & W. RINOW A931). tiberden Begriff der vollstindigen differential-
geometrischen Flachen. Comment. Mat. Helv. 3, 209-225.
H. Howards, M. Hutchings, & F. Morgan A999). The isoperimetric problem on
surfaces. Amer. Math. Monthly 106,430-439.
A. HuRwrrz A901). Sur le probleme des isoperim&res. C. R. Acad. Sci. Paris 132,
401-403.
K. ICHIHARA A982). Curvature, geodesies, and the Brownian motion on a Riemannain
manifold ii. Nagoya Math. J. 87,115-125.
K. ICHIHARA A984). Explosion problems for symmetric diffusion processes. Proc.
Japan Acad. 60, 243-245.
K. Ichihara A986). Explosion problems for symmetric diffusion processes. Trans.
Amer. Math. Soc. 298, 515-536.
M. Kanai A985). Rough isometries, and combinatorial approximations of geometries
of noncompact Riemannian manifolds. J. Math. Soc. Japan 37, 391-413.
M. Kanai A986a). Analytic inequalities, and rough isometries between noncompact
Riemannian manifolds. In Curvature and Topology of Riemannian Manifolds,
K. Shohama, T. Sakai, & T. SunaDa, cds., Lecture Notes Math. 1201,
122-137. Berlin: Springer-Veriag.
M. Kanai A986b). Rough isometries and the parabolicity of Riemannian manifolds.
J. Math. Soc. Japan 38,227-238.
Bibliography
259
L. Karp A984). Noncompact manifolds with purely continuous spectrum. Mich.
Math. J. 31, 339-347.
L. KARP & P. Li. The heat equation on complete Riemannian manifolds. Preprint.
B. Kawohl A985). Rearrangements and Convexity of Level Sets in PDE, Lecture
Notes Math. 1150. Berlin: Springer-Veriag.
H. KNOTHE A957). Contributions to the theory of convex bodies. Mich. Math. J. 4,
39-52.
E. KRAHN A925). Uber cine von Rayleigh formulierte Minimaleigenschafte des
Kreises. Math. Ann. 94,97-100.
P. Li A980). On the Sobolev constant and the p -spectrum of a compact Riemannian
manifold. Ann. Sci. tc. Norm. Sup. Paris 13,419-435.
P. Li A986). Large time behavior of the heat equation on complete manifolds with
nonnegative Ricci curvature. Ann. Math. 124,1-21.
P. Li & S.T. Yau A986). On the parabolic kernel of the Schrodinger operator. Ada
Math. 156, 153-201.
E.H. LiEB & M. LOSS A996). Analysis. Providence, RI: American Math. Soc.
H. LlEBMANN A900). Ober die Verbiegung der glossenen Flachen positiver
Krummung. Math. Ann. 53,81-112.
V.G. Maz'ya A960). Classes of domains and embedding theorems for functional
spaces (in Russian). Dokl. Acad. Nauk. SSSR133,527-530. Engl. transl., Soviet
Math. Dokl. 1 A961), 882-885.
J. MlLNOR A968). A note on curvature and the fundamental group. J. Dig. Geom. 2,
1-7.
F. MORGAN A988). Geometric Measure Theory: A Beginner's Guide. Boston:
Academic Press.
J. MOSER A964). A Harnack inequality for parabolic differential equations. Comm.
PureAppl. Math. 17, 101-134.
J. MOSSINO A984). Inigalitis isopirimitriques et application en physique. Paris:
Herman.
R. NaRASIMHAN A968). Analysis on Real and Complex Manifolds. Amsterdam:
North Holland.
J. Nash A958). Continuity of solutions of parabolic and elliptic equations. Amer.
J.Math. 80, 931-954.
M.N. NDUMU A986). An elementary formula for the Dirichlet heat kernel on
Riemannian manifolds. In From Local Times to Global Geometry, Control and
Physics, K.D. ElwORTHY, ed., n -Pitman Res. Notes Math. 150,320-328. Essex:
Longman Scientific & Technical.
L. Nirenberg A959). On elliptic partial differential equations. Ann. Scuola Norm.
Sup. Pisa 13,115-162.
J. OPREA A997). Differential Geometry and its Applications. Upper Saddle River, NJ:
Prentice Hall.
Y. Oshima A992). On conservativeness and recurrence criteria of Markov processes.
Preprint. Potential Analysis 1, 115-131.
R. OssERMAN A978). The isoperimetric inequality. Bull. Amer. Math. Soc. 84,
1182-1238.
R. OSSERMAN A979). Bonnesen-style inequalities. Amer. Math. Monthly 86, 1-29.
M. Pang A988). L' properties of two classes of singular second order elliptic
operators. J. London Math. Soc. 38,525-543.
M. Pang A996). L' and L2 spectral properties of a class of singular second order
elliptic operators with measurable coefficients on R". J. Diff. Eq. 129,
1-17.
260
Bibliography
P. PanSU A982). Une inegalit? isoperimetrique sur le groupc de Heisenberg.
C. R. AceuL Sci. Paris 295,127-130.
L.E. PAYNE A967). Isopcrimetric inequalities and their applications. SIAMRev. 9,
453-488.
G. P6lya & G. SzbgO A951). Isoperimetric Inequalities in Mathematical Physics,
Ann. Math. Studies 27. Princeton, NJ: Princeton Univ. Press.
M.H. Protter & H.F. Weinberger A984). Maximum Principles in Differential
Equations. New York: Springer-Verlag, 2nd edn.
(Lord) J.W.S. RAYLEIOH A877). The Theory of Sound. New York: Macmillan.
Reprinted, New York: Dover A945).
M. REED & B. SIMON A975). Functional Analysis (Methods of Mathematical Physics,
Vol. II). New York: Academic Press.
M. REED & B. SIMON A980). Functional Analysis (Methods of Mathematical Physics,
Vol. I). New York: Academic Press, 2nd edn.
R.C. REILLY A977). Applications of the Hessian operator in a Riemannian manifold.
Indiana Univ. Math. J. 26,459-472.
F. Rffisz & B. Sz. Nagy A955). Functional Analysis. New York: Frederick Ungar.
A. Ros A988). Compact surfaces with constant scalar curvature and a congruence
theorem. J. Diff Geom. 27,215-220.
W. RUDIN A966). Real and Complex Analysis. New York: McGraw-Hill.
L. SalOFF-Coste A992). A note on Poincani, Sobolev, and Hamack inequalities.
Duke Math. J. 65, International Mathematics Research Notices, 27-38.
E. SCHMIDT A948,1949). Der Brunn-Minkowskische Satz und sein Spiegel-theorem
sowie die isoperimetrische Eigenschaft der Kugel in dereuklidischen und
nichteuklidischen Geometrie I, II. Math. Nachr. 1, 81-157; 2, 171-244.
L.M. SIMON A984). Lectures on Geometric Measure Theory. Canberra, Australia:
Centre Math. Anal., Australian Nat. Univ.
E.M. Stein A970). Topics in Harmonic Analaysis, Ann. Math. Studies 63. Princeton,
NJ: Princeton Univ. Press.
J. STE1NER A838). Einfache Beweise der isoperimetrische Haupts&tze. J. Reine Angew.
Math. 18,281-296. Reprinted, Gesammelte Werke. Bronx, NY: Chelsea A971)
(reprint of 1881-1882 edn.), Vol. 0, 75-91.
J. STEINER A881). Uber Maximum und Minimum. In Gesammelte Werke. Bronx, NY:
Chelsea A971) (reprint of 1881-1882 edn.).
D. Sullivan A987). Related aspects of positivity in Riemannian geometry. J. Diff.
Geom. 25, 327-351.
M. Takeda A989). On a martingale method for symmetric diffusion processes and its
applications. Osaka Math. J. 26,605-623.
M. Takeda A991). On the conservativeness of the Brownian motion on Riemannian
manifolds. Bull. London Math. Soc. 23,86-88.
G. Talenti A993). The standard isoperimetric theorem. In Handbook of Convex
Geometry, Vol. A, P.M. Gruber & J.M. Wills, eds., 73-123. Amsterdam: North
Holland.
P. TOPPING A997). The optimal constant in Wente's L"° estimate. Comment. Mat.
Helv. 139,316-328.
P. Topping A998). Mean curvature flow and geometric inequalities. J. Reine Angew.
Math. 503,47-61.
P. Topping A999). The isoperimetric inequality on a surface. Manuscripta Math. 100,
23-33.
N.TH. VAROPOULOS A983). Potential theory and diffusion on Riemannian manifolds.
In Conf. on Harmonic Analysis in Honor of A. Zygmund, W. BECKNER et al., eds.
Wads worth.
Bibliography 261
N.TH. VAROPOULOS A984). Brownian motion and random walks on manifolds Ann
Inst. Fourier Grenoble 34,243-269.
N.Th. VAROPOULOS A985). Isoperimetric inequalities and Markov chains J Fail
Anal. 63,240-260. ' "
N.Th. VAROPOULOS A986). Hardy-Littlewood theory for semigroups. J. Fcnl. Anal.
66,406-431.
N.TH. VAROPOULOS A989). Small time Gaussian estimates of heat diffusion kernels
Part i: The semigroup technique. Bull. Soc. Math. France 113. 253-277.
S.T. Yau A975). Isoperimetric constants and the first eigenvalue of a compact
manifold. Ann. Sci. tc. Norm. Sup. Paris 8,487-507.
S.T. Yau A976). Some function-theoretic properties of complete Riemannian
manifolds, and their applications to geometry. Indiana Univ. Math. J. 25,
659-670. Also cf. Ibid. 31 A982), 307.
S.T. Yau A978). On the heat kernel of a complete Riemannian manifold. J. Math.
PuresAppL 57,191-201.
S.T. Yau A994). On the Hamack inequalities of partial differential equations. Comm.
Anal, and Geom. 2,431-450.
S.T. Yau A995). Harnack inequality for non-self-adjoint evolution equations. Math.
Res. Lett. 2, 387-399.
K. YOSIDA A978). Functional Analysis. Berlin: Springer-Verlag, 5th edn.
W.P. Ziemer A989). Weakly Differentiable Functions. New York: Springer-Verlag.
Author Index
Adams, C, 29
Adams. R.A.. 29. 224
Alexandrov,A.D.,51
Almgren,F..51,99
Arede, T., 224
Aubin.T, 184
Aubin, T., 224
Azencott, R., 224
Baemstein, A., 99
Bakry.D., 183,254
Bandle, C, 183. 254
Barlow, M., 254
Bendabdallah, A.. 224
Benjamini, I., 29, 233
Berard, PH., 184,254
Berger. M., 29,99
Besson, G., 254
Blaschke, W., 28
Brooks, R., 232
Burago, Y, 3.28,99
Burchard, A., 99
Buser.P., 155
Cao, J., 29
Caratheodory, C, 99
Carleman, X, 51
Carlen, E.A., 254
Carron. G.. 184
Chavel, I., 29,99,155, 183-185, 224, 233,
253,254
Cheeger.J., 183,253
Cheng, S.Y., 183
Coulhon.T. 155, 183, 184,233,
254
Courant, R., 28
Croke,C, 155
Davies, E.B., 224. 254
Dierkes, U., 28
DodziulcJ.. 184,224.254
Faber, C, 99
Fabes, E., 254
Federer. H., 29,51,99, 116.183
Fegan. H.D., 224
Feldman, E.A.. 184.233,254
Figiel, T. 29
Fischer, H.R., 224
Fleming. W.H., 51, 183
Gaffney, M.P., 224
Gage. M., 29
Gallot, S., 254
Gilbarg. D., 29,224
Giusti, E, 99. 100
Grigor'yan, A.A., 155. 156. 184,224.
233,254
Gromov, M., 29.51. 184, 253
Hadwiger. H., 28
Hasminkii, R.Z., 224
Hildebrandt, S.. 28
Hirsch, M.W., 29
Holopainen, I., 156
Hopf,H.,51.155
Howards. H.. 29
Hurwitz, A.. 29
Hutchings, M., 29
lchihara, K.. 224
Jungster, J J., 224
Kanai.M., 154, 156. 177, 184
Karp, L., 224,253
Kawohl, B., 99, 183
Knothe, H, 51
Krahn. E., 99
KUrster. A.. 28
Kusuoka. S., 254
Ledoux,M., 183
U. P., 183,222,224,253,254
263
264
Author Index
Ueb, E.H.. 29.99
Liebmann. H., 31
Lindenstrauss, J., 29
Loss. M.. 29.99
Mandouvalos, N., 224
Maz'ya.V.G.,51
Milman. V.D.. 29
Milnor.J., 143
Morgan, E, 29,99. 116
Moser, J., 183
Mossino, J.. 183
Nagy,B.Sz..221
Narasimhan, R., 29
Nash. J., 183,254
Ndumu, M.N., 224
Nirenbcrg, L., 183
Noguchi, M., 224
Oprea.J.,51
Oshima, Y., 224
Osserman. O.. 28,29
Osserman, R., 29
Pang, M.. 224
Pansu. P.. 248
Payne, L.E., 183
Polya.G.,99,183
Proner, M.H., 29,224
Qian. Z.. 254
Rayleigh. Lord. 99
Reed, M., 224,254
ReiUy.R.C.,51
Riesz, E, 221
Rinow, W.. 155
Robbins. H., 28
Ros, A., 51
Rudin, W., 29
Saloff-Coste, L., 155,183. 184.254
Schmidt, E. 29
Simon, B., 224,254
Simon, L., 99,116
Stein. E.M., 254
Steiner, J.. 99
Stroock, D.W., 254
Study. E., 99
Sullivan, D., 224
SzegO.G.,99,183
Takeda, M., 224
Talenti, G.. 28.99
Taylor, M.. 253
Topping. P.. 29
Trudinger, N.S., 29, 224
Varopoulos, N.Th., 156, 184,224,
253,254
Weinberger, H.E, 29,224
Williams, F.L., 224
Wohlrab, O.. 28
Yau, S.T, 224
Yau, ST., 131,224.254
Yosida, K.. 224
Zalgaller, V.A., 3.28.99
Ziemer. W.P., 29.99
Subject Index
i-cover, 102
f-thickening, 15.54
immeasurability, 101
o -algebra, 100
approximate identity, 229
arc length function, 4
area
of boundaries in graphs, 142
integral geometric, 53
of metric sphere in Riemannian manifold,
125
lower. 125
Minkowski, 58
surface, 2, 3, 17.25,31
boundaries in graphs, 142
area of. 142
boundary conditions, vanishing Dirichlet,
196
bounded geometry
for graphs, 140
for Riemannian manifolds, 136
Cheeger's constant, 127 <
in compact case, 162
modified. 130
circumdisk, 57
circumradius, 53
combinatorial
length of. 140
metric, 140
path. 140
complete, geodesically, 120
connection. 121
Levi-Civita, 121
constant
alternate Sobolev
in compact case. 163
Cheeger's, 127
in compact case, 162
modified. 130
isoperimetric
of compact Riemannian manifold. 162
of graphs. 144
modified, of Riemannian manifold,
130
of R\ 44,45
of Riemannian manifold, 127
Lipschitz.20
Sobolev
in compact case, 162
of graphs, 173
ofR\44.45
of Riemannian manifold, 131
convergence of sets in Z.1, 81
convex
function, 22
hull of. 28
linear combination, 27
set, 27
coordinates
Euclidean. 17
geodesic spherical. 125
Riemann normal, 123
countable additivity, 100
countably subadditive, 101
curvature
Gauss, 32
mean, 32.36,44
of path in R2, 5
Ricci, 122
sectional, 122
constant, 123
tensor, 121
cut locus, domain inside, of a point. 125
differential operator
elliptic, 19
uniformly, 19
Dirichlet energy integral, 195
discretization of Riemannian manifold, 147
covering radius of, 147
separation radius of, 147
265
266
Subject Index
Subject Index
267
distance
combinatorial, between points, 140
Hausdorff, between compact sets. 54
Riemannian, between points, 119
domain, 3
Lipschitz, 87
exponential map, 120
formula
Cauchy's, for area of boundaries of convex
domains, 26
co-area
for perimeter, 89
for smooth functions, 25
for smooth mappings, 25
Fourier transform, 203
Frenet formulae, 5
function
of bounded variation, 82
characteristic, 13
differential of. on graphs, 144, 170
discretization of, 178
gradient of, on Riemannian manifold, 157
indicator, 13
Laplacian of, on Riemannian manifold, 193
acting as L1 distribution, 198
Friedrichs extension of, 195
Lipschitz, 19
mean value, 162
polynomial decay, 252
smoothing of. 179
weak derivative of, 23
Z.2,195
functional
isoperimetric, 36
fundamental form
first, 31
second. 32
fundamental tone. 78
Gauss map, 32
geodesic, 119
completeness. 120
flow, 126
kiuematic density of, 127
Lkxiville's theorem, 127
spherical coordinates, 125
graph, 140
with bounded geometry, 140
Cayley, of group, 141
combinatorial path in, 140
distance between points, 140
Hausdorff
dimension, 105
distance between compact sets, 54
measure, 102
standard, 104
heat equation
homogeneous, 201
inhomogeneous. 201
uniqueness property. 212
heat flow, 214
heat kernel, 202
closed, 208
conservation of heat property of, 208
Dirichlet, 209
Feller property of, 208
minimal positive, 211
positive, 208
stochastic completeness of, 208
symmetric. 208
heat operator associated with the Laplaciai
201
hyperplane
separation by, 28
strict, 28
supporting, 28
incompressible flow, 39
inequality
arithmetic-geometric mean, 38,49
Bonnesen, 4
Brunn-Minkowski, 62
Buser's, 136
Crake's, 136
eigenvalue A-isoperimetric, 169
Faber-Krahn, 79
of Euclidean type, 166
geometric g-isoperimetric, 168
isodiametric, 61
isoperimetric, 2-4
for C1 surface area, 47,51
eigenvalue A-, 249
geometric g-. 249
for Minkowski area. 63
for Minkowski area in R", 77
for Minkowski length in R2.74
in model space, 4
for perimeter, 94
inR2.8,9
Wirtinger-s, 8. 29
injectivity radius of
point, 120
Riemannian manifold, 120
inradius, 130
isodiametric
inequality, 61
isometry
quasi-, of metric spaces, 140
quasi-, of Riemannian manifolds, 128
of Riemannian manifolds, 123
rough, of metric spaces, 142
isoperimetric
constant
of compact Riemannian manifold,
162
of graphs, 144
modified, of Riemannian manifold,
130
of R\ 44,45
of Riemannian manifold, 127
function, 254
functional. 1,11.36. 117
C* external of the. 31
uniqueness of C2 extremal of, 39
inequality
forC1 surface area. 47.51
eigenvalue A-, 249
geometric g-, 249
for Minkowski area. 63
for Minkowski area in R", 77
for Minkowski length in R2, 74
in model space, 4
for perimeter, 94
in R2.8,9
problem, 2
in model space, 4,29
solution to the C*,31
uniqueness of C2 solution to. 36
Laplacian on Riemannian manifold, 193
acting as L2 distribution. 198
Dirichlet, 196
Friedrichs extension of. 195
Lebesgue set, 96
length of
path in Riemannian manifold. 119
vector in Riemannian metric, 118
linear operator
adjoint of, 185
closable. 185
closed, 185
closure of. 185
extension of, 185
minimal, 185
resolvent of, 187
resolvent set of. 187
self-adjoint, 186
approximate eigenfuctions of, 189
essentially. 186
spectral family of, 187
semibounded from below, 186
Friedrichs extension of. 186
spectrum of, 187
discrete, 188
essential, 188
point, 188
symmetric, 186
nonnegative, 186
Lipschitz
constant, 20
domain. 87
function. 19
manifold
closed. 161
compact, 161
measure, 100
R* -valued, 15
absolutely continuous, 15
Radon, 16
total variation of, 15
counting, 142
Hausdorff, 102
5-, 102
standard, 104
standard J-, 104
inner regular, 16
kinematic, of geodesic flow, 127
locally finite. 16
outer, 101
Borel regular, 101
metric, 101
regular, 16, 101
Radon. 16
regular, 16
volume, on graphs, 142
metric
combinatorial, 140
Riemannian, 118
word, on group, 141
model space. 124
isoperimetric inequality in, 4
isoperimetric problem in. 4,29
mollifier, 17
natural basis of tangent spaces,
118
norm
on group
displacement. 141
word. 141
orthogonal projection, 187
perimeter. 88
geometric, 81
set with locally finite, 88
point, critical, 18
principle
Cavalieri. 14
Duhamel's, 207
strong maximum
elliptic. 19
parabolic. 207
product Riemannian structure, 118
268
Subject Index
quasi-isometry
of metric spaces, 140
of Riemannian manifolds, 128
Riemann normal coordinates, 123
Riemannian
distance between points, 119
manifold, 118
discretization of. 147
length of path in. 119
metric. 118
length of vector in, 118
rough isometry
of metric spaces, 142
semigroup, one-parameter, 190
contractive, 190
generator (infinitesmal), 191
domain of, 191
sesquilinear form, 190
nonnegative, 190
semibounded from below, 190
set
Cacciopoli, 88
t -separated, 146
partition of, IS
Sobolev constant
alternate, 180
in compact case. 162
of graphs. 173
ofR\44,45
of Riemannian manifold, 131
Sobolev spaces, 23
surface area, 2, 3, 17,25,31
symmetric decreasing rearrangement of
functions, 70
symmetrization
Schwarz, 69
Steiner, 59
tensor
curvature, 121
Ricci, 122
theorem
Alexandrov's, 42,51
Bishop's comparison, 126
Bishop-Gromov comparison,
126
Blaschke selection, 55
CaratModory's. 101
Coulhon extrapolation, 241
divergence
Riemannian, 32,193
2-dimensional, 9
Federer-Fleming, 45,51
in Riemannian manifolds, 131
Helly selection, 73
Lebesgue density, 17
Liouville's, 127
maximal, 237
Mercer's, 221
Mcyers-Serrin, 196.224
Rademacher, 20
Radon-Nikodym, 16
Riesz representation, 16
Ricsz-Thorin interpolation, 236
Sard. 18
spectral, 187
value
critical, 18
regular, 18
vanishes at infinity, function that, 69
vector field
admissible, 82
divergence of, on Riemannian manifold,
192
radial, 128
volume growth. 143