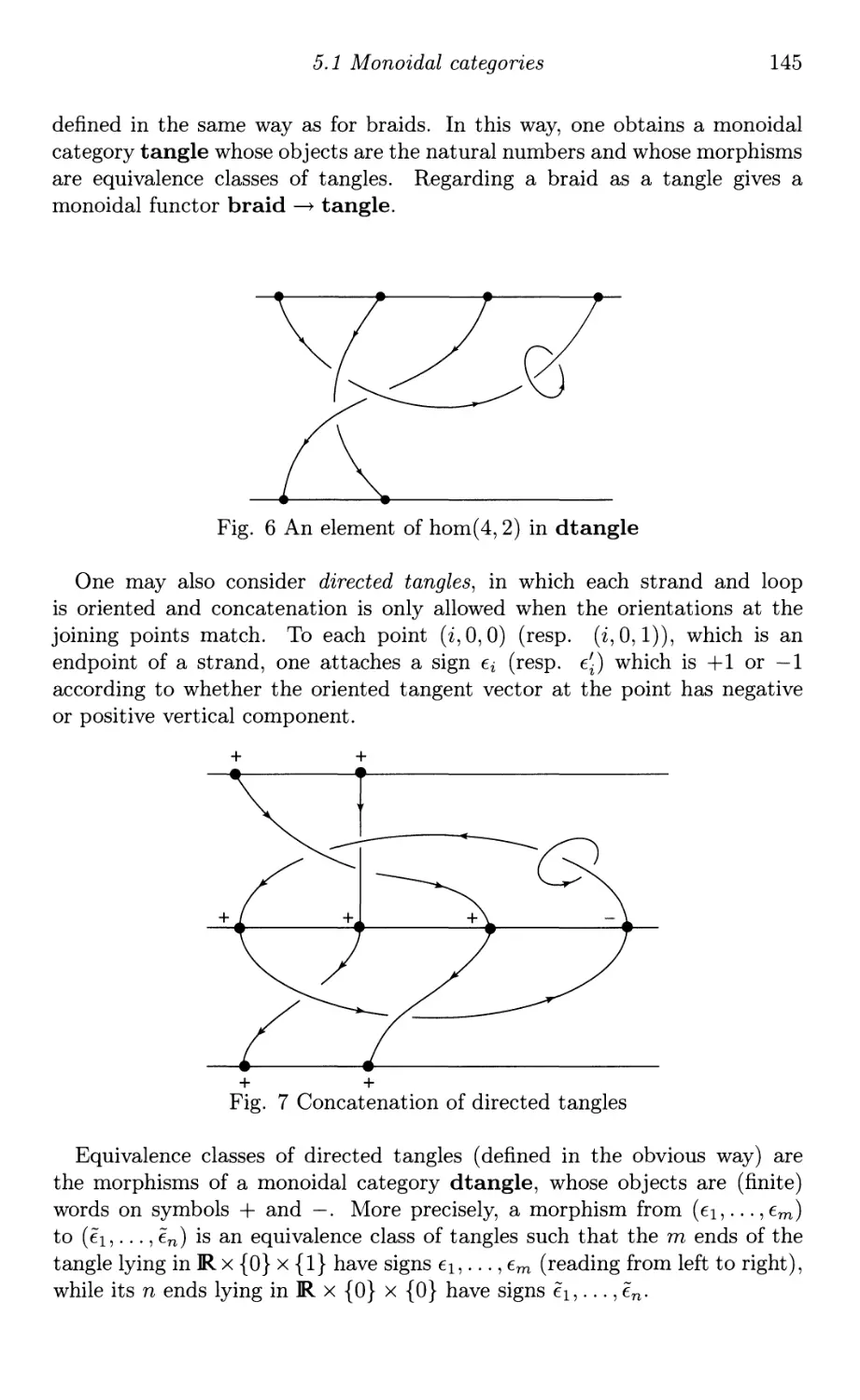
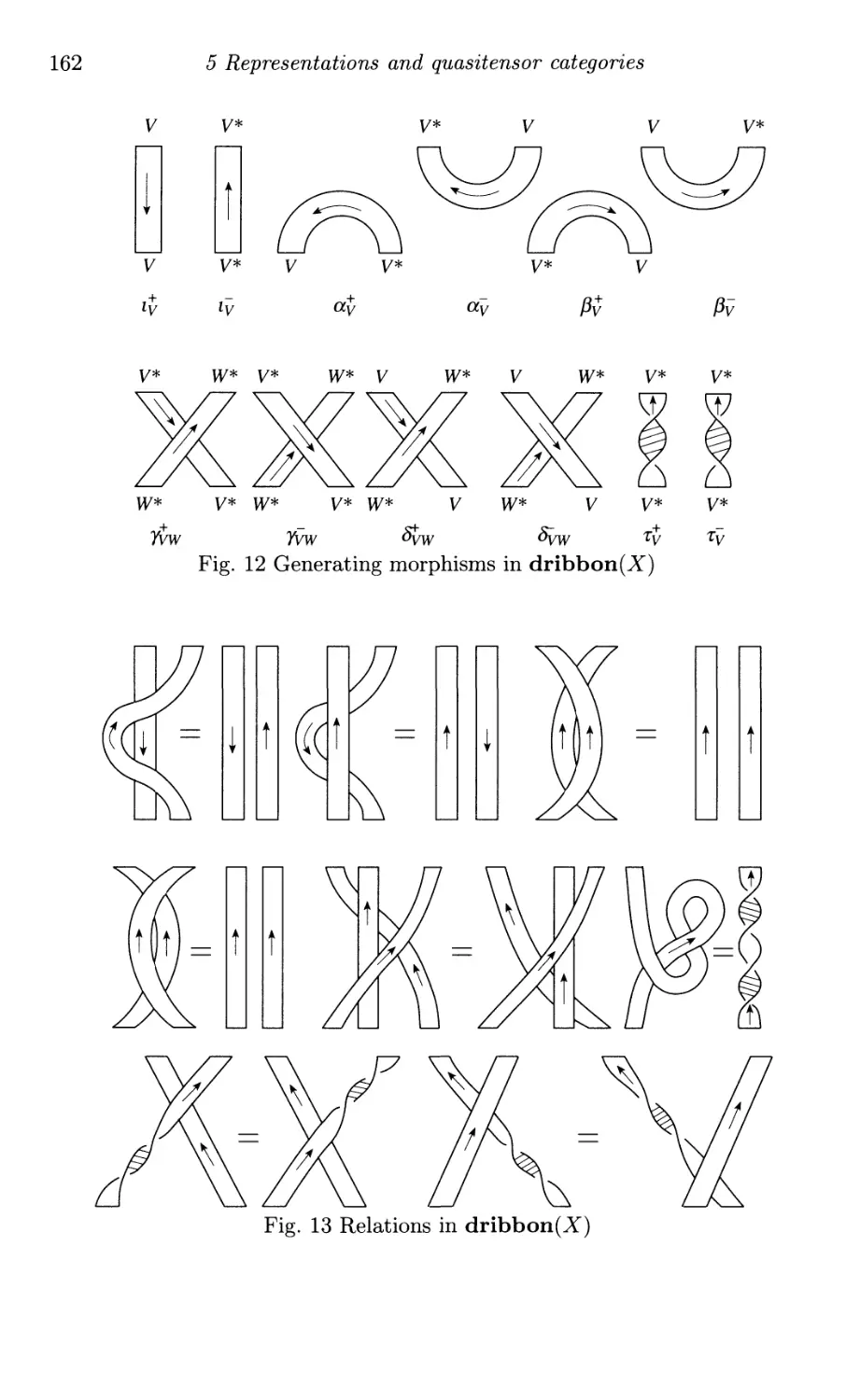
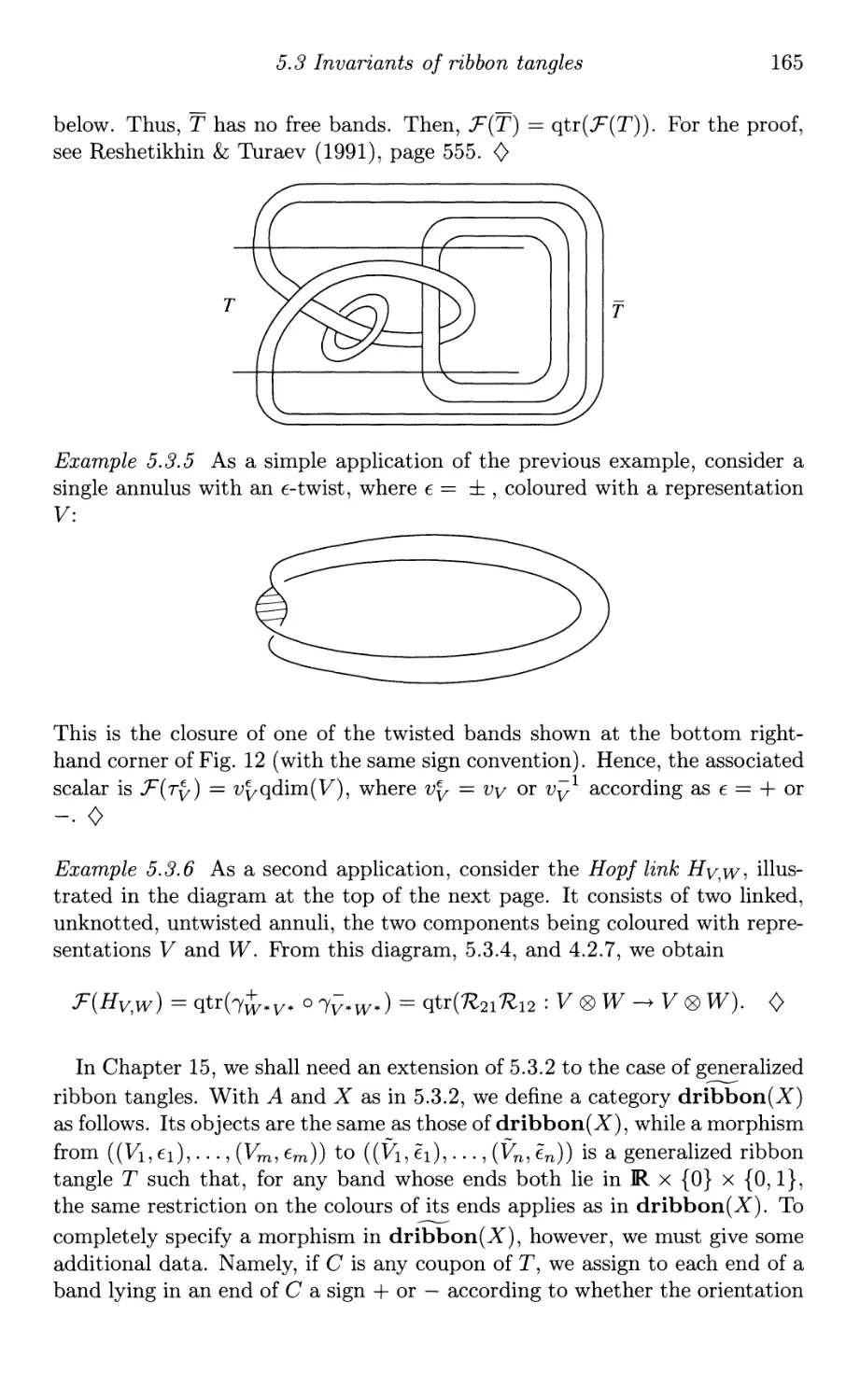
Текст
A GUIDE TO QUANTUM GROUPS
A GUIDE TO
QUANTUM GROUPS
Vyjayanthi Chari
University of California, Riverside
Andrew Pressley
King's College, London
Cambridge
UNIVERSITY PRESS
Published by the Press Syndicate of the University of Cambridge
The Pitt Building, Trumpington Street, Cambridge CB2 1RP
40 West 20th Street, New York, NY 10011-4211, USA
10 Stamford Road, Oakleigh, Melbourne 3166, Australia
© Cambridge University Press 1994
First published 1994
First paperback edition (with corrections) 1995
Printed in Great Britain at the University Press, Cambridge
Library of Congress cataloguing in publication data available
British Library cataloguing in publication data available
ISBN 0 521 43305 3 hardback
ISBN 0 521 55884 0 paperback
To our parents
Contents
Introduction 1
1 Poisson-Lie groups and Lie bialgebras 15
1.1 Poisson manifolds 16
A Definitions 16
B Punctorial properties 18
C Symplectic leaves 18
1.2 Poisson-Lie groups 21
A Definitions 21
B Poisson homogeneous spaces 22
1.3 Lie bialgebras 24
A The Lie bialgebra of a Poisson-Lie group 24
B Manin triples 26
C Examples 28
D Derivations 32
1.4 Duals and doubles 33
A Duals of Lie bialgebras and Poisson-Lie groups 33
B The classical double 34
C Compact Poisson-Lie groups 35
1.5 Dressing actions and symplectic leaves 36
A Poisson actions 36
B Dressing transformations and symplectic leaves 37
C Symplectic leaves in compact Poisson-Lie groups 39
D The twisted case 41
1.6 Deformation of Poisson structures and quantization 43
A Deformations of Poisson algebras 43
B Weyl quantization 44
C Quantization as deformation 46
Bibliographical notes 48
2 Coboundary Poisson-Lie groups and the
classical Yang-Baxter equation 50
2.1 Coboundary Lie bialgebras 50
viii Contents
A Definitions 50
B The classical Yang-Baxter equation 54
C Examples 55
D The classical double 58
2.2 Coboundary Poisson-Lie groups 59
A The Sklyanin bracket 60
B r-matrices and 2-cocycles 62
C The classical R-matrix 67
2.3 Classical integrable systems 68
A Complete integrability 68
B Lax pairs 69
C Integrable systems from r-matrices 71
D Toda systems 75
Bibliographical notes 77
3 Solutions of the classical Yang-Baxter
equation 79
3.1 Constant solutions of the CYBE 80
A The parameter space of non-skew solutions 80
B Description of the solutions 81
C Examples 82
D Skew solutions and quasi-Frobenius Lie algebras 84
3.2 Solutions of the CYBE with spectral parameters 87
A Classification of the solutions 87
B Elliptic solutions 90
C Trigonometric solutions 91
D Rational solutions 95
Bibliographical notes 98
4 Quasitriangular Hopf algebras 100
4.1 Hopf algebras 101
A Definitions 101
B Examples 105
C Representations of Hopf algebras 108
D Topological Hopf algebras and duality 111
E Integration on Hopf algebras 115
F Hopf *-algebras 117
4.2 Quasitriangular Hopf algebras 119
Contents ix
A Almost cocommutative Hopf algebras 119
B Quasitriangular Hopf algebras 123
C Ribbon Hopf algebras and quantum dimension 125
D The quantum double 127
E Twisting 129
F Sweedler's example 131
Bibliographical notes 133
5 Representations and quasitensor categories 135
5.1 Monoidal categories
A Abelian categories
B Monoidal categories
C Rigidity
D Examples
E Reconstruction theorems
5.2 Quasitensor categories
A Tensor categories
B Quasitensor categories
C Balancing
D Quasitensor categories and fusion rules
E Quasitensor categories in quantum field theory
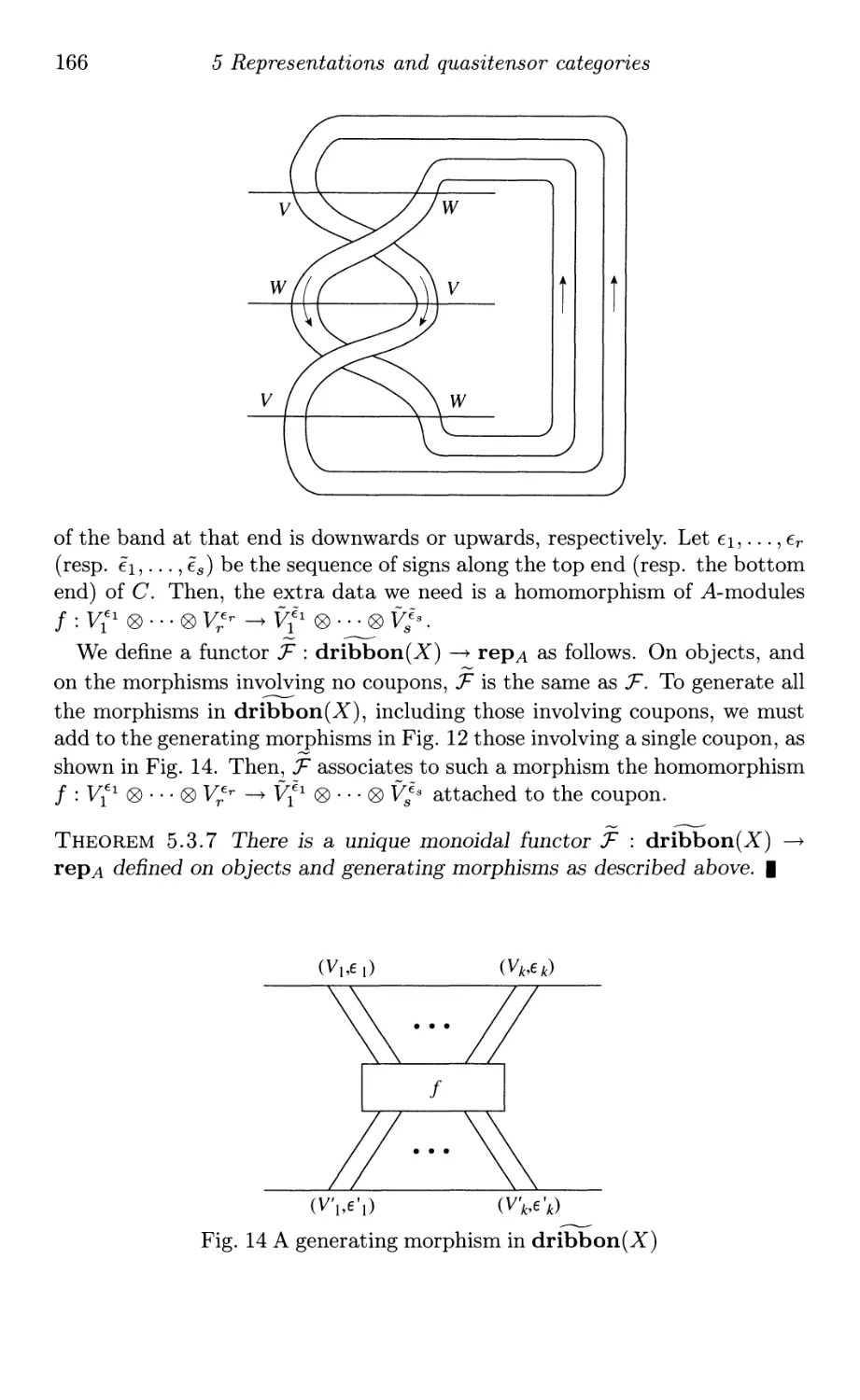
5.3 Invariants of ribbon tangles
A Isotopy invariants and monoidal functors
B Tangle invariants
C Central elements
136
136
138
139
140
147
149
149
152
154
154
157
161
161
166
168
Bibliographical notes 168
6 Quantization of Lie bialgebras 170
6.1 Deformations of Hopf algebras 171
A Definitions 171
B Cohomology theory 173
C Rigidity theorems 176
6.2 Quantization 177
A (Co-) Poisson Hopf algebras 177
B Quantization 179
C Existence of quantizations 182
6.3 Quantized universal enveloping algebras 187
A Cocommutative QUE algebras 187
B Quasitriangular QUE algebras 188
x Contents
C QUE duals and doubles 189
D The square of the antipode 190
6.4 The basic example 192
A Construction of the standard quantization 192
B Algebra structure 196
C PBW basis 199
D Quasitriangular structure 200
E Representations 203
F A non-standard quantization 206
6.5 Quantum Kac-Moody algebras 207
A The standard quantization 207
B The centre 212
C Multiparameter quantizations 212
Bibliographical notes 213
7 Quantized function algebras 215
7.1 The basic example 216
A Definition 216
B Abasisof ^(SX2(<C)) 220
C The R-matrix formulation 222
D Duality 223
E Representations 227
7.2 R-matrix quantization 228
A Prom R-matrices to bialgebras 228
B Prom bialgebras to Hopf algebras: the quantum determinant 231
C Solutions of the QYBE 233
7.3 Examples of quantized function algebras 234
A The general definition 234
B The quantum special linear group 235
C The quantum orthogonal and symplectic groups 236
D Multiparameter quantized function algebras 238
7.4 Differential calculus on quantum groups 240
A The de Rham complex of the quantum plane 240
B The de Rham complex of the quantum m x m matrices 242
C The de Rham complex of the quantum general linear group 244
D Invariant forms on quantum GLm 245
7.5 Integrable lattice models 246
A Vertex models 246
B Transfer matrices 248
Contents xi
C Integrability 249
D Examples 251
Bibliographical notes 253
8 Structure of QUE algebras:
the universal R-matrix 255
8.1 The braid group action 256
A The braid group 256
B Root vectors and the PBW basis 258
8.2 The quantum Weyl group 262
A The sl2 case 262
B The relation with the universal R-matrix 263
C The general case 265
8.3 The quasitriangular structure 266
A The quantum double construction 266
B The sl2 case 267
C The general case 271
D Multiplicative properties 274
E Uniqueness of the universal R-matrix 275
F The centre of Uh 275
G Matrix solutions of the quantum Yang-Baxter equation 276
Bibliographical notes 278
9 Specializations of QUE algebras 279
9.1 Rational forms 280
A The definition of Uq 280
B Some basic properties of Uq 282
C The Harish Chandra homomorphism and the centre of Uq 284
D A geometric realization 285
9.2 The non-restricted specialization 288
A The non-restricted integral form 289
B The centre 290
C The quantum coadjoint action 293
9.3 The restricted specialization 296
A The restricted integral form 297
B A remarkable finite-dimensional Hopf algebra 301
C A Probenius map in characteristic zero 304
D The quiver approach 307
xii Contents
9.4 Automorphisms and real forms 309
A Automorphisms 309
B Real forms 309
Bibliographical notes 311
10 Representations of QUE algebras:
the generic case 313
10.1 Classification of finite-dimensional representations 313
A Highest weight modules 313
B The determinant formula 319
C Specialization: the non-root of unity case 324
D R-matrices associated to representations of Uq 327
E Unitary representations 329
10.2 Quantum invariant theory 332
A Hecke and Birman-Murakami-Wenzl algebras 332
B Quantum Brauer-Frobenius-Schur duality 334
C Another realization of Hecke algebras 336
Bibliographical notes 337
11 Representations of QUE algebras:
the root of unity case 338
11.1 The non-restricted case
A Parametrization of the irreducible representations of Ue
B Some explicit constructions
C Intertwiners and the QYBE
11.2 The restricted case
A Highest weight representations
B A tensor product theorem
C Quasitensor structure
D Some conjectures
11.3 Tilting modules and the fusion tensor product
A Tilting modules
B Quantum dimensions
C Tensor products
D The categorical formulation
339
339
344
348
351
351
357
359
359
361
361
365
367
370
Bibliographical notes 372
Contents xiii
12 Infinite-dimensional quantum groups 374
12.1 Yangians and their representations 375
A Three realizations 375
B Basic properties 380
C Classification of the finite-dimensional representations 383
D Evaluation representations 386
E The sl2 case 388
12.2 Quantum affine algebras 392
A Another realization: quantum loop algebras 392
B Finite-dimensional representations of quantum loop algebras 394
C Evaluation representations 399
12.3 Frobenius-Schur duality for Yangians and
quantum affine algebras 403
A Affine Hecke algebras and their degenerations 403
B Representations of affine Hecke algebras 405
C Duality for Ue(sln+i(<E)) - revisited 408
D Quantum affine algebras and affine Hecke algebras 410
E Yangians and degenerate affine Hecke algebras 413
12.4 Yangians and infinite-dimensional classical groups 414
A Tame representations 415
B The relation with Yangians 416
12.5 Rational and trigonometric solutions of the QYBE 417
A Yangians and rational solutions 418
B Quantum affine algebras and trigonometric solutions 423
Bibliographical notes 426
13 Quantum harmonic analysis 428
13.1 Compact quantum groups and their representations 430
A Definitions 430
B Highest weight representations 433
C The sl2 case 435
D The general case: tensor products 437
E The twisted case and quantum tori 439
F Representations at roots of unity 442
13.2 Quantum homogeneous spaces 445
A Quantum G-spaces 445
B Quantum flag manifolds and Schubert varieties 447
C Quantum spheres 448
xiv Contents
13.3 Compact matrix quantum groups 451
A C* completions and compact matrix quantum groups 451
B The Haar integral on compact quantum groups 454
13.4 A non-compact quantum group 459
A The quantum euclidean group 459
B Representation theory 462
C Invariant integration on the quantum euclidean group 463
13.5 g-special functions 465
A Little g-Jacobi polynomials and quantum SU2 466
B Big g-Jacobi polynomials and quantum spheres 467
C g-Bessel functions and the quantum euclidean group 469
Bibliographical notes 473
14 Canonical bases 475
14.1 Crystal bases 476
A Gelfand-Tsetlin bases 476
B Crystal bases 478
C Globalization 480
D Crystal graphs and tensor products 481
14.2 Lusztig's canonical bases 486
A The algebraic construction 486
B The topological construction 488
C Some combinatorial formulas 490
Bibliographical notes 492
15 Quantum group invariants of knots
and 3-manifolds 494
15.1 Knots and 3-manifolds: a quick review 495
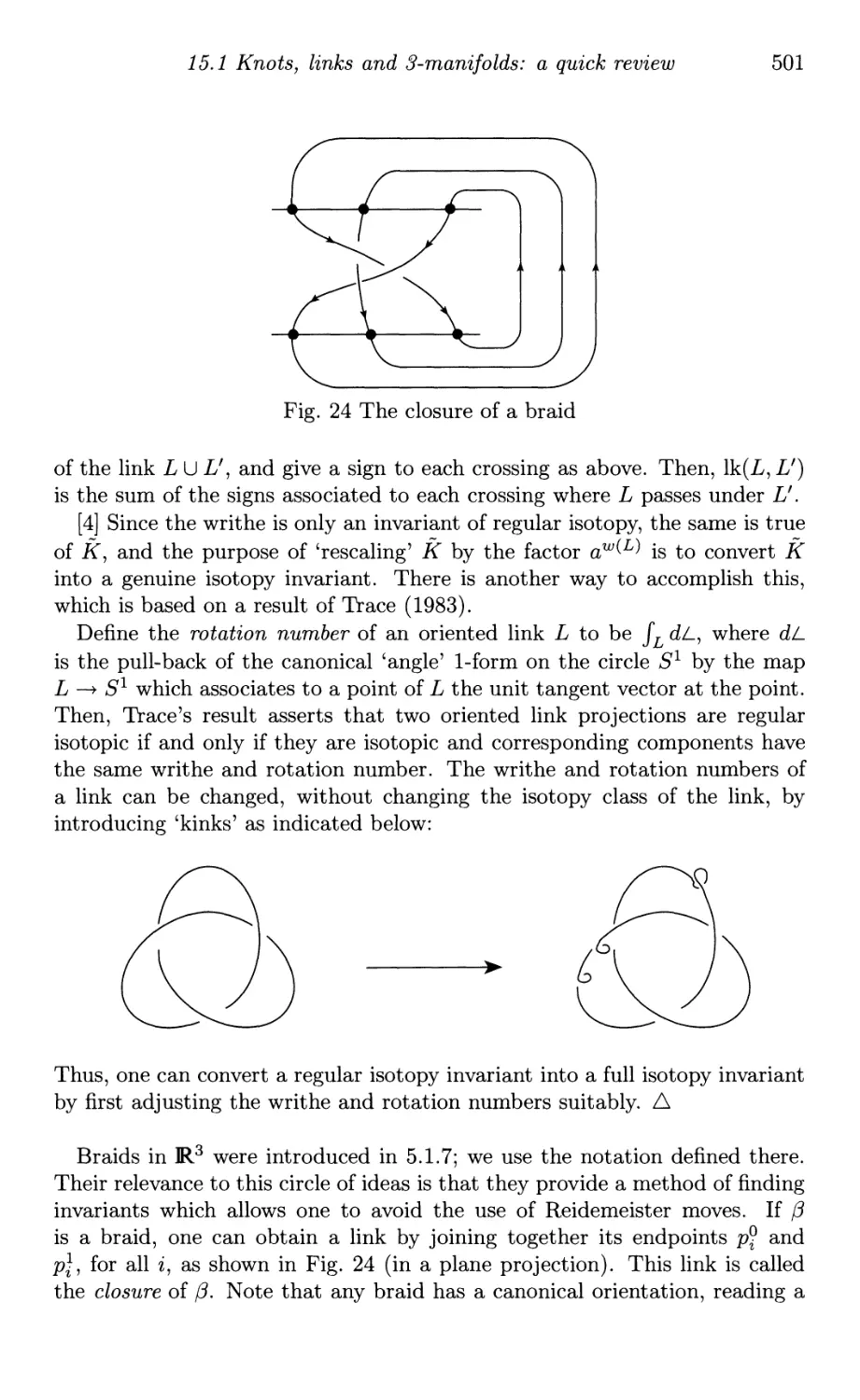
A From braids to links 496
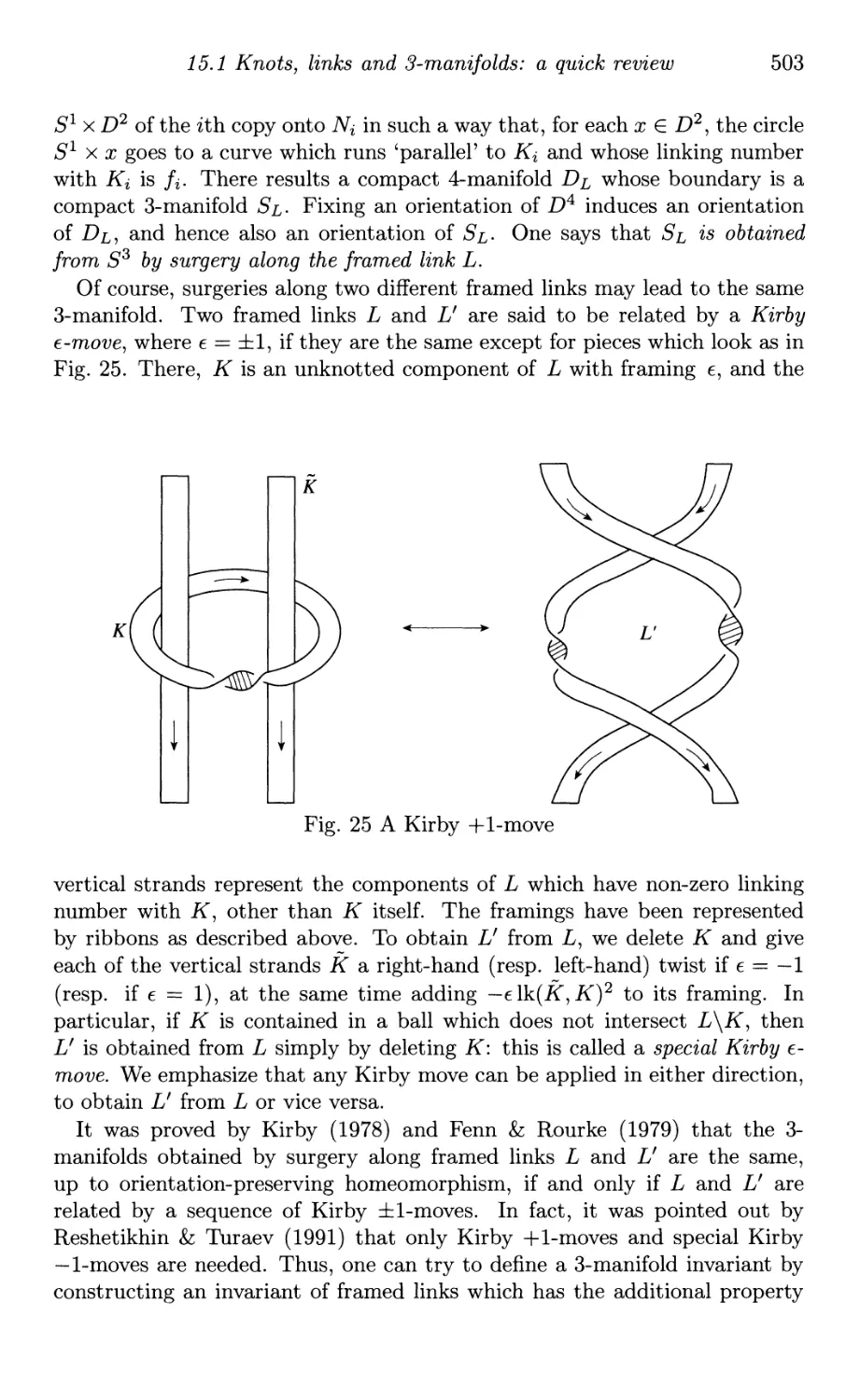
B From links to 3-manifolds 502
15.2 Link invariants from quantum groups 504
A Link invariants from R-matrices 504
B Link invariants from vertex models 510
15.3 Modular Hopf algebras and 3-manifold invariants 517
A Modular Hopf algebras 517
B The construction of 3-manifold invariants 522
Bibliographical notes 525
Contents xv
16 Quasi-Hopf algebras and the
Knizhnik-Zamolodchikov equation 527
16.1 Quasi-Hopf algebras 528
A Definitions 529
B An example from conformal field theory 533
C Quasi-Hopf QUE algebras 534
16.2 The Kohno-DrinfePd monodromy theorem 537
A Braid groups and configuration spaces 537
B The Knizhnik-Zamolodchikov equation 539
C The KZ equation and affine Lie algebras 541
D Quantization and the KZ equation 543
E The monodromy theorem 549
16.3 Affine Lie algebras and quantum groups 550
A The category OK 551
B The tensor product 552
C The equivalence theorem 555
16.4 Quasi-Hopf algebras and Grothendieck's esquisse 556
A Gal(Q/Q) and pro-finite fundamental groups 557
B The Grothendieck-Teichmuller group and
quasitriangular quasi-Hopf algebras 559
Bibliographical notes 560
Appendix Kac-Moody algebras 562
A 1 Generalized Cartan matrices 562
A 2 Kac-Moody algebras 562
A 3 The invariant bilinear form 563
A 4 Roots 563
A 5 The Weyl group 564
A 6 Root vectors 565
A 7 Affine Lie algebras 565
A 8 Highest weight modules 566
References 567
Index of notation 638
General index 643
Introduction
Quantum groups first arose in the physics literature, particularly in the work
of L. D. Faddeev and the Leningrad school, from the 'inverse scattering
method', which had been developed to construct and solve 'integrable' quan-
quantum systems. They have excited great interest in the past few years because
of their unexpected connections with such, at first sight, unrelated parts of
mathematics as the construction of knot invariants and the representation
theory of algebraic groups in characteristic p.
In their original form, quantum groups are associative algebras whose defin-
defining relations are expressed in terms of a matrix of constants (depending on the
integrable system under consideration) called a quantum R-matrix. It was
realized independently by V. G. Drinfel'd and M. Jimbo around 1985 that
these algebras are Hopf algebras, which, in many cases, are deformations of
'universal enveloping algebras' of Lie algebras. A little later, Yu. I. Manin
and S. L. Woronowicz independently constructed non-commutative deforma-
deformations of the algebra of functions on the groups SX2((C) and SU2, respectively,
and showed that many of the classical results about algebraic and topological
groups admit analogues in the non-commutative case.
Thus, although many of the fundamental papers on quantum groups are
written in the language of integrable systems, their properties are accessible
by more conventional mathematical techniques, such as the theory of topo-
topological and algebraic groups and Lie algebras. Our aim in this book is to
present the theory of quantum groups from this latter point of view. In fact,
we shall concentrate on the study of the 'Lie algebras' of quantum groups,
which seems to be the approach which has proved most powerful, particularly
in applications, but we shall also discuss, in rather less detail, their relation
with 'non-commutative algebraic geometry and topology'.
We shall now describe what a quantum group is, beginning by trying to
explain the motivation for the use of the adjective 'quantum'.
In classical mechanics, the phase space M of a dynamical system is a Pois-
son manifold. This means that the space T(M) of (differentiate) complex-
valued functions on M is equipped with a Lie bracket { , } : F(M) x T{M) —>
F(M) (satisfying certain additional conditions), called the Poisson bracket.
The dynamical equations defining the time evolution of the system are equiv-
equivalent to the equations
for / e F{M), where Hc\ is a fixed function on M called the (classical)
2 Introduction
hamiltonian, and m(t) G M is the 'state' of the system at time t. For example,
for a single particle moving along the real line, M is the cotangent bundle
T*AR), and if q is the coordinate on JR. ('position') and p the coordinate in
the fibre direction ('momentum'), the Poisson bracket is
In particular, the Poisson bracket of the coordinate functions is
A) {*>,<?} = 1.
In quantum mechanics, the space M is replaced by the set of rays in a com-
complex Hilbert space F, and the space Jr(M) of functions on M by the algebra
Op(V) of (not necessarily bounded) operators on V. The time evolution of
an operator A is given by
? =[«,», A\
for some operator Hqu G Op(F), called the (quantum) hamiltonian. For
example, in the case of a single particle moving along the real line, V is the
space L2AR) of square-integrable functions of q, and the operators P and Q
corresponding to the coordinate functions p and q are given by
P = —ydY^—^ q — multiplication by q,
dq
where h is 1/2tt times Planck's constant. Note that
B) [P,Q] =-v^lh id v.
The question is: how to pass from the classical to the quantum description
of a system. This is the problem of quantization. Ideally, one would like a
map Q which assigns to each function / G Jr(M) an operator Q(f) on V.
Moreover, since time evolution in the classical and quantum descriptions is
given by taking the Poisson bracket and commutator with the hamiltonian,
respectively, Q should satisfy the relation
(the normalization comes from A) and B)). Unfortunately, it is known that,
even for the simplest case of a single particle moving along the real line, no
such map Q exists.
There is, however, an alternative formulation of the quantization problem,
introduced by J. E. Moyal in 1949. This begins by noting that the fun-
fundamental difference between the classical and quantum descriptions is that
Introduction 3
T{M) is a commutative algebra, whereas Op(V) is non-commutative (when
dim(V) > 1). Moyal's idea is to try to reproduce the results of quantum
mechanics by replacing the usual product on T{M) by a non-commutative
product */j, depending on a parameter /i, such that *^ becomes the usual
product as h —>¦ 0, just as 'quantum mechanics becomes classical mechanics
as Planck's constant tends to zero', and such that
C) ^A*J»-/»«Ji={/i/a}
If we think of T{M) with the Moyal product *^ as a non-commutative alge-
algebra of functions ^(M), we find ourselves in the realm of non-commutative
geometry in the sense of A. Connes. The philosophy here is that any 'space'
is determined by the algebra of functions on it (with the usual product). For
example, every affine algebraic variety over (C is determined (up to isomor-
isomorphism) by the commutative algebra of regular functions on it, whereas every
compact topological space is determined by its commutative C*-algebra of
complex-valued continuous functions. More precisely, the category of 'spaces'
in these examples is dual to the category of the corresponding algebras. Thus,
a non-commutative algebra should be viewed as the space of functions on a
'non-commutative space', and we can say that Moyal's construction gives a
deformation of the classical phase space M to a family of non-commutative
(or 'quantum') spaces Mh such that Th{M) is the algebra of functions on
Mh.
The category of quantum spaces, then, might be defined as the category
dual to the category of associative, but not necessarily commutative, algebras.
To define the notion of a quantum group, let us first return for a moment to
the classical situation. If G is a group, the multiplication n : G x G —> G
of G induces a homomorphism fi* = A : ^(G) —» T{G x G) of algebras
of functions. Now, if we define the algebra F(G) and the tensor product
appropriately, T{G x G) will be isomorphic to T{G) <S> F{G) as an algebra.
For example, if G is an affine algebraic group over (C, and F(G) is the algebra
of regular functions on G, the ordinary algebraic tensor product will do.
Thus, we have a comultiplication A : T{G) —» F(G) <S> F{G). (The reason
for this terminology is that the multiplication on T(G) can be viewed as a
map J-'(G) 0 ^(G) —> T(G).) Similarly, the inverse map i : G —> G induces
a map t* = S : T(G) —* .F(G), called the antipode, and evaluation at the
identity element of G is a homomorphism e : T{G) —> (C, called the counit.
The maps A, S and e satisfy certain compatibility properties which reflect
the defining properties of the inverse and the associativity of multiplication
in G, and combine to give T{G) the structure of a Hopf algebra.
We might therefore define the category of quantum groups to be the category
dual to the category of (not necessarily commutative) Hopf algebras. (We said
'might' here, and in our tentative definition of a quantum space, because,
4 Introduction
to ensure that the categories of quantum spaces and quantum groups have
reasonable properties, it would be necessary to impose some restrictions on
the class of algebras which are acceptable as 'quantized algebras of functions'.
Manin suggests that one should work with 'Koszul algebras', but we shall not
discuss this point here.) As is common practice in the literature, we shall
often abuse terminology by referring to a Hopf algebra itself as a quantum
group.
As the preceding discussion suggests, one way to try to construct non-
classical examples of quantum groups is to look for deformations, in the cat-
category of Hopf algebras, of classical algebras of functions T(G). Just as the
classical Poisson bracket can be recovered as the 'first order part' of Moyal's
deformation (see C)), so it turns out that the existence of a deformation
Th{G) of F(G) automatically endows the group G itself with extra struc-
structure, namely that of a Poisson-Lie group. This is a Poisson structure on G
which is compatible with the group structure in a certain sense. Conversely,
to construct deformations of F{G), it is natural to begin by describing the
possible Poisson-Lie group structures on G and then to attempt to extend
these 'first order deformations' to full deformations. This is the approach
taken in this book. Poisson-Lie groups are also of interest in their own right,
for they form the natural setting for the study of classical integrable systems
with symmetry.
There is another Hopf algebra associated to any Lie group G, namely the
universal enveloping algebra C/(g) of its Lie algebra g. This is essentially the
dual of T(G) in the category of Hopf algebras. In general, the vector space
dual ^4* of any finite-dimensional Hopf algebra A is also a Hopf algebra: the
multiplication A* <S> A* —> ^4* is dual to the comultiplication A : A —> A 0 A
of A, and the comultiplication of ^4* is dual to the multiplication of A. Note
that ^4* is commutative if and only if A is cocommutative, i.e. if and only if
A (A) is contained in the symmetric part of A <S> A. If, as is usually the case
in examples of interest, A is infinite dimensional, this duality often continues
to hold provided the dual and tensor product are defined appropriately. To
a deformation Th{G) of T{G) through (not necessarily commutative) Hopf
algebras therefore corresponds a deformation C/^(g) of C/(g) through (not
necessarily cocommutative) Hopf algebras.
In fact, only non-cocommutative deformations of C/(g) are of interest, since
any deformation of C/(g) through cocommutative Hopf algebras is necessarily
of the form U($h) for some deformation g^ of g through Lie algebras. How-
However, many interesting Lie algebras have no non-trivial deformations. This is
the case, for example, if g is a (finite-dimensional) complex semisimple Lie al-
algebra, such as the Lie algebra s/2((C) of 2 x 2 complex matrices of trace zero.
This follows from the fact that the condition of semisimplicity is open, so
that any small deformation of g will still be semisimple, whereas the semisim-
semisimple Lie algebras are discretely parametrized (by their Dynkin diagrams, for
example).
Introduction 5
The first example of a non-cocommutative deformation of this type was
discovered by P. P. Kulish and E. K. Sklyanin in 1981 in the case g = 5/2(C)
(although the importance of its Hopf structure was not realized until later).
Note that 5/2 (C) has a basis
whose Lie brackets are given by
Ea) [X+, X~] = if, [H, X±] = ± 2X±.
The comultiplication is given on these basis elements by
Eb) ± ±
an assignment which extends uniquely to an algebra homomorphism A :
U{sl2{<?)) -> U(sl2{<?)) 0 U{sl2{<?)). The deformation Uh{sl2(C)) is gener-
generated by elements if, X^, which satisfy the relations
hH _
_
Fa) X+X- - X~X+ = —r 7—, ifX± - X±H = ± 2X±.
It has a non-cocommutative comultiplication given on generators by
Formally, at least, it is clear that Fa) and Fb) go over into Ea) and Eb) as
h —> 0. The Hopf algebra defined in Fa,b) is called 'quantum sl2((?)\ (See
Chapter 6 for the formulas for the antipode and counit of Uh{sl2((C)), and
for a way to make sense of expressions such as ehH.)
The Hopf algebra dual to Uh(sl2{<E)), the 'algebra Jrh{SL2(<E)) of functions
on quantum ST^CC)', was discovered by L. D. Faddeev and L. A. Takhtajan
in 1985. It is the associative algebra generated by elements a, fr, c, d with the
following multiplicative relations:
G) ab = e~hba, ac = e~hca, bd = e~hdb, cd = e"hdc,
(8) be = cb, ad-da + (eh - e~h)bc = 0,
(9) ad-e~hbc=l,
and comultiplication
A(a) =a(g>a + b<g)C, A(b) = a(g)b + b®d1
Introduction
A(c) =c®a + d®c, A(d) =
Note that, when /i —> 0, the relations G), (8) and (9) just say that the matrix
a b
c d
has commuting entries and determinant one. Thus, -7^EX2 (<?)) is a defor-
deformation of the algebra of functions on the group SL2 (<C) of 2 x 2 complex
matrices of determinant one.
As we mentioned at the beginning of this introduction, the algebra structure
of ThiG) can be described by a matrix of constants, namely
eh
0
0 e
0
0
1
,h _ e-f
0
0
0
1 1
0
0
0
0
e'
In fact, if
T=Z \c d
the relations G) and (8) are equivalent to
A1) (T 0 1)A 0 T)R - R{\ 0 T)(T 0 1).
Note that T 0 1 and 1 0 T do not commute, since the entries of T do not
commute (if h ^ 0); note also that R is most naturally viewed as an element
of End((C2 0 (C2). It is in the form A1) that quantum groups usually appear
in the theory of integrable systems.
For the dual Hopf algebra ?4 (s/2 (<?)), the quantum R-matrix expresses, as
one would expect, the non-cocommutativity of the comultiplication. Namely,
let Aop(x) be the result of interchanging the order of the factors in A(x),
for any x G Uh(sl2{(E))> It turns out that there is an invertible element
1Z G Uh(sl2{?)) 0 Uh(sl2((E)), called the 'universal R-matrix', such that
for all x G ?4(«s/2(<C)) (actually, 1Z is a formal infinite sum of elements of the
algebraic tensor product). The relation between 1Z and R is very simple: the
reader will easily verify that, if we replace X± and H by X± and H in D),
we obtain a matrix representation of ?4(«s/2(<C)); applying this representation
to 1Z gives the matrix R.
Quantum groups might have remained a curiosity to the mathematical
community at large but for their surprising connections with other parts of
Introduction 7
mathematics, most notably the theory of invariants of links and 3-manifolds,
and the representation theory of Lie algebras in characteristic p.
The former depends on the classical relation between braids and links.
Recall that a braid on m strands is a collection of m non-intersecting strings
in IR3 joining m fixed points in a plane to m fixed points in another parallel
plane. Joining corresponding points in the two planes in a standard way
associates to any braid a link (called its 'closure'), i.e. a collection of non-
intersecting circles in IR3. Joining braids end to end makes the set of isotopy
classes of braids into a group Bm. The relation with quantum groups arises
because there is a simple way to associate to any quantum R-matrix R G
End(V 0V)a representation pm of Bm on V®m for all m > 2. This depends
on the fact that R satisfies the quantum Yang-Baxter equation
R12R13R23 — -R23-R13-R12 ;
here, R12 means R <S> id G End(V®3), etc. To obtain an invariant of links,
one needs a family of 'traces' trm : End(V®m) —> C such that trrn(prn(b)) —
trn{pn{bf)) whenever the closures of the braids b G Sm and bf G Bn are
equivalent links. Thanks to a classical theorem of A. Markov, it is known
precisely which pairs (b, bf) have the latter property (and for this reason, the
trm are usually called 'Markov traces'). Using the quantum R-matrix A0)
and a suitable Markov trace, one obtains in this way the celebrated Jones
polynomial In fact, this is essentially Jones's original construction, except
that he obtained his R-matrix by using a 'Hecke algebra' instead of a quantum
group (but we shall see that Hecke algebras should probably be regarded as
'quantum' objects).
The application to 3-manifolds is based on the well-known fact that every
compact, oriented, connected 3-manifold without boundary can be obtained,
up to homeomorphism, by performing surgery on a link in the 3-dimensional
sphere. One shows that a cleverly chosen combination of the quantum invari-
invariants of this link depends only on the 3-manifold, and not on the choice of the
link along which surgery is performed.
The application of quantum groups to representations of Lie algebras in
characteristic p is no less remarkable. It makes use of a certain 'standard' de-
deformation Uh{o) of ?/(g), where g is any finite-dimensional complex semisim-
ple Lie algebra (and which reduces, when g = 5/2 (CC), to the algebra found
by Kulish and Sklyanin). To describe the relation with characteristic p, it is
convenient to replace the deformation parameter h by e = eh, and to write
?/e(g) for Uh{§)- It then turns out that the representation theory of f/e(g) de-
depends crucially on whether e is a root of unity or not. In the latter case, the
theory is essentially the same as the representation theory of g itself (over (C),
but in the former it resembles the modular representation theory of g. This is
more than an analogy: if e is a primitive pth root of unity, where p is a prime,
there is a ring homomorphism from f/e(g) to the enveloping algebra ?% (g)
8 Introduction
of g over the field JFP of p elements (this is obtained essentially by replacing e
by 1 G IFp), and, under certain additional conditions, representations of t/e(g)
can be 'specialized' to give representations of Uwp(§)- Thus, both the modu-
modular representation theory of g and the characteristic zero theory are reflected
in the representation theory of the family of Hopf algebras f/e(g) (over (C).
Using this relation, substantial progress has been made toward the solution
of several long-standing conjectures in the modular theory.
We should also mention the roles played by quantum groups in physics,
which go well beyond their origins in inverse scattering theory. Perhaps the
most interesting of these is the relation between quantum groups and con-
formal and quantum field theories. The first evidence of this was the exper-
experimental observation that the 'fusion rules' of certain conformal field theories
can be reproduced by considering the decomposition of tensor products of
representations of the quantum groups t/e(g) when e is a root of unity. Fur-
Further evidence came from a remarkable theorem of T. Kohno and Drinfel'd on
the relation between the Knizhnik-Zamolodchikov (KZ) equation and f/^(g).
The KZ equation is a system of first order partial differential equations for
a function of m complex variables with values in the tensor product Vm,
where V is a representation of g. The KZ system has regular singularities
along the hyperplanes Zi = Zj in (Cm, for all i ^ j, and can be viewed as a
connection on a bundle over the complement Vm of these hyperplanes, with
fibre y®m. Moreover, this connection has a symmetry property which means
that there is an induced connection on a bundle over the space Cm of orbits
of the obvious action of the symmetric group Em on T>m. The crucial prop-
property of the KZ equation is that this connection is flat, which implies that
the monodromy of its solutions defines a representation of the fundamental
group of Cm on V®m. The latter group is exactly the braid group Bm that
we discussed above, where we noted that a representation of Bm on V®m
could also be obtained by using a quantum R-matrix. According to Kohno
and Drinfel'd, if we use the R-matrix given by the action of the universal
R-matrix of f/^(g) on V <8) V, where h is 'generic', these two representations
of Bm coincide.
The importance of the KZ equation in conformal field theory is that it is
satisfied by the cm-point functions' of the theory. Thus, the Kohno-Drinfel'd
theorem indicates a connection between f/^(g) and conformal field theory.
This has recently been extended by D. Kazhdan and G. Lusztig, who have
shown that the KZ equation is intimately related to the category of repre-
representations of the 'specialized' algebras f/e(g) when e is a root of unity. This
result provides an 'explanation' for the coincidence between the fusion rules
arising in conformal field theory and those arising from quantum groups at
roots of unity.
These and other examples to be discussed in this book show that the the-
theory of quantum groups occupies an important place in the mainstream of
mathematics and mathematical physics.
Introduction 9
We now describe the contents of the book systematically. In Chapter 1, we
give the definition and basic properties of Poisson-Lie groups, and of their in-
infinitesimal counterparts, Lie bialgebras. We describe, among other examples,
a standard family of Lie bialgebra structures on every (finite-dimensional)
complex simple Lie algebra. These induce Poisson-Lie group structures on
the associated compact Lie group K. Like all Poisson manifolds, K has a
canonical decomposition into symplectic submanifolds, called its symplectic
leaves, and it turns out that they have a beautiful description in terms of the
so-called Bruhat decomposition of K.
In the last section of this chapter, we describe the formulation of quanti-
quantization as a deformation of Poisson structure. We discuss only the simplest
example of a single particle moving along the real line, since our aim is mainly
to motivate the treatment of the deformation theory of Hopf algebras in Chap-
Chapter 6.
Chapter 2 returns to the discussion of Lie bialgebras. We show that Lie
bialgebra structures on a Lie algebra g can be constructed from solutions
of the 'classical Yang-Baxter equation' (CYBE), and that in some cases,
for example when g is complex semisimple, all Lie bialgebra structures arise
in this way. We also discuss the relation between the CYBE and classical
integrable systems.
Chapter 2 shows the importance of the problem of classifying the solutions
of the CYBE. In Chapter 3, we give an essentially complete description of
the solutions with values in g (g) g, where g is a complex simple Lie algebra.
The discussion requires more familiarity with Lie theory than the other early
chapters of the book, and, since most of the results will not be needed later,
we recommend that this chapter be omitted on a first reading.
Chapter 4 begins with a summary of the general results about Hopf algebras
we shall need. We have already mentioned that quantum groups are usually
non-cocommutative as Hopf algebras. However, they (or their duals) are often
'quasitriangular': this means that the comultiplication of the Hopf algebra
A is conjugate to the opposite comultiplication by an invertible element 1Z
of A <S> A, called its universal R-matrix. The element 1Z satisfies certain
additional conditions, including the quantum Yang-Baxter equation (QYBE).
We discuss the general properties of quasitriangular Hopf algebras and their
relation with the QYBE.
One of the most important general properties of a Hopf algebra A is that
there is a natural way to make the tensor product of two representations of A
into another representation of A. This means that the category rep^ of rep-
representations of A is a monoidal category. If A has additional properties, these
will be reflected in rep^ and vice versa. For example, if A is quasitriangular,
rep^ is a quasitensor category, which means roughly that the tensor product
operation is associative and commutative up to isomorphism. We discuss the
basic properties of quasitensor categories in Chapter 5, and give a number of
examples arising from algebra, topology and physics.
10 Introduction
The idea that the properties of a Hopf algebra are encoded in, and might be
recovered from, its representations is called Tannaka-Krein duality, and this
will be a guiding principle throughout this book. We prove a Tannaka-Krein
type theorem valid for a large class of Hopf algebras.
We meet our first examples of quantum groups in Chapters 6 and 7. We
begin by discussing the general theory of deformations of Hopf algebras, con-
concentrating on universal enveloping algebras and function algebras. We show
that any deformation f/^(g) of t/(g) gives rise to a Lie bialgebra structure on
g, and that every finite-dimensional Lie bialgebra arises as the 'classical limit'
of some deformation in this way. To make sense of formulas such as those in
Fa,b), one interprets ?4(g) as an algebra over the ring (C[[h]\ of formal power
series in an indeterminate h.
In Chapter 6, we 'derive' the deformation Uhishi^)) described above and
show that it can be extended to a deformation of the universal enveloping
algebra of any symmetrizable Kac-Moody algebra, using the fact that such
algebras are generated by certain 5/2 (C) subalgebras.
In Chapter 7, we construct deformations of the algebras of functions on the
classical complex Lie groups using the quantum R-matrix method outlined
above. We also discuss the duality relation between these quantized function
algebras and the quantized universal enveloping algebras of Chapter 6. For a
large class of quantum R-matrices, we construct an analogue of the de Rham
complex, which can be viewed as a theory of 'differential calculus' on the
associated quantum group. In the final section of this chapter, we discuss
the relation between the quantum Yang-Baxter equation and certain models
in statistical mechanics, where the QYBE plays the role of an integrability
condition.
In Chapter 8, we obtain a formula for the universal R-matrix of the quan-
quantum groups Uh(o) defined in Chapter 6, assuming that g is finite dimensional.
We make use of an action of a (generalized) braid group on any quantum group
of this type, which is analogous to the well-known action of (a finite covering
of) the Weyl group of g on ?/(g) in the classical situation.
Chapters 9, 10 and 11 are devoted to the structure and representation
theory of the 'specialization' t/e(g), where e G (Cx. The definition of U€(q)
requires some effort, for f/^(g) is defined over the algebra of formal power
series in /i, so that the only specialization which appears to make sense is
h = 0. In fact, as we show in Chapter 9, the specialization to f/e(g) can
be carried out in two ways, called 'restricted' and 'non-restricted'. The two
specializations coincide if e is not a root of unity, but not otherwise. We also
study the relation, hinted at above, between Ue(q) when e is a root of unity
and Lie algebras in characteristic p.
In Chapter 10, we give the classification of the finite-dimensional irreducible
representations of f/e(g) when g is a finite-dimensional complex simple Lie
algebra and e is not a root of unity. It turns out that, up to a rather trivial
twisting by certain outer automorphisms, the parametrization, and even the
Introduction 11
characters, of such representations are exactly the same as in the classical
case.
There are some differences when compared with the classical situation,
however. We show, in particular, that in the quantum analogue of the classical
Frobenius-Schur duality between representations of the (special or general)
linear groups and symmetric groups, the role of the symmetric group is played
by a Hecke algebra.
In Chapter 11, we study the representation theory at a root of unity. For
the restricted specialization ?/eres(g), the finite-dimensional irreducible repre-
representations are discretely parametrized as in the classical case (in characteristic
zero), but their structure (and dimensions) are different in general. On the
other hand, for the non-restricted specialization f/e(g), we can say, oversim-
oversimplifying a little, that there is an irreducible representation of U6(q) associated
to each point of the Lie group G with Lie algebra g, and that representations
which are associated to points of the same conjugacy class are equivalent up
to twisting by an element of a certain infinite-dimensional group of automor-
automorphisms of C/e(g).
The tensor product of two irreducible representations of ?/Jes(g), when e is
a root of unity, is not in general completely reducible. However, essentially
by discarding those indecomposable pieces of the tensor product which are
not irreducible, we obtain a 'truncated' tensor product which has very inter-
interesting properties. We show that the resulting truncated representation ring
is an example of a fusion ring, a new algebraic structure first encountered in
conformal field theory. As we mentioned earlier in this introduction, this co-
coincidence was one of the first indications of the connection between quantum
groups and conformal and quantum field theories.
In Chapter 12, we return to the case of generic e, but consider quantiza-
quantizations of some infinite-dimensional groups, namely quantum affine algebras
and Yangians. It is important to classify the finite-dimensional irreducible
representations of these quantum groups, for to such a representation one
can associate a solution of the quantum Yang-Baxter equation with spectral
parameters:
Here, R(u) is a function of a complex variable u with values in End(F<S) V); it
is a rational or trigonometric function of u according as V is a representation
of a Yangian or a quantum affine algebra, respectively.
We also describe some surprising connections between quantum affine
algebras and Yangians, and the classical representation theory of p-adic
groups.
In Chapter 13, we return to quantized algebras of functions. Classically,
the algebra J~{G) is commutative, so all of its irreducible representations are
one-dimensional; in fact, there is a one-dimensional representation of J~{G)
12 Introduction
associated to each point of G (given simply by evaluating a function at the
point). However, J~h(G) is non-commutative in general, and the represen-
representation theory of J~h(G) replaces, to some extent, the study of G as a point
set.
We study the case where G is a complex simple Lie group, and replace
FhiG) by a suitable specialization Tt{G). We classify the representations
which are unitary with respect to a conjugate-linear involution on Jre{G)
whose classical limit is the involution which defines the compact real form of
G (for such representations to exist, it is necessary that e G 1R).
There is a natural G*-norm on ^e(G), and the C*-completion Ce(G) of
J-e(G) can be regarded as a quantization of the algebra of continuous func-
functions on G. This makes contact with the theory of compact matrix quantum
groups (or matrix pseudogroups) of Woronowicz. Compact quantum groups
are closely related to cKac algebras', the theory of which is the culmination of
a long effort to generalize Pontryagin duality to locally compact groups which
are not necessarily abelian. Apart from a number of technical differences, per-
perhaps the most important structural difference between the two theories is that
in the theory of Kac algebras the existence of a Haar integral is postulated,
whereas this is one of Woronowicz's main theorems about compact quantum
groups. We give a simple definition of the Haar integral by making use of the
representation theory of Ue(§).
In the final section of this chapter, we show that several q-special func-
functions are related to the representations of compact or non-compact quantum
groups. This was first noticed by L. L. Vaksman and Ya. S. Soibelman in
1986, who showed that the 'little g-Jacobi polynomials' are essentially the
matrix elements of the irreducible unitary representations of ^(ST^C)).
Thus, almost 150 years after the birth of the theory of g-special functions,
their representation-theoretic meaning was found.
In Chapter 14, we show how the results of Chapters 9 and 10 can be used to
give a solution to a classical problem in the theory of complex semisimple Lie
algebras, namely that of giving a basis of any finite-dimensional irreducible
representation of such an algebra g which is in some sense canonical. If
g is of type A, B, C or D, one solution to this problem is given by the
Gel'fand-Tsetlin basis, although this cannot be extended to the algebras of
exceptional type. We describe a solution to this problem, due independently
to M. Kashiwara and Lusztig, for arbitrary g in the quantum case, which,
specializing to h = 0, also solves the classical problem. As a by-product,
one obtains a graphical algorithm for decomposing the tensor product of two
irreducible representations of g. It is perhaps worth emphasizing that this
construction cannot be carried out purely in the classical setting: one must
pass to the quantum case and then specialize.
Chapter 15 describes the application of quantum groups to the construc-
construction of invariants of links and 3-manifolds, outlined above. This is due to
Introduction 13
N. Yu. Reshetikhin and V. G. Turaev, but strongly motivated by the work of
V. F. R. Jones and E. Witten.
The final Chapter 16 describes a generalization, due to Drinfel'd, of the
notion of a Hopf algebra, called a quasi-Hopf algebra. The category of quasi-
Hopf algebras is in some ways simpler than the category of Hopf algebras
because of the existence of a kind of 'gauge symmetry' on the former category,
which often allows one to 'twist' a given quasi-Hopf algebra into a simpler
one with the 'same' representation theory.
One of the main results of Chapter 16 is the theorem of Kohno and Drin-
Drinfel'd mentioned earlier. This is proved by using the Knizhnik-Zamolodchikov
equation to construct a certain quasi-Hopf algebra which is isomorphic to a
twist of the QUE algebra f/^(g). We give an introduction to Kazhdan and
Lusztig's generalization of this theorem, including the construction of their
new tensor product of representations of affine Lie algebras.
We also describe briefly some recent work of Drinfel'd relating quasi-Hopf
algebras to the absolute Galois group of Q. This can be regarded as the
fulfilment of part of A. Grothendieck's 'Esquisse d'un programme'.
The book concludes with an Appendix, which establishes the notation re-
relating to complex simple Lie algebras (and, more generally, to Kac-Moody
algebras), which will be used throughout the book.
As a distinct area of study, the theory of quantum groups is still less than
10 years old, and it is perhaps still possible to give an account of all its main
lines of development from a single point of view. One of the peculiarities of
our subject is that, even though most of the foundational results were stated
by Drinfel'd in his 1986 talk at the International Congress of Mathematicians,
for many of them there is no detailed exposition in print. On the other hand,
the results obtained since 1986, including those due to Drinfel'd himself, are
generally well-covered in journal articles. Although we certainly do not claim
to have filled all the gaps in the existing literature, our aim has been to
provide a full account of the foundations, while for the more advanced topics
we have usually been content to state the most important results and give a
sketch of the main ideas of the proof, together with detailed references to the
literature. We have tried not to assume too much familiarity on the part of
the reader with the classical theory of Lie groups and Lie algebras, at least
in the first half of the book. We hope that, as a result, the book will serve as
an introductory text for those readers meeting quantum groups for the first
time, and will provide more experienced readers with a survey of all the major
developments in the subject, together with a guide to where the details can
be found. This approach has made it necessary to include a rather extensive
bibliography, and, although we have tried to make this reasonably complete,
some gaps are inevitable, and we apologise to those authors whose relevant
work has inadvertently been omitted.
14 Introduction
We have learned about quantum groups from many sources, but we would
like to thank in particular V. G. Drinfel'd for two inspirational lectures at
Luminy in 1988 which ignited our interest in the subject, N. Yu. Reshetikhin
for drawing our attention to some of the relevant work in the physics litera-
literature, C. de Concini and V. G. Kac for explaining to us their work on quantum
groups at roots of unity, and S. Donkin for help with the relation between
roots of unity and modular Lie algebras.
1
Poisson-Lie groups
and Lie bialgebras
As we mentioned in the Introduction, one reason for the terminology used
to describe 'quantum groups' is that their relation to ordinary Lie groups
is analogous to that between quantum mechanics and classical mechanics.
One of the principal messages of this book is that this is more than a formal
analogy, and we begin our treatment of quantum groups by discussing the
formulation of classical mechanics for a dynamical system whose phase space
is a group.
The traditional geometric framework for classical dynamics is that of sym-
plectic manifolds. Recall that a smooth manifold M is said to be symplectic
if it is equipped with a closed 2-form uj which gives a non-degenerate bilinear
form on the tangent space at each point of M. A hamiltonian system on
M is then specified by giving a smooth real-valued function 7i on M, the
hamiltonian. By using the 2-form cj, one can associate to the 1-form dH a
vector field X^, whose flow describes the time evolution of the system.
It is clear that what is essential in this formulation is to have some way
to associate to every 1-form on M a vector field on M. For this we need
a bivector on M, i.e. a section of the second tensor power of the tangent
bundle of M, for then we can contract the 1-form against the bivector to
obtain a vector field. A Poisson manifold is a smooth manifold equipped
with a bivector with certain properties analogous to those which assert that
the symplectic form uj is skew and closed, but without any requirement of
non-degeneracy.
Every symplectic manifold M has a natural Poisson structure, for the sym-
symplectic form uj allows one to identify 1-forms and vector fields, and hence 2-
forms and skew bivectors. In fact, it is exactly the everywhere non-degenerate
Poisson structures which arise in this way. The most general Poisson man-
manifold, however, has a canonical decomposition into symplectic submanifolds
(not all of the same dimension in general), called its symplectic leaves.
The Poisson manifolds which will be of most interest to us are the Poisson-
Lie groups, introduced in Section 1.2. These are Lie groups G which have
Poisson structures which are compatible with the group operations in a certain
sense. We shall see that such Poisson structures never arise from symplectic
structures.
The most important examples of Poisson-Lie groups, at least for the study
16 1 Poisson-Lie groups and Lie bialgebras
of quantum groups, concern the case in which G is a compact group (or its
complexification). We construct in Section 1.4 a canonical family of Poisson-
Lie group structures on G whose symplectic leaves have a beautiful description
in terms of the Bruhat decomposition of G. Moreover, there are induced
Poisson structures on each coadjoint orbit O of G whose symplectic leaves
are exactly the Schubert cells in O.
The infinitesimal versions of Poisson-Lie groups are called Lie bialgebras.
More precisely, if G is any Poisson-Lie group, the dual g* of its Lie algebra
g turns out to have a natural Lie algebra structure, which is compatible
with that of g itself, in a certain sense; together, these are said to form
a Lie bialgebra structure on g. Conversely, if G is connected and simply-
connected, every Lie bialgebra structure on g arises from a unique Poisson-
Lie group structure on G. The basic properties of Lie bialgebras are described
in Sections 1.3 and 1.4, but we postpone the discussion of their classification
until Chapters 2 and 3.
Section 1.4 describes an equivalent formulation of the notion of a Lie bial-
bialgebra in which g and g* play symmetric roles; it allows us to give simple
explicit descriptions of a number of important examples of Lie bialgebras. It
also shows that g* and the direct sum (of vector spaces) g 0 g* inherit natural
Lie bialgebra structures from that on g itself. It follows that the Poisson-
Lie group G* with Lie algebra g* acts on G. This so-called dressing action,
studied in Section 1.5, is the basis for the application of Poisson-Lie groups
in the theory of integrable systems, which will be described in Section 2.3.
It also allows one to give a simple description of the symplectic leaves of a
Poisson-Lie group.
Section 1.6 is an introduction to the interpretation of quantization of clas-
classical hamiltonian systems in terms of a deformation of the Poisson structure
on the phase space of the system. The discussion provides some motivation
for the adjective in the term 'quantum group'.
1.1 Poisson manifolds
In this section, we describe those aspects of the theory of Poisson manifolds
that will be needed later.
A Definitions Let M be a smooth manifold of finite dimension m. We
denote by C°°(M) the algebra of smooth real-valued functions on M.
Definition 1.1.1 A Poisson structure on M is an IR-biiinear map
{ , }M : C
LI Poisson manifolds 17
called the Poisson bracket, which satisfies the following conditions:
B) {/i, {/2,/a}} + {/2,{/s,/i}} + {/a, {/i,/2}} = 0,
I (j ) "i/1 / 9 « T1^ f — /I "i / 9 i / "-t i "T" l / 1 i / *} f / 9 i
for all fi, /2, /3 G C°°(M). (We omit the subscript on the Poisson bracket
whenever this will not lead to confusion.)
The skew-symmetry property A) and the Jacobi identity B) together mean
that { , } is a Lie bracket on C°°(M). Property C), the Leibniz identity,
means that, for all / G C°°(M), the map g —> {g, /} is a derivation of
C°°(M); hence, there a vector field X/ on M such that X/(#) = {g,f} for
all #. (A vector field which arises in this way is called a hamiltonian vector
field.) In particular, {g, /} depends only on the differential of g and, in view
of the skew-symmetry of the Poisson bracket, on the differential of /. It
follows that there is a well-defined map of bundles Bm • T*M —> TM, where
TM (resp. T*M) denotes the tangent bundle (resp. the cotangent bundle)
of M, such that BM(df) = Xf for all / G C°°(M). Equivalently, there is a
skew-symmetric 2-tensor wm G TM®2, called the Poisson bivector, such that
{/>#}m — ((df ® dg),WM)- (Here, and elsewhere in this book, ( , ) denotes
the natural pairing between a vector space, or bundle of vector spaces (in this
case TM®2), and its dual.) The Jacobi identity B) for the Poisson bracket
is equivalent to the vanishing of the so-called Schouten bracket [w,w] (see
Schouten A940)).
It follows from these remarks that, in local coordinates (#i,..., xm) on M,
the Poisson bracket can be written in the form
v^ / \ df dg
/ j •* dx' dx'
where the locally defined functions Wij are the coefficients of the Poisson
bivector __
, , d d
Since u> is skew,
and the Jacobi identity is equivalent to
E
Wri~K r UJri— h UJrk—: — U.
18 1 Poisson-Lie groups and Lie bialgebras
It was in this form that Poisson structures were first introduced by Lie A888-
93), although the special case in which M = ]R2n with bracket
df dg dg df
Xi dxi+n
was introduced by S. D. Poisson early in the 19th century.
B Functorial properties A smooth map F : N —> M between Poisson
manifolds is called a Poisson map if it preserves the Poisson brackets of M
and JV, i.e. if
D) {/i, Mm °F = {hoFJ2o F}N
for all /i, /2 E C°°(M). Equivalently, F should take the Poisson bivector of
N to that of M:
E) (Fx <g> Fx)(wN)x = (wm)f(x),
where Fx is the tangent linear map of F at the point x ? M.
A submanifold S of dimension s of a Poisson manifold M has a Poisson
structure such that the inclusion map S <-+ M is a Poisson map if and only if,
at each point x ? S, the Poisson bivector of M lies in the subspace (TXS)®2
of (TXM)®2, and in this case S is said to be a Poisson submanifold of M (the
equivalence is easily seen by writing out the equation
{fl\s, f2\s}s — {/ij/2}m|s
in coordinates (q±,..., qm) such that S is given locally by the equations qs+i =
•••=<Zm=0).
If M and N are Poisson manifolds, their product M x TV is a Poisson
manifold in a natural way: for /1? f2 ? C°°(M xN),xeM,yeN, the
product Poisson structure is given by
F) {/i,/:
Examples of Poisson submanifolds are given in 1.1.2 and 1.1.3. Product
Poisson structures will be used in the next section.
C Symplectic leaves Every manifold admits the trivial Poisson structure
{f,g} = 0, for which the map B — 0. At the opposite extreme, M is said
to be symplectic if B is an isomorphism of bundles, or, equivalently, if the
Poisson bivector w is everywhere non-degenerate as a bilinear form on T*M.
In this case, u = (B ® B)~1(w) is a non-degenerate 2-form on M, and it is
easy to check that the Jacobi identity for { , } is equivalent to u being closed.
1.1 Poisson manifolds 19
Conversely, a non-degenerate 2-form u on M defines a bundle isomorphism
B' : TM -> T*M by B'(X) = u(X, ), and then w = (B' ® B')-l{u) is
the Poisson bivector of a Poisson structure on M. In general, the rank of a
Poisson structure at a point x e M is defined to be the rank of the linear
map Bx : T*M —> T^M. Thus, a Poisson structure is symplectic precisely
when its rank is everywhere equal to the dimension of M.
The first non-trivial result in this chapter asserts that every Poisson man-
manifold is a disjoint union of symplectic manifolds in a canonical way.
Definition-proposition 1.1.2 Let M be a Poisson manifold. Define an
equivalence relation ~~ on M as follows: x ~~ y if and only if there is a
piecewise smooth curve in M joining x to y, each smooth segment of which
is part of an integral curve of a hamiltonian vector field on M. Then, the
equivalence classes of ~~ are (immersed) symplectic Poisson submanifolds of
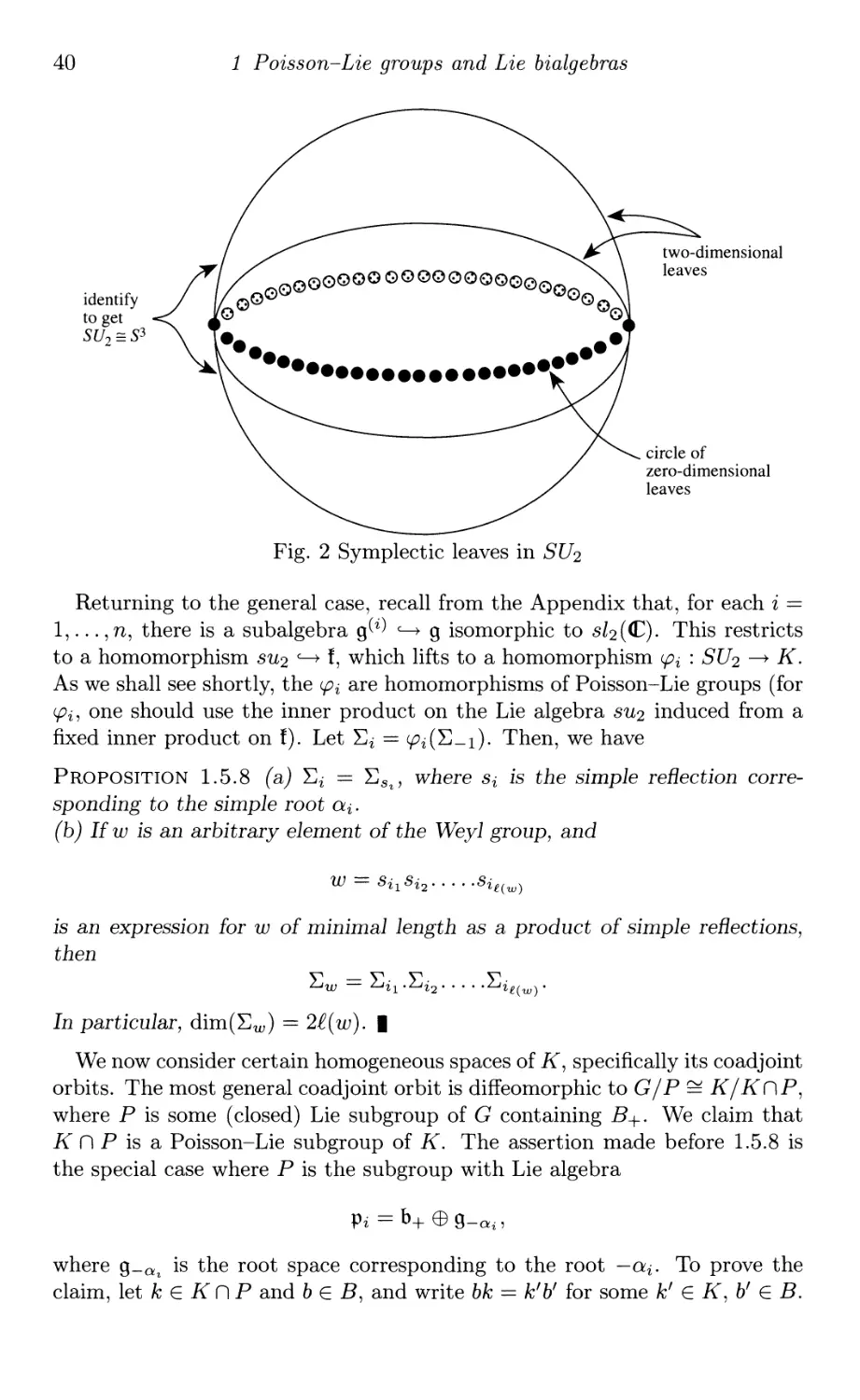
M, called its symplectic leaves (see Fig. 1). |
Fig.l Symplectic leaves
Example 1.1.3 Let g be any finite-dimensional (real) Lie algebra with Lie
bracket [ , ]. Since g* is a vector space, the tangent space of g* at any point
can be identified canonically with g* itself, so the differential df of any smooth
function / on g* is a map g* —> (g*)* = g; thus we can set
G) {fij2}@ = (l(dfih(df2h)},0
for all ^Gg*.
If Xi,..., Xm is a basis of g, we may regard xi,..., xm as (global) coordi-
coordinates on g*. It is easy to see that
20 1 Poisson-Lie groups and Lie bialgebras
where
k
and the c^ are the structure constants of g:
= / j
Obviously, Wij = —Wji\ on the other hand,
r
is zero because the sum over r vanishes by the Jacobi identity in g. Thus,
{ , } is a Poisson structure on g*: it is called the Lie-Poisson structure.
To determine the symplectic leaves of g*, let G be a connected Lie group
with Lie algebra g. We denote by Ad (resp. Ad*) the adjoint (resp. coad-
coadjoint) representation of G on g (resp. on g*), and by ad (resp. ad*) the
corresponding actions of g. With this notation, the integral curve rji of the
hamiltonian vector field Xx%, associated to the function X{ on g*, and passing
through ? ? g* at time t = 0, is given by rji(t) = Ad*(exp(-?#;))(?). Indeed,
for any x ? g, we have
Thus, the integral curve of XXx passing through ? at t = 0 is the solution of
the differential equation
with initial condition 77^@) = ?, from which our assertion follows. Finally,
since the image of the exponential map exp : g —> G generates G as a group,
and since the hamiltonian vector field Xf associated to any smooth function
/ ? C°°(g*) is a linear combination of the Xx%,
it follows that the symplectic leaves of g* are precisely the orbits of the coad-
coadjoint action of G. In particular, we recover the well-known fact that the
coadjoint orbits of any Lie group are symplectic manifolds. <C>
Remark A complex Poisson manifold is a Poisson manifold which has a com-
complex structure J which preserves the Poisson bivector w of M:
(J®J)(w) = w.
1.2 Poisson-Lie groups 21
The symplectic leaves of a complex Poisson manifold M are complex sub-
manifolds of M, and their complex and symplectic structures are compatible,
i.e. if uj is the symplectic form, we have u(JX, JY) = u(X,Y) for all tan-
tangent vectors X, Y. This means that each symplectic leaf is a pseudo-Kahler
manifold. A
1.2 Poisson-Lie groups
We now turn to the particular class of Poisson manifolds of interest to us.
A Definitions A Poisson-Lie group is a Lie group and a Poisson manifold,
the two structures being compatible in the following sense.
Definition 1.2.1 (a) A Poisson-Lie group is a Lie group G which has a
Poisson structure { , } such that the multiplication map \x : G x G —> G
(lJL(9i->92) — 9192) of G is a Poisson map (of course, G x G is given the
product Poisson structure).
(b) A homomorphism $ : G —> H of Poisson-Lie groups is a homomorphism
of Lie groups which is also a Poisson map.
Of course, the trivial Poisson structure on any Lie group is a Poisson-Lie
group structure. For a non-trivial example, let 9 be any Lie algebra and give
its dual 9* the Lie-Poisson structure described in 1.1.3. Then g*, regarded
as an abelian Lie group under addition, is a Poisson-Lie group. Moreover, if
I) is another Lie algebra, the homomorphisms of Poisson-Lie groups I)* —> 9*
are exactly the duals of the Lie algebra homomorphisms 9 —> I). (Although
these assertions can be checked directly, they follow immediately from 1.4.1
below.)
Warning If G is a Poisson-Lie group, the inversion map 1 : G —> G (t(g) =
g~l) of G is not a Poisson map unless G has the trivial Poisson structure. In
fact, it follows from 1.2.1 that it is an anti-Poisson map, i.e.
for all fuf2eC°°(G).
Moreover, left translations Lg : G —> G and right translations Rg : G —> G
by elements g e G are not Poisson maps in general. ¦
The condition that a Poisson structure on a Lie group G should be com-
compatible with the group structure in the sense of 1.2.1 can be expressed simply
in terms of the Poisson bivector w of G. In fact, recalling the definition of
the product Poisson structure in F), the condition is
{/1, ftW) = {/1 o Lg, h o Lg}(g') + {A o Rg,,f2 o Rg,}(g)
22 1 Poisson-Lie groups and Lie bialgebras
for all /i, f2e C°°(G), g, g' G G. This is equivalent to
(wgg'i (dfi)ggf ® (df2)gg') = (wg>,d(fi o Lg)g» <g> d(/2 o Lg)g>)
o Rg,)g ® d(/2 o Rg,)g),
which in turn is equivalent to
(8) wggl = {{Lg)'g, ® (Lg)'g>)(wg,) + {{Rg,)'g ® (Rg.)'g){wg).
We have proved
Proposition 1.2.2 A Poisson structure on a Lie group G is a Poisson-Lie
group structure if and only if, for all g, gf G G, the value of its Poisson
bivector at gg' is the sum of the left translate by g of its value at g' and the
right translate by g' of its value at g. |
Taking g and g' equal to the identity element e of G, we deduce
Corollary 1.2.3 The rank of the Poisson structure of a Poisson-Lie group
is zero at the identity element of the group. In particular, the Poisson struc-
structure of a Poisson-Lie group is never symplectic. |
B Poisson homogeneous spaces A Lie subgroup H of a Poisson-Lie group
G is said to be a Poisson-Lie subgroup of G if H is also a Poisson submanifold
of G. In this case, it is clear that H is itself a Poisson-Lie group and that the
inclusion H <-+ G is a homomorphism of Poisson-Lie groups. The quotient
G/H is then called a Poisson homogeneous space.
Proposition 1.2.4 Let G/H be a Poisson homogeneous space. Then G/H
can be given a unique Poisson manifold structure such that the natural pro-
projection map 7T : G —> G/H is a Poisson map.
Proof Define a bivector wG/h on G/H by
where g G G and wq is the Poisson bivector of G. To show that wq/h is
defined, note that
(wG)gh = ((Lgyh ^ (Lgyh)(wG)h + ((Rhyg 0 (Rhyg)(wG)9
by 1.2.2, and that
ix o Lg = Lg o 7T and n o Rh —
1.2 Poisson-Lie groups 23
for g e G, h G H (we use Lg to denote both left translation by g G G on G
and on G/H). Applying ^gh^^gh to tne second term on the right-hand side
of A0) therefore gives (wG)g, while applying it to the first term gives
((Lg)'eH®(LgyeH)(ir'h®ir'h){wG)hj
which vanishes because (wg)h ? T^H ® T^H. This proves that
Define a bracket { , }G/H on C°°(G/H) by
{/i, Me/if (##) = ((™g/h)9h , (d/iU ® (df2)gH}>
From the definition of Wg/Hi one easily shows that
{/l , I2JG/H ° 7T = {/l O 7T , /2 O 7r}G.
From this, and the fact that tt is a submersion, it follows immediately that
satisfies the Jacobi and Leibniz identities. |
The following example exhibits the Hopf fibration as a Poisson homoge-
homogeneous space.
Example 1.2.5 Let G = SU2, the group of 2 x 2 unitary matrices of determi-
determinant one, and let H be the diagonal subgroup of G. The homogeneous space
G/H is diffeomorphic to the Riemann sphere CP1.
Introduce the elements /
F- I ° M F- (
of the Lie algebra SU2, consisting of the 2x2 skew-hermitian matrices of trace
zero. Define a bivector on SU2 by
(WG)g = ((Lgye ® (Lgye - (Rgye ® (i?9)'e)(r),
where r = E&F — F&E. It follows from 2.1.2 that this is a Poisson bivector
(this can also be verified directly). It is easy to check that (Adg®Adg)(r) = 0
when g G H, so that the bivector wq vanishes on H. In particular, H is a
Poisson-Lie subgroup of G.
Let us compute the induced Poisson structure on CP1. It follows from the
definition of wq that the value of Wq/h at 9H, for any g G SU2, is the left
translate by Lg of the bivector
24 1 Poisson-Lie groups and Lie bialgebras
in Ten(GI'H)<g>TeH(GjH). Choose a local coordinate system (x, y) such that
any point near the 'north pole' [1,0] G CP1 has homogeneous coordinates
[l,x -f yf—\y\. Then, for
a b
x —b a
we find that
GTg 0 7Tg)(r — (Ad 0 Ad~1)(r)) = A — \a\2 + \b\2
Note that this vanishes precisely when g ? H. It follows that the induced Pois-
Poisson structure on CP1 has rank zero at the north pole, but is non-degenerate
elsewhere. <C>
We shall return to this example in Section 1.5.
1.3 Lie bialgebras
This section is devoted to the infinitesimal analogues of Poisson-Lie groups,
called Lie bialgebras.
A The Lie bialgebra of a Poisson-Lie group It is natural to ask what
structure on the Lie algebra g of a Lie group G is associated to a Poisson-
Lie group structure on G. In fact, if G is a Poisson-Lie group, there is a
canonical Lie algebra structure on g*: if ?i, ?2 ? 9*> choose /1, J2 ? C°°(G)
with (dfi)e = ?i, and set
A1) [6,&]g-=(d{/l,/2})e.
Assuming for a moment that [ , ]g* is well defined, it is obviously skew-
symmetric and satisfies the Jacobi identity because { , } has the same prop-
properties. That the right-hand side of A1) only depends on ?1? ?2 is a consequence
of the following alternative description of [?i,?2]g*-
Let wR : G —» 9 0 9 be the right translate of the Poisson bivector w of G
to the identity, and let 6 : g —> g 0 9 be the tangent linear map of wR at e.
Then, we have
A2) &,&]„• =«*F
In fact, for any g ? G,
1.3 Lie bialgebras 25
Differentiating this equation at g = e in the direction X ? g, and using the
fact that wR(e) = 0 by 1.2.3, gives
Furthermore, in terms of wR, (8) becomes
wR(gg') = (Ad, ® Adg)(wR(g')) + wR{g).
This means that wR is a 1-cocycle of G with values in g ® g (on which G acts
by the adjoint representation in each factor). Its derivative 6 at e is therefore
a 1-cocycle of g with values in g ® g, i.e.
A3) 6[X, Y] = (adx <S> 1 -f 1 <8> adx)<5(y) - (ady <g> 1 + 1 <g> ady)^(X).
This motivates the first part of
Definition 1.3.1 Let g be a Lie algebra.
(a) A Lie bialgebra structure on g is a skew-symmetric linear map <5g : g —>
g 0 g, called the cocommutator, such that
falj <5* : g* 0 g* —> g* is a Lie bracket on g*,
(a2) 6Q is a 1-cocycle of g with values in g ® g.
(b) A homomorphism of Lie bialgebras p : g —> I) is a homomorphism of Lie
algebras such that
A4) (<p <8> <p) o ?g = fyo<p.
Remarks [1] In this definition, and in the rest of this chapter, Lie algebras
may be defined over any field of characteristic zero, except where stated or
implied otherwise (for example, for Lie algebras of Lie groups, which are
usually regarded as real Lie algebras).
[2] A Lie bialgebra structure is determined by the Lie algebra structures
on g and g*. Thus, we shall sometimes denote the Lie bialgebra by the pair
(g,g*), and sometimes by the pair (g,<5g).
[3] If (g, 6Q) is a Lie bialgebra, so is (g, kSQ) for any scalar k. In particular,
taking k = — 1 gives the opposite Lie bialgebra gop of g.
[4] Condition (al) makes sense even if g is infinite dimensional, since
g*0g* c (g<S>g)*.
[5] The kernel f of a homomorphism of Lie bialgebras p : g —> I) is a Lie
bialgebra ideal of g, i.e. a Lie algebra ideal of g such that <5g(f) C g ® f -f f ® g.
The quotient g/f has a canonical Lie bialgebra structure such that the natural
map g/f —> I) is an isomorphism of Lie bialgebras. The proof is obvious. A
The motivation for part (b) of the definition derives from
26 1 Poisson-Lie groups and Lie bialgebras
Theorem 1.3.2 Let G be a Lie group with Lie algebra g. If G is a Poisson-
Lie group, then g has a natural Lie bialgebra structure, called the tangent
Lie bialgebra of G. If$:G^Hisa homomorphism of Poisson-Lie groups,
and 1) is the tangent Lie bialgebra of H, the derivative of $ at the identity
element e of G is a homomorphism of Lie bialgebras g —> I).
Conversely, if G is connected and simply-connected, every Lie bialgebra
structure on g is the tangent Lie bialgebra of a unique Poisson structure on
G which makes G into a Poisson-Lie group. Moreover, if <p : g —> I) is a
homomorphism of Lie bialgebras, and H is a Poisson-Lie group with tangent
Lie bialgebra \), there is a unique homomorphism <I> : G —> H of Poisson-Lie
groups with <J>'e = ip.
PROOF We have shown above that the Lie algebra of a Poisson-Lie group
has a natural Lie bialgebra structure. The condition that a homomorphism
<I> : G —> H is a Poisson map is
A5) {&g®Vg){wG)g = (wH)Hg)
for all g ? G. Using 1.2.3, we find that the derivatives of the left- and right-
hand sides of this equation at g = e are (ip <8> ip) o SQ and 6^ o <^, respectively,
whence ip satisfies A4).
For the converse, we use the fact that, if G is connected and simply-
connected, every 1-cocycle of g with values in g ® g can be 'integrated' to
a unique 1-cocycle of G with values in g ® g (see Bourbaki A972)). It follows
immediately that, with these assumptions on G, every Lie bialgebra struc-
structure on g comes from a unique Poisson-Lie group structure on G. Further, if
(p : g —> I) is a homomorphism of Lie bialgebras, there is a unique homomor-
homomorphism of Lie groups <I> : G —> H such that <J>'e = ip. To show that <I> is also a
Poisson map, we must show that A5) holds. For this, it suffices to note that
both sides define 1-cocycles of G with values in I) ® I), and, by the previous
argument, their associated Lie algebra cocycles are equal. |
Remark A complex Poisson-Lie group is a complex Lie group such that the
tangent Lie bialgebra structure SQ : g —> g ® g is complex linear. Theorem
1.3.2 holds as stated for complex Poisson-Lie groups and Lie bialgebras.
One must beware, however, that complex Poisson-Lie groups are not com-
complex Poisson manifolds unless the Poisson bracket is identically zero! In fact, if
J is the complex structure of G, differentiating the condition (J®J)(wG)g =
{wg)9 for a complex Poisson manifold at g = e, we see that (J ® J) o SQ = 6Q.
But, for a complex Poisson-Lie group, the left-hand side is equal to SQ o J. A
B Manin triples The definition we have given of a Lie bialgebra (g, g*)
conceals the fact that g and g* play a symmetric role. This is revealed by the
following definition, which we shall see is equivalent to 1.3.1.
1.3 Lie bialgebras 27
Definition 1.3.3 A Manin triple is a triple of Lie algebras (p,p^,p-) to-
together with a non-degenerate symmetric bilinear form ( , ) on p invariant
under the adjoint representation ofp, such that
(i) p+ and p_ are Lie subalgebras ofp,
(ii) p = p+0p_ as vector spaces,
(Hi) p+ and p_ are isotropic for ( , ).
Proposition 1.3.4 For any finite-dimensional Lie algebra g, there is a one-
to-one correspondence between Lie bialgebra structures on g and Manin
triples (p.p^.p-) such that p+ — g.
Proof If (g, g*) is a Lie bialgebra, we set p+ = g, p_ = g*, and take the
inner product on p = g 0 g* determined by
A6) (X,OP = (X,O, (X,X)p = (?,Op = 0
for X G g, ? G g*. For the converse, the inner product determines an isomor-
isomorphism of vector spaces p_ = p+, and hence a Lie algebra structure on p+.
Thus, both parts of the proposition follow from the following lemma. |
Lemma 1.3.5 Suppose that g and its dual space g* are Lie algebras, and
define an inner product on g0 g* by A6). There is a Lie algebra structure on
g 0 g* (direct sum of vector spaces) such that g and g* are Lie subalgebras
and which leaves the inner product invariant if and only if (g, g*) is a Lie
bialgebra, and in this case the Lie algebra structure is unique.
Proof Choose a basis {Xr} of g, and let {?r} be the dual basis of g*.
Suppose that
[Ar,Xs\ = crsXt, If ,f ] = 7t € •
(Throughout the proof, summation over repeated indices is understood.) To
determine [fr,Xs], we use the fact that the bilinear form ( , ) on g 0 g* is
invariant under g and g*. This implies that
so that the g-component of [?r,Xs] is —7j>tX$. Similarly, the g*-component
is c?tf*, so that
[f ,XS\ = cstf -7S Xt.
Note that the bracket on g 0 g* is uniquely determined. We must prove
that it satisfies the Jacobi identity if and only if the dual SQ of the Lie bracket
on g* is a 1-cocycle on g with values in g ® g. Clearly, 6Q(Xr) = 7^X5 <S> Xt.
Hence, the cocyle condition
69([Xr,Xs}) = Xr.69(Xs) - Xs.69(Xr)
28 1 Poisson-Lie groups and Lie bialgebras
can be written
r1 ^ab X 6d Xu — >ypq X (X 6?) X ) — >ypq X ( X (9) X )
Equating coefficients of Xa 0 X^ the cocycle condition is
(-\7\ r1 rvab — ra ^Pb j_ J> rvaQ _ ra ^Pb _ J> ^aQ
V-1-1/ ^rs /^ ^rp is i^ ^rg /s ^sp ir ^sq ir '
On the other hand, to verify the Jacobi identity for the bracket on g0g*,
we must show that
[^ , [Ar, AsjJ -h [As, [4 , Arjj + [Ar, [As,4 JJ = U,
together with a similar relation involving two ?'s and one X. Expanding the
left-hand side, we get
4.
= 0.
Equating coefficients of ^p gives a relation equivalent to the Jacobi identity in
g; equating coefficients of Xp gives a relation which is easily seen, on suitably
re-naming the indices, to be equivalent to A7). Similarly, the other Jacobi
relation in g 0 g* is equivalent to A7) together with the Jacobi identity in
Remark If dim(g) = oc, the formulations in 1.3.1 and 1.3.3 are not equivalent.
If (p,p+,p_) is a Manin triple with p+ = g, the Lie bracket on p_ induces
a map pi —> (p_ ® p_)*. This gives a Lie bialgebra structure on g provided
that it maps g C p!_ into g 0 g C pi 0 pi C (p_ ® P-)*. A
C Examples The definition in terms of Manin triples is very convenient for
constructing examples of Lie bialgebras.
Example 1.3.6 Let G be a Lie group with the trivial Poisson structure. Its
tangent Lie bialgebra (g, g*) is obtained by giving g* the zero Lie bracket.
Dually, let g be a finite-dimensional abelian Lie algebra. Then, the Lie bial-
bialgebra structures on g are in one-to-one correspondence with the Lie algebra
structures on g*. 0
Example 1.3.7 Let g be the two-dimensional non-abelian Lie algebra. Then,
every skew-symmetric linear map <5:g—>g(g)gisa Lie bialgebra structure on
1.3 Lie bialgebras 29
g, but, up to isomorphism and scalar multiples, there are only two distinct
non-trivial structures. Indeed, one can choose a basis {X, Y} of g such that
[X,Y] = X; then 6(X) = aX A Y, 8{Y) = CX A Y for some scalars a, C
(X AY means I®7-70l). If a ± 0, setting X' = X, Y' = Y - ? X
gives <S(X') = al; A Y'\ 6(Y') = 0 and [X', F'] - Xf. It is easy to check that
in both cases we do indeed have a Lie bialgebra structure. Drinfel'd A987)
calls the second structure the 'non-degenerate' case, but this should not be
confused with our use of this term in the next chapter. <)
Example 1.3.8 Let g = q(A) be the Kac-Moody algebra associated to a
symmetrizable generalized Cartan matrix A. We use the notation in the
Appendix. There is a unique Lie bialgebra structure on g, called the standard
structure, with cocommutator
A8) W) = 0, «(A) = 0, 6(X?)=diX?AHi.
Uniqueness is immediate from the cocycle property of 8 and the fact that the
Hi, Di and Xz generate g as a Lie algebra. To prove the existence of this
Lie bialgebra structure, we use Manin triples.
Let p = g0g (direct sum of Lie algebras), let p+ be the diagonal subalgebra
of p, let
p_ = {(#, y) ? b_ 0 b+ 11)—component of x + y is zero},
and define an inner product on p in terms of the standard inner product ( , )g
on g by
for x, #', 2/, y' G g. Using the facts that g = b+ + b_, I) = b+ D b_ and n±
are isotropic for ( , )g, it is easy to check that (p,p+,p_) is a Manin triple.
Thus, if dim(g) < oc, it follows that g = p+ has a Lie bialgebra structure. In
fact, the following computation of the cocommutator 6 shows, in view of the
remark at the end of Subsection 1.3B, that this is true even if dim(g) = oc.
The first equation in A8) follows from the equation
F{Hi,Hi), (X,Y) ® (X',Y')) = -(Hu [X,X']) + (Hh [?,?'}) = 0
for X, X; G b+, y, 7' €b_, which in turn follows from the fact that (f),n±) =
0. The proof of the second equation is similar. Finally, we must have 8(X^~) =
X^~ AH for some H G I), since the only elements of g which have non-zero inner
product with X+ are multiples of X~, and since the equation [X, X'} = X+
can be satisfied with X, X' e b+ only if X, X' e C.X+ + I). To determine
H, we compute both sides of the equation
, l(o,xn, {H3,-H3)})
p.
30 1 Poisson-Lie groups and Lie bialgebras
This gives
2d71(H,Hj) = d-1aji,
from which it follows that H — \diHi. Thus, the standard structure can be
obtained from the Manin triple (p.p^.p-) by multiplying the inner product
on p by two.
As we shall see in the next chapter, these are not the only Lie bialgebra
structures on g (up to isomorphism and scalar multiples), even when g =
sh (C). They are characterized by the fact that the two-dimensional Lie
subalgebras bf of g spanned by H\, Xf1, equipped with the non-degenerate
Lie bialgebra structure of 1.3.7 (suitably normalized), are sub-Lie bialgebras
of g (i.e. the inclusions bf <—> g are homomorphisms of Lie bialgebras). <)
Example 1.3.9 Let a be a finite-dimensional complex simple Lie algebra, and
set g = a[u] = a ® C[tx], where u is an indeterminate. The Lie bracket on g is
defined pointwise (viewing g as the space of polynomial maps C —> a). Fix an
invariant inner product ( , )a on a, and let t e a ® a be the Casimir element,
i.e. t corresponds to the identity element id e End(a, a) = a* ® a under the
isomorphism a* = a induced by ( , )a. Define 6 : g —> g ® g by
A9) S(f)(u,v) = (ad/(u) ® 1 -f 1 <8> adf(v)) (^
Note that, although the right-hand side of A9) appears to be a rational
function of u and v with a pole along u — i>, it is actually a polynomial
because
(adx ® l + l®adx)(?) = 0
for all X ? a (this is equivalent to the a-invariance of ( , )a).
The corresponding Manin triple is (a ((it)), a [u], a [[w]]), i.e. p+ = g,
p_ is the space of formal power series in u~x with coefficients in a, and
p = p+0p_. The inner product on p is
here 'reso' means the u~l coefficient.
This example is related to the quantum groups called Yangians, which we
all study in Chapter 12. <)
Example 1.3.10 Let g be a Lie algebra with non-trivial centre 3, and assume
that [g, [g, g]] 7^ 0. Then, g has a family of non-trivial Lie bialgebra structures
given by
= ZA[X,Y],
for any Y G g, Z G 3. It is straightforward to check that this does define a
Lie bialgebra structure on g (this is most easily seen using 2.1.2).
1.3 Lie bialgebras 31
For example, we can take g to be the Virasoro algebra Vir, the central
extension (with one-dimensional centre) of the Lie algebra VectEx) of smooth
complex vector fields on the circle 51 defined by the 2-cocycle
This means that Vir = Vect(S1) 0 (C.c as a vector space, where the element
c is central and
Example 1.3.11 Let i/;DO be the vector space of formal pseudo-differential
operators of the form P = Ylk™-ooPk(@)Dk, where the pk lie in the space
CooE1) of smooth functions on the circle and D = d/dO. The residue of P
is defined by res(P) = p~\.
Leibniz's rule provides an associative algebra structure on tpDO: from
Do f = df/dO -f/oD (where / and df/dO G CooE1) are regarded as
multiplication operators), we obtain D o / = f o D~x — D~l o & oD,
and hence by iteration
We regard i\)DO as a Lie algebra in the usual way: [P , Q] = PoQ-QoP. It
is clear that the subspaces DO of differential operators and INT of integral
operators (i.e. those formal series involving no negative powers of D, or only
negative powers of D, respectively) are subalgebras of i\)DO.
There is a derivation V of i\)DO such that V(Dk) = 0 for all k and
fc=i
Formally, the right-hand side of this equation is obtained by 'integrating
[D, /] with respect to D\ so V may be thought of as 'log(D)'.
The formula
w(P,Q) = / res{V(P)oQ)d6
Jo
is a 2-cocycle on ipDO, and thus defines a central extension i\)DO of ipDO by
adjoining a central element c. (This is a generalization of the central extension
in the preceding example: it is easy to see that the restriction of u to the
subalgebra of ipDO consisting of the smooth vector fields, i.e. the elements
32 1 Poisson-Lie groups and Lie bialgebras
of tpDO which are homogeneous of degree 1 in D, isjjjnultiple of the cocycle
considered in 1.3.10.) The derivation V extends to ipDO by setting V(c) = 0,
and we let g be the semidirect product tpDO X CD.
Let g± be the subalgebras of g defined by g+ = ?>O0(C.c, g_ = INT®<?.V.
We then have g — g+ 0 g_ as vector spaces. Further, the formula
,2tt
(Pi + AiP -f flic, P2 + A2?> + fjL2c) = 2 res (Pi o P2) dO + Ax/i2 + A2/ii
Jo
defines a non-degenerate invariant symmetric bilinear form on g for which g±
are isotropic subspaces. Hence, (g,g+,g_) is a Manin triple.
There is a group G_ which, formally at least, has g_ as its Lie algebra. An
element of G_ is a formal expression P = (l + Ylk=-ooPk{Q)DkH Da, where
a ? JR. The multiplication in G_ is defined by
k
Taking a = 0, we obtain a subgroup with Lie algebra INT, while the tangent
vector at D° = 1 to the one-parameter group a i—>• Da is formally given by
(d/da)\a=0(Da) =log(D) =V.
Thus, 1.3.2 suggests that G_ should have a Poisson-Lie group structure
whose tangent Lie bialgebra is g_. Khesin & Zakharevich A992) have shown
that this is formally the case, and that the required Poisson structure on G_
is (a generalization of) the so-called 'second Adler-Gel'fand-Dickii' Poisson
structure, which is of central importance in the theory of soliton equations.
See, for example, Gel'fand & Dickii A976) and Adler A979). 0
D Derivations An automorphism of a Lie bialgebra (g, g*) is a Lie algebra
automorphism a : g —> g such that a* : g* —> g* is also a Lie algebra
automorphism. Thus, it is natural to make the following definition.
Definition 1.3.12 A derivation of a Lie bialgebra (g,g*) is a linear map
D : g —> g such that D is a derivation of § as a Lie algebra, and D* is a
derivation of g* as a Lie algebra.
If D is a derivation of a finite-dimensional Lie bialgebra (g, g*), then etD is
a one-parameter group of automorphisms of (g, g*). This follows immediately
from the corresponding statement for Lie algebras.
The purpose of this subsection is to observe that every Lie bialgebra has a
canonical derivation (which may be zero).
Proposition 1.3.13 Let (g, 6) be a Lie bialgebra, and let D : g —> g be
the composite of the cocommutator 6 : g —> g <S> g and the Lie bracket [ , ] :
g 0 g —> g. Then, D is a derivation of (g, 6).
1.4 Duals and doubles 33
Proof Let x, y ? g and write
Then, using the cocyle property of <5, we have
-f
by the Jacobi identity. The first term on the right-hand side of the last
equation is [D(x),y], the second [x,D(y)].
This proves that D is a derivation of g. Applying the preceding argument
to g* instead of g proves that D* is a derivation of g*. |
Examples 1.3.14 For the trivial Lie bialgebra structure on a Lie algebra g,
we have D = 0.
For the standard Lie bialgebra structure on a complex simple Lie algebra
g, we find that D = ad//, where H is the element of the Cartan subalgebra
\) of g such that (a*, H) = —Adi for all simple roots a* {—\H corresponds to
the sum of the positive roots of g under the isomorphism g = g* induced by
the standard invariant bilinear form on g - see the Appendix).
For the Lie bialgebra structure on the polynomial Lie bialgebra a[u] defined
in 1.3.9, D = d/du. <}
1.4 Duals and doubles
A Duals of Lie bialgebras and Poisson-Lie groups The formulation
in terms of Manin triples shows that the notion of a Lie bialgebra is self-
dual. In fact, if (p,p+,p_) is a Manin triple, it is obvious that (p,p-,p+)
is one too (with the same inner product). It follows that, if g is a finite-
dimensional Lie bialgebra, so is g*, and that g** = g as Lie bialgebras. In
view of 1.3.2, there is a contravariant functor G —» G* on the category of
connected, simply-connected (finite-dimensional) Poisson-Lie groups, such
that G** = G, covering the functor g —> g* on the level of tangent Lie
bialgebras. In general, a Poisson-Lie group G* with tangent Lie bialgebra g*
is called, following Drinfel'd, a dual Poisson-Lie group of G.
34 1 Poisson-Lie groups and Lie bialgebras
Here is a simple example of a dual of a Poisson-Lie group; we give some
more interesting examples later in this section.
Example 1.4-1 From 1.3.6, it follows that a dual of the trivial Poisson struc-
structure on a Lie group G is given by the vector space g*, regarded as an abelian
Lie group under addition, with the Lie-Poisson structure of 1.1.3. <)
B The classical double As well as showing that the notion of a Lie bial-
gebra is self-dual, the formulation in terms of Manin triples also shows that,
if (g,g*) is a Lie bialgebra, there is a Lie algebra structure on g 0 g* which
leaves invariant the natural inner product. In fact, more is true.
Proposition 1.4.2 Let (g,g*) be a finite-dimensional Lie bialgebra. Then
there is a canonical Lie bialgebra structure on g 0 g* such that the inclusions
into the two summands are homomorphisms of Lie bialgebras.
With this Lie bialgebra structure, g 0 g* is called the double of g, and is
denoted by V(§). By 1.3.2, there is a corresponding notion of the double
V{G) of a Poisson-Lie group G.
Proof Let r G g (8> g* C T>{q) ® ?>(g) correspond to the identity map g —> g.
The cocommutator of g 0 g* is defined by
$v(u) — (adu ® id -f id ® adM)(r)
for all u G T>{q). We shall prove in 2.1.11 that this is a Lie bialgebra structure
on T>{q). Let us verify that it has the stated properties.
With the notation used in the proof of 1.3.5, and using the summation
convention, we have r = Xt ® ?*, so that
= c?stXp
since the remaining terms cancel after interchanging the summation indices
p and t.
Comparing with the proof of 1.3.5, we see that 6^(X3) = 6q(X3), so that
the inclusion g ^-> T>(§) is a homomorphism of Lie bialgebras. The proof for
the inclusion (g*)op ^-> T>(q) is similar. |
Example 1.4-3 The Lie bialgebra structure on a symmetrizable Kac-Moody
algebra g defined in 1.3.8 can almost be realized as a double, as follows. With
the notation in 1.3.8, let q = g 0 I) (direct sum of Lie algebras) and
c\± — {(#> h) G q | x G b±, ± h = I)-component of x}.
1.4 Duals and doubles 35
Note that q± = b±. Define an inner product on q by
As in 1.3.8, it follows from the orthogonality properties of the inner product
on g that (q, q+, q_) is a Manin triple. Thus, we have Lie bialgebra structures
on q± and onP(q+) = g©I). The cocommutator can be found by a calculation
similar to that in 1.3.8: one finds that 6^^ = 0 and
Thus, 0 © 1) is a Lie bialgebra ideal of ?>(q+), and since ?>(q+)/@ © I)) = g as
Lie algebras, we have a Lie bialgebra structure on g given by
= ±diX?AHi, 6^ = 0.
Multiplying by two gives the standard structure. 0
We shall now show that the complex simple Lie algebra g, regarded as a real
Lie algebra, is exactly the double of a Lie bialgebra structure on its compact
real form.
C Compact Poisson—Lie groups Let G be the complexification of a con-
connected, simply-connected compact Lie group K. The Lie algebra g of G is
then a complex semisimple Lie algebra, and we shall assume that it is actually
simple. Moreover, if t is a maximal abelian subalgebra of the Lie algebra I
of K, then I) — t © \/=Tt is a Cartan subalgebra of g, b = \/—It © n+ is a
solvable (real) Lie subalgebra of g, and g = I © b as (real) vector spaces. In
terms of the standard (C-basis {-Hi}i=i,...,n U {^alaeA+ °f 9 described in the
Appendix, we can take f to be the IR-linear span of the set
i,...^ U {Ea}aeA+ U {Fa
where Ea = X+ - X~, Fa = y/^iX* + X~). Then, {x/^ffi^i,...^ is an
IR-basis oft, and f is generated by {v^~T-Hri?-^al?-^al}i=i,...,n-
For example, if K = SUn+i then g = s/n_|_i((C), I) is the diagonal matrices
in s/n_(-i((C), t is the matrices in I) with purely imaginary diagonal entries, and
n_(- is the strictly upper triangular matrices in g.
Returning to the general case, set p = g, regarded as a real Lie algebra,
p_i_ = f and p_ = b. As inner product on p, we take
36 1 Poisson-Lie groups and Lie bialgebras
the imaginary part of the standard inner product on g. Using the formulas
for this inner product given in the Appendix, and the above bases, it is easy
to check that
and it follows immediately that (p, p_|_, p_) is a Manin triple. This defines Lie
bialgebra structures on g, f and b, and Poisson-Lie group structures on G, K
and the connected subgroup B of G with Lie algebra b. Thus, G is a double
of K and B is a dual of K.
The Lie bialgebra structure <5r on g defined in this way can be computed
explicitly by the method used to calculate the standard Lie bialgebra structure
6 in 1.3.8. We find that <5r = y/^16. The presence of the factor \/^l
guarantees that this Lie bialgebra structure takes f into I ® I. In fact,
«R(ffi) = 0, SR(Eat) = diEat 0 y/^lHi, S^{FaJ = diFa% <g> V^T^-
Remark It is shown by Ginzburg and Weinstein A992) that B is isomorphic
as a Poisson manifold to the Lie-Poisson structure on f* defined in 1.1.3. The
proof uses cohomological techniques.
Of course, B and f* are not isomorphic as Poisson-Lie groups, since f* is
abelian and B is not. A
We shall study compact Poisson-Lie groups further in Subsection 1.5C,
where we shall describe their symplectic leaves.
1.5 Dressing actions and symplectic leaves
Having introduced several examples of Lie bialgebras in the preceding sec-
sections, we now study the geometrical properties of the associated Poisson-Lie
groups. The main tool needed to describe their symplectic leaves is an action
on the groups of their dual groups.
A Poisson actions We remarked in Subsection 1.2A that, if G is a Poisson-
Lie group, left translations by elements of G do not usually preserve the
Poisson structure of G. However, they do define Poisson actions of G on
itself in the sense of the following definition.
Definition 1.5.1 Let G be a Poisson-Lie group and M a Poisson manifold.
A left action A : G x M —> M of G on M is called a Poisson action if A
is a Poisson map, G x M being given the product Poisson structure. Right
Poisson actions are defined similarly.
Thus, left (and right) translations in a Poisson-Lie group G are Poisson
actions of G on itself. More generally, let H be a Poisson-Lie subgroup of G.
1.5 Dressing actions and symplectic leaves 37
Then, by 1.2.4, the homogeneous space G/H has a unique Poisson structure
such that the natural projection tt : G —> G/H is a Poisson map. The natural
left action of G on G/H is a Poisson action. Indeed, this follows immediately
from the following commutative diagram, in which the horizontal arrows are
the natural actions of G on itself and on G/H, since all the arrows other than
the map G x G/H —> G/H are already known to be Poisson maps:
GxG > G
idXTT 7T .
G x G/H > G/H
B Dressing transformations and symplectic leaves The Poisson ac-
actions which are of most interest to us in this section arise from the notion of
the double of a Poisson-Lie group, introduced in Subsection 1.4B.
Let G be a connected Poisson-Lie group, let G* be its connected, simply-
connected dual Poisson-Lie group, and let V(G) be the connected, simply-
connected double of G. (Without the assumption of simple-connectedness,
the following constructions can be carried out locally in a neighbourhood of
the identity of the groups concerned.) By 1.3.2 and 1.4.2, there are homo-
morphisms of Lie groups
G ^ V(G) <-- G*
lifting the inclusion maps
g ^ P(g) ^ g*
of Lie algebras. Thus, we can define a product map G x G* —> ?>(G), which
is a diflFeomorphism onto a neighbourhood of the identity in *D(G). We shall
assume from now on that this map is a (global) diffeomorphism of G x G*
onto T>(G). This holds, for example, if G is compact and the image of G* in
T*(G) is closed (see Lu & Weinstein A990) for the simple proof). (Again, even
if this hypothesis is not satisfied, the constructions we are going to make can
still be carried out locally.) We shall identify V(G) with G x G* as a manifold
from now on, and denote by prG : V(G) —» G and prG* : V(G) —> G* the
projections onto the two factors.
If g G G and 7 G G*, the product 7.G in *D(G) can be factorized
7 • 9 = 91 • 7g
for some g1 G G, j9 G G*. If 71, 72 G G*, we can compute 71.72 . g G V(G)
in two ways; this gives
38 1 Poisson-Lie groups and Lie bialgebras
Projecting onto G shows that the map
A : G* x G -> G
defined by
A(#,7) =?7
is a left action of G* on G. (Similarly, we get a right action of G on G*.)
Definition 1.5.2 The right action ofG* on G given by
for g G G, 7 G G*, is called the dressing action of G* on G.
One of the most important geometric applications of dressing transforma-
transformations is to the determination of the symplectic leaves in Poisson homogeneous
spaces. We begin with the case of Poisson-Lie groups.
Proposition 1.5.3 The dressing action ofG* onG is a Poisson action whose
orbits are exactly the symplectic leaves of G. |
Corollary 1.5.4 The symplectic leaf of G passing through g G G is the
image under prG of the left coset G* . g in T>(G).
Proof This follows immediately from the proposition, together with the
definition of the dressing action. |
The dressing action gives a simple characterization of Poisson-Lie sub-
subgroups of a given Poisson-Lie group.
Proposition 1.5.5 A closed Lie subgroup H of a Poisson-Lie group G is a
Poisson-Lie subgroup of G if and only if H is invariant under the dressing
action of G* on G. |
It follows that, if H is a Poisson-Lie subgroup of a Poisson-Lie group G,
then the dressing action of the dual Poisson-Lie group G* on G induces a
right action of G* on G/H. We have the following generalization of 1.5.3.
See Semenov-Tian-Shansky A985) for a proof.
Theorem 1.5.6 Let H be a Poisson-Lie subgroup of a Poisson-Lie group
G. Then, the dressing action of the dual Poisson-Lie group G* of G on G/H
is a (right) Poisson action, and its orbits are exactly the symplectic leaves of
G/H. |
1.5 Dressing actions and symplectic leaves 39
C Symplectic leaves in compact Poisson—Lie groups Our aim in this
subsection is to apply the results on dressing transformations we have just de-
described to determine the symplectic leaves of the compact Poisson-Lie groups
K described in Subsection 1.4C, and of certain of their Poisson homogeneous
spaces. We use the notation introduced in Subsection 1.4C.
Recall that the product map K x B —> G is a (global) diffeomorphism (see
Helgason A978)). Hence, by 1.5.4, the symplectic leaf of K passing through
k e K is the image of the left coset Bk under the projection prK ofG = KxB
onto K. To describe this more explicitly, let B+ = TB = BT and recall the
Bruhat decomposition of G into double cosets modulo B+ :
G=
wew
(See Helgason A978) again.) Here, w runs through the Weyl group W =
N(T)/T of K, where N(T) is the normalizer of T in K (as usual, we do not
distinguish between an element of N(T) and its coset modulo T). Since W
normalizes T, the Bruhat decomposition is equivalent to
G = JJ tBwB.
For each w E W, let Y,w be the symplectic leaf prK(Bw); it is clear that
Y*w C BwB. The most general J5-orbit in G is of the form tBwb for t E T,
w e W and b G B, and its projection onto K is obviously t.T,w. Thus, we
have:
Proposition 1.5.7 The symplectic leaves of K are parametrized byWxT.
The leafT>w with parameter (w, 1) is the projection of Bw C G = K x B onto
K; that with parameter (w,t) is t.T>w. The symplectic leaft.T,w is contained
in the piece Kw = K n B+wB+ of the Bruhat decomposition of K. |
We can give a still more explicit description of Ew, but we first discuss the
simplest example K = SU2. Since the Weyl group of SU2 has two elements
{±1}, the symplectic leaves are parametrized by the disjoint union of two
circles. Those associated to the identity element 1 are the single points
t 0
0 r1
for t G 51 = {t G C I |?| = 1}; those associated to —1 are the two-dimensional
discs
The zero-dimensional leaves form a common 'binding circle' for the 2-dimen-
sional leaves ('pages'); see Fig. 2.
40
1 Poisson-Lie groups and Lie bialgebras
identify
to get
S
*•••••••••••••••••••?*
two-dimensional
leaves
circle of
zero-dimensional
leaves
Fig. 2 Symplectic leaves in SU2
Returning to the general case, recall from the Appendix that, for each i =
1,... ,n, there is a subalgebra g(^ ^ g isomorphic to 5/2(C). This restricts
to a homomorphism SU2 ^ f, which lifts to a homomorphism ipi : SU2 —> if-
As we shall see shortly, the ipi are homomorphisms of Poisson-Lie groups (for
(/9j, one should use the inner product on the Lie algebra SU2 induced from a
fixed inner product on f). Let ?$ = <^(?_]_). Then, we have
Proposition 1.5.8 (a) ?$ = T,St, where Si is the simple reflection corre-
corresponding to the simple root oli .
(b) If w is an arbitrary element of the Weyl group, and
w =
is an expression for w of minimal length as a product of simple reflections,
then
In particular, dim(Ew) = 2?(w). |
We now consider certain homogeneous spaces of K, specifically its coadjoint
orbits. The most general coadjoint orbit is diflFeomorphic to G/P = K/KnP,
where P is some (closed) Lie subgroup of G containing B+. We claim that
K D P is a Poisson-Lie subgroup of K. The assertion made before 1.5.8 is
the special case where P is the subgroup with Lie algebra
where g_az is the root space corresponding to the root — c^. To prove the
claim, let k G K n P and b e B, and write bk = k'V for some k' e K,bf ? B.
1.5 Dressing actions and symplectic leaves 41
Then,
prK(bk) = k' = bk(b')-1 ? K n P.
Thus, K n P is invariant under the dressing action of B on if and hence, by
1.5.5, is a Poisson-Lie subgroup of K.
Proposition 1.5.9 Every coadjoint orbit O of K has a canonical Poisson
structure such that the natural map K —> O is a Poisson map. Moreover, if
O = G/P, where P is a Lie subgroup of G containing J5+, the decomposition
ofO into its symplectic leaves coincides with the Schubert cell decomposition
of G/P:
G/P = |J BwP/P,
where Wp is the Weyl group of P.
Proof The first part follows immediately from 1.5.6. For the second part,
we simply recall that the Bruhat decomposition of G induces the following
decomposition of G/P:
G/P= (J B+wP/P= (J BTwP/P= (J BwP/P,
wew/wP
and that the pieces BwP/P of this decomposition are topological cells (see
Helgason A978)). |
Warning These Poisson structures on the coadjoint orbits are not symplectic,
in general. In particular, they are not the same as the (symplectic) Poisson
structures described in 1.1.3. Khoroshkin, Radul & Rubtsov A993) show that
the Poisson structures given by 1.1.3 and 1.5.9 are compatible, in the sense
that any linear combination of them is also a Poisson structure, if and only
if O is a hermitian symmetric space. ¦
To illustrate 1.5.9, we return to the example K = SU2. Up to diffeo-
morphism, there are two types of coadjoint orbit, namely single points and
2-spheres. Let O be any 2-sphere orbit. The projection map tt : SU2 —> O =
SU2/T is the Hopf fibration, (cf. 1.2.5). There are two symplectic leaves in
(9, a single point, say N (the 'north pole'), and the complementary 2-disc
0\{N}. The map tt sends each zero-dimensional leaf in SU2 to N, and maps
each two-dimensional leaf Dt diffeomorphically onto 0\{N}, preserving the
symplectic structures.
D The twisted case The Poisson-Lie group structure on a compact group
K we have described is not the only one (up to a scalar multiple), except in the
case K = SU2- In fact, we have the following result, which is a consequence
of the classification of the Lie bialgebra structures on complex simple Lie
algebras described in Chapter 3.
42 1 Poisson-Lie groups and Lie bialgebras
Proposition 1.5.10 Let <Sr : f —> I® I be the tangent Lie bialgebra structure
of the Poisson-Lie group structure on the compact group K defined above.
Then, for any a G 1R and any u G A2(t), the formula
defines a Lie bialgebra structure on i. Conversely, every Lie bialgebra struc-
structure on i is isomorphic to 6ajU for some a, u. |
The results proved above dealt with the case a ^ 0, u = 0. We now
summarize briefly the corresponding results in the remaining cases.
First, suppose that a and u are both non-zero. By regarding u G t0t
as a linear map t* —> t and using the standard inner product, we obtain an
endomorphism u of t. For any element w of the Weyl group W, let
tw = (u — w~1uw)(t),
and let Tw = exp(tw) be the corresponding subgroup of T.
Proposition 1.5.11 Let K be a compact Lie group with the Poisson-Lie
group structure defined by 6ajU, where a and u are non-zero. Then, iftET
and w G W, the symplectic leaf passing through the point t.w G K is Tw.t.Y*w,
where Ew is as in 1.5.7. The leafTw.t.Y*w is contained in the piece Kw of the
Bruhat decomposition. |
Remark For generic u and w ^ 1, the symplectic leaf Tw.t.T,w is equal to Kw
if n is even, and dense in Kw if n is odd. In particular, there is always a
symplectic leaf which is dense in K (namely, that associated to the longest
element wq of the Weyl group W). A
Consider finally the case a = 0, u ^ 0. The symplectic leaves are now unre-
unrelated to the Bruhat decomposition. To describe them, let n be the orthogonal
complement of t in f with respect to the standard inner product. Then we
have
f*=t*0n*,
with the understanding that linear functionals on t or n are extended to f by
making them vanish on the complementary subspace. If ? e T, we denote by
(?, u) the element (f <g> id)(w) G t.
Proposition 1.5.12 Let K be a compact Lie group with the Poisson-Lie
group structure defined by 6q,u, where u G A2(t) is non-zero. Then, the
symplectic leaf passing through a point k G K is
1(O, «» | ? € I*}.
1.6 Deformation of Poisson structures and quantization 43
(Here, if u = ?r tr ® t'r, with tr, tfr G t, then (?, u) = ?r (& tr)t'r.) I
Remark The double of K in this case is the semidirect product KIX f *, where
K acts on the additive group f* by the coadjoint representation Ad*. A
1.6 Deformation of Poisson structures and
quantization
In this section we give a brief introduction to the formulation of quantization
as deformation of Poisson structure, due to Moyal A949). Since our main
aim is to motivate the study of deformation of Hopf algebras in Chapter 6,
we shall not attempt to be completely precise.
A Deformations of Poisson algebras If A is an associative algebra, a
deformation of A is a family of bilinear associative maps
*h : A x A —> A,
depending on a parameter h, such that *o is the given multiplication of A.
Ideally, we would like */j to depend smoothly or analytically on h in some
sense. However, most of the algebras A one is interested in deforming are
infinite dimensional, in which case even the meaning of 'smooth' or 'analytic'
is problematic. Thus, we shall ignore such difficulties by considering only
formal deformations. This means that we treat h as an indeterminate and
expand *^ in a formal power series
oo
a\ */i fl2 — / hn7rn[ai, a2)
71 = 0
for certain bilinear maps ?rn : A x A —¦»¦ A. The associativity of *^ is equivalent
to
^2 7rrGrs(aua2),a3) = ^ 7rr(ai,7rs(a2,a3))
r-\-s=n r+s=n
for all ai, a2, a3 G A and all n > 0.
Now suppose that A is a commutative Poisson algebra, i.e. A is commuta-
commutative as an algebra, and, in addition to its associative algebra structure, A is
equipped with a skew-symmetric bilinear map { , } : A x A —> A, the Poisson
bracket, which satisfies the Jacobi identity
{au {a2, a3}} + {a2, {a3, ai}} + {a3, {aua2}} = 0
and the Leibniz identity
2, a3} = ai{a2, a3} -f {ai, a3}a2
44 1 Poisson-Lie groups and Lie bialgebras
(cf. (l)-C); of course, the algebra of C°° functions on any Poisson manifold
is a Poisson algebra). Then, we say that *^ is a Poisson algebra deformation,
or quantization, of A if
di *h a2 - a2 *h Q>i f , f , , v
= {ai,a2} (mod h).
= {ai,a
This makes sense because
a\ *h a2 = ai<22 (mod h)
so that
a>i *h &2 — U2 *h &i = 0 (mod h)
because A is commutative.
We shall have much more to say about Poisson algebra deformations in
Chapter 6, but to justify this definition, and to give an important example,
we turn now to the interpretation of quantization in terms of deformation
theory.
B Weyl quantization The case of interest in the study of quantization
is A = C°°(M), where M is a Poisson manifold. In Chapter 6, we shall be
interested in the case where M is a Poisson-Lie group, but for now we consider
only the simplest case M = 1R2 with coordinates p, q and the (symplectic)
Poisson structure
We can interpret M as the phase space of a single particle moving along the
real line, with position q and momentum p.
Quantum mechanics textbooks tell us that to quantize this system, one
wants to associate to the coordinate functions p and q of IR2 self-adjoint
operators P and Q on some Hilbert space TL such that the commutator
[P,Q} = PQ-QP is given by
B1)
¦Hi
where h is 1/2tt times Planck's constant. More generally, one would like to
associate to any real-valued function / on IR2 a self-adjoint operator F on TL
such that [Fi,F2] is, in some sense, approximately the same as the operator
associated to the Poisson bracket {/i, f2} (we have already mentioned in the
Introduction that 'approximately' cannot be replaced by 'exactly' here).
Equation B1) means that P and Q determine a hermitian representa-
representation <j) of the three-dimensional Heisenberg Lie algebra I), the vector space
0 V^T^ © R with the Lie bracket
2,a),(yi,y2,&)] = @,0,
1.6 Deformation of Poisson structures and quantization 45
namely
(/>(xi,X2,a) = xiP + x2Q - V-
Under mild assumptions, (f) can be 'exponentiated' to a unitary representation
$ of the Heisenberg group H, the space R©R®R with multiplication
Note that H has one-dimensional centre, spanned by c = @,0,1).
The quantization procedure of Weyl A927) is essentially to extend $ to
the group algebra of H. More precisely, for a function f(p, q), Weyl takes the
associated operator to be
JJ ? dr),
where
( 1 \2 ff
= ( 2?r ) //
is the Fourier transform of /. The operator $(/) is, at least formally, self-
adjoint if / is real-valued, and is well-defined and of trace class if / is in
the Schwartz space 5AR2), i.e. if / is C°° and decreases, together with all
its derivatives, faster than the reciprocal of any polynomial at infinity. Of
course, one wants to define $(/) for /'s more general than this (for example,
for the coordinate functions p and q\). If / is C°° and grows, together with
all its derivatives, at most polynomially at infinity, then $(/) will in general
be a densely defined unbounded operator.
Every unitary representation of H on a Hilbert space H on which the central
element c acts as exp(—\/—T/i)id^ is isomorphic to a direct sum of copies of
the representation on the space L2(]R) of square-integrable functions tp of q
given by
In this representation, to the coordinate functions p and q are associated the
operators —\f^\hdjdq and multiplication by g, respectively. More generally,
the operator associated to any polynomial / in p and q is the differential
operator obtained by replacing each monomial prnqn in / by the average,
over all orderings of the m + n terms, of the product of m differentiation op-
operators — y^lhd/dq and n operators of multiplication by q. The map $
is one-to-one on the space of functions / which do not grow too fast at
infinity.
46 1 Poisson-Lie groups and Lie bialgebras
C Quantization as deformation Moyal A949) interpreted the Weyl quan-
quantization procedure as a deformation of the algebra A = C°°(]R2). In fact, he
computed the product *^ on A such that
*(/i */> h) = *(/i)*(/2)
as follows (h is now treated as an indeterminate). The right-hand side is given
by
mQ))
x d^driid&dm-
The product of the two exponentials may be written as a single exponential
by using the Baker-Campbell-Hausdorff formula for H. This is quite simple
since [I), [I), I)]] = 0; one finds that
exp^exp^) - exp(X! + X2 + \[XUX2})
for Xi, X2 € I). Writing ? = ?i + ?2, ^ = 771 + 772, the integral therefore
becomes
B2)
////¦
If we now expand the exponential exp[\/—Tft(?i^2 ~~ ?2^1)/2] in powers of ?1,
771, ?2 and 772, we find that
where, for any / E C°°(]R2), and any r, s > 0, we set
When we perform the integrals in B2) over ?1 and 771, we therefore find the
convolution of f['r and f?s, i.e. the Fourier transform of the product fi^f^-
It follows that
r,s=(
Bibliographical notes 47
This equation can be written more concisely by regarding the Poisson
bracket B0) as a bidifferential operator II acting on C°°(]R2) x C°°(]R2) by
Then, writing n°(/i, /2) for the ordinary product /1/2, the preceding equation
is equivalent to
n=0
i.e.
B3) h *h h = exp ( -^n I (A, f2).
It is clear that *^ is a deformation of the associative algebra C°°(]R2) in
the sense of the definition given at the beginning of this section, for
/1 *h h = /1/2 (mod ft)
and, since $ is one-to-one, the associativity of *^,
/1 */i (h *h fs) = (/1 *h /2) *h /3,
follows from the associativity of multiplication of the operators
and
The Moyal bracket { , J^ on C°°(]R2) is the Lie bracket defined by the
multiplication *^:
{flj2}h = fl*hf2-f2*h fl-
flit is clear from the formula for *^ given in B3) that
{fit f2}h r n n ^ / , , x
-1—j^J- = {fij2} (mod ft).
Thus, the product *^ w a Poisson algebra deformation o/C°°(]R2) ty^ft the
Poisson bracket B0).
The discussion we have given can be generalized from ]R2 to arbitrary
symplectic manifolds (see the notes below), but for our purposes we need not
pursue this discussion any further (see, however, Subsection 6.2C).
48 1 Poisson-Lie groups and Lie bialgebras
Bibliographical notes
1.1 The general notion of a Poisson manifold was introduced by Lie A888-
93). In this work, Lie also defined the Lie-Poisson structure on the dual of
a Lie algebra, and gave the proof of 1.1.2 for Poisson structures of constant
rank; the general case is due to Kirillov A976). For further information on
Poisson manifolds in general, see Weinstein A983). For the application of
Poisson and symplectic manifolds in hamiltonian mechanics, see Abraham &
Marsden A978) and Arnold A978).
1.2 The basic references for Poisson-Lie groups are Drinfel'd A983a,b), in
which they are called Hamilton-Lie groups, and Semenov-Tian-Shansky
A985). Further details may be found in Kosmann-Schwarzbach & Magri
A988) and Lu & Weinstein A990). There are a number of generalizations
of the notion of a Poisson-Lie group: for quasi-Poisson-Lie groups, see
Kosmann-Schwarzbach A991b), and, for symplectic groupoids, see Coste,
Dazord & Weinstein A987) and Weinstein & Xu A992).
1.3 The basic references for this subsection are the same as those mentioned
in the previous paragraph.
1.4 The notion of the double of a Lie bialgebra is a special case of that of
a matched pair of Lie algebras, introduced by Takeuchi A981). A pair of
Lie algebras (possibly infinite dimensional) is matched if there is a weakly
non-degenerate pairing between them, and if they act on each other in a
'compatible' fashion. If each Lie algebra is the dual of the other, and both
actions are coadjoint actions, one recovers the situation discussed in this
section. See also Majid A988).
For further information on compact Poisson-Lie groups, see Lu & Weinstein
A990).
1.5 For the proofs of 1.5.3, 1.5.5 and 1.5.6, see Semenov-Tian-Shansky A985)
and Lu & Weinstein A990), which also contain further information about
Poisson actions and dressing transformations.
The description we have given of the symplectic leaves in a compact Lie
group G is due to Vaksman & Soibelman A988) in the case of SU2, and
\jM & Weinstein A990), Levendorskii & Soibelman A991a) and Soibelman
A991a) in the general case. For the results on the 'twisted' structures see
Levendorskii A990, 1992) and Levendorskii & Soibelman A991a).
1.6 The transition from functions on phase space to operators on a Hilbert
space is, of course, basic to quantum mechanics. The formulation we have
given appears in Weyl A927). Its interpretation in terms of a deformation of
the algebra structure on the space of functions is due to Moyal A949).
It is natural to ask whether the Poisson algebra deformation of C°°(]R2)
described in Section 1.6 is the only one. The work of Vey A975), Bayen et
al. A978), Lichnerowicz A981, 1982), and others, has shown that the Moyal
Bibliographical notes 49
deformation is indeed the only one, at least if one imposes some reasonable
conditions on the deformations one is willing to consider. In the other di-
direction, de Wilde & Lecomte A988) have extended the construction of the
deformed product to arbitrary symplectic manifolds. For more recent work
on Poisson deformations, see Rieffel A989, 1990a,b), Huebschmann A990)
and Karasev & Maslov A993).
2
Coboundary Poisson-Lie groups
and the
classical Yang-Baxter equation
As we mentioned in the Introduction, the existence of a quantization of a Lie
group G implies the existence of a Lie bialgebra structure on its Lie algebra g.
We recall from Chapter 1 that a Lie bialgebra structure on g is a linear map
6 : g —> g®g, which is, among other things, a 1-cocycle. Among the 1-cocycles
of g with values in g 0 g are the 1-coboundaries, for which S(X) = [X , r] for
some r e g 0 g. An element r E g 0 g defines a Lie bialgebra structure in this
way if and only if the symmetric part of r is a g-invariant element of g 0 g,
and the expression
[[r,r]} = [r12,r13] + [ri2,r23] + ha,^]
is a g-invariant element of g 0 g 0 g. (The meaning of 7*12 etc. is fairly obvi-
obvious, but will be explained in Section 2.1.) The latter condition is satisfied, in
particular, if [[r,r\] = 0: this is the classical Yang-Baxter equation (CYBE).
The CYBE first appeared explicitly in the literature on integrable hamilto-
nian systems, but it is a special case of the Schouten bracket in differential
geometry, introduced in 1940.
These results are proved in Sections 2.1 and 2.2, in which we also re-examine
the examples of Lie bialgebras given in Chapter 1 to see which of them are
coboundary.
In the final Section 2.3, we show the importance of the CYBE in the study
of classical hamiltonian systems, where it plays the role of an integrability
condition. We illustrate the discussion with an example of Toda lattice type.
2.1 Coboundary Lie bialgebras
A Definitions We recall from 1.2.4 that a Lie bialgebra structure on a Lie
algebra g is a linear map 6 : g —> g 0 g, its cocommutator, which satisfies the
following conditions:
(a) 6 is skew-symmetric,
2.1 Coboundary Lie bialgebras 51
(b) 6* : g* 0 g* —> g* is a Lie bracket on g*,
(c) 8 is a 1-cocycle.
(As in the previous chapter, the Lie algebras we consider are assumed to be
defined over any field of characteristic zero, except where stated or implied
otherwise.)
From now on, we shall write the action of an element X E g on an element
v of a representation V of g as X.v, provided the action is understood. Thus,
the cocycle condition (c) is
6({X,Y]) = X.8(Y)-Y.6(X)
for all X, Y E g, with the adjoint action in each factor of the tensor product
g 0 g understood.
Among the 1-cocycles of g with values in g 0 g are the 1-coboundaries, for
which
A) S(X) = X.r
for some r E g 0 g and all X E g.
Definition 2.1.1 A coboundary Lie bialgebra is a Lie bialgebra g whose
cocommutator is a 1-coboundary.
Proposition 2.1.2 Let § be a Lie algebra and let r E g 0 g. The map 6
defined by A) is the cocommutator of a Lie bialgebra structure on g if and
only if the following conditions are satisfied:
(i) r*i2 + ?i is a g-invariant element of g 0 g,
(ii) [[r, r]] = [ri2, ri3] + [n2, r23] + [n3, r23] is a g-invariant element
(The action of g on g 0 g and on g 0 g 0 g is by the adjoint representation in
each factor.)
Before proving this result, let us explain the notation. Suppose that
B) r
for some a^, bi E g. Then in (i), 7*12 is simply r, while
is obtained by applying to r the flip cr of the two factors in the tensor product.
In (ii), we have
r23] = V'ai0aj0[&iJ
52 2 Coboundary Poisson-Lie groups and the CYBE
Remarklt is obvious from A) that, if r E g®g defines a Lie bialgebra structure
on g, and if r' E g 0 g differs from r by a g-invariant element, then r' defines
the same Lie bialgebra structure as r. By condition (i) in 2.1.2, it follows
that every coboundary Lie bialgebra can be obtained from a skew-symmetric
r. A
We now turn to the proof of 2.1.2.
Proof The proof that r satisfies (i) if and only if the map 6 defined by A)
satisfies condition (a) above is completely straightforward. To prove that (ii)
is equivalent to (b) (in the presence of (a)), we first introduce some notation.
For any linear map 8 : g —> g 0 g, and any X ? g, let
c.p.
where c^c ' means the sum of the term which follows the summation sign
and the two similar terms obtained from it by cyclic permutation of the factors
in the tensor product g 0 g 0 g. If we define a bracket on g* by
then, since
it is clear that [ , ]g* satisfies the Jacobi identity if and only if Jac^ is the
zero map. It therefore suffices to prove
Lemma 2.1.3 Let g be a Lie algebra and let r ? g 0 g have ^-invariant
symmetric part. Define 6 : g —> g 0 g by A). Then
C) Jac6(X)+X.[[r,r]] = 0
for all leg.
Proof By direct computation, making repeated use of the invariance prop-
property of r and the Jacobi identity in g. If we write out the left-hand side of C)
explicitly, we find that Jac$(X) is a sum of twelve terms and that A\[[r, r]] is a
sum of nine terms. After rearranging the terms suitably, we obtain, using the
expression B) for r and with a summation over repeated indices understood,
[[X, ai],aj] 0 bi 0 bj + [[X, ai],bj] 0 6,0 clj + [X, [a*, a,]] 0 b{ 0 bj
, bi] 0 [au clj] 0 bj + [X, a,i] 0 [b^ clj] 0 6^
i] 0 a,- 0 [ai? fy] + [X, a*] 0 dj 0 [&*, fy]
+ [ai? fy] 0 [X, &*] 0 aj + [au dj] 0 [X, bi] 0 fy
2.1 Coboundary Lie bialgebras 53
+[di,dj] <8> bj <8> [X,bi] + [a^aj] <8> 6* <8> [X,&,]
+a^ <g> [[X, a*],fy] <8>6i H- a,- (8) [aubj] (8) [X,6*] + a, <8> [X, [&*,%]] (8) b3
+di <8> [bi, dj] (8) [X, fy] + a» (8) [X, dj] (8) [&«, fy] + a* (8) %• (8) [X, [bi, bj]]
+bj (8) 6i (8) [[X, a*], a,-] + fy (8) [X, &*] (8) [ai? dj]
+bi (8) [[X, a*], a,j] (8) &j + &i (8) aj (8) [[X, a^], 6^].
Interchanging the indices i and j in the first term and using the Jacobi identity
in g, the sum of the first three terms becomes
-dj <8> &i <8> [[X, ai],bj] - bj (8) h (8) [[X, a,], a,-].
Next, the sum of the fourth and fifth terms is
-(A (8) adaj )([X, bi] (8) a*+[X, a,] (8) bi)) (8) fy
= (A (8) adaj )(a, (8) [X, bi] + &i (8) [X, a*])) (8) ^j
= a, (8) [aj, [X, 6^]] (8) fy + ft« (8) [%•, [X, a^]] (8) ftj,
using the invariance property
X(ai(8)&i + fti(8)ai) = 0.
Similarly, the sum of the sixth and seventh terms becomes
di (8> dj (8> [bj, [X, bi]] + ft* (8> a^ (8) [ftj, [X, a*]],
and that of the eighth and ninth terms
-bj (8> [X, bi] (8> [a», dj] - aj (8> [X, bi] (8) [a«, fy].
Finally, the sum of the tenth and eleventh terms is obviously zero (inter-
(interchange the indices i and j in one term).
Inserting these results, we find that the expression on the left-hand side of
C) can be written in the form X^(a« ®ui + h <8>^), where u^ Vi G 9. In fact,
m = [[X, aj], 6J ® 6j + [X, [bi, aj]] <g> ^ + [flj, [X, 6J] ® 6^-
+ [djM] ® [^, 6j] + [6i,flj] ® [X, 6j]
+ [X, dj) ® [6i} fej] - ^ ® [[X, dj], bi] - [X, 6j] ® [flj-, 6i]
+ flj (8) [X, [&*, 6j]] + dj (8) [6j, [X, 6^]].
On the right-hand side, the sum of the first three terms is zero by the Jacobi
identity in g, and that of the next two terms is zero by the skew-symmetry
of the Lie bracket in g. The sum of the next three terms is
A (8) ad6J([X, dj] (8) bj+bj (8) [X, dj] + [X, bj] (8) a3)
= -A ® adfcJK ® [X, bj]) = -a,- ® [6i, [X, ^]],
54 2 Coboundary Poisson-Lie groups and the CYBE
using the invariance property of r again. Hence,
m = aj ® ({X, [bu b3}} + [bjt [X, h}} - [bu [X, bj]]),
which vanishes by the Jacobi identity in g. A similar, but shorter, argument
proves that Vi = 0. |
Remarks [1] We have already observed that, in considering coboundary Lie
bialgebras, we may restrict attention to skew-symmetric elements r. It is
not hard to show that in this case [[r, r]] is skew too (i.e. [[r, r]] E /\ 9 if
re A2 9)-
[2] An argument similar to that used to prove the lemma shows that, if r,
s ? 9 0 9 are such that r is skew and s is ^-invariant, then [[r -f s, r -f s]] =
[[rir]] + [Is > S]]- This result will be used later.
[3] Two coboundary Lie bialgebras 91 and g2 defined by r\ E 91 0 91 and
^2 E 92 0 92 are isomorphic if and only if there is an isomorphism of Lie
algebras a : 91 —> 92 such that (a 0 a)r\ — r2 is 92-invariant. A
B The classical Yang—Baxter equation Of course, the simplest way to
satisfy condition (ii) in 2.1.2 is to assume that
This is the classical Yang-Baxter equation (CYBE). A solution of the CYBE
is often called a classical r-matrix, the terminology deriving from the example
9 = End(V), where V is a vector space, in which case r E End(V 0 V) may
be viewed as a matrix. A (coboundary) Lie bialgebra structure which arises
from a solution of the CYBE is said to be quasitriangular; if it arises from a
skew solution of the CYBE, it is said to be triangular. This terminology is
borrowed from the 'quantized' situation, discussed in Chapter 4.
The following result will be needed later. Its proof, like that of 2.1.2, is
elementary, and we leave it to the reader.
Proposition 2.1.4 Suppose that (9, 8) is a quasitriangular Lie bialgebra,
where 8 is given by A) for a solution r E 9 0 9 of the CYBE. Let p : 9* —> 9
be the linear map associated to r by
where ?, 77 E 9*. Then, p is a homomorphism of Lie algebras (q* has the Lie
algebra structure defined by 8*). |
More generally, suppose that 9 is equipped with a non-degenerate symmet-
symmetric bilinear form ( , ), invariant under the adjoint action of 9. Then, there is
a canonical 9-invariant element of /\ 9*, namely
D) (X,Y,Z)^([X,Y],Z).
2.1 Coboundary Lie bialgebras 55
If, in addition, dim(9) < oo, we can identify 9 and 9* as representations of 9,
so we obtain a canonical 9-invariant element u) of f\ 9. Then condition (ii)
in 2.1.2 will be satisfied if
E) [M] = -w.
This is the modified classical Yang-Baxter equation (MCYBE). It is clear that
the CYBE is the limiting case of the MCYBE as the bilinear form ( , ) on 9
'tends to infinity'.
There is a close relationship between the solutions of the CYBE and those
of the MCYBE. The bilinear form may be regarded as an element of (9^9)* —
9* 0 9*, and hence, using the isomorphism 9 = 9*, as an element ? € 9 <g) 9 (t
is called the Casimir element). Then t is 9-invariant and symmetric, and a
simple computation shows that
F) [[*,«]] =w-
Remark [2] following the proof of 2.1.2 implies that r is a skew-symmetric
solution of the MCYBE if and only if r -\-t is a solution of the CYBE. (This
is the reason for the choice of sign in E).)
C Examples We shall now interpret the examples of Lie bialgebras given in
Chapter 1 in the light of 2.1.1.
Example 2.1.5 If 9 is abelian, only the trivial Lie bialgebra structure is
coboundary. <C>
Example 2.1.6 We saw in 1.3.7 that the two-dimensional non-abelian Lie
algebra 9 has, up to isomorphism and scalar multiples, exactly two non-trivial
Lie bialgebra structures. Choosing a basis {X, Y} of 9 such that [X, Y] = X,
the structures are given by
and
6(X) = X A y, 6(Y) = 0.
The first structure is coboundary (in fact, triangular): it arises from the
solution r = Y A X of the CYBE. The second structure is not coboundary.
Example 2.1.7 If 9 is a finite-dimensional complex simple Lie algebra, every
1-cocycle of 9 with values in any finite-dimensional representation of 9 is
a coboundary by Whitehead's lemma (see Jacobson A962), page 77). In
particular, every Lie bialgebra structure on 9 is coboundary. In fact, since
56 2 Coboundary Poisson-Lie groups and the CYBE
g has, up to a scalar multiple, exactly one non-degenerate invariant bilinear
form, it follows from the remarks at the end of the preceding subsection that
every Lie bialgebra structure on g is quasitriangular.
For the standard Lie bialgebra structure defined in 1.3.8, the r-matrix can
be defined as follows. Let t be the Casimir element of g <S> g, and write
t = ?_| + to + t |_, where to ? 1) ® I), ?_| G n+ 0 n_ and t |_ Gn_0n+.
Then the standard structure is defined by
It is quasitriangular but not triangular. We postpone the proof of these
assertions until after 2.1.11.
The description of the Lie bialgebra structures given in 1.3.8 is valid for
any symmetrizable Kac-Moody algebra g. However, the element r which
should serve as the r-matrix is now given by an infinite sum of elements of
g ® g. Drinfel'd describes g as 'pseudotriangular' in this case. The example
of (untwisted) affine Lie algebras is discussed in 2.1.10. <C>
Example 2.1.8 We mentioned in 1.3.8 that the standard structures on a
finite-dimensional complex simple Lie algebra g do not exhaust the (non-
trivial) Lie bialgebra structures on g. To illustrate this, we shall describe all
the Lie bialgebra structures in the simplest case g = 5/2 (C).
It suffices to find elements r ? f\2 sl2(<E) such that [[r,r]} ? f\3 sl2(<E) is
s/2(C)-invariant. But since sl2((E) is simple and dim (/\ sfaity) — 1, the
whole of (\ 5/2(C) is s/2(C)-invariant. Thus, condition (ii) in 2.1.2 imposes
no condition on r. Furthermore, j\ sl2 (C) is isomorphic to the adjoint rep-
representation of 5/2(C) (the isomorphism is given by the Lie bracket), so the
5/2 (C)-invariant part of f\ sl2 (C) is zero. Hence, the Lie bialgebra structures
on 5/2 (C) are parametrized by the three-dimensional vector space f\ sl2 (C).
Moreover, it is not difficult to check that r satisfies the CYBE if and only if,
when r is regarded as an element of sl2((E), we have det(r) = 0. The solutions
of the CYBE thus form a quadric cone in /\ sl2((E).
By Remark [3] following the proof of 2.1.2, the Lie bialgebra structures
defined by ri, r2 ? /\ sl2 (<C) are isomorphic if and only if there exists an
automorphism a of sl2((E) such that r2 — (a®a)ri is s/2((C)-invariant. By the
discussion in the preceding paragraph, this is possible only if r2 — (a <g) a)r\.
Since every automorphism of sl2(<E) is given by the adjoint action of some
element of the group SL2((E), we see that the isomorphism classes of Lie
bialgebra structures on sl2((E) are parametrized by the orbits of the adjoint
action of SL2(<E) on sl2(<E). These orbits are of three types:
(i) The one-parameter family of non-zero semisimple orbits, represented by
A 0
0 -A
2.1 Coboundary Lie bialgebras 57
for A G (Cx. This corresponds to
where
+ _/o i\ x-_(o o
x -\o oj' x -
These are multiples of the standard structure.
(ii) The single orbit consisting of the non-zero nilpotent elements, represented
by X+. This corresponds to
where
1 0
H- \o -i
which is a skew solution of the CYBE, and defines a triangular Lie bialgebra
structure on 5/2 (C).
(iii) The orbit consisting of the zero element, corresponding to the trivial
structure r — 0. <C>
Example 2.1.9 Let g = a[ix], where a is a finite-dimensional complex simple
Lie algebra and u is an indeterminate. In 1.3.9 we defined a Lie bialgebra
structure on g. Formally, this arises from the r-matrix
G) r=—L-,
where t G a ® a is the Casimir element. Here, we view g ® g = a[ix] <8> a[u] =
(a 0 a)[ixi, U2] as the space of polynomials in ui, 112 with coefficients in a ® a.
Of course, r is not a polynomial, i.e. r does not lie in the algebraic tensor
product g®g. Nevertheless, it gives rise, as we have seen in 1.3.9, to a genuine
Lie bialgebra structure on g. In fact, this structure is pseudotriangular, for r
satisfies the CYBE. Indeed, this is an easy consequence of the relations
[*12, *13 + *23] = [*23, *12 + *13] = 0,
which follow from the fact that t is invariant under the adjoint action of a.
The r-matrix in G) is the simplest rational solution of the CYBE. We shall
discuss the classification of such rational solutions in Chapter 3, and shall
meet the r-matrix in G) again in Chapters 12 and 16. 0
58 2 Coboundary Poisson-Lie groups and the CYBE
Example 2.1.10 Suppose that g is the untwisted affine Lie algebra associated
to a complex simple Lie algebra a. We recall from the Appendix that
g = a [u, u'1} 0 (C.c 0 <C.D
as a vector space, where c is central and
for / ? a[u, u'1]. The Lie bracket on g is given in terms of that of a by
[/, g}(u) = [/(«), g(u)} + res0
where ( , ) is an invariant inner product on a, and 'reso' means the u~l
coefficient.
To describe the standard Lie bialgebra structure on g, one checks first that
(/ + Ac + /xD, g + ?c + rjD) = reso(f(u), g(u)) + Xrj + ^
is a non-degenerate invariant inner product on g. Hence, in the notation of
2.1.7, we have
and, since
n%=na±@u±1a[u±1],
we have
where {X\} is an orthonormal basis of a. Formally, this gives the standard
r-matrix of g in terms of that of a by
_ 1
2
As in the previous example, we see a rational function of u\ and U2 with a
pole along U\ — U2. 0
D The classical double The following result will enable us to justify 2.1.7
and to complete the proof of 1.4.2.
2.2 Coboundary Poisson-Lie groups 59
Proposition 2.1.11 Let g be a finite-dimensional Lie bialgebra. Then, the
double 22 (g) of g is a quasitriangular Lie bialgebra.
PROOF The Lie bialgebra structure of 22(g) was defined in 1.4.2 (although
we have still to prove that it is a Lie bialgebra structure). We continue to
use the notation introduced in the proofs of 1.3.5 and 1.4.2.
Thus,
[[r, r]] = ]T([XS, X?] ® ?' ® ?* + ** ® [Z°,Xt] ® e + Xs ® Xt ® [?*, ?*])
s,t,p
After suitably re-naming the indices, and using the skew-symmetry property
(?st = _cfs, we find that [[r,r]\ = 0.
The X)(g)-invariance of the symmetric part of r is also easily checked; in
fact, the symmetric part of r is half the Casimir element of 22(g) 0 22(g). |
We can now prove the assertions made in 2.1.7, using the fact, proved
in 1.4.3, that the standard Lie bialgebra structure on a complex simple Lie
algebra g can 'almost' be realized as the double 22(b+). With the notation in
the Appendix, the r-matrix of V(q+) is
da(X+,0)
To get the r-matrix of g, we must project onto g®g and then multiply the
result by two, since the Lie bialgebra structure on 22(q+) induces \ that on
g. Thus,
2=1
This is the r-matrix written down in 2.1.7. Note that it follows from 2.1.11
without further calculation that rQ satisfies the CYBE.
2.2 Coboundary Poisson-Lie groups
In this section, we describe the special properties of those Poisson-Lie groups
whose tangent Lie bialgebras are coboundary.
60 2 Coboundary Poisson-Lie groups and the CYBE
A The Sklyanin bracket If g is a finite-dimensional coboundary Lie bial-
gebra, its cocommutator is given, for X e g, by
S(X) = (adx 0 1 + 10 adx)(r),
where we may and shall assume, without loss of generality, that r G g0g
is skew-symmetric (see the remark following 2.1.2). If G is a Lie group with
Lie algebra g, to describe the Poisson structure on G associated to 8 we must
'integrate' 8 to a 1-cocycle of G with values in g 0 g. But this is easy: it is
trivial to check that
wR(g) = (Adg 0 Adg)(r) - r
has the correct derivative at the identity element of G and the cocycle prop-
property
wR(gg') = (Ad5 0 Adg)(wR(g')) + wR(g)
for g, g' ? G. We recall from Section 1.2 that the Poisson bivector wg ?
Tg(G) 0 Tg(G) is the right translate of wR(g) to g, and that the associated
Poisson bracket is given, for /i, /2 € C°°(G), by
Hence, we have proved
Proposition 2.2.1 Let G be a finite-dimensional Lie group with Lie algebra
g. Suppose that rG/\ g defines a Lie bialgebra structure on g via A). Then
the corresponding Poisson-Lie group structure on G is given by
(8)
Remark A Poisson bracket of the form (8) associated to a skew-symmetric
r-matrix is called a Sklyanin bracket on G. A
It will be useful to express (8) a little more explicitly. Let {Xs} be a basis of
g and let {X^} (resp. {XR}) be the corresponding left (resp. right) invariant
vector fields on G. Then, if
s,t
we have
2.2 Coboundary Poisson-Lie groups 61
Remark We can be even more explicit if G = GLn(JR) (or, more generally,
if G is a matrix group). Let t^ be the matrix entries in GLn(R), regarded
as functions on GLn(JR). The Poisson bracket is clearly determined by the
brackets of these matrix elements. We find that
XL(tl3) = (TXJJ, XR{tl3) =
where T = (Uj). It follows that
tkb ~ riakbtajtw).
a,b
One usually writes
so that the preceding equation can be written
This is the basic equation of classical inverse scattering theory. See Section
2.3. A
An element r G g®g gives rise to other Poisson structures on G, as the
following proposition shows.
Proposition 2.2.2 Let G be a finite-dimensional Lie group with Lie algebra
g. Let r e Q<g)Q be skew-symmetric. Using the above notation, define, for f\,
(9)
s,t
Then the following are equivalent:
(i) { , }L is a Poisson structure on G,
(ii) { , }R is a Poisson structure on G,
(Hi) r is a solution of the CYBE.
PROOF This follows immediately from
62 2 Coboundary Poisson-Lie groups and the CYBE
Lemma 2.2.3 Let {Va} be any finite set of (smooth) vector fields on a Lie
group G, and define
{fij2}V =
for /i, f2 € C°°(G), where the constants pa$ satisfy pa$ = -pPa. Then,
+ {V-yfl)(Vaf2)([VS,Vf,]f3)).
PROOF Straightforward, making use of the skew-symmetry of the coefficients
Pa0. i
Remark The Poisson bracket { , }L (resp. { , }R) on G arising from 2.2.2
is left (resp. right) invariant, in the sense that left (resp. right) translations
are Poisson maps G —> G. However, neither of these Poisson brackets is a
Poisson-Lie group structure on G (unless r — 0). A
B r-matrices and 2-cocycles The following corollary of 2.2.2 gives an
interesting alternative geometric interpretation of the CYBE. It applies to
elements r G 9<8>9 which are non-degenerate, which means that the associated
linear map 9* —> 9 is a vector space isomorphism.
Corollary 2.2.4 Let G be a finite-dimensional Lie group with Lie algebra
9, and let r ? 9 ® 9 be skew-symmetric and non-degenerate. Then, r is a
solution of the CYBE if and only if the inverse of the isomorphism 9* —> 9
induced by r, regarded as a bilinear form on 9, is a 2-cocycle.
We recall that a bilinear form a; on a Lie algebra 9 is a 2-cocycle if
for all X, y, Z e 9.
Proof By 2.2.2, r satisfies the CYBE if and only if (9) defines a left-invariant
Poisson structure on G. It is clear that the Poisson bivector of (9) is every-
everywhere non-degenerate if and only if the matrix (rst) is invertible. As we
mentioned in Section 1.1, a non-degenerate Poisson structure is the same
thing as a symplectic structure. Finally, a left-invariant symplectic form on
G is determined by its value at the identity element of G, which is a 2-cocycle
on 9. I
Of course, there exist non-zero elements r ? 9 <g) 9 which are both skew and
non-degenerate only if dim (9) is even. Apart from this, it might be thought
that non-degeneracy is not a serious restriction. If one is looking for solutions
of the CYBE, however, this is not so. For example, we have
2.2 Coboundary Poisson-Lie groups 63
Proposition 2.2.5 If g is a finite-dimensional complex semisimple Lie alge-
algebra, every skew-symmetric solution of the CYBE in g 0 g is degenerate.
PROOF Fix a non-degenerate invariant symmetric bilinear form ( , ) on g.
Suppose for a contradiction that r G g <g) g is non-degenerate, skew-symmetric
and satisfies the CYBE. Let u be the 2-cocycle on g associated to r by 2.2.4.
Since ( , ) is non-degenerate, we can write uj{X,Y) — (?(X),Y) for some
linear map C : g —> g. One checks that the cocycle property of a; is equivalent
to C being a derivation of g. As g is semisimple, C is an inner derivation, i.e.
C(X) = [L,X] for some L G g and all X G g. But then L lies in the kernel of
a;, contradicting non-degeneracy. |
On the other hand, non-degeneracy can always be achieved by passing to
a subalgebra:
Proposition 2.2.6 Let g be a finite-dimensional Lie algebra, and let r G g<8>g
be a skew-symmetric solution of the CYBE. Then there is a Lie subalgebra
go of g such that r lies in go <8) go and is non-degenerate when regarded as an
element of this subspace of g <g) g.
PROOF If r is non-degenerate there is nothing to prove. So let m > 1 be
the dimension of the kernel of r, regarded as a skew-symmetric bilinear form
on g*. Then it follows from elementary linear algebra that we may choose a
basis
{Xi,..., Xn, Y\,..., Yn, Z\,..., Zm)
of g such that
2=1
We must show that the linear subspace go of g spanned by the Xi and Yi for
1 < i < n is a Lie subalgebra of g.
Since r satisfies the CYBE, we have
i®Yj - [XUYO] 0 Y% 0 X3 - [Y^Xj] 0 X%
+ Xi 0 [Yi,Xj] 0 Yj -Xi® [Yi,Yj] ® Xj
- x2 0 y, 0 [y2,x,] - y2 ® x3 ® [xj5y2] + y2 0 y, 0 [x^x,-]) - 0.
Suppose, for example, that [Xi, Xj] in the first term in the sum involves some
Zk- A moment's inspection shows that none of the other eleven terms involves
Zk 0 Yi (g) Yj, which is a contradiction. |
We conclude this section with a very interesting application of the idea of
2.2.4 to the problem of constructing Lie bialgebra structures on the infinite-
dimensional Lie algebra of vector fields on the circle.
64 2 Coboundary Poisson-Lie groups and the CYBE
Example 2.2.7 Witten A988a) attempts to construct Lie bialgebra structures
on the Lie algebra VectjRE1) of smooth real-valued vector fields on the circle
S1 by inverting 2-cocycles uj on VectjRE1). Note that, for the proof of 2.2.4 to
go through in this infinite-dimensional situation, uj must be non-degenerate
in the strong sense, that the linear map VectRE1) —> VectRE1)* induced by
uj must have a well-defined inverse.
The first observation is that a 2-cocycle uj on Vect^S1) can be non-
degenerate only if it is a coboundary. The dual space VectRE1)* is a space of
quadratic differentials on S1 (pairing a vector field and a quadratic differential
gives a 1-form, which can be integrated over S1). Then, a; is a coboundary if
there is a quadratic differential <]> such that
for all X,Y ? VectRE1). If we write X = f(d/d0), Y = g(d/d0), <$> =
Lpd9(&d9, where /, g and ip are functions on 51, we find, after an integration
by parts,
A0) u>(f,g)=
The most general 2-cocycle is obtained by adding to A0) a term cjfg'"d9
for some c G IR (see Kirillov A976)). The kernel of the resulting cocycle is
the space of solutions of the differential equation
A1) cg'" + 2<pg' + <p'g = 0
which have period 2tt. One may argue heuristically, with Witten, that if c ^ 0
and (f = 0, the only periodic solutions of A1) are g — constant, so the kernel
has dimension 1. But the dimension modulo 2 of the kernel of a skew form is
a topological invariant, so if c ^ 0 the kernel has dimension 1 or 3 for all (p.
For a rigorous argument, see Kirillov A976).
We assume from now on that c — 0. We must also assume that (p has
at least one zero, for otherwise g — (p~1/2 is a solution of A1) and so u is
still degenerate. With this assumption, the map VectRE1) —> VectRE1)*
induced by u, which is given by
A2) u(g) = 2<pg' + <p'g,
is injective. To prove surjectivity, we must solve, for any given ^, the differ-
differential equation
<p'g =
i.e.
A3)
2.2 Coboundary Poisson-Lie groups
65
Formally, the inverse of u; is therefore the map r : VectRE1)* —> VectRE1),
given by
A4)
The preceding argument is only heuristic, partly because the existence of
zeros of tp makes it unclear whether A4) makes sense, and partly because
we have been too vague about the definition of the space VectRE1) and its
dual. In fact, a closer analysis shows that there are obstructions to making
the argument rigorous.
It turns out to be easier to work, at least in the first instance, with a space
Vect(cE1) of complex vector fields on S1. The precise definition of Vect(cE1)
is as follows. For any a > 1, we consider the space Va of holomorphic vector
fields on the annulus Aa = {z G C | 1 < \z\ < a}, provided with the compact-
open topology. Then, Vect(cE1) is the direct limit of the Va as a tends to
1.
Changing coordinates from 6 to z = e^~^e, A3) becomes
A5)
d
We assume that, for some a > 1, (p has no zeros in Aa. Because of the
presence of square roots, we must work on the double cover Aa of Aa. Let zo
be any fixed point of Aa. Then the solution of A5) can be written
A6)
dw +
where 7|o is a path in Aa from zo to z. Let z\ be the other point in Aa with
the same image z in Aa as zo, let 7^ be a path in Aa from zq to z\ of winding
number 1 about the origin, and let 7^ be its image in Aa (see Fig. 3). For
A6) to define a genuine function on Aa, we must have g(zo) — g(z\), i.e.
A7)
dw H-
There are two cases to consider. If ip has even winding number about the
origin, then >Jip(zo) = >J<p(z\) and A7) forces
A8)
66
2 Coboundary Poisson-Lie groups and the CYBE
Fig. 3 Paths in Aa and in its double cover Aa
This cannot hold for all 0, since Vect(cE1) is dense in the space of continuous
vector fields on S1. Hence, w is not surjective in this case.
If ip has odd winding number, so that >Jip(zo) — —\ftp(z\), then A7) has
a unique solution for g(zo). Reinterpreting the resulting formula on Aa, we
see that in this case A5) has the unique solution
A9)
This is the rigorous version of A4).
Passing to the direct limit as a tends to 1, one finds that A9) defines a
continuous linear map r : Vect(cE1) —> Vect(cE1). Finally, one shows that
Vect(cE1) is isomorphic to its (continuous) dual, so r may be regarded as a
map Vect(cE1)* —> Vect(cE1). This gives a genuine Lie bialgebra structure
on Vect<cEfl), except that its cocommutator does not take values in the alge-
algebraic tensor product Vect<cE'1)(8)Vect<cE'1) but only in a suitable completion
of it.
Returning now to the real case, we can of course regard VectjRE1) C
Vect<cE'1) as the vector fields which are real valued on the circle, but the
question is whether r(VectjRE1)) C VectjRE1). In fact, this is never the case,
so the construction does not yield any Lie bialgebra structures on VectRE1).
This is easiest to see when tp has a zero of order greater than 1 on 51, say
at zq. In that case, it is obvious from A2) that uj(g)(zo) — 0 for all g.
2.2 Coboundary Poisson-Lie groups 67
Hence, if ip(zo) ^ 0, then r{ijj) ? VectRE1). If all the zeros have order 1, we
argue as follows. The integral in A9) depends continuously on z. Hence, if
r(ip) E VectRE1), then r(ip)(z) is continuous even at a zero z$ of <?, so the
integral in A8) must vanish. As we noted above, this cannot happen for all
*l>. 0
C The classical R-matrix Although we have described a number of spe-
special properties of Poisson-Lie groups G whose tangent Lie bialgebras g are
coboundary, we have not yet identified the geometric object on G which cor-
corresponds to the classical r-matrix r G g (g> g. To do so, we shall make the
slightly stronger assumption that r satisfies the CYBE and that r + a(r) is
non-degenerate. One says that g is factorizable in this case (the reason for
this terminology will appear in a moment).
As in the previous subsection, we may regard r and —<r(r) as linear maps
g* —> g, and, by 2.1.4, these linear maps are actually Lie algebra homo-
morphisms (note that —<r(r) defines the same Lie bialgebra structure on g
as r because r -f a{r) is g-invariant). Assuming that G and its double G*
are connected and simply-connected, these homomorphisms lift to group ho-
momorphisms S and Sa from G* to G. Let T : G* —> G be defined by
T{x) = S(x)Scr(x)~1; since r + a(r) is non-degenerate, T is a local diffeomor-
phism near the identity elements of G* and G. One says that G is factorizable
if T is a (global) diffeomorphism, since in this case every element g G G admits
the factorization g = g+gl1, where g+ = 5(T~1(^)), #_ = 5cr(T(^)).
Proposition 2.2.8 Let G be a factorizable Poisson-Lie group and define
the classical R-matrix R.GxG^GxGby
R(g, h) = (h_gh~_l, (/i_^/il1);1ft(/i_^/il1)+).
Then, R is a Poisson diffeomorphism if G is equipped with the Poisson struc-
structure of G*, using T to identify G and G* (see above). Moreover, R is a
solution of the quantum Yang-Baxter equation (QYBE):
In this equation, R\2 means the map GxGxG^GxGxG given by
and the meaning of Ris and of R23 is similar. Thus, the QYBE asserts the
equality of two composites of three maps from G x G x G to itself.
Example 2.2.9 Consider the group ??/n+i with the standard Poisson structure
described in Subsection 1.4C, and let G be its connected, simply-connected
double Poisson-Lie group. Then, G = 5Ln+i(C) as a Lie group. It is easy to
68 2 Coboundary Poisson-Lie groups and the CYBE
check that the factorization g — g+gZ1 is exactly the Gram-Schmidt process,
with g+ G ?C/n+i, g- G B, where B is the group of upper triangular matrices
in 5Ln+i(C) with positive (real) diagonal entries. Thus, G is factorizable,
and the map R denned in 2.2.8 is a solution of the QYBE. <0>
Example 2.2.10 Let G be a connected, simply-connected complex Lie group
whose Lie algebra g is simple. Give g the Lie bialgebra structure denned in
1.3.8, and give G the corresponding complex Poisson-Lie group structure.
With the notation of that example, let N± and H be the complex Lie sub-
subgroups of G with Lie algebras n± and I). It is clear from 1.3.8 that the dual
of G is the subgroup of G x G given by
G* = {(/m+ , n-h~l) G G x G \ n± G N±, h G H}.
The maps S and Sa are the projections onto the two factors, so
T(hn+ , n-h'1) = n+/i2(n_).
Hence, T is a 2 to 1 map onto the 'big cell' JV+ifiVL C G. Thus, although g
is factorizable, G is not. However, the factorization g = g+gZl is still valid
for elements g in the big cell, and, because g+ and g- are well denned up to
a sign, it is clear that the R-matrix in 2.2.8 is still uniquely determined. But
it is not clear whether it satisfies the QYBE. 0
Remark We shall meet the QYBE again when we discuss the quantization of
Poisson-Lie groups. In that case, the role of G is played by a representation
of the quantized group, and R is a linear map instead of a Poisson diffeomor-
phism. The reason for the terminology 'quantum Yang-Baxter equation' is
easy to see in that situation. For, if we look for solutions of the QYBE of the
form R — id + /ir, where h is a 'small' parameter, then the QYBE is satisfied
identically up to order h, and is satisfied to order h? if and only if r satisfies
the CYBE. A
2.3 Classical integrable systems
We conclude this chapter with a brief discussion of the relationship between
the CYBE and the theory of classical hamiltonian systems, where it plays the
role of an integrability condition.
A Complete integrability We begin by recalling the notion of a completely
integrable hamiltonian system. If a hamiltonian system is modelled by a
Poisson manifold M (the phase space of the system) and a hamiltonian H G
2.3 Classical integrable systems 69
C°°(M), its time-evolution is given by following the integral curves of the
hamiltonian vector field X^ on M corresponding to TL. We recall that
for all / e C°°(M). It follows that
!-<«•'>¦
(This equation is shorthand for (d/dt)f(m(t)) — {TL, f}(m(t)), where ra(?) is
any integral curve of Xn.) In particular, an observable / is conserved, or a
constant of the motion, if {TL, /} = 0. More generally:
Definition 2.3.1 Two observables /i, /2 ou a Poisson manifold M are in
involution if {/i, /2J = 0.
Note that every integral curve m(t) of X^ lies entirely in some symplectic
leaf of M. Hence, we might as well assume that M is symplectic, and we do
so from now on.
A hamiltonian system is completely integrable if it has the maximum num-
number of conserved quantities in involution.
Definition 2.3.2 The dynamical system defined on a 2m-dimensional sym-
symplectic manifold M by a hamiltonian TL G C°°(M) is completely integrable
if there exist m independent conserved quantities /i,...,/m G C°°(M) in
involution.
Remarks [1] The meaning of 'independent' is that the set of critical values
of the map / = (/i,...,/m) : M —> lRm is of (Lebesgue) measure zero
(a point c G lRm is a critical value of / if c = f(p) for some p such that
ffp : Tp(M) —> Tc(lRm) is not surjective). Intuitively, this means that there
should be no functional relation betwen the fa.
[2] Usually, the hamiltonian TL is taken to be one of the fa. In any case, TL,
and any other conserved quantity in involution with the fa, is 'functionally
dependent' on the fim A
The importance of complete integrability, as the terminology implies, is
that systems with this property can be 'solved' completely. In fact, one of
the most important results about such systems asserts that if b G IRm is a
regular value of/, and if the level submanifold /-1(b) is compact, then each
of its connected components can be identified with an m-dimensional torus
Tm = S1 x • • • x S1 by a diffeomorphism which carries the flow of X^ on
/~1(b) to a rotation at constant speed in each factor of Tm.
B Lax pairs One of the principal tools used to construct and solve com-
completely integrable systems is the Lax pair.
70 2 Coboundary Poisson-Lie groups and the CYBE
Definition 2.3.3 A Lax pair for a hamiltonian system on a symplectic man-
manifold M is a pair (L, P) of C°° functions on M with values in a real Lie algebra
g such that the equations of motion of the system are equivalent to
B0) f = [L,P],
where [ , ] is the Lie bracket on g.
It is easy to produce conserved quantities for systems which admit a Lax
pair. In fact, let / be a polynomial function of degree n on g which is invariant
under the coadjoint action of g. Then, /(L,..., L) is conserved:
^-f(L, ...,L) = f(dL/dt, L,..., L) + ¦ ¦ ¦ + f(L, L,..., dL/dt)
at
= adP(/)(L,L,...,L)
= 0.
To produce conserved quantities of this type in involution, we assume fur-
further that
B1) {L,L} = [r,L1+L2}
for some r G g (?> g. Here, L\ — L 0 1, L2 — 1 <8> L, and the Poisson bracket
is extended to g-valued functions in the obvious way: if {Xs} is a basis of g,
and
where /f,/| e C°°(M), then
s,t
Assume for simplicity that g = sZn+i(R) for some n > 1 (we could dispense
with this assumption by taking a representation g —> sZn+i(R)). Then, the
functions
fk(X)=tmce(Xk), A; = 1,2,...
are obviously invariant polynomial functions on g. Moreover, the observables
fk(L) and fi(L) are in involution for any k,l. Indeed,
{/fc(L), fi(L)} = (trace 0 trace){Lfc, L1}
k-i1-1
= (trace 0 trace) ]T ^(L^^L^'^iL, L}(L\LJ2)
i=0 j=0
k-l/-I
= (trace 0 trace) ^^(L^-*-1^-1)^, Li +L2](LiLJ2)
i=0 j=Q
= /cZ(trace<8)trace)(Li~1[r,Li + L2JL2),
2.3 Classical integrable systems 71
where the second equality used the derivation property of { , }, the third
equality used B1), and the last equality used the invariance property of the
trace. The last expression vanishes because, for example,
= (trace® ^([r,^]).^-1
= 0.
Remark Equation B1) imposes restrictions on the element r G g ® g. In
fact, it is easy to show that the skew-symmetry property and Jacobi identity
satisfied by the Poisson bracket { , } are equivalent to
b"l2 + 7*21 , Ll + L2] = 0
and
[[[r,r]],L1+L2 + L3] = 0,
respectively. Note that these conditions will hold if ri2 4- r2\ and [[r, r]] are
g-invariant elements of g 0 g and g ® g ® g. In view of 2.1.2, this is a strong
indication of the close relationship between coboundary Lie bialgebras and
integrable hamiltonian systems. A
C Integrable systems from r-matrices We now reverse the preceding
discussion and give a general procedure for constructing completely integrable
hamiltonian systems starting from an r-matrix.
Let g be a finite-dimensional real Lie algebra and let ( , ) be a non-
degenerate invariant symmetric bilinear form on g. Let r G g ® g be a skew-
symmetric solution of the MCYBE E). We may regard r as a linear map
g* —> g, and hence as a linear map p : g —> g, identifying g* with g by using
the inner product ( , ).
Proposition 2.3.4 With the above notation, let r G g 0 g be a skew-
symmetric solution of the MCYBE and define, for X, Y e g,
B2) [X,Y]r = \p(X),Y] + [X,p(Y)].
Then [ , ]r is a Lie bracket on g.
Proof Skew-symmetry is obvious, and the Jacobi identity is a straightfor-
straightforward verification. |
Remark Since r satisfies the MCYBE, it defines via A) a Lie bialgebra struc-
structure on g, and hence a Lie algebra structure on g*. Identifying g with g*
using the inner product, we get another Lie algebra structure on g. This is
the Lie bracket defined in the proposition. A
72 2 Coboundary Poisson-Lie groups and the CYBE
To avoid confusion, we denote by gr the vector space g with the Lie bracket
[ , ]r, by adr the adjoint action of gr on itself, and by ad* the corresponding
coadjoint action. Note that ad* can be expressed in terms of ad*:
B3) (adrK,@ = ad;w(?) + p*(adx(l-)).
We also denote by G (resp. Gr) a connected Lie group with Lie algebra g
(resp. gr).
By 2.3.4 and 1.1.3, we have two Poisson-Lie group structures on the vector
space g* (viewed as an additive group), namely
B4) {/i,/2}
and
B5) {/l,/2}r
for/i,/2€C00(g*).
The next result shows that the functions / on g* which are invariant under
the coadjoint action of G give examples of observables in involution. Note
that the infinitesimal expression of the invariance of / is
B6) <#(O,ad^)) = 0 (leg, ? e g*).
Proposition 2.3.5 The C°° functions on g* which are invariant under the
coadjoint action of G are in involution with respect to both Poisson brackets
{ , } and { , }r on g*.
Proof Suppose that /i, /2 ? C°°(g*) are invariant under the coadjoint
action of G. Then,
0, #2@1,0 = (dh{i)
by B6).
On the other hand,
= 0.
This proposition, and the definition of complete integrability, suggest that
we consider a dynamical system on g* with the Poisson bracket { , }r, using
2.3 Classical integrable systems 73
as hamiltonian a function H satisfying the invariance condition B6). The
equations of motion are then, for any / G C°°(g*),
by B3). But the second term on the right-hand side vanishes because
= o,
by the invariance of H. Hence, the equations of motion are
B7) |
Note that B7) implies that the integral curves of the equations of motion
lie on the coadjoint orbits of Gong*. By the choice of Poisson bracket, they
also lie on the coadjoint orbits of Gr.
We shall now show that the equations of motion B7) can be written in Lax
form. Let L : g* —> g be the canonical map associated to the chosen inner
product on g, and let P(?) = p(dH{Cj). Note that ?,(?) = (? <8> l)(t), where
t ? 9 0 g is the Casimir element (not to be confused with the time ?!). Then,
by the adg-invariance of t, and hence
This proves the first part of
Proposition 2.3.6 Let H be a smooth function on g* which is invariant
under the coadjoint action of G, and let r G g 0 g be a skew-symmetric
solution of the MCYBE. Then, the hamiltonian system on g* with Poisson
bracket { , }r and hamiltonian TL admits a Lax pair (L,P). Moreover,
{L,L}r = [r,L<g)l + l<g>L].
Proof Let {Xs} be a basis of g and let {Xs} be the dual basis with respect
to the inner product on g. Suppose that
r = ]T rstXs 0 Xt = - ]T r*SXS 0 X*.
s,t s,t
74 2 Coboundary Poisson-Lie groups and the CYBE
Then,
Hence, since
where Ls(?) = (Xs,0, we have
{L, L}r@
S,t
S,t
s,t
Hence, {L, L}r(?) is the sum of two terms:
B8)
On the other hand,
B9)
Now, the g-invariance of t = Y^u Xu 0 Xu implies that
S V"Wl ,0s "V _|_ V^ /O\ [ VS "V l\ f\
Applying ? ® 1 gives
Hence,
Interchanging the roles of s and u in the last sum, we see that [r, Li] is equal
to the second sum on the right-hand side of B8). Similarly, [r, L2] is equal to
the first sum on the right-hand side of B8). This proves that
{L,L}r = {r,L1+L2\. I
2.3 Classical integrable systems 75
D Toda systems We illustrate these constructions with an example of Toda
lattice type.
Example 2. 3. 7 Let g be a finite-dimensional complex simple Lie algebra of
rank n, and take the standard inner product on g. We use the notation in
the Appendix.
Let gR be a split real form of g (if g = s/n+i((C), then gR = sZn+i(R)).
The elements
C0) {5ji=l nU^U
form a basis of gR over R. Let I)R be the R-linear span of the Hi.
We take the skew solution
r=\ ? daX+AX~
of the MCYBE (see 2.1.7); note that r G gR (g) gR. Using the formulas in the
Appendix, the associated linear map p : gR —> gR is easily found to be
p(Hi)=0, \
and the Lie bracket [ , ]r to be
[Hi,Hi]r = Q, [HuX}r = (a,al)X,
F1) *
[Xa ,Xp]r = ±CapXa+f3, [X+, Xp }r = 0,
for some constants Ca/3.
To describe the Poisson bracket { , }r on (gR)*, we introduce the coordinate
functions
for ^G (gR)*. We find that
{hi,hj}r = 0, {hi,x±}r = --
\XX
Our example is essentially a symplectic leaf (i.e. a coadjoint orbit) of this
system. In fact, we take the linear submanifold g^ C (gR)* defined by the
equations
x+ = x~ if a G II, x± = 0 if ae A+\IL
76
2 Coboundary Poisson-Lie groups and the CYBE
We must show that g^ is preserved by the coadjoint action of the group GR
with Lie algebra gR. For this, it suffices to show that (adr)^@ G g^ for all
X G gR, ? G g^, and it is enough to check this when X runs through the
basis C0) of gR. The verification is straightforward, using the relations C1)
and the fact that a sum of two positive roots cannot be simple.
Note that the discussion in this section implies that if we take as hamilto-
hamiltonian the restriction to g^, of any GR-invariant function on (gR)*, the resulting
system is completely integrable. Indeed, this follows from 2.3.6 and the fact
that there are n — |dim(g^) independent GR-invariant polynomials on gR.
One natural choice for the hamiltonian is the manifestly GR-invariant func-
function
This function also admits a simple interpretation in terms of the Lax pair.
Indeed, the Lax operator L for this problem is
where {Hi} is the basis of I)R dual to {Hi} with respect to the inner prod-
product. It is clear that H = ^(L), where f2 is the GR-invariant quadratic
polynomial on gR given by the inner product.
To interpret this hamiltonian, let us introduce coordinates on g^. The most
obvious choice is the set of functions hi and Xi = x^, i — 1,..., n. Their
Poisson brackets are given by
C2) {hi,hj}r = 0, {hi,Xj}r = --(auaj)xj, {xi,Xj}r = 0.
If we introduce new coordinates pi,... ,pn, #i,..., qn on the open subset of
g^ where the Xi are positive by
hi — pi,
exp
we find that the pi and q^ satisfy the canonical commutation relations
C3) {ft,ft}r=0, {Pl,qj}r=^j, {K,q3}r = 0.
In these canonical coordinates, the hamiltonian is given by
C4)
1
Bibliographical notes 77
where B is the inverse of the symmetrized Cartan matrix (d~laij) = (Hi, Hj)
of g. Since the quadratic form ^ . BijPiPj is positive definite, there is a linear
change of coordinates
such that the Pi and Qi still satisfy the canonical commutation relations C3),
and
Thus, H may be regarded as the hamiltonian for a system of n particles with
positions Qi and momenta Pi interacting via a potential given by the second
term on the right-hand side of C4).
The simplest case, where gR = 5/2 (R)> can easily be solved by ad hoc
methods. We leave it to the reader to check that every integral curve of
H = h2 + x2 is of the form
2Exo
h = E (E + ho)e -(?-
o-hEt
where E2 is the constant value of H along the curve, and xq and ho are the
coordinates at time t = 0.
The solution in the general case can be reduced to a 'factorization' problem,
but we shall not pursue this further. <)
Bibliographical notes
2.1 The CYBE first arose in the literature on inverse scattering theory; see
Faddeev & Takhtajan A987) for a thorough exposition. The algebraic results
described in this section are due mainly to Drinfel'd A983b) and Semenov-
Tian-Shansky A983, 1984).
2.2 The main references here are again Drinfel'd A983b) and Semenov-Tian-
Shansky A983, 1984). See also Lu & Weinstein A990).
The idea for the construction of coboundary Lie bialgebra structures on the
Lie algebra of vector fields on the circle described in 2.2.7 is due to Witten
A988a), and its rigorous formulation to Beggs & Majid A990).
78 2 Coboundary Poisson-Lie groups and the CYBE
For the classical R-matrix, see Weinstein & Xu A992), where the proof of
2.2.8 can be found.
The QYBE was first encountered by C. N. Yang A967), where it played
a crucial role in his computation of the eigenfunctions of a one-dimensional
fermion gas with delta function interactions. A little later, the QYBE arose
in the solution, by R. J. Baxter A972), of the eight vertex model in sta-
statistical mechanics. The terminology 'quantum Yang-Baxter equation' was
apparently coined by L. D. Faddeev around 1980. (Strictly speaking, it was
the quantum Yang-Baxter equation 'with spectral parameters' which played
a role in the work of Yang and Baxter - see Subsection 7.5C.)
2.3 For the notion of complete integrability for dynamical systems, see Abra-
Abraham & Marsden A978). For a more detailed discussion of its relation to
the classical Yang-Baxter equation, see Semenov-Tian-Shansky A983, 1984,
1985).
For further information on systems of Toda lattice type, see Kostant A979),
Reyman & Semenov-Tian-Shansky A979, 1981), Adler & van Moerbecke
A980) and Symes A980a,b).
3
Solutions of the
classical Yang-Baxter equation
In Chapter 2, we saw the importance of describing the solutions r of the
classical Yang-Baxter equation with values in g ® g, where g is a Lie algebra.
On the one hand, solutions of the CYBE lead to integrable dynamical systems.
On the other hand, if the symmetric part of r is g-invariant, then r gives rise
to a Lie bialgebra structure on g. Moreover, in certain cases, for example
if g is a finite-dimensional complex simple Lie algebra, every Lie bialgebra
structure on g arises in this way. In this chapter, we give several results
which parametrize and, in some cases, explicitly describe, all the solutions of
the CYBE for certain Lie algebras g.
We begin in Section 3.1 by classifying all the solutions of the CYBE when
g is a finite-dimensional complex simple Lie algebra. It turns out that rather
different methods are required, depending on whether the solutions one is
looking for are skew-symmetric or not. In the latter case, the classification
is completely explicit; in particular, we shall see that the generic solution
depends on \n(n — 1) parameters, where n = rank(g). In the skew case,
the classification is rather less explicit; it depends on the classification of the
quasi-Frobenius Lie subalgebras of g, i.e. those subalgebras which admit a
non-degenerate 2-cocycle (with values in C).
In Section 3.2, we study the case where g is a Lie algebra of functions on a
space U with values in a Lie algebra a. The solutions of the CYBE may then
be regarded as functions r{u\, u^) on U x U with values in a®a. The variables
U\ and U2 are called spectral parameters in the physics literature. If U is an
open subset of the complex plane, g is a complex simple Lie algebra and r is
a meromorphic function on U x U then, under a mild additional hypothesis,
it turns out that every solution rB/1,^2) is equivalent, in a certain natural
sense, to a function which is elliptic, trigonometric (i.e. a rational function
of eUl and eU2) or rational. In the elliptic and trigonometric cases, we give
explicit descriptions of all the solutions.
Throughout the remainder of this chapter, g denotes a finite-dimensional
complex simple Lie algebra. We use freely the notation established in the
Appendix.
80 3 Solutions of the CYBE
3.1 Constant solutions of the CYBE
A The parameter space of non-skew solutions We begin with the clas-
classification of the non-skew-symmetric solutions of the CYBE with values in
g 0 g, which is due to Belavin & Drinfel'd A982, 1984a,b). As we remarked
in Subsection 2.IB, this is equivalent to solving the system of equations
A) ri2 + r2i =t, [[r,r]]=0,
where t is the Casimir element of g 0 g corresponding to a non-degenerate
invariant bilinear form ( , ) on g (this can be any non-zero multiple of the
standard bilinear form denned in the Appendix). Note that, if a is any
automorphism of g, then (a 0 cr)(r) satisfies A) if r does. We shall say that
two solutions of A) are equivalent if they can be obtained from each other by
applying an automorphism in this way.
To describe the parameter space of equivalence classes of solutions of A),
we make the following definition. Fix a set II of simple roots of g.
Definition 3.1.1 A quadruple (IIi,IIo,r,r°), where IIi, n0 C II, r is a
bijection II i —> n0, and r° E I) 0 I), is said to be admissible if it satisfies the
following conditions:
A) (t(<*),t(C)) = (a,/?) for all a, /? G IIi (we also use ( , ) to denote the
inner product on I)* induced by that on \));
(ii) for every a G IIi, there exists m G N such that a, r(a),..., rrn~l{a) G IIi
butr^ia) ?lli;
(iii) r?2 + r§! = t0, the component oft in \)®2 C g®2 = (n_ © \) © n+)®2;
(iv) (r(a) <g> l)(r°) + A0 a)(r°) = 0 for all a G IIi.
We shall aiso say that a triple (IIi, n0, r) satisfying conditions (i) and (ii)
is admissible.
For a given admissible triple (IIi,IIo,t), the solutions r° of the system
of inhomogeneous linear equations (iii) and (iv) form an affine space whose
dimension may be computed as follows. Since the simple roots form a basis
of I)*, r° is completely determined by the matrix of complex numbers (r^)
defined by
r°/3 = (a®/3)(r°) (a,/? en).
Conditions (iii) and (iv) are equivalent to the following equations:
B) r% + r°a = (a,/3), if a, 0 Gil,
C) r-°(a)/3+r°a = 0, if a 6 UU C G IT.
3.1 Constant solutions of the CYBE 81
Now, every simple root 7 G II can be expressed uniquely in the form 7 =
r~rn(a) for some integer m > 0 and some a G n\ITi (if 7 ^ III, take m — 0;
if 7 G IIi, use condition (ii)). If 6 = t~'(/?), with I > 0 and C G II\IIi, it
follows from B) and C) that
T-1(a) + ---+Ti-m(a),/3) ifm>i,
'7 6 ~ ra/3
' 0 if m = Z,
and that, conversely, if we prescribe r° ^ for a,/? G II\IIi arbitrarily, subject
only to B), and then determine r° by using the preceding formulas, then
conditions (iii) and (iv) are satisfied. Hence, for a given admissible triple
(Iii, IIo, r), the (complex) dimension of the space of solutions of (iii) and (iv)
is \k(k - 1), where k = |II\IIi|.
The parameter space of solutions of A) is essentially the space of admissible
quadruples:
Theorem 3.1.2 The parameter space of equivalence classes of solutions of
A) is the quotient of the space of admissible quadruples by the natural ac-
action of the group of automorphisms of the Dynkin diagram of g. It has a
stratification into finitely many strata, indexed by the orbits of the group of
diagram automorphisms of g on the set of admissible triples. The stratum
corresponding to the triple (IIi,no,T) is of complex dimension \k(k — 1),
where k = |II\IIi|. |
Remarks [1] A more precise statement of the last part of the theorem is that
the stratum corresponding to the admissible triple (IIi, IIo, t) is the quotient
of a complex affine space of dimension \k(k — 1) by an action of the group of
diagram automorphisms of g which fix (IIi,IIo,t).
[2] Since the invariant bilinear form on g is unique up to scalar multiples,
it follows that the parameter space of non-skew-symmetric solutions of the
CYBE is the cone over the parameter space of solutions of A) corresponding
to a fixed invariant bilinear form.
[3] There is a unique stratum of maximal dimension, corresponding to Iii =
IIo — 0- In this case, conditions (i), (ii) and (iv) in 3.1.1 are vacuous, and the
most obvious solution of (iii) is r° = |^o- This corresponds to the standard
Lie bialgebra structure on g. The most general solution of (iii) is obtained by
adding to the standard solution an arbitrary element of [\ (I)). This shows,
as predicted by 3.1.2, that the dimension of this stratum is |n(n — 1), where
n = rank(g). A
B Description of the solutions We now turn to the explicit description
of the solution of A) corresponding to a point (Iii, IIo, t, r°) of the parameter
space.
82 3 Solutions of the CYBE
For any subset E C II, let gs be the 'diagram' subalgebra of g generated
(as a Lie algebra) by the X^, Ha for a G E. Explicitly, gs is spanned (as
a vector space) by the Ha for a G E and the root spaces qa for a G As,
where As is the set of roots whose expression in terms of the simple roots
only involves roots from E.
If (III, IIo, t) is an admissible triple, there is an isomorphism of Lie algebras
^ : 9ni -> 9n0 such that
for all a G IIi (the existence of ip follows from condition (i) in 3.1.1). Choose
elements E±a G g±a such that
(Ea,E-a) = l if ae A+,
(p(Ea) = ET(a) if aeAni.
Finally, introduce a partially denned ordering < on II by saying that a < C
if there is a positive integer m such that C = ^(a) (notice that, for this
to make sense, we must have a G IIi, r(a),..., rm~1(a) G IIo H IIi, and
Ceuo).
Theorem 3.1.3 If (IIi,IIo,r,r°) is an admissible quadruple, then, with the
above notation,
E-a A
a,[3eA+,a</3
is a solution of A) (here, E~a A Ep means E-a 0 Ep — E1^ 0 E-a).
Conversely, every solution of A) is equivalent to a solution of this type. |
We have nothing to add to the detailed proof available in Belavin & Drin-
fel'd A982, 1984a).
C Examples We now make 3.1.2 and 3.1.3 explicit in the cases of 5/2 (<C)
and 5/3 (C).
Example 3.1.4 If g — ^(C), we take \) (resp. n+) to be the diagonal matrices
(resp. the strictly upper triangular matrices). Then, there is a unique simple
root a, so either n0 = II1 = 0 or n0 = II1 = {a}. But the second choice does
not satisfy condition (ii) in 3.1.1. Taking the inner product to be the trace
form
(X,r)=trace(Xr),
we obtain the unique solution
4
3.1 Constant solutions of the CYBE 83
in the notation of 2.1.8. Passing to the skew-symmetric part, we see that this
corresponds to the standard structure 2.1.8(i) (with A = —\). Note that the
non-trivial triangular Lie bialgebra structure 2.1.8(ii) is not included in the
Belavin-Drinfel'd classification. 0
Example 3.1.5 The simplest examples not treated in Section 2.1 appear when
g = 5/3 (C). Taking I), n+ and the inner product to be as described in the
previous example, and writing an element of I) as diag(xi, X2, #3)? the positive
roots are a = x\ — #2, P — %2 — ^3, ol + /? = X\ — ?3. Thus, II = {a,/?}.
Writing Eij for the elementary matrix with 1 in the ith row and jth column
and zeros elsewhere, we take
Ea+p = ^13, E-a-p = ?1, i/o; — En — E12, Hp = E22 — E33.
Then,
^0 = 3^ ® ffa + 3^ ® Hp + -fl^ ® ffa + g#0 ® ^/3-
There are three admissible triples:
(a) ITo = III = 0. Condition (iv) in 3.1.1 is vacuous and the most general
solution of (iii) is
r° = i*0 + XHa A Hp
for A € C. The resulting r-matrix is
r = -to + A#a A ff/3 + ?_a ® ^a + ^-/3 ® Ep + ^_a-/3 ® ^a+/3-
(b) Ilo = {a}, 111 = {/?}• Conditions (iii) and (iv),
have the unique solution
The
T —
resulting
\Ha <8> H
o !„
r-matrix is
1 TT TT
a + ifTg ® ffa
F« + -HP
+ \Hp®h
-Hp ® Hp.
84 3 Solutions of the CYBE
(c) ITo = {/?}, Ill = {&}• The r-matrix in this case is obtained by interchang-
interchanging a and j3 in (b).
There is a unique non-trivial diagram automorphism of 5/3 (C), which inter-
interchanges a and j3. Thus, the solution of type (c) is equivalent to the solution
of type (b), and the solution of type (a) with parameter A is equivalent to
that with parameter —A. The parameter space of solutions of A) is thus the
union of the upper half-space
{A G C I 3(A) > 0 or A > 0}
together with a single point (9?(A) denotes the imaginary part of a complex
number A). 0
D Skew solutions and quasi-Probenius Lie algebras We now consider
briefly the problem of constructing skew-symmetric solutions of the classical
Yang-Baxter equation. In view of 2.2.4 and 2.2.6, this problem is equivalent
to that of finding pairs (go,u;), where go is a Lie subalgebra of g and u is a
non-degenerate 2-cocycle on go- In general, a Lie algebra f which admits a
non-degenerate 2-cocycle u is called quasi-Frobenius] it is Frobenius if u is a
coboundary, i.e. if u(X, Y) = C([X, Y}) for some C G f* and all X, Y G f.
Since any scalar multiple of a skew solution of the CYBE is also a solu-
solution, it is convenient to weaken the notion of equivalence of solutions slightly
compared with that used for solutions of the MCYBE. We shall say that two
skew solutions r\ and r2 of the CYBE are equivalent if r2 is equivalent in the
old sense to a non-zero scalar multiple of r\.
Proposition 3.1.6 Let § be a finite-dimensional Lie algebra. There is a
(non-zero) skew-symmetric solution of the CYBE with values in g 0 g asso-
associated to every (non-zero) quasi-Frobenius Lie subalgebra (f, u) of g. The
solutions associated to (fi,u;i) and ([2,^2) are equivalent if and only if there
is an inner automorphism a of g such that a(fi) = [2 &nd a.*(u2) — u\ is a
coboundary. |
Thus, we have the following algorithm for constructing (equivalence classes
of) skew solutions of the CYBE:
(a) classify the quasi-Frobenius Lie subalgebras f of g up to inner automor-
automorphisms (such subalgebras must, of course, be even dimensional);
(b) for each such f, compute #Lie(f), the Lie algebra cohomology of f (the
space of 2-cocycles modulo the space of coboundaries);
(c) classify the orbits of the action of the normalizer N(\) of f on #Lie(f) (note
that the centralizer C(f) acts trivially on #Lie(f));
(d) determine whether a cohomology class in each orbit has a representative
cocycle which is non-degenerate.
3.1 Constant solutions of the CYBE 85
Example 3.1.7 The only non-trivial even-dimensional Lie subalgebra of g =
s/2(C) up to conjugacy is the Borel subalgebra b consisting of the upper
triangular matrices. In fact, the Lie algebra cohomology H^ih) — 0, so b is
Probenius and there is, up to equivalence, a unique solution associated to it.
It is easy to see that this solution is r = H A X+ in the notation of 2.1.8(ii).
o
Example 3.1.8 The quasi-Probenius Lie subalgebras of g = 5/3 (C) are of the
following types.
(i) Up to conjugacy, the only six-dimensional Lie subalgebra of 5/3 (C) is
(the *'s represent arbitrary complex numbers, subject only to the condition
that the trace is zero). Since Hlie(p) = 0, p is Probenius and there is a unique
skew solution of the CYBE associated to it.
(ii) The four-dimensional subalgebra
is Probenius. We have Hlie(x) = ^» an<^ tne quotient N(x)/C(x) of the
normalizer of r in SX3(<C) by its centralizer is Z2. Thus, there is a one-
parameter family of solutions associated to r.
(iii) The two-parameter family of four-dimensional subalgebras
(ai 0 0 \ /0**>
0 a2 0+00*
0 0 a3j \0 0 0j
are quasi-Probenius. We have
= i
C if {aua2, a3) = @,1, -1) or A,1, -2),
0 otherwise,
and ^(qai5a25a3)/Cf(qai,a2,a3) = <CX for all (ai,a2,a3). There are two solu-
solutions associated to each of cjo,i,-i and 91,1,-2, and one to c\ai^a2^az in each of
the remaining cases.
(iv) The two-dimensional non-abelian Lie algebra embeds in sls((C) in the
following ways.
86 3 Solutions of the CYBE
(a) the one-parameter family of subalgebras
/A 0 0 \ /0 * 0N
bA = * I 0 A-l 0 + I 0 0 0 | , (AGC);
\0 0 1-2A/ \0 0 0
(b) the subalgebra
(I 0 0 \ /O 1 0N
b(°) = * 0 0 0 + * 0 0 1 | ;
\0 0 -1/ \0 0 0
(c) the subalgebra
/2 0 0 \ /O 0 *'
b^1) = * I 0 —1 1 + I 0 0 0 I ;
\O 0 -1/ \O 0 0.
(d) the subalgebra
B 0 0 \ /O 1 T
bW = * 0 -1 1 +* 0 0 0 | .
\0 0 -1/ \0 0
In each case, i^Lie = ^ anc^ there is a unique associated solution.
(v) The two-dimensional abelian Lie algebra has Hlie = <C. In fact, 0 is the
only 2-coboundary, so Hlie is simply the space of all skew bilinear forms. In
particular, the zero class in Hlie has no non-degenerate representative. The
possible embeddings are as follows:
(a) the Cartan subalgebra
the group N(i))/C(i)) is trivial, so this gives a one-parameter family of solu-
solutions;
(b) the subalgebra
1
0
0
0
1
0
0 \
0 H
-2/
h 0
\o
*
0
0
0
0
0
3.2 Solutions of the CYBE with spectral parameters 87
this time, N(i)^)/C(i)^) = Cx, and there is a unique associated solution;
(c) the subalgebras
and
/O 1 O\ /O 0 *
t/1'1) = * 0 0 1 + 0 0 0
\0 0 0/ \0 0
for which N(l)@'V)/CH)@'V) = NftV'^/CftW) = Cx x Cx; there is a
unique solution associated to each subalgebra. <0>
3.2 Solutions of the CYBE with spectral parameters
A Classification of the solutions There is a generalization of the classical
Yang-Baxter equation, which is particularly important in physical applica-
applications of the theory, in which the r-matrix r is a function on U x [/, for some
set [/, with values in 9 0 9, satisfying
+ [r{uu)r{uu)] = 0.
This is usually called the CYBE with spectral parameters u\ and ti2, but we
shall refer to it simply as the CYBE in this section. Thus, the previous section
was concerned with constant solutions.
In this section, we shall consider solutions of D) for which 9 is a finite-
dimensional complex simple Lie algebra, as in the previous section. We shall
further assume that
(a) U is an open subset of the complex plane, and r is a meromorphic function
on U x [/, and
(b) rA11,112) is non-degenerate for at least one point A11,112) ? U x U (see
Subsection 2.2B; we shall simply say that r is non-degenerate if this condition
is satisfied).
It follows from 2.2.5 that skew-symmetric constant solutions cannot be non-
degenerate.
Note that D) and conditions (a) and (b) are preserved if we replace r by
an equivalent r-matrix, as described in the following definition.
88 3 Solutions of the CYBE
Definition 3.2.1 Let r and f be two solutions of the CYBE which are
meromorphic on open sets U xU and U xU, respectively. Then, r and r are
said to be equivalent if there exists a holomorphic map a : U —> Aut(g) and
a non-constant biholomorphic function f : U —> U such that
r(ui,u2) = {(*(ui) ® <x(u2)){r{f{ui), f{u2)))-
Note that the group Aut(g) of Lie algebra automorphisms of g is a complex
Lie group, so this definition makes sense.
We have already met examples of solutions of the CYBE D) in Section 2.1.
In 2.1.9 we encountered the rational solution
E) r(uuu2) =
U\ —
and in 2.1.10 another rational solution
F) r(ttliO2)=r9
where rg is the standard r-matrix for g found in 2.1.6 (we have passed to the
quotient of the affine Lie algebra by its centre to obtain a solution with values
in 9(8)9).
Note that the solution in E) is a function of u\ — u2 only, while that in F)
depends only on ui/u2, and, hence, making the change of variable u\ •—> eUl,
u2 •—> eU2, is equivalent to a solution which is a function of u\ — u2 only. In
general, we have:
Proposition 3.2.2 Every solution of the CYBE satisfying conditions (a)
and (b) is equivalent to one which can be continued meromorphically to the
whole complex plane and which depends only on the difference of the spectral
parameters. |
We shall assume from now on that r(ui,u2) = r(u\ — U2) for some mero-
meromorphic function r(u) on C with values in g 0 g. Thus, we have to solve
+ [^(^ - U3), r23(^2 - u3)] = 0.
Non-degenerate meromorphic solutions of G) have the following regularity
properties.
Proposition 3.2.3 Let r{u) be a non-degenerate meromorphic solution of
G). Then, up to equivalence,
(i) r has a simple pole at u = 0 with residue the Casimir element t (for some
choice of non-degenerate invariant bilinear form on q). Moreover, all the poles
ofr are simple;
3.2 Solutions of the CYBE with spectral parameters 89
(ii) r satisfies the unitarity condition
r\2(u) + r2i{-u) = 0;
(Hi) there is no proper subalgebra go of g such that r(u) G go <S> go for
all u. |
The central result for the analysis of solutions of the CYBE is:
Theorem 3.2.4 Let r(u) be a non-degenerate meromorphic solution of the
CYBE G). Then, the set of poles of r form a discrete subgroup F of the
additive group of <C. There is a homomorphism \ : F —> Aut(g) such that
(8) r(u + 7) = (XG) ® l)(r(u)) = A ® xh))~X(r(u))
for aii u e <C, 7 G I\
There are three possibilities, as follows.
(i) rank(T) = 2: this is possible only when g = s/n+i((C) for some n>l,
and then r(u) is an elliptic function of u with period lattice (n + 1)F; more-
moreover, for each 7 G F, xii) JS an automorphism of g of finite order, and the
automorphisms {xWKer have no common fixed vector.
(ii) rank(T) = 1: then r(u) is equivalent to a rational function ofecu for some
c G Cx (such functions are called trigonometric).
(Hi) F = 0: then r(u) is equivalent to a rational function of u.
Outline of proof To show that, up to equivalence, only elliptic, trigono-
trigonometric or rational solutions are possible, one proceeds as follows. Writing
u = u\ —U2, v = u2 — us, the CYBE becomes
(9) [ruin) ~ r23{v), r13(u + v)} = [r23(v), r12{u)\.
We regard (9) as an inhomogeneous system of linear equations for 7*13A1 + u),
with r 12A1) and r2%(v) playing the role of coefficients. One shows that, at
least for sufficiently small u, v, the associated homogeneous system
A0) [ri2(u) - r23(v), s13} = 0
has only the trivial solution s = 0. Assuming this for a moment, it follows
that r(u + v) is a rational function of r(u) and r(v). One now appeals to
the generalization to vector-valued functions, due to Myrberg A922), of the
classical theorem of Weierstrass, according to which a meromorphic function
f : <? ^ (?, which satisfies a functional equation of the form
P(f(u),f(v),f(u + v)) = 0
90
3 Solutions of the CYBE
for some polynomial P, is necessarily elliptic, trigonometric or rational.
To prove the assertion about the system A0), it is enough by continuity to
consider the case u = v = 0 when, by 3.2.3, A0) becomes
[tl2 -*23,Sl3] =0.
It is easy to see that this equation is equivalent to
[X ® 1, s] == [1 <8> X , s]
for all X G g. Taking X G I), this implies that
s =
Hi
aGA+
for some Si G I), A^1 G C Taking X = X^1, and considering terms whose
second factor lies in 1), one sees that X^ — 0 for all /3 G A", and then that
5 = 0. |
In the remainder of this section, we shall describe how solutions of the
CYBE of the three possible types are constructed.
B Elliptic solutions Let {71,72} be a basis of the lattice F in 3.2.4(i) and
set Xi — xili)' Thus, \i and X2 are commuting finite order automorphisms
of g with no common fixed vector. By using the classification of finite order
automorphisms of complex simple Lie algebras, one shows that there is an
isomorphism of Lie algebras g = sZn+i(C) under which xi and X2 E° over
into conjugation by the matrices
(I
0
0
I 0
0
e
0
0
0
0
e2
0
0
0
0
0
en~
\
and
X =
/O
0
0
\1
1
0
0
0
0 •••
1 •••
o ...
0 •••
0\
0
1
respectively, where e — exp[27T\/—T/(n -f 1)]. We assume that xi —
X2 — ^ from now on.
Note that the matrices XjZk for (j,k) ^ @,0) form a basis of sln+i{<E)
consisting of simultaneous eigenvectors of xi and X2, with eigenvalues e~j
and e~k, respectively. Let <pjk be the unique meromorphic function on C
such that
(ii)
u + ji) =ej(pjk(u), y?jfc(w + 72) =ek(pjk(u),
has simple poles at the points of F, no other poles, and residue 1 at
(Condition (i) comes from (8) and (ii) from 3.2.3.)
3.2 Solutions of the CYBE with spectral parameters 91
Proposition 3.2.5 With (fjk as above, the function
-. n+l
A1) r{u) = —— Y, e-jkV3k(u)X-iZ~k®XJZk
71+1 ^-^
is a non-degenerate solution of the CYBE with values in s/n+i((C)®2. It has
simple poles at the points of the lattice T — Z.71 -f Z.72.
Conversely, non-degenerate meromorphic solutions of the CYBE with val-
values in g®2 and whose poles form a lattice of rank 2 exist only when g =
sln+i(<E) for some n > 1, and every such solution is equivalent to one of the
form A1). I
Thus, for each n > 1, there is, up to equivalence, exactly one non-degen-
non-degenerate elliptic solution of the CYBE with values in sZn+i(C) 0 s/n+i(C).
C Trigonometric solutions It turns out that the classification of the non-
degenerate trigonometric solutions of the CYBE is very similar to that of the
constant solutions described in the previous section. This may explained by
the following observations.
Note first that, by 3.2.3(i), every solution is of the form
A2)
where r(u) is holomorphic. A direct computation shows that, iff is constant,
then r satisfies the CYBE if and only if f satisfies A).
Secondly, we have seen in 2.1.10 (see also F)) that trigonometric solutions
of the CYBE arise by considering Lie bialgebra structures on the affine Lie
algebra associated to g. It is well known that the structure of affine Lie
algebras resembles closely that of the finite-dimensional complex simple Lie
algebras.
To describe the classification of trigonometric solutions, we must first re-
recall certain results about the finite order automorphisms of g (see Helgason
A978)). Let g be an automorphism of the Dynkin diagram of g. We may view
a as an element of the quotient group Aut(g)/Inn(g) of the automorphism
group of g by the subgroup of inner automorphisms. An automorphism 7 of
finite order in the coset of g modulo Inn(g) is called a Coxeter automorphism
of the pair (g, g) if
(a) its fixed point subalgebra is abelian;
(b) 7 has minimal order among the elements of the coset of g which satisfy
(a).
92 3 Solutions of the CYBE
The order ha of 7 is called the Coxeter number of the pair (g, a). Let
e — exp[27^^/^l/h(T] and let g^j be the eJ-eigenspace of 7 on g. Then,
ha~l
9= © &r,j.
The abelian subalgebra g^o will play a similar role to that of the Cartan
subalgebra, and we denote it by i)a from now on. Let taj be the projection
of t onto the part g^j 0 9<7,-j of 9 ® 9- Then,
ha-l
t= Y2 l^r
j=o
For any a G I)*, and any j = 0,1,..., hG — 1, let
9^. = {X G g^ I [H,X] = a(ff)X for all ff G
Then, dim(g^}j) < 1 for a ^ 0, and
Let 11^ = {a G I)* I g^4 ^ 0}. Then, 0 ^ Ua. The elements of Ua are
called the simple weights of (g, cr). Unlike the simple roots of g, they are not
linearly independent, but satisfy a single linear relation with positive integer
coefficients.
The pair (g, a) can be recovered from its Dynkin diagram, which is con-
constructed from the simple weights in the same way as the Dynkin diagram of g
is constructed from the simple roots. Namely, the Dynkin diagram of (g, a) is
a graph with one vertex for each simple weight, the vertices corresponding to
weights a and f3 being joined by 4(a,/3J/(a, a)(/3,f3) bonds, with an arrow
pointing toward vertex f3 if (a, a) > (/3, E).
To describe the parameter space of (equivalence classes) of trigonometric
solutions of the CYBE, we make the following definition, which is analogous
to 3.1.1.
Definition 3.2.6 A quintuple (III, n0, r, r°, a), where a is an automorphism
of the Dynkin diagram of g, no,IIi C 11^, r : III —> n0 is a bijection, and
r° efya^ha, is said to be admissible if it satisfies conditions (i)-(iv) of 3.1.1
(in condition (Hi), t should be replaced by ta$). The quadruple (IIi, n0, r, a)
is admissible if it satisfies conditions (i) and (ii).
As in the case of constant solutions, the set of admissible quintuples has a
decomposition into finitely many strata, indexed by the admissible quadru-
quadruples, the stratum associated to (IIi,IIo,r, a) being a complex affine space of
dimension \k(h — 1), where k = \Iia\Ili\.
3.2 Solutions of the CYBE with spectral parameters 93
One must take into account the action of the group of automorphisms of g
on these data. Let Aut7(g) be the centralizer of the Coxeter automorphism
7 in Aut(g), and Inn7(g) the subgroup generated by 7 and the inner auto-
automorphisms given by conjugation by elements of exp(I)). Then, Inn7(g) is a
normal subgroup of Aut7(g), and Aut7(g)/Inn7(g) is isomorphic to the group
of automorphisms of the Dynkin diagram of (g, a).
Proposition 3.2.7 The equivalence classes of non-degenerate trigonometric
solutions of the CYBE are in one-to-one correspondence with the union, over
the set of automorphisms a of the Dynkin diagram of g, of the quotients of
the spaces of admissible quintuples (III, n0, r, r°, a) by the natural action of
the group of automorphisms of the Dynkin diagram of (g, a). |
We shall now describe the solution of the CYBE associated to an admissible
quintuple (IIi,IIo,r,ro,cr). Let gnz be the subalgebra of g generated by the
subspaces g?}1 for a elli. Then, gnz is the sum of certain of the g?j. Hence,
there is a canonical projection map P : g —> gnx such that P(g^) = 0 if
c?j <fi gni • One shows that there is an isomorphism 6 : gnx —> gn0 of Lie
algebras such that 0(g?i) = 9^ 1 f°r a^ a E IIi. Moreover, the operator
6 o P : g —> g is nilpotent, so it makes sense to define / : g —> g by
Theorem 3.2.8 For any admissible quintuple (IIi, n0, r, r°, a),
0 3 1
3=0 3 = 1
is a non-degenerate solution of the CYBE with poles at the points 2'K\J~—\1L.
Moreover,
r{u + 27rv/::T) = G ® l){r(u)) = A 0 7)(r(u)).
Conversely, every non-degenerate meromorphic solution of the CYBE
whose poles form a lattice of rank 1 is equivalent to a solution of this form. |
Remark The role played by g in the proof of 3.1.3 is played in that of 3.2.8
by the loop algebra L(g) of Laurent polynomial maps Cx —> g. A
Example 3.2.9 For each automorphism a of the Dynkin diagram of g, there
is a standard solution, corresponding to n0 = IIi = 0, r° = |^,o> namely
j=0
94 3 Solutions of the CYBE
Example 3.2.10 If g = s/2(C), the identity is the only diagram automorphism
of g, and the Coxeter automorphism 7 is conjugation by the element
1 0
0 -1
of SL2((C) of order hi — 2. Thus, \)i is the usual Cartan subalgebra of sZ2(<C),
and 9i5i consists of the matrices
0 *\
* 0)'
The simple weights are ± a, where a is the usual simple root of sfoiQ?)- The
Dynkin diagram of (s/2(C), 1) is
There are three admissible quadruples:
(i) n0 = III = 0: then, in the notation of 2.1.7, we have gn0 = Qiii = 0,
/ = 0, th0 = \H®H, tlfl = X+ ®X~ +X~ ® X+, r° - ^1,0, and we
obtain
r(u) — -coth f -u I H <g> H
(ii) n0 = {a}, nx = {-a}: then, gn0 = C.X+, qUi = CJ". Choose (9 such
that 0(X") = X+. Then, / is given by
/^A J = A , J \A ) = /v-"/ := ^*
We obtain
1 /I
rW - 4cot ^2W
(iii) IIq = {—a}, III = {a}: the solution in this case is obtained by inter-
interchanging X+ and X~ in (ii).
There is a unique non-trivial diagram automorphism of (g, 1), which inter-
interchanges a and — a. Thus, the solution of type (iii) is equivalent to that of
type (ii), and the parameter space of solutions consists of two points. <0>
3.2 Solutions of the CYBE with spectral parameters 95
D Rational solutions Prom 3.2.3(i) and 3.2.4, it follows that every non-
degenerate rational solution is equivalent to one of the form
A3) r(ui,u) h()
(i,2) (i,2),
U\ — U2
where f is a polynomial in U\ and u<i with values in g <g> g. As in the trigono-
trigonometric case, a computation shows that, if r is constant, then A3) holds if
and only if r is a skew-symmetric solution of the CYBE. The following result,
conjectured by Drinfel'd, shows that in one sense the general case is not much
more complicated.
Proposition 3.2.11 Every non-degenerate rational solution of the CYBE is
equivalent to a solution of the form A3), in which f is a polynomial of degree
at most one in each of u\ and U2. I
This result is a consequence of a prescription for constructing all non-
degenerate rational solutions of the CYBE due to Stolin A991a-d). We shall
only outline his results.
Let C^u]] be the algebra of formal power series in an indeterminate
u with complex coefficients, and let C((w-1)) be its field of fractions. We
introduce the Lie algebra of formal power series q((u~1)) = g <g) C((u-1))
and its subalgebras g^u]] = g C^C^u]] and g[u] = g <g)<C[u]. We define
an inner product on g ((u~1)) by
where 'res0' is the u~l coefficient, and the inner product ( , ) on the right-
hand side is that on g. Note that u^g [f^]] is a lagrangian subspace of
g ((u)), i.e. it is equal to its orthogonal complement.
Proposition 3.2.12 There is a natural one-to-one correspondence between
non-degenerate rational solutions of the CYBE and subspaces W C g ((u~1))
such that
(i) W is a Lie subalgebra of g((u~1));
(ii) W 0 q[u] = g ((w)) and W D u~Nq [[u]] for some N > 1;
(Hi) W is lagrangian.
Moreover, the solutions associated to subspaces W\ and W2 are equivalent if
and only if W2 ~ ol(u).W\ for some a G Aut(g)[u].
Outline of proof By using the inner product, we may identify the vector
space dual of g[u] with u-1g [["U]]- We associate to any rational solution of
the form A3) the graph W(r) of r thought of as a map g [u]* —> g [u]. That W
is a Lie subalgebra follows from the fact that r satisfies the CYBE, and that
W is lagrangian follows from the skew property ^12(^1,^2) = —^21(^25^1)
96
3 Solutions of the CYBE
of r. Conversely, any W such that W 0 g [u] = g ((u l)) is the graph of a
map g [u]* —> g [u], and the second condition in (ii) is a 'continuity' condition
which guarantees that this map comes from an element of g [u] <S> g [u]. |
To simplify the presentation, we shall restrict ourselves from now on to the
case g = s/n+i(C).
Proposition 3.2.13 Every subspace W C sln+iAE)((u~1)) satisfying the
conditions of 3.2.12 is contained in g~l .sln+i(<E)[[u~l]].g for some invertible
matrix g e GLn+i(C((u))). |
Since applying an element of SXn+i (C[w]) to W gives an equivalent solution
of the CYBE, and since 5/n+i(C)[[w~1]] is preserved by the adjoint action of
GLn+i(C[[u~1]]), we are in the situation of the
BlRKHOFF FACTORIZATION THEOREM 3.2.14 Every g e GLn+i(C((u~1)))
can be written as a product
/ukl 0 ••• 0 \
0 uh* ••• 0
9 = 9
7
< fcn+i.
w]]), and kuk2,.
Moreover, (fci, /C2,.
,fen+i are
, fcn+i) is
\ 0 0
where g+ e GLn+i(C[u]), g" E GZ
integers satisfying k\ < &2 <
imiqueiy determined by g. |
It follows that we may restrict ourselves to subspaces W which are con-
contained in g~l.sln^-i((C)[[u~1]].g, where g is a diagonal matrix of powers of u.
In fact, it is easy to see that condition (ii) in 3.2.12 implies that \k{ — kj\ < 1
for all i,j, so that g is of the form
/I \
1
\ UJ
where k is the number of ones. By applying the non-trivial diagram auto-
automorphism of s/n_|_i(C) if necessary, we may assume that 0 < k < [(n 4-1)/2].
If
we say that W', or the corresponding solution of the CYBE, is of class k.
Define Lie subalgebras pk of s/n+i(C), for 0 < k < n-f-1, by po — ^/n+i((
and, for k > 0,
* *
0 *
where the zero matrix is (n 4-1 — k) x k.
3.2 Solutions of the CYBE with spectral parameters 97
Proposition 3.2.15 There is a one-to-one correspondence between non-
degenerate rational solutions of the CYBE of class k with values in s/n+i
(C)®2, where 1 < k < [(n-h l)/2], and pairs (f, to), where f is a Lie subalgebra
of s/n+i(C) and uj is a 2-cocycle on f which is non-degenerate on f D p^.
Moreover, the solutions associated to pairs (fi,u;i) and (f2,^2) are equiv-
equivalent if and only if there is an inner automorphism a of s/n+i((C) such that
a(fi) = h and a*(^2) - wi is a coboundary
Finally, solutions of class 0 are equivalent to solutions A3) in which r is
constant.
Outline of proof The statement about class 0 solutions follows from 3.1.6
and the remarks at the beginning of this subsection. We assume from now
on that k > 0.
Note that sln+iWlu-^/u-tsln+iiQlu-1]]) = sln+1(€{e}/(e2)); we de-
note this Lie algebra by s/n+i(e). As a Lie algebra,
s/n+i(e) ^s/n+i(CHad,
the semidirect product in which s/n+i(C) acts on its adjoint representation
ad, thought of as an abelian Lie algebra. Note that the inner product on
s/n+i(C(('U~1))) induces one on s/n+i(e).
Given W of class fc, note that, since W is lagrangian,
Let We be the projection of dk.W.d^1 to s/n+i(e), and let f be its further
projection to s/n+i(C). Then, W€ C f 0 ead, and, since W€ is easily seen to
be lagrangian, it follows that We D ef-1. Hence, We is determined by giving
a subspace Ve C (f 0 eadj/ef-1 = f 0 e(ad/f-L) = f 0 ef*. Since We projects
onto f, it follows that Ve does also, and hence that Ve is the graph of a map
/ : f —> f*. Moreover, since W is a subalgebra of ,s/n+i(C)((^~1)), it follows
that W€ is a subalgebra of s/n+i(e) and that V€ is a subalgebra of f 0 f*. The
latter condition is equivalent to
for all x, y G f. If we regard / as an element of f* (S>f*, this in turn is equivalent
to / being a 2-cocycle.
Finally, the condition that W is of class k implies that
We 0 (pfc 0 ep?) = s/n+i(e).
It is not difficult to see that this is equivalent to requiring that / is non-
degenerate on f H pk and f + pfc = s/n+1(e). |
98 3 Solutions of the CYBE
Example 3.2.16 For s/2(C), the only possible choice of f is s?2(C) itself. This
gives the class 0 solution
r(uuu2) = + -H A X+
ui-u2 2
and the class 1 solution
() + ^H
r(«i,«2) + ^H®X^
U\ - U2 2 2
(We are taking the inner product on 5/2(<C) to be the trace form.) <0>
Example 3.2.17 For 5/3 (<C), the class 0 solutions can be read off from 3.1.8.
In the class 1 case, there are two choices for f, namely 5/3(<C) itself and
'* 0 oN
* * *
* * *
In both cases, i^Lie(f) = 0> so ^ne associated solution is unique up to equiva-
equivalence. Using the notation of 3.1.5, the associated solutions are, respectively,
r(ui, u2) = —t— + ^-(Ha + 2H0)
X+ - ui X+ ® X+ + l-{Ha - Hp)AX-+X+AX++0,
^(tf* + 2H0)
— u-2
X A (fTa + 2^) + l-X~ A BFQ + H0),
the Casimir element again being computed for the trace form.
Bibliographical notes
3.1 The classification of the non-skew-symmetric constant solutions of the
CYBE (or, equivalently, of the skew-symmetric constant solutions of the
MCYBE) for a complex simple Lie algebra is due to Belavin & Drinfel'd
A982, 1984a,b), where complete details of the proofs may be found. The
case of skew solutions of the CYBE is due to Stolin A991a,c,d).
Bibliographical notes 99
3.2 The classification theorem 3.2.4, as well as the explicit description of the
elliptic and trigonometric solutions of the CYBE, are again due to Belavin &
Drinfel'd A982, 1984a,b) although, as in the case of constant solutions, many
examples had appeared earlier in the physics literature. In particular, all the
elliptic solutions had been found by Belavin A981) by taking the 'classical
limit' of the solutions of the quantum Yang-Baxter equation associated to
the 'Zn-symmetric' lattice model in statistical mechanics (see Section 7.5).
The rational solutions were classified by Stolin A991a,b,d).
4
Quasitriangular Hopf algebras
The space T(M) of C°° functions on a smooth manifold M forms a commuta-
commutative algebra under pointwise addition and multiplication. If G is a Lie group,
the multiplication and inverse maps of G endow J-{G) with extra structure,
namely the comultiplication map J~(G) —> J-(G) <g> J-(G) and the antipode,
a map J~{G) —> J-(G) (one must define the tensor product appropriately
here). These maps satisfy certain compatibility conditions reflecting the as-
associativity of multiplication in G and the defining properties of the inverse.
Abstracting these properties leads to the notion of a Hopf algebra (which need
not be commutative as an algebra).
In fact, to any Lie group G one can associate a second Hopf algebra, the
universal enveloping algebra U(§) of the Lie algebra g of G. The universal
enveloping algebra is not commutative (unless G is), but is always cocom-
mutative, which means that the comultiplication of ?/(g) takes values in the
symmetric part of U(q) 0 U(q).
Before the advent of quantum groups, very few Hopf algebras which are
neither commutative nor cocommutative were known (apart from tensor prod-
products of function algebras and enveloping algebras), but the theory of quantum
groups provides a large class of natural examples.
We summarize the main facts about Hopf algebras in Section 4.1. This
rather lengthy section should probably not be read linearly, but referred to
when necessary.
The comultiplication map A —> A 0 A of an arbitrary Hopf algebra A al-
allows one to define the tensor product V 0 W of two representations V and
W of A. If A is not cocommutative, V 0 W and W 0 V are not necessar-
necessarily isomorphic as representations of A, although they are isomorphic for the
special class of quasitriangular Hopf algebras, discussed in Section 4.2. Such
Hopf algebras contain a distinguished invertible element 1Z e A 0 A, called
the universal R-matrix, from which the isomorphism V<g>W-*W(g>V is
constructed. Most of the quantum groups we shall encounter (or their duals)
are quasitriangular, and many of the applications of the theory of quantum
groups make essential use of their universal R-matrices. The crucial prop-
property of 7Z in these applications is that it satisfies the quantum Yang-Baxter
equation
4-1 Hopf algebras 101
4.1 Hopf algebras
A Definitions An algebra with unit over a commutative ring k (always as-
assumed to have a unit itself) is a /c-module A together with a way of multiplying
two elements ai, a2 G A to give their product a\.a2 ? A. The multiplication
should be bilinear over k and associative. The unit element 1 of A has the
property a.l = l.a = a for all a G A We shall now reformulate this in terms
of commutative diagrams.
Definition 4.1.1 An algebra over a commutative ring k is a k-module A
equipped with k-module maps /iA : A <g> A —> A, the multiplication, and
k
iA : A —> A, the unit, such that the following diagrams commute:
*1 h 4
id id
A 0 A 0 A > A 0 A
i I-
(we omit the superscript on /i, i and the subscript on the tensor product when
this will not lead to confusion).
Of course, in terms of the more familiar description of an algebra given
earlier, we have i(\) = Al, fi{ai <g> 02) = a\.a2> The first two diagrams
express the properties of the unit element and the third the associativity of
multiplication.
The condition that an algebra be commutative can similarly be expressed
by the commutativity of the diagram
A® A > A® A
•1 i-
A > A
id
where a : A® A —> A® A is the k- linear map such that a{a\ <S> A2) — a2 ® Q>i
for ai, a2 G A. In general, if we set /iop = /i o cr, then (A, z,/iop) is also an
algebra, called the opposite of A and denoted by Aop. Note that k itself is a
commutative algebra over k.
102 4 Quasitriangular Hopf algebras
If A and B are algebras over fc, their tensor product A (g> B is also an
algebra. The product operation
in A (g) B can be expressed as the composite
(A® B) <8> (A® B) —^ A <8> A <8> i? <8> i? > A^B,
where cr23 is a applied to the second and third factors of the tensor product,
and the unit of A <g) B is the composite
k -^k^k -—1-+ A <8> JB.
We leave it to the reader to give a diagrammatic formulation of the defini-
definition of a homomorphism of algebras.
The purpose of the reformulation of the definition of an algebra we have
given is that it leads naturally to the 'dual' notion.
Definition 4.1.2 A coalgebra over a commutative ring k is a k-module A
equipped with k-module maps AA : A —> A <g> A, the comultiplication, and
eA : A —> k, the counit, such that the following diagrams commute:
I A ,] JA
A < A A < A
id id
A(g)id
A® A® A < A® A
T T
id(g)A A
A® A < A
A
The commutativity of the third diagram is usually referred to as the coas-
sociativity of A.
A coalgebra A is called cocommutative if the following diagram commutes:
A® A < A® A
id
4-1 Hopf algebras 103
in other words, if A (A) is contained in the symmetric part of A <g) A. In
general, if we set Aop = joA, then (A, e, Aop) is also a coalgebra, called
the opposite of A and denoted by Aop. Note that k itself is a cocommutative
coalgebra over A;, with ek = id& and Afc : k -+ k(&k the natural isomorphism.
If A and ?? are coalgebras, then A 0 B is a coalgebra with
= eA(a)eB{b);
i.e. if AA(a) = ?\ a* (8> a< and AsF) = ?\ fy ® 6J, then
If A and j9 are coalgebras, a /c-module map <p : A —> B is a homomorphism
of coalgebras if
A Hopf algebra has compatible algebra and coalgebra structures and one
extra structure map.
Definition 4.1.3 A Hopf algebra over a commutative ring k is a k-module
A such that
(i) A is both an algebra and a coalgebra over k;
(ii) the comultiplication A : A —» A <8 A and the counit e : A —> k are
homomorphisms of algebras;
(Hi) the multiplication \x : A <8 A —> A and the unit i : k —> A are homomor-
homomorphisms of coalgebras;
(iv) A is equipped with a bijective k-module map SA : A —> A, called the
antipode, such that the following diagrams commute:
5(g)id id<g>,S
If A and j9 are Hopf algebras, a /c-module map ip : A —> 5 is a homo-
homomorphism of Hopf algebras if it is a homomorphism of both the algebra and
coalgebra structures of A.
A Hopf ideal of a Hopf algebra A over k is a two-sided ideal / of A as an
algebra such that
/0A-f-A0/, e( J) = 0, 5G) C 7.
104 4 Quasitriangular Hopf algebras
The quotient /c-module A/1 then inherits a Hopf algebra structure from A
in the obvious way. The kernel of any homomorphism of Hopf algebras is a
Hopf ideal.
The tensor product A(& B ot two Hopf algebras is a Hopf algebra with the
algebra and coalgebra structures defined above, and with antipode
If A is a Hopf algebra, there are three associated Hopf algebras Aop, Aop
and A°v. Their algebra and coalgebra structures have already been defined,
and their antipodes are EA)~1, EA)~1 and SA, respectively.
Remarks [1] Conditions (ii) and (iii) in the definition are equivalent (in the
presence of the other conditions). Omitting condition (iv) in the definition
gives the notion of a bialgebra. If a bialgebra has an antipode satisfying (iv),
then it is unique.
[2] A homomorphism of Hopf algebras ip : A —» B automatically satisfies
SB o p = ip o SA (see Hazewinkel A978), Proposition 37.1.10).
[3] The antipode S is automatically an anti-automorphism of A, i.e. S :
A —> A°v is an isomorphism of Hopf algebras. Thus, S2 is an automorphism
of A. It can be shown that, if A is either commutative or cocommutative,
then S2 is the identity map (see Abe A980), Theorem 2.1.4), but we shall
encounter many Hopf algebras in this book for which S2 is non-trivial.
[4] The defining property of the antipode S can be interpreted in terms of
the convolution algebra structure on the set of /c-module maps A —> A. If /,
g G End(A), their convolution is the map / • g : A —> A defined by
/ • g = ft o (/ <g> g) o A.
The two commutative diagrams in part (iv) of 4.1.3 assert that S is the inverse
of the identity map for the convolution product The last sentence in Remark
[1] above is a consequence of this observation.
[5] In the literature on Hopf algebras, a slightly weaker definition is used:
the antipode is not required to be bijective. It is known that the antipode
of every Hopf algebra in this weaker sense is necessarily bijective if the Hopf
algebra is either commutative or cocommutative. Indeed,- it seems to be
bijective in essentially all naturally occurring examples. A
There are several variants of the definition we have given. In some situa-
situations, A and A® A (as well as the ground ring k) are equipped with topologies
for which the /c-module structure maps of A are continuous. In that case, one
usually replaces the algebraic tensor product A <g> A by a suitable completion,
and requires that the Hopf algebra structure maps are continuous.
The most important example of such a situation for us is where the ground
ring is k[[h]], the ring of formal power series in an indeterminate h over a
4-1 Hopf algebras 105
field k. Every k[[h]]-module V has the h-adic topology, which is characterized
by requiring that {ftnV|n>0}isa base of the neighbourhoods of 0 in V,
and that translations in V are continuous. It is easy to see that, for mod-
modules equipped with this topology, every k[[h]]-module map is automatically
continuous.
Definition 4.1.4 A topological Hopf algebra over A;[[ft]], the ring of formal
power series in an indeterminate ft over a field k, is a complete k[[h]]-module
A equipped with k[[h]]-linear maps i, /i, e, A and S satisfying the axioms of
4.1.3, but with the algebraic tensor products replaced by their completions
in the h-adic topology.
We study topological Hopf algebras further in Subsection 4.ID.
A second variant of 4.1.3 applies to the case where A is a graded A:-module.
This means that there are A:-submodules An of A, for n G N, such that
A — y^ An.
nGN
One says that A is a graded Hopf algebra if the usual axioms are satisfied,
except that a is replaced by its graded version
a(a 0 a!) = (-l)mn a1 0 a, if a G Am, a' G An
(thus changing the algebra structure on Atg) A), and that the structure maps
of A are required to preserve the graded structure, i.e. i{k) C Ao, e(An) = 0 if
n > 0, S(An) = An, //(Am 0 An) C Am+n and A(An) C ®p+q=nAp 0 Aq. As
we shall see in a moment, the graded case preceded the usual case historically,
even though the latter is a special case of the former (by regarding an ordinary
Hopf algebra as being concentrated in degree zero).
B Examples There are several natural constructions which associate Hopf
algebras to groups of various kinds, and we shall discuss some of these now.
Example 4.1.5 The simplest case is that of a finite group G. The group algebra
k[G] of G over a commutative ring k is the free fc-module with basis G and
algebra structure obtained by extending linearly the product on G. There is
a Hopf algebra structure on k[G] defined by extending linearly the formulas
z(l) = e (where e is the identity element of G), e(g) = 1, A(g) = g 0 g and
S(g) = g~l• Note that k[G] is always cocommutative, but is commutative
only if G is commutative.
The second Hopf algebra associated to G is the set T(G) of k-valued func-
functions on G. The A:-module and algebra structures of T(G) are defined point-
wise, and the counit and antipode are given by e(f) = f(e) and S(f)(g) =
fig'1), respectively. To define the comultiplication, note that T[G x G) =
106 4 Quasitriangular Hopf algebras
> F{G) as algebras over k: if /i, f2 G ^(G), the isomorphism takes
/i ® /2 to the function on G x G given by (#1, #2) •—> f 1(91) 12(92)- We set
A(f)(gi,g2) — f(9i92)' Note that ^"(G) is always commutative, but is co-
commutative only if G is commutative. ^
Remark Because of the first of these examples, an element a of an arbitrary
Hopf algebra A is called group-like if A(a) = a® a. A
Example 4.1.6 Let G be an affine algebraic group over a field k (i.e. an affine
variety over k such that the group operations are morphisms of varieties),
and let T{G) be its algebra of regular functions. Then it is still true that
T(G x G) = 3~(G) <S> ^(G), and one can define a Hopf algebra structure on
T(G) exactly as in 4.1.5. For example, if G = GLn{k), then T(G) is the
commutative algebra with generators x^, 1 < i, j < n, and D~\ and the
single relation
D~\detX = 1,
where X is the n x n matrix with entries Xij. The comultiplication is defined
on generators by
k=l
and the remaining structure maps are given by e(xij) = 6ij, S(xij) =
(X~l)ij. It follows from the multiplicative property of the determinant that
D~l is group-like and that S(D~l) = D. <}
Example 4.1.1 Let G be a compact topological group and let T(G) be the
algebra of continuous real- (or complex-) valued functions on G. If we use the
same definitions as in the previous two examples, we do not get a Hopf algebra
in the sense of 4.1.3 because the comultiplication takes values in T(G x G),
which is 'bigger' than T(G) <S>J-(G). One solution is to modify our definition
of a Hopf algebra, taking into account the natural topology on J-(G) (defined
by the sup norm). Since the algebraic tensor product T{G) <g) F{G) is dense
in T(G x G), we can regard T(G x G) as a completion of T(G) 0 F{G).
Alternatively, we can replace T(G) by a smaller algebra. In fact, let p : G —>
GLn(JR) be any continuous representation of G on Rn, and let pij = Xij o p
be the matrix elements of p. Then the p^, as p runs through all finite-
dimensional representations of G, generate a subalgebra Rep(G) of ^(G),
called the algebra of representative functions of G. We know by the Peter-
Weyl theorem that Rep(G) is dense in J-(G). Also, Rep(G x G) is isomorphic
to the algebraic tensor product Rep(G) 0 Rep(G), and it is easy to see that
the usual maps make Rep(G) into a genuine Hopf algebra. ^
Example 4.1.8 Let g be a Lie algebra over a field k. The universal enveloping
algebra ?/(g) of g is the quotient of the tensor algebra T(g) = ®n>o9®n by
4.1 Hopf algebras 107
the two-sided ideal generated by the elements x 0 y — y 0 x — [x, y] for all
x, y G g. The Poincare-Birkhoff-Witt theorem asserts that, if {xi}iei is
any basis of g, where the index set / is totally ordered, the set of monomials
{xixXi2.. -Xik}, where k > 1 and i\ < %2 < • • • < ik, is a basis of U(q). It
follows that the composite of the natural map g —> T(g) with the canonical
projection T(g) —> ?/(g) gives an embedding of g into J7(g), and we usually
identify g with its image under this map. Since g clearly generates C/(g) as an
algebra, to define a Hopf structure on U(q) it is enough to give the structure
maps on elements of g:
A(x) = x0 l + 10x, S(x) = -x, e(x) = 0 (x G g).
In fact, g can be characterized as the set of primitive elements of ?/(g), i.e.
the set of elements x for which A(x) = x0l + l0x.
Of course, one must check that these formulas respect the algebra structure:
for example,
A(xy - yx) = A(x)A(y) - A(y)A(x)
= (x 0 1 + 1 0 x)(y 01 + 10 2/)-B/01 + 10 y)(x 0 1 + 1 0 x)
= (xy - yx) 0 1 + 1 0 (xy - yx)
= [x, 2/] 0 1 + 1 0 [x, ?/]
Note that i/(g) is cocommutative, since A(g) is obviously contained in the
symmetric part of ?/(g) 0 U(q), which is a subalgebra of U(q) 0 ?/(g). But
f/(g) is commutative only if g is commutative. <0>
Example 4.1.9 Let V be a graded vector space over a field k of characteristic
t^ 2. If V is concentrated in even degrees, its symmetric algebra Sym(V)
is the quotient of the tensor algebra T(V) by the two-sided ideal generated
by v 0 v' — v' 0 v for all v, z/ G V. If V is concentrated in odd degrees, its
exterior algebra f\(V) is the quotient of T(V) by the two-sided ideal generated
by v 0 z/ + v1 0 v for all v, z/ E V.
The symmetric and exterior algebras are multiplicative, in the sense that,
for any two (appropriately graded) vector spaces V and W, there are canonical
isomorphisms
Sym(F ®W)^ Sym(F) 0 Sym(W), A(V ®W)^ A(V) 0 A(W)
of graded algebras. Hence, the diagonal map V —> V0 V, v —> (v,v), induces
comultiplications on Sym(V) and A(F). If we set e(v) = 0, S(v) = —v, for
v G V, then Sym(F) and A(F) become graded Hopf algebras over k.
Note that Sym(F) and A(V) are commutative and cocommutative (in the
graded sense). Conversely, it can be shown that every graded Hopf algebra A
108 4 Quasitriangular Hopf algebras
over a field of characteristic ^ 2 which is both commutative and cocommu-
tative, and for which dim(Ao) = 1 and dim(An) < oc for all n, is isomorphic
to the tensor product of a symmetric algebra and an exterior algebra. <0>
Example 4-1-10 Let G be a connected, finite-dimensional Lie group, and let
H*(G, k) be the homology of G with coefficients in a field k of characteristic
zero. Then, H^ (G, A:) is a graded Hopf algebra: the multiplication in H^ (G, A:)
(called the Pontryagin product) is induced by the product G x G —+ G (note
that H^ (G x G, k) = H^ (G, k) 0 H* (G, A:) as graded algebras by the Kiinneth
theorem); the comultiplication is induced by the diagonal map G —+ G x G;
the antipode by the inversion map G —* G\ and the counit is the projection
onto the degree zero part, which is one-dimensional because G is connected.
Moreover, the algebra H*(G, k) is graded commutative and cocommutative,
and finite dimensional because G is finite dimensional. Hence, the result
stated in the previous example implies that H^ (G, A:) is isomorphic to the
tensor product of a symmetric algebra and an exterior algebra. But, since
H^ (G, k) itself (and not just its graded components) is finite dimensional, the
symmetric part must be trivial, whence Hopf's theorem that if*(G, A:) is an
exterior algebra on odd-dimensional generators.
This example provided the original motivation for the study of Hopf alge-
algebras, as well as the terminology. <0>
C Representations of Hopf algebras If A is an algebra over a commu-
commutative ring A:, a A:-module V is called a left A-module if there is a A:-module
map Ay : A <g> V —> V such that the following diagrams commute:
A®A®V M<gI V) A®V k®V '<gI V> A®V
A
¦1
A®V > V V > V
A idv
(as usual, we omit the subscript if this is unambiguous). Equivalently, a i—>
X(a <S> •) should be a homomorphism of algebras from A into the endomor-
phisms of V. We shall sometimes write X(a<S>v) as a.v if the action is under-
understood. Right A-modules are denned similarly.
If A is a coalgebra over a commutative ring A:, a A:-module V is called a
right A-comodule if there is a A:-module map py '- V —> V 0 A such that the
following diagrams commute:
V <S> A<S> A < V <S> A V <g> k < V 0 A
I T' -I 1-
V®A < V V < V
4-1 Hopf algebras 109
Left A-comodules are defined similarly.
If V is itself an algebra or a coalgebra, it is natural to require that these
module and comodule structures should respect the extra structure on V.
Assume that A is a bialgebra. An algebra V is a left A-module algebra if it is
a left A-module and
a.(vw) = ^^(ai.v)(al.w), a.l = €a((iI
for all a G A, i?, w G V, where A^(a) = J^ a^ (g) a\ A coalgebra V is a left
A-module coalgebra if it is a left A-module and
-V3 ^rf-V'*, €y(a.v) = e^
for all a G A, v G F, where Ay(v) = ?]. Vj <g> vJ'. We leave it to the reader
to formulate these definitions diagrammatically, and to define the notions of
a right A-comodule algebra and coalgebra.
Example 4.1.11 Let A: be a field of characteristic zero, and let G be an affine
algebraic group over k. Let ip : G —+ GL(V) be a representation of G on a
finite-dimensional A:-vector space V (in the usual sense). Choosing a basis
{vi} of V defines an isomorphism GL(V) = GLn(k), and allows us to regard
(p as a homomorphism <p : G —> GLn(k). One says that <p is rational if the
pull-backs (fij = Xij o ^ of the coordinate functions ar^ on GLn(k) are regular
functions on G (cf. 4.1.6); it is easy to see that this criterion is independent of
the choice of basis of V. For such a representation, the map p : V
denned by
is also independent of the chosen basis of F, and defines a right F{G)-
comodule structure on F. <0>
A representation of a Hopf algebra A over a commutative ring A: is a
left A-module (A being regarded simply as an algebra). The terms sub-
representation, irreducible representation, etc., have their usual meanings.
A corepresentation of A is a right A-comodule. We shall use the terms
(co)representation and (co)module interchangeably.
Remark It is only necessary to consider left A-modules, for if p : V <S> A —> V
is a right A-module, then A = po (idy 0 S) is a left A-module, and conversely.
A similar remark applies, of course, to comodules. A
110 4 Quasitriangular Hopf algebras
Example 4A. 12 The trivial representation of a Hopf algebra A on a, A;-module
V is given by
) v) = e(a)v.
More generally, an element v of an arbitrary representation of A is said to be
invariant under the action of A if the preceding equation holds for all a G A.
Similarly, the trivial corepresentation is denned using the unit i of A. <0>
Example 4.1.13 The adjoint representation of a Hopf algebra A on itself is
given by
ad(a 0 a7) =
where A(a) = J2i Gi®al- The reader will easily verify that this makes A into a
left A-module algebra, and that it reduces, in the case of a group algebra or a
universal enveloping algebra, to the action of a group on itself by conjugation
or to the usual adjoint representation of a Lie algebra, respectively. <0>
Example 4-1.14 The regular representation of a Hopf algebra A on itself is the
multiplication // of A] it makes A into a left A-module coalgebra. Similarly,
the regular corepresentation is the comultiplication A of A ; it makes A into
a right A-comodule algebra. <0>
Although the definition of a representation of a Hopf algebra A only makes
use of its algebra structure, the remaining structure maps still play an im-
important role in representation theory. In fact, we have already seen that the
counit allows one to define the trivial representation of A. More significantly,
the comultiplication allows one to take the tensor product of representations:
if V and W are representations of A, then V<S> W is naturally a representation
of A 0 A,
(a\ (g) 02).(v <8> w) = a\.v
and we make V<8)^ into a representation of A by
a.(v <S> w) = A(a).(v <g> w).
Finally, the antipode allows one to turn the dual V* = Horn*; (V, A;) of a
representation V of A into a representation of A
A) (a4,v) = (?,S(a).v),
where a G A, v G V', ? G V* (( , ) is the natural pairing between V and V*).
One checks without difficulty that the canonical A:-module map V* <g> V —> k
commutes with the action of A. If A; is a field and V is finite dimensional,
the same is true for the canonical map k —» V 0 V*, which takes 1 G k to
X^ ^z 0 vl if {^z} is a basis of V and -{V} the dual basis on V* (this remains
4.1 Hopf algebras 111
true for any commutative ring k if V is finitely generated and projective over
&, by the 'dual basis lemma' - see 5.1.3). However, the canonical A:-module
maps F0F* —> k and k —> V* <g> V do not commute with the action of A in
general. Note finally that, since S is a coalgebra anti-automorphism of A, if
V and W are representations of A, the canonical isomorphism of A:-modules
(V <g> W)* = W* ® F* also commutes with A.
If V and VF are representations of A, we make Honifc(V, W) into a repre-
representation of A by setting
for / G llomk(V,W), v G V, where A(a) = ?]• a* <g> a*. If W is the triv-
trivial representation, this is of course the dual V*. We leave it to the reader
to check that, if A: is a field (say), the canonical vector space isomorphism
Homfc(V, W) = W <g> V* is actually an isomorphism of representations of
A (but this is not true for the vector space isomorphism Homfc(V, W) =
V*®W\).
Once again, the reader will easily verify that, in the case of group algebras
and universal enveloping algebras, these definitions reduce to the usual ones
for groups and Lie algebras, respectively.
Remark One can define another action of A on Hom.fc(V, W) by replacing S by
S~x in the above formulas. In particular, if W = k this gives a representation
V of A. To distinguish V* from V7, we call them the left and right duals of
V, respectively. It is clear that, if dim(V) < oc, the canonical isomorphisms
of k-modules V*' = V = Vf* commute with the action of A.
There is a simple condition on A which guarantees that V* = V as repre-
representations of A for all V: namely, that the automorphism S2 of A is inner.
In fact, if u is an invertible element of A such that S2(a) = uau~l for all
a e A, the map F* —> V given by f h-» u~1.^ commutes with the action of
A (the dot denotes the action of A on V*). In particular, if dim(F) < oc,
V** = V = V" in this case. We shall see in the next section a large class
of Hopf algebras which have this property, and in Chapter 12 some which do
not. A
D Topological Hopf algebras and duality If A is a coalgebra (assumed to
be defined over a field k for simplicity), its vector space dual A* is naturally an
algebra. In fact, the comultiplication A of A induces a map A* : (AfgiA)* —>
A*, and the multiplication of A* is obtained by restricting A* to the subspace
A* 0 A* of (A <g> A)*. The unit of A* is the dual of the counit of A. That
these maps do define an algebra structure on A follows from the fact that the
commutative diagrams in 4.1.1 are obtained from those in 4.1.2 by 'reversing
the arrows'.
112 4 Quasitriangular Hopf algebras
Moreover, if p : V —> V <g> A is a right A-comodule, one defines a left
A* -module structure on V by
X(a 0 v) =
where a G ^4*, i> G V and p(v) = J] vi ® al-
In the finite-dimensional case, one passes from algebras to coalgebras (and
from modules to comodules) in a similar way. Combining this with the previ-
previous remarks, one sees that the dual A* of any finite-dimensional Hopf algebra
A is a Hopf algebra in a natural way (the antipode of the dual is the dual of the
antipode), and one has a canonical isomorphism of Hopf algebras (A*)* = A.
Moreover, the categories of representations of A and of corepresentations of
A* are canonically equivalent.
Example 4-1-15 If G is a finite group and A: is a field, the pairing
T(G) x k[G] -> k,
given, for / G T{G), g{ G G, A* G fc, by
induces isomorphisms of Hopf algebras T{G)* ^ k[G] and k[G\* = T(G). 0
In the infinite-dimensional case, however, the dual of a Hopf algebra A
cannot in general be given a Hopf algebra structure by the above procedure,
since the dual of the multiplication of A might not take values in the subspace
.4* <g>A* of (A<S> A)*.
Example 4-1-16 Let g be a Lie algebra over a field k of characteristic zero,
and let {xi,#2, • • • ,Xd} be any basis of g (we assume that dim(g) = d < oo
for simplicity). For any A = (Ai, A2,..., A^) G Nd, set
^.Ai A2 ™A<2
* Ai! A2!'" Ad!'
Then, by the Poincare-Birkhoff-Witt theorem, {xaJagn^ 1S a basis of ?/(g),
and it is not difficult to show that
B) A(sA) =
where the addition of elements of Nd is performed componentwise (see
Dixmier A977), Proposition 2.7.2).
4.1 Hopf algebras 113
Now define ?A G U(q)* by fA(xM) = <5A#1. Then B) implies that
Let ?i,..., ?d be indeterminates, and let k[[^\,..., ?<J] be the algebra of formal
power series in ?i,..., ?<$• It is clear that the assignment ?A i—> ^ 1?22 • • • ^d
defines an algebra isomorphism U(cyj* —> A;[[?i,... , ?d]]-
Assume now that g is abelian. Then,
where
Hence, the comultiplication on ?/(g)* should be given by
Identifying ?/(g)* with fc[[^i,..., ^d]]» this means that Ajj* is defined by tak-
taking the & to be primitive and extending to an algebra homomorphism. As
expected, however, Au* does not take values in the algebraic tensor product
MKi, • • •»&*]P2, but only in its 'completion' k[[?u ...,&,^,...,&]]. Thus,
U(q)* is a Hopf algebra, provided we are willing to interpret ?/(g)* 0 f (g)*
as an appropriately completed tensor product. <0>
Despite these difficulties, there is a way to define the dual of any Hopf
algebra, finite dimensional or not. We set A° = {a G A* \ //*(ce) G A* 0i*}.
It is easy to see that A* <g> A* is a subalgebra of (A <g> A)*; hence, A° is a
subalgebra of A*. One proves that n*(A°) C A°®A°, that A*(A°®A°) C A°,
and that S*(A°) C A°. Hence, with the obvious structure maps, A° is a Hopf
algebra, called the Hopf dual of A.
This construction has a simple representation-theoretic interpretation. In
fact, it can be shown that A° is exactly the space spanned by the matrix
elements of all finite-dimensional representations of A. This suggests the fol-
following generalization of the Hopf dual. Suppose that we have a set X) of
finite-dimensional representations of A which contains the trivial representa-
representation and is closed under taking (left) duals, direct sums and tensor products.
Let A^ be the space spanned by the matrix elements of all representations in
E. Then, A^ is a Hopf subalgebra of A°, and every Hopf subalgebra of A° is
of this form.
114 4 Quasitriangular Hopf algebras
One can also give a topological interpretation of A° (and similarly of A^).
Let
X = {ker(p) | p : A —» End(V) is a finite-dimensional left A-module}.
Then, for any a ? A, {/-ha | /Gl} forms a base of neighbourhoods of a
for the X-adic topology on A. If we define a topology on A 0 A in the same
way using the family of ideals A<g> I + J <g> A, where I, J e X, and give the
field k the discrete topology, then all the structure maps of A are continuous.
Moreover, A° is the set of continuous linear maps A —> k.
Example 4.1.17 Let G be a connected, simply-connected affine algebraic
group over <C, and let e be the identity element of G. The elements of the
Lie algebra g of G may be regarded as left-invariant vector fields on G; more
generally, any X G U(q) defines a left-invariant differential operator on G.
The pairing U(q) x J^(G) -+ C given by (XJ) *-> (X.f)(e) induces linear
maps G(g) —> ^(G) and .F(G) —* ?/(g)*. Both maps are injective, and it is
easy to see that their images are contained in T{G)° and ?/(g)°, respectively.
Inside T{G)°, we have the evaluation maps / »-> /(#) (/ G ^*(G), # G G),
and these, together with ?/(g), generate T{GH as an algebra (see Abe A980),
Theorem 4.3.13.). For an equivalent formulation of this result, note that G
acts on g by the adjoint action, and that this extends to an action on C/(g)
by Hopf algebra automorphisms. Extending by linearity gives ?/(g) a left
<C[G]-module algebra and coalgebra structure. Then, !F(GH is isomorphic to
the semi-direct product ?/(g) (t C[G], which is ?/(g) <8><C[G] as a coalgebra, and
with algebra structure and antipode denned by
(a 0 x){b 0 y) = Y^ a(xi.b) 0 x\y, S(a 0x)=^ S(xi).S(a) 0 5(x-),
where A(x) = ^^ x^ (8) x^ and the dot denotes the action of (C[G] on ?/(g).
On the other hand, the map ^(G) —* U(q)° is an isomorphism of Hopf
algebras if g is semisimple. <0>
As this example suggests, it is often convenient to bypass these delicate
duality questions by working with the weaker notion of a non-degenerate pair-
pairing of two Hopf algebras (A, tA^A,eA, AA,SA) and {B,lb, {iB,eB,AB,SB).
This is a pairing ( , ) : A x B —» fc, bilinear over the ground ring k, which is
non-degenerate in the sense that (a, b) = 0 for all a G A (resp. for all b € B)
implies that b = 0 (resp. a = 0), and which satisfies the following conditions:
a2), b) = (ai 0 a2, A
(SA(a),b)=(a,SB(b)),
4.1 Hopf algebras 115
for all a, ai, a2 G A, 6, 6i, 62 G B. In the second pair of equations, the pairing
is extended to one between A®i and B 0 B in the obvious way:
It is clear that, if A and B are finite dimensional and k is a field, such a pairing
induces injective homomorphisms of Hopf algebras A —» B* and B —» A*; in
this case, the existence of such a pairing is thus equivalent to the statement
that each of A and B is the dual of the other.
E Integration on Hopf algebras A (left-invariant) integral on a Hopf
algebra A over a field k is a linear functional H on A such that
D) (a®H,A(a)) = (a,l)(H,a)
for all a G A, a G A*. It can be shown that, if an integral exists, it is unique
up to a scalar multiple. Right-invariant and bi-invariant integrals are defined
in the obvious way.
An integral H on A is said to be normalized if (if, 1) = 1.
Example 4.1.18 Let G be a compact topological group and let Rep(G) be
its algebra of real-valued representative functions (see 4.1.7). Let d\i be a
left-invariant Haar measure on G, and set
(H,f)= f
Jg
f
g
for / G Rep(G). Then, D) follows from left invariance of the measure, and
the normalization condition is equivalent to dfi being normalized in the usual
sense, that the integral of the constant function 1 over G is equal to 1. Note
that the integral is positive definite, in the sense that for any / G Rep(G) the
integral of /2 is positive unless / is identically zero.
The integral in this example can also be expressed algebraically. If p : G —*
End(F) is an irreducible representation of G on a finite-dimensional complex
vector space V, we may choose a positive-definite hermitian form ( , ) on V
which is invariant under G:
(9'Vi,g.v2) = (vi,v2) (g G G, vi,v2 G V).
If {vi} is an orthonormal basis of V with respect to ( , ), the matrix elements
of p are the functions pij : G —» C defined by
= (9'Vj,Vi).
116 4 Quasitriangular Hopf algebras
We recall that the Schur orthogonality relations tell us that
and that, if a is another finite-dimensional irreducible representation of G,
with matrix elements cr^/, then, if p and a are not equivalent,
(#, pijdTi) = 0,
for all z, j, /c, /.
Let E be the set of matrix elements {pij}, as p runs through the set of
finite-dimensional irreducible representations of G (one from each equivalence
class). It follows from the Schur orthogonality relations that E is linearly
independent. On the other hand, any product of matrix elements PijCTki is a
matrix element of p 0 cr, and therefore belongs to the linear span of E, every
finite-dimensional representation of G being completely reducible. Thus, E
is a basis of Rep(G).
Further, by the orthogonality relations again,
= <
1 if p is trivial,
0 otherwise.
Since E is a basis of Rep(G), these formulas uniquely determine a linear map
H : Rep(G) —> 1R, and it is easy to see that H is a normalized integral. <C>
This example has a converse which is a classical example of Tannaka-Krein
duality.
Example 4.1.19 Let A be a commutative Hopf algebra over JR. Then the set G
of algebra homomorphisms A —> IR is a group with product g\.g2 — (gi^92)°
A and inverse g~x = g o S. Suppose now that A is equipped with a positive-
definite left-invariant integral, and assume that G separates the points of A
(i.e. if a and a' are distinct points of A, there exists g G G such that g(a) ^
g{a')). Then, G is a compact topological group in the finite-open topol-
topology (for which the sets N(a±,..., an, e,#) = {gf G G \ \gf(ai) — g{ai)\ < e}, for
ai,..., an G A, e > 0, form a basis of the neighbourhoods of g G G). More-
Moreover, the map which assigns to an element a G A the evaluation of a repre-
representative function at a is an isomorphism of Hopf algebras A —>• Rep(G).
If, in addition, A is finitely generated as an algebra, then G can be given
the structure of a compact Lie group, and conversely. <0>
We shall discuss Tannaka-Krein duality in more detail in Section 5.1.
4.1 Hopf algebras 117
F Hopf *-algebras If A is an associative algebra with 1 over <E, a *-structure
on A is a conjugate-linear map * : A —> A, written a —> a*, such that
(a*)* = a, (involutive)
(^1^2)* — a2ai> (ant i-multiplicative)
1* = 1, (unital)
for all a, ai, a2 G i. A homomorphism ip : A —> B between *-algebras is a
*-homomorphism if
(p(a*) = <p{a); (a G A).
If A and 5 are *-algebras, then so is A(& B:
The canonical example is, of course, the algebra B(V) of bounded linear
operators on a Hilbert space V, the *-structure being given by
where (, ) is the inner product on V.
A Hopf *-algebra is a Hopf algebra A over C equipped with a *-algebra
structure which is compatible with the coalgebra structure of A in the sense
that the comultiplication A : A —> A <g> A and counit e : A —> C are *-
homomorphisms (A0 A being given its natural *-algebra structure, and C the
*-structure given by complex-conjugation). The pair (A, *) is also sometimes
called a real form of A (see below). These two conditions imply that
In fact, they imply that * o S~x o * satisfies the axioms 4.1.3(iv) for the
antipode, so the assertion follows from the uniqueness of the antipode (see
Remark [2] following 4.1.3).
Two real forms (A, *) and (A, f) are said to be equivalent if there is a Hopf
algebra automorphism a of A such that
a(at) = a(a)*
for all a G A.
If A is a finite-dimensional Hopf *-algebra, then the dual Hopf algebra A*
(with a different meaning of * !) is also a Hopf *-algebra. In fact, if a G A*,
one defines
a*(a) = a(S(a)*),
the bar denoting complex-conjugation.
118 4 Quasitriangular Hopf algebras
A representation p of A on a separable complex Hilbert space V is unitary
with respect to a given *-structure on A, or simply a * -representation, if
p : A —>• jB(V) is a homomorphism of *-algebras, i.e. if
A corepresentation cr : F —> A ® V is unitary if, given an orthonormal basis
{vi} of V, so that
for some a^- G A, we have S(dij) = a*^.
Example 4.1.20 Let G be a complex algebraic group with Lie algebra g.
Then, there is a one-to-one correspondence between the following three types
of objects:
(i) real forms of G;
(ii) Hopf *-structures on f/(g);
(iii) Hopf *-structures on T{G).
Indeed, a real form of G determines a real form g^ of g, i.e. a real Lie
subalgebra of g such that g = g^ 0 >/—TgR. Conjugation with respect to
gR defines a conjugate-linear map * : g —> g, which extends uniquely to a
Hopf *-structure on f/(g). Conversely, given a Hopf *-structure on f/(g), the
compatibility with the comultiplication implies that * preserves the space g
of primitive elements of f/(g), and the fixed points of * on g define a real
form.
Similarly, to define the Hopf *-structure on T{G) corresponding to a real
form Gr of G, take a regular function on G, restrict it to Gr, take the
pointwise complex conjugate of this restriction, and then extend the resulting
function on Gr to a regular function on G. Conversely, given a Hopf *-
structure on T(G), every *-homomorphism T{G) —» C is of the form / —»
f(x) for some x G Gr.
The Hopf *-structures on T(G) and f/(g) corresponding to a given real
form of G are, of course, dual to each other.
If G = SX2(C), there are exactly two real forms (up to equivalence):
(a) The compact real form
d = a, c——b
If we regard the matrix entries a, 6, c and d as generators of F(SL2((E)), the
corresponding *-structure is given by d = a*, c = —b*.
4- 2 Quasitriangular Hopf algebras 119
(b) The non-compact real form
= a, 6 = 6, c = c, d =
for which the corresponding *-structure on Jr(SL2((C)) is given by a* = a,
6* = 6, c* = c, d* = d. <0>
4.2 Quasitriangular Hopf algebras
There are several results in the literature which assert, under some additional
technical hypotheses, that every cocommutative Hopf algebra is isomorphic to
the universal enveloping algebra of a Lie algebra (and, dually, that every com-
commutative Hopf algebra is isomorphic to the algebra of functions on a group).
The theory of quantum groups provides a large family of Hopf algebras which
are neither commutative nor cocommutative. However, many of these exam-
examples (or their duals) are 'almost cocommutative' in a certain sense. In this
section, we give a number of ways of constructing almost cocommutative Hopf
algebras, and we describe some of their properties.
A Almost cocommutative Hopf algebras A Hopf algebra is almost co-
cocommutative if its comultiplication and its opposite comultiplication differ by
conjugation by a distinguished invertible element of A ® A.
Definition 4.2.1 A Hopf algebra A over a commutative ring k is said to be
almost cocommutative if there exists an invertible element 1Z ? A® A such
that
E) Aop(a) = n&(aIl-1
for all a ? A.
Remarks [1] It is obvious that if A is commutative and almost cocommutative,
then it is actually cocommutative. For example, the algebra J-(G) of functions
on a non-abelian group G (in any of the categories we have considered) is not
almost cocommutative.
[2] If \y : A —> Endfc(y) and \\y • A —» End/e(W) are representations of an
almost cocommutative Hopf algebra (A, K), the tensor products V ®W and
W® V are isomorphic as representations of A. In fact, it is easy to check that,
if a : V ® W -> W 0 V is the flip of the two factors, then a o (Ay 0 \w)(R>)
is an isomorphism V (&W —> W ®V which commutes with the action of A.
We shall develop this remark much further in the next chapter.
[3] If A is a topological Hopf algebra over k[[h)) (see 4.1.4), one says that
A is topologically almost cocommutative if there exists an element 1Z in the
/i-adic completion of A 0 A with the properties in 4.2.1. A
120 4 Quasitriangular Hopf algebras
If A is almost cocommutative, then 1Z is of course unique up to right mul-
multiplication by an element of the centralizer C of A(A) in A ® A. Obviously,
C2Z(g)Z, where Z is the centre of A. In the other direction, we have
Proposition 4.2.2 Let ip : A® A —> A be the k-module map defined by
ip(ai ® a2) = ai5(a2). Then, y(C) C Z.
PROOF Give A the natural left (A 0 A)-module structure:
(ai 0 a2) * a =
Note that (/;(x) = x * 1 for any x ? A® A, and that A(a) * 1 = e(a)l by the
commutative diagrams in 4.1.3. More generally, if c G C and a G A,
A(a) * <p(c) = A(a) * (c * 1) = (A(a)c) * 1
= (cA(a))*l = c*(A(a)*l)
= e(a)(c*l) = e(a)y?(c).
Now define, for fixed c G C, a /c-module map ^:^4(g)^4(gO4—>Aby
<8) a2 0 a3) =
We compute ^((A ® id)A(a)) = ^((id 0 A)A(a)) for any a G A. Writing
A (a) = J2i ai ® a% i we
id)A(a)) =
= if(c) (e <g> id)A(a) = <p(c) a,
A)A(a)) = ^ Oiip(c).ti(S ® id)A(ai)
= (id 0
Thus, (p(c) commutes with every element aG A |
Applying the flip map a to both sides of E), we see that IZ21R, G C, and
hence that ^{U2iTi) G Z (here, 1Z2i = <r(ft)). The next result will allow us
to refine this observation.
Proposition 4.2.3 Let u = /i(S®id)G?2i)- Tiien, u is an invertible element
of A and, for all a G A,
F) S2(a) = uau'\
Proof We show first that
G) ua = S2(a)u
4-2 Quasitriangular Hopf algebras 121
for all a G A Write
(A 0 id)A(a) = ^2^®^® a".
i
Equation E) implies that
(Tl 0 1) f ^2 ai ® ai ® ai ) =
Writing 1Z = ^2 rj ® r3\ we have
= ^ a
Applying id 0 S 0 *S2 to both sides and reversing the order of the factors, we
obtain
which we rewrite as
(8)
Now,
Y2 s(ai) ai ® a" = (fi 0 id)E 0 id 0 id)((A 0 id)A(a))
= (e0id)A(a) = 1 0 a.
Hence,
so the right-hand side of (8) is equal to S2(a)u. Similarly,
/ 0>i 0 (X^DyOL- ) = (Z 0 1,
i
from which we deduce that the left-hand side of (8) is equal to ua. This
proves G).
To complete the proof, we show that v = l~i{S~l 0 id)G^^11) is the inverse
of u. Indeed, let 1Z~1 = ^/e sk® sh. Then,
1
122 4 Quasitriangular Hopf algebras
(the second equality follows from F)). Taking a = v in G) gives S2(v)u = 1.
Since u has both a left and a right inverse, it is invertible. |
Similar arguments show that, if
u2 = fi(S 0 id)(^~1), u3 = //(id 0 5~1)GJ2i), u4 = //(id
then S2(a) = Uiau~l for all a G A and i = 2,3,4. Setting ^i = u, we deduce
Corollary 4.2.4 The elements ui e A commute with each other and the
elements Uiuj1 are in the centre of A, for i,j = 1,2,3,4. |
Remarks [1] It can be shown further that
Moreover, S(ui) = u^1, S(u2) = uj, ^(^3) = ^J1, 5Ax4) — ^a-
[2] The central element ^(^21^) of A encountered above is equal to
[3] If E0 5)GJ) = 7J, then ux = /xE0 id)GJ2i) = /i(id(gM-1)(^2i) = tx3,
and similarly u2 =1*4. If 7^2i = T^, a similar argument shows that u\ — u<i
and us = U4. A
Proposition 4.2.3 has a number of interesting consequences for the represen-
representation theory of A. For example, from the discussion at the end of Subsection
4.ID, we immediately deduce
Corollary 4.2.5 The left and right duals of any representation of an almost
cocommutative Hopf algebra are canonically isomorphic. |
Proposition 4.2.3 also enables one to define a new notion of dimension for
a representation p : A —> End/e(F) when A is almost cocommutative and,
more generally, of the trace of any /c-module map / : V —» V. We recall from
Subsection 4.1C that there is a canonical isomorphism Endfc(V) = V 0 V*
of representations of A. The trace of / would normally be defined as the
image of / under the canonical pairing V ®V* —> /c, but this is unnatural
from a Hopf algebra viewpoint because this pairing does not commute with
the action of A in general. However, if A is almost cocommutative and V is
finitely generated and projective as a /c-module (for example, if k is a field
and dim(F) < 00), 4.2.3 and the discussion in Subsection 4.1C imply that
V = V** as representations of A. We may therefore think of / as an element
of V**®V* and use the canonical pairing V** ®V* —> /c, which does commute
with the A-action. We leave it to the reader to check that the image of /
under this map is trace(p(u) o /). One drawback of this new trace, however,
is that, if V is another representation of A and / G End/e(Vr), the new trace of
/ 0 / G Endfc(y 0 V) is not in general equal to the product of the new traces
4-2 Quasitriangular Hopf algebras 123
of / and /, because u is not in general group-like. In Subsection 4.2C, we shall
see how to circumvent this difficulty for a large class of almost cocommutative
Hopf algebras.
B Quasitriangular Hopf algebras It is clear that the element 1Z in E)
cannot be arbitrary since we know that Aop is a Hopf algebra. In fact,
(Aop 0 id)Aop(a) = fti2.(A 0 id)(ft).(A 0 id)A(a).(A
(id ® Aop)Aop(a) = ft23-(id 0 A)(ft).(id <g> A)A(a).(id <
Hence, a sufficient condition for coassociativity of Aop is
(9) ft12(A <8> id)(ft) = ft23(id ® A)(ft).
Similarly, a sufficient condition for the properties (e 0 id) o Aop = id and
(id 0 e) o Aop = id of the counit to hold is that (e 0 id) (ft) = (id 0 e) (ft) = 1.
It will turn out to be convenient to make a slightly stronger assumption.
Definition 4.2.6 An almost cocommutative Hopf algebra (A, 1Z) is said to
be
(i) coboundary iflZ satisfies (9), ft2i = ft and (e 0 e)(ft) = 1;
(ii) quasitriangular if
A0)
A1)
(Hi) triangular if it is quasitriangular, and, in addition, ft.21 = ft.
If A is quasitriangular, the element 1Z is called the universal R-matrix of
Remarks [1] If (A, ft) is quasitriangular, so is (A, ft^1).
[2] If (A, ft) is quasitriangular, so are (Aop,ft2i), (Aop,ft2i) and (A?p,ft).
[3] Examples of non-cocommutative quasitriangular Hopf algebras are given
in Subsection 4.2F. However, those of most importance for us are studied in
Subsection 6.4D and Section 8.3.
[4] The notion of a topologically quasitriangular (or coboundary, or trian-
triangular) Hopf algebra is defined in the obvious way (see Remark [3] following
4.2.1). A
If A is a quasitriangular Hopf algebra, the central elements of A constructed
in the previous subsection reduce essentially to the single element uS(u).
124 4 Quasitriangular Hopf algebras
In fact, it follows from the remarks following 4.2.5 that u\ = u3 = u and
u2 = U4 = Sfa)'1. Hence, the central elements Uiuj1 are either trivial
or equal to uS(u) or its inverse. Moreover, using 4.2.3 and the following
proposition, it is not difficult to show that
A2) A(u) = (n2lnl2)-\u ®u) = (u® u)(n2lnl2)-1.
The next proposition also implies that any triangular Hopf algebra is co-
boundary.
Proposition 4.2.7 Let (A, TV) be a quasitriangular Hopf algebra. Then,
A3) nl2nl3n23 = n23nl3nl2,
A4) (e®id)(ft)=l = (id<8>e)(ft),
A5) (S®id)(ft) =1Z~1 = (id®
A6)
Proof By E), we have
n12n13n23 = n12.(A 0 id) (ft) = (Aop 0 id)(ft).fti2.
Applying a12 to both sides of A0), we find that (Aop 0 id)(ft) = H23H\3,
proving A3).
Next, A4) follows immediately by applying e 0 id 0 id and id 0 id 0 e to
both sides of A0) and A1), respectively.
To prove the first equation in A5), we compute
U.(S 0 id)(ft) = (/i 0 id)(id ® S (
= (/i 0 id)(id 0 5 0 id)(A 0 id)(ft)
= (e0id)(ft) = l
(the second equality follows from A0)). The second equation in A5) follows by
applying the same argument to the quasitriangular Hopf algebra (Aop,ft2i)-
Finally, A6) follows immediately from A5). |
Remark Let A be a Hopf algebra and let 1Z G A 0 A. Define / : A* —> A by
/(a) = (a0id, ft),
i.e. if ft = J2j rj ® r'j, then /(a) - ^.(a, r3)r'r Then:
(a) Equation A0) and the first equation in A4) are equivalent to / being a
homomorphism of algebras;
4-2 Quasitriangular Hopf algebras 125
(b) if A is finite dimensional (so that A* inherits a coalgebra structure from
the algebra structure of A), A1) and the second equation in A4) are equiva-
equivalent to / : A* —> Aop being a homomorphism of coalgebras.
The verification is straightforward. For example, A0) implies that
/(a/3) = (<*/?& id, ft)
= (a (8) /? (8) id, (A <g> id)(ft))
= (a<8>/3<8>id,fti3ft23)
= (a (8) id, ft) (/? (8) id, ft)
= /(<*)/(/?),
for alia, /? G A*. A
We have already encountered A3), called the quantum Yang-Baxter equa-
equation, or QYBE, in 2.2.8. Note, however, that the R-matrices which arise in
the study of Hopf algebras are linear maps of /c-modules, while those in 2.2.8
are nonlinear.
We remarked in Subsection 2.2C that the CYBE can be regarded as the
'classical limit' of the QYBE. We shall have much more to say about this
in Chapter 6, where we study the relation between the terms triangular,
quasitriangular and coboundary in the classical and quantum situations, as
well as the question of when a classical r-matrix occurs as the 'first order
part' of a quantum R-matrix.
C Ribbon Hopf algebras and quantum dimension Prom A2), it follows
that if A is a triangular Hopf algebra, the element u = /j(S 0 id)(ft2i) is
group-like. Prom the discussion at the end of Subsection 4.2A, we see that
the new notion of trace defined there is multiplicative with respect to tensor
products. In fact, if we are willing to modify this notion of trace slightly, we
are able to preserve this multiplicative property for a somewhat larger class
of quasitriangular Hopf algebras.
Definition 4.2.8 A ribbon Hopf algebra (A, ft, v) is a quasitriangular Hopf
algebra (A, ft) equipped with an invertible central element v such that
v2=uS(u), S(v) = v, e(v) = l,
where u = /i(S(8> id)(ft2i).
Note that, by A2) and the remarks following 4.2.4, if (A, ft) is a triangular
Hopf algebra, then (A, ft, 1) is a ribbon Hopf algebra. The reason for the
picturesque terminology will appear in Section 5.3.
126 4 Quasitriangular Hopf algebras
Although not every quasitriangular Hopf algebra is a ribbon Hopf algebra,
every quasitriangular Hopf algebra A can be enlarged to a ribbon Hopf algebra
by formally adjoining a square root of uS(u). In fact, let A = A 0 A as a
k-module, and define
(ai, a2)(a'l, a2) = (aia[ 4- a2a2uS(u), a\o!2 4-
A(ai,a2) = (A(ai),0,0, &(a2)(n21n12)~l),
5(ai, a2) = E(ai), S(a2)), e(ai, a2) = (e(ai), e(a2)).
In the second equation, the first component of the right-hand side is in the
tensor product of the first factors in A® A = (A0AH(A©A), and the last
component is in the tensor product of the second factors. It is not difficult
to check that these definitions make A into a ribbon Hopf algebra containing
A as the Hopf subalgebra A 0 0, and with v = @,1).
See 8.3.16 for an important example of a ribbon Hopf algebra.
Let us now return to the question of traces. Let A be a ribbon Hopf algebra,
and let p : A —> Endk(V) be a representation of A. We assume for simplicity
that V is a free /c-module of finite rank. In Subsection 4.2A, we saw that
it was natural to consider trace(p(w) o /). The crucial property of u here is
that S2 is given by conjugation by u. But, since v is in the centre of A, S2 is
also given by conjugation by the element g = v~lu, so we could just as well
consider trace(p(#) o /). Moreover, A2) implies that g is group-like, so the
latter trace will be multiplicative with respect to tensor products.
Definition 4.2.9 Let (A,TZ,v) be a ribbon Hopf algebra and let p : A —>
Endfc(Vr) be a representation of A which is a free k-module of finite rank. If
f : V —> V is a k-linear map, its quantum trace is defined to be
qtr(/) =trace(p(flf)/),
where g = v~1u and u = ji(S 0 id)G2.21)• In particular, the quantum dimen-
dimension ofV is
qdim(T/) = trace(p(#)).
Of course, if A is cocommutative, we may take 1Z = 10 1, u = v — g = 1,
and then the quantum trace becomes the ordinary trace.
Remarks [1] As we mentioned above, the quantum trace is multiplicative, i.e.
if Vi and V2 are representations of A and /i G EncU(Vi), f2 G Endfc(V2), then
the quantum trace of /i <g>/2 G EncU(Vi ®V2) is qtr(/i <g>/2) = qtr(/i)qtr(/2).
[2] The quantum trace qtr : Endfc(Vr) —> k is a homomorphism of represen-
representations of A, where Endk(V) is made into a representation of A as described
in Subsection 4.1C, and k is the trivial representation. In fact, qtr is the
composite
y 0 y* ^ y** 0 y* -> /c.
4-2 Quasitriangular Hopf algebras 127
Each of these maps is a homomorphism of representations of A. (The maps are
all canonical except the isomorphism V —> y**? which is defined by v \—> v',
where (t/,?) = (?,, p(g)(v)) for all ^GV*; that this commutes with A is the
statement that S2 is conjugation by g.) A
D The quantum double In Section 2.1, we showed that the double
of any Lie bialgebra 9 is a quasitriangular Lie bialgebra. We recall that
is the direct sum 9 0 9* as a vector space, but not as a Lie algebra. Now, for
a direct sum of Lie algebras 9 0 I), I7(g © ^) is isomorphic as a Hopf algebra
to 17(9) 017A)). Hence, it is not surprising that we shall need to use a certain
'twisted' tensor product of Hopf algebras to define the quantum double.
Let B and C be Hopf algebras over a commutative ring /c, and let 1Z be an
invertible element of C 0 B such that
(Ac®id)(n)=n13n23, (\d
{ ' {i&®sB){n)=K-1, (s
Proposition 4.2.10 If 11 e C®B satisfies A7), then B&C, with the usual
algebra structure and with comultiplication
AF 0 c) = ft23Af3(fe)A^4(c)ft^31,
antipode
S(b 0 c) = ll2i(SB(b) 0 5c(c))ft2i,
and counit
e(b®c) = 6B{b)ec(c),
is a Hopf algebra, which we denote by B 0 C'.
Outline of proof Let us check, for example, that /xE 0 id) A = ze. For
be B, ceC, write
Then,
/xE0id)A(&0c) = fi(n^\(sB 0 sc 0 id 0 id)(n23Af3(b)Ag(c)n^).n2i)
= J2 b'sBib^bkbib'pV 0 clSc{ci)Sc{c1)Sc{ci)ckcf1.
Now,
^ Sc(Cl)ck 0 ftfc&i = EC 0 id)(ft.Ec~1 0 id)(ft))
~1) = 1(8I.
128 4 Quasitriangular Hopf algebras
Hence,
id)A(b®c)= J2 blSB{bp)b'pV ®clSc(cj)Sc(c1)c'
1)c1
= eB(b)ec(c) J2 blV
3,1
= eF<g>c). |
Suppose now that A is a finite-dimensional Hopf algebra over a field k. We
apply the preceding construction with B = A*, C — Aop.
Lemma 4.2.11 The canonical element 1Z e Aop 0 A* associated to the iden-
identity map A —> A satisfies the conditions in A7).
Outline of proof Let us verify, for example, the first of the four equations
in A7). Let {a^} be a basis of A and let {a1} be the dual basis of A*. Thus,
*. Write
Note that
(a*ak , ai) = (a*
so that
Hence,
(A 0 i
Thus, we may define the quantum double of A to be
V(A) = {A* ®Aop)*.
Note that V{A) = A ® A* as & coalgebra (and, in particular, as a vector
space). Further, it is not hard to see that the canonical embeddings
A ^ V{A) ^ {A*)op
4-2 Quasitriangular Hopf algebras 129
are homomorphisms of Hopf algebras (cf. 1.4.2).
It will be useful to have a more explicit description of the multiplication in
V(A). The problem is to express a product a.a, where a G A and a G (A*)op,
as a linear combination of products a'.a1. Write
{S~l 0 id)A(a) = ^ a
Then, one finds that
where ( , ) denotes the natural pairing between A and its dual.
The importance of quantum doubles is that they have a simple quasitrian-
quasitriangular structure.
Proposition 4.2.12 The double V(A) of a finite-dimensional Hopf algebra
A over a field k is quasitriangular, with universal R-matrix the canonical
element of A® A* C V(A) 0 V(A) associated to the identity map A —> A. |
The proof is a straightforward, but tedious, computation similar to those
given in 4.2.10 and 4.2.11.
If A is infinite dimensional, one must define the duals in an appropriate
sense and suitably complete the tensor products. The element 1Z will then lie
in some completion of the algebraic tensor product A® A°. Apart from this,
the construction of V(A) and 4.2.12 is still valid. One may even work over
any commutative ring. We shall see some examples of doubles of infinite-
dimensional Hopf algebras in Section 8.3.
E Twisting There is a way to construct quasitriangular Hopf algebras by
starting with a cocommutative Hopf algebra A and 'twisting' it with an ele-
element T G A 0 A satisfying certain conditions. This will be used in Chapter
6 to construct quantizations of a large class of Lie bialgebras.
Proposition 4.2.13 Let (A,/i, z, A,e, S) be a Hopf algebra over a commu-
commutative ring. Let T be an invertible element of A<g> A such that
A8) J=i2(A 0 id)(JO = ^23(id 0
A9) (e<
130 4 Quasitriangular Hopf algebras
Then, v = /i(id ® S)^) is an invertible element of A with
Moreover, if we define Ar : A ^ A<S> A and S^ : A —> A by
B0) A^(a) = JzrA(a)Jr-1, Sr{o) = vS(a)v~\
then (A, //, z, A-77, e, 5fjr) is a Hopf algebra, denoted by AT and called the twist
of A by JF. |
This result is proved by arguments similar to those used earlier in this
section. We leave the details to the reader. The following special case will be
of most interest to us.
Corollary 4.2.14 If A is a cocommutative Hopf algebra and T is an in-
invertible element of A ® A satisfying A8) and A9), then Ar is a triangular
Hopf algebra with universal R-matrix
B1) n = Jr21Jr-\
PROOF It is obvious that AT is almost cocommutative with universal R-
matrix B1), and that H2\ = U~l. Let us check that (Ajr(g)id)(^) = 1Z131Z23.
This equation reduces to
Applying the flip a23 to both sides and using the cocommutativity of A, the
preceding equation is equivalent to
jr13.<723(A ^ idHF2i) - ^2i-^-^23-(id
by A8). It is easy to see, using the cocommutativity of A again, that applying
o\2 to the left-hand side of the preceding equation gives JF23(id(g) A)(^*), and
applying it to the right-hand side gives T\2 (A (8)id)(^-*). So the result follows
on using A8) once again. |
Another variant of 4.2.13 is
Corollary 4.2.15 Suppose that A and T are as in 4.2.13, but assume
in addition that A is quasitriangular with universal R-matrix 1Z and that
T2\ = T and T\2T\zT2z — T2zT\zT\2. Then, AT is quasitriangular, with
universal R-matrix Vf = T^
Remark If we drop condition A8), then A^ is not coassociative in general.
However, it is 'almost coassociative' in the sense that
(id 0 A^)A^(a) = ^.(A^ 0 id)Ajr(a).$,
4-2 Quasitriangular Hopf algebras 131
where <l> is the invertible element of A ® A ® A given by
Weakening the coassociativity condition in the definition of a Hopf algebra
to almost coassociativity leads to the notion of a quasi-Hopf algebra, which
we shall study in detail in Chapter 16. A
F Sweedler's example As we remarked in the Introduction, before the
advent of quantum groups, very few examples of Hopf algebras which are
neither commutative nor cocommutative were known (except for those ob-
obtained by taking tensor products of the standard commutative and cocom-
cocommutative examples). However, Sweedler A969) constructed an interesting
four-dimensional example, which we shall use to illustrate some of the con-
concepts introduced in this chapter.
Sweedler's Hopf algebra A is defined as follows (we assume that the ground
ring k is a field of characteristic ^ 2). As an associative algebra with unit, it
has generators g and x with defining relations
g2 = i, x2 = 0, gxg = -x,
coalgebra structure given by
A(g) = g® g, A(x) = x® g + l®x,
e(g) = 1, e(x) = 0,
and antipode given by
S(g) = g, S(x) = -x.
The reader should verify that this definition of A on the generators of A
extends to a homomorphism of algebras A —> i^i, etc. The elements
{l,x,g,gx} are a basis of A over k. Obviously, A is neither commutative nor
cocommutative. The following properties hold.
(a) A* = A as Hopf algebras. In fact, let {l,~g,x,'gx} be the basis of A*
dual to the basis {1, g, x, gx} of A. Setting 7 = 1 — 77, ? = x + 7fx, we have
72 - 6, e = 0,
=7(8O,
7A) = 1,
132 4 Quasitriangular Hopf algebras
For example,
= 1,
(g2,x) = (j(z
= 0,
5 7,A(?
9 -(9
<D7,? 0
^ 7> @ ^
0) =
,9
5 + 1
= 0,
proving that 72 = e. The other formulas are established by similar calcula-
calculations.
(b) The non-zero group-like elements of A are 1 and g. In fact, one finds
that a = \1 + fix + i/g + pgx, with A, /i, 1/, p G fc, satisfies A(a) = a 0 a if
and only if
/i = p = 0, Az/ = 0, A2 = A, z/2 = 1/,
from which the assertion follows. Similarly, the most general element y G A
such that
B2) A(y) =y0l-h#0 y
is y = Xgx for some X e k (this result will be needed later).
(c) The element A + g)x is a left-invariant integral for A, and x(l -f g) =
A—<?):r Z5 a right-invariant integral. The verification of this is straightforward.
Since these integrals are not scalar multiples of each other, A has no (non-
(nonzero) bi-invariant integral.
(d) A is not isomorphic to a quantum double. For if A = V{H) for some
Hopf algebra if, then H is 2-dimensional, and any such Hopf algebra is both
commutative and cocommutative (commutativity is obvious since H is gen-
generated as an algebra by a single element, and cocommutativity follows by
applying the same argument to H*). Since V(H) = H 0 (#*)op as coalge-
bras, it follows that V(H) is cocommutative. But A is not cocommutative.
(e) A is quasitriangular (in many ways). In fact, for any A G /c,
K\ = -(\®l + l®g + g®l-g®g) + -
is a universal R-matrix of A, and every universal R-matrix of A is of this
form. The former statement can, of course, be verified by direct computation.
Now recall from the remark following 4.2.7 that if 1Z is a universal R-matrix,
4-2 Quasitriangular Hopf algebras 133
the map / : A* —> Aop given by f(rj) — (rj 0 id, 7?) is a homomorphism of
bialgebras. All such maps are of the following types (identifying A* with A):
(i) /oo(a) = e(a)l, for all a G A;
(ii) /A(#) = #, /A(x) = Xgx, for some Aefc.
Case (i) would correspond to the universal R-matrix TZqq = 10 1, which is
impossible since A is not cocommutative; and case (ii) corresponds to 7Z\. To
see the assertion about bialgebra maps / : A* —> Aop, note that f(g) is group-
like, and hence equal to 0, 1 or g by part (b). But f(g) = 0 is incompatible
with the relation g2 = 1, while /(<?) = 1 and the relation gxg = —x force
f(x) = 0, and then we are in case (i). If f(g) = g, then y = f{x) satisfies
B2), and hence is of the form y = Xgx by part (b) again.
(f) For any A G k, (A,H\) is a ribbon Hopf algebra with distinguished
central element v = g. In fact, in the notation of Subsection 4.2C, we have
u — S(u) — g.
(g) Assume now that k is algebraically closed. Then, A has (up to isomor-
isomorphism) exactly four indecomposable representations, namely two one-dimen-
one-dimensional representations given by
# i—> ± 1, xhO,
and two two-dimensional representations given by
±1 0 \ /0 1
0 zpij' x^ [o 0
To see this, observe that, since g2 = 1, any A-module V splits as the direct
sum T/+ 0 V~ of the ± 1-eigenspaces for g, and that the relation gxg =
—x implies that x interchanges T/+ and V~. Hence, the A-module V is
determined by a pair of linear maps X± : V± —> VT such that
X~X+ = 0. Choose linear subspaces W± C Vr± such that ker(X±)
F±. Then, V is the direct sum of the A-invariant subspaces ker(X+) 0 W~
and ker(X~) 0 W+. Assume now that V is indecomposable. In that case,
it follows that either X+ is injective and X" = 0, or X~ is injective and
X+ = 0. By considering im(X±), a similar argument shows that we can
replace 'injective' by 'surjective' in the last statement. Thus, either X+ is an
isomorphism and X~ — 0, or X" is an isomorphism and X+ = 0. It follows
easily that we must have dim(F+) = dim(y~) = 1.
Evaluating the universal R-matrix 7Z\ in the two-dimensional representa-
representations gives the two one-parameter families
±1
0
0
0
0
1
0
0
0
0
1
0
A
0
0
of matrix solutions of the quantum Yang-Baxter equation.
134 4 Quasitriangular Hopf algebras
Bibliographical notes
4.1 The notion of a Hopf algebra was introduced by Hopf A941). The basic
references are Milnor & Moore A965) (where the proof of the result stated
in 4.1.9 can be found), Quillen A969), Sweedler A969) and Abe A980). For
topological Hopf algebras, see Takeuchi A985) and Abe & Takeuchi A992).
See van Daele A993) for a discussion of duality in the context of Hopf *-
algebras. See Northcott A968), Chapter 9, for more information on the X-
adic (and /i-adic) topology. See Hochschild A965), Section II.3, for the result
in 4.1.19.
4.2 The notion of a quasitriangular Hopf algebra, and that of the quantum
double, is due to Drinfel'd A987). Majid A990g) surveys the properties and
applications of quasitriangular Hopf algebras in physics. See Radford A992,
1993) for a discussion of finite-dimensional quasitriangular Hopf algebras. The
more general notion of an almost cocommutative Hopf algebra is discussed in
Drinfel'd A990a) and Reshetikhin A990b). See Reshetikhin A990a) for the
notion of twisting.
5
Representations
and
quasitensor categories
It is well known that the properties of the operation of taking direct sums (of
vector spaces, of group representations, ...) can be abstracted in the notion
of an abelian category. Abstracting the properties of the tensor product
operation (on vector spaces, on group representations, ...) leads to the notion
of a monoidal category. Although the basic theory of such categories was
developed in the early 1960s by S. MacLane, the subject has attracted the
attention of a wide audience only recently, largely because of the discovery
of interesting new examples. It is no surprise that many of these are related
to quantum groups, for we saw in Chapter 4 that, from an abstract point of
view, a Hopf algebra may be regarded as an algebra A equipped with the extra
structure necessary to define tensor products (and duals) of representations
of A. We describe the basic theory of monoidal categories in Section 5.1. As
well as the categories of representations of Hopf algebras, we give a number
of geometric examples related to knot theory.
There are several results which assert, roughly speaking, that a monoidal
category with some additional properties 'is' the category of representations
of some group: this is Tannaka-Krein duality. Perhaps the simplest example
is the Pontryagin duality for locally compact abelian groups. For such groups
G, all representations are direct sums of 1-dimensional representations, or
characters. The set of characters of G can itself be given a natural structure
of a locally compact abelian group G. Pontryagin's theorem asserts that G
can be recovered completely from G: in fact, G is isomorphic to the character
group of G. At the end of Section 5.1, we give a duality result of this type
for a general Hopf algebra.
In many naturally occurring examples of monoidal categories, the tensor
product operation is commutative up to isomorphism, and the commutativity
isomorphisms are involutive: one then has a tensor category. For example,
the category of representations of a group obviously has this property. More
generally, we saw in Chapter 4 that the category of representations of any
triangular Hopf algebra is a tensor category. If we weaken 'triangular' to 'qu-
asitriangular', the tensor product is still commutative, but the commutativity
136 5 Representations and quasitensor categories
isomorphisms are no longer involutive, in general. The category of represen-
representations is then said to be a quasitensor (or braided monoidal) category. In
Section 5.2, we describe the basic properties of tensor and quasitensor cate-
categories. Many, but not all, of the monoidal categories encountered in Section
5.1 are quasitensor.
In a semisimple abelian quasitensor category, the tensor product is de-
determined by the decomposition into simple objects of the tensor product of
any two simple objects, and hence by a collection of non-negative integers
which satisfy certain conditions which reflect the commutativity and asso-
associativity properties of the tensor product. Combinatorial data of this kind
were encountered in the study of conformal field theories, where they were
called fusion rules. At the end of Section 5.2, we give a somewhat schematic
discussion of the role played by quasitensor categories in physics.
In Section 5.3, we describe an application of the theory of quasitensor
categories to the construction of topological invariants of ribbon tangles, which
are essentially collections of non-intersecting rubber bands in 1R3, either closed
or open, and with finite width but zero thickness. Ribbon tangles can be
organized into a quasitensor category, and the invariants are obtained by
constructing a functor from this category to the category of representations
of a particular type of quasitriangular Hopf algebra. If we forget the width
of the bands, and consider only ribbon tangles with no free ends, we obtain
as a special case invariants of links in 1R3. The celebrated Jones polynomial
can be constructed in this way.
5.1 Monoidal categories
In this section, we attempt to axiomatize the properties of the direct sum and
tensor product operations in the category of representations of a Hopf algebra.
This leads to the notions of abelian and monoidal categories, respectively.
A Abelian categories This subsection is meant only as a summary of the
basic definitions and results on abelian categories. For further discussion, the
reader is referred to one of the standard sources, such as MacLane A971).
As we mentioned above, the notion of an abelian category is designed to
capture the properties of direct sums of vector spaces, of group representa-
representations, etc. In general, a category C admits (finite) direct sums if, for any
finite set of objects U\,...,Un of C, there is an object U and morphisms
TCi : U —> Ui such that, for any object V and morphisms fi : V —> ?/*, there is
a unique morphism / : V —> U such that TCi o / = fi for all i. The object U
is then unique up to isomorphism; we write U = (&iUi and / = ®ifi.
A category which admits direct sums is called additive if, for any objects U
and V, the set Homc(?/, V) of morphisms from U to V is an abelian group,
5.1 Monoidal categories 137
and if the compositions
A) Homc(tf, V) x Homc(F, W) -
are bi-additive.
To define the stronger concept of an abelian category, we need the notions
of the kernel and cokernel of a morphism. If C is an additive category, a
morphism / G Homc(f/, V) is a monomorphism (resp. an epimorphism) if, for
any g G Homc(VF, ?/), fog = 0 implies # = 0 (resp. for any g G Homc(V, W),
go/ = 0 implies # = 0). A kernel of a morphism /:?/—> V is an object ker(/)
and a morphism n : ker(/) —> ?/ such that f o k = 0 and, if g G Homc(VF, ?/)
is such that / o g = 0, then g = n o h for some ft, G Homc(VF, ker(/)). The
dual notion of a cokernel coker(/) is defined in the obvious way. The kernel
and cokernel of a morphism are unique, up to isomorphism, if they exist.
An additive category C is abelian if
(a) every morphism has a kernel and a cokernel;
(b) every monomorphism is the kernel of its cokernel, and every epimorphism
is the cokernel of its kernel;
(c) every morphism is expressible as the composite of an epimorphism followed
by a monomorphism.
A morphism in C which is both mono and epi is an isomorphism. A pair of
morphisms
u -L> w ^v
in C is a short exact sequence if g o f = 0 and if the morphisms U —> ker(#)
and coker(/) —> V, given by the defining properties of the kernel and cokernel,
are isomorphisms.
We shall occasionally need the stronger notion of a k-linear category, where
k is a commutative ring. This is an abelian category for which the sets
of morphisms Homc(U,V) are /c-modules, and the compositions A) are k-
bilinear.
The concepts of an irreducible, or completely reducible, representation (of
a group, say) have analogues in any abelian category C. In fact, an object U
of C is simple if every non-zero monomorphism V —> U is an isomorphism,
and every non-zero epimorphism U —> W is an isomorphism. Any non-zero
morphism between simple objects is an isomorphism. An object is semisim-
ple if it is a (finite) direct sum of simple objects. The category C itself is
called semisimple if every object of C is semisimple. In a semisimple abelian
category, every short exact sequence splits (the meaning of this is clear).
The direct sum operation of an abelian category C is encoded in its
Grothendieck group Gr(C). Let J~{C) be the free abelian group with gen-
generators the isomorphism classes of objects of C, and let [U] be the element
138 5 Representations and quasitensor categories
of .F(C) corresponding to an object U of C. Then, Gr(C) is the quotient of
.F(C) by the subgroup generated by the elements of the form [W] — [U] — [V]
for all short exact sequences
in C. Note that, if C is semisimple, the defining relations of Gr(C) are simply
[U 0 V] = [U] + [V]; moreover, Gr(C) is generated as an abelian group by
the simple objects of C.
We shall see some examples of abelian categories in Subsection 5.ID.
B Monoidal categories We now turn to the axiomatization of the prop-
properties of the tensor product of vector spaces, of representations of a Hopf
algebra, etc.
Definition 5.1.1 A monoidal category is a category C together with a func-
functor (8 : C x C -> C, written (U, V) i-> U®V for objects U and V of C, which
satisfies the following conditions:
(i) there are natural isomorphisms otjj,v,w '- U <S> (V <S> W) —> (U <S> V) <S> W
such that the diagram
U®{V®{W®Z)) -^ (U (8) V) 0 (W 0 Z) -^ {(U®V)®W)®Z
I T
id®a a®id
u ® {(v ® w) ® z) > (u®(y®w))®z
commutes for all U, V, W, Z;
(ii) there is an identity object 1 in C and natural isomorphisms pu : ?/<g)l —> U
and Xu ' 1 <8 U —> [/ such tiiat the diagram
p®id
id® A p®id
C/(8F >
id
commutes for all U, V.
An abelian ("resp. /c-linearj monoidal category is a monoidal category which
is abelian (resp. k-linear) and such that (8 is a bi-additive functor (resp. a
k-bilinear functor).
A functor $ : C —> C between monoidal categories is a monoidal functor
if there are natural isomorphisms
5.1 Monoidal categories 139
for all U, V, such that $A) = 1', and such that the following diagrams
commute:
A' p
Since the subscripts on the structure maps a, </?, etc. appearing in these
commutative diagrams are obvious, we have omitted them. For example, the
upper left horizontal arrow in the diagram in (i) is otuy,w®z-
Condition (i) is usually called the pentagon axiom, or associativity con-
constraint. Its significance is that, according to a theorem of MacLane A971),
it implies that any two iterated tensor products of objects in C (in the same
order) are isomorphic by a canonical isomorphism. The identity object 1 is
unique up to isomorphism.
Another theorem of MacLane A971) asserts that every monoidal category is
equivalent to one in which the associativity morphisms a and the morphisms
p and A are the identity maps. A monoidal category with this property is
called strict.
If C is an abelian monoidal category, its Grothendieck group Gr(C) is a
ring with product given by
[U].[V] = [U®V],
and unit [1]. The associativity of this product, and the basic property [1]. [f/] =
[?/].[l] = [U] of the unit, follow from the existence of the isomorphisms otjjy^Wi
pu and \\j in 5.1.1.
C Rigidity The next step is to incorporate the notion of the dual of a
representation into the categorical framework.
If C is a monoidal category, an object U* is said to be a (left) dual of an
object U in C if there are morphisms evu : U* ® U —> 1 and ttjj : 1 —> U ® J7*
such that the following diagrams commute:
7r(g)id id(SOr
U
id
U
(J7® U*) <
t/<3 (?/*<§
DC/)
J7* —
-1
U* <—
—> U*d
— (?/*
[•
140 5 Representations and quasitensor categories
(We have suppressed the isomorphisms A and p for simplicity.) If ?7 has a
dual object, it is unique up to isomorphism.
Suppose now that every object in C has a dual object. If ip : ?7 —» V is a
morphism in C, then the composite
)?7*-?7*
is a morphism ip* : F* —» ?7* (we are now abusing notation by omitting the
associativity maps). Thus we obtain a contravariant functor C —» C, called
the dual object functor, which takes ?7 to ?7* and ip to ^*.
Definition 5.1.2 A monoidal category C is rigid if every object in C has a
dual object, and if the dual object functor C —> C is an anti-equivalence of
categories.
Remarks [1] If C is a rigid monoidal category, it is easy to see that, for all
objects ?7, V and W of C, the map which assigns to a morphism ^ : ?7® V —>
W the morphism ?7 —» W (8 V* given by
?7 =
is bijective; if C is /c-linear, this bijection is an isomorphism of /c-modules. In
particular, there is a bijection between morphisms ?7<8>F —> 1 and morphisms
?7 —> F*, and between morphisms V —+ W and morphisms 1 —> W ® V*.
[2] The dual object functor in a rigid monoidal category has a natural
monoidal structure. In fact, the composite
{V* (g)?7*)(8
corresponds to a morphism F* (8) ?7* —> (?7 ® V)*, while
TTr/
TTr/ idfy®7rv®idLr
1—>U®U* = ?7 (8) 10 ?7* > (?7 ® F) ® (F* ® ?7*)
corresponds to a morphism W —> ?7 (8 V, where VF* = F* ® ?7*. It is easy to
see that the dual of the latter morphism is the inverse of the former, so that
(?7 (8 V)* is naturally isomorphic to F* eg) ?7*.
[3] If ?7 is an object of a rigid category C, ?7** is not isomorphic to ?7,
in general. We shall see examples of this non-reflexivity in Chapter 12 (see
Remark [4] following 12.1.11). A
D Examples We begin with four examples of monoidal categories of an
algebraic nature.
Example 5.1.3 The category of all modules over a commutative ring k is an
abelian monoidal category with the obvious associativity maps and identity
5.1 Monoidal categories 141
object k. The same is true for its full subcategory modfc consisting of the
finitely-generated projective modules. However, only the latter category is
rigid (even if k is a field). The dual of a k-module U is U* = Homk(U,k)
as usual, and the map evjj is the obvious pairing which evaluates an element
of U* on an element of U. To define ttu, we need the 'dual basis lemma' for
finitely-generated projective modules, according to which, for any set {ui}iei
of generators of ?/, there exists a set of elements {?2}^ej in U* such that
u = J2iei ui?(u) for a11 u e U- We set M1) = Ezg/ ui®C-
Two special cases are of particular interest to us. If k is a field, modfc is
simply the category of finite-dimensional vector spaces over k (and the dual
basis lemma gives the dual basis in the usual elementary sense). On the other
hand, if k = F[[h]] is the ring of formal power series in an indeterminate h
over a field F, then, since F[[h]] is a local ring, modpp]] consists of the free
F[[/i]]-modules of finite rank. We shall usually call such F[[h]]-modules 'finite
dimensional' from now on. 0
Example 5.1.4 If A is a Hopf algebra over a commutative ring /c, the cat-
category of all representations of A is an abelian monoidal category with the
same associativity maps as in the previous example. The identity object is /c,
regarded as the trivial representation of A. The full subcategory rep^ con-
consisting of the representations of A on finitely-generated projective fc-modules
is also rigid abelian monoidal. The dual of a representation U of A is the
/c-module dual U* defined in the preceding example, provided with the action
of A given by
for a G A, u G ?/, ? G U*, where S is the antipode of A (see Subsection 4.1C).
The forgetful functor rep^ —> mod/- is monoidal.
One defines in an analogous way the category corep^ of A-comodules
which are finitely generated and projective as k-modules. It is also rigid
abelian monoidal. 0
Example 5.1.5 Suppose that A is a Hopf algebra over a commutative ring fc,
and let A^ be the twist of A by an element T G A® A satisfying equations
A8) and A9) in Chapter 4 (see Subsection 4.2E). Then rep^ and rep^
are equivalent as monoidal categories. In fact, let pu : A —> End(?/) and
pv : A —> End(F) be representations of A. We leave it to the reader to
check that setting $(?/) = U and <pu,v = {pu ® pv){J~~l) defines a monoidal
functor $ : rep^ —> repA^. 0
Example 5.1.6 Let G be a finite group and let buiic be the category of
finite-dimensional complex vector bundles over G. Thus, an object V of
buriG is a family (Vg)g(zQ of finite-dimensional vector spaces, and a morphism
/ : V —> W is a collection of linear maps fg'-Vg—+ Wg. If we define direct
142 5 Representations and quasitensor categories
sums componentwise, it is easy to see that bunc becomes an abelian category;
it is clearly semisimple.
We define the tensor product of two objects of bunc by
{V®W)g= 0 Vgi®Wg2.
9i92=9
If we take the associativity maps
(<*v,v,w)g: kB Ugi®(Vg2®Wg3)-+ ^ (Ugi®Vg2)®Wg3
919293=9 9i9293=9
to be the identity maps, and the identity object to be
C iig = e,
0 otherwise,
then bunc becomes an abelian monoidal category.
More generally, let c : G x G x G —¦> (Cx be any function and take (a
to be c(<7i, <72>#3) times the identity map on the component U9l (8) V92 (g) W93.
Then, the pentagon axiom 5.1.1(i) is equivalent to
for all <7i, g2, ^3, #4 ? G, in other words, to c being a 3-cocycle (in the group
cohomology of G with coefficients in the trivial module). Thus, for any such
cocycle, one obtains another abelian monoidal category.
This example is analogous to the theory of quasi-Hopf algebras, which is
the subject of Chapter 16. 0
We now give three topological examples of monoidal categories which are
important for the relation between quantum groups and knot theory discussed
at the end of this chapter, and, in more detail, in Chapter 15.
Example 5.1.7 Choose a plane P° in 1R3, and fix m distinct points pj,... ,p^
in P°. Let Pl be the parallel plane obtained by translating P° by a distance t
perpendicular to P°, and let p},... ,p^ be the points in P1 corresponding to
P?>--->Pm- A braid P on m strands is the union of m disjoint piecewise
smooth curves in the region X between P° and P1, each of which joins
some p® to some pj, so that j 1—> i is a permutation of {1,..., m}. We also
assume that, for each 0 < t < 1, the plane Pl cuts each curve transversely in
exactly one point. Two braids /3 and C' are said to be equivalent if there is
a diffeomorphism of X which maps each plane P*, for 0 < t < 1, into itself,
which fixes each of the points p?,. • • ,P^,Pi, •. • ,p^, and which maps f3 to /?'.
5.1 Monoidal categories
143
Although braids are objects in three-dimensional space, it is useful to have
a way of representing them in two dimensions. For this, we choose a plane Q
perpendicular to P°, and project each braid /? perpendicularly onto Q. By
choosing Q suitably, we can assume that the projection consists of n piecewise
smooth curves which intersect transversely, and that every line in Q parallel
to P° fl Q meets each curve in the projection exactly once. To be able to
recover the equivalence class of /? from its projection, one must include an
extra piece of information at each point where the projected curves cross.
Namely, if we think of the direction perpendicular to Q as 'vertical', then
the curve which lies below is shown broken in the projection (see Fig. 4). A
similar convention will be used in the other topological examples discussed
below.
Fig. 4 A braid on four strands
Equivalence classes of braids can be regarded as the morphisms in a cat-
category braid whose objects are the natural numbers, so that Hom(ra, n) is
empty unless m = n in which case it is the set of equivalence classes of braids
on m strands. Composition of morphisms is induced by concatenation of
braids, i.e. /?'/? is obtained by putting f3 'on top of f3' and shrinking the ver-
vertical coordinate by a factor of two. Moreover, if we define the tensor product
/?® f3' of two braids by putting them 'side-by-side', with /?' to the right of /?,
then braid becomes a monoidal category @ is the identity object).
It is easy to see that braid is rigid. In fact, every object m in braid is
self-dual, and the morphisms evm and 7rm are as shown in Fig. 5 (for m = 3).
0
Remark Although we do not need it at the moment, we should mention that
the set of equivalence classes of braids has a natural group structure. The
product is defined by concatenation as above, and the inverse of (the equiv-
equivalence class of) a braid is obtained by reflecting the braid in the plane P1/2.
The resulting group Sm has generators Ti,...,Tm_i given, with their in-
inverses, by the diagrams
144
5 Representations and quasitensor categories
i i+l
and the expression of an arbitrary braid as a product of these generators can
be obtained by dividing the plane projection into horizontal strips so that
each strip contains just one crossing point. For example, the braid in Fig. 4
defines the element T^1T3T2T^1 e $4. It is an easy exercise to check that
if \i - j\ >
if i-j\ =
In fact, these relations define Sm as an abstract group.
Assigning to a braid the permutation j 1—> i of its endpoints defines a
homomorphism from Sm to the symmetric group Em on m letters. Its kernel
is the pure braid group Vm- A
m* (= m)
Fig. 5 Rigidity of braid
Example 5.1.8 A tangle is similar to a braid except that the strands may now
have both their endpoints on the same plane; one also allows embedded circles,
called loops. Equivalence, concatenation and tensor products of tangles are
5.1 Monoidal categories
145
defined in the same way as for braids. In this way, one obtains a monoidal
category tangle whose objects are the natural numbers and whose morphisms
are equivalence classes of tangles. Regarding a braid as a tangle gives a
monoidal functor braid —> tangle.
Fig. 6 An element of homD,2) in dtangle
One may also consider directed tangles, in which each strand and loop
is oriented and concatenation is only allowed when the orientations at the
joining points match. To each point (i,0,0) (resp. (i,0,1)), which is an
endpoint of a strand, one attaches a sign e* (resp. e[) which is +1 or —1
according to whether the oriented tangent vector at the point has negative
or positive vertical component.
Fig. 7 Concatenation of directed tangles
Equivalence classes of directed tangles (defined in the obvious way) are
the morphisms of a monoidal category dtangle, whose objects are (finite)
words on symbols + and -. More precisely, a morphism from (ei,...,em)
to (ei,..., en) is an equivalence class of tangles such that the m ends of the
tangle lying in 1R x {0} x {1} have signs ei,..., em (reading from left to right),
while its n ends lying in 1R x {0} x {0} have signs ei,..., en.
146 5 Representations and quasitensor categories
The categories of tangles and directed tangles are rigid, with the morphisms
ev and n being given by the obvious analogues of Fig. 5 (in the directed case,
one must change the signs on passing to the dual).
Forgetting orientation gives a monoidal functor dtangle —> tangle. 0
Example 5.1.9 A ribbon tangle in JR3 is a 'thickened tangle'. More precisely, it
is a disjoint union of oriented bands and annuli, where a band is an embedding
[0,1] x [0,1] -> R3, an annulus is an embedding S1 x [0,1] -> R3, and
'orientation' has its usual meaning for surfaces in 1R3. The ends of a band
are the images of {0} x [0,1] and {1} x [0,1]. The union of the ends of the
bands must be of the form
Finally, the positively oriented normal must point towards the reader near
the end of each band. In pictures, the upper side of each band or annulus is
white, the other side shaded.
Fig. 8 A ribbon tangle
Equivalence of ribbon tangles is defined in the obvious way. As in the case
of tangles, there is a monoidal category ribbon whose objects are the same
as in tangle and whose morphisms are equivalence classes of ribbon tangles.
The core of a ribbon tangle is the union of the images of [0,1] x {^} for
each band and of S1 x {^} for each annulus. Assigning to a ribbon tangle its
core defines a monoidal functor ribbon —> tangle.
A directed ribbon tangle is a ribbon tangle with a directed core. Directed
ribbon tangles are the morphisms in a monoidal category dribbon whose
objects are the same as in dtangle, and with the same rules for concatenation.
To each end of each band of a ribbon tangle, one can associate a sign ± 1
by applying the construction in 5.1.8 to its core. Both ribbon and dribbon
are rigid.
For some purposes, it is convenient to consider ribbon tangles with 'free'
bands, called coupons. We require that any two coupons are disjoint, and that
5.1 Monoidal categories
147
the ends of the coupons do not intersect R x {0} x {0,1}. The intersection of
the bands other than coupons with ]R x {0} x {0,1} is a set of the form B) as
before, and the remaining ends of bands other than coupons are contained in
the ends of coupons. We call a collection of bands, annuli and coupons with
these properties a generalized ribbon tangle. They form a category ribbon
in the obvious way. Directed generalized ribbon tangles and the category
dribbon are defined in the same way. <0
Fig. 9 A generalized ribbon tangle
Example 5.1.10 If X is any set, we can define a category dribbon(^f) by
attaching to each annulus, and to each end of each band, of a ribbon tangle an
element of X (a 'colour'). Thus, the objects of dribbon(X) are (finite) words,
including the empty word, in the elements of the set X x {+, -}. A morphism
from an object (xi, ei),..., (xm, em), where the Xi G X and the €i = ± , to
an object (xi, l\),..., (xn, en) is a morphism in dribbon from ei,..., em to
ei,..., en (i.e. a ribbon tangle) satisfying the following additional condition.
If a band of the ribbon tangle has both ends at the top, i.e. in ]R x {0} x {1},
these ends being the ith and jth along this line, then Xi = x^\ and similarly
for bands with both ends in ]R x {0} x {0}, and for those with one end at the
top and one at the bottom.
Colourings of generalized ribbon tangles will be considered in Subsection
5.2B. 0
E Reconstruction theorems We have seen that, starting from a Hopf alge-
algebra A, we can construct a rigid monoidal category. The following result shows
essentially that the Hopf algebra can be reconstructed from this categorical
data, and gives a rather general instance of Tannaka-Krein duality.
Theorem 5.1.11 Let k be a commutative ring, let C be an essentially small,
k-linear, rigid, abelian, monoidal category, and let $ : C —> mod/- be a k-
linear exact faithful monoidal functor. Then, there exists a Hopf algebra A
148 5 Representations and quasitensor categories
over k and an equivalence ofk-linear categories C —> corep^ whose composite
with the forgetful functor corep^ —> modfc is $.
A category is essentially small if it is equivalent to a small category, i.e.
one whose class of objects is a set. A functor is faithful if it is injective on
sets of morphisms and exact if it takes exact sequences of morphisms to exact
sequences.
Outline of proof We describe how the Hopf algebra A is recovered from
the categorical data.
If M is a finitely-generated projective &;-module, let $ ® M be the functor
C —> modfc given by U —> $(J7) ® M. Let Nat($, $ ® M) be the A:-module
of natural transformations $ —> $ ® M. It can be shown that the functor
M —> NatC> , $® M) is represent able, i.e. there is a A:-module A and natural
isomorphisms
rM : Horn,-(A, M) -> Nat($ , $ ® M).
The comultiplication A : A —> A <g> A and the counit e : A -^ k of A are
defined by
where 5 = ^(id^) and e : $ —> $ ® A: is the canonical isomorphism.
Next, define $2:CxC-4 modfc to be the functor A7, V) »-> $A7) ® $(V)
and define r^ : Homfc(A ® A, M) -> Nat($2 , $2 ® M) by
(8) i
It can be shown that r^ is an isomorphism. Let ra^y be the composite
$A7) <g> $(V) ^ $(J7 ® F) -t $(J7 <g> V) ® M ^ $(J7) ® $(V) ® M,
where the isomorphisms use the fact that $ is monoidal. Then, m is a natural
transformation from $2 to $2 ® A, and we define the multiplication /x :
A-> A of A to be (rli)~1(m).
The unit 2 : k —> A of A is the composite
k ^
Finally, define isomorphisms pu : $(J7)* —>• $(i7*) to be the composites
<t(t/)*(t/)
$(J7)* ^ $(/7)* ® fc > $(/7)* ® $(/7) ® $(/7*)
5.2 Quasitensor Categories 149
If d e Nat($, $ ® M), the morphism d\j : $(U) —> $(?/) (8) M corresponds,
via p, to a morphism d[/:3>([/)*—>$({/) *®M. In view of the canonical
isomorphisms
Homfc($(J7), $(J7) <g> M) ^ Homfc($(J7)*, $(?/)* ® M),
the assignment d ^ d defines a map from Nat($ , <? ® M) to itself, and hence
also a map from Horn/-(A, M) to itself. These maps are natural in M and
A:-linear, and so correspond to a A:-linear map S : A -^ A. The invertibility of
S follows from the fact that U i—> U* is an anti-equivalence of categories.
It is not difficult to show that (A, 2, //, e, A) is a Hopf algebra over fc, and
that U i—> (^(f/), Su) is an equivalence of categories. |
Remark In view of this theorem, it is natural to ask what further conditions
on C will guarantee that it is equivalent to the category of representations (or
corepresentations) of a Hopf algebra of some special type. When A: is a field
of characteristic zero, Deligne A991) gives sufficient conditions for C to be
the category of representations of a proalgebraic group scheme. On the other
hand, Gel'fand & Kazhdan A992) show that Deligne's theorem fails if k has
finite characteristic (see also Andersen A992c)). Their counterexamples are
closely related to a category of quantum group representations discussed in
Section 11.3. A
5.2 Quasitensor categories
In many monoidal categories, such as the categories of vector spaces and of
group representations, the tensor product is commutative up to isomorphism.
In this section, we incorporate this symmetry into the categorical framework
which we introduced in the preceding section.
A Tensor categories We begin with
Definition 5.2.1 A tensor category is a monoidal category C which is
equipped with natural isomorphisms o\jy : U ® V —> V ® U, for all objects
U and V of C, such that
(i) the diagrams
° W®{U®V)
id(g)cr
a
-X-
U®(W®V) > (U®W)®V > (W®U)®V
a a<g)id
150 5 Representations and quasitensor categories
(V.
I"
T 7" ^*™^. /t r T JT 7" \ /t r ^*~-v T!T^\ T T t r ^^ /^ T )T 7" v*\
commute for all U, V, W;
(ii) the diagrams
commute for all U;
(Hi) Oyjj O G\jy — \<&.\j®v f°r &H U, V.
If C is abelian (resp. k-linear), o is required to be bi-additive (resp. k-
bilinear).
A monoidal functor $ : C —> O between tensor categories is a tensor
functor if the diagram
commutes for all U, V.
Remark It is easy to see, by using condition (iii), that if one of the diagrams
in (i) or (ii) commutes so does the other. We have included these redun-
redundant conditions partly to make the definition more symmetric, and partly for
convenience later. A
Clearly, mod/- is a tensor category with the obvious commutativity maps
crjjy .' U 0 V —> V <S> U given by o\jy (u 0 v) = v 0 u; the associativity maps
are the identity maps. The same is true (with the same maps) for rep^ for
any cocommutative Hopf algebra A, and the forgetful functor rep^ —> mod/-
is a tensor functor. More generally, we have
Example 5.2.2 Let (A,Tl) be a triangular Hopf algebra over a commutative
ring k. Then rep^ is still a tensor category, but the commutativity maps o\jy
5.2 Quasitensor Categories 151
are no longer the obvious ones, which would not commute with the action of
A in general. If pu : A —> End(?/) and pv : A —> End(V) are representations
of A, the correct choice is
&u,v = cr o {pu ® pv)(R).
Let us verify that Guy ls a morphism in rep^. Indeed, if a E A, u E 17,
Using the equation Aop(a) = ^A(a)^, we obtain A(aO?2i = 7?2iAop(a).
Hence,
a.(auy(u <g> v)) - 7?2i Aop(a).(> <g> w)
The commutativity constraint oy^j o cr^y = id^/^y follows immediately
from IZ21R — 1- Finally, going one way round the first hexagon diagram in
where ^123 is the cyclic permutation of the factors. Going the other way
round,
Thus, the hexagon axiom follows from A0) in Chapter 4 (note that A0) and
A1) are equivalent in the triangular case). 0
Example 5.2.3 The category bun^ is tensor if and only if G is abelian (we
take the associativity maps to be identity maps). Indeed, for any g E G,
let E(g) be the object of bun^ such that E(g)gt is C if g' — #, and zero if
g' ^ g. Then, if g\ and g2 are elements of G which do not commute, the only
non-zero component of E(gi) <S> E{g2) is the (#i<72)th, so E(g{) <S> E(g2) is not
isomorphic to E(g2) ® E(gi).
On the other hand, if G is abelian, we can take (cuy)g to be the obvious
map of vector spaces
heG heG
in which the arrow is the obvious flip map. This is not, however, the only
possible choice of auy- Let us take the simplest non-trivial case when G is
152
5 Representations and quasitensor categories
the group Z2 — {0,1} with two elements. Since bunz2 is semisimple, and
since E@) = 1 and ?"A) = X (say) are, up to isomorphism, the only simple
objects of bunz2, it suffices by condition 5.2.1(ii) to define crx,x'-> note that
X 0 X = 1. There are two possibilities:
(a) crx,x = idi;
(b) o~x,x = -idi.
In case (a), bunz2 is the category of ^-graded vector spaces; in case (b), it
is the category of super vector spaces. <0
B Quasitensor categories In view of the notion of a quasitriangular Hopf
algebra introduced in 4.2.6, Example 5.2.2 strongly suggests that one should
consider the effect of dropping condition (iii) in 5.2.1.
Definition 5.2.4 A quasitensor category is a monoidal category C equipped
with functorial isomorphisms o\jy : U 0 V —>V 0/7 which satisfy conditions
(i) and (ii) in 5.2.1.
Examples 5.2.5 The definition is designed, of course, so that the category of
representations of any quasitriangular Hopf algebra (A, 71) on free modules
of finite rank is a quasitensor category. The commutativity isomorphisms are
defined in the same way as in the triangular case (see 5.2.2). One needs A1)
from Chapter 4 to verify commutativity of the second hexagon diagram. In
fact, one can weaken 'Hopf to 'quasi-Hopf, as we shall see in Chapter 16.
All of the geometric categories braid, tangle and ribbon, as well as their
directed versions, are quasitensor categories (but not tensor categories). The
switch map o~x,y in ribbon, for example, is shown schematically in Fig. 10.
The verification of the axioms of a quasitensor category will be an entertaining
exercise for the reader. <0
U
U V
Fig. 10 Commutativity maps in ribbon
5.2 Quasitensor Categories
153
Remark If C is a rigid tensor (or quasitensor) category, then, for all objects
U of C, there is a morphism ju : U —> ?/** corresponding to evjj o cr^jy* :
17 (8) U* —> 1 (see the remarks following 5.1.2). If (A,7J) is a quasitriangular
Hopf algebra and U is an object of rep^, we find that
where u — [i{S <S> id)G^2i)- A
The family of isomorphisms o\jy is called the braiding of C (and quasiten-
quasitensor categories are often called braided monoidal categories). In the tensor
case, the braiding is often called the symmetry of the category. The reason
for this terminology is as follows.
Let us assume for simplicity that C is strict. Let J7, V and W be objects of
C. There are six possible tensor products of these objects, with each object
occurring once, as shown in the following diagram:
® c
uw
U ® V ®W
/® a
U ® W ® V
v,v
W ®U <8>V
It follows from 5.2.1 (i) that the top and bottom triangles commute, and
the commutativity of the middle rectangle follows from the naturality of the
braiding. If we write o\ (resp. a 2) for the braiding applied to the first two
(resp. last two) factors in a triple tensor product, we have shown that
This is the defining relation of the braid group S3 (cf. 5.1.7); if C is actually
a tensor category, then o\ — o\ — 1, and we have the defining relations of the
symmetric group ?3. Note that the pure braid group V3 acts on [/V0 W,
but that a general element /3 e B3 takes U 0 V 0 W to the tensor product of
17, V and W in some other order, determined by the element of ?3 associated
to/?.
154 5 Representations and quasitensor categories
C Balancing The morphisms ju : U —> ?/**, defined in the preceding re-
remark for all objects U of any rigid quasitensor category C, do not, in general,
respect the tensor product. However, under the following additional condi-
condition, these morphisms can be modified to become monoidal.
Definition 5.2.6 A rigid quasitensor category C is balanced if it is equipped
with an automorphism by of U, for every object U of C, such that the fol-
following conditions hold:
C) by 0 by = O~yy O Gyy O by^y,
D) by* = (buY,
E) 6i = idi.
Of course, if C is actually a tensor category, we can take by — idjy for all
U.
It is easy to see that, in any balanced rigid quasitensor category, the mod-
modified morphisms ky — jy °b^}1 satisfy
(we use the identification A7<g>V)** = U**®V** given by Remark [2] following
5.1.2).
Example 5.2.7 Let (A, 1Z, v) be a ribbon Hopf algebra (see 4.2.8), and let
C = rep a- If Pu : A —> End(U) is a finite-dimensional representation of A,
we set by = pu(v). Since v is central, by commutes with the action of A
on U. Then, C), D) and E), respectively, follow from the following defining
properties of v:
S(v) = v,
e(v) = 1.
The morphisms kjj : U —>• f/** are given by
ku = Pu(g),
where g — uv~l. As we noted in Subsection 4.2C, the element g is group-like,
so property F) is clear in this case. <0>
D Quasitensor categories and fusion rules Fusion rules are a new kind
of algebraic structure, which can be interpreted as giving the 'structure con-
constants' of a quasitensor category.
5.2 Quasitensor Categories 155
Definition 5.2.8 Let A be a set equipped with an involution A i—> A* and a
distinguished element lj such that cj* = u. A set of fusion rules indexed by A
is a collection {Nx^,v}x,v,veA of non-negative integers satisfying the following
conditions:
(i) for each X, \x G A, Nxn,v = 0 for all except finitely many v;
(n) Nx^v = N^xy,
(m) Y,aeAN^,pN^a = EaeA^^'
(iv) NXuJ^ = Nux^ = 8xy
(v) Nxil,v = N^*x*,v*;
(vi) Nx^,uj = 6x,v
Before we see the connection between fusion rules and quasitensor cate-
categories, we shall re-interpret the definition. Let T be the free abelian group
with basis a set of formal symbols {/a}aga- Define a bi-additive product
T x T -> T by setting
Condition (i) asserts that this is well defined, and conditions (ii) and (iii) that
the product is commutative and associative. Thus, T is a commutative ring
and, by condition (iv), /^ is its identity element. We call T the fusion ring
associated to the fusion rules Nx^^u-
To interpret the last two conditions in 5.2.8, extend the involution of A to
an additive involution * of T such that f? = fx*, and define an additive map
ev : T —> Z by setting ev(fx) = <$a,u;- Then, (v) asserts that ev(/*) = ev(/)
for all / G T, and (vi) that ev(fUJ) = 1. Moreover, setting
(/,/') = ev(/7')
defines a bi-additive inner product ( , ) : T x T —¦> Z such that
(//',/") = (/',/*/") (/,/',/"en
and for which {fx} is an orthonormal basis.
Remark The fusion ring has a natural representation, defined as follows. Let
Na, the fusion matrices, be the A x A matrices given by
Then, condition (iii) is equivalent to
156 5 Representations and quasitensor categories
so that /a i-> Nx is a matrix representation of T. Since T is commutative,
NANM = NMNA
for all A, fi e A.
Note further that
NA. = N*A.
In fact,
(NA. W = JVa-m,^ = (/a-//» , U) = (U> /a/.) = JW = (naW-
In particular, if the involution * is the identity map, the fusion matrices are
symmetric. A
It is time we gave some examples of fusion rules. The following example is
very familiar.
Example 5.2.9 Let G be a compact topological group, and let A be the set of
isomorphism classes of finite-dimensional irreducible complex representations
of G. Since every representation of G is completely reducible (because it
admits an invariant inner product, for example), if [/, V G A, we can write
w
for some non-negative integers Njjv,w- Further, let V* = Hom(V, <C) be the
dual of V (with the usual action of G), and let lj be the one-dimensional triv-
trivial representation. Then, {Nuv,w} is a set of fusion rules. In fact, properties
(i) and (iv) in the definition are obvious; (ii) and (iii) follow from the commu-
tativity and associativity of the tensor product; (v) follows from the fact that
taking the dual commutes with the tensor product; and (vi) follows from the
equality between the multiplicity of the trivial representation in U ® V* and
the dimension of the space of G-module maps V —> U. <0>
It is clear that the fusion ring in this example is the representation ring of
G, i.e. the Grothendieck ring of the category of finite-dimensional complex
representations of G. In this form, the example has the following generaliza-
generalization.
Proposition 5.2.10 Let k be a commutative ring, and let C be a rigid,
semisimple, k-linear, quasitensor category. Assume that the identity object
of C is simple, and that Homc(X, X) = k for all simple objects X of C.
Then, the Grothendieck ring Gr(C) is a fusion ring. Moreover, every fusion
ring arises in this way.
Remark Note that the assumption on Homc(X,X) is satisfied in the cat-
category of finite-dimensional representations of any algebra defined over an
algebraically closed field (by Schur's lemma).
5.2 Quasitensor Categories 157
PROOF Let C be as in the proposition, and let {X\}\ea be the set of (iso-
(isomorphism classes of) simple objects of C; we suppose that X^ = 1. Define
* : A-> A by Xx* = X%.
Since C is semisimple,
G) Xx 0 X^ '--
for some JVA/ljl/ G N. Note that Homc(I,,IA 0 X^) ^ kNx»>». Property (i)
in 5.2.8 is obvious; (ii) and (iii) follow from the fact that the tensor product
is commutative and associative, up to isomorphism; and (iv) follows from the
defining property 5.1.1 (ii) of the identity object. Finally, (v) and (vi) are
consequences of the remarks following 5.1.2, which imply that (X\ 0 X^)* =
and that there is an isomorphism of /c-modules Homc(l, X\<g)X^) =
For the converse, let {N\^^}x^^eA be a set of fusion rules. We define a
category C as follows. The objects of C are the maps X : A —> N such that
X(X) = 0 for all but finitely many A. If X and Y are two objects of C, we
set
Homc(X, Y) = 0Homfc(fcx^ , fcy<A>).
A
Composition of morphisms is denned in the obvious way. The direct sum of
two objects X and Y is
(X 0 Y)(A) = X(X) + Y(A) (A G A).
Then, X = (&\XX , where the object X\ maps A to one and all other
elements of A to zero. We define Xx = X\* and X\ 0 X^ by G), and extend
additively to give the dual and tensor product of arbitrary objects of C. The
identity object is X&.
We leave it to the reader to check that these definitions make C into a
rigid, fc-linear, quasitensor category. It is obviously semisimple, with the X\
being the simple objects. |
E Quasitensor categories in quantum field theory We conclude this
section with a simplistic account of how quasitensor categories arise in quan-
quantum field theory. For a more serious discussion of the physical background,
see Haag A992) and Frohlich & Kerler A993), for example.
Traditionally, observables in relativistic quantum field theory are 'operator-
valued distributions' J(x) defined on Minkowski spacetime M (thus, M = IRn
equipped with an inner product of signature (H • • • —)). This means that,
if / is a smooth real-valued function on M of compact support, then
J(f) = f J(x)f{x) dx
JM
158 5 Representations and quasitensor categories
should be a bounded operator on some separable Hilbert space. The von
Neumann algebra A(O) of observables localized in a bounded subset O C M
then consists of all bounded functions of operators of the form J(f) for which
SUPP(/) C O. The local algebras A(O\) and A(O2) associated to space like-
separated regions O\ and O2 commute (recall that O\ and O2 are 'spacelike-
separated' if || x\ — x2 ||2< 0 for all x\ G O\, x2 G O2). If S is any, not
necessarily bounded, subset of M, one sets
o
the union being over all bounded sets Oc«S, and the closure being in the op-
operator norm topology. In particular, A = A(M) is the algebra of all localized
observables of the theory. Since the theory is to be relativistic, there should
be a representation of the Poincare group Q (i.e. the group of isometries of
M) by *-automorphisms of A such that
g.A(S) = A(g.S)
for all g G G, S C M.
In order to qualify as a 'local quantum field theory', these data are required
to satisfy a number of axioms which imply, among other things, that there
is a distinguished ^representation pVac : A —> End(TY) on a Hilbert space 7Y,
called the vacuum representation, which is both faithful and irreducible. All
*-represent at ions p of A which have a physical meaning have the following
properties:
(i) p is unitarily equivalent to pVac when restricted to A(O'), for some bounded
region O (possibly depending on p); here, O' denotes the set of points of M
which are spacelike-separated from every point of O. In particular, the Hilbert
space of p can be identified with H.
(ii) p is covariant, in the sense that there is a unitary representation n of Q
on H such that
for all g G G, A G A
Representations satisfying these conditions are called physical representations.
The axioms further imply that, if p is a physical representation (whose
Hilbert space we may as well assume is 7Y), there exists a *-endomorphism tp
of A such that
P = Pvac O If,
where = means 'unitarily equivalent'. Moreover, the set of *-endomorphisms
which arise in this way is closed under taking composites. It is this last
property which is crucial for us, for it implies that, from any two irreducible
5.2 Quasitensor Categories 159
physical representations pi = pvac ° <Pi and p2 = Pvac ° ^2, we may construct
a third, pvaco y?i o y?2. We shall write the latter representation as pi"x"p2. The
following properties of "x" follow from the axioms:
(PI) if p and a are irreducible physical representations, then
pxa = crxp;
(P2) there are non-negative integers Np(TiT such that
where p, a and r run through the set of irreducible physical representations;
(P3) for each irreducible physical representation p, there exists a physical
representation p* such that pxp* contains the vacuum representation exactly
once (i.e. Npp*iPvBC = 1).
These data may be encoded in a category QFT whose objects are the
physical representations of the theory, the set of morphisms from pi to p2
being, in the above notation,
HomQFT(pi,P2) = {AeA I A<pi(B) = if2(B)A for all B G A}.
The operation ~x~ makes QFT into a rigid monoidal category: the tensor
product of morphisms A G Hoiiiqft(pi,P2)> A' G HomQFT(p/i,p2) is
(it is easy to check that A~xA' is in HoniQFT(pi^pi, P2^P2))- From property
(PI) above, QFT is actually quasitensor. Note that QFT is also strict.
With this background in place, we can state the following fundamental
theorem of Doplicher & Roberts A990).
Theorem 5.2.11 Associated to every local quantum Geld theory in four or
more spacetime dimensions is a compact group G whose representation ring
is isomorphic to the fusion ring of the theory. |
The discussion preceding 5.2.11 applies to two-dimensional conformal field
theories, if one replaces spacetime M by the circle S1, thought of as a com-
pactified light ray, and the Poincare group by the group PSL2(IR) of Mobius
transformations of S1 ('spacelike-separated' should be interpreted as 'dis-
'disjoint') (see Prohlich & Gabbiani A992)). However, the theorem of Doplicher
& Roberts is no longer valid:
Example 5.2.12 One of the simplest conformal field theories is that which
describes 'the scaling limit of the Ising model at the critical point'. This
160 5 Representations and quasitensor categories
has been worked out in detail by Mack & Schomerus A990). They find
three physical representations po, P1/2 and pi, with po being the vacuum
representation. The fusion rules are given by:
Pl/2xPl/2 = PO ©Pi, Pl/2X Pi = PlX Pl/2 = Pl/2, PlXpi=p0,
Pox ps = psx po = ps, for 5 = 0, -, 1.
2
The quasitensor category associated to this theory certainly cannot be equiva-
equivalent to the category of finite-dimensional representations of anything for which
the tensor product has its usual meaning on the level of vector spaces. For,
comparing dimensions in the above isomorphisms would lead us immediately
to the absurd conclusion that dim(pi/2) = >/2-
Nevertheless, we shall see in 11.3.22 that the fusion ring of the category
arising from this example is isomorphic to that of the category of representa-
representations of a quantum group, provided with a certain 'truncated' tensor product.
Moreover, the quantum dimension of the representation corresponding to p\j2
(in the sense of 4.2.9) is indeed equal to y/2\ 0
Although it does not quite fit into the above discussion of categories and
quantum field theories, we include the following example, which shows that a
fusion ring is essentially the same thing as a A + l)-dimensional topological
quantum field theory (TQFT) in the sense of Witten A988b) (see also Atiyah
A988)).
Example 5.2.13 A A + l)-dimensional TQFT associates to each compact
oriented 1-manifold X (i.e. a disjoint union of circles, possibly empty) a
complex vector space Vx, and to each oriented 2-manifold with boundary Y
a vector vy G Voy- We shall not write down all the axioms which the vy
and Vx must satisfy, but we note that V0 = (C, that if X* denotes X with
the opposite orientation, then Vx* = {Vx)*, and that Vx jix = Vx1 ® Vx2-
Thus, a surface Y with dY = X{ ]J X2 defines a linear map vy : Vx1 —> Vx2 •
It is not hard to see that giving such a theory is equivalent to giving a unital,
commutative, associative algebra A together with a linear form ev : A —> C
such that the bilinear form (a, a') i—> ev{aaf) on A is non-degenerate (this
remark is due to R. H. Dijkgraaf A989) and G. B. Segal). In fact, A is the
vector space associated to a single circle (with a definite orientation), and
the multiplication, unit element and linear form correspond to the diagrams
shown in Fig. 11.
It is clear from our earlier discussion that the complexification T^ — T§§<&
of a fusion ring T for which the involution * is the identity map is an algebra
satisfying these conditions. 0
5.3 Invariants of ribbon tangles 161
Fig. 11 Multiplication, unit element and linear form in a TQFT
5.3 Invariants of ribbon tangles
In this section, we consider ribbon tangles coloured with the set X of represen-
representations of a ribbon Hopf algebra A. We construct a functor from dribbon(X)
to rep^. This amounts to associating to each coloured ribbon tangle an iso-
topy invariant which is a homomorphism between representations of A.
A Isotopy invariants and monoidal functors Let A be a ribbon Hopf
algebra over a commutative ring /c, and let X be the set of objects of the
category rep^. To construct a functor dribbon(X) —+ rep^, we need the
following topological result, which gives a description of the morphisms in
dribbon(X) in terms of 'generators and relations'. It is a consequence of
classical work due to Reidemeister A932) and others (see Subsection 15.1A).
Proposition 5.3.1 Every morphism in dribbon(X) can be obtained from
the morphisms in Fig. 12 by taking compositions and tensor products. The
relations between morphisms in dribbon(X) shown in Fig. 13 hold, and every
relation is a consequence of them. |
We can now state the main result of this section.
Theorem 5.3.2 Let A be a ribbon Hopf algebra defined over a commutative
ring k, with universal R-matrix 1Z and distinguished central element v, and
let X be the set of objects of rep a- There is a unique monoidal functor
T : dribbon(X) —> rep^ such that
(i) on objects, T is given by
Cl), . . . , (Vn,tn)) = V? ® • • • ® V?,
where V+ = V and V~ = V* (T takes the empty word to k);
(ii) on generating morphisms, T is given as follows (the notation is as in
162
5 Representations and quasitensor categories
V V*
Pv
w*
w* v w* v
\y* y* y*
W* y* \y* y* \y* y \y* y y* y*
Yvw Yvw $vw $vw Tv Tv
Fig. 12 Generating morphisms in dribbon(X)
Fig. 13 Relations in dribbon(X)
5.3 Invariants of ribbon tangles
163
Fig. 12):
,) = TTy : /c -
r) = 7Ty : k -
/-) = a o i?y.
W
(a~) = evy : F*
\-i
o c
oa,
\-i
Here, i?y vy is the endomorphism of V <g) W given by the action of 1Z, vy
the endomorphism ofV given by the action ofv, and a the operator which
interchanges the order of the factors in a tensor product. The morphisms
evy and ny are defined in 5.1.3, and their 'twisted' versions evy and fry are
defined as follows: if {ei} is a basis ofV and {e1} is the dual basis ofV*,
= (ej,v
ny(l) =
Outline of proof The uniqueness follows immediately from the first part
of 5.3.1. To prove existence, we must first check that the endomorphisms on
the right-hand side of the formulas in the theorem are actually morphisms in
i.e. that they commute with the action of A. This is straightforward:
and lvw> we nave carried out most of the necessary computa-
computa, , y, one must use the fact that v lies in the centre of
A.
To complete the proof, we must verify that T is compatible with the re-
relations in Fig. 13. As an example, we do this for the relation shown in the
following diagram:
for oty,
tions in 5.2.2, and, for Ty,
164 5 Representations and quasitensor categories
The horizontal lines show how to express the left-hand side of this relation as
a composite of tensor products of generating morphisms. Its image under T
is therefore the endomorphism of F* given by
(idy* <S) evv)((Rv*v*)~1 ° & ® idy)(idy* ® a o Rvv*)(ldv* ® Try).
br, K~l = J2S cs ® ds. The effect of the preceding endo-
endo]Tr ar
morphism on a basis vector e^ of V is
-> el<g)breJ'(&arej \-> csbreJ'(&dsel(&arej \-> csbreJ(dsel, arej)
(repeated indices are to be summed over). This is the same as the action on
V of the element it; = csbrS~1(ar)ds G A. Since the image under .T7 of the
right-hand side of the relation to be checked is Vy, we must show that w =
v2 = S(u)u, where u = //(S® id)GJ2i), i-e. that S(ds)arS(csbr) = S(S(u)u).
But
S(ds)arS(csbr) = S(ds)arS(br)S(cs) = S(ds)S(u)S(cs) = S(csiids),
where the second equality is a consequence of the remarks following 4.2.4.
Recalling that S2 is given by conjugation by u, we must show that
S(u) = csS2(ds) = /x(id 0 52)(^).
But, from A5) in Chapter 4, (id <S) S2)AZ~1) = (id 0 S)(H), so our assertion
follows from the formula for S(u) used earlier in the proof. |
Example 5.3.3 It is interesting to compute the image under T of an annulus
coloured by a representation V. Using the decomposition of the annulus
shown below,
7Tv evy
it follows that the image is the composite k > F®7* > fc, which is
multiplication by the trace of the action of the element v~lu on V. Comparing
with 4.2.9 shows that this is exactly the quantum dimension of V. 0
Example 5.3.4 As a generalization of the preceding example, let T be an
endomorphism of an object ((Vi, ei),..., (Vn, en)) of dribbon(X). Let T be
the ribbon tangle obtained by 'closing' the coloured ribbon tangle T as shown
5.3 Invariants of ribbon tangles
165
below. Thus, T has no free bands. Then, F(T) = qtr(JF(T)). For the proof,
see Reshetikhin & Turaev A991), page 555. <0>
Example 5.3.5 As a simple application of the previous example, consider a
single annulus with an e-twist, where e = ± , coloured with a representation
V:
This is the closure of one of the twisted bands shown at the bottom right-
hand corner of Fig. 12 (with the same sign convention). Hence, the associated
scalar is T(jy) = ^qdim(F), where v^ = vy or Vy1 according as e = + or
-. o
Example 5.3.6 As a second application, consider the Hop} link Hyw, illus-
illustrated in the diagram at the top of the next page. It consists of two linked,
unknotted, untwisted annuli, the two components being coloured with repre-
representations V and W. From this diagram, 5.3.4, and 4.2.7, we obtain
V®W-+V®W).
In Chapter 15, we shall need an extension of 5.3.2 to the case of generalized
ribbon tangles. With A and X as in 5.3.2, we define a category dribbon(X)
as follows. Its objects are the same as those of dribbon(X), while a morphism
from ((Vi, ei),..., (Vm, em)) to ((Vi, ei),..., (Vn, en)) is a generalized ribbon
tangle T such that, for any band whose ends both lie in 1R x {0} x {0,1},
the same restriction on the colours of its ends applies as in dribbon(X). To
completely specify a morphism in dribbon(X), however, we must give some
additional data. Namely, if C is any coupon of T, we assign to each end of a
band lying in an end of C a sign + or — according to whether the orientation
166
5 Representations and quasitensor categories
of the band at that end is downwards or upwards, respectively. Let ei,..., er
(resp. ei,..., es) be the sequence of signs along the top end (resp. the bottom
end) of C. Then, the extra data we need is a homomorphism of A-modules
/ : Vf1 ® • • • ® V*r -> Vf1 ® • • • ® V*s.
We define a functor T : dribbon(X) —> rep^ as follows. On objects, and
on the morphisms involving no coupons, T is the same as T. To generate all
the morphisms in dribbon(X), including those involving coupons, we must
add to the generating morphisms in Fig. 12 those involving a single coupon, as
shown in Fig. 14. Then, T associates to such a morphism the homomorphism
/ : V]61 <S> - • • <S> Vrr —> Vi1 ® * • • ® Vss attached to the coupon.
Theorem 5.3.7 There is a unique monoidal functor T : dribbon(X) -^
defined on objects and generating morphisms as described above. |
Fig. 14 A generating morphism in dribbon(X)
5.3 Invariants of ribbon tangles
167
B Tangle invariants The following result is an analogue of 5.3.2 for
coloured tangles instead of coloured ribbon tangles.
Theorem 5.3.8 Let (A,1Z,v) be as in 5.3.2. There is a unique monoidal
functor Q : dtangle(X) —> rep^ such that
(i) on objects, Q is given by
where V+ = V and V~ = V*;
(ii) on the generating morphisms,
y* \y* y* \y* y* \y* y
y* \y* y* \y* v* \y* y*
Q is given as follows:
Q(a+) =7ry:k^V®V*, G(ay) = evv : V* 0 V -> fc,
3+) = jtv : fc _ F* 0 F, a^) = evv : V 0 F* ^ fc,
A /mfc is simply a tangle with no free ends. Hence, this theorem gives
isotopy invariants of links with values in the algebra Hom^(A:, k) = A:, i.e.
numerical invariants. To give a non-trivial example of such an invariant, we
must anticipate a result from the next chapter. In Section 6.4, we construct
a topological ribbon Hopf algebra Uhishi^C)) over the algebra C[[/i]] of for-
formal power series in an indeterminate h. It is a 'deformation' of the universal
enveloping algebra of sl2((C) and, like sl2{(C) itself, it has exactly one irre-
irreducible representation of each positive dimension. Taking A =
168
5 Representations and quasitensor categories
and X to consist of a single 'colour', namely the two-dimensional irreducible
representation of ^(^(C)), 5.3.8 gives a link invariant with values in C[[/i]].
It turns out that its values actually lie in the subalgebra consisting of the Lau-
Laurent polynomials in t = ehl2. If the normalization of the invariant is adjusted
so that its value on a single unknotted circle is 1, it becomes the Jones poly-
polynomial, discovered by V. F. R. Jones A985).
We shall study link invariants in much more detail in Chapter 15.
C Central elements In the statement of 5.3.2, we only allowed colourings
by finite-dimensional representations of A. This restriction was necessary to
be able to define the image of an annulus under T, which involves taking a
(quantum) trace. However, it can be relaxed as far as the bands are concerned.
In particular, we may colour the bands with the (left) regular representation
of A (which is infinite dimensional in most interesting cases).
Let us consider ribbon tangles with just one band: if the tangle contains
annuli, they must be coloured with finite-dimensional representations of A.
The image under T of such a ribbon tangle is a map / : A —> A, which,
by the nature of its construction, is of the form f(a) = za for some z € A.
Obviously, this map commutes with the action of A on itself if and only if z
lies in the centre of A. More generally, if we consider ribbon tangles with n
bands, we obtain elements of the centralizer of A^n\A) in
Z\ Z2 Z3 Z4
For example, the central elements of A corresponding to the four ribbon
tangles shown above are given, respectively, by
z\ = brS2(as)bsar, z2 = tracer (arbsS{bt)at)bras,
z3 = tmcey {bqarbsapS(bt)at)aqbrasap, z± = apbqarS(bt)atbpaqbr,
where 1Z = ar (& br (repeated indices are to be summed over). We leave it to
the reader to check that z\ = (uS^)).
Bibliographical notes
5.1 For the general background in category theory, which is assumed known
in this section, see MacLane A971). For monoidal categories, see Saavedra
Bibliographical notes 169
Rivano A972), Deligne & Milne A982), Joyal & Street A986), Yetter A990)
and Deligne A991). The reconstruction theorem 5.1.11 is due to Ulbrich
A990).
5.2 For fusion rules in quantum and conformal field theory, see, for exam-
example, Verlinde A988), Witten A990), Gawedski A991), Kerler A992a,b) and
Prohlich & Kerler A993).
5.3 The results of this subsection are taken from Reshetikhin A990b) and
Reshetikhin & Turaev A990, 1991). See also Rosso A992c). For other con-
constructions of central elements in quasitriangular Hopf algebras, see Drinfel'd
A990a).
6
Quantization of Lie bialgebras
The most important examples of quantum groups are deformations of univer-
universal enveloping algebras and of algebras of functions on groups. The purpose
of this chapter is to lay the foundations of the deformation theory of Hopf al-
algebras, paying particular attention to the first of these examples. Quantized
algebras of functions will be discussed in the next chapter.
The obstructions to the existence and uniqueness of deformations of a given
class of mathematical objects are generally described by some cohomology
theory of the objects concerned. In Section 6.1, we describe the appropriate
theory for Hopf algebras, which is a combination of the Hochschild coho-
cohomology theory of associative algebras and the dual theory for coalgebras.
This cohomology theory implies, among other things, that, for semisimple
algebraic groups and Lie algebras over fields of characteristic zero, every de-
deformation of the algebra of functions has unchanged coalgebra structure and
every deformation of the universal enveloping algebra has unchanged algebra
structure.
In the next two sections, we concentrate on deformations of enveloping
algebras, which are called quantized universal enveloping algebras, or simply
QUE algebras, and on deformations of the algebra of functions on a Lie group.
We argued in Chapter 1 that to quantize a Lie group or Lie algebra one
should equip it with extra structure, namely a Poisson-Lie group structure
or Lie bialgebra structure, respectively. Incorporating this into the universal
enveloping algebra leads to the notion of a co-Poisson-Hopf algebra. We
show that every deformation of a universal enveloping algebra induces on it
a co-Poisson-Hopf structure, so the Lie bialgebra structure is in fact 'built
in' to the deformation, and can be obtained from it by taking an appropriate
'classical limit'.
In Section 6.2, we show that every finite-dimensional Lie bialgebra can be
quantized. The proof is completely algebraic. We also outline an analytic
proof of the same result in the triangular case, which uses the ideas of Moyal
described in Section 1.6, and perhaps provides some justification for the use
of the term 'quantization' in this context.
After describing some general properties of QUE algebras in Section 6.3,
we give in Section 6.4 the standard quantization of s/2(C) (with its standard
Lie bialgebra structure). We show explicitly that its algebra structure is un-
unchanged, and that it is quasitriangular as a Hopf algebra. The importance
of this example is that a large class of QUE algebras, namely the quantum
6.1 Deformations of Hopf algebras 171
Kac-Moody algebras, can be constructed from it. We describe these algebras
in Section 6.5, and show further that, by suitably 'twisting' these standard
quantizations, one obtains a quantization of the 'generic' Lie bialgebra struc-
structure on any finite-dimensional complex simple Lie algebra.
6.1 Deformations of Hopf algebras
A Definitions The notion of a deformation of an associative algebra was
introduced informally in Section 1.6. We now give a more precise definition
adapted to the case of Hopf algebras.
Definition 6.1.1 A deformation of a Hopf algebra (A,z,/i,e, A, 5) over a
field k is a topological Hopf algebra (Ah, ih, HH-, ?h, A^, Sh) over the ring k[[h]]
of formal power series in an indeterminate h over k, such that
(i) Ah is isomorphic to A[[h]] as a k[[h]]-module;
(ii) fih = /i (mod h), Ah = A (mod h).
Two deformations Ah and A'h are equivalent if there is an isomorphism
fh'. Ah —> A'h of Hopf algebras over k[[h]\ which is the identity (mod h).
Remarks [1] The notation A[[h]] means the algebra of formal power series in
h with coefficients in A:
A) ah = ao + a\h + a2h2 H (a0, ai, a2,... G A).
Note that, unless A is finite-dimensional, A[[/i]] is 'bigger' than i%fc[[/i]]: in
fact, it is the completion of the latter in the /i-adic topology (see Subsection
4.1A).
[2] The definition does not mention the unit, counit and antipode of Ah.
In fact, it can be shown that any deformation is equivalent to one in which
the unit and counit are obtained simply by extending &;[[/i]]-linearly those of
A. Further, any deformation of A as a bialgebra (i.e. forgetting the antipode)
is automatically a Hopf algebra.
[3] If fh • Ah —> A!h is an equivalence, we shall write A!h = fh * Ah- Note
that gh * (fh * Ah) = (ghfh) * Ah.
[4] The simplest deformation of A, called the null deformation, is obtained
simply by extending k[[h]]-linearly the structure maps of A. Any deformation
equivalent to the null deformation is said to be trivial A
Since /i^ and A^ are k[[h]]-module maps, they are determined by giving
their values on elements A) for which a\ = a2 = • • • = 0. Condition (ii)
172 6 Quantization of Lie bialgebras
requires that, for a, a! G A,
B) fih(a <g> a') = fi(a ® a') + /ii(a <g> a')ft + /i2(a 0 a')/?2 H
C) Ah (a) = A(o) + Ai(o)ft + A2(a)/i2 + • • • ,
for some &;-module maps fa : A® A-+ A, Ai : A-+ A® A.
Similarly, an equivalence of deformations fa : Ah —> A'h can be written on
elements of A as
fa(a) = a + hfxia) + /i2/2(a) + • • • .
Note that
/h-1(a) = a-ft/i(a) + - .
The associativity condition for /i^ is
D) /i/i(/i/i(ai ® a2) 0 a3) = /i^(ai (g) /i/l(a2 0 a3))
for all ai, a2, 03 G ^4. Writing both sides of this equation as formal power
series in /i, we get an infinite number of conditions on the components \±i of
fih; the component of order h gives
E) /ii(aia2 0 a3) -f /ii(oi 0 a2)a3 = ai/ii(a2 0 a3) + /ii(«i 0 a2a3).
Similarly, the coassociativity condition for A^ is
F) (Ah 0 id)Ah(o) = (id 0 A^)A^(a)
for all a G ^4, the component of order h in which is
G) (A (g> id)Ai(a) + (Ai 0 id)A(a) = (id 0 A)Ai(a) + (id 0 Ai)A(a).
Finally, the condition that A^ is a homomorphism of algebras is
(8) Ah(/ih(ai ® 02)) = (/ih ® /ih)Ai3(oi)A^4(o2),
the term of order h in which gives
A(/ii(ai <8) a2)) 4- Ai(aia2) = (/i0^i+/ii0 /i)A13(ai)A24(a2)
+ A1(ai)A(a2) + A(ai)A1(a2).
A pair of A;-module maps (/ii, Ai) is called a deformation (mod h2) of ^4 if it
satisfies E), G) and (9). (Deformations (mod h2) are usually called infinites-
infinitesimal deformations in the literature on deformation theory.) More generally,
a 2n-tuple (/ii,..., /in, Ai,..., An) of A;-module maps is a deformation (mod
/in+1) of A if D), F) and (8) hold (mod /in+1). Thus, any deformation of A
6.1 Deformations of Hopf algebras 173
induces a deformation (mod /in+1) for all n. However, a deformation (mod
/in+1) does not in general extend to a genuine deformation.
We shall see shortly that E), G) and (9) admit a cohomological interpreta-
interpretation, but first we examine in a little more detail the notion of equivalence of
deformations. The conditions for a &;[[/i]]-module isomorphism fh'.Ah—* A'h
to be an equivalence of deformations are
Working to first order as usual, the equations become
A0) /ii(ai <g> a2) = /ii(ai <g> a2) 4- /i(aia2) - ai/i(a2) -
A1) A;(a) = Ai(a) - A(A(a)) + (/i 0 id + id ® /i)A(a).
Two deformations (mod h2) of A, say (/ii, Ai) and (fi[,A[), are said to be
equivalent if there is a A;-module map fi:A-+A satisfying A0) and A1).
B Cohomology theory The calculations in the previous section suggest
the following definition of Hopf algebra cohomology, which is modelled on
the Hochschild cohomology of associative algebras.
For z, j > 1, define the space of (i,j)-cochains of a Hopf algebra A to be
C*i = Homk(A®\A®i) and define /c-module maps d'{j : Cij -^ C{+lj and
d'(- : C1^ —> Cz<7+1 as follows (we shall usually omit the subscripts on d'^ and
A2) + ^(~l)r7(ai ® • • • ® ar_i 0 arar+i
r=l
= (/^W ® 7)(Aii+i(oi)A2l+2(a2)...
A3) + ^(-l)r(id®r ® A
r=l
Here, ^ : ^40Z —>• ^4 and A^) : A —> A®i are the iterated multiplication and
comultiplication maps:
A(j)(a) = (id <g> • • • <g> id <g> A) • • • (id <g> A)A(a)
(with j — 1 As). The meaning of the notation A^ i+k ia) is obvious, namely the
element of A®21 which has 1 in all positions except the A:th and the (i + fc)th,
where it has the components of A(o).
The following result can be proved by direct computation.
174 6 Quantization of Lie bialgebras
Definition-proposition 6.1.2 (C",d',d") is a bicomplex, i.e. one has
d! o df = d" o d" = d! o d" + d" od! = 0.
Set d = d^- + (-1)^4 and Cn = ei+^n+iC^'. Then, d : Cn -^ Cn+1
and (C'yd) is a complex whose cohomology groups (actually k-modules) we
denote by H'(A,A). |
To see what this definition means, suppose first that /i G C11. Then,
<g> a2) = ai/i(a2) + /i(ai)a2 -
d"(/i)(a) = (/! 0 id + id 0 A)A(a) - A(A(a)).
Comparing with A0) and A1), we see that a deformation (mod h2) (/ii,
is trivial if and only if it is a 2-coboundary.
Next, for any [i\ G C21 and Ai G C12,
a3) = ai/ii(a2 0 a3) - iii{aia2 <8> a3)
4- /ii(ai 0 a2a3) — /ii(oi 0 a2)a3,
a2) = (/x <8) /ii + /ii <8) /i)A13(ai)A24(a2) - A(/ii(ai 0 a2)),
a2) = Ai(oi)A(o2) - Ai(oio2) + A(oi)Ai(o2),
d/;(Ai)(o) = (id 0 Ai)A(a) - (A 0 id)Ai(o)
+ (id <g> A)Ai(a) - (Ai 0 id)A(a).
Comparing with E), G) and (9) shows that (/ii,Ai) is a deformation
(mod h2) of A if and only if it is a 2-cocycle.
We have proved the first part of
Proposition 6.1.3 Let A be a Hopf algebra over a field k.
(i) There is a natural bijection between H2(A,A) and the set of equivalence
classes of deformations (mod h2) of A.
(ii) If H2(A,A) = 0, every deformation of A is trivial.
Proof We know from part (i) that, if H2(A, A) = 0, then every deformation
Ah of A is trivial (mod h2); we must prove that it is actually trivial.
Write the multiplication and comultiplication maps of Ah as in B) and
C). Choose a 1-cochain /A) : A -> A such that d/A) = (/ii,Ai). Let
A'h = (id + hf^)*Ah. Then, /![ = A[ = 0. Repeating the calculations which
led to E), G) and (9) (but now looking at the h2 terms) shows that (/i2, A2)
is again a 2-cocycle. Choose a 1-cochain f^ such that df^ = (/i2, A2) and
define a deformation A^ = (id + ft2/B)) *^/l- Then /// = //2' = A'/ = A'2' = 0.
Let f^\ f^2\ /C), ... be the sequence of 1-cochains obtained by iterating
this process indefinitely, and set
4°°> = (• • • (id + hnfW) • • • (id + /t3/C))(id + />2/B))(id + hfW)) * Ah.
6.1 Deformations of Hopf algebras 175
Note that the infinite product makes sense as an element of -A [[/&]]. Since
A^° is the null deformation, this completes the proof. |
Example 6.1.4 If A is the group algebra k[G] of a finite group G over a field
k of characteristic zero, one can show (by a spectral sequence argument) that
H2(A, A) = 0. Thus, k[G] is non-deformable as a Hopf algebra. 0
The cohomology theory of Hopf algebras that we have defined is modelled,
as we have said, on the Hochschild cohomology of algebras and coalgebras.
In fact, the cohomology H&lg(A,A) of A as an algebra is that of the com-
complex (C1,^), and its cohomology iJcoalg(A, A) as a coalgebra is that of the
complex (C1', d"). Moreover, the proof of 6.1.3 contains that of the following
corollary.
Corollary 6.1.5 IfH%lg(A,A) = 0 (resp. if #c2oalg(A, A) = 0), every defor-
deformation of A is isomorphic to A[[h]] as an algebra (resp. as a coalgebra). |
The 'space' of genuine deformations of a Hopf algebra A is generally smaller
than the space H2(A, A) of its deformations (mod h2). In fact, if (/xi, Ai)
extends to a genuine deformation of A, or just a deformation (mod /i3), then
equating h2 terms in D), F) and (8) gives
ai ® a2) <S> a3)
-d"A2(a) = (id® Ai)Ai(a) - (Ai ®id)Ai(a),
d'A2 + d"/x2 = Ai(/xi(ai <g>a2)) - (/xi <8)//i)A13(ai)A24(a2) - Ai(ai)Ai(a2)
-(/x ® /ii + /n ® /x)(A}3(a1)A24(a2) + A13(a!)A24(a2)),
respectively. It is not difficult to check that the right-hand sides of these
equations define, for any 2-cocycle (//i, Ai), a 3-cocycle, whose cohomology
class depends only on the cohomology class of (/xi, Ai). One therefore has a
quadratic map Sq : H2(A, A) —> H3(A, A) such that a deformation (mod h2)
of A extends to a deformation (mod h3) if and only if its image under Sq is
zero.
In general, if one has a deformation (mod hn) of A, the obstruction to
extending it to a deformation (mod /in+1) is again an element of H3(A, A).
In particular, we obtain
Proposition 6.1.6 If H3(A,A) = 0, every deformation (mod h2) of A ex-
extends to a genuine deformation of A. |
Unfortunately, for most of the Hopf algebras of interest to us, H3(A, A) is
non-zero, and the question of whether a given deformation (mod h2) extends
is often non-trivial.
176 6 Quantization of Lie bialgebras
C Rigidity theorems We shall be particularly interested in deformations
Ah of the universal enveloping algebra C/(g) of a Lie algebra g, and of the
algebra J~(G) of regular functions on an algebraic group G. For these Hopf
algebras A, H2(A,A) is (fortunately!) non-zero in general, so non-trivial
deformations are possible.
Definition 6.1.7 A Hopf algebra deformation of the universal enveloping
algebra C/(g) of a Lie algebra g is called a quantized universal enveloping
algebra, or simply a QUE algebra.
A Hopf algebra deformation of the algebra J-{G) of regular functions on
an algebraic group G is called a quantized function algebra, or simply a QF
algebra.
QUE algebras in general will be discussed in Section 6.3, and the most
important examples are in Sections 6.4 and 6.5. QF algebras are the subject
of Chapter 7. The justification for the adjective 'quantized' will be discussed
in the next section.
The following result shows that, in constructing QUE algebras or QF alge-
algebras in the semisimple case, one may assume at the outset that the algebra
or coalgebra structure is unchanged (although it is often not convenient to
do this).
Theorem 6.1.8 Let G be a reductive algebraic group over a field k of char-
characteristic zero, and let g be its Lie algebra. Let Am(g)9 be the subspace of
Am(g) consisting of the elements which are invariant under the adjoint action
ofg.
(i) For all m > 1,
Hm(T(G),T(G)) * Am(g)/ A- (g)°, H™alg(T(G),f(G)) = 0.
Hence, every deformation of J~(G) is isomorphic to J~{G)\[h\\ as a coalgebra.
(ii) If g is semisimple,
H2(U(q) , U(q)) ~ A2(g), H3(U(q) , C/(g)) S A3(g)/ A3 (g)",
Hence, every deformation of C/(g) is isomorphic to U($)[[h]] as an algebra. |
Remarks [1] Part (ii) does not hold for arbitrary reductive g, as the example
of the Heisenberg Lie algebra shows. In fact, let g be the three-dimensional
abelian Lie algebra, let {X, Y, Z} be a basis of g and define a Lie bracket on
a[M by
[X,Y] = hZ, [X, Z] = [F, Z] = 0.
With this Lie algebra structure, C/(g [[h]]) is a deformation of C/(g) (when
completed in the /i-adic topology), but is non-commutative while i/(g)[[/&]] is
commutative.
6.2 Quantization 177
[2] In spite of this theorem, for most of the QUE algebras we shall study
later in the book, no explicit equivalence with a deformation with unchanged
algebra structure is known. A
6.2 Quantization
A (Co-) Poisson—Hopf algebras We argued in Section 1.6 that a 'quanti-
'quantization' of a Poisson manifold M might be interpreted as a deformation ^(M)
of the Poisson algebra !F(M) of C°° functions on M, such that the 'first order
part' of the commutator of two elements of Th{M) is equal to the Poisson
bracket of their classical limits. If G is a Poisson-Lie group, then T{G) is
also a Hopf algebra (modulo questions of completeness, which we ignore for
the moment), and the two structures are compatible. In fact, at the group
level the compatibility condition is
{/l ° rn, f2 o m}GxG = {/i , f2}G ° rn,
where /i, f2 G T{G\ m : G x G —> G is the multiplication in G and { , }gxG
and { , }g are the Poisson brackets ofGxG and G. Since fa o m = A(/^),
the preceding equation becomes
{A(/i),A(/2)}GxG = A({/i,/2}).
This suggests the following definition.
Definition 6.2.1 A Poisson algebra over a commutative ring k is a com-
commutative algebra A over k equipped with a skew-symmetric k-module map
{, }a '• A(& A —> A, the Poisson bracket, such that:
(i) the Jacobi identity
{ai,{a2,a3}A}A + {^3, {ai,^}^}^ + {^2,(^3,^1}^}^ = 0
holds for all a\, a2, a% G A;
(ii) the Leibniz identity
{aia2 , a]a = {^i, a}Aa2 + ai{a2 , a]a
holds for all ai7 a2, a G A.
A Poisson-Hopf algebra over a commutative ring k is a Poisson algebra
(A, { , }a) over k, which is also a Hopf algebra (A, z, /x, 6, A, S) over k, the
two structures being compatible in the sense that
178 6 Quantization of Lie bialgebras
(Hi) for all cl\, a2 G A,
, A(a2)}A®A = A({ai, a2}A).
The Poisson bracket { , }a®a on A ® A is defined by
{ai <8> a[ , a2 0 a^A^A = {«i, g2}a 0 o!xo!2 + aia2 ® {a'x , a!2}A-
To discuss the corresponding structures on universal enveloping algebras, we
must dualize 6.2.1.
Definition 6.2.2 A co-Poisson algebra over a commutative ring k is a co-
commutative coalgebra (A, e, A) equipped with a skew-symmetric k-module
map 8 : A —> A <8> A, the Poisson co-bracket, satisfying the following condi-
conditions:
(i) the composite
6 6<g)id c.p.
A —> A <g> A > A <8) A <g> A > A® A<g> A
is zero, where 'c.p.' means the sum over cyclic permutations of the factors in
the triple tensor product (this is the co-Jacobi identity);
(ii) the co-Leibniz identity
(A 0 id) 6 = (id <8> 6)A + cr23(<5 <8> id)A
holds.
A co-Poisson-Hopf algebra is a co-Poisson algebra (A, e, A, S) which is also
a Hopf algebra (A,i, fi, e, A, 5), the two structures being compatible in the
sense that
(Hi) for all a\, a2 G A,
<5(aia2) = <5(ai)A(a2) + A(ai)<5(a2).
Since Poisson-Hopf structures on T(G) correspond to Poisson-Lie group
structures on G, which in turn correspond to Lie bialgebra structures on the
Lie algebra of G, it is natural to expect
Proposition 6.2.3 Let g be a Lie algebra over a field k of characteristic
zero. If its universal enveloping algebra C/(g) has a co-Poisson structure 8,
making it a co-Poisson-Hopf algebra, then <5(g) c g <8) g and 8\Q is a Lie
bialgebra structure on g. Conversely, any Lie bialgebra structure 8 : g —> g<8>g
extends uniquely to a Poisson co-bracket on U(q), which makes C/(g) into a
co-Poisson-Hopf algebra.
Proof Let 8 : U(q) —> U(q)®U(q) be a Poisson co-bracket on ?/(g). To show
that <5(g) c g <8> g, let x e g and write 8(x) = Yliai® a'i-> where a^, a[ G C/(g).
6.2 Quantization 179
We may assume that the o!i are linearly independent. By condition (ii) in
6.2.2,
]T A(a») <8> a[ = 1 <8> <5(x) + a <g> 5A) + a23(8(x) <8> 1 +
Taking ai = a2 = 1 in (iii) gives 8A) = 0, so
A(a») (8) a- = ^(a» (8) 1 + 1 (8) a*) (8) a-.
It follows that the ai are primitive elements of C/(g). Hence, <5(g) c
Since <5 is skew-symmetric,
<5(g) c (g 0 C/(g)) n (/7(g) 0 g) = g 0 g.
To prove that <5|g is a 1-cocycle, let x\, x2 G g and compute
, x2]) = 8(xix2 -x2xi)
= [A(x1),6(x2)}-[A(x2),6(x1)}
= x1.8(x2) -x2.8(x1),
where the dot denotes the adjoint representation of g in each factor of g (8) g
(the second equality follows from 6.2.2(iii)).
Finally, the Jacobi identity for 6* is easily seen to be equivalent to the
co-Jacobi identity for 8.
The converse is proved in a similar way, using 6.2.2(iii) to extend 8 from g
to 17(9). I
B Quantization The following definition formalizes the discussion given in
Section 1.6.
Definition 6.2.4 Let A be a commutative Poisson-Hopf algebra over a Geld
k of characteristic zero, and let { , } be its Poisson bracket. A quantization
of A is a Hopf algebra deformation Ah of A such that
axa2 - a2ai
{xi,x2} = (mod /i),
if a\, a2 G Ah reduce to x\, x2 G A (mod h).
A quantization of an algebraic Poisson-Lie group (G, { , }) is a quantization
J-h(G) of the algebra J~(G) of regular functions on G, regarded as a Poisson
algebra, and (G, { , }) is called the classical limit of fh{G).
Before giving the dual definition, which will be the most important for us,
we pause to give an interesting example.
180 6 Quantization of Lie bialgebras
Example 6.2.5 Take the Poisson-Lie group to be the dual space g* of a
real Lie algebra g, equipped with the trivial Lie bracket and the Lie-Poisson
structure (see 1.1.3). The algebra ^(g*) of polynomial functions on g* is a
commutative (and cocommutative) Poisson-Hopf algebra. Let g^ be the Lie
algebra obtained by multiplying the Lie bracket of g by ft, and let U(Qh) be
(the ft-adic completion of) its universal enveloping algebra. It is easy to see
that U(Qh) is a quantization of .F(g*). For example, if X, Y € g are regarded
as linear functions on g*, their commutator in U($h) 1S h[X, Y], where [ , ] is
the Lie bracket in g, while
\x,Y\
is their Poisson bracket in ^(g*) (see 1.1.3).
It is clear that U($h) 1S isomorphic to i/(g)[[ft]] as a Hopf algebra, at least
over the quotient field of R[[ft]]. Thus, in a sense, C/(g) is a deformation
of ^"(g*). Now, according to the well-known Kirillov-Kostant orbit principle,
the irreducible unitary representations of g should correspond to its coadjoint
orbits. Recalling that these coadjoint orbits are exactly the symplectic leaves
of g* (see 1.1.3), we might expect that there should be a generalization of the
orbit method according to which the irreducible unitary representations of a
quantization of a Poisson-Lie group G should correspond to its symplectic
leaves. In Chapter 13 we shall see that, if G is a compact simple Lie group
with the standard Poisson structure described in Subsection 1.4C, then G has
a 'standard' quantization for which this expectation is fulfilled. 0
We now turn to the dual picture.
Definition 6.2.6 Let A be a cocommutative co-Poisson-Hopf algebra over
a Reid k of characteristic zero, and let 6 be its Poisson co-bracket. A quanti-
quantization of A is a Hopf algebra deformation Ah of A such that
Ah(a)AT(a)
a
where x G A and a is any element of Ah such that x = a (mod h).
A quantization of a Lie bialgebra (g, S) is a quantization /7^(g) of its uni-
universal enveloping algebra C/(g) equipped with the co-Poisson-Hopf structure
from 6.2.3. Conversely, (g,<5) is called the classical limit of the QUE algebra
Remarks [1] Note that the condition in this definition makes sense because
C/(g) is cocommutative, so that A^(a) = A^p(a) (mod ft). Note also that this
condition only depends on the behaviour of A^ up to order ft, so it makes
sense to discuss deformations (mod ftn) for all n > 2. Similar remarks apply,
of course, to quantizations of Poisson-Hopf algebras.
6.2 Quantization 181
[2] The Lie algebra g is uniquely determined by the QUE algebra [/^(g),
being the set of primitive elements of Uh(cy)/hUh(Q)- A
The following result shows that a quantization of a Lie bialgebra is the
same thing as a QUE algebra.
Proposition 6.2.7 Let g be a Lie algebra over a Geld k of characteristic
zero and let Uh(cy) be a Hopf algebra deformation of J7(g). Define S : C/(g) —>
(mod h),
h
where x G C/(g), and a G [/^(g) reduces to x (mod h). Then (t/(g), 5) is a
co-Poisson-Hopf algebra.
Proof It is easy to see that 6 is well-defined. We shall check that it satisfies
6.2.2(i), leaving the other two conditions to the reader.
We have
(8 ® idN(x) = ^ |(Afc ® id)Afc(a) - (A°p ® id)Afc(a)-
(Afc ® id)A°p(a) + (A°p ® id)A°p(a)| (mod h).
Write
(Ah ® id)Ah(a) = ^ a4 ® a- <8> <.
Then,
(A°p ® id) Ah (a) = Y, < ® ai ® <
(Ah ® id)A°p(a) = J^ a{ ® oj' ® en
(A°hp 0 id)A°p(a) = ^ a? ® aj 0 a,.
The result is now clear. |
This result has an interesting cohomological interpretation. In fact, let g
be a Lie algebra over a field of charcteristic zero, and let r G A2(g). The map
6 : g —> g 0 g given by 6(x) = (ad^ 0 id + id 0 adx)(r) extends uniquely to a
map 6 : C/(g) —> C/(g) 0 f(g), using the formula in 6.2.2(iii). Then, Ai = 6 is
a deformation (mod h2) of C/(g). Indeed, G) is equivalent to
((A (8) id)A(a)).((A 0 id)(r) + r 0 1) = ((id 0 A)A(a)).((id (8) A)(r) + 1 (8) r).
182 6 Quantization of Lie bialgebras
The terms involving a on the two sides are equal by the coassociativity of A,
and those involving r are both equal to the result of applying the operation
'c.p.' to r (g) 1.
By 6.1.6 and 6.1.8, the obstruction to extending this to a deformation
(mod h3) is an element of A3(g)/ A3 (g)9. Explicit computation shows that
this element is exactly [[r, r]], the 'left-hand side of the classical Yang-Baxter
equation'. In view of 2.1.2, we see that the obstruction vanishes precisely
when 8 is a Lie bialgebra structure on g.
C Existence of quantizations The question of the existence of quantiza-
quantizations of Lie bialgebras was settled, only recently, by Reshetikhin A992a).
Theorem 6.2.8 Every finite-dimensional Lie bialgebra (g, g*) over a Reid k
of characteristic zero admits a quantization.
Outline of proof Let H(X,Y), for X, Y € g, be the Baker-Campbell-
Hausdorff series for g:
h(x,y) = x + y + ±[x,y) + ±[x,[x,y}}+±i
[x,[y,[
(see Bourbaki A972), Chap. 2, §6, no. 4). We shall need the following
properties of H:
(i) H = XmLi H-m where Hn is a finite linear combination of terms of the
form
[Z1,[Z2,{---[Zn^,Zn) ¦¦¦}}},
where each Zi = X or Y;
(ii) H(X,H(Y,Z)) = H(H(X,Y),Z) (associativity);
(in) H(X, -X) = 0, H(X, 0) = H(Q, X) = X.
The first property implies that (X, Y) i-> H(hX, hY) is a well-defined k-
bilinear map g x g —¦ g[[/i]]. We denote its natural extension to a k[[h]]-linear
Let ^"(g) be the algebra of polynomial functions on g, and let
^r(g)[[/i]] as a k[[h]]-algebra. Then, properties (ii) and (iii) of H imply that
^(g) has a Hopf algebra structure with comultiplication, antipode and counit
given by
for / G g* C ^(g), I
6.2 Quantization 183
Let h be a second indeterminate, independent of h. The crux of the proof
is to show that there exist a pair of Hopf algebras (Sym^(g), Sym^(g*)) over
k[[h, h]] with the following properties:
(i) Sym?(g) S Sym(g) ® k[[h,h]] and Sym?(g*) * Sym(g*) ® fc[[M]] as
_ k k
h[[h, h]]-mod\i\es (Sym(g) denotes the symmetric algebra of g);
(ii) Sym?(g) * ^(g*) ® k[[h,h]] and Sym?(g*) ^ ^(g) ® fc[[M]] as
MM] MW]
coalgebras over fc[[/i,/i]];
(iii) there exists a non-degenerate pairing of Hopf algebras
(, ) : Sym?(g) x Sym?(g*) - k[[h,h]]
such that the restriction of ( , ) to g x g* c Sym^(g) x Sym^(g*) is equal to the
canonical pairing g x g* —> k (mod (h,h)). (The notion of a non-degenerate
pairing of Hopf algebras was introduced in Subsection 4.ID.)
Note that the existence of the pairing and the known coalgebra structure
of Sym^(g) and Sym^(g*) enable one to determine completely the algebra
structure of Sym^(g*) and Sym^(g). Prom this, one deduces that Sym^(g)
admits a fc[ft][[/i]]-form, i.e. a Hopf algebra ?^(g) over fc[/i][[/&]] such that
Symfrg) S tf?(g) ® k[[h,h}}
k{h][[h}]
as Hopf algebras over k[[h, h]}. The point is that U^(q) can be specialized in
h: we set
via the homomorphism fc[ft][[/i]] —> k[[h]] of k[[h]]-modules given by sending h
to 1. This gives the desired quantization of (g, g*). |
We shall describe briefly another approach to the existence question due to
Drinfel'd A983b), since it establishes a connection between quantum groups
and the deformation-theoretic approach to the quantization of dynamical sys-
systems discussed in Section 1.6.
Theorem 6.2.9 Let g be a finite-dimensional real Lie algebra, and let r G
g <g> g be a skew-symmetric solution of the classical Yang-Baxter equation
[ri2 , r23] + [n3 , r23] = 0.
Then, there exists a deformation /7^(g) of f/(g) whose classical limit is g with
the Lie bialgebra structure defined by r. Moreover, /7^(g) is a triangular Hopf
algebra and is isomorphic to U(o)[[h]] as an algebra over R[[/i]].
Proof We start with the trivial deformation i/(g) [[/&]] and twist it with
an invertible element Th € ?^(g) [[/*]] <8> ^(g)[[^]] (completed tensor product)
184 6 Quantization of Lie bialgebras
satisfying A8) and A9) in 4.2.13. By 4.2.14, ?/(g)[[/i]]^ is a triangular Hopf
algebra with universal R-matrix IZh = T^T^1. (Here, and elsewhere in this
chapter, we shall usually write T]^ instead of {Th)i2, etc.) In order that
C/(g)[[/i]]JFh be a quantization of the Lie bialgebra structure on g defined by
r, it suffices, by 6.2.7, that
^7j e 1 0 1 (mod h) and ee —r (mod h).
h 2
Note that, by 2.2.6, we may assume without loss of generality that r is
non-degenerate. By 2.2.2, r then defines a left-invariant symplectic structure
on the connected, simply-connected Lie group G with Lie algebra g. Let { , }
be the corresponding Poisson bracket on C°°(G). The existence of Th follows
from
Lemma 6.2.10 There exist left-invariant, bilinear, bi-differential operators
Dk : C°°(G) x C°°(G) -> C°°(G),
for k>2, such that the product *^ on C°°(G)[[h}} defined by
h *h h = hh + \h{h , M + JTthkDk(f1,f2),
for fi, J2 G C°°(G), is associative with the constant function 1 as unit ele-
element.
Indeed, if we identify g with the left-invariant vector fields on G, then
left-invariant differential operators C°°(G) —> C°°(G) are identified with ele-
elements of C/(g), and bi-differential operators C°°(G) x C°°(G) -> C°°(G) with
elements of C/(g) (?> t/(g). Note that, if XL is the left-invariant differential op-
operator corresponding to X G C/(g) (and similarly for elements of ?/(g)<S>/7(g)),
then
A4) XL(/1/2) = A(X)L(/1,/2)
for h, h e C°°(G).
Let Fk € U(q) ® U(q) correspond to Dk and set
k=2
The associativity of the product *^ is equivalent to
A5) ftifufkUtJs)) = ^LAL
6.2 Quantization 185
which, in view of A4), is equivalent to
(id ® A)(A)-H3 = (A
Hence, ^ = ^ satisfies A8) in 4.2.13. Similarly, the unital property of *^
is equivalent to A9) in the same proposition. |
To prove 6.2.10, one first linearizes the problem by essentially realizing G
as a coadjoint orbit (of a larger group), and then applies the method used in
Section 1.6 to construct the Moyal product on C°°(]R2). Actually, we shall
only construct the product *^ on the space C?°(G) of germs of C°° functions
at the identity element e of G, but this is sufficient for our purposes.
Let uj be the 2-cocycle on g defined by r (recall that r is non-degenerate),
and let
0 -* R -* g -> q -> 0
be the central extension of g denned by uj. Thus, g = g®R as a vector space,
and the Lie bracket is given by
[(x,a),(y,b)] = {[x,y],u(x,y))
for x, y G g, a, b G ]R. Let G be the connected, simply-connected Lie group
with Lie algebra g. Define <^o G g* by ?o(x,a) = a, and let 7i C g* be the
hyperplane <^0 + g*. Define a : G —» H by
Note that the kernel of the central extension G acts trivially on g*, and
hence there is an induced action of Gong*. It is easy to see that a is a local
diffeomorphism in a neighbourhood of the identity: in fact, its derivative there
is a'e(X)(Y) = u(X,Y), so the assertion follows from the non-degeneracy of
UJ.
To construct the desired product on C?°(G), it suffices to construct an as-
associative unital product *^ on C°°Gi) of the form in 6.2.10 which is invariant
under the coadjoint action of G, for we can then use a to obtain a product
on C?°(G) with the desired properties. We shall make use of the Baker-
Campbell-Hausdorff map Hh : Q[[h]] x g[[/i]] —» &[[ti\] introduced earlier. Note
that, by property (i) above, it follows that H^ is invariant under the adjoint
action of G:
Hh{g.X,g-X)=g.Hh{X,Y).
Identifying leg with X = (X, 0) € g, we define the *H product of tpi,
<P2 ? C°°(W) by
= I MX)MY)exp \?±(Hh(X,YU)] dXdY,
Jqxq L n J
186 6 Quantization of Lie bialgebras
where
( dim(g)
J
—J
is the Fourier transform of (p. This product is invariant under the coadjoint
action of G because Hh is invariant under the adjoint action of G. Further-
Furthermore, since
^ (mod/i3),
it follows that
^ {Ci (mod /i2),
where { , }^ is the Poisson bracket on H denned by u (regarded as an element
ofg*®g*).
As for associativity, a direct computation shows that
3dim(g)
/ /
/
while (((/?i *^ y?2) *^ ^3)@ is given by the same formula but with the sec-
second exponential in the integral replaced by exp[^j^(Hh(Hh(Y, Z), W),?)].
Thus, the associativity of *^ follows from the associativity property (ii) of
Hh. Finally, the unital property of *n follows immediately from the unital
property (iii) of Hh • I
Remark This calculation is a generalization of that in Subsection 1.6C. There,
g is the two-dimensional abelian Lie algebra, and g is the Heisenberg Lie
algebra. The Baker-Campbell-Hausdorff map for g is given by
so that
h~lHh{X, Y)-X-Y = h(xm - x2yi)
ifX = (xux2),Y = (y1,y2)e]R2. A
6.3 Quantized universal enveloping algebras 187
There is yet another approach to the problem of quantizing Lie bialgebras
which is closer in spirit to the origins of quantum groups in inverse scattering
theory. In this approach, the problem is to construct, for a given matrix
solution r G End(V ® V) of the classical Yang-Baxter equation, where V
is a vector space over /c, a solution Rh G End(F 0 ^O[|A]] of the quantum
Yang-Baxter equation such that Rh = 1 + hr (mod h2). In Chapter 7, we
shall describe, given such a solution of the QYBE, a way to construct a
bialgebra over fc[[/i]]. It turns out that many of the 'standard' quantizations
can be obtained this way, although in general there is no guarantee that this
construction leads to a QUE algebra.
There is, however, a relation between the R-matrix approach and the def-
definition of quantization we have given, at least in the case of triangular Lie
bialgebra structures on gln(R).
Proposition 6.2.11 Let Rh e (gln(R) <8> glnQ&))[[h]] be a solution of the
QYBE such that Rh = 1 (mod h) and Rj^Rh = 1. Then, there exists an
element Fh = l-\hr (mod h2) in (U(gln(tL))®U(gln(WL)))[[h]\ satisfying A8)
and A9) in 4.2.13 such that Rh is the image of F21F^1 under the canonical
map (p : U(gln(R))[[h]] —» yZn(]R)[[/i]] (ip is the unique homomorphism of
associative R[[/i]]-aigebras which is the identity on gln(R)[[h]]). Moreover,
Fh is uniquely determined by Rh up to transformations of the form
where fh G U(gln(^))[[h]] and <p(fh) = 1. |
We give a concrete application of 6.2.9 and 6.2.11 in Subsection 6.4F.
6.3 Quantized universal enveloping algebras
In this section, we discuss some general properties of QUE algebras. Examples
will be given in the following two sections.
A Cocommutative QUE algebras The next result shows, by contrast
with 6.1.8, that, although in many cases one may restrict attention to QUE
algebras which have the 'usual' algebra structure, the coalgebra structure
must be changed.
Proposition 6.3.1 Let Ah be a cocommutative QUE algebra over k[[h]],
where k is a field of characteristic zero. Then Ah is isomorphic as a topological
Hopf algebra over k[[h]] to U($h), where Qh is a deformation of a Lie algebra
9-
The meaning of the last sentence should be clear: §h is isomorphic as a
-module to g[[/i]], and Qh/hQh = g as Lie algebras over k. It is understood
188 6 Quantization of Lie bialgebras
that U($h) means the /i-adic completion of the universal enveloping algebra
of Qh-
Outline of proof Suppose that Ah = U(o)[[h]] as a /c[[/i]]-module, where
g is a Lie algebra over k. Let iph : Ah -* Ah be the composite iph — H>h° &h-
Note that ip preserves Ih — ker(e^) C Ah, and that, for all n > 0, ip (mod
h) has eigenvalue 2n on the image in Ih/hlh of the nth symmetric power
Symn(g). It follows that
n=0
where A^h = fc[[/i]].l and, for n > 1, A}™' is the generalized eigenspace of
iph on Ih with eigenvalue 2n (the direct sum is the /i-adic completion of the
algebraic direct sum).
Observe that A)^ is the set of primitive elements of Ah. Indeed, from the
cocommutativity of A^, it follows that iph is a coalgebra homomorphism and
hence that iph(A^) C A^] 0 A^ + A{°] 0 A^] for any a G A^\ Thus,
Ah(a) = 6(g)l + l(gN for some b e A^\ But then b = (eh (8 id)Ah(a) = a.
Let §h — A-h • Then g^ is a Lie algebra deformation of g and Ah —
as Hopf algebras over
In particular, if g is a complex simple Lie algebra, every cocommutative
deformation of G(g) is trivial, since every deformation of g as a Lie algebra
is trivial (this follows from Whitehead's lemma - see Jacobson A962)).
B Quasitriangular QUE algebras It is natural to ask which QUE al-
algebras have as their classical limits coboundary, quasitriangular or trian-
triangular Lie bialgebras (see Section 2.1). We shall say that a QUE algebra
Uh(o) is coboundary, quasitriangular or triangular if there is an element
IZh ? Uh(o) <8 Uh($) such that (Uh($), IZh) has these properties as a topo-
logical Hopf algebra and IZh = 10 1 (mod h) (see 4.2.6).
Proposition 6.3.2 Let (t/^(g), 1Zh) be a coboundary QUE algebra and
define r G U(q) (8 U(q) by
r = (mod n).
n
Then r G g(8g and the classical limit ofUh(o) is the coboundary Lie bialgebra
(g, 6) defined by r, i.e.
6(x) = (adz (8 id + id (8 adx)(r)
for x G g. Moreover, if Uh($) is quasitriangular or triangular, so is (g , 6).
Outline of proof Prom the coboundary conditions
K2 = nf (id ® A)(nh), nfnh = i ® i
6.3 Quantized universal enveloping algebras 189
on IZh-, it follows immediately that
A6) r12 + (A 0 id)(r) = r23 + (id 0 A)(r),
A7) ri2 = -r2i.
We show that r G g^)g. The rest of the proof in the coboundary case
is completely straightforward. We leave the triangular and quasitriangular
cases to the reader.
We assume that g is finite dimensional for simplicity. Let {xi,x2,..
be any basis of cj, and let
XX~ Ax! A2!'" Ad!' (AGJN
be the basis of G(g) introduced in 4.1.16. Recall that
where the addition of elements of Nd is performed componentwise.
Let
A,/*
Prom A7), we have r^ = —r^x. Next, A6) is equivalent to the following
equations:
if
ii A, \i, v are all non-zero.
Let €i = @,..., 1,..., 0), with 1 in the zth place. We must show that rx^ — 0
unless \ = €i and \i — Cj for some i, j. Suppose, on the contrary, that
A = €i + Ar, where X ^ 0, and let /i^O. Then, using A8) and the skewness of
r, we have
C QUE duals and doubles We have seen in 4.1.16 that the vector space
dual C/(g)* of the universal enveloping algebra t/(g) of a Lie algebra g
can be identified with an algebra of formal power series, and that it has
a natural Hopf algebra structure, provided we interpret the tensor product
f/(g)*0t/(g)* in a suitably completed sense. In the quantum case, Drinfel'd
A987) gives the following definition.
190 6 Quantization of Lie bialgebras
Definition 6.3.3 A quantum formal series Hopf algebra (or QFSH algebra)
is a topological Hopf algebra Bh over k[[h]], where k is a Geld, such that
Bh is isomorphic as a k[[h]]-module to Map(/, A?[[/i]]) for some set I, and
Bh/hBh = A;[[?i,?2> • • • ]] as a topological algebra, for some (possibly infinite)
sequence of indeterminates ?i,?2? • • • •
As in the classical case, when appropriately defined, the dual of a QUE
algebra is a QFSH algebra, and vice versa. But Drinfel'd also constructs a
QFSH algebra inside any QUE algebra Ah. In fact, define An : Ah -» Afn
by
Then,
Bh = {aeA\ An (a) = 0 (mod hn) for all n > 0}
is a QFSH algebra. The dual of Bh is a new QUE algebra, called the QUE
dual of Ah-
If the classical limit of Ah is a Lie bialgebra g over fe, that of the QUE dual
of Ah is the dual of g in the sense of Lie bialgebras (see Section 1.4).
Moreover, if we replace the dual A^ of Ah by its QUE dual in the construc-
construction of the quantum double in Section 4.2, then the double of Ah becomes a
QUE algebra whose classical limit is the classical double T>(q) of g.
Explicit examples of QUE duals and doubles will be discussed in Section
8.3.
D The square of the antipode In 1.3.13, we showed that the composite
D of the cocommutator <5:g—>g(g>gofa Lie bialgebra g with the Lie bracket
[ > ] : 9 ® 9 ~* 9 is a derivation of g as a Lie bialgebra. We shall now show
that D is closely related to the square of the antipode of any quantization of
9-
Proposition 6.3.4 Let § be a Lie bialgebra over a field k, let Uh(o) be a
quantization of q, and let Sh be the antipode of Uh(o)- Then, h~1(Sh — id)
(mod h) is the unique derivation of U(q) as an associative algebra whose
restriction to g is equal to —D/2.
Since the antipode S of G(cj) is given by S(x) — —x for all x G g, it follows
that S^ = id (mod /i), so the statement makes sense. Formally, it is clear
that h~l{Sfl — id) (mod h) is a derivation of f/(g) since it is the 'derivative'
(dSfr/dh)h=o of a 'one-parameter family' of automorphisms.
Proof We make use of the convolution product f %h g of k[[h}}-module maps
edby
f *h g =
6.4. The basic example 191
where \±h and Ah are the multiplication and comultiplication of t//i(g), respec-
respectively (cf. Remark [4] in Subsection 4.1A). Using the Hopf algebra axioms, it
is easy to show that *h gives the set of /c[[/i]]-module maps Uh($) —» Uh($) the
structure of an associative algebra over fc[[ft]], for which %h^h is the identity
and 5^ is the inverse of the identity map.
We claim that
(S2h - id) .h Sh = -Shfih(id ® Sh)(Ah - A°hp).
In fact, if a G Uh(o) and Ah(a) = ?^ a» <g> a-,
((S2h - id) .h Sh)(a) = ^S2h(ai)Sh(afi) - iheh(a)
Sh
\ i /
= Sh\y^a'iSh{ai)-Sh{ai)a'A.
The second equality follows from the fact that Sh is an anti-homomorphism,
and the third from the identity 5^ *^ id = ih^h- This proves our assertion.
Passing to the quotient (mod /i), we obtain
V • S = -5/i(id 0 S)S,
where V = h~l(Sfl — id) (mod h) : U(q) —> U(q) and • is the convolution
product for C/(g). Applying the right-hand side to an element x G g and
writing 6(x) = ^2j Xj 0 x'^ we find that
-Sii(id^ S)(x) =
3
On the other hand,
(V • S)(ar) = V(x)S(l)
since we clearly have V(l) = 0. Finally,
because S is skew-symmetric.
This proves that T>(x) — —D(x)/2 for x G g. If we show that V is a
derivation, it will follow that the equation holds for all x G f/(g).
192 6 Quantization of Lie bialgebras
Suppose then that x, y G f7(g), and choose a, b G C7)i(9) such that x ~ a
and y = b (mod /i). Then, (mod h) we have
- V(x)y - xV(y) s ^ " *» - M^ _ «(^)-»)
= 0.
6.4 The basic example
We now describe a quantization of the standard Lie bialgebra structure on
sl2(<E) denned in 1.3.8 (one could replace C by any field of characteristic zero).
Many of the results in this section will be generalized later in the book.
A Construction of the standard quantization The 'standard' Lie bial-
bialgebra structure
AH, 6(X~) = X- AH
on sl2{€) is defined by the r-matrix r = X+ A X~ (cf. 2.1.8). Let b±
±
{) ( )
be the subalgebras of s/2(C) spanned by {H, X±}, and let \) = b+ D b~.
Obviously, 6^) C b± 0 b±, so b± are actually sub-Lie bialgebras of s/2(C).
Our strategy is to quantize the Lie bialgebras (b^^i) in such a way that
the quantizations 'fit together' to give a quantization of (s/2(<C),<5)-
We look for a quantization of b+ which is isomorphic to ?/(b+)[[/i]] as an
algebra. Since 6(H) = 0, the choice
A9)
satisfies the condition in 6.2.6. To guess A^(X+), note that ?/(b+) is a graded
vector space, with deg(i7) = 0, deg(X+) = 1, and that its comultiplication
A preserves the grading. To preserve this grading, we try
B0) Ah(X+) = X+®f + g®X+,
where /, g G f (!))[[/&]]. The condition A^ = A (mod h) forces /, g = 1 (mod
h).
It is easy to check that, for any choice of /, g, the A^ defined by A9) and
B0) extends to an algebra homomorphism
and that A^ is coassociative if / and g are group-like for A^. The ten-
tensor product on the right-hand side is understood to be completed in the
/i-adic topology (see Subsection 4. ID) - in this case, the completion is simply
6.4 The basic example 193
Lemma 6.4.1 The group-like elements f of U(f))[[h]] such that / = 1 (mod
h) are precisely those of the form f — ehflH, where \i G C[[/i]].
Proof First, we compute
n=0
oo n
\m/ n!
n=0m=0
m=0 k=0
For the converse, let
be group-like, where fn G C[[/i]]. A computation similar to that above shows
that /m+n = fmfn for all m, n > 1. Thus, if /i = A//, then / = eh^H. |
We can therefore assume that
Ah(X+) =
for some /i, v G C[[/i]]. In fact, by replacing X+ by e~huHX+, we may assume
that i/ = 0. Definition 6.2.6 then requires that \i = 1 (mod /i). The simplest
choice is \i = 1, giving
B1) A^(X+) = X+ 0 e^ + 1 0 X+.
(In fact, up to automorphisms of C[[/i]] of the form h -+ h + O(/i2), this is
the only possible choice.) It is now easy to check that, if we set
B2) Sh(H) = -H, Sh(X+) = -X+e-hH, eh(H) = eh(X+) = 0,
then Ah, 5^ and €h extend to algebra homomorphisms (an anti-homomorphism
in the case of Sh) and satisfy the Hopf algebra axioms.
Of course, (b~,<5|b-) may be quantized in the same way. As above, there
is a choice in the definition of A^(X~), and the most convenient turns out
to be
B3) Ah(X~) = X- 0 1 + e~hH 0 X~.
194 6 Quantization of Lie bialgebras
The antipode and counit are then
B4)
We take the quantization Uh(sl2(<E)) to be U(sl2(<E))[[h]\ as a C[[/i]]-
module, with the coalgebra structure defined by A9)-B4). We must choose
the algebra structure so that A^ is a homomorphism. We compute
Ah[X+,X~] = [X+ 0 ehH + 1 0 X+ , X~ 0 1 + e~hH 0 X"]
= [X+, X"] 0 ehH + e"^ 0 [X+, X'] + X+e"^ 0 e^X"
B5) - e~hHX+ ® X~ehH.
To simplify this, we use
Lemma 6.4.2 Let A be an algebra over <?[[h]], let a, b, c e A and assume
that a commutes with c. Then,
Q eh{a+c) = ehaehc.
(ii) if [a, b] — be, then
ehabe-ha = behc
Proof The first part is well known (and easy to prove). For the second,
we have ab — b(a + c), and hence anb = b(a -+- c)n by an obvious induction.
Hence,
^nh = y »_ c)n
n! ^ n! v ;
n=0
c) = behceha. |
It follows from this lemma that the last two terms on the right-hand side
of B5) cancel, so that
B6) A/l[I+,I-] = [I+,I-]0e^+e-^0[I+,I-].
Comparing with A9), we see that the classical relation [X+,X~] = H must
be changed. Recalling that e±hH are group-like, it is easy to see that taking
[X+,X~] to be any multiple of ehH - e~hH will satisfy B6). To get the
correct classical limit, we take
phH _ p-hH
We summarize our computations in
6.4 The basic example 195
Definition-proposition 6.4.3 Quantum s/2(C) is the topological Hopf
algebra Uh(sl2((E)) over (C[[h]\ defined as follows.
Let P = <?{H, X+,X~} be the algebra of non-commutative polynomials
in three generators H, X+ and X~, let I be the two-sided ideal of P[[h]]
generated by
ehH _ e-hH
[Z () [Xi, A J — ZA , [XI, A J -f- M ,
and let I be the closure of I in the h-adic topology Then, Uh(sl
P[[h]]/I as an algebra over C[[/i]].
There are homomorphisms of (?[[h]}-algebras
Ah : Uh(sl2(<?)) -f Uh(sl2(<C)) ® Uh(sl2(C)),
e/i : Uh(sh(<C)) -* <C[[h}\, Sh : Uh(sl2(<?)) -> Uh(sl2(<E)),
(an anti-homomorphism in the case Sh) given on generators by A9) and B1)-
B4), which define the structure of a topological Hopf algebra on Uh(sl2{(E)).
Moreover, Uh(sl2((E)) is a QUE algebra whose classical limit is the Lie
bialgebra structure on sl2{(E) defined by r = X+ A X~.
Remarks [1] All C[[/i]]-modules which appear are understood to have the h-
adic topology, and all tensor products to be the completion of the algebraic
tensor products.
[2] To show that A^ (say) extends to an algebra homomorphism
Ah : Uh(sl2(€)) - Uh(sl2(€)) ® Uh(sl2(€)),
note that it extends trivially to a homomorphism P[[ft]] —» ^[[^]] 0 ^[ML
and that
B8) Ah(I) C P[[h]] 0 / + / 0 P[[h]]
(it is enough to observe that A/l(ff), A/l(X+) and A/l(X~) are contained in
the right-hand side of B8)). Since A^ is C[[/i]]-linear, it follows that I is a
Hopf ideal in P[[h]]:
Ah(l)
[3] The square of the antipode of Uh{sl2(C)) is conjugation by ehH:
S2h(a) = ehHae-hH
for all a G Uh(sl2(<C). (To prove this, it is enough to verify that the equation
holds when a — if, X+ and X~.) Taking 6.3.4 into account, this agrees with
one of the examples in 1.3.16.
196 6 Quantization of Lie bialgebras
[4] To complete the proof that Uh(sl2((E)) is a QUE algebra, we must show
that it is isomorphic to U(sl2((C))[[h]} as a <C[[ft]]-module. This is discussed in
the next subsection. Note that the completeness of Uh(sl2((E)) follows from
that of .P[[ft]] and the fact that 7 is closed.
[5] We shall often abbreviate the second paragraph in 6.4.3 by saying that
Uh(sl2((?>)) is 'topologically generated by if, X+ and X~ with defining rela-
relations [?T,X+] =2X+, etc' A
B Algebra structure We begin by introducing a quantum analogue of the
Casimir element
n = 1(# +1J + x~x+ = J(# -1J + x+x~
of U(sl2((E))- (Here, and in the remainder of this section, we use bars to
distinguish elements of U(sl2((E)) from those of Uh(sl2((E)).)
Definition 6.4.4 The quantum Casimir element of Uh(sl2(<?)) is
sinhft
_ fsmh\h{H -'.
\ sinh ft
The verification that the two expressions for ft are equal is straightforward.
It is clear that ft = ft (mod ft).
Proposition 6.4.5 The quantum Casimir element is a topological generator
of the centre of Uh(sl2(<E)).
This means that the (C[[ft]]-subalgebra of Uh(sl2((E)) generated by ft is
dense in the centre of Uh(sl2((E)) in the ft-adic topology. To prove that ft
lies in the centre, it is of course enough to show that it commutes with the
generators if, X+ and X~. We leave this to the reader, as similar but more
involved computations will be carried out in the proof of the next proposition,
which also implies that ft generates the centre.
Proposition 6.4.6 There is an isomorphism
of algebras over <C[[ft]] such that
+ = /coshft(# -1)- cosh2ftVn\
^ ] \ (ErlJ4^)sih2ft J
6.4 The basic example 197
Note that the formula for (p(X+) makes sense because, if u and v are
indeterminates,
cosh u — cosh v
u1 — v2
can be written as a formal power series /(u2,i>2). Note also that <p is equal
to the identity (mod h).
PROOF To show that <p extends to a homomorphism of algebras, we must
check that
(»)
(the other relations are obvious). From the formula for fj,
+ ^_ _ /coshh(H - 1) - cosh2hVn\
)x ~" )
On the other hand, since X~(H - 1) = (H + 1)X~, it follows that
X~f(h2(H - lJ,4/i2n) 2 f2ii
and hence that
y 2sinh^ J
Subtracting gives B9).
We prove that <p is an isomorphism by constructing its inverse. First we
compute
¦^iMfl + i) +
sinn a
_ sinh2^/iEr + 1) /cosh^E + 1) - cos
sinh2/i y 2sinh2/i
sinh2/i
Let
sinn
where ix is an indeterminate. Since
smh
198 6 Quantization of Lie bialgebras
and since h2/smh2h is an invertible element of <C[[/i]], it follows that there
exists a power series g ? <C[[/i, u}} such that
g{h,g(h,u)) = g(h,g(h,u)) = u.
Define ^(g) = g, il>(X~) = X~ and
x+
It is easy to see that ip((p(X+)) = X+ and that (p(tp(X+)) = X+, so to com-
complete the proof it suffices to show that ip extends to an algebra homomorphism
if) : U(sl2(<C))[[h]] -> Uh(sl2(<E))- For this, we compute
1 /
2 \co8hh(H-l)-cosh2hy/g(h,n)
2 \vcosh/i(iJ - 1) - cosh2hy/g(h,n)^
2 y cosh /i(g + l)- cosh 2hy/g(h, ft) /
using [H, X~] = —2X~, which equals
if ((H-IJ-4g(h,Q))sinh2h \f smh2±h(H - 1)'
2 ycosh/i(iJ — 1) — cosh2hy/g(h, ft) J \ sinh h
/ 9 2 \ /
1 / ((iJ + 1) — 4^(/i,ft))sinh /i \ /_
il —
2 y cosh /i(g+l)- cosh 2h^g(h, ft) y \ sinh2/i
Now,
cosh /i(g - 1) - cosh 2h^/g{h1Q))
( 21 .2 /z
\n 2
= 2 ( sinh2i/i(iJ - 1) - ftsinh2 ft J .
Thus,
6.4 The basic example 199
This computation completes the proof of 6.4.5. For we know that ft gener-
generates the centre of U(sl2(<E))[[h]], and hence so does g(h,Q) = f2(l + O(/i2)).
It follows that ip(g(h, 0)) = ft generates the centre of [//l(s/2(C)). |
It also completes 6.4.3. For, using the isomorphism y?, we can identify
Uh(sl2((E)) with C/(s^2(C))[[ft]] as an algebra, and in particular as a <C[[/i]]-
module. Since, on the generators H, X+ and X~, <p = id, Ch = €, A^ = A
and Sh = S (mod /i), it follows that Uh(sl2((C)) is a deformation of U(sl2((E))
in the sense of 6.1.1. And of course A^ was constructed so as to give the
standard Lie bialgebra structure on 5/2(C) in the classical limit. |
C PBW basis In the structure and representation theory of Lie algebras,
an important role is played by the Poincare-Birkhoff-Witt theorem, which
associates to any (ordered) basis of a Lie algebra a basis of its universal
enveloping algebra. The following is an analogue of this result for Uh(s
Proposition 6.4.7 The monomials (X-)r?rs(X+)*, for r,s,te N, form a
topological basis of [//l(s
PROOF This can be deduced from the isomorphism 6.4.6, together with the
classical PBW theorem. However, the following direct argument, which makes
use of the comultiplication of ^E/2 (C)), is instructive. The fact that the
given monomials span is easy; the point is to prove linear independence.
First, the generators if, X± G Uh = Uh(sl2((E)) are all non-zero, for we
shall exhibit in 6.4.10 representations of Uh in which they act as non-zero
operators. To prove, say, that (X+Y ^ 0 for all t, note that Uh is a Z-graded
algebra with deg(X±) = ± 1. One now observes that the term of degree
ff ^-^-j- X+ ® ehHX+ ® e2hHX+ ® • • • ® e«
This is non-zero by the previous observation, and hence so is A^ (
If there were a linear relation
in Uh, with cs G C[[ft]], then applying the left-hand side to the vector Vq in
the representation Vm defined in 6.4.10 shows that
ms = 0
for all m > 0. This implies that all the cs are zero.
200 6 Quantization of Lie bialgebras
Suppose now that we have a linear relation between monomials Hs(XJr)t.
Taking into account the grading, we can assume the relation is of the form
s=0
where cs ^ 0. Applying A^, using the linear independence of the powers
of if, and looking for the term of maximal degree in the second factor, we
see that the term csHs ® (X")* must itself be zero. But this contradicts
previous results.
Finally, suppose that there is a linear relation between the monomials
(X~~)rHs(X~*~)t. Applying A^ and looking for the term of maximal degree in
the second factor, we see that we can assume that only one value of t occurs
in the relation. Thus, we consider a relation of the form
s=0
where cs ^ 0. Applying A^ , looking for the term of minimal degree in the
first factor and maximal degree in the third factor, we obtain
s=0
The term Hs ® 1 ® 1 occurs on the left-hand side with coefficient c^, contra-
contradicting the linear independence of the powers of H. |
D Quasitriangular structure The classical limit of Uh(sh(C)) is a quasi-
quasitriangular Lie bialgebra structure on 5/2(C), so we might expect, in view of
6.2.7, that Uh(sl2(<E)) is itself a quasitriangular QUE algebra (cf. 6.3.2). We
now show that this is indeed the case.
First, we recall the notion of q-binomial coefficients. If q is an indetermi-
indeterminate, and m > n G N, define
[n]q\ = [n]q.[n-l]q [
[m]q\
\-n\q [n]q\[m - n]qV
These symbols are well-defined elements of the field Q(<?) of rational functions
of q over Q; in fact, it is obvious that [n]q G Z[g, g]. Moreover, taking
q = eh, it is clear that [n]eh = n (mod h).
6.4 The basic example 201
Proposition 6.4.8 The Hopf algebra Uh(sl2(<E)) is topologically quasitri-
angular with universal R-matrix
C0) nh =
n=0
where
Note that IZh is a well defined invertible element of the completion of the
tensor product Uh(sl2(<E))®Uh(sl2(<E)), since Rn{h) = 2n/in/n! (mod /in+1).
PROOF First we verify that
The left-hand side of C1) can be written as a sum,
m,n>0
where Qm?n G f/(l))[[ft]] is given by
Qm,n = q-^ [m^n] Rm+n(h)(Ah 0 id)(e^^^).(l 0 emhff 0 1).
The term involving (X+)m 0 (X+)n 0 (X")m+n on the right-hand side of
C1) is Rm(h)Rn(h) multiplied by
By induction on m, we find that
[1 <g> ff ® H , (X+)m ® 1 <g> (X~)m] = -2m
and hence, by 6.4.2,
On the other hand,
202 6 Quantization of Lie bialgebras
Thus, to verify C1), it suffices to show that
q-mn
L n
and this is an easy computation.
The relation
is verified in a similar way.
To show that
for all a G [/^(^((C)), note that both sides of this equation define algebra
homomorphisms Uh(sl2((C)) —» t//i(s^(C))(8)t//l(s/2(C)), so it suffices to check
that
A°*{aIlh = TlhAh(a)
when a = H, X+ and X~. When a = X+, for example, we must show that
| W()n (8) (X~)n I .(X+ ® ehH H-1 ®
U=o J
We find that the difference between the left- and right-hand sides is
nphH _ n-np-hH
The coefficient of (X+)n+1 (8) (X~)n vanishes provided that
[n + l]qRn+i(h) = qn(q - q'^Rnih).
This relation is easily verified. |
Remark It is clear that the second part of the above computation could have
been used to actually compute 1Zh, given the general form of IZh in the state-
statement of the proposition. This suggests that there may be a uniqueness the-
theorem for the universal R-matrix; we shall discuss such a result in Subsection
8.3E. A
Prom 4.2.7, we deduce
6.4 The basic example 203
Corollary 6.4.9 The element 1Zh e Uh(sl2(<E)) <g> Uh(sl2(<?)) (completed
tensor product) defined in C0) satisfies the quantum Yang-Baxter equation
^12^I3^J3 _ ^23^I3^12 -
Kh Kh Kh — Kh Kh Kh . |
The universal R-matrix TZh can be derived by 'almost' realizing Uh(sl2(<?))
as a quantum double and using 4.2.12 (cf. the computation of the r-matrix
for the standard Lie bialgebra structure on complex simple Lie algebras in
Subsection 2.ID). We have preferred to give a direct proof in the sl2 case,
partly to show that the proof is completely elementary, and partly because
it will be convenient to have the R-matrix in the sl2 case available before we
discuss the general case. However, we shall return to the quantum double
method in Chapter 8, when we investigate the structure of the quantization
of the standard Lie bialgebra structure on an arbitrary complex simple Lie
algebra.
Remark Note that, by 4.2.3, if uh = fih(Sh <E> id)(^1), then Sl(a) = unau^1
for all a ? Uh(sl2(<?)). On the other hand, it is easy to see directly that
S^(a) — ehHae~hH when a is one of the generators X+, X~, iJ, and hence
for all a. It follows that Vh = e~hHUh = Uhe~hH lies in the centre of
Uh(sl2((C)). Moreover, since ehH is obviously group-like, it follows that
(Uh(sl2((C)),TZh,Vh) is a topological ribbon Hopf algebra (see Subsection
4.2C). A
E Representations Thanks to 6.4.6, it is easy to describe the quasitensor
category rep^ when A = Uh(sl2((C)). We recall from Section 4.1 that rep^
consists of the representations of a Hopf algebra A defined over a commutative
ring k which are finitely generated and projective as /c-modules. In this
situation, k — C[[/i]] is a local ring, so that rep^ consists precisely of the
representations which are free and of finite rank as C[[/i]]-modules. We shall
simply call such representations finite dimensional from now on.
If Vh is a representation of t//l(s/2(C)), then Vh/hVh is a representation of
sl2(<?). Conversely, if V is a representation of s/2(C), then V[[h}} is a rep-
representation of Uh(sl2(<C)), by composing the obvious action of [7(s/2(C))[[/i]]
on V[[h]] with the isomorphism Uh(sl2(<?)) —» U(sl2(<?))[[h]\ constructed in
6.4.6. Moreover, these two operations are mutually inverse, at least for finite-
dimensional representations, because it is known that such representations
of sl2(<?) admit no non-trivial deformations (see Jacobson A962)). Finally,
irreducible representations of sl2((?) correspond to indecomposable represen-
representations of Uh(sl2((?)). Of course, (non-zero) representations Vh of Uh(sl2(<?>))
which are free as <C[[/i]]-modules are never irreducible, since hVh is a proper
subrepresentation.
After these observations, it is easy to give a complete description of the
objects of rep,4 when A = Uh(sl2(<?)).
204 6 Quantization of Lie bialgebras
Proposition 6.4.10 Let Vm be the free <?[[h]]-module of rank ra + 1 with
basis {^m),..., vffi }. Then the formulas
where q = eh and v_*l = v^1^ = 0, define an indecomposable representation
of Uh(sl2((E)) on Vm- Conversely, every finite-dimensional indecomposable
representation of Uh(sh(C)) is isomorphic to one of the Vm>
PROOF The fact that C2) does define a representation of {/^(^(C)) is a
straightforward calculation, using the relations B7). Now, Vm = Vm/hVm
has basis {vq\ ..., Vm }, where Vr = Vr (mod /i), with action of 5/2 (C)
given by
H.v^ = {m-2r)vlm\ X+4m> = (m-
Thus, t^n is the (m H- l)-dimensional irreducible representation of s^C).
Proposition 6.4.10 therefore follows from the preceding discussion, together
with the well known fact that the Vm are, up to isomorphism, all of the
finite-dimensional irreducible representations of s^C). I
The next result completes the description of rep^ when A — Uh(sl2((E)),
by determining its tensor structure. It is not, of course, a consequence of
6.4.6, since Uh(sl2((E)) is not isomorphic to f (s^2(C))[[ft]] as a coalgebra (the
latter being cocommutative, the former non-cocommutative).
Proposition 6.4.11 As representations of t//l(s/2(C)), we have
min{m,n}
1=0
PROOF Note that the representation Vn contains, up to scalar multiples, a
unique eigenvector of H which is annihilated by X+, and that its if-eigenvalue
is n. Since Vm®Vn is obviously a direct sum of indecomposables, it suffices to
show that Vm 0 Vn contains, for each / = 0,1,..., minjra, n}, an eigenvector
v^ of H with eigenvalue m + n — 21 such that v^ is annihilated by X+, and
that, up to scalar multiples, these are the only eigenvectors of H which are
annihilated by X+.
Let {^m)}z=,o,...,m and {Vj}j=oi...in be bases of Vm and Vn, as in 6.4.10.
It is obvious that the eigenvalues of H on Vm 0 Vn are m + n — 21 for / =
0,1,..., m + n, and that any vector with eigenvalue m + n — 21 is of the form
I
V =
r=0
6.4 The basic example 205
for some cr G C[[ft]]. Using B1) for A^(X+), it is easy to see that X+.v = 0
if and only if
qn~2r[m -l + r + l]qcr + [n - r]qcr+i =0, r = 0,...,/- 1.
If/ > min{ra, n}, then [n — r]q = 0 or [m — Z + r + l]g = 0 for some r = 0,...,/,
and then cr = 0 for all r. On the other hand, if I < min{m, n}, these equations
imply that v is a multiple of the vector
r=0 Vr\q
This proves the proposition. |
Remarks [1] The coefficients in the summation on the right-hand side of the
last equation are examples of quantum Clebsch-Gordan coefficients. The most
general such coefficient expresses an arbitrary eigenvector of H in the com-
component Vm+n-2i of Vm (8) Vn as a linear combination of tensor products of the
standard basis vectors in Vm and Vn. Formulas in the general case can be
found in Kirillov & Reshetikhin A989).
[2] There is a much quicker proof of 6.4.11 using characters (see Subsection
10.1C), but we feel that it is instructive to give a completely direct argument.
A
It follows from this result that Vm <g) Vn = Vn <g) Vm as representations of
Uh(sh(?))- In fact, by 5.2.2, the isomorphism is the composite with the flip
map a : Vm 0 Vn —> Vn 0 Vm of the operator on Vm 0 Vn corresponding to
the universal R-matrix IZh of Uhish^C)) given in C0). Note that TZh gives
a well-defined operator on Vm 0 Vni since the elements (X1^)^ act as zero on
Vm and Vn if k > m, n.
Example 6.4-12 Let us compute this operator in the simplest case m = n = 1.
The representation V\ has a basis {^0,^1} with action
H.v\ = —fi, X+ .v\ = i>o, X .v\ = 0.
Prom C0), we find that, with respect to the basis
of V\ 0 V\, the universal R-matrix acts as
feh
0
0
0
1
eh -e~h
0
0
0
1
0
0
0
0
e}
206 6 Quantization of Lie bialgebras
Note that, by 6.4.9, this is a matrix solution of the quantum Yang-Baxter
equation.
We shall see on a number of occasions later in this book that this simple
calculation has profound implications. <0>
F A non-standard quantization We showed in 2.1.8 that there are, up to
isomorphism and scalar multiples, exactly three Lie bialgebra structures on
5/2 (C). Apart from the trivial structure, and the standard structure which
we have quantized in this section, there is a 'non-standard' structure given
by the r-matrix rns = H A X+.
Since rns is a skew-symmetric solution of the CYBE, 6.2.9 shows that
there is a quantization U^s(sl2(^C)) of the non-standard structure which is
isomorphic to ?/(s/2(<C))[|A]] as an algebra, and with comultiplication given
by Ah = Fh.A.J7^1, where A is the comultiplication of ?y(s/2(<C)), extended
C[[ft]]-linearly to /7E/2(CC))[[/i]], and Th is a certain invertible element of
(U(sl2{<C)) <8> U(sl2(<E)))[[h]]. (Strictly, we are applying 6.2.9 to the Lie bial-
bialgebra structure on 5/2(R) defined by rns, and then complexifying the result.)
Ohn A992) finds that
From the proof of 6.2.9, we know that U%s(sl2((E)) is a triangular QUE algebra
with universal R-matrix 7Z™ = T^T^1. In the two-dimensional representa-
representation p\ of Uf(sl2(<?)), one finds that
C3)
As we noted at the end of Section 6.1, it is often inconvenient to assume
that a deformation has the usual algebra structure, even when this is possible,
and in this case the explicit formula for the comultiplication of C/?s(s/2(C))
obtained from 6.2.9 would be very cumbersome. However, it is straightfor-
straightforward to check that the following formulas also define a quantization of the
non-standard Lie bialgebra structure on sl2((C):
1
0
0
0
h
1
0
0
-h
0
1
0
h2
h
-h
1
r — I TT
L I Jtl
Sh{X+)
, [H,X+]
Ah(X-)
Ah(H)
= -x+, ,
th(X+)
h
= X+ $
= x~s
= H®
sh(x-)
= eh(X
~e
51
14
=
X+
+ e-2hX +
-e-2hx+?
-e2hX+X
= eh(H) --
[H,X~]
", Sh(
= 0.
= -2X- - hH2,
H) = -e2hx+H,
6.5 Quantum Kac-Moody algebras 207
Note that the algebra structure has been changed, although by 6.1.8 it must
be isomorphic to the usual one.
Finally, let us consider the R-matrix approach to the quantization of the
classical r-matrix rns = H AX+. This is very easy to carry out, thanks to the
following amusing observation (which may be verified by direct computation).
Proposition 6.4.13 Let g be a Lie algebra consisting ofm x m matrices over
a field k of characteristic zero. Assume that rGg^g satisfies r3 = 0, where
the cube is computed using the associative algebra structure of Mm2 (fc) =
Mm(k) 0 Mm(k). Then, the m2 x m2 matrix R = exp(r) is a solution of the
QYBE. |
In our case, if we regard H and X+ as 2 x 2 matrices (in the natural
representation of s/2(C)), then HX+ = -X+H = X+ and (X+J = 0, so it
is clear that (H A X+K = 0, and hence that R™ — exp(hrns) is a solution
of the QYBE for which R™ = 1 + hrns + O(h2). In fact, Rff is exactly the
matrix C3).
However, if rns is viewed as an element of f/(g) 0 U(§), exp(hrns) does not
satisfy the QYBE, and so is not the universal R-matrix of any QUE algebra.
(This can be verified by computing the operator defined by exp(hrns) in the
three-dimensional indecomposable representation of Ufj3(shi^E))-)
6.5 Quantum Kac-Moody algebras
In this section, we quantize the standard Lie bialgebra structure 1.3.8 on an
arbitrary symmetrizable Kac-Moody algebra g.
A The standard quantization Let A be a symmetrizable generalized Car-
tan matrix, and let g = Qf{A) be the associated Kac-Moody algebra. We
recall from the Appendix that g is generated by certain distinguished subal-
gebras isomorphic to sl2(<E). In fact, using the notation in the Appendix, g is
generated by elements Hi, Xf, X~, i = 1,... ,n, satisfying certain relations
which include
[Hi,X±]= ±2X±, [X+,X~] = Hi.
When g is given the standard Lie bialgebra structure 6 defined in 1.3.8, the
subalgebra g^ spanned by i7j, X^ and X~ is a sub-Lie bialgebra:
S(Hi)=0, 6(X±)=diX±AHi.
Thus, it is reasonable to try to quantize g by 'gluing together' the quanti-
quantizations of sl2{(E) obtained in the previous section. This procedure uniquely
specifies the action of the coalgebra structure maps on the generators of the
208 6 Quantization of Lie bialgebras
desired quantization of g, as well as the 'quantum analogues' of all the defining
relations of g except the Serre relations
l-a%3
k=0
The quantum analogues of these relations must be chosen so that the comul-
tiplication extends to an algebra homomorphism. This leads to
Definition-proposition 6.5.1 Let g = q'(A) be the Lie algebra associ-
associated to a symmetrizable generalized Cartan matrix (aij)i,j=i,...,n &s m the
Appendix. Let Uh(o>) be the algebra over (C[[h]\ topologically generated by
elements Hi, X+, X~, i = 1,..., n, and with the following defining relations:
[H^ Hj] = 0, [H^ Xf] = ± aijXf,
x?x--x~xt =
3 3 l 1'3 edxh _ e-dzh
Then, [/^(g) is a topological Hopf algebra over <C[[h]] with comultiplication
defined by
C5)
Ah{X+) = Xt ® ed^H* + 1 ® X?, Ah(X~) = X~ 0 1 + e~d*hH* 0 X~,
antipode defined by
and counit defined by
Moreover, [/^(g) is a quantization of the standard Lie bialgebra structure
on g defined in 1.3.8.
For the precise meaning of the statement that [/^(g) is topologically gener-
generated by the elements Hi, X^1, see Remark [5] following 6.4.3. As in that case,
all tensor products are to be understood in the ft-adically completed sense.
Proof We must first show that the formulas for A^, Sh and e^ do define
algebra homomorphisms (or rather an anti-homomorphism in the case of the
antipode). Let us compute, for example,
, Ah(X~)} = [X+ 0 e^hH* + 1 ® X^Xr 0 1 + e"^^ 0 XJ
Xj
6.5 Quantum Kac-Moody algebras 209
By 6.4.2, the sum of the last two terms is
(ed3a3%h _ edtat3h\ e-djhH3 j?+ ^ edxhH% j?-
which vanishes because the matrix (d^a^) is symmetric. The sum of the first
two terms is
edthHt 0 edzhHz _ e-d%hH% 0 e-dthHt
ed
as we want.
The most difficult relations to check are, of course, the 'quantum Serre
relations'
C6) E (-1)* I1 ~ha%3] ^h{Xt)k^h{Xf)^h(X±)l-^-k = 0,
k=0 L K led*h
for i y^ j. For this, we shall need certain facts about g-binomial coefficients:
Lemma 6.5.2 Let q be an indeterminate. Then:
Proof Part (i) is proved by direct computation:
* Jo W-[r-k]q\
. [r-1
[k}q\[r-k]g\ q-q-1
r-k ir ~ !]«! qk - q k
As for (ii), we have, using (i),
where the first term in the brackets on the right-hand side is understood to
be zero if k = r, and the second to be zero if fc = 0. Hence, if r > 0 the
right-hand side is equal to
q k=1
which obviously vanishes (change k to k + 1 in the second sum). |
The following result, which follows immediately from part (i) by induction
on r, will be important later in the book.
210 6 Quantization of Lie bialgebras
Corollary 6.5.3 [rk] e 7l\q,q~l] ifr > k > 0. |
Returning to the proof of 6.5.1, we shall establish C6) with the -f sign, the
other case being similar. It will be convenient to abbreviate the formulas by
writing X{ for X+, q{ for ed*\ and Ki for ed*hH\ Note that
by 6.4.2.
The first step is to compute A(Xi)r; we find, by induction on r using
L rZ J G.
Hence, the left-hand side of C6) is equal to
l-a%3 k l-alJ-k
Z—/ Z—/ V / ^ I yu I I + I I g
k=0 t=0 s=0 L J</. L J9t L J Qt
v /" Yt &\ Kl Yk~l\( Y &\ K x1 /9\ Y V Ys to A^s Y1~a3 ~k~s\
We show that the sum of the terms which have Xj in the second factor of
the tensor product is zero (the argument for the remaining terms is similar).
The sum of these terms is
l-atJ k l-atJ-k
k=0 t=0 s=0
r
sBt+s-k-i)-t(k-t) 1 - aij\ \k\ 1 - dij - k
q \ k
x
Setting m = s + t, p = k — t, and noting the identity
m
* I - I m - * I - I P I - I m I ,, L * J qt
we obtain
to
E E to-1)* [71
m=o P=o \t=o LtJ91
t=o /
aml Mal l-al3-m-p
6.5 Quantum Kac-Moody algebras 211
By 6.4.2(ii), the sum over t vanishes if m > 0, while the sum of the terms
with m = 0 is equal to
which is zero by the relations C4) in [/^(g).
The proof that A^ respects the remaining relations in C4) is easy, as are
the corresponding arguments for Sh and e^.
It remains to show that Uh(o>) is a quantization of the standard Lie bialgebra
structure on g. Since A/l(iJ^) is symmetric and
f/^(g) certainly has the correct classical limit. For the proof that f/^(g) is
isomorphic to ?/(g)[[/i]] as a C[[ft]]-module, see Tanisaki A990). |
Using the rigidity theorem 6.1.8, we deduce
Corollary 6.5.4 If g is a finite-dimensional complex simple Lie algebra,
then f//i(g) is isomorphic to U(q)[[h]] as an algebra over C[[ft]], by an isomor-
isomorphism equal to the identity (mod h). |
Remarks [1] According to DrinfePd A987) and Shnider A991, 1992), it follows
from the cohomology theory of Hopf algebras outlined in Subsection 4.1 A that
the quantization f/^(g) can be characterized, up to changes in the deformation
parameter of the form h i—> h + O(/i2), by the existence of a quantum analogue
of the Cartan involution. More precisely, a quantization Ah of g is equivalent
to the standard one if there exists a commutative Hopf subalgebra Hh of Ah
and an involution Oh of Ah which preserves if^, such that the isomorphism
AhIhAh = C/(g) takes Hh/hHh isomorphically onto C/(l)), where \) is the
Cartan subalgebra of g, and such that Oh is an algebra automorphism and
a coalgebra anti-automorphism, and reduces to the usual Cartan involution
(mod h). For [/^(g), we can take Hh to be the subalgebra topologically
generated by the iJ^, and Oh to be given on the generators by the same
formulas as in the classical case:
eh(xf) = -xf, eh(Hi) = -m.
[2] We shall discuss the structure of Uh(s) when dim(g) < oc in more detail
in Chapter 8. We show, in particular, that [/^(g) is quasitriangular, and we
compute its universal R-matrix.
[3] To extend the quantization of g = q'{A) to one of g(A), one adjoins
commuting primitive elements Di satisfying the same relations with the gen-
generators Hj, X^ of Uh(o) as in the classical case (see the Appendix). A
The following refinement of 6.5.4 is proved in DrinfePd A990a).
212 6 Quantization of Lie bialgebras
Proposition 6.5.5 Let g be a finite-dimensional complex simple Lie algebra,
let Uh{h) be the subalgebra ofUh(o) topologically generated by the Hi, and
let I) be the Lie subalgebra generated by the corresponding elements of g.
Then, there is an isomorphism of algebras cp : ?4(g) —> f(g)[[ft]] over <C[[h]]
such that Lp = id (mod h) and (p\^ = id. |
As in Subsection 6.4E, this implies
Corollary 6.5.6 If g is a finite-dimensional complex simple Lie algebra,
the assignment V i—> V[[h]] is a one-to-one correspondence between the finite-
dimensional irreducible representations of g and the indecomposable repre-
representations ofUh(o) which are free and of finite rank as C[ [ft]]-modules. |
B The
centre Another consequence of the rigidity theorem 6.1.8 is
Proposition 6.5.7 If g is a finite-dimensional complex simple Lie algebra,
the centre -Z^(g) of Uh(o) is canonically isomorphic to Z(g)[[ft]], where Z(q)
is the centre ofU(o).
Proof The existence of the isomorphism in question is an immediate conse-
consequence of 6.1.8. To see that it is canonical, note that any two isomorphisms
Uh(o) — U(o)[[h]] which are the identity (mod ft) differ by an automorphism
of ?/(g)[[^]] which is a deformation of the identity automorphism of C/(g).
But, since i?Lie(g, ?/(g)) = 0, any such deformation is trivial. This means
that the isomorphisms Uh($) = f(g)[[ft]] differ by an inner automorphism,
and therefore have the same effect on Zh(o). |
Remarks [1] The vanishing of the Lie algebra cohomology group i?Lie(g, U(q))
follows from the fact that the adjoint representation of g on C/(g) is a direct
sum of finite-dimensional irreducible representations, and that, for each such
representation V, we have #Lie(9> ^0 = 0- ^ee Jacobson A962) and Dixmier
A977).
[2] A proof of 6.5.7 which does not use 6.1.8 has been given by Tanisaki
A990). A
C Multiparameter quantizations We can use the 'twisting' construction
described in Subsection 4.2E to obtain from the single deformation Uh($) of
C/(g) a family of deformations depending on (™) parameters, where n is the
rank of g.
In fact, let g be a symmetrizable Kac-Moody algebra, let \) be a Cartan
subalgebra of g, let r ? A2A)), and set Th = exp(^hr) e Uh($) <8> E^i(g)- Since
\) is commutative, the equation
-r-12 H3 -r-23 _
^ ^ ^
Bibliographical notes 213
holds trivially, and since r is skew we have T^ — T^1. Hence, all the
conditions in the statement of 4.2.15 are satisfied, and we may define as there
a new Hopf algebra [/^(g)^ with the same algebra structure and counit as
[/^(g), but with comultiplication
Since Th = 1 (8> 1 (mod /i), we clearly have
Proposition 6.5.8 If g is any symmetrizable Kac-Moody algebra and r g
A2(\)), the Hopf algebra [/^(g)^ defined above is a QUE algebra. |
To see the significance of this result, suppose that g is finite dimensional
and simple. In Section 3.1 we saw that the set of Lie bialgebra structures on g
has a stratification into finitely many pieces, with a single stratum of maximal
dimension which is an affine space of dimension (™). More precisely, any Lie
bialgebra structure in this maximal stratum is defined by a skew solution
of the MCYBE of the form r-f r°, where r° G A2(g) defines the standard
structure and r G A2(I)) is arbitrary (the formula for r° is given in 2.1.7).
Since
Th = 1(8I + -hr (mod/i2),
it is clear that [/^(g)^ is a quantization of the Lie bialgebra structure defined
by r + r°. Thus, we have described explicitly a quantization of every Lie
bialgebra structure in the stratum of maximal dimension.
Bibliographical notes
6.1 For general background in the deformation theory of algebras, see Ger-
stenhaber & Schack A988). For the particular case of Hopf algebras, see
Gerstenhaber & Schack A990, 1992), Shnider A991, 1992) and Gerstenhaber,
Giaquinto & Schack A992), where proofs of 6.1.8 may be found.
6.2 Most of the results of this section are in Drinfel'd A987). Theorem 6.2.8
is due to Reshetikhin A992a). Theorem 6.2.9 is taken from Drinfel'd A983b),
although the proof given here is a little more explicit. The existence and
uniqueness of quantizations of Lie bialgebras are also discussed in Drinfel'd
A992a).
6.3 This section is an elaboration of parts of Drinfel'd A987).
6.4 The algebra Uh(sl2(<E)) was discovered by Kulish & Sklyanin A982b),
although its Hopf structure was only understood later. Most of the statements
in this section are special cases of more general results for quantum Kac-
Moody algebras discussed elsewhere in the book, although in the general case
214 6 Quantization of Lie bialgebras
such direct proofs are not usually possible. The explicit formulas in 6.4.6
are taken (with some modification) from Jimbo A985). The non-standard R-
matrix C3) was found by Zakrzewski A991a), and the associated deformation
of U(sl2(<E)) by Lazarev & Movshev A991b) and Ohn A992).
6.5 The defining relations of Uh{$) appeared first in Drinfel'd A987) and in
Jimbo A985) (in a slightly different form - see Chapter 9), and now appear in
nearly every paper on quantum groups. Multiparameter quantizations were
constructed by Sudbery A990), Artin, Schelter & Tate A991), and others,
although it seems to have been Reshetikhin A990a) who recognized that they
could be obtained from the standard quantization by twisting.
A quantization of the infinite general linear Lie algebra gloo, and of its
central extension A^, which is an infinite rank Kac-Moody algebra, has
been constructed by Levendorskii & Soibelman A991b). Classically, Aoo is
important because all affine Lie algebras can be embedded in it, although it
is not clear whether this continues to hold in the quantum situation.
Other examples of QUE algebras will be introduced later in the book. We
mention in particular the Yangians studied in Chapter 12.
7
Quantized function algebras
Partly because of their wealth of applications, and partly as a matter of per-
personal taste, we shall concentrate most of our attention in this book on quan-
quantized universal enveloping algebras. However, the picture of the subject which
would emerge would be too biased if we did not spend some time discussing
the dual approach in terms of quantized function algebras. Accordingly, we
devote the present chapter and Chapter 13 to this subject.
We begin in Section 7.1 with an ad hoc construction, due to Yu. Kobyzev
and Yu. I. Manin, of a quantization Th(SX2(C)) of the algebra of poly-
polynomial functions on SL/2((E). The quantization is obtained by allowing the
matrix entries which generate the classical function algebra to become non-
commuting, and demanding that the usual action of SX2(C) on the spaces of
row and column vectors survives the quantization unchanged. These spaces
are themselves allowed to become non-commutative, in a way analogous to
the deformation of the torus group to the Heisenberg group.
It turns out that the multiplicative relations between the generators of
the quantized function algebra can be expressed in terms of a solution of
the quantum Yang-Baxter equation. This suggests that, conversely, given a
solution of the QYBE one might be able to construct deformations of function
algebras from it. We discuss this approach in Section 7.2.
We also show in Section 7.1 that Jrh(SL2((C)) is exactly the dual Hopf
algebra of the quantization of U(sl2 (C)) constructed in the previous chapter.
This leads us to define the (standard) quantization Th(G) of the algebra of
functions on an arbitrary complex simple Lie group G with Lie algebra g to
be the dual of the QUE algebra C7^(g) defined in Section 6.5. One is then
faced with the problem of giving an 'explicit' description of Th{G). This has
been satisfactorily accomplished only in the SXn+i((C) case, although there
are candidates for the orthogonal and symplectic cases, which are constructed
from solutions of the QYBE as described above. We discuss the present state
of affairs in Section 7.3.
There are also multiparameter deformations of GLn+i((C) which have at-
attracted a good deal of attention, although most of them are accounted for
by the twisting construction described in Subsection 4.2E. There remains a
two-parameter family of deformations: of these, one parameter is a simple
scaling of the underlying Lie bialgebra structure, while the other parameter
arises from the fact that GLn_j_i((C) has one-dimensional centre.
In Section 7.4, we outline a theory of 'differential calculus on the quantum
216 7 Quantized function algebras
general linear group'. More precisely, we describe a deformation of the de
Rham complex of GLn+i((C) which is compatible with the deformation of the
algebra of functions defined in Section 7.3.
As we mentioned in the Introduction to this book, the quantum Yang-
Baxter equation first appeared in the physics literature. In Section 7.5, we
describe briefly the theory of two-dimensional lattice models in statistical
mechanics, where the QYBE plays the role of an integrability condition. In
fact, even the defining relations of ^(G), in the form described in Section
7.2, appear explicitly in this theory.
7.1 The basic example
We begin with an elementary discussion of the Hopf algebra structure of the
space of regular functions on GL2(C) and 6X2 (C).
A Definition If we write a general element of the vector space M2(C) of
2x2 complex matrices in the form
we can think of the entries a, 6, c and d of T as complex-valued functions
on M2(<C); in fact, the algebra T(M2((E)) is simply the polynomial algebra
<C[a, 6, c, d]. Matrix multiplication endows Jr(M2((E)) with a bialgebra struc-
structure given by
B) A(T)=TQT, c(T) = l,
which means
A(a) = a®a + b®c, A(b) = a®a + b®d,
A(c) = c®a + d®c, A(d) = c®b + d®d,
e(a) = e(d) = 1, e(b) = e(c) = 0.
(See Subsection 7.1C for the general definition of EL)
As we showed in 4.1.6, one obtains the Hopf algebra Jr(GL2(<E)) of regular
functions on the general linear group GL2(<E) by localizing at the determi-
determinant det(T) = ad — be (i.e. by 'formally adjoining' the inverse of det(T)).
A straightforward calculation shows that det(T) is a group-like element of
•F(M2(C)). If one sets
A(det(T)) = det(T)-1 0 det(T)-\ e(det(T)) = 1,
7.1 The basic example 217
and defines the antipode by S(T) = T, i.e.
S(a) = detCT)-1^ 5F) = -
S(c) = -detiT)-1^ S(d) =
and 5(det(T)) = det(T), then T(GL2{<E)) becomes a Hopf algebra.
When we regard a, 6, c and d as functions on the special linear group
5X2(C), they are no longer independent because of the determinant condition
C) det(T) = 1.
Indeed, it is easy to show that the algebra Jr(SL2((E)) of regular functions
on SL2((C) is the quotient
of T(M2(C)) by the two-sided ideal / generated by det(T) - 1. Writing
D = det(T) for simplicity, we have
A(D-1) = (D-1)®1+D®(D-1), e(D-l)=0, S(D-l) = -D~l{D-l),
from which it follows that / is a Hopf ideal of Jr(M2((E)) and hence that
Jr(SL2((C)) is a Hopf algebra (cf. Subsection 4.1A).
If V is a representation of SL2(<E), the map SL2((C) xV—+V which gives
the action of SL2((C) on V induces an algebra homomorphism
Sym(F*) -> T(SL2(<C)) 0 Sym(F*),
where Sym(V*) is the symmetric algebra of V*, i.e. the algebra of polynomial
functions on V. For example, if V is the natural representation on the space
of 2 x 1 column vectors, in which case Sym(F*) = C[x,y] is a polynomial
algebra on two generators, the homomorphism is
i.e. x \^ a<g) x + b<g)y, y i-> c ® x + d<g) y.
We look for a deformation of Jr(SL2((C)) which is generated by elements
a, 6, c and d which satisfy certain relations which reduce (mod h) to those
defining Jr(SL2((C)). Our strategy is first to deform Sym(F*) and then to
require that the map D) remains a homomorphism of algebras.
As the deformation of Sym(F*) we take
*) = C{x,y}[[h]]/(xy - e~V)-
218 7 Quantized function algebras
Here, <C{x, y} is the free (non-commutative) associative algebra over C with
generators x and y, and (xy — e~hyx) is the closure in the /i-adic topology of
the two-sided ideal in <E{x, y}[[h]] generated by the element xy — e~hyx. This
is analogous to passing from the torus to the Heisenberg group (cf. Remark
[1] following 6.1.8).
We set
= <E{a,b,c,d}[[h]}/Ih,
where Ih is an ideal of relations to be determined (the meaning of (?{a, 6, c, d}
is clear). The condition that D) defines a homomorphism of algebras
SymjF*) -> Th(SL2(<C)) ® SymJF*) is
(a 0 x + 6 0 y)(c 0 # + d 0 ?/) = e-/l(c 0 # + d 0 y)(a 0 # + 6 0 ?/).
Multiplying
(ac— e~hca
This will be
out and
)®x2 +
satisfied
using
(ad-
if
E) ac = e~hca, ad
the relation xy
da + ehbc-e->
— da + ehbc — t
= e hyx,
lcb) 0 xy -
3 cb =: 0
we find
Kbd-e-hdb)®y2 = 0.
bd = e~hdb.
In fact, these relations are forced because it is not difficult to show that the
monomials {xrnyn}rrlyne]si form a topological basis of Sym^(V*). We shall
not prove this since the purpose of this discussion is only to motivate the
definition of Th(SL2(C)).
Only half the necessary relations are contained in E), for we can just as
well require that the action of SL2 (C) on the space of 1 x 2 row vectors also
survives the deformation. This amounts to requiring that the relations E)
continue to hold when the matrix T is replaced by its transpose, or
F) ab = e~hba, ad-da-\- ehcb - e~hbc = 0, cd = e~hdc.
Combining E) and F) gives
(e-h + eh)(bc-cb) =0,
which implies that b and c commute. Then, E) and F) are together equivalent
to
ac = e~hca, bd = e~hdb, ab = e~hba, cd = e~hdc,
bc = cb, ad-da + (eh - e~h)bc = 0.
Note that, if we set h = 0, the relations G) simply say that a, b, c and d
commute with each other, and thus generate the algebra ^r(Af2(C)). We shall
write
= <C{a,b,c,d}[[h}}/Jh,
7.1 The basic example 219
where Jh is the closure of the two-sided ideal generated by the relations G)
(i.e. by the elements ac—e~hca, etc.). It is easy to check that the usual comul-
tiplication map B) extends to a homomorphism of algebras J:/l(M2(C)) —->
Fh(M2(<E)) <S> ^r/l(M2(C)) (completed tensor product), and thus defines a
(topological) bialgebra structure on ^r/l(Af2(C)).
To complete the definition of ^(aSZ^C)), we need an analogue of the
determinant relation C). A straightforward computation shows that ad — be
is not a group-like element of ^r/lE'L2(C)), but that
qdet(T) = ad - e~hbc
is group-like.
We have finally arrived at
Definition-proposition 7.1.1 Let Ih is the closure of the ideal in the
<L[[h))-algebra <C{a, 6,c, d}[[h]] generated by the relations G) and
(8) ad-e~hbc=l.
The quantized algebra of functions on SX2(C) is
= <C{a,b,c,d}[[h}}/Ih.
It is a topological Hopf algebra over C[[/i]] with comultiplication, antipode
and counit defined by
A fa b\ fa b\nfa b
Ah(c d =(c d B(c d
a b\ _ fa b
c d)~\c d) ~\-e~hc
a b\ (\ 0^
€hx c d I ~ V 0 1
Remarks [1] It is easy to verify, using the relations G) and (8), that the
quantum determinant qdet(T) lies in the centre of ^r)l(M2(C)); in fact, it
generates the centre topologically.
[2] One might ask why, in the derivation of the defining relations G) and
(8) of Th(SL<i{1?)\ we assumed that D) was not deformed. An 'explanation'
for the success of this assumption lies in the duality between J:/lE'L2(C))
and the quantized universal enveloping algebra Uh(sl2((E)), discussed below,
and the fact that the formulas in 6.4.12 which define the action of Uhishi^C))
on its two-dimensional indecomposable representation are identical to those
which define the two-dimensional representation of
220 7 Quantized function algebras
[3] It is also natural to ask for the most general deformation of T{SL2{(?))
that one can construct by the above procedure. Ewen, Ogievetsky & Wess
A991) find a two-parameter family of deformations of Jr(M2(<E)), which are
discussed in Subsection 7.3D, and a 'strange' algebra whose defining relations
are given in Subsection 7.2A. A
Before proving 7.1.1, we describe briefly an alternative approach to the
definition of Th{SL2(<L)) from which the quantum determinant qdet(T) =
ad — e~hbc appears more naturally. For this, we consider a deformation of
the exterior algebra A(V*). Classically,
and if one takes the deformation to be
then one finds that the relations F) are the conditions for the natural action
of SL2(<E) on A(V*) to survive the deformation unchanged. But now it is
natural to define the quantum determinant by qdet(T) = ad — e~hbc because
) = qdet(T) ® ?77.
B A basis of J7/lEL2(C)) What remains to be proved in 7.1.1 is that
as (C[[/i]]-modules. This is a consequence of the following lemma.
Lemma 7.1.2 The set X = {a^c1, dfibPtf', a, /?, 7, 6 > 0} is a topological
basis of Th(SL2(<?)).
This means that the elements of X are linearly independent over the quo-
quotient field <E((h)) of C[[/i]], and that their C[[/i]]-linear span is dense in
J7h(SL2(<E)) in its /i-adic topology.
Proof The linear span of the set y of finite products
(9) aai dSl b?1 c71 aa2 d62 b^c12 ... (c*i, ^,... > 0)
is obviously dense in J7/lEL2(C)). By using the relations
ab = e~hba, ac = e~hca, da = ehbc + 1,
it is clear that every such product can be written as a linear combination of
products in which oti = 0 for i > 1. Similarly, using the relations
bd = e~hdb, cd = e~hdc,
7.1 The basic example 221
every product of the latter kind can be written as a linear combination of
products for which oti = Si = 0 for i > 1. Since b and c commute, it follows
that Jrh{SL2{(C)) is spanned (topologically) by the products aad6b/3c1. If a
and 6 are both positive, write
and then use the relation ad = e~hbc + 1. Iterating this procedure, one sees
that aad6b/3c1 can be written as a linear combination of elements of X.
To prove that the elements of X are linearly independent, we formalize the
preceding argument by defining a C[[/i] ]-linear 'straightening map'
X : <E{a, b, c, d}[[h}} -> <C{a, 6, c, d}[[/i]]
with the following properties:
(i) x(u) — u f°r a^ u ? X;
(ii) x(//l) = 0, where i^ is the ideal of relations defining .^(S'Z^f^)).
Evidently, this will complete the proof of the lemma, since X is certainly
linearly independent when regarded as a subset of (C{a, 6, c, d}[[ft]].
It suffices to straighten each of the elements of y, since they are obviously
a topological basis of C{a, 6, c, d}[[/i]]. To accomplish this, we 'work from left
to right'; more precisely, we define a linear map i/j from <E{a,b, c, <i}[[/i]] to
itself as follows:
1>(aabPcyay) =
Here, y is any element of y; it is clear that every element of y can be written
in exactly one of the eight forms on the left-hand sides of these equations.
Thus, i/; is well defined. It is clear that i/;(x) = x if x G X, and that applying
ip iteratively takes any element of y into X (indeed, this is the argument of
the first paragraph). Thus, we may define, for y G y,
X(y) = lim Vn0).
222 7 Quantized function algebras
It is now clear that x satisfies condition (i) above, and that this implies
that, to check condition (ii), it suffices to show that x(xr) — 0 whenever
x e X and r is one of the generators in G) and (8) of the ideal Ih. This can
be verified by direct calculation. For example,
and hence
X(aocbf3c^(ad-da-(e-h-eh)bc))=0.
An analogous, but simpler, argument shows that
K6V, cfVc7, a, /?, 7, fi > 0}
is a basis of .FEX2(C)) (over <C). This proves that ^(SZ^C)) is a genuine
Hopf algebra deformation of
C The R-matrix formulation Let Mm,n(Ah) be the <C[[/i]]-module of mxn
matrices with entries in Ah = C{a, 6, c, d}[[ft]]. There are natural maps
0 : Mmin(Ah) O MrjS(Ah) -> Mmr
given by
We shall need the following simple properties of 0:
(A 0 1)(B 0 1) = AB 0 1, A0 A)(l ®B) = l®AB,
(A 0 1)A 0 B) = A 0 B, A0 A)(B 0 1) = (j(A 0 B)a,
where cr is the flip map. However, because Ah is not commutative, it is not
true in general that (A 0 B)(C 0 D) is equal to ^C 0 BD.
We also define
? : MmiP(Ah) 0 Mp,n(A) -^ Mm,n(A
by
k=l
For example, if
€ M2t2(Ah) = M2(Ah),
eh
0
0
0
0
1
eh - e~h
0
0
0
1
0
0
0
0
eh
7.1 The basic example 223
then
(a 0 b 0\
0 a 0 6]
c 0 d 0 I' ° ~
0 c 0 d/
(the rows and columns are numbered in the order 11, 12, 21, 22). The defining
relations of ^r/l(Af2(C)) admit a simple formulation in terms of these matrices:
Proposition 7.1.3 The defining relations (8) of Jrh(M2(<E)) are equivalent
to
(T 0 1)A 0 T)Rh = Rh(l 0 T)(T 0 1),
or to
where
Rh =
and Rh = Rh&, with a being the Hip operator. |
The proof is an easy computation.
Remark Similarly, it is easy to check that the defining relations of
and of A/l(Vr*) can be written as
A - e'hR)(X eX) = 0 and A + ehR)(E 0 S) = 0,
respectively. In the first formula, for example, we think of X as the 2x1
matrix f x J, so that X 0 X is the 4x1 matrix
A
D Duality We saw in Subsection 3.ID that the algebra Jr(SL2((E)) of regular
functions on SL2 (C) is the dual Hopf algebra, in an appropriate sense, of the
universal enveloping algebra U(sl2((E)). This suggests that the dual of a
deformation of U(sl2((E)) should be a deformation of J7(SL2(<E)). We shall
now show that this is the case for the deformation of Jr(SL2(<E)) described
in 7.1.1 and that of U(sl2^C)) described in Section 6.4.
As in Subsection 4.ID, we define the dual Hopf algebra Uh(sl2(^C))° to be
the set of C[[ft]]-linear maps Uh(sl2((C)) —> C[[/i]] which are continuous when
Uh(sfa(G)) is given the T-adic topology, where X is the set of ideals ker p, for
any representation p of Uh{sl2^C)) on a free <C[[/i]]-module of finite rank.
224 7 Quantized function algebras
Theorem 7.1.4 As a topological Hopf algebra over <C[[h]], Uh(sl2(<E))° is
isomorphic to Th(SL2(<L)).
Remark The dual Uh(sl2(<E))° is not the same as the QFSH dual of Uh(sl2{<E))
as a QUE algebra, defined in Subsection 6.3C. In fact, the QFSH dual is the
quotient of the algebra of formal power series (C{{a — 1, 6, c, d — 1}}[[/i]] by
the relations in G) and (8). A
Outline of proof We shall simplify the notation a little by writing q for
e\ Th for Tk{SL2{1E)) and Uh for Uh(sl2(<C)) throughout this proof. As
above, we write Ah = <C{a,6, c, d}[[h]], so that ^ = Ah/h, where /^ is the
(closure of the) ideal generated by the relations in G) and (8).
Let p : Uh —> End(F) be the two-dimensional indecomposable CT^-module.
Writing
B(xY
D(x)
the matrix elements A, B, C, D lie in U%. We set $(a) = A, $F) = B, $(c) =
C and $(d) = -D. Then, <1> obviously extends to an algebra homomorphism
$ : v4/i —-> E/?. We must show that <1> is surjective, and that ker(<l>) = /^.
To show that <1> is surjective, we have to show that A, B, C, D generate U%
as a topological algebra. This follows from 6.4.11, which implies that every
finite-dimensional indecomposable representation of Uh(sl2((C)) occurs as a
direct summand of an iterated tensor product of copies of V.
To see that ker(<l>) D i^, we must show that A, B, C, D satisfy the relations
in G) and (8). Let us verify, for example, that
A0) AD-e~hBC = l.
To compute the left-hand side, note that, by 6.4.7,
is a topological basis of Uh- It is almost obvious that
1 if r = t = 0,
0 otherwise,
1 if r = 0and t = 1,
0 otherwise,
1 if r = 1 and t = 0,
0 otherwise,
(-1)*, ifr = * = 0,
D((X-)rHs{X+y) = { 1 if r = * = 1,
0 otherwise.
7.1 The basic example 225
Since, for x eUh,
we must compute the comultiplication A^ on the basis elements A1). Using
the formulas A9), B1) and B3) in Chapter 6, one shows, by induction on /c,
that
r=0
Ah(X+)k =
r=0
Using these formulas, we find that
{ 1 if r = s = t = 0,
2se-h ifr = t = lj
0 otherwise.
Similarly,
(BC)((X~)rHs(X+Y) =
0 otherwise.
Hence, AD — e~hBC vanishes on all basis elements A1) except the identity
element 1, on which it is equal to one. This proves A0).
We now know that <]> induces a surjective homomorphism
To prove that it is injective, it is enough to show that the homomorphisms
<>h - u°h/hnu°h
are injective for all n > 0: the sufficiency follows from the completeness of Th
as a C[[fo]]-module, which in turn follows from the completeness of Ah and
the fact that the ideal Ih is closed. Let A{^k) be the <?[[h}} / (hn)-submodu\e
of
A[n) = Ah/hnAh = <C{a, 6, c, d} 0 C[[/i]]/(/in)
consisting of the polynomials in a, 6, c, d of total degree at most k. Thus,
oo
fc=0
226 7 Quantized function algebras
Similarly, we filter T{hn) = ThlhnTh by setting T^'k) equal to the <E[[h]]/(hn)-
submodule spanned by the matrix elements of representations of Uh of dimen-
dimension at most k + 1.
By 6.4.11, &n^(A{^k)) C ^n'fc), and it clearly suffices to show that the
induced map
is injective for all n and k. It follows, by using 6.4.11 again, that <]>(n'fc) is
surjective and jr^k)^(n,k-i) .g a free (c[^]]/(/ln)_module of mnk ^ + ^2^
On the other hand, from 7.1.2 it follows that A^' n(A^} ~~ +Ih) is spanned
by
Since this set has (fc 4-1J elements, $(n'fc) must be injective.
Finally, it is a tautology that <]> is a homomorphism of coalgebras. For this
amounts to showing that
A B\ (A B\_ (A B
C D U\C D " MC D)'
where A? is the comultiplication of ?/?, or that
A{x) B{x)\(A{y) B(y)\_(A(xy) B(xy)\
C(x) D{x))\C{y) D{y))-\C{xy) D(xy))
for all x,y & Uh- But this is what it means for
' A(x) B(x
X-> C(x) D(x)
to be a representation of Uh- I
Let CrT , 0 < r, s < m, be the matrix elements of the representation Vm
of Uh(sh((E)) constructed in 6.4.10 with respect to its basis {vr }r=o,...,m:
The preceding proof implies
Corollary 7.1.5 The matrix elements Cr?\ for 0 < r,s < m, are a topo-
logical basis of Fh(SL2(<E)). I
7.1 The basic example 227
E Representations In the classical case, the algebra J7(SL2((?)) is com-
commutative, and hence its irreducible representations are all one-dimensional.
The quantized algebra Th(SL2(C)), on the other hand, is non-commutative,
and, at first sight, it seems unlikely to have any one-dimensional representa-
representations at all. In fact, it is easy to see that there is a family of one-dimensional
representations parametrized by the set of invertible elements of C[[/i]]; in ad-
addition, there are infinite-dimensional indecomposable representations in the
quantum case, as the following result shows.
Proposition 7.1.6 The algebra Jrh(SL2((?)) has two families of indecom-
indecomposable representations, each parametrized by the invertible elements t G
C[[/i]], which can be described as follows:
(a) a family rt of representations on C[[/i]] given by
(b) a family tt* of representations on the space C[[/i]]q* of sequences of elements
0/C[[/i]], all but finitely many of whose terms are zero, given by
nt(a)(ek) = A + e~kh)ek^, n(d)(ek-i) = A - e~kh)ek,
nt(b)(ek) = -e-<fc+1>ht-1efc, nt(c)(ek) = e~khtek,
where e/~ is the sequence which has 1 in the kth place and zeros elsewhere,
and e_i =0.
Proof An easy calculation. |
Remarks [1] The formulas for tt* can be made to look a little more symmetrical
by rescaling the basis {e/c}. In fact, it is easy to see that the formulas for
7Tt(a) and 7Tt(d) can be put in the form
7rt(a)(efc) = A - e-2fcfcI/2efe-i, 7rt(d)(efc-i) = A - e~2khfl2ek,
(with no change in 7Tt(b) or 7Tt(c)), provided one is willing to extend scalars
from <C[[/i]] to ^[[/i1/2]]. In this form, we shall meet the representations itt
again in Chapter 13.
[2] Note the resemblance between this result and the parametrization of
the symplectic leaves in 5/7B) with its standard Poisson-Lie group structure,
described in Section 1.4. This correspondence has already been hinted at in
6.2.5, and will be made more precise and 'explained' in Chapter 13. A
228 7 Quantized function algebras
7.2 R-matrix quantization
In this section and the next, we shall reverse the order of events in the previous
section by defining a Hopf algebra, or at least a bialgebra, starting from an
arbitrary R-matrix. In some cases, these Hopf algebras will turn out to be
quantizations of algebras of functions on complex simple groups.
A From R-matrices to bialgebras Let R be a matrix in End/c(/cm(g)/cm) =
Endfc(/cm) ® Endfc(/cm), where /cm denotes the free /c-module of rank m, and
k is any commutative ring with unit. We write R = Ra, where a is the flip
operator. We also choose an element q G kx (the set of invertible elements of
k). Motivated by 7.1.3 and the remarks following it, we make
Definition 7.2.1 (i) Sym^q is the associative k-algebra generated by ele-
elements xi,..., xm with defining relations
(l-q-1R)(XQX) = 0,
where X is the m x 1 matrix with entries xi,..., xm.
(u) ^R,q Js the associative k-algebra generated by the elements ?1?..., ?m with
defining relations
where H is the m x 1 matrix with entries ?i,..., ?m.
(Hi) JrR(Mrn) is the associative k-algebra generated by the elements tij, where
1 ^ hj ^ ^? with defining relations
A2) R(TQT) = (T®T)R,
where T = (tij).
Remark We shall be particularly interested in the case k = (C[[/i]]. In that
case, one should replace 'generated' by 'topologically generated' in all three
parts of the definition. The meaning of 'topologically generated' is explained
in 6.4.3. A
As in the basic example considered in the preceding section, we have
Proposition 7.2.2 For any matrix R e Endfc(/cm (g) k171), ^(Mm) is a
bialgebra with comultiplication and counit determined by
A(T) = TBT and c(T) = 1,
respectively.
7.2 R-matrix quantization 229
Moreover, for any q G kx, there exist unique left k-comodule algebra struc-
structures
given on generators by
X^TBX, E^TBE.
Proof We first verify that A is compatible with the defining relations A2).
Now,
A(R(T0 T)) = R(TBT)Q(TBT)
= R(T ®T)B(T®T)
= (T 0 T)J^ ? (T 0 T)
- (T0T)El(T0T)i?
(the third and fifth equalities follow from A2)). By a similar argument,
A((T 0 T)R) = (T®T)B(T® T)R.
(We recommend that the reader write out the preceding computation in com-
components to be convinced that it is correct.) The verification for e, and the
second part of the proposition, are proved by similar calculations, and are
left to the reader. |
Although FR^Mm) is a well-defined bialgebra for any R, one usually as-
assumes that R is a solution of the quantum Yang-Baxter equation (QYBE):
A3) R12R13R23 — R23R13R12'
This is a reflection of the associativity of multiplication in T^Mm). In fact,
writing Tx = T 0 1 0 1, T2 = 1 0 T 0 1, T3 = 1 0 1 0 T, one can pass from
the product T1T2T3 to the product T3T2T1 in two ways: either
TiT2T3 —> T1T3T2 —> T3TXT2 —> T3T2TU
or
TiT2T3 —> T2T{T3 —> T2T3TX —> T3T2TX.
The first sequence is effected by conjugation by Ri2R\3R23^ the second by
conjugation by R23Ri3Ri2. We assume throughout the remainder of this
section that R satisfies the Q YBE.
e~h
eh-
eh-
1
-eh
-e~h
-e~h
0
1
0
-1
0
0
1
1
0
0
0
1
230 7 Quantized function algebras
The simplest example is, of course, R = 1 and q = 1, in which case
Sym^, AR,q and TR(Mm) become Sym((fc™)*), A((fcm)*) and .F(Mm(fc)),
respectively. We shall be mainly interested in the case k = C[[ft]], and we
would like JrR{Mrn) to be a deformation of ^-*(Mm(C)), in the sense that
JrR(Mrn)/hJ7R(Mrn) = JF(Mm((C)) as bialgebras. It is thus natural to as-
assume that
A4) R = 1 (mod ft),
since then the defining relations of JrR(Mrn) will become those of Jr(Mm(C))
when we set ft = 0. Conditions A3) and A4) are satisfied if ra = 2 and i?
is the matrix in 7.1.3; as we saw in the preceding section, JrR(Mrn) is then
a (non-trivial) deformation of ^r(M2(C)). Ewen, Ogievetsky & Wess A991)
consider the example
A5) R =
This is a solution of the QYBE, first found by Demidov et al. A990), but
clearly R ^ 1 (mod h). Thus, the algebra JrR(Mrn) associated to this 'strange'
R-matrix is not a deformation of ^"(M2(C)). (Ewen et al. assert that this
strange algebra has a 'classical limit', but that is not in the sense meant in
this book: to obtain this limit, they use a change of basis which becomes
singular when ft = 0.)
Unfortunately, however, even for a matrix satisfying A3) and A4), JrR(Mrn)
is not necessarily a deformation of ^-*(Mm(C)), and there seems to be no sim-
simple criterion on R which guarantees that it is. The question has been discussed
extensively by Gerstenhaber & Schack A990, 1992) and by Gerstenhaber, Gi-
aquinto & Schack A992). We close this subsection with a simple example of
what can go wrong.
Example 7.2.3 Take m = 2 and let R be a diagonal matrix :
R =
where a, /3, 7, 8 G C[[ft]] are = 1 (mod ft). Any matrix of this form trivially
satisfies the QYBE, and, since R = 1 (mod ft), one intuitively expects that
'the relations in JrR(Mrn) go over into those of Jr(M2(<E)) as ft tends to zero'.
But the relations A2) imply that
a
0
0
0
0
0
0
0
0
0
7
0
0
0
0
6
7.2 R-matrix quantization 231
These equations imply the relation (a2 — /3^)tnti2 — 0, so that, if a2 ^ /?7,
FiiiMm) is not a deformation of .7r(M2((C)). (This argument can easily be
made precise by noting that the algebras J-R(Mrn) and ^(il^C)) are graded
by the total degree in the generators Uj and considering their Poincare series.)
0
B From bialgebras to Hopf algebras: the quantum determinant The
next step is to construct a Hopf algebra which is related to Tr^Mju) in the
same way as ^-*(GI/2(C)) is related to .7r(M2((C)). Thus, we must construct
an appropriate analogue of the determinant det(T). To do this, it will be
necessary to make an additional assumption on R.
Note first that ArjQ is a graded algebra with deg(^) = 1:
We shall say that R is Frobenius if, for some n > 1,
(FR1) A?>g ^ k and A^q = 0 for i > n;
(FR2) the multiplication map A^g 0 A^2 —> A^ g = k is a non-degenerate
pairing for all i < n.
Of course, if R = 1 and g = 1 then n = m, but we allow n^min the general
case.
Definition-proposition 7.2.4 If R e Endfc(/cm (8) /cm) is Frobenius, there
exists an element qdet(T) G JrR(Mrn), called the quantum determinant, with
the following properties:
(i) 6r(uj) = qdet(T)(g>uj for all uo G A^ q, where 6r denotes the left k-comodule
algebra structure given by 7.2.2;
(ii) A (qdet (T)) = qdet (T) <g> qdet (T) and e(qdet(T)) = 1.
Proof By its definition, Sr(A1RA) C JrR(Mrn) (8) A^g, so, since 6r is an
algebra homomorphism, <5#(A^g) C JrR(Mm) (8) A^g. Part (i) now follows
from (FR1).
Since 6r is a /c-comodule structure, (id (8) 6rNr = (A 0 id)<5ft. Applying
both sides to a non-zero element of A^ q and using (FR2) shows that qdet(T)
is group-like. The second equation in part (ii) follows in the same way. |
Example 7.2.5 We consider the 'strange' R-matrix A5), and take q = 1 (this
choice will be justified below). We find that Ar}Q has defining relations
232 7 Quantized function algebras
It follows that A2Rq = <C.(?i6), and that ^Rq = 0 for i > 2. Thus, R is
Frobenius. Moreover,
) = (*n ® 6 +112 <s> 6)(*2i ® 6 +122
Thus, qdet(T) = ?11*22 ~ ?12*21 — *n*2i- With a little more effort, one can
show that qdet(T) lies in the centre of Fr(M2). 0
We should like to construct a Hopf algebra by localizing J7R(Mrn) at
qdet(T), in the same way as F(GLi2((E)) was obtained from F(M2 ((?)). Since
we are now dealing with non-commutative rings, however, the notion of lo-
localization is a little more subtle. In general, if M. is a ring with unit and S
is a multiplicatively closed subset of A4, one can define the localization of Ai
at S only if the Ore condition is satisfied:
if m G A4, 5 G <S, there exist m' G M, / G 5 such that ms' = m's.
Apart from this problem, the localization is constructed in essentially the
same way as in the commutative case (see McConnell & Robson A987), for
example). Note that the Ore condition is satisfied trivially if M. is commu-
commutative or, more generally, if S is contained in the centre of M,.
To ensure that the Ore condition is satisfied in our case, when M. =
pRtMm) and S = {qdet(T)r}r>i, we make an additional assumption on
R. We say that R is Hecke if
A6) R2 = {q-q-l)R+l.
Of course, this holds in the trivial case R = 1, q = 1, and it is easy to check
that the R-matrix of 7.1.3 is Hecke with q = eh. The 'strange' R-matrix A5)
is also Hecke, with q — 1 (this justifies the choice of q in 7.2.5).
Lemma 7.2.6 Let R e Endfc(/cm <g> k171) be Frobenius-Hecke. Then, there
exists a matrix Q e GLm(k) such that
This result is due to Lyubashenko A986) and Gurevich A991); see also
Tsygan A993). It clearly implies the Ore condition. For the R-matrix in
7.1.3, we have Q = 1.
Thus, if Re Endfc(/cm(g>/cm) is Frobenius-Hecke, we may define FR^GLm)
to be the localization of JrR(Mrn) at qdet(T). Using 7.2.4(ii), it is easy to
see that FR^GLm) inherits a bialgebra structure from J7R(Mrn). It follows
from the equation
A(T) = TBT
7.2 R-matrix quantization 233
and the Hopf algebra axioms that, if FR,q(GLm) can be made into a Hopf
algebra, its antipode must be given by S(T) = T~l. We must therefore
prove that T is invertible in the algebra ofmxm matrices with entries in
Fix 0 ^ Q G A^q and let o;i,..., o;m be the basis of A^1 which is right
dual to the basis ?i,..., ?m of A^ q, i.e.
A7) &.«;, = «ijft.
Define elements ?^- E JrR(Mrn) by
Applying 6r to both sides of A7), we find that
T.f = qdet(T).l,
where T = (Uj). Thus, T has a right inverse in J-R^GLm). But it is easy to
see that the map t^ j—> tij induces an isomorphism of algebras
and so T also has a left inverse in TR
It is now straightforward to prove
Proposition 7.2.7 LetR be a Frobenius-Hecke R-matrix. Then, !FR,q(GLm)
is a Hopf algebra with comultiplication, counit and antipode given by
A(T) =TBT, A(qdet(T)~1) = qdet(T) 0 qdet(T),
e(T) = 1, e(qdet(T)-1) = 1,
S(T) = T'\ ^(qdet(T)-1) = qdet(T). |
One can now define JrRjq(SLrn) to be the quotient of JrRjq(GLrn) by the
two-sided ideal / generated by qdet(T) — 1. It is clear from 7.2.4(ii) and the
formulas in 7.2.7 that / is actually a Hopf ideal, and hence that JrR^q(SLrn)
is a Hopf algebra.
C Solutions of the QYBE As the results of this section indicate, it is very
desirable to write down all the solutions R e Endfc(A:m (8) ?;m) of the quantum
Yang-Baxter equation A3). Thinking of R as an m2 x m2 matrix, the QYBE
is a system of m6 cubic equations in m4 unknowns. The problem of solving
234 7 Quantized function algebras
these equations can be simplified somewhat by noting that the QYBE has a
number of 'symmetries'. Thus, it is clear that, if R is a solution of A3), so is
(i) cR, for any c G kx,
(ii) (A®A)R(A®A)-\ for any Ae GLm(k),
(iii) #21,
(iv) the transpose of R.
Let Q be the group of linear automorphisms of Endfc(/cm ® /cm) generated by
the transformations (i)-(iv). Then, the problem is to describe the space of
orbits of Q on the space of solutions of the QYBE.
Unfortunately, although there are a large number of examples of solutions
of the QYBE in the literature, little is known about the description of this
orbit space, in general. Experimental evidence suggests that, if k = C, the
diagonal solutions will form a dense open subset of the orbit space, which
will therefore have complex dimension m2 — 1, but this does not seem to have
been proved (the loss of one dimension is due to the possibility of an overall
scaling). However, if m = 2, Hietarinta A993b) has given a complete solution
to the problem. The diagonal solutions form a dense open set, but the orbit
space is highly singular, with several 'strata' of lower dimension.
It would also be interesting to know which solutions of the QYBE arise from
quantum groups. The answer, of course, will depend on how one interprets
the question. Any solution which arises by evaluating the universal R-matrix
of a quantized universal enveloping algebra in a (finite-dimensional) represen-
representation will lie on a curve of solutions passing through the identity matrix. It
is known that the flip operator cr, which is clearly a solution of the QYBE,
does not have this property. In fact, it is an isolated point in the space of all
solutions of the QYBE (this remark is due to M. Gerstenhaber, S. Majid &
S. D. Schack).
7.3 Examples of quantized function algebras
A The general definition To define a quantized algebra of functions Fh(G)
on an arbitrary complex simple Lie group G, note that we have already con-
constructed a quantization Uh(o) of the Lie algebra g of G in Section 6.5, so we
may turn 7.1.4 into a definition. Classically, the dual of U(§) is the algebra
of regular functions on the simply-connected group G (cf. 4.1.17).
Definition 7.3.1 Let G be a connected, simply-connected, finite-dimen-
finite-dimensional, complex simple Lie group G with Lie algebra g. The (standard) quan-
quantized algebra of functions ^(G) on G is the Hopf algebra dual of the QUE
algebra Uh(&) defined in 6.5.1.
7.3 Examples of quantized function algebras 235
By the Hopf dual we mean the set of continuous (C[ [ft]]-linear maps Uh{§) —>
C[[ft|], where the topology on Uh(cy) is defined using the kernels of the finite-
dimensional representations of Uh(§) (see Subsection 4.ID). Since, by 6.5.4,
Uh(&) = #(9)[[ft]] as topological algebras over <C[[ft]], and since T(G) = U(q)°
as Hopf algebras, it follows that J~h{G) = ^"(G)[[ft]] as topological coalgebras.
In particular, J~h{G) is a Hopf algebra deformation of J-(G) in the sense of
6.1.1.
Furthermore, the classical limit of the QF algebra fh{G) is the Poisson-Lie
group structure on G whose tangent Lie bialgebra structure 8 : g —> g <g) g
is the 'first order part' of the deformation Uh{(}) of ?/($) (see Chapter 1).
Indeed, let a,b ? J~h(G) and let ao, bo G J~(G) be their h = 0 limit. We have
to prove that
MW = {d{{aOj 6o})ej Xo) (mod h)
for all X G Uh(cy) which are equal to Xq G q (mod /i). From Subsection 1.3A,
we see that the right-hand side is equal to (ao®&o> <5(^o)M while the left-hand
side is
(a®b-b®a,Ah(X)) I Ah(X)-A°hp(X)
= ( a Qs) 0,
ft
) (mod /i)
as we want.
In the remainder of this section, we attempt to give a more explicit de-
description of J~h(G) in the cases in which G is a classical group of matrices.
B The quantum special linear group To construct a deformation of the
algebra of functions on S'Ln+i(C), it is natural, in view of the developments
in Section 7.2, to consider a Hopf algebra of the form J~R,q(SLn+i) for some
invertible element q G <C[[ft]] and some R G Endc(Cn+1' <g> Cn+1 )[[/*]]. We
take q = eh and
A8) R = e
where 0 < z, j < n and the Eij are the elementary matrices (i.e. Eij has 1
in the zth row and jth column and zeros elsewhere). If n = 1, this is the
R-matrix in 7.1.3. One can check directly that R satisfies the QYBE for all
m (but see the remarks below); and it is easy to see that (R,q) satisfies the
Hecke condition A6).
Furthermore, R is Frobenius. Indeed, we find that the defining relations of
are
?o2 = ?? = •' • = il = 0, tej + qtjti = 0, for i < j.
236 7 Quantized function algebras
It follows that
A?? = <C[[fc]].(&>?i • ¦ • ?«)> *R,q = 0 for i > n + 1.
Computing <5r(?o?i .. .?n), one obtains for the quantum determinant:
A9) qdet(T)= Yl (-e~Y(w)*(M0)*iii,(i) • • • tnw(nh
where ?{w) is the length of an element w of the group ?n+i of permutations
of {0,1,..., n}, i.e. the minimum number of adjacent transpositions (i, i + 1)
of which it; is a product. It follows from 7.2.4 that qdet(T) is a group-like
element of ffl(Mn+i).
Since R is Probenius-Hecke, one can define the Hopf algebra JrR^q(SLn^i),
and we can state
Theorem 7.3.2 Let R be the matrix defined in A8), and let q = eh. Then,
the Hopf algebra, JrRiq(SLn^i) is isomorphic to Jrh{SLnjri{(?)). |
The proof of this result is analogous to that of 7.1.4.
Remarks [1] The R-matrix A8) will be 'derived' in Section 8.3, where we
show that ?/fc(sZn+i((C)) is topologically quasitriangular. By 6.5.6, the finite-
dimensional representations of Uh(sln+i((E)) are all deformations of represen-
representations of sZn+i(<C). The R-matrix A8) is obtained, up to a scalar multiple,
by evaluating the universal R-matrix of Uh(sln+i((E)) in the natural repre-
representation of dimension n+ 1. In particular, it necessarily satisfies the QYBE.
[2] It follows from its defining relations that the quantum determinant lies
in the centre of ffl(Mn+i), and that it has the alternative expression
qdet(T)=
[3] The antipode of FR,q(SLn+i) is given by
S(tij) = (-e-^
where Tji is the submatrix of T obtained by omitting its jth row and ith
column, and its quantum determinant is computed using A9) (with n replaced
by n- 1). A
C The quantum orthogonal and symplectic groups A uniform descrip-
description of the R-matrix appropriate to the orthogonal and symplectic groups can
7.3 Examples of quantized function algebras
237
be given as follows. Fix an integer m > 1 and, for r = 1,..., m, let Ar G C,
crr G {+1,-1}. Let J be the diagonal matrix
J =
0
\ o
and let
0
\
Ev
[eh - e~h)
ji - (eh - e~h)
El>3>
B0)
Ern+l m+1 0 Ern±l m+1 .
2 2 2 2
Here, i' = m + 1 - z, 1 < i < m, and the last term is present only if m is odd.
The values of the parameters Ar and ar are as follows:
(a) if G = SO2n+i(<C), then ra = 2n + 1, oy = 1 for all r, and
1
1
1
=ln- -,n- -,...,-,0,--,...,-n + -I;
(b) if G = SO2n(C), then m = 2n, ar = 1 for all r, and
(Ai,..., A2n) = (n - 1, n - 2,..., 1,0,0, -1,..., -n + 1);
(c) if G = Spn((C), then m = 2n, ar = 1 for r < n, ar = — 1 for r > n, and
(Ai,...,A2n) = (n,n- 1,..., 1, -1,..., -n).
Definition-proposition 7.3.3 For R as above, let Fun# be the quotient
of TR(Mm) by the relations
(Tl is the transpose ofT). Then, Fun# is a Hopf algebra over <C[[/&]] with
comultiplication, counit and antipode given by
, e(T) = l,
respectively |
We write FunH as Fun^(SO2n+i(C)), Fun^(SO2n(C)) and
in the three cases (a), (b) and (c), respectively. Formally at least, it is clear
238 7 Quantized function algebras
that their defining relations go over into those of T(S02n+i(<C)),
and T(Spn(<E)), respectively, in the limit h = 0.
The reason for the change of notation from Th to Fun^ is twofold. First,
one would not expect that Fun^(SOm(C)) is isomorphic to t/^(som(C))°, for
in the classical case the dual of U(som((E)) is the algebra of functions on the
simply-connected group with Lie algebra som((C), i.e. ^r(Spinm(C)), which is
'larger' than T(SOm(<E)). Put another way, the h = 0 limit of Fun^(SOm(C))
is generated by the matrix elements of the natural m-dimensional represen-
representation of SOm(C), but not all irreducible representations of som((?) occur
inside the tensor algebra of the natural representation (for example, the spin
representation(s) do(es) not).
Secondly, although one would expect that Fun^(Spn(C)) = ^)l(Spn(C)),
there does not seem to be a proof of this in the literature. (However, a pair-
pairing between Uh(spn((C)) and Fun^(Spn(C)) is constructed by Reshetikhin,
Takhtajan & Faddeev A990) and Hayashi A992b).)
Remark One difficulty with the algebras Fun^(G) for the orthogonal and sym-
plectic groups is that they are not quotients, at least in any obvious way, of the
quantized algebra of functions Th(SLm((E)) (nor are the quantized universal
enveloping algebras Uh(c$), in any obvious way, subalgebras of Uh(slm((E))).
The reason for this is that the Dynkin diagrams of the orthogonal and sym-
plectic groups are not subdiagrams of the Dynkin diagram of any special linear
group. Takeuchi A989) defines non-standard quantum analogues of the or-
orthogonal and symplectic groups which are 'quantum subgroups' of quantum
linear groups. A
D Multiparameter quantized function algebras An obvious way to
construct multiparameter deformations of T(G), where G is, for the moment,
an arbitrary complex simple Lie group, is to take the dual of the deformations
Uhio)^ of U(q) constructed in Subsection 6.5C. Since Uh(§)'Fh has the same
algebra structure as Uh(gi), its dual is isomorphic to the standard quantized
function algebra Th{G) as a coalgebra. Moreover, in view of 4.2.15, the R-
matrix which one expects to give the defining relations of the dual can be
obtained from that which defines the relations in Th{G) and the image of the
element Th in the natural representation of G (at least for classical G).
Another possibility which has attracted attention applies to reductive
rather than semisimple groups. In the case of GLn+i(C), this leads to a
two-parameter family of quantizations, as follows.
Fix A, /i e C and define Rx^ e Endc(Cn+1 (g) Cn+1)[[/*]] by
oA,/i
i
OA)V2 Y Etl 0 Ejj + (e^^2 - e-^h?2) ? EtJ
7.4 Differential calculus on quantum groups 239
where 0 < i,j < n. One can check directly that Rx^ is a solution of the
QYBE for all A and //, and that it is Hecke with q = e(x+rih/2.
Proposition 7.3.4 The R-matrix Rx^ defined in B1) is Frobenius-Hecke
with q = e(x+»)h/2. Its quantum determinant is
qdet(T)= Yl
IUEEn + 1
(~e~M ) ^
The Hopf algebra TR\^ q(GLn+i) is a deformation of ^r(GLn+i(C)). Its
antipode is given by
S(tij) = (-e-^y
where Tji is the matrix obtained from T by removing its jth row and ith
column. |
Remarks [1] If A = \i — 1, then J-r\,»5<?(GLn+i) is the standard deformation
of ^r(GLn+i(C)) defined in Subsection 7.3B. The case A = 0 and \i arbitrary
is the subject of Dipper & Donkin A991). The case A + \i = 0 is discussed in
Gerstenhaber & Schack A992) in the case n — 1. In the general case, 7.3.4
is due to Takeuchi A990a).
[2] The quantum determinant qdet(T) does not lie in the centre of
J-"r\,h q(GLn+i) unless A = fi: in fact,
^qdet(T) - e^-^l-^hqdet{T)tij.
[3] It is easy to identify the corresponding construction in the context of
enveloping algebras. In fact, U(gln+i((E)) is obtained from U(sln+i((E)) by
adjoining a primitive central element (equal to the identity matrix in the
natural representation of g/n+i(C)). To obtain a two-parameter family of de-
deformations of f/(p/n+i(C)), one first replaces h by Xh in the defining relations
of Uh(sln+i((E)) and then adjoins a primitive central element c. The comul-
tiplication is unchanged on the generators i7^, and on the X~~ it becomes
Ah(X+) = X+ 0 CeXhH + C~l 0 X+,
= X~ ® C~l + Ce~XhH O X",
where C = e^-x^hc.
[4] One can combine the two-parameter deformation of GLn+i(C) with the
\n(n— l)-parameter deformation of f(SLn+i(<E)) discussed at the beginning
240 7 Quantized function algebras
of this subsection to give a family of deformations of ^(GLn+i (<C)) depending
on \n(n — 1) + 1 parameters (modulo rescalings of h). This has been worked
out by Artin, Schelter & Tate A991). A
7.4 Differential calculus on quantum groups
Our aim in this section is to construct an analogue for 'quantum' general
linear groups of the (algebraic) de Rham complex of GLm(k), where k is any
commutative ring with unit. It is natural to define at the same time the de
Rham complex of the 'quantum' plane which is the natural representation of
quantum GLm(k).
We work in the setting of Section 7.2. Thus, we fix an invertible element
q ? k and a matrix R G Endk(km (g) /cm), and we assume throughout this sec-
section that R satisfies the quantum Yang-Baxter equation A3) and the Hecke
relation A6); we assume also that q2 + 1 is not a zero divisor. The algebras
SymRq and Tr^GL^) defined in Section 7.2 are thought of as the 'alge-
'algebras of functions' on the 'quantum' plane and the 'quantum' general linear
group. As in the classical case, their de Rham complexes will be generated,
as differential graded algebras, by SymRq and pR^GLm).
We recall that a differential graded algebra is a graded associative algebra
A = @°^0^ over ^ equipped with k-linear maps d : A1 —> A1^1 such that
d2 = 0 and
d(a.b) = d{a)b+(-l)deg{a)ad(b)
for any two homogeneous elements a, b G A.
A The de Rham complex of the quantum plane We begin by defining
a complex n*(Sym^9) which, when R = 1 and q = 1, becomes the usual de
Rham complex of km. It will be convenient to define an analogous complex
for AR,q at the same time, which can be thought of as the de Rham complex
of the 'odd' quantum plane (in the language of 'supergeometry').
Definition 7.4.1 (i) Q*(SymRq) is the associative algebra over k with gen-
generators xi,..., xm and dx\,..., dxm, and defining relations
XGdX = ()
dXGdX = -qR{dX 0 dX).
(ii) ^*(Ajr5q) is the associative k-algebra with generators &, d?i, 1 < i < m,
7.4 Differential calculus on quantum groups 241
and defining relations
dE®dE = q~lR(dE 0 dE).
The notation is as in Section 7.2. For example, X is the m x 1 ma-
matrix with entries X\,... ,xm, and X 0 X is the ra2 x 1 matrix with entries
2 2
? XiX X2X\ X
Proposition 7.4.2 O*(Symie>9) (resp. 0*(AR,q)) has a unique structure of
a differential graded algebra with grading given by deg(a^) = 0, deg(dxi) = 1
(resp. deg(^) = 1, deg(d^) = 2) and differential d such that d(xi) — dxi
(resp. d(?i) = d?i).
Outline of proof We give the proof for SymH q; that for A^q is similar.
It is clear that Q* {SyuiRq) is a graded algebra. To show that d is compatible
with its defining relations, note that applying d to the difference between the
left- and right-hand sides of the first relation in 7.4.l(i) gives
A - q-lR)(dX 0 X + X 0 dX) = A - 9 A)(l + qR){dX 0 X) = 0,
where the first equality uses the second relation in 7.4.l(i) and the second
equality the Hecke relation A6). The rest of the proof is easy, for it is clear
that applying d to the second relation in 7.4.l(i) gives the third relation, both
sides of which are annihilated by d. |
Example 74.3 For the R-matrix A8) (and with q = eh G <C[[/i]]), one finds
that r^*(Sym^q) has defining relations
j — q~lXj.Xi,
= 0, for all i,
j dXjXi, "j
i.Xj = q~lXj.dxi - (q — q~l)dXj.Xi, > for i < j,
dxi.dxj = —qdxj.dxi, )
and that fi*(AjRj9) has defining relations
&.d& - d&.&, (&J = 0, for all z,
d?,i-?,j = q?,j.d?>l-(q-q-1)d?)j.?>l, \ for i < j. <>
242 7 Quantized function algebras
B The de Rham complex of the quantum m x m matrices Recall
that, if (A, dA) and (B, (Ib) are differential graded algebras over /c, the tensor
product algebra A <g) B is a differential graded algebra with grading given by
k
3=0
and differential
dA®B(a <g> 6) = dA(a) 0 b + (-l)deg^a)a ® dB(b),
for homogeneous elements a G ^4, 6 G B. Recall also that a homomorphism
of differential graded algebras / : A —> B is a homomorphism of algebras for
which f(Al) C ??* for all i and such that / commutes with the differentials
of A and B.
In the classical situation, pulling back differential forms via the natural
representation GLm(k) x km —> km gives a homomorphism of differential
graded algebras
B2) n*(Sym((fcm)*)) - ^(GLm(A:))^*(Sym((A:m)*)).
The complex r^*(^rR(Mm)) must be defined so that it contains ^R(Mm) as
a subalgebra (the quantum 0-forms!), and such that there is an analogue of
the homomorphism B2). In the literature, the latter property is expressed
by saying that the resulting 'differential calculus' is covariant
The appropriate definition is the following.
Definition-proposition 7.4.4 n*(^ie(Mm)) is the associative algebra
over k with generators tij and dtij for 1 < i,j < m, and defining relations
R(TGT) =
TGdT = R(dT 0 T)R,
dTGdT = -R(dT 0 dT)R.
It has a unique structure of a differential graded algebra with deg(tij) = 0,
deg(dUj) = 1 and d(Uj) = dtij.
Outline of proof As in the proof of 7.4.2, the main point is to show that
applying d to the first relation in 7.4.4 gives the second relation. Now,
d[R,
= [R,dT 0T + R(dT OT)R]
= [R, dT®T] + ((<? - q-^R + l){dT 0 T)R
- R(dT OT)((q- q-
7.4 Differential calculus on quantum groups 243
where the first equality used the second relation in 7.4.4, and the third equal-
equality used the Hecke relation A6). |
As we mentioned above, the definitions of f2*(Sym^ q) and Q,* (Fn^Mm))
have been chosen so that
Proposition 7.4.5 There exist unique homomorphisms of differential
graded algebras
such that
The proof of this result rests on a computation similar to, though rather
more difficult than, that used to prove 7.4.4.
Example 7.4-6 For the R-matrix in A8), one finds that the defining relations
of ^*(jrH(Mm)) are as follows:
Ujdtij = q2dtijtij, (dtijJ = 0,
for all i, j,
tij.tkj = q~~ tkj.tij, Uj.dtkj = qdtkjUj,
dtij.tkj = q~1tkj.dtij — (q — q~1)dtkj.tij,
dtij.dtkj = —qdtkj-dtij,
for z < /c and all j,
^j-^i/ = Q~1Ui-Uj^ Uj.dtu = qdtuUj,
dUj.Ui = q~~ltu.dUj - (q - q~l)dtu.tij,
dtij.dtu = —qdtu.dtij,
for j < / and all z, and
[^,*fcj] = 0, [Uj,tki] = -(g - q'^tkjUu
Uj.dtki = dtkhUj, \Pkj,dtu] = [^,dtfcj] + (g — q~1)dtkiUj,
tkidUj = dUjtki + (q- q~1)(dtkjtu + dtutkj) + (<? - q~1JdtkiUj,
dtijdtki = -dtkidUj, dtjkdtu + dtudtjk = -(q - q~1)dtkidtij,
for i < /c and j < I. 0
Remark When i? is the R-matrix in A8) and /c is a field, the cohomology of
the complex n*(^(Mm)) has been computed by P. Feng. If q is not a root
of unity,
244 7 Quantized function algebras
concentrated in degree zero, while if q is a primitive ?th root of unity, where
? is odd and > 3, then
where o^ = 0 or 1, a{j G ?N, is a basis of /f*(ft*(.FjR(Mm))) (the grad-
grading is the obvious one). We shall encounter such 'root of unity phenomena'
frequently in later chapters. A
C The de Rham complex of the quantum general linear group In this
subsection, we assume that R is Frobenius. As we saw in Subsection 7.2B, this
enables one to define J-R,q(GLm), the algebra of functions on the 'quantum
general linear group', to be the localization of J-R(Mm) at the quantum de-
determinant qdet(T). In the same way, we should like to define Sl*{J-R,q{GLm))
to be the localization of ft*(TR(Mm)) at qdet(T) G VfP(TR(M7n)). For this,
we need the following analogue of 7.2.6, which is due to Tsygan A993).
Lemma 7.4.7 There exists an invertible element ft G k such that
T.Q-1 = pq2Q~1 .dT.qdet(T),
where Q G GLm(k) is defined in 7.2.6. |
Together with 7.2.6, this lemma clearly implies that the Ore condition is
satisfied for the multiplicative subset {qdet(T)r}r>i of the ring Q* (T^Mm)),
so we may define ^(JrR^q(GLm)) to be the localization of Q*(JrR(Mm)) at
the quantum determinant.
Proposition 7.4.8 r^*(^rR^(GLm)) is a Hopf algebra with comultiplication,
counit and antipode determined by
A(T) = T? T, A(dT) ^
c(T) = l, e(dT) = 0,
S(T) = T~\ S(dT) = d(S(T)).
Moreover, the differential graded algebra structure of fT(J~R(Mm)) extends
uniquely to Sl*(J-R,q(GLm)), and then A and e (resp. S) are homomorphisms
(resp. is an anti-homomorphism) of differential graded algebras (k is concen-
concentrated in degree zero and has the zero differential).
Outline of proof The main point is to show that there is a homomorphism
of algebras 5 : r^*(^rR^(GLm)) —> ^*(f^(GLm))op given on the generators
by the formulas in the proposition. Recalling from Subsection 7.2B that there
is an isomorphism of algebras {Tra)op = Tr-i^-i, we have to show that,
if we replace T by T~l and R by (R~lJ — crR~~1cr, the defining relations in
7.4 Differential calculus on quantum groups 245
7.4.4 continue to hold. We do this for the second relation, as the other two
are similar but easier.
We start with the second relation in 7.4.4 in the form
(T 0 l)R(dT 0 1) = A 0 dT)R-\l 0 T~l).
Multiplying both sides on the left by cr(lQT~l) and on the right by (T~lQl)cr,
and using the relation A QA)(BQl) = a(A 0 B)a, we get
{T~l 0 T~l)(jR{dT.T-1 0 l)cr = cr(l 0 T~l.dT)R-l(j{T-1 0 T~l).
Using the first relation in 7.4.4, the left-hand side of this equation is equal to
(T~l 0 T~l)(j(T 0 T)R(T 0 T)-l(dT.T~l 0 l)a
= {T~l 0 T~l)(j(T 0 T)R{1 0 T-l){T-l.dTT-1 0 l)a
= (T~l 0 T~l)(j{T 0 T)R(j(T-1 0 T-l.dT.T~l)
= {T~l 0 r)(l 0 T)(T 0 l^i^T 0 T^AT.T'1)
0T1 .dTT~l).
Similarly, the right-hand side is equal to (T^.dT.T'1 ©T)^^ Noting
that ^(T) = -T~l.dT.T-1 completes the proof. |
D Invariant forms on quantum GLm Finally, we consider briefly the
problem of defining right-invariant forms in f?*(J-R,q(GLm)) (left-invariant
forms are defined similarly). We begin by formulating the right-invariance
condition algebraically in the classical situation.
Suppose then that G is a Lie group, and let uj be an n-form on G. Then,
uj is right-invariant if Rg(u;) = uj for all g ? G, where Rg : G —> G is right
translation by g. Let m : G x G -> G be the multiplication map of G, and
define maps pg : G -^ G x G by pg{h) = (h,g). Then, Rg = m o pg so
right-invariance is equivalent to /o*(m*(o;)) = a; for all g ? G. Note that m*
is precisely the comultiplication A in the Hopf algebra ?2*(G), and that p*
kills all bigraded components of A (a;) except that of degree (n, 0). Suppose
that
The right-invariance condition is thus Yla fa(d)^a = u, for all g G G. As-
Assuming, as we may, that the uja are linearly independent, this implies that
the fa are constant, and hence that
B3) A(o;)n'° = a;®l.
Returning to the quantum situation, an element uj e ^n(^rR,9(GLm)) is
called right-invariant if it satisfies B3), where A is the comultiplication de-
defined in 7.4.8. It is clear that the set Q*nv(J-R^q(GLm)) of such forms is a
differential graded subalgebra of ^*(^rR?9(GLm)) (in the obvious sense). We
state without proof
246
7 Quantized function algebras
Proposition 7.4.9 The entries of the matrix ft = dT.T~l are right-invariant
1-forms and generate fl^nv(J:rRiq(GLrn)) subject to the relations
o
0
0
7.5 Integrable lattice models
In this section, we shall indicate briefly the origin and meaning of the relations
A2) and of the quantum Yang-Baxter equation A3) in one area of the theory
of integrable systems, namely two-dimensional lattice models in statistical
mechanics.
A Vertex models We consider a collection of 'atoms' located at the vertices
of a 2-dimensional lattice. Each atom interacts only with its nearest neigh-
neighbours with an energy which depends on the 'state' of the bonds joining each
pair of neighbouring atoms. If the possible states of the bonds are labelled
by the elements of a finite set {1,..., n}, we write the interaction energy of
an atom as ?*j if the states of the bonds connected to the atom are as shown
in Fig. 15.
Fig. 15 Labelling of the bonds
Usually, ?lj?f will depend on parameters other than the bond states, such as
the values of external electric or magnetic fields, but we shall assume that this
function does not depend on the location of the vertex itself. A knowledge of
the Sty specifies the model.
A state of the lattice is an assignment of a state to each bond, and the
energy ? of such a state is simply the sum of the ?^J over all the atoms in
the lattice. For an infinite lattice, this sum will usually diverge, so one works
with finite lattices, say an M x TV rectangular array of atoms, keeping in mind
7.5 Integrable lattice models
247
that one is interested ultimately in what happens when M and TV tend to
infinity. For finite lattices, one must impose boundary conditions on the states
of the bonds at the edges; we shall always use periodic boundary conditions,
as indicated in Fig. 16.
/¦ i
im \
g
%
4
l2 f
• t
h
\ i
i {
9 \
1 d
? %
h
h
) (
1 4
1 t
h
| |
| 4
\ 4
9 1
| |
| 4
1 4
| |
1 |
//V
Fig. 16 Periodic boundary conditions
The statistical mechanical properties of such a system are encoded in its
partition {unction
B4)
Z = 2^ exp(-^(state)),
states
where C = 1/kT is the reciprocal of Boltzmann's constant k times the tem-
temperature T. The principle is that ^e~^s is the probability that the system is
in a particular state, so that the average value of any physical quantity Q is
given by
Z^states °
For example, the average energy of the system is
(?(system)) = /cT2—lnZ.
Thus, one would like an 'explicit' formula for Z\ if this can be found, one says
that the model is exactly solvable.
Note that
exp(—fi?(state)) = IT exp(—PS^1).
vertices
The quantities in the product are called Boltzmann weights] we denote them
by
248
7 Quantized function algebras
B Transfer matrices To evaluate B4), we first sum over all possible states
of the bonds in the first row, excluding the two free bonds (which we tem-
temporarily allow to have different states):
*1
h
h
1 i
h
k d
f \
h
kN-\
rN-\
\ i
9 %
kN
f
In
Thus, we form
B5)
Before we lose control of the indices, we introduce an auxiliary iV-dimensional
vector space V with basis {vi,..., v^}, and define R G End(V 0 V) by
and T G End(F 0 V®N) by
Then, B5) can be written
B6) T = R01R02 - • •
where, as usual, Rij means R acting in the ith and jth factors of the tensor
product V 0 T/0iV, the first factor being labelled 0 and the rest 1,..., N.
Recalling that periodic boundary conditions are assumed, we have i\ = i[
and the result of summing over the states of all bonds in the first row is
The endomorphism tracey(T) is called the row-to-row transfer matrix.
The result of summing the contributions to B4) over all states of bonds in
the first two rows is therefore
Summing over the vertical bonds joining the first two rows thus gives
7.5 Integrable lattice models
249
4\
i\
7i
i i
h
72
| 4
*2 ' ' * *
h
Jn-\
f (
7yv
i
kN
1 '
Continuing in this way, it is clear that
((tracey(T)O
n'..'i>
is the result of summing over all bond states except the free vertical bonds
on the bottom and top rows. Imposing periodic boundary conditions li = l[
and summing over these free bonds, we finally obtain
Proposition 7.5.1 The partition function Z of a vertex model can be ex-
expressed in terms of its transfer matrix T by
Z = tracey®iv((tracey(T))M). |
Remark The way that the partition function is built up row by row using the
transfer matrices is reminiscent of the way, discussed in Subsection 5.3A, that
an endomorphism of a representation of a ribbon Hopf algebra is associated
to a ribbon tangle by breaking up the ribbon tangle into 'elementary tangles'.
We shall see in Section 15.2 that this similarity is not accidental. A
It follows from this proposition that, if kn is the largest eigenvalue (as-
(assumed to be simple) of tracey(T) G End(V0iV), then for large M we have
the asymptotic estimate
7 ^ KM
Thus, one would like to find the eigenvalues of tracey(T), or at least the
largest. This is complicated, of course, by the fact that the size of the matrix
tends to infinity with N. It would help if we knew a large family of operators
commuting with tracey(T), for then we could restrict attention to their com-
common invariant subspaces. We shall now give a condition which guarantees the
existence of such operators.
C Integrability Recall that the vertex energies ?*j, and hence also R and T,
may depend on the values of external parameters. We shall write an element
of this parameter space as A, //, v, etc.
250 7 Quantized function algebras
Definition 7.5.2 A vertex model is integrable if, for each \x, v, there is a X
such that
B7) Rl2(X)RMR23(v) = R23{v)Rl3&)Rl2W
as endomorphisms ofVCV(&V.
In some examples, A, \x and v are complex numbers, and it turns out that
the parametrization can be chosen so that B7) holds with X — \x — v\
B8) R12(X - fl)Rl3(X ~ u)R23(fJL " ^) = #23(M " ^)#13(A " V)R12{\ - /X).
This is called the quantum Yang-Baxter equation with spectral parameters. It
should be compared to the CYBE with spectral parameters studied in Section
3.2, to which it reduces if
where h is a vanishingly small quantity.
The importance of the integrability condition is explained by the following
result and its corollary.
Proposition 7.5.3 Consider an integrable vertex model, and let X, \i and v
be as in 7.5.2. Then,
ii(A)(l ® r(/i))G» 0 1) - G» ® 1)A ® T(fi))R(X)
as endomorphisms ofV®V® V®N, where R(X) acts on the first two factors
of the tensor product.
Corollary 7.5.4 For an integrable vertex model for which R(X) is invertible
for all X, tracey(T(/x)) commutes with tracey(T(z^)) for all fi, v.
Proof of 7.5.4 Simply note that
Taking tracey^y on both sides gives
tracey(T(z/))tracey(T(//)) = tracey(T(/x))tracey(T(^)). |
Proof of 7.5.3 We label the first two factors in V 0 V 0 V®N as 0 and 0
and the remainder as 1,..., N. Then, from B6), we have
To = R01R02 • • •
7.5 Integrable lattice models
251
* \
k i
P * '
1 » 4
1 » 1
1 < I
1 > (
k i
) * (
i * 4
Fig. 17 A possible arrangement of dipoles for the six vertex model
Thus,
= R(i5(X)R5l{n)RS2(fj) ...Rm
. R0N(u),
... R0N{v)
where the penultimate equality uses the fact that Roiif) commutes with
.Rg^/i) for i = 2,..., N, and the last equality uses the QYBE. Bringing
to the left in the same way, using the QYBE to re-order the product
and then using the fact that
commutes with i?Q1(//), we obtain
Bringing Roz(v),. • •, Ron(v) successively to the left in the same way, we even-
eventually obtain
as we want. |
D Examples We consider two examples, in both of which there are just two
possible states for each bond. We can imagine that two nearest neighbour
atoms interact by means of an electron cloud which can be either 'close' to
one atom or to the other. The two possibilities can be represented by means
of an arrow (or dipole) pointing (say) from the region of low charge density
to the region of high charge density (see Fig. 17).
252
7 Quantized function algebras
\-qX
Six vertex model (XXX model) In this, perhaps the simplest, model, one as-
assumes that all Boltzmann weights are zero except those which correspond
to configurations which have two arrows pointing towards the atom and two
pointing away (a possible arrangement of dipoles on the whole lattice is shown
in Fig. 17). There are six such configurations (hence the name of the model),
and we take their Boltzmann weights to be as shown above (the spectral
parameter A is an arbitrary complex number; q is an auxiliary non-zero pa-
parameter). The auxiliary vector space has dimension 2, and we label its basis
by {1,2}, where 1 corresponds to arrows which point up or to the left, and 2
to arrows with the opposite orientation. Then, the R-matrix is
1
0
0
0
1
0
A
-q~
0
XA
1
0
-q\
A
0
0
0
0
I
This model is integrable, for a direct calculation shows that B7) holds if
B9)
A -
(the value of q is the same for all three R-matrices).
There are two interesting special cases. If we take A = \x — v — q~l, then
B9) is satisfied and so R(q, q~l) is a constant solution of the QYBE for each
q. In fact, if we replace q by eh, then qR{q, q~l) is exactly the R-matrix which
defines the standard deformation Th{M2{^)) (see 7.1.3).
On the other hand, if we take q = 1 and set
A
V =
we find that B9) is equivalent to
A = jl — i>.
Thus, i?(l, j^--) is a rational solution of the QYBE B8), and the model is
accordingly called the rational six vertex model. We shall see in Chapter 12
Bibliographical notes
253
that this R-matrix is associated to a two-dimensional representation of the
Yangian of s?2(C).
Eight vertex model (XYZ model) In this model, one relaxes the conditions
on the Boltzmann weights by allowing them to be non-zero for the eight
configurations in which the number of arrows pointing towards each atom is
even. One also assumes that the weights are unchanged when all the arrows
are reversed. The following weights lead to an integrable model:
jl)
sn(jj)
Here, sn is a jacobian elliptic function and k is its modulus. The R-matrix is
0
0
Again, there are a number of interesting special cases. As fi —> 0, we get
the rational six vertex solution above (up to a scalar multiple and a change
of sign of the parameter). As k —> 0, the elliptic function sn becomes the
trigonometric function sin and we have the trigonometric six vertex model.
Bibliographical notes
7.1 Our discussion of Jrh(SL2(<E)) is taken from Manin A988). The proof
of 7.1.2 is adapted from Meister A992), and that of 7.1.4 from Vaksman &
Soibelman A988).
7.2 The most important references for this section and the next are Manin
A988), Reshetikhin, Takhtajan & Faddeev A990) and Tsygan A993); see
also Gurevich A991). See Majid A990g) for another method of passing from
bialgebras to Hopf algebras. Lambe & Radford A993) contains an extensive
discussion of various algebraic structures related to the QYBE.
For a catalogue of solutions of the QYBE, pre-dating quantum groups, see
Kulish & Sklyanin A982a).
254 7 Quantized function algebras
7.3 Theorem 7.3.2 is stated in DrinfeFd A987) and in Reshetikhin, Takhtajan
& Faddeev A990), although neither reference contains a complete proof. One
can give a proof along the same lines as that of 7.1.4, but the details are more
unpleasant. Takeuchi A990a) gives a more general result.
Our discussion of the orthogonal and symplectic cases is again based on
Reshetikhin, Takhtajan & Faddeev A990). Further details may be found in
Hayashi A992b). The former reference also defines quantum orthogonal and
symplectic vector spaces on which the quantum orthogonal and symplectic
groups act, generalizing their classical realizations as groups which act on
a vector space preserving a non-degenerate symmetric or skew-symmetric
bilinear form.
To define Fun^(G) when G is an exceptional group, the first step is to com-
compute a suitable R-matrix. When G is of type G2, the image of the universal
R-matrix of Uh(o) in the deformation of the seven-dimensional representation
of G is computed in Kirillov & Reshetikhin A989).
Multiparameter quantizations have been studied by a number of authors,
including Sudbery A990), Takeuchi A990a) and Artin, Schelter & Tate
A991).
7.4 A 'quantum' analogue of differential calculus was first introduced by
Woronowicz A989), in the context of 'compact matrix pseudogroups' (see
Chapter 13). In the form we have presented them, the results are due to
Tsygan A993), where further details and omitted proofs may be found. Ex-
Examples 7.4.3 and 7.4.6 can be found in Maltsiniotis A990), Wess & Zumino
A991) and elsewhere.
There is, of course, a complex of 'differential forms' associated to any k-
algebra, namely its Hochschild complex (see Chapter 4), but this is different
from the de Rham complex we have described. For quantized function alge-
algebras, the Hochschild complex has been studied in detail by Feng & Tsygan
A991).
7.5 This section is essentially an extract from Baxter A982). In Baxter's
book, the QYBE is called the 'star-triangle relation', because of a graphical
interpretation which we do not discuss in this book (although it appears,
unannounced, in Section 15.2). See also Faddeev A980, 1984), and Majid
A990g) for more details on the connection with Hopf algebras.
8
Structure of QUE algebras:
the universal R-matrix
The Weyl group W of a complex simple Lie algebra g acts as a group of
reflections on the Cartan subalgebra i) of g. It is well known that this action
extends to an action of a finite covering W of W as a group of Lie algebra
automorphisms of g, and hence to an action on the universal enveloping al-
algebra U(q) by Hopf algebra automorphisms. It is important for a number of
reasons. For example, it enables one to define root vectors in g associated to
every root, only the simple ones being 'given' as generators of g. This in turn
enables one to formulate and prove results such as the Poincare-Birkhoff-
Witt theorem, which is crucial for the representation theory of g.
In this chapter, we discuss the analogues and applications of these results in
the quantum situation. The algebra E/(I))[[ft]] of formal power series in h with
coefficients in the classical universal enveloping algebra ?/(!)) is a subalgebra
of Uh(o)i but the obvious action of W on ?7(I))[[ft]] only extends to an action
on Uh(o) of an infinite covering of W, called the braid group BQ of g (if
g = sin+i(C), then BQ is Artin's braid group on n + 1 strands). However, one
can still define root vectors in Uh(o) associated to every root of g: in fact,
for any given root, there is one root vector corresponding to each choice of a
decomposition of the longest element w$ of W (which takes positive roots to
negative roots) as a product of a minimal number of simple reflections. Using
these root vectors, one can construct a (topological) basis of Uh(gi) analogous
to the Poincare-Birkhoff-Witt basis of U($). This basis depends, however, on
the choice of the decomposition of iu0, for, contrary to the classical situation,
the different choices for a given root vector are not even proportional to each
other. (We show in Chapter 14 how to construct a basis independent of such
choices.)
Another difference between the classical and quantum situations is that
the braid group action on ?4(g) preserves its algebra structure, but not its
coalgebra structure, so that it is not obvious how to find the action of the
comultiplication on non-simple root vectors. This problem can be solved by
means of another interpretation of the braid group action. In fact, there is a
Hopf algebra Uh(o), called the quantum Weyl group of ?4(g), which contains
Uh{o) as a Hopf subalgebra, and is such that the braid group action is given
by conjugation by certain elements Wh of Uh(s?)> This is analogous to the
256 8 Structure of QUE algebras: the universal R-matrix
fact that the classical action of W on q is given by the adjoint action of
certain elements of the group G with Lie algebra q. The incompatibility of
the braid group action with the coalgebra structure of Uh(q) is reflected in
the failure of the elements Wh to be group-like: the extent of this failure can
be precisely described, and this enables one to compute the comultiplication
on arbitrary root vectors. The incompatibility also means that there is no
finite-dimensional Hopf subalgebra of Uh(q) which has the group algebra of
W as its classical limit: one can only define the quantum analogue of the
'crossed product' of U(q) with W.
One of the most important properties of Uh(q) is that it is quasitriangular.
Indeed, we show that Uh(q) can 'almost' be realized as a quantum double
(the classical analogue of this statement was proved in 1.4.3). Its universal
R-matrix can therefore be computed by the method of Subsection 4.2D. To
perform this calculation, one needs an explicit basis of Uh(q) and to know the
action of the comultiplication in this basis. As we have seen, the quantum
Weyl group is precisely the tool which enables one to carry this out.
Note Unless indicated otherwise, q denotes in this chapter a finite-dimensional
complex simple Lie algebra, and Uh(q) denotes the QUE algebra defined in
6.5.1. We denote Uh(q) by Uh if this will not lead to confusion.
8.1 The braid group action
A The braid group Let A = (a>ij)i<i<n be a symmetrizable generalized
Cartan matrix, and let q = q'(A) be the associated Kac-Moody algebra (see
the Appendix). Let m^ be equal to 2, 3, 4, 6, or infinity, if a^aji is equal to
0, 1, 2, 3, or is at least 4, respectively. We begin with
Definition 8.1.1 The braid group BQ associated to q has generators Tiy
1 < i < n, and defining relations
r m j r m i r m i f t j r m t f jt t f # j r m t
i j i j ' ' ' = j i j i ' ' '
for all i ^ j such that rrtij < oo, where there are rriij T's on each side of the
equation.
Note that, if g is finite dimensional, the products a^aji, for i ^ j, are all
equal to 0, 1, 2 or 3.
Remarks [1] The Weyl group W of q is generated by the simple reflections s^:
A) SiiHj) = Hj - ajiHi
(in this formula, the Hi are the standard generators of q - see the Appendix).
Its defining relations are those in 8.1.1 (with Ti replaced by Si), together with
8.1 The braid group action 257
sf = 1. Hence, W is a quotient of BQ. On the other hand, there is a surjective
homomorphism BQ —> Z given by 7$ >—> 1 for all i\ in particular, i3g is an
infinite group.
[2] If g is of type An, the relations become
T T — T T if U — i'l ^ 1
These are the defining relations of Artin's braid group on n + 1 strands (see
the remark following 5.1.7). A
For any integer r > 0, and for 1 < i < n, define
The ^-factorial [r]g! is defined in Subsection 6.4D.
Theorem 8.1.2 There is an action of the braid group BQ by algebra auto-
automorphisms of Uhis) defined on the standard generators (see 6.5.1) as follows:
TiiXf) = -X-ed*hH% Ti(Xr) = -e-^^Xf, T^H,) = H3 - ajzHu
r=0
r=0
This can be proved by direct verification. Of course, it is enough to consider
the case when g has rank 1 or 2.
Remarks [1] Note that the action of Ti on the Hj is the 'same' as that of the
simple reflections s^ € W on the corresponding generators of q.
[2] The inverses of the automorphisms Ti are given by
T~\Xt) = -e-W'Xr, Tr^Xr) = -X+ed<hH% T'^Hj) = Hj - aJZHt,
xt^Xt){'atJ'r) if i±h
r=0
[3] The Ti are not Hopf algebra automorphisms of Uh> We shall see in the
next section, however, that they are 'almost' Hopf algebra automorphisms,
in the same sense as Uh is 'almost' cocommutative.
258 8 Structure of QUE algebras: the universal R-matrix
[4] The Ti can be expressed in terms of the Hopf algebra adjoint represen-
representation of Uh and that of the opposite coalgebra U^p (see 4.1.13):
[5] In the sequel, we shall make use of the (C-algebra anti-automorphism
and the C-algebra automorphism </> of Uh defined on generators by:
co(X+) = X-, oj(X~) = X+, u(Hi) = Hi, u(h) = -h,
The action of B$ is compatible with these involutions, in the sense that:
ujoTi=TiOu;, (f)oTi=T-1 ocf). A
Recall from the Appendix that any element w € W can be written as a
product w = Si1Si2 ... Sik of simple reflections; the expression is reduced if
its length k is minimal among all such expressions for w, and this minimal
length is denoted by ?(w).
The following classical result shows that the natural surjective homomor-
phism BQ —> W which sends Ti to Si has a canonical section (which is not a
homomorphism). See Bourbaki A968), Chap. 4, § 1.5, Proposition 5.
Proposition 8.1.3 Let w = silsi2... sie(w) be a reduced expression of an
element w € W. Then, the automorphism Tw = ThTi2 ... Til{w) of Uh($)
depends only on w, and not on the choice of reduced expression. |
B Root vectors and the PBW basis The classical Poincare-Birkhoff-
Witt theorem associates to any (ordered) basis of a Lie algebra a basis of its
universal enveloping algebra. In the case of a quantized universal enveloping
algebra such as E/h(g), one has no underlying Lie algebra, much less a basis
of it, so it is not immediately clear how to obtain an analogue of the PBW
theorem for ?/h(g). The most natural basis of the classical enveloping algebra
U(q) is the PBW basis associated to the basis of g given by a basis of the
Cartan subalgebra f) C g together with a root vector in each root space of g.
In Uh(o)i one has an analogue of the basis of I), namely {i^}i=i,...,n5 but one
is only given 'root vectors' Xf associated to the simple roots c^ (and their
negatives). Thus, to construct a basis of Uh{$) of PBW type, one must define
analogues of root vectors associated to the non-simple roots of g. As we recall
in the Appendix, if g is finite dimensional, non-simple root vectors of g can
be defined by using the action of (a finite covering of) the Weyl group W on
g. This is based on the fact that, if
B) w0 = silsi2...siN
8.1 The braid group action 259
is a reduced decomposition of the longest element of W, then every positive
root occurs exactly once in the following set:
C) f3l=ail, f32 = sh(ai2),..., f3N = shsi2 .. .siN_1(aiN).
In the quantum case, the action of the Weyl group is replaced by that of the
braid group i3g, and we make
Definition 8.1.4 Let q be a Unite-dimensional complex simple Lie algebra.
Fix a reduced decomposition B) of the longest element wq ? W, and define
/?i,..., /3n as in C). Define elements X^ ? C4(g) as follows:
The X~q (resp. X^ ) are called the positive (resp. negative) root vectors of
If g is an infinite-dimensional Kac-Moody algebra, it is no longer true
that every root lies in the Weyl group orbit of a simple root, and the above
procedure for defining root vectors fails. (See Beck A993), however, for the
case when g is affine.) For the remainder of this chapter, we assume that g
is finite dimensional.
One important difference between the classical and quantum situations is
that, in the classical case, the root vectors defined in this way are indepen-
independent, up to sign, of the choice of the reduced decomposition B), whereas, in
the quantum case, the root vectors corresponding to different reduced decom-
decompositions of wo are not even proportional to each other, in general.
Example 8.1.5 If g is of type A2, there are two choices for the reduced
decomposition of wq:
(i) wq = S1S2S1: then the positive root vectors are
X+, TX(X+) = -X+X+ + e-hX+X+, TXT2{X+) = X+ ;
(ii) wo — S2S1S2'. then the positive root vectors are
X+, T2{Xt) = -X2+Xt + e-hXtX+, T2T1(X2+) = X+. 0
Let U^ , U® and U^ be the (C[[/i]]-subalgebras of Uh topologically generated
by the Xf, by the Hi and by the X~, respectively.
Proposition 8.1.6 (i) Let w eW be such that w(cti) e A+ for some simple
root a*. Then, Tw(Xf) eU^. Ifw(ai) = a, is simple, then Tw(Xf) = Xf.
(ii) In particular, for any choice of reduced decomposition ofwQ, the positive
(resp. negative) root vectors lie in U^ (resp. U^).
260 8 Structure of QUE algebras: the universal R-matrix
(iii) The braid group action preserves U® and induces on it the classical action
of the Weyl group. |
The meaning of the third part is that, if j3 = X^ /c^ ^ Qi an(^ ^ we
define Hp = J2ikiHii then TW(HP) = Hw(f3) for all w G W. Note that, if
0 = /3r ? A+ is a positive root (in the notation of C)), the vectors {Hpr,X^}
satisfy the defining relations of Ud h(sh(^))'- this follows by applying the
automorphism Ti±Ti2 .. .Tir_1 to the relations satisfied by {Hir,Xf}.
Now that we have quantum analogues of all the root vectors of g at our
disposal, we can use them to construct a topological basis of Uh- Fix a choice
of positive and negative root vectors as in 8.1.4. Define, for r = (ri,..., rjy) ?
and for s = (si,..., sn) G Nn,
Proposition 8.1.7 The elements (X~)r, Hs and (X+)\ for r, t e
s e Nn, form topological bases of U^, U® and U?, respectively, and the
products (X~)rHs(X+)t form a topological basis ofUh- I
This result has the following immediate
Corollary 8.1.8 Multiplication defines an isomorphism of (C[[h]]-modules
u~ ®u°h® u+ - uh
(completed tensor products). |
Proposition 8.1.7 was first proved by Rosso A989) when g = sin+i((C),
using a definition of the root vectors due to Jimbo A986a), which did not
of course use the braid group action. Lusztig A990a) deals with the case
in which q is simply laced, and Lusztig A990b) considers the general case.
Berger A992) gives a proof using the 'diamond lemma' in ring theory (see
Bergman A978)). S. Z. Levendorskii has given a proof using the next result,
which is also used in the computation of the universal R-matrix of Uhis) (see
Section 8.3). Although we shall make use of 8.1.7 in the proof of this result,
Levendorskii gives an independent proof by making use of a weak version of
8.1.7, which in turn is established by the argument used to prove 6.4.7.
8.2 The quantum Weyl group 261
Proposition 8.1.9 If 0 < r < s < N, we have
S^ ^s-i fy+ \tr+1
)~l
where the sum is over all ?r+i,..., ?s_i gN, and all but finitely many of the
c(tr+i,... ,ts-i) e <C[[h]] are zero.
Proof By 8.1.7, we know that there is an expression of the form
xtxt.= E <tl,..
ti,...,tjv=O
Suppose that there is a p < r and a non-zero coefficient c@,..., 0, tp,...,
with tp =? 0; and choose p minimal with this property. Applying (T^ ... Tip
to both sides and using 8.1.6(i), we see that every term lies in U? except those
with tp ^ 0, which give a term of the form ET~1(Xip), where E E U^ is non-
nonzero. Since T-l{X\p) = (-e-d*phH*pXryP, this contradicts 8.1.7. Similar
Op \ Ip ' \ %p / '
arguments show that c(?i,..., t^) = 0 unless t\ — • • • = tr-\ = ts+i = • • • =
tjv = 0, and that, if these equalities hold, then c(ti,... ,?jv) = 0 unless tr
and ts are both non-zero. For weight reasons, we then have the equation in
the statement of the proposition, except that the coefficient eh^r^s^ must
be replaced by an as yet unknown scalar k, say. To determine k, apply
(Th .. -Tir)~l to both sides. The right-hand side is in ?/+, while the left-
hand side is
where E = Tir+1 . ..Tis_1(X+) ? U+ has weight sir(f3s
Thus, the left-hand side becomes
Writing E as a linear combination of monomials in the Xj~, j = l,...,n,
we see that EX~ - X~E € U%.U?. It follows by using 8.1.7 again that
as required.
262 8 Structure of QUE algebras: the universal R-matrix
8.2 The quantum Weyl group
Classically, the action of (a finite covering of) the Weyl group on g is given
by the adjoint action of certain elements of the group G with Lie algebra q.
In this section, we show that essentially the same result holds in the quantum
case, the role of the group elements being played by certain elements of T^,
the dual of the quantized algebra of functions on G. Conjugation by invertible
elements of T^ makes sense, because T^ is an algebra and there is a natural
embedding Uh —> T^.
A The sl2 case We recall from 7.1.5 that the matrix elements CrT of the
representations Fm of Uh = Uh(sl2((E)) are a topological basis of the dual
Hopf algebra Th of Uh- It therefore makes sense to define a linear functional
WhEfhi the ful1 C[[ft]]-module dual of Th, by
1 " otherwise.
Since T^ is an algebra, the following result makes sense.
Lemma 8.2.1 In JF*, we have
X+ —1 h V— V— —1 —h V+ TT —1 TT
^wh — — e X , WhX wh = — e A^, WhHwh = —if.
Proof Let us prove the first formula. We have
t
Now, by 6.4.10,
(X+ , CM) = [m-s + l]q6r,s-u (X- , CM) = [s + l]^r>fl+
where q = eh. Hence,
M+ , CM) = 5^(-l)reihm2+r^r+t>m[m - s + i\q6t,a-i
t
= (-iyeihm*+rh[m - s + i)qsr+a,m+1.
On the other hand,
- -Ph\r\ (-'
8.2 The quantum Weyl group 263
Thus, whX+ = -ehX~wh. |
Now define Wh G T^ to be the product
E) wh = Wh exp —— = exp —— wh
(the latter equality follows from 8.2.1).
Proposition 8.2.2 Let T be the generator of the braid group of sl2(<?).
Then, for all a eUh, we have
T(d) = WhCiw^1.
Proof It suffices to check this when a is one of the generators of Uh> It is
obvious when a = H. By 6.4.2,
exp PH x exP -^ = X^xplhiH ± 1I.
L 4 J L 4 J
The result now follows from 8.2.1 and the definition of T in 8.1.2. For example,
= -X~e
~ehH
(the second equation follows from 8.2.1, and the third equation from 6.4.2). |
B The relation with the universal R-matrix Although the elements
CrT are linearly independent, there are many multiplicative relations be-
between them. In fact, in the Clebsch-Gordan decomposition 6.4.11 of the
tensor product Vm 0 Vn as a direct sum of indecomposable representations
Vp, we can express any basis vector v\ of any Vp which occurs as a linear
combination of tensor products Vr ®Vs of basis vectors in Vm and Vn, and
vice versa. By considering the action of Uh on both sides, one then obtains
relations of the form
(a\ Mrn)r(n) _ ST^ mnp
y°) ^rr> Css> - Z^Crstys
t,t'
These relations allow one to compute the action on Wh of the comultiplication
Ah dual to the multiplication on Fh.
264 8 Structure of QUE algebras: the universal R-matrix
Proposition 8.2.3 For the element Wh G T^ defined in D), we have
G) Ah(wh) = nj;1(wh®wh),
where IZh is the universal R-matrix ofUh defined in 6.4.8.
Outline of proof It suffices to show that the two sides of G) agree on any
tensor product C{™) <g> C^). The left-hand side gives wh{C^)C{^)), which
can be computed using F). The right-hand side is
> — l\
where
which can be computed using the formula for the R-matrix in 6.4.8. See
Kirillov & Reshetikhin A989) for the details. |
Similar calculations give the action of the counit and antipode on Wh:
Sh(wh) = whehH, eh(wh) = 1.
Remarks [1] This result shows that T is 'almost' a Hopf algebra automorphism
of Uh- In fact, for a eUh,
Ah(T(o)) = A
(8) = Tl
where
_ h(H®H)v
(9) ~ h
°° /i —2h\
7rj
=y
by 6.4.8.
[2] One can 'explain' 8.2.3 as follows. Recall that the Poisson bracket
on T = F(SL2 (C)) induced by the quantization Uh is given by {/, g} =
h~1(fh9h ~ 9hfh) (mod ft), where fh, gh € J7^ have classical limits /, g € T.
Now, if it;/! € Uh were group-like, we should have wh(fh9h) = ™h(fh)wh(gh),
and hence {/ , g}(w) = 0 for all /, g, where w € W is the classical limit of Wh-
But we saw in Section 1.4 that the Poisson bracket on ST2(C) vanishes only
8.2 The quantum Weyl group 265
at the points of the diagonal (Cartan) subgroup of 5L2(C) (strictly speaking,
we discussed SU2 rather than 5L2(C) in Section 1.4, but the same result
holds). Since the Poisson bracket is determined by the classical r-matrix, it
is natural that the extent to which Wh fails to be group-like is measured by
the universal (quantum) R-matrix. A
It follows from 8.2.3 and the above remarks that the subalgebra Uh of J-^
topologically generated by Uh and Wh (or, equivalently, by Uh and Wh) is a
topological Hopf algebra. Moreover, every finite-dimensional representation
of Uh-, being a direct sum of indecomposables, is naturally a representation of
Uh- The topological Hopf algebra Uh is called the quantum Weyl group of Uh-
Note that, unlike the classical situation, in which the group algebra of the
Weyl group is itself a Hopf algebra, 8.2.3 shows that neither the subalgebra
of Tfr topologically generated by Wh-, nor that topologically generated by Wh-,
is a topological Hopf algebra.
Another difference from the classical situation is that neither Wh nor Wh is
an involution. The corresponding fact in the quantum situation is
Proposition 8.2.4 The square w\ of the quantum Weyl group element Wh
lies in the centre of Uh • In fact,
w2h = e-hHuh(J,
where Uh = Hh{Sh® id^T?^1) and a is the central element of J7^ given by
for all r, s = 0,...,ra,ra>0 (we write IZf^ instead of Alh) 21 f°r typograph-
typographical convenience).
Outline of proof The first statement is immediate from 8.2.1. The fact
that e~hHUh lies in the centre of Uh was shown in the remark at the end of
Subsection 6.4D. The formula for w\ is proved by a direct computation. |
C The general case Turning now to the algebra Uh = Uh(o) f°r an ar^^~
trary finite-dimensional complex simple Lie algebra g, we use the fact that
Uh is generated topologically by the subalgebras Uh,i, • • •, ?4,n of Uh(sh(<C)),
where Uh,i is the subalgebra topologically generated by Hi, X+ and X~;
note that Uh,% — Udth(sh(?))- The inclusions Uh,i -^ Uh induce projections
Th -^ 3~h,i of the dual Hopf algebras, and hence the element Wh,i G J~h i
constructed in Subsection 8.2A may be regarded as an element of T^. We set
Then, we have
266 8 Structure of QUE algebras: the universal R-matrix
Proposition 8.2.5 For all a eUh and i = 1,..., n,
The proof is by explicit computation. See Kirillov & Reshetikhin A990a)
for the details.
We also have the following generalization of 8.2.5.
Proposition 8.2.6 For % = 1,... ,n,
where
fZf~j % KA )
n=0 [Tl^'
and q{ = edih. |
As in the 5/2 case, this result implies that the subalgebra Uh of T^ topo-
topologically generated by Uh and w/^i,..., Wh,n is a topological Hopf algebra. It
is called the quantum Weyl group of Uh.
Remarks [1] One can show that the Wh,i satisfy the braid relations in 8.1.1.
Together with 8.2.5, this gives another proof of 8.1.2.
[2] Levendorskii & Soibelman A990) define an element Wh € J~h (in the 5/2
case) directly as a matrix element of an infinite-dimensional representation of
Th- In fact, in the notation of 7.1.6, one sets Wh(f) equal to the 00 matrix
element of / G Th acting in the representation tt_i. A
8.3 The quasitriangular structure
In this section, we show that ^(9) is 'almost' a quantum double, deduce that
it is topologically quasitriangular and compute its universal R-matrix.
A The quantum double construction We recall from Subsection 4.2D
that the double V(A) of any finite-dimensional Hopf algebra A is a Hopf
algebra isomorphic to A<g)(A*)op as a coalgebra, and that it is quasitriangular
with the element of A <S> (A*)op C V{A) B) V(A) corresponding to the identity
map A —> A being the universal R-matrix. As explained in Subsection 6.3C,
when A is a QUE algebra, the tensor products must be understood in the
completed sense, and A* must be the QUE dual of A.
The crucial observation for the proof that Uh = Uh{s) is topologically
quasitriangular is the following result, which shows that Uh is 'almost' a
quantum double. We write U^° = U%.U?, U^° = U^.[/?. It is obvious that
C/^°, U% and U^° are Hopf subalgebras of Uh.
8.3 The quasitriangular structure 267
Proposition 8.3.1 There is a surjective homomorphism of topological Hopf
algebras
*°
The image of the universal R-matrix of T>(U^ ) under the homomorphism
in 8.3.1 will clearly be a universal R-matrix for Uh- This not only proves that
Uh is topologically quasitriangular, but also gives an explicit formula for its
universal R-matrix.
Remark In fact, there is an isomorphism of topological Hopf algebras
V(U^°) —> Uh ® U^
(completed tensor product) and the homomorphism in the proposition is ob-
obtained by composing this isomorphism with id ® e/i, where Ch is the counit of
As explained above, one of our first tasks is to describe the QUE dual of
h
Proposition 8.3.2 The QUE dual ofU^°, with the opposite comultiplica-
tion, is isomorphic to U^° as a topological Hopf algebra over <C[[/&]].
We prove 8.3.1 and 8.3.2 in detail in the s/2(<C) case to bring out the main
ideas of the quantum double method, and then outline the general case where
the quantum Weyl group is used.
B The 5/2 case In this subsection, g = 5/2 (C). By 8.1.7, the monomials
HS(X+Y, 5, t > 0, are a topological basis of U^ • We recall from Subsection
6.3C that the QUE dual of U^° is the Hopf algebra dual of a QFSH subalgebra
Proposition 8.3.3 The QFSH subalgebra Uh,>0 ofU^° defined in Subsec-
Subsection 6.3C is the subalgebra topologically generated, in the sense of formal
power series over <C[[ft]], by H = hH and X+ = hX+.
Proof By the discussion in Subsection 6.3 C, an element a G U^ lies in
the QFSH subalgebra Uh,>o provided that An(a) = 0 (mod hn) for all n > 1,
where An = ir®nA^ and n : U^° —> U^° is the <E[[h]]-module projection
which sends 1 to 0 and fixes each monomial HS(X+Y for which s + t >
0. Consider an element a = fsj(h)Hs(X+)t G U^0, where s + t > 0 and
fs,t(h) G C[[fe]]. Applying As+t, we obtain a sum of terms with exactly one
H or one X+ in each position in the tensor product. In particular, the term
268 8 Structure of QUE algebras: the universal R-matrix
occurs with coefficient s\t\fs+t{h). It follows that a lies in Uh,>o if and only
if fa,t(h) is divisible by hs+l. |
Note that
A0) Ah(H) = H®l + l®H, A/l(X+)=X+®e" + l®X+,
and that eH is not in the /i-adic completion of the subalgebra of U^ generated
bytf.
To describe the QUE dual of Uj^°, let ? and r\ be the linear functional on
Uh,>o which are equal to one on X+ and H, respectively, and equal to zero on
all other monomials HS(X+)K Then, the QUE dual of U^° is topologically
generated by ? and rj.
Lemma 8.3.4 Let ( , ) be the natural pairing between Uh,>o &nd its dual.
Then,
(Z'rf , Hs'{X+)tf) = 6a,a,6t,t,8\ g-i*^-1) [t]q\,
where q = eh.
Proof Consider first the case t = 0. From A0), it is clear that
can be non-zero only if tf — 0, and that in this case it is equal to the coefficient
of H 0 • • • (8) H in
This vanishes unless s = s;, in which case it is equal to s\.
Similarly, {rf , ?P'(X~f)t') clearly vanishes unless sr = 0 and ?; = ?, in
which case it is equal to the coefficient of the term in the product
which has exactly one X+ in each factor. Thus, we are considering an ex-
expression
(ai +a2^ VatI
in which aidj = q2djdi if i < j, and we require the coefficient ct of a\a2 ... a^,
all products being written so that the a^ occur in increasing order. An obvious
induction on t shows that
= ct(l + ^ + ^ + • • • + ^t),
8.3 The quasitriangular structure 269
from which we find that
Ct = q-it(t-i)[t]ql
To prove the formula in the general case, we must consider the term in
Ah(Hs'(X+)*') which has s #'s (and no X+'s) in the first factor, and t X+ 's
(and no H's) in the second factor. Such a term exists only if s' = s and t' = t,
in which case it is simply Hs ® (X+)t. It follows that
(CV, HS'(X+/) = (ti^H*')^, (X+/). I
We can now describe the Hopf algebra structure of the QUE dual of U^ •
Lemma 8.3.5 In the QUE dual ofU^°, we have
(a) [€,v] = ~V,
(b) Afc(O = ?<8>1 + 1<8>?, Ah(r)) = rj <g> e^ + 1 (g) rj.
PROOF For (a), we must compute ?77 and 77^. The only non-zero pairings are
(?77, HX+) = (
The formula ^r] — r]^ = —rj is now clear.
To prove the second formula in (b) (the proof of the first is similar but
easier), note that, since rj vanishes on all monomials HS(X+ )l except that for
which 5 = 0 and t — 1, it follows that Ah(v) vanishes on all tensor products
of such monomials except two:
(Ah(V), X+ 0 Hs) = G7, X+Hs) = (rj, (H - 2h)sX+) = (-2h)s. |
We can now prove 8.3.2 in the sl2((E) case. In fact, it is clear from the
preceding lemma that the map
H^2?, X~ ^rj
defines an isomorphism of Hopf algebras from U^° to the QUE dual of U^°
with the opposite comultiplication.
Remark At first sight, this result seems paradoxical, since the classical ana-
analogue U-° of ?//p, being non-commutative, is certainly not isomorphic to the
270 8 Structure of QUE algebras: the universal R-matrix
classical analogue ((C7^°)*)op of ((^°)*)op, which is commutative. However,
we are taking the QUE dual here, i.e. the dual of the QFSH algebra Uh,>o
generated by H and X+. Since
[H, X+] = 2/iX+, Ah(X+) =I+0e^ + l®I+,
the classical limit of Uh,>o is the commutative algebra of formal power series
in two variables H and X+, with the non-cocommutative coalgebra struc-
structure A0). Hence, the classical limit of [/? >0 is cocommutative but non-
commutative, and of course U-° has the same properties. A
We are finally in a position to describe the algebra structure in T>{U^ )
Lemma 8.3.6 The following relations hold in
Outline of proof We prove the first formula. According to the description
of the algebra structure in the double T>{A) given in Subsection 4.2D, if a G ^4
and a G (,4*)op, and if
(S^1 0 id)Ai2) (a) = J2 <*i ® «i ® <, Af (a) = ^ a, 0 aj 0 <,
i 3
then
In our case, we have
(S^1 0 id)A|l2)(X+) = -e~hHX+ 0 ehH 0 ehH + l 0 X+ 0 ehH+ 1 0 1 0 X+,
A^2) G7) = 77 0 1 (8) 1 + e^ 0 i) 0 1 + e~2/l* 0 e~2^ 0 77.
Each term in A^ (^+) pairs with exactly one term in A^ G7), and we find
that
= X^r/-
ehH -,
We can now prove 8.3.1 in the s/2(<C) case. In fact, the required homomor-
phism V(UJ^°) —> Uh is given by
8.3 The quasitriangular structure 271
It is now a simple matter to compute the universal R-matrix of Uh> By
8.3.4, the basis of J7?>0 dual to the basis {HS(X+Y} of U^° is
S\[t]q\ *
Hence, the universal R-matrix of T>(Uj^°) is
Applying the homomorphism A1), we find that the universal R-matrix of Uh
oo oo -| / h
= E E "W7 U
is
^ -I t=o l J^'
This is the same as the formula in 6.4.8.
Remark The formula for 1Zh can also be written as follows:
where J5? = e~hHX+, F = ehHX~. A
C The general case For an arbitrary finite-dimensional complex simple Lie
algebra g, one follows the same procedure as in the 5/2 (<C) case, the additional
difficulty arising from the need to use root vectors corresponding to all the
positive roots, not just the simple roots, and the fact that the comultiplication
in Uh is known a priori only on the simple root vectors.
The solution to the latter problem is contained in 8.2.5 and 8.2.7. Let -X*^,
X~p2,... ,X~jN be the root vectors defined in 8.1.4, corresponding to some
choice of a reduced decomposition of the longest element of the Weyl group
of g. The first root which is not simple is /?2, and by 8.2.5 and 8.2.6 we have
)
272 8 Structure of QUE algebras: the universal R-matrix
This procedure can clearly be iterated to compute the effect of the comulti-
plication on all the root vectors. To state the general result, set
for every positive root /3r.
Proposition 8.3.7 For any positive root /3, we have
Ah(x+) = n^<p(x+ ® ehHe +1® xpnh^
where, if C = J2{ fc^ G Q, then Hp = J^ dikiHi. |
To determine the QUE dual of C/^°, we must first describe its QFSH sub-
algebra Uh,>o- As in 8.3.3, one finds that Uh,>o is generated by the elements
Hi = hHi, i = l,...,n, and Xt = hXt as /3 runs through the positive
roots of g. Define elements ?i,..., ?n, rjp1,..., rjpN in U% >0 by requiring that
(?i, Hi) = (rj/3r , X^r) = 1, and ^ and r]pr give zero when paired against any
other monomial of the form H{x ... H^(X+N)tN ... (X^f1. Then, we have
the following generalization of 8.3.4. It is proved by induction, making use of
8.3.7.
Lemma 8.3.8 For any si,s[,.. .,tN,t'N e N, we have
i=lr=l
where qp = edf3h and dp = di if the positive root j3 is Weyl group conjugate
to the simple root a^. |
Using this result, the Hopf algebra structure of U? >0 can be determined
and 8.3.2 proved in the general case. In fact, one finds that the isomorphism
uh° -> uh,>ois given by
To prove 8.3.1, one shows that the following defines a homomorphism of Hopf
algebras V{U}°) - Uh:
8.3 The quasitriangular structure 273
where B is the matrix (d~ldij).
Finally, the universal R-matrix of T>(U^°) is, by 8.3.8,
oo n N i1st+trnhtr(tr-'L)
Z^ 1111 a.\\f 1 !
Applying the homomorphism A3), we find that the universal R-matrix
of Uh is
t1,...,tN=Or=l i"'Wr-
The order of the factors in the product is such that the /3r-term appears to
the left of the /3s-term if r > s.
The expression for IZh can be written more concisely by making use of the
^-exponential
OO L.
X
A4)
k=o l'"iq'
Then, we obtain
Theorem 8.3.9 For any finite-dimensional complex simple Lie algebra g,
is topologically quasitriangular with universal R-matrix
where the product is over all the positive roots of g, and the order of the
terms is such that the f3r-term appears to the left of the f3s-term ifr>s (see
8.1.4). |
Remark The r-matrix r = h~lAZh — 1 0 1) (mod h) which is the classical
limit of 1Zh is clearly given by
n N *
r=l
This agrees with the formula in 2.1.7, since the inner products of the gener-
generators are given by
(see the Appendix). A
274 8 Structure of QUE algebras: the universal R-matrix
D Multiplicative properties Recalling the 'partial' R-matrices ilh,p de-
defined in A2), we deduce from 8.3.9 the following multiplicative formula for the
universal R-matrix of ?4(g) in terms of those of its ?4(s/2(<C))-subalgebras •
Proposition 8.3.10 The universal R-matrix ofUh(g>) is given by
nh =
We can obtain a third formula for the universal R-matrix of Uh if we recall
the remark at the end of Section 8.2, according to which the Wh,i satisfy the
defining relations of the braid group of g. As in 8.1.3, this implies that there
is a canonical element of the quantum Weyl group of Uh associated to any
element of the Weyl group of g. In particular, if
w0 = shsi2 ...siN
is a reduced expression of the longest element of the Weyl group, we have a
canonical element
of the quantum Weyl group. Now, by 8.2.6,
where
This proves
Proposition 8.3.11 The universal R-matrix ofUh(§) is given by
Uh = exp ft YJ.B-^ijHi 0 Hj (wh,0
2j "^
Corollary 8.3.12 The universal R-matrix ofUh(&) defined in 8.3.9 is in-
independent of the choice of reduced expression of the longest element of the
Weyl group of g. |
It would be interesting to find a proof of 8.3.11 and 8.3.12 which does not
require one to compute the R-matrices involved.
8.3 The quasitriangular structure 275
E Uniqueness of the universal R-matrix The solution to the problem
of finding an invertible element TZh in (some completion of) Uh ® Uh such
that A^p = IZh-^h-^h1 *s certainly not unique (see the discussion preceding
4.2.2). However, the next result shows that any solution TZh, which is of the
same form as that in 8.3.9, coincides with that solution up to a scalar multiple
(cf. the remark following the proof of 6.4.8).
Let U® be the field of fractions of the subalgebra of U® <g) U® generated by
elements of the form ehH* <g> 1, 1 <g> ehH* and ehH*®Hi, i = 1,..., n. Let U^ be
the set of formal infinite sums, with coefficients in [/?, of monomials of the
form
( Y+ ^iSiV ( Y+ \Sl &\ ( Y~ V1 (Y~ \1^
vxpN) •••(A/?J ®(A/?J ¦••yApN)
such that the total weight of the terms in each monomial appearing in a given
formal sum is bounded, i.e. if mp^ is the multiplicity of a simple root a* in
a positive root /?, then
< constant.
It is not hard to see that Uj^ is an associative algebra over C[[/i]]. Moreover,
the R-matrix in 8.3.9 clearly lies in U^.
Proposition 8.3.13 IfR'h € U^ is such that n'h./±h.(nfh)-1 = A°hp, then
lZ'h is a scalar multiple of the R-matrix in 8.3.9. |
F The centre of Uh If Uh = Hh(Sh® id)(R-hJ1, where TZh is the universal
R-matrix given by 8.3.9, then by 4.2.4 and the remarks following it, Zh =
UhSh(uh) = Sh(uh)uh lies in the centre of Uh- This element is closely related
to the Casimir element of the classical enveloping algebra U. Note that, since
TZh = 1 ® 1 (mod h), we have Zh = 1 (mod h), so that it makes sense to define
Ch = -^ln(^).
h
Proposition 8.3.14 The element Ch € C/"^(g) corresponds, under the iso-
isomorphism in 6.5.5, to the Casimir element of J7(g).
The square of the antipode S^, which is given by conjugation by Uh (see
4.2.3), can be computed directly, and this leads to another central element of
Uh- In fact, let p* be the unique element of t) C Uh(i)) such that Qi(p*) = 2di
for i = 1,..., n. (If J2 kiai ^s ^ne sum °f ^ne positive roots of g, then p* =
J2kid>iHi.) Prom the definition of Sh in 6.5.1, it is easy to see that S%(a) =
ehp ae~hp for all a € C/^(g) (it is enough to check this when a = X^). It
follows that Vh = e~hp Uh is in the centre of Uh- The central element Vh is
not really new, however, for we have
276 8 Structure of QUE algebras: the universal R-matrix
Proposition 8.3.15 zh = v\.
Corollary 8.3.16 The topologically quasitriangular Hopf algebra
with the central element Vh described above, is a topological ribbon Hopf
algebra. |
We shall prove 8.3.14 and 8.3.15 in Subsection 10.1B.
G Matrix solutions of the quantum Yang-Baxter equation We know
from 4.2.7 that 1Zh satisfies the quantum Yang-Baxter equation
-r>12-r> 13-r>23 1?22>'T? 13-r>12
Kh Kh Kh — Kh Kh Kh •
If p : Uh —> End(V) is a finite-dimensional representation of Uh, then ob-
obviously R^ = (p (g) p)AZh) will be a solution of the QYBE with values in
End(V (g) V), i.e. a 'matrix' solution. Computing i?? is not easy, however,
since one needs to know the action on V of all the root vectors of Uh, not
just the simple ones. We outline one such calculation:
Example 8.3.17 Let g = s/n+i(C) and let p\:Uh-^ End(V^) be the natural
(n -f l)-dimensional representation of Uh- This means that V^ has a basis
{i>o, vi,..., vn} with respect to which the generators of Uh act as follows:
A5) p{(Hi) = Ei-U-i-Eii, pl{X?) = Ei-u, p\{X~) = En-!
(Eij is the elementary matrix with one in the zth row and jth column and
zeros elsewhere). Using 6.5.1, one verifies directly that these formulas do
define a representation of Uh', its lh = 0 limit' is clearly the natural represen-
representation of s/n_|_i(C) (in fact, the formulas in A5) are exactly the same as in
the classical case). Prom the discussion in Subsection 6.4E, it follows that V%
is indecomposable.
We must now compute the action of the remaining root vectors X^ on V%.
We take the reduced decomposition of wo to be
• 5n_i . . . S1S2S1.
The positive roots, in the order in which they appear in C), are
A6) A)l? AJi • • • > A)ni/?12> • • • ,Pln, • • • , Pn-2n-li Pn-2n, Pn-ln,
where Aj — ai+i + ai+2 H + otj. Noting that a product of the form
Bibliographical notes Til
vanishes unless each difference zr+i — ir = 1 (and similarly for the p^(X~)),
it is not difficult to see that
Hence,
Remembering to write the terms in the reverse of the order A6), we see that
all the cross terms vanish and so
A7)
The action of the remaining factor exp[h^2i j(B~1)ijHi 0 //j] is quite easy
to compute, since we already know the action of all the Hi. We find that it
gives
A8) e-Wn+V le» ^ E.. 0 E.. + ^ ?« a ?.,.
Multiplying A7) and A8), we obtain finally that (p\ 0 p\)(R,h) is equal to
e^ y^ En 0 ?"ii + y^ ?"ii 0 ?"jj + (e^ — e~h)
Apart from the unimportant scalar factor e /l/(n+1O this is the same as the
R-matrix in equation A8) of Chapter 7. 0
If g is of type B, C or D, the calculation proceeds along similar lines. The
main point is that the indecomposable representation of C/^(g) which is a
deformation of the natural representation of g is again given, in a suitable
basis, by precisely the same formulas as the natural representation of g. We
leave it to the reader to check that this is a consequence of the following
observations:
(a) the matrices representing the simple root vectors X.f' of g in the standard
realization of its natural representation all have square zero (see Varadarajan
A974), Section 4.4, for example);
(), , p);
(b) the eigenvalues of the generators Hi of g in the natural representation
all 0, 1 or -1.
are
One finds that the image of the universal R-matrix IZ^ of C/^(g) is given, up
to a scalar multiple, by the R-matrices written down in Subsection 7.3C.
278 8 Structure of QUE algebras: the universal R-matrix
Bibliographical notes
8.1 The braid group action on C/^(g) was introduced by Lusztig A988), and
its detailed properties were proved in Lusztig A990a,b, 1993). Further details,
and the omitted proofs, of the results in this section may be found in these
references.
8.2 The quantum Weyl group was introduced by Vaksman & Soibelman
A988) in the s/2 case, by Soibelman A990b) in the s/n+i case, and by Kirillov
& Reshetikhin A989, 1990a), and Soibelman A991b) in the general case. We
have mainly followed Kirillov & Reshetikhin, where the proofs of the results
of this section may be found.
8.3 The fact that Uh(o) is 'almost' a quantum double was pointed out by
Drinfel'd A987), where the formula for the universal R-matrix in the s/2 case
can also be found. The universal R-matrix in the s/n+i case was computed by
Rosso A989), and in the general case by Kirillov & Reshetikhin A990a) and
Levendorskii & Soibelman A990). Proposition 8.3.13 is due to Khoroshkin &
Tolstoy A992b).
9
Specializations of QUE algebras
Intuitively, one thinks of the quantized universal enveloping algebras
studied in Chapters 6 and 8 as families of Hopf algebras (over <C) depending
on a parameter h. Strictly speaking, however, this does not make sense,
for an algebra defined over the formal power series ring C[[/i]] cannot be
specialized to any value of h except h = 0. To remedy this situation, we
introduce a new algebra Uq(§), defined over the field of rational functions of an
indeterminate q, which is a kind of 'rational' counterpart of the 'formal' object
Uh(o)' The main advantage of Uq(q) over C/"^(g) is that one can specialize q
to any transcendental complex number. In fact, with a little more effort, one
can construct an 'integral' form of the algebra, denned over Z[q, g], which
enables one to specialize q to any non-zero complex number e. Moreover, the
definition and properties of Uq(g) closely resemble those of C/^(g). In addition,
Uq(§) is in some ways technically simpler than C/^(g): for example, one no
longer has to worry about fo-adic topologies, completed tensor products, etc.
We discuss two such integral forms of C/^(g), called the 'non-restricted' and
'restricted' forms. We shall see that the resulting specializations coincide
when e is transcendental, in fact even when e is not a root of unity, but have
very different properties when e is a root of unity. In the former case, the
properties of the specialization closely resemble those of the classical universal
enveloping algebra. On the other hand, it turns out that the specializations
at a root of unity provide a characteristic zero analogue of the classical Lie
algebras in characteristic p. Indeed, this is more than an analogy: we shall
formulate some precise results relating the two theories in this chapter and
Chapter 11.
The non-restricted specialization U€(q) is the easiest to define: one simply
replaces q by e in the defining relations of Uq(o). The crucial fact about
C/€ (g), when e is a primitive fth root of unity (? > 1), is that it is finite
dimensional over its centre Ze; in particular, the representation theory of
C/C(g) reduces essentially to that of a finite-dimensional algebra. We show
that Ze is the algebra of regular functions on a complex algebraic variety
Ze, and that Ze is a finite (ramified) covering of the 'big cell' in the group
G with Lie algebra g. (Recall that the centre of E/(g) is much smaller: it
is a polynomial algebra on rank(g) generators.) We also exhibit an infinite-
dimensional group Q of automorphisms of C/€(g) for which the induced action
on Z€ corresponds, in a precise sense, to the adjoint action of G on itself.
We shall see in the next chapter that, conjecturally at least, this leads to a
280 9 Specializations of QUE algebras
picture of the representation theory of ?/"e(g) which is in some ways analogous
to that provided for G by the Kostant-Kirillov 'orbit method'.
The definition of the restricted specialization ?/eres(g) mimics that of the
Chevalley-Kostant Z-form of the universal enveloping algebra C7(g), which is
itself central to the classical characteristic p theory. When e is a primitive
^th root of unity, we show that ?/eres(g) has a remarkable finite-dimensional
Hopf subalgebra ?/efin(g) such that the 'quotient' of ?/eres(g) by ?/efin(g) is iso-
morphic to the classical universal enveloping algebra U(q). Thus, as in the
non-restricted case, the representation theory of ?/J"es(g) reduces to that of a
finite-dimensional algebra. Moreover, if ? — p is an odd prime, then, after
taking the quotient Ufn(§) of Ufn(§) by a small subalgebra of its centre and
reducing (mod p), ?/<fn(g) becomes what is usually called the 'restricted' uni-
universal enveloping algebra in the characteristic p theory (hence the terminology
used for this specialization). Conjecturally, Ufn(o) has the same representa-
representation theory (in characteristic zero) as the restricted enveloping algebra in
characteristic p (if p is not too small).
Note Unless indicated otherwise, g denotes in this chapter a finite-dimensional
complex simple Lie algebra. We use freely the notation in the Appendix.
9.1 Rational forms
A The definition of Uq If g is a finite-dimensional complex simple Lie
algebra with Cartan matrix (a^), we let di be the coprime positive integers
such that the matrix (didij) is symmetric. Let q be an indeterminate, and
let Q(#) be the field of rational functions of q with coefficients in Q. Write
q% — qd% •
The definition of Uq(§) is modelled on that of C/^(g) in 6.5.1.
Definition-proposition 9.1.1 Let g be a finite-dimensional complex sim-
simple Lie algebra. Then ?/g(g) is the associative algebra over Q(g) with gener-
generators X*, X~, Ki and K~l, 1 < i < n, and the following defining relations:
is ts iy iy is zz"~~l zv~l is 1
J\iKj = KjKi, J^iJ^i = J^i J^i = 1,
(o\ y+ y- y- y+ _ k l ~ i
\z) A2 Aj ~ Aj Ai — °i,j _ _i ^
Qi ~~ Qi
C) EVl)
r=0
There is a Hopf algebra structure on Uq($) with comultiplication Aq, an-
9.1 Rational forms 281
tipode Sq and counit eq defined on generators as follows:
Aq(X+) =X+®Ki + l®X+, Aq(X~) =
D) \ + +
Proof The verification that the formulas for Aq, Sq and eq do extend to
algebra homomorphisms (an anti-homomorphism in the case of the antipode)
is analogous to the case of Uh($) treated in Section 6.5. |
Remarks [1] We shall omit the subscript q on Aq, Sq and eq, and will denote
Uq(§) simply by Uq, whenever this will not lead to confusion.
[2] If we let q{ = ed*h and K{ = ed*hH% the relations in 9.1.1 are conse-
consequences of those in 6.5.1. For example, by using 6.4.2, it is clear that relations
A) above are consequences of the relations [Hi, Xf] = ± a^X^ in 6.5.1.
[3] The same relations and coalgebra maps serve to define Uq(q) when
g = g'(A) is the Kac-Moody algebra associated to an arbitrary symmetrizable
Cartan matrix A (see the Appendix).
[4] There are other rational forms of J7^(g), which bear the same relation
to C/g(g) as the various complex Lie groups with Lie algebra g bear to the
adjoint group of g. The largest of these, the simply-connected rational form,
is obtained by adjoining to Uq(o) invertible elements L^, i = 1,... ,n, such
that Ki = Y\j Lafx\ the relations in A) are replaced by
r y±t-1 _ ±<$zj y±
LiJij L{ — qi Aj .
More generally, if M is any lattice such that Q C M C P, there is a rational
form C/^4"(g) obtained by adjoining to C/q(g) the elements Kp = Y\j L™3 for
every /3 = J2j rnij^j ^ M, where Ai,..., An are the fundamental weights of
g. Thus, Uq(o) is the adjoint form C/^(g). When g = s/2(<C), for example,
P/Q = Z2, so there are only two rational forms, the adjoint form and the
simply-connected form. The latter is obtained from the former by adjoining
a square root of K\.
We shall deal only with the adjoint rational form f7q(g), as is customary in
most of the literature, although for some purposes the simply-connected form
is more convenient. Note that, as in the case of ?/(g), one cannot distinguish
adjoint and simply-connected forms of J7^(g).
[5] One can define a rational form Tq of the coordinate algebra as follows.
Let X be the set of finite-codimensional two-sided ideals / of Uq such that, for
some r € N and alH = 1,...,n, YTs=-AKi ~ Qi) e L Then, Tq is the set of
all Q(g)-linear maps Uq —> Q(#) whose kernel contains some ideal / € X. It
is not difficult to show that the comultiplication (resp. the antipode) dual to
282 9 Specializations of QUE algebras
the multiplication (resp. to the antipode) in Uq maps Tq into Tq <g) Tq (resp.
into Tq), so that Tq is a well-defined Hopf algebra over Q(g). A
B Some basic properties of Uq As we mentioned above, many of the
results we have established for Uh have counterparts for Uq. Most of these
translations are obvious, and we shall not write them all down. We content
ourselves with two examples, which will be especially important in the sequel.
First, we translate the braid group action on Uh discussed in Section 8.1.
Proposition 9.1.2 The braid group BQ of g acts by Q(g)-aigebra automor-
automorphisms on Uq as follows:
Tt(X+) = -X-Kt, Ti(Xr) = -K^X+, T^Kj) = KjK'^,
The divided powers (Xf)^ are denned as in Subsection 8.1 A.
The formulas in this proposition are obtained in an obvious way from those
in 8.1.2. For example,
TAK) = TAed:)hH3) = ed3hH3e~d3(l3thHj
= ed3hHJe-dtatjhH3 _ X K~a%3
(note that we used the fact that (didij) is symmetric).
Root vectors Xp can now be denned exactly as in 8.1.4. We let U^ Uq
and U~ be the Q(g)-subalgebras of Uq generated by the X^~, the K~ and
the X~, respectively, and write U^° = U°.U+, U^° = U~.U®. Further, for
P = T,i kiai € Q> we let KP = Ui Kki%\then^ TW(K0) = Kw{C) for all weW.
We have the following analogue of 8.1.7 and 8.1.8:
Proposition 9.1.3 Multiplication defines an isomorphism of vector spaces
over Q(#)
u- ® u°q ® u+ - uq.
Moreover:
(i) theproducts (X+)t-(X+v)*-(X+vi)*—.. .(X+)*S wheret=(t1,... ,tN)
€ NN? form a basis ofU+;
(ii) the products Ks = K^K? ... Ksnn, where s = (sx,..., sn) € Zn, form a
basis
9.1 Rational forms 283
(iii) the products (X')r = (X^(X^ ... (X^Y*, wherer = (n,..., rN)
e NN, form a basis ofU~. |
One should not think, however, that every property of Uh translates into a
property of Uq, and vice versa. We give three (counter) examples.
First, while C/^(g) is isomorphic as an algebra to f/(9)[[ft]] (if dim(g) < oo),
it is not true that Uq($) <g) <C(q) is isomorphic to J7(g)®C(g). This follows,
Q() ?
for example, from the fact that, for any Lie algebra g over a field, the only
invertible elements of U(g) are the non-zero scalar multiples of the identity
(see Bourbaki A972), Chap. 1, §2, Exercise 2a). Nevertheless, we shall see in
the next chapter that, up to a rather trivial twisting, there is still a one-to-one
correspondence between the finite-dimensional representations of Uq(§) and
those of g.
The second property concerns the twisting just mentioned. Since it will be
used later, we formulate it as
Proposition 9.1.4 For each sequence of signs (<7i,..., an) E { ± l}n, there
is an algebra automorphism of Uq given by
The proof is an easy verification. Note that, except for the identity auto-
automorphism corresponding to A,..., 1), there are no analogous automorphisms
of Uh- For, if there were such automorphisms, mapping Hi to rji say, then on
reducing the equation
a edihHi _ edthrjz
(mod ft), we obtain that Oi — \. Note also that, again except for the identity,
these algebra automorphisms do not respect the coalgebra structure of Uq.
Let us formulate 9.1.4 a little more invariantly. Let Q% be the group of
homomorphisms Q —>Z2 = {=tl} (the product is pointwise multiplication).
Then, the assertion is that Q% acts as a group of automorphisms on Uq by
a.K0 = a(f3)K0, a.X+=a(a)X+, a.X~ = X~
for all a € A+, /3 € Q, a € Q\. Note that W acts on Q\:
moreover, the action of QJ on Uq obviously extends to an action of the semidi-
rect product W KQ^-
Finally, the universal R-matrix does not quite translate to Uq. For the q-
exponentials appearing in 8.3.9 involve infinite sums, and so are not elements
284 9 Specializations of QUE algebras
of Uq(&Uq. Furthermore, there is no element of Uq <S> Uq corresponding to the
factor
in 1Z. We shall see in Subsection 10.ID, however, that even though the
universal R-matrix does not exist as an element of Uq (8>[/q, it nevertheless
acts on any tensor product of finite-dimensional t/q-modules!
C The Harish Chandra homomorphism and the centre of Uq We now
discuss briefly the centre Zq of Uq. Proofs and further details will be given
in the next chapter, after certain necessary facts about the representation
theory of Uq have been obtained.
Any element z € Zq can, of course, be written as a linear combination of
the basis elements of Uq given in 9.1.3. Since z commutes, in particular, with
the Ki for all z, it follows that
E) z=
where the ipr^ € Uq and
= <(mu...,mN) € N^ | ^771^ = 771
^ i '
The proof of the following result is almost exactly as in the classical case.
Definition-proposition 9.1.5 The map hq : Zq -» C/J defined by hq(z) =
ytyo is a homomorphism of algebras, called the Harish Chandra homomor-
homomorphism. I
Any element tpG [/J may be regarded as a Q(g)-valued function on the
weight lattice P in an obvious way: if (p = YYi=i K\% > wnere ^1^2, • • • ,tn € Z,
set
and extended to C/J by linearity. Define an automorphism of Q(g)-algebras
7q : Uq —>• Uq by setting ^yq(Ki) = qiKi. It is clear that
for all (f G Uq, where p is half the sum of the positive roots of 9 (see the
Appendix).
As we saw in the previous subsection, the semidirect product W X Q% acts
as a group of automorphisms of Uq . Let W be the subgroup generated by all
conjugates aWa~l of W by elements a ? Q%-
9.1 Rational forms 285
Theorem 9.1.6 The homomorphism 7 ohq : Zq —> U® is injective, and its
image is precisely the set U® w of fixed points of the action ofWonU®. |
Thus, an element (/?o,o ? U® occurs as the '[/? part' of an element z G Zq as
in E) if and only if 7~1((/?o,o) ? U®w. In this case, there is an inductive pro-
procedure for calculating the remaining coefficients tprj in E), but this, like the
proof of 9.1.6, will have to wait until Subsection 10.IB. We content ourselves
at this point with the following example.
Example 9.1.7 Let g = sZ2(<C). Then, W = W and U™ consists of the
Laurent polynomials in K\ which are invariant under K\ »-> K{*. Thus,
W is generated as an algebra over Q(g) by
r- 1
It is easy to check that the quantum Casimir element
lies in Zq) and, since 7q 1(hq(Q)) = (/?, it follows from 9.1.6 that Q generates
Zq as a Q(g)-algebra. 0
We conclude this subsection with the quantum analogue of Harish Chan-
Chandra's theorem on the central characters of the classical enveloping algebra U.
Note that any weight A G P defines a homomorphism Uq —> Q(g) by sending
Ki to q(a%'A) (cf. the discussion following 9.1.5); let \q,\ '• Zq ~* Q(^) be its
composite with the homomorphism 7 o hq in 9.1.6.
Theorem 9.1.8 Let X, /j e P. Then, xq,a = Xq^ if and only if ji = w{X) for
some w G W. |
D A geometric realization We conclude this section by outlining an inter-
interpretation, due to Beilinson, Lusztig & MacPherson A990), of Uq(sln+i(<E,))
in terms of spaces of flags in vector spaces over finite fields. It is based
on a rather general combinatorial construction, which has other interesting
applications.
In fact, suppose that F is a finite group which acts transitively on a finite
set X. Let F be the free vector space over a field k with basis the set A of
orbits of the diagonal action of F on X x X. We define a k-algebra structure
on F as follows. For 0, Of', O" G A, choose (x1,x2) G O" and let cg"o, be
the number of elements xGl such that (xi, x) G 0 and (x, X2) G 0' (this is
286 9 Specializations of QUE algebras
obviously independent of the choice of (xi, x2)). Then, one defines a product
on F by
O"
The unit element of F is the diagonal in X x X (which is a single F-orbit).
As an example, let X = F with the action given by left multiplication.
Then, it is easy to see that F is the group algebra k[T] of F. Another example
can be found in Subsection 10.2A.
We now show how this construction, with some modifications, can be used
to construct Uq. Let V be a vector space of dimension m over a finite field
with r elements, and let Flagn(V) be the set of (n -f l)-step nitrations
F = @ = VQCV1CV2C-..CVn+1 = V).
The finite general linear group GL(V) acts naturally on Flagn(V), and its
orbits are the fibres of the map which associates to the flag F the (n-hl)-tuple
of integers
(dim(VVV&),dim(V'2/Vri),... ,di
If we have a second flag
f' = (o = y0' c v{ c y2' c • • • c v^i = v),
the subspaces Wij = V^_i-|-(VinV^/) form an (n H- lJ-step filtration of V:
0 = Wio C Wn C • • • C Wm+i = W20 C • • • C Wn+ln+1 = V.
Let Aij = dim(Wij/Wi!7-_i), 1 < 2, j < n-l-1 (we interpret Wio as Wi_in+i).
Obviously, J^^ A^ = m.
Proposition 9.1.9 Tl2e map \yi2ici2 associates to a pair of flags (F, F') the
matrix A = (Ai<7-) is a bijection between the set Om,n of orbits of the diagonal
action of GL{V) on Flagn(F) x Flagn(F) and the set Am,n of all (n + l)x
(n+1) matrices with non-negative integer entries, the sum of whose entries
is m. |
Let O{A) be the orbit in Flag(V)n x Flagn(Vr) corresponding to a matrix
A e Am,n. If A, A' and A" e A^n) choose (Fi,F2) G O(A") and let c^(r)
be the number of flags F such that (FUF) G O(A) and (F, F2) G O(A').
Proposition 9.1.10 For any A, A', A!' e Am,n, there exist integers c0,
ci,..., q, for some ? > 0, such that
ca'a> (r) = co + cir H 1- c^?
9.1 Rational forms 287
whenever r is a prime power. Define c\ A, G Q(g) by
Let Fm,n be the free vector space over Q(g) with basis An,n- Then, the
formula
c?A,A"
defines the structure of an associative algebra over Q(g) on /^m,n with unit
element Yl^, as A runs over the diagonal matrices in Am,n- I
It is convenient to renormalize the structure constants cA A, by multiplying
them by certain powers of q. In fact, for A G An,n> set {A} = q~sA G Fm^ni
where
and the sum is over {z, j, /c, / | i > /c, j < I}. Then, we have
for some cAA, G
Let An be the set of (n + 1) x (n 4- 1) matrices with integer entries, the
off-diagonal entries being non-negative. If A G An and ? G Z, set
where / is the identity matrix. If A, A', A" G *4n are such that the sum of
the entries in A, in A! and in A!' are the same, then, by taking t sufficiently
large, we can obviously arrange that tA, tA! and tA!' G An,n for some m.
Proposition 9.1.11 Let q' be an indeterminate independent of q. There is
a unique element Ia'a1^^') ^ Q(<l)W} sucn that
for all sufficiently large t if the sum of the entries in A, in Af and in A" are
the same, and jA A, (g, q') =0 otherwise.
Let Fn be the free (Q(q)-vector space with basis An (we write [A] for the
basis element corresponding to A ? An to avoid confusion). Then, the for-
formula
A"eAn
288 9 Specializations of QUE algebras
defines the structure of an associative algebra (without unit) over Q(g) on
Fn. |
One thinks oiFn as being a kind of limit of the F^^ as m —> oo.
Finally, let A^ be the set of all (n-h 1) x (n-h 1) matrices with non-negative
integer entries and all diagonal entries equal to zero. For A e A^ and integers
ri,..., rn+i, consider the formal infinite sum of elements of Fn given by
A(n, . . . , rn+1) - ? ^ir1 + ...+dn+1rn+1 [A + ^
D
where the sum is over all diagonal matrices D = diag(di,... ,dn+i) with
integer entries. Let F?° be the free Q(g)-vector space with basis the elements
A(r\,..., rn+i) above. One shows that the product of two elements
computed term-by-term using the product in Fn, is well defined and in
Thus, F^ is an associative algebra over Q(g). It has a unit given by
as D runs through all the diagonal matrices with integer entries.
Theorem 9.1.12 There is an isomorphism Uq —> F?° of algebras over
given on the generators of Uq by
where, in the first (resp. second) sum, A runs over all the matrices in An
with 1 in the ith row and (i + l)th column (resp. in the (i + l)th row and ith
column) and zeros elsewhere, and in the third sum, D = diag(di,..., dn+i)
runs over the diagonal matrices in An. |
Related results can be found in Subsection 9.3D.
9.2 The non-restricted specialization
To obtain from Uq a well-defined Hopf algebra by specializing q to an arbitrary
non-zero complex number e, one constructs an integral form of Uq. This is an
*4-subalgebra Ua of Uqi where A = Z[q, q~1), such that the natural map
A
is an isomorphism of Q(g)-algebras. One then defines
9.2 The non-restricted specialization 289
using the homomorphism A —> C taking q to e. One could replace C by Q(e)
here, or even by Z[e, e], and we shall find it necessary to do this in the next
section.
There are two candidates for f/4 which lead to different specializations
(with markedly different representation theories) for certain values of e. We
shall discuss them in this section and the next.
A The non-restricted integral form Introduce the elements
jy~ nrn K~^~n~rn
F) [tfi;m]* = ^ *i * eUo (m>0),
Qi-Qi
where qi — qd%.
Definition-proposition 9.2.1 The algebra f/4 is the A-subalgebra of Uq
generated by the elements X*, X~, K^1 and [Ki; 0}qt for 1 < i < n. With
the maps A, S and e defined on the first three sets of generators as in 9.1.1,
and with
G) A,([tf4; 0],,) = [*•<; 0],, ® K{ + K~x ® [K{; 0],,,
(8)
(9)
Ua becomes a Hopf algebra. Moreover, Ua is an integral form ofUq. |
Remarks [1] The defining relations for Ua are as in 9.1.1, but replacing B)
by
and adding the relation
A0) (qi-q
[2] The elements [Ki; m]qt are in Ua f°r aU ^n G N, for it is easy to see
that
[Ki; m]q% = [Ki; 0]qtqrm + Ki[m)q%. A
We now define, as above, Ue = f/^0C for any e e<Cx. Define f/e+, U~ and
A
U® in the obvious way.
Proposition 9.2.2 If e2d% 7^ 1 for all i, then Ue is generated over C by
elements Xf, X~ and K^1 with defining relations obtained from those in
9.1.1 by replacing q bye. Moreover, in this case, the products {X~)rK8{X+)t
in 9.1.3 are a basis ofUe over C |
One might expect that the specialization U\ (g) would be isomorphic to the
classical universal enveloping algebra U($). In fact, this is not quite true.
Note that, by A), the Ki are in the centre of f/i, and by A0) that Kf = 1 in
U\. From this, it is easy to deduce
290 9 Specializations of QUE algebras
Proposition 9.2.3 The quotient of Ui(q) by the ideal generated by the
Ki - 1 is isomorphic to the classical universal enveloping algebra U(cy). |
On the other hand, the specialization U^~ (g) of U+(q) has generators Xf
and defining relations C), and hence is isomorphic to the universal envelop-
enveloping algebra of the nilpotent subalgebra n+ of g generated by the classical
analogues of the Xf. In particular, since U(n+) is an integral domain, so is
U^~ (g). Similar remarks apply, of course, to [7-j~, and it is obvious that U® is
an integral domain. This proves the first part of
Proposition 9.2.4 The rings Uq and Ua are integral domains. If e2d% ^ 1
for all i, then Ue is also an integral domain. |
B The centre Suppose first that e G <CX is not a root of unity. Let Ze denote
the centre of Ue, and define U®w and the Harish Chandra homomorphism
he : Ze —> U® as in Subsection 9.1C, and the homomorphism 7e : [7e° —> U® by
"Ye(Ki) = €d%Ki. Further, for any A G P, let Xe,A : Ze -* (C be the composite
of 771 o he : Ze —* f/e° with the homomorphism f/e° —> C which sends ^ to
e(^ , A) xhen, as in 9.1.6, we have
Proposition 9.2.5 Suppose that e G <CX is not a root of unity Then, the
map 7e~x o foe is injective and its image is U® w. Moreover, if X, fi G P, we
have Xe,A — Xe,^ if and only if \i — w(X) for some w G W. |
Note In the remainder of this section, we assume that e is a primitive ?th root
of unity, where ? is odd, and ? > di for all i.
Our aim is to describe the structure of the centre Ze of Ue. We shall use
a different approach from that used in the generic case, for the following rea-
reason. One can show that the inductive procedure which, in the generic case,
associates to each element tp G U®w an element z^ G Zq (see the discus-
discussion following 9.1.6), can be specialized to give a well-defined homomorphism
U®w —> Ze. This homomorphism is injective but, unlike the generic case, it
is not surjective (see Remark [4] following 9.2.19). Thus, the Harish Chandra
approach now captures only a part of the centre.
We begin our study of Ze with
Proposition 9.2.6 Theelements (X±)? fora G A+, andK[ fori = 1,... ,n,
lie in Ze.
Outline of proof The second part is obvious, for it is enough to prove
that K[ commutes with each X^, and this is immediate from the equation
KiXfK'1 = e±d'a^Xf. The first part follows from certain relations in U€
proved in Lusztig A990b). |
9.2 The non-restricted specialization 291
For a e A+, C e Q, let x^ = (X^)e, kp = K^\ we shall often write xf for
x^t. Let Zq (resp. Z^, Zq) be the subalgebra of Ze generated by the x^ and
the kf1 (resp. by the z±, by the fcf1).
Proposition 9.2.7 (i) We have Z± c Vf and Z$ c J7e°.
Cii^) Multiplication defines an isomorphism of algebras
^Q Q9 ^Q (X) ^Q > ^0*
fiiij Zq is the algebra of Laurent polynomials in the ki, and Z^~ is the poly-
polynomial algebra with generators the x^ .
(iv) We have Zq = XJf n Ze.
(v) The subalgebra Zo of Ze is preserved by the action of the braid group
automorphisms Ti.
(vi) Ue is a free ZQ-module with basis the set of monomials (X~)rK8(X+)t
in the statement of 9.1.3 for which 0 < r^ , s^, tk < ?, for i = l,...,n,
Outline of proof Parts (i), (ii), (iii) and (vi) follow from 9.2.2 and the
analogue of 8.1.6 for Ue. Part (iv) is proved by considering the action of Zo
on 'diagonal' ?/e-modules (see Subsection 11.1A). Part (v) follows from part
(iv) and 8.1.6(i). |
The preceding proposition shows that Ue is a noetherian Zo-module. It
follows that Ze C Ue is finitely generated over Zq , and hence integral over Zq .
By the Hilbert basis theorem, Ze is a finitely-generated algebra. Thus, the
amne schemes Spec(Ze) and Spec(Zo), namely the sets of algebra homomor-
phisms from Ze and Zq to C, are algebraic varieties. In fact, it is obvious that
Spec(Zo) is isomorphic to (C2iV x (<Cx)n, a complex amne space of dimension
equal to that of g with n codimension one hyperplanes removed. Moreover,
the inclusion Zo ^ Ze induces a projection map r : Spec(Ze) —> Spec(Z0)
and, by the Cohen-Seidenberg theorem, r is a finite (surjective) map. More
precisely, we have
Proposition 9.2.8 Spec(Ze) is a normal affine variety and r : Spec(Ze) -»
Spec(Zo) is a finite map of degree ?n. |
This means that the fibres of r have at most ?n points, and that the generic
fibre has precisely ?n points. The computation of the degree of r is carried
out in Subsection 11.1 A; it depends on the representation theory of Ue.
Example 9.2.9 Suppose that g = «s/2((C) and that ? is odd. Then, Ze contains
the quantum Casimir element
"" ~~ / i \ o "T~ ¦**¦ 1 -^»-1 •
292 9 Specializations of QUE algebras
By an easy induction on r, one shows that
Taking r = ?, we obtain the relation
_ r+r-
It is not difficult to show that the left-hand side is a polynomial in 12, all of
whose coefficients are complex numbers (not involving K\), except the term
independent of 12, which is equal to
fci + fcf1
In fact, Ze is generated over Zq by Q subject to the single relation A1). 0
We conclude this subsection by discussing the relation between the centre
and the Hopf structure of Ue. To compute the effect of the comultiplication
on the ?t\i powers, we need the following lemma, which is easily proved by
induction.
Lemma 9.2.10 Suppose that a and b are elements of an associative algebra
over C such that ab = e2ba, where e e <CX. Then, for all ?>0,
i-k
: ' ' \k\ uu
k=0
In particular, if e is a primitive ith root of unity and ? is odd, then (a 4- h)* =
p , i p _
<r -f ?r. |
It follows immediately that, if Ae denotes the comultiplication of f/e,
Unfortunately, there is no such simple formula for A(x^) when a is a non-
simple root. Nevertheless, one can prove
Proposition 9.2.11 Zo is a Hopf subalgebra of Ue, as are Z§, Z^° and
y<0 .
The meaning of the notation is clear: Z§ — ZqZ^ , Z§ — ZqZq .
It follows from 9.2.11 that Spec(Z0) inherits a Lie group structure from the
Hopf structure of Ue. In fact:
9.2 The non-restricted specialization 293
Proposition 9.2.12 The formula
, zz' - z'z
{z , z } — lim , ^ _ _^.
defines a Poisson bracket on Zq which gives Spec(Zo) the structure of a
Poisson-Lie group. |
The chosen normalization of the Poisson bracket will enable us, in the next
subsection, to identify Spec(Zo) with a Poisson-Lie group studied in Chapter
1.
C The quantum coadjoint action In this subsection, we assume that e
is a primitive ?th root of unity, where ? is odd and ? > di for all i. We set
Define derivations x_f of Uq by
\iZ) ±.% \u) ~
Note that, if we specialize to q = e, we obtain at first sight an indeterminate
result, since the (Xf)? are central and [?\eJ> — 0. However, we have
Proposition 9.2.13 On specializing to q = e^ A2) induces well-defined
derivations ofUe. In fact, we have the following explicit formulas:
\ E
and x~ is obtained from x_f by using
r^T r
o^i -'-wo — ±-i
where i •—> i is the permutation of the nodes of the Dynkin diagram of g such
that wo(cti) = — ai- |
We should like to exponentiate these derivations to obtain automorphisms
of Ue. To do this, we must enlarge Ue. Let Zq be the algebra of formal power
series in the xj, a G A+, and the kf1, i = 1,..., n, which define holomorphic
functions on C2iV x (<Cx)n. Let
Ze = Ze ® Zo.
Zq
Then, another direct computation gives
294 9 Specializations of QUE algebras
Lemma 9.2.14 The series
n=0
converge, for all t G (C, to well-defined automorphisms of the algebra Ue over
C. |
Let Q be the group of automorphisms of Ue generated by the one-parameter
groups of automorphisms appearing in the previous lemma.
Proposition 9.2.15 The action of Q on Ue preserves the subalgebras Ze
and Zq, and (hence) acts by holomorphic automorphisms on the complex
algebraic varieties Spec(Zo) and Spec(Ze). Moreover, the action of Q on Ue
is normalized by that of the braid group transformations Ti.
Outline of proof For the first statement, it is enough to show that ZQ is
preserved by the derivations x^. This is proved for the xf by direct compu-
computation, and the general case is deduced from this by using the braid group
action. For the second statement, one proves by a direct computation that
the Ti normalize the Lie algebra generated by the derivations x^. |
The group Q is 'infinite dimensional', and at first sight there seems little
prospect of understanding its action on Spec(Zo). We shall now see, however,
that its orbits are very closely related to the conjugacy classes in the Lie group
with Lie algebra g.
Let G be the adjoint group of g (i.e. the connected complex Lie group with
Lie algebra g and trivial centre), let H be a Cartan subgroup of G, and let
N± be the unipotent subgroups of G with Lie algebra n±. Note that H is
canonically identified with Spec(Zg) by the pairing
(exp(ry), ki) = expB7r¦y/^ia
for rj €t), the Lie algebra of H. The product G° — N-HN+ is well known to
be a dense open subset of G (in the complex topology), called the big cell.
We define maps
X± : Spec(Z^) -+ JV±, K : Spec(Zg) -> H
and a map
7T =XKX+ : Spec(Zo) - Spec(Z0") x Spec(Z^) x Spec(Z+) -> G°
as follows. Fix a reduced decomposition wq = s^ ... SiN, and let X^,..., X^N
be the corresponding negative root vectors of g (see the Appendix: we have
changed notation to X^ to avoid confusion with the generators of U€). Let
9.2 The non-restricted specialization 295
which we regard as a complex-valued function on Spec(Zo). Then, we define
maps X± : Spec(Z^) -> N±, K : Spec(Z0) = H -> H = Spec(Z0) to be the
products
X~ =
(heH).
In the formula for X+, the action of To = T^ ... T^ on g is as described in
the Appendix.
Proposition 9.2.16 The product map n = X~ifX+ : Spec(Z0) -> G° is
independent of the choice of reduced decomposition of wq, and is an (un-
ramified) covering of degree 2n. The set of fixed points of Q on Spec(Z0) is
precisely the pre-image under n of the identity element of G. |
Example 9.2.17 When G = PSL2(C) is the adjoint group of sZ2(C), the map
7T is given by
°\ (ki ° A (l xt\ a
Since tt is a covering map, vector fields on G° can be lifted to vector fields
on Spec(Zo). In particular, we may regard the Chevalley generators Xf~ of g
as left-invariant vector fields on G°, and hence as vector fields on Spec(Zo).
On the other hand, the derivations xf may also be regarded as vector fields
on Spec(Zo). One has the following remarkable relations, which are proved
by direct computation (it is enough to do the cases in which g has rank 1 or
2).
Theorem 9.2.18 As vector fields on Spec(Z0), we have
where the k{ are regarded as complex-valued functions on Spec(Zo). |
This is the basic link between the quantum object, namely the action of
Q on Spec(Zo), and the classical action of G on itself by conjugation. The
following consequences are almost immediate.
Corollary 9.2.19 (i) The action of Q in the tangent space at each of its
fixed points induces the coadjoint action of G on g* (cf 9.2.20(i)).
(ii) If F is a conjugacy class in G, the connected components of 7r~1(F) are
Q-orbits in Spec(Zo).
296 9 Specializations of QUE algebras
(Hi) If O is a Q-orbit in Spec(Zo), the connected components of r~l{O) are
G-orbits in Spec(Ze). |
Remarks [1] Because of part (i), the action of Q on Spec(Zo) is called the
quantum coadjoint action.
[2] Part (ii) makes sense since every conjugacy class in G intersects G°
(because, for example, every element of G is conjugate to an element of the
Borel subgroup B+ = HN+).
[3] Corollary 9.2.19 is analogous to the description of the centre of the
universal enveloping algebra in characteristic p - see Kac & Weisfeiler A976).
[4] One can show that the image of the map U®w —> Ze described at the
beginning of Subsection 9.2B is exactly the (/-invariant part of Ze. A
We conclude this section by showing that the Poisson-Lie group structure
on Spec(Zo) described in the previous subsection is closely related to that on
G defined in 1.3.8. In fact, when G is equipped with the Poisson-Lie structure
described in that example (or any non-zero multiple of it), it is clear that the
subgroup of G x G given by
G* = {(n_?, n+t~l) \n± e N±,te H}
is a dual Poisson-Lie group of G. Define a map ip : Spec(Zo) —¦> G* by
Note that n = n o -0, where n : G* —> G° is the unramified covering of degree
2n given by n(b- , 6+) = 6_F+)~1. We have
Theorem 9.2.20 Let G be a complex simple Lie group equipped with the
Poisson-Lie group structure defined in 1.3.8, but with the standard bilinear
form on the Lie algebra of G replaced by the Killing form. Let G* be the
dual Poisson-Lie group of G defined above. Then:
(i) the map ip : Spec(Z0) —> G* is an isomorphism of Poisson-Lie groups;
(ii) the orbits of Q on Spec(Zo) are precisely its symplectic leaves. |
If we recall from Subsection 1.5B that the symplectic leaves of Poisson-Lie
groups are the orbits of the dressing transformations, it is tempting to think
that the action of Q on Spec(Z0) should factor through the dressing action
of G on G*. However, there does not seem to be any homomorphism Q —* G
with this property.
9.3 The restricted specialization
In this section, we discuss the second of the two specializations mentioned in
the introduction.
9.3 The restricted specialization 297
A The restricted integral form The restricted integral form is defined as
follows. As usual, qi = qdl.
Definition-proposition 9.3.1 The algebra U^s(q) is the A-subalgebra of
Uq{q) generated by the elements {X+)(r\ (X~)^ and Kfl for 1 < i < n
and r > 1. It is an integral form of Uq(§) and a Hopf algebra over A with
comultiplication given by
k=0
k=0
counit given by
eq{Kt) = l,
and antipode given by
S(K) = K
sq((x-){r)) = {-iyqr(r+l\x-)^Ki. i
The proof that U^s really is an integral form of Uq is non-trivial. It proceeds
by constructing an ^4-basis of f/^s, analogous to the Q(g)-basis of Uq given in
9.1.3. To do this, one first shows that the root vectors X^ defined in Section
9.1 lie in U^s. This follows from the following lemma.
Lemma 9.3.2 For i = 1,... ,n, T^C/Jf8) - U%s.
Proof It suffices to show that Ti and T~l take each generator of U^s into
U^s. This is a straightforward computation. |
Fix a reduced expression wq = s^ ... SiN of the longest element of the Weyl
group of g and, for r G N, set
Let UrJ(s + (resp. U^s~) be the Asubalgebra of U%s generated by the (X+)(r)
(resp. by the (X")(r)) for alH - 1,... ,n, r G N, and let U%s0 be the A-
subalgebra of U^s generated by the Kfl and the
for alH = 1,..., n, c G Z and r G N. (It follows from A3) below that these
elements of U® do, in fact, belong to U^s.) Then, we have the following
result, which includes 9.1.3 as a special case.
298 9 Specializations of QUE algebras
Proposition 9.3.3 For any choice of reduced decomposition ofwo,
(i) the set of products
where tu t2,..., tN G N, form an A-basis ofUTj;s+ and a Q(g)-basis ofU\es + ;
(ii) the set of products
where v\, r2,..., rN G N, form an A-basis ofU^s ~ and a (Q(q)-basis ofUvqes ~;
(Hi) the set of products
where si,..., sn G N and each Oi is zero or one, form an A-basis of U^
and a <§(q)-basis ofUTqes0;
(iv) multiplication defines an isomorphism of A-modules
In particular, U%s±, U%s0 and U%s are free A-modules. |
Remarks [1] The bases described in this proposition depend on the choice
of the reduced expression of wo. We shall describe in Chapter 14 certain
'canonical' bases which are independent of any such choices.
[2] The importance of the elements K^c derives from the following
L Si Jqt
identity in U™s:
Ki;2t-s-r] fY+^r-t)
t
This can be proved by induction on r for fixed s, after first proving the case
r = 1 by induction on s. A
Using the elements introduced above, one can give a description of U^s in
terms of generators and relations. For simplicity, we restrict ourselves to the
case where g is simply laced, i.e. di = 1 for all i (thus, g is of type A, D or
E). We number the nodes of the Dynkin diagram of g as in Bourbaki A968),
Chaps 4, 5 and 6, except in the Dn case, when we compose the numbering in
Planche V with the permutation i \-> n — i + 1. For any a G A+, let g(a) be
the largest index of any simple root which occurs in a, let ca be the coefficient
of that simple root, and let h(a) = c height (a).
9.3 The restricted specialization 299
Theorem 9.3.4 Suppose that g is of type A, D or E. Then U™s is isomorphic
to the associative A-algebra with generators (X^)^r\ K^1 and J;c , for
a G A+, i = l,...,n,cGZ and r, t G N, and the following defining relations:
the generators K\f1, l' commute with each other,
, r > 0, c> 0,
0<s<r L " J Q L' "J Q
0<s<r ~~~H L' SU
0<t<r,s
T lq
±)W if (a, a,) = 0, i < g(a), h(a) G Z,
r,s>t>0
r,s>t>0
300 9 Specializations of QUE algebras
where, in the last four relations, we assume that (a,af) = —1 and either
a' = oti and i < g(a)
or
height (c/) = height (a) + 1 and g(a') = g(ct). I
As in the non-restricted case, one can now define, for any e G Cx, the
restricted specializations
?/Jf = UT ® Z[e, e-1], Urtes = UrJs ® Q(e)
(it is important for later results to work over Z[e, e] or Q(e) rather than <C).
Hopf algebras f/eres±, C/^^, t/eres0 and U^° are defined in a similar way.
If e is not a root of unity, it is clear that the restricted and non-restricted
specializations coincide,
U€ ^ Urees ^ C,
since in that case [r]e ^0 for all r > 1. But if e is a root of unity, these two
algebras are not isomorphic, as will become clear later in this section.
Note From now until the end of Subsection 9.3C, we assume that e is a
primitive ^th root of unity, where ? is odd and greater than di for all i.
The following result is the counterpart of 9.2.6 in the restricted case.
Proposition 9.3.5 In U^, we have
(i) (X±Y = 0 for all a G A+;
(ii) K[ is central and K?e = 1 for i = 1,..., n.
Proof Part (i) is obvious, since (X±)? - (X±)W[?\q\ in t/J3, and [?}e\ = 0.
The first assertion in (ii) is also obvious, and the second follows on specializing
the relation
p p
\Kl;
r=l r=l L
in t/^es. |
Remarks [1] It is clear from its definition that, if 0 < Si < ?, |^;0 lies in
L J et
the Q(e)-subalgebra of ?/eres generated by Kf1, and that, for all Si G N,
9.3 The restricted specialization 301
It follows that f/eres'° is generated as a Q(e)-algebra by the Kfl and the
hi-
res
A
[2] We define the restricted integral form and specialization of the coordi-
coordinate algebra Tq as follows (cf. Remark [5] at the end of Subsection 9.1A).
Let U\ be the set of all Q[g,g~1]-linear maps U%?
and let Ta -^H U\. We define
Ti = TA <g> Q(e).
Taking e = 1, one can show that
is the coordinate algebra of the simply-connected complex algebraic group
with Lie algebra g. A
B A remarkable finite-dimensional Hopf algebra In this subsection,
we show that ?/eres can be 'factorized' into a kind of 'product' of the classical
universal enveloping algebra and a very interesting finite-dimensional Hopf
algebra. This has important implications for the representation theory of
?/eres, as we shall see in Chapter 11. We define this finite-dimensional Hopf
algebra in this subsection, and describe the factorization in the next.
The origin of the factorization is the following property of e-binomial coef-
coefficients, which is easily deduced from the identity
771—1 771
k=Q k=0
in Q(e)[?], ? being an indeterminate, and the observation that
k=0
Lemma 9.3.6 Let e be a primitive ?th root of unity, where ? is odd and
greater than one. Let r, s ? N, and write r = ro + ?r\, s = so 4- ?s\, where
0 < r0, s0 < ?, ri, si > 0, r > s. Then,
where ( ^ I is an ordinary binomial coefficient. |
Now, in C/Js we have the following evident identity (already noted in 9.3.4):
302 9 Specializations of QUE algebras
Using the lemma, we deduce that, in ?/eres,
(f) (f)
It follows that Urees is generated as a Q(e)-algebra by the Xf, (Xf)^\ Kfl
and \K^° , where 0 < r^ < ? and i = 1,..., n. The factorization will essen-
essentially be into the part generated by the Xf1 and the remainder consisting of
the ^th divided powers.
More precisely, let Ufn (resp. Uf%) be the Q(e)-subalgebra of Urees (resp.
the Z[c, c-^-subalgebra of U\%) generated by the Xf, Kfl and \Kf] ,
where 0 < n < I, i = 1,..., n. Define subalgebras Uf^~, U?%°, and U^ of
Ufj? in the obvious way. The following result is analogous to 9.3.3 (although
it is not a consequence of it).
Proposition 9.3.7 Suppose that g is of type A, D or E, and that e is a
primitive ?th root of unity, where ? is odd and greater than one. Then, for
any choice of reduced decomposition ofu>o,
(i) Uf%+ is a free Z[e, e~1]-module of rank ?N with basis the set of products
where 0 < t\, ?2, • • •, tjsf < ?;
(ii) Uf%~ is a free Z[e, e~l]-module of rank ?N with basis the set of products
where 0 < ri, r2,..., rjy < ?;
(iii) Uf^0 is a freeZ[e, e~1]-mociuie of rank B?)n with basis the set of products
where 0 < Si < ? and each Oi is zero or one;
(iv) multiplication defines an isomorphism ofZ[e, e~l]-modules
A similar, but more complicated, result holds when g is not simply laced.
Remark One shows in a similar way that the Hopf algebra Ufn has finite
dimension 2n?2N+n over Q(e). The basis is as in the preceding proposition. In
this case, however, the elements in part (iii) may be replaced by the products
9.3 The restricted specialization 303
where 0 < s{ < 21, since the [K^°] for 0 < st < I clearly lie in the Q(e)-
subalgebra of Ufn generated by the K^1, and since Kf^ = 1 (we are still
assuming that g is simply laced). A
One can also describe Ufn in terms of generators and relations.
Proposition 9.3.8 Suppose that g is of type A, D or E. Then, Ufn is
isomorphic to the associative Q(e) -algebra with generators X^ and Kf1, for
a e A+, i = 1,..., n, and the following defining relations:
Y- Y- V+ — X ^ Kj
i^OLj ~~ ^OLj^OLi — Oi,j _ I
X = XX
±, if (a, at) = 0, i < g(a), h(a) €
(Xa ) = 0, K{ = 1,
w^here, in the last three relations, we assume that (a, a') = — 1, i < g(a) and
either
or
height (a7) = height (a) + 1 and g(af) = g(a). |
We conclude our discussion of Ufn with
Proposition 9.3.9 The finite-dimensional Hopf algebra Ufn is quasitrian-
gular, with universal R-matrix 7Ze given by
a€A+\r=0 Ue-' /
Here, ea = edi if a is in the Weyl group orbit of the simple root a^; Kp =
Qi = < ^^miai | 0 <rrii < ? for all
This formula is due to Rosso A992c), who proved it by using the quantum
double method (see Section 8.3). We shall omit the details, but we note that
304 9 Specializations of QUE algebras
the formula cannot be deduced directly from the formula for the universal
R-matrix of f/^(g) obtained in Chapter 8 since, as we observed at the end of
Subsection 9.IB, that formula cannot be translated to U*es, and hence cannot
be specialized.
It is unlikely that ?/fes is quasitriangular in the strict sense, since the quan-
quantum double method would suggest that any potential R-matrix would be an
infinite sum of elements of U*es <g) ?/eres. See, however, Subsection 10.ID.
C A Frobenius map in characteristic zero The definition of ?/eres mimics
that of the Chevalley-Kostant Z-form Uz of the classical universal enveloping
algebra U (over <C). We recall that Uz is the subring of U generated by the
divided powers
(jf) = ) reN.
(Here, and elsewhere in this section, we use a bar to distinguish the generators
of U from those of ?/eres.)
The following result gives a simple relation between Uz and U^s. Let
U[es = U%s <g> Q
be the Hopf algebra over Q obtained by specializing q to 1, and let U[es be
the quotient of U{es by the ideal generated by the Ki — 1 (it is clear that the
Ki are central in U{es). The following result is the analogue for the restricted
specialization of 9.2.3.
Proposition 9.3.10 There is an isomorphism of Hopf algebras over Q
which takes Xf to Xf. I
Suppose now that p G N is an odd prime, and let Fp be the field with p
elements. The Hopf algebra
over Fp is the hyperalgebra of the algebraic group Gjfp over Fp associated to
g. This is clearly analogous to the construction of t/J j from U^s. The next
result shows that this is more than an analogy.
Let Ul^l be the quotient of U\^ by the ideal generated by the K\ — 1, and
let ?/]pn, the restricted enveloping algebra, be the subalgebra of U?p generated
by the Xf~ (we shall see the reason for the term 'restricted' in Subsection
11.2B).
9.3 The restricted specialization 305
Proposition 9.3.11 Suppose that ? — p is an odd prime. Then, as Hopf
algebras over Wp,
Note that, since e is a primitive pth root of unity in this situation, there is
a well-defined ring homomorphism TL[e1e~l] —> 1FP which takes e to 1.
Recall that there is a homomorphism of Hopf algebras over 1FP
Fr:UWp->UFp,
called the Frobenius map, such that
jf ±)(*7p) if p divides r,
^ 0 otherwise,
(see Jantzen A987), for example). Moreover, the kernel of Pr is the two-sided
ideal of Uwp generated by the augmentation ideal of [7jpn (the kernel of its
counit).
The following result provides an analogous map for U*es (in characteristic
zero!). For the remainder of this subsection, we assume, in addition to the
usual conditions on ?, that if Q is of type G2, then ? is not divisible by three.
Theorem 9.3.12 (i) There is a unique homomorphism
FYe:t/fs-t/Q|Q(e)
of Hopf algebras over Q(e) such that Pre(Ki) = 1
0 otherwise.
(ii) The kernel of Pre is the two-sided ideal of f/eres generated by the augmen-
augmentation ideal ofllfn (the kernel of its counit).
(Hi) Pre restricts to a homomorphism of'Z[e, e~ ^-modules
FYe:U™i^Uz®Z[e,6-1}. |
Remarks [1] Suppose that ? — p is an odd prime. Since Fre(Ki) — 1, there is
an induced homomorphism
306 9 Specializations of QUE algebras
By 9.3.11, if we tensor over 1FP, the source and target algebras both become
C/ifp, and clearly Pre becomes Fr. This gives the first proof, working directly at
the algebra level, of the existence of a homomorphism U^p —> Uwp satisfying
A4). The classical proof goes via the algebraic group G^p over Wp associated
to g: taking the pth. power of each of the matrix entries of G^p (in a suitable
matrix representation) defines an endomorphism of the coordinate algebra
lFp[GiFp]; one checks that the dual of this map preserves the hyperalgebra
Uwp C Fp[GiFp]*, and that it is given by the formulas in A4).
[2] Parts (i) and (ii) of the theorem make precise the 'factorization' property
mentioned at the beginning of Subsection 9.3B.
[3] Dualizing the Probenius map Pre, we obtain an embedding
^q <8> Q(e) C Te
Q
of Hopf algebras over Q(e). Thus, the classical coordinate algebra Tq appears
as a Hopf subalgebra of the quantum coordinate algebra Te.
[4] Despite the analogies between Ups and Ujpp1 there are some differences.
These are reflections of the differences between 9.3.6 and its characteristic p
analogue. In fact, let r, s G N with r > s, and write
k=0 fc=0
where 0 < r/c, Sk < p (of course, all but finitely many of the r^ and Sk are
zero). Then, we have the well-known congruence property
0 s (:)(::)(;:) •¦¦<-">¦
(Note that, even if r > s, it may happen that r^ < Sk for some k; in this case,
the binomial coefficient rM is understood to be zero.)
Although formula A5) closely resembles that in 9.3.6, note that there are
only two factors on the right-hand side of the formula in 9.3.6, whereas there
is no bound (independent of r and s) on the number of factors on the right-
hand side of A5). This is reflected in the fact that f/eres is finitely generated,
but C/jFp is not (to generate the latter algebra, one needs all of the divided
powers Xf, (^f)(p), {Xf){p2\ ...). Note also that, whereas all the factors
on the right-hand side of A5) are of the same kind, those on the right-hand
side of the formula in 9.3.6 are not, one being an e-binomial coefficient and
one an ordinary binomial coefficient. This is reflected in the fact that Pr is a
map from U^p to itself, whereas Pre is a map between two different algebras.
In particular, while in the classical case one can consider the iterates Prfc of
the Probenius map, in the quantum situation this is meaningless. A
9.3 The restricted specialization 307
D The quiver approach We conclude this section by describing a combi-
combinatorial realization of the subalgebra U*es-° of Ups, for certain (algebraic)
values of e. We assume throughout this subsection that g is simply laced, i.e.
that the Dynkin diagram F of g has only single bonds.
Fix an orientation of F, i.e. attach an arrow * ^ 3m to each edge * 3m of
F. A representation p of F over a field IF is a collection of finite-dimensional
vector spaces Vi over IF, one for each vertex (or node) of F, and IF-linear
maps Tij '• Vi —> Vj, one for each oriented edge * ^ 3m of F. The dimension
of p is the n-tuple dim(p) = (dim(Vi), dim(V2),..., dim(Fn)). We shall often
identify dim(p) with the element ]T\ dim(F^) cti G Q.
If p' is another representation of F, given by vector spaces V( and linear
maps T[p a morphism from p to p' is a collection of IF-linear maps <\>i : Vi —> F/
such that the diagram
commutes for every oriented edge * v 3m of F. Subrepresentations, quotient
representations, direct sums of representations, etc., are defined in the obvious
way. This makes the category of representations of F and morphisms between
them into an abelian category repr-
The simplest examples of representations of F, apart from the zero repre-
representation for which Vi — 0 for all i, are the representations e$ for which
( 0 otherwise.
This representation is obviously irreducible, and every irreducible represen-
representation of F is isomorphic to some e$. The category repr is not semisimple,
however, for the representations e^, defined, for every oriented edge * y3m
of F, by ""
Vk = {? " = -r,, ^
[ 0 otherwise,
are clearly indecomposable but not irreducible. In general, one has the fol-
following fundamental result of Gabriel A972).
Theorem 9.3.13 A representation pofT is indecomposable if and only if
dim(p) G A+. Conversely, for every a G A+, there is, up to isomorphism, a
unique indecomposable representation pofT such that dim(p) — a. §
Remark The oriented Dynkin graphs F are examples of quivers. In general,
a quiver T is a set of vertices joined by (oriented) arrows, but possibly with
more than one arrow joining each pair of vertices:
308 9 Specializations of QUE algebras
One can then define an abelian category repr of representations of T exactly
as above. It is known that every finite-dimensional representation of T can
be written uniquely as a sum of indecomposables (in particular, this holds for
r).
According to another fundamental result of Gabriel A972), the oriented
Dynkin graphs are characterized as the quivers T for which repr has only
finitely-many indecomposables. A
Suppose from now on that IF is a finite field with m elements. Let Rep(F)
be the complex vector space with basis the set of isomorphism classes of
representations of F, and define a bilinear product on Rep(F) by
where cp, „ is the number of subrepresentations of p isomorphic to p" for
which the quotient representation is isomorphic to p'. This gives Rep(F) the
structure of an associative algebra with unit element (the zero representation),
called the Hall algebra associated to F.
As an exercise, the reader may like to verify the following relations in
Rep(F):
eij = eiej - ejei-> eieij = meijei, e^ei = me^e^.
It follows that
efej — (m -f l^e^ + meje? — 0,
eie'j - (m + 1)^6^- + rae^e; = 0.
We note the similarity between these identities and some of the defining
relations of Uq(§) in 9.1.1.
To make this observation precise, let
(as a complex vector space), and define an associative algebra structure on
Rep(F) by requiring that Ure\®2 and Rep(F) are subalgebras, and that
9.4 Automorphisms and real forms 309
for peRep(F), where (a^) is the Cartan matrix of g and dim(p) = (ri,... ,rn).
Then, we have the following result of Ringel A990).
Theorem 9.3.14 Choose integers fci,..., kn such that ki - k3¦, — 1 whenever
* y 3m is an oriented edge ofT. Then, there is an algebra isomorphism
which takes Kfl to Kfl and X? to K^ei for all i. |
Note that, since m1//2 is not a root of unity, Ure\p^ is generated by the
K~-x and the X2+, so the isomorphism in the theorem is uniquely determined.
Theorem 9.3.14 is important for the construction of 'canonical' bases in
Chapter 14.
9.4 Automorphisms and real forms
The main purpose of this section is to classify the real forms of the Hopf
algebras U€(§). This is necessary for the discussion of unitary representations
of quantum groups in Chapters 10 and 13. In the case in which e is a primitive
^th root of unity, we assume that ? is odd and ? > 2d{ for all i.
A Automorphisms We begin by determining all the automorphisms of
f/e(g) as a Hopf algebra. Recall that a diagram automorphism of g is a
permutation /i of the set {l,...,n} of vertices of the Dynkin diagram of
g such that a^)^) = a^ for all i, j.
Proposition 9.4.1 Let ci,... ,cn E <CX, and let n be a diagram automor-
automorphism of g. Then, there is a unique Hopf algebra automorphism p of C/e(g)
such that
p{Ki)=Klx{i), r
and every Hopf algebra automorphism of f/e(g) is of this form. |
We shall comment on the proof of 9.4.1 after the statement of the next
result.
B Real forms The definition of a real form (or *-structure) on a Hopf
algebra may be found in Subsection 4.IF.
Proposition 9.4.2 The Hopf algebra f/e(g) has real forms if and only if
|e| = l, e e R or e e v/IITR.
310 9 Specializations of QUE algebras
(i) If \e\ — 1, the Hopf ^-structures on E/e(g) are of the form
where fi is a diagram automorphism of g such that n2 = id and the non-zero
complex numbers ci satisfy c^Ci = 1. A second ^-structure, given by data
c[ and n', is equivalent to this one if and only if \i and y! are conjugate in the
group of diagram automorphisms.
(ii) If e G 1R, the Hopf ^-structures on Ue(§) are of the form
k; = k,{1), {xtr = ciX-^K^, (x-y = c^k^
where \i is a diagram automorphism of g such that n2 — id and the non-zero
complex numbers q satisfy c^ —C{. A second ^-structure, given by data c[
and [i1, is equivalent to this one if and only if there is a diagram automorphism
v such that ufi = n'v and <^c~/^ > 0 for all i such that n(i) — i.
(Hi) Ifee v^-TRj then f/e(g) has real forms only if g = soBn+ 1, C). In this
case, any Hopf ^-structure on L^e(g) is of the form
K*=KU (XtY = ciX-Ku (X-)* = (-l)d>c-1K-lX+,
where the non-zero complex numbers Ci satisfy Ci — (—1)^q. A second *-
structure, given by data c[, is equivalent to this one if and only if c[c~l > 0
for all i. |
The main point of the proofs of 9.4.1 and 9.4.2 is to show that any map
77 : f/e(g) —> E/e(g) such that G7 (8) tj) o A = A o 77, and e o 77 = 77 takes K{ to
K1% for some 7^ G J^ N.aj-; note that automorphisms and *-structures both
enjoy this property. If 77 is bijective, the 7^ must be simple roots, and from
this point the proofs are straightforward.
Example 9.4-3 The Hopf algebra automorphisms of ?/e(s/2(C)), for any e G
Cx, are of the form
Ki^Ku X±^c±lX±
for some c ? (Cx. Up to equivalence, there are exactly five *-structures:
e € R : K{ = KU {X+Y = Xfi^i, (Xf)* = K^X+ ;
eelR: K1 = KU (X+)* = -X^Ku (Xf)* = -K^X+ ;
|c| = 1 : K{ = Klt (X+)* = -X+, (Xf)* = -Xf ;
/rTlR: K{=KX, (X?)* = ^ ^
The first three are usually called quantum su2, quantum su^i and quantum
)i respectively (if we let e —* 1 through the appropriate ranges, we obtain
Bibliographical notes 311
*-structures on 5/2 (C), and the sets of elements x G 5/2 (C) for which x* = — x
are su2, st/i,i and s/2(IR), respectively). Note that, whereas st/i?1 and s/2(IR)
are isomorphic as real Lie algebras (cf. 4.1.20), there is no question of their
quantum versions being isomorphic, as they are defined for different values
of e. Note also that the last two *-structures have no classical limit, since
1 i v/irTlR. 0
Remark Masuda et al. A990a) (and a number of other authors) find only
the first three of the real forms because they work with the simply-connected
version f/ep of Ue (cf. Remark [4] in Subsection 9.1A). This is obtained by
adjoining to Ue a square root L\ of K\. For any *-structure on f/p, L\ — L\,
but then it is clear that the last two *-structures above are incompatible with
the relations L^L'1 = e±lxf in J7€p. A
Bibliographical notes
9.1 The rational form Uq was first introduced by Jimbo A985). Theorem
9.1.8 was proved by Rosso A990b); the explicit description of the centre in
9.1.6 is due to De Concini k Kac A990) and Joseph k Letzter A992) (we
have followed De Concini & Kac). See these papers, as well as Lusztig A988,
1993), for the omitted proofs.
9.2 The results of this section can be found in De Concini k Kac A990)
and De Concini, Kac k Procesi A992a). See Kac k Weisfeiler A976) for the
analogous classical theory in characteristic p.
9.3 The restricted integral form of Uq was introduced by Lusztig A988). The
basic properties of /7eres are in Lusztig A989). The Poincare-Birkhoff-Witt
bases, the description of C/4 and its specializations, and the characteristic
zero Frobenius map, including the description of the finite-dimensional Hopf
algebra Ufn and its relation with the classical characteristic p theory, were
obtained in Lusztig A990a) in the simply-laced case, and in Lusztig A990b)
in the general case. Full details of the proofs of all the results stated in
Subsections 9.3A-C may be found in these papers, and in Lusztig A993).
See Jantzen A987) for the analogous classical theory in characteristic p.
See Feng k Tsygan A991) and Ginzburg k Kumar A992) for information
on the cohomology of f/eres(g) when e is not, or is, a root of unity, respectively.
For the basic properties of quivers, see Gabriel A972) and Bernstein,
Gel'fand k Ponomarev A973). Their connection with quantum groups was
noticed by Ringel A990). We have followed the discussion in Lusztig A990d).
See Ringel A992, 1993) for further information.
9.4 The classification of the automorphisms and real forms of Ue is due to
312 9 Specializations of QUE algebras
Twietmeyer A992) in the general case. In fact, he classifies the automor-
automorphisms and real forms of Ue($) when g is an arbitrary symmetrizable Kac-
Moody algebra. Several authors had previously considered the 5/2 case. See
Lyubashenko A992) for a different approach, based on category-theoretic
considerations.
10
Representations of QUE algebras:
the generic case
This chapter and the next are devoted to the representation theory of QUE
algebras. In the present chapter, we discuss C/g(g) and its specialization U€(q)
when e is not a root of unity, leaving the root of unity case to Chapter 11.
In the former case, it turns out that the representation theory is closely
parallel to that of g itself, although one sometimes has to work a little harder
than in the classical case to establish the basic results. A notable example is
the complete reducibility of finite-dimensional f/e(g)-modules when e is not a
root of unity. In the classical case, complete reducibility is most easily estab-
established by transcendental methods: one uses Weyl's unitary trick, regarding
representations of g as representations of the compact Lie group K whose
complexified Lie algebra is g, and then making use of integration over K. In
the quantum case a purely algebraic argument must be found.
The basic facts about the representation theory of f/e(g) when e is not a
root of unity are given in Section 10.1. In Section 10.2, we disuss the quantum
analogue of the Probenius-Schur duality between the representations of the
special linear and symmetric groups. The role of the latter in the quantum
situation is played by the Hecke algebra.
Note Unless indicated otherwise, g denotes in this chapter a finite-dimensional
complex simple Lie algebra. We use the notation in the Appendix, and write
Uq for Uq(cy) when this will not lead to confusion.
10.1 Classification of finite-dimensional
representations
Classically, the finite-dimensional irreducible representations of g are parame-
parametrized by their highest weights. The main result of this section is that, up to
a rather trivial twisting, this continues to hold for Uq(o).
A Highest weight modules In this subsection and the next, we work with
the Hopf algebra C/g(g) over the field Q(g) of rational functions of an indeter-
indeterminate q, defined in 9.1.1. We begin by describing the analogues for C/g(g) of
some of the definitions and results concerning highest weight representations
of g.
314 10 Representations of QUE algebras: the generic case
By a weight, we mean an n-tuple lj — (o;i,... ,u;n) G (Q(#)x)n. If a/ is
another weight, we write lJ < lj if u;^~ u^ = q(a% '^ for some /? G Q+ and all
i = l,...,n.
If F is a (left) [/^-module, its weight spaces are all the non-zero Q(g)-linear
subspaces of V of the form
Xi, — {v G V | i^.v = UiV, i = 1,..., n},
where a; is a weight. A primitive vector in V is a non-zero vector v G V such
that X2+.f = 0 for all i, and v G Fu for some lj.
A highest weight Uq-module is a [/^-module V which contains a primitive
vector v such that V — Uq.v. It follows immediately from 9.1.3 that, if v G K,,
then
and that dim<Q(g)(T?,) = 1. In particular, lj is uniquely determined by V; it is
called the highest weight of V, and t> is called a highest weight vector.
For any weight a/, define the Verma module Mq(u)) to be the quotient of Uq
by the left ideal generated by X+ and Ki - u^l, for i = 1,..., n. Obviously,
Mq (w) is a highest weight module with highest weight a; and canonical highest
weight vector vw equal to the image of 1 G Uq. Moreover, every highest weight
module with highest weight lj is isomorphic to a quotient of Mq(ui). It follows
from 9.1.3, as in the classical case, that Mq(Lj) is a free [/"-module generated
by Vfjj. Finally, since dim(M9(o;)u,) = 1, it follows by the well-known classical
argument that Mq (lj) has a unique irreducible quotient Vq (lj) , and hence that
every irreducible highest weight module is isomorphic to some Vq(ui).
We shall be interested mainly in modules with highest weight LJa^\ of the
form
A) vi=a(ai)q(a*>x\
where a G Q^ ^ ^ P- (We recall from Subsection 9.IB that Q\ is the set of
homomorphisms Q —> { ± 1}.) Note that the partial ordering we have denned
induces, on the weights LJa,\ of a fixed type <r, the usual partial ordering on
P- b/a x < LJa,\ if and only if A — A7 G Q+. In particular, the weights of a
[/^-module with highest weight o/^a are all of the form ljo^ with \i < A. The
reason for the importance of such weights is contained in the next proposition.
As in the classical case, we say that a [/^-module is integrable if it is the
direct sum of its weight spaces, and if the X^ act locally nilpotently on V,
i.e. if, for any v G V, we have (X^)r.v — (X~)r.v = 0 for sufficiently large r.
Proposition 10.1.1 The irreducible Uq-module Vq(lj) with highest weight
lj is integrable if and only if lj — LJa,\ for some a G Q%, ^ € P+ • I
The proof of this result is very similar to that of its classical analogue (cf.
Humphreys A972), Sect. 21, for example). As in the classical case, the reason
for the importance of integrable modules is:
10.1 Classification of finite-dimensional representations 315
Proposition 10.1.2 Every finite-dimensional irreducible Uq-module V is
integrable and highest weight.
Proof The fact that V is highest weight will be proved at the same time as
10.1.7 below. We may thus assume that V = Vq(u)) for some a; G (Q(<7)x)n;
let Vv be a highest weight vector of Vq(ui). Since the vectors (Xi )r'.v^ have
distinct i^-eigenvalues Wiqf2r for all r, they are linearly independent if non-
nonzero. Thus, the local nilpotence of Xf follows from the finite dimensionality
of V. |
Note that the module Vq(u>afi) is one dimensional, the action on the highest
weight vector being
Moreover, it is easy to see that
as ^-modules, where l(a^) = 1 for all i. Thus, it is enough to consider
modules of type 1. If doing so will not lead to confusion, we shall abuse
notation by referring to a weight lji\ simply as A, and Vq(uJii\) as Vq(X).
If W is any highest weight Uq-module with highest weight A G P, its
character ch(W) G Z[P] is denned, as in the classical case, by
ch(W) =
where eM denotes the basis element of the group algebra Z[P] of P corre-
corresponding to /i G P.
Remark If W is as above, one proves, as in the classical case, that the centre
Ze acts on W by the central character Xe,x+p (see Subsection 9.2B). It follows
from 9.2.5 that if two irreducible highest weight modules with highest weights
A and /i have the same central characters, then p + p = w(X + p) for some
Weyl group element w G VF. In particular, by 10.1.2, the finite-dimensional
irreducible L^-modules are separated by their central characters. A
Example 10.1.3 There are exactly two irreducible ^(^(C))-modules of each
(finite) dimension A + 1 > 1, namely the modules ^(oi^a)? & — il, with
basis {^q ,..., vx } on which the action of the generators of Uq is as follows:
The vector Vq is a highest weight vector of Vq(u)a^\). Note that, if a — 1,
these formulas are the counterparts for Uq of those in 6.4.10 for Uh (recall
316 10 Representations of QUE algebras: the generic case
that, to make the translation, one puts q — eh and K\ — ehH). Those with
a = — 1 have no analogues for Uh (cf. 9.1.4 and the discussion following it).
0
Note that the formulas in this example describing the
Vq{Mi,\) become, in the limit q —> 1, the formulas describing the (A + 1)-
dimensional irreducible representation of 5/2 (<C) (one thinks of K\ as LqH').
Our main aim in this subsection is to make this argument rigorous, and to
show, for arbitrary g, that the structure of the ?/g(g)-modules Vq(X) with
A G P+ is exactly parallel to that of the corresponding highest weight g-
modules. For this, we must specialize q to 1, and hence must first find an A-
submodule of Vq(X) preserved by the action of U^s (it makes little difference
whether we work with the restricted form U^s or the non-restricted form Ua
here, cf. 9.2.3 and 9.3.10).
Proposition 10.1.4 Let V be a highest weight Uq-module with highest
weight vector v, and let V^s = U%*.v. Then
(i) V?s is a U%s-submodule ofV;
(ii) V^es is an A-form of V, in the sense that the natural map
vr® q(«) ^v
A
is an isomorphism of vector spaces over Q(g);
(Hi) Vys is the direct sum of its intersections with the weight spaces of V,
and each such intersection is a free A-module of finite rank. |
The proof is straightforward, making use of 9.3.3.
If V is as in 10.1.4, let
be the Q-vector space obtained by specializing q to 1. By part (i) of 10.1.4,
V is a {7{es-module, where
"* A
Moreover, by our assumption on the highest weight of V, the eigenvalues
of the Ki on V are powers of g, hence the images of the Ki in U[es, which
we also denote by K^ act as the identity on V. Hence, V is naturally a
?7{es-module, where U{es is the quotient of U{es by the ideal generated by the
central elements Ki — 1, i = 1,..., n.
By 9.3.10, V becomes a module for the classical enveloping algebra U (over
Q). It is clear that V is highest weight as a [/-module, with highest weight
10.1 Classification of finite-dimensional representations 317
vector the image v of v in V. Moreover, the highest weight of V is the same
as that of V. For,
in Vies, and hence, using bars to distinguish generators of U from those of
Hi.v = (XJX, - X% Xj).v = lim
^^1
The following is a more precise result:
Proposition 10.1.5 Let Vq(X) be the irreducible highest weight Uq-module
with highest weight A G P+. Then, Vq(X) is the irreducible U-module with
highest weight A. Moreover,
for all 11 G P. In particular, the character of Vq(X) is given by the classical
Weyl character formula.
PROOF To prove that Vq(X) is irreducible, note that, by 10.1.2, the Xf act
locally nilpotently on Vq(X), and Vq(X) is the direct sum of its weight spaces.
Hence, Vq(X) is an integrable [/-module. But it is well known that every
integrable highest weight [/-module is irreducible.
The statement about the dimensions of the weight spaces follows from
10.1.4. |
Corollary 10.1.6 Every finite-dimensional highest weight Uq-module is ir-
irreducible and has highest weight in P+.
PROOF By 10.1.1 and 10.1.2, the highest weight A of W lies in P+. From
the proof of 10.1.5, we see that W is a finite-dimensional [/-module with the
same highest weight. But a finite-dimensional highest weight [/-module is
irreducible. It follows, as above, that ch(W) is given by the Weyl character
formula. But the same argument applies to the unique irreducible quotient W
of W. Hence, W and W have the same character. It follows that W — W,
and hence that W is irreducible. |
An important consequence of this is
Theorem 10.1.7 Every finite-dimensional Uq-module is completely re-
reducible.
318 10 Representations of QUE algebras: the generic case
Outline OF PROOF We shall prove simultaneously that every finite-dimen-
finite-dimensional irreducible ^-module is highest weight.
Suppose first that 9 = s/2(<C). Let V be a finite-dimensional irreducible
L^-module. Let Q(#) be the algebraic closure of Q(#), let V = V
and define Uq similarly; then, V is a ?/9-module. Since we are now working
over an algebraically closed field, there is a if-eigenvector 0 ^ v ? V with
eigenvalue uj ? Q(g), say. Then,
since the right-hand side is a non-zero submodule of V. Since dim-rp-(V') <
00, there is a maximal r = r0 (say) such that Kvro ?" 0- Replacing v by a
non-zero vector in Vu;q2r0) we may therefore assume that X^~.v = 0.
Suppose for a contradiction that u <? ± qz. Define vr = (Xf)r.'D/[r]9! for
r ? N. Then,
i^i.tV = ujq~2rvr,
By the assumption on cj, all the coefficients on the right-hand sides of these
equations are non-zero. From the third equation, it follows that vr 7^ 0 for all
r, and from the first that the vr are linearly independent. This contradicts
Thus, u e±qz and, in particular, u ? Q(g). Hence, there is a vector v ? V
of weight cj. Then, i; is primitive, and V is a highest weight module.
Now suppose, for a contradiction, that V is a finite-dimensional Uq-modu\e
which is not completely reducible, and that V has minimal dimension among
^-modules with this property (we are still in the 5/2 case). An argument
with Jordan-Holder series shows that V belongs to a short exact sequence
C) 0 ^ Vq(n) ^V^ Vq{\) -+ 0.
In fact, by a classical argument (see, for example, Serre A965), LA 6.5-6.6),
one may even assume that A = 0. Thus, we have a short exact sequence
0 -+ Vq(ji) - V -> Q(g) -> 0,
where Q(g) is the trivial L^-module. Let {vq , v± ,..., vjf } be the basis
of Vq(/j,) as in 10.1.3, and denote the images of these vectors in V by the
same symbols. Let v' be any vector in V such that V — Vq(/j,) 0
10.1 Classification of finite-dimensional representations 319
as Q(<7)-vector spaces. Then, K\.vr = v' + J2r=oarvr f°r some ar G
r = 1,..., /x. If /x is odd, the vector
r=0 *
is an eigenvector of K\ of eigenvalue 1, so we may as well assume that K\.v' =
vr. In the case where /x is even, the same conclusion holds, since the relation
KiX+K^1 = q2Xi~ forces afl/2 = 0. The remaining relations now x>rce
Xf.vf = 0 (the even case again causes a little more difficulty than the odd
case). Thus, v' generates a highest weight submodule V° of V of highest
weight 0. By 10.1.6, V° is irreducible. It follows that V = Vq{fi) 0 1^@),
contrary to hypothesis.
We now turn to the case where g is arbitrary. We first prove that every
finite-dimensional irreducible Uq-modu\e V is highest weight. By considering
V as a module for the Uqt(sl2(<E)) subalgebras of Uq generated by Xf, Kf1
for i — 1,..., n, and using the 5/2 case proved above, it follows that V is the
direct sum of its weight spaces. But if vu G V is a vector of maximal weight
a;, then ifo is primitive, and so V is a highest weight module.
For the proof of complete reducibility, we are reduced, as in the 5/2 case,
to considering a short exact sequence of the form C), in which V is assumed,
for a contradiction, not to be completely reducible. We prove that A < /x
(there is now no particular advantage in assuming that A = 0). Since V is
the direct sum of its weight spaces, there is a vector v' G V which projects to
a highest weight vector in V{\). If A ^ /x, then X*.vf maps to zero in Vq(\),
hence is in the image of Vq(fjb), and hence must be zero since it has weight
A + oci, which is not < /x. Thus, v' is a primitive vector. As in the 5/2 case,
10.1.6 implies that v1 generates a submodule of V isomorphic to V^A), which
contradicts our hypothesis.
By taking duals in C), it follows that we also have —wo(fi) < —wo(\),
i.e. /x < A. This contradicts the conclusion of the preceding paragraph, and
completes the proof of complete reducibility. |
Remark The argument reducing the proof of complete reducibility to the
statement in 10.1.6 is due to A. Borel. A
B The determinant formula In this subsection, we establish some im-
important results about Verma modules and use them to sketch the proof of
9.1.6.
We must first introduce the quantum analogue of another familiar notion
from the classical theory. If V is a Q(^)-vector space, a hermitian form on V
is a bi-additive form ( , ) on V such that
(vi, v2) = (v2 , ^i), (^i , cv2) = c{v\ , ^2),
320 10 Representations of QUE algebras: the generic case
for c G Q(g), vi, V2 G V. Here, the bar denotes the homomorphism of Q-
algebras Q(g) —> Q(g) such that q = q~l. If V is a [/^-module, a hermitian
form (, ) on V is said to be contravariant if
for all v\, V2 EV, x eUq, where u is the Q-algebra anti-automorphism of Uq
such that
(cf. the automorphism of Uh with the same name defined in Subsection 8.1A).
Proposition 10.1.8 The Verma module Mq(X), for A G P, has a unique
contravariant hermitian form (, ) such that (v\ , v\) = 1, wiiere v\ is the
canonical highest weight vector of Mq{\). Its kernel is the unique maximal
proper submodule of Mq(X).
Outline of proof This is exactly as in the classical case. In fact, by 9.1.3,
we have a decomposition of Q(g)-vector spaces
where U^ = XT=i XtUqh- Let n be the projection of Uq onto C/J. Then,
we set
{xi.vx , x2.v\) = ir(uj(x2)xi)
for all #1, #2 G f7^~. I
The last sentence of 10.1.8 implies
Corollary 10.1.9 Every highest weight Uq-module V admits a contravari-
contravariant hermitian form. If V is irreducible, the form is non-degenerate. |
It follows immediately from the definitions of (, ) and of u that distinct
weight spaces of Mq(X) are orthogonal:
For r] G Q+, let detqjT](X) denote the determinant of the restriction of (, )
to the (finite-dimensional) weight space Mq(X)\-v, computed in the basis
)- We recall that
Par(r?) = {r = (n,... ,rN)
10.1 Classification of finite-dimensional representations 321
Proposition 10.1.10 For A e P,rj G Q+, the determinant detg ^(A) is given
by
l/3GA+
llm=0
The proof of 10.1.10 is almost identical to that in the classical case (see
Kac A983), for example). As in that situation, we deduce
Corollary 10.1.11 The Verma module Mq(X), A G P, is irreducible if and
only if 2(A + p, /?) ^ ra(/3, /?) for aii /? G A+, ra G N. |
In fact, this is just the condition for detg57?(A) to be non-zero for all rj G Q+.
One can also deduce conditions for inclusions of Verma modules, and for the
occurrence of irreducible highest weight modules as subquotients of Verma
modules. We shall not write down these conditions since they are exactly the
same as in the classical case.
We shall now apply these results on the structure of Verma modules to
complete the discussion of the centre Zq of Uq begun in Subsection 9.1C. As
we mentioned there, any z G Zq can be expressed in the form
E) z= E E
where (/v,t G Uq. The ParG7) x ParG7) matrix tp^ = (yv,t) can be computed
by induction on r) G Q+, as follows.
We consider the action of z on a Verma module M9(A), A G P. Since
z-v\ = (A),o(A)^a and z G Zq, it follows that z acts as the scalar </fyo(A) on
the whole of Mq(X). For 0, r] E Q+, let G^57?(A) be the endomorphism of the
weight space Mq(\)\-V induced by the action of the element
r,tePar@)
Note that Ge^(X) = 0 unless 0 < r). Hence, the fact that z acts as the scalar
<#o,o(A) on Mg(A)A-r7 translates into the equation
F) G^(X)
Let H71(X) (resp. G^57?(A)) be the matrix of the contravariant form ( , )
(resp. of GejT1(X)) in the basis {{X~)8.v\}separ(<r]) of Mq(X)\-ri. Then, we
have
G) G,,,(A)
322 10 Representations of QUE algebras: the generic case
In fact, since
we have
t,rGParG7)
and hence
Combining F) and G), we have
(8) ?
0<T]
Assume that (po is known for all 0 < rj. Then, Gq^ is known for all 6 < rj, and
hence (8) determines y?^, provided that Hv is invertible. By 10.1.10, inverting
Hv involves introducing denominators of the form
— m
for C G A+ (qp — q^^)). A priori, therefore, the inductive procedure gives
elements (prt lying in S~1Uq, where S is the set of products of terms as in
(9).
The crux of the proof of 9.1.6 is to show that, starting with an arbitrary
element (foo G Uq, the inductive procedure leads to elements </v,t G U® if and
only if (poo G lq(JJ®w)- When this condition holds, the resulting element
z G Uq lies in Zq because it acts as a scalar on every Verma module.
We shall not prove this last statement, but we give the following example,
which may help to clarify the preceding argument.
Example 10.1.12 Suppose that g = 5/2 (C). The expansion E) now takes the
form
z = y>o + XiViX* + (Xf) V2(X1+J + ... ,
where <po, <pi,... G Uq are now thought of as Laurent polynomials in K\ with
coefficients in Q(g). The inductive procedure leads to the following equations:
A0)
[m]q[m - l],[#i; 1 - m],[^i; 2 - m]qip2(q-2m+i Ki)
[m],![/ri; 1 - mlJ/sTi; 2 - m], ... [Id ; 0]^m(JftT1).
10.1 Classification of finite-dimensional representations 323
We have used A3) from Chapter 9 to compute the elements Gq^ G U®.
Taking m = 1, we find
in particular, the left-hand side must be divisible by K\ - iff1 in U®. The
choice
1
has this property and gives <pi(Ki) = 1. It now follows from A0) for m > 1,
by considering the degrees of the various terms in K\, that <p2 = (f3 = • • • = 0.
Thus, the central element we obtain is
the quantum Casimir element (cf. 9.1.7). 0
The discussion in this subsection can be given for Uh just as well as for Uq,
and we use it to give the
Proof of Proposition 8.3.15 We use the notation of Subsection 8.3E.
The equation to be proved is equivalent to
Sh(e-h<>* uh) = e-h<>* uh.
In view of the results of this subsection, and those of Subsection 9.1C (which
also apply to Uh), it is enough to show that both sides of this equation act
by the same scalar on any finite-dimensional indecomposable t/^-module Vh.
It suffices to consider the highest weight vector v of Vh, and if this vector has
weight AgP, say, we have, using the formula for the universal R-matrix in
8.3.9,
since p* G f) corresponds to 2p G I)* under the standard invariant bilinear form
( , ). But Sh{e~hp*Uh) acts on Vh as e~hp*Uh acts on the (left) dual module
V?, which has highest weight —wq(X), where w$ is the longest element of the
Weyl group of g. Thus, our assertion follows from the computation
e-/i(-ti;o(A),-ti;o(A)+2p) = e-h(X,X-2w0(p)) _ e-/
324 10 Representations of QUE algebras: the generic case
where we have used the invariance of (, ) and the fact that wo(p) = —p. |
We can also prove 8.3.14. Let C be the image of Ch under the canonical
isomorphism between the centres of Uh(o) and f/(g)[[/i]] (see 6.5.7). By the
preceding proof, C acts by the scalar (A, A -f 2p) on any g-module of highest
weight A. But it is well known that the classical Casimir element also has this
property and, by the classical analogue of 9.2.5, that an element of the centre
of t/(g) is determined by its action on all the highest weight representations
of 9- I
C Specialization: the non-root of unity case In this subsection, e de-
denotes a non-zero complex number which is not a root of unity. We examine
the extent to which the results of the previous two subsections carry over
from Uq to Ue.
We can define highest weight modules V whose highest weight is any n-
tuple of non-zero complex numbers c*/ = (ui,..., un): V should be generated
as a /7e-module by a vector vu such that U^.v^ = 0 and Ki.v^ = uJiV^ for
i = 1,..., n. Any such module is the direct sum of its weight spaces
VJ = {v G V | Ki.v = uj[v, i = 1,..., n}.
The Verma module Me(c*/), defined in the obvious way for any a/, is the uni-
universal highest weight module with highest weight w. By 9.2.2, it is a free
G"-module with basis {(-^"^.^IteN^- Moreover, it has a unique irreducible
quotient Ve(ui).
We shall usually be interested in the case where uji = e^z'A^ for some
A G P. We shall then denote Me(ai) by Me(A), etc. Note that, by the
preceding remarks, ch(Me(A)) is the same as in the classical case.
Suppose that e is transcendental. Then all the arguments of Subsection
10.1 A carry over verbatim to Ue. In particular, one can specialize e to 1 to
obtain from each highest weight /7e-module V a highest weight /7-module V
(over Q). Then, we have the following result, whose proof is exactly the same
as that of 10.1.5.
Proposition 10.1.13 Assume that e g <Cx is transcendental Let Ve(X) be
the irreducible highest weight Ue-module with highest weight A G P+. Then,
Vg(A) is the irreducible highest weight U-module with highest weight A. |
In the same way, complete reducibility also holds when e is transcendental.
In fact, we have the following stronger result.
Theorem 10.1.14 Suppose that e g Cx is not a root of unity. Then, ev-
every finite-dimensional Ue-module is completely reducible, and every finite-
dimensional irreducible Ue-module is highest weight.
Outline of PROOF As we have just noted, if e is transcendental, the proof
given in the previous subsection carries over verbatim to the Ue case. If e
10.1 Classification of finite-dimensional representations 325
is algebraic (but not a root of unity), the proof we gave for Uq(sl2((E)) still
works for Ue(sl2((E)) (note, in particular, that the vector denned in D) still
makes sense when q is replaced by e - this might not be the case if e were a
root of unity). The passage to the case of arbitrary g relied on 10.1.6, which
in turn was deduced from 10.1.5. Unfortunately, however, the latter result
does not even make sense when e is algebraic, since one cannot then specialize
e to 1. Thus, we must find a proof of the analogue of 10.1.6 for Ue when e is
algebraic, but not a root of unity.
We first look at the Verma modules Me(A), A G P. If v^ is a primitive
vector in Me(A) of weight /i, then we see by considering the action of Ze
that \e,x = Xe,/x- By 9.2.5, /i -f p G W(X + p). As in the classical case
(see Humphreys A972), for example), one sees by considering Jordan-Holder
series that ch(Me(A)) is a linear combination of characters ch(Ve(/i)) for /i G
Px = {^ g P | /i<A, /i + pG W(X -f p)}, and that these relations can be
inverted to obtain an expression for ch(Ve(A)) as a linear combination of the
ch(Me(/i)) for /i E P\.
Suppose now that V is any finite-dimensional /7e-module with highest
weight A. As in the proof of 10.1.6, to prove that V is irreducible, it is
enough to show that ch(V) is given by the Weyl character formula. By con-
considering Jordan-Holder series as before, we see that ch(V) can be written as
a linear combination of the ch(Ve(/i)) for /i G Pa- Hence,
ch(V) = J2 C-(A) ch(Me(w(A + p) - p))
for some cw(X) G Q(e).
The next step is to show that
dimQ(e)(y/x) = dimQ(e)(K;/x)
for all w G W. In fact, the proof of this is exactly as in the classical case
(see Humphreys A972), Sects 7.2 and 21.2). It uses complete reducibility
under Ue(sl2((C)), but this is already known. It now follows as in the clas-
classical case that cw(X) — sign(w), where sign(u>) = (—l)k if w = s^s^ ... Sik.
Finally, since the characters ch(Me(A)) are the same as the characters of the
classical Verma modules, it follows that ch(V) is given by the Weyl character
formula. |
From the proof, we note
Corollary 10.1.15 Suppose that e g Cx is not a root of unity, and let
X E P+. Then, ch(Ve(A)) is given by the classical Weyl character formula. |
Remark We shall see later in this chapter that 10.1.14 and its corollary,
10.1.15, are both false in general when e is a root of unity (this holds for
both the restricted and non-restricted specializations). A
Let us give an application of 10.1.14 and 10.1.15.
326 10 Representations of QUE algebras: the generic case
Proposition 10.1.16 Suppose that e e <CX is not a root of unity, and let A,
fi G P+. Then
1/GP+
where the multiplicities mv are the same as in the decomposition of the tensor
product V(X) 0 V(/x) of the irreducible representations of g with highest
weights A and /x.
Proof Note first that, if Ve and We are any two finite-dimensional Ue-
modules, then
Ch(ye 0 We) = ch{Ve)ch{We)
(this follows from the fact that, if v G Ve and to G We are weight vectors, then
the weight ofv<g>w is the sum of the weights of v and w, which in turn follows
from the fact that the Ki are group-like). From this remark and 10.1.15, we
deduce that
Thus, if nv are the multiplicities in the classical case, we have, using 10.1.15
again,
Since finite-dimensional g-modules are determined by their characters, we
have
But mv (for example) is the dimension of the space of g-module homomor-
phisms from V{y) to the left-hand side. Hence, mv — nv for all v. |
Suppose now that |e| = 1. Then, a contravariant form on a Ue-mod\i\e V
is a hermitian form ( , ) on V (in the usual sense) such that
(x.vi , v2) = {vi , v(x).v2),
where uj is the anti-automorphism of Ue defined by the same formulas as in
the Uq case. Arguing as in 10.1.8 and 10.1.9, we see that the Verma module
Me(A) admits such a form whose kernel is the unique maximal submodule of
Me(A). It follows that every highest weight C/e-module of type 1 with highest
weight AgP admits a non-zero contravariant form.
Let dete?7?(A) be the determinant of the restriction of the contravariant
form on Me(A) to the weight space Me(A)A-r?, r\ G Q+, computed in the basis
y
10.1 Classification of finite-dimensional representations 327
Proposition 10.1.17 Suppose that \e\ — 1 and that e2dt ^ 1 for i = 1,..., n.
Then, detEjT](X) is obtained by replacing q by e in the formula in 10.1.10. |
D R-matrices associated to representations of Uq We observed at the
end of Subsection 9.IB that the universal R-matrix
N f-t _ -2ur
a^ —f—^ ;—\XJ ) 0 (Xft ) r
of 17^ does not translate to give an element of C79 0 /7g (the notation is that of
Subsection 8.3C). In fact, there are two problems, which must be discussed
separately. Let
€h -
The first difficulty is that, although each term in IZh is meaningful as an
element of Uq 0 Uq, the sum is infinite. This problem is easily overcome by
taking a suitable completion of Uq. In fact, for any r > 1, let
upr = 0 W*
{/3GQ|height(/3)>r}
where (t/+)/3 = {u e U+ \ KiuK~l = q^^u for i = 1,... ,n} is the sub-
space of U* consisting of elements of weight f3 (recall that height(^ miOLi) =
Y^i mi)- The appropriate completion of Uq is
Uq = KmUq/UqU+>r.
We define the completed tensor product Uq{Q)®Uq{Q) to be Uq($ 0 g), the
subspaces Uq(q 0 g)+'r C U+ 0 17+ being defined in the obvious way, using
the height function height (J^ rrii a i, ^2j rij a j) = Ylimi ~t"Sjnj- Higher
completed tensor products are defined similarly. It is then easy to check
that the algebra structure on Uq extends naturally to Uq, that the coalgebra
structure maps extend to the appropriate completions, and that the Hopf
algebra axioms are satisfied, provided one replaces 0 by 0. Moreover, IZh is
obviously a well-defined element of Uq(&Uq, and as such we denote it by TZq.
The second, and more serious, difficulty is that the exponential term Eh
cannot be interpreted as an element of Uq 0 Uq (or its completion). The way
328 10 Representations of QUE algebras: the generic case
to overcome this problem was pointed out by Tanisaki A992). We consider
the automorphism ^h of Uh <8> Uk given by
It is easy to show, using 6.4.2, that
where K{ = edzhH\ and that these formulas define an algebra automorphism
tyq of Uq <S> Uq which extends to an automorphism of Uq®Uq. The following
result was proved by Tanisaki A992) by direct computation.
Lemma 10.1.18 We have;
(i) 1Zq is an invertible element ofUq®Uq;
(ii) ^q(Aop(x)) = 1iq.A(x).1iql for all x G Uq;
(iii) (^J3G^3).7^3 = (A (
(iv) (\?q) 12(It13).TZ12 = (id (
Suppose now that p : Uq —> End(V) and p' : Uq -+ End(V;) are finite-
dimensional irreducible Uq-modules of type 1. From the results of Subsection
10.1 A it is clear that all but finitely-many terms in TZq act as zero on V and
V, and hence that (p (8) p){lZq) = RP,Pf is a well-defined invertible operator
on V(8>V. Moreover, V and V are the direct sums of their weight spaces V\,
V^, A, /x G P, so we may define an invertible operator EPiP' on V (8) V which
acts as the scalar g(A'^) on the subspace V\ 0V^. Set RP,P' = Ep^pi Rp,p> •
Proposition 10.1.19 With the above notation, Rp,p> is an invertible oper-
operator on V (8) V such that
for aii x E Uq. Moreover, Rp,p> satisfies the quantum Yang-Baxter equation.
Outline of proof The operator Epy is defined so that it 'implements' the
automorphism \?g, in the sense that
A1) (p®p')(*q(x)) = E-1pl(p®p')(x)Ep,p,
for all x E Uq(&Uq. To prove this, it suffices to check that the two sides agree
on V\ (8) V^ for all A, /i; we may also assume that x is one of the generators
Xf 0 1, 1 (8) Xf, Kfx (8) 1 or 1 (8) Kf1 of Uq®Uq. For example, taking
x = Xf (8) 1, the left-hand side of A1) gives
VX®V'
10.1 Classification of finite-dimensional representations 329
while the right-hand side gives
Thus, A1) holds in this case.
The first part of the proposition follows immediately from A1) and 10.1.18
(ii). The second part follows in a similar way using 10.1.18(iii) and (iv). |
In category-theoretic language:
Corollary 10.1.20 The category of finite-dimensional Uq-modules of type
1 is a quasitensor category, with the commutativity isomorphism V ® V —>
V' ® V given by o o Rp^p,. |
Since the matrix of Rp,p' with respect to any Q(#) bases of V and V has
entries in Q(g), the preceding results also apply when q is specialized to any
transcendental number e ? (Cx. In fact, we could have replaced Uq by U^s
in the preceding discussion, noting that tyq takes U^s to U^s and that each
term in TZq is an element of U^s 0 U^s, so that the conclusion of 10.1.20
applies to ?/eres for arbitrary e (see Lusztig A993) for further discussion of
this point).
E Unitary representations We conclude this section by considering briefly
the classification of the unitary representations of Ue. See Subsection 4. IF for
the definition of a unitary representation of a Hopf *-algebra, and Subsection
9.4B for the classification of the Hopf *-structures on Ue. We shall work over
C, and accordingly set Uf = Ue <g> C The complexification V^A) of K(A),
Q(<0
for any A G P, is an irreducible Uf-module.
We first consider the standard Hopf *-structure on Uf, defined, for e G 1R,
by
k; = kz, (x+y = x-Kz, (x-)* = ^-1x+.
Proposition 10.1.21 Let e > 0 and let V^(X) be the finite-dimensional
irreducible Uf -module with highest weight A ? P+. Then, V^(X) is unitary
with respect to the standard ^-structure on Uf.
Outline of proof One first shows, as in 10.1.8 and 10.1.9, that V^A)
admits a non-degenerate hermitian form ( , )e such that
(x.Vi , V2)e = (Vi , X*.^2)e
for all x e Uf, vu v2 e V^(\). By 10.1.15, one can identify V^(X) and
yc(A) as vector spaces over (C, where V(L(X) denotes the irreducible Uc-
module with highest weight A. Thus, we may regard ( , )e as a family of
330 10 Representations of QUE algebras: the generic case
hermitian forms on the fixed vector space FC(A), parametrized by the set
1R+ of positive real numbers. Equivalently, we may consider the family Te of
self-adjoint operators on FC(A), where
{Vl , V2)e = {Vl , Te(v2))l.
It suffices to prove that all the eigenvalues of Te are positive for all e ? IR+.
Suppose for a contradiction that Te is not positive definite for some e G IR+.
Then, for some e' € IR+ between 1 and e, Te> has a zero eigenvalue. But then
ker(Te/) is a proper C/J'-submodule of V^A), contradicting irreducibility. |
For the non-standard *-structures (i.e. those which are not equivalent to
the standard structure), the question of unitarity of representations seems
to be open in general. In the 5/2 (C) case, however, we have the following
negative result.
Proposition 10.1.22 There are no non-trivial finite-dimensional unitary
representations for any of the non-standard Hopf ^-structures on Uf (s^2((C))l
The proof is a straightforward exercise, using complete reducibility and the
explicit description of the irreducible t/^-modules (cf. 6.4.10) and of the Hopf
*-structures (cf. 9.4.3).
The question of infinite-dimensional unitary representations is more inter-
interesting, and seems still to be open in general. We content ourselves with
the following examples, which give quantum analogues of the discrete and
continuous series representations of su\^.
Example 10.1.23 Suppose that e is real and > 1 and consider the *-structure
K\ = Ku (X+)* - -Xf/fi, (Xf)* = -K^lX+ (quantum suhl). Then,
there are three families of infinite-dimensional irreducible unitary representa-
representations:
(i) Lowest weight discrete series The Hilbert space with orthonormal basis
{v\, V2, •. • } and action
/ K-2.r-l _ K-2A-r\ V2
Ki.Vr = AC 6 Vr, X{.Vr = K€ I [r\e ^_ _1 I Vr+i,
where ac is a real constant greater than 1. (The formula for the action of X±
can, of course, be deduced from those above using unitarity.)
(ii) Highest weight discrete series The same Hilbert space as in (i), with
action
/ K-2fr K2f-r\1/2
Ki.vr = k e vr, X{.vr = Aee Mr - 1J€ 3T vr-\,
\ e -e J
where 0 < k < e and vq = 0.
10.1 Classification of finite-dimensional representations 331
(iii) Continuous series The Hilbert space with orthonormal basis {vr}r^z
and action
-2
o 2r -\r-\- 1 t I ri
«e v X .vr = Aee I c -f- [j
-2 r-1 2 l-r\V2
j
where 1 < ac < e and c > 0. <0
Remark There are *-algebra structures on Ue which are not Hopf *-algebra
structures, and the definition of a unitary representation makes sense for
them. For example, if |e| = 1 the following formulas define a *-algebra struc-
structure on Ue:
A2) #i* = #r\ (x1+r = x1-, (Xf)* = x+,
although this is not compatible with the coalgebra structure on Ue. The
classification of the unitary representations in this case is rather startling.
Suppose that e = e^*9, where 0 < 0 < 1. Let
be the continued fraction expansion of ^, where t\, ^2,. •. G N, and let o?i = ti,
o?2 = ^2^1 + 1, 0C = tst2ti -f ^3 + ti,... be the sequence of denominators of
the successive convergents
1 t2 t3t2 +1
H-13 + *i
Then, the 7n-dimensional irreducible representation of C/c is unitary for the
*-structure A2) (with respect to some inner product) if and only if m belongs
to the sequence
,..., dk
For example, if 0 = ^(V^ ~ 1)» ^ne possible dimensions form the Fibonacci
sequence 1, 2, 3, 5, 8, .... A
332 10 Representations of QUE algebras: the generic case
10.2 Quantum invariant theory
One of the most beautiful results from the early years of the representa-
representation theory of Lie groups is the duality, established by Probenius and Schur,
between the representation theory of general linear groups and symmetric
groups. An analogous theory was developed by Brauer for the orthogonal
and symplectic groups. In this section, we describe a quantum analogue of
these theories.
A Hecke and Birman-Murakami-Wenzl algebras First, we briefly re-
recall the classical theory. Let V^ be the natural (n + l)-dimensional represen-
representation of s/n+1((C), and let ? > 1. One is interested in the algebra Int((V^)®?)
of intertwining operators of the representation (V^)®e, i.e. the linear maps
from (V^)^ to itself which commute with the action of s/n+i((C). Accord-
According to Frobenius and Schur, this algebra is generated by the permutations
of adjacent pairs of factors in the tensor product. More precisely, assigning
to the transposition (i,i -f 1) in the symmetric group E^ the flip of the zth
and (z-fl)th factors in (V^)®1 defines a surjective homomorphism of algebras
For the orthogonal (resp. symplectic) groups, the natural representation
V^ is equipped with a non-degenerate symmetric (resp. skew-symmetric)
bilinear form. This enables one to identify V^ and (V^)* as representations,
and hence also End(V^) and End(V^)*. Let r G End(V^ ® V^) correspond to
the map End(V^) -> End(V^) given by T ^ trace(T).idy^. Then, Brauer's
assertion is that the algebra of intertwining operators of (V^)®e is generated
by the flips oi and the maps r^, 1 < i < ?, where Ti is r acting in the zth and
(i + l)th factors in
We now turn to the quantum situation, beginning with the s/n+i case. The
role of the symmetric group in the Frobenius-Schur theory is played in the
quantum theory by the algebra defined as follows.
Definition 10.2.1 The Hecke algebra He(e), where e e C and ? > 1, is the
associative algebra over C with generators <Ji,..., <j^_i and defining relations
A3)
A4)
A6)
(We set Hi (e) = C.
O~i(Jj
= aial if i-j\> 1,
Remarks [1] Putting e = 1 in A3), A4), A5) and A6) gives the denning
relations of the symmetric group E^. Further, it is known that dimG-^(e)) =
?\, so Hi(e) may be regarded as a 'deformation' of the group algebra
10.2 Quantum invariant theory 333
[2] Since He(l) = C[E^] is semisimple, and since semisimplicity is an 'open'
condition on an algebra (for it is equivalent to the non-degeneracy of the
Killing trace), one expects that He(e) is semisimple for 'generic' values of e.
In fact, it is known that 7^(e) = C[E^] as algebras, provided e ? (Cx is not a
root of unity (this is a sufficient, not a necessary, condition for semisimplicity).
[3] Historically, Hecke algebras arose in connection with algebraic groups
over finite fields. Let G = GL^(fc), where k is a finite field with r elements,
and let B be the Borel subgroup of G consisting of the upper triangular
matrices. We apply the construction given at the beginning of Subsection
9.ID with X = G/B. Using the Bruhat decomposition
G=
it is easy to see that the orbits of the diagonal action of G on X x X are
parametrized by E^, with representatives (wB,B). The algebra F defined
in Subsection 9.ID is generated by the orbits indexed by the transpositions
Si — (z, z + 1), 2 = 1, ...,?— 1, and in fact assigning to &i the orbit of (siB, B)
defines an isomorphism of algebras He(r) —> F. A
Before discussing the quantum analogues of Brauer's algebras, we mention
another algebra, closely related to the Hecke algebra, which plays an impor-
important role in this circle of ideas. It was introduced by Temperley & Lieb A971)
in their discussion of certain lattice models in statistical mechanics.
Definition 10.2.2 The Temperley-Lieb algebra T?*(A), where A e (Cx, is
the united associative algebra over C with generators ti,..., tg-\ and defining
relations
t2i = tu titi±1U = XU, Utj = tjU if \i - j\ > 1.
Proposition 10.2.3 If e2 ^ — 1, there is a surjective homomorphism of
algebras He(e2) —>¦ T?^((e -fe)) given on generators by
A7) <n >-> e2 - (e2 + l)U. |
The proof is a straightforward verification that the assignment A7) respects
the defining relations of 7ii{e2). It is easy to see that the homomorphism in
the proposition is an isomorphism if ? = 2, but not if ? > 2.
For the quantum orthogonal and symplectic groups, the Hecke algebras are
replaced by the algebras defined as follows.
334 10 Representations of QUE algebras: the generic case
Definition 10.2.4 Let e, r e Cx. The Birman-Murakami-Wenzl algebra
BMWi(r,e) is the associative algebra over C with generators <ji, ... ,<j?_i
and defining relations A3), A4), A5) and
A8) na^r-1^
A9) f^^
where
T -1 _
Remark The Hecke algebra 7i^{e2) is a quotient of BAiWi(r, e) for all r. In
fact, the map &i »—> e^, r^ ^ 0 obviously extends to a surjective homomor-
phism BMWt{r,e) -+ He{e2). A
B Quantum Brauer—Frobenius—Schur duality Let g be of type An, Bn,
Cn or Dn and assume that e ? (Cx is not a root of unity. From Subsection
10.1C, we know that there is a representation p\ : C/e(g) —> End(V^) which has
the natural representation ft of g as its classical limit. In fact, as we observed
in Subsection 8.3G in the case of [/^(g), V^ = V^ as a vector space and, in
a suitable basis, p\ is given by the same formulas as ft. The arguments in
Subsection 10.ID show that, although we do not have a universal R-matrix
for C/c(g), we can associate to p\ a matrix Re e End(V^ 0 V^) which satisfies
the quantum Yang-Baxter equation and is such that Ie — a o Re commutes
with the action of C/C(g) on V^ 0 V}. In fact, up to a scalar multiple, Re can
be obtained from the R-matrices written down in A8) and B0) of Chapter 7
by replacing eh by e.
Theorem 10.2.5 Suppose that e is not a root of unity let g be of type An,
Bn, Cn or Dn, and let p\ : C/e(g) —> End(^) be the natural representation of
U€(q). Let Re e End(^ 0 V%) be the result of replacing eh by e in A8) and
B0) of Chapter 7, and let Ie = a o Re, where a is the Rip operator.
(i) If g is of type An, setting rji(ai) — e/*2+1 deRnes a representation rj? of
He(e2) on (V^)®*. Moreover, each of the operator algebras ^GY^(e2)) and
(p\)®l(Ufl) is the commutant of the other.
(ii) If g is of type Bn, Cn or Dn, setting /3i(o~i) = e/*2+1 deRnes a represen-
representation pe ofBMWe(r,e2) on (V^)®e, where
e2n if g is of type Bn,
r = { _6Bn-i)/2 if g is of type Cn^
_e-2n-l if n is C
10.2 Quantum invariant theory 335
Moreover, each of the operator algebras Ci(BMWe(r, e2)) and (p\)®e(U®e) is
the commutant of the other. |
Let us make the 5/2 case a little more explicit. Prom 6.4.12, we recall that
the natural representation V^ has a basis {^0,^1} on which the action of
Ue(sl2(<E)) is given by
Ki.vo = ev0, Xf.vo = 0, X^.v0 = v±,
Ki.vi = e~1vi, Xf.vi = vo, X^.vi = 0.
With respect to the basis {vo 0 vo, v\ 0 vo, uo^^b v\®v\} of V} 0 V^, the
R-matrix is given by
It is easy to verify directly that the matrices
(e2 0 0
0 0
acting in the ith and (i + l)th places, satisfy the denning relations of He(e2).
In fact, they satisfy a stronger condition:
Proposition 10.2.6 Let V} be the natural representation ofUe(sl2(<E)), and
let ?>2. Then, the representation r}? of"He(e2) on (V})®? given by 10.2.5
factors through the Temperley-Lieb algebra TLi{(e + e)").
Outline of proof We send U to the matrix
0
0
0
0
0
1
e
€o+1
0
e
e2+1
e o1
o\
0
0
o)
acting in the zth and (i + l)th places in (V^)®?. It is easy to check that this
is compatible with B0) and the homomorphism A7), and that the images of
the ti satisfy the defining relations of TL^e + e)) (it is obviously enough
to do the case ? = 2). |
From this and the comment following 10.2.3, it follows that r\t is not faithful
336 10 Representations of QUE algebras: the generic case
C Another realization of Hecke algebras The description of the Hecke
algebra given in the third remark following 10.2.1 can obviously be generalized
by replacing GLi(k) by an arbitrary reductive algebraic group over the finite
field k. In particular, taking G to be the group over k associated to a complex
simple Lie algebra g, we obtain Hecke algebras HQ(e): then 7^(e) is the special
case g = sle((E). Restricting ourselves to the simply-laced case for simplicity,
7Yg(e) is defined by generators <Ji,..., on and relations A3), A4) (if a^ = 0),
A5) (ifdij = -1) and A6).
It turns out that there is a realization of 7Yg(e~2), for any (simply-laced)
g, in terms of intertwining operators of C/e(g) (although this is quite different
from the realization in 10.2.5 when g is of type A, B, C or D). We recall the
action of the braid group BQ on C/e(g) from 9.1.2 (we continue to assume that
e is not a root of unity). If V is a finite-dimensional irreducible Ue-modu\e of
type 1, we can twist V by the automorphism Ti to get new representations
V% of Ue on the same underlying vector space. Note that
for any /iGP, where Si is the zth fundamental reflection in the Weyl group
of g. But, by 10.1.15, the dimension on the right-hand side is given by the
Weyl character formula. Since, in the classical case, the dimensions of the
weight spaces of a finite-dimensional irreducible g-module are invariant under
the action of the the Weyl group on the weights, it follows that
for all jLtGP. Since V and V1 have the same character, they are isomorphic as
?/e-modules (this follows from 10.1.15 and the corresponding classical state-
statement). Hence, there are isomorphisms &i G End(V), unique up to a scalar
multiple, such that
o-i(x.v) =Ti(x).(Ti(v)
for all x G Ue, v G V. From the defining relations of /3g, it is obvious that
OiOjOi = Cij(Tj<Ti(Tj if dij = -1,
(JiO-j = CijCTjCTi if dij = 0,
for some non-zero scalars Qj.
Proposition 10.2.7 Assume that e is not a root of unity and that g is of
type A, D or E. Let 6 be the highest root of g. When suitably normalized, the
intertwiners <7i, restricted to the zero weight space Ve(9)o of the irreducible
U€(q)-module of highest weight 0, satisfy the defining relations of HQ(e~2). |
Note that, by 10.1.15, the character of VeF) is the same as that of the
adjoint representation of g. In particular, dim(VeFH) = rank(g).
Bibliographical notes 337
Bibliographical notes
10.1 Most of this subsection is based on Lusztig A988). One alternative
approach, using cohomological methods, can be seen in Andersen, Polo &
Wen A991), and another, using methods from non-commutative ring theory,
can be found in Joseph & Letzter A992).
Complete reducibility in the quantum case was first proved by Rosso
A990b), and it is his proof we have presented, simplified using some remarks
from Lusztig A990c). Different proofs are given by Andersen et al. A991)
and by Joseph & Letzter A992). See also Lusztig A993).
The quantum analogue of the Harish Chandra homomorphism and the
description of the centre of Ue are essentially due to Rosso A990b). The latter
was made more precise by De Concini & Kac A990), who also obtained the
quantum analogue of the determinant formula.
Example 10.1.23 and the remark which follows it are taken from Vaysleb
A992).
10.2 The connection between Hecke algebras and representation theory was
first noticed by Iwahori A964). The BMW algebra was introduced by Mu-
Murakami A987) and Birman & Wenzl A989). A good exposition of the theory
of Hecke and BMW algebras can be found in Goodman, de la Harpe & Jones
A989). See Wenzl A988b) for the theory of Brauer's algebras in the classical
situation.
Theorem 10.2.5 is due to Jimbo A986a) for type A, and to Kirillov &
Reshetikhin A989) in the remaining cases; see also Hayashi A992b). Jimbo
even defines quantum analogues of Young symmetrizers; further steps in this
direction are taken by Goodman & Wenzl A990). It is interesting to note
that Jimbo obtained the R-matrix Re without the benefit of the universal
R-matrix.
Representations of Hecke and BMW algebras have been used to construct
link invariants. This goes back, in the 5/2 case, to Jones A987).
Proposition 10.2.7 was noticed independently by Levendorskii & Soibelman
A990) and Lusztig A990c).
11
Representations of QUE algebras:
the root of unity case
In this chapter, we study the representation theory of Uq(§) when q is spe-
specialized to a root of unity e. We have seen in Chapter 9 that there are two
ways to carry out this specialization, leading to two different algebras, t/c(g)
and ?/Jes(g). Their representation theories turn out to be very different, both
from each other and from that of Uq(o) (or of g).
The first important difference between the representation theory of the
non-restricted specialization U€(q) and that of g is that most of the repre-
representations of Ue(g) are neither highest nor lowest weight. Every irreducible
representation has, of course, a well-defined central character, and we shall
see that, conversely, there are a finite number of representations (at least
one) of ?/e(g) with any given central character, whereas for g only a discrete
set of central characters arise from finite-dimensional representations. Using
the fact, proved in Chapter 9, that the centre of ?/e(g) is essentially (but
not quite) a polynomial algebra on dim(g) generators, it follows that there
are a finite number of irreducible representations of U€(q) associated to each
point of a complex algebraic variety of dimension equal to that of g. Almost
all of these representations have the same dimension ?N, and all the others
have strictly smaller dimension. The methods used to establish these results,
which we describe in Section 11.1, come from the theory of finite-dimensional
associative algebras, which applies to this situation because Ue(o) is finite
dimensional over its centre.
Although the representation theory of C/C(g) differs so markedly from that
of g, we show that there is a remarkable connection between the quantum and
classical situations. In fact, one can associate to every irreducible representa-
representation of C/C(g) an element of the classical (adjoint) complex Lie group G whose
Lie algebra is g, in such a way that representations which are associated to
conjugate elements of G are essentially 'the same', in the sense that they are
related by twisting with an automorphism of C/e(g). One expects that the
structure of a representation of C/C(g) will be reflected in the geometric prop-
properties of the corresponding conjugacy class in G. In particular, it has been
conjectured that the dimension of a representation should be divisible by ?d
if the (complex) dimension of the associated conjugacy class is 2d.
To test this conjecture, it is important to describe the representations of
C/C(g) as explicitly as possible. This problem is only partially solved, but we
review what is currently known.
11.1 The non-restricted case 339
In Section 11.2, we turn to the representation theory of the restricted spe-
specialization U*es(§). This time, the finite-dimensional irreducible representa-
representations are parametrized by dominant weights, exactly as in the representation
theory of g. However, the structure of such a representation of t/eres(g), in-
including its dimension, is in general different from that of the representation
of g with the same highest weight. The characters of the irreducible represen-
representations are given, rather implicitly, by a formula conjectured by Lusztig and
proved by Kazhdan and Lusztig. We discuss the conjecture in this chapter,
and its proof in Chapter 16.
The study of the irreducible representations can be reduced to that of two
special cases, namely that in which all the components of the highest weight
are less than ?, and that in which all the components are divisible by L In
fact, every irreducible representation is isomorphic to a tensor product of rep-
representations of the two types. This result is analogous to a classical theorem
of Steinberg in characteristic p, adding to the evidence seen in Chapter 9 of
a close connection between quantum groups at roots of unity and classical
groups in characteristic p.
In Section 11.3, we study tensor products of representations of U*es(§).
Such tensor products are not, in general, completely reducible, but we show
that if one discards the part of the tensor product which has quantum di-
dimension zero, the resulting 'truncated' tensor product is a direct sum of
irreducibles. This new tensor product is of interest because it leads to the
construction of quasitensor categories whose fusion rings, at least in some
cases, are found experimentally to be the same as those which arise from
certain quantum and conformal field theories. This coincidence is strong
evidence of a deep connection between quantum groups and quantum field
theory, a connection which is under very active investigation at the present
time.
Note In this chapter, g denotes a finite-dimensional complex simple Lie alge-
algebra. We use the notation in the Appendix.
11.1 The non-restricted case
In this section, we assume that e is a primitive ?th root of unity, where ? is
odd and greater than di for all i. We use the notation set up in Section 9.2.
All representations are on complex vector spaces.
A Parametrization of the irreducible representations of Ue We begin
by observing that every irreducible ^-module V is finite dimensional. Indeed,
let Z(V) be the subalgebra of the algebra of intertwining operators of V given
by the action of the elements of the centre Ze of Ue. Since, by 9.2.7, Ue is
finitely generated as a Ze-module, V is finitely generated as a i?(V)-module. If
340 11 Representations of QUE algebras: root of unity case
0 y^ / € Z{V), then f(V) — V, otherwise /(V) would be a proper submodule
of V. Hence, by Nakayama's lemma, there exists an endomorphism g € Z(V)
such that (l-fg)(V) = 0, i.e. / is invertible. Thus, Z(V) is a field. It follows
easily (by using Hilbert's Nullstellensatz, for example) that Z(V) consists of
scalar operators. Thus, V is a finite-dimensional vector space.
Since Ze acts by scalar operators on V, there is a homomorphism \v '•
Ze —> C, the central character of V, such that
z.v = Xv(z)v
for all z € Ze, t; € V. Isomorphic representations obviously have the same
central character, so assigning to a t/g-module its central character gives a
well-defined map S : Rep(?/e) —> Spec(Ze), where Rep(?7e) is the set of iso-
isomorphism classes of irreducible t/e-modules, and Spec(Ze) is the set of algebra
homomorphisms Ze -+ C
To see that S is surjective, let /ex, for \ ? Spec(Ze), be the ideal in Ue
generated by
{z-x(z).l I z e Z€}.
To construct V € H-1(x) is the same thing as to construct an irreducible
representation of the algebra U* = Ue/I* ; note that U* is finite-dimensional
by 9.2.7(vi) and non-zero by Nakayama's lemma. Thus, we may take V, for
example, to be any irreducible subrepresentation of the regular representation
off/*.
However, H is not quite injective:
Theorem 11.1.1 There is a (non-empty) closed proper subvariety V of
Spec(Ze) such that
(i) if x € Spec(Ze)\D, thenH~1(x) consists of a single irreducible Ue-module
of dimension ?N;
(ii) ifx € V, then'S~l(x) consists of a finite number of irreducible Ue-modules
of dimensions strictly less than ?N.
The remainder of this subsection is devoted to an outline of the proof of
this theorem. The strategy is to reduce it to the representation theory of
certain associative algebras over a field.
Note first that, since Ue is an integral domain (see 9.2.4), so is Ze, and we
may consider the field of fractions Q(Ze) of Ze. Then,
Q(Ue) = Ue® Q(Ze)
is a division algebra, finite-dimensional over its centre Q(Ze) by 9.2.7 again.
Let IF be a maximal commutative subfield of Q(U€); then IF is a finite ex-
extension of Q(Ze) of degree m, say. It follows from standard results in the
11.1 The non-restricted case 341
theory of associative algebras (see, for example, Pierce A982)) that Q(Ue)
has dimension m2 over Q(Ze), and that Q(Ue) ® IF is isomorphic to the
Q{Z)
algebra Mm(W) of all m x m matrices over IF. Thus, if x € U€, we may regard
x as an m x m matrix and consider its characteristic polynomial
det(A - x) = Am - (trx)\rn-1 + • • • + (-l)mdetz.
It follows from the next result that all the coefficients of the powers of A on
the right-hand side of this equation are in Ze (see Bourbaki A985), Chap. 5,
§1, no. 6, Corollaire 1).
Proposition 11.1.2 Ue is integrally closed and (hence) so is its centre Ze. |
We can now define the subvariety V C Spec(Ze) in the statement of the
theorem: it is the set of zeros of the ideal in Ze generated by the elements
det (tr(uiUj)), where w1?... ,wm2 are any elements of Ue. By standard asso-
associative algebra techniques applied to the algebras ?/*, one shows
Lemma 11.1.3 (i) Ifx € Spec(Ze)\D, then U} is isomorphic to Mm(<E), and
(hence) there is, up to isomorphism, exactly one irreducible Ue-module Vx
with character \- One has dim(V^) = m.
(ii) If x € V, then dim(t/ex) > m2, but the dimension of every irreducible
U*-module is strictly less than m. |
It only remains to prove that m = ?N; at the same time, we shall prove
that the canonical projection r : Spec(Ze) —> Spec(Zo) has degree ?n (see
9.2.8).
It is enough to show that there is an open subset O C Spec(Zo) (in the
complex topology) such that, for every x € T~1(?*)> ^-1(x) consists of irre-
irreducible modules of dimension ?N, for r~1(O) obviously cannot be contained
in V. But ?2N+n = m2degr, since
()) =degr,
dimQ{Ze)(Q(Ue)) = m2,
dimQ{Zo)(Q(Ue))=?2N+n.
Here, the first equality is a definition, the second has been pointed out above,
and the third follows from 9.2.2.
To construct O, we begin by considering the Verma modules M€(lj), lj €
(Cx)n, which are defined exactly as in Subsection 10.1A. Note that, since
the elements x^ = (Xp)e, C G A+, are in Ze, the vectors Xp.vu € M€(lj) are
primitive, where vu is a highest weight vector of M€(lj). Let M€(lj) be the
quotient of M€(lj) by the f/e-submodule generated by all such vectors. Note
that the central elements x^ act as zero on M€(lj) for alia;.
342 11 Representations of QUE algebras: root of unity case
It follows from 9.2.2 that {(X^)*1 ... (XpN)tN .vu,}o<tr<e,r=i,...,N is a basis
of Me(«i/); in particular, M€(lj) has dimension ?N. Moreover, M€(lj) is irre-
irreducible for generic lj. In fact, it follows from 10.1.17 that M€(lj) is irreducible
if and only if J^e2{P^)-m{^) ^ x for all /? G A+, 0 < ra< L This condition
obviously holds, in particular, if the central elements &r| G Zo act as scalars
^ 1 on Me(cj) for all /? G A+. To summarize, we have shown that, if
H = {x e Spec(Zo) | x(^) = 0, and x(k}) ^ 1 for all /? G A+},
then (t oH)~1(W) consists of representations of dimension ?N.
The desired open set O C Spec(Z0) is manufactured from TL by using the
action of the automorphism group Q on Ue = ?/e 0 Zo (see Subsection 9.2C). If
<fi : U€ -+ End(F) is any irreducible t/e-module, the central elements x^j, k^1
act as scalars on V, and hence Zo, which consists of holomorphic functions
of these elements, also acts on V. Thus, V is naturally a f/e-module. We
can therefore 'twist' V by any element 7 G ^ to get a new representation
cfO = 0 o 7 on the same vector space. In particular, every representation in
(t o'E.)~1(Q.H) has dimension ?iV. The proof of 11.1.1 is thus completed by
the following lemma, which is proved by using the explicit formulas in 9.2.13
for the action of Q on Ue.
Lemma 11.1.4 Q.TL contains an open subset O of Spec(Zo) (in the complex
topology). I
Remark The modules M€(lj) used in the proof of 11.1.1 are called diagonal.
The reason is clear: under the map n : Spec(Zo) —> G° defined in Subsection
9.2C, their Zo-characters go to elements of the Cartan subgroup H of G
(we recall that G is the adjoint group of g). Similarly, one can define an
irreducible C/g-module to be triangular if it contains a (non-zero) vector which
is annihilated by the Xf and is a common eigenvector for the K^i — 1,..., n.
The image of the Zo-character of such a module under n is an element of the
Borel subgroup B+ — HN+ of G. Corollary 9.2.19, together with the fact
that every element of G is conjugate to an element of #+, implies that if V
is any irreducible C7e-module, there is an automorphism 7 G Q such that the
twist of V by 7 is triangular. A
Theorem 11.1.1 gives an adequate parametrization of the irreducible rep-
representations of U€, but gives little idea of their structure. In particular, one
does not know the dimensions of the representations inS~1(P). However, de
Concini, Kac and Procesi A992a) make the following interesting conjecture:
Conjecture 11.1.5 Let V be an irreducible representation of U€, and let
gv be the image ofV under the composite map ttotoH: Rep(?/e) —> G. Let
11.1 The non-restricted case 343
Cy be the conjugacy class of gy in G, and let dim(CV) be its dimension (as
a complex manifold). Then, dim(F) is divisible by ?2dim(cv).
More generally, one expects that the structure of a representation V will
be reflected in the geometric properties of Cy.
The conjugacy classes in G of maximal dimension are those of the regular
elements, and their dimension is 2N. For such classes, the conjecture is true:
Theorem 11.1.6 With the notation in 11.1.5, suppose that dim(CV) = 2N.
Then, \v € Spec(Ze)\V. |
In the next subsection, we shall test 11.1.5 by giving some explicit con-
constructions of representations of Ue. But first, we discuss the simplest example,
namely E/c(sZ2(C)).
Example 11.1.7 By elementary methods, one can easily show that every
irreducible representation of ?/e(s/2(<C)) is isomorphic to exactly one of the
following:
(i) the ^-dimensional representation V(A, a, 6), where A G (Cx, a, b G C, with
basis {i>o, i>i, •.., V?-i} and action
K\.Vj — Xc ^Vjf X^ .Vj = Vj-fi, J' < ? -— 1, X^ -V?—i = by®,
^+ f (Xel~j — X~1ej~1)(ej — e~~j) \ __,
Xi'vj = 7 TTv5 ^ ab vj-ii X{.Vq = avi-x ;
(ii) the (r + l)-dimensional representation V^, where 0 < r < ?-1 and cr = ±,
with basis {v0, ^i,..., vr} and action
Kx.Vj = aer-2jVj, Xf .Vj = <r[r -j + l]e^-i, X~.Vj = [j + l]€vj+1
(v-i =vr+i =0).
The discriminant set V consists of the ?—1 points x^, r = 0,1,..., ^(? —3),
where
cf) = O, Xr(fci)=±1> x^(^)=±
If X G Spec(Ze)\D, S x(x) consists of a single representation, namely the
F(A, a, 6) such that
344 11 Representations of QUE algebras: root of unity case
V(!-3)/2 • V(l- 1 )/2 VA-3I2 • VG_ i)/2
I ^ points ^ *
V0 * Vl-2
Spec(Z6)
Fig. 18 The space of representations of U€(sl2((E))
On the other hand, there are exactly two representations with any given
central character in V. In fact, Sr1(xt) = {K*, V^_r_2}.
We can visualize Rep(?/e) and Spec(Ze) as shown in Fig. 18.
Note finally that, since every irreducible representation with central char-
character outside V has dimension ?, and every non-trivial conjugacy class in
PSL2(<E) has (complex) dimension 2, 11.1.5 is true for U€(sl2(<E)). <>
B Some explicit constructions In this subsection, we make the additional
assumption that ? is coprime to the determinant of the symmetrized Cartan
matrix (didij) of q.
We should like to have an explicit description of the irreducible represen-
representations of Ue(§) for arbitrary g analogous to that given for U€(sl2((E)) at the
end of the preceding subsection. Unfortunately, this problem is only partially
solved. We shall restrict ourselves to the construction of representations of
the following kind.
Definition 11.1.8 An irreducible representation V of Ue is cyclic if the
elements (X^Y € Zq act as non-zero scalars on V.
The reason for this terminology is clear: in a cyclic representation of
U€(sl2((E)) 1 for example, one can get from any weight vector of V to (a non-
nonzero multiple of) any other by applying some power of X^~ or X^, in contrast
to the linear structure of the representations of U(sl2((E)) (see Fig. 19).
We note the following simple observation:
Proposition 11.1.9 If V is a cyclic representation of U€, all the weight
spaces ofV have the same dimension and (hence) dim(F) is divisible by ?n.
11.1 The non-restricted case
345
Fig. 19 Cyclic representations of U€(sl2((E)) vs. representations of
Proof Let Vx = {v eV \ Ki.v = e^^v, for i = 1,... ,n} and V^ be two
non-zero weight spaces of V. Then, A — /i = ^ fc^i for some ^ G Z. Write
if ki > 0,
*' if fci <0,
if ki = 0.
Then, X*1X%2 ... X^j1 is an invertible operator V^ —> V\- In particular,
Since V is the sum of its weight spaces, the last part will follow if we can
show that V\ — V^ iff A — \i € ?Q. But the condition that V\ = V^ is clearly
that
2_"didijkj = 0 (mod ?)
j
for all i. By the assumption on ?, this holds if and only if kj = 0 (mod ?) for
all j. I
Thus, the dimension of a cyclic representation of Ue is > ?n. The next two
results show that the dimension ?n is realized if g is of type An, Bn or Cn,
but not otherwise. To state them, we first introduce an auxiliary quantum
algebra.
Definition 11.1.10 C€[x, z, x", z~l] is the associative algebra over C with
generators x, x~l, z, z~l and defining relations
ZX — € XI
XX l = X 1X — ZZ l = Z l Z = 1.
We shall also use the following notation: if u is an invertible element of a
ring,
{u} — u + u~l.
346 11 Representations of QUE algebras: root of unity case
Proposition 11.1.11 The following formulas define homomorphisms of al-
algebras:
(i) (q of type An) U€2($) -> (g)^1 <Le[x3,x-\zhzj1},
(ii) (q of type Bn) Ue2 (g) -> (g)^ Ve[Xj,xj\ z^zj1),
z , Xi , Ki, i < n, map as in (i),
(iii) (q of type Cn) U€(q) - <g?=1 ^[
X+, X~, K^ i < n, map as in (i),
The numbering of the simple roots is as in Bourbaki A972). The proof is
a direct verification.
Representations of Ue can now be constructed by pulling back representa-
representations of tensor products of copies of Ce[x, x~l, z, z~x\ by the homomorphisms
denned in the proposition. It is an easy exercise to show that every irre-
irreducible representation V of <Ee[x,x~1, z, z~l] is of dimension ?, and is given,
in a suitable basis {v0, v\,..., t^-i}, by
for some A, \i € Cx (the indices are counted (mod ?)). We denote this
representation by
Proposition 11.1.12 (i) The pull-back of a representation ®]=I
of ^j'^Cgfxj,^, Zj, z~l] by the homomorphism in ll.l.ll(i) is the direct
sum of ? irreducible representations of Ue2(q) of dimension ?n, namely the
eigenspaces of z\z^ ... ?n+i•
(ii) The pull-back of a representation ^=1V(Xj,/jlj) of Q^ifcelxj,xjx,
Zj,z~l] by the homomorphisms in 11.1.11 (ii) and (iii) are irreducible.
(iii) If § is of type An, Bn or Cn, every cyclic representation of Ue(§) (or
Ue2 (§)) of dimension ?n arises, up to isomorphism, in this way.
11.1 The non-restricted case 347
(iv) If g is not of type An, Bn or Cn, the minimal dimension of a cyclic
representation ofU€(§) is strictly greater than ?n. |
See Chari and Pressiey A991c) for the proof, and Arnaudon & Chakrabarti
A991a) for an alternative approach.
It is interesting to examine this result in light of 11.1.5. The minimal
dimension d of a non-trivial conjugacy class is given below:
An Bn Cn Dn E6 E7 Es F4 G2
In In In 4n - 6 22 34 58 16 6
Except in the Bn case, d is the dimension of the conjugacy class of the unipo-
tent element exp(X^"), where X'q is a root vector corresponding to the highest
root 6 (it is known that this latter dimension is 4(p, 6)/F,#)); in the Bn case,
it is the dimension of the conjugacy class of the exceptional semisimple ele-
element diag(-l, -1,..., —1,1) in S0Bn + 1). Note that d — 2n when q is of
type An, Bn or Cn, so that 11.1.12 is in agreement with 11.1.5.
Further, it is known that there are at most a finite number of conjugacy
classes of dimension d, except for type An when there is a one-parameter
family of semisimple classes of minimal dimension. The general theory out-
outlined above would therefore lead us to expect a d-parameter family of minimal
cyclic representations except in the An case, when there should be a (d + 1)-
parameter family. Inspection of 11.1.12 shows that this is indeed the case
(there is apparently a Bn + 2)-parameter family in the An case, but the rep-
representations are unchanged, up to isomorphism, by replacing A^ for all i by
AAi, for any A € Cx).
It is not known how to construct the minimal cyclic representations for
arbitrary g. But, for type D4, the prototype of the cases not covered by
the preceding proposition, we have the following result. It confirms the ex-
expectation that the minimal dimension should be ?5, and that the minimal
representations should depend on ten parameters.
Proposition 11.1.13 Suppose that q is of type D4.
(i) The minimal dimension of a cyclic representation ofUe(§) is ?5.
(ii) The following formulas define a homomorphism of algebras Ue2 (g) —>
1, X+
1Z2Z3(CO + C(^
(e2 - e~2J
—l
'(e2-V2J
348 11 Representations of QUE algebras: root of unity case
where i runs from 1 to 3 and
Q> = e2x^1z^1 +Z51 +X51, b = x5, c=z5, c0 = 2
e2)
d=xs1(l + 6~2z5), d0 = x^(x^(e-4z5 + e2)
(Hi) Pulling back a representation 0^=1 V(Aj, /ij) 0 V(A5, 25) of
®$=l<Ce[xj,Xj1,Zj,Zj1]®<C€2[xs,Xs1,Z5,Z51]
under the homomorphism in (ii) gives an irreducible representation
and every cyclic representation of dimension ?6 arises, up to isomorphism, in
this way |
The proof may be found in Chari and Pressley A992, 1994a).
Let us now turn to representations of maximal dimension ?N. The following
result is due to Date et al. A991b). It will be convenient to use the notation
u- u~x
[]
Proposition 11.1.14 Let q be of type An. For any n,... ,rn e Cx, there
is a homomorphism of algebras Ue2 (g) —> 0i<z<j<nCe[x^, x^1, Zij, z~^\ given
by
n
¦&i l~^> / \rizijzij-lzj-l j-izj+i j\xijxij + l • • •xiri')
3=1
i+l-j n+l-jXi+2-j n+2-j ' ' 'Xin '
(one sets x^ and z^ equal to one if i or j is > n).
Pulling back a representation ®ijV(\ij, fiij) of^ijCe^^,^, Zij, z^1} un-
under these homomorphisms gives (irreducible) cyclic representations of Ue2 (g)
of dimension ?N. Their Zq-characters fill a Zariski open subset of Spec(Zq).
C Intertwiners and the QYBE We recall from 5.2.5 that, if (A, 11) is a
quasitriangular Hopf algebra and p\ : A —* End(Vi) and pi : A —> End(V^)
are two finite-dimensional representations of A, the tensor products V\ ® V2
and V2 0 V\ are isomorphic as representations. In fact, as we saw in 5.2.2,
the map
/ = cr o (px (g) p2)(H) : Vi 0 V2 -> V2 0 Vi
is an intertwiner, i.e. it commutes with the action of A. It follows almost
immediately that
11.1 The non-restricted case
349
Proposition 11.1.15 U€(q) is not quasitriangular.
Proof Let V\ and V2 be irreducible ?/e-modules. From 9.2.11, it is clear
that, if Vi 0 V2 = V2 0 Vi as ?/e-modules, the Z0-characters of Vi and V2
commute in the group Spec(Zo). Since Spec(Zo) is not commutative, and
since the map which assigns to an irreducible C/e-module its Z0-character is
surjective, this completes the proof. |
Remark For later purposes, it is useful to make this argument a little more
explicit. We note first that the central elements xf = (Xf)e and ki — Kf
act as scalars on any tensor product Vi 0 V2 of irreducible representations
of U€, even though this representation cannot be irreducible in general, for
dimensional reasons (see 11.1.1). Taking a —
9.2.10, we have
and b — 1
> v+
in
(pi
pi(h) + 1 0 p2(xt)-
Thus, a necessary condition for V± 0 V2 and V2 0 V\ to be isomorphic as
representations of Ue is
B) Pl(xt)p2(kl)+p2(xi) = P2(xt)Pi(h)+Pi(xt)
for all i. Similarly, by considering the action of the X~, we find the necessary
conditions
C)
pi(kl)-1P2(x~) =
~). A
Despite the lack of a universal R-matrix for Ue, the following general result,
which will also be needed in Chapter 12, allows one to obtain matrix-valued
solutions of the QYBE by restricting to a set of representations of Ue on which
the tensor product operation is commutative (up to isomorphism).
Proposition 11.1.16 Let {V(v)}v^\; be a family of representations of a
Hopf algebra A, all with the same underlying vector space V and parametrized
by the elements v of some set V, such that:
(i) for all vi, v2 € V, there is an isomorphism of representations
I(vi,v2) : V>i) ® V(V2) - V(v2)
(ii) for all Vi, v2, v% € V\ the only isomorphisms of representations
V(vx) 0 V(v2) 0 V(v3) -> V{v{) 0 V(v2) 0 V(v3)
are the scalar multiples of the identity
350
11 Representations of QUE algebras: root of unity case
Then, if R — a o /, where a is the interchange of the factors in the tensor
product,
D)
where c is a scalar (possibly depending on v\, v2 and V3).
Proof In the diagram
V{vi)®V(v3)®V(v2)
V(vs)®V{vi)®V(v2)
the composite of the maps on the left-hand side gives the intertwiner
while the right-hand side gives the intertwiner 123(^1, ^2)^12(^1, ^3)^23(^2,
By property (ii), these can differ only by a scalar multiple:
1, V2) •
It is easy to see that this is equivalent to D). |
Note that the intertwiners / are only determined up to a scalar multiple,
so that it may be possible to normalize them so that c = 1. In this case, D)
is the QYBE with spectral parameters.
In practice, the hypotheses of this proposition are a little too restrictive.
Typically, V is an open set in the complex plane, I(vi,v2) is a meromorphic
function on V\ x V2, and conditions (i) and (ii) hold for generic values of the
parameters. But then E) also holds generically, and hence identically since
both sides are meromorphic functions.
Returning to Ut(sl2(<?)), we note that B) and C) are satisfied if p\(k\) =
P2(ki) = 1. This suggests that we consider the family X of representations of
Ue on which k\ — 1 and xf 7^ 0. The latter condition guarantees that all the
11.2 The restricted case 351
representations in X have dimension ?, and that they are uniquely determined
by their central character. Date et al. A991c) show that the tensor product is
indeed commutative on X, compute the intertwiners and show, using 11.1.16,
that they lead to solutions of the QYBE.
To state their result precisely, we need to modify our description 11.1.7 of
the representations V(A, a, b) in X. For a, C € Cx, set
a = a(-— _1— I, b = a~lf
and define a new basis {vi} of F(A, a, b) by Vi — fiiVi, where the constants
are such that
e -
Proposition 11.1.17 Let V\ = V(l,ai,6i), V2 = V(l,a2,&2) be represen-
representations in X. There is an intertwiner I : Vi ® V2 —> V2 ® Vi, unique up to
scalar multiples, given, with respect to the basis {v^ ® V{2} of V\ ® V2 defined
above, by
w(
V
wijere
The matrix R = a o I satisfies the quantum Yang-Baxter equation.
The functions VF(?)r and VF(^)r are the Boltzmann weights of the model
of Fateev & Zamolodchikov A982) in statistical mechanics.
11.2 The restricted case
In this section we continue to assume that e is a primitive ?ih root of unity,
where ? is odd and greater than di for all i. We use the notation defined in
Section 9.3. Except in Subsection 11.2D, all representations are on complex
vector spaces.
352 11 Representations of QUE algebras: root of unity case
A Highest weight representations If V is a finite-dimensional represen-
representation of ?/eres, then K\,... ,Kn act by commuting operators on V, and, by
9.3.5(ii), these operators are simultaneously diagonalizable with eigenvalues
in the set { ± er}r=o,i,...,?-i. As in Subsection 10.1A, by tensoring with a
one-dimensional representation, we may and shall restrict attention to repre-
representations on which K\ — 1 for all i\ such representations are said to be of
type 1.
Following the discussion for Uq, one is tempted to define the weight spaces
of V to be
Vx = {v G V | Ki.v = eix^v for all i}, (A G P).
But this definition is unsatisfactory, for V\ would be equal to V^ whenever
A — fi G ?P, so the sum of the weight spaces would not be direct. The 'reason'
for this is that the Kf1 do not generate a maximal abelian subalgebra of E/Jes.
In fact, the elements Ky° commute with each other and with the Ku and,
by Remark [1] following 9.3.5, these elements together generate C/Jes'°.
Lemma 11.2.1 If V is a finite-dimensional U*es-module of type 1, then
(i) the (Xf)^ act nilpotently on V;
(ii) the eigenvalues of the Ky° on V are integers.
Outline of proof It is enough to do the s/2 case. Since K\ and Kl?'°
are commuting operators on V and K[ = 1, we can write V = 0mo,miKno,mi 5
where K\ = em°.id and Kl/° — mi is nilpotent on Vmn mi; here, mo G Z,
L t Je
0 < mo < ? and mi G <C.
Using the relations in 9.3.4, it follows that
(X1+)^.Fmo,mi C]/m0)mi+2,
if m0 + 2 < ?,
with similar results for X± and (Xf)^). Since dim(V) < cxo, the possible
values of mi lie in a bounded set, so the first inclusion implies (i).
Now assume, for a contradiction, that Vrmo>mi ^ 0 for some mi G C\Z,
and that mo +&t(m{) is maximal with this property Eft(mi) denotes the real
part of mi). The above inclusions show that X^ and (X^~)^ both increase
the latter quantity by 2, so must annihilate Vmo,m1- It follows that Vrm0)mi
is annihilated by (X^~)^ for all k > 1. On the other hand, part (i) implies
that VmQ,m1 is annihilated by ((Xf )^))r for some r, and hence by (X^)^r\
Applying both sides of the relation in A3) of Chapter 9 (with r and s both
11.2 The restricted case 353
replaced by ?r) to Fm0)Tni, it follows that K^° also annihilates Vrno^rni.
But, by an inductive argument using the third and fifth relations in 9.3.4, it
is not difficult to prove the identity
Ir . r! n
in ?/Jes. Since V —mi is nilpotent on Vrno^rni^ it follows that mi belongs
L J e
to the set {0,1,..., r — 1}, contrary to our hypothesis. |
In view of this lemma, if v is a simultaneous eigenvector for the elements
of ?/eres'°, then
7V lnl 0 15
A^.z; = e{ ' v, \ \ .v = m^iv,
L J e%
where m^o5 mi,i ^ ^5 an(i, without loss of generality, 0 < ra^o < $>• It follows
from 9.3.6 that, if rrii — m^o + -^m^i, then [7nit]e = rrii,i> This suggests the
following definition.
We write, as usual, a — 2a/(a, a) for any root a; in particular, on — d~lai.
Definition 11.2.2 The weight spaces V\ (X e P) of a U*es-module V of
type 1 are defined by
If V is finite-dimensional, its character ch(V) is the element of the group ring
Z[P] given by
ch(V) = 2_\ dim(VA) eA.
AGP
Remark It follows from the relations in 9.3.4 that Kyc acts on Vx as
Proposition 11.2.3 IfV is a finite-dimensional irreducible Urees-module of
type 1, then V is the direct sum of its weight spaces.
Proof By 9.3.4,
F) X?(Vx)<zVx±a%, (X?)«\Vx)cVx±la%.
It follows that YlxeP ^x 1S a submodule of V. To see that the sum is direct, we
note that, by 9.3.6, if m, m' e Z are such that ef1 = ef and I"™ j = I71}] ,
then m = m!. |
Later in the chapter, we shall need to know that, as in the classical case,
characters are multiplicative:
354 11 Representations of QUE algebras: root of unity case
Proposition 11.2.4 IfV and W are finite-dimensional Urees-modules of type
1, then
ch(V <g> W) = ch(V) <g> ch(W).
Proof It suffices to show that, if v\ e V and w^ e W are vectors of the
indicated weights, then v\ 0 w^ has weight A + /i. For this, we might as well
assume that g = 5/2(^M so that A, fi € Z. We must show that Ki.{v\^>w^) =
eA+^A 0 wM) and that [*J;0] .(vA 0 wM) - [*+"] (vA 0 wM). The first
equation is obvious since K\ is group-like. To prove the second, we use the
identity
for t € N, which is easily proved by induction on t. Then, taking t — -?, what
we must prove is
( ' A
This follows easily from 9.2.10 by expanding both sides of
The definition of highest weight t/^-modules now proceeds as in the Uq
theory. Namely, a ?/Jes-module V of type 1 is a highest weight module if it
is generated by a primitive vector, i.e. a vector v\ € V\, for some A € P,
such that X?.v\ = {Xf)W.v\ = 0, i = 1,..., n. It is obvious from 9.3.3(iv)
and F) that V — 0m<aV^, so that A is the highest weight of V; moreover,
V\ — <C.V\. It follows by the usual argument that V has a unique irreducible
quotient module.
Let V^(A) be the irreducible [/^-module with highest weight A G P and high-
highest weight vector v\ (see Section 10.1). Let V^es(A) be the f/^fs-submodule
of V^(A) generated by v\, and define the Weyl module
via the homomorphism A —» C given by q 1—> e. This is clearly a highest weight
t/Jes-module with highest weight A, but it is not necessarily irreducible.
11.2 The restricted case 355
Proposition 11.2.5 Suppose that AgP+. Then:
(i) dim(VFeres(A)) < oc;
(ii) the character of VFeres(A) is given by the Weyl character formula;
(Hi) VFeres(A) is irreducible if either
(a) (A + p, a) < ? for all positive roots a, or
(b) \=(?-l)p + tfj, for some \i e P+.
Outline of Proof Parts (i) and (ii) follow immediately from 10.1.5. Part
(iii) is proved in Andersen, Polo & Wen A991). |
In general, since VFeres(A) is a highest weight module, it has a unique irre-
irreducible quotient module T/res(A). From 11.2.5 we obtain immediately
Corollary 11.2.6 If A e P+, then dim(Vrcres(A)) < oc. If, in addition, A
satisfies one of the conditions in 11.2.5(iii), the character of V/es(A) is given
by the Weyl character formula. |
Example 11.2.7 Suppose that g = s/2(C). For any integer n, write n —
no + ?ni, where no, n\ € Z and 0 < no < ?. Then, if m G N, the Weyl
module VFeres(m) with maximal weight m has a basis {vq ,.. •, Vm } on
which the action of C/Jes is given by
(XrflvM = (n + l)v(r% (X+)W.vW = ((m - r)x + 1)^.
Let V be the subspace of VFeres(m) spanned by the Vr such that mo < ro < ?
and T\ < mi. Then, it is not difficult to see that:
(i) V is the unique proper ?/eres-submodule of Weres(ra);
(ii) V' ^ V7es(ra'), where m' - ? - 2 - m0 + ?(mx - 1);
(iii) VFf^m)/!/7 9* F/es(m).
It is clear from these remarks that VFeres(m) is irreducible if (and only if)
either m < ? or ra0 = ? - 1, confirming 11.2.5(iii) in this case. Note that, by
(i), if Weres(m) is reducible, it is not completely reducible.
xr x
17 15 13 11 9 7 5 3 1 -1 -3 -5 -7 -9 -11 -13 -15 -17
356 11 Representations of QUE algebras: root of unity case
As a specific example, take ? = 5, m — 17. The weight structure of T/resA7)
is shown above, in which the solid circles denote basis vectors of T/resA7)
with the indicated weights, and the open circles denote the basis vectors of
the unique maximal submodule of VFeresA7), which is isomorphic to T/res(ll).
Note that dim(T/resA7)) = 12. In general, it is clear from the above de-
description that dim(Vr/) = m\(? — rao — 1), so that
dim(V7es(m)) = m + 1 - m^i - m0 - 1) = (m0 + l)(rai + 1). 0
We now prove the main result of this subsection.
Theorem 11.2.8 Every finite-dimensional irreducible U*e& -module V of type
1 is isomorphic to Feres(A) for some (unique) A G P+.
Proof This follows closely the proof of the analogous result in the classical
situation. By 11.2.3, V is the direct sum of its weight spaces. Let A G P
be maximal among the weights of V. Then, any non-zero vector v\ G Va
is primitive, and, since V is irreducible, it follows that v\ generates V and
hence that V ^ F/es(A).
It remains to prove that A G P+. By 11.2.1 (i) and the fact that
/ -rr- \ (rmP\ ->-
in C/Jes, it follows that there exists m > 1 such that
(X-)iim~m-vx ? 0, (X-)ime)-Vx = 0.
Applying (X^~)^ to the second equation and using the relations in 9.3.4, we
find that
Hence, r(*.«*)-(™-i)*l = q. By 9.3.6, this implies that (m-l)? < (A,di) <
m?; in particular, (A, oti) > 0. |
Remark One can also obtain V/es(A) by a Verma module construction. Let
Meres(A) be the quotient of ?/eres by the two-sided ideal generated by the fol-
following elements:
Then, Mfs(A) is a highest weight U*es-module, and Veres(X) is its unique
irreducible quotient. A
11.2 The restricted case 357
B A tensor product theorem For any A G P+, we can find unique Ao,
Ai e P+ such that A = Ao + ?Xi and 0 < (Ao , a*) < ? for i = 1,..., n.
The following theorem reduces the study of Veres(X) to that of Kres(A0) and
Theorem 11.2.9 Let A e P+ and write A = Ao +?\i as above. Then, there
is an isomorphism of Ue-modules
v;res(A) 9* veres{\0) 0 Kres(^i)-
Before we can sketch the proof of this theorem, we need to gain some
understanding of the structure of the modules V/es(Ao) and VJes(?\i).
The representations of the first kind are essentially the representations of
the finite-dimensional Hopf subalgebra Ufn of Urees generated by the Xf~ and
Kf1 (see Subsection 9.3B).
Proposition 11.2.10 Let AgP+ satisfy 0 < (A, a*) < ? for i = 1,... ,n.
As a Ufu-module, V7es(A) is irreducible. In fact, restriction to Ufu sets up
a one-to-one correspondence between the finite-dimensional irreducible U*es-
modules of type 1 whose highest weights satisfy the above condition and the
irreducible Ufn-modules on which the Kf act as 1. In particular, Ufn has,
up to isomorphism, exactly ?n irreducible representations. |
Remark It follows by an argument used in the proof of 11.2.8 that, if V/es(A)
is as in the preceding proposition and v\ is a highest weight vector in V/es(A),
then (Xr)W.vx = 0. A
To describe the modules of the second kind, we need the Frobenius ho-
momorphism Fre from U*es to the classical enveloping algebra U defined in
9.3.12 (we extend the base field from Q(e) to <C).
Proposition 11.2.11 Let A e P+ and let V(X) be the irreducible U-module
with highest weight A. Then, VJes(?X) is isomorphic as a U*e&-module to the
pull-back of'V(X) by Fre. |
Remark It follows from this that the character of VJes(?X) can be deduced from
the Weyl character formula. In fact, recall from 9.3.12 that Fr€(Ki) — 1, and
note that Fre([Ky°]e ) = Hi (to see this, compute Fre{[(Xf)W,(Xr)W])
using 9.3.12 and A3) from Subsection 9.3A). It follows that the weights of
V*es(?X) are obtained (with the same multiplicities) exactly by multiplying
those of V(A) by ?.
This implies, in particular, that Xf1 and K{ — 1 are zero on VJes(?X). A
We can now give an
358 11 Representations of QUE algebras: root of unity case
Outline of proof of 11.2.9 We first show that F/es(A0)®V;res(^Ai) (= v,
say) is a highest weight ?/eres-module with highest weight A. Let v0, v\ be
highest weight vectors in Veres(X0) and F/es(Ai), respectively. By 9.2.10 and
the preceding remark, it follows that
Ki.(vo 0 vi) = Ki.vo 0 Ki.vi.
(In fact, this is true even if vo and v± are not highest weight vectors.) From
the first of these equations and A3) from Subsection 9.3A, we deduce that
.v0 ® vi + v0
^ J
These equations imply that vo 0 V\ is a primitive vector in V of weight A =
To show that v0 0vi generates V, let v0 € V7es(A0), t>i G V7es(?\i). Then,
z;o = ^o-^o, v[ = xi.^i, where xo (resp. xi) is a linear combination of products
of elements X~ (resp. (X~)^^), i — 1,..., n. By the remark following 11.2.10
and the fact that the (X~)^ behave like primitive elements on V, we have
X0.(^0 0 ^l.^i),
and, since X~ acts trivially on V7es(^Ai), this equals
X0.^0 0 X\.V\ — v'o 0 ^.
It remains to prove that V is irreducible. Let F7 be a proper submodule
of V, and let A' be maximal among the weights of V'. Any non-zero vector
v' e Vy is primitive. Fix a vector space basis {w1?..., wp} of F/es(-?Ai) and
write
T—\
Arguing as above, we have
0 = Xf.v' =
r=l
so X* ,ur = 0 for all r and all i. Hence, ur is a multiple of Vo and t/ = vo
for some v[ € VJes(?Xi). The same argument now gives (X^)^.Vi — 0, so
v[ is a multiple of V\. Hence, V contains vo 0 t>i, which generates V. Thus,
V = V, a contradiction. |
Theorem 11.2.9 is analogous to a theorem of Steinberg in the representation
theory of the hyperalgebra Uwp (see Subsection 9.3C). It is known that the
irreducible representations of Uwp are again parametrized by P+ (every such
representation is finite dimensional); let Vfp(X) be the irreducible module
associated to A € P+.
11.2 The restricted case 359
Steinberg's tensor product theorem Let X e P+ and write
X = Ao + pAi + p2X2 + h pkXk,
where 0 < (Aj , di) < p for i = 1,..., n, j = 0,1,..., k. Then, as Ujpp-
modules,
Vfep(A) = Ffp(A0) 0 Vfcp(Ai)*r <8> FFp(A2;r 0 • • • ® Vtp(Afc)w ,
where Vjpp (X)Fr3 is the twist of Vjpp (A) by the jth iterate of the Frobenius map
Ft. I
This theorem reduces the study of the representations Vfp(X) to the special
case in which 0 < (A, di) < p for all i: the irreducible representations whose
highest weights satisfy this condition are called restricted.
The most obvious difference between this result and 11.2.9 is that there is
no upper bound (independent of A) on the number of factors in the tensor
product in Steinberg's theorem, whereas there are only two factors in 11.2.9.
The 'reason' for this is the fact, already noted at the end of Subsection 9.3C,
that f/Jes is finitely generated, but Ujpp is not. Note also that, unlike the
characteristic p Frobenius map, Pre is a map between two different spaces,
and so cannot be iterated.
C Quasitensor structure We remarked at the end of Subsection 10.ID
that, although we do not have a universal R-matrix for f/Jes, the conclusion
of 10.1.19 holds for [/?es, even when e is a root of unity. We record this result
here.
Proposition 11.2.12 With the usual operations of direct sum, dual and ten-
tensor product, the category of finite-dimensional f/eres-modules of type 1 which
are the direct sums of their weight spaces is a rigid, (C-linear, quasitensor
category |
D Some conjectures The results of Subsection 11.2B reduce the study
of the finite-dimensional irreducible representations of f/eres to those of the
finite-dimensional Hopf algebra f/efin. Recall from 9.3.11 that, if ? = p is an
odd prime, there is a close relationship between the Z[e, e-1]-algebra Uf%,
the quotient of U^\ by the ideal generated by the K\ — 1, and f/pn, the
subalgebra of the hyperalgebra UFp generated by the Xf1 (recall also that bars
are used to distinguish generators of Ujpp from those of f/eres). It is known that
the irreducible representations of U^n are parametrized by (Z/pZ)n; in fact,
these representations are exactly the restricted modules Vpp(A), whose highest
weights are of the form A = ]T\ t-A^, where 0 < r* < p. For this reason, ?/jpn
360 11 Representations of QUE algebras: root of unity case
is called the restricted enveloping algebra of g over Wp. By 11.2.10, the same
set (Z/pZ)n parametrizes the finite-dimensional irreducible representations
of Uf% (i.e. those which are free and of finite rank as Z[e, e~1]-modules). To
make this connection on the level of representations, note that if V is a finite-
dimensional irreducible /7^-module, and if V has parameter (highest weight)
A, the second isomorphism in 9.3.11 allows one to regard V as a ?/jpn-module,
and as such it has a unique irreducible quotient corresponding to the same
parameter A. Lusztig A990a) conjectures that V is actually irreducible as a
?/jpn-module, and in fact
Conjecture 11.2.13 If ? = p is an odd prime, and p is sufficiently large,
then U^n and U^n have identical representation theories.
This conjecture has largely been proved by Andersen, Jantzen & Soergel
A992). They show that every irreducible ?/jpn-module arises by reduction
(mod p) from an irreducible [/^-module, provided that p is sufficiently large
(although no bound is given on how large p should be). We shall discuss their
work in a little more detail at the end of this subsection, but, before doing so,
we describe a second conjecture of Lusztig A989), relating the representation
theory of C/?es(c$) to that of the affine Lie algebra g (see the Appendix).
This conjecture enables one to determine (in principle) the characters of the
modules VJe8(X). A proof of the preceding conjecture would then determine
(in principle) the characters of the irreducible representations of ?/jpn and
hence, by Steinberg's tensor product theorem, those of Ujpp- It is known that
this would completely determine the rational representation theory of the
algebraic group (over the algebraic closure of JFp) associated to g.
To state Lusztig's conjecture, we assume for simplicity that g is of type A,
D or E. Let
Here, I) is the Cartan subalgebra of g, p is half the sum of the positive roots
and 0 is the highest root. Then, A^ is a simplex bounded by the hyperplanes
The reflections s0, si,...,sn in these planes generate the affine Weyl group
We of g; the length ?(w) of an element w G We is defined in the obvious way. If
A G I)*, there is a unique w\ G We of minimal length such that w^1(X) G A^.
If wr is any element of We, we set \w* = w/(w^1(X)).
For any wf, w G We, let Pw>,w G Z[q] be the associated Kazhdan-Lusztig
polynomial (see Humphreys A990), Chap. 7). We recall that Pw>,w = 0 unless
wf < w, where < is the Bruhat ordering on We-
11.3 Tilting modules and the fusion tensor product 361
Conjecture 11.2.14 Let A e P+. Then, in the Grothendieck group of
finite-dimensional U*es -modules,
where the sum is over {wf G Wt \ wf < w\, \w> G
Remark The equality in 11.2.14 implies that
By 11.2.5, the characters of the Weyl modules W*es(\wr) are given by the
Weyl character formula, so a knowledge of the coefficients Pw',Wx(l) enables
one to compute the characters of the irreducible modules V7es(A). A
Conjecture 11.2.14 has been proved by Kazhdan & Lusztig A991). They
show that the category of finite-dimensional ?/eres(g)-modules is equivalent, as
an abelian quasitensor category, to a certain category of representations of g
of level — ? — h, where h is the Coxeter number of g (see the Appendix). The
main point is to construct a new kind of tensor product <g) on this category,
which has the property that the tensor product of two representations of level
—? — h is again of level — ? — h (of course, with the usual tensor product, the
levels add). We shall outline their arguments in Chapter 16.
Conjecture 11.2.14 resembles another conjecture of Lusztig A980), concern-
concerning the characters of representations of g in characteristic p. It follows from
the work of Andersen et al. A992), and the proof of 11.2.14, that this con-
conjecture is equivalent to an analogous conjecture about representations of the
(classical) affine Lie algebra g of level —p — h. A proof of this last conjecture
was announced by Casian A993), and his arguments have been completed by
Kashiwara & Tanisaki A994).
11.3 Tilting modules and the fusion tensor product
In this section, we discuss tensor products of representations of U^es(q) and
show that it leads to a remarkable new algebraic structure. We assume that
e is a primitive ^th root of unity, where, as usual, ? is odd and greater than
di for all i. We also assume that ? > h, the Coxeter number of g, and that ?
is not divisible by three if g is of type G2. All representations are on complex
vector spaces.
A Tilting modules We begin by introducing an important technical tool.
362 11 Representations of QUE algebras: root of unity case
Definition 11.3.1 A finite-dimensional U™8-module V of type 1 has a Weyl
filtration if there exists a sequence of submodules
0 = Vo C Vi c • • • C Vp = V
with VrlVr-x ^ W*es(Xr) for some Xr ? P+, r = 1,... ,p.
A finite-dimensional UveQS-module V of type 1 is a tilting module if both V
and its dual F* have Weyl filtrations.
Example 11.3.2 Define the principal alcove
C? = {\eP+ | (A + p, d) < ? for all a G A+},
where p is half the sum of the positive roots of g. Suppose that A G C|.
Then, by 11.2.5, W*es(\) = Veres(X) is irreducible, and so trivially has a Weyl
filtration. But Veres(A)* ^ V7es(-w0(A)), and it is clear that -wo(\) € C?.
Hence, V7es(A) is a tilting module in this case. 0
The next result lists some of the basic properties of tilting modules.
Proposition 11.3.3 (i) The dual of a tilting module is tilting,
(ii) Any (finite) direct sum of tilting modules is tilting.
(Hi) Any direct summand of a tilting module is tilting,
(iv) Any (finite) tensor product of tilting modules is tilting.
Outline of proof Parts (i) and (ii) are obvious, and part (iii) is nearly
so. Part (iv) is proved by Paradowski A992), using the theory of canonical
bases, which we discuss in Chapter 14. |
In view of parts (ii) and (iii) of this proposition, we may restrict our atten-
attention to indecomposable tilting modules. These are parametrized by P+:
Proposition 11.3.4 For any A e P+, there exists, up to isomorphism, a
unique indecomposable tilting module Te(A) with the following properties:
(i) the set of weights of Te(X) is contained in the convex hull of the Weyl
group orbit of X;
(ii) A is the unique maximal weight of Te(A);
(iii) the weight space Te(X)\ is one-dimensional;
(iv) Tc(\y * Te(-wo(X)).
Conversely, every indecomposable tilting module is isomorphic to some
(unique) Te(A).
Outline of proof We indicate briefly how Te(A) is constructed. To do so,
we shall need the following criterion for the existence of a Weyl filtration.
11.3 Tilting modules and the fusion tensor product 363
Lemma 11.3.5 A finite-dimensional U*es-module V of type 1 has a Weyl
filtration if and only if, for all A G P^~, every short exact sequence of U*es-
modules
0 -+ Wfs(A) -> V -> F -> 0
splits. |
Fix A G P+ and let Vi = Weres(A). If Vi* has a Weyl filtration, we set
^e(A) = V\. Otherwise, by the lemma, there is a non-split extension
for some fie P+. This forces A > /i (since W*es(\) and Weres(/i) are deforma-
deformations of irreducible representations of g, it is enough to prove the analogous
assertion in the classical situation, which is well known). Since 0 C V\ C V2
is a Weyl filtration of V2, if V2 nas a Weyl filtration, we may take Te(X) = V2.
Iterating this procedure, one eventually arrives at the desired module Te(A);
there can be only finitely many iterations, because there are only finitely many
dominant weights less than A. |
Propositions 11.3.3 and 11.3.4 have a number of interesting corollaries.
Corollary 11.3.6 Let T be a tilting module for f/eres. Then,
G) T^ 0 Te(A)en*(T\
where the multiplicities n\(T) are uniquely determined by T.
Proof It is immediate from 11.3.3 and 11.3.4 that T is a direct sum of
Te(A)'s. For the last part, note that, if A is a maximal weight of T, then Te(A)
must occur in any decomposition of T of the form G). The result now follows
by an obvious induction on dim(T). |
Essentially the same argument proves
Corollary 11.3.7 Let Tx and T2 be tilting modules for ?/eres, and suppose
that ch(Ti) = ch(T2). Then, Tx and T2 are isomorphic.
Proof In fact, the hypothesis implies that T\ and T2 have the same weights,
hence the same maximal weights. So we can use the same argument by
induction on dim(Ti) = dim(T2) as above. |
This result and 11.2.4 immediately give
Corollary 11.3.8 lfTx andT2 are tilting modules for Urees, then Tx <g> T2
and T2 <g) T\ are isomorphic as U*es-modules. |
Of course, this result is also contained in 11.2.12, but the present proof
makes no use of R-matrices.
364
11 Representations of QUE algebras: root of unity case
Example 11.3.9 If g = s/2(C), 11.3.2 shows that the tilting modules TC(A)
with maximal weights in the range 0 < A < ? — 1 are irreducible (we identify
X G P with the integer (A, a), a being the positive root of g). When ? — 1 <
A < 2? - 2, Te(A) can be described explicitly as follows. First, by 11.2.5,
Wrees(? - 1) is irreducible, so Te(? - 1) = Veres(? - 1). If ? < A < 2? - 2, T€(A)
is the 2^-dimensional module with basis {tr}r=o,i,...,AU{^}r=o,i,...,2^-2-A and
the following action (as usual, we write r = r$ + -fri with 0 < ro < ?, r\ = 0
or 1):
A-2r,
,tr =
Xf.tr = [A-r + 1
[Xf)W.tr = ((\-
Ki.t'r = t
= [r
?-2r-2-A ,r
t
4 = o,
r_^, if 0 < r < 2? - 2 - A,
X~.t'r = [r + l]c<+i, if 0 < r < 2? - 2 - A, (Xfj^.^ = 0,
r / — 1
t+.t'0=i\-i- - ¦ — '
(Vectors tr and tr with r outside the appropriate range are understood to be
zero.)
Fig. 20 The tilting module Tc(8) for Urees(sl2(C)), e = e
11.3 Tilting modules and the fusion tensor product 365
The structure of Te(A) for ? < A < 2? - 2 is illustrated in Fig. 20, where
dots represent basis vectors, the horizontal level indicates the weight, and
upward (resp. downward) sloping arrows indicate the action of X^~ (resp. of
Xf). It is clear that Te(A) is indecomposable, that the tr span a submodule
of Te(A) isomorphic to W€res(A), and that the quotient, spanned by the t'r,
is isomorphic to WreesB? - 2 - A). Thus, TC(A) has a Weyl filtration. The
structure of Te(A)* can be understood essentially by turning Fig. 20 upside
down, which makes it clear that Te(A)* has a Weyl filtration involving the
same Weyl modules as that of Te(X). Hence, Te(X) is a tilting module.
Note that A is the unique maximal weight of Te(A), but that Te(X) is not
a highest weight module, because it is not generated by the maximal weight
vector to. Note also that the character of Te(X) can be written down without
further computation:
ch(Weres(A)) + ch(WeresB^ - 2 - A)), if ? < X < 2? - 2,
the characters of the Weyl modules being given by the Weyl character formula.
0
B Quantum dimensions By analogy with the discussion leading to 8.3.15,
we define the quantum trace of an endomorphism / of a finite-dimensional
?/eres-module V to be
qtr(/) = traced* /),
where, if ]T\ r^, r^ G TL, is the sum of the positive roots of g, then Kp* =
Yl{ K[%. Taking / = idy, we get the quantum dimension
qdim(F) = trace(ifp*).
Note that we do not have a universal R-matrix for f/eres, much less a ribbon
Hopf structure, so this is not, strictly speaking, an application of the theory
in Subsection 4.2C.
Example U.S. 10 Since, by 11.2.5, the character of the Weyl module W*es(X)
with highest weight A G P+ is given by the Weyl character formula, it is easy
to compute its quantum dimension. One obtains a 'quantum Weyl dimension
formula':
the product being over all the positive roots j3 of g. It follows that Weres(A)
has non-zero quantum dimension if and only if, for all f3 > 0, (A + p, C) is
not divisible by ?. <C>
Example 11.3.11 Let us compute the quantum dimension of the tilting mod-
modules Te(A) for sl2(C) described in 11.3.9. If A < ?, we find, using the preceding
366 11 Representations of QUE algebras: root of unity case
example, that qdim(Te(A)) = [A + l]c; in particular, qdim(Te(^ - 1)) = 0. On
the other hand, if I < A < 2? - 2, we have, using the Weyl filtration of Te(A),
qdim(Te(A)) = qdim(Weres(A)) + qdim(WeresB^ - 2 - A))
= [A + l]e + [2^-A-l]c = 0. 0
It is obvious that, if A G C^ the condition on A in the last sentence of 11.3.10
is satisfied, and hence W*es(\) = V7es(A) = Te(X) has non-zero quantum
dimension. Example 11.3.11 shows that the converse of this assertion is also
true if g = s/2(<C) and A is not too large. In fact,
Proposition 11.3.12 Let A e P+. Then, qdim(Te(A)) ^ 0 if and only if
\?C?. |
See Andersen A992a) for the proof.
Corollary 11.3.13 Let A e P+\C? and let f : Te(A) -+ T€(\) be a homo-
morphism of U*es-modules. Then, qtr(/) = 0.
Proof Since Te(A) is indecomposable, / is the sum of a scalar operator
and a nilpotent operator. The quantum trace of the former vanishes by the
proposition, and that of the latter vanishes because Kp* f is nilpotent if / is
nilpotent, Te(X) being the direct sum of its weight spaces by 11.2.3. |
We shall need one further corollary of 11.3.12 in the next subsection.
Corollary 11.3.14 Let A e P+\Ct and let V be any Ul™-module of type
1. Then, every direct summand of Te(A) 0 V has quantum dimension zero.
Outline of proof By considering the projection onto a direct summand,
it is enough to prove that qtr(/) = 0 for all t/^es-module homomorphisms
/ : Te(A) (g) V -> Te(A) <g> V. Consider the following isomorphisms of Urees-
modules:
End(Te(A) 0 V) 9i (Te(A) 0 V) 0 (Te(A) 0 V)*
Applying the quantum trace End(F) —>> C, which is a ?/eres-module homo-
morphism, to the middle factor in the last module, we obtain a f/eres-module
homomorphism / : Te(A) —> Te(A). It is easy to check that
qtr(/)=qtr(/).
But the right-hand side vanishes by 11.3.13. |
11.3 Tilting modules and the fusion tensor product 367
C Tensor products We would like to understand how to 'decompose' tensor
products V^es(A) <g) V*es(/i) for A, \i G P+. Of course, we cannot expect that
such a tensor product is a direct sum of irreducible modules, since U*es-
modules are not completely reducible in general (see 11.2.7). However, it
follows from 11.3.2, 11.3.3 and 11.3.6 that, if A, /i G d, then yeres(AHF€res(/i)
can be expressed as a direct sum of indecomposable tilting modules. Thus, one
could try to define a 'semisimple' tensor product by discarding those tilting
components which are not irreducible. Unfortunately, this procedure does
not lead to an associative tensor product (see the remark following 11.3.17).
However, a small modification of it does.
We begin to make this precise with the easy, but important,
Proposition 11.3.15 LetTx andT2 be tilting modules. Then,
(8) Ti ®T2 <* @ Feres(A)em*) 0Z,
where the multiplicities m\ G N and Z is a U*es-module with the property
that qtr(/) = 0 for all homomorphisms of U*es-modules f : Z —> Z (in
particular, qdim(Z) = 0).
Proof By 11.3.3, Tx ® T2 is a tilting module, and hence, by 11.3.6,
for some n\ G N. We take m\ — n\ if A G Ci and set
Z=
\€P+\Ci
The required property of Z follows from 11.3.13. |
Example 11.3.16 If c$ = s/2(C) and 0 < A,// < i — 1, the decomposition of
the tensor product V7es(A) (8) VJes(fi) into indecomposable tilting modules is
as follows:
v=\\-n\
+ Li (mod 2)
if A + fi < ? - 2, and
vps(v) e
i/=|A-/x| i/ = f-l
+ jz (mod 2) i^ = A + ax (mod 2)
368 11 Representations of QUE algebras: root of unity case
\i?-l<\ + H<2?-2. To verify this, it is enough, by 11.3.7, to check that
the modules in question have the same character. This is straightforward,
since the characters of all modules appearing are already known from 11.3.9.
Returning to the general case, 11.3.15 suggests that we can 'make T\ 0 T2
completely reducible' by redefining the tensor product to be the result of dis-
discarding Z on the right-hand side of (8). More precisely, if T is any tilting
module, let T be the sum of the indecomposable summands in a decomposi-
decomposition G) of T whose maximal weights lie in Ci\ then T is well defined up to
isomorphism. Further, if T\ and T2 are tilting modules, define a new kind of
tensor product of T\ and T2 by
Proposition 11.3.17 LetTl7T2 and T3 be tilting modules for Urees. Then,
as U*es-modules:
(iij 7i0 (T20T3) 9*
Proof Part (i) is immediate from 11.3.8. For part (ii), we have
where n\{Z{) = nx(Z3) = 0 for all A G C?. By 11.3.14, nA(Ti <g> Z2)
nx(Z3 (g) T3) = 0 if A e Ci. Hence,
(Ti®T2) 0T3 = (Ti0T2) 0T3, since Z30T3 - 0,
(T2
(T2
= Ti<g> (T2®T3), since Ti^Zi = 0.
Remark Let ^ = 5. From 11.3.16, we find that
F/esB) ® F/esB) ^ F/es@) 0 F/esB) 0 F/esD),
FeresB) 0 F/esD) ^ F/esD) 0 TeF),
F/esD) 0 F/esD) ^ V7esD) 0 TeF) 0 Tc(8).
Thus, if we define a tensor product 0 by discarding those indecomposable
tilting components which are not irreducible, we have
D) ^ (Kres@) 0 KresB) ® Kr
^ F/esD) 0 F/esD) 0 F/e
11.3 Tilting modules and the fusion tensor product 369
whereas F/esB)(8)(l/eresB)(8)l/eresD)) ^ VeresB)(8)l/eresD) ^ F/esD). Thus, <§>
is not associative, even up to isomorphism. On the other hand,
VeresB)®(VeresB)®VeresD)) = 0 = (yeresB)^KresB))^VeresD). A
The module T associated to a tilting module T is well defined only up to
isomorphism, for the decomposition of T into indecomposables is not unique,
in general (although the maximal weights of the summands are unique). It is
important, especially for the categorical arguments presented below, to make
a canonical choice of a module in the isomorphism class of T. This can be
done as follows.
Let T~ be the unique maximal submodule of T, all of whose composition
factors are of the form Feres(A) for A G Cf. We note that T~ is completely
reducible. Indeed, we might as well assume that T is indecomposable, and
then the highest weights of all the composition factors of T belong to the same
orbit of the affine Weyl group on P - this follows from the 'linkage principle'
(see Andersen, Polo & Wen Kexin A991)). In particular, this is so for Tv, but
all its composition factors have highest weights in C^, no two distinct points
of which are in the same orbit. Hence, all composition factors of T~ are the
same, and our assertion now follows from the remarks made in the proof of
11.3.4.
Similarly, let T~ = TjV be the largest quotient of T which has all its
composition factors of the form Feres(A) for A G C^. The argument in the
preceding paragraph shows that T" is also completely reducible.
The following result was pointed out to us by D. Kazhdan. We include the
proof, which was given to us by S. Donkin, since it does not seem to be in
the literature.
Proposition 11.3.18 The image ofTdT in T = T/Tf is isomorphic to
T.
Proof We first show that Te(Xy C Te(A)' for any A g P+\Ce. Indeed, if
Te(A)~is not contained in Te(A)', then, since Te(Xy is completely reducible,
there is an irreducible submodule V of Te(\y which is not contained in Te(A)'.
Since Te(A)~is completely reducible, we have
re(A) v@Te(\y w
Te(\y Te(\y ^ Te(\y
for some submodule W of T containing Te(A)'. Hence, Te(A) = V + W,
and, by counting dimensions, one sees that the sum is direct. Since Te(A) is
indecomposable, W — 0. But then T(X)f = 0, which contradicts the fact that
If T is any tilting module, write T = T\ 0 • • • 0 Tr, where the Tj are
indecomposable and their maximal weights Xj lie in Ct if 1 < j < s (say), but
370 11 Representations of QUE algebras: root of unity case
not if s + 1 < j < r. Now, the highest weights of all the composition factors
of T/ 0J>S Tj are in Ct, so that T C ®j>sTj. Hence, @j<aTj = ®j<sTf
maps injectively into T/T1. On the other hand, by the result of the previous
paragraph we have TfC Tj C Tf for j > s, so that @j>sTf maps to zero in
r/r. i
From now on, T will mean the module described in the statement of 11.3.18.
D The categorical formulation Let tilt^ be the full subcategory of the
category of finite-dimensional ?/eres-modules of type 1 whose objects are the
tilting modules for ?/eres. Proposition 11.3.3 shows that tilt^ is closed under
taking direct sums, duals and tensor products. Thus, from 11.2.12, it follows
that
Proposition 11.3.19 tilt^ is a rigid, (C-linear, quasitensor category. |
Now let tilt^ be the full subcategory of tilt^ consisting of the finite-
dimensional ?/eres-modules all of whose weights lie in
{X e P | (A + p, d) < ? for all roots a}.
From 11.3.2 and 11.3.4, it follows that tilt^ is a semisimple, C-linear category.
Proposition 11.3.20 Let tilt^ be the full subcategory of tilt ? consisting of
the tilting modules T for which T = 0. Then;
(i) tilt^ = tilt^ 0 tilt^, i.e. every tilting module is, in exactly one way, the
direct sum of objects in tilt^ and
(ii) tilt^ is an ideal in tilt^, i.e. ifT' is in tilt^ and T is any tilting module,
thenT®T' is in tiltj;
(iii) ifTi, T2 G tilt*, V e tilt^ / <e Homtiit^Ti,^) andg G Homtiit,(T',T2),
then g o / = 0.
Proof Part (i) is immediate from the definitions. For part (ii), note that,
by 11.3.13, if T is an object of tilt^, then qtr(/) - 0 for all ?/eres-module
endomorphisms of T. But, the proof of 11.3.14 shows that, if / is a t/eres-
endomorphism of T 0 T', then qtr(/) = qtr(/) for some / <E End(T/). Thus,
(ii) follows.
Finally, since tilt^ is semisimple, it is enough to prove (iii) when T\ and T2
are irreducible; also, we might as well assume that T\ = T2, since if T\ and
T2 are not isomorphic the result is trivial. But then if g o / ^ 0, T\ —T2—T
would be a summand of Tr, which is impossible since T has non-zero quantum
dimension. |
From this, we deduce that tilt^ is a 'quotient category' of tilt^.
11.3 Tilting modules and the fusion tensor product 371
Theorem 11.3.21 With the usual operations of direct sum and dual, and
with the tensor product 0 defined in Subsection 11.3C, tilt^ becomes a rigid,
semisimple, (C-linear, quasitensor category.
Outline of proof Let C be the category whose objects are those of tilt^,
but whose sets of morphisms are given, as C-vector spaces, by
Homc(Ti,T2) - Homtiit,(T1,r2)/Hom;ilt^(r1,r2),
where Horr4iIt/,(Ti,T2) consists of the morphisms / : T\ —+ T2 which factorize
as / = g o h, where g <E Homtiit, (T',T2), h G Homtnt^T^T') and V is an
object of tilt^ (it is easy to see that Homiiit^(Ti,T2) is a vector subspace of
Homtnt^(Ti,T2)). By using 11.3.20, it is easy to see that this makes C into
a C-linear category.
Moreover, there is a functor T : tilt^ —> C which is the identity on objects,
and the natural projection
Homtiit<(Ti,T2) - Homtiit,(Ti,T2)/Hom;ilt?(Ti,T2)
on morphisms. If one defines commutativity and associativity isomorphisms
in C to be the images of those in tilt^, then C becomes a C-linear, quasitensor
category. Rigidity is also easily checked.
Restricting T to tilt^ gives an equivalence of categories T : tilt^ —> C.
Indeed, to prove this, it is enough to show that every object of C is isomorphic
to the image under T of an object of tilt^, and that T is a bijection on sets
of morphisms (see MacLane A971), page 91). Both assertions follow easily
from 11.3.20. Since C is a rigid, C-linear, quasitensor category, so is tilt^. |
It is natural to ask for a description of the fusion ring of the quasitensor
category tilt^ (see Subsection 5.2D). According to D. Kazhdan (private com-
communication) , this fusion ring is isomorphic to the quotient of the Grothendieck
ring of the category of finite-dimensional g-modules by the ideal generated by
the irreducible modules whose highest weights lie on the upper wall
ofCe.
Example 11.3.22 We consider the fusion ring associated to t/eresE/2(C)) for
e = \/—T. Unfortunately, this example is not covered by the results of this sec-
section, since we have always assumed that ? is odd. However, it is easy to check
directly that there are exactly three irreducible Lf^^(s/2(C))-modules of type
1 with non-zero quantum dimension, namely the representations V^-@),
V^~(l) and V^yB) of the indicated highest weights (and given by the
usual formulas). Their dimensions are 1, 2 and 3, and their quantum dimen-
dimensions are 1, y/2 and 1, respectively. Defining the truncated tensor product (8)
372 11 Representations of QUE algebras: root of unity case
as usual by discarding summands of quantum dimension zero, it is easy to
check that
), for A = 0, 1, 2.
Comparing with the formulas in 5.2.11, we see that this fusion ring is iso-
morphic to that of the 'scaling model of the Ising model at the critical
point': one should identify the physical representation ps in 5.2.11 with the
?7^E*2(C))-module VJ^Bs).
This coincidence strongly suggests that Ur%j(sl2(<E)) should act on the
Hilbert space of the Ising model as a 'quantum symmetry group'. Mack &
Schomerus A990) show that this is indeed the case. 0
Bibliographical notes
11.1 The main references for Subsection 11.1A are De Concini & Kac A990)
and De Concini, Kac & Procesi A992). For the proof of 11.1.6, see De Concini,
Kac & Procesi A993a).
The irreducible representations of U€(sl2((E)) were first described explicitly
by Roche & Arnaudon A989). See Arnaudon A990), Date, Jimbo, Miki &
Miwa A990, 1991a,b) and Arnaudon & Chakrabarti A991b) for the sln case,
Arnaudon & Chakrabarti A99la,c) and Chari & Pressley A991c) for minimal
cyclic representations, Schnizer A992) for maximal cyclic representations of
the quantum orthogonal and symplectic groups, and Chari & Pressley A992,
1994a) for the construction of some representations of intermediate dimension.
11.2 Most of the results and conjectures in this section are taken from Lusztig
A989, 1990a-c). We have refrained from entering into the cohomological
theory of representations of t/eres (Borel-Weil-Bott theory). For this, see
Andersen, Polo & Wen Kexin A991, 1992), and Andersen & Wen Kexin
A992).
For a sophisticated treatment of the (classical) characteristic p theory, see
Jantzen A987).
11.3 For further details on tilting modules for E/?es, see Andersen A992a).
Similar results, when ? is a prime, have been obtained by Gel'fand & Kazhdan
A992). The proof of 11.3.21 was taken from this last reference. The theory of
tilting modules for classical algebraic groups is due to Donkin A993), whose
Bibliographical notes 373
work is based on Ringel A991). The idea of taking truncated tensor products
seems to have appeared first in the physics literature, where the representa-
representations of quantum dimension zero are regarded as 'unphysical'; see Pasquier
& Saleur A990). See Frohlich & Kerler A993) for further discussion of the
relation between Ups and quantum field theory.
12
Infinite-dimensional quantum groups
All the quantum groups we have considered in detail so far are deformations
of the universal enveloping algebra of some finite-dimensional Lie algebra (or
of the algebra of functions on the associated group). In this chapter, we look
at two families of infinite-dimensional quantum groups, called Yangians and
quantum affine algebras.
Classical affine algebras are the simplest infinite-dimensional Kac-Moody
algebras. They are more interesting and tractable than arbitrary Kac-Moody
algebras because they have another realization besides that given by the usual
generators and relations; namely, they are central extensions of the Lie algebra
of maps Cx —> g, where g is finite dimensional. One of the crucial results
in this chapter gives another realization of quantum affine algebras which,
although still in terms of generators and relations, retains many of the features
of a space of maps. For example, in some cases, one can 'evaluate' an element
of a quantum affine algebra at a point of Cx, although this is more subtle
than in the classical case.
We discuss the structure and representation theory of quantum affine al-
algebras in Section 12.2, but we begin with Yangians, which are deformations
of the Lie algebra of maps C —+ g. They are similar to, but in some ways
simpler than, quantum affine algebras. For one thing, they involve no cen-
central extension; for another, one can scale away their deformation parameter
completely, so that one is dealing with a single algebra (over C) instead of a
one-parameter family (in particular, there is no 'root of unity phenomenon'
for Yangians). Finally, Yangians may be viewed as 'degenerate' versions of
quantum affine algebras. In Section 12.1, we summarize what is known about
the structure and representation theory of Yangians, giving a classification
of their finite-dimensional irreducible representations analogous to that of
finite-dimensional complex simple Lie algebras in terms of highest weights.
In Section 12.3, we describe a duality between quantum affine s/n+i(<C) and
affine Hecke algebras, analogous to the classical Frobenius-Schur duality be-
between s/n+i(<C) and symmetric groups. Affine Hecke algebras arise classically
in connection with the representation theory of p-adic groups, so these results
give a surprising connection beteween the quantum and p-adic worlds. There
is also a parallel theory relating the Yangian of sZn+i(C) and 'degenerate'
affine Hecke algebras.
In Section 12.4, we mention briefly a second connection between Yangians
and the representation theory of classical objects, namely the orthogonal
12.1 Yangians and their representations 375
groups of infinite-dimensional (real) Hilbert space.
The main reason for the importance of Yangians and quantum affine alge-
algebras, at least historically, is that from their finite-dimensional representations
one can construct rational and trigonometric solutions of the quantum Yang-
Baxter equation, respectively. This is despite the fact that neither Yangians
nor quantum affine algebras are quasitriangular in the sense used in this book.
However, they both have 'pseudo-universal R-matrices' which, although not
well-defined elements of the tensor product of the algebra with itself (even
after /i-adic completion), give well-defined operators on the tensor product
of finite-dimensional representations, after being suitably 'renormalized'. We
describe the properties of these pseudo-universal R-matrices, and the result-
resulting solutions of the QYBE, in Section 12.5.
Note In this chapter, g denotes a finite-dimensional complex simple Lie alge-
algebra.
12.1 Yangians and their representations
A Three realizations If g is any Lie algebra over C and u is an indeter-
indeterminate, the set g[tx] = g 0 C[tx] may be identified with the set of polyno-
polynomial maps / : C —> g, and is clearly a Lie algebra under pointwise opera-
operations. In case g is finite dimensional and simple, a Lie bialgebra structure
8 : g[tx] —> a\u] 0 g[tx] = (g 0 g)[^,v] (where v is a second indeterminate,
independent of u) was defined in 1.3.9:
8(f) (u, v) = (ad/(u) 0 id + id ® ad/(v)) ( —— ) ,
where t G Sym2(g) is the Casimir element of g associated to a fixed invariant
bilinear form ( , ) on g. More explicitly, if {x\} is any orthonormal basis
of g with respect to ( , ), then t = Ylx xa 0 %\- Note that, if we view
Sym2(g) as a subset of t/(g), t is identified with the central (Casimir) element
Now g[/u] is a graded Lie algebra:
Moreover, with the induced grading on g[tx]0g[tz], 8 lowers degree by one, so it
is natural to look for quantizations Uh(§[u]) of (g[tx], 8) which are homogeneous
in the sense that there is a dense <C[[/i]]-sub-Hopf algebra E//i(g[u]) of t/^gl/u])
such that
376 12 Infinite-dimensional quantum groups
(a) Uh(^[u]) is a graded associative algebra over C[[/i]] (setting deg(/i) = 1);
(b) Uh(^[u])/hUh(^[u]) = U(q[u]) as graded algebras over C.
The next result shows that there is an essentially unique quantization with
these properties.
For any elements z\, z^, z^ of any associative algebra over C, set
{21,22,23} = —
TV
the sum being over all permutations n of {1, 2, 3}.
Theorem 12.1.1 Let § be a finite-dimensional complex simple Lie algebra.
Fix a (non-zero) invariant bilinear form ( , ) on 9, and let {x\} be an or-
thonormal basis of 9 with respect to ( , ). There is, up to isomorphism,
a unique homogeneous quantization Uh((}[u]) of (q[u],6). It is topologically
generated by elements x, J(x), for x G 9, with the following defining relations:
A) [x,y] (inUh(Q[u])) = [x,y] (in §),
B) J(ax + by) = aJ(x) + bJ(y),
C) [:
D) h ^2
[[J(a:), JB/)], [^, J(W)]] + [[J(z), J(w)], [x,
E) h2 ^([a;,a;A], [[y,x)J\)[[z,w},xu]\){x\)xIJ,) J(xu)} ,
for all x, y, z G 9, a, b G C
The Hopf structure ofUh($[u]) is given by
F)
G) A/l(J(x)) - J(x) 0 1 + 10 J(x) + ^ft[x 0 1,*],
(8) Sh(x) = -x, Sh(J(x)) = -J(x) + ^cx,
(9) eh(x) = eh(J(x))=0.
Here, c is the eigenvalue of the Casimir element t G U(q) in the adjoint
representation of 9 (in G), we regard t as an element ofU(c\)®2).
The grading on Uh(^[u\) is given by
deg(x)=0, deg(J(x)) = 1. I
12.1 Yangians and their representations 377
Remarks [1] Although the defining relations of Uh{o>[u}) depend on the choice
of the inner product ( , ), it is easy to see that, up to isomorphism, the Hopf
algebra Uh($[u\) does not. The right-hand sides of D) and E) are independent
of the choice of orthonormal basis of g.
[2] If g = sl2(C), D) is a consequence of (l)-C), while if g ? sl2(<C), E)
follows from (l)-D).
[3] The fact that Uh($[u\) is a genuine deformation of E/(g[tz]), i.e. that
Uh{^[u]) = E/(g[tz]) as C[ [ft]]-modules, is a consequence of 12.1.8. A
The relations in 12.1.1 can be 'derived' as follows. Using the fact that
[g5 g] = g5 it is easy to see that g[tz] is generated as a Lie algebra by the
elements x, xu = Jq(x) (say) for x G g, and that these elements satisfy the
relations obtained by putting ft — 0 in those of 12.1.1. To motivate the
definition of A^, note that since 6(x) = 0, it is natural to take A/l(x) to be
given by the classical formula. On the other hand,
6(Jq(x)) = \8l + l8
u — v
U r _ V
, t].
u — v u — v
But, since t lies in the centre of ?/(g), [x 0 1, t] — — [1 0 x, t], so
It is now clear that G) is the simplest way to satisfy
)-AHJ(,))
ft
The right-hand sides of D) and E) are designed to make A^ extend to a
homomorphism of algebras Uh(§[u]) —+ Uh(^[u]) 0 Uh(§[u]) (cf. the proof of
6.4.3).
Let f//i(g['u]) be the <C[ft]-subalgebra of Uh(^[u]) generated (in the usual
sense, not topologically) by the x, J(x) for x G g. Then, ^(g^]) is a
graded Hopf algebra over C[ft], and we may now specialize ft to any complex
number e. However, the resulting Hopf algebra E/€(g[tx]) (over C) is essentially
independent of e, provided that e ^ 0. In fact, if e, e' G <CX, the map
E/€(g[tx]) —¦»• t/e/(g[tx]) given by x i—> x, J(x) i—»• ^J(x) is clearly an isomorphism
of Hopf algebras. Thus, we might as well take e = 1. (On the other hand,
^o(gM) = E/(g[tx]) is certainly not isomorphic to E/e(g[tx]) if e ^ 0, since
C/€(g[tx]) is not cocommutative.)
Definition 12.1.2 For any finite-dimensional complex simple Lie algebra
g, the Yangian y(g) is the Hopf algebra over C with generators x, J(x) for
378 12 Infinite-dimensional quantum groups
x G g arid defining relations and coalgebra structure given by setting h = 1
in (l)-(9) (we drop the subscripts on the coalgebra maps from now on).
Although C/(g[tz]) is given by the generators and relations of 12.1.1 with
h — 0, this description obscures the fact that §[u] is a space of maps C —+ g.
It is more natural to take as generators of E/(g[tz]) the elements Xfur, Hiur
for i = 1,... , n, r G N, where {Xf-, Hi} are the usual generators of g (see
the Appendix). Drinfel'd A988b) gives a second realization of Y(§) in terms
of generators which have the X^ur, HiUr as their classical limit.
From now on, we fix the inner product on g to be the standard one, and
define root vectors X^ G g for all positive roots ft as described in the Ap-
Appendix.
Theorem 12.1.3 The Yangian Y(§) is isomorphic to the associative algebra
with generators Xfr1 Hir, i = 1,... ,n, r G N, arid the following defining
relations:
A0) [Hi,r , HJtS] = 0,
A1) [Hifi,X?<s]=±diaijXl;a,
f1O\ \U yi 1 \ zj y± 1 I j ~ ( u y± | y± rj \
{LA) [/l^r_|_i , Ajs\ — [rLi^r , j\^s+1\ — It —(liaij{fliirj\j^s -+- A^^il^r-J,
A5) \ ^fj^^ fJ^^" f-X"^" .X"^" 1 • • • 11 := 0
for ail sequences of non-negative integers n,..., rm, where m = 1 — a^j
the sum is over all permutations ir of {1,..., m}.
The isomorphism ip between the two realizations of Y(§) is given by
where
Xf,
12.1 Yangians and their representations 379
Remarks [1] Multiplying the right-hand sides of A2) and A4) by ft, one obtains
another presentation of Uh(Q[u\); replacing the right-hand sides of A2) and
A4) by zero gives another presentation of C7(g[ix]).
[2] The reader will have noticed that we have not given the formulas for the
coalgebra structure of Y(q) in this new realization. While this is determined,
in principle, by the isomorphism ip and equations F)-(9), no explicit formula
for the action of the comultiplication on the generators Xfr, Hi,r is known.
A
There is a third realization of the Yangian, at least when g = sZn+i((C),
which preceded the other two historically. We take the simple root vectors in
sZn+i((C) to be Xf = i?ii+i, X~ = Ei+n, and the basis vectors of the Cartan
subalgebra to be Hi = Ea — Ei+n+i. Here, Eij is the (n-fl)x(n-fl) matrix
with one in the zth row and jth column and zeros elsewhere. The standard
inner product in this case is just the trace form (x, y) = trace(xy).
Let T be the free associative algebra over (C with generators t\j, where
r > 1, 1 < i,j < n + 1. Introduce the formal power series
r=l
and define the quantum determinant of the matrix T(u) = (Uj(u)) by
qdet(T(im = > sgnGr)tin(i\(u-\—)t2nB)(u~^ 1) • • • tn+in(n+i}(u )
At At A
the sum being over all permutations of{l,2,...,n + l}. The quantum de-
determinant of any square submatrix of T(u) is defined in an analogous way,
taking care to preserve the ordering of the rows and columns.
Theorem 12.1 A The Yangian y(sZn+i((C)) is isomorphic to the quotient of
T by the two-sided ideal generated by the following relations:
A7) R(u - v)(T(u) 0 T(v)) = (T(u) 0 T(v))R(u - v),
A8) qdet(T(iO) = 1.
In the first relation, R(u) = a - A <g> l)u~l e (Mn+i((C) (g> Mn+^C))^], a
being the flip of the two factors in (Cn+1 <g> Cn+1.
There is an isomorphism %p between this realization and that of 12.1.3 given
by
) = ai(u)-l(n{u + ly^ai-^u + -)ai+1(u + -).
380 12 Infinite-dimensional quantum groups
Here, Xf{u) = E~o^r""r' H^u) = l + ZZo H*,^^1, and at(u)
(resp. bi(u), resp. Ci(u)) denotes the quantum determinant of the i x i
submatrix of T(u) formed by the entries tjk(u) for which 1 < j, h < i + 1
and j, k ^ i + 1 (resp. j ^ i + 1, k ^ i, resp. j ^z i, k ^ i + 1). (We set
a0 = a_i = l.J |
Remarks [1] The two relations A7) and A8) are equivalent to the infinitely
many relations which result from expanding both sides in powers of u and v.
For the meaning of T(u) 0 T(v), see Subsection 7.2A.
[2] Let Y(gln+iAE)) be the quotient of T by the relations A7). Then
qdet(T(ix)) lies in the centre of Y(gln+iAE)). Moreover, Y(gln+i(<C)) is a
bialgebra with comultiplication and counit given by
A(T(u)) = T(u) ? T(u), e(T(u)) = 1
(see Subsection 7.2A again for the meaning of these formulas), and qdet(T(u))
is a group-like element of Y(gln+i((E)). Finally, the antipode of Y(gln+i(<E))
is given by S(T(u)) = T(u)~l, and we have S(qdet{T{u))) = qdet(r(w))-1.
[3] The matrix R(u, v) = a o R(u — v) = 1 ®1 — a/(u — v) is the simplest
(non-const ant) rational solution of the quantum Yang-Baxter equation with
spectral parameters
A9) R\2(u - v)Ris(u - w)R23(v - w) = #23^ - w)Ri3(u - w)Ri2(u - v).
In Section 12.5, we show how, conversely, given a finite-dimensional repre-
representation of a Yangian Y(§), one can construct a rational solution of the
QYBE. Using these solutions, one can extend 12.1.4 to arbitary g, although
the description is not quite so explicit in the general case. The possibility of
constructing rational solutions of the QYBE is one of the main motivations
for the study of the representations of Yangians, which we take up later in
this section. A
B Basic properties To obtain interesting results about Yangians, one of-
often has to use more than one of the realizations 12.1.2, 12.1.3 and 12.1.4
simultaneously. While 12.1.3 reminds one that the classical limit of Y(q) is
a space of maps, the others have the advantage that the comultiplication is
known on all of their generators. As an example of this interplay, we prove
the following result, which provides a quantum analogue of the 1-parameter
group of translation automorphisms of q[u] given by u h-> u + a, a G (C.
Proposition 12.1.5 There is a one-parameter group of Hopf algebra auto-
automorphisms ra ofY(q), a G (C, given by
B0) ra(ffi|r) =
12.1 Yangians and their representations 381
Proof The first step is to define ra in terms of the presentation 12.1.2:
B1) ra(x) = x, ra(J(x)) = J{x) + ax (xe g).
This is the most obvious quantum analogue of the translation u h-> u + a,
since the classical limits of x and J(x) are x and xu, respectively. It is easy
to see that this definition is compatible with the relations (l)-E) and the
Hopf structure F)-(9).
To prove the formulas in B0), we proceed by induction on r, using the
isomorphism A6) and the definition B1) for the cases r = 0 and 1, and the
relations
for the inductive step. |
Remark The automorphisms ra are closely related to the antipode of Y(q): by
checking on the generators x, J(x) in 12.1.2, it is easy to see that S2 = nc.
We have not so far made use of the fact that Uh{Q[u]) is a graded algebra.
In fact, this grading was lost when we set ft = 1, since ft had positive degree.
However,
Proposition 12.1.6 The Yangian Y(q) has the structure of a filtered alge-
algebra, such that the associated graded algebra is isomorphic to U(q[u\).
Proof Using realization 12.1.3, let Y($)ri for r G N, be the linear span of
all monomials in the generators X^s, Hi^s for which the sum of the indices s is
at most r. It is clear that Y($)r C y(g)r+i and that Y(o)r.Y(Q)s C y(g)r+s.
The associated graded algebra has generators X^r, Hir satisfying the
same relations as in 12.1.3, except that the right-hand sides of A2) and A4)
are replaced by zero. By Remark [1] following 12.1.3, this algebra is just
U(Q[u}). I
Corollary 12.1.7 The centre of F(g) consists of the scalar multiples of the
identity element.
Proof Let z be an element of the centre of l^(g), and suppose that z G
F(g)r\y(g)r_i (we set F(g)_i = 0). By the proposition, z corresponds to a
non-zero element of the centre of ?/(g[ix]) of degree r. But it is known that
?/(g[i/]) has trivial centre (cf. Chari & Ilangovan A984)), so we must have
r = 0. |
It will be important for the discussion of the representations of Yangians
to have available an analogue of the Poincare-Birkhoff-Witt theorem. For
382 12 Infinite-dimensional quantum groups
E/(g[iz]), the most obvious PBW basis consists of ordered monomials in the
elements X^ur and HiUr, for i = 1,..., n, C G A+, r gN. Thus, to construct
a PBW basis for ^(g), we must define quantum analogues of the X^ur. Now,
the root vectors Xp of g are defined in terms of the simple root vectors Xi
by formulas of the form
where c is a non-zero complex number. For each r G N and each /c > 1,
choose any partition r = r± + • • • + Tk of r into a sum of k non-negative
integers, and define
XC,r ~ ClXiliri > iXi2,r2 ' • • ' ' [^fc-i,rfc_i ' Xik,r
Although the Xpr depend on the choice of partition of r, this dependence is
rather weak, for one can show that, if X^r are the elements obtained using
a different partition, then X^ — X^r G y(g)r_i.
Proposition 12.1.8 Fix a total ordering on the set
Then, the set of all ordered monomials in the elements of E is a vector space
basis of y(g).
Outline of proof It is straightfoward to prove that E spans y(g). To
prove that the elements of E are linearly independent, one makes use of the
automorphisms ra. See Levendorskii A993) for the details. |
Remark A similar argument shows that E is also a topological basis of
Uh(Q[u]). This proves that Uh(Q[v]) is a genuine quantization of g[ix], i.e.
that Uh(Q[u]) ^ ?/(g[ix])[[ft]] as <C[[h]]-modules. A
Let y^ (resp. Y°) be the subalgebra of y(g) generated by the Xf~r (resp.
by the i7i?r), i = 1,..., n, r G N. If we choose the total ordering in the propo-
proposition to be such that each X~r precedes each HjSi which in turn precedes
each X?v we obtain
Corollary 12.1.9 (i) The ordered monomials in the X^r, C G A+, r G M
(resp. in the Hi r, i = 1,..., n, r G UST) form a vector space basis ofY± (resp.
ofY°).
(ii) Multiplication induces an isomorphism of vector spaces
12.1 Yangians and their representations 383
C Classification of the finite-dimensional representations In this sub-
subsection, we describe a classification of the finite-dimensional representations
of y(g) analogous to the classical theory for g in terms of highest weights.
Let hi,r, for i = 1,..., n, r G N, be complex numbers, collectively denoted
by ft. If V is a y(g)-module, its weight spaces are the subspaces
Vh = {v G V | Hi^.v = h^rv for all z, r}.
A primitive vector in F is a non-zero vector v € Vh, for some ft, such that
X^~r.v = 0 for all z, r. One says that V is a highest weight module with highest
weight ft if V = y(g).i> for some primitive vector i> G V^.
Note that there is a homomorphism of Hopf algebras t : t/(g) —> F(g) given
by *,(#) = x for all x G g. In particular, we may regard any representation of
y(g) as a representation of g.
Proposition 12.1.10 Every finite-dimensional irreducible Y(o)-module V
is highest weight. |
The proof of this result is similar to, but simpler than, that of Proposition
12.2.3 below.
Highest weight y(g)-modules can be constructed by the usual methods.
Define the Verma module M(h) to be the quotient of Y(q) by the left ideal
generated by the elements X^~r and Hir — /ii,r.l, for i = 1,... ,n, r G M.
By 12.1.9(ii), M(h) = Y~.l. It follows that, regarded as a g-module, the
weight space of M(ft) with weight Yli^^^i^i is one-dimensional (the \
are the fundamental weights of g - see the Appendix). By the standard
classical argument, this implies that M(h) has a unique irreducible quotient
y(g)-module, say V(h).
It only remains to determine which of the V(h) are finite dimensional.
Theorem 12.1.11 The irreducible Y($)-module V(h) of highest weight ft is
finite dimensional if and only if there exist polynomials Pi G (C[u] such that
B3) Piju + dj) ^
in the sense that the right-hand side is the Laurent expansion of the left-hand
side about u = oo. |
We sketch the proof of a result very similar to 12.1.11 in the next section
(see 12.2.6).
Remarks [1] It is clear that the highest weight ft determines the polynomials
Pi up to a scalar multiple. Thus, 12.1.10 and 12.1.11 show that the finite-
dimensional irreducible representations of Y(q) are parametrized by the set
of n-tuples of monic polynomials.
384 12 Infinite-dimensional quantum groups
[2] Let A be the unique maximal weight of V(h) as a g-module. Using the
isomorphism ip in 12.1.3, we find that hi^ = diX(Hi). On the other hand,
from B3) we obtain h^o = dideg(Pi). Hence, deg(P^) = \(Hi).
[3] If p : Y(q) —> End(F) is a finite-dimensional irreducible module with
associated polynomials Pi(u), the twist pora by the translation automorphism
ra defined in 12.1.5, which we denote by r*(V), has polynomials Pi(u — a)
(this follows easily from the formulas B0)).
[4] If V is any finite-dimensional representation of F(g), the remark follow-
following 12.1.5 implies that the canonical isomorphism of vector spaces
V** =* t!c(V)
is an isomorphism of representations of Y(q) (the * on the left-hand side
indicates the left dual). Prom the preceding remark, it follows that F** 3* V
in general (cf. Remark [3] following 5.1.2). A
The 'simplest' highest weight y(g)-modules are those whose associated
polynomials are of smallest degree. We shall say that a finite-dimensional
irreducible Y(g)-module is fundamental if its associated polynomials are given
by
B4) P'M-{l-c ViVi,
for some i = 1,... ,n; the corresponding representation will be denoted by
V(\i,a). It follows from the preceding remarks that, as a g-module, V(\i,a)
has A^ as its unique maximal weight, and so contains the irreducible g-module
V(\i) with multiplicity one. We shall describe the structure of the V(\i,a)
in more detail later in this section.
The justification for the adjective 'fundamental' is contained in
Proposition 12.1.12 Let V and W be finite-dimensional Y($)-modules and
let v eV, w eW be primitive vectors of weights hy and h\y- Then, v<g>w is
a primitive vector in V 0 W of weight hy®w, where
p _ p. p. Jxr
the monic polynomials Pty^w, Pty &nd Pi,w being related to the weights
hy®w, hy andhw &s in B3).
In fact, this result has the almost immediate
Corollary 12.1.13 Every finite-dimensional irreducible Y(§)-module is iso-
morphic to a subquotient of a tensor product of fundamental representations.
Proof Consider a finite-dimensional module V(h) with associated polyno-
polynomials Pi, i = 1 , n. Let a^, ai2,. • • be the roots of Pi (counted with multi-
multiplicity). By the proposition, the tensor product v of the highest weight vectors
12.1 Yangians and their representations 385
in the fundamental representations V(Ai,an), V(Ai,ai2),..., V(An,ani),...
(in any order) is a primitive vector of weight h. Hence, V(h) is a quotient of
the submodule Y($).v of ®ijV(\i,aij). |
We note also the obvious
Corollary 12.1.14 Let V and W be finite-dimensional irreducible Y(q)-
modules and assume that V 0 W is also irreducible. Then,
(i) the polynomials Piy^w, Piy and P%%w associated to V 0 W, V and W
are related by Piy®w — PiyPiyv]
(ii) V 0 W and W 0 V are isomorphic as representations ofY(q). |
Remark We shall see later in this section that there are finite-dimensional
irreducible representations of Y(q) on which the tensor product operation is
not commutative. A
We conclude this subsection with an
Outline of proof of 12.1.12 This is an easy consequence of the follow-
following, still not quite explicit, formulas for the comultiplication of Y(q) in the
realization 12.1.3. Let iV+ = Y<irXtrY* = T,irY+Xtv Then> modulo
B5)
s=l
This is proved by induction on r, using F)-(9) and the isomorphism (p in
12.1.3 to check the cases r = 0, 1, and the relations B2) for the inductive
step.
To see that these formulas imply 12.1.12, note that it follows from the first
formula that v 0 w is annihilated by the X^r, and from the second that v 0 w
is an eigenvector of the H^r with eigenvalues
h>i,r,
V<8>W —
(in an obvious notation). It is easy to see that the scalars on the right-hand
side of this equation are the coefficients in the Laurent expansion of
r_i
386 12 Infinite-dimensional quantum groups
D Evaluation representations We now consider the problem of giving 'ex-
'explicit' descriptions of the finite-dimensional modules V(h). Before attempting
this, it is instructive to consider what happens in the classical limit.
The most obvious way to construct representations of q[u] is to use the
homomorphisms eva : q[u] —> g which evaluate a g-valued polynomial at a
point a G C If V is a finite-dimensional irreducible g-module, its pull-back
by eva is still irreducible because eva is obviously surjective. In fact, it can
be shown that every finite-dimensional irreducible representation of q[u] is
isomorphic to a tensor product of such 'evaluation representations' (cf. Chari
& Pressley A986)).
Thus, it is natural to try to find an analogue of the homomorphisms eva for
y(g). Using the realization 12.1.2 and recalling that the classical limit of J(x)
is xu, the most obvious guess is eva(x) — x, eva(J(x)) = ax. Unfortunately,
one finds that this map respects the defining relations of Y(q) only if g =
s/2 (C). In general, we have
Proposition 12.1.15 A) If g = sfailE), there is a unique homomorphism of
algebras eva : Y(q) —> ?/(g), for all a G (C, such that
eva(x) = x, eva(J(x)) = ax
for all x G g.
(ii) If g = sZn+i((C), where n > 1, there is a unique homomorphism of algebras
eva : Y(q) —> U(q), for all a G (C, such that
B6) eva(x) = x, eva( J(x)) = ax + -
A,m
for all x G g. Jfere, {x\} is an orthonormal basis of g, and the trace is
computed by multiplying together x, x\ and x^, thought of as (n-fl) x (n + 1)
matrices.
(Hi) If g is not of type An for any n, there is no homomorphism of algebras
1 ev
ev : y(g) —> ?/(g) such that the composite C7(g) —> F(g) —>• ?/(g) is the
identity map. |
The first two parts are proved by direct verification; the last part will
become clear later in this section.
Remarks [1] The maps eva in (i) and (ii) are not homomorphisms of Hopf
algebras.
[2] The reason for the special role played by type An, n > 1, in this result
derives from the following strange fact. Consider the tensor product g 0 g of
two copies of the adjoint representation of g. This always contains at least one
copy of the adjoint representation, since the Lie bracket g <g> g —> g commutes
with the action of g (this assertion is equivalent to the Jacobi identity). But
12.1 Yangians and their representations 387
if g is of type An, n > 1, and only in that case, there is a second copy of g in
g 0 g. The projection n onto this second copy is given by
2
tt(x 0y) = xy + yx tiace(xy).l.
n + 1
The mysterious extra term on the right-hand side of the formula B6) for
eva(J(x)) is \ Y,\ n(z ® x\)x\-
[3] If n > 1, there is a second family of evaluation homomorphisms eva :
y(sZn+i(<C)) -+ /7(s/n+i((C)), which also act as the identity on ?/(sZn+i(<C))
C y(s/n+i(C)), and which are given by
evo(» = z, eva(J(x)) =ax- -
A,At
In fact, eva = Su ° eva+ic o 5y, where SV and Sy are the antipodes of
C/(sZn+i(<C)) and y(s/n+i(C)), respectively. If n = 1, we set eva = eva. A
In general, if g is of type A and V is a representation of g, the represen-
representation of y(g) obtained by pulling back V by an evaluation homomorphism
eva : y(g) —> U(q) (resp. eva : Y(q) —> ?/(g)) is called an evaluation repre-
representation, and denoted by Fa (resp. F0). It is clear from the second remark
following 12.1.11 that, if V = V(Xi) is the irreducible g-module with highest
weight a fundamental weight A^, any associated evaluation representation is a
fundamental representation V{\i, b) of Y(q) for some b. Hence, from 12.1.13,
we obtain
Corollary 12.1.16 If g = sZn+i(C), every finite-dimensional irreducible
Y(o)-module is isomorphic to a subquotient of a tensor product of evaluation
representations (which we may assume are all of the form Va, or all of the
form Va, if we wish). |
Later in this section, we give a much more precise result in the 5/2 case,
but first we consider what happens when g is not of type An.
Proposition 12.1.17 Let mi be the multiplicity of the simple root c^ in
the highest root 0 of g, and let do — d{ if 6 is conjugate to o.i under the Weyl
group of g. If mi = 1 or de/di, the fundamental representation V(Xi) of g
can be made into a fundamental representation of Y(q) by letting J(x) act
as bx for any b G (C.
Proof Let p : y(g) —> End(y) be the fundamental representation of y(g)
with associated polynomials B4). Then, as a g-module,
v * v(\i)
388 12 Infinite-dimensional quantum groups
for certain multiplicities r^ > 0. Now, the map g(g)F^7 given by x ® v —>
p(J(x))(t;) commutes with the action of g (this follows from relation C)).
The proposition therefore follows from the following facts:
(i) if rrii = 0 or dg/di, and /i is a dominant weight less than A^, there is no
non-trivial g-module map g ® V(Xi) —> V(/jl);
(ii) for any fixed fundamental weight A* of g, any g-module map g® V(Xi) —>
V(Ai) is a scalar multiple of the action of g on V(Xi).
The first of these can be checked case-by-case; the second is an easy exercise. |
Inspecting the tables in Bourbaki A968), we see that this result covers
all the fundamental representations if g is of type An (where, of course, we
already know the result) or Cn, as well as the natural and spin representations
if g is of type Bn or Dn. It also covers nodes 1 and 6 for ?, node 7 for E7i
node 4 for F4 and node 2 for G2 (numbering as in Bourbaki A968)). The
structure of the remaining fundamental representations in the Bn and Dn
cases is given by
Proposition 12.1.18 Let g be of type Bn or Dn+i. Then, for any a e (C,
[i/2]
as ^-modules. |
For the proof of this result, and the description of the fundamental repre-
representations of Y(q) when g is of exceptional type, see Chari & Pressley A991a).
Inspecting the results of that work shows that the converse of 12.1.17 is also
true, i.e. if rrii does not satisfy the conditions in the proposition, the fun-
fundamental representation V(Xi,a) is reducible as a g-module. Further, in the
Cn case, the adjoint representation of g (which is not fundamental) does not
extend to an action of Y(q) (on the same space). This result, and those on
the Yangians of the exceptional Lie algebras obtained in Chari & Pressley
A991a), prove part (iii) of 12.1.15. See also Drinfel'd A985).
E The 5/2 case We conclude this section by describing the finite-dimensional
irreducible representations of Y(sl2((E)) in more detail.
Let V(r)a be the pull-back by eva of the (r + l)-dimensional irreducible
s/2(<C)-module V(r). Let us compute the polynomial associated to V(r)a.
There is a basis {i?o,..., vr} of V(r) on which the action of 5/2(C) is given by
Xf.v3 = (r - s + 1K_i, X^.Vs = E + lK+i, Hx.Vs = (r - 2s)vs
for s = 0,1,..., r (we set t?_i = vr+i = 0). Since J(x) acts on V(r)a as
ax acts on V(r), the action of Y(sl2((E)) is determined. But to compute the
12.1 Yangians and their representations 389
associated polynomial, we must describe the action of the generators X^k
and Hi^ of the realization 12.1.3. We claim that
k
/ 1
Xlk.v8= [a+-r-s--
B7) ' V 2
Hi,k.v8 = ((a + ^r - s - -)k(r - s)(s + 1)
To prove this, one checks first that these formulas do define a representation
of y(s/2(C)), and then, by using the isomorphism tp in 12.1.3, that they agree
with the known action of x and J(x) for x = X^1 and Hi (recall that the
relation in D) does not have to be checked in the s/2 case because it is a
consequence of the other relations).
From B7), we read off the eigenvalues of the H\k on the highest weight
vector vo of V(r)a:
from which we find that the monic polynomial satisfying B3) is
r-l
s=0
Note that the roots of P\ form a 'string' of length r, i.e. a sequence z$,
z\,..., zr-\ of complex numbers such that zs+\ — zs = 1 for all s.
We shall need a simple combinatorial property of such strings, whose proof
may safely be left to the reader. Let us say that two strings S\ and S2 are in
special position if their union is a string which properly contains S\ and S2]
otherwise, S\ and S2 are in general position. For example, the strings S(r)a
and S(s)b associated to evaluation representations V(r)a and V(s)b are in
special position if and only if a — b or b - a = \{r + s) — k + 1 for some
0 < k < min{r, s}.
Lemma 12.1.19 Any finite set of complex numbers with multiplicities can
be written as a union of strings in general position. Moreover, the resulting
set of strings is unique. |
The 'union' here is in the sense of sets with multiplicity: the multiplicity of
a complex number z in the union of Si and S2 is the sum of its multiplicities
in Si and in S2.
Continuing to imitate the representation theory of «s/2(C)[ii], we next con-
consider tensor products of evaluation representations. The crucial result, proved
in Chari & Pressley A990b), is
390 12 Infinite-dimensional quantum groups
Lemma 12.1.20 A (finite) tensor product ®jV(rj)aj of evaluation represen-
representations is irreducible if and only if, for all j, k7 the strings S(rj)aj and S(rk)ak
are in general position. |
We can now prove
Theorem 12.1.21 Every finite-dimensional irreducible Y(sl2(<E>))-module is
isomorphic to a tensor product of evaluation modules. Moreover, two such
tensor products are isomorphic if and only if one is obtained from the other
by a permutation of the factors.
Proof Let V be a finite-dimensional irreducible Y (sl2((E))-mod\i\e with as-
associated polynomial P. The set of roots of P, counted with multiplicity, can
be written as a union of strings in general position. By 12.1.20, the tensor
product of the evaluation representations corresponding to these strings (in
any order) is irreducible, and by 12.1.12 it has associated polynomial P, and
is therefore isomorphic to V. The second statement follows immediately from
12.1.12 and the uniqueness part of 12.1.19. |
Although we shall omit the proof of 12.1.20, it will be instructive to examine
the simpler case of the tensor product of two evaluation modules in more
detail.
Proposition 12.1.22 The representation V = V(r)a <g> V(s)b ofY(sl2(<E))
is reducible if and only if
a — b or b — a — —(r + s) — j + 1 for some 0 < j < min{r, s}.
In this case, V has a unique proper subrepresentation W. Moreover:
(i)ifa-b=±(r + s)-j + l,
W = V(r-j)a+j/2®V(s-j)b_j/2
W/V * V(j - l)o_(r_j+i)/2 ® V{r + s - j + lN+(
(ii)ifb-a= l(r + s)-j + l,
W/V S V(r - j)Q_i/2 ® V(s - j
Outline of proof As an sZ2(C)-module,
min{r,s}
V(r
3=0
12.1 Yangians and their representations 391
If Wj is the unique (up to a scalar multiple) «s/2(C)-primitive vector of weight
r -\- s — 2j in V(r)a ® V(s)b, one checks by a direct computation that Wj is
a y(«s/2(C))-highest weight vector if and only if a — b = ^(r + s) — j + 1.
This gives the necessary and sufficient condition for V(r)a ® V(s)b to have a
y(«s/2(C))-submodule not containing the tensor product of the highest weight
vectors in V(r)a and V(s)b.
On the other hand, V(r)a (g) V(s)b has a proper submodule containing the
tensor product of these highest weight vectors if and only if
b — a = - (r + s) — j + 1 for some 0 < j < min{r, «s}.
In fact, V(r)a (g) V(s)b has such a submodule if and only if the (left) dual
(V(r)a (8) V(s)by ^ (V(s)b)* 0 (V(r)o)* has a submodule which does not
contain the tensor product of the highest weight vectors in (V(s)b)* and
(V(r)o)*. But (V(r)a)* = V(r)o_i : this follows from the fact that the
antipode S of Y(sl2((E)) satisfies evo o S = S o evo_i (this is easily checked
on the generators of the realization 12.1.2). Our assertion thus follows from
the first part. |
Corollary 12.1.23 Suppose that a-borb-a= |(r + s) - j + 1 for some
0 < j < min{r, s}. Then:
(i) V(r)a 0 V(s)b is not completely reducible;
(ii) V{r)a 0 V(s)b is not isomorphic to V(s)b 0 V(r)a. |
Remarks [1] We have already encountered failure of complete reducibility in
Chapter 11, but it is worth pointing out that its failure here has nothing
to do with any 'root of unity phenomenon'. In fact, the category of finite-
dimensional representations of the Lie algebra §[u] is not semisimple either.
For example, it is easy to see that, if k > 1 and a G C, the natural represen-
representation of g[u] on the space of /c-jets
MQ)=Q[u]/(u-a)k+1Q[u]
is indecomposable but not irreducible (since (u - a) Jfc(g) is a proper sub-
submodule). However, tensor products of evaluation representations of §[u] are
always completely reducible.
[2] Part (ii) implies that Y(sl2((E)) is not quasitriangular (or even almost
cocommutative). In fact, it implies that the category of finite-dimensional
representations of Y(sl2((C)) is not quasitensor. Nevertheless, we shall see
in Section 12.5 that Y(§) (for arbitrary g) is quasitriangular in a certain
'limiting' sense. A
392 12 Infinite-dimensional quantum groups
12.2 Quantum affine algebras
Many of the results in this section are analogues of those obtained for Yan-
gians in Section 12.1, or of those obtained for finite-dimensional Lie algebras
in Chapters 9 and 10, so we shall keep our discussion brief to avoid too much
repetition. The term 'affine Lie algebra' will always mean untwisted affine
Lie algebra.
A Another realization: quantum loop algebras The affine Lie algebra
g associated to a finite-dimensional complex simple Lie algebra g is an exam-
example of a Kac-Moody algebra g'(^4), where A is a symmetrizable generalized
Cartan matrix (see the Appendix). Thus, 6.1.5 gives a quantization Uh(o) of
9-
But affine Lie algebras are simpler, and better understood, than arbitrary
Kac-Moody algebras because they have another realization. Namely, g is a
central extension, with one-dimensional centre, of the loop algebra L(g) =
g[it, it], where u is an indeterminate; note that L(g) may be thought of as
the space of Laurent polynomial maps Cx —> g. As in the case of Yangians,
Drinfel'd A988b) gave another realization of Uh(o) which, although still in
terms of generators and relations, is closer to the description of affine Lie
algebras as a space of maps. It will be more convenient for us to work with
Uq(o) than with t/^cj); we refer to Uq(o), or any of its specializations, as a
quantum affine algebra. The following presentation of Uq(q) is proved in Beck
A993).
Theorem 12.2.1 Let g be the untwisted affine Lie algebra associated to a
finite-dimensional complex simple Lie algebra g. The standard quantization
Uq(o) of g defined in 9.1.1 is isomorphic, as an algebra over C(g), to the
algebra Aq with generators C±1/27 Kf1, H^r, 1 < i < n, r e Z\{0} and X±r,
1 < i < n, r G Z, and with the following defining relations:
— /v^ l\>i — 1, L ' C ' = 1,
are central,
K,j\ —
± y±
_ -
12.2 Quantum affine algebras 393
k=0
for all sequences of integers n,..., rm, where m = 1 — a^ and the elements
$fr are determined by equating coefficients of powers ofu in the formal power
series
r=0 \ s=l
Let 0 = Y^i=i miai be the highest root of g7 set qe = qi if 0 is Weyl group
conjugate to aiy and set Kq — IlILi K-T% - Suppose that the root vector
of g is expressed in terms of the simple root vectors as
tor some A € (C. Define maps wf1 : Uq(o) —> C/q(g) by
f(a) =
wf(a) = ? ^
Then, there exists an isomorphism of <E-(q)-algebras f : Uq(o) -+ Aq defined
on generators by
f(K0) = CKTS\
f(X+) = nw- ...
where \i G C(g) is determined by the condition
o J ~
Qe -
Remarks [1] To obtain the analogous result for Uh(o) given in Drinfel'd
A988b), one replaces the generators /Q and C1/2 by new generators Jii$
and c/2. The element c is central and the third and fifth sets of relations
above are replaced by
j r.
The remaining relations are the same as those above, except that qi is replaced
bye^andC1/2 by ehc/2.
[2] If A is the generalized Cartan matrix of g, then Uq(q) — Uq($'(A)).
To obtain an analogous presentation of Uq($(A)), one introduces additional
394 12 Infinite-dimensional quantum groups
generators V±l and relations
VV~l = V~lV = 1,
V-1 = <fWz,r, [P, /Q] = [V,C] = 0,
[3] By replacing q by any transcendental number e G Cx, one obtains from
12.2.1 another presentation of the specialization ?/e(g).
[4] Setting
deg(/Q) = deg(C) - 0, deg(Wz,r) = deg(A?) - r, deg(q) - 0
gives Uq(o) the structure of a graded algebra.
[5] The elements $fr are given in terms of the HjiS by formulas of the form
$% = ±>C?1((qi - qr1)'Hi,r + 0<tr(Wi,±i> • • •, Wi,±(r-i))),
where ^r are polynomials, with coefficients in C(g), which are homogeneous
of degree r with respect to the above grading. A
Beck A993) also gives an analogue of the Poincare-Birkhoff-Witt theorem
for Uq(o). We state only the following weak version, which follows easily from
12.2.1.
Proposition 12.2.2 Let e e Cx be transcendental. Let Uf (resp. U®)
be the subalgebras of Ue(§) generated by the elements X^r (resp. by the
elements C±x/2, Kf1, H%,r) for all i, r. Then,
Note that, by the Remark [5] following 12.2.1, U® is also generated by the
l Kfl and <P±r.
B Finite-dimensional representations of quantum loop algebras For
the remainder of this section, e G Cx is assumed to be transcendental.
We shall say that a representation V of Ue(q) is of type 1 if the generators
Ko, K\y..., Kn act semisimply on V with eigenvalues which are integer pow-
powers of e, and if C1/2 acts as 1 on V. As in 9.1.4, there are 2n+1 (C(g)-algebra
automorphisms of Ue(o) given on generators by
B8) Ki^ViKi, X+~atX+, Xr^xr,
for any set of signs cro,..., crn E { ± 1}. We shall also make use of the auto-
automorphism given by
B9)
12.2 Quantum affine algebras 395
Proposition 12.2.3 (i) Every finite-dimensional irreducible representation
V of Ue(o) can be obtained from a type 1 representation by twisting with a
product of some of the automorphisms B8), B9).
(ii) Every finite-dimensional (non-zero) type 1 representation V ofUe(o) con-
contains a non-zero vector v which is annihilated by the X^r for all i, r, and is
a simultaneous eigenvector for the elements of
PROOF Let V be a finite-dimensional representation of ?/e(g), and let
V° = {v G V | X+r.v = 0 for all i, r}.
Assume for a contradiction that V° = 0. Let w be any non-zero joint eigen-
eigenvector of K\,..., Kn. By the assumption, there is an infinite sequence of pairs
(ip, rp), p = 1,2,..., such that the vectors w, X~^ri .w, X^r2X^ri.w,... are
all non-zero. Since these vectors have different weights for the action of Ue($),
they are linearly independent, contradicting the finite dimensionality of V.
Let 0 7^ v G V°. By considering the !7ez(«s/2(C))-subalgebra of U€(q) gener-
generated by Xf, Kf1, and using 10.1.6, it follows that
Ki.v — <Jiqs%v, i = 0,1,... ,n,
for some &i = ± 1, s^ G Z, where so < 0, si,..., sn > 0. Hence,
On the other hand, considering V as a representation of Ue%(sl2((E)) via the
homomorphism Ue%(sl2^C)) —>• ^4(9) given by
one sees that we must have
/ n \
r ( s° ~*~ 5Z m^ ) + Si -
V i=l /
for all r GZ. Thus, .so + JZ^ m^«s^ = 0 and
C.v = a
1=1
By twisting with an automorphism B8), we can assume that G{ = 1 for
i = 0,1,...,n, and then C.v = v. If V is irreducible, C acts as 1 on V,
and hence either C1/2 = 1 on V or C1/2 = —1 on V. The second case can
396 12 Infinite-dimensional quantum groups
be transformed into the first by twisting with the automorphism B9). This
proves (i).
If V is of type 1, it follows from the fourth set of relations in 12.2.1 that the
elements of U® act on V as commuting operators, and from the fifth and sixth
relations that these operators preserve V°. Any simultaneous eigenvector
v ? V° for the action of U® satisfies the requirements in part (ii). |
Thus, studying the finite-dimensional irreducible representations of Ue(o)
reduces to studying the representations of the quantum loop algebra [7e(L(g)),
the quotient of U€(q) by the ideal generated by C1/2 — 1. Proposition 12.2.3
also suggests
Definition 12.2.4 A typel representation V ofUe(L(g)) is pseudo-highest
weight if it is generated by a vector vo which is annihilated by the X^r, and
is a simultaneous eigenvector for the /Q and the Hi,r, i = l,...,n, r /0.
If<pfr.vo = <pfrvo, the collection of complex numbers (p^r, denoted by (p, is
called the pseudo-highest weight ofV.
Remark We use the term 'pseudo-highest weight' because this notion does
not reduce in the classical limit to the usual notion of highest weight for
representations of Kac-Moody algebras. See Chari A985) for a discussion of
this point in the classical case. A
The proof of 12.2.3 gives
Corollary 12.2.5 Every finite-dimensional irreducible type 1 representa-
representation V ofUe(L($)) is pseudo-highest weight. |
Note that vtoVTo — 1? and that ipfr — 0 for r < 0, ip~r = 0 for r > 0.
pfr —
One proves, as in the case of Yangians, that for any collection of scalars
ip — {(/^l^i^.^^z satisfying these conditions, there is a unique irreducible
C/e(L(g))-module V(ip) with pseudo-highest weight (p.
We can now state the following analogue of 12.1.11.
Theorem 12.2.6 Let V be a finite-dimensional irreducible Ue(L(a))-module
of type 1, let vo be a pseudo-highest weight vector of V, and define (pi r G
C, for i = l,...,n, r ? Z, as in 12.2.4. Then, there exist unique monic
polynomials Piy ? (?[u], i = 1,..., n, all with non-zero constant term, such
that
in the sense that the left- and right-hand sides are the Laurent expansions
of the middle term about 0 and oo, respectively. Moreover, every n-tuple
(Pi)i=i,...,n of monic polynomials with non-zero constant term arises from a
finite-dimensional irreducible Ue(L(g))-module of type 1 in this way.
12.2 Quantum affine algebras 397
Moreover, if V and W are finite-dimensional type 1 representations of
Ue(L(o)) such that V (g>W is irreducible, then
In particular, V <8> W = W <8> V.
Outline of proof This is based on the following lemma. To state it, let
Lemma 12.2.7 Define elements V^±r G U®, for i = 1,... ,n, r > 0, induc-
inductively by setting Vf0 = 1 and, for r > 0,
n
Hi Hi S=Q
Then,
V- = (-
C2)
-r-Cr-^
s=0
\r-\( y- \r r
the congruences being (mod N+). |
The proof is by induction on r. See Chari & Pressley A991b) for the details
(only the s/2 case is treated there, but the proof in the general case is the
same).
It is convenient to formulate the definition C0) by introducing the formal
power series
r=0 r=0
in {/"[[u*1]]. Then, we have
C3) *f(.)-AJ
398 12 Infinite-dimensional quantum groups
Suppose then that V(<p) is finite dimensional with pseudo-highest weight
<p, and let vq be a pseudo-highest weight vector. Then,
for some ri G N. From the results of Section 10.1, it follows that the Ue(§)-
submodule of V(<p) generated by vq is isomorphic to the irreducible module
Ve(X), where A = Yliri^i- I*1 particular, we have (X~0)r%+1.VQ = 0. From
C1), we obtain
V?(u).vo = Pi(u)vo
for some polynomial Pi(u) = Y^r=oPhrUr of degree r*. The first equation in
12.2.6 now follows from C3).
To prove the second equation, apply both sides of C2), with r = r* + 1, to
vq. Since {X~i)ri+1 .vq = 0 for weight reasons, we get
s=0
Applying X^'_s_1 for s > 0 and using the relation
TV+ V-1 _ i,r+s ~ z,r+s
we find that
S Vi—S
Y^V^-tPi^-s+t = Yl vttPi,r%-s
t=Q t-0
for 0 < s < ri, and that
s
for s > Ti. Note that, by C0) (with r replaced by r^ — s), the right-hand side
of the first of these equations is equal to qllq~ Pi,r%-s- Multiplying the
sth equation by ur%~s and summing from s = 0 to oo, we find
\t=0
as required.
The proof that every n-tuple {Pi)i=i,...,n of monic polynomials with non-
nonzero constant term arises in this way is very similar to the classical proof,
given in Humphreys A972), for example, that the irreducible g-module V(A)
12.2 Quantum affine algebras 399
of highest weight A G P+ is finite dimensional. See Chari & Pressley A994c)
for the details. (A constructive proof is given in the next section in the special
case g = s/n+i(C).)
The multiplicative property of the polynomials Pi follows by an argument
identical to that used for Yangians in 12.1.12.
Remark We have made no use of the V~ in this proof. In fact, similar argu-
arguments show that V~ .vq — P~v (u~1)vo for some polynomials P~v, and that
r=0 -i,V\™ I
It follows that, up to a scalar multiple, P~v(u) — uTlPiy(u~l). In particular,
the action of the ^~_r on the highest weight vector vq is determined by that
of the#+r, i = l,...,n, r > 0. A
As for Yangians, the last part of 12.2.6 suggests that we define a finite-
dimensional irreducible Ue(L(o))-modu\e of type 1 to be fundamental if its
associated polynomials are given by
1 if j ^z i7
u — a if j — z,
for some i — l,...,n,a(E<C; the corresponding representation will be denoted
by Ve(Xi, a). As a f/e(g)-module, K(^i7 ^) has A^ as its unique maximal weight,
and so contains the irreducible f/e(g)-module Ve(Xi) with multiplicity one. In
view of 12.2.6, it is clear that
Corollary 12.2.8 Every finite-dimensional irreducible Ue (L(g))-module is
isomorphic to a subquotient of a tensor product of fundamental representa-
representations. I
C Evaluation representations Recalling that the generators X^r have
classical limits Xfur, the bar denoting elements of g, we might hope that,
for any a € (C, there is a homomorphism of algebras Ue(L(q)) —> Ue(q) such
that X^r *—> arxf: for all i. In fact, this does not work for any g. Nevertheless,
Jimbo A986a) defined a quantum analogue of the latter homomorphism when
g — sZn+i(C). It takes values in an 'enlargement' of Ue(sln+i(<E)).
Fix a square root e1/2 of e and, for any elements w, v of an algebra over C,
set
400 12 Infinite-dimensional quantum groups
Definition-proposition 12.2.9 Ue(gln+i(<?)) is the associative algebra
over C with generators xf, i — 1,..., n, tf1, r — 0,1,...,n, and the fol-
following defining relations:
j. j.—l 1 ±—l ±
lypij, 1 tr 67-*,
]el/2]el/2=0 if\i-j\ =
[xf,xf]=O if\i-j\>
\nr' t» 1 — A. . ^
where ki — U-\ti l.
There is a Hopf algebra structure on Ue(gln+i(<E)) given by the same for-
formulas as in 9.1.1, together with
A(tr) = tr®tr, S(tr) = t~\ e(tr) = l. I
The proof is straightforward. Note that there is a homomorphism of Hopf
algebras Ue(sln+i((E)) —> Ue(gln+i((E)) which takes X~ to x^ and Ki to ki.
Proposition 12.2.10 For any a e<C, there exist unique homomorphisms of
algebras eva and eva from Ue(L(sln+i(<E))) to Ue(gln+i(<E)) such that
eva(X±) = ( ± l)n-16=F(n
CV-^) = ( ± l)n-lcT(n+l)/2a±l [xf? [xT? . . . ^ [xj_1? X^]el/
The proof is a direct verification that eva and eva respect the defining
relations of Ue(L(sln+1((C))) (in the form 9.1.1).
Remarks [1] The homomorphism eva was given in Jimbo A986a). The ho-
homomorphism eva — ao eva o or, where a and a are the automorphisms of
Ue(gln+i((E)) and Ue(L(sln+i((?))), respectively, which are given on genera-
generators by
a(x±) - x± att^) - tTl
and
= Xn_i+lr, a(Hi,r) = Wn-l+i,r, a(/C- )
12.2 Quantum affine algebras 401
Alternatively, eva may be obtained from eva essentially by twisting with the
antipodes 5 and 5 of Ue(gln+i(<E)) and ?/e(Z/(s/n+i(<C))), respectively: by
checking on the generators Xj^, one finds that
where b= {-IO1-1 ae-n+l.
[2] Neither eva nor eva is a homomorphism of Hopf algebras.
[3] If n = 1, eva - eva for all a G Cx. A
Fix an (n + l)th root el^nJrl^ of e. We say that a representation W of
Ue(gln+i((C)) is of type 1 if the following conditions are satisfied:
(a) W is of type 1 regarded as a representation of C/e(sZn+i(C));
(b) the tr act semisimply on W with eigenvalues which are integer powers of
(c) toti... tn acts as the identity on W.
It is easy to see that the restriction to ?/e(s/n_|_i(C)) is an equivalence
from the category of finite-dimensional type 1 representations of Ue(gln+i((C))
to the category of finite-dimensional type 1 representations of Ue(sln+i((C)).
Thus, if W is a finite-dimensional type 1 representation of Ue(sln+i((C)), we
may regard W as a type 1 representation of Ue(gln+i((C)). We denote by Wa
(resp. Wa) the pull-back of W by eva (resp. by eva). Both Wa and Wa are
called evaluation representations.
If W is irreducible as a representation of f/e(s/n+i(C)), it is obvious that
both Wa and Wa are irreducible representations of Ue(L(sln+i(<E))), for all
a G Cx. Using the formulas in 12.2.2 and 12.2.9, one can compute the
polynomials associated to Wa and Wa, as in 12.2.5.
Example 12.2.11 Let a e Cx, r G N, and let W = K(r) be the (r + 1)-
dimensional irreducible type 1 representation of Ue(sl2((E>))> In the usual
basis {^0 7 vi,..., vn}, the action of Ue(gl2((C)) on K@ is given by
Using these formulas, and the method used in Subsection 12.IE, it is not
difficult to compute the polynomial Pi associated to Ve(r)a'
u-a-h2^-1). 0
P=i
This example suggests the following definition.
402 12 Infinite-dimensional quantum groups
Definition 12.2.12 Let a e Cx, r e N. The e-segment E(r)a with centre
a and length r is the r-tuple (ae~r+1, ae~r+3,..., aer~l).
The general result, proved in Chari & Pressley A993d), is given in
Proposition 12.2.13 Let W be the finite-dimensional irreducible type 1
representation of Ue(sln+i((E)) with highest weight A = ^r^A^ and let a €
Cx. Then,
(i) ifn = 0, we have PiiWa = Pi}Wa = 1;
(lij if r* > 0, the roots of Pi,wa (resp- of Pi,wa) form, when suitably ordered,
the e-segment of length V{ and with centre
-1 *~1 XT y^n (
Ci — a e n+1 ^j=iv
(resp. witii centre
It follows immediately from this computation that every fundamental rep-
representation of Ue(L(sln+i((E))) is isomorphic to an evaluation representation.
By 12.2.7, we have
COROLLARY 12.2.13 Every finite-dimensional irreducible type 1 representa-
representation of f/e(L(s/n+i(C))) is isomorphic to a subquotient of a tensor product of
evaluation representations. |
This result establishes the converse of the first part of 12.2.5 in the case
9 = s/n+i(C).
Corollary 12.2.14 can be made much more precise in the s/2 case.
Proposition 12.2.15 Let the notation be as in 12.2.10 and 12.2.11.
(i) Every finite-dimensional irreducible type! representation ofU€(L(sl2((E)))
is isomorphic to a tensor product
C4) K(ri)a^--^K(rfc)afe
of evaluation representations.
(ii) Two such irreducible tensor products are isomorphic if and only if one is
obtained from the other by a permutation of the factors.
(Hi) An arbitrary tensor product C4) is reducible if and only at least one pair
of e-segments E(r^)a., E(rj)aj is in special position, in the sense that their
union is an e-segment which properly contains them both. |
The proof of this result is similar to that of 12.1.21; see Chari & Pressley
A990b) for the details.
There is also an analogue of 12.1.22. For example, V€(r)a 0 Ve(s)b is re-
reducible if and only if r/s or s/r — er+s~2k+2 for some 0 < k < min{r, s},
12.3 Duality for Yangians and quantum affine algebras 403
in which case it has a unique proper submodule. In particular, whenever
K(^)a®K(s)b is reducible, it is not completely reducible, nor is Ve(r)a®Ve(s)b
— Ve(s)b ® Ve(r)a. Thus, f/e(L(g)) is not quasitriangular, although, as in the
case of Yangians, it turns out to be quasitriangular in a certain 'limiting'
sense.
Remark The close similarity between the representation theory of Yangians
and quantum loop algebras is 'explained' by the following observation of Drin-
fel'd A987). Let Uh(L(q)) be the deformation of U(L(q)) generated by el-
elements Hi,r, X\~r for i — 1,... , n, r € TL and with defining relations as in
12.2.1, but with q replaced by e\ /Q by ed*hn*>° and C1/2 by 1. Let <p be the
composite map Uh(L(q)) —> U(L(q)) —> U(q) given by first setting h — 0 and
then u = 1. Finally, let A be the C[[/z]]-subalgebra of Uh(L(o)) 0 C((h))
C[[/]]
generated by Uh{L(q)) and /z~1ker(^). Then, A/hA = F(g). A
12.3 Frobenius-Schur duality for Yangians and
quantum affine algebras
In this section, we describe analogues, for Yangians and quantum affine al-
algebras, of the classical duality between the representation theories of special
linear and symmetric groups (another such analogue is discussed in Subsection
10.2B). We first introduce the algebras which play the role of the symmetric
groups in the infinite-dimensional (quantum) theory.
Throughout this section, e ? Cx is assumed to be transcendental.
A Affine Hecke algebras and their degenerations We begin with
Definition 12.3.1 Fix ? > 1, e e Cx. The affine Hecke algebra H?(e)
is the associative algebra over C with generators erf1, af1,... ,crf\, zf1,
z^ 1, • •., Zg l, and the following defining relations:
-i _ -i _ -|
- <0 = o,
Z3Zj
ZjZk =
Zj&i — GiZj if j t^ i or i -f 1,
404 12 Infinite-dimensional quantum groups
Note that the first four sets of relations define the Hecke algebra Hi(e) (see
10.2.1). Hence, there is a natural homomorphism Hi(e) —> Hi(e). It follows
from 12.3.6 below that this map is injective.
Remark Affine Hecke algebras arise classically in connection with the theory
of p-adic groups. Let G — GZ^(QP), and let C be the set of locally constant
functions / : G/B —> C of compact support. Then, C is a representation of
G by left translation, and an algebra under the convolution product
(/i */2)@)= ( h{x)f2(x-lg)dx,
JG
where dx is left-invariant Haar measure on G (note that, since the integrand
is locally constant and compactly supported, the integral is actually a finite
sum).
Let B be the compact open subgroup of G given by
B = {g= (9ij) e GL?(QP) | 9ij e Zp for i > j}.
The Hecke algebra Hi(G,B) of G with respect to B is the subalgebra of C
consisting of the i?-bi-invariant functions:
H?(G,B) = {feC\ f(bigb2) = f(g) for all bu b2eB,ge G}.
It was proved by Bernstein & Zelevinsky A977) that Hi(G,B) = Hi(p).
If W is a (right) Hi(G, i?)-module, we may define the induced representa-
representation
Cw = W 0 C
He(G,B)
of G, regarding C as a (left) Hi(G, B)-modu\e by the convolution product.
It is known that Cw is an admissible representation of G, and that W is
irreducible if and only if Cw is irreducible. We shall obtain an analogous
result later in this section in which G is replaced by Ue(L(sln+i(<E))) (see
12.3.13).
See Cartier A979) for the notion of an admissible representation and for
further background information on p-adic groups. A
Let Uj — A — Zj)/(e — 1). Rewriting the defining relations of Hi(e) in
terms of the Oi and Uj, clearing denominators and dividing both sides of each
relation by the highest power of e — 1, and finally replacing e by 1, one obtains
the following relations:
GiGi — Gi Gi = 1, CFi — 1,
OiOj = GjCJi if \i - j\ > 1,
1,
12.3 Duality for Yangians and quantum affine algebras 405
Definition 12.3.2 The degenerate affine Hecke algebra A^ is the asssocia-
tive algebra with generators af1,..., vflv ui,... ,ui, and the above defining
relations.
Note that the first three sets of relations above are the defining relations
of the symmetric group E^ (take oi to be the transposition (i, z + 1)). Hence,
there is a canonical homomorphism C[?^] —> A^.
It will be convenient to introduce the elements
In terms of these elements, the defining relations of A^ take the following
form:
C5)
B Representations of affine Hecke algebras It is known that when e
is transcendental (or simply not a root of unity), the Hecke algebra Hg(e) is
isomorphic as an algebra to the group algebra C[?^]. Its irreducible repre-
representations are therefore parametrized by the partitions of L To describe this
correspondence explicitly, we make use of certain elements of Hg(e) introduced
by Kazhdan & Lusztig A979).
Let w ?Y>i and let
C6) w = rilTi2...ritiw)
be a reduced expression of w as a product of the simple transpositions Ti —
(z,i + 1) (see the Appendix). It follows from the defining relations in Hi(e)
that, if C6) is any reduced expression for w, the element
depends only on w, and not on the choice of reduced expression (see 8.1.3:
in fact, this statement is a consequence of the corresponding assertion for
the braid group of s/n+i(C), since He(e) is the quotient of the group algebra
of the braid group by the two-sided ideal generated by (a* -h l)(o"i — e) for
i = l,...,?—1). Let < be the Bruhat ordering on E^ determined by the choice
of generators t~i, ... ,r^_i, and for wf < w let Pw^w be the Kazhdan-Lusztig
406 12 Infinite-dimensional quantum groups
polynomial (see Humphreys A990), Chap. 7, for background information).
Define elements Cw ? 7ii(e), for all w G E^, by
Let ? = ?i + ?2 H h^bea partition tt of t, with each 4 > 0, and let EJ
be the subgroup E^ x • • • x E^p of E^ which fixes tt. Let wr be the longest
element of the subgroup E^r, i.e. the permutation which reverses the order
of
Set ww — W1W2 .. .wp and let Iw be the right ideal in Hi(c) generated by CWlT.
PROPOSITION 12.3.3 For every partition n of?, 1^ has a unique irreducible
quotient Jn in which CWix has non-zero image. Every finite-dimensional irre-
irreducible representation ofTLi{e) is isomorphic to exactly one Jn. |
See Rogawski A985) for a proof.
Turning now to affine Hecke algebras, we first introduce a family of 'uni-
'universal' representations, analogous to the Verma representations of quantum
groups (see Chapter 9). Let a — (ai,..., a^) € (Cx)^, and let
the quotient of Hi(e) by the right ideal 7ia generated by Zj—ctj.l, j — 1, ...,?.
The following result is proved in Rogawski A985).
Proposition 12.3.4 (i) Every finite-dimensional irreducible (right) Hi(e)-
module is isomorphic to a quotient of some Ma.
(ii) For all a (E ((Cx)?, the natural map Hi(e) —> Ma is an isomorphism of
Hi(e)-modules (where Hi(e) acts on itself in the right regular representation).
(Hi) Ma is reducible as an Hi(e)-module if and only if ctj — eafc for some j,
k. I
Zelevinsky A980) and Rogawski A985) identified certain distinguished quo-
quotients of the Ma, for certain a, which exhaust the irreducible representations
of Hi(e):
Theorem 12.3.5 Let s — {si,..., sp} be any (unordered) collection
segments, the sum of whose lengths is ?. Let ?r be the length of sr, and
denote by tt(s) the partition ? = ?\ + • • • -h ?p. Let a = S1S2 • • • $p € (<EX Y be
the result of juxtaposing the segments in s. Then,
(i) /^(s) is an Hi(e)-submodule of Ma (this makes sense in view of 12.3.4(ii));
(ii) with the He(e)-module structure inherited from Ma, In^ has a unique
irreducible subquotient Va in which CWn(s) has non-zero image.
12.3 Duality for Yangians and quantum affine algebras 407
Moreover, every finite-dimensional irreducible right Hi(e)-module is iso-
morphic to some Va. |
The next proposition allows one to give a simple construction of some, but
not all, of the irreducible representations of Hi(e). We shall see in 12.3.15
that the similarity between this result and 12.2.10 is not accidental.
Proposition 12.3.6 For any a E Cx, there exist unique homomorphisms
eva and eva from Hi(c) to Ht(c) such that
The proof is straightforward.
If M is any Hg(e)-module, pulling back M by eva (resp. by eva) gives an
7i!^(e)-module Ma (resp. Ma) which is isomorphic to M as an 7^(e)-module.
In particular, Ma and Ma are irreducible if M is irreducible. If ? > 1, a
module Ma is not in general isomorphic to any module of the form M'a,. We
call Ma and Ma evaluation representations of Hi(e) (the justification for this
terminology appears in 12.3.15).
One can extend the class of 'constructive' W^(e)-modules by using a kind
of tensor product, the definition of which is based on the following easy ob-
observation:
Proposition 12.3.7 For any ?i, ?2 ^ ^-, there exists a unique homomor-
phism of algebras
such that
hu?2(<7i ® 1) = <7i, hul2(Zj <g> 1) = Zj,
for i — 1,... ,^1 — 1, j — 1,... ,?1, and
Clearly, Z^^ restricts to give a homomorphism itx^ : Hi^e) 0W/2(e)
Suppose now that Mi (resp. M2) is an H^(e)-module (resp. an Hi2(e)-
module), and let Mi 0 M2 be their outer tensor product (an H^ (e) 0 Hi2 (e)-
module). Then, we define an 7i!^1+^2(e)-module Mi^M2, sometimes called
the Zelevinsky tensor product of M\ and M2, to be the induced module
= (Mi <g> M2)
408 12 Infinite-dimensional quantum groups
The Zelevinsky tensor product E3 of representations of Hecke algebras is de-
defined in the same way. Standard properties of induced modules show that the
Zelevinsky tensor products are associative up to isomorphism (but we shall
see that ISI is not commutative, in general).
Remark We have already noted that Hi(e) is isomorphic to C[?^] as an al-
algebra. Thus, Hi(e) has a Hopf algebra structure. This gives another way
to take tensor products of Hecke algebra modules, quite different from the
Zelevinsky tensor product. A
To understand these constructions, the reader may find it useful to establish
the result of the following example.
Example 12.3.8 Let <C be the one-dimensional trivial representation of H\ (e) =
C (on which 1 € H\(e) acts as 1). Then, for any a = (ai,..., ai) ? (Cx)^,
as 7i^(e)-modules. <)
All of the above constructions have analogues for degenerate affine Hecke
algebras. For example, using the limiting procedure described in Subsection
12.3A by which A^ is obtained from Hg(e), it is easy to deduce the existence
of a homomorphism A^ 0 A^2 —> A^1+^2 such that
fc = l fc = l
Using this, one can define a tensor product of degenerate affine Hecke algebra
modules analogous to 13.
We leave it to the reader to find in a similar way the homomorphisms
A^ —> C[E^] which are the e = 1 limits of eva and eva (see Drinfel'd A986b)
for the answer).
However, the classification of the finite-dimensional irreducible A^-modules
cannot be deduced so easily from that for Hg(e). See Cherednik A988b).
C Duality for Ue(sln+i((C)) — revisited We begin our discussion of quan-
quantum Frobenius-Schur duality with the case of Ue(sln+i(<E)). Recall from
Section 10.2 that Ue(sln+i((C)) has a natural (n -f 1)-dimensional irreducible
type 1 representation V^ with basis {^o, • • • > vn} and action given by
Ki.Vr = 66r'l~1~6r^Vr, Xf.Vr = 6ryiVr-i, X~ .Vr = 6r,i-iVr+i
(we set v-i — vn+i = 0). A finite-dimensional representation of [7e(s/n+i(C))
is said to be of level ? if each of its irreducible components is isomorphic to
12.3 Duality for Yangians and quantum affine algebras 409
some irreducible component of (V^)®^ (recall from 10.1.7 that every finite-
dimensional representation of U€(sln+i((E)) is completely reducible). The
level of a representation is not, in general, uniquely defined, but the following
result shows that the level is unique if it is < n.
Proposition 12.3.9 The finite-dimensional irreducible U€(sln+i(<E))-
module V€(X) is of level ? < n if and only if its highest weight A = Yl7=i ri^i>
where Ym-i ^ri — ^-
Outline of proof By the results of Chapter 10, it suffices to prove the
analogous classical result, which is not difficult. |
Let I€ : (V*)®2 -> (V?)®2 be the linear map defined by
{evr <g)vs if r = s,
vs®vr if s > r,
vs 0 vr + (e — e)^ 0 vs if r > s.
We saw in 10.2.5(i) that there is an action of He(e2) on (V*)®e such that
(Ji acts as ele on the ith and (i + l)th factors and as the identity on the
other factors. Thus, if M is any right ?-^(e2)-module, the natural action of
U€(sln+i((C)) on {V^)®^ induces an action of ?/e(s/n+i((C)) on the vector space
M 0 ?'
We have the following more precise result, due to Jimbo A986a).
Theorem 12.3.10 Fix ?, n > 1. There is a functor J from the category of
finite-dimensional right Hi(e2)-modules to the category of finite-dimensional
left Ue(sln+i(<E))-modules of level ? such that, if M is an Hi(e2)-module,
J(M) = M 0
equipped with the natural Ue{sln+i{<E))-module structure induced by that on
(V*)®e.
If ? <n, J is an equivalence of categories. |
In view of complete reducibility, J is determined by its effect on the Jn
(see 12.3.3).
Proposition 12.3.11 Let 1 < ? < n and let ?1+?2J\ \-?p be a partition
7T of?. Then,
as representations of U€ (sln+i (C)).
Outline of proof It is proved in Kazhdan & Lusztig A979) that
Cw(Ji = — Cw if wTi < w.
410 12 Infinite-dimensional quantum groups
Using the formulas in C7), this implies that, if v G (V^)®e has vr <g) vr in the
ith and (i + l)th positions, for some r = 0,1,..., n, then in J(Jn) we have
C8) CWn <g> v = 0.
By 12.3.10, there exists a partition tt' of ?, say ^ = ?\ H h C> sucn tnat
It is easy to see that the weight space of (V^)®e of weight A^ +•• • + Xip is
spanned by the permutations of the vector
If v is such a vector, it follows from C8) that CWn, 0v = O unless the first ?[
components of v are distinct, as are the next t!2, ..., and the last ?'m. Since
Cwn, 0 v must be non-zero for some such v, it follows that nf = n. |
The functor J is clearly one of (C-linear categories, but it also captures
part of the tensor structure of the category of f/e(s/n+i(C))-modules.
Proposition 12.3.12 Let n, ?ly ?2 > 1, and let Mj (resp. M2) be a Rnite-
dimensional H?1(e2)-module (resp. Hi2(e2)-module). Then, there is a canon-
canonical isomorphism of'Ue(sln+i(<?))-modules
The proof is straightforward.
D Quantum affine algebras and affine Hecke algebras The follow-
following result, due to Chari & Pressley A993b), is an analogue of 12.3.8 for
?/c(L(s/n+i(C))). Let Ke = KXK2 ...Kne U€(sln+1(€)), and let Xf be the
operators on V^ defined by
Theorem 12.3.13 Fix ?, n > 1. There is a functor T from the category of
finite-dimensional right 7i^(e2) -modules to the category of finite-dimensional
left U€(L(sln+i((?)))-modules which are of level ? as Ue(sln+i((?))-modules,
defined as follows. IfM is an H^e2)-module, F(M)=J(M) as a t7€(sZn+i(C))-
module, and the action of the remaining generators of U€(L(sln+i(<C))) (in
the presentation 9.1.1) is given by
K0.(m 0 v) = m <
12.3 Duality for Yangians and quantum affine algebras 411
for all me M,v G {V})®1, where the operators Zf on (Ve^)®? are defined by
Z+ = id®' 0 X~ 0 (Ko1)®'-',
ZJ = Kf3'1 ® Xj ® id®*"''.
If f : M -* M' is a homomorphism ofHi{e2)-modules, then T{f) : T{M)
F(M') is defined by
The functor T is an equivalence of categories if ? < n.
Outline of proof To see that the action of Xq (say) is well defined, we
must show that, as operators on J{M\ we have
? ?
D0) ^ (TiZj (g> Zf = ^ Zj (8) Zt<7i.
If j ^ i or z + 1, the jth terms on the left- and right-hand sides of D0) are
equal, since G{Zj = z^oi and &iZf = Zf&i. Hence, we must show that
GiZi (g) Zf + (TiZi+1 ® Z^: = Zi (g) Z2+(J^ -f Z;+1 (g) Z2^_ 1Gj.
Using the relation €2a~1 = <j^ — e2 + 1, this reduces to
e2zz+1 0 (trr^t - Z^a'1) + * 0 faZ^ - Z+a,) = 0.
Thus, it suffices to prove that cFiZf+1 — Zfo~i, i.e. that
This equation is easily checked.
The fact that the formulas in the theorem define a ?/e(L(s/n+i((C)))-module
is proved by directly verifying those defining relations of U€(L(sln+i((C)))
which involve Xq~, Xq or Kq.
Suppose now that ? < n, and let W be a finite-dimensional representation
of U€(L(sln+i(<C))) of level L By 12.3.8, we may assume that W = J(M)
as a representation of U€(sln+i((C)), for some 7i?(e2)-module M. Since the
permutations of the vector
clearly span the subspace of (V^)®^ of weight A^, it follows that there exists
C~ € Endc(M) such that
V2 0 •
J" (m) 0 vi 0 i;2 0 • • • 0 ^j-i 0 ^o 0 ^j 0 ^j+i 0 • • • 0 V?-i
412 12 Infinite-dimensional quantum groups
for all m ? M. Similarly, there exists C/ ? Endcc(M) such that
X^.(m 0 ^n-?+l 0 • • • 0 Vn-e+j-i ®Vo® Vn-?+j 0 • • • 0 Vn-l)
= C/(™) ® ^n-?+l 0 ' ' ' 0 ^n-?+j-l 0 ^n 0 Vn-?+j 0 • • • 0 Vn_i.
One shows that letting z^1 act as (^ for j = 1,..., ? defines an 7i^(e2)-module
structure on M, and that one then has W = !F(M). |
The following result determines the action of T on the irreducible repre-
representations of He(e2). See Chari & Pressley A993b) for the proof.
Theorem 12.3.14 Let s = {si, s2,..., sp} be a collection of e-segments, the
sum of whose lengths is L Let ar be the centre of sr and ?r its length. Let
a = S1S2 • • .sp ? (<?XY be the result of juxtaposing si,..., sp, and let Va be
the irreducible H^e2)-module defined in 12.3.5. Then, if ? < n, ^(Va) is the
irreducible Ue(L(sln+i((?)))-module whose associated polynomials Pi (as in
12.2.6) are
{r\er=i}
The simplest representations of 7i^(e2) are the 'evaluation representations'
defined in 12.3.6 and the remarks following this proposition. The following
result justifies this terminology.
Proposition 12.3.15 Let 1 < ? < n and let M be a finite-dimensional
Hi(e2)-module. Then, there are canonical isomorphisms of U€(L(sln+i(<E)))-
modules
•F(Mac-«/(»+o) ^ J(M)a, f(Mae~2e/(n+1)) * J(M)a.
Outline of proof In the first case, we know by 12.3.13 that J(M)a =
T(N) for some 7Y?(e2)-module A^ which is isomorphic to M as an Hi(e2)-
module. It suffices to prove that z\ ? ^(e2) acts as the scalar ae~2^n+1) on
N. To see this, one computes the action of X$ on m®vo 0i;n_^_j_i (g>vn^?+2 ®
• • • 0 tVi-i, for all m ? M, in two different ways. First, by the definition of
T, we have
X?.(m ®Vo® Vn-?+l <8) Vn-?+2 0 ' ' * 0 Vn-l)
= m.Zi 0Vn0 Vn-?+i 0 Vn-?+2 0 • • • 0 Vn-l-
On the other hand, let
fn = [X~,[X~__V . . . ,[X2 ,X^]€i/2 - "]€i/2]€i/2 ? Ue{gln+i{<L)).
12.3 Duality for Yangians and quantum affine algebras 413
Then, by 12.2.10,
X?.(m ®V0® Vn-?+1 ® Vn-?+2 0 ' ' • 0 Vn-l)
= m ® evapQj").(t/o 0 vn-*+i ® vn-e+2 (8) •
= ae-(n)/2-2?/(n+1)m ® /n.(t/0 0 ^n-?+i
Finally, as in 12.3.12, T respects the tensor product operations on the
categories involved: it is straightforward to prove
Proposition 12.3.16 Let ?i, ?2 > 1, and let Mx (resp. M2) be a Gnite-
dimensionalH?1(e2)-module (resp. 7i^2(e2)-module). Then, there is a canon-
canonical isomorphism of U€(L(sln+i(<C)))-modules
We conclude this subsection with
Example 12.3.17 Let C be the one-dimensional trivial representation of
Hi(e) = C It is easy to see that J(C) = V*. By 12.3.15, for any a e Cx,
By 12.3.8 and 12.3.16, we see that, for any a = (au ...,a?)e (<CX)?,
By 12.3.4(i) and 12.3.13, it follows that every finite-dimensional irreducible
representation of U€(L(sln+i((E))) of level ? < n is isomorphic to a quotient
of a tensor product of representations of the form (V^)a. <}
E Yangians and degenerate affine Hecke algebras In view of the re-
remark at the end of Section 12.2, and the discussion preceding 12.3.2, it
is not surprising that there is an analogue of 12.3.13 relating the Yangian
F(s/n+i((C)) to the degenerate affine Hecke algebra A^.
Let V^ be the (n + l)-dimensional irreducible representation of s/n+i((C).
We say that a finite-dimensional representation W of sZn_|_i(C) is of level ?
if every irreducible component of W occurs in (V^)®*. Recall that there is a
canonical homomorphism s/n+i((C) —> y(sZn_j_i(C)), so that any representa-
representation of y(s/n+i((C)) may be regarded as one of sZn_j_i(C).
414 12 Infinite-dimensional quantum groups
Theorem 12.3.18 Let ?, n > 1. There is a functor V from the category
of finite-dimensional right Ai-modules to the category of finite-dimensional
Y(sin_j_i((C))-modules which are of level ? as sin+i((C)-modules, defined as
follows. If M is a Ai-module, then, as a vector space,
V(M) = M ® (V*)®1,
C[E<]
where T,? acts on (V^)®e by permuting the factors. The action of s/n+i((C)
on V(M) is induced by that on (y^)®e, while the action of the generators
J(x) (x e sln+i(<E)) in 12.1.2 is given by
for all m e M, wi,... ,W? eVK
If ? < n, V is an equivalence of categories. |
Note that it follows from C5) that the action of J(x) is well-defined.
This result is due to Drinfel'd A986b). The same work also contains an ana-
analogue of 12.3.16 for Yangians, whose formulation we leave to the reader. The
finite-dimensional irreducible A^-modules have been classified in Cherednik
A988b), so 12.3.18 gives a description of all irreducible y(s/n+i(C))-modules
which are of level < n for s/n+i((C).
Nazarov A993b) gives an analogue of 12.3.18 for the orthogonal Yangians
Y{son{<L)).
12 A Yangians and infinite-dimensional
classical groups
The second instance of a relation between Yangians and classical represen-
representation theory concerns the infinite-dimensional classical group Oqo consisting
of the N x N matrices of the form
D1)
(A 0 0 0
0 10 0
0 0 10
\o o o ¦•.
where A ? On for some n > 1; we identify On with the subgroup of Oqo
consisting of the matrices D1). We define the Lie algebra Ooo of Ooo to be
the union of the Lie algebras on of On under the same embeddings.
12.4 Yangians and infinite-dimensional classical groups 415
A Tame representations A representation p of Ooo on a complex Hilbert
space V is said to be tame if every vector v ? V can be approximated arbi-
arbitrarily closely by a vector fixed by On for some sufficiently large n. If x ? Ooo,
let pr{x) be the skew-symmetric operator such that exp (tp'{x)) = p(exp (tx))
for all t ? IR. This gives an action of Ooo, and hence of its universal enveloping
algebra f7(ooo)> on V.
It is not difficult to construct tame representations. The most obvious
example is the complexification of the natural representation of Ooo on the
real Hilbert space of all square-summable sequences (?]_, ?2, • • ¦) (thought of
as N x 1 column vectors). Let us denote this representation by Vnat: it is
clearly tame. More generally, let (ynat)®fc be the fc-fold Hilbert space tensor
product of \/nat, i.e. the completion of the fc-fold algebraic tensor product
equipped with the inner product
{vi ® • • • ® vk , v[ ® • • • <g> v'k) = (vi, v[)... (vk , v'k).
The symmetric group ?& acts on (v™*)®*5 by permuting the factors, and
this action obviously commutes with that of Ooo. It is known that, if n is
any irreducible representation of ?&, the isotypical component of (Vnat)®fc of
type 7T is a direct sum of dimGr) copies of an irreducible representation Vn of
Ooo- Further, Vn is tame, and every tame irreducible representation of Ooo
is isomorphic to some V71".
Remarks [1] This result obviously resembles the Frobenius-Schur duality be-
between the representations of symmetric groups and those of finite-dimensional
general linear groups. We shall see an explanation for this at the end of this
section.
[2] It is perhaps worth emphasizing that the tensor products (Vnat}®k do
not decompose into irreducibles in the 'same' way as in the case of finite-
dimensional orthogonal groups. For example, the inner product
( , ) : Fnat 0 Fnat -> C
clearly does not extend to a continuous linear form (\/nat)®2 —+ (C. This
implies that the representation (Vnat)®2 of Ooo does not contain a copy of
the trivial representation. A
One would like to study tame representations by infinitesimal methods.
For example, one would like to classify them by their central characters.
Unfortunately, it is known that the centre of ?/(ooo) contains only the scalars.
However, there is a way to enlarge the enveloping algebra in such a way that
it still acts on tame representations.
Definition 12.4.1 Fix m e N and let Xm be the set of all sequences x\,
X2, ?3,. •. such that
416 12 Infinite-dimensional quantum groups
(i) xn e U(on) is invariant under the adjoint action of the subgroup
o -
of On for all n > m;
(ii) the degrees of the xn are bounded (the degree of an element x of an
enveloping algebra U(q) is the minimal fc^N such that x is in the image of
the canonical embedding §®k -» U(q) - see 4.1.8);
(Hi) if p is any tame representation of Oqo, the strong limit limn^oo pf(xn)
exists (and is then necessarily a bounded operator).
Two sequences (#i, #2, X3, • • • )> B/i? 2/2? 2/3> • • •) ? Xm are said to be equiv-
equivalent if
lim p'(xn) = lim p'(yn)
n—kx> n—>oo
for aii tame representations p. The set of equivalence classes is denoted by
UmiOoo)'
Since Om+i5n C O^^, there are natural enbeddings Um{ooo) ^ C^m+i(°c»)
and we define
Note that Um{ooo) nas an obvious algebra structure, corresponding to com-
componentwise multiplication of sequences in Xm, and hence so does ^7(ooo). Note
also that there is an embedding Ufooo) ^> t/(ooo) which associates the se-
sequence (#,?,?,...) to any element x G J7(ooo). It is tautologous that Ufooo)
acts by bounded operators on any tame representation of Ooo, extending the
action of
B The relation with Yangians With these preparations, we can state the
main result of this section, which shows that the extended enveloping algebra
Uiooc) is closely related to Yangians.
Theorem 12.4.2 Let Z be the centre ofU(ooo). Then, for all m>l, there
are isomorphisms of algebras
These isomorphisms are compatible with the natural embeddings
Um(ooo) — ?Wi(ooo) and Y(glm(€))^Y{glm+1(€)).
Thus, the infinite Yangian
Y(gloo(<L))=\imY(glm(<L))
12.5 Rational and trigonometric solutions of the QYBE 417
acts on any tame representation of Ooo.
Remarks [1] The last sentence of the theorem implies that
and hence that the centre of Y(gloo((?)) is trivial (cf. 12.1.7).
[2] The structure of the centre Z of U(ooo) is known. Let Zm be the sub-
algebra of the polynomial algebra <C[zi,..., zm] consisting of the polynomials
which are symmetric in the variables z\ — \, Z2 — 2,..., zm — m. Restricting a
polynomial in Zm to the hyperplane ?m = 0 in (Cm defines a homomorphism
Zm -+ Zm_i, and
[3] The resemblance between the theory of tame representations of 0^
and that of the representations of finite-dimensional general linear groups is
explained to some extent by the following alternative description of U(ooo).
Let Un = U(gln(<E)) and regard Un as a subalgebra of Un+i in the usual
way. Let [7™, for each m < n, be the centralizer in Un of the elementary
matrices Eij with m < i,j < n. Then, U™~1 C U™ for all m < n. It is
easy to see that, if In is the left ideal in Un generated by E\n, E2n, - • •»Enni
then U™'1 = Un-i 0 In. If we restrict the isomorphism U™~1 /In —> C/n_i to
C/^1, we obtain a homomorphism U™ —> C/n_i whose image clearly lies inside
G^.!. We define
in the category of filtered algebras. Thus, an element of ?/m is a compatible
sequence (xm,xm+i,...) with xn ? ?7™, such that the degrees of the xn are
bounded. There are obvious embeddings U171 ^-> Urn+l and one shows that
in the category of filtered algebras. A
12.5 Rational and trigonometric solutions
of the QYBE
We have seen that Yangians and quantum affine algebras are not quasitrian-
gular. However, we show in this section that these Hopf algebras are 'pseu-
dotriangular' (this terminology is due to Drinfel'd A987)), and that, as for
quasitriangular Hopf algebras, this property is sufficient to guarantee that
there is a solution of the quantum Yang-Baxter equation associated to the
tensor product of any pair of finite-dimensional representations.
418 12 Infinite-dimensional quantum groups
A Yangians and rational solutions We recall from Subsection 12.1 A (see
also 1.3.9) that the Lie bialgebra structure on $[u] of which Uh($[u]) is the
quantization is given by
D2) 6(f)(u, v) = (ad/(n) 0 id + id 0 ad/(w)) (
u — v
where t is the Casimir element of g ® g. Although this formula defines a
Lie bialgebra (q[u] , <5), it does not imply that it is quasitriangular because
r = t/(u — v) is not an element of the algebraic tensor product §[u] 0g[it] =
]
However, let A be an indeterminate and let g[i/]((A~1)) be the extension
of §[u] to a Lie algebra over the field of formal power series in A. The
translation f(u) »—> f(u + A) is a well-defined automorphism of g[i/]((A~1)),
which we denote by r\, and the coefficients of powers of A in the formal power
series
r(A) = (rA ® id) (-J-) = _L^ = f> - uYA-r-H
do belong to (g 0 g)[^, v]. Thus, replacing t/(u — v) on the right-hand
side of D2) by r(A) gives a genuinely coboundary Lie bialgebra structure
on g[i/]((A)). Note that r2i(A) = -r12(-\).
The translation automorphisms of q[u] have been 'quantized' in 12.1.5. If
we replace the complex number a in B0) by the indeterminate A, we obtain
a well-defined algebra automorphism t\ of y(g)((A-1)). From the preceding
remarks, it is reasonable to expect that y(g)((A-1)) has a universal R-matrix
1l(X) satisfying Tl2i(X) = ^^(-A). This expectation is fulfilled:
Theorem 12.5.1 There is a unique formal power series
oo
D3) Tl(X) = 1 <g> 1 + | +
x r=1
with the following properties:
(a ® id)(n(\)) = n13(x)n23(\), (id ®
(rA ® id)(A°») = n(X).((rx ® i
for aiJ a € ^(g)- Moreover, 1Z(X) is a triangular solution of the QYBE:
- X2)K13(Xi - X3)n23(X2 - A3) =
D4) TZ23(X2 - A3Ol13(A1 - Xa^u^ - X2),
12.5 Rational and trigonometric solutions of the QYBE 419
We shall call TZ(X) the pseudo-universal R-matrix of Y(g).
Remark In principle, it should be possible to compute the pseudo-universal
R-matrix 7Z(X) by means of the quantum double method, which we used in
Chapter 8 to compute the universal R-matrix of f7^(g). As in that case, to
carry out the computation, it would be necessary to calculate the action of
the comultiplication on all of the basis elements of Y(cy) given in 12.1.9. As
we noted in Remark [1] following 12.1.1, this has not been achieved, even for
the generators of Y(g) given in 12.1.3. A
In view of D3) and D4), if p : Y(g) —> End(V) is a representation of F(g),
then RP{X) = (p <8> p)(Tl(X)) G End(V <8> V')[[A~1]] will be a matrix solution
of the QYBE, with Ai, A2, A3 playing the role of spectral parameters, of the
form
00
-1 , V^ o x-r-l
D5) RP(X) = 1 ® 1 + (p ® p){t)X~l +
r=l
Unfortunately, since no explicit expression for TZ(X) is known, this result does
not allow one to actually compute RP(X).
However, 11.1.16 gives another method of constructing solutions of the
QYBE from representations of Hopf algebras. To apply this to Yangians, we
need a one-parameter family of finite-dimensional irreducible representations
of Y(q) on a fixed underlying vector space. If p : Y(§) —* End(V) is any finite-
dimensional representation, we can take the family poTa, which we denote
by t*{V). Then, we expect that, if I(a,b) : T*a{V) ® T6*(F) - rb*(F) ® t*(V)
is a suitably normalized intertwining operator, then R — a o /, where a is
the map which interchanges the factors in the tensor product, is a solution of
the QYBE, the spectral parameters now being complex numbers rather than
indeterminates. The following result shows that this expectation is fulfilled,
and that the resulting solutions of the QYBE are the same as those obtained
by applying p to the universal R-matrix
Theorem 12.5.2 Let p : Y(g) —> End(F) be a finite-dimensional irreducible
representation of Y(g). Then, up to a scalar multiple, RP(X) = (p<8> p)(R,(X))
is the Laurent expansion about 00 of a rational function of X, and thus Rp(a)
is a well-defined element of End(V 0 V) for all except finitely many values
of a G (C. Moreover, except for finitely many values of a — b, Ip(a,b) =
a o RP{a - b) is the intertwining operator ra*(V) 0 rb*(V) -» rb*(V) 0 ra*(V)
(up to a scalar multiple). |
Remark It is clear a priori that, up to a scalar multiple, every intertwining
operator /(a, b) : r*(F) <g) rb*(V) -» rb*(V) (g) r*(V) is a rational function of
a — b. For, using the description B1) of ra, the condition that I(a,b) is an
420 12 Infinite-dimensional quantum groups
intertwiner is that
(p 0 p)(x 0 1 + 1 0 x)I(a, b) = /(a, b)(p 0 p)(x 0 1 + 1 0 x),
D6) (P ® P)(( J(a:) + &z) ® 1+1 ® (J(z) + ax) + - [z 0 1, t])I(a, b) =
/(a, b)(p 0 /9)(( J(x)+ax) 0 1 + 10 (J(x) +6a;) + -[x0l, *]),
z
for all x G g. Using the first equation in D6), the second is equivalent to
(J(x) + (a-b)x) + -[x®l
/(a, b)(p 0 p){(J{x) + (a - 6)x) 0 1 + 10 J(x) + -[x 0 1, t]).
Letting x run through a basis of g, we see that the equations D6) are equiva-
equivalent to a finite system of linear equations for the entries of the matrix /(a, 6),
the coefficients of which are polynomials in a — b. For elementary reasons, the
solution I(a,b) must therefore be a rational function of a — b (up to a scalar
multiple). A
It is natural to ask which rational solutions R(X) G End(V 0 V) of the
QYBE arise from representations of Yangians in this way. An obvious neces-
necessary condition is that, up to a scalar multiple, the Laurent expansion of R(X)
about A = 00 is of the form D5) for some representation p of g on V. The
next result shows that this condition is also sufficient.
Theorem 12.5.3 Let R(X) be a rational solution of the QYBE of the form
D5) for some finite-dimensional representation p of g. Then, there is an
extension of p to a representation p : Y(q) —* End(F) on the same vector
space such that R(a) is a scalar multiple of RP(a) for all but finitely many
a G (C. Moreover, p is uniquely determined by R(X) and p up to twisting with
one of the automorphisms t\,. |
Remark The condition D5) is natural from another point of view, for the
most obvious way to construct rational solutions of the CYBE is to apply
representations p of g to the classical r-matrix t/(u — v) of §[u\. Then, D5)
gives a 'quantization' of this classical r-matrix (see 6.2.11). To see this, it is
necessary to work with Uh(Q[u\) rather than F(g), i.e. to avoid specializing
h to 1. If one does that, one finds that the analogue of D5) is
RP(\) = 1 ^ 1 + h{p 0 p){t)X~1 + J2
r=l
so that {p®p){t/X) = ft-1(jR^(A) - 1 0 1) (mod h). A
12.5 Rational and trigonometric solutions of the QYBE 421
We now turn to the problem of actually computing the R-matrix associated
to a given representation of Y(q). In general, this is far from solved. If
g = SI2 (C), however, we can give a complete answer:
Proposition 12.5.4 Let a\,..., ak e <C, r*i,..., rk eN, k > 1, satisfy the
condition in 12.2.15(Hi), so that
is an irreducible representation of Y(sl2{(C)). The R-matrix associated to V
can be described as follows. Choose s^C)-primitive vectors Vj in V(r)®V(s)
of weight r+s — 2j, whenever 0 < j < max{r, s}, such that (X^<g>i).Vj — Vj-i
for all j > 0, and let Pj's : V(r) <8> V{s) -» V(s) <8> V(r) be the unique
homomorphism of si 2 {<?¦)-modules such that PJ's(vj) = ct(vj) and Pj's(vk) =
0 if k / j (a is the Hip operator). Define
I(r, a;s,b): V(r)a ® V(s)b -f V(s)b ® V(r)a
by
min{r,s} /j —1 T , 1
Then, the R-matrix associated to V is
D7) R(a-b)
wLere tLe operator I in the (i,j)th term acts in the (i +j — \)th and (i+j)th
factors in the 2k-fold tensor product, and the (i,j)th term appears to the
right of the (if,jf)th term if and only if i > i' or i — i' and j < j'.
The possibility of choosing primitive vectors Vj satisfying the conditions in
the proposition will be established in the course of the proof.
Proof Let I{r,a; s,b) : V(r)a (8) V(s)b —> V(s)b <%> V(r)a be the unique
intertwining operator of y(s/2(<C))-modules which flips the tensor product of
highest weight vectors in V(r)a and V(s)b- The unique intertwining operator
Ta (V) <8) t?(V) —> rfe*(V) 0 r*(V), between the tensor products of the twists
of V by ra and T&, which permutes the 2/c-fold tensor product of highest
weight vectors, can be computed as the product of the intertwiners which
successively move each of the k factors in t?(V) to the left of each of the k
factors in r*(V). The result is the product in D7).
Thus, it suffices to compute I(r,a; 5,6). Since this operator commutes
with the action of 5/2 (C), we must have
min{r,s}
I(r,a;s,b)= ? CjPj's
422 12 Infinite-dimensional quantum groups
for some scalars Cj\ by the chosen normalization, cq — 1. Let Vj be an sh(C)-
primitive vector in V(r) 0 V(s) of weight r + s — 2j. If j > 0, it is easy to see
that (X^ (8> l).^j is an s^(C)-highest weight vector of weight r + s — 2j + 2; it
is non-zero, for otherwise Vj would be annihilated by X^ (gI and l^Xj1", and
hence would have to be a tensor product of highest weight vectors in V(r)
and V(s), contradicting the assumption that j > 0. Hence, if we normalize
the Vj suitably, we may assume that
D8) (X+ <g> l).Vj = t;,-!
for j > 0. From the proof of 12.1.22, Vj is a Y(s/2(?))-highest weight vector
in V(r)Q ® V(s)b if a - b = \(r + s) - j + 1. It follows from G) that, in
V(r)a®V(s)b,
J(X+).Vj = (a-b-±(r + s)+j-
If ^- = cr(^j) G V(s)b 0 V"(r)a, we find by the same argument that
J{Xt).v'3 = (b - a - l(r + s) + j - l) (X+ 0 1).^-,
and from D8) that (X^ (g) 1).^ = -Vj_v The equation
/(r, a ; s, b)(J(X+).v3) = J(X+).(/(r, a ; s, 6)(Vj))
now gives
Cj b - a -h \{r -h s) - j -f 1
and hence the stated formula for /(r, a ; 5, 6). |
Remarks [1] The expression for R(a-b) in 12.5.4 was first obtained by Kulish,
Reshetikhin & Sklyanin A981), using methods of inverse scattering theory.
Even when the evaluation representations V(r)a are all two-dimensional (i.e.
r — 1), the resulting solutions of the QYBE are related to interesting phys-
physical models (the quantum non-linear Schrodinger equation, the Heisenberg
ferromagnet (XXX model), Toda chains, ...).
Kulish et al. apparently proved that R(a — b), as defined above, satisfies the
QYBE by a direct verification (which is not entirely trivial). For us, however,
this follows from 11.1.16 without further computation. The hypotheses (i)
and (ii) in that proposition (for generic values of the parameters) follow from
12.1.20 and 12.1.21, and the scalar c in equation D) in the same proposition
is equal to 1 because the products of the R-matrices on both sides of D)
preserve the tensor products of highest weight vectors.
12.5 Rational and trigonometric solutions of the QYBE 423
[2] The kind of direct computation used to prove 12.5.4 is impractical for
general g, except for the simplest representations. However, the R-matrices
associated to most of the fundamental representations of Y(q) are known.
See Ogievetsky, Reshetikhin & Wiegmann A987), Ogievetsky & Wiegmann
A986), Reshetikhin & Wiegmann A987) and Chari & Pressley A991a). The
arguments used in the first three references depend on the assumption of
'the physical consistency of certain quantum field theories', but most of their
results are proved in the last reference by Lie-theoretic methods. A
B Quantum affine algebras and trigonometric solutions Like Yan-
gians, (untwisted) quantum affine algebras also turn out to be pseudotrian-
gular. In principle, their pseudo-universal R-matrices can be constructed by
the quantum double method used in Chapter 8, but there are two difficulties
caused by differences between the structure of the root system of an affine
Lie algebra g and that of its underlying finite-dimensional Lie algebra g.
The first important difference is that, unlike the situation for g, not every
root of g can be obtained by applying an element of the Weyl group of g to a
simple root. This means that the procedure used in Section 8.1 to define non-
simple root vectors in E/h(g) cannot be used for ?/h(g). The other difference
is more obvious: g has infinitely many positive roots. Thus, if one is to
prove a formula like that in 8.3.9 for the universal R-matrix Ti of Uh{§), the
coefficients in its fo-adic expansion will be formal infinite linear combinations
of products of root vectors. There would then be no guarantee that 1Z would
act on a tensor product of representations of C/^(g) (and is why we obtain
only a 'pseudo-universal' R-matrix).
Despite these objections, we have the following result of Drinfel'd A987).
Let A be an indeterminate and let t\ be the automorphism of
given by
Theorem 12.5.5 There exists an element 1l(X) e {Uh($) <S>Uh($)){(\)) such
that, if p : Uh{§) —> End(V) is an indecomposable representation ofUh{§) on
a free <C[[h]]-module V of finite rank, then RP(X) = {p <8> p){{r\ <E> id)G^)) is
a well-defined element of End(V 0 V)((A)) which satisfies the QYBE in the
form
D9) R^X/^R^X/^R^/v) = R^^/v)R{z{X/v)Rpl2{X^).
Up to a scalar factor, a o RP(X) is a rational matrix-valued function of X and
is an intertwining operator between the representations (p 0 p)(t\ 0 id) and
Remarks [1] As in the Yangian case, it is clear a priori that the intertwining
operator referred to in the theorem is, up to a scalar multiple, a rational
function of A.
424 12 Infinite-dimensional quantum groups
[2] The form D9) of the QYBE can be brought to the more usual form A9)
simply by making the change of variable A = eu, \i = ev, v = ew. Then, Rp
becomes a rational function of eu: this is what is meant by a 'trigonometric'
function.
[3] Khoroshkin & Tolstoy A992a) give a formula for TZ(X) for arbitrary
(untwisted) quantum affine algebras. They define the root vectors of Uh(o)
without using the braid group action, using instead the notion of a normal
ordering of the positive roots of g. Levendorskii, Soibelman and Stukopin
A993) obtained the formula in the s^ case essentially by using the braid
group action to define the root vectors, but replacing the non-existent longest
element of the Weyl group of g by the pair of infinite expressions
ToTiToTiTo ..., TiToTiToTi.... A
Even though an 'explicit' formula for the pseudo-universal R-matrix is avail-
available, it is not easy to compute its action in any but the simplest represen-
representations. Thus, to determine RP(X) (up to a scalar factor), one computes the
intertwiner directly.
The proof of the following result is similar to that of 12.5.4. Let Vh{r) be
the indecomposable representation of Uh(sl2^C)) of dimension r + 1.
Proposition 12.5.6 Letai,...,afc G <C[[/i]]x, n,... ,rfc G N, k > 1, sat-
satisfy the obvious analogue of 12.2.15(iii), and let p be the indecomposable
representation
V = Vh(r1)ai®'-®Vh(rk)ak
ofUh(sl2{(?))> Choose Uh(sl2((E))-primitive vectors Vj G Vh(r) ® V^(s) (resp.
Vj G Vh(s) ® Vh(r)) of weight r + s — 2j, whenever 0 < j < max{r, s}, such
that (X+ 0 l).Vj = Vj-± (resp. (Xf (8> 1).^- = v'5_ J for all j > 0. Let Pp
Vh(r) 0 Vh(s) —> Vh{s) (8) Vh(r) be the unique homomorphism ofUhisi^
modules such that Pj's(vj) = vfj and Pj's(vk) = 0 if j ^ k. Define
/(r, a ; s, b) : Vh(r)a 0 Vh{s)b -> Vh(s)b 0 Vh{r)a
Then,
Rp(X) = Aa°l f
where A is a scalar and the operator I in the (i,j)th term acts in the
(i+j — l)th and (i+j)th factors in the 2k-fold tensor product, and the (i,j)th
12.5 Rational and trigonometric solutions of the QYBE 425
term appears to the right of the (if\jf)th term if and only if i > if or i = i'
and j <f. |
Example 12.5.7 Let us compute the intertwiner
Vh(l)a 0 Vh(l)b - Vh(l)b ® Vh(l)a.
If {v0, vi} is the usual basis of Vh(l) (see 6.4.12), we find that the maps P^1'1,
j = 0, 1, are given by
= v0 <8> v0, -Pj'1^! <E> vi) = vi (8)^1,
D,i/ ^ x ei;o (8) vi -h vi (8) ^o Di,i, ^ x ^o <E) ^i 4- eh
Di,i/ ^ x e~hi;o (8) vi -h vi (8) ^o Di,i, ^ x ^o <E) ^i 4- ehvx
and
Pi"'1(^o 0 ^o) — P\:1(vi 0 ^i) = 0,
11/ ^ ^0 0^1 — ^10 Vo 11/ &~
P, ' (l)Q 0^1] = r r , Pi ' (l^i 0 ^o) ^
respectively. The formula in 12.5.7 gives the intertwiner as
0
a{eh-e-h)
b-ae~2h
a(en-e-n) b-a(e"l-l+e
with respect to the basis {^o 0 vq, v\ 0 vq, vq 0 v\, v\ 0 ^i}. Note that J?^ has
a 'pole' when b/a = e~2h; further, one checks that Rh fails to be invertible
when b/a — e2h. On the other hand, from the analogue of 12.2.14 (or by
a direct computation), one finds that Vh(l)a 0 Vk(l)b fails to be isomorphic
to Vh{l)b 0 Vh{l)a precisely when b/a — e±2h, i.e. precisely when Rh has
'singularities'.
The R-matrix Rp{\) found by Levendorskii, Soibelman & Stukopin A993)
for this example can be obtained, up to a scalar multiple, by putting a = A2,
b = 1 in the formula for Rh. 0
426 12 Infinite-dimensional quantum groups
Bibliographical notes
12.1 The two realizations 12.1.1 and 12.1.3 are due to Drinfel'd A987,1988b).
For the R-matrix realization 12.1.4, see Kirillov & Reshetikhin A986).
Theorem 12.1.11 appears in Drinfel'd A988b). Fundamental representa-
representations of Y(q) were introduced, and their structure investigated, in Chari &
Pressley A991a). Evaluation representations of Y(sl2((E)) were implicit in
Kulish, Reshetikhin & Sklyanin A981), although they did not prove that
every irreducible representation is a tensor product of evaluation representa-
representations: this was done in Chari & Pressley A990b). Proposition 12.1.17 was
stated in Drinfel'd A985).
The results 12.1.8 and 12.1.9 of Poincare-Birkhoff-Witt type are due to
Levendorskii A993).
12.2 The classification of pseudo-highest weight representations 12.2.6 is due
to Chari & Pressley A991b). Evaluation homomorphisms and representations
for quantum affine algebras were introduced by Jimbo A986a). Little seems to
be known about representations of quantum affine algebras at roots of unity,
except for the representations obtained from evaluation representations of
U6(q) when g is of type A. See, however, Tarasov A992).
For results on 'standard' highest weight representations of quantum affine
algebras, see Lusztig A993). For the construction of such representations
using quantum analogues of vertex operators, see Frenkel & Jing A988) and
Jing A990).
For another realization of quantum affine algebras, analogous to the re-
realization of Yangians in 12.1.4, see Reshetikhin & Semenov-Tian-Shansky
A990).
Readers unfamiliar with classical affine Lie algebras should see Kac A983)
for background information.
12.3 For proofs of the results in Subsections 12.3A and 12.3B, and for fur-
further information about affine Hecke algebras, see Zelevinsky A980) and Ro
gawski A985). The relation between Ue(sln+i((C)) and 7ie(e2) is due to Jimbo
A986a). The results in Subsection 12.3D are due to Chari & Pressley A993b,
1994b). See Cherednik A987a) for related results. The relation between affine
Hecke algebras and Yangians is due to Drinfel'd A986b).
12.4 The relation between Yangians and infinite-dimensional classical groups
is due to Olshanskii A988, 1989, 1991, 1992b). For other connections between
Yangians and classical representation theory, see Nazarov A991), which gives
a Yangian-theoretic interpretation of the classical Capelli identities (see Weyl
A939), Chap 2, §4), and Nazarov A993b), which relates Yangians and pro-
jective representations of symmetric groups.
12.5 Theorems 12.5.1-12.5.3 are due to Drinfel'd A985, 1987). The compu-
computation 12.5.4 is taken from Chari & Pressley A990b). Theorem 12.5.5 is due
Bibliographical notes 427
to Drinfel'd A987).
See Levendorskii, Soibelman & Stukopin A993) for the computation of the
pseudo-universal R-matrix for /7/l(8/2(C)), and Khoroshkin & Tolstoy A991a,
1992a) for an alternative, and more general, approach. See Tolstoy A990) for
more on normal order ings.
For a list of some solutions of the QYBE, of rational, trigonometric and
elliptic type, see Kulish & Sklyanin A982a). The connection between elliptic
solutions of the QYBE and quantum groups is still something of a mys-
mystery (see, however, Prenkel & Reshetikhin A992a)). More recently, solutions
R(u, v) of the QYBE have been found for which the spectral parameters are
points of an algebraic curve of genus > 1, in contrast to 3.2.4, which allows
only rational, trigonometric and elliptic solutions of the CYBE. See, for ex-
example, Au-Yang et al. A987). These solutions are related to representations
of Ue(§) for e a root of unity (see Subsection 10.1C); see Date et al. A990,
1991a,c).
13
Quantum harmonic analysis
In this chapter, we return to the study of quantized algebras of functions be-
begun in Chapter 7. Classically, the assumption that groups are compact leads
to a more complete theory than for topological groups in general, one of the
main reasons for this being the existence on such groups of a normalized Haar
measure. For quantum groups, one must formulate the notions of compact-
compactness and Haar measure algebraically, for one has no space on which to put a
topology or measure. We saw how to deal with the question of compactness in
Subsection 4. IF: the algebra of functions on a real form of a complex simple
Lie group G, and a compact real form K in particular, can be characterized
as the set of fixed points of a conjugate-linear involution on the algebra T{G)
of representative functions on G. Thus, one may define a compact quantum
group to be a quantized algebra of functions equipped with a conjugate-linear
involution such that the involution on T{G) obtained by taking the classical
limit corresponds to a compact real form of G. A Haar integral may then
be described as a linear functional having certain invariance and positivity
properties.
As in previous chapters, we find it more convenient to work with a spe-
specialization ^(G), rather than the formal deformation Th{G). It follows from
the results of Subsection 9.4B that, to be able to define an involution with
classical limit a compact real form, one must assume that e is real. Thus,
with the possible exception of e = — 1, which we shall ignore, there are no
'root of unity phenomena'. We shall prove the existence and uniqueness of
Haar functionals on Te(G), and deduce quantum analogues of a number of
well-known classical applications of the Haar measure, such as the Schur or-
orthogonality relations for the matrix elements of finite-dimensional irreducible
representations of G.
The *-structure also allows one to discuss unitary representations. In the
classical theory, there is a (one-dimensional) unitary representation of J~{G)
associated to every point of the real form of G corresponding to the involution,
given simply by evaluating a function at the point. In the quantum case, one
has no 'points', so the study of the unitary representations replaces, to some
extent, the study of the space itself. In the case of compact quantum groups,
it turns out that the unitary representations of Te{G) are parametrized by
pairs (w , t), where w is an element of the Weyl group of G and t is an element
of the maximal torus of the compact real form K of G; these representations
are one-dimensional when w is the identity element, but infinite-dimensional
13 Quantum harmonic analysis 429
otherwise. Comparing this with the results of Subsection 1.5C, one sees that
there is a one-to-one correspondence between the irreducible unitary repre-
representations of J-e(G) and the symplectic leaves of the Poisson-Lie group which
is the classical limit of Fe(G). This provides support for the tentative gener-
generalization of the 'orbit principle' of Kirillov and Kostant which we discussed
in 6.2.5. However, we shall see that this principle fails when we discuss the
'twisted' Poisson-Lie group structures on G.
Section 13.2 gives a brief discussion of the notion of a quantum G-space.
Classically, an action of a group G on a space M is a map G x M —> M
satisfying certain properties; it therefore gives rise to a homomorphism of
algebras J-(M) —> F(G) <8> J-(M). We thus define a quantum G-space to
be an algebra A together with a homomorphism a : A —> J-e{G) <8> A; the
defining properties of the classical action translate into the requirement that
a is an ^7e(G)-comodule algebra structure on A (see Section 4.1). The exam-
examples which have been studied most extensively, apart from quantum groups
themselves (in which case a is given by the comultiplication of J-e(G)) are
the quantum analogues of odd-dimensional spheres. Classically, such spheres
can be realized as the homogeneous spaces SUn+i/SUn; in the quantum case,
they are *-subalgebras of jFe(SXn+1((C)), the *-structure being the one which
defines the compact quantum group. The case of even-dimensional spheres is
more difficult: classically, they arise as homogeneous spaces SO2n+i/SO2n,
but, as we have mentioned earlier in the book, Ue(so2n(&)) is not in any ob-
obvious way a subalgebra of t/e(s02n+i({C)), so it is not clear how to define the
corresponding quantum homogeneous space. However, one can define quan-
quantum 2-spheres, essentially because they can be realized as quantum (complex)
projective lines.
The elements of J-e(G) all act by bounded operators in any unitary rep-
representation. This fact allows one to introduce a C*-norm on Fe{G). In the
classical theory, the Peter-Weyl theorem tells us that the completion of the
algebra of representative functions in the corresponding norm is the space
of continous functions on G. Thus, we define the quantized algebra of con-
continuous functions to be the completion of J-e{G) in its norm. The resulting
C*-algebras are examples of the compact matrix quantum groups first stud-
studied by Woronowicz, quite independently of the theory of quantized universal
enveloping algebras. We present some of his results in Section 13.3.
In Section 13.4, we discuss briefly an example of a non-compact quantum
group, i.e. a *-structure on J-e(G) whose classical limit defines a non-compact
real form of G. As one would expect, the definition of the Haar integral on
such a quantum group is more delicate than in the compact case, necessitat-
necessitating the definition of a space of quantized functions which vanish sufficiently
rapidly at infinity.
The chapter concludes with a discussion of the relation between quantum
groups and the theory of (/-special functions. The classical theory of special
functions originated in the work of Euler and the Bernoullis in the early 18th
430 13 Quantum harmonic analysis
century, but its connection with representation theory was not noticed until
the 1930s, by Elie Cartan. The theory of (/-special functions is more recent,
dating back to the introduction of g-hypergeometric series by Erich Heine
in 1847. Although some isolated results had been obtained a little earlier,
the proper representation-theoretic setting for (/-special functions was found
only in 1986, when L. Vaksman and Ya. Soibelman observed that the matrix
elements of finite-dimensional *-represent at ions of Uq(sl2) could be expressed
in terms of little (/-Jacobi polynomials. (So one could say that, after more
than 100 years of work on (/-special functions, it has finally been discovered
what the '(/' stands for!). More recently, several other families of (/-special
functions have found interpretations in terms of the representation theory of
quantum groups, and we outline a few of these in Section 13.5.
13.1 Compact quantum groups and their
representations
In this section, g denotes a finite-dimensional complex simple Lie algebra and,
except in Subsection 13.IF, e is a positive real number. All Hopf algebras and
their representations are defined over C We shall often denote C/C(g) by Ue
provided this is unambiguous.
A Definitions The quantized algebra of functions J~h(G) on the connected,
simply-connected, complex Lie group G with Lie algebra g was defined in
7.3.1 as the dual of the formal deformation Uh(o) of the universal enveloping
algebra U(q). By analogy, we make
Definition 13.1.1 The quantized function algebra Te{G) is the sub&lgebm
of the Hopf algebra dual of U€(q) generated by the matrix elements of the
finite-dimensional C/e(g) -modules of type 1.
We shall denote J~e{G) simply by Te when the group G is understood.
Remarks [1] If V is a finite-dimensional ?/e(g)-module, and {i>o,^i, • • • ,vk}
is a basis of V, the corresponding matrix elements are the functions C^,
0 < r, s < ?;, where
(xeUe(g)).
The CYS, 0 < r,s < k, depend on the choice of basis, but the subspace they
span does not.
13.1 Compact quantum groups and their representations 431
[2] Since the trivial representation is of type 1, and tensor products and
duals of representations of type 1 are of type 1, it follows that Te is actually
a Hopf subalgebra of the Hopf dual U°.
[3] If we dropped the restriction to type 1 representations, the resulting dual
Hopf algebra would be generated by Te together with n group-like elements
corresponding to the one-dimensional representations Xf~ »—> 0, Kj i—> 1 if
j ^ i, Ki*-* -1, where i = 1,..., n (cf. Takeuchi A992a)).
[4] There is an isomorphism of Hopf algebras Te = Te-\. This is because
there is an isomorphism of Hopf algebras Ue = C/e-i, namely
This is easily checked directly using the relations in 9.1.1. Thus, we shall,
without loss of generality, assume throughout this section that e > 1, except
in Subsection 13.IF. A
As we saw in Subsection 4.IF, the appropriate language for discussing the
algebra of (complex-valued) functions on a real form of G, or the enveloping
algebra of a real form of g, is that of Hopf *-structures. Throughout this
section, we shall use the standard structure
A) K* = Kh (Xt)*=er1X-Ku (Xry=eiK~1X+
on Ue. (This is slightly different from, although equivalent to, the standard
structure used in Subsection 10.IE. The normalization in A) is convenient in
this chapter.) The classical limit of * is given by
the bars denoting elements of g. The corresponding real form
{x E g | x* — — x}
is the compact real form ! of g, so-called because the Lie subgroup K of G
with Lie algebra ! is compact.
By 13.1.1 and Subsection 4.IF, A) induces a Hopf *-structure, also denoted
by *, on jFe.
Definition 13.1.2 The pair (Fe(G), *) is the quantized algebra of functions
on the compact real form K of G.
Remark In the literature, the pair {Te{G), *) is often denoted by Fe(K), but
we find this abuse of notation confusing, and we shall avoid it. A
As usual, for any A E P+, we denote by V^(A) the irreducible ?/e-module of
type 1 with highest weight A. Recall from 10.1.21 that V€(X) is unitarizable,
i.e. it admits a positive-definite hermitian form ( , ) such that
(x.vi , v2) = (vi, x*.v2)
432 13 Quantum harmonic analysis
for all Vi, v2 <G V^A), x E Ue (the algebra denoted by Uf there is denoted by
Ue here). Fix an orthonormal basis {v7^} of each weight space V^A)^, \i ? P;
their union is then an orthonormal basis of Ve(X). Let
be the associated matrix elements of Ve(X). To simplify the notation, we omit
the subscript r (resp. s) if dim(Vre(A)M) = 1 (resp. if dim(ye(A)^) — 1).
Proposition 13.1.3 (i) The matrix elements CxS]fir, where A runs through
P+ and (//,r) and (^, s) run independently through the index set of a basis
of Ve(X), form a vector space basis of Fe(G).
(ii) The action of the involution * of J-e(G) in this basis is given by
(Cx Y =
\ v,s;/j,,r/
— v,s;—fi,r'
(Hi) The comultiplication and counit of J-e(G) are given by
7T,p
respectively
Outline of proof It is clear that Te{G) is spanned as a vector space by
the Cxs.fir. Indeed, this follows from the complete reducibility of finite-
dimensional ?/e(g)-modules proved in 10.1.14, and the fact that the product
of two such matrix elements is a matrix element of a tensor product of two
U6(q) -modules.
Now let A1,..., Xk be distinct elements of P+. By Wedderburn's theorem,
the homomorphism
U€ -> End(Fe(A1)) x • • • x End(Fe(Afc)),
given by the action of Uei is surjective. This means that the space spanned
by the matrix elements Cxs;fir of Ve(X^I for j = l,...,fc, has dimension
Ilj=i dim(Ve(Xj)J. Since this is the number of matrix elements in question,
they must be linearly independent.
Part (ii) follows by a straightforward calculation, using the isomorphisms of
?/e-modules Ve(X)* = Ve(—WoX), and the fact that the square of the antipode
of Ue is given by conjugation by Kp* (see Subsections 8.3F and 11.3B).
Part (iii) is obvious. |
Remark The antipode Sjre of Te is computed in the proof of 13.3.1. A
13.1 Compact quantum groups and their representations 433
A representation of Te on a complex vector space V is said to be unitarizable
if V admits a positive-definite hermitian form ( , ) such that
{f-vi, v2) = Oi , f*.v2)
for all / G !Fe, i>i, v2 G V. If V is complete in the inner product ( , ) and
Te acts by bounded operators, the representation is said to be unitary, or a
*-representation. Two unitarizable (or unitary) representations V and V are
equivalent if there is an invertible operator T : V —> V which commutes with
the action of Te and is unitary:
(T(vi), T{v2))v = (vi, v2)v, (vi, v2 E V).
The following result follows from the classification of the unitarizable rep-
representations of Te described below.
Proposition 13.1.4 Every irreducible unitarizable representation V of
J~e{G) extends to a unitary representation on the completion of V. More-
Moreover, this sets up a one-to-one correspondence between the irreducible uni-
unitary representations ofJre(G) on separable Hilbert spaces, and its irreducible
unitarizable representations. |
B Highest weight representations We are going to describe a para-
metrization of the irreducible unitarizable representations of jFe(G) by highest
weights. An analogous description of the representations of C/e(g) was given
in Chapters 10 and 11, but the ^-theory presents a number of interesting
differences. For example, we shall see that there are several subalgebras of Te
which have the right to be called Cartan subalgebras, but they are not equiva-
equivalent, and different representations must in general be described by characters
of different Cartan subalgebras.
Let JF+ be the subalgebra of Te generated by the matrix elements C^s.x
for all A, //, 5, and let T~ — {T^Y. We shall also need the subalgebra
T^ C T^ obtained by restricting A to the set P++ of regular dominant
weights (i.e. those A ? P+ such that X(Hi) > 0 for all i = 1,... ,n); we set
T~~ - (^e++)* C T~. The following result is a kind of Poincare-Birkhoff-
Witt factorization.
Lemma 13.1.5 We have Te = Te .^e++. A fortiori, the same result holds
ifF++ and T~~ are replaced by T+ and T~. |
We shall see that T+ plays a role in the representation theory of Te anal-
analogous to that played by the 'Borel subalgebra' C/e-° of Ue (cf. Subsection
9.IB). In particular, we make
434 13 Quantum harmonic analysis
Definition 13.1.6 A representation V of Fe(G) is highest weight if there
exists a vector v E V such that
(i)V = Fe(G).v;
(ii) T+{G) preserves the line <E.v in V.
The homomorphism \ '• F^(G) —>• C such that f.v — x(f)v (which exists
by (ii)) is called the highest weight ofV.
The main result of this subsection is
Theorem 13.1.7 Every irreducible unitary representation of F€{G) on a
separable Hilbert space is the completion of a unitarizable highest weight
representation. Moreover, two such representations are equivalent if and only
if they have the same highest weight.
Outline of proof Let p : Fe(G) —> End(V) be an irreducible ^represen-
^representation (assumed to be non-trivial). By 13.1.5, there exists A E P++ such that
p(C^ s.x) 7^ 0 for some //, s. Choose a \i with this property which is minimal
for the usual partial ordering on P (it will turn out that this \i is unique).
The first step is to prove the following relation in T<r.
This is done by analysing the isomorphism from Ve(X) 0 V€(X) to itself given
by the universal R-matrix of [/^(g). (One has to be a little careful here, since
this universal R-matrix cannot be specialized to give a well-defined element
of C/e(g) 0 ?4(g)> but this problem can be overcome by using the results in
Subsection 10.1D.)
Since e > 1 and p(C^s.x) is bounded, it follows that (A, A) = (//,//) and
that p(C^ s.x) is a normal operator. Since A E P++, the first equality implies
that \i — wX for some w E W, the Weyl group of g (in particular, \i is a
weight of multiplicity one).
The next step is to study the spectrum D of the operator p(C*xx). One
shows that it is contained in the unit disc {z E C | \z\ < 1}, that it intersects
the unit circle \z\ — 1 in a unique point, say zq, and that 0 is its only possible
limit point. Thus, H\{0} is contained in the discrete spectrum, and in fact is
equal to it since one can show that kerp(C^x.x) — 0. Thus, we have
where Vz — {v E V \ p(C^x.x)(v) — zv}. Although this decomposition
depends on A and if, it turns out that VZo is actually independent of A.
Moreover, it is one-dimensional and is preserved by T^'.
This completes our sketch proof of the first part of the theorem. The
uniqueness statement is proved by constructing, for each character x'- J~t ~* ^>
13.1 Compact quantum groups and their representations 435
a 'Verma module' Me(x) with highest weight x, and proving as usual that
Me(x) has a unique irreducible quotient. |
The complete details of the proof of 13.1.7 may be found in Vaksman &
Soibelman A988) in the SU2 case, Vaksman & Soibelman A991) in the SUn+i
case, and Levendorskii & Soibelman A991a) and Soibelman A991a) in the
general case.
In the course of a complete proof, one obtains a more precise result. For
any w E W, A E P+, let Je(w,\) be the two-sided *-ideal in Te generated
by the matrix elements C^s.x such that v^ ? U^°.Ve(X)w\. Then, for any
irreducible ^representation p : Te —> End(V), there exists w E W (possibly
depending on p) such that, for all A E P+:
(i)p(Je(w,X))=0;
The subalgebra T^w oiTe generated by the C^A;A for A E P+ plays the role of
a Cartan subalgebra of T^, for it can be shown that p(J-€,w) is a commutative
subalgebra of End(V). As we mentioned above, different Cartan subalgebras
may thus be required to describe different representations.
When (i) and (ii) hold for the Weyl group element w, Levendorskii,
Soibelman and Vaksman say that p corresponds to the Schubert cell Sw —
B+wB+/B+ in G/B+ (cf. Subsection 1.5C). The reason for this terminology
is discussed in Subsection 13.2B.
In view of the last part of the proof, it seems natural to try to parametrize
the irreducible ^representations of Te by determining when the irreducible
quotient of the Verma module Me(x) is unitarizable. This seems to be rather
difficult, however, and we shall take a different approach, beginning with the
5/2 case.
C The 5/2 case The algebra Jre(SL2(<C)) is generated by the matrix elements
a b
c d
of the two-dimensional type 1 representation V} of [4E/2 (?)) with basis
{^o > vi} given by
0
As in 7.1.4, one shows that the denning relations of jFeEL2(<C)) are
ab — e~1ba, bd — e-1db, ac — e~1ca, cd — e~1dc,
B) bc = cb, ad-da + (e-e~1)&c-0,
ad — e~1bc — 1,
436 13 Quantum harmonic analysis
and its coalgebra structure
(a b\-(a b\n(a b\
'a b\ _ f d -eb\ ^ /a 5\_/l 0
The *-structure on Te dual to the standard structure on Ue is:
D) a* = d, 6* = -e^c.
To prove the second formula, for example, one checks, as in Subsection 7.ID,
that
Hence,
By the method used in Subsection 7.ID, this is equal to
(-lf+V-'-.e^Ao = -^.i^oc8.
On the other hand,
The equality b* = -e~1c follows.
It follows immediately from D) and the last relation in B) that
E) aa* + 66* = 1.
Thus, it is clear in this case that every unitarizable representation p of
J-e{S'Z/2(C)) extends to a representation by bounded operators on the com-
completion, for E) obviously implies that || p(a) ||< 1 and || p(b) ||< 1, and then
D) shows that p(c) and p(d) are bounded too. Equations D) and E) also
imply that the spectra of p{a) and p(b) lie inside the unit disc (cf. the proof
of 13.1.7).
If A denotes the highest weight of V^, it is easy to check that the matrix
elements C^.x — a and C^A.A = c. Further, since every finite-dimensional ir-
irreducible Ue(sl2((E>))-module of type 1 is a direct summand of a tensor product
of copies of V} (see 10.1.16), T~? is the subalgebra of Te generated by a and
c. Note that, by B) and D),
F) ac = e~lca, a*a + c*c=l.
It is now straightforward to prove
13.1 Compact quantum groups and their representations 437
Proposition 13.1.8 Every irreducible ^-representation of Jre(SL2(<E)) is
equivalent to a representation belonging to one of the following families, each
of which is parametrized by S1 — {? E (C | \t\ = 1}:
(i) the family of one-dimensional representations rt given by
rt(a) = t, rt{b)=Tt{c) = 0, rt(d)=t-1;
(ii) the family nt of representations on I2 (N) given by
nt(a)(ek) - A - 6fcI/2efc_1, nt(b)(ek) = -e'^r1^,
7Tt(c)(ek) = e-Hek, nt(d)(ek) = A - e^
Here, {ek}keN is the natural orthonormal basis of ?2(N), in which ek is the
vector with one in the kth position and zeros elsewhere (and e_i = 0).
These representations are all mutually inequivalent.
Proof It is easy to check that these formulas do define *-represent at ions of
^7eEI/2(C)). The highest weight of rt is obviously given by
X(a) = t, x(c) - 0.
For 7Tt, Ceo is the unique line preserved by JF+, so its highest weight is given
by
X(a) = 0, X(c) = t.
In view of 13.1.7, it is enough to prove that these are the only characters x
of T^ which arise from *- represent at ions.
Prom the first equation in F), it is clear that x(a) = 0 or x(c) = 0. If
x(c) = 0 and x(a) = a ^ 0, say, there exists a vector v such that a.v — av,
c.v = 0. The second equation in F) now implies that |a| — 1. Similarly, if
X(a) = 0, then |x(c) | = 1. I
This result should be compared with the description in Subsection 1.5C
of the symplectic leaves of the Poisson-Lie group structure on SU2 which is
the classical limit of Ue(sl2((C)). Both the symplectic leaves of SU2 and the
irreducible *- represent at ions of Jre(SL2 (C)) are parametrized by the disjoint
union of two circles. We shall now extend this correspondence to J~e{G) for
arbitrary G.
D The general case: tensor products The embedding U€t(sl2AE>)) —>
C/e(g) given by i^i ^ Kj, Xf —> Xf induces, by passing to the dual, a
surjective homomorphism J-e(G) —>• Jr6i(SL2((E)). Composing the represen-
representation tt_i of Jrei(SL2((?)) with this homomorphism gives a representation
of J~e(G) on -?2(N), which, for reasons which will soon become clear, we shall
438 13 Quantum harmonic analysis
denote by 7rSt, where Si is the ith fundamental reflection in the Weyl group
WofG.
On the other hand, there is a family of one-dimensional ^representations
rt of Te(G) parametrized by the elements t of the maximal torus T of K (we
may assume that the complexification of the Lie algebra t of T is our chosen
Cartan subalgebra of g). In fact, if t = expB7T\/—lx) for some x E t,
It is clear that the representations rt are associated to the zero-dimensional
Schubert cell Se, where e is the identity element of the Weyl group W of g.
Theorem 13.1.9 Let w — s^s^ ...Sik be a reduced decomposition of an
element w of the Weyl group W of G. Then,
(i) the Hilbert space tensor product
Pw,t — 7Tstl 0 KSi2 0 • • • 0 7TSik 0 Tt
is an irreducible * -representation ofJre(G) which is associated to the Schubert
cen &ijj j
(ii) up to equivalence, the representation pwj does not depend on the choice
of the reduced decomposition ofw;
(Hi) every irreducible ^-representation of Te(G) is equivalent to some pW}t- I
Although we shall not prove this result, we comment briefly on part (ii).
In view of a classical result which we have already used in Subsection 8.1 A
(see Bourbaki A968), Chap. 4, § 1.5, Proposition 5), it is enough to prove
Proposition 13.1.10 Let (a^) be the Cartan matrix of g. Then:
KSt 0 7TSj = 7TSj 0 7TSt ifdij = 0,
7TSt 0 7TSj 0 7TSi = 7TSj 0 7TSi 0 TXSj if dijdji = 1,
GTSt 0 7TSj)®2 * GTSj 0 7TSJ®2 if Oijdji = 2,
GTflt 0 7TSj)®3 *? GTSj 0 7TSi)®3 if dijdji = 3.
(All tensor products are Hilbert space tensor products.) |
This can be proved by directly computing the highest weights of the rep-
representations involved and appealing to 13.1.7.
Remarks [1] Using 13.1.3, 13.1.8 and 13.1.9, one can show that the intersection
of the kernels of the representations pwj is trivial, which implies that their
direct integral
0 / Pw,tdt
13.1 Compact quantum groups and their representations 439
is a faithful representation.
[2] Theorem 13.1.9 is the starting point for another approach to the quan-
quantum Weyl group, which we discussed in Section 8.2. In fact, let Wi be the
Gel'fand-Naimark-Segal state
where / 6 Te, vSi is a normalized highest weight vector of ?rs., and ( , ) is the
inner product on nSi. Then, 13.1.9 immediately implies that the wi satisfy
the braid relations (i)-(iv) in 8.1.1. As in Subsection 8.2C, one proves that
conjugation by the wi agrees, at least up to a scalar multiple, with Lusztig's
automorphisms Ti; this gives another proof of 8.1.2.
[3] We saw in 1.5.7 that the set W x T which, by 13.1.9, parametrizes
the irreducible ^representations of ^-*e(G), also parametrizes the set of sym-
plectic leaves of the Poisson-Lie group structure on the maximal compact
subgroup K of G. In fact, comparing 13.1.9(i) with 1.5.8, it appears that
multiplication of symplectic leaves 'corresponds' to taking tensor products
of representations. One might view this as support for a general principle,
according to which the symplectic leaves of a Poisson-Lie group K (not nec-
necessarily compact) should 'correspond' to the irreducible representations of a
quantization of the algebra of functions on K. We explained in 6.2.5 that
this would be a generalization of the 'orbit principle' of Kirillov and Kostant,
according to which the unitary representations of a group should 'correspond'
to its coadjoint orbits. Just as the Kirillov-Kostant principle, while very suc-
successful in some situations, fails in others, so we shall now see a situation where
its putative generalization also fails. A
E The twisted case and quantum tori We saw in 1.5.10 that the most
general Lie bialgebra structure on the Lie algebra ! of a compact simple Lie
group K is of the form
?a,u(aO = a6^(x) + (adz ® id + id <g) adx)(u),
where a gR, u ? A2(t), and <5r is the standard Lie bialgebra structure on
!, a quantization of which we have used above. We now consider briefly the
corresponding theory for this most general Lie bialgebra structure.
We suppose first that a ^ 0 and u/0; in this case, we may as well assume
that a = 1. A quantization of the Lie bialgebra (g, #ijW), where 6iiU is
extended complex-linearly to g, can be obtained by the twisting construction
of Subsection 4.2E. In fact, the desired quantization U^u(q) is identical to the
standard quantization C/^(g) as an algebra over C[[/i]], but its comultiplication
is given in terms of that of f/^(g) by
G) &hu(o) = e-hu/2Ah{a)ehu/2.
440 13 Quantum harmonic analysis
We shall not need the formula for the antipode, but it can be found in 4.2.13.
The usual formulas A) define a *-structure on UhjU(o), if one uses the conju-
conjugation on C[[/i]] given by chk i—> chk for c ? C, k ? N. One is then forced to
take H* = Hi, and hence u* = u, so that A^u is a *-homomorphism.
Unfortunately, it is not immediately clear how to specialize this twisted
quantization, since the expression eu/2 is meaningless. However, as we have
seen in Section 10.1, the whole of the representation theory of U€(g) can be
carried through for Uh{o) with only notational changes. For example, as
we have already seen in the 5/2 case (see Subsection 6.4E), there is a one-
to-one correspondence between irreducible type 1 representations of Ue and
the indecomposable representation of Uh- Further, the indecomposable Uh-
module Vh(\) with highest weight A G P+, which is free and of finite rank as a
<C[[/i]]-module, has an invariant hermitian form (with values in C[[/i]]), which
induces an isomorphism of <C[[/i]]-modules V^(A) —> V^(A)*, where V^(A)*
denotes the dual of Vh with the conjugate (C[[/i]]-module structure. Thus, if
{v1^} is a basis of V^(A), and {??} is the dual basis of V^(A)*, we can define
the matrix elements
as before.
Since U^u(q) is the same as Uh(s) as an algebra, it has the same set of
indecomposable representations, and hence one can define matrix elements for
it with the same names as those of E/fc(g). However, because the coalgebra
structure of UhjU is different from that of [7^, the algebra structure on the
space of such matrix elements is different in the twisted case: from G), it
follows that
=exp f-(u, i/®i/
where the • on the right-hand side denotes the multiplication in the untwisted
case. It is now clear how to define the twisted function algebra Tl'u{G) (over
C):
Definition 13.1.11 Let u e A2(t). The twisted function algebra ^^(G) is
the algebra over C spanned by the matrix elements C*jS;M>r? with multiplica-
multiplication given by
where the • on the right-hand side is the multiplication in the untwisted
algebra F€(G).
It is clear that T\'u inherits a Hopf *-structure from that on U\'u(§). Note
that, since e > 1, the scalar on the right-hand side of (8) makes sense even if
the exponent is complex.
13.1 Compact quantum groups and their representations 441
One can now define the notion of a representation of T\'u corresponding
to a Schubert cell Sw exactly as in the untwisted case, and, as in that case,
we have
Proposition 13.1.12 Every irreducible ^-representation of T\'u corre-
corresponds to a unique Schubert cell. |
The 'Cartan subalgebras' T\^ of T\'u are defined in exactly the same way
as the T^w, but in the twisted case their images under a ^representation are
no longer commutative in general.
Lemma 13.1.13 The following relations hold in T\^:
CwX;X
where
Moreover, the elements Z* = C*x.x •u (C*A;A)* = (C*A;A)* mu C*x.x are in
the centre
It follows from this lemma that the central subalgebra of T\^ generated
by the Z^, A e P+, is already generated by Z*1,..., Z^n, where the A^ are
the fundamental weights of g. As in the proof of 13.1.7, one shows that,
if p is any irreducible ^representation of T\-u on a separable Hilbert space
V, the joint spectrum of the commuting self-adjoint operators p{Z*1) is of
the form E^ U {0}, where S^ is a discrete subset of R+ with 0 as its only
possible limit point. We partially order the joint eigenvalues z = (zi1..., zn)
of Z*1,..., Z*n by z > z* if and only if zi > z[ for all i.
Lemma 13.1.14 The n-tuple A,1,..., 1) is the unique maximal joint eigen-
eigenvalue of the Z*1 onV.t
In view of this lemma, the action of T\^ on the maximal joint eigenspace Vb
of the Z^ factors through its quotient T^u by the two-sided *-ideal generated
by the Z^ — 1. The resulting irreducible ^representation of T^u on Vb
is called the highest weight of (p, V) (note that Vb is not necessarily one-
dimensional).
Theorem 13.1.15 Two irreducible ^-representations of Tl'u{G) correspond-
corresponding to a Schubert cell Sw are equivalent if and only if their highest weights
are equivalent. Conversely, given w ? W and an irreducible unitary repre-
representation p0 ofT^u, there exists an irreducible ^-representation of ^^(G)
which corresponds to Sw and has highest weight po- I
442 13 Quantum harmonic analysis
If po is the highest weight of an irreducible ^representation corresponding
to Sw, the operators t\ = Po(C*x.x) generate pv(T^u), and, by 13.1.13 and
13.1.14, they obviously satisfy
(9) txt*x = t*xtx = 1, txtp = <r(A, ii)tx+li.
A *-algebra with generators t\ for A in some lattice P, and defining relations
(9) for some <r(A, /jl) = eK(Xjfl\ where k, : P x P —> y/^TR is a skew-symmetric
biadditive form, is called a quantum torus. See Rieffel A990a).
The correspondence between irreducible ^representations and symplectic
leaves fails, in general, in the twisted case. Recall from 1.5.11 that, for generic
u ? A2(t), if KljU is the Poisson-Lie group with tangent Lie bialgebra (!, #ijW),
the symplectic leaves of KljU (resp. their closures) are parametrized by W
if n is even (resp. odd). One finds that, again for generic w, there is a one-
to-one correspondence between W\{e} and the set of kernels of irreducible
^representations of T\'u of dimension greater than one. However, an irre-
irreducible unitary representation is not uniquely determined by its kernel, in
general. This is related to the type of T\'u', or rather that of a suitable
completion of it, as a C*-algebra. We shall discuss this question in Section
13.3.
We conclude this subsection by considering briefly the family of Lie bialge-
bialgebra structures 6otU. One can define a quantization U^u(q) of 50,u by twisting
the null deformation ?/(g)[[A]] by ehul2 as in G). This leads to a Hopf *-
algebra T^'U(G) as before. However, there is now no relation between the
representations of T^'u and Schubert cells. This is not unexpected, since we
saw in 1.5.12 that there is no relation between the Bruhat decomposition and
the symplectic leaves of the Poisson-Lie group KOjU with tangent Lie bialge-
bialgebra (f, #o,u). One finds that there is an irreducible ^representation of J^jU
associated to each pair (tt,x), where n is an irreducible unitary representa-
representation of the classical algebra of functions F(G) and x ^s an irreducible unitary
representation of a certain quantum torus. Moreover, every such representa-
representation of T^'u arises in this way. For a precise statement, and proofs of this
and of the other results in this subsection, see Levendorskii A990, 1992) and
Levendorskii & Soibelman A991a).
F Representations at roots of unity Although our main interest in this
chapter is in unitary representations, for which e must be real, in this subsec-
subsection we consider briefly the structure and representation theory of Te when e
is a root of unity.
We assume, then, that e is a primitive fth root of unity, where ? is odd,
greater than all the d^, and not divisible by three in case g is of type G?2-
Unlike the case when e > 1, we do not define the quantized function algebra
13.1 Compact quantum groups and their representations 443
to be the Hopf dual of C/e(g) - this would be too big in the root of unity
case. To define it, we first introduce a new rational form of Uq, namely the
,4-subalgebra U%* of Uq generated by {Xf)^\ Kf\ and
Ki
-S+1
where i = l,...,n,iGN. (Although we do not need it, we remark that U^s
properly contains U^s.) One then defines Tj± to be the set of *4-linear maps
<p : U^s —> A such that ker((^) contains an ideal / such that
(a) there is a free *4-module M of finite rank such that U^s = I © M as
A- modules,
(b) there exists k ? N such that I"Ir=-fc(^ ~ #0 ^ I ^or ^ = ^-' • • • >n*
Note that ^4 is contained in the Hopf dual {U^s)° (see Subsection 4.ID).
One can show that it is actually a Hopf subalgebra of (U^s)°-
The specializations are now defined in the obvious way:
A A
via the homomorphism A —> C which takes q to e.
Lemma 13.1.16 There is a non-degenerate pairing of Hopf algebras
Te 0 Urees -> <C. I
e
The following result is analogous to 9.3.11.
Proposition 13.1.17 There is a surjective homomorphism of Hopf algebras
from UTees to the classical universal enveloping algebra U such that
if p divides t,
otherwise. |
As usual, bars denote generators of U.
Passing to the dual, using 13.1.16, and recalling from 4.1.17 that the Hopf
dual of the classical enveloping algebra U is the classical function algebra T,
we obtain an injective homomorphism \i\ T' —> (?/eres)°; let J-q be its image.
444 13 Quantum harmonic analysis
Theorem 13.1.18 The Hopf algebra To over C defined above is contained
in the centre of Te. Moreover, Te is a finitely generated algebra over To of
degree ?N, where N is the number of positive roots of g, and a projective
T0-module of rank ^dim(9). |
Remark This result is 'dual' to those in Section 9.2. We found there that
the centre of the non-restricted specialization Ue contains a subalgebra Zo for
which Spec(Z0) has the structure of a complex Poisson-Lie group. Moreover,
this group is the dual, in the sense of Poisson-Lie groups, of the standard
Poisson-Lie group structure on G, which underlies the quantization Uq(o).
A
Example ISA. 19 If G = 5L2(C), To is the subalgebra of Te generated by
the ?\\\ powers of the generators a, 6, c and d (cf. Subsection 13.1C). The
isomorphism To(sl2{(E)) —> T(SL2((C)) is given by a? i—> a, 6^ i—^ 6, c? i-> c,
de^d. 0
It follows from 13.1.18 that, if V is an irreducible (complex) representation
of Te, then dim(V) < ?N. In order to state a more precise result, note that To
acts by scalars on F, so to F there corresponds an element gy ? Spec(^-o) —
G.
Proposition 13.1.20 Assume, in addition to the usual restrictions, that ? is
coprime to the coefficients in the expression of the highest root of g in terms
of the simple roots. Let V be an irreducible representation of Te (over (C),
and let gy be the associated element of G. Then:
(i) there is a dense open subset Go ofG such that, if gy ? Go, then dim(F) =
?N;
(ii) for any V, dim(F) is divisible by ?2dirn(°\ where O is the symplectic leaf
of G passing through gy. |
Remark The symplectic leaves of G have been described by Hodges & Lev-
asseur A993). They are parametrized by triples (^wi,!^), where t is an
element of the Cartan subgroup of G and w\, w2 are elements of the Weyl
group of G. This should not be confused with the study of the symplectic
leaves of the compact real form of G in Subsection 1.5C, although the two
theories are, of course, closely related. A
To actually construct some representations of Te, we can proceed as fol-
follows. If G = 51/2(C), the formulas in 13.1.8(ii) define an infinite-dimensional
representation of ^*eEL2((C)) (we take t = 1 and the branch of the square
root which is continuous on the complement of the negative real axis, and
such that y/T = 1). Since 7Ti(a)(e^) = 0, the vectors {e^,e^+i,...} span a
13.2 Quantum homogeneous spaces 445
subrepresentation; let V be the ^-dimensional quotient. It is clear that V is
irreducible.
One passes to the general case as in Subsection 13.ID. Namely, if G is
arbitrary, there is a canonical homomorphism Te{G) —> Jr€iE1/2(C)), for
each i = l,...,n, induced by the natural inclusions Uqt(sl2{(E)) —> Uq(g).
Pulling back V by these homomorphisms gives representations Vs% of Fe(G).
If w = si± ... 5^(w) is a reduced expression of an element w of the Weyl group
W of g, we can form
We have the following analogue of (part of) 13.1.9.
Theorem 13.1.21 The representation Vw defined above depends, up to iso-
isomorphism, only on the element w G W, and not on its reduced decomposition
w = si± .. .Sik. The representations Vw, for w 6 W, are irreducible and mu-
mutually non-isomorphic. |
In contrast to 13.1.9, however, this theorem does not describe all the irre-
irreducible representations of Te. Other examples are constructed in de Concini
& Lyubashenko A993), from which the results of this subsection were taken,
and to which the reader should refer for proofs and further details.
13.2 Quantum homogeneous spaces
In this section, we assume that e is a real number greater than 1.
A Quantum G-spaces Classically, if a Lie group G acts on a smooth man-
manifold M, then the Lie algebra g of G, thought of as the left-invariant vector
fields on G, acts by derivations on C°°(M):
Z\hh) = (Z./i)/2 + fi(Z.f2), (Z e g, A,h e C°°(M)).
The action of g extends uniquely to one of /7(g), and the preceding equation
generalizes to
z.(hf2) =
where A is the comultiplication of /7(g) and \i is the multiplication in C°°(M).
This equation says that C°°(M) is a /7e(g)-module algebra (see Subsection
4.1C).
We are now in a position to extend the notion of an action of a group on
a space to the action of a quantum group on a 'quantum space'.
Definition 13.2.1 Let C/e(g) be the standard quantization of the Lie algebra
g of a complex simple Lie group G. A quantum G-space is an associative
446 13 Quantum harmonic analysis
algebra A equipped with a U€(o)-module algebra structure. A morphism
(p : A\ —> A2 of quantum G-spaces is a map which is a homomorphism of
algebras and of ?/e(g) -modules.
Remark Classically, an action of G on M can also be defined as a map
a : G x M —> M such that a(gig21m) = a(gi1a(g21m)) for all gi, g2 ? G,
m e M. This translates into the commutativity of the diagram
.F(M) > J^(G) 0 .F(M)
A0) a* I
where a* : F(M) —> ^"(G) 0 J-'(M) is the homomorphism induced by a (we
ignore the question of the precise definition of 0).
Replacing F(M) by A and ^(G) by ^(G) thus gives another reasonable
definition of a 'quantum G-space'. However, this is simply the 'transpose' of
13.2.1: modulo questions about duality of infinite-dimensional Hopf algebras,
the two definitions are equivalent. A
Of course, we expect that a quantum group will act on itself by translations.
The most obvious such action is
where Z e ?/c(g), / 6 JFe(G) and Ajr (/) = ^fc f'k ® K- We leave it: to the
reader to check that this is a C7e-module algebra structure. Unfortunately,
however, it is a right action of U€. For psychological reasons, we prefer to
work with the left action
A1) Z*Lf
This is a C/^p-module algebra structure. We could also have worked with the
left action
(Ha) Z*R
Whether the reader prefers A1a) or A1) will depend on whether (s)he prefers
to define a left action of G on C°°(G) by g.f{h) = f(hg) or by g.f{h) =
f{g~~1h), to which they reduce in the classical limit.
Example 13.2.2 As in Subsection 7.1B, it is easy to see that Jr€(SL2{(C)) is
spanned by the products a^dfib^c1 for a, /?, 7, S ? N (in fact, a basis is given
13.2 Quantum homogeneous spaces 447
by the subset described in the statement of 7.1.2, but we shall not need this
here). A rather tedious computation shows that the action of U€(sl2((E)) on
is given by the following formulas:
Xf *L c^aad6 = -e-^pkc^+Vd*-1 - e^-^c^^/V+V. 0
In the next two subsections, we give a number of less trivial examples of
quantum G-spaces.
B Quantum flag manifolds and Schubert varieties A classical (general-
(generalized) flag manifold F\ is the orbit of a highest weight vector in the projective
space P(V(A)) of the irreducible representation V(A) of a complex simple Lie
group G of highest weight A ? P+. The group G obviously acts transitively
on F\, so that Fx = G/P\, where P\ is the stabilizer of the highest weight
vector in P(V(A)); note that P\ obviously contains ??+. The terminology
derives from the case G = 5Ln+i(<C), when such an orbit can be identified
with the set of sequences of subspaces
0 = Vo C Vi C V2 C • • • C Fn+1 = (Cn+1,
the dimensions of the Vj depending only on j and A.
We shall define the quantum analogue of the 'affine' version of Fx, i.e. the
orbit of the highest weight vector in the vector space V(A).
Definition-proposition 13.2.3 For any AeP+, the subalgebra ofF€(G)
generated by the matrix elements C^ s.x for all is, s is called the quantized
algebra of functions on the flag manifold F\, and is denoted by Fe{F\). It
is a quantum G-space, and the inclusion T^Fx) c-> Te{G) is a morphism of
quantum G-spaces.
PROOF We have to check that F€{F\) is a Ge(g)-submodule of Te{G). But
this is immediate: the formula for the comultiplication of T^G) given in
13.1.3 implies that
is an element of F€{F\) for all X e U€(q). I
Remark ^F€{F\) is not a *-subalgebra of ^(G), as one sees immediately from
the description of the *-structure on Te{G) in 13.1.3. A
It is possible to describe the algebra structure of ^(Fx) quite explicitly.
Let
448 13 Quantum harmonic analysis
(the * indicating the dual representation!), and define an algebra structure
on VeA by using the maps
ve(j\y ® ve(k\y -> ve(U + *oa)*
which project onto the (unique) highest component of the tensor product.
Since these projections are surjective, VA is generated as an algebra by the
basis elements ?? of V^A)* defined by ^(v) = (v, v7^), where (, ) is the
invariant hermitian form on
Proposition 13.2.4 The map ?? i-> CAr.A extends to an isomorphism of
algebras and ofU€-modules VA —> ,Fe(F\). Moreover, the ideal of relations of
VA is generated by elements which are homogeneous quadratic functions of
the$. |
The ideal of relations in VeA (or, equivalently, in ,Fe(F\)) can also be de-
described explicitly - apart from the relations which define VeA as a 'quan-
'quantum vector space' (cf. Subsection 7.1A), there are quantum analogues of the
Plucker relations in the classical theory. See Soibelman A992c).
We now turn to the quantum analogue of Schubert varieties. The varieties
5A we have in mind are the closures in the projective space of V(X) of the B+-
orbits of the vector of weight wX (which is unique, up to a scalar multiple).
If A G P++, then 5A = Sw is the closure of a Schubert cell.
The following definition is motivated by the description of the classical
Schubert varieties S^ using 'standard monomial theory' (see Lakshmibai &
Seshadri A991) for a recent survey).
Definition-proposition 13.2.5 For X e P+, w e W, let J€(w,X) be the
two-sided ideal in ^(Fx) generated by the matrix elements C*AS.A such that
v j? wX. Then, the quotient algebra T^Fx)/' Je{w, A) is called the quantized
algebra of functions on the Schubert variety S^, and is denoted by ^E^).
Restricting the C/e(g)-structure of J-e(Fx) to E/e(b+) induces the structure of
a quantum B+-space on ^(S^) such that the natural projection ^(Fx) —>
^Fe{§w) JS a morphism of quantum B+-spaces. |
Remark Note the similarity of the ideals J€(w1 A) to the ideals Je{w, A) defined
at the end of Subsection 13.IB. In fact, it is clear that Je{w,X) C Je(w,X)
and that the two ideals coincide in the 5/2 case. This is the motivation for
the notion of a ^representation of ^(G) 'corresponding to a Schubert cell
Sw\ In fact, such a representation induces a representation of ^E^) for all
A 6 P+, and so is 'supported' on these quantum Schubert varieties. A
C Quantum spheres The classical odd-dimensional sphere g2n+1 can be
realized as the orbit under the action of the compact group SUn+i of the
13.2 Quantum homogeneous spaces 449
highest weight vector vq in its natural (n + l)-dimensional representation V^.
If trs, 0 < r, s < n, are the matrix entries of V\ the algebra of functions
on the orbit is generated by the entries in the 'first column' tso and their
complex conjugates. In fact, ^E2n+1) is the quotient of the polynomial
algebra (C[tOo, • • •> *no> ?oo> • • •>*no] by the relation
To define a quantum analogue of ^E2n+1), we observe that ,Fe(SXn+i((C))
is generated by the matrix entries in its natural representation V^, since every
irreducible Ue (si n+i(<E))-module occurs in a tensor product of copies of V^.
In fact, we have
Proposition 13.2.6 The Hopf algebra 7*eELn+i((C)) is given by the same
generators and relations as in Subsection 7.3B, with e±h replaced by e±1.
The ^-structure is given by
Ks = (-e)r-sqdet(frs),
where frs is the matrix obtained by removing the rth row and sth column
from T. |
Following the above discussion, we make
Definition-proposition 13.2.7 The *-subalgebra of 7*eELn+i((C)) gen-
generated by the elements tso and ?*0, for s = 0,..., n, is called the quantized
algebra of functions on the sphere 52n+1, and is denoted by J-e(S2n+1). It is
a quantum SXn+i((C)-space.
Outline of proof The last part follows from the comultiplication formulas
A^€ {ts0) = Y,tsr® *rO, A^e (tjo) = ^ t*r 0 t*rQ,
as in the proof of 13.2.3. |
We set zs = tso from now on. Using 13.2.6, it is easy to see that the
following relations hold in J^eE2n+1):
zrzs = e~1zszr, if r < s, zrz*s = e~1z*zr, if r ^ s,
ZrZ;-Z*rZr + (e - 1)^^ = 0,
s>r s=0
Proposition 13.2.8 7*eE2n+1) has A2) as its defining relations.
450 13 Quantum harmonic analysis
This follows from the representation theory of ^7eE2n+1), which we now
discuss.
The most obvious way to construct representations of Jre(S2n+1) is, of
course, to restrict representations of ,Fe(SXn+i((C)). The following result
shows that every irreducible ^representation of ^-*eE2n+1) arises in this way.
Theorem 13.2.9 Every irreducible ^-representation of Jre(S2n+1) is equiva-
equivalent to exactly one of the following:
(i) the one-dimensional representations poj, t G S1, given by
PoA4) = t~\ po,t«) = 0, ifr>0;
(ii) the representations prj, 1 < r < n, t G S1, on the Hilbert space tensor
product ?2(?l)®r, given by
Pr,t(z*s)(ekl®---®ekr) =
2(g)...(g)e^ jf g < ^
if s > r.
The representation po,t JS equivalent to the restriction of the representation
rt of J-e(SLn+i((E)) (cf 13.1.9); and, for r > 0, pr^ is equivalent to the
restriction of ttSi (g) nS2 <g> • • • <g> 7rSr ® rt.
Outline of proof of 13.2.8 Let T be the quotient of the free associa-
associative algebra over (C with generators zr, z*, r = 0,... ,n, by the two-sided
ideal generated by the relations in A2). We have to show that the canonical
surjective homomorphism of algebras ip : T —> J-e(S2n+1) given by the com-
comments following 13.2.7 is injective. One shows first that the subalgebra H of
T generated by the elements zrz*, r = 0,... ,n, is commutative, and that
the monomials Zq° ... z%n, where the exponents pr are either zero, one or *,
form an W-basis of^T7. Next, one checks that the formulas in 13.2.9 define
representations of T in which Ji acts diagonally. An explicit computation
finally shows that no non-trivial linear combination of the Zq° ... z^71 with
coefficients in H can be annihilated by all the pr?t. |
Outline of proof of 13.2.9 One proves by induction on n that the
representations in (i) and (ii) exhaust the irreducible ^representations of
7*eE2n+1). The case n = 1 is 13.1.8, for it is easy to see that 7*eE3) is the
whole of Jre(SL2(<C)) (SU2 = S3\), and the inductive step follows from the
observation that Jre(S2n~1) is isomorphic to the quotient of JFeE2n+1) by the
two-sided ideal generated by zn and z* (this is immediate from 13.2.8). |
13.3 Compact matrix quantum groups 451
In the classical case, the orbit of the highest weight vector of SUn+i in
the projective space of its natural representation V^ is the entire complex
projective space P(V^) = (CPn. Thus, it is natural to define JFe((CPn), the
quantized algebra of functions on the projective space (CPn, to be the 'homo-
'homogeneous' version of ^7eE2n+1), i.e. the *-subalgebra of ^7eE2n+1) consisting
of the fixed points of the *-automorphisms zr i-» (zr, ( ? S1. Taking n = 1
gives our first example of the algebra of functions on an even-dimensional
quantum sphere JFeE2). We study it in detail in Subsection 13.5B.
13.3 Compact matrix quantum groups
The Hopf *-algebra J~e(G) is a quantum analogue of the algebra J~(K) of
representative functions on the compact real form K of G. If K is realized as a
closed subgroup of a unitary group t/m, an element of F(K) is a polynomial in
the matrix entries and their complex conjugates. There is another approach to
quantized algebras of functions, originally developed by Woronowicz A987a)
independently of the study of quantized enveloping algebras, which studies
the properties of a quantum analogue of the algebra of continuous functions
on K. We do not discuss this approach in detail in this book, but we shall
now outline its relation to quantized enveloping algebras.
A C* completions and compact matrix quantum groups Since one
does not have any 'geometric' realization of quantum groups, one cannot de-
define quantized continuous functions in a topological way. Classically, however,
the Peter-Weyl theorem gives an essentially algebraic characterization of the
algebra of continuous functions on K as a completion of the algebra generated
by the matrix elements of the unitary representations of K. This provides
the motivation for
Definition-proposition 13.3.1 The quantized algebra of continuous func-
functions on K is the C*-completion Ce(G) of the *-algebra ^(G) with respect
to the norm
|| / || = sup || p(/) ||, (/GJFC(G)),
p
where p runs through the ^-representations of !Fe(G) and the norm on the
right-hand side is the operator norm.
Proof It suffices to show that || / || is finite for all / ? ^(G), for it is clear
that || || is a C*-norm, i.e. || //* || = || / ||2.
We have already proved this fmiteness property in the s/2 case: it was a
consequence of the relation in E). Although we do not know all the defining
relations of Te in the general case, we shall prove that the following relations
452 13 Quantum harmonic analysis
hold for all A ? P+:
A3) Y,c^Ac^tY = ^^t-
Taking fj, — k and r = t, and then applying any *-representation p of JFe, we
find that || p(C^s.^ r) \\ < 1 for all A, fi, z/, r and s, proving our assertion.
To prove A3), fix an invariant hermitian form ( , ) on Ve(A) and let T\ be
the matrix of the representation Ve(X) with respect to an orthonormal basis
{v1^}. Then, A3) is equivalent to
where (Tj)* is the result of applying the *-structure of Te to each entry of
the transpose of the matrix T\. Now, as in the s/2 case considered at the end
of the proof of 7.1.4, it is tautologous that
Using the relation ^^e(id 0 Sjre)Ajre = e^e, we obtain T\Sjre(T\) = ejre(T\).
But,
since the basis {v7^} is orthonormal. Hence, T\S^e(T\) = 1.
To prove A4), we are thus reduced to proving that
The (/i, r; z/, s) entry of the right-hand side, when applied to an element x ?
C/e, is equal to
which is equal to the (/i, r; z/, 5) entry of 5^e (T\). I
Remarks [1] One can define the twisted C*-algebra C\'U(G) in the same way.
[2] Prom the definition of the norm on Ce(G), it is obvious that every mis-
misrepresentation of J-'e(G) extends to a continuous ^representation of Ce(G).
[3] One can define CeE2n+1), the quantized algebra of continuous func-
functions on 52n+1, by completing ^7eE2n+1) in the same way as we defined
Ce(SXn+i((C)) by completing ^reELn+i((C)). It is obvious that every *-
representation of 7*eE2n+1) extends to CeE2n+1). A
We have now made contact with the theory of compact matrix quantum
groups in the sense of Woronowicz A987a) (he originally used the term 'com-
'compact matrix pseudogroup').
13.3 Compact matrix quantum groups 453
Definition 13.3.2 A compact matrix quantum group is a unital C*-algebra
A together with an m x m matrix T = (Trs) of elements of A such that
(i) the *-subalgebra of A generated by the Trs is dense in A;
(ii) there is a unital C*-homomorphism A : A —* A(g>A for which A(T) =
T®T;
(Hi) there is a linear anti-homomorphism S : A —> A such that S(S(a*)*) = a
for allaeA and S{T)T = TS{T) = 1.
The tensor product A®A in (ii) is defined by completing the algebraic
tensor product A® A with respect to the norm defined by
|| x || = sup || {pi ®p2)(x) ||,
Pl,P2
where x E A(& A and p\ and p2 run through the ^representations of A.
Proposition 13.3.3 The C*-aIgebra Ce(G) is a compact matrix quantum
group.
Outline of proof One may take the matrix T in 13.3.2 to be the matrix
of the representation Ve — ®iVe(\i) with respect to the orthonormal basis
obtained by taking the union of the usual bases of the Ve(\i) (here, Ai,..., An
are the fundamental weights of g). Now, every finite-dimensional irreducible
Ue-modu\e of type 1 is a direct summand of a tensor product of a sufficiently
large number of copies of Ve (this follows from 10.1.16 and the classical fact
that every finite-dimensional irreducible g-module is a direct summand of a
tensor product of fundamental representations). It follows that the entries of
T generate Te.
To show that J-e is dense in Ce, we must show that || / || = 0 only if / = 0.
This follows from the existence of a faithful ^representation (see the first
remark following 13.1.10).
Finally, the comultiplication A^e of Te obviously extends continuously to
Ce. For, if / ? Te, then, by the definition of the norm on
and this is < || / || because (pi 0 p2) ° Ajre is a ^representation of J-e. |
Remark Note that S is not assumed to be continuous. In fact, it is already
clear in the SL2 case that the antipode Sjre of Te does not extend continuously
to Ce. For, 5jre is given by (see Subsection 13.1C)
and the relations || Sj?e(bk) \\ = ek \\ bk ||, || Sj?e(ck) \\ = e~k \\ ck \\ imply that
5jre is unbounded. A
454 13 Quantum harmonic analysis
We conclude this subsection by discussing some of the properties of Ce as
a C*-algebra.
In the classical case, the C*-algebra C(G) is obviously of type I, since it is
abelian. The following result, however, is much less trivial:
Proposition 13.3.4 (i) The C*-aIgebra Ce{G) is of type I.
(ii) The C*-algebra C^U(G) is of type I if and only if, for all X, fi ? P,
(u, A 0 [i - wX 0 wfi) e ——-Q. |
me
In the untwisted case, we have seen that there is a one-to-one correspon-
correspondence between the symplectic leaves of K and the irreducible ^represen-
^representations of Te. On the space of symplectic leaves, there is a natural quotient
topology, which one might hope is reflected in the topology of Ce. In fact,
there is a natural topology, the Jacobson topology, on the set prim(Ce) of
primitive ideals of Ce, i.e. the kernels of the irreducible ^representations of
Ce. The closed sets of this topology are those sets of primitive ideals which
contain some fixed, but arbitrary, subset of Ce.
Example 13.3.5 We consider the case G = SX2(C). Using the notation
in 13.1.8, it is easy to see that the kernels of the representations rt and nt
of Jre(SL/2((E')) are all distinct. Thus, there is a one-to-one correspondence
between irreducible ^representations and primitive ideals: in an obvious no-
notation, prim(CeEL2((C))) = S* ]JSl is the disjoint union of two circles.
The Jacobson topology on prim(CeEL2((C))) can be computed directly (see
Meister A992) for the details). The most general closed set is either a closed
set of 5* in its usual topology as a subset of (C, or the disjoint union of
S]. with a closed set in the usual topology of S\. Comparing with Fig. 2,
and recalling that the representations Tt (resp. 7Tt) are associated with the
zero-dimensional (resp. two-dimensional) symplectic leaves, we see that the
topology on the space of symplectic leaves is identical with that on prim(Ce).
0
Remarks [1] Note that prim(CeEL2((C))) and its topology are independent
of e. In fact, Woronowicz A987b) proves that the C*-algebra Ce(SL2(C)) is
itself independent of e, up to isomorphism, provided that e ? R+\{1}.
[2] See Hodges & Levasseur A993) for a description of the primitive ideals
of CeEL3(C)). A
B The Haar integral on compact quantum groups Following the dis-
discussion in Subsection 4.IE, we say that a linear functional H : ^Fe(G) —> (C is
a normalized bi-invariant integral, or simply a Haar integral, if H(l) = 1 and
A5) (H ® Z, A^e (/)) = {Z ® H, ATe (/)) = H(f)eUe (Z)
forall/€^(G), ZeUe(q).
13.3 Compact matrix quantum groups 455
Proposition 13.3.6 The quantized algebra of functions 7*e(G) admits a
unique Haar integral.
Proof We first establish uniqueness; in the process, we shall obtain an ex-
explicit description of the Haar integral.
Suppose, then, that H is a Haar integral. We prove first that H satisfies
the 'left-invariance' condition
H(Z *L f) = eUe(Z)H(f)
for all Z ? C/e(g), / ? J-e(G), where *L denotes the action of Ue on Te defined
in A1). We shall need the following identity, which is easily checked:
A6) A^(Z*l f) = (Z®l)*LAre(f)-
Then,
l.H(Z *L /) = (id ® H)((Z ® 1) *L
= Z*L ((id®ff)A.(
= €Ut(Z)H(f),
proving our assertion.
We now use A6) to show that H(C^S.^ r) = 0 unless A = 0. In fact, using
the identity H(Ki *L /) = #(/), we find that
which implies that i^(C^s;/i r) = 0 unless v = 0. Similarly, from the identity
H(X+ *L /) = 0, we obtain
0 = H(X+ *L
where ( , ) is the inner product on V^A). But, if A ^ 0, no non-zero vector in
the 0-weight space Ve(A)o can be annihilated by all the X2+, otherwise Ve(X)
would have a primitive vector of weight 0, contradicting its irreducibility.
Hence, the preceding equation implies that H{C^t.^r) = 0 for all n, r, t.
Combining these two observations, it follows that H must be given by
if A = 0,
otherwise.
Thus, H is uniquely determined.
Conversely, it is easy to check that A7) does define a Haar integral on
456 13 Quantum harmonic analysis
Remarks [1] Note that we have actually shown that H is uniquely determined
by the normalization and left-invariance conditions. Thus, every normalized
left-invariant integral on J~e{G) is right-invariant, and conversely.
[2] In the quantum case, the Haar integral is non-central, i.e. H(fif2) ^
H(f2fi) in general. A
Woronowicz A987a) proves a result more general than 13.3.6 in the context
of compact matrix quantum groups:
Theorem 13.3.7 Let (A, T) be a compact matrix quantum group. Then,
there exists a unique normalized, bi-invariant integral H on A. Moreover,
H(a) > 0 if a > 0, and H(S(d)) = H(a) for every a in the dense subalgebra
of A generated by the matrix entries ofT. |
By a bi-invariant integral on A, we mean a linear functional H : A —> (C
satisfying A5) for all continuous linear functional Z on A and all / ? A. An
element a e Ais positive if a = 66* for some 6 ? A, and a > 0 if a is non-zero
and positive.
In view of 13.3.3, this last result has the following corollary, which is also
easy to prove directly.
Corollary 13.3.8 The Haar integral on J~e{G) is positive, in the sense that,
for all f ? ,FC(G), H(f) > 0 if f > 0. Moreover, H(S(f)) = H(f) for all f
and H extends to a continuous linear functional on Ce(G). |
Although the description of H given by A7) is, in a sense, 'explicit', one
would like a formula for H in terms of a more economical set of generators
of JFe, such as those used in the proof of 13.3.3. Unfortunately, no such
description seems to be known except in the sl2 case.
Example 13.3.9 Prom the proof of 7.1.2, it follows that Jre(SL2((C)) is spanned
by the monomials aad6b^c1, where a, /?, 7, 6 ? N. The Haar integral is given
by
( (_ey3e2a(/3+l)/i _ 2\(e2;e2)a(e2;e2)p .f _ g , ^
H{aad6bPc<) = \ [ ] [ ] {*2;*2)«+0+i it <* - 0 ana p - 7,
@ otherwise.
Here, we have used the symbol
[1 if fc = 0.
To prove this formula, one first observes, using the invariance of H under
the left and right actions of K\ ? Ue, that H(aad6b^3c1) = 0 unless a = 5 and
C = 7. Now, any monomial aadab^c^ can be written as a linear combination
of powers of be (cf. the proof of 7.1.2). Thus, it is enough to compute
13.3 Compact matrix quantum groups 457
H((bc)P). This is done by induction on /?. For example, using the right-
invariance condition, we have
H(bc).l = (H
= (H 0 id)(a 0 b + b 0 d)(c 0 a + d 0 c))
= H(ad)bc + H(bc)da
= H(e~lbc + lNc + H(bc)(ebc + 1).
Since #A) = 1, we obtain H(bc) = — l/(e + e). In general, this argument
gives a recurrence relation between i^(Fc)/3+1) and H(bc)P, from which we
find that
The general formula can easily be deduced from this.
The reason for writing the previous fromula as we have is that, if z = ebc
and / is a polynomial in z, it implies that
where q = e and
/"
k=0
is the Jackson integral from (/-analysis. We shall see further connections
between quantum groups and (/-analysis in Section 13.5. 0
Perhaps surprisingly, although no explicit formula for the Haar integral is
known for general g, the quantum analogues of the classical Schur orthogo-
orthogonality relations can be obtained rather easily.
Proposition 13.3.10 We have
H((rX vrx x = *A,A^^A^-2^
where the sum is over the set of weights A ofVe(X).
Proof Let {??} be the basis of Ve(A)* dual to the orthonormal weight basis
{^} of yc(A), and define a basis {??} of V;(A) similarly. Then, if Z G Ue and
458 13 Quantum harmonic analysis
This is a matrix element of the representation Ve(X)* 0 V€(X). By A7),
^((^,s;^,r)*^5/x r) w^ vanish unless this representation contains the triv-
trivial representation, that is, unless A = A. Assuming this, the trivial component
is spanned by a linear combination of the vectors ^0^, and it follows that
,\ii,rYcofriJL,T) = ° unless fi = ft, v = i),r = r and s = s.
Finally, since Fe(A)* 0 Ve(X) ^ Homc(K(A)/, Ve{X)*) as t/e-modules (see Sub-
Subsection 4.1C), we can interpret H((C^s.^ryC^s.^r) as a matrix element of
an intertwining operator $ : Ve(X)' —> V^(A)*. Now, by the discussion pre-
preceding 8.3.15, 3> is a multiple of the map ? i—>¦ Kp*.?, where the dot denotes
the action in V(A)* and Kp* = fJi ^' if 2p = ^» na». It follows that
for some constant ca, the value of which is fixed by relation A3) to be as
stated in the proposition. |
Example 13.3.11 If G = 5L2((C), 13.3.10 gives
[^ + J-Je
(as usual, we identify a weight AgP with the integer (A, a), where a is the
positive root of sfailE))- Noting that C\.i = a, C*.^ = 6, Clia = c and
Cl1._1 = <i, it is easy to check that this formula is in agreement with that in
13.3'.9. 0
13.4 A non-compact quantum group 459
13.4 A non-compact quantum group
The Hopf *-algebra J-e(G) discussed in the preceding section may be called
a 'compact' quantum group, because the classical limit of its *-structure de-
defines the compact real form of G. In this section, we look at a non-compact
quantum group.
We continue to assume that e is a real number greater than one.
A The quantum euclidean group The group E2 of orientation-preserving
isometries of the plane 1R2, equipped with its usual euclidean metric, is the
semidirect product SO2 K IR2 of the group SO2 of rigid rotations with the
group 1R2 of translations, with SO2 acting on ]R2 in its natural representation.
The group E2 is solvable, and is not among the groups for which we have
given deformations, either on the enveloping algebra or function algebra level.
However, it is possible to write down a deformation of E2 by imitating the
following classical construction whereby E2 is obtained as a 'limit' of the
simple group SO3 (or, equivalently, SO3 is realized as a deformation of E2).
We regard SO3 as the group of rotations of the sphere in ]R3 with centre
@,0, R) and radius R. In the limit as R —> 00, rotations about an axis
passing through @,0, R) and parallel to the xy-jA&ne induce translations in
the tangent plane 1R2 to the sphere at the origin, while rotations about the
z-axis induce rotations in 1R2 (see Fig. 21). More explicitly, recall that every
rotation is a product of a rotation through an angle i\) about the z-axis,
followed by a rotation 9 about the ?/-axis, followed by a rotation (f about the
z-axis, where (ip,6,(p) are the Euler angles. The rotation about the y-&xis is
given by
(x , y , z) i-> (x cos 9 — (z — R) sin 9, y , x sin 9 + (z — R) cos 9 + R).
Writing 9 = r/R, where r is fixed, and letting R —> 00, we obtain the trans-
translation (x, y, 0) 1—> (x + r, y, 0).
Since SU2 is a double covering of 5O3, we obtain a double covering E2 of
E2 as a limit of SU2 (E2 is obtained simply by replacing SO2 by its double
cover).
At the level of (complexified) Lie algebras, this geometric construction
amounts to replacing the generators X^ of 5/2 (C) by RX^. Letting R —> 00
gives the Lie algebra with defining relations
This is clearly isomorphic to the (complexified) Lie algebra t2 of E^ if r+, r_
and p are, respectively, the generators of translations along the x- and y-axes
and of rotations, set H = 2\/—lp, X± = \{t+ ± yf^irJ).
Turning now to the quantum case, the preceding discussion suggests
460
13 Quantum harmonic analysis
Fig. 21 E2 as a limiting version of SO3
Definition-proposition 13.4.1 (i) The quantized universal enveloping al-
algebra of the euclidean group E2 is the associative algebra t/e(e2) over C with
generators L±l, X^ and the following defining relations:
A8) LX±L~1 = e±2X±, [X+ , X~] = 0.
It is a Hopf *-algebra with structure maps given by
A9)
= X+ <8> L2
) = L®L,
AUt (X~) =X
eUt(L) = l, eUt{X±) = O,
and ^-structure
B0) L* = L, (X+)* = e-1X
, (X~y = eL'2X+.
(ii) The quantized algebra of functions on the euclidean group E2 is the
associative algebra ^(?'2) over C with generators a, b, c, d and the following
defining relations:
B1)
ob = e 16a, ac = e lca, bd = e 1d6, cd = e 1dc,
be = cb, ad = da = 1.
13.4 A non-compact quantum group 461
It is a Hopf *-algebra with coalgebra structure
a (a
\c d
B2)
V (a b\ ( d -eb\ fa b\ (\ 0
) { J )
and ^-structure
B3) a* = d, 6* - -e~lc.
The quantized algebra of functions on the euclidean group E2 is the sub-
algebra Te{E<2) of Te{E<2) spanned by the products of an even number of
generators. It is a sub-Hopf *-algebra of Te{E<2). |
Remark The formulas in A8) and A9) are obtained from those defining the
'simply-connected' form of Uq(sl2((E)) by replacing Li by L and Xf by RX±
and letting R —> oc (see Remark [4] following 9.1.1). Similarly, the formulas
in B1)-B3) are obtained from those in B)-D) by replacing a, 6, c and d by
a, R~lb, R~lc and d, respectively, and letting R —> oc. A
Of course, we expect that ^(^2) will be isomorphic to an appropriately
denned dual of Ue(t2)- We shall be content with the following slightly weaker
result. Let E1!2 be the positive square root of E.
Proposition 13.4.2 There is a unique non-degenerate pairing of Hopf al-
algebras (, ) : C/e(e2) x JFe(E2) —> C which is zero on all pairs of generators
except
<L,a) = e1/2, (L,d) = e~V\ (X+ , b) = e^\ (X~ , c) = e1/2.
The notion of a non-degenerate pairing of Hopf algebras is defined in Sub-
Subsection 4. ID.
Outline of proof It is not difficult to show that p),
is a basis of Ue{t2)-> and that the elements albmcn, for / Gl, m, n gN, form
a basis of JTe(?^2) (if I < 01 a1 is interpreted as d~'). The pairing is denned
on basis elements by
(Lp(X+)r(X-)s ,albmcn)
ll{22)\e \ e ){^ ' ? )
)n
One can check that the pairing B4) is invariant and non-degenerate
462 13 Quantum harmonic analysis
Remark One can define a quantized algebra Ce(E2) of continuous functions
on E/2 which 'vanish at infinity'. However, this is technically more difficult to
work with than in the compact case because it is a non-unital C*-algebra. In
addition, we shall see shortly that the matrix elements of ^representations
of t/e(e2) do not usually belong to Ce{E<2) since they are 'unbounded'. This
difficulty can be overcome by working with elements 'affiliated' with Ce{E<2).
See Podles & Woronowicz A990) and Woronowicz A991b). A
B Representation theory We now turn to the representation theory of
Ue{t2) and JTe(?^2)- As one would expect, this is a kind of 'limit' of the
representation theory of U€(sl2((C)) and J-e(SL2 ((?)).
Theorem 13.4.3 (i) Every irreducible unitarizable representation ofUe(t2)
on which L acts semisimply with finite-dimensional eigenspaces is equivalent
to exactly one of the following:
(a) for v G IR\{0}, the one-dimensional representation ov given by
(b) for X, fx G 1R with A > 0 and 1 < \/jl\ < e, the representations p±^ on the
Hilbert space ?2 (Z) given by
in terms of the standard orthonormal basis {ek}ke% of?2(Z) (the reason for
writing A in the last formula is explained below).
(ii) Every irreducible unitarizable representation of J-e(E2) is equivalent to
exactly one of the following:
(a) for t ? S1, the one-dimensional representation rt given by
rt(a) = t, rt(b)=Tt(c) = 0, rt(d)=r1;
(b) for t G (C, the representation Kt on ?2 (Z) given by
7rt(a)(ek) = ek-i, 7rt(b)(ek) = ie~k~1eki
Kt(c)(ek) = te~kek, 7Tt(d)(ek) =
Remarks [1] The formulas in (i)(a) define an irreducible unitarizable repre-
representation p±^ whenever A G Cx and fx G 1RX. However, it is easy to see that
one has the following equivalences of representations:
13.4 A non-compact quantum group 463
(ii) p^ ^ p±A)/i for any v G C with \v\ = 1;
(iii) pY <* p^ for all reZ.
Using these observations, one sees that every p±'M is equivalent to one for
which the parameters A and fi satisfy the stated restrictions. Moreover,
with these restrictions, the representations p±'M are mutually inequivalent,
as one easily sees by looking at the eigenvalues of the operators p±^(L) and
[2] The representation p+' is a limit of the finite-dimensional representa-
representations of Ue(sl2AE))- In fact, one writes the basis of the Bk + l)-dimensional
irreducible representation as e^, e^_i,..., e_/e (instead of the more customary
i>o, Vi,..., V2k) and takes the radius of the sphere to be
R =
-*-¦)'
so that R —> oc as k —> oo. Similarly, the representations p+' can be
obtained as a limit of the even-dimensional irreducible representations of
Ue(sl2((E)). Finally, the representations p^1 and p^€ can be obtained by
starting with representations of Ue(sl2^C)) which are not of type 1.
[3] The operators p±^(L), p^(X+) and p^(X~) are clearly unbounded.
However, all the operators in p±'/i(C/e(e2)) obviously have the set of finite
linear combinations of the e^ as a common domain of definition.
[4] The algebra C/e(e2) has a three-parameter family of automorphisms
given by arbitrary rescalings of the generators L, X^. It is clear that the
representations p±M can all be obtained from p^1 (say) by twisting with an
automorphism of this type. A
We shall study the representations of Ue(t2) and J-e(E2) further in the next
subsection.
C Invariant integration on the quantum euclidean group The clas-
classical euclidean group E2 is unimodular, i.e. it admits a bi-invariant positive
measure. Of course, since E2 is non-compact, one can only integrate continu-
continuous functions which 'vanish sufficiently rapidly at infinity'; in particular, the
measure cannot be normalized. We will now show how to obtain analogous
results in the quantum case.
We recall that Fe(E2) has a basis consisting of the monomials albmcn for
/ G Z, m, n G N. Equivalently, we may take the monomials alcm(c*c)n
and az(c*)m(c*c)n. To define the appropriate class of quantized functions
464 13 Quantum harmonic analysis
'vanishing at infinity', we introduce the e-derivative of a power series tp
For r > 0, let J~e consist of all formal power series in the generators of
Te{E<2) of the form alcrn(p(c*c) or al(c*)m(p(c*c), where (f is a holomorphic
function on C satisfying the following condition: for all j G N, s > 0, there
exists a constant C(j, s) for which
^ )(l + 62/e)"s, for all fcel
Lemma 13.4.4 For all r > 0, Te is a *-algebra (with multiplication and
^-structure obtained by extending those of Te(E2) in the obvious way). |
Now define linear functionals Hr : Te —> C by
oo
Hr(al(c or c*)mip{c'c)) = 6lflSm,0
k= — oo
(cf. 13.3.9).
Proposition 13.4.5 For all r > 0, Hr is a Haar integral on T^r\ i.e.
Hr(Z *L /) = eUe(Z)Hr(f) = Hr(Z ** /)
foralizeue(t2),fertr)- I
As in the case of compact quantum groups, one can use these Haar func-
functionals to prove analogues of the Schur orthogonality relations.
Proposition 13.4.6 Let a and r be irreducible ^-representations ofUe(t2)
on which K acts semisimply with finite-dimensional eigenspaces, and denote
their matrix elements by cFjk, rst- Assume that the products &jkT*t and r*t(jjk
all lie in Te for some r.
(i) If a and r are inequivalent, then
for all j, k, s, t.
13.5 q-special functions 465
(ii) We have
Hr(rstT*v) = c{K~x, Ttv}8s,u, Hr(r*tTuv) = c{K~x, TusNt,v
for some constant c independent of s, t, u and v. |
13.5 q-special functions
In this section, we describe the relation between three types of g-special func-
functions and the representation theory of quantum groups and their quantum
homogeneous spaces, with one example drawn from each of Sections 13.1,
13.2 and 13.4. We continue to assume that e > 1, and set q = e~l.
All the g-special functions we shall be concerned with are special cases of
the q-hypergeometric series, which are defined as follows. We have already
defined the symbol
3=0
Note that, since q < 1, the limit
(a; q)oo = lim (a; g)fc
exists. Set
(ai,a2,.. .,ar; q)k = (ai; g)/c(a2 ; <?)/c • • • (ar ; <?)fc-
Then, the general g-hypergeometric series are the power series in a complex
variable z given by
B5)
The terminology is justified by the observation that, if we replace a^, bi and z
in the right-hand side of B5) by qa\ qhl and A — qI+s~rz, respectively, and
then let q ] 1 in each term of the sum, we obtain the power series expansion
of a classical hypergeometric function.
For generic values of the upper parameters ai,..., ar and lower parameters
&i,..., bs, the radius of convergence of this series is 0, 1 or oo according to
whether r — s > l,r — s = lorr — s< 1, respectively. However, if one of
the upper parameters is equal to q~n for some n G N, the series becomes
a polynomial because (q~n; q)k = 0 if k > n. Further, if one of the lower
parameters is equal to q~n for some n G N, then the series is well defined
only if one of the upper parameters is equal to q~m for some 0 < m < n.
466
13 Quantum harmonic analysis
A Little g-Jacobi polynomials and quantum SU2 In our first example,
we compute the matrix elements C*.^ of the irreducible C/e(«s/2((C))-module
Ve(X) with highest weight AgN, with respect to an orthonormal basis (see
Subsection 13.1 A for the relevant definitions). It turns out that they are
related to the little q- Jacobi polynomials, defined by
pn(z; a, p;q)=2<Pi
qz
Proposition 13.5.1 The matrix elements C*;/i of the irreducible Ue(sl2((C))-
module of highest weight A are given as follows:
(i) if [i + v > 0 and jjl > v,
(ii) if fi + v > 0 and n <v,
;A =a(/i+i/)/26(i/-/x)/29(A-i/)(/i-i/)/4 2(
l_2(
(iii) if// + z/ < 0 and fi < V,
^
J^
Jq*
(iv) if 11 + z/ < 0 and // > z/,
Jq*
Jq*
Proofs of these formulas may be found in Vaksman & Soibelman A988),
Masuda, Mimachi, Nakagami, Noumi & Ueno A988, 1991), and Koornwinder
A989a), the first of which is closest in spirit to the methods used in this book.
13.5 q-special functions 467
Remark One interesting special case is that in which A is even and fi = v = 0.
Then, one obtains
which is a little q-Legendre polynomial with argument — q 1bc. A
Substituting the formulas in this proposition into the quantum Schur or-
orthogonality relations in 13.3.11, one obtains the orthogonality relations for
the little q-Jacobi polynomials:
Corollary 13.5.2 For k, I, m, n e N and 0 < q < 1, we have
>; qk, ql\ q) pn(z; qk, ql; q)zk(qz; q)tdqz =
f
Jo
where Jo dqz denotes the Jackson integral defined in 13.3.9. |
There are other connections between quantum SU2 and g-special functions,
but we do not have the space to discuss them here. We mention only the rela-
relation between quantum Clebsch-Gordan coefficients and q-Hahn polynomials
obtained by Kirillov & Reshetikhin A989), Koelink & Koornwinder A989)
and Vaksman A989).
B Big q- Jacobi polynomials and quantum spheres Our second instance
of the connection between the quantum and q-worlds concerns the quantized
algebra J-e{S2) of functions on the 2-sphere, introduced at the end of Section
13.2. We recall that Te{S2) is the subalgebra of Jre(SL2(<E)) consisting of
the fixed points of the *-automorphisms given by a 1—> ("a, b 1—> C^ c I~H> Cc>
d 1—>C^, CEaS1. The reader may check that an equivalent description is
B6) F({S2) = {xe Fe(SL2(C)) \K1*Rx = x}.
(This is analogous to the description of S2 as the homogeneous space SU2/S1,
where Sl is the diagonal matrices in SU2.) It is easy to see that ^reE2) is
generated, as an algebra over (C, by the elements x = eafe, y = ecd and
z = — ebc. Further, by using B), one checks that these generators satisfy the
following relations:
B7)
xz = e 2zx, yz = e2zy,
xy = — e 1z(l — e 2z), yx = — ez(l — z).
By D), the *-structure on JreE2) is given by
B8) x* = -e~ly, y* = -ex, z* = z.
In fact, we have
468 13 Quantum harmonic analysis
Proposition 13.5.3 Jre(S'2) is isomorphic to the associative algebra over C
with generators x, y, z, defining relations B7) and ^-structure B8). The
monomials yizkxl, with j, k, I G N, are a basis of ^(S2) over (C. Moreover,
J-e(S2) is a quantum SL2((?)-space.
Outline of proof The last statement follows from the fact that the co-
multiplication of Te{SL2(O:)) maps Te(S2) into Fe(SL2(<C)) 0^(S'2). This
assertion in turn follows from the description of J-e{S2) given in B6), together
with the analogue of A6) for *# instead of *^:
A^(Z*fl/) = (l®Z) *R A^e(/). |
It is well known that the algebra of polynomial functions on the classical
2-sphere, as a representation of SO3, contains each irreducible representation
exactly once. Precisely the same result holds in the quantum case:
Proposition 13.5.4 As an Jre(SL2(<E))-comodule, Te(S2) decomposes into
irreducibles as follows:
AG2N
where V€(X) is the irreducible Te(S2)-comodule of dimension A + 1.
Outline of proof Since Te{S2) is a quantum 5L2(C)-space, it is a
C/e(s/2(<C))-module. Computing the action of C/e, one checks that the only
elements of ^(S*2) which are killed by X+ and are eigenvectors of Ki are the
scalar multiples of powers of x, and that K\ *? xr = e2rxr. If we knew that
Te(S2) is completely reducible, it would follow immediately that Te(S2) de-
decomposes as stated as a [/e(sZ2(<C))-module, or equivalently as an JTe(S'L2(C))-
comodule. But since Te(S2) is infinite dimensional, we cannot immediately
deduce complete reducibility from 10.1.14. However, one can check that the
finite-dimensional subspace Tf of J-e(S2) spanned by the monomials yizkxl
with j; + k + / < d is a C/e(«s/2(C))-submodule of J-e(S2), and so is completely
reducible by 10.1.14. It follows that the same is true of J-e(S'2), since
d
It follows from this proposition that there is a unique basis {S^} of ^
where ji = A, A — 2,..., —A, A G 2N, such that S® = 1 and
B9) A^)
The S^ are q-analogues of spherical functions.
The main result of this subsection gives a formula for the S^ in terms of
big q-Jacobi polynomials, which are defined as follows:
p/ ox (q-n,qn+laC,qaz
Pn(z;a,C; q) = 3(p2[ ] q,q
13.5 q-special functions
469
Proposition 13.5.5 The q-spherical functions S^ are given by the following
formulas:
(i) if ix > 0,
-1/2
-(A+)i)(A-3/i+6)/8
|(A-^)Jq2
-1/2
The proof is a direct verification that the elements S^ ? Te{S2) defined by
these formulas satisfy B9). This uses certain properties of the big g-Jacobi
polynomials which we shall not write down here.
Remark The quantum 2-sphere which we have studied is a special case of
a two-parameter family introduced by Podles A987). In the form given by
Noumi & Mimachi A990c), the defining relations for the most general quan-
quantum 2-sphere are
xz = e~2zx, yz — e2zy,
xy = -e(a
yx = -e(a + z)(C - z),
where a and /3 are real constants (the *-structure is still given by B8)). Our
quantum 2-sphere is the special case a — 0, /3 — 1. A
C g-Bessel functions and the quantum euclidean group We first recall
the connection between the representations of the classical euclidean group
E2 and the Bessel functions
Jn(z
1 f2
= /
27r Jo
^l(zsin9 -n0))d0 (n € Z, z € <C).
We define, for any 5 ? <C, a representation ps of E^ on the Hilbert space
L2EX) of square-integrable functions on the unit circle, as follows. The most
general element of E2 is a product of a rotation through an angle a about the
origin, followed by a translation of ]R2 by a vector (r cos 0, r sin 0); we denote
this element by g(r, 0, a). Then, if / ? L2EX),
- exp(rscos@ -
- a).
470 13 Quantum harmonic analysis
This representation is irreducible if s ^ 0, and unitary if s is purely imaginary.
Moreover, every irreducible unitary representation of E2 is equivalent to ps
for some s ^ 0, or to a (one-dimensional) irreducible component of p°.
Bessel functions enter as matrix elements of ps for s^O. In fact, if
P'mn{9) = (
it is easy to see that
psmn(g(r, cj>, a)) = (>/=l)n-Tnexp[-/=I(na + (n
There are several g-analogues of Bessel functions in the literature, but we
shall only be concerned with the Hahn-Exton q-Bessel functions
It can be shown that
limJn((l-^; q) = JnBz).
The following result gives the first connection between these g-Bessel func-
functions and the representation theory of Ue(z2)- It is easily proved using the
formulas in 13.4.3(ii) and the pairing B4).
p' d e
Proposition 13.5.6 The following formulas give the matrix elements of the
representations p+' and
(i) for j > k,
(ii) for j <k,
Remark Note that these matrix elements do not belong to Te{E2) because
they are not given by polynomials in the generators a, 6, c and d. However,
13.5 q-special functions 471
they are all contained in the space Tf^(E2) consisting of the formal linear
combinations
Z,ra,n
where / G Z, ra, n G N, and where the constants 7/,m,n vanish for all ra, n
except for finitely many values of /. One can check that the multiplication in
^(^2), as well as the left and right actions of C/e(e2), extend to Tf^i^^)-
Moreover, J^xt(E2) contains the domains Te of all the Haar functionals Hr.
A
Using 13.5.6 and the unitarity property J2iPk,iPj,i — 6ij f°r P — P+1 and
p+' , one obtains the Hansel-Lommel orthogonality relations:
Corollary 13.5.7 The Hahn-Exton q-Bessel functions Jn(z ; q) satisfy the
following identities:
Jn+k(z] q)Jm+k{z; q) = 6rn,nq~n,
for \z\ < q~1/2, m,neZ. |
Although these orthogonality relations were known before the advent of
quantum groups, we conclude this section by giving an 'addition formula' for
the Hahn-Exton g-Bessel functions, which was discovered by Koelink A991b)
using quantum group methods.
Theorem 13.5.8 The Hahn-Exton q-Bessel functions satisfy the following
identity:
for all A > 0, I, m, n, p G TL.
Outline of proof The idea is to start with the identity
in ^xt(?^2)- Applying the representation tti (8) tti to both sides gives an
equation between operators on the Hilbert space tensor product ^2(Z)<g)^2(Z),
from which we extract a scalar identity by applying both sides to two cleverly
chosen vectors and then taking inner products.
472 13 Quantum harmonic analysis
In a little more detail, we define the vector
A direct computation shows that
C0) (tt! ® 7n)A^ (c*C)(/r)=<?2m/r-
Moreover, /jm is a unit vector: the proof of this uses the q-Hankel orthogo-
orthogonality relations
^ i+fc) 5 q) = 6m,nq-n
for r > — 1, to, n ? Z, which follow from the Schur orthogonality relations in
13.4.6.
Now we compute each side of the inner product:
C1)
On the one hand, the right-hand side can be computed directly using the
formulas in 13.5.6; one finds that it is equal to
v+2* Jfc(AA _ q2)qU-i . q2)Jk_n{X(l - <?)q"-n-l ; q2)
nm-v+k+n . 2\ c
On the other hand, the property C0) of fj71 enables one to compute the action
of the hypergeometric series in 13.5.6 on /zm. Using this, and the fact that
tti is a ^representation, one finds that, if n > 0, the left-hand side of C1) is
equal to
_ q2)qn+m-l .
-1)"-* f
Taking u — v = l — n, replacing A by Ag1/2, and renaming the indices suitably,
the equality of the last two expressions can be seen to be equivalent to the
identity in the statement of the theorem. |
Bibliographical notes 473
Remark Because the matrix elements involved are given by formal power
series, the argument leading to the formula in 13.5.8 must be supplemented
by an analytic proof. This has been supplied by Kalnins, Miller & Mukherjee
A994) and Koelink & Swarttouw A994). Different addition formulas are
proved in Koornwinder & Swarttouw A992). A
Bibliographical notes
13.1 The representation theory of compact quantum groups began with the
work of Vaksman & Soibelman A988) on the sl2 case. For the s/n+i case,
see Soibelman A990a) and Vaksman & Soibelman A991), and, for the gen-
general case, see Levendorskii & Soibelman A991a). For the twisted case, see
Levendorskii A990, 1992) and Levendorskii & Soibelman A991a).
The 5/2 case has been developed by a number of authors by starting with the
definition of Jre(SL2(C)) in terms of generators and relations. See, for exam-
example, Masuda, Mimachi, Nakagami, Noumi & Ueno A988, 1991) and Koelink
& Koornwinder A989). The s/n+i case is treated by the same methods by
Koelink A991a).
The ^representations tt* of Jre(SL/2((E)) were studied by Arik & Coon
A976) and Feinsilver A987) in connection with a g-analogue of the
Schrodinger representation, independently of quantum groups.
The results on quantized function algebras at roots of unity are taken from
de Concini & Lyubashenko A993).
13.2 Quantum spheres were first introduced by Podles A987); see also Po-
dles A989) and Noumi & Mimachi A990c); we have followed the latter refer-
reference. For quantum flag manifolds and Schubert varieties, see Lakshmibai &
Reshetikhin A991, 1992) and Soibelman A992c).
13.3 The theory of compact matrix quantum groups is due to Woronowicz,
and the reader should refer to his papers in the references, beginning with
Woronowicz A987a,b).
The fact that Ce(G) is of type I was proved by Vaksman & Soibelman A988)
in the sl2 case, by Bragiel A989) in the sZ3 case, and by Koelink A991b) in
the sZn+i case; it is stated in Levendorskii & Soibelman A991a) in the general
case. For the twisted case, see Levendorskii A990, 1992) and Levendorskii &
Soibelman A991a).
The Haar integral on Jre(SL2(C)) has been computed by a number of au-
authors: see, for example, Woronowicz A987a) and Masuda et al. A988, 1991).
Proposition 13.3.10 is due to Soibelman & Vaksman A992).
474 13 Quantum harmonic analysis
13.4 The results of this section have been taken from Koelink A991b); see
also Koelink A994a,b) and Vaksman & Korogodskii A989). A number of
other non-compact quantum groups have been treated in the literature. See
Masuda et al. A990a, b) and Soibelman & Vaksman A992) for quantum
S77M, and Podles & Woronowicz A990) and Takeuchi A992b) for the quan-
quantum Lorentz group. A discussion of the difficulties in dealing with quantized
algebras of continuous functions on non-compact quantum groups is given in
Woronowicz A991b).
13.5 The connection between quantum sl2 and little g-Jacobi polynomials
was first noticed by Vaksman & Soibelman A988); see also Masuda et al.
A988, 1991) and Koornwinder A989a). For the connection between quantum
Clebsch-Gordan coefficients and g-Hahn polynomials, see Koelink & Koorn-
Koornwinder A989) and Vaksman A989). Our discussion of quantum 2-spheres
and big g-Jacobi polynomials is taken from Noumi & Mimachi A990c). The
relation between g-Bessel functions and the quantum euclidean group is due
to Vaksman & Korogodskii A989) and Koelink A991b); we have followed the
latter.
For an excellent general survey of the connections between quantum groups
and g-analysis, see Koornwinder A990). For general background in the clas-
classical theory of g-special functions, see Exton A983) and Gasper & Rahman
A990).
14
Canonical bases
This is the first of three chapters which describe some applications of quantum
groups to problems in 'classical' mathematics. The problem addressed in
this chapter is that of giving a 'canonical' basis of any (finite-dimensional)
representation of a complex simple Lie algebra g. Roughly speaking, this
means bases which are independent of any arbitrary choices, at least up to
an overall scalar multiple. Such bases should also have good properties: for
example, the action of the generators of g in the basis should be 'simple', the
bases should behave well under tensor products, etc.
The construction of canonical bases goes back, at least, to the work of
W. V. D. Hodge in the slm case in the 1940s, subsequently elaborated into
'standard monomial theory' by V. Lakshmibai, C. Musili and C. Seshadri,
which applies to any g of classical type. Another canonical basis, and perhaps
the simplest, is that of I. M. Gel'fand & M. L. Tsetlin; it applies when g — slm
or sOm. There are several other classical approaches to this problem, but all
of them seem to be restricted to the case when g is of classical type, and often
to the slm case. Thus, it is remarkable that the approaches using quantum
groups we shall discuss apply when g is an arbitrary symmetrizable Kac-
Moody algebra.
In Section 14.1, we discuss the construction of crystal bases, due to M.
Kashiwara. These are bases of any finite-dimensional ?/g(g)-module V with
the surprising property that the action of the generators Xf of Uq($) on the
crystal basis of V, when suitably 'renormalized', makes sense at q = 0 (we
continue to assume that g is finite dimensional, although, as we have said,
Kashiwara's construction extends to the infinite-dimensional case). In fact, it
was an observation, by E. Date, M. Jimbo and T. Miwa, that one can make
sense of the action of Uq(slm((E)) on its finite-dimensional representations at
q — 0, and that the quantum analogue of the Gel'fand-Tsetlin basis then
becomes drastically simpler, that provided the starting point for Kashiwara's
theory. In the application of quantum groups to vertex models in statistical
mechanics (see Section 7.5), the parameter q essentially plays the role of
temperature, so crystal bases are related to the behaviour of the model at
'absolute zero', whence their name.
The construction of crystal bases is completely algebraic, making use only
of the structural properties of C/g(g)-modules developed in Chapter 10. One
of the most important properties of crystal bases is that they behave very
simply under tensor products: this leads to a simple graphical algorithm for
476 14 Canonical bases
decomposing tensor products of irreducible representations of Uq($). Spe-
Specializing q to 1, we obtain a solution of the corresponding classical problem
which is completely different in nature from that provided by the well-known
formula of R. Steinberg.
G. Lusztig gave a quite different construction of canonical bases, which
we outline in Section 14.2. It is based on the relation between quivers and
quantum groups discussed in Subsection 9.3D. The set of isomorphism classes
of representations of a given dimension of a quiver can be naturally identified
with the set of orbits of an algebraic group on a finite-dimensional vector
space. The coefficients of the canonical basis elements in terms of the elements
of a Poincare-Birkhoff-Witt basis (see 9.1.3) turn out to be essentially the
Euler characteristic of the local intersection cohomology of the closures of
these orbits. Note that the PBW bases themselves are not canonical, for they
depend on the choice of a reduced decomposition of the longest element of
the Weyl group of g.
We begin our discussion of Lusztig's canonical bases by constructing them
using an elementary algebraic method, although the topological approach
seems to be necessary to derive many of their most important properties. In
fact, we construct a basis of the subalgebra U+ of Uq($) which has the prop-
property that, when this basis is applied to the lowest weight vector of any finite-
dimensional irreducible ?/g(g)-module V, the result is precisely the canonical
basis of V (together with zero). It turns out that this is the same as the basis
produced by Kashiwara's theory.
It is perhaps worth emphasizing that, while these bases specialize to give
canonical bases of all the finite-dimensional irreducible g-modules, the con-
construction of crystal bases, as well as the algebraic construction of Lusztig's
bases, can only be carried out at the quantum level. Thus, quantum groups
appear to be essential for the solution of the classical problem with which we
began this introduction.
We also remark that Lusztig's construction is very reminiscent of the well-
known construction of special bases for Hecke algebras, due to D. Kazhdan
and G. Lusztig. This supports the idea, already suggested by the results of
Section 10.2, that Hecke algebras should be thought of as 'quantum' objects.
14.1 Crystal bases
A Gel'fand-Tsetlin bases Perhaps the most well-known classical construc-
construction of canonical bases is that due to Gel'fand & Tsetlin A959a,b). We begin
with a brief description of the quantum analogue of this construction, as it
provides motivation for the introduction of crystal bases later in this section.
It is based on the following result (see Jimbo A986a)). Note that there are
14-1 Crystal bases 477
embeddings Uq(sln(V)) -> Uq(sln+1(C)) given by Kt ^ Ku Xf ^ Xf for
i — 1,..., n — 1 (see Section 9.1 for the definition of the Q(g)-Hopf algebra
0,(9)).
Lemma 14.1.1 Let V be a finite-dimensional irreducible type 1 C/g(sZn+i (C))-
module, and regard V as a Uq(sln((E))-module via the above embedding.
Then, each irreducible Uq(sln(<E))-module which occurs in V does so with
multiplicity one. |
This result implies that the decomposition of V into irreducible Uq(sln((E))-
modules
is unique. Hence, GT bases may be constructed by induction on n: one simply
takes the GT basis of V to be the union of the GT bases of the V^r\ The
induction starts with Uq{sl2{(?)). If we choose the bases of the irreducible
representations of Uq(sl2((E>)) as in 14.1.6 below, the resulting GT basis is
uniquely determined up to scalar multiples.
Remark In the classical situation, GT bases also exist for representations
of son((?), since the classical analogue of 14.1.1 holds for the natural inclu-
inclusions son((?) <—> son_|_i(C). However, there is no obvious homomorphism
Uq(son((E)) —> Uq(son+i((C)) which might have the property 14.1.1, essen-
essentially because the Dynkin diagram of son(<?) is not a subdiagram of that of
son_i_i((C) (of course, this is true classically, but there we have a 'geometric'
description of son((C)). Thus, it is unclear how to construct bases of GT
type for Uq(son((E))-modules (see, however, Takeuchi A989)). And for the
algebras of exceptional type, GT bases do not even exist in the classical case.
A
Let V? be the natural irreducible (n-hl)-dimensional Uq(sln+i(<E))-module
with basis {t>g,..., v^} and action:
A) Ki.v] = tf^-'-'v), X+.v) = 6itiv)_x, X'.v) = 6itj+1v*j+1.
Lemma 14.1.2 IfV is a finite-dimensional irreducible Uq(sln+i(<?))-module
of type 1, then every irreducible Uq(sln+\((L))-module which occurs in V®V?
does so exactly once. |
This follows, as in the classical case, from the fact that the non-zero weight
spaces of V? all have dimension one. (Alternatively, one may deduce the quan-
quantum statement from the classical one using the fact that the decomposition
of tensor products of [/g(sZn+i(C))-modules is the 'same' as for sZn+i(C)-
modules (see 10.1.16).)
478 14 Canonical bases
With V as in the lemma, let V' be any irreducible component of V 0 V^,
and let {vfa}, {vp} and {v^} be the GT bases of V, V and Vq\ respectively.
Then,
for some constants c^7 ? Q(g). By computing the coefficients c^7 explicitly,
Date, Jimbo & Miwa A990) made the following striking observation. Let A0
be the subring of Q(#) consisting of the rational functions which are regular
at q = 0.
Proposition 14.1.3 With the above notation, the constants c^7 € A0 for
all a, f3, 7. In fact, for each a, c^7 ? qA° except for precisely one pair (/?, 7)
(depending on a). |
Corollary 14.1.4 Let V be any irreducible component of an iterated tensor
product (V$)®k for some k>2, and let {vp} and {v\} be the GeVfand-Tsetlin
bases ofV and Vq\ respectively Let
7ivi7fc
Then, c^'"lk ? A0 and, for each C, c^'"lk ? qA°, except for precisely one
k-tuple G1,..., 7^) (depending on C). |
In other words, 'at q — 0', each GT basis vector of V becomes, up to a scalar
multiple, a 'monomial' i^ ® • • • ® v^k in the GT basis vectors of V$. This is
the first suggestion that the representations of Uq(sln+i((?)) are meaningful,
and drastically simpler, when cq — 0'. The crystal bases described in the
remainder of this section are the natural development of this observation.
Remark By using the Robinson-Schensted correspondence, it is possible to
describe exactly which monomial v^ (g) • • • ® v^k is equal to vp at q = 0. See
Date, Jimbo & Miwa A990). A
B Crystal bases Throughout the rest of this section, g will denote a finite-
dimensional complex simple Lie algebra. We denote the Q(g)-Hopf algebra
Uq(o) simply by Uq from now on if there is no risk of ambiguity.
If V is a finite-dimensional {^(g)-module of type 1, we may regard V as a
module for the {/^(^(G^O-subalgebra of Uq($) generated by Xz and K^1.
By the results of Chapter 10, any such module is generated by its primitive
vectors, i.e. vectors lying in some weight space V\ of V which are annihilated
by X^~. By the Poincare-Birkhoff-Witt decomposition 9.1.3, we thus have
14-1 Crystal bases 479
where the sum runs over the pairs (A,r) G P x TL such that (A,&i) > r > 0
(recall that 6l{ = d^). We may therefore define operators x^ G End(V)
by
for any v G Va fl ker X^~ and any (A, r) as above.
Definition 14.1.5 A crystal basis of a finite-dimensional Uq($)-module V
is a pair (V°, By) consisting of a free A0-module V° and a basis By of the
(^-vector space V°/qV° with the following properties:
(i) V° is an A0-form ofV, i.e. V^V°
A0
(u) V° = 0AFA0 and By = \Jx B\, where Bx = By n (Vg/qVg) and VA0 -
v°nvx;
(iii) xf(V°) C V° and xf(By) C By U {0};
(iv) for any i — 1,..., n and any u, v G J3y, one has v = x~ (u) if and only if
u = xf(v).
Before we address the question of the existence and uniqueness of crystal
bases in general, let us consider the s/2 case.
Example 14-1-6 Let Vq(ni) be the (m+l)-dimensional irreducible t/g(s/2(C))-
module of type 1. Thus, Vq(ni) has a basis {v0,..., vm} such that
Ki.vr = qm~2rvr, X+.vr = [m - r + l]qvr-U X{.vr = [r + l]gvr+i
(we set v_i = vm+i = 0). The operators xf in this case are given by
xf(vr) — fr=Fi. We may therefore take Vq(m)° to be the free ^-module
with basis {t>o,..., vm}, and the images of these vectors in Vq(m)°/qVq(m)°
as the basis BVq(my In fact, it is clear that, up to an overall scalar multiple,
this is the only possible choice for BVq^my 0
Returning to the general case, denote as usual by V^(A) the irreducible
t/g(g)-module of type 1 with highest weight A G P+ (see Chapter 10). Let
V^(A)° be the ^-submodule of V^(A) generated by the vectors of the form
x~ o- • -ox" (v\), where k > 0 and v\ is the highest weight vector of V^(A), and
let By (A) = B(X) consist of the images of these vectors in Vq(\)°/qVq(\)°,
deleting those which are zero. We can now state the main result of this
section.
Theorem 14.1.7 With the above notation, the pair (Vq(\)°, B(X)) is a crys-
crystal basis ofVq(\). More generally, ifV = 0aVq(A) is a finite direct sum of
irreducible modules, and we define V° = 0aV^(A)°, By = UxB(X), then
(V°, By) is a crystal basis ofV.
Conversely, let V be a finite-dimensional Uq($)-module of type 1, and let
V = 0aK?(A) be a decomposition ofV into irreducible modules. If(V°, By) is
480 14 Canonical bases
any crystal basis ofV, there is an isomorphism V° = ®\Vq(\)° of A0-modules
which carries By bijectively onto JJA B(X). |
We shall not discuss the proof of this theorem, which is given in complete
detail in Kashiwara A991).
C Globalization We now show how to 'melt' a crystal basis (V°,BV): we
shall obtain, from the basis By of V°/qV°, a basis of V itself. This is done
by first constructing a basis of U~ (cf. Section 9.1) which has some of the
properties of a crystal basis, and then using the fact that V is generated as a
[/^"-module by its primitive vectors (this follows from 9.1.3).
We begin with the following simple lemma.
Lemma 14.1.8 For any X G U~ and any i = 1,... ,n, there exist unique
elements Y{, Z{ g U~ such that
B) + KtY% K/
Outline of proof Uniqueness is a consequence of 9.1.3. As for existence,
since any element of U~ is a linear combination of products of X~'s, and
since we can take Y{ — Z{ = 0 if X = 1, it is enough to show that, if the
result holds for X, it also holds for any product XJX. This is proved by a
simple computation. |
We may therefore define endomorphisms yi and Z{ of U~ by y%(X) = 1^,
Zi(X) = Zi for all X G U~, with Y{ and Z{ as in B).
Lemma 14.1.9 For all i = 1,... ,n, we have
r=0
This is analogous to the statement that every finite-dimensional Uq-module
V is generated by its primitive vectors. Thus, we can imitate the construction
of crystal bases of V by defining endomorphisms xf of U~ by
for all r > 0 and X G ker yi% Note that, by 14.1.9, xfox~ = id. Let Uq be the
^-submodule of U~ generated by the elements of the form x~ o • • • o x~k A)
for all k > 0, and let Bo be the set of images of these elements in Uq jqU^,
discarding those which are zero. Then, we have the following analogue of the
properties in 14.1.5:
H.l Crystal bases 481
Proposition 14.1.10 With the above notation,
(i) Bo is a basis of the (^-vector space Uo~ /qU0~;
(ii) xf(Uo) C Uo~ and xf(B0) CB0U {0} (in fact, x~ (Bo) C Bo);
(Hi) if a, b G Bo, then a = xf(b) if and only ifb = x~{d). |
Kashiwara A991) calls (Uo~,Bo) the crystal basis ofU~.
The next proposition is the crucial result which allows one to 'melt' a crystal
basis of a finite-dimensional t/g-module V to obtain a genuine basis of V over
). To state it, let ~ be the Q-algebra automorphism of Uq defined by
let A = TL\q,q~x\, and let U^s~ be the .4-subalgebra of Uq generated by the
(X~)(r\ i = 1,..., n, r > 1 (see Section 9.3).
Proposition 14.1.11 The natural map
n t/0" n
is an isomorphism of (^-vector spaces. |
Let 7T : UQ~~/qUQ~~ —> (t/Ts~ ® Qfes*?]) H C/(T fl C/^" be the inverse of the
.4.
isomorphism in 14.1.11, and let Bo — tt(J50).
Theorem 14.1.12 With the above notation, Bo is an A-basis ofU^s~, and
a Q(g)-basis ofUq. Moreover, for every element b G Bo, we have b = b. |
We can now describe a canonical basis, over Q(g), of any finite-dimensional
irreducible Uq-modu\e V of type 1. In fact, we obtain an .4-basis of the A-form
V^es = U™s~ .vo of V, where Vo is a highest weight vector of V.
Theorem 14.1.13 Let V be a finite-dimensional irreducible Uq-module, and
let vo be a highest weight vector ofV. Let By be the set of non-zero vectors
in V of the form n(b).vo, where b runs through the basis Bo ofU^s ~ described
before 14.1.12. Then, By is an A-basis ofVJ?s and (hence) a Q(#)-basis of
V. Moreover, ifV° is the A°-submodule ofV with basis Bo, and if By is the
image of By in V°/qV°, then (V°,BV) is a crystal basis ofV. |
Kashiwara A991) calls By the global crystal basis ofV.
D Crystal graphs and tensor products We have not yet considered the
behaviour of crystal bases under tensor products. This is the subject of the
next result. As a corollary, we shall give a new combinatorial algorithm
for decomposing into irreducibles any tensor product of finite-dimensional
representations of g.
482
14 Canonical bases
Proposition 14.1.14 Let (Vf,BVl) and (V2,BV<2) be crystal bases of two
finite-dimensional Uq-modules V\ and V2 of type 1. Let V° = Vi° <g> V? and
A0
A0
Bv = BVl <g> BV2 = {h <g> b2 | h e BVl, b2 € By2}. Then, (V°,BV) is a
crystal basis of V\ (?) V2. Moreover, we have
Qfa)
b2)
\ 6i ® ^~
g> b2 if 3k > 1 with {xj)k(b{) ^ 0, (xf)h(b2) = 0,
(b2) otherwise,
(b2) if3k> 1 with (xf)k(b2) ^ 0, (ir)fc(&i) = °»
g) 6o otherwise. I
We shall now reformulate this result graphically. By a coloured oriented
graph, we mean a set V of vertices, a set ? of ordered pairs of elements of
V, called arrows, and a set C of colours, together with a map k : ? —> C. If
a = (?(a), /i(a)) is an arrow of the graph, we call t(a) the tazZ of a, and /i(a)
its /lead. Finally, a said to have colour c G C if «(a) = c. We leave it to the
reader to formulate the notion of an isomorphism of coloured oriented graphs.
Fig. 22 An admissible coloured oriented graph
The coloured oriented graphs we shall encounter have one further property.
To state it, let us say that a (non-coloured) oriented graph is a string if it is
of the following type:
The length of a string is the number of arrows it contains.
A coloured oriented graph Q is admissible if, for each colour c, the oriented
sub-graph Qc consisting of all the vertices, but only the arrows of colour c, is
a disjoint union of strings.
lJf.,1 Crystal bases
483
Example 14-1-15 Fig. 22 shows an admissible coloured oriented graph, in
which the dots represent the vertices, and there are two colours, represented
by the solid and dashed arrows. 0
There is a tensor product operation on admissible coloured oriented graphs,
which may be described as follows. First, we define the tensor product of
strings as indicated in the diagram which follows; the result is a disjoint
union of strings.
More generally, if (non-coloured) oriented graphs S\ and Si are disjoint
unions of strings, their tensor product is the union of the graphs obtained by
taking the tensor product of each component of S\ with each component of
Suppose now that Q\ and Q2 are admissible coloured oriented graphs. For
each colour c, we form the tensor product Q\ <S> G? as indicated above. Then,
the tensor product Q\ ® Q2 is the union of the Q{ <g> Q%, with the colour c
attached.
Example 14.. 1.16 Let Q\ — Q2 be the coloured oriented graph shown below.
The sub-graph corresponding to the solid arrows is
and the tensor product with itself is
484 H Canonical bases
Similarly, the sub-graph corresponding to the dashed arrows gives
Taking the union, we see that Q\ <g> Q2 is precisely the coloured oriented graph
shown in Fig. 22. 0
Returning now to representation theory, let V be a finite-dimensional Uq(o)-
module of type 1, and let (V°,BV) be a crystal basis of V. The crystal
graph Qy of V is the coloured oriented graph with set of vertices By, set of
colours C = {1,..., n}, and set of arrows of colour i the pairs F, bf) such that
b' = x~(b) (or, equivalently, b = xf(b')).
The following result is fairly clear from what we have said above.
Proposition 14.1.17 The crystal graph QVq (A) of the finite-dimensional Uq-
module Vq(X) of highest weight A has the following properties:
(i) it is admissible;
(ii) it is connected (regarded as a non-coloured, non-oriented graph);
(Hi) the vector vx G B(X) of weight A is the unique source of Gvq(x) (by
a source, we mean a vertex which is the tail of any arrow of which it is a
component);
(iv) the component containing v\ of the sub-graph Qy ,A) of colour i is a string
of length (A,&i).
Moreover, the crystal graph Gvq(\)®vq(n) oi the tensor product of the irre-
irreducible finite-dimensional Uq-modules of highest weights A and \i is isomor-
phic to the tensor product Gvq(\) ® Qy (M) of the crystal graphs ofVq{\) and
14-1 Crystal bases 485
This result gives the following algorithm for decomposing Vq(X) ® Vq(ii).
Note that, by 10.1.16, the decomposition of this tensor product into irre-
ducibles is the 'same' as in the classical case (the proof of 10.1.16 is given for
Ue when e ? Cx is not a root of unity, but the same result and proof are valid
for Uq).
Kashiwara's tensor product algorithm 14.1.18 Let Vq(X) and Vq(fi)
be the irreducible finite-dimensional Uq-modules of the indicated highest
weights. For each connected component Q ofQvq(\) ®Gvq(ii)i locate the unique
source s in Q, and, for each colour i, let Vi be the length of the string in Q
containing s. Define a weight v G P+ by (V, &*) = i^. Then, Vq(X) ® Vq(fi) is
isomorphic to the direct sum of the Vq(v), as Q runs through the connected
components ofQVqW ® Gvq{»)' I
Example 14-1-19 We consider the natural 3-dimensional irreducible represen-
representation V^(Ai) of Uq(sls(<E)). Then, V^(Ai) has a basis {^0,^1,^2} on which
the action of the Xf is given by A) (with n = 2). The crystal graph of T^(Ai)
is thus
v0 vi v2
where solid arrows are coloured 1 and dashed arrows are coloured 2. Hence,
^Vq(Ai) ® ^Vq(Ai) is the graph shown in Fig. 22. It has two connected compo-
components. In the component
the unique source is the top left vertex, and the strings of colours 1 and 2
originating at this vertex are of lengths 2 and 0, respectively; so this sub-
subgraph is the crystal graph of the Uq-modu\e V^BAi). The source of the other
component
t
t
486 14 Canonical bases
is the upper vertex, and the strings of colours 1 and 2 originating at this
vertex have lengths 0 and 1, respectively; so this component is the crystal
graph of Vq(\2). Kashiwara's algorithm thus gives the isomorphism
K,(Ai) ® Vq{\!) = V,BAi) 0 Vq(\2)
(Ai and A2 are the fundamental weights of g - see the Appendix.) 0
14.2 Lusztig's canonical bases
In this section, we describe another construction of canonical bases using a
method which looks quite different from that used to produce crystal bases.
Eventually, however, we shall see that the two bases are the same.
We assume throughout this section that g is a complex simple Lie algebra
of type An, Dn or En.
A The algebraic construction We have seen in 9.3.3 that the set BG of
products
forms an *4-basis of U^s + ; here, t = (ti,..., ?tv) € N^, and N is the number
of positive roots of g. This basis is certainly not canonical: as our notation
suggests, it depends on the choice of a reduced decomposition a of the longest
element Wo of the Weyl group of g, for it is only by using such a decomposition
that one can define the root vectors X? (see Subsection 9.IB).
Our aim is to modify the basis Ba in order to obtain a new basis which is
independent of a. Let U+ be the Z[g~1]-submodule of [/+ generated by Ba.
Proposition 14.2.1 TheZ[q-1}-submodulel(+ ofU+ is independent of the
reduced decomposition a, and may therefore be denoted byU+.
Moreover, if tt :U+ —> U+j'q~lU+ is the canonical projection, then n(Ba)
is a Z-basis B of U+ /q~1UJr which is independent of a. |
Remark It is only the set 7r(Ba) which is independent of <r, not the individual
elements tt(X^). If a' is another reduced decomposition of wo, there is a
(generally non-trivial) bijection R<? : NN -» NN such that R°'(t) =t if and
only if 7t(X^t) = ft(X^,t,). These permutations will play an important role
in Subsection 14.2C. A '
We can now state the main result of this section. We recall the ring auto-
automorphism ~~ of Uq defined before 14.1.11.
14-2 Lusztig's canonical bases 487
Theorem 14.2.2 The restriction of tt toU+ P\U+ induces an isomorphism
of7L-moduleslA+C\U+ —> IA+/'q^lA^'. Moreover, if X^ is the unique element
ofU+DU+such that tt(X+) = 7r(X+t), then X+ - ~X+ and {X+}t€Niv is
(i) aTL[q-l]-basisofU+;
(ii)anA-basisofUrXs + ;
(iii) a <§(q)-basis ofU+. |
The proof, given in Lusztig A990d), uses the relation between quantized
universal enveloping algebras and quivers described in 9.3.14.
We call the basis B — {X?}t<^n given by this theorem Lusztig's canonical
basis. Prom Chapter 9, we know that the specialization of [/+ to q = 1 gives
the classical enveloping algebra U+. Theorem 14.2.2 thus gives a canonical
basis of U+ over Q.
Examples 14-2.3 If g is of type Ai, B consists of the g-divided powers {X^)^\
for all t e N.
If g is of type A<i, B consists of the monomials of the form
(X1+)^(^2+)('/)(^i+)(t'/) and (X2+)^(X1+)^)(X2+)^//\
where t, t', t" G N satisfy t' > t + t". These elements are, in fact, all distinct,
except when t' = t + tn', when one has the relation
(this is a g-analogue of a classical identity due to D. N. Verma).
If g is of type A3, B contains some elements which are not monomials, such
as
(node 2 is the middle node of the Dynkin diagram of g). 0
Lusztig's canonical basis has many remarkable properties, some of which
we shall now describe. The first result shows that the structure constants of
the algebra t/^s+ with respect to B are 'positive'.
Proposition 14.2.4 The product of any two elements of Lusztig's canon-
canonical basis B is a linear combination of elements of B with coefficients in
Specializing to q = 1, we see that the structure constants of the classical
enveloping algebra ?/+, with respect to its canonical basis, are non-negative
integers.
The next result shows that B is beautifully adapted to the study of repre-
representations of Uq (cf. 14.1.13). Let p : Uq —> End(V) be a finite-dimensional
488 14 Canonical bases
irreducible t/^-module of type 1. Then, V is generated as a ?/+-module by a
lowest weight vector, i.e. a weight vector Vqq G V which is annihilated by X~
for all i — 1,... ,n. This follows from the corresponding results in Chapter
10 for highest weight vectors, using the involution of Uq, as a Q(g)-algebra,
given by X? ~ Xf, Jfc h-> ffr1.
Theorem 14.2.5 Wjtii the above notation, the non-zero vectors in p(B)(voo)
are a Q(q)-basis ofV. |
Specializing to q — 1 gives, of course, a canonical basis of any finite-
dimensional irreducible g-module.
The proofs of the last two results make use of another construction of 6,
using topological methods, which we outline in the next subsection. This also
yields an 'explicit' formula for the elements of Lusztig's canonical basis.
Before doing this, however, we shall establish the connection between B and
the basis Bo of U~ constructed in 14.1.10. The existence of such a connection
is strongly suggested by similarities between the construction of the two bases
(cf. 14.1.12 and 14.2.2), and between their properties (cf. 14.1.13 and 14.2.5).
We must first make sure that we are comparing two bases of the same
space. By applying to Bo the Q-algebra automorphism of Uq given by
we obtain an *4-basis of ?/J, and a Q(g)-basis of [/+, which we denote by
Boo-
Theorem 14.2.6 Kashiwara's basis B^ is identical to Lusztig's basis B. |
This is proved in Lusztig A990e).
B The topological construction To describe the second construction of
Lusztig's canonical basis, we need to recall the discussion of quivers in Sub-
Subsection 9.3D.
Fix an orientation of the Dynkin graph of g, and denote the resulting
quiver by F. We must choose a reduced decomposition wo = Si± ... SiN which
is adapted to this orientation, in the following sense. Say that a vertex i is
a sink of F if there is no oriented edge * Jm in F; in this case, let Si(T)
be the orientation obtained by reversing every oriented edge of F that has
vertex i as its head. Then, wo = si:L ... siN is adapted to the orientation
F if i\ is a sink of F and if, for each r — 1,..., N — 1, ir+i is a sink of
It can be shown that there is at least one reduced decomposition of wo
adapted to any given orientation of the Dynkin graph. It is easiest to describe
such a decomposition when w$ lies in the centre of W (this holds when g is of
type Ai, Dn for n even, E7 and Eg). Then, one can define a Coxeter element
14-2 Lusztig's canonical bases 489
c = sil ... sin for which {zi,..., in} = {1,..., n} and such that Jm y\ in F
implies j < j' (see Bernstein, Gel'fand & Ponomarev A973)). In this case,
the order ft of c is even and
w0 = (sh ... sin)(sil ... sin)... (sh ... sin) (ft/2 times)
is a reduced decomposition adapted to F.
We reformulate slightly the notion of a representation of F, introduced in
Subsection 9.3D; we work over an algebraic closure F of a finite field IF. If
m= (mi,... , ran) G Nn, let
A representation of F on Ir is a linear map T : Ir —> Ir such that T(IF *) C
IF 3 whenever \ Jm is an oriented edge of F; in other words, T is an element
of the vector space
Em =
Moreover, the group
acts on Em by (g.T)ij = 9jTijg~l, where g = (gi,..., gn) G GLm(IF), and T^-
is the component of T in Homp(IF * , IF °). The set of isomorphism classes
of representations of F of dimension m is in one-to-one correspondence with
the set of orbits of GLm(W) on Em.
Let Cr = silsi2 ... Sir_1(air), r = 1,..., N, be the positive roots of g. Let
epr be the indecomposable representation of F corresponding to /3r, as in
Gabriel's theorem 9.3.13, and, for any t— (ti,..., tw) G N^, let
r=l
Let m = dim(F*), and let Ot be the GLm(IF)-orbit in Em corresponding to
V*. Define a partial order on N^ by saying that i < t if and only if Of is
contained in the Zariski closure of Ot and dim(Vt) = dim(F*').
Fix a prime p G N which is non-zero in F, and denote by Qp the field of p-
adic numbers. Let x be an IF-rational point of Ot, and let IC^(Ot) be the stalk
at x of the &th cohomology sheaf with coefficients in Qp of the intersection
cohomology complex of the closure of Ot (see Beilinson, Bernstein & Deligne
A982)).
490 14 Canonical bases
Theorem 14.2.7 Let a be a reduced decomposition of w0 adapted to the
chosen orientation ofT, and let the other notation be as above. Then:
(i) IC*(Pt) =0 if k is odd.
(ii) Ift, H e ?iN, define <*' G Z[q, q-1] by
V dim(IChx(Ot))qk =
k even
if if < t, and (| = 0 otherwise. Then, the canonical basis element Jr(X*t) is
given by
t'<t
(cf. 14.2.1). |
This result is a consequence of a more abstract construction of the canonical
basis in terms of perverse sheaves. For each t ? N^, one defines a certain
category of perverse sheaves on IF, and forms the free .4-module A(V) with
basis the set V of objects of these categories, for all t G N^. One then defines,
by cohomological methods, an associative algebra structure on A(P), and
proves that it is isomorphic to U^s^~. Since A(V) has a natural basis, namely
V, so does U^s + . The final step is to show that this basis is independent of
the choice of orientation of the Dynkin graph.
For complete details, see Lusztig A990d, 1991, 1993).
C Some combinatorial formulas We conclude this chapter by describing a
combinatorial formula for the dimension of any finite-dimensional irreducible
Uq-module which can be derived using Lusztig's canonical basis.
To state it, we first choose a partition of the set of vertices of the Dynkin
diagram of g into a disjoint union of two subsets, say V and V", with the
property that a^ = 0 whenever i ^ j are both in V;, or both in V" (it is
easy to see that there is a unique such partition for any connected Dynkin
diagram). Let |V;| = &, |V/;| = n — k. We may assume that the vertices are
numbered so that V = {1,..., k} and V — [k + 1,..., n}. Then
Wo =
is a reduced decomposition, say cr, and
is another reduced decomposition, say o'. These reduced decompositions are
both adapted to the unique orientation of the Dynkin graph for which the
vertices in V1 are all sinks, and those of V" are all sources (i.e. sinks for the
orientation obtained by reversing all the arrows).
14-2 Lusztig's canonical bases 491
Now recall the bijection R° introduced in the remark following 14.2.1. For
any m G Nn, let Z(m) be the set of pairs (t,1f) G N^ x N^ satisfying the
following conditions:
(i)/#(*)=*,
(ii) tr < mr if 1 < r < k,
(iii) t'r < mn-T+\ if 1 < r < n — k.
Then, we have
Proposition 14.2.8 Let Vq(X) be the finite-dimensional irreducible Uq-
module with highest weight X, and define m = (rai,...,ran) G Nn by
rrii = (A,a«). Then,
Note that, by the results of Chapter 10, the dimension of V^(A) is the same
as that of the g-module V(X) with the same highest weight.
As it stands, 14.2.8 does not give a purely combinatorial way of computing
dim(V^(A)), since the bijection RGG is defined rather implicitly in terms of the
relation between the canonical basis of XJq and its Poincare-Birkhoff-Witt
bases. However, a combinatorial description of R%\ for any two reduced
decompositions o and cr', can be given as follows.
We first define RGG in two special cases:
(a) a' can be obtained from a by replacing 3 consecutive reflections SiSjSi in
cr, such that ctij = —1, by SjSiSj: then Raa (t) =if, where i is the same as t
except in the three positions where a and a' differ, while if (tx, v, w) are these
three positions in t, then those in if are
(v + w — min(w, w), min(w, w), u + v — min(w, it;)).
(b) a' can be obtained from a by replacing two consecutive reflections SiSj
in cr, such that a^ = 0, by SjSi'. then R°'(t) = if, where if is the same as t
except in the two positions where a and a' differ, while if (u, v) are these 2
positions in t, then those in if are (v, u).
It is classical that, given any two reduced decompositions a and cr;, there is
a sequence a = 0*1, 0*2,..., ot — a' such that any pair of consective reduced
decompositions in the sequence satisfy one of the conditions (a) or (b); then
B!7' = Rat R!7*-1 Ra<2
Example 1+.2.9 Let g be of type A2. We take V = {1}, V" = {2}. Then,
the two reduced decompositions are
a : wo = S1S2S1, o' : wo — S2S1S2.
492 H Canonical bases
From the preceding description, the bijection Rf? is given by
We use 14.2.8 to compute the dimension of the adjoint representation of g.
Since m= A,1), conditions (ii) and (iii) above become
If ti = 0, then t[ = t2 + t3, giving the three possibilities t = @,0,0), @,1,0),
@,0,1). If h = 1 and t3 = 0, then ^ = t2, giving t = A,0,0) or A,1,0).
Similarly, if ^ = t3 = 1, thent= A,0,1) or A,1,1), andif ^ = 1 and t3 = 2,
thent= A,0,2). Thus, \Z(m)\ = 8-0
Remark Lusztig A990e) proves a formula similar to that in 14.2.8 for the
multiplicities of the irreducible components in the tensor product of two
finite-dimensional irreducible C/g-modules. This is of a different nature from
Kashiwara's tensor product algorithm 14.1.18. A
Bibliographical notes
14.1 The notion of a crystal basis was introduced in Kashiwara A990b),
where their existence was proved when g is of type A, B, C or D. Misra &
Miwa A990) exhibited a crystal basis of the quantum analogue of the basic
representation of affine sln, indicating the possibility of extension to infinite-
dimensional g. Finally, Kashiwara A990c) announced the proof of the exis-
existence of crystal bases for integrable representations of arbitrary symmetriz-
able quantum Kac-Moody algebras. Detailed proofs appeared in Kashiwara
A991). (A representation of Uq(o) is 'integrable' if it is the direct sum of
its weight spaces, these weight spaces being finite dimensional, and if, when
regarded as a representation of the ?7^E/2(C))-subalgebra of Uq(o) gener-
generated by X^, K^1, for each i = l,...,n, it is a sum of finite-dimensional
representations.)
Although we have presented Kashiwara's results linearly, he proves most of
them simultaneously, by an inductive argument, in what he calls the 'grand
loop'.
For an application of crystal bases to vertex models in statistical mechanics
(see Section 7.5), see Kang et al. A992a-c).
14.2 Most of the results of this section are taken from Lusztig A990d,e),
where further details and complete proofs can be found. In these papers
Bibliographical notes 493
(and in our treatment), it is assumed that g is of type A, D or E, but
Lusztig A991) deals with the case where g is any Kac-Moody algebra with
a symmetric generalized Cartan matrix. The fact, proved in Lusztig A990e),
that his basis coincides with Kashiwara's basis in the A, D, E cases, together
with the fact that the latter is defined for any symmetrizable quantum Kac-
Moody algebra, strongly suggested that Lusztig's results should hold in this
generality. This was shown to be the case in Lusztig A993), where a very
thorough treatment of the whole subject of canonical bases can be found. To
pass from symmetric to merely symmetrizable generalized Cartan matrices,
one has to take into account the action of a certain cyclic group.
See Lakshmibai & Reshetikhin A991, 1992) for a quantum analogue of
standard monomial theory.
See Mathieu A992) for a simplified discussion of the topological construc-
construction in Subsection 14.2B, dealing directly with the specialization to q = 1.
15
Quantum group invariants
of knots and 3-manifolds
One of the most remarkable developments in the story of quantum groups
was the discovery, due essentially to V. F. R. Jones, that they can be used
to construct new isotopy invariants of knots (and, more generally, of links)
in the 3-sphere S3. In fact, the crucial ingredient in Jones's construction is
a solution of the quantum Yang-Baxter equation, from which it is easy to
obtain a representation of Artin's braid group #m on m strands, for all m.
Since every link can be obtained by joining the free ends of a braid (in a
standard way), one has an operator associated to each link. This operator
will depend on the braid used to represent the given link, but Jones observed
that, by taking a suitable 'Markov trace' of the operator, one could obtain a
scalar which depends only on the isotopy class of the link.
We have seen on several occasions throughout this book that quantum
groups provide a machine for producing solutions of the QYBE. Although
Jones actually obtained his R-matrix by another method, it turns out that it
is the R-matrix associated to the two-dimensional irreducible representation
of Uq E/2 (<C)). One thus obtains an isotopy invariant of links which depends on
the deformation parameter q. After suitable rescaling and reparametrization,
this becomes the Jones polynomial. It is natural to try to generalize this
construction to any finite-dimensional representation of Uq(o), for any simple
Lie algebra g. The difficulty lies in the construction of a suitable Markov
trace, and, although it has not yet been carried out in complete generality,
V. Turaev succeeded in the case of the natural representations of Uq(gi) when
9 is of classical type. He showed that, when 9 is of type An, the resulting
sequence of polynomial invariants can be organized into a single two-variable
invariant, the HOMFLY polynomial; when 9 is of type Bn, Cn and Dn, he
obtained the KaufTman polynomial.
Meanwhile, E. Witten gave, in the heuristic language of Feynman inte-
integrals, a construction of invariants of links in an arbitrary compact oriented
3-manifold. In the case when the ambient 3-manifold is the sphere, these in-
invariants reduce to the HOMFLY polynomial; at the opposite extreme, when
the 3-manifold is arbitrary but the link is empty, they give new invariants of 3-
manifolds. N. Yu. Reshetikhin and V. Turaev showed how Witten's invariants
could be obtained from the quantum group approach, by using the fact that
any 3-manifold can be obtained by performing surgery along a 'framed link'
15.1 Knots, links and 3-manifolds: a quick review 495
in S3. A framed link is the same thing as a ribbon tangle, to which invariants
were attached in Section 5.3 using ribbon Hopf algebras, and Reshetikhin and
Turaev showed that there is an essentially unique combination of these ribbon
tangle invariants which depends only on the given 3-manifold, and not on the
surgery used to construct it.
After summarizing, in Section 15.1, the background results on links and 3-
manifolds we shall need, in Section 15.2 we describe Turaev's construction of
the HOMFLY polynomial: using what we now know about quantum groups
and their associated R-matrices, the construction reduces to a fairly easy
exercise in linear algebra. We also describe another construction, due to
Jones but based heavily on ideas of L. H. Kauffman, which works directly
with a plane projection of a link, and does not depend on the relation with
braids. This essentially involves formulating vertex models, which we studied
in Section 7.5, on an arbitrary 4-valent graph instead of a rectangular lattice
(such a formulation was given earlier by R. J. Baxter for other purposes).
3-Manifold invariants are discussed in Section 15.3. The ribbon tangle
invariants, from which the 3-manifold invariants are constructed, depend on
a choice of a 'colouring' of the ribbon tangle, i.e. a choice of a representation
of some fixed ribbon Hopf algebra for each component of the link. One has to
impose some restrictions on the allowable colourings, which lead to the notion
of a modular Hopf algebra. We show that the 'simply-connected covering' of
the finite-dimensional subalgebra Ufn(sl2((E)) of the restricted specialization
of Uq(sl2((E)) at any root of unity e of odd (and sufficiently large) order gives
a modular Hopf algebra, and hence a 3-manifold invariant. The proof of
this relies on the properties of tilting modules for [/Jes(s/2(C)), discussed in
Section 11.3. The work of Witten strongly suggests that this result should
generalize to arbitrary g.
Since the quantum group constructions we are going to describe are all ul-
ultimately two-dimensional in nature, it is perhaps worth recalling that part of
the motivation for Witten's work on link invariants was the desire to give an
intrinsically three-dimensional description of the Jones polynomial, indepen-
independent of a choice of plane projection. Witten accomplished this by his quantum
field theoretic approach, but it seems that this has not yet been completely
translated into rigorous mathematics. On the other hand, J. S. Birman and
X. S. Lin have show very recently that the quantum group invariants are
closely related to invariants constructed by V. A. Vassiliev by a completely
different method.
15.1 Knots, links and 3-manifolds: a quick review
The purpose of this section is to collect the definitions and notations we shall
use in the two sections which follow. For proofs and further details, the reader
should consult the references mentioned in the Bibliographical notes.
496
15 Quantum group invariants of knots and 3-manifolds
A From braids to links A link in R3 (or the 3-sphere S3) is a one-
dimensional smooth compact submanifold of IR3 (or 53), in other words,
a disjoint union of embedded circles. A knot is a connected link. A link is
oriented if each of its connected components is oriented. Two oriented links
L and V are equivalent (or ambient isotopic) if there exists an orientation-
preserving difTeomorphism / of R3 (or S3) such that f(L) = V', and such
that / takes the orientation of L into that of L'.
Links L can be pictured in two dimensions by projecting perpendicularly
onto a plane, chosen so that the projection L has only transversal crossings,
none of which have more than two branches (we shall always assume that
our link projections have these properties). The equivalence class of the
link can be recovered from a projection provided one includes certain extra
information at each crossing in the projection (cf. the discussion of braids
in 5.1.7). Namely, if we think of the direction perpendicular to the chosen
plane as 'vertical', the branch of the link which lies 'below' the branch which
it crosses in the projection is shown broken in the two-dimensional picture.
See Fig. 23.
Fig. 23 Plane projection of the Whitehead link
Two oriented link projections define equivalent links if and only if they can
be obtained from each other by applying an isotopy of the plane together
with a sequence of Reidemeister moves:
Reidemeister I
15.1 Knots, links and 3-manifolds: a quick review
497
Reidemeister II
Reidemeister III
Here, the two link projections are supposed to be the same except for the
portion shown. All possible orientations are allowed.
Links are distinguished from each other by means of invariants. An (ori-
(oriented) link invariant is an assignment of an element of a set S to every (ori-
(oriented) link in such a way that equivalent links are assigned the same element
of S. In view of the result of the preceding paragraph, defining such an in-
invariant is the same thing as associating an element of S to every (oriented)
link projection in such a way that it is unchanged by plane isotopy and the
Reidemeister moves.
Link invariants are usually easier to define than to calculate. However,
there is a special class of invariants, the calculation of which can be effec-
effectively carried out by an inductive procedure. Three oriented link projections
L+, L_ and Lo are said td be skein related if they are the same outside a
neighbourhood of some crossing point, near which they are as shown below:
It is intuitively plausible (and also true!) that any link projection can be
transformed into that of an unlink, i.e. a disjoint union of circles, by suc-
successively changing overcrossings to undercrossings, or vice versa. Thus, of
the three link projections L+, L_ and Lq, one of them (either L+ or L_) is
'more complicated' than the other two, either because it has more crossings,
or because it is further from an unlink.
Theorem 15.1.1 There exists a unique invariant P of oriented links with
498
15 Quantum group invariants of knots and 3-manifolds
values in the ring Z[x,x 1,y,y x] of Laurent polynomials in two variables x
and y (with integer coefficients) such that P = 1 for a single unknotted circle
and
A)
xP(L+) + x-xP{L.) + yP(Lo) = 0
whenever L+, L_ and Lq are skein related. |
The invariant P is called the HOMFLY polynomial, after its discoverers
Freyd, Hoste, Lickorish, Millett, Ocneanu & Yetter A985) and Przytycki &
Traczyk A987) (unfortunately, P had been named before the contribution of
the last two authors was recognized).
By the remarks preceding this theorem, the value of P on a link L can
be calculated inductively by successively simplifying the projection L using
the skein relations. This proves uniqueness. The problem is to show that P
exists, i.e. that two different ways of simplifying the link projection lead to
the same value of P(L). We shall establish this in the next section by using
quantum groups.
Some special cases of the HOMFLY polynomial were discovered earlier.
For example, the Alexander polynomial is
A(L)(t) =
- r1'2)),
and the Jones polynomial, whose discovery by Jones A985) motivated the
construction of P, is
J(L)(t) =
Example 15.1.2 Let us compute the value of P(L) when L is the trefoil knot.
The skein relation,
T - T T — 4 ) T
Li + Li Li_~ <LJ Li 0
applied to the crossing enclosed by the dashed circle, gives
xP(L) = -x-1 - yP(Lo),
while
15.1 Knots, links and 3-manifolds: a quick review
499
LL=W
gives
Finally,
gives
Combining these equations, we find that
P(L)=y2x~2-x-4-2x-2. 0
There is another polynomial invariant of oriented links whose existence
can be proved using quantum groups, namely the Kauffman polynomial To
define it, we need to recall the notion of the writhe (or Tait number) of an
oriented link projection. We associate a sign to each crossing according to
the scheme
+ 1
-1
Then, the writhe w(L) of a link projection L is obtained by adding up the
signs of all the crossings in a projection of Z. Note that the writhe is not a
link invariant, since it is obviously changed by Reidemeister I. In general, the
500 15 Quantum group invariants of knots and 3-manifolds
equivalence relation on links generated by plane isotopy and Reidemeister II
and III is called regular isotopy. Thus, writhe is a regular isotopy invariant.
Theorem 15.1.3 There exists a unique invariant K of oriented links, with
values in the ringZ[z, z~x, a, a] of Laurent polynomials in 2 variables z and
a, such that, ifL is any plane projection of a link L, then K(L) — a~
has the following properties:
(i) K(v) = 1;
(iia) if link projections L and L' are related by
then K(L ) = aK(L);
(iib) if link projections L and L are related by
thenK(L")=a-1K(Ll;
(Hi) if link projections L+, L_, Lq and L^ are related by
L+ L_ Lo L^
then K(L+) + K(LJ) = z{K{L0) + if (loo)). I
Remarks [1] Conditions (i)-(iii) do not involve the orientation of the link,
which is used only to compute its writhe.
[2] The Alexander polynomial is not a specialization of the Kauffman poly-
polynomial, but the Jones polynomial is:
J(L)(t) = -^(LX-t-1/4 - t1/4,^3/4).
[3] An invariant closely related to the writhe is the linking number lk(L, L')
of two disjoint oriented links L and V'. To define it, choose a plane projection
15.1 Knots, links and 3-manifolds: a quick review
501
Fig. 24 The closure of a braid
of the link L U L', and give a sign to each crossing as above. Then, lk(L, L')
is the sum of the signs associated to each crossing where L passes under Lf.
[4] Since the writhe is only an invariant of regular isotopy, the same is true
of K, and the purpose of 'rescaling' K by the factor aw^ is to convert K
into a genuine isotopy invariant. There is another way to accomplish this,
which is based on a result of Trace A983).
Define the rotation number of an oriented link L to be JL dL, where dL
is the pull-back of the canonical 'angle' 1-form on the circle S1 by the map
L —> S1 which associates to a point of L the unit tangent vector at the point.
Then, Trace's result asserts that two oriented link projections are regular
isotopic if and only if they are isotopic and corresponding components have
the same writhe and rotation number. The writhe and rotation numbers of
a link can be changed, without changing the isotopy class of the link, by
introducing 'kinks' as indicated below:
Thus, one can convert a regular isotopy invariant into a full isotopy invariant
by first adjusting the writhe and rotation numbers suitably. A
Braids in R3 were introduced in 5.1.7; we use the notation denned there.
Their relevance to this circle of ideas is that they provide a method of finding
invariants which allows one to avoid the use of Reidemeister moves. If /3
is a braid, one can obtain a link by joining together its endpoints p® and
pj, for all z, as shown in Fig. 24 (in a plane projection). This link is called
the closure of /3. Note that any braid has a canonical orientation, reading a
502 15 Quantum group invariants of knots and 3-manifolds
plane representation from top to bottom, so that its closure is also naturally
oriented. It was proved by J. Alexander that, up to equivalence, every oriented
link is the closure of a braid.
It is obvious that equivalent braids have equivalent closures, but the con-
converse is false. The precise conditions under which two braids have equivalent
closures were found by A. Markov. To state his result, note first that there
are obvious embeddings Bm <—> Bm+i given by adding an (ra -f l)th strand
to any braid j3 G Bm, sufficiently far away from the strands of /3 so that it is
not linked with any of them:
Let us say that two braids /?, /?' G \Jm Bm are Markov equivalent if they
can be obtained from each other by a sequence of Markov moves:
Markov I /?' ~ /J/J'/T * (/?, /?' e Bm),
Markov II C ~ CT*1 @eBm).
Then, Markov's theorem asserts that two braids have equivalent closures if
and only if they are Markov equivalent. Thus, defining a link invariant with
values in a set S is the same thing as defining a map ]Jm Bm —¦> S which is
constant on Markov equivalence classes.
B From links to 3-manifolds The construction of 3-manifold invariants
from quantum groups is based on the classical result that every compact, ori-
oriented 3-manifold (without boundary) can be obtained by performing surgery
along a framed link in S3. We shall now explain what this means, and
how to tell when two such surgeries give rise to the same 3-manifold (up
to orientation-preserving homeomorphism).
A framing of an oriented link L C S3 is an assignment of an integer to
each component of L. This is the same thing as choosing a ribbon tangle T
whose core is L (cf. 5.1.9). In fact, let S be a connected component of T with
core a component K of L. Then, if K' is one of the two components of the
boundary dS of 5, the integer associated to K is lk(K,K').
Let K\,... ,Kn be the components of a framed link L in 53, and let fi
be the integer associated to Ki by the framing. Choose disjoint tubular
neighbourhoods JVi,..., iVn of Ki,..., Kn in S3. One then attaches n copies
of D2 x D2 to the 4-ball D4 with boundary S3 by gluing the part dD2 x D2 =
15.1 Knots, links and 3-manifolds: a quick review
503
S1 x D2 of the ith copy onto Ni in such a way that, for each x G D2, the circle
S1 x x goes to a curve which runs 'parallel' to Ki and whose linking number
with Ki is fi. There results a compact 4-manifold Dl whose boundary is a
compact 3-manifold Sl- Fixing an orientation of D4 induces an orientation
of Dl, and hence also an orientation of Sl- One says that Sl is obtained
from S3 by surgery along the framed link L.
Of course, surgeries along two different framed links may lead to the same
3-manifold. Two framed links L and V are said to be related by a Kirby
e-move, where e = ±1, if they are the same except for pieces which look as in
Fig. 25. There, K is an unknotted component of L with framing e, and the
K
Fig. 25 A Kirby -hl-move
vertical strands represent the components of L which have non-zero linking
number with K, other than K itself. The framings have been represented
by ribbons as described above. To obtain V from L, we delete K and give
each of the vertical strands K a right-hand (resp. left-hand) twist if e = — 1
(resp. if e = 1), at the same time adding —elk(K,KJ to its framing. In
particular, if K is contained in a ball which does not intersect L\K, then
U is obtained from L simply by deleting K: this is called a special Kirby e-
move. We emphasize that any Kirby move can be applied in either direction,
to obtain L' from L or vice versa.
It was proved by Kirby A978) and Fenn & Rourke A979) that the 3-
manifolds obtained by surgery along framed links L and V are the same,
up to orientation-preserving homeomorphism, if and only if L and L' are
related by a sequence of Kirby ±l-moves. In fact, it was pointed out by
Reshetikhin & Turaev A991) that only Kirby +l-moves and special Kirby
—1-moves are needed. Thus, one can try to define a 3-manifold invariant by
constructing an invariant of framed links which has the additional property
504 15 Quantum group invariants of knots and 3-manifolds
of being unchanged by these Kirby moves. We shall carry out this program
in Section 15.3.
15.2 Link invariants from quantum groups
In this section, we describe two ways of constructing link invariants, starting
from representations of quantum groups. The first is based on the relation
between links and braids discussed at the end of Subsection 15.1 A, while the
second makes use of the vertex models of statistical mechanics, which we
discussed in Section 7.5.
A Link invariants from R-matrices Suppose first that V is a free module
of finite rank over a commutative ring k and that R G End(F 0 V) is an
invertible solution of the quantum Yang-Baxter equation:
Then, we obtain a representation pm of the braid group Bm on V®m by setting
Pm(Ti)(vi 0 • • • 0 Vm) — Vi 0 • • • 0 Vi-i 0 aR(Vi 0 Vi+i) 0 Vi+2 0 • • • 0 Vm,
where a G End(F 0 V) is the interchange of the two factors. Indeed, it is
easy to check that the QYBE is equivalent to the braid group relations,
= Pm{Tj) Pm{T$Pm{Tj), if \i - j\ = 1,
and the remaining relations
Tj) = pm{Tj)pm{Ti), if \% - j\ > 1,
are obvious because if \i — j\ > 1 the operators pm(Ti) and pm(Tj) act on
disjoint pairs of factors in V0rn. Note that the representations pm are com-
compatible, in the sense that they fit into commutative diagrams
Pm+1
in which the left-hand vertical arrow is the natural inclusion Ti h-> Ti, i —
l,...,m-1.
15.2 Link invariants from quantum groups
505
Example 15.2.1 Let V — C2 with basis {t>o,t>i}, and let R be the endomor-
phism given by the matrix
1 0 0
0 A 0 0
0 1-A2 A 0
,0 0 0
with respect to the basis {vq ® vo> ^i <S> t>o, ^o ® ^i> ^i ® ^i> } of V (8) V. Up to
a rescaling and a change of parameter A = e~hr, this is the exactly the result
of evaluating the universal R-matrix of %E/2((C)) in its two-dimensional in-
indecomposable representation (cf. 6.4.12). Thus, R satisfies the QYBE. The
associated representation pm of Bm resembles the well-known Burau repre-
representation of Bm. In fact, note that
/I
Pm{Ti) =
\
1-A2 A
A 0
1/
with the 1 — A2 in the B4-1 + 2,24-1 + 2) position. By an obvious change of
basis in V®m, we obtain an equivalent representation in which
/I
C)
T
\
1-A2 A2
1 0
1/
One can check that the matrices C) still give a representation of Bm if we
interpret them as being m x ra, with the 1 — A2 being in the (z, i) position.
The line spanned by the vector A,1,..., 1) is obviously preserved by all these
operators, and the (ra — l)-dimensional quotient representation can be seen
to be irreducible; this is the Burau representation. <C>
Suppose now that a link L is the closure of a braid j3 (see Fig. 24). In view
of Markov's theorem, a first attempt to construct an invariant of L might
506 15 Quantum group invariants of knots and 3-manifolds
be to take the trace of pm(f3) (we shall not distinguish between C and its
equivalence class in Bm). This is independent of the choice of m because of
the compatibility of the representations pm, and is invariant under Markov I
because conjugating an operator does not change its trace. But it will not, in
general, be invariant under Markov II. Following Turaev A988), we therefore
make
Definition 15.2.2 Let V be a free module of finite rank over a commutative
ring k. An enhanced quantum Yang-Baxter operator onV^V is a quadruple
(R, /, A, ji) consisting of
(i) an invertible solution R G End(F <g> V) of the QYBE;
(ii) an invertible operator f G End(F) such that f ® f commutes with R;
(Hi) invertible elements X, \i G k such that
trace2(J o (/ <g> /)) = A///, trace2(/~1 o (/ <g> /)) = A"V/>
where I = o o R.
Remark It is no loss of generality to assume that A = \i = 1 in 15.2.2, for if
(R, /, A, ji) is an enhanced quantum Yang-Baxter operator, (A-1i^, /x/, 1,1)
is one too. However, it is not always convenient to make this normalization.
A
Here, and in the following discussion, if 0 < j < m and F G End(F0m) ^
End(V)^-1 (g)End(V) (g)End(V)®m-^, then trace^F) G End(V®m-1) is the
result of applying the usual trace in the jth factor of the tensor product. We
record two simple properties of these traces for later use. The proofs are easy
exercises.
Lemma 15.2.3 Let F G End(V^m+1), G G End(F®m). Then, we have
D) trace(tracem+i(F)) - trace(F),
E) tracem+i((G <g> idy) o F) = G o tracem+i(F). |
There is an invariant of oriented links associated to any enhanced quantum
Yang-Baxter operator (R, /, A,//). In fact, let a : Bm —-> Z be the augmen-
augmentation homomorphism, i.e. a{Tfx) — ±1 for i — l,...,m — 1; here, Z is
thought of as an additive group. Set
where pm : Bm —> End(Vr®m) is the representation associated to R.
15.2 Link invariants from quantum groups 507
Proposition 15.2.4 The map P : \\mBm —> k is invariant under the
Markov moves of types I and II, and hence defines an invariant of oriented
links.
Proof We give the proof to emphasize how straightforward Turaev's con-
construction is.
Indeed, invariance under Markov I follows from the property 15.2.2(ii) of
/. For that implies that f®m commutes with I^+i for all i, and hence with
the whole of Pm(Bm). As for Markov II, note that, if 0 G Bm, then
Pm(f3-Tm) = (pm(/3)
Since a@.Tm) = a@) + 1,
P@.Tm) = \-«W- V~mtrace((pm(/?) ® idv) o Jmm+1 o (id®™ 0 / 0 /)
^-1 0 (I o / ^ /)) o (/®»*-i ^ idy ^ idy))) by D)
- V~mtrace(pm(/?) o (id^ 0 trace2(J o / ® /))
otf^-^idv)) by E)
- V~mtrace(pm(/?) o (id^ 0 A/x/) o (j^™ 0 idy))
by 15.2.2(iii)
One deals with p.T^1 in a similar way. |
The problem now is to find a supply of enhanced quantum Yang-Baxter
operators. We are familiar by now with the fact that there is a solution of the
QYBE associated to any finite-dimensional representation V of the standard
quantization Uh (g) of a finite-dimensional complex simple Lie algebra g, which
can be obtained, in principle at least, by evaluating the universal R-matrix
of E/&(g) in the representation. We do not know if all R-matrices which arise
in this way can be enhanced. However, this is so if g is of type An, Bn, Cn or
Dn and V is the natural representation; the R-matrices in these cases were
written down in Section 7.3. Here, we concentrate on the An case.
Proposition 15.2.5 Let R e (Mn+i(C) (8) Mn+i(C))[[ft]] be the matrix
ii® En
2=0
508 15 Quantum group invariants of knots and 3-manifolds
where Eij is the matrix with a 1 in the (i,j)-posit ion and zeros elsewhere,
and let f be the diagonal matrix
/e-nh
f =
e-(n-2)h
\ enh ,
Finally, let A = e~(n+1^ and /j, — —1. Then, (—R, /, A, /i) is an enhanced
Yang-Baxter operator.
Moreover, the associated oriented link invariant Pn satisfies the equation
F) e^hPn(L+) - e-(n+1^Pn(Z_) - (eh - e-h)Pn(L0) = 0,
whenever L+, L_ and Lo are skein related (see Subsection 15.1A).
Proof The proof of the first part is a straightforward calculation. For the
second part, note that, if L+, L_ and Lq are skein related links, we may find
a braid /3 G Bm (say) such that L+, L_ and Lq are equivalent to the closures
of Tf1/?, Ti/J and ^, respectively. Hence,
_ e-(n+i)fcpn(x;_) _ (efc - e-h)Pn(Lo)
= (-l)-m+1e(n+1)/'A-Q(/3)+1trace(/oTO(Tf1/3) ° f0m)
o
- (eh - e-h)\aWtrace{Pm@) o
= (-l)-TO+1A-Q^)trace((J-1 - I - (eh - e-h)id02) ® id0
°,M/?)°/0m))
= o,
since one easily checks that I — —aoR satisfies I — I*1 = —(eh — e~h)\d®2.
Before proceeding further, note that
Together with the skein relation F), and the discussion in Subsection 15.1 A,
this implies that Pn takes values in the subring Z[q, q~x] of C[[/i]], where
h
= eh
The final step is to regard the sequence of (Laurent) polynomials Pn in the
single variable q as a single polynomial in two variables. To make this precise,
we need
15.2 Link invariants from quantum groups 509
Lemma 15.2.6 Let L be a link with r components. Choose a plane projection
L of L, and suppose that it has c crossings. Then, ifn > 4c + 2r, one has
(q-q~1r+rPn(L)= ? pa,bqa+{n+l)h,
a,beZ
where the integers pa^ have the following properties:
(i) pa^ = 0 for all but finitely many pairs (a, b);
(ii) Pa,b = 0 if \a\ >2c + r;
(Hi) the pa^ do not depend on n.
Proof Applying the skein relation F) inductively as described in Subsection
15.1 A, one sees that Pn(L) is a linear combination, with integer coefficients,
of terms of the form
i>n(oVn+1)e(9-<r1)/,
where e, / G 2, 0 < / < c and d < c + r. Next, one uses the skein relation to
compute
(see 15.1.2). Thus, (q — q~l)c+rPn(L) is a linear combination of terms of the
form q(n+l)e^qn+l _q-n-iy(Q_Q-iy+c+r-d^ gince y + c + r_^ < / + c + r <
2c + r, the lemma is proved. |
Now, with the notation in the lemma, let t be an indeterminate independent
of q and set
P(L) = (q- q-1)-^
It follows from F) that P satisfies the skein relation
tP(L+) - rlP(L_) -{q- q-^PiLo) = 0.
Furthermore, it is clear that
~, . t-t
Thus, if we set
t'1
and write x = y/—lt, y = —y^T(q — q x), then P satisfies the skein relation
A). We have therefore proved the existence of the HOMFLY polynomial (and
15.1.1).
510 15 Quantum group invariants of knots and 3-manifolds
Theorem 15.1.3 can be proved in a similar way. One shows that the R-
matrices associated to the natural representations of %(g), when g is of type
Bn, Cn and Dn, can be enhanced, and hence define invariants. One thus
obtains three sequences of invariants which are (Laurent) polynomials in a
single variable q. By combining them in a suitable way, one obtains a two-
variable invariant which satisfies the conditions in 15.1.3. See Turaev A988)
for the details.
B Link invariants from vertex models In Section 7.4, we discussed cer-
certain 2-dimensional models in statistical mechanics, called vertex models, in
which 'atoms' located at the vertices of a rectangular lattice 'interact' with
their nearest neighbours. The energy ?%j of a particular atom is a certain
function of the 'states' i, j, k, I of the edges of the lattice incident with the
atom. The physical properties of the model can be deduced from its partition
function
n
states vertices
where the Boltzmann weights
C being a constant, and the sum is over all possible assignments of states to
the edges of the lattice.
There is an obvious generalization of these rectangular lattice vertex mod-
models, for the same functions ?^1 can be used to associate a vertex model to
any oriented 4-valent graph, provided one decides on a way of numbering the
edges which meet at a given vertex. Since a plane projection of any link is a
4-valent graph (forgetting the over/under information), the partition function
associates a number to every oriented link. One may then try to choose the
Boltzmann weights in such a way that the partition function depends only
on the equivalence class of the link.
To carry out this program, we shall have to impose some conditions on the
Boltzmann weights beyond the quantum Yang-Baxter equation required in
Section 7.5. Unfortunately, although these conditions are necessary for the
topological applications we have in mind, they do not seem to be satisfied in
physically interesting models.
Definition 15.2.7 A vertex model consists of
(a) a finite-dimensional complex vector space V equipped with a distinguished
basis S;
(b) a family of endomorphisms R±(9) G End(F(g) V) parametrized by 0 G C;
(c) a family of invertible endomorphisms L@) G End(F), also parametrized
byOeC, of the form
L@)(s) = exp{f(sH)s for all s G <S,
15.2 Link invariants from quantum groups 511
where f : S —> C
TLese data are required to satisfy the following conditions:
(i) (L(-6)®idv)R±(9)(L(-6)®idv)-1 = (idv®LF))R±(9)(idv®LF))-1 -
R±(9 + 6), for all 9, 6 <E C;
(ii) /-(O) = /-^(O) (here, i± = a o i?±, cr being as usuai the interchange of
the factors in the tensor product);
(iii) (croJR+Gr)tri).(croJR_Gr)tr2) = idy (here, tr* : End(y®2) ^ End^H2 ->
End(l^)®2 taices the transpose of the ith factor, i = 1, 2);
fiv) R±(9) satisfy the quantum Yang-Baxter equation with spectral param-
parameters
for all 0,ye<? (R = R+ or R_).
Remarks [1] Condition (i) implies that R±(9) are completely determined by
R±{0) and L(9), and that L(9) (8> L((9) commutes with R±@). Conversely, if
these lattei conditions hold and we define
R±@) = (L(-0) (g) idv)iJ±(O)(Z,(-0) 0 idy)
= (idv 1
then R±{9) satisfies (i) (one makes use of the group property L(9 + 6) =
L@)LF)).
[2] By (i) again, the QYBE with spectral parameters in (iv) is equivalent
to the QYBE
G) ^12@)^13@)^23@) = #23 @)fli3 @)iJi2@)
(R = R+ or i?_). By (ii), R-@) is determined by #+@), and obviously
satisfies the QYBE if i?_@) does. Thus, R±(9) are, in fact, determined by
L@) and the single (constant) solution R+@) of the QYBE.
[3] The condition that L(9) <S> L(9) commutes with R+{0) is reminiscent of
condition (ii) in the definition 15.2.2 of an enhanced Yang-Baxter operator.
We shall discuss the braid-theoretic interpretation of vertex models later in
this subsection. A
Forgetting the over/under information in a plane projection L of an oriented
link L gives an oriented 4-valent graph. Given a vertex model as above, a
state of this graph is a map E from the edges of the graph to S. The discussion
in Section 7.5 suggests that we define the partition function of L by
= E II
states crossings
512 15 Quantum group invariants of knots and 3-manifolds
where
The choice of whether to use R+ or R- at a particular crossing, and the
convention as to the way in which the labels z, j, k and / are attached to the
edges, is indicated below:
use R+ use R_
The way the angle 0 is determined is also shown in these diagrams; it is chosen
so that 0 < 0 < 7T.
Unfortunately, Z(L) is not an invariant in general. This is the reason for
the extra datum in 15.2.7 consisting of the map / : S —> JR. If ? is any state
of L, let /s be the locally constant function on L which is equal to /(E(e))
along the edge e.
Definition 15.2.8 Given a vertex model as in 15.2.7, and a plane projection
L of an oriented link L, the partition function of L is
The angle 1-form dL was defined in Remark [4] following 15.1.3.
Proposition 15.2.9 The partition function Z defined above is an invariant
of regular isotopy.
Outline of proof Two plane projections define oriented links which are
equivalent under regular isotopy if and only if one can transform one into the
other by an isotopy of the plane, together with Reidemeister moves II and
III. Let us check invariance under the type II move:
15.2 Link invariants from quantum groups
513
j=n
The contribution to the partition function from the portion of the diagram
on the left is
while that of the portion of the diagram on the right is
exp@(/(i) - /(j))).
Hence, we must prove that
= exp(8(f(i) -
-1JR+W(idv-
Now,
kl
by condition (i) in 15.2.7. Similarly,
Thus, the equation to be proved is
This is obviously equivalent to condition (ii) in 15.2.7.
The other type II Reidemeister move
is dealt with in the same way. Invariance under the type III move
514 15 Quantum group invariants of knots and 3-manifolds
follows from conditions (i) and (iv), but for the other oriented type III moves
one must work a little harder, making use of the other conditions. Finally,
invariance of Z under plane isotopy follows from condition (i) (it essentially
guarantees that Z does not depend on the angles at the crossings). |
The partition function Z is not invariant under type I Reidemeister moves
in general, and so is not an isotopy invariant. Of course, one can obtain an
isotopy invariant by introducing kinks as described in Remark [4] following
15.1.3, but there is actually a simple extra condition on the model which
guarantees full isotopy invariance:
Corollary 15.2.10 The partition function of a vertex model defines an
oriented link invariant provided the following additional conditions hold:
(8)
tracei((LB7r)<g>idv)I±@)) = idy, trace2(/±@)(idy <8>L(-2tt))) = idy. |
The proof is straightforward.
Before giving examples of vertex models, we indicate the relation between
the last two results and the braid approach to constructing link invariants.
The solution i?+@) of the QYBE defines, as usual, a representation of the
braid group Bm on V®m for all m by letting the generator Ti of Bm act
as /+@) in the zth and (i + l)th positions. We define a Markov trace on
End(F®m) by
mtr(A) = trace(L(-27r)®m o A).
By Markov's theorem, these traces will define a link invariant provided they
are unchanged by the Markov moves, i.e.
mtr(/3/3/i9-1)=mtr(/3/)
mtr(/3T±1)=mtr(/3)
if /?, /?' € Bn
The first equation follows from the fact that L(—2tt) 0 L(—2tt) commutes
with i+@), which implies that L(—27r)<g)m commutes with every element of
15.2 Link invariants from quantum groups 515
The second equation follows from property (8): for example,
trace (L(-2n)®m+1/3Tm)
= trace(tracem+i(L(-27r)®m/3(id®m ® L@1
= trace(L(-27r)®m/3(id®m-1 ® trace2(/+@)(id
= trace(L(-27r)®m/3)
by (8).
We see from this calculation that the reason the usual trace does not define
a link invariant in general, because it is not invariant under Markov II, is
the same as the reason for including the 'angular term' exp( JL /s dL) in the
definition of a vertex model.
The next result shows that there is a vertex model associated to any finite-
dimensional representation of the standard quantization Uh(Q) of any finite-
dimensional complex simple Lie algebra g.
Let 1Zh be the universal R-matrix of Uh(Q) (see Chapter 8). If Yliriai
is the sum of the positive roots of g, set Hp* = ]TV diTiHi (see Subsection
11.3B). We recall that the square of the antipode Sh of {/^(g) is given by
S2h(x) = exp(hHp.).x.exp(-hHp.) (x e Uh(g)).
We shall write the right-hand side of this equation as Ad(exp(hHp*))(x).
Proposition 15.2.11 Let T : Uh(q) —> End<c[[/i]](V) be a finite-dimensional
representation of Uh(§), and set
R+@) = (T®T){Kh), i?_@) = o-(R+@r1),
C{6) = exp(-h6Hp. /2tt), L@) = T{C{6)).
Then, R±@) and L{0) define a vertex model in the sense of 15.2.7.
It is understood that R± (9) are defined in terms of R± @) as described in
the remarks following 15.2.7.
Proof Since TZh satisfies the QYBE, so does R+(Q). Next, we have
Applying T shows that Lh@) (8) Lh@) commutes with i?+(O).
It remains to prove property (iii) in 15.2.7. For this, we shall interpret the
transpose on the algebra level.
516 15 Quantum group invariants of knots and 3-manifolds
Let &h be the anti-involution of E/j^g) given on generators by
As in the classical case, V admits a non-degenerate symmetric C[[/i]]-bilinear
form ( , ) such that
(9) (x.vi, v2) = (vi, $h(x)-v2)
for all v\, V2 G V, x G ET/^g). We recall the construction briefly. We may
assume that V is indecomposable. Let v\ be a highest weight vector in V
of weight A G ^, say, and extend A to a homomorphism of C[[/i]]-algebras
U® —> (C[[h]\ (see Subsection 8.1 A for the notation). Now, if v\ = x\.v\ and
v2 = X2.v\, with xi, X2 G J7/i(g), one defines (t'l, ^2) to be the image of
)%2 under the composite map
where we have used the Poincare-Birkhoff-Witt factorization 8.1.8.
It follows from (9) that, if we work in an orthonormal basis of V with
respect to ( , ), the matrix of T($/l(x)) is the transpose of that of T(x), for
all x G Uh(Q).
We can now proceed with the proof. Define
nt(o) = Ad(c(~e)®i)(^), n-h{0) = Ad(c(-o)®i)((^1)-1).
Then, from the remarks following 15.2.7, R±@) = (T <g> T)G^@)), and
condition (iii) will follow if we prove that
in other words, 1Z^(n)Tl'^ (nJ1 = 1 (8> 1. Using the definitions, and the group
property of ?@), this is equivalent to
But, we observed above that Ad(?(—2tt)) = Ad(e/l^*) = 5^, so our assertion
follows from A5), Chapter 4. |
Remark The vertex model given by this proposition does not satisfy the ad-
additional property (8), even in the 5/2 case. However, the invariants of regular
isotopy given by 15.2.9 and 15.2.11 can often be 'rescaled' to obtain genuine
isotopy invariants. In particular, this can be done when g is of type An, Bn,
Cn or Dn, and V is the natural representation, and the resulting sequences of
15.3 Modular Hopf algebras and 3-manifold invariants 517
invariants can be combined to give the HOMFLY and Kauffman polynomials
in a manner similar to that described in the previous subsection. A
15.3 Modular Hopf algebras and 3-manifold invariants
Suppose that a 3-manifold M is obtained by surgery along a framed link L in
S3. The methods of Section 5.3 enable us to associate to this link, equipped
with a suitable colouring, an isotopy invariant. In this section, we show
that, by taking suitable combinations of such invariants, one can construct
an invariant of M itself. We begin by describing the class of colourings we
shall need.
A Modular Hopf algebras Recall from Subsection 4.2C that a ribbon Hopf
algebra (A, 7?, v) over a field k (say) is a quasitriangular Hopf algebra (A, 7V)
equipped with an invertible central element v satisfying certain conditions
(given in 4.2.8) which imply that the element g = uv~x is group-like, where
u = fi(S ® id)G2.21 )• Recall further that, if py : A —> End(V) is a finite-
dimensional A-module, the quantum trace of a /c-linear map / : V —> V is
defined to be qtr(/) = trace(py(g) o /); in particular, taking / = idy gives
the quantum dimension qdim(F). Recall finally that the left and right duals
of V are canonically isomorphic or, equivalently, the second (left) dual F** is
canonically isomorphic to V: in fact, the isomorphism V** —> V is essentially
given by the action of g.
With these definitions in mind, we can state
Definition 15.3.1 A modular Hopf algebra is a ribbon Hopf algebra
(A,1Z,v) over a field k equipped with a distinguished family {V(\)}\ec of
irreducible A-modules, indexed by a finite set C. The set C is equipped with
an involution A i—» A* and a distinguished element 0 such that 0* = 0 and V@)
is the trivial module. Finally for each A G C, one is given an isomorphism of
A-modules
ujx : V(\)* - V(X*).
These data are required to satisfy the following conditions:
(i) qdim(F(A)) ^ 0 for all A G C;
(ii) the composite map
•T1
v(\) —> v(\*y —* v(\)** -> v(\),
the last map being the canonical isomorphism of vector spaces, is given by
the action of the element g G A;
518 15 Quantum group invariants of knots and 3-manifolds
(Hi) for any Ai,..., Ar G C, we have
(8) • • • <8> V(Ar) = Zi
as A-modules, where m\ G N and tLe module Z has the property
qtr(/) = 0
for aii A-moduie endomorphisms f of Z;
(iv) ifs\^ is the quantum trace of the map V(AH V(/i) —> V(AH V(/i) given
by the action oflZ2iTl, then the matrix (sa/z)a,/zec is invertible.
Remarks [1] In condition (iv), we are using the obvious fact that, if (A, 7ZA, vA)
and (B,7ZB ,vB) are two ribbon Hopf algebras, then their tensor product
A ® B, equipped with the usual Hopf algebra structure, is itself a ribbon
Hopf algebra, the universal R-matrix being TZi^TZ^, and the distinguished
central element vA 0 vB.
[2] Reshetikhin & Turaev A991) included an additional condition when they
introduced the notion of a modular Hopf algebra. Suppose that the central
element v acts on V(A) by the scalar v\\ this will hold if k is algebraically
closed or, more generally, if the V(A) remain irreducible over an algebraic
closure of k. Since the matrix (s\^) is invertible, there are unique scalars
(d\)\ec such that
A0) ^vxsx^dx = v^qdimiVifji)), (fi € C).
xec
Then, the additional condition was that the scalar
A1) c =
xec
is non-zero. We have omitted it because it was proved by Turaev & Wenzl
A993) that it is actually a consequence of the other conditions in 15.3.1. A
In the next subsection, we show how to associate a 3-manifold invariant to
any modular Hopf algebra, but first we describe an example.
Conditions (i)-(iii) are reminiscent of the properties of tilting modules ob-
obtained in Section 11.3, so natural candidates for modular Hopf algebras are
the quantum groups ?/eres(g) studied there, e being a root of unity, together
with the family of irreducible representations V7es(A) with highest weights A
lying in the set
Ce = {XeP+ | (A + p,d) <? for alia e A+}.
15.3 Modular Hopf algebras and 3-manifold invariants 519
These representations are irreducible under the finite-dimensional subalgebra
?/€fin(g) of ?/€res(g) by 11.2.10, and ?/€fin(g) is quasitriangular by 9.3.9. Unfor-
Unfortunately, however, these data do not define a modular Hopf algebra, since
condition (iv) is not satisfied (even when g = sl2((E))- The way to proceed
was shown by Reshetikhin & Turaev A991), at least in the s/2 case.
We work with the 'simply-connected' quantum group (see Subsection 9.1A).
Namely, we let Ufn be the associative algebra over C with generators L±l,
X± and defining relations
(X±)e = 0, Lu = 1.
Here, e = e^^71"/2^ where ? is any integer greater than one (not necessarily
odd). The Hopf algebra structure is given by
S(L) = L~\ 5(X+) = -X+L, S(X~) = -L2X~,
e(L) = l, e(X±)=0.
The following formulas define a representation of Ufn on the vector space
^"(A) with basis {fo,t>i,. •. ,v\}:
L.vr = ex~2rvr, X+.vr-[A-r+lW_i, X~.vr = [r + l]c2iv+i.
It is easy to see that the representation t^fin(A) is irreducible if and only if
0 < A < ? — 1, and that all such representations are isomorphic to their (left)
duals.
Theorem 15.3.2 The Hopf algebra U^n, together with the family of repre-
representations {Vrefin(A)}o<A<€-i? is a modular Hopf algebra.
Outline of proof The first step is to show that Ufn is quasitriangular.
For this, one verifies by a direct calculation, analogous to that used in the
proof of 6.4.8, that
e-i u-i ( 2 _ 2)n
U= pYlY. r I , en{n~l)~abLa{X+)n ® Lb{X~)n
satisfies the conditions in 4.2.1 and 4.2.6(ii) (see 9.3.9). That Ufn is actually
a ribbon Hopf algebra now follows easily from the general results on quasi-
quasitriangular Hopf algebras in Section 4.2 and the observation that the square
520 15 Quantum group invariants of knots and 3-manifolds
of the antipode S of Ufn is given by conjugation by the group-like element
Properties (i)-(iii) in 15.3.1 follow by arguments similar to those used in
Section 11.3. To verify the crucial condition (iv), we must compute the matrix
(sam). Now, using the functor T constructed in 5.3.7, with X =
we have
= JH the Hopf link
= F\ closure of
V I
A2)
(the second equality uses 5.3.6). For the last equation, we used the fact that
the endomorphism in question is a scalar, since ^"(A) is irreducible. It may
therefore be computed using the diagram
to be the composite map
t>fin(A)
I
VeRn(fj,)*
0 v;fin (//)** 0 Kfln(
VeRn(X)
15.3 Modular Hopf algebras and 3-manifold invariants 521
given by
(the notation is that used in Subsection 5.3A). We can compute this scalar
endomorphism by evaluating it on any non-zero vector. If we choose the
highest weight vector v\ of Kfin(A), then only the n = 0 terms in 1Z2i do
not annihilate va, and then only the n = 0 terms in 7^12 need be considered,
otherwise the quantum trace will vanish. Thus, we get
A 4?-l
b) f (T a+h'\
a,6,a',6/=O
Now,
4€-l /4€-l
1 V f-o.b-a'b'+\{a'+b) _ _J_ ( V^ VCA-
16?2 Z. e - 16?2 I 2^ e
a',6=0 W=0
Thus, the desired scalar is equal to
[BA + 2)(M + l)]e _ [(A
Comparing with A2), we have finally
The proof of condition (iv) is now straightforward. For the easily proved
identity
? 2
shows that the square of the matrix (sa/z) is equal to ^/2 times the identity
matrix. |
Remark Turaev & Wenzl A993) show that one can associate to ?/fn(g), for
all g of type A, B, C or D, a 'quasi-modular Hopf algebra'. This is a slightly
weaker notion than that of a modular Hopf algebra, but it still leads to 3-
manifold invariants. However, the methods of Turaev and Wenzl make use
of the special properties of certain representations of ?/efin(g) when g is of
classical type, and it would be desirable to find a proof which works for all g
simultaneously. A
522 15 Quantum group invariants of knots and 3-manifolds
B The construction of 3-manifold invariants Let M be a compact,
connected, oriented 3-manifold without boundary. Choose a framed link L
in 53, with components K\,..., ifm, such that the manifold Sl obtained by
performing surgery along L is orientation-preserving homeomorphic to M;
recall from Subsection 15.IB that Sl is the boundary of a compact 4-manifold
Dl> Fix an orientation lj of L. As we explained in Subsection 15.IB, we may
view L as a directed ribbon tangle (with annuli but no bands); by an isotopy
of 53, we can arrange that L C R2 x @,1) C R3 C 53. Fix a modular Hopf
algebra as in 15.3.1, and let A = (Ai,..., Am) G Cm be a colouring of L with
the elements of C. Theorem 5.3.7 associates to these data a homomorphism
of ^.-modules k —> &;, i.e. a scalar T{L, A) G k.
We need one further piece of topological data before we can state the main
result of this section. Consider the intersection pairing on the homology group
#2(Al;R)- This is a symmetric bilinear form; let cr<o(L) be the number of
non-positive eigenvalues in a diagonal representation.
Theorem 15.3.3 Fix a modular Hopf algebra A as in 15.3.1. Let SL be the
compact, connected, oriented 3-manifold without boundary which is obtained
from S3 by surgery along an oriented, framed link L with m components
coloured with representations V(Ai),..., V(Am) of A, where Ai,..., Am ? C.
Let
rEL,lj, L) = cT^°<L> ]T IJ dx%HL,\) G A;,
A i=l
where cr<o(L) and F(L,X) are as defined above and the scalar c is defined in
A1). Then, t(Sl->u,L) is a topological invariant of Sl-
The last sentence means that, if L' is another framed link in 53 with
orientation a/, and if Sl> is orientation-preserving homeomorphic to Sl, then
t(Sl>,u/,L/)=t(Sl,u,L).
Outline of proof By Subsection 15.IB, to show that t(M,u,L) depends
only on 5l, and not on L, it is enough to show that it is unchanged by special
Kir by — 1-moves and by Kir by -l-1-moves (we shall not discuss the proof that
r(M, a;, L) — t(M, L) is independent of the orientation lj of L).
In the former case, we start with a ribbon tangle which is the union of a
ribbon tangle (= framed link) L and an unknotted annulus if, not linked to
L, with one full right-hand twist:
The special Kirby — 1-move consists simply in deleting (or inserting) K. Let
15.3 Modular Hopf algebras and 3-manifold invariants
523
Xl be any colouring of L, \k any colouring of K, and denote the correspond-
corresponding colouring of L U K by (Al, A#). Since the functor T constructed in 5.3.7
is a monoidal functor,
T[L U K, (AL, XK)) = f(L,XL)T(K, A*)
(we have omitted the tensor product since all three endomorphisms are
scalars). Since a<0(L U K) = cr<o(L) + 1, the definition of r gives
t(SLuK,LuK)=t(Sl,L)c
-1
But, by 5.3.5,
so T{K, \k) = 1 by the definition of c in A1).
In the case of a Kirby +l-move, we have the situation in Fig. 25, where K
is now an unknotted annulus with one full left-hand twist, and the r (say)
vertical strands represent the components of the complement L of K which
are linked with K. We can assume that L is the closure of a tangle T' o T,
where T is the tangle shown in the left-hand diagram in Fig. 25, and Tf is
some tangle with r free ends at the top and bottom. The effect of the Kirby
+l-move is to delete K and replace T with a tangle f obtained by performing
a single left-hand twist of the r strands (cf. Fig. 25):
T
Let L be the closure of V o T. Denoting colourings of L U K as before, we
have
T(SLUK,LUK)= ]T dXK
\LeCri=l
by 5.3.4, and, similarly,
t(Sl,L)=
524 15 Quantum group invariants of knots and 3-manifolds
So it is enough to prove that
A3) Y, dXKqtv(HTf o T, (AL, XK))) = qtr(^(T' o f ,AL)).
Suppose first that r = 1. In this case, we have the stronger result
A4) Y, d^HT, (AL, Ax)) = f(f, AL),
from which A3) follows by using the functoriality of T and the linearity of
the quantum trace. To prove A4), let T{T, (Al, \k)) = f\L\K; note that
f\L\K is an ^4-module endomorphism of the irreducible module V(Al), and
so is a scalar. To compute it, note that, if T denotes the closure of T, then
•F(T, (Al, A*-)) = /At,A*qdim(V(AL))
by 5.3.4, while a computation similar to that in 5.3.6 shows, on the other
hand,that
F(T,(\l,\k))=vXksXlXk
in the notation of 15.3.1. Thus,
HT,(\L,\K))=vXKsXLXK(qdim(V(\L)))-\
On the other hand, we found in 5.3.5 that !F(f, \l) — v^1 - Thus, A4) is a
consequence of A0).
To prove A3) for arbitrary r, let Ai,..., Ar be the colours of the strands
incident with the top of X", and ei,..., er the signs indicating their directions.
Note that ^(T'oT, (AL, A*-)) and F(T'of,\L) are ^-module endomorphisms
of V/1 (8) • • • (g) V^ (recall that Ve = V oy V* according as e = +1 or -1; we
have written Vi for V(\i)). Write
A5) Vf1 (8) • • • (8) Vr€r ^ Z 0 0 V(A)emA
xec
as in 15.3.1(iii). Writing the endomorphisms in question in block matrix
form with respect to the decomposition A5), we must compute the sum of
the quantum traces of the diagonal blocks. Those of the Z-Z blocks vanish
by 15.3.1(iii), since they are composites
Z -^ ®V(A2)e* - ®V(\i)€* ^ Z,
where the first and last homomorphisms are the obvious inclusions and pro-
projections. As for the V(X)^rnx-V(X)^rnx blocks, it is easy to reduce to the
15.3 Modular Hopf algebras and 3-manifold invariants 525
T
T
n
case m\ = 1 by writing V(\)®mx = V(A) (8) M(X) and choosing a basis of the
multiplicity space M(A), and in that case it suffices to prove that
dXKGrvwoT(TfoT,(\L,\K))oLV{x)) = nvw°?(T'of,\L)°<>v(\),
A6)
(or in fact, just that both sides have the same quantum trace), where
and 7iV(A) are the obvious inclusions and projections. The pictures necessary
to compute the two sides of A6) are shown above, in which the upper and
lower boxes are coupons representing iy{\) and flV(A)> respectively (and here
we need the generalization 5.3.7 of 5.3.2). Equation A6) follows immediately
from these diagrams, using the r = 1 case together with the functoriality of
T. |
The construction of invariants of 3-manifolds we have outlined can be ex-
extended without much difficulty to the case of coloured ribbon tangles in ar-
arbitrary compact, oriented 3-manifolds. See Reshetikhin & Turaev A991).
Bibliographical notes
15.1 This section merely summarizes the terminology and basic results used
in the remainder of the chapter. For further information on braids and links,
the reader should consult one of the many standard sources, such as Birman
A976) for braids and links, and Rolfsen A976) for links and 3-manifolds.
15.2 The polynomial link invariant discovered by Jones A985) arises from
representations of the braid groups Bm which factor through the Hecke alge-
algebra Tim (see 10.2.1), and the Markov trace is provided by a canonical trace
526 15 Quantum group invariants of knots and 3-manifolds
on the Hecke algebra itself, discovered by A. Ocneanu. As we saw in Section
10.2, the Birman-Murakami-Wenzl algebra is to Lie algebras of type I?, C
and D as 7Ym is to type A, and in fact Birman & Wenzl A989) showed how
to associate link invariants to representations of the BMW algebra.
Our discussion of the braid-theoretic approach to link invariants is based
on Turaev A988). 'Universal' approaches to this question have been given by
Lawrence A989) and Drinfel'd A990b). The former depends on constructing
an invariant in a certain enlargement of a quantized universal enveloping
algebra which gives scalar invariants on applying suitable representations.
The latter is based on quasi-Hopf algebras, discussed in the next chapter.
Date, Jimbo, Miki & Miwa A990, 1991c) gave an analogous construction
of link invariants for the non-restricted specialization U€(q) of C/g(g) at a root
of unity e (for some g of low rank). As we saw in Section 11.1, even though
?/e(g) is not quasitriangular, certain families of its representations commute
under tensor product, and the intertwiners may still give solutions of the
QYBE. If one can construct a Markov trace, one obtains link invariants in
the usual way. Rosso A992c) gives an alternative approach by showing that
one can construct a universal R-matrix for the 'part' of G€(g) relevant to the
representations one is interested in.
Our discussion of the vertex model approach to link invariants is based
on Jones A989) and Rosso A988c). For further information, see Kauffman
A991b).
15.3 The work of Reshetikhin & Turaev A991) summarized here was moti-
motivated, as we said in the introduction, by Witten A989), although only later
were the two constructions proved to be equivalent, by Walker A991). The
invariants arising from quantum s/2 are studied in more detail by Kirby &
Melvin A991) and Kirby, Melvin & Zhang A993). The properties of the in-
invariants associated to Lie algebras of classical type by Turaev & Wenzl A993)
do not seem to have been investigated in detail yet.
As these words are being written, an understanding is beginning to emerge
of the meaning of the invariants of Witten, and Reshetikhin and Turaev, in
terms of 'classical' algebraic topology. This is based on the construction by
Vassiliev A990, 1993) of knot invariants by analysing the singularities of the
'space of all knots'. It appears that, if one replaces q (or e) by eh in a quantum
group invariant, the coefficients of powers of h in its power series expansion
are Vassiliev invariants. See Birman A993) and Birman & Lin A993).
16
Quasi-Hopf algebras
and the
Knizhnik-Zamolodchikov equation
We saw in Section 5.1 that the category of representations of a Hopf alge-
algebra is monoidal, which means essentially that it is equipped with a tensor
product which is associative up to isomorphism. In fact, the coassociativ-
ity property of a Hopf algebra means that the associativity isomorphisms
G 0 (V 0 W) —> (U 0 V) 0 W can be taken to be the natural isomorphisms of
vector spaces. This suggests that one might be able to relax the coassociativ-
ity condition and still obtain a monoidal category, perhaps with non-trivial
associativity isomorphisms. The rigidity of the category of representations of
a Hopf algebra, which depends on the properties of its antipode, might also
be retained by replacing these properties by some suitable analogue. These
suggestions are realized in the notion of a quasi-Hopf algebra, which we define
in Section 16.1. Although the category of quasi-Hopf algebras is larger than
the category of Hopf algebras, it turns out to be more manageable because
it admits a kind of 'gauge group', which sometimes allows one to 'twist' a
given quasi-Hopf algebra into an apparently simpler one, but one which has
the 'same' representation theory as the original quasi-Hopf algebra.
Section 16.2 describes the relation, due to V. G. Drinfel'd but implicit in
earlier work of T. Kohno, between quasi-Hopf algebras and a certain system
of first order partial differential equations for a function of m (say) complex
variables, called the Knizhnik-Zamolodchikov (KZ) equation. The KZ equa-
equation first appeared in conformal field theory, as the equation satisfied by the
'ra-point functions' of the theory, but it has since proved to play an impor-
important role in several areas of mathematics. Of most importance to us is that,
by considering the monodromy of its solutions along closed paths, it leads to
representations of braid groups. There is actually one KZ equation for each
solution of the classical Yang-Baxter equation with spectral parameters, but
we shall need only the one corresponding to the r-matrix underlying the Yan-
gians y(g), where g is a finite-dimensional complex simple Lie algebra (see
Chapter 12).
The main result of Section 16.2 is that, if Uh(o) is the standard QUE
algebra associated to g, and IZh is its universal R-matrix, the braid group
representation defined by IZh (see Subsection 15.2A) is equivalent to that
528 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
denned by the KZ equation. This can be viewed as a 'quantization' theorem,
since the two braid group representations arise essentially from a solution of
the QYBE and a solution of the CYBE, respectively, and indeed the proof
proceeds by using the KZ equation to construct a quantization of a certain
'quasi-Lie bialgebra'.
The Kohno-Drinfel'd theorem shows that the category of finite-dimensional
representations of Uh{$) is equivalent, as a quasitensor category, to the cat-
category of finite-dimensional representations of g itself, equipped with a qua-
quasitensor structure defined using the KZ equation. D. Kazhdan and G. Lusztig
proved an extension of this result, relating the category of finite-dimensional
representations of [/,fes(g), where e G (Cx, to a certain category of represen-
representations of level k of the (classical) afRne Lie algebra g, where e = e->/-!*¦/«;
the Kohno-Drinfel'd theorem can be viewed essentially as the e —> oo limit
of Kazhdan & Lusztig's result. It goes without saying that the quasitensor
structure on the latter category is not given by the usual tensor product of
representations of g, since under that tensor product the levels add. The
definition of the required tensor product, and the proof that it gives rise to
a quasitensor category, is rather difficult, and again makes use of (a general-
generalization of) the KZ equation. We outline this work of Kazhdan and Lusztig
in Section 16.3.
It is a consequence of Kazhdan and Lusztig's theorem that the conjecture
of Lusztig stated in Subsection 11.2C, which determines the characters of the
finite-dimensional irreducible representations of the quantum groups J7€res(g)
when e is a root of unity, is true.
A connection between quantum groups and classical affine Lie algebras
was predicted in the literature on conformal field theory, although physicists
are mainly interested in unitary representations of g, which are excluded
from the category considered by Kazhdan and Lusztig. However, there is
a parallel result, very recently proved by M. Finkelberg, which establishes
an equivalence between a category of representations of g which includes
these 'physical' representations (but not those considered by Kazhdan and
Lusztig!), and the 'truncated' category of tilting modules tilt€ discussed in
Section 11.3.
Section 16.4 sketches a remarkable relation between quasi-Hopf algebras
and algebraic number theory, specifically the structure of the 'absolute Galois
group' Gal(Q/Q). This relation was discovered by Drinfel'd, but some aspects
of it were certainly foreseen by A. Grothendieck in 1984, in his 'Esquisse d'un
programme'.
16.1 Quasi-Hopf algebras
In this section, we define a generalization of the notion of a Hopf algebra,
16.1 Quasi-Hop} algebras 529
called a quasi-Hopf algebra, and study some of their basic properties.
A Definitions The relation between quasi-Hopf algebras and Hopf algebras
is similar to that between almost cocommutative Hopf algebras and cocom-
mutative Hopf algebras. In the latter case, one weakens cocommutativity to
'cocommutativity up to conjugacy', while in the former case one does some-
something similar with associativity.
Definition 16.1.1 A quasi-bialgebra over a commutative ring k is an as-
associative algebra A over k together with homomorphisms ca ' A —> k (the
counit) and A a : A —> A<g> A (the comultiplication), and an invertible element
<&a G A 0 A 0 A (the coassociator), satisfying the following conditions (we
omit the subscripts):
A) (id <g> A)(A(a)) = ^.(A <g> id)(A(a)).<S>,
for all a G A;
B)
(A (g> id (g> id)($).(id 0 id 0 A)($) = ($ <g> l).(id <g> A
C) (e 0 id) o A = id = (id 0 e) o A;
D) (id 0e0id)($) = 1.
A quasi-Hopf algebra is a quasi-bialgebra A equipped with an anti-homo-
morphism Sa • A —¦> A (the antipode), and elements a a, Pa ? A, such that
E)
for all a e A,
F)
where
A(a) = ^ ar 0 aj., * = ^ <^a 0 ^ 0 ^, ^> = ^ ^ 0 fit ® <Pt
P
If B is another quasi-bialgebra (resp. quasi-Hopf algebra), an algebra ho-
momorphism f : A —» B is a homomorphism of quasi-bialgebras (resp. of
quasi-Hopf algebras) if
530 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
(resp. and Sb ° / = /
Remarks [1] A Hopf algebra is the same thing as a quasi-Hopf algebra for
which a = C = 1 and $ = 1 0 1 0 1.
[2] If u is an invertible element of A, and if 5, a and /? satisfy E) and F),
then so do 5, a and /?, where
G) S(a) = uS(a)u-1, a = ua, C = Cu~l.
Conversely, one can show that if 5, a, /3 and 5, a, /3 both satisfy E) and F),
there is a unique u G ^4 for which G) holds. Thus, 5, a and fi are essentially
uniquely determined, if they exist. It can be shown further that the two
equations in F) are equivalent, in the presence of conditions (l)-E). A
Proposition 16.1.2 If A is a quasi-Hopf algebra over a commutative ring
k, then the category rep a of A-modules, which are finitely generated and
projective as k-modules, is a rigid, k-linear, monoidal category
Outline of proof The associativity isomorphisms
:U®(V®W)->(U®V)®W
are given by the action of $. That the au,v,w are ^-module homomorphisms
follows from A), and the commutativity of the pentagon diagram in 5.1.1(i)
follows from B).
The trivial module k and the tensor product of A-modules are denned
using the counit and comultiplication of A, as in the case of Hopf algebras.
The fact that, for any A-module [/, the natural maps pu : U 0 k —> U
and \u : k ®U —> U are A-module isomorphisms follows from C), and the
commutativity of the diagram in 5.1.1(ii) follows from D). The (left) dual
U* of an A-module U is also defined as in the case of Hopf algebras, by using
the antipode. But the isomorphisms evu : U* ®U —> k and ixu : k —* U 0 U*
are now given by
if ( , ) is the natural pairing and {u^ and {?*} are dual bases of U and U*.
That these maps are A-module homomorphisms follows from E), and the
commutativity of the diagrams in Subsection 5.1C follows from F). |
In view of this result, and of those in Section 5.1, it is natural to ask what
further conditions on a quasi-Hopf algebra A will ensure that rep^ is a tensor
or quasitensor category.
16.1 Quasi-Hopf algebras 531
Definition 16.1.3 A quasitriangular quasi-Hopf algebra is a quasi-Hopf al-
algebra A equipped with an invertible element ft G A® A, called its universal
R-matrix, such that
(8)
(9)
A0)
(A
(id
> A)(ft) =
for all a € A. Here, if$ = J^r Vr®<Pr®Vri we define $23i = r
etc. If, in addition, ft satisfies the relations
A1) n2l=UY2\ (e®c)(ft) = l,
then A is said to be triangular.
Quasitriangular and triangular quasi-bialgebras are defined in the same
way, dropping the requirement of the existence of an antipode.
Remark The universal R-matrix of a quasitriangular quasi-Hopf algebra is a
solution of the 'quasi-quantum Yang-Baxter equation':
A2) ftl2*231lftl3*132ft23*r23 = *r32^23*312^13*213^12.
In fact, using (9) and A0), the left-hand side is equal to ft 12(A 0 id)(ft), and
the right-hand is equal to (Aop 0 id)(ft)fti2, so the result follows from (8).
A
From 16.1.2, we obtain
Corollary 16.1.4 If A is a quasitriangular (resp. triangular) quasi-bialgebra,
then rep a is a quasitensor (resp. tensor) category.
Proof The commutativity maps oyy : U 0 V —* V 0 U, for any objects U
and V in rep^, are denned exactly as in the case of Hopf algebras (cf. 5.2.2).
The axioms in 5.2.1 follow immediately from (8)—A1). |
At first sight, the category of quasi-Hopf algebras appears to be more diffi-
difficult to work with than the category of Hopf algebras, but in fact the opposite
is true, because the former category admits a kind of 'gauge symmetry', which
we have already encountered in a restricted form in Subsection 4.2E. Namely,
let A be any quasi-bialgebra and let T be an invertible element of A 0 A such
that
A3)
Set
A4)
A5) & = JF
532 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Proposition 16.1.5 Let A be a quasi-bialgebra (resp. quasi-Hopf algebra)
and T G A® A an invertible element satisfying A3), and let AT be the algebra
A, equipped with the same counit (resp. and antipode) as A, but with the
comultiplication A^ and coassociator ^ defined in A4) and A5). Then, A^
is a quasi-bialgebra (resp. a quasi-Hopf algebra).
If A is quasitriangular with universal R-matrix 1Z, then A^ is quasitrian-
quasitriangular with universal R-matrix 1Z^ — T^x^T^ -
Proof A straightforward verification. The elements a and fi in E) and F)
appropriate to A^ are given by
i? \ ^ ~~ —/ i? \ ^
s r
where Jr=Y,rfr® f'n F~l =Y,sfs® Is- ¦
We shall say that two quasi-bialgebras (or quasi-Hopf algebras) A and B
are twist equivalent if B = A^ for some T G A 0 A as above. This is an
equivalence relation, for it is easy to see that twisting with T\ and then with
JT2 is the same as twisting with J^-^i-
Twisting has a simple category-theoretic interpretation:
Proposition 16.1.6 Suppose that two quasi-bialgebras A and B are twist
equivalent. Then, rep a and reps are equivalent as monoidal categories. If A
and B are quasitriangular, then rep a and repB are equivalent as quasitensor
categories.
Proof We have to construct an equivalence of categories / : rep^ —> rep^,
together with a natural isomorphism X between the bifunctors
(U,V)~f(U®V) and (U,V) » f(U)® f(V),
and an isomorphism i : f(k) —> /c, such that the following diagrams commute:
{Tu, v <8> id f (w)) °Zu ® v, w
f((U®V)®W) > (f(U)®f(V))®f(W)
f{<XU,V,w) af(U),f(V),f(W)
f(U®{V®W)) > f(U)®(f(V)®f(W))
(id f (u) (g) Xy, w) °Zu, v ® w
f(u®k) -^ f(u)®f{k)
f(U) —^ k®f(U) f(U) ^^ f(U)®k
If B = A^, we can take / and i to be the identity, and Xjjy to be the image
We leave it to the reader to write down, and prove commutative, the dia-
diagrams necessary to establish the second part of the proposition. |
16.1 Quasi-Hopf algebras 533
B An example from conformal field theory We illustrate the preced-
preceding definitions and results with a very interesting example due to Dijkgraaf,
Pasquier & Roche A992).
Example 16.1.7 Let G be a finite group, C[G] its group algebra over the
complex numbers, and T(G) the algebra of complex-valued functions on G.
Let c:GxGxG—>Tbea 3-cocycle on G with values in the circle group
T. This means that
c(y, z, w)c{xy, z, w)~xc{x, yz, w)c(x, y, zw)~lc(x, y, z) = 1
for all x, y, z, w G G. We assume that c is normalized, i.e. that c(x, y, z) — 1
if x, y or z is equal to the identity element e G G. We define a quasi-Hopf
algebra T>C(G) as follows.
As a vector space, VC(G) = F(G) <S> C[G]. It has a basis consisting of the
elements Sg ® x, where #, x G G, and ?p denotes the 'Dirac delta function,'
i.e. 8g{h) = 1 \i h — g and ^(h) = 0 otherwise. Let
c@, x, y)c(x, y, (xy)~lgxy)
uxy)
c(x,x-1gx,y)
c(g, ft, x)c(x, x~lgx, x~lhx)
c(g,x,x~1hx)
The multiplication of VC(G) is defined by
F9®x).Fh®y) = I
0g(x, y)(Sg (8) xy) if ^x = xft,
0 otherwise,
the unit element being 1 = Ylgfig ® e). The comultiplication, counit and
antipode are defined by
AFg®x)= ^2 7x(h,k)Fh®x)®(Sk ®x), eFg ®x) = ^>e 1,
Finally,
g,h,k?G
One checks that condition B) in 16.1.1 is equivalent to the cocyle property
of c. Conditions C) and D) follow from the normalization of c, while the
534 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
associativity of multiplication, the fact that A is an algebra homomorphism,
and condition A), respectively, are consequences of the following identities:
0g(x, yNg(xy, z) = 0g(x, yzNx-igx(y, z),
gh, k)c(x~lgx, x~lhx, x~lkx) = jx(h, k)jx(g, hk)c(g, ft, fc).
These identities in turn follow by repeated use of the cocycle property of c.
It is easy to see that, if c is the trivial cocycle c(g, ft, A:) = 1, then T>C(G) is
exactly the quantum double of !F{G) (see Subsection 4.2D). Since quantum
doubles form the most important examples of quasitriangular Hopf algebras,
it is natural to expect that, for any 3-cocycle c, VC(G) is a quasitriangular
quasi-Hopf algebra. This is indeed the case, the universal R-matrix being
given by the same formula as for the quantum double:
geG
It is also natural to ask when two of the quasi-Hopf algebras T>C(G) and
T>c (G) are twist equivalent. It is not hard to see that this happens precisely
when the 3-cocycles c and d are cohomologous. In fact, if d — c = db for some
map b : G x G -> T, then Vc>'(G) = VC{G)T', where
:F=
9,h?G
Thus, the quasi-Hopf algebras VC{G) are classified, up to twist equivalence,
by the cohomology group H3(G,T).
Dijkgraaf et al. A992) show that the category of finite-dimensional rep-
representations of VC(G) is semisimple, and that its fusion ring is isomorphic
to that of an 'orbifold' conformal field theory with symmetry group G (see
Subsection 5.2E). In view of the result of the preceding paragraph and 16.1.6,
this suggests that such conformal field theories might themselves be classified
by H3(G,T). Dijkgraaf & Witten A990) proved that this is indeed the case.
(We have actually reversed the historical order of the development of these
ideas.) 0
C Quasi-Hopf QUE algebras The quasi-Hopf algebras of most interest
to us are deformations of universal enveloping algebras. By a deformation
of a quasi-bialgebra A over a field &, we mean a topological quasi-bialgebra
Ah over fc[[ft]] such that A^/hAh = A as quasi-Hopf algebras over fc, and
Ah = -A[[ft]] as A:[[ft]]-modules. We assume also that the coassociator $h of
Ah is = 1 0 1 <S> 1 (mod ft). As in the case of Hopf algebras, the adjective
'topological' means that all tensor products appearing in 16.1.1 are to be
understood in the ft-adically completed sense. Furthermore, again as in the
Hopf case (see Subsection 6.1A), one can show that any deformation of a
quasi-Hopf algebra as a quasi-bialgebra is, in fact, a quasi-Hopf algebra.
16.1 Quasi-Hop} algebras 535
Definition 16.1.8 A quasi-Hopf QUE algebra is a quasi-Hopf deformation
Ah of the universal enveloping algebra U(g) of a Lie algebra g over a field k,
such that the coassociator <f>h of Ah satisfies the following condition:
A6) Yl (^kiM2M3) = 1 <g> 1 <g> 1 (mod h2).
A quasi-Hopf QUE algebra Ah is topologically quasitriangular if it is qua-
sitriangular as a quasi-Hopf algebra and its universal R-matrix IZh G Ah® Ah
(completed tensor product) satisfies IZh = 1 0 1 (mod h).
Remarks [1] If Ah is a quasi-Hopf deformation of U(q) which has a universal
R-matrix IZh = 101 (mod ft), then condition A6) follows automatically from
(9) and A0).
[2] When we consider twists of quasi-Hopf QUE algebras Ah by elements
•Tti ? Ah 0 Ah (completed tensor product), we shall always assume that
Th = 1 0 1 (mod ft). Twisting preserves condition A6).
[3] By twisting, one can always ensure that $ft = 1 0 1 0 1 (mod ft2). This
result is proved by cohomological methods - see Drinfel'd A990b).
[4] Twisting also allows one to assume that 1Z^ = IZh (we write V?^
instead of G2^J1 here and below for typographical reasons). In fact, IZh =
T^IZhTh1 is symmetric if and only if Th = T'h.{nh{Kfnh)~l/2)l/2, where
T'h is symmetric (for, the equation (R^hJ1 = 1Z^h is equivalent to 1Zf^1Zh —
(J^1^1^J). Note that the square roots make sense because IZh = 1 ® 1
(mod ft). A
If-Aft is a quasi-Hopf QUE algebra, we define a map 6 : C/(g) —> U(q)<8>U(q)
as in the case of QUE algebras:
Ma)AW
h
where a e Ah is equal to x G U(q) (mod ft). Arguing as in the Hopf case (cf.
the proof of 6.2.3), one shows that 6 is determined by its restriction to g by
the equation in 6.2.2(iii), and that 6 : g —> A2(g) is a 1-cocycle. Moreover, if
we have arranged that $ft = 10101 (mod ft2), and we set (p = —h~2A\t($h)
(mod ft), then similar arguments show that (p G A3(g) and satisfies
A7) -Alt(<5 0 idN(x) = [x
A8) Alt(<5
Here,
Alt(xi 0 X2 0 ?3) =
536 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Definition-proposition 16.1.9 A quasi-Lie bialgebra is a Lie algebra g
equipped with a 1-cocycle 8 : g —¦> A2(g) and an element ip G A3(g) satisfying
A7) and A8).
Ifr G A2(g) and we set
8r(x) = 8(x) + [x 0 1 + 1 0 x, r],
where [[r, r]] = [r 12,^13] + [^12,^23] + [^13^23] is the left-hand side of the
classical Yang-Baxter equation, then g equipped with 6r and (fr is also a
quasi-Lie bialgebra, called the twist of g by r, and denoted by gr.
IfAh is a quasi-Hopf QUE algebra with Ah/hAh = C/(g) and $^ = 10101
(mod h2), and, if we define 6 and (p as above, then g becomes a quasi-Lie
bialgebra, called the classical limit of Ah- If A^h is the quasi-Hopf QUE
algebra obtained by twisting Ah by an element J7^, and if <&^h = 1 0 1 0 1
(mod h2), then the classical limit of A^h is gr, where r = -/i Alt(JTjFl) (mod
h). I
The only non-trivial point is to show that the element r — —h~1A\t(J-'h)
(mod h) in the last part, which a priori lies in U(g) 0 C/(g), actually belongs
to A2(g). This is proved by using the same cohomological argument as was
used to establish Remark [3] following 16.1.8.
We shall be particularly interested in quasitriangular quasi-Hopf QUE al-
algebras. In that case, it turns out that the classical limit is determined by a
g-invariant symmetric element of g 0 g.
Proposition 16.1.10 Let Ah be a quasitriangular quasi-Hopf QUE algebra
with universal R-matrix 1lh and Ah/hAh = U(q). Set
t = h-l(Jlfn}? - 1 0 1) (mod h).
Then, t is a symmetric ^-invariant element of g 0 g, and is unchanged by
twisting Ah.
Moreover, by twisting if necessary, we can assume that h~lAZh~ 101) = t/2
(mod h) and $h = 1 0 1 0 1 (mod h2), and then the classical limit of Ah is
given by 6 = 0, (p = -\[ti2 , ^23].
Outline of proof From A0) and the fact that $^ = 10101 (mod h), it
follows that
(A0id)(*) =^13 + ^23.
As in the proof of 6.2.3, this implies that t G g 0 C/(g). Since t is obviously
symmetric, t G g&g. Finally, g-invariance follows from the fact that IZ^TVj^
commutes with A/l(A/l).
16.2 The Kohno-DrinjeVd monodromy theorem 537
For the second part, we may assume by the third remark following 16.1.8
that $h = 1 0 1 0 1 (mod h2). The stated conditions can then be achieved
by a further twist by an element Th such that ^ = 101+ f (ri2 - ^21)
(mod h2). The formula for <p now follows from 16.1.3, and the vanishing of 6
follows from the g-invariance of t. |
By abuse of language, in the situation of the preceding proposition, we
shall call the pair (g, t) the classical limit of the quasitriangular quasi-Hopf
algebra Ah. Note that, if Ah happens to be a quasitriangular (Hopf) QUE
algebra, its classical limit as a QUE algebra is the Lie bialgebra (g, <5), where
8(x) = [z0l + l0z, r] andr = h~l{Jlh-l®l) (mod ft). On the other hand,
its classical limit as a quasitriangular quasi-Hopf QUE algebra is (g, 7*12 + 7*21)
(with 6 = 0).
Given a Lie algebra g and a symmetric g-invariant element t G g 0 g, it
is natural to ask whether a quantization of (g, ?) exists, i.e. whether there
is a quasitriangular quasi-Hopf QUE algebra with classical limit (g, t). This
question is completely answered by
Theorem 16.1.11 Let g^ be a Lie algebra over the ring of formal power series
k[[h]], where k is a field of characteristic zero, such that g^ = g[[ft]] as k[[h]]-
modules, for some Lie algebra g over k. Then, to any g^-invariant symmetric
element th of g/i®g/i is associated a quasitriangular quasi-Hopf algebra AQhith
over k[[h\], which is isomorphic to U($h) (completed in the h-adic topology)
as a k[[h]]-algebra. In particular, if Qh — Q[[h]] and th — t G g 0 g, then the
classical limit of AQhith = AQit is (g,?).
Conversely, if Ah is a quasitriangular quasi-Hopf QUE algebra such that
Ah/hAh — U(q) as quasi-Hopf algebras, then Ah is isomorphic to a twisting
of AQhjh, for some (g^,^) satisfying the above conditions, and with th = t
(mod h). Moreover, the isomorphism class of (g^,^) is uniquely determined
by Ah.
We shall outline the proof of the existence part of this theorem in Subsection
16.2D. Uniqueness was proved first in Drinfel'd A991), and then by a simpler
method in Drinfel'd A992b).
16.2 The Kohno-Drinferd monodromy theorem
The main topic of this section is the Knizhnik-Zamolodchikov equation and
its application to the 'quantization problem' for quasi-Hopf algebras. But we
must begin by giving yet another interpretation of braid groups, which will
also be needed in Section 16.4.
A Braid groups and configuration spaces If M is any connected smooth
manifold, let Vrn(M) be the space of all ordered ra-tuples of distinct points of
538 16 Quasi-Hop/ algebras and the Knizhnik-Zamolodchikov equation
M. Note that the symmetric group Em acts freely on Vm(M) by permuting
the points; the configuration space Cm(M) is the orbit space Dm(M)/?m. We
define the cM-braid group' Bm(M) to be the fundamental group of Cm(M).
It is clear that Bm(M) is of most interest when M is two-dimensional.
For, if dim(M) > 2, then Vm(M) differs from Mm by a submanifold of
codimension > 3, so that TTi(Vm(M)) = ?ri(M)m; it follows that 7Ti(Cm(M))
is the semidirect product of Em with ?ri(M)m (with the obvious diagonal
action).
It is fairly clear that /3m(C) is Artin's braid group Bm on m strands (the
fundamental group of Dm((C) is called the pure braid group, and denoted by
Vm): we recall that Bm has generators Ti,..., Tm-i and defining relations
In fact, in the notation of 5.1.7, if we take the intersection of such a braid
with the plane Pl and then identify Pl with P° by vertical translation, we
obtain m curves in <C, no two of which intersect at the same value of ?, and
whose endpoints are a permutation of their initial points. This is the same
thing as a closed curve in Cm((C). By a classical result of R. H. Fox, the
universal covering space of Cm(<E) is contractible, so that Cm((C) is actually
the classifying space of Bm.
The other case which will be of interest to us is the sphere braid group
Sm(CP1), which we shall denote by SBm (the fundamental group of Dm(CP1)
is the pure sphere braid group SVm). It is clear that SBm is a quotient of /3m
(and similarly for the pure groups), since any loop in CP1 can be deformed
so as to lie in C = CP1\{oo}. In fact, SBm is obtained from Bm by imposing
the additional relation
(TiT2 ... Tm_2Tm_i)(Tm_iTm_2 ... T2Ti) = 1.
Using this topological interpretation, it is easy to describe the structure
of Vm as an abstract group. Consider the projection Dm+i(C) —* Vm(<E)
which forgets the (m + l)th point. This is a fibration whose fibre over a
point (z\,..., zm) e X>m(C) is C\{z?,..., zm}. Now, in any fibration, lifting
closed paths in the base to paths in the total space defines an action of
the fundamental group of the base on that of the fibre. In our case, the
fundamental group of the fibre is obviously the free group Fm on m generators,
say /i,...,/m, and that of the base is, by definition, the pure braid group
Vm- It is not difficult to see that Vm consists exactly of the automorphisms
of Fm which fix the product f\... /m and take each fi into a conjugate of fa
and, by considering the exact sequence of fundamental groups associated to
the fibration, that ?m+i is isomorphic to the semidirect product of V
Fm- Thus, Vm is an iterated semidirect product of free groups.
16.2 The Kohno-DrinfeUd monodromy theorem 539
There is a similar description of Sm, namely as the group of automorphisms
of Fm which fix /i... /m and, for some a G Em, take each /; into a conjugate
°f fa{i)- 1^ was known to Artin A947) that Vm is generated by the elements
Pij = (Tj-i. ..Ti+i)Tf(Tj-i.. .Tlfi)-1 for 1 < i, j < m (the relations satis-
satisfied by the P^ are also known, but we shall not need them). In particular,
V2 is generated by T2, where T is the generator of the infinite cyclic group
B2, and V3 is generated by Tx2, T22 and (T^K; moreover, (T^K = (T2TiK
generates the centre of B3 and of 7^3.
B The Knizhnik-Zamolodchikov equation Let r(z) be a holomorphic
function denned for z lying in some open set M C C and with values in
the g 0 g, for some Lie algebra g. Let pk : g —» End(Vfc), /c = 1,..., m, be
finite-dimensional representations. Then, r defines a connection in the trivial
bundle V^m) over Vm(M) with fibre Vi ® • • -® Vm, i.e. a 1-form 6>r on P
with values in End(Vi ® • • • 0 Vm), by
A9) 6r = J2rMzJ ~ zk)(dzj - dzk),
3<k
where rjk(zj — Zk) means, as usual, the endomorphism of Vi 0 • • • 0 Vm which
acts as (pj 0 pk)(r(zj — Zk)) on the jth and kth factors and as the identity
on the others.
Proposition 16.2.1 The connection defined by the matrix of 1-forms 6r de-
defined in A9) is flat if and only ifr satisfies the classical Yang-Baxter equation
with spectral parameters:
[7-12B1 - z2), 7-13B1 - 23)] + [7*12B1 - 22) ,7-23(^2 - 23)]
+ [7*13B1 - 23), 7*23(^2 - 23)] = 0
for atf B1,22,23) eV3(M).
Proof We have to show that
d6r + 6r A 6r = 0.
It is obvious that d6r = 0. On the other hand, if s < t, the coefficient of
dzs A dzt in 9r A 0r is easily found to be
B0)
j>s,k>t j>s,k<t j<s,k>t j<s,k<t
where we have written rsj for rSj(zs — Zj), etc. Now, the operators r^ and
rj'k' commute if j, k, jf and kf are distinct, since in that case they act on
540 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
disjoint pairs of factors in the tensor product V\ 0 • • • 0 Fm. The only non-zero
terms in B0) are, therefore,
Yy^ r*fci+Yy^ r**i+Yy^ r*A+ Y ^r**i
, v k>t k>t j>s s<k<t
k<t
We can split up the terms in this sum according to which factors in the tensor
product they act on. There are three types: those which act on Vj, Vs and
Vt for some j < s; those for which s < j < t; and those for which t < j. The
terms of the first type come from the last three terms in B1), namely
the vanishing of which is equivalent to A9). Similarly, one finds that A9) is
also equivalent to the vanishing of the other two types of terms. |
Definition 16.2.2 The Knizhnik-Zamolodchikov (KZ) equation associated
to a classical r-matrix r as above is the system of differential equations for a
function f on Pm(M) with values in Vi 0 • • • 0 Vm given by
it
In the special case when the Vj are all equal to some representation V of
g, the connection A9) is invariant under the obvious action of the symmetric
group Em on Vrn(M) x V®171 given by permuting the coordinates of a point in
?>m(M) and the factors on the tensor product, and so defines a flat connection
on a bundle over ?>m(M)/?m = Cm(M) with fibre F0m. Equation B2) is
the condition that / is a covariant constant section of this bundle. In general,
such sections will only exist locally; global sections will be well defined only
on the universal covering space of Cm(C). More precisely, if 7 : [0,1] —>
Cm(M) is a smooth curve, then, by analytically continuing a solution /1 of
B2) defined near 7@) along the curve, we obtain a solution f% defined near
7A). If 7 is closed, then, since B2) is homogeneous, f\ and $2 differ by
an element M{^) G GL(F(glm), independent of /1, called the monodromy of
the KZ equation along 7. Since the connection 6r is flat, M(^) depends
only on the homotopy class of 7. Thus, associating to a closed curve 7 in
Cm(M) the monodromy M{^) defines a representation of the braid group
The case of interest to us is the KZ equation associated to the r-matrix
B3) r(Zl -z2) =
Z\ -Z2
16.2 The Kohno-DrinfeUd monodromy theorem 541
where t is a g-invariant symmetric element of g 0 g. We saw in 2.1.9 that r is
indeed a solution of the CYBE. In this case, M = (C, so, by the results of Sub-
Subsection 11.2A, the monodromy of the KZ equation gives us a representation
of Artin's braid group i3m on V®m, for any representation V of g.
We have seen in Subsection 5.2B that, in any quasitensor category C, the
braid group Bs acts on triple tensor products (the three objects involved
should be the same, otherwise it is only the pure braid group which acts).
If C is the category of representations of a quasitriangular Hopf (or quasi-
Hopf) algebra A, this action is given by that of the universal R-matrix 1Z of A
(see Subsection 5.2B). If A is a quantization of a universal enveloping algebra
?/(g), it is natural to expect that this action is closely related to that given
by the monodromy of the KZ equation associated to the classical r-matrix
r which is the classical limit of 71. That this is indeed the case is the main
result of this section, and to prove it we shall actually use the KZ equation
to carry out the quantization (see Subsection 16.2D).
C The KZ equation and affine Lie algebras We allow ourselves a small
digression at this point to explain the relation between the KZ equation and
the representation theory of (classical) affine Lie algebras, which is one of the
main reasons for its importance in conformal field theory. This is not strictly
necessary for our purposes, but it provides motivation for the developments
in Section 16.3.
For convenience, we work over the field (C((z)) of formal power series, and
take the affine Lie algebra g associated to a finite-dimensional complex simple
Lie algebra g to be g((z)) ® (C.c as a vector space, where g((z)) =
and c is a central element. The bracket on g is given by
\f,g](z) = [f(z), g(z)]+reso(f(z), j|
where /, g ? g((z)), ( , ) is the standard invariant bilinear form on g, and reso
means the z~x coefficient. Note that, if we view g C g((z)) as the constant
functions of z, the restriction of the cocycle
(/lff),-reso
of g to g x g vanishes; thus, g is canonically embedded in g.
As usual, we denote by D the derivation of g such that
[D,c]=0, [D,f](z) = zfz.
There are two types of representations of g which are compatible with the
derivation D, in the sense that they extend to representations of the semidi-
rect product of g with the one-dimensional Lie algebra (E.D. These are the
542 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
highest (and lowest) weight representations, together with the loop represen-
representations.
We recall (see the Appendix) that a highest weight representation W of g is
generated by a vector w ? W which is annihilated by the subalgebra ?g[[z]],
is a highest weight vector in the usual sense for the action of the subalgebra
g of g, and is an eigenvector of the central element c. Any irreducible highest
weight representation of g is characterized, up to isomorphism, by the eigen-
eigenvalue k of c (called the level) and the weight A of w for the action of g. The
conformal weight of w is defined to be
where C\ is the eigenvalue of the Casimir element of U(q) on w and g is the
dual Coxeter number of g (we assume that k + g ^ 0).
A loop representation of g, on the other hand, is of the form V((z)), where
V is a finite-dimensional irreducible representation of g, with the obvious
pointwise action of g((z)) and with c acting as zero.
In conformal field theory, a crucial role is played by the intertwining oper-
operators
where W and W are highest weight representations and V((z)) is a loop
representation. Of course, for the existence of a (non-zero) intertwiner of this
kind, it is necessary that W and W' have the same level. It will be convenient
to work with the rescaled operators
Tw'>w(*\ - rw''w(vwMA')-MA)+Mm)
Jy \z) — xv \z)z •>
where k is the level of W and Wf, A and A' are the g-weights of their highest
weight vectors, and fi is the highest weight of V.
Proposition 16.2.3 Let g be a finite-dimensional complex simple Lie alge-
algebra, and let g be the associated afRne Lie algebra. Let pj : g —» End(V^),
j — 1,..., m, be finite-dimensional irreducible representations of g, and let
Wo,..., Wm be highest weight representations of g of level k. Define an op-
operator
F : Wm -» Wo <S> Vi((zi)) <8>-'-<g> Vm((zm))
by
where the rescaled intertwining operators J™ 'W (z) are as defined above. Re-
Regard F as a linear map Wm —» Wo with values in (Vi®- • •®Kri)((^i,... ,2m)),
and let f be the matrix element of F between the highest weight vectors of Wq
16.2 The Kohno-DrinfeUd monodromy theorem 543
and Wm (with respect to bases of Wo and Wm consisting of weight vectors).
Then, f satisfies the KZ equation
where ? ? g (g) g is the canonical element associated to the standard bilinear
form, on g, and the Y^' indicates that the term with k = j is omitted from
the sum. |
The function / in the statement of this result is an example of an m-point
function. For a proof of this result and further discussion of the role played
by the KZ equation in conformal field theory, see, for example, Tsuchiya &
Kanie A988) and Frenkel & Reshetikhin A992a).
D Quantization and the KZ equation In this subsection, we shall outline
the proof of the existence part of 16.1.11. We denote by g^ and th the objects
defined there, and take Ah to be the completed universal enveloping algebra
U(Qh) as an algebra over k[[h]], and with universal R-matrix IZkz = ehth^2;
note that the comultiplication A^ of U(Qh) satisfies A^p = 7^kz-^/i-^-kz kv
the gh-invariance of t^. In view of Remark [4] following 16.1.8, to prove the
existence part of 16.1.11 it is sufficient to construct an element $h G U(Qh)®3
satisfying A), B), D), (9) and A0).
We assume initially that k = (C, and consider the 'universal' KZ equation
r)f tjk
(KZm) ?LJ2
Zj ~
where h — h/2iry/^l and / is a function of zi,..., zm with values in ?7(g/i)®m.
Of course, the usual KZ equation can be obtained from this by applying a
representation of ^(g^H771 to both sides.
Observe first that the R-matrix TZkz = ehth^2 is the monodromy of (KZ2).
More precisely, since df/dz\-\-dfjdz^ — 0, any solution of (KZ2) is of the form
f(zi->Z2) — 9(zi ~ Zci)-> where g(z) satisfies the ordinary differential equation
9 (z) = —9(z).
The monodromy of the solution g(z) = zhth — ehthlnz from the region z ^$> 0
to the region z <C 0 is e^1^^1 — ehtl2. Note that this is also the monodromy
of (KZ2), in its original form, from the asymptotic region z\ — z<i ^> 0 to the
region z\ — Z2 < 0. (Of course, g should really be considered as a function
on the universal covering of C\{0}, and the solution / of (KZ2) as a function
on the universal covering of C2((E).)
544 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
The coassociator is constructed in a similar way using (KZ3). We assume
initially that zi, Z2 and 2:3 are real. Since (KZ3) is unchanged if we subject
z\, Z2 and 2:3 simultaneously to a transformation of the form zi •-» azi + 6, it
follows that any solution of (KZ3) in the region {z\ < z2 < 2:3} is of the form
where g satisfies the differential equation
B4) g'(x) =h(t? + Jt-) g(x)
for 0 < x < 1. Similar reductions are, of course, possible in each of the
other five connected components of the complement in R3 of the hyperplanes
Zi = Zj, 1 < i < j < 3.
According to the classical theory of fuchsian differential equations, there
are unique analytic solutions g\ and g2 of B4), defined for x G C\{0,1}, and
with asymptotic behaviour
gi(x) ~ xhth as x —» 0,
g2(x) ~ A-x)^3 asx-> 1.
We should explain the meaning of 'analytic' and of the symbol ~. First, to
say that g is analytic means that, for all n G N, g(x) is equal (mod hn) to
a finite sum of products of analytic functions of x with elements of U(Qh)®3-
We shall be most interested in the case where c^ is the null deformation
Qh — g[[h}) of a Lie algebra g over /c, and then 'analytic' simply means that
n=0
where each g^ is an analytic function with values in a finite-dimensional
subspace of U(q)®3. Saying that g(x) ~ xhth , for example, means that
g(x)x~hth extends to an analytic function, in the sense we have just described,
which is defined in a neighbourhood of x = 0 and equal to 1 at that point.
Since B4) is homogeneous in g, it follows that $kz = 9\192 is a con-
constant element of U(Qh)®3- This is the desired coassociator of Ah- Note that
/i$kz = /2, where /1 and f2 are the solutions of (KZ3) in {z\ < z2 < 2:3}
with asymptotic behaviour
2, 23) ~ (*2 - 21)**" B3 - 2:1)/i(^3+^3) for 2:2 - 2:1 < 2:3 - 2:x,
2, z3) ~ B:3 - 2:2)^B:3 - 2i)*(*"+**3) for 2:3 - 2:2 < 2:3 - 2:1.
16.2 The Kohno-DrinjeVd monodromy theorem 545
Thus, <I>kz is the monodromy of (KZ3) from the asymptotic region 2:2 — ^1 <^
zs — z\ to the region 2:3 - z2 «C z3 — z\.
To verify that <I>kz has the desired properties, note first that A) is the
statement that <I>kz is 9/i-invariant, and that this follows from the uniqueness
of /1 and f2 and the g^-invariance of th- Similarly, D) follows from the fact
that (eh 0 id)(th) — (id 0 ^h)(th) = 0. Further, by replacing x by 1 — x in
B4), we see that #gg = #?z> so that A0) follows from (9)- Thus> we have
to prove equations B) and (9).
We recall that B) guarantees the commutativity of the pentagon diagram
in 5.1.1 (i). We consider the system (KZ4) in the region {z\ < z2 < zs < z4} C
R4, and distinguish five zones in this region corresponding to the vertices of
the pentagon diagram, according to the following rule:
Zone I z2 - zi < z3 - zx < z4 - z\ ((U <S> V) 0 W) 0 Z,
Zone II z3 - z2 < z3 - zx < z4 - zx (U 0 (V 0 W)) 0 Z,
Zone III z3 - z2 < z4 - z2 < z4 - 21 ^ 0 ((^ 0 W) 0 Z),
Zone IV z4 - z3 < z4 - z2 < z4 - *i J7 0 (V 0 (VF 0 Z)),
ZoneV z2 - 21 < 24-21, 2:4 - 2:3 < z4 - zx (U 0 F) 0 (VF 0 Z).
In these zones, we look for solutions / of (KZ4) with the following asymptotic
behaviour:
fll ~ (%3 — Z2) h (^3 — Zi) ^ h
(or.\ r / \htl3 („ „ \h(tl4+t
\zo/ Jill ~ V-^3 ~ Z2) \Z4 — Z2) K h
Replacing the representations at the vertices of the pentagon diagram 5.1.1(i)
by these solutions according to the above rule, and the associativity maps
between them by the appropriate elements of U(§h)®4 built out of <I>kz, we
obtain the following diagram:
(id<g>id<g>A/l)($Kz) (fcgg)(Kz)
/iv > /v > h
i
fill > fll
(idAid)(l)
Equation B) is a consequence of the following relations:
fw = /v-(id 0 id 0 Ah)(*Kz), /v = /i-(Ah 0 id 0 id)(*Kz),
B6) /IV = /m.(l
546 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
The existence and uniqueness of solutions of (KZ4) with the asymptotics in
B5) follow by standard methods in the theory of differential equations. For
example,
' z2 — z\ Z4 — 2:3N
/v =
Z4 — Z\ Z4 — Z\
where the U(Qh)®3-valued function (pv(u, v) is analytic in a neighbourhood of
@,0) and equal to 10101 at that point, and satisfies a system of differential
equations of the form
= A(u,
where A and B are analytic in a neighbourhood of @,0). Thus, proving
the existence and uniqueness of a function /v with the desired properties
reduces to solving an initial value problem for a first order system of partial
differential equations with real-analytic coefficients.
Each of the equations B6) is proved by comparing two solutions to the same
initial value problem. We first observe that /i,...,/v can De analytically
continued to the whole region {z\ < Z2 < z3 < 2:4}. To prove, for example,
that/i.($kz®1) = /ii, let
Fn = *i-(*4 " .i)-^4+^4^4).(^kz 0 I).
It is enough to prove that F\ = Fn, for [$Kz , txh4 + t2^ + ^4] = 0 by the
g^-invariance of ^kz, so that
From the asymptotics of F\ and Fq, it is clear that these functions extend
analytically to 2:4 = 00. One checks that they both satisfy the differential
system
4.12 j 13 +14 . ^24 . ^34
lh _p> lh p _ p lh ~T~lh "T lh
i-Z2 Z1-Z3
.
dz2 \z2-zi z2-z3j ' dz3 \z3-z1 z3-z2
Thus, at 2:4 = oc, both F\ and Fn satisfy (KZ3); in fact, in view of their
asymptotics, we have, in the notation introduced earlier in this subsection,
Fi = gi(x) 0 1, Fn = (g2(x) 0 l).($Kz ® I),
16.2 The Kohno-DrinfeUd monodromy theorem 547
where x — (z2 — z\)/(z3 — z\). Recalling the definition of <I>kz> we see that
F\ = Fu throughout the region {z\ < z2 < z3, z\ = 00}. But, it is easy to
check that F\ and Fu also satisfy
9F _hs^\t{\F}
2:4 - Zj
so, using the uniqueness of solutions of initial value problems once again, we
have that F\ — F\\ throughout {z\ < z2 < z3 < Z4}.
The proof of (9) proceeds along similar lines, but this time one must allow
the Zj to take complex values. In fact, we consider (KZ3) in the region
{(zuz2,z3) e <C3 I 3(*i) < 9(*2) < 9(*3), zu z2, z3 distinct},
where $s(z) denotes the imaginary part of a complex number z. Let /i,..., /vi
be the solutions of (KZ3) in this region for which
h - (*2 - *i)*"(*3 "'3
hi - (z3 - z2f™(z3
fm - (z2 - z3)ht™{z2
ftv - (z3 - z1f^\z2
fv - (zi - z3)ht"(z2
fvi - (z2 - zxf^\z2
If the Zj are real, one shows, using the definition of <I>kz as above, that
/i-$kz = /11 in the region {z\ < z2 < z3}, and hence everywhere by analytic
continuation. Similarly, one shows that /iv-^k3z — fill and fv&jtz — /vi by
considering the two regions {z\ < z3 < z2} and {z3 < z\ < z2}, respectively.
By considering complex values of the Zj, on the other hand, one shows
that fn = }m.eht™/2, fw = fv.eht^l2 and ft = fvl.eh^3^3^2. Combining
these formulas with those in the preceding paragraph immediately gives (9)
(one needs to recall that Tlh = ehth/2 and to note that Ah(th) = ^3 + t2h3).
To prove the first formula, for example, choose the branch of the logarithm
which is real on the positive real axis and holomorphic on the complement of
the negative imaginary axis (see the next diagram). We compare fu and ftu
when z2 — z3 > 0 (and hence ^(z2) = 3B3)). Thus,
for
for
for
for
for
for
\Z2-Zi\ <¦
\z3- z2\ <
\z3- z2\ <
\z3- zi\ <
\zi - z3\ <
\Z2~Zi\ <
? |Z3~Zl|,
'<\z3-zi\,
t:\z2-z1l
? \Z2-Zll
'C\z2-z3\,
Z\Z3-Z!\.
(*3 - Z2)ht" = exp((ln(z2 - z3) + y/^lir)ktf) = (z2 - z3fl" eht" >2.
Since the other factors in fu and fui are asymptotically equal in the region
being considered, and since [t2^ , t12 +1]^] = 0 by the g/j-invariance of th, it
548 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
follows that fn and fm.ehth I2 have the same asymptotic behaviour in their
common region of definition. Since they are both solutions of (KZ3), they
coincide.
This completes our outline of the proof of the existence part of 16.1.11 in
the case k = (C. The construction of $kz we have described is transcendental,
and obviously does not make sense unless the ground field k D <E. Of course,
it is possible a priori that the resulting <I>kz is actually defined over Q in
some sense, but unfortunately this is not the case. Drinfel'd A991) computes
a series expansion of <I>kz 5 among the coefficients of which feature the numbers
C(n)/nB7T\/^T)n, n G N, half of which are imaginary and all of which are
probably transcendental. Thus, a different method of proof must be used if
k ^ <C. Drinfel'd A991) uses a cohomological argument which produces a
'universal' solution defined over Q, but we shall not describe it here.
Remark Since the representations of the quasi-Hopf algebra AQhjh, whose
existence we have established, form a quasitensor category, there is an action
of the braid group Bm on V^m, for any representation ph : AQhjh —> End(V/l)
and any m > 2. This action is the same as that given by the monodromy of
(KZm) (with th replaced by (ph®Ph)(th))- To see this, it is enough to consider
the case m = 3. We fix a basepoint @,1, oo) G Cs((C), where 'oc' means a
very large positive number. We associate the representations (Vh 0 V^) 0 V^
and Vh 0 (Vh 0 Vh) with the following asymptotic zones in Cs((C):
Zone I Z2 — z\ <C ?3 — z\ (Vh 0 Vh) 0 V^,
Zone II zs — z2 <C z% - z\ Vh 0 (Vh 0 Vh).
The generator T\ G #3 is represented by a path from @,1, 00) to A,0, 00)
lying entirely in zone I, and since (KZ3) degenerates to (KZ2) when 2:3 = 00,
it follows that the monodromy along this path is 7?kz = ehth^2. This is the
same as the action of T\ on (Vh 0 Vh) 0^. On the other hand, the action of
the generator T2 is given by the composite
J kz $KZ
{Vh®Vh)®Vh >Vh®{Vh®Vh) >Vh®{Vh®Vh) >{Vh®Vh)<8>Vh.
Now T2 can be represented by the conjunction of three paths (see Fig. 26):
16.2 The Kohno-DrinfeVd monodromy theorem
549
(a) a path from @,1, oo) to (—oo,0,1), which, in terms of z = zz2_zzl, is a
straight line path from a point close to 0 to a point close to 1, followed by
(b) a small path in zone II from (—oo, 0,1) to (—oo, 1, 0), followed by
(c) a path from (—oo, 1, 0) to @,1, oo), which, in terms of z, is a straight line
path from a point close to 1 to a point close to 0.
@ 1
-oo 1 0)
Fig. 26 Paths in C3((C)
The monodromy of (KZ2) along these paths is 3>kz> ^r3z an<^ ^kz, respec-
respectively, by the definition of T^kz and 3>kz- Hence, the action of T2 is also given
by the monodromy of the KZ equation. A
E The monodromy theorem In this subsection, 9 is a finite-dimensional
complex simple Lie algebra, and Uh(§) is the associated standard (Hopf) QUE
algebra defined in Section 6.5. We can associate to any finite-dimensional
representation ph : Uh(cy) —> End(V^) two representations of the braid group
Bm on V^fm, for any m > 2, as follows.
First, let IZh e Uh(cy) ® ?4(9) be the universal R-matrix of Uhfa) (see
Section 8.3). Then, we described in Subsection 15.2A how to use the matrix
(ph (8) ph){^h) G End(T4 ® Vh) to obtain a representation pQYBE of Sm on
On the other hand, let t be the symmetric 9-invariant element of 9 ® 9
associated to the standard inner product on 9. Recall that Vh is a deformation
of a representation p : 9 —¦> End(F ® V); in particular, we may assume that
V^ = V[[ft]] as a C[[/i]]-module. We consider the KZ equation
df
We saw in Subsection 16.2B that the monodromy of this equation defines
a representation pKZ of Bm on V®m. We extend this representation
linearly to obtain a representation, also denoted by pKZ, of B
Kohno and Drinfel'd independently proved the following beautiful result:
[[
on V®m.
550 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Theorem 16.2.4 The representations p®YBE and pKZ of Bm defined above
are equivalent.
Outline OF PROOF We can consider ?7^(g) as a quasitriangular quasi-Hopf
QUE algebra over <C[[ft]] with comultiplication A^, universal R-matrix IZh
and trivial coassociator. By 16.1.6 and the remark at the end of the previous
subsection, it is enough to show that ?7^(g) is isomorphic as a quasi-Hopf
QUE algebra to a twisting of AQhj, where g^ = 9[[ft]] is the null deformation
of g and t is the invariant symmetric element of g ® g C g^ ® g^ associated
to the standard inner product on g.
By 6.5.4, Uh(§) = ?7(g)[[ft]] as an algebra over <C[[ft]]. Let Ah be the
composite homomorphism
U(9)[[h]] -=> Uh(Q) -^ Uh(Q) ® Uh(a) ^ (?7(g) ® E7(g))[[ft]].
Since A^ = A (mod ft), where A is the usual comultiplication of ?7(g),
and since i^(g, ?7(g) 0 ?7(9)) = 0 (see the first remark in Subsection 6.5B),
there exists an element Th ? (?7(9) 0 ?7(9))[[ft]] such that J-X = 1 ® 1 (mod
ft) and Ah(x) = Jr^1A(x)Jrh for all x G E7(g). Let Uh be the element of
(?7(g) <S> ?7(g))[[ft]] corresponding to lZh G ?7^(g) (8) ?7^(g). Then, twisting the
quasitriangular Hopf QUE algebra (?7(9)[[ft]], A^,^^) by Th, we obtain a
quasitriangular quasi-Hopf QUE algebra (?7(g)[[ft]], A, $^,^), say. By Re-
21
mark [4] following 16.1.8, we can assume that 1Zh = IZh by further twisting
if necessary. But, by 4.2.8 and the results of Subsection 8.3F, we have
where Ch is the element of ?7^(g) which corresponds to the Casimir element C
of ?7(g). Hence, (UhJ = nfnh = Ah(ehC"I2){e~hc"I2 0 e~hCl2). Finally, it
is clear that A(C) = C®l + l®C + ?, so that 1Zh = ehtl2. Since <f>h is unique
up to twisting by a g-invariant element of (?7(g) 0 ?7(9))[[ft]] by 16.1.11, this
completes the proof. |
16.3 Affine Lie algebras and quantum groups
The results of the previous section already indicate a connection between
quantum groups and afRne Lie algebras, for we saw in Subsection 16.2C that
the KZ equation is intimately related to representations of afRne Lie alge-
algebras, and in the Kohno-Drinfel'd monodromy theorem that it is also related
to QUE algebras. In this section, we describe Kazhdan and Lusztig's exten-
extension of this latter result, which gives an explicit equivalence between certain
categories of representations of quantum groups and afRne Lie algebras. It is
16.3 Affine Lie algebras and quantum groups 551
beyond the scope of this book to discuss this deep result in detail, and even
to state it will require considerable preparation.
Throughout this section, g denotes a finite-dimensional complex simple Lie
algebra of type A, D or E.
A The category OK Let g be the affine Lie algebra defined in Subsection
16.2A: thus, g is a central extension
0 -> C.c -f g -f g((z)) -> 0.
Let g be the subalgebra of g given by the pre-image of g[z, z~l] in g. Our aim
is to define a quasitensor structure on a suitable category of representations
of g. One difficulty which must be overcome is that the usual tensor product
of two 'randomly selected' representations of g will be 'too large'. Thus, our
first step will be to select a category of 'small' (but still infinite-dimensional)
representations of g.
Definition 16.3.1 For any «eC, letOK be the full subcategory of the cat-
category of representations of g whose objects V satisfy the following conditions:
(i) the central element c acts as the scalar n — h on V, where h is the Coxeter
number of g;
(ii) g acts locally finitely on V (i.e. for any v eV, dim(U(q).v) < ooj;
(Hi) zq[[z]] acts locally nilpotently on V (i.e. if v e V, x e z$[[z\], then
xN .v = 0 for sufficiently large N);
(iv) V is finitely generated as a Q-module.
Example 16.3.2 Let V(A) be the irreducible finite-dimensional g-module with
highest weight A e P+. Since g = g[|V|]/zg[[z]] as Lie algebras, we can
regard V(A) as a g[[z]]-module on which zq[[z\] acts trivially. Extend to a
representation of g[[z]] 0 (C.c (direct sum of Lie algebras) by making c act as
(k — /i).id, and define
WK(X) = ?7(g) 0 V(X).
U([[}}®<L)
It is not difficult to see that WK(X) e OK for all A <E P+. In fact, the only
condition in 16.3.1 which is not completely obvious is (iii), which follows from
the fact that every element of WK(X) can be written as y<8>va, where y E E7(g)
and v\ is a highest weight vector of V(A), together with the observation that,
for any x e z$[[z]], the AT-fold iterated bracket
for sufficiently large A^. It is not difficult to show further that WK(X) has a
unique irreducible quotient module VK(X), and that every irreducible object
of OK is isomorphic to some VK(X). 0
The properties of OK depend strongly on whether k is a (positive) rational
number:
552 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Proposition 16.3.3 (i) If k <? Q, then OK is semisimple (i.e. every object
ofOK is completely reducible);
(ii) if k ? Q>o> then every object ofOK has a composition series of finite
length. |
For the existence of the kind of tensor product on OK we are looking for, it
turns out to be crucial that modules in OK have finite length. Thus, for the
remainder of this section, we assume that k ? Q>o- On the other hand, the
case k G Q<o will be of particular interest to us.
If V is any g-module and N G N, let V(N) be the subspace of V consisting
of those vectors which are annihilated by all products of N elements of z§ C g.
Obviously, V(l) C VB) C • • •; we define the set of smooth vectors in V to be
V(N),
N=l
and say that V is smooth if V = V(oo).
Proposition 16.3.4 A Q-module V is in OK if and only if V is smooth and
V(l) is finite dimensional. |
One of the reasons for the importance of smoothness is that any smooth g-
module V is naturally a g-module. In fact, let / G (C((z)) and let v G V(N).
Choose g e C^,^] such that / - g G zN<C[[z]] and set (fx).v = (gx).v
for all x e g. This is well defined, for, if h G z^C^z]], then hx is a linear
combination of monomials, each of which is a product of N elements of zg.
(This is proved by induction on N: for the inductive step, one has to show
that, for any x G g, zx G [zg, g], and this is an immediate consequence of the
simplicity of g.)
B The tensor product We shall now define duality and tensor product
operations on OK, beginning with the duality, which is the simpler of the two.
The usual dual of an object V in OK is not, of course, in OK, since it has
the wrong level, namely — [k — ft), and because it is not smooth, in general.
To overcome the first difficulty, let Fw be the result of twisting V with the
automorphism uj of g given by
u(zkx) = (-z)~kx, uj{c) = -c,
for x G g, k G Z. Then, V" has level — (k — ft), and we define
F* = Horned, C)(cx>)
to be the smooth part of the vector space dual of Vw.
16.3 Affine Lie algebras and quantum groups 553
Example 16.3.5 If A ? P+ and VK(X) is the irreducible object of OK defined
in 16.3.2, then
0
Proposition 16.3.6 (i)IfV is in OK, so is F*;
(ii) V i—> V* is an exact contravariant functor OK —> OK;
(Hi) the natural map V —> F**, which associates to a vector v e V the linear
functional on V* given by evaluation at v, is an isomorphism ofq-modules. |
We now give an abstract characterization of the duality operation we have
defined.
Let gB) be the quotient of the direct sum of Lie algebras g 0 g by the
one-dimensional central ideal spanned by (c,—c). Let I^2) be the image of
the embedding g[z, z~1} ^-> g((z)) 0 g((z)) given by
zkx i-> (zhx, z~kx), (x e g, ke X).
^ f •> 9 ^ ^t^^]? the differential 1-form f dg can have poles only at 0 and
oo, so by the residue theorem,
reso( fdg) +resoo(/d#) = 0.
Thus, the cocycle defining the central extension gB) vanishes on
so that F^2^ can be regarded naturally as a subalgebra of gB).
If V and W are in OK, the usual tensor product W <g) V is naturally a
module for g 0 g, and, since the difference of the levels of V and W is zero,
this action factors through an action of gB). Hence, W 0 V may be regarded
as a rB)-module. Fix V in OK and consider the functor Vy : OK -+ vec from
OK to the category of vector spaces over (C defined by
the right-hand side denoting the largest subspace of W (8) V on which
acts trivially.
Proposition 16.3.7 The functor Vv is represented by V*, i.e. there are
natural isomorphisms
for all objects W ofOK. |
Remark It follows from this result that the space of invariants (W 0 V)r 2
is finite dimensional, for one can show that, for any objects X and Y in OK,
B.omoK (X , Y) is finite-dimensional. A
554 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
We now turn to the definition of the tensor product on OK. The usual
tensor product fails to preserve OK for the same reasons as the usual dual:
for example, the level of the usual tensor product of two objects of OK is 2k.
We begin by giving an abstract characterization of the desired tensor product
analogous to that given for the dual in 16.3.7.
Let g^3) be the quotient of the direct sum of Lie algebras g®3 by the two-
dimensional central ideal {(aic, a2C, a^c) \ a\ -f ot2 + <%3 = 0}. If R is the
algebra of regular functions on P1\{0,1, oc}, there are three obvious embed-
dings R <^-> <?((z)) given by associating to a function / E R its power series
expansions in the local parameters z at 0, z — 1 at 1 and \/z at oc. Let F^
be the image of the resulting embedding g ® R <^-> g((z))®3. If /, g E R, the
sum of the residues of / dg at 0, 1 and oc is zero, so that F^3) can be regarded
naturally as a subalgebra of gC).
If U, V and W are any three objects in OK, then gC) acts naturally on
U (8> V (8> W, so this tensor product can be regarded as a F^-module. For
fixed U, V in OK, define a functor Tjjy : OK —¦> vec by
Tt7|V(W) = (?7 ® F ® W)/F^3).(t/ 0 V 0 W).
Definition-proposition 16.3.8 For every pair of objects U and V in OK,
there exists an object U ®V in OK, unique up to isomorphism, such that
Homc(^t/,v(W),(C) is naturally isomorphic to UomoK(U (8) V, W*) for aii
objects W in OK. |
To describe [7 <8> V concretely, let g^ be the pull-back of the extension g by
the homomorphism g0^-^ 9((^)) induced by the embedding R ^ <C((z))
which associates to a regular function its expansion at 1. Associating to
such a function its expansions at 0 and oc, and mapping c i—> — c, defines
a homomorphism of Lie algebras g^ —> g^2^ (that this is a homomorphism
follows once again from the fact that the sum of the residues of a differential
1-form regular on P1\{0,1, oc} is zero). The usual tensor product W = U®V
is naturally a g^2^-module, and hence also a g^-module; note that the level
of the latter module is —(k — Ji). Let R\ be the subspace of R consisting
of the functions which vanish at 1 (and, in particular, are regular there).
For any k E N, let Wk be the subspace of W spanned by the elements
(fiXi)...(fkXk).w for /i,...,//c E i?i, xi,...,x/c E g and w E W. Then,
and we define W to be the projective limit
W = \im(W/Wk).
We now show that W has a natural g-module structure. Note that an
element of W is represented by a sequence (u>i, u>2,...) of elements of W such
16.3 Affine Lie algebras and quantum groups 555
that Wk+i — Wk E Wk for k = 1, 2,.... Let / E C((z)), fix r > 0 such that
/ E ^"r^C[[^]], and choose elements #i,#2> • • • E i? such that, for /c = 1,2,...,
the expansion of g^ at 1 differs from / by an element of (z — l)fcC[[;z]]. It is
not difficult to show that such elements exist, and that setting
gives a well-defined action of g on W. We may therefore form the g-module
Tyw(oo), which clearly has level k — h.
Proposition 16.3.9 With the above notation, the q-module Wu(oo) is in
OK and represents the functor Tjjy '• OK —> vec in the sense of 16.3.8. Thus,
Remark The most difficult point of the proof that M^oo) is in OK is to show
that it is finitely generated. It is here that the assumption that k ? Q>0 is
crucial. A
We can now state
Theorem 16.3.10 With the duality operation * and the tensor product ®,
OK becomes a rigid, (C-linear, quasitensor category. |
We cannot discuss the proof of this result here, but the reader who has
come this far will not be surprised to learn that it involves (a generalization
of) the Knizhnik-Zamolodchikov equation.
C The equivalence theorem We turn finally to the relation between quan-
quantum groups and the quasitensor category OK defined in the last two subsec-
subsections. Let e{n) = e1"^^/*, and recall the Hopf algebra ^TMg) studied
in Sections 9.3, 10.1 and 11.2. Let OK be the category of finite-dimensional
U*?\ (g)-modules V of type 1 which are the direct sums of their weight spaces.
We have shown in 10.1.20 and 11.2.12 that the tensor product and duality op-
operations induced by the Hopf structure of U*?\(§) make OK into a quasitensor
category.
Theorem 16.3.11 There is an equivalence of quasitensor categories OK =
The construction of the equivalence is outlined in Kazhdan & Lusztig
A991).
This theorem is the confirmation of the connection, conjectured by Lusztig
A989), between the representation theories of affine Lie algebras and quantum
groups. In fact, taking k E Q<o in 16.3.11, one deduces
556 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Theorem 16.3.12 Conjecture 11.2.14, on the characters of the irreducible
representations V^res(A) of ?/eres(g) when A e P+ and e is a root of unity, is
true. |
A relationship between quantum groups and classical affine algebras has
been widely predicted in the literature on conformal field theory - see espe-
especially Moore & Seiberg A988). Physicists are interested mainly in unitary
representations of affine Lie algebras, for which the level must be a non-
negative integer. Unfortunately, such representations are excluded from our
discussion of OK, since we have always assumed that k ? Q>o- However,
there is an analogue of 16.3.11 which applies to such representations.
Let intK be the category of integmble g-modules of level n — h and of finite
length: this forces k — h e N. (A representation V of g is integrable if it is
the direct sum of its weight spaces and if the Chevalley generators Xf of g
act locally nilpotently on V.) One can define a tensor product 0 on intK in a
manner analogous to that used for OK. At first sight, this seems paradoxical,
since, to define the tensor product on OK, we had to assume that k ? Q>o-
But the finiteness property, which the assumption k ? Q>o guaranteed in the
case of OK, holds automatically in intK. Georgiev & Mathieu A993) made
the following
Conjecture 16.3.13 Provided that k e N is sufficiently large, intK and
tilte are equivalent as (C-linear quasitensor categories, where e = e27rv-i/K# |
We understand that this has been proved by Finkelberg A993).
Remarks [1] We saw in Subsection 11.3D that the category tilt^ is semisimple.
This is consistent with 16.3.13, for it follows from results of Deodhar, Gabber
and Kac that intK is semisimple. On the other hand, neither of the categories
OK and OK in 16.3.11 is semisimple when -kgN.
[2] Also implicit in the literature of conformal field theory is a connection
between quantum groups and the Virasoro algebra. Such a result has not been
precisely formulated at the time of writing, but it is expected that there is an
equivalence of quasitensor categories, analogous to that in 16.3.11, between a
certain category of representations of the Virasoro algebra and the category
of finite-dimensional representations of the tensor product of two copies of
quantum 5/2 (C) at a root of unity. A
16.4 Quasi-Hopf algebras and Grothendieck's Esquisse
We conclude this chapter, and the book, by sketching a remarkable connection
between quasi-Hopf algebras and algebraic number theory. The first serious
16.4 Quasi-Hopf algebras and Grothendieck's Esquisse 557
results in this area were obtained in Drinfel'd A991), although to some extent
the connection was foreseen by A. Grothendieck in 1984 in his 'Esquisse d'un
programme'.
A Gal(Q/Q) and pro-finite fundamental groups Let X be an algebraic
variety defined over Q, and, for any field k with Q C k C (C, denote by X(k)
the set of /c-rational points of X. We assume that X((E) is connected in the
complex topology. By the generalized Riemann existence theorem, all finite
coverings of X((C) are algebraic and defined over Q, the field of all algebraic
numbers in (C (see Hartshorne A977), page 442, for example). Hence, if
r E Gal(Q/Q) is an automorphism of Q which fixes Q pointwise, any finite
Galois covering of X((?) can be 'twisted' by r to give another finite Galois
covering of X(<C). This implies that, provided the basepoint xo e
Gal(Q/Q) acts as a group of automorphisms of the pro-finite completion
0) - Urn 7
of the fundamental group of X(<C) (in the projective limit, S runs through
all the normal subgroups of tti(X((C),xo) of finite index).
To explain this in a little more detail, we must give another description
of the pro-finite completion 7ti(X((E),xo). Note that normal subroups of
tti(X((C), xo) of finite index correspond to finite Galois coverings p : X((E)P —¦>
X((C), and that lifting a closed path 7 in X((E) based at #o to X((E)P gives a
bijection jp : p~1(xo) —> p~1(xo). These bijections are compatible, in the sense
that, if p' is another finite Galois covering of X(<E) and / : X(<C)P -+ X(<E)P'
is a covering map such that the induced map X((E) —>• X((E) fixes xo, then
the following diagram commutes:
p
From these remarks, it follows that giving an element of tti(X(<E),xo) is
the same thing as giving an assignment, to each covering p of X(C), of a
bijection jp : p^) -^ p(xo), these bijections being compatible in the
above sense. The group operation on tti (X((C), xo) corresponds to the obvious
way of composing such bijections. An element r ? Gal(Q/Q) acts on a family
of bijections {jp} by
It is clear that this defines an action of Gal (Q/Q) as a group of automorphisms
of7ri(X(C),x0).
558 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
Since tti(X((C), #o) is independent of xq up to inner automorphisms, the ho-
momorphisms (fx,x0 • Gal(Q/Q) —> AutGTi(X((C),xo)) we have constructed
induce a homomorphism
independent of a choice of basepoint (Out(TTi) is the group of outer automor-
automorphisms of tti, i.e. the quotient of the group of automorphisms by the group
of inner automorphisms).
According to Grothendieck A984), the most important varieties X to con-
consider are the configuration spaces
where PGL2((?) acts diagonally on (IP1O71. The fundamental group tti (Xm((C))
is obviously isomorphic to the quotient of the pure sphere braid group SVm by
its centre (= tti(PGL2(<E)) = Z2). In particular, since PGL2(<?) acts triply
transitively on P1, X4 ^ P^O, 1, oc}; thus, 7n(X4((C)) is the free group F2
on two generators X and Y", representing loops which go once round 0 and 1,
respectively, but do not enclose any other point of {0,1, oc}.
Belyi A987) proved that the homomorphism
<pxA : Gal(Q/Q) -+ OutGr1(X4((C)))
is injective; hence, the homomorphisms (px4,x0 are also injective. Although
the precise image of (px4,x0 is not known, it was proved by Ihara A988) that
it is contained in a certain remarkable subgroup of Aut(i<2), which we shall
now describe.
Following Drinfel'd A991), we define the Grothendieck-Teichmuller group
GT to be the set of automorphisms of F2 of the form
where / lies in the commutator subgroup (F2,F2) of F2, and m lies in the
pro-finite completion
Z = lim
of the integers, and where m and / satisfy conditions (i), (ii) and (iii) below:
(ii) f(X3,X1)X?f(X2,X3)X?f(X1,X2)Xr = 1 whenever X,X2X3 = 1 in
F2;
(iii) the relation
f(Pl2, P23P24)f(Pl3P23, P34) = /(P23,
16.4 Quasi-Hopf algebras and Grothendieck's Esquisse 559
holds in the pro-finite completion of the pure braid group P4, where the P^
are the generators of V4 defined in Subsection 16.2A.
A little surprisingly, GT is actually a subgroup of Aut(F2).
Since Gal(Q/Q) is a subgroup of GT, one would like to understand more
about GT itself. In the next subsection, we describe Drinfel'd's insight, that
GT is essentially the 'universal symmetry group' of quasitriangular quasi-
Hopf algebras.
B The Grothendieck-Teichmiiller group and quasitriangular quasi-
Hopf algebras Suppose that C is a quasitensor category. We saw in Sub-
Subsection 5.ID that, if Vi, V2 and V3 are objects of C, then every element
C G #3 defines an isomorphism (V\ 0 V2) 0 V3 —> (V^i) 0 V^B)) 0 V^C),
where a G ?3 is the permutation associated to f3~l. In particular, P3 acts
on (Vi 0 V2) 0 V3. Composing the given associativity isomorphisms with
the action of an element of P3 therefore gives rise to new candidates for the
associativity isomorphisms. Similarly, composing the given commutativity
isomorphisms with the action of elements of V2 on tensor products V\ 0 V2
gives new candidates for the commutativity isomorphisms. Of course, in order
that these new commutativity and associativity isomorphisms should define
a quasitensor category, some restrictions must be satisfied.
From Subsection 16.2A, we know that every element of V2 is of the form
T2rn, where T is the generator of B2, and that every element of Vz is of the
form j^rl,Tl){T{T2fn, where f{X,Y) is an element of the free group F2
with generators X and Y. The commutativity of the hexagon diagrams in
5.2.1 forces n = 0 and the relations (i) and (ii) in Subsection 16.4A (but now
the X{ are in P3), while the commutativity of the pentagon diagram in 5.1.1
forces condition (iii) (in V4 rather than its pro-finite completion). Twisting a
quasitensor category by a pair (A, /), where A = 1 + 2m, and then by (A7, /;)
is the same as twisting by (A/;, /"), where
B7) A" = AY, /"(X, Y) = /;(/(X, Y)Xxf(X, F), FA)./(X, F),
(x,y) = xyx~xy~x denoting the commutator of two group elements x and
y. This makes the set of pairs (A, /) satisfying the above conditions into a
semigroup, which we denote by GT.
If A is a quasitriangular quasi-bialgebra over a field k of characteristic zero,
then, by 16.1.4, the category rep^ is quasitensor, and we may 'twist' it with
pairs (A, /) G GT by using the preceding construction. This is equivalent to
changing the universal R-matrix 1Z and the coassociator $ of A to (A,/).1Z
560 16 Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equation
and (A, /).$, where
(a, f).n = n.(n21nr =
B8) (a, /).$ = f(n21n12, ^.
It is time to admit that, unfortunately, conditions (i)-(iii) (in P3 and V±)
have only two solutions, namely m = ±1, / = 1 (this is not difficult to
see)! However, suppose that we replace A by a deformation Ah of A as a
quasi-bialgebra; we assume that the universal R-matrix 1Z of A is = 10
1 (mod ft). By the remarks at the beginning of Subsection 16.1C, Ah is
then a quasitriangular quasi-Hopf algebra. Then, the right-hand sides of the
formulas in B8) make sense for any m G k and any f(X,Y) in the pro-
nilpotent completion F™1 of F2. In fact, since 1Z = 1 (8 1 (mod ft), \n(lZ2i.lZ)
is a well-defined element of the completed tensor product Ah (8 Ah, as is
G^2i-^)m = exp(m\n(lZ2i.lZ)). Moreover, F™1 consists of expressions of the
form exp(jF(lnX , In F)), where T is a formal Lie series over k (see Bourbaki
A972), Chap. II, § 6, no. 3). Since $h = 1(8I(8I (mod ft), the right-hand sides
of the second equation in B8) also make sense. Finally, conditions (i)-(iii)
are also meaningful if we work in the appropriate nilpotent completions.
We therefore have an action, on the category of quasitriangular quasi-Hopf
algebras over fc[[ft]] with the above properties, of the semigroup GT{k) of
pairs (A,/) satisfying conditions (i)-(iii), where X e k and / G F-f11. The in-
vertible elements in GT(k) are precisely those for which A ^ 0, and form what
Drinfel'd A991) calls the fc-pro-unipotent version GT(k) of the Grothendieck-
Teichmuller group. This group is highly non-trivial: for example, it is known
that the homomorphism GT(k) —> kx given by (A, /) i—> A is surjective.
Remark The twisting of quasi-Hopf algebras over fc[[ft]] by elements of GT(k)
we have defined should not be confused with the twists introduced in Sub-
Subsection 16.1 A. The two are quite separate: in fact, they commute with each
other. A
Bibliographical notes
16.1 The results of this section are taken from Drinfel'd A990b).
16.2 The main sources for this section are Drinfel'd A989, 1990b, 1991) and
the papers of T. Kohno in the references. The KZ equation was introduced
in Knizhnik & Zamolodchikov A984); see also Belavin, Polyakov & Zamolod-
chikov A984) and Tsuchiya & Kanie A988). For more information on the
Bibliographical notes 561
relation between the KZ equation and the topology of complements of hyper-
planes, see Schechtman & Varchenko A991a,b) and Schechtman A992a,b).
The solutions of the KZ equation can be expressed in terms of (generalized)
hypergeometric functions - see Schechtman & Varchenko A990). For further
information on monodromy representations, see Cherednik A991a). Frenkel
& Reshetikhin A992a) define a g-analogue of the KZ equation, show that its
solutions are given in terms of g-hypergeometric functions (see Chapter 13),
and study its relation to quantum afflne algebras (see Section 12.3).
16.3 Theorems 16.3.11 and 16.3.12 were announced in Kazhdan & Lusztig
A991), and the details of this work have appeared in Kazhdan & Lusztig
A993a,b, 1994a,b) and Lusztig A994). Conjecture 16.3.13 is the subject of
the thesis of Finkelberg A993).
16.4 The literature on Grothendieck's Esquisse is extensive. As well as
Grothendieck A984), one should consult Deligne A989) and Ihara A991),
and the references there. The relation to quasi-Hopf algebras is given in
Drinfel'd A991).
Appendix
Kac-Moody algebras
In this Appendix, we summarize the results and notation relating to Kac-
Moody algebras used throughout the book.
A 1 Generalized Cartan matrices A generalized Cartan matrix is a
square matrix A = (aij)i,j=i,...,n °f integers such that, for all z, j,
an = 2, ctij < 0 if i ^ j, di3¦, = 0 if and only if d3i = 0.
A is symmetrizable if there exist coprime positive integers d\,..., dn such
that the matrix (didij) is symmetric. The d{ are then uniquely determined.
A is decomposable if, by applying a permutation to the rows of A and the
same permutation to the columns, A can be put in the form
B 0
0 C
where B and C are non-zero square matrices.
The Dynkin diagram of A is the graph with vertices (or nodes) labelled by
{1,..., n}, nodes i and j being joined by di3d3i edges (or bonds) if i ^ j, and
carrying an arrow pointing towards node i if |a^| > \dji\. A is determined by
its Dynkin diagram if di3d3i < 4 for all z, j.
A symmetrizable generalized Cartan matrix A is of finite (resp. affine) type
if and only if the matrix (didij) is positive-definite (resp. positive semi-definite
of rank n — 1) ; in the former case, A is called a Cartan matrix.
Note In the remainder of the Appendix, A denotes an indecomposable sym-
symmetrizable generalized Cartan matrix.
A 2 Kac-Moody algebras Denote by g;(^4) the Lie algebra over C (or any
field of characteristic zero) with generators Hi, Xz, i — 1,..., n, and defining
relations
[Hu Hj] = 0, [HuXf] = aijXf, [X+,X~] = SijHi,
The Xf are called the Chevalley generators of 9;(^)- The subspace g^ of
g;(^4) spanned by Hi, Xf and X~ is a subalgebra isomorphic to 5^2(<C).
Appendix Kac-Moody algebras 563
Let \)r be the linear span of the H{. Choose a vector space \)" of dimension
n — r, r = rank(yl), with basis {J9r+i,..., J9n}. Assume, by applying a
permutation to the rows and the same permutation to the columns of A, if
necessary, that the first r rows of A are linearly independent. Let q(A) be the
Lie algebra with generators i^, X^, i = 1,..., n, and 2^, i = r + 1,..., n,
and with defining relations those of q'(A) together with
[Di,Dj] = 0, [DuHj] = 0, [DuXf] = ± <^X±.
The direct sum I) = IO 0 f)" is called the Cartan subalgebra of q(A).
For any A, g'(A) = [g(A),g(A)]. We have g(A) = g'(A) if and only if
det(A) 7^ 0 if and only if q(A) is simple; in particular, if A is of finite type, then
q'(A) = q(A) is simple. Further, dim(g/(^4)) < oo if and only if dim(g(A)) <
oo if and only if A is of finite type.
Note We denote g(-A) (resp. g;(-A)) simply by g (resp. g') from now on.
A 3 The invariant bilinear form There exists a unique non-degenerate
invariant symmetric bilinear form ( , ) : g x g —> C such that, for all z, j,
(Hi,Hj) = dj1aij, (Di,Dj) = 0, (HitDj) = d'H^, (Di,Xf) = 0,
The restriction of ( , ) to g; is non-degenerate if and only if det(-A) ^ 0. Its
restriction to I) is always non-degenerate.
A 4 Roots The simple roots of g are the linear functionals o^ : \) —> C,
i = 1,... ,n, given by
They are linearly independent.
The bilinear form ( , ) induces an isomorphism of vector spaces \) = I)*,
under which oti e I)* corresponds to diH{ G I). The induced bilinear form on
I)* is given by (auaj) = dkaij.
Set II = {ai,... ,an}, and
2=1 2=1
If a = ]T\ fc^ai G Q, its height is height(a) = Yli h- Let
P = {A e ? | X(Hi) E TL for all i}, P+ = {A G I)* | A(^) G N for all i}.
564 Appendix Kac-Moody algebras
We have Q C P. There is a natural partial order on P given by A > /i if and
only if A-// G Q+.
If a G Q, define the root space
9a = {x ? 9 | [h, x] = a(h)x for all h G I)}.
Set A = {a G Q | a ^ 0, ga ^ 0}. Then, A is the set of roots of 9,
A+ =Afl Q+ the set of positive roots, A~ = — A+ the set of negative roots.
We have A = A+ ]J A~ (disjoint union).
We have the following orthogonality relations between the root spaces:
(9a, 9/?) = 0 if a+ /3 = 0, (gQ , f)) = 0 if a ^ 0.
Let n± be the subalgebras of 9 generated by the Xf. Then, we have, as
direct sums of vector spaces,
n±= K& 9a, I) = 90,
The subalgebras b± = n±0f) are the (positive and negative) Borel subalgebras
of 9.
If A is of finite type, define A; G I)*, i = 1,... ,n, by Xi(Hj) = 6{j. Then,
the A; form a basis of P and
If p is half the sum of the positive roots of g, then p = ^^ A^ and (p, a^) = d^
for all i. There is a unique maximal root 8 G A+ with respect to the partial
order on Q. The dual Coxeter number of 9 is g = 2^4 + 1.
A 5 The Weyl group Define linear maps S{ : I) —> I), called the fundamental
(or simple) reflections, by
si(h) = h-ai(h)Hi, (ft el)).
The Weyl group W of 9 is the subgroup of GL{bj) generated by si,..., sn.
The action of W preserves the bilinear form ( , ) on \).
As an abstract group, W is a Coxeter group with generators si,..., sn and
defining relations
5? = 1, (*z5jr^ =1, if z ^ J,
where the integers m^ are given by
0 1 2 3 > 4
2 3 4 6 00
Appendix Kac-Moody algebras 565
(if rriij = oo, the relation (s^O77^ = 1 is omitted). The element c =
S1S2 sn is called the Coxeter element: its order is the Coxeter number h
of g.
An expression w = s^ Sik of an element w G W as a product of simple
reflections is called a reduced expression (or a reduced decomposition) if k is
the minimal number of simple reflections which appear in any such expression
of w, and then k is called the length of w, and is denoted by l(w). If w' is
another element of W, we say that w' < w if wf = Sj1 Sj2 ... Sji, where the
sequence j'1,.7'2, • • • ,je is obtained from the sequence ii, 22, • • • , ik by deleting
some (possibly none) of its terms. Then, < is a partial ordering on W, called
the Bruhat ordering.
Identifying f) with I)* using the bilinear form, we get an action of W on I)*
given by
, (f elf).
We have W(A) = A and dim(ga) = dim(giy(Q)) for all w G W, a G A.
A 6 Root vectors In this subsection we assume that A is of finite type.
There is a unique element w0 €W of maximal length; this length is iV = | A+|;
and we have Wq = 1. If wq = s^ S{N is a reduced expression, then
A+ = {a*!, Si^a^),... jS*! • •. SiN_l(aiN)},
each positive root occurring exactly once on the right-hand side.
There are automorphisms T\,..., Tn of g such that
Ti(X+) = (-aiJ)\-1(Bdx+)-a" (X+), if i * j,
Ti(X+) = {-l)a«(-aij)r1{»Ax-)-a»{Xr), if z ^ j.
They satisfy the defining relations of the braid group BQ:
TiTj=TjTi, TiTjTi=TjTiTj, {T^f = {T^f, G\TjK = (TjTJ3,
according as a^aji = 0, 1, 2 or 3, respectively. Each Ti preserves f) and
induces on it the action of the reflection Si.
If C = Si±Si2 ... sik_1(aik) G A+, where w0 = s^ ... siN is a reduced ex-
expression, define
Then, X^ is a non-zero element of §±p for all C G A+. The X^ are indepen-
independent of the choice of reduced expression of Wo, up to sign.
566 Appendix Kac-Moody algebras
A 7 Affine Lie algebras Let g = g(-A), where A is of finite type. The
extended Cartan matrix of g is A = (a^);J=o,i,...,n, where A — (a^)^J=iv..5n,
aoo = 2 and
ai0 —
for i = 1,..., n. Then, A is a generalized Cartan matrix of affine type.
The Lie algebra g'(-A) is the affine Lie algebra g, which is isomorphic to
g[z, z~l] (&<L.c as a vector space with bracket
[Xzk,Yzl] = {X,Y]zk+l + 6k^(X,Y)c, (X,YeQ, fc.IeZ),
the element c being central. The Lie algebra q(A) is the semidirect product
of g with the one-dimensional algebra spanned by the derivation D given by
D(Xzk) = kXzk, D(c) = 0.
If c acts by a scalar fona g-module V, one says that V is of level ?.
A 8 Highest weight modules If V is a g-module and A G I)*, the weight
space
Vx = {v G V | h.v = X(h)v for all h G I)}.
Define the set of weights of V to be P(V) = {A G f)* | Vx ^ 0}.
A g-module V has highest weight A G I)* if there exists a vector i;A ? Va such
that V = U(q).vx and n+.vx = 0. The Verma module M(X) is the quotient of
C/(g) by the left ideal generated by n+ and the elements h — A(/i).l for /iGf);
it has highest weight A and is free as a ?/(n_)-module. Moreover, M(A) has
a unique irreducible quotient module V(A); up to isomorphism, V(A) is the
unique irreducible g-module of highest weight A. If \i G P(M(A)), then \i<\.
A g-module V is integrable if
y= 0 y.
and V is a sum of finite-dimensional g^-modules for each i. If V is integrable,
then W(P(V)) = P(V). The module V(A) is integrable iff A G P+. If A is of
finite type, V(A) is integrable if and only if it is finite dimensional.
References
Abe, E. A980) Hopf Algebras, Cambridge Tracts in Mathematics 74, Cambridge University
Press, Cambridge
Abe, E. & Takeuchi, M. A992) Groups associated with some types of infinite dimensional
Lie algebras, J. Algebra 146, 385-404
Abraham, R. Sz Marsden, J. E. A978) Foundations of Mechanics, Benjamin, Reading, MA
Accardi, L., Schiirmann, M. Sz von Waldenfels, W. A988) Quantum independent increment
processes on superalgebras, Math. Z. 198, 451-77
Adler, M. A979) On a trace functional for formal pseudo-differential operators and the
symplectic structure of the KdV-type equations, Invent. Math. 50, 219—48
Adler, M. & van Moerbecke, P. A980) Completely integrable systems, euclidean Lie alge-
algebras, and curves, Adv. Math. 38, 267-317
Agarwal, G. S. & Chaturvedi, S. A992) Atomic transitions in ^-deformed fields, Modern
Phys. Lett. A 7, 2407-14
Aghamohammadi, A., Karimipour, V. & Rouhari, S. A993) The multiparametric non-
standard deformation of An-i, J. Phys. A 26, L75-82
Aizawa, N. A993a) q <-*¦ q~1 invariance of ^-oscillators and new realizations of quantum
algebras, J. Phys. A 26, 1115-22
Aizawa, N. A993b) Tensor operators and Clebsch-Gordan coefficients for the quantum
algebra suq{l,l), J. Math. Phys. 34, 1937-63
Aizawa, N. & Sato, H. A991) ^-deformation of the Virasoro algebra with central extension,
Phys. Lett. B 256, 185-90
Akutsu, Y., Deguchi, T. & Wadati, M. A989) The Yang-Baxter equation: a new tool for
knot theory, in Braid Group, Knot Theory and Statistical Mechanics, C. N. Yang &; M. L.
Ge (eds), pp. 151-200, World Scientific, Teaneck, NJ
Alcalde, C. & Cadavid, A. C. A992) Quantization, characters and the star-exponential, in
Topological and Geometrical Methods in Field Theory, J. Mickelsson & O. Pekonen (eds),
pp. 1-12, World Scientific, Singapore
Alcaraz, F. C, Koberle, R. & Lima-Santos, A. A992) All exactly solvable [/(l)-invariant
quantum spin 1 chains from Hecke algebra, Intemat. J. Modern Phys. A 7, 7615—28
Aldaya, V., de Azcarraga, J. A., Bisquert, J. &, Cervero, J. M. A990) Dynamics on
5LB,R)xC/(l), J. Phys. A 23, 707-20
Aldaya, V., Loll, R. & Navarro-Salas, J. A989) BRST supergroups and quantization, Phys.
Lett. B 225, 340-6
Aldaya, V. & Navarro-Salas, J. A990) Quantization of the Virasoro group, Comm. Math.
Phys. 126, 575-95
Alekseev, A. Yu., Faddeev, L. D. & Semenov-Tian-Shansky, M. A. A992a) Hidden quantum
groups inside Kac-Moody algebras, in Quantum Groups, Proceedings of Workshops held in
the Euler International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in
Mathematics 1510, pp. 148-58, Springer, Berlin
Alekseev, A. Yu., Faddeev, L. D. & Semenov-Tian-Shansky, M. A. A992b) Hidden quantum
groups inside Kac-Moody algebras, Comm. Math. Phys. 149, 335—46
Alekseev, A. & Shatashvili, S. A989) From geometric quantization to conformal field theory,
in Problems of Modern Quantum Field Theory, Alushta, 1989, A. A. Belavin, A. U. Klimyk
& A. B. Zamolodchikov (eds), Research Reports in Physics, pp. 22—42, Springer, Berlin
Alekseev, A. & Shatashvili, S. A990) Quantum groups and WZNW models, Comm. Math.
Phys. 133, 353-68
568 References
Alishauskes, S. I. & Kulish, P. P. A985) Spectral expansion of SUC) invariant solutions
of the Yang-Baxter equation, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 145
(Russian)
Altschuler, D. & Coste, A. A992) Quasi-quantum groups, knots, three-manifolds and topo-
logical field theory, Comm. Math. Phys. 150, 83-108
Alvarez-Gaume, L. A989) Quantum groups and conformal field theories, Phil. Trans. Roy.
Soc. London Ser. A 329, 343-7
Alvarez-Gaume, L. A990a) Quantum groups and conformal field theories, in The Interface
of Mathematics and Particle Physics, Oxford, 1988, D. Quillen, G. B. Segal & S. T. Tsou
(eds), Institute of Mathematics and its Applications Conference Series New Series 24, pp.
1-7, Oxford University Press, New York
Alvarez-Gaume, L. A990b) Quantum group approach to conformal field theory, Nucl. Phys.
B Proc. Suppl. 16, 571-3
Alvarez-Gaume, L. & Gomez, C. A989) Hidden quantum symmetries in rational conformal
field theories, Nucl. Phys. B 319, 155-86
Alvarez-Gaume, L., Gomez, C. & Sierra, G. A989) Quantum group interpretation of some
conformal field theories, Phys. Lett. B 220, 142-52
Alvarez-Gaume, L., Gomez, C. Sz Sierra, G. A990) Duality and quantum groups, Nucl.
Phys. B 330, 347-98
Aminou, R. A987) Bigebres de Lie, structures de Poisson et variantes de l'equation de
Yang-Baxter, Publ. IRMA Lille 9, no. 3
Aminou, R. & Kosmann-Schwarzbach, Y. A988) Bigebres de Lie, doubles et carres, Ann.
Inst. Henri Poincare Phys. Theor. 49, 461-78
Andersen, H. H. A992a) Tensor products of quantized tilting modules, Comm. Math. Phys.
149, 149-59
Andersen, H. H. A992b) Finite dimensional representations of quantum groups, preprint
no. 14, Matematisk Institut Aarhus Universitet
Andersen, H. H. A992c) Quantum groups, invariants of 3-manifolds and semisimple tensor
categories, preprint no. 15, Matematisk Institut Aarhus Universitet
Andersen, H. H., Jantzen, J. C. & Soergel, W. A994) Representations of quantum groups
at a p-th root of unity and of semisimple groups in characteristic p: independence of p,
Asterisque 220, Societe Mathematique de Prance, Paris
Andersen, H. H., Polo, P. & Wen Kexin A991) Representations of quantum algebras, Invent.
Math. 104, 1-59
Andersen, H. H., Polo, P. & Wen Kexin A992) Injective modules for quantum algebras,
Amer. J. Math. 114, 571-604
Andersen, H. H. Sz Wen Kexin A992) Representations of quantum algebras, the mixed
case, J. reine angew. Math. 427, 35-50
Andrews, G. E. A976) The Theory of Partitions, Addison-Wesley, London
Andrews, G. E. A986) q-Series: Their Development and Application in Analysis, Number
Theory, Physics and Computer Algebra, CBMS Regional Conference Series in Mathematics
66, American Mathematical Society, Providence, RI
Andrews, G. E., Baxter, R. J. & Forrester, P. J. A984) Eight vertex SOS model and
generalized Rogers-Ramanujan-type identities, J. Stat. Phys. 35, 193-266
Andruskiewitsch, A. A992) Some exceptional compact matrix pseudogroups, Bull. Soc.
Math. France 120, 297-326
Andruskiewitsch, A. & Enriquez, B. A992) Examples of compact matrix pseudogroups
arising from the twisting operation, Comm. Math. Phys. 149, 195-208
Aneva, B. A991) A deformed quantum SUB) superalgebra, J. Phys. A 24, L455-8
Aratyn, H., Nissimov, E. Sz Pacheva, S. A992) Classical r-matrices and Poisson bracket
structures on infinite-dimensional groups, Phys. Lett. B 284, 273-82
References 569
Archer, F. J. A992) The UqslC) 6-j symbols and state sum invariants, Phys. Lett. B 295,
199-208
Aref'eva, I. Ya. &; Volovich, I. V. A991a) Quantum group chiral fields and differential
Yang-Baxter equations, Phys. Lett. B 264, 62-8
Aref'eva, I. Ya. & Volovich, I. V. A991b) Quantum group gauge fields, Modern Phys. Lett.
A 6, 893-907
Aref'eva, I. Ya. &; Volovich, I. V. A991c) Quantum group particles and non-archimedean
geometry, Phys. Lett. B 268, 179-87
Arik, M. A991) The g-difference operator, the quantum hyperplane, Hilbert spaces of
analytic functions and g-oscillators, Z. Phys. C51, 627—32
Arik, M. & Coon, D. D. A976) Hilbert spaces of analytic functions and generalized coherent
states, J. Math. Phys. 17, 524-7
Arnaudon, D. A990) Periodic and flat irreducible representations of SUC)q, Comm. Math.
Phys. 134, 523-37
Arnaudon, D. A991) Fusion rules and R-matrix for the composition of regular spins with
semi-periodic representations of SLB)q, Phys. Lett. B 268, 217-21
Arnaudon, D. A992a) On periodic representations of quantum groups, in Topological and
Geometrical Methods in Field Theory, J. Mickelsson &; O. Pekonen (eds), pp. 13-21, World
Scientific, Singapore
Arnaudon, D. A992b) New fusion rules and R-matrices for SL(N)q at roots of unity, Phys.
Lett. B 280, 31-8
Arnaudon, D. &; Chakrabarti, A. A991a) Flat periodic representations of Uq(Q), Comm.
Math. Phys. 139, 605-17
Arnaudon, D. &; Chakrabarti, A. A991b) Periodic and partially periodic representations
ofSU(N)q, Comm. Math. Phys. 139, 461-78
Arnaudon, D. & Chakrabarti, A. A991c) Periodic representations of SOE)q, Phys. Lett.
B 262,68-70
Arnaudon, D. & Chakrabarti, A. A991d) g-analogue of IU(n) for q a root of unity, Phys.
Lett. B 255, 242-8
Arnaudon, D. &; Rittenberg, V. A993) Quantum chains with Uq(sl{2)) symmetry and
unrestricted representations, Phys. Lett. B 306, 86-90
Arnold, V. I. A978) Mathematical Methods of Classical Mechanics, Graduate Texts in
Mathematics 60, Springer, Berlin
Artin, E. A947) Theory of braids, Ann. of Math. 48, 101-26
Artin, M., Schelter, W. &; Tate, J. A991) Quantum deformations of GLn, Comm. Pure
Appl. Math. 44, 879-95
Aschieri, P. & Castellani, L. A992) Bicovariant differential geometry of the quantum group
GLq{3), Phys. Lett. B 293, 299-308
Aschieri, P. &; Castellani, L. A993) An introduction to noncommutative differential geom-
geometry on quantum groups, Internat. J. Modern Phys. A 8, 1667-706
Atiyah, M. F. A988) Topological quantum field theories, Publ. Math. IHES 68, 175-86
Atiyah, M. F. A989) The Jones-Witten invariants of knots, Seminaire Bourbaki exp. no.
715, Asterisque 189-190, 7-16, Societe Mathematique de France, Paris
Atiyah, M. F. A991) Magnetic monopoles and the Yang-Baxter equation, Internat. J.
Modem Phys. A 6, 2761-74
Au-Yang, H., McCoy, B. M., Perk, J., Tang, S. & Yan, M. L. A987) Commuting transfer
matrices in the chiral Potts models: solutions of star-triangle equations for genus > 1, Phys.
Lett. A 123, 219-23
Au-Yang, H. & Perk, J. A989) Onsager's star-triangle equation: master key to integrability,
in Integrable Systems in Quantum Field Theory and Statistical Mechanics, M. Jimbo, T.
Miwa &; A. Tsuchiya (eds), Advanced Studies in Pure Mathematics 19, pp. 57-94, Academic
Press, Boston
570 References
Au-Yang, H. &; Perk, J. A991) Star-triangle equations and multicomponent chiral Potts
models, in Current Problems in Statistical Mechanics, Washington, DC, 1991, E. Domany
& D. Jasnow (eds), pp. 139-45
Avan, J. A990a) Current algebra realization of R-matrices associated to ^-graded Lie
algebras, Phys. Lett. B 252, 230-6
Avan, J. A990b) Graded Lie algebras in the Yang-Baxter equation, Phys. Lett. B 245,
491-6
Avan, J. A990c) Rational and trigonometric constant non-antisymmetric R-matrices, Phys.
Lett. B 241, 77-82
Avan, J. A991) Prom rational to trigonometric R-matrices, Phys. Lett. A 156, 61-8
Avan, J. & Tolan, M. A991) Graded R-matrices for integrable systems, Nucl. Phys. B 352,
215-49
Avancini, S. S. &; Brunelli, J. C. A993) g-deformed variational study of the Lipkin-Meshkov-
Glick model via coherent states, Phys. Lett. A 174, 358-62
Avancini, S. S. & Menezes, D. P. A993) Generating function for Clebsch-Gordan coefficients
of the suqB) quantum algebra, J. Phys. A 26, 1139-48
Baaj, S. A992) Representation reguliere du groupe quantique Efj,B) de Woronowicz, C R.
Acad. Sci. Paris Ser. 7 314, 1021-6
Babelon, O. A984) Representations of the Yang-Baxter algebra associated to Toda field
theory, Nucl. Phys. B 230, 241-9
Babelon, O. A988a) Jimbo's g-analogues and current algebras, Lett. Math. Phys. 15, 111-7
Babelon, O. A988b) Extended conformal algebra and the Yang-Baxter equation, Phys.
Lett. B 215, 523-9
Babelon, O. A989) The role of the Yang-Baxter equation in conformal field theory, in
Knots, Topology and Quantum Field Theories, Florence, 1989, L. Lusanna (ed.), pp. 447-
68, World Scientific, River Edge, NJ
Babelon, O. A990) Prom integrable to conformal field theory, Nucl. Phys. B Proc. Suppl.
18 A, 1-22
Babelon, O. A991) Universal exchange algebra for Bloch waves and Liouville theory, Comm.
Math. Phys. 139, 619-43
Babelon, O. A992) Liouville theory on the lattice and universal exchange algebra for Bloch
waves, in Quantum Groups, Proceedings of Workshops held in the Euler International
Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp.
159-75, Springer, Berlin
Babelon, O. & Bernard, D. A991) Dressing transformations and the origin of quantum
group symmetries, Phys. Lett. B 356, 387-438
Babelon, O. & Bernard, D. A992) Dressing symmetries, Comm. Math. Phys. 149, 279-306
Babelon, O. & Bonora, L. A991) Quantum Toda theory, Phys. Lett. B 253, 365-72
Babelon, O. &; Viallet, C. M. A990) Hamiltonian structures and Lax equations, Phys. Lett.
B 237, 411-6
Bacry, H. A993a) The problem of mass in the LNR quantum Poincare algebra, Phys. Lett.
B 306,41-3
Bacry, H. A993b) Classical electrodynamics on a quantum Poincare group, Phys. Lett. B
306, 44-8
Baez, J. C. A991) Differential calculi on quantum vector spaces with Hecke type relations,
Lett. Math. Phys. 23, 133-41
Baez, J. C. A992) R-commutative geometry and quantization of Poisson algebras, Adv.
Math. 95, 61-91
Ballesteros, A., Gadella, M. & Del Olmo, M. A. A992) Moyal quantization of 2 + 1 dimen-
dimensional Galilean systems, J. Math. Phys. 33, 3379-86
Ballesteros, A. &; Negro, J. A992) A characterization of functional realizations of three-
dimensional quantum groups, J. Phys. A 25, 5945-62
References 571
Balog, J., Dabrowski, L. & Feher, L. A990) Classical r-matrix and exchange algebra in
WZNW and Toda theories, Phys. Lett. B 244, 227-34
Balog, J., Dabrowski, L. &; Feher, L. A991) A new quantum deformation of SXC), Phys.
Lett. B 257, 74-8
Bantay, P. A990) Orbifolds and Hopf algebras, Phys. Lett. B 245, 477-9
Bantay, P. A991) Orbifolds, Hopf algebras and moonshine, Lett. Math. Phys. 22, 187-94
Barouch, E. A984) Lax pair for the free-fermion eight-vertex model, Stud. Appl. Math. 70,
151-62
Basu-Mallick, B. & Kundu, A. A991) Single g-oscillator mode realization of the quantum
group through canonical bosonisations of SUqB) and g-oscillators, Modern Phys. Lett. A
6, 701-5
Basu-Mallick, B. & Kundu, A. A992a) Hidden quantum group structure in relativistic
quantum integrable model, Phys. Lett. B 287, 149-53
Basu-Mallick, B. &; Kundu, A. A992b) Spectral parameter-dependent approach to quan-
quantized algebra, its multiparameter deformations and their g-oscillator realizations, J. Phys.
A 25, 4147-56
Batchelor, M. A991) Measuring coalgebras, quantum group-like objects and noncommuta-
tive geometry, in Differential Geometric Methods in Theoretical Physics, Rapallo, 1990, C.
Bartocci, U. Bruzzo & R. Cianci (eds), Lecture Notes in Physics 375, pp. 47-60, Springer,
Berlin
Batchelor, M. &; Kuniba, A. A991/2) Temperley-Lieb lattice models from quantum groups,
J. Phys. A 24, 2599-614; corrigendum, ibid. 25, 1019
Batchelor, M., Mezincescu, L., Nepomechie, R. & Rittenberg, V. A990) g-deformations of
the OC) symmetric spin-1 Heisenberg chain, J. Phys. A 23, L141-4
Baulieu, L. & Floratos, G. A991) Path integral on the quantum plane, Phys. Lett. B 258,
171-8
Baxter, R. J. A972) Partition function of the eight-vertex lattice model, Ann. Phys. 70,
193-228
Baxter, R. J. A973) Eight vertex model in lattice statistics and one-dimensional anisotropic
Heisenberg chain, Ann. Phys. 76, 1-24; 25-47; 48-71
Baxter, R. J. A982) Exactly Solved Models in Statistical Mechanics, Academic Press, New
York
Baxter, R. J., Perk, J. H. H. & Au-Yang, H. A988) New solutions of the star-triangle
relations for the chiral Potts model, Phys. Lett. A 128, 138-42
Bayen, F., Flato, M., Fronsdal, C, Lichnerowicz, A. & Sternheimer, D. A978) Deformation
theory and quantization. I. Deformations of symplectic structures, Ann. Phys. Ill, 61-110;
II. Physical applications, ibid. Ill, 111-151
Bazhanov, V. V. A985a) Trigonometric solutions of triangle equations and classical Lie
algebras, Phys. Lett. B 159, 321-4
Bazhanov, V. V. A985b) Hidden symmetry of the free fermion model, I, Theoret. Math.
Phys. 62, 253-60; II, ibid. 63, 519-27; III, ibid. 63, 604-11
Bazhanov, V. V. A987) Integrable quantum systems and classical Lie algebras, Comm.
Math. Phys. 113, 471-503
Bazhanov, V. V. & Kashaev, R. M. A991) Cyclic L operators related with 3-state R-matrix,
Comm. Math. Phys. 136, 607-23
Bazhanov, V. V., Kashaev, R. M., Mangazeev, V. V. & Stroganov, Yu. G. A991) {ZN)Xn~l
-generalization of the chiral Potts model, Comm. Math. Phys. 138, 393—408
Bazhanov, V. V. & Reshetikhin, Yu. N. A989) Critical RSOS models and conformal field
theory, Internat. J. Modern Phys. A 4, 115-42
Bazhanov, V. V. & Reshetikhin, Yu. N. A990) Restricted solid-on-solid models connected
with simply-laced algebras and conformal field theory, J. Phys. A 23, 1477-92
572 References
Bazhanov, V. V. & Reshetikhin, Yu. N. A991) Thermodynamic Bethe ansatz for RSOS
scattering theories, Nucl. Phys. B 358, 497-523
Bazhanov, V. V. &; Stroganov, Yu. G. A982) Trigonometric and Sn symmetric solutions
of triangle equations with variables on the faces, Nucl. Phys. B 205, 505-26
Bazhanov, V. V. &; Stroganov, Yu. G. A990) Chiral Potts models as a descendant of the
six-vertex models, J. Stat. Phys. 51, 799-817
Beck, J. A993) Braid group action and quantum affine algebras, preprint, MIT
Beckers, J. & Debergh, N. A992) Prom TV = 2 supersymmetry to quantum deformations,
Phys. Lett. B 286, 290-2
Bednar, M., Burdik, C., Couture, M. & Hlavaty, L. A992) On the quantum symmetries
associated with the two-parameter free fermion model, J. Phys. A 25, L341-6
Beggs, E. & Majid, S. A990) Matched pairs of topological Lie algebras corresponding to Lie
bialgebra structures on diff(S1) and diff(]R.), Ann. Inst. Henri Poincare Phys. Theor.
53,15-34
Beilinson, A., Bernstein, J. &; Deligne, P. A982) Faisceaux Pervers, Asterisque 100, Societe
Mathematique de Prance, Paris
Beilinson, A. A., Lusztig, G. &; MacPherson, R. A990) A geometric setting for the quantum
deformation of GLn, Duke Math. J. 61, 655-77
Belavin, A. A. A981) Dynamical symmetry of integrable quantum systems, Nucl. Phys. B
180, 189-200
Belavin, A. A. & Drinfel'd, V. G. A982) Solutions of the classical Yang-Baxter equation
for simple Lie algebras, Fund. Anal. Appl. 16, 159-80
Belavin, A. A. & Drinfel'd, V. G. A984a) Triangle equations and simple Lie algebras, Soviet
Scientific Reviews Sect. C 4, 93-165, Harwood Academic Publishers, Chur, Switzerland
Belavin, A. A. & Drinfel'd, V. G. A984b) Classical Young-Baxter (sic) equation for simple
Lie algebras, Fund. Anal. Appl. 17, 220-1
Belavin, A. A., Polyakov, A. M. & Zamolodchikov, A. B. A984) Infinite conformal symme-
symmetry in two-dimensional quantum field theory, Nucl. Phys. B 241, 333-80
Bellon, M. P., Maillard, J. M. & Viallet, C. A991) Infinite discrete symmetry group for the
Yang-Baxter equations. Vertex models, Phys. Lett. B 260, 87—100
Belov, A. A. & Chaltikian, K. D. A993) Q-deformation of Virasoro algebra and lattice
conformal theories, Modern Phys. Lett. A 8, 1233-42
Belyi, A. A987) On the commutator of the absolute Galois group, in Proceedings of the
International Congress of Mathematicians, Berkeley, 1986, A. M. Gleason (ed.), pp. 346-9,
American Mathematical Society, Providence, RI (Russian)
Berger, R. A991) Quantification de l'identite de Jacobi, C. R. Acad. Sci. Paris Ser. 7 312,
721-4
Berger, R. A992) The quantum Poincare-Birkhoff-Witt theorem, Comm. Math. Phys. 143,
215-34
Bergman, G. M. A978) The diamond lemma for ring theory, Adv. Math. 29, 178-218
Bergman, G. M. A985) Everybody knows what a Hopf algebra is, in Group Actions on
Rings, S. Montgomery (ed.), Contemporary Mathematics 43, pp. 25-48, American Mathe-
Mathematical Society, Providence, RI
Berkovich, A., Gomez, C. & Sierra, G. A993) g-magnetism at roots of unity, J. Phys. A
26, L45-52
Bernard, D. A989) Vertex operator representations of the quantum affine algebra Uq(Br ),
Lett. Math. Phys. 17, 239-45
Bernard, D. A990) Quantum Lie algebras and differential calculus on quantum groups,
Progr. Theor. Phys. Suppl. 102, 49-66
Bernard, D. A991a) A remark on quasi-triangular quantum Lie algebras, Phys. Lett. B
260, 389-93
References 573
Bernard, D. A991b) Hidden Yangians in 2D massive current algebras, Comm. Math. Phys.
137, 191-208
Bernard, D. A992) A propos du calcul differentiel sur les groupes quantiques, Ann. Inst.
Henri Poincare Phys. Theor. 56, 443-8
Bernard, D. &; Felder, G. A991) Quantum group symmetries in two-dimensional lattice
quantum field theory, Nucl. Phys. B 365, 98-120
Bernard, D. & LeClair, A. A989) g-deformation of SUA,1), conformal Ward identities and
g-strings, Phys. Lett. B 227, 417-23
Bernard, D. & LeClair, A. A990) Residual quantum symmetries of the restricted sine-
Gordan theories, Nucl. Phys. B 340, 721-51
Bernard, D. & LeClair, A. A991) Quantum group symmetries and non-local currents in
2D QFT, Comm. Math. Phys. 142, 99-138
Bernard, D. & LeClair, A. A992) Non-local currents in 2D QFT: an alternative to the
quantum scattering method, in Quantum Groups, Proceedings of Workshops held in the
Euler International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Math-
Mathematics 1510, pp. 176-96, Springer, Berlin
Bernard, D. & Pasquier, V. A990) Exchange algebra and exotic supersymmetry in the
chiral Potts model, Internat. J. Modern Phys. B 4, 913-27
Bernstein, I. N., Gel'fand, I. M. & Ponomarev, V. A. A973) Coxeter functors and Gabriel's
theorem, Russian Math. Surveys 28 B), 17-32
Bernstein, I. N. & Zelevinsky, A. V. A977) Induced representations of p-adic groups I, Ann.
Sci. Ecole Norm. Sup. 4e Ser. 10, 441-72
Biedenharn, L. C. A989) The quantum group SUqB) and a g-analogue of the boson oper-
operators, J. Phys. A 22, L873-8
Biedenharn, L. C. A990) A g-boson realization of the quantum group SUq{2) and the theory
of g-tensor operators, in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &
J.-D. Hennig (eds), Lecture Notes in Physics 370, pp. 67—88, Springer, Berlin
Biedenharn, L. C. A991) An overview of quantum groups, in Group Theoretical Methods
in Physics, Moscow, 1990, V. V. Dodonov & V. I. Manko (eds), Lecture Notes in Physics
382, pp. 147-63, Springer, Berlin
Biedenharn, L. C. & Lohe, M. A. A990) Some remarks on quantum groups - a new variation
on the theme of symmetry, in From Symmetries to Strings, Rochester NY, 1990, A. Das
(ed.), pp. 189-206, World Scientific, Teaneck, NJ
Biedenharn, L. C. & Lohe, M. A. A991) Quantum groups and basic hypergeometric func-
functions, in Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), 123-32, World
Scientific, Singapore
Biedenharn, L. C. & Lohe, M. A. A992a) Induced representations and tensor operators for
quantum groups, in Quantum Groups, Proceedings of Workshops held in the Euler Inter-
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics
1510, pp. 197-209, Springer, Berlin
Biedenharn, L. C. &; Lohe, M. A. A992b) An extension of the Borel-Weil construction to
the quantum group Uq(n), Comm. Math. Phys. 146, 483-504
Biedenharn, L. C. & Tarlini, M. A990) On g-tensor operators for quantum groups, Lett.
Math. Phys. 20, 271-8
Bilal, A. A991) Toda theories, W-algebras and their branching and fusion properties, in
Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), 258-74, World Scientific,
Singapore
Bincer, A. M. A991) Casimir operators for suq(n), J. Phys. A 24, LI 133-8
Birman, J. S. A976) Braids, Links and Mapping Class Groups, Annals of Mathematics
Studies 82, Princeton University Press, Princeton
Birman, J. S. A993) New points of view in knot theory, Bull. Amer. Math. Soc. 28, 253-87
574 References
Birman, J. S. & Lin, X. S. A993) Knot polynomials and Vassiliev's invariants, Invent.
Math. Ill, 225-70
Birman, J. S. & Wenzl, H. A989) Braids, links and a new algebra, Trans. Amer. Math.
Soc. 313, 239-45
Bogoliubov, N. M. & Bullough, R. K. A992) Completely integrable model of interacting
g-bosons, Phys. Lett. A 168, 264-9
Bogolyubov, N. N., Mikityuk, I. V. & Prikarpatskii, A. K. A991) Verma modules over the
quantum Lie algebra of currents on the circle, Soviet Math. Dokl. 42, 424-8
Bogoyavlenskii, O. I. A976) On perturbations of the periodic Toda lattice, Comm. Math.
Phys. 51, 201-9
Bonatsos, D., Argyres, E. N., Drenska, S. B., Raychev, P. P., Roussev, R. P. & Smirnov, Yu.
F. A990) SUqB) description of rotational spectra and its relation to the variable moment
of the inertia model, Phys. Lett. B 251, 477-82
Bonatsos, D., Argyres, E. N. & Raychev, P. P. A991) SUq(l,l) description of vibrational
molecular spectra, J. Phys. A 24, L403-8
Bonatsos, D., Brito, L. & Menezes, D. A993) The g-deformed Moszkowski model: RPA
modes, J. Phys. A 26, 895-904
Bonatsos, D. &; Daskaloyannis, C. A993) Equivalence of deformed fermionic algebras, J.
Phys. A 26, 1589-600
Bonatsos, D., Daskaloyannis, C. & Kokkotas, K. A992) WKB equivalent potentials for
g-deformed harmonic and anharmonic oscillators, J. Math. Phys. 33, 2958-65
Bonatsos, D., Faessler, A., Raychev, P. P., Roussev, R. P. & Smirnov, Yu. F. A992a) An
exactly soluble nuclear model with SUqC) D SUqB) D SOqB) symmetry, J. Phys. A 25,
L267-74
Bonatsos, D., Faessler, A., Raychev, P. P., Roussev, R. P. & Smirnov, Yu. F. A992b)
B(E2) transition probabilities in the g-rotator model with SUq{2) symmetry, J. Phys. A
25, 3275-86
Bonechi, F., Celeghini, E., Giachetti, R., Sorace, E. & Tarlini, M. A992) Heisenberg XXZ
model and quantum Galilei group, J. Phys. A 25, L939-44
Bonneau, P. A992) Cohomology and associated deformations for not necessarily co-
associative bialgebras, Lett. Math. Phys. 26, 277-84
Bonneau, P., Flato, M. & Pinczon, G. A992) A natural and rigid model of quantum groups,
Lett. Math. Phys. 25, 75-84
Bordemann, M. A990) Generalized Lax pairs, the modified classical Yang-Baxter equation
and affine geometry of Lie groups, Comm. Math. Phys. 135, 201—16
Borisov, N. V., Ilinski, K. N. & Uzdin, V. M. A992) Quantum group particles and paras-
tatistical excitations, Phys. Lett. A 169, 427-32
Bourbaki, N. A968) Groupes et Algebres de Lie, Chapitres 4, 5 et 6, Hermann, Paris
Bourbaki, N. A970), Algebre, Chapitres 1 a 3, Hermann, Paris
Bourbaki, N. A972) Groupes et Algebres de Lie, Chapitres 2 et 3, Hermann, Paris
Bourbaki, N. A985) Algebre Commutative, Chapitres 5 a 7, Masson, Paris
Bouwknegt, P., McCarthy, J., Nemeschansky, D. & Pilch, K. A991) Vertex operators and
fusion rules in the free field realizations of WZNW theories, Phys. Lett. B 258, 127-33
Bouwknegt, P., McCarthy, J. & Pilch, K. A990a) Quantum group structure in the Fock
space resolutions of sl(n) representations, Comm. Math. Phys. 131, 125-55
Bouwknegt, P., McCarthy, J. & Pilch, K. A990b) Free field realizations of WZNW models.
The BRST complex and its quantum group structure, Phys. Lett. B 234, 297-303
Bowcock, P. & Watts, G. M. T. A992) On the classification of quantum W-algebras, Nucl.
Phys. B 379, 63-95
Bozejko, M. & Speicher, R. A991) An example of a generalized Brownian motion, Comm.
Math. Phys. 137, 519-31
References 575
Bracken, A. J., Gould, M. D. & Tsohantjis, I. A993) Boson-fermion models for osp(l,2)
and Uq(osp{l,2)), J. Math. Phys. 34, 1654-64
Bracken, A. J., Gould, M. D. & Zhang, R. B. A990) Quantum supergroups and solutions
of the Yang-Baxter equation, Modern Phys. Lett. A 5, 831—40
Bracken, A. J., McAnally, D. S., Zhang, R. B. & Gould, M. D. A991) A g-analogue of
Bargmann space and its scalar product, J. Phys. A 24, 1379-91
Braden, H. W., Corrigan, E., Dorey, P. E. & Sasaki, R. A992) Affine Toda field theory: S-
matrix vs. perturbation, in Quantum Groups, Proceedings of Workshops held in the Euler
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathemat-
Mathematics 1510, pp. 210-20, Springer, Berlin
Braden, H. W., Corrigan, E., Dorey, P. E. & Sasalu, R. A991) Aspects of affine Toda field
theory, in Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 275-305, World
Scientific, Singapore
Bragiel, K. A989) The twisted SUC) group. Irreducible ^representations of the C*-algebra
C(S^UC)), Lett. Math. Phys. 17, 37-44
Bragiel, K. A990) The twisted SU(N) group. On the C*-algebra C(S^U(N)), Lett. Math.
Phys. 20, 251-7
Bragiel, K. A991a) On the Wigner-Eckart theorem for tensor operators connected with
compact matrix quantum groups, Lett. Math. Phys. 21, 181-91
Bragiel, K. A991b) On the spherical and zonal functions on the compact quantum groups,
Lett. Math. Phys. 22, 195-202
Bratelli, O., Elliot, G. A., Evans, D. E. & Kishimoto, A. A991) Non-commutative spheres
I, Intemat. J. Math. 2, 139-66
Brauer, R. A937) On algebras which are connected with the semisimple continuous groups,
Ann. of Math. 38, 857-72
Brzezinski, T. A993) Quantum group related to the space of differential operators on the
quantum hyperplane, J. Phys. A 26, 921-6
Brzezinski, T., Dabrowski, H. &; Rembielinski, J. A992) On the quantum differential cal-
calculus and the quantum holomorphicity, J. Math. Phys. 33, 19—24
Brzezinski, T. & Majid, S. A993) Quantum group gauge theory on classical spaces, Phys.
Lett. B 298, 339-43
Brzezinski, T. &; Rembielinski, J. A992) g-integrals on the quantum complex plane, J.
Phys. A 25, 1945-52
Brzezinski, T., Rembielinski, J. & Smolinski, K. A. A993) Quantum particle on a quantum
circle, Modern Phys. Lett. A 8, 409-16
Bullough, R. K., Pilling, D. J. &; Timonen, J. A988) Soliton statistical mechanics, in Soli-
tons, Tiruchirapalli, 1987, M. Lakshmanan (ed.), Springer Series in Nonlinear Dynamics,
pp. 250-81, Springer, Berlin
Bullough, R. K. &; Timonen, J. A991) Quantum groups and quantum complete integra-
bility: theory and experiment, in Differential Geometric Methods in Theoretical Physics,
Rapallo, 1990, C. Bartocci, U. Bruzzo & R. Cianci (eds), Lecture Notes in Physics 375, pp.
71-90, Springer, Berlin
Burdik, C., Cerny, L. &; Navratil, O. A993) The g-boson realization of the quantum group
Uq(sl(n+ 1,C)), J. Phys. A 26, L83-6
Burdik, C., Havlicek, M. & Vancura, A. A992) Irreducible highest weight representations
of quantum groups Uq(gl(n,(?)), Comm. Math. Phys. 148, 417—23
Burdik, C. Sz Hellinger, P. A992a) Universal R-matrix for a two-parametric quantization
of 0/B), J. Phys. A 25, L629-32
Burdik, C. & Hellinger, P. A992b) The universal R-matrix and the Yang-Baxter equation
with parameters, J. Phys. A 25, L1023-8
Burdik, C. & Hlavaty, L. A991) A two-parametric quantization of sl{2), J. Phys. A 24,
L165-8
576 References
Burdik, C. & Navratil, O. A990) The boson realizations of the quantum group Uq(slB)),
J. Phys. A 23, L2105-8
Burroughs, N. A990a) The universal R-matrix for Uqsl(S) and beyond, Comm. Math. Phys.
127, 109-28
Burroughs, N. A990b) Relating the approaches to quantized algebras and quantum groups,
Comm. Math. Phys. 133, 91-117
Burroughs, N. A991) The quantum group methods of quantizing the special linear group
5L2(C), in Differential Geometric Methods in Theoretical Physics, Davis, 1988, L. L. Chau
& W. Nahm (eds), NATO Advanced Science Institutes Series B: Physics 245, pp. 513-39,
Plenum, New York
Buzek, V. A991) Dynamics of a g-analogue of the quantum harmonic oscillator, J. Modern
Optics 38, 801-12
Buzek, V. A992) The Jaynes-Cummings model with a <?-analogue of a coherent state, J.
Modern Optics 39, 949-59
Cahen, M., Gutt, S., Ohn, C. &; Parker, M. A990) Lie-Poisson groups: remarks and exam-
examples, Lett. Math. Phys. 19, 343-53
Cahen, M., Gutt, S. & Rawnsley, J. A992) Nonlinearizability of the Iwasawa Poisson-Lie
structure, Lett. Math. Phys. 24, 79-83
Caldero, P. A993) Elements ad-finis de certains groupes quantiques, C. R. Acad. Sci. Paris
Ser. I 316, 327-9
Caldi, D. G. A991) SUqB) and SUB) as hamiltonian symmetries, in Quantum Groups,
T. Curtright, D. Fairlie & C. Zachos (eds), pp. 236-46, World Scientific, Singapore
Caldi, D. G., Chodos, A., Zhu, Z. & Barth, A. A991) The classical suB) invariance of the
sitB)9-invariant XXZ chain, Lett. Math. Phys. 22, 163-6
Carow-Watamura, U., Schlieker, M., Scholl, M. & Watamura, S. A990) Tensor represen-
representation of the quantum group SLqB,<E) and quantum Minkowski space, Z. Phys. C 48,
159-65
Carow-Watamura, U., Schlieker, M., Scholl, M. & Watamura, S. A991) A quantum Lorentz
group, Internat. J. Modern Phys. A 6, 3081-108
Carow-Watamura, U., Schlieker, M. & Watamura, S. A991) SOq(N) covariant differential
calculus on quantum space and quantum deformation of Schrodinger equation, Z. Phys. C
49, 439-46
Carow-Watamura, U., Schlieker, M., Watamura, S. &; Weich, W. A991) Bicovariant differ-
differential calculus on quantum groups SUq(N) and SOq(N), Comm. Math. Phys. 142, 605-41
Carow-Watamura, U. & Watamura, S. A993) Complex quantum group, dual algebra and
bicovariant differential calculus, Comm. Math. Phys. 151, 487-514
Cartier, P. A979) Representations of p-adic groups: a survey, in Automorphic Forms, Rep-
Representations and L-Functions, Proceedings of Symposia in Pure Mathematics 33, Part I,
pp. 111-55, American Mathematical Society, Providence, RI
Cartier, P. A990) Developpements recents sur les groupes de tresses. Applications a la
topologie et a l'algebre, Seminaire Bourbaki exp. no. 716, Asterisque 189—190, 17-67,
Societe Mathematique de Prance, Paris
Casian, L. A990) Kazhdan-Lusztig multiplicity formulas for Kac-Moody algebras, C R.
Acad. Sci. Paris Ser. 7 310, 333-7
Casian, L. A993) Kazhdan-Lusztig conjecture in the negative level case (Kac-Moody al-
algebras of affine type), preprint
Castellani, L. A992a) Bicovariant differential calculus on the quantum D = 2 Poincare
group, Phys. Lett. B 279, 291-8
Castellani, L. A992b) Gauge theories of quantum groups, Phys. Lett. B 292, 93-8
Castellani, L. A993) R-matrix and bicovariant calculus for the inhomogeneous quantum
groups IGLq(n), Phys. Lett. B 298, 335-8
Cateau, H. & Saito, S. A990) Braids of strings, Phys. Rev. Lett. 65, 2487-90
References 577
Celeghini, E., Giachetti, R., Kulish, P., Sorace, E. & Tarlini, M. A991) Hopf superalgebra
contractions and R-matrix for fermions, J. Math. Phys. A 24, 5675-82
Celeghini, E., Giachetti, R., Reyman, A., Sorace, E. & Tarlini, M. A991) SOq(n+l,n-l)
as a real form of SOq{2n,<E), Lett. Math. Phys. 23, 45-9
Celeghini, E., Giachetti, R., Sorace, E. & Tarlini, M. A990) Three dimensional quantum
groups from contractions of SUB)q, J. Math. Phys. 31, 2548-51
Celeghini, E., Giachetti, R., Sorace, E. & Tarlini, M. A991a) The quantum Heisenberg
group H(l)q, J. Math. Phys. 32, 1155-8
Celeghini, E., Giachetti, R., Sorace, E. & Tarlini, M. A991b) The three dimensional eu-
clidean quantum group EC)q and its R-matrix, J. Math. Phys. 32, 1159-65
Celeghini, E., Giachetti, R., Sorace, E. & Tarlini, M. A992) Contractions of quantum
groups, in Quantum Groups, Proceedings of Workshops held in the Euler International
Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp.
221-44, Springer, Berlin
Celeghini, E., Palev, T. D. & Tarlini, M. A991) The quantum superalgebra Bq@\l) and
g-deformed creation and annihilation operators, Modern Phys. Lett. B 5, 187—93
Celeghini, E., Rasetti, M. & Vitiello, G. A991) Squeezing and quantum groups, Phys. Rev.
Lett. 66, 2056-9
Chaichian, M., De Azcarraga, J. A., Presnajder, P. & Rodenas, F. A992) Oscillator real-
realization of the g-deformed anti-de Sitter algebra, Phys. Lett. B 291, 411-7
Chaichian, M. & Demichev, A. P. A993) Quantum Poincare group, Phys. Lett. B 304,
220-4
Chaichian, M. & Ellinas, D. A990) On the polar decomposition of the quantum group
SU{2) algebra, J. Phys. A 23, L291-6
Chaichian, M., Ellinas, D. & Kulish, P. A990) Quantum algebra as the dynamical symmetry
of the deformed Jaynes-Cummings model, Phys. Rev. Lett. 65, 980—3
Chaichian, M., Ellinas, D. & Popovich, Z. A990) Quantum conformal algebra with central
extension, Phys. Lett. B 248, 95-9
Chaichian, M., Isaev, A. P., Lukierski, J., Popovich, Z. & Presnajder, P. A992) g-deforma-
tions of Virasoro algebra and conformal dimension, Phys. Lett. B 262, 32-8
Chaichian, M. & Kulish, P. A990) Quantum Lie superalgebras and g-oscillators, Phys. Lett.
B 234, 72-80
Chaichian, M., Kulish, P. & Lukierski, J. A990) g-deformed Jacobi identity, g-oscillators
and g-deformed infinite-dimensional algebras, Phys. Lett. B 237, 401—6
Chaichian, M., Kulish, P. & Lukierski, J. A991a) Supercovariant g-oscillators, in Nonlinear
Fields: Classical, Random, Semiclassical, Karpacz, 1991, P. Garbaczewski & Z. Popowicz
(eds), pp. 336-45, World Scientific, Singapore
Chaichian, M., Kulish, P. & Lukierski, J. A991b) Supercovariant systems of g-oscillators
and g-supercovariant Hamiltonians, Phys. Lett. B 262, 43-8
Chaichian, M., Popovich, Z. & Presnajder, P. A990) q-Virasoro algebra and its relation to
the g-deformed KdV system, Phys. Lett. B 249, 63-5
Chaichian, M. & Presnajder, P. A992a) Sugawara construction and the g-deformation of
Virasoro algebra, in Quantum Groups and Related Topics, R. Gierlak et al. (eds), pp. 3-12,
Kluwer, Dordrecht
Chaichian, M. & Presnajder, P. A992b) Sugawara construction and the g-deformation of
Virasoro (super) algebra, Phys. Lett. B 277, 109-18
Chair, N. & Zhu, C. J. A991) Tetrahedra and polynomial equations in topological field
theory, Internat. J. Modem Phys. A 6, 3571-98
Chakrabarti, A. A991) g-analogs of IU{n) and f/(n,l), J. Math. Phys. 32, 1227-34
Chakrabarti, A. A993) Canonical structure in SOD)q and relations to EC)q and 5OC, l)q,
J. Math. Phys. 34, 1964-85
578 References
Chakrabarti, A. &; Jagannathan, R. A991a) On the representations of GLp,qB), GLv,q(l\l)
and noncommutative spaces, J. Phys. A 24, 5683-701
Chakrabarti, A. & Jagannathan, R. A991b) On the representations of GLq(n) using the
Heisenberg-Weyl relations, J. Phys. A 24, 1709-20
Chakrabarti, A. &; Jagannathan, R. A991c) A (p, g)-oscillator realization of two-parameter
quantum algebras, J. Phys. A 24, L711-8
Chakrabarti, A. &; Jagannathan, R. A992a) A (p, g)-deformed Virasoro algebra, J. Phys.
A 25, 2607-14
Chakrabarti, A. & Jagannathan, R. A992b) On the number operators of single mode q-
oscillators, J. Phys. A 25, 6393-8
Chakrabarti, A. & Jagannathan, R. A992c) A two-parameter deformation of the Jaynes-
Cummings model: path integral representation, J. Phys. A 25, 6399-408
Chang, D., Phillips, I. &; Rozansky, L. A992) R-matrix approach to quantum superalgebras
suq{m\n), J. Math. Phys. 33, 3710-5
Chang, Z. A992a) The quantum multiboson algebra and generalized coherent states of
SUq(l,l), J. Phys. A 25, L707-12
Chang, Z. A992b) The quantum g-deformed symmetric top: an exactly solved model, J.
Phys. A 25, L781-8
Chang, Z. A992c) Quantum group realized in a symmetric top system, Phys. Rev. A 45,
4303-11
Chang, Z., Chen, W. & Guo, H. Y. A990) SUq->0B) and SUq{2), the classical and quantum
g-deformations of the SUB) algebra, J. Phys. A 23, L4185-90
Chang, Z., Chen, W., Guo, H. Y. & Yan, H. A990a) SUq->0B) and SUqB), the classical
and quantum g-deformations of the SUB) algebra II, J. Phys. A 23, 5371-82
Chang, Z., Chen, W., Guo, H. Y. & Yan, H. A990b) SUq^oB) and SUq{2), the classical
and quantum g-deformations of the SU{2) algebra III, J. Phys. A 24, 1427-34
Chang, Z., Fei, S. M., Guo, H. Y. & Yan, H. A991) SUq->0B) and SUq{2), the classical
and quantum g-deformations of the SU{2) algebra IV, J. Phys. A 24, 5435—44
Chang, Z., Guo, H. Y. & Yan, H. A991) The g-deformed oscillator model and the vibrational
spectra of diatomic molecules, Phys. Lett. A 156, 192-6
Chang, Z., Guo, H. Y. & Yan, H. A992) The g-Hermite polynomial and the representations
of Heisenberg and quantum Heisenberg algebras, J. Phys. A 25, 1517-25
Chang, Z., Wang, J. X. & Yan, H. A991) The realization of quantum groups of An-\ and
Cn types in g-deformed oscillator systems at classical and quantum levels, J. Math. Phys.
32, 3241-5
Chang, Z. & Yan, H. A991a) The SUq{2) quantum group symmetry and diatomic mol-
molecules, Phys. Lett. A 154, 254-8
Chang, Z. & Yan, H. A991b) Quantum group-theoretic approach to vibrating and rotating
diatomic molecules, Phys. Lett. A 158, 242-6
Chang, Z. & Yan, H. A991c) HqD) and SUq{2) symmetries in diatomic molecules, Phys.
Rev. A C) 43, 6043-52
Chari, V. A985) Integrable representations of affine Lie algebras, Invent. Math. 81, 317-37
Chari, V. & Ilangovan, S. A984) On the Harish-Chandra homomorphism for infinite-
dimensional Lie algebras, J. Algebra 90, 476-94
Chari, V. & Premet, A. A993) Indecomposable restricted representations of quantum 5/2,
Publ. Res. Inst. Math. Sci. (to appear)
Chari, V. &; Pressley, A. N. A986) New unitary representations of loop groups, Math. Ann.
275, 87-104
Chari, V. & Pressley, A. N. A990a) Notes on quantum groups, Nucl. Phys. B Proc. Suppl.
18 A, 207-28
Chari, V. & Pressley, A. N. A990b) Yangians and R-matrices, L'Enseignement Math. 36,
267-302
References 579
Chari, V. Sz Pressley, A. N. A991a) Fundamental representations of Yangians and rational
R-matrices, J. reine angew. Math. 417, 87-128
Chari, V. Sc Pressley, A. N. A991b) Quantum affine algebras, Comm. Math. Phys. 142,
261-83
Chari, V. Sz Pressley, A. N. A991c) Minimal cyclic representations of quantum groups at
roots of 1, C. R. Acad. Sci. Paris Ser. 7 313, 429-34
Chari, V. Sz Pressley, A. N. A991d) Introduction to quantum groups, in Proceedings of
International Conference on Algebraic Groups, Hyderabad, India, December, 1989, S. Ra-
manan, C. Musili Sz N. Mohan Kumar (eds), pp. 81-122, Manoj Prakashan, Madras
Chari, V. Sz Pressley, A. N. A992) Fundamental representations of quantum groups, Lett.
Math. Phys. 26, 133-46
Chari, V. Sz Pressley, A. N. A993a) Representations of modular Lie algebras through
quantum groups, C. R. Acad. Sci. Paris Ser. 7 317, 728-9
Chari, V. Sz Pressley, A. N. A993b) Quantum affine algebras and affine Hecke algebras,
Pacific J. Math, (to appear)
Chari, V. Sz Pressley, A. N. A994a) Representations of quantum SO(8) and related quan-
quantum algebras, Comm. Math. Phys. Comm. Math. Phys. 159 29—49
Chari, V. Sz Pressley, A. N. A994b) Small representations of quantum affine algebras, Lett.
Math. Phys. 30, 131-45
Chari, V. Sz Pressley, A. N. A994c) Quantum affine algebras and their representations, in
Proceedings of the Canadian Mathematical Society Annual Seminar - Representations of
Groups, Banff, 1994 (to appear)
Chen, Y. X. Sz Ni, G. J. A991) General theory of quantum statistics with internal degrees
of freedom in two dimensions, Phys. Rev. D 43, 4133-41
Cheng, Y., Ge, M. L. Sz Xue, K. A991) Yang-Baxterization of braid group representations,
Comm. Math. Phys. 136, 195-208
Cherednik, I. V. A980) On the method of constructing factorized S-matrices in elementary
functions, Theoret. Math. Phys. 43, 117-9 (Russian)
Cherednik, I. V. A982) On the properties of factorized S-matrices in elliptic functions,
Soviet J. Nucl. Phys. 36, 320-4
Cherednik, I. V. A983) Backlund-Darboux transformations for classical Yang-Baxter bun-
bundles, Fund. Anal. Appl. 17, 155-7
Cherednik, I. V. A984) Factorizing particles on a half line and root systems, Theoret. Math.
Phys. 61, 977-83
Cherednik, I. V. A985) Some finite-dimensional representations of generalized Sklyanin
algebras, Fund. Anal. Appl. 19, 77-9
Cherednik, I. V. A986a) On R-matrix quantization of formal loop groups, in Group Theo-
Theoretical Methods in Physics, Vol. II, Yurmala, USSR, 1985), V. V. Dodonov, V. I. Manko
Sc M. A. Markov (eds), pp. 161-80, VNU Science Press, Utrecht
Cherednik, I. V. A986b) On the quantum deformations of irreducible finite-dimensional
representations of g/jv, Soviet Math. Dokl. 33, 507—10
Cherednik, I. V. A987a) A new interpretation of Gel'fand-Tzetlin bases, Duke Math. J.
54, 563-77
Cherednik, I. V. A987b) On irreducible R-algebras, Soviet Math. Dokl. 34, 446-50
Cherednik, I. V. A988a) g-analogues of Gel'fand-Tzetlin bases, Fund. Anal. Appl. 22, 78-9
Cherednik, I. V. A988b) On special bases of irreducible finite-dimensional representations
of the degenerate affine Hecke algebra, Fund. Anal. Appl. 20, 87-8
Cherednik, I. V. A989) Quantum groups as hidden symmetries of classic representation
theory, in Differential Geometric Methods in Mathematical Physics, Proceedings of the 11th
International Conference, Chester, 1988, A. I. Solomon (ed.), pp. 47—55, World Scientific,
Teaneck, NJ
580 References
Cherednik, I. V. A990a) Generalised braid groups and local r-matrix systems, Soviet Math.
Dokl. 40, 43-8
Cherednik, I. V. A990b) Calculation of the monodromy of some ^-invariant local systems
of type B, C and D, Fund. Anal. Appl. 24, 78-9
Cherednik, I. V. A991a) Monodromy representations for generalized Knizhnik-Zamolod-
chikov equations and Hecke algebras, Publ. Res. Inst. Math. Sci. 27, 711-26
Cherednik, I. V. A991b) Integral solutions of trigonometric Knizhnik-Zamolodchikov equa-
equations and Kac-Moody algebras, Publ. Res. Inst. Math. Sci. 27, 727-44
Cherednik, I. V. A991c) A unification of Knizhnik-Zamolodchikov and Dunkl operators via
affine Hecke algebras, Invent. Math. 106, 411-31
Cherednik, I. V. A991d) Affine extensions of Knizhnik-Zamolodchikov equations and
Lusztig's isomorphisms, in Special Functions, Okayama, 1990, M. Kashiwara Sz T. Miwa
(eds), pp. 63-77, Springer, Tokyo
Cherednik, I. V. A992a) Double affine Hecke algebras, Knizhnik-Zamolodchikov equations,
and Macdonald's operators, Duke Math. J. Internat. Math. Res. Notices 2, 171-80
Cherednik, I. V. A992b) Degenerate affine Hecke algebras and two-dimensional particles,
in Infinite Analysis, A. Tsuchiya, T. Eguchi Sz M. Jimbo (eds), Advanced Series in Math-
Mathematical Physics 16, pp. 109-40, World Scientific, Singapore
Cherednik, I. V. A992c) Quantum Knizhnik-Zamolodchikov equations and affine root sys-
systems, Comm. Math. Phys. 150, 109-36
Chernyak, V. Ya., Grigorishin, K. I. Sz Ogievetsky, E. I. A991) Triangle equation and
quantum algebra representations, Phys. Lett. A 158, 291—4
Chernyak, V. Ya., Grigorishin, K. I. Sz Ogievetsky, E. I. A992a) Universal R-matrix and
representation theory for quantum groups, Phys. Lett. A 164, 389-97
Chernyak, V. Ya., Grigorishin, K. I. Sz Ogievetsky, E. I. A992b) Quantum group bootstrap
approach and infinite-dimensional factorized scattering matrices, Phys. Lett. A 164, 398-
407
Chernyak, V. Ya., Grigorishin, K. I. Sz Ogievetsky, E. I. A992c) Quantum group bootstrap
approach. Application to extended Heisenberg group, Phys. Lett. A 164, 408-15
Chernyak, V. Ya., Kozhekin, A. E. Sz Ogievetsky, E., A993) 5C/A, l)-invariant solutions of
the quantum Yang-Baxter equation, J. Phys. A 26, 1313-6
Chiu, S. H., Gray, R. W. & Nelson, C. A. A992) The g-analogue quantized radiation field
and its uncertainty relations, Phys. Lett. A 164, 237-42
Chryssomalokos, C. A992) Coproduct of vector fields on the quantum Lorentz group, Mod-
Modern Phys. Lett. A 7, 2851-6
Chryssomalokos, C, Drabant, B., Schlieker, M., Weich, W. Sz Zumino, B. A992) Vector
fields on complex quantum groups, Comm. Math. Phys. 147, 635-46
Chung, H. J. Sz Koh, I. G. A991) Solutions to the quantum Yang-Baxter equation for the
exceptional Lie algebra with a spectral parameter, J. Math. Phys. 32, 2406-8
Chung, Z., Guo, H. Y. Sz Yan, H. A991) The g-deformed oscillator model and the vibrational
spectra of diatomic molecules, Phys. Lett. A 156, 192-6
Codrianski, S. A991) Comments on (/-algebras, Internat. J. Theoret. Phys. 30, 59-76
Codrianski, S. A992) SUB)q in a Hilbert space of analytic functions, Internat. J. Theoret.
Phys. 31, 907-24
Cohen, M. A992) Hopf algebra actions - revisited, in Deformation Theory and Quantum
Groups with Applications to Mathematical Physics, M. Gerstenhaber Sz J. Stasheff (eds),
Contemporary Mathematics 134, pp. 1—18, American Mathematical Society, Providence,
RI
Connes, A., Flato, M. Sz Sternheimer, D. A992) Closed star products and cyclic cohomology,
Lett. Math. Phys. 24, 1-12
Cornwell, J. F. A992) Multiparameter deformations of the universal enveloping algebras
of the simple Lie algebras Ai for all/ > 2 and the Yang-Baxter equation, J. Math. Phys.
References 581
33, 3963-77
Corrigan, E., Fairlie, D. B., Fletcher, P. Sz Sasaki, R. A990) Some aspects of quantum
groups and supergroups, J. Math. Phys. 31, 776-80
Coste, A., Dazord, P. Sz Weinstein, A. A987) Groupoides symplectiques, Publications du
Departement de Mathematiques, Universite Claude Bernard-Lyon I 2A, pp. 1-62
Cotta-Ramasino, P. A992) Link diagrams, Yang-Baxter equations and quantum holonomy,
in Deformation Theory and Quantum Groups with Applications to Mathematical Physics,
M. Gerstenhaber Sz J. Stasheff (eds), Contemporary Mathematics 134, pp. 19—44, American
Mathematical Society, Providence, RI
Cotta-Ramasino, P. Sz Rinaldi, M. A991) Multi-parameter quantum groups related to link
diagrams, Comm. Math. Phys. 142, 589-604
Couture, M. A991) On some quantum R matrices associated with representations of
Uq(slB,<C)) when q is a root of unity, J. Phys. A 24, L103-7
Couture, M., Cheng, Y., Ge, M. L. Sz Xue, K. A991) New solutions of the Yang-Baxter
equation and their Yang-Baxterization, Internat. J. Modern Phys. A 6, 559-76
Crane, L. A991) 2-d physics and 3-d topology, Comm. Math. Phys. 135, 615-40
Cremmer, E. Sz Gervais, J.-L. A990) The quantum group structure associated with non-
linearly extended Virasoro algebras, Comm. Math. Phys. 134, 619-32
Crivelli, M., Felder, G. Sz Wieczerkowski, C. A993) Generalized hypergeometric functions
on the torus and the adjoint representation of Uq(sl2), Comm. Math. Phys. 154, 1-24
Cuerno, R. A991) Quantum symmetries in the free field realization of Wn algebras, Phys.
Lett. B 271, 314-20
Cummins, C. J. Sz King, R. C. A992) Characters of An-\ Hecke algebras at roots of unity,
J. Phys. A 25, L789-98
Curtright, T. I. A991) Deformations, coproducts and U, in Quantum Groups, T. Curtright,
D. Fairlie Sz C. Zachos (eds), pp. 72-96, World Scientific, Singapore
Curtright, T. I., Ghandour, G. I. Sz Zachos, C. K. A991) Quantum algebra deforming maps,
Clebsch-Gordan coefficients, coproducts, R and U matrices, J. Math. Phys. 32, 676-88
Curtright, T. I. Sz Zachos, C. K. A990) Deforming maps for quantum algebras, Phys. Lett.
B 243, 237-44
Dabrowski, L. Sz Dobrev, V. K. A993) Positive energy representations of the conformal
quantum algebra, Phys. Lett. B 302, 215-22
Dabrowski, L. Sz Wang, L. Y. A991) Two-parameter quantum deformation of GLA|1),
Phys. Lett. B 266, 51-4
Dai, J. H., Guo, H. Y. Sz Yan, H. A991) The g-deformed differential operator algebra, a
new solution to the Yang-Baxter equation and quantum plane, J. Phys. A 24, L409-14
Damaskinskii, E. V. Sz Kulish, P. P. A991) Deformed oscillators and their applications,
Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 189 (Russian)
Damaskinskii, E. V. Sz Kulish, P. P. A992) Hermite ^-polynomials and g-oscillators, Zap.
Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 199 (Russian)
Daskaloyannis, C. A992) Generalized deformed Virasoro algebras, Modern Phys. Lett. A
7, 809-16
Date, E., Jimbo, M., Kuniba, A., Miwa, T. & Okado, M. A987) Exactly solvable SOS
models: Local height probabilities and theta function identities, Nucl. Phys. B 290, 231—
73
Date, E., Jimbo, M., Kuniba, A., Miwa, T. Sz Okado, M. A988) Exactly solvable SOS
models: II. Proof of the star-triangle relation and combinatorial identities, in Conformal
Field Theory and Solvable Lattice Models, Kyoto, 1986, A. Tsuchiya, T. Eguchi Sz M. Jimbo
(eds), Advanced Studies in Pure Mathematics 16, pp. 17-122, Academic Press, Boston
Date, M., Jimbo, M. Sz Miki, K. A990) A note on the branching rule for cyclic representa-
representations of Uq(gln), preprint, RIMS, Kyoto
582 References
Date, E., Jimbo, M., Miki, K. Sz Miwa, T. A990) R-matrix for cyclic representations of
C/g(sZC,C)) at q3 = 1, Phys. Lett. A 148, 45-9
Date, M., Jimbo, M., Miki, K. Sz Miwa, T. A991a) Generalized chiral Potts models and
minimal cyclic representations of Uqgl(n,<?), Comm. Math. Phys. 137, 133-47
Date, E., Jimbo, M., Miki, K. Sz Miwa, T. A991b) Cyclic representations of Uq(sl(n + 1))
at qN = 1, Publ. Res. Inst. Math. Sci. 27, 347-66
Date, E., Jimbo, M., Miki, K. Sz Miwa, T. A991c) New R-matrices associated with cyclic
representations of Uq(A^), Publ. Res. Inst. Math. Sci. 27, 639-55
Date, M., Jimbo, M., Miki, K. Sz Miwa, T. A992) Braid group representations arising from
the generalized chiral Potts models, Pacific J. Math. 154, 37-66
Date, E., Jimbo, M. Sz Miwa, T. A990) Representations of Uq(gl(n,<?)) at q — 0 and the
Robinson-Schensted correspondence, in Physics and Mathematics of Strings, L. Brink, D.
Priedan Sz A. M. Polyakov (eds), pp. 185-211, World Scientific, Teaneck, NJ
De Concini, C. Sz Kac, V. G. A990) Representations of quantum groups at roots of 1, in
Operator Algebras, Unitary Representations, Enveloping Algebras and Invariant Theory,
A. Connes, M. Duflo, A. Joseph Sz R. Rentschler (eds), pp. 471-506, Birkhauser, Boston
De Concini, C, Kac, V. G. Sz Procesi, C. A992a) Quantum coadjoint action, J. Amer.
Math. Soc. 5, 151-89
De Concini, C, Kac, V. G. Sz Procesi, C. A992b) Representations of quantum groups at
roots of 1: reduction to the exceptional case, in Infinite Analysis, A. Tsuchiya, T. Eguchi Sz
M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp. 141—50, World Scientific,
Singapore
De Concini, C, Kac, V. G. Sz Procesi, C. A993a) Some remarkable degenerations of quan-
quantum groups, Comm. Math. Phys. 157, 405-27
De Concini, C, Kac, V. G. Sz Procesi, C. A993b) Some quantum analogues of solvable
groups, preprint, RIMS, Kyoto
De Concini, C. Sz Lyubashenko, V. A993) Quantum function algebra at roots of 1, preprint
Deguchi, T. A989) Braid group representations and link polynomials derived from gener-
generalized SU(n) vertex models, J. Phys. Soc. Japan 58, 3441—4
Deguchi, T. A990) Braids, link polynomials and transformations of solvable models, Inter-
nat. J. Modern Phys. A 5, 2195-239
Deguchi, T. & Akutsu, Y. A992) Colored braid matrices from infinite-dimensional repre-
representations of Uq(g), Modem Phys. Lett. A 7, 767-79
Deguchi, T., Pujii, A. Sz Ito, K. A992) Quantum superalgebra Uq(ospB,2)), Phys. Lett. B
238,242-6
De la Harpe, P. A988) Introduction to knot and link polynomials, in Fractals, Quasicrys-
tals, Chaos, Knots and Algebraic Quantum Mechanics, Maratea, 1987, A. Amann, L.
Cederbaum Sz W. Gans (eds), NATO Advanced Science Institutes Series C: Mathemat-
Mathematical and Physical Sciences 235, pp. 233—63, Kluwer, Dordrecht
Delbecq, C. Sz Quesne, C. A993a) Nonlinear deformations of su{2) and su(l, 1) generalizing
Witten's algebra, J. Phys. A 26, L127-34
Delbecq, C. Sz Quesne, C. A993b) Representation theory and (/-boson realizations of Wit-
ten's suB) and su(l, 1) deformations,Phys. Lett. B 300, 227-33
Delbecq, C. Sz Quesne, C. A993c) A cubic deformation of suB), Modern Phys. Lett. A 8,
961-6
Deligne, P. A989) Le groupe fondamental de la droite projective moins trois points, in
Galois groups over Q, P. Cartier et al. (eds), Publications of the Mathematical Sciences
Research Institute 16, pp. 79-298, Springer, Berlin
Deligne, P. A991) Categories Tannakiennes, in Grothendieck Festschrift, Vol. 2, P. Cartier
et al. (eds), pp. 111-95, Birkhauser, Boston
Deligne, P. Sz Milne, J. A982) Tannakian categories, in Hodge Cycles, Motives and Shimura
Varieties, P. Deligne, J. S. Milne, A. Ogus Sz K. Shih (eds), Lecture Notes in Mathematics
References 583
900, pp. 101-228, Springer, Berlin
Del Sol Mesa, A., Loyola, G., Moshinsky, M. Sz Velasquez, V. A993) Quantum groups and
the recovery of UC) symmetry in the Hamiltonian of the nuclear shell model, J. Phys. A
26, 1147-60
Demidov, E. E. A991a) Function algebras on quantum matrix supergroups, Fund. Anal.
Appl. 24, 238-40
Demidov, E. E. A991b) Multiparameter quantum deformations of the group GL(n), Rus-
Russian Math. Surveys 46 D), 169-71
Demidov, E., Manin, Yu. I., Mukhin, E. E. Sz Zhdanovich, D. V. A990) Non-standard
quantum deformations of GL(n) and constant solutions of the Yang-Baxter equation, Progr.
Theor. Phys. Suppl. 102, 203-18
Deodhar, V. V., Gabber, O. Sz Kac, V. G. A982) Structure of some categories of represen-
representations of infinite-dimensional Lie algebras, Adv. Math. 45, 92-116
Destri, C. Sz de Vega, H. J. A992a) Bethe ansatz and quantum groups: the light cone lattice
approach, I. Six vertex and SOS models, Nucl. Phys. B 374, 692-719
Destri, C. & de Vega, H. J. A992b) Bethe ansatz and quantum groups: the light cone
lattice approach, II. From RSOS (p + l)-models to p-restricted sine Gordon field theories,
Nucl. Phys. B 385, 361-91
Devchand, Ch. Sz Saveliev, M. V. A991) Comultiplication for quantum deformations of the
centreless Virasoro algebra in the continuum formulation, Phys. Lett. B 258, 364-8
De Vega, H. J. A988) Quantum groups (YBZF algebras), integrable field theories and
statistical mechanics, in Two-dimensional Models and String Theories, E. Abdalla Sz M.
C. B. Abdalla (eds), pp. 86-160, World Scientific, Singapore
De Vega, H. J. A989a) Yang-Baxter algebras, integrable theories and quantum groups,
Intemat. J. Modern Phys. A 4, 2371-463
De Vega, H. J. A989b) Yang-Baxter algebras, integrable quantum field theories and con-
formal models, in Differential Geometric Methods in Theoretical Physics, Chester, 1988,
A. I. Solomon (ed.), pp. 3-11, World Scientific, Teaneck, NJ
De Vega, H. J. A990a) Yang-Baxter algebras, integrable theories and Bethe ansatz, in
Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner Sz J.-D. Hennig (eds), pp.
129-82, Lecture Notes in Physics 370, Springer, Berlin
De Vega, H. J. A990b) Yang-Baxter algebras, integrable theories and Bethe ansatz, Inter-
not. J. Modern Phys. 4, 735-801
De Vega, H. J. Sz, Fateev, V. A. A991) Factorizable S-matrices for perturbed V^-invariant
theories, Intemat. J. Modern Phys. A 6, 3221-34
De Vega, H. J. Sz Nicolai, H. A990) The octionic S-matrix, Phys. Lett. B 244, 295-8
De Vega, H. J. Sz Sanchez, N. A989) Quantum group generalization of string theory, Phys.
Lett. B 216, 97-102
De Wilde, M. Sz Lecomte, P. A988) Formal deformations of the Poisson Lie algebra of a
symplectic manifold and star-products. Existence, equivalence, derivations, in Deformation
Theory of Algebras and Structures and Applications, M. Hazewinkel (ed.), pp. 897-960,
Kluwer, Dordrecht
D'Hoker, E., Floreanini, R. Sz Vinet, L. A991) (/-oscillator realizations of the metaplectic
representation of quantum ospC,2), J. Math. Phys. 32, 1427—9
Dijkgraaf, R. A989) A Geometrical Approach to Two-dimensional Conformal Field The-
Theory, Doctoral Thesis, University of Utrecht
Dijkgraaf, R., Pasquier, V. Sz Roche, P. A992) Quasi-quantum groups related to orb-
ifold models, in Integrable Systems and Quantum Groups, M. Carfora, M. Martinelli Sz A.
Marzuoli (eds), pp. 75-98, World Scientific, Singapore
Dijkgraaf, R. Sz Witten, E. A990) Topological gauge theories and group cohomology,
Comm. Math. Phys. 129, 393-429
584 References
Dimakis, A. & Miiller-Hoissen, F. A992) Quantum mechanics on a lattice and g-deforma-
tions, Phys. Lett. B 295, 242-7
Dimakis, A., Miiller-Hoissen, F. Sz Striker, T. A993) Non-commutative differential calculus
and lattice gauge theory, J. Phys. A 26, 1927-50
Dipper, R. A991) Polynomial representations of finite general linear groups in nonde-
scribing characteristic, in Representation Theory of Finite Groups and Finite-dimensional
Algebras, Bielefeld, 1991, G. O. Michler Sz C. M. Ringel (eds), Progress in Mathematics
95, pp. 343-70, Birkhauser, Basel
Dipper, R. Sz Donkin, S. A991) Quantum GLn, Proc. London Math. Soc. 63, 165-211
Dipper, R. & James, G. D. A989) The g-Schur algebra, Proc. London Math. Soc. 59, 23-50
Dipper, R. Sz James, G. D. A991) (/-tensor space and g-Weyl modules, Trans. Amer. Math.
Soc. 327, 251-82
Dixmier, J. A977) Enveloping Algebras, North-Holland, Amsterdam
Djemai, A. E. F. A992) Quantum mechanical Galilei group and Q-planes, Modern Phys.
Lett. A 7, 3169-78
Dobrev, V. K. A989) Character formulae for Uq(slC,<?)) representations, in Knots, Topol-
Topology and Quantum Field Theories, Florence, 1989, L. Lusanna (ed.), pp. 539—47, World
Scientific, Singapore
Dobrev, V. K. A990) Classification and characters of ?/g(s/C,C)) representations, in Quan-
Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner Sz J.-D. Hennig (eds), Lecture
Notes in Physics 370, pp. 107-17, Springer, Berlin
Dobrev, V. K. A991) Singular vectors of quantum group representations for straight Lie
algebra roots, Lett. Math. Phys. 22, 251-66
Dobrev, V. K. A992a) Singular vectors of representations of quantum groups, J. Phys. A
25,149-60
Dobrev, V. K. A992b) Duality for the matrix quantum group GLp^q{2), J. Math. Phys.
33, 3419-30
Dobrev, V. K. A993) Canonical (/-deformations of non-compact Lie (super-) algebras, J.
Phys. A 26, 1317-34
Doebner, H.-D., Hennig, J.-D. Sz Liicke, W. A990) Mathematical guide to quantum groups,
in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner Sz J.-D. Hennig (eds),
Lecture Notes in Physics 370, pp. 29—63, Springer, Berlin
Donin, J. Sz Gurevich, D. A993) Quasi-Hopf algebras and R-matrix structures in line
bundles over flag manifolds, Selecta Mathematica 12, 37-48
Donkin, S. A993) On tilting modules for algebraic groups, Math. Z. 212, 39-60
Doplicher, S. Sz Roberts, J. E. A990) Why there is a field algebra with a compact gauge
group describing the superselection structure in particle physics, Comm. Math. Phys. 131,
51-107
Dorey, P. A991) Root systems and purely elastic S-matrices, Nucl. Phys. B 358, 654-76
Dorey, P. A992) Root systems and purely elastic 5-matrices II, Nucl. Phys. B 374, 746-61
Dorey, P. A993) Partition functions, intertwiners and the Coxeter element, Intemat. J.
Modem Phys. A 8, 193-208
Dorfel, B. D. A988) Quantum integrable systems and the inverse scattering method,
Fortschr. Phys. 36, 281-333
Drabant, B., Schlieker, M., Weich, W. Sz Zumino, B. A992a) Complex quantum groups
and their quantum universal enveloping algebras, Comm. Math. Phys. 147, 625-33
Drabant, B., Schlieker, M., Weich, W. & Zumino, B. A992b) Complex quantum groups
and their dual Hopf algebras, in Quantum Groups and Related Topics, R. Gierlak et al.
(eds), pp. 13-22, Kluwer, Dordrecht
Drinfel'd, V. G. A983a) Hamiltonian structures on Lie groups, Lie bialgebras and the
geometric meaning of the classical Yang-Baxter equations, Soviet Math. Dokl. 27, 68-71
References 585
Drinfel'd, V. G. A983b) On constant quasiclassical solutions of the Yang-Baxter quantum
equation, Soviet Math. Dokl. 28, 667-71
Drinfel'd, V. G. A985) Hopf algebras and the quantum Yang-Baxter equation, Soviet Math.
Dokl. 32, 254-8
Drinfel'd, V. G. A986a) On quadratic commutation relations in the quasiclassical case, in
Mathematical Physics, Functional Analysis, V. A. Marchenko (ed.), pp. 25-34, Naukova
Dumka, Kiev (Russian)
Drinfel'd, V. G. A986b) Degenerate affine Hecke algebras and Yangians, Fund. Anal. Appl.
20, 62-4
Drinfel'd, V. G. A987) Quantum groups, in Proceedings of the International Congress of
Mathematicians, Berkeley, 1986, A. M. Gleason (ed.), pp. 798—820, American Mathemat-
Mathematical Society, Providence, RI
Drinfel'd, V. G. A988a) Quantum groups, J. Soviet Math. 41, 18-49
Drinfel'd, V. G. A988b) A new realization of Yangians and quantized affine algebras, Soviet
Math. Dokl. 36, 212-6
Drinfel'd, V. G. A989) Quasi-Hopf algebras and the Knizhnik-Zamolodchikov equations,
in Problems of Modern Quantum Field Theory, A. A. Belavin, A. U. Klimyk Sz A. B.
Zamolodchikov (eds), pp. 1-13, Springer, Berlin
Drinfel'd, V. G. A990a) On almost cocommutative Hopf algebras, Leningrad Math. J. 1,
321-42
Drinfel'd, V. G. A990b) Quasi-Hopf algebras, Leningrad Math. J. 1, 1419-57
Drinfel'd, V. G. A991) On quasitriangular quasi-Hopf algebras and a certain group closely
connected with Gal(<$,<$), Leningrad Math. J. 2, 829-60
Drinfel'd, V. G. A992a) On some unsolved problems in quantum group theory, in Quantum
Groups, Proceedings of Workshops held in the Euler International Mathematical Institute
1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 1-8, Springer, Berlin
Drinfel'd, V. G. A992b) On the structure of the quasitriangular quasi-Hopf algebras, Fund.
Anal. Appl. 26, 63-5
Du, J. A991) The modular representation theory of g-Schur algebras II, Math. Z. 208,
503-36
Du, J. A992a) Canonical bases for irreducible representations of quantum GLn, Bull.
London Math. Soc. 24, 325-34
Du, J. A992b) The modular representation theory of g-Schur algebras, Trans. Amer. Math.
Soc. 329, 253-71
Du, J., Parshall, B. Sz Wang, J. P. A991) Two-parameter quantum linear groups and the
hyperbolic invariance of g-Schur algebras, J. London Math. Soc. 44, 420—36
Dubois-Violette, M. A988) Derivations et calcul differentiel non commutatif, C. R. Acad.
Sci. Paris Ser. I 307, 403-8
Dubois-Violette, M. A990) On the theory of quantum groups, Lett. Math. Phys. 19, 121-6
Dubois-Violette, M., Kerner, R. Sz Madore, J. A990) Noncommutative differential geometry
of matrix algebras, J. Math. Phys. 31, 323-30
Dubois-Violette, M. Sz Launer, G. A990) The quantum group of a non-degenerate bilinear
form, Phys. Lett. B 245, 175-7
Durhuus, B., Jakobsen, P. Sz Nest, R. A992) Topological quantum field theories from gener-
generalized 6,7-symbols, in Topological and Geometrical Methods in Field Theory, J. Mickelsson
Sz O. Pekonen (eds), pp. 121-34, World Scientific, Singapore
Dutta-Roy, B. Sz Ghosh, G. A993a) Geometric phase in g-deformed 'quantum mechanics',
Phys. Lett. A 173, 439-41
Dutta-Roy, B. Sz Ghosh, G. A993b) Curvature of Hilbert space and g-deformed quantum
mechanics, Modern Phys. Lett. A 8, 1427-32
Efthimou, C. J. A993) Quantum group symmetry for the 3>i2-perturbed and 3>2i-perturbed
minimal models of conformal field theory, Nucl. Phys. B 398, 697-740
586 References
Egusquiza, I. L. A992) Quantum group invariance in quantum sphere valued statistical
models, Phys. Lett. B 276, 465-71
Elashvili, A. A983) Frobenius Lie algebras, Fund. Anal. Appl. 16, 94-5
Ellinas, D. A990) Studies in Lie and quantum algebras, Soc. Sci. Fenn. Comment. Phys.-
Math. 120, 11pp.
Enock, M. Sz Schwartz, J.-M. A992) Kac-Algebras and Duality of Locally Compact Groups,
Springer, Berlin
Enriquez, B. A992) Rational forms for twistings of enveloping algebras of simple Lie alge-
algebras, Lett. Math. Phys. 25, 111-20
Ewen, H. Sz Ogievetsky, O. A992) Jordanian solution of simplex equations, Lett. Math.
Phys. 26, 307-14
Ewen, H., Ogievetsky, O. Sz Wess, J. A991) Quantum matrices in two dimensions, Lett.
Math. Phys. 22, 297-305
Exton, H. A983) q-Hypergeometric Functions and Applications, Ellis Horwood, Chichester,
UK
Faddeev, L. A980) Quantum completely integrable models in field theory, Soviet Scientific
Reviews Sect. C 1, 107-55, Harwood Academic Publishers, Chur, Switzerland
Faddeev, L. D. A984) Integrable models in A + l)-dimensional quantum field theory, in
Recent Advances in Field Theory and Statistical Mechanics, Les Houches, Session XXXIX,
1982, J.-B. Zuber Sz R. Stora (eds), pp. 561-608, North-Holland, Amsterdam
Faddeev, L. D. A989) Quantum groups, Bol. Soc. Brasil. Mat. (New Series) 20, 47-54
Faddeev, L. D. A990) On the exchange matrix for WZNW model, Comm. Math. Phys.
132,131-8
Faddeev, L., Reshetikhin, N. Sz Takhtajan, L. A988) Quantization of Lie groups and Lie
algebras, in Algebraic analysis, Vol. 1, M. Kashiwara Sz T. Kawai (eds), pp. 129-39, Aca-
Academic Press, New York
Faddeev, L., Reshetikhin, N. Sz Takhtajan, L. A989) Quantum groups, in Braid Group,
Knot Theory and Statistical Mechanics, C. N. Yang Sz M. L. Ge (eds), pp. 97-110, Advanced
Series in Mathematical Physics 9, World Scientific, Singapore
Faddeev, L., Sklyanin, E. K. Sz Takhtajan, L.A. A979) The quantum inverse problem I,
Theoret. Math. Phys. 40, 194-220 (Russian)
Faddeev, L. D. Sz Takhtajan, L. A979) The quantum inverse scattering method of the
inverse problem and the Heisenberg XYZ model, Russian Math. Surveys 34 E), 11—68
Faddeev, L. Sz Takhtajan, L. A987) Hamiltonian Methods in the Theory of Solitons,
Springer, Berlin
Fairlie, D. B. A990a) Quantum deformations of SU{2), J. Phys. A 23, L183-7
Fairlie, D. B. A990b) Quantum groups or the uses of algebraic computational programs in
the suggestion and verification of algebraic conjectures, in Strings '89, R. Arnowitt et al.
(eds), pp. 334-40, World Scientific, River Edge, NJ
Fairlie, D. B. A991a) Polynomial algebras with g-Heisenberg operators, in Quantum
Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 133-42, World Scientific, Singapore
Fairlie, D. B. A991b) (/-analysis and quantum groups, in Symmetries in Science V, B.
Gruber Sz H.-D. Doebner (eds), pp. 147-57, Plenum, New York
Fairlie, D. B. Sz Zachos, C. A991) Multiparameter associative generalizations of canonical
commutation relations and quantized planes, Phys. Lett. B 256, 43—9
Fateev, V. A. Sz Lukyanov, S. L. A992a) Poisson-Lie groups and classical W'-algebras,
Internat. J. Modern Phys. A 7, 853-76
Fateev, V. A. Sz Lukyanov, S. L. A992b) Vertex operators and representations of quantum
universal enveloping algebras, Internat. J. Modern Phys. A 7, 1325—59
Fateev, V. A. Sz Zamolodchikov, A. V. A982) Self-dual solutions of the star-triangle rela-
relations in TLjsj-models, Phys. Lett. A 92, 37—9
References 587
Fei, S. M. A991) Hopf algebraic structures of SUq-+oB) and SUqB) algebras, monopoles
and symplectic geometry on 2D manifolds, J. Phys. A 24, 5195—214
Fei, S. M. & Guo, H. Y. A991) Symplectic geometry of 5C/g_>0B) and SUqB) algebras, J.
Phys. A 24, 1-10
Fei, S. M., Guo, H. Y. Sz Shi, H. A992) Multiparameter solutions of the Yang-Baxter
equation, J. Phys. A 25, 2711-20
Fei, S. M. Sz Yue, R. H. A993) New algebra related to non-standard R-matrix, J. Phys. A
26, L217-20
Feigin, B. Sz Frenkel, E. A990) Quantization of Drinfeld-Sokolov reduction, Phys. Lett. B
246, 75-81
Feinsilver, P. A987) Discrete analogues of the Heisenberg-Weyl algebra, Monatsh. Math.
104, 89-108
Feinsilver, P. A989) Elements of g-harmonic analysis, J. Math. Anal. Appl. 141, 509-26
Feinsilver, P. A990) Lie algebras and recurrence relations III: (/-analogs and quantized
algebras, Ada Appl Math. 19, 207-51
Felder, G., Frohlich, J. Sz Keller, G. A989) Braid matrices and structure constants for
minimal conformal models, Comm. Math. Phys. 124, 647—64
Felder, G. Sz Leclair, A. A992) Restricted quantum affine symmetry of perturbed minimal
conformal models, in Infinite Analysis, A. Tsuchiya, T. Eguchi Sz M. Jimbo (eds), Advanced
Series in Mathematical Physics 16, pp. 239-78, World Scientific, Singapore
Felder, G. Sz Wieczerkowski, C. A991) Topological representations of the quantum group
Uq(sl2), Comm. Math. Phys. 138, 583-605
Felder, G. Sz Wieczerkowski, C. A992) Fock space representations of A^ ' and topological
representations of Uq(sl2), in New Symmetry Principles in Quantum Field Theory, J.
Frohlich et al. (eds), NATO Advanced Science Institutes Series B: Physics 295, pp. 513-22,
Plenum, New York
Feng, P. Sz Tsygan, B. A991) Hochschild and cyclic cohomology of quantum groups, Comm.
Math. Phys. 140, 481-521
Fenn, R. Sz Rourke, C. A979) On Kirby's calculus of links, Topology 18, 1-15
Filippov, A. T., Gangopadhyay, D. Sz Isaev, A. P. A991) Harmonic oscillator realization of
the canonical ^-transformation, J. Phys. A 24, L63-8
Filippov, A. T. Sz Isaev, A. P. A992) Para-grassmann analysis and quantum groups, Modern
Phys. Lett. A 7, 2129-41
Finkelberg, M. A993) Ph. D. Thesis, Harvard University, Cambridge, MA
Finkelstein, R. J. A992) g-deformations of the oscillator, J. Math. Phys. 33, 4259-66
Fiore, G. A992) SOq (N, R)-symmetric harmonic oscillator on the N dim real quantum
euclidean space, Intemat. J. Modern Phys. A 7, 7597—614
Fivel, D. A990) Interpolation between Fermi and Bose statistics using generalized commu-
commutators, Phys. Rev. Lett. 65, 3361-4
Fivel, D. A991) Quasi-coherent states and the spectral resolution of the g-Bose field oper-
operator, J. Phys. A 24, 3575-86
Flato, M., Lichnerowicz, A. Sz Sternheimer, D. A975) Deformations 1-differentiables des
algebre de Lie attachees a une variete symplectique ou de contact, Compositio Math. 31,
47-82
Flato, M. Sz Lu, Z. A991) Remarks on quantum groups, Lett. Math. Phys. 21, 85-8
Flato, M. Sz Sternheimer, D. A991) On a possible origin of quantum groups, Lett. Math.
Phys. 22, 155-60
Fletcher, P. A990) The uniqueness of the Moyal algebra, Phys. Lett B 248, 323-8
Fletcher, P. A991) The Moyal bracket, in Quantum Groups, T. Curt right, D. Fairlie & C.
Zachos (eds), pp. 143-57, World Scientific, Singapore
Floratos, E. G. A989) Representations of the quantum group GLqB) for values of q on the
unit circle, Phys. Lett. B 233, 395-9
588 References
Floratos, E. G. A990) Manin's quantum spaces and standard quantum mechanics, Phys.
Lett. B 252, 97-100
Floratos, E. G. A991) The two anyon system and the (/-oscillator, in Quantum Groups, T.
Curtright, D. Fairlie Sz C. Zachos (eds), pp. 158-65, World Scientific, Singapore
Floreanini, R., Leites, D. A. Sz Vinet, L. A991) On the defining relations of quantum
superalgebras, Lett. Math. Phys. 23, 127-31
Floreanini, R., Spiridonov, V. P. Sz Vinet, L. A990) Bosonic realization of the quantum
superalgebra ospq(l,2n), Phys. Lett. B 242, 383-6
Floreanini, R., Spiridonov, V. P. Sz Vinet, L. A991a) (/-oscillator realizations of the quantum
superalgebras slq(m,n) and ospq(m,2n), Comm. Math. Phys. 137, 149-60
Floreanini, R., Spiridonov, V. P. Sz Vinet, L. A991b) (/-oscillator realizations of quantum
superalgebras, in Group Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov Sz
V. I. Manko (eds), Lecture Notes in Physics 382, pp. 208-14, Springer, Berlin
Floreanini, R. Sz Vinet, L. A990) (/-analogues of the para-Bose and para-Fermi oscillators
and representations of quantum algebras, J. Phys. A 23, L1019—23
Floreanini, R. Sz Vinet, L. A991a) (/-orthogonal polynomials and the oscillator quantum
group, Lett. Math. Phys. 22, 45-54
Floreanini, R. Sz Vinet, L. A991b) Braid group action on the (/-Weyl algebra, Lett. Math.
Phys. 23, 151-8
Floreanini, A. Sz Vinet, L. A992a) (/-oscillators and quantum superalgebras, in Topological
and Geometrical Methods in Field Theory, J. Mickelsson Sz O. Pekonen (eds), pp. 147-52,
World Scientific, Singapore
Floreanini, A. Sz Vinet, L. A992b) (/-conformal quantum mechanics and (/-special functions,
Phys. Lett. B 277, 442-6
Floreanini, A. Sz Vinet, L. A992c) Addition formulas for g-Bessel functions, J. Math. Phys.
33, 2984-8
Floreanini, R. Sz Vinet, L. A992d) The metaplectic representation of slqB) and the q-
Gegenbauer polynomials, J. Math. Phys. 33, 1358-62
Floreanini, R. Sz Vinet, L. A992e) Using quantum algebras in (/-special function theory,
Phys. Lett. A 170, 21-8
Foda, O. Sz Miwa, T. A992) Corner transfer matrices and quantum affine algebras, in Infi-
Infinite Analysis, A. Tsuchiya, T. Eguchi Sz M. Jimbo (eds), Advanced Series in Mathematical
Physics 16, pp. 279-302, World Scientific, Singapore
Fordy, A. P., Reyman, A. G. Sz Semenov-Tian-Shansky, M. A. A989) Classical r-matrices
and compatible Poisson brackets for coupled KdV systems, Lett. Math. Phys. 17, 25—9
Forger, M. A989) Solutions of the Yang-Baxter equation from field theory, in Differential
Geometric Methods in Theoretical Physics, Chester, 1988, A. I. Solomon (ed.), pp. 36-46,
World Scientific, Teaneck, NJ
Fradkin, E. S. Sz Netsaev, R. R. A990) Quantum R-matrix in the relativistic string model
in a space of constant curvature, Modern Phys. Lett. A 5, 1329-38
Frahm, H. A991) On the construction of integrable XXZ Heisenberg models with arbitrary
spin, Contemp. Math. 122, 41-5
Frappat, L. Sz Sciarrino, A. A992) A quasi-parafermionic realization of G2 and Uq(G2), J>
Phys. A 25, L383-6
Frappat, L., Sorba, P. Sz Sciarrino, A. A991) (/-fermionic operators and quantum excep-
exceptional algebras, J. Phys. A 24, L179-83
Freidel, L. Sz Maillet, J.-M. A991a) Quantum algebras and integrable systems, Phys. Lett.
B 262, 278-84
Freidel, L. Sz Maillet, J.-M. A991b) On classical and quantum integrable field theories
associated to Kac-Moody current algebras, Phys. Lett. B 263, 403-10
Freidel, L. Sz Maillet, J.-M. A992) The universal R-matrix and its associated quantum
algebra as functionals of the classical r-matrix. The sfo case, Phys. Lett. B 296, 353-60
References 589
Prenkel, E., Kac, V. Sz Wakimoto, M. A992) Characters and fusion rules for W-algebras
via quantized Drinfeld-Sokolov reduction, Comm. Math. Phys. 147, 295-328
Frenkel, I. B. Sz Jing, N. A988) Vertex representations of quantum affine algebras, Proc.
Natl Acad. Sci. USA 85, 9373-7
Frenkel, I. B. Sz Moore, G. A991) Simplex equations and their solutions, Comm. Math.
Phys. 138, 259-71
Prenkel, I. B. Sc Reshetikhin, N. Yu. A992a) Quantum affine algebras and holonomic dif-
difference equations, Comm. Math. Phys. 146, 1-60
Frenkel, I. B. Sz Reshetikhin, N. Yu. A992b) Quantum affine algebras, commutative systems
of difference equations and elliptic solutions to the Yang-Baxter equation, in Proceedings
of the XX International Conference on Differential Geometric Methods in Theoretical
Physics, S. Catto Sz A. Rocha (eds), World Scientific, Singapore
Freund, P. G. O. & Zabrodin, A. V. A992a) Macdonald polynomials for Sklyanin algebras:
a conceptual basis for the p-adics — quantum group connection, Comm. Math. Phys. 147,
277-94
Freund, P. G. O. & Zabrodin, A. V. A992b) Zn-Baxter models and quantum symmetric
spaces, Phys. Lett. B 284, 283-8
Freyd, P. J. & Yetter, D. N. A989) Braided compact closed categories with applications to
low dimensional topology, Adv. Math. 77, 156-82
Freyd, P. J., Hoste, J., Lickorish, W. B. R., Millet, K. C, Ocneanu, A. & Yetter, D. N.
A985) A new polynomial invariant of knots and links, Bull. Amer. Math. Soc. 12, 239-46
Friedlander, E. Sz Parshall, B. A986) Cohomology of Lie algebras and algebraic groups,
Amer. J. Math. 108, 235-53
Frishman, Y., Lukierski, J. & Zakrzewski, W. J. A993) Quantum group a models, J. Phys.
A 26, 301-12
Frohlich, J. A988) Statistics of fields, the Yang-Baxter equation and the theory of knots and
links, in Non-perturbative Quantum Field Theory, Cargese, 1987, G. 't Hooft, A. Jaffe, G.
Mack, P. K. Mitter & R. Stora (eds), NATO Advanced Science Institutes Series B: Physics
185, pp. 71-100, Plenum, New York
Frohlich, J. & Gabbiani, F. A990) Braid statistics in local quantum theory, Rev. Math.
Phys. 2, 251-353
Frohlich, J. Sz Gabbiani, F. A992) Operator algebras and conformal field theory, preprint
ETH-TH/92-30, Zurich
Frohlich, J. Sz Kerler, T. A993) Quantum Groups, Quantum Categories and Quantum
Field Theory, Lecture Notes in Mathematics 1542, Springer, Berlin
Frohlich, J. Sz King, C. A989) Two-dimensional conformal field theory and three-dimen-
three-dimensional topology, Intemat. J. Modern Phys. A 4, 5321—99
OFronsdal, C. A991) Normal ordering and quantum groups, Lett. Math. Phys. 22, 225-8
Fronsdal, C. A992) glq(n) and quantum monodromy, Lett. Math. Phys. 24, 73-8
Fronsdal, C. & Galindo, A. A993) The dual of a quantum group, Lett. Math. Phys. 27,
59-72
Fu, H. C. & Ge, M. L. A992a) Verma modules of the quantum group GL(n)q and its
g-boson and Heisenberg-Weyl realizations, J. Phys. A 25, L389-96
Fu, H. C. Sz Ge, M. L. A992b) The g-boson realization of parametrized cyclic representa-
representations of quantum algebras at qp = 1, J. Math. Phys. 33, 427-35
Fu, H. C. Sz Ge, M. L. A992c) g-boson realization of quadratic algebra A\ and its repre-
representations, J. Phys. A 25, LI233-8
Fu, H. C. & Ge, M. L. A993) Reflection quadratic algebra associated with Z2 model, J.
Phys. A 26, L233-8
Fuchs, J. Sz van Driel, P. A990) WZW fusion rules, quantum groups and the modular
matrix 5, Nucl. Phys. B 346, 632-48
590 References
Furlan, P., Ganchev, A. Ch. &; Petkova, V. B. A990) Quantum groups and fusion rules
multiplicities, Nucl. Phys. B 343, 205-27
Furlan, P., Ganchev, A. Ch. & Petkova, V. B. A991) Remarks on the quantum group
structure of the rational c < 1 conformal field theories, Intemat. J. Modern Phys. A 6,
4859-84
Furlan, P., Hadjiivanov, L. K. &; Todorov, I. T. A992) Quantum deformation of the ladder
representations of U(l, 1) for \q\ — 1, J. Math. Phys. 33, 4255-8
Furlan, P., Stanev, Y. S. & Todorov, I. T. A991) Coherent state operators and n-point
invariants for Uq(slB)), Lett. Math. Phys. 22, 307-19
Gabriel, P. A972) Unzerlegbare Darstellungen I, Manuscripta Math. 6, 71-103
Ganchev, A. Ch. Sc Petkova, V. B. A989) Uq(slB)) invariant operators and minimal theories
fusion matrices, Phys. Lett. B 233, 374-82
Ganchev, A. Ch. Sc Petkova, V. B. A990) /7q(s/B))-invariant operators and reduced poly-
polynomial identities, in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &; J.-D.
Hennig (eds), Lecture Notes in Physics 370, pp. 96—106, Springer, Berlin
Gangopadhyay, D. A991) On canonical ^-transformations with two ^-oscillators, Modern
Phys. Lett. A 6, 2909-16
Gasper, G. & Rahman, M. A990) Basic Hypergeometric Series, Cambridge University
Press, Cambridge
Gavrilik, A. M. & Klimyk, A. U. A991) g-deformed orthogonal and pseudo-orthogonal
algebras and their representations, Lett. Math. Phys. 21, 215-20
Gawedzki, K. A991) Classical origin of quantum group symmetries in Wess-Zumino-Witten
conformal field theory, Comm. Math. Phys. 139, 201-13
Ge, M. L. A992) New solutions of Yang-Baxter equations and quantum group structures, in
Quantum Groups, Proceedings of Workshops held in the Euler International Mathematical
Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 245-58, Springer,
Berlin
Ge, M. L., Gwa, L. H., Piao, F. Sz Xue, K. A990) Braid group representation associated
with the 10-dimensional representation of 5/7E) and its Yang-Baxterization, J. Phys. A
23, 2273-86
Ge, M. L., Jing, N. H. & Liu, G. G. A992) On quantum groups for ^-models, J. Phys.
A 25, L799-806
Ge, M. L., Li, Y. Q., Wang, Y. Y. & Xue, K. A990) The braid group representations
associated with some non-fundamental representations of Lie algebras, J. Phys. A 23,
605-18
Ge, M. L. & Liu, G. G. A992a) A new kind of R-matrix associated with the Hopf algebra
Uq(A2(fi)), Phys. Lett. A 167, 161-4
Ge, M. L. & Liu, G. G. A992b) Construction of a new quantum double and new solutions
to the Yang-Baxter equation, Lett. Math. Phys. 24, 197-203
Ge, M. L., Liu, G. G. & Sun, C. P. A991a) Nonstandard R-matrices for the Yang-Baxter
equation and boson representations of the quantum algebra slqB) with qp = 1, Phys. Lett.
A 155,137-9
Ge, M. L., Liu, G. G. & Sun, C. P. A991b) The g-boson realization of new solutions of
the Yang-Baxter equation associated with the quantum algebra Uq(sl(S)) at qp = 1, Phys.
Lett. A 160, 433-6
Ge, M. L., Liu, G. G. & Sun, C. P. A991c) New boson representations of the slqB) with
multiplicity two and new solutions to the Yang-Baxter equation at qp = 1, Lett. Math.
Phys. 23, 169-78
Ge, M. L., Liu, G. G. & Sun, C. P. A992) Representations of quantum matrix algebra
MqB) and its g-boson realization, J. Math. Phys. 33, 2541-5
Ge, M. L., Liu, G. G., Sun, C. P. & Xue, K. A991) General solutions of RJi(x) and
quantum group structure, J. Phys. A 24, 4955—63
References 591
Ge, M. L., Liu, G. G. Sz Xue, K. A991) New solutions of the Yang-Baxter equations:
Birman-Wenzl algebra and quantum group structures, J. Phys. A 24, 2679-90
Ge, M. L., Liu, X. F. Sz Sun, C. P. A992) The cyclic representation of the quantum algebra
Uq(ospB,1)) in terms of the Zn-algebra, J. Phys. A 25, 2907-10
Ge, M. L. & Su, G. A991) The statistical distribution function of the g-deformed harmonic
oscillator, J. Phys. A 24, L721-3
Ge, M. L., Sun, C. P. & Wang, L. Y. A990) Weight conservation and quantum group
construction of the braid group representation, J. Phys. A 23, L645-8
Ge, M. L., Sun, C. P. & Xue, K. A992a) New R-matrices for the Yang-Baxter equation
associated with the representations of the quantum superalgebra Uqosp(l, 2) with q a root
of unity, Phys. Lett. A 163, 176-80
Ge, M. L., Sun, C. P. Sz Xue, K. A992b) Construction of general colored R matrices for
the Yang-Baxter equation and g-boson realization of quantum algebra slqB) when q is a
root of unity, Intemat. J. Modem Phys. A 7, 6609-22
Ge, M. L. Sz Wang, Y. W. A993) More about the non-standard R-matrix associated with
SUqB), J. Phys. A 26, 443-7
Ge, M. L., Wang, L. Y. & Kong, X. P. A991) Yang-Baxterization of braid group rep-
representation associated with the seven-dimensional representation of G2, J. Phys. A 24,
569-79
Ge, M. L., Wang, L. Y., Xue, K. & Wu, Y. S. A989) Akutsu-Wadati link polynomials from
Feynman-Kauffman diagrams, Internat. J. Modern Phys. A 4, 3351-73
Ge, M. L. Sz Wu, A. C. T. A992/3) Quantum groups constructed from the non-standard
braid group representations in the Faddeev-Reshetikhin-Takhtajan approach: I, J. Phys. A
24, L725-32; II, J. Phys. A 25, L807-16
Ge, M. L., Wu, Y. S. Sz Xue, K. A991) Explicit trigonometric Yang-Baxterization, Internat.
J. Modern Phys. A 6, 3735-79
Ge, M. L. & Xue, K. A990) Braid group representations related to the generalized Toda
system, Phys. Lett. A 146, 245-51
Ge, M. L. Sz Xue, K. A991a) Exotic solutions of the Yang-Baxter equation and the quantum
group structure, in Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 97-
112, World Scientific, Singapore
Ge, M. L. Sz Xue, K. A991b) New solutions of braid group representations associated with
Yang-Baxter equation, J. Math. Phys. 32, 1301-9
Ge, M. L. Sz Xue, K. A991c) Rational Yang-Baxterization and factorized S matrix, Phys.
Lett. A 152, 266-72
Ge, M. L. & Xue, K. A993a) Trigonometric Yang-Baxterization of coloured .R-matrix, J.
Phys. A 26, 281-92
Ge, M. L. Sz Xue, K. A993b) Extended Birman-Wenzl algebra and Yang-Baxterization, J.
Phys. A 26, 1865-74
Ge, M. L., Zhao, Q. Sz Zhang, Y. J. A993) Yang-Baxter equations associated with scattering
from kaleidoscopes, Phys. Lett. A 175, 199-202
Gel'fand, I. M. & Cherednik, I. V. A983) Abstract hamiltonian formalism for classical
Yang-Baxter bundles, Russian Math. Surveys 38 C), 1—22
Gel'fand, I. M. & Dickii, L. A. A976) Fractional powers of operators and hamiltonian
systems, Fund. Anal. Appl. 10, 259-73
Gel'fand, I. M. Sz Dorfman, I. Ya. A979) Hamiltonian operators and algebraic structures
connected with them, Fund. Anal. Appl. 15, 173-87
Gel'fand, I. M. Sz Dorfman, I. Ya. A982) Hamiltonian operators and the classical Yang-
Baxter equation, Fund. Anal. Appl. 16, 241—8
Gel'fand, I. M. & Fairlie, D. B. A991) The algebra of Weyl symmetrized polynomials and
its quantum extension, Comm. Math. Phys. 136, 487-99
592 References
Gel'fand, I. M. & Tsetlin, M. L. A959a) Finite dimensional representations of the group of
unimodular matrices, Dokl. Akad. Nauk. USSR 71, 825-8 (Russian); English translation
in /. M. Gel'fand. Collected Papers, Vol. II, pp. 653-6, Springer, Berlin, 1988
Gel'fand, I. M. & Tsetlin, M. L. A959b) Finite dimensional representations of the group of
orthogonal matrices, Dokl. Akad. Nauk. USSR 71, 1017-20 (Russian); English translation
in /. M. Gel'fand. Collected Papers, Vol. II, pp. 657-61, Springer, Berlin, 1988
Gel'fand, S. I. & Kazhdan, D. A992) Examples of tensor categories, Invent. Math. 109,
595-617
Georgiev, G. &; Mathieu, O. A992) Categorie de fusion pour les groupes de Chevalley, C.
R. Acad. Sci. Paris Ser. 7 315, 659-62
Gepner, D. A991) Fusion rings and geometry, Comm. Math. Phys. 141, 381-411
Gerdjikov, V. S. A987) The Zakharov-Shabat dressing method and the representation
theory of semisimple Lie algebras, Phys. Lett. A 121, 184—8
Gerstenhaber, M., Giaquinto, A. Sz Schack, S. D. A992) Quantum symmetry, in Quantum
Groups, Proceedings of Workshops held in the Euler International Mathematical Institute
1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 9-46, Springer, Berlin
Gerstenhaber, M. &; Schack, S. D. A988) Algebraic cohomology and deformation theory,
in Deformation Theory of Algebras and Structures and Applications, M. Hazewinkel (ed.),
pp. 11-264, Kluwer, Dordrecht
Gerstenhaber, M. &; Schack, S. D. A990) Bialgebra cohomology, deformations and quantum
groups, Proc. Natl Acad. Sci. USA 87, 478-81
Gerstenhaber, M. & Schack, S. D. A992) Algebras, bialgebras, quantum groups and al-
algebraic deformations, in Deformation Theory and Quantum Groups with Applications to
Mathematical Physics, M. Gerstenhaber &; J. Stasheff (eds), Contemporary Mathematics
134, pp. 51-92, American Mathematical Society, Providence, RI
Gervais, J.-L. A985) Transport matrices associated with the Virasoro algebra, Phys. Lett.
B 160, 279-82
Gervais, J.-L. A990a) The quantum group structure of 2D gravity and minimal models I,
Comm. Math. Phys. 130, 257-83
Gervais, J.-L. A990b) The quantum group of Virasoro conformal theories, in Recent De-
Developments in Conformal Field Theories, Trieste, 1989, S. Randjbar-Daemi, E. Sezgin &;
J.-B. Zuber (eds), pp. 143-59, World Scientific, Singapore
Gervais, J.-L. A990c) Lie and quantum group structures common to integrable and con-
conformal theories, in Mathematical Physics, Islamabad, 1989, F. Hussain &; A. Qadir (eds),
pp. 138-53, World Scientific, Singapore
Gervais, J.-L. A991a) Solving the strongly coupled 2D gravity: I. Unitary truncation and
quantum group structure, Comm. Math. Phys. 138, 301-38
Gervais, J.-L. A991b) On the algebraic structure of quantum gravity in two dimensions,
Intemat. J. Modern Phys. A 6, 2805-27
Gervais, J.-L. A992a) Quantum group symmetry of 2D gravity, in Quantum Groups, Pro-
Proceedings of Workshops held in the Euler International Mathematical Institute 1990, P. P.
Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 259-76, Springer, Berlin
Gervais, J.-L. A992b) Two-dimensional gravity: quantum group structure of the continuum
theory, Classical and Quantum Gravity 9, S97-116
Gervais, J.-L. Sz Rostand, B. A991) On two-dimensional supergravity and the quantum
super-Mobius group, Comm. Math. Phys. 143, 175-99
Giaquinto, A. A992) Quantization of tensor representations and deformations of matrix
bialgebras, J. Pure Appl. Algebra 79, 169-90
Giler, S., Kosinski, P., Majewski, M., Maslanka, P. & Kunz, J. A992) More about the
g-deformed Poincare algebra, Phys. Lett. B 286, 57-62
Giler, S., Kosinski, P. &; Maslanka, P. A991) Remarks on differential calculi on Manin's
plane, Modern Phys. Lett. A 6, 3251-4
References 593
Ginzburg, V. L. Sz Kumar, S. A993) Cohomology of quantum groups at roots of unity,
Duke Math. J. 69, 179-98
Ginzburg, V. L. Sz Weinstein, A. A992) Lie-Poisson structure on some Poisson-Lie groups,
J. Amer. Math. Soc. 5, 445-53
Glockner, P. Sz von Waldenfels, W. A989) The relations of the non-commutative coefficient
algebra of the unitary group, in Quantum Probability and Applications IV, L. Accardi &
W. von Waldenfels (eds), Lecture Notes in Mathematics 1396, pp. 182-220, Springer, Berlin
Golenishcheva-Kutuzova, M. Sz Lebedev, D. A992) Vertex operator representations of some
quantum tori Lie algebras, Comm. Math. Phys. 148, 403-16
Gomez, C., Ruiz-Altaba, M. & Sierra, G. A991) New R-matrices associated with finite-
dimensional representations of Uq(slB)) at roots of unity, Phys. Lett. B 265, 95-8
Gomez, C. & Sierra, G. A990a) Quantum group meaning of the Coulomb gas, Phys. Lett.
B 240,149-57
Gomez, C. Sz Sierra, G. A990b) Comments on rational conformal field theory, quantum
groups and towers of algebras, in Quantum Groups, Clausthal, Germany, 1989, H.-D.
Doebner Sz J.-D. Hennig (eds), Lecture Notes in Physics 370, pp. 278-306, Springer, Berlin
Gomez, C. Sz Sierra, G. A991a) The quantum group symmetry of rational conformal field
theories, Nucl. Phys. B 352, 791-828
Gomez, C. & Sierra, G. A991b) Quantum groups, Riemann surfaces and conformal field
theory, in Differential Geometric Methods in Theoretical Physics, Rapallo, 1990, C. Bar-
tocci, U. Bruzzo Sz R. Cianci (eds), Lecture Notes in Physics 375, pp. 120-30, Springer,
Berlin
Gomez, C. Sz Sierra, G. A991c) Integrability and uniformization in Liouville theory: the
geometrical origin of quantized symmetries, Phys. Lett. B 255, 51-60
Gomez, C. & Sierra, G. A992) Integrability and quantum symmetries, in Integrable Systems
and Quantum Groups, M. Carfora, M. Martinelli & A. Marzuoli (eds), pp. 37-50, World
Scientific, Singapore
Gomez, C. Sz Sierra, G. A993) Quantum harmonic oscillator algebra and link invariants,
J. Math. Phys. 34, 2119-31
Gong, R. A992) Path integral formalism for SUqB) coherent states, J. Phys. A 25, LI 145-
50
Gonzalez-Ruiz, A. Sz Ibort, L. A. A992) Induction of quantum group representations, Phys.
Lett. B 296, 104-8
Goodman, F. M., de la Harpe, P. Sz Jones, V. F. R. A989) Coxeter Graphs and Towers of
Algebras, Mathematical Sciences Research Institute Publications 14, Springer, New York
Goodman, F. M. Sz Wenzl, H. A990) Littlewood-Richardson coefficients for Hecke algebras
at roots of unity, Adv. Math. 82, 244-65
Gora, J. A992) Two models of a g-deformed hydrogen atom, J. Phys. A 25, L1281-6
Gould, M. D. A992a) Quantum groups and diagonalization of the braid generator, Lett.
Math. Phys. 24, 183-96
Gould, M. D. A992b) Reduced Wigner coefficients for Uq(gl(n)), J. Math. Phys. 33, 1023-
31
Gould, M. D. Sz Biedenharn, L. C. A992) The pattern calculus for tensor operators on
quantum groups, J. Math. Phys. 33, 3613-35
Gould, M. D., Links, J. & Bracken, A. J. A992) Matrix elements and Wigner coefficients
for Uq(sl{n)), J. Math. Phys. 33, 1008-22
Gould, M. D., Zhang, R. B. & Bracken, A. J. A991a) Generalized Gel'fand invariants and
characteristic identities for quantum groups, J. Math. Phys. 32, 2298-303
Gould, M. D., Zhang, R. B. Sz Bracken, A. J. A991b) Lie bi-superalgebras and the graded
classical Yang-Baxter equation, Rev. Math. Phys. 3, 223-40
Grabowski, J. A990) Quantum 5/7B) group of Woronowicz and Poisson structures, in
Differential Geometry and its Applications, Brno, 1989, J. Janyska Sz D. Krupka (eds),
594 References
pp. 313-22, World Scientific, Teaneck, NJ
Gracia-Bondia, J. M. A992) Generalized Moyal quantization and homogeneous symplectic
spaces, in Deformation Theory and Quantum Groups with Applications to Mathematical
Physics, M. Gerstenhaber & J. Stasheff (eds), Contemporary Mathematics 134, pp. 93-114,
American Mathematical Society, Providence, RI
Granovskii, Ya. I. Sz Zhedanov, A. S. A992) 'Twisted' Clebsch-Gordan coefficients for
SUqB), J. Phys. A 25, L1029-30
Granovskii, Ya. I. Sz Zhedanov, A. S. A993a) Linear covariance algebra for SLqB), J. Phys.
A 26, L357-60
Granovskii, Ya. I. Sz Zhedanov, A. S. A993b) Production of Q-bosons by a classical current:
an exactly solvable model, Modern Phys. Lett. A 8, 1029-36
Gray, R. W. & Nelson, C. A. A990) A completeness relation for the ^-analogue coherent
states by ^-integration, J. Phys. A 23, L945—50
Greenberg, O. W. A991) g-mutators and violations of statistics, in Quantum Groups, T.
Curtright, D. Fairlie & C. Zachos (eds), pp. 166-80, World Scientific, Singapore
Gromov, N. A. A993) The matrix quantum unitary Cayley-Klein groups, J. Phys. A 26,
L5-8
Gromov, N. A. Sz Manko, V. I. A991) Contractions and analytic continuations of the
irreducible representations of the quantum algebra SUqB), in Group Theoretical Methods
in Physics, Moscow, 1990, V. V. Dodonov Sz V. I. Manko (eds), Lecture Notes in Physics
382, pp. 225-8, Springer, Berlin
Gromov, N. A. Sz Manko, V. I. A992) Contractions of the irreducible representations of
the quantum algebras suqB) and soqC), J. Math. Phys. 33, 1374-8
Grossman, R. & Radford, D. A992) A simple construction of bialgebra deformations, in
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M.
Gerstenhaber Sz J. Stasheff (eds), Contemporary Mathematics 134, pp. 115—7, American
Mathematical Society, Providence, RI
Grothendieck, A. A984) Esquisse d'un programme, mimeographed notes, Universite de
Montpelier
Groza, V. A. Sz Kachurik, I. I. A990) Addition and multiplication theorems for
Krawtchouk, Hahn and Racah ^-polynomials, Dokl. Akad. Nauk. Ukrain. SSR Ser. A 89,
3-6 (Russian)
Groza, V. A., Kachurik, I. I. & Klimyk, A. U. A990) On Clebsch-Gordan coefficients and
matrix elements of representations of the quantum algebra Uq(su2), J. Math. Phys. 31,
2769-80
Gruber, B. Sz Smirnov, Yu. F. A991) On quantized Verma modules, in Symmetries in
Science V, Lochau, 1990, B. Gruber, L. C. Biedenharn & H.-D. Doebner (eds), pp. 293-
304, Plenum, New York
Guadagnini, E. A992) The universal link polynomial, Intemat. J. Modern Phys. A 7,
877-946
Guadagnini, E., Martellini, M. Sz Mintchev, M. A990a) Chern-Simons holonomies and the
appearance of quantum groups, Phys. Lett. B 235, 275-81
Guadagnini, E., Martellini, M. Sz Mintchev, M. A990b) Braids and quantum group sym-
symmetry in Chern-Simons theory, Nucl. Phys. B 336, 581-609
Guadagnini, E., Martellini, M. & Mintchev, M. A990c) Chern-Simons field theory and
quantum groups, in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner Sz J.-D.
Hennig (eds), pp. 307-17, Lecture Notes in Physics 370, Springer, Berlin
Guan, X. W., Xiong Zhuang Sz Zhou, H. Q. A992) Classical Yang-Baxter equations and
quantum gl(p, g)-Gaudin model, Modern Phys. Lett. 7, 1647-50
Guil, F. A990) Commuting differential operators over integrable hierarchies, in Integrable
and Superintegrable Systems, B. Kuperschmidt (ed.), pp. 307-20, World Scientific, Teaneck,
NJ
References 595
Gurevich, D. I. A986) The Yang-Baxter equation and a generalization of formal Lie theory,
Soviet Math. Dokl. 33, 758-62
Gurevich, D. I. A989a) Hecke symmetries and quantum determinants, Soviet Math. Dokl.
38, 555-9
Gurevich, D. I. A989b) On Poisson brackets associated with the classical Yang-Baxter
equation, Soviet J. Fund. Anal. 23, 68-9
Gurevich, D. I. A990) Equation de Yang-Baxter et quantification de cocycles, C. R. Acad.
Sci. Paris Ser. I 310, 845-8
Gurevich, D. I. A991) Algebraic aspects of the quantum Yang-Baxter equation, Leningrad
Math. J. 2, 801-28
Gurevich, D. I., Radul, A. & Rubtsov, V. A992) Noncommutative differential geometry re-
related to the Yang-Baxter equation, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov
199 (Russian)
Gurevich, D. I. &; Rubtsov, V. A992) Yang-Baxter equation and deformation of associative
and Lie algebras, in Quantum Groups, Proceedings of Workshops held in the Euler Inter-
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics
1510, pp. 47-55, Springer, Berlin
Gurevich, D. I., Rubtsov, V. & Zobin, N. A992) Quantization of Poisson pairs: the R-matrix
approach, J. Geom. Phys. 9, 25-44
Gyoja, A. A986) A ^-analogue of Young symmetrizer, Osaka J. Math. 23, 841-52
Haag, R. A992) Local Quantum Physics, Springer, Berlin
Hadjiivanov, L. K., Paunov, R. R. & Todorov, I. T. A991) Quantum group extended chiral
p-models, Nucl. Phys. B 356, 387-438
Hadjiivanov, L. K., Paunov, R. R. & Todorov, I. T. A992a) Extended chiral conformal field
theories with a quantum symmetry, in Quantum Groups, Proceedings of Workshops held
in the Euler International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes
in Mathematics 1510, pp. 277-302, Springer, Berlin
Hadjiivanov, L. K., Paunov, R. R. &; Todorov, I. T. A992b) Uq covariant oscillators and
vertex operators, J. Math. Phys. 33, 1379-94
Hadjiivanov, L. K. &; Stoyanov, D. T. A991) On a class of infinite-dimensional representa-
representations of Uq(slB)), J. Phys. A 24, L907-12
Hakobyan, T. S. & Sedrakyan, A. G. A993a) R-matrices for highest weight representations
of sl^&C) at roots of unity, Phys. Lett. B 303, 27-32
Hakobyan, T. S. & Sedrakyan, A. G. A993b) Some new spinor representations of quantum
groups Bq(n), Cq{n), GqB), J. Math. Phys. 34, 2554-60
Hartshorne, R. A977) Algebraic Geometry, Graduate Texts in Mathematics 72, Springer,
Berlin
Hayashi, T. A990) ^-analogues of Clifford and Weyl algebras - spinor and oscillator repre-
representations of quantum enveloping algebras, Comm. Math. Phys. 127, 129-44
Hayashi, T. A991) An algebra related to the fusion rules of Wess-Zumino-Witten models,
Lett. Math. Phys. 22, 291-6
Hayashi, T. A992a) Quantum groups and quantum determinants, J. Algebra 152, 146-65
Hayashi, T. A992b) Quantum deformations of classical groups, Publ. Res. Inst. Math. Sci.
28, 57-81
Hazewinkel, M. A978) Formal Groups and Applications, Academic Press, New York
Hazewinkel, M. A991) Introductory recommendations for the study of Hopf algebras in
mathematics and physics, CWI Quart. 4, 3-26
Helgason, S. A978) Differential Geometry, Lie Groups and Symmetric Spaces, Academic
Press, New York
Hennings, M. A. A993) On solutions to the braid equation identified by Woronowicz, Lett.
Math. Phys. 27, 13-6
596 References
Hibi, T. Sz Wakayama, M. A991) A g-analogue of Capelli's identity for GLB), preprint,
Hokkaido University
Hietarinta, J. A992) All solutions to the constant quantum Yang-Baxter equation in two
dimensions, Phys. Lett. A 165, 245-51
Hietarinta, J. A993a) Some constant solutions to Zamolodchikov's tetrahedra equations,
J. Phys. A 26, L9-16
Hietarinta, J. A993b) Solving the 2-dimensional constant quantum Yang-Baxter equation,
J. Math. Phys. 34, 1725-56
Hinrichsen, H. & Rittenberg, V. A992) A two-parameter deformation of the SUA\1) su-
peralgebra and the XY quantum chain in a magnetic field, Phys. Lett. B 275, 350-4
Hinrichsen, H. & Rittenberg, V. A993) Quantum groups, correlation functions and infrared
divergences, Phys. Lett. B 304, 115-20
Hlavaty, L. A985) Solution to the Yang-Baxter equation corresponding to the XXZ models
in an external magnetic field, Communications of the Joint Institute for Nuclear Research,
5 pp., Dubna
Hlavaty, L. A987) Unusual solutions to the Yang-Baxter equations, J. Phys. A 20, 1661-7
Hlavaty, L. A991) Two-dimensional quantum spaces corresponding to solutions of the Yang-
Baxter equations, J. Phys. A 24, 2903-12
Hlavaty, L. A992a) Yang-Baxter matrices and differential calculi on quantum hyperplanes,
J. Phys. A 25, 485-94
Hlavaty, L. A992b) New constant and trigonometric 4x4 solutions to the Yang-Baxter
equations, J. Phys. A 25, L63-8
Hlavaty, L. A992c) On the solutions of the Yang-Baxter equations, in Quantum Groups
and Related Topics, R. Gierlak et al (eds), pp. 179-88, Kluwer, Dordrecht
Hlavaty, L. A992d) On solutions of the Yang-Baxter equation without additivity, J. Phys.
A 25,1395-7
Hlavaty, L. A993) A remark on quantum supergroups, Modern Phys. Lett. A 7, 3365—72
Hochschild, G. P. A965) The Structure of Lie Groups, Holden—Day, San Francisco
Hodges, T. J. A990) Ring theoretical aspects of the Bernstein-Beilinson theorem, in Non-
commutative Ring Theory, Athens, Ohio, 1989, S. K. Jain &; S. R. Lopez-Permouth (eds),
Lecture Notes in Mathematics 1448, pp. 155—63, Springer, New York
Hodges, T. J. & Levasseur, T. A993) Primitive ideals of Cq[SLC)], Comm. Math. Phys.
156, 581-605
Hojman, S. A. A991) Quantum algebras in classical mechanics, J. Phys. A 24, L249-54
Hollowood, T. A993) Quantizing SL(N) solitons and the Hecke algebra, Intemat. J. Mod-
Modem Phys. A 8, 947-81
Hollowood, T. & Mansfield, P. A990) Quantum group structure of quantum Toda conformal
field theories (I), Nucl. Phys. B 330, 720-40
Hopf, H. A941) Uber die Topologie der Gruppen-mannigfaltigkeiten und ihre Verallge-
meinerungen, Ann. of Math. 42, 22—52
Hou, B. Y., Hou, B. Y. & Ma, Z. Q. A991a) Solutions to the Yang-Baxter equation for the
spinor representations of q-B\, J. Phys. A 24, 1363—77
Hou, B. Y., Hou, B. Y. & Ma, Z. Q. A991b) The XXZ model with Beraha values, J. Phys.
A 24, 2847-61
Hou, B. Y., Hou, B. Y. & Ma, Z. Q. A992) Quantum Clebsch-Gordan coefficients for
non-generic q-values, J. Phys. A 25, 1211-22
Hou, B. Y., Hou, B. Y., Ma, Z. Q. & Yin, Y. D. A991) Solutions of Yang-Baxter equation
in the vertex model and the face model for octet representation, J. Math. Phys. 32, 2210—8
Hou, B. Y., Li, K. & Wang, P. A990) General solutions to fundamental problems of SU{2)k
WZW models, J. Phys. A 23, 3431-46
Hou, B. Y., Lie, D. P. & Yue, R. H. A989) Quantum group structure in the unitary minimal
model, Phys. Lett. B 229, 45-50
References 597
Hou, B. Y. & Ma, Z. Q. A991) Solutions to the Yang-Baxter equation for the spinor
representations of q-Bt, J. Phys. A 24, 1363-77
Hou, B. Y., Shi, K. J., Wang, P. & Yue, R. H. A990) The crossing matrices of WZW 5/7B)
model and minimal models with the quantum 6j symbols, Nucl. Phys. B 345, 659—84
Hou, B. Y., Shi, K. J. & Yang, Z. Z. A992) slq{n) quantum algebra as a limit of the elliptic
case, in Infinite Analysis, A. Tsuchiya, T. Eguchi Sc M. Jimbo (eds), Advanced Series in
Mathematical Physics 16, pp. 391-404, World Scientific, Singapore
Hou, B. Y., Shi, K. J., Yang, Z. Z. & Yue, R. H. A991) Integrable quantum chain and the
representation theory of the quantum group SUqB), J. Phys. A 24, 3825-36
Hou, B. Y., Shi, K. J. Sc Yue, R. H. A990) Explicit expressions for fusion and braid matrices
in the unitary minimal model, High Energy Phys. Nucl. Phys. 14, 802-9
Hou, B. Y., Wang, P. & Yue, R. H. A990) The crossing matrices of WZW SUB) model
and minimal models with the quantum 6j symbols, Nucl. Phys. B 345, 659—84
Hou, B. Y. & Wei, H. A989) Algebras connected with the Zn elliptic solution of the Yang-
Baxter equation, J. Math. Phys. 30, 2750-5
Hou, B. Y. & Yang, Z. X. A991) The Bethe ansatz solutions to the XXZ model and the
highest weight states of quantum groups, J. Northwest Univ. 21, 7-11 (Chinese)
Hou, B. Y. & Zhou, Y. K. A990) Fusion procedure and Sklyanin algebra, J. Phys. A 23,
1147-54
Howe, R. A988) The Classical Groups and invariants of binary forms, in The Mathemat-
Mathematical Heritage of Hermann Weyl, R. O. Wells Jr. (ed.), Proceedings of Symposia in Pure
Mathematics 48, pp. 133-66, American Mathematical Society, Providence, RI
Huang, Y. Z. Sc Lepowsky, J. A992) Toward a theory of tensor products for representa-
representations of a vertex operator algebra, in Proceedings of the 20th International Conference on
Differential Geometric Methods in Theoretical Physics, S. Catto &; A. Rocha-Caridi (eds),
pp. 344-54, World Scientific, Singapore
Huebschmann, J. A990) Poisson cohomology and quantization, J. reine angew. Math. 408,
57-113
Humphreys, J. E. A972) Introduction to Lie Algebras and Representation Theory, Gradu-
Graduate Texts in Mathematics 9, Springer, New York
Humphreys, J. E. A990) Reflection Groups and Coxeter Groups, Cambridge University
Press, Cambridge
Idzumi, M., Tokohiro, T., Iohara, K., Jimbo, M., Miwa, T. & Nakashima, T. A993) Quan-
Quantum affine symmetry in vertex models, Internat. J. Modern Phys. A 8, 1479-511
Ihara, Y. A988) Galois groups over Q and monodromy, in Prospects of Algebraic Analysis,
RIMS Report 675, pp. 23-34 (Japanese)
Ihara, Y. A991) Braids, Galois groups and some arithmetic functions, in Proceedings of
the International Congress of Mathematicians, Berkeley, 1986, A. M. Gleason (ed.), pp.
99—120, American Mathematical Society, Providence, RI
Ikeda, K. A991) The Hamiltonian systems on the Poisson structure of the quasi-classical
limit of GLq(oo), Lett. Math. Phys. 23, 121-6
Iosifescu, M. & Scutaru, H. A988a) Degenerate representations from quantum kinematical
constraints, in Group Theoretical Methods in Physics, Varna, 1987, H.-D. Doebner, J.-D.
Hennig & T. D. Palev (eds), Lecture Notes in Physics 313, pp. 230-7, Springer, Berlin
Iosifescu, M. Sc Scutaru, H. A988b) Second degree kinematical constraints associated with
dynamical symmetries, J. Math. Phys. 29, 742—57
Iotov, M. S. & Todorov, I. T. A991) On the universal R-matrix for C/9(sZr+i), Lett. Math*
Phys. 23, 241-50
Isaev, A. P. &; Popowicz, Z. A992) g-trace for quantum groups and g-deformed Yang-Mills
theory, Phys. Lett. B 281, 271—8
Isaev, A. P. Sc Malik, R. P. A992) Deformed traces and covariant quantum algebras for
quantum groups GLqpB) and GLqp(l|l), Phys. Lett B 280, 219-26
598 References
Itoh, T. Sc Yamada, Y. A991a) Explicit exchange relations in the SLB) Wess-Zumino-
Witten model, Internat. J. Modern Phys. A 6, 3283-91
Itoh, T. Sc Yamada, Y. A991b) Exchange relations in Wess-Zumino-Novikov-Witten model
and quantum groups, Progr. Theoret. Phys. 85, 751—8
Itoyama, H. A989) Symmetries of the generalized Toda system, Phys. Lett A 140, 391-4
Itoyama, H. & Moxhay, P. A991) Thermodynamic Bet he ansatz, sine Gordan theory and
minimal models, in Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp.
306-20, World Scientific, Singapore
Itoyama, H. & Sevrin, A. A990) Braiding matrices of conformal blocks and coset models,
Internat J. Modern Phys. A 5, 211-22
Ivanov, I. T. &: Uglov, D. B. A992) R-matrices for the semicyclic representations of
Uq{sl{2)), Phys. Lett A 167, 459-64
Iwahori, N. A964) On the structure of a Hecke ring of a Chevalley group over a finite field,
J. Fac. Sci. Univ. Tokyo Sect. 110, 215-36
Iwahori, N. &; Matsumoto, H. A965) On some Bruhat decompositions and the structure of
the Hecke ring of p-adic Chevalley groups, Publ. Math. IHES 25, 5-48
Iwao, S. A990) Spectroscopy in Witten's quantum universal enveloping algebra of SU2 and
strength of deformation of its representation space, Progr. Theor. Phys. 83, 363-72
Izergin, A. G. &; Korepin, V. E. A981) The inverse scattering method approach to the
quantum Shabat-Mikhailov model, Comm. Math. Phys. 79, 303-16
Izergin, A. G. & Korepin, V. E. A982) Quantum inverse scattering method, Soviet J.
Particles & Nuclei 13, 207-23
Izergin, A. G. & Korepin, V. E. A984a) The quantum inverse scattering approach to
correlation functions, Comm. Math. Phys. 94, 67-92
Izergin, A. G. &: Korepin, V. E. A984b) The most general L-operator for the R-matrix of
the XXX model, Lett. Math. Phys. 8, 259-65
Izergin, A. G. &: Korepin, V. E. A985) Correlation functions for the Heisenberg XXZ
ferromagnet, Comm. Math. Phys. 99, 271-302
Jacobson, N. A962) Lie Algebras, Wiley (Interscience), New York
Jagannathan, R., Sridhar, R., Vasudevan, R., Chaturvedi, S., Krishnakamuri, M., Shanta,
P. & Srinivasan, V. A992) On the number operators of multimode systems of deformed
oscillators covariant under quantum groups, J. Phys. A 25, 6429-54
Jain, V. &; Ogievetsky, O. A992) Classical isomorphisms for quantum groups, Modern Phys.
Lett. A 7, 2199-209
Jannussis, A., Brodimas, G. Sz Mignani, R. A991) Quantum groups and Lie-admissible
time evolution, J. Phys. A 24, L775-8
Jannussis, A., Brodimas, G., Sourlas, D., Papaloucas, L., Poulopoulos, P. &; Siafarikas, P.
A982) Generalized q Bose operators, Lett. Nuovo Cim. 34, 375-9
Jannussis, A., Brodimas, G., Sourlas, D., Vlachos, K., Siafarikas, P. Sc Papaloucas, L.
A983) Some properties of ^-analysis and application to noncanonical quantum mechanics,
Hadronic J. 6, 1653-86
Jannussis, A., Brodimas, G., Sourlas, D. Sz Zisis, V. A981) Remarks on the ^-quantization,
Lett Nuovo Cim. 30, 123-7
Jantzen, J. C. A987) Representations of Algebraic Groups, Academic Press, Boston
Jarvis, P. D. & Baker, T. A993) q-deformation of radial problems: the simple harmonic
oscillator in two dimensions, J. Phys. A 26, 883—94
Jarvis, P. D., Warner, R. C, Yang, C. M. & Zhou, R. B. A992) BRST cohomology for
Uq(slB)) representations, J. Phys. A 25, L895-900
Jimbo, M. A985) A ^-difference analogue of U(Q) and the Yang-Baxter equation, Lett
Math. Phys. 10, 63-9
Jimbo, M. A986a) A ^-analogue of U(gl(N 4- 1)), Hecke algebra and the Yang-Baxter
equation, Lett. Math. Phys. 11, 247-52
References 599
Jimbo, M. A986b) Quantum R-matrix related to the generalized Toda system: an algebraic
approach, in Field Theory, Quantum Gravity and Strings, H. J. de Vega &: N. Sanchez (eds),
Lecture Notes in Physics 246, pp. 335-61, Springer, Berlin
Jimbo, M. A986c) Quantum R-matrix for the generalized Toda system, Comm. Math.
Phys. 102, 537-47
Jimbo, M. (ed.) A989a) Yang-Baxter Equation in Integrable Systems, World Scientific,
Singapore
Jimbo, M. A989b) Introduction to the Yang-Baxter equation, in Braid Group, Knot Theory
and Statistical Mechanics, C. N. Yang &; M. L. Ge (eds), Advanced Series in Physics 9, pp.
111-34, World Scientific, Singapore
Jimbo, M. A989c) Introduction to the Yang-Baxter equation, Internat. J. Modern Phys.
A 4, 3759-77
Jimbo, M., Kuniba, A., Miwa, T. & Okado, M. A988) An A^lx family of solvable lattice
models, Comm. Math. Phys. 119, 543-65
Jimbo, M., Misra, K. C. &: Miwa, T. A990) Crystal base for the basic representation of
Uq(sin), Comm. Math. Phys. 134, 79-88
Jimbo, M., Misra, K. C, Miwa, T. &: Okado, M. A991) Combinatorics of representations
of Uq(sl(n)) at q = 0, Comm. Math. Phys. 136, 543-66
Jimbo, M. &; Miwa, T. A985) Classification of solutions to the star triangle relation for a
class of 3 and 4 state IRF models, Nucl. Phys. B 257, 1-18
Jimbo, M., Miwa, T. &: Okado, M. A988a) Local state probabilities of solvable lattice
models: an A^_x family, Nucl. Phys. B 300, 74-108
Jimbo, M., Miwa, T. & Okado, M. A988b) Solvable lattice models related to the vector
representation of classical simple Lie algebras, Comm. Math. Phys. 116, 507—25
Jimenez, F. A990) Quantum group symmetry of N = 1 superconformal field theories, Phys.
Lett. B 252, 577-85
Jimenez, F. A991) The quantized symmetries of N = 2 superconformal field theories, Phys.
Lett. B 273, 399-408
Jing, N. H. A990) Twisted vertex representations of quantum affine algebras, Invent. Math.
102, 663-90
Jing, N. H. A991) On a trace of g-analog vertex operators, in Quantum Groups, T. Cur-
tright, D. Fairlie & C. Zachos (eds), pp. 113-22, World Scientific, Singapore
Jing, N. H. A992) Quantum groups with two parameters, in Deformation Theory and
Quantum Groups with Applications to Mathematical Physics, M. Gerstenhaber &; J. Stash-
eff (eds), Contemporary Mathematics 134, pp. 129-38, American Mathematical Society,
Providence, RI
Jing, N. H., Ge, M. L. &; Wu, Y. S. A991) A new quantum group associated with a
'nonstandard' braid group representation, Lett. Math. Phys. 21, 193-203
Jing, N. H. &; Xu, J. J. A991) Comment on the g-deformed fermionic oscillator, J. Phys.
A 24, L891-4
Jing, S. A993) The Jordan-Schwinger realization of two-parametric quantum group s/9)SB),
Modem Phys. Lett. A 8, 543-8
Jing, S. &: Fan, H. A993) A new completeness relation in the g-deformed two-mode Fock
space, J. Phys. A 26, L69-74
Jones, V. F. R. A985) A polynomial invariant for knots via von Neumann algebras, Bull.
Amer. Math. Soc. 12, 103-11
Jones, V. F. R. A987) Hecke algebra representations of braid groups and link polynomials,
Ann. of Math. 126, 335-88
Jones, V. F. R. A988) Subfactors and related topics, in Operator Algebras and Applications,
Vol. 2, D. E. Evans &; M. Takesaki (eds), London Mathematical Society Lecture Note Series
136, pp. 103-18, Cambridge University Press, Cambridge
600 References
Jones, V. F. R. A989) On knot invariants related to some statistical mechanical models,
Pacific J. Math. 137, 311-34
Jones, V. F. R. A990) Baxterization, in Yang-Baxter Equations, Conformal Invariance
and Integrability in Statistical Mechanics and Field Theory, M. N. Barber &: P. A. Pearce
(eds), pp. 1-13, World Scientific, Singapore
Jones, V. F. R. A991) Subfactors and Knots, CBMS Regional Conference Series in Math-
Mathematics 80, American Mathematical Society, Providence, RI
Jordan, D. A. A993) Iterated skew polynomial rings and quantum groups, J. Algebra 156,
194-218
Joseph, A. &: Letzter, G. A992) Local finiteness of the adjoint action for quantized en-
enveloping algebras, J. Algebra 153, 289-318
Joyal, A. &; Street, R. A986) Braided monoidal categories, Macquarie Mathematics Reports
no. 860081
Joyal, A. &; Street, R. A991a) Tortile Yang-Baxter operators in tensor categories, J. Pure
Appl. Algebra 71, 43-51
Joyal, A. & Street, R. A991b) The geometry of tensor calculus I, Adv. Math. 88, 55-112
Joyal, A. &: Street, R. A992) An introduction to Tannaka duality and quantum groups, in
Category Theory, Como, 1990, A. Carboni, M. C. Pedicchio &; G. Rosolini (eds), Lecture
Notes in Mathematics 1488, pp. 413-92, Springer, Berlin
Jurco, B. A990) Classical Yang-Baxter equations and quantum integrable systems (Gaudin
models), in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &; J.-D. Hennig
(eds), pp. 219-27, Lecture Notes in Physics 370, Springer, Berlin
Jurco, B. A991a) On coherent states for the simplest quantum groups, Lett. Math. Phys.
21, 51-8
Jurco, B. A991b) Differential calculus on quantized simple Lie groups, Lett. Math. Phys.
22, 177-86
Jurco, B. &; Stovicek, P. A993) Quantum dressing orbits on compact groups, Comm. Math.
Phys. 152, 97-126
Kac, V. G. A983) Infinite Dimensional Lie Algebras, Birkhaiiser, Boston
Kac, V. G. &: Wakimoto, M. A988) Modular and conformal invariance constraints in rep-
representation theory of affine algebras, Adv. Math. 70, 156—236
Kac, V. G. &: Weisfeiler, B. A976) Coadjoint action of a semi-simple algebraic group and
the center of the enveloping algebra in characteristic p, Indag. Math. 38, 136-51
Kachurik, I. I. &: Klimyk, A. U. A990) On Racah coefficients of the quantum algebra
Uq(su2), J- Phys. A 23, 2717-28
Kachurik, I. I. &: Klimyk, A. U. A991) General recurrence relations for Clebsch-Gordan
coefficients of the quantum algebra Uq(su2), J. Phys. A 24, 4009-15
Kalnins, E. G., Manocha, H. L. &; Miller, W. A992) Models of ^-algebra representations:
I. Tensor products of special unitary and oscillator algebras, J. Math. Phys. 33, 2365-83
Kalnins, E. G., Miller, W. &; Mukherjee, S. A994) Models of ^-algebra representations: the
group of plane motions, SIAM J. Math. Anal. 25, 513-27
Kang, S. J., Kashiwara, M., Misra, K. C, Miwa, T., Nakashima, T. &: Nakayashiki, A.
A992a) Vertex models and crystals, C. R. Acad. Sci. Paris Ser. I 315, 375-80
Kang, S. J., Kashiwara, M., Misra, K. C, Miwa, T., Nakashima, T. &; Nakayashiki, A.
A992b) Affine crystals and vertex models, in Infinite Analysis, A. Tsuchiya, T. Eguchi &;
M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp. 449-84, World Scientific,
Singapore
Kang, S. J., Kashiwara, M., Misra, K. C, Miwa, T., Nakashima, T. &; Nakayashiki, A.
A992c) Perfect crystals of quantum affine Lie algebras, Duke Math. J. 68, 499-607
Kang, S. J., Misra, K. C. &; Miwa, T. A993) Fock space representations of the quantized
universal enveloping algebras UqiC^), Uq(A$) and Uq{D(^l), J. Algebra 155, 238-51
References 601
Karasev, M. V. A987) Analogues of objects of Lie group theory for non-linear Poisson
brackets, Math. USSR Izvestiya 28, 497-527
Karasev, M. V. &: Maslov, V. P. A993) Nonlinear Poisson Brackets: Geometry and Quan-
Quantization, Translations of Mathematical Monographs 119, American Mathematical Society,
Providence, RI
Karimipour, V. A993) The quantum double and the universal R-matrix for non-standard
deformation of A^n_x), J. Phys. A 26, L239-44
Karimipour, V. &; Aghamohammadi, A. A993) Multiparametric quantization of the special
linear superalgebra, J. Math. Phys. 34, 2561-71
Karowski, M. A990) Yang-Baxter algebra - Bethe ansatz - conformal quantum field theories
- quantum groups, in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &; J.-D.
Hennig (eds), pp. 183-218, Lecture Notes in Physics 370, Springer, Berlin
Karowski, M., Miiller, W. &; Schrader, R. A992) State sum invariants of compact 3-
manifolds with boundary and 6j-symbols, J. Phys. A 25, 4847-60
Karowski, M. &: Schrader, R. A992) A quantum group version of quantum gauge theories
in two dimensions, J. Phys. A 25, LI 151-4
Karowski, M. &; Schrader, R. A993) A combinatorial approach to topological quantum field
theories and invariants of graphs, Comm. Math. Phys. 151, 355—402
Kashaev, R. M. & Mangazeev, V. V. A990) The four state solution of the Yang-Baxter
equation, Phys. Lett. A 150, 375-9
Kashaev, R. M. & Mangazeev, V. V. A992) iVn(n-1)/2-state intertwiner related to
Uq(sl(n)) algebra at q2N = 1, Modem Phys. Lett. A 7, 2827-36
Kashaev, R. M., Mangazeev, V. V. & Stroganov, Yu. G. A991) Cyclic eight-state R-matrix
related to Uq(slC)) algebra at q2 = -1, Modern Phys. Lett. A 6, 3437-43
Kashaev, R. M., Mangazeev, V. V. & Stroganov, Yu. G. A992) iV3-state R-matrix related
with Uq(slC)) algebra at q2N = 1, in Infinite Analysis, A. Tsuchiya, T. Eguchi & M.
Jimbo (eds), Advanced Series in Mathematical Physics 16, pp. 485—92, World Scientific,
Singapore
Kashiwara, M. A990a) Kazhdan-Lusztig conjecture for a symmetrizable Kac-Moody alge-
algebra, in Grothendieck Festschrift, Vol. II, P. Cartier et al. (eds), Progress in Mathematics
87, pp. 407-33, Birkhaiiser, Boston
Kashiwara, M. A990b) Bases cristallines, C. R. Acad. Sci. Paris. Ser. /311, 277-80
Kashiwara, M. A990c) Crystalizing the g-analogue of universal enveloping algebras, Comm.
Math. Phys. 133, 249-60
Kashiwara, M. A991) On crystal bases of the g-analogue of universal enveloping algebras,
Duke Math. J. 63, 465-516
Kashiwara, M. &; Miwa, T. A986) A class of elliptic solutions to the star-triangle equation,
Nucl. Phys. B 275, 121-34
Kashiwara, M. &: Tanisaki, T. A990) Kazhdan-Lusztig conjecture for a symmetrizable Kac-
Moody algebra II, in Operator Algebras, Unitary Representations, Enveloping Algebras
and Invariant Theory, A. Connes, M. Duflo, A. Joseph &: R. Rentschler (eds), Progress in
Mathematics 92, pp. 159—95, Birkhaiiser, Boston
Kashiwara, M. &; Tanisaki, T. A994) Characters of negative level highest weight modules
for affine Lie algebras, preprint
Kassel, Ch. A992) Cyclic homology of differential operators, the Virasoro algebra and a
g-analogue, Comm. Math. Phys. 146, 343-56
Kato, M. A990) Flat connection, quantum field theory and quantum group, in Differential
Geometric Methods in Theoretical Physics, Davis, 1988, L. L. Chau &: W. Nahm (eds),
NATO Advanced Science Institutes Series B: Physics 245, pp. 251-6, Plenum, New York
Katriel, J. &: Solomon, A. I. A991) A ^-analogue of the Campbell-Baker-Hausdorff expan-
expansion, J. Phys. A 24, L1139-42
602 References
Kauffman, L. H. A991a) From knots to quantum groups and back, in Quantum Groups,
T. Curtright, D. Fairlie & C. Zachos (eds), pp. 1-32, World Scientific, Singapore
Kauffman, L. H. A991b) Knots and Physics, World Scientific, Singapore
Kauffman, L. H &; Saleur, H. A992) Fermions and link invariants, in Infinite Analysis, A.
Tsuchiya, T. Eguchi &; M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp.
493-532, World Scientific, Singapore
Kazhdan, D. &; Lusztig, G. A979) Representations of Coxeter groups and Hecke algebras,
Invent. Math. 53, 165-84
Kazhdan, D. &: Lusztig, G. A991) Affine Lie algebras and quantum groups, Duke Math. J.
Intemat. Math. Res. Notices 2, 21-9
Kazhdan, D. &; Lusztig, G. A993a) Tensor structures arising from affine Lie algebras I, J.
Amer. Math. Soc. 6, 905-47
Kazhdan, D. &; Lusztig, G. A993b) Tensor structures arising from affine Lie algebras II, J.
Amer. Math. Soc. 6, 949-1011
Kazhdan, D. &: Lusztig, G. A994a) Tensor structures arising from affine Lie algebras III,
J. Amer. Math. Soc. 7, 335-81
Kazhdan, D. &: Lusztig, G. A994b) Tensor structures arising from affine Lie algebras IV,
J. Amer. Math. Soc. 7, 383-453
Kazhdan, D. &; Soibelman, Ya. S. A992) Representations of the quantized function algebras,
2-categories and Zamolodchikov tetrahedra equation, pre-print, Harvard University
Kazhdan, D. &: Wenzl, H. A993) Reconstructing monoidal categories, pre-print, Harvard
University
Kekalainen, P. A992) Step algebras of quantum sl(n), J. Algebra 150, 245-53
Keller, G. A991) Fusion rules of Uq(slBX)), q™ = 1, Lett. Math. Phys. 21, 273-86
Kempf, A. A993) Quantum group symmetric Bargmann-Fock space: integral kernels, Green
functions, driving forces, J. Math. Phys. 34, 969—87
Kennedy, T. A992) Solutions of the Yang-Baxter equation for isotropic quantum spin
chains, J. Phys. A 25, 2809-18
Kerler, T. A992) Non-Tannakian categories in quantum field theory, in New Symmetry
Principles in Quantum Field Theory, J. Frohlich et al. (eds), NATO Advanced Science
Institutes Series B: Physics 295, pp. 449-85, Plenum, New York
Kerov, S. V. A992a) Characters of Hecke and Birman-Wenzl algebras, in Quantum Groups,
Proceedings of Workshops held in the Euler International Mathematical Institute 1990, P.
P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 335-40, Springer, Berlin
Kerov, S. V. A992b) A ^-analog of the Hook walk algorithm and random Young tableaux,
Fund. Anal. Appl. 26, 179-87
Kerov, S. V. &: Vershik, A. M. A989) Characters and realizations of representations of an
infinite dimensional Hecke algebra and knot invariants, Soviet Math. Dokl. 38, 134-7
Khesin, B. &: Zakharevich, I. A992) Lie-Poisson group of pseudodifferential symbols and
fractional KP-KdV hierarchies, preprint IHES/M/92/71
Khoroshkin, S. M., Radul, A. &; Rubtsov, V. A993) A family of Poisson structures on
hermitian symmetric spaces, Comm. Math. Phys. 152, '299—315
Khoroshkin, S. M. &: Tolstoy, V. N. A991a) Universal R-matrix for quantized (super)
algebras, Comm. Math. Phys. 141, 599-617
Khoroshkin, S. M. &: Tolstoy, V. N. A991b) Universal R-matrix for quantum supergroups,
in Group Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov & V. I. Manko
(eds), Lecture Notes in Physics 382, pp. 229-32, Springer, Berlin
Khoroshkin, S. M. &; Tolstoy, V. N. A992a) Extremal projector and universal R-matrix for
quantized contragredient Lie (super) algebras, in Quantum Groups and Related Topics, R.
Gierlak et al. (eds), pp. 23-32, Kluwer, Dordrecht
Khoroshkin, S. M. &: Tolstoy, V. N. A992b) Uniqueness theorem for universal R-matrix,
Lett. Math. Phys. 24, 231-44
References 603
Kim, J. D., Koh, I. G. & Ma, Z. Q. A991) Quantum R matrix for E7 and F4 groups, J.
Math. Phys. 32, 845-56
Kirby, A. A978) A calculus for framed links, Invent. Math. 45, 35-56
Kirby, R. & Melvin, P. A991) The 3-manifold invariants of Witten and Reshetikhin-Turaev
for sZB,C), Invent. Math. 105, 473-505
Kirby, R., Melvin, P. & Zhang, X. A993) Quantum invariants at the sixth root of unity,
Comm. Math. Phys. 151, 607-18
Kirillov, A. A. A976) Local Lie algebras, Russian Math. Surveys 31 D), 55-75
Kirillov, A. N. A988) Clebsch-Gordan quantum coefficients, Zap. Nauchn. Sem. Leningrad
Otdel. Mat. Inst. Steklov 9, 67-84 (Russian)
Kirillov, A. N. & Reshetikhin, N. Yu. A986) The Yangians, Bethe ansatz and combinatorics,
Lett. Math. Phys. 12, 199-208
Kirillov, A. N. & Reshetikhin, N. Yu. A987) Exact solution of the integrable XXZ Heisen-
berg model with arbitrary spin. II. Thermodynamics of the system, J. Phys. A 20, 1587-97
Kirillov, A. N. & Reshetikhin, N. Yu. A989) Representations of the algebra Uq{slB)), q-
orthogonal polynomials and invariants of links, in Infinite-dimensional Lie Algebras and
Groups, V. G. Kac (ed.), pp. 285-339, World Scientific, Singapore
Kirillov, A. N. &; Reshetikhin, N. Yu. A990a) g-Weyl group and a multiplicative formula
for universal R-matrices, Comm. Math. Phys. 134, 421—31
Kirillov, A. N. & Reshetikhin, N. Yu. A990b) Representations of Yangians and multiplicities
of occurrence of the irreducible components of the tensor product of representations of
simple Lie algebras, J. Soviet Math. 52, 3156—64
Klimcik, C. & Klimcik, E. A993) On macroscopic energy gap for g-quantum mechanical
systems, J. Phys. A 26, L289-92
Klimek, M. A993) Extension of g-deformed analysis and g-deformed models of classical
mechanics, J. Phys. A 26, 955-68
Klimek, S. &; Lesniewski, A. A992a) Quantum Riemann surfaces I. The unit disc, Comm.
Math. Phys. 146, 103-22
Klimek, S. & Lesniewski, A. A992b) Quantum Riemann surfaces II. The discrete series,
Lett. Math. Phys. 24, 125-40
Klimyk, A. U. A992) Wigner-Eckart theorem for tensor operators of the quantum group
Uq(n), J. Phys. A 25, 2919-27
Klimyk, A. U. &; Pakuliak, S. Z. A992) Representations of the quantum algebras Uq(ur,s)
and Uq{ur+a) related to the quantum hyperboloid and sphere, J. Math. Phys. 33, 1937-47
Klimyk, A. U., Smirnov, Yu. F. &; Gruber, B. A991) Representations of the quantum
algebras Uq(suB)) and Uq(su(l, 1)), in Symmetries in Science V, B. Gruber &; H.-D.
Doebner (eds), pp. 341-68, Plenum, New York
Knizhnik, V. &; Zamolodchikov, A. A984) Current algebra and Wess-Zumino model in two
dimensions, Nucl. Phys. B 247, 83-103
Kobayashi, T. & Uematsu, T. A993) g-deformed superconformal algebra on quantum su-
perspace, Phys. Lett. B 306, 27-33
Koelink, H. T. A991a) On ^representations of the Hopf *-algebra associated with the
quantum group Uq(n), Compositio Math. 77, 199-231
Koelink, H. T. A991b) On quantum groups and g-special functions, Thesis, University of
Leiden
Koelink, H. T. A992) Quantum group theoretical proof of the addition formula for con-
continuous g-Legendre polynomials, in Deformation Theory and Quantum Groups with Ap-
Applications to Mathematical Physics, M. Gerstenhaber & J. Stasheff (eds), Contemporary
Mathematics 134, pp. 139-40, American Mathematical Society, Providence, RI
Koelink, H. T. A994a) The quantum group of plane motions and the Hahn-Exton g-Bessel
function, Duke Math. J. 76, 483-508
604 References
Koelink, H. T. A994b) The quantum group of plane motions and basic Bessel functions,
Indagationes Math, (to appear)
Koelink, H. T. & Koornwinder, T. H. A989) The Clebsch-Gordon coefficients for the quan-
quantum group S[j,UB) and q-Hahn polynomials, Nederl. Akad. Wetensch. Proc. Ser. A 92,
443-56
Koelink, H. T. & Koornwinder, T. H. A992) ^-special functions: a tutorial, in Deformation
Theory and Quantum Groups with Applications to Mathematical Physics, M. Gerstenhaber
&: J. Stasheff (eds), Contemporary Mathematics 134, pp. 141-2, American Mathematical
Society, Providence, RI
Koelink, H. T. & Swarttouw, R. F. A994) A ^-analogue of Graf's addition formula for the
Hahn-Exton g-Bessel function, J. Approx. Theory (to appear)
Koh, I. G. & Ma, Z. Q. A990) Exceptional quantum groups, Phys. Lett. B 234, 480-6
Kohno, T. A985) Serie de Poincare-Koszul associee aux groups de tresses pures, Invent.
Math. 82, 57-75
Kohno, T. A986) Homology of a local system on a complement of hyperplanes, Proc. Japan
Acad. Sci. Ser. A 62, 144-7
Kohno, T. A987a) Monodromy representations of braid groups and Yang-Baxter equations,
Ann. Inst. Fourier (Grenoble) 37, 139-60
Kohno, T. A987b) One parameter family of linear representations of Artin's braid groups,
Adv. Stud, in Pure Math. 12, 189-200
Kohno, T. A988a) Linear representations of braid groups and classical Yang-Baxter equa-
equations, in Braids, Santa Cruz, 1986, J. S. Birman &; S. Libgober (eds), Contemporary Math-
Mathematics 78, pp. 339-63, American Mathematical Society, Providence, RI
Kohno, T. A988b) Hecke algebra representations of braid groups and classical Yang-Baxter
equations, in Conformal Field Theories and Solvable Lattice Models, Kyoto, 1986, M.
Jimbo, T. Miwa &: A. Tsuchiya (eds), Advanced Studies in Pure Mathematics 16, pp.
255—69, Academic Press, Boston
Kohno, T. A989a) Integrable systems related to braid groups and Yang-Baxter equation,
in Braid Group, Knot Theory and Statistical Mechanics, C. N. Yang & M. L. Ge (eds),
Advanced Series in Mathematical Physics 9, pp. 139-45, World Scientific, Singapore
Kohno, T. A989b) Monodromy representations of braid groups, Sugaku 41, 305-19
Komata, S., Mohri, K. &: Nohara, H. A991) Classical and quantum extended superconfor-
mal algebra, Nucl. Phys. B 359, 168-200
Konishi, Y. A992) A note on actions of compact matrix quantum groups on von Neumann
algebras, Nihonkai Math. J. 3, 23-9
Konishi, Y., Nagisa, M. &; Watatani, Y. A992) Some remarks on actions of compact matrix
quantum groups on C*-algebras, Pacific J. Math. 153, 119-27
Koornwinder, T. H. A989a) Representations of the twisted SU{2) quantum group and
some g-hypergeometric orthogonal polynomials, Nederl. Akad. Wetensch. Proc. Ser. A 92,
97-117
Koornwinder, T. H. A989b) Continuous g-Legendre polynomials are spherical matrix ele-
elements of irreducible representations of the quantum SU{2) group, CWI Quart. 2, 171—3
Koornwinder, T. H. A990) Orthogonal polynomials in connection with quantum groups,
in Orthogonal Polynomials: Theory and Practice, P. Nevai (ed.), NATO Advanced Science
Institutes Series C: Mathematical and Physical Sciences 294, pp. 257-92, Kluwer, Dordrecht
Koornwinder, T. H. A991a) The addition formula for little g-Legendre polynomials and
the SUB) quantum group, SIAM J. Math. Anal. 22, 295-301
Koornwinder, T. H. A991b) Positive convolution structures associated with quantum
groups, in Probability Measures on Groups X, Oberwolfach, 1990, H. Heyer (ed.), pp.
249-68, Plenum, New York
Koornwinder, T. H. A992) ^-special functions and their occurrence in quantum groups, in
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M.
References 605
Gerstenhaber & J. Stasheff (eds), Contemporary Mathematics 134, pp. 143-4, American
Mathematical Society, Providence, RI
Koornwinder, T. H. & Swarttouw, R. F. A992) On g-analogues of the Fourier and Hankel
transforms, Trans. Amer. Math. Soc. 333, 445-61
Korenskii, S. V. A991) Representations of the quantum group SLjB), Russian Math.
Surveys 46 F), 221-2
Korepin, V. E. A983) The analysis of the bilinear relation of the six-vertex model, Soviet
Phys. Dokl. 27, 1050-1
Korogodskii, L. I. & Vaksman, L. L. A992) Quantum G-spaces and Heisenberg algebra, in
Quantum Groups, Proceedings of Workshops held in the Euler International Mathematical
Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 56-66, Springer,
Berlin
Kosmann-Schwarzbach, V. A990a) Quantum and classical Yang-Baxter equations, Modern
Phys. Lett. A 5, 981-90; errata, ibid. 6 A991), 3373
Kosmann-Schwarzbach, V. A990b) Groupes de Lie-Poisson quasitriangulaires, in Ge-
ometrie Symplectique et Mecanique, Colloque International La Grande Motte, France, 23-
28 Mai, 1988, C. Albert (ed.), Lecture Notes in Mathematics 1416, pp. 161-7, Springer,
Berlin
Kosmann-Schwarzbach, V. A991a) From 'quantum groups' to 'quasi-quantum groups', in
Symmetry in Science V, B. Gruber & H.-D. Doebner (eds), pp. 369-93, Plenum, New York
Kosmann-Schwarzbach, V. A991b) Quasi-bigebres de Lie et groupes de Lie quasi-Poisson,
C. R. Acad. Sci. Paris Ser. I 312, 391-4
Kosmann-Schwarzbach, V. & Magri, F. A988) Poisson-Lie groups and complete integra-
bility, I. Drinfeld algebras, dual extensions and their canonical representations, Ann. Inst.
Henri Poincare Phys. Theor. 49, 433-60
Kosmann-Schwarzbach, V. & Magri, F. A990) Poisson-Nijenhuis structures, Ann. Sci.
Henri Poincare Phys. Theor. 53, 35-81
Kostant, B. A979) The solution to the generalized Toda lattice and representation theory,
Adv. Math. 34, 195-338
Kosuda, M. &; Murakami, J. A992) The centralizer algebras of mixed tensor representations
of Uq(gln) and the HOMFLY polynomial, Proc. Japan Acad. Ser. A Math. Sci. 68, 148-51
Kowalski, K. & Rembielinski, J. A993) Coherent states for the quantum complex plane, J.
Math. Phys. 34, 2153-65
Kruglyak, S. A. A984) Representations of a quantum algebra connected with the Yang-
Baxter equation, in Spectral Theory of Operators and Infinite-dimensional Analysis, Yu.
M. Berezanskii (ed.), pp. 111-20, Akad. Nauk Ukrain. SSR, Inst. Mat., Kiev
Kuang, L. M. & Wang, F. B. A993) The suq(\, 1) ^-coherent states and their nonclassical
properties, Phys. Lett. A 173, 221-7
Kulish, P. P. A985) Integrable graded magnets, Zap. Nauchn. Sem. Leningrad Otdel. Mat.
Inst. Steklov 145 (Russian)
Kulish, P. P. A989) Quantum Lie superalgebras and supergroups, in Problems of Mod-
Modern Quantum Field Theory, A. A. Belavin, A. U. Klimyk &: A. B. Zamolodchikov (eds),
Research Reports in Physics, pp. 14—21, Springer, Berlin
Kulish, P. P. A990a) A two-parameter quantum group and a gauge transformation, Zap.
Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 23, 89—93 (Russian)
Kulish, P. P. A990b) Clebsch-Gordan coefficients for a quantum superalgebra of rank one
I, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 180 (Russian)
Kulish, P. P. A991a) The quantum superalgebra ospB\\), J. Soviet Math. 54, 923-30
Kulish, P. P. A991b) Finite-dimensional Fateev-Zamolodchikov algebra and g-oscillators,
Phys. Lett. A 161, 50-2
Kulish, P. P. A991c) Contraction of quantum algebras and g-oscillators, Theoret. Math.
Phys. 86, 108-10
606 References
Kulish, P. P. A991d) Quantum algebras and symmetries of dynamical systems, in Group
Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov &: V. I. Manko (eds),
Lecture Notes in Physics 382, pp. 195-8, Springer, Berlin
Kulish, P. P. &: Damashinsky A990) On the q oscillator and the quantum algebra suq(l, 1),
J. Phys. A 23, L415-9
Kulish, P. P. & Reshetikhin, N. Yu. A982) On GL3-invariant solutions of the Yang-Baxter
equation and associated quantum systems, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst.
Steklov 120 (Russian)
Kulish, P. P. & Reshetikhin, N. Yu. A983) Quantum linear problem for the sine-Gordon
equation and higher representations, J. Soviet Math. 23, 2435—41
Kulish, P. P. &: Reshetikhin, N. Yu. A989) Universal R-matrix of the quantum superalgebra
osp{2\l), Lett. Math. Phys. 18, 143-9
Kulish, P. P., Reshetikhin, N. Yu. & Sklyanin, E. K. A981) Yang-Baxter equation and
representation theory I, Lett. Math. Phys. 5, 393-403
Kulish, P. P., Sasaki, R. &; Schwiebert, C. A993) Constant solutions of reflection equations
and quantum groups, J. Math. Phys. 34, 286-304
Kulish, P. &; Sklyanin, E. K. A982a) Solutions of the Yang-Baxter equation, J. Soviet
Math. 19, 1596-620
Kulish, P. &; Sklyanin, E. K. A982b) Quantum spectral transform method. Recent de-
developments, in Integrable Quantum Field Theories, Tvarminne, 1981, J. Hietarinta & C.
Montonen (eds), Lecture Notes in Physics 151, pp. 61-119, Springer, Berlin
Kulish, P. & Sklyanin, E. K. A991) The general Uq(slB)) invariant XXZ integrable quan-
quantum spin chain, J. Phys. A 24, L435-9
Kulish, P. &: Sklyanin, E. K. A992) Algebraic structure related to the reflection equations,
J. Phys. A 25, 5963-76
Kumari, M. K., Shanta, P., Chaturvedi, S. & Srinivasan, V. A992) On g-deformed para-
oscillators and para-g-oscillators, Modern Phys. Lett. A 7, 2593—600
Kundu, A. &: Basu-Mallick, B. A991) g-deformation of the Holstein-Primakoff transforma-
transformation and other bosonisations of the quantum group, Phys. Lett. A 156, 175-8
Kundu, A. & Basu-Mallick, B. A992a) Solutions of the non-additive YBE by spectral
parameter factorization and re-Yang-Baxterization, J. Phys. A 25, 6307-16
Kundu, A. &; Basu-Mallick, B. A992b) Construction of integrable quantum lattice models
through Sklyanin-like algebras, Modern Phys. Lett. A 7, 61-9
Kundu, A. &; Basu-Mallick, B. A993) Classical and quantum integrability of a derivative
non-linear Schrodinger model related to quantum groups, J. Math. Phys. 34, 1052—62
Kuniba, A. A990) Quantum R-matrix for G2 and a solvable 175 vertex model, J. Phys. A
23, 1349-62
Kuniba, A. A993) Thermodynamics of the Uq(Xr ) Bethe ansatz system with q a root of
unity, Nucl. Phys. B 389, 209-46
Kuniba, A. &; Nakanishi, T. A992) Fusion RSOS models and rational coset models, in
Quantum Groups, Proceedings of Workshops held in the Euler International Mathematical
Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 303-11, Springer,
Berlin
Kuniba, A., Nakanishi, T. &: Suzuki, J. A991) Ferro- and antiferro-magnetizations in RSOS
models, Nucl. Phys. B 356, 750-74
Kunz, J., Maslanka, P. & Giler, S. A991) Quantum BRST cohomology, J. Phys. A 24,
4235-9
Kuperschmidt, B. A. A991) Quasiclassical limit of quantum matrix groups, in Mechan-
Mechanics, Analysis and Geometry: 200 Years after Lagrange, M. Francaviglia (ed.), pp. 171-99,
North-Holland, Amsterdam
Kuperschmidt, B. A. A992a) The quantum group ThGL(n), J. Phys. A 25, L911-4
References 607
Kuperschmidt, B. A. A992b) Trace formulae for the quantum group GLq{2), J. Phys. A
25, L915-20
Kuperschmidt, B. A. A992c) The quantum group GLhB), J. Phys. A 25, L1239-44
Kuperschmidt, B. A. A993a) A ^-analogue of the dual space to the Lie algebras glB) and
slB), J. Phys. A 26, Ll-4
Kuperschmidt, B. A. A993b) All quantum group structures on the supergroup GLA|1), J.
Phys. A 26, L251-6
Kuperschmidt, B. A. A993c) A quantum analogue of the group of motions on the plane
and its coadjoint representation, Phys. Lett. A 174, 81-4
Lacki, J. A989) Algebres de dimension infinie, groupes de tresses et groupes quantiques
dans les theories conformes a deux dimensions, Riv. Nuovo Cim. 12 C), 52pp.
Lakshmibai, V. &: Reshetikhin, N. Yu. A991) Quantum deformations of flag and Schubert
schemes, C. R. Acad. Sci. Paris Ser. I 313, 121-6
Lakshmibai, V. &: Reshetikhin, N. Yu. A992) Quantum flag and Schubert schemes, in
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M.
Gerstenhaber &; J. Stasheff (eds), Contemporary Mathematics 134, pp. 145—81, American
Mathematical Society, Providence, RI
Lakshmibai, V. &: Seshadri, C. S. A991) Standard monomial theory, in Proceedings of Inter-
International Conference on Algebraic groups, Hyderabad, India, December, 1989, S. Ramanan,
C. Musili &: N. Mohan Kumar (eds), pp. 279-322, Manoj Prakashan, Madras
Lambe, L. A. A992) Homological perturbation theory, Hochschild homology and formal
groups, in Deformation Theory and Quantum Groups with Applications to Mathematical
Physics, M. Gerstenhaber &; J. Stasheff (eds), Contemporary Mathematics 134, pp. 183-
218, American Mathematical Society, Providence, RI
Lambe, L. A. &: Radford, D. E. A993) Algebraic aspects of the quantum Yang-Baxter
equation, J. Algebra 154, 228-88
Larson, R. G. A971) Characters of Hopf algebras, J. Algebra 17, 352-68
Larson, R. G. &: Towber, J. A991) Two dual classes of bialgebras related to the concepts
of 'quantum group' and 'quantum Lie algebra', Comm. Algebra 19, 3295-345
Larsson, T. A. A992) Universal solutions to the simplex equations, Nucl. Phys. B 380,
575-87
Lawrence, R. J. A989) A universal link invariant, in The Interface of Mathematics and
Particle Physics, Oxford, 1988, D. Quillen, G. B. Segal & S. T. Tsou (eds), Institute of
Mathematics and its Applications Conference Series New Series 24, pp. 151—6, Oxford
University Press, New York
Lawrence, R. J. A990) Homological representations of Hecke algebras, Comm. Math. Phys.
135, 141-91
Lawrence, R. J. A992) On algebras and triangle relations, in Topological and Geometrical
Methods in Field Theory, J. Mickelsson & O. Pekonen (eds), pp. 429-48, World Scientific,
Singapore
Lawrence, R. J. A993) A functorial approach to the one-variable Jones polynomial, J. Diff.
Geom. 37, 689-710
Lazarev, A. Yu. &: Movshev, M. V. A991a) Deformations of Hopf algebras, Russian Math.
Surveys 46 A), 253-4
Lazarev, A. Yu. &: Movshev, M. V. A991b) On the quantization of certain Lie groups and
Lie algebras, Russian Math. Surveys 46 F), 225-6
Leblanc, Y. &; Wallet, J.-C. A993) R-matrix and g-covariant oscillators for Uq(sl(n\m)),
Phys. Lett. B 304, 89-97
LeClair, A. A989) Restricted sine-Gordon theory and the minimal conformal series, Phys.
Lett. B 230, 103-7
LeClair, A. A991) Taming the integrable zoo, in Quantum Groups, T. Curtright, D. Fairlie
& C. Zachos (eds), pp. 247-57, World Scientific, Singapore
608 References
LeClair, A. &; Smirnov, F. A. A992) Infinite quantum group symmetry in massive 2D
quantum field theory, Intemat. J. Modern Phys. A 7, 2997-3022
Lee, H. C. A992a) On Seifert circles and functors for tangles, in Infinite Analysis, A.
Tsuchiya, T. Eguchi &: M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp.
581-610, World Scientific, Singapore
Lee, H. C. A992b) Tangle invariants and the centre of the quantum group, in Knots 90,
Osaka, 1990, A. Kawauchi (ed.), PP- 341-61, De Gruyter, Berlin
Lee, H.-C., Ge, M.-L., Couture, M. J. & Wu, Y. S. A989) Strange statistics, braid group
representations and multipoint functions in the iV-component model, Intemat. J. Modern
Phys. A 9, 2333-70
Leites, D. A. & Serganova, V. V. A983) On classical Yang-Baxter equation for simple Lie
superalgebras, Soviet J. Theor. Math. Phys. 17, 69-70
Le Man Kuang A992) The g-supercoherent states of the g-deformed SUB) superalgebra,
J. Phys. A 25, 4827-34
Lenczewski, R. A993a) A ^-analog of the quantum central limit theorem for SUqB), q
complex, J. Math. Phys. 34, 480-9
Lenczewski, R. A993b) On sums of ^-independent SUqB) quantum variables, Comvn. Math.
Phys. 154, 127-34
Lenczewski, R. &: Podgorski, K. A992) A ^-analog of the quantum central limit theorem
for SUqB), J. Math. Phys. 33, 2768-78
Lesniewski, A. & Rinaldi, M. A993) Tensor products of representations of C(SUqB)), J.
Math. Phys. 34, 305-14
Levendorskii, S. Z. A990) Twisted function algebras on a compact quantum group and
their representation, Fund. Anal. Appl. 24, 330-2
Levendorskii, S. Z. A992) Twisted function algebras on a compact quantum group and
their representation, St. Petersburg Math. J. 3, 405-23
Levendorskii, S. Z. A993) On PBW bases for Yangians, Lett. Math. Phys. 27, 37-42
Levendorskii, S. Z. & Soibelman, Ya. S. A990) Some applications of quantum Weyl groups,
J. Geom. Phys. 7, 241-54
Levendorskii, S. Z. & Soibelman, Ya. S. A991a) Algebras of functions on compact quantum
groups, Schubert cells and quantum tori, Comm. Math. Phys. 139, 141-70
Levendorskii, S. Z. & Soibelman, Ya. S. A991b) Quantum group Aoo, Comm. Math. Phys.
140, 399-414
Levendorskii, S. Z. & Soibelman, Ya. S. A991c) The quantum Weyl group and a multi-
multiplicative formula for the R-matrix of a simple Lie algebra, Fund. Anal. Appl. 25, 143-5
Levendorskii, S. Z., Soibelman, Ya. S. & Stukopin, V. A993) The quantum Weyl group and
the universal quantum R-matrix for affine Lie algebra A^ , Lett. Math. Phys. 27, 253-64
Leznov, A. N. & Mukhtarov, M. A. A987) The internal symmetry algebra of completely
integrable dynamical systems in the quantum regime, Theoret. Math. Phys. 71, 370—5
Li, Y. Q. A992a) Representations of a braid group with transpose symmetry and the related
link invariants, J. Phys. A 25, 6713-22
Li, Y. Q. A992b) General form of BGR associated with An and its Yang-Baxterization,
Phys. Lett. A 161, 411-5
Li, Y. Q. A993) Yang-Baxterization, J. Math. Phys. 34, 864-74
Li, Y. Q. & Ge, M. L. A991) Polynomials from non-standard braid group representations,
Phys. Lett. A 152, 273-5
Li, Y. Q., Ge, M. L., Xue, K. & Wang, L. Y. A991) Weight conservation condition and
structure of the braid group representation, J. Phys. A 24, 3443-53
Li, Y. Q. & Sheng, Z. A992) A deformation of quantum mechanics, J. Phys. A 25, 6779-88
Li, Y. Q., Wang, L. Y. & Zhang, J. A992) Representations of braid group and Birman-
Wenzl algebra, Phys. Lett. A 162, 449-52
References 609
Liao, L. &: Song, X. C. A991a) Quantum Lie superalgebras and 'nonstandard' braid group
representations, Modern Phys. Lett. A 6, 959-68
Liao, L. Sz Song, X. C. A991b) ^-deformation of Lie superalgebras B(m, n), B@, n), C(l+n)
and D(m, n) in their boson-fermion representations, J. Phys. A 24, 5451—63
Lichnerowicz, A. A981) Existence and invariance of twisted products on a symplectic man-
manifold, Lett. Math. Phys. 5, 117-26
Lichnerowicz, A. A982) Deformations d'algebres associees a une variete symplectique (les
iv-produits), Ann. Inst. Fourier 32, 157-209
Lickorish, W. B. R. A991) Three-manifold invariants and the Temperley-Lieb algebra,
Math. Ann. 290, 657-70
Lickorish, W. B. R. A993) Distinct 3-manifolds with all SUB)q invariants the same, Proc.
Amer. Math. Soc. 117, 285-92
Lie, S. A888-93) Theorie der Transformationsgruppen, Bd. 1-3, Teubner, Leipzig
Lienert, C. R. &: Butler, P. H. A992a) Racah-Wigner algebra for (/-deformed algebras, J.
Phys. A 25, 1223-36
Lienert, C. R. &: Butler, P. H. A992b) Recursive calculation of the R-matrices of q-deformed
algebras, J. Phys. A 25, 5577-86
Liguori, A. & Mintchev, M. A992) Spectral parameters of the quantum Yang-Baxter equa-
equation, Phys. Lett. B 275, 371-4
Lin, Z. A993) Induced representations of Hopf algebras: applications to quantum groups
at roots of 1, J. Algebra 154, 152-87
Links, J. R. &: Gould, M. D. A993) Raising and lowering operators for Uq(sl(n)), J. Math.
Phys. 34, 1577-86
Links, J. R., Gould, M. D. Sz Tsohantjis, I. A993) Baxterization of the R-matrix for the
adjoint representation of Uq[DB,1; a)], Lett. Math. Phys. 27, 51-8
Liskova, N. A. & Kirillov, A. N. A992) Clebsch-Gordan and Racah-Wigner coefficients for
Uq(SU(l,l)), in Infinite Analysis, A. Tsuchiya, T. Eguchi &; M. Jimbo (eds), Advanced
Series in Mathematical Physics 16, pp. 611-22, World Scientific, Singapore
Liu, K. A991) Quantum central extensions, C. R. Math. Rep. Acad. Sd. Canada 13,
135-40
Liu, K. A992) Characterizations of the quantum Witt algebra, Lett. Math. Phys. 24, 257-
66
Liu, Z. J. & Qian, M. A990) Classical R-matrix and semi-simple Lie algebras, in Nonlinear
Physics, Shanghai, 1989, Chao Hao Gu, Yi Shen Li & Gui Zhang Tu (eds), Research
Reports in Physics, pp. 146-51, Springer, Berlin
Liu, Z. J. & Qian, M. A992) Generalized Yang-Baxter equations, Koszul operators and
Poisson-Lie groups, J. Diff. Geom. 35, 399-414
Lu, J. F. & Ge, M. L. A987) The Yang-Baxter algebra in a nonlinear chiral model, Kexue-
Tongbao 32, 1853-6 (Chinese)
Lu, J. H. & Weinstein, A. A989) Groupoides symplectiques doubles des groupes de Lie-
Poisson, C. R. Acad. Sd. Ser. I 309, 951-4
Lu, J. H. & Weinstein, A. A990) Poisson-Lie groups, dressing transformations and Bruhat
decompositions, J. Diff. Geom. 31, 501-26
Lu, J. H. & Weinstein, A. A991) Comm. Math. Phys. 135, 229-31; appendix to Sheu
A991)
Lu, Z. C. A992a) Star products and phase space realizations of quantum groups, Lett.
Math. Phys. 25, 51-60
Lu, Z. C. A992b) Quantum algebras on phase space, J. Math. Phys. 33, 446-53
Lukierski, J. & Nowicki, A. A992a) Real forms of Uq(OSp(l\2)) and quantum D = 2
supersymmetry algebras, J. Phys. A 25, L161-70
Lukierski, J. &: Nowicki, A. A992b) Quantum deformations of D = 4 Poincare algebra, in
Quantum Groups and Related Topics, R. Gierlak et al. (eds), pp. 33—44, Kluwer, Dordrecht
610 References
Lukierski, J. Sz Nowicki, A. A992c) Quantum deformations of D = 4 Poincare and Weyl
algebra from g-deformed D = 4 conformal algebra, Phys. Lett B 279, 299-307
Lukierski, J., Nowicki, A. &: Ruegg, H. A991) Real forms of complex quantum anti-de
Sitter algebra Uq(SpD,<C)) and their contraction schemes, Phys. Lett B 271, 321-8
Lukierski, J., Nowicki, A. Sz Ruegg, H. A992a) Quantum deformations of Poincare alge-
algebra and the supersymmetric extensions, in Topological and Geometrical Methods in Field
Theory, J. Mickelsson & O. Pekonen (eds), pp. 202-26, World Scientific, Singapore
Lukierski, J., Nowicki, A. &: Ruegg, H. A992b) New quantum Poincare algebra and k-
deformed field theory, Phys. Lett. B 293, 344-52
Lukierski, J., Ruegg, H., Nowicki, A. Sz Tolstoy, V. N. A991) ^-deformation of the Poincare
algebra, Phys. Lett. B 264, 331-8
Lukyanov, S. & Shatashvili, S. L. A993) Free field representation of the classical limit of
the quantum affine algebra, Phys. Lett. B 298, 111-5
Lusztig, G. A980) Some problems in the representation theory of finite Chevalley groups,
in Finite Groups, Santa Cruz, 1979, J. S. Birman & S. Libgober (eds), Proceedings of
Symposia in Pure Mathematics 37, pp. 313—7, American Mathematical Society, Providence,
RI
Lusztig, G. A988) Quantum deformations of certain simple modules over enveloping alge-
algebras, Adv. Math. 70, 237-49
Lusztig, G. A989) Modular representations and quantum groups, in Classical Groups and
Related Topics, Beijing, 1987, A. J. Hahn, D. G. James Sz Zhe Xian Wan (eds), Contem-
Contemporary Mathematics 82, pp. 59—77, American Mathematical Society, Providence, RI
Lusztig, G. A990a) Finite-dimensional Hopf algebras arising from quantized universal en-
enveloping algebras, J. Amer. Math. Soc. 3, 257-96
Lusztig, G. A990b) Quantum groups at roots of 1, Geom. Dedicata 35, 89-113
Lusztig, G. A990c) On quantum groups, J. Algebra 131, 466-75
Lusztig, G. A990d) Canonical bases arising from quantized enveloping algebras, J. Amer.
Math. Soc. 3, 447-98
Lusztig, G. A990e) Canonical bases arising from quantized enveloping algebras II, Progr.
Theor. Phys. Suppl. 102, 175-201
Lusztig, G. A991) Quivers, perverse sheaves and quantized enveloping algebras, J. Amer.
Math. Soc. 4, 365-421
Lusztig, G. A992a) Introduction to quantized enveloping algebras, in New Developments in
Lie Theory and their Applications, J. Tirao Sz N. Wallach (eds), Progress in Mathematics
105, pp. 49-66, Birkhauser, Boston
Lusztig, G. A992b) Problems on canonical bases, preprint, MIT
Lusztig, G. A992c) Affine quivers and canonical bases, Publ. Math. IHES 76, 111-63
Lusztig, G. A993) Introduction to Quantum Groups, Progress in Mathematics 110, Birk-
Birkhauser, Boston
Lusztig, G. A994) Monodromic systems on flag manifolds, preprint, MIT
Lyakhovsky, V. D. Sz Mudrov, A. A992) Generalized quantization scheme for Lie algebras,
J. Phys. A 25, LI 139-54
Lyubashenko, V. V. A986) Hopf algebras and vector symmetries, Russian Math. Surveys
41 E), 153-4
Lyubashenko, V. V. A992) Real and imaginary forms of quantum groups, in Quantum
Groups, Proceedings of Workshops held in the Euler International Mathematical Institute
1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 67-78, Springer, Berlin
Lyubashenko, V. V. Sz Majid, S. A992) Fourier transform identities in quantum mechanics
and the quantum line, Phys. Lett. B 284, 66-70
Ma, Z. Q. A990a) Representations of the braid group obtained from quantum 5/C) en-
enveloping algebra, J. Math. Phys. 31, 550—6
References 611
Ma, Z. Q. A990b) New link polynomials obtained from octet representation of quantum
5/C) enveloping algebra, J. Math. Phys. 31, 3079-84
Ma, Z. Q. A990c) Rational solution for the minimal representation of Gi, J- Phys. A 23,
4415-6
Ma, Z. Q. A990d) The spectrum-dependent solutions to the Yang-Baxter equation for
quantum E6 and E7, J. Phys. A 23, 5513-22
Ma, Z. Q. A991) The embedding eo and the spectrum dependent R-matrix for q-F$, J.
Phys. A 24, 433-49
McConnell, J. C. A990) Quantum groups, filtered rings and Gel'fand-Kirillov dimension,
in Non-commutative Ring Theory, Athens, Ohio, 1989, S. K. Jain Sz S. R. Lopez-Permouth
(eds), Lecture Notes in Mathematics 1448, pp. 139-47, Springer, Berlin
McConnell, J. C. & Robson, J. C. A987) Noncommutative Noetherian Rings, Wiley, Chich-
ester, UK
MacFarlane, A. A989) On ^-analogues of the quantum harmonic oscillator and the quantum
group SUB)q, J. Phys. A 22, 4581-8
MacFarlane, A. A992) Spectrum generating quantum group of the harmonic oscillator,
Intemat. J. Modern Phys. A 7, 4377-93
MacFarlane, A. & Majid, S. A991) Quantum group structure in a fermionic extension of
the quantum harmonic oscillator, Phys. Lett. B 268, 71-4
MacFarlane, A. &: Majid, S. A992a) The superalgebra osp(l/2) and a related quantum
group structure for harmonic oscillator systems, in Topological and Geometrical Meth-
Methods in Field Theory, J. Mickelsson & O. Pekonen (eds), pp. 227-36, World Scientific,
Singapore
MacFarlane, A. & Majid, S. A992b) Spectrum generating quantum group of the harmonic
oscillator, Intemat. J. Modern Phys. A 7, 4377-94
Mack, G. &: Schomerus, V. A990) Conformal field algebras with quantum symmetry from
the theory of superselection sectors, Comm. Math. Phys. 134, 139-96
Mack, G. & Schomerus, V. A991) Quasi quantum group symmetry and local braid relations
in the conformal Ising model, Phys. Lett. B 267, 207-13
Mack, G. & Schomerus, V. A992a) Quasi Hopf quantum symmetry in quantum theory,
Nucl. Phys. B 370, 185-230
Mack, G. & Schomerus, V. A992b) Action of truncated quantum group algebras on quasi-
quantum planes and a quasi-associative differential calculus, Comm. Math. Phys. 149,
513-48
MacKay, N. H. A991a) Rational R-matrices in irreducible representations, J. Phys. A 24,
4017-26
MacKay, N. H. A991b) New factorized 5-matrices associated with SO(N), Nucl Phys. B
356, 729-49
MacKay, N. H. A992a) On the classical origins of Yangian symmetry in integrable field
theory, Phys. Lett. B 281, 90-7
MacKay, N. H. A992b) The full set of Cn-mvariant factorized S-matrices, J. Phys. A 25,
LI343-9
MacKay, N. H. A992c) The fusion of R-matrices using the Birman-Wenzl-Murakami alge-
algebra, J. Math. Phys. 33, 1529-37
MacLane, S. A971) Categories for the Working Mathematician, Graduate Texts in Math-
Mathematics 5, Springer, Berlin
Madivanane, S. & Venkata-Satyanarayana, M. A984) A note on the relation between q-
algebras without interaction and Weyl commutation relations, Lett. Nuovo Cim. 40, 19-22
Maekawa, T. A991) On the Wigner and Racah coefficients of suqB) and suq(l, 1), J. Math.
Phys. 32, 2598-604
Maillard, J. M. A986) Automorphisms of algebraic varieties and Yang-Baxter equations,
J. Math. Phys. 27, 2776-81; erratum, ibid. 28 A987), 1209
612 References
Maillet, J. M. A985) Kac-Moody algebra and extended Yang-Baxter relations in the O(N)
nonlinear cr-model, Phys. Lett. B 162, 137-42
Maillet, J. M. A986) New integrable canonical structures in two-dimensional models, Nucl.
Phys. B 269, 54-76
Maillet, J. M. A990) Lax equations and quantum groups, Phys. Lett. B 245, 480-6
Maillet, J. M. & Nijhoff, F. A989) Gauging the quantum groups, Phys. Lett. B 229, 71-8
Majid, S. A988) Hopf algebras for physics at the Planck scale, J. Classical and Quantum
Gravity 5, 1587-606
Majid, S. A989) Matched pairs of Lie groups and Hopf algebra bicrossproducts, Nucl. Phys.
B Suppl. 6, 422-4
Majid, S. A990a) Quasi-quantum groups as internal symmetries of topological quantum
field theories, Lett. Math. Phys. 21, 330-2
Majid, S. A990b) Matched pairs of Lie groups associated to solutions of the Yang-Baxter
equation, Pacific J. Math. 141, 311-32
Majid, S. A990c) Representation-theoretic rank and double Hopf algebras, Comm. Algebra
18, 3705-12
Majid, S. A990d) On g-regularization, Internat. J. Modern Phys. A 5, 4689-96
Majid, S. A990e) Physics for algebraists: non-commutative and non-cocommutative Hopf
algebras by a bicrossproduct construction, J. Algebra 130, 17-64
Majid, S. A990f) More examples of bicrossproduct and double crossproduct Hopf algebras,
Israel J. Math. 72, 133-48
Majid, S. A990g) Quasitriangular Hopf algebras and Yang-Baxter equations, Internat. J.
Modem Phys. A 5, 1-91
Majid, S. A990h) Fourier transforms on A(G) and knot invariants, J. Math. Phys. 31,
924-7
Majid, S. A990i) Quantum group duality in vertex models and other results in the theory
of quasitriangular Hopf algebras, in Differential Geometric Methods in Theoretical Physics,
Davis, 1988, L. L. Chau & W. Nahm (eds), NATO Advanced Science Institutes Series B:
Physics 245, pp. 373-85, Plenum, New York
Majid, S. A991a) Some Physical applications of category theory, in Differential Geometric
Methods in Theoretical Physics, Rapallo, 1990, C. Bartocci, U. Bruzzo & R. Cianci (eds),
Lecture Notes in Physics 375, pp. 131—42, Springer, Berlin
Majid, S. A991b) Braided groups and algebraic quantum field theories, Lett. Math. Phys.
22, 167-76
Majid, S. A991c) Hopf-von Neumann algebra bicrossproducts, Kac algebra bicrossproducts
and the classical Yang-Baxter equations, J. Func. Anal. 95, 291-319
Majid, S. A991d) Reconstruction theorems and rational conformal field theories, Internat.
J. Modern Phys. A 6, 4359-74
Majid, S. A991e) Representations, duals and quantum doubles of monoidal categories,
Suppl. Rend. Circ. Mat. Palermo Ser. II 26, 197-206
Majid, S. A991f) Examples of braided groups and braided matrices, J. Math. Phys. 32,
3246-53
Majid, S. A991g) Quantum groups and quantum probability, in Quantum Probability and
Related Topics, L. Accardi (ed.), pp. 333-58, World Scientific, Singapore
Majid, S. A991h) Quasi-quantum groups and internal symmetries of topological quantum
field theories, Lett. Math. Phys. 22, 83-90
Majid, S. A991i) Doubles of quasitriangular Hopf algebras, Comm. Algebra 19, 3061-73
Majid, S. A992a) Tannaka-Krein theorem for quasi-Hopf algebras and other results, in
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M.
Gerstenhaber & J. Stasheff (eds), Contemporary Mathematics 134, pp. 219-32, American
Mathematical Society, Providence, RI
References 613
Majid, S. A992b) Braided groups and duals of monoidal categories, Canadian Math. Soc.
Conf. Proc. 13, 329-43
Majid, S. A992c) Rank of quantum groups and braided groups in dual form, in Quantum
Groups, Proceedings of Workshops held in the Euler International Mathematical Institute
1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 79-89, Springer, Berlin
Majid, S. A992d) An open problem in quantum groups, in Quantum Groups, Proceedings
of Workshops held in the Euler International Mathematical Institute 1990, P. P. Kulish
(ed.), Lecture Notes in Mathematics 1510, pp. 391-2, Springer, Berlin
Majid, S. A992e) C-statistical quantum groups and Weyl algebras, J. Math. Phys. 33,
3431-44
Majid, S. A993a) Braided momentum in the g-Poincare group, J. Math. Phys. 34, 2045-58
Majid, S. A993b) Anyonic quantum groups, in Proceedings of the 2nd Max Born Syposium,
Wroclaw, Poland, 1992, A. Borowiec et al. (eds), Kluwer, Dordrecht
Majid, S. A993c) Beyond supersymmetry and quantum symmetry (An introduction to
braided groups and braided matrices), in Proceedings of the 5th Nankai Workshop, Tianjin,
China, June, 1992, M. L. Ge (ed.), World Scientific, Singapore
Majid, S. & Soibelman, Ya. S. A991a) Chern-Simons theory, modular functions and quan-
quantum mechanics in an alcove, Internat. J. Modern Phys. A 6, 1815-27
Majid, S. & Soibelman, Ya. S. A991b) Rank of quantized universal enveloping algebras
and modular functions, Comm. Math. Phys. 137, 249-62
Malikov, F. A992) Quantum groups: singular vectors and BGG resolution, in Infinite Anal-
Analysis, A. Tsuchiya, T. Eguchi & M. Jimbo (eds), Advanced Series in Mathematical Physics
16, pp. 623-44, World Scientific, Singapore
Maltsiniotis, G. A990) Groupes quantiques et structures differentielles, C. R. Acad. Sci.
Paris Ser 1311, 831-44
Maltsiniotis, G. A992) Groupoides quantiques, C. R. Acad. Sci. Paris Ser I 314, 249-52
Maltsiniotis, G. A993) Le langage des espaces et des groupes quantiques, Comm. Math.
Phys. 151, 275-302
Manin, Yu. I. A987) Some remarks on Koszul algebras and quantum groups, Ann. Inst.
Fourier (Grenoble) 37, 191-205
Manin, Yu. I. A988) Quantum Groups and Non-commutative Geometry, Centre de
Recherches Mathematiques, Montreal
Manin, Yu. I. A989) Multiparameter quantum deformation of the general linear super-
supergroup, Comm. Math. Phys. 123, 163-75
Manin, Yu. I. A990) Quantized theta functions, Progr. Theor. Phys. Suppl. 102, 219-28
Manin, Yu. I. A991a) Quantum groups, Nederl. Akad. Wetensch. Versla Afd. Natuurk.
100, 55-68
Manin, Yu. I. A991b) Topics in Non-commutative Geometry, Princeton University Press,
Princeton
Manin, Yu. I. A991c) Quantum groups and non-commutative de Rham complexes, preprint
MPI/91-47, Bonn
Manin, Yu. I. A991d) Notes on quantum groups and quantum de Rham complexes, pre-
preprint, MPI/91-60, Bonn
Manin, Yu. I. &; Schechtman, V. V. A986) Higher Bruhat orderings connected with the
symmetric group, Funkts. Anal, i Prilozhen 20, 74-5 (Russian)
Manko, V. I., Marmo, G., Solimeno, S. &; Zaccaria, F. A993) Correlation functions of
quantum ^-oscillators, Phys. Lett. A 176, 173-5
Manocha, H. L. A990) On models of irreducible q- represent at ions of s/B,C), Appl. Anal.
37, 19-47
Marchiafava, S. & Rembielinski, J. A992) Quantum quaternions, J. Math. Phys. 33, 171-3
Marcinek, W. A992) Graded algebras and geometry based on Yang-Baxter operators, J.
Math. Phys. 33, 1631-5
614 References
Markov, A. A941) Uber die freie Aquivalenz geschlossener Zopfe, Recueil Math. Moscow
1, 73-8
Martin, P. P. A992) On Schur-Weyl duality, An Hecke algebras and quantum sl(N) on
(g)n+1CiV, in Infinite Analysis, A. Tsuchiya, T. Eguchi &: M. Jimbo (eds), Advanced Series
in Mathematical Physics 16, pp. 645-74, World Scientific, Singapore
Martin-Delgado, M. A. A991) A physical interpretation of the quantum group Uq(SUB)),
J. Phys. A 24, L807-13
Masuda, T., Mimachi, K., Nakagami, Y., Noumi, M. & Ueno, K. A988) Representations of
quantum groups and a (/-analogue of orthogonal polynomials, C. R. Acad. Sci. Paris Ser.
I 307, 559-64
Masuda, T., Mimachi, K., Nakagami, Y., Noumi, M. & Ueno, K. A991) Representations of
the quantum group SUqB) and the little g-Jacobi polynomials, J. Func. Anal. 99, 357-86
Masuda, T., Mimachi, K., Nakagami, Y., Noumi, M., Saburi, Y. &. & Ueno, K. A990a)
Unitary representations of the quantum group 5^A,1): structure of the dual space of
Uq(slB)), Lett Math. Phys. 19, 187-94
Masuda, T., Mimachi, K., Nakagami, Y., Noumi, M., Saburi, Y. & Ueno, K. A990b) Unitary
representations of the quantum group SUq(l, 1): II - matrix elements of unitary represen-
representations and the basic hypergeometric functions, Lett Math. Phys. 19, 195-204
Masuda, T., Nakagami, Y. & Watanabe, J. A990) Non-commutative differential geometry
on the quantum SUB), I. An algebraic viewpoint, K-theory 4, 157—80
Masuda, T., Nakagami, Y. & Watanabe, J. A991) Non-commutative differential geometry
on the quantum 2-spheres of Podles, I. An algebraic viewpoint, K-theory 5, 151-75
Masuda, T. & Watanabe, J. A991) Sur les espaces vectoriels topologiques associes aux
groupes quantiques SUqB) et SUq(l,l), C. R. Acad. Sci. Paris Ser. 7 312, 827-30
Matheus-Valle, J. L. & Monteiro, M. A. R. A993a) Quantum group generalization of the
heterotic QFT, Phys. Lett B 300, 66-72
Matheus-Valle, J. L. Sz Monteiro, M. A. R. A993b) Quantum group generalization of the
classical supersymmetric point particle, Modern Phys. Lett. A 7, 3023—8
Mathieu, O. A992) Bases des representations des groupes simples complexes, Seminaire
Bourbaki exp. no. 743, Asterisque 201-203, 421-42, Societe Mathematique de Prance,
Paris
Mathur, S. D. A992) Quantum Kac-Moody symmetry in integrable field theories, Nucl.
Phys. B 369, 433-60
Matsuo, A. A993) Jackson integrals of Jordan-Pockhammer type and quantum Knizhnik-
Zamolodchikov equation, Comm. Math. Phys. 151, 263—74
Matsuzaki, T. & Suzuki, T. A992) A representation of Uq(su(l, 1)) on the space of quasi-
primary fields and correlation functions, Phys. Lett B 296, 33-9
Matthes, R. A991) An example of a differential calculus on the quantum complex n-space,
Seminar Sophus Lie 1, 23—30
Matthes, R. A992) 'Quantum group' structure and 'covariant' differential calculus on sym-
symmetric algebras corresponding to commutation factors on Zn, in Quantum Groups and
Related Topics, R. Gierlak et al. (eds), pp. 45—54, Kluwer, Dordrecht
Mayer, M. E. A988) Groupoids and Lie bigebras in gauge and string theories, in Differ-
Differential Geometrical Methods in Theoretical Physics, K. Bleuler & M. Werner (eds), NATO
Advanced Science Institutes Series C: Mathematical and Physical Sciences 250, pp. 149-64,
Kluwer, Dordrecht
Mayer, M. E. A991) From Poisson groupoids to quantum groupoids and back, in Differen-
Differential Geometric Methods in Theoretical Physics, Rapallo, 1990, C. Bartocci, U. Bruzzo &
R. Cianci (eds), Lecture Notes in Physics 375, pp. 143-54, Springer, Berlin
Meister, A. A992) The C*-algebra obtained by completing the quantum group Funq
(SUB)), J. Math. Phys. 33, 4177-89
References 615
Menezes, D. P., Avancini, S. S. & Providenca, C. A992) Quantum algebraic description of
the Moszkowski model, J. Phys. A 25, 6317-22
Merkulov, S. A. A991a) Quantum m x n matrices and the ^-deformed Binet-Cauchy for-
formula, J. Phys. A 24, L1243-7
Merkulov, S. A. A991b) Quantum deformation of compactified Minkowski space, Z. Phys.
C52, 583-8
Mezincescu, L. &: Nepomechie, R. I. A990) Unitarity and irrationality for the quantum
algebra Uq[SUB)}, Phys. Lett. B 246, 412-6
Mezincescu, L. & Nepomechie, R. I. A991a) Integrability of open spin chains with quantum
algebra symmetry, Intemat. J. Modern Phys. A 6, 5231-48; addendum, ibid. 7, 5657-9
Mezincescu, L. & Nepomechie, R. I. A991b) Integrable higher-spin chains with SUqB)
symmetry, in Quantum Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 206-35,
World Scientific, Singapore
Mezincescu, L. & Nepomechie, R. I. A991c) Quantum algebra structure of exactly soluble
quantum spin chains, Modern Phys. Lett. A 6, 2497-508
Mezincescu, L. & Nepomechie, R. I. A991d) Integrable open spin chains with non-sym-
non-symmetric R-matrices, J. Phys. A 24, L17-23
Michaelis, W. A980) Lie coalgebras, Adv. Math. 38, 1-54
Mikami, K. A991) Symplectic double groupoids over Poisson (ax + b) groups, Trans. Amer.
Math. Soc. 324, 447-63
Milnor, J. W. & Moore, J. C. A965) On the structure of Hopf algebras, Ann. of Math. 81,
211-64
Mir-Kasimov, R. M. A991a) SUq(l, 1) and the relativistic oscillator, J. Phys. A 24, 4283-
302
Mir-Kasimov, R. M. A991b) Relativistic oscillator = g-oscillator, in Group Theoretical
Methods in Physics, Moscow, 1990, V. V. Dodonov & V. I. Manko (eds), Lecture Notes in
Physics 382, pp. 215-20, Springer, Berlin
Misra, K. C. & Miwa, T. A990) Crystal base for the basic representation of Uq(sl(n)),
Comm. Math. Phys. 134, 79-88
Molev, A. I. A992) Representations of twisted Yangians, Lett. Math. Phys. 26, 211-8
Moore, G. & Reshetikhin, N. Yu. A989) A comment on quantum group symmetry in
conformal field theory, Nucl. Phys. B 328, 557-74
Moore, G. & Seiberg, N. A988) Classical and quantum conformal field theory, Comm.
Math. Phys. 123, 177-254
Montgomery, S. & Smith, S. P. A990) Skew derivations and Uq(slB)), Israel J. Math. 72,
158-66
Moreno, C. A990) Produits star sur certain G/K kahleriens. Equation de Yang-Baxter et
produits star sur G, in Geometrie Symplectique et Mecanique, Colloque International La
Grande Motte, France, 23-28 Mai, 1988, C. Albert (ed.), Lecture Notes in Mathematics
1416, pp. 210-34, Springer, Berlin
Morosi, C. A992) The R-matrix theory and the reduction of Poisson manifolds, J. Math.
Phys. 33, 941-52
Morton, H. R. & Strickland, P. A991) Jones polynomial invariants for knots and satellites,
Math. Proc. Camb. Phil Soc. 109, 83-103
Moyal, J. E. A949) Quantum mechanics as a statistical theory, Proc. Camb. Phil. Soc. 45,
99-124
Mukhin, E. E. A991) Yang-Baxter operators and the non-commutative de Rham complex,
Russian Math. Surveys 46 D), 192-3
Miiller, A. A992) Classifying spaces for quantum principal bundles, Comm. Math. Phys.
149, 495-512
Muller-Hoissen, F. A992) Differential calculi on the quantum group GLp,qB), J. Phys. A
25, 1703-4
616 References
Murakami, J. A987) The Kauffman polynomial of links and representation theory, Osaka
J. Math. 24, 745-58
Murakami, J. A989) Solvable lattice models and algebras of face operators, in Integrable
Systems in Quantum Field Theory and Statistical Mechanics, M. Jimbo, T. Miwa & A.
Tsuchiya (eds), Advanced Studies in Pure Mathematics 19, pp. 399—415, Academic Press,
Boston
Murakami, J. A990) The representations of the ^-analogue of Brauer's centralizer algebras
and the Kauffman polynomial of links, Publ. Res. Inst. Math. Sci. 26, 935-45
Murakami, J. A992a) The multi-variable Alexander polynomial and a one-parameter family
of representations of Uq(slB,C)) at q2 = —1, in Quantum Groups, Proceedings of Work-
Workshops held in the Euler International Mathematical Institute 1990, P. P. Kulish (ed.),
Lecture Notes in Mathematics 1510, pp. 350-3, Springer, Berlin
Murakami, J. A992b) The free-fermion model in presence of field related to the quantum
group Uq(sl2) of affine type and the multi-variable Alexander polynomial of links, in Infinite
Analysis, A. Tsuchiya, T. Eguchi & M. Jimbo (eds), Advanced Series in Mathematical
Physics 16, pp. 765—72, World Scientific, Singapore
Myrberg, P. J. A922) Uber Systeme analytischer Funktionen welche ein Additions-theorem
besitzen; Preisschrift gekront und herausgegeben von der Furstlich Jablonowskischen
Gesellschaft zu Leipzig
Nagy, G. A993) On the Haar measure of the quantum SU(N) group, Comm. Math. Phys.
153, 217-28
Nakabo, S. A993) An invariant of links in a handlebody associated with the spin j repre-
representation of Uq(siB, <C)), Proc. Amer. Math. Soc. 118, 645-56
Nakashima, T. A990) A basis of symmetric tensor representations for the quantum analogue
of the Lie algebras Bn, Cn and Dn, Publ. Res. Inst. Math. Sci. 26, 723-33
Nakashima, T. A993) Crystal base and a generalization of the Littlewood-Richardson rule
for classical Lie algebras, Comm. Math. Phys. 154, 215-43
Nakatsu, T. A991) Quantum group approach to affine Toda field theory, Nucl. Phys. B
356, 499-529
Nanhua, X. A993) Special bases of irreducible modules of the quantized universal envelop-
enveloping algebra Uv(gl(n)), J. Algebra 154, 377-86
Narganes-Quijano, F. J. A991a) The quantum deformation of SUA\1) and the dynamical
symmetry of the anharmonic oscillator, J. Phys. A 24, 1699-707
Narganes-Quijano, F. J. A991b) Cyclic representations of a ^-deformation of the Virasoro
algebra, J. Phys. A 24, 593-601
Nazarov, M. L. A991) Quantum berezinian and the classical Capelli identity, Lett. Math.
Phys. 21, 123-31
Nazarov, M. L. A992) Yangians of the 'strange' Lie superalgebras, in Quantum Groups,
Proceedings of Workshops held in the Euler International Mathematical Institute 1990, P.
P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 47-55, Springer, Berlin
Nazarov, M. L. A993a) Yangians of the queer Lie superalgebra, in Quantum Groups, Pro-
Proceedings of the 2nd Wigner Symposium, Goslar, 1991, Springer, Berlin
Nazarov, M. L. A993b) Young's symmetrizers for projective representations of the sym-
symmetric group, preprint, RIMS, Kyoto
Nazarov, M. L. A993c) Yangians and Gel'fand-Zetlin bases, preprint, RIMS, Kyoto
Ndimubandi, J. A993) A note on ^-deformations and supersymmetric quantum mechanics,
Modern Phys. Lett. A 8, 429-34
Nelson, J. E. &; Regge, T. A991) Quantum gravity and quantum groups, in Mechan-
Mechanics, Analysis and Geometry: 200 Years after Lagrange, M. Francaviglia (ed.), pp. 503-12,
North-Holland, Amsterdam
Nelson, J. E. & Regge, T. A992) SUB)q and 2-|-l quantum gravity, in Integrable Systems
and Quantum Groups, M. Carfora, M. Martinelli &: A. Marzuoli (eds), pp. 173-81, World
References 617
Scientific, Singapore
Neskovic, P. V. & Urosevic, B. V. A992) Quantum oscillators: applications in statistical
mechanics, Internat. J. Modern Phys. A 7, 3379—88
Ng, Y. J. A990) Comment on the ^-analogues of the harmonic oscillator, J. Phys. A 23,
1023-7
Nijhoff, F. W. &: Capel, H. W. A992) Integrable quantum mappings and non-ultralocal
Yang-Baxter structures, Phys. Lett. A 163, 49-56
Nomura, M. A988) Relations among n-j symbols in forms of the star-triangle relation, J.
Phys. Soc. Japan 57, 3653-6
Nomura, M. A989a) Relations for Clebsch-Gordan coefficients in suqB) and Yang-Baxter
equations, J. Math. Phys. 30, 2397-405
Nomura, M. A989b) Yang-Baxter relations in terms of n-j symbols of suq{2) algebra, J.
Phys. Soc. Japan 58, 2694-704
Nomura, M. A990a) An alternative description of the quantum group SUqB) and the
g-analog Racah-Wigner algebra, J. Phys. Soc. Japan 59, 439-48
Nomura, M. A990b) Recursion relations for the Clebsch-Gordon coefficient of quantum
group SUqB), J. Phys. Soc. Japan 59, 1954-61; addendum, ibid. 60, 726
Nomura, M. A990c) Various kinds of relations for 3n-j symbols of quantum group SUqB),
J. Phys. Soc. Japan 59, 3851-60
Nomura, M. A990d) Representation functions c^fc of U[slq{2)\ as wave functions of 'quan-
'quantum symmetric tops' and relationship to braiding matrices, J. Phys. Soc. Japan 59, 4260-71
Nomura, M. A990e) A Jordan-Schwinger representation of quadratic relations for SUqB)
operators and of the (/-analog Wigner-Eckart theorem, J. Phys. Soc. Japan 59, 2345-54;
erratum, ibid. 59, 3805
Nomura, M. A991a) Concepts of tensors in Uq(slB)) and a van der Waerden method for
quantum Clebsch-Gordan coefficients, J. Phys. Soc. Japan 60, 789-97
Nomura, M. A991b) Co- and contra-variant tensors of a general rank in quantum matrix
algebras suqB) expressed by creation and annihilation operators I, J. Phys. Soc. Japan
60, 3260-70; II, ibid. 60, 4060-70
Nomura, M. A992) Covariant exchange algebras and quantum groups I, J. Phys. Soc.
Japan 61, 1485-94
Nomura, M. &; Biedenharn, L. C. A992) On the g-symplecton realization of the quantum
group SUqB), J. Math. Phys. 33, 3636-48
Northcott, D. G. A968) Lessons on Rings, Modules and Multiplicities, Cambridge Univer-
University Press, Cambridge
Noumi, M. A991) Quantum groups and ^-orthogonal polynomials - towards a realization of
Askey-Wilson polynomials on SUq{2), in Special Functions, Okayama, 1990, M. Kashiwara
& T. Miwa (eds), pp. 260-88, Springer, Berlin
Noumi, M. & Mimachi, K. A990a) Big g-Jacobi polynomials, g-Hahn polynomials and a
family of quantum 3-spheres, Lett. Math. Phys. 19, 299-305
Noumi, M. & Mimachi, K. A990b) Askey-Wilson polynomials and the quantum group
SUq{2), Proc. Japan Acad. Ser. A Math. Sci. 66, 146-9
Noumi, M. & Mimachi, K. A990c) Quantum 2-spheres and big g-Jacobi polynomials,
Comm. Math. Phys. 128, 521-31
Noumi, M. & Mimachi, K. A991) Rogers' g-ultraspherical polynomials on a quantum 2-
sphere, Duke Math. J. 63, 65-80
Noumi, M. & Mimachi, K. A992a) Askey-Wilson polynomials as spherical functions on the
quantum group SUqB), in Quantum Groups, Proceedings of Workshops held in the Euler
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathemat-
Mathematics 1510, pp. 98-103, Springer, Berlin
Noumi, M. & Mimachi, K. A992b) Spherical functions on a family of quantum 3-spheres,
Compositio Math. 83, 19-42
618 References
Noumi, M., Yamada, H. &; Mimachi, K. A989) Zonal spherical functions on the quantum
homogeneous space SUq(n + l)/SUq(n), Proc. Japan Acad. Ser. A Math. Sci. 65, 169-71
Nowicki, A., Sorace, E. &: Tarlini, M. A993) The quantum deformed Dirac equation from
the K>Poincare algebra, Phys. Lett. B 302, 419-22
Ocneanu, A. A988) Quantized groups, string algebras and Galois theory for algebras, in
Operator Theory and Applications, Vol. 2, D. E. Evans & M. Takesaki (eds), London
Mathematical Society Lecture Note Series 136, pp. 119-72, Cambridge University Press,
Cambridge
Odaka, K. A992) Fermionic ^-oscillators and associated canonical ^-transformations, J.
Phys. A 25, L39-44
Odesskii, A. V. A986) An analogue of the Sklyanin algebra, Fund. Anal. Appl. 20, 152—4
Odesskii, A. V. & Feigin, B. L. A989) Sklyanin's elliptic algebras, Fund. Anal. Appl. 23,
207-14
Oevel, W. A988) R-matrices and related involution theorems, in Finite-dimensional Inte-
grable Nonlinear Dynamical Systems, Johannesburg, 1988, P. G. L. Leach & W. H. Steeb
(eds), pp. 60-73, World Scientific, Teaneck, NJ
Oevel, W. A989) R-matrices and higher Poisson brackets for integrable systems, in Nonlin-
Nonlinear Physics, Shanghai, 1989, Chao Hao Gu, Yi Shen Li & Gui Zhang Tu (eds), pp. 136-45,
Springer, Berlin
Oevel, W. & Ragnisco, O. A989) R-matrices and higher Poisson brackets for integrable
systems, J. Phys. A 161, 181-220
Ogievetsky, E. A992) Differential operators on quantum spaces for GLq(n) and SOq(n),
Lett. Math. Phys. 24, 245-55
Ogievetsky, E., Reshetikhin, N. Yu. & Wiegmann, P. A987) The principal chiral field in
two dimensions and classical Lie algebras, Nucl. Phys. B 280, 45-96
Ogievetsky, E., Schmidke, W. B. & Wess, J. A991) Six generator g-deformed Lorentz
algebra, Lett Math. Phys. 23, 233-40
Ogievetsky, E., Schmidke, W. B., Wess, J. & Zumino, B. A992) g-deformed Poincare alge-
algebra, Comm. Math. Phys. 150, 495-518
Ogievetsky, E. & Wess, J. A991) Relations between GLp^s, Z. Phys. C 50, 123-31
Ogievetsky, E. Sz Wiegmann, P. A986) Factorized S-matrix and the Bethe ansatz for simple
Lie groups, Phys. Lett. B 168, 360-6
Ogievetsky, E. & Zumino, B. A992) Reality in the differential claculus on q-Euclidean
spaces, Lett. Math. Phys. 25, 121-30
Oh, C. H. &; Singh, K. A992) Conformal properties of primary fields in a (/-deformed theory,
J. Phys. A 25, L149-56
Ohn, C. A992) A *-product on SL{2) and the corresponding nonstandard quantum
U{sl{2)), Lett. Math. Phys. 25, 85-8
Okado, M. A990) Quantum R-matrices related to the spin representations of Bn and Dn,
Comm. Math. Phys. 134, 467-86
Okado, M. & Yamane, H. A991) R-matrices with gauge parameters and multi-parameter
quantized enveloping algebras, Special Functions, Okayama, 1990, M. Kashiwara &; T.
Miwa (eds), pp. 289-93, Springer, Tokyo
Olive, D. & Turok, N. A985) Local conserved densities and zero-curvature conditions for
Toda lattice field theories, Nucl. Phys. B 257, 277-301
Olshanskii, G. I. A988) Extension of the algebra U(Q) for the infinite-dimensional classical
Lie algebras g and the Yangians Y(gl(m)), Soviet Math. Dokl. 36, 569-73
Olshanskii, G. I. A989) Yangians and universal enveloping algebras, J. Soviet Math. 47,
2466-73
Olshanskii, G. I. A991) Representations of infinite-dimensional classical groups, limits of
enveloping algebras and Yangians, in Topics in Representation Theory, A. A. Kirillov (ed.),
References 619
Advances in Soviet Mathematics 2, pp. 1—66, American Mathematical Society, Providence,
RI
Olshanskii, G. I. A992a) Quantized enveloping superalgebra of type Q and a super exten-
extension of the Hecke algebra, Lett. Math. Phys. 24, 93-102
Olshanskii, G. I. A992b) Twisted Yangians and infinite-dimensional classical Lie algebras,
in Quantum Groups, Proceedings of Workshops held in the Euler International Mathemat-
Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 104-19,
Springer, Berlin
Omori, H., Maeda, Y. & Yoshioka, A. A992a) Existence of a closed star product, Lett.
Math. Phys. 26, 284-94
Omori, H., Maeda, Y. & Yoshioka, A. A992b) Deformation quantization of Poisson alge-
algebras, Proc. Japan Acad. Ser. A Math. Sci. 68, 97-100
Ottinger, H. C. &; Honerkamp, J. A982) Note on the Yang-Baxter equations for generalized
Baxter models, Phys. Lett. A 88, 339-43
Ozawa, T. A990) Quantization of a Poisson algebra and polynomials associated to links,
Nagoya Math. J. 120, 113-27
Palev, T. D. & Tolstoy, V. N. A991) Finite-dimensional irreducible representations of the
quantum superalgebra Uq(gl(n/1)), Comm. Math. Phys. 141, 549-58
Pan, F. A991) Irreducible tensor operators for the quantum algebra suB)q, J. Phys. A 24,
L803-6
Pan, F. A993) Quantum deformation of SUC) and subalgebras, J. Phys. A 26, L257-62
Pan, F. & Chen, J. Q. A992) Symmetric irreducible representations in the SUB)q x C/(l)
basis and some extensions to SU(N)q x C/(l), J. Phys. A 25, 4017-24
Paradowski, J. A992) Filtrations of modules over quantum algebras, preprint
Parashar, P., Bhasin, V. S. & Soni, S. K. A993) Covariant differential calculi on quantum
symplectic and orthogonal planes, Modern Phys. Lett. A 8, 389-98
Parashar, P. &; Soni, S. K. A992) Covariant differential calculus on the quantum exterior
vector space, Z. Phys. C 53, 609-11
Pareigis, B. A981) A noncommutative, noncocommutative Hopf algebra in 'nature', J.
Algebra 70, 356-74
Parshall, B. & Wang, J. P. A990) On bialgebra cohomology, Bull. Soc. Math. Belg. Ser.
A 42, 607-42
Parshall, B. & Wang, J. P. A991) Quantum Linear Groups, Memoirs of the American
Mathematical Society 439, American Mathematical Society, Providence, RI
Parshall, B. k, Wang, J. P. A992) Cohomology of infinitesimal quantum groups I, Tohoku
Math. J. 44, 395-423
Parthasarathy, R. &; Viswanathan, K. S. A991) A g-analogue of the supersymmetric oscil-
oscillator and its g-superalgebra, J. Phys. A 24, 613-7
Pasquier, V. A988a) Etiology of IRF models, Comm. Math. Phys. 118, 355-64
Pasquier, V. A988b) Continuum limit of lattice models built on quantum groups, Nucl.
Phys. B 295, 491-510
Pasquier, V. A992) Quantum groups in lattice models, in New Symmetry Principles in
Quantum Field Theory, J. Frohlich et al. (eds), NATO Advanced Science Institutes Series
B: Physics 295, pp. 355-81, Plenum, New York
Pasquier, V. &; Saleur, H. A990) Common structures between finite systems and conformal
field theories through quantum groups, Nucl. Phys. B 330, 523-56
Perk, J. H. H. A989) Star-triangle equations, quantum Lax pairs, and higher genus curves,
in Theta Functions, Bowdoin, ME, 1987, L. Ehrenpreis &; R. C. Gunning (eds), Proceedings
of Symposia in Pure Mathematics 49, Part I, pp. 341-54, American Mathematical Society,
Providence, RI
Pierce, R. S. A982) Associative Algebras, Graduate Texts in Mathematics 88, Springer,
Berlin
620 References
Podles, P. A987) Quantum spheres, Lett. Math. Phys. 14, 193-202
Podles, P. A989) Differential calculus on quantum spheres, Lett. Math. Phys. 18, 107-19
Podles, P. A991) Complex quantum groups and their real representations, preprint RIMS-
754, Kyoto
Podles, P. A992a) Quantization reinforces interaction. Quantum mechanics of two particles
on a quantum sphere, in Infinite Analysis, A. Tsuchiya, T. Eguchi & M. Jimbo (eds),
Advanced Series in Mathematical Physics 16, pp. 805-12, World Scientific, Singapore
Podles, P. A992b) The classification of differential structures on quantum 2-spheres, Comm.
Math. Phys. 150, 167-80
Podles, P. A992c) Complex quantum groups and their real representations, Publ. Res. Inst.
Math. Sci. 28, 709-46
Podles, P. &; Woronowicz, S. L. A990) Quantum deformation of Lorentz group, Comm.
Math. Phys. 130, 381-431
Polychronakos, A. P. A990) A classical realization of quantum algebras, Modern Phys.
Lett. A 5, 2325-33
Polychronakos, A. P. A991a) Aspects of g-Virasoro algebra, in Quantum Groups, T. Cur-
tright, D. Fairlie & C. Zachos (eds), pp. 194-205, World Scientific, Singapore
Polychronakos, A. P. A991b) Consistence conditions and representations of a g-deformed
Virasoro algebra, Phys. Lett. B 256, 35-40
Pressley, A. N. A992) Quantum groups, Hamburger Beit rage zur Mathematik, Heft 16
Przytycki, J. A992) Quantum group of links in a handlebody, in Deformation Theory
and Quantum Groups with Applications to Mathematical Physics, M. Gerstenhaber &,
J. Stasheff (eds), Contemporary Mathematics 134, pp. 235-45, American Mathematical
Society, Providence, RI
Przytycki, J. & Traczyk, P. A987) Conway algebras and skein equivalence of links, Proc.
Amer. Math. Soc. 100, 744-8
Pusz, W. A989) Twisted canonical anticommutation relations, Rep. Math. Phys. 27, 349-
60
Pusz, W. A991) On the implementation of S^UB) action in the irreducible representations
of twisted canonical commutation relations, Lett. Math. Phys. 21, 59-67
Pusz, W. A993) Irreducible unitary representations of quantum Lorentz group, Comm.
Math. Phys. 152, 591-626
Pusz, W. & Woronowicz, S. L. A989) Twisted second quantization, Rep. Math. Phys. 27,
231-57
Qian, Z. H., Qian, M. &, Guo, M. A992) A new type of Hopf algebra which is neither
commutative nor cocommutative, J. Phys. A 25, 1237—46
Quan, X. C. A991) Compact quantum groups and group duality, Ada Appl. Math. 25,
277-99
Quano, Y. H. & Pujii, A. A991) Generalized Sklyanin algebra, Modem Phys. Lett. A 6,
3635-40
Quesne, C. A991) Coherent states, K-matrix theory and g-boson realizations of the quan-
quantum algebra suq{2), Phys. Lett. A 153, 303-7
Quesne, C. A992) Complementarity of suqC) and uqB) and g-boson realization of the
suqC) irreducible representations, J. Phys. A 25, 5977-98
Quesne, C. A993a) Raising and lowering operators for uq(n), J. Phys. A 26, 357-72
Quesne, C. A993b) Sets of covariant and contravariant spinors for SUq{2) and alternative
quantizations, J. Phys. A 26, L299-306
Quesne, C. A993c) Two-parameter versus one-parameter quantum deformation of su{2),
Phys. Lett. A 174, 19-24
Quesne, C. A993d) g-bosonic vector operators for soqC) and a g-deformed uC) algebra,
Phys. Lett. B 304, 81-8
References 621
Quesne, C. A993e) g-bosonic operators as double irreducible tensors for uq(n) -\-uq(m),
Phys. Lett. B 298, 344-50
Quillen, D. A969) Rational homotopy theory, Ann. of Math. 90 B), 205-95
Quispel, G. R. W. &; Nijhoff, F. W. A992) Integrable two-dimensional quantum mappings,
Phys. Lett. A 161, 419-22
Radford, D. E. A976) The order of the antipode of a finite dimensional Hopf algebra is
finite, Amer. J. Math. 98, 333-5
Radford, D. E. A992) On the antipode of a quasitriangular Hopf algebra, J. Algebra 151,
1-11
Radford, D. E. A993) Minimal quasitriangular Hopf algebras, J. Algebra 157, 285-315
Rajagopal, A. K. &; Gupta, V. A992) Uncertainty principle, squeezing and quantum groups,
Modern Phys. Lett. A 7, 3759-64
Rajeswari, V. &; Srinivasa Rao, K. A991a) Generalized basic hypergeometric functions and
the g-analogues of 3 - j and 6 - j coefficients, J. Phys. A 24, 3761-80
Rajeswari, V. & Srinivasa Rao, K. A991b) Note on the explicit forms of the Clebsch-Gordan
coefficients of the quantum group SUq{2), J. Phys. Soc. Japan 60, 3583-4
Ralchenko, Yu. V. A992) g-deformed paracommutation relations, J. Phys. A 25, L1155-8
Ram, A. A991) A Frobenius formula for the characters of the Hecke algebras, Invent. Math.
106, 461-88
Ramirez, C, Ruegg, H. & Ruiz-Altaba, M. A990) Explicit quantum symmetries of WZNW
theories, Phys. Lett. B 247, 499-508
Ramirez, C, Ruegg, H. k, Ruiz-Altaba, M. A991a) The contour picture of quantum groups:
conformal field theories, Nucl. Phys. B 364, 195-233
Ramirez, C, Ruegg, H. &, Ruiz-Altaba, M. A991b) Coulomb gas realization of simple
quantum groups, in Group Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov
& V. I. Manko (eds), Lecture Notes in Physics 382, pp. 199-203, Springer, Berlin
Recknagel, A. A993) Fusion rules from algebraic K-theory, Internat. J. Modern Phys. A
8, 1345-57
Reidemeister, K. A932) Knottentheorie, Springer, Berlin
Rembielinskii, J. A992a) Differential and integral calculus on the quantum C-plane, in
Quantum Groups and Related Topics, R. Gierlak et al. (eds), pp. 129-40, Kluwer, Dordrecht
Rembielinskii, J. A992b) Quantum inhomogeneous groups related to Manin's plane, Phys.
Lett B 296, 335-40
Rembielinskii, J. & Tybor, W. A992) Polar decomposition of the twisted de Rham complex
for Cq, J. Phys. A 25, L1209-11
Reshetikhin, N. Yu. A983) The functional equation method in the theory of exactly solvable
quantum systems, Soviet Phys. JETP 57, 691-6
Reshetikhin, N. Yu. A985a) Integrable models of quantum 1-dimensional magnetics with
O(n) and 5pB/c)-symmetry, Theoret. Math. Phys. 63, 555-69
Reshetikhin, N. Yu. A985b) OGV)-invariant quantum field theoretical models: exact solu-
solution, Nucl. Phys. B 251, 565-80
Reshetikhin, N. Yu. A987) The spectrum of the transfer matrices connected with Kac-
Moody algebras, Lett. Math. Phys. 14, 235-46
Reshetikhin, N. Yu. A990a) Multiparameter quantum groups and twisted quasitriangular
Hopf algebras, Lett. Math. Phys. 20, 331-5
Reshetikhin, N. Yu. A990b) Quasitriangular Hopf algebras and invariants of tangles,
Leningrad Math. J. 1, 491-513
Reshetikhin, N. Yu. A992a) Quantization of Lie bialgebras, Duke Math. J. Internat. Math.
Res. Notices 7, 143-51
Reshetikhin, N. Yu. A992b) The Knizhnik-Zamolodchikov system as a deformation of the
isomonodromy problem, Lett. Math. Phys 26, 153-65
622 References
Reshetikhin, N. Yu. A992c) Jackson-type integrals, Bethe vectors, and solutions to a dif-
difference analog of the Knizhnik-Zamolodchikov system, Lett. Math. Phys. 26, 167-77
Reshetikhin, N. Yu. & Faddeev, L. D. A983) Hamiltonian structures for integrable field
theory models, Teoret. Mat. Fiz. 56, 323-43 (Russian)
Reshetikhin, N. Yu. & Semenov-Tian-Shansky, M. A. A988) Quantum R-matrices and
factorization problems, J. Geom. Phys. 5, 533-50
Reshetikhin, N. Yu. &; Semenov-Tian-Shansky, M. A. A990) Central extensions of quantum
current groups, Lett. Math. Phys. 19, 133-42
Reshetikhin, N. Yu. & Smirnov, F. A990) Hidden quantum group symmetry and integrable
perturbations of conformal field theories, Comm. Math. Phys. 131, 157-77
Reshetikhin, N. Yu., Takhtajan, L. A. & Faddeev, L. D. A990) Quantization of Lie groups
and Lie algebras, Leningrad Math. J. 1, 193-225
Reshetikhin, N. Yu. & Turaev, V. G. A990) Ribbon graphs and their invariants derived
from quantum groups, Comm. Math. Phys. 127, 1-26
Reshetikhin, N. Yu. &, Turaev, V. G. A991) Invariants of 3-manifolds via link polynomials
and quantum groups, Invent. Math. 103, 547—97
Reshetikhin, N. Yu. & Wiegmann, P. B. A987) Towards the classification of completely
integrable quantum field theories (the Bethe ansatz associated with Dynkin diagrams and
their automorphisms), Phys. Lett. B 189, 125-31
Reyman, A. G. & Semenov-Tian-Shansky, M. A. A979) Reduction of hamiltonian systems,
affine Lie algebras, and Lax equations I, Invent. Math. 54, 81-100
Reyman, A. G. & Semenov-Tian-Shansky, M. A. A981) Reduction of hamiltonian systems,
affine Lie algebras, and Lax equations II, Invent. Math. 63, 423-32
Reyman, A. G. k, Semenov-Tian-Shansky, M. A. A988) Compatible Poisson structures for
Lax equations: an r-matrix approach, Phys. Lett. A 130, 456—60
Rideau, G. A992) On the representations of the quantum oscillator algebra, Lett. Math.
Phys. 24, 147-54
Rieffel, M. A. A989) Deformation quantization of Heisenberg manifolds, Comm. Math.
Phys. 122, 531-62
Rieffel, M. A. A990a) Non-commutative tori: a case study of non-commutative differ-
entiable manifolds, in Geometrical and Topological Invariants of Elliptic Operators,
Brunswick, ME, 1988, J. Kaminker (ed.), Contemporary Mathematics 105, pp. 191—211,
American Mathematical Society, Providence, RI
Rieffel, M. A. A990b) Deformation quantization and operator algebras, in Operator Theory:
Operator Algebras and Applications, Durham, NH, 1988, W. V. Arveson &; R. G. Douglas
(eds), Proceedings of Symposia in Pure Mathematics 51, Part I, pp. 411—23, American
Mathematical Society, Providence, RI
Rieffel, M. A. A992) Category theory and quantum field theory, in Noncommutative Rings,
S. Montgomery &; L. W. Small (eds), Mathematical Sciences Research Institute Publications
24, pp. 115—29, Springer, Berlin
Ringel, C. M. A990) Hall algebras and quantum groups, Invent. Math. 101, 583-92
Ringel, C. M. A991) The category of modules with good filtrations over a quasi-hereditary
algebra has almost split sequences, Math. Zeit. 208, 209-25
Ringel, C. M. A992) From representations of quivers via Hall and Loewy algebras to quan-
quantum groups, in Proceedings of the International Conference on Algebra, Part 2, Novosi-
Novosibirsk, 1989, L. A. Bokut, Yu. L. Ershov &; A. I. Kostrikin (eds), Contemporary Mathematics
141, pp. 381-401, American Mathematical Society, Providence, RI
Ringel, C. M. A993) The composition algebra of a cyclic quiver. Towards an explicit de-
description of the quantum group of type An, Proc. London Math. Soc. 66, 507-38
Rittenberg, V. k, Scheunert, M. A992) Tensor operators for quantum groups and applica-
applications, J. Math. Phys. 33, 436-45
References 623
Rittenberg, V. &; Schutz, G. A991) Patterns of Uq(SUB)) symmetry breaking in Heisenberg
quantum chains, Helv. Phys. Ada 64, 871-6
Rocek, M. A991) Representation theory of the nonlinear SUB) algebra, Phys. Lett. B 255,
554-7
Roche, P. & Arnaudon, D. A989) Irreducible representations of the quantum analogue of
SU{2), Lett. Math. Phys. 17, 295-300
Rodriguez-Plaza, M. J. A991) Casimir operators of UqslC), J. Math. Phys. 32, 2020-7
Rodriguez-Plaza, M. J. A992) Universal 1Z matrix for quantum A2, ?2 and G2, in Topo-
logical and Geometrical Methods in Field Theory, J. Mickelsson &; O. Pekonen (eds), pp.
337-46, World Scientific, Singapore
Rogawski, J. D. A985) On modules over the Hecke algebra of a p-adic group, Invent. Math.
79, 443-65
Roger, C. A990) Deformations universelles des crochets de Poisson, in Geometric Symplec-
tique et Mecanique, Colloque International La Grande Motte, France, 23-28 Mai, 1988,
C. Albert (ed.), Lecture Notes in Mathematics 1416, pp. 242-54, Springer, Berlin
Rolfsen, D. A976) Knots and Links, Publish or Perish, Berkeley
Rosenberg, A. L. A992) The unitary irreducible representations of the quantum Heisenberg
group, Comm. Math. Phys. 144, 41-52
Rosso, M. A987a) Representations irreductibles de dimension finie du g-analogue de
l'algebre enveloppante d'une algebre de Lie simple, C. R. Acad. Sci. Paris Ser. I 305,
587-90
Rosso, M. A987b) Comparaison des groupes de Drinfel'd et de Woronowicz, C. R. Acad.
Sci. Paris Ser. I 304, 323-6
Rosso, M. A988a) Finite dimensional representations of the quantum analog of the en-
enveloping algebra of a complex simple Lie algebra, Comm. Math. Phys. 117, 581-93
Rosso, M. A988b) Groupes quantiques de Drinfel'd et Woronowicz, Publ. Res. Inst. Math.
Univ. Strasbourg 38, 67-82
Rosso, M. A988c) Groupes quantiques et modeles a vertex de V. Jones en theorie des
noeuds, C. R. Acad. Sci. Paris Ser. I 307, 207-10
Rosso, M. A989) An analogue of P.B.W. theorem and the universal R-matrix for Uh,sl(N +
1), Comm. Math. Phys. 124, 307-18
Rosso, M. A990a) Algebres enveloppantes quantifiers, groupes quantiques compacts de
matrices et calcul differentiel non commutatif, Duke Math. J. 61, 11—40
Rosso, M. A990b) Analogues de la forme de Killing et du theoreme d'Harish-Chandra pour
les groupes quantiques, Ann. Sci. Ecole Norm. Sup. 23 D), 445—67
Rosso, M. A990c) Koszul resolutions and quantum groups, Nucl. Phys. B Proc. Suppl. 18
B, 269-76
Rosso, M. A991) An analogue of the B. G. G. resolution for the quantum SL{N) group,
in Symplectic Geometry and Mathematical Physics, Aix-en-Provence, 1990, P. Donato,
C. Duval, J. Elhadad & G. M. Tuynman (eds), Progress in Mathematics 99, pp. 422-32,
Birkhauser, Boston
Rosso, M. A992a) Representations des groupes quantiques, Seminaire Bourbaki exp. no.
744, Asterisque 201-203, 443-83, Societe Mathematique de France, Paris
Rosso, M. A992b) Certaines formes bilineaires sur les groupes quantiques et une conjecture
de Schechtman et Varchenko, C. R. Acad. Sci. Paris Ser. I 314, 5—8
Rosso, M. A992c) Quantum groups at a root of 1 and tangle invariants, in Topological
and Geometrical Methods in Field Theory, J. Mickelsson & O. Pekonen (eds), pp. 347—58,
World Scientific, Singapore
Ruegg, H. A990a) A simple derivation of the quantum Clebsch-Gordan coefficients for
SUqB), J. Math. Phys. 31, 1085-7
Ruegg, H. A990b) Polynomial basis for SUqB) and Clebsch-Gordan coefficients, in Quan-
Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &, J.-D. Hennig (eds), Lecture
624 References
Notes in Physics 370, pp. 89-95, Springer, Berlin
Ryang, S. A992) Vertex operators for Uq(suB)) correlation functions, Phys. Rev. D 45
C), 3873-6
Saavedra Rivano, N. A972) Categories Tannakiennes, Lecture Notes in Mathematics 265,
Springer, Berlin
Salam, M. A. &; Wybourne, B. G. A991) The g-deformation of symmetric functions and
the symmetric group, J. Phys. A 24, L317-21
Saleur, H. A990a) Zeroes of chromatic polynomials. A new approach to Beraha conjecture
using quantum groups, Comm. Math. Phys. 132, 657-79
Saleur, H. A990b) Representations of Uq(slB)) for q a root of unity, in Number theory and
Physics, Les Houches, 1989, pp. 68-76, Springer, Berlin
Saleur, H. A990c) Quantum osp(l,2) and solutions of the graded Yang-Baxter equation,
Nucl. Phys. B 336, 363-76
Saleur, H. A991) Level-rank duality in quantum groups, Nucl. Phys. B 354, 579-613
Saleur, H. & Zuber, J. B. A991) Integrable lattice models and quantum groups, in String
Theory and Quantum Gravity, Trieste, 1990, M. Green, R. Iengo, S. Randjbar-Daemi, E.
Sezgin & H. Verlinde (eds), pp. 1-53, World Scientific, River Edge, NJ
Sanchez, N. A991) String theory, quantum gravity and quantum groups, in Group Theo-
Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov &; V. I. Manko (eds), Lecture
Notes in Physics 382, pp. 204-7, Springer, Berlin
Schechtman, V. A992a) Vanishing cycles and quantum groups I, Duke Math. J. Internat.
Math. Res. Notices 2, 39-49
Schechtman, V. A992b) Vanishing cycles and quantum groups II, Duke Math. J. Internat.
Math. Res. Notices 2, 207-15
Schechtman, V. k, Varchenko, A. A990) Hypergeometric solutions of the Knizhnik-
Zamolodchikov equations, Lett. Math. Phys. 20, 279-83
Schechtman, V. k, Varchenko, A. A991a) Quantum groups and homology of local systems,
in Algebraic Geometry and Analytic Geometry, Proceedings of the International Congress
of Mathematicians Satellite Conference, Tokyo, 1990, pp. 182—91, Springer, Berlin
Schechtman, V. &, Varchenko, A. A991b) Arrangements of hyperplanes and Lie algebra
homology, Invent. Math. 106, 134-94
Schirrmacher, A. A991a) The multiparametric deformation of GL(n) and the covariant
differential calculus on the quantum vector space, Z. Phys. C 50, 321-7
Schirrmacher, A. A991b) Multiparameter R-matrices and their quantum groups, J. Phys.
A 24, L1249-58
Schirrmacher, A. A992) Remarks on the use of R-matrices, in Quantum Groups and Related
Topics, R. Gierlak et al. (eds), pp. 55-66, Kluwer, Dordrecht
Schirrmacher, A., Wess, J. &; Zumino, B. A991) The two parameter deformation of GLB),
its differential calculus and Lie algebra, Z. Phys. C 49, 317-24
Schlieker, M. &; Scholl, M. A990) Spinor calculus for quantum groups, Z. Phys. C 47,
625-8
Schlieker, M., Weich, W. & Weixler, R. A992) Inhomogeneous quantum groups, Z. Phys.
C53, 79-82
Schmeing, N. C. A991) A Hopf algebra based on the Patera-Zassenhaus grading of An, J.
Phys. A 24, 1971-7
Schmidke, W. B., Vokos, S. P. & Zumino, B. A990) Differential geometry of the quantum
supergroup GLq(l\l), Z. Phys. C48, 249-55
Schmidke, W. B., Wess, J. & Zumino, B. A991) A g-deformed Lorentz algebra, Z. Phys.
C52, 471-6
Schmiidgen, K. A991a) Eine Einfiihrung in die Theorie der Quantenmatrixgruppen, Sem-
Seminar Sophus Lie 1, 3-21
References 625
Schmiidgen, K. A991b) Noncommutative covariant differential calculi on quantum spaces
and quantum groups, Seminar Sophus Lie 1, 125-32
Schneider, H.-J. A990) Principal homogeneous spaces for arbitrary Hopf algebras, Israel
Math. J. 72, 167-95
Schnizer, A. W. A992) Roots of unity: representations for symplectic and orthogonal quan-
quantum groups, preprint RIMS-864, Kyoto
Schouten, J. A. A940) Uber differentialkomitanten zweier kontravarianter Grossen, Nederl.
Akad. Wetensch. Proc. Ser. A 43, 449-52
Schiirmann, M. A991a) White noise on involutive bialgebras, in Quantum Probability and
Related Topics, L. Accardi (ed.), pp. 401-19, World Scientific, River Edge, NJ
Schiirmann, M. A991b) Quantum q-white noise and a g-central limit theorem, Comm.
Math. Phys. 140, 589-615
Schupp, P., Watts, P. & Zumino, B. A992a) The two-dimensional quantum Euclidean
algebra, Lett Math. Phys. 24, 141-6
Schupp, P., Watts, P. &; Zumino, B. A992b) Differential geometry on quantum linear
groups, Lett. Math. Phys. 25, 139-47
Schwenk, J. A991) Differential calculus for the iV-dimensional quantum plane, in Quantum
Groups, T. Curtright, D. Fairlie &; C. Zachos (eds), pp. 53—61, World Scientific, Singapore
Schwenk, J., Schmidke, W. B. & Vokos, S. P. A990) Properties of 2 x 2 quantum matrices
in Z2-graded spaces, Z. Phys. C 46, 643-6
Schwenk, J. &; Wess, J. A992) A g-deformed quantum mechanical toy model, Phys. Lett.
B 291, 273-7
Sciarrino, A. A992) g-oscillators realization of FqD) and GqC), J. Phys. A 25, L219-26
Sie-Qwon Oh A993) Finite dimensional simple modules over the coordinate ring of quantum
matrices, Bull. London Math. Soc. 25, 427-30
Semenov-Tian-Shansky, M. A. A983) What is a classical R-matrix ?, Fund. Anal. Appl.
17, 259-72
Semenov-Tian-Shansky, M. A. A984) Classical r-matrices and quantization, J. Soviet Math.
31, 3411-6
Semenov-Tian-Shansky, M. A985) Dressing transformations and Poisson-Lie group actions,
Publ. Res. Inst. Math. Sci. 21, 1237-60
Semenov-Tian-Shansky, M. A986) Poisson groups and dressing transformations, Zap.
Nauch. Sem. Leningrad Otdel. Mat. Inst. Steklov. 150, 119-42, 221-2 (Russian)
Sen, S. &; Chowdhury, A. R. A991) Yang-Baxter equation and non-ultralocal integrable
system, Phys. Scripta 44, 409-11
Sergeev, S. M. A991) Spectral decomposition of ^-matrices for exceptional Lie algebras,
Modern Phys. Lett. A 10, 923-7
Serre, J.-P. A965) Lie algebras and Lie Groups, Benjamin, Reading, MA
Shabanov, S. V. A992a) The Poisson bracket for g-deformed systems, J. Phys. A 25,
L1245-50
Shabanov, S. V. A992b) Path integral for the g-deformed oscillator and its interpretation,
Phys. Lett. B 293, 117-22
Sheu, A. J. L. A991) Quantization of the Poisson SUB) and its Poisson homogeneous
space the 2-sphere, Comm. Math. Phys. 135, 217-32
Sheu, A. J. L. A992) Quantum Poisson SUB) and quantum Poisson spheres, in Deforma-
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M. Gersten-
haber &; J. Stasheff (eds), Contemporary Mathematics 134, pp. 247-58, American Mathe-
Mathematical Society, Providence, RI
Shibukawa, Y. A992) Clebsch-Gordan coefficients for Uq(su(l, 1)) and Uq(slB)) and lin-
linearization formula of matrix elements, Publ. Res. Inst. Math. Sci. 28, 775-808
Shibukawa, Y. &; Ueno, K. A992) Completely Z-symmetric R-matrix, Lett. Math. Phys.
25, 239-48
626 References
Shigano, H. A977) A correspondence between observable Hopf ideals and left coideal sub-
algebras, Tsukuba Math. J. 1, 149-56
Shigano, H. A982) On observable and strongly observable Hopf ideals, Tsukuba Math. J.
6, 127-50
Shiraishi, J. A993) Free boson representation of Uq(sl2), Phys. Lett. A 171, 243-8
Shnider, S. A991) Bialgebra deformations, C. R. Acad. Sci. Paris Ser. I 312, 7-12
Shnider, S. A992) Deformation cohomology for bialgebras and quasi-bialgebras, in Defor-
Deformation Theory and Groups with Applications in Mathematical Physics, M. Gerstenhaber
&; J. Stasheff (eds), Contemporary Mathematics 134, pp. 259—97, American Mathematical
Society, Providence, RI
Siafarikas, P., Jannussis, A., Brodimas, G. & Papaloucas, L. A983) g-algebras without
interaction, Lett. Nuovo Cim. 37, 119-23
Sierra, G. A989) Duality and quantum groups, in Knots, Topology and Quantum Field
Theories, Florence, 1989, L. Lusanna (ed.), pp. 417-45, World Scientific, River Edge, NJ
Siopsis, G. A991a) Quantum groups in WZW and Chern-Simons theories, in Quantum
Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 181-93, World Scientific, Singapore
Siopsis, G. A991b) On the quantum group structure in WZW models and Chern-Simons
theories, Modern Phys. Lett. A 6, 1515-23
Sklyanin, E. K. A982a) Quantum variant of the method of inverse scattering problem, J.
Soviet Math. 19, 1546-96
Sklyanin, E. K. A982b) Some algebraic structures connected with the Yang-Baxter equa-
equation, Fund. Anal. Appl. 16, 263-70
Sklyanin, E. K. A983) Some algebraic structures connected with the Yang-Baxter equation.
Representations of quantum algebras, Fund. Anal. Appl. 17, 273-84
Sklyanin, E. K. A984) The Goryachev-Chaplygin top and the method of the inverse scatter-
scattering problem, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 133, 236—57 (Russian)
Sklyanin, E. K. A985) Classical limits of SUB) invariant solutions of the Yang-Baxter
equation, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 146 (Russian)
Smirnov, F. A. A990) Quantum groups and generalized statistics in integrable models,
Comm. Math. Phys. 132, 415-39
Smirnov, F. A. A992) Dynamical symmetries of massive integrable models, in Infinite
Analysis, A. Tsuchiya, T. Eguchi &; M. Jimbo (eds), Advanced Series in Mathematical
Physics 16, pp. 813-38 & 839-58, World Scientific, Singapore
Smirnov, Yu. F. & Tolstoy, V. N. A990) Extremal projectors for usual, super and quantum
algebras and their use for solving Yang-Baxter problem, in Selected Topics in Quantum
Field Theory and Mathematical Physics, Liblice, 1989, J. Niederle &, J. Fischer (eds), pp.
347-59, World Scientific, Singapore
Smirnov, Yu. F. & Tolstoy, V. N. A991a) Projection-operator method and the q-analog
of the quantum theory of angular momentum. Racah coefficients, 3j and 6j symbols, and
their symmetry properties, Soviet J. Nuclear Phys. 53, 1068-86
Smirnov, Yu. F. &; Tolstoy, V. N. A991b) Projection operator method and Q-analog of
angular momentum theory, in Group Theoretical Methods in Physics, Moscow, 1990, V.
V. Dodonov & V. I. Manko (eds), Lecture Notes in Physics 382, pp. 183-94, Springer,
Berlin
Smirnov, Yu. F. & Tolstoy, V. N. A992) The quantum algebra UqC), Soviet J. Nuclear
Phys. 54, 437-45
Smirnov, Yu. F., Tolstoy, V. N. & Kharitonov, Yu. I. A991) Method of projection operators
and the q-analog of the quantum theory of angular momentum. Clebsch-Gordan coefficients
and irreducible tensor operators, Soviet J. Nuclear Phys. 53, 593-605
Smirnov, Yu. F. & Wehrhahn, R. F. A992) The Clebsch-Gordan coefficients for the two-
parameter quantum algebra SUp,qB) in the Lowdin-Shapiro approach, J. Phys. A 25,
5563-76
References 627
Smit, D.-J. A990) A quantum group structure in integrable conformal field theories, Comm.
Math. Phys. 128, 1-37
Smith, S. P. A992) Quantum groups: an introduction and survey for ring theorists, in Non-
commutative Rings, S. Montgomery &, L. W. Small (eds), Mathematical Sciences Research
Institute Publications 24, pp. 131—78, Springer, Berlin
Sochen, N. A991) Integrable models through representations of the Hecke algebra, Nucl.
Phys. B 360, 613-40
Soibelman, Ya. S. A990a) Irreducible representations of the algebra of functions on the
quantum group SU(n) and Schubert cells, Soviet Math. Dokl. 40, 34-8
Soibelman, Ya. S. A990b) Gel'fand-Naimark-Segal states and Weyl group for the quantum
group SU(n), Fund. Anal. Appl. 24, 253-5
Soibelman, Ya. S. A991a) The algebra of functions on a compact quantum group, and its
representations, Leningrad Math. J. 2, 161—78; correction, ibid. 2, 256
Soibelman, Ya. S. A991b) Quantum Weyl group and some of its applications, Rend. Circ.
Mat. Palermo Suppl. 26 B), 233-5
Soibelman, Ya. S. A992a) Two problems in quantized algebras of functions, in Quantum
Groups, Proceedings of Workshops held in the Euler International Mathematical Institute
1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510, p. 393, Springer, Berlin
Soibelman, Ya. S. A992b) Selected topics in quantum groups, in Infinite Analysis, A.
Tsuchiya, T. Eguchi & M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp.
859-88, World Scientific, Singapore
Soibelman, Ya. S. A992c) On quantum flag manifolds, Funct. Anal. Appl. 26, 225-7
Soibelman, Ya. S. &; Vaksman, L. L. A992) On some problems in the theory of quantum
groups, in Representation Theory and Dynamical Systems, A. M. Vershik (ed.), Advances
in Soviet Mathematics 9, pp. 3-55, American Mathematical Society, Providence, RI
Solomon, A. I. & Katriel, J. A990), On g-squeezed states, J. Phys. A 23, L1209-12
Song, X. C. A992) Spinor analysis for the quantum group SUqB), J. Phys. A 25, 2929-44
Song, X. C. & Li Liao A992) The quantum Schrodinger equation and the g-deformation of
the hydrogen atom, J. Phys. A 25, 623-34
Soni, S. K. A990) g-analogues of some prototype Berry phase calculations, J. Phys. A 23,
L951-5
Soni, S. K. A991a) Differential calculus on the quantum superplane, J. Phys. A 24, 619-24
Soni, S. K. A991b) Comment on the differential calculus on quantum planes, J. Phys. A
24, L169-74
Soni, S. K. A991c) Covariant differential calculus on the quantum superplane and gener-
generalization of the Wess-Zumino formalism, J. Phys. A 24, L459—62
Soni, S. K. A992) Classical spin dynamics and quantum algebras, J. Phys. A 25, L837-42
Sorace, E. A992) Construction of some Hopf algebras, in Quantum Groups and Related
Topics, R. Gierlak et al. (eds), pp. 67-82, Kluwer, Dordrecht
Spiridonov, V. A992a) Exactly solvable potentials and quantum algebras, Phys. Rev. Lett.
69, 398-401
Spiridonov, V. A992b) Deformed conformal and supersymmetric quantum mechanics, Mod-
Modem Phys. Lett. A 7, 1241-52
Srinivasa Rao, K. &; Rajeswari, V. A991) Some aspects of angular momentum coefficients
in SUqB), in Group Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov & V.
I. Manko (eds), Lecture Notes in Physics 382, pp. 221-4, Springer, Berlin
Stachura, P. A992) Bicovariant differential calculi on SMB), Lett. Math. Phys. 25, 175-88
Stanev, Ya. S., Todorov, I. T. & Hadjiivanov, L. K. A992) Braid invariant rational confor-
conformal models with a quantum group symmetry, Phys. Lett. B 276, 87-94
Stasheff, J. A992a) Drinfel'd's quasi-Hopf algebras and beyond, in Deformation Theory
and Quantum Groups with Applications to Mathematical Physics, M. Gerstenhaber &;
628 References
J. Stasheff (eds), Contemporary Mathematics 134, pp. 297—307, American Mathematical
Society, Providence, RI
Stasheff, J. A992b) Differential graded Lie algebras, quasi-Hopf algebras and higher homo-
topy algebras, in Quantum Groups, Proceedings of Workshops held in the Euler Interna-
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics 1510,
pp. 120-37, Springer, Berlin
Steinberg, R. A965) Regular elements of semi-simple algebraic groups, Publ. Math. IHES
25, 49-80
Stolin, A. A991a) On rational solutions of the classical Yang-Baxter equation, Thesis,
Matematiska Institutionen, Stockholms Universitet
Stolin, A. A991b) On rational solutions of the Yang-Baxter equations. Maximal orders in
loop algebra, Comm. Math. Phys. 141, 533-48
Stolin, A. A991c) Constant solutions of the Yang-Baxter equation for slB) and s/C), Math.
Scand. 69, 81-8
Stolin, A. A991d) On rational solutions of Yang-Baxter equation for sl(n), Math. Scand.
69, 57-80
Stovicek, P. A993) Quantum line bundles on S2 and the method of orbits for SUqB), J.
Math. Phys. 34, 1606-13
Su, G. & Ge, M. L. A993) Thermodynamic characteristics of the g-deformed ideal boson
gas, Phys. Lett. A 173, 17-20
Sudbery, A. A990) Consistent multiparameter quantisation of GL(n), J. Phys. A 23, L697-
704
Sudbery, A. A991) Non-commuting coordinates and differential operators, in Quantum
Groups, T. Curtright, D. Fairlie & C. Zachos (eds), pp. 33-52, World Scientific, Singapore
Sudbery, A. A992) Canonical differential calculus on quantum general linear groups and
supergroups, Phys. Lett. B 284, 61—5
Sun, C. P. &; Pu, H. C. A989) The g-deformed boson realization of the quantum group
SU(n)q and its representations, J. Phys. A 22, L983-6
Sun, C. P., Pu, H. C. & Ge, M. L. A991) The cyclic representations of the quantum
superalgebra UqospB,1) with q a root of unity, Lett. Math. Phys. 23, 19-27
Sun, C. P. k, Ge, M. L. A991a) The g-analog of the boson algebra, its representation on
the Fock space, and applications to the quantum group, J. Math. Phys. 32, 595—8
Sun, C. P. &; Ge, M. L. A991b) The cyclic boson operators and new representations of the
quantum algebra slqB) for q a root of unity, J. Phys. A 24, L969-73
Sun, C. P. &, Ge, M. L. A991c) The g-deformed boson realization of representations of
quantized universal enveloping algebras for q a root of unity: I. The case of Uq(SL(l)), J.
Phys. A 24, 3265-80
Sun, C. P. k, Ge, M. L. A992) The g-deformed boson realization of representations of
quantized universal enveloping algebras for q a root of unity: II. The subalgebra chain of
Uq{Ci), J. Phys. A 25, 401-10
Sun, C. P., Liu, X. F. k, Ge, M. L. A991) A new g-deformed boson realization of quantum
algebra slqB) and nongeneric slqB) R-matrices, J. Math. Phys. 32, 2409—12
Sun, C. P., Liu, X. F. &; Ge, M. L. A992) Cyclic boson algebra and g-boson realization of
cyclic representations of the quantum algebra slqC), J. Phys. A 25, 161—8
Sun, C. P., Liu, X. F. &, Ge, M. L. A993) A new quasitriangular Hopf algebra as the non-
trivial quantum double of a simplest C algebra and its universal R-matrix for Yang-Baxter
equation, J. Math. Phys. 34, 1218-22
Sun, C. P., Liu, X. F., Lu, J. F. & Ge, M. L. A992) A g-deformed oscillator system with
quantum group SLq{l) symmetry, J. Phys. A 25, L35-8
Sun, C. P., Lu, J. F. &; Ge, M. L. A990) Structure of regular representation of quantum
universal enveloping algebra SLqB) with qp = 1, J. Phys. A 23, L1199-204
References 629
Sun, C. P., Lu, J. F. &; Ge, M. L. A991a) g-analogues of Verma representations of quantum
algebras for q a root of unity: the case of Uq(slC)), J. Phys. A 24, 3731-40
Sun, C. P., Lu, J. F. &; Ge, M. L. A991b) g-deformed Verma representations of quantum
algebra slqC) and new type Yang-Baxter matrices, Sci. China Ser. A 34, 1474-83
Sun, X. D. &; Wang, S. K. A992) Bicovariant differential calculus on the two-parameter
quantum group GLp,qB), J. Math. Phys. 33, 3313-30
Sun, X. D. & Wang, S. K. A993) Yang-Baxter matrix and *-calculi on quantum groups of
,4-series, J. Phys. A 26, L293-8
Sun, C. P., Xue, K., Liu, X. F. & Ge, M. L. A991) Boson realization of non-generic slqB).
R-matrices for the Yang-Baxter equation, J. Phys. A 24, L545—8
Sweedler, M. E. A969) Hopf Algebras, Benjamin, New York
Symes, W. A980a) Hamiltonian group actions and integrable systems, Phys. D 1, 339-74
Symes, W. A980b) Systems of Toda type, inverse spectral problems and representation
theory, Invent. Math. 59, 13-51; addendum, ibid. 63 A981), 519
Szymczak, I. &; Zakrzewski, S. A990) Quantum deformations of the Heisenberg group
obtained by geometric quantization, J. Geom. Phys. 7, 553-69
Taft, E. J. A992a) Quantum deformation of the flag variety, in Quantum Groups, Pro-
Proceedings of Workshops held in the Euler International Mathematical Institute 1990, P. P.
Kulish (ed.), Lecture Notes in Mathematics 1510, pp. 138-41, Springer, Berlin
Taft, E. J. A992b) Unsolved problems, in Quantum Groups, Proceedings of Workshops
held in the Euler International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture
Notes in Mathematics 1510, p. 394, Springer, Berlin
Taft, E. J. &; Towber, J. A991) Quantum deformation of flag schemes and Grassmann
schemes I. A ^-deformation of the shape algebra for GL(n), J. Algebra 142, 1-36
Taft, E. J. & Wilson, R. L. A980) There exist finite dimensional Hopf algebras with an-
antipodes of arbitrary even order, J. Algebra 62, 283-91
Takata, T. A992) Invariants of 3-manifolds associated with quantum groups and Verlinde's
formula, Publ. Res. Inst. Math. Sci. 28, 139-67
Takeuchi, M. A981) Matched pairs of groups and bismash products of Hopf algebras,
Comm. Algebra 9, 841-82
Takeuchi, M. A985) Topological coalgebras, J. Algebra 97, 505-39
Takeuchi, M. A989) Quantum orthogonal and symplectic groups and their embedding into
quantum GL, Proc. Japan Acad. Ser. A Math. Sci. 65, 55-8
Takeuchi, M. A990a) A two-parameter quantization of GLn (Summary), Proc. Japan Acad.
Ser. A Math. Sci. 66, 112-4
Takeuchi, M. A990b) Matric bialgebras and quantum groups, Israel J. Math. 72, 232-51
Takeuchi, M. A990c) The ^-bracket product and quantum enveloping algebras of classical
types, J. Math. Soc. Japan 42, 605-29
Takeuchi, M. A992a) Some topics on GLq{n), J. Algebra 147, 379-410
Takeuchi, M. A992b) Finite dimensional representations of the quantum Lorentz group,
Comm. Math. Phys. 144, 557-80
Takeuchi, M. A992c) Hopf algebra techniques applied to the quantum group Uq(slB)), in
Deformation Theory and Quantum Groups with Applications to Mathematical Physics, M.
Gerstenhaber &; J. Stasheff (eds), Contemporary Mathematics 134, pp. 309—23, American
Mathematical Society, Providence, RI
Takeuchi, M. &; Tambara, D. A991) A new one-parameter family of 2 x 2 quantum matrices,
Proc. Japan Acad. Ser. A Math. Sci. 67, 267-9
Takhtajan, L. A. A984) Solutions of the triangle equations with TL^ xZjy symmetry as ma-
matrix analogues of the Weierstrass zeta and sigma functions, Zap. Nauchn. Sem. Leningrad
Otdel. Mat. Inst. Steklov 133, 258-76 (Russian)
Takhtajan, L. A985) Introduction to algebraic Bethe ansatz, in Exactly Solvable Problems
in Condensed Matter and Relativistic Field Theory, Panchgani, 1985, B. S. Shastry. S. S.
630 References
Jha & V. Singh (eds), Lecture Notes in Physics 242, pp. 175-219, Springer, Berlin
Takhtajan, L. A. A989a) Quantum groups and integrable models, Adv. Stud. Pure Math.
19, 435-57
Takhtajan, L. A. A989b) Noncommutative homology of quantum tori, Fund. Anal. Appl.
23, 147-9
Takhtajan, L. A. A990) Introduction to quantum groups, in Quantum Groups, Clausthal,
Germany, 1989, H.-D. Doebner &; J.-D. Hennig (eds), Lecture Notes in Physics 370, pp.
3-28, Springer, Berlin
Takhtajan, L. A. A992) Lectures on quantum groups, in Introduction to Quantum Group
and Integrable Massive Models of Quantum Field Theory, M. L. Ge &; B. H. Zhao (eds),
pp. 69-197, World Scientific, Singapore
Tanisaki, T. A990) Harish-Chandra isomorphisms for quantum algebras, Comm. Math.
Phys. 127, 555-71
Tanisaki, T. A991) Finite-dimensional representations of quantum groups, Osaka J. Math.
28, 37-53
Tanisaki, T. A992) Killing forms, Harish-Chandra homomorphisms and universal R-mat-
rices for quantum algebras, in Infinite Analysis, A. Tsuchiya, T. Eguchi &; M. Jimbo (eds),
Advanced Series in Mathematical Physics 16, pp. 941-62, World Scientific, Singapore
Tarasov, V. O. A985a) Irreducible monodromy matrices for the R-matrix of the XXZ model
and local lattice quantum hamiltonians, Theoret. Math. Phys. 63, 440-54
Tarasov, V. O. A985b) Structure of the quantum L operators for the R-matrix of the XXZ
model, Theoret. Math. Phys. 63, 1065-72
Tarasov, V. O. A988) An algebraic Bethe ansatz for the Izergin-Korepin R-matrix, Theoret.
Math. Phys. 76, 793-804
Tarasov, V. O. A992) Cyclic monodromy matrices for the R-matrix of the six-vertex model
and the chiral Potts model with fixed spin boundary conditions, in Infinite Analysis, A.
Tsuchiya, T. Eguchi &; M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp.
963-76, World Scientific, Singapore
Temperley, N. &; Lieb, E. A971) Relations between the 'percolation' and 'colouring' problem
and other graph-theoretical problems associated with regular planar lattices: some exact
results for the 'percolation' problem, Proc. Roy. Soc. Ser. A 322, 251-80
Thams, L. A993) Two classical results in the quantum mixed case, J. reine angew. Math.
436, 129-53
Tiraboschi, A. A991) Compact quantum groups G<z, F4 and Es, C. R. Acad. Sci. Paris
Ser. I 313, 913-8
Tjin, T. A992) Introduction to quantized Lie groups and Lie algebras, Internat. J. Modern
Phys. A 7, 6175-214
Todorov, I. T. A990) Quantum groups as symmetries of chiral conformal algebras, in
Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner &; J.-D. Hennig (eds), Lecture
Notes in Physics 370, pp. 231-77, Springer, Berlin
Todorov, I. T. A991) Extended chiral conformal models with a quantum group symmetry,
in Group Theoretical Methods in Physics, Moscow, 1990, V. V. Dodonov & V. I. Manko
(eds), Lecture Notes in Physics 382, pp. 299-313, Springer, Berlin
Tolstoy, V. N. A990) Extremal projectors for quantized Kac-Moody superalgebras and
some of their applications, in Quantum Groups, Clausthal, Germany, 1989, H.-D. Doebner
&; J.-D. Hennig (eds), Lecture Notes in Physics 370, pp. 118-25, Springer, Berlin
Tolstoy, V. N. &; Khoroshkin, S. M. A992) The universal R-matrix for quantum nontwisted
affine Lie algebras, Fund. Anal. Appl. 26, 69-71
Trace, B. A983) Reidemeister moves of a classical knot, Proc. Amer. Math. Soc. 89, 722-4
Tracy, C. A. A985a) Complete integrability in statistical mechanics and the Yang-Baxter
equations, Phys. D 14, 253-64
References 631
Tracy, C. A. A985b) Embedded elliptic curves and the Yang-Baxter equations, Phys. D
16, 203-20
Truini, P. &; Varadarajan, V. S. A991) The concept of a quantum semisimple group, Lett.
Math. Phys. 21, 287-92
Truini, P. &; Varadarajan, V. S. A992) Universal deformations of simple Lie algebras, Lett.
Math. Phys. 24, 63-72
Tsuchiya, A. &; Kanie, Y. A988) Vertex operators in conformal field theory on P1 and
monodromy representations of braid groups, in Conformal Field Theory and Solvable Lat-
Lattice Models, Kyoto, 1986, A. Tsuchiya, T. Eguchi &; M. Jimbo (eds), Advanced Studies in
Pure Mathematics 16, pp. 297-372, Academic Press, Boston
Tsukuda, H. A992) Functional realization of quantum affine algebras, J. Math. Phys. 33,
3848-64
Tsygan, B. A993) Notes on differential forms on quantum groups, Selecta Mathematica
12, 75-103
Turaev, V. G. A988) The Yang-Baxter equation and invariants of links, Invent. Math. 92,
527-53
Turaev, V. G. A989a) Algebras of loops on surfaces, algebras of knots and quantization,
in Braid Group, Knot Theory and Statistical Mechanics, C. N. Yang & M. L. Ge (eds),
Advanced Series in Physics 9, pp. 59-95, World Scientific, Singapore
Turaev, V. G. A989b) The category of oriented tangles and its representations, Fund.
Anal. Appl. 23, 254-5
Turaev, V. G. A990a) The Yang-Baxter equation and invariants of links, in New Devel-
Developments in the Theory of Knots, T. Kohno (ed.), pp. 175-201, World Scientific, Teaneck,
NJ
Turaev, V. G. A990b) Operator invariants of tangles and R-matrices, Math. USSR Izv.
35, 411-44
Turaev, V. G. A991) Quantum invariants of 3-manifolds and a glimpse of shadow topology,
C. R. Acad. Sci. Pans Ser. I 313, 396-8
Turaev, V. G. A992) Shadow links and face models of statistical mechanics, J. Diff. Geom.
36, 35-74
Turaev, V. G. & Viro, O. Y. A992) State sum invariants of 3-manifolds and quantum
6j-symbols, Topology 31, 865-902
Turaev, V. G. & Wenzl, H. A993) Quantum invariants of 3-manifolds associated with
classical simple Lie algebras, preprint
Tuszynski, J. A., Rubin, J. L., Meyer, J. &; Kibler, M. A993) Statistical mechanics of a
g-deformed boson gas, Phys. Lett. A 175, 173-7
Twietmeyer, E. A992) Real forms of Uq(Q), Lett. Math. Phys. 24, 49-58
Ubriaco, M. R. A992) Non-commutative differential calculus and g-analysis, J. Phys. A
25, 169-74
Ubriaco, M. R. A993) Quantum deformation of quantum mechanics, Modern Phys. Lett.
A 8, 89-96
Ueno, K. A990a) Representation theory of quantum groups, Sugaku 42, 68—73
Ueno, K. A990b) Spectral analysis for the Casimir operator on the quantum group
SUq(l,l), Proc. Japan Acad. Ser. A Math. Sci. 66, 42-4
Ueno, K., Masuda, T., Mimachi, K., Nakagami, Y., Noumi, M. & Saburi, Y. A990) Matrix
elements of unitary representations of the quantum group SUq(l, 1) and the basic hyperge-
ometric functions, in Differential Geometric Methods in Theoretical Physics, Davis, 1988,
L. L. Chau & W. Nahm (eds), NATO Advanced Science Institutes Series B: Physics 245,
pp. 331-43, Plenum, New York
Ueno, K. &; Shibukawa, Y. A992) Character table of Hecke algebra of type A^-i and
representations of the quantum group Uq(gln+i), in Infinite Analysis, A. Tsuchiya, T.
632 References
Eguchi &; M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp. 977-84, World
Scientific, Singapore
Ueno, K. &; Takebayashi, T. A992) Zonal spherical functions on quantum symmetric spaces
and Macdonald's polynomials, in Quantum Groups, Proceedings of Workshops held in
the Euler International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in
Mathematics 1510, pp. 142-7, Springer, Berlin
Ueno, K., Takebayashi, T. & Shibukawa, Y. A989) Gel'fand-Zetlin basis for Uq{gl{N + l))
modules, Lett. Math. Phys. 18, 215-21
Ueno, K., Takebayashi, T. & Shibukawa, Y. A990) Construction of Gel'fand-Zetlin basis
for Uq(gl(N + 1)) modules, Publ. Res. Inst. Math. Sci. 26, 667-79
Ui, H. &; Aizawa, N. A990) The g-analogue of boson commutator and the quantum groups
SUqB) and SUq(l, 1), Modern Phys. Lett. A 5, 237-42
Ulbrich, K.-H. A990) On Hopf algebras and rigid monoidal categories, Israel J. Math. 72,
252-6
Vainerman, L. I. A992) Relations between compact quantum groups and Kac algebras, in
Representation Theory and Dynamical Systems, A. M. Vershik (ed.), Advances in Soviet
Mathematics 9, pp. 151-60, American Mathematical Society, Providence, RI
Vaksman, L. L. A989) ^-analogues of Clebsch-Gordan coefficients and the algebra of func-
functions on the quantum group SUB), Soviet Math. Dokl. 39, 467-70
Vaksman, L. L. &; Korogodskii, L. I. A989) The algebra of bounded functions on the
quantum group of the motions of the plane and q-analogues of Bessel functions, Soviet
Math. Dokl. 39, 173-7
Vaksman, L. L. &; Korogodskii, L. I. A991) Spherical functions on the quantum group
SUA,1) and a g-analogue of the Mehler-Fock formula, Fund. Anal. Appl. 25, 48—9
Vaksman, L. L. &; Soibelman, Ya. S. A988) Algebra of functions on the quantum group
SU{2), Funct. Anal. Appl. 22, 170-81
Vaksman, L. L. &; Soibelman, Ya. S. A991) Algebra of functions on the quantum group
SU(N + 1) and odd-dimensional quantum spheres, Leningrad Math. J. 2, 1023-42
Van Assche, W. &; Koornwinder, T. H. A991) Asymptotic behaviour for Wall polynomials
and the addition formula for little g-Legendre polynomials, SIAM J. Math. Analysis 22,
302-11
Van Daele, A. A991a) The operator a^H^fl when ab = \ba, preprint, K. U. Leuven
Van Daele, A. A991b) Quantum deformation of the Heisenberg group, in Current Topics
in Operator Algebras, Nara, 1990, pp. 314-25, World Scientific, Singapore
Van Daele, A. A993) Dual pairs of Hopf *-algebras, Bull. London Math. Soc. 25, 209-30
Van Daele, A. &; Van Keer, S. A991) The Yang-Baxter and pentagon equation, preprint,
K. U. Leuven
Van der Jeugt, J. A992a) The g-boson operator algebra and g-Hermite polynomials, Lett.
Math. Phys. 24, 267-74
Van der Jeugt, J. A992b) On the principal subalgebras of quantum enveloping algebras
glq{l + 1), J. Phys. A 25, L213-8
Van der Jeugt, J. A992c) Knot invariants and universal R-matrices from perturbative
Chern-Simons theory in the almost axial gauge, Nucl. Phys. B 379, 172-98
Van der Jeugt, J. A993a) Dynamical algebra of the (/-deformed three-dimensional algebra,
J. Math. Phys. 34, 1799-806
Van der Jeugt, J. A993b) R-matrix formulation of deformed boson algebra, J. Phys. A 25,
L405-13
Varadarajan, V. S. A974) Lie Groups, Lie Algebras and their Representations, Prentice-
Hall, Englewood Cliffs, NJ
Vassiliev, V. A. A990) Cohomology of knot spaces, in Theory of Singularities and its
Applications, V. I. Arnold (ed.), pp. 23-69, American Mathematical Society, Providence,
RI
References 633
Vassiliev, V. A. A993) Complements of Discriminants of Smooth Maps: Topology and Ap-
Applications, Translations of Mathematical Monographs 98, American Mathematical Society,
Providence, RI
Vaysleb, E. A992) Representations of quantum *-algebras slt(N + 1,R), in Representation
Theory and Dynamical Systems, A. M. Vershik (ed.), Advances in Soviet Mathematics 9,
pp. 57—65, American Mathematical Society, Providence, RI
Vaysleb, E. A993) Infinite-dimensional ^representations of Sklyanin algebra and of the
quantum algebra Uq(slB)), Selecta Mathematica 12, 57-73
Verdier, J.-L. A987) Groupes quantiques, Seminaire Bourbaki exp. no. 685, Asterisque
152-153, 305-19, Societe Mathematique de Prance, Paris
Verlinde, E. A988) Fusion rules and modular transformations in 2D conformal field theory,
Nucl. Phys. B 300, 360-75
Vey, J. A975) Deformations du crochet de Poisson d'une variete symplectique, Comm.
Math. Helv. 50, 421-54
Vinteler, E. A991) Extended braid group in higher dimensional integrable theories, Phys.
Lett B 254, 103-5
Viswanathan, K. S., Parthasarathy, R. &; Jagannathan, R. A992) Generalized g-fermion
oscillators and ^-coherent states, J. Phys. A 25, L335—40
Vladimirov, A. A. A993) A method for obtaining quantum doubles from the Yang-Baxter
R-matrices, Modern Phys. Lett. A 8, 1315-22
Vokos, S. P. A991) Multiparameter deformations of GL(N) and Jordan-Schwinger con-
constructions, J. Math. Phys. 32, 2979-85
Vokos, S. P., Zumino, B. &; Wess, J. A990) Analysis of the basic matrix representation of
GL9B,C), Z. Phys. C 48, 65-74
Vorobev, Yu. M. &; Karasev, M. V. A988a) Corrections to classical dynamics and quan-
quantization conditions arising in the deformation of Poisson brackets, Soviet Math. Dokl. 36,
594-8
Vorobev, Yu. M. &; Karasev, M. V. A988b) Poisson manifolds and the Schouten bracket,
Fund. Anal. Appl. 22, 1-9
Vorobev, Yu. M. &; Karasev, M. V. A990) Deformation and cohomologies of Poisson brack-
brackets, in Global Analysis - Studies and Applications, 4, Yu. G. Borisovich & Yu. E. Gliklikh
(eds), Lecture Notes in Mathematics 1453, pp. 75-89, Springer, Berlin
Wadati, M. &; Akutsu, Y. A988) Prom solitons to knots and links, Progr. Theoret. Phys.
Suppl 94, 1-41
Wadati, M., Deguchi, T. &; Akutsu, Y. A992) Yang-Baxter relation, exactly solvable models
and link polynomials, in Quantum Groups, Proceedings of Workshops held in the Euler In-
International Mathematical Institute 1990, P. P. Kulish (ed.), Lecture Notes in Mathematics
1510, pp. 373-88, Springer, Berlin
Walker, L. A991) On Witten's three-manifold invariants, preprint
Wallet, J.-C. A992) R-matrix and covariant g-superoscillators for Uq(gl{l\l)), J. Phys. A
25, L1159-66
Wambst, M. A992) Complexes de Koszul quantiques et homologie cyclique, C. R. Acad.
Sci. Paris Ser. I 314, 977-82
Wang, F. B. &; Kuang, L. M. A993) Even and odd ^-coherent states and their optical
staistics properties, J. Phys. A 26, 293-300
Wang, J. P. A991) A survey of the theory of quantum groups, Adv. Math. (China) 20,
424-54
Wang, K. W. A991) ^-determinants and permutations, Fibonacci Quart. 29, 160-3
Ward, R. S. A985) Generalized Nahm equations and the quantum Yang-Baxter equation,
Phys. Lett. A 112, 3-5
Wasserman, A. A988) Coactions and Yang-Baxter equations for ergodic actions and sub-
factors, in Operator Algebras and Applications, Vol. 2, D. E. Evans & M. Takesaki (eds),
634 References
London Mathematical Society Lecture Note Series 136, pp. 203—36, Cambridge University
Press, Cambridge
Waterhouse, W. C. A975) Antipodes and group-likes in finite Hopf algebras, J. Algebra
37, 290-5
Wei, H. A990) Structure constants of the quantum algebra and the Yang-Baxter relation
for the Zn symmetric statistical model, Ada Phys. Sinica 39, 1357—62
Weinstein, A. A983) The local structure of Poisson manifolds, J. Diff. Geom. 18, 523-57
Weinstein, A. &: Xu, P. A991) Extensions of symplectic groupoids and quantization, J.
reine angew. Math. 417, 159-89
Weinstein, A. &; Xu, P. A992) Classical solutions of the quantum Yang-Baxter equation,
Comm. Math. Phys. 148, 309-43
Weisfeiler, B. &; Kac, V. G. A971) On irreducible representations of Lie p-algebras, Funct.
Anal. Appl. 5, 28-36
Wenzl, H. A988a) Hecke algebras of type An and subfactors, Invent. Math. 92, 349-83
Wenzl, H. A988b) On the structure of Brauer's centralizer algebras, Ann. of Math. 128,
173-93
Wenzl, H. A988c) Derived link invariants and subfactors, in Operator Algebras and Appli-
Applications, Vol. 2, D. E. Evans &; M. Takesaki (eds), London Mathematical Society Lecture
Note Series 136, pp. 237—40, Cambridge University Press, Cambridge
Wenzl, H. A989) Unitarization of solutions of the quantum Yang-Baxter equation and
subfactors, in IXth International Congress on Mathematical Physics, Swansea, 1988, B.
Simon, A. Truman &; I. M. Davies (eds), pp. 434-43, Adam Hilger, Bristol
Wenzl, H. A990a) Quantum groups and subfactors of type B, C and D, Comm. Math.
Phys. 133, 383-432
Wenzl, H. A990b) Representations of braid groups and the quantum Yang-Baxter equation,
Pacific J. Math. 145, 153-80
Wenzl, H. A992) Unitary braid representations, in Infinite Analysis, A. Tsuchiya, T. Eguchi
&; M. Jimbo (eds), Advanced Series in Mathematical Physics 16, pp. 985—1006, World
Scientific, Singapore
Wess, J. &; Zumino, B. A991) Covariant differential calculus on the quantum hyperplane,
Nucl. Phys. B Proc. Suppl. 18 B, 302-12
Weyers, J. A990) The quantum group GLq(N) and Weyl-Heisenberg operators, Phys. Lett.
B 240, 396-400
Weyl, H. A927) Quantenmechanik und Gruppentheorie, Z. Phys. 46, 1-46
Weyl, H. A939) The Classical Groups, Princeton University Press, Princeton
Witten, E. A988a) Coadjoint orbits of the Virasoro group, Comm. Math. Phys. 114,
1-53
Witten, E. A988b) Topological quantum field theory, Comm. Math. Phys. 117, 353-86
Witten, E. A989) Quantum field theory and the Jones polynomial, Comm. Math. Phys.
121, 351-99
Witten, E. A990) Gauge theories, vector models and quantum groups, Nucl. Phys. B 330,
285-346
Woronowicz, S. L. A980) Pseudospaces, pseudogroups and Pontriagin duality, in Proceed-
Proceedings of the International Conference on Mathematics and Physics, Lausanne, 1979, K.
Osterwalder (ed.), Lecture Notes in Physics 116, pp. 407—12, Springer, Berlin
Woronowicz, S. L. A986) Group structure on noncommutative spaces, in Fields and
Geometry, Karpacz, 1986, A. Jadczyk (ed.), pp. 478-96, World Scientific, Teaneck,
NJ
Woronowicz, S. L. A987a) Compact matrix pseudogroups, Comm. Math. Phys. Ill, 613-
65
Woronowicz, S. L. A987b) Twisted SUB) group. An example of a non-commutative dif-
differential calculus, Publ. Res. Inst. Math. Sci. 23, 117-81
References 635
Woronowicz, S. L. A988) Tannaka-Krein duality for compact matrix pseudogroups. Twisted
SU(N) group, Invent Math. 93, 35-76
Woronowicz, S. L. A989) Differential calculus on compact matrix pseudogroups (quantum
groups), Comm. Math. Phys. 122, 125-70
Woronowicz, S. L. A991a) A remark on compact matrix quantum groups, Lett. Math. Phys.
21, 35-9
Woronowicz, S. L. A991b) Unbounded elements affiliated with C*-algebras and non-
compact quantum groups, Comm. Math. Phys. 136, 399-432
Woronowicz, S. L. A991c) Quantum EB) group and its Pontryagin dual, Lett. Math. Phys.
23, 251-63
Woronowicz, S. L. A991d) New quantum deformation of <SXB, <C). Hopf algebra level, Rep.
Math. Phys. 30, 259-69
Woronowicz, S. L. A991e) Solutions of the braid equation related to a Hopf algebra, Lett.
Math. Phys. 23, 143-5
Woronowicz, S. L. A992a) Operator equalities related to the quantum EB) group, Comm.
Math. Phys. 144, 417-28
Woronowicz, S. L. A992b) Quantum SUB) and EB) groups. Contraction procedure,
Comm. Math. Phys. 149, 637-52
Woronowicz, S. L. &; Zakrzewski, S. A992) Quantum Lorentz group having Gauss decom-
decomposition property, Publ. Res. Inst. Math. Sci. 28, 809-24
Xi, N. H. A990) Finite dimensional modules of some quantum groups over Fp(v), J. reine
angew. Math. 410, 109-15
Yamane, H. A988) A Poincare-Birkhoff-Witt theorem for the quantum group of type An ,
Proc. Japan Acad. Ser. A Math. Sci. 64, 385-6
Yamane, H. A989) A Poincare-Birkhoff-Witt theorem for quantized universal enveloping
algebras of type AN, Publ. Res. Inst. Math. Sci. 25, 503-20
Yamane, H. A991) Universal R-matrices for quantum groups associated to simple Lie
superalgebras, Proc. Japan Acad. Ser. A Math. Sci. 67, 108—12
Yan, H. A990) (/-deformed oscillator algebra as a quantum group, J. Phys. A 23, LI 155-60
Yan, H. A991) On (/-deformed oscillator systems and the (/-oscillator algebra HqD), Phys.
Lett. B 262, 459-62
Yan, H., Zhou, Y. & Zhu, T. H. A993) Two-parametric solutions to graded Yang-Baxter
equation and two-parametric deformed algebra Uuvgl(l\l), J. Phys. A 26, 935-42
Yang, C. M. A993) The modified classical Yang-Baxter equation and supersymmetric
Gel'fand-Dickii brackets, Modern Phys. Lett. A 8, 129-38
Yang, C. N. A967) Some exact results for the many-body problem in one dimension with
repulsive delta-function interaction, Phys. Rev. Lett. 19, 1312-4
Yang, Q. G. &; Xu, B. W. A993) Energy spectrum of a (/-analogue of the hydrogen atom,
J. Phys. A 26, L365-8
Yeh, E. H. Y. A989) Quantization of the semisimple Lie group, Nucl. Phys. B Proc. Suppl.
6, 436-9
Yetter, D. N. A988) Markov algebras, in Braids, Santa Cruz, 1986, J. S. Birman & A. Lib-
gober (eds), Contemporary Mathematics 78, pp. 705-30, American Mathematical Society,
Providence, RI
Yetter, D. N. A990) Quantum groups and representations of monoidal categories, Math.
Proc. Camb. Phil. Soc. 108, 261-90
Yetter, D. N. A992) Framed tangles and a theorem of Deligne on braided deformations
of monoidal categories, in Deformation Theory and Quantum Groups with Applications to
Mathematical Physics, M. Gerstenhaber &; J. Stasheff (eds), Contemporary Mathematics
134, pp. 325-49, American Mathematical Society, Providence, RI
Yoshinaga, S. A991) An invariant of spatial graphs associated with C/9(sZB,(C)), Kobe
Math. J. 8, 25-40
636 References
You, H. Q. & Zhou, S. Y. A990) On the quantum R-matrix on a Uq (si B, <E))-modu\e,
Modern Phys. Lett. A 5, 2465-72
Yu, Y., Zhu, Z. &; Lee, H. C. A993) Flat connections on quantum bundles and fractional
statistics in geometric quantization, J. Math. Phys. 34, 988-96
Yu, Z. R. A991a) Some realizations of the quantum algebra Uq(SUB)), J. Phys. A 24,
L1321-5
Yu, Z. R. A991b) A new method of determining an irreducible representation of quantum
SLq{3) algebra, J. Phys. A 24, L399-402
Yu, Z. R. A992) g-Usui operator of some quantum algebras, Phys. Lett. A 162, 5-6
Zabrodin, A. A992) Integrable models of field theory and scattering on quantum hyper-
boloids, Modern Phys. Lett. A 7, 441—6
Zachos, C. A991) Quantum deformations, in Quantum Groups, T. Curtright, D. Fairlie &;
C. Zachos (eds), pp. 62-71, World Scientific, Singapore
Zachos, C. A992a) Elementary paradigms of quantum algebras, in Deformation Theory
and Quantum Groups with Applications to Mathematical Physics, M. Gerstenhaber &;
J. Stasheff (eds), Contemporary Mathematics 134, pp. 351-77, American Mathematical
Society, Providence, RI
Zachos, C. A992b) Altering the symmetry of wave functions in quantum algebras and
supersymmetry, Modern Phys. Lett. A 7, 1595-600
Zakrzewski, S. A985) A differential structure for quantum mechanics, J. Geom. Phys. 2,
135-45
Zakrzewski, S. A990a) Quantum and classical pseudogroups, part I. Union pseudogroups
and their quantization, Comm. Math. Phys. 134, 347-70
Zakrzewski, S. A990b) Quantum and classical pseudogroups, part II. Differential and sym-
plectic pseudogroups, Comm. Math. Phys. 134, 371—95
Zakrzewski, S. A991a) A Hopf *-algebra of polynomials on the quantum 5LB,R) for a
"unitary" R-matrix, Lett. Math. Phys. 22, 287-9
Zakrzewski, S. A991b) Matrix pseudogroups associated with anti-commutative plane, Lett.
Math. Phys. 21, 309-21
Zakrzewski, S. A992) Poisson-Lie groups and pentagonal transformations, Lett. Math.
Phys. 24, 13-20
Zelevinsky, A. V. A980) Induced representations of reductive p-adic groups II. On irre-
irreducible representations of GL(n), Ann. Sci. Ecole Norm. Sup. 4e Ser. 13, 165-210
Zhang, M. Q. A991) How to find the Lax pair from the quantum Yang-Baxter equation,
Comm. Math. Phys. 141, 523-31
Zhang, R. B. A991a) Graded representations of the Temperley-Lieb algebra, quantum
supergroups and the Jones polynomial, J. Math. Phys. 32, 2605-13
Zhang, R. B. A991b) Invariants of the quantum supergroup Uq(gl(m/1)), J. Phys. A 24,
L1327-32
Zhang, R. B. A991c) Multiparameter dependent solutions of the Yang-Baxter equation, J.
Phys. A 24, L535-43
Zhang, R. B. A992a) Universal L operator and invariants of the quantum supergroup
Uq{gl{m/n)), J. Math. Phys. 33, 1970-9
Zhang, R. B. A992b) A two-parameter quantization of ospD/2), J. Phys. A 25, L991-6
Zhang, R. B. A992c) Braid group representations arising from quantum supergroups with
arbitrary q and link polynomials, J. Math. Phys. 33, 3918-30
Zhang, R. B. A993) Finite-dimensional irreducible representations of the quantum super-
supergroup Uq{gl{m/n)), J. Math. Phys. 34, 1236-54
Zhang, R. B. &; Gould, M. D. A991) Universal R-matrices and invariants of quantum
supergroups, J. Math. Phys. 32, 3261-7
Zhang, R. B., Gould, M. D. &; Bracken, A. J. A991a) Quantum group invariants and link
polynomials, Comm. Math. Phys. 137, 13-27
References 637
Zhang, R. B., Gould, M. D. & Bracken, A. J. A991b) Solutions of the graded classical
Yang-Baxter equation and integrable models, J. Phys. A 24, 1185—97
Zhang, R. B., Gould, M. D. & Bracken, A. J. A991c) Prom representations of the braid
group to solutions of the Yang-Baxter equation, Nucl. Phys. B 354, 625-52
Zhang, R. B., Gould, M. D. & Bracken, A. J. A991d) Solution of the graded Yang-Baxter
equation associated with the vector representation of Uq(osp(m\2n)), Phys. Lett. B 257,
133-9
Zhang, R. B., Gould, M. D. &; Bracken, A. J. A991e) Generalized Gel'fand invariants of
quantum groups, J. Phys. A 24, 937-43
Zhang, S. &; Duan, Y. A992) The quantum group SUq{2) and the ^-analogue of angular
momenta in classical mechanics, J. Phys. A 25, 5135—40
Zhang Y. J. A992) A remark on the representation theory of the algebra Uq(sl(n)) when
q is a root of unity, J. Phys. A 25, 851-60
Zhedanov, A. S. A992a) 'Non-classical' g-oscillator realization of the quantum SU{2) alge-
algebra, J. Phys. A 25, L713-8
Zhedanov, A. S. A992b) The 'Higgs algebra' as a 'quantum' deformation of 5C7B), Modern
Phys. Lett. A 7, 507-12
Zhedanov, A. S. A992c) Quantum SUqB) algebra: 'Cartesian' version and overlaps, Modern
Phys. Lett. A 7, 1589-93
Zhedanov, A. S. A992d) Bogoliubov ^-transformation and Clebsch-Gordan coefficients for
a g-oscillator, Phys. Lett. A 165, 53-7
Zhedanov, A. S. A993a) On the realization of the Weyl commutation relation HR = qRH,
Phys. Lett. A 176, 300-2
Zhedanov, A. S. A993b) Q rotations and other Q transformations as unitary nonlinear
automorphisms of quantum algebras, J. Math. Phys. 34, 2631-47
Zheng, Q. R. & Zhang, D. H. A993) Solutions of the quantum three-simplex equation
without spectral parameters, Phys. Lett. A 174, 75-80
Zhong, Z. Z. A992a) The hyperbolic complexification of quantum groups and the isomor-
phic relations, J. Phys. A 25, L397-402
Zhong, Z. Z. A992b) A remark on the classical realization of the double quantum group
SUq(<q,J), J. Phys. A 25, L867-70
Zhong, Z. Z. A993) Non-commutative analysis, quantum group gauge transformations and
gauge fields, J. Phys. A 26, L391-400
Zuber, J. B. A990) Conformal field theories, Coulomb gas picture and integrable models, in
Champs, Cordes et Phenomenes Critiques, Les Houches, 1988, E. Brezin &; J. Zinn-Justin
(eds), pp. 247-79, North-Holland, Amsterdam
Zumino, B. A991) Deformation of the quantum mechanical phase space with bosonic or
fermionic cooordinates, Modern Phys. Lett. A 6, 1225-35
Index of notation
Roman symbols
ad
ad*
Ad
Ad*
Ao
A°p
Ao
AT
A(s)
A
A0
A(L)
aXJ
B+
braid
Bm
bu
BQ 256,
BMWe(r,e)
Bv
B(X)
Bo
Bo
Ba
B
Boo
corep^
ch
Ce
c
C
cw
Ce(G)
V(G)
20
20
20
20
101
103
113
130
158
288
478
498
562
39
141
143
143
154
282, 565
334
479
479
481
481
486
487
488
16
141
226
315, 353
362
376
392
406
432
451
452
34
34
V(A)
dtangle
dribbon
dribbon
dribbon(X)
det<7,r?(A)
dete)r?(A)
V
dL
DL
dx
T>m
di
evu
expg
eva
eva
eva
eva
F(G)
FR{Mm)
FR,q(GLm)
fR,q(SLm)
fh{G)
Funn
Fun^
Fr
Fre
T
Te{G)
?t
?7
Tt+
Fe
Fe,w
Tz'u(G)
J^'U(G)
?A
Fe
Fe{Fx)
Te{S2n + 1)
128
145
146
147
147
321
326
341, 414
501
503
518
538
562
139
273
386, 400
387, 400
407
407
106
228
232
233
234-5
237
237
305
305
410
430
433
433
433
433
435
440
442
443
443
447
449
Index of notation 639
460-1 ?i 392
461 K(L) 500
KZm 543
464
L_ 497
25 L+ 497
(9,9*) 25
G* 33 ^o 497
Gr(C) 137 L°° 500
? 294 lk(L,L0 501
qO 294 t(w) 565
GF 304 modfc 141
$/ 484 M«M 314
gB) 553 M^M 324
gC) 554 M^X) 324
GT 558 M^ 383
GT 559 M« 4°6
g'(A) 562 m^ 564
g(V 562 M(A) 566
9a 564 n 562
564 ^ 565
Hi 84 °~ 414
HL(A,A) 174 ^ 414
H- (A, A) 175 a* 551
alg ParG?) 320
H^^A) 175 W 383
H* 182 PtV 396
1: Z 4 -
W,(e) 332 pnm 454
H 378 Pn{z;a,/3;Q) 466
He{€) 403 P(L) 497-8
height^) 563 Q^ 159
h 565 qdet(T) 231
int. 556 Q^ *
,-„ 9. 289
JU 153 Q 563
J(^ 376 Q+ 563
^ 4°6 Rep(G) 106
J{ , ™ n 119,123
J^W'X) 435 repA 141
J-^ 47° ribbon
J(L) 498 riSTon 147
fcc/ 154 ^, 264
K" 282 7eh 201,271
fc" 291 Hh< 266
^ 365 repr 307
640
Index of notation
Rep(r)
S
Sym(V)
Spec(Zo)
Spec(Ze)
S(r)a
*.(r)
SL
Si
TM
T*M
t
tangle
Te(X)
T
tilt^
tracej
U
v
jjOW
Ut
U?
308
418
423
487
543
103
107
228
291
291
389
435
488
503
518
564
17
17
55
145
256, 282
333
362
368, 370
370
370
370
506
107
208
260
260
260
275
280-1
282
282
282
285
289
289
290
289
289
u;
Ue
UT°
f/res
UTeeS+
f/resO
jjves
U{es
L/efin
Vq(u>)
VqW
yres
Ve(u>)
Ve(X)
289
293
297
297
297
297
300
300
300
300
300
300
300
300
302
302
302
302
302
304
304
304
304
340
376
392
394
396
399-400
416
443
460
486
486
519
276
314
314
315
316
324
324
332
Index of notation 641
yeres(A)
Vf (A)
Vh
V(h)
V(Xi,a)
Va
ya
v(v)
yn&t
Vq
v°
VK(X)
V(oo)
Va
V(X)
wM
Wh
Wh,i
™h,0
VKeres(A)
We
w(L)
WK(L)
W
wo
xf
XL
XR
(xf)(r)
xt
xa
xf
X±
x±
i,r
xXt
xt
Xm
y(9)
Y+
y°
y-
334
355
358
383
383
384
387, 401, 407
387, 401, 407
396
415
477
479
551
552
566
566
18
262
263
265
265
274
354
360
499
551
564
565
17
60
60
257
259
291
293
378
392
486
487
558
377-8
382
382
382
Y(glooi
Zq
Ze
Z+
zo
zo
Zo
Ze
Z(L)
auvw
a
a
OLA
7
7e
rC)
6
sR
6a u
A
Aop
6r
A+
A~
e
e
L
A(V)
Xu
AR,q
A^
A4
Mop
[i]
n
Kt
n^
7T1
;C)) 416
284
290
291
291
291
293
293
512
Greek symbols
138
353
506
529
563
284
290
553
554
25, 178
42
42
102, 564
103
231
564
564
102
293
564
101
107
138
228
405
564
101
101
340
80
138
227, 437, 462
438
557
642 Index of notation
PU
p* 275 Miscellaneous symbols
Ph { , } 16, 177
p\ 334 ;\ 17
504 {T®T}
138
275
276
334
462
504
564
39
149
332
402
462
522
227, 437, 462
291
380
384
258
392-3
465
529
544
285
290
240
240-1
242
244
245-6
258, 320, 552
196
314
\ ' )
[' 11
IT <9> 1
{ . }L
{,}R
/ mg
1
*h
[n]q
\n] !
in jq
0
?
\Ki-m
I r J
(*/ ^ LJ
{u}
\u v]
M
I2SJ
M
I2SJ
*L
•
61
61
104
138, 315
184
200
n 227, 437, 462 [n]q\ 200
r 291 [™] 200
222
222
289
297
314
345
368
X<?'A 285 \u,v]^l/2 399
Xe'A — rs^ 407
408
446
446
456
u 258, 320, 552 Jo "I" 457
q 196 ; 481
554
, < A 564
General index
absolute Galois group 557-60
admissible 80, 92, 482
affiliated element 462
affine Hecke algebra 403
relation with p-adic groups 404
representations 405-8, 410-3
affine Lie algebra 58, 541-3, 550-6,
565-6
Alexander polynomial 498, 500
algebra 101-2
deformation 43
opposite 101
ambient isotopy 496, 514
angle 1-form 501
antipode 103, 529
square of 190—2
arrow 482
associativity constraint 139
Baker-Campbell-Hausdorff formula
46, 182, 185-6
big cell 294
Birkhoff factorization theorem 96
Birman-Murakami-Wenzl algebra
334, 526
Boltzmann weight 247, 351, 510
bond 246
braid 142-4
closure 501
braid group 143-4, 153, 256
action 257, 282, 336
and configuration spaces 538
Brauer-Probenius-Schur duality
(see Probenius—Schur duality)
Bruhat decomposition 39, 41
Bruhat ordering 360, 405, 565
Burau representation 505
Capelli identity 426
Cart an matrix 562
extended 565—6
Casimir element 196, 275-6
category
abelian 136-7, 307
additive 136-7
balanced 154
braided monoidal 153
essentially small 148
/c-linear 137
monoidal 138-47, 530
quasitensor 152-3, 329, 359, 370,
531, 555, 559-60
rigid 139-40, 530, 555
semisimple 137, 391, 556
small 148
strict 139
tensor 149-52, 531
C* -completion 451—2
type of 454
central character 290, 315, 340
central elements 122, 124, 168-9,
284, 321-3
character 317, 325-6, 353-4, 361,
363
characteristic p 296, 304-6, 358-61,
555-6
classical limit
of a QF algebra 179
of a quasi-Hopf QUE algebra
536-7
of a QUE algebra 180-2
classical r-matrix 54, 181-2, 183-4
and 2-cocycles 62-3
and inte.grable systems 71-7
non-degenerate 62, 87
classical R-matrix 67—8
classical Yang-Baxter equation
(CYBE) 54, 125, 182, 187
and Lie bialgebras 51
class of solution of 96
equivalent solutions of 80, 84, 88
modified 55
644
General index
solutions of 80-98
with spectral parameters 87
Clebsch-Gordan decomposition
204, 326
coadjoint orbits 20, 40-1
coalgebra 102-3
coassociativity 102
coassociator 529
coboundary 51, 84, 174
cochain 173
cocommutator 25, 535
cocycle 25, 62, 174, 533
cohomology of Hopf algebras 173-7
rigidity theorems for 176-7, 212
co-Jacobi identity 178
cokernel 137
co-Leibniz identity 178
comodule 108
comodule algebra 109
comodule coalgebra 109
compact matrix pseudogroup
(see compact matrix quantum
group)
compact matrix quantum group
453-4
Haar integral 454-8
complete integrability 68-9
complete reducibility 318-9, 324-5
comultiplication 102
configuration spaces 537-8, 558
conformal field theory 159, 371-2
orbifold 534
conformal weight 542
conserved quantities 69
in involution 69
continued fraction 331
continuous series 331
contravariant form 320
convolution product 104
co-Poisson algebra 178
co-Poisson Hopf algebra 178
core 146
corepresentation 110, 141
regular 110
unitary 118
Coxeter automorphism 91
Coxeter element 489, 565
Coxeter number 92, 489, 565
crystal basis 478-86
global 480-6
crystal graph 484
deformation
(mod hn) 172
of algebras 43
of bialgebras 171
of Hopf algebras 171
of Poisson algebras 44
quantization 44, 46-7
degenerate affine Hecke algebra 405
de Rham complex
homology of 243-4
of quantum GLm 244-5
of quantum m x m matrices 242-3
of quantum plane 240-1
derivation 190-2
determinant formula 321, 327
diagonal module 342
diagram automorphism 309
differential graded algebra 242
directed tangle 145
direct sum 136
discrete series 330
discriminant 340-1
dressing action 37-8
and symplectic leaves 38—41
dressing transformation 37-8
dual Coxeter number 564
dual basis lemma 141
dual object 139
dual object functor 140
Dynkin diagram 92, 562
Dynkin graph 307
eight vertex model 253
elliptic solutions
of the CYBE 90-1
of the QYBE 427
enhanced quantum Yang-Baxter
operator 506
epimorphism 137
equivalence
of deformations 171
of solutions of the CYBE 80, 84, 8?
General index
645
euclidean group 459
evaluation homomorphism
for affine Hecke algebras 407
for quantum loop algebras 399-
401
for Yangians 386-7
evaluation representations
of affine Hecke algebras 407
of quantum loop algebras 399-
403
of Yangians 386-91
exterior algebra 107-8
Fateev-Zamolodchikov model 351
Fibonacci sequence 331
Frobenius Lie algebra 84
Frobenius map 305-6, 357, 359
Frobenius—Schur duality
classical 332
for quantum affine algebras
410-3
for U€(g) 334-5, 408-10
for Yangians 413-4
framing 502
fuchsian differential equations 544
functor
exact 148
faithful 148
monoidal 138-9
tensor 150
fundamental reflection
(see simple reflection)
fundamental representations
of quantum loop algebras 399
of Yangians 384, 387-8
fundamental weight 564
fusion matrices 155
fusion ring 155, 159, 160, 371
fusion rules 154-7, 160
fusion tensor product 371, 552-5
Gabriel's theorem 307-8, 489
Gel'fand-Naimark-Segal state 439
Gel'fand-Tsetlin basis 476-8
generalized Cartan matrix 562
graphs
admissible 482
coloured oriented 482
crystal 484
tensor products of 483-6
Grothendieck group 137-8
Grothendieck ring 139, 156
Grothendieck-Teichmuller group
558-9
and quasi-Hopf algebras 559-60
group algebra 105, 112, 175
group cohomology 533-4
group-like 106, 193
Haar integral
(see integral, invariant)
/i-adic topology 105
hamiltonian 68—9
hamiltonian vector field 17
Harish Chandra homomorphism
284, 290, 321-4
and quantum coadjoint action
296
Harish Chandra's theorem 285, 290
Hecke algebra 332-6, 404, 476
representations 405—6
Heisenberg ferromagnet
(see XXX model)
Heisenberg group 45, 218
Heisenberg Lie algebra 44-5, 176, 186
hermitian symmetric space 41
highest weight 314, 354, 383, 434,
441
highest weight module 314, 324,
354, 542
for QF algebras 434, 441
for Yangians 383
highest weight vector 314, 383
Hilbert space tensor product 415
Hochschild cohomology 174, 254
HOMFLY polynomial 497-8,
509, 517
for trefoil knot 498-9
*-homomorphism 117
Hopf algebra 103-5
almost cocommutative 119
coboundary 123
cocommutative 102
cohomology 173-7
646
General index
deformations 171
dual 111-5, 131-2, 223-6, 234-5
graded 105
integral on 115-6, 132
quasitriangular 123, 129-30
representations 108—12
ribbon 125, 133
*-structure 117-9, 309-11, 329,
431-2
topological 105, 114, 123
triangular 123, 150-1
Hopf ideal 103-4
Hopf link 165-6
Hopf's theorem 108
hyperalgebra 304, 358, 359-60
identity object 138
infinite-dimensional orthogonal
group 414-7
infinitesimal deformation 172
integral 115—6
invariant 115
non-central 456
normalized 115
integral form
non-restricted 289
restricted 297
intersection cohomology 489
intertwiner 151, 348-51, 542
invariant bilinear form 563
orthogonality properties 564
invariant differential form 245—6
Ising model 371-2
Jackson integral 457, 467
Jacobi identity 17
Jacobson topology 454
jets 391
Jones polynomial 168, 498, 500
Kac-Moody algebra 562
Kashiwara's tensor product
algorithm 485-6
Kauffman polynomial 499, 500,
510, 517
Kazhdan-Lusztig element 406
Kazhdan—Lusztig polynomial 360
Kazhdan-Lusztig tensor product
552-5
kernel 137
kink 501
Kirby move 503, 522-5
special 503
Kirillov-Kostant principle
{see orbit principle)
Knizhnik-Zamolodchikov equation
539-41
and hyperplane complements 561
and ra-point functions 542—3
and quantization 543—9, 555
knot 496
Kohno—Drinfel'd monodromy
theorem 549-50
lattice model
exactly solvable 247
integrable 246-53
Lax pair 69-71, 73, 76
left dual 111, 122
Leibniz identity 17
length 565
level 408-9
for affine Lie algebras 566
Lie bialgebra 24-33
automorphism 32
coboundary 50-9
cocommutator of 25
derivation 32—3
double 34-5, 58-9
dual 33-4
factorizable 67
homomorphism 25
ideal 25
opposite 25
pseudotriangular 56
quasitriangular 54
quotient 25
standard 29-30, 34-6, 55-6, 59,
81, 93
tangent 26
triangular 54
Lie—Poisson structure 19—20, 21
linking number 500—1
link invariants 167-8, 497
General index
647
from R-matrices 504-10
from vertex models 510—7
links 167
equivalent 496
oriented 496
skein related 497
local algebra 158
loop representation 542
Lusztig's canonical basis
algebraic construction 486—8
positivity property 487
topological construction 488—90
Lusztig's conjectures 359—61
3-manifold invariants 522-5
Manin triples 26-32
infinite-dimensional 28
Markov equivalence 502
Markov moves 502
Markov trace 506
matched pair 48
matrix elements 106, 116, 430
and little g-Jacobi polynomials
466
and little g-Legendre polynomials
467
and g-Bessel functions 470-3
modified classical Yang-Baxter
equation (MCYBE) 55
equivalent solutions 80
modular Hopf algebra 517-21
module 108
module algebra 109
module coalgebra 109
monodromy 540
monodromy theorem 549-50
monoidal functor 138-9
monomorphism 137
non-linear Schrodinger equation
422
non-restricted integral form 289
non-restricted specialization 288—96
and conjugacy classes 295—6,
342-3, 347
and R-matrices 348—51
automorphisms 293—5
centre 290-2
defining relations 289
relation with ?7(9) 290
representations 339-48
opposite
algebra 101
coalgebra 103
orbit principle 180, 439, 442
Ore condition 232, 244
pairing of Hopf algebras 114—5,
224-6, 461
partition function 247, 249, 510
pentagon axiom 139
perverse sheaves 490
Peter-Weyl theorem 451
Pliicker relations 448
Poincare-Birkhoff-Witt 199-200,
260, 282-3, 291, 298, 302,
382, 394, 433
Poisson action 36—7
Poisson algebra 43, 177
deformation 44
Poisson bivector 17
Poisson bracket 16—7
Poisson homogeneous space 22-4
Hopf fibration as 23—4
symplectic leaves of 38
Poisson-Hopf algebra 177-8
Poisson-Lie group 21-4, 292-3, 296
coboundary 59—68
compact 35-6
complex 26
double 34, 37-8, 43
dual 33-4, 37-8, 296
factorizable 67
homomorphism 21
Lie bialgebra of 26
subgroup 22
Poisson manifold 16—21
complex 20—1
Poisson map 18
Poisson structure 16—7
compatible 41
product 18
rank of 19, 22
648
General index
second Adler-Gel'fand-Dickii 32
symplectic 18
trivial 18
twisted 42-3
Poisson submanifold 18
Pontryagin product 108
Pontryagin duality 135
primitive element 107
primitive ideal 454
primitive vector 314, 354, 383
principal alcove 362
pro-finite fundamental group 557
pseudo-differential operators 31-2
pseudo-highest weight 396
pseudo-universal R-matrix 419, 423
pure braid group 144, 153, 538
pure sphere braid group 538
g-Bessel function 470
addition formula 471
Hansel-Lommel orthogonality
relation 471
g-binomial coefficient 200, 209, 301
^-derivative 464
^-exponential 273
^-factorial 200
QF algebra 176, 216-27, 234-40, 430
admits a faithful representation
438-9
and classical function algebra
306, 443-4
at roots of unity 301, 442-5
centre 219
differential calculus on 240—6
highest weight representations
227, 433-8, 441-2
multiparameter 238—40
PBW factorization 433
rational form 280—1
^representations 433, 437-8,
441-2
*-structure 431—2
twisted 439-42
QFSH algebra 190, 267-8
g-Hahn polynomial 467
g-hypergeometric series 430, 465, 561
^-integral (see Jackson integral)
g-Jacobi polynomial
big 468-9
little 466-7
g-Legendre polynomial 467
^-number 200
g-spherical function 468—9
quantization
deformation 46-7
homogeneous 375-6
Moyal 46-7, 183-7
multiparameter 212-3, 238-40
non-standard 206-7
of co-Poisson—Hopf algebras 180
of Lie bialgebras 180—9
of Poisson—Hopf algebras 179
of Poisson—Lie groups 179
of quasi-Hopf algebras 537
R-matrix 187, 222-3, 228-34
standard 195, 208, 234-5
Weyl 44-5
quantized algebra of continuous
functions 451—2
vanishing at infinity 461-2
quantized function algebra
(see QF algebra)
quantum affine algebra 392-4
PBW basis 394
pseudotriangular structure 403,
423-5
quantum Casimir element 196, 285,
291-2, 323
quantum Clebsch-Gordan
coefficient 205, 467
quantum coadjoint action 293-6
and conjugacy classes 295-6
quantum coordinate ring (see QF
algebra)
quantum determinant 219, 220,
231-3, 236
quantum dimension 122-3, 126,
365-6, 371
quantum double 127-9, 132
quantum euclidean group 459—62,
469-70
automorphisms 463
Haar integral 463-5
representations 462-3
General index
649
quantum field theory 157-60
quantum flag manifolds 447-8
quantum G-space 445—7
quantum Kac-Moody algebras
207-13
automorphisms 309
centre 212, 284-5, 290-3, 321-4
geometric realization 285-8,
308-9
real forms 309-11
representations 313-31
quantum loop algebras 396
relation with Yangians 403
representations 394-403
quantum orthogonal group 236-8
quantum plane 217-8, 228, 240-1
quantum projective space 451
quantum R-matrix 133, 205, 276-7
elliptic 427
Frobenius 231
Hecke 232
rational 380, 419-23
singularities 425
strange 230
trigonometric 424
quantum Schubert variety 448
quantum Schur orthogonality
relations 457-8
quantum Serre relation 209
quantum sl2 192-206, 216-27
algebra structure 196
and little g-Jacobi polynomials
466-7
automorphisms 309
basis 199, 220-2, 226
centre 285, 291-2, 321-3
matrix elements 466
quantum Weyl group 262-3
quasitriangular structure 201-3
real forms 309-11
representations 203-6, 330-1,
343-4
tilting modules 364-6
universal R-matrix 201, 263-5
Weyl modules 355-6
quantum special linear group 235-6
quantum spheres 448-51, 467-9
quantum symplectic group 236—8
quantum torus 442
quantum trace 122-3, 126-7,
365-6, 370
quantum Weyl group 262-6, 439
and central elements 265
and universal R-matrix 263—5
for quantum affine algebras 424
quantum Yang-Baxter equation
(QYBE) 67, 124-5, 187, 203,
229, 250
and braid groups 504—5
and intertwiners 348—51
space of solutions of 233—4
with spectral parameters 250,
348-51, 380, 419-25, 511
quasi-bialgebra 529
quasitriangular 531
triangular 531
quasi-Frobenius Lie algebra 84
quasi-Hopf algebra 130-1, 529
quasitriangular 531
triangular 531
quasi-Hopf QUE algebra 534-7
quasitriangular 536
quasi-Lie bialgebra 536
quasi-modular Hopf algebra 521
quasi-Poisson—Lie group 48
quasi-quantum Yang-Baxter
equation 531
QUE algebra 176, 187-92
coboundary 188
cocommutative 187-8
quasitriangular 188
rational form 280—1
triangular 188
QUE double 190, 266-7, 270
QUE dual 190, 267, 268-70
quiver 307, 488-90
rational form 280-1
adjoint 281
and R-matrices 327-9
simply-connected 281
real form 117-9
compact 431
equivalent 117
650
General index
reconstruction theorem 147-9
reduced decomposition 565
adapted 488
regular dominant weight 433
regular isotopy 500, 512
Reidemeister moves 496-7
representation
adjoint 110
and symplectic leaves 180, 439,
442, 454
characters 315
completely reducible 391
corresponding to a Schubert cell
435, 441, 448
cyclic 344-8
dual 110-1
faithful 438-9
highest weight 314, 324, 433
integrable 314, 492, 556, 566
physical 158
pseudo-highest weight 396
regular 110
restricted 359
tame 415
tensor products 110
trivial 110
type 314, 394, 401
unitarizable 433
unitary 118, 329-31, 433
¦-representation 433, 437-9, 441-2
representative functions 106, 116
restricted enveloping algebra 304,
360
restricted integral form 296-7
basis 298
generators and relations 299-300
of a representation 316
restricted representation 359
restricted specialization 300
and affine Lie algebras 360-1
centre 300
representations 351-61
ribbon Hopf algebra 125-7, 133,
161, 276, 517
central elements 168-9
ribbon tangle 146-7, 502
closure 164—5
coloured 147
directed 146-7
isotopy invariants 161-6
right dual 111, 122
rigidity theorems 176-7, 212
Robinson-Schensted
correspondence 478
root 563
root space 564
root vector 259, 282, 565
rotation number 501
Schouten bracket 17
Schubert cell 41, 435, 441, 448
segment 402
short exact sequence 137
simple object 137
simple reflection 564
simple root 563
sink 488
six vertex model 252-3
rational 252
trigonometric 253
skein invariant 498
skein relation 497
Sklyanin bracket 60
smooth vector 552
soliton equations 32
source 484
sphere braid group 538
state 246
strange algebra 220, 230-2
Steinberg's theorem 359
string 389-90, 482
length 482
surgery 503
Sweedler's example 131—3
symmetric algebra 107—8
symmetrizable 562
symplectic groupoid 48
symplectic manifold 15, 18, 184
symplectic leaves 18-21, 296, 444
and dressing transformations 38
and representations 180, 439,
442, 444, 454
in compact Poisson-Lie groups
39-43, 227
General index
651
in Poisson homogeneous spaces
38
multiplicative properties 274
uniqueness 275
Tait number 499
tame representation 415
tangles 144
isotopy invariants of 167-8
Tannaka-Krein duality 116, 135,
147
Temperley-Lieb algebra 333, 335
tensor product theorem 357-9
tilting modules 361-72
and quantum dimension 365-6
Toda system 75-7
topologically generated 196
topological quantum field theory
160-1
transfer matrix 248—9
triangular module 342
trigonometric solutions of the
CYBE 91-4
trivial deformation 171
truncated tensor product 160,
368-71
twisting 129-31, 183-4, 439, 532,
536, 537
and group cohomology 534
of a quasitensor category 559-60
type
of a C*-algebra 442, 454
of a representation 314, 394, 401
universal enveloping algebra" 107,
112-3
universal R-matrix 123, 129-31,
201, 263-6, 271-5, 283-4,
327, 531
at a root of unity 303-4
vacuum representation 158
Vassiliev invariants 526
Verma module 314, 320-1, 356,
435, 566
Verma's identity 487
vertex model 246-7, 510-4
and link invariants 512-4
integrable 250
Virasoro algebra 31, 64-7, 556
weight 314, 353, 383, 566
Weyl character formula 317, 325,
355, 357, 361
Weyl filtration 362
Weyl group 564
Weyl module 354-6, 362
quantum dimension of 365
Whitehead's lemma 188, 212
writhe 499
XXX model 252-3, 422
XYZ model 253
Yangians 30, 375-80
and infinite-dimensional groups
414-7
automorphisms 380-1, 384
centre 381
finite-dimensional representations
383-91
infinite 416-7
PBW basis 382
pseudotriangular structure 385,
391, 418-23
Zelevinsky tensor product 407—8