Текст
А. И. ЛУРЬЕ
АНАЛИТИЧЕСКАЯ
МЕХАНИКА
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЬЕ
МОСКВА 1961
12-5-4
Лурье Анатолий Исаакович.
Аналитическая механика.
Редактор Д. Р. Меркин.
Техн редактор К Ф. Брудно. Корректор Л. О. Сеиеико.
Сдано в рабор 24/XI 1960 г. Подписано к печати 26/V 1961 г. Бумага 60х92/,„. Физ. печ. л. 51.5.
Условн печ. л 51,5. Уч.-изд. л. 49,9 Тираж 18 000 экз. Т-03162. Цена книги 2 р. 70 к.
Заказ 2072.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой УПП Ленсовнархоза.
Ленинград, Измайловский пр., 29.
ОГЛАВЛЕНИЕ
Предисловие 9
Глава 1. Основные определения И
1. 1. Связи П
1. 2. Обобщенные координаты 13
1. 3. Обобщенные скорости и ускорения 17
1. 4. Избыточные координаты 20
1. 5. Квазискорости и квазикоординаты 22
1. 6. Виртуальные перемещения 26
1. 7. О переставимости операций d и о («правило db — Ыь) ... 29
1. 8. Вариации квазикоординат 32
1. 9. Некоторые свойства трехиндексных символов 33
1.10. Вычисление трехиндексных символов для двускатной те-
тележки 35
Глава 2. Кинематика твердого тела. Основные сведения
40
2. 1. Определение положения твердого тела 40
2. 2. Преобразование координат 43
2 3. Эйлеровы углы 44
2. 4. Самолетные и корабельные оси 47
2. 5. Применение умножения матриц к составлению таблиц коси-
косинусов ; . 53
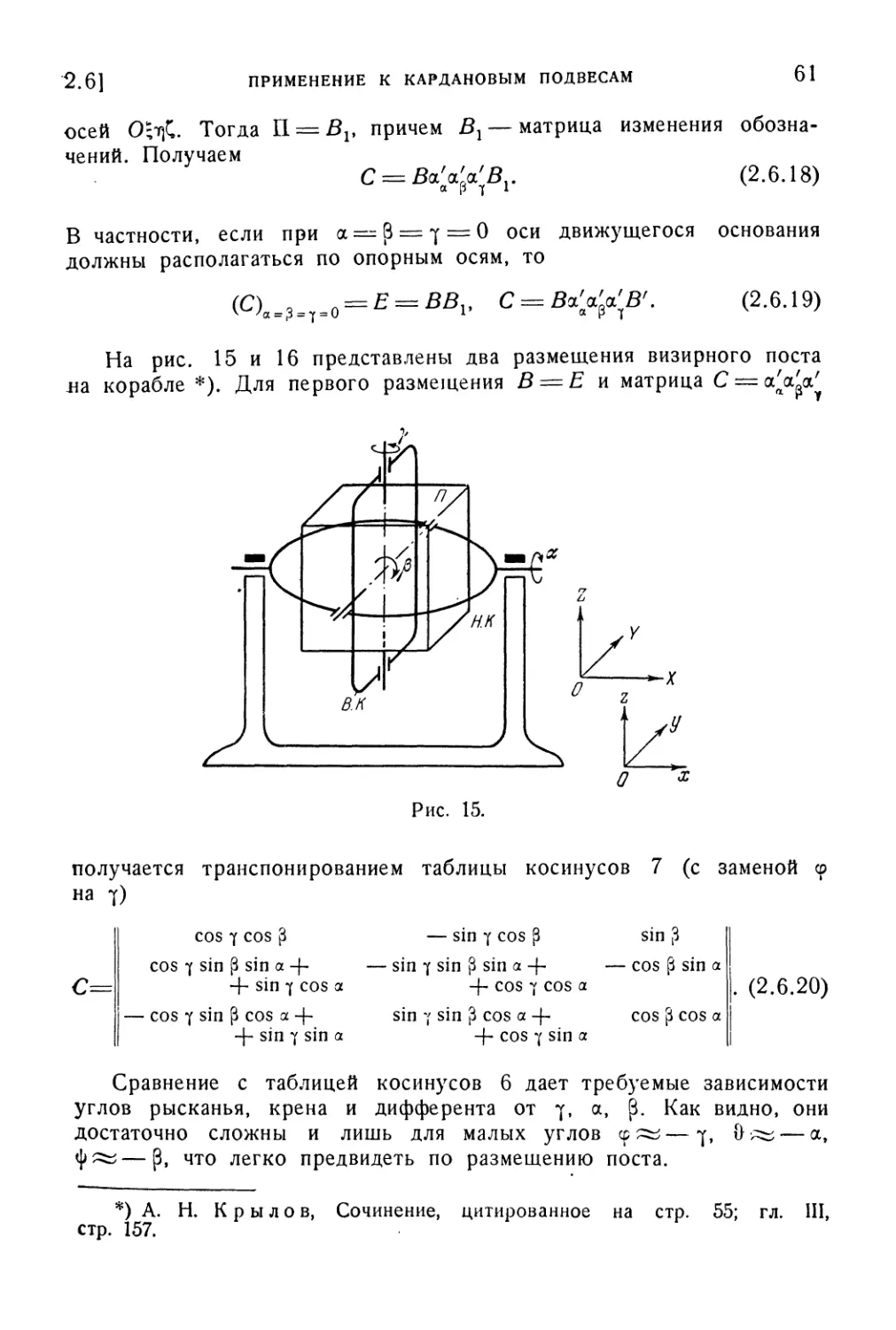
2. 6. Применение к кардановым подвесам 55
2. 7 Распределение скоростей в твердом теле 63
2. 8. Вектор бесконечно малого поворота 65
2. 9. Выражение вектора угловой скорости через производные
эйлеровых углов 66
2.10. Применение к вычислению трехиндексных символов .... 68
2.11. Распределение ускорений в твердом теле 74
2.12. Матричная запись формул распределения скоростей и уско-
ускорений в твердом теле 75
2.13. Дифференцирование вектора в подвижной системе осей . . 79
2.14. Относительное движение 80
2.15. Абсолютное ускорение точки, движущейся по вращающейся
Земле 82
4 ОГЛАВЛЕНИЕ
2.16. Катание тела по неподвижной плоскости 85
2.17. Сложение движений твердого тела 93
2.18. Движение натурального триэдра пространственной кривой . 96
Глава 3. Теория конечных поворотов твердого тела 10Э
3. 1. Формула Родрига и вектор конечного поворота 100
3. 2. Параметры Родрига — Гамильтона 103
3. 3. Сложение конечных поворотов 105
3. 4. Вычитание конечных поворотов ПО
3. 5. Переставимые конечные повороты 111
3. 6. Выражение конечного поворота и параметров Родрига — Га-
Гамильтона через эйлеровы углы . . . 112
3. 7. Приложения формул конечного поворота 114
3. 8. Выражение вектора угловой скорости через конечный пово-
поворот 118
3. 9. Параметры Кейли — Клейна 121
ЗЛО. Выражение угловой скорости тела через параметры Кейли —
Клейна 126
3.11. Определение положения твердого тела по угловой скорости 127
3.12. Уравнение Дарбу 130
3.13. Пример. Определение положения твердого тела при самовоз-
самовозбуждении 133
Глава 4. Основные динамические величины : . . . . 137
4. 1. Кинетическая энергия системы 137
4. 2. Союзное выражение кинетической энергии 141
4. 3. Тензор инерции 143
4. 4. Преобразование тензора инерции 147
4. 5. Главные оси инерции 150
4. 6. Эллипсоид инерции 153
4. 7. Кинетическая энергия твердого тела 156
4. 8. Главный вектор и главный момент количеств движения твер-
твердого тела 158
4. 9. Кинетическая энергия системы при относительном движении 160
4.10. Энергия ускорений • 162
4.11. Энергия ускорений твердого тела 166
4.12. Примеры вычисления кинетической энергии системы тел . . 169
4.13. Примеры вычисления кинетической энергии и энергии уско-
ускорений при наличии неголономных связей 179
Глава 5. Работа и потенциальная энергия 188
5. 1. Обобщенные силы 188
5. 2. Элементарная работа сил, действующих на твердое тело . . 190
5. 3. Потенциальная энергия 193
5. 4. Силы, линейно зависящие от координат 199
5. 5. Потенциальная энергия сил тяготения 201
ОГЛАВЛЕНИЕ О
5. 6. Фигура Земли' 205
5. 7. Силы упругости 211
5. 8. Вычисление потенциальной энергии стержневых систем . . 215
5. 9. Потенциальная энергия изогнутого, скрученного и сжатоге
стержня 221
5.10. Мощность 231
5.11. Диссипативная функция 232
5.12. Примеры вычисления диссипативной функции 235
5.13. Силы сопротивления воздуха 243
Глава 6. Общее уравнение динамики. Аналитическая статика . . 248
6. 1. Уравнения Лагранжа первого рода 248
6. 2. Идеальные связи 252
6. 3. Общее уравнение динамики и центральное уравнение Ла-
Лагранжа 253
6. 4. Преобразование центрального уравнения Лагранжа .... 256
6. 5. Равновесие системы материальных точек 259
6. 6. Примеры на уравнения равновесия и определение реакций
связей 263
Глава 7. Дифференциальные уравнения Лагранжа 282
7. 1. Вывод дифференциальных уравнений Лагранжа второго рода 282
7. 2. Интеграл энергии 285
7. 3. Структура уравнений Лагранжа 288
7. 4. Явная форма уравнений Лагранжа 289
7. 5. Геометрическое истолкование движения материальной точки 291
7. 6. Движение материальной точки по поверхности ....... 295
7. 7. Примеры 297
7. 8. Геометрическая интерпретация уравнений движения системы 304
7. 9. Примеры на составление уравнений Лагранжа 307
7.10. Определение и исключение множителей связей 319
7.11. Примеры 321
7.12. Обобщенные реакции отбрасываемых связей 327
7.13. Геометрическое истолкование обобщенных реакций связей . 331
7.14. Применение к плоским стержневым системам 333
7.15. Циклические координаты 344
7.16. Функция Рауса 347
7.17. Структура функции Рауса 350
7.18. Примеры 355
7.19. Квазициклические координаты 364
Глава 8. Другие формы дифференциальных уравнений движения 368
8.1. Дифференциальные уравнения Эйлера — Лагранжа 368
8.2. Примеры составления уравнений движения неголономных
систем 372
б ОГЛАВЛЕНИЕ
8. 3. Катание без скольжения твердого тела по неподвижной пло-
плоскости 379
8. 4. Случай тела, ограниченного поверхностью вращения .... 385
8. 5. Дифференциальные уравнения Аппеля 392
8. 6. Уравнения Аппеля в квазискоростях . 395
8. 7. Явная форма уравнений Аппеля. Уравнения Чаплыгина . . . 398-
8. 8. Применение к не! олономным системам 402
8. 9. Явная форма уравнений Эйлера — Лагранжа 411
8.10. Уравнения движения свободного твердого тела 413
8.11. Уравнения движения вращающегося снаряда 420
Глава 9. Динамика относительного движения 42<>
9. 1. Дифференциальные уравнения движения несущего тела . . 425
9. 2. Дифференциальные уравнения относительного движения
носимых тел 433
9. 3. Относительное равновесие 436
9. 4. Равновесие вращающегося гибкого вала 439
9. 5. Относительное равновесие гироскопа в кардановом подвесе
на движущейся платформе 445
9. 6. Относительное движение твердых тел 451
9. 7. Примеры 459
9. 8. Уравнения движения твердого тела с полостью, заполнен-
заполненной жидкостью 468-
9. 9. Уравнения движения деформируемого тела 474
9.10. Колебания вращающегося стержня 482
9.11. Уравнения движения ракеты 488
9.12. Гироскопическая платформа 492
Глава 10. Канонические уравнения и теорема Якоби 49Э-
10. 1. Преобразование Лежандра 499
10. 2. Канонические уравнения движения 502
10. 3. Явная форма канонических уравнений 507
10. 4. Примеры составления канонических уравнений 50&
10. 5. Скобки Пуассона и скобки Лагранжа 512
10. 6. Теорема Пуассона 516
10. 7. Канонические преобразования 518
10. 8. Производящие функции 521
10. 9. Инвариантность канонических переменных 525
10.10. Примеры канонических преобразований 527
10.11. Канонические уравнения относительного движения .... 529
10.12. Каноническое преобразование и процесс движения .... 532
10.13. Теорема Якоби 535
10.14. Разделимость переменных в уравнении Якоби — Гамильтона.
Теорема Штеккеля , , 541
10.15. Кеплерово движение 551
ОГЛАВЛЕНИЕ I
Глава И. Теория возмущений 560
11. 1. Метод вариации постоянных 560
11. 2. Канонические уравнения возмущенного движения 563
11. 3. Движение материальной точки в поле силы тяжести вра-
вращающейся Земли 565
11. 4. Движение материальной точки в среде с сопротивлением . 572
11. 5. Влияние малых возмущений на колебания системы около
положения равновесия 574
11. 6. Влияние неуравновешенности на движение волчка 589
11. 7. Вращение искусственного спутника Земли вокруг центра
инерции 585
И. 8. Уравнения возмущенного кеплерова движения 595
11. 9. Возмущенное движение центра инерции искусственного
спутника Земли 599
11.10. Уравнения в вариациях. 605
11.11. Об интегрировании уравнений в вариациях 609
11.12. Уравнения возмущенного движения материальной точки . . 611
11.13. Возмущенное кеплерово движение по круговой орбите . . 616
11.14. Уравнения возмущенного движения материальной си-
системы .... 622
11.15. Системы с двумя степенями свободы 626
11.16. Системы с тремя степенями свободы 630
11.17. Установившиеся невозмущенные движения 633
11.18. Примеры 635
Глава 12. Вариационные принципы механики 642
12. 1. Действие по Гамильтону 642
12. 2. Принцип Гамильтона — Остроградского 644
12. 3. О характере экстремума действия по Гамильтону . .* . . . 649
12. 4. Применение принципа Гамильтона — Остроградского к не-
голономным системам 665
12. 5. Уравнения движения распределенных систем 672
12. 6. Приближенное определение частот и форм свободных ко-
колебаний 688
12. 7. Примеры приближенного расчета частот и форм свобод-
свободных колебаний 697
12. 8. Главная функция Гамильтона 702
12. 9. Асинхронное варьирование 707
12.10. Принцип стационарного действия Лагранжа 709
12.11. Принцип стационарного действия в форме Якоби 712
12.12. Метрика элемента действия и метрика кинематического
элемента 715
12.13. Возмущение траекторий 721
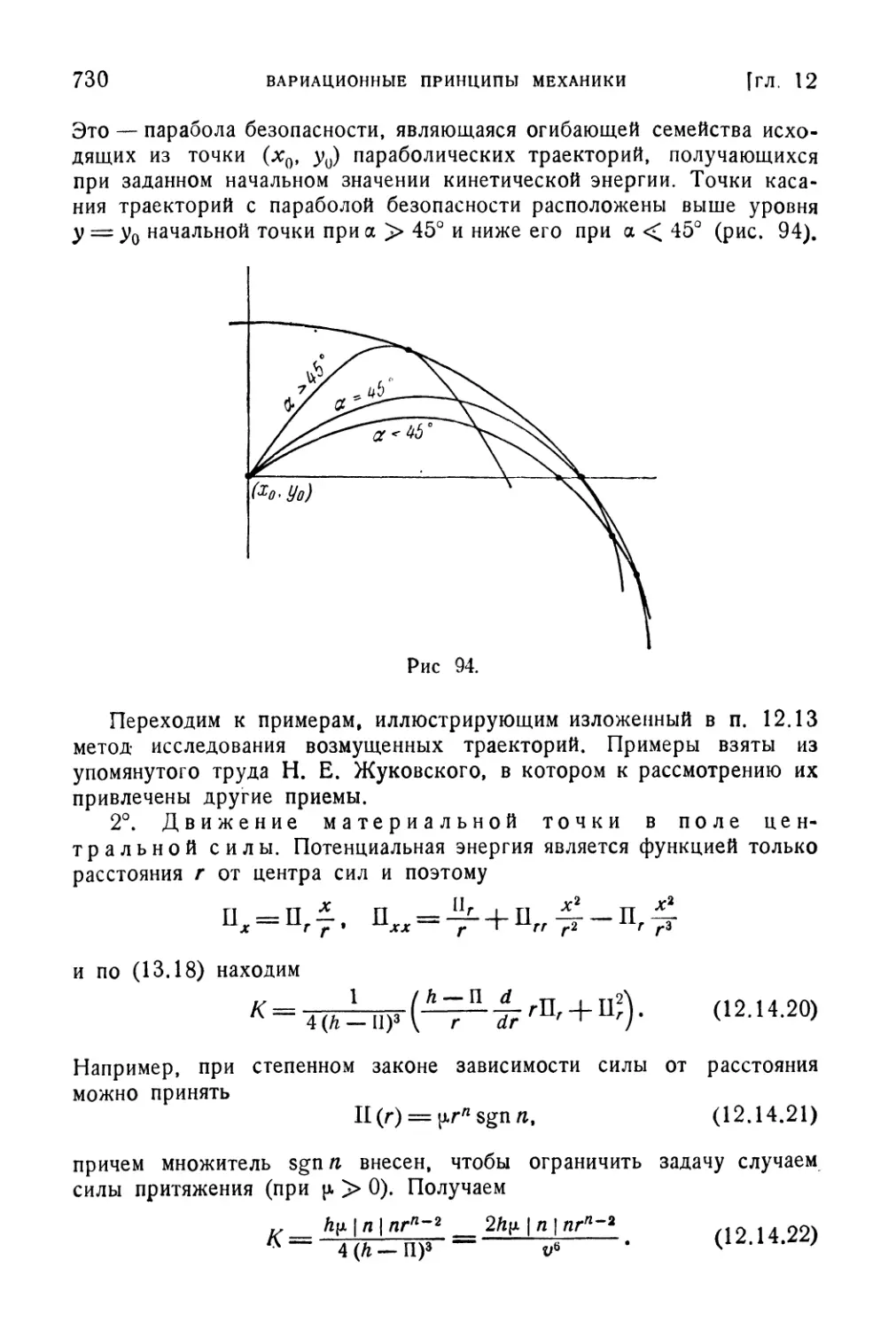
12.14. Примеры 726
8 ОГЛАВЛЕНИЕ
12.15. Вращение вблизи вертикали тяжелого твердого тела с не-
неравными моментами инерции 734
12.16. Характеристическая функция Гамильтона 738
12.17. О характере экстремума действия по Лагранжу 748
Приложение 1. Элементарные сведения из теории матриц ... 755
П. 1. 1. Определения 755
П. 1. 2. Действия над матрицами 760
П. 1. 3. Обращение матриц 768
П. 1. 4. Матричное представление операций векторной алгебры . 775
П. 1. 5. Дифференцирование матрицы 776
Приложение 2. Сведения из тензорного анализа 778
П. 2. 1. Косоугольные координаты 778
П. 2. 2. Векторы в косоугольных координатах , . 781
П. 2. 3. Тензоры второго ранга в косоугольных координатах . . . 782
П. 2. 4. Криволинейные координаты точки 784
П. 2. 5. Ковариантное дифференцирование 787
П. 2. 6. Пример неортогональных криволинейных координат . . . 790
П. 2. 7. Формулы теории поверхностей 791
П. 2. 8. Кривизна линий на поверхности 795
П. 2. 9. Ковариантная производная вектора на поверхности . . . 797
П, 2.10. Ортогональные криволинейные координаты 800
П. 2.11. Евклидово пространство конечного числа измерений . . 805
П. 2.12. Риманово пространство п измерений 808
П. 2.13. Риманово подпространство Rn в евклидовом Ет . . . . 811
П. 2.14. Тензор Римана — Кристоффеля 817
Именной указатель 820
Предметный указатель 821
ПРЕДИСЛОВИЕ
По сложившейся традиции в курсы аналитической механики вклю-
включают общие уравнения движения голономных и неголономных систем,
вариационные принципы, теорию канонических преобразований, кано-
канонические уравнения с теорией интегрирования их (теорема Гамиль-
Гамильтона — Якоби), интегральные инварианты, теорию последнего множи-
множителя и т. п.; основные законы механики считаются известными и не
подвергаются обсуждению.
В настоящей книге из этого комплекса вопросов рассмотрены те,
которые, по нашему мнению, наиболее близки к инженерным задачам.
Применение методов аналитической механики к решению нетри-
нетривиальных задач требует уже при составлении уравнений подробных
сведений по вопросам, на которых, как правило, останавливаются
весьма кратко. В связи с этим в книге значительное внимание уде-
уделено способам введения обобщенных координат, теории конечных
поворотов, методам вычисления кинетической энергии и энергии уско-
ускорений, потенциальной энергии сил различной природы, рассмотрению
сил сопротивления. После этих вводных глав, имеющих в известной
степени и самостоятельное значение, рассмотрены методы составле-
составления дифференциальных уравнений движения голономных и неголоном-
неголономных систем в различных формах, причем обсуждаются вопросы их
взаимной связи; подробно рассмотрены вопросы определения реакций
связей и некоторые задачи аналитической статики. Мы считали полез-
полезным привести геометрическое рассмотрение движения материальной
системы, как движение изображающей точки в римановом простран-
пространстве; этот материал нашел, далее, применение в задачах теории возму-
возмущений. Специальная глава отведена динамике относительного движе-
движения, к которому приводятся многочисленные прикладные задачи. Далее
рассмотрены канонические уравнения, канонические преобразования
и вопросы интегрирования. Значительное место уделено теории воз-
возмущений и ее разнообразным применениям. Последняя глава посвя-
посвящена принципу Гамильтона—Остроградского, принципу наименьшего
действия Лагранжа и теории возмущений траекторий.
Общие методы поясняются примерами, некоторые из которых,
по нашему мнению, сами по себе не лишены интереса. К последним
10 ПРЕДИСЛОВИЕ
можно отнести задачу о движении твердых тел на движущемся осно-
основании, движение твердого тела с полостью, заполненной жидкостью,
задачу о движении ракеты, применение принципа Гамильтона—Остро-
Гамильтона—Остроградского к системам с распределенными массами и т. п. Специально
рассмотрены вопросы, связанные с возмущенным движением искус-
искусственного спутника Земли.
Приведенные в книге примеры подтверждают важность методов
аналитической механики для самых различных приложений; показать
это являлось одной из целей, которую ставил перед собой автор
книги. При рассмотрении примеров на первый план выдвигалась
постановка задачи и составление уравнений движения; интегрирова-
интегрированию их и исследованию результатов уделено меньше места.
Для облегчения чтения книга снабжена приложениями, в которых
читатель может найти краткие сведения из теории матриц и тензор-
тензорного исчисления.
В подстрочных "примечаниях отмечены относящиеся к предмету
изложения основные литературные источники (составление исчерпы-
исчерпывающего списка таких источников не входило в задачу автора).
Некоторую часть книги составляет содержание лекций по анали-
аналитической механике и теории колебаний, которые автор свыше двух
десятков лет читает для механических специальностей физико-меха-
физико-механического факультета Ленинградского политехнического института
им. М. И. Калинина. Но. книга не согласована с программными тре-
требованиями и не предназначена быть учебником для высшей школы.
Однако автор позволяет себе выразить надежду, что книга окажется
не бесполезной для учащейся молодежи и научных работников в мно-
многочисленных областях техники.
Проф. Д. Р. Меркин, любезно взявший на себя труд редакти-
редактирования книги, дал автору большое число ценных указаний и сове-
советов. Большую помощь при оформлении рукописи и рисунков оказали
А. К. Гибянская и К. А. Лурье. Выполняя приятный долг, автор
приносит этим лицам глубокую благодарность.
ГЛАВА 1
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
1.1. Связи
Материальная система рассматривается в динамике как собрание
материальных точек. Приспособления, осуществляющие зависимости
между величинами, определяющими положение и скорости точек
системы, называются связями. Наличие связей обусловливает выполне-
выполнение этих зависимостей при движении системы, каковы бы ни были
действующие на систему силы и начальные условия ее движения.
Так, собрание материальных точек, остающихся на неизменных
расстояниях друг от друга, что можно мыслить обеспечивающимся
с помощью лишенных массы нерастяжимых стерженьков, соединяю-
соединяющих эти точки, является подчиненной связям системой. Такова модель
абсолютно твердого тела в динамике *). При отсутствии связей система
материальных точек называется свободной. Примерами служат солнеч-
солнечная система (солнце и планеты рассматриваются как материальные
точки), упругое тело, сжимаемая жидкость.
Положение точки Mt системы определяется координатами этой
точки в инерциальной декартовой системе осей Oxyz**). Вектор -ра-
-радиус OMt обозначается через rv Индекс / принимает значения
1, 2, ..., N, причем TV обозначает число точек в системе.
Простейший и наиболее важный класс представляют позиционные
связи; они осуществляют зависимости между координатами то'чек
системы и аналитически выражаются соотношениями вида
/»(*!• УГ ZX XN' Уг gN> 0 = ° <'=1- •••• ')• 0-1.1)***)
*) Термин «абсолютно твердое тело» в дальнейшем заменяется на
«твердое тело».
**) Если не оговорено противное, то координатный триэдр считается
ортогональным.
***) В нумерации формул первое число указывает главу, второе — пара-
параграф этой главы, третье — номер формулы в параграфе. При ссылках на
формулу в данном параграфе указывается только последнее число; формула
другого параграфа той же главы помечается вторым и третьим числами;
номер воспроизводится полностью при ссылке на формулу другой главы.
12
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
[ГЛ. I
называемыми уравнениями связей. Через г обозначено число уравнений
связей. Конечно, r^,3N, причем равенству соответствовало бы дви-
движение системы по заранее предписанному закону во времени.
Точка М, закрепленная в конце нити длиной /, второй конец
которой закреплен в начале координат, подчинена связи
Р— (
выражающей, что расстояние точки М от начала координат не пре-
превосходит /. Связи подобного рода, называемые неудерживающими
(или односторонними), аналитически задаются неравенствами. В даль-
дальнейшем рассматриваются удерживающие (двусторонние) связи, зада-
задаваемые равенствами.
Позиционные связи называются также голономными\ система,
все связи которой голономны, называется голономной. Неголономные
(или кинематические) связи выражают зависимости между скоростями
точек системы, не сводящиеся к зависимостям между ее координа-
координатами. Классическим примером системы, подчиненной неголономным
связям, является твердое тело, принужденное катиться по поверх-
поверхности, не допускающей проскальзывания по ней тела в точке кон-
контакта. Мы ограничимся рассмотрением неголономных связей, линей-
линейных относительно проекций скоростей точек системы. Уравнения
таких связей имеют вид
N
2 (alhkk
bikyk
cikik
A.1.2)
причем величины aik, blk, cik, gt зависят от координат точек и вре-
времени t. Эквивалентной B) является форма записи
N
2
(aikdxk
i
ik
dyk + cikdz.k)-\-gldt =
A.1.3)
Равенство этого вида выражает неголономную связь, если оно неин-
тегрируемо, т. е. не сводится к конечному соотношению вида A).
Если соблюдены условия
4k dais
fix*
dbi
ik
dt
dt
dzs
_ dCjs
dt
dgi
A.1.4)
для всех k и s, пробегающих значения 1, ..., TV при фиксирован-
фиксированном /, то i-e уравнение C) интегрируемо, так как в этом случае
I 2] ОБОБЩЕННЫЕ КООРДИНАТЫ 13
всем равенствам D) можно удовлетворить, положив
п — dfi h — dfl r — dfi о- — dfi (\ 1 Ъ
а—Щ ь*-^ С*—Щ g^~f AЛ5)
где f^—функция координат и времени; уравнение C) при таких
условиях выражает, что полный дифференциал dft равен нулю,
т. е. ft сохраняет постоянное значение Ct. Соотношение
/.(*,, yv zv .... xN, yN, zN; t)-Ct = O A.1.6)
' в этом случае служит уравнением голономной связи. Заметим, что
условия D) являются достаточными, но отнюдь не необходимыми
условиями интегрируемости; их несоблюдение еще не указывает на
неинтегрируемость /-го уравнения связи (возможно существование
интегрирующего множителя) *).
Голономные связи называются стационарными или склероном-
ними, если время t не входит в их уравнения A). Им противопо-
противопоставляются зависящие от времени нестационарные, или реономные
связи. Неголономная связь склерономна, если коэффициенты aik, blk%
clk в уравнениях B) не зависят явно от времени, а ^. = 0. В про-
противном случае (при gt Ф 0) она считается реономной, так как t вхо-
входит в запись уравнения C) через dt, и в том случае, когда все коэф-
коэффициенты aik, bik, cik, gt не зависят от t явно. Целесообразность
такой классификации неголономных связей следует уже из того, что
в частном случае, когда выполняются условия D) и уравнение него-
лономной связи интегрируемо, gt будет отличной от нуля постоянной
и конечное соотношение F) приобретет вид
//(*,. Уг *i xn- Уд,. *N)-St-Ci = 0, A.1.7)
т. е. представит реономную голономную связь.
1.2. Обобщенные координаты
Для укорочения последующих записей условимся о следующем
обозначении координат:
v 3v2 yv 3vl v 3v ( ) ()
Тогда уравнения позиционных связей A.1) представятся в виде
/*(?, w 0=° (f- = 1 r)- (L2-2>
Предполагается, что эти уравнения независимы, т. е. что функции
/j, . . ., /г не связаны соотношением вида
/,) = 0. A.2.3)
*) О необходимых и достаточных условиях интегрируемости см*
Ш. Ж. де ла В а л л е-П у с с е н, Курс анализа бесконечно-малых, II, § 311,
ГТТИ. 1933. *
14
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
[ГЛ. 1
Это значит, что ранг якобиевой матрицы*) (П. 1.1.7)
pfx dfr
~W
%3/V
dfr
•злг
A.2.4)
в области определения переменных Si, . . ., £злг и при любом / должен
быть равен г (дефект матрицы D) равен нулю). Пусть, например,
отличен от нуля якобиан
J--=
A.2.5)
Тогда система уравнений B) будет разрешима относительно Elt . . ., <г;
они могут быть выражены через остальные 3N — г координат
£/ч ь .... £злг и время t. Получим соотношения вида
Е* = ЕлEг+ь .... feyv; 0 (ft =1, .... г). A.2.6)
в которых координаты £г+ь ..., £3уу независимы друг от друга.
Их число п = ЗА/ — г, если система голономна (т. е. неголономных
связей нет), называется числом степеней свободы системы. Соотноше-
Соотношения F) определяют остающиеся координаты !;,, ..., 1Г через незави-
независимые. При наличии также и неголономных связей числом степеней
свободы системы называют разность п — г' между числом независимых
параметров, определяющих конфигурацию системы, и числом уравне-
уравнений неголономных связей.
Описанный способ введения независимых координат, как правило,
не является пригодным для приложений. Нет нужды пользоваться
декартовыми координатами Sr + ь ..., ^ как независимыми; можно
вместо них ввести в рассмотрение любые другие независимые вели-
величины <7ь ..-, Qn = Q3N-n в их совокупности определяющие конфи-
конфигурацию системы. Это могут быть как расстояния, так и углы, гаус-
гауссовы координаты точки на поверхности, площади и другие величины,
в числе которых могут быть и такие, которые лишены непосредст-
непосредственного геометрического истолкования. Важно лишь, что введение
этих величин должно допускать установление соотношений
0
A.2.7)
*) Основные определения и действия теории матриц изложены в При-
Приложении 1. Ссылки на формулы приложений содержат букву П перед номе-
номером Например, (П. 1.2.2) указывает на вторую формулу второго параграфа
первого Приложения.
1.21
ОБОБЩЕННЫЕ КООРДИНАТЫ
15
определяющих через них независимые декартовы координаты. Эти
соотношения должны удовлетворять условию необращения в нуль
якобиана
dqx
dqx
Ф0.
A.2.8)
выражающему независимость величин %r+k и разрешимость уравне-
уравнений G) относительно qv . .., qn.
Теперь выражения G) можно подставить в правые части уравне-
уравнений F), в результате декартовы координаты всех точек системы
окажутся выраженными через величины qv . . ., qn, называемые обоб-
обобщенными координатами, и через время t. Возвратившись к перво-
первоначальным обозначениям, можно теперь написать
xl = xl(ql
qn\ t)t
qn; t\
gn; t)
или короче
t=l, .... N),
qn; t).
A.2.9)
A.2.10)
Если связи стационарны, то можно так распорядиться выбором
обобщенных координат, т. е. соотношений G), чтобы время t не вошло
в уравнения (9). В последующем, говоря о стационарных связях,
мы предполагаем, что такой выбор координат произведен; поэтому
соотношение A0) в случае стационарных связей будет записываться
в виде
»-, = »•,(?,. .... <?„) (/=1 N). A.2.11)
где, напомним, rt обозначает вектор-радиус точки Мь по отношению
к началу инерциальной системы координат.
Исключив из 3N уравнений (9) обобщенные координаты, придем
к 3iV — п уравнениям позиционных связей. Исключение возможно,
поскольку дефект якобиевой матрицы
Dl
A.2.12)
согласно (8) равен нулю.
Нельзя утверждать, что связи нестационарны, если t входит явно
в уравнения (9), поскольку форма этих уравнений связана с выбором
обобщенных координат. Если исключение этих координат из ура-
уравнений (9) приводит к таким соотношениям между декартовыми
16 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ fГЛ. 1
координатами (в инерциальной системе), в которые t явно не вхо-
входит, то связи стационарны, в противном случае — нестационарны.
Сказанное можно пояснить простым примером. Рассмотрим криво-
кривошип ОМ длиной г, вращающийся в плоскости Оху вокруг непо-
неподвижного шарнира О. За обобщенную координату выберем угол ф
между этим кривошипом и прямой,-вращающейся с постоянной угло-
угловой скоростью со вокруг той же точки. Тогда декартовы координаты
конца М кривошипа будут
х = г cos (со^ + ф), у = г sin (at 4~ ф).
Уравнение связи, выражающее постоянство длины кривошипа, будет
Оно получено исключением ф из выражений декартовых координат
и не содержит t, т. е. связь, как это было очевидно, стационарна.
Это подтверждается также тем, что если за обобщенную координату
принять угол ср = ш£-|-ф кривошипа с осью Ох, то t не войдет
в уравнения, связывающие декартовы и обобщенные координаты, т. е.
эти уравнения будут иметь вид A1).
Вышеописанная процедура введения обобщенных координат не
должна воспроизводиться при рассмотрении частных задач. Нет нужды
обычно и в составлении уравнений позиционных связей. Следует,
руководствуясь природой задачи, с самого начала задаться обобщен-
обобщенными координатами в числе, необходимом и достаточном для опре-
определения • конфигурации механической системы. Соотношения вида (9)
составляются, если в том есть надобность, с помощью геометрических
или иных соображений.
Объектом рассмотрения в аналитической механике являются мате-
материальная точка, система конечного числа свободных (в небесной
механике) или подчиненных связям материальных точек, одно или
несколько связанных друг с другом твердых тел. Геометрическая
конфигурация таких систем задается конечным числом обобщенных
координат. Распространение уравнений и методов аналитической меха-
пики оказывается возможным на некоторый класс электрических и
электромеханических систем, поведение которых может быть описано
конечным числом геометрических величин и величин зарядов на про-
проводниках; те и другие в их совокупности принимаются за обобщен-
обобщенные координаты системы.
В предмет аналитической механики обычно не включается рас-
рассмотрение систем, состояние которых не может быть строго описано
заданием конечного числа параметров. Таковы задачи механики
сплошной среды. Они могут быть введены в рамки методов аналити-
аналитической механики, если представляется возможность с достаточным
приближением ограничиться конечным числом параметров. Например,
1.3]
ОБОБЩЕННЫЕ СКОРОСТИ И УСКОРЕНИЯ
17
ч}юрма оси упругого стержня в положении равновесия или при коле-
колебаниях около этого положения строго задается лишь счетным мно-
множеством *) коэффициентов тригонометрического ряда, которым пред-
представляется уравнение этой кривой; с помощью конечного числа
коэффициентов может быть описано поведение динамической системы,
приближенно заменяющей этот упругий стержень. Эти коэффициенты
и принимаются за обобщенные координаты.
1.3. Обобщенные скорости и ускорения
Производные по времени обобщенных координат называются
обобщенными скоростями и обозначаются qv . . ., qn. Вообще точка
над буквой служит знаком дифференцирования по времени; например,
если задана функция обобщенных координат и времени
= /(?,
то / обозначает величину
?„;').
0.3.1)
Последнее слагаемое представляет производную по явно входящей
в функции A) букве t.
Вектор скорости vt точки Mt> как известно, представляет про-
проП
изводную по времени вектор-радиуса
используя B.10), получим
.,=2
дг1
rt этой точки. Поэтому,
дг*
В случае стационарных связей выражение rt может быть взято
в виде B.11); тогда последнее слагаемое в C) отпадает, вектор vt
становится однородной линейной формой обобщенных скоростей qs
A.3-4)
Важным следствием формул B) и C) являются часто исполь-
используемые далее зависимости
dqs dqs dqs dqs
*) Множество называется счетным, если элементы его могут быть зану-
занумерованы числами натурального ряда 1, 2, ...
2 Зак. 2072. А. И. Лурье
18 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. I
В дальнейшем мы будем иногда рассматривать вектор
5 = 1
который условимся называть виртуальной скоростью. Это — ско-
скорость, вычисленная в предположении, что t в выражении B.10)
зафиксировано, т. е. связи как бы мгновенно остановлены. Конечно»
в случае стационарных связей нет нужды вводить эту величину.
Заметим, что, условившись обозначать
можно выражение вектора скорости C) записать в виде
5 = 1
Это замечание позволяет сокращать записи соотношений, относящихся
к нестационарным связям, и распространять на них результаты, по-
получаемые для стационарных связей.
Вторые производные обобщенных координат по времени назы-
называются обобщенными ускорениями qv ..., qn. Вектор ускорения
точки wt получим, дифференцируя по времени выражение C) вектора
скорости:
dqsdt 4s~^ dt2 ' v1-^-^
5=1
Это же выражение получаем сразу дифференцированием соотноше-
соотношения (8)
л + 1 п 11 пf1
5 = 1 k = l 5-1 R *
Легко проверяются также используемые ниже равенства
J__drL__d_^rL_dvL
dt dqs ~ dqs dt ~ dqs '
Действительно, из равенства B) имеем
dt dqs ~ £l dq.dq 4k~^ dtdqs '
1.3] ОБОБЩЕННЫЕ СКОРОСТИ И УСКОРЕНИЯ
а, с другой стороны, по C)
)п tin *k I
19
dq$df
откуда и следуют соотношения A1). Конечно, подобные же равенства
имеют место для любой функции обобщенных координат и времени.
В заключение выразим через обобщенные скорости уравнения A.2)
неголономных связей. Замечая, что
п п п
dqs / '
= 0 (/=!.....0. 0.3.12)
5 = 1
получим соотношения вида
n N
Qs ^ yaik $qs "T" ik fiqs \ cik
k = \
N
которые при обозначениях
N
B; =
dqs j'
Принимают вид
или, в другой форме записи,
Связь является интегрируемой при соблюдении условий
A.3.13)
A.3.14)
A.3.15)
dqk — dqs ' d/ — d^ * (У.бЛЬ)
В случае стационарной неголономной связи коэффициенты Bls
не зависят от времени явно, а 5^ = 0.
При рассмотрении частных задач уравнения неголономных связей
составляются сразу через обобщенные скорости, т. е. в форме A4).
2*
20
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
[ГЛ. I
1.4. Избыточные координаты
В некоторых задачах оказывается целесообразным задавать конфи-
конфигурацию механической системы параметрами qv . .., qn, ..., qn+m>
взятыми в числе, превосходящем необходимое п. Тогда т из этих
п-\-т параметров называются избыточными обобщенными коорди-
координатами. Конечно, между п-\-т параметрами qx Яп+т суще-
существуют т соотношений, которые могут содержать и время
Яп
= 0 (*=1.
т).
A.4.1)
Эти соотношения, представляющие обобщенные уравнения связей,
должны быть разрешимы относительно т из т-\-п величин qs, т. е.
дефект якобиевой матрицы
дЯп
A.4.2)
должен быть нулем. Так, если отличен от нуля якобиан
П
¥=0,
A.4.3)
то из уравнений A) избыточные координаты qn+v ..., qn+m
быть определены через qv . . ., qn и время t
О —- п (п п • f\ ([ | ffi} (| А 4Л
Выражения декартовых координат через обобщенные будут иметь вид
0.
0
A-4.5)
Подстановка сюда значений избыточных координат D) приведет
к форме B.9) этих соотношений, но последняя часто будет гораздо
более сложной, чем E). Например, конфигурация двукривошипнога
механизма (рис. 1) определяется заданием одного угла срх; но при
введении еще двух углов ср2 и ср3 выражения декартовых координат
1.4]
ИЗБЫТОЧНЫЕ КООРДИНАТЫ
21
точки С на шатуне станут весьма простыми
х = ах cos срj + с cos ср2, у = ах sin срх —j— ^r sin cp2.
Уравнения связей A) также легко составить
F х — ах cos cpj -(- а2 cos cp2 -f- а3 cos ср3 — d = 0,
F2 = ах sin cpj -f~ a2 sin cp2 — a3 sin cp3 = 0,
A.4.7)
но исключение ср2 из выражений F), т. е. переход к соотношениям
вида B.9), привело бы к громоздким формулам.
.Более общим является пример твердого тела, имеющего непо-
неподвижную точку *). Его положение может 0ыть задано таблицей девяти
косинусов aik углов, составляемых осями, связанными с телом, с осями,
неизменного направления. Уравне-
Уравнениями связей служат шесть хо-
хорошо известных соотношений, три
из которых выражают равенство
единице суммы квадратов косину-
косинусов углов каждой из трех связанных
с телом (подвижных) осей с не-
неподвижными осями, а три других—
условия взаимной ортогонально-
ортогональности подвижных осей. Выражения
координат любой точки тела в не-
неподвижных осях через косинусы aik
более компактны, чем формулы,
которые мы получили бы, заменив косинусы через эйлеровы углы,
являющиеся тремя независимыми параметрами, определяющими по-
положение тела. Отметим еще, что последнее может быть задано
также с помощью четырех параметров Родрига (см. C.2.9)), выра-
выражаемых через эйлеровы углы по формулам C.6.6). Уравнением
связи A) здесь служит соотношение C.2.7). Выражения координат
точек твердого тела через эти параметры более симметричны, чем
через эйлеровы углы.
Рассмотрение избыточных координат позволяет дать постановку
задач динамики, при которой необходимость введения декартовой
координатной системы отступает на второй план: конфигурация опре-
определяется п-\-т параметрами qv ..., qn+m> система подчинена т
Рис. 1.
*) Здесь и в дальнейшем предполагается знакомство читателя с основ-
основными положениями кинематики твердого тела в объеме, не превосходящем
сведений, сообщаемых в общих курсах теоретической механики, например,
в книге «Курс теоретической механики» Л. Г. Лойцянского и А. И. Лурье
(ч- 1,в Гостехиздат, 1955). Краткая сводка этих сведений дается в главе 2.
В ней, а также в главе 3 излагаются и более специальные вопросы кине-
кинематики.
2 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
голономным и гг неголономным связям, уравнения которых соответ-
соответственно будут:
\ A.4.8)
2
5=1
Число степеней свободы равно п — г\
1.5. Квазискорости и квазикоординаты
Кон фигурация системы задается п независимыми параметрами
<7], . ... <7„; при определении скоростей ее точек в большом числе
задач предпочтительно пользоваться не непосредственно обобщенными
скоростями qv . . ., qn% а некоторыми линейными их формами с коэф-
коэффициентами, зависящими от обобщенных координат
®s = as\4\ + ••• +азпЯп E=1, .... л). A.5.1 )
Число этих формул считаем равным п\ если бы их было пг < п, то
за формы о)л»4 ь . . ., о)л можно было бы просто принять <7rtr + b • • •» 9Г^«
Величины («5 называются квазискоростями. Примером могут
служить проекции Wj, (o2, (о3 вектора угловой скорости тела со на
связанные с телом оси Ox'y'z' или проекции на эти же оси вектора
скорости <v0 полюса 0. За обобщенные координаты qv . .«., qe сво-
свободного твердого тела могут быть приняты координаты полюса х0,
yQ, zQ в неподвижной системе осей Oxyz и эйлеровы углы, а обоб-
обобщенными скоростями являются производные этих величин по времени.
Выражения через них указанных квазискоростей имеют вид
ш1 = ^ cos ср —|— ф sin ^ sin ср,
оJ = — 9 sin ср-j-isin 9 cos ср, \ A.5.2)
0K = cp-|-tyCOSu J
и соответственно
V0x' = X0a
A.5.3)
где aik — косинусы углов осей Ox'y'z' с неподвижными осями (на-
(например, а23—косинус угла оси Оуг с Oz), которые должны быть
выражены через эйлеровы углы по формулам, приведенным в таб-
таблице 2 п. 2.3. Через квазискорости весьма просто выражаются иногда
1.5)
КВАЗИСКОРОСТИ И КВАЗИКООРДИНАТЫ
23
другие величины, например, проекции скорости любой точки тела
на оси Ox'y'z' представляются следующими формулами:
= Vox'
vy> =
VZ' =
A.5.4)
где х\ у'', zf — координаты точки по отношению к этим осям,
остающиеся, конечно, неизменными при движении тела. Из сказан-
сказанного видно, сколь громоздкие выражения приняли бы формулы D)
при записи их через обобщенные скорости. Точно так же выражения
важнейших динамических величин, как кинетическая энергия твердого
тела и проекции его главного момента количеств движения, простые
и наглядные при записи их через квазискорости, становятся трудно-
труднообозримыми, если квазискорости заменить их выражениями через
обобщенные скорости.
Содержание рассматриваемой частной задачи подсказывает, какие
линейные формы обобщенных скоростей следует выбрать в качестве
квазискоростей. При наличии неголономных связей полезно в число
квазискоростей внести линейные формы обобщенных скоростей, обра-
обращающиеся в нуль в силу самих уравнений этих связей. Иными
словами, если последние имеют вид
^i<7i + • • • +ctsnqn = 0 E=1 г'),
A.5.5)
то при обозначении A) уравнения неголономных связей будут иметь
вид
оM = 0 E=1, ..., г'). A.5.C)
Принимается, что матрица -коэффициентов ask форм
11 ... а\п
а =
... ап
A.5.7)
— невырожденная, т. е. что ее определитель \а\ отличен от нуля;
тогда уравнения A) разрешимы относительно обобщенных скоростей
Матрица
Ъ = \
является обратной а, т. е.
соя (г=1, ..., п).
и ... *1Л
... ^
A.5.8)
A.5 9)
A.5.10)
'24 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
где Е — единичная матрица; иными словами, обозначая через bsr сим-
.вол Кронекера
имеем
2А ^ 2)
Предполагается, что соотношения A) неинтегрируемы; напомним,
что если говорить об s-й квазискорости, то случай интегрируемости
будет иметь место при соблюдении условий
dasr_ ( k=l } A.5.13)
Несоблюдение этих условий, как уже говорилось, не указывает на
то, что правая часть выражения о>5 не может быть проинтегрирована.
Наряду с A) рассмотрим линейные формы дифференциалов обоб-
обобщенных координат
di:s = asldql^r ... + asndgn E=1, . ... п). A.5.14)
Величины dizs называются дифференциалами квазикоординат; по-
поскольку соотношения A) неинтегрируемы, величины izs как функ-
функции координат не существуют. Например, Wj dt представляет про-
проекцию на ось Ох' вектора бесконечно малого поворота 6 твердого
тела-, но нет такого угла, дифференциал которого был был равен Ьх>
(исключая тривиальный случай вращения тела вокруг оси, неподвиж-
неподвижной в теле и в пространстве). Однако чисто условное введение
обозначений тг5 и именование этих символов квазикоординатами не
лишено смысла, так как позволяет сократить записи с|орм;л и сло-
словесные формулировки. Мы условимся обозначать
причем нулик (вместо точки) над буквой ks напоминает, что идет
речь об условно введенных обозначениях, а не о дифференцировании
по времени величин тг5. Если выражения A), или A4) интегрируемы,
то мы придем к соотношениям вида
^5 = ^(^1. •' " Яп) E=1, .... Л),
указывает лишь на переход к новым обобщенным координатам.
л 1.5]
квазискорости и квазикоординаты
25*
Пусть cp(<7j qn) — функция обобщенных координат. Выраже-
Выражение ее полного дифференциала с помощью (8) и A4) может быть
представлено в виде
Г=1
T-\
A.5.16)
Здесь принято условное, но естественное обозначение
для коэффициента при dizs в выражении г/ср; это «частная произ-
производная ф по квазикоординате тг5».
В частности,
через квазискорости
■%. 0-5.19)
/=1
Это позволяет представить вектор скорости
в виде
п п
>-/° , дг,
Отсюда следуют еще соотношения, аналогичные C.5):
dvt * dri
A.5.20)
Соотношения, обратные A7) и A8), понадобятся ниже. Они имеют
вид
п п
дЧг
До сих пор за квазискорости принимались линейные однородные
формы обобщенных скоростей, коэффициенты которых зависели от
обобщенных координат. Более общим будет определение квазиско-
квазискоростей с помощью линейных соотношений
a)* = *si?i+ ••• -\-*sJin + as.n+i (s=l, .... л), A.5.22)
содержащих также свободные члены aSt л+1; при этом ask могут еще
явно зависеть от времени. Нет нужды здесь повторять сказанное^
26 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
ранее, достаточно использовать обозначение C.7) и дополнить B2)
еще одной строкой
%+i = Qn+i = 1 («„+,, г = К^,гУ О.5.23)
Придем к выражениям
п+1
<»,= 2!я,*?* E=1,..., /i + l), A.5.24)
и приведенные выше формулы сохранят свой вид, если заменить
в них п на п-\- 1.
Соотношения, обратные B4), имеют вид
п л + 1
?г= 2 *r*(°>* —e*.»+i) = S *г*ю* (г^1 «). A-5.25)
где обозначено
1.6. Виртуальные перемещения
Обобщенные координаты <7i» •••• Qn представляют функции вре-
времени, определяемые интегрированием при заданных начальных усло-
условиях дифференциальных уравнений движения, выражающих законы
механики. Этой совокупностью функций времени
?i@. •■..?„(') 0.6.1)
определяется истинное движение системы. Дифференциалы dqs обоб-
обобщенных координат представляют их бесконечно малые изменения
в истинном движении, пропорциональные промежутку времени dt
dqs='qsdt. A.6.2)
При формулировании общих положений механики оказывается
полезным ввести в рассмотрение бесконечно малые величины иной при-
природы. Совокупность величин A) определяет в фиксированный мо-
момент времени t конфигурацию системы. Отвлекаясь от движения,
зададимся вопросом, какое множество конфигураций в этот момент
времени допускают связи системы. Если ограничиться рассмотрением
конфигураций бесконечно близких к истинным и через bqv ..., bqn
обозначить бесконечно малые приращения обобщенных координат,
называемые их вариациями, то упомянутое множество определится
совокупностью величин
q\ = qn it) + bqn< A.6.3)
1.6] ВИРТУАЛЬНЫЕ ПЕРЕМЕЩЕНИЯ 27"
где в случае голономной системы вариации bqk совершенно произ-
произвольны. Мы можем сказать, что в момент t связи такой системы,
имеющей п степеней свободы, допускают со" конфигураций.
При наличии неголономных связей, задаваемых уравнениями
п
^askdqk + asdt==^ (s=\ г'). A.6.4)
вариации bqk связаны rr условиями
2«Л = 0. A.6.5)
так как, поскольку t фиксируется, следует в D) принять Ы = 0. Связи
этой системы с п —г' степенями свободы допускают оол-гГ конфи-
конфигураций.
Рассмотрим точку системы Mt, задаваемую вектор-радиусом rv
Изменение гь за промежуток времени dt определяется дифферен-
дифференциалом
^s + ^dt, A.6.6)
s-\
представляющим бесконечно малое перемещение точки Mi в истин-
истинном движении системы. Ему противопоставляется виртуальное или
возможное перемещение точки Mit обозначаемое or,.. Этот беско-
бесконечно малый вектор представляет изменение вектор-радиуса точки
при мысленном переведении системы из рассматриваемой конфигура-
конфигурации в одну из (оол или оо/1~г') допускаемых связями бесконечно
близких конфигураций; он (бесконечно малый вектор Ьг^ вычисляется
в фиксированный момент t с точностью до первых степеней относи-
относительно вариаций bqk:
A.6.7)-
Если связи не зависят от времени, то в выражениях F) и в урав-
уравнениях неголономных связей D) отпадают последние слагаемые.
Дифференциалы drt связаны теми же соотношениями E), что и ва-
вариации brit и истинное перемещение
принадлежит множеству виртуальных или возможных перемещений.
В случае же нестационарных связей сравнение выражений F) и G),.
^28 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
а также D) и E) показывает, что drt не принадлежит этому множе-
множеству. Недостаток терминологии (из нее следует, что «истинное пере-
перемещение невозможно») устраняется, если отбросить наименование
«возможный» *). Мы в дальнейшем считаем термины «виртуальный»
и «возможный» синонимами, так как второй достаточно хорошо
передает содержание французского слова virtuel**).
Сказанное о вектор-радиусе распространяется на любую функ-
функцию обобщенных координат и времени 9(<7i» •••» Qn> *)• Дифферен-
Дифференциал ее — это приращение функции в процессе движения за проме-
промежуток времени dt\
а вариация
— бесконечно малое изменение, обусловленное переходом в фикси-
фиксированный момент времени к бесконечно близкой конфигурации си-
системы.
Дифференциалы квазикоординат были определены соотношени-
соотношениями E.14); при более общем задании квазискоростей E.22) эти фор-
формулы примут вид
Заменив в них dqk на bqk и полагая при t фиксированном Ы = О,
получаем выражения вариаций квазикоординат
Ъп3 = asl bq} -f- ... -\-asnbqn (s = 1 ri). A.6.12)
Обратные формулы будут
bqr = bn Bttj 4- . . . 4- bTn Ъъп (r=\ ..., n). A.6.13)
Выражение виртуального перемещения через вариации квазикоорди-
квазикоординат имеет.вид
/г = 1
*) Некоторые авторы (Г. К. Суслов, Теоретическая механика,
§ 169, Гостехиздат, 1944) вводят в рассмотрение три неравнозначных друг
другу термина: истинное, возможное и виртуальное перемещения.
**) Е. Л. Николаи (Теоретическая механика, ч. II, седьмое издание,
§ 53, ГОНТИ, 1939) и А. И. Некрасов (Курс теоретической механики, ч. 2,
§ 112, Гостехиздат, 1953) пользуются термином «возможный». В посмертном
девятом издании книги Е. Л. Николаи A951), вышедшем под редакцией
Н. Д. Моисеева, применено слоео < виртуальный».
1.7] О ПЕРЕСТАВИМОСТИ ОПЕРАЦИЙ й( И 8 («ПРАВИЛО d% = bd») 29
где «частные производные rt по квазикоординатам» были определены
выше формулами E.18).
Рассмотренный в этом параграфе способ варьирования, заключаю-
заключающийся в сравнении конфигураций системы, допускаемых связями,
в фиксированный момент времени t> называется синхронным варьиро-
яанием. Можно рассмотреть более общую операцию асинхронного
варьирования, когда истинная конфигурация в момент / сравнивается
•с бесконечно близкой, допускаемой связями в момент t-\-bt, отлич-
отличный от t.
1.7. О переставимости операций d и 8* («правило db = bd»)
В дальнейшем мы будем считать вариации bqs дифференцируемыми
.функциями времени t. Тогда, дифференцируя выражение F.7) вир-
виртуального перемещения, получим
5=1
«С другой стороны, варьируя выражение C.3) вектора скорости,
найдем
#=1 5=1 5=1 5=1
Составив разность этих выражений, придем к соотношению
п
$rty - 8», = 2 -щ; №*У - ЧЬ A-7.3)
5 = 1
«ли в дифференциальной форме
fy A.7.4)
5 = 1
Теперь рассмотрим траекторию Ct точки Mi в ее истинном дви-
движении. Отметим положения Мь и Mft этой точки в моменты t и
* (рис. 2). Тогда, называя через rt вектор-радиус точки Mit
30
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
[ГЛ. 1
будем иметь MiM'i = dri и вектор-радиус точки М\ будет равен
ri + dri- Далее отметим положения М* и А1'* точки в варьирован-
варьированных конфигурациях системы, отнесенных к тем же моментам вре-
времени; эти точки М\ и Mf* находим с помощью операции варьиро-
м;
Рис. 2.
вания 8 вектор-радиусов соответствующих им точек истинной траек-
траектории. Поэтому
A1LM^ = brit
Вектор-радиус точки М*, по сказанному, равен ^-f-8rt.. При
построении вариационных принципов механики и использовании
методов вариационного исчисления существенно необходимо рассмат-
рассматривать совокупность варьированных положений Ж!, М'? и т. д. как
новую варьированную траекторию С*. Учитывая, что положению М*.
отвечает момент времени t, а Ж'.*—момент t-\-dt и предполагая
дифференцируемость векторов-радиусов точек варьированной траек-
траектории, имеем
Щг lrt) = drt
Теперь, учитывая очевидное равенство
dr-t -f- br i
получаем
или
Теперь по D) получим
п
\-dbrlt
(*=1 Ю-
A.7.5)
1.7] О ПЕРЕСТАВИМОСТИ ОПЕРАЦИЙ flf И 8 («ПРАВИЛО db = bd») 31
Проектируя эти векторные соотношения на оси и пользуясь обозна-
обозначением B.1) декартовых координат, можем написать также
Вспоминая, что дефект якобиевой матрицы B.12) равен нулю, заклю-
заключаем, что система уравнений G) не имеет отличных от нуля реше-
решений относительно разностей dbqs — bdqs. Итак, следствием соотно-
соотношений E) являются равенства
dbqs — bdqs = O (s=\, .... п). A.7.8)
Обратно из (8) следуют соотношения E).
Формулы (8), или в иной записи
(bqs)'—bqs = O E=1, .... я), A.7.9)
выражают переставимость действий дифференцирования и варьиро-
варьирования— правило «db = bd». Оно упрощает выводы теорем механики,
сокращая промежуточные выкладки. Его применение неизбежно
в вариационном исчислении, чем, по мнению Гамеля, объясняется
многократное использование этого правила в «Аналитической меха-
механике» Лагранжа.
Равенство db = bd является следствием принятых правил варьи-
варьирования, и можно ввести другие правила, при которых это равенство
яе будет иметь места. Так как уравнения движения не должны зави-
зависеть от того или иного правила варьирования, то можно заранее
предвидеть, что разности d bqs — 8 dqs выпадут из этих уравнений.
3 этом мы ниже будем не раз иметь случай убедиться. Вместе
с тем вывод правила основывался на введении варьированной траек-
траектории, т. е. на не вызываемом необходимостью расширении понятия
виртуального перемещения.
При использовании правила (9) соотношение C) принимает вид
(brt) =bvt. A.7.10)
Пусть далее <f(qv .... qn\ t)— функция обобщенных координат и
времени. Повторив вычисление, проделанное для вектор-радиуса,
Получим подобно C)
^^-Ьд51 A.7.11)
5 = 1
применив правило (9),
A.7.12)
32 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
1.8. Вариации квазикоординат
Перейдем теперь к вычислению разностей (Втс^)* — Scd5, в которых
вариации квазикоординат определены по F.12), а квазискорости
по E.1). Коэффициенты ask считаем не зависящими явно от t. Имеем
п п
(8*,)' = ^ (a3k bqj = 2 ask (bqj J
ft = l £ = 1 /f = l Г=1
и далее
A.8.1)
Во второй сумме обобщенные скорости qr и вариации обобщен-
обобщенных . координат заменим через квазискорости и вариации квазикоор-
квазикоординат, воспользовавшись формулами E.8) и соответственно F.13).
Получим
п п п п
да
ft-l г-
Для упрощения этой записи введем в рассмотрение трехиндексные
символы Больцмана
*.*.«=! «)■ 0.8.2)
Тогда выражения A) примут вид
г п
Т. ^) V^ (!) Q/j£ A.8.3)
k = \ ~" " " t=l m=l tm t m*
причем первая сумма отпадает, если используется «правило db = Ы».
В этом выводе предположено, что квазискорости были опре-
определены однородными линейными формами обобщенных скоростей,
а коэффициенты ask не зависят от времени явно. При более общем
определении E.22) следует заменить в формулах C) и B) число п
1.9] НЕКОТОРЫЕ СВОЙСТВА ТРЕХИНДЕКСНЫХ СИМВОЛОВ 33
на п-\-\\ вспомним при этом E.23) — E.26) и учтем соотношения
Получаем
/2 + 1 п + \ /2+1
„ = 2 в,* W Ы 22
k=\ t-\ /72
= 2 «.* [(8^)' - S?ft] 4- S 2 й,«, 8тст + 2 ^ ^„. A-8.4)
/г = 1 / = 1 m = l m=l
где по B)
/2+1 /2 + 1
t jL± jLA \ да dqh I r'r
k = \ r=\ v r k '
km
. d.8.5)
При этом нетрудно также проверить, что трехиндексные символы
в соотношениях D) могут быть вычислены по формулам B). Дей-
Действительно, имеем
/2-fl /2 + 1
Urn
V
/I
V / fas, /2 + 1 E^lhXh h I ( daS, П + l
h
1 Л
Учитывая E.26), возвращаемся к формулам B).
1.9. Некоторые свойства трехиндексных символов
Значения трехиндексных символов ^*т зависят лишь от принятого
определения квазискоростей через обобщенные скорости, но не от
структуры и движения механической системы. Если, в частности,
для данного s выполнены условия интегрируемости E.13), то из (8.2)
следует, что все трехиндексные символы обращаются в нуль. Этого
и следовало ожидать, так как тогда tzs становится функцией обоб-
обобщенных координат, а со5 ее производной по времени.
Матрицы
Ти • • • Tin
v5 Vs
J/2l *ПП
3 Зак. 2072. А. И. Лурье
34 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
кососимметричны. Действительно, по (8.2)
а11 dask
dq dq
k=\ r=i x r * ' r=i k=i
и сравнение с (8.2) дает
Vt = — T/ (s, тш t=l. .... п). A.9.2)
В частности,
1^ = 0 (s, f=l, .... я). A.9.3)
He считая равных нулю диагональных элементов матрицы, для
каждого 5 подлежат вычислению -^п{п— 1) трехиндексных символов.
Общее число их равно -^-п2(п—1). Вычисление громоздко, если
непосредственно пользоваться формулами (8.2). В каждом частном
случае следует предпочесть воспроизводить ход вывода формул (8.3)
и определять f*m как коэффициенты при произведениях ^8тгт в раз-
разности (8т:5)' — 8оM. Нет нужды в .этом вычислении отказываться от
пользования правилом db = bd, так как значения трехиндексных сим-
символов ничем не связаны с этим правилом.
Выражения трехиндексных символов можно преобразовать к виду,
отличному от (8.2). Дифференцируя соотношения E.12), имеем
п п п п
С dasr u V _ dbrt
\} daSk . vi dbkm У dasr , >П
2л ~do7 °km ~ ~ Ad a*k ~do7 * ал ~Ш7 °rt — — 2л as*
dqr иь™~ AJ"sk dqr * АЛ dqb rt~~ АЛ ^r dq '
k=\ k=l r=\ R r=l R
и подстановка в (8.2) дает
п п
A.9.4)
Это выражение трехиндексных символов используется для соста-
составления выражений разностей «вторых производных по квазикоорди-
квазикоординатам» от функции cp(#lf ..., qn\ t). По определению E.17) имеем
п п п п
dbrk -
h ** 1 h
srk dg dq "+" °
^ dKk — Za u* ~d^Zj ur« d^r —^л La \u^rk s^d^ -r "ts sfi- -dfj •
Теперь, учитывая E.21), получаем
n n n n n
d2f ^T1 V^ и l. ^2cp V^ ду \Г^ ^f и dbrk
dKs д-Kk ^ Zu ts rk dqt dqr ' ^ dnm AA AA ts dqt mr
ВЫЧИСЛЕНИЕ ТРЕХИНДЕКСНЫХ СИМВОЛОВ 35
dbrs
J±_h s \
dqt °tk dqt )amr>
откуда по D) приходим к искомым соотношениям
1^щ ~ <*** а«, — 2л
-я.
Отметим еще важный для приложений частный случай: пусть
в рассмотрение введено пь квазискоростей
*з=аа\Я\+ ••• +азтЯт (S = l т)> С1'9'6)
причем коэффициенты^ зависят от qv . . ., qm, но не от qm+v . . ., qn.
Для симметрии полагаем
*m+j = km+j С/=1. >-•> П — т). A.9.7)
Тогда все трехиндексные символы
1*q (s. t, q=l9 .... т) A.9.8)
определятся формулами (8.2), в которых суммирование ведется от 1
до т. Все остальные символы (в которых один из индексов s, t, q
превосходит т) будут равны нулю.
1.10. Вычисление трехиндексных символов
для двускатной тележки*)
На рис. 3 показан вид в плане двускатной тележки. Конфигура-
Конфигурация ее задается восьмью параметрами — координатами х, у шар-
шарнира В, углами 0 и % и углами поворота колес cplf cp2» Тз» ?4- Если
считать, что между дорогой и колесами нет проскальзывания, то
система будет иметь шесть неголономных связей; две из них выра-
выражают отсутствие боковых составляющих скоростей точек А и В,
четыре—отсутствие скоростей точек соприкасания колес с доро-
дорогой. Система имеет две степени свободы.
Уравнения неголономных связей запишем в соответствии с E.6)
в форме
<о1 = 0, оJ = 0, <o3 = 0f <о4 = 0. о>5 = 0, со6 = 0, A.10.1)
*) R. S t и с к 1 е г, Ober die Berechnung der an rollenden Fahrzcugen
Wirkenden Haftreibungen, Ingenieur-Archiv, 1955, 23, № 4, стр. 279—28/.
36
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
[ГЛ. 1
причем выражения этих квазискоростей имеют вид:
«1 = —xsin(» + x) + ycos(»+Z). A.10.2)
ш2 = —xsinft -f-ycosft — /ft, A.10.3)
<o3 = icos&-|-ysin» —aft — r,cplf A.10.4)
oL = xcos ft+y sinft+aft — rxy2% A.10.5)
A.10.6)
A.10.7)
Уравнения B) и (З) представляют записи выражений (равных нулю)
составляющих скоростей точек ЗиЛ вдоль осей соответствующих
колесных скатов; слагаемые -
х cos ft -\- у sin ft — aft, x cos ft ~\- у sin ft -|- a^
в уравнениях D) и E) равны скоростям центров колес / и 2, а сами
эти уравнения выражают условия обращения в нуль скоростей точек
|/
Рис. 3.
этих колес, соприкасающихся с дорогой. Аналогичное значение для
колес 3 и 4' имеют уравнения F) и G); в них слагаемые
представляют скорости центров колес 3 и 4.
Вводим еще в рассмотрение квазискорости
8 х
первая из которых равна скорости шарнира В.
Принимая нумерацию
A.10.8)
A.10.9)
= 1. 2, 3, 4), A.10.10)
f#l0] ВЫЧИСЛЕНИЕ ТРЕХИНДЕКСНЫХ СИМВОЛОВ 37
Представим матрицу коэффициентов ask в виде
a =
— sin (d + x
— sin 0
cos %
cos &
COS(& + X)
cos (v —J- x)
COS (v —|— x)
0
) cos(S + x)
COS %
sin %
sin»
sin (& + x)
sin (ft + Z)
sin (ft + x)
0
0
— /
— a
a
— с
с
0
0
0
0
0
0
— с
с
0
1
0
0
— г,
0
0
0
0
0
0
0
0
— г,
0
0
0
0
0
0
0
0
~г2
0
0
0
0
0
0
0
0
— Г 2
0
0
A.10
.11)
Матрицу b = a l построим, непосредственно решив уравнения
B—8) относительно обобщенных скоростей, что не представляет
труда вследствие простоты структуры этой системы. Сначала по B)
и (8) находим
х = — «Isin(ft + x)+aOcos(ft + x),
A.10.12)
у = a)! cos ((ft + x) + <o7 sin (ft + x),
после чего определяются
7^*Л' A.10.13)
— х sin ft -\-у cos 8 = o)j cosx "h0^ s*n X- 1
Теперь по C) находим ft, a no D) и E) обобщенные скорости с^,
<р2. Наконец, по F), G), (8), (9), зная 8, определяем ср3> ср4. Резуль-
Результат представлен матрицей A4)
-sin(O+yJ 0 0 0 0 0 (cosi>+-x) 0
cos(& + y) 0 0 0 0 0 sin(x> + x) 0
— cosx -у 0 0 0 0 —sin у 0
0 0 0 0 0 0 0 1
0
1
Ь—
—(SinX+TC0SX) 7J "/7 ° 0 0 _^cosy-y sin/)
~L (sin x-f cosx) ~% 0
О 0 JL(cosy + —cosv ) 0
~ г, r,\~i sln Ч ~7Г
.COS/ «oo о -J- J-fi+
A.10.14)
38 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ [ГЛ. 1
При составлении уравнений движения понадобятся, как увидим
ниже, трехиндексные символы с нижними индексами 7, 8. Применив
формулу (9.4), получим
Y* —
ь -
8 8
г=1 г=1
так как все элементы восьмого столбца постоянны, а седьмого зави-
зависят только от $ = qz и х = Яа> лричем Ьгъ==0, £48=1. Получаем
Vis = - asx sin (» + X) 4- as2 cos @ + у) +
H^C0SZ a (sinX + cosx) + ^
и, обратившись к матрице A1), найдем
7*8=1. 7re=sindsin(&+Z) + cos
7^ = — cos ft sin (ft + x) + sin ft cos (ft -f- ^) — y- cos x -
+ sin
и т. д. Получаем
Тк = -Т|7=1. Tf8 = ° (s = 2 8). A.10.15)
Остальные трехиндексные символы вычислим, непосредственно находя
разность фк3У — 8оM. Имеем по A4) и (9)
* = j 0°i cos X — Ш2 4- ^7 sin X). X = Ш8-
Поэтому
(ЪкхУ — Ьпх = — cos(» + х) №Ф +Ь—х(^ 4-h)\ —
— sin (» 4- х) [8у (ft 4- X) — У $ь 4- h)\ =
— — 8те7 [a>8 + j (a)! cos / — «>2 + «>7 sin X)J +
4- a), [(k8 -f- у (Sitj cos x — Щ- biz7 sin x)l
j.10] ВЫЧИСЛЕНИЕ ТРЕХИНДЕКСНЫХ СИМВОЛОВ 39
я так далее. Отличными от нуля оказываются следующие трехин-
дексные символы:
1 cos X 1 yl 1 1 11
1fl7— 171 / * 127 7 / ' 178 187 '
9 1 о 9 / о о O
T71 * 17 / ' 112 * 21 —^" / ' 127 172 /
T12— T21— / • T72— T27— / W —6» V*
k k __ J_ fe ^ sin x k k 1
T12 — T21'— 1 ' T71 — T17 — / • Tsi — Tis — A
(£ = 5, 6, 7, 8).
A.10.16)
Другие примеры вычисления трехиндексных символов, а также
составления уравнений неголономных связей, будут приведены во вто-
второй главе (п. 2.10, п. 2.16).
ГЛАВА 2
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
2.1. Определение положения твердого тела
Твердое тело и системы твердых тел, как выше уже говорилось,
являются важнейшими объектами рассмотрения аналитической меха-
механики. Поэтому представляется полезным кратко перечислить здесь
в нескольких параграфах основные положения и формулы кинематики
твердого тела и более подробно остановиться на некоторых ее спе-
специальных вопросах, обычно не рассматриваемых в общих курсах
механики.
Вместе с инерциальной (неподвижной) системой осей Oxyz в рас-
рассмотрение вводится система подвижных осей Ox'y'z', неизменно
связанных с телом и имеющих начало (полюс) О в произвольно
выбираемой точке тела *). Положение этой системы осей задается
координатами ее полюса л:0, yQt z0 (или вектором-радиусом его rQ = OO)
и таблицей косинусов углов между осями Oxyz и Ox'y'z'.
Таблица косинусов 1
—*х у г
X ОСi ] ОС12 «IЯ
у' «21 «22 «23
2' «31 «32 «33-
Единичные векторы осей системы Oxyz обозначаются через ls>
а осей Ox'y'z' — через i's E=1,2,3). Как видно из таблицы,
*) Для упрощения записи некоторых формул мы будем также пользо-
пользоваться обозначениями Оххх2хъ для инерциальной системы и Ох^х^х^ — для
системы осей, связанных с телом. Когда желательно избежать штрихов
над буквами, для . инерцизльных осей применяются обозначения О^С
(или Оё^з) и Oxyz (или 0*1*2*3) — для осей, связанных с телом.
2.1] ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТВЕРДОГО ТЕЛА 41
to ь представляет проекцию i's на направление ik, т. е.
п /' / с Ъ 19 4 /о 1 h
(точка между векторами означает скалярное умножение).
Отсюда следует, что вектор i'5 может быть представлен следующим
разложением по единичным векторам системы Oxyz:
з
Векторы iv f2, /3 — единичные и взаимно ортогональные (образуют
ортонормированную систему векторов). Применяя обозначение сим-
символа Кронекера, запишем это в форме
Отсюда находим
3 3 3
#/ ., утл ^г\ «> V1
и поскольку тройка векторов irs также ортонормированна, то
2«,Л* = 8,|- Bл-4)
Таковы шесть соотношений, связывающих девять косинусов
таблицы 1. В развернутом виде они записываются так:
аи + а?2 + а?з = 1 • апа21 + а12О22 + а13а23 = О,
а21 + а22 + а23 = ' • °^21а31 Ч- а22а32 + а23аЗЗ = °»
a3i + а12 + азз = 1 • a3iaii + a32ai2 + а33а13 = 0.
B.1.5)
Векторное произведение il X *2 представляет единичный вектор,
перпендикулярный плоскости перемножаемых векторов, направленный
по положительной оси Oz\ иными словами, ix X h = 'з- Запись шести
формул вида
X 'X' = —'3 и т- Д- Bл-6)
Ъюжно сократить, вводя в рассмотрение символ Леви — Чивита €"/тл,
определяемый следующим образом: а) б"/тл = 0, если в числе индек-
индексов /, ту я, принимающих значения из совокупности чисел 1, 2, 0,
имеются одинаковые; б) £^дая=1, если индексы /, т, /г различны и
расположены в порядке 123 или получающемся из него круговой
«орестановкой (т. е. 231, 312); в) €tmn = —l. если в следовании
42 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
различных индексов /, тУ п этот порядок нарушается. Формулы F)
получают вид
hXh = €klJm или im = €mklikXh V^.l)
Очевидно, что
€■«» = ** • (Н X im) = *« • Vm X »ft) = im • (h X *,)•
Такие же формулы могут быть написаны для единичных векто-
векторов ifv *2> *з в предположении, что системы осей Oxyz и Oxfy'z' —
одноименные:
Выражая в последнем соотношении единичные векторы подвижных
осей через iv i2> iz по формулам B), получим
2 rqq rst 2
q = l k — \
т. е. девять формул вида
3 3
2 askatl
1 1
Например,
з
2
«=l
al2 =
или
<х12 = а23а31 — а21а33 = — (а33а21 — а31а23).
Таким образом, в определителе
:П «12 а\
a =
«21 a22 a23
«31 a32 a33
B.1.10)
каждый элемент равен своему алгебраическому дополнению. Так,
элементы первой строки определителя равны проекциям на оси Oxyz
единичного вектора i'y а их алгебраические дополнения проекциям
на те же оси равного ему векторного произведения /2 X iy Отсюда
следует, что
i*i=';-(^x/3)='i-'i=i- B.1-10
Матрица
«=1К11 С *=1. 2. 3) B.1.12)
называется матрицей поворота — точнее, матрицей, осуществляющей
совмещение системы осей Oxyz с системой Ox'y'z' (начала считаются
<2#2] преобразование координат 43
-совпадающими). Из сказанного следует, что эта матрица ортого-
ортогональна: ей обратная совпадает с транспонированной (П. 1.4.)
а~1=а/. B.1.13)
С помощью символа Леви — Чивита векторное произведение двух
векторов а и Ь записывается в виде
aXb=% i>asbSsXir=2 2 *А^гА- С2-1-14)
5=1 Г=1 S=l Г=1
2.2. Преобразование координат
Вектор-радиус ОМ точки М твердого тела в инерциальной системе
осей Oxyz обозначается через г, его проекции на эти оси, т. е.
координаты точки в этой системе — через х, у, z. Через х\ у\ zf
обозначаются остающиеся неизменными при движении тела коорди-
координаты той же точки М по отношению к осям Ox'y'z', связанным
с телом; г' = ОМ — вектор-радиус в этой системе. Таким образом,
г = xix + yi2 + zlb% г' = х% + y'ir2 + г%. B.2.1)
Через г0=ОО обозначается вектор-радиус полюса О. Тогда,
проектируя на оси инерциальной системы очевидное геометрическое
равенство
г = г0 + г' = г0-|- х% + у% + z%, B.2.2)
придем к равенствам вида
г • h = го • h 4- *%' h + У% • 'i 4- г% • /,,
представляющим формулы преобразования координат
B.2.3)
Формулы обратного преобразования найдем, проектируя соотно-
соотношение B) на оси системы Ox'y'z'\ т. е. умножая обе части B)
последовательно на irv i'v i'r Получим
х' = an (х — х0) + a12 (у — yQ) -f- a13 (z — z0),
у = a21 (at — дг0) + a22 (y — y0) -ha23 (z — zQ). B.2.4)
zr = a31 (л: — xQ) + a32 (y — y0) -}- a33 (z — zQ).
Матрицу-столбец с элементами х% у, z обозначим через \% а с эле-
элементами х', у\ zr — через х. Приходится прибегнуть к этому
у = уо + al2x' + a22/
z = z0 + а13
44 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
обозначению, так как штрих в матричных записях обозначает транспо-
транспонирование; £' и х1 представляют матрицы строки из указанных
элементов.
Формулы D) принимают вид
х = а£ — у. B.2.5)
а формулы C) вследствие ортогональности матрицы поворота а будут
5 = ^-1-а'*. B.2.6)
2.3. Эйлеровы углы
В дальнейшем будем говорить о двух положениях твердого тела —
начальном, в котором оси Ox'y'z1', связанные с телом, совпадают
с осями неизменного направления Oxyz (начала О систем осей совпа-
совпадают), и конечном, соответствующем рассматриваемому положению
тела. Переход триэдра осей Oxfyrzr из начального положения в ко-
конечное можна осуществить с помощью трех поворотов, производи-
производимых в определенной последовательности вокруг надлежащим образом
выбранных осей. Углы этих поворотов, называемые эйлеровыми
углами, представляют три независимые величины, через которые могут
быть выражены девять косинусов cx.sk (таблица 1), связанных шестью
соотношениями A.5).
В теоретической механике чаще всего применяется описываемый
ниже способ выбора эйлеровых углов. Условимся раз навсегда поло-
положительным направлением поворота называть поворот, осуществляемый
в правой системе осей (левой системе) против часовой стрелки (по
часовой стрелке) для наблюдателя, смотрящего с положительного
конца оси, вокруг которой производится поворот. Предполагается
также, что, говоря о производимом повороте, мы подразумеваем
поворот, производимый в положительном направлении.
Первый поворот на угол ф, причем 0 ^ ф ^ 2тг, производится
вокруг оси Oz\ после него единичные векторы iv i2, оставаясь в пло-
плоскости Оху, примут направления единичных векторов п и пх% первый
из которых располагается по прямой, называемой ^HJdQ^y3Aoe^jONp
и определяет положительное направление на этой оси (рис. 4). Из
сказанного следуют формулы
п = ix cos ф -f- h sin Ф» n\ — — h sin ф-f-/2 cos Ф- B.3.1)
Второй поворот на угол 0, причем 0<;fr^7c, производится вокруг
линии узлов; векторы пх и /3» к неЙ перпендикулярные, займут поло-
положения nf и i'v причем последний определяет ось Ozf в ее конечном
положении. Имеем по сказанному
п' = пх cos 0 -f ё3 sin », 1'3 = — пх sin » + i3 cos 0. B.3.2)
2/6]
ЭЙЛЕРОВЫ УГЛЫ
45
Плоскость векторов я, п\ перпендикулярная Oz\ представляет
плоскость Ох'у'. Чтобы построить в ней единичные векторы i'v i'2
осей Ох' и Оу', следует совершить еще один поворот на угол ср
(причем 0 <; ср <; 2тг) вокруг оси Oz\ приводящий векторы п и пг
в совпадение с i[, i'Y Имеем
;J = /icoscp-f-/*' sin cp, *2 = — n sin cp-[-/*'cos cp. B.3.3)
Углы ф, ft, cp называются углами прецессии, нутации и чистого
вращения. Пользуясь соотношениями A), B), C), легко составить
Рис. 4.
выражения косинусов углов olsU между осями триэдров Ox'y'z'
и Oxyz. Например,
an — *#i • **! = (л cos <р + п' sin ф) * h =
= (ix cos ф + f2 sin ф) • /j cos cp -f- («! cos & -f- /3 sin 0) • ij sin cp =
= cos ф cos cp -j- /tj • /j cos 0 sin cp = cos ф cos cp — sin ф cos 9 sin cp
и т. д. Таблица косинусов 1 принимает вид таблицы 2.
Таблица косинусов 2
^' cos <p cos ф — sin cp sin ф cos ^ eos cp sin ф + sin cp cos ф cos ^ sin cp sin 0
У' —БИкрсовф — cos cp sin фсов 0 —sin cp sin ф-f cos cp cos ф cos 0 coscpsinu
*' sin 0 sin ф — sin 0 cos ф cos 0
46
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Существенное значение при определении эйлеровых углов имело
построение ортонормированных систем векторов — «полунеподвиж-
«полунеподвижной» пУ nv /3 и «полуподвижной» п, п\ /д. Описанный способ вве-
введения этих углов отнюдь не является единственным, но во всех
разнообразных приемах их определения, применяемых в динамике
самолета, корабля, теории гироскопических устройств, легко разо-
разобраться, руководствуясь следующими общими положениями: -
а) Назначаются основные оси—одна неподвижная, вторая—при-
вторая—принадлежащая телу. Они могут быть одноименными (как в вышерас-
смотренном случае Oz и Ozr) или разноименными (например, Оу
..-/7
Рис. 5.
и Охг). Перпендикулярные основным осям плоскости назовем основ-
основными; в них назначаются отсчетные оси (выше это б#ли 'плоскости
Оху и Ох'у' и оси Ох и Oxf).
б) Вводится в рассмотрение линия пересечения основных плоско-
плоскостей — линия узлов; на ней назначается единичный вектор п. Для
построения этого вектора проще всего, спроектировав подвижную
основную ось на неподвижную основную плоскость, определить по
направлению этой проекции единичный вектор —щ; тогда п будет
направлен по перпендикуляру к^ в неподвижной основной плоскости
так, чтобы триедр я, nv неподвижная основная ось, был одноимен-
одноименным с iv i2, /3.
В подвижной основной плоскости после этого строится единичный век-
вектор п!\ перпендикулярный п\ при этом триедр я, п\ подвижная основная
ось, должен быть одноименным с i'^iy Вектор п' расположится по про-
проекции неподвижной основной оси на подвижную основную плоскость.
в) Тремя углами, определяющими положение системы осей Ox'y'z',
являются: 1) угол между неподвижной и подвижной основными
осями; вместо него может быть взят угол, составляемый векто-
вектором— пх с подвижной основной плоскостью (их сумма равна тс/2),
2.4]
САМОЛЕТНЫЕ И КОРАБЕЛЬНЫЕ ОСИ
47
2) угол отечетной оси в неподвижной основной плоскости с
вектором п (иногда с nv или —пх), 3) угол между векто-
вектором п (иногда nf) и отсчетной осью подвижной основной пло-
плоскости. Отсчет этих углов производится соответственно вокруг п
(или —я), неподвижной основной оси и подвижной основной оси,
причем первому даются значения в промежутке 0, тс или —у, ^-»
а двум другим в промежутке 0, 2тс.
Известным примером применения углов Эйлера в астрономии
являются углы «Q,, /, определяющие положение плоскости орбиты и
угол (о, служащий для задания направления некоторой отсчетной оси
в этой плоскости (рис. 5). Первый из этих углов, <Q> представляет
долготу восходящего узла TV планеты, он играет роль прецессии;
угол /, определяющий наклон плоскости орбиты к отсчетной непо-
неподвижной плоскости О;т], является углом нутации. Угол о) предста-
представляет чистое вращение и, если упомянутая отсчетная ось направлена
к перигею планеты П (ближайшая точка орбиты к притягивающему
центру О), то о) является угловым расстоянием перигея от восходя-
восходящего узла.
2.4. Самолетные и корабельные оси
В динамике самолета оси неизменного направления принято напра-
направлять так: ось Ос, — по предположенной линии курса в плоскости
горизонта, Оч\—по восходя-
восходящей вертикали в точке О,
ось ОС— вправо для наблю-
наблюдателя, смотрящего вдоль О;
(начало О помещается в ме-
месте старта). Ось Ох систе-
системы самолетных осей Oxyz
направлена по строитель-
строительной оси самолета от хвоста
к кабине летчика, пер-
перпендикулярная к ней ось
Оу располагается в плос-
плоскости симметрии самолета
и, наконец, Oz — перпен-
перпендикулярно этой плоскости
(по размаху крыла) впра- Рис. 6.
во для летчика (рис. 6). _
Начало О системы осей О£т]С мыгленно поместим в О. За основ-
основные оси принимаются Оч\ и Ох. Проектируя, как указано в п. 2.3,
Ох на основную плоскость ОС£, строим вектор — пх и расположенный
48
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
в той же плоскости вектор п так, что iv п, пх образуют орто-
нормированный правый триэдр (рис. 7). Вектор nf расположен по
проекции i2 на основную плоскость Oyz; его проще всего разыскать,
построив направление, перпендикулярное к i[ в плоскости основных
осей Ох и От, (в ней же расположен и вектор nj.
Углы ф, ft, 9» называемые углами рысканья, тангажа и крена,
строятся так: ф— угол между О; и —nv отсчитываемый вокруг Oiq,
ср — угол, на который надо повернуть вектор пг вокруг Ох, чтобы
совместить его с Оу; тангаж ft определяется как угол между векто-
векторами — пх и i'v отсчитываемый вокруг —п.
3 динамике самолета, наряду с самолетными рассматривают ско-
скоростные оси Ox*y*z*. Ось Ох* этой системы направлена по вектору
скорости точки О (обычно центра инерции самолета), Оу* — в пло-
плоскости симметрии самолета перпендикулярно Ох*; ось Oz* — перпен-
перпендикулярно плоскости осей Ох* и Оу* и образует с ними правую
систему. Положение скоростных осей относительно неподвижных ОЬ\^
задается углами X, p., v, определяемыми в точности тем же построе-
построением, каким углы ф, ft, ср определяли самолетные оси. Углы \, {х,
Рис. 7.
Рис. 8.
задающие направление вектора скорости (оси Ох*) подобно тому,
как ф и ft давали направление оси самолета Ох, называются углом
курса и углом подъема; угол v может быть назвав скоростным
креном.
Построение самолетных осей, когда заданы скоростные, дости-
достигается путем введения двух углов: скольжения C и атаки а. Повернув
плоскость осей Oz*x* вокруг оси Оу* на угол C, определим еди-
единичные векторы шиШ] (рис. 8), после чего поворот вокруг т на
2.4] САМОЛЕТНЫЕ И КОРАБЕЛЬНЫЕ ОСИ 49
угол а совместит вектор тх с осью самолета Ох. Вспомнив те-
теперь, что плоскость осей Ох и Оу* является плоскостью симметрии
самолета, найдем в ней ось Оу под углом а к оси О у* и ~ -f- а
к вектору mv Ясно также что вектор т = /3, так как он перпен-
перпендикулярен плоскости симметрии самолета.
Для вычисления таблицы косинусов углов самолетных осей с не-
неподвижными составляем вспомогательные соотношения
— n = iz cos ф + ix sin ф, — пх = — /3 sin Ф + h cos Ф» ]
я' = щ sin ft -p-r'gCOsO, ix =— «jCosO -)- f2 sin ft, j, B.4.1)
/^ = я' cos cp — я sin cp, /3 = — n1 sin cp — я cos cp, J
после чего находим
ij = /2 sin ft + cos 0 (— /3 sin ф -\- ix cos ф) =
= ix cos ф cos 0 -\- i2 sin П — r3 sin ф cos ft,
что определяет первую строку таблицы косинусов. Аналогично
получаем
^ —coscp^ sin ft —f— /2 cos 0) —f— sin cp (/3 cos ф —)— ix sin ф) =
= coscp sin 0 (/351пф—ix cos ф)-}-^ cos ^ cos 9+^3 sin
и коэффициенты при iv /2, /3 составляют вторую строку таблицы,
и т. д.
Таблица косинусов самолетных углов 3
jc cos ф cos Ь sin & — sin ф cos &
у sin cp sin ф — cos cp cos ф sin Ь cos Ь cos 9 sin cp cos ф + cos cp sin ф sin Ь
г cos cp sin 6 + sin cp cos ф sin \> — cos 0 sin cp cos cp cos ф — sin cp sin'L sin Ъ
Конечно, для составления таблицы косинусов углов скоростных
Осей с неподвижными надо заменить в таблице 3 углы ф, 0, ср
на \, p., v. Таблица косинусов скоростных осей с самолетными
имеет вид:
Таблица косинусов скоростных осей 4
х* cos a cos 3 — cos [J sin a sin ^
У* Sin a COS а О
z* — cos a sin 3 sin p sin я cos
4 Зак. 2072. А. И Лурье
50 кинематика твердого тела, основные сведения [гл. 2
Имея таблицы 3 и 4, можно составить соотношения, выражающие
углы X, [х, v через ф, 8, cp и углы а, р. Например,
cos(x*, E) =
+ cos(x*, у) cos (у, £)-}-cos(a**, z)cos(z, ?)
и т. д. Эти формулы значительно упрощаются, если считать углы
атаки и скольжения малыми и заменить таблицу 4 таблицей 5:
Таблица
г~> х
х* 1
V* а
косинусов
У
— а
1
5
z
0
г* — р 0 1
Пользуясь этой таблицей, находим:
cos Xcos jx = cos ф cos 0 — аEШф sin cp — со5фсо5ср sinf))-j-
-f- p (sin ф cos cp -f- cos ф sin cp sin Л)^
cos[xcos v = asin 0 -f-cos8coscp, sin jx = sin 8—-cos 8 (acoscp-|~P sin cp).
Имея в виду, что X, р,, v отличаются от ф, 0, ср малыми величинами
того же порядка, что а и р, легко получим
cos X cos jx = cos (X — ф -f- ф) cos ({x — 0 -|~ Л) да
да [cos ф — (X — ф) sin ф] [cos 0 — (jx — 8) sin ♦>] да
да cos ф cos 0 — (X — ф) sin ф cos 0 — (|х — 8) cos ф sin 8„
cos jx cos v да cos 8 cos cp — (jx — 8) sin 8 cos cp — (\ — cp) cos 8 sin cp,
sin {x да sin 8 -f- (p. — 8) cos 8.
Сравнивая соответствующие выражения, найдем соотношения
(X — ф) sin ф cos 8 -f- ((х — 8) cos ф sin 0 да
да (a sin cp — р cos cp) sin ф — (a cos cp —|— р cos cp) cos ф sin 8„
((х — 0) cos cp sin 8 -(- (v — cp) cos 8 sin cp да — a sin 8,
(|x — 8) cos 8 да — (a cos cp —|— p sin cp) cos 8,
приводящие к формулам, связывающим скоростные и самолетные
углы:
[х — 8 = — (a cos cp —|— р sin cp), ^
1 } B 4 2)
X — ф = ^ (a sin cp—р cos cp), v—ср=(—a sin cp+P cos cp) tg 8. I
2.4]
САМОЛЕТНЫЕ И КОРАБЕЛЬНЫЕ ОСИ
51
Оси, применяемые в теории корабля (корабельные оси), только
обозначениями отличаются от самолетных осей. На рис. 9 показано
построение системы осей, примененных А. Н. Крыловым: корабель-
корабельные оси Oxyz направлены
соответственно от кормы
к носу (Ох), к левому борт)
(Оу) и в диаметральной пло-
плоскости корабля (Oz). В поло-
положении равновесия корабля
они совпадают с осями О£т]С.
За основные приняты оси От\
и Oz. Вектор —пх получен
проектированием основной
оси Oz на плоскость <ХЕ;
перпендикуляр к нему в той
же плоскости определяет
единичный вектор линии уз-
узлов п, расположенный по ли-
линии пересечения основных
плоскостей (Х£ и Оху. Углы
<[> и ft, отсчитываемые вокруг
осей От) и п, определяют
дифферент и крен, а угол ср,
отсчитываемый от п к оси Ох вокруг Oz,—рысканье корабля.
Выражения косинусов углов корабельных осей с неподвижными при-
приведены в таблице 6.
Таблица косинусов корабельных углов 6
5 -ц С
cos ф cos 9 + sin 6 sin9 sin & sin 9 cos Ь —cos 9 sin <L + sin 9 cos <!> sin Ь
— cos ф sin 9 -J- sin 6 cos 9 sin ft cos 9 cos ft sin 9 sin 6-f cos 9 cos ф sin d
cos % sin 6 — sin ft cos ft cos ф
Рис. 9.
X
У
z
Описанный выбор самолетных и корабельных осей обладает тем
свойством, что при малом изменении первоначально прямого угла
между основными осями, два угла (рысканье и тангаж, дифферент и
крен) остаются малыми. Этим такой выбор выгодно отличается от
эйлеровых углов, когда лишь один угол нутации ft остается малым
при малом отклонении подвижной основной оси от неподвижной. Так.
приняв в случае самолета, одноименные оси О£ и Ох за основные,
мы при малом отклонении от курса могли бы считать малым только
этот угол между основными осями, а не два угла рысканья и тангажа,
остающиеся малыми при произвольном крене при выборе самолетных
52 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
осей. Точно так же конец мачты на корабле (ось Oz) при слабом
волнении моря ходит вкруговую; взяв за основные оси Oz и верти-
вертикаль ОС, т. е. введя эйлеровы углы, мы могли бы малым считать
лишь один угол нутации, тогда как углы прецессии и чистого вращения
могут принимать произвольные значения; при выборе же корабель-
корабельных осей малыми останутся оба угла: дифферента и крена, а произ-
произвольным останется лишь угол рысканья.
При малом отклонении тела от начального положения все три:
угла, определяющие самолетные или корабельные оси, остаются
малыми. Если же пользоваться эйлеровыми углами, то малому откло-
отклонению от начального положения будет соответствовать малость угла О
и суммы углов ср —|— ф. Действительно, поскольку одноименные оси
мало отклонены друг от друга, диагональные элементы таблицы 2
могут лишь малыми второго порядка отличаться от единицы. Это
приводит к требованиям
cos 0 ^ 1, cos (ф -j- ср) ^ 1,
и таблица 2 примет вид:
Таблица косинусов 2*
х 1 ф + ср Ь sin ср
У — (Ф + ?) * ^ cos 9
z 0 sin ф — 0 cos ^ 1.
Углы ср и ф по отдельности могут иметь любые значения, но одно-
одноименные оси останутся близкими друг к другу, а разноименные при-
приблизительно взаимно перпендикулярными. Структура же таблиц 3 и б
существенно иная. Чтобы сделать их диагональные члены отличаю-
отличающимися от единицы малыми второго порядка, необходимо малыми
считать все три угла; тогда и недиагональные члены будут малыми
первого порядка.
Например, таблица 3 примет вид:
Таблица косинусов 3*
|— * 6 ч С
х 1 0 — ф
у —Ь 1 <р
2.5]
СОСТАВЛЕНИЕ ТАБЛИЦ КОСИНУСОВ
2.5. Применение умножения матриц к составлению
таблиц косинусов
Вернемся к формуле B.5) и рассмотрим ее простейшие виды.
Пусть поворот осуществляется вокруг оси £ на угол сра; таблица
косинусов углов между осями систем Oxyz и О£т]С будет иметь вид.
ф""
X
У
Z
б
1
0
0
•п
0
COS ф!
— sin со,
С
0
sin
cos
II COS 92
л ft
2 ==
II S^n ?2
0
1
0
— sin
0
COS cp
<P2 1
L
2 II
«3 =
COS (p3
— sin cp3
0
sin cp3
coscp3
0
0
0
1
Поэтому, называя через аг матрицу, осуществляющую этот поворот
имеем
1 О О
О cos cpi sin cp
О — sin cpi cos «j
а матричная запись формул преобразования координат будет (при £0 = 0>
x = afi. B.5.2)
Матрицы, осуществляющие поворот вокруг оси Ог\ на ср2 или
вокруг ОС на ср3, соответственно будут
B.5.3>
В общем случае поворот твердого тела вокруг неподвижной точки
осуществляется как последовательность трех поворотов. Так, опре-
определяя положение тела с помощью эйлеровых углов ф, ft, cp, мы
осуществляем первый поворот вокруг оси ОС на угол ф. При таком
повороте оси £, т], С займут положение xv yv zv причем zx сов-
совпадает с С, ^! — с линией узлов, ^i —с перпендикуляром к ней
(вектор пг). Матричная запись B) формул преобразования координат
будет
причем а^—матрица, имеющая структуру а3 (угол ср3 заменяется на ф).
Следующий поворот на угол 8- вокруг линии узлов, т. е. оси Охи.
переводит систему осей Oxlylzl в Ox2y<1z<1 (оси Ох2 и Охх совпа-
совпадают, Оу2 ложится по вектору п', ось Oz2 займет ^ положение Oz).
Так как теперь на месте остается ось Oxv то матрица поворота а^
будет типа а, (замена сра на 0) и формулы преобразования координат-
в матричной записи примут вид
54 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
Остается третий поворот, переводящий систему осей Ox2y2z2
в систему Oxyz. Он осуществляется матрицей а , также типа а3,
— на месте остается ось Oz3:
х = %х2.
Теперь получаем
х = %Х2 = \Ч*\ = афа*яФ* = «Е- B.5.4)
Таким образом, матрица а, осуществляющая поворот системы осей О;т]С
в систему Oxyz, оказывается равной произведению матриц
а = а?а^аф, B.5.5)
где а а$, аф — матрицы типов а3, а^ а3. Следует отметить, что
в матрице-произведении множители следуют слева направо в порядке,
обратном последовательности поворотов. Из D) имеем по A.13)
? = а'дс = а;а;а;*. B.5.6)
Здесь использовано правило транспонирования произведения матриц.
Конечно, развернув матрицу E), придем к таблице косинусов 2,
а развернув матрицу (б)—к той же таблице, но с записью на гори-
горизонтали букв х, у, г, а по вертикали с, т\, С.
Таблица косинусов 3 самолетных осей записывается в виде про-
произведения матриц
B.5.7)
в которой а^ — типа av а# — типа а3, а^—типа а2. Для корабель-
корабельных осей
а = афа^аф, B.5.8)
причем а —типа а3, а^ — типа olv аф — типа а2. Развернув матрицу (8),
получим таблицу косинусов б.
Вернемся к случаю самолета. Выражение матрицы поворота непо-
неподвижных осей в скоростные дается матрицей вида G):
а* = а,о^ах. B.5.9)
Скоростные оси Ox*y*z* совмещаются с самолетными с помощью
матрицы
Т = ааа3, B.5.10)
где аа и otp—матрицы типа а3 и av Итак,
х = ух* = ?а*£ = aS, 7a* == a»
или
a* = fa, ava^ax = a^a^a^ *). B.5.11)
Развернув это матричное равенство, получим выражения углов курса,
*) Следует обратить внимание на то, что таблица 4 дает к' (в ней по
горизонтали записаны х, у, z, а по вертикали х\ у*, г*).
2.6]
ПРИМЕНЕНИЕ К КАРДАНОВЫМ ПОДВЕСАМ
55
подъема и скоростного крена через углы рысканья, тангажа и крена,
а также атаки и скольжения. Эти формулы выше были получены
в предположении, что углы р и а малы. Тогда ?' дается таблицей
косинусов 5 и следующие за ней в п. 2.4 формулы могут быть
получены умножением матриц.
2.6. Применение к кардановым подвесам
1. Карданов подвес*). Это устройство (рис. 10) служит
для закрепления тела на неподвижной или движущейся относительно-
земли платформе (корабле, самолете); оно состоит из двух колец —
наружного (н. к.) и внутреннего (в. к.). Подшипники /, V оси вра-
вращения наружного кольца закреп-
закреплены на платформе, тогда как внут-
внутреннее кольцо имеет ось вращения
с подшипниками 2, 2' на наружном
кольце. Оси вращения наружного
и внутреннего колец перпендику-
перпендикулярны друг другу и пересекаются
в центре О обоих колец, так что эта
точка остается неподвижной отно-
относительно платформы. Тело (прибор)
закрепляется на внутреннем кольце.
В гироскопических устройствах внут-
внутреннее кольцо, выполненное в виде
кожуха, несет подшипники оси ро-
ротора, вращающегося в этом кожухе. Схематически это показано на
рис. 11, на котором изображен вид с оси вращения кожуха. Ось
ротора располагается перпендикулярно оси вращения внутреннего
кольца в наружном и проходит через точку пересечения О осей
этих колец.
Относительно платформы внутреннее кольцо имеет две степени
свободы: его положение можно определить углами поворота а наруж-
наружного кольца и C внутреннего кольца в наружном. Пусть О^С — триэдр
осей, связанных с платформой, причем Ь\ — ось вращения наружного^
кольца; оси системы Ox*y*z*t связанной с внутренним кольцом,,
в начальном положении совпадают с С£т]£. При повороте наружного
кольца (рис. 12) на угол а ось вращения в нем внутреннего кольца
займет положение Оч\' (или Оу*), а перпендикуляр к плоскости
наружного кольца — положение ОС. (Для наглядности изображения,
углов рис. 12 повернут относительно рис. 11 на 90°.)
Рис. 10.
*) А. Н. Крыло в, Карданов подвес на корабле, Собрание трудов, 12,
ч. 1, стр. 193—258. Изд-во АН СССР, 1955.
А. Ю. Ишлинский, Механика специальных гироскопических систем
гл. I, Изд-во АН УССР, Киев, 1952.
56
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Следующий поворот внутреннего кольца вокруг оси Оу* на угол C
лает положение системы осей Ox*y*z*. На рис. 11 изображено по-
зернутое на угол а наружное кольцо, причем ось Оу% направлена
Рис. 11.
Рис. 12.
иерлеидикулярно чертежу от читателя. Внутреннее кольцо представ-
представлено кожухом; в нем заключен ротор, подшипники которого рас-
расположены на оси Oz*. Пусть Oxyz — система осей, связанных с рото-
ротором (оси Oz и Oz* совпадают); она получается поворотом осей Ox*y*z*
на угол ср вокруг Oz*. Матрицы, осуществляющие повороты на углы
<а,
ср, соответственно равны:
1
0
0
0
COS a
— Sin a
a
0
sin a
COS a
—
COS
sin
0
с
sin cp
COS cp
0
cosp
0
sinp
0
0
1 1
0
1
0
-*- sin
0
cos
B.6.1)
Элементами их являются косинусы углов между осями систем — свя-
связанной с поворачиваемым телом и связанной с телом, относительно
которого рассматривается поворот. Матрицей аа наружное кольцо
ориентируется относительно платформы, о^ — внутреннее кольцо в на-
наружном, ol9 — ротор в наружном кольце (кожухе).
По правилу умножения матриц находим
Icos p sin p sin a — sin p cos а
О COS а sill а . B.6.2)
sin р — cos p sin а cos P cos а |
2.6]
ПРИМЕНЕНИЕ К КАРДАНОВЫМ ПОДВЕСАМ
6Т
Это — таблица косинусов между осями систем О^С и Ox*y*z* (причем ^
т), С должны быть записаны по горизонтали, х*, у*, z*— по вертикали).
Остается умножить араа на а слева. Получаем искомую таблицу
косинусов.
Таблица косинусов углов в кардановом подвесе 7
J—> б f] С
X cos cp cos р cos cp sin р sin a-f sin cp cos а —cos cp sin p cos a -f sin cp sin <x.
у —sin cp cos p —sin cp sin p sin a-f-cos cp cos a sin <p sin fi cos а+cos ? sin*.
z sin p —cos p sin a cos p cos а
2. Двойной карданов подвес. На корабле установлены
два кардановых подвеса, внутренние кольца которых стабилизированы
в плоскости горизонта; ось наружного кольца первого подвеса распо-
расположена по продольной оси корабля Ох, а ось наружного кольца-
второго— по поперечной оси корабля Оу\ углы по ворота наруж-
наружных колец относительно корабля обозначаются а}, а2. Через эти углы
надо выразить таблицы косинусов корабельных осей Oxyz с осями.
Рис. 13.
систем 0{x*y*z* и О2л:*у*г*, связанных с внутренними кольцами под-
подвесов*) (рис. 13).
Матрицы, осуществляющие поворот системы осей Oxyz в системы
Oxx\y\z\ и соответственно в O2x*y*z*, равны a^a^ и ap aa , причем
Рг Р2—подлежащие определению углы поворота внутренних колец
первого и второго подвесов во внешних. Первая из этих матриц
определяется по F.2) с заменой а, [3 на av p1#^Вторая равна
B.6.3)
II
= °
1 0
0
cos p2
— sin p2
0
sinp2
cos р2
COS a2
0
sin а2
0
1
0
— Sfn а2
0
COS a2
стр
*) А. Ю. И ш л и н с к и й. книга, цитированная на стр. 55, гл. L
. 9—17.
•58
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
так как теперь поворот на угол а2 делается вокруг оси Оу.
Получаем
COS а2 0 — sin а2 II
sin p2 si*1 а2 cos ^2 sin p2 cos а2 I B.6.4)
cos j32 sina2 — sin fJ cos fJ cos a2 II
Поскольку внутренние кольца подвесов остаются горизонтальными,
третьи строки этой матрицы и таблицы 7, определяющие косинусы
углов вертикали с корабельными осями, равны друг другу:
sin Pj — cos p2 sin a2, cos ^ sin ах = sin fJ, cos p1cosa1 = cos p2cosa2.
B.6.5)
Одно из этих равенств является следствием двух других. Из них находим
tg ^ = cos ax tg a2, tg p2 = cos a2 tg onv B.6.6)
или
где
COS
COS a2 sin
R
= e
— sin2 ax sin2 a2,
B.6.7)
B.6.8)
и е=±1, причем во всех выражениях G) берется вследствие
третьего уравнения E) одинаковый знак.
Матрицы поворота а« аа и а^аа примут вид
B.6.9)
aQa =
p, ОС j
a8aa =
COS a2 COS aj sin «i sin a2
0
cos a{ sin a2
COS a2
COS a2 sin aj sin a2
COS a! sin a2
COS a!
COS a2 sin ai
Л
0
COS cxj
Л
cos a2 sin с
COS2 a
sin a2
К
sin
cos a2 c
R
cos2
*! COS
«1
OS aj
- sin a2
a2 sin aj
R
*i COS a2
R
R
R
B.6.10)
Их третьи строки одинаковы, а прочие отличны друг от друга. Это
указывает на то, что системы осей внутренних колец повернуты
лруг относительно друга вокруг оси Oxz*x (или O2z*). Пусть f
2.6] ПРИМЕНЕНИЕ К КАРДАНОВЫМ ПОДВЕСАМ 59
обозначает угол, на который надо повернуть систему Oxx\y[z*v чтобы
совместить ее с системой O2x*2y'2z*2. Поэтому
Icos 7 sin f О II
-sinT cosT 0 a3aai. B.6.11>
О 0 1 I
Отсюда, приравнивая элементы первых строк, находим
cos a2 = cos a* cos 7, 0 = £2L1 COs ax sin аг sin a2 -f- sin 7 cos alt
sin a2 = ^jp- cos2 ax sinea2 -(- sin f sin a1#
Получаем (вспомнив выражение R)
cos f = /?, sin -[ = — sin ax sin a2. B.6.12).
Конечно, оказываются равными и элементы вторых строк.
Третий столбец таблицы косинусов б определяет косинусы углов
восходящей вертикали с корабельными осями; но эти же косинусы
даются третьей строкой матрицы (9) или A0). Это приводит к соот-
соотношениям
При отсутствии рысканья
tg» = —tga1§ tg^ = — tga2cos0, B.6.14)
что дает основание называть углы —аг и —а2 приборным креном
и приборным дифферентом. При малых углах крена ф« — а2. Заме-
Заметим еще, что согласно F) и A4), tg ф == — tgpj, т. е. дифферент
может быть измерен по углу поворота внутреннего кольца первого-
подвеса.
3. Площадка на кардановом подвесе. Площадка П
монтируется на движущемся основании С (самолете, корабле) с по-
помощью карданова подвеса. Наружное кольцо подвеса имеет подшип-
подшипники на одной из осей основания (самолетных, корабельных), внутрен-
внутреннее кольцо — на наружном, площадка П — на внутреннем кольце. Эти
три оси взаимно перпендикулярны и пересекаются в точке О. Ориен-
Ориентация триэдров осей Oxyz и Oabc, связанных с основанием и с пло-
площадкой, задается в опорной системе осей О^С (инерциальных или
земных). Требуется составить выражения косинусов углов осей си-
системы Oxyz с • опорными осями через косинусы углов осей Oabc
с теми же осями и через углы поворота колец и площадки во внут-
внутреннем кольце.
60
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Пусть П и С — матрицы, осуществляющие поворот триэдра О;?]С
.в Oabc и соответственно в Oxyz. Тогда
а = Щ, x = Ci, а = ПС'х, B.6.15)
.и матрица ПС осуществляет поворот триэдра Oxyz в Oabc. Через а
назовем угол поворота наружного кольца карданова подвеса отно-
относительно основания С, через C—угол поворота внутреннего кольца
в наружном и через f — угол поворота платформы во внутреннем
кольце (в таблице косинусов 7 он был обозначен через ср). Назовем
через OXYZ триэдр осей, связанных с основанием; его оси лишь
наименованиями отличаются от»осей триэдра Oxyz (например, про-
лольной осью корабля может оказаться OZ). Матрицу, осуществляющую
Рис. 14.
-поворот системы OXYZ в Oxyz, обозначим через В\ ее можно
назвать матрицей изменения обозначений. Ее элементами являются
.нули и ± 1. Например, для систем осей, показанных на рис. 14,
0 1 0
0 0 1
1 0 0
Ось ОХ является осью вращения наружного кольца подвеса,
.а по осям вращения внутреннего кольца и площадки в начальном
их положении располагаются оси OY и OZ. В этом положении
площадки триэдры OXYZ и Oabc совпадают.
По сказанному, называя через а матрицу, определяемую таблицей
.косинусов 7, имеем
а = 1Л^аВ'х, B.6.16)
откуда по A5) приходим к искомому соотношению
ааа В' = ПС С =
**л\
B.6.17)
Рассмотрим площадку, стабилизированную в системе опорных осей
так, что оси триэдра Oabc лишь наименованиями отличаются от
■2.6]
ПРИМЕНЕНИЕ К КАРДАНОВЫМ ПОДВЕСАМ
61
осей О\т\^. Тогда YL = BV причем Вг — матрица изменения обозна-
обозначений. Получаем
C = Ba'aftBv B.6.18)
В частности, если при а = р = f = 0 оси движущегося основания
должны располагаться по опорным осям, то
С = В*'*'а'В'. B.6.19)
На рис. 15 и 16 представлены два размещения визирного поста
ла корабле *). Для первого размещения В = Е и матрица С = а'аа'р.'
Рис. 15.
получается транспонированием таблицы косинусов 7 (с заменой ср
на 7)
cos y cos
sin
— sin f cos
cos 7 sin P sin a + — sin 7 sin [J sin a + — cos p sin a
+ sin 7 cos a + cos 7 cos a
— cos y sin p cos a +
-)- sin y sin a
sin 7 sin p cos a + cos [J cos a
+ c^s 4 sin a
. B.6.20)
Сравнение с таблицей косинусов 6 дает требуемые зависимости
углов рысканья, крена и дифферента от f, a, C. Как видно, они
достаточно сложны и лишь для малых углов ср^—f, &^ — а,
ф^—р, что легко предвидеть по размещению поста.
*) А. Н. Крыло в, Сочинение, цитированное на стр. 55; гл. III,
стр. 157.
62 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
Для второго размещения
10 0 — 1 II
0 1 0 ,
10 0 1
и по A9) получаем
[гл. 2
г>
cos p cos a — sin y sin p cos a — cos y sin C cos a —
— cos y sin a — sin y sin a
cos P sin a — sin y sin p sin a +
cos 7 sin p sin a
-f- cos y cos a
— sin p — sin y cos P
+ sin v cos a
cos y cos p
B.6.21)
Для малых углов ср = — a, ф = — p, 0 = f. Для объяснения знака О-
заметим, что отсчеты малых углов f и 0 происходят вокруг проти-
противоположно направленных осей (Z и л:).
Рис. 16.
Полученные соотношения облегчают рассмотрение и более слож-
сложных вопросов. Пусть, например, площадка не полностью стабилизи-
стабилизирована, а ее оси Oabc получаются поворотом на малые углы X, jx, v
вокруг осей системы O2HZ, отличающихся наименованиями от
опорных О£т]С.. Тогда
а =
1 V
V 1
[д. —Л
11 =
1
12.7) РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ТВЕРДОМ ТЕЛЕ
и соотношение A7) дает
1
1
[A — 1
1
B[N.
63
B.6.22)
Полагая, что при строго стабилизированной площадке а=р = f = 0
и оси движущегося основания расположены по опорным осям O£tjC,
получаем ВВ^—Е, Brx = Bf. При малых углах приходим к равен-
равенству
1
|
= В
1
|
I
в котором матрица В определяется монтажом подвеса.
2.7. Распределение скоростей в твердом теле
Дифференцируя векторное соотношение B.2) по времени и учиты-
учитывая, что х'', у\ z' постоянны, придем к соотношению
в котором
= v = xix
dL
-\-ztz, r0 =
dt '
0i2
B.7.1)
B.7.2.)
представляют векторы скорости точек Ж и О (полюса) тела.
Векторы -— представим в форме разложений по единичным
векторам irr
Подлежат определению элементы u>sr матрицы ш. Эта матрица
кососимметрична; действительно, дифференцирование соотношений
дает
dt
dt
Но из C) следует, что правая часть этого равенства представляет
левая же равна a)rs, что и требуется доказать.
64
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Представив кососимметричную матрицу о) в виде (П. 1.2.3)
О — оK о
ОK
0
О
B.7.4)
можем теперь записать предыдущие формулы иначе:
dL
B.7.5)
3* J
Здесь через со обозначен вектор, сопоставляемый матрице о) и назы-
называемый вектором угловой скорости; со,, u>2, u>3 обозначают проек-
проекции (о на оси системы Ox'y'z' *). Три формулы E) можно записать
также в форме
B.7.6)
откуда следует, что
ИЛИ
dt.
B.7.7)
Таковы выражения проекций угловой скорости через косинусы аш
и их производные. В развернутом виде имеем формулы
0)j = a31a2l + а32а22 Н~ аЗЗа23 == (а21а31 + <*22а32 "+" а23а3з)
и т. д.
Формула A) распределения скоростей в твердом теле при исполь-
использовании выражений E) принимает вид
или
B.7.8)
*) Возможность сопоставления кососимметричной матрице w вектора «о
с проекциями o>i, о>2, со3 будет оправдана, если мы докажем, что эта тройка
величин преобразуется при переходе к новой координатной системе по тому
же закону, по какому преобразуются проекции вектора. См. п. 2.12.
2.81 ВЕКТОР БЕСКОНЕЧНО МАЛОГО ПОВОРОТА 65
причем, как следует из хода вывода, второе слагаемое в этих фор-
формулах выражает производную по времени вектора г':
^- = ^ = юХг' = юХ(г-г0). B.7.9)
2.8. Вектор бесконечно малого поворота
Рассматривается такое положение твердого тела, имеющего непод-
неподвижную точку О, которое бесконечно близко к заданному. Век-
Вектор бесконечно малого перемещения 8г точки тела М (конца вектора
г= ОМ) перпендикулярен г\ это следует из того, что так как длина
вектора г в твердом теле неизменна, то
Поэтому можно представить вектор Ьг в виде
8г=бХГ B.8.1)
где 8—бесконечно малый вектор, одинаковый для всех точек тела.
Действительно, предположив обратное и написав для двух точек
тела соотношения
получили бы
= F, — 82) • (г, X г2).
Но левая часть представляет вариацию скалярного
произведения гг • г2, а так как величина векторов гх и
г2 и угол между ними неизменны, то эта вариация равна
нулю. Итак,
(в1-е2).(г1х>-2) = о,
т. е. Gj — 62 = 0, поскольку вектор гх X г<>—про-
г<>—произвольный.
Возвращаясь к A) и обращаясь к рис. 17, видим, что в соотно-
соотношении
Ьг = | 6 | г sin a,
величина |8| вектора 8 выражает бесконечно малый угол поворота
всевозможных векторов г в рассматриваемом бесконечно малом пере-
перемещении твердого тела; итак, 8 представляет вектор бесконечно
малого поворота *).
*) Определение вектора конечного поворота дается ниже в главе 3
(п. 3.1).
5 Зак. 2072. А. И. Лурье
66 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
В случае твердого тела, имеющего неподвижную точку О, имеем
<Р0 = 0, г' = г, вследствие чего формула распределения скоростей G.8)
принимает вид
tf = coX''. B.8.2)
Поэтому, полагая br = vdt, т. е. сопоставляя бесконечно малому
перемещению тела промежуток времени dt, в течение которого мы
мыслим совершившимся это перемещение, получаем (сравнивая A)
и B))
b = tadt. B.8.3)
Это равенство связывает введенный выше вектор (о с вектором
бесконечно малого поворота 8 и объясняет наименование (О вектором
угловой скорости.
Пусть Gj и 82— два последовательных бесконечно малых пово-
поворота, которым подвергнуто твердое тело, имеющее неподвижную
точку. Тогда после первого поворота вектор г станет равным
а после второго
Сохранение малой величины второго порядка 82 X Ф\ X Г) было бы
не только излишне, но и неверно, так как в исходных определениях
величинами этого порядка мы пренебрегали. Получаем
г" —r = @I-+-82)Xr = 8Xr,
где через 8 обозначен бесконечно малый поворот, осуществляющий
сразу перемещение Ъг = г'г — г. Итак,
6 = 61 + 62 = 62-f 6,, B.8.4)
т. е. бесконечно малые повороты подчиняются закону сложения
векторов. Вследствие соотношения C) то же самое можно утвер-
утверждать об угловых скоростях.
2.9. Выражение вектора угловой скорости через производные
эйлеровых углов
Рассмотрим два положения твердого тела, имеющего неподвижную
точку: первое определяется значением ф, ft, cp эйлеровых углов,
второе, бесконечно близкое к первому, их значениями ф + 8ф,
ft + Sfli, cp —|— Sep. Можно осуществить переход из первого положения
во второе с помощью трех бесконечно малых поворотов, векторы
которых даются выражениями
2.91
ВЫРАЖЕНИЕ ВЕКТОРА УГЛОВОЙ СКОРОСТИ
67
Согласно (8.4) результирующий бесконечно малый поворот опре-
определяется геометрической суммой слагаемых
Н-^8ср. B.9.1)
По (8.3) получаем выражение вектора угловой скорости
B.9.3)
B.9.2)
Его проекции на оси, связанные с телом, поэтому будут
оI = со • i'x = ф sin ft sin cp -\- ft cos cp,
oJ = со • /2 = ф sin ft cos cp — 8 sin cp,
и = со • /' = ф cos ft 4- cp.
Проекции (о на неподвижные оси обозначаем Wj, co2, со3. Они равны
o)j = со • /j = ft cos ф -f- ? sin ft sin ф,
u>2 = <o . /2 = ft sin ф — cp sin ft cos ф,
t = со - /3 = ф —(— cp cos ft.
B.9.4)
Аналогичные формулы можно составить для проекций вектора
бесконечно малого поворота, надо лишь в равенствах C) и D) заме-
заменить производные ф, ft, cp вариациями 8ф, 8ft, 8cp. Получаем выраже-
выражения проекций в на оси, связанные с телом
6j = sin ft sin cp 5ф -f cos cp 8ft,
02 = sinftcoscp8^ — sin cp 8ft,
03 = cos ft
B.9.5)
и на неподвижные оси
02 = — sin l> cos ф 89-f-sin ф 8ft,
B.9.6)
cos
Отметим еще, что угловые скорости «полунеподвижного» п> nlt i^
и «полуподвижного» я, п\ /3 триэдров соответственно равны ф/3 и
формулам G.5) находим
= фл1в /i1=— фя, ^ = 0 B.9.7)
5*
68 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
и также
A = ^1 = ^(/t/cos& — ^sin ft), п' =— флсовй + Ц, }
di's . . > B.9.8)
-^ = фл sin & — ft/*'.
Выражения вариаций 8я, 8/^, 8я', 8^, т. е. бесконечно малых пере-
перемещений концов векторов п, nv n\ i'3 при бесконечно малом пово-
повороте б получим, заменив в формулах G) и (8) величины ф, ft, <р
на 8ф, 8В, оср.
2.10. Применение к вычислению трехиндексных символов
Как указывалось в п. 1.5, при рассмотрении движения твердого
тела за квазискорости естественно принять проекции вектора угловой
скорости оM на оси, связанные с телом, и проекции vos вектора ско-
скорости полюса на эти оси. Для первой группы квазискоростей сохра-
сохраним обозначение (о1э оJ, оK, а для второй примем обозначение оL, w5, u>6.
Подлежат вычислению -у • б2 • 5 = 90 трехиндексных символов..
1°. Квазискорости первой группы связаны с обобщенными ско-
скоростями формулами (9.3). Обратные соотношения имеют вид
()isin ? + ^cos ^'
0 = o)j cos cp — оJ sin cp,
ср = — (o)j sin cp —|— ci>2 cos cp) ctg ft -f- oK.
B.10.1)
Вариации квазикоординат 8-rcj, 8u2, 8^3 равны проекциям на оси,
связанные с телом, вектора бесконечно малого поворота; их выра-
выражения через вариации 8ф, 8ft, Щ обобщенных координат определены
соотношениями (9.5). Обратные соотношения получим из A), заме-
заменив ф, Л, ср вариациями 8ф, 8е)э 8ср, a ws на 65.
Имеем
(81^)" = (sin ft sin cp Вф-f- cos ср ВО)", Ьтх = 8(ф sin ft sin cp-j-ft cos cp),
и учитывая при составлении разностей этих величин «правило db = Ы»,
находим
фт^)' — 8o)j = (ft 8ф — ф 89) cos ft sin cp -|-
-f- (ср 8ф — ф 8ср) sin ft cos cp —|— @- Scp — ср 89) sin cp #
В этом равенстве надо заменить обобщенные скорости их значе-
значениями A) через квазискорости, а вариации обобщенных координат
2.10] применение к вычислению трехиндексных символов 69
по аналогичным формулам через вариации квазикоординат. Проделав
это вычисление и аналогичное для разностей
придем к формулам
и по A.8.3) получим
»yl »yl 1 <у2 -__- <у2 _— 1 <уЗ ___. #уЗ -Ц^2 I B 1 О О )
132 »23 ' »13 131 ' 121 П2 v ' ' у
Остальные символы с индексами 1, 2, 3 равны нулю.
2°. Можно было бы провести аналогичное вычисление, основан-
основанное на формулах
получающихся при проектировании выражения G.2) вектора скорости
полюса О на связанные с телом оси. Однако оно было бы очень
громоздким. Его можно упростить, использовав соотношения
а также формулы дифференцирования G.5) единичных векторов и
соответствующие формулы варьирования
В формулах D) через Ъг0 обозначен вектор бесконечно малого
перемещения полюса. Напомним еще, что проекции 8 на оси, связан-
связанные с телом, обозначены через Втг^. Имеем
(S+,)' =(Sro)' • *'а+К ■ (» XQ. ь»а+а= ъ%• i's+ vQ. (вxg.
учитывая теперь соотношение A.7.10), находим
(Чт,У-Ч^ = (8гоХ««>-«>оХб)Ч; B.10.6)
придавая s значения 1, 2, 3, получаем соотношения
(W — 8оL = ^3 §7Г5 — Ш2 §7Гб — (Ш5 Sir3 — ^6 8тс2>» J
(8тсб)' — 8(О5= wi §7Г6 — ^з §7Г4 — (W6 8tci — Ш4 ^з)' > B.10.7)
(<J7U6)' 8оN = @2 6тГ4 (Oj Sil5 (U>4 07U2 OM SiCj). j
70
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Напомним, что и>4, ш5, со6 обозначают проекции вектора v0 на оси,
связанные с телом, а 8тс4, 8тг5, 8тгб—вектора 8г0. Отличными от нуля
оказываются двенадцать величин
*35 *53 А' Тб2 »26— 1*
B.10.8)
3°. Если за квазискорости примем проекции со^ вектора угловой
скорости на неподвижные оси, то, исходя из формул (9.4) и им
обратных
= o)j cos ф -\- оJ sin ф,
B.10.9)
ф = (о3 — ctg 0 (o)j sin ф — <о2 cos ф),
придем, повторив вычисление, проведенное выше, к соотношениям
(8тс2)" — Sco2 = со3 BtTj — о)х
B.10.10)
Трехиндексные символы отличаются знаком от определенных
выше, когда за квазискорости были приняты проекции вектора на
оси, связанные с телом. Теперь
4°. Составление уравнений движения твердого тела часто значи-
значительно облегчается при использовании триэдра подвижных осей, не
связанных с телом. Примером может служить «полуподвижный» триэдр
векторов я, п\ i'3, введенный в п. 2.3. Вектор угловой скорости
его равен
(о'= ЙяЧ-ф/3 = &л-|-<Ипвл' -НфсоэЦ. B.10.12)
Вектор же угловой скорости тела будет
се = со'-Ид?- B.10.13)
За квазискорости тела примем проекции о> на оси полуподвижного
триэдра:
0^ = 6, <o2=<j>sinft, со3 ^= 4>cos 0 -|— ср. B.10.14)
Тогда вариациями квазикоординат будут служить величины
ottj = 50, 8тг2 = sin 0 8ф, 8т:3== 8ср-)-8фсо5&. B.10.15^
2.10] применение к вычислению трехиндексных символов 71
Отличными от нуля будут трехиндексные символы
^ = -^=1. B.10.16)
Трехиндексные символы с верхним значком 1 равны нулю, так как
0—«истинная» координата.
5°. Примем еще за квазискорости проекции вектора скорости
полюса v0 на оси «полунеподвижного» триэдра п, nv /3
B.10.17)
oL = v0. n = x0 cos ф ■+- y0 sin ф,
oM == v0 • «j = — л:0 sin ф -hy0 cos ф,
Последнее выражение интегрируемо и трехиндексные символы с верх-
верхним значком б равны нулю. Квазискорость со2 определим соотноше-
соотношением A4). Тогда
(оти4)* — 5со4 = — (ф 8л:0 — х0 8ф) sin ф + (ф 8у0 — у0 S ]>) cos ф =
= ф 8iu5 — <о5 8ф = —-у (со2 8тс5 — со5 8тг2).
Получаем
?* = —& =-Ш- й = -Т|4 = ^. B-10.18)
Классическими примерами систем, подчиненных неголономным
связям, являются шар и обруч, катящиеся без скольжения по непод-
неподвижной плоскости. Приведем для этих случаев записи уравнений
связей в форме A.5.6) обращения в нуль соответствующих квази-
квазискоростей и вычислим трехиндексные символы.
6°. Качение без скольжения шара по плоскости.
Положение шара определяется пятью параметрами, за которые при-
принимаем координаты xQ, yQ центра шара О в системе неподвижных
осей Oxyz и три эйлеровых угла. Ось Oz (единичный вектор /3) на"
правлена по перпендикуляру плоскости, по которой катится шар.
Уравнения неголономных связей выражают условия обращения в нуль
вектора скорости vp точки Я, в которой шар соприкасается с пло-
плоскостью. По формуле G.8)
так как гр—го = — i3a, где а—радиус шара; через а>5, как и выше,
обозначаются проекции вектора угловой скорости на неподвижные оси.
Уравнения неголономных связей будут
х0 — ао>2 = 0, у0 -(- acoj = 0.
B.10.1?)
72 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
Система имеет три степени свободы. За квазискорости примем (Oj,
<о2, о*з и введем еще в рассмотрение величины
оL = xQ — <ш2 = х0— a (ft sin ф — ср sin ft созф),
со. = у0+ #<*>! = у0-|-а(&со8ф + ? sin^ sin ф),
обращающиеся в нуль в силу уравнений неголономных связей. Имеем
и по A0) получаем'
Tl, = —Тз1 = а' Т|3 == — Т|2 = ^- B10.20)
Прочие трехиндексные символы определяются по A1). Общая
задача о катании по неподвижной плоскости тела, ограниченного
произвольной выпуклой поверхностью, рассмотрена в п. 2.16.
7°. Качение обруча по плоскости. Положение обруча
задается теми же пятью параметрами xQt yQ, ф, ft, rf, что и в случае
Рис. 18.
шара (рис. 18). Координата z0 центра обруча выражается через угол 0
с помощью соотношения
z = a sin ft. B.10.21)
В рассматриваемом случае
rp — rQ = — an', B.10.22)
где а — радиус обруча, пг — единичный вектор полуподвижного
триэдра п, п'\ /д» направленный здесь по прямой наибольшего ската
плоскости обруча (вверх). Скорость точки обруча Р, соприкасающейся
с плоскостью по G.8), равна
= v^ — a (лш1 + n^z -f- i^) X n'.
2.10] применение к вычислению трехиндексных символов 73
Здесь использовано соотношение A2) и приняты обозначения квази-
квазискоростей A4). По условию отсутствия скольжения имеем
vp = v0 — ai^+an^ = 0. B.10.23)
Уравнения неголономных связей запишем, проектируя это соот-
соотношение на оси «полунеподвижной системы» п, пх. Используя обо-
обозначения A7), получим
<о4 + асо3 = 0, <о5 + flcoj sin 0 = 0. B.10.24)
Проектирование же на ось Oz дает интегрируемое соотношение
(о6—flo)jcos0=0 или 20 = a0-cos0, B.10.25)
являющееся следствием равенства B1). Вместо оL и оM в рассмотре-
рассмотрение удобно ввести новые квазискорости <о* и со*:
ш* = а>4 -+- #<*>3, ш* = ш_ -f- flcoj sin f), B.10.26)
обращающиеся в нуль в силу уравнений неголономных связей. Таким
образом, пятью квазискоростями, которые здесь используются,
являются три величины A4) и две B6).
Трехиндексные символы, соответствующие первой группе этих
величин, даются формулами A6). Далее имеем по A8) и B)
(«ф — всо* = —-j (ш2 §т:5 — оM отт2) + а (оJ StCj — ^ 8т:2).
Заменив здесь Втг5 и и>5 их значениями по B6), получим
(Цу-осо^^со^-ш*^). B.10.27)
Замечая еще, что выражение о)х sin 0 = 0 sin 0- интегрируемо, по A8)
лолучим
(8тс5)" — К = — ШГ¥ (Ш2 В7Г4 — ^4 ^2)>
или, заменив Stt4 и оL их значениями A8),
Трехиндексные символы оказываются равными
V4 ^4 /О 1 a OQ\
i 25 '52 „-п а » \£. ixj.Zo)
лг5 уЪ ^_ V5 __ V5 /О 1() 9Q'i
Н2 124 sin ft ' »23 132 sin ft * ^llUt^^
74 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
2.11. Распределение ускорений в твердом теле
Дифференцируя по времени соотношение G.8), дающее формулу
распределения* скоростей и замечая, что производная по времени
вектора скорости точки определяет вектор ускорения ее w = vt при-
придем, используя также G.9), к равенству
ю = юо+юХг/+юХ(юХг/). B.11.1)
Здесь wQ = vQ—вектор ускорения полюса, w—вектор ускорения
точки тела с вектор-радиусом г'= г — г0. Вектор со—производная
по времени вектора угловой скорости — называется вектором угло-
углового ускорения) он обозначается далее через е:
•=*=:§(«/.)•.
Применив формулы дифференцирования единичных векторов G.5),
получим
Таким образом, проекции es вектора углового ускорения твердого
тела на связанные с телом оси равны производным по времени от
проекций на эти оси вектора угловой скорости; выражения ss через
эйлеровы углы и их первые и вторые производные по времени
получаются дифференцированием равенств (9.3). Конечно, проек-
проекции es вектора е на неподвижные оси равны также производным
проекций со5 вектора со на эти оси.
Рассмотрим теперь триэдр подвижных осей, не связанных с телом;
пусть l*s обозначают единичные векторы этого триэдра, со' — вектор
его угловой скорости, со* = (о-/*— проекции вектора угловой ско-
скорости тела на оси /*. Тогда, повторив сделанное выше вычисление»
получим
3 3
6 = со = 2 ">*/* + <■>' X <■> = 2 «#* — (со — со') X <■>. B.11.3)
S=l 5=1
Здесь со — со' — угловая скорость тела по отношению к триэдру /*.
Например, в случае «полуподвижного» триэдра векторов п, п\ i^
е = Яп -Иф sin в)" п' -+-(ф cos в +ф)# 1'г — *з<Р X № + п'ф sin 0 +
+ Сг (ф cos в + ср)] = (& 4- ^ ф sin fi) л + (ф sin ° + Ф ® cos 8 — Т ®)п' +
^ B.11.4)
2.12] матричная запись формул скоростей и ускорений 75
В формуле распределения ускорений A) второе слагаемое еХ^
называется вращательным ускорением, а третье (о X ((о X г')— центро-
центростремительным ускорением. Отложим вектор (о по оси, проходящей
через полюс О, и через h назовем расстояние рассматриваемой точки
до этой прямой; тогда величина центростремительного ускорения
будет
| <■> X (<■> X г') | = со2/*. B.11.5)
Оно направлено по перпендикуляру, опущенному из точки на ось
вектора угловой скорости.
Выражение центростремительного ускорения может быть записано
еще в виде
<■> X (<■> X г') = (о (to • г7) — wV = (*>» — £»•©). г'. B.11.6)
Здесь wo) — диадное произведение, £ — единичный тензор*).
2.12. Матричная запись формул распределения скоростей
и ускорений в твердом теле
Напомним введенные в п. 2.2 обозначения: через £ была обозна-
обозначена матрица-столбец координат точки в системе неподвижных
осей О£т]С, через х — матрица-столбец этих координат в системе
осей Oxyz, связанных с телом; t0—матрица-столбец координат
полюса О. Матрица, осуществляющая поворот триэдра О£т]С
в триэдр Oxyz, была названа а; ее элементами были косинусы углов
между осями системы; &sk — косинус угла 5-й оси триэдра Oxyz
с &-й осью триэдра О£т]С.
Формулы преобразования координат—проекций вектор-радиуса,
записываются в виде
5—5о = а'х, * = аE —5о). B.12.1)
Точно так же составляются формулы преобразования проекций любого
вектора а: если а—столбец его проекций as на неподвижные оси,
а—столбец проекций as на оси Oxyz, то
а = ь'а а=ш. B.12.2)
Дифференцируя (I) по времени, получаем
k—^i'x. B.12.3)
так как х от времени не зависит; !•—Ео представляет столбец
v — vQ проекций вектора v — v0 на оси системы О;т]С. Поэтому,
согласно B)
v — vo=a(v—vQ) = a(k—ko) = a'a'x. B.12.4)
*) Элементы диадного исчисления кратко изложены в гл. 4, п. 3.
76 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
Это — формула распределения скоростей в твердом теле. Матрица
оса'—кососимметрична; это следует из того, что
(аа')' = аа' = — аа',
причем последнее равенство проверяется дифференцированием соот-
соотношения ал! = Е.
Таким образом можно положить
ш = аа', B.12.5)
причем кососимметричная матрица
О) =
@2i = GK ^22 == 0 ^23 — '
CO31 = 0J 6K2 = (Oj 6K3 = 0
B.12.6)
определяется заданием трех величин
оI = — со23 = а>32, о>2
или, в более короткой записи, с применением символа Леви—Чивита
*r=-€rAt (/•=!. 2, 3). B.12.7)
Ниже показывается, что <ог можно трактовать как проекции на
оси вектора о> — это вектор угловой скорости. Формула D) прини-
принимает вид
V — vo = (qx B.12.8)
и определяет матричную запись векторной формулы распределения
скоростей в твердом теле G.8), если спроектировать ее на оси,
связанные с телом. Заменив в (8) столбец х его выражением A) и
умножив обе части на а! слева, согласно B) получим соотношение
а/ (V _ *g = g _ ^ = а'ia « — у, B.12.9)
представляющее результат проектирования векторной формулы рас-
распределения скоростей в твердом теле на неподвижные оси. Косо-
Кососимметричная матрица
со= a'wa = a/aa/a = a'a B.12.10)
определяет столбец сог проекций вектора о> на оси неподвижной си-
системы, причем подобно G)
»r=-€rst"st- B.12.11)
2.12]
МАТРИЧНАЯ ЗАПИСЬ ФОРМУЛ СКОРОСТЕЙ И УСКОРЕНИЙ
77
Надо проверить, что тройки величин о)г и со5 связаны законом пре-
преобразования проекций вектора, т, е.
з
= 2 asr°v
Имеем
по
Проделав
@ =
k=
A0)
@ =
ОС ОHС .
умножение матриц, получим
-л
Сославшись на
или
kl
а' =
i
3
2
формулу A
@ =
3
k=l
=
9), это можно
L
и
3
V « ~
—
3
2
3
S askatl{
записать в виде
B.12.12)
что и требовалось.
Определяя положение твердого тела эйлеровыми углами и пред-
представляя матрицу поворота а в форме E.5), можно записать матрицу
угловой скорости E) в виде
03 = \аЛ [аХат]' = %К + аЛаК + асра^аФаФаК- B.12.13)
Здесь, в соответствии с определением матриц а , а$, ol^
а =
rj?
— sin cp — cos cp 0
cos ср — sin cp О
О 0 0
а а = со
ср ср Т
0
1
0
— 1
0
0
0
0
0
и т. д. После вычисления по формуле A3), находим
0—10
1 О О
О 0 0
О
cos ■
0
0
0
0
0
1
0
— 1
0
о! 4- фа ас
ср I T со £
0—10
1
о о||а;а; =
— Ор + фcos'
о
о оо[|
ф sin ft cos ср — ft sin cp
— (ф sin % sin cp -|- Ь cos ср) ||э
0
|!— (ф sin ft cos cp — ft sin cp) ф sin ft sin cp + ft cos cp
B.12.14)
что согласно G) эквивалентно формулам (9.3). Аналогично вычисляется
матрица со.
Переходим к записи формулы распределения ускорений. По (9)
и A0) имеем
6-4 = 2F-«. B.12.15)
7Й КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ fГЛ. 2
Дифференцируя это равенство по времени, получим
где
е=(ш)" B.12.17)
— кососимметричная матрица, составленная по правилу A1) из
столбца проекций es вектора углового ускорения на неподвижные
оси. Имеем также
2 |1 ~2 i ~2 ~~ ~
■ G) -4- О)< О), О)л О), (Oq
1 1 I Z х о
0
— Ю2
0
со2
0
= fa/ СО -)- С0(|/ ,
где со'— строка Рю,, со2, щ\\. Это же соотношение непосредственно
следует из формулы (П. 1.4.7). Итак,
\ —\ = К — £ 5' ш + е) (? — у. B.12.18)
Рто — матричная запись векторной формулы распределения ускоре-
ускорений П1.1), если спроектировать ее на неподвижные оси.
Столбец проекций вектора w—w0 на оси, связанные с телом,
обозначим w — w0. Было бы грубой ошибкой отождествить его
с v—v0. Имеем по B) и A)
w—wQ = a(i—'io) = a(uu' — Eu'u + B)a'x. B.12.19)
Но ао) = а), а/а7 = а/ и далее по A0) и E)
осеа' = а (со) V = а (а'соа) V = ааг со -)- (со)' -f- юаа' =
= со2 -\- (со)' -4- со (со)' = (со)" = 8,
так как (со/ = —со, поскольку со — кососимметричная матрица. Итак,
(со)' = е = aeV = а (ш)" a'. B.12.20)
Это выражение, вполне аналогичное A7), дает выражение кососим-
метричной матрицы ё углового ускорения, составленное из проекций
на оси, связанные с телом, вектора углового ускорения е; вместе
с тем показано, что проекции вектора углового ускорения на эти
оси равны производным по времени от проекций на них вектора
угловой скорости со.
Соотношение С19) принимает вид
W — Wq = (осе' — £со'со + е) а: = (ai2 -f- s) x B.12.21)
2.13] ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА В ПОДВИЖНОЙ СИСТЕМЕ ОСЕЙ 7*9"
и представляет матричную запись векторной формулы распределения
ускорений в твердом теле в проекциях на связанные с телом оси.
Выразим в заключение величины в формуле B1) через матрицу
поворота. Имеем
е = Н' = (аа7)" =аа' + аа' B.12.22)
и также
(uJ = _J/^ = —аа'аа' = — а а'. B.12.23)
Получаем
w2-{-e = aa', w — wQ = аа'л;, B.12.24)
где w — w0—столбец проекций вектора w — wQ на связанные
с телом оси. Отсюда, по B), находим также
1-% = *'х, B.12.25)
что получается и непосредственным дифференцированием формулы A).
2.13. Дифференцирование вектора в подвижной системе осей
Рассматривается вектор а, проекции которого на оси триэдра
единичных векторов i'v i*v i'v вращающегося с угловой скоростью о>,
обозначаются av а2, а3, так что
а = а/х+а/2 + а/3. B.13.1)
При дифференцировании этого вектора по времени следует
учесть формулы G.5) для производных единичных векторов. Получаем
а = axi[ + a2i'2 + а3'з + ftiw X h + «2W X к + Ч™ X Н =
= аг i[ + a2i'2 + а/3 + w X ( А & )
* г г г
Обозначим через а вектор, проекции которого на оси триэдра M2fe
равны as,
*a = ali[ + a2ili + azh. B.13.2)
Тогда предыдущее равенство примет вид
fl. B.13.3)
Вектор а можно назвать относительной или локальной производной
ог а\ слагаемым wXfl учитывается вращение триэдра осей М2*з>
на которые проектируется вектор.
Частные случаи равенства C) встречались выше: в формуле G.9)
проекции гг на оси системы Ox'y'z* постоянны и отпало первое сла-
слагаемое в формуле C), в A1.2) дифференцируется сам вектор (оииз C)
01 надает второе слагаемое.
80 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
2.14. Относительное движение
Рассмотрим движение системы материальных точек 5 по отноше-
отношению к движущемуся триэдру осей Ox'y'z1'. Предполагается, что урав-
уравнения связей, составленные в этой системе осей, не содержат явно
времени
Ъ (k=l г). B.14.1)
Тогда координаты х'г у'., z\ любой точки Mt системы 5 могут быть
выражены через п = ЪЫ — г независимых обобщенных координат
с помощью соотношений, не содержащих времени:
Ча).
B.14.2)
или в векторной записи
r\ = r'iDv •■•• Яп). B.14.3)
Индекс / далее опускаем.
Положение системы осей Ox'y'z' задается координатами полюса х0,
у0, zQ (т. е. начала этой системы осей) в системе инерциальных
осей Oxyz и тремя угловыми координатами, например, эйлеровыми
углами. Через них выражаются косинусы углов таблицы 1 в п. 2.1.
Вектор-радиус г точки системы по отношению к началу инерциаль-
инерциальных осей определяется по B.2); равенства B.4) дают выражения х',
У, z\ через х, у, z и шесть параметров, определяющих движение
триэдра Ox'y'z'. Подставив их в A), придем к уравнениям связей
в системе инерциальных осей. Надо различать два случая. Во-пер-
Во-первых, движение триэдра Ox'y'z' может быть задано, тогда t войдет
в уравнения связей через посредство соотношений
= хо С)." Уо = Уо @. *о = zo @, |
определяющих координаты полюса и угловые координаты. В этом
случае связи нестационарны и число степеней свободы равно п. Во-
вторых, движение триэдра Ox'y'z' неизвестно; тогда в г уравнений
связей войдут 3N координат точек системы в инерциальной системе
и еще шесть параметров, определяющих положение триэдра Ox'y'z'\
время t в уравнения связей не входит; связи стационарны, а число
степеней свободы равно п -(-6. Конечно, могут иметь место и про-
промежуточные случаи, когда движение системы Ox'y'z' известно ча-
частично, например, задано лишь движение полюса, но не угловые коор-
координаты.
2.14] относительное движение 81
Мысленно свяжем с системой осей Ox'y'z' твердое тело и рас-
рассмотрим точку его ЛГ, в которую в рассматриваемый момент попадает
точка М системы 5. Ясно, что скорость и ускорение точки Ж*
определяются правилами кинематики твердого тела, т. е. формулами
{7.8) и A1.1). Их называют переносной скоростью и переносным
ускорением и обозначают ve, we. Если есть в том надобность, то
векторы угловой скорости to и углового ускорения е, присоединен-
присоединенного к триэдру Ox'y'z' твердого тела, также снабжают индексом е.
Теперь мысленно остановим систему осей Ox'y'z' или, что то же
самое, представим себе, что мы наблюдаем за движением точек си-
системы S, будучи неизменно связаны с этими осями. Скорость и
ускорение точки М системы, определяемые при этом условии, назы-
называются относительными и обозначаются vr, wr. Они вычисляются,
как указано в п. 1.3, т. е. дифференцированием по t соотноше-
соотношений B) или векторного выражения C):
п п п п
Sdr' • , \\ дг' " , V V д2г> ' ' /пн^
Wsq" w'=l^^+11^^7^- BЛ45)
5=1 5 = 1 л=1£=1
Наблюдатель, находящийся в системе инерциальных осей Oxyz, опре-
определит абсолютную скорость и абсолютное ускорение <оа и wa
точки М системы S по формулам
va = r% wa = r = va. B.14.6)
Но, с другой стороны, дифференцируя по времени соотношение B.2)
r = ro + f = rQ + x'i[-\-y'i'2-\-z%t B.14.7)
придем, повторив вывод формулы распределения скоростей G.8), но
учитывая теперь, что вектор-радиус г' не остается неизменным в си-
системе осей Ox'y'z't к равенству
= ^о-т-»Хг/+г', B.14.8)
которое можно было бы написать, сославшись также на A3.3) с за-
заменой а на г'.
Замечая, что
п п
^^-^q^^ BЛ4-9)
приходим к теореме сложения скоростей:
«e = «o + «X^+vr = ^ + vr. B.14.10)
выражающей равенство абсолютной скорости геометрической сумме
переносной и относительной скоростей.
6 Зак. 2072s А. И. Лурье
82 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
Отметим, что поскольку векторы г0 и i's не зависят от обобщен-
обобщенных координат, а г' от обобщенных скоростей, из D), (8) и A0)
следуют соотношения
Дифференцируя равенство A0), приходим к теореме сложения
ускорений. При вычислении воспроизводится вывод формулы распре-
распределения ускорений в твердом теле A1.1) с применением формулы
дифференцирования A3.3) для векторов г' и vr Получаем
Но по (9) и E)
г' = *г, vf = wr B.14.12)
Поэтому
e o «V. B.14.13)
или в другой записи;;
B.14.14)
Абсолютное ускорение равно геометрической сумме переносного
ускорения we, относительного wr и добавочного или кориолисова
ускорения WcoX. Последнее определяется формулой
Wcor = 2wX*r B.14.15)
Для последующего отметим здесь формулу: пусть а — вектор,
зависящий от обобщенных координат qv ..., qn. Тогда
п
а = а-\-иХа = 1£-^д3 + и>Ха. B.14.16)
5=1
В частности,
^^ + Й)Х^- B14Л7>
2.15. Абсолютное ускорение точки, движущейся
по вращающейся Земле
Через vn, Vo, vh обозначаются северная, восточная и вертикаль-
вертикальная составляющие вектора скорости материальной точки (самолета,
снаряда) относительно вращающейся Земли; Ф и \ обозначают север-
северную широту и восточную долготу места, над которым проходит в данный
момент ючка, h ооо^начаег высоту точки над земной поверхностью —
2.15] ускорение точки, движущейся по вращающейся Земле 83
точкой О на уровне моря. Эта точка принимается за начало геоцен-
геоцентрической системы осей Oxyz. Ось Oz этой системы направлена по
восходящей вертикали, которая предполагается направленной по ра-
радиусу Земли*), ось Ох — по касательной к меридиану на север,
ось Оу—по касательной к параллели на запад. Эта система осей
вращается вместе с Землей и перемещается по поверхности Земли,
так что движущаяся точка в любой момент времени остается на оси Oz.
Обозначая через R земной радиус, имеем
vN = (R + h) Ф, vo=(R-hh)lcosO, vh = h. B.15.1)
Проекции вектора скорости v начала О геоцентрической системы
осей Oxyz на оси этой системы равны
)
vo-\-RUcosФ^, j B-15-2)
а проекции угловой скорости ее
]
\ <2Л5-3>
j
(через U обозначена угловая скорость Земли). Формулами B) и C)
определено переносное движение. Координаты точки в системе
осей Oxyz равны @, 0, h), и поэтому проекции его относительной
скорости на эти оси равны
*Vi = °> <V2 = 0. vfZ = h = vh. B.15.4)
Абсолютная скорость точки, т. е. ее скорость в системе осей,
сохраняющих неизменные направления по отношению к неподвижным
звездам (например, в геоцентрической системе места старта в момент
старта), определяется следующими выражениями ее проекций на оси
va2 — v2 — ш,Л = — vQ — (R-\-h)U cos Ф,
B.15.5)
*) Формулы, учитывающие сжатие земного сфероида, приведены в книге
. В. Булгакова «Прикладная теория гироскопа» (§ 57, Гостехиздат, 1955).
84
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ (ГЛ. 2
Переходим к вычислению ускорения. Ускорение w полюса О си-
системы осей Oxyz равно
Применив формулы G.5), получаем
-[■
или после вычисления
w, =
-з— (R + h)* l
B.15.6)
Для составления выражения переносного ускорения следует вычи-
вычислить еще вектор
s X г' +-ы X (w X г1) = е X г' +-юл . г' — ю2г',
где r/= hi'3. Проекции этого вектора на оси равны соответственно
(Sn —I— (l),(Dn) Д ( S, —I— (l)r»(l)-5^ h (i£p" —I— i£p\ h
V 2 I 1 3/ '"» • V II 2 3/» \ 1 ' 2/
причем проекции вектора углового ускорения равны производным
соответствующих проекций угловой скорости, т. е.
uOvh
(R + hJ
R + h
vN
uNuh
R + h (R + h)*'
B.15.7)
Проекции относительного ускорения зд>г на оси Oxyz равны 0, 0, vh>
а кориолисово ускорение определяется равенством
= 2@ X i'&h = 2*>2Л — 2i2^1Vh'
2.16] КАТАНИЕ ТЕЛА ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ
Теперь находим абсолютное ускорение wa. Его проекции равны
+ "W h 4" 2aJ*V
wa2 =
Проделав вычисление по вышеприведенным формулам, получим *)*
WaB = vh ЩГ}Г — 2 Uvo cos Ф — (R + h)
B.15.8)
2.16. Катание тела по неподвижной плоскости
Как еще один пример составления уравнений неголономных связей
и вычисления трехиндексных символов, а также применения резуль-
результатов п. 2.13, рассмотрим случай катания без скольжения твердого
тела по неподвижной плоскости. Предполагается, что поверхность 5
тела имеет в каждой своей точке определенную касательную плоскость.
Свяжем с телом систему осей Ox'y'z', имеющей начало (полюс)
в точке О тела; на поверхности S введем гауссовы координаты q1, q2,
и вектор-радиус точки поверхности р (имеющий начало в полюсе О)
рассматривается как известная функция q1, q2, как указано в П. 2.7.
Следуя П. В. Воронцу **), будем определять положение тела пятью
обобщенными координатами. Две из них — гауссовы координаты^1, q2
точки М, в которой поверхность 5 соприкасается с плоскостью. Еще
две — декартовы координаты х, у этой точки на плоскости в си-
системе неподвижных осей Oxyz (причем ось Oz направлена нормально-
к плоскости). Знание четырех функций времени
ql(t), q2(t); x (t), у (t)
определяет, во-первых, кривую U — геометрическое место точек со-
соприкасания М на 5 и, во-вторых, кривую L—геометрическое место
этих точек на плоскости. U и L имеют общую касательную в точке М
(единичный вектор т); мы зафиксируем положение тела, задав пятую
*) В несколько ином виде эти формулы приведены Е. Л. Николаи в ра-
работе «К теории девиаций гироскопических приборов» (Е. Л. Николаи,
Труды по механике, Гостехиздат, 1955).
**) П. В. Воронец, Уравнения движения твердого тела, катящегося,
без скольжения по неподвижной плоскости, Киев, 1903.
86
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
обобщенную координату — угол 0 вектора т с неизменным направле-
направлением (например, с осью Ох) на плоскости (рис. 19).
Слздуя сказанному в П. 2.7, введем основные векторы рг и р2
на поверхности 5 и единичный вектор нормали к ней т. Он сона-
правлен с осью Oz. Тогда, называя через to вектор угловой скоро-
скорости тела (системы осей Ox'y'z') и применив соотношение A3.3),
имеем
m = m + <oXtn = 0> B.16.1)
так как т сохраняет неизменное направление в пространстве; через т
обозначена производная вектора т в системе осей Ox'y'z'. По
(П. 2.7.24)
т = maqa = — ba$tq*, B.16.2)
где ba? — коэффициенты второй квадратичной формы поверхности,
^ рР—векторы взаимного базиса.
т
Рис. 19.
Проекция вектора to на нормаль т (угловая скорость верчения)
лалее обозначается 2 —со-т. Умножив A) векторно на т> получим
или
Но
— b^m X
— &т = 0.
=ущ(?А-?А)- B-16.3)
Здесь аа? — коэффициенты первой квадратичной формы, т. е.
.ковариантные составляющие метрического тензора поверхности;
2.16] КАТАНИЕ ТЕЛА ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ ST
а\ — его смешанные составляющие; \а\ — дискриминант первой ква-
квадратичной формы.
Получаем
^ B.16.4)
Таково выражение вектора to через величины, определяемые геоме-
геометрией поверхности и £2.
Проекции его на оси, связанные с телом, будут
»з =
1 Г/а дг> и дг'\ "i I /а дг' , дг'\ -91
Для выяснения геометрического значения величины Я заметим,
что вектор т может быть представлен в двух видах: это производ-
производная единичного вектора касательной к кривой L и поэтому
т=0тХ*. B.16.6).
С другой стороны,
i = ; + toXx = m^^ + pa^+«X^ B.16.7)
Здесь использованы соотношения (П. 2.8.3) и (П. 2.8.6); через &**
обозначены контравариантные составляющие вектора геодезической
кривизны, через do—элемент дуги кривой U. Заменив еще х его
значением (П. 2.8.2), получим равенство
to X т = Qm X 1 +ущг(Ьа1?2- ^
Слагаемое, соответствующее в G) вектору нормальной кривизны»
как следовало ожидать, сократилось. Внося полученное выражение
для со X ^ в G) и сравнивая с F), приходим к равенству
в = Q + ра. (т X т) ^*аа. B.16.8)
Имеем
р. • (ж X ч) = ^=L= lp. X (р, X Ра)] -Ь^~= уЩ (fliPfl«2-«23««i) ^г
и далее
Р. • (» X <с) **"о = у±= (ai9aa2 & /Щ &л %
"88 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
Итак,
У\(я1Ь* — д2кш1). B.16.9)
Из этого соотношения следует, что при известных q1 (/), g2(t),
угол 0 определяется квадратурой; но тогда х и у также определятся
квадратурами из соотношении
dx=cosbda, dy = sin 0 da B.16.10)
поскольку при катании без скольжения элементы дуг da кривых L
и U равны. Задача будет решена (об этом см. п. 8.3).
Пусть v обозначает вектор скорости полюса О, vs—его проек-
проекции на оси, связанные с телом. Тогда выразив, что скорость точки
-соприкасания М тела с плоскостью равна нулю, придем к трем
уравнениям:
12 = v2 + vzx' — (V' = 0, I B.16.11)
Ъ = '°ь + {*\УГ — <»2*' = 0. J
Введем еще обозначения
Х4 = w • т = 2 = ^i^i + ">2m2 -f- ^3m3» B.16.12)
Xs = ^. Хб = ?2. B.16.13)
причем (Oj, oJ, ш3 в этих соотношениях определяются по E). Вели-
Величины ^9 принимаются за квазискорости; три из них обращаются
в нуль в силу уравнений неголономных связей A1). Соответствующие
вариации квазикоординат обозначаются bns. Для сокращения записей
вводятся векторы ^ и ^> проекции которых на оси, связанные
с телом, равны xs и *Ч* для s=l, 2, 3. Тогда
р. B.16.14)
причем формулы A0.2) и A0.6) можно кратко записать в виде
6 — 8ю = О X w (8>0* — to = 8г X w — * X 0. B.16.15)
Здесь звездочка (а не точка) обозначает, что вычисляется производ-
производная вектора по времени в системе осей Ox'y'z'ь связанных с телом,
так что проекции векторов 6, (8те)* и т. д. равны производным
по времени от проекций этих векторов на указанные оси. Получаем
. B.16.16)
Теперь, заменив brt v их значениями по A4) и учитывая, что р и бр
2.16] КАТАНИЕ ТЕЛА ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ 89*
соответственно равны ра#а, ра8<7а, придем к выражению
(8я)* — »х = *« X to —х X 6 +-F?« — со ty«) X р.. B.16.17)
так как остальные слагаемые дают в сумме нуль
- F X р) X <о + (ю X р) X 6 + F X ») X Р = 0.
Остается в правой части равенства A7) заменить to и 6 их значе-
значениями по формулам D). Эти формулы перепишем в виде
w = mx4 + ^a. 6 = m&7r4 + /aV<, B.16.18)
причем векторы 1а, по сказанному выше, определяются из равенства D).
Вводя еще обозначение
^^^t B.16.19).
получим после несложного вычисления
(8*Г-»Х = (Х48*-Х Ю X т + (<7а 8те-х 8<7а) X К
B.16.20)
Правая часть теперь содержит только квазискорости \s и соответ-
соответствующие им вариации квазикоординат. Спроектировав векторное
соотношение B0) на ось Ох^ получим трехиндексные символы -[;*
как коэффициенты при произведениях Ха^р» пРичем следует иметь
в виду, что <71==Х5» ^2==:Хб п0 обозначению A3). Таблица трех-
индексных символов приводится ниже.
Остается еще определить значение разности
так как т = 0, 8т = 0, а разность 6 — 8to должна быть заменена
ее значением A0.10), но отнюдь не A0.2). Получаем, заменив 6 и о>
по A8),
(8*4)' - Ь7и = т • (/„ X h) ?e V- B.16.21)
Заменив векторы 1а и Ц их значениями, легко найдем, вспомнив
определение т,
так что
*"^*" ^ B.16.22)
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
Выражения трехиндексных символов показаны в приводимых
табличках.
\p 1
1
2
0
2
3
0
0
3
4
0
— mz
4
5
0
/it
-*„
5
6
0
-/23
/22
0
Tap
V 1
a \
1
2
0
2
3
0
0
3
4
m3
0
-«,
4
5
/.3
0
-/11
-*„
5
6
/23
0
-/21
— ^22
0
\ p
a \
1
1
2
0
2
3
0
0
3
4
-«,
».
0
4
5
-/12
/11
0
-*„
5
6
-/22
/21
0
— £23
0
Здесь Аад
например
— проекции векторов ka и /а на оси системы Ox'y'z',
_ 1 / дх' дх'\ , _ 1 I дх' дх'\
кп- Y\T\ Г" 1^~°12^гj' Л21 ~ vWГ21 д?» а221ф)'
<щ_и дх>\ i __j /* дх> — ь дх'\
" ^ 12~w)' 21 ~ /и v21 ^ 22^г)*
2.1б| КАТАНИЕ ТЕЛА ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ 91
Из трехиндексных символов с верхним индексом 4 отличны от нуля
по B0) лишь
Все трехиндексные символы с верхними индексами 5 и б, конечно,
нули, так как выражения %5 = ql и -^Q = q2 интегрируемы.
Вектор углового ускорения тела определим, дифференцируя па
времени выражение A8) вектора угловой скорости:
е = w = йт + Q* Ч- maQq« -f
По (П. 2.7.24) и (П. 2.7.19) находим
или
= y=f m У
w (*■■! 2Л ~
2
Заметив, что
получим
Как пример, рассмотрим случай твердого тела, ограниченного-
поверхностью вращения. Ось Oz' направляем по оси симметрии
поверхности; тогда (рис.20)
х' = v (s) cos ср, у = v E) sin ср, г' = г' (s).
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
За гауссовы координаты приняты дуга s, отсчитываемая по дуге
меридиана от точки пересечения меридиана с осью Oz1', и азиму-
азимутальный угол ср. Через v обозначено расстояние точки до оси Oz'.
Единичный вектор нормали т к поверхности в этом случае направлен
по нормали к меридиану (противоположно его главной нормали
на рис. 20). Если через а назвать угол вектора т с осью Oz/', то,
как нетрудно видеть,
dz'
ds
ds
—• =cosa,
ds
— — sin a.
Получаем следующие выражения проекций векторов р}, р2, т на оси
системы:
77?
Pi
р2
т
Далее
аи
а22
ьп
Ъп
Ох1
cos a cos ср
— v sin ср
sin acoscp
находим
= Pi - Pi =
= Р2-Р2 =
dm
~ ds
dm
>~ дГ
Oy'
cos a sincp
v COS cp
sin a sin cp
1, a12 = pr
da
•р2=0,
Oz'
— sin a
0
cos a.
P2 = 0,
V,
Рис. 20.
dm
= d^~ • p2 = ~ v sin a,
где через k обозначена кривизна меридиана. Отличные от нуля сим-
символы Кристоффеля второго рода для поверхности вращения равны
COS a
и составляющие вектора геодезической кривизны кривой s = s(a)t
«p = cp(a) будут
. *i d2s ( dy
da2 \ da
flo (9) получаем
и*2
dy ds cos a
ds d<s \
B,16.25)
2,17]
СЛОЖЕНИЕ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
93
Формулы D) для проекций вектора угловой скорости на оси
системы Ox'y'z' получают вид
(Oj = (Q -)- cp cos a) sin а cos y-\-ks sin cp,
uJ = (Q -j- cp cos a) sin a sin cp — ks cos cp,
uK = 2 cos a — cp sin2 a.
B.16.26)
2.17. Сложение движений твердого тела
Обобщением теории относительного движения, изложенной
в п. 2.14, является задача о сложении движений твердого тела.
•Объектом, который совершает заданное движение по отношению
к системе подвижных осей Ox'y'z', является теперь не точка Ж,
я твердое тело E). Относительное движение точки М задавалось
ранее законом зависимости ее координат х', у', z1 от времени.
Относительное же движение тела надо задать движением его полюса
(точки М на рис. 21) и угловой скоростью еог по отношению
Рис. 21.
к системе Ox'y'z1 (относительной угловой скоростью). С твердым
телом E) связана система осей Mx*y*z*\ требуется определить дви-
движение любой его точки с вектором-радиусом р = MN относительно
основной системы Oxyz. Угловую скорость твердого тела, мысленно
связываемого с осями Ox'y'z', будем теперь обозначать ые и
называть переносной угловой скоростью. Ранее она обозначалась
•через (о.
Можно непосредственно применить теорему сложения скоростей
<п. 2.14), забыв на минуту о твердом теле и фиксируя внимание на
точке Л/; тогда под переносной скоростью ve надо понимать ско-
скорость той точки мысленно соединенного с системой Ox'y'z' твердого
94 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2"
тела, через которую проходит в рассматриваемый момент
точка N
>
где г' = ОМ.
Относительная же скорость точки N в системе Ox'y'z' по формуле
распределения скоростей G.8) складывается из скорости полюса М
(она обозначалась vr) и вращательной скорости еог X р- Итак, абсо-
абсолютная скорость vA точки N равна
или
«Ъ = *Ъ + »,Х'"/+«г+(», + »г)Хр. B.17.1)
Первые три слагаемых представляют абсолютную скорость точки М,
которую мы обозначаем через va. Итак,
+ »г)Хр. B.17.2)
Пусть, в частности, точки О, О, М совпадают. Тогда va — О и ско-
скорость точки N будет
*л = Р = (», + «>г)Хр. B.17.3)
Но в этом случае, забыв о существовании осей Ox'y'z', мы могли бы
написать, что скорость точки N равна
^ = й)лХр, _ B.17.4)
где (ол — угловая скорость тела по отношению к осям, Oxyz—абсо-
Oxyz—абсолютная угловая скорость. Сравнивая C) и D), заключаем, что вслед-
вследствие произвола выбора вектор-радиуса р
ь>А = ь)е + ь)г B.17.5)
Это — теорема о сложении угловых скоростей. Отметим далее, что,
положив р = /* в C), где i*s — единичный вектор 5-й оси системы
Mx*y*z*t получим
,.*
что следует также из E) и G.5).
Вектор ь)е естественно задавать его проекциями на оси Ox'y'z',
а еог—на оси Mx*y*z*. Поэтому выражение вектора углового уско-
ускорения будет
= S («„<;+«„*о+»# х «,+(».+»,) х »г.
■S — 1
или
•л = «.+-«, + ».Х«»,. B.17.7)
2.17] СЛОЖЕНИЕ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА 95
где ег обозначает вектор, проекции которого на оси Mx*y*z* равны
производным от проекций вектора относительной угловой скорости tor
на эти оси.
Теперь, дифференцируя по времени выражение B), получим вы-
выражение абсолютного ускорения wA точки N. Дифференцирование
слагаемого va проводилось в п. 2.14 и давало выражение A4.13)
абсолютного ускорения wa точки М. В нем надо произвести замены
to на ые и в на ге. Остается вычислить производную по времени
второго слагаемого в формуле B). Использовав G) и C), получим
К
Замечая теперь, что
КХ»Г) X р4-юг XКX р) = »,Х (»,X р).
приведем предыдущее выражение к виду
К», X »,) X рГ =«, X р + •», X О», X р) -Ь«, X р + <•», X О», X р)+
+ЧХКХР).
Окончательное выражение wA может быть записано в виде
Xp)l}. B.17.8)
Величина
^Я = ^0 +*е X (Г' + р) -4-Ю, X К X (Г' +Р)] B.17.9)
представляет переносное ускорение, т. е. ускорение точки Л/,
мысленно жестко соединенной с системой осей Ox'y'z'.
Вторая группа слагаемых
B.17.10)
есть относительное ускорение точки N по отношению к осям
Ox'y'z' — оно вычисляется по формуле распределения ускорений
в твердом теле A1.1): первое слагаемое представляет ускорение
полюса М, второе и третье—вращательное и центростремительное
ускорения, вычисляемые в предположении, что оси Ox'y'z' непод-
неподвижны. Относительная скорость точки N по отношению к осям
Ox'y'z', равна
** = «V + »rXp. B.17.11)
Поэтому третье слагаемое
«»Сог = 2(Яе X [», + (», X РI = 2<Ое X VR B.17.12)
96 КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ [ГЛ. 2
является кориолисовым ускорением точки N. Снова получаем теорему
сложения ускорений
f B.17.13)
как и можно было предвидеть заранее. Однако полезно иметь в виду
и соотношение (8), так как оно подробно раскрывает значения отдель-
отдельных слагаемых в формуле A3).
2.18. Движение натурального триэдра пространственной кривой
Положение точки М пространственной кривой С задается в си-
системе неподвижных осей Oxyz вектор-радиусом г, рассматривае-
рассматриваемым как известная функция дуги а, отсчитываемой вдоль кривой от
некоторой начальной точки ее МхУ
Единичный вектор касательной кривой т, направленный в сто-
сторону возрастания а, определяется равенством
т = £. B.18.1)
Векторы т и проведенный через точку М вектор т1 =
имеющий направление касательной в бесконечно близкой к М
точке М\ определяют соприкасающуюся плоскость /7 в точке М.
Рис. 22.
бесконечно малый вектор dz перпендикулярен т и направлен в сто-
сторону вогнутости кривой; его величина |^т| = е определяет беско-
бесконечно малый угол смежности — угол между касательными кривой
в точках М и М', а отношение
\dx\ = г = 1
da da p
— кривизну кривой в точке /И; р является радиусом кривизны в этой
точке. Таким образом, вектор
n=V% BЛ8.2)
2.181 движение натурального триэдра пространственной кривой 97
является единичным, расположен в соприкасающейся плоскости
и направлен по нормали в сторону вогнутости кривой. Это — еди-
единичный вектор главной нормали кривой. По векторам чип строится
единичный вектор бинормали b = zy^n (рис. 22).
Таким образом, в каждой точке М кривой С определен ортого-
ортогональный триэдр единичных векторов т, п, Ь. Рассмотрим точку Л/",
неизменно связанную с этим триэдром; ее вектор-радиус MN отно-
относительно вершины триэдра обозначим через rf, а его проекции на
оси натурального триэдра через av a2> а3. Пусть
обозначает скорость вершины натурального триэдра. Скорость
точки N равна
V — г-\-гг = ъа-\-(пуЪ-\- a2n -f- аф) =
dn , b
С другой стороны, называя через Q вектор угловой скорости, кото-
которую приобретает натуральный триэдр при движении его вершины по
кривой С, имеем по основной формуле кинематики твердого тела G.8)
X г' = to H-T(Q2a3— ^з
+ nB3fl, — ^az) + b (Q^2-Q2^). B.18.4)
Сравнение соотношений (З) и D) позволяет, вследствие произ-
произвольности чисел av a2, #3, составить три равенства
c^. = Qzn— Q2b, a4£ = Qlb — 23т, о^ = 22х — 2гп. B.18.5)
Из первого равенства и B) следуют соотношения
3
Р
Величина Q} определяется из третьего равенства E):
(дифференцируя равенство b = т X я и учитывая B), имеем
B.18.7)
Величина
х' (а) у' (а) zf (а)
X" (а) у" (а) г" (а)
Х"'(а) /"(а) *'"(")
7 Зак. 2072. А. И. Лурье
98
КИНЕМАТИКА ТВЕРДОГО ТЕЛА. ОСНОВНЫЕ СВЕДЕНИЯ
[ГЛ. 2
называется кручением кривой. Заметим еще, что кривизна кривой,
как следует из B), определяется равенством
Учитывая E)—G), приходим к известным формулам Френе
db_ /г dn J&_ х db п /oiftcn
da ~ p ' da — T ~ p ' rfa — T </.ie.y;
и к выражению угловой скорости натурального триэдра
B.18.10)
Величина в скобках называется вектором Дарбу. Заметим, что из
третьей формулы (9) следует, что при смещении из точки М в бес-
бесконечно близкую точку Мг соприкасающаяся плоскость кривой повора-
чивается вокруг касательной т на угол
так что нормаль к ней Ь приобретает
при 7>0 приращение db% направлен-
направленное противоположно п.
Рассмотрим теперь движение твер-
твердого тела (самолета), точка которого
(полюс М) движется по кривой С. При-
Принимая обозначения п. 2.4, введем си-
систему скоростных осей Mx*y*z*> по-
положение которой в системе непо-
неподвижных осей О£т]£ определим углами
X, [a, v. Ось Мх* сонаправлена с т,
поэтому плоскость My*z* совпадает с нормальной плоскостью траекто-
траектории; через х обозначается угол, на который следует повернуть еди-
единичные векторы п, Ь вокруг т, чтобы совместить их со скоростными
осями My* и Mz* (рис. 23). Поэтому, называя через &>' вектор угло»
вой скорости скоростных осей, имеем
Рис. 23.
^cosx, B.18.11)
причем is—единичные векторы системы скоростных осей. С другой
стороны, из определения углов X, |х, v легко получить выражения
проекций ш\ вектора ео' на скоростные оси /*:
вектора &>' на скоростные ^~., ^.
ы'^ = X sin |x -\- v,
:i>2* = X cos |x cos v -|- [х sin v,
^з* = —X cos |x sin v 4~|x cos v.
B.18.12)
2.18] движение натурального триэдра пространственной кривой 99
Получаем три соотношения
B.18.13)
Из двух последних находим
^-sinx= X cos (a cos v —(— [a sin v, B.18.14)
= —Xcos|x sin v-(- [a cos v. B.18.15)
*-= V^2 _J- X2 COS2 [A, B.18.16)
cos(x—v) = p-rL= ^
V \>-2+ A2 COS2 |X '
' B.18.17)
. / ч ACOS(X к COS fx i
sinfe —v) = p—r^^ . ^
a |/ ^2^x2 cos2 (x J
Дифференцируя первое равенство A7) и воспользовавшись вторым,
а также выражением х — -v» получаемым из A3), придем к соот-
соотношению
* ^^° + t^^)cos B.18.18)
Формулы A6) и A8) определяют элементы движения натурального
триэдра при заданных в функции времени курсовом угле X и угле
подъема [х. Направления осей натурального триэдра, когда известны
скоростные оси, находятся по формулам A7).
О построении скоростных осей по осям, связанным с телом, гово-
говорилось в п. 2.4 и п. 2.5.
ГЛАВА 3
ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА
3.1. Формула Родрига и вектор конечного поворота
Твердое тело, имеющее неподвижную точку О, подвергается пово-
повороту на угол ^ вокруг оси, направление которой задается единичным
вектором е\ это направление на оси выбирается так, чтобы, смотря
с его конца, видеть поворот на угол <; 180° происходящим в поло-
положительную сторону (против часовой стрелки
для правой системы осей, принятой в этой
книге).
Рассмотрим вектор-радиус точки тела
ОМ = р до поворота. После поворота он
займет положение ОМ1 = р', так что вектор
'= р' — р
C.1.1)
представит перемещение точки М при пово-
повороте тела; это перемещение требуется выра-
выразить через величины (угол % и вектор е),
определяющие поворот, и вектор р.
Очевидно, что векторы р и р' являются
образующими кругового конуса, по оси ко-
которого направлен единичный вектор е% как
показано на рис. 24. Составляющая вектора р по оси поворота,
т. е. вектор ее-р> очевидно, не изменяется при повороте, т. е.
ер = ер\ C.1.2)
и остается проследить за изменением составляющей, перпендикуляр-
перпендикулярной оси,
Ро = Р — ее-р C.1.3)
в вектор
3.1] ФОРМУЛА РОДРИГА И ВЕКТОР КОНЕЧНОГО ПОВОРОТА
По рис. 25 (вид с конца ё) имеем
101
или pJ = -g-
Заметив, что вектор SM' по величине равен
правление векторного произведения
получим
или
Воспользовавшись теперь соотношениями C) и D), заменим
здесь р^ и р0 через р' и р, в результате чего придем к формуле
Родрига
| Xptg|-. C.1.5)
Остается решить это уравнение относительно р; для этого умножим
обе части его векторно слева на е. Тогда, заметив, что по B)
придем к уравнению
Исключив из E) и F) вектор е X р'» получим
|. C.1.6)
|.]. C.1.7)
Эту формулу можно переписать в виде
р' = " о- 2
1 + tg21
— ptg^i]. C.1.8)
102 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ.
Два последних слагаемых представляют произведение
вследствие чего еще одну запись формулы G) можно представить так:
C.1.9)
Введем теперь в рассмотрение вектор 6, имеющий направление
единичного вектора оси поворота е и равный по величине удвоен-
удвоенному тангенсу половины угла поворота
e = |6| = 2tg£. C.1.10)
Тогда получим формулу в окончательном виде, также данную Род-
ригом:
6х(р + 4вХ) C.1.11)
Введенный здесь вектор
| C.1.12)
условимся называть вектором конечного поворота*). К нему при-
применимы все действия векторной алгебры. Так, представляя е в форме
разложения по единичным векторам осей Oxyz
е = ix cos а + '2 cos Р ~т~ h cos 7»
где а, р, т — углы е с этими осями, можно написать
в = Vi+U> '2+Vs. C.1.13)
причем величины
01 = 2tg-|cosa, 02 = 2tg-|cosp, 63 = 2tg^cosT C.1.14)
представляют проекции вектора 6 на указанные оси. Однако было бы
ошибочно трактовать запись A3) как утверждение, что конечный
поворот, определяемый вектором 6, реализуется с помощью трех
поворотов вокруг координатных осей на углы, определяемые
по в^2, б3 согласно A0). Это имело бы место, если бы .конечные
повороты подчинялись тому же закону сложения векторов (пра-
(правилу параллелограмма), что, скажем, силы или скорости. В действи-
действительности закон сложения поворотов более сложен (п. 3.3).
*) Слово «конечный» будем опускать, когда это не может привести
к недоразумению.
3.2] ПАРАМЕТРЫ РОДРИГА—ГАМИЛЬТОНА 103
3.2. Параметры Родрига—Гамильтона
Будем считать, что вектор р связан с подвижной системой осей
Ox'y'z'* которая до поворота совпадала с неподвижной системой
осей Oxyz. Вектор 6 осуществляет поворот системы Oxyz в Ox'y'zf\
поэтому, приняв р = *у, будем иметь р = /5 и "о A.11)
i' i\e
C.2.1)
_1
4
Поворот — 6 осуществляет переход системы Ox'y'z' в Oxyz.
Тогда p = i's и p' = is; получаем соотношение, обратное A),
is = ts V— в Х(й— i в X С). C.2.2)
1 i * ПО \ ^ /
Из этих формул, равно как из A.2), следует, что
е.£ = е.<„ C.2.3)
т. е. проекции вектора поворота на одноименные оси системы Oxyz
и получающейся из нее при этом повороте системы Oxfyrzr друг
другу равны:
05=65 E=1,2,3). C.2.4)
Выражение A.13) может быть поэтому записано в одном из двух
видов:
6 = 6, /; -f 92 *2 4- 63 /з = М, 4- 62 'г -+- 9з ^з- C-2.5)
Формулы теории конечных поворотов приобретают более сим-
симметричный вид, если пользоваться не проекциями вектора поворота,
а пропорциональными им величинами
Коэффициент пропорциональности выбирается по условию
х2-ьх?+х!-4-х!=1. C.2.7)
Его геометрическое значение легко обнаружить; действительно, имеем
по A.10)
С другой стороны, из F) и G) последовательно получим
104 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Сравнивая оба выражения, будем иметь
I l C.2.8)
у 1+т62
Таким образом, вектор поворота 6 будет определяться четырьмя
параметрами Родрига — Гамильтона:
\ =cos asin-^ , Х2 = cos p sin-^-, Х3 = cos f sin ~, X0 = cos-^-t
C.2.9)
связанными одним условием G). Здесь a, C, f — углы оси поворота
с осями координат (одинаковые в системах Oxyz и Ox'y'z'), % — угол
поворота. Выражение 6 и формулы A) и B) принимают вид
3 3
2
S
i's = 2 (
2 \it X (V, + 2 \iq X /,) • C.2.11)
/ = 1 \ q = 1 /
3/3 \
is = i's— 2 2V/X M— 2 \lqXis • C.2.12)
Вспомнив определение символа Леви — Чивита и использовав равенство
преобразуем соотношения A1) и A2) к виду
is = is + 2 (>•„ 2 etteV« + Х^ 2 Ve - *s 2 ^) • C.2.13)
/3 3 3 \
is = is-2 x0 S e*M—x^ 2 vi+<i 2 ^ • C.2.И)
Отсюда находим значения косинусов углов между осями координат
той и другой систем:
*,*=^** = 8,*( 1-22 ^2)+2Х0 2 ^Л + 2ХЛ> C.2.15)
4s = is'i'k = \b-^ 2 ^)-2Х0 2 €tsk\ + 2\sXk. C.2.16)
\ q = 1 / / = 1
Остается вспомнить значение символов Леви — Чивита и воспользо-
воспользоваться соотношением G), чтобы получить таблицу косинусов L
3.3] СЛОЖЕНИЕ КОНЕЧНЫХ ПОВОРОТОВ 105
Она составляется по строкам с помощью A5) или по столбцам
с помощью A6).
Таблица косинусов через параметры Родрига — Гамильтона 1
4— -> х у
х-
у'
С помощью A5) можно также дать краткую запись формул преоб-
преобразования координат
2 2 е„л**+2К S Ч**.
C.2.17)
3 3 3
*5 = (Хо - х?—х!—х!) х'в — 2\ 2 2 е*А** 4- 2xs 2 ^**i-
C.2.18)
Заметим, что преобразование координат A8) представляет результат
проектирования на оси системы Oxyz формулы Родрига A.11). Преоб-
Преобразование A7) получается при проектировании на оси системы Ox'y'z'
соотношения
V(JA C.2.19)
Р РV
l + i-62
представляющего результат обращения формулы Родрига и выражаю-
выражающего, что вектор р' переходит в р при повороте — 6, с помощью
которого система осей Oxry'zr совмещается с Oxyz.
3.3. Сложение конечных поворотов
Твердому телу, имеющему неподвижную точку О, сообщается
поворот, задаваемый вектором Ьх (на угол у^\ вокруг оси, опреде-
определяемой единичным вектором ег). После этого телу сообщается вто-
второй поворот 62 (угол Хг. ось ^г) *)• ^гол (меньший 180°) между осями
обозначается Ф, т. е.
I^X^I2^11*' C.3.1)
*) Векторы еи е2 не связаны с телом.
106 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Известно, что всякое перемещение твердого тела, имеющего
неподвижную точку, можно осуществить с помощью одного пово-
поворота вокруг оси, проходящей через эту точку (теорема Эйлера —
Шаля). Этот поворот (вектор 6, угол х» ось ё) требуется выразить
через векторы 6Р 62.
На единичной сфере концы векторов ev e2, в образуют сфери-
сферический треугольник ЛВС (рис. 26,а). Его вершина С является точ-
точкой сферы, сохраняющей положение при последовательности пово-
поворотов 8Т, 62. Такая точка может быть построена в пересечении дуг
больших кругов АС и ВС, составляющих углы -^-Xi и -^ х2 с ду-
дугой АВ, как показано на рис. 26. Действительно, при повороте 6j
Рис. 26.
точка С займет положение С, а Сг при повороте 62 вернется в С
вследствие равенства по построению сферических треугольников ABC
и ABC\ Из построения ясно видна некоммутативность поворотов:
при последовательности 62, Ь1 сохранит свое положение на сфере С\
а не С.
Таким образом определено направление оси (вектор е) резуль-
результирующего поворота; остается найти угол х- Обратимся к рис. 26,E.
Точка Л, остающаяся неподвижной в первом повороте, займет при
втором повороте положение А'\ это же положение она примет и при
результирующем повороте 6 на угол ^- Поэтому угол в вершине С
сферического треугольника ABC оказывается равным -^ Bтс — x)==z
1
= *— 2-Х-
Теперь надо составить формулы, соответствующие приведенным
геометрическим построениям. Мы будем пользоваться формулами
3.3] СЛОЖЕНИЕ КОНЕЧНЫХ ПОВОРОТОВ 107
сферической тригонометрии (рис. 26) *)
cos с = cos a cos Ъ -\- sin a sin b cos С, C.3.2)
sin а sin Ь sin с .« о о\
cos С = — cos Л cos Б -f- sin A sin.5 cos с C.3.4)
Применив последнее соотношение к сферическому треуголь-
треугольнику ABC рис. 26а, получим
cos -| = cos ^ cos -^ — sin -^ sin ^ cos Ф, C.3.5)
что по A) и A.12) записывается также в виде
) C.3.6)
Мы получили выражение угла результирующего поворота; остается
выразить вектор е\ представим его в виде разложения по некомпла-
некомпланарным векторам ev е2, £2X#i:
+ ^2Хе1 C.3.7)
с коэффициентами а, [3, f» подлежащими определению. Последний
из них f положителен, так как вектор е (рис. 26) должен быть
отклонен от плоскости векторов ev e2 в сторону е2 X €\> Случай
7 < 0, согласно приведенному пояснению, соответствует последова-
последовательности поворотов 62, 61#
Из соотношения G), поскольку е—единичный вектор, имеем
или
Чтобы, не решая никаких уравнений, определить аир, умножим
обе части G) скалярно на е2 X (#2 X #i) и соответственно на
ei X (#2 X ^i)- Первый из них перпендикулярен £2 и ^2X^i» ^ вто-
второй ^ и е2 X ^i- Поэтому получаем
* • [*2 X (^2 X е})] = а^х • \е2 X (^2 X ^)Ь
е • to X (^ X ^i)l = P^2 • [*i X (^ X ^i)]
, *) Последняя из этих формул для косинуса угла менее известна, чем
остальные* Проще всего ее получить, применив B) к поЛярному сфериче-
сферическому треугольнику А*В*С* — его вершины расположены в полюсах боль-
больших кругов, образующих стороны данного треугольника ЛВС.
108 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
и далее по рис. 26, а и формулам A), B):
е • [е2 X (*2 X ех)] = е - е2ех е2 — ее] =
= cos a cos Ф — cos b = — sin a sin Ф cos -^-,
Л Г /% \/ | Л \/ Л |1 ■ ■ ■ ■■■ Л # Л —_ & л & & л & ■ ——
& * 1*^1 /Ч \*^2 /\ I/* — 2 11 2 —
= cos а — cos £ cos Ф = sin & sin Ф cos 4p ,
^i • [£2 X (^2 X ^i)] = (*i X ^г) * (*2 X ^i) = — sifl2 Ф.
Теперь, воспользовавшись еще соотношениями C), находим
• Xi • Х2
sin —?^— . . sin ~^z
Х2 2 /2 л sin & _. . y, 2
Vo 2 to n sin c? v 1
cos -~ = cos 4r. P = sr cos -^- =
2 у 2 r sin Ф 2
a = ^- cos -~ = cos 4r. P = sr cos -^-
sin Ф 2 . у 2 r sin Ф 2 x
sin -|- sin^-
C.3.9)
и по (8) вычисляем y:
sin Ф sin —^
X j/'sin» |—sin2 ^ cos2 I -sin2 ^ cos2 Ц--2 sin^. sin ^-cos^-cos^ .
Заменив здесь sin2y=l—cos2-|- его значением по E), после про-
простых преобразований найдем
sin -^- sin Щ-
Т = у ' C-ЗЛ0>
sinT
Остается подставить выражения (9) и A0) в соотношение G):
^sin^-sin^), C.3.11)
которое, вспоминая определение вектора поворота, можно записать
еще в виде
C.3.12)
cos -£-
3.3] СЛОЖЕНИЕ КОНЕЧНЫХ ПОВОРОТОВ 109
Теперь по F) приходим к формуле, выражающей правило сложе-
сложения конечных поворотов:
J
Наличие в ней слагаемого 62 X ©i указывает на некоммутативность
конечных поворотов. Результирующий поворот последовательности
поворотов 62, 6j определяется по формуле
•'= Л-
Отметим, что в частном случае последовательных поворотов вокруг
одной и той же оси формулы A3) или A4) выражают теорему сло-
сложения тангенсов: при
имеем
6 = 6'"= — (tg -~ -f- tg -#-) = 2g tg * 2 . C.3.15)
l — tg-^tg-^2- V 7 ^
Нетрудно составить также выражение параметров Родрига—Га-
Родрига—Гамильтона результирующего поворота (обозначим их v0, v1$ v2, v3) no
параметрам Xo, Xlf X2, X3 и |x0, |xlt |x2, |x3 слагаемых поворотов. Вы-
Вычислим сначала по B.8) и A3) величину
Г)-
Замечая, что
| в2 х в! |2 = е?е| — (вх - в2J.
получим
и можно принять
ПО ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Теперь по A3) получаем
(
~\ + Т + V7 &
з з
.5=1
или
3 3
Из A61 и A7) получаем систему формул *)
C.3.18)
3.4. Вычитание конечных поворотов
Конечные повороты обладают свойством ассоциативности. Это зна-
значит, что последовательность поворотов 61э 62, 63 можно осуществить
как путем сложения результирующего поворотов bv Ь2 и пово-
поворота 63, так и складывая 6Х с результирующим поворотов 62 и 63.
Имея это в виду, рассмотрим последовательность поворотов — в1#
Ь{, 62, эквивалентную, очевидно, повороту 62. Она же эквивалентна
последовательности —6Х и 6. Поэтому, заменив в C.13) векторы 6
на б2, 6j на — 6j и 62 на 6, придем к формуле вычитания поворотов
(вв + вХв) C.4.1)
позволяющей по заданному результирующему повороту и первому
из слагаемых поворотов определить второй слагаемый поворот.
Если же требуется по результирующему повороту и второму сла-
слагаемому повороту определить первый слагаемый поворот, то рассу-
рассуждение можно провести так: последовательность поворотов — 62, — 6Х
эквивалентна результирующему повороту — 6. Поэтому, воспользо-
воспользовавшись A), получим
1 + 1
или
C.4.2)
*) Это — формулы умножения кватернионов.
3.5] ПЕРЕСТАВИМЫЕ КОНЕЧНЫЕ ПОВОРОТЫ 111
3.5. Переставимые конечные повороты
Заключение о некоммутативности поворотов было сделано в пред-
предположении, что направления осей слагаемых поворотов фиксированы
в системе осей, не связанных с телом. Отказываясь от этого предпо-
предположения, можно прийти к выводам, существенно облегчающим при-
применения теории конечных поворотов. Докажем теорему *): последо-
последовательность конечных поворотов, определяемых векторами
C.5.1)
эквивалентна последовательности
6; = 62 = 2е2 tg ■£-, 6; = 2е[ tg Ц-, C.5.2)
где е'х—единичный вектор, в который переходит ех при повороте 62.
Этот вектор может быть определен по формуле A.11):
C.5.3)
\ х Г7
и следовательно,
^
В выражение в скобках можно добавить вектор 62; тогда по C.13)
получим
1» «
C.5.4)
Теперь по C.13) надо составить результирующий поворот, назо-
назовем его 6', последовательности поворотов B). Для этого сначала
отметим, что по D)
е;.б;=б2.б2 = е2.б1. C.5.5)
*) См. А. И. Лурье, О теории конечных поворотов твердого тела.
Прикладная математика и механика, 21, № 4, 1957, стр. 371—373.
112 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Получаем
4
j r 1-4 e, .
6 +1-0, X 0
, X 02
1 - 1 0, • 62
В выражение в скобках внесем равный нулю вектор
Тогда, применив C.13), можно будет написать
°' = е+5
e
C.5.6)
В выражении в квадратных скобках заменим теперь 8 его значе-
значением C.13); получим вектор
°i)° 4°2хо, —
коллинеарный 82; поэтому подстановка в F) дает
6 = в/. C.5.7)
что я доказывает эквивалентность последовательностей поворотов A)
и B).
3.6. Выражение конечного поворота и параметров
Родрига — Гамильтона через эйлеровы углы
Конечное положение связанного с твердым телом триэдра еди-
единичных векторов i's получается из начального его положения, опре-
определяемого неподвижным триэдром is с помощью последовательности
трех поворотов
0i = 2*8tg^. 62 = 2tttg-J, 63 = 2^tg|. C.6.1)
3.6] ВЫРАЖЕНИЕ КОНЕЧНОГО ПОВОРОТА ЧЕРЕЗ ЭЙЛЕРОВЫ УГЛЫ 113
на углы ф, 9,- <р вокруг оси Oz, линии узлов п и оси Oz'. Резуль-
Результирующий поворот можно получить, дважды применяя последовательно
формулу сложения C.13). Но мы избежим этого вычисления, восполь-
воспользовавшись теоремой о переставимых поворотах. При повороте 62 ось
вектора *3 переходит в *3. Поэтому, согласно упомянутой теореме,
последовательность поворотов A) эквивалентна последовательности
i | ej = 2^tgi. C.6.2)
Но два последних поворота происходят вокруг одной и той же оси..
Они, согласно C.15), заменяются одним поворотом на угол ф-f-cp:
Теперь, заметив, что n*i'3 = 0t получаем по C.13)
b = 2(ntg^+i'3tg± + *-±n'tg±tgl+±), C.6.4)
так как /^Х я ==/*'. Спроектировав это соотношение на оси i'v i'v
i'y получаем
в = 2 [i\ tg i (cos cp + sin cp tg
cos
2 C.6.5)
Коэффициенты при i's в этом выражении представляют проекции
вектора поворота 6 как на оси Ox'yfzf9 так и на оси системы Oxyz.
Величина угла поворота у определяется по B.8). Имеем
и далее
cos2 -£- = cos2 тг cos2 т ' ' , cos -k- = cos тг
COS
Знак параметра Хо может быть выбран произвольно. Поэтому из E)
B.6), B.8) получаем
Ао = cos -g- cos т ^ ' , Xt = sin -g- cos T Y
.0.6 — cp . О.
= sin у sin ' 2 , X3 = cos -j sin
C.6.6)
Таковы выражения параметров Родрига — Гамильтона через эйле-
эйлеровы углы.
8 Зак. 2072. А. И. Лурье
114
ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА
[гл.
3.7. Приложения формул конечного поворота
1°. Ротор в кардановом подвесе. Очевидно, что поло-
положение оси ротора в кардановом подвесе не зависит от последова-
последовательности поворотов колец подвеса. Проверим это, применив теорему
о переставимых поворотах. Назовем через ех, еъ ег триэдр осей,
связанных с платформой подвеса, причем единичный вектор ех напра-
направлен по оси вращения наружного кольца; iv /2, h — триэдр осей,
связанных с наружным кольцом (ix = ex); i'v i'v i'z — с внутренним
кольцом (i2 = /2). Ось вращения ротора во внутреннем кольце имеет
направление /£. В начальном положении все триэдры совмещены.
Надо проверить эквивалентность последовательностей поворотов
ei = 2i,tg£, 62 = 2/;tg| C.7.1)
= 2*; tgf.
C.7.2)
так как /j— то положение, которое займет вектор ix после пово-
поворота 6', = 62.
Результирующий поворот последовательности A)
равен
е = 2 (/, tg £ + i'2 tg 4+1'2 x /, tg I tg 1), C.7.3)
а последовательности B) —
б' = 2 (i'2 tg| -f- /; tg | -h i[ X i'2 tg | tg I). C.7.4)
Надо проверить, что имеет место тождество
Расположение векторов, стоящих в этом выражении, показано на
рис. 27 (вид с конца fy; из него следует
и дело сводится к проверке тождеств
3.7]
ПРИЛОЖЕНИЯ ФОРМУЛ КОНЕЧНОГО ПОВОРОТА
115
Параметры Родрига — Гамильтона, соответствующие повороту 6,
равны
3 В
C.7.5)
v0 = cos-2-cosir » vi = sin-2-C0ST'
a . 3 . a . 3
v2 = cos -к sin -j , Vo = sin -g- sin -£-.
Эти же выражения можно получить по C.18), заметив, что по B)
ft о
X0 = cos^-, X1 = 0, X2 = sin-^-, X3 = 0,
С помощью таблицы косинусов 1 этой главы, зная величины E).
легко восстанавливается матрица B.6.2).
2°. Поворот геоцентрической системы осей. Опре-
Определение этой системы осей дано в п. 2.15. Пусть Фо, Хо—северная
широта и восточная долгота начала О системы в момент t = t0, а Ф
и X — в момент t. Требуется опре-
определить вектор поворота, совмещаю- I
щий начальное положение системы
с конечным.
Речь идет о сложении поворотов
C.7.6)
Здесь е2 — единичный вектор, пер-
перпендикулярный плоскости меридиана
X = Xq и направленный на запад,
е—единичный вектор оси мира,
АХ = X — Xq -f- U (t — tf0), причем U—
угловая скорость Земли (рис. 28).
Первый поворот этой последова-
последовательности соответствует смещению
по меридиану Хо из точки с широ-
широтой Фо на широту Ф, второй — по параллельному кругу широты Ф.
По теореме о переставимых поворотах последовательность F) может
быть заменена на
Л^-, e; = 2*'tgiq^, C.7.7)
Рис. 28.
где е'2 — единичный вектор, перпендикулярный плоскости меридиана X,
направленный на запад; в него переходит е2 при повороте 62 = 6J.
Последовательности G) соответствует смещение сначала по парал-
116
ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА
[ГЛ.
лельному кругу широты Фо, потом по меридиану X на параллельный
круг Ф. Поскольку конечное положение триэдра никак не связано
с тем, как мы мыслим происходящими смещения, теорема о пере-
переставимых поворотах наглядно подтверждается этим примером.
Имеем
ДХ , _v , _ , ДХ , Ф — Фп
C.7.8)
Проверка тождества 6 = 6' выполняется, как в предыдущем примере.
Заметив, что
е = ех cos Фо -f- ег sin Фо, е X e<i = — €х sin Фо -f- e3 cos Фо,
где во, е^—единичные векторы восходящей вертикали и направле-
направления на север, получаем
2
COS.
i cos
C.7.9)
Параметры Родрига — Гамильтона равны
—Фо
cos-
= cos
Фо . ДХ
sin
sin
, . Ф—Фо
А2 = sin ^—- (
ДХ
Х3 = sin
. ДХ
sin ~y~ .
C.7.10)
3°. Ориентация оси уравновешенного ротора в кар-
дановом подвесе относительно геоцентрической
системы осей*). Известно, что ось уравновешенного ротора
в кардановом подвесе сохраняет неизменное направление в простран-
пространстве. Зададим это направление в геоцентрической системе Oxyz
места старта (Фо, Xfl) в момент t = t0 углами азимута а0, отсчитывае-
отсчитываемого по направлению север — запад (от ех к е2), и подъема р0 над
плоскостью горизонта. Здесь а0 представляет угол поворота наружного
кольца подвеса вокруг восходящей вертикали, а — C0 есть угол пово-
поворота внутреннего кольца вокруг его оси, расположенной в плоскости
горизонта и направленной вначале (при ао = О) на запад. Надо соста-
составить формулы, определяющие углы а, C оси ротора в геоцентриче-
*) Д. Р. М е р к и н,
стр. 145—158.
Гироскопические системы, Гостехиздат, 1956>
3.71 приложения формул конечного поворота 117
ской системе осей Ox'y'z' места с северной широтой Ф и восточной
долготой X в момент t.
Координаты конца единичного вектора, расположенного по оси
ротора и сохраняющего неизменное направление в системе стартовых
осей Oxyz, в системах Oxyz и Ox'y'z' равны
х = cos а0 cos р0, у = sin а0 cos po, z = sin p0,
х'= cosacosp, у' = sin a cos p, zf = sin p.
По формулам B.17) получаем
cos a cos р = (Хо 4"^i — ^2 — Xl) cos a0 cos Po 4~
4- 2 (Х0Х3 + XjX2) sin a0 cos p0 + 2 (— X0X2 4- Х^,3) sin p0,
sin a cos p = 2 (— X0X3 -j- X^) cos a0 cos po 4"
sin p = 2 (X0X2 4- XjXg) cos a0 cos po 4-
4- 2 (— X0X! 4- ^2X3) sin a0 cos Po 4- (Ao + X3 — X? — \
где Xo, Xp X2, X3 определены по A0). В частных случаях эти фор-
формулы упрощаются. Например, если в начальный момент ось ротора
была в плоскости горизонта и направлена на восток, то ао = — -к-тг,
Р0 = 0 и формулы A1) принимают вид
cos p cos a = — sin ДХ sin Ф, sin a cos p = — cos ДХ, j
sin p = sin AX cos Ф. j
Если же в начальный момент ось ротора расположена в плоскости
меридиана (а0 = 0) и приподнята над горизонтом на угол ро, то вычи-
вычисление по формулам A1) дает равенства
0 — р0) 4~cos ДХ sin Ф 81п(Ф0 — ро),
sin a cos р = — sin ДХ sin (Фо — р0), 1 C.7.13)
sin р = sin Ф cos (Фо — р0) — cos ДХ cos Ф sin (Фо — ро). j
Наиболее прост случай начального расположения по оси мира;
тогда Ф0=^р0 и по A3) получаем
cos a cos p = cos Ф, sin a cos p = 0, sin C = sin Ф,
или a = 0, р = Ф — ось ротора остается направленной по оси мира,
поворачиваясь вокруг оси внутреннего кольца на угол, равный изме-
изменению широты.
П8 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
3.8. Выражение вектора угловой скорости
через конечный поворот
Положение твердого тела (системы связанных с ним осей Ox'y'z')
задается вектором конечного поворота 6, осуществляющего совмещение
системы осей Oxyz с системой Ox'y'z'. Положение же тела, бесконечно
«близкое к рассматриваемому, может быть получено двумя способами:
или путем сообщения телу бесконечно малого поворота, обозначае-
обозначаемого &'6, из рассматриваемого положения, или же путем сообщения
телу поворота 6 —j— S6 из начального положения. Здесь бесконечна
малый вектор ЪЬ обозначает приращение, которое получает вектор 6,
когда телу сообщается дополнительный бесконечно малый поворот,
так что 6-4-йб представляет результирующий поворот последователь-
последовательности двух поворотов: конечного 6 и бесконечно малого ЪГЬ. Послед-
Последний поэтому может быть найден по формуле вычитания поворо-
поворотов D.1). При пренебрежении малыми величинами второго порядка
эта формула дает
1
Выражение £6 через Vb проще всего получить по формуле D.2):
гь = Ь'в 4- ■§-ь'® X 6 4- j 66. Ь'в =
= Ъ'Ъ A 4- \ в2) — ^ 6 X (§'6 4 -g- 8'в X б). C.8.2)
Вектор угловой скорости <о связан с вектором бесконечно малого
поворота соотношением tadt = b'b. Поэтому, основываясь на фор-
формуле A), приходим к соотношению, связывающему (о с вектором
конечного поворота,
(о=—\—(б-t iexeV C.8.3)
1 4- | 02 V ^ }
4
Производная же по времени вектора поворота выражается через
вектор угловой скорости по формуле
6 = to 4- \ » X 6 + j 66 • и. C.8.4)
Дифференцируя, выражение B.10) вектора 6 и учитывая соотно-
соотношение B.8), получим
= 2 [ (ХОХХ — W
3.8]
ВЫРАЖЕНИЕ УГЛОВОЙ СКОРОСТИ ЧЕРЕЗ КОНЕЧНЫЙ ПОВОРОТ
1 19
где iv i2, *з—единичные векторы неподвижных осей Oxyz. Поэтому
проекции вектора (О на эти оси.по C) будут
ш, = 2 (ко\ —
ш2 = 2 (Х0Х2 —
i3 = 2 (Х0Х3 - Х3Х0 + Х,Х, —
C.8.6>
Проектируя же на оси системы Oxyz равенства B), придем к соот-
соотношениям:
2 (XoXi — XiXo) == щ (X? + Ф + ^2 (Х0Хз + Х^) 4" ^>з (—
2 (ХоХ2 — Х2Х0) = (Oj (— XqX3 4- ^i^2> -Ь W2 (Хо 4" ^)
2 (ХсХ3 — хДо) = о>1 (ХоХ2 4- ^з) 4- ^г (— ХоХ! + Х2Х3)
1^з).
C.8.7)
Воспользовавшись теперь уравнением связи B.7) и вытекающим
него соотношением
4- ^2X2 4- hh = 0,
C.8.8)
легко найдем выражения производных параметров Родрига—Гамиль-
Родрига—Гамильтона по времени через проекции угловой скорости на неподвижные
оси:
2Хо = —
2Х] =
2Х2 = оJХ0 4" ^Xi —
2Х3 =
C.8.9>
Зная проекции вектора угловой скорости на оси Oxyz, можно
спроектировать его на оси Ox'y'z'\ связанные с телом, с помощью,
таблицы косинусов 1 п. 3.2. Получим
о), = 2 (ХОХХ — ХДО 4- ^2X3 — Х3Х2),
оJ = 2 (ХоХ2 — Х2Хо 4" ^Xi — ХхХз),
ш3 = 2 (Х0Х3 — Х3Х0 4" ^1^2 — ^2^1) •
C.8.10»
Изменился знак второй группы слагаемых. Это можно было предви-
предвидеть, так как при рассмотрении поворота — 6 системы осей Ox'y'z'
и Oxyz меняются местами, причем изменяется знак \v X2, Х3 и
120 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
вектора (о, но знак Хо сохраняется. Выражения производных пара-
параметров Родрига — Гамильтона через со^ имеют вид:
2Х0 = — (cojXj -f- co2X2 + ">зХз)
2Х, = а),Хп -4- сооХг, — соХ,
.' 10 32 23
2Х2 = со2Х0 -f- WjXg — (D3Xlf
2Х3 = со3Х0 -|— tD2^i"— ^i^*
C.8.11)
Как пример применения формулы C), определим угловую ско-
скорость геоцентрической системы осей, вектор поворота 6 которой
дается выражением G.8). Имеем
I ф ф д^
1 + 4- б2 = cos2 —2~~^ cos2 —.
Дифференцируя G.8) и учитывая, что векторы е2 и е сохраняют
неизменные направления, получим
а Ф ДХ
20 ^
cos2—2— cos2-^-
ДХ , Ф — Фо Ф , ДХ
t^
COS2-T cos--2-^
где ^ = ^Х^2 — единичный вектор, направленный по радиусу парал-
параллельного круга от его центра, так что е2, £*, е образуют правый
триэдр единичных векторов. Внесем это выражение в C):
to = е АХ -+- е2Ф cos AX -f- ej> sin AX, C.8.12)
что легко было непосредственно сообразить. Проектируя это равен-
равенство на оси геоцентрической системы, получим
<о = U ■Jrel (Xcos Фо — Ф sin AX sin Фо) -\~е2 Ф cos AX -\-
( sin фо + * sin AXcos фо>» C.8.13)
где ev e2, в^ — единичные векторы направлений на север, запад и
восходящей вертикали в месте и в момент старта; через U = Ue обо-
обозначена угловая скорость Земли.
Выражения A2) и A3) можно представить также в виде
to = е АХ +- е!2 Ф = U -\- X {е\ с о s Ф 4- е\ si n Ф) -+- е\ Ф, C.8.14)
где e'v e'v е'ъ — триэдр осей геоцентрической системы данного места
в момент t.
3.9|
ПАРАМЕТРЫ КЕЙЛИ КЛЕЙНА
3.9. Параметры Кейли — Клейна *)
121
Эти величины, определяющие положение твердого тела, пред-
представляют комплексные комбинации параметров Родрига — Гамильтона.
С их помощью повороту тела сопоставляется некоторое дробно-линей-
дробно-линейное преобразование в плоскости комплексного переменного, а задача
сложения поворотов сводится к выполнению последовательности таких
преобразований.
В дальнейшем используются два представления комплексных чисел:
представление их точками плоскости z = х -f- 1у и сопоставляемыми
им с помощью стереографической проекции точками сферической
поверхности единичного радиуса (сферы Римана).
Плоскостью ? будет служить экваториальная плоскость сферы
единичного радиуса £0, на которую проектируются из ее полюса N
точки плоскости. Система осей О*££ъ **) выбирается с началом
координат в центре сферы О так, чтобы оси ^, £2 совпадали с осями х
и у плоскости, а ось Е3 шла к полюсу сферы (рис. 29). Тогда,
Рис. 29.
выражая, что три точки TV @, 0, 1), M(tv ?2, £3) и М'(х, у, 0)
лежат на одной прямой NMM', получим соотношения
1 — (
т. е. z = .
причем £j, E2, Е3 связаны уравнением поверхности сферы
C.9.1)
C.9.2)
*) F. Klein und A. Sommerfeld, Uber die Theorie des Kreisels,
Heft I, Кар. I, S. 7—68 (Leipzig, 1897).
**) Ранее эти оси обозначались Oxyz; связанные с телом оси Ох'у'г'
Далее обозначаются Оххх2хъ.
122 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Окружности плоскости II, содержащие центр сферы, переходят
при стереографическом проектировании в большие круги сферы.
Действительно, с помощью A) и B) выражение
Л (х2 + у2) — (Вх + Су) =
преобразуется на проходящей через начало координат плоскости
в уравнение окружности
— * -г- 4Л2 в
Эта окружность содержит центр сферы, так как ее радиус
/ В2 4- С2
JR = y 1-| j^2— больше расстояния от центра окружности до
/ £2 _l Q2
1/
центра сферы, равного 1/ —^тг— • Но пересечение упомянутой
плоскости со сферой представляет окружность большого круга, что
и требовалось доказать. Нетрудно показать (мы не будем на этом
останавливаться), что стереографическая проекция любой окружности
плоскости П представляет некоторую окружность сферы. В частности,
прямые плоскости П, проходящие через начало координат, преоб-
преобразуются в большие круги, проходящие через полюсы N и S сферы;
•единичной окр} ж юсти | z | = 1 соответствует экватор, точкам | z \ < 1
внутри нее—точки нижней полусферы (£3 < 0), а точкам вне ее
\z\ > 1 —точки верхней полусферы (£3 > 0). Начало z = 0 n беско-
«ечно удаленная точка плоскости П преобразуются в полюсы 5 и N.
Возвращаясь к случаю твердого тела, имеющего неподвижную
точку О, представим себе описанную вокруг О единичную сферу 2,
неизменно связанную с телом и с системой осей Ох1х2хъ. При пово-
поворотах тела сфера £ скользит по неподвижной сфере Ёо. Большой
круг Г сферы 2 после поворота займет на £0 положение Г'. Пусть f
и f' — окружности плоскости 1J, которым соответствуют на £0 боль-
большие круги Г и Г'. Этому преобразованию окружности ] в j' сопо-
сопоставляется поворот тела (сферы 2). Но при указанном преобразовании
комплексные координаты z и zr точек окружностей ] и ]' связаны
друг с другом дробно-линейным соотношением
Коэффициенты этого преобразования а, р, f. 8 определены с точ-
точностью до произвольного множителя, так как соотношение C) не
3.9] ПАРАМЕТРЫ КЕЙЛИ КЛЕЙНА 123-
изменится при умножении числителя и знаменателя на одно и то же
число. Поэтому выбор коэффициентов можно подчинить условию-
нормирования, которое берется в форме
ьЬ— рт = 1. C.9.4>
Надо установить связь величин а, р, f, ^» называемых пара-
параметрами Кейли — Клейна, с параметрами Родрига — Гамильтона.
Для этого отметим, что дробно-линейное преобразование, при котором,
три точки zv z2, z3, определяющие окружность f, переходят
в точки z[, zfv z'v определяющие f\ может быть записано в виде
I Г I Г
Z—Zo Zo—Zx Z —Z9 Zo — ZA
± ±l \ 4C.9.5>
z—z1 z6 —
Вектор поворота 0 пересекает сферу £0 в точке Р, координаты
которой пропорциональны параметрам Родрига \v X2, Х3, и в диаме-
диаметрально противоположной точке Q. Коэффициент пропорциональности:
надо выбрать так, чтобы удовлетворялось уравнение сферы B);.
поэтому, учитывая B.7), получим выражения координат Р и Q в виде
41 l/ 2 ' 2 l/ 2 ' 3 — l/ 2 *
На плоскости П им по A) соответствуют точки Рг и Q' с коорди-
координатами
Но точки Р и Q не смещаются при повороте тела; поэтому в дробно-
линейном преобразовании E)
болюсу сферы N до поворота соответствует точка zx = oo; ее коор
динаты cj, ;2, ^з после поворота равны
£2 = 2 (— ^1 +■ Х3Х2), $3 = X? §
что следует из формул B.18), если в них принять xl = x2 =
*3 = ^*)« Теперь, учитывая B.7), по A) получаем
*) В этих формулах, в связи с изменением обозначений, xk теперь сле-
следует обозначить хъ, а лг# через ^.
24 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
эсле подстановки в E) величин
дем иметь
g (Х3-- Ар) + ^ + /Х2
следовательно,
= С(Х3-*Х0), Р = С(Х1 + /Х2). Т = С(Х1—/Хз), 8 =
Коэффициент пропорциональности С определяем по D). Оконча-
льные выражения параметров Кейли — Клейна через параметры
»дрига—Гамильтона будут:
а = Х0+/Х8. Р = — \-\-L\, Т = Х2+-/Х1, Ъ = \ — /Х3. C.9.6)'
j них видно, что а, 8, а также C, —у являются комплексными
пряженными числами; сумма квадратов модулей | а|2 -\-\ р |2 =
1^|2+1т12 Равна по D) единице.
Выражения параметров Кейли — Клейна через эйлеровы углы
F.6) имеют вид:
0 , 11
а = cos Ye
C.9.7)
Преобразование координат (xv х2, хг) в (Slt £2, £з)» выражаемое
рмулой C), может быть записано в виде:
из C) следует, что
этому обратное преобразование (tlt 52. ?3) в (л:,, дг2, х3) будет
<*,. *2, ^3)=(~8;( _J)Fi. «2. ч)- «.9.
Явное выражение преобразования (8) по A) имеет вид:
3.91 ПАРАМЕТРЫ КЕЙЛИ КЛЕЙНА 125
Сопряженное выражение будет
Si—-#2 _ о (хх — ix2) •— ? A — *3) /о п 1 о^
1—68 ~-Р(*1--'*2) + «A--*в)' V J
Перемножая A1) и A2), получим по B) и D):
1 -Из = 1 + Ка* + ft?) *з — И - ft*) *i - («If + №) ix*\
1 — «з 1 — [(«* + PT) *з — («T - Р&) х, - (оТ -f РЬ) /х2] *
откуда заключаем, что величина в квадратных скобках равна Е3.
Воспользовавшись этим значением £3» получим kx-\-&2 и ^ — /;2-
Таким образом придем к формулам преобразования
— р2 (хг — tx2) — 2а^3,
— ^2 = — Т2
C.9.13)
Обратное преобразование получаем, используя замены, указываемые
формулой A0):
/у _ р2 t5i _
2
— lx2 = — 7*(*i + «a) + a* (*, — &,) — 2TaS3, C.9.14)
В формулах линейных преобразований A3) и A4), конечно, нет
более нужды считать переменные нормированными согласно B).
В параметрах Кейли — Клейна задача сложения поворотов сво-
сводится к выполнению последовательности дробно-линейных преобразо-
преобразований: повороту 6j соответствует преобразование
C.9.15)
а следующему за ним повороту 62 соответствует преобразование
Результирующий поворот 6 соответствует преобразованию ^ в 2:"
и имеет вид
C.9.16)
Таким образом, параметры Кейли — Клейна результирующего
поворота выражаются через параметры последовательных поворотов
0j и 02 по формулам
tp P
¥2 C'9Л7)
Нетрудно проверить, что эти формулы согласуются с C.18).
126
ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА
[гл. а
3.10. Выражение угловой скорости тела через параметры
Кейли — Клейна
Переходя к определению угловой скорости, обозначим параметры
Кейли — Клейна в моменты t и t-\-dt через
а,
Им соответствуют в формулах (9.17) параметры (alf p,, fj, 8j) пер»
вого 62 и параметры (a12, p12, fi2. 812) результирующего поворота 6.
Второй поворот с параметрами (а2, р2, ^2> 82) в данном случае пред-
представляет бесконечно малый поворот 5'0 = 'д> tftf, проекции которого
на оси системы Otfi^ равны
так что с точностью до малых второго порядка
и по (9.6)
Т2 = У
По формулам C) находим
и т. д. Получаем
,M, 8=--1аK
/ ~
C.10.1)
C.10.2)
C.10.3)
2>Р-
C.10.4)
Заменив здесь проекции ш5 вектора угловой скорости на оси
OEj^ их выражениями через^ проекции со^ на оси, связанные с телом»
по формулам (9.14), получим также
Ъ = - =.
■тК
C.10.5)
3.11] ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА ПО УГЛОВОЙ СКОРОСТИ 127
Легко составляются и обратные соотношения
C.10.6)
и также
= 2/ (Р7 — оА) = 21 (8а —
со, +■/а>2 = 2/(р8 — р8),
o)j — /аJ = 2* (fa — af),
а>з = 2/ (a8 — pT) = 2/ (pi — 8i).
C.10.7)
3.11. Определение положения твердого тела
по угловой скорости
Предполагается, что проекции <Dj, oo2, оо3 вектора угловой ско-
скорости тела, вращающегося вокруг неподвижной течки на оси, свя-
связанные с ним, являются заданными функциями времени, и требуется
найти зависимость от времени параметров, определяющих положение
тела. Речь идет, таким образом, об интегрировании системы диф-
дифференциальных уравнений, дающих выражение производных упомя-
упомянутых параметров по времени через u>j, <у2, w3.
Первая форма этих дифференциальных уравнений представляется
выражениями B.10.1) производных эйлеровых углов через про-
проекции оM вектора угловой скорости:
— оJ in cp,
Ф = ——^ (w1 sin ср -(- а>2 cos ср),
ср = оK — (coj sin cp -\- oJ cos cp) ctg 0.
C.11.1)
В некоторых частных случаях интегрирование этой системы может
<>ыть проведено, но нелинейность и отсутствие симметрии затрудняют
решение и не позволяют получить выводов общего характера.
Симметрично построенную линейную систему дифференциальных
Уравнений можно получить, вводя в рассмотрение единичный век-
вектор е, сохраняющий неизменное направление в пространстве; называя
через 7i» T2» Тз его проекции на оси, связанные с телом (т. е. коси-
*ус углов е с осями Ox'y'z'), имеем
'=2.7^
123 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
Но скорость конца вектора е равна нулю, и согласно B.13.3) можно
написать
Отсюда следует, что коэффициенты при i's равны нулю; это дает
систему трех дифференциальных уравнений
Ti + °>2Тз — "УЬ = 0. Т2 + "YTi — ^Тз = °. Тз + wiT2 — ^Ti = °>
C.11.2)
очевидным следствием которой является соотношение
Сумма квадратов решений системы B) должна оставаться постоян-
постоянной, равной единице. Поэтому начальные значения fj, ^, ^з должны
быть подчинены этому условию. Итак, задача сведена к интегриро-
интегрированию системы трех дифференциальных уравнений B), допускающих
первый интеграл
? £ §
Предположив, что решение, содержащее еще две произвольные
постоянные, найдено, примем e = iv т. е. расположим вектор е по
оси Ох. Тогда, определив постоянные по начальным условиям
Ti = aii» T2 = a2i» Тз = аз1» удовлетворяющим C), где а^ — известные
косинусы углов осей системы Ox'y'z' с осью Ох в начальном
положении ее, найдем an, а21, а31, т. е. восстановим первый стол-
столбец таблицы косинусов 1 главы 2. Аналогично будут найдены по
их начальным значениям величины второго и третьего столбцов
этой таблицы.
Другой способ решения задачи заключается в разыскании пара-
параметров Родрига—Гамильтона. Тогда речь будет идти об инте-
интегрировании системы четырех дифференциальных уравнений (8.11),
допускающих первый интеграл B.7). Если ввести комплексные
комбинации (9.6) параметров Родрига—Гамильтона, т. е. принять за
величины, определяющие положение тела, параметры Кейли—Клейна,
то система (8.11) примет вид A0.5), а первый интеграл B.7) —
вид (9.4). Применение параметров Кейли—Клейна дает более про-
простую формулировку задачи. Действительно, система A0.5) распа-
распадается на две системы линейных уравнений первого порядка совер-
совершенно одинаковой структуры. Каждая из них имеет вид
i )p. ^-^P--^-*»,)*. C.11.4)
3.11] ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА ПО УГЛОВОЙ СКОРОСТИ 129
Предположим, что известны два линейно-независимых решения
этой системы, удовлетворяющие начальным условиям, образующим
единичную матрицу
*l@)=l Pl@) = 0|
=о Р2со)=1!!- (ЗЛ1-5)
Тогда решение системы A0.5) при начальных условиях
при* = 0 а = а0, р = ро, Т = То, Ъ = Ъ0, C.11.6)
удовлетворяющих соотношению
может быть записано в виде
а = аоХ] ц_ р0х2, р = aoPl + р0р2, 7 = Toxi + 8ох2« * 8 = ToPi
C.11.8)
Надо проверить лишь, что это решение удовлетворяет условию (9.4).
Вспомним для этого, что для системы дифференциальных уравнений
вида D)
х = ри (t) х + pl2 (t) у, у = р21 @ х 4- /?22 @ у
определитель Вронского имеет вид
t
Но для системы D) сумма /?11 + /?22=:0» а для взятых решений
£>@)= 1. Поэтому
*iP2
а по (8)
что и требуется.
Фактически достаточно определить лишь одну систему частных
решений Xj, рг\ тогда вторая найдется из соотношений
х2 = pj, p2 = xlt
(черточкой обозначается переход к сопряженным комплексным вели-
величинам). Действительно, xt и рх являются решениями системы диффе-
дифференциальных уравнений, получаемой из D) при замене в правых
частях / на —i\ при этом хД0)=1, ра @) == 0. Но этим же диф-
дифференциальным уравнениям и таким же начальным условиям удов-
удовлетворяют — х2 и р2.
9 Зак. 2072. А. И. Лурье
130 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА |ГЛ. 3
3.12. Уравнение Дарбу
В классическом сочинении Дарбу по теории поверхностей*) за-
задача об определении положения тела по заданной угловой скорости
сведена к разысканию одного частного решения уравнения типа Рик-
кати. Вывод этого уравнения основывается на рассмотрении стерео-
стереографической проекции плоскости на единичную сферу 20, о чем
говорилось в п. 3.9. Пусть £1§ £2, £3 — координаты точки этой сферы.
Ее координаты в системе Ох1х2хъ даются преобразованием (9.10)
или в другой форме (9.9). Дифференцируя последнее соотношение
по времени и учитывая, что zr = 0, получим
К—
или, воспользовавшись формулами A0.6)
Замечая, что по (9.3)
'*= 2i(J-ay 1^+^2 + 2^4 — z'2^-^)]. C.12.1)
_-__(T2 + 8), _£__
и воспользовавшись формулами преобразования (9.14), которые
в применении к вектору w имеют вид
o)j -|— /to2 = 1
0),
аK = *{Ъ (u)j + /аJ) — pa (a)j — /аJ) -f- (а
придем к уравнению Дарбу—Риккати
C.12.2)
(ЗЛ2.3)
Форму этого уравнения можно упростить. Подстановкой
C.12.4)
*) G. D а r b о и х, Lecons sur 1а theorie generate des surfaces, t. 1, Chap.
11, Paris, 1887.
3.12J УРАВНЕНИЕ ДАРБУ 13!
оно приводится к виду, в котором отсутствует линейный член
в правой части:
/ Г (оа dt — / ( со3 dt
t = 7г (щ—шл)е ° -4- tt(w., 4- /u>.) C2£ ^ . C.12.5)
242 17 i2V2ll/ ч 7
Далее полагаем
t
-i ( oi3dt
(AJ -f- /0)^ ^0 = Q^,
так что
S=/o)?-f со?, j==e L 0 J, д = -1. C.12.6)
Теперь, введя новую независимую переменную
t
1 = 1^2^, C.12.7)
о
монотонно возрастающую вместе с tt приведем дифференциальное
уравнение E) к виду (штрихом обозначается производная по т)
С' = —+ ?С2. C.12.8)
Покажем, что задача определения положения твердого тела, вра-
вращающегося вокруг неподвижной точки, полностью решается, если
будет найдено одно частное решение этого уравнения. Действительно,
если С = Е представляет частное решение этого уравнения, то вто-
вторым его частным решением будет —~. Тогда из известного свой-
свойства дифференциального уравнения типа Риккати следует, что функция
т) = ^^ = 4^Ц C.12.9)
удовлетворяет линейному дифференциальному уравнению первого
порядка, которое легко построить; действительно,
77^
Но из дифференциального уравнения, сопряженного с (8), следует, что
132 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
и предыдущее соотношение дает
tj £ q' t
где
с C.12.10)
вещественная функция (разность двух сопряженных величин, делен-
деленная на 21). По (9) и D) находим
t
Умножим теперь числитель и знаменатель на нормирующий множитель
- е
-I в(х)~ J CD.rf/
Тогда, полагая
а = —}*~'в'. * = 4^/вя' с = —4^вя. rf = — т*"*1- C.12.11)
где
о о
C.12.12)
придем к выражению общего решения дифференциального уравнения
Дарбу в форме дробно-линейного преобразования
с коэффициентами —d, b, с, —а, нормированными согласно (9.4).
Надо подобрать С так, чтобы z приняло вид (9.9) с параметрами
а, р. Т» ^» удовлетворяющими начальным условиям A1.6). Положив
для этого
г mz' + п
С- pz' + q >
подчиним выбор постоянных т, п, /?, q условиям
mcQ — pa0 = -[0, —/w0 ■+-gra0 = <x0.
3.131
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА ПРИ САМОВОЗБУЖДЕНИИ
133
Теперь, исключив, например, из уравнений, содержащих в правых
частях а, а0, р0 постоянные п, q, придем к соотношению, опреде-
определяющему а:
с — а
со — ао
= 0.
Таким образом, получаем выражения параметров Кейли — Клейна
в виде
a = aQ(ad0—cb()-\r%(ci0 — acQ)9
Р = а0 (bd0 — dbQ) -f- Po idao — bco)>
•j = 70 (ad0 — ^Z?o) + Bo (ca0 — acQ),
C.12.14)
Величины в скобках вычисляются по A1) и A2); с другой сто-
стороны, сравнение с формулами A1.8) позволяет отождествить их
с соответствующими решениями системы A1.4) при начальных усло-
условиях A1.5). Это приводит к соотношениям, устанавливающим связь
решений упомянутой системы со взятым частным решением уравне-
уравнения Дарбу:
, » * / и
- db0 = Pl
1
2
C.12.15)
где нуликом обозначены величины, относящиеся к начальным значе-
значениям частного решения £, a \ — V I ^o
Таким образом задача об определении положения твердого тела,
вращающегося вокруг неподвижной точки, сведена к квадратурам,
если известно одно частное решение уравнения типа Риккати (8).
3,13. Пример. Определение положения твердого тела
при самовозбуждении
Рассматривается твердое тело, вращающееся вокруг неподвижного
Центра О и находящееся под действием зависящих от времени (но
не от положения тела) моментов сил. Такие моменты могут созда-
создаваться, например, силами реакций вытекающей струи. Предполагается
наличие симметрии вращения вокруг оси Oz\ так что моменты
134
ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА
[ГЛ 3
инерции тела относительно осей Ох' и Оу' равны друг другу
(Л = В)\ момент инерции относительно оси Oz' обозначается через С.
Уравнения вращения тела вокруг неподвижной точки — уравнения
Эйлера (8.1.18)—в этом случае легко интегрируются относительно
угловых скоростей. Имеем
ЛоI -\- (С — А) оJаK = тх%
Из последнего получаем
C.13.1)
C.13.2)
а первые два можно объединить, сложив второе с произведением
первого на /, Получим линейное уравнение первого порядка
) = -д(Щ + im\)>
ciJ 4~ ^i ~\ 1— ^з (!®2
общий интеграл которого будет
СО2—|—/СО !=
C.13.3)
Простейшим является случай отсутствия моментов, т. е. вращения
тела по инерции; тело совершает (при А = В) регулярную прецессию
и закон зависимости величин, определяющих положение тела, от вре-
времени легко получить, применяя предложенный в предшествующем
пункте прием вычисления. Действительно, при тг = т2 = тъ = О
имеем
C.13.4)
где через со0 и —2е обозначены модуль и аргумент со^ —|— /со^. По фор-
формулам A2.6) и A2,7) находим
2т о;
t —
где введено обозначение
С
C.13.5)
C.13.6)
3.13] ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА ПРИ САМОВОЗБУЖДЕНИИ 135
Уравнение Риккати A2.8) принимает вид
£/ _ е21 (т ctg Х+е) _|_ е-21 (т ctg X + t^2f C.13.7)
и его частное решение легко найти в форме
где Л — постоянная, которая должна быть определена из квадратного
уравнения
A2 — 2Actgl— 1=0. C.13.8)
Его корни равны Al=ctg-^-i A2 = —*&~о~» Взяв, например, первый
корень, получим частное решение
| = ^ctg^-^Mxctgx+e)f C.13.9)
и вычисление по формулам A2.10) — A2.12) дает
Далее, по A2.15) находим
x1=sin2T^ c [e 2
= у sin \e v c x \^ 2 — e 2 / = —
и остается, обратившись к соотношениям A1.8), записать решение.
Приняв, чтобы не усложнять записей, начальные значения эйлеровых
углов равными нулю, по (9.7) получим
и далее
a=cosy^ 2 =х, р = / sin -J- ^ '2 =Pl. C.13.11)
!±±1
Остается проделать преобразования, связанные с отделением веще-
вещественных и мнимых частей этих выражений.
При движениях, отличных от регулярной прецессии, задача значи-
значительно усложняется. Рассмотрим, например, случай, когда т1 = т2=0,
но тъ Ф 0. Сохранив принятые ранее обозначения независимой пере-
переменной т и постоянных со0, е, ctgX и называя через б отношение угло-
угловой скорости оK к ее начальному значению to^ (или к ДРУгои величине,
136 ТЕОРИЯ КОНЕЧНЫХ ПОВОРОТОВ ТВЕРДОГО ТЕЛА [ГЛ. 3
имеющей ту же размерность, если бы о)!| было равным нулю), запи-
запишем выражение C) в виде
~2Ч 0~4)ctgX J Bdx+e
C.13.12)
Вместо уравнения Риккати G) обратимся к системе линейных
уравнений A1.4) и введем новые неизвестные k и г соотношениями
Ч 0~4")ctgX J 9dT+e ~l A")ctgX J 8dT+t (
k = *e L ° J, r = pe L о J C.i3.13>
Для k и г получим систему дифференциальных уравнений
k' = ikb ctg X + г, /-r = — //-0 ctg X — Л, C.13.14)
где, как выше, штрих обозначает производную по т.
При 6 = 1 возвращаемся к рассмотренному случаю регулярной
прецессии. Конечно, решение получающейся системы линейных диф-
дифференциальных уравнений, если удовлетворить условиям х@)=1г
р@) = 0, приведет к соотношениям A0).
Систему двух дифференциальных уравнений A4) первого порядка
можно привести к одному уравнению второго порядка
+62ctg2X — /в' ctg X) = 0. C.13.15)
Если, в частности, момент сил относительно оси Ozf постоянен,
то б линейно зависит от т:
9=1+-7^in^l+^. C-13.16)
и задача сводится к дифференциальному уравнению Вебера *). Можно
развить также приемы приближенного решения, выбор которых
обусловлен числовыми значениями параметров |л и X.
*) Е. Т. У и т т е к е р и Г. Н. В а т с о н, Современный анализ, т. 2,
стр. 153, ГТТИ, 1934.
ГЛАВА 4
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
4.1. Кинетическая энергия системы
Кинетическая энергия системы материальных точек равна полу-
полусумме произведений масс точек на квадраты их скоростей:
N
т=i
/=1
1=1
Выражение кинетической энергии через обобщенные скорости
получим, заменив вектор скорости vi его выражением A.3.3)
s=l
_ у V дг, drt
dfj • dfj . 1 drt 2
dqs ^s% dt * I dt
и, далее,
[п п N
5 = 1 /г = 1 1 = 1
138
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
[гл. 4
Для сокращения этой записи вводятся обозначения
N
N
N
f* l \dqs dqk^' dqs dqk~^ dqs dqk)
N
drt__ у idxt djct дУ1
N N
IV dri 2
2w =
D.1.2)
Приняв обозначения A.2.1) и полагая
i = m* = m* = m* и т. д.,
можно также записать
37V
< = 1 /=1 /=1
D,1.3)
Эти величины зависят от обобщенных координат и от времени tt но
может случиться, что переменная /, явно входящая в выражения A.2.9)
декартовых координат через обобщенные, не войдет в Ask, Bs, TQt
Кинетическая энергия представлена суммой трех слагаемых
7=72+^ + 70. D.1.4)
К первому G2) отнесены члены, квадратичные относительно обоб-
обобщенных скоростей:
п п
У^АЖЯь. D.1.5)
D.1.6)
Во второе (Тх) обобщенные скорости входят линейно
Третье слагаемое 70 не зависит от обобщенных скоростей. В слу-
случае стационарных связей обобщенные координаты выбираются так,
чтобы t не входило в выражения декартовых координат (или вектор-
радиусов rt) через обобщенные координаты. Тогда, как следует из B),
= 0. 70=0,
D.1.7)
4.11
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
139
и кинетическая энергия системы, подчиненной стационарным связям,
представляется квадратичной формой обобщенных скоростей:
Т==
D.1.8)
По определению A) кинетическая энергия является существенно
положительной величиной, могущей стать нулем лишь при обращении
в нуль скоростей vt всех точек системы. Но в случае стационарных
связей обращение в нуль всех vl влечет за собой равенство нулю и
всех обобщенных скоростей qs. Это следует из формул A.3.4), так
как дефект матрицы A.2.12) равен нулю. Поэтому квадратичная
форма (8) от обобщенных скоростей—положительная определенная,
и коэффициенты ее должны удовлетворять известным критериям
Сильвестра, выражающим положительность определителя и всех диаго-
диагональных миноров матрицы коэффициентов формы (см. (П. 1. 3.25))
А =
л
• • • S*nn И
D.1.9)
при всех значениях обобщенных координат в области их определения.
Неравенства Сильвестра имеют вид:
Д„=| А |=
A]i ... Л\п
Ап\ • • • Ann
Ao\ Ao
Я-1. 1 • • • ■"„_ |, п_1
> О, Д, = Аи > 0.
> 0, . . .
D.1 10)
Первое из этих неравенств выражает также, что матрица А — не-
невырожденная; второе, что невырожденной является матрица коэффи-
коэффициентов квадратичной формы, соответствующей кинетической энергии
системы, получающейся из заданной системы при наложении связи
д„ = const, и т. д.
В случае нестационарных связей слагаемое Т2 выражения D)
кинетической энергии также остается положительной определенной
формой обобщенных скоростей. Это следует из того, что Т2 пред-
представляет кинетическую энергию, соответствующую виртуальным ско-
скоростям v\\
N N
Г Х V ™ V2 1 V ™ <п дГ1 2 /А 1 11\
2 = ~2*^ i i =~2 Zj * I — ~dt * D.1.11)
/el l=\
140 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
т. е. кинетическую энергию воображаемого движения при мгновенно
остановленных связях.
В дальнейшем неоднократно используется теорема Эйлера об
однородных функциях. Однородной функцией степени т называется
функция cp(Xj, ..., хп) от п переменных, удовлетворяющая условию
Содержание теоремы заключается в равенстве
^l^m'fO, xn). D.1.12)
5 = 1
\\i еем по D)
5 = 1 ™ 5 = 1
откуда, согласно A2), следует
5 = 1 S
При стационарных связях получаем многократно используемое
ниже тождество
п
Перейдем к составлению выражения кинетической энергии чере»
квазискорости. Сначала остановимся на случае стационарных связей
и примем, что квазискорости определены однородными формами
обобщенных скоростей A.5.1). Тогда, использовав выражения ско-
скоростей
5 = 1
получим
п п
Г=41] 2Л**ШЛ' D.1.16)
5 = 1 k = \
где, подобно B),
4.2]
СОЮЗНОЕ ВЫРАЖЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
14!
Если связи нестационарны, а квазискорости определены соотноше-
соотношениями A.5.22), то вектор скорости vt равен
Я4-1 Я Ч-1/7 + 1
уч dri • у у drt .
= V
Получаем
п п
=т2
5=1
где в дополнение к A7) приняты обозначения
ы\
5 = 1
D.1.19)
D.1.20)
Выражения кинетической энергии через квазискорости при
кажущейся сложности их структуры во многих случаях имеют значи-
значительно более простой вид, чем через обобщенные скорости. Ниже
мы неоднократно будем иметь случай в этом убедиться.
В случае стационарных связей в выражениях B0) отпадают сла-
слагаемые, содержащие -~ ; при нестационарных связях, но при введе-
введении квазискоростей с помощью однородных выражений A.5.1), от-
отпадают слагаемые с коэффициентами bSt n+v
4.2. Союзное выражение кинетической энергии
Важное значение в аналитической механике голономных систем
имеют величины, называемые обобщенными импульсами. Обобщен-
Обобщенный импульс, отнесенный к координате gs, обозначается через ps.
По определению он равен производной кинетической энергии по
соответствующей обобщенной скорости q's [см. также далее A0.2.1)],
=1. .... п).
D.2.1)
142 основные динамические величины |гл 4
В случае стационарных связей импульсы представляют однородные
линейные формы обобщенных скоростей:
п
п V и л (Л о 9\
а при нестационарных связях
п
п V л ~ __|_ п /'4 9Ч^
Ps — ^-J sk4 k "i s' \^.£.o)
Эти уравнения разрешимы относительно обобщенных скоростей, по-
поскольку, как указывалось выше, матрица А — невырожденная и,
следовательно, существует обратная матрица А .
В матричной записи выражение кинетической энергии имеет по
(П. 1.2.32) вид
Т= i- q'Aq -\-q'B ■+- TQt D.2.4)
где q — столбец, qr — строка обобщенных скоростей, В — столбец
коэффициентов Bs. Вводя еще столбец р обобщенных импульсов,
получаем вместо C)
p=Aq + B, D.2.5)
откуда находим также выражения обобщенных скоростей через им-
импульсы:
q = A'l(p — B). D.2.6)
В случае стационарных связей имеем
откуда следует еще, что
q' = р' {А~1)' = р'А~1, D.2.8)
поскольку матрицы А и А'1 — симметричные. Поэтому выражение
кинетической энергии через импульсы (обозначаемое через V)
будет
V = 4 p'A-lAA-lp = i p'A-lp. D.2.9)
Оно называется союзным выражением кинетической энергии. На-
Например, для системы, имеющей две степени свободы,
D.2.10)
4.3] тензор инерции 143
и союзное выражение кинетической энергии будет
Отметим еще билинейное представление кинетической энергии
р = I q'p = i- p'q. D.2.12)
В случае нестационарных связей представляет интерес выражение
через импульсы не кинетической энергии, а величины
Т=^ pJts—T=2T2+Tx-T=T2-T^. D.2.13)
Здесь использовано соотношение A.13). В матричной записи союзное
выражение для Т легко получить, используя D) и F):
или
Г =±(р' - В') А'1 (р- В)- То. D.2.14)
Приведем еще матричную запись выражения кинетической энергии
через квазискорости. Переписывая соотношения A.5.1) и им обрат-
обратные в виде
w = aq, q ==a~1m = dm, D.2.15)
и подставляя их в D), получаем выражение
7=
1
В КОТОРОМ П X /!
соотношениями
t матрица
D 1
/Э —
А*
-То-
и «
— а
XI
столбец j
В* 4-7V D.2.
.16)
3^ определяются
D.2.17)
первое представляет иную запись формул A.17), а второе—формул
A.20) при ад.я+1 = 0.
4.3. Тензор инерции
При рассмотрении движения материальной системы важное значе-
значение имеют величины и понятия, характеризующие распределение масс
материальных точек, образующих эту систему.
Простейшим из них является понятие о центре инерции —
геометрической точке, положение которой (вектор-радиус гс)
144 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ |ГЛ. 4
определяется равенством
JV
Здесь через
TV
М = 2 /И/ D.3.2)
обозначена масса системы — сумма масс ее точек. Положение центра
инерции при движении изменяется не только по отношению к инер-
циальным осям Oxyz, но и по отношению к точкам самой системы.
Исключительным является случай твердого тела; тогда
N
где rQ=00—вектор-радиус полюса осей Ox'y'z', связанных с те-
телом, г'с = ОС—вектор-радиус центра инерции С в этой системе
осей, остающийся в ней неизменным.
Более сложно понятие о тензоре инерции Q0 системы матери-
материальных точек в точке О.
Определение тензора второго ранга дано в П. 1.4; в том же При-
Приложении несколько ранее (П. 1.2) вводилось в рассмотрение диадное
произведение аЬ векторов а, Ь (диада). Диада представляет пример
тензора второго ранга, так как ее произведение справа или слева на
вектор с дает вектор (аЪ • с или с • ab).
Правила действий над тензорами облегчаются введением диад
единичных векторов isik принятой системы координатных осей. Обо-
Обозначая через Psk составляющие тензора Р в этих осях, можно пред-
представить его суммой девяти диад:
3 3
Р = 2 2 Pskhh* D.3.4)
так как при такой записи сохраняется принятое в определении
(П. 1.4.8) свойство тензора давать при умножении его на вектор
новый вектор
3 3 3 3 3
s=\k=\ S S 5=1 ^^=1 5 5=1
Простейшим примером тензора является единичный тензор
(\ О О
Е=
1
U о 1
D.3.5)
4.3] тензор инерции 145
Его диадное представление имеет вид
E = ixix + i2i2-+-hiz. D.3.6)
Более общим является диагональный тензор
Q = Q^ + Q2t2i2 4- QsMs- <4-3-7)
Если при том Q1 = Q2t то диагональный тензор может быть записан
в виде
Q = QXE 4-(Q3- Qi)
В П 1.4 вводились в рассмотрение тензоры второго ранга
РХа и «ХР. D.3.9),
Их можно назвать векторными произведениями вектора а на тензор Р
слева и соответственно справа. Пользуясь диадным представлением
тензора D), получаем
о о о
Р X а = 2 2 2 /WfcA'r. D-3-10)
о о о
Легко проверить, что таблица составляющих этого тензора совпа-
совпадает с матрицей (П. 1.4.14).
Отметим еще формулы (П. 1.4.15) и (П. 1.4.16):
(аХР)-* = вХР-&. (РХ«):» = Р'(вХ»). D.3.12)
Вспомнив это, рассмотрим диадное представление тензора в си-
системе ортогональных осей, вращающихся с угловой скоростью (о
относительно инерциальной системы. Тогда, применив формулы диф-
дифференцирования единичных векторов B.7.6), получим
2 2|,,«»[(;);Их;)]!
S — 1 /2—1
= P + wXP-PXw. D.3.13)
Через Р обозначен тензор с составляющими в подвижных осях, рав-
равными производным составляющих Р в этих осях. Формула A3) яв-
является обобщением правила дифференцирования вектора в подвиж-
подвижной системе осей на тензор второго ранга.
10 Зак. 2072.. А. И. Лурье
146 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Тензор второго ранга называется симметричным, если
Psk = Pks (/5,5=1, 2, 3). D.3.14)
В случае симметричного тензора произведения а-Р и Р -а опре-
определяют один и тот же вектор. Выражение
3 3
а-Р-а=2 2 VA D.3.15)
S=l ft=l
дает представление квадратичной формы проекций вектора а, коэф-
коэффициенты которой определяются симметричным тензором Р.
Напомнив эти определения, перейдем к рассмотрению тензора
инерции материальной системы в точке О — начале принятой системы
осей. Зададим в этой точке направление единичного вектора е на
оси ОЛ. Моментом инерции материальной системы относительно оси
называется сумма произведений масс ее точек на квадраты их рас-
расстояний ht до оси.
Имеем
е • ri = ricosat, ht = гг sina{l hj^r2. — (е- а^J,
где rL—вектор-радиус рассматриваемой точки, а1 — угол, образуе-
образуемый им с осью ОЛ. Момент инерции относительно этой оси равен
IV N
Joa= 2 /и/Л? = S rni\r] — {rref\.. D.3.16)
Квадрат скалярного произведения rt • е можно представить в виде
(Г/ • ef = (е • г,) {гге) = е- гЛ • е, D.3.17)
выделяя диаду гггь. Далее можно еще записать
е - Е • е= 1, г\ = е • Ег] - е. D.3.18)
Теперь, замечая, что вектор е может быть вынесен за знак суммы
A6), получаем представление момента инерции относительно оси
N
= e- 2 т* {r% — riri) • e D.3.19)
в виде квадратичной формы проекций е (т. е. косинусов углов оси
ОЛ с координатными осями); эта квадратичная форма образуется
с помощью симметричного тензора второго ранга
N
0° = 2 mi № — riri\ D.3.20)
4.4] ПРЕОБРАЗОВАНИЕ ТЕНЗОРА ИНЕРЦИИ 147
определенного для точки О и называемого тензором инерции мате*
риальной системы в этой точке.
Таблица составляющих тензора инерции в точке О в системе
-осей, имеющих начало в этой точке, имеет, согласно B0) (см. П. 1.2.21),
вид:
W N \
ei2 = -- 2 «лу/ 0i3 = - 2 т*м
,00 =
— 2 mi*iyi е22 = 2 mi (*? + -*?) е2з = — 2
1 \ Ы\ /1
TV N N
2 mlzixi 632 = — 2 т1У1*1 °зз = 2 mi{A + У
/=1 i=l i=l
D.3.21)
Диагональные члены этой таблицы представляют моменты инерции
относительно осей координат:
®п===^х9 ®22== «V ®зз==г Л* D.3.22)
Недиагональные (взятые со знаком минус)—называются центробеж-
центробежными моментами инерции и обозначаются
^12 = ®21==—/лгу' в23=вз2= Jyg, ©31 = ®13= ~~'Ллг* D.3.23)
В этих обозначениях тензор инерции представится в следующей
форме:
Jx ~~Jxy —Jx2\
Jyx Jy -Jy*\. D.3.24)
Jzx Jzy J г '
При движении системы составляющие тензора инерции изменяются
вместе с расположениями точек системы друг по отношению к другу
и по отношению к принятой системе осей. Исключением является
случай твердого тела, если тензор инерции его вычисляется в системе
осей, связанных с этим телом.
В случае сплошного тела суммы в формулах A) и B1) выра-
выражаются через определенные интегралы по объему тела.
4.4. Преобразование тензора инерции
Предполагая известным тензор инерции 0° в точке О, определим
*го значение 0°' в точке О'. Достаточно для этого в выражении
<3.20) сделать замену
10*
148 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4-
где ОО' = г0—вектор-радиус нового начала О' относительно ста-
старого, а г'г — вектор-радиус О'Mt рассматриваемой точки по отноше-
отношению к О''. Имея в виду, что
придем к соотношению
0° = 2 «, (Е/-;2 - rf.)+Er\ S m,+2г0.2 «/Г;е -
/1 t l il
(\
— 2 **/■; r0 - r0 2 m r; — roro 2 m,
или по C.2) и C.3)
[4 )]. D.4.1)
Это соотношение значительно упрощается, когда за точку О' принят
центр инерции. Тогда г'с = 0 и
где гс— вектор-радиус ОС центра инерции по отношению к началу О.
Формула C.20) дает определение тензора инерции в точке О,
не зависящее от выбора осей, имеющих начало в этой точке. Соот-
Соотношение A) связывает значения тензоров инерции в двух точках О
и О'. Предполагая, что координатные оси, имеющие начало в О и О',
соответственно параллельны друг другу, найдем из A) следующие
формулы, определяющие составляющие тензора инерции в точке О
(моменты инерции и центробежные моменты) через его составляю-
составляющие в точке О':
i*ci + х02ХС2 + хозхсг) *ik — i (x0lx'ck + xcixok)] • D-4-3>
Здесь через xQV x02, хог обозначены координаты точки О' в системе
осей Оххх2Хъ (с началом в О), через x'cv x'cv x'C3—координаты
центра инерции в осях О'х[х'2х'у параллельных первым (с началом
в О'). Когда за (У принят центр инерции С системы, то xrCi = 0
и xol = xCi\ формула C) принимает вид
Щ )Ь1к — хС1хСк]. D.4.4)
Например,
4 4] ПРЕОБРАЗОВАНИЕ ТЕНЗОРА ИНЕРЦИИ 149"
Первая из этих формул составляет содержание известной теоремы
Штейнера о моменте инерции относительно параллельной оси, про-
проходящей через центр инерции.
Перейдем к составлению формул, связывающих составляющие
тензора инерции в точке О в двух системах осей О^^3 и Ох1х2хЗУ
построенных в этой точке. Назовем а матрицу косинусов, осуще-
осуществляющую поворот, приводящий к совпадению первой системы са
второй. Тогда
лг = а?, t = a'x, D.4.6)
где х и £—столбцы координат некоторой точки М\ в дальнейших
записях отбрасывается индекс /.
Переходя к матричным обозначениям, вводим матрицу инерции
в точке О; согласно C.20) и соотношениям (П. 1.2.19) и (П. 1.2.21)
она может быть представлена формулой
е = 2т(Щ~^). D.4.7)
Элементы 9^ этой матрицы отнесены к осям О^2£3. Составляющие
тензора инерции в той же точке О, но отнесенные к осям Охгх2х^
образуют матрицу, обозначаемую 9*. Последняя равна
9* = 2 т (Ех'х — хх') D.4.8)
или по F)
9* = 2 т (E^a'rt — аК'а') = 2 т (EV% — а^V).
Поскольку Е'£—скаляр, можно написать
и далее
в* = 2 т {tEVW — аК'а') = а [2 т (Е\'\ — Ю] *'*
так как матрицы а и а' одинаковы для всех слагаемых суммы. По-
Получили
9* = <х9а/, 9 = а'9*а. D.4.9)
Таковы соотношения, связывающие матрицы инерции в двух систе-
системах осей, имеющих общее начало. По правилу умножения матриц
находим теперь формулы, связывающие элементы этих матриц, т. е.
составляющие тензора инерции:
о о
в^ЕЗв^А. D.4.10)
Например,
3а12а13 + 2е31а13ап. D.4.
150
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
[гл 4
Это — известная формула, дающая выражение момента инерции от-
относительно некоторой оси (в данном случае Охг) через моменты
инерции и центробежные моменты в принятой системе координат
Ос^з и косинусы углов ап, а12, а13, составляемых этой осью
с координатными осями.
Поскольку 9ц остается (по определению) положительным при
любых вещественных значениях трех переменных ап, а12, а13,
то квадратичная форма, образованная с помощью матрицы в, является
знякоопределенной положительной, т. е. величины 9^ удовлетворяют
■неравенствам Сильвестра
еп > о.
>0. D.4.12)
Развернутое выражение формулы преобразования центробежных
моментов имеет вид:
= впапа2,
в22а12а22
12 (апа22 + ai2a2i) +
(а12а23 Н- а13а22> -+~ ®31 (а13а21 +аПа2з)- D.4.13)
4.5. Главные оси инерции
Следствием равенств D.10) является соотношение
<х9 = 9 а или
2 «rtew Н 2
D.5.1)
"Известно, что направления осей Ojc1JC2Ar3, т. е. матрицу а, можно
определить так, чтобы матрица инерции 9* в точке О стала диаго-
малъной:
е =
0
0
0
e*2
0
0
0
в*
D.5.2)
Такие оси называются главными осями инерции в точке О, а диа-
диагональные элементы матрицы 9* — главными моментами инерции
в этой точке. 9Л -*— это момент инерции относительно главной оси
Oxs. Равенства A) для этой оси (т. е. при фиксированной строке s)
лают три уравнения:
3 3
2 *Sk®kt = &s*st = В* 2 hflsk s=={> 2> 3- D.5.3)
4.51
ГЛАВНЫЕ ОСИ ИНЕРЦИИ
15Г
Опуская временно индекс s и полагая ask = рл, можно переписать-
эти уравнения в виде
2 h (©*, - ht&) = 0 (* = 1. 2, 3), D.5.4)-
причем
D.5.5>
Определитель системы D) должен быть равен нулю, так как
5 р П
вследствие E) в числе величин
ходим к уравнению
©11 ©* ©12
12 ^22 ^
3 ^23
имеются отличные от нуля. При-
При©23
е33-е*
= 0,
выражающему равенство нулю определителя матрицы
/(в*) = в — EQ*.
D.5.6>
D.5.7>
Доказывается, на чем мы не останавливаемся, что все три корня Qs
этого кубического уравнения вещественны, поскольку матрица в
симметрична.
Надо различать три случая:
а) Корни уравнения F) различны. Тогда дефект матрицы G) равен,
единице, т. е. существует для каждого 5=1, 2, 3 минор второго-
порядка определителя F), отличный от нуля. Пусть таковым будет
минор элемента в33—©. т. е.
е„ —в;
©12
©22 ©с
¥=0,
где Qs—один из корней. При этом условии из двух первых урав-
уравнений D) неизвестные рь р2 могут быть выражены через (Зз, а по-
последнее определится далее из условия нормирования E). Получаем
(для 5=1, 2, 3) три направления, образующие матрицу Ш\\
Р{ Й Рз
q2 д2
Р2 V2
Р! Рз
D.5.8).
и* остается проверить взаимную ортогональность этих направлений^
Для этого достаточно заметить, что по D)
(<=1. 2, 3),
152 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
откуда следует, что
££р$е„=е:£р?р?
/=lfc = l t=\
или, при перемене индексов s w r местами:
Но левые части этих равенств одинаковы, в чем легко убедиться,
поменяв места индексов суммирования k и t и учитывая, что Qkt = Qtk.
Поэтому
(в;- в;
откуда, поскольку Н5 Ф Нг, следует
т. е. ортогональность направлений, соответствующих различным глав-
главным осям. Матрица (8) может быть отождествлена с искомой матри-
матрицей поворота а.
б) уравнение F) имеет два равных корня Oi = ©2; тогда дефект
матрицы G) при в = 9i = в2 равен двум; существует минор первого
порядка, пусть ви — %i = 9И — вг, не равный нулю. Для каждой
тройки величин ф\ и §\ имеем по одному уравнению D), соответ-
соответствующему t=lt и по одному уравнению E). Эти величины можно
связать также соотношением
№1=о,
выражающим ортогональность направлений, определяющих первую и
вторую главные оси инерции. Направление третьей главной оси
определится единственным образом, как указано выше в п. а); таким же
путем проверяется его ортогональность направлениям первой и второй
оси. Неопределенность одной из величин $k и рд соответствует тому,
что одна из главных осей (первая или вторая) может иметь произ-
произвольное направление в плоскости, перпендикулярной третьей главной
оси. Матрица а определяется с точностью до поворота вокруг
этой оси.
в) Все корни уравнения F) равны друг другу. Тогда обращаются
в нуль все миноры третьего порядка определителя F), т. е. все его
элементы; уравнения D) удовлетворяются тождественно и девять эле-
элементов матрицы (8) можно лишь связать шестью соотношениями,
выражающими ортонормированность триэдра направлений главных
4 б] эллипсоид инерции 153
осей. Матрица а остается неопределенной-;—любые три взаимно
ортогональных направления могут быть приняты за направления глав-
главных осей инерции в точке О.
Если направления главных осей в точке О определить единичными
векторами £, то диадное представление тензора инерции в этой точке
приобретает диагональную форму C.16)
Ортонормированный триэдр направлений i\% i^ i3 определяется
единственным образом, когда главные моменты инерции различны.
Если 'в* = вг ф вз, то он определен с точностью до поворота
вокруг и. Тензор инерции может быть, согласно C.8), в этом слу-
случае записан в виде
Q0 = elE+(Ql-e*i)&ii D.5.10)
Наконец, при равенстве трех главных моментов инерции тензор
инерции приобретает вид произведения главного момента инерции на
единичный тензор
0° = е;Е D.5.11)
и триэдром главных осей является любой ортогональный триэдр.
4.6. Эллипсоид инерции
Вспомогательным средством для иллюстрации понятия тензора
инерции в точке О служит построение эллипсоида инерции. Отложим
вдоль оси ОЛ, направление которой задается единичным вектором е>
отрезок ОК длины р, обратно пропорциональный квадратному корню
из момента инерции относительно этой оси:
D6D
Координаты точки К — конца этого отрезка—равны
V JOA V JOA У JOA
где а, р, у — косинусы углов вектора е с осями системы Oxyz. Они
играют роль косинусов ап, а]2, а13 в формуле D.11), если заменить
в ней в*п на Jqa- Сделав эту замену и внося значения а, р и у из B),
получим после очевидных упрощений
вп*2 + в22у2 + езз22 + Щ2ху + 2в23^ + 2%хгх = 1. D.6.3)
Это уравнение поверхности второго порядка, являющейся геоме-
геометрическим местом концов отрезков A). Из неравенств D.12) следует,
154 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ fГЛ. 4
эта поверхность представляет эллипсоид, центр его расположен
в точке О. Он называется эллипсоидом инерции в этой точке. Если
за координатные оси х, у, z принять главные оси инерции x*t y*t z*
в этой точке, то уравнение эллипсоида инерции примет вид
Таким образом, оси эллипсоида инерции имеют направления главных
осей инерции в точке О; длины полуосей согласно A), равны
а=уц> Ь=УЩ' С=:УЩ' <4-6-5>
Эллипсоид инерции, построенный в центре инерции С, назы-
называется центральным, главные оси инерции в этой точке будут глав-
яыми центральными осями инерции, главные моменты инерции —
главными центральными моментами инерции. Если линейные раз-
размеры однородного твердого тела имеют наименьшую протяженность
т направлении оси Cx*t а наибольшую — в направлении оси Cz*% то
откуда следует, что
! £. D.6.6)
Таким образом, центральный эллипсоид инерции вытянут по напра-
направлению оси Oz* и сжат по оси Ох* — он в этом смысле «повторяет»
форму тела. При а = Ь = с эллипсоид инерции обращается в шар,
что соответствует «кубообразному телу».
Случай вз = 0 может иметь место для материального бесконечно
тонкого стержня, эллипсоид инерции вырождается в круговой цилиндр
«с осью Oz*.
Заметим, что всегда
6*<в2-[-вз, то есть ^2<тг+т. D.6.7)
причем знак равенства может иметь место при ^тх*2 — 0, т. е.
когда тело представляет бесконечно тонкую пластинку в пло-
плоскости Cy*z*.
Введем в рассмотрение величины (считая 6i не равным нулю)
а2 е: J е'
б! = —= -—, 4 = -j = -^. D.6.8)
Неравенства F) дают
1.61
ЭЛЛИПСОИД ИНЕРЦИИ
155
На плоскости sv е2 (рис. 30) они определяют область, расположен-
расположенную внутри равнокатетного треугольника ОАБ (причем ОА = АВ = 1).
На такую область отображаются все мыслимые эллипсоиды (не обя-
обязательно эллипсоиды инерции), для которых а ^Ь О. Границе ее О А
(т. е. е2 = 0, с = оо) соответствуют эллиптические цилиндры с осью Cz*\
на ОБ имеем эллипсоиды вращения вокруг оси Cx*t сплющенные
вдоль этой оси (а ^ b = с)\
эллипсоиды вращения вокруг
оси Сг*, для которых а = Ь^с,
представляются отрезком АВ.
Точка В соответствует шару,
А — круговому цилиндру с
осью Cz*.
Обращаясь теперь к нера-
неравенству G), которое можно
переписать в виде
видим, что эллипсоидам инер-
инерции соответствует лишь заштри-
заштрихованная часть АСВ области,
Определяющей все мыслимые q
Эллипсоиды. Граница АС— вы-
высота треугольника ОАВ из вер- Рис. 30.
Шины А\ она представляет эл-
эллипсоиды инерции, соответствующие телам, массы которых распре-
распределены по плоской области, расположенной в плоскости Cy*z*.
В точке С имеем е, = е2 = 0,5, т. е. в! = 2в'2 = 2в1 Интересна
отметить, что эллипсоид Ковалевской *), для которого ®*\ = Ql = 2Ql*
расположен в точке К—основании перпендикуляра, опущенного из С
Ш АВ. Для эллипсоида, соответствующего точке L пересечения бис*
сектрисы угла В со стороной АС,
\Г2-
' V2
т. е. в2 = 0.707вь вз = 0B93в1.
Э*о.— эллипсоид инерции, наиболее уклоняющийся от эллипсоида
вращения •♦).
*) Он не является центральным.
**) Графическое представление области параметров, определяющих эл-
иды инерции, несколько отличающееся от приведенного, дается также
JLS4?*e в- Д- Мак-Миллана, Динамика твердого тела, Изд-во иностраи-
«°п «атературы, 1951; стр. 43—44.
156 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
4.7. Кинетическая энергия твердого тела
Рассмотрим сначала случай твердого тела, имеющего неподвиж-
неподвижную точку О. Распределение скоростей точек тела определяется
известной формулой кинематики B.7.8) при vQ = 0:
v, = »Xr;. Г4.7.1)
Поэтому кинетическая энергия равна
N N
1=1 /=1
1- • v\ х (• х ^я=т
Это выражение преобразуется подобно C.16):
«v/ - (. • г;) (. ■ г;.) = . • ( /-;2е - /•;<.)...
Вспомнив определение тензора C.20), придем к формуле
D.7.2)
где 0° — тензор инерции твердого тела в точке О. Кинетическая
энергия представляется квадратичной формой проекций о^, a>2, а>3
вектора угловой скорости (о с коэффициентами, определяемыми сим-
симметричным тензором 0°. В матричной записи
7=|со'в<4 D.7.3)
где со — столбец, а/ — строка проекций (о на принятые оси коорди-
координат, 0°—матрица инерции.
Если, в частности, за оси координат принимаются оси Ox'y'z'\
неизменно связанные с телом, то Qst — постоянные величины, и упо-
упомянутая форма имеет постоянные коэффициенты.
В развернутом виде формула B) (или C)) будет
7= -у @ци>1 —|— ©22^2 "~Г~ ©ЗЗ^З ~~\~~ 29i2(JI)lttJ —(~ 2023(O2(JIK ~\~ 2©31(JIK(JI)l)'
D.7.4)
Она существенно упрощается, когда за оси, связанные с телом,
принимаются главные оси инерции в точке О:
1 / * 2 * 2 i; 2\
7—Tj- (OiODi -\~ 02(О2 + ©з^з)* D.7.5)
4.7] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА 157
Таковы выражения кинетической энергии через квазискорости^
Если же использовать обобщенные скорости ф, Ь, ср, то выражение
кинетической энергии примет труднообозримый вид даже для случая,
когда за оси принимаются главные оси инерции:
cos2 cp 4- 82 sin2 ?) ft2 + Озер2 + 2взфср* cos 0 +
-f- 2 (Ol — 62) sin cp cos cp sin Щ }. D.7.6)
Переходим к общему случаю движения твердого тела. По фор-
формуле распределения скоростей в твердом теле
и, следовательно,
v », = *>1+2 К х ») • г; +(« х г;) ■ (» х /•;>
Поэтому, использовав B), а также определения C.2) и C.1), получим
Здесь ^0—скорость полюса О, г^—вектор-радиус ОС центра инер-
инерции тела в системе осей, имеющих начало в полюсе О, 0° — тензор
инерции тела в этой точке.
Наиболее простая развернутая запись формулы G) получается
при пользовании осями, неизменно связанными с телом. Это связано
с введением проекций vov z>02, vQ% скорости полюса О на эти оси,
т. е. опять таки квазискоростей; в главных осях инерции в точке О
получаем выражение в виде квадратичной формы шести квазискоростей
— г>01«>з) УС + (t>01«>2 — «02«>l) z'C] -f- et<l>l + в2«>2 }
D.7.8)
с постоянными коэффициентами.
Дело упрощается, когда за полюс принят центр инерции тела.
Тогда x'c = y'c = z'c = 0 и
Т = i M {v\x + </2с2 + viz) + -§■ (9Wi + &Wi + вУз)- D.7.9)
i M {v\x + </с2 + viz) + -§
Отметим еще частный случай вращения твердого тела вокруг не-
неподвижной точки О, когда эллипсоид инерции в точке О является
158 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ Ф
эллипсоидом вращения с осью, определяемой единичным вектором е.
Тогда по E.10) и B) получим
7=1[е^+(вз—вО(<о.*J]. D.7.10).
где со • е—проекция угловой скорости на ось вращения эллипсоида
инерции; вз, 6i — моменты инерции относительно этой оси и перпен-
перпендикулярного ей направления, т. е. осевой и экваториальный моменты
инерции.
4.8. Главный вектор и главный момент количеств движения
твердого тела
Известно, что вектор т{0{, равный произведению массы материаль-
материальной точки на ее скорость, определяет количество движения этой
точки. Главный вектор количеств движения точек системы обозна-
обозначается через Q и он, по определению, равен
Q = 2 mivi = 2 miri- D.8.1)
/ = 1 /= 1
Замечая, что по C.1)
N
W D.8.2)
где vc — скорость центра инерции, получаем
D.8.3)
т. е. главный вектор количеств движения системы равен произ~
ведению ее массы на скорость центра инерции.
Главный момент количеств движения точек системы относи-
относительно точки О, т. е. геометрическая сумма моментов относительна
этой точки количеств движения точек системы, обозначается через K°i
_ я
*° = £ лу, X *,. D.8.4)
Будем рассматривать далее движение системы материальных точек не
по отношению к инерциальным осям Oxyzt а но отношению к системе
осей Ox'y'z', движение которой задается скоростью v0 ее полюса О
и угловой скоростью со. Тогда по теореме сложения скоростей
Q = Mvc = M(v0 + to X r'c) + Mv'c = Qe + Qr, D.8.5)
где г'с = ОС — вектор-радиус центра инерции в этой системе осей,
4.8] ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ .МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ 159
4Q ,— его абсолютная, v'c — относительная скорость,
Q, = ^K + WX^), Qr = Mv'c D.8.6)
— главные векторы переносного и относительного количеств
движения.
Выражение момента количеств движения можно представить в виде
К° = 2 », ('о -Ь '',) X (»0 + » X г\ + v\) = Мг0 X (»0 + *> X /-'с) +
i x <■„ + S »y; x (» x-•;) + S »v; x *;.
Имеем
2
где 0° — тензор инерции системы в точке О. Замечая, что по D)
N
2 m/. X *>; = *? D.8.7)
представляет главный момент относительных количеств движения
относительно точки О, приходим к равенству
D.8.8)
В случае, когда рассматриваемая система представляет твердое
тело, а оси Ox'y'z' — неизменно с ним связаны, .имеем v'i=0 и
поэтому
Qr = 0, Af° = O.
Получаем
Q=M(vo + *Xr'c). D.8.9)
К° =r0X Q + Мг'сХ*0 + в° • », D.8.10)
.где 09 — тензор инерции твердого тела в полюсе О системы осей,
с ним связанных. Если, в частности, за этот полюс принят центр
Пиерции С, то r'c = Qt rQ = rc и далее
td. D.8.11)
же твердое тело имеет неподвижную точку О и эта точка
Принимается совпадающей с О, то го = О, ^0 = 0. Получаем
D.8.12)
160 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
В проекциях на оси координат Ox'y'z', связанные с телом»
последнее выражение имеет вид *)
К? = вц©! + в12оJ -f- ©1з«>з.
К2 = &2\®\ -f-
D.8.13)
Если же за эти оси принять главные оси инерции в точке О, то
АГ? = вТсо1# /С2° = 020J, /Сз° = в3и>3. D.8.14)
Как выше в п. 4.7, интересно отметить частный случай тела,
вращающегося вокруг неподвижной точки О, когда эллипсоид инер-
инерции в этой точке — эллипсоид вращения. Тогда
К9 = в! (ю — to • ее) + 8з<о • ее. D.8.15)
где е — единичный вектор оси вращения эллипсоида инерции, а вектор
в скобках представляет проекцию вектора ео на плоскость, перпен-
перпендикулярную этой оси — поперечную составляющую вектора угловой
скорости.
4.9. Кинетическая энергия системы
при относительном движении
Исходим из теоремы о сложении скоростей, записываемой в виде
где vQ — скорость полюса О движущейся системы осей, (о — ее"
угловая скорость, *о\ — скорость точки по отношению к этой системе
осей, a vt—абсолютная скорость точки. Тогда, пользуясь известным
равенством (а X Ь) • с = а • (#Х с)> получим
Теперь по G.7), (8.6) и (8.7) находим
N
m.v'.2- D.9.1)
*) Напомним, что центробежные моменты равны в^ (при s Ф t), взятым
со знаком минус.
4.9] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ ПРИ ОТНОСИТ. ДВИЖЕНИИ 161
Первая строка этого выражения представляет кинетическую энер-
энергию Те переносного движения. Формально ее выражение не отли-
отличается от кинетической энергии, которую мы приписали бы системе,
если бы точки ее были неизменно связаны с подвижной системой
осей Ox'y'z'. Надо, однако, иметь в виду, что здесь тензор инер-
инерции 0° в точке О не остается постоянным при движении (что было бы
в случае твердого тела, неизменно связанного с этими осями)
Слагаемое
представляет кинетическую энергию относительного движения.
Итак,
K? + Tr. D.9.3)
Определяя положение точек системы по отношению к движущимся
осям обобщенными координатами qv q2 qn и полагая
r'i=r'i(?v qv .... Яя). D.9.4)
имеем
ft n N /
Щ-5Г-* D.9.5)
dqs
ft n N . f
*r?=2 m^ x ^=2 'i, 2 «/ix dJr • D-9-6)
i-l 5=1 /»1
Эти величины — линейные относительно обобщенных скоростей;
поэтому совокупность слагаемых
п
r-t-ft) • /Гг = 2j &s4s* D.9.7)
в которых
N i ft t
1=1 S i=l
представляет линейную часть выражения кинетической энергии (I Л),
обозначаемую через Тг. Кинетическая энергия относительного движе-
движения является однородной квадратичной формой обобщенных скоростей:
п п ft ^_/ Л /
Наконец, кинетическая энергия переносного движения Те не зависит
от обобщенных скоростей qs и представляет часть То выражения A.4)
Ц <*ак. 2072, А. И. Лурье
162 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
4.10. Энергия ускорений
Составление дифференциальных уравнений движения в форме,
предложенной Аппелем, предполагает, что составлена величина
D.10.1)
называемая, по аналогии с кинетической энергией, энергией ускоре-
ускорений. Нет нужды в полном знании величины 5, так как диффе-
дифференциальные уравнения Аппеля содержат производные лишь по
обобщенным ускорениям qs, вследствие чего слагаемые, от qs не
зависящие, можно в выражении 5 отбросить. В дальнейшем
через S* обозначается выражение 5, в котором эти слагаемые уже
отброшены.
Сначала остановимся на случае стационарных связей. По A.3.9)
имеем
д ri drt
Вспоминая теперь выражение A.2)
находим
dri drt
dqT -bmi\ dqr dqs dqk ^ dqs dq, d
Изменив здесь индексы г, s, k в круговом порядке, получим еще
два соотношения
_V_ / av, drt drt d*r(
— A m' \ dqs dqk dqr ^ dqk dq$ dqr
dq.
dArs \ч
4.10] ЭНЕРГИЯ УСКОРЕНИЙ 163
Вычитая теперь первое выражение из суммы второго и третьего,
получим
Выражения в правой части представляют символы Кристоффеля
первого рода для матрицы коэффициентов ||Л^||. Они обозначаются
[kt s; r] = [s, k; г], вследствие чего называются также прямыми
скобками кристоффеля — см. (П. 2.4.14):
D.10.3)
Теперь получаем
п п п п п
Таким образом, если известно выражение кинетической энергии Т,
то составление 5* по правилу, указываемому формулами C) и D),
не может вызвать затруднений *).
В случае нестационарных связей суммирования по s и k надо
проводить от 1 до п в первой сумме и по г — во второй (так как
qn+l = 0); во второй сумме суммирования по 5 и k проводятся от I
до п-\- 1. Имеем
л+1 п+1 п п
2 2 [s> k\ r]qsqk=^ 2 Is* k\ r\qsqk-Ar
д-i k=i s=i k=l
n
Учитывая, что
N N
V, дг}
получаем D.10.5)
2[ +» i
дТ0
dqr '
*) А. И. Лурье, Заметки по аналитической механике, Прикладная
математика и механика, XXI, вып. 6, 1957.
U*
164
Поэтому
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
St k;
[гл. 4
5=1
Г дТ0\ " /Л 1 A ^\
Таково выражение 5* при нестационарных связях; для его составле-
составления также достаточно лишь знать коэффициенты, входящие в 7.
Пергходим к составлению энергии ускорений через квазиускоре-
квазиускорения о)г И здесь достаточно знать лишь ту часть 5* величины 5,
которая зависит от квазиускорений. Ограничимся случаем стационар-
стационарных связей и однородных зависимостей вида A.5.1) квазискоростей
от обобщенных скоростей. Тогда, продифференцировав по времени
формулу A.15), найдем
Поэтому можно записать
п п N
дп«
д2г д2г
при этом следует помнить, что 3—4— Ф з—г см- A-9.5). Даль-
Ullfc 011$ V^s V^k
нейшее вычисление ведется подобно проведенному выше. Имеем
по A.17)
ГЛ . rl^^rll. . ГЛ- J ,
N
D.10.8)
4.10] ЭНЕРГИЯ УСКОРЕНИЙ 165
Вспомнив правило «дифференцирования по квазикоординате» A.5.17)
и вводя обобщенные символы Кристоффеля, имеем
1 (дА'„ дА\г дА\Л 1 у Л 6А
„
3^ дщ.
m=l
дА* дА* \
Теперь вычтем третье соотношение (8) из суммы первого и второго
Получим
1 \ч dr. I d2r. d2r.
D.10.10)
Но разности «вторых производных»
д2г, d2rt
могут быть выражены по A.9.5) через «первые производные»:
Получаем
= у f drt
дпг дпг dns ±U* д
i d \ д д д d )
1 У т ЛИ . (
2 *шА i dns \
— Zj T^ ij '" "^7 d^7 "~ 2
и, аналогично,
2 Li Mi ~fr^' \ dizs dnr ~~ dnr dizj— 2 Zi ЧгзЛкГ
1*1 /=1
166 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Подстановка в A0) дает (напомним, что m\lrk = — TJ^-I
*=1 D.10.11)
Теперь, возвратившись к G), приходим к выражению для S*:
( п \
п п п
D.10.12)
Применение этой формулы требует знания выражения кинетической
энергии Т через квазискорости и трехиндексные символы.
Как пример рассмотрим случай твердого тела, вращающегося вокруг
неподвижной точки О. По G.5), когда за оси координат приняты
главные оси инерции в точке О,
A*k = Qsk — 0 при s Ф k, A*ss = Qs = const.
Поэтому все выражения \s, k\ r]7C = 0. Получаем, вспомнив B.10.3),
S* = 1 (в! i? + в2Ш2 + вз^з) +
+ ш^зсоз (93 — в2) + ш2аз3(о1 (в, — в3) + <W2 (в2 — в,). D.10.13)
Выражение S* через обобщенные ускорения было бы очень громоздко.
4.11. Энергия ускорений твердого тела
Выражение энергии ускорений (точнее говоря, величины S*) твер-
твердо! о тела легко составить и непосредственно, исходя из формулы
распределения ускорений в твердом теле.
Начнем со случая твердого тела, имеющего неподвижную точку О,
которую примем за начало системы осей, связанных с телом. Имеем
Удерживая лишь слагаемые, содержащие со, получим
N N
'=* '-I D.11.1)
Первое слагаемое отличается от рассмотренного при вычислении ки-
кинетической энергии Т лишь заменой to на со. Поэтому, согласно G.2)
7V
i = l
4.И] ЭНЕРГИЯ УСКОРЕНИЙ ТВЕРДОГО ТЕЛА 167
Величина под знаком второй суммы преобразуется так:
(» х^) • [» х(» х<)] =(» х г;) • (»»• r;-u>2r;)=
Здесь учтено, что
(«х^-г; = о, (»хrf.)■ с» = (их»)• /■;, (»х»)-»=о.
Поэтому
^(юХ^-^Х^Х rj)] =
/ = 1 ' ^ \ '/ ' D.11.3)
где К0 по (8.4) представляет главный момент количеств движения
твердого тела относительно неподвижной точки О. Вспомнив его
выражение (8.12), приходим к равенству
\ . . \ . .
«S* = "тгw * 0^ • w 4~ w • (to х К j== "о" ft) * 0 * ft) 4~ ft) * (ft) X 0° * ft))-
D.11.4)
Последнее слагаемое может быть записано также в виде (со X <*>) • 0° • со,
т. е. представляет билинейную форму проекций векторов wXw и w
с коэффициентами, определяемыми тензором 0°.
В матричной записи равенство D) имеет вид
S* = yi/e°(D 4-<о'<!>во<о. D.11.5)
где о)' — строка проекций вектора со, (о — столбец проекций вектора со,
о)—сопоставляемая ему кососимметричная матрица по правилу
(П. 1.2.3).
Выражение S* через проекции векторов со и to и составляющие
тензора 0° легко составляются по D) или E):
^з — "У^з) (ви»! + в12аJ -г- в13аK) 4"
@K")! — Wgcoj) (в21ш, 4- ©22^2 +• ©гз^з) +
4- (аз^з — (Ojcojj) (83^! 4" взгв>2 4- ©зз^з)- D-! ^ -б)
Конечно, когда оси, .связанные с телом, являются главными осями
инерции, приходим к выражению A0.13).
168 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ 4
Составим выражение S* в общем случае движения твердого тела,
В формуле распределения ускорений
wt = w0 4- <о X г\ + о) X (ю X г;) D.11.7)
первое и второе слагаемые отличаются от слагаемых формулы рас-
распределения скоростей заменой v0 и со на wQ и to. Поэтому соответ-
соответствующие члены S* получим, сделав эти же замены в выражении G.7)
кинетической энергии Т. Остаются еще два слагаемых в 5*: одно из
них получается от скалярного умножения (при возведении wt в квад-
квадрат) второго слагаемого G) на третье. Оно дается формулой C) или
вторым членом формулы D). Второе слагаемое сразу же вычисляется:
N
2 mtwQ • [to X (ю X П)] = Mw0 • [to X (ю X fc)] =
Таким образом, в общем случае движения твердого тела
+ у <о • 0° • w 4-((i) X ю) • 0° • w. D.11.8)
Значительное упрощение получается, когда за полюс системы
осей, связанных с телом, принимается его центр инерции С. Тогда
rj, = O и поэтому
S* = -i Ж^2С +у A). 0е . со +- (со X со) • 0е • со. D.11.9)
Однако в эти выражения могут войти ненужные члены, т. е.
члены, не зависящие от ускорений, часть которых уже была отбро-
отброшена. Вспомним, что по известной формуле дифференцирования
вектора
*
X *о.
где проекции вектора, обозначенного через vQ, на оси, связанные
с телом, равны производным по времени vQs проекций вектора v0.
Поэтому в (8) можно произвести замены
на
4.121 примеры вычисления кинетической энергии 169
сохранив лишь слагаемые, содержащие квазиускорения (т. е. векторы v0
и to). Получаем после простого преобразования
{Xw)'0°-w. D.11.10)
4.12. Примеры вычисления кинетической энергии системы тел
1°. Гироскоп в кардановом подвесе. Описание устрой-
устройства и применяемые ниже обозначения даны в п. 2.6. Платформа,
несущая подшипники оси наружного кольца, считается неподвижной.
Тогда кинетическая энергия наружного кольца, вращающегося с угло-
угловой скоростью а вокруг оси О£ платформы, будет
где Ах—момент инерции наружного кольца относительно оси О;.
Угловая скорость внутреннего кольца (кожуха) задается векторс^м
(О2 = ai} -f- fy = ifi cos р 4- (Ц + 'з* sin P'
где ц — единичный вектор оси вращения наружного кольца, i's — еди-
единичные векторы осей системы Ox*y*z*> связанных с внутренним коль-
кольцом. Считая, что триэдр этих векторов определяет главные оси инер-
инерции и называя через А2, В2, С2 главные моменты инерции кожуха,
получаем
Т2 = -1 (А2*2 cos2 р + Я2р2 + С2о? sin2 p).
Остается составить выражение кинетической энергии ротора. Вектор
его угловой скорости равен
оK = <о2 4- 4 <р = *"i a cos р 4- ? 4 4- 4 *> sin ?■+-?)•
Представляя тензор инерции его в точке О выражением вида E.10),
получим
7 <V
1 Л(i2 coS2 р + р*) |1
= 1 Л3(i2 coS2 р + р*) -|-1С
3
a sin
Кинетическая энергия системы равна
7"= -j (Л, + Л2 cos2 р + С2 sin2 p -4-у48 cos2P)а2 +
+ i-(B2 + ^3)p2 + ^c3(cp + asinpJ. D.12.1)
2°. Оболочка, несущая маховики. Рассматривается твер-
твердое тело (оболочка), вращающееся вокруг неподвижной точки О.
170 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ 4
Если А, В, С обозначают главные моменты инерции этого тела
в точке О, а (О—его вектор угловой скорости, то по G.5)
Оболочка несет оси вращения п маховиков. Сначала рассмотрим про-
простейший случай — маховики полностью уравновешены. Это значит,
что центр инерции каждого маховика расположен на оси вращения
(маховики сбалансированы статически) и последняя является одной
из главных центральных осей инерции (динамическая уравновешен-
уравновешенность). Через е{ назовем единичный вектор оси вращения /-го махо-
маховика; этот вектор имеет неизменное направление в оболочке, задавае-
задаваемое косинусами а,, р/5 r\i его углов с главными осями Oxyz оболочки.
Вектор-радиус центра инерции Si маховика обозначается через гг = OS;',
наконец, ср^ представляет вектор угловой скорости маховика отно-
относительно оболочки; его абсолютная угловая скорость равна
Считая экваториальные моменты маховика равными друг другу
(Ai = Bi) и называя через Ct осевой момент инерции, по G.9) и G.10)
имеем
= т^й • (Е^ • rt — rtr^ • to -+- At [аз2 — (to • ^J] -(-£*(<*>• ^ -
D.12.2)
Кинетическую энергию системы получим, складывая эти выраже-
выражения с кинетической энергией оболочки. Имеем:
п
— 1 Ж. 1 •
7— a v f\O I ^ /"* / I О I I \2 /Л 1 О О\
ч" to * fc» * to —г~~ *л~ / . О • ( (D-i ОС/ —(~~ tDnp • —t— ОЗоТ/ —1— Ср • I ( Т". 1 ^.. OI
/ = ]
причем 0° — тензор с составляющими
-(-^•(з^ + г2;)],
D.12.4)
и т. д.
Ь°. Кинетическая энергия тела, несущего неурав-
неуравновешенный маховик. Ось маховика (единичный вектор ё)
проходит через точку О, положение которой задается в теле векто-
вектором г = 00. Через а, Ьу с обозначаются единичные векторы триэдра
4.12]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
171
главных осей тензора инерции маховика в точке О. Принимаем рас-
расположение, показанное на рис. 31; на том же рисунке показан триэдр
единичных векторов ev e2> е, имеющих неизменные направления в обо-
оболочке. Угол ср, составляемый плоскостью единичных векторов Ь, с
с плоскостью е, ev является углом поворота маховика, X— угол
Рис. 31.
главной оси инерции с с осью вращения. Положение центра инер-
инерции 5 маховика задается вектором р = 05, проекции которого на
оси а, Ь, с обозначаются ev s2, e3.
Обратимся к формуле (9.1). Первая группа слагаемых этой
формулы представляет кинетическую энергию переносного движения.
В ней
v0 = (о X г, в° = А\<ш + ВХЬЬ + Схсс
и поэтому .
-\-АгAй- аJ + В\ ((о • ЬJ 4-Сх ((о • сJ. D.12.5)
Кинетическая энергия относительного движения определяется
выражением
2Тг = у2е- (Лгаа-+-ВХЬЬ-\-Clcc)-e =
sin
cos2\)f, D.12.6)
представляющим кинетическую энергию твердого тела, вращающегося
вокруг неподвижной оси; когда рассматривается относительное дви-
движение, неподвижной является ось е.
Остается вычислить в выражении (9.3) слагаемые, обусловленные
как переносным, так и относительным движением. По (8.12) и (8.3)
имеем
Bxbb -\-Схсс) -е^ = (—
sin
l cos X) у,
172 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Поэтому
<о. д^4-*>, - Qu = (— £1<D-£sinX-f-C1?i>-ccosX)cp4-
+ /»(»Хг).(*Хр)ф. D.12.7)
Складывая выражения E), F), G) и добавляя к ним кинетическую
энергию оболочки, найдем
[Ло>* + 5o)j 4 Cur; + m | о> X г |2 + Л (со аJ
Т= -j [Ло>* + 5o)j -4- Cur; + m | о> X г |2 -+- Л, (со • аJ 4-
-+- i^j (со . b — <р sin XJ 4- С, (со . £ +■ ср cosXJ) 4-
^pV D.12.8)
Для вычислений по этой формуле требуется задание матрицы
поворота g осей Oxyz, связанных с оболочкой, в триэдр направле-
направлений ev е2у е и матрицы поворота k этого триэдра в триэдр а, Ь% с
главных осей инерции маховика
|<*п а12 а13
а2) а22 а23
аЗ) а32 аЗЗ
sin ср — cos ср О
cos \ cos cp cos \ sin ср — sin X
sin X cos cp sin \ sin 9 cos X
Матрица поворота осей Oxyz в триэдр а, Ь% с равна kg.
Введем в рассмотрение строки
i;=||l 0 0||. Ц=|[0 1 0||, Ц=||0 0 1|| D.12.9)
и соответствующие им столбцы. Тогда строки а\ b'% с' проекций
векторов а, Ь% с на направления осей Oxyz будут
a'=i;*g, b'=V2kgt c'=Vkg D.12.10)
и поэтому
<D-a=lj&£C0, A>-6=12^Ш, Ю«С= l^ftgW. D.12.11)
где со — столбец проекций со на указанные оси.
Через х обозначается столбец проекций х, у, z вектора г,
через р — вектора р на оси Oxyz; столбец проекций elt e2, s3 век~
тора р на направления а, Ь, с обозначается е, так что
Получаем
| о> X г р = &> • (Е^* • г — гг) • (о = с
(ю X /•) • II» 4- ^Т) X Pi = » • (Ер • г — рг). (со 4- еу) =
D.12.12)
4.12] ПРИМЕРЫ ВЫЧИСЛЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ 173
Не останавливаемся на продолжении этих вычислений; развернутое
выражение кинетической энергии, записываемое формулой (8), было
бы очень громоздким. Она несколько упрощается, когда g=E и
ось вращения (вектор е) параллельна оси Ог. Тогда
о> * а = 1 J/гш = (Dj sin ср — со2 cos 9.
w • b = 1 ?&a> = :os X (ш1 ;os ср —|— о>2 sin ср) — <*>3 s*n ^»
оо - £ = 1 лк\й = sin А (о), ;os ср —(— а>2 sin cp) -)- оK cos X.
При наличии только статической неуравновешенности (X = 0) и
при Л, = В} выражение кинетической энергии будет
wXr|2 +
-\-mu>' (Ex'k'e — к'гх')(& -\-ylz). D.12.13)
Не жертвуя общностью, в этом случае можно считать s2 = 0; при-
примем также, что ось вектора с является главной осью инерции в точке
пересечения ее с перпендикулярной к ней плоскостью, содержа-
содержащей центр инерции маховика. Эту точку можно принять за начало
триэдра а, Ь, с\ тогда е3 = 0, e = e1l1 и вычисление дает
тчь1 {Ех'к'г— k'bx')(<& -f-cpl3) = тгх {coscpj((iK-(-cp)(co22: —ш3у) —
~ ">1 (со^ — оJлг)) — sin ср [со2 (о),у — oKx) — (со3 4-ср) (ю3^ ~ ^i^)!}-
Конечно, этот же результат получили бы, раскрывая векторное
выражение
К»Хг) X (« 4-^I -р
и замечая, что проекции р на оси Oxyz равны SjSincp, —©jcoscp, 0.
4°. Платформа, несущая кожухи с заключенными
в них роторами. Подшипники оси вращения наружного кольца
карданова подвеса расположены на движущемся заданным образом
теле 5„. Внутреннее кольцо, ось которого расположена в наружном,
представляет платформу Я, используемую для размещения на ней
гироскопов — вращающихся роторов, заключенных в кожухах, могу-
могущих поворачиваться относительно платформы (рис. 32).
Предполагается, что оси вращения наружного и внутреннего
колец перпендикулярны друг другу и пересекаются в центре инер-
инерции наружного кольца С. Скорость последнего (вследствие движе-
движения тела *S0) задается вектором V; через 2 обозначается вектор
угловой скорости тела So.
С наружным кольцом связан ортогональный триэдр единичных век-
векторов is, причем ix имеет направление оси вращения этого кольца, а /2 —
направление оси вращения в нем внутреннего кольца — платформы /7.
174
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
[гл. 4
Направления осей системы Cx'y'z\ связанных с платформой, задаются
единичными векторами /^, причем i'2 = i2- Подшипники осей враще-
вращения кожухов Кк закреплены на платформе; в ортогональном триэдре
единичных векторов ak% bk, ck% связанных с кожухом Kk, вектор ak
направлен по оси вращения кожуха, a ck — по оси вращающегося
в нем с угловой скоростью cpfe ротора Pk. Угол поворота кожуха Kk
вокруг оси ak обозначается через ~[k, а положение точки пересече-
пересечения Ck осей вращения ротора Pk и кожуха Kk задается на плат-
платформе вектор-радиусом CCk = r'k. Эта точка является центром
Рис. 32.
инерции ротора Pk, тогда как центр инерции кожуха Kk, снабжаемого
точечным противовесом, несколько отнесен от Ck по направлению
оси ck.
Кинетическая энергия системы складывается из кинетической
энергии наружного кольца, платформы, кожухов с противовесами и
роторов.
а) Наружное кольцо. Скорость его центра инерции равна V,
а угловая скорость Q + ^a, где a — угол поворота вокруг оси iv
Поэтому
б) Платформа. Ее угловая* скорость равна
D.12.14)
где р — угол поворота платформы в наружном кольце.
4.12] ПРИМЕРЫ ВЫЧИСЛЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ 175
Вектор-радиус центра инерции платформы (имеющий начало
в точке С) назовем г*. Ее кинетическая энергия по G.7) равна:
в) Кожух Kk. Угловая скорость кожуха и скорость точки Ck
равны соответственно
Вектор-радиус центра инерции Sk кожуха CkSk = skck. По G.7)
кинетическая энергия T'k кожуха Kk дается выражением
Здесь 0Г * — тензор инерции кожуха в точке Ck. Предполагая ра-
равенство экваториальных моментов инерции A'k, B'k кожуха (относи-
(относительно осей ak, bk), имеем
г) Ротор Pk. Его угловая скорость равна
а центр инерции по условию расположен в точке Ск, Получаем
4- («>„ \ с
причем
с
— тензор инерции ротора в точке Ck.
В выражение кинетической энергии платформы и размещенных
на ней тел входит слагаемое, пропорциональное V2:
J
L
Слагаемое, содержащее множитель VXwn» будет
»„> • [ м2г*+s к+о *■;+s »; v *] •
L «=1 «=1 J
176 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Разместив на платформе надлежащим образом противовесы, можно
добиться того, чтобы центр инерции платформы, роторов и кожухов
(при sk = 0) совпал с точкой С:
Тогда выражение слагаемого, содержащего VXwn, примет вид
Переходим к слагаемым, квадратичным относительно (оп. Это
будут
1
[Е Лй + (Ск - Ak) ckck
Через Лл и Cfe здесь обозначены суммы А'к-\- А'к и С^ -|—С^. По-
Постоянную часть тензора в фигурных скобках обозначим Q. Тогда
вычисляемое слагаемое кинетической энергии примет вид
п
Далее выделим слагаемые, зависящие от угловых скоростей ко-
кожухов *\k относительно платформы. Это будут
Остаются слагаемые, содержащие угловые скорости роторов
1 Я*
где Я; — С^срА обозначает «собственный кинетический момент ро-
ротора».
4.12]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
177
Добавив к вышеприведенным выражениям кинетическую энергию
кольца, получим
= у (Ж, -+- М) V2 +1 (Q + /,а) • 0,с • (Q + *,а
| <оп
Ak)ckc
k)ckck
+■
k=\
D.12.15)
5°. Четырехгироскопная вертикаль. Как пример при-
применения формулы A5), рассмотрим представленную на рис. 33 схему
1*_
л.
У////к
V///A
Рис. 33.
четырехгироскопной вертикали при начальном расположении плат-
платформы и кожухов*). Принимаем основание неподвижным, так что
V=0, Q = 0. Оси вращения кожухов, проходящие через точки Cv
С2> ^3» С4, перпендикулярны плоскости i'y i'2 платформы; их единич-
единичные векторы, при принятых на рис. 33 направлениях отсчета углов ть,
будут '*
*) Д. Р. М е р к и н, Гироскопические системы, Гостехиздат, 1956, стр. 108.
12 Зак. 2072. А. И. Лурье
178 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Кожухи попарно связаны между собой, так что их повороты проис-
происходят на равные углы fi = Тг« 7з = Т4- Это достигается или с по-
помощью зубчатой передачи или (при малых углах поворота) механиз-
механизмом антипараллелограмма, как показано на рисунке. Роторы в свя-
связанных между собой кожухах вращаются в противоположные стороны
(против часовой стрелки, если смотреть на них с концов векторов ck).
Вектор-радиусы точек Ck равны
r[ = ai'x + Ц + с1'а. r2 = — ai\ + Щ + с1'й.
r'3 = ai[ - Ы'2 + cl'3. r\ = - ai\ - Ы'2 + ci'r
Массы и моменты инерции всех кожухов (т\ А\ С) так же, как
и заключенных в них роторов (mf\ Affy С"), принимаются равными
друг другу. Противовесы отсутствуют. Угловая скорость платформы
равна
еоп = i[i cos p + Q-+- i'za sin p.
Составим еще выражения векторов:
сг = /j sin fx — if2 cos 7lt c2 = i[ sin fx +1'2 cos fv
c3 = — i[ cos 7з —1'2 sin Тз, cA = i[ cos Тз — ir2 sin Тз.
Остается проделачь вычисления, диктуемые формулой A5), кото-
которая в рассматриваемом случае значительно упрощается и принимает
вид
4
+ 2Л (i* + И -4-j (С - А)
4
in.^J. D.12.16)
Считая углы а, р, fi и ^з малыми, при вышеприведенных выра-
выражениях векторов wn, r'k и ^fe, получим *)
= \ [©и 4- е214- 2Л 4- 2С 4- 4« (б2 4- c2)l i2 4-1 [вв 4- 2Л 4-
4- 2С + 4т (с« 4" а2)] р+А (ft + i) -t у С" K<Pi + «Ti ~ PJ +
+ (% + a*Ti + РJ 4- (<Рз — « — РТзJ 4- («Р4 4- i — РЪJЬ D.12.17)
*) Это выражение (при других обозначениях) приводится на стр. 113*
книги Д. Р. Меркина.
4.13] ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ И ЭНЕРГИИ УСКОРЕНИЙ 179
Здесь вп — момент инерции наружного кольца относительно его
оси вращения; 021, в22 — моменты инерции платформы в точке С
относительно направлений i'v i'2; Л — сумма экваториальных момен-
моментов инерции кожуха и ротора; С и С" — их осевые моменты инер-
инерции; т — масса кожуха с ротором.
4.13. Примеры вычисления кинетической энергии и энергии
ускорений при наличии неголономных связей
Обратимся к рассмотренным в пп. 2.10 и 1.10 примерам неголо-
неголономных систем. Как будет показано ниже, для составления уравне-
уравнений движения системы с неголономными связями понадобятся два
выражения кинетической энергии: первое при отброшенных неголо-
неголономных связях и второе, когда наличие их учтено. При составлении
энергии ускорений неголономные связи учитываются.
1°. Шар. Принимая, что центр инерции шара совпадает с его
геометрическим центром, по G.7) имеем
e(Zl + Zl + u§, D.13.1)
где в — момент инерции шара относительно оси, проходящей через
его центр. Для сплошного шара
в = | Ма2.
о
Использовав выражения B.10.19) квазискоростей ш4 и оM, получим
Т= -g- М \-г а2 (о)? -f- щ) + -g- п2щ + 2аоJоL — 2аоIсо5 -|- щ -|- u>| I.
D.13.2)
Для составления энергии ускорений обратимся к A1.9). Для шара
2
0 . со = -=- Ма2ы\
о
следовательно, направления векторов 0 • со и со совпадают, так что
(со X ю) • 0 • w = 0.
и последнее слагаемое в равенстве A1.9) отпадает. По B.10.19)
имеем далее
Поэтому
2 *2 *2 2/*2 * 9\ * * • •
We = хо -J- уо = щ + &5 + a i^i -К &2J Ч" 2aaJ &4 — 2aSi1&5.
Слагаемое у со • 0 • со в равенстве A1.9) отличается от соответствую-
соответствующего слагаемого выражения кинетической энергии заменой вектора
12*
180 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ 4
со на to; этому при использовании проекций вектора на неподвиж-
неподвижные оси (как в настоящем случае) или на оси, связанные с твердым
телом, отвечает замена величин ш5 на &s. Итак,
1 12 / • 2 • 2 • 2\
Получаем
S*=T(&)9 D.13.3)
т е. для составления энергии ускорений в этом примере достаточно
заменить в выражении B) квазискорости (bs квазиускорениями &s.
2°. Обруч. Для вычисления кинетической энергии обратимся
к формуле G.7). Принимая, что центр инерции совпадает с геоме-
геометрическим центром обруча, имеем г'с = 0. По формулам B.10.26) и
B,10.25) получаем далее
«У- = О)^ -j- loi -I- <»б = («^ пМ^2 Н" (Ш5 а(°1 Sil1 ^
= cof -+- (of +a2((o^ + o>i) — 2я<о3а>* — 2^0),«о* sin ft. D.13.4)
Моменты инерции бесконечно тонкого обода относительно оси,
перпендикулярной его плоскости, и произвольно направленной оси,
расположенной в его плоскости, равны соответственно Ма2 и 0,5Жа2
(оси проходят через центр обруча О); поэтому тензор инерции
в точке О равен
( \) D.13.5)
Вспомнив еще представление B.10.13) вектора со и обозначения
B.10.14), получим
Итак,
. D,13.6)
Сложнее вычисление энергии ускорений; применение формулы
A1.9) требует знания ускорения центра инерции обруча и углового
ускорения. Начнем с первого, причем при вычислении учтем нали-
наличие неголономных связей, уравнения которых имеют вид B.10.24).
Используя обозначения B.10.17), имеем следующее представление
вектора скорости в «полунеподвижной» системе nt nv iz:
<vQ = (о4# 4" Ш5Я1 4" °V3 == — а ^шзя Н~ Ш1 s*n ^ п\ — Ш1 cos
4.13] ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ И ЭНЕРГИИ УСКОРЕНИЙ 181
По B.9.7), учитывая обозначения B.10.14), получаем
и, следовательно,
^0 = -гу0= —а[(оK — «vo2)*H-(«>, sinti -+-u>f cos fr
— (со, cos ft — u)^ sin О-) /3 I.
При вычислении wlQ отбрасываются члены, не содержащие о),. Полу-
Получаем
w20 = a2(oVf -\-u]) + 2aV;(w1u>3 — а),^). D.13.7)
Переходим к вычислению вектора углового ускорения. По B.10.13)
имеем
(о = ш1/|-4-^2/|/Н" ша'з D.13.8)
и, вспомнив формулы B.9.8), получим
D.13.9)
Для вычисления последнего слагаемого в формуле A1.9) достаточно
учесть здесь лишь члены с ш>9. Имеем с этой точностью
Далее,
qo.<o = Ma? (j со,» -+- у «зп7 + o)^
и, следовательно,
(<i> X »)• 0°- «о = -g- Л1а2оK(ш^з — u>ico2). D.13.10)
Представим теперь вектор w в виде
со
со 4-е, £==0J@K — ю2 ctg &) л — о), (оK — ш2 ctg &) л'.
где со — вектор, проекции которого на оси «полусвязанного» триэдра
равны соответственно оIэ оJ, оK. Имеем (отбрасывая слагаемые, не
содержащие ш5)
рб «=:|(о 0. со Н- е • 0 • ю = ~ Ма2 Г( ^ + у ^>; +
D.13.11)
182 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
Сложив выражения G), A0), A1), причем первое умножается на 0.5Л1,
получаем
4 • D.13.12)
3°. Двускатная тележка (п. 1.10). При вычислении кине-
кинетической энергии при отброшенных неголономных связях надо при-
принять отличными от нуля как составляющие скоростей точек А и В
вдоль осей колесных скатов, так и скорости точек контакта колес
с дорогой. Условимся вычисляемые так скорости обозначать малыми
буквами; большие буквы соответствуют скоростям в движении, про-
происходящем при наличии связей.
Система состоит из шести тел: оси заднего ската, неизменно
соединенного с мостом АВ, оси переднего ската и четырех колес.
Нам понадобится знание скоростей точек А, С, В и центров колес.
Имеем по обозначениям п. 1.10 и при показанных на рис. 3 напра-
направлениях единичных векторов tv /2, i'v i'2:
*°А = h (— Ш1 Sin X + ^7 C0S X) + *>2' VA = *>7 C0S X'
Через их (и соответственно через U^ обозначается угловая скорость
оси заднего ската, равная по п. 1.10
щ =tj> = т^гcosx + ^7sinx—^2)f3» u\ = j ^7s{ttXh^ D.13.13)
где /3 — единичный вектор, перпендикулярный плоскости дороги.
Скорости центров колес заднего ската равны соответственно
^i = ^ + ttiX ha = va — ha^>
V}=VA — ix j o>7 sin x = oO (cos x — j sin x) ix.
v2 = vA — ulX ha = va + ha^*
У2 = va +■ h j Ш7 sin Z = шт (c°s x + f sin /
Их угловые скорости, отмечаемые индексами 3 и 4, складываются из*
угловой скорости оси их (и соответственно Ux) и угловых скоростей
4.13| ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ И ЭНЕРГИИ УСКОРЕНИЙ 183
вокруг оси, равных
у sinx)w?] 'V
D.13.14)
у-^2 — w4+(cosx4--f si
D.13.15)
если связи не учитываются; при учете связей надо принять a>j == ш2 =
= оK = оL = 0. Получаем
h
h
«4 = «1 + ЧЪ = ^ + *V? ^ = ^ + '
где 1^! и V2—величины векторов Vt и V2.
Угловая скорость оси переднего ската равна
Щ = (в 4- X) '3 = у (Ш1 cos X + ^ sin X — Ш2 + /a)s) h>
где оз8 = х- Скорости центров колес определяются равенствами
v3 = vB + u2Xt'2c = vB-c(b
V3 = [a>7 A — у sin Х) — ca>8] /J,
а их угловые скорости
Здесь
у sinx)^? — ca)8> D.13.16)
«> ш|A +in) + c D.13.17)
Переходим к составлению кинетической энергии. Через Mv M2 обозна-
обозначим массы заднего и переднего скатов (без колес), через 91 и в2 —
их моменты инерции относительно осей, перпендикулярных дороге и
184 основные динамические величины [гл. 4
проходящих через точки А и В; массы колес обозначаются через тх
(задний скат) и тг (передний). Тензоры инерции колес в их центрах
соответственно равны
r J'z V'A+Уз) ■+• Wr
Теперь, применив формулы G.7) и G.8), записываем выражения
кинетических энергий:
оси заднего ската с мостом
Ту = т mxv\ + ж, (vA х «о • г;+1 е,»2,
где г'с = /^ = /j^C; кинетическая энергия колес этого ската равна
Т, + Г4 = \ тх {у\ + \ 1 $ ^
оси переднего ската
и колес его
Собирая значения вышеприведенных величин, найдем
27= (Ж, + 2«j) [(— ш, sin х + о7 cos хJ 4- <о«] 4- 2M,»2»s 4"
4-(в, 4- 2от,а2 4- 2У() Й* 4" (Л12 4- 2т2) (ш* -+ а>2) +
^^+^). D-13.18)
причем й, ср5 надо заменить их выражениями A3)—A7).
При учете неголономных связей получили бы выражение
2Г= (|х + !Vin2 X) ®7 + /va)8+ 2va)8aO sin X. D.13.19)
где обозначено
9 / 9 /
р = Ж, 4- 2», + ^2 + 2от2 + 41 + ^ •
Г] Г2
1*1 = -р- (©, + 2mja2 4- 2^' + в2 + 2т3с2 + 270 - Ж, —
D.13.20)
При вычислении энергии ускорений, как указывалось выше, связи
учитываются. Поэтому далее используются выражения скоростей
4.13] ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ И ЭНЕРГИИ УСКОРЕНИЙ 185
и угловых скоростей в происходящем движении. При дифференци-
дифференцировании надо иметь в виду соотношения
. D.13.21)
. DЛ3.22)
Получаем: ускорение точки А и угловое ускорение оси заднего ската
2
а>7
WA = VА = 1г (а>? cos % — а>7а>8 sin х) + h~T~ s*n X cos x»
й\ = н у Кsin х+<°7а>8cos x;
ускорения центров колес этого ската и угловые ускорения колес
Wl=Vx= ix [i7 (cos x — ~ sin x) — <d7o>4 (sin x + у cos x)J +
2
+l* ~T (cos Z - тsin x)sin X = Wi 4- /2^i2^
W2 = V2 = ix p7 (cos x -H-f sin x) — w7u>8 (sin x у cos x)J -f
+12 -y- (cos x -f- j- sin x) sin x = ^U721 -+- i2W22>
Для переднего ската:
/ / «7
4 i'2 (-^ sin x + «*) [«7 A - j sin x) - сш8] = W3Vi[
W4 == ^4 = *i [Ш7 (! 4--f sin x) + y- <u7o>8 cos X 4 cu>8J -J-
-Н'2(т sinx4«)8)[<o7(l +7sinX) +■
&2 = hу К si" Z 4- ">7°>8 cos X 4 Й)■
Энергия ускорений оси заднего ската находится по формуле A1.8)>
так как центр инерции С не совпадает с полюсом А Для осталь-
остальных тел— оси переднего ската и колес — используется формула A1.9).
186 ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ [ГЛ. 4
В рассматриваемом плоском движении равенство A1.8) записывается
в виде
В дальнейшем надо учесть лишь слагаемые, содержащие ш7 и о)8.
Тогда среднее слагаемое отпадет; получаем
S\ = у ^0J -+- у ^ Л^ j (ш* sin2 х -4- 2oOoOoj8 sin x cos x).
Вычисление для оси переднего ската дает
1 • 1 й
5* = -к ^2(D7 ~^~ "Т ~7^~ (Ш7 S^°2 X ~Ь 2oOciOo)g sin x cos x + /2w2 -|-
cos х + 2/о)8 оO sin
Для кол^с на заднем скате получаем
... , 27,
■[£-(• -*)(-■+f )]<»?*
а на переднем
X (^ si ^878x ^7 x)}
Сложив эти выражения и применив обозначения B0), получим
2S* = (|х + |х, sin2 x) <i>2 + /v^ _f- 2voi/ oi8 sin z +
-f- 2|XjaO(D7a)8 sin x cos x + 2vo)8uOo)g cos x« D.13.23)
Первые три слагаемых можно получить при замене в выражении
кинетической энергии A9) происходящего движения квазискоростей оO
и о)ь квазиускорениями о>7 и о)8. Еще два слагаемых соответствуют
дополнительным членам в формуле A0.12).
Эти дополнительные члены разбиваются на две группы. Пер-
Первая Rx содержит прямые скобки Кристоффеля; в рассматриваемом
случае коэффициенты выражения кинетической энергии A8) зависят
лишь от/одной обобщенной координаты q4 — %, причем по A.10.14)
лишь &48=1, тогда как остальные элементы четвертой строки
матрицы Ь равны нулю. Формула A0.9) принимает вид:
! k !
4.131 ВЫЧИСЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ И ЭНЕРГИИ УСКОРЕНИЙ 187
и отличными от нуля могут быть те скобки, в которые хотя бы
один раз входит индекс 8:
1 дА
1 дА*
is.
1 дА*
[8. 8; i% =
дА*
1 дА*
D.13.24)
[St 8; 8], = [8, s\ 8]. = О. [8, 8; 8]тс = т
Выписываем теперь первую группу слагаемых:
#1 = <Ц(ш|[7, 7; 7]тс+2(о7о)8[7, 8; 7]я + <«>|[8, 8»
+ /ч//ч2Г7 7. Q1 I О/ ч / \ Г 7 Q. Ql I /.v2 ГО Q. О, \
A) I A) I / /I О| —р ^ID (Do I / • О, О I —i* Ш I о» О» Ol )•
о \ 7 тс 7о Тсо Jic/
Ho no A9)
и по B4) получаем
/?] = aOB|x1(D7a)8 sinx^osx + vw^cosx) —p-j^g^sinxcosx. D.13.25)
Надо перейти к вычислению второй группы дополнительных членов
в формуле A0.12), т. е. к четырехкратной сумме
г s k I
= ш7«)8 2 2
? 2
т'т8=(w—»7ш8) 2
Здесь были использованы равенства A.10.15). Остается определить
из выражения кинетической энергии A8) значения Л*г и А*г; находим
Ап = Ь sin X cos X. ^8i = v cos Z-
Получаем
R2 = (оOо)8 — ы^) (^г(о7 sin x cos x + vco8 cos x) D.13.26)
и далее
/?г —|— /?2 == [х1аOоOа)8 sinx cosx + va)80Oa)8cosX- D.13.27)
Таким образом, восстановлено выражение B3). Мы привели это
вычисление с целью показать, что вычисление энергии ускорений
возможно без знания распределения ускорений точек системы; доста-
достаточно иметь выражения кинетической энергии (вычисленной при отбро-
отброшенных связях^ и трехиндексных символов. Требуемый результат
Достигается путем вычисления, диктуемого правилом A0.12).
ГЛАВА 5
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
5.1. Обобщенные силы
Сумма элементарных работ сил Fv приложенных в точках Mt
рассматриваемой системы, на виртуальных перемещениях brt этих
точек из положений, занимаемых ими в фиксированный момент вре-
времени, равна
8^ = 2 Ff 8г,. E.1 1)
Обозначение 8' применено с целью отметить, что речь идет о
бесконечно малой величине, не являющейся, однако, вариацией некото-
некоторой величины W.
Заменив в A) виртуальные перемещения их выражениями A.6.7)
через вариации обобщенных координат bqs, получим
/-1 5-1 5-1 /-1
Величина
1ш\
называется обобщенной силой, отнесенной к обобщенной коорди-
координате qs. Выражение элементарной работы через обобщенные силы
по B) имеет вид
W = JiQabqe9 E.1.4)
откуда следует, что обобщенная сила Qs равна коэффициенту при
вариации 8^ соответствующей обобщенной координаты в выражении
суммы элементарных работ сил, приложенных к точкам системы, на
виртуальном перемещении этих точек из рассматриваемого положения.
5.П ОБОБЩЕННЫЕ СИЛЫ 189
Мысленно сообщив точкам системы наиболее общие виртуальные
перемещения — такие, при которых варьируются одновременно все
обобщенные координаты, найдем по D) все п обобщенных сил. Если
же подлежит определению обобщенная сила Qk(k — фиксировано), то
достаточно выделить из совокупности виртуальных перемещений та-
такое, в котором варьируется лишь обобщенная координата qk, а все
прочие сохраняют неизменные значения. Тогда элементарная работа
(§'W)k будет по D) пропорциональна bqk:
(b'W)k = Qkbqkt E.1.5)
и обобщенная сила Qk определится как множитель при bqk в так вы-
вычисленном выражении элементарной работы. Практически целесооб-
целесообразно все Qk вычислять по очереди указанным приемом.
При применении квазикоординат виртуальное перемещение brt
определяется по A.6.14), и выражение элементарной работы пред-
представится в виде
^ РМ, E-1.6)
Величина
N
EЛ.7)
будет обобщенной силой, отнесенной к квазикоординате ns. Пре-
Преобразуя ее выражение и пользуясь соотношением A.5.17), найдем
Обратные соотношения имеют вид:
п — V л Р EЛ.9)
^
где ars—элементы матрицы A.5.7).
Если речь идет об относительном движении системы материаль-
материальных точек, так что положение точки Mt в инерциальных осях опре-
определяется в общем случае равенством
ql qn; t), E.1.10)
190 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
в котором г0 — заданная функция времени, то виртуальным переме-
перемещением по определению будет Ъг'г Вариации векторов гг и г'г равны
друг другу и выражение обобщенной силы может быть записано
в виде
><-ж- EЛЛ1)
5.2. Элементарная работа сил, действующих на твердое тело
Рассматривая свободное твердое тело, назовем действующие на его
точки силы Fv F2, . .., Fn. Виртуальное перемещение точки Мь тела
определяется соотношением
8г| = 8г0+вХг|, E.2.1)
в котором Ьг0—виртуальное перемещение полюса О системы осей
Ox'y'z't связанных с телом, 0 — вектор бесконечно малого поворота
тела, Г/ = OMi—вектор-радиус рассматриваемой точки.
Поэтому
bfW=2Frbri=2Frbr0+2Fr(eXr'l) =
2^/7г E.2.2)
E.2.3)
/si
Замечая, что
N
представляет главный вектор рассматриваемой системы сил, а
N
2^Х/Г, = 1»° E.2.4)
- — ее главный момент относительно полюса О, получаем выражение
элементарной работы в виде
VW= V-bro-\-m° Q E.2.5)
Если за обобщенные координаты принять координаты xQ, у0, z0
полюса О в системе неподвижных осей Oxyz и эйлеровы углы ф, 0\ ср,
то
5.2] ЭЛЕМЕНТАРНАЯ РАБОТА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО 191
Здесь, как и ранее, is — единичные векторы неподвижных осей,
i's — подвижных осей; через п обозначается единичный вектор линии
узлов. Соотношение E) приводится к виду:
VW = V, Ьх0 + V2 Ьу0 +- V3 bz0 -+-
+ т° ■ <з Ц -+- т° ■ п Ш + т° ■ i'3 89. E.2.7)
Согласно A.4) имеем
Ql = Vl, Q2 = V2, Q3 = VZ, E.2.8)
т. е. обобщенными силами, отнесенными к координатам х0, у0, z0,
являются проекции главного вектора на оси неподвижной системы
Oxyz. Далее,
Q4= т° • /3 = m3, Q5 = т° • п = тм, Q6 = m° • /3 = m3. E.2.9)
Таким образом, обобщенные силы, соответствующие эйлеровым углам
ф, Ь, ср, представляют проекции главного момента системы сил на
ось 0z, ось узлов и ось Oz\ т. е. главные моменты системы сил
относительно этих осей.
Теперь выразим скалярные произведения в выражении E) через
проекции векторов на оси Ox'y'z'', связанные с твердым телом:
b'W = Vx фго)г + V2фгоJ + Vz (8roK -+- <8, 4 «?8, + ^03. E.2.10)
Здесь (8гоI$ .... 03 представляют вариации квазикоординат, соот-
соответствующих квазискоростям, которые были введены соотношениями
A.5.2) и A.5.3). Принимая нумерацию, использованную в п. 2.10,
т. е. полагая
. 8^ = 6^ Stt2 = 02, Stc3=03, 8тс4 = (8го),, \
получим
Р1 = т1. Р2 = гп2, Ръ = тъ. P4 = VV P5 = V2, P6 = V*. E.2.12)
Таким образом, обобщенными силами, отнесенными к квази-
квазикоординатам AП, являются главные моменты системы сил
относительно связанных с телом осей и проекции на эти оси
ее главного вектора. В записях (8) и A2) применены обозначения
вида тх вместо т°, так как проекция момента пг° на некоторую
ось, т. е. момент относительно оси, не зависит от выбора центра
моментов на этой оси.
Если за квазискорости приняты проекции вектора угловой ско-
скорости на оси Oxyz с началом (полюсом) О в точке тела, но сохра-
сохраняющие неизменные направления в пространстве, то соответствующими
обобщёнными силами будут главные моменты системы сил т1% т2,
Щ относительно этих осей.
192
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Установим связь этих величин с моментами /% ^/v. Щ — обоб-
обобщенными силами, отнесенными к эйлеровым углам. Имеем
т° = mlil -I- m2i2
но, конечно,
т° Ф m3
E.2.13)
так как направления г3, п, if.6 не образуют ортогонального триэдра.
Правильное представление имеет вид
1
rO =
— w3cos Ь) i3 + (/п3 —
, E.2.14)
как нетрудно проверить, с помощью формул (9) *). Действительно,
умножая обе части A4) скалярно последовательно на п, /3, /3» при-
придем к указанным формулам.
Из A4), вспоминая зависимости B.3.1)—B.3.3), получим
т1 = mN cos ф 4~ Щ ~~-—\ — тъс^ ^ s*n Ф»
т2 = mN sin ф — тг cos ^ 4~ Щ ctg * cos Ф»
E.2.15)
a no A3) и (9) — обратные соотношения
озф 4~ Щ sin Ф»
= ml sin 0 5тф — т
mN =
= тъ.
E.2.16)
Аналогично получаются равенства
тх = mN cos cp 4- w3 -4^ — w3 ctg » sin cp,
-f- w3 -^j|- — m3ctg ^ cos cp,
E.2.17)
и обратные зависимости
mN = A/ij cos cp — m2 sin cp,
Щ =
= (m, sin cp 4- m2 cos cp) sin fr 4- w3 cos Ь.
E.2.18)
*) Более подробное разъяснение различия между составляющими век-
вектора по осям (неортогональной) системы координат и его проекциями на
оси дается в П. 2.2.
5.3] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 193
5.3. Потенциальная энергия
Выше было введено понятие об элементарной работе на вирту-
виртуальных перемещениях точек системы. Аналогично определяется эле-
элементарная работа на действительных перемещениях:
N
drW= 2 Frdrt. E.3.1)
Пользуясь этой величиной, определяем работу сил на конечном
перемещении точек системы как интеграл
B) B) N
Wl2 = f d'W= / S /=1 • dri9 E.3.2)
A) A) Ы\
пределы которого задаются значениями координат точек системы
в начальном A) и конечном B) положениях. Этот интеграл может
быть вычислен, если движение известно; тогда подынтегральное выра-
выражение станет известной функцией времени, а пределы интеграла най-
найдутся по заданию моментов времени tx и t2, соответствующих началь-
начальному и конечному положениям системы.
Рассмотрим случай сил, зависящих только от положений точек
в инерциалъной системе осей. Эти силы называются потенциаль-
потенциальными, если существует однозначная и дважды дифференцируемая по
всем ее аргументам функция
П = П (xv yv zv ..., xNi yN, zN\ E.3.3)
такая, что проекции на координатные оси силы, действующей на точку
Mi (xt, yt, zt)y равны взятым со знаком минус частным производным
от II по координатам этой точки:
F — — — F — дп р — дп /53 4^
Предполагается, что функция II зависит только от координат
точек и время не входит явно в ее выражение; тогда из равенств D)
следует, что она определена с точностью до аддитивной постоянной.
Эта функция называется потенциальной энергией.
Вектор, проекции которого на координатные оси равны частным
производным некоторой функции ср координат по xt, ylt zt точки Mit
называется градиентом функции ср в этой точке и обозна-
обозначается gradjcp. Поэтому
F; = —gradjll. E.3.5)
13 Зак. 2072. А. И. Лурье
194 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
Согласно A) и D), элементарная работа потенциальных сил на
действительных перемещениях равна
N ' N
* = 1 / = 1
= — </П, E.3.6)
где dll—полный дифференциал потенциальной энергии.
Работа потенциальных сил на конечном перемещении согласно B)
и F) равна
B) B)
W12 = f d'W = — f dll = II, — II2. E.3.7)
U) (i)
Из этого выражения следует, что потенциальная энергия равна
работе, которая была бы произведена потенциальными силами
на конечном пути из рассматриваемого положения системы
в положение, где она условно мооюет быть принята равной нулю.
Рассмотрим случай стационарных связей. Тогда, согласно A.2.11),
в выражения декартовых координат через обобщенные время не вой-
войдет, и потенциальная энергия после соответствующей замены в C)
станет функцией только обобщенных координат
П = П(?1 qn). E.3.8)
Элементарная работа потенциальных сил на виртуальном переме-
перемещении согласно F) равна
^bqs. E.3.9)
5=1
Сравнивая с A.4) и учитывая независимость вариаций обобщен-
обобщенных координат, приходим к выражению обобщенных сил через
потенциальную энергию
Пусть определены обобщенные силы Q, Qn, и они оказа-
оказались зависящими только от обобщенных координат qv .... qn. Как
следует из последних равенств, признаком потенциальности сил
является выполнение следующих условий:
F, 5=1 п). E.3.11)
dQs ^_
dqk dqs
Если эти условия не выполнены, то силы непотенциальны. Если же
они выполнены, то элементарная работа d'W представляет полный
дифференциал некоторой функции координат, и силы потенциальны,.
5.3] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 195
если эта функция однозначно определена. Для пояснения приведем
известный пример. Пусть проекции силы F на оси Оху равны
Легко непосредственно проверить, что условия A1) удовлетворены
и элементарная работа равна
Так как функция arctg— не определена в начале координат О, то
сила F непотенциальна в области, содержащей точку О.
При введении квазикоординат имеем по A.8):
_ rs-~ E.3.12)
или, вспомнив обозначения A.5.17),
Иногда обобщенные силы можно представить формальным равен-
равенством
аналогичным A0), в котором, однако, функция П зависит не только
от обобщенных координат, но также и от времени
П = П(<71 qnj). E.3.14)
Это будет, в частности, иметь место при нестационарных связях
при подстановке в C) выражений A.2.9) декартовых координат через
Обобщенные. Другим примером будет случай силы, зависящей явным
образом только от времени. Например, если
то
Функцию A4) назовем обобщенной потенциальной энергией.
Элементарная работа сил на действительном перемещении вы-
выражается через обобщенную потенциальную энергию следующим
образом:
13*
196
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
и, следовательно, не является полным дифференциалом функции A4);
соотношение G) также не имеет места.
В дальнейшем, по ходу изложения, будет ясно, в каком случае
рассматривается потенциальная энергия или обобщенная потенциаль-
потенциальная энергия. Поэтому для краткости слово «обобщенная» будет
опускаться.
Простейшим примером потенциальных сил являются силы неиз-
неизменной величины и направления. Такова сила тяжести вблизи поверх-
поверхности Земли. Потенциальная энергия системы в поле силы тяжести
определяется выражением
N
п = g 2 щ*1 =
E.3.16)
где zc — координата центра тяжести, отсчитываемая по восходящей
вертикали от поверхности Земли. Действительно, A6) равно работе,
которую произвели бы силы веса при переходе точек системы из
рассматриваемого положения их на поверхность
Земли.
Выражение A6) можно представить также
в форме
E.3.17)
Рис. 34.
где g—направленный по нисходящей верти-
вертикали вектор ускорения свободного падения,
гс — вектор-радиус центра инерции системы.
Более общим является предложение: потенциаль-
потенциальная энергия системы сил Ft неизменного напра-
направления и постоянной величины, приложенных
КТ в точках Mt системы, определяется равенством
N
i. E.3.18)
^
Как пример рассмотрим систему двух стержней ОХО2 и О2Ог$
шарнирно сочлененных в точке О2, причем конец Ох первого стержня
закреплен в неподвижном шарнире Ох, а к свободному концу О3
второго стержня приложена сила Т постоянной величины (рис. 34).
Положение системы определяется обобщенными координата ми —
углами cpj и ср2 стержней с осью Охх\ через (J обозначается угол
силы Т с тем же направлением.
Элементарная работа силы Т равна
= Г [cos C8 (lx cos <pj 4- /2 cos T2) 4~ sin № Wi sin ¥1 + h sin ¥2I
5.3] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 197
и, следовательно,
VW = Т[1г sin (Р — ?1) 8?1 +/2 ^п (Р — ср2) 8ср2],
т. е. обобщенные силы равны
Q1=T/1sin(p —Tl). Q2=7/2sin(p —ср2). E.3.19)
Они будут потенциальными при условии A1)
/х cos (р - ?1) ^ = /2 cos (р - %) ^ • E.3.20)
Оно выполняется, в частности, когда р = const, т. е. в случае силы
постоянного направления, а не только величины. Такая сила — потен-
потенциальна и потенциальная энергия равна
cos (p — ?2)]. E.3.21)
В случае же постоянной по величине силы 7\ составляющей
постоянный угол а с направлением стержня О203. имеем р = ос —]— ср2
и далее
Qj = Т1г sin (ос —1— ср2 — cpj), Q2 = 7/2 sin a.
Такая «следящая сила» (ее можно осуществить с помощью авто-
автоматически действующей следящей системы) представляет пример
позиционной, но не потенциальной силы.
Возвращаясь к формуле A8), рассмотрим два положения твер-
твердого тела, имеющего неподвижную точку О,—начальное и конеч-
конечное, получающиеся из начального при сообщении телу конечного
поворота, задаваемого вектором в. Силы F\, ..., Fn, приложенные
в точках тела с вектор-радиусами rj, ..., г°, сохраняют при пово-
повороте тела свои величины и направления в пространстве. Надо соста-
составить выражение потенциальной энергии этой системы сил в конеч-
конечном положении тела.
По формуле Родрига вектор-радиусы r°k после поворота станут
равными
и по формуле A7)
*=1
. E.3.22)
198 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
Слагаемое По — потенциальная энергия в начальном положении — мо-
может быть отброшено; через
обозначен момент относительно полюса О силы Fk в начальном поло-
положении тела. Результат может быть записан в виде
П = \ < + i 4nre-Q0'e- E.3.23)
Здесь т° обозначает главный момент системы сил относительно
полюса О в начальном положении тела, через Q0 обозначен тензор
E.3.24)
Выражая с помощью формул C.2.8) и C.2.10) вектор 0 через
параметры Родрига — Гамильтона, можно еще представить фор-
формулу B3) в виде
з з з
5=1 S ° ^ = 1Лг = 1
Здесь is — единичные векторы связанного с телом триэдра осей
в начальном положении, Qsk — составляющие тензора Q0 по этим
осям.
Пусть, например,
Тогда
и по B5), подставив значения C.6.6) параметров Родрига через
эйлеровы углы, получим
= — Z^^Tq sin 0 sin ty-\-Fxo(l —cos ф cos cp -f- sin ф sin cp cos fl).
К этому же результату, конечно, пришли бы, исходя из соотно-
соотношения
где х — координата точки приложения силы после поворота тела.
Ее легко найти с помощью таблицы косинусов 2 гл. 3 по форму-
формулам преобразования координат
х = xQ (cos cp cos ф — sin cp sin ф cos 8) -\- z0 sin 0 sin ф.
5.4] СИЛЫ, ЛИНЕЙНО ЗАВИСЯЩИЕ ОТ КООРДИНАТ 199
5.4. Силы, линейно зависящие от координат
Рассмотрим пример позиционной силы F, проекции которой на
оси декартовой системы координат Охгх2х3 задаются линейными
функциями координат
*3 (*= 1.2,3). E.4.1)
где Psk постоянны.
Введя в рассмотрение тензор Р и вектор-радиус г, можно эти
выражения записать в виде (П. 1.4.10)
F=Pr. E.4.2)
Пусть Р' обозначает транспонированный тензор, т. е. такой,
составляющие которого Р1к равны Pki. Соотношение
Р = \ (Р + Р') +1 (Р — Р0 E-4-3)
определяет разбиение тензора Р на симметричную часть
S = I(P-|-P') E.4.4)
с составляющими
E.4.5)
E.4.6)
И
в
*
кососимметричную
Q=i(
которой *
О * Р Р
^1 = ^32 ^2з)'
Sik = -(Pik-
Р-Р0=(
\
\
У2 = у (Р
т- ^ft/)
0
^8
0
3l)'
о /
дз= 2
Теперь выражение силы F записывается в виде
^S-r + Q-r, E.4.7)
причем по A) и F) второе слагаемое, т. е. вектор Q-r, имеет
проекции на оси координат
^3*2 + ^2*3» *3*1 *1*3» ^2*1 + **\Х2*
Если ввести в рассмотрение вектор Q, проекции которого на
оси системы Oxxx2xz равны соответственно Qj, 122, &3*)» т0 пРеД~
ставление силы G) может быть переписано в виде
r. E.4.8)
*) Законность такого определения обосновываемся тем, что величины Qs
ири преобразовании поворота координатной системы преобразуются по тому
же закону, что и проекции вектора. См. п. 2.12.
200
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Первое слагаемое представляет вследствие соотношений E) градиент
квадратичной формы
3 3
т. е. представляет потенциальную часть силы F
E.4.10)
Второе слагаемое — непотенциальная сила, называемая также циркуля-
циркуляционной или силой радиальной коррекции (последний термин при-
применяется в теории гироскопа). Она направлена перпендикулярно век-
вектор-радиусу точки приложения силы. Простейшим является случай
силы, проекции которой задаются
равенствами
Fx = — ky, Fy = kx. E.4.11)
Примером является, как доказывается
в гидродинамической теории смазки,
главный вектор реакций масля-
масляной пленки на вращающийся шип
(рис. 35). Здесь при полном охвате
шипа подшипником, согласно теории
Зоммерфельда,
F=
E.4.12)
Рис. 35.
где е ==(/?'—R)—разность радиусов
подшипника и шипа, j* — коэффи-
коэффициент вязкости смазки, Х=—, to— угловая скорость шипа. В от-
отличие от A1) коэффициент пропорциональности здесь не постоянен,
а зависит от г. Сила F показана на рис. 35 приложенной в центре
шипа О'. Надо однако иметь в виду, что реакции пленки на шип
статически эквивалентны главному вектору F и главному моменту т°\
пропорциональному и противоположно направленному вектору (о.
Поэтому точка приложения равнодействующей реакций пленки от-
отлична от О1'. При вращении вертикально нагруженного (сверху вниз)
шипа точка О' смещается по горизонтали вправо от О для наблю-
наблюдателя, которому вращение шипа представляется происходящим
против часовой стрелки. Тогда реакция F будет направлена верти-
вертикально вверх.
5.5]
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СИЛ ТЯГОТЕНИЯ
201
5.5. Потенциальная энергия сил тяготения
Сила тяготения, с которой на материальную точку М массы т
действует материальная точка массы т0 (центр притяжения) опре-
определяется равенством
F=—f mm° — E 5 1)
в котором г— расстояние между точками, г— вектор-радиус точки М%
имеющий начало в центре притяжения. Через / обозначена постоян-
постоянная тяготения, равная в системе CGS
/ = 6,67 . 10"8 смъ\г • сек2, E.5.2)
Элементарная работа силы ^на виртуальном перемещении точки Ьг
равна
Замечая, что
> = ^ог
■2
/•or,
имеем
Д
Отсюда по C.9) следует, что потенциальная энергия сил тяготения
двух материальных точек опреде-
ляется выражением ^
_ _ ^ Vf*
^ E.5.3)
Перейдем к вычислению по-
потенциальной энергии материаль-
материальной точки Ж, притягиваемой твер-
твердым телом, имеющим конечные
размеры, но достаточно удален-
удаленным от точки М. Начало системы
осей поместим в центре инер-
инерции G тела, а оси Gx, Oy, Gz
направим по его главным центральным осям инерции. Тогда по C)
Рис. 36.
где ть—массы материальных точек Mt, составляющих притягиваю-
притягивающее тело, rt — их расстояния от притягиваемой точки М. Положе-
Положение точки Mt в теле задается вектор-радиусом pt = GMt (рис. 36)
202 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
Обозначая еще GM = r, получаем
и далее
Г; Г \ Г2 ^ Г2 I
Заметив, что
г . р. = хх. 4- VV- -A-zz. о2. = х2. 4- у? + z1.
где х, у, z обозначают координаты точки Ж, a xit y-r zt — точки M-L,
ограничимся в разложении выражения E) в ряд по степеням —
членами, содержащими лишь квадраты этого, по предположению,
малого отношения. Придем к равенству
1 _ W I _1_ Г • р' * р< _,_ 3 (г-р«J | \ _
— 1 I
— г -г
При подстановке этого выражения в D) следует учесть, что начало
координат G выбрано в центре инерции, т. е.
N N N
2 "*Л = 2 "W = 2 mlzl = 0t
i=\ /=1 /=1
а координатные оси являются главными осями инерции
/V JV JV
i = 1 i = 1 / = 1
Получаем
Здесь w0—масса тела. Заметив далее, что по D.3.21)
£+*?) (
А'
5.5] ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СИЛ ТЯГОТЕНИЯ 203
и т. д., где 0j, 02, в3—главные центральные моменты инерции,
получаем
| г ~Т~ 2/-5 IV 2 1 3 1/ \\ 3 ~Г~ 1
— 202)у2 + @1 + 02 — 293)г2]} + ... E.5.6)
Действующая на притягиваемую точку М сила F* определяется
равенством C.6). По принципу равенства действия и противодействия
сила F, с которой тело притягивается точкой М, равна F* по ве-
величине, противоположна ей по направлению и действует по той же
прямой, т. е. проходит через точку А1. Итак, тело конечных раз-
размеров в поле точечного притягивающего центра находится под дей-
действием сил притяжения, главный вектор которых и главный момент
относительно центра инерции тела соответственно равны
>= —/7* = gradn, mG=rXgradn. E.5.7)
Проекции главного вектора на оси системы Gxyz поэтому будут
77 он 011 jfti /f\ 1 r\ 0O1 \ У /t^ к q\
Г ., = —^—= I —^ r-frFq-f-o, ZO0 , (O.O.o)
У ду L *"
где обозначено
r t- -^ l<@2 + ©з - 20,) x2 +- (вз + в, - 292) f +
+ (ei + O2-2e3)z2l}. E.5.9)
Главные моменты относительно этих осей равны
my = zFx—xFz = ^(Q1 — e3)zx, \ E.5.10)
лгг, == хг„ — vr „ = ■
При рассмотрении движения твердого тела действующие на него
силы и моменты должны быгь выражены через параметры, опре-
определяющие положение этого тела, тогда как полученные формулы
содержат координаты притягивающего центра Л1, отнесенные к си-
системе осей, связанных с телом. Следует ввести поэтому непод-
неподвижные оси Ж?т]С (рис. 37) с началом в притягивающем центре;
204
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
положение центра инерции О в этой системе определяется вектор-
радиусом MG = — г или координатами его 5, ?], С. Направления
осей Gxyz, связанных с твердым телом, задаются эйлеровыми углами,
через которые определяются косинусы углов aik этих осей с не-
неподвижными осями.
Спроектировав вектор г на оси системы Gxyz, получим равенства
х = — (anS + a127] -|- a13C),
у = —(a215-ba224 + a23t),
- a33C).
E.5.11)
Их надо подставить в выражение F) потенциальной энергии или
непосредственно в формулы (8) и A0). Тогда придем к выражениям
Рис. 37.
Рис. 38.
через обобщенные координаты обобщенных сил Ps, отнесенных к квази-
квазикоординатам. Формулы весьма громоздки, более отчетливые резуль-
результаты получаются, если центральный эллипсоид инерции тела является
эллипсоидом вращения. Пусть ось Gz служит его осью вращения,
за положительное направление на ней примем то, которое составляет
острый угол 6 с вектором GM = г (рис. 38).
Поскольку 9j = 02, имеем теперь
m =-^L(ei-e3)**> тг = 0. E.5.12)
Вектор т°, перпендикулярный по G) вектору г, теперь перпенди-
перпендикулярен оси z (единичному вектору Q. Он может быть представлен
в виде
E.5.13)
5.6] фигура земли 205
По условию z > 0, поэтому при в3 < в], т. е. когда эллипсоид
инерции вытянут по оси вращения, момент т° действует в сторону
совмещения оси Gz с направлением на центр притяжения М. Сила F
(поскольку mz = 0) действует в плоскости, проходящей через ось Gz
и точку М. Проекции F на оси по (8) и (9) равны
E.5.14)
Теперь введем «полусвязанный» с телом ортогональный триэдр еди-
единичных векторов п, п\ *з' причем п перпендикулярен плоскости г,
i'y а п' направлен по проекции г на плоскость Gxy, как показано
на рис. 38. Тогда
- A—5 cos2 6I sin 6,
E.5.15)
mn = j&-(e3 — ei)sin2e, тя/=0, mz = 0. E.5.16)
Для изображенного на рис. 38 случая 93 < ®i момент тп < 0.
5.6. Фигура Земли
Вопрос о форме земной поверхности имеет значение для теории
гироскопических приборов, в задаче о движении искусственного
спутника Земли и в других динамических исследованиях. С другой
"стороны, рассмотрение его дает превосходный пример применения
понятия о потенциальной энергии*).
Поверхность нормального сфероида, которой аппроксимируется
поверхность Земли, представляет поверхность уровня поля силы
тяжести, слагающегося из силы притяжения Землей и центробежной
силы, происходящей от вращения Земли.
Нормальный сфероид мало отличается от сферы; в приводимом
ниже вычислении мы ограничиваемся учетом первых степеней малых
величин, характеризующих и обусловливающих это отклонение.
Через г, &, X обозначаются сферические координаты точки — рас-
расстояние от центра Земли, полюсное расстояние, отсчитываемое по
*) Изложение этого параграфа основывается на материале гл. 5 книги
Н. И. Идельсона «Теория потенциала и ее приложение к вопросам гео-
геофизики* (ГТТИ, 1932).
206 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
меридиану (дополнение до широты), долгота. Полагая, что нормаль-
нормальный сфероид является телом вращения (Oz — ось вращения) и обо-
обозначая через А = ®г = в2 его экваториальный, через С = в3 — поляр-
полярный моменты инерции, согласно E.6) имеем следующее выражение
потенциальной энергии силы притяжения на точку единичной массы
. E.6.1)
Здесь через М обозначена масса Земли. Как увидим ниже (9.2.6),
при рассмотрении движения или равновесия по отношению к системе
осей, вращающихся вместе с Землей, следует учесть потенциальное
поле центробежных сил. Потенциальная энергия центробежных сил
вращения Земли, отнесенная к точке единичной массы, равна
у2) = — jU2r2 sln4, E.6.2)
где U — угловая скорость Земли. Сложив выражения A) и B) и
введя в рассмотрение длину Ro, которую назовем средним радиусом
Земли, придем к равенству
/М ( /?0 , С-А //?0\з u2R30 i r \2
cos2f>|-
До 1 г ^ 2М Д§
~Л) / Д0\з
/ Д0\з
\ г /
В теории фигуры Земли принимаются обозначения
3(C—A) UR\
=т, — о-Н ^ = а» E.6.3)
fM 2МЩ ' 2/М
в которых предыдущее равенство записывается в виде
Эквивалентной является запись
5.6] фигура земли 207
в которой P2(cos^) обозначает второй полином Лежандра
р2 (cos ») = I C cos2 0 — 1). E.6.6)
Произведения и квадраты малых величин т и а в последующем
вычислении отбрасываются. Их учет мог бы иметь смысл лишь при
сохранении отброшенных слагаемых в выражении потенциальной
энергии сил притяжения E.6).
Величина
представляет ускорение «средней силы тяжести» — силы притяжения
невращающейся сферической Землей радиуса RQ. Поэтому
E.6.8)
равно отношению центробежной силы на экваторе к средней силе
тяжести.
Введенную выше величину Ro теперь определим как радиус
сферы £0 — такой, что потенциальная энергия По притяжения ею
точки единичной массы равна среднему значению на этой сфере по-
потенциальной энергии. П:
где
do = /?§ sin f) d\) d\
— элемент поверхности сферы So. Поэтому, согласно E),
-4a //>,<совв)
«п
так как по свойству полиномов Лежандра
Г P2(cos&)sin0d» = 0.
208 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
В дальнейшем условимся рассматривать вместо П его отклонение
от этого значения По:
Нормальный сфероид Клеро определяется как тело, на поверх-
поверхности которого потенциальная энергия равна потенциальной энергии
сферы So — «средней сферической Земли». По этому определению,
называя через R* радиус-вектор поверхности нормального сфероида,
имеем
(П-П0)г=/?, = 0. E.6.10)
Это уравнение определяет R* как функцию угла 8. Его решение
будем искать в виде
/?' = /?0[1+7(»)Ь
Величина 7@), характеризующая уклонение нормального сфе-
сфероида от средней сферической Земли, имеет тот же порядок малости,
что ант. Сохраняя лишь первые степени этих величин, получаем
по A0)
— 7 (9) — у аР2 (cos 8) = 0,
и уравнение поверхности нормального сфероида приобретает вид
/?* = /?0[l — |-a/>2(cos0)]. E.6.11)
На экваторе и полюсах, т. е. при & = -тт и & = 0:
(-•§«)• E-6-12)
Величины а и с называются экваториальным и полярным радиусами
нормального сфероида, а — его сжатием:
а — с а — с
а = •
До а '
Поверхности нормального сфероида и средней сферической Земли
пересекаются по параллельным кругам, на которых Р2(&) обращается
в нуль, т. е. при
cos Ь = ± j/"!, ft, = 35° 16', ft2 =144° 44'.
Можно уравнение нормального сфероида записать еще в виде
= a(l —acos2»). E.6.13)
5.6]
фигура земли
209
Назовем Ь* угол нормали к поверхности нормального сфе-
сфероида с его осью вращения Oz. Пусть р и ^ обозначают цилиндри-
цилиндрические координаты точки; на поверхности нормального сфероида они
равны
р* = а A — a cos2 Ь) sin %t z* = а(\ — а cos2 8) eos Ь.
Поэтому
dz*
1 — За cos2 Ь
ИЛИ
= 8 —8* = a
. E.6.14)
Переходим к вычислению силы в рассматриваемом потенциальном
поле. По C.6) находим ее проекции на оси сферической системы
координат:
дг
<^П Г/ ^\/^oV , /И Г
где g0 определено формулой G). В точках сфероида получаем
Составляющие силы тяжести по нормали п к сфероиду и по
касательной т к его меридиану равны
Гп = F*r соs е —
F\=F*r sin е+
l sin s « Fft
cos e = — ^oa sin
+ F\ = 0.
Последний результат служит проверкой вычисления, так как вектор
gradll направлен по нормали к уровенным поверхностям П = const,
одной из которых ограничен нормальный сфероид. Выражение F*
можно записать еще в виде
E-6.17)
где
14 Зак. 2072. А. И. Лурье
210 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
— ускорение силы тяжести на экваторе, а постоянная Клеро C имеет
значение
р = |./и_а. E.6.19)
Составим еще уравнение нормального сфероида в цилиндриче-
цилиндрических координатах р*, «г*. Имеем по A3)
#*2 = р*2 -f z*2 = а2 A — a cos2 ОJ да а2 A — 2а cos2 0) да а2 — 2аг*2
или
*2 ^*2
Но по A2)
и, следовательно,
При принятой точности вычисления поверхность нормального
сфероида Клеро совпадает с поверхностью эллипсоида Клеро, опре-
определяемой уравнением B0).
В заключение приведем некоторые численные данные. Постоян-
Постоянные а и а, определяющие размеры и форму нормального сфероида
Клеро, имеют значения
а = 6378,4 /см, а да -т^-тг да 0,003375. E.6.21)
Постоянные т \\ $ равны
т= 2^ = 0,00347, р = 0,00529. E.6.22)
Имея а и /тг, по C) находим
Из теории предварения равноденствий известно также значение
величины
■^=^-=0,003275. E.6.24)
Последние два значения дают
С
MR*
= 0,334 E.6.25)
вместо 0,4 для однородного шара; это указывает, что средняя плот-
плотность Земли возрастает к ее центру.
5.7] силы упругости 211
Значение разности географической ^ — 0* и геоцентрической
Л 0 широт дается формулой A4). Ее максимальное значение на
широте 45° равно а. При более точном рассмотрении оказывается
efflax = -232 *
6.7. Силы упругости
Ограничивая рамки аналитической механики изучением движений
систем, имеющих конечное число степеней свободы, приходится рас-
рассматривать упругое тело как лишенный массы источник силовых
воздействий — упругих реакций на точки материальной системы, при-
присоединенных к упругому телу или находящихся с ним в контакте.
Становясь здесь на эту точку зрения, мы в последующем (гл. 12)
приведем примеры приближенного учета массы сплошных (в частности,
упругих) тел, основанного на замене последних моделями, конфигу-
конфигурация которых может быть достаточно хорошо определена конечным
числом параметров.
Свойством идеально упругого тела является то, что возникающие
при изменении его формы и размеров упругие реакции на материаль-
материальную систему оказываются зависящими только от величин, опреде-
определяющих положение точек системы, но не от их скоростей, пред-
предшествующей истории деформирования тела и т. п. Поэтому в даль-
дальнейшем принимается, что обобщенные силы упругих реакций являются
функциями лишь обобщенных координат системы
Упругие силы — потенциальны. Это физическое допущение является
выражением свойства упругого тела накоплять при постоянном на-
гружении потенциальную энергию и возвращать ее без потерь, когда
тело при постепенном разгружении возвращается в исходное натураль-
натуральное состояние, в котором восстанавливаются его размеры и форма.
Итак, принимается, что функции координат A) представимы
в виде
Qs^~Ws s==l п- E-7-2)
где n(^j, q2, ..., qn) — потенциальная энергия упругих тел, вклю-
включенных в систему. Следствием B) являются указанные ранее соотно-
соотношения C.12)
которым должны удовлетворять обобщенные потенциальные силы.
В дальнейшем предполагается, что отсчет обобщенных коордшчат
ведется от той конфигурации системы, в которой упругие тела
14*
212 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
находятся в натуральном состоянии. Иначе говоря, упругие реакции
исчезают, когда обращаются в нуль обобщенные координаты:
Q5@, .... 0) = 0. E.7.4)
Основным физическим законом математической теории упругости
является обобщенный закон Гука, выражающий наличие линейных
соотношений между величинами, определяющими напряженное со-
состояние (нормальные и касательные напряжения) в упругом теле,
и величинами, характеризующими его деформацию (относительные
удлинения и сдвиги). Это свойство идеально-упругого (гукова) тела
соблюдается для большого числа материалов при достаточно малых
деформациях.
Можно ли утверждать, что выполнение закона Гука предопреде-
предопределяет также линейную зависимость между перемещениями точек упру-
упругого тела и приложенными к нему силами и, как следствие, между
обобщенными силами упругих реакций и обобщенными координатами?
Многочисленные простые примеры убеждают, что это не так. Реакция
упругой среды на вдавливаемый в нее твердый шарик пропорцио-
пропорциональна не первой, а полуторной степени перемещения центра шарика.
Конец вертикального стержня под действием сжимающей осевой силы,
если она достаточно велика (превосходит эйлерово критическое зна-
значение), перемещается вниз и в сторону; эти перемещения сложным
образом зависят от силы и отнюдь не будут малы, хотя закон Гука
и малость деформаций имеют место.
Тем не менее, рассмотрение большого числа задач теории упру-
упругости, основанное на применении закона Гука, приводит к линейным
соотношениям между силами, приложенными к упругому телу, и
перемещениями его точек. Это дает основание принять видоизменен-
видоизмененный обобщенный закон Гука, в котором зависимости упругих сил
от координат задаются линейными соотношениями
п
Qs = —1> cskqk = — (cslqx + ... + csnqn) (s = 1 , и), E.7.5)
k = l
где csk — постоянные коэффициенты, совокупность которых образует
матрицу жесткостей
|Сц С12 ... С1п
с21 с22 ... с2п и E.7.6)
СП\ СП2 • - • СПП
Симметричность этой матрицы является следствием потенциаль-
потенциальности упругих сил. Действительно, из C) и E) получаем соотношения
csk = cks (ft. 5=1 л). E.7.7)
Конечно, уравнения E) применимы лишь при достаточно малых
значениях обобщенных координат (отсчитываемых, напоминаем, от
5.7]
СИЛЫ УПРУГОСТИ
213
натуральной конфигурации системы). Это соответствует предпосылке
о малости деформаций в законе Гука и предположению, что упругая
система не допускает больших изменений размеров и формы.
Вариация потенциальной энергии упругих сил по B) и E) равна
п
=- 2
E-7-8)
5 = 1
Выражение потенциальной энергии легко восстановить по ее пол-
полной вариации (8), но это вычисление было бы излишним, так как
согласно (8) потенциальная энергия представляет квадратичную форму
обобщенных координат (постоянное слагаемое может быть отброшено).
Билинейное выражение этой формы через обобщенные координаты
и обобщенные силы легко составляется
по теореме об однородных функциях /
D.1.12):
5 = 1
E.7.9)
после чего по E) получаем
=т?'с?- <5-7-10>
5 = 1
Здесь q — столбец, qr — строка обобщен-
обобщенных координат; аналогичное значение Рис. 39.
для обобщенных сил имеют Q и Q/.
Свойством упругого тела является положительность работы сил
упругих реакций при восстановлении натуральной конфигурации,
т. е. положительность потенциальной энергии во всякой конфигура-
конфигурации, отличной от натуральной. Поэтому квадратичная форма A0)
знакопостоянна и положительна. Но говорить, что она является
знакоопределенной функцией обобщенных координат системы, допу-
допустимо лишь при надлежащих оговорках — см. (п. 1.3). Прежде всего
следует условиться, что под qx qn в формулах A0) и пред-
предшествующих подразумеваются не все независимые параметры, опре-
определяющие конфигурацию системы, а лишь те, которые входят в эти
формулы. И эти последние должны быть выбраны так, чтобы нату-
натуральной конфигурации упругих тел, входящих в систему, соответ-
соответствовало обращение в нуль каждой из координат. На рис. 39 пред-
представлен иллюстрирующий это условие пример. Твердая пластинка S
соединена шарниром О с концом упругого стержня, другой конец
214 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
которого жестко заделан. Положение пластинки в ее плоскости,
перпендикулярной к оси шарнира, определяется тремя параметрами.
За таковые можно принять проекции перемещения uo = qx и vo = q2
точки О на оси Ох и Оу и угол поворота <? —<7з пластинки. В этом
случае потенциальная энергия П будет положительной знакоопреде-
ленной квадратичной формой qx и gj2, a q3, конечно, не войдет в ее
выражение. Но за обобщенные координаты можно принять также проек-
проекции на оси Мх* и My* перемещения точки М пластинки q* = uM и
q* = vM, и тот же угол y = q3. Тогда, считая угол ср малым, имеем
и II будет положительной знакопостоянной функцией трех перемен-
переменных q*v q*v q3 (но не знакоопределенной, так как она обращается
в нуль при q*x — bqy q\ = — а#з)*
В дальнейшем предполагается, что П—положительная знако-
определенная квадратичная форма обобщенных координат, входящих
в ее состав. Тогда элементы csk матрицы жесткостей будут удовле-
удовлетворять неравенствам Сильвестра (П. 1.3.25), одно из них — положи-
положительность дискриминанта |с| квадратичной формы — гарантирует
существование обратной матрицы
|] а11 а12 ••. а\П
а21 «22 ... «2Л f E.7.11)
аП\ ап2 ♦ • • аПП !
называемой матрицей влияния] через эту матрицу записываются
выражения, обратные E):
п
?, = — S«rtQft = — («,!«!+ ••• +«snQn) (S=l «).. E.7.12)
k = 1
Матрица, обратная симметричной, симметрична, т. е.
asfc = afcs (k, s=l, ..., п). E.7.13)
Эти соотношения выражают теорему взаимности Максвелла.
Подставив в билинейное выражение потенциальной энергии (9)
значения qs через обобщенные силы, придем к союзному представле-
представлению 11 через обобщенные силы
п п п
11=- т 2 Qj* - i 2 Ц as*Q°Qk = i Q'aQ- <5-7-14>
6'»1 5 = 1 k = \
Из него и A2) следует теорема Кастильяно
*Л = ^ {s=\,...,n). E.7.15)
5.8] ВЫЧИСЛЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СТЕРЖНЕВЫХ СИСТЕМ 215
5.8. Вычисление потенциальной энергии стержневых систем
Вычисление матриц влияния и жесткостей проводится методами
теории упругости и строительной механики. Мы приводим в этом
и следующем параграфах несколько примеров.
1°. Стержневая статически определимая система.
Рассматривается твердая пластинка S, шарнирно подвешенная в точ-
точках Ох и О2 к двум фермам. Каждая из ферм представляет стати-
статически-определимую систему шарнирно-соединенных по концам стерж-
стержней. В положении равновесия системы стержни будут напряжены,
Рис. 40.
так как, во-первых, на ферму передаются силы, приложенные к пла-
пластинке (ее вес, например), во-вторых, натуральные длины стержней
могут отличаться от тех, которые они приобрели при монтаже фермы.
Мы пренебрегаем этими начальными напряже-
напряжениями, т. е. отождествляем изображенное на
рис. 40 положение равновесия с натуральной
конфигурацией упругой системы. Вес стержней
не учитывается.
Предполагается, что пластинка, перемещаясь
в своей плоскости, весьма мало отклоняется
от положения равновесия. За обобщенные ко-
координаты
принимаются угол поворота пла-
пластинки ср и координаты xQ, yG полюса G.
Рис. 41.
Последние следует отсчитывать в неподвижной
системе осей GQxy, начало которых совпадает с начальным положе-
положением полюса (рис. 41). Однако проекции перемещения полюса на
оси Gx'yf% связанные с пластинкой,
= xg cos ¥
sin <
отличаются лишь слагаемыми второго порядка малости от xQ и yG%
Поэтому в дальнейшем отождествляем эти величины. Проекции
216
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
перемещений шарниров Ох и О2 на оси GQxy с такой же степенью
точности равны
Переходим к составлению выражений потенциальных энергий
упругих реакций левой и правой ферм через xQ, у0 и соответ-
соответственно х0 , у0 .
Мысленно загрузим ферму (рис. 42)
в шарнире Ох единичной силой ^=1,
направленной по положительной оси х\
далее проводим с помощью графиче-
графических или аналитических способов строи-
строительной механики расчет усилий в стерж-
стержнях фермы; усилие в k-u стержне
обозначается \k. Подобным же обра-
образом отдельно определяются усилия pk
в стержнях при загружении единичной
Рис. 42.
силой К=1. Зная \k и
находим
усилия Sk в стержнях фермы при загружении ее в шарнире О
силами X и Y произвольной величины
E.8.2)
и потенциальную энергию фермы (всех т стержней)
т су „/ т . , т
E.8.3)
Здесь Fk — площадь поперечного сечения /г-го стержня, Ек — модуль
Юнга. Обозначая через
т
E.8.4)
коэффициенты влияния, определяемые по конструктивным размерам
и материалам стержней фермы, и замечая, что внешние силы X, У
лишь знаками отличаются от обобщенных сил Q1§ Q2, отнесенных
к обобщенным координатам xQt y0 (горизонтальная и вертикальная
проекции перемещения загруженного шарнира О), находим
1
E.8.5)
5.8] ВЫЧИСЛЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СТЕРЖНЕВЫХ СИСТЕМ 217
Выражение П через обобщенные координаты х0, у0
х°= ~~ Ж = ~(cCllQl+auQ2)' Уо==2~Ж^~(cC2lQl+a22Q2>
имеет вид
П = ±(спх1 + 2с12х0у0 + с22у1), E.8.6)
причем коэффициенты матрицы жесткостей равны
_ 1 _ 1 _ 1
^11 — ~[7|~а22> ^12— "у^~|" а12» ^22 — ~y^yalV
Возвращаясь к примеру, изображенному на рис. 40, имеем
П = { (с[Л, + 2<2*о,УО, + <-fo) +
+ \ КХЬ, 4- 2<2*OiyOj + с;2уЪ), E.8.7)
где c'ik и ск—коэффициенты матрицы жесткостей левой и правой
ферм. Остается по формулам A) выразить xQ, ..., у0 через обоб-
обобщенные координаты
Получаем
3 3
5 = 1 ^ = 1
где обозначено
С сг -Х- г" С — с' -Х- с"
^11 — С11 ' С11» ^22 С22"| С22»
С33 = ЫСи + аЮ22 + 2ab (c[2 - Q,
— С
\2
Г *^12 ~t~ a (с22 Сй) ■
E.8.9)
2°. Статически неопределимая стержневая система.
Пример такой системы стержней, сходящихся в сферическом шар-
шарнире Мо и присоединенных к неподвижным опорам сферическими
шарнирами Ov O2, ..., OIV показан на рис. 43. Натуральные длины
стержней равны /?, ..., fn\ направление OkMQ задается косинусами
ak> Рл> Тл Углов> составляемых им с осями неподвижной системы MQxyz.
218
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Требуется определить потенциальную энергию упругих сил при малом
смещении и = М0М точки Мо в положение М с координатами xt у, z.
При этом смещении стержень OkMQ, повернувшись на малый
угол г°к, приобретает длину Lk — OkM = OkAV'. Его удлинение
Рис. 43.
fk = Lk — lk\ пренебрегая малыми величинами второго порядка (отно-
(относительно х, у, z)y можно принять угол при вершине Мг треуголь-
треугольника М0М'М равным 90°. Поэтому, обозначая через е\ единичный
вектор направления OkM0, имеем
и потенциальная энергия оказывается равной
п
п=
k= I
где жесткость /г-го стержня ck равна продольной силе, сообщающей
ему удлинение, равное единице длины:
Итак,
П = ~2
E.8.10)
5.8]
где
ВЫЧИСЛЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СТЕРЖНЕВЫХ СИСТЕМ 219
с =
п
<п=2
12 — 2j
22 = 2j
С23
__ 'Vl
k= [
n
>=2
E.8.11)
Рассмотрим теперь ту же стержневую систему, но в предполо-
предположении, что в начальном ее положении длины стержней (монтажные
длины) lk отличны от натуральных /#. Обозначая по-прежнему через fk
удлинение k-vo стержня из начального положения, имеем
Lk - ll = (Lk -1,) +{lk - Ц) = fk + %,
где bk — изменение длины при монтаже (bk > 0 при растяжении).
Потенциальная энергия k-vo стержня равна
и для вычисления второго слагаемого с учетом членов второй сте-
степени относительно х, у, z необходимо иметь выражение fk с этой
степенью точности. Замечая, что координаты точек Ok и М соот-
соответственно равны (—ад,/^, —р^/д,, —7/А) и (JC» У* z)> имеем
akl!:f + (у
J + (z
a.x+ 8. у -Ь т.г л:2 + у2
h
4- -
"'-']
При разложении радикала в ряд учитываем слагаемые второй, сте-
степени относительно ху у, z. Находим
2*) + f (Т
Отбрасывая постоянное слагаемое, соответствующее потенциальной
энергии системы в начальном состоянии, получим теперь
|||*. У- г\\С
E.8.12)
220
где
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
|Сц Ci2 С13
Q?l С22 С23
с с с
^31 Ь32 ^33
причем
E.8.14)
Заметим, что величина
= ^
23» ^13 ==
E.8.15)
равна начальному усилию в k-м стержне; поэтому Rv R2, /?3 пред-
представляют суммы проекций на координатные оси усилий, сходящихся
в узле MQ. Начальная конфигурация будет равновесной (если в точке Мо
не приложены другие силы) при условиях
#! = (), /?2 = 0, /?3 = 0. E.8.16)
Потенциальная энергия представляется однородной квадратичной
формой, входящей в состав выражения A2). Эта форма может и не
быть знакоопределенной. Это объясняется тем, что отсчет потен-
5.9]
ЭНЕРГИЯ ИЗОГНУТОГО, СКРУЧЕННОГО И СЖАТОГО СТЕРЖНЯ
221
циальной энергии ведется теперь не от натуральной, а от равновес-
равновесной конфигурации; в последней потенциальная энергия принимается
/ А/
gH У У У У УЧ ГУ V V V V Мр £
Рис. 44.
равной нулю. Поэтому при смещении из этой конфигурации П может
уменьшиться и стать отрицательной.
Как простейший пример рассмотрим массу между двумя предва-
предварительно поджатыми на 8 одинаковыми пружинами (рис. 44). В этом
случае
1 Р О 8 8 8
—- Сп ===: С
и по приведенным формулам находим
E.8.17)
5.9, Потенциальная энергия изогнутого, скрученного
и сжатого стержня
Рассмотрим в натуральной конфигурации упругий стержень, ось
которого (геометрическое место центров тяжести сечений) предста-
представляет пространственную кривую (рис. 45). Концевое сечение жестко
Рис. 45.
заделано, т. е. предотвращены его перемещение и поворот. Другим
своим концом М стержень жестко заделан в твердое тело S, с кото-
которым связана система осей М£т£. Требуется определить потенциальную
энергию упругих реакций стержня на тело «S, возникающих при
22
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Ггл. 5
сообщении телу поворота 6 и поступательного перемещения и. Триэдр
Л1£т}С при этом займет положение Mrt,fy\V. Заметим, что задача о конеч-
конечных перемещениях и поворотах не решена полностью (для неплоского
случая) даже для стержня с первоначально прямолинейной осью,
поэтому мы ограничимся рассмотрением малых перемещений и пово-
поворотов, т. е. будем считать проекции и, v, w вектора перемещения и
на оси системы М£т]С, равно как и проекции на них а, C, f вектора
поворота 6, малыми величинами, произведения которых отбрасы-
отбрасываются; заметим, что а, р, т являются углами, на которые надо по-
повернуть триэдр М£т£ вокруг осей М%, Mr\, MC, безразлично в какой
последовательности *), чтобы его оси стали параллельными осям три-
триэдра мтус.
Эти шесть величин примем за обобщенные координаты
' = ЯЧ, OL
■q^ p = (
Им соответствующими обобщенными упругими реакциями будут проек-
проекции на оси М£т]С главного вектора V0 и главного момента L0 упру-
упругих реакций стержня на тело
Vl = Qv V°4 = Q2. V? = Q3. £? = Q4. L\ = QS, L? = Q6. E.9.2)
Здесь — V° и — L° представляют главный вектор и главный момент
сил, приложенных к стержню в сечении М, при медленном и посте-
постепенном возрастании которых совершается переход от натуральной
Рис. 46.
конфигурации стержня к равновесной (напомним, что массой стержня
мы пренебрегаем).
Рассмотрим (рис. 46) часть стержня Л+О, отделенную мысленно
в сечении А. Главный вектор и главный момент сил, действующих
в этом сечении, обозначим —V, —L. Часть стержня МЛ_ будет
находиться в равновесии под действием силы и момента —Vго, —L0
ротов.
:) Это следует из свойства коммутативности бесконечно малых пово-
5.9] ЭНЕРГИЯ ИЗОГНУТОГО, СКРУЧЕННОГО И СЖАТОГО СТЕРЖНЯ 223
в сечении М и V, L — в сечении Л_. Уравнения равновесия ее,
выражающие равенство нулю главного вектора всех сил и главного
момента относительно точки М, будут
V— V° = 0,
или
V=V°, L = L°—r(s)XV°. E.9.3)
Через r(s) обозначен вектор-радиус точки А оси стержня, имеющий
начало в М; 5 — дуга МЛ, отсчитываемая по оси стержня; проек-
проекции г (s) на оси М£т]С обозначаются через $(s), f\(s)t £(s). Мы рас-
рассматривали равновесную конфигурацию стержня, и вектор г (s) должен
быть определен в этой неизвестной конфигурации, в чем и состоит
трудность задачи о конечных перемещениях. В решении, относящемся
к случаю малых перемещений и поворотов, r(s) отождествляется
с. вектор-радиусом МЛ точки А в натуральной конфигурации
стержня, тогда £(s), tj(s), C(s) будут известными функциями дуги s,
причем последняя также отсчитывается по оси недеформированного
стержня. В точке А (центре тяжести поперечного сечения) строится
система осей Axyz, оси хну которой направлены по главным осям
инерции поперечного сечения, а ось Az — по касательной к оси
стержня. Косинусы aik углов между осями этой системы и осями
системы Ж?т]С также должны рассматриваться как заданные функции
дуги s.
Проектируя второе соотношение C) на оси системы A]£t£, полу-
получим уравнения
E.9.4)
Проекции вектора L на оси системы Axyz — изгибающие мо-
моменты Lx, Ly и крутящий момент Lz — находятся по формулам пре-
преобразования координат
E.9.5)
Потенциальная энергия стержня, складывающаяся из потенциаль-
потенциальной энергии изгиба и кручения, равна
224
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Здесь А — Е1Х, В = Е1у — жесткости на изгиб (произведения модуля
Юнга Е на моменты инерции 1Х, 1у сечения относительно соответ-
соответствующих осей), С — постоянная, зависящая от геометрической формы
сечения и пропорциональная модулю сдвига; она называется жест-
жесткостью на кручение. Через / обозначена длина стержня. Заметим, что
в выражении F) мы пренебрегали, как это обычно делается, сла-
слагаемым, учитывающим потенциальную энергию растяжения стержня
(ось стержня считаем нерастяжимой).
Подставив в F) значения Lx, Ly, Lz по формулам E) и D) и
заменив в последних L\ V® их значениями B), получим выра-
выражение II в виде квадратичной формы обобщенных сил
E-9J)
1 k=\
причем элементы $sk матрицы влияния р *) (число их равно 21) будут
выражены определенными интегралами от величин, являющихся извест-
известными функциями дуги s, зависящими от геометрической формы оси
стержня в натуральной конфигурации и от прочностных параметров
А, В, С. Матрицу жесткостей с = ф~1 определяем как обратную
матрицу влияния.
Для более подробного выяснения структуры матрицы влияния
перейдем к матричным записям: пусть L, Zo, Vo, $ обозначают столбцы
проекций на оси М£т]С векторов L, Z,0, V°, r(s). Через \ обозна-
обозначается кососимметричная 3 X 3 матрица, сопоставляемая столбцу $
согласно правилу (П. 1.2.3), через а — матрица, осуществляющая
совмещение системы осей M^rjt. с осями, параллельными Axyz. Урав-
Уравнения D) и E) запишутся так:
L = Zo — \VQ9 L = aZ = aZ0 — a|l/Ol
E.9.8)
где L — столбец проекций вектора L на оси Axyz. Вводится в рас-
рассмотрение диагональная матрица податливостей стержня
о =
A
0
0
0
1
* в
0
0
0
1
с
E.9.9)
*) Через ask в этом параграфе обозначены косинусы углов между
осями — элементы матрицы поворота а.
5.9]
ЭНЕРГИЯ ИЗОГНУТОГО, СКРУЧЕННОГО И СЖАТОГО СТЕРЖНЯ
225
с помощью которой образуется квадратичная форма проекций век-
вектора L на оси Axyz, равная потенциальной энергии, отнесенной
к единице длины оси стержня
Учитывая, что
E.9.10)
получаем
L'aL = L'oa'
'o \a'aaLQ — L'Qa'aabV0 — Vfi
E.9.11)
Если теперь ввести в рассмотрение матрицы
?! = — f ia'aaikds, -\= — j droa\dst $2= f a'aads, E.9.12)
0 0 0
то выражение потенциальной энергии F) представится в виде
i
П = I / L'oL ds = ± (V^V0 + Vfr'Zo + L'^V, + Ltffy E.9.13)
0
причем равные друг другу второе и третье слагаемые можно
объединить.
Чтобы перейти к записи в форме G), введем 6 X 1 столбец Q
обобщенных сил
и сложную 6X6 матрицу
Pi Г
Т Р2
E.9.14)
E.9.15)
которая, как легко проверить, симметрична. Тогда, заметив, что
Vn
'V oLo\\
получим по A3)
E.9.16)
т. е. соотношение G). Последовательность вычисления матрицы влия-
влияния р указывается формулами A2) и A5). Перейдем к рассмотрению
частных случаев.
15 Зак. 2072. А. И. Лурье
226 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
\°. Плоская кривая. Вычисление значительно упрощается,
когда ось стержня в натуральной конфигурации представляет плоскую
кривую, причем одна из главных осей инерции сечения стержня лежит
в плоскости кривой, а другая перпендикулярна этой плоскости.
Изменяя введенные в этом параграфе обозначения, мы совместим
плоскость оси стержня с плоскостью Мщ. Ось х системы Axyz
направим по касательной к оси стержня; оси у и z — по главным
осям инерции поперечного сечения — первую в плоскости №%% а вто-
вторую параллельно оси С. Уравнения кривой будут:
и таблица косинусов aik примет вид (штрихом обозначается произ-
производная по s)
х 6' V О
у -V 6' 0 •
z 0 0 1
Формулы D) и E) разбиваются на две группы. В первую входят
величины, определяющие изгиб стержня в его плоскости, т. е. v\9
К Lb
LZ = L,, L, = Ll — S(s)VS1 + t](s)V£ E.9.17)
Изменяя обозначения B), вводим обобщенные силы упругих реак-
реакций и соответствующие им обобщенные координаты
V\ = QV V\=Q2% L? = Q3; ?i = «. b = v, ?з = 7- E.9.18)
Вторая группа формул соответствует изгибу стержня, в котором
точки его оси выходят из плоскости уИ£т], причем изгиб сопро-
сопровождается кручением. Эта группа содержит v\, L^ Lv Имеем
по D) и E)
L,-i# + LJ. I,-1*-,WV«U 1
причем теперь
Vl = Q4, L°, = Q5, L? = Q6; w = q,, p = fe a = qQ. E.9.20)
Выражение потенциальной энергии также разбивается на два сла-
слагаемых
ц=п1+п2, п1=
5.9] ЭНЕРГИЯ ИЗОГНУТОГО, СКРУЧЕННОГО И СЖАТОГО СТЕРЖНЯ 227
Полагая
3 3 3 3
!2 2 2S№^+3. E-9.21)
получаем следующие выражения элементов матрицы влияния
i i i
—- f
— J
L ВО)
Е1г ' Pl3
0 0
О О
Выражения C^ более сложны:
E.9.22)
Г12
Pi
ds>
т-т) ^ds-
E.9.23)
Для прямолинейного в натуральном состоянии стержня т\
получаем
= 0 и $'= 1;
— J ^77 ' Р23 — J Е1г ' РЗЗ — ./ £/,
E.9.24)
15*
228
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Остальные элементы обращаются в нуль. При учете растяжимости
стержня получили бы еще
E.9.25)
где F — площадь поперечного сечения стержня. Выражение потен-
потенциальной энергии разбивается на четыре слагаемых
1
E.9.26)
Здесь выражения П2 и П3 с коэффициентами одинаковой структуры
соответствуют изгибу в плоскостях ir\ и С£, rtj — растяжению, ^ — кру-
кручению стержня.
2°. Спиральная винтовая пружина. В натуральной кон-
конфигурации ось стержня представляет винтовую линию на поверх-
поверхности кругового цилиндра радиуса а. Ось цилиндра примем за ось ОС,
Рис. 47.
а в плоскости его сечения расположим оси 0% и Ог\. Тогда уравне-
уравнения осевой линии пружины будут (рис. 47)
S COS a
S COS а
E.9.27)
где а — угол подъема, 5 — дуга, отсчитываемая вдоль винтовой линии.
В начальной точке s = 0 (t = a, т] = С—0) пружина заделана в жест-
жесткую пластинку 5, расположенную в плоскости О£т]. Другой конец
5.9] энергия изогнутого, скрученного и сжатого стержня 229
пружины заделан неподвижно. Пружина сделана из куска проволоки
длины / с круговым поперечным сечением радиуса г.
Предполагается, что на пластинку действует пара с моментом L0
и в точке О к ней приложена сила V0. Требуется определить, сохра-
сохраняя предположения о малости перемещений и поворотов, перемеще-
перемещение точки О и поворот пластинки. В системе осей Axyz ось Ах
имеет направление единичного вектора касательной т к винтовой
линии: оси Ах и Ау можно направить по ее главной нормали п и
бинормали Ь, так как любые два взаимно перпендикулярных напра-
направления в плоскости круглого поперечного сечения будут направле-
направлениями главных осей инерции. Если г—вектор-радиус точки А, то
по B.18.2)
dr d2r u
где р—радиус кривизны. Имеем поэтому
5 COS a S COS а
Т£ = — cos а sin , т^ = cos а cos =— , тс = sin а
и далее
о 9 *S COS а р 9 . 5 COS а
tit = cos2 а cos —= , пъ = — — cos2 а sin , /г, = О,
причем, определяя р условием, что п — единичный вектор, находим
р = —2~ . Теперь получаем таблицу косинусов
C°S —* ^ ч с
х (п) — cos ср — sin cp О
у (b) sin a sin 9 — sin а cos cp cos а
z (х) — cos о sin cp cos а cos cp sin ot,
где ср = . Проекции на оси системы Axyz момента в сече-
сечении А определяем теперь по D), E) и B7). Вычисление, кроме
некоторой длинноты, не представляет труда. Ограничимся случаем
действия осевой силы и осевого момента
Соответствующие обобщенные координаты
Представляют перемещение пластинки 5 по оси OQ и угол поворота
ее вокруг этой оси.
230 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
Находим по упомянутым формулам
U = — aVl sin ср, 1Л = aV\ cos <р, £; = £?,
/,* = 0, Ly = — dV\ sin a -+ L\ cos а, L2 = aV\ cos a -f- L? sin а
и далее
=la\-c - -в)si
sinаcosa«
cos2 a sin2 a
E.9.28)
Обратная матрица будет
c =
Си = -z-~2 (^ cos2 a + & Sin2 a) f 12 = j— (B — C) Sin a COS a
= C\2
C22 = — (C Sin2 a + В COS2 a)
. E.9.29)
Таким образом, обобщенные упругие реакции пружины равны
Qi =
С cos2 a -f В sin2 a
В —С
la2
sin a cos a,
В — С
la
w cos a sin a
E.9.30)
Для круглой проволоки
о 7i£r4 c
4 • с ~ 4(l+v) '
где v — коэффициент Пуассона.
Приложение одной лишь осевой силы вызывает не только осевое
перемещение w, но и поворот пластинки на угол
С—В w . v sin a cos a w ,~ Л о л ч
- sin a cos а = — ^—, , E.9.31)
С sin2 a-f- В cos2 a a
1 + v cos2 a a
т. е. сжатая пружина правого хода раскручивается.
Обратно, приложение крутящего момента создает не только пово-
поворот 7» но и осевое перемещение
(С — В) sin a COS a v sin a COS a
w = Ccos2a + £sin2a aT ~ — 1 + N bin2 a
E.9.32)
Эти эффекты пропорциональны sin a, т. е. малы при малом угле
подъема.
5.10] мощность 231
5.10. Мощность
Мощностью в действительном движении системы называется
сумма скалярных произведений векторов сил на скорости точек
их приложения
&«.+т?) E-10Л)
или, по определению A.3) обобщенных сил,
п N
5=1 i=\
Первое слагаемое — виртуальная мощность
п
Nr = ^Qsqs E.10.3)
5=1
— получается при замене в определении мощности действительной
скорости vt точки ее виртуальной скоростью v'r
При стационарных связях понятие мощности в действительном
движении и виртуальной мощности совпадают.
Выражение мощности через квазискорости составим, использовав
соотношения A.5.8) и A.8):
5=1 Г=1 Г=1
Здесь предположено, что квазискорости связаны с обобщенными ско-
скоростями однородными линейными соотношениями A.5.1).
Например, мощность сил, действующих в точках твердого тела,
согласно формулам п. 5.2, можно представить в одном из двух
видов: через обобщенные силы и обобщенные скорости
N = Vl х0 ■+- V2y0 ■+- V3z0 + mj> + т3ф + т$ E.10.5)
или через квазискорости и обобщенные силы, отнесенные к квази-
квазикоординатам:
232 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
5.11. Диссипативная функция
К числу диссипативных сил относятся силы сопротивления дви-
движению точек системы, направленные противоположно их скоростям.
Мы рассмотрим случай сил сопротивления, представимых в виде
где vt — величина скорости точки Mt\ kt и ft (vt) — положительные
функции от обобщенных координат и соответственно от скоростей vt.
По A.3) и A.3.5) соответствующие этим силам обобщенные силы
определяются равенствами
/ = 1 / = 1
Заметив, что
dvt 1 д \ dv\
находим
N N Vi
дФ
if fi(u)du = -
i = i -•" ~ 1 л -t _ | q dqs
(s=l ti\ E.11.2)
где через Ф обозначена величина, называемая диссипативной функцией
/ E.11.3)
i«1 О
Заметим, что Ф^О, так как подынтегральные функции положи-
положительны.
Обобщенные силы, отнесенные к квазикоординатам, по A.8) равны
rsQr^-^brs^^-J^ (S=l Л), E.11.4)
где сОу — квазискорости.
Диссипативная функция была введена в классическом труде Релея
«Теория звука» для сил сопротивления, пропорциональных первой
степени скорости. Здесь это понятие обобщено на силы более общего
вида.
В случае одночленной степенной зависимости сил сопротивления
от скорости
f(vt) = vf E.11.5)
5.11] диссипативная функция 233
диссипативная функция
E.11.6)
5=1
будет однородной функцией {т-\-\) степени от обобщенных скоро-
скоростей, которую легко выразить через мощность диссипативных сил
i^=~(m+1)O- EЛ1-7)
5=1 5=1 ^
Здесь применена теорема Эйлера D.1.12). Отметим, что т = 0 соот-
соответствует кулонову (сухому) трению, т = 1 — силам вязкого трения,
пропорциональным первой степени скорости (случай Релея), т — 2 —
силам квадратичного сопротивления.
При составлении обобщенных сил по формуле B) необходимо
иметь в виду, что дифференцируются выражения, содержащие модуль
обобщенных скоростей. Например, при сопротивлении, пропорцио-
пропорциональном четной степени скорости и п= \
Q = — k'q2s Щ±- = — kq2s sgn q,
дд
где sgn ср означает знак функции ср (sgn ср = —)— 1, если ср > 0 и
sgn ср = —1, если ср < 0).
Будем рассматривать движение системы относительно движущихся
осей Ox'y'z'\ но примем, что в выражение вектор-радиусов r't
точек системы по отношению к полюсу О время / явно не входит.
Силы сопротивления, действующие на точки системы, определяются
их скоростями относительно окружающей среды, которые в общем
случае не будут совпадать со скоростями v'. в системе осей Ox'y'z'.
Пусть, например, рассматривается движение математического маят-
маятника, точка подвеса которого имеет по отношению к земле ско-
скорость vQ\ движение происходит в набегающем со скоростью V воз-
воздушном потоке, скорость маятника относительно системы осей, дви-
движущихся поступательно вместе с точкой подвеса, равна vr. Абсолютная
скорость маятника (по отношению к земле) равна vo-\-v\ а его ско-
скорость относительно потока равна vo-{-v'—V. В формулу A) для
силы сопротивления должно входить это выражение скорости
Например, при V=0 (воздух неподвижен) сила сопротивления опре-
определяется абсолютной скоростью точки, которая в этом случае является
234 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [ГЛ. 5
ее скоростью относительно воздуха; при v0 = 0, v' = 0 на точку
действует сила, направленная по скорости потока
Возвращаясь от частного примера к общим определениям, запишем
выражение силы сопротивления, вместо A), в виде
где V*. — геометрическая разность векторов переносной скорости и
абсолютной скорости точек среды Vl в той точке движущейся си-
системы, через которую в рассматриваемый момент проходит точка Mt.
Векторы V* могут зависеть от времени t и обобщенных координат,
определяющих положение точек материальной системы в системе
осей Ox'y'z', но не от обобщенных скоростей qs\ векторы v'. пред-
представляют линейные формы обобщенных скоростей.
В частности, v*. могут равняться нулю, и тогда силы сопротивле-
сопротивления будут зависеть только от относительных скоростей. Это может
иметь место в тех случаях, когда среда, в которой происходит дви-
движение, перемещается вместе с системой Ox'y'z'.
Диссипативная функция вводится и при задании сил сопротивле-
сопротивления зависимостью (8) формулой того же вида C), что и ранее.
Сохраняется также формула B), с помощью которой обобщенные
силы определяются через диссипативную функцию. Сказанное следует
из гого, что выражение обобщенной силы можно взять в форме A.11),
а вместе с тем
дг\ dv\ д
=
поскольку я?* не зависит от обобщенных скоростей. Повторив с этим
изменением вывод формулы C), получаем
где теперь
i * ' i
A \vt+vi\
/ /(«)*«• E.11.10)
6.12]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ ДИССИПАТИВНОЙ ФУНКЦИИ
235
При одночленной степенной зависимости функции / от ее аргу-
аргумента диссипативная функция сохранит однородность относительно qs
лишь при v*t = 0, например, при движении системы осей Ox'y'z'
вместе со средой (предполагается возможным движение среды как
твердого тела).
Мощность диссипативных сил в действительном движении равна
причем vt—вектор абсолютной скорости, vie—переносной. Первое
слагаемое представляет виртуальную мощность, определяемую по E.10).
Получаем
N
i=\
E.11.11)
причем Qs дается формулой (9).
5.12. Примеры вычисления
диссипативной функции
1°. Двойной математический маят-
маятник с квадратичным законом сопро-
сопротивления. Составить выражение диссипативной Рис.48,
функции и обобщенных сил сопротивления, когда
система представляет двойной математический маятник (рис. 48),
точка подвеса которого О движется со скоростью v0 в неподвижном
воздухе, а силы сопротивления воздуха принимаются пропорциональ-
пропорциональными квадратам скоростей относительно воздуха.
Движение системы будем определять относительно поступательно
движущейся со скоростью v0 системы осей Ох'у'. Квадраты абсо-
абсолютных скоростей точек равны
v<\ ~ I vi ~г" vo |2 = (^о cos а — ^i?i s*n ?iJ 4~ (^о s^n а "i~ ^i?icos ?iJ ==
= tf2-f-^?J + 2tfo/1cp1 sin Га — срЛ, E.12.1)
-f- (v0 sin a -\- /jCpj cos cpx -f- /2rf 2 cos cp2J =s
Vl =
in(a -
sin
cos (?! - ?2)- E-12-2)
236
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
В данном случае
и выражение диссипативной функции по A1.10) будет
ф=т(*1°1+*24
Обобщенные силы равны
Q, = — Vi [ЧЬ + «\Аsin (а — Ъ)] —
— k2v2 [/ft, + Vi sin (а — cp,) + /,^2 cos (cp, — <p2)]
E.12.4)
Q2 = — *2«2 [%2 + г»0/2 sin (a — cp2) + /1/2ф1 cos (cp, — cp2)J.
При относительном равновесии ср, = cp2 = 0 и обобщенные силы будут
Q0 = ^ + Ц ^ sin (?0 _ a), Q0 = Д.^2^ sin (c?0 _ a)>
что легко проверить непосредственным вычислением элементарной
работы сил—ktvQvQ на виртуальных перемещениях Ьгх и Ьг2. Эле-
Элементарная работа сил веса на этих виртуальных перемещениях равна
- Рг1г sin cpO8cPl - Р2 Aг sin ср^ + /2 sin ?208ср2),
и обобщенные силы веса равны
<?i = - (pi + р2) ^isin ??. Ql = - phsin ?l
Из уравнений равновесия (о них говорится ниже в п. 6.5)
легко найти теперь значения ср? и
[kx +
sin a
ctgepg = ctga-
sin a
E.12.5)
Выражения обобщенных сил D) получились весьма сложными.
Они значительно упрощаются, если рассматривать малые колебания
системы около положения относительного равновесия и считать как
углы £j = <Pj — <р?» £2 = ?2 — ^2' отсчитываемые от этого положения,
так и соответствующие угловые скорости slt e2 малыми первого
порядка. Тогда, пренебрегая произведениями и квадратами этих
величин и считая для упрощения в записи формул а = —, получим
C0S ??
V2 = V0
C0S ?1
C0S ?2
5.191 примеры вычисления диссипативной функции
и далее
237
о _
^ . 7,2 tcr го° —-=- 7!г
~~ Pt+P2 V°" tg^-—P2V<>-
Вследствие этих равенств имеем
Подстановка в формулы D) дает теперь
^-A + cos 2cpJ) у - 2 VoV2 cos cpj cos срО X
S
Эти формулы сохраняют смысл при т/0, отличном от нуля и
достаточно большом, так как при t/0 = 0 в выражения v\ и v\ войдут
только квадратичные относительно гх и s2 •
слагаемые. 1^
2°. Кулоново трение. Рассматри-
Рассматривается плоское движение твердой пластинки S,
прижатой к неподвижной шероховатой плите, г
Требуется определить мощность, потребную 1
для сообщения пластинке угловой скорости со^, у
а полюсу О скорости <&0 (рис. 49).
Сила кулонова трения, действующая на
элемент do площади соприкасания, равна
У/////7//////Л
////////////////
— fpdo-,
{+~z
Рис. 49.
где / — коэффициент трения (который счи-
считаем не зависящим от скорости), р — давле-
давление, предполагаемое равномерно распределенным. В выражении A1.6)
суммирование заменяется интегрированием по площади соприкаса-
соприкасания 5, т. е.
Ф
-/'Я
vdo.
E.12.7)
238
Имеем
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[гл. 5
V = VQ
X Г
или в проекциях на оси Оху, связанные с пластинкой,
= V
Поэтому
Ф = /р
Здесь
Qy
E.12.8)
— координяты мгновенного центра скоростей. Обозначив расстояние
Рис. 50.
элемента do от мгновенного центра скоростей через г, а силу, при-
прижимающую пластинку к плите, через G, можем написать
»г\г\ E.12.10)
E.12.11)
причем имеющая размерность длины величина г* равна
Г = — I I Г(
II
S
Принимая мгновенный центр скоростей за начало полярной системы
координат (г, X) с полярной осью ОР, имеем do = rdrd\. Поэтому,
если мгновенный центр расположен внутри 5, то (рис. 50, а)
г =
E.12.12)
ПРИМЕРЫ ВЫЧИСЛЕНИЯ ДИССИПАТИВНОЙ ФУНКЦИИ
239
где r\k) = PM, M — точка контура. Если же он расположен вне S,
то (рис. 50,E)
^2
* = -gj / [i М - *1 М] Л.
E.12.13)
где r2(k) = PN, rx(k) = PM, a Xj и Х2 — углы, составляемые каса-
касательными из Р к контуру с прямой РО.
И
Рис. 51.
Величина г* зависит, таким образом, от формы контура пластинки
и от положения мгновенного центра скоростей. Для круглой пла-
пластинки радиуса а в первом случае (рис. 51, а) имеем
r*=(R cos X +- ]/V--#2sin2XK = #3 cos3 X+3/?2 cos2 X Va2—R2 sin2X+
-f- 3/? cos X (a2 — #2 sin2 X) -f (a2 — /?2 sin2 XK/a,
где R = OP. Замечая, что интегралы, соответствующие первому и
третьему слагаемому, обращаются в нуль, получим
где К и Е — полные эллиптические интегралы первого и второго
рода от модуля
Во втором случае (рис. 51, tf) имеем
>% ~г\ = (г2 - г,) [4 (г, + ^^J ~ ггг2] = MN ЩРО?-(РТ)Ч =
= 2 J/ а2 — Я2 sin2 X Dfi2 cos2 X — Я2 + а2)
240 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [г'л. 5
и далее
r* = 4& f К^2 — R2 sin21 D cos2 X — 1 + -g-) dk.
6
Подстановкой
R iX = a sin
это выражение приводится к виду
71 J i/ i _ ^L sin2 e ' ^
Получаем
E.12.15)
где К и £ — полные эллиптические интегралы от модуля
В формулах A4) и A5)
Предельный случай т/0 = 0, соответствующий вращению вокруг
неподвижной оси, проходящей через центр круга О, получаем из A4)
при R = 0. Тогда
E@) = tf@) = -i-ic. r' = -g.fl. Ф=-|/Оа|шг|, E.12.17)
что легко проверить элементарным расчетом.
Второй предельный случай — поступательное движение. Вспомнив
разложения в ряды
+
получим из A5) при предельном переходе
и далее
Ф = /О(/г|ш,|)^оо = /О«г0, E.12.18)
что и требуется.
5.12J примеры вычисления диссипативной функции 241
В \случае качения круга без скольжения R = a. Тогда из A4)
или A5) найдем
где vQ — скорость центра колеса. Это выражение легко также полу-
получить непосредственно по A1), принимая r(X) = 2acosX и нижний
предел равным ^ , а верхний у
Обобщенные силы трения, отнесенные к квазискоростям vOx и vQyt
т. е. проекции главного вектора сил трения на оси Ох и Оу, связан-
связанные с пластинкой по A1.4) и A6), равны
dФ dФ dR
dR dvOx
дФ dk2
dФ dk2
dk2 W
n ___ ^ОУ
y ~ К I "о dk2 dR '
Применив соотношения
dK _ 1 E— A — k2)K dE
dk2
2 (\ — k2)k2 ' dk2
1 K—E
2 k2 '
получим
_
Vo
Рэ р =
E.12.19)
4 . Жа.
Здесь обозначено
E.12.20)
Обобщенную силу Р^ (вращающий момент) проще всего найти по
выражению мощности
т. е.
Находим
Р^ Sgn 0)^ =
__4/G
E.12.21)
16 Зак. 2072. А. И. Лурье
242
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[гл. 5
где sgna^ обозначает знак <ог : sgna);B= 1 при <ог > 0 и sgn со = — 1
при сог < 0. Предельные переходы в этих формулах дают:
а) при вращении вокруг неподвижной оси, проходящей через
центр пластинки,
Р = 0. P^l
б) при поступательном движении (/?->
P = fG, Рш =
в) при качении без скольжения (R = a
р _ 8/G n 8/G
оо)
E.12.22)
E.12.23)
E.12.24)
что эквивалентно силе величины Р, приложенной в точке, отстоящей
4
на -j-a от мгновенного центра
скоростей; направление силы
противоположно скорости точки
приложения силы.
Элементарно, хотя и гро-
громоздко, вычисление Ф в случае
пластинки, ограниченной поли-
полигональным контуром. На рис. 52
показан пример прямоугольной
пластинки со сторонами 2а и
Рис. 52. 2£. Рассматривая простейший
пример вращения вокруг не-
неподвижной оси, проходящей через центр симметрии О, по A2) получим
2а
где в этом случае
Здесь, как и для любого полигонального контура, дело сведется
к суммированию выражений, содержащих интегралы вида
В нашем примере найдем
| + ^)|]}. E.12.25)
5. i&l силы сопротивления воздуха 243
5.13. Силы сопротивления воздуха
Изучение сил, действующих на движущееся в воздухе тело
(снаряд, самолет), представляет предмет теоретической и экспери-
экспериментальной аэродинамики. В книге по аналитической механике рас-
рассмотрение этих вопросов возможно лишь в самых общих чертах; оно
имеет целью дать представление о характере и степени трудности
задач механики, возникающих при учете этих сил.
Ниже, следуя Нильсену и Синджу*), мы рассматриваем систему
аэродинамических сил, действующих на движущийся в покоящемся
воздухе вращающийся снаряд. Движение снаряда (по отношению
к земле) задается вектором скорости v полюса О и вектором угло-
угловой скорости со. В исследованиях по баллистике за полюс обычно
принимают центр инерции снаряда. Такой выбор нелогичен, так как
положение центра инерции определяется распределением масс в сна-
снаряде, тогда как аэродинамические силы обусловлены геометрической
формой поверхности вращения, ограничивающей тело снаряда. По-
Поэтому в дальнейшем за полюс — начало О связанной со снарядом
системы осей Oxyz — примем центр тяжести Объема снаряда (центр
величины), расположенный на оси снаряда Oz. Впрочем, можно было
бы полюсом О считать любую точку на оси снаряда; целью после-
последующего является дать такую формулировку зависимостей главного
вектора F и главного момента т° аэродинамических сил от векто-
векторов v и со, которая сохранялась бы независимо от выбора полюса.
Проекции v и (о на ось снаряда обозначаются через г>3 и а>3;
предполагается, что они весьма велики по сравнению с г% и о^ —
величинами проекций ю% и @^ этих векторов на плоскость Оху.
Векторы F и т° также представим в виде
F=F, + kFz, mP=m° + kmt E.13.1)
где /%, т^ —проекции F и т на плоскость Оху — поперечная сила
и поперечный момент; через k обозначен единичный вектор оси Oz.
Принимается, что осевая сила Ръ и осевой момент т° имеют вы-
выражения
m$ = — pa4 gsv^ E.13.2)
где через р обозначена плотность воздуха, а — радиус (полукалибр)
снаряда; /3 и g3— безразмерные аэродинамические функции, опре-
определяемые экспериментально; они зависят от безразмерных величин
чУс и ааK/с, где с — местная скорость звука, и, возможно, от числа
Рейнольдса. От этих же величин принимаются зависящими остальные
*) К. L. NielsenanJ J. L. Synge, On the motion of a spinning shell
(Quarterly of Applied Mathematics, IV, № зэ 1946).
16*
244 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ [гл. 5
вводимые ниже аэродинамические функции, обозначаемые буквами /
и g с соответствующими индексами.
Поперечные составляющие силы и момента считаются зависящими
линейно от v^ и (О+, причем расположение осей Ох и Оу, вследствие
симметрии вращения, никак не должно влиять на формулировку этих
зависимостей. Поэтому наиболее общими являются такие предста-
представления:
в которых каждый из векторов Ft и т° предполагается составлен-
составленным из четырех слагаемых; направления двух слагаемых определяются
направлениями v^ и оол, а двух других — направлениями перпенди-
перпендикулярных к ним векторов k X ^* и * X <*>*» лежащих в плоскости Оху.
Слагаемые Ьхк X V* и схы^ поперечной силы и — afa и d[k X <*>*
поперечного момента характеризуют так называемые эффекты Маг-
Магнуса, возникающие вследствие вращения снаряда вокруг оси Oz.
Поэтому коэффициенты bv cv a'v d'x принимаются пропорциональ-
пропорциональными оK; в запись прочих коэффициентов в формулах C) вносится
множитель vz. Итак, полагаем
a[ = />aK, b[ = f2vv c[ = g[avy d[ = ^a>3.
Тогда выражения поперечной силы и момента примут вид
) ( }
Как указывалось выше, десять безразмерных аэродинамических
функций
/,. U gv 8V f'v f'v g'v Sr Л- S3, E-13-5)
входящих в формулы B) и D), зависят от vjc, аы3/с. Знаки рас-
расставлены так, чтобы с уверенностью мэжно было утверждать, что
не зависящие от эффектов Магнуса коэффициенты fv gv f'v gfx
положительны, когда центр давления снаряда расположен впереди
центра величины; знаки прочих коэффициентов умозрительно пред-
представляются также положительными.
При переходе к аэродинамическим функциям, отнесенным к центру
инерции снаряда С, надо иметь в виду, что главный вектор F оста-
остается неизменным, тогда как главный момент тс должен быть опре-
определен соотношением
тс =т° +ek^F=^m° -\-ekXF,, E.13.6)
5.13] силы сопротивления воздуха 245
где ek = CO—вектор-радиус точки О, имеющий начало в центре
инерции С (который также расположен на оси снаряда). Сила F
и момент тс теперь должны быть выражены через скорость центра
инерции
£ E.13.7)
и через вектор (о, не зависящий, как известно, от выбора полюса.
Подобно A), имеем
с = т;
ik = m°-\-
тс =
откуда следует, что соотношения B) и, значит, аэродинамические
функции /3 и g3 сохраняются при переходе к новому полюсу:
/зС==/з> e%=g*. E.13.8)
Теперь, подставляя в выражение /^ значение ©# по формуле G),
придем к выражению
F^ = F% = pa2 [- /л k° + ek X »J +
*>3fc X Wl -h ek X <*0 + gxa\^ + g2fl^3* X »J,
которое приводится к виду
F, = pa2 (— /fг>з«£ + /2СаоK^ X i£ + ^^2oKto, -f gc2av,k X »J.
E.13.9)
где обозначено
Имеем также
mc = раз [_ /jaaK ^c + eft x »*) — /&* X (rf + ^ X ».) —
— ^ot3»# + ^fl(o3ft X <*>*] -\-pa4k X (— /ftytf -h /2^w3^ X ^c +
+ ^^2aK(o, -f g^a^ft X «>*)
и это выражение приводится к виду
тс = р^з (_ /;сасо3*£ - /Jc©8* X *£ — «;с^3«# + ^Cfl2(D3* X »•).
E.13.11)
где обозначено
ffCf'\e
E.13.12)
246
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
[ГЛ. 5
Система сил и моментов, определяемых формулами B) и D) или B),
(9), A1), является (при предположении о линейной зависимости по-
поперечной силы и момента от поперечных составляющих векторов
скорости и угловой скорости) наиболее общей. Применение ее вслед-
вследствие ее сложности и трудности экспериментального определения
/есяти аэродинамических функций E) вряд ли практически возможно
и целесообразно. Обычно в первую очередь пренебрегают эффектами
Магнуса. При таком пренебрежении формулировка зависимостей аэро-
аэродинамических сил от скорости и угловой скорости снаряда остается
неизменной при переходе к новому полюсу. Действительно, если
принять равными нулю коэффициенты /2, gv f[ и g'v то, как сле-
следует из соотношений A0) и A2), обратятся в нуль такие же ко-
коэффициенты, содержащие индекс С. Поэтому при указанном прене-
пренебрежении выражения силы и момента, отнесенные к произвольно вы-
выбранному полюсу, имеют вид
F= pa (— kf3vl — fxvzv* -f- g2avzk X
m° = — pa3 (kgsausv3 -f- fr2vzk X v* + g[
E.13.13)
если под v* условимся понимать поперечную составляющую скорости
этого полюса и считать, что к нему отнесены аэродинамические функции.
Важнейшим исследованием по аэродинамике вращающегося сна-
снаряда, содержащим наиболее полные для своего времени эксперимен-
экспериментальные данные полигонных стрельб,
является опубликованная в 1922 году
работа четырех английских авторов
(Фоулер, Гэлопп, Локк и Ричмонд) *).
Перевод ее на русский язык в той
части, которая содержит описание
и результаты опытов, включен
А. Н. Крыловым в его известное
сочинение о вращательном движе-
движении снаряда **).
Система сил и моментов, суще-
существование которых экспериментально
подтверждено указанными авторами,
представлена на рис. 53. На нем
показаны: вектор скорости v цент-
центра инерции, единичный вектор к
оси снаряда, составляющий угол 8 с вектором скорости, единич-
РИс. 53.
*) R. H. Fowler, Е. О. Gallop, С. Н. L о с k, H. W. R i с h m on d,
The Aerodynamics of a Spinning Shell (Philosophical Transactions of the Royal
Soc:ety of London, 221—222; 1921—1922).
**) О вращательном движении продолговатого снаряда во время полета.
Собрание трудов акад. А. Н. Крылова (IV изд. АН СССР, 1937).
5.13] силы сопротивления воздуха 247
ный вектор iv имеющий направление поперечной проекции v# век-
вектора скорости, и единичный вектор /2 = &X*V ^гол ^ прини-
принимается малым (cos&^l, sin $^8), так что величина скорости может
быть отождествлена с v3. В плоскости векторов iv i2 показан также
вектор ы^ поперечной угловой скорости снаряда.
Аэродинамические силы приводятся к двум силам R и L и мо-
моментам М и И.
Сила R представляет лобовое сопротивление; она принимается
равной
Я = - ?a2fRvsv = - pa2 (fRkv\ + f Rvp.)t E.13.14)
так как v = kv3-\-v^.
Боковая сила L по величине равна
Согласно рис. 53 она может быть представлена в виде
L = pa2fL (— v4ix -f v44) » — pa2fLvsv*, E.13.15)
Мы пренебрегли здесь слагаемым, пропорциональным 82, и приняли
v4ix == vvjtx ^ v^.
Моменты — опрокидывающий М и гасящий Н—определяются равен-
равенствами
М = — 9a*fMvsk Xv*. H= — ра4У>3<о,. E.13.16)
Выражения главного вектора F и главного момента тс аэроди-
аэродинамических сил относительно центра инерции снаряда получаются
в виде
тс = — pa3 (/^з* X ^* + fHavs<fi,). \
Эти соотношения позволяют установить связь аэродинамических функ-
функций в формулах A3) с коэффициентами сопротивления, подъемной
силы опрокидывающего и гасящего момента:
/зС = /Я- /? = /*+"/,. /;С = /ж> S[C = fH. E.13.18)
Вместе с тем надо принять
£3 = 0, ££ = 0. E.13.19)
Логическое несовершенство системы сил A7), хотя практически
она может оказаться достаточно точной, заключается в неинвари-
неинвариантности последнего соотношения A9): принимая отсутствие сла-
слагаемого вида v*k Xw, в выражении F% когда за полюс принят центр
инерции, мы тотчас же получим подобное слагаемое при переходе
к новому полюсу.
ГЛАВА б
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ.
АНАЛИТИЧЕСКАЯ СТАТИКА
6.1. Уравнения Лагранжа первого рода
Реакции связей — это прилагаемые к точкам рассматриваемой
системы силы, которые при мысленном уничтожении связей обеспе-
обеспечивают движения точек системы, осуществляемые при наличии связей.
Введя в рассмотрение реакции связей, условимся различать две кате-
категории сил, действующих на точки системы: реакции связей и актив-
активные (или задаваемые) силы. Равнодействующая реакций связей, при-
приложенных к точке М1 системы, обозначается через Rt, а активных
сил через Ft.
Введение реакций связей позволяет записать дифференциальные
уравнения движения любой точки в форме второго закона Ньютона —
уравнений движения свободной (освобожденной от связей) матери-
материальной точки:
mlwi = Fi + Rl (/==1, ..., N). F.1.1)
Сказанное составляет содержание принципа освобождав мости от
связей. Через mt обозначена масса материальной точки Mt, через
4®i — вектор ускорения в инерциальной системе осей Oxyz:
wi = vi = ri. F.1.2)
В проекциях на оси координат и в обозначениях A.2.1) уравне-
уравнения A) имеют вид
mX = /\ + /?v (v=l ЗЛО, F.1.3)
причем tn3s-2 = mzs-i = m3s ПРИ 5= 1, 2, . . ., Л/. К системе 3N
дифференциальных уравнений надо присоединить г уравнений голо-
номных связей
ных
зуу
= 0 (А=1, ..., г'). F.1.5)
6.1] УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА 249
Неизвестными в уравнениях C) — E) являются 37V координат
\ ..., £здг и такое же число проекций реакций связей. Число не-
неизвестных 67V превышает число уравнений ЪИ -\-г* -\-г на 37V —
— г — г', т. е. на число степеней свободы. Чтобы задача стала
определенной, неизбежно введение некоторых предположений о ха-
характере связей.
Выражение элементарной работы сил реакций связей Rt на вир-
виртуальных перемещениях точек системы из рассматриваемых поло-
положений в момент t имеет вид
N SN
b'W = 2 ^ • 8г, = 2 R Д,. (б. 1.6)
Поскольку связи сохраняются в варьированных состояниях, т. е. на-
наряду с D) имеют также место равенства
то обращаются в нуль также и вариации bfk функций fk
N
= S grad/ /* ■ 8r, = 0 (ft=l, .... г). F.1.7)
/ = 1
Уравнения E) накладывают на вариации &£v еще г' условий
N
37V
2/;
* = 1
N
2
/ = i
2 «г, = о I F_ j 8)
j
(*=1 г').
Здесь ^Л/—вектор с проекциями akl, bki, cki на оси системы Oxyz.
Докажем теперь, что достаточным условием обращения в нуль
элементарной работы F) сил реакций связей является представимость
этих сил в виде линейных функций градиентов связей D) и век-
векторов еы\
или, в другой записи,
=i..... зло.
250 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. б
Коэффициенты Х^ и Х^ называются множителями Лагранжа или
множителями связей—голономных и неголономных; число каждых
из них равно числу уравнений соответствующих связей.
Достаточность проверяется непосредственно; подставляя выражения
реакций A0) в выражение элементарной работы F) и учитывая G)
и (8), имеем
3N 3/V
v = l
г 3N г' 3/V
k=l v=l * = 1 v--=l
что и требуется.
Обратно, если сумма элементарных работ сил реакций связей
равна нулю, то всегда можно выбрать r-\-rr коэффициентов \k
и Vk таких, что 37V величин Rv могут быть представлены линейными
соотношениями A0). Действительно, умножив каждое из равенств G)
и (8) соответственно на —Xk и —Х^ и сложив полученные произ-
произведения с F), придем к равенству
3N г 37V r' SN
k=i
Выберем теперь r + r7 коэффициентов Х^ и Х^ так, чтобы обра-
обратились в нуль r-\-rr слагаемых суммы A1); не нарушая общности,
можно считать, что это будут первые r-\-rr скобок.
Получим
В силу общих предположений о связях эти уравнения имеют
решение относительно Х^ и Х^.
Равенство A1) теперь получает вид
5 1] УРАВНЕНИЯ ЛАГРАНЖА ПЕРВОГО РОДА 251
причем SN—r—r' вариаций Ь^ независимы друг от друга. Поэтому
коэффициент при каждой из этих вариаций в выражении A3) дол-
должен быть нулем, т. е.
'ьК, (v = r + r' + l. .... 3/V). F.1.14)
Совокупность равенств A2) и A4) доказывает предложение.
Итак, если элементарная работа всех сил реакций связей на
всяком виртуальном перемещении точек системы равна нулю, то
ЗА/" реакций выражаются через r-\-rf множителей связей \k и У
вследствие чего дифференциальные уравнения движения точек си-
системы C) принимают вид
или, в векторной форме,
г г'
2 Кен- F-1.16)
k1
k=l k=1
Это—уравнения Лагранжа первого рода. Задача становится опре-
определенной, так как ЗЛ/ уравнений A5) совместно с r-\-rr уравне-
уравнениями связей D), E) содержат такое же число неизвестных:
Ч W» \> • • •• \'> К* • • •• К"
В последующем придется неоднократно возвращаться к доказан-
доказанной в этом пункте теореме: достаточным условием обращения в нуль
дифференциального выражения
п
2*,8*,. F.1.17)
в котором вариации bxs связаны линейными соотношениями
п
2 яА = о (* = 1 г) F.1.18)
является представимость функций Xs через г независимых множи-
множителей Лагранжа \ \ в виде
г
*, = 2 h"k* E=1 «). F.1.19)
k=\
Обратно, если выражение A7) равно нулю, то всегда можно вы-
выбрать г коэффициентов \k так, чтобы функции Л^ были представимы
линейными соотношениями A9).
252 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. 6
6.2. Идеальные связи
Связи — голономные и неголономные,—удовлетворяющие требо-
требованию обращения в нуль элементарной работы сил их реакций на
любом виртуальном перемещении точек системы, называются идеаль-
идеальными связями или связями без трения.
Связи, обеспечиваемые контактом гладких поверхностей, связи,
сохраняющие неизменность расстояний точек системы и т. п., являются
идеальными. Например, реакциями связей в абсолютно твердом теле
являются внутренние силы взаимодействия его частиц, принуждаю-
принуждающие сохранять неизменность расстояний между последними. По прин-
принципу равенства действия и противодействия главный вектор и главный
момент внутренних сил равны нулю, вследствие чего по формуле
E.2.5) обращается в нуль и элементарная работа их, т. е. связи
в абсолютно твердом теле идеальные. Реакция R гладкой поверхности
(неподвижной или движущейся) на движущееся по ней тело на-
направлена по нормали к поверхности и, следовательно, перпен-
перпендикулярна виртуальному перемещению Ьг точки соприкасания тела
с поверхностью; элементарная работа R • Ьг равна нулю — гладкая
поверхность представляет идеальную связь. Абсолютно шероховатая
поверхность, обеспечивающая качение по ней тела без проскальзывания,
дает пример идеальной неголономной связи; в этом случае R • Ьг
обращается в нуль, вследствие обращения в нуль второго множи-
множителя — виртуальное перемещение точки соприкасания тела, катя-
катящегося по шероховатой поверхности, с этой поверхностью равно
нулю. •
Динамика несвободной системы точек, начиная с Даламбера и
Лагранжа, основывается на предположении об идеальности связей.
Причиной этого служит, во-первых, то, что достигаемая точность
достаточна для описания явлений природы и большого числа техни-
технических процессов движения. Во-вторых, это предположение позволяет,
оставаясь на почве основных принципов Ньютона и Даламбера, дать
такую теорию движения материальных тел, в которой необходимость
обращаться к опытным данным ограничивается формулированием за-
законов активных (задаваемых) сил.
Например, учет неидеальности контактных связей, т. е. сил тре-
трения в приспособлениях, реализующих связи, производится путем от-
отнесения этих сил к категории активных. Это сопряжено с необходи-
необходимостью введения экспериментального закона трения, с помощью
которого устраняется несоответствие числа уравнений механики и
числа неизвестных в них при неидеальных связях.
Во всем дальнейшем, когда не оговорено противное, прини-
принимается предположение об идеальности связей, т. е. об обращении
в нуль суммы элементарных работ их реакций на любом виртуальном
6.3] ОБЩЕЕ УР-НИЕ ДИНАМИКИ И ЦЕНТРАЛЬНОЕ УР-НИЕ ЛАГРАНЖА 253
перемещении:
3N N
2 /?v8?v = S Rrbrt = 0. F.2.1)
v=l / = 1
Заменив здесь brt выражениями A.6.7) или A.6.14) через вариа-
вариации обобщенных координат или вариации квазикоординат, получим
^ £ = 0. F.2.2)
5=1 / = 1 5=1 i=\
По определению E.1.3) и E.1.7) внутренние суммы в этих ра-
равенствах представляют обобщенные силы реакций связей:
i
/ = 1 i = 1
и равенства B) принимают вид
2 Q!bqs = 0, 2 P*sЬка = 0. F.2.4)
5=1 5=1
Если, в частности, qv ..., qn—независимые обобщенные коорди-
координаты и неголономные связи отсутствуют, то вариации bqs (а также
вариации &тг5 квазикоординат) независимы; тогда следствием D)
является обращение в нуль всех обобщенных реакций связей
Q* = 0 или Р* = 0 E=1 п). F.2.5)
6.3. Общее уравнение динамики и центральное уравнение
Лагранжа
Исходим из дифференциальных уравнений движения системы
материальных точек A.1)
(/=1,...,Л0. F.3.1)
Общее уравнение динамики представляет соотношение, получающееся
при исключении реакций связей из этих уравнений. Благодаря этому
задача о нахождении движений под действием активных сил от-
отделяется от задачи определения реакций (по крайней мере, в случае
голономных связей). Последняя может рассматриваться после того, как
решена первая.
Исключение реакций связей достигается весьма просто, когда
связи—идеальные. Достаточно, вспомнив определение B.1) идеаль-
идеальности связей, скалярно умножить каждое из уравнений A) на brt
254 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. 6
и, сложив произведения, получить соотношение
N N
2 miwi • 8г, = 2 Ff be F.3.2)
которое Лагранж назвал общим уравнением динамики. Вывод его
основывался на принципе освобождаемое™, позволившем составить
уравнения A), и на определении идеальных связей. Никаких ограни-
ограничений на кинематические свойства связей не было наложено. Поэтому
общее уравнение динамики применимо как к позиционным, так и
к неголономным идеальным связям.
Согласно A.4.5) при наличии т избыточных координат
и общее уравнение динамики приводится к виду
/V п + т N п+т
/=1 S=\ /el 5=
или, вспомнив определение обобщенной силы,
п+т IN
Вариации bqs связаны m-\-rf соотношениями
О' k Ъ _ /Л / L. 1
s = l
n+ m
2 aksbgs = O (ft=l. .... г'). F.3.6)
*=i
получающимися как следствие т конечных и гг неголономных усло-
условий A.4.8).
Использовав теорему, сформулированную в п. 6.1, придем к си-
системе п-\-т уравнений
JV - т
/1 *1 й1
F.3.7)
содержащих всего п-\-2т-\-г' неизвестных, т. е. n-j-m обобщен-
обобщенных координат, т множителей конечных и rf неголономных связей.
6 3] ОБЩЕЕ УР-НИЕ ДИНАМИКИ И ЦЕНТРАЛЬНОЕ УР-НИЕ ЛАГРАНЖА 255
Число неизвестных соответствует числу уравнений, так как к G) сле-
следует еще присоединить т-\-гг уравнений A.4.8).
Напомним, что в равенствах D) и G) под Qs подразумеваются
обобщенные силы, отнесенные к обобщенным координатам qv ...
Qn+m> B числе которых имеется т избыточных.
В случае голономной системы и при отсутствии избыточных
координат уравнения G) упрощаются и приобретают вид
N
Сумму
т
W dFk
можно в уравнении G) откинуть даже и в том случае, когда в числе
введенных в рассмотрение обобщенных координат имеются избыточ-
избыточные, так как она может быть включена в состав слагаемых
Поэтому в дальнейшем число обобщенных координат можно обо-
обозначать через я, независимо от того, являются ли они независимыми
или связаны конечными соотношениями.
Остается дать представление левых частей равенств G) или (8)
через обобщенные координаты. Это будет сделано ниже, а здесь мы
обратимся к другой форме записи общего уравнения динамики B),
называемой центральным уравнением Лагранжа.
Имеем
d
ttl:Wj • ОГ, = ntfV: • ОГ, = -jr ttl/V, • Oft — ntiV} • (off) =
= —rr tUiVi • bft — tttiVi • Ъф, -\-tttiVi • \Ь*оi — (bf,) 1. Г6.3.9)
dt l l * l l l ' t t l t \ is i \ /
Последнее слагаемое исчезает, если применить правило переставимо-
сти A.7.10) действий варьирования и дифференцирования. Заметив
еще, что
приведем общее уравнение динамики B) к виду
W Л N
256 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. 6
ИЛИ
^^ i F.3.10)
где Т—кинетическая энергия, ЬТ—ее вариация, b'W — элементарная
работа активных сил. Это соотношение представляет центральное
уравнение Лагранжа.
Отбросив правило переставимости A.7.5), получили бы вместо A0)
соотношение
& • {{Ьг'у - ^ь F-3-1 {)
которое, следуя Гамелю, назовем общим центральным уравнением.
6.4. Преобразование центрального уравнения Лагранжа
Выражение
/V
2ад-^- F.4.1)
можно трактовать, согласно E.1.1), как «элементарную работу векто-
векторов количеств движения mtvt (импульсов)» на виртуальных переме-
перемещениях brt точек системы. Поэтому, в точном соответствии с тем,
как вводились обобщенные силы Qs, можно определить обобщенные
импульсы ps. Они выражаются через импульсы mivl как обобщенные
силы Qs через силы Fiy т. е. по формуле E.1.3):
N
При этом соотношению E.1.4) сопоставляется равенство
N п
^ mivi ■ brt = ^ ps bqs. F.4.3)
i=l s=l
Воспользовавшись преобразованием A.3.5), можно переписать B)
в виде
N IV N
или же
0<Js
5.4] ПРЕОБРАЗОВАНИЕ ЦЕНТРАЛЬНОГО УРАВНЕНИЯ ЛАГРАНЖА 257
Обобщенный импульс равен производной кинетической энергии по
обобщенной скорости. Такое определение было принято ранее —
см. формулу D.2.1).
Запись центрального уравнения Лагранжа C.10) теперь приво-
приводится к виду
^8?.- F-4.6)
5 = 1 5 = 1
Если силы потенциальны, то по E.3.9)
8Г-+- 8'ИР = ЬТ— 8П = 8 (Г— П). F.4.7)
Функцию обобщенных скоростей, обобщенных координат и времени,
равную разности кинетической и потенциальной энергий, называют
кинетическим потенциалом или функцией Лагранжа: она обозна-
обозначается через L
L{qv .... qn. qv .... qn\ 9=Г—П. F.4.8)
Время t может входить в функцию Лагранжа как через кинети-
кинетическую энергию Т, так и через обобщенную потенциальную энер-
энергию П.
Итак*, в случае потенциальных сил центральное уравнение Лагранжа
приводится к виду
5=1
Отбрасывая правило переставимости «db = bd», следует правые части
выражений F) или (9) дополнить слагаемым
N N п
Ы\ 5 =
N
S
5*1
Здесь использованы формулы A.7.3) и B). Общее центральное урав-
уравнение представится теперь в виде
п п п
5 = 1
17 Зак. 2072. А. И. Лурье
258
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. б
В последующем понадобится выразить это уравнение через квази-
квазискорости и вариации квазикоординат. Повторив в точности преобра-
преобразование E.1.6), получим
N
2 rnpi -80 = 2 PsЬЯ3 = 2 P*s К-
где p*s связывается с рг равенством, аналогичным E.1.8)
F.4.12)
Величины /?*, т. е. производные кинетической энергии по квазиско-
квазискоростям, будем называть обобщенными импульсами, отнесенными к квази-
квазискоростям. Отметим, например, что в случае твердого тела, имею-
имеющего неподвижную точку,
дТ
—-. = виоу1 -(- 012со2 -(- в13со3 = К?,
дТ
— = в21ш1 4- в22ш2 4- ©зз^з =
_ = е^ш, 4- в32со2 4- ©зз^з =
F.4.14)
как это следует из выражений D.7.4) и D.8.13). Таким образом,
импульсами, отнесенными к проекциям угловой скорости, оказываются
проекции на соответствующие оси главного момента количеств дви-
движения твердого тела относительно неподвижной точки. Это служит
иллюстрацией важности величин /?* в механике.
Соотношения, обратные A3), будут:
г = 1
Поэтому, воспользовавшись формулами A.8.4), имеем
п п п
5=1 /-=1 ' S = l
п ( п п п 1
= 2 tf ((Ч)'-Ч-2 2 т?лЧ -jSej8«г J.
F-4.15)
F-4-»в)
6.5] РАВНОВЕСИЕ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 269
и общее центральное уравнение A1) принимает вид
5=sl 5 = 1
Если активные силы потенциальны, то два слагаемых в правой части
можно объединить
п
bT+'%PsbTzs = b(T—n)=bL. F.4.18)
Ssl
Заметим еще, что, поскольку потенциальная энергия не зависит
от обобщенных скоростей, можно записать выражения E) и A3)
также в виде
6.5. Равновесие системы материальных точек
В случае равновесия обращаются в нуль ускорения wt всех точек
материальной системы по отношению к инерциальным осям Oxyz.
Применяя принцип освобождаемости, вместо A.1) получим
Fi + Ri = Q ('=1 АО- F.5.1)
Отсюда, сославшись на A.15), можно записать 3N уравнений
равновесия
Конечно, предполагая наличие равновесия, надо принять здесь, что
уравнения связей A.4) и A.5) не содержат явно времени и, кроме
того, в уравнениях A.5) отсутствуют свободные члены gk — в про-
противном случае было бы невозможно одновременное обращение в нуль
всех скоростей.
Считая задаваемые силы известными, имеем SN уравнений равно-
равновесия, содержащих ЗЛ/' —|— г —f— r' неизвестных: 3jV декартовых коор-
координат точек системы и г-\-г' множителей связей. К числу уравнений,
которыми мы располагаем, надо отнести еще г уравнений A.4) ко-
конечных связей; уравнения же неголономных связей A.5) при равно-
ресии, когда все £v обращаются в нуль, удовлетворяются тождественно.
Задача о равновесии системы, подчиненной идеальным связям, является
17*
260 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. 6
определенной только при отсутствии неголономных связей; она теряет
определенность при наличии таких связей: г1 из 3N -\-r -\-rr величин
остаются неопределенными.
Определяя положение системы п-\~т обобщенными" координатами,
связанными т уравнениями конечных связей
F* (?i qn+J = 0 (* = 1 "О F.5.3)
и гг уравнениями неголономных связей
2>aksqs = 0 (k=l r'), F.5.4)
получим, полагая в левых частях уравнений C.7) ускорения wt рав-
равными нулю, п -\-т уравнений равновесия
Они выражают обращение в нуль сумм задаваемых обобщенных сил
и обобщенных сил реакций связей
Задача является определенной при отсутствии неголономных связей.
Заметим, что первая сумма в правой части выражения F) может быть
записана в виде
так как, вследствие уравнений C), слагаемое
т
отпадает.
Рассмотрим случай потенциальных сил; тогда
где П — потенциальная энергия системы. Поэтому, учитывая G),
можно уравнения равновесия при отсутствии неголономных связей
записать также в виде
-а
\kFk]=:Q (s=\ /г). F.5.9)
6.5] РАВНОВЕСИЕ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 261
Это — уравнения относительного экстремума функции
— U(gv ..., qn+m)
при наличии т добавочных условий C).
При отсутствии избыточных координат и неголономных связей
уравнения равновесия
Qs = 0 0= 1, ..., п) F.5.10)
выражают условия обращения в нуль всех обобщенных сил; в случае
потенциальных сил они превращаются в уравнения
определяющие экстремумы (стационарные значения) потенциальной
энергии системы. В положении равновесия системы, подчиненной
идеальным связям и находящейся под действием только потенциаль-
потенциальных сил, потенциальная энергия системы имеет стационарное значение;
это значит, что при отклонении системы из положения равновесия
<7р ..., фп в бесконечно близкое положение
приращение потенциальной энергии
ДП = П {$ 4-4 #4- 4.) - П (q\, .... <7°п) F.5.12)
будет величиной порядка не ниже второго относительно вариаций bqs
обобщенных координат. Сказанное следует из того, что в разложении
величины АН в ряд по степеням oqs слагаемые первого порядка
вследствие уравнений A1) отпадут.
Характер равновесия системы при действии потенциальных сил
определяется характером экстремума функции П. Равновесие может
быть устойчивым или неустойчивым. Согласно фундаментальной тео-
теореме Лагранжа — Дирихле, оно устойчиво, если потенциальная энер-
энергия в положении равновесия имеет минимум. Обратные предложения
о неустойчивости равновесия, если экстремум не есть минимум, дока-
доказаны с почти исчерпывающей полнотой А. М. Ляпуновым и Н. Г. Че-
таевым. Изложение этих вопросов и точное определение понятия
устойчивости выходит за рамки этой книги. Оно является предметом
специальных сочинений по теории устойчивости движения *).
Мы сформулировали задачу о равновесии, пользуясь принципом
освобождаемости при отсутствии ускорений точек системы (wt = 0)
и ссылаясь на следствия из общего уравнения динамики C.2). Исходя
*) Н. Г. Ч е т а е в, Устойчивость движения, Гостехиздат, 1955;
И. Г. М а л к и н, Теория устойчивости движения, Гостехиздат, 1952 г.
262 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. $
непосредственно из этого уравнения и полагая в нем wt = 0, придем
к принципу виртуальных перемещений:
N
2/7..^ = О F.5.13)
— сумма работ активных сил на виртуальных перемещениях точек
системы, подчиненной идеальным связям, из рассматриваемого поло-
положения равновесия равна нулю (напомним, что мы рассматриваем
только удерживающие связи).
Если в числе активных сил имеются потенциальные, то принцип
возможных перемещений записывается в виде
N
— 8П + 2 Pi • К = 0. F.5.14)
Вернемся к уравнениям F) в предположении отсутствия неголо-
номных связей. Выберем обобщенные координаты так, чтобы уравне-
уравнения связей приобрели наиболее простую форму:
Л = ^+1-9°я+1-° Fm = 4n+m-q°n+m = 0, F.5.15)
где q°n k — постоянные значения избыточных координат. Тогда
( ° + ЬФ s,
dqs -*n+k,s
и уравнения равновесия примут вид
т
или подробнее
Qx = 0. ..., Qrt = 0, X1 = —дя+1. .... lm = -Qn+m. F.5.16)
Пусть, например, рассматривается равновесие точки на поверхности.
Вводя пространственные криволинейные координаты ql, q2y q'6, такие,
что q3 = ql соответствует рассматриваемой поверхности, вычислим,
предполагая точку свободной, элементарную работу приложенной к ней
активной силы F. В обозначении (П. 2.7.2) получим
где rs — основные векторы поверхности. Уравнения равновесия A4)
дадут
/7.^ = 0, /?.*-2 = 0, \X = — F.rb.
Эти уравнения имеют место в точках поверхности, т. е. при q3 = q^
Из представления вектора активной силы через его ковариантные со-
составляющие
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 263
следует, что равновесие может иметь место, если активная сила имеет
направление г3, нормальное поверхности. Поскольку F= — /?, где
R—реакция поверхности, заключаем, что множитель связи при сде-
сделанном выборе координат равен ковариантной составляющей /?3
реакции.
6.6. Примеры на уравнения равновесия и определение
реакций связей
Г. Трехстержневая система. Рассмотрим систему трех
соединенных последовательно друг с другом с помощью шарниров А
и В тяжелых стержней ОЛ, АВ, ВС; шарнир О неподвижен и си-
система удерживается в равновесии в вертикальной плоскости Оху
с помощью трех горизонтальных нитей, причем углы стержней с нисхо-
нисходящей вертикалью имеют значения
cpj, ср2. ?з (Рис- 54). Требуется опре-
определить натяжения 7\, T2, Т3 нитей.
Активными силами являются веса
стержней Gv O2, О3. Потенциальная
энергия равна
П = — (G1xl 4~ G2x2 4~ ^з-Гз)»
где хг, х2, хъ — координаты х цен-
центров тяжести стержней:
х2 = /j cos cpj -\- s2 cos cp2>
xs = lx cos cpj -f- /2 cos cp2 + s3 cos cp3.
Через /j, /2, /3 обозначены длины
стержней; sY, s2, s3—расстояния их Рис.54,
центров тяжести от шарниров О, А,
В; cpj, cp2, ср3—углы стержней с нисходящей вертикалью при мыслен-
мысленном освобождении системы от связей, налагаемых наличием нитей.
Этих связей три и уравнения их можно записать в форме E.15):
Получаем
П = — (О151 4- 02*1 + °3/i) cos ?i — (°2^2 + G3/2) cos cp2 — G3s3 cos cp3
и по E.16) находим множители связей
X3 = G3S3 Sil
V | F.6.
1)
264
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
Таковы множители связей — обобщенные реакции связей. Но это
отнюдь не искомые натяжения нитей. Чтобы найти последние, не
прибегая к общим формулам, выразим, что элементарная работа этих
сил при виртуальном перемещении точек приложения их Л, В, С из
положения равновесия равна элемен-
элементарной работе обобщенных реакций:
циях 8с
равнять
Находим
Замечая, что
F.6.2)
/2 cos cp2 8cp2,
/2 cos ср2 &92 4-
Ьув = /j cos cpj
Ьус = 1г cos <p,
^ис# ^' и приравнивая в уравнении B) коэф-
коэффициенты при независимых вариа-
вариаполучим систему трех уравнений (в них <р5 надо при-
при77
= (О2 |-Ь О3) tg ср°-Оз^-tg ср°,
s3
F.6.3)
Проверить эти выражения можно, убедившись, что сумма моментов
всех сил веса Gt и натяжений нитей Tt относительно неподвижного
шарнира О равна нулю.
2°. Равновесие тяжелого стержня, скользящего
своими концами по гладкой поверхности. Стержень
веса О и длины / может скользить своими концами А, В по внут-
внутренней поверхности чаши. Направляя ось Oz по восходящей верти-
вертикали, представим эту поверхность уравнением
* = /(*. у). F.6.4)
Требуется определить положение равновесия стержня и реакции
стенок чаши (рис. 55).
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 265
Обозначим через xv yv zx и х2> у2, z2 координаты концов стержня.
Три уравнения связей будут:
F, = (х2 -
F.6.5)
■ ()J2 — 3>lJ + (*2 — Z\f — Р = °- j
Через р, q будем обозначать частные производные функции f (х, у)
по х и у\ индексы 1 и 2 указывают, что эти величины отнесены
к точкам А и В. В соответствии со сказанным в п. 1.4 следует
рассмотреть матрицу
-/?, —qx 10 0 0
0 0 0 —p2—q2 1
В ней можно выделить квадратную 3 X 3 субматрицу
~qx 1 0
0 0 — р2
с определителем, который, как видно будет далее, отличен от нуля.
Поэтому уравнения E) могут быть разрешены относительно трех
из шести введенных величин.
Обозначим через т единичный вектор нормали поверхности D),
направленный в ту сторону, куда z возрастает, черев а, [), *[ — коси-
косинусы его углов с осями координат. Тогда
а = — . _Z
. F.6.6)
Единичный вектор, направленный по стержню от Л к Б, обозначим
через е\ ev e2, ег—косинусы его углов с координатными осями:
х2 —
* —Уч — У*
I
F.6.7)
Центр тяжести стержня считаем расположенным в его середине;
поэтому потенциальная энергия силы тяжести равна
При обозначениях F) и G) шесть уравнений равновесия E.9)
будут
~ G,
F.6.8)
266
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
Решив их относительно Хт, Х^ Х3, получим
2
1
*lT[2 — *3«2
X, = "ТтГ 0^ = 7Г О^г
1 ""' 1
Два последних равенства приводятся к виду
6\ 0L\ &2
F.6.9)
F.6.10)
F.6.11)
При этом з^довлетворяются также два из равенств (9). Соотноше-
Соотношения A1) выражают, что векторы нормалей mv m2 к поверхности D)
расположены в вертикальной плоскости, проходящей через стержень.
Действительно, обозначая через k единичный вектор восходящей
вертикали и через п вектор нормали к указанной плоскости, доста-
достаточно убедиться, что вектор п перпендикулярен к т1 и т2. Имеем
п =
и, далее,
п - mi =
1
I e a » I I ^ А » I
что и требовалось.
Знаменатели формул (9) и A0) пропорциональны проекциям век-
вектора п на оси Ох и Оу. Действительно, по сказанному,
е X пц
\exmt\
и, следовательно,
\ехпц\
Вектор п параллелен плоскости Оху, поэтому хотя бы одно из этих
выражений отлично от нуля; заметим еще, что определитель упомя-
упомянутой выше субматрицы как раз пропорционален пг.
Еще одно соотношение, являющееся следствием формул (9),
имеет вид:
Ь__ , J[2__. 2^1
а, ~" а2 ех
или i + ^L^2—. F.6.12)
Pi P2 #2
Смысл этого соотношения выясняется ниже.
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 267
Таким образом, получены три уравнения A1) и A2); положения
равновесия существуют, если эти уравнения совместно с уравнениями
связей E) имеют решения.
Переходим к определению реакций. Равнодействующую реакций Ri9
приложенных к каждому из концов Л и В стержня, можно опре-
определить по формуле A.9), которая в нашем случае дает
#i = \ gradj Fx 4- Х3 gradj F3, R2 = h, grad2 F2 + X3 grad2 Fz,
так как Fl зависит только от xv yv zv a F2 от x2, y2, z2. Первые
слагаемые этих выражений представляют реакции стенки чаши Nv М2,
вторые — реакции стержня Тх = —Т2. Получаем для /==1, 2
Nix = 1 Geiai , A^<v = i °e2h Q , Nb = K F.6.13)
и, далее,
Т2 = —Тх=*Ще. F.6.14)
Учитывая условия A1) и A2), легко проверить, что силы Л^, N2,
G находятся в равновесии.
3°. Стержень в эллиптической чаше. Рассмотрим
частный случай, когда поверхность чаши представляет эллипсоид
вращения вокруг оси Ог*).
Беря начало координат в вершине эллипсоида, имеем
Z = (
Г~ Д? + у2
у 1 JJL.
В случае поверхности вращения вертикальную плоскость, в кото-
которой при равновесии располагается палочка, можно принять за пло-
плоскость О£х. В приведенных формулах тогда надо положить ух = у2 =* 0.
Для определения неизвестных xv x2 получим уравнения
cc j (Х2 X2 — X\
причем
Заметив, что
(х2 —
СХ
*) Эта задача под наименованием «задача Н. Д. Брашмана» рассмотрена
в университетском курсе Н. Е. Жуковского «Собрание сочинений. Лекции»
( 6 4548 1939)
урстетсо курсе Н
(вып. 6, стр. 45—48, 1939).
268
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
и полагая х = a sin и, приведем эти уравнения к виду
~ь~ „ I ^~ ,. _ О С2 COS W2— COS И,
i u2 — sin i
/2
(sin u2 — sin иjJ -| y (cos u2 — cos uxJ — —^.
Если ввести в рассмотрение полусумму и полуразность углов и2, аг
а =
то эти соотношения можно представить в форме
sin a (cos2 р
2 р —
/2
cos2 а) = 0, sin2 р A — ^2 cos2 а) = ~ ,
причем
Пусть эллипсоид вращения — вытянутый (с > а, 0 < е2 < 1). Поло-
Положение равновесия а = 0 невозможно, так как а существенно положи-
положительно; возможно положение равновесия
а = тс, #2-|-tfj = 2пг. Это, как видно из
рис. 56, соответствует горизонтальному
положению равновесия АХВХ\ угол р и
положение палочки определится условием
и задача имеет решение (равновесие воз-
возможно) при
А2В2
/ < 2a у 1 — Л
что и очевидно.
Второе положение равновесия
имеет место при сое2 р = е2 cos2 а, тогда
определится условием l — 2a sin1 p. Можно
доказать, что палочка при этом должна
проходить через фокус эллипса *).
Если эллипсоид вращения сплюснут (с < а, е2 < 0), то горизон-
горизонтальное положение равновесия (a«=ir) — единственно возможное.
4°. Равновесие твердого тела в поле центральной
силы. Потенциальная энергия тела дается выражением E.5.6);
поскольку мы рассматриваем равновесие, то в этой формуле г = const;
надо найти, nptf каких значениях величин, определяющих ориентацию
Рис. 56.
*) Простое геометрическое доказательство и построение положения
равновесия в этом случае дается в «Лекциях» Н. Е. Жуковского.
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 269
триэдра центральных осей Gxyz (рис. 37) относительно осей неиз-
неизменного направления М%т£*у потенциальная энергия П имеет стацио-
стационарные значения. Эти величины — эйлеровы углы О, ф, ср входят
в выражение П через посредство отношений -i, X, JL 9 равных
косинусам а, C, f углов, образуемых вектором MG с осями си-
системы М $7]С.
Согласно E.11) искомые положения триэдра Gxyz определяются
условиями
Обращаясь к формулам E.2.18), это можно записать в виде
m1 cos ср — m2 sin ср = О,
(mx sincp-f-/n2coscp) sin ft -f-m3cos0 = 0,
m?j = 0,
причем mv m2, тг определяются формулами E.5.10). Таким образом,
имеются возможности:
а) тх =0, /и2 = 0, т3 = 0;
б) /я3 = 0, sin^ = 0, /njCoscp — /n2sincp = 0.
Рассмотрим случай а). Он реализуется при условиях
Два из трех косинусов а, C, ? должны быть нулями, чтобы удовле-
удовлетворить всем трем равенствам. Это значит, что в положениях равно-
равновесия одна из главных осей инерции должна быть направлена
вдоль MG. Например, если а = (В = О, |-f|=l, то х = у = 0 и
в системе осей Gxyz отлична от нуля только координата z точки М\
вдоль MG направлена ось Gz эллипсоида инерции.
В случае б) направим ось М^ по направлению MG; тогда
^а= t]G = 0 в формулах E.5.11) и, поскольку sin0 = 0, получаем
т. е. возвращаемся к одному из рассмотренных случаев.
Эти же условия равновесия можно получить, не прибегая к вычи-
вычислению обобщенных сил, а разыскивая экстремумы потенциальной
энергии. По E.5.6) она лишь аддитивной постоянной и несуществен-
несущественным положительным множителем отличается от квадратичной формы
l-£l-l)T2]. F.6.15)
270
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
Здесь приняты обозначения D.6.8) в предположении D.6.6) — наи-
наименьшая ось эллипсоида инерции направлена по оси Gx, средняя —
по оси Gyr наибольшая — по оси Gz.
Вследствие неравенств п. 4.6, которым удовлетворяют е1 и s2,
2 — ej — е2 > 0, 2е2 — ег — 1 < 0.
Что касается коэффициента при р2, то он может быть как положи-
положительным, та*, и отрицательным. Оба случая реализуемы, так как
прямая' L (рис. 57)
2ег — е2 — 1 = 0
пересекает область возможных значений параметров Sj, s2 и разбивает
ее на две зоны; в зоне под L указанный коэффициент положителен,
над L — отрицателен.
£г Места экстремумов квадратичной формы F%
когда а, р, f связаны условием
Ф = а2 -4- р2 -|- -у2 — 1=0.
_ ХФ) = 0,
разыскиваются по условиям
Рис. 57.
JL (Р _ Хф) = 0
а = 0, BSJ —82—1 —X) р = 0,
— Sj—1—Х)Т = 0. F.6.16)
не обращаются одновременно в нуль; поэтому возможны
X = 2е2 — гх — 1 < 0,
Но а, р, у
три случая:
а) а = р = 0,
б) р = Т = 0, Х = 2 — ег — 82>0,
в) 7 = а = О, X = 2sj — s2 — 1 ^ 0.
Этим определены положения равновесия тела. Вместе с тем известно,
что найденные значения X равны экстремальным значениям F. Дей-
Действительно, умножив уравнения A6) соответственно на а, C, f и
сложив произведения, получим
Таким образом, случаю а) соответствует минимальное, а случаю б) —
максимальное значение потенциальной энергии. По теореме Лагранжа —
Дирихле первому из них отвечает устойчивое равновесие — вдоль MG
легла «длинная» ось эллипсоида инерции; случаю б) — расположению
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 271
по MG «короткой» оси — отвечает, согласно теореме Ляпунова,
неустойчивое равновесие. Характер равновесия в случае в) зависит
от соотношения между величинами моментов инерции.
5°. Равновесие твердого тела, подвешенного на
упругих стержнях. Твердое тело удерживается в покое систе-
системой упругих, невесомых стержней, присоединенных к телу сфери-
сферическими шарнирами в точках М1% ..., Мт. Другие концы стержней
таким же образом закреплены в неподвижных точках Sv ..., Sm,
Определить, как сместится тело из этого начального состояния при
нагружении его силами, постепенно и весьма медленно нарастающими
от нуля до значений Fv ..., Fn. Иными словами, предполагается,
что переход из начального состояния (когда силы Ft отсутствуют)
в конечное осуществляется через непрерывную последовательность
равновесных конфигураций. В начальном состоянии стержни не
напряжены.
Пусть Oxyz — система осей, связанных с телом, V — главный
вектор, т — главный момент относительно полюса О системы сил
Fv ..., Fn\ через rk обозначаются вектор-радиусы OMk шарни-
шарниров Mk. Аналогичная задача для системы сходящихся стержней рас-
рассматривалась в п. 5.8. В отличие от нее теперь следует учесть при
вычислении потенциальной энергии стержней, что вследствие поворота
тела векторы перемещений uk шарниров Мк отличны друг от друга
и равны
Мы ограничиваемся рассмотрением лишь малых поворотов и переме-
перемещений. Тогда с точностью до первых степеней этих величин удли-
удлинение k-vo стержня будет
/*=«*• < = «о • < + в • (rk X е») F.6.17)
и далее
Потенциальная энергия упругих стержней представится в виде
-*«„• % сА«х *■>)■<>}• F.6Л8)
}• F.6Л
J
272
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
Это—квадратичная форма проекций векторов и0, 0, безразлично,
при принятой точности, на какие оси — связанные с телом или непо-
неподвижные. Через ck обозначены жесткости стержней на растяжение.
Как сумма положительных слагаемых -~ ck/l, потенциальная энер-
энергия представляет знакоопределенную квадратичную форму. Критерии
Сильвестра всегда будут выполнены. Поэтому положение равновесия
при отсутствии сил Fs, согласно теореме Лагранжа — Дирихле,
устойчиво.
Согласно E.14) при равновесии имеет место равенство
_ ail -f- V. Ьи0 -+- т° • ЬЬ = 0.
Поэтому получим
тп
2
m
:-2'
X гк) ■ О -, V,
F.6.19)
Эти уравнения равновесия можно было, конечно, непосредственно
составить, не вычисляя потенциальной энергии, а выражая \еловия
обращения в нуль главного вектора и главного момента относительно
полюса О системы сил —Tv ..., —Тт, Fr . ..,/7л, приложенных
т
к телу. Достаточно заметить, что реакция
и ее момент относительно полюса О равны
Tk стержня на тело
и заменить fk его выражением A7).
Уравнения A9) можно записать в матричном виде
Ql"°h
где А, В, С обозначают матрицы
е
—
А В |
В1 С |
«о
0
__
V
пг°
W* ■
B=
Определение столбцов и0, 6 сводится к решению системы шести
линейных уравнений или, что то же самое, к обращению матрицы Q.
Обратная матрица существует, так как определитель |Q| отличен
от нуля — он положителен по первому из критериев Сильвестра.
6°. Случай первоначально напряженной системы*).
Рассматривается, как в предыдущем пункте, тело, подвешенное на
*) См/Г. И. Николенко, Колебания первоначально напряженных
упругих систем. Инженерный сборник, 11, 1952, стр. 79—94.
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 273
упругих стержнях и находящееся в равновесии под действием упру-
упругих реакций этих стержней и некоторых заданных сил; их главный
вектор и главный момент относительно полюса О обозначаются Vo
и т^. Стержни приобрели из своею натурального состояния удли-
удлинения f)k. Рассматривается переход из этой равновесной конфигура-
конфигурации 50 в конфигурацию S, получающуюся
при новом нагружении тела системой сил,
задаваемой главным вектором V и главным
моментом т° (относительно того же по-
полюса О). Иначе говоря, разыскиваются век-
вектор и{] перемещения полюса О и вектор по-
поворота 6, когда тело переходит в новое
равновесное положение из старого.
Потенциальная энергия k-го стержня
в конфигурации S, как указывалось в п. 5.8,
равна
}
Рис. 58.
Поэтому удлинение fk должно быть опре-
определено с точностью до величин второго по-
порядка; считая вектор поворота 0 малым, сле-
следует теперь учесть в формуле Родрига C.1.11) для перемещения пово-
поворота точки М^ лишь слагаемые второй степени относительно 6.
Тогда получим
»* = яо + ех»-4+-2-®х (ох *■*) = *;
По рис. 58 получаем
Ч = (<°* + hf = Ч2 + «; + Ч< • »*■
Решение этого уравнения ищем в виде
в котором первое слагаемое представляет выражение A7), a ek по-
поправку к нему в членах второго порядка. Подстановка дает
Выражение* §ft
равным
| ek X F X rk) |2-2 (a0 X
ft, вычисленное с указанной точностью, оказывается
^ X Ф X rk)\ -+-1\ (e'i X 6) • (в X rk)\.
F.6.20)
18 Зак. 2072. А. И. Лурье
274 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА (ГЛ. 6
Будем считать, что приложенные к телу в конфигурации So силы
Fy .... F°n сохраняют неизменную величину и направление при
переходе в конфигурацию 5. Тогда изменение потенциальной энергии
этой системы сил, вычисленное с точностью до малых величин вто-
второго порядка включительно, по E.3.23) будет равно
причем тензор Q0 определяется по E.3.24).
В выражении потенциальной энергии стержневой системы
mm m
п=т
первое слагаемое дается формулой A8), так как наличие добавочного
члена в выражении B) для fk может дать лишь поправку в членах
третьего порядка в /|. Второе слагаемое обозначается АП1. Третье
слагаемое представляет несущественную аддитивную постоянную (зна-
(значение потенциальной энергии в конфигурации 50) и может быть
отброшено. Получаем
Поскольку конфигурация 50 — равновесная, вариация потенциаль-
потенциальной энергии при и0 = 0 и 6 = 0 должна быть нулем. Эта вариация
равна
и обращение ее в нуль (вследствие произвольности 8»0, S6) приводит
к уравнениям
/A2o ^A*<
5=1 5=1
выражающим, конечно, что в конфигурации SQ реакции первоначально
напряженных стержней уравновешиваются с приложенными силами.
Следствием уравнений B2) является обращение в нуль линейных
слагаемых в выражении потенциальной энергии. Теперь, объединяя A8)
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 275
с квадратичными слагаемыми в формуле B1), приведем выражение
потенциальной энергии к виду
П=±[и'0(А + А1)и0-{-2и'0(В-\-В1)Ъ-\-9'(С-\-С1)В]. F.6.23)
где выражения матриц Л, В, С приведены выше, а матрицы Av Bv
Cj определяются выражениями
= V Ck]k (E c\c
С, = -
1 J/g^ \ К К К К /•
F.6.24)
Напоминаем, что rk обозначают вектор-радиусы шарниров в кото-
которых стержни соединены с телом, r°k — вектор-радиусы точек,
приложения сил F® в равновесной конфигурации 50; е\ — единичные
векторы SkMQk стержней в этой конфигурации, /^ — длины этих
стержней; знаком' rk обозначается кососимметричная 3X3 матрица,
сопоставляемая вектору rk по правилу (П. 1.2.3); а и а/ — столбец
и строка проекций вектора а.
Столбцы проекций вектора перемещения и поворота следует
разыскивать из уравнений того же вида, что в предшествующем при-
примере с соответствующей заменой матриц на А-\- Av B-\-Bl и С-\-С1.
Вопрос о знаке квадратичной формы B3), представляющей сумму
слагаемых
не может быть решен заранее, как это было при первоначально не-
ненапряженной системе стержней. Критерии Сильвестра для матрицы
Ах
F.6.25)
для одних значений начальных удлинений bk будут удовлетворены,
а для других — нарушены. Равновесная конфигурация SQ в первом
случае окажется устойчивой, во втором — неустойчивой.
18*
276 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. б
Ограничимся рассмотрением сочетания параметров, удовлетворяю-
удовлетворяющих всем критериям Сильвестра, кроме одного — определитель | М \
матрицы М равен нулю. Тогда система уравнений, определяющих
векторы #0, 0, не будет иметь решения при произвольно назначен-
назначенных V и т°\ равновесных конфигураций S, близких к So, не
существует. Известно вместе с тем, что неоднородная система линей-
линейных уравнений с определителем, равным нулю, может им^ть решения
при специальных условиях, налагаемых на правые части (свободные
члены). Если при том один из первых миноров определителя отличен
от нуля, то эти решения определены с точностью до слагаемых,
пропорциональных произвольному параметру с. Таким образом, в нашем
случае мыслимо указать соотношение значений V и т°, которым
соответствует непрерывная серия равновесных конфигураций, про-
пропорциональных произвольному параметру — это то, что можно назвать
безразличным равновесием.
7°. Равновесие при наличии кулонова трения. Твер-
Твердая пластинка сжата по торцам двумя плитами. Линия действия
активной силы F, приложенной к пластинке, расположена (для устра-
устранения перекоса) в средней плоскости пластинки. Рассматривается пре-
предельное равновесие пластинки при учете силы трения, развивающегося
на торцах *). Виртуальное перемещение пластинки задается вектором
Ьг0 виртуального перемещения полюса О системы осей Oxyz и век-
вектором бесконечно малого поворота G = бг/3 вокруг оси Oz% Элемен-
Элементарная работа активной силы F на этом виртуальном перемещении
равна
b
где m°z — момент силы F относительно оси Oz.
Силы трения на элементарной площадке do контакта пластинки
с плитой равны по величине fpdo, где / — коэффициент трения,
р — давление. Направление силы трения противоположно скорости v,
которую приобрела бы рассматриваемая площадка при нарушении
предельного равновесия. Элементарная работа сил трения, распре-
распределенных по двум площадям контакта 5, поэтому представляется
выражением
*) Задача рассматривалась Н. Е. Жуковским в работе «Условие равно-
равновесия твердого тела, опирающегося на неподвижную плоскость некоторой
площадкой и могущего перемещаться вдоль этой плоскости с трением» 1896 г.
(Собрание сочинений, 1, ОНТИ, 1937; стр. 433 — 449). В несколько иной
постановке этот вопрос рассмотрел Мак-Миллан в книге «Динамика твердого
тела» (стр. 141—153), цитированный на стр. 155.
>.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 277
&десь г — вектор-радиус площадки. Введя в рассмотрение вектор-
>адиус гр мгновенного центра скоростей Р, можно представить век-
ор скорости v и его модуль v формулами
* = '>* X (г — rp), v = \ux(r — rp)\.
\h2lk сог, т. е. -\-\ при сог > 0 и —1 при о)^ < 0, обозначается
[ерез s. Тогда
'еперь, записав, что согласно принципу возможных перемещений
[ приравнивая нулю коэффициенты при независимых вариациях Sr0, 02,
[ридем к двум уравнениям
о о
[ричем последнее выражение преобразуется также к виду
f ffp\r — rp\do. F.6.27)
5 I Я I
Замечая, что
ЦГр • (Г - Гр) = Гр X [/3 X (А" - Гр)].
[ принимая во внимание выражение силы F, имеем еще
1усть гг — вектор-радиус точки на линии действия силы F\ тогда
i3mo =» г' X F. нтР = (г' - гр) X F,
де т^ — момент силы F относительно оси, проведенной через мгно-
;енный центр скоростей параллельно Oz. Формула B7) теперь пре-
>бразована к виду
mpz= 2s J J fp | r — rp | do. F.6.28)
5
~1адо еще составить выражения проекций силы F на координатные
)си. Заметив, что
'] ' \Н X (г — гр)] = — (у — ур), «2 • [/3 X (г — rp)J = х — хр,
278 ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА [ГЛ. 6
и заменив модуль разности \г — гр\ его выражением
получим
• — rp\do.
S ' ' 5
Итак, если ввести в рассмотрение функцию
F.6.29)
- ур\2 do, F.6.30)
5
то выражение силы F и ее момента тР можно представить в виде
Fx = eP~> Fv= —s^-» mP = eW(xp, ур). F.6.31)
Предполагая известным закон распределения нормальных давлений
р (х, у) и вычислив ч7(лгр, ур\ можно по C1), задавшись коор-
координатами мгновенного центра скоростей, определить величину, на-
направление и линию действия силы F% приложение которой при на-
нарушении равновесия создает начальное вращение вокруг этого мгно-
мгновенного центра (в направлении, которым следует задаться). Если же
задать величину и направление силы Т7, то из первого и второго
соотношений C1), можно определить хру ур (а также знак uJ) и далее
из третьего соотношения найти, по какой линии действия следует
приложить силу, чтобы начальное вращение осуществлялось вокруг
этого мгновенного центра скоростей. Отметим еще, что, поскольку
ЧГ > 0, тР имеет знак со^.
Найдем, при каком условии начальное перемещение пластинки
будет поступательным; элементарная работа сил трения в общем
случае равна
f
s
и принцип возможных перемещений дает
.,- , „,(._^И3. F.6.32)
5
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 279
Если ввести в рассмотрение центр давлений — точку, положение
которой определяется вектор-радиусом гс, равным
J J fprdo
^(б.б.ЗЗ)
fpdo
то выражение момента m°z представится в виде
z
F.6.34)
Он равен нулю, если сила проходит через центр давления.
Таким образом, начальное поступательное движение в направлении
силы будет иметь место, когда сила имеет максимальную величину,
при которой еще может быть равновесие:
Fm = 2fffpdo, F.6.35)
5
и проходит через центр давления пластинки.
Рассмотрим теперь действие пары сил. Тогда F=0 и по C1)
■^ = 0, -^ = 0, F.6.36)
дхр дур v
г. е. ч7 имеет экстремум, который представляет минимум. Последнее
обнаруживается по знаку второй вариации 82ч7—приращения, кото-
которое получает ч7 при изменении xpt yp в хр-\-Ъхр, ур-\-Ьур:
/
S
j тг [(У — Ур) Ьхр — (х~ хр) ЬУР\2 d0-
s
Величина в квадратных скобках может стать равной нулю при
всех х и у только тогда, когда площадка представляет прямую линию
У — Ур
X — Хр
■ const.
Если исключить этот случай, то &2ч7 > 0, что и требовалось дока-
доказать. Н. Е. Жуковский называет точку (x*pt y*p\ определяемую
условиями C6), полюсом трения. При приложении к телу пары сил,
равной
т? = гч7 (х*р, ур) = еч7т1п, F.6.37)
280
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ СТАТИКА
[ГЛ. 6
начальное вращение происходит вокруг полюса трения. Равновесие
не может иметь места, если абсолютная величина момента пары
превосходит ч7т|П. Поскольку функция ч7 может иметь только мини-
минимумы, то ее минимум — единственный. Возможно существование
только одного полюса трения *).
При равномерном распределении давления по поверхности кон-
контакта функция ч7 записывается в виде
, (b.6.38)
где О — сила, прижимающая плиту, а величина г* была введена
в п. 5.12 при рассмотрении диссипативной функции сил трения. Вы-
Вычисление г* производится по формулам E.12.12) и E.12.13). При
контакте по круговой площадке радиуса а
где R = rp, выражения ф при R <^ а и R^> а даются формулами
E.12.14) и E.12.15), а ее производная ф' по аргументу фор-
формулой E.12.20), в которой надо теперь отбросить множитель /О.
Приводим таблицу значений ф и <]/.
Таблица функций ф(—) и А' (—)
/?
а
0
0,1736
0,3420
0,5000
0,6428
0,7660
0,8660
0,9397
0,9848
0,6667
0,6817
0,7247
0,7897
0,8677
0,9487
1,0227
1,0814
1,1189
у D)
0
0,1730
0,3369
0,4838
0,6076
0,7047
0,7744
0,8188
0,8420
а
1
1,0154
1,0642
1,1547
1,3054
1,5557
2,0000
2,9238
5,7588
оо
1,1318
1,1449
1,1870
1,2669
1,4038
1,6375
2,0631
2,9665
5,7797
оо
--'(-£)
0,8488
0,8550
0,8714
0,8942
0,9199
0,9452
0,9677
0,9851
0,9962
1
Центром давления является, конечно, центр круга О; в нем же
расположен полюс трения. Последнее следует из того, что ф' @) = 0
и ясно по соображениям симметрии. Начальное поступательное дви-
движение будет иметь место при приложении силы величины Fm = f
*) В работе, цитированной на стр. 276, Н. Е. Жуковский, исследуя по-
поверхности \Г = const, получает ряд интересных предложений о свойствах
равновесия тела.
6.6] ПРИМЕРЫ НА УРАВНЕНИЯ РАВНОВЕСИЯ И ОПРЕДЕЛЕНИЕ РЕАКЦИЙ 281
проходящей через центр площадки, а начальное вращение вокруг
центра круга при приложении пары с моментом Fmaty@)=0t667Fma.
В общем случае можно вследствие симметрии считать ось Ох сона-
правленной с силой F% тогда по C1) получим
Поскольку 0<<*/<1, равновесие возможно при F < Fт. Линия
действия силы пересекает ось Оу в точке
а
♦■D).
а.
Н. Е. Жуковский рассмотрел случай соприкасания по двум весьма
малым площадкам.
ГЛАВА 7
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
7.1. Вывод дифференциальных уравнений Лагранжа
второго рода
Дифференциальные уравнения движения в обобщенных коорди-
координатах можно сразу же получить, если воспользоваться центральным
уравнением Лагранжа. Мы дадим вывод в двух предположениях,
считая первый раз, что правило переставимости операций d и 8
не имеет места, и второй раз, что оно соблюдается. В первом слу-
случае, когда db Ф bd, нужно воспользоваться центральным уравнением
в форме F.4.11). Тогда, учитывая, что кинетическая энергия Т
представляет функцию обобщенных координат и скоростей, можно
написать
Имеем также
п п
5=1 5 = 1
и подстановка в F.4.11) дает
п
5 = 1 5 = 1
После сокращения подчеркнутых слагаемых приходим к равенству
п
VI / d дТ дТ
7.1] ВЫВОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЛАГРАНЖА ВТОРОГО РОДА 283
Рассмотрим теперь случай, когда справедливо правило d& == Id.
В этом предположении нужно воспользоваться центральным уравне-
уравнением Лагранжа в форме F.4.6). При выполнении тех же действий
последнее принимает вид
Подчеркнутые слагаемые сокращаются, так как согласно правилу
переставимости (£qsY = 8^. Приходим к равенству C). Таким обра-
образом, мы видим (об этом уже говорилось в п. 1.7), что при выводе
уравнений движения вопрос о правиле переставимости операций d и Ь
не имеет принципиального значения — оно, сокращая промежуточные
записи, ничего не вносит в конечный результат. Можно о нем и
не упоминать, если ставится цель получить дифференциальные урав-
уравнения движения системы, подчиненной идеальным связям, исходя из
принципа освобождаемости."
Равенство C) имеет такую же общность, что и общее уравнение
динамики F.3.2). Оно представляет результат формального преобра-
преобразования последнего и применимо поэтому как к голономным, так и
неголоножъш системам. В случае голономшх связей и независимых
обобщенных координат вариации bqs независимы, вследствие чего
коэффициент при каждом &qs в сумме C) должен быть по отдель-
отдельности равен нулю. Получаем систему дифференциальных уравнений
движения, выраженных в обобщенных координатах:
Ttirs~^=Qs {s==1 п)- GЛ-4).
Это — уравнения Лагранжа второго рода. Число их равно числу
обобщенных координат, т. е. числу степеней свободы голономной
системы.
Если же имеются неголономные связи, задаваемые соотношениями
п
2вь?, + в» = ° (Л=1. .... О, G.1.5)
5=1
то следствием равенства C), согласно сформулированной в п. 6.1
теореме, будут уравнения
Это — уравнения Лагранжа второго рода при наличии неголоном-
чых связей. Общее число уравнений E) и F) равно п-\-1\ оно на
удвоенное число связей 2/ больше числа степеней свободы п — /,
г. е. разности между числом независимых параметров qv ..., qn%
284 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
определяющих конфигурацию системы, и числом уравнений неголо-
номных связей. Уравнения E) и F) содержат п-\-1 неизвестных:
п обобщенных координат qv . . ., qn и / множителей связей \ \.
Форму записи уравнений C) можно сохранить, как указывалось
в п. 6.3, и при введении избыточных координат, если включить
в число уравнений E) равенства, получающиеся при дифференциро-
дифференцировании по времени конечных соотношений между обобщенными коор-
координатами.
Другой вывод уравнений Лагранжа основан на преобразовании
левых частей уравнений F.3.7). Вспомнив многократно использован-
использованное соотношение A.3.5), имеем
дГ} d dvi d дг/
1 l dqs dt l l dqs l l dt dqs
Но, согласно A.3.11),
d drt dvt
dt dqs ~dqs '
Поэтому
тли, • —- = — m,Vi • —r1 m{ol L =
' ' dqs dt l l dqs l l dqs
d д 1 ^1
dt dqs 2 l l l dqs 2 l l l
и далее
N N 2 ^ N l
v д
или, учитывая определение кинетической энергии D.1.1),
£ l dqs dt dqs dqs
что и требовалось.
Рассматривая функцию обобщенных координат, обобщенных ско-
скоростей и времени
/(<7i Qn- Qi Чп> 0.
условимся для краткости писать
dt dqs oqs
и называть $>s — эйлеровыми операторами над /. В частности,
если / не зависит от обобщенных скоростей, то
7.2] интеграл энергии 285
Ясно, что
в, С/г
Уравнения Лагранжа D) в этой записи будут
$s(T) = Qs (s=l, .... п\ G.1.11)
а в случае потенциальных сил, учитывая (9), A0) и F.4.8),
$s(L) = 0 (s = I, . . ., п), G.1.12)
где L — кинетический потенциал (L—T—И).
Если наряду с потенциальными силами имеются непотенциальные
и в их числе допускающие диссипативную функцию Ф, то уравне-
уравнения движения Лагранжа по A1), A2), E.11.2) записываются в виде
$s{l)==Qs—^- E=1 п). G.1.13)
Запись уравнений Лагранжа F) при наличии неголономных свя-
связей E) имеет вид
^v/ ^5 | ^u'^kaks xi v5" ~ * а)- G.1.14)
Слагаемые
i
2V**5 G.1.15)
в уравнениях A4) представляют обобщенные реакции неголономных
связей.
7.2. Интеграл энергии
Уравнения движения Лагранжа второго рода представляют
систему п обыкновенных дифференциальных уравнений второго
порядка — в них входят обобщенные координаты, их первые и вто-
вторые производные по времени (обобщенные скорости и обобщенные
ускорения) и, может быть, явно время t. Эта система линейна отно-
относительно обобщенных ускорений и последние могут быть из нее
определены через обобщенные координаты, обобщенные скорости
и время
b = fs(Qi Яп> Я\ Яп* О. G.2.1)
Явная форма записи этих соотношений приведена ниже G.4.7).
Рассмотрим функцию обобщенных координат, скоростей и времени
Яя> Яг Яп* 0. G.2.2)
286 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. Т
Ее производной по времени, составленной в силу уравнений дви-
движения, называется выражение
в котором обобщенные ускорения заменены их значениями A) из
уравнений движения, т. е.
Эта функция ф от обобщенных координат, скоростей и времени
будет первым интегралом уравнений движения, если ее производная
по времени, составленная в силу этих уравнений, равна тождественно
нулю. Тогда сама функция ф сохраняет постоянное значение при
движении системы.
Составим теперь производную по времени в силу дифферен-
дифференциальных уравнений A.14) от функции L—кинетического потенциала.
Имеем
п
dL dL , V4 / dl •• , dL • \ dL .
Мы заменили здесь производные L по обобщенным координатам их
значениями из уравнений движения. Теперь можно, вспомнив A.5),
записать
п п I п
dL__dL^ , d_ у dL_ •
или, на основании F.4.19) и E.10.3),
Уравнения движения допускают первый интеграл, называемый инте-
интегралом энергии, если все активные силы потенциальны, время t не
входит в выражение кинетического потенциала и уравнения неголо-
номных связей не содержат свободных членов ak. Тогда правая
часть равенства D) обращается в нуль и, обозначая через h
7.2] интеграл энергии 287
постоянную величину, приходим к соотношению
п п
jLqs-L = h. G.2.5)
q
s=l s=l qs
Предположение, что L не содержит t явно, и все ak == 0, отнюдь
не равнозначно с предположением о стационарности связей, так как t
может не входить в [, а все ak обращаться в нуль и при нестацио-
нестационарных связях. Примеры, когда L явно не содержит t при нестацио-
нестационарных связях, приведены ниже.
Теперь, обратившись к соотношению D.1.13) и вспомнив значе-
значения ps и Z,, получаем вместо E)
или Г2 + П — TQ = h. G.2.6)
Таково выражение интеграла энергии в общем случае. Если же
связи стационарны, то Т2 = Т, Т0 — 0 и соотношение F) прини-
принимает вид
= /г, G.2.7)
т. е. выражает закон сохранения полной механической энергии Е
(суммы кинетической и потенциальной энергий) при движении системы,
подчиненной стационарным связям и находящейся под действием лишь
потенциальных активных сил.
Возвращаясь к равенству D), предположим связи стационарными
и что L не зависит от t явно (при стационарных связях время t
может войти явно в L через обобщенную потенциальную энергию П).
Тогда, преобразовав, как только что было сделано, выражение
в левой части, придем к соотношению
J-
G.2.8)
где N—мощность, соответствующая непотенциальным силам, отлич-
отличным от тех, которые выражаются через диссипативную функцию, а
^, = -(т + 1)Ф G.2.9)
— мощность, затрачиваемая на преодоление диссипативных сил;
последнее равенство в (9) имеет место, когда диссипативные силы
выражаются одночленной степенной зависимостью от скоростей точек.
Физическое содержание равенства (8) ясно: изменение полной
механической энергии системы, подчиненной стационарным связям,
V единицу времени равно мощности непотенциальных приложен-
приложенных сил.
288 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
7.3. Структура уравнений Лагранжа
Ограничиваясь случаем голономных связей, запишем уравнения
Лагранжа в виде
$S(L) = QS (s=l п). G.3.1)
Развернутое выражение кинетического потенциала можно записать
в виде
L = T — 11 = Г2+7\ — (И- Го) = Т2 + Тг—П.\ G.3.2)
где П* зависит от обобщенных координат и в общем случае от
времени
П* = П — То. G.3.3)
Величину И* будем называть измененной потенциальной энергией.
Такое всегда возможное формальное отнесение части кинетической
энергии к потенциальной, как увидим ниже, имеет полезное физи-
физическое истолкование.
Уравнения движения A) теперь могут быть записаны в виде
Т2 — определенно положительная квадратичная форма обобщенных
скоростей qx qn и ее можно трактовать как кинетическую
энергию некоторой системы. Поэтому все члены, стоящие в правых
частях уравнений движения D), в том числе и —ёДТ^). допустимо
рассматривать как некоторые обобщенные силы. По A.8) и D,1.6)
имеем
dt
Величины
n n
dBk • dBs , у / dBk dBs_
образующие кососимметричную матрицу
Yin
G.3.7)
О Ti2 ... Tin
Т21 0 ... Y2/I
Ы Тл2
7.4] ЯВНАЯ ФОРМА УРАВНЕНИЙ ЛАГРАНЖА 289
называются гироскопическими коэффициентами, а выражение
2 G-3.8)
— обобщенной гироскопической силой; его слагаемые ^skqk — гиро-
гироскопическими силами.
Уравнения движения D) теперь записываются в виде
-^.-^. (*=1 а). G.3.9)
причем последнее слагаемое отпадает, когда t не входит в L явно.
Обобщенные скорости входят в этом случае в левые части уравне-
уравнений (9) лишь квадратично (об этом см. п. 7.4); наличие линейных
относительно обобщенных скоростей слагаемых, если исключить те,
которые могут входить в выражения обобщенных сил Qsf обусло-
обусловлено гироскопическими силами. При этом в s-e уравнение не входит
обобщенная скорость qs (так как ^ = 0), а обобщенные скорости qk
в него входят с коэффициентами, обратными по знаку тем, с кото-
которыми qs фигурирует в уравнениях для координат qk. Это свойство
часто используется при проверке, что уравнения движения правильно
записаны.
Виртуальная мощность (п. 5.10) гироскопических сил равна
нулю; действительно, по (8) и F) имеем
.5=1 5=1 k = \
Этим объясняется исчезновение слагаемого Тг в выражении интеграла
энергии B.6).
7.4. Явная форма уравнений Лагранжа
Теперь остается записать в раскрытом виде правые части
уравнений движения C.4), Имеем по D.1.5)
п п
2 £ mml
fe-1 m=l - £=1
19 Зак. 2072. А. И. Лурье
290 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
причем последнее слагаемое (линейное относительно обобщенных
скоростей) отпадает, когда t не входит в Т явно.
Заметим далее, что
dA
\dqm
km
dAms dAk
где величины
_ dAkm\
d У
уже ранее введенные в п. 4.10, представляют символы Кристоффеля
первого рода для матрицы А коэффициентов квадратичной формы Т.
Уравнения движения C.9) теперь записываются в виде
k=\ m=l
(*=i »)• G-4.1)
Обобщенные ускорения, как уже говорилось в п. 7.2, входят в них
линейно и они разрешимы относительно обобщенных ускорений,
так как матрица D.1.9) невырожденная. В п. 4.2 была введена
обратная ей матрица Л; элементы последней равны (см. (П. 1.3.13))
A7ll = JT\ С *=1. •••. л). G.4.2)
где Д^у—алгебраическое дополнение элемента Als определителя |Л|
матрицы А.
Теперь, умножив на AJtl каждое из уравнений A) и просумми-
просуммировав по всем 5 эти произведения, получим
так как
5-1 S=l
7.5] ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ ДВИЖЕНИЯ ТОЧКИ 291
Вводя далее величины
п
1 { 1 \ I 1 \
G.4.4)
представляющие символы Кристоффеля второго рода (волнистые
скобки) для матрицы Л, придем к уравнениям движения в обобщен-
обобщенных координатах, разрешенным относительно обобщенных ускорений:
G.4.5)
В случае стационарных связей уравнения Лагранжа A) и E)
упрощаются и принимают вид
п п п
2 21 [k' m> s^k4m = Qs — -^-s (s=l я). G.4.6)
7.5. Геометрическое истолкование движения
материальной точки
Уравнения движения Лагранжа в форме D.6), D.7) допускают
интересное и плодотворное истолкование в терминах тензорного
анализа и римановой геометрии *). Начнем с рассмотрения простей-
простейшего случая — движения свободной материальной точки. Будет удобно
ввести вместо декартовых координат х, у, z пропорциональные им
величины
х' = У"тх% y' = Ymy, z' = Vmz, G.5.1)
где т—масса точки. Условимся называть вектор-радиусом точки,
ее скоростью и ускорением — векторы, отличающиеся от их истинных
значений тем же множителем пропорциональности У т. Мы сохраним
за этими векторами привычные обозначения
v = rt w = v = rt G.5.2)
*) Необходимые для понимания последующего сведения изложены
в Приложении 2.
19*
292 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
где is — единичные векторы декартовой системы осей Ox'y'z*.
Выражение кинетической энергии будет иметь вид:
где ds — «элемент дуги» траектории точки. Вводя криволинейные
координаты q1, q2, q3
r = r(q\ q2, q% G.5.4)
получим
r = v = rsqsi G.5.5)
где rs — базисные векторы (П. 2.4.4) и знак суммы по немому
индексу 5 опущен. Обобщенные скорости, таким образом, являются
контравариантными составляющими вектора скорости v. Выражение
кинетической энергии через них получает вид
так что роль ковариантных составляющих метрического тензора пере-
переходит к коэффициентам выражения кинетической энергии (ранее
обозначенным Ask), а основной квадратичной формы — к величине
(dsJ = 2T(dtf = gskqsqk. G.5.7)
Элементарная работа силы F, приложенной к точке, на возмож-
возможном перемещении ее из рассматриваемого положения равна
b'W = F.£= = -±=F.rsbq* = Qsbq*. G.5.8)
у m у m
Условимся называть далее вектором силы вектор
У m
Величины Qs являются, в принятом ранее определении, обобщен-
обобщенными силами; они здесь представлены как ковариантные составляю-
составляющие «силы» Q; ее контравариантные составляющие равны
Qs = gskQk- G-5-10)
Теперь надо составить выражение вектора w. Дифференцируя E)
по времени и используя правило дифференцирования (П. 2.4.9) базис-
базисных векторов, получим
7.5] ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ ДВИЖЕНИЯ ТОЧКИ 293
Величины в скобках представляют контравариантные составляю-
составляющие ws вектора w:
ws='qs-\-\t%\qtq*. G.5.12)
Второй закон Ньютона при введенных наименованиях векто-
векторов w и Q принимает форму: ускорение равно силе, приложенной
к точке:
w = Q G.5.13)
или, согласно A0) и A2),
4s + Ц №kk = QS = gskQk. G.5.14)
Пришли к разрешенным относительно обобщенных ускорений урав-
уравнениям Лагранжа в форме D.7). Уравнения Лагранжа в форме D.6)
и в их обычной форме A.11) получим, рассматривая соотноше-
соотношение A3) в ковариантных составляющих.
Действительно,
, t\ s\'qmqK G.5.15)
учитывая еще, что
=irgsmqm ~ Ч?qmqt- [Ч^ -{т' *'• s])qmqt=i
— qmqt
и вспомнив выражение (б) кинетической энергии, получим также
d дТ дТ /т г 1 г\
Ws==-Z7'TT7 71- G.5.16)
dt dqs dqs
Выражение второго закона Ньютона в ковариантных соста-
составляющих принимает вид уравнений Лагранжа
G.5.17)
dt dq* dqs s
или тех же уравнений в явной форме D.6)
. t; s\q^ = Qs. G.5.18)
Перейдем к записи уравнений движения в естественной форме.
Выражение вектора скорости E) представим в виде
= rkl£-'s. G.5.19)
где ds — элемент дуги, определяемый по формуле G). Вектор
* = rk*£- G.5.20)
294 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
dqk
с контравариантными составляющими —j— направлен по касательной
a s
траектории в сторону возрастания s\ из G) следует, что -с — единич-
единичный вектор. Получаем
v = z's, w = v = zs-}-s2 |j. G.5.21)
Теперь имеем
~~ k
d^_dTk_dg^_ (d2qk {ь\ dqm dq' \_
ds dqm ds ~ k \ ds2 ""^ W'l ds ds ) —
ds ~~ k ds2 "•" ds dqm ds
G.5.22)
Этот вектор называется вектором кривизны. Величины
аг_ <**ЯГ ■ ID dq™ dq'
к ~~ ds2 ~T~\rnt) ds ds
являются его контравариантными составляющими, а величина
* = Vgsmkskm G.5.23)
равна кривизне траектории. Единичный вектор п представляет ее
главную нормаль. Получаем
;(# 4££)*]. .7.5.24)
Вектор ускорения представлен геометрической суммой двух
составляющих — касательного ускорения w^ и нормального W(ny
„,„ _
Представляя вектор Q аналогичным разложением
G-5.26)
()
по B0) найдем
QM^Q., = rt^Q/:r,^ = Q,HlL^r, G.5.27)
и далее
п —О О —г (О* О dqt dqk\—rO(pkt d<? d(ik\ п^2Ъ\
Естественные уравнения движения теперь записываются в виде
Преобразуя первое из них в случае потенциальных сил
-•_ ds • d s2 дП dq1 dil_
ds ds 2 dq( ds ds
7.6] ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ПОВЕРХНОСТИ 295
после интегрирования получим
52 = 2(Л—П), G.5.30)
где постоянная h представляет полную энергию материальной точки.
Теперь, по исключении s2 из уравнения C0) и второго уравнения B9),
придем к дифференциальным уравнениям траекторий точки
в потенциальном силовом поле:
dV , IM dVm *ЧЧ 1 дП k
\g ds ds)'
~d^'^\mk\ ds ~ds — 2(h-d)
Их надо рассматривать, конечно, совместно с соотношением
dql dq'* _
G.5.
7.6. Движение материальной точки по поверхности
Простейшим примером движения системы, подчиненной связям,
может служить движение материальной точки по поверхности. Урав-
Уравнение поверхности будем считать заданным в виде (П. 2.7.1)
Р = Р(<71. <72). G.6.1)
где qa — гауссовы координаты (греческие индексы принимают зна-
значения 1, 2). Скорость
v = ?j* G.6.2)
представляет вектор на поверхности. Однако вектор, равный произ-
производной вектора скорости по времени, не будет таковым. Обратив-
Обратившись к формулам (П. 2.7.19), найдем
A' U1 )\-тЬЛ£*я\ G.6.3)
где т — единичный вектор нормали поверхности, Ьа^ — коэффициенты
ее второй квадратичной формы. Символы Кристоффеля вычисляются
здесь с помощью метрического тензора, ковариантные составляющие
которого аа!з представляют коэффициенты первой квадратичной
формы поверхности
ds2 = aa, dq« dq? = pa • p3 dq* dq$ = 2Tdt'\ G.6.4)
где T—кинетическая энергия точки. Вектор v представляет полное
ускорение.
Формула C) представляет полное ускорение в виде суммы двух
векторов: во-первых, вектора ускорения на поверхности w с контра-
вариантными составляющими
296 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
получающегося при ковариантном дифференцировании контравариант-
контравариантных составляющих скорости; во-вторых, ускорения, нормального
к поверхности,
^ ^£- ^ = s*km. G.6.6)
Здесь, согласно (П. 2.8.4), величина k представляет нормальную
кривизну
k=b'?dfiq\. G.6.7)
Ковариантные составляющие ускорения на поверхности преобра-
преобразуются к виду
Перейдя в выражениях E) контравариантных составляющих wa век-
вектора ускорения w на поверхности к независимой переменной s,
получим
причем через k*a обозначены контравариантные составляющие век-
вектора геодезической кривизны, определяемые формулой (П. 2.8.6).
Соответствующий ему единичный вектор п* определяет направление
геодезической нормали траектории. Итак,
w = st-\-s2k*n*, G.6.10)
где геодезическая кривизна k* задается формулой (П. 2.8.8). Вектор
ускорения на поверхности представлен суммой двух взаимно перпен-
перпендикулярных, согласно (П. 2.8.13), векторов — касательного ускоре-
ускорения и геодезического нормального ускорения.
К точке приложены активная сила F и реакция поверхности /?,
направленная по нормали к последней (предполагается, что сила
трения отсутствует). Элементарная работа этих сил равна
b'W = -tL (F + R) • or = ^L- F- pjjq* = Qj>q*. G.6.11)
Как и ранее, вводим в рассмотрение вектор Q с ковариантными
составляющими Qa, равными обобщенным силам. Но теперь равен-
равенство E.9) уже не имеет места, так как активная сила F может
содержать еще составляющую по нормали поверхности:
F=F'?a + F{m)m. G.6.12)
7.7] примеры 297
Второй закон Ньютона в наших обозначениях принимает вид
у т
Таким образом, приходим, во-первых, к уравнениям движения
'W = q'-*-{»l)q9qi = a'9Q9 G.6.13)
или, в ковариантных составляющих,
jLJZL_^L = Qa. G.б.п)
dt dq« dq«
Во-вторых, находим выражение нормальной реакции
/? = (— F{m)+Vm^l)m, G.6.15)
причем наличие множителя ]/т объясняется выбором масштаба длин
согласно соотношениям E.1).
Уравнения движения точки по поверхности имеют тот же вид,
что и свободной точки. Если «ничего не знать» о реакции поверх-
поверхности и «забыть» о существовании нормальной к поверхности
составляющей активной силы, то уравнения A3) и A4) можно истол-
истолковать как запись второго закона в форме равенства E.13) векто-
векторов силы и ускорения на поверхности.
Повторив сказанное в предыдущем пункте, можно записать также
уравнения движения на поверхности в форме, соответствующей
естественным уравнениям движения
^r i
d*q* <a] dql dqt\ -2 _ ( . dql dq*\ <7-6Л6)
в проекциях на касательную и геодезическую нормаль траектории.
Если Q = 0, то скорость сохраняет постоянную величину. Усло-
Условимся называть такое движение инерционным; инерционное движение,
как следует из A6), происходит по геодезической линии поверх-
поверхности.
7.7. Примеры
1°. Движение свободной точки в неортого-
неортогональной системе криволинейных координат. Соста-
Составим уравнения движения тяжелой точки в системе вращающихся осей,
начало которых равномерно перемещается по вертикали (см. при-
пример в П. 2.6).
298 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Использовав формулы E.12) и выражения (П. 2.6.6) символов
Кристоффеля, получаем контравариантные составляющие ускорения
в виде
wl = х1 4- 2 { и! х2х3 4- {зз} х3х3 = х1 — 2тх2х3 — хЧ2 (х3/2,
2 9 i О 1*4 9 9 / " Ч\9
V* ^ 1 / ~* V* * V* ^ -., , V* Т I V* 1
где т—постоянный коэффициент, связывающий угол поворота осей
с вертикальным перемещением.
Если движение происходит в поле силы тяжести и ось Ог напра-
направлена вертикально, то (для точки единичной массы)
II = gz = gx3,
и ковариантные составляющие силы Q будут
Ее контравариантные составляющие равны
Уравнения движения имеют вид
х1 — 2тх2х3 — хЧ2 (х3J = —
х2 4- 2тх!х3 — х2х2 (х3J = gxx1, G.7.1)
X = g.
Чтобы записать уравнения движения в ковариантных составляющих,
составляем выражение кинетической энергии
4-
х2^з _ 2тх2х3 — т2х! (х3J = 0, \
х2 -+- тх]х3 -г- 2тх2х3 — т2х2 (х3J = 0, i G.7.2)
т=1
Тогда
*2 1
s — 2 &ibx
получим
Нетрудно проверить, что проекции ускорения w точки на (вра-
(вращающиеся) оси Ох1 и Ох2 равны его ковариантным составляю-
составляющим wv w2, а на ось Ог—контравариантной составляющей w*.
7.7] примеры 299
Сложность полученных систем уравнений объясняется выбором системы
координат. В неподвижной системе осей движение представляет паде-
падение тяжелой точки в пустоте. Если за плоскость Ozx принять
плоскость траектории (вертикальную плоскость, в которой располо-
расположен вектор начальной скорости v0) и начало координат совместить
с начальным положением точки, то
x = vQJ9 z = vJ—\ gt*
и далее
хх = v()xt cos тх3, х2 = — vOxt sin тх3, х3 = vOzt — -^ gt2.
Эти выражения, конечно, тождественно удовлетворяют уравнениям A)
или B).
2°. Уравнения движения точки в ортогональ-
ортогональных криволинейных координатах. В ортогональных кри-
криволинейных координатах уравнение движения свободной точки E.18)
для координаты ql имеет вид
3J = O1. G.7.3)
где ht—коэффициенты Ляме. Два других получаем при соответ-
соответствующей замене индексов. Здесь использованы выражения (П. 2.10.8)
символов Кристоффеля. Запись в контравариантных составляющих,
т. е. в форме уравнений E.14), получается при делении C) на
коэффициент h\ при ql.
Как пример рассмотрим в плоскости Оху ортогональную систему
криволинейных координат ql = а и q2 = $, образующих изотерми-
изотермическую сеть. Это значит, что выражение декартовых координат
через а, р может быть представлено в форме
G-7-4)
где /(f)— некоторая функция комплексного переменного 'у = а
Предполагается, что ее производная /' (f) не обращается в нуль
в области изменения переменной -у. Тогда
их +■ ids, = f (T) (d« 4- WP). ds\ = I /' (т)
Таким образом, для изотермических координат коэффициенты Ляме ha
и h? равны, причем
hi = А| = | /' (Т) j2 - /' (ТO' (т> = А2 («. Р) G-7.5)
(черточкой обозначается сопряженная комплексная величина). При
вращении плоскости Оху вокруг оси Ох получают пространственную
300
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛЛГРАНЖА
[ГЛ. 7
систему координат, в которой квадрат элемента дуги задается выра-
выражением
(dsf = ti2 (a, p) {do? + df) + hi (а,
ц
где ср—азимутальный угол и h9 равно квадрату мнимой части
h\= | Iw/(j)|2- G.7.6)
Уравнения движения C) в координатах а, р, о будут иметь вид
<Э1П/2 .^
_ ЯЛ _J_ О « R „2 _____ ^
Р-
da
din Л .
d3 (Р
(a*—
• а В —
h2 dot
G.7.7)
Предположено, что Q? = 0.
Из последнего уравнения получаем интеграл площадей
?
Г
G.7.8)
где /г — постоянная. Исключив с помощью этого соотношения ср и
предполагая, что силы потенциальны, получим
д In h
In h
din Я
Теперь, использовав интеграл энергии
1
1 d
G.7.9)
G.7.10)
легко преобразовать первое уравнение (9) в виду
Аналогично записывается второе уравнение. Получаем систему урав-
уравнений
£(A»i)» = 2i!-*»(E0-II--4V ]
at оо. \ и 2ftJ /
G.7.11)
7.7] примеры 301
допускающую дальнейшее интегрирование, если величина в скобках
оказывается равной сумме функций, зависящих от а и р по отдель-
отдельности. Это, например, имеет место в задаче о плоском движении
точки под действием сил притяжения двух центров. Располагая эти
центры Fx и F2 на оси Ох и называя через 2с расстояние между
ними, будем определять положение движущейся точки М криво-
криволинейными координатами, вводимыми соотношением
х -\- iy = с ch (а +- *Р) = с (ch а cos р -|- / sh а sin C).
Тогда
/*2 = c2(ch2a — cos2p).
Расстояния гх и г2 точки М от притягивающих центров находим из
равенств
rj = с | ch (а + /Р) 4- 1 | = с (ch а -h cos р),
— I | = c(cha —cosp).
Теперь, учитывая, что потенциальная энергия равна
П Й—^ ch.ico,.ptC
где /j и /2—постоянные, и что в плоском движении &ф = 0, получим
h2 (EQ— U) = c2 (eq ch2 a 4-^4^ ch a) — c1 (eq cos2 p +f-r^1 cos p) ,
и уравнения A1), после интегрирования, принимают вид
/г4а2 = 2с2 (£о ch2 a 4~ f-~^- ch a 4~ Ti) «
COS
Сложив эти равенства и воспользовавшись интегралом энергии, легко
найдем -^4-72 = 0- Получаем систему двух уравнений
(day (d$J 2 (dty
302
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
из которой находим еще два интеграла
1
1 da —
-cos,
\ G.7.1
ioc— 72) 2 da —
Решение задачи, содержащее четыре произвольных постоянных
£0, С, Ео, 72» сведено к вычислению этих эллиптических интегралов *).
Задача о двух притягивающих центрах принадлежит к числу тех,
возможность сведения которых к квадратурам была указана Лиувил-
лем. Системами типа Лиувилля называются такие, для которых
Л2 = Л?(а) + л1(Р), /г2П(а, р) = ЧГ, (а) +ЧГ2(р). G.7.13)
Более полное определение систем Лиувилля будет дано в п. 10.14.
Возвращаясь к уравнениям A1) и повторив проведенное вычисление,
получим для систем Лиувилля
Е0А? - ЧГ,
f (EQhl -W2
= С
= f
~ da 4-
G.7.14)
3°. Уравнения движения точки по поверхности вра-
вращения. Эти уравнения имеют вид
Здесь приняты обозначения, приведенные в конце пункта П. 2.10, и
использованы вычисленные там значения символов Кристоффеля. Если
ось поверхности вращения направлена по вертикали, а движение
происходит в поле силы тяжести, то
*) Подробное исследование задачи о движении материальной точки
в поле сил притяжения двух центров дано в курсе небесной механики Шарлье
(С. L. Char Пег, Die Mechanik des Himmels, т. I, стр. 117—166; Leipzig,
1902).
7.7] примеры 3J33
Тогда, проинтегрировав второе уравнение и исключив из первого ср2,
получим
2 * 2 е " | 1 4'2 d I flte /7 7 i c\
rcprcp 5 + ^cp^ = — g^j. G.7.16)
Из последнего уравнения находим интеграл энергии
G.7.17)
Здесь z и г рассматриваются как функции дуги, отсчитываемой по
меридиану, h — постоянная интегрирования. Решение задачи сводится
к квадратурам. Для задачи о сферическом маятнике
z = R cos », г = Л sin Я = 1/7?2 —z2,
и получающееся дифференциальное уравнение
? = 2 (Л — #г) (Я2 — /) — гЗ$
может быть проинтегрировано с помощью эллиптических функций.
К интегрированию в эллиптических функциях сводятся также задачи
о движении точки по поверхности кругового конуса
z = scosa, r = ssina
(a—половина угла раствора конуса; вершина снизу), параболоида
вращения
r2 = az
и по некоторым другим поверхностям *).
4°. Движение по развертывающейся поверхности.
Рассмотрим еще случай движения материальной точки по разверты-
развертывающейся поверхности. Длина дуги и геодезическая кривизна траекто-
траектории, будучи инвариантами изгибания поверхности, сохраняют свою
величину при развертывании поверхности на плоскость. Геодезиче-
Геодезическая кривизна становится кривизной плоской траектории точки. По-
Поэтому уравнения движения по развертывающейся поверхности записы-
записываются в форме уравнений движения точки по плоскости под
действием активной силы, равной составляющей, приложенной к точке
силы в касательной плоскости к поверхности.
Например, на тяжелую точку, движущуюся по поверхности пря-
прямого кругового конуса с вертикальной осью, действует направленная
по образующей конуса сила величины gcosa. При развертывании
конуса на плоскость приходим к задаче о плоском движении мате-
материальной точки под действием центральной силы постоянной величины
*) Е. Т. Уиттекер, Аналитическая динамика, § 55, ГТТИ, 1937.
304 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
(центр силы соответствует вершине конуса). В полярных координа-
координатах 5, ф уравнения движения будут
5 — $ф2 = q: g cos a, — $2ф = 0,
где верхний знак (сила притяжения) соответствует расположению
вершины конуса снизу, а нижний (сила отталкивания)— сверху; углы ф
и ср (азимут на поверхности конуса) связаны соотношением ^ = ^sina.
Как и требуется, получаем
s2 = 2 (/г q: gs cos a) ^— .
7.8. Геометрическая интерпретация уравнений
движения системы
Ограничиваемся рассмотрением системы материальных точек *),
подчиненных стационарным голономным связям. Как и в п. 7.5, усло-
условимся определять положение точки М( массы tni величинами, про-
пропорциональными ее декартовым координатам в неподвижной системе
осей:
^-2= И "*>/> ^i-\=Vrniyii 1ы=Ущг1 (/=1, .... N).
G.8.1)
Можно сказать, что положение системы в данный момент времени
задается точкой (£lf .... £злг) евклидова пространства Bsjy. Вектор-
радиус этой «изображающей» точки обозначается через г; числа ^v
рассматриваются как его проекции на оси декартовой системы коор-
координат в Ем\. Соотношение
r = r(q\ .... q»)t G.8.2)
выражающее декартовы координаты через обобщенные qxt ..., qn,
выделяет в Езм риманово многообразие Rn. Задача состоит в предста-
представлении движения материальной системы с помощью терминов геоме-
геометрии Rn. Здесь будет в значительной мере повторено сказанное в п. 7.6,
когда шла речь о движении точки на поверхности и все, о чем
говорилось, имело непосредственную наглядность. Перенесение этого
геометрического языка на систему материальных точек сообщает
законам движения ее «условную наглядность». Во всем последующем
*) Конспективный обзор работ, посвященных применению геометриче-
геометрических методов к задачам динамики, содержится в книге Д. Л. Синджа ^Тен-
зорные методы в динамике» (Гос. изд-во иностранной литературы, 1947).
Подробное изложение основных идей и применений дано в работе того же
автора «О геометрии динамики» (J. L. S у n ge, On the Geometry of Dynamics,
Phil. Transactions of the Roy. Soc. of London Ser. A, vol. 226, Pp. 31—106).
Литературные указания см. в упомянутой книге Синджа.
7.8] ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ УР-НИЙ ДВИЖЕНИЯ СИСТЕМЫ 305
не надо лишь забывать, что слова вектор-радиус, скорость, ускоре-
ускорение обозначают понятия, относимые к изображающей точке, а отнюдь
не к какой-то материальной точке системы.
Координатный базис в каждой точке Rn определяется системой п
векторов
(греческие индексы принимают значения 1, ..., п). Вектор, предста-
представленный в виде аага, принадлежит Rn; aa—контравариантные соста-
составляющие этого вектора. Так, дифференцируя B) по времени, получим
вектор скорости
r = v=raq*, G.8.4)
принадлежащий Rn; обобщенные скорости qa— его контравариантные
составляющие.
Кинетическая энергия системы материальных точек равна половине
квадрата модуля вектора скорости v изображающей точки. Дей-
Действительно,
N 3/V
~ IV / • *> , • 2 , • 2\ 1 V1 ;2 1 • • 1 о
Т= у 2и mi W +■ У1 +-Zi) = -2 2и ^ = ~2 гог = ~2 v •
/=1 v=l
Выразив v по формуле D), получим
Т= у г^фф = 1 аф*ф , G.8.5)
где aai3—ковариантные составляющие метрического тензора простран-
пространства Rn.
Активные силы Ft, действующие на точки материальной системы,
-заменяются в их совокупности вектором Q, называемым силой,
относимой к изображающей точке. Этот принадлежащий Rn вектор
определяется его ковариантными составляющими, равными обобщен-
обобщенным силам
Q=Qar\ G.8.6)
где ra — векторы взаимного базиса. Возможность такого введения
понятия силы обусловлена тем, что элементарная работа всех актив-
активных сил Ft на виртуальном перемещении точек системы равна эле-
элементарной работе «силы» Q на виртуальном перемещении Ьг:
Q.or = QarVp 6/ = Qaal V = Qa bq\
Вектор ускорения w определяется как принадлежащий Rn вектор
w = w*ra = war« G.8.7)
^0 Зак. 2072. А И. Лурье
306 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
с контравариантными составляющими w'x% получаемыми путем кова-
риаитного дифференцирования по времени контравариантных соста-
вляющих q* вектора скорости v:
{^}^Я^ G.8.8)
Можно сказать, ссылаясь на случай движения точки по поверхности,
что w представляет ту часть вектора v (производной v по времени)»
которая принадлежит Rn *).
Ковариантные составляющие wa вычисляются теперь по известному
правилу
Повторив вычисление п. 7.5, можно записать это выражение еще
в виде
Wa=*^l-—?L. G.8.10)
Теперь, основываясь на этих определениях, можно сформулиро-
сформулировать закон движения в форме второго закона Ньютона: вектор уско-
ускорения равен вектору силы:
w = Q. G.8.11)
В контравариантной записи получаем
^ = fl"pC?p. G-8.12)
Пришли к уравнениям движения в форме D.7), разрешенным
относительно обобщенных ускорений. В ковариантной записи получим
уравнения Лагранжа второго рода. Таким образом, последние выра-
выражают закон Ньютона для движения точки, изображающей рассматри-
рассматриваемую систему материальных точек в пространстве Rn с метрикой,
определяемой квадратичной формой 2Tdt2. Тем самым законам
движения придано «условно наглядное» геометрическое пояснение.
Так, словесно повторив сказанное в пп. 7.5 и 7.6, можно записать
уравнения движения в форме естественных уравнений, непосредственно
следующей из E.29):
*) Следует обратить внимание на заключительное замечание в пункте
П.2.12.
7.9] ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА 307
В «инерционном» движении, т. е. при Q = 0, движение проис-
происходит с постоянной скоростью по геодезическим линиям многообра-
многообразия /?л, для которых
Следствием естественных уравнений является указанное Синджем
обобщение теоремы Бонне, относящейся к движению материальной
точки*). Пусть под действием каждой из сил QA)f QB), ..., Q(m)
в отдельности изображающая точка может описывать одну и ту же
траекторию С. Кинетические энергии каждого из этих движений обо-
обозначим через 7(i), 7B) 7(т). Тогда та же траектория С может
описываться при одновременном действии всех сил Q(i), ...,Q(m),
причем кинетическая энергия в этом движении равна сумме кинети-
кинетических энергий отдельных движений.
Действительно, учитывая E.24) и E.22), можно записать есте-
естественные уравнения движения в виде
-J^4 + 2TU)kn=Q{i) (/=1, ..., m), G.8.15)
где, по условию, векторы т, kn одинаковы для всех /. Складывая
эти соотношения, получим требуемый результат.
7.9. Примеры на составление уравнений Лагранжа
1°. Двойной математический маятник при движе-
движении точки подвеса и при наличии квадратичного
сопротивления. Рассматривается движение в вертикальной пло-
плоскости двух тел столь малого размера, что можно считать их мате-
материальными точками Mv М2. Точка Мх с помощью гибкой и нерастя-
нерастяжимой нити ОМХ длиной /j связана с точкой подвеса О, вторая
такая же нить М1М2 длиной /2 соединяет точку М2 с Mv Точке
подвеса О сообщается движение в вертикальной плоскости ОМХМ2.
Скорость точки О обозначается через v0, угол вектора vQ с нисхо-
нисходящей вертикалью обозначается через а. Требуется составить уравне-
уравнения движения системы, учитывая силы веса и силы сопротивления
неподвижного воздуха, которые принимаются пропорциональными
квадратам скоростей точек. Массой нитей пренебрегают (рис. 48).
Вычисление диссипативной функции и обобщенных сил сопроти-
сопротивления приводилось выше в п. 5.12. Там же были получены фор-
формулы E.12.2) для квадратов скоростей точек. Воспользовавшись ими,
*) Уиттекер, Аналитическая динамика, §51.
308 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
записываем выражение кинетической энергии
7[(m+m
+ г;0 [(/^ + т2) /^ sin (а — ?1) + /ю2/2<р2 sin (а — ср2)] +
4-1^+^)^=72 + ^ + 7^. G.9.1)
Наличие слагаемых Тг и Т2 является следствием нестационарности
связей. Вычисляем эйлеровы операторы от Т2:
+m2/l/2;p2COS(C?l~ CP2) + /n2/l/2C?2 Sitl 0l — ?2)«
^i cos (?!—<p2) — "МЛ?? sin (9l — cp2).
При вычислении $^G^) величины vQ и а рассматриваются как
заданные функции времени. Находим
г G-9-2)
S2 (Г,) = m2l2 [vQ sin (a — cp2) + i;oa cos (a — cp2)]. j
Исчезновение гироскопических членов обусловлено тем, что
в выражении 71, коэффициент при cpi зависит лишь от срр а при
ср2 — лишь от ср2. Слагаемое Го не зависит от обобщенных координат
и ему соответствующие эйлеровы операторы обращаются в нуль.
Потенциальная энергия сил веса равна
П = — m>xglx cos cpj — m2g (ix cos cp2 +12 cos cp2), G.9.3)
и уравнения движения принимают вид
(m] 4- m^j Щ^х + m2lx /2cp2 cos (cpj —92) + m2lx /2cp^ sin (cpj —cp2) =
= — (mj + m2) /j [t;0 sin (a — cpx) + t;oa cos (a — cp2)] —
— g(mlll + m2l2)sin(pl-\-Qv \ G.9.4)
= — m2l2 [vQ sin (a —cp2) + vQa cos (a—cp2)] —gm2l2 sin cp2 + Q2>
причем выражения обобщенных сил сопротивления даются формулами
E.12.4).
В дальнейшем ограничиваемся рассмотрением этих уравнений
в предположении равномерного горизонтального движения точки под-
подвеса и малых отклонений точек М} и М2 от положений относитель-
относительного равновесия. Тогда, полагая в уравнениях D)
7.9] ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА 309
и воспользовавшись выражениями E.12.6) обобщенных сил сопроти-
сопротивления, а также уравнениями относительного равновесия E.12.5),
придем к системе линейных дифференциальных уравнений с постоян-
постоянными коэффициентами
«22 S
22 S2
где обозначено
ап = (т1+т2I2и а12 = а21 = m2lxl2 +!l'l— , а22 =
У{1 + L)(\+Ц)
ьп = г*, + *,) v? ^|. ьп = ь21 =
2 2
1 . .2
1 -f- А2
^l] I— ,
К 1 4- а?
Здесь —Xj и —Х2 обозначают тангенсы углов нитей с вертикалью
в положении относительного равновесия
1 (mx+m2)g ^ m2g
так что, считая эти углы по абсолютному значению меньшими 90°,
имеем
о 1 о 1
COS Ср! =—г_ COS Ср2 = —-
Vi + x] V1 + -4
Можно рассматривать дифференциальные уравнения E) как урав-
уравнения Лагранжа, составленные по кинетической энергии, диссипатив-
ной функции и потенциальной энергии, определяемым квадратичными
формами
Т. = Т (ап^? + 2а,2*Я + а^. Ф. == 1 (V* -f 2й12ё,е.2 + ЦЦ),
Нетрудно проверить, что эти квадратичные формы — положитель-
положительные знакоопределенные. Поэтому из уравнения энергии B.8), которое
в нашем случае имеет вид
можно заключить, что полная механическая энергия монотонно убывает.
310
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
Колебания, возникающие при нарушении относительного равно-
равновесия, поэтому будут затухающими. К этому же можно прийти,
интегрируя известными приемами систему уравнений E).
2°. Движение согнутой нити. Рассматривается движение
сложенной нерастяжимой нити (рис. 59), по правой ветви которой
с постоянной относительной скоростью движется материальная точка М
с массой т *). Предполагается, что созданы такие начальные условия,
при которых сложенная нить может двигаться поступательно в вер-
вертикальном направлении, причем одновременно правая ветвь укорачи-
укорачивается, а левая — удлиняется. Через х и у обо-
обозначаются в момент t высоты концов правой и
левой ветвей, а через z— высота точки К, в ко-
которой сложена нить. Длина нити равна /.
Между величинами г, х, у имеется легко
устанавливаемое по рис. 59 соотношение
z — x-\-z— у = /,
К
Т
м
и, следовательно, система имеет две степени сво-
свободы.
Если ввести в рассмотрение величину
и = х — у, G.9.6)
то это соотношение может быть записано в виде
'У////////////////////-
Рис. 59.
G.9.7)
Вследствие нерастяжимости нити скорости точек каждой ее ветви
одинаковы и равны х для правой, у — для левой ветви. Кинетическая
энергия системы равна
~m(x +
и) +■ и2
Через р обозначена масса единицы длины нити, через £ — расстояние
в момент t точки М от конца правой ветви нити.
Выражение потенциальной энергии силы веса будет
+• const.
— -2 lu — -£и2) + mg(*
*) Задача в предположении, что масса m отсутствует, рассмотрена
на стр. 264 книги Гамеля «Theoretische Mechanik» (Berlin, Springer, 1949).
7.9J ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА 311
Учитывая, что по условию I постоянно, получаем дифференциаль-
дифференциальные уравнения движения, записываемые в виде
4-и) = и{1 + + \
Исключив из них x-{-g, придем к уравнению
Оно имеет частное решение и = О, соответствующее случаю сообще-
сообщения концам ветвей сложенной нити одинаковых начальных скоростей
xQ = yQ. Из уравнений (8) и F) получим тогда х = у — — g. Нить
совершает вертикальное равнозамедленное движение, при неизменных
длинах ветвей. Это тривиальное решение не представляет интереса.
Возвращаясь к уравнению (9), примем и за независимое пере-
переменное; тогда
du -
du
и уравнение (9) после сокращения на отличный от нуля множитель и
допускает разделение переменных
du 1 du . 1 da
и2 I Л-и 2 1 1 2^ и'
?
Примем, что в начальный момент времени (t = 0) нить сложена
пополам, а разность начальных скоростей точек правой и левой
ветвей положительна:
Тогда после интегрирования получим
/
2SL)
ij G.9.10)
По смыслу задачи величина и не может превзойти /, причем это
значение она приобретает в момент распрямления нити, монотонно
увеличиваясь от нуля.
312
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
Выражение t через а легко получить интегрированием уравне-
уравнения A0):
Интеграл вычисляется просто, но выражение его не представляет
интереса; важно лишь отметить, что промежуток времени ^ до рас-
распрямления нити — конечный. Он соответствует значению и — 1 верх-
верхнего предела интеграла. Значение и# величины и в этот момент равно
.-</■
77
1L
2т
G.9.11)
Переходим к вычислению натяжений ветвей нити. Дифференциаль-
Дифференциальное уравнение движения мысленно отделенной части правой ветви
нити длины sj < £ имеет вид
или
где S[— натяжение нижней части правой ветви.
Рассматривая участок правой ветви части длины sj' > с, надо
учесть наличие на кем массы т. Тогда
ps"x + тх = S'[ — ps[g — tug или 5[ = (ps^ ■+ m) (x -\- g).
Заменив здесь величину х-\~ g ее значением по (8) и учитывая
соотношения (9) и A0), найдем
l
G.9.12)
Для участка длиной s2 левой ветви нити
1
2 = ?S2(y + g) = ?S2(X + g — U) = -o
P /
G.9.13)
7.9]
ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА
313
Точке К соответствуют по G)
s'[ = z — х = y (I — и), s2 = z — у = -g- (* + й)
и в этой точке
G.9.14)
В любой момент времени натяжение во всех сечениях нити поло-
положительно; это указывает на осуществимость рассматриваемого движе-
движения. В момент распрямления нити натяжение 5^ в точке К равно
|^. G-9.15)
В рассмотренном Гамелем случае т = 0
Это соответствует известным фактам разрушающего действия быстро
выпрямляющейся нити. По мнению Гамеля, решение задачи дает
приемлемое разъяснение удивительного циркового номера: по бро-
брошенной примерно так, как принято в условиях задачи, струне взби-
взбирается мальчик!
3°. Гироскоп в кардановом подвесе. Выражение кине-
кинетической энергии системы (ротор, кожух, наружное кольцо) составлено
в примере Г п. 4.12. К кожуху (внутреннему кольцу) на продолжении
Рис. 60.
оси ротора прикреплен точечный груз массой т. Составим уравнения
движения при двух предположениях: а) ось наружного кольца гори-
горизонтальна, б) — вертикальна. Соответствующие начальные положения
представлены на рис. 60, а и б.
314
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
К выражению кинетической энергии D.12.1) следует добавить
кинетическую энергию груза. Вектор скорости этой точки равен
v = w2 X i'3h = h (— i!2a cos p +■ /jp),
где h — расстояние ее от точки пересечения осей подвеса. Слагаемое,
о котором идет речь, оказывается равным
COS2
А2 и В2 кожуха. Далее A2-\-mh2, B2~\--mh2
и, как следовало ожидать, дело сводится к добавлению члена mh2
к моментам инерции 2 2 у 2
обозначаются через А'2 и В'т
Расположение осей показано на рис. 61;
О;т£— оси неизменного направления, связан-
связанные с неподвижным основанием прибора, при-
причем О; — ось вращения наружного кольца.
Ц Триэдр единичных векторов i'v i't), i'z свя-
связан с внутренним кольцом. В случае а)
ось Ос, горизонтальна, а в случае б) — вер-
7 тикальна. Потенциальная энергия в первом
случае равна
П = mg^ = mgh cos a cos p,
а во втором
II = mg\ = mgh sin p.
Это следует из матрицы косинусов B.6.2)
и легко проверяется по рис. 61.
Применив A.12), получим дифференциальные уравнения Лагранжа
рассматриваемой системы
Рис. 61
(ах -+- Ь cos2 р) а — £оф sin 2р + Съ(? + а sin p) p cos
^oc2 sin 2p —
sin 3) i cos p = —
3( + P)
где обозначено
al = Al+ Cv a2 = B\-\-Ay b = A\
Последнее уравнение A6) допускает интеграл
G.9.16)
— С r
G.9.17)
7.9] ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА 315
выражающий постоянство кинетического момента ротора — проекции
на ось ротора его главного момента количеств движения относительна
неподвижной точки О. Используя этот интеграл, можно записать
уравнения A6) в виде
(а, + Ьcos2 ?)а — b'4 sin 2? -+-Сгг$ cos р = — -g-,
-i- йа2 sin 2? — С3г0а cos р = — -^.
G'9Л8>
Члены —C3r0[3cos[3 и C3r0acosj3 играют роль обобщенных гироско-
гироскопических сил. Они появились здесь, хотя связи стационарны и сла-
слагаемое Тг в выражении кинетической энергии отсутствует, вследствие
исключения из уравнения движения обобщенной скорости ср. Подроб-
Подробнее об этом говорится ниже в п. 7.17 (преобразование Рауса).
Интеграл энергии B.7) имеет вид
Т + П = 1 [(«,+& cos2P)i2 +^+ П=£0, G.9.19)
причем слагаемое -^Сг^ включено в EQ.
При вертикальной оси вращения система допускает еще один
первый интеграл. Тогда П не зависит от а, а поскольку а йе входит
и в выражение кинетической энергии, то первое уравнение A8),
которое можно записать в виде
dt да
дает интеграл
дТ
— = (а _|_ ь cos2 P) a + C3r0 sin (В = АГр. G.9.20)
да
Здесь АГ: — проекция на ось 01 главного момента количеств движе-
движения системы К0- Эта проекция сохраняет постоянное значение, так
как момент внешних сил — веса и реакций подшипников наружного
кольца — относительно вертикальной оси этого кольца равен нулю.
Обращаясь к случаю а), будем предполагать, что отклонения
колец от начального положения, представленного на рис. 60, а,
остаются малыми. Тогда малы углы а и р, и уравнения движения A8)
в линейном приближении будут
• (a1-\-b)a-\-C3r$ = mghoi, #2р — C3r0<x= mgh$. G.9.21)
Частное решение этой системы линейных дифференциальных урав-
уравнений первого порядка, следуя известным правилам, разыскиваем
в виде
a = Dx cos (kt -\-ф), р = D2 sin (kt -\- ф). G.9.22)
316 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Для определения постоянных DY и D2 получаем два линейных одно-
однородных уравнения
Нетривиальное решение существует при обращении в нуль определи-
определителя этой системы
А (k2) = [(а, + Ь) k2 + mgh] {a2k2 + mgh) — C\r\k\ G.9.23)
Если h < 0 (груз расположен снизу), то
Д@)>0, д(_
и уравнение B3) имеет два положительных корня. Меньший назо-
2 2 2
вем k\, больший ki* Т
чем большая из величин
()
2 2 2 9
вем k\, больший ki* Тогда k\ меньше, чем меньшая, a ki больше,
mgh mgh
а2
При h > 0 (груз сверху) уравнение B3) имеет вещественные корни
при условии
. {С{г\ _(«,+* + а2) mghf > AntgW (a, + b) а2.
Выражение в скобках должно быть положительно; в противном
2 2
случае оба корня k\ и ki отрицательны. Приходим к неравенству*)
Съ | го\ > от^й (V^fb + /^2J. G.9.24)
являющемуся необходимым и достаточным условием положитель-
2 2
НОСТИ &1 И ki.
При положительных /г! и k} общее решение системы дифферен-
дифференциальных уравнений B1) будет
а = D(!1} cos (kxt +- <M + M2) cos (V + ф2).
n. fai + b) k2 -f тр-/г ,.л (а, 4- b) k2, -f mgh
pD Д sin (v+w+m0 A+; -
и входящие в него четыре постоянных Di1*, D'f}, ф1} ф2 определяются
по начальным условиям. Движение представляет наложение гармони-
гармонических колебаний с частотами кх и к2. Если же (при h > 0) нера-
неравенство B4) не имеет места, то а и р не останутся при t—>oo
*) В. В. Румянцев в работе «Об устойчивости движения гироскопа
в кардановом подвесе» II (Прикладная математика и механика 22, 1958,
стр. 499—503) получил это условие гироскопической стабилизации другим
путем.
7.9] ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА 317
ограниченными, и переход к линеаризированным дифференциальным
уравнениям B1) лишен смысла. Рассмотрение допустимости линеари-
линеаризации уравнений движения, когда решения линейных уравнений
ограничены как в этом, так и в последующих примерах, выходит
за рамки этой книги.
При вертикальной оси вращения наружного кольца, исключая а
из интегралов A9) и B0) и полагая sin p = и, придем к дифферен-
дифференциальному уравнению с разделяющимися переменными
G.9.25)
решение которого приводит к гиперэллиптическим квадратурам.
Случай уравновешенного гироскопа (h = 0) подробно рассмотрел
Е. Л. Николаи*); в статье Н. Г. Четаева **) даются указания, отно-
относящиеся к интегрированию уравнения B5) при h Ф 0. Исследование
устойчивости вертикального положения оси ротора j3 = -~- (рис. 60, б)
проведено К. Магнусом и В. В. Румянцевым ***).
Второе уравнение A8) при вертикальной оси вращения наружного
кольца принимает вид
-1 ba2 sin 2р — C3r0a cos p -f- mgh cos p = 0. G.9.26)
Из него, и из уравнения A8) следует существование частного решения
которому соответствуют равномерное вращение наружного кольца
и вертикальное положение оси ротора. Полагая
и линеаризируя уравнение B6) по предполагаемой малой величине г,
получим
*) Е. Л. Николаи, О движении уравновешенного гироскопа в кар-
дановом подвесе A939). Труды по механике, Гостехиздат, 1955, стр. 455—496.
**) Н. Г. Ч е т а е в, О гироскопе в кардановом подвесе, Прикладная
математика и механика 22, 1958, стр. 379—381.
***) К. Магнус, Об устойчивости движения, симметричного гироскопа
в кардановом подвесе, Прикл. матем. и мех. 22, 1958, стр. 173—178;
В. В. Румянцев, Об устойчивости движения гироскопа в кардановом
подвесе, там же, стр. 374—381. В последней работе рассмотрена также
устойчивость регулярной прецессии.
318 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Движение оси ротора будет гармоническим колебанием около верти-
вертикального положения при условии
/(ао) = — Ьа?-\~С.6г0а0— m£h >°- G.9.27)
Квадратный трехчлен /(а0) имеет вещественные корни (ао)х и (аоJ
при условии
C\r\ > 4btngh = 4tngh(A2-\-A3— C2) G.9.28)
и будет положительным, если угловая скорость а0 наружного кольца
заключена между границами
(«o)i < «о < («оJ- G-9.29)
Эти условия устойчивости вертикального положения оси волчка
в кардановом подвесе получены в упомянутых
работах К. Магнуса и В. В. Румянцева.
4°. Двухстержневая система. Рас-
Рассматривается плоская двухстержневая система,
показанная на рис. 62. За обобщенные коор-
координаты принимаются углы ср2 и tyx стержней АХВХ
и ВХС с осью Ахх\ через $х обозначается
разность ф1 — срг Моменты инерции стерж-
стержней АХВХ и ВХС относительно осей, перпендику-
перпендикулярных плоскости Ахху и проходящие,—пер-
проходящие,—первая через неподвижный шарнир Ах, а вторая—■
через шарнир Вх, обозначаются Jx и вх; масса
второго стержня названа тх. Требуется опре-
Рис. 62. делить угловые ускорения стержней, когда
в шарнире Вх приложена сила Fv направле-
направление которой перпендикулярно АХВХ. Длины стержней АХВХ и ВХС
обозначены через гх и рх% расстояние BXGX центра тяжести Gx второго
стержня от шарнира Вх — через sv
Кинетическая энергия системы равна
7"=-9"^1cfi ~т~"о"(wiriTi "+" 2лтг1/'15>1ср1ф1 cos $x ~\- &{$[). G.9.30)
Первое слагаемое — кинетическая энергия стержня AXBV вращающе-
вращающегося вокруг неподвижной оси А. Кинетическая энергия стержня ВХСУ
представленная группой слагаемых в скобках, вычислена по фор-
формуле D.7.7).
Элементарная работа силы Fx равна Fxrx 8cplf т. е. в нашем
примере
При обозначениях
* A12 = m1rlslcos$1, A22 = Ql G.9.31)
7.10]
ОПРЕДЕЛЕНИЕ И ИСКЛЮЧЕНИЕ МНОЖИТЕЛЕЙ СВЯЗЕЙ
319
приходим к уравнениям движения
К (О = Anb + Ai
¥г =
G.9.32)
Сравнивая с уравнениями D.6), имеющими в данном примере вид
= Q2,j
G.9.33)
причем индексы 1 и 2 отнесены соответственно к координатам о\
и tyj, находим, что отличными от нуля являются в рассматриваемом
случае следующие прямые скобки:
12,2; l] =
[1, 1; 2] = mlr
1. G.9.34)
Это легко проверить и непосредственным вычислением по фор-
формулам D.10.3).
Решив уравнения C2) относительно обобщенных ускорений,
получим
= i [A22Firi
Sftl
/i5isin Pi (?1ли — Ф?Л12)]-
G.9.35)
тде Д = ЛцЛ22 — ^i2- Конечно, эти же выражения получили бы,
шчислив по D.4) волнистые скобки. Составленные формулы исполь-
вуются ниже в п. 7.11.
7.10. Определение и исключение множителей связей
Вернемся к уравнениям Лагранжа A.6):
k=l
E=1,-....
G.10.1)
будем предполагать, чтобы не усложнять записей, что все связи —
яономные и неголономные — стационарны, так что уравнения A.5)
иисываются в виде
= 0 (*=1. .... 0.
G.10.2)
320
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
В числе этих уравнений могут быть и интегрируемые; так, если для
фиксированного к выполнены условия
да
■ks
да
kr
(г, s= 1, /г),
dqr dqs
то уравнение &-й связи может быть заменено конечным уравнением
Fktii. ■... ?л) = 0. G.10.3)
причем
aks =
G.10.4)
Число избыточных координат равно числу интегрируемых уравнений B).
Существенным является предположение, что уравнения B) раз-
разрешимы относительно / из п обобщенных скоростей, т. е. что дефект
матрицы
#11 #12 • • • а\п
#21 #22 • • • #2/2
а =
G.10.5)
#л #/2 ... atn !
равен нулю.
Тогда из / уравнений, взятых из общего числа п уравнений A),
например из уравнений
E=1. .... /),
G.10.6)
#11
#12
#21
#22
#2/
... #/1
... #/2
можно определить множители связи. Это следует из того, что квад-
квадратная / X ^ матрица
G.10.7)
— невырожденная, так как она является транспонированной по отно-
отношению к / X ^ подматрице а^ матрицы E). Пусть aqr обозначает
алгебраическое дополнение элемента aqr r-ft строки и #-го столбца
определителя | а* | матрицы G). Тогда
G.10.8)
и при подстановке этих значений \k в (п — /) остальных уравне-
уравнений A) найдем
2 (r=l п-1). G.10.9)
7.111 примеры 321
причем величина
Л/f+г = —Vr ^ akSak, t+r GЛ0-1°)
представляет разделенный на | а* | определитель, получающийся из|а*|
при замене в последнем 5-й строки строкой величин
ai,i+r> •••> ai,i+r G.10.11)
Сумма
i
Q* = ^\aks E=1, ..., п) G.10.12)
представляет обобщенную силу реакций связи, отнесенную к коорди-
координате qs. Это следует хотя бы из того, что при мысленном уничто-
уничтожении связей, выражаемых уравнениями B), и включении их реакций
в число активных сил, мы записали бы 5-е уравнение A) в виде
G.10.13)
С другой стороны, поскольку связи идеальны, они удовлетворяют
условию F.2.4), в котором вариации bqs связаны соотношениями
п
^aksbqs = 0, G.10.14)
S=\
и на основании теоремы, доказанной в п. 6.1, величины Q* пред-
ставимы формулами A2).
Таким образом, обобщенные реакции связей определяются ра-
равенствами
Q] = $s(T) — Qs (s=l I),
S^+,fe,(^-QJ (л=1 n-l).
G.10.15)
Уравнениями движения, в которых реакции связей исключены,
являются равенства (9). К ним должны быть присоединены уравнения
связей B).
7.11. Примеры
1°. Четырехстержневая система. Рассмотрим изображен-
изображенную на рис. 63 четырехстержневую систему *). Для определения ее
конфигурации достаточно задать два угла ср2 и ср2- ^ак вспомога-
вспомогательные величины введем еще избыточные координаты — углы ty} и ф2,
*) R. Beyer, Dynamik der Mehrkurbtlgetriebe, Zeitschrift fur ange-
wandte Mathematik und Mechanik, 8, № 2, 1926.
21 Зак. 2072. А И. Лурье
322
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
(гл. 7
связанные с ср2 и ср2 зависимостями
Фг = a-j cos cpj -f- pj cos ф1 — r2 cos cp2 — po cos ф2 = 0,
Ф2 = Г! sin cpj -+- pj sin ф, — r2 sin cp2 — p2 sin ф2 — a = 0,
G.11.1)
получаемыми при
проектировании замкнутого пятиугольника
А1В1СВ2А2А1 на координатные оси. Обо-
значения указаны на рис. 63.
*] Кинетическая энергия системы по
(9.30) и (9.31) записывается в виде
где индексы A) и B) относятся к парам
стержней АгВг, ВХС и соответственно А2В2%
В2С. Обобщенные силы равны (считаем,
что Fl±A1Bl и F2±A2B2)
рис. бз. "~ хГ" "~ 2/' ф'~ (ф;~.3)
Не повторяя вычисления, а основываясь на уравнениях (9.32),
можем написать равенства
4-
sin
sln
sin
sin
G.11.4)
Принимая нумерацию координат
запишем матрицу A0.5) в виде
Определитель I a! | равен
I'
—pi sin ф,
p2 Sin ф2
COS
— Г2 COS cp2
Pl созф!
p2 cos Ф2
= P1P2sin (f^l —
7.11] примеры
откуда, по правилу, сформулированному в п. 7.10, получаем
— Г\ sin <p, rx cos
р2 sin ф2 — р2 cos ф2
323
ал
— rx sin с
cos <pi
Аналогично находим
Sin (ф2
1
2
Г\
?2
Р1
sin
sin
sin
sin
sin
(?i
(Ф1
№.
(?i — фг)
-ф»)'
4 Pl sin (ф2 — фО ' 4 р2 sin (ф, —
и уравнения движения A0.9) принимают вид
sin (
sin (
sin (
tfi — M , 9
ф.-ф2) ' (
Фг — ?г) . g
Ф1— Ф2)
(Т) Г2
^ ?2
sin (ф 1
sin f^i
sin (ф!
sin (ф,
— Ф0
— ?2>
G.11.5)
Конечно, их следует рассматривать совместно с уравнениями свя-
связей A). Величины в правых частях этих уравнений представляют
обобщенные реакции связей Q* и Q*g. Обобщенными реакциями
связей Q*t и Q*a являются 8Ф| (Г) и §..,, (V).
Уравнения E) легко получить из весьма простых соображений:
отбросив мысленно шарнир С, заменим действие стержневой системы
А2В2С на АХВХС реактивной силой, проекции которой на оси обо-
обозначаются через X, Y\ к системе Л2В2С прикладывается сила про-
противоположного направления.
Элементарная работа сил, приложенных к двустержневой системе
АХВХС, равна
VW = Рггг 6ср1 И- ХЬ (г, cos cpj + р1 cos ф^ -f- УЪ (гг sin <рх + рх sin ф,) =
= г1(/7, — A'sincpj-f К cos «pj) Вер, -f- pj (—^
и уравнения движения будут
К (T) = r1 (Z7, — X sin ь + ^ cos
Для системы стержней А2В2С аналогично найдем
Ьр. (Г) = г2(F2 -f-^ sin cp2 — К cos<p2). 8Ф, (Г) = р2(Л' sin ф2 — Y :os ф2).
Исключение неизвестных X, Y приводит к уравнениям E). Преиму-
Преимуществом предшествующего рассмотрения является сведение «к общим
324
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
формулам, простое развитие которых дает все уравнения, необходи-
необходимые для решения каждой задачи» *).
2°. Плоское движение тяжелого твердого тела
на нити, проходящей через неподвижное кольцо.
Требуется составить уравнения движения тяжелого твердого тела,
снабженного двумя кольцами Ои /1 (рис. 64), через которые про-
пропущена гибкая, нерастяжимая и замкнутая нить, проходящая также
внутри неподвижного кольца Ov
Массой нити пренебрегаем; предпо-
предполагается, что центр тяжести С тела
расположен в плоскости треуголь-
треугольника ОХОА и что движение тела
происходит параллельно этой вер-
вертикальной плоскости. Общую длину
нити обозначим через L, расстоя-
расстояние О А между кольцами на теле рав-
равно /, вес тела Q, его момент инерции
относительно оси, перпендикулярной
плоскости движения и проходящей
через точку О, обозначим через 60.
Система имеет две степени сво-
свободы, так как положение тела мо-
может быть определено заданием положения полюса О системы
ocel Оху, связанных с телом, т. е. длиной s — ОХО участка нити и
углом наклона его ср к вертикали Ох;. Действительно, длины двух
других сторон треугольника ОЛ = / и OXA — L — / — 5 известны,
так что, зная положение точек Ох и О, можно построить этот тре-
треугольник, чем определяется положение тела, а значит и угол ф,
составляемый стороной ОА с горизонтальной прямой. Замечая далее,
О те
что угол при вершине и треугольника равен -^ — i
имеем
или
F(s, ф, cp) =
— 2l)L = 0. G.11.6)
Это уравнение связи между параметрами s, ф, ср. Можно было бы,
гользуясь им, выразить 5 через ф и ср, но это усложнило бы
форму выражения кинетической и потенциальной энергий и написание
уравнений движения. При сохранении всех трех параметров уравне-
уравнения хотя и остаются достаточно сложными, но все же обозримы.
Кинетическая энергия твердого тела, совершающего плоское дви-
движение, согласно D.7.7) равна
Т= ^- \rnvl -\- 90о)^ + 2^аJ(^о хс — ^оигУг)]» G.11.7)
*) Ж.-Л. Л а г р а н ж, Аналитическая механика, т. I, Предисловие автора.
7.11] примеры 325
причем в нашем случае а>2 = ф, а через хс и ус обозначены коор-
координаты центра тяжести тела в системе осей Оху.
Замечая, что координаты полюса О равны
Ео = 5 cos ср, т]0 =—5 sin ср,
находим
t0 = s cos cp — scp sin s, т]0 = — 5 sin cp — scp cos cp
и далее
vOx = £0 cos ф 4" ^o s*n Ф ~ 5 cos (? H~ Ф) — S(? sin (cp 4~ Ф).
vOy = —£0 sin ф 4" ^]ocos Ф — — 5 sin (cp 4~ф) — scpcos (cp 4~Ф)-
Выражение кинетической энергии принимает вид:
Т= ^ {ms2~\- ms2^2-\- 90ф2 — 2тф [sa(c) -\-s^af (a)]}. G.11.8)
Для краткости здесь обозначено
а(о) — хс sin o-{-yccosG, а' (а) = хс ;osa — ус sin a, о=ср4"ф» G.11.9)
причем а"(о) = — а (а). Потенциальная энергия равна
II = — mg\c = ~mg (;0 4- хс cos ф — ус sin ф) =
= — Q(s cos cp 4- Xq cos Ф — Ус sin Ф)*
Вычисление дает
t^(T) = m\s — а (о) ф — а7 (а)ф2 — s^2\,
tt(T) = m[s2:i—sa'{G)^-+-2s?-+s^2a(G)}, G.11.10)
&ф G) == m Г-— ф — i'a (a) — af (a) scp — 2icpa7 (a) 4~ sa (а) с^2
и далее
Qs = mg cos cp, Q9 = — /rcgs sin cp, Q±= — mg(xc sin ty-{-ус cos ty).
G.11.11)
Дифференцированием уравнения связи F) получим соотношение
s[L — / — / sin (cp -j- ф)] — si (cp 4- Ф) cos (ср 4~ ф) = 0,
приводящееся с помощью того же уравнения F) к виду
-о~г 1— (ср —|— Ф) cos (ср —{— ф) = 0. G.11.12)
Вторичное дифференцирование дает
sin(<р4^)=0. G.11.13)
326 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Из A2) получаем также
д* _ (L-2l)L д±__х G\\\А\
ds ~ 2s4 cos (ф + <f) ' ду ~ l ' ;
Теперь по A0.9), считая ф избыточной координатой, получим
5 S 2s^l COS (ср Ч~ Ф) т ' i /7 1 1 1 Рч\
^^^; > (/.11.10)
Эти уравнения движения надо рассматривать совместно с F), A2)
и A3). Заметим, что
i—%= —т8 (хс sin ^+Ус cos ^~s sin c?)= —mgf\c = m?\ G.11.16)
т. е. эта разность равна моменту силы веса относительно оси О^.
Поэтому последнее уравнение A5) выражает теорему о моменте
количеств движения
*<,(Т) — $9(Т) = К?'. G.11.17)
где К?,1—проекция момента количеств движения относительно точки Ох
на ось OjC. По D.8.10) она равна
К?1 = %Q^ - 7]0Qe + m (xcvOy — ycvOx) + воф, G.11.18)
причем по D.8.9) проекции вектора количеств движения Q равны
Qz = m (% — фгСТ]), Qri = m (v^ + фгс6), G.11.19)
где через rc^, rCri обозначены проекции вектора гс = ОС на оси
системы О^т]:
rc: = xccos^ — ус sin ф, rCrj = xc sin ф-(-УсС05Ф- G.11.20)
Теперь, применив приведенные выше формулы для проекций скорости
полюса и использовав обозначения A1), получим
К°* = m\— s2y + stya' (a) — sa(a) — stfa' (о) + ^Ц. G.11.21)
Вычислив производную по времени, придем к соотношению A7),
где I, и I определены по A0). Это служит проверкой вычисления.
Дифференциальные уравнения A5) допускают один первый инте-
интеграл—интеграл энергии
Выражения Г и И приведены выше.
7.12] ОБОБЩЕННЫЕ РЕАКЦИИ ОТБРАСЫВАЕМЫХ СВЯЗЕЙ 327
7.12. Обобщенные реакции отбрасываемых связей*)
Рассматривается система, подчиненная голономным связям, имею-
имеющая п степеней свободы. Ее конфигурация задается обобщенными
координатами q}f ..., qn. Мысленно отбросим некоторое число свя-
связей, реакции которых подлежат определению. Число степеней свободы
возрастет до п-\-т и для задания конфигурации понадобится ввести
еще т обобщенных координат gn + v ..., qn+m- Выбор их подчиним
условию, чтобы их нулевые значения приводили к первоначальной
системе. Иными словами, движение системы рассматривается с при-
привлечением избыточных координат qn+1, .... Яп+т, причем уравнениям
связей A.4.8) придается максимально простой вид
Этот прием уже применялся в п. 6.5 при рассмотрении статических
задач. Обращаясь к A0.4), имеем
a"+-=^ff =bn+r,s (r=l m; 8=1...., « + «) G.12.2)
.и по A0.12) обобщенные реакции связей будут
т
e:=2ww,=o с- .*| G|23)
Q',u=Ku « = ' "■>■)
Уравнения движения A0.1) примут вид
t.(T) = Q. (s = i я); 1
&n+r(T) = Qn+r + ln+r (r=l, .... m). J (- -V
Здесь кинетическая энергия и обобщенные силы составляются
в предположении, что связи, задаваемые уравнениями A), отсутствуют.
Уравнения D) должны, после того, как они составлены, рассматри-
рассматриваться совместно с уравнениями связей. Это значит, что в уравне-
уравнениях D) следует принять
<7л+г = 0, дп+г = 0, 9„+г = 0 (г=1 т). G.12.5)
*) А. И. Лурье, Заметки по аналитической механике, Прикл. матем.
и механика, 21, № 6, 1957, стр. 760—768.
328 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ 7
В явной форме, в случае стационарных связей, уравнения движе-
движения имеют вид D.6)
п - т п-^тплт
2 А&Я*+ 2 2 la> PI s]qaq, = Qs E=1 п), G.12.6)
а=\ с=1 р=1
п т пл т пл т
2 An+rJ.+ 2 -2 [о. Pi n+r]q,qP = Qn+r+h+r G.12.7)
а=1 а= 1 р = 1
(г= 1, . . ., /я).
Рассмотрение нестационарных связей не повлекло бы других
осложнений, кроме удлинения записей. Теперь, учитывая E) и обо-
обозначая нуликом сверху значения функций от q} Яп+т> когДа
qn + li ..., qn+m делаются равными нулю, получим вместо F) и G)
(s= 1, .. ., п), G.12.8)
п
%А
о = 1
п
Ч
2
а =
5а а
1 П
п
а = 1
.„л
/г
р = 1
а
V
ч:
s]°q
(г =
я —Q
i р ^
1, .•.,
j
?
/Л).
В уравнениях F) и G), составленных по выражению кинетиче-
кинетической энергии
п т п + т
5=1 а=1
m n mm
п п
5 = 1 а=1 /-=1 о = 1 r=1 t = ]
G.12.10)
коэффициенты Л5а представляют функции всех переменных q] Qn+m
Обобщенные силы в этих уравнениях вычислялись по выражению
элементарной работы активных сил на виртуальных перемещениях,
определяемых совокупностью всех вариаций 8^, ..., %
-г8<7/| + г- G.12.11)
5=1 Г=1
Кинетическая энергия 7° первоначальной системы получается из вы-
выражения A0) при qn+r и qn+r (г = 1, .... т), равных нулю:
/г /г
7° = — ^ ^ л^Л* G.12.12)
5=1 а=1
7.12] ОБОБЩЕННЫЕ РЕАКЦИИ ОТБРАСЫВАЕМЫХ СВЯЗЕЙ 329
Полагая нулями величины qn + r в выражения v обобщенных сил, найдем
их значения, стоящие в уравнениях (9) и (8). При этом QJ, ..., Q®
равны обобщенным силам, которые получили бы, составляя уравнения
движения первоначальной системы. Эти уравнения имеют по D.6)
и по определению прямых скобок вид
а=1 с=1р=1
Прямые скобки в уравнениях (8) равны
и нулик указывает, что qn + l, . . ., qn+m делаются нулями после диф-
дифференцирования, тогда как в скобках при составлении уравнений A3)
они приняты равными нулю до дифференцирования. Но это не имеет
значения, так как дифференцирование ведется по переменным qs, для
которых 5=1, ..., п, а нулями становятся прочие переменные.
Итак, уравнения движения (8) тождественны с уравнениями движения
первоначальной системы A3).
Отметим еще, что по только что указанной причине прямые
скобки в уравнениях (9) определяются так:
. 1() 1 /<Иг,л-гг . дА?,п+г
>?Р <>q3 dqn.
= ■0 ir^H ?r^ (з11^) I G.12.14)
и для вычисления их требуется знать значения коэффициентов AQ0
в выражении A0) кинетической энергии лишь с точностью до членов
первой степени включительно относительно переменных qn+r\ значения
же An + rj0 должны быть известны лишь при qn + r, равных нулю (т. е.
надо знать А}п fr 5). Знания коэффициентов An + rrjA_t(r, t=\ т)
не требуется.
В формулах (9), дающих значение обобщенных реакций отбрасы-
отбрасываемых связей, обобщенные ускорения могут быть заменены их вы-
выражениями по уравнениям (8). Согласно D.7) имеем
р=1 Х=1 р=1
330
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
причем волнистые скобки вычислены для матрицы коэффициентов
квадратичной формы A2), (А~1\о—элементы обратной матрицы»
Подстановка в формулы (9) дает
0=1
p = l X = l
n n
G.12.16)
В дальнейшем обозначим
о=1
(r=l т\ р=1 п\ G.12.17)
Эти величины вычисляются так: заменим в определителе — дискрими-
дискриминанте квадратичной формы A2)
\А*\
р-ю строку строкой коэффициентов
^21
А°
А12 .,
^22 • •
..Al
-An
• тгп
**П + Г, 1» fin+T, 2» • • • » J*n t Г, П'
G.12.18)
G.12.19)
Частное от деления полученного определителя на \А°\ равно М9п+Г.
Вспомнив далее значения D.4) волнистых скобок, имеем по A7)
п
V
а=1 т=1
т=1
G.12.20)
и подстановка в выражения A6) после некоторых перемен индексов
приводит к равенствам
К+г = 22 Я«Я> {[^ Р; п + г]° - 2 М; нг [р, а; х
а=1 р=1 ' I т=1
(r=l, .... т). G.12.21)
Вывод этих формул был нашей целью; они дают выражения обоб-
обобщенных реакций отбрасываемых связей через задаваемые силы (по
ним определяются Q^ Q^J и через обобщенные скорости. От
7.13] ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ РЕАКЦИЙ СВЯЗЕЙ 331
последних (в рассмотренном случае стационарных связей) обобщен-
обобщенные реакции зависят квадратично.
Каждая из величин Х/| + г определяется формулами B1) независимо
от остальных. Поэтому можно находить Хл + 1, ..., Хл+т поочередно,
вводя избыточные координаты по одиночке.
7.13. Геометрическое истолкование обобщенных реакций связей
Примером плодотворного использования терминов геометрии рима-
нова пространства применительно к задаче динамики может служить
рассмотренная в предыдущем пункте задача о нахождении обобщен-
обобщенных реакций связей.
Необходимые для понимания последующего сведения даны
в пункте П. 2.13. Рассматриваемой системе материальных точек сопо-
сопоставлено, как объяснено в п. 7.8, риманово многообразие Rn с квад-
квадратичной формой Т° (dtJ\ ковариантные составляющие метрического
тензора в нем обозначены через аа^. Многообразие Rn является
частью многообразия Rn+m с квадратичной формой T(dtf\ это значит,
что точки Rn+m, которым соответствуют фиксированные значения
обобщенных координат
qn + \=qn~\% ш#в> qn-m = qn~m^ G.13.1)
принадлежат Rn. Иными словами, рассматриваемая система мате-
материальных точек может быть получена из системы, соответствую-
соответствующей Rn+m, при наложении на последнюю пг связей, задаваемых
соотношениями A). Полагая в выражении кинетической энергии
системы Rn+m
T(dt)* = ±(ga}dq*dqt + 2ga,n+sdrdq»+*+gn+Stn+^
G.13.2)
(суммирование по греческим индексам от 1 до п, по латинским —
от 1 до т) дифференциалы dqn+s равными нулю, придем к 7° —
кинетической энергии рассматриваемой системы. Таким образом
(£«з)о = *«р- G.13.3)
Сила, относимая к изображающей точке в многообразии Rn+m, за-
задается вектором Q + A c ковариантными составляющими Qa,
Qn+s-\-An+s\ при этом элементарная работа задаваемых сил на воз-
возможном перемещении точек освобожденной от связей A) системы Rn
равна
Q9bq*-\-Qn+s*q"+*9 G.13.4)
тогда как
&n+sbqn+s G.i3.5)
332 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
представляет элементарную работу реакций освобожденных связей.
Величины (QaH представляют ковариантные составляющие вектора Q
в точках многообразия Rn, т. е. обобщенные силы для рассматри-
рассматриваемой системы.
Второй закон Ньютона для Rn+m записывается в виде
G.13.6)
и остается найти значение вектора ускорения w в точках Rn. Вектор
скорости в Rn+m равен
Его производная по времени будет
Но в точках Rn+m, принадлежащих Rn, согласно A) имеем
gn+S = Q gn+S — Qe G.13.7)
Итак,
где pa = (raH — базисные векторы Rn. Теперь, обратившись к соот-
соотношению (П. 2.13.21), заменим вектор (гарH его значением. Приходим
к соотношению
-M\u\z, C; tfa)q° <&«+'. G-13.8)
Напомним, что индексом а обозначаются величины, вычисляемые
с помощью метрики Rn. Поэтому, согласно (8.7) и (8.8), первая
группа слагаемых в (8) представляет вектор ускорения (<wa) в Rn:
= ?У- G.13.9)
Вторая группа слагаемых определяет вектор
юо = 9е?"([«. Р; «+a-^ia. P; т1в)^х/- G.13.Ю)
Поскольку
вектор Wo следует назвать ортогональным пространству /?rt. Вектор Tt^
в формуле (8) представляет ускорение в точках Rn + m, принадлежа-
принадлежащих Rn. Он равен геометрической сумме вектора ускорения в Rr и
ортогонального пространству Rn, но рассматриваемого в его точках»
вектора ускорения w0. Соотношение (8) обобщает формулу F.3),
относящуюся к движению точки на поверхности. Уместно вспомнить
7.14] ПРИМЕНЕНИЕ К ПЛОСКИМ СТЕРЖНЕВЫМ СИСТЕМАМ 333
здесь, что вычисление коэффициентов второй квадратичной формы
поверхности Ьа^ проводится по правилу, содержащемуся в формуле A0).
Об этом говорилось в конце пункта П. 2.13.
Теперь, обращаясь к соотношению (П. 2.13.28), представим вектор
силы Q -\- Л в точках Rn в виде
Q + A = (Q%Pa + [(Qn+t)o+(An+t)o-Ml.1(QX]f"¥t- G.13.11)
Первое слагаемое вычислено в метрике Rn; оно равно #ai3(Q)pPa» т. е.
не содержит составляющих вектора А. Теперь надо записать в раз-
развернутом виде второй закон Ньютона, т. е. равенство F)
= (<?")* Pa + [№л+,)о -+" (Л.+/)о - Man+t (Qa)J rS+t. G.13.12)
Таким образом, получаем уравнения движения в Rn в известной
форме (8.12)
и выражения ковариантных составляющих ортогонального простран-
пространству Rn вектора силы реакции
— [(<?Я+Д)—ЛС/«2„)в) (^=1 «). G.13.13)
Пришли, если учесть изменения обозначений, в точности к выраже-
выражениям A2.21). В отнесении к ранее известным соотношениям опреде-
определенных (хотя бы словесно) геометрических образов и заключается
поучительность нового вывода. Силы реакции идеальных связей
ортогональны пространству, в котором движется изображающая
точка; они определяются ортогональным этому пространству слагае-
слагаемым вектора ускорения. Разыскание движения требует знания лишь
той части вектора V, которая принадлежит Rn. Снимая связи, обна-
обнаруживаем другие составляющие этого вектора; полностью содержание
вектора v раскрывается при освобождении системы от всех связей,
т. е. в пространстве £"зуу-
7.14. Применение к плоским стержневым системам
Г. Физический маятник. Рассматривается тяжелое твердое
тело веса G, имеющее вертикальную плоскость симметрии и могущее
вращаться вокруг неподвижной оси О, перпендикулярной этой пло-
плоскости— физический маятник (рис. 65). Проведем мысленно сече-
сечение SKS, отделяющее в маятнике тела 7 и 2. Требуется определить
334
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
главный вектор и главный момент реактивных сил в этом сечении —
тех сил, которые обеспечивают объединение тел / и 2 в одно
(маятник).
Кинетическая энергия маятника и потенциальная энергия силы веса
равны
T° = -icQoq\t T\° = — Gccosqv G.14.1)
где 0О — момент инерции маятника относительно оси вращения,
ОС = с—расстояние центра тяжести С от этой оси.
После отделения тело 2 приобретает три степени свободы; за
параметры, определяющие его положение, примем отрезки q2 и qz%
Рис. 65.
отсчитываемые по перпендикуляру к линии ОК и вдоль нее, а также
угол qx-\-qA между прямой К"С и нисходящей вертикалью. В перво-
первоначальной конфигурации q2, qz, q4 равны нулю, что соответствует
условиям A2.1) выбора избыточных координат.
Для упрощения последующих вычислений предполагаем, что центры
тяжести Сх и С2 тел 1 п 2 расположены на прямой, проходящей
через точку О; на этой же прямой ОС расположен центр тяжести
маятника.
Кинетическая энергия системы, освобожденной от связей, т. е.
1ела 2 и маятника 1 дается выражением
G.14.2)
где во — момент инерции маятника / относительно оси вращения О,
вс2 — момент инерции тела 2 относительно параллельной оси, про-
проходящей через центр инерции С2 этого тела, т2 — его масса, vc<> —
скорость точки б
7.14] ПРИМЕНЕНИЕ К ПЛОСКИМ СТЕРЖНЕВЫМ СИСТЕМАМ 335
Координаты этой точки равны
хс.2 = a cos qx — q2 sin qx + qz cos qx + c2 cos {qx + <74),
уCa = a sin ^ -+- q2 cos ^ + qz sin ^ + c2 sin (^ -f- #4).
Поэтому
*c, = 49 + У с., = [(« + Я + 2 («
+ 2c2 (a
причем невыписанные слагаемые не представляют интереса, так как
они содержат квадраты и произведения q2, q3, q4, произведения их
на #1 и на обращающиеся вместе с q2, q3, qA в нуль множители,
а также члены, пропорциональные фу но с множителями более высо-
высокого порядка, чем первый, относительно q2, qz, q4.
Получаем
Здесь
в0 = вЬ + вс,-+- т2 {а + с2J
представляет, как, надо было ожидать, момент инерции маятника от-
относительно оси вращения О. Далее,
Аи = т2(а-\- с2), Л°13 = О, А°ы = вСз + т2с2 (а + с2).
Потенциальная энергия системы равна
= — G1c1 cos qx — G2 [(a + q3) cos ^j — q2 sin ^ -f- ^2 cos {qx -|- 74)] =
= —-Gc cos ^! — G2q3 cos ^ + G2 (q2 + c2^4) sin ^ -f-,
причем
Gc = OlCl+G2(c2
Поэтому
Q°i = — Gcsinqx, Q% = — G2 sin qx, Q°z =
По формулам A2.17) имеем также
Кроме того,
li. 1; 3]и = —.
336
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
Остальные прямые скобки равны нулю. Вычисление по формулам A2.21)
приводит к выражениям
1 L G во
\ == [т2 {п ~+~ С2) Я\ + ^2 C0S #l] '
~r с п " ^ s*n Q\-
и w0 j
В этом примере Х2 представляет поперечное усилие, Х3— продоль-
продольное, Х4— изгибающий момент в сечении SKS\ это — обобщенные силы,
отнесенные к координатам q2, qs, q4. Положительные направления
усилий и момента (если рассматривать действие на отсекаемую часть)
совпадают с направлениями отсчета соответствующих координат.
2°. Обобщенные реакции связей в плоских меха-
механизмах. Начнем с рассмотрения разомкнутой цепи из п звеньев,
имеющей п степеней свободы. На
рис. 66 изображена цепь, состоя-
состоящая из последовательно соединен-
соединенных звеньев, но нижесказанное
имеет место и для цепей с боко-
боковыми ответвлениями. Звено цепи
условно изображается отрезком
прямой, соединяющей два после-
последовательных шарнира, но это не
ограничивает общности, так как
мы не будем считать центр тя-
тяжести звена расположенным на
этой прямой. Ведущим будем на-
называть звено, имеющее неподвиж-
неподвижную ось вращения, ему приписы-
приписывается индекс 1; индекс / имеет
звено, соединяющее шарниры Аь
и А1+1. Точка А1 принимается за
начало системы осей, связанных
с /-м звеном; направления этих
векторами е[ и е1Т причем вектор elv
составляет угол ср/ с неподвижной от-
е/
х
Рис. 66.
осей задаются единичными
направленный от At к А1+1,
счетной осью Ахх. Положение центра тяжести Ct звена в этой си-
системе осей задается вектор-радиусом
Векторы скорости vt шарниров связаны рекуррентным соотношением
7.141 применение к плоским стержневым системам 337
где /j_j — длина отрезка А.ь_^Аг. Кинетическая энергия /-го звена
вычисляется по формуле D.7.7)
= m.v\ -+- 2mtft (s[vi - ey_ — spt - e[) 4- в,#. G.14.5)
где mt—масса звена, В/—его момент инерции относительно оси
шарнира At\ через k обозначен единичный вектор, перпендикулярный
плоскости цепи, kyt— вектор угловой скорости /-го звена.
Таким образом,
7, = I 6^, Т2 = -1 в.^2 -+- 4 m./^+m.^SYPt D2)cos pa-^> sin pa).
y «
i ^гЪ cos Рм)
) C0S P3I - 43) Si" ?3l) -H l2b (Sf C0S ^32 - 43) Sitl Р32)]
и т. д.,. где введено обозначение разностей углов
Вычисляя сумму выражений вида E), получим выражение кине-
кинетической энергии цепи в виде однородной квадратичной формы:
причем коэффициенты Akk постоянны, а Л5Й зависят лишь от
так что
= Т7о^-- G.14.8)
Элементарная работа активных сил, действующих в точках /-го звена,
приводится к виду E.2.5)
l'Wt= Vl -S^-f-mU^, G.14.9)
где V'—главный вектор этих сил, пг1г—их главный момент отно-
относительно оси шарнира At\ brt — виртуальные перемещения шарни-
шарниров Ah связанные соотношениями, подобными D):
ог, = 8г/-1+/|.1^8ср/| 8г, = 0 (/ = 2, .... /г). G.14.10)
Элементарная работа активных сил для всей цепи представится ра-
равенством
3'r = 2Q,5?s^Q1ocp1+2Qi5cPi. G.14.11)
5=1 5=2
22 Зак. 2072. Л. И. Лурье
338 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Рассматриваемая цепь /г-звенная становится механизмом при нало-
наложении п—1 связей; уравнения этих связей
/%(<Pi <Рл) = 0 (А=1 л—1) G.14.12)
можно предположить разрешенными относительно ср2, ..., срл
?5 = /,(<Pi) (* = 2> •••■ «)• G.14.13)
Тогда
К G.14.14)
и выражение кинетической энергии G) запишется в виде
7° = ^в'(?,)#. G.14.15)
Здесь
называется моментом инерции механизма, приведенным к оси Лг ве-
ведущего звена. Нуликами указывается, что рассматриваемые величины
вычислены для значений ср2, . .., срл, определяемых уравнениями связей.
Элементарная работа активных сил A1) становится равной
G.14.17)
причем mz называется приведенным к ведущему звену механизма
вращающим моментом. Уравнение движения механизма теперь можно
записать в виде
0 вЧ?1)?1+4-^Т? = %. G.14.18)
Освободим мысленно механизм от связей. Тогда вместо соотноше-
соотношений A3) и A4) можно принять
причем, имея целью определение обобщенных реакций отброшенных
связей, достаточно в последующих вычислениях удержать слагаемые
не выше первой степени относительно qs и qs.
7.141
ПРИМЕНЕНИЕ К ПЛОСКИМ СТЕРЖНЕВЫМ СИСТЕМАМ
339
Начнем с составления кинетической энергии; для этого в ее выра-
выражении G) следует заменить ср5 и ср5 их значениями A9). Найдем
г-2
(A.
/i),
G.14.20)
причем в соответствии с (8)
п
и кинетическая энергия механизма, освобожденного от связей, пред-
представится (с указанной выше точностью), согласно G) и A6), равен-
равенством
Здесь учтено, что
п п
5 = 2 k = <2
A°lsqs
L5 = 2
5=2
2 2
5-2 £ = 2
'• 1
JkQs •
у
5-2 k = 2 5 = 2
Выражение A1) элементарной работы должно быть взято в виде
b'W = Q?
5=2
" (f's
[+2q2%. G.14.23)
5 = 2
Теперь налицо все данные, чтобы применить формулу «'12.21). В нашем
случае п=\ и она принимает вид
M\mx—Q* (r = 29 ..., я).
G.14.24)
22*
340 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Коэффициенты выражения кинетической энергии приведены к виду
г,.
Поэтому
имеем
Далее,
I1 1 ч ^
Обобщенная реакция г-й связи оказывается равной
_ (dAir\° f> _ V ( dAkr у f, f,
и учитывая, что
* 2 й=2
G.14.25)
3°. Кривошипный механизм (рис. 67). Этот механизм
можно получить из трехзвенной цепи при наложении связей
sin ср2 = — jjl sin ?1, ?3 = 0 (р = b^j . G.1 4.26)
Из этих уравнений имеем
^ JiiL9i f> f Ощ G.14.27)
3 3
COS3 *f
7 14]
ПРИМЕНЕНИЕ К ПЛОСКИМ СТЕРЖНЕВЫМ СИСТЕМАМ
341
Из вышеприведенных выражений Tv Т2, 73 получаем значения коэф-
коэффициентов Aik
2 _ 2 л г\
/\ = {у^ —|— (/7^2 Ч~ ^з) 1' 22 ==~ 2 i~ ^3^2» 33 ~~:: 3'
у410 = m2l\ {s\~] cos p2i — S2 sin p21) -j- rn^xl2 cos C21,
Приведенный момент инерции и его производная по cpi равны
в'(ср1) = Л11-
и выражения обобщенных реакций связей по B5) принимают вид
G.14.28)
Обобщенная реакция Х2 представляет реактивный момент, при-
прикладываемый к шатуну пои неизменном значении с;3 = 0; реактивный
Рис. 67.
момент, не допускающий поворота ползуна, при сохранении первой
из связей B6), обозначен через Х3*).
*) Подробно, по другим путем, задачи этого рода рассмотрены в содер-
содержательной книге Хейна. См. К. Heun, Lehrbuch der Mechanik, I Teil, Kine-
matik, Sammlung Schubert, Leipzig, 1906, стр. 133—153.
342
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
Реактивный момент Х2 легко получить, используя уравнения дви-
движения двухзвенной цепи (9.32). Второе из них надо теперь записать
в виде
так как частная производная по -?г может быть заменена взятой со
знаком минус производной по р21. Остается подставить
и заменить ср2 его значением по уравнению движения механизма A8).
4°. Двухстержневая система. Требуется определить реак-
реакцию в шарнире Л2 двухстержневой системы, представленной на рис. 68,
нагруженной силой F в точке Л3.
Отделив второй стержень в шар-
шарнире А2, обозначим через q^ и д4 про-
проекции на оси х и у вектора, мысленно
сообщенного этой точке перемещения.
Тогда скорость ее будет
где /j, /2—единичные векторы осей х
и у. Кинетическая энергия первого
стержня равна
л =4 ад-
рис gg При вычислении кинетической энер-
энергии второго стержня достаточно сохра-
сохранить слагаемые не выше первой степени относительно q3, q4, так
как для вычисления обобщенных реакций связей остальные члены не
имеют значения:
Г2 = {в2^2 + т2 {1\я\ + 21\Ч\Я* cos ^1 — 2/i<^3 sin ^1) +
+ 2m2sq2 [Itf^ cos (^r2 — qx) — g3 sin q2 + ^4 cos g2]|,
где 5 обозначает расстояние центра тяжести С2 от шарнира А2. Итак,
Т= 70 + 2Л?з^дз + 2Л?4д^4 + 2Л^з + 2Л^4, G.14.29)
где через Т° обозначена кинетическая энергия исходной двухстер-
двухстержневой системы:
Т° = 1 {Allq2i+'2Al2qlq2 + A22q22)t G.14.30)
7.14]
ПРИМЕНЕНИЕ К ПЛОСКИМ СТЕРЖНЕВЫМ СИСТЕМАМ
343
причем коэффициенты этого выражения не отличаются от их значе-
значений при q3 = q4 = 0:
Аи = 0J + mj\% Л22 = в2, АХ2 = m2slx cos (q2 — qx).
Остальные коэффициенты равны
13 = — m2ll sin qv
\\ = m2lx cos qv
А°2з = — m2s sin q2,
A-24 = m2s cos q2.
Надо еще составить выражение элементарной работы силы F
и обобщенные силы будут
Ql = —Xvnql +-Ycosqv
Q2 = — X sin q2 ~\- Y cos q2,
Формулы A2.21) при п = 2 имеют вид
Q4 = Y.
^2([l, 2; rj°—Л1М1. 2; 1]° —Ж?[1, 2; 2]°L-
+ VKl2. 2; r]°—Mj[2, 2; 1]°—Ж?[2, 2; 2]°) +
+ yMjQ? + M^-Q°. G.14.31)
где /- = 3,4. В нашем случае отличны от нуля скобки
[2, 2; 1]° = — m2lxs sin (q2 —
[1, 1; 31° = — m2lxcosqv
[1, 1; 4]° = — m^sin^,
Имеем также
[1, 1; 2]° = m2lxs sin (q2 — qx),
[2, 2; 3]° = — tn2s cos q2,
[2, 2; 4J° = —
sin q2.
Ли А12
АХ2 А22
и далее, в соответствии с A2.17) и сформулированным вслед за этой
формулой правилом,
т2
! Sin i
Al2
', sin q2
A22
м\-.
m2
L{ cos qx s cos q2
m2
I A°
m2
j-
\
I
1
/.
I COS
An
sin
4\
s
An
s sin
AX2
cos q2
42
•
344 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ 7
Остается сделать подстановку в формулы C1). Ограничимся напи-
написанием значения Х3 в предположении, что сила F отсутствует.
Получаем
Лз = ~~ "УЖ] {Лп И22 cos Яг — m2s2 sin 4<i ^п (q2 — q})\ —
— mffis2 cos (q2 — qx) cos q^ q\ — -~^- {A22 [ An cos q2 -+-
+ m2l\ sin qx sin (q2 — qj\ — m]l\s2 cos (q2 — q^ cos qx]q\.
Конечно, это же выражение Х3 получили бы, составив уравнение дви-
движения центра инерции стержня А2Аг
т2х°с = Х3, x°c = — ll (qx sin qx + q\ cos qx) — s (q2 sin q2 -f- q] cos ^2),
причем qx и ^2 надо заменить их значениями по уравнениям движе-
движения двухстержневой системы, т. е. (при надлежащих изменениях обо-
обозначений) выражениями (9.35). Это решение было бы короче, но
автоматизм расчета был бы утрачен.
7.15. Циклические координаты
Обобщенную координату qs голономной системы условимся назы-
называть циклической при соблюдении следующих условий: соответствую-
соответствующая ей обобщенная сила Qs равна пулю, а выражения остальных
обобщенных сил, равно как и выражение кинетической энергии
П. е. То и коэффициенты Ask, Bs) не зависят от этой координаты.
Обобщенная скорость, соответствующая циклической координате,
будет циклической обобщенной скоростью. Нециклические координаты
называются позиционными. Если силы потенциальны, то в соответ-
соответствии с приведенным определением циклическими будут те коор-
координаты, которые не входят в выражение кинетического потенциала L.
Пусть в системе с п степенями свободы, конфигурация которой
определяется обобщенными координатами qx qn, позиционными
являются координаты qv . . ., qm, а остальные qm + v . . ., qn — цикли-
циклическими. Тогда
Уте+1 = 0 Qn = °'> Qs = Qs(Qi Vm)(s=l m) G.15.1)
и
T=T{qx, ....qm; qv .... qn; t)9 G.15.2)
а в случае потенциальных сил
L = L{qi qm> «7, qn, t). G.15.3)
7 15] ЦИКЛИЧЕСКИЕ КООРДИНАТЫ 345
Выражение кинетической энергии может быть разбито на слагаемые:
= т; + и + г.; +• т; +.г;* + то(дх qn- t). рл5.4)
Здесь Т* и Г*"—квадратичные формы позиционных и соответственно
циклических скоростей, U — билинейная форма тех и других:
7"
2
1 2
_ 1
~2
1
~~ 2
т
у
fe=l
п-т
т
5=1
п-т
1
5=1 fe=l
s> m+k4m+s4m+k'
im + k-
G.15.5)
Линейная часть кинетической энергии также представлена двумя сла-
слагаемыми
т п — т
= 2j В q , I = £j Bm+sqm+s. G.15.6)
5=1 5 S 5=1
Квадратичные формы 7* и Т** образованы с помощью квадратных
матриц
А„
А
лпг+1, п
... -А.
. G.15.7)
Эти матрицы — невырожденные, так как их определители \ Л*\ и | Л** |
представляют диагональные миноры определителя | А |, положительные,
согласно неравенствам Сильвестра D.1.10).
Обратимся к дифференциальным уравнениям движения. Замечая,
что
=0
E=1, .... л —т),
G.15.8)
и учитывая A), разобьем их на две группы: для позиционных
координат
d дТ дТ „ 1
—:—. —- = QS (s=l m) G.15.9)
dt dqs dqs ч '
и для циклических
— --^—= 0 E=1 n — m). G.15.10)
dt ciqm+s
346 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА fГЛ. 7
Эта группа уравнений сразу интегрируется. Получаем п—т первых
интегралов уравнений движения
^ («=1. .... «-/»). f7.15.ll)
выражающих, что обобщенные циклические импульсы сохранят
при движении постоянные значения, обозначенные $m+s. В более
подробной записи уравнения A1) имеют вид
дТ? dU дТ\*
^ + hi P (s=l n — m) G.15.12)
m
2 4. ft<7fc — Bm+S G 15.13)
или
п — т
^■J tn+si m + k* m + k Ym + s ш*А
k = l k=l
E=1 п — m).
Эта система линейных уравнений вследствие положительности ее
определителя | Л**| допускает решение относительно циклических
обобщенных скоростей. Последние будут зависеть от позиционных
обобщенных координат и скоростей, постоянных циклических импуль-
импульсов и времени
qm+r = fm + r(qv . .., qm, qv ..., qm\ $m + v ..., ря; t) G.15.14)
(r=l. .... n—m).
Разности ^m+5—Вщ+s и Яи в эти соотношения входят линейно.
Более подробно: пусть
1, п
G.15.15)
АП. Г72+1 ^ АПП
представляют матрицу, обратную Л**, т. е.
Am+s. m + k I a
где km+k,m+s—алгебраическое дополнение элемента Ат+ь, m+s опре-
определителя |Л**|. Тогда
п—т т п—т
'п V/Q Я N. Am + r> m+s V ^ V Л дт + r, rr+s
Чт+г — .£J VPm+5 Dm+s) n ^ 4k Zi ^m+s, kH
G.15.17)
347
G.15.18)
представляют частное от деления на |Л**| определителя, получаю-
получающегося из | Л** | при замене в нем элементов /*-й строки
А А
величинами
7.16]
Величины
Nm+r
Mkm+r
п — т
n-m
_ у
ФУНКЦИЯ
9.,,-
Л,„,И
РАУСА
Bm + s)Am+r,m+St ■
и соответственно
Получаем
^«+,—SAl*+r^ (/"-I л —я»). G.15.19)
fel
Таковы более подробные выражения функций A4). Если подставить
их в уравнения движения (9)
то в их запись войдут позиционные обобщенные скорости и коорди-
координаты, время t и постоянные циклические импульсы. Можно было бы
осуществить в общем виде эту подстановку, но проще идти другим
путем, позволяющим представить эти уравнения в легко обозримой
и знакомой форме уравнений Лагранжа второго рода.
7.16. Функция Рауса
Упомянутый в конце предыдущего пункта способ записи диффе-
дифференциальных уравнений движения принадлежит Раусу. Он основан на
введении вместо кинетической энергии Т другой функции R, зави-
зависящей от позиционных координат и скоростей, времени t и цикли-
циклических постоянных импульсов. Эта функция определяется так:
0 =
- GЛ6Л)
Составим выражения производных
dR dR dR (b~\ — —
348 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРЛНЖА | ГЛ. 7
учитывая, что в правые части равенства A) аргументы qk, qk, [im+r
входят и непосредственно, и через функции /m+r. Получаем
dR
так
как
дТ
дЧ
по
п-
t
A5.
-m
?
- с
.11)
дТ (
и A5.
^fm-\
14)
г
дТ
n — m
й
э ^.
fm + r
k
дТ
G.16.2)
и суммы в предыдущем равенстве сокращаются. Это же вычисление
повторяется при дифференцировании по qk
dR дТ
(k= 1, .... m). G.16.3)
Аналогично находим
п — т п — т
V дТ dfm+r _ * _ V
Л df d' 4m+S ^
и, следовательно,
ir— (s=l n—m). G.1R.4)
Подставив выражения производных B) и C) в дифференциальные
уравнения для позиционных координат A5.9), получим
g AT) = &S(R) = — -^ — = QS E=1 m). G.16.5)
Эти уравнения, данные Раусом, имеют структуру уравнений Лагранжа,
причем роль кинетической энергии играет функция Рауса R; они
содержат лишь позиционные координаты и соответствующие этим
координатам обобщенные скорости и ускорения. Способ Рауса поэтому
называется способом игнорирования циклических координат, а сами
эти координаты—игнорируемыми или скрытыми. В противопостав-
противопоставление этому позиционные координаты называют явными.
Проинтегрировав систему т дифференциальных уравнений второго
порядка, определим обобщенные координаты и скорости как функции
времени t, п — т постоянных $m+s и еще 2т постоянных интегри-
интегрирования:
) G.16.6)
. . "J л \ ' Ш Г I ' - - ' \ W I ' - - - » - Z.IIL/ \~ » ---» •
7.16] ФУНКЦИЯ РАУСА 343
Эти значения надо подставить в равенства D); тогда определение
циклических координат приведется к квадратурам
(s=1 n~mh GЛ6-7)
Уравнения D), F), G) представляют полную систему интегралов
исходной системы дифференциальных уравнений движения, содержа-
содержащую 2п произвольных постоянных. Наличие п — т циклических
координат позволило понизить порядок интегрируемой системы до 2т
и свести задачу к интегрированию этой системы E) и к выполне-
выполнению п — т квадратур G). Надо к этому добавить, что от выбора
обобщенных координат зависит и число циклических координат;
например, при задании положения материальной точки в поле цен-
центральной силы декартовыми координатами х, у, z циклические
координаты отсутствуют, тогда как при применении сферических
координат одна из них (долгота) будет циклической (пример 1°
п. 7.18).
Конечно, выражения циклических координат можно записать,
используя A5.19), и в виде
^J } G.16.8)
В случае потенциальных сил, вычитая из обеих частей равен-
равенства A) выражение потенциальной энергии II (qx, ..., qm) и заме-
замечая, что
/W=T^—. G.16.9)
0(l
вводим кинетический потенциал Рауса L%
J * G.16.10)
Дифференциальные уравнения движения E) принимают вид
$s(LR)= — -A~—^ = 0 E=1. .... m). G.16.11)
dt dqs dqs
Если в выражение LP время / явно не входит, то, повторив вычи-
вычисление п. 7.2, получаем для уравнений A1) интеграл энергии
Д^_£я = А. G.16.12)
350 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Из A) и A5.19) следует, что функция R может быть разбита на три
слагаемых
Я = Я2-|-#,-|_ Яо§ G.16.13)
где R2— квадратичная, Rt— линейная однородные формы обобщен-
обобщенных скоростей qv . . ., qmi a Ro от последних не зависит. Поэтому,
подобно B.6), выражение интеграла энергии приводится к виду
/?0 = А. G.16.14)
7.17. Структура функции Рауса
Надо вычислить значение суммы
= 2T? + U + T?. G.17.1)
Поэтому, вспомнив определение функции Рауса A6.1) и воспользо-
воспользовавшись введенным ранее разбиением выражения кинетической энер-
энергии A5.4), получим
К— I 2-f- U -f- I 2 -\г I х-\- I х -h /0 Л 2 ^ /j
или
/< /2 /2 "Т" / ! -Г уо» \1.\.IU)
причем циклические обобщенные скорости, входящие в /?, должны
быть заменены их выражениями A5.17).
Особенно отчетливую форму выражение B) принимает в случае
стационарных связей. Тогда
R=Ti—f?t G.17.3)
т. е. функция Рауса представляет разность входящих в выражение Т
квадратичных форм от обобщенных скоростей, соответствующих
позиционным и циклическим координатам. Однако после замены в Т<±
обобщенных циклических скоростей их выражениями A5.17), причем
для стационарных связей Бт+5 = 0, функция Рауса, выраженная через
обобщенные скорости qk (&=1, 2 ш), уже не останется квад-
квадратичной формой этих скоростей, а приобретет структуру, указывае-
указываемую формулой A6.13).
7.17] СТРУКТУРА ФУНКЦИИ РАУСА 351
Эту замену проведем для общего случая нестационарных связей,
т. е. в формуле B). Имеем *)
п — т п — т
5=1 Г=1
п-т п-т
— 2 Zu Zjj
s=\ r=i
m m
т. e. 7*" будет суммой трех слагаемых: функции, не зависящей от
обобщенных скоростей:
п-т п-т
ф = \ N А N N G.17.5)
5=1 Г=1
линейной формы этих переменных:
т п — т п — т
*1 = — 2W* 2 2 Ли+s. т+г^т+Ж+, G.17.6)
и их квадратичной формы:
т т п — т п — т
1 V V ' V V Л k хЛ
(л ——; у т п 1 п- / 7 А /\А АЛ • (i 17 7^
2 О / j / j *j yj*/ ^ ^^j ^^j 'ш + 5, nt-f-r1'л т -г S* Т *■ /72 -f- " V, .-1' •'/
k=l 1=1 5=1 Г=1
Соответственно этому выражение B) функции Рауса примет вид
а в случае стационарных связей
R = (T*2— Ф2)— Фх — Ф0 = /?2 + /?14-/?0. G.17.9)
В выражении Фо проведем замену величин Nm+r их значениями
ло соотношениям A5.18). Из последних следует
n — m
$m+s-Bm+s= 2 4В+ЛЯ,+Л„+, G.17.10)
и, обратившись к E), имеем
дФ» =й _5 G 17 11)
*) См. также цитированную на стр. 177 книгу Д. Р. Меркина (стр. 21
и след.).
352 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Теперь, сославшись на формулы D.2.9) и D.2.12), можно запи-
записать выражение квадратичной формы Фо величин Л/"т+г в союзной
форме и в билинейном представлении
п — т п-т
5 = 1 Г=1
п-т
G.17.12)
Отметим еще, что ксадратичная форма Фо, как следует из E),
образована с помощью той же матрицы А**, что и Т2 . Поэтому
Фо — знакоопределенная положительная форма.
Коэффициенты линейной формы Фг преобразуются с помощью A0);
получаем вместо F)
тп п-т
*i = — 2<7* 2 M*m±s$m+S—Bm+S). G.17.13)
k=l 5=1
Теперь составим выражение кинетической энергии системы через
обобщенные скорости, соответствующие позиционным координатам.
Для этого в выражении
п — т
G.17.14)
заменим qm+s по формулам A5.18), a R по (8), причем исполь-
используем A3) и билинейное представление Фо, т. е. второе выраже-
выражение A2).
Получаем
т п — т
k=l 5=1
5=1 5=1 \ k=l I
G.17.15)
Заменяя в левой части Т суммой
7= 72-+-Г, 4-^о, G.17.16)
а в ней Тг его значением
n-m / m
G.17.17)
2 ft9ft 2 т+^т+, = г; + 2 Bm+S [Nm+S- 2
7.17] СТРУКТУРА ФУНКЦИИ РАУСА 353
придем, после приведения в правой части A5) подобных членов,
к соотношению
Т2
s--\ \ k = \
m n — rn
= (T2 - %) + rx - 2
Л=1 5=1
5=1
или, вспомнив A2) и (8),
72 = #2 + Ф0. G.17.18)
Из этого представления следует, что
mm Г n-m n-m
^2 = Т2 ~~ Ф2 = ^J ^ ^Л^/ М*/ ~~ ^J ^J ^т+
k=l 1=1 L 5=1 r=l
G.17.19)
является положительной знакоопределенной формой обобщенных ско-
скоростей qx qm, соответствующих позиционным координатам.
Об этом можно заключить из таких соображений: зададим обобщен-
обобщенным скоростям qk начальные значения q°k, не равные одновременно
нулю, а циклические импульсы $m+s примем равными начальным зна-
значениям коэффициентов Bm+S:
при t = t0 Bm+Stf. .... 9°m; <0) = Pm+, G-17-20)
(s= 1 n — m).
Тогда по A5.18) и A5.17) начальные значения циклических обоб-
обобщенных скоростей будут
lm+r
J
k=\
G.17.21)
При таких начальных данных Фо станет нулем, а /?2 равным Т2,
т. е. будет положительным. Но выбор начального момента £0 и началь-
начальных значений q°x q°m позиционных координат и соответствующих
им скоростей <7? Ят ничем не ограничен; это и доказывает
положительную знакоопределенность квадратичной части R2 функции
Рауса. Было бы значительно труднее сделать такое заключение непо-
непосредственно по коэффициентам этой квадратичной формы в ее пред-
представлении A9).
23 Зак. 2072. А. И. Лурье
354 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Подведем итог сказанному для случая стационарных связей. Функ-
Функция Рауса представляется в виде
tf? R2+ /?,+/?„. G.17.22)
где квадратичная относительно обобщенных скоростей qx qm
функция R2 знакоопределенна и положительна; линейная часть Rx
функции Рауса по (9) и A3) равна
т п- т
Я.= 2?* 2 Mkm+$m,s, G.17.23)
причем коэффициенты Mm+S определяются через коэффициенты выра-
выражения кинетической энергии Т по правилу, указываемому форму-
формулой A5.17). Наконец, свободный член
п- m n-m
1 \^ V1 дт+з,т + га Q /7 17O/I4
будет зиакоопределенной отрицательной формой циклических импуль-
импульсов; при обращении в нуль слагаемого О в выражении кинетической
энергии системы Т циклические импульсы будут, согласно A5.12),
#* • ##
производными /2 по qm+s, т. е. квадратичная форма /2 будет союз-
союзной по отношению к — Ro:
п- m n- m
^=4 2 £ Am+s,m+rK+sh+r = -K- G-17.25)
5=1 Г=1
Уравнения движения для позиционных (явных) координат приво-
приводятся к виду
J_dRL_dRL = Q +т +д^ (ft=1 m) G.17.26)
dt dqk dqk VA ^ k ^ dqk
где Г^ — гироскопические силы (п. 7.3), соответствующие Rx\ R2 можно
трактовать как кинетическую, а —/?0 как потенциальную энергию.
Согласно B5) она равна по величине кинетической энергии Г2* скрытых
движений (если U = 0). При потенциальных задаваемых силах интег-
интеграл энергии A6.14) в случае стационарных связей выражает постоян-
постоянство суммы кинетической R2 и измененной потенциальной энергии
системы II—/?0. С фактом появления гироскопических сил при исклю-
исключении циклических координат мы встретились уже в примере 3° п. 7.9.
В механике Герца потенциальная энергия любого силового поля
трактуется как кинетическая энергия скрытых движений *).
*) Г, Герц, Принципы механики, изложенные в новой связи, 1894 г.
Русский перевод в изд. АН СССР, 1959 г.
7.18] примеры 355
Предположим, что нам доступно наблюдение только за движениями,
соответствующими явным координатам; мы установим, во-первых,
изменение величин и распределений масс в системе (так как R2 отлично
от Т*\ во-вторых, появление гироскопических сил, в-третьих, изме-
изменение поля потенциальных сил, определяемого теперь измененной
потенциальной энергией. Таковы влияния скрытых движений на явные
наблюдаемые.
При /?! = 0 гироскопические силы отсутствуют, система назы-
называется гироскопически несвязанной. По B3) и A5.18) это во всяком
случае будет иметь место при
Am+s,k = ° (s=l n — m\ k=\ m\ G.17.27)
т. е., когда в выражении кинетической энергии Т отсутствуют произ-
произведения циклических скоростей и скоростей, соответствующих пози-
позиционным координатам (при U = 0).
7.18. Примеры
1°. Движение материальной точки в поле централь-
центральной силы (кеплерово движение). Уравнение движения в векторной
записи имеет вид
где г — вектор-радиус движущейся точки, имеющий начало в притя-
притягивающем центре О; f (г) — закон зависимости силы от расстояния;
ее момент относительно точки О, конечно, равен нулю
и, следовательно,
т. е. момент количества движения точки относительно центра О
сохраняет неизменное значение
К0 = г X tnr.
Отсюда следует, что траекторией точки служит кривая, расположен-
расположенная в плоскости, перпендикулярной вектору Кэ и проходящей через
центр притяжения. Примем последний за начало полярной системы
координат г, <р в этой плоскости. Выражения кинетической и потен-
потенциальной энергии в этих координатах имеют вид .
^ + гУ;, 11= j f(r)dr. G.18.1)
22*
356 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
Координата ср—циклическая, соответствующий ей интеграл
тг*ч = $9 G.18.2)
представляет известный закон площадей, выражающий постоянство
величины вектора Кэ* Кинетический потенциал Рауса имеет вид
LR=f2-f?-TL = \m'r* -£fc- ff(r)dr, G.18.3)
Го
и дифференциальное уравнение движения будет
^ = 0. G.18.4)
Оно допускает первый интеграл — интеграл энергии
J f(r)dr = h, G.18.
5)
которы можно непосредственно записать и по A6.14).
Если положение точки определить сферическими координатами —
радиусом R сферы с центром в центре притяжения О, полюсным
углом ft (дополнение до широты) и долготой X, то, разлагая вектор
скорости точки v на составляющие по радиусу vR, по касательной
к меридиану v$ и по касательной к параллельному кругу vx, имеем
vR=R, vt = RU, <yx = /?Xsinft.
Выражения кинетической и потенциальной энергии будут
= f f(R)dR. G.18.6)
Координата X—циклическая, соответствующий ей первый интеграл
имеет вид
Рх = Ц- = mRA sin2 ft, G.18.7)
д\
и кинетический потенциал Рауса определяется выражением
1
7.18] примеры 357
Дифференциальные уравнения движения будут
G.18.9)
Они допускают первый интеграл, который можно записать и сразу
по A6.14):
С помощью этого интеграла из первого уравнения (9) исключаются О
и ft. К рассмотрению задачи о кеплеровом движении мы вернемся
позже.
2°. Волчок. Рассматривается движение тяжелого твердого тела,
имеющего неподвижную точку О на оси Oz, являющейся осью сим-
симметрии эллипсоида инерции тела в точке О. Вводим «полуподвижную»
систему осей п, nf, i'3, о которой говорилось в разделе 4° п. 2.10,
и за квазискорости аI( со2, оK примем проекции вектора w на эти оси.
Тогла, полагая
° 'y G.18.11)
где Л — экваториальный, С — полярный моменты инерции, по D.7.4)
получим
1 | G.18.12)
и, если определять положение тела эйлеровыми углами ф, 0, ср, то
по B.10.14) найдем
7'=li4(»2 + fsin20) + -5-C(?-b4>cos&J- G.18.13)
Потенциальная энергия равна
II = Mglc = Mgz cos », G.18.14)
где ^ — координата центра инерции, отсчитываемая по восходящей
вертикали ОС, z — его координата по оси симметрии тела Oz. Цикли-
Циклическими являются координаты ф и ср. Соответствующие им интегралы
будут
>1ф sin2 » -|- С (ср -f-ф cos ») cos в = рф, C(cp + <j>cos») = p9, G.18.15)
и кинетический потенциал Рауса определяется равенством
358
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА
[ГЛ. 7
Интеграл энергии будет иметь вид
A sin2 ft
G.18.17)
Полагая cos ft = и, приходим к известному дифференциальному урав-
уравнению для косинуса угла нутации:
Аи* = 2(h — Mgzu) (I
G.18.18)
Мы не будем останавливаться на интегрировании этого уравнения и
на исследовании движения; эти вопросы подробно рассматриваются
в многочисленных курсах механики и в специальных трудах*).
Большой интерес представляет случай почти вертикального волчка,
когда угол ft остается малым (задача о «спящем волчке»); выбор
в качестве обобщенных координат эй-
эйлеровых углов здесь малопригоден, так
как угол ф может иметь любое значение
(не остается малым); затруднение создает
также наличие множителя sin2 П в зна-
знаменателе выражения A7). За обобщен-
обобщенные координаты надо принять два угл.и
определяющие положение оси Oz вол-
волчка, остающиеся малыми при помчи
вертикальном ее положении. Таковыми
7 являются корабельные углы п. 2.4.
Здесь они обозначаются через а и р;
а — угол оси Oz с плоскостью ОС?»
Р — угол проекции оси Oz на эту
плоскость с осью ОС. Третьей обобщен-
обобщенной координатой служит угол с? пово-
поворота тела вокруг оси Oz. «Полусвязан-
«Полусвязанная» с телом система трех единичных
векторов п, п'', /д теперь определяется так: п расположен в пло-
плоскости ОС; по перпендикуляру к проекции оси Oz на эту плоскость,
составляя углы р и у+Cсосями О: и ОС; п' — в плоскости, содер-
содержащей оси Oz и Ог\ под углом а к последней; i'y как и ранее,—по
оси тела (рис. 69). Проекции вектора угловой скорости о на эти
направления выражаются через обобщенные скорости а, C, ср по фор-
формулам
(ол = (Oj = — а, а)л'= аJ = [В cos а, а). / = аK = ср-(—р sin а. G.18.19)
з
Рис. 69.
*) В. В. Голуб ев, Лекции по интегрированию уравнений движения
тяжелого твердого тела около неподвижной точки, ГТТИ, 1953.
7.181 примеры 359
Ниже понадобится также таблица косинусов углов осей полусвя-
полусвязанного триэдра с осями:
п cosC 0 —sin p
п' —sin a sin p cos а —sin а cos [
/£ cos а sin р sin а cos a cos {
G.18.20)
Теперь выражения кинетической и потенциальной энергии принимают
вид:
Т = ^ ^(i2 + P2cos2a) + 4C^P+ psinaJ, П == Mgz cosa cos p ,
u только координата ср будет циклической; угол р входит в выраже-
выражение II. Интеграл, соответствующий циклической координате, и кинети-
кинетический потенциал Рауса будут
]
1 . В2 G.18.21)
^B + p22)+Ppi^^fp j
Интеграл энергии имеет вид
Л (а2 + р2 cos2 a) + 2Mgz cos a cos р = 2/г. G Л 8.22)
Первый циклический интеграл A5), который мы получили при
пользовании эйлеровыми углами, выражает постоянство проекции на
вертикаль ОС главного момента количеств движения—внешними
силами, действующими на волчок, являются сила веса и реакция
неподвижной точки О, а их моменты относительно упомянутой непо-
неподвижной оси равны нулю. При выборе в качестве обобщенных коор-
координат углов аир этот интеграл моментов непосредственно (т. е. по
выражениям Т и II) не обнаруживается. Учитывая, что проекции
главного момента количеств движения на оси полусвязанного триэдра
п, п', /д равны
Аго]=—Аа, Ло>2 = Л'р cos а, (Ж = С (ср +- Р sin a) = р^, G.18.23)
получаем при проектировании на ось ОС,
Acl sin p — Лр cos a sin a cos p + p^ cos a cos p = 7, G.18.24)
где y — постоянно.
Уравнения движения, соответствующие кинетическому потенциалу
Рауса B1), имеют вид
Л (а + Р2 cos a sin а) — р^р cos а — Mgz sin a cos p = 0, )
.... \ G.18.25)
Л (р cos2 а —2а р sin a cos a)+p a cos a—Mgz cosa sin p = 0. J
360 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
При малых значениях аир получаем систему двух линейных диф-
дифференциальных уравнений *):
А* — (^C — Mgza = 0, Лр -f p?i — MgzC = 0. G.18.26)
3°. Система двух волчков. Первый волчок, имеющий не-
неподвижную точку Ох, вращается с угловой скоростью, задаваемой
вектором «о; тензор инерции волчка в точке Ох обозначается 0lt
центр тяжести Сх расположен на оси симметрии Oxzx в точке с абсцис-
абсциссой zv Точка О2 на оси Oxzx является точкой опоры второго волчка;
угловая скорость его задается вектором Si, тензор инерции в точке О2
обозначается через 02, расстояние ОгО2—через /, абсцисса центра
тяжести С2, расположенная на оси симметрии O2z2% — через z2.
Вводим в рассмотрение две «полусвязанные» системы осей, о кото-
которых говорилось в предшествующем примере: оси nt n\ i'y отнесенные
к первому волчку, и я*, я*', /*' — ко второму. Система имеет шесть
степеней свободы, за обобщенные координаты принимаются «корабель-
«корабельные» углы
Квазискоростями в соответствии с A9) являются проекции Wj, cd2, od3
вектора w и и>4, о>5, и>6—вектора Q на оси соответствующей полу-
полусвязанной системы.
Кинетическая энергия первого волчка дается выражением A2)
G.18.27)
Кинетическая энергия второго волчка вычисляется по фор*
муле D.7.7)
{ |02-2. G.18.28)
Здесь М2—масса, vQ —вектор скорости точки опоры, i*3'z2 — вектор-
радиус центра тяжести второго волчка, имеющий начало в О2. Имеем
*0i=<oX«;, г&, = /2[»2-(»-*аJ]='2Ов1 + в>2) G-18.29)
и далее
*) Об интегрировании их см., например: Л. Г. Лойцянский и
А. И. Л у р ь е, Курс теоретической механики, т. 2, стр. 569, Гостехиздат, 1955.
См. также пример 3° в п. 7.9. Применение интегралов B2) и B4) к исследо-
исследованию устойчивости движения почти вертикального волчка дано в книге
Н. Г. Четаева «Устойчивость движения» (стр. 27, Гостехиздат, 1955).
у |gj ПРИМЕРЫ
- "'wi + »«»• 1 G ! 8 30)
Замечая, что
3 (
q X Г3' = («у + «У + VT) X С = - я*
находим
v0 • B X С) =z K'V1' • "*' + ^s» ' "* — ^
и кинетическая энергия системы будет
-f-^((Oja)^' -Я*' -(-ш2аMл • Л*— со2ш4# . л*' — (OjO)^' • Л*), G.18.31)
где Л{ = Ах -\- М2Р, В = M2lzT Чтобы выразить ее через обобщен-
обобщенные скорости и обобщенные координаты, используем формулы вида A9)
и таблицы косинусов B0), записанные для первого и второго волчков.
Получим
Т= \ [Л[ (i? + Picos2 aj) + Л2{i22 4- ?! cos2 a2) -f-С, (^
sin
] +^ fai a2
-f- Pi ^2 C0S al COS a2 C0S P + al ?2 C0S a2 S*n al Sin P —
— a2Pj cosocj sina2sinp], G.18.32)
где p = p2—Pj. Потенциальная энергия равна
TI = QjC^ 4- Q2*^=Qi^i cos aj cos ^lJrQ2 (I cos a2 cos Cj 4-^2 cos a2 cos P2)»
где ^Cx и CCi — отсчитываемые по восходящей вертикали О^ абсциссы
центров тяжести волчков, Q} — вес первого, Q2—вес второго волчка.
Итак,
II = (Q{Zl 4- Q2/) COS ax COS pj 4- Q2^2 C0S a2 COS ?2- G-l 8'33)
Циклическими являются координаты cpj и ср2; соответствующие им
интегралы будут
C1co3 = C1(?1-hP1slna1) = 7lf C2co6 = C2(^2-l-^2sina2)=72. G.18.34)
Функция Рауса имеет согласно A7.22) вид
R = Tl-Tl* = ±. [А[ (Ц + р? cos2 a,) -ЬЛ2(аЦ-р1 cos^ a2) +
4-^B[a1a2(cosa1 cos a2 4-sin 04 sin a2 соз PL~Pi P2 cos aj cos a2 cos^ 4~
-j- ax p2 cos a2 sin a2 sin p — a2 p'j cos aj sin a2 sin pj 4- Ti Pi sin ai +
1 72 1 72
^i2 + /?0, G.18.35)
362 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
и интеграл энергии будет
/?2-|-11 = /г. G.18.36)
Может быть составлен еще интеграл моментов количеств движения
относительно вертикальной оси О^. Вычисление главного момента
количеств движения К ' относительно неподвижной точки опоры
проводится по формуле D.8.10). Для первого волчка
*f * = 0г<о = Аг (ш,я -f- "У*') + СаУ'з- G.18.37)
Для вычисления Кч' надо иметь выражение главного вектора Q2
количеств движения второго волчка
Q2 = M2ve, = М2 (со X «з + й X г^'). G.18.38)
Получаем, учитывая формулы B9) и C0),
+ В [^ X (- %и*' + »5я*) -f- if X (- «»,«' + »2«)j +
-f Л2(а./+ш/')+С2^(* G.18.39)
Остается вычислить проекцию /С?1 суммы векторов
на вертикаль. Обозначая через k единичный вектор восходящей верти-
вертикали, имеем
k X *з = л' sin Pj — /г sin aj cos [^ 1
jfe X С = я*' sin ?2 — tC sin a2 cos P2 j G-! 8'40>
и далее
k • (/3 X n*f) = (ft X *з) • «r* = яг • л*г sin Pj — /г • /г*г sin ttl cos p, ==
= cos a, cos a2 sin p2 -f- sin a2 sin a2 sin P2
и т. д. Получаем
^р1 = — { Л[ (C0j Sin Р2—|- Ш2 Sin al C0S PO+A (aL Sitl ?2 + ^o Sitl a2 COS
-\- B\w4 (cos aj cos a2 sin p2 -f- sin a2 sin a2 sin p2) -(- coj (cos aj cos a2 sin p2 -(-
+ sinotj sina2 sin px) -)— a>5 sin a1 cos p2 + W2 sin^cospj) +
+ Сгшъ cos aj cos Pj 4- C2co6 cos a2 cos p2 = 7. G.18.41)
где ic — постоянная. При нашем выборе обобщенных координат этот
интеграл не является циклическим. Определив положение волчков
эйлеровыми углами f)lt фр <рх для первого и Р2, ф2, ср2 для второго»
получили бы вместо C3)
2/) cos P j -f- Q2
7 181
ПРИМЕРЫ
363
где ftj и f>2 — углы осей волчков с восходящей вертикалью OXL
В выражение коэффициентов кинетической энергии вошли бы углы 01$ 02
(подобно а1 и а2) и разность и = ф2 — ^ углов ф2 и ф1§ подобно
Р = ?2—Pi B C2). Поэтому, если принять
то циклической будет координата )г, не входящая в выражения кине-
кинетической и потенциальной энергий. Соответствующий ей интеграл
как раз выражает постоянство проекции главного момента количеств
движения на ось О^. Корабельные углы портят в этом смысле выра-
выражение потенциальной энергии; но они существенно облегчают исследо-
исследование случая почти вертикальных волчков.
В этом случае, сохраняя в выражении R лишь члены второй сте-
степени относительно предполагаемо малых величин a/f (^ и ait [3/t полу-
получаем (отбрасывая постоянные)
II =-y
и уравнения движения будут
2В (к, «
)]
G.18.42)
G-18.43)
G.18.44)
где обозначено
\ 2 1 2 1 2
G.18.45)
Их можно свести к системе двух дифференциальных уравнений вто-
второго порядка относительно неизвестных
= *2, G.18.46)
представляющих комплексные числа, определяющие положения «вер-
«вершин» волчков (концов векторов ¥г и /*') на плоскости, параллельной
Ofcr\. Эти уравнения имеют вид
z) H-fti^+^i^i — с1-2г1 = 0, z2-\-b2\
Частное решение разыскивается в виде
гг = Zxe™t z2 =
— c2z2 = 0. G.18.47)
9 G.18.48)
364 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
где Zj, Z2, X—постоянные. Подстановка в D7) приводит к системе
линейных однородных уравнений
Zx (X2 -Ь sxl -f- сг) + Z2bx\2 = О,
2 = 0, )
G.18.49)
допускающей нетривиальное решение относительно Zx и Z2, если ее
определитель равен нулю. Это условие приводит к уравнению четвер-
четвертой степени относительно X:
(Х2 -f- sx\ -{- сх) (к2 -f- s2l -f- с2) — bxb2lA = 0. G.18.50)
Каждому из четырех корней \k соответствует частное решение D8),
в котором постоянные Zlt Z2 связаны условием
jt- = ^ = Ту . (/.1О.01)
Общее решение системы уравнений движения D7) поэтому может
быть записано в виде
*i=2 CftVS*'V, ^2—2C,D + ^ + O^'V. G.18.52)
Необходимым условием существования режима движения, в кото-
котором оси волчков сохраняют почти вертикальные положения, является
ограниченность по модулю величин zx и z2 *). Она будет иметь место
(если не накладывать специальных требований на начальные условия)
лишь в том случае, когда все корни уравнения E0) — вещественные»
Действительно, при существовании комплексного корня X будет суще-
существовать и ему сопряженный Г, вследствие чего вещественная часть
одного из чисел /X, /X окажется положительной и соответствующее
частное решение будет с ростом t неограниченно возрастать по
модулю **).
7.19. Квазициклические координаты
Для некоторого класса задач динамики оказывается полезным
обобщение определения циклических координат. Допустим, что в числе
обобщенных координат имеются такие qm+x, ..., qn> которые не
входят в выражения кинетической энергии и обобщенных сил, но
обобщенные силы Qm+1, . . ., Qn; к ним отнесенные (в отличие от слу-
*) Вопрос о достаточности этого условия более сложен и мы оставляем
его открытым.
**) Критерии вещественности всех корней уравнения четвертой степени
через коэффициенты уравнения приведены в книге А. К. Сушкевича «Основы
высшей алгебры» (ОНТИ, 1937, § 130, стр. 222). Они имеют весьма слож-
сложный вид.
7.19] КВАЗИЦИКЛИЧЕСКИЕ КООРДИНАТЫ 365
чая циклических координат), не равны нулю. Условимся называть
такие координаты квазициклическими. Как пример можно назвать
твердое тело, снабженное маховиком, вращающимся вокруг неподвиж-
неподвижной в теле оси и имеющим центр тяжести на этой оси. Если
qv .... #6—обобщенные координаты, определяющие положение тела
(например, координаты полюса и эйлеровы углы), а ср — угол поворота
маховика в теле, то эта координата будет квазициклической, когда
с целью управления вращением маховика к нему прикладывается
(осуществимый с помощью следящих систем) момент, зависящий от
обобщенных координат qs.
Пусть qv ..., qm — позиционные, <7m+1, •••> Яп— квазицикличе-
квазициклические координаты. Дифференциальные уравнения движения разбиваются
на две группы
ts{T)=^s-Ws=QM' Ят) (s=h •••• m)> GЛ91)
Pm+s=Qm+sDl' ■■■' Ят) (S = l П — ш), G.19.2)
где через pm+s обозначены квазициклические импульсы
Pm+s=-p E=1, ..., п — т). G.19.3)
Они не остаются при движении постоянными, но все формальные
рассмотрения пп. 7.15—7.17 сохраняются. Надо заменить лишь Pm+S
на Pm+s-
Так, разрешив систему линейных уравнений C) относительно квази-
квазициклических обобщенных скоростей
4m + s = fm + sDl. '••• Ят' Я\> •••• ?«• Pm + L •••- Рп> 0. G.19.4)
можно по правилу A6.1) составить функцию Рауса
GЛ9.5)
и с ее помощью записать дифференциальные уравнения движения
в виде
l^R) = Tt^—s^ = QAqv '■- ° (s=u '••' т)* GЛ9)
^ . G.19.7)
Системы дифференциальных уравнений F) и B) должны рассма-
рассматриваться совместно. Определив из них позиционные обобщенные
координаты, соответствующие им обобщенные скорости, а также
квазиимпульсы, найдем далее из G), с помощью п — т квадрат) р,
366 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЛАГРАНЖА [ГЛ. 7
квазициклические координаты. Преимущество, даваемое методом Рауса,
заключается в этом сведении задачи к рассмотрению системы диф-
дифференциальных уравнений {п-\-т) порядка и последующим квадра-
квадратурам.
Вычисление функции Рауса проще, чем по E), проводится (огра-
(ограничиваемся рассмотрением стационарных связей) по формуле
R^Rx + R0, G.19.8)
где Г* и 7**—части кинетической энергии, зависящие, первая — от
обобщенных скоростей, соответствующих только позиционным коор-
координатам, вторая — только от квазициклических обобщенных скоростей.
В состав квадратичной формы R2 от обобщенных скоростей
<7], ..., qm квазициклические импульсы не входят; это следует из
выражения A7.19) этой формы и правила составления A5.17) вели-
величин Mkm+S- Слагаемое RY представляет билинейную форму
т п — т
«i=2 2 Mkm^qhPm¥s G.19.9)
k = l 5 = 1
от позиционных обобщенных скоростей и квазициклических импуль-
импульсов, а /?0 — квадратичную форму последних, записываемую в соответ-
соответствии с A7.24) в виде
п — т п — т
*о = —у 2 2 Am+S' ""P^sP^ G-19.10)
Таким образом, имеем, учитывая B),
V=l 5=1
n—m n-m
*m + s
5 = 1
Mkm+sQm+s, G.19.11)
где Г^ — обобщенные гироскопические силы. Уравнения (б) поэтому
записываются в виде
п-т
$k(R2) = Qk-\-Fk— 2 M*m+aQm+s + ^S (k=l. .... т). G.19.12)
5 = 1
Рассмотрим случай потенциальных обобщенных сил, отнесенных
к обобщенным позиционным координатам,
Q* = ~W* (k^] "l)- G.19.13)
7.19] КВАЗИЦИКЛИЧЕСКИЕ КООРДИНАТЫ 367
Равенства E.3.12) дают в этом случае
Ou G.19.14)
Поэтому, если исключить случай постоянных обобщенных сил Qm+S,
в системе с квазициклическими координатами обязательно наличие
непотенциальных сил.
Отметив теперь соотношение
dt — Li dqk q*^ Zd dpm.,s qk
k=l S=\ k=l 5=1
dqk ч*^~ jU dpm.,sy^s — jUdqk 4* "^ AA dpm+s
+$>
G.19.15)
воспроизведем над дифференциальными уравнениями A2) вычисление
п. 7.2, с помощью которого был получен интеграл энергии. Придем
к равенству
—т п-т
V qk 2 Мат+sQm+s
(R2 + II - RQ) = - V -qk 2 Мат+sQm+s -
Л=1 s=l s=\
m
Но, поскольку в состав R2 не входят обобщенные импульсы:
_i<*±M=_ ж=- 9
°Pm + s °Pm + s
то соотношение A6) служит для определения мощности непотенциаль-
непотенциальных сил Qm+5 в системе с квазициклическими координатами:
п-т
(Л + и/?„). G.19.13)
ГЛ АВА 8
ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ДВИЖЕНИЯ
8.1. Дифференциальные уравнения Эйлера — Лагранжа
Эти уравнения движения, отличающиеся от уравнений Лагранжа
введением квазискоростей вместо обобщенных скоростей, были почти
одновременно получены Больцманом *) и Гамелем **). Последнему
принадлежит и принятое здесь наименование этих уравнений. В урав-
уравнениях движения, которыми пользовался П. В. Воронец ***), также
рассматриваются квазискорости, но по форме они несколько отли-
отличаются от уравнений Эйлера — Лагранжа.
Уравнения Эйлера — Лагранжа преимущественно применяются при
рассмотрении неголономных систем; они и были введены с этой целью,
как видно из наименований работ Больцмана и Воронца. Однако их
значение не ограничивается этими специальными задачами, так как они
позволяют в значительной мере упростить форму и процесс составле-
составления уравнений движения и в голономных задачах. Мы неоднократно
будем иметь случай убедиться, насколько плодотворно применение
уравнений Эйлера — Лагранжа в вопросах динамики систем твер-
твердых тел.
Будем исходить из общего центрального уравнения F.4.17). Тре-
Требуется лишь развернуть его левую часть
dt
*) L. В о 1 z m a n n, Ober die Form der Lagrange'chen Gleichungen fur
nichtholonome generalisierte Koordinaten. Sitzungsberichte der Wiener Akade-
mie der Wissenschaften, 111, Dez. 1902.
**) G. Hamel, Die Lagrange-Eulerschen Gleichungen der Mechanik,
Zeitschrift fur Mathematik und Physik, Bd. 50, 1904.
***) П. В. Воронец, Уравнения движения твердого тела, катящегося
без скольжения по неподвижной плоскости, Киев, 1903.
8.1] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА ЛАГРАНЖА 369
и заменить ЬТ в правой части его значением
(8.1.2)
5
Теперь подстановка в F.4.17) дает
п п
Yg A^L-4-V— (Ь У —
5=1 5=1
5=1 5=1
П П П П П
' дТ » V V
Г = \ / = 1 5 = 1 Г = 1 5 = 1
После сокращения подчеркнутых членов приходим к соотношению
П г П П П -|
У 8ТС iL.f*Zl + у у г дт ш | у zr дТ дТ р _ о (Q I j)
5=1 L ^ Г=1/=1 Г=\ J
Предполагаем, что избыточные координаты не введены и рассмотрим
случаи голономной и неголономной системы по отдельности.
В первом случае все вариации bizs независимы и следствием D)
является обращение в нуль коэффициентов при них в этом соотно-
соотношении. Получаем уравнения движения Эйлера — Лагранжа
d дТ , V V г дТ , V» г дТ дТ
г=1/=1 г=1
(8.1.5)
к которым должны быть присоединены кинематические соотношения
A.5.25)
л + 1
?,= 2 *,*<■>* E=1,..., Л), (8.1.6)
fe=l
дающие выражения обобщенных скоростей через квазискорости. Полу-
Получили систему 2п обыкновенных дифференциальных' уравнений первого
порядка относительно такого же числа неизвестных
">i <V. Qv •••• Яп- (8.1.7)
24 Зак 2072. А. И. Лурье
370 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. S
Уравнения упрощаются и принимают вид
п п
d дТ t tw ;, —со —^L = p (S= I, .... п), (8 1 8>
п
^ Д>*<°* E=1 я), (8.1.9)
если квазискорости введены с помощью однородных линейных форм
A.5.1) с коэффициентами, не содержащими t явно, а не с помощыа
более общих соотношений A.5.22).
При наличии неголономных связей, как говорилось в п. 1.5,
в число квазискоростей вносятся линейные формы обобщенных ско-
скоростей, обращающиеся в нуль в силу самих уравнений неголономных
связей. Последние тогда будут иметь вид A.5.6) или в более общем
случае, если исходить из формы записи A.5.22),
п
Тогда имеем также
п
%ns = 2 askbqk = 0 E=1,...,/), (8.1.11)
где /—число уравнений неголономных связей. Суммирование по 5
и / в равенстве D) поэтому должно производиться от / -f-1 до m
г, г- п п п т
V s iL^L_L.y у r^ZLcoi_y r дТ дт р —о
(8.1.12)
и, поскольку вариации Вти^ при s = /-|-l, ..., п независимы, вели-
величины в квадратных скобках должны быть нулями. Получаем п — /
уравнений движения
п п п
d дТ ,
~dtd^~^
2 *.£',+!£;*.-&-
l l \
число которых равно числу степеней свободы. К ним надо присоеди-
присоединить п кинематических соотношений
л + 1
Чз= 2 bskuk E=-l. .... п). (8.1.14)
8.1] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА ЛАГРАНЖА 371
Всего имеем 2п — / уравнений первого порядка, содержащих такое
же число неизвестных
ш/+1. •• •» <V Qv •••• 4п- (8.1.15)
Для составления уравнений A3) достаточно знать лишь те сим-
символы Yt<;> B которых нижние индексы соответствуют номерам квази-
квазискоростей, не обращающихся в нуль вследствие уравнений неголо-
номных связей. Уравнения A3) содержат производные кинетической
энергии Т по всем квазискоростям, в том числе и по тем, которые,
согласно AС), обращаются в нуль. Поэтому при составлении выра-
выражения Т неголономные связи нельзя учитывать, они принимаются
во внимание лишь после вычисления производных Т по квазискоро-
квазискоростям, т. е. квазиимпульсов /г\ Вспоминая выражение D.1.19) кинети-
кинетической энергии, можно, однако, добавить, что в нем достаточно
сохранить лишь линейные относительно квазискоростей
<!>!, . . ., О), (8.1.16)
слагаемые, т. е. не выписывать произведений и квадратов этих
величин, так как после вычисления квазиимпульсов соответствующие
слагаемые все равно отпадут в силу уравнений A0). Отметим еще,
что в числе линейных относительно величин A6) слагаемых имеются
их произведения на <*>/+1, ..., ш^. Эти члены, конечно, надо сохра-
сохранить в выражении Т.
Уравнения движения E) и (8) обращаются в уравнения Лагранжа
G.1.4), если все квазискорости а>5 являются обобщенными скоростями
u>s = qs (s=l, ..., п), (8.1.17)
так как тогда, как указывалось в п. 1.9, все символы Yts и е^ будут
нулями, а «производные Т по квазикоординатам» станут производ-
производными по обобщенным координатам qs. Было бы, однако, ошибочно
думать, что уравнение Эйлера — Лагранжа, соответствующее номеру
квазискорости, равной обобщенной скорости (когда это равенство
имеет место не для всех s), обращается в уравнение Лагранжа. Чтобы
понять это, достаточно заметить, что номер уравнения E) или (8)
не совпадает с верхним индексом символа yts. Но в частном случае
задания квазискоростей соотношениями A.9.6), A.9.7) все символы,
в которых один из индексов превосходит тпу обращаются в нуль.
Тогда уравнения движения распадаются на две группы: группу урав-
уравнений Эйлера—Лагранжа для номеров 1, . . ., m и уравнений Лагранжа
для пг -\- 1 я.
Мы отметили выше, что структура выражения кинетической энер-
энергии через квазискорости, как правило, гораздо более проста, чем
через обобщенные скорости. Этим и объясняется, что уравнения
движения в форме Эйлера — Лагранжа оказываются более простыми
24*
372 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
по форме и симметричными для значительного класса задач, чем
уравнения Лагранжа. Затруднения, связанные с вычислением трех-
трехиндексных символов, не столь велики и, во всяком случае, не принци-
принципиальны; кроме того, это вычисление при выбранном задании квазиско-
квазискоростей через обобщенные скорости производится один раз навсегда.
Наглядный пример, иллюстрирующий сказанное, представляет
случай вращения твердого тела вокруг неподвижной точки. Выра-
Выражение кинетической энергии через обобщенные скорости дается фор-
формулой D.7.6) и, составив по нему уравнения Лагранжа
d дТ дТ _~
dt дф ~~ cty — тз»
d дТ дТ __
d дТ дТ _
dt ду ду ~ 3'
в которых правые части определены по E.2.9), пришли бы к ли-
лишенным симметрии труднообозримым соотношениям. Если же, вос-
воспользовавшись выражением кинетической энергии Т в форме D.7.5)
и значениями B.10.3) трехиндексных символов, составить уравнения
Эйлера — Лагранжа, то придем к известным уравнениям Эйлера вра-
вращения тела вокруг неподвижной точки
J
82ш2 +- (в, — 63) «Vй! = ^2. } (8.1.18)
являющимся непосредственным выражением теоремы об изменении
главного момента количеств движения. Этим следует объяснить
принятое наименование рассматриваемой формы уравнений движения;
в них наглядность и симметрия эйлеровых уравнений соединены
с лагранжевым автоматизмом хода вычислений.
8.2. Примеры составления уравнений движения
неголономных систем
Мы рассмотрим с помощью уравнений Эйлера — Лагранжа те
задачи, для которых ранее в пп. 2.10 и 1.10 были составлены выраже-
выражения трехиндексных символов, а в п. 4.13 — кинетической энергии.
1°. Шар, катящийся по шероховатой плоскости.
Учитывая сделанные выше замечания, можно выражение кинетической
энергии D.13.2) записать в виде
1+ .... (8.2.1)
8.2] СОСТАВЛЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ НЕГОЛОНОМНЫХ СИСТЕМ 373
где не выписаны слагаемые квадратичные относительно о>4 и а>5, так
как соответствующие им члены в уравнениях движения обратятся
в нуль в силу уравнений неголономных связей. Следует еще иметь
в виду, что квазискорости, не обращающиеся в нуль в силу урав-
уравнений неголономных связей, здесь занумерованы первыми индексами,
а в уравнениях A.13) — последними.
Для составления уравнений движения надо знать трехиндексные
символы с нижними индексами 1, 2, 3. Они даются формулами B.10.11)
и B.10.20). Принимая в расчет уравнения неголономных связей
B.10.19), можно написать
Z (jp *Z (8.2.2)
и далее
/?* = |.МЛ>з, p\ = MaZ2% p\ = — Mcmv (8.2.3)
Выражение элементарной работы приложенных к шару активных
сил записывается, если вспомнить, что o)j, со2, оK обозначают про-
проекции вектора угловой скорости о) на оси неизменного направле-
направления Oxyz, в виде
оТ = V • Ьг0 + т° • 6 = 9гЬх
Но по B.10.19)
= in°-\-aVlt Ръ = т%. (8.2.4)
Поэтому обобщенные силы, отнесенные к квазикоординатам, будут
Pl=m? — aV2, P2 = in°-\-aVlt Ръ = т%
Первое уравнение Эйлера — Лагранжа A.13) имеет вид
Надо разыскать в числе трехиндексных символов, с правым нижним
индексом 1, отличные от нуля. Таковыми являются
Т31 ~ * ♦ Т21zz=z *» Т31rrr: a-
Получаем
7 ал 2~ I дт ~ дт ~ дт ~ п (л
Но по B) и C)
дт ~ дт ~ дт ~ лл 2/7 2 1 i
374 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Аналогично составляются уравнения Эйлера—Лагранжа для квази-
квазискоростей о>2 и оK. Получаем три уравнения
-=- M#2a>j = mi — aV2,
(8.2.5)
К ним присоединяются кинематические соотношения B.9.4) и урав-
уравнения неголономных связей B.10.19). Всего имеем 8 дифференци-
дифференциальных уравнений первого порядка для определения такого же числа
неизвестных
шх, оJ, оK, ф, ft, ср, *0, у0.
Составим для этой же задачи уравнения Лагранжа с множителями
в форме G.1.6). Теперь выражение кинетической энергии надо составить
через обобщенные скорости. Оно будет согласно B.9.4) и D.7.6)
иметь вид
Уравнения неголономных связей будут
xQ — а @- sin ф — ср sin ft cos ф) = 0, |
уо4- ^(^созф -(- ср sin 0 ^пф) =0. )
Чтобы избежать ошибки при назначении наименований коэффициен-
коэффициентов aks, составим общее уравнение динамики F.3.4). Оно будет
иметь вид:
М (£о8*о + Уо8Уо) +4 Ма<1 $ +*? sin fi)S& +| ж<*2(ф
О
-f- ^ cos 0 — <p& sin ^)8ф + Е
— 1^,8*0 — V2hy0 — т?5ф — mJv8& — ^Scp = O. (8.2.7)
Мз уравнений неголономных связей найдем
Ьх0 — a (sin ф 8$ — *1п ^ cos ф Scp) = 0,
8у0 -f- а (cos ф 8ft 4~ sin ft cos ф 8cp) = 0.
Прибавив произведения левых частей этих соотношений на множи-
множители связей —Xj и —Х2 к левой части G) и приравнивая затем
8.2] СОСТАВЛЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ НЕГОЛОНОМНЫХ СИСТЕМ 375
нулю коэффициенты при вариациях обобщенных координат, получим.
пять уравнений движения
cos
= т% — а (\ sin ф — Х2 cos ф),
— АИ sin П) =
— cprf sin 8) =
(8.2.8>
Из двух первых уравнений находим Х}, Х2. Тогда после подстановки
в три остающихся уравнения получим
■^ Ма2 (ft -f- ф ср sin ft) + Ма (х0 sin ф — у0 cos ф) =
= ^дг -+- a (Vx sin ф — V2 cos ф),
4- Ma2 (<? -f- ф cos П — ф4 sin ft) — Ma (x0cos ф -f- y0 sin ф) =
= ml — a sin 8 (V\ соэф -j- У2 sin Ф)»
— Ma2 (ф -f- cp cos ft — cp ft sin ft) = ml.
(8.2.9>
J
Сюда надо присоединить дяа уравнения неголономных связей F);
с их помощью из уразнений (9) могут быть исключены х0, у0.
Система уравнений, к которой мы придем, должна быть эквивалент-
эквивалентной системе E). Совпадение третьего уравнения (9) и третьего урав-
уравнения E) устанавливается сразу; сложнее проверить, что два остаю-
остающихся уравнения (9) являются следствием E). Мы не будем оста-
останавливаться на этом, так как целью было показать, насколько слож-
сложными и трудно доступными для дальнейшего исследования являются
уравнения Лагранжа с множителями даже в применении к простей-
шеЛ задаче с неголономными связями.
2°. Обруч. Выражение кинетической энергии, если опустить
слагаемые квадратичные относительно со* и ок, согласно D.13.6)
имеет вид
; sin ft] . (8.2.10)
Здесь, напомним, по B.10.14)
376 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
а уравнения неголономных связей B.10.26) имеют вид
со* = оL-(—аоK = 0, со! = оM -\- #(Dj sin ft = 0, (8.2.11)
причем через со4 и о>5 обозначены проекции скорости центра обруча
на ось узлов и перпендикуляр к ней в неподвижной плоскости бху*
Мы учтем только силу веса. Потенциальная энергия равна
И = Mgz = Mga sin i\ (8.2.12)
Учитывая, что в данном случае тгт = Ь, найдем
Имеем
\ . Р*5 = — Ма(ах sin &.
Производные
дТ дТ дТ
diii ' дтс2 ' дтс3
обращаются в нуль в силу второго уравнения неголономной связи.
Остается выписать значения трехиндексных символов, правый ниж-
нижний индекс которых равен соответственно 1, 2, 3. Имеем, по B.10.16),
B.10.28) и B.10.29):
(8.2.13)
а
^23 sin {} *
Получаем систему дифференциальных уравнений
2" ^2 +
(8.2.14)
2оK — @^2 = 0. ]
Если за независимую переменную принять вместо t угол t>, то,
вспомнив, что & = (i)j, получим
^=0L E=1, 2, 3),
2.8] СОСТАВЛЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ НЕГОЛОНОМНЫХ СИСТЕМ 377
причем штрихом обозначена производная по Ь. Второе и третье
уравнения A4) примут вид
Ц-f-w2 ctg & — 2оK = 0, 2а>з = а>2. (8.2.15)
Исключив а>2, придем к уравнению
а>з + ">з ctg ft — оK = 0. (8.2.16)
При начальных условиях
/ = 0, » = ^0, со, = coj, oJ = (!>о = 2a>3°, а>, = а>° (8.2.17)
общее решение дифференциального уравнения A6), интегрируемого
с помощью гипергеометрического ряда, будет иметь вид
оK = /=■(», 1>0, («о, оH), (8.2.18)
после чего а>2 определится дифференцированием. Теперь первое
уравнение A4) приведется к виду
Т Чь ^ = ~~ Т cos й + ^ ct£ ° — 2 ^з»
откуда (Dj (ft) определится квадратурой. Еще одно интегрирование
определит Ь как функцию t *).
3°. Двухскатная тележка. Кинетическая энергия опреде-
определяется выражением D.13.18), в котором значения величин Ь и ср5
даются формулами D.13.13)—D.13.17). Уравнения движения по
A.13) имеют вид
8 8
d дт _i_ V V г дт дТ — р
r=\ s=l
dt д<*8 ' Z Z ^ ^
Вспомнив равенства A.10.15), получим
А_дт__дт_^ _
dt дщ дщ
7 <b8 ~" 8* J
Теперь надо вычислить импульсы /?*, /?*, р^ и, найдя их, учесть
уравнения неголономных связей
и> = и>2 = о>з = оL = оM = о)б = 0. (8.2.20)
*) П. А п п е л ь, Теоретическая механика, т. 2, стр. 222—227, Физмат-
гиз, 1960.
*378 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Находим
\
sin2
^7/о= ([Х
(-3—) = v/a)ft -f- voO sin
\ <К /о 8 т 7
sin
(8.2.21)
*и из хода действий видно, что уже при вычислении Т можно было
принять квазискорости а>2, . . ., а>6 равными нулю (но не coj). Это,
конечно, значительно сократило бы составление выражения Т. Теперь
по A.5.17) и A.10.14) находим еще
дТ
дТ
7 ~~А ^'
г-\
дТ
(8.2.22)
Здесь использовано значение Г, вычисленное при наличии всех свя-
связей, т. е. выражение D.13.19). Сделав подстановку в A9), придем
теперь к уравнениям движения
v/
Sin2 у) ОO 4" ^1^>7Ш8 Sin X C0S X + va)8 Sin X =
va,7 sin x + vciOa)8 cos x = Ps-
{O.Z.
Обозначая co8 = x. ^7 = ^, причем V—величина скорости шар-
шарнира В, соединяющего скаты, перепишем эти уравнения в виде
+ p., sin2 х) V + V4VX sin х cos х 4- ^Х sin X = pv
(8.2.24)
Величина v/, как следует из ее выражения D.13.20), представляет
момент инерции переднего ската, приведенный к оси шарнира В\
Я8&Х — элементарная работа активных сил при виртуальном переме-
перемещении, определимом вариацией угла х, а обобщенная сила Я8—вра-
Я8—вращающий момент рулевого управления. К числу активных сил отно-
относится вращающий момент двигателя, действующий на ведущие колеса,
-силы трения в осях колес, силы сопротивления воздуха, силы трения
качения; Р7 представляет соответствующую им обобщенную силу.
Сила тяги ведущих колес, возникающая вследствие сцепления колес
с дорогой, принадлежит числу реактивных, а не активных сил. Ее
элементарная работа равна нулю и в уравнения B4) она не входит.
8.3] КАТАНИЕ БЕЗ СКОЛЬЖЕНИЯ ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ 379^
Рассмотрим режим движения, в котором Р7 = Ps = О, принимая
начальные условия
'' = 0. V = V0, х = Хо. х = Хп- (8-2.25)
Дифференциальные уравнения допускают два первых интеграла: один
из них
X-r-jVsinx-Xo + j^oSinXo (8-2-26)
выражает постоянство угловой скорости переднего ската; второй —
постоянство кинетической энергии системы D.13.19)
([х -+- [х, sin2 х) V2 + 2vXV sin
= (у. + ь sin2x0) VI + 24oVo sin x0 + /v&
Он преобразуется к виду
[,x + (^ - f) sin2 x] V2 + */ (i + -f sin xJ =
J- (8-2-27)
Из равенств B6) и B7) находим формулу, связывающую ско-
скорость V с углом х;
V
8.3. Катание без скольжения твердого тела
по неподвижной плоскости
Необходимые кинематические соотношения были приведены в п. 2.16.
Выражение кинетической энергии через введенные там квазискорости,
если за точку О принять центр инерции тела, записывается в виде
0.<о = М|х — <*> X р |2 + <*> • 0 • <о. (8.3.1)
Здесь )(— вектор, обращающийся в нуль в силу уравнений неголо-
номных связей B.16.11), а вектор угловой скорости <о выражается
через квазискорость ^4 и qa с помощью B.16.5). Получаем
<*> X р) +<*>•[© 4-М (Ер-р — ррI-ю. (8.3.2)
Первое слагаемое в этом выражении может быть сразу отброшено;,
второе надо сохранить, поскольку в дифференциальные уравнения
движения войдут производные по j^, ^2, у? и эти члены сохранятся
после того, как /л, ^2, ^3 будут сделаны нулями. Третье слагаемое
380
ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
представляет однородную квадратичную форму от у4, q* с коэффи-
коэффициентами, зависящими от гауссовых координат ql9 q2. Итак, полагаем
27= —
(8.3.3)
Для составления обобщенных сил внесем в выражение элементарной
работы
b b
значения Ьг (виртуального перемещения полюса О) и 6 по B.16.14)
и B.16.18), причем Втг вследствие неголономности связей следует
сделать нулем. Получим
Величина т° — р X F представляет главный момент задаваемых сил
относительно точки соприкасания тела с плоскостью. Она обозна-
обозначается через М. Итак, обобщенные силы равны
Р4 = М-т, P5 = Mlv Яб = М./2, М = т° — р X ^ (8.3.4)
Заметим еще, что выражения обобщенных скоростей через квази-
квазискорости по B.16.13) и B.16.9) имеют вид
Поскольку Т не зависит от ft, имеем
дщ
1
дк5
Теперь обращаемся к составлению уравнений движения в форме
A.13)
1гА
А_^!_1-У У т'
dt ^X5 ^ ^ T/5
у дт* -р
lt dq{ ~~ 5'
dt д1б
Т/б dXr Zr <ty2 —
(8.3.6)
Суммирование по г производится до 4, так как трехиндексные сим-
символы с верхними индексами 5, 6 обращаются в нуль; в записи урав-
уравнений учтено, что после составления их ^р ^2» Хз делаются нулями.
8.3] КАТАНИЕ БЕЗ СКОЛЬ>лЕНИЯ ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ 381
Развернем двойные суммы в уравнениях F), воспользовавшись
значениями трехиндексных символов, приведенными в табличках
п. 2.16:
4 6
V V г дТ дт ,и х и ч i дт <и . и ч ,
^^Л ^^Л \ 14 /y-y A.* /i-y v 1 1A.0 I ZIA.O7 I H-y ^ 1/A.D ' cLrJQ' •
4 6
1 <ЭГ / дТ , , дТ t
12
4 6
дГ f. * дТ ь .дТ . \ , 4 дГ*
^ «19 -t- ^ R\3)JL4 i Тй5 ^
Теперь отметим легко получаемое из C) соотношение
Но по B.16.18) и B.16.19)
= — Х4Ра +^=" Ш ^^п2а ~~ *?2Л1«)- (8.3.7)
Получаем
4 6
VI V* дТ .. • , Ms
£J ^я4 *ti dir V\a\
4 б
4 6
X
2 2 T« "£• X/ = ^P • P2X4 —
l/4 Г
■=l/=4
Вдесь
e = »j • p
382 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
равно расстоянию от центра инерции О до плоскости, по которой
катится тело; можно также написать
где р — модуль вектора, р — расстояние от полюса О до точки со-
прикасания с плоскостью.
Окончательная форма уравнений движения F), полученная
П. В. Воронцом *), будет
- -]=- \(qxf (bnal2 — bl2au) +
d дТ дТ ,
: h
dt dql dgl
— ^22fln)l — -57- U1/t^T ^ = J
dt dq2 dq2
dq2 Y\a\
(8.3.8)
В обозначении Г отброшена звездочка; теперь под Г подразумевается
кинетическая энергия при катании без скольжения, т. е. выраже-
выражение B) при х = 0.
Общий интеграл системы уравнений (8), содержащий пять по-
постоянных, дает значения
в функции времени. Правая часть выражения B.16.9) становится
известной функцией времени и угол 0 из него определяется квадра-
квадратурой, вносящей еще одну постоянную 00; далее квадратурами из
B.16.10) находятся как функции времени координаты х, у следа L
точки соприкасания тела с плоскостью на этой плоскости. Эти инте-
интегрирования внесут еще две постоянные. Всего в решение войдет
восемь постоянных и этим задача интегрирования исчерпывается.
Эйлеровы углы между осями связанного с телом триэдра Ox'y'z' и
неподвижного триэдра Oxyz определяются через ql, q2t ft. Действи-
Действительно, мы можем считать известным положение в каждый момент
*) Уравнения движения, из которых исходил П. В. Воронец, отличаются
от уравнений Эйлера — Лагранжа. Вывод в тексте поэтому отличен от при-
приведенного в работе, цитированной на стр. 85.
8.31
КАТАНИЕ ВЕЗ СКОЛЬЖЕНИЯ ПО НЕПОДВИЖНОЙ ПЛОСКОСТИ
383
времени «полунеподвижного» триэдра единичных векторов:
т 1 р X Р т = о — mYt = k dg* (8 3 9)
в котором векторы ка определены по B.16.19), а элемент дуги
Таблица косинусов углов триэдра Oxryrzr с осями триэдра
т, т, /»Х^ дается матрицей
(8.3.10)
тогда как матрица, осуществляющая поворот, совмещающий триэдр
Oxyz с полунеподвижным триэдром, равна
0 0 II]
cos ft sin ft 0 . (8.3.11)
— sin ft cos ft 0
m3
Pal
Р*2
Pa3
dq*
dz
dq13
dqn
dz
dqn
v°" dz
dq*
**3 dz
Поэтому матрица
(ра1 cos ft —-
sin ft)
dq*
~dz~~
cos ft j -~ m\
J aa
(pa2 cos ft — &a2 sin ft)
(pa3 cos ft — ka3 sin ft)
—j- I pa2 sin ft+^a2 cos ft) -4-
) dz
sin
cos
>y
m3
(8.3.12)
представляет таблицу косинусов углов осей Ox/y/z/ с осями Oxyz.
Остается составить формулы для определения координат xQ, yQ, z0
полюса О в системе неподвижных осей Oxyz. Для этого достаточно
спроектировать на оси этой системы векторное соотношение
? котором гм—вектор-радиус ОМ точки соприкасания поверхности
тела с плоскостью; его проекции на оси системы Oxyz равны
х, у, О. Приходим к формулам
= х — (auxf + a21/ +
(' + / + а32^Г), (8.3. 13)
У О = У — (a1
zo= — (a13xr + a23y
^O = — m • p = — e.
384 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Проекции реакции Рг, Р2, Р3 плоскости на связанные с телом
оси Ox'y'z' можно определить по уравнениям Эйлера—Лагранжа,
составленным для квазискоростей ^,, х2, Хз- Эти уравнения имеют
вид:
6 3
rts^TXt = Ps E=1.2,3), (8.3.14)
причем для Т должно быть взято выражение C). Суммирование по г
ведется от 1 до 3, поскольку все трехиндексные символы с верх-
верхним значком 4 и одним из нижних <; 3 обращаются в нуль. Для
5=1, используя таблички п. 2.16, получаем
-d- (to X p)i + \m2 (to X Р)з — Щ (» X РJ1 Х4 +
+ [/,2 (» X Р)з—'l3 (» X РJ1 Х5 + 1*22 (» X РK-^23 (» X рJ1 Хб = ~ J '
(8.3.15)
Здесь ms, /l5, /2^» (ю X РM обозначают проекции на оси системы
Ox'y'z' векторов.m, lv l2, «Хр; производные по времени величин
(to X рM представляют проекции вектора (<о X р)*, т. е. производ-
производные вектора to X р в системе осей, связанных с телом. Поэтому
соотношение A5) является результатом проектирования на ось Ох'
векторного равенства
(to X p)* + (mQ + /a<7*)X(<o X Р) = ~ЖР'
Первый множитель во втором слагаемом по B.16.18) равен to. Итак,
X(«Xp) = -^-/>. (8.3.16)
Конечно, к такому же результату приводит применение теоремы
количеств движения. Действительно, вследствие отсутствия скольже-
скольжения в точке соприкасания тела с плоскостью
v0 + со X Р = 0, v0 = — to X P.
где v0 — скорость полюса О, за который был принят центр инер-
инерции тела. Поэтому
что совпадает с A6).
В равенстве A6) вектор to должен быть заменен его значением
*
B.16.18). Выражение вектора углового ускорения to дается форму-
8.4] СЛУЧАЙ ТЕЛА, ОГРАНИЧЕННОГО ПОВЕРХНОСТЬЮ ВРАЩЕНИЯ 385
лой B.16.24). Вектор <*>Хр определяется следующим вычислением:
ИЛИ
mbatf*q*.
Нормальная составляющая реакции равна
ИЛИ
причем
M\-ka.
a'
p / dp
~ VTTT val W~~u(l
al
l — ba2q«mq2
(8.3.17)
p], (8.3.18)
(8.3.19)
где, как указывалось, р — модуль вектора р. Напомним, что
w — внешняя нормаль поверхности. Если тело давит на плоскость,
то N < 0.
Сила трения катящегося тела
Гтрт (8.3.20)
может быть определена ее ковариантными составляющими
= М
Ajf (8.3,21)
где CaT?, обозначает символ Леви-Чивита, определяемый по (П. 2.1.16).
Катание без скольжения будет иметь место, если величина силы
трения не превосходит критического значения f \ N \, т. е. при выпол-
выполнении неравенства
сПьТ^Ть < /W2. (8.3.22)
8.4. Случай тела, ограниченного поверхностью вращения
Принимается, что оси триэдра Ox'y'z' (причем Ozr — ось сим-
симметрии поверхности вращения) являются главными центральными
осями инерции; главные центральные моменты инерции обозначаются
через Л, В, С. Необязательно Л — Б, так как распределение масс
в теле может и не быть симметричным относительно оси Oz'.
25 Зак 2072 А И. Лурье
386
ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ fГЛ. 8
Кинетическая энергия тела вычисляется по формуле C.3)
27=to • [0-ЬМ (Ер • р—рр)] • ю=Л1ш1Ч-£1ш]-|-С1и>3 —М (й> • рJ, (8.4.1)
причем
А] = Л + /Ир2 = Л + М (г/2 + v2) (8.4.2)
и т. д., а скалярное произведение со • р согласно C.19) и формулам
п. 2.16 для поверхности вращения определяется равенством
со • р = £m- р-+ <7Чх • Р— ^е +■ ,- sina(—z' sin a 4-v cos a), (8.4.3)
где е = v sina-f ^cosa. Выражение кинетической энергии упро-
упрощается, если Л = В Тогда
27= Дсо2 + (С — Л — Mz'2) ш] — Л/№а>] — 2Mz'weu>i
где в соответствии с B.16.26)
со2 = &2 -|~ ср2 sin2 a -|- &2s\ оK = Q cos a — ср sin2 a,
(d^ = (S -f- cp cos a) sin a.
Потенциальная энергия силы тяжести равна
(8.4.4)
(8.4.5)
s\na + z'cos7) (8.4.6)
и дифференциальные уравнения C.8) катания тяжелого твердого тела,
ограниченного поверхностью вращения, по неподвижной плоскости
принимают вил
d дТ ,. , .. ч*/-ч1
—тт -зтт — № (v c°s a — z sin a) sbl 4-
/7A ЛУ
4- ^W (v sin a 4~ 2' cos a) (— &v 4- sin a) scp == 0,
; \- М{у cos a — z sin а) L22 —
dt ds ds
— М (v sin а 4~ z' cos a) S<p sin а —
sin a =
dt
(v sin a 4
= — Mgk (v cos a — zf sin aM
^sina 0
(8.4.7)
Здесь к—кривизна меридиана; при А = В координата ъ не входит
в выражение 7 и слагаемое -т— в последнем уравнении отпадает.
Вместо второго уравнения можно рассматривать интеграл энергии
7*4-П=Е. (8.4.8)
Тогда при Л — В, переходя к независимой переменой s, остающиеся
8.4] СЛУЧАЙ ТЕЛА, ОГРАНИЧЕННОГО ПОВЕРХНОСТЬЮ ВРАЩЕНИЯ
уравнения следует представить в виде
-—гтг- — М (v cos a — zf sin a) Q -4-
ds cJiii
-(- Ж (v sin a -f- 2' cos a) ( — &v -(- sin a) <p = 0,
I -\'J- rlT
-|- Ж (v sin a 4~ 2' cos a) v2& --| & sin a = 0.
337
(8.4.9)
Из этих двух дифференциальных уравнений первого порядка ве-
величины '^ и 2 должны быть определены как функции от s; тогда
задача определения 5 как функции времени из интеграла энергии
будет сведена к квадратурам.
Рассмотрим, в частности, тело, опирающееся на горизонтальную
плоскость своим закругленным по
поверхности сферы концом *). При-
Примем Л = В и (рис. 70)
zf = h ■+■ a cos a, v = a sin a,
где h — расстояние от центра инер-
инерции О до геометрического центра
сферической поверхности, а—ра-
а—радиус этой поверхности, так что
k = a~l> s — aa. Уравнения (9) при-
примут вид
±-*L-\- Mah D- + cos a) 2 sin a +
da d<p > '
+ -gsina = 0. (8.4.10)
Исключив из этих уравнений Ма/г2, придем к оотношению
d дТ Г/ а . \ d dT дТ . ] л
^^~Lb + cosa)^^-"^sinaJ = 0-
Оно допускает интеграл
(8.4.11)
*) Этот случай интегрируемости в задаче о катании тела по неподвиж
ной плоскости указан С. А. Чаплыгиным в известной работе «О движении
тяжелого тела вращения на горизонтальной плоскости», впервые опублико-
опубликованной в 1897 г. См. С. А. Чаплыгин, Исследования по динамике него-
лономных систем, серия «Классики естествознания», Гостехиздат, 1949,
стр. 9—27. Уравнения С. А. Чаплыгина отличаются от использованных здесь
уравнений П. В. Воронца.
25*
388 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ 8
представляющий линейное соотношение между ср и 2, позволяющее
одну из этих величин выразить через другую. Исключив теперь ср
из первого уравнения A0), прилем к линейному относительно й диф-
дифференциальному уравнению первого порялка, всегда интегрируемому
в квадратурах; ср и 2 оказываются выраженными через а, но сле-
следующий этап решения — определение а как функции времени по
интегралу энергии, хотя и сводящийся к квадратурам, может быть
достаточно полно рассмотрен лишь при некоторых специально подо-
подобранных начальных условиях, даже в предположении, что h = 0 *).
В этом последнем случае
27= Аи&+2АиЩ -+- Atf? + А,.;а\ (8.4.12)
причем
Алл = С cos2 а 4- A sin2 а, AV) =— (С — Л) cos а sin2 а, )
V /О Л 1Q\
А22 = (A cos2 а + С sin2 а + Ма2) sin2 а, Л33 = Л + Ma2 J ( * ' }
и дифференциальные уравнения A0) дают
iZ! = B = const, —-^-f/Ha22sina4-3sina = 0. (8.4.14)
Второе из них после исключения ср и соответствующих упрощений
приводится к виду
d- А (с
da Т АС + Ma* (A sm* а + С cos* а)\Г А
и после интегрирования дает
^ С08Я » (8.4.16)
где ^ — новая постоянная, а величина X определяется равенством
\ — С~А Ма*
С~+~Ш* А '
Теперь первое уравнение A4) позволяет найти
COS a — -
1- cos a + f —- " - /. (8.4.17)
*) Эту задачу в предположении, что в шаре заключен вращающийся
ротор, рассмотрел Д. К. Бобылев в работе «О шаре с гироскопом внутри»
(Математический сборник, 16, 1892). См. также работу Н. Е. Жуковского
«О гироскопическом шаре Бобылева» A894; Собрание сочинений, 1, стр. 352,
Гостехиздат, 1948). В работе С. А. Чаплыгина «О катании шара по гори-
горизонтальной плоскости» A903) доказана сводимость к квадратурам задачи
о капшии юла, ограниченного сферической поверхностью при h = 0 и
A jz В Ф С- См. чипцованную на стр. 387 книгу (стр. 72 — 99).
8.4] СЛУЧАЙ ТЕЛА, ОГРАНИЧЕННОГО ПОВЕРХНОСТЬЮ ВРАЩЕНИЯ 389
Остановимся на рассмотрении частного решения
существующего при наличии легко получаемого из интеграла энер-
энергии соотношения между постоянными C, у, Е, а0. Точка соприкаса-
соприкасания в этом случае описывает на шаре параллельный круг а = а0.
По B.16.25) получаем далее
f) = 9 + ср cos a0, ft = B + ср cos а) t -\- ft0,
и по B.16.10) след точки соприкасания на плоскости будет окруж-
окружностью
, ay sin ап . п #Ф sin cLn о
X = XQ ~\ ■*-: Sin О, У — Уо -Ч ^ COS ft.
Q + ф cos <х0 Q + ф cos a0
Наконец, ср = ф/-)-ср0. Решение содержит семь постоянных а0, р, у,
00, х0, ^0, cf0, восьмая а0 = 0, т. е. рассматриваемое движение осу-
осуществляется, если вектор сообщаемой телу начальной угловой ско-
скорости расположен в плоскости меридиана (<о°=0).
Менее общим является случай, когда следом точки соприкасания
на шаре служит меридиан. Тогда ср = 0 и это возможно, как сле-
следует из A7), лишь при p = f = O; поэтому и 2 = 0. Поскольку
геодезическая кривизна меридиана равна нулю, из B.16.25) следует,
что 0=0 и ft сохраняет постоянное значение ftQ: следом точки
соприкасания на плоскости является прямая. Закон изменения угла а
во времени находится из уравнения энергии; последнее при ср = 0,
й = 0 принимает вид
и, следовательно, a = aQt-\-aQ. Решение содержит шесть постоянных:
а0, а0, ср0, '(H и две постоянные х0, у0, определяющие начальное по-
положение следа точки соприкасания на плоскости. Движение осуще-
осуществляется, если вектор начальной угловой скорости перпендикулярен
плоскости меридиана.
С небольшими изменениями вычислений частные решения рассмо-
рассмотренного вида (катание по параллельному кругу, катание по мери-
меридиану) определяются и в задаче о катании без скольжения по непо-
неподвижной плоскости тела, ограниченного произвольной поверхностью
вращения (при А = В).
Возвратимся к рассмотрению движения твердого тела, ограничен-
ограниченного сферической поверхностью, в предположении, что центр инер-
инерции тела не совпадает с геометрическим центром сферы (h ф 0).
390
ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Тогда вместо A3) получим следующие выражения коэффициен-
коэффициентов кинетической энергии:
Аи = С cos2 а 4- (Л 4- Mh2) sin2 а,
Al2 = [(А — С) cos а 4- Mh (a 4- h cos а)] sin2 а,
Л22 = [С sin2 а + Л cos2 а-\- М(а-\- h cos аJ) sin2 а,
Л33 = Л 4~ Л! (а2 4- ^2 + 2а/г cos а).
Интеграл A1) теперь записывается в виде
[Аа sin2 а-\- C(h-\-acosa) cos а] £2 -[-
4- И0 cos а — С (/г 4- 0 cos а)] ср sin2 а = fjj/г, (8.4.19)
а первое уравнение A0) будет
-т- (Лцй 4" А2Т) ~f~ М#/г Й sin a = 0. (8.4.20)
Вычисление упрощается, если вместо ср sin2 а ввести в рассмотрение
проекцию (iK вектора угловой скорости to тела на ось симметрии Oz\
определяемую по E):
ш3 = Q cos а — ср sin2 а. (8.4.21)
Уравнения A9) и B0) преобразуются тогда к виду
(8.4.22)
(8.4.23)
—C{h-\-
причем cos a = y»
Переписав эти уравнения в виде
_ ( а — С 4- Mh2) <о3 = 0
и исключив из них -^-, получим легко интегрируемое линейное урав-
уравнение первого порядка
4- \СМа (h 4- 07) — AMa2i] ш, = 0. (8.4.24)
Из него сразу находим
-г-
8.4] СЛУЧАЙ ТЕЛА, ОГРАНИЧЕННОГО ПОВЕРХНОСТЬЮ ВРАЩЕНИЯ 391
Теперь из B2) получаем
q_JM_ i ?2[Aa-( — C(h + ai)] (8 4 26)
Аа Аа[АС + Ма2А A — f) + MC(h + a^J]42
Выражение кинетической энергии через 2, оK и а преобразуется к виду
2T{[A
(8.4.27)
Остается составить интеграл энергии; подставив в него выражения B5)
и B6) квазискоростей 2 и и>3, приведем задачу определения -[, как
функции времени, к квадратурам, выполнение и исследование которых
было бы весьма сложно. Ограничимся рассмотрением движений, в ко-
которых ось симметрии Ozr мало уклоняется от вертикали *); тогда
можно положить
^^^- ..., (8.4.28)
где Yj — мало. Обозначив через rQ значения и>3 и 2 при ^ = 1, по-
получим
АМа2 — МС (а + h) а
I Г [Aa-C(a + h)YM С-Ал Л (8.4.2У)
" — Г« I ~" I ЛС (Л + vW (а + А)*] Л" J Ч "Г • • • f • j
причем знания последующих членов разложения не понадобится.
Выражение в скобках в формуле B7), если провести вычисление
f
с точностью до if, оказывается равным
^
(8.4.30)
Возвращаясь к углу а, получим
или
(8.4.31)
*) Задача об устойчивости этого движения рассмотрена в работе
Л. С. Исаевой «О достаточных условиях устойчивости вращения волчка
„тип-топ", находящегося на абсолютно шероховатой плоскости» (Прикладная
математика и механика 23, № 2, стр. 403—406, 1959).
392 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ fГЛ. 8
Потенциальная энергия равна
Yl = Mg(a + h cos a), (8.4.32)
так что выражение интеграла энергии записывается в виде
(8.4.33)
Из него дифференцированием по времени получаем
f ri Г С 4- M (а 4- fi) a "j2 I Crl — \Mgh )
При /г < 0 (центр инерции расположен ниже центра сферы) угол a
изменяется по гармоническому закону с частотой
+ М (а + hY J ~^T A + M(a + h)* J " W-™°>
Положительность подкоренного выражения является необходимым
условием устойчивости вертикального положения оси при h > 0, когда
центр инерции расположен выше центра сферы.
8.5. Дифференциальные уравнения Аппеля *)
Рассматривается система материальных точек, конфигурация кото-
которой задается п независимыми обобщенными координатами qx, ..., qn.
Уравнения неголономных связей, если таковые имеются, записываются
в виде
2«*Я-М* = 0 (ft=l О, (8.5.1)
S = \
где aks и ak в общем случае представляют функции обобщенных
координат и времени. Уравнения A) должны быть разрешимы отно-
относительно / обобщенных скоростей qv ..., qh т. е. дефект прямо-
прямоугольной ly^n матрицы G.10.5) должен быть нулем. Тогда, выразив/
обобщенных скоростей через остальные п — /, получим систему ра-
равенств
(r=l /). (8.5.2)
*) См. Р. А р р е 11, Sur une forme generate des equations de la dynamique.
Memorial des Sc. Math. № 1, Paris, 1925. Там же подробный указатель лите-
литературы, посвященной уравнениям Аппеля. Впервые они были опубликованы
в 1899 г.
8.5] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ АППЕЛЯ 393
Уравнения, связывающие зариации обобщенных координат
п
2аЛ = 0 (*=1 0. (8-5-3)
5 = 1
позволяют выразить также вариации Ъд{, ..., bqt через (п — /) ва-
вариаций <^+1 Ьдп, которые уже будут независимыми. Подобно B)
получим
8?г = 2>,,!нЛ+, ('•=1 О- (8.5.4)
Дифференцируя уравнения B), найдем выражения обобщенных
ускорений
п-1 п-1
Яг = 2 br.i+jli+s + S К. i+sQi+z + К (8-5-5)
Этими равенствами мы воспользуемся, чтобы исключить qr из выра-
выражения A.3.9) вектора ускорения точки системы Mt. Имеем
где многоточием отмечены слагаемые, не зависящие от обобщенных
ускорений. Воспользовавшись соотношениями E), перепишем это
равенство в виде
/ п-1 п-1
дг, ••
Г-1 5=1 5=1
П-l I I
Теперь, обозначив
r=i г
получим
п-1
5 = 1
и, поскольку невыписанные слагаемые от обобщенных ускорений не
зависят, приходим к используемым далее равенствам
Нетрудно сообразить, что виртуальные перемещения brt выражаются
через независимые вариации bql+s с помощью линейных соотношений
394 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ 8
с теми же коэффициентами chlhs. Действительно, использовав D),
имеем
п I п-1
wkb^=
или по G) и (9)
221^-^'+*- (8-5Л0)
21^
5 = 1 5 = 1 ^l + s
Применим соотношения A0) к преобразованию левой части общего
уравнения динамики F.3.2). Имеем
/V TV n-l
? 9/+,
i=\ / = 1 ,у = 1 ^/ + ^
Х>,«'г^- (8.5.11)
5=1 /=1 4l+S
Замечая, что
.V /V
_i-=_--^«j«|.«l=-5=-. (8.5.12)
придем к равенству
TV П-l
в котором S, согласно D.10.1), представляет энергию ускорений.
При вычислении S, как видно из хода вывода, учтено наличие него-
лономных связей; с помощью уравнений этих связей из выражения <S
исключены обобщенные ускорения qlt ..., qt.
Остается преобразовать правую часть общего уравнения дина-
динамики— выражение элементарной работы задаваемых сил
b'W = 2 Fr brt = 2 Ft ■ 2 ct, l+s bql+s = 2 Ql+S ogl+s. (8.5.14)
/=1 i=\ s=\ 5=1
Здесь
N
Qi+s = Hcitl+s'F, (s=\ n — l) (8.5.15)
/ -1
— обобщенные силы для независимых вариаций обобщенных
8.6] УРАВНЕНИЯ АППЕЛЯ В КВАЗИСКОРОСТЯХ 395
координат. В соответствии с G) их выражениям можно придать вид
N I I \
[ dri 1 V дП ъ
\ dqr+ ^ Zj dqr °r>l+s
/=1 \ l+s r=\ I
или, по E.1.3),
Qi+s = Qi+s+2ibr.i+sQr (s=l> •••• л —0. (8.5.16)
r = l
где Ql + S, Qr — обобщенные силы, вычисляемые в предположении, что
все вариации независимы.
Общее уравнение динамики теперь преобразовано к виду
п-1
(й)=0' (8>5Л7)
(w
откуда вследствие независимости вариаций bql+s следуют уравнения
движения в форме Аппеля
*L (s=l. .... п — 1). (8.5.18)
Число их равно числу степеней свободы системы. Это дифферен-
дифференциальные уравнения второго порядка относительно обобщенных коор-
координат ql+l, ...%qn\ но в общем случае в их состав входят все
обобщенные координаты и скорости. Совместно с уравнениями него-
лономных связей, которые можно записывать в виде B) или A),
имеем систему п дифференциальных уравнений, содержащую столько же
неизвестных. Порядок этой системы равен 2(п — I) -\~ 1 = 2п — /.
Напомним, что уравнения Лагранжа с множителями при наличии /
неголономных связей представляют систему дифференциальных урав-
уравнений, порядок которой равен 2/г + /.
Уравнения Аппеля применимы и при отсутствии неголономных
связей. Ниже будет показано, что в случае голономной системы они
в точности совпадают по форме с уравнениями Лагранжа второго
рода G.1.4). Конечно, при составлении выражения 5 следует учесть
лишь слагаемые, содержащие обобщенные ускорения; нет нужды загро-
загромождать вычисление членами, их не содержащими.
8.6. Уравнения Аппеля в квазискоростях
Вычисление энергии ускорений и составление уравнений Аппеля
значительно упрощается при применении квазиускорений вместо обоб-
обобщенных ускорений.
Пусть o)j, ..., о)/2 обозначают квазискорости, причем уравнения
неголономных связей выражаются равенствами
О)я=0 E= 1, ...,/). (8.6.1)
396 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Тогда вектор скорости точки системы по A.5.19) представится ра-
равенством
Дифференцируя его, получим вектор ускорения
п-1
<"< = 2-^ "<-+••" (8-6-3)
причем точками обозначены члены, не зависящие от обобщенных
ускорений. Следствием C) являются соотношения
(8.6.4)
С другой стороны, учитывая, что при наличии неголономных свя-
связей A)
§i:s = 0 (s= 1, ...,/), (8.6.5)
по A.6.14) имеем
%%
Поэтому
w . J&-
/г-/ N
с — 1 ^ ' " / 1
о — X f = 1
ИЛИ
TV я-/
(8-6.7)
где 5—энергия ускорений. Остается заметить, что по E.1.6) эле-
элементарная работа активных сил может быть представлена равенством,
имеющим вследствие соотношений E) вид
п-1
8'W = 2^,S1t;+J, (8.6.8)
s=\
где Р^8 — обобщенные силы, отнесенные к квазикоординатам; они,
равно как и S, вычисляются с учетом неголономных связей.
8.6] УРАВНЕНИЯ АППЕЛЯ В КВАЗИСКОРОСТЯХ 397
Общее уравнение динамики преобразовано к виду
п-1
2 (-^ Pi+s) Stc/+j = °. (8-6-9>
и из него вследствие независимости вариаций Ъъц.5 следуют уравне-
уравнения Аппеля в квазискоростях
-4^- = Pl+S (s = 1, . . .. п — /). (8.6.10)
К этой системе п — / уравнений первого порядка, содержащей
первые производные по времени и>/+5 квазискоростей и сами эти квази-
квазискорости, а также, в общем случае, все обобщенные координаты
qv ..., qn, надо присоединить систему п уравнений первого по-
порядка A.5.25)
П-1 1 1
определяющих первые производные по времени обобщенных коорди-
координат через квазискорости.
Конечно, уравнения Аппеля A0) с успехом применимы и к со-
составлению уравнений движения голономных систем.
По форме уравнения Аппеля A0), как показывается ниже, ничем
не отличаются от уравнений Эйлера—Лагранжа A.13). Применение
тех или иных уравнений— вопрос вычислительного удобства. Поль-
Пользование уравнениями Эйлера — Лагранжа предполагает предваритель-
предварительное нахождение трехиндексных символов; кинетическая энергия должна
вычисляться без учета наличия неголопомных связей, что усложняет
структуру этого выражения; само написание уравнений требует вни-
внимания в расстановке индексов. При применении уравнений Аппеля
основная трудность состоит в вычислении энергии ускорений; тре-
требуется внимание, чтобы не упустить слагаемых, содержащих квази-
квазиускорения. При рассмотрении неголономных систем дело облегчается
возможностью учитывать наличие этих связей. Не следует переоце-
переоценивать значения правил D.10.4) и D.10.12) составления энергии уско-
ускорений S по кинетической энергии Т, так как применение второго
из них требует знания трехиндексных символов и выражения Т, вы-
вычисленного при отброшенных связях, а применение первого для соста-
составления уравнений Аппеля в форме E.18) воспроизводит выкладки,
которые надо проделать при написании уравнений Лагранжа второго
рода (если неголономные связи отсутствуют). Важное значение имеют
в задачах динамики твердого тела правила составления S, данные
в п. 4.11. Уравнения Аппеля легко запоминаемы, а процесс
398 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
написания их, когда 5 составлено, уже не представляет никакого
труда.
Мы не рассматриваем в этой книге систем, подчиненных нелиней-
нелинейным неголономным связям. Уравнения Аппеля*), равно как и с неко-
некоторыми видоизменениями уравнения Эйлера — Лагранжа **), применимы
к рассмотрению таких систем.
8.7. Явная форма уравнений Аппеля. Уравнения Чаплыгина
Будем исходить из представления D.10.6) кинетической энергии
ускорений. При отсутствии неголономных связей E.1) уравнения
Аппеля E.18) в соответствии с E.16) принимают вид
#- = Qr (r=l. .... п). (8.7.1)
dqr
Обратившись к D.10.6), получим
s=l s=\ *=l
AST дВг дВЛ- дВг дТ0
dt ' да, да
s = \
Но, обратившись к равенству G.4.1) и вспомнив G.3.5), нетрудно
заметить, что правая часть его представляет не что иное, как выра-
выражение в развернутой записи эйлерова оператора $Г(Т). Теперь урав-
уравнения A) можно представить еще в форме
~- = Ъг(Т) = Qr (r=U ..., п). (8.7.3)
dqT
Итак, в случае голономных связей уравнения Аппеля тождественны
с уравнениями Лагранжа второго рода — ничего другого не могло
и быть, так как правые части их представляют те же обобщенные
силы.
При наличии связей, выражаемых соотношениями E.2), дифферен-
дифференцируя, найдем
причем точками обозначены слагаемые, не содержащие обобщенных
ускорений. Энергия ускорений <S теперь зависит от обобщенных
*) См. книгу Аппеля, указанную в подстрочном примечании на стр. 392.
**) См. курс Гамеля (подстрочное примечание к стр. 310), § 8, гл. 9.
8.7]
ЯВНАЯ ФОРМА РАВНЕНИЙ АППЕЛЯ. \ РАВНЕНИЯ ЧАПЛЫГИНА
399
ускорений <7л л» как явн0 входящих в ее выражение D.10.6), так и
входящих в 5 через посредство qr. Поэтому
, V^ , dS
или
dS
(8.7.5)
r=\
и уравнения Аппеля E.18), если учесть еще E.16), могут быть за-
записаны в виде
/
dS
= 1 0. (8.7.6)
Легко предвидеть, что эта запись уравнений Аппеля тождественна
с уравнениями движения G.10.9), получающимися после исключения
множителей связи из уравнений Лагранжа. Надо лишь убедиться
в наличии равенств
bnl+k = — Nrl+* (r=l, ..., /; k=l. .... n — l). (8.7.7)
Действительно, выражения E.2) получены из решения системы урав-
уравнений
I п-1
2 qrQr ^Q, i
r-\ k=\
с матрицей коэффициентов
— aq
012
О>2\
(q =
аи
02/
(8.7.8)
и определителем
0/1 0/2 ... 0//
= | а* I. Алгебраическое дополнение а^ эле-
элемента uqr q строки и г столбца этого определителя равно обозначен-
обозначенному в и. 7.10 также через aqr алгебраическому дополнению эле-
элемента q строки и г столбца определителя I a[ | транспонированной
матрицы а*. Решение системы уравнений (8) имеет вид
п-1
(8-7-9)
400 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
то есть
и остается сослаться на формулу G.10.10), чтобы убедиться в нали-
наличии равенств G).
Вместо описанной процедуры составления уравнений Аппеля, можно
было бы сначала исключить из выражения энергии ускорений D.10.6)
все qr (г = I /) с помощью уравнений D), а потом проделать
дифференцирование по остающимся обобщенным ускорениям qUk.
Это и предполагалось в записи E.18) уравнений Аппеля, которые
мы теперь запишем в виде
^=«- <*-■ °- <8-7л"
обозначив через S выражение энергии ускорений после упомянутого
исключения величин qr
Через Т обозначим результат исключения из выражения кинетической
энергии Т обобщенных скоростей qr определяемых по E.2). Было бы,
однако, грубо ошибочно предположить, при наличии неголономных
связей, что
(У о л? /т^ч
Если бы это было так, то в соответствии с F) разности
Л/+л (8.7.12)
были бы нулями. Убедимся, что они отличны от нуля. Это вычисле-
вычисление, следуя С. А. Чаплыгину *), проводим в предположении, что
связи стационарны и как в выражение Т, так и в выражения коэффи-
коэффициентов brtl+k не входят обобщенные координаты qx ql% Тогда
имеем
+ \>
*) О движении тяжелого тела вращения на горизонтальной плоскости
A897), Сборник статей С. А. Чаплыгина «Исследования по динамике
i-iei олономных систем» в серии «Классики естествознания» (Гостехиз-
1Ш
8.7) ЯВНАЯ ФОРМА УРАВНЕНИЙ АППЕЛЯ. УРАВНЕНИЯ ЧАПЛЫГИНА 401
откуда следуют равенства
у дТ
дТ дТ у дТ
i i
d дТ d дТ у d дТ у дТ ;
^ "l+k dt dk + £ dk "
dt dkl+k dt dql+k \^ "l+k dt
df _ ОТ ,у_дТ_ у • dbnl+
aqr
Теперь, учитывая, что
получаем
n-l
Но
так что по F) и E.16) получаем
Q^^.,, (S.7..4,
(* = 1, .... П — 1).
Эта система дифференциальных уравнений движения системы, подчи-
подчиненной неголоиомным связям, тождественна с уравнениями Чаплы-
Чаплыгина. Как видно из нее, предварительное исключение из выражений
кинетической энергии Т при составлении уравнений Лагранжа обоб-
обобщенных скоростей qr по уравнениям связей E.2) привело бы к оши-
ошибочным результатам. В так составленные уравнения должны быть
внесены корректирующие слагаемые
I п-1
дт \}(dbm+k dbr,l+m
dqf L { dqt,m dql+h
/■ = 1 m = 1
{k=\ П — 1).
26 Зак. 207'£ Л И. Лурье
402 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Они обращаются в нуль, когда
dbId±lL_dbr,l+m =() j
Но в этом случае существуют функции /r(<7/+i» •••» <7rt). такие, что
K,i+k = ^~ (Г=\ /; к=\ я-0.
и уравнения связей E.2) будут интегрируемыми (по предположению
связи стационарны), так как
одп
или
4r = fA4i+v •••• ?«) (^=1' •••• О-
Координаты <7Р •••» ^; являются избыточными. В этом случае пред-
предварительное исключение qT из выражения Т естественно является
законным — можно было их не вводить с самого начала.
8.8. Применение к неголономным системам
Вернемся к трем примерам составления дифференциальных урав-
уравнений движения, рассмотренным в п. 8.2. Убедимся, что эти же
уравнения можно получить методом Аппеля.
1°. Шар. Энергия ускорений шара, катящегося без скольжения
по неподвижной плоскости, по D.13.3) имеет выражение
причем отброшены слагаемые, обращающиеся в нуль в силу уравне-
уравнений неголономных связей:
(Б4 = (Ь5 = 0.
Левые части уравнений Аппеля F.10) равны
dS 7 лл о~ dS 7 АЛ 21 dS 2
Mauv г МацJ, j
5 д(Ь2 5 д(Ь3 5
(8.8.1)
Обобщенные силы определяются выражениями B.4). Приходим
к уравнениям движения B.5).
8.8] ПРИМЕНЕНИЕ К НЕГОЛОНОМНЫМ СИСТЕМАМ 403
2°. Обруч. Энергия ускорений дается выражением D.13.12). Из
него получаем
-1 ш2 ctg ft),
-^- = Ma2 (- w2 — o^ + - 0)^2 ctg
o>co2 \ 2 2
—:— = Ma2 Bco3 — 0)^2).
(8.8.2)
Потенциальная энергия определяется по B.12). Из нее получаем
выражения обобщенных сил, после чего записываются уравнения
движения B.14).
3°. Двухскатная тележка. Дифференцированием по со7 и со8
выражения D.13.23) энергии ускорений получаем левые части диф-
дифференциальных уравнений движения B.23).
4°. Уравнения Чаплыгина в задаче о шаре. Выражение
кинетической энергии Т через обобщенные скорости и уравнения
неголономных связей, как указывалось в п. 8.2, имеют вид
(8.8.3)
хо = а (Я sin ф — 9sin ^ cos ф), Уо = — а (Й cos ф 4~ Т sin 0 sin ф). (8.8.4)
Уравнения Чаплыгина применимы, поскольку связи стационарны,
а х0 и у0 не входят ни в выражение 7, ни в уравнения связей.
Исключив х0 и у0 из 7 с помощью уравнений связей, получим
Т=±- Ma2 [-^ ft2 4- ?2 sin2 ft 4- -| (ф2 4- f + 2срф cos ft)J.
Принимая нумерацию обобщенных координат
получаем
5
$3 G) = -| Жа2 (ф 4- 9 cos ft — c^ft sin ft),
S4 G1) = Ma2 (j ft — 92 sin ft cos 0 4~|- <рф sin
$5 G) = Ma2 (i sin2 ft 4- 2^ft sin ft cos ft 4- -| 9 4- ~ ф cos ft — | ф?> sin ft].
Обобщенные силы Q2+r» определяемые по E.16), равны
Q3 = Щ> Q\ = mN 4-a (V\ ™ Ф — ^2 cos ф),
Q5 = mz — a (Vx cos ф-f V2 sin ф).
404
ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Остается вычислить величины
з
/71 = 1
dq2i
Их значения указаны в табличке
5=1 — a ( ft cos'i»-f 9 sin 0- sin b) a cos -L- (I 4- <P cos ft) a ($sin ft sin <p - ftcos ft cos i)
5=2 —a (ft sin ф— cp sin 0- cos |) я sin ф (ф Ч-9 cos ft) — a ( ^sin ft cos ф-f ft cos 0 sin ф
Заметив еще, что
получаем следующие значения двойных сумм в правых частях уравне-
уравнений G.14):
г=\ О
г = 2 — Ма1'^ (ф -Ь ср cos П) sin &,
г = 3 Жа2а (ф ■+- ср cos 0) sin ft,
и после некоторых упрощений уравнения Чаплыгина примут вид
4 Ма2 (ф 4- Ф cos ft — if) cos ft):
о
I
(8.8.5)
7 -. • ^> -w
-^- Ma2 (ft -|- срф sin ft) = myv — «(V/1 sin ф — V2 cos ф),
Ma2 U sin2 {) +2^ 4-1 (jicosft + 9ft sin ft cos ft —-^ фП sin ^ =
= //i3 — а (У х cos ф 4- ^2 sin Ф)-
Конечно, этот же вид приобретают уравнения B.9), если в них за-
заменить jc0, y0 их значениями, получающимися при дифференцировании
равенств D). К простой и компактной форме B.5) уравнения E)
приводятся при перепроектировании на оси Oxyz, для чего надо
использовать формулы вида E.2.15).
По формулам G.10.15) составим еще выражения обобщенных
реакций связей
* = мх, -
: = му{, - v,,
Q* =-- а \— М (х0 sin <|> — у0 cosф) + (V, sin
с?; = о.
V2 cos ф)].
Q* == а \М (х0 cos ф -4- У„ sin ф) — (Vj cos ф + V2 sin ф)].
(8.8.6)
8.8] ПРИМЕНЕНИЕ К НЕГОЛОНОМНЫМ СИСТЕМАМ 405
Сложность самих уравнений движения (8.5) и вычислений, свя-
связанных с их получением даже в столь простой задаче, как катание
шара, служат объяснением тогсТ, что сам С. А. Чаплыгин при рас-
рассмотрении частных задач не пользовался уравнениями G.14) — он
привел их с целью предупредить ошибку, могущую произойти при
исключении из выражения Т «лишних» обобщенных скоростей, и
указал форму корректирующего члена G.15).
5°. Плоское движение материальной точки. Приведем
еще один поучительный и простой пример применения уравнений Эйле-
Эйлера— Лагранжа и Аппеля. Условимся, следуя Аппелю, определять поло-
положение движущейся точки М на плоскости ее вектор-радиусом г = ОМ
и удвоенной площадью а сектора ОМ()А1, описанного вектор-
радиусом в предшествующем движении (ОМ{) — начальное положение
вектор-радиуса). Обозначая через ср угол М0ОМ, имеем выражение
удвоенной секториальной скорости
о = г\, (8.8.7)
так что кинетическая энергия точки (считая массу равной единице)
будет
(> + ty)±(t+£) (8.8.8)
Соотношение G) является неинтегрируемым уравнением, определяю-
определяющим квазискорость а через обобщенную скорость ср. Называя еще
w>l=r, со2 = а, Stcj = 8г, 8тг2 = 8а = г2 8ср,
имеем
2
(8ти2)" — 8аJ = 2rr 8ср — 2гср Ьг = — (а^ Stt2 — co2 8tuj)
и по A.8.4) находим
2
ТГг ~ 4r2i===~r' (8.8.9)
Элементарная работа силы, приложенной к точке, равна
VW = F,br + F^r 8cp = Fr Ь*х + ^ отг2.
Теперь по A.13) составляем уравнения движения
d дТ дТ F9
dt д(*2 "■ П2 до>2 l~ r '
Вычисление дает
# г — ^- -uii — F A__^i_ i l*'r If
406 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ (ГЛ. 8
Получили уравнения движения
г' —-£ = /%, о o = rF9. (8.8.10)
Составление же уравнений Лагранжа по выражению кинетической
энергии (8) привело бы, конечно, к неверным уравнениям, поскольку
уравнение связи G) неинтегрируемо.
Заметив далее, что
w = г — г '2 = г — — w = - (г2')' = '—
составляем выражение энергии ускорений
и уравнения Аппеля F.10) снова дают найденные ранее соотноше-
соотношения A0).
6°. Фрикционный редуктор*). Составим уравнения движе-
движения в форме Аппеля для изображенного на рис. 71 механизма, осу-
осуществляющего передачу вращения от пала / барабану С, жестко
Рис. 71.
насаженному на вал 2. Диск А закреплен на валу / жестко, а коле-
колесико В может свободно вращаться на иевращающемся валике 3, но
не смещается поступательно вдоль оси этого валика. Центробежный
*) Этот пример системы, подчиненной неголономной связи, приведен
в статье В. С. Новоселова «Пример нелинейной неголономной связи, не
относящейся к типу Н. Г. Четаева» (Вестник Ленинградского университета,
№ 19, 1957, стр. 106—112)
8.8] ПРИМЕНЕНИЕ К НЕГОЛОНОМНЫМ СИСТЕМАМ 407
регулятор Р вращается на одном валу с барабаном С; перемещение
его муфты D с помощью тросика, пропущенного по неподвижным
роликам Ох и О2, передается валику 3; вследствие этого колесико В
при изменении угловой скорости ср2 вала 2 (разгоне или торможении)
будет смещаться вместе с валиком 3 по диску Л (к его центру или
в противоположную сторону); допускается, что вследствие этого
должно восстанавливаться исходное значение <р2. Требуется составить
дифференциальные уравнения движения системы.
Положение системы может быть определено тремя обобщенными
координатами: углами поворота ср,, ср2 валов / и 2 и расстоянием х
муфты D от шарнира L; расстояние же р = SQ центра Q колесика В
от оси вала / легко выразить через х. Эту связь можно получить,
замечая, что сумма длин ветвей OXD и О2К тросика (т. е. длины
тросика, уменьшенной на отрезок OjO2) постоянна. Имеем
OXD = OXL — х, О2К == O2S + p — KQ
и, поскольку отрезки OXL, O2S, KQ постоянны, будет постоянной
и разность
х — р = с. (8.8.11)
Выражая теперь условие равенства окружных скоростей точек
соприкасания колесика В с диском Л и барабаном С (при отсутствии
проскальзывания), получаем уравнение неголономной связи
P?1 = /??2. (8.8.12)
Система имеет две степени свободы.
Переходим к вычислению энергии ускорений, конечно, сохраняя
лишь слагаемые, содержащие обобщенные ускорения. Энергии уско-
ускорений диска Л, барабана С, колесика В и муфты D соответственно
равны
% i& ^E ) \rnDx\ (8.8.13)
Более сложно вычисление кинетической энергии ускорений шаров.
Назовем а угол стержня LN с осью вала 2, так что
х = 2/cos а.
Рассмотрим проекции ускорения Wn центра шара на три взаимно-
перпендикулярных направления: направление стержня LN, перпенди-
перпендикуляра к нему в плоскости механизма центробежного регулятора и
перпендикуляра к этой плоскости. В выражение первой из этих
проекций обобщенные ускорения не входят, вторая, как видно из
рис. 71, равна
/а — /<р2 sin а cos а,
а третья .. . .
/ср2 sin а -(- 2ср2/а cos а,
408 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
причем второе слагаемое представляет ускорение Кориолиса. Таким
образом, в выражение энергии ускорений двух шаров входят сла-
слагаемые:
-^-2mNl2(a2— 2аср2 sin а cos а -\- ср| sin2 а-(-4ср2ср2а sin а cos а). (8.8.14)
Обобщенное ускорение срх исключается из выражения энергии
ускорений с помощью уравнения неголономной связи A2); получаем
На законность этой процедуры при составлении уравнений Аппеля
указывалось в п. 8.7. Имеем также
ос — —
~" 4/2 sin2 а т 4/3 sin4 a
Теперь, складывая выражения A3) и A4), получим S в виде
[1 • 2/2jc2 l
ycP2+D/2_;c2JJ- (8.8.15)
R2
Переходим к обобщенным силам. Через ср^ и х0 обозначим значе-
значения ср2 и х в некотором стационарном режиме. Пружина регулятора,
поскольку тросик должен быть растянут, будет в этом режиме иметь
длину /х —|— Sj, большую натуральной (она должна быть предварительно
растянута), а пружина, упирающаяся в колесико В — длину /2 — о2
(она предварительно сжата). При отклонении от стационарного режима
длины пружин станут равны
h + 8i •+•х — хо> 12 — Ь2 + Р — Ро = к — \ + х — хо-
Изменения их длин (отсчитываемые от натурального состояния) равны
^-(-л: — х0 и й2—х-\-х{), так что потенциальная энергия yupyi их
сил с точностью до постоянного слагаемого будет
II = -2 с, (Oj + х — х0J + -j с,2 F2 — х + х0J =
« ! б)
8.8] ПРИМЕНЕНИЕ К НЕГОЛОНОМНЫМ СИСТЕМАМ 409
Элементарная работа моментов тх и т2, прилагаемых к валам / и 2,
по A2) равна
VW = тх 8<р, + т2 Ц2 =
и обобщенные силы, отнесенные к координатам ср2 и х, будут
+ т Q (^ + С) (х х) (СА с
= т
\ -j~=
Остается записать дифференциальные уравнения движения, пользуясь
схемой E.18):
в (х) ср2 — Ф (х)ху2 = т} 1- т2ч
2Рх • о
т (х) х + т
(8.8.17)
причем приняты обозначения
Для проверки и сравнения составим теперь те же уравнения
движения, используя способ Чаплыгина; это возможно, поскольку срг
не входит ни в выражение кинетической энергии, ни в уравнение
неголономной связи. Легко составляется кинетическая энергия системы
причем первый член
выражения приведенного момента инерции й (х) получился исключе-
исключением cpj с помощью уравнения неголономной связи A2) из слагаемого
Уравнения Чаплыгина будут
*л( 7") = <?*, + £,>,. bx(T) = Q* + Rx. (8.8.19)
410 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
где корректирующие члены, вычисляемые по G.15), равны в нашем
случае
R R2
D __ й • • d I R \
JZ 7\з
d I R \ R2
$x = — ел?т Ъ-^ \x — c ) = ®л J^Z~cf c
Теперь нетрудно убедиться в тождественности систем уравнений
A9) и A7).
Уравнения движения в установившемся режиме — уравнения относи-
относительного равновесия регулятора — получим, полагая в A7)
х = х0, х = 0, х = 0, 92 = ^2- Ь = °-
Приходим к соотношениям
г> 1
т0 tl Lm'1 П m v- rnO2 , . ft .ft /л ГЙ 8 9П
Вводя в рассмотрение величины, определяющие отклонения от уста-
установившегося режима,
^ * * о
и считая их малыми, получим, учитывая B1), систему линейных
дифференциальных уравнений
в (*0) 2 - ХОФ (*0) q + -Lt/- q =
m°}R
^ (^o)? +1 ^.v?? (^ +■ 22) + (c2 + c2) q = 0,
причем
(8.8.22)
/72 о — /72^,
Рассмотрим соответствующую однородную систему (\ь1 = [х2 = 0).
Разыскивая ее частное решение в виде
придем лля определения X к характеристическому уравнению:
в (*0) т(я-0)ХЗ + [в (х0) [сх + с2 + ^ /*„<#) + т^0Ф (х0) ?o-J K +
4- mv^-<^ = 0. (8.8.23)
Здесь т^ заменено через т\ с помощью первого уравнения относи-
относительного равновесия B1). Недостаток слагаемого, содержащего X2,
8.9] ЯВНАЯ ФОРМА УРАВНЕНИЙ ЭЙЛЕРА ЛАГРАНЖА 411
может быть восполнен, если предположить наличие катарракта на
регуляторе — приспособления, создающего силу сопротивления движе-
движению муфты, пропорциональную ее скорости. Тогда во втором урав-
уравнении B2) появится слагаемое, содержащее д. Устойчивость стацио-
стационарного режима может быть достигнута, когда к валу 2 подводится
мощность (а»^ ^ О)» з вал / является ее приемником (т®у® < 0Y
Устойчивость будет иметь место, если коэффициенты уравнения B3)
удовлетворяют известному критерию Гурвица; для уравнения третьей
степени дело сводится к рассмотрению диаграммы Вышнеградского *).
8.9. Явная форма уравнений Эйлера — Лагранжа
Ограничимся рассмотрением стационарных связей и задания квази-
квазискоростей с помощью однородных линейных форм A.5.1) от обоб-
обобщенных скоростей. Имея выражение D.1.16) кинетической энергии,
найдем
и подстановка в A.8) приводит к уравнениям
п п п п
к-\
r-l *=1
1 дАть \
Можно, применив обозначение D.10.9), записать двойную сумму
в виде
гГу
1 V V I sr l ^* дАкг 1 V V i »,
*) И. А. В ыш н е г р а д с к и й, О регуляторах прямого действия, Сбор-
Сборник «Теория автоматического регулирования» в серии «Классики науки»,
Изд-во АН СССР, 1949. стр. 43—87. См. также любой из курсов теории
автомат ического perулировании.
412 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Получаем
(8.9.1)
Естественно, что в точности к этим же уравнениям пришли бы, за-
записав уравнения Аппеля F.10) по выражению кинетической энергии
ускорений D.10.12).
При наличии / уравнений неголономных связей вида
u)m = 0 (т= 1 /) (8.9.2)
уравнения A) приобретают вид
п t п п ( п \
7, Л ,оо, н— 7, У, а)«,о), < >1 у. Л . -4- г. /г: s\ \=jt (о 9 oi
(s = / —j— 1 n).
Для определения обобщенных реакций Xm связей служат соотношения
п п п ( п \
Л СО —f— У, У. OihUL{ 7, Т /1 —Н |Г ^ Wl > И —|— Л
mk k ' ^eJ ^hJ R t \ jaU »tm tr ' l ' I tn > tn
(tn=\ /), (8.9.4)
в которых оо/г должны быть заменены их значениями из уравнений C).
Как пример определим реакции неголономных связей в задаче
об обруче. Надо определить реакции Х4, Х5; отличные от нуля коэф-
коэффициенты выражения кинетической энергии D.13.6) с индексами 4 и
5, равны
Лз4 = — Ма, ^15 = — /Wa sin и.
Интересующими нас трехиндексными символами являются -^ и Т^з*
По B.10.28) и B.10.29) они равны
?24 sin Ь ' "^25 sin ft '
Рассмотрение формул D.10.9) показывает, что отличной от нуля
будет лишь одна из прямых скобок
[1, 1; 5],=—^ = -
Получаем
L=Ма(— шз + о)^),
/ • coco \ \ (8.9.5)
/ .— Ма — о)! sin 0 ?—I со? cos ft ).
5 V 1 sin» . 1 J
8.10] УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА 413
Эти же выражения легко получить, применив теорему количеств
движения; имеем, использовав «полунеподвижную систему» осей,
описанную в п. 2.10,
Q = Mv0 = M (uL/i + о)^ i
Учитывая, что
найдем
пл = -^
' sin
или, по B.11),
Q = Me [(- «, + u)lUJ) я - (щ sin ft + «of cos
Проекции главного вектора внешних сил V на направления п и
пх как раз представляют искомые реакции.
В формулах E) производные о»3 и ш1 надо заменить их значе-
значениями по уравнениям движения B.14). Найдем
1
(8.9.6)
— -§--£ sin 0 cos Ol.
За J
8.10. Уравнения движения свободного твердого тела
При составлении уравнений движения в форме Эйлера — Лаг-
ранжа будем исходить из выражения кинетической энергии D.7.8)
Т=\\М
Здесь г>01,
}. (8.10.1)
01 (J 03 р р
ных осей инерции Ox'y'z' в полюсе О; оо^ cjd2, ш3 — проекции на
них угловой скорости; х'с, у'с, z'Q— координаты центра инерции
тела в этих осях. Значения необходимых трехиндексных символов
даются формулами B.10.3) и B.10.8), причем квазискоростям vol,
v(J, у03 по B.10.4) приписываются номера 4, 5, 6. Имеем
-^ = М (y'cvm - z'cvvi)
414 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
и аналогичные равенства, получаемые при круговой перестановке
индексов.
Отличны от нуля следующие трехиндексные символы с правыми
нижними индексами 1 и 4:
• 31 1* »21 lj *61 — " 1} T51 — l* T34— if T24— l'
Поэтому, обратившись к уравнениям Эйлера — Лагранжа, получим
d дТ
дТ
дТ
d дТ
dt dcoi
дТ
dt dvQl
+
дТ
дТ
■=m?
(8.10.3)
J
и другие аналогичные уравнения. Правые части записаны в соответ-
соответствии с равенствами E.2.12). После подстановок получим две группы
уравнений по три уравнения в каждой.
Уравнения первой группы имеют вид
+ ш1(ш2у/с + ш/с) = ^-. (8.10.4)
Два других получаются с помощью круговой замены индексов.
Первое уравнение второй группы будет
- в;) со2ш3 + М [у'с (vm + ш, vm - oJz»03) -
К этим же уравнениям придем, обратившись к выражению D.11.10)
энергии ускорений. Перепишем его в виде
). (8.10.6)
Пользуясь правилами дифференцирования
a b —
das
4- a2b2 + a3b3) = bs,
да i
(8.10.7)
8.10] УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА 415
получим теперь, составив производные по квазиускорениям vQs и u>Sf
уравнения Аппеля F.10) в виде
4^ = М [r'cX (vo + » Xvo)l4-@° • » + » X 0° • wM = m?
E=1, 2, 3).
Конечно, это — те же соотношения D) и E). Ясно видно, что урав-
уравнения движения свободного твердого тела представляют два
векторных соотношения
М [vo + to X *>о + » X r'c + <о X (to X rfc)\ = V, (8.10.8)
0° . to + to X 0° • » + Л^ X D + <° X v0) = т° • (8.10.9)
Первое из них выражает теорему количеств движения, второе—тео-
второе—теорему моментов количеств движения относительно полюса О. Действи-
Действительно, вспоминая выражение D.8.9) главного вектора количеств
движения Q и формулы дифференцирования B.7.9) и B.13.3), по-
получим
Q = A1 [»;, + « Xvd + «X^ + »X(»Xr'c)] = V, (8.10.10)
т. е. (8) является записью теоремы количеств движения.
Теорема об изменении момента количеств движения имеет вид
где О — неподвижный центр моментов, а момент количеств движения
относительно него определяется выражением D.8.10); дифферен-
дифференцируя его, получим
4-0° •to-t-'jDXO0 ъ) = т°, (8.10.11)
причем использовано также правило дифференцирования тензора
D.3.13) и соотношение D.3.12)
@°X»)'W = 0°'(«Xw) = 0.
Теперь по известной теореме статики и уравнению A0) имеем
тР =т° +г0Х V=m° +r0XQ. (8.10.12)
416 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
С другой стороны.
и после упрощения с помощью этих формул уравнение A1) совпа-
совпадет с (9), что и требовалось. Небесполезно отметить, что в ходе
этого вывода уравнений движения свободного твердого тела из общих
теорем динамики — количеств движения и моментов количеств движе-
движения — надо было осторожно обойти ряд затруднений: дифференциро-
дифференцирование векторов и тензора 0° в подвижной системе осей, необходи-
необходимость прибегнуть к выражению момента количеств авижения относи-
относительно неподвижного центра (так как полюс связанной с телом
системы осей не совпадает с центром инерции), применение теоремы
статики о переносе центра момента. Этому противопоставляется при-
присущий методам аналитической механики автоматизм вычисления,
которым отличается вывод, основанный на уравнениях Аппеля. То же
можно повторить (еще в большей мере) в отношении уравнений
Эйлера — Лагранжа. Преимущества общих методов аналитической
механики еще в большей мере обнаруживаются при составлении
уравнений движений более сложных систем, например системы, со-
состоящей из нескольких твердых тел.
Уравнения (8) и (9) существенно упрощаются, если совместить
полюс О с центром инерции тела С. Тогда г^ = 0и уравнения дви-
движения свободного твердого тела принимают вид
M(^c.+ wX^c)= V, 0е - со-ИоХО0• м = тс. (8.10.13)
Мысленно отделим от тела S часть S} поверхностью раздела а.
Пусть М} обозначает массу этой части, г'с =СС} — вектор-радиус
центра инерции ее Сг г'к = СК—вектор-радиус точки на поверх-
поверхности о; тензор инерции тела S} в его центре инерции обозна-
обозначается через 0i'.
Назовем еще V и т^ — главный вектор и главный момент отно-
относительно точки К активных сил, прикладываемых к телу S в точках
тела Sv a R и Мк— главный вектор и главный момент относительно
той же точки реакций отделенной части тела S на Sv т. е. системы
сил, распределенных по поверхности раздела а, обеспечивающих неиз-
неизменяемость тела 5.
Уравнение движения тела Slt принимая С за полюс, можно по (8)
записать в виде
'Ct)] =
(8.10.14)
8.10] УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА 417
Учитывая A3), получаем
R = -V{l)+^V + Ml[»Xr'Ci+f*X(«>Xr'Ci)]. (8.10.15)
По упомянутой теореме статики A2)
+ A!-f (rK-rc) X
Поэтому, принимая для составления уравнения вращения тела S} за
полюс его центр инерции, по второму уравнению A3) и по A5)
находим
. (8.10.16)
Вектор углового ускорения (о следует исключить из A5) и A6)
с помощью уравнения A3). Общие выражения можно записать, пе-
перейдя к матричным обозначениям и вводя в рассмотрение матрицу
@е), обратную матрице инерции 0е. Мы ограничимся рассмотре-
рассмотрением случая тела вращения.
Векторы, входящие в уравнения движения тела вращения, усло-
условимся разлагать на составляющие—продольную по оси симметрии
тела /*з и поперечную в плоскости единичных векторов i'v i'2
а = аА -ь *А +■ аА = аЛ+а*.
Рассматривая далее плоскость /^ как плоскость комплексных чисел,
условимся вектору а>::, расположенному в этой плоскости, сопо-
сопоставлять комплексное число (вектор)
а2 (/ = У^Т).
Тогда вектору
i'3 X а = 1'ъ X а* = i'2ax — i[av
расположенному в этой же плоскости, должно быть сопоставлено
комплексное число ш*. Теперь, возвращаясь к уравнениям движе-
движения A3), перепишем их в виде
(8.10.17)
Здесь через Л и С обозначены экваториальный и осевой централь-
центральные моменты инерции тела; так что
27 Зак. 2072. А II. Лурье
At. -f C/>3 + (^ + *>3) X
418 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Отделив в уравнениях A7) продольные и поперечные составляю-
составляющие векторов и перейдя к комплексным векторам, получим две
группы уравнений движения — уравнения осевых движений
М(^сз + <^С2— <^ci)=^3> Сыг = т% (8.10.18)
з *л *> (8.10.19)
ш^ = т j
и уравнения поперечных движений
c*-r v з с,
Таковы уравнения движения свободного тела вращения. Переходя
теперь к вычислению реактивных силы R и момента Мк, примем,
что отделяющей тело Sx поверхностью о является плоскость, пер-
перпендикулярная оси тела и расположенная на расстоянии | h | от центра
инерции тела 5 (рис. 72). Тело Sx будет также
/ телом вращения вокруг оси симметрии i'3i его центр
s. /TS инерции Сг расположен на этой оси на расстоянии \s\
Ы) от с-так что
и, кроме того,
<:, = <>. r'K = i'A
Из уравнений A8) и A9) имеем теперь
Q
Рис.72. <i3=^, *. = ^№+(С—А)Ш^.\. (8.10.20)
Эти выражения надо подставить в A5). Придем к выражениям про-
продольного усилия в сечении о
^(? 2) (8.10.21)
и комплексного вектора поперечного усилия в этом сечении
^==-V(,).+-^-V. + %-(-/»f+C«o3«.J. (8.10.22)
Переходя к уравнению A6), предварительно находим
f' •» = и,—с,) ш3*з х ».,
X
8.10] УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА 419
Теперь по A6) получаем крутящий момент в сечении а
Ж^ = ^-^зС— /и*3 (8.10.23)
и комплексный вектор изгибающего момента
ллк к- i A\+Mi(s — h) s r , М{ , /ч.т7 ,
м* = ~т*)*+ X —< + -ж(? — Ь)М.+
+ j{C{Al + Ml($ — h)s}-ClA\o>?^. (8.10.24)
Как простейший пример рассмотрим движение тяжелого однород-
однородного твердого тела, которому сообщено начальное вращение, под
действием только силы тяжести. Движение центра инерции тела
в этих условиях будет параболическим движением тяжелой точки
в пустоте, а вращение тела вокруг центра инерции—вращением по
инерции (случай Эйлера), так как тс = 0.
В формуле A5) в этом случае
так как вес V(d отделенной части S: пропорционален ее массе. Далее
"'A) V С, К)/^ (I) М \ С, К) ^ У'
поскольку сила V^ приложена в центре инерции Сх тела Sv Фор-
Формулы A5) и A6) получают вид
Cl ' , } (8.10.25)
is I У\ *\ « I
'I Л. / /
При поступательном движении тела /? и Мк, как и следовало ожи-
ожидать, становятся равными нулю; каждая мысленно отделенная часть
движется без силового воздействия другой части тела.
Для тела вращения формулы B1) — B4) в рассматриваемом слу-
случае принимают вид
R3 = — M:s (о)! -|~ oJJ, M3 = 0,
MxC
(8.10.26)
Mf = ~{C [A, + Mx (s - h) s] — CXA) шЛ.
Поперечное усилие и поперечный момент становятся равными нулю
при отсутствии вращения вокруг продольной оси (о»3 = 0).
27*
420 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
8.11. Уравнения движения вращающегося снаряда
При выводе уравнений движения предполагается отсутствие ветра,
не учитываются вращение Земли и изменение силы тяжести ни по
величине, ни по направлению. Принимаются наиболее общие выра-
выражения аэродинамической силы и момента E.13.2) и E.13.4). Урав-
Уравнения движения центра инерции снаряда будут составляться в си-
системе осей натурального триэдра траектории, описанной в п. 2.18,
а уравнения вращения — в системе осей i'v i'v /g, связанных со сна-
снарядом (i'3—ось симметрии; в п. 5.13 этот единичный вектор обо-
обозначался через k\ На рис. 73 показано расположение этих триэдров,
причем аир можно назвать углами атаки и скольжения; ^ пред-
представляет угол поворота триэдра, связанного с телом, вокруг его
л\
Рис. 74.
оси /д по отношению к натуральному триэдру. Построение почти
полностью повторяет сказанное в п. 2.4. На рис. 74 показаны
углы X, [х, v, определяющие положение натурального триэдра т, п, b
в неподвижной системе осей О\ч\\ (ось От\ по восходящей вертикали).
Связь триэдров единичных векторов т, п, b и i'v i'y i!3 дается
в приводимой таблице косинусов; при составлении ее учтена малость
углов а и р. Это предположение было использовано в п. 5.13 при
рассмотрении аэродинамических сил.
Таблица косинусов
ф— -> т п Ъ
— a COS
a sin у
1
I sin x cos x sin x
1 cos x — sin у cos x
8.11] УРАВНЕНИЯ ДВИЖЕНИЯ ВРАЩАЮЩЕГОСЯ СНАРЯДА 421
Угловая скорость триэдра осей, связанных со снарядом, относи-
относительно натурального триэдра определяется вектором (отбрасываются
величины второго порядка малости)
<о' = я(р+ха) + йа+<сх. (8.11.1)
Выражение вектора угловой скорости натурального триэдра будет
(рис. 74)
Q = х (v -\- X sin |л) -(- п (к cos [л cos v -f- jx sin v) -[—
(— Xcosjji sin v-f-|icosv), (8.11.2)
и сравнение с формулой B.18.10) дает соотношения:
-± = Q. = — X cos и sin v -(- a cos v,
(8.11.3)
0 = Qn = X cos [x cos n -(- [a sin
Т
r- = Qx = ч _l_ X sin
где через /? обозначен рад-иус кривизны траектории центра инерции
снаряда.
Вектор угловой скорости снаряда <о равен геометрической сумме
векторов ъ)' и Q. Находим
^ (а — ^cosp- sin \> -(-{jlcosv). (8.11.4)
Отсюда, воспользовавшись таблицей косинусов, можно получить вы-
выражение п-родольной составляющей ш3
со3 =^ X. —I— ^ —I— ^ si-n р- — ^({jlcosv— Xcosp- sin v) (8.11.5)
и комплексного вектора ш^, соответствующего поперечной соста-
составляющей (О# вектора to:
cos м — Xcos p- sin
+ Р + & + i ф -f- ia) (X sin |л + v)] ^-гх. (8.11.6)
В состав выражения Л входит слагаемое
(р- cos v — X cos p- sin v) = i -~,
и, если траектория не очень крутая, это слагаемое можно считать
величиной того же порядка малости, что и прочие, и пренебрегать
ее произведениями на а и C; малость величины Л следует из пред-
предположений, принятых при выводе аэродинамической силы и момента.
422 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
Переходим к вектору скорости центра инерции. Имеем, исполь-
используя первый столбец таблицы косинусов,
vc = vcz = vc[l\ (— acosx + p sin J) + i'2(a sin 1 + Рcos*) + Q
и, следовательно, при принятой точности
vzc = vc% (8.11.7)
а комплексный вектор vc^ определяющий поперечную составляю-
составляющую vc# вектора скорости, равен
*>с* = v\c + lv2C = vc (— а + /Р) е-ч. (8.11.8)
Легко проверить, что проекции вектора vc* (отнюдь не vc\) на напра-
направления nub равны вещественной и мнимой части комплексного
числа vc^ely-t так что
vc* = vc(— ал + Р*). 5c, = tFc(—а + /р), (8.11.9)
причем Vq^ обозначает комплексный вектор с вещественной осью п
и мнимой Ь. Сказанное верно в отношении любого вектора первого
порядка малости, расположенного в поперечной плоскости снаряда,
но не для конечного вектора, так как плоскости п, b и i'v i'2 не
совпадают. Малыми первого порядка предполагаются поперечная
сила /^ и момент т%. Поэтому, обратившись к их выражениям
E.13.4), получим следующие их комплексные представления:
F* = /Vх = ?а [— fxvc (— а + *Р) + /2Д<№ (— « + 'Р) +
+ g^VjA + g2tavcA\t (8.11.10)
тс = 9а4-ч [— f[a^vc (— а + /?) - /^с (— а + /Р) -
^ ^A]. (8.11.11)
Вектор силы тяжести определяется выражением
j\4gl2 = — Mg(*z siri[x-|-«cos[xcos v — 6cos[x sin v). (8.11.12)
Для составления уравнений движения центра инерции остается
отделить коэффициенты при векторах т, п, b в векторном уравнении
(8.11.13)
8.11] УРАВНЕНИЯ ДВИЖЕНИЯ ВРАЩАЮЩЕГОСЯ СНАРЯДА 423
причем вещественная и мнимые части F^ представляют, по сказан-
сказанному, проекции /^ на направления п и Ь, Приходим, вспомнив C),
к трем уравнениям
'°с = — ^w^c — gsinn, (8.11.14)
A COS V — X COS JX Sin V = ■§- COS A COS V + (/i /3) -g- VCO.
-f- g? v-jt- [X cos [x sin v — {л cos v — a — C (X sin jx -f- v)], (8.11.15)
t ^ °)з [a -f- ^ cos v — X cos (x sin v -)— p (X sin jx -|— v)] -f-
+ ^2?^[P — a(Xsin|i + v)]. (8.11.1С)
Остается составить уравнение вращения вокруг продольной оси
^3=—9~g3v^3 (8.11.17)
и комплексное уравнение A0.19) поперечного вращения
А (Ае- </)' — НС — А) (о3Л*- 'х = mf.
Оно, если учесть A1), приводится к виду
A — i-j a>3A + i (oK — х)Л =
(- a + Р) + /2 Ч ( + Р) + g[c
(8.11.18)
Величины Лих определяются из соотношений F) и E). К уравне-
уравнениям движения A4) — A8), которых всего шесть (A8) содержит два
уравнения), присоединяется кинематическое соотношение— второе
уравнение C). Получим семь уравнений с таким же числом неиз-
неизвестных
а, р, [л, X, v, аK, vc. (8.11.19)
Траектория центра инерции при столь общих предположениях об
аэродинамических силах не будет плоской кривой, так как требо-
требование обращения в нуль кручения у, определяемого третьим урав-
уравнением C), привело бы к увеличению числа уравнений при том же
числе неизвестных.
424 ДРУГИЕ ФОРМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ [ГЛ. 8
При менее общем предположении E.13.17) о законе аэродина-
аэродинамических сил получили бы вместо A0) и A1)
F. = F/* = ^ (fR + fL) (а - /р) vl
/а) - />«CA], j ^ *
причем
F3 = —ра2/^. т£ = 0, (8.11.21)
так что из уравнений A7) и A0.18) следует, что угловая скорость
снаряда вокруг его оси симметрии сохраняет постоянное значение а>^
Повторив приведенное выше вычисление, придем к системе уравне-
уравнений движения центра инерции
[xcosv — Xsinvcos[x = — cos \i cos v-\-fL -^t- *>£<*, \ (8.11.22)
с
и к уравнению вращения
А - i-j (о3Л+/(аK-х)А- ~ /л«МР + 'а> — JLX^ ^Л. (8.11.23)
Предположение, что траекторией центра инерции является плоская
кривая в вертикальной плоскости Х = Х0, требует выполнения равенств
Х = Х0, v = 0. (8.11.24)
При этом отпадает упомянутое кинематическое соотношение, а фор-
мулы E) и F) в предположении, что ^ = -5 малая величина, зна-
чительно упрощаются и дают
а>о = х. A = /(jl+a-/p). (8.11.25)
Но тогда из третьего уравнения B3) при отличном от нуля коэф-
коэффициенте подъемной силы fL следует, что C = 0; это несовместимо
с уравнением вращения B3), так как оно приняло бы вид
.... С
где {л определено предшествующими уравнениями; a не было бы
вещественным.
Итак, наличие только подъемной силы (так как она дает боковую
составляющую) создает необходимость учета отклонения центра инер-
инерции снаряда от плоской траектории. При пренебрежении подъемной
8.11] УРАВНЕНИЯ ДВИЖЕНИЯ ВРАЩАЮЩЕГОСЯ СНАРЯДА 425
силой (fL = 0) задача резко упрощается: из общеизвестных уравне-
уравнений внешней баллистики
. g
Р = — ^ГС05? (8.11.26)
vc = AT vc—
движение центра инерции определяется независимо от вращения сна-
снаряда, после чего для определения вращения приходим к уравнению
а _ ф _ _ ,ш. (а _ /р) + 1_^ Vc (а _ /р) _ i__ fM V2c (а _ /р) =
Ma2 \ Is Cdi ]
/J+l^j. (8.11.27)
правая часть которого получена с помощью B6). Уравнение B7)
лишь наличием слагаемого, пропорционального гасящему моменту
(член с коэффициентом /я), отличается от обычно рассматриваемого
в теории вращательного движения снаряда. Ему посвящена большая
специальная литература *).
*) См. А. Н. Крылов, сочинение, цитированное на стр. 246, а также
книгу Ф. Р. Гантмахера и А. М. Левина «Теория полета неупра-
неуправляемых ракет» (Физматгиз, 1959). Первоначальные сведения приводятся в
«Курсе теоретической механики» Л. Г. Лойцянского и А. И. Лурье
(т. 2, стр. 574—576, Гостехиздат, 1954).
ГЛАВА 9
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
9.1. Дифференциальные уравнения движения несущего тела
Рассмотрим материальную систему, состоящую из «несущего»
твердого тела и N материальных точек («носимые тела»), положение
которых относительно системы осей Oxyz, связанных с «несущим
телом», может быть задано конечным числом или даже счетным мно-
множеством (в случае сплошной среды) обобщенных координат. При
исследовании движения такой системы можно поставить две задачи.
Во-первых, движение «несущего тела» задается и требуется опреде-
определить движения «носимых тел», причем предполагается, что последние
не изменяют заданного наперед закона движения несущего тела.
Положение системы при этом может быть определено независимыми
обобщенными координатами qs, число которых обозначается через /г,
причем случай сплошной среды специально не выделяется. Такое
движение системы может встретиться, в частности, когда масса не-
несущего тела значительно превосходит массу носимых тел так, что
влияние последних на движение несущего тела можно не учиты-
учитывать (но не наоборот). Например, при изучении движения гироскопа
его влиянием на движение Земли можно безусловно пренебречь,
однако движение Земли весьма существенно сказывается на движении
гироскопа. Естественно, что этот случай может представиться также,
когда заданное движение «несущего тела» обеспечивается некоторыми
внешними силами. Тогда последние можно определить из уравнений
движения.
Второй, более общий случай состоит в том, что закон движения
несущего тела неизвестен и его нужно определить с учетом носи-
носимых тел. Положение всей системы в этом случае будет определяться,
вообще говоря, п-\-6 параметрами.
Исследование движения системы можно построить таким образом,
чтобы оба случая были охвачены одним методом, причем первый
случай будет получаться из второго простым отбрасыванием некото-
некоторых уравнений, которые мы условно назовем уравнениями движения
несущего тела. Выводу этих уравнений посвящен этот параграф.
9.1 I ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕСУЩЕГО ТЕЛА 427
Движение несущего тела будем определять вектором скорости v0
полюса О и вектором его угловой скорости со. Положение «носимой»
материальной точки М{ относительно инерциальной координатной
системы О;т]С будем определять вектор-радиусом гь, а относительно
системы Oxyz, связанной с несущим телом,—вектор-радиусом rf.\
принимается, что в выражение г', время не входит явно, так что
Обозначая через г0 вектор-радиус полюса несущего тела, имеем
ri = ro + r'i{4x Чп). (9-1.2)
причем г0, если движение несущего тела задано, является известной
функцией времени; тогда связи системы нестационарны, так как t
существенно входит в выражение гь. Если же подлежит определению
и движение несущего тела, то г0 определяется через обобщенные
координаты, которыми задается положение полюса; связи будут ста-
стационарными.
В дальнейшем многократно используется лемма п. 2.13 о диффе-
дифференцировании вектора а, заданного его проекциями на оси, неиз-
неизменно связанные с несущим телом:
а = в + *>Х0, (9.1.3)
где а — вектор, проекции которого на эти оси равны производным
от проекций на них вектора а. В частности,
Кинетическая энергия системы была в п. 4.9 представлена суммой
трех групп слагаемых
Т=Те + Тт + Тг. (9.1.5)
Здесь кинетическая энергия переносного движения Те равна
Те=\ [Mvl + 2Mv0 ■ (ш X г'с) + » • 0° • »]. (91-6)
где М — масса всей системы и Q0 — ее тензор инерции в точке О.
По внешнему виду это выражение не отличается от кинетической
энергии, которую приобрела бы система при «затвердении», когда все
тела, входящие в нее, образуют одно твердое тело. Тогда 0° и r'Q
были бы постоянны, в нашем же случае они являются функциями
428 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9'
обобщенных координат qv . . ., qn. От обобщенных скоростей
qv ..., qn величина Те не зависит.
Группа слагаемых
Г* = «0 •<?,+ »•*?, (9.1.7)
где Qr—главный вектор относительных количеств движения, а К° —
их главный момент относительно полюса О, зависит как от величин v0,
to, определяющих движение несущего тела, так и от относительных
движений заключенных в нем тел. Тт представляет линейную функцию
обобщенных скоростей qs, коэффициенты которой определяются
равенствами D.9.8). Наконец, Тг — кинетическая энергия относитель-
относительных движений; она выражается квадратичной функцией обобщенных
скоростей qs с коэффициентами, зависящими от обобщенных коор-
координат, определяемыми формулами D.9.9).
Обозначим через vQi и со/ (/=1, 2, 3,...) проекции векто-
векторов ^0 и (О на оси системы Oxyz, связанной с несущим телом.
Важно отметить, что в силу выбора параметров, определяющих дви-
движение несущего тела, кинетическая энергия системы Т не зависит от
его обобщенных координат. Поэтому мы имеем здесь как раз упо-
упомянутый в п. 8.1 случай распадения дифференциальных уравнений
движения на две группы: группу уравнений Эйлера — Лагранжа для
квазискоростей vQi, со/ и группу уравнений Лагранжа, составляемых
для координат qs.
Виртуальное перемещение любой точки Mt системы, согласно B),
равно
S ^ г;. (9.1.8)
Здесь 6 — вектор бесконечно малого поворота несущего тела, а ра-
равенство, определяющее вектор Ъг'., вполне аналогично D). Элемен-
Элементарная работа всех активных сил, приложенных как к несущему,
так и к носимым телам на виртуальном перемещении точек системы
в соответствии с E.2.5) и E.1.4), определится равенством
п
где V—главный вектор, а т° — главный момент всех активных сил
относительно полюса О.
Переходим к составлению уравнений Эйлера—Лагранжа для ква-
квазискоростей vQi, со,.. Имеем
дТ __ дТе , дТт дТ _дТе дТгп
dv{
Qi
9.1] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕСУЩЕГО ТЕЛА 429
так как Тг от квазискоростей не зависит. По F) и D.7.8) имеем
'
дТ.е
= M (v{
= М (v{
Ql
2zc — оKус),
Q2
(9.1.10)
и далее, учитывая также D.7.4),
§" = М (ycv03 - zcv,2) + eg», + eg», + в?,»,. \
eg»,+eg»,+eg»,.
(9.1.11)
Здесь xc, yc, zc — координаты центра инерции всей системы отно-
относительно осей Oxyz, Qfk — составляющие тензора инерции в точке О.
Как указывалось выше, все эти величины надо рассматривать как
известные функции обобщенных координат.
По G) имеем:
(9.1.12)
и далее
дТ„
(9.1.13)
Эти значения производных A0) — A3) надо подставить в уравнения
Эйлера—Лагранжа. Последние будут иметь тот же вид (8.10.3)
что и для свободного твердого тела:
d дТ . дТ дТ
dt dvOi ' l dv03 6 ov02
d дТ
dt
дТ
-• _дт_
'V°2 dv03
(9.1.14)
»?. (9.1.15)
так как при составлении их были использованы лишь неизменившиеся
и в этом рассмотрении трехиндексные символы для квазискоростей
vQi и о);. Вместе с тем в выражение Т не входят величины, опреде-
определяющие положение несущего тела, вследствие чего производные Т
по квазикоординатам обращаются в нуль, как и при составлении
уравнений движения свободного твердого тела.
430 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Сделав подстановку величин A0) и A2) в уравнение A4), получим
первое из группы трех уравнений для квазискоростей
¥с —
(9.1.16)
Векторной записью этого уравнения и двух других, получающихся
из него круговой перестановкой индексов, является
Она выражает теорему о движении центра инерции системы (или
теорему об изменении количеств движения). Величина в квадратных
скобках представляет, согласно п. 2.11, абсолютное ускорение wc
центра инерции системы, причем группа слагаемых
^^o + wX^ + (°X>-/c + <oX(<*>X<:) (9.1.18)
является переносным ускорением, складывающимся из ускорения по-
поцентростремительного и вращательного ускорений
wn = (о X (ю X /"с). wBp = »X/'c. (9.1.20)
Надо напомнить, что поскольку система осей неизменно связана
с несущим телом (имеет ту же угловую скорость, что несущее
тело), то
« = w + wXw = w. (9.1.21)
Слагаемое, входящее в A7),
адСог = 2w X г'с (9.1.22)
*
— ускорение Кориолиса, причем г'с — относительная скорость центра
инерции системы. Наконец,
wr=*rfc (9.1.23)
представляет его относительное ускорение. Вычисление относительной
скорости и относительного ускорения производится по формулам
B.14.5):
п . / п ( . / п
Н- (9Л }
9.1] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕСУЩЕГО ТЕЛА 431
Переходим ко второй группе уравнений движения несущего тела.
Сделав надлежащие подстановки в уравнение A5), получим (после
упрощений)
М(.Ус^оз — zc°&) + ^n^i + 6?2«>2 + ©?з">з + wiOU + оJв1°2 -f- ?
+ К?\ + Л1 [оJ (z;02xc — TF01yc) — а>з BC% — а:
2^2 + ©ЗЗ^з) W3 (©21^1 + ©22^2
[vQ2 (^1Ус~^2хс)—'иог (^3^c—^izc)]=m^ (9-l -25)
Соответствующей векторной записью является
+ Мг'с X («г0 + со X *0) - /^°. (9.1.26)
Это уравнение можно преобразовать. Для этого, вспомнив определе-
определение D.3.20) тензора инерции 0°, находим
п N
/ , дГ; 1 ^Г/ 1 ^/*/ \
5 = 1 / = 1
Поэтому, учитывая D.9.6), можно записать
или, после упрощения,
п N
5=1 1=1
так что эту совокупность слагаемых, перенесенную в правую часть
уравнения B6), можно трактовать как момент кориолисовых сил
инерции
mgor-~0o-»-wX^°. (9.1.29)
432 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Этот момент приложен к несущему телу, он возникает вследствие
относительных движений связанных с ним «носимых» тел.
С помощью уравнения A7) можно из уравнения B6) исключить
ускорение полюса. В результате легко восстановимого вычисления
приходим к соотношению
0С.(О + (оХ0с.(О==шс+шСог_^ (9Л.з0)
Здесь 0е —тензор инерции системы в ее центре инерции
вс=е° -M(Er'c -r'c — r'cr'c). (9.1.31)
Через ЛГгс обозначен главный момент относительных количеств дви-
движения относительно центра инерции
/С? = К? _ Мг>с х тг'с (9.1.32)
и через m£or—момент относительно центра инерции кориолисовых
сил инерции
тсСог = -вс-ь> — <оХ*,с. (9.1.33)
Наконец, тс представляет главный момент активных сил относи-
относительно центра инерции
тс = т°—г'сХ у (9.1.34)
Конечно, уравнение C0) может быть получено из B6) непосредственно,
если совместить полюс О с центром инерции С системы.
Мы рассмотрели первую часть задачи — составили систему урав-
уравнений движения A7) и B6) или A7) и C0) несущего тела.
Эта система уравнений не замкнута (она содержит в качестве
параметров обобщенные координаты qs), и для полного решения за-
задачи к ней нужно присоединить уравнения относительных движений
носимых тел. Конечно, при отсутствии относительных движений
уравнения A7) и B6) совпадают с уравнениями движения твердого
тела (8.10.8), (8.10.9).
Отметим еще, что если несущее тело имеет точку, движущуюся
относительно инерциальной системы координат О;т]С равномерно и
прямолинейно, то слагаемые A9) в уравнении B6), определяющие
ускорение полюса (если эту точку принять за полюс О), отпадают,
и можно считать несущее тело вращающимся вокруг неподвижной
точки О. Уравнение движения его будет
0O.i + »X0°-» + ^? = «o+«gor. (9 Л.35)
а уравнение A7) может служить для определения реакции в точке О —
силы, которая должна быть приложена, чтобы обеспечить наличие
в теле точки, не имеющей ускорения,
9.2] УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ НОСИМЫХ ТЕЛ 433
9.2. Дифференциальные уравнения относительного движения
носимых тел
Остается составить уравнения Лагранжа для координат qv . .., qn,
определяющих положение носимых тел в несущем теле. По A.5)
и A.9) эти уравнения будут
*s(Te)+bs(Tm)-\-*s(Tr) = Qs (S=l П). (9.2.1)
Начнем с вычисления первого слагаемого. Кинетическая энергия пере-
переносного движения Те не зависит от обобщенных скоростей qs: поэтому
Переходим ко второму слагаемому; по A.7) и A.8), учитывая, что
вектор #о не зависит от Qs и #5» имеем
U4s
Но по A.3.5), A.3.11) и A.3)
*/ ,/ j ^ ' **f -»*' * '
or г or г d or г or г or г or г
U L, L, L. L, | чу U /л Q о\
; —— , —— — ft) у\^ (У , Zi, О )
dqs dqs dt dqs dqs dqs dqs
и, следовательно,
d dr'c dr'r drr
dt dqs dqs 0qs
Итак,
(9.2.4)
Вектор (о также не зависит от qs и qs\ поэтому, аналогично сказан-
сказанному ранее,
. дК? [(дК?\* дК? дК?
s L\ q ) ' ^ dqs dqs
Ho
28 Зак. 2072. А. И. Лурье
434 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
и полученное выражение может быть записано в виде
дК°
$5(<о . д?)= i . _£. + <о . £(*?). (9.2.5)
dqs
где звездочкой указывается, что производимое при вычислении эйле-
эйлерова оператора дифференцирование по времени проводится в системе
осей, связанных с несущим телом.
Дифференциальные уравнения A) теперь записываются в виде
1 до0 • дК? а*, 0\
+ -(О. —.@-0). —± ю.бДдг?). (9.2.6)
2 dqs dqs
Обратимся к рассмотрению отдельных слагаемых в правых частях
этих уравнений. Вектор
S° = —Afoo = —Л1(*0 + »Х*0). (9>2.7)
приложенный в центре инерции системы, будем называть силой инер-
инерции поступательного движения. Тогда по E.1.3) величины
г'с (9.2.8)
будут обобщенными силами инерции поступательного движения, а ска-
скалярное произведение
° D ) (9.2.9)
можно рассматривать как потенциальную энергию однородного поля
этих сил.
Квадратичная форма проекций вектора угловой скорости
ГГ = —^-ео.00. (о (9.2.10)
может быть названа потенциальной энергией центробежных сил,
а величины
п« дПш 1 fi <Э0° fi zoo in
будут обобщенными центробежными силами,
9.21 УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ НОСИМЫХ ТЕЛ 435
Переходим к предпоследнему и последнему слагаемым правой
части F), не имеющим характера потенциальных сил. Надо вспомнить
выражение вектора К?'
:V n N ,
К°г = 2 тА X г\ = 2 qs 2 т.г\ X -£-, (9.2.12)
Ы\ .5 = 1 / = 1
так что
дК? . \п , ^/ д'
Вектор
СВР „. /мЛ Ч/ -'\ /Q О 1 Q\
О . — 171. I (О /\ / , 1 ^c/.Z. 1 Оу
представляет вращательную силу инерции материальной точки; по-
поэтому величины
""п N дг
(»Хт,г').—±- (9.2.14)
будут обобщенными вращательными силами инерции.
Возвращаясь к выражению A2), имеем
так что
~ h^-Xir1-' (9.2.15)
и это выражение можно представить в одном из двух видов: во-пер-
во-первых, в форме
;)-fr. (9.2Л6)
обнаруживающей, что рассматриваемое слагаемое правой части диф-
дифференциального уравнения F) является обобщенной кориолисовой
28*
436 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
силой инерции. Во-вторых, вспомнив сказанное в п. 7.3, можно
трактовать выражение A5) как обобщенную гироскопическую силу
_ о,. §: {к°) = rs = S} ЪМ (9-2.17)
со значениями гироскопических коэффициентов G.3.6)
N / г
l^wxw==-^- (9-2Л8)
S R
При введенных обозначениях система дифференциальных уравне-
уравнений носимых тел представляется в виде
д
Левые части этих уравнений зависят только от величин, определяю-
определяющих конфигурацию и движение носимых тел относительно несущего.
Уравнениям относительного движения придана форма уравнений абсо-
абсолютного движения путем отнесения в правые части к активным силам
слагаемых, обусловленных движением несущего тела и названных
силами инерции.
Уравнения A9), если движение несущего тела не задано, должны
рассматриваться совместно с уравнениями движения A.17) и A.26).
Получаем систему п-\-6 дифференциальных уравнений второго порядка
относительно обобщенных координат qv .... qn, и первого относи-
относительно шести квазискоростей vok и а^. К ним надо еще присоединить
шесть уравнений типа A.5.8), выражающих обобщенные скорости,
соответствующие обобщенным координатам несущего тела, через
квазискорости.
При задании движения несущего тела рассмотрению подлежат
лишь уравнения A9). При этом не обязательно пользоваться именно
этой формой уравнений; важно знание перечисленных в правых
частях уравнений обобщенных сил инерции. Надлежащим образом
учитывая эти силы, можно сами уравнения движения записывать
в квазискоростях, пользоваться уравнениями Аппеля и т. д.
9.3. Относительное равновесие
При рассмотрении относительного равновесия носимых тел, опре-
определяемого равенствами
qs = qo = const E=1, ..., л), (9.3.1)
естественно возникают следующие вопросы: 1) при каком движении
несущего тела осуществимо относительное равновесие; 2) как опре-
определить возможные положения относительного равновесия; 3) какие
9.31 относительное равновесие 437
положения относительного равновесия являются устойчивыми и какие
неустойчивыми. Последний вопрос в его общем виде выходит за
рамки этой книги, что же касается первого, то мы ограничимся рас-
рассмотрением таких движений несущего тела, при которых ускорение
любой его точки сохраняет неизменную величину и направление по
отношению к осям, связанным с телом. Из формулы распределения
ускорений в твердом теле B.11.1) следует, что это будет иметь
место при постоянных по величине и направлению (также относи-
относительно тела) векторах ускорения полюса w0 и угловой скорости ео.
Предполагается также, что обобщенные силы Qs в уравнениях B.19)
явно не зависят от времени.
При относительном равновесии носимых тел обобщенные относи-
относительные скорости qs и ускорения qs равны нулю; поэтому обра-
обращаются в нуль как кинетическая энергия относительных движений Тп
так и гироскопические силы Г^. Кроме того, в соответствии с при-
принятым предположением о движении несущего тела будут нулями
и обобщенные враиательные силы инерции Q^.
Из уравнения B.19) теперь следует, что обобщенные координаты q°s
удовлетворяют уравнениям
Q,—^(П + П° + 1Г) = 0 (*=1. .... «). (9.3.2)
причем если Qs зависят от обобщенных скоростей qs% то последние
нужно заменить нулями. В уравнениях B)
П° = MwQ -r'c IT = — 1 со • Q0 • со. (9.3.3)
Вектор г'с и тензор инерции 0° зависят от искомых координат q°s.
Если система п уравнений B) имеет решение A) (одно или не-
несколько), то оно определяет положение относительного равновесия.
Устойчивость найденных положений относительного равновесия иссле-
исследуется общими методами теории устойчивости движения для каждого
из возможных положений относительного равновесия по отдельности.
Сказанное можно обобщить. Пусть в числе координат, опре-
определяющих положение носимых тел в несущем, имеются как пози-
позиционные q} qm, так и циклические qm+l qn. Тогда урав-
уравнения B.19) примут вид
= Qs - -£; (И+П°+1Г)+B;+Г, (s= I «t), (9.3.4)
(/=l n — m), (9.3.5)
причем Qs, IT, П°, IIм, а также гироскопические коэффициенты и
коэффициенты ask выражения Тг зависят лишь от позиционных
438 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
координат. Это следует из определения циклических координат и из
того соображения, что уравнения B.19) представляют лишь иную
форму записи дифференциальных уравнений движения
^(^) + ^G-m) + S5G,) = Q,--gL E=1 »).
Относительным равновесием при соблюдении перечисленных
условий (wQ и (о постоянны) назовем теперь состояние движения,
в котором остаются постоянными как позиционные координаты
qs = qQs E=1 т). (9.3.6)
так и циклические обобщенные скорости
4m+i = <+i (/ = 1. .... «-«). (9-3.7)
Теперь из выражения G.4.6) эйлерова оператора
п п п
*,GV) =2 fl,*?» + 2 2 \k, J: s]qkql
и определения символов Кристоффеля следует, что для позиционных
координат
"s(Tr)
а для
n- m
/ = 1
1
2
n-m
2j i
/•=1
n — m
J^
циклических
n-m
m
n-
\
L
r—
n-
1
т/ ?т+|91Я+г = 0 (9.3.9)
(/ = 1, ..., n — m).
Вспомнив еще выражения B.17) гироскопических сил, можем
теперь записать уравнения относительного равновесия D) и E) в виде
п — т п — т
jf4
1=1 r«l
п-т
S 0 E==1 "*)■ (9-3.10)
(/=!..... я-м). (9.3.11)
9.4]
РАВНОВЕСИЕ ВРАЩАЮЩЕГОСЯ ГИБКОГО ВАЛА
439
Кососимметрический определитель системы уравнений A1)
Т/й + 2, /Я + 1 О
Т/тг \-2, п
[In, m+i
In, т + 2
Inn
(9.3.12)
обращается в нуль, когда п — т нечетно. Тогда система однородных
уравнений A1) допускает отличные от нуля решения для циклических
обобщенных скоростей и принятое определение относительного равно-
равновесия имеет смысл и значение. При четном числе циклических коор-
координат определитель A2), вообще говоря, отличен от нуля, так что
значение введенного понятия не теряется лишь для таких значений
гироскопических коэффициентов, которые обращают Dn_m в нуль.
9.4. Равновесие вращающегося гибкого вала
Рассматривается упругий стержень круглого сечения, конец ко-
которого О вставлен во вращающийся с постоянной угловой ско-
скоростью ш вокруг оси Oz патрон. В конце М стержень заделан
в твердое тело 5 (рис. 75). Конфигурация системы определяется
(при пренебрежении массой стержня) координа-
координатами и углами поворота сечения М стержня
в системе осей, связанных с несущим телом —
патроном. Предполагается, что эта конфигура-
конфигурация сохраняется, т. е. что имеет место относи-
относительное равновесие.
С телом связывается система осей Mx'y'z',
ось Mz' которой остается направленной по ка-
касательной к упругой оси стержня в точке М.
Координаты х, у последней в системе вра-
вращающихся осей Oxyz назовем #, v, пренебрегая
осадкой стержня, т. е. полагая z = /. При от-
отсутствии вращения ось стержня расположена по
оси Oz, а оси Mx'y'z' занимают положение
MoxQyozo, имея направления, параллельные осям
системы Oxyz. Через в обозначим вектор пово-
рота, при котором оси Moxoyozo становятся
параллельными осям Mx'y'z'. Как и в п. 5.9,
принимаем, что и, v, а также проекции а, C, f вектора поворота —
малые величины; через is обозначаются единичные векторы осей
Oxyz, через is — осей Mx'y'z',
Надо выразить через пять введенных обобщенных координат потен-
потенциальные энергии упругих сил II и центробежных сил ГГ. Начнем
с последней. В ее выражении B.10) заменим сначала по формуле D.4.1)
Рис. 75.
440 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
тензор инерции в точке О через тензор инерции в точке М:
в° = вм + М (Егм ■ гм - гмгм) + 2Ж [ Егм . г'с - ](V
(9.4.1)
Здесь гм = ОМ — вектор-радиус точки М, имеющий начало в О,
г'с — МС — вектор-радиус центра инерции С тела с началом в М:
В дальнейшем вычислении потребуется таблица косинусов углов
между единичными векторами триэдров is и i's. Величина Пш должна
вычисляться с точностью до квадратов обобщенных координат; это
заставляет и в выражениях косинусов сохранить вторые степени
малых величин а, C, f. Обращаясь к формуле Родрига C.2.1), имеем
и таблица косинусов с указанной точностью будет
Таблица косинусов
I > i
i\ h h
h
+ ? 1(т2 + 2) + Р
h P + ^T ~« + lpT l__^(a2+p2)
По BЛ0), заменив вектор (о его значением <л>/3, получим
ПО) 1 9 • г\~П •
= — у OJt3 • 0° • l3.
Имеем
'з • (Егм • гм — гмгм) • h = + v<2'
h • [ Егм • г'с - Т (гмг'с + rc^)] • h = гм • r'c - h' г'сгм ■ h =
= {uix + vi2) ■ r'c + й3 • r'c — /3 • r'cl = («i, + t-i2) • r'c.
Как и следовало ожидать, слагаемые, содержащие /, сократились.
Считая далее и, v также малыми величинами, можно теперь в таб-
таблице косинусов сохранить лишь линейные слагаемые. Получаем
{uix + ш2) • г'с = их'с -\- vy'c -f- (Jfg^ - у'сн) 7 + z^ («p - ш).
9.4]
РАВНОВЕСИЕ ВРАЩАЮЩЕГОСЯ ГИБКОГО ВАЛА
441
Через Qik обозначим составляющие тензора QM в осях Mx'y'z't
связанных с телом; тогда, обратившись к формуле D.4.11), получим
и с помощью таблицы косинусов найдем
-h=(%- в33) Р + (©22 - ©33) «2 + ©33
h -
Теперь, согласно B.10), потенциальная энергия центробежных сил IT
оказывается равной
м («2
v2) + 2Mz'c («Р —
'cv)] -1
2, (9.4.3)
причем последнее слагаемое, не зависящее от обобщенных координат,
может быть отброшено. Ограничившись в выражениях косинусов
лишь линейными слагаемыми, мы потеряли бы в выражении по-
потенциальной энергии существенные сла-
слагаемые.
Выражение потенциальной энергии П^
упругих сил изогнутого и скрученного
стержня выводилось в п. 5.9. Приложим
мысленно к концу М стержня силы V°Xt V°y
и изгибающие моменты L°y, L°x, как пока-
показано на рис. 76. Изгибаюшие моменты
Ly и Lx в сечении z стержня тогда равны
(9.4.4)
и потенциальные энергии, соответствующие изгибам в плоскостях zx
и yz будут
°2
442
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
[гл. 9
Коэффициенты этих квадратичных форм образуют матрицы влия-
влияния; с помощью обратных им матриц жесткости составляется выра-
выражение потенциальной энергии упругих сил через обобщенные коор-
координаты
(9.4.5)
Последнее слагаемое в нем соответствует потенциальной энергии
кручения. Пренебрегая потенциальной энергией веса тела, приходим
к уравнениям равновесия
которым в развернутой форме можно придать вид
6£/ fc\ у'с __ х'с
ц/12£/ ч /
v ( UEI А 1 Л
6£/
*с) х'сг- у'с
{ ) I \— I >
Ml2
/ \ Ж/3ОJ ^ I ) 2
^22 — ^33
» ~
Ж/2
о-
Ж/2 '
23
С
Ж/2 '
= 0.
(9.4.6)
В дальнейшем рассмотрении ограничимся случаем, когда тело,
закрепленное на упругом вале, представляет тело вращения, а ось Mz'
является его осью симметрии. Тогда
и из последнего уравнения (б) следует, что -[ = 0 — кручение отсут-
отсутствует. Вводим обозначения
3EI
1
■ = *. Т = (
Ж/2
/p = s. (9.4.7)
Заметим, что значению v = 1 соответствует угловая скорость, рав-
равная частоте свободных колебаний точечной массы М на упругом валу;
9.4] РАВНОВЕСИЕ ВРАЩАЮЩЕГОСЯ ГИБКОГО ВАЛА 443
параметр k может иметь как положительные, так и отрицательные
значения; в первом случае мы говорим, что тело — цилиндр, а во
втором—диск. Например, для однородного сплошного цилиндра k < О
при /г<г|/Г3 и k > О при h > г У~Ъ, где г — радиус, h—высота
цилиндра.
Получаем систему однородных уравнений
(9.4.8)
с определителем
v—
Здесь обозначено
() 6=4(ft-C2c). (9.4.10)
Если определитель (9) отличен от нуля, то в положении равно-
равновесия s = p = O ось стержня остается прямолинейной. Значениям пара-
параметра v2, обращающим трехчлен A(v2) в нуль, соответствуют угловые
скорости, называемые критическими. При критических угловых ско-
скоростях система уравнений (8) имеет решения, определяемые с точно-
точностью до произвольного множителя. Тогда существует серия форм
равновесия, близких к прямолинейным. Критерии Сильвестра, гаран-
гарантирующие положительную знакоопределенность квадратичной формы
U^-j-ir*. сводятся, как нетрудно видеть, к одному неравенству
A(v2)>0. Поэтому, основываясь на теореме Лагранжа — Дирихле,
можно утверждать, что прямолинейная форма будет устойчивой, когда
это неравенство имеет место; она теряет устойчивость для значений v2,
соответствующих неравенству противоположного знака.
Дискриминант трехчлена (9) может быть записан в виде
в* _ \Ъ = 9 [(Сс + j + кJ -1 (А
Он представляет квадратичную форму величин Сс -Ь-о- и * — тт и.
поскольку 4 • 3 — З2 > 0, эта квадратичная форма — положительная
знакоопределенная, обращающаяся в нуль лишь при Сс = -о- , ft =-g-.
Корни трехчлена Д (v2) всегда вещественные; только один из них v'^
будет положительным, если
£<0 или Cc>ft. (9.4.12)
444
Если же
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
Ь>0, а>0 или
[ГЛ. 9
(9.4.13)
то оба корня v^ и v^ положительны. Случай двух отрицательных
корней соответствовал бы неравенствам
£>0, а<0, . (9.4.14)
которые, однако, несовместимы. Действительно, если бы они имели
место, то второе неравенство можно было бы усилить, заменив
в нем k меньшей величиной Сс; тогда пришли бы к неравенству
Сс + Сс+у<0.
невыполнимому при вещественных Сс-
Итак, при условии A2)
а при условиях A3)
(9.4.16)
Случай только одной критической угловой скорости о^ осуще-
осуществляется всегда для дисков, так как b < 0 при k < 0. Он соответ-
соответствует явлению, называемому влиянием гироскопического эффекта на
критическую угловую скорость диска *). Если принять k = 0t £c = 0,
т. е. рассматривать точечную массу на упругом вале, то а = 1, 6 = 0;
критическая угловая скорость ш0, как показывают соотношения G)
и (9), тогда равна частоте свободных колебаний этой массы. Для
тонкого диска можно считать Сс = 0; тогда
и нетрудно проверить, что, поскольку k < 0, имеют место неравенства
2 ^ Vi <-
(надо учесть, что при k-> — со
образом,
;—ЗА —J— ...). Таким
(9.4.17)
*) К. Б. Бицено и Р. Граммель, Техническая динамика, т. 2. Гос-
техиздат, стр. 262—268. См. также Р. Граммель, Гироскоп, его теория
и применение, т. 2. ИЛ, 1952, стр. 19—29.
9.5] ГИРОСКОП В КАРДАНОВОМ ПОДВЕСЕ НА ДВИЖУЩЕЙСЯ ПЛАТФОРМЕ 445
Гироскопический эффект повышает критическую угловую скорость ш0
тонкого диска. Наименование «гироскопический» не соответствует
сущности явления, так как речь идет о центробежных, а не о гиро-
гироскопических силах.
Две критические угловые скорости ш2 и ш2, соответствующие
корням v2 и v2, имеют место при соблюдении неравенств A3), т. е.
для «цилиндров». Если через v2 назвать меньший корень трехчлена (9),
то, как показывает выражение A6), прямолинейная форма равновесия
будет устойчивой при со2 < ш2 и при ш2 > ш2; при ш2 < ш2 < ш2 она
теряет устойчивость. Не следует смешивать это явление со «встреч-
«встречным гироскопическим эффектом».
9.5. Относительное равновесие гироскопа в кардановом
подвесе на движущейся платформе
Вводим три триэдра единичных векторов: es—связанных с плат-
платформой, is — с наружным кольцом, i's — с кожухом, в который заклю-
заключен вращающийся в нем с угловой скоростью ср ротор. Подшипники
оси вращения наружного кольца расположены на оси е3 платформы,
а кожуха — на оси i2 наружного кольца, так что е3 = /3, i2 = i'2\ ось
вращения ротора располагается по единичному вектору i'x (рис. 77).
Рис. 77.
Начала всех систем осей расположены в точке пересечения О осей
вращения наружного кольца, кожуха и ротора. Эта точка является
центром инерции наружного кольца и ротора. К кожуху присоединена
добавочная точечная масса т в точке с вектор-радиусом
r^Vl + a^ + Cg^. (9.5.1)
Постоянное по величине и направлению ускорение точки О обо-
обозначается wQi а постоянный вектор угловой скорости платформы —
446 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
через (о. Чтобы учесть силу веса, вводим в рассмотрение вектор гео-
геометрической суммы
w. = «\> —ff. (9-5-2)
где g—ускорение силы тяжести. Тогда, объединив в одно слагае-
слагаемое П^ потенциальные энергии веса П^. и сил инерции переносного
поступательного движения 11°, следует в уравнения (ЗЛО) вместо
II —j— Г1° ввести величину
II. = /&«;„. г'. (9.5.3)
Чтобы упростить и сократить вычисление производных по обоб-
обобщенным координатам этой величины и ей аналогичных, рассматри-
рассматриваемых ниже, следует использовать соотношение A.3.5)
дг dv
В нашем случае
и поскольку г0 не зависит от qs% a vQt to, r' — от qs, то
Но относительная скорость г*' точки, принадлежащей твердому
телу, вращающемуся вокруг точки О с угловой скоростью ы' относи-
относительно платформы, равна со'Х**'. так что
dqs dqs dqs
поскольку rr от qs не зависит. Вектор <о' линейно зависит от обоб-
обобщенных скоростей qs% тогда как зависимость г1 от обобщенных коор-
координат определяется более сложными формулами преобразования, выра-
выражающими координаты точки в системах осей, связанных с платформой
и телом. Этим и объясняются упрощения, даваемые соотношениями E).
Через аир обозначаются, как всегда, углы поворота наружного
кольца относительно платформы и кожуха относительно наружного
кольца. Согласно рис. 11 получаем следующие таблицы косинусов:
h
h
h
COS a
— sin a
0
e2
sin a
COS a
0
ег
0
0
1
Таблица
h
h
косинусов
cos p cos a
— sin a
sin p cos a
e2
cos p sin a
COS a
sin p sin a
e3
— sinp
0
cos [
9.5] ГИРОСКОП В КАРДАНОВОМ ПОДВЕСЕ НА ДВИЖУЩЕЙСЯ ПЛАТФОРМЕ 447
и значения векторов относительных угловых скоростей (Oj, (ojp ы'ш
наружного кольца, ротора и кожуха:
(9.5.6)
Переходим к составлению уравнений C.10). Начнем с вычисления
производных от П^ по а и р. По C), E) и A) получим
да
mw*' [if х г')=mw*
Обозначая через ws проекции w^ на оси платформы, имеем
после чего с помощью таблиц косинусов придем к выражениям:
д\\
_-* = — mwl {ax cos p sin a -f- a2 cos a -f- #3 sin p sin a) -f-
-f- mw2 (пх cos p cos a — a2 sin a -f~~ ^3 sin P cos a)»
— ma, (t^n sin 8 cos a -4- w0 sin В sin a -4- Wn cos 8) +
-f- ma3 (да, cos p cos a -f- ™2 cos P sin a — te»3 sin C).
(9.5.7)
Переходим к составлению потенциальной энергии центробежных сил.
Тензоры инерции в точке О наружного кольца, кожуха с закреплен-
закрепленной на нем точечной массой и ротора представляются в виде
QO =
■ei)K*2 + [A|-T-m(°:
(9.5.8)
J
Через А я В обозначены моменты инерции относительно центральных
осей, лежащих в средней плоскости детали, а через С — относительно
448
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
[гл. 9
осей, перпендикулярных этой плоскости. В результате выражение IIй*
представится в виде
— у [С ((о • i[f + В (<о . ф* + Л (ш • Q2 — 2/»^ а2» • *> • i'2 -
1а> • ^«о • /[], (9.5.9)
— 2та2а3ь) • ^«о . /£—
причем постоянные Л, #, С легко выразить через величины, введен-
введенные формулами (8). Дифференцирование скалярных произведений (о • if
выполняется по правилу E)
да
да -
E=1, 2, 3).
(9.5.10)
В выражении Тг кинетической энергии относительного движения
(таким является только вращение ротора), как следует из уравнений
C.10), нас сейчас может интересовать только коэффициент при квад-
квадрате циклической скорости ср; он постоянный (равен -^-СШ1, и
поэтому соответствующее слагаемое в (ЗЛО) отпадает. Остается вычи-
вычислить гироскопические коэффициенты ^ и
заметим еще, что
уравнение C.11) в рассматриваемом случае является тождеством, так
как т — 0. Согласно B.18) подлежат вычислению выражения
or, or; xr\ or, дг}
Х^ 21^Х^
причем суммирование ведется по материальным частицам ротора.
Снова, обратившись к E), имеем
дг] дг,
1 ч/ £
да дер V да
III
и далее
XI ,
^ = 2.-2 «^
ди>ш д(а.
III
да
дт
Ш
д<р
(9.5.11)
9.5] ГИРОСКОП В КАРДАНОВОМ ПОДВЕСЕ НА ДВИЖУЩЕЙСЯ ПЛАТФОРМЕ 449
Теперь, вспомнив определение D.3.20) тензора инерции, найдем
N N
2 *М = Е 2 тГ\ • г\ - 0° = т Е (Э?, + 02°2 + 03°3)-0° (9-5.12)
и, в частности, для симметричного тела — ротора
N
{ — Cul)i[i[. (9.5.13)
Итак,
I а.(п I III ' V III III/ 111 V 3 •/^ 1 7 III 2 • ' I
n ., :< (9-5.14)
и далее
111 . l 2 ' 1 (9.5.15)
Гр = — Сшср (o)j sin p cos a -f- oJ sin p sin a + ^з cos p). J
Эти результаты можно было предвидеть, так как выражения A5)>
к которым мы пришли, представляют не что иное, как проекции на
оси вращения наружного и внутреннего колец вектора гироскопи-
гироскопического момента:
Теперь все подготовлено для написания уравнений C.10), опре-
определяющих углы аир при относительном равновесии. Рассмотрим
задачи о влиянии движения корабля по сферической Земле и угловой
скорости Земли на равновесное положение оси ротора в кардановом
подвесе. Единичные векторы триэдра ev e2, въ будем считать напра-
направленными по осям геоцентрической системы — на север по касательной
к меридиану (ег), на запад по касательной к параллельному кругу (е2)
и по восходящей вертикали места (е3). Тогда, обозначая через vN, vQ
северную и восточную составляющие вектора скорости платформы,
через Ф — широту места, имеем
тг- (9.5.17)
В дальнейшем ограничиваемся учетом слагаемых, пропорциональных
первым степеням проекций этого вектора; поэтому из уравнений равно-
равновесия исключаются центробежные силы инерции.
Проекции вектора W# — геометрической разности ускорений плат-
платформы и силы тяжести,—определяются с помощью формул B.15.8);
450
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
[гл.
в них отбрасываются слагаемые, зависящие от вертикальной соста-
составляющей скорости vh, и слагаемые, пропорциональные U2. Величину
скоростей vN и vQ принимаются постоянными. Получаем
\
V\rVn
(9.5.18)
ws=g —
R
— 2v^U cos Ф.
Эти выражения, поскольку в них входит широта места, представляют
некоторые функции времени; поэтому проводимое здесь рассмотрение
задачи об относительном равновесии приемлемо лишь при медленном
изменении широты и в течение небольших промежутков времени.
В выражениях G) примем
что соответствует расположению грузика в гирокомпасе Сперри (не
учитывается смещение грузика к востоку). Приходим к системе урав-
уравнений
— (wx sin a — w2 cos а) sin p = — q (^~ sin а — ~ cos а) cos p,
~
1
— (wl cos <x-\-w2 sin a) cos p sin C =
(9.5.19)
где через q обозначена конструктивная постоянная
_ CmyU
4 mga
(9.5.20)
Из этих двух уравнений могут быть определены девиации оси
ротора аир. Они должны быть достаточно малыми; пренебрегая их
квадратами, получим
и
«03
(9.5.21)
Коэффициенты этих уравнений содержат слагаемые различных
порядков величины. Малыми по сравнению с единицей будут величины
VN
RUcQS<f>' RU cos Ф*
(9.5.22)
9.6] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ 451
представляющие^отношения северной и восточной составляющих ско-
скорости корабля к скорости данного места вращающейся Земли.
Отношения составляющих кориолисова ускорения к g
2vmU cos Ф 2vnUcos$
-^—g . -^ (9.5.23)
представляют малые величины более высокого порядка, чем вели-
величины B2), так как их отношения к последним пропорциональны
RU2
малому отношению центробежной силы на экваторе к силе
притяжения.
Сохранив в уравнениях равновесия B1) только основные слагаемые,
придем к формулам
а= *N ., р = — ?sin<£, (9.5.24)
RU cos Ф r ^ v J
определяющим статические девиации — отклонение оси ротора к западу,
вызванное наличием северной составляющей скорости, и подъем ее
над горизонтом, возникающий при неподвижном основании. Если же
учесть в этих уравнениях также величины, имеющие порядок отно-
шениЛ B2), то окажется
RU cos Ф v0 RU cos Ф
1 + RU cos Ф
1+-
\ RUcos®)'
. (9.5.26)
Было бы нерационально находить следующие приближения, так
как при составлении уравнений B1) были отброшены слагаемые,
зависящие от центробежных сил. Кроме того, тогда следовало бы
уточнить переход от уравнений A9) к B1).
9.6. Относительное движение твердых тел*)
Как частный случай общих уравнений пп. 9.1 и 9.2 рассмотрим
случай абсолютно твердых носимых тел. Можно ограничиться одним
лишь носимым телом, поскольку обобщение на произвольное их число
тривиально. Приходим к задаче об относительном движении двух
твердых тел, одно из которых—«несущее», а второе — «носимое».
Напомним, что с несущим телом, которому далее приписывается
индекс 1, связана система осей Oxyz с полюсом в точке О этого
*) А. И. Лурье. Некоторые задачи динамики системы твердых тел.
Известия Ленинградского политехнического института им. М. И. Калинина,
1960 г., № 210, стр. 7—22. -
29*
452 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ* [ГЛ. 9
тела. Начало системы координатных осей C2x'y'zr % связанных с носимым
телом (индекс 2), выбирается в его центре инерции С2. Поэтому
Mr'c = M/Q + М/сг (9.6.1)
где г'с — фигурирующий в уравнении A.17) вектор-радиус центра
инерции системы, a r'Q , r'c — вектор-радиусы (с началом в полюсе О)
центров инерции несущего и носимого тел.
За обобщенные координаты носимого тела принимаются три вели-
величины qv q2, qz% определяющие положение его центра инерции в системе
осей Oxyz, и три угловые координаты q4, q5, qQ, задающие ориен-
ориентацию в этой системе триэдра осей C2x'yrz'. Итак,
*'и = 1'к(9*9у9б) (k=h 2, 3), (9.6.3)
где i'k—единичные векторы осей носимого тела.
Поскольку в системе осей Oxyz вектор-радиусг^ является по-
постоянным вектором, имеем вполне понятные равенства
#, * ** #*
Мг'с = М/Сг Мг'с = М/с%, (9.6.4)
причем по A.24)
Уравнение движения A.17) центра инерции системы тел будет иметь
вид
(9.6.6)
В него, кроме векторов v0 и (о, входят обобщенные координаты qlt
q2, q3 и соответствующие им обобщенные скорости и обобщенные
ускорения.
Переходим к составлению второго векторного уравнения — «урав-
«уравнения вращения» A.26). Прежде всего следует отметить равенство
0° = 0? + 02°, (9.6.7)
причем 0р — постоянный в системе осей Oxyz тензор, так что
§? = (>. 0°=02°. (9.6.8)
9.6] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ 453
Далее естественно вводится в рассмотрение тензор инерции Q£\ носи-
носимого тела в его центре инерции, обозначаемый для упрощения
через 02. По D.4.2) имеем
00 = 02 + м2 (Er'Cj • /^ - r'cr'c) (9.6.9)
и, использовав формулу дифференцирования тензора D.3.13), найдем
0? = »' X 02 - 02 X »' + М2 BЕг^ • г'с> - r'cr'Ci - Pcr'c). (9.6.10)
Через (о' обозначен вектор угловой скорости носимого тела в системе
осей Oxyz, связанных с несущим телом.
Главный момент относительно полюса О относительных количеств
движения К® равен по D.8.11)
«>'. (9.6.11)
так что его производная по времени в системе осей Oxyz будет
*г° = Г'С| X М/с, + ©2 • «' + ю' X 02 • »'. (9.6.12)
Здесь учтены соотношения A0) и D.3.12). Использовав теперь равен-
равенства (9) — A2), составим входящее в A.26) выражение
в0 ■ o>-f-o>Xtfr0 + /t° = <•>' X 02 • <о — 02- (<">' X ю) + «Х02- »' 4-
+ 02 • 4' + ю' X 02 • <•>' + М2 [2r'Ci ■ Рс» - r'cr'Ci ■ ы- r'cr'Ci ■ й) 4-
+ « X (rCi X ^J + r^ X>cJ- (9-6-13)
Остается еще заметить, что по G) и (9)
+ Ж2 (ГС2 ' ГС> - ГСГС, • » - » X ^Д . (О),
и учесть, что
<£>'= £'-f.ю X <»>'• (9.6.14)
Тогда после подстановки в A.26) и простейших преобразований
придем к векторному уравнению вращения рассматриваемой системы телГ
©о • w + to х Эр •» + MfCi х дао+ 02 • (» + »
454 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
в котором для краткости введены обозначения векторов ускорения
полюса О и центра инерции носимого тела
Уравнение A5) можно было бы получить, применив теорему об изме-
изменении момента количеств движения к системе двух тел и учитывая,
что вектор абсолютной угловой скорости носимого тела равен ю + о/.
Здесь и для дальнейшего полезно отметить тождество
а X 0 • Ь - Ъ X 0 • а = @ - 8Е) • Ф X я), (9.6.17)
верное для симметричного тензора второго ранга; через 0 обозначен
первый инвариант этого тензора — сумма его диагональных соста-
составляющих:
О = вп _|_ В22 _|_ езз, (9.6.18)
а Е, как всегда, — единичный тензор. Использовав это тождество,
найдем
(со + со') X 02 • (» + »') — (о X '02 • » + »' X 02 • »' +
Эта форма записи облегчает вычисление входящего в уравнение A5)
слагаемого. Дело заключается в том, что при вычислении величин,
в которых фигурирует вектор (О и тензор 02, задаваемый, естественно,
в осях носимого тела, приходится вектор а> также проектировать
на эти оси. Поэтому полезно отделить в упомянутом слагаемом члены
вида о>' X 02 * ю'» вычисление которых проще, поскольку w' также
задается в осях носимого тела.
Переходим к составлению уравнений движения носимого тела.
Они разбиваются на две группы — первая (для координат qv q2> q^
представляет три уравнения относительного движения центра инерции
носимого тела, а вторая (для координат q4, q5> q§) — его уравнение
относительного вращения.
В выражениях потенциальных энергий B.9) и B.10), поскольку
они дифференцируются в ходе составления уравнений движения B.19)
по обобщенным координатам, можно отбросить слагаемые, не зави-
зависящие от этих координат. Поэтому, учитывая A), G) и (9), имеем
(9.6.20)
Из A1) и D) для s=l, 2, 3 находим
~^г, (9.6.21)
9.6] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ 455
и по B.6) первая группа уравнений движения носимого тела будет
^i)X^^_2wX^]' -jr2- • (9'.6.22)
Заметим еще, что в рассматриваемом случае
Тг = I м}'Сг • ^+ 1 <*>' • 02 ■ со', (9.6.23)
так что
d *r дг'с^ *г дг\
dt с, ' да, с2 # да
и, воспользовавшись преобразованием B.3), найдем, как следовало
ожидать,
M?Ci.^. (9.6.24)
Уравнения движения B2) принимают вид
M2wc^ '^~- = Qs E=1,2,3), (9.6.25)
где вектор абсолютного ускорения wr центра инерции носимого
тела определяется выражением A6).
Остается рассмотреть группу уравнений движения носимого тела
для угловых координат q4, q5, q6. Порядок вычисления диктуется
уравнением B.19). Основываясь на выражениях B0), находим
dll° dtt™ 1 до2 , л к CN /С, а оа,
_т»._1.» (s = 4. 5, 6). (9.6.26)
-^-=0, _.
Выражения производных тензора инерции по координатам легко
найти, основываясь на соотношениях A0). Для этого отметим, что
вектор угловой скорости @х представляет линейную функцию обоб-
обобщенных скоростей #4, #5, qQ
коэффициенты которой
е, = Н- (9.6.28)
456 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
— векторы, зависящие от обобщенных координат q4, q5, q6. Напри-
Например, если за обобщенные координаты приняты эйлеровы углы
то вектор со7 представляется в виде
6 (9.6.29)
где /3, п, /д—единичные векторы оси Oz, линии узлов и оси C2z\
В этом случае
Использовав B7), можно записать формулу A0) в виде
и, следовательно,
■^7 = ^Х02-02Х^. (9.6.30)
Выражение обобщенной центробежной силы принимает вид
Q? =■§■»• (^X 02-02Х^)-» = (»Х^)-02-». (9-6-31)
Далее, имея в виду выражение A1) вектора К°9 получаем по B.14)
дК°
Q« = — w.—J- = — w-02.^. (9.6.32)
Определение обобщенных гироскопических сил приводится к вычи-
вычислению эйлерова оператора над вектором К°\ обратившись снова
к A1), имеем
(9.6.33)
и необходимо остановиться на вычислении вектора es. Исходим из
формул дифференцирования единичных векторов координатных осей
носимого тела:
di
(/;)* = ю' X /;. -щ) ==esXtfk (k = 1. 2, 3); (9.6.34)
продифференцируем первое по g^, a второе по времени, имея в
виду при этом, что здесь применимо соотношение вида A.3.11)
9.6] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ 457
так как векторы i'k зависят только от обобщенных координат.
Получаем
Это соотношение, учитывая тождество
можно записать еще в виде
—3|£-"'Х'.)Х*; = О. * = 1. 2. 3,
откуда следует, что
*е*=т£+*'Хе* s=4* 5> 6* (9>6-35)
Теперь выражение C3), если использовать также формулы A0), C0)
и A7), преобразуется к виду
KW) = Q2 • (»' X*,) + (»' X 02- 02X «') • *,—
- (е, X 02 - 02 X О • »' = B02 - Е^2) • (es X «') (9.6.36)
и обобщенные гироскопические силы будут
Г, = 2ео • (©2 - I Е»2) ■ («' X ^) (^ = 4, 5, 6). (9.6.37)
Гироскопические коэффициенты ^sk находим по B.17) и B7):
(^ХО (А. «= 4. 5, 6). (9.6.38)
Приходим к следующим дифференциальным уравнениям вращения
носимого тела:
Ь9(ТТ) = Q, + (w Xes) • 02 • « - и • 02 • *,+
+ 2@ • (о2 -1 Е*>2) • («' X О (^ = 4, 5, 6). (9.6.39)
Надо еще раскрыть содержание левой части этого равенства. Обра-
Обратившись к B3) и применив равенства A0), C0) и C5), найдем
= «,-е2-ю' + *,-(ю'Хв2—в2X »') •»'
— j ft)' ■ (fi, X 02- 02 Х^) • Ю' = в, ■ @2 • »' + Ю' X 02 • »')• (9.6.40)
458 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Теперь выражение C9) можно переписать еще так:
es • [о2; <*>' + со' X 02 • <*>' ■+■w X 02 * w + 02 • <*> 4-
] (?,. (9.6.41)
Заменив здесь со' на со' по формуле A4) и обратившись к тожде-
тождеству A9), приходим к другому представлению уравнений вращения
носимого тела:
е8 • [02 • (ю+(о'о+(<о-И>')Х02 • (»+»')]=<?, E=4. 5, 6). (9.6.42)
Величина в скобках представляет левую часть векторного уравнения
вращения носимого тела (в абсолютном движении)
02 • (со + со') -И» + <*>') X 02' О +- *>') = "*Сз> (9.6.43)
правая часть которого представляет главный момент внешних сил,,
приложенных к носимому телу, относительно его центра инерции С2.
При варьировании обобщенных координат #4, q5, q§ носимому
телу сообщается бесконечно малый поворот (относительно несущего
тела), определяемый по B7) вектором
б
O'=2*,8?JI (9.6.44).
5 = 4
откуда, основываясь на E.2.5), следует заключить, что
?, = wCj-e/> Qs = mc*-es (s = 4t 5, 6). (9.6.45)
Уравнения D2) легко непосредственно получить из векторного
уравнения вращения D3). Однако в формах записи C9) и D1) этих
же уравнений более отчетливо обнаруживается значение отдельных сла-
слагаемых; надо еще добавить, что в них указан более простой поря-
порядок вычисления: например, требуется вычисление вектора w\ а не со/.
Уравнения движения носимого тела B5) и D2), представленные
в форме Лагранжа, легко также записать и в виде уравнений Эйле-
Эйлера— Лагранжа. За квазискорости примем проекции на оси системы
C2x'y'z' векторов r'Q и а>'. Производная по времени вектора в системе
осей носимого тела далее обозначается крестиком над буквой; тогда
К, = гс> + *»' X г'сг <*>' = со' + о)' X <*>' = со7. (9.6.46)
Обобщенные силы в правых частях уравнений B5) теперь следует
заменить проекциями главного вектора V2 внешних сил, приложен-
9.7] примеры 459
ных к носимому телу на оси связанной с ним системы C2x'y'z'. При-
Придем к трем уравнениям движения в проекциях на эти оси; можно
заменить их одним векторным уравнением
V2, (9.6.47)
*
где vr = r'c —вектор относительной скорости точки С2.
В уравнениях вращения следует заменить Qs проекциями главного
момента mCi на оси носимого тела» а векторы es — единичными век-
векторами is. Проделав эти замены в уравнениях D1) и заменив их
одним векторным уравнением, получим уравнение вращения носимого
тела в виде
02 • ( w + ы') + со X 02 • » + »' X 02 • »' +
+ 2<*>' X @2 — 4 Е^) ' » = ^Сг- (9.6.48)
9.7. Примеры
1°. Уравнения вращения твердого тела, имею-
имеющего неподвижную точку, при учете вращения
Земли. Координатные оси Oxyz, связанные с несущим телом —
Землей,—зададим направлениями осей ev e2, въ геоцентрической системы,
описанной в п. 9.5. Их начало О — точка на поверхности Земли —
принимается за полюс системы осей Oxfyrz', неизменно связанных
с телом. Уравнения движения F.48) выведены в предположении,
что полюсом является центр инерции носимого тела; они применимы
также при неподвижном, как в настоящем случае, относительно
несущего тела полюсе (vr = 0).
Предполагаем, что за оси Oxryrz' приняты главные оси инерции
тела в полюсе О, так что
©о = Ai[i\ + Bi'/2 + Ci'/r (9.7.1)
Вектор угловой скорости несущего тела о> здесь имеет постоянные
величину и направление. В уравнении F.48) следует принять о> = 0;
проекции (О на оси носимого тела обозначаются через с
геоцентрической системы — через («у. Таким образом,
з
k = l
причем (o^t/cosO, a>2 = 0, co3=/7sin0,
где Ф — широта места, U — угловая скорость Земли.
а на
(9
(9
ОСИ
.7,
.7,
■2)
.3)
460 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Слагаемое в F.48), происходящее от ускорения Кориолиса, будет
со' Х[(Л-В - С) i[i[ + (В - С - A) i'/2 + (C~A-B) И/3]. ы =
= [ЮЯ(С—А—В) — ш'3ш2 {В— С— A)] i[ + [ю>, (А — В — С) —
—ш;ш3(С— А— В)] i'2-^[o>[Z2(B~C-A)~w'2^(A~B-C)]i'3. (9.7.4)
Остальные слагаемые — того же вида, что и в уравнениях Эйлера.
Приходим к трем уравнениям, первое из которых имеет вид:
[ + (С — В) (ш£ш£ + ш2ш3) + Л (ю^ — ш3<о£)
— В) (ш;ш3 + ш;ш2) = «,, (9.7.5)
а остальные получаются круговой перестановкой букв и индексов.
Слагаемые вида w2od3, происходящие от центробежных сил инер-
инерции, пропорциональные U2, следует отбросить; влияние . этих сил
может быть учтено путем сохранения соответствующих членов в вы-
выражении E.6.5) потенциальной энергии силы тяжести.
Приходим к уравнениям
(9.7.6)
2°. Волчок. Как пример применения общих уравнений F)
рассмотрим задачу о влиянии вращения Земли на движение волчка.
Положение его оси симметрии Ozr определим углами а, C, опи-
описанными в примере 2° п. 7.18, и применим ту же, что в указанном
примере, систему «полусвязанных» с волчком осей я, п\ i'3; через ср,
как всегда, обозначается угол поворота вокруг оси (собственное
вращение).
Уравнения F) записаны в предположении, что оси Ox'y'z' неиз-
неизменно связаны с телом; поэтому имело место второе равенство F.46).
Теперь его следует заменить на
>[ + (С — В) (gd^ + u'2Z3 + <»з">2) + Л (<*2<°3 — ^зК) = m
— С) (a£i>; + ш^1 + а,;ш3) + В (ш3а>; — S^Q = mv
— Л) (aft + а)>2 + cofo) + С Дш^ — ш2а>;) = /и3
<»'. (9.7.7)
+
в котором to' обозначает вектор, проекции которого на оси я, п\ i'3
равны производным от проекций вектора to' на эти оси (обозначае-
(обозначаемые, как и ранее, и/); вектор угловой скорости «полусвязанных
осей» А отличается от о/ отсутствием в нем составляющей собствен-
собственного вращения
А = со' —/£<р. (9.7.8)
9.7] примеры 461
Итак,
и входящие в уравнения F) величины <oj, о^, (и3 надо заменить
*' I ' *r f 'f
В таблице косинусов G.18.20) роль осей £, т\, С теперь играют
направления на север, запад и по восходящей вертикали. Поэтому,
в соответствии с B) и C), находим:
<оя = u)j = U (— sin Ф sin р 4- cos Ф cos р) = U cos (Ф + Р),
о)Л/ = (о2 = — f/ sin (Ф + р) sin а, оу = а>3 = U sin (Ф + р) cos а.
з
Момент силы веса волчка относительно его точки опоры равен
т° = — i'zzr X esQ—Qzr (— п sin p—nr sin a cos р+/3 cos a cos P) X i'3 =
= Q^ (яг sin p — я sin а cos P).
Учитывая еще, что А —В, приводим дифференциальные уравне-
уравнения F) к виду
Л (cij + <К + ^з - «У°2) + (С - Л) (о)>; + а)>3 + a)>2) =
= —Q^' sin a cos p,
Л (<о£ — 9O)j + S3o)J — Sj^g) — (С — Л) (o)joK + «>з^1 + ^^з) —
= Qz' cos p,
В случае почти вертикального волчка углы а и р, а также про-
проекции o)j, 0)^ вектора угловой скорости — малые величины; малыми
являются и величины оM, пропорциональные U. Отбросив произве-
произведения малых величин, получим два первых уравнения (9) в виде
Л (cij + уа' + ш2оK) + (С — Л) (Ц + S2) ^з = — 0^- 1
~ ~ [ (9.7.10)
Л (A)^ — СрО); — (OjO)^) — (С — Л) (<!>; + (Oj) 0)^ = QZ'$, j
причем в силу третьего уравнения (9)
<0g = const.
При принятой степени точности вычисления следует принять
<ог = исоьФ, <о2==0, <o3
o)j = — а, а)^ = р, аK = ср.
462 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Теперь система дифференциальных уравнений A0) может быть запи-
записана в форме одного линейного дифференциального уравнения вто-
второго порядка
А ф -4- &) — Ci^ ф 4- to) — Qz' Ф + to) = CyU cos Ф. (9.7.11)
Оно имеет частное решение
$ = % = --Щ^-со5Ф, (9.7.12)
соответствующее отклонению вершины волчка к югу (при <р > 0,
z' > 0). На это отклонение накладываются колебания, происходящие
с частбтами
Положительность подрадикального выражения (вещественность Хр )^)
является необходимым условием того, чтобы волчок оставался почти
вертикальным:
Сер > 2|/QAz'. (9.7.14)
Более общее условие, когда учитывается масса колец подвеса,
цается формулой G.9.24).
3°. Твердое тело, несущее вращающиеся махо-
маховики. Несущее тело предположим имеющим неподвижную точку О.
С ним связана система осей Oxyz. Маховик вращается с угловой
скоростью о/ = /з? вокруг неподвижной в несущем теле оси; на
этой оси лежит центр инерции маховика, его положение в несущем
теле задается вектор-радиусом г'с (ранее обозначался г'Л.
В уравнении F.16) теперь
Слагаемое М2г'с X ^с преобразуется к виду
» X М2 (Ег'с ■ г'с - г'сг'с) -и> + М2 (Er'c . r'c - r'cr'c) •».
Поэтому, обозначив через 0° тензор инерции в точке О системы,
состоящей из несущего тела и мысленно остановленного маховика,
Qo = Qo + м2 (Ег'с ■ г'с - г'сг'с) + 0С,
можем представить уравнение F.15), используя F.19), в виде
+ <Р @2С - Е«2С) • (i'3 X <•>) + 02С • (<&)' - «°. (9.7.15)
9.7] примеры 463
Маховик является телом вращения; обозначая через 9Х = в2, в3
его главные центральные моменты инерции, имеем
)
Поэтому
'з X 02С • 1'ъ = 0. QC . (<?*;)• = 0С . (^ + тй) х /3) =
и также
2^ хе2с'«+т (е2с - е<\с) • (/; х со)+в2с • (^у =
= 2в^ X » + Нв1 - Bв1 + вз)] 'з X » + в3^ + в,?w X /J -
= в3% + в3т<оХ^ (9.7.16)
Теперь уравнение A5) переписывается так:
0О.^) + (оХ0о.(О + в3(^ + та)Х^) = т0. (9.7.17)
За координатные оси Oxyz примем главные оси тензора 0°, так что
Тогда, проектируя на эти оси уравнения A7), придем к трел диф-
дифференциальным уравнениям:
Аа>1 -\-(С — Б) оJоK -f- в3 [аср -\- (а>2^ — оKC) ср] = т°,
В'<»2 +(Л — С) @,0)! + в31Рт + (ш3а — o)lT) ?] = т°г (9.7.18)
CtOo-J- (.о — ^4) о)|О>2 —j— xjq 1ТФ ~f~ (^1г — ^2^) т!:=:= ^ »
где а, р, т — косинусы углов направления i'z с осями системы Oxyz.
Уравнение вращения носимого тела (маховика) составим в форме
F.41). При принятых обозначениях
и далее
Остальные слагаемые в квадратной скобке формулы F.41) обра-
образуют вектор, перпендикулярный irv и не войдут в уравнение враще-
вращения маховика. Последнее будет иметь вид
464 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
что было легко заранее предвидеть. Уравнения A8) и A9) даны
Врльтерра. При наличии п маховиков они записываются в виде
/1^1 -\-(C — В) оJаK + 2 ®з [ ¥ A + ?
5ij+(л - о w3U)l + 2 e* г iftpft+?
(9.7.20)
2
<■" 3 I
и соответственно
Выражение кинетической энергии несущего тела с маховиком,
составленное в примере 2е п. 4.12, дается формулой D.12.3). Пре-
Преобразуя ее в соответствии с принятыми здесь обозначениями, получим
-^
= у a) • 0° • а) + у
При наличии д маховиков
/г
Г==|в. 0о. « + 4вз*Й + 2 (•!•*+«2?»+«.аТ»)?»]. (9.7.22)
В уравнениях B0) моменты активных сил относительно осей си-
системы Oxyz естественно принять не зависящими от углов поворота
маховиков yk.
Обобщенные силы (X будем считать зависящими от величин,
характеризующих положение и движение несущего тела; это осущест-
осуществимо с помощью систем, следящих за указанными величинами и выра-
вырабатывающих по ним моменты, сообщаемые маховикам. Тогда коор-
координаты ср# будут квазициклическими. Отнесенные к ним импульсы
равны
Pk = j?- = 91\Ъ + (">,** + «гР* + ">зТйI (А = 1....,»). (9.7.23)
Функция Рауса по G.19.3) будет иметь вид
Г, (9.7.24)
9.7] примеры 465
и составленные по ней уравнения движения в форме Эйлера—Лагранжа
будут
п
уЦ + (С-В) со2ш3 + 2 {(">27*-шзР») [Pk~ в* (««>,«* + «зР* + «>зТ»)] +
+ «ft [Q?ft - в* («ja* + »2Р* + «зТ»)]} = «?• (9-7-25)
Два других уравнения получим при круговой перестановке букв
и индексов. К ним надо добавить уравнения G.19.2)
Pk = Q4 (*=1. .... я). (9.7.26)
Если срл — циклические координаты, то обобщенные силы отсут-
отсутствуют, а импульсы pk сохраняют постоянные значения. Тогда дело
сводится к рассмотрению системы трех уравнений B5) и трех кине-
кинематических соотношений, определяющих иIэ о>2» ^з чеРез угловые
* координаты несущего тела и соответствующие им обобщенные ско-
скорости.
Возвращаясь к общему случаю, составим легко получающееся из
уравнений B5) соотношение
*(ш1ай + ш2Р*+ «зТ»J +
J
В первой строке представлена квадратичная часть R2 функции Рауса,
а выражение во второй строке с помощью B6) и B3) можно запи-
записать в виде
п п 2 n
F ■§■
Теперь, обратившись к формуле G.19.15), можно составить соотно-
соотношение, определяющее мощность активных сил:
Пример тела, снабженного маховиками, отчетливо иллюстрирует
понятие о циклических координатах. Несущее тело может быть пред-
представлено в виде замкнутой оболочки; вращающиеся маховики скрыты,
466 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
но их наличие существенно изменяет движение несущего тела,
так как оно служит причиной появления в уравнениях движения для
позиционных (явных) координат добавочных гироскопических сла-
слагаемых.
4°. Колебания точечных масс в движущейся твер-
твердой оболочке. Дифференциальное уравнение вращения F.15) при
учете соотношений F.14) и F.19), когда число носимых тел равно N,
а за полюс О принят центр инерции С несущего тела-оболочки,
можно записать в виде
2
N
rn/iXwi = mc. (9.7.28)
Здесь r'i-—CCi — вектор-радиус центра инерции Ct /-го носимого
тела. Вектор-радиус r'Q общего центра инерции оболочки и носимых
тел определяется равенством
N
а абсолютное ускорение точки G равно
N
W, Bсо х £;+";> (9.7.30)
Введем в правую часть уравнения B8) вместо тс главный мо*
мент т° относительно центра инерции О.
Имеем
/ N \
\ *=i /
N
0 X jS rnt B(o X ^ +^> (9.7.31)
9Г.7] примеры 467
Перенеся добавочные к т° слагаемые в правую часть уравнения B8)
и заменив в последнем векторы wt их значениями, придем к уравнению
N \ { N \ N
- (вн*+е22'+взз0 < х <•>+0е' •«;+»; х 0е'
+ 2«/(^-^)ХBюХг//+г;) = т°. (9.7.32)
Рассмотрим простейший пример*) — единственное носимое тело
совершает поступательное прямолинейное колебательное движение
внутри оболочки спутника Земли. Уравнение колебания центра инер-
инерции Сх этого тела записывается в виде
r'=r'0 + aes(t)9 (9.7.33)
причем среднее значение функции г{г) за достаточно большой про-
промежуток времени равно нулю, так что вектор г^ определяет среднее
положение С? центра инерции тела в оболочке. Через е обозначен
единичный вектор, определяющий направление прямой, множитель а
характеризует размахи колебания. В задаче о спутнике можно при-
принять момент mG равным нулю, считая, что главный вектор сил тяго-
тяготения в каждый момент проходит через центр инерции G, и прене-
пренебрегая силами сопротивления атмосферы.
Имеем
r'= ™ r't rf — rr= АЛМУ г\ ю/ = 0, (9.7.34)
и уравнение движения C2) запишется в виде
@е + 0Cl) • «о + о) X @е + 0СО • w =
= ™ Ж^ г' X 1<° X г' + о) X О» X П + 2аш Хе + аё'г]. (9.7.35)
Заменим здесь г1 его выражением C3), причем слагаемые
отнесем в правую часть и введем в рассмотрение тензор
ео = Qc + ec. + _^L_ {Ег'о . rl -г'/0), (9.7.36)
*) Roberson R. E., Torques on a Satellite Vehicle from Internal Mo-
Moving Parts, Journal of Applied Mechanics, 25, № 2, p. 196—200, 1958.
30*
468 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
равный, как нетрудно сообразить, тензору инерции оболочки и тела,
если бы оно было неизменно присоединено к оболочке, в общем
центре инерции их О0. Действительно, по D.4.2)
и к выражению C6) придем, сложив эти равенства и использовав
формулы C4).
Уравнение C5) теперь перепишется так:
@G° + 0f°) • со + to X @G° + 0f°) • ю = LG°. (9.7.37)
Вектор L°° можно назвать возмущающим моментом относительно
точки Go, вызванным движением массы т. Его выражение приводится
к виду
(9-7.38)
Существенно в этом выражении наличие слагаемых, среднее зна-
значение которых отлично от нуля. Таковыми будут
L*G° = — Х+т а^ 1(Е — ее) • со — со X ** • <*>]. (9.7.39)
Предполагается, что среднее значение вычисляется за промежуток
времени, содержащий достаточно большое число периодов изменения
функции e(t), но достаточно малый, чтобы можно было пренебречь
в течение этого времени изменениями со и со.
9.8. Уравнения движения твердого тела
с полостью, заполненной жидкостью *)
Здесь эта задача рассматривается как пример применения уравне-
уравнений динамики относительного движения, когда носимое тело —
жидкость, движение которой относительно несущего тела определено.
*) Н. Е. Жуковский, О движении твердого тела, имеющего полости,
наполненные однородной капельной жидкостью, Собрание сочинений, т. III,
стр. 21—186, ОНТИ, 1936. Опубликовано в 1885 году.
9.81 движение твердого тела с полостью, заполненной жидкостью 469
Ограничимся случаем одной односвязной *) полости в твердом
теле. Предполагается, что заполняющая ее целиком жидкость — идеаль-
идеальная, несжимаемая и однородная; тогда абсолютное движение ее будет
безвихревым и в рассмотрение может быть введен в системе непо-
неподвижных осей О;т]С однозначный потенциал скоростей — гармониче-
гармоническая функция Ф1 (!-, т], С) координат частиц жидкости, градиент кото-
которой равен вектору абсолютной скорости va частицы.
Пусть Oxyz— система осей, связанных с телом; можно с помощью
формул преобразования координат представить потенциал скоростей Фг
как функцию координат х, у, z, в которую теперь явно войдет и
время t:
Фг(Ъ т], С) = Ф(х, у, г% t).
Итак,
, (9.8.1)
причем Ф остается гармонической функцией х, у, z.
На поверхности 5 полости нормальные составляющие скорости
стенки полости и частицы жидкости равны друг другу. Поэтому,
обозначая через п единичный вектор нормали к 5 (направленной во-
вовне), имеем
van = n- grad Ф = (*>0 + со X rr) • п = v0 • n-f со • (г' X л), (9.8.2)
так как геометрическая сумма ^0 + (оХг' представляет вектор ско-
скорости точки твердого тела, расположенной на 5; г' — вектор-радиус
точки поверхности полости. Отметим, что, поскольку вектор v0 не
зависит от координат х, у, z, можно записать соотношение
grad(*F0./") = tf0. (9.8.3)
В рассмотрение вводится далее гармонический вектор В(х, у, z),
т. е. вектор, проекции которого Bv В2, В3 на оси системы Oxyz —
гармонические функции. Они определяются в полости V по следую-
следующим значениям на поверхности 5 их нормальных производных:
дЯ±- = упг — zn2, ^-=znx — хпг, ^- = хп2 — ynv (9.8.4)
Здесь п}, п2, пъ — проекции п на оси системы Oxyz; через
обозначены нормальные производные функций Bs.
*) Область называется односвязной, если любая взятая в ней замкнутая
кривая может быть непрерывным преобразованием сведена в точку. Область
внутри шара — односвязна, внутри тора — двусвязна.
470 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [гл! 9
Известно, что задача разыскания гармонической функции в области по
заданной на границе ее нормальной производной — задача Неймана—*
имеет единственное решение при условии
J.
Д
(9.8.5)
(do— элемент поверхности, и интегрирование производится по поверх-
поверхности S, ограничивающей область). Это условие в настоящем случае
выполнено. * Чтобы проверить это, следует вспомнить формулы пре-
преобразования поверхностного интеграла в объемный, многократно при-
применяемые ниже:
<fnldo = j -^dx, j <fn2do = J -^Л, j чЧйо = J^ dx
S V S V S V
(9.8.6)
(dx — элемент объема, интегрирование по объему V"), где ср — непре-
непрерывная и имеющая непрерывные частные производные первого порядка
функция внутри У и на его границе. В нашем случае
что и требуется.
Можно записать условия D) также в виде
л. grad Я = г' X п. (9.8.7)
Здесь введен в рассмотрение тензор gradZ?— диадное произведение
оператора
. д , . д . . д
на вектор В. Заметим, в частности, что gradr' = E, где Е — еди-
единичный тензор.
Зная вектор В, можно определить потенциал скоростей Ф соот-
соотношением
o. (9.8.8)
Это — гармоническая функция х, у, z, так как гг и В — гармониче-
гармонические векторы, a v0 и ы от координат не зависят; время входит в Ф
только через их посредство. Отсюда следует, что если вначале
покоившийся сосуд с жидкостью начнет двигаться и в некоторый
момент остановится, то остановится в этот момент и заключенная,
в нем жидкость.
Функция Ф удовлетворяет краевому условию B). Действительно,
<va = grad Ф = grad (vQ • г') + grad (В. со) = v0 + grad (В • со), (9.8.9)
9.8] ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА С ПОЛОСТЬЮ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ 471
и далее, используя C) и G), находим
nva = n- grad Ф^й.^ + ^'Х»)' ю, (9.8.10)
что и требуется.
Обозначая через г', как и ранее, скорость частицы жидкости
относительно сосуда (т. е. системы осей Oxyz), имеем
и сравнение с (9) дает
г' = grad # • (о — (о X f'. (9.8.11)
Таким образом, если движение сосуда задано» можно считать
известным движение жидкости, его целиком заполняющей, — доста-
достаточно иметь решения трех упомянутых задач Неймана, зависящие
лишь от формы сосуда.
Переходим к составлению уравнений движения системы — твердое
тело (сосуд) с заполняющей его жидкостью. Это — уравнения A.17)
и A.26). В первое из них входят относительная скорость rrQ и отно-
сительное ускорение rQ центра инерции системы. Но, поскольку сосуд
заполнен целиком, а жидкость однородна, ее перетекание по сосуду
не изменяет положения центра инерции, т. е.
* **
г — 0 г1 — О
и уравнение A.17) не отличается от уравнения движения твердого
тела
Xrfc\ = Vt (9.8.12)
причем М обозначает массу системы.
По той же причине в уравнении A.26) неизменное значение сохра-
сохраняет и тензор инерции 0° системы в точке О. Он такой же, как
если бы жидкость не перетекала по сосуду (затвердела). Поэтому
и подлежит определению момент относительных количеств движе^
ния К° и его производная по времени. Он равен по A1)
d'z. (9.8.13)
V V V
Здесь pdz = dm—элемент массы жидкости, р—ее плотность. Заме-
Заметим, что
Р / г' X (» X г') dx = со • J (Е>" • гг — rrrr) dm = w Q° (9.8.14)
472 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
представляет момент относительно полюса О количеств движения
жидкости, если бы она не перетекала по сосуду, и 0^— ее тензор
инерции в точке О. Остается вычислить интеграл
G° = p f (r' X grad Я • со) dT = ДГ° + 0° • u>. (9.8.15)
v
При неподвижной точке О вектор G0 представляет, как это сле-
следует из D.8.8), момент количеств движения (абсолютного) жидкости,
заключенной в сосуде.
Обозначая через
тензор инерции в точке О твердого тела (без заполняющей его
жидкости) и замечая, что
К? + w X К°т = — 0? • <о — со X 0? • со + G0 + (О X O°t
теперь запишем уравнение A.26) в виде
QO . (О-НОХ0? • *+Mr'cX(v0-\-t*Xv<)-\-Qo-\-'*XO0 = m°. (9.8.16)
Вычислим проекцию вектора G° на ось х. Можно сохранить и век-
векторные записи, но это усложнило бы дело. Имеем
Интегралы легко преобразуются с помощью формул F) и D)
к виду
= f'Bkd-§do. (9.8.18)
jGг) I
V S
Поэтому, вводя обозначение
f^Bkdo (/, k=l. 2, 3), (9.8.19)
s
вместо A7) получим
G°x = (До)! + Q?2oJ + Q?3(O3 (9.8.20)
и два аналогичных выражения для 0^ и G%
9.8] ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА С ПОЛОСТЬЮ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ 473
Заметим еще, что, применив преобразование F) и учитывая,
что Bt—гармонические функции, получим
V
/^-B,*>. (9.8.21)
откуда следует также, что Qik = Qki.
Проекции вектора G° оказываются линейными функциями проек-
проекций вектора @. Поэтому величины Q?k представляют составляющие
тензора второго ранга. Этот симметричный тензор второго ранга
можно назвать тензором инерции в точке О эквивалентного (жидкости
внутри полости) твердого тела, так как момент количеств движения
жидкости относительно точки О представлен в форме
G° = Q°b), (9.8.22)
подобной моменту количеств движения твердого тела с тензором
инерции Q0 в точке О.
Уравнение движения A6) теперь записывается в виде
(9.8.23)
тогда как, если бы жидкость не перетекала по сосуду, то оно
имело бы вид
) ) ci
(9.8.24)
Как пример рассмотрим случай сосуда, имеющего эллипсоидаль-
эллипсоидальную полость. Уравнение поверхности, ее ограничивающей, будет
Известно, что
п =LEL—^L — LUL — 2lL __ 1 dF = 2z
где
Первое из краевых условий записывается в виде
дВх х дВ{ у дВ{ z _ ( 1 1\
дх a2 "I" ду Ь2~^ dz c2~yZ\c* b2)'
474 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
и ему удовлетворяет гармоническая функция
_ Ь2 — с2
Аналогично получим
2~ с2 + я2 Z '
Вычисление по формулам B1) дает
о / Ь2 — с2 у - ^о __ / с2 — л - \2 D глО __( а2 — Ь2 \2
и
Через А, В, С обозначены моменты инерции покоящейся в сосуде
жидкой массы:
Л = i М (Ь2 + с2), В = 1 Ж (с2 + а2), С = 4- М («2 + Ь2).
о о о
Для шара а = Ь = с и гармонический вектор Z? обращается в нуль —
идеальная жидкость не увлекается вращением сферического сосуда.
Примеры, относящиеся к цилиндрическому сосуду, рассмотрены
в указанном труде Н. Е. Жуковского.
9.9. Уравнения движения деформируемого тела
Носимыми телами в последующем рассмотрении являются частицы
упругого тела, совершающие малые движения около тех положений,
которые они занимали бы в абсолютно твердом теле. Этот «твердый
скелет» представляет несущее тело. С ним связывается система
осей Oxyz, движение которой определяется скоростью полюса vQ и
вектором угловой скорости (о. Положение точки М скелета задается
ее вектор-радиусом ОМ = р; через rQ=OO обозначается вектор-
радиус полюса О относительно неподвижных осей с началом в точке О-
Смещение частицы, находившейся в точке Ж, задается вектором и,
зависящим от ее координат и от времени. Предполагается, и это
существенно, что время входит в а только через посредство пара-
параметров qai играющих в дальнейшем роль обобщенных координат.
Число этих параметров принимается конечным и обозначается через п.
Оставаясь в рамках методов аналитической механики систем с конеч-
конечным числом степеней свободы, следует считать также известной
(заданной) функциональную зависимость вектора а как от коорди-
координат х, у, z точки в натуральном состоянии тела', так и от обобщен-
обобщенных координат:
» = b(jc. у, г; <?, дп). (9.9.1)
9.9] УРАВНЕНИЯ ДВИЖЕНИЯ ДЕФОРМИРУЕМОГО ТЕЛА 475
Это выражение может быть представлено рядом по степеням qa:
JU"(x, у. *) + .*. 2 2?«?р&вЭ(*. У, z)+ ... (9.9.2)
<у = 1 а = 1 C = 1
Здесь учтено, что при qa = 0 вектор и равен нулю.
Хотя в последующем рассматриваются только малые движения
и в уравнениях движения сохраняются лишь линейные члены относи-
относительно qa, но было бы неосторожно отбросить квадратичные сла-
слагаемые сразу же в выражении и. При этом были бы потеряны неко-
некоторые линейные слагаемые в уравнениях движения, учитывающие
существенные эффекты. Члены более высокого порядка, чем второй,
в уравнении B) при рассмотрении линейных задач нет нужды
сохранять.
Поясним способ выбора функций а на примере нерастяжимого
упругого стержня. Направим ось Ох по оси стержня, изгибные
колебания которого происходят в плоскостях ху и zx. Линейная
часть вектора перемещения точек оси стержня при изгибе задается
в виде
п п
«о = 2 to. (*)+2 /з?я+Ж (*). Ф^-з)
а=1 а=1
где за сра(лг) и фа(л0 можно принять собственные формы колебаний
в плоскостях ху и zx, a q* и qn + a — две системы обобщенных коорди-
координат. Учтем далее поворот сечения стержня при изгибе. Через f2, ^3
обозначим углы поворота сечения вокруг осей у и z, так что
a=l a=.l
Тогда добавочное слагаемое вектора и, определяющее перемещение
точки поперечного сечения с абсциссой х и вектор-радиусом в сече-
сечении i2y-\-hz* будет равно
«1 = (*2Т2 + 'зТз) X (i2y + i&) = - h у 2 я^ (x)+*itqn, X (х) 1.
L a=l a=;l J
(9.9.4)
Таким образом, и0 не исчерпывает линейных слагаемых вектора и.
Слагаемые второй степени определяются по известной формуле для
осадки изгибаемого стержня
476 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
в которой £—проекция перемещения точек оси стержня на ось Ох,
а т] и С—на оси Оу и Oz. Предполагается, что ^ = 0 в сечении
х = 0. Использовав C), получим
Таким образом, выражение вектора и при учете квадратичных отно-
относительно обобщенных координат слагаемых приобретает вид
и=2 к [- №
a = l
п п Г * x "I
i ^ 2 2 wp / < (9 ^з«) ^+?«+л+з / ф: (о Фр«)« • с9-9-
a=l p = l L 6 0 J
Известно, что любая форма смещения точек оси стержня представима
рядом вида B) по собственным формам колебаний; в приближенном
решении число собственных форм (слагаемых ряда) может быть взято
конечным и часто весьма небольшим. Более того, в выражении C)
допустимо использование вместо собственных форм колебаний других
функций от х, разумно описывающих характер упругой линии оси
стержня. Подобного рода предположения — конечность п, допускаемый
произвол выбора функциональной зависимости вектора перемещения
от координат точек упругого тела — практически оправдываются
расчетами колебаний стержней и плит на неподвижных опорах. Нет
оснований считать их неприемлемыми при составлении общих уравне-
уравнений движения упругого тела. Первое из упомянутых предположений,
сводящее задачу к рассмотрению системы с конечным числом степе-
степеней свободы, исключает из рассмотрения вообще весьма трудно
учитываемые колебания высоких частот. Второе не должно значи-
значительно повлиять на результат, поскольку, как увидим ниже, выбо-
выбором функций, которыми задается вектор и, определяются чис-
численные значения некоторых интегральных характеристик; они мало
изменяются от этого выбора, если, конечно, он сделан достаточно
разумно.
Знак интеграла в последующем применяется в смысле «нагружен-
«нагруженного интеграла» — суммирование ведется не только по распределенным,
но и по сосредоточенным величинам*) (массам, силам и т. д.).
*) О нагруженном интеграле (это понятие тесно связывается с интегра-
интегралом в смысле Стильтьеса) см. В. И. Смирнов, Курс высшей математики,
том 4, § 95, стр. 278 (ГТТИ, 1941).
9.9] УРАВНЕНИЯ ДВИЖЕНИЯ ДЕФОРМИРУЕМОГО ТЕЛА 477
Выражение вектор-радиуса гг точки М тела в системе осей Oxyz
при введенных выше обозначениях будет
Поэтому вектор-радиус центра инерции С определяется равенством
M9c + a(qx qn)9 (9.9.7)
так что
п п
л/г*/ V1 да • .„**/ ^ да •
а = 1 а=1 а=1 C = 1 ^
Уравнения движения упругого тела составляются на основании
общих уравнений теории относительного движения A.17) и A.26)
для несущего тела и B.19) для координат qa. Уравнения должны
быть линейными относительно qa и qa. Поэтому надо сохранить
квадратичные слагаемые в тех величинах, которые придется диффе-
дифференцировать по этим переменным. Таковыми являются кинетическая
энергия относительного движения Тг, потенциальные энергии П° сил
инерции поступательного движения и 1Г°—центробежных сил. Кроме
того, в выражении вариации Ъг', необходимом для вычисления обоб-
обобщенных сил, надо учесть линейные относительно qa слагаемые;
вследствие этого в г' придется сохранить квадратичные члены. Учет
квадратичных членов в выражении г' потребуется еще при вычисле-
вычислении обобщенных вращательных сил инерции Q™.
Имеем по (8)
а=1
и совершенно ясно, что для вычисления Тг достаточно сохранить
только линейные слагаемые в формуле B). Получаем
a-Updm, (9.9.9)
<x = l 3 = 1
Обращаясь к B.5) и (8), имеем, отбрасывая не зависящее от qa сла-
слагаемое:
478 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Здесь введены обозначения
Таким образом,
/ п \
^ 4 5]аЧз )• (9-9-12)
и пренебрежение в формуле B) квадратичными членами привело бы
к потере линейных слагаемых выражений Qa.
С такой же точностью надо провести вычисление тенсора инер-
инерции 0°, через который по B.6) определяется IIе0. Имеем по D.3.20)
Q0 = f(Er'-r'-r'r')dm= f\
= j (Ер- р—рр) dm+ 2 j [Ер-и — у(
+ / (Ей-и — uu)dm,
и, чтобы сохранить все квадратичные относительно qa члены, надо
во второй группе слагаемых учесть эти члены в выражении а.
Получаем
п п п
*ъО fbO | n "V4 a a | v^ \i Г^а^/> n /'Q Q 1 (X\
a=l a=l 3=1
Здесь 0^ — тензор инерции в точке О твердого скелета; через Да
и Qa^ обозначены тензоры в этой точке, определяемые равенствами
Ла = f '\Ep-V*- ^{pU« + Vap)]dm,
m. (9.9.14)
Переходим к обобщенным силам. Задаваемые силы (кроме упру-
упругих сил, о которых говорится ниже) будем считать зависящими от
координат и скоростей точек тела; поэтому, если учитывать изме-
изменения, связанные с упругими перемещениями точек тела, следует
9.9] УРАВНЕНИЯ ДВИЖЕНИЯ ДЕФОРМИРУЕМОГО ТЕЛА 479
принять для сил выражения вида
Под F подразумеваются объемные, поверхностные, линейно рас-
распределенные и сосредоточенные силы; /^ — то значение, которое
имело бы F в абсолютно твердом теле; fa и f'a — зависящие
от координат х, у, z векторы, задание которых связано с рассматри-
рассматриваемой частной задачей. Например, поверхностные аэродинамические
силы, действующие на крыло самолета, как известно, существенно
зависят от колебаний крыла и выражаются через величины, опреде-
определяющие его упругие перемещения и их скорость. Изменение сил
гидростатического давления на тело, погруженное в тяжелую жидкость,
обусловленно изменением направления нормалей к поверхности тела
при его деформации.
Виртуальное перемещение точки тела определяется равенством
а=1
3 = 1 V т=1
и выражение элементарной работы принимает вид
( ^8?.)л. (9.9.17)
3=1 \ а=1 /
Здесь уже отброшены квадратичные относительно qa и qa слагаемые.
Интегралы — нагруженные; под dz подразумевается элемент объема,
или поверхности, или дуги.
Теперь, обозначив через V* и тР главный вектор и главный
момент относительно полюса О сил Ft, через V и т°—сил F,
придем к такому представлению выражения элементарной работы:
i (9.9.18)
480 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Здесь
()
C=1 C=1
(9.9.19)
C-1
/г
= m? + ^ (lifyp + V%)• (9.9.20)
Постоянные векторы v3, v/C, jip, fi/C определяют изменения главного
вектора и главного момента сил, обусловленные деформацией
тела; их нахождение должно служить предметом специального
исследования *).
Выражения обобщенных сил Qa в формуле A8) имеют вид
] %%). (9.9.21)
C-1
Наличие слагаемых QOa, не исчезающих вместе с деформацией,
обусловлено учетом элементарной работы «уже существующих» сил /^
на виртуальных перемещениях точек тела из их положений в твер-
твердом скелете.
Поскольку обобщенные координаты qa отсчитываются от нату-
натурального состояния тела, выражение потенциальной энергии упругих
сил представляет квадратичную форму этих переменных
aC<7a9> (9.9.22)
Теперь, учитывая формулы G) и (8) и обозначения A1), приходим
*) Определение этих величин является одной из основных задач
дисциплины, получившей название «аэроупругость». См. монографию:
Р. Л. Бисплингхофф, X. Эшли и Р. Л. Халфмэн, Аэроупругость,
ИЛ, 1958.
9.9] УРАВНЕНИЯ ДВИЖЕНИЯ ДЕФОРМИРУЕМОГО ТЕЛА 481
к такой записи уравнения движения несущего тела A.17):
П
— 2 [дл I» X аа + ю X (» X а«)] + 2?вю X в'+?.о'|. (9.9.23)
1
При qa = О приходим к уравнению движения центра инерции твер-
твердого скелета. Добавочные слагаемые обусловлены, во-первых, изме-
изменением главного вектора сил V, во-вторых, реактивными воздействиями,
обусловленными движением в самом скелете.
Для записи уравнения вращения несущего тела A.26) надо вычи-
вычислить момент относительных количеств движения К0 относительно
г
полюса О. Он равен
I п \ п п
(9.9.24)
причем через Ga обозначен вектор
G" = j pXUadx. (9.9.25)
Квадратичные слагаемые отброшены. По A.29) составляем момент
кориолисовых сил инерции, также сохраняя только линейные отно-
относительно qa члены:
п
<or = -@O-» + «XAr?) = -2y<LU-Aa + i<«>XG*V (9-9-26)
а = 1
В том, что это выражение действительно является моментом кориоли-
кориолисовых сил, убеждаемся из равенства
а 1
<*> • Л + y
которое легко получить, использовав вышеприведенные выражения A4)
и B5) величин Да и (?\
Теперь сделаем подстановки в A.26). Получаем:
* а=1 а=1
о]^а^4J
а=1 а=1
31 Зак. 2072. А. И. Лурье
482 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
Переходим к уравнениям B.19) для координат qa. В них остается
выразить обобщенные силы инерции вращательного движения Q% и
обобщенные гироскопические силы Га. Имеем по B.14)
T) [ %\Y (9.9.28)
/ \ з-i /
где введено обозначение
G^a =f(U?XUa + pX U**) dm. (9.9.29)
Выражения гироскопических коэффициентов 7аВ составляются по B.18),
и достаточно в них сохранить только величины, не зависящие от qa,
так как эти коэффициенты далее умножаются на обобщенные ско-
скорости <7р- Получаем
(9.9.30)
и уравнения B.15) в виде
2
£
(a= 1 я). (9.9.31)
Здесь применены обозначения B1), B2), A1), A4), C0), B5) и B9);
с помощью этих формул производится вычисление постоянных векто-
векторов и тензоров aa, Ga, Да и т. д. в уравнениях C1), равно как и
в уравнениях движения несущего тела B3) и B7). Сложность полу-
полученных систем уравнений является следствием их значительной
общности. В частных задачах они существенно упрощаются.
9.10. Колебания вращающегося стержня
Эта задача здесь служит примером применения общих уравнений
(9.31). Рассматриваются изгибные колебания вращающегося упругого,
нерастяжимого стержня (лопатки). Конец О стержня заделан во вра-
вращающееся с постоянной угловой скоростью to вокруг оси Ozx колесо
9.10]
КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ СТЕРЖНЯ
483
на расстоянии R от его оси вращения. Другой конец (х = Г) стержня
свободен. Надо составить только уравнения (9.31), так как движение
несущего тела (колеса) задано. Полюс системы осей, связанных
/У
-А *
Рис. 78.
с несущим телом, поместим в точке О и направим ось Ох по оси
недеформированного стержня (рис. 78). Тогда
= -w2Wi (9.10.1)
и уравнения (9.34) примут вид (вес не учитывается)
@ % *Ч (Аз
(9.10.2)
Предполагается, что точки оси стержня могут совершать как тан-
тангенциальные (по оси Оу), так и аксиальные (по оси Oz) движения.
Тогда по (9.5)
(9.10.3)
!/•*=-/, J<@ т; @d5. f/"+a- n+9 = -ix f Ф:@ % @d;
(a, p=l я).
причем
Имеем
Ц*. Р + П^ЦЬ + П, P^q ^ р—^ ###| Я)# (9.10.4)
dm = p {х) do dxt
31*
484 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ 9
где р(х) — плотность материала стержня, do — элемент площади попе-
поперечного сечения S(x). Поэтому вычисление интегралов, которые далее
встречаются, сводится к правилу
//(*. У* z)dm = f p(x)dx j f (x, y, z)do.
0 S (x)
Поскольку как функции сра (лг), фа(х)» так и законы распределения
плотности р(х) и изменения площади поперечных сечений S (х) счи-
считаются заданными, вычисление всех коэффициентов уравнений B)
выполнимо, хотя может оказаться громоздким.
В последующем мы ограничимся рассмотрением однородного приз-
призматического стержня (р и «S постоянны), не будем учитывать слагае-
слагаемых в выражениях C), обязанных своим происхождением повороту
сечений, и будем считать, что стержень не закручен; тогда главные
оси инерции всех поперечных сечений будут параллельны друг другу;
для облегчения расчета мы будем рассматривать случай, когда одна
из этих осей параллельна Оу, а другая Oz. Ось Ох является гео-
геометрическим местом центров инерции поперечных сечений стержня.
Если за функции <ра(х), <\>а(х) принять собственные формы коле-
колебаний консольного стержня с неподвижной заделкой, то при пере-
перечисленных условиях
<?„(*) эф.(*). (9.10.5)
Итак, в нашей задаче
(9Л0>6)
и количество выкладок для определения коэффициентов сокращается
вдвое. Переходим к их вычислению. По (9.9) получаем
Здесь и далее интегрирование ведется по безразмерной переменной
—т-
Проекции а* ня ось Ох векторов а\ а также составляю-
составляющие Дзз тензоров у\а, как видно из (9.11) и (9.14), обращаются в нуль;
уравнения B) оказываются однородными. Это и должно быть, так как
прямолинейный стержень на вращающемся колесе может сохранять
свою форму.
9.10] КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ СТЕРЖНЯ
Теперь по (9.11) находим еще
435
af
f<f'a(o)z'9(a)da. (9.10.8)
Обратившись к (9.14), получим
Qt = ?Slf\ c?a (S) Ь (S) - s f ?: (а) ^ (с) da
dst
QT' П^ = -
v'a (а) ^ (а) da.
(9.10.9)
J
Здесь имеется различие между коэффициентами уравнений двух групп
колебаний, оно объясняется тем, что векторы Ua и {]п+а имеют раз-
различные направления, так что входящие по (9.14) в вычисление коэф-
коэффициентов Q33 величины
[EU* • Us — \ (UkUs + UsUk)^ . /
при k, s=l, ..., n отличны от тех, которые получаются при
k, s = n+l 2л.
Потенциальная энергия изогнутого стержня выч 1сляется по изве-
известной формуле
/ i
Ue = 1Е/2 fv (х) dx + ^ E/y f w dx,
о о
где v(x) и w(x) — проекции перемещения точек оси стержня на
оси Оу и Oz, а 1г и 1у — моменты инерции поперечных сечений отно-
относительно Oz и Оу. В нашем случае найдем
q^+qn+aqn+^) f ^)^s)ds, (9.10.10)
a=l 3=1 0
откуда обнаруживаются значения коэффициентов
= ^?3. (9.10.11)
В формулах G) — A1) смешанные коэффициенты с одним индексом,
меньшим п, 2l другим, большим nt отсутствуют. Легко далее видеть,
486 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
что гироскопические обобщенные силы в данном случае исчезают.
Действительно, обратившись к формулам (9.30) и F), получим
if = i3-f(J?X U*dm = 0. (9.10.12)
Введем еще обозначения
и
1 s
J ?, (а) ?,
о
у (ds J
о о
Этот двойной интеграл с помощью известной формулы
ах а а
fdxf/(x, y)dy = fdyff(x, y)dx
0 0 0 0
приводится к однократному
1
т°* = тп + а' "+Р = i- f (\—a)(j^+\ -f-о) q/(о) <р£ (о) do. (9.10.14)
о
Сделав теперь подстановки в уравнения B), приходим к двум незави-
независимым системам уравнений: для тангенциальных
п
= 0 (а=1, .... л) (9.10.15)
[
и для аксиальных движений
%+л* + и2«%+л]==0 (Р=1 я). (9.10.16)
Р = 1
Собственные формы колебаний консольного стержня определяются
по известному дифференциальному уравнению *)
?ivE)-vi?.E) = ° (9.10.17)
при краевых условиях
<Р.@) = <@) = 0, <A) = Ч»ГA> = °- (9-10.18)
Здесь
(9.10.19)
*) См., например, И. М. Бабаков, Теория колебаний, гл. XI, Гостех-
издат, 1958.
9.101 колебания вращающегося стержня 487
причем X*—квадраты собственных частот колебаний для формы
с номером а, а через X2 обозначена величина
^ (9.10.20)
так что Х2:=Ху для тангенциальных колебаний, Х2 = Х^—для аксиаль-
аксиальных. Величины va представляют известные числа, определяемые раз
навсегда из частотного уравнения. Они равны
v,= 1,19372* v2 = 0.99610^. v3= 1,00010^.
(9.10.21)
Таким образом, формы свободных аксиальных и тангенциальных коле-
колебаний стержня тождественны; частоты их, конечно, отличаются друг
от друга. Их отношения равны
ГГ . (9.10.22)
Известно свойство ортогональности собственных форм, выражаю-
выражающееся в нашем случае в том, что интеграл от произведения двух
форм cpa(s)<fy(s) различных номеров по промежутку @,1) обращается
в нуль. Можно так выбрать множитель, с точностью до которого
определяется собственная форма, чтобы интеграл от cp^(s) по указан-
указанному промежутку стал равным единице. Итак, по G)
s = 8.p. (9.10.23)
о
где 5ар — символ Кронекера.
Обращаясь теперь к выражению A1), проделаем интегрирование
по частям
Са|3 = Г ?a (S^ fy ^ ^S ~ Ча ^ % ^ \ Г *?'а W ?7 E) ^5 ==
i ° 0
= [ ?! W ?р (S) — ?. (S) у'" (S)] + Г сра (S) ср^ E) dS.
о J
откуда, сославшись на A7), A8) и B3), находим
^ = 8^4. (9.10.24)
Теперь уравнения движения A5) и A6) значительно упрощаются и
принимают вид
п
У.+ Кй + ^^ + ^^^Г0 (a==1 ») (9.10.25)
0 = 1
488 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
для тангенциальных колебаний и
п
q _L-(^a) Яп + а + и? 2 ^qn,o = 0 (<* = 1. •••> п) (9.10.26)
для аксиальных. Здесь (\а)у и (\а)г обозначают частоты тангенциаль-
тангенциальных и аксиальных колебаний при неподвижной заделке. С помощью
этих уравнений учитывается влияние угловой скорости вращения на
частоты и формы свободных колебаний стержней. Слагаемые в урав-
уравнениях B5) и B6), содержащие коэффициенты т^, определяют вос-
восстанавливающее действие центробежных сил. Опустив в выражении
вектора перемещения и квадратичное слагаемое, мы не получили бы
существенной части этих слагаемых (с коэффициентами т^)\ смысл
задачи был бы в значительной мере утрачен.
Выражения функций сра (х), нормированные так, чтобы выполнялось
равенство B3), имеют вид
гг (х) — г г— [(sh v_ -f- sin va) (ch vas — cos v_s) —
TaV ' Sltl Va Ch Ma —COS »a Sh Vry lV a ' a/v a a/
— (ch va + cos vj (sh yas — sin vas)l, (9.10.27)
R
так что при заданном значении параметра — имеется все необходи-
необходимое для численного расчета по A4) коэффициентов т°$.
9.11. Уравнения движения ракеты*)
За несущее тело здесь принимаются неизменные части ракеты
(оболочка, снаряжение) вместе с заключающимся в ней не сгоревшим
к рассматриваемому моменту t топливом. Носимыми телами являются
газообразные продукты сгорания в канале
с/Л _ г» *>
^ ракеты, вектор г. представляет скорость
6 относительно канала /-й частицы газа. Дви-
^ ^ жение газа принимается установившимся и
р „д прямолинейным; это предположение позволяет
представить вектор относительной скорости гг
(отбрасываем индекс /) совокупности частиц газа, находящихся в не-
некотором поперечном сечении канала, в виде (рис. 79)
r' = — ev(k)t (9.11.1)
где е—единичный вектор, направленный по оси канала от его выход-
выходного сечения к носу ракеты, к—абсцисса рассматриваемого сечения,
причем Х = 0 во входном, Х = / в выходном сечении канала; вели-
\S-A--
") См. Ф. Р. Г а н т м а х е р и Л. М. Л е в и н, Об уравнениях движения
ракеты. Прикладная математика и механика, 11, 1947, стр. 301—312.
9.11] УРАВНЕНИЯ ДВИЖЕНИЯ РАКЕТЫ 489
чина относительной скорости v(k), таким образом, определяется очер-
очертанием канала и считается не зависящей от времени.
Масса ракеты Ж, уменьшающаяся вследствие расхода газов через
выходное сечение, является в нашем случае заданной функцией вре-
времени t\ предполагается известным также закон сгорания, определяю-
определяющий для каждого момента времени количество и конфигурацию налич-
наличного топлива; этим задается функциональная зависимость от времени
вектор-радиуса центра инерции r'Q и тензора инерции 0°. Массой
и моментом инерции находящегося в канале газа пренебрегаем.
Вернемся теперь к уравнениям динамики относительного движения.
В уравнении A.17) надо заменить суммы интегралами:
Mr'c = J r' dm, М?с = f r' dm, Mr'c = j г' dm. (9,11.2)
В уравнении A.26), согласно A.28) и определению вектора Af£\ соот-
соответственно будем иметь
0° • со + со X К°т = 2 j rf X (со X h dm, K°T = j r' X rr dm. (9.11.3)
Сделав эти замены, придем к уравнениям
М [^+еоХ*'о+*> X г'с 4- со X (со Xг'с)\+-2и XJV' dm-\~ f ?' dm=V9
(9.11.4).
r/ X ?dm = m°. (9.11.5)
Это — лишь другая форма записи уравнений A.17) и A.26), пока
речь идет о движении одной и той же совокупности тел. При соста-
составлении же уравнений движения ракеты следует использовать именно
уравнения D) и E), так как преобразования, которые привели исход-
исходные уравнения движения- системы материальных точек к виду A.17)
и A.26), теперь неприменимы. Так, из первого соотношения B) не
вытекает вследствие переменности М второе, а из второго—третье.
Поясним сказанное ссылкой на вывод уравнений Лагранжа в п. 7.1
из основного уравнения динамики. Ничего нельзя возразить против
соотношения
Следующий шаг заключался в замене суммы ее значением Т.
В нашем случае Т определяется формулами A.5) — A.7), в которые
входят М и 0°; теперь они рассматриваются как величины, зависящие
490 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
от времени, так как та часть топлива, которая к моменту t сго-
сгорела и в виде газообразных продуктов покинула ракету, нас не
интересует. Пока уравнения Лагранжа были записаны в форме F),
не пришло бы на ум дифференцировать по t массы mv но об этом
легко забыть после проделанных замен стоящих в F) сумм по упо-
упомянутым формулам для 7, в которые вошли интегральные величины,
подобные М, 0.
Обращаясь к уравнениям D), заметим, что выражение элементар-
*
ной массы dm, движущейся по каналу с относительной скоростью г\
может быть представлено в виде
dm = — Mdt = v(k)pSdt = pSd\t (9.117)
где М— секундный расход, р—плотность, предполагаемая постоян-
постоянной, Поэтому, учитывая A), получаем
i i
С *Г' dm = — e Г v(k)pSdl = eM Г dl = Me. (9.11.8)
о о
По A) имеем также
7' = -ev'(k)i (9Л1-9>
и далее, применив G),
i i
С г'dm = Me J v' (\)idt = Me Г v' (k) dl = Mv(I)e. (9.11.10)
о о
Здесь v(l) — величина относительной скорости газов в выходном
сечении (во входном она равна нулю).
Уравнение D) теперь принимает вид
[0 ^ с (с)] г. (9.11.11)
Здесь через Ф обозначена сила тяги (реактивная сила)
Ф = —еМу{1). (9.11.12)
Она равна по величине \M\v{l) = — Mv(l) и имеет направление е+
так как М < 0. Эффект движения газов по каналу выражается еще
в появлении кориоласовой силы
FCot = — 2(о X еШ. (9.11.13)
Остается провести соответствующие преобразования в уравне-
уравнении E). Вектор-радиус г' точки на оси канала можно представить
ч виде
—X), (9.11.14)
9.11] УРАВНЕНИЯ ДВИЖЕНИЯ РАКЕТЫ 491
где г'г — вектор-радиус точки на оси выходного сечения, имеющий
начало в полюсе О системы осей Oxyz, связанной с ракетой. Как
показано выше,
* **
г' dm = eM dk, r' dm = Mev' (к) d\. (9.11.15)
Поэтому
х (<*> х f1'W =
= Шг\ X (ю X e) I + 2 Me X ('•> X e) f(l — \)dk =
о
= 2Ж (r\ + \ el) X (со X e) I = - (r\ + \ el) X FCor (9.11.16)
и также
i i
j r' Xr* dm = M J r'tXev' (k)dl-+- M f (I — \)eXevr (k)d\ =
о о
= Mv A) r\ X e = — r\ X Ф. (9.11.17)
Приходим к уравнению вращения ракеты
©э • со + со X 0° • »+ Мг'с X (^0 + ^ X vQ) =
)/7Сог. (9.11.18)
Оно имеет вид уравнения движения свободного твердого тела, пра-
правая часть которого дополнена моментами относительно полюса О
силы тяги Ф, с точкой приложения в выходном сечении, и кориоли-
совой силы, прикладываемой в средней точке канала.
Соотношения (И) и A8) представляют искомые уравнения дви-
движения ракеты. В их выводе существенными были предположения,
что движение газа установившееся и газ несжимаем. Добавочные
слагаемые, которые должны быть внесены при отказе от этих предпо-
предположений, обычно пренебрежимо малы *).
При выводе уравнений движения можно было бы также основы-
основываться на уравнении динамики переменной массы И. В. Мещер-
Мещерского **).
*) См. упомянутую в сноске на стр. 488 статью Ф. Р. Гантмахера
и Л. М. Левина.
**) Л. Г. Л о й ц я н с к и й и А. И. Лурье, Курс теоретической
механики, часть II, гл. XXV, Гостехиздат, 1948.
492 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ. 9
9.12. Гироскопическая платформа
Несущим телом в последующем рассмотрении является платформа,
на которой размещены гироскопы — кожухи с заключенными в них
вращающимися роторами. С платформой связана система осей Oxyz,
направления которых задаются единичными векторами il% /2, /3» век"
торы угловой скорости платформы и скорости полюса О обозна-
обозначаются через со и vQ\ с каждым из кожухов связывается ортогональный
триэдр единичных векторов ак, bk, ck = ak X bk, причем вектор ak
направлен по оси вращения k-то кожуха на платформе; он имеет
неизменное направление в системе осей Oxyz, связанных с платфор-
платформой. Вектор bk направлен по оси вращающегося в кожухе ротора.
Углы поворота кожухов относительно платформы и роторов в кожу-
кожухах обозначаются y^k, cpfe; поэтому векторы угловой скорости этих
тел по отношению к системе осей Oxyz равны (см., учитывая изме-
изменение обозначений, рис. 32)
+■**?*• (9.12.1)
Производные единичных векторов триэдра ak, bk, ck в этой системе
осей будут
* ; k = ~bklk. (9.12.2)
Поэтому
i i i i. (9.12.3)
Точка пересечения Ok осей вращения кожуха и ротора предпола-
предполагается совпадающей с центрами инерции этих тел, вектор-радиус OOk
назовем г'г Массы k-то кожуха и ротора обозначаются через m'k, m'k\
выражения тензоров инерции их в точке Ок записываются в виде
Qr°k = А'кЕ+(С*- л'ь) bkbk, Q0* = AkE+(Cl - Ak) bkbk,
(9.12.4)
причем для сокращения письма принимается
Аъ = А'к + А1 Ck = C'k + C'i mk = m'k + m'i (9.12,5)
Переходим к составлению уравнений движения несущего тела —
платформы. Это — уравнения F.6) и F.15), с тем отличием, что
число носимых тел равно не двум, a 2s (s кожухов, s роторов).
Пусть т обозначает массу платформы, г'с — вектор-радиус ОСп
ее центра инерции. Тогда уравнение (fi.6) — уравнение движения
9.121 ГИРОСКОПИЧЕСКАЯ ПЛАТФОРМА 493
центра инерции рассматриваемой системы тел — будет
т [ v0 + to X «о + «* X гсп + w X (<° X гсп)] +
Слагаемые в F.6) вида r'k откинуты, так как центры инерции Ok
в системе осей Oxyz неподвижны. За полюс О примем центр инер-
инерции платформы и сосредоченных в точках Ok масс mk. Тогда
5
Wr +• 2 тУь = О (9.12.6)
и уравнение движения центра инерции будет
m(vq + u>Xv0)=V, (9.12.7)
где М — масса системы. Можно, надлежащим образом размещая про-
противовесы, поместить точку О в точку пересечения осей карданова
подвеса, с помощью которого платформа монтируется на движущемся
основании (корабле, самолете).
Переходим к уравнению вращения F.15). Через 0° обозначим
тензор инерции в точке О платформы и системы масс mk, сосредо-
сосредоточенных в точках Ok, т. е.
п * = i k^ k k k k'
Теперь, использовав равенства C), F) и обозначения E) и (8), надо
лишь внимательно выписать все слагаемые, входящие в F.15); после
вполне очевидных упрощений придем к равенству
k =
У. (9.12.9)
Перейдем к уравнениям движения носимых тел. Можно для этого
обратиться к уравнениям вида F.39), но быстрее ведет к цели непо-
непосредственное составление уравнений Лагранжа.
Кинетическая энергия &-го кожуха с ротором равна (в абсолют-
абсолютном движении)
Т> = | (« 4- akyj ■ [Е А'к 4- (С; - А'к) bkbk] ■ (т + aklk) +
-г ~ (ш + акЪ + ЬьъУ [Е А; 4- (С"к - A"k) bkbk] ■ (ш 4 aklk + ft*?*).
494 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ (ГЛ. 9
Проделав показанное вычисление, получим
Если отсутствуют специально вводимые силовые воздействия, то
обобщенная сила Qy представляет момент сил трения в оси вра-
вращения &-го кожуха, a Q —разность между вращающим моментом
и моментом трения на оси &-го ротора. Мы полагаем далее
Qy =0, Q^ =0 (*=1. ..., s). (9.12.11)
Координаты cpfe циклические, но j^k — позиционные, так как от них
зависят векторы bk. Можно составить 5 уравнений, выражающих
постоянство циклических импульсов р — кинетических моментов
роторов. Придем к соотношениям
С;4 + й)-й,) = Яй {k=\ s). (9.12.12)
Теперь по G.17.2) и G.15.4) составляем функцию Рауса
Н1 1
-^ (ft=l. . .., s) (9.12.13)
и дифференциальные уравнения
(А= 1, ..., s). (9.12.14)
Здесь использовано соотношение
Теперь легко проверить также уравнение (9) — это векторная запись
уравнений Эйлера — Лагранжа для функции Рауса
Я = 1ю.00.ю+Д/?л. (9.12.15)
Первое из этих уравнений
d dR . dR dR n
9.12] ГИРОСКОПИЧЕСКАЯ ПЛАТФОРМА 495
будет иметь вид
@° • »)i + ">2 О0 • »)з — шз @° • «Ь +
+ 51 [Ак (X>*i + »i) + (Ci - Ak) (» • ftftftM)' 4-
4- Hki>kl -j- Aklk (uJcM — ш3ай2) + (С* — Ak) (о • 6ft (<o2ftM — w3ftft2) 4-
4- Hh (w2bk3 — шз^и)] = mf.
Оно представляет проекцию на ось Ох векторного соотношения
@°4- 2ЕЛй) .« + @X0°-«4-2 M*e»x»4-^x*»Xefc4-
\ ^ = 1 / k = 1
ХА + а)Х^]}-т0. (9.12.16)
В точности к этому виду приводится уравнение (9), если заме-
заменить в нем ср& и ?* их значениями из уравнений A2) и отметить
тождество
со X ак = (о • с^ — со • V* = WX(^X cfc).
Предполагая, что роторам сообщены большие угловые скоро-
скорости cpft, тогда как угловая скорость платформы и угловые скорости пре-
прецессий yk остаются достаточно малыми, сохраним в уравнениях A4) лишь
слагаемые, содержащие кинетические моменты роторов. Получим
«>.ck = 0 (k = l, ..., s). (9.12.17)
При числе гироскопов s^>3 и при условии, что в числе векторов
ck найдутся три некомпланарных
^•(^Х^)^О (/,*,/== 1, .... 5), (9.12.18)
следствием равенств A7) является обращение в нуль угловой ско-
скорости платформы — платформа стабилизирована в пространстве:
(о = 0. (9.12.19)
Уравнение A6) теперь дает
или 2НАХа^ + тО=0 (9 Л 2.20)
k
и выражает «уравнение равновесия» платформы — геометрическая
сумма гироскопических моментов роторов и главного момента отно-
относительно центра инерции внешних сил, приложенных к платформе,
должна быть равна нулю.
496
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
[гл. 9
Как пример рассмотрим случай трех гироскопов при располо-
расположении их на платформе, изображенном на рис. 80.
L
На рис. 81 показана ориентация единичных векторов il% i2, iz>
векторов ak осей вращения кожухов и начальных положений векто-
векторов bk> ck. Из него легко получить
Cj = l3,
a2 = — i2,
1*3 «-3,
Ьг = — I, cos Zl — i2
>2 = j,cosx2
b, = — и sin
i2cosx3.
ci = h sin Zi — h cos Xi.
c2 = — ix sin y2 + /3 cos Ъ,
= — ix cos ъ -
h ^
Условие A8) принимает вид
(9.12.21)
(9.12.22)
Оно не выполняется при Xi = X3— о1» когда оси вращения рото-
роторов 3 и 1 станут параллельными друг другу, а также при х2 —it —
ось вращения ротора 2 перпендикулярна плоскости, в которой рас-
расположены оси роторов 3 и 7.
9.12]
ГИРОСКОПИЧЕСКАЯ ПЛАТФОРМА
497
Не представит теперь труда записать уравнения движения плат-
платформы и гироскопов в развернутом виде. Например, первое уравне-
уравнение A4) будет
; -А
) [о),оJ cos 2Xl + i (co|-co2) sin
— Я, (wj sin X! — oJ cos X!) = 0. (9.12.23)
Считая как углы поворота роторов, так и проекции угловой ско-
скорости платформы на оси координат малыми величинами, ограничимся
линейным приближением; тогда
(9.12.24)
В этом же приближении три уравнения, получающиеся при проекти-
А, (х2 — со2) — Я2о>3 = 0,
-h с/
"г
\«
Рис. 81.
ровании на оси триэдра ix, iv i3 векторного соотношения A6), при-
приводятся при учете соотношений B4) к виду
(9.12.25)
2 (Ш2 — Х2) = тз-
где обозначено для краткости
Q^eo+Cj+q+Лз, Q^eo-Кз+Л,. <гз=»зО+/12- (9-12.26)
Теперь от систем уравнений B4) и B5) легко перейти к системе
1-о
1 .
Щ
(9.12.27)
32 Зак. 2072^ А. И. Лурье
498 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ [ГЛ 9
В предположении постоянства проекций на оси платформы глав-
главного момента т° проекции угловой скорости будут изменяться по
гармоническому закону с частотами
X=& ^ Х= (9Л2-28>
пропорциональными угловым скоростям роторов, т. е. очень высо-
высокими. Имеем
ml=Ml sin (\xt+аг), оJ=Ж2 sin 0^+а2)9 ®г=мз sin (V+aa) (9.12.29)
и по B5)
for
777 a3) — |/ -^-M2cos(V + g2) (9.12.30)
и т. д. Углы поворота кожухов при наличии моментов тР, сколь бы
малы они ни были, будут нарастать. Чтобы избежать этого, преду-
предусматривают специальные приспособления. Одно из них (преследующее
и другие цели) показано схематически на рис. 80. На нем имеются
три двигателя Дх, Д2, Дг, создающие вращающие моменты относительно
осей вращения колец карданова подвеса и платформы; сигналы, по
которым происходит управление двигателями, поставлены в связь
с углами поворота кожухов *).
*) А. Ю. Ишлинский, К теории сложных систем гироскопической
стабилизации. Прикладная математика и механика, 22, № 3, стр. 359, 1958 г.
ГЛАВА 10
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
10.1. Преобразование Лежандра
Рассмотрим функцию Ф(х1 хп) переменных xY, ..., хп,
непрерывную и имеющую непрерывные производные первого и вто-
второго порядков по всем этим переменным. С помощью функции Ф,
называемой далее производящей, совершается преобразование от
«старых» переменных xv . . ., хп к «новым», определяемое форму-
формулами
дФ
E=1.
п).
A0.1 1)
Якобиан системы функций ys называется гессианом функции Ф
и обозначается Я(Ф). Его элементами являются вторые производные
функции Ф по переменным xk
Н(Ф) =
дх\ дх2 дхх
д2Ф д2Ф
д2Ф
дхп дхх
д2Ф
дх] дхп дх2 дхп дх\
A0.1.2)
Система уравнений A) может быть разрешена относительно ста-
старых переменных в области значений их, в которой гессиан не при-
принимает значения, равного нулю. Тогда можно получить формулы
обратного преобразования, выражающие старые переменные через
новые:
*, = *,(У1. ••-. Уп) (s=l, ..., п). A0.1.3)
Это преобразование можно записать в форме A); с этой целью
в рассмотрение вводится производящая функция W(уг, .... уп) но-
новых переменных, определяемая равенством
6=1
A0.1.4)
500 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
в котором все старые переменные заменены их значениями C). Дей-
Действительно, вычислим частную производную ч7 по ys, учитывая,
что W зависит от этого аргумента и явно и через посредство ста-
старых переменных. Находим
dys xs~r Zd ду& Ук ^U dxk dys
так как вследствие равенств A) суммы сокращаются. Итак,
*s=^-s (s=U .... п), A0.1.5)
что и требовалось. Соотношения A) и E), определяющие прямое
и обратное преобразования, образуют преобразование Лежандра.
Легко сообразить, что преобразование, обратное обратному, возвра-
возвращает нас к исходному преобразованию.
Если, в частности, производящая функция Ф — квадратичная
форма
п п
то ее гессианом является определитель | а \ матрицы а коэффициен-
коэффициентов этой формы
|а|. A0.1.7)
Если а — невырожденная матрица, т. е. \а\ отлично от нуля, то
система линейных уравнений
п
%ах (s==1 п) A0Л8)
разрешима относительно старых переменных. Обозначая через b = a~l
обратную матрицу, найдем
Из теоремы Эйлера об однородных функциях следует, что в этом
случае производящая функция W(ух уп) обратного преобразо-
преобразования получается при непосредственной подстановке выражений (9)
в форму (б). Действительно, по D) и A) имеем
к-^- — Ф^2Ф — Ф = Ф, A0.1.10)
4=1 к=\
10.11
ПРЕОБРАЗОВАНИЕ ЛЕЖАНДРА
501
причем Ф должно быть выражено через новые переменные. Итак,
5=1
5=1 fc = l
т. е. квадратичная форма Ч\ образуемая с помощью матрицы Ь,
обратной а, представляет союзное выражение квадратичной формы Ф.
Нетрудно сообразить, что форма W может быть записана в виде
определителя
W = —
1
flu
«21
а22
A0.1.12)
anl an2 . . . ann yn
У\ Уг • • • Уп О
Примером применения преобразования Лежандра может служить
обобщенная теорема Кастильяно. Рассматривается равновесное поло-
положение системы с идеальными связями, на которую действуют актив-
активные силы двух видов: потенциальные силы, определяемые потенци-
потенциальной энергией II (qx qn), и силы Fv ..., Fjy, называемые на-
нагрузками. Сумма элементарных работ всех сил на виртуальных пере-
перемещениях точек системы из положения равновесия должна быть нулем:
лг п
k=\
5=1
4'де Qs — обобщенные силы нагрузок. Отсюда при независимых ва-
вариациях bqs следуют уравнения равновесия
(s=\....,n),
A0.1.13)
которые можно рассматривать как преобразование, определяющее но-
новые переменные — обобщенные силы нагрузок, через старые — обоб-
обобщенные координаты qs системы в положении равновесия под дейст-
действием этих нагрузок. Потенциальная энергия II является производя-
производящей функцией этого преобразования; производящей функцией об-
обратного преобразования R (Qv ..., Qn) будет величина
N
R(Ql9 ..., 0я) =
5 = 1
A0.1.14)
называемая дополнительной работой. Соотношения E) здесь будут
dR
E=1,
П).
A0.1.15)
Они имеют более общее значение, чем сформулированная в п. 5.7
известная теорема Кастильяно, которая и выражает эту теорему в част-
частном. случае, когда потенциальная энергия является квадратичной
502 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. Ю
формой обобщенных координат. Тогда, согласно A1), дополнитель*
ная работа R будет союзным выражением потенциальной энергии
и теорема Кастильяно приобретает ее общепринятую формулировку.
Конечно, практическое применение обобщенная теорема Кастильяно
имеет в тех случаях, когда есть возможность непосредственного пред-
представления дополнительной работы через обобщенные силы, так как
если пришлось бы решать уравнения равновесия A3) относительно
обобщенных координат, то не было бы нужды в определении их
с помощью формул A5). Это замечание, конечно, можно повторить
и в отношении любого преобразования Лежандра — оно ни в какой
мере не облегчает задачи решения системы уравнений A) относительно
старых переменных, а указывает лишь на возможность представле-
представления их с помощью производящей функции, выраженной через новые
переменные.
10.2. Канонические уравнения движения
Рассматривается материальная система, связи которой голономны,
имеющая п степеней свободы. Уравнения Лагранжа движения этой
системы представляют систему п дифференциальных уравнений вто-
второго порядка относительно обобщенных координат, разрешимую от-
относительно вторых производных qs, как указывалось в п. 7.4. Мно-
Множеством способов можно заменить рассмотрение этой системы уравне-
уравнений системой 2п уравнений первого порядка. Достаточно, например,
обозначив qs = rs, ввести в рассмотрение 2п переменных qs, rs, кото-
которые в дальнейшем могут играть роль независимых величин, опре-
определяющих поведение системы. Системой 2п уравнений движения пер-
первого порядка были бы п уравнений Лагранжа, определяющие г s через
qs,rs, и п уравнений qs = rs. Конечно, никакого значения эта три-
тривиальная замена обозначений не имела бы, сказанное преследует лишь
цель указать, что рассмотрение вместо п дифференциальных уравне-
уравнений второго порядка 2п уравнений первого порядка позволяет счи-
считать все 2п переменных независимыми друг от друга. Пример пло-
плодотворного перехода к уравнениям первого порядка представляют урав-
уравнения Эйлера—Лагранжа, позволяющие при удачном выборе квазиско-
квазискоростей дать более наглядную и симметричную запись уравнений движения,
чем уравнения Лагранжа.
В качестве 2п переменных системы дифференциальных уравнений
движения первого порядка могут быть приняты обобщенные коорди-
координаты qlt . . ., qn и линейные функции обобщенных скоростей qs—обоб-
qs—обобщенные импульсы рг, ..., рп. Последние были уже определены
в п. 4.2:
10.2] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ 503
При таком выборе переменных уравнения движения, когда активные
силы потенциальны, записываются в весьма симметричной и компакт-
компактной форме, называемой канонической; это облегчает исследование
общих свойств движения и допускает сведение задачи интегрирования
канонических уравнений к разысканию полного интеграла некоторого
уравнения в частных производных первого порядка (теорема Якоби).
Переменные qs, ps являются независимыми и симметрично входят
в последующие записи и преобразования.
Кинетическая энергия Т, рассматриваемая как функция обобщен-
обобщенных скоростей, играет роль производящей функции от старых пере-
переменных qs к новым ps. Ее гессианом будет определитель матрицы А
коэффициентов квадратичной формы Г2, входящей в состав выраже-
выражения Т. Было показано в п. 4.1, что этот определитель не может
быть нулем (он положителен); поэтому уравнения A), линейные от-
относительно обобщенных скоростей qit разрешимы относительно них.
Получаем соотношения D.2.6)
qs=qs(pv .... /V gv ...,qa;t), A0.2.2)
линейные относительно обобщенных импульсов. Они и представляют
первую группу канонических уравнений — систему п дифференциаль-
дифференциальных уравнений первого порядка, определяющих производные по вре-
времени обобщенных координат через обобщенные импульсы, обобщенные
координаты и время t.
Преобразование Лежандра позволяет представить уравнения B)
в другой записи. Для этого составим, согласно A.4), производя-
производящую функцию обратного преобразования
п
? = 2ws-^% д„. Pi Рп. *). (Ю.2.3)
s = l
в которой, конечно, обобщенные скорости заменены их выражениями
B) через обобщенные импульсы. Тогда по A.5) получим
^="ёг (s==u "■••п)ш A0<2-4)
Важно, что с помощью этой же функции Т составляется вторая группа
уравнений движения. В противоположность уравнениям D), представ-
представляющим лишь запись формул преобразования, уравнения второй
группы служат выражением общего уравнения динамики. Последнее
здесь предпочтительно записать в форме центрального уравнения
Лагранжа F.4.6)
504 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
ИЛИ С ПОМОЩЬЮ C)
п п
^ ^s^s- 00.2.6)
5=1 5 = 1 5 = 1
Получаем
п п ~
P Ц Ь
5=1 5=1
ИЛИ
п
Q)8^+'f (Ьду s^] fc
5 = 1
- s^] - fc - ж)Ьр^ = °-
Последняя группа слагаемых исчезает вследствие соотношений D),
а предпоследняя—вследствие переставимости действий варьирования
и дифференцирования (правило db = bd)\ как указывалось ранее,
можно было бы и не прибегать к этому правилу, применив вместо
центрального у равнения Лагранжа общее центральное уравнение F.4.11).
Пришли бы к тому же результату
5 = 1
Из него, вследствие независимости вариаций bqs, находим
Ps.^_-^-4-Qs (s=\ /i). (Ю.2.7)
Такова вторая группа канонических уравнений движения для системы
переменных qs, ps. Она переходит во вторую группу канонических
уравнений Гамильтона, когда силы потенциальны. Подобно тому как
уравнения Лагранжа могут быть в этом случае записаны с помощью
одной лишь функции L — кинетического потенциала, достаточно
также одной функции /У, называемой функцией Гамильтона, чтобы
составить каноническую систему. Эта функция определяется так:
qn, Рх рп\ /)=f+n=2w,-?tU (Ю.2.8)
5 = 1
ИЛИ
п
Н= 2л^—i=r+-n. A0.2.9)
v=l
Функция И зависит от обобщенных координат, обобщенных импуль-
импульсов и времени; обобщенные скорости исключены с помощью соот-
соотношений B).
10.21
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ
505
Полезно заметить, что время / может войти явным образом
в функцию Гамильтона И как через Т (при нестационарных связях),
так и через обобщенную потенциальную энергию II.
Учитывая, что потенциальная энергия не зависит от обобщенных
импульсов, имеем теперь вместо D) и G)
дН
дТ
дП
dqs
дИ
dqs
Мы получили систему канонических уравнений Гамильтона
• __ дН • __ _ дН
q' ~ dps Ps~~ dqs
(s= 1,
п). A0.2.10)
Переменные qs и ps, удовлетворяющие системе канонических урав-
уравнений Гамильтона, называются каноническими.
Если связи стационарны, то Т— квадратичная форма обобщенных
скоростей; тогда, согласно сказанному в предыдущем пункте, Т яв-
является союзным выражением кинетической энергии; оно в п. 4.2 было
обозначено через Т. Итак, при стационарных связях
Н=Т'-\-П,
A0.2.11)
т. е. функция Гамильтона представляет выраженную через обобщен-
обобщенные координаты и обобщенные импульсы полную механическую
энергию. Заметим, что по A.12) составление Т сводится к раскрытию
определителя
1
2\А\
А2\
. . . Л
2п
Л/II Лп2 . . . Лпп рп
Р\ Р2 .-. Рп 0
A0.2.12)
При нестационарных связях, как отмечалось в и. 4.1,
Ps = ^+^
и из (9) следует, что
A0.2.13)
причем, конечно, Т2 должно быть выражено через импульсы.
В случае стационарных связей импульсы входят в Т\ и поэтому
в И, лишь квадратично; при нестационарных связях Т2—квадра-
Т2—квадратичная форма обобщенных скоростей, но выражения последних,
506 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ 10
являясь линейными функциями обобщенных импуЛьсов, содержат сво-
свободные члены; поэтому Н разобьется на слагаемые: квадратичное,
линейное и не зависящее от импульсов; соответствующие выраже-
выражения Т даются формулами D.2.13) и D.2.14). В первой из них
через Т обозначена разность Т2— То, выраженная через обобщенные
скорости и координаты; эта разность, выраженная через импульсы,
в формуле D.2.14) обозначена Т2.
Составим полную производную функции Гамильтона по времени
в силу канонических уравнений A0)
dH дИ Y / дН ' i дН
dt л
n
дН
- dt тЛ1й}, dps dps dqs}— dt * <—'
Поэтому функция Гамильтона И остается при движении постоянной,
если t явно не входит в ее выражение. Получаем интеграл уравне-
уравнений движения
H(ql qn, p, pn)=zh. A0.2.15)
называемый интегралом энергии. Для системы со стационарными свя-
связями он выражает постоянство суммы кинетической и потенциальной
энергии системы.
Если координаты <7т+1, .... qn циклические, то из равенств
pm+/=-__!^L. (/=l п — т), A0.2.16)
являющихся следствием определения, данного в п. 7.15, и выраже-
выражения A3) функции Гамильтона, можно заключить, что соответствующие
обобщенные импульсы сохраняют при движении постоянные значения
(/= 1 п — т). A0.2.17)
Рассмотрению подлежит в этом случае система 2т уравнений первого
порядка
^=■^7 P* = --dj7 (S=1 «). (Ю.2.18)
содержащая такое же число неизвестных величин— позиционных коор-
координат и соответствующих им импульсов. Если предположить, что эта
задача решена, то определение циклических координат из уравнений
=1 п-т) A0219)
сведется к квадратурам, так как правые части этих уравнений станут
известными функциями времени.
10.3] ЯВНАЯ ФОРМА КАНОНИЧЕСКИХ УРАВНЕНИЙ 507
10.3. Явная форма канонических уравнений
Сопоставляя движению материальной системы, подчиненной стацио-
стационарным связям, движение изображающей точки в римановом многооб-
многообразии с метрикой, определяемой квадратом линейного элемента
ds2 = Tdt2 = 1 аар dq* dqK
мы ввели в рассмотрение формулой G.8.4) вектор скорости v этой
точки с контравариантными составляющими, равными обобщенным
скоростям qa. Связь ковариантных составляющих с контравариант-
контравариантными дается общим правилом (П. 2.2.3) и в данном случае будет
•я дТ
п^Я ~df = Pa- (Ю.3.1)
Таким образом, обобщенные импульсы (при принятом в п. 7.8 выборе
масштабов) представляют ковариантные составляющие скорости изо-
изображающей точки. Из A) получаем обратные соотношения
q* = a**pi. A0.3.2)
представляющие первую группу канонических уравнений. Союзное
выражение кинетической энергии будет
7" =у aepa"i/y*e^8 = -2- а*р,рь% A0.3.3)
откуда, учитывая, что в выражение потенциальной энергии импульсы
не входят, приходим к другой записи уравнений B)
Вторая группа канонических уравнений представляет закон движения
G.8.11)—«ускорение изображающей точки равно действующей
силе» — в ковариантной записи
Здесь, аналогично G.8.8), дифференцируя выражение вектора ско-
скорости ф—р^г* по правилу П.2.4.19, имеем
и соотношение
dll * Г В )
р> = - -W + ат {«т f р*Ръ A0-3-5)
представляет развернутое выражение второй группы канонических
уравнений. Чтобы проверить это, рассмотрим выражение
Oq« 2 oq*
508 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ 10
Тогда, вспомнив теорему Риччи (П. 2.5.8) и правило ковариантного
дифференцирования (П. 2.5.6), можно записать
так что
и сравнение с E) дает
• = д(П+Г) ^ дН
^а . dqrj dqrj '
что и требовалось. Итак, в явной записи канонические уравнения
имеют вид:
{Д}—IP- (Ю.3.6)
10.4. Примеры составления канонических уравнений
1°. Движение материальной точки в поле цен-
центральной силы. Вводя сферические координаты R, ft, X, имеем
выражения G.18.6) кинетической и потенциальной энергии. Из них
получаем
pR = mR, pb = mR2by px = m\R2s\n2b. A0.4.1)
Функция Гамильтона будет
U44) <10-4-2)
Первая группа канонических уравнений представляет, как указыва-
указывалось выше, уравнения A), разрешенные относительно обобщенных
скоростей:
дрр т ' др^ mR2 ' дрх mR2 sin2 tt " ^ '
Вторая группа уравнений будет
дН 1 / ., . р\ \ дп
i
(ЮЛА)
5 sin3
Имеются интегралы энергии и циклический интеграл рк = const.
10.4]
ПРИМЕРЫ СОСТАВЛЕНИЯ КАНОНИЧЕСКИХ УРАВНЕНИЙ
509
2°. Канонические уравнения движения волчка при
заданном движении его точки опоры (рис. 82). Вектор
скорости центра инерции волчка равен
<ос = v0 + фп + ф sin fin') X i^z'c = v{) + z'c (— Ьп' +- ф sin ЯЛ).
Здесь введена система «полуподвижных» единичных векторов п, п\ i'z%
рассмотренная в 2.10. Через vQ обо-
обозначен вектор скорости точки опо-
опоры О. Получаем
2z'c (—
sin
и выражение кинетической энергии
системы будет
Т = -i ^4 (О2 -|- ф2 sin2 0) -+-
(—fltf0 • л7 + ф sin П«г0 • л) +
A0.4.5)
Рис. 82.
причем через Л и С обозначены экваториальный и осевой моменты
инерции в точке О.
Обобщенные импульсы равны
р = Лф sin2 f) + Mz'cv0 • л sin Я + С (<р + Ф cos '0 cos (C>»
» 4 cos b).
Отсюда находим
1
~ Р* cos
sin
- Р, cos П - Mzc% •п sin ft>
A0.4.6)
Составив по B.13) функцию Гамильтона, получим
cos
510 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Здесь С0@ — высота точки опоры над некоторым уровнем. Наличие
слагаемых
в выражении Н никакого значения не имеет.
При составлении второй группы канонических уравнений следует
учитывать зависимость векторов п и п' от углов ф и ft:
п = ix cos ф + /2 sin Ф» л' = (— h sin Ф + Ь cos Ф)cos & + 'з sin **»
/3 = — (— ix sin ф -)- i2 cos ф) sin ft -|- /3 cos ft,
где ij, /2, i3 — единичные векторы осей неизменного направления.
Отсюда следуют соотношения
дп дп' ди дС
° ® ' fi&- A0-4-8>
Учитывая эти равенства, получаем
= Mz'c (v0 • л sin ft)' — Мг^о • n sin ft,
где se>0 = 5>0 — ускорение полюса О. Второе уравнение приводится
к виду
дН cos Ь , а „_/ .а\9
Р (С0Ь ^»s&)
sin Ь + Ж4 («0 • i4 cos & —
Последнее слагаемое можно записать еще в следующей форме:
Вводя теперь в рассмотрение величины
Pi = />ф — Л^о * л sin &. Р* =
можно записать канонические уравнения в виде:
первая группа
♦ (';^сояв> &
р? cos»
10.4] ПРИМЕРЫ СОСТАВЛЕНИЯ КАНОНИЧЕСКИХ УРАВНЕНИЙ 51i
вторая группа
р* = — Mz'cw0 • п sin Ь,
pi = -а^т с; - рч cos ь) (picos n - p)+
A0.4.10)
-f~ Mgz'c sin ft -(- Mz'cw0 • n',
Остается заметить, что согласно (8)
Таким образом, в полном соответствии со сказанным в п. 9.2 и
формулой (9.2.9) движение точки опоры можно учесть, включая
в выражение потенциальной энергии слагаемое
Уравнения (9) и A0) представляют канонические уравнения для
функции Гамильтона
1 1 *2
2А sin2 ft v Ф ^<р / ' 2Л ^ '
+ -2^-/?24-Mg2:'ccosft -}-Mz'cttJQ • i'v A0.4.11)
причем
wQ • /g = (a:0 sin ф — y0 cos ф) sin ft + z0 cos 0, A0.4.12)
где x0, y0, z0 — проекции ускорения полюса О на оси неизменного
направления.
3°. Канонические уравнения движения волчка,
несущего вращающийся маховик. Предполагается, что
подшипники оси маховика расположены на оси симметрии Oz' волчка.
Обозначая через / угол поворота маховика (чтобы сохранить обо-
обозначение ср для угла чистого вращения волчка), имеем в фор-
формуле D.12.3)
и выражение кинетической энергии системы будет:
1 1
Т = -п- А (&^ -|— ф^ sin^ ft) —j—рг- С (ср —(— ф cos ft)^ —\-
+ у ®зХ2 + ®зХ (? + Ф cos l^)- (Ю.4.13)
Здесь Л и С — экваториальный и осевой моменты инерции волчка и
мысленно остановленного маховика относительно осей, проведенных
512 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
через точку опоры волчка, в3—момент инерции маховика относи-
относительно его оси вращения. Получаем
рь = /1ft, /?ф = Лф sin2 ft + С (ср + ф cos ft) cos 0 + в3х cos О,
Р9 = с (? + Ф cos lC}) + ®зХ» Рх = взХ + ®з (? + Ф cos Ь)>
откуда легко находим
~~~~А* У A sin2
'г == ~~Г 1л л ~;~э a C0S "» X :=== "i
A0.4.14)
—Н3) *
Это — первая группа канонических уравнений. Функция Гамильтона
равна
1 Г/4 (^-PycosdJ
77 ~ 2 [ Л ~1~ Л sin2 0 "^
^)] A0.4.15)
где Q — вес волчка с маховиком, z'c — абсцисса центра тяжести
системы, расположенного на оси волчка.
К первой группе канонических уравнений можно присоединить
четыре интеграла: интеграл энергии
H = h A0.4.16)
и три циклических интеграла
Задача сводится к квадратурам, причем отличие от задачи о волчке
обнаруживается только в определении угла ср; выражение угла %
записывается сразу же
g^fe O0.4..8)
10.5. Скобки Пуассона и скобки Лагранжа
Рассматриваются две функции иу v от двух групп независимых
переменных, каждая из которых содержит п переменных:
tf = afolf .... qnt р1ш ..., Рп) = и(р\д), ) g
v = v(gl9 ..., qn, pv .... pn) = v(p\q). J
Составляется выражение
du dv . du dv / du dv . du dv
10.5] СКОБКИ ПУАССОНА И СКОБКИ ЛАГРАНЖА 513
называемое скобками Пуассона от этих функций и обозначаемое
Из определения сразу же следуют простейшие свойства скобок
Пуассона
(и, v) = — {vy и), (и, и) = 0, (и, с) = 0, A0.5.3)
если с не зависит от рассматриваемых переменных. Имеем также
(и, Vl + v2) = (u, vx) + (u, v2). A0.5.4)
Частные производные функции и по qs и ps можно представить
в форме скобок Пуассона
ди . ч да . ч /in к к\
-^-=-(ps,u). -^- = (qs,u), (Ю.5.5)
что позволяет, в частности, записать канонические уравнения Гамиль-
Гамильтона в виде
Ъ = (Ч*. я). Л = (Л. Н) (s=l я). A0.5.6)
Наконец, отметим еще значения скобок Пуассона
(Qs> Яг) = 0. (Ps. Pt) = 0. fe, ft) = 85/, (Ю.5.7)
где 8^ — символ Кронекера. Эти скобки называются фундамен-
фундаментальными.
В обозначении скобок Пуассона, если в этом есть необходимость,
индексами можно указать независимые переменные, т. е. писать
В последующем будет применено тождество Якоби
(и, {v, w)) + (v, (w, u)) + (w, (и, v))*=0. A0.5.8)
Чтобы избежать в доказательстве громоздких записей, заметим,
что каждое слагаемое левой части этого тождества содержит вторую
производную одной из функций и, v, w. Обратим внимание на вто-
вторые производные w\ они входят в сумму двух первых скобок, но
не в третью скобку. Эту сумму можно, согласно C), записать
в виде
(и, (vt w)) — {у, (и, w)). A0.5.9)
ЯЧ Зак. 2072. А. И. Jlvobe
514
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Скобки (v, w) и (и, w) представим в виде линейных форм первых
производных от w:
п
dw \
<...»-а <»=2
*
.„•
dw
ч др т-"п+к-щ-у
где обозначено
С/U т-ъ (J (J л \)ЬЬ л
Тогда
— (v, (и, w))= A\B(w)\ — B[A(w)] =
5=1
■В.
dw
др.
К
dw
A0.5.10)
A0.5.11)
5=1 /f=l
d2w
причем многоточием показаны члены, не содержащие вторых произ-
производных w. Выражение, стоящее под знаком двойной суммы, меняет
знак при замене индексов суммирования 5 на k и к на s\ отсюда
заключаем, что эта сумма равна нулю и в выражении (9) вторые
производные от w сокращаются. Повторив рассуждение для функций
и, v, найдем, что должны сократиться вторые производные всех
функций и, v, но каждое слагаемое содержит производную одной
из трех функций, значит, сократятся попарно все слагаемые, что и
требовалось доказать.
Еще одно свойство' скобок Пуассона будет использовано ниже;
если и, v зависят также и от переменной /, то
0
dt ^ '
то легко проверить, основываясь на определении скобок Пуассона.
10.5]
СКОБКИ ПУАССОНА И СКОБКИ ЛАГРАНЖА
515
Переходим к рассмотрению выражений
и dv "■ * * '
qn дрп
-(■
dql дрх
ди dv ' ' ' du dv \ dv du
называемых скобками Лагранжа и обозначаемых
* * * + dv du)*
£=1
В частности, аналогично G), имеем
\Яз> Як\ = °> \Qs> Pk\ = bsk> IPs*
St k=l П).
A0.5.14)
Это — фундаментальные скобки Лагранжа. В обозначении скобок
Лагранжа, когда есть в том нужда, индексами указывается система
переменных q, p, по которым строятся скобки.
Пусть теперь
uv vv . . ., ип, vn A0.5.15)
п пар функций от п пар переменных
Я1. Рх Яп> Рп- A0.5.16)
Можно также считать величины A6) фулкциями переменных A5).
Рассмотрим 4/г2 скобок Пуассона
(«л, us). (ukt vs)t (vk, us), (vk, vs)
(k, 5=1, .... /г), A0.5.17)
являющихся элементами квадратной матрицы Пуассона Р
(П. 1.1.28):
Р =
(«i.
... (м,, ип)
(Ил, И,) ... (Ы„, 1/„)
(V!, W,) ... A/,, Ы„)
A/„, Ы,) ... (У„, Мл)
(и.,
... («I, vn)
(Unt Vi) ... (Мл, Vn)
(Vl.
A0.5.18)
(vn, v^ ... (vn, vn)
Аналогично определяется матрица Л, элементами кстэрой служат
скобки Лагранжа
\uk, usl \uk vs]t [vk, us], [vkJ vs]. A0.5.19)
Обе эти кососимметричные матрицы могут быть записаны в форме
сложных 2X2 матриц от п X п матриц [(П. 1.1.23) и (П. 1.1.28I
((и, и)) ((и, v))
((v, и)) ((v, v))
А =
\[и,и\\ [{u,v}\
\[vtu]\ [[v,v]\
A0.5.20)
где ((и, и)), ((и, v)) и т. д.—матрицы, отделенные пунктирными
ЗЭ*
516 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
линиями в записи формулы A8); аналогичное значение имеют ма-
матрицы [[и, и]], [[и, v]] и т. д. Заметим, что матрицы Я и Л меняют
знак при транспонировании
Р' = — Р, Л' = — Л, A0.5.21)
что следует из свойств скобок Пуассона, и Лагранжа менять знак
при замене порядка функций и, v.
В Приложении I рассматривается произведение матриц АР, при-
причем доказывается используемое ниже свойство матриц Пуассона и
Лагранжа (П. 1.2.39)
— Е2п. A0.5.22)
Эта запись эквивалентна четырем матричным равенствам
((«, и))[[и, н]| + ((н. v))[[v, «]] = — £„,
((н. н))[[«, «]]+((«, v))[[v. V}) = 0,
5
г>, v))\[v, и}} = 0,
((v, и))[[и, v
Первое, например, из этих равенств в развернутом виде предста-
представляется так:
2 {(«„ uk) [ик, иг] + («„ г;,) К, «,!} = - Ьзг. A0.5.24)
10.6. Теорема Пуассона
Рассмотрим функцию ср от 2/г переменных q и р и явно входящего
и ее выражение времени z1. Полная производная ср по t, составленная
в силу канонических уравнений движения Гамильтона B.10), равна
• ду . V / <ty дН д^р дН \
9 + ^
или, вспомнив определение скобок Пуассона,
<?=-§- + (?. «)• (Ю.6.1)
Поэтому, если
<Р = <?(?!/>; 0 A0.6.2)
представляет интеграл уравнений движения т. е. ср сохраняет при
движении постоянное значение с, то
|?- + (ср, Н) = 0. A0.6.3)
Это равенство удовлетворяется при всех значениях входящих в него
аргументов qs, ps, tt т. е. является тождеством.
Ю.6] ТЕОРЕМА ПУАССОНА 517
Основываясь на тождестве Якоби и на соотношении E.12), легко
доказать теорему Пуассона: если
^(q\p\t) и o2(q\p;t) A0.6.4)
— два интеграла канонических уравнений, то скобки Пуассона
Ф = (?1. Ъ) A0.6.5)
сохраняют при движении системы постоянное значение с.
Действительно, по условию теоремы, согласно C), имеем тождества
^L+(?I,//) = 0, -§*- + (%,//) = 0 (Ю.6.6)
и надо проверить, что
Это соотношение по E.12) и F) приводится к тождеству Якоби
— ((?1, Я), ?2) —(?1, (%, Я)) + ((ср1, ср2), Я) =
= (ср2, (ср1} Я)) + (?1, (Я, %)) + (//, (<р2, ср,)) = О,
что и требовалось доказать.
Величина ф или представляет новый интеграл канонических урав-
уравнений, или не дает такового, так как она может оказаться функцией
ранее известных интегралов, в частности интегралов D)
Ф = Ф(?1.«Р2) = Ф(с1.с2). (Ю.6.7)
или же тождественно обращается в постоянную, которая может быть
и нулем.
Рассмотрим случай Я, не содержащего t явно. Тогда имеется
интеграл энергии B.15), комбинируя который с интегралом B) полу-
получим на основании теоремы Пуассона
где а постоянно; воспользовавшись теперь равенством C), найдем
новый интеграл
% = -а. A0.6.8)
Продолжив это рассуждение, получим интеграл
dt2 —a\
и т. д. Если же ср = с — интеграл, не содержащий t явно, то выра-
выражение (И, ср), которое, согласно C), тождественно обращается в нуль,
не дает нового интеграла.
518
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
Отметим также, что, комбинируя интегралы C.4), соответствующие
циклическим координатам, с каким-либо из интегралов системы C.5)
?(?> я*, Рх Рт. Pm+1. .... Р„; Ъ = с. (Ю.6.9)
приходим к не дающему нового интеграла тождеству
(<?. Рт+г) = -гр-^0- A0.6.10)
Теореме Пуассона в классических «Лекциях по динамике» *) Якоби
посвящена тридцать четвертая лекция. По словам Якоби, «это одна из
замечательнейших теорем всего интегрального исчисления, а в частном
случае, когда положено Н= Г-f-Il, это есть основная теорема анали-
аналитической механики». Чтобы, комбинируя некоторый интеграл с ранее
известным, получать новый интеграл, надо, указывает Якоби, чтобы
«он был интегралом, специально принадлежащим рассматриваемой
частной задаче. Но первые интегралы, которые отыскивались для
какой-нибудь предложенной задачи, были, как правило, те, которые
следовали из общих принципов (например, из принципа сохранения
площадей); поэтому они не принадлежали специально именно к рас-
рассматриваемой задаче и нельзя требовать, чтобы из них должны были
выводиться все первые интегралы».
10.7. Канонические преобразования
Рассматриваются две системы переменных: переменные
qv ..., qn; pv ..., рп, A0.7.1)
называемые старыми, и переменные
Q,. .-.,<?„;/>, р„. ■ (Ю.7.2)
называемые новыми; они рассматриваются как функции старых пере-
переменных и времени t\
//,; Pi Р/
/»; Pv •••• P*
(s== 1, ....
A0.7.3)
причем предполагается, что эти соотношения разрешимы относительно
старых переменных
= qk(Q\P;t),
pb(Q\P; t)
=l,...,n). A0.7.4)
*) Имеется русский перевод: К. И к о б и, Лекции но динамике, ОНТИ, 1936.
10.7] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 519
Преобразование C) называется каноническим, если соблюдено
условие: выражение
Ър*ЬЧь-ЪР№1 (Ю.7.5)
является вариацией некоторой функции старых и новых пере-
переменных и времени t. Последнее при варьировании считается фикси-
фиксированным, так что, варьируя, например, первую группу соотноше-
соотношений D), имеем
и выражение E) может быть представлено в виде
Преобразование будет каноническим, если соблюдены три системы
соотношений: во-первых, производная по Qt коэффициента при 6Qi
в выражении G) должна быть равна производной по Q,- коэффициента
при bQ}
V№ %JLn d2qb \ dPi - V ( dP* 6qk 1 n ^ °P
*U \dQi dQ- "^ ^ dQz dQ/ / dQz ~~ ^ VdQ/ dQ, "^ Pk dQt dQt
k\ A 1
Во-вторых, должны быть равны производные по Pf и Pt коэффициен-
коэффициентов при оР. и оР}
А ^ \ _ V d d д2
э, дР, ' dPtdPj Fk!~ J*d\dP, дР, т ИкдР,д1
и, в-третьих, требуется равенство производных по Я; и Qt коэффи-
коэффициентов при oQt и oPj
^w \ дР, oQ, ' ^^ dPfdQj) дР/ dmd \ 6Qf дР/ Pk dQiOP/ I '
Теперь, учитывая, что новые переменные Pt, Qt независимы, т. е
dQj = Oj 1PJ = °«f
и вспоминая определение скобок Лагранжа E.13), приходим к равен-
равенствам
520 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
при соблюдении которых преобразование C) будет каноническим.
Эти условия являются необходимыми и достаточными. Свойство пре-
преобразования быть каноническим обратимо: если преобразование C)
каноническое, то и обратное D) — также каноническое. Это следует
из того, что в условие E) старые и новые переменные входят вполне
равноправно.
В новых переменных Qt, Pt равенства E.14) для фундаментальных
скобок Лагранжа могут быть представлены в виде
Таким образом, вместо (8) можно записать соотношения
выражающие инвариантность фундаментальных скобок Лагранжа при
каноническом преобразовании.
Матрица Лагранжа Л системы функций Qs, Ps от старых пере-
переменных в соответствии с (8) записывается в виде
-Еп 0
A0.7.11)
где 0 обозначает нуль п X я матрицу. По E.22) теперь легко заклю-
заключить, что такую же структуру A1) имеет и матрица Пуассона, т. е.
наряду с (8) имеют место равенства
(Q/tQ,) = 0, (Я,, Я,) = 0, {QltPl) = bil (/, /= 1, . . ., п). A0.7.12)
Они представляют другую запись необходимых и достаточных усло-
условий каноничности преобразования C). Фундаментальные скобки Пуас-
Пуассона E.7) также являются инвариантами канонического преобразования.
Более общий характер имеет следующее предложение: функции ut v
рассматриваются сначала как зависящие от старых переменных,
потом — от новых, связанных со старыми каноническим преобразова-
преобразованием. Тогда
(и, v)qp = (u% v)Qp. A0.7.13)
Это проверяется непосредственным вычислением. Действительно, выра-
выразив в скобках Пуассона
п
да ди ди dv \
>ЧР £Uqhdpk dpkdqk
10.8] производящие функции 521
частные производные по старым координатам через частные производ-
производные по новым с помощью формул вида
после подстановки и суммирования по к придем к равенству
которое в случае канонического преобразования, т. е. при соблюдении
условий A2), дает
V V / ди ду ди dv \ *
п
ди dv да dv
г=1
как и требовалось. Аналогично доказывается инвариантность относи-
относительно канонического преобразования скобок Лагранжа
A0.7.15)
10.8. Производящие функции
Возвращаемся к определению канонического преобразования. Функ-
Функция, вариация которой дается выражением G.5), называемая
далее производящей, может зависеть от всех An аргументов qs, ps,
Qs, Ps и, кроме того, от t. Но, поскольку имеются соотношения G.3)
и G.4), достаточно считать ее зависящей от 2/г аргументов и вре-
времени t\ при этом п аргументов должно быть старых и п новых.
Таким образом, приходим к рассмотрению четырех типов произво-
производящих функций:
Vi(?.Q;0. V2{q,P;t). Vz{p,Q;t)t V4(p, Я; t). A0.8.1)
522
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
В соответствии с выбором производящей функции условие канонич-
каноничности преобразования G.5) предпочтительно записать в одном из
четырех видов:
п.
2 (Л Ч — Р, Щ) = 8V, (q, Q; t).
2
Г п I
L '=i J
Q; 0-'
= 8К4(р.
A0 8.2)
. p-t), <ю.8.з)
Q; 0. A0.8.4)
A0.8.5)
Отсюда получаем такие системы канонических преобразований, осуще-
осуществляемых производящими функциями каждого из типов:
дУ2
dqt
dp,
и, наконец,
1 i
Q,=
Q,=
dV2
dPi
dV3
dQ,
dP,
(/=1..
(/=1..
(/=1..
... n).
... я).
... n)
A0
A0
A0
.8
.8
.8
•6)
•7)
.8)
(/=1.
n). A0.8.9)
Рассмотрим, например, преобразование (б). Задавшись функцией
M?i> •••* Я» Pi Рп> «
и составив формулы F), следует для построения выражений G.3)
новых переменных через старые разрешить первую группу уравне-
уравнений F) относительно Qt. Это возможно при неравенстве нулю якобиана
dqn
'" dQndqn
Ф0.
A0.8.10)
Таково требование, налагаемое на производящую функцию V^ Выра-
Выражения новых переменных Qs через старые qh pt, найденные из первой
группы уравнений F), должны быть подставлены во вторую группу
этих уравнений. Это даст вторую группу равенств G.3), определяю-
определяющую Ps через старые переменные.
10.8]
ПРОИЗВОДЯЩИЕ ФУНКЦИИ
523
Аналогично записываются условия, которым должен быть подчинен
выбор остальных производящих функций. Например,
д2У2
д*У2
"' dPxdqn
dPndqn
A0.8.11)
а процедура построения формул преобразования G.3) сводится к опре-
определению новых переменных Ps из первой группы уравнений G) и
подстановке этих значений во вторую группу этих уравнений.
Соотношения, связывающие производящие функции, указаны в фор-
формулах B) — E). В дальнейшем чаще других будет рассматриваться
функция Vo. Выражение через нее остальных производящих функций
имеет вид
Vx(q,Q; 9 =
A0.8.12)
Q; t) = V2(q, P; t) —
/=1
;t) = V2(q,P; t)
(Ю.8.13)
A0.8.14)
Отметим, что если V2(q, P\ t) рассматривать как производящую функ-
функцию преобразования Лежандра от q и Р к р и Q, то —Уг будет
производящей функцией обратного преобразования от р и Q к q и Р.
Для частичных преобразований только одной группы переменных
в другую — от q к р и соответственно от Р к Q, осуществляемых
производящей функцией V2, функциями, определяющими обратные
преобразования, являются —V4 и —Vv
Из соотношений F) — (9) следует система равенств
д/ 0Qs
_ dpi _
dpi dQs
dQs
dP±
dqt •
dPs
dqtdPs
dp± \
dp, dPs
db__dQs
'dP.
dpi '
A0.8.15)
A0.8.16)
Используя эти равенства, вычислим якобиан канонического преобразо-
преобразования *)
i,..., (?Я;-Р| Pn\=D(Q\P\
*) С Caratheodory, Variationsrechnung und partielle Differentiat-
gleichungen erster Ordnung, Bd. I, Leipzig, 1956, p. 92.
524 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
По известному свойству якобианов можно написать
q\p
\
q\Q)' D(q\
[ГЛ. 10
A0.8.17)
С другой стороны,
D
Q\P
0qx "' dqn
dQn " dQn
dqx '" dqn
дРх дРх
\ 1 ... О
О ... 1
о ... о
дРп дРп
dq{ "' dqn
Точно так же получаем
Я\Р\_
О ... О
_Р>
Чп
tY
Q
i Рп\
u.... Qn)'
и первое соотношение A5) дает
Из A7) следует теперь, что искомый якобиан преобразования
(Q, P)->(q, p) равен единице. Но известно, что произведение якобиа-
якобианов прямого и обратного преобразований также равно единице. Итак,
= 1. A0.8.19)
Ч\Р
Следствием этого предложения является теорема Лиувилля об инва-
инвариантности выражения интеграла
J ... fdqx ...dqndPl ...dpn
In
но некоторому объему v пространства канонических переменных (q, p)
(фазового пространства) относительно канонического преобразования
этих переменных (q, p)->(Q, P). При любом преобразовании
J ... j dql...dqndp1... dpn =
. . . dQndPx . . . dPh.
10.9] ИНВАРИАНТНОСТЬ КАНОНИЧЕСКИХ ПЕРЕМЕННЫХ 525
где интегрирование справа производится по объему 1/, в который
переходит при этом преобразовании v. Для канонического преобразо-
преобразования по A9)
f ... fdqt... dqndPl ...dpn = f... fdQt . . . dQndP, . . . dPn.
In 2n
A0.8.20)
10.9. Инвариантность канонических переменных
Напомним, что переменные, удовлетворяющие системе канониче-
канонических уравнений, — обобщенные координаты qs и обобщенные импульсы
ps — называются каноническими переменными. Важное значение кано-
канонических преобразований в аналитической механике определяется сле-
следующей теоремой: переменные Qs, Ps, связанные с каноническими
переменными qs, ps каноническим преобразованием, являются
каноническими, т. е. удовлетворяют системе канонических уравнений
Гамильтона
Здесь К — функция Гамильтона, зависящая от новых канонических
переменных Qs и Ps и времени t,— выражается через функцию Гамиль-
Гамильтона Н для старых переменных соотношением
К = Н + -^-, A0.9.2)
где Vt — производящая функция рассматриваемого канонического
преобразования. В частности, если последняя явно от t не зависит,
то
К = Н. A0.9.3)
Рассмотрим преобразование с производящей функцией Vx(q, Q; t).
Переменные qsi Qs, t в ней рассматриваются как независимые, и, при-
применяя это преобразование, следует считать
dQs =0. A0.9.4)
dt
Вместе с тем из второй группы формул (8.6) имеем
dPs
Г
dtdQs
Будем теперь рассматривать Qs, Ps как функции времени и старых
канонических переменных, определяемые уравнениями (8.6), Тогда,
526
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
основываясь на соотношениях F.1), D) и E), можно записать
равенства
A0.9.6)
4S — \4S. "Jgp. < S~ dQsdt
которые вследствие инвариантности скобок Пуассона при канониче-
канонических преобразованиях, выражаемой соотношениями G.13), а также
при использовании свойств E.5) скобок Пуассона, могут быть запи-
записаны в виде
dH
dPs>
dQs dt
. h)qp = - -^(^-
A0.9.7)
Остается отметить, что, поскольку Vx не зависит от Ps,
dPs = dPs \ dt ■
Итак, обозначая
dV{
приходим к системе канонических уравнений A)
dK
dPs>
р ~—
dQs
(s=l /г),
что и требовалось. Ничего не изменилось бы в этих рассуждениях
при использовании производящей функции V3.
В случае производящей функции V2 (то же рассмотрение приме-
применяется для V4) вместо D) и E) надо принять
Qvs _ v у2 ors п
dt dPsdt' dt ~~ '
вследствие чего вместо F) и G) получим
так как Qs не входит в выражение V2{q,P\ t). Полагая
приходим к каноническим уравнениям A).
Итак, доказано, что канонические уравнения сохраняются при
канонических преобразованиях переменных.
10.101
ПРИМЕРЫ КАНОНИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
527
10.10. Примеры канонических преобразований
Г. Для функции старых координат и новых импульсов (не содер-
содержащей t)
п
V2(qtP) = ^iPsfs(ql qn) A0.10.1)
условие (8.11) принимает вид
dfi
dfn Ofn
dqx • "' dqn
Ф0.
A0.10.2)
Если оно соблюдено, то Vt можно принять за производящую
функцию канонического преобразования, причем вторая группа
равенств (8.7)
Qs = JW*- = fs(qlt . .., qn) E=1, .... п) A0.10.3)
определяет точечное преобразование обобщенных координат. Выра-
Выражения новых импульсов Ps через старые обобщенные координаты и
импульсы, согласно первой группе упомянутых равенств, получаются
из рассмотрения системы линейных уравнений
5=1
%*- (/=.1 я).
A0.10.4)
которая имеет решение, так как ее определитель B) отличен от нуля.
Будем, например, рассматривать движение материальной точки
в поле центральной силы с помощью цилиндрических координат z,
г, X. Кинетическая и потенциальная энергии равны
± П =
и выражение функции Гамильтона будет
Чтобы осуществить переход к сферическим координатам, надо рас-
рассмотреть функцию
V2 - Рх
2 arctg 7
A0.10.6)
528 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
которая может быть принята за производящую функцию канониче-
канонического преобразования, так как условие B) выполняется. Получаем
по C)
YWP ^ = fti q3 = X, A0.10.7)
где /?, ft, X—сферические координаты. По формулам D) находим
теперь
и выражение функции Гамильтона в новых переменных получим пу-
путем подстановки в E) этих выражений
где pRi рь, рх—новые импульсы, соответствующие сферическим
координатам G). Это значение Н приводилось в примере 1° п. 10.4.
2°. Рассмотрим преобразование
Q, = ?,. ps = Ps—$j;- A0Л0-9)
в котором F—функция от qv . . ., qn и t. Чтобы проверить, является ли
оно каноническим, составим выражения скобок Пуассона G.12).
Имеем
(р рЛ—\(дЕл-дРг__дР8 дР/
dqk dpk dPk dqk
qr ) ~ dqr
5 g
dqk dqs '» ~f" ** dqk dqr ) ~ dqr dqs ^ dqs dqr
ft = l
Точно так же
«?„ Qr) = (qs, qr) = 0
и, наконец,
= 0.
qk dpk dpk dpJ — Zi °**°r* — °sr
Преобразование — каноническое. За производящую функцию можно
принять
1 я п. о- (io.io.io)
10.11] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 529
10.11. Канонические уравнения относительного движения
Кинетическая энергия системы представляется согласно D.9.1),
D.9.5) и D.9.6) в виде
П I
Т— it Mi>l -\- -у to • 0° • to -|- М (v0 X w) * г'с ~Ь ^l^o' ^j "л— Qs ~~l~
5=1
где /"[.(#!, ..., ^w)—вектор-радиус точек по отношению к полюсу О
системы координат, связанной с несущим телом, движение которого,
определяемое скоростью полюса v0 и вектором угловой скорости со,
предполагается заданным; г'с обозначает вектор-радиус центра инер-
инерции системы с началом в О. Через Тг обозначена кинетическая энер-
энергия относительного движения, являющаяся квадратичной формой
обобщенных скоростей.
Выражения импульсов имеют вид
A0Л1-2)
и функция Гамильтона по B.13) равна
H=Tr + U-T0=: Г + П —lfD-00. to + М(ь>Х^)'ГгсA0Л\.г)
так как слагаемое -^ Mv\, входящее в Г, зависящее лишь от вре-
времени, можно отбросить. Величина Т'г представляет результат замены
в выражении Тг обобщенных скоростей импульсами. Обозначая через
В = А~] матрицу, обратную матрице А коэффициентов квадратич-
квадратичной формы Тг, имеем по B)
S=\ k=1
Здесь введены величины
^=ps--^-MvQ-r'c (s=\ a). A0.11.5)
34 Зак. 2072. А. И. Лурье
530 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Если принять еще
Qs = Qs E=1. ...> п\ A0.11.6)
то преобразование, связывающее новые переменные Ps, Qs со ста-
старыми ps, qs, будет каноническим вида A0.9), причем
y'c-±.v^z'cy A0.11.7)
Производная F по явно входящей букве t равна
-^- = N1 [v01xc-+-v02yc + %гс) = Mv0 -rc, A0.11.8)
и функция Гамильтона К для системы канонических переменных по
(9.2) и C) оказывается равной
где с соответствии с обозначениями (9.2.10) и (9.2.9) через 11Ш и Иа
обозначены потенциальные энергии центробежных сил и сил инерции
поступательного движения. Величина Т'г определяется формулой D).
Система канонических уравнений относительного движения
теперь записывается в виде
qs = ~, Ps = —^- E=1,..., п), A0.11.10)
причем приняты прежние обозначения обобщенных координат.
Действие центробежных сил и сил инерции поступательного дви-
движения учтено внесением слагаемых 11* и П° в выражение потенциаль-
потенциальной энергии. Кориолисовы силы и вращательные силы инерции, не
являющиеся потенциальными, автоматически учитываются введением
новых импульсов Ps. Было бы ошибочно отожествлять их с импуль-
импульсами в относительном движении
Союзное выражение кинетической энергии через эти величины пред-
представляется квадратичной формой
s=l k
и сравнение с D) дает
=\...., л), (io.ii.i3)
10.11] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 531
так что
/ = 1
Здесь использованы формулы дифференцирования вида
Замечая, что
можем переписать A4), вспомнив (9.2.14), в форме
)- A0Л115)
Правые части второй группы канонических уравнений A0) имеют
вид:
дК dfr dll dTV° дП°
причем при вычислении производной от величины Тг, даваемой фор-
формулой D), надо учесть зависимость от qs как через посредство коэф-
коэффициентов Bsk, так и через посредство величин
N /
так что по D), A3) и первой группе уравнений A0)
Атг л п п.
4^ 1 у
4^ = 1 у У^
dqs 2 jU Zi dq
i i k \
АТ''
П N
532 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
причем первое слагаемое представляет производную от определяемой
по формуле A2) величины Т'г, когда при вычислении этой произ-
производной предполагается независимость относительных импульсов от
обобщенных координат.
Теперь вторая группа уравнений A0), если вспомнить обозначения
п. 9.2, приобретает вид
ИЛИ
A0.11.13)
а первая по A2) представляется равенствами
дт'
<1 ) Ю1119)
Систему уравнений A8), A9) можно было бы составить, основы-
основываясь на уравнениях движения B.4) и B.7) и рассматривая лишь
относительное движение с учетом сил инерции, определяемых дви-
движением системы отсчета Oxyz.
Система уравнений A0), полученная путем канонического преобра-
преобразования канонических уравнений абсолютного движения, представляет
промежуточную запись между последними и уравнениями относитель-
относительного движения A8), A9). В ней, благодаря внесению слагаемых IIй*
и 11° в выражение функции Гамильтона, учтены силы инерции потен-
потенциального характера, а остальные силы инерции явно не выделены,
что позволило сохранить гамильтонову форму этих уравнений.
10.12. Каноническое преобразование и процесс движения
Предполагается, что известно общее решение системы канониче-
канонических уравнений
Ч*=-§£- Р° = ~1Щ; <S=l П)- A0Л2Л)
Это решение дает выражения обобщенных координат и импульсов
как функций времени и 2и произвольных постоянных, обозначаемых
Ч и h-
| ш 122)
10.12] КАНОНИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ И ПРОЦЕСС ДВИЖЕНИЯ 533
Система этих уравнений должна быть разрешимой относительно по-
постоянных ak, $k; иными словами, требуется, чтобы был отличен от
нуля якобиан
D (?ь .... Яп\ Ри ...,Рп) ф 0> A0.12.3)
В противном случае решение B) не было бы общим, так как не все
постоянные были бы независимы между собой.
Решение системы уравнений B) относительно постоянных ak и §k
запишем в виде
3.12.4)
Будучи постоянными, эти выражения представляют все 2м интегра-
интегралов канонической системы уравнений A). Поэтому, согласно теореме
Пуассона, любая из скобок Пуассона
К. «*). К- Р*). (Р,. Ра) A0.12.5)
или постоянна, в частности, тождественно обращается в нуль, или
выражается через те же постоянные а/} pj. В противном случае
в числе скобок E) содержался бы Bм-f- 1)-й независимый интеграл,
что невозможно.
Теперь предположим, что нами взята не любая система 2м неза-
независимых интегралов канонической системы уравнений A), а ее пол-
полный интеграл Коши. Это значит, что постоянные as и Р5 определены
как значения обобщенных координат и импульсов в некоторый мо-
момент времени t = t0:
Тогда, вспомнив определение скобок Лагранжа E.13), получим, на-
например,
п
ra q 1 _ V / дЯг дРг dqr дрг
и, значит,
п п
r=l S ' г=1
Таким же образом найдем
[а,, алЬ t =0, [pjt рл] =0.
534 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Из этих равенств тотчас же, основываясь на соотношении E.22)
или, что то же самое, на формулах вида E.24), получим такие же
выражения скобок Пуассона
Но, как выше отмечалось, все скобки Пуассона E) сохраняют посто-
постоянные значения, так что полученные соотношения должны иметь место
при любом t. Итак,
К. P*) = 8s*. («s> a*) = 0. (Ps. Рл) = 0, A0.12.6)
и выполнение этих равенств показывает, что соотношения B), пред-
представляющие интеграл Коши канонических уравнений, являются фор-
формулами канонического преобразования переменных ak, §k в qs, ps.
Обратное преобразование D) также каноническое.
Движение голономной системы, на основании сказанного, является
каноническим преобразованием значений обобщенных координат и
импульсов в некоторый момент времени t = t0 в их значения в те-
текущий момент t. В этом смысле говорят, что движение есть посте-
пенно разворачивающееся каноническое преобразование.
Естественно, что большой интерес представляет вопрос, какой
■смысл можно приписать производящей функции рассмотренного кано-
канонического преобразования. Мы вернемся к нему в п. 12.8.
В заключение приведем два иллюстративных примера.
1°. Система уравнений
представляет интеграл Коши системы канонических уравнений с функ-
функцией Гамильтона
± A0.12.8)
Это — свободное колебание простейшего вибратора (грузика на пру-
пружине). Вычислением скобок Лагранжа проверим, что уравнения G)
представляют каноническое преобразование. Имеем
что и требовалось, так как для системы с одной степенью свободы
остальные скобки Лагранжа отпадают.
10.131 теорема якоби 535
2\ В задаче о параболическом движении тяжелой точки (единич-
(единичной массы) в пустоте выражения координат х, у и импульсов х, у
имеют вид
o) g( oy, | A0129)
X = Хо, y = yQ — g(t — tQ). )
Эти равенства представляют интеграл Коши системы канонических
уравнений с функцией Гамильтона
Я=4(^2+У2) + £У. A0.12.10)
Проверим, что преобразование (9) — каноническое. Надо найти,
как видно из таблицы, аналогичной E.18), всего -^-(^п2— 2/г) = 6
скобок Лагранжа
1*0' Уо1 1*0' *<I 1*0' 3\)Ь
и простое вычисление обнаруживает, что все условия G.8) выполнены.
Например,
\у ti 1 — -^£. _?£. _^£- J*~ -j- _^Z_ _^i. _ Al- AL — о
l*o» Уо\— дХо дуо дуо дХо i- dXQ дуо дуо дХо — и
и т. д.
10.13. Теорема Якоби
В п. 10.9 было доказано, что при каноническом преобразовании
Qs = Q*(9\P: t), Ps = Ps(q\p; t) (s=l я) A0.13.1)
новые переменные Qs, Ps удовлетворяют системе уравнений Гамильтона
^ = Ж' Р^~Ж (s=1 п)' AОЛЗ-2>
образованной функцией Гамильтона
^. A0.13.3)
Здесь //—функция Гамильтона для исходных канонических пере-
переменных
дН дН t. 1 ч /1А1о/1\
536 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
а V — производящая функция преобразования. Конечно, К должно
быть выражено через новые канонические переменные Qs, Ps.
Таким образом, задаваясь производящей функцией V, мы сводим
задачу интегрирования исходной системы уравнений движения D)
к новой задаче B), которая может оказаться более простой, чем
лервая. Естественно, возникает вопрос о таком выборе производящей
функции V, которому соответствует значение К, равное нулю (или,
что безразлично, постоянной). Тогда, согласно B), Qs и Ps будут
иметь постоянные значения
Qs = as, Ps=$s (s=\, ..., п). A0.13.5)
Поэтому, если выбрать в качестве производящей функцию типа V2,
зависящую от старых координат qs и новых импульсов V2(q, P; О,
то ее определение, согласно C), сведется к задаче разыскания решения
уравнения в частных производных — уравнения Якоби — Гамильтона
4г+«(« »•■■& £;<)=<>■ <«>•■>••>
в котором pj, в соответствии с формулами преобразования (8.7),
заменены частными производными искомой функции V по обобщенным
координатам
Рн = -Т~ (А=1. .... я). A0.13.7)
Речь идет о таком решении уравнения F), которое содержит п по-
постоянных pj рл, т. е. о полном интеграле уравнения Якоби —
Гамильтона F). Он должен удовлетворять еще условию (8.11), ко-
которое в принятых теперь обозначениях имеет вид
д2У д2У
Ф0. A0.13.8)
В частности, если хотя бы одна из п постоянных входит в V адди-
аддитивно, т. е. если.
V = V(qv ..., qn\ Pj, ..., рл_!*, О + Ря.
то якобиан (8) будет нулем и такое решение не будет требуемым
полным интегралом.
Зная полный интеграл уравнения Якоби — Гамильтона, по (8.7)
приходим к системе равенств
|£ = ал, ^~;=Pk (k=l *)• (Ю.13.9)
Первая из этих систем уравнений разрешима, согласно (8), относительно
qv . .., qn\ она дает их выражения через t w 2п постоянных о^, р^;
10.13] теорема якоби 537
подставив эти значения координат во вторую систему, найдем
импульсы как функции тех же величин t, a5, р5:
) п01310)
( }
Это — общий интеграл канонической системы уравнений D), так как
он содержит 2/1 независимых постоянных.
Приходим к теореме Якоби: задача разыскания общего инте-
интеграла канонической системы уравнений D) эквивалентна задаче
построения полного интеграла уравнения в частных производных
Гамильтона — Якоби F), т. е. решения его, содержащего
п произвольных постоянных и удовлетворяющего условию необра-
необращения в нуль якобиана (8). Зная этот полный интеграл, нахо-
находим общий интеграл канонической системы, решив составляемую
по нему систему конечных уравнений (9).
Отметим, что получаемый с помощью теоремы Якоби общий ин-
интеграл канонической системы в форме A0) представляет каноническое
преобразование переменных ak, $k в переменные qs, ps, производимое
с помощью производящей функции V. Всякий другой общий интеграл
ее вида
qs = qs(t\ Cv . .., Сп; Dv ..., Dn), 1
pa=p3(t. С,. .... Cn; D]t ..., Dn) (,= !..... я). J A0ЛЗЛ1>
где Ck и Dk — произвольные постоянные, не имеет этого свойства,
и его знание не позволяет непосредственно составить полный инте-
интеграл уравнения Якоби — Гамильтона, так как соотношения A1) не
представляют, вообще говоря, канонического преобразования. Исклю-
Исключением, согласно доказанной в п. 10.12 теореме, является случай»
когда Ck и Dk равны начальным значениям координат и импульсов.
Задачи построения полного интеграла уравнения Гамильтона —
Якоби и общего интеграла канонической системы, как доказывается
в теории дифференциальных уравнений, математически эквивалентны.
Степень трудности их, вообще говоря, одинакова. Однако может
быть отмечен ряд частных случаев, когда уравнение Гамильтона —
Якоби может оказаться более податливым, чем каноническая система.
Об этом говорится в п. 10.14. Более важно то обстоятельство, что
решение A0), получаемое с помощью теоремы Якоби, является кано-
каноническим преобразованием, а это, как мы увидим в главе 11, зна-
значительно упрощает форму уравнений возмущенного движения.
Особо следует остановиться на случае существования интеграла
энергии, когда t явно не входит в выражение функции Гамильтона.
Тогда можно удовлетворить уравнению F) Гамильтона—Якоби, полагая
V = — ht-\-W(ql9 ..., qn)9 A0.13.12),
538
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
причем подстановка этого выражения в F) приводит к уравнению
в частных производных Гамильтона — Якоби для функции W, имею-
имеющему вид
dW\
я„'>
dW
A0.13.13)
Оно составляется путем замены в записи интеграла энергии И = h
импульсов частными производными искомой функции W по соответ-
соответствующим координатам.
Теперь задача сведена к разысканию полного интеграла урав-
уравнения A3), содержащего, кроме /г, еще п — 1 постоянных
W = W(qx qn; p, ря.„ К) A0.13.14)
и удовлетворяющего условию
d2W d2W
dfo dq{
d'2W
dfa dqn
фО.
A0.13,15)
dh dq] '" dh dqn \
Зная его, составляем уравнения (9). Они принимают вид
-~- = аь (£=1, .... я—1), A0.13.16)
0W А л
dh
oqk
n).
A0.13.17)
A0.13.18)
Постоянные h и tQ играют роль [jn и ап.
Уравнения A6) представляют п—1 не содержащих t зависимо-
зависимостей между обобщенными координатами qx, ..., qn. Они дают сово-
совокупность всех траекторий в /г-мерном пространстве этих перемен-
переменных, зависящую от 2п—1 постоянных. Возможность непосред-
непосредственного нахождения траекторий, минуя обычный процесс исклю-
исключения t из уравнений движения, является замечательной особенностью
метода Якоби,
Легко видеть, что по крайней мере один минор, соответствующий
элементу последней строки якобиана A5), отличен от нуля— в про-
противном случае неравенство A5) не имело бы места. Можно принять
d2W
10.13] ТЕОРЕМА ЯКОБИ 539
Тогда из уравнений A6) найдем параметрическое представление траек-
траекторий
я8 = я*(Яп> «1 «л-i; Pi Рл-i. л) (io.i3.i9)
E=1, ..., П— 1),
где qn играет роль параметра. При подстановке этих выражений
в левую часть уравнения A7) в последней останется лишь коорди-
координата qn\ решив относительно нее это уравнение и воспользовавшись
снова уравнениями A9), придем к уравнениям движения
gs = gs(t-t0; а,, ..., a^; р„ ..., рЛ_,. h) A0.13.20)
E=1, . . . , П).
Их можно получить, конечно, решая в какой-либо другой последо-
последовательности систему уравнений A6) и A7)—разрешимость ее следует
из условия A5). После подстановки выражений B0) в правые части
уравнений A8), получим
Рз = Рз(! — *о> alf ..., ал_1; р„ ..., $n_v h) A0.13.21)
E=1, .... я).
Соотношения B0) и B1) представляют каноническое преобразование
переменных $k, h, а.к> —10 к переменным qs, ps, определяемое про-
производящей функцией
V = -ht-\-W(qlt .... дп, р„ .... рл_„ К) A0.13.22)
типа V2 от координат qx qn и новых импульсов р,, . . ., Pw_ls /г.
Если координаты ^т+1, ..., ^7П—циклические, то уравнение
Гамильтона—Якоби A3) принимает вид
/У j,, ..., Jm, -3—, ..., ~s—, •••, -л—) — h> A0.13.23)
V1 Чт dqx dqm dqn ) y }
и его решение следует разыскивать в форме
^ qm). A0.13.24)
Подстановка в B3) приводит к уравнению Гамильтона — Якоби для
функции W*:
.)=*• A0ЛЗ-25)
Речь будет идти о разыскании полного интеграла этого уравнения,
содержащего, кроме п—т постоянных рш, ..., fyn-v /г, еще т—1
540
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
постоянных
якобиан
-i' причем отличным от нуля должен быть
d2W*
д$\ dqn
d2W*
d2W*
dh dqx
dh dqn
Ф0.
A0.13.26)
Выше в качестве производящей была выбрана функция вида V2.
Остановившись на функции типа Vv запишем, чтобы сохранить соот-
соответствие обозначений ak и фк координатам и импульсам, выражение
полного интеграла уравнения Гамильтона — Якоби F) в виде
A0.13.27)
У = У(Я\ Яп> ai *п> О-
Тогда по (8.6) получим вместо (9) систему уравнений
k (k=\. .... я), A0.13.28)
дУ
дУ
причем по (8.10) должно иметь место условие вида (8), в котором
буквы $k заменены на ak.
Для производящих функций типа Vz по E) получили бы
Тогда по (8.8)
дУ
l. ..., рп; ах а„; 0- (ЮЛ3.29)
\s = — ~ E=1, .... п), A0.13.30)
О(Х о
и уравнение Якоби — Гамильтона надо было бы рассматривать в виде
■^ + #(—4^-...., — 4^-, pv .... рп; Л = 0. A0.13.31)
dt ' \ dpx dpn ri r n i v y
Здесь через частные производные искомой производящей функции по
импульсам заменены входящие в функцию Гамильтона И обобщенные
координаты. Если речь идет о канонической системе, определяемой
функцией И произвольного вида, то нет основания предпочесть урав-
уравнение F) уравнению C1). Для канонической системы уравнений
динамики дело обстоит иначе, так как импульсы ps в функцию
Гамильтона Н входят вполне определенным образом (квадратично),
а координаты—как угодно. По этой причине производящая функция У3
(равно и V4) малопригодна для нашей цели, хотя могут быть и
исключения.
10.141 РАЗДЕЛИМОСТЬ ПЕРЕМЕННЫХ В УРАВНЕНИИ ЯКОВИ ГАМИЛЬТОНА 541
Возвращаясь к уравнению A4), зафиксируем в нем значения
постоянных pif ..., Рл_!, /г, тогда соотношение
W(q\ .... q\ pif .... p^j, Л) = Т> A0.13.32)
где 7 — переменный параметр, можно рассматривать как уравнение
семейства гиперповерхностей риманова многообразия Rn (индексы
поставлены сверху, так как здесь применяются обозначения тензорного
анализа). На поверхности -\ = const
■^■V=0. A0.13.33)
причем вариации lqs представляют контравариантные составляющие
бесконечно малого вектора перемещения Ьг по этой поверхности, так
что br = rsbqs, где rs—базисные векторы, и bqs = rs -%г. Теперь,
вспомнив равенства A8), можем записать C3) в виде
™-г*.Ъг = р/*.Ъг = Ь. A0.13.34)
Таким образом, вектор импульса (или скорости изображающей
точки)
v = psrs, A0.13.35)
ортогонален поверхности постоянного W и по A8) равен гра-
градиенту этой функции
p = gradW. A0.13.36)
Особенно наглядное значение это равенство приобретает при рассмо-
рассмотрении движения свободной материальной точки в потенциальном поле.
Тогда
p = mv = grad W. A0.13.37)
Траектории точки ортогональны поверхностям W = const.
10.14. Разделимость переменных в уравнении
Якоби — Гамильтона. Теорема Штеккеля
Полный интеграл уравнения Гамильтона — Якоби можно найти
в некоторых случаях для функции Гамильтона специального вида,
допускающего разделение переменных, т. е. представление полного
интеграла как суммы функций, зависящих каждая лишь от одной из
обобщенных координат.
Рассматривается случай стационарных связей. Тогда союзное
выражение кинетической энергии будет квадратичной формой обоб-
обобщенных импульсов. Предполагается, что эта форма содержит, лишь
квадраты импульсов, а попарные произведения их отсутствуют. Тогда
542 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
уравнение Гамильтона — Якоби A3.13) будет иметь вид
Речь идет о том, при какой структуре функций Ak и П это урав-
уравнение допускает полный интеграл вида
W = Wl(ql)-{-W2(q2)+ ... +Wn(qn) A0.14.2)
(содержащий необходимое число постоянных).
Начнем с рассмотрения некоторых примеров.
1°. Кеплерово движение. Предполагая известным, что тра-
траектория материальной точки в поле силы притяжения к неподвижному
центру—плоская кривая, будем определять положение точки в этой
плоскости полярными координатами г, ср. Тогда выражение функции
Гамильтона будет (для точки единичной массы)
Полный интеграл уравнения Гамильтона — Якоби
следует разыскивать, в соответствии с A3.24), в виде
^)9 A0.14.4)
где R(r) должно быть определено из дифференциального уравнения
A0.14.5)
Получаем
U^ = fi^cp ± / I/ 2h~\-- -Ц-rfr. A0.14.6)
Нижний предел не фиксируется, так как W определяется с точно-
точностью до аддитивно входящей постоянной. По A3.17) и A3.16) находим
уравнение траектории и уравнение времени:
A0.14.7)
10.14] РАЗДЕЛИМОСТЬ ПЕРЕМЕННЫХ В УРАВНЕНИИ ЯКОВИ — ГАМИЛЬТОНА 543
Верхний или нижний знак берется в зависимости от того, возра-
возрастает или убывает г в рассматриваемом интервале изменения t — tQ.
Указание знака перед радикалом в дальнейшем опускается; выбор
знака определяется в ходе исследования получаемых соотношений.
2е. Кеплерово движение в сферических коорди-
координатах. Вспоминая выражение функции Гамильтона, приведенное
в примере 1° п. 10.4, имеем (полагая ;п=\):
Разыскивая решение в виде B)
придем к равенству
4-
которому можно удовлетворить лишь в предположении, что лева>!
и правая части этого равенства постоянны. Обозначив эту постоян-
постоянную через рз, получим два соотношения:
и полный интеграл уравнения Якоби — Гамильтона будет
W =
Ч ^; О u dft»
A0.14/i)
Из него получаем: уравнения траектории
A0.14.1
и уравнение времени
dR
J V R R2
A0.14.11)
544 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
3°. Движение материальной точки при действии
ньютонова притяжения двух центров. Эта задача уже
рассматривалась в п. 7.7. Применим теперь метод Якоби. Пусть
притягивающие центры Ох и О2 расположены на оси Oz цилиндриче-
цилиндрической системы координат г, ср, z\ расстояние ОХО2 обозначается
через 2с. Положение движущейся материальной точки М в меридио-
меридиональной плоскости ср == const определим обобщенными координатами
qv q2, связываемыми с декартовыми координатами z, r в этой пло-
плоскости равенствами
причем l-^^^oo, —\^q2<C\. Кривые qx = const, q2 = const
будут софокусными эллипсами и гиперболами
^2 Г2 <у2 г2
л | ^ 1 _f _J[ 1
2 О2 ' 2/ О2 Л 2 О2 2/i 02>k
с фокусами в центрах притяжения z=±c. Поскольку сумма гг-\-г2
и разность гх — г2 расстояний точки от притягивающих центров зави-
зависят соответственно лишь от qx и q2 (так как сумма постоянна на
эллипсе #i = я\* а разность на гиперболе q2 = q% сами расстояния
будут связаны простыми соотношениями с ^ и q2. Действительно,
г, = c(ql+ q2), r2 = c(ql — q2).
Выражение потенциальной энергии будет иметь вид
Легко вычисляется также кинетическая энергия:
Функция Гамильтона получается равной
1—1 —— I _; 1 i_ 1 — — I
11 2с2 2 2 2 2 ^^ (п^ \\(\ а^\
Разыскивая полный интеграл уравнения Гамильтона — Якоби в виде
10.14] РАЗДЕЛИМОСТЬ ПЕРЕМЕННЫХ В УРАВНЕНИИ ЯКОБИ ГАМИЛЬТОНА 545
придем к уравнению
\2
- Ъс [(/1 4- /2) <7i 4- (/2 - /i) <721 =
из которого легко заключить, что переменные qx и q2 разделимы
Действительно, полагая
придем к соотношению
которому можно удовлетворить, приравнивая каждую его часть по-
постоянной —р. Получаем
Выражение W представляется теперь в виде
w = № + f V~^ ^~ + f V~FM -j^ • A0.11.13)
где
M +2c (А +ДН - PI - K-
Уравнения траекторий и уравнение времени будут иметь вид
й_в Г d<?i -р
J VFi (?.) J Vf* Ы °
A0.11.14)
35 3jk. 2072 А. И.
546
КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ
(ГЛ. 10
Необходимые и достаточные условия разделимости переменных,
т. е. представимости полного интеграла уравнения A) в форме B)
даются теоремой Штеккеля *).
Для сокращения записей обозначаем далее
р k = ~. A0.14.15)
Предположим, что
W — W (qx qn% pv . . ., ря«1, п)
есть полный интеграл уравнения A); тогда, подставив это выражение
в A), придем к тождеству, которое можно продифференцировать
по каждой из величин ^, ..., fyn-v h. Это дает систему уравнений
п
5>^Ж- = ° <*=! п-1).
.9=1
Jtmt лл * Oft
A0.14.16)
Р\
dh
Рп
dh
= Р\
линейных относительно As с определителем
до.
Р>~... Рп^
Рп
dqx
dqn
dhdqn
который по A3.15) отличен от нуля. Из нее находим
А. — -=^- (s=l, .... «),
A0.14.17)
A0.14.18)
где Д^—алгебраическое дополнение элемента п строки, 5 столбца
определителя A7). Подставив эти значения As в уравнение A), найдем
выражение II
п
^-/»V A0.14.19)
По предположению, полный интеграл уравнения A) должен иметь
вид B); поэтому в /5-й столбец определителя A7) может входить
лишь переменная qk> т. е. должны иметь место равенства
A0.14.20)
*) С. Char Пег, стр. 76—81 (см. сноску на стр. 302).
10.14] РАЗДЕЛИМОСТЬ ПЕРЕМЕННЫХ В УРАВНЕНИИ ЯКОБИ — ГАМИЛЬТОНА 547
причем п2 функций 95^ (<7$) произвольны; требуется лишь, чтобы был
отличен от нуля составленный по ним определитель A7)
<Рп (Я\) ... Ьп(Яп)
Д= . A0.14.21)
9п\(Я\) ... Чпп(Яп)
Следствием B) и A5) являются соотношения
С другой стороны, равенства B0) позволяют написать
Р\ = 2 РЛ* («Л + 2ht*nk (?*) + Цк (?*). (Ю.14.23)
5 = 1
где ^()фй П
—я произвольных функций. Получаем
/2-1
Dk)
07*) dqk.
A0.14.24)
это — полный интеграл, так как в него входит п постоянных, причем
определитель A3.15) не равен нулю. Он, согласно A7), лишь мно-
множителем, не равным нулю, отличается от определителя B1). Остается
отметить еще, что выражение II можно по A9) и B3) записать
в виде
Но по свойству определителя
откуда следует равенство
A0-14-25)
k=i
Приходим к теореме Штеккеля: задаваясь п(п-\-1) функциями
4sk (Як) и Фл (Яи)* можно построить уравнение Гамильтона — Якоби
вида A), в котором коэффициенты As и выражение П определяются
по формулам A8) и B5), причем kns представляют алгебраические
дополнения элементов последней строки определителя B1). Формула
35*
548
КАНОНИЧЕСКИЕ \ФЛВНЕНИЯ И ТЕОРЕМА ЯКОБИ
[ГЛ. 10
B4) представляет полный интеграл этого уравнения. Обратно: если
полный интеграл уравнения Гамильтона — Якоби A) представим суммой
B), то существуют п(п-\-\) функций ysk{qk) и tyk(qk), через которые
по упомянутым формулам A8) и B5) должны выражаться коэффи-
коэффициенты As и потенциальная энергия П в уравнении A), причем пол-,
ный интеграл последнего дается выражением B4).
Остается отметить, что система уравнений, дающих общий интег-
интеграл канонической системы уравнений для случая разделимых перемен-
переменных, имеет вид
(S— 1 П— 1),
dw
-1 t —
| A0.14.26)
J
Теорема Штеккеля полностью определяет класс уравнений Гамиль-
Гамильтона— Якоби вида A) с разделяющимися переменными. Однако, имея
заданное уравнение, можно лишь в простых случаях ответить на во-
вопрос, принадлежит ли оно к этому классу, так как трудность возни-
возникает при восстановлении функций ysk(qk) и tyk(qk) по заданным
выражениям As и П. Согласно A6) и B0), дело сводится к разыска-
разысканию такой системы коэффициентов ysk% чтобы при заданных As
удовлетворить системе уравнений
=0.
A0.14.27)
Эта задача может быть решена лишь при определенной структуре
функций As; множественность решений снижается требованием, чтобы
коэффициенты каждого столбца зависели лишь от переменной, соот-
соответствующей его номеру. В окончательной записи B4) решения W
различие в выборе функций ysk (qk) и фй (qk) изменяет лишь обозна-
обозначение постоянных $s.
10.141 РАЗДЕЛИМОСТЬ ПЕРЕМЕННЫХ В УРАВНЕНИИ ЯКОБИ — ГАМИЛЬТОНА 549
Как пример рассмотрим систему Лиувилля — динамическую
систему, кинетическая и потенциальная энергии которой задаются
выражениями *)
— ~2~ ^ sVis'Tst ~
где с и Ь — суммы вида
п п
с (о ^ Ь — / Ь
Функция Гамильтона будет иметь вид
я-ivi-L-
A0.14.28)
A0.14.29)
A0.14.30)
и матрица функций ysk, удовлетворяющая системе уравнений B7)
-III i i Ьп __г>
11L
может быть выбрана так:
ах — а2 0 ... 0
0 а2 — аъ ... 0
0 0 0 ... ап_{ —ап
ахЪх a2b2 аъЬг ... ал_,6/?_, а„6„
Остается подобрать строку функций tyk(qk) по условию B5). Получаем
Теперь в формуле B4) имеем
(* = и).
Чтобы упростить запись, положим
*) Определение систем Лиувилля, данное в п. 7.7 формулами G.7.13),
имеет менее общий характер.
550 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
так что при этих обозначениях постоянных
п-\
г = 1
причем теперь
п
2 К=0' A0.14.31)
Полный интеграл уравнения Якоби — Гамильтона запишется в виде
(отбрасываем штрих в обозначении коэффициентов $k)
W =
Вернемся к движению точки в поле притяжения двух центров.
При плоском движении эта задача принадлежит к классу Лиувилля,
причем
q\ - 1 • 1 - q\ •
г /i +/2 /2-— /1
Получаем
+ 2^ ^£__ ,
У 1 — ^2
где pi-(_p2 = O. Это лишь обозначением отличается от ранее полу-
полученного выражения.
В общем случае неплоского движения задача не включается в класс
систем Лиувилля. Система уравнений B7) теперь приобретает вид
921 (*1 -
Функции ср53 не могут зависеть от третьей координаты ср; поэтому
они постоянны. Полагаем ср13 = ср23 = — 1, ^=0. Тогда
10.151
КЕПЛЕРОВО ДВИЖЕНИЕ
551
и можно удовлетворить этим соотношениям, принимая, что каждая из
величин в скобках постоянна и эти постоянные противоположны по
знаку. Для s = \ и s = 2 полагаем соответственно
Ф0
?-о—
Матрица функций cp5fe (gfe) оказывается такой:
1 1
?
я\ —
9 2
— 1
— 1
о
Для функций tyk принимаем, как и ранее, значения
Я\
л 9 *
1 — qi
Выражение W по B4) будет
что при замене обозначений постоянных приводится к виду A3).
10.15. Кеплерово движение
Вернемся к задаче о движении материальной точки под действием
центральной силы ньютонова притяжения. В системе полярных коор-
координат г, ср, располагаемой в плоскости траектории с началом в центре
притяжения, решение дается формулами A4.7):
г
J
Vf(r)
= л, A0.15.1)
552 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
причем
/(г) = 2Л + ^—А. A0.15.2)
Импульсы определяются дифференцированием выражения A4.6) по
координатам
Pr = -r==±YJjr), P<f = r^ = $f. A0.15.3)
Функция /(г), входящая под знак корня, должна оставаться поло-
положительной. Отсюда следует, что квадратный трехчлен г2/ (г) может
иметь лишь вещественные корни rx, r2, так как в противном случае,
будучи отрицательным при достаточно малых г, он сохранил бы этот
знак при всех вещественных г. Полагая гг < г2, можно этот трех-
трехчлен записать в виае
r2f(r) = — 2h(r — rl)(r2 — r), A0.15.4)
причем
Г1 + г2 = -^, ,у2 = -А. (Ю.15.5)
При h > 0 знаки корней различны, а при h < 0 оба корня положи-
положительны. В последнем случае, рассмотрением которого мы ограни-
ограничимся, г в процессе движения будет, как это следует из D), не
меньше гх и не больше г2:
'1ОО2. A0.15.6)
Значениям гх и г2 расстояния г от притягивающего центра соот-
соответствуют точки, называемые перигеем и апогеем орбиты.
Пусть при ^ = 0
Тогда в течение некоторого промежутка времени @, tQ) радиус-век-
радиус-вектор г будет убывать от начального значения г0 до гх и первая фор-
формула A), в которой радикал должен быть взят с нижним знаком, дает
A0.15.7)
r)
t0—момент прохождения через перигей конечен, так как
знаменатель подынтегральной функции хотя и обращается в нуль, но
пропорционально Vr — /у
Отсчитывая t от момента tQt следует в упомянутой формуле при-
принять гг за нижний предел интеграла и перед радикалом взять знак
10.15] КЕПЛЕРОВО ДВИЖЕНИЕ 553
плюс, пока г, возрастая от значения rlt не достигнет значения г2
в апогее
dr . L Г dr
Vf(r) ° и ./ Yf(r) 1 °'
Начиная от момента tv имеем снова
Г dr , . Г dr . .
— / , =-t — Л и / - = to — t.t
J Yf(r) J Yf(r)
г, Ту
где t2 — новый момент прохождения перигея. Будет видно ниже, что
возвращение в перигей и апогей соответствует прохождению через
те же точки плоскости (ср приобретает приращение 2т:). Это значит,
что орбита — замкнутая, а движение — периодическое. Промежуток
времени
A0.15.8)
равен полупериоду движения на орбите.
Вычисление интегралов в формулах типа A) основывается на вве-
введении вместо г новой переменной w с помощью соотношения
70) 40) I 1
r^z-jcos2 у f r2 sin2 -g- = у (гг + r2) — у (г2 — гг) cos ку. A0.15.9)
Нетрудно проверить, что неравенства F) будут при этом удовлетво-
удовлетворены для вещественных w. Поэтому подстановка (9) применяется
с успехом во всех случаях, когда заранее известно, что иссле-
исследуемая величина заключена между двумя предельными значениями
(в нашем случае rlt /*2). В задаче Кеплера переменная w называется
эксцентрической аномалией. В перигее и апогее она прини-
принимает значения 0 и тс.
Запись равенства (9) упрощается, если для суммы и разности
г\ + Гс1 и Г2 — ri ввести обозначения
rl + r2 = 2a, r2 — rl = 2ae, A0.15.10)
причем, очевидно, 0< е < 1. Тогда получим
r = a(\ — ecosw). A0.15.11)
Равенства E) и A0) позволяют теперь значительно упростить запись
выражения D); находим
г2/ (г) = \iae2 sin2 w,
554 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
после чего соотношения A) приведутся к виду
f /dr =-^J- f(l—ecosw)dw = t — L, A0.15.12)
г, О
T W
<F=l/"li«(l— e2) f _^= = Кь=^2 С-л — . A0.15.13)
T r r v J r Yf(r) J 1-е cos w v '
T\ 0
Здесь учтено, что
W(l-e*). A0.15.14)
а а принято равным нулю, что соответствует отсчету угла ср (его
называют истинной аномалией) от направления из притягивающего
центра на перигей. Теперь по A2) и (8) находим
Т= 2™fJ , „=*L = J^L. A0.15.15)
Эти формулы для периода обращения Т и частоты п (называемой
также средним движением) служат выражением третьего закона Кеп-
Кеплера. Возвращаясь к A2), приходим к уравнению Кеплера
w — es\nw = n(t — to) = ^ A0.15.16)
служащему для определения эксцентрической аномалии в функции
времени. К его решению мы вернемся ниже. Величина С называется
средней аномалией.
Произведя интегрирование выражения A3), найдем формулу, свя-
связывающую истинную аномалию ср с эксцентрической w:
Из нее находим
лГ~% о sin 9 /ia ic ю\
= у I—e1T-x ~— (ЮЛ5Л8)
r 1 + e cos cp
е 4- cos ф .
-j-^- -*—, sin w = у I—eT-x
1 + e cos cp r 1 + e cos
и обратные формулы
cos w — e . i/z n sin w
\n Y I e2
1 — ecosw ' 1—e cos w
/ia ik ion
A0.15.19)
Теперь сразу видно, что орбитой служит эллипс с фокусом в при-
притягивающем центре, причем введенные выше постоянные awe пред-
представляют большую полуось и эксцентриситет этого эллипса. В самом
10.15]
КЕПЛЕРОВО ДВИЖЕНИЕ
555
деле, заменив cosw в A1) его значением A8), придем к уравнению
эллипса в полярных координатах (рис. 83) с началом в фокусе F:
1 + е cos <р 1 + е cos ср'
A0.15.20)
Через р обозначен параметр эллипса — ордината в фокусе.
В найденное решение, выражаемое формулами B0), A6), A7),
входят три постоянные а, е, t0. Общее же решение уравнений дви-
движения точки в пространстве должно содержать шесть постоянных.
За остальные постоянные примем три эйлеровых угла, определяющих
Рис. 83.
положение плоскости орбиты и осей ее на этой плоскости в системе
осей неизменного направления О£т£ (в звездной системе), имеющей
начало в притягивающем центре.
Направления осей системы Oxyz зададим единичными векторами ev
е2, ег, причем ех направлен из притягивающего центра к перигею,
е2 — в плоскости орбиты перпендикулярно ех в сторону возрастания ср,
ез==е\У,е2— перпендикулярно этой плоскости. Эйлеровы углы обо-
обозначаются через Q, i, со (рис. 5, стр. 46). Угол <Q, определяет на
плоскости О£т] направление прямой, по которой эта плоскость пересе-
пересекается с плоскостью траектории. Это — линия узлов, и точка N, в кото-
которой ее встречает движущаяся от апогея к перигею точка, называется
восходящим узлом; поэтому угол <Г£ представляет долготу восходящего
узла. Угол / определяет наклон плоскости орбиты к плоскости О1т\,
а угол со — между линией узлов (направлением на восходящий узел)
и осью Ох (направлением на перигей).
556 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Записав теперь выражение вектор-радиуса движущейся точки
в виде
r=elr cos Y+^2r s*n ? = #[ei (cosw — e)-\-e2V\ —£2 sin w\ A0.15.21)
ii проектируя его на оси системы О;тI, придем к выражениям коор-
координат ;, т{, С-движущейся точки, содержащим шесть постоянных — эл-
эллиптических элементов орбиты
я, е% t0, ft, i, со. A0.15.22)
Эти выражения, мы не станем их здесь выписывать, можно также
получить при рассмотрении задачи в сферических координатах, исходя
из решений A4.10) и A4.11)*).
Имея в виду, что по A6), A5) и A1)
=i/~JL-Lf A0.15.23)
w=,
1 — е cos w
найдем дифференцируя выражение B1)., вектор скорости точки
\j V* — ^2cos w} A0.15.24)
Зеличина вектора скорости и его угол с вектор-радиусом г опре-
определяются равенствами
esmw A0.15.25)
— е cos w rv Y\ e2 cos2 w
Теперь легко определить постоянные а, е, wQ (через последнюю из
уравнения Кеплера определится t0) по начальным значениям г0> vQ, a.
г!айдем
— lJ
lJsin2a, cos wo= 2?~ * . A0.15.26)
1десь через р обозначена величина
$=—-. A0.15.27)
Если притягивающим центром является Земля, то, заменив \i =
по форму,
обозначая
Г)
по формуле E.6.7) его значением gRo, где Rq — радиус Земли, и
A0.15.28)
:) Классическое изложение дано в двадцать четвертой лекции «Лекций
пс 'пнамнке, Якоби. См. ссылку на стр. 518.
10.15] КЕПЛЕРОПО ДВИЖЕНИЕ 557
получим
о _ го ( Щ \2
Н~ М7~ • A0.15.29)
\ ОО /
Величина г^ называется «скоростью из бесконечности»,— эту ско-
скорость приобретает точка, падающая «из бесконечности» на Землю под
действием земного притяжения; эту же скорость надо сообщить на
Земле точке, чтобы удалить ее «в бесконечность». При сообщении
на Земле (г0 = /?0) горизонтальной скорости (cos а = 0), равной
VgR0 = 0,707 Voo, как видно из формул B6), орбитой будет окруж-
окружность с радиусом, равным земному.
Эллиптические движения, начинающиеся с поверхности Земли
(г0 = /?0), можно в зависимости от начальной скорости vQ разбить на
два вида. К первому относятся «земные движения», для которых
l>£>cosa,
A0.15.30)
Эти движения происходят по отрезкам эллипсов, пересекающим по-
поверхность Земли в начальной точке и точке падения, причем началь-
начальная точка близка к апогею, т. е. центр Земли расположен в удален-
удаленном от нее фокусе орбиты; второй фокус близок к поверхности Земли.
Параболическое движение в однородном поле земного притяжения
(/?0 = оо) соответствует левым предельным случаям неравенств C0).
т. е. C = 0, е=\, wo = 'k.
Эллиптические орбиты движений второго вида — «космических
движений» — определяются неравенствами
A0.15.31)
cosa<£<l,
Фокус, являющийся центром Земли, расположен ближе к перигею
орбиты, чем второй фокус, находящийся от точки старта на расстоя-
расстоянии, большем земного радиуса. Движение рассматриваемого вида со-
совершает искусственный спутник Земли. Левым предельным случаям
неравенств C1) соответствует, при горизонтальном бросании (cos a = 0),
упомянутый выше случай круговой орбиты; правым — параболическая
орбита с фокусом в центре Земли. При vo > ^со, т. е. [3 > 1, движе-
движение уже не принадлежит к классу эллиптических; орбитами являются
гиперболы.
558 КАНОНИЧЕСКИЕ УРАВНЕНИЯ И ТЕОРЕМА ЯКОБИ [ГЛ. 10
Остается рассмотреть уравнение Кеплера A6). Из многочисленных
способов его решения наиболее совершенным является представление
разности эксцентрической и средней аномалии
w — t = esiriT0 A0.15.32)
в виде тригонометрического ряда по синусам аргументов, крат-
кратных
С:
™ — ^= 2 я* smut. A0.15.33)
Возможность такого представления следует из того, что за период
обращения, когда С получает приращение 2тг, такое же приращение
приобретает w, а при перемене знака С уравнение Кеплера не изме-
изменяет вида, если изменить одновременно знак w. Поэтому w — С будет
нечетной периодической функцией С, представимой рядом C3). Коэф-
Коэффициенты его вычисляются по формуле
2 /»
&k — ~zr■ / (w — Q sin ^ Л-
о
Интегрируя по частям и используя уравнение Кеплера, получим
а, — ?_ (w — С) cos К
— /cos К d(w—Q =-т- /
JO
cos/гС
= — I cos /г (-о; — е sin 10)
2
i
о
Функции, определяемые интегралами вида
7С
J.(x) = -1
1 Г
'п(х) = — / cos {nw—х sin w) dw, A0.15.34)
о
впервые были введены в рассмотрение (и именно для решения урав-
уравнения Кеплера) Бесселем и названы впоследствии его именем. Итак,
n &C. A0.15.35)
Из уравнения Кеплера находим теперь
= j V A^LsinAC. A0.15.36)
sin w j
k=i
10.15] КЕПЛЕРОВО ДВИЖЕНИЕ 559
Способ вычисления применим к вычислению других функций от w.
Например, cosw является четной периодической функцией С и пред-
представим в виде
оо
cos w = -j- -f- £ bk cos kL
Коэффициенты его определяются по формулам
I cos<ny(l—^cosi^)^^ = —
о о
-£ = — / coswd^=— I cos<ny(l—^cosi^)
о
7i те
bk—— cos w cos k(, d^ =-г- / s*n & sin w dw =
о и
1 \ Г Г
— ~h\ / cos(&£ — w)dw— / cos (&£ -j- w) dw —
L о о
j 7U 1С \
—{ / cos[(/2 —1)^ — kesmw]dw— cos[(k-\-l)w—kes\nw]dw)
\ J
и по C4)
, A0.15.37)
ГЛАВА 11
ТЕОРИЯ ВОЗМУЩЕНИЙ
11.1. Метод вариации постоянных
Наряду с заданной системой уравнений движения
(s==l п)
рассматривается вспомогательная (или упрощенная) каноническая
система
ж
(ПЛ-2)
Предполагается, что функция Гамильтона Но в системе уравнений B)
выбрана так, что может быть найдено ее общее решение, содержа-
содержащее 2п постоянных
ъ=ъ(*; <*! «„. Pi Р„).
Как и в п. 10.12, предполагается, что эта система уравнений
разрешима относительно ak, Cft:
aft = M<7i Я„- Р\ P«i 0.
Рг Р„; 0 (k=\ я). |( ' ' ;
Тогда, как указывалось там же, любая из скобок Пуассона
(aft, a,), (aft, p,), (рл, р,) A1.1.5)
или постоянна, в частности равна нулю, или выражается через эти же
величины ak, §k\ ни одна из скобок не содержит явно ни t, ни пере-
переменных gs, ps. Заметим еще, что по A0.6.3) можно записать 2п
тождеств
Перейдем к заданной системе уравнений A). Идея метода вариа-
вариации постоянных состоит в том, что общее решение исходных
11.1] МЕТОД ВАРИАЦИИ ПОСТОЯННЫХ 561
уравнений A) разыскивается в той же форме C), но предполагается,
что as и р5 являются не постоянными, а функциями времени. Тогда
уравнения C) можно рассматривать как формулы преобразования
новых переменных о^, (^ в старые qs, ps, а уравнения D)—как фор-
формулы обратного преобразования. Речь теперь идет о составлении
системы дифференциальных уравнений, которым должны удовлетво-
удовлетворять эти новые переменные, если предположить, что старые переменные
должны представлять решения исходных уравнений A), а не уравнений
B) — тогда «новые переменные» были бы постоянными по условию.
Тождества F) при этом сохраняются, так как форма уравнений D),
в силу которых они являются теждествами, не изменилась. Не изме-
изменяют своего вида по этой же причине и скобки Пуассона E).
Надо составить выражения производных по времени новых пере-
переменных в силу системы дифференциальных уравнений A). Дифферен-
Дифференцируя выражения D), получим
Здесь учтены тождества F), a qk и pk заменены их значениями из
уравнений A). Аналогично вычисляются §s. Приходим к системе
уравнений
A1.1.7)
называемых уравнениями возмущенного движения. Конечно, их пра-
правые части предполагаются выраженными с помощью формул C) через
переменные afe, рл.
Можно привести уравнения G) к другому виду, воспользовавшись
формулой A0.7.14) преобразования скобок Пуассона. В ней надо
теперь заменить Qs, Ps на a5, C5, а и, v на as и И — Но. Получим
Учитывая, что
36 Зак 2072. А. И Лурье
562 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
приходим к равенству
Точно так же
^<ь. М-
Система дифференциальных уравнений возмущенного движения G)
теперь приводится к виду
(s = 1, .... n).
A1.1.10)
Преимущество этой записи заключается в том, что скобки Пуассона,
в ней фигурирующие, или постоянны, или выражаются через ak, рЛ.
До сих пор речь шла о замене системы дифференциальных урав-
уравнений A) другой системой A0); предположив, что решение последней
известно, сразу же по формулам C) найдем решение предложенной
задачи A). Очевидно, что такой прием может быть плодотворным,
когда система A0) легче поддается решению (хотя бы и приближен-
приближенному), чем исходная. Приближенное решение будет эффективным,
если можно так выбрать вспомогательную систему уравнений B),
чтобы она отличалась лишь второстепенными малыми слагаемыми от
подлежащей рассмотрению системы A). Тогда величины а5, $k, кото-
которые в решении вспомогательной системы B) были постоянными, будут
в задаче A) мало отличаться от постоянных. Сказанное можно
сразу же усмотреть и из уравнений A0) — производные по вре-
времени а5, р5 имеют тот же порядок, что и предполагаемо малые
Н—Яо, Qk; поэтому а5, Р5 оказываются медленно изменяющимися
функциями времени и к интегрированию системы уравнений возму-
возмущенного движения A0) становятся применимыми многочисленные при-
приближенные методы, в частности метод последовательных приближений
Пикара. Так, обозначив для краткости правые части уравнений A0)
через ФДа|р; t) и ч75(а|р, t)t можно в соотношениях
t t
> (а|р; t)dt9 В =К+ (ХНр; t)dt% A1.1.11)
11.2] КАНОНИЧЕСКИЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ 563
непосредственно получающихся из этих уравнений, заменить под зна-
знаком интеграла ak, $k их начальными значениями a°k, $® (при t=0).
Такая замена медленно изменяющихся величин постоянными не может
привести к заметной погрешности, по крайней мере, если t невелико.
Задача сводится к квадратурам
t t
• (П.1.12)
Этот процесс может быть продолжен — значения ols и ^, определен-
определенные по A2), снова подставляем в A1) и т. д.*).
Для разыскания периодических движений предложены способы,
основанные на замене (когда ищутся первые приближения) правых
частей уравнений возмущенного движения A0) их средними значе-
значениями за некоторый промежуток времени Т:
г г
Л«1Р; t)dt, Ф>|р)=-1у ЧГ,(а|Р; f)dt,
о о
A1.1.13)
причем а^, $k при вычислении интегралов справа считаются постоян-
постоянными. Задача сводится к рассмотрению системы уравнений
а5=Ф>|Р), р, = Ф5(а|р) E=1, ...,л) A1.1.14)
с малыми правыми частями, не зависящими от времени.
11.2. Канонические уравнения возмущенного движения
Система уравнений возмущенного движения упрощается в том
случае, когда решение A.3) вспомогательной системы уравнений A.2)
представляет каноническое преобразование величин ak, §k в qs, ps.
Это будет иметь место, как говорилось в гл. 10, в двух случаях:
во-первых, когда решение A.3) представляет интеграл Коши для
системы дифференциальных уравнений A.2), то есть а5, $s—началь-
$s—начальные значения переменных gs, ps\ во-вторых, когда решение A.3)
представляет общий интеграл канонической системы A.2), полученный
из полного интеграла уравнения в частных производных Якоби —
Гамильтона.
Для канонического преобразования, согласно A0.7.12),
0V «*) = 0. (а„ р») = 8,Л. (р„ pft) = 0. A1.2.1)
*) Мы не останавливаемся на рассмотрении вопросов сходимости. Метод
в ряде случаев не утрачивает значения, когда описанный процесс—расходя-
процесс—расходящийся. Свидетельством служит практика астрономических вычислений. См.
Г. Н Д у б о ш и н, Введение в небесную механику, ОНТИ, 1938, стр. 256.
564 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
вследствие чего форма уравнений возмущенного движения A.10) резко
упрощается. Они приобретают вид
A1.2.2)
15 dns { ^ dpk ^k K J
В частности, если
Q^ = 0 {k= 1, . . ., я),
т. е. когда уравнения A.1) — канонические, то каноническими в ого-
оговоренных выше случаях будут и уравнения возмущенного движения
•а = д(Н-И0) ^ • = д(И-И0) E=1 п) A1 2 3)
Сославшись теперь на соотношения A0.8.16) — в них надо лишь
заменить Qs, Ps cuuibeiLibehHO на а5, ^5,—можно уравнения B)
записать также в виде
_д(И~И0) у^ dqk ^
A1.2.4)
д(Н-Щ) у
Для записи уравнений D) не требуется знания обратного преобра-
преобразования A.3); в этом состоит их преимущество перед уравнениями B).
Если обобщенные силы Qs зависят только от времени (в частно-
частности, постоянны), то уравнения возмущенного движения приобретают
каноническую форму
л] (*=!..... я). (П.2.5)
Конечно, это легко было предвидеть, так как и исходные урав-
уравнения движения A.1) записываются в форме канонических уравнений
с функцией Гамильтона (см. определение обобщенной потенциальной
энергии п. 5.3)
^Qkqk. (П.2.6)
11.31 ДВИЖЕНИЕ ТОЧКИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ ВРАЩАЮЩЕЙСЯ ЗЕМЛИ 565
Метод вариации постоянных изложен в пятом отделе первого
тома «Аналитической механики» Лагранжа *). Приведены уравнения
возмущенного движения как в форме A.10), так и C), хотя канони-
канонические уравнения не были известны Лагранжу. Он следующими сло-
словами характеризует сущность метода: «обычно первое решение
(в задачах механики) находят, принимая во внимание только главные
силы, действующие на тела, а для того чтобы это решение распро-
распространить на другие силы, которые можно назвать возмущающими,
проще всего сохранить форму первого решения, но рассматривать
входящие в него произвольные постоянные как переменные величины.
Ибо если величины, которыми мы пренебрегли и которые хотим
теперь учесть, очень малы, то новые переменные будут почти
постоянными и к ним можно будет применять обычные методы при-
приближения».
Эти идеи Лагранжа развивали выдающиеся математики первой
половины девятнадцатого столетия — Пуассон, Якоби, Остроградский.
11.3. Движение материальной точки в поле силы тяжести
вращающейся Земли
Положение точки определяется в системе «стартовых осей» Oxyz,
начало которой помещено в точке О, определяемой на земной поверх-
поверхности полюсным углом 00 (дополнение до широты) и долготой Хо.
Ось Oz направлена из центра Земли О в точку О по вектор-
радиусу /?*, оси Ох и Оу — в касательной плоскости в точке О
к сфере радиуса /?*— первая по касательной к меридиану этой сферы
в сторону уменьшения угла ^0, а вторая — по касательной к парал-
параллельному кругу также в сторону уменьшения Хо. Это — направления
на север и на запад, если пренебречь несферичностью Земли.
Начнем с вычисления функции Гамильтона К, определяемой соот-
соотношением A0.11.9); по ней будут составлены канонические уравнения
движения A0.11.10). Надо записать в форме A0.11.4) выражение
кинетической энергии точки единичной массы. Замечая, что в нашем
случае
где, как всегда, U — угловая скорость Земли, имеем
» ' (г' X -£-) = U ft sin Ьо -[- /3 cos »0). (г' X h) = — Uу cos »0,
аналогично
= г/У sin
*) Стр. 412—437 русского перевода (Гостехиздат, 1950)
566 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
и по упомянутой формуле
Г = 1 К^ + Uу cosft0J + [P2—U(хcos\ — z sin \)}2 +
_(/ysin»0J}. A1.3.1)
Переходим к вычислению отдельных слагаемых выражения A0.11.9)
функции Гамильтона К. Имеем (при т=\)
@-0- (о = г' со2—(r'-(oJ= U2(х2-\-у2-\-z2) — U2(xsm§0-\-zcosiHJ —
= U2 [(z sin i% — x cos V
(to X v0). r' = U [(^ sin »0 + /3 cos 00) X (- i2R*0U sin »0)| . r< =
= t/2/?; sin fr0 (— 2: sin frQ + x cos »0)f
так как вектор v0 — скорость полюса стартовой системы осей —
равен
*
Это — постоянная величина; поэтому слагаемое, содержащее v0, отпа-
отпадает. Получаем
— у w ' 9 ' w + т (*» X vo) • r' =
= -\ W Kz sin %-* cos^oJ + Щiz sin ^o - x cos *o) +
+ Rf Sin2 »Q+ y2] + I /?fG2 sin2 &o = _ |
причем, конечно, постоянное слагаемое можно отбросить; через
h2 обозначен квадрат расстояния точки до оси вращения Земли
А2 = КЛо + г) sin &0 - х cos &о
Поэтому величина
П, = II — i- со • 0 • со + т(to X v0) • г' = П — i U2h2+const, A1.3.2)
согласно E.6.2), представляет потенциальную энергию силы тяжести,
т. е. сумму потенциальных энергий сил притяжения и центробежной
силы. П^ определяется равенством E.6.9); в него входят расстояние г
от центра Земли и дополнение 0 до широты места, где находится
точка. Имеем
г = г0 + гг = i3Rl + 1гх + /2у + *у, cos & = ~ • (^ sin &0 + h cos
и, следовательно,
cos 0 = 1 j-jf Sin bQ + (/?; + Z) COS »„].
11.3] ДВИЖЕНИЕ ТОЧКИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ ВРАЩАЮЩЕЙСЯ ЗЕМЛИ 567
Здесь, согласно E.6.11),
причем Ro— средний земной радиус, а R*Q—радиус нормально!
сфероида в точке О.
Имеем
г Г- . 2г . x2 + y2 + z2 4 П/ лч/, , -г \|!/*
16 R*
l+ + /
^^0^ 2RI ^
В этом вычислении отношения -^-, ~-, -^- считаются малыми первого
^\0 Ко Ко
порядка, а число а (и далее т) — второго порядка. Удерживаются
слагаемые до третьего порядка включительно. Имеем
3
[г2 г (х2 -}- у2) \ z
_ . £ л:2 + У2 — 2г2 Зг (х* + у2) — 2г3
При вычислении слагаемых в E.6.9), умножаемых на т или а, до-
достаточно в этих разложениях удержать члены первого порядка.
Находим, учитывая E.6.3) и E.6.7)
т Г / г \2
- aP2 (cos 9) + (| т - За) ~- Р2 (cos »„),
568 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
причем Р2 (cos ft) следует заменить выражением
Р2 (cos ft) = Р2 (cos 1%) + (—^ cos ^ ) (cos ^ — cos *o) =
= P2 (cos \) 4-3 ~ cos fl0 sin 8 ,
Подстановка в E.6.9) дает теперь
~ ^0 [ ^^ +2P~~2Z* — -| Р^Р2 (C0S &o) —
h«... (П.З.З)
где p — постоянная Клеро, определяемая по E.6.19).
Функция Гамильтона К теперь представляется в виде
cos »0 — Р3 sin &0)у — Р2(хcos &0 — z sin &0)] +
8J
[^ + (Х C0S 8о -
f
f $z2 (cos0) xcos»0 sin »
2axcos»0 sin (
(n.3.4)
В дальнейшем отбрасывается слагаемое К , определяемое сжатием
геоида и действием центробежных сил вращения Земли, величина
которых сравнима, как указывает Аппель *), с притяжением точки
Луной. Кориолисовы силы, пропорциональные первой степени угло-
угловой скорости Земли, учтены слагаемым К \ которое далее считается
имеющим первый порядок малости.
Упрощенную систему уравнений определим слагаемым Кт. По-
Получаем
— ]' У~ дР2 ~^2i z~ дР3 —^З'
(П.3.5)
2 ду 3 ^<г
*) П. А п и е л ь, Теоретическая механика, т. 2, Физматгиз, 1960, стр. 254.
11.3] ДВИЖЕНИЕ ТОЧКИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ ВРАЧУЮЩЕЙСЯ ЗЕМЛИ 569
Это — уравнения движения тяжелой материальной точки без учета
вращения Земли. Их решения имеют вид
-3.6)
причем cLt и р^ представляют начальные значения координат и импуль-
импульсов для системы уравнений E).
Уравнения возмущенного движения B.3) составляются с помощью
функции Гамильтона К , в которой координаты и импульсы должны
быть заменены выражениями F):
a,) cos По -f
з - 4 go*2) ^n Po
. (П-3.7)
К{1) = U [ф, cos 00 - S3 sin 90) (У -+- a2) -
(У + «з) sin в0 + p2
Получаем систему трех канонических уравнений возмущенного дви-
движения для величин а.
- = — Uclx cos d0 -\- Ua3 sin &0 -\-
A1.3.8)
и трех уравнений для
= - ^i cos ft0 + Щъ sin fi0 -
A1.3.9)
570
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
Заменив в правых частях этих уравнений alt $t их начальными
значениями ofi, ро, согласно A.12), придем к приближенным реше-
решениям вида
if (т W3 + а°Л) •
cos &0 -
п т. д.; подставив их в F), получим значения координат
у = a° + р - U (*\t + р°/2) cos »0 + U
sin f>0 -
sin
Ro V* 6 "^ a3 T 24 )
и импульсов
P, =
P2 =
t sin
A1.3.11)
= po _ t^ sin !>o + ^ (po I + aot _
Относительные обобщенные импульсы, равные для точки единич-
единичной массы проекциям х, у, z скорости ее на оси системы Oxyz,
могут быть вычислены по формулам A0.11.13). Находим
х = Р, + Uу cos \ » />, + t/ (a» + P^) cos J>0,
у = />2- f/ (jc cos »0—г sin 00) « P2-1/ (aj+p?/) cos
z=P3— Uу sin «0 ^ Ря — t/ (ag + $t) sin Яо.
A1.3.12)
Эти же соотношения можно получить, дифференцируя равенства A0).
Постоянные aj, a§, a^ представляют начальные значения координат;
572 теория возмущений [гл. 11
По формулам A0) получаем
х = vot cos В cos 8 -\- Uv0t2 cos S sin s cos fr0,
у — vot cos Ь sin 8 — Uv0t2 cos В cos s cos fr0 -f-
-|-Lfo0f2sin8sin00 — i- UgQts sin §Q% 5" (H.3.16)
I
я = i/0£ sin В— Uv0t2 cos В sin s sin ^0 — — gQt2.
Расположив ось O£ в плоскости бросания, а ось Оч\ перпендику-
перпендикулярно к ней под углом s с направлением на запад, найдем, вместо
двух первых выражений,
£ =z vot cos В -f- UvQt2 sin S sin i>0 sin s —-~ Ug0t3 sin l>0 sin s,
7] = — Uv0t2 (cos В cos ^0 — sin о sin f)Q cos г) — у ^0^3 sin fr0 cos 8.
Последнее равенство определяет отклонение от плоскости бро-
бросания.
11.4. Движение материальной точки в среде
с сопротивлением *)
Пренебрегаем влиянием вращения Земли и изменением силы
тяжести с высотой. Тогда (для точки единичной массы), направив
ось х горизонтально, а ось у по восходящей вертикали, имеем
Сила сопротивления направлена противоположно скорости точки и
ее проекции на оси Ох и Оу равны
причем х = рх, У = РУ- При пренебрежении силами сопротивления
получаем
*) Hamel G., Theoretische Mechanlk, Berlin, 1949, p. 310.
11.3] ДВИЖЕНИЕ ТОЧКИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ ВРАЩАЮЩЕЙСЯ ЗЕМЛИ 571
постоянные же ф®, ро, Щ определяются по начальным значениям ско-
скоростей из соотношений
х0 = ро -f- t/«§ cos &0> у0 = Щ - U*\ cos \
s
Пусть, например, рассматривается падение точки вблизи поверх-
поверхности Земли с высоты h без начальной скорости. Тогда
aJ = O, a0 = 0, al = ht р° = 0, po = — f/Л sin »0, p° = 0
и, пренебрегая членами, зависящими от изменения силы тяжести
с высотой, найдем по A0)
A1.3.13).
х = — U2ht2 sin fr0cos fr0 та 0, у = — -^ ^/3 sin &0,
= /г — у ^2 + ^72/г^2 sin2
Удержание слагаемых, пропорциональных £/2, не имело бы смысла
при принятой точности вычисления. Мы получили выражение восточ-
восточного отклонения падающего тела. При бросании вертикально вверх
начальные условия будут
ао _ о а0 = 0 а0 = О В0 — О В0 — 0 В0 — z
и из A0) получим
I z = z4 — \g&. (Н.3.14)
В момент достижения наибольшей высоты, то есть при z = 0, вели-*
чина западного отклонения будет
/ = |t/J-sinft0. A1.3.15)
Рассмотрим еще случай бросания с поверхности Земли со ско-
скоростью vQt составляющей угол о с плоскостью горизонта; проекция vQ
на эту плоскость составляет угол s с направлением на север. Тогда
<^ = 0, а^ = 0, а§ = 0,
РУ = ^Ocos Ь cos е, Рз= vo cos 8 sin £» Рз = ^о sin S*
574 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
11.5. Влияние малых возмущений на колебания системы
около положения равновесия
Мы остановимся в этом параграфе на трудностях, возникающих
в методе последовательных приближений, которые частично можно
устранить, применяя метод осреднения. С целью упрощения изложе-
изложения самого метода мы рассмотрим его на примере учета влияния
малых возмущений на колебания системы около положения равно-
равновесия.
Рассматривается материальная система со стационарными связями,
способная совершать малые движения около положения равновесия.
Обозначая через qs обобщенные координаты, отсчитываемые от поло-
положения равновесия, представим выражения кинетической энергии
системы и потенциальной энергии в виде
<"■»•■>
5=1 k = \
Здесь из коэффициентов выражения кинетической энергии Ask (qv ..., qn)
выделены постоянные слагаемые ask, так что a*k представляют раз-
разности
В выражении потенциальной энергии члены первого порядка отсут-
отсутствуют, так как нулевым значениям координат соответствует, по
условию, положение равновесия, и по F.5.11) имеем
4s /о
Разложение в степенной ряд выражения П^ начинается с членов
не ниже третьей степени.
Известно, что две квадратичные формы
п п п п
-У Ус
2 АЛ ZaC*
5=1 k=l 5=1 k=\
из которых одна знакоопределенная, могут быть одновременно с по-
помощью линейного преобразования приведены к виду, в котором
отсутствуют произведения переменных *). Мы предположим далее»
*) См., например, Л. Г. Лойцянский и А. И. Лурье, Курс теоре-
теоретической механики, том 2, Гостехиздат, 1954, стр. 498. -
11.4] ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СРЕДЕ С СОПРОТИВЛЕНИЕМ 573
Уравнения возмущенного движения B.4) поэтому будут
A1.4.2)
Если сопротивление мало, то при интегрировании можно считать
..., C2 в правых частях этих уравнений постоянными. Тогда
где
Для интегрирования вводим новую переменную X
I
X = ($® —
Тогда
и решение уравнений A) представится в виде
*==а0 + р°*+(-^-) /(shX—shp.)/(PJchX)rfX,
— ) / (shX—shu/
V-o
где обозначено
P2
A1.4.3)
Вычисление, например, для квадратичного закона сопротивления
f(v) = cv2 не представит труда, хотя и будет сопряжено с громозд-
громоздкими выражениями.
11.5] ВЛИЯНИЕ МАЛЫХ ВОЗМУЩЕНИЙ НА КОЛЕБАНИЯ СИСТЕМЫ 575
что такое преобразование к этим, называемым главными, координатам
проведено; сохраним для главных координат то же обозначение qs.
Тогда вместо A) получим выражения
5=1
A1.5.2)
Предполагается, что малые движения происходят около положения
устойчивого равновесия; тогда П — знакоопределенная функция, по
крайней мере для достаточно малых \qs\, и все коэффициенты будут
положительными. Конечно, положительны также коэффициенты as.
Их отношения
\1 = ^ E=1, ....*) A1.5.3)
as
представляют квадраты частот главных колебаний системы около рас-
рассматриваемого положения устойчивого равновесия.
Кроме потенциальных сил, на систему действуют непотенциальные
силы. Соответствующие им обобщенные силы Qs будут в общем
случае зависеть от координат qs, обобщенных скоростей qs и вре-
времени.
Импульсы ps вводятся с помощью соотношений
и из этой системы линейных уравнений обобщенные скорости выра-
выражаются через импульсы. Обобщенные силы Qs поэтому далее можно
считать выраженными через время, обобщенные координаты и
импульсы.
За функцию Гамильтона вспомогательной задачи A.2) естественно
принять выражение
Тогда разность Н—Но определится равенством
5=1 \ S / 5=1 *-1
A1.5.6)
в котором, конечно, qs предполагаются выраженными через импульсы
576 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. П
с помощью системы уравнений D). Было бы ошибкой отбросить
в этом выражении первую (одинарную) сумму.
Упрощенная каноническая система A.2) имеет вид
Я8 = ~> Ps = — Cs4s (s=l ") (П.5.7)
и ее интеграл Коши будет
qs = ascos X/ + A- sin X/, ps = — asasls sin \st + $s cos X/, A1.5.8)
так что as и $s — начальные значения обобщенных координат и им-
импульсов. Поэтому уравнения возмущенного движения можно записать
в форме B.4)
(H.5.9)
причем, конечно, И— Ho и Qs здесь должны быть выражены через а^,
р^ с помощью выражений (8).
Прием интегрирования этой системы уравнений, основывающийся
на замене в их правых частях неизвестных afe, $k постоянными зна-
значениями, малопригоден в задачах колебаний, так как, давая количе-
количественно верное для достаточно малого промежутка времени решение,
он не допускает суждения о качественном характере движения. Более
приспособлен к задачам этого рода метод осереднения правых частей
уравнений (9), являющийся в настоящее время одним из наиболее
важных средств решения задач нелинейной теории колебаний. Он был
разработан Н. М. Крыловым и Н. Н. Боголюбовым *) и развит
в многочисленных трудах других ученых **).
Имея целью лишь пояснить причину возникновения трудностей, мы
ограничимся рассмотрением линейной системы с двумя степенями сво-
свободы; поэтому величина Н—Но далее отбрасывается. Как возмущаю-
возмущающие силы далее рассматриваются силы сопротивлений, линейно зави-
зависящие от скоростей и определяемые положительной знакоопределенной
диссипативной функцией
) (П.5.10)
с малыми коэффициентами bl% h, b2. Вычисление далее ведется с учетом
слагаемых первой степени относительно этих коэффициентов.
*) Н. М. Крылов и Н. Н. Б о г о л ю б о в, Введение в нелинейную
механику, Киев, 1937.
**) Н. Н. Боголюбов и Ю. А. М и т р о п о л ь с к и й, Асимптотиче-
Асимптотические методы в теории нелинейных колебаний, гл. V, Физматгиз, 1958.
11.5]
ВЛИЯНИЕ МАЛЫХ ВОЗМУЩЕНИЙ НА КОЛЕБАНИЯ СИСТЕМЫ
577
В обобщенных силах
дФ
дФ
x = — —г- = — (blql -4- hq2),
дФ
дФ
2 = —-y- = — (hqx + b2q2)
следует выразить обобщенные скорости через импульсы. Получим
Уравнения возмущенного движения B.4) примут вид
. h \s\n\\t а /6, , /г
sinM
1
Справа надо подставить значения импульсов по формулам (8). Заменив
в получающихся выражениях произведения тригонометрических функ-
функций вида cosXj/cosX^ через тригонометрические функции от суммы
и разности аргументов, придем к уравнениям
257 а" + fe ai C0S 21
Х2) * - cos (X, - Х2) /1
sin 2X,/
[sin
sin (X,
A1.5.13)
— 9— ^2 'C0S ^ ~t~ ^2) ^ + cos Оч — ^2) ^1»
соответственно заменяя индексы, получим уравнения для <х2, C2.
Если бы теперь мы заменили а5, Р5 в правых частях этих урав-
уравнений постоянными значениями аР, C^, то в результат интегрирования
вошли бы слагаемые
2.CL] * 2Л] ^
содержащие t вне знака тригонометрических функций — вековые
члены. Такие решения, пригодные для вычисления в течение корот-
короткого промежутка времени, представляют первые члены разложения
точного решения в ряд по степеням t. О характере движения, пред-
представляющего, как хорошо известно, затухающий колебательный про-
процесс, ничего нельзя было бы . сказать,. Возникающая трудность
37 Зак. 2072. А. И. Лурье
578
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. If
устраняется в методе осреднения. Чтобы укоротить записи, поясним
идею на примере двух уравнений первого порядка
xl = Pfl(xl' Х2' 0. x2=Pf2(XV XV 0. (П.5.14)
где (л — малый параметр, а функции ft представимы в виде рядов
v x2)sin\t] (/=1,2). A1.5.15)
Например, в уравнениях A3) степени и произведения косинусов
и синусов были заменены суммами косинусов и синусов частот 2Х1э
2Х2, Xj ± Х2. В состав функций ft входит, таким образом, часть
<p?(*i» хЛ, медленно изменяющаяся во времени, так как таковыми
являются аргументы хг, х2, и накладывающиеся на нее колебательные
члены с медленно изменяющимися коэффициентами cp(v), ф^). Это на-
наводит на мысль заменить правые части уравнений A5) их средними
значениями за достаточно большой промежуток времени, принимая
при вычислении средних значений х1 и х2 постоянными. Тогда
т
Um т f fi(x^> x» t)dt = <$(xv x2) A1.5.16)
о
Г->оо
и в этом приближении уравнения A5) заменяются уравнениями
Г Х2)~ (П.5.17)
Так в примере системы A3) эти дифференциальные уравнения будут
иметь вид:
Их решение будет
и подстановка в (8) дает
2а с
A1.5.18)
11.5] ВЛИЯНИЕ МАЛЫХ ВОЗМУЩЕНИЙ НА КОЛЕБАНИЯ СИСТЕМЫ 579
Это еще очень грубое приближение. Достаточно указать на то, что
наличие слагаемого 2hq]q2 в выражении диссипативной функции, кото-
которое обусловливает связь движений, соответствующих главным коор-
координатам <7i. #2> никак не отражено в решении A8).
Более точное приближение естественно определить так. Полагаем,
возвращаясь к системе A4),
A1.5.19)
где Sj являются, как и выше, решениями системы уравнений A7):
Это значит, что решение представляется суммой «нулевого прибли-
приближения» ^ и интеграла по t от остающихся в правых частях системы A4)
колеблющихся слагаемых, причем при вычислении этого интеграла хх%
х2 заменены на £1§ £2 и, поскольку последние медленно меняются,
не учтено их изменение во времени. Можно доказать, что построен-
построенное этим способом решение удовлетворяет системе дифференциальных
уравнений A4) с ошибкой, имеющей порядок (а2. Это устанавливается
дифференцированием выражения A9)*).
Проведем намеченное вычисление для системы A3). Находим
по A9)
2axa2\x W [ h + X2
I COS (Л,— Х2)П
Г" X, — X2 J
cos (Xt — X2) / 1
X,-X2 J
A. Me-jt * Г sin (Xi + h) t , sin (X! — X2) f
~2a2 W 2 L h+h "^ X,Х
! — X2) f\
*) Описание способа построения следующих приближений и обоснование
метода даны в гл. V и VI книги Н. Н. Боголюбова и Ю. А. Митропольского.
См. сноску на стр. 576.
37*
580 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 1
Лодставив эти значения в (8), после упрощений найдем
Выражение q2 получим при соответствующей замене индексов:
A1.5.21)
Задача о колебаниях диссипативной системы с двумя степенями
свободы около положения равновесия рассмотрена в книге Уиттекера *)
непосредственным интегрированием уравнений движения с учетом
диссипативных сил. При вычислении частот Уиттекер пренебрег сла-
слагаемыми, пропорциональными, квадратам коэффициентов диссипативной
функции и получил выражения qv q2, которые совпадают с приве-
приведенными в тексте, если в последних отбросить подчеркнутые слагаемые.
11.6. Влияние неуравновешенности на движение волчка
К почти 1 вертикальному волчку присоединена на весьма малом
расстоянии е от его оси симметрии Ог точечная масса т. Требуется
определить возмущение, вносимое наличием этой неуравновешенности
в движение волчка, ограничиваясь рассмотрением величин, пропор-
пропорциональных первой степени эксцентриситета е.
Положение волчка определим, как в примере 2° п. 7.18, кора-
корабельными углами, которые теперь будут обозначены X и [х (причем
X = a, JX = Р) и углом собственного вращения ср. Координаты при-
присоединенной массы в системе осей Oxyz, связанных с телом, обозна-
обозначим через x0=ecosz, yo=e sin 8, z0. Ее кинетическая энергия равна
. ,Tj = j т [(шуг0 — шгУоJ + (согл:0 —
*) Аналитическая динамика, § 94, стр. 260—262, ОНТИ НКТП, 1937.
11.6] ВЛИЯНИЕ НЕУРАВНОВЕШЕННОСТИ НА ДВИЖЕНИЕ ВОЛЧКА 581
причем величины, пропорциональные е2% не выписаны. Вспомнив
выражения проекций угловой скорости
ых = — X cos ср -4- |i cos X sin cp,
шу = X sin ср —j— [х cos X cos cp,
o)z = cp —I— jjl sin X.
найдем, что кинетическая энергия системы — волчка с присоединен-
присоединенной массой — равна
Т = -1 {А (X2 + <i2 cos2 X) + С (ф -Ь £ sin XJ —
— 2ez0m (^-{-р sin X) |— Xcos (cp —|— г) —|—jjl cos X sin (cp-f-s)]}, A1.6.1)
где через, А обозначен экваториальный момент инерции системы,
через С — осевой момент инерции волчка.
Обозначая через к единичный вектор восходящей вертикали,
составляем выражение потенциальной энергии
П = Qxzck • /3 + mgk • Aгх0 + i2y0 + i3zQ) =
= (QYzc -{- tngZo) cos X cos [x -f- mge (k • ix cos e -|- ft • /2 sin s),
где Qj — вес волчка. Пусть Q—вес,, z* — координата по оси Oz
центра тяжести системы. Заметив, что
i}=n cos cp -f- n' sin cp, i2 = — n sin cp -|- n' cos cp,
найдем
ll=Q2:*cos Xcos jjl—mge [sin ^ cos (cp—|—©)—|~sin X cos ^ sin (cp—J—s)]. A1.6.2)
Теперь по A) получаем
Px = AX -(- m^z0 (cp —|— jjl sin X) cos (cp -|- s),
p^ = ^ sin X -f- Л[л cos2 X — m^0 (cp -f- ц sin X) cos X sin (cp -f- e),
p = С (cp 4- (j- sin X) — m£20 [— X cos (cp -j- e) -f- |j- cos X sin (cp -\- e)],
Ъткуда, с принятой точностью,
Х = £--3?Ч co.fr+ .).
/?а — р9 sin X
АсовП ^-A
p >
582
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. II
и выражение функции Гамильтона будет
Н=~2
р!
cos (т+в)
sin
— mge [sin [x cos (cp —J— e) —|— sin \ cos (j- sin
Для почти вертикального волчка
Л
e)J
= Ho-\-H1.
Н\= -jT^ [p\P cos (cp -\- е) — (р^ — Хр ) Ру sin
— mge № cos (cp -f- e) +1 sin (cp -f- e)].
Канонические уравнения невозмущенного движения волчка
1.6.4)
A1.6.5)
Рч Pv- ~~
приводятся к виду
j» 4- /x = -j- (p^ — P?i 4- iP}),
0 + Qz
A1.6.6)
Обозначая теперь через qx и q2 корни квадратного уравнения
A1.6.7)
и через а^, ах> р , рх начальные значения координат и импульсов,
придем к равенствам
1* + /Х = -
1
A1.6.8)
11.6] ВЛИЯНИЕ НЕУРАВНОВЕШЕННОСТИ НА ДВИЖЕНИЕ ВОЛЧКА 583
Из последнего приближенного равенства F) имеем еще
где а —начальное значение ср. Полагая е = 0, что, конечно, не на-
нарушает общности, теперь можем представить возмущающую функцию
в виде
^ ll)e^] = Hl(a[lt ах, а?, р,, рх, ^; t).
A1.6.10)
Переменные а^, .... ^ здесь являются начальными значениями коор-
координат и импульсов. Поэтому уравнения возмущенного движения имеют
каноническую форму B.3). Их легко составить, заменив в A0) коор-
координаты и импульсы по формулам (8) и (9). В дальнейшем вычислении
ограничимся случаем быстро вращающегося волчка, когда имеет место
неравенство
и корни квадратного уравнения D1) приближенно равны
_ Q*c ^K_ A16 11)
Первый из них соответствует медленному движению — прецессии,
второй — быстрым нутационным дрожаниям оси волчка.
При этом условии формулы (8) можно упростить, приняв
ipx _ tAqi (а^ _|_ /ал (рШ _ р^.^ -4- С11 -6-12)
и представить Их в виде
4-(^— Pf«x 4-^
у [. fax)
*> 4-^ (K~
584
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. П
Переходя к составлению канонических уравнений возмущенного
движения
заметим, что Нх зависит от р^, (Зх, а^, ах через посредство величин
и им сопряженных С}, С2. Поэтому
дНх дИ1 , д'Я,
дН\ _ о / дН\ , дНх \ . . / дЯ,
что позволяет записать упомянутые уравнения в виде
дНх\
#2 /
Сложнее запись остающихся двух уравнений
дНх
В = ' =
<?2г; ая,
1 дЯ!
^4 dq2
t
~С
A1.6.14)
' J
A1.6.15)
Первое из них определяет возмущение кинетического момента; при.
составлении второго учтено, что Нх зависит от ^ как через посред-
посредство этой явно входящей в запись A3) буквы, так и через посред-
посредство <7i> #2» ?• ^3 (9) и A5) "находим, что вызываемое наличием,
добавочной массы изменение угловой скорости собственного вращения
равно
Аср = ср — — =а + — 5 — -) -- -— - + — (И.6.16)
11.7] ВРАЩЕНИЕ СПУТНИКА ЗЕМЛИ ВОКРУГ ЦЕНТРА ИНЕРЦИИ 585
и из A3) следует, что оно представляет наложение колебаний
с частотами
"Г = 9о.
= ?0
Возвращаясь к уравнениям A4), упростим их, пользуясь малостью qY
ло сравнению с q2. Величины [3 и а в правых частях этих уравне-
пий рассматриваются как постоянные, причем -=г = ср0. Получаем,
- „ тег*
обозначая через х малый параметр —д—
. а-с • л
л-с
A1.6.17)
Из этих соотношений следует, что при А = С, когда эллипсоид
инерции в точке опоры представляет шар, в выражения возмущений
войдут растущие пропорционально времени слагаемые.
11.7. Вращение искусственного спутника Земли вокруг
центра инерции
В п. 5.5 было показано, что силы центрального поля, действую-
действующие на движущееся в нем тело, приводятся не только к главному
вектору /\ но и главному моменту т° относительно центра инерции G
тела. Выражение момента mG, в предположении, что центральный
эллипсоид инерции тела представляет эллипсоид вращения, дается
формулой E.5.13). При отсутствии момента mG вращение тела вокруг
его центра инерции было бы регулярной прецессией. Совершая ре-
регулярную прецессию, тело вращается с постоянной угловой скоростью
вокруг оси вращения эллипсоида инерции, а последняя в свою оче-
очередь вращается также с постоянной угловой скоростью вокруг неиз-
неизменного направления вектора главного момента количеств движения К°,
составляя с ним постоянный угол. Задача о возмущении регулярной
прецессии, вызываемом наличием момента mG, принадлежит к числу
классических вопросов небесной механики, дающих объяснение явле-
явления лунно-солнечной прецессии земной оси и предварения равноден-
равноденствий. Вращение вокруг центра инерции искусственного спутника
Земли, являющегося вытянутым по оси симметрии телом вращения,
586 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
также представляет возмущенную регулярную прецессию; рассмотрение
этой задачи дает интересный пример применения теории возмущений *).
Назовем С и Л осевой и экваториальный центральные моменты
инерции спутника. Движение его происходит в поле сил притяжения
Землей, которая здесь рассматривается как однородный шар. Тогда
по E.5.6) потенциальная энергия поля притяжения будет равна
-+ ±-(С-A) (x*
где p = fM— произведение постоянной тяготения на массу Земли.
Заменив х2-\-у2 через г2— г2 и отбрасывая в выражении II ту часть,,
которая не зависит от ориентации системы осей, связанных со спут-
спутником, и в этом рассмотрении не может нас интересовать, получим.
П = ^(С-А)^. A1.7.1)
Пусть ег обозначает единичный вектор направления MG от центра
Земли к центру инерции спутника, /3 — единичный вектор по оси
вращения Gz его эллипсоида инерции, составляющий с ет угол Ь
(рис. 38). Тогда
и выражение II приобретает вид
^А)^. A1.7.2)
Введем в рассмотрение ортогональный триэдр единичных векто-
векторов ev e2, вг с началом в центре Земли — фокусе эллиптической
орбиты спутника; ех направлен к перигею орбиты, е2 в плоскости
орбиты параллельно ее малой оси и в сторону движения от перигея
к апогею; единичный вектор ^3 = ^j X ^2 имеет направление перпен-
перпендикуляра к плоскости орбиты. Возмущениями элементов орбиты спут-
спутника пренебрегаем; тогда векторы ех, е2, £3 остаются неизменно
направленными в пространстве. Заметим еще, что
A1.7.3)
*) Элементарное рассмотрение задачи о лунно-солнечной прецессии дана
в книге Р. Граммеля «Гироскоп, его теория и применение» (т. 2, гл. 3, § 10,
стр. 253—265). Весьма полно она (а также задача о либрации луны) изло-
изложена в классическом сочинении по небесной механике Тиссерана (F. T i s-
serand, ТгаНё de mecanique celeste, 2, chap. 22—28, p. 371—475; Paris, 1891).
В применении к спутнику вопрос рассмотрен в работе В. В. Белецкого
«Движение искусственного спутника Земли относительно центра масс»
(сборник «Искусственные спутники Земли», № 1, стр. 25—43, Изд-во АН СССР,
1958). В этой работе рассмотрено возмущающее действие не только грави-
гравитационных, но и аэродинамических сил, а также изменяемости орбиты центра
инерции спутника.
11.7] ВРАЩЕНИЕ СПУТНИКА ЗЕМЛИ ВОКРУГ ЦЕНТРА ИНЕРЦИИ 587
где а обозначает теперь истинную аномалию — угол вектора ет с на-
направлением на перигей.
Ориентацию осей триэдра Oxyz (единичные векторы ilt i2% /3),
связанных со спутником, задаем эйлеровыми углами ф, ft, ср. Тогда
ег • f3 = sin ft sin ф, е2 • f3 = — sin ft cos ф, e3 • /3 = cos ft A1.7.4)
и далее по C)
cos 6 = er • /3 = sin ft (sin ф cos a — costy sin a) = sin ft sin(ф — a). A1.7.5)
Теперь, обозначая через а большую полуось орбиты и вспоминая
{10.15.15), получим
II = |- п2 ^ (С — A) sin2 ft sin2 (ф — a), A1.7.6)
где п — среднее движение спутника.
Выражение кинетической энергии вращательного движения твер-
твердого тела вокруг его центра инерции хорошо известно. Оно имеет вид
(П.7.7)
Записав еще выражение Т в виде
и замечая, что С — Л<0 для вытянутого по оси Gz тела вращения,
получим
| II | Зп2 а3 А • 9а . о/, ч / 3 я3 (А
(П.7.8)
Для существующих спутников отношение (— I представляет малую
величину; это обстоятельство делает допустимым применение метода
теории возмущений, причем первое приближение (вспомогательная
задача) соответствует регулярной прецессии, имеющей место при
11 = 0. Для Земли по E.6.34)
С —А
С
При притяжении Солнцем
= 0-0033.
ш" 366
11 соответственно
28"
588 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. It
для притяжения Луной. Отношение у оказывается весьма малым.
В задаче о спутнике соотношения менее благоприятны для применения
теории возмущений.
Из выражений F) и G) следует, что ср является циклической коор-
координатой; поэтому соответствующий ей обобщенный импульс
/>Ф = С(9 + фсо5П) = Р9 A1.7.9)
сохраняет постоянное значение (в основной, а не только во вспомо-
вспомогательной задаче).
Составив выражение импульсов
/>Ф= i4^sin» + P9cos»f Ръ = АП, A1.7.10)
найдем
Ра . р,\, —
Функция Гамильтона оказывается равной
2
A1.7.12)
о 2
Мы отбросили в ее выражении постоянное слагаемое -^~. Для вспо-
вспомогательной задачи функция Гамильтона равна
1 Г р\ (Р'Ь — Эсоcos ^J 1
что, как указывалось, соответствует движению регулярной прецессии.
Здесь координата ф также оказывается циклической
Я=--^- = °. P* = h- (И.7.14)
Вектор момента количеств движения тела может быть представлен
в виде
К= А (пМ 4-я'Ф sin fl) -4-С/3 (ср-+-фсо5 Я),
где п, п\ /3—как обычно, «полуподвижный триэдр» единичных
векторов линии узлов, перпендикуляра к ней в экваториальной пло-
плоскости и оси Gz, a
а)„ —(V, av=^sinO, оK = ср —|— ф cos О-
— проекции вектора угловой скорости на эти направления. По (9),.
A1) и A4) получаем
h — h cos 8
'< 2% Ь'зР9. (П.7.15)
11.7] ВРАЩЕНИЕ СПУТНИКА ЗЕМЛИ ВОКРУГ ЦЕНТРА ИНЕРЦИИ 589
Поскольку момент внешних сил относительно центра инерции равен
нулю (т°=0), вектор К остается неизменным по величине и напра-
направлению. Это следует из теоремы об изменении момента количеств
движения. Не ссылаясь на эту теорему, а используя только канони-
канонические уравнения движения A1), A4) и остающееся уравнение
можно проверить сказанное непосредственным дифференцированием
выражения A5) вектора К- Для этого напомним, что вектор угловой
скорости «полуподвижного» триэдра единичных векторов п, п', /3
равен
о>0 = пЬ + л'ф sin 0 + /3Ф cos 0 =
1/ Рь — рф cos 0- р6 —Derosa \
= -Апръ + п! Р* \ Из -и cos») A1.7 17)
А \ ™ ' sin Ь ' 6 sin2 0 / v 7
и, следовательно,
Pdj— Pep cos ^ / COS ^ \
0 /х Л sin 0 \ sin О V
Находим
A1.7.18)
A1.7.19)
в чем убеждаемся подстановкой значений (И), A6) производных fl
и р$, а также выражений производных единичных векторов. Заметим
еще, что из A5) следует
h-*=% e3-K=%. A1.7.20)
причем первое из этих равенств показывает, что ось Gz тела сохра-
сохраняет постоянный угол с неизменным направлением вектора /f. Поэтому,
направив на минуту вектор е3 вдоль К и обозначив при таком выборе
неподвижной оси эйлеровы углы ф, 0, ср соответственно через ЧГ, 9, Ф,
получим по B0)
A1.7.21)
590 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
а по (И) и (9)
* — A sin* е0 ~ Л ' ф — С ^ cos и0 — лс Д cos w0.
A1.7.22)
Первое выражение представляет угловую скорость оси Gz в движении
регулярной прецессии вокруг неизменного направления вектора Л\
второе — угловую скорость собственного вращения тела в этом дви-
движении.
Пусть k обозначает единичный вектор направления К. Вектор
конечного поворота 6 оси тела /3 за время t из начального положе-
положения ее /з по определению C.1.12) равен
0 = 2fttg-^ = 2fttg-g-, A1.7.23)
и по формуле Родрига C.1.11) получим
«з= ЙЧ ЦтГ I tg \k X ЙЧ-2 tg2 f-ft X (ft X ЙI. A1.7.24)
1+tg2^- J
По A5), учитывая, что К—неизменный вектор, имеем
где р^ — начальное значение (в момент ^ = 0) импульса /?#, а нуликом
обозначены начальные значения прочих величин. Проделав вычисление,
получим
/3 = $ cos W -f /fe X й sin ¥ + A — cos ¥) ftft • il
или
A.(l—cos\F)J. A1.7.26)
С помощью этого соотношения легко теперь получить выражения
эйлеровых углов 0, ф при регулярной прецессии в функции времени
(угла W) и начальных значений этих углов, что является нашей целью.
Для этого достаточно спроектировать вектор /3 на оси неизменного
направления. Вспомнив формулы
. e1 = sin ft sin ф, /3 • e2 = — sin Л cos ф, i3 • ^3 = cos Л,
^1==со5ф0, ^ • ex = —
e2 = cos ф0 cos Q"o$ л° • e3 = 0,
= cos фп, nf0 -e}= — sin <k cos Лп; w° • e9 = sin <
11.7] ВРАЩЕНИЕ СПУТНИКА ЗЕМЛИ ВОКРУГ ЦЕНТРА ИНЕРЦИИ 591
придем после элементарных преобразований к выражениям
.. A1.7.27)
sinF /t3,, рф cos
sin f> sin q>:=sin »0 sin ф0cos ^H—[
1 — COS W _ /_ Эф —PcbCOSi „
A1.7.28)
sin & cos ф = sin ft0 cos ф0 cos ¥ -f-
sin ЧУ / В 8 cos Ол \
H jt- ( -^r sin Фо -f- p{> cos fH cos <b0) 4-
l-cosV. , . p.-P. сое». , (n
Первую из этих формул можно получить интегрированием выражения
интеграла энергии, вторую и третью — интегрированием выражения A1)
угловой скорости ф. Приведенный вывод, основывающийся на простых
формулах регулярной прецессии и на преобразовании координат,
конечно, значительно более прост и отвечает существу дела. Напо-
Напомним еще, что
Присоединим к формулам B7) — B9) соотношения
] A1.7.31)
второе из которых получено дифференцированием выражения B7).
Мы получили обобщенные координаты и импульсы в движении регу-
регулярной прецессии, выраженные через время и начальные значения
переменных, т. е. интеграл Коши вспомогательной системы канониче-
канонических уравнений. Поэтому уравнения возмущенного движения для вели-
величин Ра, рф, ft0, ф0 будут каноническими. По A1.2.3) и A2) эти
уравнения будут
с- __ д\\ • ^11 а dll a _ <Ш m ~2\
Мы не будем заниматься этими уравнениями, а остановимся на дру-
другом способе расчета. Начнем с рассмотрения величины главного мо-
момента количеств движения в исходной, а не во вспомогательной задаче.
По формулам A2) и A5), причем в последней надо заменить р^ на/?ф
(этот импульс не постоянен теперь), имеем
^2 _ 3^2 ^- А (С — A) sin2 & sin2 (ф — а) A1.7.33)
592 ТЕОРИЯ ВОЗМУЩЕНИЙ |ГЛ II
и, поскольку имеется интеграл энергии,
2КК =2К-к= — Ъп2А (С — А)—^- sin2 ft sin2 (ф — с). A1.7.34)
Канонические уравнения исходной задачи можно записать в виде
Рь = (А>)о — Ж = <Л>)о — 3 -^ (С — Л) sin ft cos ft sin2 (ф — a),
A1.7.35)
причем (p&H определяется по A6). Уравнения A1), равно как и фор-
формулы дифференцирования A8), после замены C^ на р^ сохраняют
вид. Поэтому, вычисляя производную вектора К, получим вместо A9)
выражение
К = — Злг2 ^ (С — A) sin ft sin (ф—a) [n cos 0 sin (ф—a) -+-п' cos (ф — a)],
A1.7.36)
так как результат остальных дифференцирований по A9) тождественно
равен нулю. Получаем
-(С— Л) cos» sin ft sin (ф — a) sin a,
п2 % (С — A) cos ft sin ft sin (ф — a) cos a,
К • e3 = — 3/г2 ^ (C — A) sin2 ft sin (ф — a) cos (ф — a).
e2 =
A1.7.37)
Далее мы ограничиваемся рассмотрением только вековых возму-
возмущений движения регулярной прецессии, т. е. слагаемых, величина
которых монотонно нарастает с течением времени. Периодические
возмущения не учитываются. Заметим, что правые части уравнений C7)
содержат две группы периодичностей — по аргументу а с периодом
обращения спутника по орбите и по аргументу ЧР* с периодом пре-
прецессии оси спутника; по условию, последний меньше первого. Не
учитывая ни долгопериодических, ни короткопериодических возмуще-
возмущений, следует правые части упомянутых уравнений осреднить по обоим
аргументам а и W. Придем к соотношениям вида
2тс 2тс
К.ех = 1~% З/г2 (С—A) f ^ sin ado j sin ft cos ft sin (ф—a) dW. A1.7.
о
38)
Чтобы получить более точную картину возмущенного движения, сле-
следует учесть долгопериодические колебания, ограничившись осредне-
11.71
ВРАЩЕНИЕ СПУТНИКА ЗЕМЛИ ВОКРУГ ЦЕНТРА ИНЕРЦИИ
593
нием лишь переменной W и пренебрегая при таком осреднении изме-
изменением величин, зависящих от а, — #пи в течение периода перемен-
переменной W не изменяются значительно.
Величина вектора К сохраняет постоянное значение уже при таком
осреднении, что следует из соотношения C4). Осредняя его правую
часть по переменной W, получим
2КК = — Ъп2А(C—A)^fdw£-tja sin2 ft sin2(ф — о) =
Т = 2*
А (С — A) fj sin2 ft sin2 (ф — а) ~ = О, A1.7.39)
так как sin ф sin ft и cos ф sin ft no B8) и B9) — периодические функ-
функции W.
Переходим к вычислению интегралов вида C8). При осреднении
по переменной а следует по A0.15.20) заменить -у значением
~= A_^2K О +^cosaK. A1.7.40)
Больших затруднений в интегрирование это не вносит, но осложняет
запись формул; поэтому дальнейшее вычисление проводится для кру-
круговой орбиты (£ = 0). В задаче о спутнике это не повлечет суще-
существенной количественной ошибки, так как эксцентриситеты существую-
существующих спутников малы. После осреднения по а получаем
Кех = —
cosft sin ft cos
27t
, = — -т- (С — A) / cos ft sin ft sir
4тс J
о
A1.7.41)
К -ez = — ^2(C — A) J sin2 fl dW j sin 2 (ф — a) da = 0. A1.7.
42)
Проекция вектора К на нормаль еъ к плоскости круговой орбиты
оказывается не имеющей вековых возмущений. Остается в соотноше-
соотношениях D1) заменить выражения под знаком интеграла их выражениями
B7) — B9); при вычислении интеграла следует, конечно, считать
38 Зак. 2072. А. И. Лурье
594
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
постоянными входящие в эти выражения величины (Зф, р&, fr0, ф0, яв-
являющиеся медленно меняющимися функциями времени. Имеем
cos
/ ft ft \ г ft ft
f> sin ft cos ф = cos2 W (cos fl0 jrj-J sin i>0cos ф0 -)- -^~ sin ф0
PT (Pt — Рф cos *o)
)
cos
sin «ft, -
- p, cos fl0 cos
cos Ф
причем слагаемые, которые после интегрирования по W дадут нуль,
не выписаны.
Проделав интегрирование и последующие упрощения, получим
, — Рф cos
A1.7.43)
и аналогично
Эти соотношения легко представить в более отчетливой форме. По B5)
находим
Pep — Рф COS
sin
Pep Рф COS ^о
A1.7.44)
Поэтому, учитывая B0) и обозначая через в0, Хо постоянные углы
вектора К с осью спутника и с перпендикуляром к плоскости орбиты
(при регулярной прецессии), через г0 — постоянную угловую скорость
собственного вращения тела, определяемую по формуле (9), получим.
К *е\ = — "Г" ~Т7- cos в0 A — 3 cos2 90)
е2,
A1.7.45)
Эти соотношения показывают, что вектор момента количеств движе-
движения К вращается с угловой скоростью, определяемой вектором
(И.7.46)
направленным параллельно нормали еъ к плоскости траектории *).
Этот результат указан в цитированной выше работе В. В. Белецкого.
11.8] УРАВНЕНИЯ ВОЗМУЩЕННОГО КЕПЛЕРОВА ДВИЖЕНИЯ 595
Спутник совершает регулярную прецессию вокруг прецессирую-
щего с угловой скоростью Q вектора К, сохраняющего постоян-
постоянную величину. Эффект возмущения регулярной прецессии объясняется
лесферичностью (Л Ф С) эллипсоида инерции спутника.
11.8. Уравнения возмущенного кеплерова движения
Кеплерово движение — движение материальной точки в поле
центральной силы ньютонова притяжения
FQ = -£er A1.8.1)
— рассмотрено в п. 10.15. Одной из основных задач небесной меха-
механики является вычисление возмущений кеплерова движения, вызывае-
вызываемых действием на точку малых по сравнению с Fo добавочных сил.
К их числу принадлежит, например, задача о возмущении движения
Луны, вызываемом притяжением Солнца, являющаяся частным случаем
знаменитой задачи трех тел. Движение искусственного спутника воз-
возмущается силой сопротивления атмосферы и добавочной силой притя-
притяжения, объясняемой несферичностью Земли.
Обратимся к выводу уравнений возмущенного кеплерова движе-
движения *). Исходим из выражений вектора-радиуса г и вектора скорости v
планеты A0.15.21) и A0.15.24) в невозмущенном движении. Переходя
в этих формулах от эксцентрической аномалии w к истинной ср
•с помощью соотношений A0.15.18), .получим выражения
а п е2\ / Т[ ]
г = егГ-г —, v = J/ — Г —\ег е sin cp-i-f? A Л-е cos cp)],
г 1 +£cos о у а лГ\_п2 1 Т Y ' <Р v > тл>
v e A1.8.2)
первое из которых хорошо известно; е —единичный вектор перпенди-
перпендикуляра к вектор-радиусу г, направленный в сторону возрастания ср
и расположенный в плоскости невозмущенной орбиты — соприкасаю-
соприкасающейся плоскости «оскулирующей» орбиты. Векторное произведение
ers/Ke(? обозначается через е3. Триэдр ег е?, е3 получается поворо-
поворотом вокруг ez на угол ср триэдра ev e2, е^ (ех — направление
из притягивающего центра на перигей невозмущенной орбиты);
ориентация осей последнего по отношению к неподвижным осям, как
*) Вывод уравнений возмущенного кеплерова движения, основывающийся
на изящном вычислении скобок Лагранжа для эллиптических элементов
орбиты, дан в десятой главе первого тома курса небесной механики Тиссе-
рана (см. сноску на стр. 586). Геометрические построения, проследить за
которыми нелегко, использованы в выводах А. Н. Крылова «Sur la variation
des elements des orbites elliptiques de planetes» A915, Собрание трудов, 6,
стр. 249—266) и Г. Н. Дубошина (сноска на стр. 563). Приводимый здесь
вывод опубликован в заметке автора «Уравнения возмущенного движения
в задаче Кеплера» (Прикладная математика и механика, 23, № 2, стр.
412—413, 1959).
38*
596 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
указывалось в п. 10.15, задается эйлеровыми углами Д, /, и>—
долготой восходящего узла, наклоном плоскости орбиты и углом
линии узлов с направлением на перигей.
Следуя идее метода вариации постоянных, сохраним для векто-
векторов г и v в возмущенном движении те же выражения B), что и
в невозмущенном движении, считая теперь эллиптические элементы
A0.15.22) не постоянными, а искомыми функциями времени. Они
должны быть определены так, чтобы дифференцирование по времени г
приводило к указанному выражению V, а дифференцирование послед-
последнего давало вектор ускорения, определяемый геометрической суммой
сил притяжения Fo и возмущающей силы F.
Пусть со обозначает вектор угловой скорости триэдра ev е2, е%;
тогда вектор угловой скорости триэдра еп е , ег будет со + ^зТ- По
известным формулам дифференцирования единичных векторов B.7.5)
получим
е9 = <^з —(<°з + ?)*г. } A1.8.3)
е3 = (со -Ьejp) X еъ = ">/г — шге9. ]
Здесь wr, со , оK определяются по формулам B.9.3), выражающим
проекции со через производные эйлеровых углов
i . dl , л ■ • . ^
tor = (Oj COS Cp —1— 0L>2 Sin cp = — COS U-\~ hi Sin I Sin U, '
) = — oI sin cp -+- ^2cos ? = — ^7 sin w~b A sin icos w»
K = Ш + Д C0S ''t
A1.8.4)
причем
a = <D-f-cp A1.8.5)
— угол вектор-радиуса г с направлением на восходящий узел.
В невозмущенном движении триэдр £r, e , £3 имеет угловую ско-
скорость #3?°» конечно, отличную от составляющей е3у вектора угловой
скорости этого триэдра в возмущенном движении. Формулы C) в не-
невозмущенном движении поэтому получают вид
Дифференцируя выражение B) вектора г, получаем по сказанному
•п а(\—е2) . а A-е2) -п .
<p4 +^^ CS
11.8] УРАВНЕНИЯ ВОЗМУЩЕННОГО КЕПЛЕРОВА ДВИЖЕНИЯ 597
причем два первых слагаемых представляют значение г° производной,
вычисляемое для невозмущенного движения. Они, конечно, дают зна-
значение вектора V, определяемое формулой B). Нетрудно проверить
это, заменив ср° ег0 значением
определяемым по A0.15.3) и A0.15.14) или непосредственно по тео-
теореме площадей. Добавочные слагаемые в формуле G) должны, по
сказанному выше, давать нуль; нулями должны быть коэффициенты
при ег, е^ ег. Это приводит к первой группе уравнений возмущен-
возмущенного движения
«\р = — -77™п uJr &Z sin i cos и = 0, A1.8.9)
ср = 9° — < = <Р° — ("> 4- U cos 0. С11.8.10)
о)^ sin ср + YZrjF Bе + cos ср + е2 cos ср) — -^- (\-\-e cos cp)=O, A1.8.11)
причем в записи уравнения A1) использовано значение ср — ср° из
уравнения A0).
Переходим к дифференцированию вектора v. Используя F) и (8),
составим сначала выражение v°—производной v в невозмущенном
движении
= 'f° у ^ y-j—^ \ere cos -f — eve sin ср + е^е sin ср— er (\+e cos ц,)\ =
-у^=ег = -^ег = Р0, A1.8.12)
как и следовало ожидать. Остается составить равенство
i* + F^ + F,e,. A1.8.13)
Замечая еще, что вследствие (9) и A0) выражение вектора
принимает вид
w+^ = Vr + ?4 A1.8.14)
находим теперь
■598 теория возмущений [гл. 11
и вторая группа уравнений возмущенного движения будет
Hi • /~~п \Г\ г*
г dt ' и r fx 1 + ^ cos cp ^ v '
sin cp — ~ e sin cp — (d3* cos9 = j/~- V\ — e2 /%. A 1.8.18)
e sin cp (d3* cos9 = j/
Из уравнений (9) и A6) получаем
dl ,/~дГ У\ —е2
1/ ^
F.cos и, О sin £=1/ —fn /% sin 0,A1.8.19)
3 ° г р 1 + е cos cp 6 v 7
=^ F.cos и, О sin £=1/ fn
1 + ^ cos ср 3 ° г р. 1 + е cos cp
из A1), A7) и A8)
COS Ср
, A1.8.21)
■ш Га У*1—^2 / г- i 2 + £ cos ср „ . \ л о ОГ|Ч
(о-=|/ — —Fr cos cp -f- —-f- ^-/7(osincp). A1.8.22)
3 rjx ^ V г ^^'l+^COScp^P T/ v 7
Шестое уравнение возмущенного движения для времени прохож-
прохождения t0 через перигей будет получено в п. 11.9. Вывод его основан
на соотношении A0). Последнее, если учесть значение Д, даваемое
вторым уравнением A9), а также формулы D), E) и (8), преобра-
преобразуется к виду
i_0+ecoS,y WtinuwO—Y. AL8.23)
а а A __ ^2yV, fx A+^cos 'f K v '
Используя это выражение, перейдем в уравнениях A9) — B2) к не-
независимому переменному и. Получим уравнения возмущенного движе-
движения в виде
w/ Fa cos и dSl. Fosinu
^ = О~ . -^ = Отт-7— г--г. (П.8.24)
du 1+^coscp du A -\-e cos tp) sin / v '
A1.8.25)
^ = G(Frsino+ 1
da \ r ' ' 1 + 0 cos <p
Й ? A1.8.26)
A1.8.27)
Здесь для краткости обозначено
О 1*0-"Г A1.8.28)
Г [х A +^COS cpJ> v
11.9] ВОЗМУЩЕННОЕ ДВИЖЕНИЕ ЦЕНТРА ИНЕРЦИИ СПУТНИКА ЗЕМЛИ 599-
а уравнение B7) получено из B2), B4) и последнего соотношения D).
Приведенный вывод уравнений возмущенного движения, не связан-
связанный с геометрическими построениями, требует проведения естественно-
диктуемых методом вариации постоянных несложных вычислений.
В уравнениях B3) — B8) угол ср определяется по E) как разность
углов и и со. В системе шести уравнений B3) — B8) пять уравнений
B4) — B8), если /%, F?, F3 не зависят явно от времени, отделяются
от уравнения B3); последнее дает выражение времени через пере-
переменную и, после того как уравнения B4) — B8) проинтегрированы.
11.9. Возмущенное движение центра инерции
искусственного спутника Земли
Мы ограничимся рассмотрением возмущений кеплерова движения
центра инерции спутника, вызываемых нецентральностью поля притя-
притяжения Земли *).
Потенциальная энергия добавочной силы притяжения, обусловлен-
обусловленной сжатием геоида, по E.5.6) при 03 = С и Ql = в2 = Л опре-
определяется формулой
Ц_ ** С~Л (t2 I TJ2 ОГ2Ч 3 С-А /1 С2\
Начало системы осей О£т]С взято в центре Земли, ось (% перпенди-
перпендикулярна плоскости экватора. Заменив С — Л по формуле E.6.23),
получим
U{^rt) A1.9.1)
где s = 0,00164 — постоянная теории фигуры Земли. Малость этой,
величины обусловливает медленность изменения элементов орбиты.
Величины, пропорциональные s2 в выражении A), не учтены и не учи-
учитываются в последующем рассмотрении.
*) Влиянию сопротивления атмосферы посвящена работа Д. Е. Охоцим-
ского, Т. М. Энеева, Г. П. Таратыновой «Определение времени существова-
существования искусственного спутника Земли и исследование вековых возмущений
его орбиты» (Успехи физических наук 63, № 1, 1957, стр. 33—50). В этой же
статье рассмотрены вековые возмущения, вызванные нецентральностью поля
тяготения. В работе Г. П. Таратыновой «О движении искусственного спут-
спутника в нецентральном поле тяготения Земли с учетом сопротивления атмо-
атмосферы» (там же, стр. 50—58) учтено одновременное влияние этих двух факто-
факторов. Средствами, отличными от классической теории возмущений, задача
о влиянии нецентральности поля тяготения на движение спутника трактуется
в работах L. Blitzer, M. Weisfeld, A. Wheelon «Perturbations of a Satellite's
Orbit, due the Earth's Oblateness» (Journal of Applied Physics, 27, № 10, 1956,
p. 1141—1149) и L. Blitzer «Effect of Earth's Oblateness on the Period oi
a Satellite» (Jet Propulsion, April 1957, p. .405—406).
•600 теория возмущений |гл. 11
Имеем
•где k — единичный вектор оси 01. Заметив, что
— = ker= sin 7 sin и, k • е = sin / cos uy k • e3 = cos /, A1.9.3)
•найдем
Fr = — e~r A — 3 sin2 / sin2 и),
F =_e!^sln2/sin2«, } (H.9.4)
'' i I
Fo = — s —-г- sin 2/ sin и. г
3 r4 j
Величина Г оказывается равной
f1 — | _j 2s f 1 —I в cos cc} sin2 и (\ 1 9 5}
Она понадобится ниже, а при составлении уравнений возмущенного
движения (8.24) — (8.27) можно принять Г=1. Подставив в них
выражения сил D), придем к системе уравнений
^■ = — Ц- sin 2/A -\-е cos cp) sin 2at A1.9.6)
A1.9.7)
4- sin2 / sin 2u (e +-2 coscp-f-^cos2cp)(l -f-^coscp)], A1.9.8)
--— = — Sj [A — 3 sin2// sin2/) sin cp A -\- e cos cpJ -f-
-+- sin2 / sin 2u(\+e cos cpK], A1.9.9)
~p~ == — [A — 3 sin2 и sin2 /)A -\- e cos cpJ cos cp —
— sin2 / sin 2u sin cp B -f- £ cos cp) A ~\-e cos cp) -f-
4-2^ sin2 и cos2/A -r-^coscf)]. A1.9.10)
Здесь обозначено
*1 = «„„1*^- A1.9.11)
Ограничиваясь лишь определением вековых возмущений, мы заме-
.ним правые части этих уравнений их средними значениями за один
sin2
11.9] ВОЗМУЩЕННОЕ ДВИЖЕНИЕ ЦЕНТРА ИНЕРЦИИ СПУТНИКА ЗЕМЛИ 60!
оборот спутника, т. е. за промежуток изменения @, 2к) переменной и. *
При осереднении элементы а, ел /, со эллиптической орбиты счи-
считаются постоянными, а угол ср следует заменить его значением и— со.
Рассмотрим, например, процесс осереднения величины в квадратных,
скобках в выражении (8). Переписываем ее в виде
у sin2/4~-o" cos2# sin2/) sin <p —|— ^ sin2cp—(- — £2(sin cp-f-sin 3<p) -(-
in2 i sin 2u [-| e + (^e2 + 2) cos cp -f-1 e cos 2<p -f- -^- cos 3cp] =
= у e sin2 / (cos 2и sin 2cp + sin 2u cos 2cp) -f- . . .
. . . — -^- ^ sin2i sin Da — 2со)„+ . . „
Точками обозначены слагаемые, среднее значение которых, как сразу-
видно, равно нулю. Подобное вычисление дает
i^^O, -£- = 0, -£- = 0. A1.9.12>
du da da v r
Таким образом, эллиптические элементы а, е, i лишены вековых
(пропорциональных и) слагаемых; они представляют периодические
функции и. Отличными от нуля оказываются средние значения
производных
dS)j da I
^ = _eicos/, ^--^s^l-Scos2/). A1.9.13)
Восходящий узел и угол направления на перигей с линией узлов-
за N оборотов спутника изменяются на величины
£lN= — гтге^ cos /, aN = — ттДГе1 A—5 cos2 i). A1.9.14)
Значительно сложнее вычисление изменения шестого эллиптического
элемента — времени прохождения перигея. Заметим сначала, что соот-
соотношение A0.15.17), дающее выражение истинной аномалии ср через
эксцентрическую w, является интегралом уравнений невозмущенного
движения, содержащим три постоянные е, а, /0 — две последние,
входят через уравнение Кеплера A0.15.16). Поэтому, согласно
островной идее метода вариации постоянных, * форма интеграла
A0.15.17) сохраняется в возмущенном движении при непостоянных:
Имея это в виду и дифференцируя по времени уравнения A0.15.17)
и A0.15.16), получим^
Ф = T/ Г — e2 ~Л г- -Л ~ , w = -л , A1.9.1 э)
т у 1 — е cos w ' 1 — е2 ' 1 — е cos w '
где C = /i(/ —/q).
'602 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
Исключив из них до и заменив cos до и sin до по формулам A0.15.18),
получим
С A-I-£ cos срJ . е sin ср /Ск . ч /л л п , _ч
ср = —2—L _rz_ ^ т. B -L. е cos ср). A1.9.16)
Но по (8.23)
Z O + ^osy)» Г г_ 4«1
и подстановка в A6) дает
Правая часть этого уравнения с помощью E), A0) и (8) приводится
i< виду
лв] ^ ,f™S2V [A — 3 sin2 и sin2 /) Bе — cos ср — е cos2 ср) -|-
+ sin2 / sin 2u sin ср B + е cos ср)]. A1.9.19)
Выражение в левой части при использовании соотношения B3)
ю уравнения Кеплера преобразуется так:
Замечая еще, что
±^ = _ 3 rfa A1.9.21)
n da 2a du K '
« заменив дои sin до их значениями A0.15.17), A0.15.18), придем
к следующему дифференциальному уравнению:
Ж = /^^2 arct£ VlTT ^ f + /2 OP). A1 -9-22)
в котором
Ji (?) = tEV A +^ coscpJ [(l — |-sin2 / -(-у cos 2u sin2 /) e
sin
4_ (i 4. * cos cp) sin2 / sin 2wJ, A1.9.23)
—COScp A _^2)_^(
sin2 / sin 2u sin cp [2 + e2-\- e cos cp A -+- 2^2)l|. A1.9.24)
11.9] ВОЗМУЩЕННОЕ ДВИЖЕНИЕ ЦЕНТРА ИНЕРЦИИ СПУТНИКА ЗЕМЛИ 603
Среднее значение функции /2(<р) за период обращения спутника легка
вычисляется:
2т:
^- / /2 (ср) rfcp = _
sin^ / cos 2«>] .
A1.9.25)
Функция Д (ср) представляется тригонометрической суммой
А (?) = T=
sin
cos
1.9.26)
Свободный член, как и в первом соотношении A2), отсутствует.
Коэффициенты при косинусах, как увидим далее, не будут приме-
применяться в дальнейшем вычислении (если ограничиться рассмотрением
вековых членов). Коэффициенты при синусах оказываются равными
я =(l _ 3 sin2 Л е2-\-[\ +4 *2) sin2 / cos 2<о,
3 5
а4 = у е2 sin2 / cos 2ш, аь = -rg- еъ sin2 i cos 2a>.
Теперь, замечая, что
(U.9.27)
-f- e cos 6 '
и используя известное преобразование последовательности интегри-
интегрирования, имеем
1 г /—j——
о- / (аЛ sin &ср -f- £Л cos ft-f) 2 arctgl/ -j—— tg -2- rfcp =
2tc
Sin
I i/* liji I t /» • t i
ЛЛ l/"i 2" / C0S т ^т 1 I ^fe l/l 2~ I Sln ^T " .
Л I 2% J \ -\- #cos ^ I A J I -{- e cos 6
L 0 J 0
604 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
Интегралы
Jk~2^J T+J~i
cos ф
о
с помощью подстановки ^ = а преобразуются к виду
/ 2 £ °kdz 2
/ = £ &
k 2тл J ез2 + 2а + е~~ 2ш е J (а — о,) (з — о2)'
где интегрирование ведется по единичному кругу; через о, и о2
обозначены корни трехчлена в знаменателе
о, = -11 —
причем | Oj | < 1 и |о2| > 1. По теореме Коши получаем
2of (i_/i_^2)^
^ (ai — а2>
с)то — вещественное число; поэтому
2*
2я J l+^cos'>~^ ^ fco/fe -I/-1 ^2 ' 2tz J l+£cos<!> —
о г о
XI 1.9.28)
По B2) и B5) приходим к уравнению, определяющему вековое изме-
изменение времени прохождения через перигей
dt0 __ 3s, у ak\ k
^1 ], (П.9.29)
— ^
где ak определяются по формулам B7). Ограничиваясь при вычисле,-
пии членами первой степени относительно е% найдем *):
п ^ = — е, A + Зе) A — 3 sin2 a> sin2 /). A1.9.30)
*) Эта формула указывается в статье И. М. Яцунского «О влиянии гео-
геофизических факторов ча движение- спутника» (Успехи физических наук 63,
№ 1, 1^7, стр. 59—7i>.
11 10] УРАВНЕНИЯ В ВАРИАЦИЯХ 605
11.10. Уравнения в вариациях
Дифференциальные уравнения возмущенного движения B.4), полу-
получаемые методом вариации постоянных, вполне точны. Когда вспомо-
вспомогательная задача (для функции Гамильтона Ио) отличается от исход-
исходной малыми слагаемыми, то новые переменные в этих дифферен-
дифференциальных уравнениях — они были постоянными во вспомогательной
задаче — представляют медленно изменяющиеся функции времени,
вследствие чего оказываются применимыми приемы приближенного
интегрирования. В противоположность этому, излагаемый далее спо-
способ рассмотрения возмущенного движения основывается на составле-
составлении приближенных дифференциальных уравнений относительно пред-
предполагаемо малых отклонений (вариаций) возмущенного движения от
заданного невозмущенного движения. При учете лишь первых степе-
степеней этих отклонений задача сводится к рассмотрению системы линей-
линейных дифференциальных уравнений, называемой системой в вариа-
вариациях. Интегрирование ее облегчается возможностью непосредствен-
непосредственного написания некоторых частных решений в числе, равном числу
произвольных постоянных в решении задачи о невозмущенном дви-
движении, отклонения от которого рассматриваются*).
Рассматривается система дифференциальных уравнений первого
порядка
qs = Qstei я„) (s=i я). (п.10.1)
Предположение, что t не входит явно в выражения правых частей
этих уравнений, существенно.
Пусть известно некоторое частное решение системы A), содер-
содержащее k ^ п независимых постоянных
?, = /,(< —'о. С, Ck) (s=l и). A1.10.2)
называемое далее невозмущенным движением. Начальные значения
переменных qs в невозмущенном движении обозначаются через /£:
при t = tQ qs = fs = fs(pt Clt .... Ck). A1.10.3)
Различие возмущенного и невозмущенного движений обусловливается,
во-первых, изменениями начальных условий, во-вторых, изменениями
самих дифференциальных уравнений — вносятся дополнительные сла-
слагаемые в правые части уравнений A). О близости в том или ином
смысле этих движений можно говорить, конечно, только в предпо-
предположении малости тех и других изменений. Например, зная движе-
движение снаряда на невращающейся Земле и некоторые расчетные
*) Метод сведения задачи о возмущенном движении к рассмотрению
решений, бесконечно близких к известному решению системы дифференци-
дифференциальных уравнений, развит Пуанкаре в применении к задаче трех тел.
606 теория возмущений [гл. И
начальные условия, можно говорить о возмущенном движении его при
учете вращения Земли и при малых отличиях начальных данных ог
расчетных. Теория возмущенного движения должна, например, ука-
указать способ внесения поправок в выражение дальности, полученное
из решения задачи о невозмущенном движении. Но нельзя ожидать,
что эта теория даст удовлетворительные результаты при учете силы
сопротивления воздуха, когда невозмущенное движение определено
в пустоте.
Итак, наряду с системой A), введем в рассмотрение систему
дифференциальных уравнений
7, = <?,(?! qJ+v-Qsti Яп> 0 (*=1 «)• (п.10.4>
где {х — малый параметр. Возмущенным движением назовем решение
этой системы, удовлетворяющее начальным условиям:
при t = tQ qs = f°s+x». A1.10.5)
где f°s — начальные данные C) невозмущенного движения, а х®— ма»
лые величины, называемые начальными возмущениями.
Вместо qs введем новые переменные — возмущения xs — с помощыо
формул
Qs = fs(t-to> С,. .... Ck) + xs (s=l, ..., п). A1.10.6)
Дифференциальные уравнения D) переписываются в виде
/,+*,=Q*(A+*i /«+*я)+1*ф,СЛ + *1 /«+*«; 0.
A1.10.7)
Но, по условию, функции fs являются решениями системы A), т. е.
fs^Qsifi /«). (И.10.8)
так что
Л/1 + *1, .... fn + xn) (s=U .....л). A1.10.9)
Эта система дифференциальных уравнений совместно с начальным»
условиями
при t = t0 xs = x°s A1.10.10)
определяет возмущенное движение. Конечно, это — лишь другая
запись задачи D) — E); следующий шаг состоит в том, чтобы, исполь-
используя предполагаемую малость возмущений, хотя бы на ограниченном
промежутке времени
'о<*<'о+^ A1.10.11)
заменить точные уравнения (9) их разложениями в ряды по степеням xs*
11.10] УРАВНЕНИЯ В ВАРИАЦИЯХ 607
Тогда придем к системе уравнений
A1.10.12)
где нуликом указывается, что в рассматриваемые величины должны
быть подставлены выражения B) переменных qs в невозмущенном
движении, а в состав функций Rs входят как члены более высокой
степени, чем первая, относительно возмущений xs, так и линейное
относительно них слагаемое
A1Л0ЛЗ)
г=1
Поскольку оно умножается на малый параметр [i, его можно счи-
считать малой величиной более высокого порядка, чем явно выписанные
в уравнениях A2) члены. Приходим в первом приближении к рас-
рассмотрению системы линейных неоднородных уравнений
/i. •••• /„;') (s=i п) (ii.io.i4)
с коэффициентами, зависящими от времени, называемой уравнениями
в вариациях.
Возможность вышеприведенных построений обосновывается теоре-
теоремой о непрерывной зависимости решений системы дифференциальных
уравнений от входящих в них параметров и от начальных данных:
пусть дана система дифференциальных уравнений
gs = QsDv •••• я» '; 1*1 tv> (*=1' •••• *)• (ii.io.i5)
Бравые части которых непрерывны относительно всех входящих в них
.аргументов qr, tt \ъ( и допускают непрерывные частные производные
по этим аргументам в некоторой области D. Тогда интегралы этой
системы, принимающие значения q°s при t = tQt сами являются непре-
непрерывными функциями tQt q°s, {x/ и имеют непрерывные частные произ-
производные по tQt q°s, (а. в достаточно малой области 8 *).
Содержание теоремы надо понимать так: пусть
4,(t.to,f\ /0; ,*0, .... ^ (s=i п) (Ц.10.16)
— решение системы дифференциальных уравнений A5) при фиксиро-
*) Э. Г у р с а, Курс математического анализа 3, часть I. ГТТИ, 1933,
стр. 9—28; В. В. Степанов, Курс дифференциальных уравнений, ГИТТЛ,
1945, стр. 255-259 и 285-293.
608 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 1
ванных значениях ц9 параметров \iit принимающее значения qs=f°s при
t = tQ. Тогда, задавшись достаточно малыми положительными числами est
можно определить положительные числа \ и Mt такие, что при
К —/2| < \. |^-^?|<Ч (s=l л; 1=1, ..., р)
A1.10.17)
решение упомянутой системы
qs(t.tn-<fi С«\.---р„) (* = ».••••«) (ii.io.i8)
в некотором промежутке времени A1) будет удовлетворять неравенствам
j^C- *о-«? ^ ^ ^ — ^(^ /0. /о /о;|4о |*5)|<в,
E=1, .... п). A1.10.19)
Важно отметить, что величины тM и N\l% определяемые по наперед
заданным е5, вообще говоря, зависят от Т, Естественно, что они
будут тем меньше, чем больше Т. Если же \ и М1 можно выбрать
так, чтобы неравенства A9) сохранялись при любом сколь угодно
большом t > tQ, то невозмущенное движение A6) будет устойчивым
по Ляпунову *). Существенно, что наличие или отсутствие устойчи-
устойчивости по Ляпунову может быть установлено из рассмотрения уравне-
уравнений в вариациях (исключая так называемые особые случаи).
Вопросы теории устойчивости движения не входят в рамки этой
книги. Мы довольствуемся возможностью рассмотрения возмущенного
движения на конечном интервале времени, подтверждаемой теоремой
о непрерывной зависимости решений от начальных данных и пара-
параметров. С этой точки зрения было бы законно рассмотреть, напри-
например, задачу о движении маятника около положения его неустойчи-
неустойчивого равновесия (верхнего положения). Решение A6) здесь будет
q = 0t д = 09
где q— угол, отсчитываемый от верхнего положения. Можно, задав-
задавшись, например, значениями е=1°, е=\0/сек, определить столь
малые значения начального отклонения q0 и начальной скорости q0,
чтобы в течение промежутка времени Т= 1 час соблюдались нера-
В6НСТВа A9) \q\<*. k|<s
и для таких начальных данных искать решение уравнений возмущен-
возмущенного движения. Конечно, этот пример **) лишь указывает на необхо-
необходимость разумного выбора задач, рассматриваемых методом уравне-
уравнений в вариациях, и иллюстрирует, с другой стороны, фундаменталь-
фундаментальное значение понятия устойчивости по Ляпунову.
*) Ляпунов рассматривал лишь зависимость от начальных данных.
**) И. Г. М а л к и н, Теория устойчивости движения, Гостехиздат, 1952*
стр. 11.
11.11] ОБ ИНТЕГРИРОВАНИИ УРАВНЕНИИ В ВАРИАЦИЯХ 609
11.11. Об интегрировании уравнений в вариациях
Рассмотрим систему линейных однородных уравнений
соответствующую системе уравнений в вариациях A0.14). Следующее
замечание существенно облегчает разыскание частных решений,
а в некоторых случаях и полное интегрирование системы A): частные
производные по каждой из постоянных Ct решения A0.2) системы
уравнений невозмущенного движения A0.1)
т$=-щ (s=l «; 1=\ к). A1.11.2)
а также его производная по времени
Ч?+1) = Д A1.11.3)
являются частными решениями системы линейных однородных урав-
уравнений A).
Для проверки продифференцируем по Сь и по t тождества A0.8).
Получим
dfs = у dQs dfr j V dQs j
L J £ J
dCt —jLi dfr dCt 9
r = l
или, в другой записи,
Пришли к уравнениям A), что и подтверждает сказанное. Заметим,
что при k = п частное решение C) входит в совокупность реше-
решений B), так как его можно получить дифференцированием по посто*
янной tQ, входящей в решение A0.2).
Предположим теперь известным интеграл Коши системы уравнений
невозмущенного движения A0.1)
так что
39 Зак. 2072. А. И. Лурье
610
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
где bis — символ Кронекера. Из соотношений B) получаем теперь
полную систему решений однородной системы A)
(П.П.7)
Они удовлетворяют начальным условиям
образующим единичную матрицу (полагаем to=O). Известно, что
определитель Вронского для системы линейных дифференци-альных
уравнений равен *)
4
Я)
dQ
и, поскольку D@)=l, он отличен от нуля. Решения G) образуют
фундаментальную систему — систему независимых решений с единич-
единичной матрицей начальных условий для однородной системы диффе-
дифференциальных уравнений A). Поэтому
*,= 2*ЭДЛ)(') (*=!.•■•. п) A1.11.10)
представляет ее интеграл Коши.
Интеграл Коши системы линейных уравнений в вариациях A0.14)
/•=1
теперь легко находится методом вариации постоянных. Полагаем
A1.11.12)
причем Ck должны быть определены из системы уравнений
(ii.ii.i3)
Из нее и из (9) следует
/•=1
*) В. В. Степанов, Курс дифференциальных уравнений, стр. 265.
11.12] УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ 611
причем АгА, (/) — алгебраическое дополнение элемента г строки и k
столбца определителя (9). Теперь по A2) получаем интеграл Коши
системы дифференциальных уравнений в вариациях A1)
. A1.11.15)
11.12. Уравнения возмущенного движения материальной точки
Уравнения невозмущенного движения рассматриваются в форме
естественных уравнений (масса принимается равной единице)
5 = /%, — = Fn, 0 = Fb. A1.12.1)
Траекторию С точки Ж в этом движении назовем опорной кри-
кривой; р — радиус кривизны кривой С в точке Ж; т, п, b — единич-
единичные векторы натурального триэдра, о—-дуга, отсчитываемая по
траектории. Через F обозначена сила, действующая на точку в невоз-
невозмущенном движении.
Наряду с невозмущенным рассматривается возмущенное (околь-
(окольное) движение. Его можно трактовать как движение «другого экзем-
экземпляра» Ж* точки, находящейся под действием силы F\ Силы F и F\
Рис. 84.
а также начальные данные движений точек Ж и Ж* мало отличаются
друг от друга; это позволяет рассматривать уравнения окольного
движения в вариациях к опорному (рис. 84).
Положение точки М на опорной кривой определяется вектор-
радиусом /"(о). Пусть нормальная плоскость П опорной кривой, про-
проведенная через Ж*, пересечет эту кривую в точке Мх с вектор-радиусом
39*
612
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
г(о-\-е)\ через xlf nlt bY назовем единичные векторы натурального три-
триэдра опорной кривой в точке A\Y\ проекции вектора Л^Ж*, лежащего
в плоскости /7, на направления пх, Ьх обозначаются v, C. Тогда
#ектор-радиус г* точки М* можно представить в виде
г* = г{р + г)+п? + Ь$. A1.12.2)
Используя формулы Френе B.18.9), получим
и, следовательно, с точностью до квадратов малых величин
+ -£). A1.12.3)
При вычислении векторов скорости и ускорения точки М* ограни-
ограничиваемся членами первого порядка малости. Получаем
A1.12.4)
причем штрихами обозначается дифференцирование по дуге о. Запи-
Записав теперь векторное уравнение движения в виде
получим три дифференциальных уравнения в вариациях
р О р I ^ Р Р I j Р Р* Р /'"II 1 О f^\
X I /2 /2 I Т п т ' ^1 1 i 1^1 *-s J
,. (П.12.6)
A1.12.7)
11.12] УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ 613
В этой записи о и о2 заменены их значениями из уравнений не-
невозмущенного движения A). Как следует из хода вывода, F*, Z7*, F*
обозначают проекции силы Z7*, действующей на точку ЛГ (в воз-
возмущенном движении), на оси натурального триэдра в точке М. На
вычислении этих проекций надо остановиться подробнее.
Из выражения B) вектора г*, определяющего положение точки Ж*,
следует, что величины
0i = o-|-e, <72 = v, <73 = P A1.12.8)
можно рассматривать как криволинейные координаты. Невозмущенное
движение соответствует значениям их ql0 = a, q^^=zq^=zO. Базисные
векторы этой системы координат определяются по формулам (П. 2.4.4).
Получаем
дг\
откуда с помощью формул Френе, отбрасывая слагаемые второго
порядка, находим
p .-.-,■• . О1-12-9)
Эти же формулы можно получить, дифференцируя выражение C)
по г, v, р.
Ковариантные составляющие метрического тензора будут
1 2V Р V
£н—1 р » ^12— т"' ^13 — Т"'
«зз= !•
Они вычислены с учетом членов первого порядка. С этой же точ-
точностью находим по (П. 2.1.11) контравариантные составляющие
614
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
и по ним, пользуясь формулами (П. 2.1.14), векторы сопряженного
базиса
A1.12.10)
Вектор силы F* представляется через его ковариантные соста-
составляющие F*s выражением (П. 2.2.4)
F* = F*/* = F* • r/s. A1.12.11)
В случае потенциальных сил
F*. 5г* = р .уе V = — oil = — -^ 8^.
причем потенциальная энергия II рассматривается как известная функ-
функция криволинейных координат. Получаем
F*—
s—
dqs
A1.12.12)
В невозмущенном движении
и, следовательно,
(дП\ _
где llo = II(<7j, ql> <7^ = П(а, 0, 0) — значение потенциальной энер-
энергии на опорной кривой. Возвращаясь к выражению силы A2), имеем
или, учитывая A3),
dql
an
an
da
dp
"
A1.12.14)
11.12] УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ 615
Теперь по A-3) и A0) получаем
_(_
dq*\T
dq1
an
dq2
dq* T
~ dq2 T dq*~T n
r(dm\
? \ d$2 H'
A1.12.15)
Эти выражения надо подставить в правые части уравнений E) — G) *).
Таким образом, составление уравнений в вариациях требует знания
сил на опорной траектории и значений вторых производных на ней
потенциальной энергии
д2П\
W~)
\ /
дЧ1
Jo' V д?2 H •
Рассмотрим еще случай силы сопротивления, зависящей от ско-
скорости,
/* = — /&*)**. A1.12.16)
Здесь по D)
V = о -4- е
1 * . /•£<: Ва \ 1
В невозмущенном движении
A1.12.17)
= 0. A1.12.18)
Заметив еще, что
*) Уравнения этого вида рассматривал Г. А. Гринберг в задаче о фоку-
фокусировке электронных пучков. См. Г. А. Гринберг, Избранные вопросы
математической теории электрических и магнитных явлений, Изд-во АН СССР,
1948; стр. 507—535.
616
получим
ТЕОРИЯ ВОЗМУЩЕНИЙ
- /\ = — /' О
F* — ^(°) Л*, I £а _ РС\
[гл. 11
A1.12.19)
11.13. Возмущенное кеплерово движение по круговой орбите
В поле центральной силы
^= —Ф(г>7 A1.13.1)
материальная точка может при некоторых начальных условиях совер-
совершать движение по круговой орбите. На этой орбите
и, следовательно,
A1.13.2)
A1.13.3)
Второе уравнение показывает, что скорость точки в этом движе-
движении сохраняет постоянную величину, равную, согласно первому урав-
уравнению
У A1.13.4)
Таким образом, круговое движение осуществляется, если точке сооб-
сообщена начальная скорость, перпендикулярна'я вектор-радиусу и опре-
определяемая по величине равенством D). В возмущенном движении
вектор-радиус точки г* задается выражением A2.3), в котором теперь,
надо принять р = г, Т=оо. Получаем
-Щ. A1.13.5)
Потенциальная энергия центрального поля в возмущенном движении,
равна
г*
A1.13.6),
Требуется найти значения на опорной (круговой) орбите вторых про-
производных этого выражения, входящих в формулы A2.15). Для этого>
1.13] ВОЗМУЩЕННОЕ КЕПЛЕРОВО ДВИЖЕНИЕ ПО КРУГОВОЙ ОРБИТЕ 617
заметим, что
Поэтому
-^1 -
д? ~ г*
A1.13.7)
Уравнения в вариациях A2.5), если учесть A2.15), C) и G),
теперь представятся в виде
;+Ш{3 = 0.
A1.13.8)
В частности, в задаче о возмущении круговой орбиты спутника Земли
■£.
и уравнения (8) принимают вид
V2
г2
1 = 0
или
Здесь введена новая независимая переменная
A1.13.9)
= 0. A1.13.10)
A1.13.11)
618
ТЕОРИЯ ВОЗМУЩЕНИЙ
[гл. 11
—угол поворота вектор-радиуса, который условимся отсчитывать
от восходящего узла круговой орбиты. Решение системы уравне-
уравнений (9) будет
*L = з Bv0 - e£) + 2 Bs; - 3vQ) cos и + 2v^ sin «.
v = 4v0_2s; + Bs;-3v0)cosW + v;sin^,
A1.13.12)
Первое из них определяет возмущение орбитальной скорости, второе
и третье — радиальное и нормальное (к плоскости опорной орбиты)
отклонения.
При учете нецентральности поля тяготения, создаваемого сжатием
геоида, надо внести в правые части уравнений (9) силы, определяе-
определяемые выражениями (9.4); при этом, как говорилось в п. 11.10, доста-
достаточно рассмотреть их значения на опорной траектории:
sin2 / sin 2u,
Фл = a-^- (l — -| sin2 / +J- sin2 / cos 2«) »
= — а —~ sin 2/ sin u.
A1.13.13)
I
Здесь / — угол плоскости орбиты -с плоскостью земного экватора;
через а обозначен малый параметр — постоянная фигуры Земли, ранее
обозначенная s.
Измеряя отклонения от круговой орбиты в долях земного радиуса,
обозначая
и переходя снова к независимой переменной и, получаем систему
уравнений
du2
f — 2 -jl- = — аг sin2 / sin 2u,
^252
-^- —382 = ai(l—
sin2
■!*! sin2/ sin 2u,
+ ьз = — ai sin 2i sin u.
A1.13.15)
Возмущенное движение представляет наложение движения A2),
определяющего эффект начальных возмущений, на движение, обу-
обусловленное действием возмущающих сил. В плоскости опорной орбиты
эти силы имеют постоянную составляющую и составляющие с частотой^
11.13] ВОЗМУЩЕННОЕ КЕПЛЕРОВО ДВИЖЕНИЕ ПО КРУГОВОЙ ОРБИТЕ 619
вдвое большей частоты обращения спутника на невозмущенной
орбите. Возмущающая сила, перпендикулярная плоскости орбиты,
имеет частоту обращения спут-
спутника на орбите— здесь имеются
условия резонанса.
Рис. 85.
Рис. 86.
Решение системы уравнений A4) при нулевых начальных данных
имеет вид
5Х = 2аа A — -г- sin2 пи — A ~- sin2 / ] sin и -J- -~г sin2 / sin 2и\,
Ь2 = — ctj Г^1 — у sin2 Л cos и — -!г sin2 / cos 2u — 1 +у sin2 /1,
83 = -н- otj sin 2/ (й cos w — sin w).
A1.13.16)
Вектор-радиус точки в возмущенном движении определяется равен-
равенством 1
•следующим из B) и A4) и A2.3). Соответствующий единичный век-
вектор е* будет р
е* = — " + ~г (*с8, -+- 683). A1.13.18)
Пусть w, /wlf ^ обозначают единичные векторы линии узлов для
невозмущенной орбиты, перпендикуляра к ней в плоскости экватора
и перпендикуляра к этой плоскости. Тогда (рис. 85 и 86)
т = — т sin и + cos и (ml cos / -(- & sin /),
я = —mcosu — sin «(/Wj cos/-(-ft sin/), }• A1.13.19)
b = — m1 sin / -f- ft cos /
620 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
и выражение е* принимает вид:
е\=т(cos и ± Ьх sin u\ +
+ ml (cos / sin и + -^г Si cos / cos и — ^f- Ьг sin Л +
+ k (sin / sin a + -^- ^ cos a sin / -|—^°- 83 cos Л . A1.13.20)
По условию, при и = 0 спутник проходит через восходящий узел;
значение аргумента и, соответствующее следующему прохождению
восходящего узла, обозначим через 2тг —|— ф, где Ф — мало. В этом
положении косинус угла 6 — дополнения до широты — равен нулю:
R R
cos б = ё\ • & — sin i sin u-\ 8j cos и sin i-\
Отсюда получаем
и далее
Выражение ё*т при этом значении а будет
^* r=n m -\- 2ътх < -т^— cos / + (—-) а cos /12 ^ sin2 /) — sin2 / cos / >
или
42 a cos/. A1.13.22)
Обозначая через у угловое перемещение узла за один оборот спут-
спутника, получаем
(|) DJi. A1.13.23)
Это в точности совпадает с формулой (9.14) при е — 0.
Введем в рассмотрение переменную х, определив ее равенством
A1.13.24)
Из сказанного следует, что cos 0, являясь периодической функ-
функцией и с периодом 2т: -f- ф, будет относительно переменной х иметь
период 2тг. Обращаясь к B0), получим
cos 0 = е*г • k = sin / (sin х -\- -^ cos xj + -^- (82 cos w sin / -f- o3 cos i)p
11.13] ВОЗМУЩЕННОЕ КЕПЛЕРОВО ДВИЖЕНИЕ ПО КРУГОВОЙ ОРБИТЕ 621
причем в последнем слагаемом, пренебрегая малыми второго порядка,
следует заменить и на х. Пользуясь формулами B1), и A6), находим
( /?2 Г / 2 \
cos 6 = sin /sin л; 1 ^ а B—^ sin2 /J cos x —
— -g- cos2 x sin2 / + cos2 /11. A1.13.25)
Имеем также, обозначая через X долготу спутника,
sin 6 cos X == е*г • т — cos х — -^- sin х Ьг (х) sin jc,
sin
s\n\ = e*' m1 = cos / (sin x -)- -|^- cos д:) -f-
n
Ч [^i (x) cos jc cos / — S3 (jc) sin /]
или, использовав указанные формулы,
sin 6cosX =
f г 2 "I]
—ro<s *! 1 -I a jc to- irns2 / -J sin2 jc -pr sin2 / sin2 jc (
Г2 Ь ' COS X 6
sin б sin X =
—cos / sin jc 1 la \x ctg JC-f-( 2— ^ sin2 / jcos x—^sin2 / cos2 jc—sin2 / |
A1.13.26)
и, следовательно,
[ ^2 Г
c j 1 — ~ a j
^ 2 —-g-sin»/ n 1!
\g X = cos / tg jc j 1 — ~ a jc (ctg jc+tg jc cos2 04 —— -g- sin2 / .
A1.13.27)
Теперь выразим переменную jc через время t. Долгота X не входит
в выражение потенциальной энергии возмущающих сил. Поэтому
в возмущенном движении имеет место интеграл момента количеств
движения относительно оси ОС:
Но в начальный момент возмущения 8lf 82, Ьг и их производные равны
нулю, так что постоянную рх можно вычислить для движения по
круговой орбите со скоростью v:
h = (r X w) • k = — rv (n X O • ft = rv cos /.
Итак,
\= rvcosi A1.13.28)
r2 sin2 6 '
622 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
С другой стороны, дифференцируя выражение B7), получим
I . Г
\
cos2
2 —4sln2/
A -j-sin2 jc) —
Н (l+sin*) ^sin/ .
1 COS JC V ' У 6 J J
Определив отсюда х и заменив X и sin 6 cos X по B8) и B6), а также
учитывая, что по A7)
г*2 = г211 + 2-^-a |~(l —g-sin2 /)cos x—g-sin2 / cos 2x — 1+ysin2 /] j,
A1.13.29)
после вычисления получим весьма простое выражение
jc = y I +TaC—4sin2/)l ' (И.13.30)
Отсюда получаем
r\ ^(|)] A1.13.31)
где t0—момент прохождения через восходящий узел. Следующее
прохождение через восходящий узел (в его новом положении) будет
при х = 2тг. Называя периодом Т этот промежуток времени, получим *)
A1.13.32)
причем 70—период невозмущенного движения по круговой орбите:
11.14. Уравнения возмущенного движения
материальной системы
В п. 7.8 было дано геометрическое истолкование движения си-
системы материальных точек (голономной со стационарными связями),
как движения изображающей точки в римановом многообразии Rn,
определяемом заданием квадрата элемента дуги
A1.14.1)
*) В работе Блитцера, указанной в примечании на стр. 599, дана фор-
формула для периода, отличающаяся от C2).
11.14] УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ СИСТЕМЫ 623
Обобщенные координаты в невозмущенном движении qs предпола-
предполагаются известными функциями времени
qs = qs(t) E=1 я). A1.14.2)
Эти соотношения представляют частное решение дифференциаль-
дифференциальных уравнений движения, которые мы запишем в виде G.8.12):
?я" = Яа = а\ A1.14.3)
выражающем равенство контравариантных составляющих векторов
ускорения изображающей точки и вектора силы. Уравнения B) можно
рассматривать как параметрические уравнения траектории изображаю-
изображающей точки — опорной траектории. Единичный вектор касательной т
к траектории определяется контравариантными составляющими
dq« 1 .
* = -fc=jq: (П.14.4)
В возмущенном движении обобщенные координаты обозначаются через
q*-\-xa, причем возмущения ха можно рассматривать как контрава-
риантные составляющие вектора возмущения р
? = х*га, A1.14.5)
где га — базисные векторы.
Уравнения возмущенного движения получим, заменив в C) обоб-
обобщенные координаты qa на qa-\-xa и относя входящие в них величины
(символы Кристоффеля, силы) к этой точке:
Здесь {х — малый параметр, вследствие чего значения добавочных сил,
задаваемых их контравариантными составляющими Фа, рассматриваются
в уравнениях в вариациях в точках опорной траектории. С точностью
до первых степеней возмущений имеем
причем силы предполагаются зависящими от обобщенных координат
и скоростей.
Приходим к системе уравнений в вариациях
A1.14.8)
624 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
которой можно непосредственно пользоваться при рассмотрении от-
отдельных задач. Однако представляет интерес предложенное Синджем *)
преобразование, раскрывающее тензорный характер входящих в урав-
уравнения (8) величин.
В рассмотрение вводятся векторы скорости и ускорения возму-
возмущения. Дифференцируя по правилу (П. 2.6.1) выражение E), получим
A1.14.9)
\ ^pi ) /
и далее
Заменив здесь q$ их значениями из уравнений невозмущенного дви-
движения C), получим
<11Л4Л0>
Коэффициенты при га в выражениях р и р представляют контра-
вариантные составляющие этих векторов; обозначим их через ха и х°-\
Теперь заменим ха и х* в уравнениях (8) через х* и ха. Принци-
Принципиальное значение этого преобразования состоит в том, что здесь
проводится переход к составляющим инвариантных величин —
векторов скорости и ускорения возмущения. Приходим, предполагая
фа~0, а силы Qa зависящими только от координат, к уравнениям
(пл4лз)
*) См. вторую из указанных в сноске на стр. 304 работ Синджа.
11.14] УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ СИСТЕМЫ 625
Выражение
A1.14.14)
представляет ковариантную производную контравариантных составляю-
составляющих вектора силы Q. Далее надо вспомнить определение (П. 2.14.2)
тензора Римана — Кристоффеля
Ы U?J
Уравнения в вариациях теперь записываются в форме
д^а I ГУ''<а />Т v* п^ v°U Г^Р" П ( \ \ \ А \ ал.
X —р- *\уоЗ v -^ v -^ * оЦ: — ^« ^ 1 1.1 т. i Dj
В ковариантных составляющих, используя теорему Риччи (П. 2.5),
получим
I. A1.14.17)
Ковариантные составляющие тензора Римана — Кристоффеля опреде-
определяются формулами (П. 2.14.5). Из них следуют свойства:
1) симметричность относительно пар индексов уЬ и pa
R^ = R^fo> A1.14.18)
2) антисимметричность относительно индексов j и S, р и a
Rfbfo — — ^8у?ср ^y8j>3 =—^-^cp A1.14.19)
3) тождество Риччи
#т83, + ^Та + Я?Т5а = О' (П.14.20)
выражающее свойство циклической симметрии относительно трех
ковариантных индексов.
В случае потенциальных сил уравнения A7) принимают вид
"у 8 *Р
^ ^ ^
о
д211
) т | <Ш\
A1.14.21)
Интеграл энергии, который теперь можно составить, в невозмущен-
невозмущенном движении имеет вид
г в возмущенном
40 Зак. 2072. А. И. Лурье
626 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 1
где Ъ/г — вариация постоянной энергии. В последнем выражении
Здесь использовано представление производных от аа^ через прямые
скобки Кристоффеля, указанное в (П. 2.4). Учитывая теперь A1),
получаем
Т.-Т = 1*. Т;
и соотношение, выражающее вариацию интеграла энергии, приобре-
приобретает вид
aa^ + ^x- = bh. A1.14.22)
11.15. Системы с двумя степенями свободы
Более подробно остановимся на голономних консервативных систе-
системах с двумя и (в следующем параграфе) с тремя степенями свободы.
Обобщение на более сложные системы потребовало бы сообщения
дальнейших сведений из римановой геометрии.
Надо помнить, что исходными данными являются, во-первых,
составляющие метрического тензора а^ и, во-вторых, уравнения
невозмущенного движения A4.2) при д = 2. Базисный вектор га,
имеющий направление касательной к координатной линии, вдоль кото-
которой изменяется параметр qa, уже не является производной по qa при-
принадлежащего многообразию вектора г\ последний может быть опре-
определен лишь в евклидовом многообразии, включающем рассматривае-
рассматриваемое риманово.
По упомянутым данным с помощью формул A4.4) определяется
по его контравариантным составляющим единичный вектор касатель-
касательной т опорной кривой; единичный вектор первой нормали п в рима-
римановой геометрии вводится с помощью первой формулы Френе, пред-
представляющей иную запись уравнения G.5.22)
х = юл, со = ka. A1.15.1)
Здесь k — первая кривизна. Вторую формулу Френе (для п = 2)
п=:—^ A1.15.2)
легко получить, дифференцируя соотношение т»я = 0 и учитывая,
что вектор п имеет направление т (или противоположное), так как
11 15] системы с двумя степенями свободы 627
п.п = 0. Следует заметить, что A) и B) эквивалентны соотношениям
вида
та = (о/га, па =— (ота; та = ата, па — — «>та A1.15.3)
между контравариантными или ковариантными составляющими векто-
векторов т, п и п, т. Здесь звездочка (а отнюдь не точка) подобно A4.11)
определяет операцию вида
^}xV. A1.15.4)
Теперь представим вектор возмущения в виде
p = eT + vtt. A1.15.5)
Тогда по A) и B) получим
р = (S — 0)v) T -f- (v -\- 0)s) Я,
р == (s — 2v(i) — v(i) — soJ) U -f- (v -)- 2so) -[-so) — voJ) я.
Из этих равенств получаем соотношения вида
ё — (ov = р • т = гаха . т°га = ааахат3.
Приходим к четырем формулам
* * •
ааал;ат0 = е — wv, ааохапа = v-f-eo, A1.15.6)
^f'^!""^1' j A1.15.7)
Возвращаясь к уравнениям в вариациях A4.21) и учитывая, что
xS = exS+v^, ^r=axr, A1.15.8)
придем к другой записи этих уравнений
* -f- v^) T^vsna = 0, A1.15.9)
'v _j_ 2eco 4-еш — vco2 + o2/?^?a (exYx8x V + vxT/i8xV) +
+ ;s:6-f-v^)wav5IIa=:O. A1.15.10)
Чтобы в последующем не возвращаться отдельно к случаю я = 3,
займемся рассмотрением инварианта
/С (а, £0 = /?Т53ятта8х1У, A1.15.11)
определяемого двумя выбранными единичными векторами а, с.
628 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 1
Для вычисления этого инварианта введем в рассмотрение тензор
Риччи, — симметричный тензор второго ранга, — определяемый равен-
равенствами
= -^С € кт8?а, A1.15.12)
где £*хт5 — символы Леви — Чивита, вводимые равенствами (П. 2.1.16)—
(П. 2.1.17). Пользуясь их свойствами и учитывая соотношения A4.18)
и A4.19), легко получить формулы
л 11 * /~> ,119 1 /~> л ]3 ^
— у—у #2331'
а
м /?3131' л23~"м
A1.15.13)
Л33 = - '
где, как всегда, |а| = |аар|. В формулах A3)'перечислены все шесть
независимых составляющих тензора Римана — Кристоффеля для /г=3.
При п = 2 имеется, как видно из (П. 2.14.5), лишь одна независимая
составляющая /?Ш2» и в этом случае
R]212
A1.15.14)
В теории поверхностей К представляет гауссову кривизну.
Из соотношений A2) можно получить выражение тензора Римана —
Кристоффеля через тензор Риччи
R^o = exf)€^\ A1.15.15)
Для проверки воспользуемся легко устанавливаемым тождеством
€if£ l=^ro^—o68:r, (П. 15.16)
где Щ — символы Кронекера. Теперь, заменив в A5) тензор Риччи
его значением A2), получим
j <Гхт5еЬре,^Х,™ = |(ь;Ч - ЩШь: - Щ) /?„„„,. (ii.i5.i7)
и чтобы прийти к A5) остается раскрыть скобки и использовать
свойства A4.18), A4.19) тензора Римана — Кристоффеля.
Инвариант A1), подлежащий вычислению, записывается в виде
К (a, c) = Ah^xf^aeix?Jc\
Теперь, сославшись на представление (П. 2.2.7) векторных произве-
произведений
чХа=Р) >zXc = q, A1.15.18)
11.15] СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 629
получаем
К (a, c) = Ahxpxglx. A1.15.19)
Из этой формулы следует, что
К(а, ч) = К(ч, с) = К(т, т) = 0. A1.15.20)
Пусть далее
а = с = п,
где п — единичный вектор нормали кривой. Тогда
К(п, п) = £Чф^ A1.15.21)
где 6 = :XW — единичный вектор, который будем называть второй
нормалью; его ковариантные составляющие равны
&x = €V^3. A1.15.22)
Точно так же
K{bt b) = Ahinxri^ K(n, Ь) = — ^Чуп^ = К(Ь9 п). A1.15.23)
Эти формулы соответствуют п = Ъ. При /1 = 2 в рассмотрение вво-
вводится лишь К(п, п), так как по A9)
К(ч, я) = 0, /С(т, т) = 0. A1.15.24)
Векторы т и п, принадлежащие R2, имеют лишь составляю-
составляющие т1, т2 и соответственно /г1, п2 (напомним, что kna определено
как ковариантная производная та). Поэтому единичный вектор b
(не принадлежащий /?2) имеет лишь единственную составляющую
Ьг = У[а\ {^п2 — т2/г!), A1.15.25)
равную единице — площади квадрата, построенного на единичных
векторах т, п. Итак, при п = 2 по A4) и B1)
К (п. п) = ^1212 2 =К. A1.15.26)
Теперь возвратимся к уравнениям (9) и A0). По B4) и B6) они
приобретают вид:
e(O_vo>* a'v 'f v«- ЯЧ1 - ) AU5>27)
где обозначено
ЛОТТ / _ \ Г\ГТ
A1.15.28)
'630 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
Интеграл энергии по A4.22), E) и F) будет:
о (ё — va>) -f (ex* + v/ie) -ут = bh- A1.15.29)
Заметим теперь, что в невозмущенном (опорном) движении, как сле-
следует из G.5.29),
а= — -|^-та, оо) = — ~п\ A1.15.30)
dq° oq* v '
Пользуясь ими, можно, продифференцировав выражение B9), прийти
к первому уравнению B7); поэтому, имея интеграл энергии, его
можно из рассмотрения исключить. При указанном дифференцирова-
дифференцировании производные та и па по времени определяются с помощью фор-
формул C); точно так же и производная по времени от ковариантной
составляющей силы — -^ в опорном движении вычисляется по пра-
правилу ковариантного дифференцирования.
Используя C0), запишем интеграл энергии в виде
A1.15.31)
Далее, дифференцируя по времени второе уравнение C0) и исполь-
используя первое, найдем:
goo -\--оо) = "з~оГ ^ — ахб/га115а
или
2аа) -f gш = — ат§/гаП5а. A1.15.32)
Ур1внение B7) теперь, если учесть соотношения C1), C2) и A),
получает вид:
v + v (о2К + З^2^2 + пьп°1\,)-\-2kbh = 0. A1.15.33)
Оно содержит лишь v и известные по опорному движению величины.
Задача определения е, по уравнению энергии C1), если предположим,
что v определено, сводится к квадратурам
s = 2g f kvdt + obh Г4^+е0^-, A1.15.34)
J J a2 an
О 0 °
где е0, a0 — значения е и о в момент ^ = 0 сообщения начального
возмущения.
11.16. Системы с тремя степенями свободы
Теперь в рассмотрение вводятся единичные векторы касательной *,
первой нормали п и второй нормали Ь, причем п, как и ранее,
определяется формулой Френе A5.1), а Ь — как векторное произведе-
произведение тХ#. так что *» л, Ь определены в каждой точке /?3 и
11.16]
СИСТЕМЫ С ТРЕМЯ СТЕПЕНЯМИ СВОБОДЫ
63 Г
образуют ортонормированный триэдр. Первую формулу Френе теперь
запишем в виде
T = o)qj^, O)q) = &d)<3, (ll.16.iy
где &(!) — определяемая по G.5.22) и G.5.23) первая кривизна.
Индекс 1 заключен в скобки, так как он указывает номер величины,.
а не ее ковариантный характер. Дифференцируя теперь соотноше-
соотношение п • т = 0, получим
и учитывая, что п»п = 0, можно написать
Здесь введен множитель a)B)J он равен, как следует из B),
П • Ь = С0/Оч.
Теперь, имея в виду, что
и, применив A) и B), получим третью формулу Френе
Через о)B) обозначено произведение &B)<з, причем /гB) называется
второй кривизной кривой в /?3.
С помощью формул Френе A), B), D), представив вектор возму-
возмущения р в виде
р = zi -j- v# -j- p&, A1.16.5).
получим вместо A5.6) и A5.7)
и далее
^ 0 " • о 0J СО СО В
пппхап° = v-4- со/пе — ^го\Р -t- 2convS — 2о)/9,8 —
= p -1- u)B)v + 2<ep>v -f-
\ V»
A1.16.7)
632 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 1
Дифференциальные уравнения A4.21) при обозначениях A5.11)
учитывая соотношения A5.20), запишем в виде
ё _; i)V _ 2u,A); - 0,2 )S -
= 0, A1.16.8)
=0, A1.16.9)
2<V
-\-K(b, 6)p]+(sT" + v«S + ^5)^no8 = 0. A1.16.10)
Интеграл энергии A4.22) будет:
^L(aa^) = 8/?. A1.16.11)
Вместо A5.30) уравнения невозмущенного движения надо записать
в виде
5—£* ;•...=-■&-. »=-f »■■ <it.i6.iso
Дифференцируя по времени второе соотношение, найдем с помощью
формул Фрепе и двух остающихся уравнений A2):
Ц«—2-|^T-a,AL-«»x'aIIe, = 0, A1.16.13)
а из третьего соотношения A2) после ковариантного дифференци-
дифференцирования получим
awu)WB)+£V<;iIa, = 0. A1.16.14)
Соотношения A2) позволяют также записать интеграл энергии A1)
в виде
as — as = 2oa)A)V-j-o^, A1.16.15)
не отличающемся от A5.31).
Теперь, используя A5), A4), A3), можно преобразовать уравне-
уравнения (9) и A0)
v 4" v р/С (Л. Я) + Зо)^ - оJ2) + IISj/lV] +
-f р[о2/С(л, 6) —шB)+П85/гУ] —2a>B)p-f 2АA)8Л===0, A1.16.16)
+ V[/C(/I, 6)a2+wB) + n§^V] + 2a)B)V =0. A1.16.17>
Б эти уравнения величина е не входит; она определяется с помощью
11.17] УСТАНОВИВШИЕСЯ НЕВОЗМУЩЕННЫЕ ДВИЖЕНИЯ 633
квадратуры из интеграла энергии A5) по формуле A5.34). Уравне-
Уравнение (8) из рассмотрения исключается, так как оно может быть полу-
получено дифференцированием выражения A5).
Напомним, что инварианты К (п, п), К F, Ь) — квадратичные
формы па и соответственно Ьа, а К (п, Ь) — билинейная форма этих
величин. Эти формы определяются по A5.21) и A5.23); коэффи-
коэффициенты их представляют составляющие тензора Риччи, вычисляемые
по A5.13).
11.17. Установившиеся невозмущенные движения
Невозмущенное движение, в котором позиционные обобщенные
координаты и циклические обобщенные скорости сохраняют
постоянные значения, называется установившимся.
Если невозмущенное движение — установившееся, то в уравне-
уравнениях A6.16) и A6.17) все коэффициенты постоянны, причем и>B) = О*
Они приобретают вид
3A 0, 1 (Ш7
P + ftP + ^ + 2<oB)v = 0, I
причем
]
Р2 = - WB) + (aH;3+Hfip) №. } (П.17.2)
q =(_^? + Пв?)^я!, J
где А&9—ковариантные составляющие тензора Риччи. Интеграл энер-
энергии A5.34) будет t
^ + -^+в0. A1.17.3)
о
Невозмущенное установившееся движение Синдж, следуя Раусу
и Томпсону и Тэту, называет кинематически устойчивым, если
величина вектора возмущения
A1.17.4)
остается ограниченной при любом t, как бы велико оно ни было.
Частное решение системы однородных уравнений, соо!встствующей
системе A), ищем в виде
v = Neirt, $ = Beirt. A1.17.5)
Получаем систему однородных уравнений
A1.17.Ь)
fK4 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 11
Характеристическое уравнение будет
(Рг - r2) (P2- r2)-q2-A*22)r2 = г4-(Л+р2 + Н}) г2 + pxp2-q2 = 0.
A1.17.7)
Корни этого биквадратного уравнения назовем г2 и г2. При
р}р2— q2 = 0 уравнение G) имеет двукратный нулевой корень и
в решение системы неоднородных уравнений A) входят слагаемые,
пропорциональные t2. Если г2 (или г2\ окажется отрицательным или
комплексным, то одно из значений /г, (или /г2) будет положительным
или иметь положительную вещественную часть; соответствующее
частное решение E) неограниченно возрастает в'месте с t. Поэтому
положительность корней г2 и г2 биквадратного уравнения является
необходимым условием устойчивости в вышеприведенном определении.
Она имеет место при выполнении неравенств
А+р2 + 4аJ2) > 0, (Р] +^ + 40)^J > A{Plp2-q2)> 0. A1.17.8)
Этого было бы достаточно при Ь/г = О для малых возмущений, при
которых полная механическая энергия с точностью до первых степе-
степеней этих возмущений остается неизменной. Тогда свободный член
в уравнениях A), а вместе с ним слагаемое в C), пропорциональное t,
исчезают. Если же ЪНФО, то частное решение системы A) будет:
2kn)bh 2k(l)bh
^^—2" Р2 (П.17.9)
и е останется ограниченным при соблюдении равенства
Частоты колебаний около состояния установившегося движения
будут равны а*! и /*2. Было бы ошибочно считать, что неравенства (8)
сами по себе гарантируют ограниченность v и р, так как уравнения
в вариациях A) выведены в предположении, что е остается огра-
ограниченным.
Аналогичное рассмотрение более простого случая двух степеней
свободы приводит при S^ = 0 к неравенству
р1 = ^ + ЗаJ + П§а/г3^>0, A1.17.11)
представляющему условие устойчивости (по Синджу) установившегося
невозмущенного движения. При Ь/г Ф 0 к этому неравенству присо-
присоединяется равенство
или Ко2 -+-П5а/Лг° — оJ = 0. A1.17.12)
Частота колебаний около состояния установившегося движения равна 2о>.
11.18]
ПРИМЕРЫ
635
11.18. Примеры
1°. Две материальные точки Mv M2 с массами тх и т2 связаны
невесомой нерастяжимой гибкой нитью длиной /. Нить пропущена
в отверстие О в гладком, горизонтальном столе, причем точка Мх
остается на столе, отрезок ОМХ нити натянут, а отрезок ее ОМ2
расположен по вертикали Oz
(рис. 87). г^*М>
Обозначим через г = ОМХ и ср ^^^ff
полярные координаты точки Мх\ па*---* —
тогда кинетическая и потенциаль-
потенциальная энергии системы будут
II = —m2g (/—/*) = w2g/* + const.
A1.18.1)
Составив по ним дифференциаль-
дифференциальные уравнения движения в форме
Лагранжа, получим
(тх -р- пц)г — тхгу>2 = — fticfg,
mxr2y-{-2mxrry — 0. A1.18.2)
Одним из частных решений ее-
устойчивость которого далее рассматривается, будет:
1Z
Рис. 87.
установившимся движением,.
ср =сро= const.
A1.18.3)
В этом движении точка М2 неподвижна, а Мх вращается по кругу
радиуса /*0 с угловой скоростью ср0. Натяжение нити во всех ее
точках равно m2g = mxr0y2.
Заметим, что движение системы можно сопоставить с движением
точки массы т = тх по поверхности конуса с вертикальной осью
(с вершиной О снизу) и с половиной угла раствора а, причем
ctga=|/ ^ A1.18.4)
Действительно, в цилиндрических координатах поверхность конуса
задается уравнением
v z = rctga. A1.18.5)
Поэтому кинетическая и потенциальная энергии точки равны
7 = -j т [г2 A -Ь-ctg2 a) + г2<р21, II = mgz = mxgr ctga = m2gj
и это совпадает с выражениями A), если обозначить 9 = g Л/ —^
°* ° Г 1712
теория возмущений [гл. 11
Далее рассматривается движение изображающей точки в римано-
вом многообразии R2\ ковариантные составляющие метрического
тензора в этом многообразии равны
аи = тг-{-п12, al2 = 0, а22 — тхг2. A1.18.6)
Уравнения невозмущенного установившегося движения A4.2) здесь
имеют вид:
qi = r0, Я2 = 'У. A1.18.7)
Квадрат скорости о2 в этом движении равен
^ A1.18.8)
а контравариантные составляющие единичного вектора касательной
равны
Ti = 0, т2 = ^- = -Ь-. A1.18.9)
UJ a
Этот вектор — единичный, так как согласно (8)
,о 09 О • 0 1
a тЧ? = а(>)т2т2 = т, п -т- = I.
ар 22 1 U _2
Символы Кристоффеля второго рода находим, сравнивая B) с урав-
уравнениями движения в форме A4.3). Отличны от нуля будут лишь
Теперь по формулам A5.3) получаем
и в нашем случае
1 | М ' ?0 т1Г0?0 2 л /1 1 ю их
am1 = { оо > а-^- = г; ат2 = 0. A1.18.11)
I22) а2 (m, +w2)a v 7
Величина со = &з определяется по условию, что « — единичный вектор
Находим
-. / ^1 ! 1 2 п
о) = ■. , =^ = 1/ ср0, /г1 = , /г2 = 0.
ъ\ т\-\- т2 у т\ +т2 У Ш\ -\~ т2
A1.18.12)
Вычисление по формулам A5.26) и (П. 2.14.5) дает АГ = 0—этого
.следовало ожидать, так как гауссова кривизна поверхности конуса
11.18] примеры 637
равна нулю. Остается заметить еще, что и выражение 11^пьп? обра-
обращается также в нуль, так как
п --^5-U l\m -о
пп— дг2 -r\nfW —и*
Уравнение A5.33) приобретает вид
;* Ъ1г = О, A1.18.13)
V^ + т
Устойчивость в смысле Синджа невозмущенного движения возможна
лишь для возмущений, при которых полная энергия системы сохра-
сохраняется Fh = 0), так как равенство A7.12) не соблюдается. Заметим
еще, что в рассматриваемой задаче
2А = 2 G-f II) = (тх -t- m2) г2 + mxr2f + 2w2gr
и, следовательно, поскольку в невозмущенном движении г~0, учи-
учитывая C), получим
2g)or + m}r\^ Ц = тх Bro<pg or + ^Т
где C = т^2^ — главный момент количеств движения системы отно-
относительно оси Oz\ поэтому ЪН обращается в нуль для возмущений,
оставляющих момент количеств движения неизменным. Такое возму-
возмущение можно осуществить, сообщая точкам системы Мх и М2 им-
импульсы, направленные вдоль нити. Невозмущенное движение тогда
в вышеприведенном определении устойчиво.
Переходя к уравнениям A5.33) и A5.34), примем начальные
условия
x* = xl = (bf)Qt Х2 = х1 = {ц^ j
причем, по условию
Надо найти начальные значения величин v, v, e, г. Обратившись
к A5.5), A2) и (9), имеем
* = v/i = — , x = ez = e il
У Mi Л~ т2 а
и, следовательно,
Y Y' A1.18.16)
Далее, по A4.11) и A5.6)
^j^j^x1^ (8 —
638 ТЕОРИЯ ВОЗМУЩЕНИЙ [ГЛ. 1 I
откуда получим
г = Ущг0Ъу, A1.18.17)
что, конечно, легко найти, дифференцируя соотношения A6). Усло-
Условие A5) в связи с A2) теперь дает
so = 2vocd. A1.18.18)
Общее решение уравнений A5.33) и A5.34) записывается в виде:
= v0cos ]/ Ы -f -Д— sin
Л/ Зсо
(ИЛ8.19>
и легко проверяется, что условие A8) выполняется. Возмущения
полярного радиуса 8г и угловой скорости 8ср точки определяются
по A9), A7) и A6):
Ьг = (8гH cos УЗЫ -f- -^— sin У ЗЫ,
-30) ьг - • (П.18.20)
г0 8ср = — 2ср0 (8гH cos ]/Зсо/ -(- —?- sin V^3co/ ==—2ср0 or.
Момент количеств движения системы относительно оси Oz сохраняется,
как отсюда видно, в возмущенном движении в любой момент времени.
Конечно, выражения B0) легко было бы получить непосредственно,
варьируя интеграл энергии (при неизменной с точностью до первых
степеней возмущений полной энергии) и учитывая наличие интеграла
моментов количеств движения в невозмущенном и в возмущенном
движении. Вышеприведенное вычисление имело целью дать иллюстра-
иллюстрацию вычислений, которые надо провести, рассматривая задачу меха-
механики в терминах геометрии Римана.
2J. Рассмотрим задачу об устойчивости регулярной прецессии
тяжелого гироскопа — симметричного тела, вращающегося вокруг
неподвижной точки. Определяя положение системы осей, связанных
с телом эйлеровыми углами 0 = ^, ф = ^2, ср = #3, имеем следующие
выражения кинетической и потенциальной энергии:
Г = -i- [ Л (О2 -|- ф2 sin2 0) -+- С (9 -j- ф cos »J1. II = Q,zc cos 0 A1.18.21)
и, следовательно,
аи = Л, ап = 0,
11.18] примеры 639
Записав уравнения Лагранжа, разрешенные относительно ft, ф, ср,
С — А . С . . Qzn
j2fH + i^= —^- sin &, A1.18.23)
= 0' A1.18.24)
находим из них
{32i} —
A1Л8-26)
В установившемся движении регулярной прецессии угловые ско-
скорости прецессии ф и собственного вращения ср и угол нутации Ь
сохраняют постоянные значения. Полагая ф = ф0> ср —ср0 и 0 = 00,
мы удовлетворим уравнениям B4) и B5), а уравнение B3) определит
соотношение, которое должно связывать эти величины, чтобы регу-
регулярная прецессия осуществлялась:
С — А . С . . Qzr
-A-fo^\ + -J%%=~T-' (П.18.27)
Это уравнение имеет, при условии
(С%J > 4 (А — С) Qzc cos »0, A1.18.28)
два вещественных корня относительно ф0
2 (А-С) cos 90
К + УС9О - 4 (Л - С) Qzc cos ■%], A1.18.29)
определяющих две регулярные прецессии — медленную и быструю.
В возмущенном движении полагаем
Уравнения возмущенного движения запишем в форме A4.8), причем
теперь xl = x, х2 = %, xz = r\. Учитывая, что символы Кристоффеля
зависят только от ^! = 0, находим
= О при а==2'3'
640
ТЕОРИЯ ВОЗМУЩЕНИЙ
[ГЛ. 11
так как необращающиеся в нуль символы Кристоффеля с верхним
индексом 2 или 3 содержат нижний индекс 1, а в невозмущенном
движении ft = q1 = 0.
Получаем следующие уравнения:
cos 2t>o
хcos
— -^гcos а
Здесь учтено, что
Два остающихся уравнения будут
<Ш Qzr
так как а11 = A~
ИЛИ
где а и р — постоянные. Они могут быть выражены через вариа-
вариации SB и 86ф циклических постоянных
дТ
и будут нулями, если предположить, что при сообщении возмущения
моменты количеств движения твердого тела относительно его оси
симметрии и относительно вертикальной оси сохраняют те же значе-
значения, что и в невозмущенном движении. Это будет иметь место при
возмущении импульсом (ударом) в вертикальной плоскости, проходя-
проходящей через ось гироскопа.
Теперь, подставив значения B6) символов Кристоффеля, придем
к системе уравнений
С — А . . С Qzr
2[> + ^
A1.18.30)
Tj-f-X —
11.18] примеры 641
Остается подставить полученные выражения £, т] в первое уравне-
уравнение C0). Тогда, исключив еще с помощью B7) угловую скорость
собственного вращения ср0, придем к дифференциальному уравнению
i'-f<j,2(l — 2{xcos.cH -±-^)х = 0, A1.18.31)
в котором
|i=-4|. A1.18.32)
Возмущенное движение около регулярной прецессии представляет
гармоническое колебание угла нутации с частотой
со = ф0 Vl — 2jxcos 00 + {J-2- (П.18.33)
ГЛАВА 12
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
12.1. Действие по Гамильтону
Исходные положения динамики — аксиомы Ньютона и принцип
Даламбера—позволяют сформулировать законы движения в виде
дифференциальных уравнений движения. Этим, однако, не исчерпы-
исчерпываются возможность и способы количественного познания законов
движения материальных тел. Равноправными оказываются вариацион-
вариационные формулировки, устанавливающие стационарные свойства некото-
некоторых величин и позволяющие полностью заменить упомянутые поло-
положения.
Аналогично мы поступаем в геометрии — средством определения
объекта может явиться задание его дифференциальных свойств, опи-
описываемых соответствующими дифференциальными уравнениями, а мо-
может служить и некоторое вариационное требование. Так, геодезиче-
геодезическая линия определяется как кривая на поверхности, главная нормаль
в точках которой сонаправлена с нормалью поверхности и это не-
немедленно приводит к записи дифференциальных уравнений геодези-
геодезических линий; но последнюю можно полностью определить как кри-
кривую, дающую кратчайшее расстояние между двумя достаточно близкими
точками на поверхности. Требование, чтобы интеграл, определяющий
длину линии на поверхности, имел стационарное значение, является
гариационной формулировкой задачи о геодезических.
В статике при разыскании формы равновесия тяжелой однород-
однородной цепи с закрепленными в двух точках концами (цепной линии)
можно исходить из дифференциальных уравнений этой кривой, полу-
получаемых из рассмотрения сил, действующих на мысленно выделяемый
элемент цепи. Другое определение основано на том, что центр
тяжести искомой кривой должен занимать наинизшее возможное поло-
положение. Такова вариационная формулировка задачи о цепной линии.
Пусть
<7i@ qn(f) A2.1.1)
представляют функции от времени, являющиеся в действительно
происходящем движении обобщенными координатами материальной
12.1] ДЕЙСТВИЕ ПО ГАМИЛЬТОНУ 643
системы, подчиненной голономным, идеальным связям. Активные (за-
(задаваемые) силы потенциальны. Будем говорить, что совокупность
функций A) определяет истинный путь системы, а любая из ос"
допускаемых связями конфигураций, бесконечно близких к истинному
пути
где вариации bqs являются произвольными бесконечно малыми диф-
дифференцируемыми функциями времени, определяет окольный путь.
Через L, как всегда, обозначим кинетический потенциал — раз-
разность кинетической и потенциальной энергий. На истинном пути
L(qx Ч„ дг. ....?я, t) A2.1.3)
представляет некоторую известную функцию времени. Вариация кине-
кинетического потенциала при переходе к одному из ооп окольных путей
равна
Здесь использовано правило «hd = dh>, содержание которого было
пояснено в п. 1.7.
Из всей совокупности мыслимых окольных путей выделим такие,
которые в два фиксированных (но произвольно выбираемых) момента
времени t0 и tx совпадают с истинным путем, так что.
Теперь ьведзм в рассмотрение величину 5, называемую действием
по Гамильтону за промежуток времени (/0, tY) и определяемую вы-
выражением
и
Ldt. A2.1.6)
Размерность действия — произведение энергии на время (кгмсек).
Действие по Гамильтону представляет функционал, определяемый
выбором совокупности п функций времени qs(t)\ на истинном пути 5
принимает вполне определенное числовое значение S^, и тогда вхо-
входящие в подынтегральное выражение функции qs(t) и qs(t) опреде-
определяются как обобщенные координаты и скорости в действительном
движении.
Перейдем к вычислению приращения, которое приобретает дей-
действие 5 при переходе от истинного пути к одному из оол окольных.
Надо в выражение F) подставить значение кинетического потенциала
41*
644 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
на этом окольном пути, т. е., если ограничиться рассмотрением вели-
величин первого порядка относительно bqs и bqs, заменить L на L-\~bL.
Итак, приращение действия, вычисленное в указанном приближе-
приближении,— вариация действия 85 — определяется равенством
= J (L-\-bL)dt = J Ldt-\- С
dt.
Согласно D), получаем
Л п
t 7^1 L dqs dqs
Интегрируя по частям и учитывая наложенное ограничение E) на
выбор окольных путей, имеем
J dqs dqs J dt dqs J dt dqs
s
J dqs dqs
lO O O 0
A2.1.8)
Итак, вариация действия дается выражением
причем использовано обозначение G.1.8) эйлерова оператора.
12.2. Принцип Гамильтона—Остроградского
Обращаясь к выражению A.9) вариации действия, мы можем
теперь вести рассуждение двояким путем. Во-первых, можно, став
на точку зрения соблюдения аксиом Ньютона и принципа Даламбера,
сказать, что qs(t) в истинном движении удовлетворяют уравнениям
Лагранжа
$s(L) = 0 E=1 п) A2.2.1)
и поэтому
bS = O. A2.2.2)
Во-вторых, возможна другая точка зрения — равенство B) выста-
выставляется как самостоятельное требование. Это приводит к формули-
формулировке принципа Гамильтона — Остроградского — признака, устанавли-
устанавливающего некоторое свойство происходящих в действительности дви-
движений и отличающего их от всех мыслимых (допускаемых связями)
движений.
12.2] ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО 645
Если задан функционал вида A.6)
J= /f^iW' •••• ^W. У[(х)9 .... yfn(x), x)dxt
то говорят, что совокупность функций ys(x) сообщает этому функ-
функционалу стационарное значение, если вариация этого функционала,
обусловленная заданием приращений (вариаций) §ys функциям ys(x)
и вычисленная с точностью до величин первого порядка относительно
этих вариаций, — равна нулю.
Таким образом, принцип Гамильтона — Остроградского при-
приобретает следующую формулировку: действие по Гамильтону S
имеет стационарное значение на истинном пути системы, если
к сравнению с ним привлекается многообразие окольных путей,
совпадающих с истинным в начальный и конечный моменты вре-
времени tQ и tv
Мы покажем, что принцип Гамильтона — Остроградского содер-
содержит в себе многократно упомянутые исходные положения динамики,
если установим, что уравнения движения Лагранжа A) являются след-
следствием равенства B). Рассуждение ведется так. В силу независимости
вариаций bqs можно принять за окольный путь такой, в котором
а bqk ф 0. Тогда уравнение B) примет вид
- f' tk(L)bqkdt= f(jL_jLAL\bqkdt = O. A2.2.3)
;•' i \% dt dqk)
Теперь допустим, что величина
dt dqk dqk
лри t = t.¥. Тогда можно определить содержащий момент t^ проме-
промежуток времени (^.0, £#1) такой, что в нем $k(L) сохраняет знак. Но
%qk — произвольная функция времени. Выберем ее так, чтобы она
обращалась в нуль при
'о < **о и ПРИ К\ < fi
11 сохраняла знак в указанном промежутке. Тогда
646 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Выражение под знаком интеграла, по условию, сохраняет знак, и
интеграл не может быть нулем. Пришли к противоречию, а это зна-
значит, что предположенное неравенство D)-не соблюдено. Итак,
и, конечно, приведенное рассуждение пригодно для любого k=\,...
. . ., /г; это и требовалось доказать.
Гамильтон в работах по динамике и оптике, относящихся к сере-
середине тридцатых годов девятнадцатого столетия, сформулировал прин-
принцип стационарного действия для свободной системы материальных
точек и системы точек, подчиненных стационарным связям. Это огра-
ограничение в 1848 г,*) было снято Остроградским, который, не зная ра-
работ Гамильтона, опубликованных в мало распространенных тогда тру-
трудах Ирландской Академии наук, с полной ясностью изложил принцип
в работе о дифференциальных уравнениях изопериметрической задачи,
распространив его и на нестационарные связи.
Приведем еще основанный на принципе Гамильтона — Остроград-
Остроградского вывод канонических уравнений движения. Исходим из равен-
равенства A0.2.9)
]£f 2W,-"- A2.2.5)
Из него следует
^JM-|784 A2-2-6)
.9=1 S=\
Но равенства
W {s=l n)> A2>2J)
т. е. первая группа канонических уравнений, ни с какими положе-
положениями механики не связаны — это лишь форма записи соотношений
между обобщенными скоростями и импульсами. Поэтому
s = \
*) Основоположные классические работы по вариационным принципам
механики собраны в сборнике «Вариационные принципы механики) (под ре-
редакцией Л. С. Полака, Москва, Ф,лзматгиз, 1959). См. в этом сборнике
(стр. 353) письмо М. В. Остроградского к Н. Д. Брашману; в нем принцип
стационарного действия излагается в почти современных терминах.
12.2] ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО 647
Далее, учитывая A.5), имеем
f Ps(bgsydt = psbqs\- f psbqsdt = -j psbqsdt
и, следовательно,
ч . ^-)bqsdt = O. A2.2.9)
5 = 1
Теперь, повторив рассуждение, которое позволило из равенства B)
получить уравнения Лагранжа, приходим ко второй группе канони-
канонических уравнений Гамильтона
ps = —-jL (S=\ /г), A2.2.10)
что и требовалось.
Аналогичный прием применим и к выводу уравнений Эйлера —
Лагранжа (8.1.8). В рассмотрение вводятся с помощью формул A.5.1)
и A.6.12) квазискорости со5 и вариации квазикоординат bns. Тогда,
используя выражение кинетической энергии через квазискорости
D.1.19) и вспомнив определение «производной от функции по квази-
квазикоординате» A.5.17), придем к следующей записи вариации кинети-
кинетического потенциала:
5=1 U"
Заменив здесь 8со5 через (Siu^)" по формуле A.8.3) и учитывая пра-
правило «db = bd», а также свойство A.9.2) трехиндексных символов,
имеем п п
Всо5 = (8тг5)" -|— ^j ^j ^s со 8т: A2.2.11)
/=ir=i r r
и далее
п п Г
дG"-П)
■•]•
5=1 5=1 L ^-1 r=l
Остается проделать интегрирование по частям
и отметить, что вследствие условий A.5) и A.6.12) вариации квази-
квазикоординат обращаются в нуль при t = t0 и t = tl
8ic,(fo) = O, 8ic, (*,) = <) (s=l я). A2.2.12)
648 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Получаем соотношение
f[££g]
/0 5=1 L /=1 Г=1 J
A2.2.13)
откуда вследствие независимости величин Ьт:5 следуют уравнения
движения (8.1.8); к ним надо присоединить соотношения (8.1.9), даю-
дающие выражения обобщенных скоростей ч-ерез квазискорости. Этот
способ позволяет, например, получить уравнения движения свобод-
свободного твердого тела из принципа Гамильтона — Остроградского*).
При наличии непотенциальных сил соотношение, аналогичное прин-
принципу Гамильтона — Остроградского, записывается в виде
Qsbqsdt = Q. A2.2.14)
Но, как следует из ранее сказанного,
/
0 s = \ t0 5 = 1 t0
A2.2.15)
и равенство A4) приводится к виду
.f\iit) <i2-2i6>
5 = 1 0
откуда тотчас же получаем уравнения Лагранжа. Если же ввести
в рассмотрение вариации квазикоординат и представить выражение
элементарной работы в виде E.1.6)
п
VW = ^Psbi:s% A2.2.17)
5 = 1
то, использовав представление A3) вариации действия, придем к диф-
дифференциальным уравнениям движения Эйлера — Лагранжа.
Следует обратить внимание на принципиальное отличие равен-
равенства A4) от предшествующих ему соотношений B) или (9). В по-
последних речь шла о функционале 5 и о разыскании необходимых
*) "Вывод уравнений движения твердого тела, основывающийся на соот-
соотношениях между вариациями проекций угловых скоростей и производными
от проекций вектора бесконечно малого поворота, дан в классических лек-
лекциях Г. Кирхгоффа (G. Kirchhoff, Vorlesungen uber mathematische Phy-
sik, Mechanik; Leipzig, 1876, S. 54—61).
12.3] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ 649
условий стационарности этого функционала; тем самым задача меха-
механики сводилась к задаче вариационного исчисления. В противополож-
противоположность этому в равенстве A4) содержится лишь утверждение об обра-
обращении в нуль величины
Л
i'Wdt= f(bT—bU + b'W)dt, A2.2.18)
но функционала R не существует, так как нет величины, вариация
которой равна b'R. Это — не вариационная формулировка задач!.
Соотношение A3) также не является вариационной записью, так как
в правую часть его входят вариации квазикоординат.
Следует отличать вариационный принцип Гамильтона — Остро-
Остроградского от более общей точки зрения на этот принцип в меха-
механике. Первый, как указывалось, имеет место для систем, подчинен-
подчиненных голономным связям, при действии потенциальных сил. Принцип
Гамильтона — Остроградского в механике имеет более общее значе-
значение. Он применим при наличии непотенциальных сил и, как увидим
ниже, к неголономным системам.
12.3. О характере экстремума действия по Гамильтону
• Известно, что в точках, в которых функция f {хх, ..., хп) при-
принимает стационарное значение, полный дифференциал df равен нулю.
Различение характера этих точек стационарности (минимум, макси-
максимум, отсутствие минимума или максимума) производится по знаку
второго дифференциала d2f, а в исключительных случаях по членам
более высокого порядка. Подобно этому обращение в нуль вариа-
вариации о5 является лишь необходимым условием стационарности дей-
действия по Гамильтону на истинном пути. Установление же характера
экстремума связано с рассмотрением знака второй вариации 825,
причем минимум действия осуществляется при b2S > 0. Ограничиваясь
случаем стационарных связей, сравнительно нетрудно установить на-
наличие минимума действия S при достаточно малом промежутке
времени tx —t0. Для этого составим выражение приращения ДА ки-
кинетического потенциала при переходе к окольному пути, вычислен-
вычисленного с точностью до квадратов вариаций bqs и bqs:
п п
s=\k=l
г^2
650 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 12
Но при стационарных связях кинетическая энергия — квадратичная
форма обобщенных скоростей; поэтому последняя группа слагаемых
может быть представлена в виде
где T(bq) обозначает результат замены в выражении Т обобщенных
скоростей qs их вариациями bqs. Итак,
п п п п
\ yfr] ^п д2 (Т II)
b2L = -л- Л Л $qs oqk-
dqs dqk
Но учитывая, что bqs(to) = Ot имеем
t
dt
где $s — максимум модуля bqs при tQ < t < tv Поэтому при достаточно
малом промежутке времени tx — tQ слагаемое T(bq)9 как превалирую-
превалирующее в выражении A), будет определять его знак:
так как квадратичная форма Т— положительная знакоопределенная.
Итак,
J T(bq)dt>0, A2.3.2)
что и требовалось доказать.
Напомним теперь, что истинный путь в принципе Гамильтона —
Остроградского был определен как движение системы между двумя
наперед заданными ее положениями Ао и А19 определяемыми заданиями
обобщенных координат q°s в момент t = tQ и qls в момент t = ty за
фиксированный промежуток времени. На окольных путях система
в указанные моменты времени проходит через те же упомянутые
положения. Из этого определения следует, что нет основания ни
утверждать, что такой путь существует, ни что он — единственный,
если существует. Действительно, в теории дифференциальных урав-
уравнений устанавливается при оговариваемых там условиях, выполняю-
выполняющихся в задачах механики (хотя могут быть и исключения), един-
единственность и существование решения при заданных начальных условиях
(интеграл Коши).
Разыскание же истинного пути представляет краевую задачу —
надо так определить начальные импульсы (или начальные обобщенные
12.3] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ 651
скорости), чтобы система за назначенный промежуток времени прошла
из начального положения в конечное. Эта задача может иметь одно
решение или ни одного; иметь несколько решений, или даже беско-
бесконечное множество.
Важное значение имеет рассмотрение случая существования между
положениями системы Ао и А} соединяющих их бесконечно близких
истинных путей, проходимых за одно и то же время. Такие два
положения системы называются сопряженными кинетическими фоку-
фокусами. Известный пример представляет движение точки при отсутствии
сил на поверхности сферы. Такое движение происходит по большому
кругу сферы (геодезической линии) с постоянной скоростью. Сопря-
Сопряженными кинетическими фокусами будут положения точки на концах
одного и того же диаметра сферы, так как их можно соединить
бесконечно близкими большими полукругами, прохождение которых
осуществляется за один и тот же промежуток времени при задании
одинаковых по величине скоростей.
Вернемся к неравенству B), соблюдающемуся при достаточно
малых интервалах времени tx — tQ. Назовем t* то значение tv при
котором в первый раз обратится в нуль вторая вариация b2S,
вычисленная по окольному пути А0НАг (рис. 88), пересекающему
Рис. 88.
истинный путь А0ВАг (в моменты t = tQ и t = t*^. Действие на истин-
истинном пути А0ВА} обозначим через 5^; на любом окольном пути, пере-
пересекающем истинный в точках Ао и Av оно отличается от S^ величиной
второго порядка малости; на окольном же пути А0НАг, по условию,
действие равно S^ с точностью до величин второго порядка малости
включительно (так как на нем В25 = 0). Покажем, что этот окольный
путь является истинным. Предположим обратное — путь А0НАг не
истинный; тогда, соединив две достаточно близкие точки его Е и F
истинным путем ERF, по доказанному выше найдем, что действие
на пути ERF меньше, чем на EHF. Поэтому действие на пути AJERFAX
будет меньше, чем на пути AQEHFAV и, следовательно, меньше,
чем S^. Но это противоречит условию, что Аг — первое положение
на истинном пути ABAV в котором вариация b2S на пересекающих
его окольных путях становится нулем.
652 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Итак, положения А и Ах соединены двумя бесконечно близкими,
истинными путями, т. е. являются сопряженными кинетическими фоку-
фокусами. Вместе с тем доказано, что действие есть минимум, если ко-
конечное положение проходится системой ранее того момента, когда
достигается сопряженный рассматриваемому начальному положению
кинетический фокус *).
Пусть А и Ах— сопряженные кинетические фокусы. Рассмотрим,
истинный путь ABAXQ, в котором конечное положение Q (рис. 89)
Рис. 89.
проходится после того, как пройден фокус Av Действие на этом
пути уже не является минимумом. Это следует из возможности по*
строения окольного пути, действие по которому будет меньшим, чем
по истинному ABAXQ. Для доказательства возьмем на ранее по-
построенном истинном пути АНАХ положение N, столь близкое к Q,
чтобы действие по соединяющему эти положения истинному пути NTQ
было минимальным; тогда
Sntq
Поэтому
, q = SABAr -\-$Аг<э = Saha, -\-Saxq =
= Sahn + S/vAt + 5д q > Sahn + Sntq = Sahntq,
т. е. действие на прямом пути оказывается большим, чем на по-
построенном окольном.
Проведенное геометрическое рассмотрение позволило установить
наличие минимума действия по Гамильтону на истинном пути, не
проходящем через сопряженный кинетический фокус, и отсутствие
минимума на пути, его содержащем. Однако оно не дает средств
для разыскания сопряженного данному начальному положению кине-
кинетического фокуса и не решает вопроса о его существовании.
*) Это доказательство, воспроизводящее идею рассуждения Якоби («Лек-
(«Лекции по динамике», стр. 41, ОНТИ, 1936), относящееся к частному случаю
материальной точки на сфере, приведено в книге Уиттекера «Аналитическая
динамика» (стр. 281—283, ОНТИ, 1937).
12.3] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ 653
Перейдем к аналитическому рассмотрению *). Выразив L через
канонические переменные
5=1
s—H^i ?„. Pi Рп)
и заменив при переходе к окольному пути qsi ps на qs-\~bqsi ps-\-bps,
получим
5=1 5=1k=\
A2.3.3)
причем, конечно, вторые производные функции Гамильтона Н вычи-
вычисляются на истинном пути. Для квадратичной формы, входящей
в выражение 82L, примем обозначение
5=1k=l
5 = 1
с помощью которого равенство C) можно записать в виде
5=1 5=1
A2.3.5)
Поэтому, учитывая условия выбора окольных путей
bqs(to) = O, ty,('i) = 0 (s=l я). A2.3.6)
придем к выражению
/
0 5 = 1
Ниже мы вернемся к этому выражению, а сначала рассмотрим
уравнения движений, бесконечно близких к рассматриваемому движению,
*) Д. К. Б о б ы л е в, О начале Гамильтона или Остроградского и о на-
начале наименьшего действия. Приложение к LXI тому Записок Российской
Академии наук, 1889.
654 вариационные принципы механики [гл. 12
т. е. уравнения в вариациях для канонической системы уравнений
ь=ж- ^=~Ш (s=l ">■ A2-3-8)
Составив их, как указывалось в п. 11.10, получим
^ = ^- и*=~ш; {s=l-- ■■'n)' A2-3-9)
где xs и us обозначают вариации координат и импульсов, а 2 — вве-
введенная выше квадратичная форма D). Отметим еще, что для урав-
уравнений Лагранжа, которые можно записать в виде
Ps=-^~> Л = 7^" (*=1. •••.*). A2.3.10)
dqs dqs
система уравнений в вариациях будет:
Здесь F— квадратичная форма, выражение которой имеет вид:
F(xi хп> xv •••• хп) = Y 2j 2u \
+
\ dqs dqk
d2L • , d2L • •
ХХ+хХ
n n
^ T H Y* (uskXsxk + 2*./Л** + Cskxsxk)- 02-3-1 2>
Вторая вариация S2L, как видно из формулы A), представляется
той же формой F от переменных bqk и В^, так что
§2S = I F (bqlf ..., В<7/г> 8gr1 bqn)dt. A2.3.13)
Мы предполагаем известным интеграл Коши системы дифференциаль-
дифференциальных уравнений движения (8)
д*~ЧЛ<7 Г ai> "" a"' и' "" ь\ (s=l, ...,n),\ A2.3.14)
Рз=РбУ—*0* Л1. ••" аЛ' Pi' ••'» P/l) J
причем ak и pft — значения при t — t0 обобщенных координат и им-
импульсов. Тогда, по сказанному в п. 11.11, функции времени
{.т= d(ls ^ ^m= dPs m_ dqs ^m _ dps A2 3 15)
(s, m= 1, . .., п)
12.31
О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ
655
представят систему частных решений линейных уравнений в вари-
вариациях (9).
Поскольку уравнения A4) можно рассматривать как формулы
канонического преобразования переменных (ak, $k) в (qk, pk), может
быть использовано соотношение A0.8.19)
i\ ••• s? il ... ч?
п
i,.... «я. к .
Рп
уП о1
= 1
и, следовательно, решения A5) линейно независимы. Заметим еще,
что, по определению интеграла Коши,
Нам понадобится также равенство A0.7.8) для скобок Лагранжа
Имея решения A5) и пользуясь их свойствами A6), легко запи-
записать интеграл Коши системы уравнений в вариациях:
,= 2
=l п).
A2.3.17)
Вернемся теперь к выражению G) второй вариации действия.
Она обратится в нуль, если будут соблюдены равенства
lb $ (s=1 nl A2-ЗЛ8)
Но это — та же система уравнений в вариациях (9), если сделать
замену xs и us на bqs и bps. Отсюда следует вывод, который ранее
был получен из геометрических соображений, — окольные пути, на
которых b2S делается нулем, принадлежат к числу истинных,
бесконечно близких к истинному пути A4).
Перейдем к вопросу о существовании окольных путей, на кото-
которых §2S=0. Из сказанного ясно, что положительный ответ может быть
дан, если уравнения в вариациях A8) имеют нетривиальные решения.
656
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
При указанной замене, удовлетворяя первой группе условий F), по-
получим по A7)
Ч @ = 2 Um (*„) 1,» (t). bps = £ Um (tQ) «« @ (S = 1,...,«).
ftl—\ TTl = 1
A2.3.19)
Теперь в рассмотрение должен быть введен определитель, играю-
играющий в дальнейшем основную роль,
Ц\ dqx
. *<>) =
4i.-.4?
A2.3.20)
причем А(^о, /0) = 0, как видно из равенств A6).
Обращаясь ко второй группе упомянутых условий, приходим по
A9) к системе линейных однородных уравнений
п
§7s('i)=2«m(g\m('0 = O' (s=l я). A2.3.21)
допускающей относительно неизвестных начальных значений вариаций
импульсов um(t0) отличные от нуля решения, если
А(^, *0) = 0. A2.3.22)
Здесь через tx обозначен ближайший к t0 корень уравнения k(t, to) = O<
При условии B2) неизвестные um(t0) находятся с точностью до по-
постоянного множителя. Этим определяется пучок путей A9), являю-
являющихся истинными и бесконечно близкими к рассматриваемому истин-
истинному пути. На всех этих путях действия по Гамильтону, вычислен-
вычисленные с точностью до малых величин второго порядка включительно,
равны друг другу. Они пересекаются в моменты t0 и tx в сопряжен-
сопряженных кинетических фокусах; положения последних определяются по
формулам A4):
?Л'о) = а5. ^('i) = ?5('i-'o. °Ч' •••■ а*. Pi РЛ) E=1, ..., я).
A2.3.23)
Теперь остается доказать, что при любом t в промежутке (/0, tx)t
когда, по условию, соблюдается неравенство
(tQ<t<tl),
A2.3.24)
действие по Гамильтону имеет минимум на истинном пути. Речь идет
об установлении положительности второй вариации §2S не при доста-
достаточно малом промежутке времени, как было установлено ранее,
а на конечном отрезке времени, определяемом неравенством B4).
12.3] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ 657
Будет доказано, что при условии B4) квадратичная форма F, стоя-
стоящая под знаком интеграла A3), имеет знак формы
п п
UJ'rt^^WX). A2.3.25)
s=l k=l
т. е. остается положительной знакоопределенной *).
Рассмотрение основывается на введении в форму F вместо bqs
новых переменных vs:
п
8^ = ^+2т,г8?г (s=l. ...,«) A2.3.26)
г = \
м внесении под знак интеграла квадратичной формы вида
*8^*- A2-3-27)
представляющей полную производную по времени. Очевидно, что
в силу условий F) это не изменяет величины интеграла A3). Послед-
Последний по A2) примет вид:
r=l
n n n
CskVsVk -h Csk
r=l h=\
br A2.3.28)
м цель заключается в таком выборе функций времени ^sr и \sk, чтобы
это выражение стало равно:
*> п п '.
82S = t/ 2 Sc^^^= fT(v)M>0. A2.3.29)
причем знак равенства по B5) может иметь место только при vs — 0
для всех s=l, ..., п. Поэтому необходимо будет убедиться, что
*) Для п = 2 доказательства приведены в книгах Н. М. Гюнтера «Курс
вариационного исчисления» (стр. 151—161, Гостехиздат, 1941) и Э. Гурса
«Курс математического анализа» (т. III, ч. 2, стр. 248—252, ГТТИ, 1934). Мы
следуем изложению (для любого п), данному в курсе С. Jordan «Cours d'ana-
lyse de l'Ecole Polytechnique» (t. Ill, p. 504—529, Paris, Gauthier — Villars,
1887), значительно упростив его.
42 Зак. 2072. А. И. Лурье
658
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[ГЛ. 12
тогда и все bqs будут нулями, т. е. обращение %2S в нуль возможна
лишь на прямом пути A4). Итак, надо удовлетворить условиям
Я** +■ 2
2
r=l
r=\.h=\
S, k= 1, .... Я),
A2.3.30)
причем вторая группа условий преобразуется с помощью условий
первой группы к виду
2
/1=1
5, ft=l, .... л). A2.3.31)
Матрица коэффициентов Х5А, квадратичной формы B7), конечно, сим»
метрична, тогда как bsk Ф bks. Поэтому к уравнениям C0) надо при-
присоединить еще уравнения
= O (ft. s = l, .... я).
A2.3.32)
Остается теперь показать, во-первых, что полученные уравнения имеют
решение, и, во-вторых, что при vs = 0 все bqs также будут нулями.
Заметим, что при vs = 0 по B6)
=l я).
A2.3.33)
Вернемся к установлению некоторых свойств решений A5) урав-
уравнений в вариациях. Положим
i?=2g,*1?. fi?= —2/^? («. m = l. .... я). A2.3.34)
где gsk, lsk—некоторые функции времени, которые при условии B4)
могут быть найдены из написанных соотношений (для каждого фикси-
фиксированного s). Матрица lsk симметрична. Это проверяется подстановкой
в A0.7.8):
п п / п п
т-\ г=1 '
= 2
'2.3] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ 659
откуда, применив дважды условие B4), получаем
hk = hr (*• r=l n). A2.3.35)
Теперь выясним связь функций gks, lks с коэффициентами дифферен-
дифференциальных уравнений A1). Из первой группы этих уравнений, под-
подставляя в них для любого /я=1, ..., п вместо us и xs частные
решения flm и т|™, имеем
5
П
2 « = 2kW+<^П = 2
1 / 1 1\
/с —
ИЛИ
Снова обратившись к B4), найдем
A2.3.36)
Имеем также из соотношений C4) и второй группы уравнений A1)
»?=-2 (« + ^* 2 г»х) = 2 («,*ч?+*», 2 g,Am) •
Приравняв коэффициенты при т]^ и использовав C6), придем к ра-
равенствам
п п
L + «,* - 2 2 crhgrsghk = 0 (s, k = 1 .....я). A2.3.37)
Сравнивая C6), C7) с уравнениями C0), C2) и C1), находим, что
лоследним можно удовлетворить, приняв
bk = gsk* Kk = *sk (s.k=U..., n). A2.3.38)
Таким образом, с помощью функций времени gsk, Xsk, опреде-
определяемых из уравнений C4), осуществляется линейное преобразование
переменных B6), позволяющее привести выражение второй вариа-
вариации b2S к виду B9). Остается отметить, что уравнения C3), которые
теперь записываются в виде
8ъ=2«,*8?л E=1, ..., я), A2.3.39)
42*
660
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
при условиях F) имеют лишь тривиальное решение. Действительно,
из первой группы равенств C4) следует, что решения этой системы,,
обращающиеся в нуль при t = tQi будут
bqs= 2 СтХ1' A2.3.40)
а из второй группы условий F), при необращении в нуль опреде-
определителя B0), получаем:
= 0 (т=\, .... я).
A2.3.41)
Подведем итог сказанному:
1. Если в промежутке времени [tQ, tx\ определитель B0) не обра-
обращается в нуль (т. е. истинный путь не проходит через кинетический
фокус), то действие по Гамильтону имеет минимум и существует
единственное решение краевой задачи.
2. Если
= 0, то положения Ао и Av проходимые
ф
v
в моменты t0 и tv являются кинетическими фокусами и суще-
существуют другие бесконечно близкие пути, реализующие условие
стационарности действия) краевая задача имеет бесчисленное мно-
множество решений.
В вариационном исчислении условие B4) называется условием
Якоби, а B9) — условием Лежандра. В задачах механики последнее
оказывается требованием положительной знакоопределенности кине-
кинетической энергии и поэтому всегда соблюдается; условие Якоби вы-
выполняется на истинных путях, не проходящих через соответствующий
начальному положению кинетический фокус.
Для разыскания кинетических фокусов можно применить также
следующее простое рассуждение. Не нарушая общности, примем £0 = 0
и ^° = 0. Тогда движение системы определится равенствами
Я, = Ъ('- Р\ Р°п) (s=1 ")• A2,3.42)
где />° — начальные импульсы. Для разыскания истинного пути надо
определил их значения из системы уравнений
Я\=Я$[}УР\ Р°п) (s=l я). A2.3.43)
гдс q\ — обобщенные координаты в положении Av Якобиан
др\
dqn
A2.3.44)
12.3]
О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ
661
будет тождественным нулем при t = О, так как в этот момент урав-
уравнения D2) тождественно удовлетворяются при произвольно задаваемых
импульсах р°.
Задавая начальным импульсам значения p°s-\-%p°s, причем Ьр® —
произвольные бесконечно малые величины, получим
\ п
A2.3.45)
где точками обозначены слагаемые не ниже второго порядка малости
относительно Ър°к. Если окажется, что при непрерывном возрастании t
от t = 0 якобиан D4) при t = tx (отличном от t = to = O) снова ста-
станет нулем, то система уравнений
(s=i
A2-з-4б>
будет иметь отличные от нуля решения относительно bp°k. Тогда па
D5) и D2) получим
^(V />? /„)+••• 02.3.47)
(s=l, .... я).
Итак, если в момент t = tl якобиан D4) становится нулем, то
существуют две системы начальных значений импульсов
сообщение которых по двум бесконечно близким истинным путям — па
пути D2) и по пути
приводит систему в положение .Аг или в отличающееся от нега
малыми величинами не ниже второго порядка. Ах является сопряжен-
сопряженным с начальным положением кинетическим фокусом.
Проверим это на упомянутом выше примере движения материаль-
материальной точки по поверхности сферы при отсутствии сил. Принимая радиус
сферы равным единице и выбирая систему координат так, чтобы
в начальном положении А точка была
на экваторе
= ^- и
назовем \, \ проекции начальной скорости на направ-
направления касательных к меридиану и экватору. Тогда движение
^662 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
точки будет происходить по большому кругу, наклоненному к пло-
плоскости экватора под углом /, причем
о) (о О I 0'
где о) — постоянная по величине скорость точки. Пройденная на боль-
большом круге дуга равна u>t и из сферического треугольника AMQ
(рис. 90) имеем
Ь \
cos ft = °- sin u< sin ft cos X = cos u^, sin ft sin X = — sin Ы,
@ @
так что
д$ 1
sin ft —7- = — (Xjj sin at -\- ft^o)^ cos озЛ,
sin ft —— = ° ° • (— sin at -\- at cos о)Л,
cos2 X
1
cosU dX0 со8 \ ° cos2(
Якобиан D4) оказывается равным
-те
-и обращается в нуль при tx = —, что соответствует положению
\}1 = — и \ = tz, т. е. точке F, диаметрально противоположной Л.
Как второй пример рассмотрим задачу о свободных колебаниях
простейшего вибратора. Движение определяется равенством
q = 0LCOsat +-£■ sinutf, A2.3.48)
где а и р — начальные значения обобщенной координаты и скорости,
о) -- частота колебаний. По D4) имеем
так что кинетический фокус достигается в момент tx = — в положе-
положении qx = — а. Действительно, выражение
q = a cos Ы +- (р + 8р) sin < A2.3.50)
12.3]
О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ
663
где Ъ$—произвольная бесконечно малая величина, является решением
дифференциального уравнения движения вибратора и представляет
прямой путь, бесконечно близкий к прямому пути D8) и пересекаю-
пересекающий его в кинетическом фокусе. Применяя термины вариационного
исчисления, можно сказать, что уравнение E0) представляет пучок
экстремалей, исходящих из
точки qo = a и снова пересе-
пересекающихся в кинетическом фо-
фокусе.
На этом примере проведем
вычисление, подтверждающее
вышеприведенное геометриче-
геометрическое доказательство отсутствия
минимума действия по Гамиль-
Гамильтону на пути, по которому
проходится кинетический фо-
фокус, соответствующий началь-
начальному положению. Пусть конеч-
конечная точка прямого пути D8)про-
D8)проходится в момент t= — -\-T:.
Окольный путь составим из
. двух отрезков: на прямом пути
E0) берем его отрезок, прохо-
проходимый за время т; конец рис gQ
этого отрезка соединим также
прямым путем с конечной точкой заданного прямого пути D8), так"
что эта часть окольного пути должна проходиться за время 2т.
Действие по Гамильтону на ней будет минимально (это требовалось
в упомянутом доказательстве) при 2х < ~ .
Итак, обозначая обобщенную координату на окольном пути через
q* (t), имеем
f
причем q*(t) в указанном промежутке времени задается выраже-
выражением E0). Положения конечных точек пути q*(t) и прямого пути D8)
задаются равенствами
^ (^ ) A2.3.52)
€64 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Функция #* @ является решением дифференциального уравнения
колебаний
q* = Сх cos со/ -f- C2 sin °^'
в котором постоянные Сх и С2 должны быть определены по усло-
условиям E2) и E3). Приходим к системе уравнений
I
С, cos озх — С2 sin озх = a cos сох (В -\- SB) sin cox,
(л)
С, cos сох -4- Со sin сох = а cos сот —i В sin сох,
из которой следует
причем, как сказано, 2шх < тт. Итак,
q\ (t) = (а—^ tg шт) cos Ы + ^ (р + j p) sin
- + x). A2.3.54)
Остается подсчитать действия по Гамильтону на прямом и окольном
путях:
к
— ^ 1
A2.3.55)
С целью облегчить это вычисление, заметим, что действие за проме-
промежуток времени (t0, tx) для гармонического колебания
q = A cos to/ -| Б sin (
равно
сг- sin со (
cos ш
sin
A2.3.56)
12.3]
.О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ГАМИЛЬТОНУ
66S
Пользуясь этой формулой, легко вычислить выражения фд). Получим
82 — a2.
a2oJ) cos сот — 2офиз sin an], S* = S ^j-^- tg an.
Итак 1
о — 5 = -^ (ору tg cox > U, A2.3.57)
что и требовалось доказать.
Составление определителя B0) предполагает знание интеграла
Коши системы дифференциальных уравнений движения. Если же
известно общее решение этой системы, содержащее 2п постоянных,
но не представляющее интеграла Коши
qs = gs(tt cv ..., с2п) E=1 /t), A2.3.58)
то к разысканию кинетических фокусов применимы такие соображе-
соображения: уравнения E8) определяют при фиксированных cv . . ., с2п неко-
некоторый истинный путь Со; значениям ck-\-bck этих постоянных соот-
соответствует совокупность путей С> бесконечно близких к Со и также,
истинных. На этих путях
2/2
Если пути С пересекают Со в моменты t — t0 и t = tv то соответ-
соответствующие конфигурации системы ^°), qW будут сопряженными кине-
кинетическими фокусами. Приходим к однородной системе 2п линейных
уравнений:
2л
2л
г=1
допускающей нетривиальное решение относительно Ьсг при обраще-
обращении в нуль ее определителя
(ддл / dgx \
\0сх )х ' ' ' \дс2п )х
(ПЯл) ( dq» \
\ дс, )х ' ' \ дс2п )г
/дул ^ ^ / dqx \
\дсх /о ' V дс2п /о
/^\ /^я \
V ^^1 /0 ' \ ^2/г /0
= 0.
A2.3.59)
Отсюда находится момент t} прохождения кинетического фокуса,
соответствующего начальному положению системы *).
*) См. упомянутую в ссылке на CTfL 653 работу Д. К. Бобылева.
•666 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ . [ГЛ. 12
12.4. Применение принципа Гамильтона — Остроградского
к неголономным системам
При наличии неголономных связей, задаваемых уравнениями
п
2 *,= О E=1 /), A2.4.1)
2
выбор вариаций bqk, определяющих окольный путь, кроме усло-
условий A.5), должен быть подчинен уравнениям
п
%askbqk = O (s=l, ...,/). A2.4.2)
Эти уравнения определяют мгновенно фиксируемую конфигурацию
системы, допускаемую связями. Если же рассматривается не мгно-
мгновенно фиксируемая конфигурация системы, а ее движение, то на
окольном пути уравнения связей A) должны также соблюдаться
для варьированных значений обобщенных координат; иными словами,
должны иметь место наряду с A) соотношения
-\-as(q1-\-bql, . . ., qn-\-§qn', t) = 0 (s = 1 /). A2.4.3)
Отсюда, учитывая A) и ограничиваясь членами первого порядка
малости, находим
aj ^j if^Qk^Qr + ask^k H~^j ~^~^ЯГ = 0. A2.4.4)
С другой стороны, дифференцируя уравнения B), имеем
&bqr = O. A2.4.5)
^7]
k=lГ=1 L J Г=\
Почленно вычитая соотношения E) из D) и используя правило
d = od», приходим к уравнениям
(s=l I),
A246)
называемым условиями кинематической осуществимости смеж-
смежного движения*). Они выделяют из класса вариаций bqk, подчиненных
*) Н. В. Роз е, Лекции по аналитической механике, ч. I. Издание
Ленинградского университета, 1938, стр. 29—32.
12.4] ПРИМЕНЕНИЕ ПРИНЦИПА ГАМИЛЬТОНА ОСТРОГРАДСКОГО 667
условиям B), накладываемым на допускаемые связями смежные
конфигурации, более узкий класс вариаций, допускающих также
осуществление смежных с истинным движений. Заметим, что при
соблюдении условий интегрируемости
dasr das dasr
(r, ft= 1 л; s= 1 /) A2.4.7)
уравнения F) выполняются автоматически; поэтому для голономных
связей всякая смежная конфигурация осуществима в смежном дви-
движении.
Обратимся теперь к выражающему принцип Гамильтона — Остро-
Остроградского соотношению
f
=0- A2.4.8)
Надо ли требовать, чтобы вариации bqk, определяющие переход
к окольному пути, удовлетворяли, кроме условий B), еще и усло-
условиям F)? На это дается отрицательный ответ, так как формули-
формулировка общего уравнения динамики (см. п. 6.3 и п. 1.6) не содер-
содержит сравнения истинного движения с движениями, допускаемыми
связями, а ограничивается сравнением только двух положений си-
системы — положения ее в совершающемся движении с бесконечно
близким положением, допускаемым связями в тот же момент времени.
Такое же толкование понятия вариаций должно быть принято и при
применении принципа Гамильтона — Остроградского, если считать era
следствием исходных положений динамики.
Вывод уравнений движения неголономных систем из соотноше-
соотношения (8) теперь уже не вызывает сомнений. Можно идти двумя пу-
путями. Или выразить из уравнений B) вариации bqv ..., bqt через
остающиеся независимые вариации 8^+1, ..., %qn, подставить эти
выражения в равенство (8) и получить из него п — / уравнений,
приравняв нулю множители при указанных назависимых вариациях.
Придем, конечно, к уравнениям движения G.10.9). Или использовать-
метод множителей Лагранжа — каждое из уравнений B) умножается
на неопределенный множитель Х5 и сумма этих произведений (рав-
(равная нулю) вносится под знак интеграла (8). Приходим к равенству
A2.4.9)
Далее проводится известное рассуждение: за счет выбора множи-
множителей \ Х^ обращаем в нуль / выражений в прямых скобках;
f668 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ 1ГЛ. 12
остающиеся под знаком интеграла п — / вариаций независимы, и
множители при них также должны быть нулями. Приходим к урав-
уравнениям движения вида G.1.6)
8* (*-) + 2 М** = ° (*=1. •••' л), A2.4.10)
5 = 1
которые следует рассматривать совместно с уравнениями связей A).
При введении квазискоростей ws и представлении уравнений
неголономных связей в виде
*s= 2 *,*?* = <> E=1, ....0 A2.4.11)
условия B), накладываемые на вариации квазикоординат, будут
п
Ч=2*,*8?* = 0 (s=l, ...,/). A2.4.12)
п=\
В равенстве B.13) отпадают слагаемые, в которых индексы s
и t пробегают значения 1, ...,/. Вариации Ъъ8 при 5 = / -f-1, . . ., п'
никакими условиями не связаны, поэтому можно приравнять нулю стоя-
стоящие при них множители; получим уравнения движения вида (8.1.13)
d дТ i V V г дТ дТ д[1 / /II ч /ю л юч
К ним надо присоединить кинематические соотношения
п
?,= 2 »,*«>* E=1. .... л). A2.4.14)
* / 1
Важно заметить, что при составлении выражения кинетической
энергии наличие связей не должно учитываться — в уравнения A3)
входят слагаемые, содержащие -^- и при г= 1, ...,/. Точно так же
было бы ошибочно, учитывая наличие связей A), исключить / обоб-
обобщенных скоростей qv ..., qx из выражения L до того, как про-
проделаны дифференцирования, проводимые при составлении уравнений
движения A0). Этот вопрос был рассмотрен в п. 8. 7.
Интеграл (8), в котором од^ связаны соотношениями B), не яв-
является вариацией некоторого интеграла. То же можно сказать об
интеграле (9). Требование обращения в нуль этого интеграла выра-
выражает, как и в случае системы, в которой действуют непотенциальные
1*2.4] ПРИМЕНЕНИЕ ПРИНЦИПА ГАМИЛЬТОНА ОСТРОГРАДСКОГО 669
силы, принцип Гамильтона — Остроградского, но не вариационный
принцип *).
Возникает вопрос, можно ли принцип Гамильтона—Остро-
градского при наличии неголономных связей трактовать как
связанную задачу вариационного исчисления — изопериметрическую
задачу Лагранжа о разыскании стационарного значения функционала **)
S=JLdt A2.4.15)
при наличии условий A).
При решении задачи Лагранжа в рассмотрение вводится функция
п \
2**1#* + <Ч' A2.4.16)
5=1 " \k=\ I
где \is— неопределенные множители, и составляются уравнения
экстремалей для функционала
A2.4.17)
Надо вычислить вариацию этого интеграла. Имеем
«• A2.4.18)
Второй интеграл справа отпадает, так как внутренние суммы
в силу уравнений связи A) равны нулю. Заметив это и проделав
интегрирование по частям с учетом условий выбора окольных
путей A.5)
U i 1
k=l
л / г п
* dt = — / 2 2 (^а
t0 5=1 L ЛГ = 1
*) Вывод уравнений движения системы, подчиненной неголономным
связям, основанный на этом воззрении, дан О. Гельдером в классической
работе «О принципах Гамильтона и Мопертюи» (Сборник «Вариационные
принципы механики», Физматгиз, 1959, стр. 538—563).
**) Н. М. Г юн тер, Курс вариационного исчисления, стр. 241, Гос-
техиздат, 1941.
670 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
приведем правую часть выражения A8) к виду:
/, / п /\ I Г п
-/22i1^*8**л+/ 2 м 2<**8а**-*
/0 5=1 Л = 1 /0 5 = 1 Lft = l
A2.4.19)
Остается преобразовать выражение под знаком суммы
п
r=i
Оно обращается в нуль, если учесть условия кинематической воз-
возможности окольного движения (б). Обозначив еще \is через \s, при-
приходим к соотношению
8Л = J 8ФЛ= J bLdt— f ^ Ь,2 *А<И =
Снова пришли к равенству (9) и, следовательно, к уравнениям дви-
движения A0). Итак, эти уравнения получаются из рассмотрения свя-
связанной задачи вариационного исчисления при условии, что на искомых
экстремалях учтены условия кинематической осуществимости околь-
окольного движения. Однако такая попытка сохранить вариационную
формулировку принципа Гамильтона—Остроградского, вообще говоря,
не приводит к цели, так как требования кинематической осуществи-
осуществимости смежного движения могут оказаться совместимыми с условиями
B) и уравнениями связей A) только в случае интегрируемости этих
уравнений. Это показывается на простом примере движения матери-
материальной точки при наличии неголономной связи *)
alx + a2y-\-a3z = a*v = 0t A2.4.21)
где функции координат av a2, я3 рассматриваются как проекции
вектора а. Скорость точки должна оставаться перпендикулярной
линиям векторного поля а. Связь будет интегрируемой (голономной)
*) Этот пример рассмотрен в статье О. Гельдера и в «Теоретической
механике» Г. К. Суслова (Гостехиздат, 1944, стр. 362—363).
12.4]
ПРИМЕНЕНИЕ ПРИНЦИПА ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
671
при существовании интегрирующего множителя М (л:, у, z). Тогда
выражение
М {ах dx + a2 dy -f- аъ dz)
будет полным дифференциалом и, следовательно,
rot Ma = М rot a — grad M X # — 0>
и условие интегрируемости (получаемое при исключении М) будет
A2.4.22)
Уравнение F), следуя ходу его вывода, в этом примере можно за-
записать в виде
(v ~j- bv) — а • v — а • (Ьг)' — а • Ьг = v Ьа — а - Ъг = 0.
A2.4.23)
Имеем
дх
где через Va = grada обозначен тензор второго ранга (см. п. 9.8)
с таблицей составляющих*)
dax
дх
дах
ду
dax
dz
да2
дх
да2
ду
да2
dz
4-
da
з
dx
da3
ду
даъ
dz
1
с
с
с
ь
dz
1
2
0
<
9
дах
ду
dz
да2
dx
дх
да
dx
4-
da2
dx
da2
dz
да2
дх
даг
dx
0
da2
dx
9
da2
dz
dy
da3
dv
dac.
dy
I
1
da?
dx
da3
dy
dax
dy
da3
dy
п
da3
dx
dy
dax
dz
da2
dz
, 6ax
1 dz
1 dz
о даъ
~ dz
rlpf n
+ 0.
Через defa (деформация вектора а) и 0 обозначены симметричная
и кососимметричная части тензора Va. Уравнение B3) теперь
*) Н. Е. К о ч и н, Векторное исчисление и начала тензорного исчисле-
исчисления, ГТТИ, 1934, стр. 321.
672 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
записывается в виде
v • la — а • Ьг = (v • def а • Ьг — Ьг • def a • v) +
+ do • 0 • Ьг — or . 0 • v) = 0.
Величина в первой скобке исчезает, так как для всякого симме-
симметричного тензора Q
а . Q . b = Ь • Q • а,
а выражение во второй скобке можно записать в виде
v • 0 • Ьг — Ьг • 0 • v =
= [у X 4 rot а) * Ьг — ( Ьг X тг rot a) . v = v • (rot а X 8/0,
так что условие кинематической осуществимости движения B3) выра-
выразится равенством
*>. (rota X 8г) = 0. A2.4.24)
Уравнение B) в рассматриваемом примере будет:
а-Ьг = 0, A2.4.25)
что позволяет представить Ьг как векторное произведение
Ьг = а X Ь,
причем b — вектор, направлением которого можно распорядиться.
Поэтому, используя уравнение связи B1), можно записать усло-
условие B4) в виде
v • (rot 0Х8/О = v • [rot aX(aX b)] =
= v • ab • rot a — v • ba • rot a = — v • 6a • rot a = 0.
Выбрав вектор 6 не перпендикулярным v, получаем
а • rot a = 0, A2.4.26)
т. е. единовременное выполнение условий B5) и B4) приводит к тре-
требованию интегрируемости связей.
12.5. Уравнения движения распределенных систем
Распределенными системами здесь мы называем материальные си-
системы, конфигурация которых не может быть определена заданием ко-
конечного числа обобщенных координат. Примерами, если ограничиться
одноразмерными телами, могут служить гибкая, нерастяжимая нить,
струна, упругий стержень. Принцип Гамильтона — Остроградского
12.5]
УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
673
представляет наиболее простой и естественней способ составле-
составления уравнений движения таких систем. Теперь это будут уравнения
в частных производных по двум независимым переменным — вре-
времени t и непрерывно изменяющейся по протя-
протяжению тела (нити, стержня) координаты, за-
задающей положение точки (поперечного сечения)
на этом теле.
1°. Колебания висящей цепи с гру-
грузом на конце (рис. 91). Рассматривается
гибкая, нерастяжимая, однородная тяжелая цепь
длиной /, конец О которой неподвижен; на
конце N цепь несет точечный груз с массой т.
Положение точки М цепи задается ее абсцис-
абсциссой а = ОМ в положении равновесия. Рассма-
Рассматривая плоские колебания цепи, обозначим через
и, v проекции перемещения точки М на оси Ох
и Оу\ знание этих функций и {а, /), v(a, t) опре-
определяет как движение любой точки цепи (при
фиксированном я), так и форму кривой С', по
которой располагается цепь (при фиксирован-
фиксированном f). Проекции перемещения груза — точки
N— равны u(l, t)y i/(/, f).
Условие нерастяжимости цепи приводит к не-
некоторому соотношению между функциями a, v,
представляющему здесь уравнение связи. Мы
получим его, выразив, что длина da элемента цепи остается неизмен-
неизменной. Положение 1W точки М в момент t определяется ее декарто-
декартовыми координатами
Рис. 91.
= а-\-а(а, t), y = v(a, t).
A2.5.1)
Это — параметрическое уравнение кривой С при фиксированном /.
Дифференциал дуги da этой кривой, по условию, равен da, так что
do = V(dx?
Отсюда находим
Г \ * да ) ~\да )
da.
da
да
= — -Т\\1Г-) + (тН • A2.5.2)
2 IV да / ' V да 1 I v y
Ограничиваясь рассмотрением малых отклонений цепи от вертикали,
будем считать и, v и производные этих функций по а и по t ма-
малыми величинами. Тогда, считая v, v\ v (далее частные производ-
производные по а обозначаются штрихом, а по t — точкой) малыми первого
порядка, следует на основании B) принять, что а, и\ и имеют
43
2072. А. И. Лурье
674 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
второй порядок малости; поэтому, пренебрегая величиной и'2 четвер-
четвертого порядка малости, можно записать уравнение связи B) в виде
и' = — \-vf\ A2.5.3)
Кинетическая энергия системы в таком же приближении равна
=h J\»2
2 da + ±-mv2(l> t), A2.5.4)
о
где р — масса единицы длины цепи. Потенциальная энергия силы
веса дается выражением
П = — £/рл:ц — mgxNt
где хц — координата центра инерции кривой С, xjy — координата
конца, несущего груз; имеем
i it i
/л:ц = (a-\-u)da= / ada-\- I uda = ~Y+ uda, xn=1-\-u(IJ).
0 0 0 0
С помощью уравнения связи исключим и из этих выражений. Учиты-
Учитывая, что и@, t) = 0, имеем
U(l9 t)= I и' (a;t)da = — ~ j' v'2dat
о о
/ I II
/ uda= au\ — / аи' da = — jl v'2 da -+- -^ / avf2 da =
о о 6 6
— a)v'2da.
Итак, откинув несущественную постоянную, найдем
/ / i
11=1 g9 f (I— a)v'2da + jrng f vf2da = \gp j\l+lx-a)v'2dat
5 ° 5 A2.5.5)
где обозначено т
и sx — отношение весов груза и цепи.
12.5] УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ 675
Кинетический потенциал L получает выражение
L = ±?{ J [fr— g(l + ll— a)v'2\da + lp*i!, t)} A2.5.6)
Теперь вариационная задача, к которой приводит принцип Гамиль-
Гамильтона— Остроградского, формулируется так: из всех функций v(a, t)
непрерывных и имеющих непрерывные производные по а и t при
О ^ а ^ / и при t > О, удовлетворяющих краевому условию
v@, 0 = 0, A2.5.7)
определить такую, которая сообщает стационарное значение выраже-
выражению действия
л л ( i
S= fLdt = ±P J' dt{ f [v> — g{l-\-lx— tiv'^da + lftiL t) \
iQ t0 V 6
A2.5.8)
«Истинный путь» здесь определяется искомой функцией v(a, t),
а окольный — функцией v-\-bv(a, t), причем вариация bv{a, t) пред-
представляет произвольно задаваемую при 0 < а ^ / и t0 < t < tx непре-
непрерывную, вместе с (bv)' и (bv)\ функцию, удовлетворяющую условиям
bv(at to)-=O, bv(a, tx) = 0t bv@, 0 = 0. A2.5.9)
Из них первые два выражают условие A.5) выбора окольных путей
в принципе Гамильтона — Остроградского, а последнее является след-
следствием краевого условия G), так как в допускаемых к сравнению
формах кривой С точка а — 0 должна оставаться неподвижной.
Вариация действия равна
U ( I ч
bS=p fdt{ j [v bv — g (/ -f lx— a) vr bvf]da + lxv (/, t)bv(l, t) \
tQ io j
и далее надо с помощью интегрирований по частям избавиться от
производных bv по а и по t. При этом используется правило «rf8 = bd»
для обеих переменных. Получаем, используя (9),
\—a) V Wda = (l + l^—a) vr bv — Jbv^ (l+lx—a) vr da=
° 6
6
= lxv' (/, /) bv (I, I) - f bv A (/ + /, - a) v da
о
43*
676 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
и также
v bv dt = v bv — I zj Si; tf£ — — I z; Sz; dt.
/ ^° / /
Теперь применение принципа Гамильтона — Остроградского приводит
к равенству
U ( I
85= р Jdt\ [[-i + g^
1
— /i [£*'('. O + v(Z,O]8v(Z. O>. A2.5.10)
Поскольку вариация bv, рассматриваемая как функция tt произвольна,
выражение под знаком интеграла по t должно быть нулем. Но bv(a, t)
для 0<а</ равно# как и bv{lyt) — также произвольно задаваемы.
Поэтому должны обращаться порознь в нуль величины в квадратных
скобках как под знаком интеграла по а, так и вне его. Это при-
приводит, во-первых, к дифференциальному уравнению движения цепи
в частных производных
i=g-^\(l + h-a)v;\ A2.5.11)
и, во-вторых, к краевому условию на конце а = /
lAgv'iL ') + £(/. 01 = 0. A2.5.12)
Краевое условие на конце а = 0 выражается равенством G).
Заметим, что при /, = 0, т. е. при отсутствии груза на конце цепи,
условие A2) заменяется требованием конечности v и его производных
по а и по t при а = 1.
Как во всякой задаче механики, должны быть заданы также
начальные условия, определяющие положение и скорость любой точки
системы в начальный момент времени
v(a, 0) = /(a), v(at 0) = g(a). A2.5.13)
Здесь f (а) и g(a) — непрерывные функции от а, конечно, такие,
что /@) = 0, g@) = 0.
Ход решения получившейся краевой задачи, относящейся к теории
дифференциальных уравнений математической физики, вкратце такой.
Функция v(at f) разыскивается в виде суммы частных решений vk(a, t)t
каждое из которых представляет гармоническое колебание (главное
собственное колебание) пока неизвестной частоты ш^:
vk(a, 0 = <l>ft(«HVOS(V + BftsinuV)- A2.5.14)
12.5]
УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
677
Здесь функция Фк(а), определяющая распределение амплитуд рас-
рассматриваемого колебания — его форму, разыскивается как решение
дифференциального уравнения
■f— ФЛ(а) = 0 (* = 1. 2...) A2.5.15)
при краевых условиях
2
Фй@) = 0, ФИО — -^Ф»@ = 0 (*=1. 2...). A2.5.16)
При замене независимой переменной а с помощью подстановки
дифференциальное уравнение A5) приводится к уравнению Бесселя
общее решение которого записывается в виде
где Jo (а) и No (а) — функции Бесселя первого и второго рода. Замечая
еще, что
можем записать краевые условия A6) в виде
где обозначено
A2.5.17)
** = ■
. A2.5.18)
Система уравнений A7) допускает нетривиальное решение относи-
относительно неизвестных Clk, C2k, если обращается в нуль ее определитель.
Приходим к трансцендентному уравнению
A2.5.19)
корни которого (они все простые) определяют по A8) искомые
частоты свободных колебаний. Число этих корней бесконечно.
[
678 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Решение vk(a, t) теперь можно записать в виде
vk (a, t) = /Vo (xk) Jo yxk у 1 — YTT) —
— JQ(xk)No(xk\/ 1 — ) \(Akcosukt-\-Bk s\nukt), A2.5.20)
так что
Постоянные ^4fe и /?£ определяются по начальным условиям A3):
g(a)-
-s^«-i/-^
A2.5.21)
так что речь идет о представлении заданных функций / (а) и g (a)
в виде рядов по формам колебаний Ф^(^).
Решение этого вопроса основывается на свойстве обобщенной
ортогональности системы функций Фк(а), выражающемся равенствами
i
f Фк (а) Фт (a) da + /,ФЛ (/) Фт (/) = 0 {k Ф т). A2.5.22)
о
Действительно, обратившись к дифференциальному уравнению A5),
можем написать
2 1 1
-у /ф* W фт (a)da + f [(/ + lx-a)Ф'к{а)] Фт(a)da = 0.
После двукратного интегрирования по частям и использования (для
функций Фт(а)) уравнения A5) с краевыми условиями A6), получим
{а) da+ l
откуда при т Ф k следует соотношение B2). Для т = k вводится
обозначение
i
Кт= f Ф2m(a)da + llФ2m (/). A2.5.23)
12.5] УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ 679
Теперь, учитывая, что по B2) и B3)
ОО р /
ф*ф-da+zi
) =
J
получаем
1
(ОМ A2.5.24)
и аналогично
и решение v(atf) полностью определено*). Численные расчеты
могут быть выполнены при задании отношения [х весов груза и цепи.
Они значительно упрощаются, когда груз отсутствует, т. е. [л = О
или /j = 0. Тогда
и о обращается в нуль на нижнем конце цепи. Решение уравнения
Бесселя надо теперь взять в виде
так как при сохранении в этом выражении функции Бесселя второго
рода (функции Неймана) решение не оставалось бы конечным при
о = 0. Уравнение частот, получаемое из краевого условия G), будет
. A2.5.26)
Его корни хорошо известны. Первые три корня равны
^ = 2,4048. jc2 = 5,520, хъ = 8,654,
так что
о), = 1,2024 ]/~f , ш2 = 2,760 |/"^- , со3 = 4,327 |/~^ .
Выражения форм колебаний принимают вид
=1. 2..0. A2.5.27)
*) Мы не останавливаемся на обосновании законности проведенных
операций и доказательстве сходимости рядов, представляющих решение.
680 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
Равенства B2) и B3) теперь дают
[гл. 12
J * + *.
так что
^ = 0,269/, ЛГ2 = 0,116/, ЛГ3 = 0,074/.
Решение выражается рядом
v{a, 0 =
k=l
причем по B4)
Я —
A2.5.28)
A2.5.29)
Движение цепи представляет наложение главных колебаний, пред-
представляющих гармонические колебания с частотами со^. Форма &-го
главного колебания задается функцией Фк(а). Эта функция, как
видно из ее выражения B7), имеет, кроме корня а = 0, еще k—1
корней, определяемых равенствами
-2.) (т=1, 2 k—l). A2.5.30)
Это — узловые точки k-Pi формы. Например, вторая форма имеет
один узел
г2*
af)=lll g-j«0,8n.
третья — два узла
= 0,923/,
= 0,595/
и так далее. Первая форма колебаний — безузловая.
2°. Колебания вращающегося упругого стержня.
Эта задача рассмотрена в п. 9.10. Конец О упругого .однородного
стержня постоянного сечения заделан во вращающееся вокруг непо-
неподвижной оси Oz с постоянной угловой скоростью со колесо радиуса R.
Другой конец стержня а = I свободен. Требуется составить, считая
12.5]
УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
681
стержень нерастяжимым и невесомым, дифференциальные уравнения
изгибных колебаний — тангенциальных по оси Оу и аксиальных по
оси ~Oz (рис. 92) *).
Обозначая через и вектор перемещения точки М стержня, через и,
v, w — его проекции на оси вращающейся системы Oxyz, имеем
Рис. 92.
следующее выражение вектора-радиуса гг точки М\ которая до де-
деформации стержня находилась в точке М:
Здесь а = ОМ, и, v, w — искомые функции а и t. Условие нерастя-
нерастяжимости стержня имеет вид
«' = —Д-
A2.5.31)
Оно выводится в точности так же, как и уравнение B) для цепи.
Скорость (абсолютная) точки стержня равна
где vr — ее относительная скорость. Получаем
vy =
*) Л. А. Ш у б е н к о, О влиянии центробежных сил на частоту свобод-
свободных колебаний лопаток паровых турбин. Труды Ленинградского индустри-
индустриального института, 1937, № б, стр. 53—68,
682 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ, 12
и выражение кинетической энергии будет
+ 2оJ (R + а) и +- оJ (R 4- аJ + ^21 •
Здесь сохранены лишь слагаемые второго порядка малости (напом-
(напомним, что и имеет второй порядок малости, a v ww — первый). Заме-
Замечая, что
f
^ а} аи' da =
и отбрасывая в выражении Т несущественное постоянное слагаемое,
получим
Т=^р fda |o)V4- v24- 2о)^(R 4-a) —
'24-<t£/2L-^2}. A2.5.32)
Потенциальная энергия изгиба дается известным выражением
== -л* / \fi'£) -\~Е'уУ!) )аа, A2.О.ОО)
6
и выражение действия по Гамильтону принимает вид
= ~р f
dt / da
J
tQ о
_C02(/_a) ^ ^ (^24-^2) ^^2 ^^/2J. A2.5.34)
Искомые функции v(a,t) и w(a,t) подчинены краевым условиям
v @, 0 = 0, ^@,0 = 0, г;'@.0 = 0, -а;'@, 0 = 0. A2.5.35)
12.5] УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ 683
Дифференциальные уравнения колебаний и краевые условия на
конце а = 1 получим, выразив, что вариация действия 85 обращается
в нуль, Имеем
и i
bS = р / dt / da\ vbv -\- -пуй'Ш-f-uPvlv-j-о)(R -f- a) bv —
6
2R + l + a Elz
— u)^ (I — cl) к (vfovf -4— wrowr) vrbv —
У ff*\ !! I /Л / 1 Г» С О Р \
— W 0W = U ( 1 Z O.oO)
p J • v 7
После интегрирований по частям, учитывая условия
bvr (a, g = 0, bw' (a, tQ) = 0, bv' (a, tx) = 0, hw' (a, ^) — 0,
равенство C6) преобразуется к виду
= p f dt fda{— 5 + (o4r
a)
t0 0
bw -\-.EIz / dt [vm (/, 0 8<у (/, 0 — v" (I, 0 ^ (^ 01 +
+ EIy f dt \wm (/, 0 8w (/, 0 — w" (/, 0 ^' (^ 01 = 0.
Приходим к следующим дифференциальным уравнениям в частных
производных и краевым условиям: для тангенциальных колебаний
v + ~yv ~ ^v~ * [у — а> g ^J— ' i(l2.5.37)
-у @,0 = 0, г;'@,0 = 0, ^"(/,0 = 0, v'"{lt 0 = 0 )
и для аксиальных
Ely 0Г 2/? + ^ + ^ У
W —I t£J — СО I (/ — Cl) Wr I — О
Р L4 2 J A2.5.38)
Мы не будем останавливаться на задаче интегрирования этих
уравнений (см. п. 9.10).
684
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
3°. Колебания цепной линии. Рассматриваются малые
колебания около положения равновесия тяжелой, однородной, нера-
нерастяжимой цепи, концы которой закреплены неподвижно на одном
уровне (рис. 93).
В положении равновесия цепь располагается, как известно, по
цепной линии. К этому можно прийти из рассмотрения вариационной
задачи о минимуме потенциальной
U 2а *н энергии силы тяжести цепи:
а
П = Т ГУ do =
= 7
Здесь f — вес единицы длины цепи,
±а — абсциссы закрепленных точек,
da = У 1 -|- у'2 dx — элемент дуги
искомой кривой у(х). Заменив мыс-
мысленно с целью использовать привыч-
ные в динамике обозначения х на /,
у на q и П на 5, будем иметь дело
с «движением» системы с одной степенью свободы, кинетический
потенциал L которой, задаваемый выражением
Рис. 93.
не содержит независимого переменного х. Но тогда «уравнение дви-
движения» Лагранжа, т. е. уравнение Эйлера для рассматриваемой ва-
вариационной задачи, допускает интеграл энергии G.2.5); в нашем
случае это будет соотношение
У
ду'
VT+.
где постоянная у0 — значение у в низшей точке (в ней у' = 0)
кривой равновесия цепи. Итак,
откуда дифференцированием получаем
4
Уо
12.51 УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ 685
Четное относительно х решение этого уравнения, равное у0 при х = О,
будет
y = yochj-. A2.5.39)
Отсюда находим
y' = sh —, de = c\\— dx, A2.5.40)
у Уо Уо к }
так что длина цепи / оказывается равной
а
1= fch — dx = 2y0sh — или -0— = sh (^- -4~)- A2.5.41)
J Уо ^° Уо Ьо \ I 2у0 ) к }
-а
Неизвестное -^— должно быть определено из этого трансцендентного
2а
уравнения по заданному отношению —г-.
В дальнейшем понадобятся формулы
cosa = 4^ = —-—, sina = th—, A2.5.42)
d° chJL Уо
Уо
где a—угол касательной с осью Ох; из них находим
^L^ychJL, ^ = I = _J , (i2.5.43)
где р—радиус кривизны цепной линии.
Переходим к составлению дифференциального уравнения колеба-
колебаний. Обозначая через и вектор перемещения точек цепи из равно-
равновесного положения, через jjl, v, C — его проекции на касательную,
главную нормаль и бинормаль цепной линии (перпендикуляр к вер-
вертикальной плоскости, в которой расположена цепь). Тогда
-|-C&, r = ro + ut A2.5.44)
где г0 — вектор-радиус точки цепной линии, г—вектор-радиус ее
в смещенном положении. Дифференцируя это соотношение по дуге a
и используя формулы Френе для плоской кривой, получим
da \ р ' да ) ' \ р ' да ] ' да
Для нерастяжимой цепи \dr\ = da; поэтому
или, после простого преобразования
686 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Такой вид имеет условие нерастяжимости цепи — уравнение связи
нашей задачи. Для малых колебаний, если не учитывать слагаемых
второго и более высокого порядков,
■l=*i „ли v = -^. A2-5-46)
р да да v '
а при сохранении членов второго порядка
Переходим к составлению выражения потенциальной энергии.
Координата по вертикальной оси Оу точки кривой по D4) равна
7] = );-[-{jLsina-)-v cos a,
где у— координата этой же точки при равновесии (на цепной ли-
линии). Поэтому, учитывая нерастяжимость цепи, имеем
П = т Г y\dG= 7 Г yda-\- -f f (ц sin a -f- v cos a) da =
«0
= II0 —{— 7 Г ([x sin a -|- v cos a) p da,
-ao
где По — значение потенциальной энергии в положении равновесия.
Пределы интегрирования соответствуют значениям а на закрепленных
концах. Заменив v по формуле D7), получим
ао
И —П0 = Т J ^Sina + !£
+h
-«о
Линейное слагаемое здесь должно быть нулем, так как в поло-
положении равновесия потенциальная энергия имеет стационарное значе-
значение. Действительно, заменив sin a, cos a, p их значениями D2), D3)
для цепной линии, получим
~аУ
12.5] УРАВНЕНИЯ ДВИЖЕНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ 687
так как (i=0 при х = ± а. Итак,
^J + (^-J]^. A2.5.48)
Кстати говоря, этим подтверждается, что в положении равновесия
потенциальная энергия имеет минимум. Кинетическая энергия колеб-
колеблющейся цепи равна
Здесь использовано соотношение D6) и отброшены величины четвер-
четвертого порядка малости.
Теперь, введя безразмерные переменные
Уо Уо
и обозначая производные по этим переменным соответственно точкой
и штрихом, получим следующее выражение кинетического потен-
потенциала:
4
+ <П /(P2ch5 —р'*)«. A2.5.50)
-I
Здесь использованы равенства D2) и D3) и через £0 обозначено зна-
значение % при л: = а (в месте закрепления). Искомые функции ц и р
удовлетворяют краевым условиям
при £=±S0 ц = 0, ii/ = 0, р = 0. A2.5.51)
причем второе является следствием равенства D6).
Теперь выразив, что вариация действия is обращается в нуль,
и проделав интегрирования по частям с целью замены производных
от вариаций 8[х и Щ самими вариациями, причем используются крае-
краевые условия E1) для вариаций, получаем дифференциальные урав-
уравнения малых колебаний цепи
— |? ch2 £ — Зр/ ch £ sh £ + 2р/ sh 5 + 5^ ch £ +
-j- 4^ Sh 5 + jj.iv ch I = 0, A2.5.52)
p ch £ — p^ = 0. A2.5.53)
688 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Если принять теперь
ji = М (?) sin (It -\-а), Р = В (?) sin (со/ + а),
то определение частот и форм колебаний цепи около положения рав-
равновесия приведется к двум следующим краевым задачам*) для коле-
колебаний цепи в ее плоскости:
MIV ch % -f- AM"' sh £ + E +12 ch Q M" ch $ +
-f-B-+-3X2 ch £) AI'sh £ — 12M = O, A2.5.54)
)
и для колебаний, перпендикулярных ее плоскости:
) = 0. A2.5.55)
12.6. Приближенное определение частот и форм
свободных колебаний
В п. 12.5 были показаны способы составления дифференциальных
уравнений малых колебаний одноразмерных тел около положения
равновесия в поле потенциальных сил. Это были уравнения в част-
частных производных относительно неизвестной функции v(x,t)t где
х — координата точки в равновесном положении, t — время. Реше-
Решение задачи проводилось в два этапа. На первом этапе в рассмотре-
рассмотрение вводилось семейство частных решений
vk (х, t) = vk (x) (Ck cos ukt 4- Dk sin co^), A2.6.1)
каждое из которых представляет гармоническое колебание — так
называемое главное колебание; отысканию подлежали частоты глав-
главных колебаний со^ и функции vk(x)—их формы. При подстановке
выражения A) в дифференциальное уравнение переменные х и t
в рассмотренных задачах отделялись и определение vk(x) сводилось
к однородной краевой задаче, т. е. к разысканию таких значений
входящего в однородное линейное дифференциальное уравнение па-
параметра, пропорционального со^, которым при однородных краевых
условиях соответствуют ненулевые решения vk(x). На втором этапе
речь шла о выполнении начальных условий: решение задачи пред-
представлялось рядом по главным колебаниям vk (x, t), причем постоян-
постоянные Ck и Dk определялись по заданной начальной форме смещений
точек и распределению их начальньх скоростей.
*) Определению частот свободных колебаний цепи в ее плоскости по-
посвящена работа D. Saxon and A. S. Cahn «Modes of vibration of a suspended
chain» (Quarterly Journal of Mechanics and applied Mathematics, vol VI,
part. 3, September, 1953). Дифференциальное уравнение E4) составлено для
независимой переменной а.
12.6] ПРИБЛИЖЕННОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТ СВОБОДНЫХ КОЛЕБАНИЙ 689
Принципиальная выполнимость перечисленных операций может
быть доказана; однако представление решения через хорошо изу-
изученные и табулированные функции возможно лишь для ограниченйого
круга задач; в примерах 2° и 3° п. 12.5 оно было невыполнимо,
так как дифференциальные уравнения для собственных форм коле-
колебаний не принадлежали к известным типам. Возникает задача при-
приближенного определения частот и форм главных колебаний. Конечно,
приходится ограничиться разысканием конечного числа частот и соот-
соответствующих им форм колебаний. В приложениях в первую очередь
важно знание низших частот и форм, главным образом, первой —
наинизшей. Распределенная система при этом рассмотрении заменяется
системой с конечным числом степеней свободы, равным числу ра-
разыскиваемых форм колебаний; начальные условия тогда можно за-
задать в таком же числе точек.
Начнем с рассмотрения системы, имеющей конечное число степе-
степеней свободы, могущей совершать малые колебания около положения
устойчивого равновесия в поле потенциальных сил. В этом случае
кинетическая и потенциальная энергии представляют квадратичные
формы обобщенных скоростей и соответственно обобщенных коор-
координат с постоянными коэффициентами
-, п п -,
= 2 * П
1 kl
22 2 ,*?*?, 22 2^5?*- A2.6.2)
5=1 k^l 5 = 1 £ = 1
Предполагается известным, что в числе движений, реализуемых
в этой системе при надлежащим образом подобранных начальных
условиях, имеются колебания
E=1, .... п), A2.6.3)
в которых все координаты изменяются в одинаковой фазе со/ —f— ос —
главные колебания. Ставится задача получить с помощью принципа
Гамильтона — Остроградского систему алгебраических уравнений, опре-
определяющую величины ш и Cs. Конечно, исходя из этого принципа
и из выражений B) кинетической и потенциальной энергии, можно
получить дифференциальные уравнения движения
п
&s (L) = S (askqk + cskqk) = 0' (s = 1..... п) A2.6.4)
# = 1
и после подстановки в них значений C) обобщенных координат
прийти к искомым соотношениям
2 Ck (- a*ask + csk) = О E = 1, .... я). A2.6.5)
Однако речь идет о том, чтобы избежать составления дифферен-
дифференциальных уравнений, а, задаваясь формой решения, разыскать
44 Зак. 2072. А. И. Лурье
690 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
«прямым методом» входящие в него величины, опираясь на принцип
Гамильтона — Остроградского *).
Выражениями C) задается «прямой путь»; гармонические коле-
колебания с частотами и амплитудами, бесконечно мало отличающимися
от искомых, образуют «окольный путь»
q's (t) = С; sin (co'f + а') = qs + lqs =
= qs-\- sin H + °0 8C5 + Csba cos (o>* + a) + Cstbu cos (со* -f-a).
Итак,
bqs = bCs sin (a>* + a) + (Cs8a + C/8co) cos (со/ -f- a) E=1,..., n).
A2.6.6)
Принцип Гамильтона — Остроградского следует записать в форме
O, A2.6.7)
которая при фиксированных t0 и tv конечно, сводится к требованию
л
85 = 0, S = JLdt. A2.6.8)
Если же t0 и tx зависят от варьируемых величин, то эти формы
записи не эквивалентны. Тогда, учитывая изменяемость пределов
интеграла, имеем
^ A2.6.9)
to
и требование G) приводится к виду**)
bS + (L)tmtobt0 — (L)t.t№i = 0. A2.6.10)
Примем, что моменты tx и t0 отличаются на один период:
'.='о + ^. «^Ц-^-йш. A2.6.11)
*) Г. Ю. Джанелидзе и А. И. Лурье, О применении инте-
интегральных и вариационных принципов механики в задачах колебаний. При -
кладная математика и механика, т. XXIV, вып. 1, стр. 80—87, 1960 г.
**) По существу эта же форма принципа Гамильтона — Остроград-
Остроградского приводится в «Аналитической динамике> Е. Т. Уиттекера (стр. 280,
ОНТИ, 1937).
12.6] ПРИБЛИЖЕННОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТ СВОБОДНЫХ КОЛЕБАНИЙ 691
Имея в виду соотношение
'. п *
= ~2 f&s(L)bqsdt-X-
5 = 1
OL
можем, вследствие периодичности величин——, принять
S?,(^i) —^,(^o) = O E=1. .... п), A2.6.13)
а не считать равной нулю каждую из этих вариаций. Тогда соотно-
соотношение A2) приведет к уравнениям Лагранжа, что и требуется.
Запись A0) этого соотношения вследствие периодичности L и ра-
равенств A1) может быть еще представлена так:
A2.6.14)
Возвращаясь к F), имеем
bqs (^) == bCs sin (u>£0 -)- a) -f- C5oa cos (u>£0 -|- a) -j- C^j&w cos (co^0 -|- a),
bqs (tQ) — bCs sin (co^0 -f- a) -f- Csoa cos (ш^0 -)- a) -j- Cstobu> cos (to^0 -|- a),
и, поскольку /0 —11=£0, надо для выполнения условий A3) на
окольных путях принять
Ы0 + а = ^-. A2.6.15)
Выражение L при подстановке в него значений C) обобщенных
координат примет вид:
L = coTcos2 (со^ —|— ос) — U sin2 (co^-J-a). A2.6.16)
Здесь Г и U — квадратичные формы, получающиеся из Т и II при
замене их аргументов qs и qs на Cs
п п
1 "" *СА- A2.6.17)
Их можно назвать амплитудами кинетической и потенциальной энер*
гий. Получаем
5= f Ldt = — (<№—U) A2.6.18)
J ^
to
и далее,
0. A2.6.19)
692 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Замечая еще, что по A6) и A5)
запишем теперь соотношение A4), выражающее принцип Гамиль-
Гамильтона— Остроградского, в виде
(г — -£г) 8о) + ~ О2^ — 8t/) = 0. A2.6.20)
Воспользуемся еще интегралом энергии
оJГ cos2 (Ы ~{-(х)-\- U sin2 (со/ -\- a) = const,
причем постоянную определим по значению левой части при t — t0.
Найдем
coTcos2 (со/ + а) = U [ 1 — sin2 (со/ + а)]
или
а>2Г=£/, A2.6.21)
так что соотношение B0) оказывается возможным представить
в виде
оJ&Г — bU = 0. A2.6.22)
Поэтому, если ввести в рассмотрение величину
R=-^S = u2T — U, A2.6.23)
то ее вариация b'R, вычисленная при фиксированном а), будет нулем
С* = 0- A2-6-24)
Отсюда, вследствие произвольности вариаций bCs, действительно
получаем, обратившись к A7), систему соотношений E). Началь-
Начальная фаза а, одинаковая в рассматриваемом главном колебании для
всех координат, в выражение R не входит; а является произволь-
произвольной постоянной в частном решении C).
Итак, оказалось возможным избежать составления дифферен-
дифференциальных уравнений движения и прийти к строгой системе конеч-
конечных соотношений, определяющих главное колебание C), потребовав
обращения в нуль вариации b'R величины /?, вычисляемой при
фиксированном со. В конечном счете этот результат равнозначен
принципу Гамильтона — Остроградского, но R и вариационное требо-
требование B4) не являются ни действием по Гамильтону, ни непосред-
непосредственным выражением принципа в форме B.2). Заметим, что вслед-
вследствие B1) величина R на истинном пути оказывается равной нулю.
12.6] ПРИБЛИЖЁННОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТ СВОБОДНЫХ КОЛЕБАНИЙ 693
Пусть Г# и U^ вычислены для произвольно взятых значений C%s
величин Cs. Величину
< = -^~ A2.6.25)
называют квадратом первой (низшей) частоты по Релею *). Можно
доказать, на чем не останавливаемся, что вычисляемая так величина
не меньше о>2 (квадрата истинного значения частоты); она больше со2
и становится равной аJ, когда все коэффициенты С*5 равны С5, т. е.
определяют первую форму колебаний.
Равенство B4) является исходным для разъяснения приближен-
приближенного прямого метода разыскания главных колебаний, называемого
методом Ритца. Коэффициенты Cv ..., Сп считаются не неза-
независимыми величинами, а задаются как линейные однородные формы
меньшего числа k параметров (Xj, ..., p,ft:
k
Cs=^qsrpr (s=l, .... n), A2.6.26)
r = \
причем числовая прямоугольная п X k матрица qsr предполагается
надлежащим образом выбранной. Тогда Г и U станут квадратичными
формами параметров \хГ и равенство B4) примет вид
A2.6.27)
откуда при произвольных Ь^г приходим к однородной системе ли-
линейных относительно (хг уравнений
"^-fH0 ('=1 k)- A2-6-28)
Требование обращения в нуль ее определителя приводит к част-
частному уравнению, которое будет k-ft степени относительно оJ и,
вообще говоря, дает k различных значений со2, .. ., ш2 частот (они
окажутся положительными). Каждому из значений о>2 соответствует
система значений (хИ, .. ., р,£) параметров, определенная с точностью
до произвольного множителя; тогда по B6), с точностью до этого мно-
множителя, найдутся и коэффициенты С^г\ соответствующие форме
колебаний частоты а)г.
В описанном приближении исходная система, имеющая п степе-
степеней свободы, заменена фиктивной с k степенями свободы. Однако
практика применения метода показывает, что, руководствуясь при
*) При некоторых условиях, налагаемых на выбор C*s, это будут
квадраты второй, третьей и т. д. частот по Релею.
694 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
выборе чисел qsr соображениями, вытекающими из приемлемого пред-
представления об искомом движении, можно получить близкие к действи-
действительности значения частот и форм. Так, принимая k = 2, обычно
получают надежные значения о>2 и первой формы; при & = 4 можно
рассчитывать на получение удовлетворительных сведений и об со^ и
второй форме.
Все сказанное переносимо на распределенные системы. Мы будем
рассматривать задачи, в которых кинетическая и потенциальная
энергии задаются функционалами вида
i /
Т=~ f 9(x)F(v, v')dx, П = 4" / ф(^ v'> v")dx, A2.6.29)
6 о
где р(х) —масса единицы длины одноразмерного тела, Г и Ф — ква-
квадратичные формы их аргументов. Полагая
v(x, t) = V(x)s\n(vt-\-a)9 A2.6.30)
получаем выражение L вида A6), причем теперь
о
, V')dx, U = ^ f Ф(У, V't V")dx. A2.6.31)
о
Величина R определяется по B3); вариации амплитуд кинетической
и потенциальной энергии преобразуютея с помощью интегрирований
по частям к виду
f
о
Vdx-\--~-v^ibV , A2.6.32)
— 2 J
12.6] ПРИБЛИЖЕННОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТ СВОБОДНЫХ КОЛЕБАНИЙ 695
Получаем
i
*,г» 1 Г Г <>( д? d dF \ дФ . d дФ d2 дФ
и дело сводится к однородной задаче для линейного дифференци-
дифференциального уравнения
^)w+ife^-^rfi^=0 A2-6-35)
с краевыми условиями: первая группа при х — 0 и х = 1
9 dF дФ , d дФ * /1О а осч
"P^l^-W^ + ^dT^^0 A2.6.36)
ИЛИ
V = 0; A2.6.37)
и вторая группа
W*=0 A2.6.38)
ИЛИ
У' = 0. A2.6.39)
Условия C6) и C8) являются силовыми, а C7) и C9) — геометри-
геометрическими.
При приближенном рассмотрении задачи задаемся, аналогично B6),
выражением формы колебаний в виде
^ = SlVPr(*). A2.6.40)
где cpr(x) — некоторые функции, удовлетворяющие геометрическим
краевым условиям. После подстановки этого выражения в формулы
C1) и проведенного интегрирования получим Г и U как квадратичные
формы параметров |i1 ]xk. Останется составить уравнения B8),
из которых указанным выше путем находятся k частот о>^, . . ., со^
и к систем соответствующих им параметров ^\ . . ., ^\ По ним,
с точностью до постоянного множителя, находятся формы Vr(x).
Вместо предложенного здесь способа непосредственного вычисле-
вычисления Г и U и последующего составления по ним уравнений B8)
можно, обратившись к равенству C4) и заменив в нем вариацию bV
ее выражением
A2.6.41)
696 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 12
получить те же уравнения B8), приравняв нулю коэффициенты при
независимых вариациях 8jxr. Придем к равенствам
дФ
_#Г__ dU _ 1 Г\ 2( dF_ d dF\
дрг фг — Т ,/ Г V dV~ dx9 ~dVr)
о
d дФ d2 дФ "I . , J_[7 о dF дФ
^"dx~ dV ~~dtf dV''\4rWax~r 2 L\ P Wr ~~ ~dV
| = ° C-=l, .... *). A2.6.42)
0
Здесь, конечно, V должно быть заменено выражением D0). Такое
видоизменение последовательности вычисления в методе Ритца ука-
указано Галеркиным.
Заметим, что во внеинтегральных слагаемых
dF дФ , d дФ
уравнений D2) автоматически отпадают члены, относящиеся к гео-
геометрическим краевым условиям (те и на том из краев, где они за-
заданы), так как выбор функций <рг(х) был этим условиям подчинен.
Если же в числе краевых условий имеются силовые, то, опустив
в уравнении D2), как часто делают, внеинтегральные слагаемые
1 Г Г 2
о
dF d dF \ дф
Jf=0 (r=1
следует подчинить выбор функций срг(х) также и силовым краевым
условиям. В методе же Ритца, т. е. при записи уравнений в форме B8),
силовые краевые условия, как видно из тождеств D2), автомати-
автоматически входят в требования стационарности функционала /?.
Способ записи D4) уравнений Галеркина легко запоминаем и
прост: в рассматриваемом дифференциальном уравнении
ТA/, V, V", ...) = 0
искомая функция V заменяется ее приближенным представлением
вида D0), причем срг(х) должны удовлетворять всем краевым усло-
условиям. После этого составляется k (по числу взятых функций) со-
соотношений
V\ V'\ ...)b(x)dx = Q (r=l, ..., k),
12.7] ПРИБЛИЖЕННЫЙ РАСЧЕТ ЧАСТОТ И ФОРМ СВОБОДНЫХ КОЛЕБАНИЙ 697
из которых определяются неизвестные параметры. В этой формулировке
способ Галеркина применяется к самым разнообразным задачам,
тогда как возможность применения метода Ритца ограничивается
дифференциальными уравнениями, получающимися на основании вариа-
вариационного принципа *).
12.7. Примеры приближенного расчета частот и форм
свободных колебаний
1°. Колебания висящей цепи с грузом на конце.
Амплитуды кинетической и потенциальной энергий по E.4) и E.5)
равны
Будем искать V в форме полинома
V = ^х~ -^-^-^--f-^TT» A2.7.3)
причем функции
5=1. 2, 3)
удовлетворяют геометрическому краевому условию V@) = 0. Полу-
Получаем после вполне элементарного, хотя и громоздкого, вычисления
квадратичную форму параметров (xfe:
A2.7.4)
*) Вопросы сходимости решений, получаемых методами Ритца и Галер-
Галеркина, и оценок даваемых ими приближений рассматриваются в многочислен-
многочисленных работах и монографиях. См. книги: Л. В. Канторович и
В. И. Крылов, Приближенные методы высшего анализа, Гостехиздат, 1949
и С. Г. Михли н, Прямые методы в математической физике, Гостех-
Гостехиздат, 1950.
698 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
где через х обозначено отношение весов груза и цепи (обозначенное
в п. 12.5 через [i). Уравнения F.28) теперь легко составить; при-
приравнивая нулю их определитель, получим кубическое уравнение
относительно о>2, все корни которого будут положительны. Таким
образом определяются три формы Vr(x) свободных колебаний, при-
причем Vj и V2 будут давать приемлемое приближение. Проведение
этих выкладок заняло бы много места. Ограничимся в случае х ф О
только первым приближением, сохранив в C) лишь одно слагаемое
Это соответствует замене цепи твердым стержнем. Тогда
«-W(t+")-*(t+
и приближенное значение квадрата частоты будет
Постоянная [Xj, конечно, остается неопределенной. При х = 0 получаем
тогда как числовой коэффициент в точном решении п. 12.5 равен 1,2024.
Результат при взятом весьма грубом приближении — достаточно хоро-
хороший. Приняв в точном и приближенном выражениях форм колебаний
отклонение конца цепи равным единице, получим
так что в середине цепи
o(fif)~O,4. ^D) = 0.5.
Различие форм довольно значительное. Во втором приближении при
ъ = 0 приходим к системе уравнений
Частотное уравнение
I
3
12.7] ПРИБЛИЖЕННЫЙ РАСЧЕТ ЧАСТОТ И ФОРМ СВОБОДНЫХ КОЛЕБАНИЙ 699
имеет корни
о>!=у -|- 1,2025 оJ = ]/ -у-3,037,
что дает почти полное совпадение с точным значением первой ча-
частоты и мало удовлетворительное значение второй частоты (в точ-
точном решении числовой множитель равен 2,760).
Подставив в F) числовое значение (ор получим для отыскания
коэффициентов р,*1) и [а*1) первой формы колебания систему уравнений
,0282^) = 0, 0,028.2^) — 0,0441^) = 0,
определитель которой, как и должно быть, равен нулю. Находим
и приближенное выражение первой собственной формы, нормирован-
нормированное так, чтобы перемещение конца х = 1 было равно 1, будет
В приводимой табличке сопоставлены численные значения точного
и приближенного выражений первой формы.
а
1
0
0,25
0,50
0,75
1,00
Ф. (а)
0
0,178
0,398
0,670
1,000
Vl(a)
0
0,177
0,403
0,678
1,000
Совпадение достаточно хорошее. Чтобы с удовлетворительной
точностью получить вторую частоту и форму, надо сохранить в выра-
выражении C) четыре слагаемых.
2°. Колебания вращающегося стержня. Ограничимся
рассмотрением тангенциальных колебаний. Пользуясь выражением 85
в п. 12.5, имеем
о
v]V (a) \
[Vм (/) W (/) — У" (/) W (/)] = 0, A2.7.7)
700 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
где через \2 обозначен квадрат искомой частоты. Приняв теперь
A2.7.8)
мы удовлетворим геометрическим условиям на заделанном конце
стержня. После подстановки в равенство F) и приравнивания нулю
множителей перед вариациями 8^ и 8|i2, придем к уравнениям
A2.7.9)
так как при взятом приближении VlV обращается в нуль.
Примем сначала аJ = 0, т. е. рассмотрим невращающийся одно-
однородный стержень с одним заделанным и вторым свободным концом;
частоты и формы колебаний в этом случае хорошо известны и это
позволит оценить взятое приближение. Система уравнений (9) при-
приводится к виду
A2.7.10)
где обозначено
z =
Elz
Составив частотное уравнение, найдем его меньший корень
A2.7.11)
тогда как в точном решении числовой множитель равен 3,5160. При
о> Ф 0 приходим к частотному уравнению
12.7] ПРИБЛИЖЕННЫЙ РАСЧЕТ ЧАСТОТ И ФОРМ СВОБОДНЫХ КОЛЕБАНИЙ 701
рассмотрение которого позволяет оценить влияние угловой скорости
вращения на низшую частоту свободных колебаний стержня.
3°. Колебания математического маятника. В выра-
выражении потенциальной энергии математического маятника
сохраним написанные слагаемые и вместо t введем безразмерную
независимую переменную у -j-t, обозначаемую ниже также через t.
Тогда с точностью до постоянного множителя выражение кинетиче-
кинетического потенциала будет
Требуется найти движение маятника при начальных условиях:
при / = 0 <р = %, <р = °- A2.7.14)
В линейном приближении решение имеет вид
A2.7.15)
При сохранении в выражении A3) последнего слагаемого изменяется
частота колебаний и в решении должна быть учтена гармоника
утроенной частоты. При тех же начальных условиях A4) полагаем
ср = (ср0 + а) cos It — а cos Ш. A2.7.16)
Пользуясь принципом Гамильтона — Остроградского, найдем \ и а.
Имеем
8<р = Ъа (cos It — cos Ш) — 18Х [(<р0 -f- а) sin It — За sin 3W],
так что Scp обращается в нуль при t = tQ — O и £ = /1 = у=Г.
Верхний предел в выражении действия зависит. от определяемого
параметра X; поэтому следует использовать соотношение F.14)
^0^8Х = 0. A2.7.17)
Имеем
ср = — X (сро + а) sin M+ ЗХа sin 3W A2.7.18)
и, следовательно,
/7\ п *ч те 5Х / 1 о ^ Л *
(^=0 IT Ы = — "XT" [y К — 24 Ч?j •
702 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Далее, подставив в A3) значения A6) и A8), найдем
т
Параметр а, как увидим ниже, имеет порядок cpg. Поэтому в про-
проведенном вычислении отброшены степени а выше второй и произве-
произведения а2 на ср0. Получаем
Отбросив слагаемые, пропорциональные а2, приходим к двум
уравнениям для определения а и X
« - Ж <?3) = 0.
-^-(cpo + 2a - ^ срз)= 0.
Сохранив в решении этой системы низшие степени ср0, получим
х==1—ж<& а=ш^
и движение маятника в рассматриваемом приближении определяется
равенством
A2.7.20)
12.8. Главная функция Гамильтона
В выражении действия по Гамильтону будем считать верхний
предел переменным, а кинетический потенциал представим через функ-
функцию Гамильтона Н
д„. Pv •••- р„; t). A2.8.1)
s = \
Тогда
S={
1
qn. рг. .... Рп\ t)\dt. A2.8.2)
J
12.8]
ГЛАВНАЯ ФУНКЦИЯ ГАМИЛЬТОНА
703
и выражение вариации этого интеграла будет
' п
-^Zps)dt. A2.8.3)
Использовав канонические уравнения движения
' — J*IL ' — дН
4s dps ' ^s dqs
преобразуем это равенство к виду
/ п t
qs) at = I a
to
E=1 Л).
A2.8.4)
s = 1 s=l A2.8.5)
Здесь через as и $s обозначены начальные значения обобщенных
координат и импульсов
при t=:t0 qs = as, ps = $s E=1 п). A2.8.6)
Вспомним теперь определение A0.7.5) канонического преобразова-
преобразования и выражение A0.8.2) вариации производящей функции канони-
канонического преобразования типа V1 (g, Q; t)\ тогда, рассматривая 5 как
функцию текущих и начальных значений координат, времени t и фикси-
фиксированного момента tQ
S = S(qv . ... qnt al§ ..., ая; t. t0), A2.8.7)
следует, основываясь на равенстве E), заключить, что она является
производящей функцией указанного типа канонического преобразова-
преобразования, определяемого соотношениями
Решив эти уравнения относительно координат qs и импульсов ps,
что предполагает необращение в нуль Гессиана:
d2S
G —
dqn Ool{ " ' dqn дап
придем к равенствам
= PsV' *0> а1. •••• an> Pi. •••• PJ.
A2.8.9)
A2.8.10)
дающим интеграл Коши системы канонических уравнений движения.
В п. 10.12 уже доказывалось, что соотношения A0) представляют
704 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
формулы канонического преобразования начальных значений обобщен-
обобщенных координат и импульсов в их текущие значения. Здесь это заме-
замечательное предложение снова доказано другим способом, дающим
вместе с тем ответ на поставленный там вопрос: производящей функ-
функцией этого преобразования является действие по Гамильтону, вычисляе-
вычисляемое при переменном верхнем пределе и выраженное через начальные
и текущие значения обобщенных координат, как указано в записи G).
Так, построенную функцию 5 Гамильтон назвал главной функцией.
Все сведения о движении, которые можно почерпнуть из интеграла
Коши, т. е. из 2п уравнений A0), заключены в одной-единственной
главной функции *).
Имея явное выражение главной функции, можно сразу же с по-
помощью формул (8) ответить на вопрос: какие начальные импульсы
надо сообщить системе в начальном положении, чтобы она
в назначенный момент времени пришла в заданное конечное поло-
положение. По словам Гамильтона «вся математическая динамика сво-
сводится к изучению и отысканию главной функции».
Из равенств B), G) и (8) имеем
dS dS . V dS - V * ^r V< dS •
s=l s=l s=l
откуда, после сокращения слева и справа одинакового слагаемого,
получаем
dS ,
Главная функция удовлетворяет уравнению Якоби и предста-
представляет тот его полный интеграл вида A0.13.27), в котором
постоянные av ..., ап равны начальным значениям обобщенных
координат qlt . . ., qn.
Если известен интеграл Коши A0), то вычисление по формуле B)
даст выражение действия 5 через начальные значения обобщенных
координат, импульсов и время.
Главную функцию 5 получим, исключив из этого выражения
начальные импульсы рл. Последние надо найти из первой группы
уравнений A0).
Другой способ построения главной функции основан на исполь-
использовании какого-либо полного интеграла уравнения Якоби:
а ч т • /) -I— т A2 8 12")
*) Главной функции посвящен «Второй очерк об общем методе
в динамике» Гамильтона (Сборник «Вариационные принципы механики»,
cjp. 235 — 28^).
12.8] ГЛАВНАЯ ФУНКЦИЯ ГАМИЛЬТОНА 705
где ifj, ..., Тл — постоянные; аддитивно входящую постоянную *(п+1,
которую всегда можно внести, так как функция V входит в уравне-
уравнение Якоби только через ее производные, определим так, чтобы V
было нулем при t = t0 и qs = ols. Тогда
V = 4T(9l, ..., qn. Tl Тл; t)-W(av .... an, Tl 7я; g.
A2.8.13)
Примем постоянные в первой системе равенств A0.13.28) равными
нулю. Тогда придем к системе уравнений
дУ _ дЧ>(ди .,., дт ?ь ..., Ы О _ ^(аь •••» a/z> Ть ...> Tm *o) _ q
(k=l n), A2.8.14)
из которых обобщенные координаты qv ..., qn найдутся через их
начальные значения а1э ..., ал, время и постоянные fi» •••» 7я-
Исключив же последние из уравнений A3) и A4), придем к полному
интегралу уравнения Якоби, зависящему от времени, текущих и началь-
начальных значений обобщенных координат. Это и будет главной функцией
Гамильтона.
Приведем для иллюстрации построение главной функции в задаче
о движении тяжелой материальной точки в пустоте. Использовав
выражения A0.12.9) интеграла Коши, получим
j [D + yl) (t -10)+1 g*(t - g3- 2gy0 {t-t,f - 2gy0 (t - g].
Подставив сюда значения начальных импульсов из первой группы
уравнений A0.12.9)
найдем
(
A2.8.15)
Теперь с помощью формул (8) можно найти текущие и начальные
импульсы; легко проверить также, что 5 удовлетворяет уравнению
Якоби.
45 Зак. 2072. А. И. Луоье
706 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 12
Построение S с помощью полного интеграла уравнения Якоби
несколько сложнее. Это уравнение в рассматриваемом примере имеет
вид:
дУ л l [( dV\2 I (dV\2
и его полный интеграл, записываемый в форме A3), будет
V=—й(*-*<^ЬР(*-*о)-^^
A2.8.16)
Система уравнений A4), если обозначить для краткости
приводится к виду
с // / л — yi <п у* v J—. /''я тЛ ft a / ^
Заметив теперь, что т]2 — 7]2==2^(у0 — у\ легко найдем
и далее
A2.8.18)
Остается подставить эти выражения в A6). Придем к ранее полу-
полученному значению A5).
При гармоническом колебании вибратора
q = ?0cos a)(/- g + -^- sin a) (^ _ g, И= 1 (р2 + аJ^2).
Вычислив главную функцию, получим
Д = 2 sin **t-10) [ (^ + ^o)cos cu(/-10)- 2?Go], A2.8.19)
и соотношения (8), A1) легко проверяются.
Сопряженные кинетические фокусы можно найти по выражению
главной функции, приравнивая нулю обратную величину гессиана (9)
■^- = 0. A2.8.20)
Проще всего это выводится из таких соображений: дифференцируя
вторую группу уравнений (8) по $т и учитывая, что левые их части
12.9] АСИНХРОННОЕ ВАРЬИРОВАНИЕ 707*
зависят от Рт только через посредство обобщенных координат qk%
имеем п
d*S dqk _ % П9Я9П
^TSfc—1 A2821>
Но эти соотношения можно записать в форме произведения определи-
определителей
—1 0 ... 0
0 —1 ... 0
G^(t, to) =
0 0 ... —1
= (—1)л, A2.8.22)
где A (t, t0) определяется по C.20) и по C.22) становится нулем
в сопряженных кинетических фокусах. Приходим к соотношению B0).
Например, из A5) следует, что в движении материальной точки
в однородном поле силы тяжести кинетические фокусы отсутствуют.
Формулы A9) и B0) дают ранее найденный по C.49) момент дости-
достижения кинетического фокуса в движении вибратора (п. 12,3).
12.9. Асинхронное варьирование
Сопоставление конфигураций системы на ее истинном пути и на
каком-нибудь из окольных путей не обязательно относить, как это
делалось до сих пор, к одному и тому же моменту времени. Иными
словами, задавая положение системы в ее действительном движении
обобщенными координатами qs(t)t мы можем определить ее бесконечно
близкое и допускаемое связями положение в окольном движении зада-
заданием функций q*s(t-\-M), причем разности
4*sV) — qsV) = tqs A2.9.1)
представляют синхронные вариации обобщенных координат, которые
вводились выше. Учитывая лишь величины первого порядка малости,
имеем
ql(t + W = q]V) + fc(f)M = qs(t) + bqs + qs(t)bt, A2.9.2)
так что
q*s(t + M)-qs(t) = bqs(t) = bqs+js(t)bt (s=l. ..., п). A2.9.3)
Этими равенствами определяется асинхронное варьирование, обозначае-
обозначаемое символом А. Можно, конечно, их применить к любой функции
времени
Д/ = 8/-|-/Д*. A2.9.4)
В частности,
45*
708
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[ГЛ. 12
В соотношениях C) величины А/—произвольные дифференцируемые
бесконечно малые функции времени. Поэтому
так что
A2.9.6)
= (bqsy + qs Д* + qs (Д/)' = Д^ -f qs (M)'. A2.9.7)
Таким образом, операции Д и d непереставимы (в отличие от 8 и d).
Применив формулу D) к интегралу
fFdt,
придем к равенству
С другой стороны,
0 0 О
Исключив из этих равенств выражение
t t
о
приходим к соотношению
/ t
f F dt = f
о о
Заметив теперь, что
и
J Fdt = j F dt — j Fdtt
тотчас же находим
A2.9.8)
. A2.9.9)
tm0.
A2.9.10)
Д J Fdt= f[bF + F(M)u]dt. A2.9.11)
12.10] ПРИНЦИП СТАЦИОНАРНОГО ДЕЙСТВИЯ ЛАГГАНЖА 709
12.10. Принцип стационарного действия Лагранжа
Рассматривается материальная система с голономными стационар-
стационарными связями; активные силы предполагаются потенциальными, так
что в процессе движения полная механическая энергия сохраняет
постоянное значение
А. A2.10.1)
Принимается, что это соотношение выполняется и на всех околь-
окольных путях, соединяющих два фиксированных положения q№ и qM на
истинном пути. Поскольку условие A) налагает некоторое ограниче-
ограничение на скорости точек системы в окольном движении, было бы оши-
ошибочно здесь относить конфигурацию системы q*s на окольном пути,
соответствующую конфигурации ее qs на истинном пути, к одному
и тому же моменту времени. В частности, нельзя требовать, чтобы
переход системы из начального положения в конечное по окольному
пути совершался за тот же промежуток времени tx—10, что и по
истинному пути.
Например, при прямолинейном движении материальной точки
в отсутствии сил движение по истинному пути определяется равен-
равенством
-/!'■
т
и нельзя по окольному пути прийти за одинаковое время tl в то же
положение xlt что и на истинном пути, сохраняя неизменной постоян-
постоянную энергии h.
Итак, условие A) делает обязательным применение асинхронного
варьирования.
Для последующего отметим соотношение, получающееся варьиро-
варьированием равенства A) с учетом формулы (9.4):
Д(Т+П)===8(Т+П) + (Т4-11)'Д^=8(Г4-П)===ДА==8Л=0. A2.10.2)
Обратимся теперь к центральному уравнению Лагранжа F.4.9);
имеем по B)
Заменив здесь bqs по (9.3) и замечая, что для стационарных связей
s=\
710 вариационные принципы механики [гл. 12
получим по (9.4)
п
d \ч d T л •
5=1 A2.10.3)
Теперь, интегрируя обе части в пределах t0, tx, вспомнив фор-
формулу (9.11) и замечая, что
Д^(*0) = 0, Д^(/,) == 0 E=1, ..., п), A2.10.4)
так как окольные пути пересекают истинные в моменты времени t0
и tv приходим к равенству
Л
А Г 2Tdt = 0. A2.10.5)
/о
Величина
А= J 2Tdt A2.10.6)
to
называется действием по Лагранжу. Для одной материальной точки
/. Л >.
А= Г mv-vdt= Г mv-dr= Г mvds, A2.10.7)
причем пределам интеграла соответствуют начальное и конечное поло-
положения точки. Это же выражение А сохраняется и для любой системы
материальных точек, если «вектор скорости» v определить по G.8.4),
т. е. рассматривать скорость изображающей точки в римановом много-
многообразии G.8.2), в котором квадрат элемента дуги равен 2T{dtJ. Можно
также определить действие А как сумму работ векторов количеств
движения по истинному пути, соединяющему начальное и конечное
положения точек системы
A) N
А= f 2 "/*/•<»"/• A2.10.8)
@) / = 1
Равенство E) выражает принцип стационарного действия: действие
поЛагранжу между двумя фиксированными положениями системы
имеет стационарное значение на истинном пути, когда на при-
привлекаемых к сравнению окольных путях сохраняется одно и то же
постоянное значение полной механической энергии *).
*) Впервые в неясной форме принцип сформулировал Мопертюи. Исто-
История развития принципа и возникших в связи с ним в XVIII веке научных
дискуссий изложена Л. С. Полаком в Сборнике «Вариационные принципы
механики» (Физматгиз, 1959, стр. 784—803).
12.10] ПРИНЦИП СТАЦИОНАРНОГО ДЕЙСТВИЯ ЛАГРАНЖА 711
В вышеприведенном рассуждении принцип стационарного действия
был получен как следствие центрального уравнения Лагранжа. Но
можно стать на другую точку зрения — принять этот принцип как
исходное положение динамики голономной системы со стационарными
связями при действии потенциальных сил и из него выводить уравне-
уравнения движения системы. Приходим к изопериметрической задаче Ла-
Лагранжа о разыскании необходимых условий стационарности функцио-
функционала F) при условии A). В п. 12.4 указывалось, что дело сводится
к составлению дифференциальных уравнений экстремалей для функ-
функционала *)
qr= J [27 + ХGЧ-П —A)]rf/= f Fdt, A2.10.9)
где обозначено
F = 2T-\-\(J+\\ — h) A2.10.10)
и к — неопределенный лагранжев множитель.
По (9.11) и (9.4) имеем
№ = J[Д/7 4-/=" (ДО'] dt=
to tQ
= J* [bF -f (F ДО'] dt= j hFdt +
tQ to t0
Интеграл, входящий в это выражение, преобразуется по формулам
A.4), A.8), A.9), надо лишь заменить букву L на F. Применив также
формулу (9.3), получим
Последнее слагаемое отпадает по условиям D). Итак
д\1Г = _ J ^$s(F)oqsdt + l F — ^^gs jM =0. A2.10.11)
t0 5=1 \ S«l ^ / t0
Поскольку (ДО! и (Д02 независимы и отыскивается стационарное
*) См. упомянутые в подстрочном примечании на стр. 666 «Лекции»
Н. В. Р о з е (стр. 88—89).
712 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
значение функционала W, содержащего лагранжев множитель X, следует
(повторив многократно проведенное рассуждение) считать равными
нулю множители при (^t)l и (ktJ, а также при каждом bqs под зна-
знаком интеграла. Получаем, во-первых, п уравнений Лагранжа для
функции F:
4^-~ = 0 E=1. .... л) A2.10.12)
и, во-вторых, соотношения на концах, называемые в вариационном
исчислении условиями трансверсальности:
-i^) =0. A2.10.13,
Вспомним теперь, что следствием уравнений Лагранжа было равен-
равенство G.2.4), которое для функции F примет вид:
Здесь использованы равенства A0) и A). Итак, величина в скобках
сохраняет постоянное значение; но она равна нулю при t = tQ и t = tx
и, значит, остается нулем при всех t:
^ = 0- A2.10.14)
Подставив сюда значение F и воспользовавшись только что упомя-
упомянутыми равенствами, найдем
27-|-ХG+П — К) — D7+2X7) = — 27A +Х) = 0.
Итак, Х = —1 и по A0) получаем F = L -\-h. Уравнения A2) оказы-
оказываются уравнениями движения Лагранжа, что и требовалось доказать.
12.11. Принцип стационарного действия в форме Якоби
Трудности, связанные с необходимостью применения асинхронного
варьирования и теории связанных задач вариационного исчисления,
устраняются, если исключить время из выражения принципа стацио-
стационарного действия. Возможность этого обусловлена наличием интеграла
энергии A0.1); последний может быть представлен в форме
2 7 Kdtf =S 2 ask {qx qn) dqs dqk = 2 (Л - П) (dt)\ A2.11.1)
1 kl
12.11] ПРИНЦИП СТАЦИОНАРНОГО ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ 713
позволяющей выразить dt через дифференциалы координат:
Это значение dt подставляется в выражение действия по Лагранжу;
получаем:
Л 0) Г п п
А= J2Tdt= j у 2(h — U)^i^askdqsdqk. A2.11.3)
@) ' 5=1
причем пределы @) и A) соответствуют начальному и конечному
положениям системы. Якоби предложил принять одну из обобщенных
координат за независимую переменную; пусть это будет qv Тогда А
запишется в якобиевой форме:
>=/
A2.11.4)
причем функция R имеет выражение
я = 2<л-пJ!Se^ =
5 = 1 k-\
п + 22 а,Х+2 2 askq'A A2.11.5)
«У — 2. s — 2 k — 2 /
(штрихи обозначают дифференцирование по qx). Принцип наимень-
наименьшего действия сводит задачу определения траекторий системы
к разысканию экстремалей функционала D). Дифференциальные
уравнения траекторий — это дифференциальные уравнения Эйлера — Ла-
гранжа для этих экстремалей. Нет нужды их выводить, так как доста-
достаточно сделать замену обозначений: роль L в принципе Гамильтона —
Остроградского здесь играет R, а независимое переменное t заменено
на qv Приходим к дифференциальным уравнениям траекторий
в форме Якоби для голономной системы со стационарными связями
при потенциальных силах
А_дУн__дУЪ^
dqx dqs dqs
Время определяется квадратурой из интеграла энергии B):
„@)
714 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ 12
Решение содержит 2п постоянных: т, h и 2п— 2 постоянных, полу-
получающихся при интегрировании системы F).
Уравнения движения более общего вида можно получить, рассма-.
тривая подынтегральное выражение, входящее в лагранжево действие C),
как элемент дуги do некоторого риманова многообразия /?*. Полагаем
{dcf = 2 (А — II) ask dqs dqk = bsk dqK dqk A2.11.8)
(применяются обозначения тензорного анализа; знаки сумм по повто-
повторяющимся снизу и сверху индексам отбрасываются), так что величины
bsk = 2(h — U)ask (s, k=l. .... п) A2.11.9)
являются ковариантными составляющими метрического тензора в /?^.
Действие по Лагранжу теперь записывается, вместо C), в виде
A» A) О)
А= f bsk^^£do= f Ф do= Jdo = a^—a^t A2.ПЛО)
F) ч F) @)
где введена квадратичная форма
«Дуга» о, принятая за независимую переменную, представляет дей-
действие по Лагранжу от начальной до текущей точки траектории. В соот-
соответствии с принципом стационарного действия истинный путь, соеди-
соединяющий точки @) и A) многообразия /?*, является экстремалью
функционала A0). Можно сразу же записать дифференциальные урав-
уравнения экстремалей (в упомянутой только что аналогии L заменяется
на Ф, t на о):
da
Они совпадают с дифференциальными уравнениями (П. 2.8.12) геоде-
геодезических линий многообразия /?*, выражающими обращение в нуль
ковариантных составляющих вектора кривизны многообразия /?* вдоль
экстремалей. В контравариантной записи уравнения имеют вид (П. 2.8.7)
причем символы Кристоффеля составляются для многообразия R
с квадратичной формой (8).
Независимая переменная о не входит явно в выражение Ф; это
позволяет без нарушения общности принять, что в начальном поло-
12.12] МЕТРИКА ЭЛЕМЕНТА ДЕЙСТВИЯ 715
жении системы о = 0 через ог обозначено значение о в конечном ее
положении, т. е. действие на всем рассматриваемом пути. Общий
интеграл системы A2) содержит, кроме заданной постоянной h (речь
идет о краевой задаче разыскания истинного пути между двумя точ-
точками в R*\ еще 2п постоянных ck:
?4=<75(о, cv ..., с2п; К) (s=l, .... п) A2.11.14)
и для определения 2п-\-\ постоянных cv ..., с2п, h имеем 2п крае-
краевых условий вида
(^@) = 95@, cv .... с2п, h\ (q^ = qs(Olicv .... £г2
и уравнение A1), являющееся интегралом системы A2), не содержа-
содержащим новых постоянных. Оно является условием нормирования, позво-
позволяющим установить связь между введенными при интегрировании
системы A2) постоянными. Уравнение времени но B) и (8) будет:
A2:П16)
При отсутствии сил и при п = 2 многообразие /?* превращается
в /?2 — поверхность в трехмерном пространстве. Задача о движении
по инерции точки по поверхности сводится к разысканию геодези-
геодезических линий на этой поверхности. Дифференциальные уравнения A2)
выражают далеко идущее обобщение этого известного факта. Прин-
Принцип стационарного действия сводится к утверждению, что истинный
путь отличается от окольных тем, что вектор кривизны вдоль
него обращается в нуль. Истинный путь — «прямейший» из всех
бесконечно близких к нему допускаемых путей, имеющих с ним общие
концы. Эта форма выражения принципа стационарного действия в при-
применении к случаю отсутствия задаваемых (инерционному движению)
сил принадлежит Герцу.
12.12. Метрика элемента действия и метрика
кинематического элемента
Нам известно, что движение материальной системы, подчиненной
голономным стационарным связям, можно представить в виде движения
изображающей точки в римановом многообразии Rn, элемент дуги
которого — кинематический элемент по терминологии Синджа, опре-
определяется выражением кинетической энергии (п. 7.8)
ds2 = 2Tdf2 = askdqdq\ A2.12.1)
716 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
При наличии только потенциальных сил движению той же мате-
материальной системы сопоставляется изображающая точка в многообра-
многообразии /?* с метрикой элемента действия
da2 = bsk dqs dqk = 2 (/г — П) ds2 = 2 (А — П) ask dqs dqk. A2.12.2)
Траекториями изображающей точки в метрике /?* являются геодези-
геодезические линии этого многообразия. Связь ковариантных составляющих
метрических тензоров в /?* и Rn дается формулами
bsk = 2(h-U)ask. A2.12.3)
Поэтому между определителями матриц b и а и алгебраическими
дополнениями Bsk> Ask соответствующих их элементов имеются соот-
соотношения
\ЬЛ\ = [2 (h - П)]я \ask\, Bsn = [2 (А - И)]" Лй,
так что связь между контравариантными составляющими метрических
тензоров в /?* и Rn будет
v'V**' A2Л2'4)
Квадрат длины вектора а в метрике /?* представляется в виде
а2 = bskasak = ask /2 (А — II) as ]/(А —П) а^= лдЛ^ал =
= ^fl/x. = a5fe г п$ , uk = askasak A2.12.5)
s k /2 (A —II) /2 (A —II) s k
и это позволяет сопоставить вектору а в /?* вектор а в Rn по пра-
правилам
£ = /2 (А-II)с*. ZS=^JJ!-—. A2.12.6)
причем множитель "|/ (А — П) равен величине «скорости точки».
Заметим, что формулы F) удовлетворяют требуемому соотношению
связи между контра- и ковариантными составляющими вектора
—II) а* =
askZ /2 (А II) а , ^.
А* 2 (/г — П) V K J f2 (/г — II) *
Скалярное произведение а • & векторов в /?* инвариантно при пере-
переходе в метрику /?д
а • b = а^5 = а5й5 = а • й.
Отсюда и из E) следует сохранение утла между векторами при пе-
переходе из /?* в /?л.
12.12] МЕТРИКА ЭЛЕМЕНТА ДЕЙСТВИЯ 717
Соответствие символов Кристоффеля первого рода в метриках
многообразий R*n и Rn устанавливается формулой
= 2(А —П)[р. Т;а1 —(арвПт + от.Пр —ортП.), A2.12.7)
где, как и ранее, знаком ~ обозначается величина в метрике кине-
кинематического элемента, а Па обозначает производную Па по qa. Соот-
Соотношение между символами второго рода будет
Рассмотрим некоторую траекторию материальной системы — гео-
геодезическую линию многообразия /?*; пусть х — единичный вектор каса-
касательной к ней; тогда в соответствии с B) и F)
~~ dz ~ /2 (/г — II) ~ds ~ /2 (/г — П)
Дифференциальные уравнения A1.12) являются уравнениями парал-
параллельного переноса вектора х по траектории; они выражают обраще-
обращение в нуль геодезической кривизны и имеют в ковариантной записи
вид
*«Р !£" + №• ?; aJT^T = °. A2.12.10)
Понятие единичного вектора первой нормали, вводимое форму-
формулой A1.15.1), теряет смысл на геодезической линии, так как кри-
кривизна A(i) обращается в нуль. Подобно этому лишено смысла говорить
о главной нормали прямой в пространстве Евклида. Для последующего
имеет, однако, значение введение в рассмотрение единичных нормаль-
нормальных х векторов с, параллельно переносимых вдоль траектории.
По п. 2.9 производная такого вектора по дуге геодезической линии
обращается в нуль; поэтому его контравариантные составляющие удо-
удовлетворяют системе линейных дифференциальных уравнений парал-
параллельного переноса, аналогичной A0)
*aP"^+iP. V а]Лг = 0. A2.12.11)
Одно частное решение ее известно, именно, с^ — т?, так как уравне-
j k
ния A0) и A1) при такой подстановке совпадают. Пусть с, с— векторы,
; k
удовлетворяющие уравнениям A1). Их скалярное произведение с-с
сохраняет постоянное значение вдоль геодезической линии; это
718 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
следует хотя бы из того, что уравнения A1) выражают обращение
в нуль производной с по дуге о геодезической линии, та что
£c.c = %L.c + c-£ = 0. A2.12.12)
Поэтому, рассматривая систему (п—1) независимых частных ре-
1 л-1
шений са, ..., са дифференциальных уравнений A1), определяющих
1 /i-i
векторы е, . . ., с% можно подчинить выбор этих решений начальным
условиям
k j к j f 0 (ft Ф J),
WW (VeP) ( {k = Jy A2.12.13)
l /гi
Система векторов и, с, ..., с образует сопровождающий траекторию
ортогональный д-эдр параллельно переносимых единичных векторов,
принадлежащих многообразию /?*,
k
^1 = 0, -^- = 0 (ft=l, .... п— 1). A2.12.14)
Этот я-эдр определяется с точностью до поворота вокруг и. Если
вектор р, заданный на этом многообразии, представить разложением
+%,-?• A2.12.15)
то его производная по а будет
■*а=«^+в^+ ... +a{n_"f A2.12.16)
(штрихи обозначают производные по а). В этом смысле я-эдр парал-
параллельно переносимых векторов заменяет оси неизменного направления.
Уравнения A0), руководствуясь правилами, выражаемыми фор-
формулами F) — (8), можно преобразовать к виду:
1/2 (А —II) аа3 — т + [В, у; а] ?тг —
V ; a?^s /2 (А —11) ^^ '
^^1^-7^ 02.12.17)
Здесь использованы соотношения
?^ ^;~9 ~i=xe-g-. A2.12.18)
12.121 метрика элемента действия 719
так как ЕЦ — ковариантные составляющие вектора grad П. Заметив
еще, что ~ ~а ~ ~
а т*г —т./» — О Л9 19 1 ал
и подвергнув аналогичному преобразованию уравнения (И), получим
dV
Векторная запись уравнений A7) и B0) имеет вид
dz 1 / HIT ~ ^^ ^ ^с ~* grad П • с i о i о о i \
Вспомнив первую формулу Френе и учитывая, что 2 (/г — II) равно
квадрату скорости изображающей точки, а—grad П по G.8.6) —
действующей на нее «силе» Q, легко узнать в первом уравнении B1)
естественное уравнение движения
ftA)£ = -L(Q — Q.xx) = \ Q.nii, A2.12.22)
где п — первая нормаль траектории, &A)—первая кривизна ее
(конечно, в метрике кинематического элемента она отлична от нуля).
Второе уравнение B1) указывает, что производная по дуге 5
вектора с в метрике кинематического элемента имеет направление и.
Таково важное свойство в метрике кинематического элемента единич-
единичных векторов, параллельно переносимых в метрике элемента дейст-
действия. Вектор первой нормали п% будучи переведен в метрику эле-
элемента действия, не является параллельно переносимым по траектории.
Вводим теперь в рассмотрение местную систему ортогональных
I л-1
осей х, с с в точке М траектории; положение двух беско-
бесконечно близких точек N и ЛГ, взятых в окрестности Му причем N
расположена на гиперплоскости, нормальной к траектории в точке М%
z N' — в точке ЛГ, бесконечно близкой к Ж, задается векторами MN
и MN\ соответственно равными
n-l k п-\ k k
\ A2.12.23)
так что квадрат линейного элемента (NN'Jt далее обозначаемый ds* ,
будет:
п-\
k k
720
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[ГЛ. 12
причем нулик указывает, что величина рассматривается на опорной
траектории.
k
Учитывая ортогональность единичных векторов т, е, получим
п-\ * V
гgrad П • с
A2.12.24)
k=\
Г gfad П • С 1
[ 2 (Л-II) Jo
В частном случае п = 3 вводим в рассмотрение единичные векторы п
и b первой и второй нормалей траектории. Тогда можно записать
равенства
1 ^ ^ 2
с = Hi cos ф + Ь sin ф, с = — п sin ф + Ь cos ф A2.12.25)
и с помощью формул Френе A1.16.1)—A1.16.4) получаем
2
dc_
ds
2
A2.12.26)
С другой стороны, из B5) и B2) следуют равенства
II • с = —j Q• с =—% Q• пcosф = &A)cosф,
-2(A-n)gradII^==-^Q^^-^-Q<
и подстановка ео второе уравнение B1) дает:
»sin Ф = — *(»sin Ф.
A2.12.27)
Теперь сравнение с B6) приводит к соотношению, связывающему
УГОЛ ф СО ВТОрОЙ КрИВИЗНОЙ ЙB)
i
A2.12.28)
Когда метрика кинематического элемента — евклидова, то, как дока-
доказывается в теории поверхностей, из этих формул следует, что семей-
12.13] ВОЗМУЩЕНИЕ ТРАЕКТОРИЙ 721
1 2
ства нормалей с, с образуют развертывающиеся поверхности, имею-
имеющие рассматриваемую траекторию ребром возврата *).
1 2
Выражение B5) линейного элемента в местной системе осей т, с, с
принимает вид
1 2
+v()[J + Jl
A2.12.29)
12.13. Возмущение траекторий
Задача об устойчивости заданного движения материальной системы
может рассматриваться с различных точек зрения. Речь может идти,
во-первых, о разыскании оценок отклонений обобщенных координат
и обобщенных скоростей от их значений в опорном движении в любой
момент времени, когда начальные возмущения достаточно малы.
Об основывающемся на этом воззрении определении устойчивости
движения по Ляпунову кратко говорилось в п. 11.10, а составлению
уравнений возмущенного движения — уравнений в вариациях — были
посвящены пп. 11.14—11.17. Во-вторых, может рассматриваться лишь
орбитальная устойчивость, когда вопрос о протекании во времени
возмущенного движения отодвигается на второй план, а изучаются лишь
траектории возмущенного движения и устанавливаются критерии их
близости к опорной траектории. При этом часто, ограничивая поста-
постановку задачи, рассматривают только консервативные возмущения —
такие, при которых на возмущенных траекториях сохраняется то же
самое значение постоянной энергии /г, что и на опорной траектории.
Принцип стационарного действия Лагранжа оказывается при этой
постановке задачи наиболее приспособленным методом исследования
орбитальной устойчивости, поскольку траекториями как опорного,
так и возмущенного движений являются геодезические линии много-
многообразия /?* элемента действия, т. е. простейшие геометрические
объекты этого многообразия, соответствующие прямым в пространстве
Евклида. В основу исследования орбитальной устойчивости этот прин-
принцип положен в известном труде Томсона и Тэта **) и в исследовании
Н. Е. Жуковского ***) (в последнем рассмотрены и неконсервативные
возмущения).
*) См., например, книгу: А. П. Н орден, Дифференциальная геомет-
геометрия, Учпедгиз, 1948, стр. 113.
**) W. Thomson and P. G. T a i t, Treatise on Natural Philosophy.
Vol. I. Part I, p. 416, 1879.
***) H. E. Жуковский, О прочности движения A882). Полное собра-
собрание сочинений, т. I, ОНТИ, 1937, стр. 110—208.
722 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12/
Вывод дифференциальных уравнений в вариациях возмущенных
траекторий в значительной мере повторяет сказанное в пп. 11.14—
11.17, с той разницей, что независимым переменным теперь является
не время t% а действие по опорной траектории — отсчитываемая по ней
дуга а в метрике элемента действия; конечно, все вычисление ведется
в той же 'метрике, а не в метрике кинематического элемента.
Пусть р— вектор возмущения, ха— его контравариантные соста-
составляющие, а ха, ха—контравариантные составляющие первой и вто-
второй производной вектора р по дуге а. Их выражения после упомя-
упомянутых замен обозначений даются формулами A1.14.9)—A1.14.12)
* **
для величин, обозначенных там ха, ха
A2.13.1)
В этих обозначениях уравнения в вариациях, подобные уравне-
уравнениям A1.14.17), будут
*aP*a+/WT^ = 0, A2.13.2)
причем /?v5pp—ковариантные составляющие тензора кривизны Римана —
Кристоффеля в многообразии /?*.
Более подробно остановимся на случае систем с двумя и тремя
степенями свободы.
1°. п = 2. В дифференциальных уравнениях A1.15.27) теперь
надо в соответствии с A2.14) принять wA) = ok^) = 0. Получаем
уравнения
5-=°- -&+**=<>. <12ЛЗ-з>
где е и v — составляющие вектора возмущения по ъ и с. Последний
при п = 2 представляет единственный принадлежащий /?* нормаль-
нормальный ъ единичный вектор. Мы ограничимся рассмотрением возмущений
нормальных к траекториям, т. е. примем е = 0. Тогда вектор воз-
возмущения представится в виде
p = vc, A2.13.4)
1
где v — «длина» в метрике элемента действия, так как с — единичный
вектор в этой метрике. В метрике кинематического элемента, т. е.
поверхности R2 (не /?*!) с линейным элементом dst длина вектора
12.13] ВОЗМУЩЕНИЕ ТРАЕКТОРИЙ 723
возмущения должна, как следует из A2.2), вычисляться по формуле
у= - v = -- A2.13.5)
"|/2(Л —П) v
В уравнении C) через К обозначена гауссова кривизна много-
многообразия /?*; по A1.15,26) она равна
К= Rl212 2 . A2.13.6)
Томпсон и Тэт называют опорную орбиту устойчивой, если при сооб-
сообщении достаточно малого консервативного возмущения нормальное
отклонение v остается по всей траектории ограниченным. Это .же
определение «прочности движения» принимает Н. Е. Жуковский.
Надо добавить, что уравнение C) может дать лишь необходимый
критерий орбитальной устойчивости, а разыскание также и достаточ-
достаточных критериев требует сохранения в уравнениях возмущенных траек-
траекторий нелинейных относительно v слагаемых. Необходимым (но недо-
недостаточным) условием того, чтобы величина v, определяемая уравне-
уравнением C), оставалась ограниченной, является положительность К
во всем интервале изменения а; для установившихся движений, когда К
постоянно вдоль траектории, оно будет и достаточным.
2°. п = 3. В уравнениях A1.16.8)—A1.16.10) теперь, в соответ-
соответствии с A2.14), надо принять шA) = 0, шB) = 0. Тогда при консер-
консервативном возмущении (bh = 0) получим уравнения в вариациях возму-
возмущенных траекторий в виде
1 2
Г, C)vB) = l
rf.v._. 2 1 2 2 A2.13.7)
где vA), vB) представляют составляющие вектора возмущения
A2.13.8)
1 2
по единичным векторам нормалей с, с, параллельно переносимым
вдоль опорной траектории. Коэффициенты при vA) и v^2) в уравне-
уравнениях G) определяются по правилам A1.15.21)—A1.15.23) и предста-
1 2
вляют квадратичные формы от составляющих векторов с и с с коэф-
коэффициентами, определяемыми тензором Риччи.
Остановимся более подробно на случае евклидовой метрики кине-
кинематического элемента. Тогда за qa могут быть приняты обычные
прямоугольные декартовы координаты ху у, zt так что
ask = 0 (s^k), ass=l (s. ft=l. 2, 3). A2.13.9)
724
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
В метрике элемента действия-по A2.7) имеем (равные нулю скобки
не выписаны):
[1, 1; 1]=-Н* [1, 2; 1]=-Пу, [1, 3; 1]=- П2, [2, 2; 1]=Г1^ [3, 3; 1]=П^ ^
[2, 2; 2]=-Пу, [2, 3; 2]=-П* [2, 1; 2]=— П^, [3, 3; 2] = Пу, [1, 1; 2]=Пу, V
[3, 3; 3]=— Пг, [3, 1; 3]=— IT,, [3, 2; 3]=— Пу, [1, 1; 3J=n^, [2, 2; 3]= Пг. )
A2.13.10)
Вычисление тензора Риччи по этим формулам, формулам A1.15.13)
и (П. 2.14.5) приводит к следующим значениям его контравариант-
ных составляющих:
Ass = 8 (/, ^ дL [(/г — П) АП + (grad П)Ц + Bss9 Ask = Bsk, A2.13.11)
причем А— лапласов оператор, а через Bsk обозначены контра-
вариантные составляющие добавочного симметричного тензора вто-
второго ранга, даваемые таблицей
1
8 (/г —IIL
(А-П)
(Л-П)Пуу f|
A2.13.12)
В инвариантной форме тензор В представим выражением
г^ 3 grad 1J fifrad 11 1 , , __ ,т ю io\
В = — -jg- * „ _* 4 8 (Л —II)8 gradgradn» A2-13.13)
где первое слагаемое представляет диадное произведение gradll на
себя, а второе — градиент вектора градиента — тензор второго ранга,
формально записываемый в виде диадного произведения символиче-
символического вектора grad на grad II .
12 12
Ковариантные составляющие сх, сх единичных векторов с и с
в системе координат ха элемента действия удовлетворяют соотношениям
1 V f 1 (i-Щ A2.13.14)
О Aфк)
2(л-п)
следующим из A2.4) и (9). Теперь по A1.15.21) и A1.15.23) находим
4(h-
2 2
12
(С. С) = -
- U) Д11 + (grad an
11
12
A2.13.15)
12.13]
ВОЗМУЩЕНИЕ ТРАЕКТОРИЙ
725
Дальнейшее преобразование основано на переходе от декартовых
координат х, у, z к местной координатной системе опорной траек-
траектории. Используя A3) и A2.6), можно записать квадратичные формы
в правых частях соотношений A5) в виде
i — — I
1.8 (Л-II)8
—rr^ с • grad grad П . с
1 2
8 (h — Il)!
с • grad П с • grad П -f-
П •
A2.13.16)
Дело сводится к вычислению проекций вектора grad П на направле-
1 2
ния единичных векторов с, с и составляющих тензора gradgradll по
этим направлениям. Принимается, что потенциальная энергия, задан-
заданная как функция х, у, z, выражена в окрестности опорной траек-
траектории через дугу 5 и расстояния vA), vB), отсчитываемые по нор-
нормалям с, с. Лапласиан в формулах A5) надо также выразить через
производные по этим переменным. Все величины должны быть опре-
определены на опорной траектории; поэтому, проделав указанные вычи-
вычисления, следует принять v2 и v2 равными нулю.
Коэффициенты Ляме линейного элемента A2.29) равны
откуда следует, что
j тт ~ дП ,
grad II = ъ \-
2 (А — И)
дп
VB)
д\\
2 (Л -II)
1
~ дП.
с т
дП
с • grad И = ——
Тензор grad grad II представим в виде диадного произведения
~ г)
С —^г~
VB)
>~ дп
с
hbds
откуда следует
k
с • grad grad II =
v(*)
an
и поскольку единичные векторы т, с, с не зависят от
можно
726
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
сразу же заключить, что
I I
с • grad grad П • с =
дЧ\
Лапласиан от П составляется по известной формуле
= 1 Г д bh
hih2h3ldv(i) hx
cbB) h2 (
и оказывается при vA) = vB) = 0 равным
_d_ hxh2 дП
ds hz ds
д2И , ОТ! , дЧ\
h1 (h2 ' ds2 2(h — l
Теперь, сделав подстановки в формулы A5) и A6), придем к выра-
выражениям *)
1 1
4 (ft —
Г 1
L 4 (/г —
i
3 д[1 д[1 1
-ИK dv, (^v2 Jo
A2.13.17)
Замечание. Отбросив в таблице A0) выражения, не содержа-
содержащие индекса 3, получим символы Кристоффеля первого рода при
п = 2, когда метрика кинематического элемента — евклидова. По F)
и (П. 2.14.5) приходим к формуле для гауссовой кривизны
12.14. Примеры
1°. Траектории материальной точки в поле силы
тяжести. Когда речь идет об одной материальной точке, метрика
кинематического элемента определяется простейшим образом форму-
формулами A3.9) и дифференциальные уравнения траекторий A2.10), если
*) Аналогичные формулы приведены в цитированном на стр. 721
сочинении Н. Е. Жуковского (стр. 165), где они получены после остроумного,
но трудно воспроизводимою геометрического построения.
12.141 примеры 727
использовать выражения A3.10) символов Кристоффеля первого рода,
запишутся в виде
2 ф — П) х" — x/2Ux -[- (у'2 -[- z'2) П^ — 2лг'у'Пу — 2x'z'II 2 = 0,
A2.14.1)
причем штрихи обозначают производные по а. Два других уравнения
системы выписываются по аналогии. Первый интеграл по A1.11)
будет
2(А — и)(х'* + у'*-\-г'*)=1 A2.14.2)
и, пользуясь им, легко преобразовать систему уравнений A) к виду:
A2.14.3)
В случае однородного поля силы тяжести можно ограничиться
рассмотрением плоского движения; направив ось у по восходящей
вертикали, придем к двум уравнениям
^ j igy)=0. A2.14.4)
Проинтегрировав первое и исключив у' из второго с помощью
интеграла B), получим
причем e = sgny'=± 1. Введя обозначение
7] = е|/*2(/г — gy) — С2, A2.14.6)
приведем второе уравнение E) к легко интегрируемому виду
— — (r\2 + C2)dri = da. A2.14.7)
Таким образом, действие по Лагранжу оказывается представленным
выражением
[ ] A2.14.8)
Здесь т]0 — начальное значение tj:
-gyu)-C\ eo=egn/o. A2.14.9)
728 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Примем у'о > 0, тогда so = s=l на восходящей ветви траектории,
на которой у возрастает от у0 до значения у^ обращающего в нуль
подрадикальное выражение
2/i —С2
На нисходящей ветви у убывает от значения у^ и е = — 1.
Постоянная С может быть выражена через начальное значение х'о
производной х'\ заменив далее do в E) его значением G), придем,
после интегрирования, к уравнению траектории:
^-(yio — rl). A2.14.10)
Итак, на восходящей ветви
-У~2(к- gy) - 4 (h - gyQf x'o2] , A2.14.11)
в вершине
х. = х0 + 2 (h - gy0) -^ У2 {h - gyQ) - 4 {h - gyQJ x'* A2.14.12)
и на нисходящей ветви
х = хо+ 2 (Л - gJ>0) -у- [^2(Л - gy0)- 4(Л - gyQf x
4(A-gyoJ<2]. A2.14.13)
Решение содержит при фиксированном /г три постоянных xQ, yQ, xfQ —
это пучок траекторий с вершиной в точке х0, у0; отдельная кри-
кривая С пучка задается наклоном х'о. На бесконечно близкой к ней
кривой С'того же пучка наклон равен x'Q-\-bx'Q и вариация Ьх, опре-
определяющая переход от С к С\ определяется равенством
ЬХ = ^7ЬХ' A2.14.14)
дх0
Из уравнений A1 —13) получаем
дх х — хп \ 4 (h — gyn) x'rs
— = т-2- 1 ± —^ i^L_£_ I A2.14.15)
12.14]
ПРИМЕРЫ
729
причем верхний знак относится к восходящей, нижний — к нисходя-
нисходящей ветви; в вершине траектории
1 —
2(Л —
A2.14.16)
Из A4) и A5) следует, что вариация Ьх становится нулем при
отличном от нуля Ъх'о при значении у = ух, обращающем в нуль
величину в квадратных скобках A5); по A3) находим соответствую-
соответствующее значение х = хх. Получаем
2 (Л - £у0) 4
У\ = -7 — \т
h
Хл — Х(\
h
-^ — Уо
A2.14.17)
/2
х0
2(h-gy0) x0
ё Уо
J
Итак, бесконечно близкие изоэнергетические траектории пересе-
пересекаются в точке (хх, ух) — кинетическом фокусе, соответствующем
начальной точке (х0, у0). Для единовременных путей кинетических
фокусов при движении в поле силы тяжести, как указывалось
в п. 12.8, не существует.
Выражения координат кинетического фокуса A7) можно пред-
представить в более отчетливой форме, заметив, что
/ _ dx —
dx
v2di
Xo COS a
= —5"
где vQ — величина вектора начальной скорости, а — его угол с осью х.
Придем к формулам
хх = хо-\ ctga, у j = у0 —|— -^— A—ctg2a), A2.14.18)
легко получаемым из элементарного рассмотрения. Исключив из них а.
получим уравнение геометрического места кинетических фокусов,
соответствующих начальной точке при всевозможных углах бросания,
у;? юг /jr, —хЛ2 h а (у, —х~\2
A2.14.19)
730
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
Это — парабола безопасности, являющаяся огибающей семейства исхо-
исходящих из точки (xQ, y0) параболических траекторий, получающихся
при заданном начальном значении кинетической энергии. Точки каса-
касания траекторий с параболой безопасности расположены выше уровня
у == yQ начальной точки при а > 45° и ниже его при а < 45° (рис. 94).
Рис 94.
Переходим к примерам, иллюстрирующим изложенный в п. 12.13
метод исследования возмущенных траекторий. Примеры взяты из
упомянутого труда Н. Е. Жуковского, в котором к рассмотрению их
привлечены другие приемы.
2°. Движение материальной точки в поле цен-
центральной силы. Потенциальная энергия является функцией только
расстояния г от центра сил и поэтому
Y \\ Y2 Г*
и по A3.18) находим
is
A2.14.20)
Например, при степенном законе зависимости силы от расстояния
можно принять
II (г) = р.гЛ sgn л. A2.14.21)
причем множитель sgnn внесен, чтобы ограничить задачу случаем
силы притяжения (при |х > 0). Получаем
К— 4 (Л — ПK ~ w»
A2.14.22)
12.14]
ПРИМЕРЫ
731
Необходимым условием устойчивости орбиты является положитель-
положительность произведения hn. В частности, для круговой орбиты
так что
1
и указанный критерий приводит к неравенству п > — 2. Случай п = — 1
соответствует силе ньютонова притяжения; тогда
и по A3.3)
: v0 cos
~ -f- v'
sin
A2.14.23)
Переход к зависимости от времени в этом случае очень прост
-^^ A2.14.24)
Период возмущения совпадает с периодом прохождения невозмущен-
невозмущенной орбиты, как и следовало ожидать.
3°. Движение материальной
точки по поверхности конуса.
Тяжелая материальная точка двигается по
поверхности конуса, ось которого составляет
угол X с нисходящей вертикалью; угол рас-
раствора конуса равен 2[х, причем (рис. 95)
(х< X, X—|—и- < \-
Невозмущенное движение происходит по
нижней (ОА) или верхней (ОВ) образующей,
начинаясь из вершины конуса. Составить урав-
уравнения возмущенных траекторий.
Положение точки М на поверхности ко-
конуса задается ее расстоянием / = ОМ от
вершины, отсчитываемым по образующей, и рис 95
углом ср, который составляет вертикальная
плоскость, содержащая ось конуса, с плоскостью, проходящей через
точку и эту ось.
Кинетическая и потенциальная энергия равны
/
П = — gz = — gl (cos {x cos X -f- sin {X sin X cos cp)
i
A2.14.25)
732 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Постоянная h = 0t по условию, и квадрат элемента действия будет
do2 = — 211 ds1 = — 2П (dP + P sin2 p df). A2.14.26)
Метрика на поверхности конуса — евклидова, поэтому формула A3.18)
кривизны многообразия элемента действия сохраняется, причем, конечно,
вычисление входящих в нее лапласиана и квадрата градиента должно
быть проведено в криволинейных координатах /, ср:
= — ~
— ~ ctg |a (cos X sin [a — sin X cos [x cos cp),
= g2 [ (cos ja cos X -f- sin ja sin X cos cpJ -|~ sin2 X sin2 cp].
Значение К должно быть определено на опорных траекториях, т. е.
при ср = О и ср = тс. На них
— U = gl cos (X q: ja), АП = ± ■—- ctg ja sin (X zp ja),
и подстановка в A3.18) дает
IS 4- Sin X
4gl3 sin (a cos2 (\ ; jx) '
где верхний (нижний) знак отнесен к нижней (верхней) образующей
конуса. Дифференциальное уравнение C) принимает вид:
d2v + sinX
da2 4gl3 sin (a cos2 (X + p)
и остается выразить / в опорном движении через независимую пере-
переменную о. По B6) получаем
О:
/3 = 932
cos (К + (а)
о
и далее
%L± 2 «пХ ^ = 0 A2.14.27)
dz2 9 cos (X q: (a) sin (a a2 v
Пришли к интегрируемому в квадратурах уравнению типа Эйлера;
его решение имеет вид:
2 sirTX
sin (a cos (X
12.14] примеры 733
Величина \ неограниченно возрастает вместе с о. Для опорного дви-
движения по верхней образующей этого надо было ожидать, так как
на ней К < 0; в случае нижней образующей /С, хотя и остается
положительным, но имеет пределом нуль при о->оо, и необходимый
критерий прочности также не соблюдается.
Величина v — «длина» в метрике элемента действия — связана
с нормальным отклонением
v = / sin |л Scp
движущейся точки от опорной траектории равенством A3.5); поэтому
Scp = v . = Ъ = -И— -L (Cxaq + C2o~q).
I sin fi Y2gl cos {I + [i) 3a sin (x Звш^/а 1 ' 2
На нижней образующей q < -^ и Вер —> 0 при a->oo.
4°. Движение по кругу в поле притяжения двух
центров. Движение материальной точки по кругу радиуса а про-
происходит под действием сил притяжения двух центров F и Fl% рас-
расположенных на расстоянии 2Ь так, что линия FFX проходит через
центр круга и перпендикулярна его плоскости. Потенциальная энер-
энергия сил притяжения задается формулой B1). Исследуется устойчивость
круговой траектории.
Поскольку опорная траектория — плоская кривая, угол ф, опре-
определяемый по A2.28), можно принять равным нулю; по A2.25) век-
1 £
торы с, с имеют направления главной нормали траектории и ее
бинормали; в рассматриваемом случае они направлены к центру
круга и по перпендикуляру к его плоскости; по этим же направлениям
отсчитываются отклонения vA) и vB) от опорной траектории.
На круговой траектории потенциальная энергия равна
и не зависит от положения (дуги s) точки на траектории. При малом
отклонении точки
J* (г» + г*) sgn л = р {\(а -
~)': + ф + vB))г] } sgn n =
[(а — v~(I
sgn п.
734 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
В разложении П в ряд по степеням vA), \B^ достаточно удержать
квадратичные члены. Находим:
я —2) (g+V |sgn"
и далее
=0.
О
A)^B) /о
=0.
Для определения постоянной h составляется уравнение движения
по опорной траектории:
г/2 _ 2 (h — П)
Теперь по формулам A3.17) находим коэффициенты уравнений возму-
возмущенного движения A3.7)
( ' }
Движение по опорной траектории устойчиво при соблюдении условий
л>-2+4^, *>!_-£. A2.14.29)
12.15. Вращение вблизи вертикали тяжелого твердого тела
с неравными моментами инерции
Использование представлений геометрии многообразия элемента
действия для изучения возмущенных траекторий в применении к си-
системам с числом степеней свободы /г>»3 становится весьма трудным.
Быстрее и надежнее к цели — составлению дифференциальных урав-
уравнений возмущенных траекторий — приводит применение уравнений
Якоби A1.6), хотя при этом теряются геометрический язык и ком-
компактность и изящество записей тензорного анализа.
12.15] вращение вблизи вертикали тяжелого твердого тела 735
Выражение (П.о) функции R при обозначении A1.9) записывается
в виде
Обобщенные координаты q2, ..., <?„ предполагаются выбранными
так, чтобы опорному движению соответствовали их нулевые значения.
На возмущенных траекториях как эти координаты, так и их произ-
производные q'v .... qn no <7i малы. Поэтому в дифференциальных урав-
уравнениях возмущенных траекторий—в уравнениях в вариациях, должны
быть сохранены лишь первые степени величин q2 qn, q'v ..., q'n%
Это позволяет заменить коэффициенты bsk их разложениями в ряды
по степеням q2, ..., qn, причем ряд для Ьп должен быть вычислен
с точностью до квадратов этих величин включительно, для Ьи— до
первых степеней, а в bsk при 5 и ^>2 достаточно сохранить часть,
не зависящую от q2, ..., qn.
С этой степенью точности составляется входящее в уравнения A1.6)
выражение У R:
5=2 ' м 5=2 £ = 2
Нуликом указывается, что величина рассматривается для значений
q2 qn> равных нулю.
Переходим к вычислению входящих в эйлеров оператор произ-
производных от У R. Следует при этом помнить, что коэффициенты bsk
зависят от ql% как явно входящего, так и входящего через посред-
посредство q2 qn, поскольку последние здесь являются искомыми
функциями qv Имеем (s = 2t .... п)
п.
bSk bXsblk
d dR _ д bls , V _/ / д bls \ , у / bsj^ blsb^, „
n
dY~R
blk
736 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Приходим к системе линейных дифференциальных уравнений
в вариациях
153)
sk blsbxk \ >' \ ( д bls д blk
^U* /^ dqs V~b7
dqs
В качестве примера далее рассматривается случай вращения около
вертикали тяжелого твердого тела, имеющего неподвижную точку О.
Через Д В, С обозначаются главные моменты инерции относительно
осей связанной с телом системы координат Oxyz, причем в опорном
движении ось Oz, на которой расположен центр инерции тела, напра-
направлена по вертикали ОС. В возмущенном движении положение тела
определяется эйлеровыми углами ф, 0, ср, причем угол 0 будет малым.
Проекции угловой скорости тела на связанные с ним оси равны:
ш^ = 0 cos ср -\- ф sin 0- sin ср, ш = — 0 sin ср —[— ф sin i) cos cp,
U>^ = Ср —|— ф COS i>.
Н. Е. Жуковский *) указал замену переменных, позволяющую
в выражении кинетической энергии тела
избежать (при малом 0) появления слагаемых, содержащих косинусы
и синусы угла ср. Полагаем
Ф =====
тогда формулы для проекций угловой системы можно записать в виде
ш^ = 0 cos ср -|- (Ф — ср) 0 sin ср = ф cos cp)' -f- Ф^ sin ср,
ш — — 0 sin ср —|— (Ф — ср) 8 cos ср = — (Ь sin ср)" —f- Ф 0 cos cp,
Теперь, вводя новые переменные — проекции единичного вектора
оси ОС на оси Ох и Оу
л: == i> sin cp, y=9coscp,
получим
х ф ху — ух • с.9
tgcp = —. —-т-= 2 » уЪ2 = ху — ух.
to Т у COS2Cp у2 т
*) <О прочности движения), стр. 186—191. См. ссылку на стр. 721.
12.15] ВРАЩЕНИЕ ВБЛИЗИ ВЕРТИКАЛИ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА 737
Итак,
--о(ху — ух)*
и выражение кинетической энергии принимает вид:
+ (С — 2В) <у + Л/2 + В*'2] ,
причем штрихом обозначается дифференцирование по Ф. Потенциаль-
Потенциальная энергия равна
где Q — вес, / — абсцисса центра инерции тела. Теперь из интеграла
энергии находим значение постоянной h в опорном движении (при 0=0)
где Фо = (<ozH. Это же значение постоянной энергии сохраняется при
консервативном возмущении. Получаем
и теперь по A) получаем выражение функции R
'2\. A2.15.4)
Таким образом, с требуемой точностью имеем, приписывая коорди-
координате х индекс 2, а у — индекс 3,
A2.15.5)
Уравнения движения C), после сокращения на множитель Фо,
будут:
Вх" 4- (
В — А) у'— (£L + А
Ау" — (С — В — А) х' — l¥j -f В —С
-Ь=0-
47
/Z А. И. Лурье
738 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Разыскивая частное решение в виде
х = М sin (ХФ + а), у = N cos (ХФ -|-а),
приходим к характеристическому уравнению для определения X:
^
= АВ\* — \ЛВ-{~(А — С) (В — С) —
и необходимым условием устойчивости вертикального положения
2 2
оси является положительность его корней Хь Х2; это приводит
к коэффициентным критериям
A2.15.7)
Пусть / = 0, что соответствует случаю вращения вокруг не-
неподвижного центра инерции. Тогда характеристическое уравнение
распадется на два множителя и его корни будут
и устойчивым будет вращение вокруг оси наибольшего или наи-
наименьшего момента инерции.
При А = В и />0 приходим к уже известному условию устой-
устойчивости вертикального волчка
^о ^ с2 '
Оно получается, например, из формулы G.9.28), если принять
А2 = С'2 = 0 и перейти к обозначениям этого параграфа.
12.16. Характеристическая функция Гамильтона
Здесь, как в предшествующих параграфах, рассматривается мате-
материальная система со стационарными, голономными связями, находя-
находящаяся под действием потенциальных сил.
В этом случае функция Гамильтона Н не содержит явно времени
и главная функция Гамильтона, введенная в п. 12.8, будет полным
12.16]
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ ГАМИЛЬТОНА
739
интегралом дифференциального уравнения Якоби
dS dS
qa,
зависящим от времени и начальных и текущих значений обобщенных
координат as, qs. В интеграл Коши (8.10) системы дифференциаль-
дифференциальных уравнений движения время может входить лишь через посред-
посредство аргумента t — tQ, так как эти уравнения не содержат t явно
и не изменяют вида при замене t на t — tQ. Итак,
S = S(qx qn. а, а„; t-t0). A2.16.2)
С другой стороны, полный интеграл уравнения Якоби A) можно
по A0.13.12) — A0.13.14) представить, добавляя аддитивную постоян-
постоянную -f/r в виДе
V = -ht + W{qx qn. Ь, .... Тя_„ +
или при надлежащем выборе ^п в виде
.... qn, Tl, ....
-W{a, an, Tl
По (8.14) для определения постоянных
t—10 составляется п уравнений
_
_„ h)-
Тя_„ h). A2.16.3)
fi» •••» Тл-i и времени
-W (alt
qn,
Tlt
(*= 1 л— 1).
A2.16.4)
Из них находим постоянные
Тя-i»
подставив которые
в C), получим главную функцию Гамильтона. Но можно поступить
иначе—из уравнений D) выразить t—10, fv. . ., 7,2-1 через ap. . ., ая, /г
и после исключения их из C) получить равенство вида
где 5 — главная функция Гамильтона.
Определенная таким образом функция А представляет, как сле-
следует из A0.13.13), полный интеграл уравнения в частных производных
*..-з£ W^h< A2Л6-6)
в котором постоянные аг ап обозначают начальные значения
обобщенных координат.
47*
740 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Функция
А(Ях* •••• Яп> *]. ••- аЛ> Л)=.
= 5(?„ .... qn% alt ..., ая. * — *0) + Л(*_*0) A2.16.7)
называется характеристической функцией Гамильтона. Как ука-
указывалось в п. 12.8, главная функция 5 является особой формой
действия по Гамильтону. Подобно этому характеристическая функция
представляет форму действия по Лагранжу. Действительно, по (8.1)
и (8.2) при наличии интеграла энергии
имеем
/ t t
S = JLdt= f (T—H)dt = f 2Tdt — h(t — tQ) = A — h (t —10).
to t0 t0
A2.16.8)
Записывая здесь действие по Лагранжу в виде A1.3) или A1.4)
f 2 %skk f A2.16.9)
@) L J
и выражая его через начальные и текущие значения обобщенных
координат, придем, подразумевая под 5 главную функцию Гамиль-
Гамильтона, к формуле E).
Из (9) видно, что для построения характеристической функции
Гамильтона можно также идти другим путем: подставив в выражение
Я
f
общее решение дифференциальных уравнений Якоби A1.6)
Qs = Qs(Qv cv ..., с2п_2) (s = 2, .... д), A2.16.10)
выразить входящие в него постоянные c]t . .., с2л-2 чеРез Я\* • • •» Яп*
а,, .... ал. Для этого надо использовать как уравнения A0), так
и начальные условия
<*, = ?,(«]. clt .... с2п_2) E = 2, .... п). A2.16.11)
Свойства характеристической функции, аналогичные свойствам (8.8)
главной функции, получим, варьируя основное соотношение E). Здесь
имеется в виду общий случай асинхронного варьирования, когда
сравниваются положения системы
12.16] ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ ГАМИЛЬТОНА 741
при различных значениях h и h-^-bh постоянной энергии; обозна-
обозначение Д#5 определено формулой (9.4).
Получаем:
dqs ^s ' day 5/ ' dh
. A2.16/12)
причем по (9.4)
п
5 = 1
и аналогично
я
п
5 = 1
п
5 = 1
5=1
5=1
5 = 1
dS . \i dS • , ,\Л>
l3^hr ll^ 1
5=1 \ 5=1 / 5=1
Соотношение A2) представится в виде
5=1
_4- B7— L — h)M + Г^- — (* — *0I bh = 0.
Коэффициент при Л/ исчезает в силу интеграла энергии G). По пер-
первому уравнению D) и по E) имеем также
j£- = t — t0. A2.16.13)
Остается приравнять нулю кооэффициенты при независимых вариа-
вариациях oqs, oa9. Тогда, вспомнив также (8.8), приходим к соотношениям
-з— = 1— = Л. -5—=л— = ~Р. E=1, ...,л;, A2.16.14)
742 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
где ps—обобщенные импульсы, $s— их начальные значения. Таким
образом, подобно главной функции, характеристическая функция
Гамильтона дает ответ на вопрос, какие начальные импульсы
были сообщены материальной системе {при заданной постоянной
анергии /г), если известны ее начальное и конечное положения,
и каковы значения импульсов в этом 'конечном положении.
Заметим также, что из п уравнений второй группы A4) незави-
независимых будет только п—1. В противном случае из этих уравнений
были бы получены выражения текущих значений всех координат
°\> •••» Яп чеРез постоянные величины alf ..., ап, Clt . .,, CЛ, /г,
тогда как они позволяют лишь выразить п—1 координат q2, ..., qn
через qv Характеристическая функция содержит в себе интеграл Коши
системы A1.6) дифференциальных уравнений траекторий, но не диф-
дифференциальных уравнений движения.
Вспоминая, что импульсы ps являются ковариантными составляю-
составляющими вектора скорости v изображающей точки в римановом про-
пространстве с метрикой кинематического элемента 2Tdt2t можно первую
группу уравнений A4) записать также в виде
# = grad А.
Рассмотрим случай свободной материальной точки; в начальном
положении ей сообщается произвольно направленная скорость, квадрат
модуля которой фиксируется значением постоянной энергии h. Можно
говорить не об одной точке, а о бесчисленном множестве тожде-
тождественных экземпляров, разбрасываемых во всевозможных направле-
направлениях. Все эти экземпляры попадут (но не одновременно) на поверх-
поверхность А = const, причем скорость каждого будет нормальна к этой
поверхности и задается координатой (х, у, г) той точки ее, где этот
экземпляр оказался. В оптической аналогии, которой руководство-
руководствовался Гамильтон в своих динамических исследованиях, поверхности
А = const — волновые поверхности (на них t — to = const), а траек-
траектории точек — нормальные к ним траектории лучей света. Принципу
стационарного действия сопоставляется оптический принцип Ферма,
выражающий требование стационарности интеграла
B)
I п(х, у, z)ds,
(i)
где п — показатель преломления рассматриваемой неоднородной, изо-
изотропной среды. Сравнение с A0.7) показывает, что ему в динамике
соответствует модуль вектора количества движения
12.161 ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ ГАМИЛЬТОНА 743
Иначе говоря, траектория светового луча совпадает с траекторией
материальной точки, движущейся в поле с потенциальной энергией *)
"■=*-£•
Перейдем к примерам построения характеристической функции.
1°. Движение в поле силы тяжести. В задаче о движении
материальной точки в однородном поле силы тяжести значение дей-
действия было представлено выражением A4.8):
A2.16.15)
~/ j
причем по A4.6), A4.9) и A4.10)
s> \
у у» (*Г) _____ f\\ Y) 1/ О (fa (УМ \ ^*2 I
ё | A2-16.16)
yi^Ycl{h — gy) — a. J
Характеристическую функцию получим, исключив С2 из выраже-
выражения A5), так как тогда действие будет выражено через координаты
начального (л:0, у0) и конечного (х, у) положений точки и постоянную
энергии h.
Вычисление проводится так**): имеем
и пользуясь тождеством
■nl+-л2 = i К-% + -пJ+(ъ - -пП,
приходим к уравнению для С2
^J* + ^=^. A2.16.17)
Из него, обозначая для сокращения записей
yon A2.16.18)
*) Подробнее об оптической аналогии, имевшей большое значение для
развития волновой механики, см. в книгах: Е. Т. У и т т е к е р, Аналитиче-
Аналитическая динамика, ОНТИ, 1937. стр. 319—324; Ф. Клейн, Лекции о развитии
математики в XIX столетии, т. I, ОНТИ, 1937, стр. 232—249.
**) Г. К. С у с л о в, Теоретическая механика, ГТТИ, 1944, стр. 458—460.
744
найдем
ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
[гл. 12
М ± У М2 — N2
* (л -
A2.16.19)
Записав теперь A5) в форме
А = а = j (т1о - tj) [| GH + r)J -I- -jj
У —Уо
12
у (Ж ± 1/М2— Л/2) 4-
—Л/)BМ ± |/ Ж2 — /V2),
придем к выражению характеристической функции
L
а =
-L
+aoj/j + (Ж - /v)J/i].
В начальной точке траектории 7V = 0, и, взяв верхний знак, имеем
А — О. Верхний знак сохраняется, пока N не станет равным Ж.
Нетрудно проверить, использовав формулы A4.17), что это про-
произойдет в кинетическом фокусе. Итак,
A2.16.20)
A2.16.21)
до достижения кинетического фокуса и
после прохождения кинетического фокуса.
В соответствии с A3) имеем
=N) = t-t0. A2.16.22)
Это — уравнение кривой, на которой распо/ш аются в заданный момент
времени все экземпляры, разбрасываемые из начальной точки во
12.16] ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ ГАМИЛЬТОНА 745
всевозможных направлениях с одинаковой по величине скоростью.
По A4) находим начальные импульсы
-— = - у [VmTN + VM=N] + A2.16.23)
Каждое из этих равенств представляет уравнение пучка изоэнерге-
тических траекторий, исходящих из точки (лг0, у0); отдельной кривой
пучка С соответствует фиксированное значение наклона xQ или у0.
Замечая еще, что
± Vm~="
приходим к элементарно получаемой записи равенств B3)
2°. Кеплерово движение. В задаче о кеплеровом эллипти-
эллиптическом движении (п. 10.15) интеграл A0.14.6) уравнения в частных
производных Якоби, обращающийся в нуль в начальной точке (г0, ср0)
траектории, имеет вид
./ -f 2к__^, A2.16.24)
и равенство D) будет
г
■4^- = «Р — <Ро — Р- / г ЛГ = = °- A2.16.25)
Это — уравнение пучка изоэнергетических траекторий, исходящих
из точки (г0, (f0). Используя его, приведем выражение B4) к виду
г
= f
A2.16.26)
Характеристическая функция должна быть получена путем исклю-
исключения fl (при сохранении h) из равенств B5) и B6). Для упрощения
последующих записей введем обозначения
2А = -£, р; = (шA-*-) = №• A2.16.27)
746 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
где а — большая полуось, е — эксцентриситет, "р—параметр эллип-
эллиптической орбиты.
Квадратный трехчлен в интегралах B5) и B6) приведется к виду
2hr2 + 2i*r — Щ = £ [2ar — г2 — а2 A — е2)].
Теперь при обозначениях
■\/2ar — r2 — a2(\—e2) = l, V2arQ — г2 — а2(\ — е2) = С, A2.16.28)
придем после вычисления к равенствам
e2rr0cos(y — ?0) = A-«2)^ + (fl — /- — ае*)(а-гъ-ае*)% A2.16.29)
(a — r)(a-ro)]|. A2.16.30)
Из формул B8) следуют тождества
A — е2) 7, )
\ A2.16.31)
а A — е>) — г = Vr2e2 — A — е2) 7, )
, \
(l2) Vg2(l2)C§ J
используя которые, приведем B9) к виду
A-r0cos(?-cp0) — Vr4i — (\— e0
Теперь, возвысив обе части в квадрат, отбрасывая общий мно-
множитель е1 и снова применив тождества C1), приходим к не содер-
содержащему иррациональностей соотношению
е*г*г\ [1 + cos2 (<? - <р0)] - 2/-r0cos (? - ?0) [а A — е*) - г\ X
i;2) = 0> A2.16.32)
представляющему квадратное относительно параметра р уравнение,
определяющее значение его на эллипсе пучка, проходящем через
заданные точки (г0, ср0), (а*, ср):
= Г -^- -Ь -р -^— cos (ср — ср0) 1
4^
4-[ 1-cos (? — 9о)]2 = О. A2.16.33)
Находим два решения
п — 1 —cos(y — ?0) Г
>2 1 1 2cos(? —ср0) I
cos(y — с
_*_ _. 2 cos (у — y0) L 2a ~ r ~ r0
-i-i;4 I;]. (.2.16.34)
12.16]
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ ГАМИЛЬТОНА
747
соответствующие двум кривым, соединяющим эти точки. При фикси-
фиксированной вершине пучка (г0, ср0) в той точке (rlt cpj), в которой
кривые сливаются, подрадикальное выражение обращается в нуль,
т. е. уравнение C3) имеет кратный корень. Этим определяется геоме-
геометрическое место сопряженных вершине кинетических фокусов изо-
энергетических траекторий. Его уравнение будет:
г л =
4а Bа — г0)
4а — го
1 —
A2.16.35)
cos (cpt — с
Поскольку г0 < 2а, величина
0<е =
4а —г 0
1;
кривая C5) представляет эллипс, а г — его эксцентриситет. Один
из фокусов расположен в при-
притягивающем центре, а второй —
на расстоянии от него, равном
Pi
4a Ba — r0)
4a —r0
где a — большая полуось, рх —
параметр. Подставив значение г,
найдем, что фокусное расстоя-
расстояние 2as = г0 — второй фокус
эллипса C5) расположен в на-
начальной точке, а его большая
ось 2а равна
2а = -^- = 4а — г0. A2.16.36)
На рис. 96 эллиптическая
траектория обозначена бук- Рис. 96.
вой С, а эллипс C5) буквой Е.
Пусть Flt F2 представляют фокусы эллиптической траектории,
М^ — сопряженный начальной точке Мо кинетический фокус (рис. 96).
По свойству эллипса
так что
+ MJF2 = 4а — r0 — rv
A2.16.37)
748 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
С другой стороны, по свойству эллипса C5) с фокусами Fx и Мо
имеем
M^FX -\- М^М0 = гг -\- М^М0 = 2а, М^М0 = 2а — гх = 4а — r0 — rlt
и сравнение с C7) дает
откуда следует, что отрезок М0М^ соединяющий сопряженные кине-
кинетические фокусы Мо и М*, проходит через второй фокус F2 эллип-
эллиптической траектории; на это построение сопряженных фокусов (через
начальную точку Мо и фокус F2 проводится прямая, пересекающая
траекторию в сопряженном кинетическом фокусе) указал Якоби *).
Остается заметить, что, подставив в C0) одно из значений C4)
параметра р и заменив е2 его значением 1— —, придем к выражению
характеристической функции Гамильтона Л, .которое используется,
пока текущая точка М не прошла через сопряженный кинетический
фокус; после этого р заменяется его вторым значением.
Для вычисления времени по характеристической функции служит
по A3) соотношение
*-'o = -^- = -TL —• A2.16.38)
0 dh да \l v • /
а для текущих и начальных значений импульсов — формулы A4)
12.17. О характере экстремума действия по Лагранжу
В п. 12.10 было установлено, что действие по Лагранжу между
двумя фиксированными положениями системы имеет стационарное
значение на истинном пути, если на привлекаемых к сравнению
окольных путях сохраняется то же значение постоянной энергии h.
Является ли это стационарное значение минимальным? Будем движе-
движению системы сопоставлять движение изображающей точки в много-
многообразии /?* с метрикой элемента действия; тогда утвердительный
ответ заключается в теореме, что геодезическая линия, соединяющая
две достаточно близкие точки этого многообразия, короче всякой
другой линии, соединяющей эти точки.
Доказательство теоремы проводится следующим образом. Фикси-
Фиксируется начальное положение системы (qs)Q и рассматривается семей-
*) «Лекции по динамике», стр. 42, ОНТИ, 1936. Геометрические построе-
построения, связанные с сопряженными кинетическими фокусами в эллиптическом
движении, приведены также в «Теоретической механике» Г. К. Суслова
(стр. 489 издания, указанного в сноске на стр. 743).
12.17] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ЛАГРАНЖУ 749
ство гиперповерхностей A(qst q^, h}% на каждой из которых харак-
характеристическая функция Гамильтона принимает постоянное значение.
Все траектории, из множества ооп~1 траекторий пучка с вершиной
в начальном положении (q%, пересекают ортогонально каждую из
гиперповерхностей в каждой ее точке. Исходя из точек пересечения
траекторий с некоторой гиперповерхностью А = Л0, отложим на них
отрезки одинаковой длины о0. Геометрическим местом концов этих
отрезков будет одна из гиперповерхностей того же семейства, так
как отрезок дуги геодезической линии /?* равен изменению на нем
действия по Лагранжу. Тем самым в примыкающей к вершине пучка
достаточно малой области построена система «параллельных» гипер-
гиперповерхностей и нормальных к ним кривых. Положение точки на
гиперповерхности — многообразии (п—1) измерений — можно задать
(п—1) параметрами л:1, ..., хп~1 и можно ввести систему коор-
координат х1 xn~l, xn = at где а — дуга, отсчитываемая по траек-
траекториям от вершины пучка, определяющих положение любой точки
многообразия /?* в указанной области. Элемент дуги этого много-
многообразия зададим квадратичной формой
п-\
ds* = gsk dx* dx* = gnn dx« dx» + 2% gin dx* dx» +
i l
/z-1 n-\
+ 22 gskdxsdxK A2.17.1)
Оставаясь на гиперповерхности Л = const, т. е. полагая dx1 = ...
... = dxn~l = 0 и двигаясь по траектории, имеем
ds2 = da2 = gnn dxn dxn
и, следовательно,
«„«=1. A2.17.2)
Вместе с тем,
gln = 0 (t=lt .... п— 1). A2.17.3)
Это следует из ортогональности касательной т к траектории к любому
бесконечно малому вектору Ьг на поверхности А = const, проходя-
проходящему через рассматриваемую точку и из определения gin как ска-
скалярных произведений базисных векторов на т. Итак, на произволь-
произвольной кривой многообразия R*
/1-1 Л-1
A2.17.4)
причем выражение
Л-1 /Z-1
2 2 gskdx*dxkt
750 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
будучи квадратом элемента дуги на поверхности А = const, пред-
представляет знакоопределенную квадратичную форму дифференциалов dxs.
Поэтому длина дуги любой кривой многообразия
A) A) г- л-1 л-1 -iV2
s{l) — s{d)=Jds= f U^ + ^S&ftrf*5*** >
@) @) L s = lk = l J
0)
@)
чем и доказывается, что геодезическая кривая представляет кратчай-
кратчайшее расстояние двух точек, взятых в области, примыкающей к вы-
выбранной начальной точке.
Геометрическое место кинетических фокусов, сопряженных началу
рассматриваемого пучка траекторий, представляет сопряженную этому
началу фокальную поверхность. Так, в примере движения материаль-
материальной точки в поле силы тяжести этой «поверхностью» служила
парабола безопасности A4.19), а в случае эллиптического кеплерова
движения — эллипс A6.35). От расположения этой фокальной по-
поверхности относительно начала пучка зависит протяженность примы-
примыкающей к нему «достаточно малой области», о которой выше гово-
говорилось. Ее граница определяется той поверхностью семейства
Л = const, на которой расположен ближайший к началу кинетический
фокус. Нет нужды доказывать, что действие по Лагранжу на траек-
траектории, соединяющей начальное положение с конечным, расположенным
за кинетическим фокусом, не является минимумом, так как доказа-
доказательство свелось бы к дословному повторению сказанного в п. 12.3
и иллюстрируемого рис. 89.
Вопрос о характере экстремума действия по Лагранжу на избран-
избранной траектории Со пучка связывается с рассмотрением устойчивоеги
этой траектории. Ограничимся случаем п = 2 и рассмотрим семей-
семейство интегралов дифференциального уравнения возмущенных траек-
торий A2.13.3)
|^ = O, A2.17.5)
обращающихся в нуль при a = a0. Решение дифференциального урав-
уравнения E) называется неколеблющимся на отрезке (ах, о2), если оно
обращается в нуль на этом отрезке не более чем один раз. Известна
теорема *): если
при a1<o<o2 /C<0, A2.17.6)
то решение дифференциального уравнения будет неколеблющимся на
всяком отрезке (a*, a*J, заключенном внутри отрезка (о}, о2). Это
*) Дж. С а н с о н е, Обыкновенные дифференциальные уравнения, т. I,
стр. 165, ИЛ, 1953.
12.17] О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ЛАГРАНЖУ 751
значит, что не- существует бесконечно близкой к Со возмущенной
траектории С', начинающейся в точке g = Gq (такой, чтб ох < с0 < а9)
и пересекающей С на указанном отрезке — на нем нет сопряженных
кинетических фокусов, и действие по Лагранжу на куске траектории
(а*, а*) минимально.
Пусть, например, К=- — т? =■ const; границы о2 и а2 отодви-
отодвигаются в —оо, оо, а за отрезок (а*, о*\ на котором нет кинети-
кинетических фокусов, может быть взят такой, для которого решение
v = ^shm(a-a0) A2.17.7)
оставалось бы по модулю меньшим наперед заданного сколь угодно
малого числа е, что достигается надлежащим выбором v^# Этим га-
гарантируется, что С остается траекторией, соседней с С, а на ука-
указанном отрезке последней нет пересечений с С, так как функция G)
не обращается в нуль при а Ф а0.
Пусть теперь
при Ol<a<o2 Kmax>K>Kmin>0. A2.17.8)
Тогда по теореме Штурма *) расстояние между двумя последователь-
последовательными нулями решения дифференциального уравнения E) меньше
чем „тс и больше, чем —г^=-. Поэтому, взяв обращающееся
при а = а0, в нуль решение, можно утверждать, что если
о,<-7==-. **>-,§=-. а1<а0<а2, A2.17.9)
то на отрезке ах, а2 траектории Со найдется сопряженный а0 кинети-
кинетический фокус.
Сказанное, в сопоставлении с приведенным в п. 12.13 определе-
определением орбитальной устойчивости по Томсону и Тэту, поясняет утвер-
утверждение Н. Е. Жуковского: «действие будет наименьшим между вся-
всякими двумя положениями в непрочном движении и не будет обладать
этим свойством при прочном движении» **).
Возвращаясь еще раз к примеру движения в поле силы тяжести,
напомним, что в обозначениях п. 12.14 интеграл энергии в этом
движении имеет вид:
*) В. В. Степанов, Курс дифференциальных уравнений, стр. 244.
Гостехиздат, 1945.
■-•■•*) «О прочности движения», стр. 111 в издании, цитированном на
стр. 721.
752 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
откуда следует, что
g(y — Уо)<* —«Уо. A2.17.10)
причем знак равенства возможен лишь при вертикальном движении
в момент достижения наивысшего положения.
Теперь в соответствии со сделанным выше замечанием найдем
минимум расстояния вершины (*0, yQ) пучка траекторий до параболы
безопасности A4.19), т. е. минимум величины
(*» - х0? + (у, - уоJ = 4 (А - у0J - 4 (А - Уо) (У1 - Уо) +
. A2.17.11)
Учитывая неравенство A0), легко заключить, что искомый минимум
достигается при значении у = уг, обращающем это неравенство в ра-
равенство; из A4.19) следует теперь, что х1 — х$. Итак, ближайшая
к началу точка параболы безопасности лежит на пересечении ее
с вертикалью, проведенной через начало. Это следует, конечно, и
из того, что вертикаль, проходящая через начало пучка,, является
нормалью к параболе безопасности.
Подставив значения координат
* = *<>. У==у = У1 A2.17 12)
в формулу A6.20), найдем значение постоянной в уравнении кривой
А = const:
^ g (у, + Уо) + g I Ух ~ Уо 11>Л -
— \2h-g(у, + у„)-g \ у, - у0|]"л} = -I: [2(А -gy,)\'\
Найденная кривая
-~г
Q) — g V (T^~7oj2 + (у - уоу f} =
A2.17.13)
изображена на рис. 97*). Это — замкнутая кривая; на всякой траек-
траектории пучка, конечная точка которой лежит в области G, ограни-
*) В е б с т е р А. Г., Механика материальных точек, твердых, упругих
и жидких тел, ГТТИ, 1933, стр. 121.
12 171
О ХАРАКТЕРЕ ЭКСТРЕМУМА ДЕЙСТВИЯ ПО ЛАГРАНЖУ
753
ченной этой кривой, действие по Лагранжу имеет минимум. Все кри-
кривые семейства
при
A2.17.14)
также замкнутые, расположены в области G и стягиваются к началу
пучка по мере уменьшения *у; «кривая» ^ = 0 вырождается в точку
xQ, yQ. Траектории пучка ортогональны этим кривым.
Рассмотрим теперь кривые A = f для значения постоянной
Т>Т*-
Зафиксируем точку (х*, у*Л параболы безопасности, на которой
происходит смена знака в уравнении характеристической функции
Рис. 97.
Гамильтона — переход от уравнения A6.20) к A6.21); в ней, напо-
напоминаем, M = N. Тогда, воспользовавшись также уравнением A4.19),
найдем значение постоянной
Искомые уравнения будут иметь вид:
A2.17.15)
АО Ъ„„ ОЛ-1 А Л Л
754 ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ [ГЛ. 12
Верхнему знаку в этой формуле соответствует на рис. 97 ветвь Av
а нижнему—ветвь А2. На том же рисунке отмечены две траекто-
траектории С#, касающиеся параболы безопасности в точках (± x*v y*\
Будем говорить, что они разделяют траектории пучка на «высокие»
и «пологие». Любая точка области, ограниченной кривыми С# и Av
может быть соединена пологой траекторией с началом пучка — дей-
действие по Лагранжу по этим траекториям минимально. Вместе с тем,
через каждую точку области, ограниченной параболой безопасности
и кривой Av проходит высокая траектория пучка траекторий, орто-
ортогональная ветви А2. Действие по куску этой траектории, содержа-
содержащему сопряженный началу кинетический фокус, не будет мини-
минимальным.
ПРИЛОЖЕНИЕ 1
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ*)
П. 1.1. Определения
Совокупность ту^п величин aik, записываемых в форме прямо-
прямоугольной таблицы
^22
ат\ пт2 • • • <W
содержащей т строк и п столбцов, образует прямоугольную ма-
матрицу порядка ту^п. В записи элемента матрицы aik первый
индекс указывает номер строки, второй — номер столбца. В даль-
дальнейшем матрица элементов alk будет обозначаться одной буквой а;
этим указывается на то, что в рассмотрение вводится вся совокуп-
совокупность этих элементов. В теории матриц устанавливаются правила
действий над такими совокупностями,
С целью отметить, что речь идет о матрице элементов aik> а не
о каждом из них по отдельности, вышеприведенная таблица поме-
помещается между двумя параллельными полосками. Таким образом,
запись ту^п матрицы осуществляется в виде
С1\\ п\2 . . . #1Л
#21 #22 • • • #2Л
ат\ атг
(П. 1.1.1)
*) Мы ограничиваемся простейшими определениями и понятиями, исполь-
используемыми в тексте книги. Теории матриц посвящено большое число специаль-
специальных сочинений. См. А. И. Мальцев, Основы линейной алгебры, Гос-
техиздат, 1955; Р. Фрезер, В. Дункан, А. Коллар, Теория матриц
и ее приложения, ИЛ, 1950; Ф. Р. Г а н т м а х е р, Теория матриц, Гостех-
издат, 1953. В книге Б. В. Булгакова «Колебания» (Гостехиздат, 1954) по-
подробное изложение матричного исчисления предпослано рассмотрению урав-
уравнений аналитической механики и теории колебаний.
48*
756 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
Для экономии места мы будем также писать
a = \\aik\\ (/==1 т\ k=\ п). (П. 1.1.2)
Равными считаются две матрицы одинакового порядка w X #.
соответственные элементы которых равны, т. е.
а = Ь при aik = biff A=1 т; k=\ п). (П. 1.1.3)
Матрица, все элементы которой равны нулю, называется нуль-
матрицей и обозначается обычным образом через 0.
Матрица, число строк которой равно числу столбцов, называется
квадратной.
Примеры: 1, Рассмотрим /г-мерный вектор х, определяемый
совокупностью п величин xv x2% ...> xn Эту совокупность можно
записать в столбец и рассматривать как (п X 1)-матрицу, обозна-
обозначаемую буквой х
х2
(П. 1.1.4)
или же в строку; тогда получим A X /О"матрицу, обозначаемую
через х1
2. Имея систему т функций от п переменных xv ..., хп
fr = fr(xv .... хп) (г=1. ..., т), (П. 1.1.6)
можно определить прямоугольную (т X я)-матрицу, обозначаемую
Ш = \Ш;\ С-=1..... «:*=! я) (П. 1.1.7)
и называемую якобиевой матрицей этой системы функций. Если,
в частности,
то получаем квадратную (п X п)-гессову матрицу
H=S^ {r's={ п)- (П-1Л-8)
сопоставляемую функции Ф.
3. Совокупность символов Кронекера
0 AФ k)
! (i = k) С *=1- •••• ^ (П. 1.1.9)
п. 1.1]
ОПРЕДЕЛЕНИЯ
757
образует квадратную единичную матрицу, обозначаемую Еп (или
просто Е, когда число измерений ясно по тексту):
Еп=\\Ъш\\ (/, ft=l, .... я). (П. 1.1.10)
Диагональные элементы Еп равны 1, недиагональные — нулю.
Возвращаясь к общим определениям, рассмотрим прямоугольную
(s X 0-матРицУ. составляемую из элементов некоторых s строк и t
столбцов матрицы а
(П. 1.1.11)
*',**
где tv i2t .... is — любые из чисел 1, 2, . .., m, a klt k2, ..., kt —
любые из чисел 1, 2, .... п. Конечно, s^m, t^n. (s X 0-матрица
(П. 11) называется субматрицей а и обозначается
1И„ C = 'i. h ^ k = kv ft2. .... ft,). (П. 1.1.12)
Для квадратной субматрицы s = t. Определитель, составленный из
элементов этой субматрицы, записанных в той же последовательности,
в какой они записаны в субматрице, называется минором 5-го по-
порядка матрицы а. Очевидно, что наивысший порядок минора
\т X я)-матрицы равен меньшему из чисел ту п.
Пусть а—квадратная (п X я)-матрица. Определитель, составлен-
составленный из элементов этой матрицы, записанных в том же порядке,
в каком они записаны в а, называется определителе м-матрицы
(П. 1.1.13)
Определитель квадратной (я X я)-матрицы представляет один из
ее миноров я-го порядка — тот, в котором числа iv . . ., in и
k]t . . ., kn следуют в порядке чисел натурального ряда 1, 2, . . ., я.
Очевидно, что остальные миноры я-го порядка этой матрицы лишь
знаком могут отличаться от ее определителя.
Квадратная матрица с определителем, отличным от нуля, назы-
называется невырожденной, в противном случае — вырожденной.
Возвращаясь к случаю прямоугольной (т X я)-матрицы, отметим
наивысший порядок г ее отличного от нуля минора; разность между
меньшим из чисел т, п и числом г называется дефектом матрицы.
Если, например, /й^йи определители всех (т X ^-субматриц ||а||
равны нулю, то1да как имеется (т— 1) X (т—: 1)-субматрица
и
обозначается
а
или
\а\ =
det a
= det a =
-
а2]
ап1
а>\2
а22
ап2
... а1п
\'\п2П.
... апп
758
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
II # || _ с определителем, отличным от нуля, то дефект а равен 1;
ее дефект равен нулю, если имеется отличный от нуля минор т-го
(при т^п) или я-го (при п^т) порядка.
4. Рассмотрим якобиеву матрицу (П. 7), в которой т < /г, с де-
дефектом, равным нулю. Тогда существует отличный от нуля якобиан
dfx
дхь
df2 df2
dxb
dfx
df2
dxh
Jfm
dxh
dfm
dxh
Jfm
dxh
=£0, (П. 1.1.14)
и по известной теореме анализа из системы уравнений
/г(хх, х2, . . ., хя) = 0 (г=1,.,„л) (П. 1.1.15)
могут быть выражены через остающиеся
т величин xk , . . ., >
п — т величин х. , ..., х. .
/я + 1 п
Проведем в матрице а некоторое число горизонтальных и верти-
вертикальных прямых (перегородок). Тогда образуются субматрицы, в ко-
которых индексы следуют в порядке натурального ряда чисел. В обо-
обозначении таких субматриц условимся нижние индексы помещать
в скобки; кроме того, мы их снабжаем верхними индексами, указы-
указывающими номера их начальных строк и столбцов. Например,
k+t
• k+t
i+s, k + i
a
i+s, k + t
(П. 1.1.16)
Так, проведя в матрице а перегородки — горизонтальную под
s-й строкой и вертикальную справа от /-го столбца, мы можем пред-
представить а в виде
II я II
II л ||
A,1)
(s, t)
"(s+T'i)"
(m-s, t)
,A, t+\)
II л II
(m-s, n — t)
(П. 1.1.17)
Мы рассматривали до сих пор матрицы, элементами которых
являются числа (вещественные или комплексные). Но оказывается
целесообразным и рассмотрение сложных матриц—элементами их также
являются матрицы. Так, если в выражении (П. 17), являющемся лишь
п 1.1]
ОПРЕДЕЛЕНИЯ
759
формой записи матрицы а, уберем перегородки, то придем (в этом
примере) к сложной квадратной B X 2)-матрице
II я II
II я II
A,1)
(s, t)
(m-s, t)
II Я II
II * II
О, '+D
(s, n-t)
E + 1, t + \)
(m-s, n — t)
(П. 1.1.18)
Действия над такой сложной матрицей во многих отношениях,
при соблюдении некоторых правил, эквивалентны действиям над ма-
матрицей а.
5. Скобками Лаграижа системы функций qr, prno переменным а, р
называется выражение, обозначаемое [а, C] и имеющее вид:
Очевидно, что
[а, а] = 0.
(П. 1.1.20)
Рассматривая теперь систему 2п функций qr, pr от 2я перемен-
переменных аг, Рг:
Рт = РАч «.;Р, Р.).
составим квадратную Bя X 2я)-матрицу Л Лагранжа
[«1.
[a2.
[«Я.
[pi.
[Рг,
[P«.
al]
«.]
«.]
«.]
«.]
«l]
[a,, a2]
[«2, «»]
[Pi. «2]
[p2, a2j
[р«.«г]
... К an]
... [a2. a«]
...' [«я,'«я]
... [P.. «„]
• ■ • [Pi. ««]
••• IP«. a«]
[«1. P.)
К Pi]
[«„, Pi]
[Pi. Pi]
[P2, P.]
[?«. Pi]
[«1.
[«4.
: cot
[Рг,
[p«.*
P*]
P2]
P.]
P.]
P2]
CO-
... к
... [<h,
'.'•'. [«„.'
... [Рь
... [P..
'.'.'• IP».'
Ря] 1
OQ-
Ря]
Ря]
Ря]
P«]
(П. 1.1.22)
Она, естественно, подразделяется показанными перегородками на
четыре яХя матрицы, обозначаемые [[аос]], [[сф]], [[ра]], [[рр]]:
1м] |
l[pp]]
В предположении, что якобиан отличен от нуля
,..., Чт Pi, •■., Рп)
¥=0
(П. 1.1.23)
(П. 1.1.24)
760 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
система функций (П. 21) разрешима относительно аг, рг:
_ (г=1. .... я). (П. 1.1.25)
Скобками Пуассона двух функций а, р по переменным pr, qr на-
называется выражение вида
г = 1
Из определения следует
(а, а) = 0. (П. 1.1.27)
Матрица Пуассона Р вводится аналогично матрице Лагранжа — ее
элементами являются скобки Пуассона (ait ak)t (at, $k), (P/f ak)t (^, pfe).
Запись, аналогичная (П. 23), имеет вид
(М)
р
П. 1.2. Действия над матрицами
(П. 1.1.28)
а. Транспонирование. Имея {т X я)-матрицу а, можно опре-
определить (п X ^-матрицу а', строками и столбцами которой являются
столбцы и строки матрицы а; а' называется транспонированной
матрицей по отношению к а. Ясно, что транспонирование матрицы а'
приводит к а
(а'У = а.
В квадратной матрице элементы аи называются диагональными.
Если элементы квадратной матрицы, симметрично расположенные
относительно диагональных, попарно равны друг другу, то квадратная
матрица симметрична', симметричная матрица равна своей транспо-
транспонированной
а = а'. (П. 1.2.1)
Примером может служить гессова матрица (П. 1.8).
Квадратная матрица, диагональные элементы которой равны нулю,
а элементы, симметрично расположенные относительно диагональных,
равны по величине, но противоположны по знаку, называется косо-
симметричной.- Примерами являются матрицы Лагранжа (П. 1.22)
и Пуассона (П. 1.28). Кососимметричными будут также матрицы
|[аа]|, [[C[3]j или ((аа)), (C3)), входящие в состав этих матриц.
Заметим, что но известному свойству определителей
ja 1 = 1^1. (П. 1.2.2)
П. 1.2] ДЕЙСТВИЯ НАД МАТРИЦАМИ 761
Пример 1. С трехмерным вектором а с проекциями av a2, а$
может быть сопоставлена кососимметричная C X 3)-матрица
О — <23 а2
а =
аъ О — ах
-а2 ах О
(П. 1.2.3)
Матрица а применяется в матричных записях векторных операций.
Пример 2. Транспонированной по отношению к (яХО-матрице-
столбцу х является A X я)-матрица-строка х''.
б. Сложение и вычитание матриц. Эти действия опре-
определяются для матриц одинакового порядка ту^п. Суммой (разностью)
двух таких матриц а и b называется матрица с, элементы которой
равны сумме (разности) соответствующих элементов матриц а и Ь:
с = а±Ь, если clk — aik±bik (/=1, ...,m; k=l п).
(П. 1.2.4)
Очевидно имеют место свойства
Определение суммы и разности распространяется на сложные ма-
матрицы; конечно, требуется, чтобы одинаково расположенные матрицы,
входящие в состав сложных слагаемых матриц, имели одинаковые
порядки.
в. Умножение матрицы на число. Произведением ма-
матрицы а на число X называется матрица, элементы которой равны
произведениям элементов а на это число. Эта матрица обозначается \а\
ка= \\\aik\\ (/= 1, . . ., т\ к= 1, .. ., п). (П. 1.2.5)
В частности (при к = —1), через — а обозначается матрица элемен-
элементов — aik. Поэтому при трансполировании кососимметричной матрицы
имеем
а' — --а. (П. 1.2.6;
Например,
а' = — а. (П. 1.2.7)
Тождества
аш = \ aik"+- akr> + 7 ("tk — akd С * = 1. - • •. л),
согласно приведенным определениям, могут быть записаны в виде
а = 1(а+а/)+^(я —я') (И- L2'8)
и определяют разбиение квадратной (яХя)-матРиЦЬ1 а на симметричную
762 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
и кососимметричную части
i(fl — п')' = — ^{а — а')=^^(а' — а). (П. 1.2.10)
Пример 3. При транспонировании матрицы [[а{3]], входящей
в состав матрицы Лагранжа (П. 1.23), приходим, согласно (П. 1.20)
и (П. 1.22), к равенству
И«Р]1' = — ПИ- (П. 1.2.11)
Аналогичное соотношение имеет место для матриц, входящих в состав
матрицы Пуассона (П. 1.28):
г. Умножение матриц. Рассмотрим (т X /?)-матрицу а и
(р X я)-матрицу Ь—число столбцов а равно числу строк Ь. Такие
матрицы, взятые в указанной последовательности а, Ь, называются
конформными. Действие умножения определено для конформных
матриц. Произведением их c = ab называется (т X я)-матрица, эле-
элемент clk /-й строки и k-то столбца которой ра^ен сумме произведе-
произведений элементов /-й строки матрицы а на элементы k-vo столбца ма-
матрицы b
р
cik=^aisbsk A= 1, ..., т\ k=l, .. ., п). (П. 1.2.12)
s-=i
Конечно, действие умножения некоммутативно; так, при т Ф п
запись Ьа вообще лишена смысла. При tn — nab определяет квад-
квадратную (я X я)-матрицу — произведение а на b справа, а Ьа—квад-
Ьа—квадратную (р X /?)-матрицу — произведение а на b слева. Только квад-
квадратные матрицы могут быть коммутативными. Например, единичная
^-матрица коммутирует с любой квадратной (п X я)-матрицей
аЕп = Епа = а. (П. 1.2.13)
Свойство ассоциативности умножения сохраняется для матриц:
если а, Ь, с представляют (т X Р)> (РХ^)» (я X я)-матрицы, то
матрицы (ab)c и a (be) друг другу равны
(ab)c = a(bc) = abc. . (П. 1.2.14)
Имеет место и свойство дистрибутивности умножения
(П. 1.2.15)
Соотношения (П. 14) и (П. 15) проверяются непосредственно по фор-
формуле (П. 12), служащей определением операции умножения. Эта же
формула применяется для проверки правила транспонирования про-
произведения матриц
(aby = bra'. (П. 1.2.16)
п. 1.2]
ДЕЙСТВИЯ НАД МАТРИЦАМИ
763
С помощью (П. 14) правило (П. 16) распространяется на произведение
любого числа матриц
(abcy = с'Ь'а'.
Пусть а и Ь — квадратные матрицы. Сопоставляя правило (П. 12)
с правилом умножения определителей и учитывая (П. 2), можно записать
равенства
аЬ | = | Ьа | = | а \ \ Ь | = | а' \ \ Ъ \ = \ а \ \ V \ = \ аг \ \ V |. (П. 1.2.17)
Пример 4. По заданным векторам х и у определим
A X я)-матрицу-строку х' и (я X 1) матрицу-столбец у. Их произве-
произведение представляет A X 1)-матрицу, т. е. скаляр, равный по (П. 12)
у/«, у «, I Y х) \ \ у .. «/у /Т~] 1 О 1 Q4
^Л/ V w\r л у л |" »Л^ О Vo " I • • • " I *Л/ *j V *j V «^ • IXlile^ilO/
Таким образом, скалярное произведение двух векторов а и Ь
представляется в одном из двух видов
(П. 1.2.19)
Пример. 5. Произведение хуг представляет квадратную
матрицу
хуг =
х2у2
(П. 1.2.20)
Напомним, что диадным произведением двух трехмерных векторов
а и Ъ называется тензор второго ранга, обозначаемый аЪь с таблицей
составляющих
аф2 a2bz
аф2 а%Ъъ
)
(П. 1.2.21)
Эта таблица совпадает с матрицей ab', и в этом смысле можно запи-
записать равенство
ab = abr. (П. 1.2.22)
Умножив матрицу аЪг справа на (ЗХ1)"столбец с, сопоставляемый
вектору с, придем по (П. 19) к выражению
ab'c = ab * с,
(П. 1.2.23)
764 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. I
определяющему столбец, соответствующий произведению вектора а
на скаляр b • с. Точно так же при умножении abf на строку сг слева
найдем
c'ab' =-C- ab (П. 1.2.24)
— строку, соответствующую вектору с • ab. Таким образом, опреде-
определяется произведение диадного произведения ab на вектор с справа
и слева: в первом случае приходим к вектору, имеющему направление
левого вектора диады, во-втором — правого.
Пример 6. Рассмотрим произведение кососимметричной ма-
матрицы а, сопоставляемой по (П. 3) вектору я, на столбец Ь. Имеем
0
— а2
— #з
0
а>\
а2
— л,
. 0
II ^ 1'
Ьг =
1 ьъ ||
— аъЬ2 + a2b
аф \ — п\Ь
— <2о^1 -\- й\Ь
ИЛИ
аЬ = с. (П. 1.2.25)
Здесь с — матрица-столбец с элементами
с1 = а2Ьг — аф2% c2 = azbl — ахЬъ, cz = alb2 — b2av (П. 1.2.26)
которой может быть сопоставлен вектор с, равный векторному про-
произведению
с=аХЬ. (П. 1.2.27)
Матрица-строка, сопоставляемая с вектором с, по (П. 7) и (П. 16)
равна
с'- = — Ь'а. (П. 1.2.28)
Пример 7. Рассмотрим произведение (тХл)"Матрицы а на ма-
матрицу 0гХ1)-столбец х\ получаем (/г*Х1)-столбец
г = ах (П. 1.2.29)
с элементами
п
zi=^iaikxk A=1 т). (П. 1.2.30)
Умножив z на AХ#0-СТРОКУ У' слева, получим скаляр
т п
yrz = y'ax = £i 2 aikyixk — х'а'У> (П. 1 231)
представляющий билинейную форму переменных xlt х2, . . ., хп и
У\, у2* • ••» Ущ- Последнее равенство в (П. 31) написано на основании
(П. 16), так как, транспонируя скаляр, придем к нему же.
П. 1.2] ДЕЙСТВИЯ НАД МАТРИЦАМИ 765
Пример 8. Рассмотрим случай квадратной матрицы и у=х. Тогда
придем к рассмотрению квадратичной формы переменных хх хп
п . п
ср (jCj, х2 хп) = х'ах = х'а'х = 2 2 ^л:^, (П. 1.2.32)
/ = 1 k = 1
образованной с помощью матрицы а. Эта квадратичная форма будет
нулем, если матрица а кососимметрична; действительно, тогда по (П. 6)
х'ах = — х' а' х = — хахг = О,
что и непосредственно ясно, так как в этом случае каждому сла-
слагаемому aikxixk при / Ф k сопоставляется противоположное по знаку
слагаемое akixkxit а слагаемые, содержащие квадраты переменных»
отсутствуют, поскольку аи = 0. Поэтому в тождестве
х'ах = -у х' (а-\-а') х -\- -у- хг (а — а') х
можно отбросить второе слагаемое в правой части; иными словами,
не нарушая общности, матрицу а, с помощью которой образована
квадратичная форма, можно считать симметричной.
Дискриминантом квадратичной формы Д называется определи-
определитель квадратной матрицы, с помощью которой образована форма:
При преобразовании квадратичной формы к новым переменным z,
вводимым с помощью линейного преобразования
х = hz или xr = zfhf
с квадратной матрицей /г, получаем
х'ах = z'h'ahz = z'bz% (П. 1.2.33)
где Ь = h'ah.
Нетрудно проверить, что b—симметричная матрица, когда а —
симметрична:
V = h'a'h = h'ah = b.
Заметим, что по (П. 17) и (П. 2)
|а| = |Л'||а||Л| = |Л|2|а|. (П. 1.2.34)
т. е. дискриминант формы при указанном преобразовании умножается
на квадрат определителя матрицы преобразования.
Матрицы b и а, связанные соотношением (П. 33), называются
подобными.
766
ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
д. Умножение сложных матриц. Рассмотрим конформные
матрицы: (т X /?)-матрицу а и (/? X я)-матрицу Ь. Проведя перего-
перегородки, представим а и b как сложные матрицы вида
а =
тх X Р\
т2Хр\
mtX pi
Р\Хп{
Р2Хпх\
Ps Хпх
' mi X Р\ \
\т2Хр2:
mtXP2[
Р\ X п2
Р2 X П2
PsX п2
• • • \mxXps
• • • \т2Х Ps
• . • \mtXps
\ • • • \P\Xnq
\ ' ' ' \P2Xnq
\ * * * \PsXnq
(П. 1.2.35)
причем
пх+ ... -\-nq = n.
В этой записи отмечены только порядки субматриц; разбиение
произведено так, что субматрицы в строках матрицы а конформны
субматрицам столбцов Ь. Пусть С обозначает сложную матрицу
с элементами
Сы = (mk X Pi) Oi X nt) + (mk X P2) O2 X nt) + .. .
<^), (П. 1.2.36)
представляющими (mk X я^-матрицы. Порядок матрицы С равен
(т1 + т2 + • • • + Щ) X {пх + д2 + . ,+л?) = /»Х л; такой же по-
порядок имеет произведение ab = c. Легко проверить, что С = 6, т. е.
при перемножении двух сложных матриц можно формально обра-
обращаться с субматрицами, входящими в их состав, как с числами при
перемножении числовых матриц.
Пример 9. Определим произведение АР матриц Лагранжа и
Пуассона (П. 1.23) и (П. 1.28). По правилу (П. 36) получаем
АР =
[[00]] ((аа)Н-
"[[Ра]] ((аа")) +
а)) ; [[?а]] ((а?)) +
((??))
(П. 1.2.37)
Вычислим (д X /г)-субматрицы, входящие в состав этой сложной
матрицы. Имеем
k=i
(s, г=1. ....
„ аг)}
П. 1.2] ДЕЙСТВИЯ НАД МАТРИЦАМИ 767
Вспомнив определения скобок Лагранжа и Пуассона (П. 1.20; и
(П. 1.26), получим
= V V
т_ т __ ^l .^ (Л. _^l _ _^ ^
as dak das dak ) \ dqt dpt dpt dqt
| (dqm dpm dpm dqm \ / d$k dar d$k dar \i
~ ^ ^ da, dpt £i \
m = \ Ы\ L ^ = 1
dak дрт д?г \
dak dqt ^ d$k dqt
d^ d / ~
das dqt -U \ daik dpt ' d^ dpt
i даь , dpm dftk \
dpt dfifc dpi )
lm даь j. dqm d$k \l
Теперь, замечая, что
n
УA
У _ JL _ _ _
JU \ dak dqt "+" dh dqt ) ~ dqt
dak . dqm d^\ _ dq^
n
У
dpt
*t I dpt
h \ _ dpm
ot ) dpt
dak dqt
768 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
получим
1т даг дрт даг \ _
дрт da
/п = 1
и, следовательно,
[[аа]]((аа)) + [[ар]](фа)) = -^. (П. 1.2.38)
Матрица в правом нижнем углу (П. 37) отличается от рассмотренной
лишь перестановкой букв а и р. Она также поэтому равна —Еп.
Как выше, убедимся далее, что матрица
= О,
т. е. представляет нуль-матрицу, равно как и получающаяся из нее
перестановкой букв аир матрица во второй строке первого столбца
(П. 37). Итак,
АР-
(П. 1.2.39)
Вспомнив, что Л и Р — кососимметричные матрицы, можно написать
также
А'Р = ЛР' = Е2п. (П. 1.2.40)
П. 1.3. Обращение матриц
а. Присоединенная матрица. Рассмотрим |#| = det0, где
а—квадратная (я X л)-матрица. Известно, что алгебраическим до-
дополнением Aik элемента aik этого определителя называется определи-
определитель, получающийся из | а | при вычеркивании /-Й строки и k-vo
столбца и снабженный знаком (—\)l'¥k.
Составим (п X /О-матрицу А ал!ебраических дополнений Akl (об-
(обратить внимание на следование индексов)
ll ^21 . ♦ • А-п\ I
, А„ ... Ап2 [ (П_ 13Л)
I \п Л2п ... Лпп II
Эта матрица называется присоединенной к а. Составим матриц) аА\
се элемент r-й строки и Л-го столбца равен
П 1.3] ОБРАЩЕНИЕ МАТРИЦ 769
т. е. сумме произведений элементов r-й строки | а | на алгебраиче-
алгебраические дополнения соответствующих элементов s-й строки; при г Ф s
эта сумма равна произведению элементов г-й строки на алгебраиче-
алгебраические дополнения другой строки, т. е. нулю, а при r = s она равна |а|.
Итак,
(aA)rs = ors\ а | или аЛ = \ а \ Е. (П. 1.3.2)
Точно так же получим
Ла = \а\Е: (П. 1.3.3)
б. Обратная матрица. Предположив, что а — невырожден-
невырожденная матрица, т. е. | а | Ф О, иримем обозначение
Т7Г = в- (ПЛ-3-4)
Тогда из B) и C) получим
аа-1 = а~1а = Е. (П. 1.3.5)
Квадратная пу^п матрица а~1 называется обратной а\ только не-
невырожденная квадратная матрица имеет обратную.
Пусть а и Ь — невырожденные п X п матрицы. Тогда по (П. 2.17)
невырожденной будет и c = ab. Обе части последнего равенства
умножим на b~l а слева и на с'1 справа. Получим
или по (П. 2.13)
~l = b~lbc~l = Ее
Итак, если ab = c% то b~la~l = с'1.
Таково правило обращения произведения матриц. Его можно за-
записать в виде
(ab)~l = b~la-1. (П. 1.3.6)
В частности,
Е~1 = Е = (аа~1)~1 = (а)^1,
и сравнение с (П. 5) показывает, что (а~1)~1 = а, т. е. матрица, об-
обратная обратной, есть исходная. Отметим также, что по (П. 5)
и (П. 2.17)
|^| = 1=|а||а-1|, т. е. \а-*\ = \а\~1 = -^-. (П. 1.3.7)
Применим к соотношению (П.5) правило транспонирования про-
произведения (П. 2.16)
Умножив обе части этого равенства справа на {a'j~lt получим
Е (я/) = (а)' а' «Г1 = (я)'
или
(аГ1 = {а-у. (П. 1.3.8)
49 Зак. 2072. А. И. Лурье
770 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. I
т. е. матрица, обратная транспонированной, равна транспонированной
обратной матрице.
в. Решение системы линейных уравнений. Систему
линейных уравнений
п
2 askxk = bs (s = 1, . . ., п) (П. 1.3.9)
можно, введя (п X л)-матрицу а и (яХ 1)-столбцы х и Ь, записать
в матричной форме
ах = Ь. (П. 1.3.10)
Если а — невырожденная матрица, то, умножив это соотношение
слева на я", найдем
a'lax = Ex = a"lbt т.е. х = а~}Ь. (П. 1.3.11)
Вспомнив (П. 4), получим в развернутом виде
**й* {s={ п)' <ПЛ;ЗЛ2>
причем для элементов обратной матрицы е — а~1 введены обозначения
в** = та"/4** (s-&=1 «)• (П. 1.3.13)
г. Союзная квадратичная форма. Пусть
п п
askxsxk = у x/aA: (П. 1.3.14)
5=1 Л=1
— квадратичная форма, образованная с помощью невырожденной сим-
симметричной п X я матрицы а.
Введем новые переменные
в****' Т- е- У = аХ- СП. 1.3.15)
Квадратичная форма преобразуется к виду
1 , 1 ,
причем по (П. 2.33) и (П. 8)
е = (a-l)faa'1 = {а~1)гЕ = (а')~1 = а~\
Итак,
^ х'ах = ±у'а-*у. (П. 1.3.16)
т. е. выражение квадратичной формы в переменных, определяемых
П. 1.3] ОБРАЩЕНИЕ МАТРИЦ 771
согласно (П. 15), называемое союзным* по отношению к ее выраже-
выражению в старых переменных, образуется с помощью матрицы, обрат-
обратной а.
Союзное выражение формы <p(xv . .., хп) обозначается через
<?'0>i» •••» Уп)- Заметим, что
Л E=1. ••.. *). (П. 1.3.17)
где esk — элементы матрицы а~1 — определены по (П. 13).
Отметим также билинейное представление квадратичной формы
I xax = ^xy = j^xsys, (П. 1.3.18)
причем последнее равенство можно записать по (П. 15) и (П. 17)
в одном из двух видов
5=1 5=1
выражающем теорему Эйлера об однородных функциях (в случае
квадратичной формы).
д. Знакоопределенная квадратичная форма. Квад-
Квадратичная форма п переменных
п п
9 = -2хах= -J Z
5=1 £ = 1
называется знакопостоянной, если она сохраняет знак при всех ве-
вещественных значениях переменных. Таковы формы трех переменных
и т. д. Знакопосто жная форма, обращающаяся в нуль тогда и только
тогда, когда все переменные xv x2> ..., хп равны нулю, называется
знакоопределенной. Такова форма в первом примере; второй же
пример представляет только знакопостоянную, но не знакоопреде-
ленную форму — обращение ее в нуль имеет место на прямой
хх = х2 = лг3, проходящей через начало координат, а не только
в последнем. Точно так же, рассматривая формы трех перемен-
переменных хг, х2, х3, должно считать форму
обращающуюся в нуль на прямой хх = х2 = 0 (на оси хг) знако-
знакопостоянной, но не знакоопределенной.
49*
772 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. t
Целью последующего является вывод теоремы Сильвестра, оп-
определяющей необходимые и достаточные критерии положительности
квадратичной формы. Пусть сначала х2 = . . . = хп = 0; тогда
ср = -^ аих^ будет при хх Ф 0 положительным лишь при ап > 0, и
это неравенство должно войти в число критериев Сильвестра. При
соблюдении его можем написать
где ср2 зависит от переменных х2 хп, но не от xv Положим
теперь
Тогда
(? ) = <Р2(*2. 0 0) = 1
откуда следует, что F2 > 0 и форму ср2 можно также представить
в виде
•_[_ р / . ^23 _|_ _|_ ^2/г V _| / ч
ср2 * '2 I 2 ~1 "^~" -^3 "Т" • • • "I ~р Хп\ —р срз (-^з» *^4' * * * ♦ *^/|/ •
Продолжив это рассуждение, представим форму ср суммой произ-
произведений положительных чисел au = Flt F2, ..., Fn на полные
квадраты линейных функций \s от переменных (xv x2, ...,хп),
(х2 хп), . . . , хп, имеющих вид:
«23-^3 Ч- • • • Ч- U2nXn,
(П. 1.3.20)
где alk можно последовательно выразить через коэффициенты ask
формы ср в исходных переменных; в новых переменных эта форма
записывается так:
4(^ ^| +...+^2). (П. 1.3.21)
Поэтому неравенства
an = Fx>^ /72>0, .... Fn>0 (П. 1.3.22)
являются искомыми необходимыми и достаточными условиями поло-
положительной знакоопределенности формы. Эти неравенства надо выразить
через коэффициенты ask.
П 1 3] ОБРАЩЕНИЕ МАТРИЦ
Линейное преобразование (П. 20) можно записать в виде
Е = их,
где и — «треугольная» матрица
I «12 «13 ... «U
0 1 и23 ... и2п
773
и =
0 0 1
0 0 0
1
Ее определитель, как легко видеть, равен единице. Введя еще диа-
диагональную матрицу
Z7, 0 ... 0
0 /^ ... 0
F =
можем записать B1) в виде
и, следовательно,
О О
a = u'Fu.
(П КЗ.23)
Назовем Д/1 = |д| дискриминант формы ср (выраженной через исход-
исходные переменные), а &n-v Дл_2, . . ., А1 — дискриминанты форм
T/i-i» ?л-2» •••• ?1» получающихся, если принять в ср переменные
л:л = 0, V,=Oh^ = 0, . .., х2 = х3= ... =хп_} = хп = 0.
Ясно, что Ал_5 являются главными диагональными минорами
определителя | а\ = А:
а,,
, А, = ах.
(П. 1.3.24)
Остается заметить теперь, что по (П. 23) и (П. 2.34)
Положив теперь ?„ = хп = 0, получим
?„==?„_,== 0 и, следовательно, хп_}—хп = 0, имеем
50 Зак. 20. А. И Лурье
774 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
и т. д. Последним в этой цепи равенств будет
Отсюда находим
А/г-1 р А/г
^
и условия (П. 22) принимают вид:
Д, > О, Д2 > 0, .'. ., Л^! > О, Д;| > 0. (П. 1.3.25)
Таковы необходимые и достаточные критерии положительной знако-
знакоопределенности квадратичной формы <f, выраженные через коэффи-
коэффициенты этой формы.
Замечание. Из приведенного вывода легко заметить, что в слу-
случае знакоопределенной отрицательной квадратичной формы
Д, < 0, Д2>0, /Ц< 0. •••' (— {)П\ >0' (П. 1.3.26)
Г. е. знаки в последовательности этих величин должны чередоваться,
причем ап = Д2 < 0.
Отметим еще, что матрица, образующая знакоопределенную
форму — невырожденная, так как Д„ = | а | =£= 0.
Если же Дл = | а | = 0, тогда как остальные Д; > 0 (для /— 1,
2, ..., п—1), то ср — вырожденная, знакопостоянная положительная
форма. Она обращается в нуль при ^ = £2 = ... =^/7_1 = 0 и при
произвольном Ъп — хп. При Дл = 0 и Art_j = 0, но Д; > 0 G = 1,
2, ..., п — 2), имеем Fn = Fn_^ = 0, и знакопостоянная положи-
положительная форма выражается суммой (п — 2) квадратов Ц, ..., ^_о,
умноженных на положительные коэффициенты F}, ..., Fn_2, т. е.
обращается в нуль при Sj = ... =^_2:г:=^ и ПРИ произвольных ^„j
и с/г И так далее.
е. Ортогональные матрицы. Невырожденная матрица а
называется ортогональной, если ей обратная а~х равна транспони-
транспонированной
а-1=^а'. (П. 1.3.27)
Г ля ортогональной матрицы
ааг = аа-1 = Е и а'а = а~1а -= Е. (П. 1.3.28)
Отсюда из (П. 2.2) и (П. 2.17) следует, что квадрат определителя
ортогональной матрицы равен единице.
Произведение двух ортогональных матриц представляет ортого-
ортогональную матрицу. Это следует из такого вычисления, в котором ис-
используются соотношения (П. 27) и (П. б)
(ab)'= b'a' = b-la-l = {ab)-1. (П. 1.3.29)
П. 1.41 МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАЦИЙ ВЕКТОРНОЙ АЛГЕБРЫ 775
П. 1.4. Матричное представление операций векторной алгебры
Как указывалось выше (см. (П. 2.19), (П. 2.25), (П. 2.27)), основ-
основным операциям векторной алгебры — скалярному, векторному и диад-
ному умножению векторов— сопоставляются матричные записи
a-b = arb = bra, (П. 1.4.1)
c = ab = ^-ba9 С = — Ь'а = а'Ь, (П. 1.4.2)
ab = aV% ba = ba\ (П. 1.4.3)
Здесь с — столбец (с' — строка) проекций векторного произведения
с — ау<Ь, через а обозначена кососимметричная C X 3)-матрица
(П. 2.3).
Тождествам
соответствуют записи
a'be = b'ca = c'ab9 (П. 1.4.4)
а тождеству
аХ(ЬХс) = Ь(а-с) — с (а • Ь) = Ьа • с — b • ас
соответствует запись
dbc = barc — ca'b = (pa' — Ea'b) с. (П. 1.4.5)
Поскольку столбец с произволен, можно приравнять друг другу
C X 3)-матрицы, стоящие множителем перед с; приходим к тож-
тождеству
ab = ba' — Ea'b (П. 1.4.6)
и, в частности,
а2 = аа'—Еа'а. (П. 1.4.7)
Рассмотрим линейные функции проекций av a2, а3 вектора а
(П. 1.4.8)
Если при произвольном векторе а величины сх, с2, съ также
можно рассматривать как проекции на те же оси некоторого
вектора с, то говорят, что совокупность девяти величин
(П. 1.4.9)
определяет тензор Р, причем Pik являются составляющими его в этих
осях.
776 ЭЛЕМЕНТАРНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ [ПРИЛОЖ. 1
Вектор с называется произведением тензора Р на вектор а справа
и соотношения (П. 8) записываются в виде
с = Ра. (П. 1.4.10)
Матричное представление этого соотношения имеет вид
с = Ра, (П. 1.4.11)
где Р обозначает C X 3)-матрицу, задаваемую такой же таблицей
(П. 9), а с и а — C X 1)-столбцы, сопоставляемые векторам с и а.
Транспонированию соотношения (П. 11)
с' = а'Рг (П. 1.4.12)
соответствует операция умножения транспонированного тензора Р'
на а слева
с = а-Р'. (П. 1.4.13)
Умножению матриц
II — а3Р21 + а2Р3] — аъР22 + а2РЪ2 — а3Рг2 + а2Ръг |
1 (П. 1.4.14)
ставится в соответствие образование тензора а X Р- Можно теперь
написать
«X(P-ft) = (eXP)-ft. (П. 1.4.15)
так как обе части этого векторного равенства в матричной записи
имеют вид аРЬ.
Матричной записи РаЪ соответствует векторная операция
(РХа)-Ь = Р-(аХЬ). (П. 1.4.16)
П. 1.5. Дифференцирование матрицы
Рассмотрим матрицу а, элементами которой служат функции пе-
переменной t. Рассматривая разность значений матрицы при значениях
параметра t-\-kt и t, имеем по определению разности матриц
Теперь, воспользовавшись определением умножения матрицы на ска-
1
ляр —, имеем
а (/ + AQ - a jt) _ || aik (t + AQ - aik @ II
и — 1 дг И •
При переходе к пределу Д£->0 элементы матрицы, стоящей справа,
станут равными производным элементов матрицы а. Поэтому
п. 1.5]
ДИФФЕРЕНЦИРОВАНИЕ МАТРИЦЫ
777
естественно называть это предельное значение производной а по t:
а= \\'alk\\ A= 1 т\ k=lt .... п). (П. 1.5.1)
Например, сопоставляя вектор-радиусу г столбец х (или
строку х'), следует столбец v (строку v'), соответствующий вектору
скорости v = r, определить как производную х по времени:
v = x. v' = x'. (П. 1.5.2)
Если г зависит от t как явно, так и через посредство аргумен-
аргументов qv q2 qn
r = r (Я\* - - •. Яп> 0 или х — х (Яг* • • •. Яп> 0.
то вектор скорости определится столбцом
дх • , , дх •
-^- (П. 1.5.3)
Этому равенству можно придать вид
дх - . дх
vg+
(П. 1.5.4)
дх
где ^ — столбец элементов qs(s = 1, ..., /г), а -т— представляет
C X я)-матрицу
дх2 дх2
дх,
дх2
дх*
дх
(П. 1.5.5)
дх3 дх3
dq] dq2
.Из (П. 4) следует соотношение
civ дх дх
dq dq dq *
являющееся матричной записью векторных равенств
dv дг дг
(П. 1.5.6)
(П. 1.5.7)
ПРИ ПО ЖЕНИ Е 2
СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА*)
П. 2.1. Косоугольные координаты
Рассматриваются три некомпланарных вектора ev e2, ег, обра-
образующих координатный базис; модули этих основных или базисных
векторов могут быть различны (векторы еь — не единичные). Вслед-
Вследствие некомпланарности базисных векторов величина
v = er(e2X е3) = е2 • (е3 X ег) = е,. {ех X е2) (П. 2.1 Л)
отлична от нуля и при надлежащем порядке нумерации векторов
положительна. Она равна объему параллелепипеда, построенного на
основных векторах.
Векторы, взаимные с основными (образующие взаимный коор-
координатный базис), определяются равенствами
е2Хеь. e ezXev е е,Хе2. (П. 2.1.2)
Они перпендикулярны координатным плоскостям основного базиса
e*.ek = 0 (вФк), (П. 2.1.3)
причем, согласно (П. 1), -
es-e,= \. (П. 2.1.4)
Определения основного и взаимного базиса обратимы, т. е. базис
взаимный взаимному совпадает с основным. Чтобы проверить это,
вычислим векторное произведение
е2Хе3 = ±г (е3 X ех) X (в, X е2) =
= ^г [«1*2 • («з X в,) — е2е, • (ея X е,)| = - в,
*) Мы ограничиваемся сообщением лишь основных сведений, использу-
используемых в изложении нашего предмета. Отсылаем читателя к книгам:
Н. А. К и л ь ч е в с к и й, Элементы тензорного исчисления и его приложения
к механике, Гостехиздат, 1954 и Э. К а р т а н, Геометрия римановых про-
пространств, ОНТИ, 1936. Элементарные сведения по тензорному анализу со-
сообщаются также в книге: Н. Е. К о ч и н, Векторное исчисление и начала
тензорного исчисления, ГТТИ, 1938.
П. 2.1] КОСОУГОЛЬНЫЕ КООРДИНАТЫ 779
и величину
*, = е1 ■ (е2 Хе3)=--^е1-е1 = ^. (П. 2.1.5)
Приходим к равенствам
е =-Le2Xe\ е2 = — е3Хе\ е3^ — е*Хе\ (П. 2.1.6)
что и требовалось.
Основное значение в дальнейшем имеют скалярные произведения
es-ek = gsb=gks, es-ek = gs\ es-ek = gl (П. 2.1.7)
причем, согласно (П. 3) и (П. 4)
т. е. матрица
— единичная.
Локажем, что симметричные матрицы
обратные, т. е. g* = g~1. Надо вычислить для этого суммы
3
ет = es • 2 ekek • ет =
m - ek\ =
v /г = 1
Но нетрудно видеть, что
> о \У £>k \о \У (о Ч/ р \ _1 о \/ (р \/ р \ р (р \/ р W П
/ j t> fe /\ t> \г> j /\ \t>2 s^ 3' i 2 ^ \*^3 •'^ и " 3 ^ 1 ^ 2'' —
(П. 2.1.9)
и, следовательно,
з
J-и ^ s == ^ ИЛИ ^^' = Ь, g' == g » A1. z. 1. 1U)
что и требовалось. Из сказанного следует теперь, что
g*s = S. (П. 2.1.11)
780 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
где Gsk — алгебраическое дополнение элемента gsk определителя \g\
матрицы g. С другой стороны, например,
gia = е1 • е2 = ^ (е2 X ег) ■ (ег Хех) = ^ (е2 • егег -е1~е1- e2ez • ег) =
— ! ( \— °12
и сравнение с (П. 11) приводит к соотношению
v = VTg\- (П. 2.1.12)
В дальнейших записях (в этом Приложении) условимся опускать
знаки суммирования по повторяющимся сверху и снизу индексам
(немым индексам). Например, формула (П. 10) в этой записи примет
вид
gskgkm=g?. (П. 2.1.13)
Пользуясь введенными величинами (П. 7), можно наряду с (П. 2)
и (П. 6). установить следующие соотношения между векторами основ-
ного и взаимного базисов:
es = gskek, es=gskek (П. 2.1.14)
(знаки суммирования опущены). -Для проверки достаточно умножить
обе части первого соотношения на еК а второго на ev Получим
pis -— psk pi — psl p — p pk — p
что и требуется.
При использовании косоугольных координат удобно обобщить
определенные в п. 2.1 символы Леей—Чивита. Вводим два вида
этих символов
Sstq = es' (fit X eq) и е«* = es ■ {* X &). (П. 2.1.15)
Они отличны от нуля, если в числе индексов s, /, q нет одинаковых.
Если же эти индексы различны и следуют в порядке 1, 2, 3 или
получающемся из него круговой перестановкой, то
- (п. 2.1.1б>
При нарушении указанного порядка расстановки индексов
€«,=-V\g\. €** = -у±=. (П. 2.1.17)
Формулы (П. 2) и (П. 6) теперь записываются в виде
«,Хв, = €щеч, е°X<? = etqer (П. 2.i.18)
П. 2.2] ВЕКТОРЫ В КОСОУГОЛЬНЫХ КООРДИНАТАХ 781
П. 2.2. Векторы в косоугольных координатах
Задаваясь координатным базисом ev e2, еъ, можно двояким обра-
образом определить произвольный вектор а. Во-первых, представить его
в форме разложения по базисным векторам
a = ases (П. 2.2.1)
и, во-вторых, задать три скалярных произведения
as = a-es (s = 1, 2, 3). (П. 2.2.2)
Величины а5 называются контравариантнымп, as — ковариантными
составляющими вектора а. Их геометрическое значение очевидно:
отрезки
(не суммировать по s\) равны ребрам параллелепипеда, построенного
на основных векторах и имеющего вектор а диагональю; отрезки
1*1 VIZ
представляют проекции а на основные векторы.
Из соотношений (П. 1), (П. 2) и (П. 1.14) следуют формулы, свя-
связывающие контра- и ковариантные составляющие
as = gskak, as = a-es = gskak. (П. 2.2.3)
Легко получить теперь соотношения
а = akek = akgkses = ase\ (П. 2.2.4)
которые вместе со второй группой формул (П. 3) позволяют опре-
определить контравариантные и ковариантные составляющие вектора
в основном координатном базисе как ковариантные и контравариант-
контравариантные составляющие во взаимном базисе.
Условимся называть основной базис е3 старым, взаимный es
новым. Сопоставление формул
as = gSkak и es = gskek
показывает, что соотношения, связывающие ковариантные составляю-
составляющие вектора в старом и новом базисе, тождественны с теми, кото-
которые связывают старые и новые базисные векторы. Из формул же
as = gskuk и es _ gsk6k
следует, что контравариантные составляющие в старом базисе свя-
связаны с такими же составляющими нового базиса соотношениями
перехода от новых базисных векторов к старым. Сказанное остается
верным, если в качестве нового базиса принять не взаимный с основным,
782 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
а произвольно ориентированную тройку векторов e'v e'v е'ъ% Этим
объясняются наименования составляющих вектора: коварианг-
ный — изменяющийся, как базисные векторы, контравариантный —
обратно базисным векторам.
В ортогональной декартовой системе координат при \es\=\
различие между ко- и контравариантными составляющими исчезает.
Выражение скалярного произведения двух векторов может быть
записано в одном из трех видов
а . Ъ = asb5 = gskasb* = gs*asbh. (П. 2.2.5)
В частности,
а2 = a*as = gska*ak = gskasak. (П. 2.2.6)
Векторное произведение с = аУ^Ь записывается в форме
с = ctel = asbkes Xek = asbk€sktel
или же
с = cfet = asbkes Xek = asbkesktet.
Таким образом, ковариантные и контравариантные составляющие
векторного произведения оказываются равными
ct = €skflsbk* ct = €Ш"А- ^П- 2-2-7)
Например,
V 4 2Ьг - * А) (П. 2.2.8)
и т. д.
П. 2.3. Тензоры второго ранга в косоугольных координатах
Тензор второго ранга был определен (см. П. 1.4 и П. 4.3) как
величина, задаваемая девятью составляющими, с помощью которой
осуществляется преобразование вектора а в другой вектор с. В орто-
ортогональных декартовых координатах тензор второго ранга может быть
задан его диадным представлением D.3.4). При переходе к косо-
косоугольным координатам диады вида isik следует заменить одной
из диад вида
*^ s kу • S * к'
в связи с чем возможны четыре диадных представления тензора
р = Pskesek = P>*ese* = Р8.ке*ек = P\keeR A1. 2.3..1)
с помощью контравариантных составляющих Psk, ковариантных Psk,
и двух типов смешанных составляющих Р% и P's — контравариант-
контравариантных по первому индексу и ковариантных по второму, или наоборот.
Легко получить, пользуясь соотношениями (П. 1.14), формулы связи
между составляющими тензора различного рода; для этого умножим
2.3] ТЕНЗОРЫ ВТОРОГО РАНГА В КОСОУГОЛЬНЫХ КООРДИНАТАХ 783
скалярно выражения (П. 1) справа сначала на ет% потом на е1. При-
Придем к формулам
pim _ g5lg*mpsn = gkmp[k = g'lP'sm. (П. 2.3.2)
Аналогично получим
Р1 — glsP =g Р1к = Цк1 g P's, (П 2.3.4)
Р'1 = цб1Р =g Pki' = g gklP* . (П. 2.3.5)
В этих формулах ?аключены правила операций опускания и под-
поднятия индексов, автоматизирующие вычисления с тензорными вели-
величинами.
Тензор второго ранга будет симметричным, если Psk = Pks\
тогда, как видно из приведенных формул, такие же соотношения
будут иметь место для контравариантных составляющих Psk = Pks
и смешанных Ps.k = P'ks; их можно тогда обозначать Psk, так как
указание последовательности индексов (первый, второй) становится
ненужным.
Примером симметричного тензора второго ранга является фунда-
фундаментальный тензор g: его ковариантные составляющие gsk, контра-
вариантные gsk и смешанные gsk определены выше через векторы
основного и взаимного базисов по формулам (П. 1.7).
Представление вектора
с = Р-а (П. 2.3.6)
через его контравариантные или ковариантные составляющие при
заданном представлении а можно получить, выбирая одну из форм
записи Р. Например, ковариантные составляющие с, если заданы
такие же составляющие а, получаем так:
с = cses = P'*esek • атет = P'skakes,
т. е.
и т. д. Аналогично следует поступать при умножении Р на а слева.
Тензор второго ранга будет кососимметричным, если Psk = —Pk\
тогда PSk — — Pks и Plk = —P'sk- Кососчмметричный тензор задается
тремя составляющими. Вводя определенные в (П. 2.1) символы Леви-
Чивита, можно принять обозначение
ps* = _€isk^ p^ = _6шу| (п. 2.3.7)
где wz и to/ — некоторые величины.
784
СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА
[ПРИЛОЖ. 2
При умножении кососимметричного тензора на вектор а справа
имеем
с=Р • а
или
kaki»1, (П. 2.3.8)
cs = Pskak = — €l
т. е. в развернутом виде
cs = Pskak = -
с1 =
—j (^з — co3fl2). сг = V\J\ (со2а3 — со3а2)
и т. д.
Но к этим же формулам пришли бы, согласно (П. 2.8), рассма-
рассматривая (о как вектор и составив векторное произведение его на а.
Итак, при обозначениях (П. 7) имеем в случае кососимметричного
тензора
9
П. 2.4. Криволинейные координаты точки
Положение точки в пространстве трех измерений будет задаваться
тремя числами ql, q2, qz — ее криволинейными или обобщенными
координатами; это значит, что вектор-радиус г точки должен рас-
рассматриваться как вектор-функция этих величин
r = r{q\ <72, ?3). (П. 2.4.1)
В декартовых (или любых косоугольных) координатах это соотноше-
соотношение может быть записано в форме трех равенств
= x(q\q\q*), у = у (q\ q2, ?3),
z(q\q\q*). (П. 2.4.2)
Область изменения переменных qlt q2, q3 предполагается опреде-
определенной так, чтобы эти уравнения были однозначно разрешимы отно-
относительно qlt q2% q6. Иными словами, в этой области якобиан
J:=-
дх
W
ду
dql
dz
дх
dq2
ду
dq2
dz
дх
dq3
ду
dq3
dz
dq1 dq2
(П. 2.4.3)
отличен от нуля. Его можно считать положительным, если принять
надлежащую последовательность в нумерации переменных qs.
Выбранной системе криволинейных координат сопоставим тройку
векторов
rs = W E=1.2,3). (П. 2.4.4)
П. 2.4] КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ ТОЧКИ 785
Эти векторы некомпланарны, так как величина
гг = г1.(г2Хг3). (П. 2.4.5)
равная якобиану У, отлична от нуля (и положительна).
Векторы rs примем за основные в?кторы координатного базиса
в рассматриваемой точке. Векторы взаимного базиса обозначаются
через rs. Все формулы и определения, приведенные в предшествую-
предшествующих параграфах этого Приложения, сохраняются, конечно, с тем раз-
различием, что рассматриваемые теперь величины (равно как и коорди-
координатный базис) изменяются при переходе из одной точки пространства
в другую.
Выражение вектора dry соединяющего две бесконечно близкие
точки, имеет по (П. 4) вид:
dr = rsdqst (П. 2.4.6)
и, следовательно, квадрат расстояния между этими точками рлвен
ds2 = dr-dr = rs.rk dqs dqk = gsk dq* dq<\ (П. 2.4.7)
т. е. ковариантные составляющие фундаментального тензора могут
быть определены как коэффициенты квадратичной формы в выраже-
выражении ds2\ они определяют метрику в выбранной системе криволиней-
криволинейных координат в окрестности рассматриваемой точки; тензор g по
этой причине называется метрическим.
Основное значение в последующем имеют формулы дифференциро-
дифференцирования базисных векторов rs и взаимных им rs.
Начнем с вычисления векторов
rsk = ^JL = f =^ = rk, (П. 2.4.8)
sk dqk dqkdqs dqs ks У J
Представление этих векторов через базисные векторы может быть
выражено формулами
{ЛК- (П. 2.4.9)
Коэффициенты, обозначенные волнистыми скобками, называются
символами Кристоффеля второго рода. Из (П. 8) следует свойство
симметрии этих величин по нижним индексам
{лиг}- (п-2-4ло)
Из (П. 9) имеем
rst.rt = \ m\gmt (П. 2.4.11)
и далее, по (П. 1.13)
= *"rc*.r,. (П. 2.4.12)
786 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Скалярные произведения в правой части этих равенств обозначаются
так:
rsk.rt = \s4 k\ t\ = [k, s; t\. (П. 2.4.13)
Эти величины называются символами Кристоффеля первого рода
или прямыми скобками. Для символов Кристоффеля часто приме-
применяются также обозначения
I*, ft; t\ = vskth
Имеем по (П. 13)
dq! oql
Меняя Гуквы s, k, t в круговом порядке, получим также
HL*L = \k4 s; t] + [t, s; kl -Щ- = у. k\ 5|-U|s, k\ t\.
d,f dqk
Вычитая теперь первое равенство из суммы второго и третьего и
учитывая симметрию прямых скобок относительно двух первых индек-
индексов, придем к формуле, определяющей символы Кристоффеля пер-
еого рода через производные ковариантных составляющих метриче-
метрического тензора
|5, Л; ,, = !/_%+ *Цц_Щ\ (П 2.4.14)
1 ] 2 \ dqk T dqs dq< ) У *
Из (П. 12) и (П. 13) имеем
K = g"\s, k\ t\. (П. 2.4.15)
Следствием формул (П. 15) являются равенства
(*■ ft; t\ = gtm\?ll\- (П. 2.4.16)
Вычисление производных
г* = 4гт (П. 2.4.17)
s dqs v 7
проще всего проводится так: имеем по (П. 9)
или
г\ •г/ = — | ^|, (П. 2.4.18)
т. е. величины справа формально можно трактовать как ковариантные
составляющие векторов r*s. Поэтому
rts=-{'si}rl. (П. 2.4.19)
П. 2.5] КОВЛРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ 787
Отметим, что символы Кристоффеля обращаются в нуль тогда и
только тогда, когда величины gsk постоянны, т. е. основные век-
векторы rs координатного базиса сохраняют неизменные величины и
направления.
П. 2.5. Ковариантное дифференцирование
Предметом рассмотрения в механике и математической физике
являются инвариантные величины; они не зависят от выбора коорди-
координатного базиса и определяются собственными свойствами изучаемого
объекта. Инварианты могут быть скалярами (энергия, работа, масса,
температура), векторами (скорость, ускорение, сила), тензорами (тен-
(тензор инерции в точке тела, тензоры деформаций и напряжений
в сплошной среде), а также их функциями—диадное, скалярное и
векторное произведения векторов, произведение тензора на вектор
и т. д.
Проведение вычислений с векторными и тензорными величинами
требует введения координатного базиса и составляющих той или иной
природы (контравариантных, ковариантных, смешанных) по основным
векторам этого базиса. Изменения инварианта при.переходе отточки
к точке или с течением времени обусловлены лишь свойствами этого
инварианта; иначе обстоит дело, ьогда рассматриваются составляю-
составляющие — их изменения обусловлены еще и изменением величин и напра-
направлений основных векторов взятого координатного базиса. Пусть,
например, аь не зависят от координат; их частные производные по
координатам равны нулю, но было бы грубой ошибкой считать, что
в этом случае век'юр а не испытывает изменений при переходе от
точки к точке. Верно и обратное: при постоянном а составляющие as
(или as) не сохраняют постоянных значений. Задачей последующего
является введение таких характеристик изменяемости составляющих
векторов и тензоров, в которых учитывались бы как изменения самих
этих функций, так и координатного базиса, к которому они отнесены.
Это достигается введением операции ковариантного (или абсолютного)
дифференцирования.
Рассмотрим производную вектора а по одной из переменных qs.
Начнем со случая задания вектора его контравариантными составляю-
составляющими. Тогда
д" — д akr
dqs ~ dq* п ГЪ'
Не возникает сомнения в том, что при дифференцировании инвари-
инварианта (вектора я, диадного произведения ab и т. д.) сохраняются
общеизвестные формальные правила дифференцирования суммы, про-
произведения и т. д. Поэтому, учитывая формулы (П. 4.9),
788 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ 2
Аналогично получим, исгользовав формулы (П. 4.19)
^e. = r*4^-_eJ k\rm = rm(^f-\ k\ak). (П. 2 5 2)
dqs dqs k\sm) \ dqs \sm\ k) v •*■•"•*->
Итак,
-^=rm4sam = r»4sam, (П. 2.5.3)
причем выражения
•называются ко вариантными (или абсолютными) производными от
контравариантных а™ и соответственно ковариантных aw составляю-
составляющих вектора а.
Вычисление легко обобщить на тензоры любой кратности. Огра-
Ограничимся здесь, как и ранее, тензорами второго ранга. Имеем, исполь-
используя диадное представление тензора,
Аналогично поступаем при задании тензора его ковариантными или
•смешанными составляющими. Приходим к формулам
^P=V^ = ^%PW = V-'V>.V (П. 2.5.5)
причем ковариантные производные величин Pkt, Pw P*t определяются
по формулам
dpkt
V Pk = —- 4-1 I Pm —\ }Pk
ys^.t dqs^lsm) -t 1st) -ru-
-rust\
По этим формулам, например, вычисляются ковариантные производ-
производные составляющих диады, т. е. произведений вида akbt\ отсюда
легко видеть, что при ковариантном дифференцировании произведения
сохраняется правило
Сказанное относится и к ковариантному дифференцированию произве-
произведения составляющих тензоров. Например,
П. 2.5] КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ 789
Ковариантная производная скаляра равна производной его
Например, в случае скалярного произведения двух векторов имеем
по (П. 6)
так как второе и третье слагаемые сокращаются.
Важное значение в тензорном анализе имеет теорема Риччи:
ковариантные производные ковариантных, смешанных и контрава-
риантных составляющих метрического тензора равны нулю. Действи-
Действительно, применяя вторую формулу (П. 6) к величинам gkv имеем
по (П. 4.16) и (П. 4.14)
(П. 2.5.7)
Смешанные составляющие glk постоянны по величине (равны нулю
или единице). Поэтому
Вычисляя их ковариантную производную по последней формуле (П. 6),
получим
V ,t-__\rn) ( t \ m__i М , i M 0
Остается рассмотреть контравариантные составляющие. Проще всего
исходить из соотношения (П. 1.13). Имеем по (П. 7)
При фиксированных sat получили однородную систему линейных
уравнений с определителем \g\, отличным от нуля. Поэтому
Итак,
Отсюда следует, что составляющие метрического тензора ведут себя
при ковариантном дифференцировании как постоянные величины; их
можно вносить под знак и выносить из-под знака Vs. Это видно,
например, из формул (П. 5)
что и требуется.
790 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Рассмотрим тензор, равный сумме трех диад
rl+r2+r3w- (П2-5-9>
Формулы (П. 3) дают диадное представление этого тензора
да „ „ т-т ел г 1 ^ч
rs -T—Z- = rsrj4cam = rsrmV а„. (П. 2.5.10)
fiqs m s s m \ )
Величины Vsam и Vsam являются коэффициентами диадного предста-
представления тензора (П. 9). Поэтому их следует рассматривать как соста-
составляющие тензора — первую, как смешанную (ковариантную по 5 и
контравариантную по т), вторую, как ковариантную по обоим
индексам.
Частные производные от а1 и aL no qs не являются составляю-
составляющими тензора.
П. 2.6. Пример неортогональных криволинейных координат
Чтобы иллюстрировать ход вычислений, рассмотрим такой пример:
пластинка, плоскость которой остается параллельной плоскости Оху,
перемещается вдоль оси Oz, вращаясь вокруг нее, причем угол по-
поворота y = iz, где т постоянно. В плоскости пластинки располагаем
взаимно перпендикулярные оси Ох1 и Ол;2 и положение точки про-
пространства определяем координатами л;1, л;2, x3 — z, играющими
роль ql, q2, q6. Уравнения (П. 4.2), выражающие декартовы коор-
координаты х, у, z в системе неподвижных осей через обобщенные,
в этом случае будут
х — л;1 cos тл;3 — л;2 sin тл;3, y = xlsmzx3-{-x2cosrzx3, z — x3,
(П. 2.6.1)
поэтому проекции основных векторов координатного базиса на эти
оси будут
г2: — sin тл;3 cos тл;3 0
г3: — ту тл: 1.
Ковариантные составляющие метрического тензора равны
«и=1» £i2 = 0« £\з = — хх?> !
«22=1. «23=^. [ (П. 2.6.2)
«зз=1+^[(^1J + (^2J]. I
Теперь имеем
1 0 - ™2
= 1 (П. 2.6.3)
П. 2.7] ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 791
и далее
gU =
(П. 2.6.4)
Все прямые скобки, не содержащие индекса 3, равны нулю. Не рав-
равными нулю оказываются
[3, 3; 11 = — xh\ [3, 3; 2) = - Л2,
[2, 3; 1) = 13, 2; 11 = —т, [1, 3; 2] = [3, 1; 2]=х,
[1, 3; 3] = [3, 1; 3\ = х1т?, [2, 3; 3] = [3, 2; 31 = — х2х2.
(П. 2.6.5)
Остается по (П. 4.15) составить выражения волнистых скобок;
получаем
Ц}--" {i)~~- (П266)
113
Остальные равны нулю. Вычисление можно упростить, непосред-
непосредственно определяя производные основных векторов. Имеем
гх = ix cos ххъ + /2 sin xjc3, r2 = — /2 sin тл:3 -f- i2 cos тх3,
откуда
/j = r1 cos tjc3 — r, sin тх3, /2 = гг sin xjc3 -f- r2 cos тд:3,
и далее
г3 = х (— /jy 4- i2x) = ^ (x1^ — x2ri)- (П. 2.6.7)
Поэтому
rn = r12 = r22 = 0, r13 = x (— ^ sin xjc3 -f- /2 cos хд:3) = xr2,
Г23 = — ТГ1« Г33 = T (-^lr23 ~ ^2ri3) = — т2 (^ 1г1 4" ^2>-
(П. 2.6.8)
Теперь, обратившись к формулам (П. 4.9), приходим к тем же
значениям (П. 6) символов Кристоффеля второго рода.
П. 2.7. Формулы теории поверхностей
Обозначая через qx и q1 гауссовы координаты точки на поверх-
поверхности и через р — вектор-радиус этой точки, запишем векторное
уравнение поверхности в виде
? = ?(д\ <72). (П. 2.7.1)
792 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Можно записать теперь систему соотношений, повторяющих до опре-
определенного места сказанное в предшествующих пунктах; при этом
применяемые ниже греческие индексы могут получать одно из двух
значений A или 2).
Определяются основные векторы на поверхности
Ра = -^г. (П. 2.7.2)
имеющие направления касательных к координатным линиям поверх-
поверхности. Через них определяются бесконечно малое перемещение по
поверхности и квадрат его величины
dp = padq*. \d9\* = (do? = tu.9id<rdq* = a^d<rdqtt (П. 2.7.3)
где
0«р = Р«'Рр (П. 2.7.4)
представляют ко вариантные составляющие метрического тензора
поверхности. Его контравариантные составляющие, подобно (П. 1.11),
вычисляются по формулам
где через | а | обозначен определитель
. | #11 #12
так что, как и ранее,
пап а\2> (П. 2.7.6)
#12 #22
0 (<*Ф Т).
1 <а=т>- (а2'7'7)
В рассмотрение вводятся еще взаимные векторы
р* = а«Ррр. (П. 2.7.8)
Они, как и основные, представляют векторы на поверхности (т. е.
лежат в ее касательной плоскости). При этом
Ра-Рр = ^. (П. 2.7.9)
т. е. р1 и р2 соответственно перпендикулярны р2 и рг Заметим еще,
что
|P1Xp2|2 = P?Pl-fpI-p2)l = l«|. (П. 2.7.10)
откуда следует, что элемент площади поверхности do =y\a\ dqldq2.
Любой вектор с на поверхности (т. е. лежащий в касательной
плоскости к ней) может быть определен его контравариантными са
или ковариантными составляющими са:
с = с«?A = с«?*> (П. 2.7.11)
П. 2.7] ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 793
причем
с* = с-ра, с* = с-?\ (П. 2.7.12)
Сказанное здесь является повторением того, о чем говорилось
ранее в теории пространственных криволинейных координат. Для
определения действия дифференцирования векторов на поверхности
этого недостаточно — дело в том, что производная такого вектора
является вектором, уже не принадлежащим поверхности, так как
последний имеет составляющую, нормальную поверхности.
Единичный вектор нормали поверхности обозначается через т.
Очевидно имеем
т= plXp2 ^-^L-p^Xpo (п- 2-7-13)
I Pi XP2I V\a\ *1/NW
и, следовательно,
pe.m = 0. (П. 2.7.14)
Дифференцируя эти соотношения по q$% получим
Квадратичные формы дифференциалов dqa гауссовых координат
I=(dof = a^dq«dqK II = b^dq«dq$ (П. 2.7.16)
называются первой и второй квадратичной формами поверхности.
Ниже станет ясным, что вторая квадратичная форма, подобно пер-
первой, имеет инвариантное (не зависящее от выбора гауссовых коор-
координат) геометрическое значение. Поэтому ее коэффициенты Ь^
являются ковариантными составляющими тензора; его смешанные
составляющие будут
а контравариантные
b^ = abaa^hv (П. 2.7.18)
Переходим к выводу формул, определяющих вторые производ-
производные ра? вектор-радиуса р. Выше указывалось, что ра^ не является
вектором на поверхности. Поэтому его представление должно со-
содержать составляющую по нормали к поверхности. Полагаем
fl- (П. 2.7.19)
Тогда, учитывая (П. 14) и (П. 15), легко видеть, что Ьа$ в этих
формулах являются только что введенными коэффициентами второй
квадратичной формы. Далее имеем согласно (П. 14) и (П. 4)
P.?-P» = {a]lK- (П. 2.7.20)
51 Зак. 2072. А. И. Лурье
794 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Как и ранее, полагаем
И£ ££) СП. 2.7.2,,
причем последнее выражение получается при точном воспроизведе-
воспроизведении вывода, приведенного в П. 2.4 для случая трех измерений.
Из (П. 20) и (П. 7) следует также
{Jp}=«r5[a. P: 81. (П. 2.7.22)
Величины
1«. Р; т1 и Ц}
'представляют символы Кристоффеля первого и второго рода для рас-
рассматриваемой поверхности (прямые и волнистые скобки). Они вы-
вычисляются по коэффициентам первой квадратичной формы; наоборот,
величины #ар не могут быть выражены через эти коэффициенты.
К сказанному следует добавить соотношения
та-т = 0, (П. 2.7.23)
выражающие, что производная единичного вектора перпендикулярна
этому вектору; поэтому та, как вектор на поверхности, может быть
представлен через векторы рР или рр. Учитывая соотношения (П. 12),
(П. 15) и (П. 17), имеем
= — *2рэ- (П. 2.7.24)
Составим еще формулы дифференцирования векторов взаимного
базиса, т. е. выражения
до*
«а —
Ре ~~ dqt e
Повторив вычисление, которое привело к формуле (П. 4.18),
найдем
Далее имеем
так как все остальные слагаемые вектора, получающегося при диф-
дифференцировании выражения #агрт, перпендикулярны т. Следствием
(П. 25) и (П. 26) являются искомые соотношения
- (П. 2.7.27)
п. 2.8] кривизна линий на поверхности 795
П. 2.8. Кривизна линий на поверхности
Линия на поверхности задается уравнениями
ql=ql(t). <72 = <72(O. (П. 2.8.1)
выражающими, что гауссовы координаты поверхности являются функ-
функциями одного параметра t. Векторное уравнение линии на поверх-
поверхности поэтому записывается в виде (П. 7.1) в предположении, что q1
и q2 определены их значениями (П. 1).
В дальнейшем за параметр примем длину дуги о рассматриваемой
линии. Единичный вектор х касательной к ней равен
Обозначая через k кривизну линии, через п единичный вектор глав-
главной нормали, имеем по первой формуле Френе
Заменив здесь pa4 по (П. 7.19), получим
Вектор кривизны kn здесь представлен слагаемым по нормали к по-
поверхности— вектором нормальной кривизны
dqa dq^ baBdq«dq$
mk = mkn • m — mbno —i -r- = tn ——-.—-i-? (П. 2.8.4)
аи da da a^dq^dq^ v '
и слагаемым, расположенным в касательной плоскости к ней.
По известной теореме Менье величина
k = kn*m = kzosb (П. 2.8.5)
представляет кривизну нормального сечения поверхности—^плоской
кривой, получающейся в сечении поверхности плоскостью, проведен-
проведенной через нормаль поверхности т и касательную х к рассматривае-
рассматриваемой кривой.
Второе из упомянутых слагаемых вектора кривизны называется
вектором геодезической кривизны
Величины в скобках представляют контравариантные составляющие
этого вектора. Они обращаются в нуль вдоль линий на поверхности,
51*
796 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
называемых геодезическими. Дифференциальные уравнения геоде-
геодезических линий на основании сказанного имеют вид
Через каждую точку поверхности в любом направлении, проведенном
через эту точку, проходит одна геодезическая линия. Это следует
из теорем существования решения системы двух дифференциальных
уравнений (П. 7) при задании начальных значений искомых функ-
функций <7а и их первых производных —J-.
Из сказанного следует также, что геодезические линии можно
определить как кривые на поверхности, главные нормали ко-
которых имеют направление нормали т к поверхности. Тогда
п=±т и k=±k9 т. е. £* = 0.
Геодезической кривизной линии на поверхности называется мо-
модуль вектора геодезической кривизны, т. е.
Va^ak^ . (П. 2.8.8)
Она обращается в нуль на геодезических линиях поверхности.
В приведенном вычислении были использованы контравариантные
составляющие вектора т. Его ковариантные составляющие можно
представить в виде
\ da
где через Ф обозначена квадратичная форма
m \ dq* dqr$ _ 1 /п 9 я 1 m
ф = та«?-^--^~т- (П- 2-8Л0)
Теперь получаем, использовав формулы (П. 7.27),
-г
ИЛИ
Kn—V\d* A dq« da da
L 6~dT
Вспомнив соотношение
П 2.9] КОВАРИАНТНАЯ ПРОИЗВОДНАЯ ВЕКТОРА НА ПОВЕРХНОСТИ 797
и заметив, что
dq?> I d<z dz
2 dq* dz dz dq°- '
получим теперь
Г" /4 Л/tS лгп 1 /У/7^ ///73
ttlU„о —; ;— • (П. 2.8.1 1)
дФ дФ
Выражения в скобках — ковариантные составляющие вектора геоде-
геодезической кривизны — обращаются в нуль на геодезических линиях.
Приходим к другой форме записи дифференциальных уравнений
этих линий:
4--^г 4^- = ° (а=1,2). (П. 2.8.12)
dz . dqa oqa v J v '
Отметим еще, что вектор х и вектор геодезической кривизны
перпендикулярны друг другу. Действительно,
-с. k* = -с • (kn — kmm • п) = 0. (П. 2.8.13)
П. 2.9. Коварианткая производная вектора на поверхности
Составим выражение приращения dc вектора с, заданного на по-
поверхности его контравариантными составляющими са, при переносе
начала вектора из точки (q\ q2) в бесконечно близкую ql-\-dql,
q2-\-dql. Применив формулы дифференцирования (П. 7.19), получим
(IJ{Tp})^w- (П- 2-9л)
Слагаемое
dqU-b^m (П. 2.9.2)
представляет составляющую dc по нормали поверхности; вектором
на поверхности является совокупность слагаемых
d*c = dq^^,c\ (П. 2.9.3)
где
SUk (П-2-9-4)
798 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
— ковариантная (абсолютная) производная контравариантных вели-
величин са.
Вдоль линии L на поверхности
«). ft. ^
dz dz dq? dz
и выражению d*c придается вид
Говорят, что вектор с перенесен параллельно вдоль Z,, если
d*c = 0, т. e. Vfa = O. (П. 2.9.6)
В частности, когда за с принят единичный вектор касательной т
к L, то по (П. 8.6)
«■ = £. ^М^Ш^Н^ (П.2.9.7,
Имея это в виду, рассмотрим изменение скалярного произведе-
произведения с • х вдоль Z,. Учитывая, что с и х — векторы на поверхности,
имеем
с • т = 0, х«т = 0
и поэтому
rf (с . х) = г . dz + х • dc = с . rf4 +- х • Л. (П. 2.9.8)
Отсюда следует, что при параллельном переносе с вдоль L
d(c-z) = c-k*dG, (П. 2.9.9)
а в частности, когда L — геодезическая линия, то
z) = 0. (П. 2.9.10)
Если с — вектор постоянной длины, то при параллельном переносе
он сохраняет неизменный угол с геодезической линией. Например,
при параллельном переносе вектора по прямой линии на плоскости
угол вектора с этой прямой сохраняется.
Задавая вектор с его ковариантными составляющими, имеем
2 (П. 2.9.11)
п. 2.9] ковариантная производная вектора на поверхности 799
причем величины в скобках представляют ковариантную производную
ковариантных величин са. Теперь, повторив проведенные выше пре-
преобразования, получим
т. е. при параллельном переносе вектора с вдоль кривой L на по-
поверхности
*± \т\И£с (П. 2.9.13)
Знание элемента дуги любой линии на поверхности, которое дои
стигается измерениями, производимыми на самой поверхности т
доступными «двумерным существам, на ней обитающим», определяе-
первую квадратичную форму поверхности и с нею внутреннюю гео-
геометрию поверхности; к внутренней геометрии принадлежат составляю-
составляющие метрического тензора и все величины, определяемые по ним,
т. е. элемент площади, символы Кристоффеля первого и второго
рода, геодезическая кривизна линии на поверхности. Задачи разыска-
разыскания геодезических линий, определения операций ковариантного диф-
дифференцирования и параллельного переноса вектора на поверхности
также относятся к внутренней геометрии. При изгибании поверхности,
не сопровождаемом изменением длин линий на ней, перечисленные
величины остаются неизменными — они представляют инварианты изги-
изгибания. Нормальная кривизна не является, конечно, инвариантом изги-
изгибания. Этим объясняется, что коэффициенты второй квадратичной
формы принципиально не могут быть вычислены при задании только
метрического тензора. Их определение было связано с введением
вектора нормали т поверхности.
Пусть рассматриваемой поверхности соответствует значение q* = qZ
в пространственной системе криволинейных координат q1, q2, #3; таким
образом,
Тогда (напоминаем, что греческие индексы принимают значения 1 и 2)
и далее
т = (riД^2)о = 1/ i^jg- Г3, = AL_ гз (П. 2.9.14)
Y\a\ У l«l ° /^зз о
800 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Здесь использовано соотношение вида (П. 1.2). Теперь имеем
д 1 1 drl
+ —-• (п- 2.9.15)
Заметив, что
ддЧо~ ''^' '° **"' '°
'о 17;-» Jo l^PJo
и учитывая соотношения
о . гт = py . г3 =0
придем к равенству
1 ( Q \
(П. 2.9.16)
\
«э jo
Здесь
{3} 3t«. Р; 3]0 (П. 2.9.17)
и для вычисления величины [а, р, 3]0 требуется знание производной
от gap по <73- Поэтому определение коэффициентов /?ар предполагает
известными значения составляющих метрического тензора ga3 при
q3 — q3 и составляющих ga3 с точностью до членов первого порядка
относительно q'6 — q^:
Поверхность пришлось «покинуть»; нельзя определить вторую квад-
квадратичную форму, оставаясь на ней.
П. 2.10. Ортогональные криволинейные координаты
В случае взаимной ортогональности базисных векторов rv r2, гъ
недиагональные составляющие gsk метрического тензора обращаются
в нуль; диагональные составляющие gss обозначаются через h2:
0 О Ф k),
,2 ; (П. 2.Ю.1)
Величины hs называются коэффициентами Ляме. Имеем теперь
|g-| = h\h:2h\f (П. 2.Ю.2)
откуда следует, что
gss = — rs = ^-. (П. 2.Ю.З)
П. 2.10] ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 801
Выражение вектора а представляется в одном из двух видов:
а = asrs = asrs = -^rrs- (П. 2.10.4)
Физические составляющие а^ вектора определяются как коэффи-
коэффициенты представления его по единичным векторам is базисных на-
направлений:
h = ir = hsrS> а = а(*Iз- (П. 2.10.5)
Таким образом
a(s) = ashs = -^- (П. 2.10.6)
(не суммировать по s\).
Выражение квадрата элемента дуги имеет вид
(dsJ = h2 (dqvJ + h2 (dq2f + h\ (dqzJt (П. 2.10.7)
т. е. коэффициент Ляме hs представляет множитель, на который
следует умножить dqs, чтобы получить элемент дуги координатной
линии, по которой отсчитывается qs.
Отличны от нуля следующие символы Кристоффеля первого и
второго рода (не суммировать!)
lc b' с I \ b с • с 1 h £— I
s o<lk \ss) h\ dqk
(П. 2.10.8)
Is, s\ s] = hs-^f-9 ( s \ d\nhs
q \ss) dqs
Как пример рассмотрим сферические координаты R, ft, cp; здесь
R — радиус сферы, на которой расположена рассматриваемая точка,
О — угол, отсчитываемый по меридиану сферы от северного полюса
@ <С ft ^ тс), ? — азимут меридиана @ ^ cp ^ 2тг), отсчитываемый от
плоскости Ozx к Oyz (на восток).
Коэффициенты Ляме равны
hR=\4 hb = R% h(p = Rsm?t> (П. 2.10.9)
так как при умножении их на dR, db, do получаем длины элемен-
элементарных отрезков на радиусе, меридиане и по параллельному кругу.
Базисные векторы
rR = 1r> гь = Riv ro = K sin ni* (П. 2.10.10)
802
СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА
[прилож. 2
где единичные векторы /#, /&, ц имеют направления радиуса, каса-
касательной к меридиану и касательной к параллельному кругу в сторону
возрастания аргументов /?, 0, ср. Теперь находим
\Rb \ r» + \w (г<р = :я г» =
•r =
^"aci
=={»Лг*+{в9}гв+Ц}г1>=
= — sin
sin Э
cos
0).
(П.2.10.11)
J
Нет нужды повторять сказанное для ортогональных гауссовых
координат на поверхности. Единичные векторы -г- р1э -г- р2, т обра-
образуют в этом случае ортогональный триэдр, так что
Отсюда следует, что
Рассмотрим три вектора: р2, m и m* = m-\-m1dql. Последний пред-
представляет вектор нормали поверхности в точке поверхности (ql-\-dql, q2)>
бесконечно близкой к рассматриваемой точке (qlt q2). Произведение
векторов
(pi X«)'«' = (pi X«)*«i dq\
пропорциональное bl2, представляет объем параллелепипеда, построен-
построенного на векторах plf m, m*. Оно обращается в нуль, если эти век-
векторы компланарны, что будет иметь место тогда и только тогда,
когда векторы т и т* пересекаются или параллельны. Это свой-
свойство определяет линии кривизны поверхности. Например, таковыми
будут меридианы и параллельные круги поверхности вращения. Вели-
П. 2.10] ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 803
чина bl2, как следует из сказанного, обращается в нуль, если за коор-
координатные линии приняты линии кривизны, но не для всякой сети
ортогональных линий на поверхности.
Обращаясь к формулам (П. 9.17) и считая, что рассматриваемая
поверхность соответствует значению qz = q^ в тройной ортогональной
системе координат, получим теперь (не суммировать по а)
Итак,
bl2 = 0. (П.2.10.12)
Последнее равенство показывает, что поверхности тройной ортого-
ортогональной системы пересекаются по линиям их кривизны (теорема
Дюпена). Например, для поверхности сферы радиуса /?0, полагая
ql = bt q2 = yt <73 = /?j имеем
и согласно (П. 8.4) значение нормальной кривизны будет
Отличны от нуля, согласно (П. 11), только два символа Кристоффеля
i *l = ctgftt \ dl = —sinftcosft.
и контравариантные составляющие вектора геодезической кривизны
будут
*•»=*»-Ш1 «in Осей». Л*= ^ + 2^-#-«*»■
da2 \dc ) dz2 ' da da s
Например, вдоль меридиана
dc = Rodb. %i = 0, ^ = 0, т. е. k*» = k*f = 0,
0 da2 da
т. е. меридиан является геодезической линией. Для параллельного
круга
da = #0 sin fttfcp, fc** =V *
и по (П. 8.8) и (П. 8.3)
h — Vk*
что и требовалось.
804 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Как второй пример рассмотрим поверхность прямого кругового
конуса {) = »»0. Полагаем ^r1 = cp, q2 = R, <73 = ^- Тогда по (П. 12)
*99 — — R sin 00 cos 00, £w = 0
и значение нормальной кривизны линии на конусе будет
1
1 И2 sin*
Отличны от нуля символы Кристоффеля
Поэтому контравариантные составляющие вектора геодезической кри-
кривизны будут
и геодезическая кривизна параллельного круга (da = R sin 00 dy)
равна -д—эта кривизна дуги окружности, в которую преобразуется
параллельный круг при развертывании конуса на плоскость.
Рассмотрим также случай поверхности вращения. Положение точки
на ней определяется дугой ql = s, отсчитываемой по меридиану и
углом плоскости меридиана q2 = ^ с отсчетной плоскостью, проходя-
проходящей через ось вращения (азимутом). Коэффициенты Ляме равны
hx = 1, h2 = r(s),
где г (s) — расстояние точки от оси вращения.
Отличны от нуля символы Кристоффеля
г
и уравнения геодезических линий на поверхности вращения будут
d2s г / dy \2 л d2y (^ ~ г' dy ds ^
~d^~~rr УНТ/ = ' ~d^ ' г ~ch ~dz = '
где 0 — дуга по геодезической линии. Нетрудно найти два первых
интеграла
dy i ds \2 Cj
и решение приводится еще к двум квадратурам.
П. 2.11] ЕВКЛИДОВО ПРОСТРАНСТВО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ 805
П. 2.11. Евклидово пространство конечного числа измерений
В аналитической геометрии предметами изучения служат мно-
множества, состоящие из чисел, пар чисел, троек чисел. Полученные
алгебраические результаты, перенесенные на точечные множества,
истолковываются геометрически.
Естественным обобщением является рассмотрение многообразия,
элементы которого.составляют упорядоченные системы вещественных
чисел, состоящие из т чисел xlt ..., хт% взятых в определенной
последовательности. Условимся эти числа называть координатами
точки в декартовой ортогональной системе осей, и говорить, что
множеству всех систем чисел (xv ..., хт) сопоставлено простран-
пространство т измерений. Если расстояние MN между двумя точками
этого пространства М(хг хт) и N (yv ..., ут) определено
формулой
MN=V(x1-ylf+ ... +{хт-ут)\ (П. 2.11.1)
то пространство называется евклидовым пространством Ет.
Изложение последовательности определений и выводов, допускаю-
допускающих перенесение понятий отрезка, вектора, угла, площади, объема
и т. д. на Ет, в этой книге было бы неуместно. Достаточно сказать,
что привычный геометрический язык Е3 сохраняется в Ет. Так, пре-
преобразование координат определяется при неизменном начале О с по-
помощью (указанных в п. 2.1 *)) формул
т
x' = olx или x's=^dskxkt (П. 2.11.2)
k=\
где а — ортогональная ту^т матрица, осуществляющая поворот ста-
старой системы в новую, х/ — столбец новых координат, х столбец ста-
старых координат точки М. Элемент ast матрицы поворота называется
косинусом угла между осями Oxrs и Ох(, а система чисел ast при
фиксированном s определяет проекции единичного вектора i's оси Ox's
на оси старой системы Охг, ..., Охт. Свойству ортогональных
матриц
act' = £ или
2 *sPkt = Kk
геометрически соответствует ортогональность единичных векторов i's.
Система чисел as> преобразуемая при переходе к новым осям
по тем же формулам (П. 2), что и координаты xst определяет в Ет
вектор а\ сами числа as называются его проекциями. В част-
частности, xs служат проекциями вектор-радиуса г. Когда xt = ots
*) Ссылка на пункт 1 второй главы текста.
806 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
(s фиксировано), вектор-радиус превращается в единичный вектор is
оси Oxs. Вектор может быть представлен его разложением по еди-
единичным векторам
т
а= 2<yV (П. 2.11.3)
5=1 $S '
Скалярное произведение двух векторов а • b определяется числом
т
а- Ь= 2 <*А- (П. 2.11.4)
5=1
В точности в тех же выражениях, что и в Е3, в Ет вводится
понятие тензора второго ранга: это система т2 величин Pst, таких,
что линейное преобразование, осуществляемое ими над проекциями
вектора а по формулам
т
bs= %Pstat, (П. 2.11.5)
t=\
приводит к системе чисел bs, являющихся проекциями вектора Ь%
т. е. преобразующимся как координаты. Тензор может быть задан
его диадным представлением
т т
р=2 2^5/М/- (п.2.П.6)
5=1 ^=1
Примером тензора может служить диадное произведение векторов
т т
ab= 2 2<*AMV (П. 2.11.7)
5=1 ^=1
Кривая в Ет задается ее параметрическими уравнениями
xs = xs(t) или r = r(t). (П. 2.11.8)
За параметр может быть принята дуга о, отсчитываемая вдоль кри-.
вой; дифференциал дуги по (П.1) определяется формулой
!= у Hfir) dL (П- 2Л1*9)
5=1 * 5=1
Вектор
т = -^- с проекциями Tfc = ~^- (П. 2.11.10)
определяет единичный вектор касательной кривой. Его производная
определяет вектор, называемый вектором кривизны kn, имеющий на-
направление п—единичного вектора главной нормали кривой
(П. 2.11.11)
П. 2.11] ЕВКЛИДОВО ПРОСТРАНСТВО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ 807
Более сложно обобщение в Ет векторного произведения, последующих
кривизн, подобных кручению в £3, и других понятий.
Конечно, в Ет могут быть введены также косоугольные коор-
координаты с системой базисных векторов es. По ним определяется тен-
тензор с ковариантными составляющими
gsk = es-ek (s. k=l. .... т). (П. 2.11.12)
Контравариантные его составляющие gsk определяем соотноше-
соотношениями (П. 1.11), как элементы матрицы, обратной || gsk\\. Тогда сме-
смешанные составляющие (опускаем знак суммы по немому индексу)
gskgkt=gi (П. 2.11.13)
по свойству прямой и обратной матриц будут определены формулами
(П. 1.8). Теперь, по (П. 1.14) определяются векторы es взаимного
базиса
так что по (П. 12) и (П. 13)
e*-et= g*. ese< = gslgt(tglq = gslg\ = gst. (П. 2.11.14)
Вектор а может быть задан одним из представлений
a = ases = ases, as = a-es, as = a-es, (П. 2.11.15)
т. е. с помощью контравариантных или ковариантных составляющих as
и as. В отличие от того, о чем говорилось в пунктах П. 2.1 —П. 2.3,
индексы (в том числе, немые) принимают значения 1 т, а не
1, 2, 3.
В Ет можно, конечно, ввести криволинейные координаты ql, .. .,qm.
Здесь повторяется все сказанное в П. 2.4 — П. 2.5, включая опреде-
определения символов Кристоффеля и ковариантного (абсолютного) диффе-
дифференцирования. Существенно напомнить лишь, что выражение квадрата
дифференциала дуги
{dsf = gsk dqs dqk (П. 2.11.16)
может быть всегда преобразовано по самому определению Ет к виду
суммы квадратов
{dsf = (dxi? -U ... + (dxj>. (П. 2.11.17)
Для этого надо лишь от переменных qk возвратиться к декартовым
координатам xs\ при этом используются формулы преобразования,
обратные формулам
xs=xs{q\ ..., qm) или r = r(q\ .... qm)% (П. 2.11.18)
с помощью которых декартовы координаты в Ет были выражены
через криволинейные.
808 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Отметим, что такое обращение возможно, так как определитель
V\g\ =
dq1 ' dqn
dq1 ' dqm
(П. 2.11.19)
отличен по условию от нуля.
П. 2.12. Риманово пространство п измерений
Будем говорить, что соотношения
xs=xs(q\ . ... qn) E=1 nt . . ., т) (П. 2.12.1)
или, в векторной записи,
..., qn\ (П. 2.12.2)
где п < т, определяют в евклидовом пространстве Ет пространство
Римана Rn. Например, поверхность в Ег рассматривается как про-
пространство R2.
Условимся греческими индексами обозначать числа 1, ..., п\
индексы, значения которых больше, чем п, обозначаются через п -\-t,
n-\-q и т. д., причем латинские буквы (t, q и т. д.) принимают
значения 1, ..., т — п. Они понадобятся в следующем пункте.
Соотношение
dr—Wd^-^d^ (П. 2.12.3)
выделяет из всей совокупности принадлежащих Ет бесконечно малых
векторов в точке M(xv ..., хт) совокупность, принадлежащую Rn.
Векторы
Р. = -^Г (П. 2.12.4)
образуют в окрестности точки*М координатный базис пространства Rn.
Квадрат элемента дуги в Rn, поскольку Rn принадлежит к Ет, дол-
должен быть определен формулой*)
+ . . . + (dxj* = -^dq«--^ dq* = aa} dq* dq*.
(П. 2.12.5)
*) Мы ограничиваемся рассмотрением пространств с положительной
квадратичной формой (dsJ; в специальной теории относительности имеет
значение рассмотрение обобщенных евклидовых пространств с квадратичной
п
формой вида 2 са (^йJ> гЯе в числе постоянных сл имеются и отрица-
тельные.
П. 2.12] РИМАНОВО ПРОСТРАНСТВО П ИЗМЕРЕНИЙ 809
Здесь через
ЯаЗ=Ра-р3 (П. 2.12.6)
обозначены ковариантные составляющие метрического тензора. Его
контравариантные составляющие аа$ определяются как элементы ма-
матрицы, обратной ||яа;э||; обратная матрица существует, поскольку
квадратичная форма (П. 5) от дифференциалов dq*— знакоопределен-
ная (положительная). Зная аа?, можно построить в точке М взаим-
взаимный базис
р« = а^р?. (П. 2.12.7)
Вектор с в Ет называется принадлежащим Rn, если он представим
в виде разложения по векторам ра или по взаимным векторам ра:
с=сара = сар\ (П. 2.12.8)
Существенная разница между представлениями (П. 11.16) и (П. 5)
выражений квадрата дифференциала дуги в Ет и Rn заключается
в том, что в первом случае существовало преобразование от qs
к т переменным хг, . . ., хт (декартовым координатам), в которых
эта квадратичная форма выражалась суммой квадратов (П. 11.17);
форма же (П. 5), вообще говоря, непредставима суммой квадратов
того же числа п новых переменных во всей области определения
переменных qa, т. е. во всем пространстве Rn. Это осуществимо
лишь в окрестности фиксированной точки q*9 так как можно,
и не единственным образом, ввести такие линейные функции dp"
дифференциалов dq$
t\dq* = dp\ (П. 2.12.9)
чтобы выражение (dsJ приняло вид суммы квадратов
(dsJ = (dp1J +- ... +(dpnJ. (П. 2.12.10)
Поскольку система (П. 9) в общем случае неинтегрируема, т. е.
dp* представляют дифференциалы квазикоординат, выражение (dsJ
в форме (П. 10) возможно лишь локально, так как соотношения (П. 9)
интегрируемы при постоянных /* т. е. для фиксированных значений
ql, ..., qn. Геометрия Rn в бесконечно малой области, примыкаю-
примыкающей к этой точке, является евклидовой. Затруднения возникают при
сравнении величин, отнесенных к различным точкам Rn и, значит,
Ет. Здесь необходимо, как уже отмечалось в П. 2.7 — П. 2.9 для
случая многообразия R2 в Е3 (т. е. для геометрии на поверхности)
отличать внутренние свойства Rni определяемые заданием в нем
метрического тензора аа^ от обстоятельств, обусловленных располо-
расположением Rn в пространстве Ет, к которому Rn отнесено.
52 Зак. 2072. А. И. Лурье
810 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Действие ковариантного дифференцирования определяется в Rn
формулами
причем индекс «а» указывает, что символы Кристоффеля вычислены
в метрике Rn\
2.12.12)
По выражениям (П. 11) с помощью формул (П. 9.5) и (П. 9.12) со-
составляются выражения приращения d*c вектора с, заданного в Rn,
при перемещении в бесконечно близкую точку линии qa = qa (о).
Однако надо помнить, что приращение dc этого вектора в Ет отли-
отличается от d*c составляющими, нормальными к базисным векторам ра
пространства Rn в рассматриваемой точке. Об этом более подробно
говорится в следующем пункте.
Введенные в П. 2.8 и П. 2.9 для R2 определения геодезической
кривизны, геодезических линий и параллельного переноса вектора
на поверхности в том же словесном выражении повторяются в Rn.
Полезно отметить, что если в (П. 9.5) принять за вектор с один
из базисных векторов р6, то место контравариантных составляющих с*
в этих формулах займут величины
(а = 8).
Поэтому имеем соотношение
<**Р» = Р«{^}<*7р = <*?%Р». (П- 2.12.13)
Здесь введены векторы
{ } = [8. Р; 71а«"тР.. (П- 2.12.14)
которые позволительно назвать ковариантными производными базис-
базисных векторов р5 пространства Rn. Из свойств симметрии символов
Кристоффеля следует, что
(П. 2.12.15)
Соотношения (П. 14) заменяют уравнения (П. 4.9) в пространстве £т.
Можно отметить, что вычисления, производимые в Ет, переносятся
на Rnt если производную вектора с понимать в смысле ковариант-
ной производной. Так, формулы (П. 5.1) и (П. 5.2) должны записы-
записываться в виде
П. 2.13] РИМАНОВО ПОДПРОСТРАНСТВО Rn В ЕВКЛИДОВОМ Ет 811
Это значит, что «не выходя за пределы Rn», мы принуждены го-
говорить лишь о той части приращения вектора с, которая может
быть определена в Rn.
П. 2.13. Риманово подпространство Rn в евклидовом Ет
Вопрос о разыскании евклидова пространства Ет, в котором
содержится риманово пространство Rn, определяемое заданием ква-
квадрата линейного элемента, т. е. составляющих метрического
тензора аа3, сводится к нахождению в Ет вектора p(qY, ..., qn)
по уравнениям (П. 12.6), левые части которых считаются известными
функциями ql qn. Число уравнений равно -^ п(п-\-1), а число
неизвестных равно т — числу проекций (П. 12.1) вектора р на оси
координат в Ет. Если
то упомянутая система уравнений (П. 6) допускает, как может быть
доказано средствами теории дифференциальных уравнений в частных
производных, вещественные решения. Например, R2 вкладывается
в Ег, а /?3 в общем случае лишь в Е6. Но может оказаться, что Rn
вкладывается в евклидово пространство меньшего числа т = п-\-р
1
измерений, чем -^■п(п^-\); чидло р называется классом Rn.
В Еп+р вводятся криволинейные координаты qlt . . ., qn qn+P
таким образом, чтобы вектор-радиус p{qx qn) точек Еп+р, при-
принадлежащих Rn, соответствовал фиксированным значениям коор-
координат qn+l, . . ., qn+P:
piq1 qn) = r(q\ . . ., qny q"+l, . . ., q^+p), (П. 2.13.1)
Базисные векторы в Еп+р обозначаются так:
дг дг . 1 1 ч
(П. 2.13.2)
Система базисных векторов в Rn будет
= (Оо. (п- 2-13.3)
причем нуликом отмечается, что величина, определенная в Еп+р,
рассматривается в точках Rn. Например, величины
52*
812 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
в точках Rn равны соответственно
(П. 2.13.5)
Имея ковариантные составляющие метрического тензора в Еп+р, т. е.
матрицу с элементами
£<*;3 ' а * *"g» £a, n + t =1 Г* ' Г n + V &n+s, n + tz:=z rn+s " Г n + V
находим его контравариантные составляющие, т. е. элементы обрат-
обратной матрицы
р-ар р-а, П + t ptlt-S, n+t
о » о » о *
По ним находим векторы взаимного базиса *)
/*а г>ар«- _1_ оа, n + tr rn+S пП + S, а*. _1_ гтП + S, n + ty
' Ь 'вТб ' n + t' ' Ь 'а\& ' n + t'
(П. 2.13.6)
Мы напоминаем это, чтобы стала ясна ошибочность отожествления
величин gff с а^ или, например, г* с а°ррр = р* и т. д. Точно
так же величина
5МР. т; vu+^-MP. т;
т. е. символы Кристоффеля второго рода, определенные в метрике
Еп+р, но в точках Rn, отнюдь не равны этим символам, вычислен-
вычисленным в метрике Rn.
Нам известно, что векторы rn+t ортогональны га; поэтому в точ-
точках Еп+р, принадлежащих Rn, имеем равенства
Ра-^ + / = 0, (П. 2.13.7)
т. е. r^¥t представляют совокупность р векторов пространства Еп+
ортогональных всем векторам ра или, как говорят, ортогональных Rn.
Очевидно, что любой вектор, линейно выражающийся через век-
векторы r"+t, ортогонален всем ра; но можно доказать и обратное
предложение: если известно, что т«ра = 0 при а=1, ..., п, то
вектор т представим линейной формой векторов ^ + /.
Имея в виду сказанное, введем, оставаясь пока в пространстве Еп+р,
в качестве базисных векторы
га, гп+\ (П. 2.13.8)
*) Суммирование по немым греческим индексам от I до а, латинским —
от 1 до р.
П. 2.13] РИМАНОВО ПОДПРОСТРАНСТВО Rn В ЕВКЛИДОВОМ Ет 813
Вторые производные г^ вектора г представим теперь в форме раз-
разложения по векторам этого базиса
^г ?|л/+' (П. 2.13.9)
Нельзя отождествлять р^ с символами Кристоффеля второго рода.
Действительно, умножив обе части (П. 9) скалярно на г5, получим
g^ = r^rb = \^ в 81. (П. 2.13.10)
тогда как формулы (П. 4.16), по которым находятся символы Кристоф-
Кристоффеля второго рода, должны в применяемых здесь обозначениях
иметь вид
Вместе с тем из (П. 10) следует, что в точках Еп+р, принадле-
принадлежащих Rn,
откуда следует важное соотношение
(Г.тэ)о = ст![а, р; 81в = {а7р}в. (П. 2.13.11)
Мы должны перейти к определению коэффициентов Qaa,n+t.
Умножив обе части (П. 9) скалярно на rn+s, придем к системе урав-
уравнений
правые части которых можно преобразовать так: дифференцируя
по q$ и соответственно по qa соотношения
имеем
Г
откуда, сославшись на формулы (П. 4.19), найдем
или
rar?*rn+s=gn+s'i[at р; т] + §л+д>/1+/1а. Р; л + ^Ь (п- 2.13.13)
Система уравнений (П. 12) теперь принимает вид
xn+tgn+t'n+s = A^gn+S>\ (П. 2.13.14)
где для краткости обозначено
^ = [at p; Т]. (П.2.13.15)
814 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА
Квадратичная форма
[прилож. 2
п+р п + р
1R ^
п+1\ &
t, n + s
является союзной с знакоопределенной формой (dsJ, т. е. сама знако-
определенна. По теореме Сильвестра отсюда следует положитель-
положительность определителя
n + l, n
g1
Л + 1, П л р
„n+p, n + l
~n-\p, n \ p
системы уравнений (П. 14). Иными словами, эта система имеет реше-
решение и оно единственное. Будем искать его в виде
n + t ёп + иУ
Тогда, заметив, что
о pn + t, n+s I р ру, n+s— рпл-s—О
вместо (П. 14) получим соотношения
которым можно удовлетворить, определив yv как решение системы
уравнений
В точках Еп+р, принадлежащих Rn, эта система имеет вид
и мы сразу же находим
У — — aV la» Р» Tla» х° =— ar(gn+t v)o 1а» Р» Т1й- (П. 2.13.16)
Как отмечено выше, найденное решение является единственным.
Получаем
(?«р1л+Д> = 1а. Р; п + *\о — aV(gn+t,M*> Р; т1в- (п.2.13.17)
Величины
аг»(в|1+л,H = Л!л+/ (П. 2.13.18)
вычисляются так: в определителе
#11 #12 ...
\а\ =
#21 #22 ... #2/2
#/21 Я/22 ... #/2/2
(П. 2.13.19)
П. 2.13] РИМАНОВО ПОДПРОСТРАНСТВО Rn В ЕВКЛИДОВОМ Ет 815
строка ^ заменяется строкой величин
(SWi)o. •••> («я+/,п)о. (П. 2.13.20)
Отношение получающегося определителя к определителю (П. 19)
будет как раз равно M\+t. Чтобы убедиться в этом, достаточно
разложить упомянутый определитель по строке величин (П. 20) и
вспомнить, что выражения | а | avv являются алгебраическими допол-
дополнениями элементов строки -[ определителя (П, 19).
Возвратившись теперь к соотношениям (П. 9) и учитывая фор-
формулы (П. 11) (П. 17) и (П. 18), придем к таким выражениям вто-
вторых производных гар вектор-радиуса г в точках Rn
(П. 2.13.21)
Здесь
. (П. 2.13.22)
Вычисление коэффициентов представления V^pa по основным век-
векторам ра и г"+' требует, во-первых, знания величин, определяемых
внутренней геометрией Rn. Этого, конечно, недостаточно; во-вторых,
требуется знать величины gn+tta (t= I, ...,/?; a = 1, ..., я), но
только в точках Rn\ величины же g^ (a, p ===== 1 п) надо знать
не только в Rn, но и в окрестности Rn, принадлежащей En+pt
поскольку, как указано в формулах (П. 22), в определение величин
[a, p; n-\-t\Q входят значения производных ga^ по координатам qn+t
в точках Rn.
Ниже понадобится еще одно замечание. В представлении некото-
некоторого вектора b по базисным векторам (П. 8) пространства Еп+р
Ь = Ъ*Гь-\-Ъп+гп+г (П. 2.13.23)
величины Ь* и bn+t отнюдь не являются контравариантными и кова-
риантными составляющими b в метрике Еп+р. Действительно, по
определению, содержащемуся в формулах (П. 2.2) и (П. 2.3), можно
написать
£p = ft.rp=S"gepi bn+« = b . rn+« ==bn+tqn+t>n^. (П.2Л3.24)
Переходя в первой группе этих формул к точкам Еп+р, принадле-
принадлежащим Rn, получим
(П. 2.13.25)
816 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
таким образом, величины Ь* в точках Rn являются контравариант-
ными составляющими Ъ для метрики Rn. Теперь вспомним, что по
(П. 2.3)
п + р
2
9=1
и вторая группа соотношений (П. 24) принимает вид
gn+«>*ba = gn+''»+«(bn+t — bn+t). (П. 2.13.26)
Снова пришли к системе уравнений (П. 14); ее решение по (П. 16)
и (П. 17) в точках 'Rn будет:
(»/,+/)о= (»„+/)<> —Ml+t(ba)a. (П. 2.13.27)
Таким образом, представление вектора Ь, не принадлежа-
принадлежащего Rn, но в точках Rn может быть записано в виде
Ь = (Ь%?а + [(Ьп+1H — М*я+1фа)а]г'{''. (П. 2.13.28)
где (Ьа)а, (Ьа)а — контравариантные и ковариантные составляющие
вектора b в метрике Rn, (bn+tH— значение ковариантной составляю-
составляющей этого вектора в точках Rn.
Составим теперь выражение производной вектора с, заданного
в Rn. Обозначая эту производную вектором Ь, имеем
и дс да дса
(П. 2.13.29)
Обращаясь к (П. 28), видим, что величины
представляют контравариантные составляющие b в метрике Rn\ его
ковариантные составляющие в метрике Еп+р, но в точках Rn равны
— Ml+tl*. P; т1в). (П. 2.13.30)
где (Ьа)а — ковариантные составляющие в метрике Rn, т. е. величины
p^ = V«- (П. 2.13.31)
Здесь использована возможность вносить величины ащ под знак
ковариантного дифференцирования.
Ничего не изменилось бы в результативных формулах (П. 21) и
(П. 30), если бы рассматривалось вложение Rn в Rn+p (а не в Еп+р).
п. 2.14]
ТЕНЗОР РИМАНА — КРИСТОФФЕЛЯ
817
В соответствующих местах вычисления пришлось бы лишь заменить
dn + s §
векторами
V9rn+St
в метрике
векторы га?, -^, ^
/?/Нр, как указывалось в конце предыдущего пункта П. 2.12.
В частном случае /?2, вложенного в Ev т. е. для поверхности
в евклидовом трехмерном пространстве, имеем
М\ =
\а\
#11
#21 #22
где т — единичный вектор нормали к поверхности. Рассматривая
теперь определитель | g | в точках поверхности
#11 #12
\g\o =
#21 #22
находим
^32
зз
„зз •
Формула (П.21) принимает вид
1«Р )ЙП' ' 1/" 33 V
^Ча, Р; Т]в). (П. 2.13.32)
Сравнивая ее с (П. 7.19), снова получаем выражения (П. 9.16) для
коэффициентов второй квадратичной формы поверхности £а3.
П. 2.14. Тензор Римана — Кристоффеля
В Rn рассматривается последовательность двух ковариантных
дифференцирований VpVYca контравариантных величин са. Вспоминая,
что ¥.(са представляет составляющую тензора второго ранга, кова-
риантную по *[ и контравариантную по а и применяя правило кова-
риантного дифференцирования, даваемое последней формулой (П. 5.6),
получаем
S ) lA
а ) ( Ь
35
818 СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА [ПРИЛОЖ. 2
Нетрудно сообразить, что подчеркнутые слагаемые вошли бы и
в выражение VYVpca. Поэтому приходим к соотношению
VpV^« — VTVpc« = cl%^\ (П. 2.14.1)
где обозначено
*....*(« )—L( ' \ + ( М ( Ч_( Ч ( Ч (П. 2.14.2)
В левой части соотношения (П. 1) стоят составляющие тензора
третьего ранга, ковариантные по *[ и р и контравариантные по а.
Отсюда можно заключить, что величины в формуле (П. 2) предста-
представляют ковариантные по р, f. Р и контравариантные по а составляю-
составляющие тензора четвертого ранга. Это — тензор Римана — Кристоф-
феля. Несколько более просто выражаются его ковариантные со-
составляющие
ЯтР11, = *«Л$Л (П. 2.14.3)
Из (П. 1) и теоремы Риччи, рассмотренной в П. 2.5, следует теперь
Wv - Wv = с%^> (П. 2.14.4)
Выражение ковариантных составляющих тензора Римана — Кри-
стоффеля преобразуется путем перехода к символам Кристоффеля
первого рода
Далее имеем
Развернув выражения производных от прямых скобок и сделав
замены
■yf =[«. Pi v] + [p. v; a], ^f = [«. Г. *! + lT. >; *Ь
получим после подстановки
ТР^ 2 \d^d^ d<> d*
2 \d^d^ dq<> dq* dqf dq4 dqt d
— gm(V[, V-l o]K P; a] —[p, p; o][v, T, a]). (П. 2.14.5)
П. 2.14] ТЕНЗОР РИМАНА — КРИСТОФФЕЛЯ 819
Из общего числа п4 составляющих тензора Римана — Кристоф-
феля независимых (через которые выражаются остальные) будет
-=у п2 (п2—1). Так, при п = 2 получается одна составляющая /?12i2»
а при п = 3 — шесть составляющих.
Как указывалось в П. 2.11, отличительным признаком евклидова
пространства является возможность отнесения всех точек его к еди-
единой (декартовой или косоугольной) системе осей неизменного напра-
направления, в которой выражение основной квадратичной формы имеет
постоянные коэффициенты (в частности, в декартовой системе пред-
представляется суммой квадратов). Но тогда все символы Кристоффеля
обращаются в нуль, а вместе с ними и все составляющие тензора
Римана — Кристоффеля. Свойство тензора не может быть связано
с выбором системы координат; естественно, что может быть дока-
доказано обратное предположение: если тензор Римана — Кристоффеля
тождественно обращается в нуль, то многообразие является евкли-
евклидовым; иными словами, в нем могут быть введены такие коорди-
координаты д , .... дп, что выраженная в них квадратичная форма (dsJ
будет иметь постоянные коэффициенты. Необращение в нуль тен-
тензора Римана — Кристоффеля свидетельствует о том, что рассма-
рассматриваемое многообразие — не евклидово. Если (dsJ — положительная
знакоопределенная форма дифференциалов dqk, то оно — риманово
многообразие Rn.
Итак, при любом выборе криволинейных координат в Еп
V3VYca = VYV^a, (П. 2.14.6)
т. е. порядок ковариантного дифференцирования может быть изменен.
Запись условий тождественного обращения шести независимых
составляющих тензора Римана — Кристоффеля для ортогональной
системы криволинейных координат в Е3 приводит к шести известным
зависимостям Ляме для коэффициентов h2s квадратичной формы (П. 10.7)
52*
ИМЕННОЙ УКАЗАТЕЛЬ
Аппель 377. 392, 398, 568
Белецкий В. В. 586
Блитцер 599, 622
Бобылев Д. К. 388. 653, 665
Боголюбов Н. Н. 576, 579
Больцман 32, 368
Брашман Н. Д 646
Булгаков Б. В. 83, 755
Валле-Пуссен Ш. Ж. 13
Ватсон Г. Н. 136
Вебстер 752
Воронец П. В. 35, 368. 382
Вышнеградский И. А. 411
Галеркин 696
Га мель 31, 256, 368 398 572
Гамильтон 646, 704
Гантмахер Ф. Р. 488, 491, 755
Гельдер О. 669, 670
Герц Г. 354
Голубев В. В. 358
Граммель Р. 586
Гринберг Г. А. 615
Гурса 607, 657
Гэлопп 246
Гюнтер Н. М. 657, 669
Даламбер 252
Джанелидзе Г. Ю 690
Дубошин Г. Н. 563, 595
Дункан 480, 755
Жордан 657
Жуковский Н. Е. 267, 268 276, 279,
468, 474, 721, 726, 736, 751
Зоммерфельд А. 121
Идельсон Н. И. 205
Исаева Л. С. 391
Ишлинский А. Ю. 55, 57, 498
Канторович Л. В. 697
Каратеодори 523
Картан Э. 77S
Кильчевский Н. А. 778
Кирхгофф Г. 648
Клейн 121. 743
Коллар А. 755
Кочин Н. Е. 671, 778
Крылов А. Н. 55, 246, 425. 595
Крылов В. И. 597
Крылов Н. М. 576
Лагранж Ж. Л. 31, 252, 324. 565
Левин Л. М. 488, 491
Лойцянский Л. Г. 360, 425, 491, 574
Локк 246
Лурье А. И. 111, 163, 327. 360, 425 451
574, 690
Ляпунов А. М. 2Ы, 608, 721
Магнус К. 317
Мак-Миллан В Д. 155. 276
Малкин И. Г. 2о!, 608
Мальцев А. И. 755
Меркин Д. Р. 177, 351
Митропольский Ю А 576, 579
Михлин С. Г. 697
Мопертюи 710
Николаи Е. Л. 85, 31/
Николенко Г. И. 272
Нильсен К. Л. 243
Новоселов В. В. 406
Норден 721
Ньютон 252
Окунев Б. Н. 425
Остроградский М. В. 646
Охоцимский Д. Е. 599
Полак Л. С. 646. 710
Пуанкаре 605
Раусе 633
Релей 232
Ричмонд 246
Роберсон 467
Розе Н. В. 666, 711
Румянцев В. В. 317
Сансоне Дж. 750
Синдж Дж. Л. 243, 624, 633
Смирнов В. И. 476
Степанов В. В. 607, 751
Суслов Г. К. 670, 743, 748
Сушкевич А. К. 364
Таратынова Г. П. 599
Тиссеран 586, 595
Томсон 633, 721, 751
Тэт 633, 721, 751
Уиттекер Е. Т. 136, 580. 690. 743
Фоулер 246
Фрезер Р. 755
Хейн 341
Чаплыгин С. А 387, 388, 400
Четаев Н. Г. 261, 317, 360, 406
Шубенко Л. А 681
Энеев Т. М. 599
Якоби К. 518, 556, 6^2, 748
Яцунский Н. М. 604
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуда энергии кинетической 691
— — потенциальной 691
Аномалия истинная 554
— средняя 554
— эксцентрическая 553
Апогей 552
Базис координатный 778
— — взаимный 778
Бинормаль кривой 97
Вариации квазикоординат 32 и д.
— координат обобщенных 26
асинхронные 707
— синхронные 29, 707
Вектор в римановом пространстве 809
— геодезической кривизны 795
— главный количеств движения 158
относительных 159
переносных 159
системы сил 190
— Дарбу 98
— поворота бесконечно малого 65
конечного 102, 104, 110, 118
— углового ускорения 74
— угловой скорости 64. 66
Векторы основные (базисные) 778, 792
, взаимные с ними 778 792
Величины ковариантные 781
— контравариантные 781
Вертикаль четырехгироскопная 177
Возмущение траектории 721 и д.
Волчок, влияние вращения Земли 460
Вращение гибкого вала 439
— искусственного спутника вокруг центра
инерции 585 и д., 595
— тела по инерции 134
с неподвижной точкой 157, 166,
459
с неравными моментами инерции
вблизи вертикали 734 и д., 738
Галеркина метод 696
Гесса матрица 756
Гироскоп в кардановом подвесе 169. 313
— на движущейся платформе 445
Движение в однородном поле силы тя-
тяжести 743. '/51
*— в поле тяготения вращающейся
Земли 565
двух центров 733
■ центральной силы 355, 508. 527,
542, 543, 551, 730. 745
— возмущенное материальной системы 622
и д.
точки 611
Движение волчка 509
— —, влияние неуравновешенности 580
и д.
, несущего вращающийся маховик 511
— деформируемого тела 474
— кеплерово 355, 508, 527, 542, 543, 551,
730. 745
возмущенное 595
спутника Земли 599, 616
— натурального триэдра 96 и д.
—, кинематически устойчивое 633
— чевозмущенное установившееся 633
— относительнее 80 и д.
твердых тел 451 и д.
— платформы с гироскопами 496, 497
— по кругу в поле двух притягивающих
центров 733
— ракеты 488 и д.
— самолета 99
— снаряда 243, 420
— спутника Земли 599, 616
— тела деформируемого 47^ и д.
— —, несущего вращающиеся маховики
462
свободного 415, 417, 419
с полостью, наполненной жидкостью
468 и д.
— точки в среде с сопротивлением 572
плоское 405
по поверхности 297
■ вращения 302
конуса 731
развертывающейся 303
— — эллиптическое начинающееся с по-
поверхности Земли 557
Действие по Гамильтону 643
, вариация 644
, минимум 649 и д., 652
— по Лагранжу 710. 748 и д.
Дефект матрицы 757
Диада 144
Дискриминант квадратичной формы 765
ДисЬсЬерент корабля 51
Дифференциалы квазикоординат 24
Дифференципование ковариантное (абсо-
(абсолютное) 788. 810
в римановом пространство 810
вектора на поверхности 797 и д.
— матрицы 777
Закон Гука 212
Земля, вращающаяся, движение в ее поле
тяжести 565
Значение стационарное функционала 645
Импульс обобщенный 141
Интеграл энергии 286
822
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Качение без скольжения 85 и д., 379
и д.
— — — обруча 72
шара 71
Квазикоординаты 24
—, вариации 32 и д.
Квазискорости 22 и д.
Колебания маятника математического 233,
235, 307, 701
физического 333
— системы около положения равновесия
574 и д.
— тела, подвешенного на упруги* стерж-
стержнях 271
— точечных масс в движущейся твердой
оболочке 466
— упругого вращающегося стержня 482
и д. 680, 699
— цепи, висящей с грузом на конце 673,
697
— цепной линии 684
Количество движения 158
Координаты криволинейные ортогональ-
ортогональные 800 и д.
— обобщенные 15
— —, вариации 26, 29
— — избыточные 20
— — квазициклические 365
— — позиционные (явные) 344, 348
— — циклические (игнорируемые скры-
скрытые) 344, 348
Коэффициенты гироскопические 289
— Ляме 800
Крен корабля 51
Кривизна линии 96, 795
на поверхности геодезическая 796
— нормального сечения поверхности 795
Кристоффеля символы второго рода 291,
785
первого рода 163, 786
Кручение кривой 98
Линия геодезическая 796, 797
— узлов 46
Матрица, вычитание матриц 761
— Гесса 756
—, дефект 757
—, дифференцирование 777
— единичная 757
— квадратная 756
кососимметричная 760
— — Луассона 515
— — симметричная 760
— нулевая -756
— обратная 769
—. определитель 757
— ортогональная 774
— поворота 42
— присоединенная 768
— прямоугольная 755
—, сложение матриц 761
— сложная 758
—. субматрица 757
— транспонированная 760
—, умножение матриц 762
—, сложных 766
—, — на число 761
— Якоби 756
Маятник математический 233, 701
двойной с квадратичным законом
сопротивления 235, 307
— физический 333
Метод вариации постоянных 560
— Галеркина 696
Метод игнорирования циклических коор-
координат Рауса 348
— Ритца 693
Метрика элемента действия 716
Механизм 338
— двухкривошипный 20
— кривошипный 340
Момент главный количеств движения 158
относительных 159
— инерции 147, 149
главный центральный 154
— — относительно оси координат 147
центробежный 147
Мощность 231
—, выражение через квазискорости 231
— диссипативных сил 235
Неравенства Сильвестра 139
Нормаль кривой главная 97
Оболочка, несущая маховики, ее кинети-
кинетическая энергия 169
Определитель матрицы 757
Освобождаемость от связей 248
Оси инерции главные 150
— — — центральные 154
— корабельные 51
— самолетные 47
скоростные 48
Парабола безопасности 751
Параметры Кейли — Клейна 123, 124
— Родрига — Гамильтона 104
Переменные канонические 505
, инвариантность 525
Перемещение виртуальное (возможное)
27
Перенос параллельный вектора 798
Перигей орбиты 552
Платформа гироскопическая 173, 492 и д«
Плоскость соприкасающаяся 96
Поворот конечный 10?, 118 и д.
, выражение через углы Эйлера 112
и д.
— —, вычитание поворотов ПО
, параметры Родрига — Гамильтона 104,
, переставимость поворотов 111
, сложение поворотов 109
— тела вокруг неподвижной точки 53
Подвес карданов 55, 59, 114, 116
двойной 57
Подпространство евклидово 811 и д.
Поле притяжения 201, 268
Порядок матрицы 755
Потенциал кинетический 257
Рауса 349
Преобразование каноническое 519, 534
— координат 43
— Лежандра 499, 500
Прецессия регулярная 134, 638
Признак потенциальности сил 194
Принцип Гамильтона — Остроградского
045, 672
— освобождаемости от связей 248
— стационарного действия в форме Лаг-
ранжа 710
Якоби 713
Произведение векторов диадное 144, 763
скалярное 806
Производная вектора ковариантная (абсо-
(абсолютная) 788
на поверхности 799
относительная (локальная) 79
Пространство евклидово 805 и д.
— риманово 808
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
823
Пружина спиральная винтовая 228
Пуассона скобки 513, 760
Путь системы истинный 643, 715
окольный 643, 655, 715
Работа элементарная сил 188, 189,
193
потенциальных 194
Равновесие относительное 438
— при трении 276
— системы материальных точек 259 и д.
неустойчивое 261
»~ устойчивое 261
— тела, подвешенного на упругих стерж-
стержнях 271
— тяжелого стержня 264
Распределение скоростей в теле 63, 77
— ускорений в теле 74, 78
, запись матричная 75
Реакции связей 248
обобщенные 327, 331, 336
— — отбрасываемых обобщенные 327
Редуктор фрикционный 406
Решение системы линейных уравнений
770
Рысканье корабля 51
Связи 11
— голономные (позиционные) 11, 12
нестационарные (реономные) 13
стационарные (склерономные) 13
— идеальные 252
, силы реакций 333
— неголономные (кинематические) 12
реономные 13
склерономные 13
— неудерживающие (односторонние) 12
— позиционные 11, 12
—, принцип освобождаемое™ от связей
248
'—, реакции связей 248
— удерживающие (двусторонние) 12
Сила гироскопическая 289
— — обобщенная 289
— диссипативная 232
, мощность 235
— обобщенная, выражение через потен-
потенциальную энергию 194
, отнесенная к квазикоординате 189,
191
, — к обобщенной координате 188
— позиционная 197, 199
— потенциальная 193, 196
, признак потенциальности 194
— радиальной коррекции (циркуляцион-
(циркуляционная) 200
— сопротивления 233
— тяготения 201
— упругости 211 и д.
Символ Кронекера 41
— Леви — Чивита 41
Символы Кристоффеля второго рода 291,
785
первого рода 163, 786
— Леви — Чивита 780
— трехиндексные Больцмана 32, 33 и
Д., 68
Система векторов полунеподвижная 46
— — полуподвижная 46
— голономная 12
— двух волчков 360
— двухстержневая 318, 342
— Луивилля 549
— материальных точек 11
— осей геоцентрическая 82, 83
Система осей геоцентрическая, поворот
115
инерциальная (неподвижная) 40
, матрица поворота 42
подвижная 40
, матрица поворота 42
—, первоначально напряженная 272
— свободная 11
— стержневая, статически неопредели-
неопределимая 217
— —, — определимая 215
— трехстержневая 263
— четырехстержневая 321
Скобки Кристоффеля волнистые 291, 785
прямые 163, 786
— Лагранжа 515, 759
— — фундаментальные 515
— Пуассона 513, 760
фундаментальные 513
Скорость абсолютная 81
точки, движущейся по вращающейся
Земле 83
— виртуальная 18
— обобщенная 17
циклическая 17
— относительная 81
— переносная 81
точки, движущейся по вращающейся
Земле 83
—, сложение скоростей 81
— угловая 64, 118 и д., 126 и д.
, определение положения тела J27 и
Д., 130
, уравнения Дарбу 130
Сложение движений тела 93 и д.
— матриц 761
— поворотов 109, 125
Снаряд вращающийся 420
Сопротивление воздуха 243 и д.
Степени свободы 14
Стержень в эллиптической чаше 267
— изогнутый, скрученный, сжатый 221
— с .осью, являющейся плоской кривой
226
— тяжелый 264
— упругий вращающийся 680, 699
— нерастяжимый 482
Субматрица 757
Тележка двухскатная 35 и д., 182, 374,
403
Тело абсолютно твердое 11
— в поле центральной силы 268
— деформируемое 474
—, несущее неуравновешенный маховик
170
—, подвешенное на упругих стержнях 271
— с неподвижной точкой 122, 156, 197
— упругое идеальное 211
Тензор 775, 806
— второго ранга в косоугольных коорди-
координатах 782 и д.
кососимметричный 783
, представление диадное 782, 806
симметричный 146, 783
— фундаментальный 783
— инерции 144, 145
, преобразование 147 и д.
, эллипсоид инерции 154
— метрический 785. 792
— Римана — Кристоффеля 818
— Риччи 628
Теорема Кастильяно 214
обобщенная 501
— Лагранжа — Дирихле 261
824
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Теорема Лиувиллл 524
— Менье 795
— сложения скоростей 81
ускорений 82
— Пауссона 517
— Риччи 789
— Штейнера 149
— Штеккеля 547
— Штурма 751
— Эйлера — Шаля 106
— Якоби 537
Теория Зоммерфельда 200
Траектория точки в потенциальном сило-
силовом поле 295
Трение вязкое 233
— кулоново (сухое) 233, 237, 276
Триэдр натуральный 96
— — самолета 99
, элементы движения 99
Углы Эйлера 44, 47
Угол атаки 48
— дифферента 51
— крена 47, 48, 51
— курса 48
— нутации 45, 47
— подъема 48
— прецессии 45, 47
— рысканья 47, 51
— скольжения 48
— смежности 96
— тангажа 47
— чистого вращения 45, 47
Умножение матриц 762
— — сложных 766
— матрицы на число 761
Уравнение Дарбу — Риккати 130
— динамики общее 254
— Кеплера 554
— центральное Лагранжа 256
общее 256
Уравнения движения Аппеля 395, 397, 400
в квазискоростях 397
в вариациях 605, 607
f интегрирование 610
возмущенного 561, 597, 598, 611, 622
второго рода 283
канонические Гамильтона 505, 508,
564
Лагранжа первого рода 251
относительного канонические 436, 529
и д.
Рауса 348
Чаплыгина 401
Эйлера — Лагранжа 369, 411
Ускорение абсолютное 81
точки, движущейся по вращающейся
Земле 85
— вращательное 75
— добавочное (кориолисово) 82
— обобщенное 18
— относительное 81
— переносное 81
Ускорение переносное точки, движущейся
по вращающейся Земле 84
—, теорема сложения ускорений 82
— угловое 74
— центростремительное 75
Условие Лежандра 660
— Якоби 660
Условия кинетической осуществимости
смежного движения 666
Устойчивость движения 721
— регулярной прецессии тяжелого гиро-
гироскопа 638
Фигура Земли 205 и д.
Фокусы кинетические сопряженные 651,
665
Форма квадратичная, знакоопределенная
771
союзная 770
поверхности вторая 793
— первая 793
Формула Родрига 101
Формулы Френе 98, 795
Функция Гамильтона 504
главная 704, 705
характеристическая 740, 742
— диссипативная 232, 234
— Лагранжа 257
— однородная 140
— производящая 499, 521
— Рауса 348, 350 и д.
Центр инерции 144
Цепь висящая с грузом на конце 673,
697
Число степеней свободы 14
Шар, катящийся по шероховатой плос-
плоскости 179, 372, 402, 403
Элемент кинематический 715
, метрика 716
Элементы матрицы диагональные 760
— орбиты эллиптические 556
Эллипсоид инерции 153
центральный 154
Энергия кинетическая 137
— —, выражение союзное 142
, — через квазискорости 141, 156
— —t — — обобщенные скорости 137, 138,
157
— — движения относительного 161
переносного 161
системы, подчиненной стационарным
связям 139
— потенциальная 193, 194
— — обобщенная 195
сил тяготения 201
— ускорений 162
Эффекты Магнуса 244
Якобиан 758