Автор: Колмогоров А.Н. Дудницын Ю.П. Абрамов А.М.
Теги: общее школьное образование общеобразовательная школа алгебра математика учебник
ISBN: 978-5-09-019513-3
Год: 2008
Текст
математического
анализа
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО
А. Н. Колмогоров
(25.IV.1903—20.Х.1987)
Андрей Николаевич Колмогоров —
великий ученый России. Мировую изве-
стность ему принесли выдающиеся рабо-
ты, относящиеся практически ко всем
областям математики — теории вероят-
ностей и математической статистике, то-
пологии и функциональному анализу, ма-
тематической логике, теории информа-
ции и т. д.
Гений Колмогорова не ограничен ма-
тематикой и удивительно универсален.
Вслед за Ньютоном, Лапласом и Пуанка-
ре он совершил прорыв в осмыслении
проблемы вечности Солнечной системы.
Им создана теория процессов, позволяю-
щая воссоединить идеи Фурье, Ньютона,
Эйнштейна, открыт новый закон при-
роды в области турбулентности. А еще
были блестящие новаторские работы
в кибернетике, биологии, океанологии,
геологии, метеорологии, кристаллографии, истории, языкознании, стихо-
ведении. В годы Великой Отечественной войны А. Н. Колмогоров принял
активное участие в решении оборонных проблем.
Всю свою жизнь А. Н. Колмогоров посвятил науке и труду Учителя.
Он основатель известнейших научных школ, научный руководитель мно-
гих талантливых ученых. С 1930 г. до последнего дня жизни А. Н. Колмо-
горов — профессор Московского университета, создатель новых кафедр
и лабораторий, яркий лектор. С 30-х гг. он принимает самое активное уча-
стие в проведении математических олимпиад для школьников. В 1963 г.
создает физико-математическую школу-интернат при МГУ, в которую
и поныне отбираются талантливые ребята со всей страны. В этой школе он
многие годы читает замечательные лекции для школьников, ходит с ними
в походы, проводит музыкальные и литературные вечера. В 1970 г. вместе
с академиком В. К. Кикоиным создает журнал «Квант». А. Н. Колмого-
ров — автор многих статей и книг по математике для учеников и учителей
(учебник алгебры и начал анализа — одна из этих книг).
Заслуги Андрея Николаевича уже при жизни были оценены очень вы-
соко. Сам он спокойно относился и к необычайной славе, и к формам при-
знания. А их было много: академик в 35 лет, лауреат Ленинской и госу-
дарственных премий, лауреат престижнейших международных премий,
почетный член десятков международных академий и научных обществ.
В числе многих правительственных наград Золотая звезда Героя Социали-
стического Труда и семь орденов Ленина.
А. Н. Колмогоров проявлял глубочайший интерес ко всему сущему.
Он любил музыку и литературу, ходил в многодневные пешие, лодочные,
лыжные походы, в качестве научного руководителя океанологической экс-
педиции совершил кругосветное путешествие. На склоне лет он однажды
заметил: «Какую все-таки интересную жизнь я нро.жил!»
Свое жизненное кредо А. Н. Колмогоров точнее .всех сформулиро-
вал сам: «Я жил, всегда руководствуясь тем тезисом, что истина — благо,
что наш долг — ее находить и отстаивать независимо от тбго, приятна она
кому-то или неприятна».
УДК 373.167.1:[512 + 517]
ББК 22.14я72
А45
Авторы:
А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын,
Б. М. Ивлев, С. И. Шварцбурд
На учебник получены положительные заключения
Российской академии наук (№ 10106-5215/15 от 31.10.07)
и Российской академии образования (№ 01-205/5/7д от 11.10.07)
Алгебра и начала математического анализа : учеб, для
А45 10—11 кл. общеобразоват. учреждений / [А. Н. Колмо-
горов, А. М. Абрамов, Ю. П. Дудницын и др.] ; под ред.
А. Н. Колмогорова. — 17-е изд. — М. : Просвещение,
2008. — 384 с. : ил. — ISBN 978-5-09-019513-3.
УДК 373.167.1:[512 + 517]
ББК 22.14я72 + 22.161я72
ISBN 978-5-09-019513-3
© Издательство «Просвещение», 1990
© Издательство «Просвещение»,
с изменениями, 2008
© Художественное оформление.
Издательство «Просвещение», 2000
Все права защищены
ПРЕДИСЛОВИЕ
Вы начинаете изучать новый предмет. Слово «алгебра»
в его названии вам уже известно.
Принципиально новая часть курса посвящена изучению на-
чал анализа. Математический анализ (или просто анализ) — ветвь
математики, оформившаяся в XVIII столетии и включающая
в себя две основные части: дифференциальное и интегральное ис-
числения. Анализ сыграл громадную роль в развитии естествозна-
ния — появился мощный, достаточно универсальный метод иссле-
дования функций, возникающих при решении разнообразных при-
кладных задач. Знакомство с начальными понятиями и методами
анализа (производная, дифференцирование, первообразная, инте-
грал, метод поиска максимумов и минимумов функций) — одна из
важных целей курса.
Несколько замечаний о том, как пользоваться учебником.
Оглавление и предметный указатель, помещенные в конце книги,
помогут вам быстро найти нужный раздел, определение или теоре-
му. Ответы и указания к упражнениям приведены в соответст-
вующем разделе. Для знакомства с основными идеями решения
предлагаемых задач приводится множество примеров решения,
выделенных значками | и . Отметим также, что задачи, вклю-
ченные в каждый пункт, делятся на две части. Задачи, входящие
в первую часть, необходимо уметь решать для получения удовлет-
ворительной оценки, они задают обязательный уровень подготов-
ки. Остальные задачи чуть сложнее.
Чтобы помочь вам при подготовке к контрольной работе,
в конце каждой главы приведены вопросы и задачи на повторение
основного материала. Ответы на вопросы и примеры решения та-
ких задач можно найти в тексте соответствующих пунктов.
О происхождении изучаемых понятий, терминов и символов,
о людях, создававших математический анализ, вы можете узнать,
прочитав разделы «Сведения из истории».
Дополнительный материал теоретического характера содер-
жится в некоторых пунктах учебника, он выделен значками
и
По окончании школы вам предстоит сдавать выпускные эк-
замены. Как известно, теоретический материал за курс средней
школы кратко изложен в книге «Математика. Справочные мате-
риалы». Практические упражнения для повторения курса помеще-
ны в главе «Задачи на повторение». Задачи повышенной трудно-
сти содержит заключительная глава.
3 Предисловие
Алгебра
и начала
математического
анализа
I
Учебник
для 10-11 классов
общеобразовательных
учреждений
Под редакцией А. Н. Колмогорова
Рекомендовано
Министерством образования и науки
Российской Федерации
17-е издание
Москва
«Просвещение»
2008 |
Mr в.
Обозначения,
встречающиеся
в учебном пособии
N — множество всех f (х) — значение функции f
Z Q R натуральных чисел — множество всех целых чисел — множество всех неотрицательных целых чисел — множество всех рациональных чисел — множество всех D(f) E(f) Ах — Д/(х0), Д/ — Г(х0) в точке x - область определения функции f - область значений функции f приращение аргу- мента X приращение функ- ции f в точке xQ производная функ-
[а;Ь] действительных чисел, числовая прямая — замкнутый про- sin — cos — tg ции f в точке х0 функция синус функция косинус функция тангенс
(а; Ь) (а; Ь], [а; Ь) межуток (отре- зок) с концами а и Ь, а < Ъ — открытый проме- жуток (интервал) с концами а и 6, а < Ъ — полуоткрытые ctg — e — l°Sa функция котангенс число е, основание показательной функ- ции, для которой (ех)' = ех логарифм с основа- нием а
(а; оо), , [а; оо), промежутки с концами а и Ь, а < Ъ — бесконечные 1g — In — десятичный лога- рифм натуральный лога- рифм (логарифм
( сю; Ь), (—оо; fe] промежутки с основанием е)
( оо; оо) — бесконечный max f — наибольшее значение
а промежуток, числовая прямая — обозначение век- [a; 6] min f — функции f на отрез- ке [а; Ь] наименьшее значе-
(а -6; а + 6) тора — 6-окрестность [a; b] ние функции f на отрезке [я; 6]
И точки а — целая часть b J f(x)dx — интеграл функции f
{*} числа х — дробная часть a arcsin a — в пределах от а до Ь арксинус числа а
|х| числа х — модуль (абсолют- ная величина) числа х arccos a — arctg a — arcctg a — арккосинус числа а арктангенс числа а арккотангенс числа а
Тригонометрические
функции
।
§ 1.
Тригонометрические функции
числового аргумента
1. Синус, косинус, тангенс и котангенс
(повторение)
1. Радианная мера. Вы уже знакомы с радианной
мерой углов. Угол в 1 радиан — это такой центральный угол, дли-
на дуги которого равна радиусу окружности (рис. 1). Радианная
и градусная меры связаны зависимостью 180° = л радиан; угол в п°
равен радиан.
При радианном измерении углов упрощается ряд формул.
Так, для окружности радиуса г длина I ее дуги в а радиан нахо-
дится по формуле
I = ar-, (1)
площадь S сектора круга радиуса г, дуга которого содержит а ра-
диан, такова:
S=~- (2)
Формулы (1) и (2) проще аналогичных формул I =
180
о ЛГ2П
и о = -- для вычисления длины дуги окружности и площади
360
сектора, дуги которых (величиной и°) заданы в градусной мере.
Наличие у радианной меры ряда преимуществ (см. также п. 17)
привело к тому, что в тригонометрии предпочитают пользоваться
радианной, а не градусной мерой.
Из курса алгебры вы знаете, как опре-
деляется поворот на угол в а радиан, где
а — действительное число. Знакомы вам
и определения синуса, косинуса, тангенса
и котангенса а (а — угол или число).
Пример 1. Найдем значения синуса,
косинуса, тангенса и котангенса угла
Рис. 1
5 Тригонометрические функции
а В
Рис. 2
Рис. 3
В прямоугольном треугольнике с углом в 30° противолежа-
щий ему катет равен половине гипотенузы с (рис. 2). Пусть с - 1,
тогда:
Поэтому
а _ 1
с 2’
tg^=|=73, ctg"- =
о tz 3
cos J =
3
а _ 1
ь уГз'
Вообще значения основных тригонометрических функций
острого угла а могут быть найдены так, как это делалось в курсе
геометрии (рис. 3):
cosa=-, sinct= —, tga=—, ctga=—.
с с b а
Приближенные значения синуса, косинуса, тангенса и ко-
тангенса произвольного угла находятся с помощью калькулятора
или таблиц. (Здесь и далее имеются в виду «Четырехзначные ма-
тематические таблицы» В. М. Брадиса.)
Задача нахождения значений синуса, косинуса, тангенса
и котангенса произвольного угла путем применения известных
вам формул сводится к нахождению значений sin a, cos a, tg a,
ctg a, где 0<a<^. Так, например, может быть заполнена табли-
ца (см. с. 5).
2. Основные формулы тригонометрии. Из определений
синуса, косинуса, тангенса и котангенса сразу следуют основные
тригонометрические тождества:
sin2 a + cos2 a = 1;
tga = sinu; ctga=£osn;
cos a sin a
tg a ctg a = 1;
tg2 a + 1 = - 1 ; ctg2 a + 1 = —1—
cos z a sin £ a
Тригонометрические функции
а 0 Л 6 71 4 Л 3 л 2 2л 3 3 л 4 5 л 6 71
sin а 0 1 2 У2 2 Уз 2 1 Уз 2 У2 2 1 2 0
cos а 1 Уз 2 У2 2 1 2 0 1 2 У2 2 Уз 2 -1
tg а 0 1 Уз 1 Уз — -УЗ -1 1 Уз 0
ctg а — Уз 1 1 Уз 0 1_ Уз -1 -у[3 —
а 7л 6 5 л 4 4 л 3 3 л “Г 5 л 3 7л 4 11л 6 2л
sin а 1 2 _У1 2 _Уз 2 -1 Уз 2 _У1 2 1 2 0
cos а Уз 2 _У1 2 1 2 0 1 2 У2 2 Уз 2 1
tg а 1 Уз 1 Уз — -Уз -1 1 Уз 0
ctg а Уз 1 1 Уз 0 1_ Уз -1 -Уз —
Основой для вывода остальных формул являются формулы
сложения’.
cos (а - Р) = cos а cos р + sin а sin Р;
cos (а + Р) = cos а cos Р - sin а sin Р;
sin (а - Р) = sin а cos Р - cos а sin Р;
sin (а + Р) = sin а cos р + cos а sin Р;
1®<“+₽>=гтАН-
1 - tg а tg Р 1 + tg а tg р
7 Тригонометрии.. ьие функции
Рис. 4
и котангенса
Из формул сложения, полагая Р = ~
где п е Z, получаем
формулы приведения для преобразования выражений вида
sinf — ±ct\ cosf—±а\ tgf— ±а\ ctgf — ±а\ п е Z.
12 J I. 2 J I 2 J ° \ 2 J
Для запоминания этих формул удобно пользоваться таким
мнемоническим правилом:
а) перед приведенной функцией ставится тот знак,
который имеет исходная функция (рис. 4), если
О <а <-;
2
б) функция меняется на «кофункцию», если п нечет-
но; функция не меняется, если п четно. (Кофунк-
циями синуса, косинуса, тангенса и котангенса на-
зываются соответственно косинус, синус, котангенс
и тангенс.)
Например:
sin — - а = cos а;
12 J
tg — + а = - ctg а; cos
cos — - а I = sin а;
\2 J
I — -а I = -sinа и т. п.
<2 )
Вам известны также формулы суммы и разности синусов
{косинусов):
_ о. а+Р а-Р
sin а + sin Р = 2 sin —-— cos-- ;
' 2 2
• о о • а -Р а + Р
sin а - sin Р = 2 sin —-— cos -;
н 2 2
cosa + cosp = 2 cos — —
a - P
cos ——;
Ci
„ . a-p . a+p
cosa - cosP = - 2 sin - - sin
H 2 2
8 Тригонометрические функции
Из формул сложения, полагая а = р, выводятся формулы
двойного аргумента'.
sin 2а = 2 sin a cos а;
cos 2а = cos2 а - sin2 а;
cos 2а = 1 - 2 sin2 а; cos 2а = 2 cos2 а - 1;
1 - tg 2 а
Подставляя в формулы cos 2t = 1 - 2 sin2 t и cos 2t =
= 2 cos2 t - 1 значение t = “, получаем формулы половинного аргу-
мента'.
. о о 1 - cos а
Sin2 — =---------;
2 2
9 а 1 + cos а
cos2 — =---------.
2 2
(3)
(4)
Пример 2. Найдем значение sin — без помощи таблиц
по формуле (3):
sin2
1 - cos —
л ___6
12 2
i_V3
___2
2
4
Так как 0 < —
12
sin > 0, получаем
. л V о „
sin — = -------. Ответ
12 2
л
2
можно упростить:
л/2-Уз _ 74-2V3 _ 7(V3-1)2 _ 44, -I _ 4в-42
2 2 42 2 42 2 42 4
Разделив почленно равенство (3) на (4), получаем:
tg2 « =
s 2
1 - cos а
1 + cos а
(5)
находим:
Умножая числитель и знаменатель правой части равенства
sin —
tg ~ =----— на 2 cos
2 cos « 2
2
sin — 2 sin — cos —
tg a _2 __________2 2 _ sina
2 cos— 2 cos2— 1+cosa’
2 2
tg— = sin a
2 1 + cos a
(6)
Тригонометрические функции
на 2 sin , приходим к формуле
Аналогично, умножая числитель и знаменатель правой части
sin"
(X 2
равенства tg - =----
2 cos"
2
tg -
& 2
1 -cos а
sin а
(7)
Пример 3. Найдем значение tg
без помощи таблиц:
tg2
1-сок5я
4
1+ cos —
4
V2
2
/2
2
(V2 + 1)2 =(л/2 + 1)2
2-1
Заметим,
tg =-(V2 + 1).
О
Пример 4. Найдем
что
л.
Поэтому tg < О,
и, следовательно,
sin —,
2
cos и tg
—, если известно,
2
5 л
8
л < 5 л
2 8
что cos а = 0,8 и 0 < а < —.
2
Угол находится в первой
cos > 0, tg > 0. Поэтому
£ £
четверти, и, значит, sin > О,
1-0,8
sin “ =
2 V 2
__„ а
COS — =
2
1+0,8
2
tgf =
1 °’- = -- «0,3333.
1 + 0,8 3
Упражнения
В каждом пункте упражнения разделены на две части. За-
дачи, приводимые в первой части, характеризуют обязательный
уровень подготовки по данной теме: подобные упражнения необхо-
димо уметь решать для получения удовлетворительной оценки.
В большинстве случаев со способами решения этих задач можно
ознакомиться, рассмотрев примеры, разобранные в тексте соответ-
ствующего пункта.
1.— Выразите в радианной мере величины углов:
|а) 45°, 36°, 180°; б) 120°, 310°, 360°;
в) 60°, 72°, 270°; г) 150°, 216°, 90°.
Тригонометрические функции
2.— Выразите в градусной мере величины углов:
л Зл х 5л Зл _7л
6’5’’ ’ 4 ’ 2 ’ 12
3.—
Найдите числовое
a) sin 0 + cos — + sin:
2
в) 6 sin — - 2 cos 0 + tg:
6
значение
2 Л.
4’
.2 Л.
3’
выражения:
б) 3 sin — + 2 cos л + ctg2 — ;
6 6
г) 3 tg — - sin2 — + cos2 -.
4 3 6
4.—
Существуют ли числа a, p и у, для которых:
а) sin a = -0,5 , COS P : = V3, tg у = -2,5;
б) sin _ V5 a 2 ’ COS P = -2,2, tg у = 0,31;
в) sin a = 1,3, COS P = Ло 4 ’ tg у = 5,2;
г) sin a =--, 9 cos p = л /2^5, tg у = -7,5?
5.
8.
Могут ли синус и косинус одного и того же числа быть рав-
ными соответственно:
а) —А и б) 0,4 и 0,7;
Могут ли тангенс и котангенс одного и того же числа быть
равными соответственно:
a) -f и -|; б) (ТЗ-2) и (V3 + 2);
5 о
в) 2,4 и -А; г)
Найдите значения других трех основных тригонометриче-
ских функций, если:
a) sin а = -0,8, п < а < —;
7 2
д/fi ‘ТГ
б) cosa =—, - <а<л;
4 2
в) sina= —, 0<а<—; г)
3 2
Упростите выражение:
a) cos2 a - cos4 a + sin4 a;
в) (sin2 a + tg2 a sin2 a) ctg a;
cosa= — —
cosa K, 2
6)
r)
1 - 2 cos2 p .
cosp + sinp’
sin2 t - 1 ,
------ - + tg2t.
cos t
1 1 Тригонометрические функции
9.
Вычислите:
cos — cos — - sin — sin —
15 15 15 15
а) -------------------------------------,
cos0,3n sin0,2n + sin0,3rc cos0,2n
tg + tg —
в) —10 20 .
1 - tg -E- tg ^E
10 20
• 5 л
sin —
18
tg -2^ - tg 5 л
6) -----3------12_;
1 4 tg tg 5 Я
3 12
cos — - sin — cos —
9 9 18
cos^'
12
r)
sin sin Ze _ cos 5л
12 12 12
10.
Вычислите sin 2a, cos 2p, sin (a - P) и cos (a + P), если:
a) sina =4 cosp = -—, —
5 H 13 2
6) cos a = 0,6, sinp = -jy,
Упростите выражение:
. 2 sin a cos p - sin (a - p).
a}
cos (a —P) —2 sina sinp
E+al
4 J
a < л,
3n<a
2
11.4?
б)
в)
2 sin —+a'' 14 ) | - V2 sin a
г)
12.
13.
14.
л
2
Зл
2
1 - cos a + cos 2 a
sin2a - sina
ctg2 а (1 - cos 2а) + cos2 а.
Преобразуйте данное выражение таким образом, чтобы
аргумент соответствующей тригонометрической функции
принадлежал промежутку 0;
2
7 л
a) sin —, cos
7 8
6) tg —, sin [
5 \
-Д, tg 0,6л,
3 )
\ cos 1,8л,
9 )
ctg (-1,2л);
ctg 0,9л.
Найдите числовое значение выражения:
а)
б)
в)
8 sin cos tg ^E ctg Ze;
6 3 6 3 4
5л „„„ 7л.
4 4 ’
6
10 ctg — sin ™ cos ™
4 A *
sin2 (л - £)
1 + sin Д+ tl I 2 J
-cos (2 л -t).
Верно ли равенство:
sin^E-sin^- = Д
12 12 2
sin HE + sin Z? = cos ZE;
18 18 9
COS — + COS — = V2 cos — ?
8 8 8
а)
в)
г)
б) cos ii’L -cos — = -sin —;
24 8 24
Тригонометрические функции
15.—
16.
17.
Найдите sin cos^1, tg если:
a) cos a = , л < a < —; 6) sina= —, — < a < л;
13 2 5 2
в) cosa=—, — <a<2jt; r) sin a = , л < a < —.
’ 25 2 ’ 17 2
С помощью калькулятора или таблиц найдите значения
sin a, cos a, tg a, ctg a, если:
a) a = 0,19; 6) a = 1,37; в) a = 0,9; r) a = 1,2.
С помощью калькулятора или таблиц найдите:
а) радианные меры углов 17°; 43°24'; 83°36'; 72°12';
б) градусные меры углов 0,384; 0,48; 1,11; 1,48.
18.— Вычислите длину дуги, если известны ее радианная мера a
и радиус R содержащей ее окружности:
а) a = 2, R = 1 см; б) а = —, R = 6 см;
4
в) a = 0,1 и R = 1 м; г) a = —, R = 10 м.
’ '10
19 .— Вычислите площадь сектора, если известны радиус R кру-
га и радианная мера а центрального угла сектора:
а) а = 0,1, R = 1 м; б) а-^-, R = 3 м.
20 .— а) Найдите радианную меру центрального угла сектора,
если длина соответствующей дуги равна диаметру круга,
б) Длина дуги сектора втрое меньше его периметра.
Найдите радианную меру его центрального угла.
Найдите значения выражений (21—22).
21 .— а) 3 sin I 2a - — 1 + 2 cos (3a - л), если a=-^;
V 4 j 4
б) sin2 f a+ 3 tgf — \ если a=^;
I 3J <42 J 3’
в) 4 cos 3a - — + ctg a + — , если a = —;
I 6 J I 12/ 6
r) cos (a + tg2 ^2a + если a=-^.
22.-1 a) 1+ tga , если cosa=—, — <a<2n;
1+ctga 13 2
J sin a + cos a , 5
X 6) -------, если tg a = —;
sin a - cos a 4
cos a + ctg a 1 3 л
V в) ------- , если cos a = —, л < a < ——;
ctg a 3 2
I r) sin2 a - cos2 p, если cos2 a - sin2 p = 0,5.
13 Тригонометрические функции
23.—
Докажите, что при 0 < а < ~ справедливо равенство:
a) sin а д/1 + tg2a =-. - -;
cos ayl + tg-2a
/1+ cos a 11 - cos a
б) Л ---------J------=2 ctga;
V 1-cosa vl+cosa
Vl-Sin2 a = cosa .
sina д/l- cos2 a
r) д/sin2 a + tg2a sin2 a = — — 1
д/cos2 a + ctg2 a cos2 a
Докажите тождества (24—26).
tga+ tgP + tga-tgP = 2
tg(a + P) tg(a-P)
25.— a) (sin2 t + 2 sin t cos t - cos2 t)2 = 1 - sin 4t;
cosa-2 sin3a-cos5a , „
6) . _ „----s;-----= tg 3a;
sin5a-2 cos3a-sma
в)
1-4 sin21 cos21
cos21- sin2 t
= cos 2t;
sina + 2 sin2a + sin3a
cos a + 2 cos2a + cos 3a
= tg 2a.
l-tg2| 2tg|
26.— a) cos t =-----; 6) sin В =-—.
l+tg2| l+tg2|
27.— Вычислите (без помощи таблиц и калькулятора):
a) sin ~ cos —; б) ( sin — - sin — 1: cos —;
12 12 I 18 18 J 9
I/ \2 cos 11Л _ cos ?
в) I sin2 - -cos2 — I ; r) -------—-------
I 8 8 J «,„5я
2. Тригонометрические функции
и их графики
1. Функции синус и косинус. Окружность радиуса 1
с центром в начале координат называют единичной окружностью.
Пусть точка Ра единичной окружности получена при повороте
точки Ро (1; 0) на угол в а радиан. Нетрудно понять, что ордината
точки Ра — это синус угла а, а абсцисса этой точки — косинус
угла а (рис. 5).
Тригонометрические функции
Ц Пример. Найдем значения синуса, косинуса, тангенса
3 л
и котангенса угла — радиан.
4
Координаты точки Р3п (рис. 6) нетрудно найти, воспользо-
4
вавшись свойством равнобедренного прямоугольного треуголь-
2 -\1~2 п Зл л/2 Зл V2
ника: х = , ц - —. Поэтому sin - - - —, cos = -—,
2*2 4 2 4 2
tg^=-l, ctg^=-l.
4 4
Далее мы считаем, что все углы измерены в радианной ме-
ре, и поэтому обозначение рад, как правило, опускается. Дого-
ворившись считать единицу измерения углов (1 радиан) фикси-
рованной, определяем, например, синус числа х как синус угла
в х радиан; косинус числа х как косинус угла в х радиан и т.д.
Определение. Числовые функции, заданные
формулами у = sin х и у = cos х, называют соответ-
ственно синусом и косинусом [тл обозначают sin
и cos).
Область определения этих функций — множество всех дейст-
вительных чисел. Областью значений функций синус и косинус
является отрезок [-1; 1], поскольку и ординаты, и абсциссы точек
единичной окружности принимают все значения от -1 до 1. Будем
обозначать область определения функции f через D (/), а область
значений через Е (/). Тогда
D (sin) = D (cos) = R; Е (sin) = Е (cos) = [-1; 1].
Напомним следующие известные вам свойства функций си-
нус и косинус:
Для любого х справедливы равенства:
1) sin (-х) = -sin х, cos (-х) = cos х;
2) sin (х + 2лп) = sin х, cos (х + 2пп) = cos х
(п — произвольное целое число).
Тригонометрические функции
2. Синусоида. Построим график функции синус на отрезке
[0; 2л]. Для этого отметим на оси ординат точки (0; -1) и (0; 1),
а на оси абсцисс точку с абсциссой 2л (обратите внимание: длина
отрезка [0; 2л] приближенно равна 6,28). Разделим отрезок [0; 2л]
и единичную окружность на 16 равных частей (рис. 7). Для по-
строения точки графика с абсциссой а воспользуемся определени-
ем синуса: отметим точку Ра на единичной окружности и проведем
через Ра прямую, параллельную оси абсцисс (рис. 7). Точка пере-
сечения этой прямой и прямой х - а искомая, так как ее ордината
совпадает с ординатой точки Ра, а по определению sin а равен ор-
динате Ра.
На рисунке 7 показано построение 16 точек графика. Соеди-
няя их плавной кривой, получаем эскиз графика синуса на отрезке
[0; 2л]. Для построения графика синуса вне этого отрезка заметим,
что sin (х + 2лп) = sin х (п — произвольное целое число). Поэтому
во всех точках вида х0 + 2лл, где 0 < х0 < 2л, значения синуса сов-
падают, и, следовательно, график синуса на всей прямой получает-
ся из построенного графика с помощью параллельных переносов
его вдоль оси Ох (вправо и влево) на 2л, 4л, 6л и т. д. (рис. 8). Гра-
фик синуса называется синусоидой. Отрезок [-1; 1] оси ординат,
с помощью которого мы находили значения синуса, иногда назы-
вают линией синусов.
Для построения графика косинуса напомним, что cos х =
= sin х + — . Следовательно, значение косинуса в произвольной
точке х0 равно значению синуса в точке х0 + |. Это означает, что
график косинуса получается из графика синуса с помощью парал-
^6 Тригонометрические функции.
лельного переноса на расстояние
— в отрицательном направле-
нии оси Ох. Поэтому график функции у = cos х (рис. 9) также
является синусоидой.
3. Функции тангенс и котангенс и их графики.
Определение. Числовые функции, заданные
формулами у = tg х и у = ctg х, называют соответст-
венно тангенсом и котангенсом (и обозначают tg
и ctg).
Областью определения функции тангенс является множество
всех чисел х, для которых cos х 0, т. е. все числа х, не равные
л
2
+ лп (п «пробегает» все множество целых чисел Z). Область опре-
деления котангенса состоит из всех чисел х, для которых sin х О,
т. е. из всех чисел, не равных ли, где п е Z.
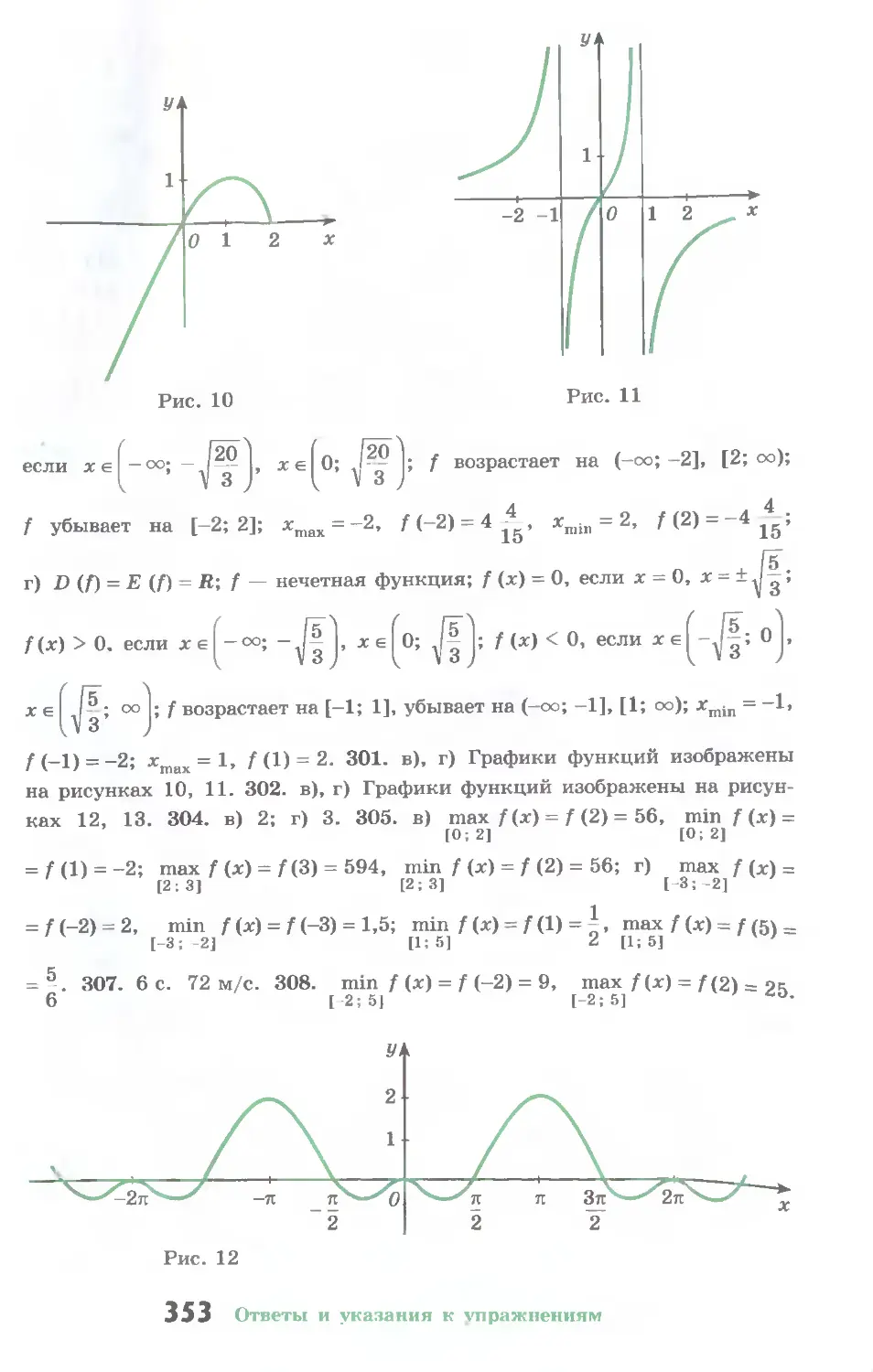
Проведем касательную I к единичной окружности в точке Ро
(рис. 10). Пусть а — произвольное число, для которого cos а 0.
Тогда точка Ра (cos a; sin а) не лежит на оси ординат, и, следо-
вательно, прямая ОРа пересекает I в некоторой точке Та с абсцис-
сой 1. Найдем ординату этой точки.
Для этого заметим, что прямая ОРа проходит через точ-
ку О (0; 0) и Ра (cos a; sin а). Поэтому она имеет уравнение
у = х tg а. Абсцисса точки Та, лежащей на этой прямой, рав-
на 1. Из уравнения прямой ОРа находим, что ордината точки Та
равна tg а. Итак, ордината точки пересечения прямых ОРа и I рав-
на тангенсу а. Поэтому прямую I и называют линией тангенсов.
Нетрудно также доказать, что абсцисса точки Са пересечения
прямой ОРа с касательной т к единичной окружности, проведен-
ной через точку Рл (рис. 11), равна ctg а при sin а#0. Поэтому
2
прямую т называют линией котангенсов.
Область значений тангенса (котангенса) — вся числовая пря-
мая. Докажем это для функции tg. Пусть у0 — произвольное дей-
ствительное число. Рассмотрим точку Т (1; у0). Как только что
было показано, тангенс угла ТОх равен у0. Следовательно, функ-
ция tg принимает любое действительное значение у0, что и требо-
валось доказать.
Напомним следующие известные вам свойства функций tg
и ctg:
1) tg (—х) = -tg х; ctg (-х) = -ctg х;
2) tg (х + ял) = tg х; ctg (х + ял) = ctg х, п е Z.
Построение графика тангенса на интервале ~ j (рис. 12)
аналогично построению, описанному в случае синуса. (Значение
функции tg в точке находится с помощью линии тангенсов.)
18 Тригонометрические функции
тервале
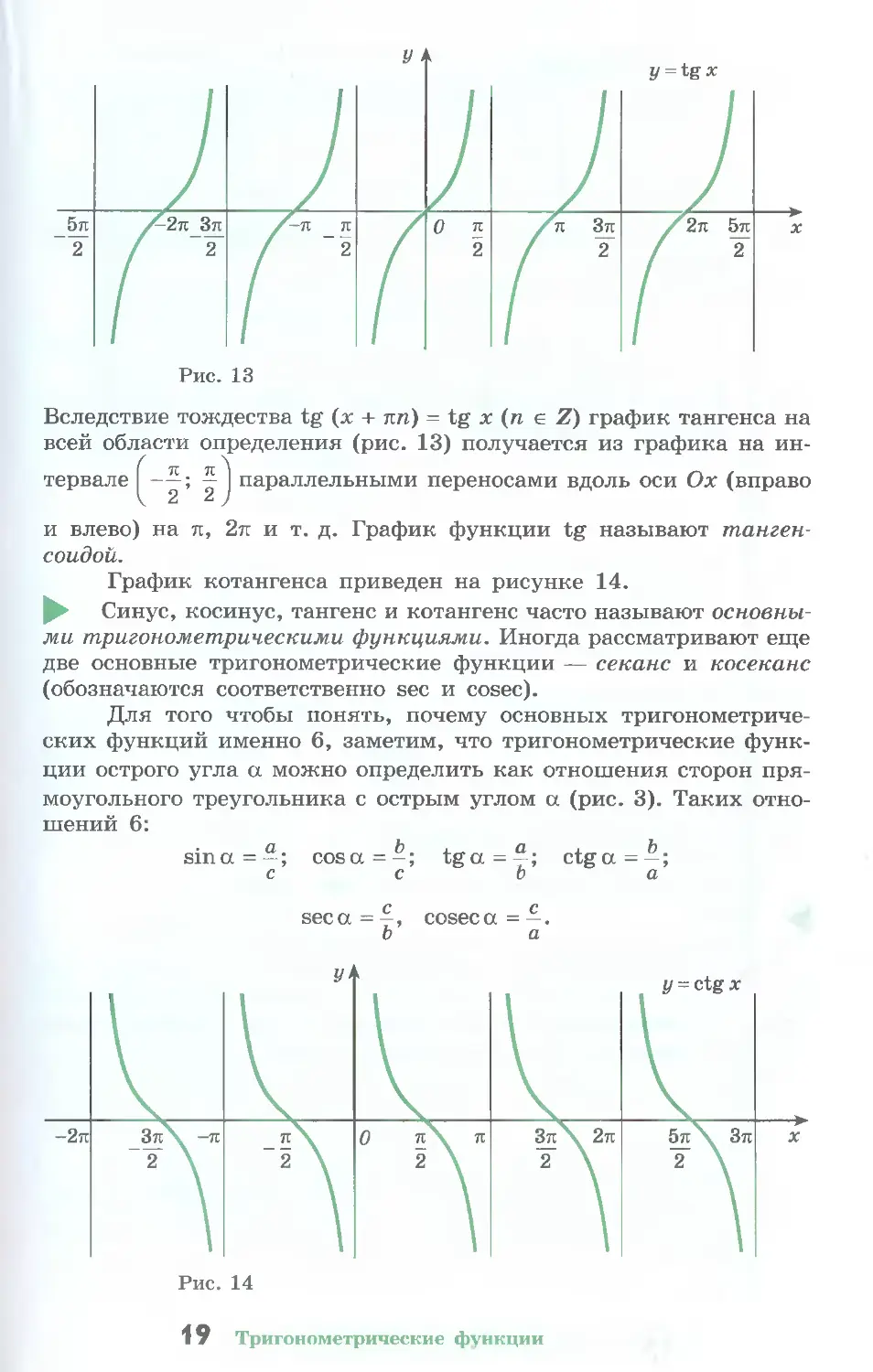
Вследствие тождества tg (х + ли) = tg х (п е Z) график тангенса на
всей области определения (рис. 13) получается из графика на ин-
—; параллельными переносами вдоль оси Ох (вправо
2 2 J
и влево) на л, 2л и т. д. График функции tg называют танген-
соидой.
График котангенса приведен на рисунке 14.
► Синус, косинус, тангенс и котангенс часто называют основны-
ми тригонометрическими функциями. Иногда рассматривают еще
две основные тригонометрические функции — секанс и косеканс
(обозначаются соответственно sec и cosec).
Для того чтобы понять, почему основных тригонометриче-
ских функций именно 6, заметим, что тригонометрические функ-
ции острого угла а можно определить как отношения сторон пря-
моугольного треугольника с острым углом а (рис. 3). Таких отно-
шений 6:
sina=~; cosct=-; tga= —; ctga=—;
с c b а
19 Тригонометрические функции
Упражнения
28.— Отметьте на единичной окружности точку Р , если:
а) а=^, б) а=Т’ а=л, а=-£;
о z 4 4 £
в) а=^, а=Д^, а =~~; г) а=--, а=2л, а=Д^.
3 2 4 6 4
29.— Найдите координаты точки Ра единичной окружности, если
а равно:
* а) -, -, -л; б) --, — 2 4 6 3 2
в) -, Зл; г) —, 2 3 4 3 2
30.- - В какой четверти координатной плоскости расположена
точка Ра, если а равно:
а) Зтг 8л _2 7 б) 5л j 8 _3 2;
8 7 7 3
в) 1,9; г) -2,3л, 3,7?
4 5 9
31. Найдите знак числа:
a) sin^" cos^ tg2,3n; б) sin 1 cos 3 tg 5;
7 8
в) sin 1,3л cos tg2,9; r) sin 8 cos 0,7 tg 6,4.
32. Найдите значения синуса и косинуса а, если а равно:
а) 4л, -л; б) -5,5л;
в) л, -2л; г) -^.
2 2
33.- Постройте график функции:
I Зл I
а) у = cos I — + х I;
в) i/=cos^-xj;
б) у = -sin (х + л);
г) у = tg (х + л).
34.—
На единичной окружности отметьте точку Ра (х; у), коор-
динаты которой удовлетворяют условию:
а) у = 0,5, х > 0;
в) х = —3, у > 0;
б) х = -~, у > 0;
г) У = ~~-, х < 0.
35.—
На миллиметровой бумаге постройте единичную окруж-
ность, а затем центральный угол а, такой, что:
a) sin а = -0,5; б) cos а = 0,3;
в) cos а = -0,4; г) tg а = 2.
Тригонометрические функции
Найдите область определения и область значений данной
функции. Постройте ее график (36—37).
36.— а) в) у = 2 + sin х; у = cos х - 1; б) г) у = 1 + tg х; у = 3 + sin х.
37.- а) у = 2 sin х; б) и = -icosx; а 2
в) у = 0,5 tg х; г) у = -1,5 sin х.
Найдите координаты точек пересечения с осями координат
графика функции (38- -39).
38. 4 а) у = sin х; б) у = 1 + cos х;
в) у ~ cos х; г) у = sin х - 1.
39. а) у — х2 - Зх; б) у = sin х - 1,5;
в) у = 2,5 + cos х; г)
§2.
Основные свойства функций
3. Функции и их графики
1. Числовая функция. С понятием функции вы позна-
комились в курсе алгебры. При изучении начал анализа удобно
принять следующее определение:
Определение. Числовой функцией с областью
определения D называется соответствие, при кото-
ром каждому числу х из множества D сопоставляет-
ся по некоторому правилу число у, зависящее от х.
Функции обычно обозначают латинскими (а иногда гречески-
ми) буквами. Рассмотрим произвольную функцию f. Независимую
переменную х называют также аргументом функции. Число у,
соответствующее числу х, называют значением функции f в точ-
ке х и обозначают f (х). Область определения функции f обозна-
чают D (f). Множество, состоящее из всех чисел f (х), таких, что х
принадлежит области определения функции f, называют областью
значений функции f и обозначают Е (f).
Чаще всего функцию задают с помощью какой-либо фор-
мулы. При этом если не дано дополнительных ограничений, то
областью определения функции, заданной формулой, считают
множество всех значений переменной, при которых эта форму-
ла имеет смысл. Например, формула f(x) = — имеет смысл при
х
Тригонометрические функции
всех х * О, поэтому областью определения функции f (х) = - счи-
тают множество всех не равных нулю действительных чисел.
Область ее значений совпадает с областью определения и являет-
ся объединением интервалов (—оо; 0) и (0; оо).
► Вообще объединением множеств А и В называется множест-
во, состоящее из всех элементов, которые принадлежат хотя бы
одному из множеств А или В. Объединение множеств А и В обозна-
чается так: ЛиВ. Например, объединением отрезков [0; 2] и [1; 3]
является отрезок [0; 3].
Символом U удобно пользоваться для обозначения числовых
множеств, которые можно представить в виде объединения число-
вых промежутков. Так, для функции /(х) = i
х
D(f) = E (f) = (-оо; 0) U (0; оо).
интервалов вида
Область определения функции у = tg х — объединение всех
-—+ тш; — + пп , где п е Z; область ее значе-
2 2 J
ний — вся числовая прямая, т. е. Е (tg) = (-оо; оо).
Функции вида f (х) = р (х), где р (х) — многочлен, называют
целыми рациональными функциями, а функции вида f (х) = —-
9(х)
где р (х) и q (х) — многочлены, называют дробно-рациональными
функциями. Частное ----- определено, если q (х) не обращается
9(х)
в нуль. Поэтому область определения дробно-рациональной функ-
ции f (х) =------множество всех действительных чисел, из кото-
9(х)
рых исключены корни многочлена q (х).
Пример 1. Найдем область определения дробно-рацио-
нальной функции
., 7х8 -5х6 + Зх2 -4х
f(x) =
х3 - Зх2 + 2х
Корни многочлена х3 - Зх2 + 2х — числа 0, 1 и 2. Поэтому
D (f) = (-оо; 0) и (0; 1) и (1; 2) U (2; оо).
2. График функции. Графиком функции f называют мно-
жество всех точек (х; у) координатной плоскости, где у = f (х),
а х «пробегает» всю область определения функции f.
Подмножество координатной плоскости является графиком
какой-либо функции, если оно имеет не более одной общей точки
с любой прямой, параллельной оси Оу. Например, множество,
изображенное на рисунке 15, не является графиком функции, так
как оно содержит две точки с одной и той же абсциссой а, но раз-
ными ординатами Ь1 и Ъ2. Если бы мы сочли это множество графи-
22 Тригонометрические функции
ком функции, то пришлось бы считать, что эта функция имеет при
х = а сразу два значения Ьг и Ь2, что противоречит определению
функции.
Часто функцию задают графически. При этом для любого х(|
из области определения легко найти соответствующее значение
Уо = f (х0) функции (рис. 16).
3. Преобразование графиков. Запас функций, графики кото-
рых вы умеете строить, пока невелик — это функции у = kx + Ъ,
у = ах2 + Ьх + с, у = \ у = sin х, у = cos х, у = tg х, у = ctg х. Пока-
жем, что, применяя известные из курса геометрии сведения о пре-
образованиях фигур, этот список можно существенно расширить.
1) Рассмотрим сначала параллельный перенос на вектор
(0; Ъ) вдоль оси ординат. Обозначая здесь и далее через (х'; у') ко-
ординаты точки, в которую переходит произвольная точка (х; у)
плоскости при данном преобразовании, получим известные вам
формулы
х' = х,
(1)
У = У + Ь.
Пусть f — произвольная функция с областью определения
D (/). Выясним, в какую фигуру переходит график этой функции
при данном переносе. Из формул (1) сразу получаем, что произ-
вольная точка (х; f (х)) графика переходит в точку (х; f (х) + Ь).
Это означает, что график f переходит в фигуру, состоящую из всех
точек (х; f (х) + Ь), где х е D (f).
По определению графика функции эта фигура является гра-
фиком функции у = f (х) + Ь. Сказанное позволяет сформулировать
правило:
Для построения графика функции f (х) + Ь, где
b — постоянное число, надо перенести график f на
вектор (0; Ь) вдоль оси ординат.
Пример 2. Построим графики функций: а) у = sin х + 2;
б) у = х2 - 5.
23 Тригонометрические функции
а) В соответствии с правилом
переносим график функции у = sin х
на вектор (0; 2), т. е. вверх по оси Оу
на 2 единицы (рис. 17).
б) Построение осуществляется
переносом параболы у = х2 на век-
тор (0; -5), т. е. вниз по оси Оу
(рис. 18).
2) Новым для вас преобразова-
нием является растяжение вдоль оси
Оу с коэффициентом k, которое зада-
ется формулами
(2)
I У' = ky.
Для построения точки М', в ко-
торую переходит данная точка М
при растяжении, надо построить на
прямой AM, где А — проекция М на
ось Ох (рис. 19, а), точку, гомотетич-
ную М относительно центра А (коэффициент гомотетии равен ко-
эффициенту k растяжения). На рисунке 19, б показано построение
точек, в которые переходят данные при растяжениях с коэффици-
ентами - и -2.
2
Выясним, в какую фигуру переходит график функции f при
растяжении. Из формул (2) сразу получаем, что произвольная точ-
ка (х; f (х)) графика f переходит в точку (х; kf (х)). Отсюда следует,
что график f переходит в фигуру, состоящую из всех точек
(х; kf (х)), где х е D (/). Эта фигура является графиком функции
у = kf (х). Доказано следующее правило:
Для построения графика функции у = kf (х) надо ра-
стянуть график функции у = f (х) в k раз вдоль оси
ординат.
Пример 3. Построим графики функций у = -2х2 и у = A cos х.
3
Тригонометричес кие функции
у>'
'►ЛГ(х0; ky0)
В
Г"
АЧхр У1)"
N' (хх; kyj I
«М(х0; у0)
Рис. 19
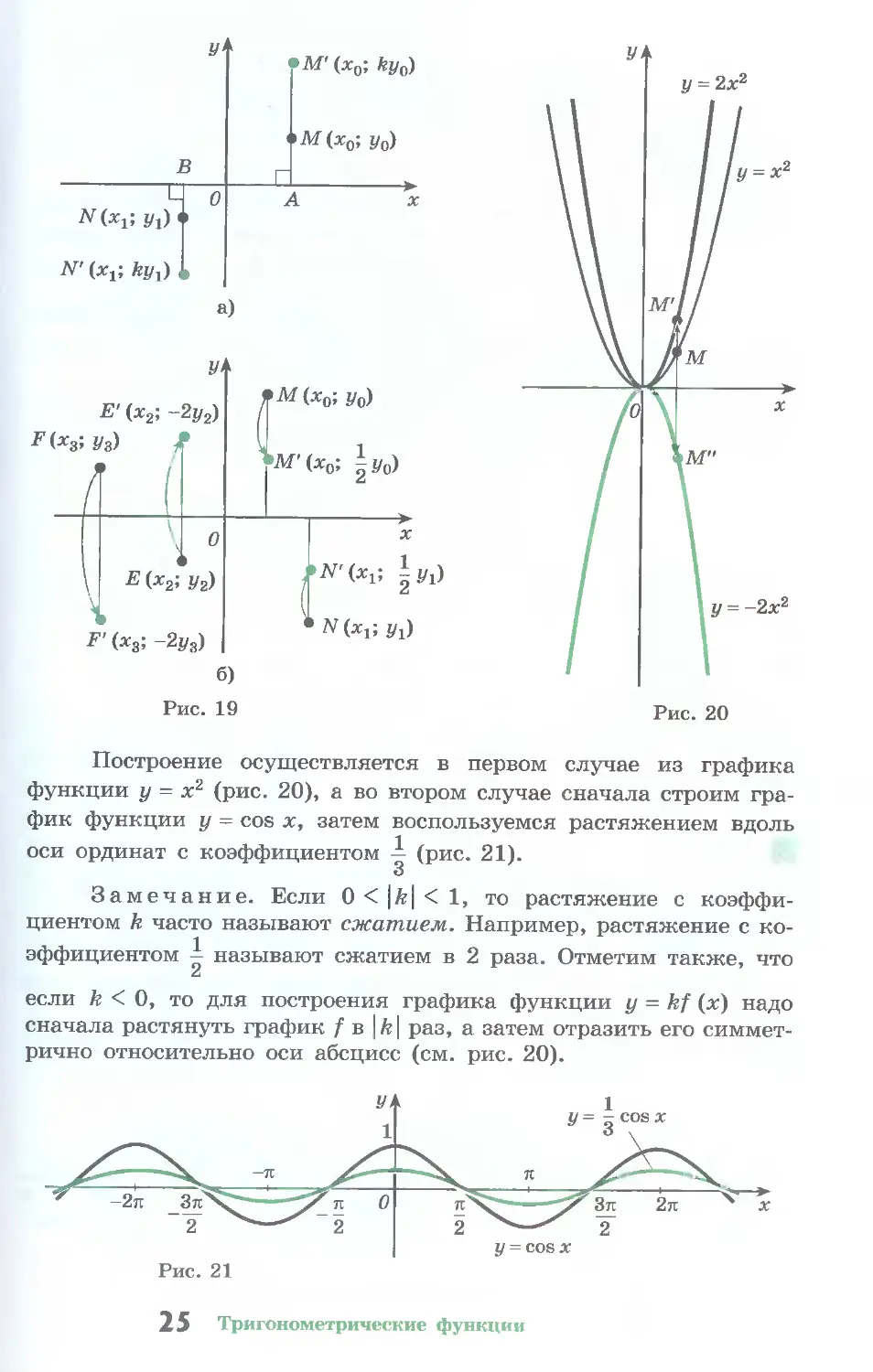
Построение осуществляется в первом случае из графика
функции у = х2 (рис. 20), а во втором случае сначала строим гра-
фик функции у = cos х, затем воспользуемся растяжением вдоль
оси ординат с коэффициентом — (рис. 21).
Замечание. Если 0 < |й| < 1, то растяжение с коэффи-
циентом k часто называют сжатием. Например, растяжение с ко-
эффициентом называют сжатием в 2 раза. Отметим также, что
если k < 0, то для построения графика функции у = kf (х) надо
сначала растянуть график f в |fe| раз, а затем отразить его симмет-
рично относительно оси абсцисс (см. рис. 20).
Рис. 21
25 Тригонометрические функции
3) Параллельный перенос вдоль
оси абсцисс на вектор (а; 0) зада-
ется формулами
[х'=х + а,
1г/' =у-
Каждая точка графика функ-
ции f переходит согласно форму-
лам (3) в точку (х + a; f (х)). Поэто-
му с помощью переменных х', у'
можно записать, что график f пере-
ходит в фигуру Ф, состоящую из точек (х'; f (х' - а)), где х' прини-
мает все значения вида х + а (х «пробегает» D (/)).
Именно при этих значениях х' число х' - а принадлежит
D (/) и f (х' - а) определено. Следовательно, фигура Ф есть график
функции у = f (х - а). Итак, можно сделать вывод:
График функции у = f (х - а) получается из графи-
ка f переносом (вдоль оси абсцисс) на вектор (а; 0).
Обратите внимание: если а > 0, то вектор (а; 0) направлен
в положительном направлении оси абсцисс, а при а < 0 — в отри-
цательном.
Пример 4. Построение графиков функций у = -Ух+1 и
у =cos Х-— I показано на рисунках 22 и 23.
\ 4)
4) Растяжение вдоль оси Ох с коэффициентом k задается
формулами
Произвольная точка графика функции / переходит при та-
ком растяжении в точку (/ex; f (х)). Переходя к переменным х', у',
можно записать, что график у = f (х) переходит в фигуру, состоя-
щую из точек х'; /[ — )], гДе х' принимает все значения вида
Тригонометрические функции
Эта фигура есть график функции у = / — . Итак:
\k J
Для построения графика функции у = f — надо
у k )
подвергнуть график функции f растяжению с коэф-
фициентом k вдоль оси абсцисс.
Пример 5. Построение графиков функций у = cos 2х и
у = sin — х показано на рисунках 24 и 25.
3
4. Отображение. Функцию с областью определения D и об-
ластью значений Е называют также отображением множества D
на множество Е. Можно сказать, например, что формула у = sin х
задает отображение множества R действительных чисел на отрезок
[-1; 1]. Слова «функция» и «отображение» — синонимы.
Нередко рассматривают функции (отображения), область
определения или область значения которых (а возможно, и оба
этих множества) не являются числовыми множествами. С такими
примерами, по существу, вы уже встречались в курсе геометрии.
Например, областью определения функции «Площадь многоуголь-
ника» при фиксированной единице измерения площадей является
множество многоугольников плоскости. Область значений этой
функции — множество неотрицательных чисел (площадь 0 имеют
«вырожденные» многоугольники, например отрезок).
Движение (так же как и преобразование подобия), переводя-
щее фигуру F в фигуру F', также является отображением, его об-
ласть определения F и область значений F' состоят из точек.
Понятие отображения часто относят к числу основных поня-
тий всей математики. С его помощью можно дать такое определе-
27 Тригонометрические функции
ние функции: функцией с областью определения D и областью зна-
чений Е называется отображение множества D на множество Е,
при котором каждому элементу множества D соответствует один
вполне определенный элемент множества Е и каждый элемент
множества Е поставлен в соответствие некоторому (хотя бы одно-
му) элементу множества D.
Упражнения
40.— Найдите значения функции:
a) f (х) - х + — в точках -1, 10;
х 2
б) f (х) = 3 cos | х - — | в точках 0, л;
к 4 J 4
< в) f (х) = д/бх - х2 в точках 0, 1, 2;
г) f (х) = 2 - sin 2х в точках 0,
41.
Запишите значения функции:
a) f (х) = х2 + 2х в точках х0, t + 1;
б) f (х) = tg 2х в точках a, b - 1;
в) f (х) = — + 1 в точках хп, а + 2;
х
г) f (х) = 2 cos * в точках z, h + л.
О
28 Тригонометрические функции
42.— Является ли графиком функции фигура, изображенная
на рисунке 26, а—гЧ
43.—
44.-
45.
46.
47.
Найдите область определения каждой из функций (43—44).
х — 1 qA -f I — • 6) f (x) = Vx2 -9;
' ' ’ x2 — 4x + 3 ’
в) 5-х2 f(x)~ ; x2 +2x-8 r) /(x) = V36-x2
a) f (x) = 4; XA 6) f (x) = 2 tg x;
в) f (x) = 1 + ctg x; r)
х
Найдите область определения и область значений каждой
из функций:
a) j/= 2 cos (хб) у = 2 + —Цр
в) у = - -1; г) у = 3 + 0,5 sin^x + -j
Найдите область определения и область значений функции,
график которой изображен на рисунке 27, а—г.
Начертите график какой-нибудь функции /, для которой:
a) D (/) = [-2; 4], Е (/) = [-3; 3];
б) D (/) = (-5; 3), Е (f) = [2; 6].
Рис. 27
29 Тригонометрические функции
48.—
В одной и той же системе координат постройте графики
функций:
а) у =-, у = — + 2, у = ~^;
х х х-2
б) у = cos х, у = cos х - 3, у = cos х + — ;
\ 4 7
в) у = -х2, у = 4 - х2, у = - (х - 2)г;
г) у = sin х, у = sin х + 2, у = sin ( х +
49.
50.
Постройте графики функций (49—50).
а) у = -^-д; X о б) у = (х - 2)2 - 4;
в) У = 1 - (X + 2)2; г) у=2 + —. X
а) у = 1 + 2 sin х; б) у = V х + 1 -1;
в) у = 0,5 cos х - 1; г) у = 2 + у/ х-1.
51.—
Найдите значения функции:
[ х, если х > 0, 1
a) f (х) = -! в точках -2; - —; 0; 5;
[-х, если х<0, 3
б) /(х)=|Х если х 1’ в точках -2; -1; 0; 4;
[1-х, если х < -1,
. „ , , [sinx, если х>0, _
в) f(x)=l в точках 0; п-.
[cosx-1, если х < 0, 2 3 6
52.—
а) Основание АС треугольника АВС равно Ь, высота BD
равна h. Через точку К высоты BD проведена прямая,
параллельная АС. Выразите площади фигур, на которые
делит эта прямая данный треугольник, как функции от
расстояния ВК = х.
б) Радианная мера центрального угла равна х, радиус кру-
га равен R. Выразите площадь соответствующего сегмента
как функцию от х.
в) Радианная мера центрального угла сектора равна а, ра-
диус равен г. Выразите периметр сектора как функцию
от угла а.
г) Прямая, параллельная диагонали квадрата, делит его
на две фигуры. Задайте формулой зависимость между пло-
щадью каждой фигуры и длиной х меньшего отрезка, отсе-
каемого данной прямой от диагонали, если сторона квадра-
та равна а.
30 Тригонометрические функции
53.—
Найдите область
определения функции:
б) У = ~ 2
16-xz
г) У =
1-2х
54.- - Найдите область определения и область значений функции:
а) в) у = 1 + sin2 х; у = ^х2 + 4; б) г) X- 1 у =—; X у = 1,5 - 0,5 cos2 х.
55.-1 Постройте графики - а) у = |х - 11; в) у = у/2х-2; функций (55—56). |х2-4, если х> 2, о) у = < [2-х, если х < 2; „ 1 3 - х2, если х > 1, г) у = < [х-2, если х < 1.
56. а) в) у = sin Зх - 1; у = 1 + cos 2х; б) г) у = - х3 +2; у 2 у = 1 + - -/х. у 2
4. Четные и нечетные функции.
Периодичность тригонометрических функций
1. Четные и нечетные функции. Рассмотрим функции,
области определения которых симметричны относительно начала
координат, т. е. для любого х из области определения число (-х)
также принадлежит области определения. Среди таких функций
выделяют четные и нечетные.
Определение. Функция f называется четной,
если для любого х из ее области определенья
f(-x) = f(x) (рис. 28).
*4
31 Тригонометрические функции
Определение. Функция f называется нечет-
ной, если для любого х из ее области определения
f (-ж) = f М (рис. 29).
Пример 1. Функция f (х) = х4 четная, а функция
g (х) = х3 нечетная. Действительно, область определения каждой
из них (это вся числовая прямая) симметрична относительно точки
О и для любого х выполнены равенства f (-х) = (-х)4 = х4 = f (х),
g (-х) = (—х)3 = -х3 = -g (х). Графики функций изображены на ри-
сунках 30 и 31.
При построении графиков четных и нечетных функций бу-
дем пользоваться следующими известными из курса алгебры свой-
ствами:
1°. График четной функции симметричен относи-
тельно оси ординат.
2°. График нечетной функции симметричен относи-
тельно начала координат.
Из этих двух правил вытекает следующее: при построении
графика четной или нечетной функции достаточно построить его
часть для неотрицательных х, а затем отразить полученный гра-
фик относительно оси ординат (в случае четной функции) или на-
чала координат (в случае нечетной).
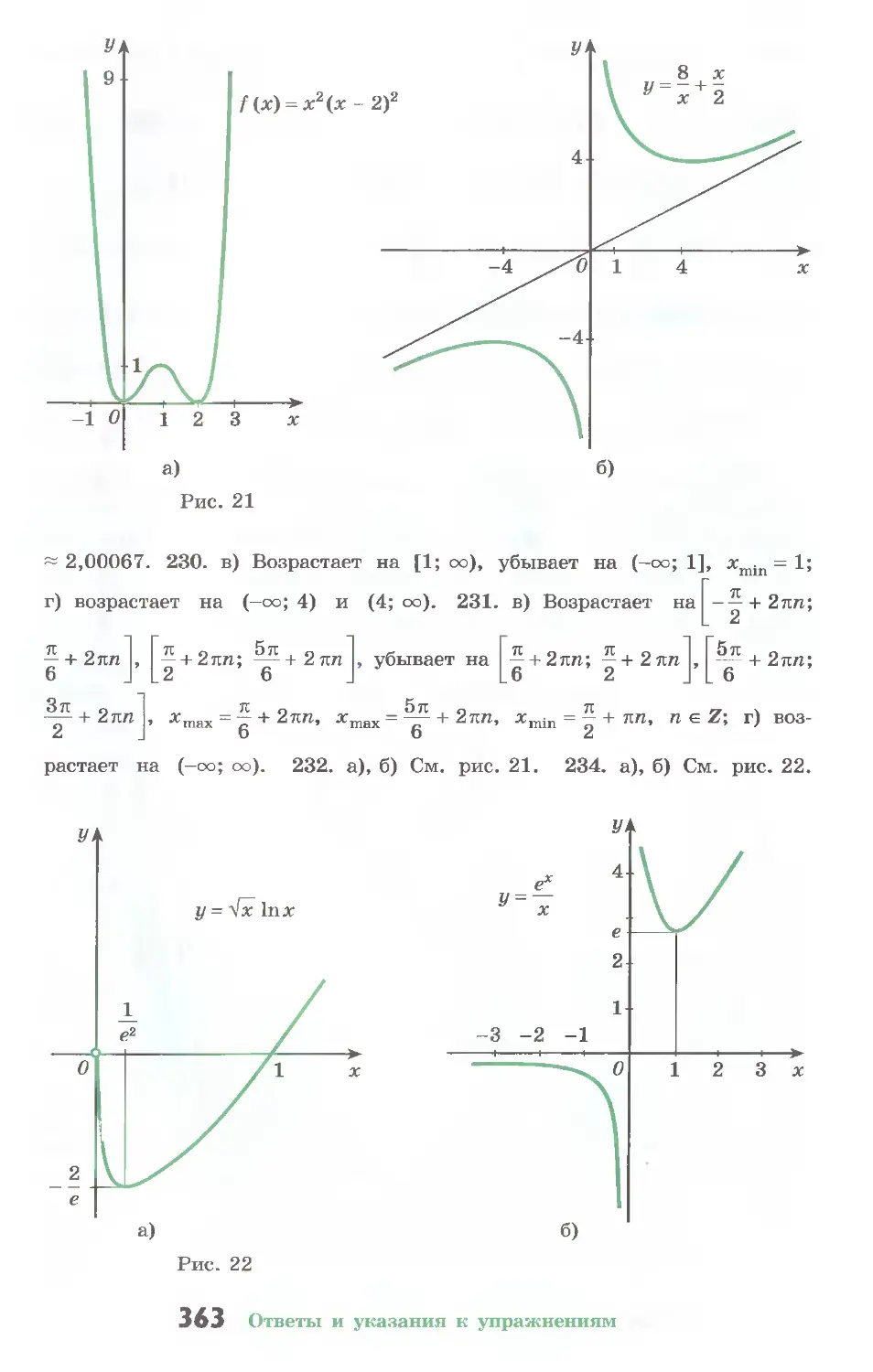
П ример 2. Функция f(x) = x + — нечетная (докажите это
х
самостоятельно). Ее график симметричен относительно начала ко-
ординат (рис. 32).
Основные тригонометрические функции синус, тангенс и котан-
генс являются нечетными, а косинус — четной функцией (см. п. 2).
32 Тригонометрические функции
Поэтому графики синуса, тангенса и котангенса (рис. 8, 13, 14)
симметричны относительно начала координат, а график косинуса
(рис. 9) симметричен относительно оси ординат.
Х^ + X
Пример 3. Функция f (х) = —----четная, так как ее об-
х3 -х
ласть определения симметрична относительно точки х = О (она со-
стоит из всех чисел, отличных от -1, 0 и 1) и для всех х е D (J)
выполнено равенство
/ <-«) - '’7'4 - =4^ - «*’•
(-х)3 (-х) х-х3 х3-х
График этой функции симметричен относительно оси Оу
(рис. 33).
Пример 4. Функция f (х) = х2 + х не является ни четной,
ни нечетной. Ее область определения симметрична относительно
точки 0, но, например, при х = 1 не выполнено ни равенство
f (1) = / (- 1), ни равенство f (1) = -f (-1), поскольку f(l) = 2,
a f (-1) = 0.
2. Периодические функции. Очень многие процессы и явле-
ния, с которыми мы встречаемся на практике, имеют повторяю-
щийся характер. Так, взаимное расположение Солнца и Земли
повторяется через год. Положения маятника в моменты времени,
отличающиеся на период колебания маятника, одинаковы.
Такого рода процессы называют периодическими, а функ-
ции, их описывающие,— периодическими функциями.
33 Тригонометрические функции
Известные вам основные тригонометрические функции —
периодические. Так, для любого числа х и любого целого k выпол-
нено равенство sin (х + 2л/г) = sin х. Отсюда следует, что 2 л/г — пе-
риод функции синус (k Ф 0 — произвольное целое число).
Вообще, говоря о периодичности функции Д полагают, что
имеется такое число Т * 0, что область определения D (f) вместе
с каждой точкой х содержит и точки, получающиеся из х па-
раллельными переносами вдоль оси Ох (вправо и влево) на рассто-
яние Т. Функцию f называют периодической с периодом Т * О,
если для любого х из области определения значения этой функции
в точках х, х - Т и х + Т равны, т. е. f (х + Т) = f (х) = f (х - Т).
Поскольку синус и косинус определены на всей числовой
прямой и sin (х + 2л) = sin х, cos (х + 2л) = cos х для любого х, си-
нус и косинус — периодические функции с периодом 2л.
Тангенс и котангенс — периодические функции с перио-
дом л. В самом деле, области определения этих функций вместе
с каждым х содержат числа х + л и х-л и верны равенства
tg (х + л) = tg х, ctg (х + л) = ctg х.
Очевидно, что если функция f периодическая с периодом Т,
то при любом целом п 0 число пТ тоже период этой функции.
Например, при п = 3, воспользовавшись несколько раз определе-
нием периодической функции, находим:
f (х + ЗТ) = f ((х + 2Т) + Т) = f (х + 27) = f ((х + Т) + Т) =
= f (х + Т) = f (х).
Докажем, что:
а) наименьший положительный период функций
у = sin х и у = cos х равен 2л;
б) наименьшим положительным периодом функций
у = tg х и у = ctg х является число л.
| а) Как уже отмечалось, число 2л является периодом функций
sin и cos. Поэтому остается доказать, что положительное число,
меньшее 2л, не может быть их периодом. Докажем это.
Если Т — произвольный период косинуса, то cos (а + Т) =
= cos а при любом а. Полагая а = 0, находим cos Т = cos 0=1.
Наименьшее положительное число Т, для которого cos х = 1,
есть 2л.
Пусть Т — произвольный положительный период синуса.
Тогда sin (а + Т) = sin а при любом а. Полагая а = , получаем
sin Т + — = sin— = 1. Но sin х = 1 только при х = — + 2ли, п 6 Z.
I 2 J 2 2
Поэтому Т = 2лп. Наименьшее положительное число вида 2лп
есть 2л.
34 Тригонометрические функции
У,'
w vwv
-2T -T 0 т 2T 3T x
Рис. 34
б) Если T — положительный период тангенса, то tg Т =
= tg (0 + Т) = tg 0 = 0. Так как на интервале (0; л) тангенс нулей
не имеет, Т > л. Ранее доказано, что л — период функции tg,
и, значит, л — это ее наименьший положительный период. Для
функции ctg доказательство аналогично.
Как правило, слова «наименьший положительный период»
опускают. Принято, например, говорить, что период тангенса ра-
вен л, а период синуса равен 2л.
Периодичностью основных тригонометрических функций мы
уже фактически пользовались ранее, при построении графиков.
Справедливо следующее утверждение:
Для построения графика периодической функции
с периодом Т достаточно провести построение на
отрезке длиной Т и затем полученный график парал-
лельно перенести на расстояния пТ вправо и влево
вдоль оси Ох (рис. 34, здесь п — любое натуральное
число).
Действительно, пусть (х0; у0) — точка графика периодиче-
ской функции f. Тогда точка х0 + пТ при любом целом п принад-
лежит области определения f (см. замечание в начале пункта)
и вследствие периодичности f справедливо равенство f (х0 + пТ) =
= f (хо) = Уо- Значит, точка (х0 + пТ; у0), полученная при парал-
лельном переносе точки (х0; у0) вдоль оси Ох на вектор (пТ; 0),
тоже принадлежит графику f.
Пример 5. Построим график функции f (х) = 2 cos х + 1.
Для построения воспользуемся тем, что функция f периодическая
с периодом 2л. Действительно, функ-
ция f определена на всей прямой,
и, значит, вместе с произвольной
точкой х0 ее область определения со-
держит точки, получающиеся из х0
параллельными переносами вдоль
оси Ох вправо и влево на 2л. Кроме
того, вследствие периодичности ко-
синуса f (х + 2л) = 2 cos (х + 2л) + 1 =
= 2 cos х + 1 = f (х). Пользуясь свой-
35 Тригонометрические функции
ством графиков периодических функций, строим график f сначала
на отрезке [0; 2л] (для этого в соответствии с известными правила-
ми преобразования графиков растягиваем график косинуса вдоль
оси Оу в 2 раза и сдвигаем его на 1 вверх (рис. 35), а затем с по-
мощью параллельных переносов продолжаем его на всю числовую
прямую (рис. 36).
► Пример 6. Докажем, что функция f (х) = tg I 2х - — I пе-
и «л 71
риодическая и ее наименьший положительный период равен -.
Тангенс определен при всех значениях аргумента, не равных
+ лп, п е Z. Поэтому область определения данной функции состо-
ит из таких х, что 2х- — * - + ли, т. е. х * — + —, п g Z. Отсюда
4 2 8 2
следует, что D (/) наряду с произвольным х0 содержит и все точки
вида х0 + ™, х0-~, п е Z. Очевидно, что число является пе-
-'l = tg f 1^2 х + л|=
4 1 I k 4/ j
риодом f, так как f \ х + — = tg 2 х + —
V 2J < 2
= f (х). Остается доказать, что число — наимень-
ший положительный период f. Допустим, что периодом f является
такое число То, что То < Тогда для любого х е D (f) справедливо
равенство /(х + То) = tg 2 (х + То) -
4
2
= tg 2 х - —
\ 4
=f(x)=
= tg ^2 х - J, поскольку Tq — период f. Но это означает, что 2^, —
период функции tg. По предположению То < , т. е. 270 < л. Про-
тиворечие с доказанным ранее: наименьший положительный пе-
риод тангенса равен л. Справедливо и общее утверждение:
Если функция f периодическая и имеет наименьший
положительный период Т, то функция Af (kx + b), где
A, k и b постоянны, a k 0, также периодична, при-
т
чем ее наименьший положительный период равен —г.
I ь I
36 Тригонометрические функции
Из этого утверждения сразу получаем, что, например, перио-
является число —, а период функции
3
дом функции sin I Зх - —
\ 2
cos
равен 4л.
Упражнения
Докажите, что функции являются четными (57—58).
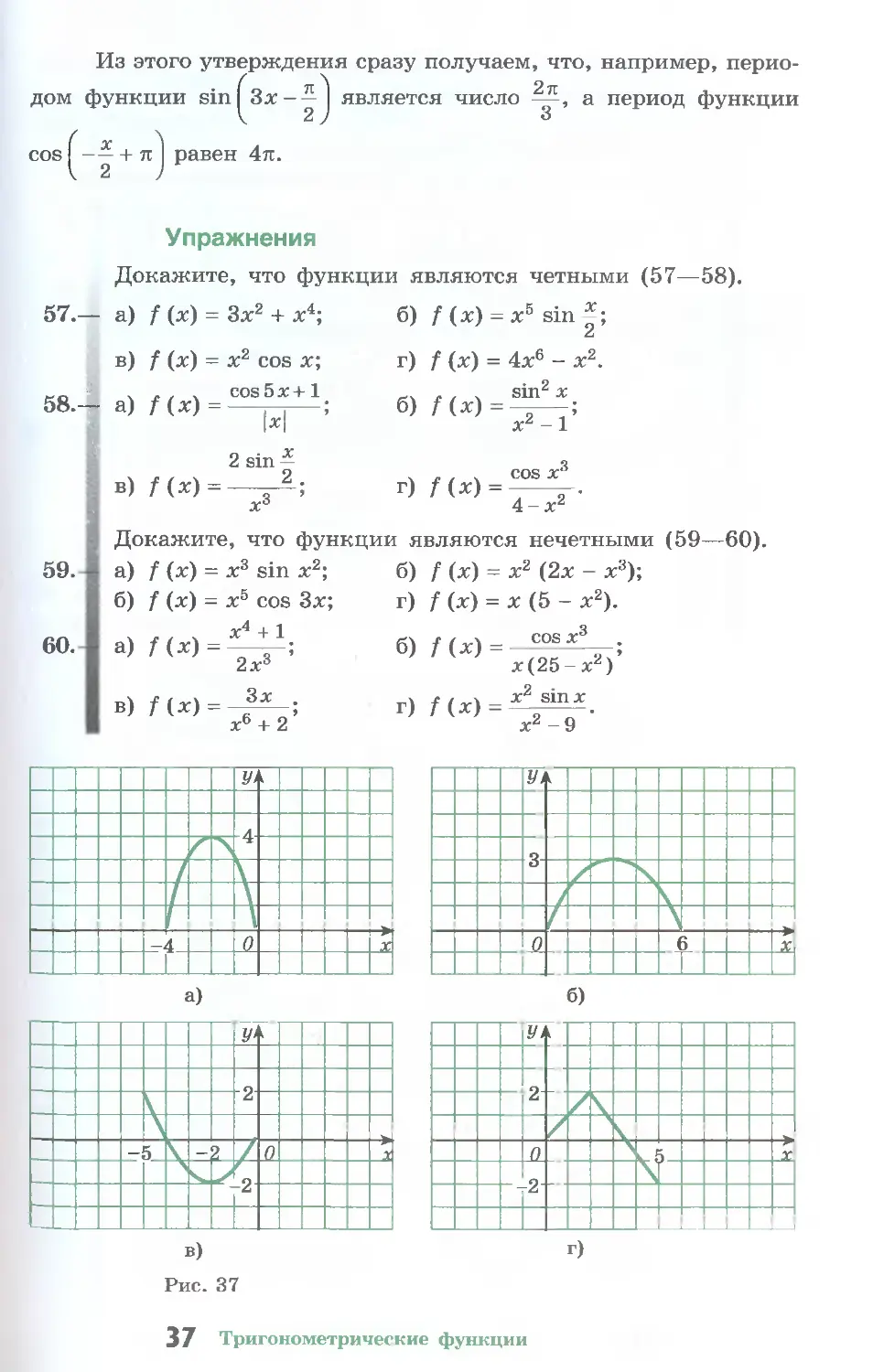
57.- - а) f (х) = Зх2 + х4; б) f (х) = х5 sin
в) f (х) = х2 cos х; г) f (х) = 4х6 - х2.
58. - а) . , . cos 5 х + 1 |,| б) sin2 х f(x)- 2 ; -1
в) 2 sin — f(x)=—^-2; X6 г) ... COS X3 2- 4-х^
Докажите, что функции являются нечетными (59—60).
59. а) f (х) = х3 sin х2; б) f (х) = х2 (2х - х3);
б) / (х) = х5 cos Зх; г) f (х) = х (5 - х2).
60. а) 1 (х) = х4 + 1 2х3 б) f(x) = cos*3 ; x(25-xz)
в) f (х) = Зх . х6 + 2 ’ г) /(x) = x^sinx. xz - 9
Рис. 37
б)
г)
37 Тригонометрические функции
61.— На рисунке 37, а—г построен график функции f для всех х,
удовлетворяющих условию х > О (х < 0). Постройте гра-
фик функции f, если известно: 1) f — четная функция;
2) f — нечетная функция.
62.— Докажите, что число Т является периодом функции f,
если:
63.
64.
65.
а) / (х) = sin Т = 4л; б) f (х) = 2 tg Зх, Т =
2 о
в) f (х) = 3 cos 4х, Т = ~; г) f(x) = ctg* Т = Зл.
2 о
Докажите, что функция f является периодической:
a) f (х) = 2 - cos х; б) f (х) = tg 2х;
в) f (х) = sin х + cos х; г) f (х) = 3 + sin2 х.
Найдите наименьший
положительный период каждой из
функций (64—65).
а) У = | sin J;
в) у = 4 cos 2х;
б) у = 3 tg 1,5х;
г) У = 5 tg *
о
а) у = sin х cos х;
в) у = sin2 х - cos2 х;
б) у = sin х sin 4х - cos х cos 4х;
г) у = sin Зх cos х + cos Зх sin х.
38 Тригонометрические функции
66.— На рисунке 38, а—г изображена часть графика функции,
имеющей период Т. Постройте график этой функции на
промежутке [-1,57; 2,57].
67.— Найдите наименьший положительный период и постройте
график функции:
а) у = sin 2х;
в) У = tg
б) У = cos
О
г) у = sin 1,5х.
68.
Для функции f ученик проверил справедливость двух ра-
венств и сделал вывод, что Т является периодом f. Прав ли
ученик, если:
a) f (х) = sin х,
б) f (х) = cos х,
sin^=l, sin I * + 2’4 = 1, 7 = 2^;
6 2 <6 3 ) 2 3
cos 77 = 0, cos f — + л | = 0, 7 = n;
2 12 J
, ,, „ x + 1, если x < 1,
B)
I 3-х, если x > 1,
f (-1J =0,5, f J-l + 3J = 0,5, 7 = 3;
r) /(x) = x + |x|, / (-4) = 0, f (-4 + 3) = 0, 7 = 3?
Какие из указанных ниже функций являются четными,
какие — нечетными, а какие не являются ни четными, ни
нечетными (69—70)?
I я I
69.— а) у = sin х + ctg х - х; б) у ------—!;
sin х cos х
в) У = х4 + tg2 х + х sin х; , tg X - ctg X Г) У = Г-,— |х|
70.— а) sinx . б) у = х + sin х _
У X3 - 1’ х - sin х
в) У = 71-х2 _ г) у = X + tgx
1-х ’ X COS X
71.
72.—
Докажите, что данная функция является четной или нечет-
ной, и постройте ее график:
а) У = ~~', б) </ = -1 .
xz ха
Функции fug определены на множестве всех действитель-
ных чисел. Является ли функция h четной или нечетной,
если:
a) h (х) = f (х) g2 (х), f — четная функция, g — нечетная;
б) h (х) = f (х) - g (х), fug — четные функции;
в) h (х) = f (х) + g (х), fug — нечетные функции;
г) h (х) = f (х) g (х), f и g — нечетные функции?
39 Тригонометрические функции
73 .— Найдите наименьший положительный период функции:
а) у = sin2 х; б) у = tg х ctg х;
f А2
в) у = sin4 х - cos4 х; г) у = I sin + cos I
74 .— Постройте график функции:
а) у = 1 - cos 1,5х; б) t/ = sin^2x-^;
в) у = 2 + sin г) y=tg^2x-^.
75 . Ч Докажите, что если функция у = f (х) периодическая, то
и функция у = kf (х) + b периодическая.
76 .- Докажите, что число 2 не является периодом функции:
а) у = х2 - 3; б) у = cos х; в) у = Зх - 5; г) у = |х|.
5. Возрастание и убывание функций.
Экстремумы
1. Возрастание и убывание функций. Вы уже зна-
комы с понятием возрастающей и убывающей функций. Так, на
рисунке 39 изображен график функции, определенной на отрезке
[-1; 10]. Эта функция возрастает на отрезках [-1; 3] и [4; 5], убы-
вает на отрезках [3; 4] и [5; 10]. Известно, что функция у = х2 убы-
вает на промежутке (-оо; 0] и возрастает на промежутке [0; оо).
График этой функции при изменении х от -оо до оо сначала «опус-
кается» до нуля (значение функции в точке 0 равно нулю), а затем
«поднимается» до бесконечности (см. рис. 20).
Определение. Функция f возрастает на мно-
жестве Р, если для любых хх и х2 из множест-
ва Р, таких, что х2 > хт, выполнено неравенство
f (*2) > f (xi)-
Определение. Функция f убывает на мно-
жестве Р, если для любых х1 и х2 из множест-
ва Р, таких, что х2 > хг, выполнено неравенство
Иными словами, функция f называется возрастающей на
множестве Р, если большему значению аргумента из этого множе-
ства соответствует большее значение функции. Функция f называ-
ется убывающей на множестве Р, если большему значению аргу-
мента соответствует меньшее значение функции.
40 Тригонометрические функции
| Пример 1. Докажем, что
функция f (х) = х" (п е N) при не-
четном п возрастает на всей чис-
ловой прямой, а при четном п
функция f (х) = хп возрастает на
промежутке [0; оо) и убывает на
промежутке (-оо; 0].
Докажем сначала, что функ-
ция f (х) = хп возрастает на проме-
жутке [0; оо) при любом натураль-
ном п. Пусть х2 > Xj > 0. Тогда по
свойству степени х2 > х". Теперь
рассмотрим случай четного п.
Пусть xt < х2 < 0. Тогда -хг > -х2 > 0 и (-Xj)" > (х2)" > 0, т. е.
xf > х2. Тем самым доказано, что функция f (х) = хл убывает на
(-оо; 0] при четном п. Осталось рассмотреть случай нечетного п.
Если Xj < 0 < х2, то Xj” < 0 < х£. Если хх < х2 < 0, то -хг > -х2 > 0
и потому (-Х!)” > (-х2)" > 0, т. е. -х" > -х£, откуда следует,
что х2 > х[. Итак, доказано, что для нечетного п из неравенст-
ва х2 > хх следует неравенство х2 > х^. Согласно определению
функция f (х) = х" при нечетном п возрастает на всей числовой
прямой.
Пример 2. Докажем, что если функция у = f (х) возраста-
ет на множестве Р, то функция у = -f (х) убывает на множестве Р.
Пусть X; и х2 — любые два числа из множества Р, такие, что
х2 > хР Надо доказать, что -f (х2) < -f (Xj), т. е. f (xj < f (х2). Но
это — очевидное следствие условия: f возрастает на множестве Р.
Пример 3. Функция f (х) =— убывает на каждом из про-
х
межутков (-оо; 0) и (0; оо) (докажите самостоятельно). Однако эта
функция не является убывающей на объединении этих промежут-
ков. Например, 1 > —1, но /(!)>/(-!).
При исследовании функций на возрастание и убывание при-
нято указывать промежутки возрастания и убывания максималь-
ной длины, включая концы (если, конечно, они входят в эти про-
межутки). Так, можно было сказать, что функция f (х) = — убы-
х
вает на отрезке [2; 100]. Это верно, но такой ответ неполон.
Замечание. Для четных и нечетных функций задача на-
хождения промежутков возрастания и убывания несколько упро-
щается: достаточно найти эти промежутки при х > 0 (рис. 40).
Пусть, например, функция f четна и возрастает на проме-
жутке [а; Ь], где t> > а > 0. Докажем, что эта функция убывает на
промежутке [ Ь; -а].
Тригонометрические функции
a)
Рис. 40
Действительно, пусть -а х2 > хг > -Ь. Тогда f (-х2) = f (х2),
f (-xi) = f (Xj), причем а < -х2 < -xr < fe, и поскольку f возрастает
на [а; &], имеем f (~xr) > f (-х2), т. е. f (хг) > f (х2).
2. Возрастание и убывание тригонометрических функций.
Докажем сначала, что синус возрастает на промежутках
[ТС , q , 71 .
—— + z тш; —ь
2 2
, п е Z. В силу периодичности синуса доказа-
тельство достаточно провести для отрезка
. Пусть х2 > хг
Применяя формулу разности синусов, находим:
X, + х2 . х2 - х, ...
sin х9 - sin х, = 2 cos — -sm —---. (1)
2i 2 2
и
Из неравенства < хг < х2 <
Л < Х1 + х2 < 71
2 2 2’
„ Хо X-t тг
следует, что О < —-— < —
__ X, + Хо . Хо — Xi
Поэтому cos—1----— >0, sin—------ > 0. Из (1) вытекает, что
разность sin х2 - sin х1 положительна, т. е. sin х2 > sin xv Тем са-
мым доказано, что синус возрастает на указанных промежутках.
Аналогично доказывается, что промежутки Г^+2лн; ^ + 2лп1,
п е Z, являются промежутками убывания синуса.
Заметим, что полученный результат легко проиллюстриро-
л
2
вать с помощью единичной окружности: если —
<t2 < —, то
2 2
< t
точка Р. имеет, естественно, ординату, большую, чем ордината
точки Pt (рис. 41, а). Если — < t1<t2 , то ордината точки Pt
1 2 2 2
меньше ординаты точки Р. (рис. 41, б).
Г1
Промежутками возрастания косинуса являются отрезки
[-л + 2ли; 2лп], где п е Z, а промежутками убывания — отрезки
Тригонометрические функции
Рис. 41
[2лп; л + 2лп], где п е Z. Доказательство можно провести пример-
но так же, как и в случае синуса. Проще же воспользоваться фор-
мулой приведения cosx = sin ^х + Из нее сразу следует, напри-
мер, что промежутками возрастания косинуса являются проме-
жутки, полученные из промежутков возрастания синуса сдвигом
на — влево.
2
Докажем, что функция тангенс возрастает на промежутках
| - — + лп; — + ли I, где п е Z. В силу периодичности тангенса дока-
<2 2 J
зательство достаточно провести для интервала
Пусть Xj и х2 — произвольные числа из этого интервала,
такие, что х2 > хг. Надо доказать, что tg х2 > tg хг Имеем
sin х2 cos Xj - sin Xj cos х2 sin (х2 - хх)
COS X2 COS Xj cos x1 cos x2
< Xj < x2 < Поэтому cos Xj > 0,
cos x2 > 0. А так как 0 < x2 - Xj < л, то и sin (x2 - xx) > 0. Следо-
вательно, tgx2 -tgXj >0, t. e. tg x2 > tg Xj, что и требовалось до-
казать.
Аналогично доказывается, что ctg убывает на промежутках
(ли; л + ли), где п е Z.
Л . 7Г
2’ 2
sin х2 sin Xj
tgx2 - tgXj =----------
COS x2 COS Xj
По предположению
3. Экстремумы. При исследовании поведения функции вбли-
зи некоторой точки удобно пользоваться понятием окрестности.
Окрестностью точки а называется любой интервал, содержащий
эту точку. Например, интервал (2; 6) — одна из окрестностей точ-
ки 3, интервал (-3,3; -2,7) — окрестность точки -3.
Изучая график рисунка 39, можно прийти к выводу, что
наиболее «заметными» точками области определения являются
43 Тригонометрические функции
такие точки х, в которых возрастание функции сменяется убы-
ванием (точки 3 и 5) или, наоборот, убывание сменяется возраста-
нием (точка 4). Эти точки называют соответственно точками мак-
симума (хтах = 3 и хтах = 5) и минимума (xmin = 4).
При построении графиков конкретных функций полезно
предварительно найти такие точки. Например, для функции sin
это точки вида ±— + 2 ли, п е Z. Возьмем для определенности
Эта точка является правым концом промежутка возраста-
ния синуса, и поэтому 1 = sin х0 > sin х, если
< х < \ Кроме
того, х0 = — левый конец промежутка убывания, и, следователь-
но, sin х < sin х0 при £ < х < Итак, sin^ > sinx для любого х
(х х0), лежащего в окрестности
Зл
2
х0 = — точка максимума функции синус.
В точке наоборот, убывание функции меняется на возра-
стание (слева от функция убывает, а справа возрастает). Анало-
гично для любого х из некоторой окрестности точки (х * х0)
точки х0 = J, и поэтому
71
и поэтому — точка минимума
функции синус. Дадим точные определения точек экстремума.
имеем sin х > sin
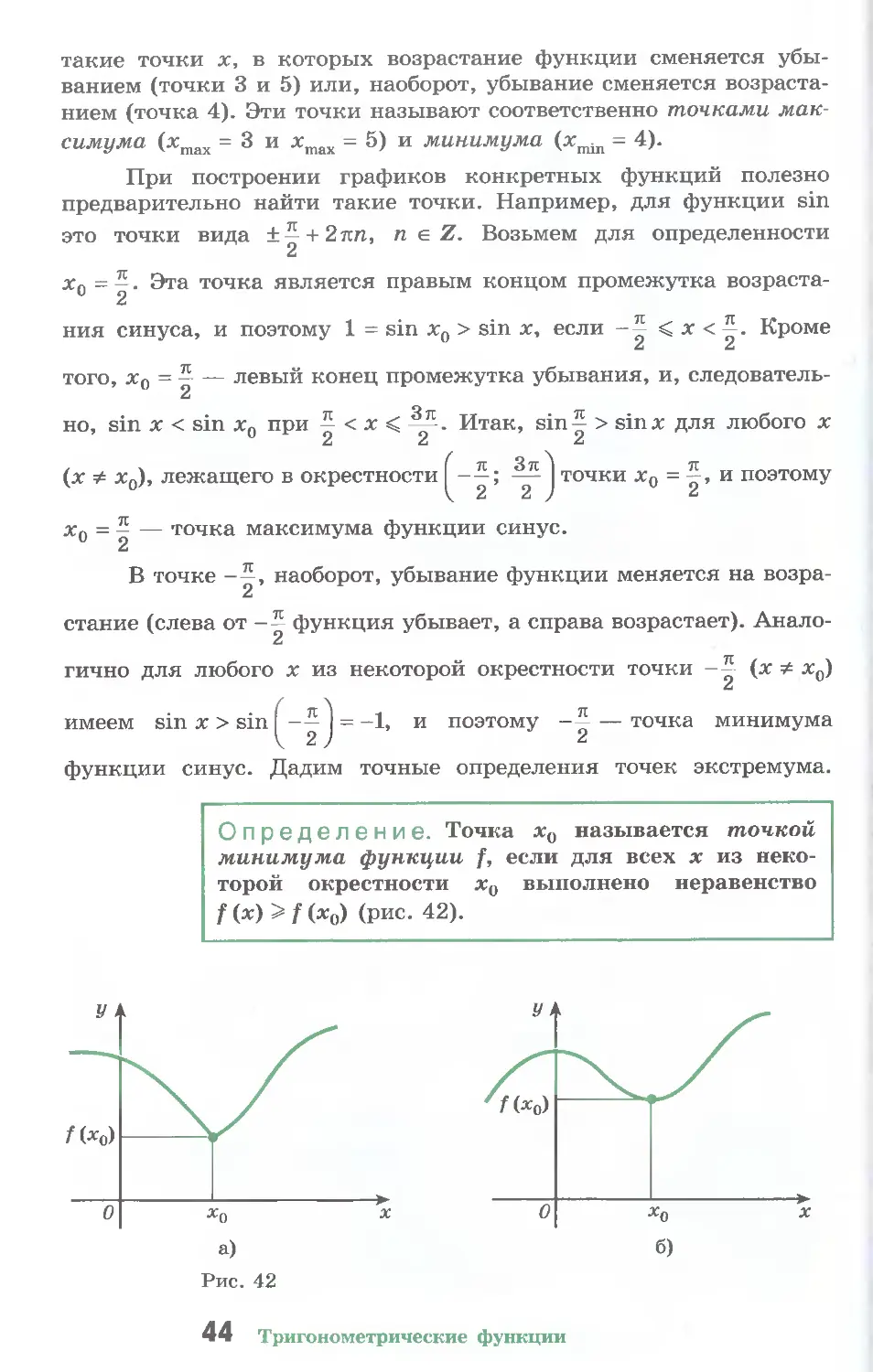
Определение. Точка х0 называется точкой
минимума функции f, если для всех х из неко-
торой окрестности х0 выполнено неравенство
/ (х) > f (х0) (рис. 42).
Тригонометрические функции
Определение. Точка х0 называется точкой
максимума функции f, если для всех х из неко-
торой окрестности х0 выполнено неравенство
f (х) < f (х0) (Рис- 43)-
По определению значение функции f в точке максимума х0
является наибольшим среди значений функции из некоторой
окрестности этой точки, поэтому график функции в окрестно-
сти х0, как правило, имеет вид гладкого «холма» (рис. 43, а
и рис. 44 — точки хл, х2, х3) или заостренного «пика» (рис. 43, б).
В окрестности точки минимума графики, как правило, изобра-
жаются в виде «впадины», тоже
или гладкой (рис. 42, б — точ-
ка х0, рис. 44 — точки х4, х5), или
заостренной (рис. 42, а — точка х0
и рис. 44 — точка х6).
Другие примеры поведения
графиков функций в точках макси-
мума или минимума приведены на
рисунках 45 (а — точка максиму-
ма), 46 (а — точка минимума) и 47
(здесь каждая точка промежутка
(-1; 0) является как точкой мини-
мума, так и точкой максимума).
45 Тригонометрические функции
Для точек максимума и минимума функции принято общее
название — их называют точками экстремума. Значение функ-
ции в этих точках называют соответственно максимумами и мини-
мумами функции (общее название — экстремум функции). Точки
максимума обозначают хтах, а точки минимума xmin. Значения
функции в этих точках обозначаются соответственно t/max и </min-
Упражнения
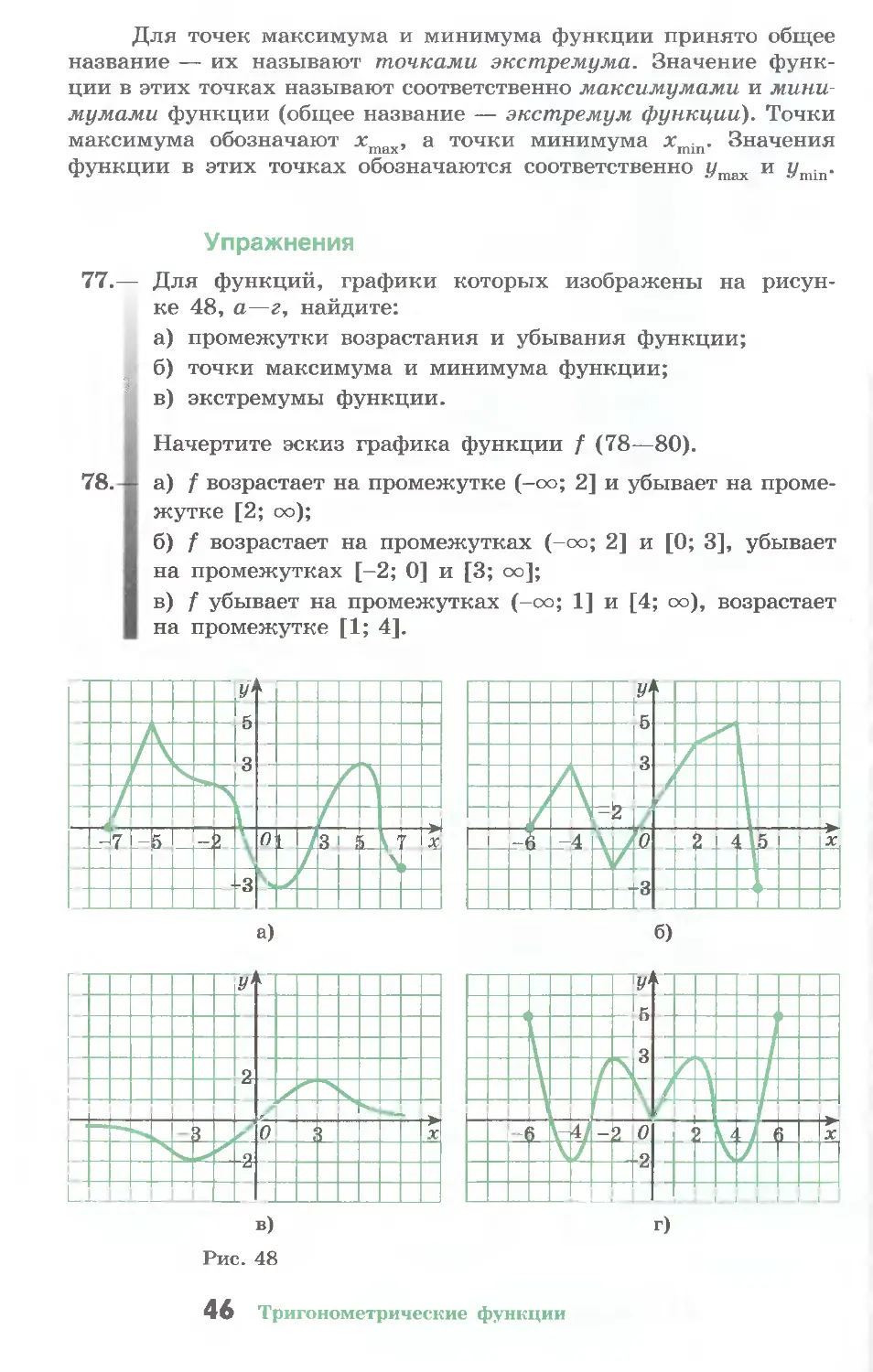
77.— Для функций, графики которых изображены на рисун-
ке 48, а—г, найдите:
а) промежутки возрастания и убывания функции;
б) точки максимума и минимума функции;
в) экстремумы функции.
Начертите эскиз графика функции f (78—80).
78.
a) f возрастает на промежутке (-оо; 2] и убывает на проме-
жутке [2; оо);
б) f возрастает на промежутках (-оо; 2] и [0; 3], убывает
на промежутках [-2; 0] и [3; оо];
в) f убывает на промежутках (-оо; 1] и [4; оо), возрастает
на промежутке [1; 4].
Рис. 48
б)
46 Тригонометрические функции
79 .- a) xmax = -3, xmin = 4, f (-3) = 5, f (4) = -5;
6) *min = -2’ *min = 2, *max = 0,
f (-2) = f (2) = -3, f (0) = 2;
B) xmin = -5, xmax = 2,
/(-5)=1, / (2) = 6;
r) *,„ax = -4, *max = 3, xmin = -1,
f (-4) = 5, f (3) = 2, f (-1) = -2.
80 .— a) f — четная функция, xmax = -3, xmin = 0,
| f (-3) '= 4, f (0) = 0;
s 6) f — нечетная функция, xmax = 2, xmin = 5,
f (2) = 3, f (5) = -4;
в) f — четная функция, xmin = 4, xmax = 0,
f (4) = -2, f (0) = 2;
r) f — нечетная функция, xmin = -4, xmax = -1,
f (-4) = -3, f (-1) = 1.
81.— Докажите, что функция у = kx + b:
а) возрастает на множестве R при k > 0;
I б) убывает на множестве R при k < 0.
I Найдите промежутки возрастания и убывания, точки мак-
симума и точки минимума функции, ее максимумы и ми- ! нимумы (82—85).
82.1 а) у = —х2 + 6х - 8; б) у = (х + 2)4 + 1;
в) у = х2 - 4х; г) у = (х - З)4.
83. а) у = -^—; б) у = (х + З)5; х-2
в) У = г) у = (х - 4)3. ОС "Ь о
84. а) у = 3 sin х - 1; б) у = -2 cos х + 1;
в) у = 2 cos х + 1; г) у = 0,5 sin х - 1,5.
85. а) у = 1 + 2 tg х; б) у = sin х + 1;
86. в) у = -tg х; г) у = cos х - 1. Сравните числа:
a) cos — и cos —; б) sin — и sin ’ 7 9 7 8
в) tg и tg г) sin и sin^. ( о У о
87. Расположите числа в порядке возрастания: a) sin 3,2, sin 3,8, sin 1,3; б) cos 0,9, cos 1,9, cos 1,3; в) tg 0,5, tg 1,4, tg (-0,3);
r) sin 1,2, sin (-1,2), sin 0,8.
47 Тригонометрические функции
Найдите промежутки возрастания и убывания, точки экст-
ремума и экстремумы функции (88—89).
88.— а)
в)
89.— а)
в)
(х-2)2
у = —Цг-2;
(х+ I)3
у — cos
t/= sin
б) у = 4 | х | - х2;
г) у = х2 - 2 | х |.
б) у = 1 - sin х -
г) у = 2 + cos Г х -
90—
Расположите числа в порядке возрастания:
a) cos 2^, sin 4—, cos—, cosf-—\
’ 9 5 9 I 9 J
б) v’ctg 1F’ ЧчО
в)
ctg^,ctgl|\ tg^, ctg
iu о о io
cos1 — , sin 5л, sin1^.
I 12 J 24 24 6
91—
92—
Докажите, что функция:
a) f (x) = x4 + Зх возрастает на [0; оо);
6) f (х) = -х3 - 2х убывает на R;
в) f (х) = х6 - 0,5 убывает на (-оо; 0];
г) f (х) = х5 + 1,5х возрастает на R.
Докажите следующие утверждения:
а) если f — четная функция, х0 — точка максимума,
то -х0 является точкой максимума;
б) если f — нечетная функция и на промежутке [а; Ь] она
убывает, то и на промежутке [-fe; -а] функция f убывает;
в) если f — нечетная функция, х0 — точка минимума,
то -х0 является точкой максимума;
г) если f — четная функция и на промежутке [а; Ь] функ-
ция возрастает, то на промежутке [-Ь; -а] она убывает.
6. Исследование функций
1. Построение графиков функций. Ранее вы строили
графики функций «по точкам». Во многих случаях этот метод дает
хорошие результаты, если, конечно, отметить достаточно большое
число точек. Однако при этом приходится составлять большие таб-
лицы значений функции, а главное, можно не заметить существен-
ных особенностей функции и в итоге ошибиться при построении
графика.
Тригонометрические функции
Предположим, например, что, вычислив значение функции
в 15 точках и отметив соответствующие точки графика на коорди-
натной плоскости, мы пришли к рисунку 49. Естественно предпо-
ложить, что эскиз графика близок к непрерывной кривой, прохо-
дящей через все эти точки (рис. 50). Однако «настоящий» график
(естественно, проходящий через все эти точки) может быть совер-
шенно не похож на этот эскиз (рис. 51—53).
Для того чтобы избежать ошибок, надо научиться выявлять
характерные особенности функции, т. е. предварительно провести
ее исследование. Пусть, например, о функции f нам известно,
что она:
— определена на объединении промежутков (-оо; -10),
(-10; 10), (10; оо);
— обращается в нуль в точках -11 и 0, отрицательна на ин-
тервалах (-оо; -11), (-10; 0) и положительна на интервалах
(-11; -10); (0; 10) и (10; оо);
— возрастает на промежутках (-оо; -10), (-10; 10), [12; 15]
и убывает на промежутках (10; 12] и [15; оо);
— имеет минимум в точке 12, причем f (12) = 16, и макси-
мум в точке 15, причем f (15) = 19;
— наконец, значения f при приближении значений аргумен-
та к -10 и 10 неограниченно возрастают по абсолютной величине.
Эти сведения позволяют понять, что эскиз графика функции
примерно таков, каким он изображен на рисунке 53.
Тригонометрические функции
Рассмотрим еще один пример: исследуем функцию
f (*) =
1
X2 + 1
1) Найдем область определения функции. В данном случае
D (f) — вся числовая прямая, поскольку знаменатель х2 + 1 не об-
ращается в нуль.
2) Заметим, что функция f четная: для любого х
Н-х)
1
(-х)2 + 1
1
X2 + 1
= /(х).
Поэтому достаточно исследовать функцию и построить ее график
при х > О, затем остается отразить построенную часть графика от-
носительно оси ординат.
3) Найдем точки пересечения графика / с осями координат.
Ось ординат график f пересекает в точке (0; f (0)). Значение f (0)
равно 1. Поэтому график f проходит через точку (0; 1).
Для того чтобы найти точки пересечения графика функции f
с осью абсцисс, надо решить уравнение f (х) = 0 (его корни называ-
ют нулями функции). Уравнение —— = 0 не имеет корней. Зна-
х2 +1
чит, график f не пересекает ось абсцисс.
4) Выясним, на каких промежутках функция f принима-
ет положительные, а на каких — отрицательные значения; их
называют промежутками знакопостоянства функции. Над эти-
ми промежутками график функции лежит выше (соответствен-
но ниже) оси абсцисс. В данном случае, поскольку при любом х
значение х2 + 1 положительно, f (х) > 0 на всей числовой пря-
мой.
5) Существенно облегчают построение графика сведения
о том, на каких промежутках функция возрастает или убывает
(эти промежутки называют промежутками возрастания или убы-
вания функции). Докажем, что для рассматриваемой функции
промежуток возрастания — это (-оо; 0], а промежуток убыва-
ния — [0; оо).
Пусть Xj и х2 — два значения из промежутка [0; оо), причем
х2 > Xj. Поскольку X, и х2 положительны, из условия х2 > хг сле-
дует х2 > х2, xf + 1 > х2 + 1 и, наконец,
1
х2 +1
——. Итак,
х2 +1
f (х2) < f (xj, т. е. функция f убывает на промежутке [0; оо).
На промежутке (-оо; 0] функция f возрастает. Доказательст-
во проводится аналогично (можно также воспользоваться четно-
стью данной функции).
6) Найдем значения функции в точках, в которых возраста-
ние сменяется убыванием или наоборот. В нашем случае имеется
Тригонометрические функции
лишь одна точка, принадлежащая одновременно и промежутку
возрастания, и промежутку убывания,— это точка 0. Точка 0 —
точка максимума функции f (х) = —-—; f (0) = 1.
х2 +1
7) Заметим, наконец, что при неограниченном увеличении х
значение х2 + 1 неограниченно возрастает, а потому значения
f (х) =- — (оставаясь положительными) приближаются к нулю.
х2 +1
Полученных в ходе исследования свойств функции
f (х) = —i— достаточно для построения ее графика.
х2 +1
Построим точку графика (0; 1). Мы установили, что
[0; оо) — промежуток убывания функции f. Поэтому правее точки
с абсциссой 0 график рисуем в виде кривой, которая «идет вниз»
(рис. 54). Так как f (х) > 0 при любом х, эта кривая не может опу-
ститься ниже оси абсцисс, причем (см. п. 7 исследования) при про-
должении вправо график неограниченно приближается к оси абс-
цисс. Остается воспользоваться четностью функции f: график f
получаем, отразив построенную для х > 0 кривую симметрично от-
носительно оси ординат (рис. 55).
2. Схема исследования функций. При исследовании функ-
ций мы будем придерживаться описанной схемы. В общем случае
исследование предусматривает решение следующих задач:
1) Найти области определения и значений данной
функции f.
2) Выяснить, обладает ли функция особенностями,
облегчающими исследование, т. е. является ли функ-
ция f: а) четной или нечетной; б) периодической.
3) Вычислить координаты точек пересечения графи-
ка с осями координат.
4) Найти промежутки знакопостоянства функции f.
5) Выяснить, на каких промежутках функция f воз-
растает, а на каких убывает.
51 Тригонометрические функции
6) Найти точки экстремума, вид экстремума (мак-
симум или минимум) и вычислить значения f в этих
точках.
7) Исследовать поведение функции f в окрестности
характерных точек, не входящих в область определе-
ния (например, точка х = 0 для функции f (х) = — ),
и при больших (по модулю) значениях аргумента.
Необходимо заметить, что этот план имеет примерный ха-
рактер. Так, для нахождения точек пересечения с осью абсцисс
надо решить уравнение f (х) = 0, чего мы не умеем делать даже
в случае, когда f (х), например, многочлен пятой степени. (Суще-
ствуют, правда, методы, которые позволяют найти число корней
такого уравнения и сами корни с любой точностью.) Поэтому часто
тот или иной этап исследования приходится опускать. Однако по
возможности в ходе исследования функций желательно придержи-
ваться этой схемы.
Наиболее трудным этапом исследования является, как пра-
вило, поиск промежутков возрастания (убывания), точек экстре-
мума. В следующей главе вы познакомитесь с общими методами
решения этих задач, основанными на применении методов матема-
тического анализа.
Вертикальные прямые, к которым неограниченно приближа-
ется график функции f (например, прямая х = 0 для функции
/(х) = — или прямые х - ± 10 для графика функции, изображен-
х
ного на рисунке 53), называют вертикальными асимптотами.
Чаще всего график имеет вертикальную асимптоту х = а
в случае, если выражение, задающее данную функцию, имеет вид
дроби, знаменатель которой обращается в нуль в точке а, а числи-
тель нет. Например, график функции f (х) = - имеет вертикаль-
х
ную асимптоту х = 0. Для графика функции f (х) = tg х вертикаль-
ными асимптотами являются прямые х = ^ + пп, где п € Z.
Если график функции неограниченно приближается к не-
которой горизонтальной (в случае функции f (х) = —-— это пря-
хг +1
мая у = 0, см. рис. 55) или наклонной (прямая у = х для графика
функции f(x)=x + —, см. рис. 32) прямой при неограниченном
X
возрастании (по модулю) х, то такую прямую называют горизон-
тальной (соответственно наклонной) асимптотой.
3. «Чтение» графиков. В большинстве разобранных выше
примеров и задач на построение графиков функций вы встре-
чались с такой ситуацией: функция задана формулой, требуется
52 Тригонометрические функции
исследовать ее свойства и построить график f. Представляет зна-
чительный практический интерес другая задача: задан график f,
с помощью которого требуется перечислить основные свойства
этой функции.
Подобные задачи часто решаются в ходе экспериментальных
исследований. Построение графиков при этом осуществляется раз-
ными методами. Например, по точкам, найденным эксперимен-
тально. Существуют также многочисленные приборы-самописцы.
Это, например, осциллографы, на экранах которых электрические
колебания преобразуются в наглядные графические изображения.
Другим примером прибора, позволяющего получить наглядное
графическое описание, служит кардиограф; «прочитывая» полу-
ченную с его помощью кардиограмму, врачи делают выводы о со-
стоянии сердечной деятельности.
С довольно типичным примером трудностей, возникающих
при исследовании реальных процессов, для описания которых нет
точных теорий, вы можете познакомиться, рассмотрев рисунок 56.
Здесь приведены графики среднесуточного хода температур по Мо-
сковской области в феврале 1974 г. Толстой линией изображены
«теоретические кривые» А и Б, фиксирующие результаты долго-
срочного прогноза (поскольку прогноз дается с точностью до 5°,
кривых две). «Читая» этот график, мы находим, например, что
предполагались три «волны холода» (в период с 4 по 10, с 17 по 19
и с 23 по 26 февраля). Предполагалось также отсутствие оттепелей
и в целом холодная (до -17°... -22°) погода. Однако в действитель-
ности (график фактического хода температур изображен тонкой
линией В) температура была выше нормы на 5—10° (климатиче-
ская норма, являющаяся результатом многолетних наблюдений,
задана линией Г), в период с 4 по 8 февраля было потепление, а не
похолодание и т. д. Эти и другие сведения о прогнозе и реальной
картине вы можете получить, «читая» графики, приведенные на
рисунке 56.
Рис. 56
Тригонометрические функции
Упражнения
93.— Проведите по общей схеме исследование функции, задан-
ной графиком (рис. 57).
94.— Постройте график функции /, если известны ее свойства
(см. табл, на с. 55).
Проведите по общей схеме исследование каждой из функ-
; ций и постройте ее график (95—99).
а 95.4 а) f (х) = 5 - 2х; б) f (х) = 3 - 2х - х2;
в) f (х) = Зх - 2; г) f (х) = х2 - Зх + 2.
96. а) 1 ^1 Н II 'к' б) f (х) = - (х - З)4;
в) х+ 2 г) f (х) = х3 - 1.
97. а) f (х) =-7х-3; б) f (х) = 4х - х2;
в) f (х) = Vx+ 1; г) / (х) = 4 - х2.
в) г)
Рис. 57
54 Тригонометрические функции
Свойство функции а) 6) в) r)
1 Область опреде- ления Область значе- ний [-6; 6] [-2; 5] [-5; 4] [0; 6] [-4; 4] [-3; 6] [-5; 3] [0; 5]
2 Точки пересече- ния графика: а) с осью Ох б) с осью Оу А (-4; 0), В (-2; 0) С (0; 2,5) o (0; 0) A (-4; 0), В (-1; 0), C (2,5; 0) D (0; -2) A (3; 0) В (0; 4,5)
3 Промежутки знакопостоян- ства: a) f (х) > 0 б) f (х) < 0 [-6; -4), (-2; 6] (-4; -2) [-5; 0), (0; 4] (-4; -1), (2,5; 4] (-1; 2,5) [-5; 3)
4 Промежутки: а) возрастания б) убывания [-3; 1], [4; 6] [-6; -3], [1; 4] [-5; -2], [0; 4] [-2; 0] [-4; -2], [1; 4] [-2; 1] [-3; 1] [-5; -3], [i; 3]
5 Точки максимума, максимум функции Точки минимума, минимум функции 1, f (1) = 3 -3, f (-3) = -2 4, f (4) = 1 -2, f (-2) = = 2 0, f (0) = 0 -2, f (-2) = = 2 1, / (1) =-3 1, /(1) = 5 -3, /(-3) = 2
6 Дополнительные точки графика f (-6) = 3 f (6) = 5 f (-5) = 0,5 f (4) = 6 f (4) = 6 f (-5) = 3
98.— a) f (x) = x4 + 4x2; 6) f (x) = l-Vx + 4;
в) f (x) = x3 + x; r) f (x) = л/х -2 -2.
99.— a) f (x) = x2 - 2 | x | + 1; 6) . x+1
x-1
в) f (x) = | x | - x2; r) xz x 2x+l f (x) = . X
Тригонометрические функции
7. Свойства тригонометрических функций.
Гармонические колебания
1. Исследование тригонометрических функций. Свой-
ства изучаемых функций удобно записывать согласно приведенной
в предыдущем пункте схеме. Сведем уже известные вам свойства
функций синус, косинус, тангенс и котангенс в таблицу. (Всюду
предполагается, что п е Z.)
Функция
f (х) = sin х f (х) = COS X f (х) = tg X f (х) = ctg X
1.1 R R 1 71 Я 1 --+ пп;- + лп (лп; л + лп)
1.2 [-1; 1] [-1; 1] R R
2.1 Нечетная Четная Нечетная Нечетная
2.2 2л 2л Л л
3.1 (лп; 0) (^ + пп; о) (лп; 0) (j+,m;0) 1
3.2 (0; 0) (0; 1) (0; 0) Нет
4.1 (2лп; л + 2лп) (-^ + 2лп; + 2nnj (лп; + лп) (лп; + лп)
4.2 (-л + 2лп; 2лп) (| + 2лп; + 2лп) (“ 2" + л/г) (-^ + лп; лп)
5.1 (-+ 2 лп; + 2 лп) [-л + 2лп; 2лп] (-j + лп;| + лп) Нет
5.2 (| + 2лп;^- + 2лп) [2лп; л + 2лп] Нет (лп; л + лп)
6.1 - + 2лп л + 2пп Нет Нет
6.2 -1 -1 Нет Нет
6.3 + 2лп 2лп Нет Нет
6.4 1 1 Нет Нет
В таблице принята следующая нумерация свойств функции f:
1.1 — область определения;
1.2 — область значений;
2.1 — четность (нечетность);
2.2 — наименьший положительный период;
3.1 — координаты точек пересечения графика f с осью Ох;
3.2 — координаты точек пересечения графика f с осью Оу;
Тригонометрические функции
4.1 — промежутки, на которых f принимает положительные зна-
чения;
4.2 — промежутки, на которых f принимает отрицательные зна-
чения;
5.1 — промежутки возрастания;
5.2 — промежутки убывания;
6.1 — точки минимума;
6.2 — минимумы функции;
6.3 — точки максимума;
6.4 — максимумы функции.
Свойства тригонометрических функций часто применяются
при решении задач.
Пример 1. Расположим в порядке возрастания числа
sin (-1), sin 1, sin 2, sin 3, sin 4.
Пользуясь формулами приведения, запишем эти числа в та-
ком виде, чтобы значения аргумента принадлежали одному из
промежутков возрастания синуса — отрезку
2Е-
2’ 2J'
sin 2 = sin (л - 2), sin 3 = sin (л - 3), sin 4 = sin (л - 4).
Очевидно, что <-1<л-4<л-3< 1 < л - 2 < —, по-
2 2
этому sin (-1) < sin (л - 4) < sin (л - 3) < sin 1 < sin (л - 2). Итак,
sin (-1) < sin 4 < sin 3 < sin 1 < sin 2.
Рассмотрим график функции f (x) =2 sin I Зх - — | (рис. 58).
Он получается при помощи следующей последовательности преоб-
разований:
а) сжатием графика функции у = sin х в 3 раза вдоль оси абс-
цисс получаем график функции у = sin Зх (рис. 59);
57 Тригонометрические функции
получаем график функции у = sin 3
б) переносом графика функции у = sin Зх на вектор | О
л
4
(рис. 60);
I, т. е. u = sin|3x--^
1 ’ у I 4
Рис. 60
( Зл ।
в) растяжением графика у = sin Зх-в 2 раза вдоль оси
к 4 J
( Зл
ординат получаем график функции у = 2 sin Зх----(рис. 61).
к 4 J
58 Тригонометрические функции
При преобразованиях, изученных в п. 3, «форма» кривой
сохраняется (так же как при движениях и преобразованиях по-
добия). Поэтому синусоидой называют не только график синуса,
но и любую кривую, полученную из него при помощи сжатий (рас-
тяжений) вдоль осей и последующих движений или преобразова-
ний подобия. Это же замечание справедливо для других кривых,
например параболы или гиперболы.
То обстоятельство, что свойства функций вида f (х) =
= A sin (kx + b) и f (х) = A cos (kx + b) аналогичны свойствам си-
нуса (или косинуса), позволяет сравнительно быстро провести
исследование таких функций: главное — найти их период и точ-
ки, в которых значения равны 0 и + А.
Пример 2. Исследуем функцию f (х) = 2 sin I Зх - —
\ 4
и
построим ее график.
Период функции f равен — (см. п. 4). Синус обращается
3
в нуль в точках вида пп, п е Z, поэтому f (х) = 0 при Зх- — = пп,
4
т. е. при х = ^ + —, п е Z. Затем, решая уравнения f (х) = -2
и f (х) = 2, получим sin (Зх - — । = -1 при Зх - —
V 4 J 4
п е Z; sin|3x-—| = 1 при Зх- — = — + 2тгп,
I 4 J 4 2
— = +2пп, от-
4 2
куда х = —+ , i
12 3
откуда х = — + 2 —,
12 3
абсцисс. Достаточно
периоду. В данном случае удобно
п е Z. Отметим полученные точки на оси
рассмотреть отрезок, длина которого равна
взять
конец которого является точкой
нимума функции (рис. 62). Далее
суем график функции f, возрастаю-
щей от -2 до 2 на отрезке
и убывающей от 2 до -2 на отрезке
[5п Зя 1
—; — . График пересечет
и | ; О I. Эскиз
112 )
графика функции / на всей числовой
прямой получается из графика рисун-
ка 62 сдвигами на 2 , п е Z, вдоль
3
оси абсцисс (рис. 58).
ми-
ри-
ось абс-
цисс в точках ( —; О
\ 4
4
59 Тригонометрические функции
2. Гармонические колебания. Величины, меняющиеся со-
гласно закону
f (t) = A cos (cat + ф) (1)
или
f (t) = A sin (cot + ф),
(2)
играют важную роль в физике. По такому закону меняется коор-
дината шарика, подвешенного на пружине (рис. 149). Говорят, что
шарик совершает гармонические колебания.
Функцию (2) тоже можно записать в виде (1):
A sin (at + ф) = A cos
at + ф - —
2
Параметры А, со и ф, полностью определяющие колебание (1),
имеют специальные названия: А называют амплитудой коле-
бания, со — циклической (или круговой) частотой колебания,
ф — начальной фазой колебания (обычно берут ф е [0; 2л)). Период
функций A sin (cot + ф) и A cos (cot + ф), равный —, называют пери-
со
одом гармонического колебания.
Свойства функций (1) и (2) удобно проиллюстрировать на
следующем примере из механики. Пусть точка М движется равно-
мерно по окружности радиуса R = А с угловой скоростью со (при
со > 0 вращение против часовой стрелки, а при со < 0 — по часовой
стрелке), причем в начальный момент времени t = 0 вектор ОМ со-
ставляет угол ф с положительным направлением оси абсцисс
(рис. 63). Рассмотрим две следующие функции от t — координаты
проекций точки на оси абсцисс и ординат — функции х (t) и у (t).
В момент времени t вектор ОМ составляет с положительным
направлением оси Ох угол ф (t), при этом ф (t) = ф + cot согласно за-
кону равномерного движения по окружности. По определению
функций синус и косинус
х (t) = A cos ф (t), т. е. х (t) =А cos (cot + ф),
у (t) = A sin ф (t), т. е. у (t) = A sin (cot + ф).
Изучим свойства этих функций,
опираясь на кинематические сообра-
жения. Их период равен, очевидно, вре-
мени Т, за которое точка совершает
один оборот. Длина окружности равна
2лА, а линейная скорость v равна oiA,
поэтому
_2 лА _2 л
v и
Рассмотрим один из моментов
времени t0, в который точка М занима-
60 Тригонометрические функции
ет крайнее правое положение. Тогда х (t0) = А, у (t0) = 0. Начиная
с этого момента времени функция х (t) будет попеременно убы-
вать от А до -А на первой половине периода и возрастать от -А
до А на второй половине периода. При этом точки максимума
функции х (t) — это те моменты времени, когда точка занимает
крайнее правое положение; точки минимума соответствуют край-
нему левому положению, а нули — верхнему и нижнему положе-
ниям.
Аналогичными свойствами обладает и функция у (t); ее точ-
ки максимума и минимума соответствуют верхнему и нижнему
положениям точки на окружности, а нули — правому и левому
положениям.
Отметим, что при А = 1, со = 1 и<р = О функции х (t) и у (t)
равны соответственно cos t и sin t. Проверьте самостоятельно,
что известные вам свойства этих функций легко получить, рас-
сматривая соответствующее движение точки по единичной окруж-
ности.
Упражнения
100.— Пользуясь свойствами тригонометрических функций, за-
мените выражение равным ему значением той же тригоно-
метрической функции наименьшего положительного аргу-
мента:
a) tgi^, sin^;
5 3
в) sin Г-1^1 tg
\ D 7 о
6) COsf-i^l, Ctgf- —
V 8 ) V 5
r) cos —, ctg
7 s 9
101
102.
103.
Найдите область определения и область значений функции:
а) / (х) = 3 cos 2х - 1; б) f (х) = 2 - ctg Зх;
в) / (х) = 2 tg г) f (х) = 1 + 0,5 sin
И z
Найдите промежутки знакопостоянства и нули функции:
а) / (%) = -sin 3 х; б) f (х) = tg —;
3
в) f (х) = cos г) f (х) = ctg 2х.
Найдите промежутки возрастания, убывания, точки макси-
мума и минимума функции:
a) f (х) = 4 cos Зх; б) f (х) = 0,5 ctg —;
4
в) f (х) = 2 tg г) f (х) = 0,2 sin 4х.
61 Тригонометрические функции
104.
105.—
106, t
Исследуйте функцию и постройте ее график (104—105).
a) f (х) = - cos б) f (х) = -2 sin 2х;
2 3
в) f (х) = -1,5 cos Зх; г) f (х) = 3 sin
a) f (х) = tg2x; б) f (х) = -3 cos 3
в) f (X) = -2 ctg f; г) f (х) = 2,5 sin
О о
Координата движущегося тела (измеренная в сантиметрах)
изменяется по указанному закону. Найдите амплитуду, пе-
риод, частоту колебания. Вычислите координату тела в мо-
мент времени tr, если:
а) х (t) = 3,5 cos 4nt, c;
6)
x (t) = 5 cos
fsitf+ -1
I 6 J
tj = 4,5 c;
в) x (t) = 1,5 cos 6rct, t, = 1^ c;
О
г)
x (t) = 0,5 cos
Ttt , 7t I
2 +3/
tj = 8 c.
107.
108.
109.
110.
Найдите амплитуду, период, частоту силы тока, если она
изменяется по закону (сила тока измерена в амперах, вре-
мя — в секундах):
a) I (t) = 0,25 sin 50ftt; б) I (t) = 5 sin 20nt;
в) I (t) = 0,5 sin 10nt; г) I (t) = 3 sin 30n<.
Найдите амплитуду, период и частоту напряжения, если
оно изменяется по закону (напряжение измерено в вольтах,
время — в секундах):
a) U (t) = 220 cos 60nt; б) U (t) =110 cos 30nt;
в) U (t) = 360 cos 20nt; r) U (t) = 180 cos 45nt.
Расположите в порядке возрастания числа:
a) cos 4, cos 7, cos 9, cos (-12,5);
6) tg (-8), tg 1,3, tg 4, tg 16;
в) sin 6,7, sin 10,5, sin (-7), sin 20,5;
r) ctg 3,5, ctg (-9), ctg 5, ctg 15.
Найдите область определения функции:
а) у = —4—; б) у = /sin2 £ -cos2 £;
1 - sin х V 2 2
в) у = —- - ; г) у = д/tgx + ctgx.
cos х -1
62 Тригонометрические функции
111.— Найдите область значений функции:
I— ч
а) у = sin х - V3cosx; б) у = S—;
1+ tg2 х
в) I/= ^/1-cos 4х; г) j/=---.
1+ ctgz X
Исследуйте функцию и постройте ее график (112—113).
112.— a) f (х) = 2 cos х + — ;
\ 4)
в) f (х) = tgfx-y\
113 .— a) f (х) = sin ^2х\
у 3 J
в) f (х) = 4 cos f- + — \
I 3 3J
б)
f (х) = i sin
2
f (х) = 1,5 cos
б) f (х) = ctg[j + ^j:
г) /(x) = tgf—-Зх
\ 4
114 .— По графику, изображенному на рисунке 64, определите
(амплитуду силы тока (или напряжения), период колеба-
ния. Запишите закон зависимости силы тока (или напря-
жения) от времени.
63 Тригонометрические функции
115 .— В какой ближайший момент времени t (t > 0), считая
от начала движения, смещение точки, совершающей гар-
монические колебания по закону x(t) =5 cos — + -
^4 3
а) максимально; б) равно 2,5;
в) равно 0; г) равно -5?
§3.
Решение тригонометрических
уравнений и неравенств
8. Арксинус, арккосинус и арктангенс
1. Теорема о корне. Сформулируем важное утверж-
дение, которым удобно пользоваться при решении урав-
нений.
Теорема (о корне). Пусть функция / возрастает
(или убывает) на промежутке I, число а — любое
из значений, принимаемых f на этом промежутке.
Тогда уравнение f (х) = а имеет единственный ко-
рень в промежутке 1.
Доказательство. Рассмотрим возрастающую функцию f
(в случае убывающей функции рассуждения аналогичны). По
условию в промежутке I существует такое число Ь, что f (Ъ) - а.
Покажем, что Ъ — единственный корень уравнения / (х) = а.
Допустим, что на промежутке I есть еще число с Ф Ъ, такое,
что f (с) = а. Тогда или с < Ь, или с > Ъ. Но функция f возрастает
на промежутке I, поэтому соответственно либо f (с) < f (fe), либо
f (с) > f (Ъ). Это противоречит равенству f (с) = f (b) = а. Следова-
тельно, сделанное предположение неверно и в промежутке I, кро-
ме числа Ь, других корней уравнения f (х) = а нет.
Пример 1. Решим уравнение х3 + х = 2.
Функция f (х) = х3 + х возрастает на R (это сумма двух возра-
стающих функций). Поэтому уравнение f (х) = 2 имеет не более
одного корня. Легко видеть, что корнем является х = 1.
2. Арксинус. Как вы знаете, функция синус возрастает на
отрезке
и принимает все значения от — 1 до 1. Следова-
тельно, по теореме о корне для любого числа а, такого, что |а| < 1,
в промежутке
существует единственный корень b уравне-
64 Тригонометрические функции
ния sin х = а. Это число Ъ называют арксинусом числа а и обозна-
чают arcsin а (рис. 65).
числа а называ-
—; I, синус кото-
2 2 I
Определение. Арксинусом
ется такое число из отрезка —
рого равен а.
х/2
Пример 2. Найдем arcsin^-.
Пример 3. Найдем arcsin
Число
промежутка
синус которого есть - —,
равно Поэтому arcsin
3. Арккосинус. Функция косинус убывает на отрезке [0; л]
и принимает все значения от -1 до 1. Поэтому для любого числа а,
такого, что |а| < 1, на отрезке [0; л] существует единственный
корень Ъ уравнения cos х = а. Это число b называют арккосинусом
числа а и обозначают arccos а (рис. 66).
Определение. Арккосинусом числа а назы-
вается такое число из отрезка [О; л], косинус ко-
торого равен а.
Пример
Пример
е [0; л].
"V 3 д/ 3
4. arccos -— = —, так как cos — = -— и — е ГО; л].
2 6 6 2 6 1 J
к ( 42} Зл Зл 42
5. arccos-=—, так как cos — = -— и
I 2 ) 4 4 2
65 Тригонометрические функции
4. Арктангенс. На интервале функция тангенс воз-
растает и принимает все значения из R. Поэтому для любого числа
а на интервале I ; — I существует единственный корень b уравне-
(2 2 J
ния tg х = а. Это число b называют арктангенсом числа а и обозна-
чают arctg а (рис. 67).
Определение. Арктангенсом числа а назы-
вается такое число из интервала тангенс
которого равен а.
4
Пример 6. arctg 1 = -, так как tg у = 1 и ~ е
4 4 4
Пример 7. arctg(—УЗ) = так как tg -
О \
Д. Л 1
2 ’ 2 J'
I = —Уз и
3
7Г. Д
2’ 2
5. Арккотангенс. Функция котангенс на интервале (0; л)
убывает и принимает все значения из R. Поэтому для любого чис-
ла а в интервале (0; л) существует единственный корень Ь уравне-
ния ctg х = а. Это число b называют арккотангенсом числа а и обо-
значают arcctg а (рис. 68).
Определение. Арккотангенсом числа а назы-
вается такое число из интервала (0; л), котангенс
которого равен а.
Тригонометрические функции
Пример 8. arcctg:L=^, так как ctg " =-L и ^е(О;л).
уз з 3 у/З о
Пример 9. arcctg (УЗ) = так как ctg = —/3 и
о о
^е(О;л).
Упражнения
Сколько корней, принадлежащих данному промежутку,
имеет каждое из уравнений (116—117)?
116 .— а) х7 = 3, х е (-оо; оо); б) -А- = -5, хе (-оо; 1);
х-1
в) х6 = 4, хе (-оо; 0]; г) —=2, х е (-2; оо).
117 .— а) (х - З)3 = -4, х е (-оо; оо);
б) 2 sin х = 1,5, х е
в) (х + 2)4 = 5, хе [-2; оо); г) 0,5 cos a = -|, х е [0; л].
118.
119.
120.
Отметьте на единичной окружности точки Р(, для которых
соответствующее значение t удовлетворяет данному равен-
ству. Найдите значение t, принадлежащее указанному про-
межутку (118—120).
а) sin t = y[2 Г_2Е- 25.1- T’ L 2’ 2 J’ 6) sin t = i to I l-> 1 | Я M |S 1 1
в) sin t = Уз Гл. л"1. 2 ’ L 2’ 2J’ r) sin t = й
а) cos t = -1. [0;«); 6) cos t = f. [0; »];
в) cos t = -f, [0; я]; r) cos t = 0, [0; л].
а) tg t = ’I 2 ’ 2 / 6) ctg t = УЗ, (0; л);
в) tg t = ’ J3, -1; I 2 2) r) ctg t = -1, (0; л).
Вычислите (121—123).
121.
a) arcsin 0;
в) arcsin 1;
б) arcsin
г) arcsin
67 Тригонометрические функции
122.—
a) arccos
в) arccos
72
6) arccos —;
’ 2
r) arccos 1.
123.— a) arctg
-Уз
в) arctg 0;
6) arctg (-1);
r) arctg л/З.
124.—
125.4
126. J
127.-1
128.-
129.
Имеют ли смысл выражения (124—125)?
a) arcsin 1; б) arccos-Уб; в) arcsin 1,5;
a) arccos л; б) arcsin (3--У20);
в) arccos (—УЗ); г) arcsin 4
Найдите значения выражений
a) arcsin 0 + arccos 0;
. 73 73
arcsin — + arccos —;
2 2
г) arccos
(126—128).
,, . ( У2 V 1
6) arcsin------+ arccos-;
I 2 J 2
•Уз
г) arcsin (-1) + arccos
а) arccos (-0,5) + arcsin (-0,5);
б) ( № 'I arccos I 2 J -arcsin (-1);
в) ( УзЛ arccos -— I 2 . I • ( 1 I 2 J
г) У2 . Уз arccos - arcsin —. 2 2
а) arctg 1 - arctg -УЗ; 6) arctg 1 - arctg (-1);
в) arctg (—Уз) + arctg 0; r) arctg = + arctg -Уз. 73
Сравните числа:
ч - Г 1Л Уз
a) arcsin — и arccos —;
к 2 J 2
б) arccos и arctg (-1);
в) arctg -Уз и arcsin 1;
г)
I 731 -1
arccos -— и arcsin -.
I 2 J 2
130.— С помощью калькулятора или таблиц найдите значение
выражения:
(a) arcsin 0,3010; arctg 2,3;
б) arccos 0,6081; arctg 0,3541;
Тригонометрические функции
в) arcsin 0,7801; arccos 0,8771;
г) arctg 10; arcsin 0,4303.
131.— Вычислите:
6)
в)
г)
a) 2 arcsin
+ arctg (-1) + arccos —;
arctg (—УЗ) + arccos
3 arcsin - + 4 arccos
2
-arcctg (—Уз);
/3
2
+ arcsin 1;
3 1
arcsin (-1) — arccos - + 3 arctg
2 2
1
Гз
132.—
133.-
Докажите, что для любых чисел хг и х2 из промежутка
[-1; 1] из неравенства хг < х2 следует неравенство:
a) arcsin хх < arcsin х2; б) arccos х, > arccos х2.
Докажите, что для любых чисел хг и х2 из неравенства
х, < х2 следует неравенство:
a) arctg х, < arctg х2; б) arcctg хх > arcctg х2.
Расположите числа в порядке возрастания (134—135).
134. U a) arcsin—, arcsin (0,3), arcsin 0,9;
6
I 6) arcsin (-0,5), arcsin (-0,7), arcsin^;
1°
в) arccos 0,4, arccos (-0,2), arccos (-0,8);
r) arccos 0,9, arccos (-0,6), arccos
5
a) arctg 100, arctg (-5), arctg 0,7;
6) arcctg 1,2, arcctg n, arcctg (-5).
9. Решение простейших тригонометрических
уравнений
1. Уравнение cost = a. Очевидно, что если |о| > 1,
то уравнение
cos t = а (1)
не имеет решений, поскольку |cos t| < 1 для любого t.
Пусть |а | < 1. Надо найти все такие числа t, что cos t = а.
На отрезке [0; л] существует в точности одно решение уравне-
ния (1) — это число arccos а.
69 Тригонометрические функции
Косинус — четная функция, и, значит, на отрезке [-л; 0]
уравнение (1) также имеет в точности одно решение — число
-arccos а. Итак, уравнение cos t = а на отрезке [-л; л] длиной 2л
имеет два решения: t = ± arccos а (совпадающие при а = 1).
Вследствие периодичности функции cos все остальные реше-
ния отличаются от этих на 2лп, (п g Z), т. е. формула корней
уравнения (1) такова:
t = ± arccos а + 2лп, п е Z. (2)
(Обратите внимание: этой формулой можно пользоваться только
при |а| < 1.)
Решение уравнения (1) можно проиллюстрировать на еди-
ничной окружности. По определению cos t — это абсцисса точ-
ки Pt единичной окружности. Если |а| < 1, то таких точек две
(рис. 69, а); если же а = 1 или а = -1, то одна (рис. 69, б).
При а = 1 числа arccos а и -arccos а совпадают (они равны
нулю), поэтому решения уравнения cos t = 1 принято записывать
в виде t = 2лп, п е Z.
Особая форма записи решений уравнений (1) принята также
для а = -1 и а = 0:
cos t = — 1 при t = л + 2ли, п е Z;
cos t = 0 при t = + пп, п е Z.
Пример 1. Решим уравнение cos х = | •
По формуле (2)
х = ± arccos i + 2лп, п g Z.
2
Поскольку arccos
—, приходим к ответу
3
X = ± — + 2пп, п G Z.
3
Тригонометрические функции
Пример 2. Решим уравнение cos х =—0,2756.
По формуле (2)
х = ±arccos (-0,2756) + 2пп, п е Z.
Значение arccos (-0,2756) находим с помощью калькулятора;
оно приближенно равно 1,8500. Итак,
х = ±х0 + 2лп, п е Z, где х0 ® 1,8500.
Пример 3. Решим уравнение cos[<2х-—'1 =
По формуле (2)
। лАз ।
2х - — = ± arccos -— + 2 ли,
4 I 2 )
п е Z, т. е. 2х-—=±“ + 2лп, откуда
4 6
__ л , 5 л . __и „ п
X — — +-+ ЛИ, И G Z.
8 12
2. Уравнение sin t = а. Уравнение
sin t = а
(3)
не имеет решений при
При | ct | < 1 на отрезке
а| > 1, так как |sin t[ < 1 для любого t.
уравнение (3) имеет в точности
одно решение tx = arcsin а. На промежутке
л
2
3— функция sin
убывает и принимает все значения от -1 до 1. По теореме о корне
уравнение (3) имеет и на этом отрезке один корень. Из рисун-
ка 70, а видно, что этот корень есть число t2 = л - arcsin а. Дейст-
вительно, sin t2 = sin (л - Ij) = sin tx = а. Кроме того, поскольку
-- < t, < -, имеем -- < -t, < - и л-- < л-t, < л + т. е. при-
2 1 2 2 1 2 2 1 2 2
Г 71 Зтс П
надлежит отрезку —; —- .
Рис. 70
Тригонометрические функции
Итак, уравнение (3) на отрезке
имеет два решения:
Zj = arcsin а и t2 = п - arcsin а (совпадающие при а = 1). Учитывая,
что период синуса равен 2л, получаем такие формулы для записи
всех решений уравнения:
t = arcsin а + 2ли, (4)
t = л - arcsin а + 2лп, п е Z. (5)
Удобно решения уравнения (3) записывать не двумя, а одной
формулой:
t = (-l)fc arcsin а + nk, k e Z. (6)
Нетрудно убедиться, что при четных k = 2п из формулы (6)
находим все решения, записанные формулой (4); при нечетных
k = 2п + 1 — решения, записываемые формулой (5).
Решение уравнения (3) удобно иллюстрировать на единичной
окружности. По определению sin t есть ордината точки Pt единич-
ной окружности. Если |а| < 1, то таких точек две (рис. 70, а); при
а = ± 1 — одна (рис. 70, б).
Если а = 1, то числа arcsin а и л - arcsin а совпадают, по-
этому решение уравнения
sin t = 1
принято записывать так:
t =— + 2лп, п е Z.
2
При а = -1 и а = 0 принята следующая запись решений:
sin t = -1, если t = - — + 2лп, п & Z.
2
sin t = 0, если t = пп, п е Z.
J2
Пример 4. Решим уравнение sinx= ^ .
/9
По формуле (6) х = (-1)А arcsin ~ + л/г, k е Z, т. е.
х =(-!)* - + л/г, /г g Z.
4
Пример 5. Решим уравнение sin х = 0,3714.
Согласно формуле (6)
х = (-I)71 arcsin 0,3714 + тт, п е Z.
С помощью калькулятора находим arcsin 0,3714 « 0,3805.
Пример 6. Решим уравнение sin f—.
110 2J 2
Функция синус нечетна. Поэтому
Тригонометрические функции
По формуле (6)
=(-1)А arcsin f-— |+ nk, keZ.
2 10 ' ’ I 2 I
Так как arcsin I | = имеем:
I 2 I 4
— - — = (-1)* + nfe, x = + (-1)* + 1 — + 2nk, k e Z.
2 10 v 4 J 5 v ' 2
3. Уравнение tgt = a. При любом а на интервале
имеется ровно одно такое число t, что tg t = а, — это arctg а.
Поэтому уравнение
tg t = а (7)
имеет на интервале ; — длиной л единственный корень. Функ-
<2 2 J
ция тангенс имеет период л. Следовательно, остальные корни
уравнения (7) отличаются от найденного на лп (п е Z), т. е.
t = arctg а + лп, п е Z.
(8)
Решение уравнения tg t = а удобно проиллюстрировать с по-
мощью линии тангенсов (рис. 71). Напомним, что tg t — это ор-
дината точки Tt пересечения прямой ОР(, с линией тангенсов
(см. п. 1). Для любого числа а на линии тангенсов есть лишь
одна точка с ординатой а, это точка Т (1; а). Прямая ОТ пересе-
кается с единичной окружностью в двух точках; при этом интер-
валу ; — 1 соответствует точка Р. правой полуокружности, та-
I 2 9 J ч
кая, что = arctg а.
Пример 7. Решим уравнение
tg х = л/З.
По формуле (8) находим реше-
ние х = arctg -Уз + лп, п е Z, а так как
arctg л/з = —, приходим к окончатель-
3
ному ответу:
х = — + лп, п е Z.
3
Пример 8. Решим уравнение
tg х = 5,177.
Из формулы (8) следует, что
х = arctg 5,177 + лп, п е Z.
С помощью калькулятора нахо-
дим arctg 5,177 « 1,3800.
Рис. 71
73 Тригонометрические функции
Пример 9. Решим уравнение ctg х = —Уз.
Это уравнение равносильно уравнению tg х = — — , которое
Уз
решаем с помощью формулы (8):
( 1 А ~
х = arctg —— + тт = + пп, neZ.
V УЗ J 6
Упражнения
Решите уравнения (136—143).
136.- - а) У2 cos х = -—; 2 6) cosx = 2
в) cosx = —; 2 r) cos x = -1.
137.- - а) 2 cos х + 73 = 0; 6) V2 cos x -1 = 0;
в) 2 cos х + л/2 = 0; r) 2 cos x - 1 = 0.
138— а) sinx = i; 2 6) Уз sinx = --—; 2
в) sinx = 2 Г) sin x = -1.
139. а) -У2 sin x + 1 = 0; 6) 2 sin x + -Уз = 0;
в) 2 sin x - 1 = 0; r) 2 sin x + V2 = 0.
140. а) tg x = Уз 6) ctg x = -УЗ;
в) tg x = 1; r) tg x = 0.
141. а) tg x + л/З = 0; 6) ctg x + 1 = 0;
в) -Уз tg x -1 = 0; r) -Уз ctg x -1 = 0.
142. а) • 0 J2 sin2x = —; 2 6) cos - = 3 2
в) • X 1 sin - 4 2 r) cos 4x = 0.
143. а) sin x = -0,6; 6) ctg x = 2,5;
в) cos x = 0,3; r) tg x =-3,5.
144.—
Решите уравнения (144—147).
a) = б) tg(-4x)=-jL;
\ о/ л/ 3
в) cos (-2х) = г) ctg Г——= 1.
2 v 2 J
7 4 Тригонометрические функции
145.—
146.—
б) 2 sin |Зх — — ] = -y[2;
I 4 J
r) sin f — - —+ 1 = 0.
I 2 6 J
6) 2 sinf---^1 = V3;
<3 4 J
r) 2 cos | —-3x | = V2.
147.—
v 3
a) sin 3x cos x - cos 3x sin x = —;
6) sin2 — - cos2 — = 1;
4 4
в) sin 2x cos 2x = -
r) sin — cos — -cos sin
’ 3 5 3 5 2
148.—
Для каждой из функций
и
у = 2 cos I 2 x - —
к 3
у = sin
X Л. |
2 4 7
149.
150.
найдите координаты общих точек ее графика с прямой:
а) х = 4,5л; б) у = -1; в) у = 1; г) у = 0.
Решите уравнения cos - 2х^ = ^, sin ^2х + = -1
и найдите для каждого из них:
а) наименьший положительный корень;
б) корни, принадлежащие промежутку
Зл!
2 J’
в) наибольший отрицательный корень;
г) корни, принадлежащие промежутку -л; —
Докажите, что все решения уравнения ctg t = а находятся
по формуле t = arcctg а + лп, п е Z.
10. Решение простейших
тригонометрических неравенств
Решение неравенств, содержащих тригонометрические
функции, сводится, как правило, к решению простейших нера-
венств вида sin t < a, cos t > a, tg f > о и т. п.
Рассмотрим на примерах способы их решения.
Н Пример 1. Решим неравенство sint > -.
Все точки Pt единичной окружности при значениях t, удо-
влетворяющих данному неравенству, имеют ординату, большую
75 Тригонометрические функции
или равную Множество всех таких точек — дуга I, выделенная
на рисунке 72. Найдем условие принадлежности точки Р( этой
дуге.
Точка Pt лежит на правой полуокружности, ордината Pt рав-
1 1 1
на , и, следовательно, в качестве fj удобно взять значение
Zj = arcsin
—. Представим себе, что мы совершаем обход
6
1
2
дуги I ОТ ТОЧКИ К Р(
и, как легко понять, t2 = л - arcsin
решения неравенства, принадлежащие промежутку
против часовой стрелки. Тогда t2 > tv
—. Таким образом, полу-
6
чаем, что точка Pt принадлежит дуге /, если < t < —. Итак,
ной 2л, таковы: . Вследствие периодичности синуса
6 6
остальные решения получаются добавлением к найденным чисел
вида 2лп, где п е Z. Приходим к ответу:
+ 2яп < t < — + 2 ли, п е Z.
6 6
V2
Пример 2. Решим неравенство sin/<—.
Это неравенство означает, что все точки Pt единичной окруж-
ности при значениях t, удовлетворяющих данному неравенству,
у[2
имеют ординату, меньшую —. Множество всех таких точек —
дуга I, выделенная на рисунке 73. Концы ее Р, и Р. не входят
11 Г2
в рассматриваемое множество, поскольку их ординаты не меньше,
л/2
а равны —Чтобы найти условие, при котором точка Р( при-
7 6 Тригонометрические функции
надлежит указанному множеству, найдем t. и t9. Возьмем
, • 42 п
t, = arcsin — = —.
1 2 4
Рассмотрим обход дуги I от точки Р( к Р( в направлении
42 5тг
по часовой стрелке; t2 < tx, и t2 = -л - arcsin — = —Все реше-
промежутка ^-^4 длиной 2л
<t <—. Учитывая периодичность синуса, получаем все реше-
4 4
ния неравенства:
- — + 2 ли < t < — + 2 ли, п е Z.
4 4
таковы:
ния неравенства из
Пример 3.
Решим неравенство cos t < ~.
Множество точек единичной окружности, абсциссы которых
меньше i, лежат левее прямой х = Значит, множество всех та-
ких точек есть дуга I, выделенная на рисунке 74 (концы ее Pt^ и Pt?
не входят в это множество). Находим tx и t2. Точка Pt расположе-
на на верхней полуокружности, абсцисса Pt равна следователь-
но, tx = arccos - = —. При переходе от точки Pt к Р( по дуге I вы-
2 3 12
полняем обход против движения часовой стрелки, тогда t2 >
и t9 = 2л - arccos --- —. Точка принадлежит выделенной дуге I
6 2 3
(исключая ее концы) при условии, что - <t <—. Решения нера-
3 3
венства, принадлежащие промежутку [О; 2л] длиной 2л, таковы:
— </<—. Вследствие периодичности косинуса остальные решения
3 3
получаются добавлением к найденным чисел вида 2лл, где п е Z.
Приходим к окончательному ответу:
— + 2 лл <t < — + 2 ли, п е Z.
3 3
Пример 4. Решим неравенст-
во tg t < 1.
Период тангенса равен л. Поэто-
му найдем сначала все решения данно-
го неравенства, принадлежащие про-
межутку а затем воспользу-
емся периодичностью тангенса. Для
выделения всех точек Pt правой полу-
окружности, значения t которых удо-
77 Тригонометрические функции
к
влетворяют данному неравенству, обратимся
Если t является решением неравенства, то
равная tg t, должна быть меньше или равна
точек Т — лучАТ (рис. 75). Множество точек Pt, соответствующих
точкам этого луча, — дуга I, выделенная
внимание: точка Pt принадлежит, а Р п не
2
риваемому множеству). Находим условие,
7Г. _Л
2’ 2
принадлежит дуге I. t
t. = arctg 1 = —. Значит,
4
~ < t < Все решения
линии тангенсов,
ордината точки Т,
1. Множество таких
на рисунке (обратите
принадлежит рассмат-
при котором точка Pt
и tg tj = 1, следовательно,
t должно удовлетворять условию
данного неравенства, принадлежащие
Л
2* 2
тангенса, получаем ответ:
промежутку
, таковы:
. Учитывая периодичность
Л
2
— + ЛП, п G Z.
4
/и
Пример 5. Решим неравенство cos 2х>
Го
Обозначив 2х через t, получим cost>-^-. На рисунке 76
выделена соответствующая дуга I. Находим tr = arccos
J2
2
= 3_
4 ’
t2 = -“, откуда
4
--^ + 2xn<t<-^ + 2xn, п е Z.
4 4
Переходя к переменной х, получаем:
-~ + 2тт <2х <-^ + 2лп, -Зл + лп<
4 4 8
Зл
8
78 Тригонометрические функции
Пример 6. Решим нера-
венство 3 tg ( — — — | < л/З.
к 3 2)
Преобразовав данное нера-
венство, получим:
Обозначим — - — через t, тогда tg t > . На рисунке 77 выделена
2 3 3
соответствующая дуга I. Так как tr =
получаем
+ т < t
6
< — + пл. Перейдем к переменной х:
ТС I — п / ТС I
---+ Т1П < — — — <------h Tin,
6 2 3 2
— + 2лп < х < —- + 2лп, п е Z.
3 3
Упражнения
На единичной окружности отметьте точки Pt, для кото-
рых соответствующие значения t удовлетворяют данному
неравенству. Найдите множество значений t, удовлетворя-
ющих неравенству и принадлежащих указанному проме-
жутку (151—153).
151J j а) sin t > j, t e [0; л]; 6) sin t e [-л; 0];
в) sin t V2 t > —, t e 2 [0; л]; r) sin t < t e 2 [-л; 0].
152.- а) cos t _2£. 71 2’ 2_ ; 6) cos t '-I-'6! 71. Зл ~l. 2 ’ 2 J’
в) cos t 7L. Tel. 2’ 2_r r) cos t <-^3, tepE; ЗлТ 2 l_2 2 J
153. а) tg t > -л/З, t e _7t. 7C 2’ 2y j; 6) tg t /3 I 1 to Is to |s
в) tg t > Vi . ( 1 to to |s r) tg t ' ~1» t E to Is to Is
79 Тригонометрические функции
Решите неравенства
(154—157).
154.- - а) V2 sin х > ; 2 6) sin x < - Уз. 2 ’
в) sin х> 2 r) sin x < - V2 2 ‘
155.— а) 4 cos х~> 2 6) cos X < — z 2 .
в) . Уз cos х > -—; r) COS X < - V2
2 2
156. а) tg х < 6) tg X > 1_. [3 ’
в) tg х > r) tg X < -1.
157. а) 2 cos х -1 > 0; 6) 2 sin x + У2 > 0;
в) 2 cos x - Уз < 0; r) 3 tg x + д/ ^3 > 0.
Решите неравенства (158 —163).
158.- - а) sin 2x < i; 6) cos - > Vi.
2 3 2 ’
в) sin 2 2 r) tg 5x > 1.
159.— - а) 2 cos | 2 x + — | < 1; б) Уз tg Гзх + ^У
I 3 J V 6 J
в) У2 sin ( - + -^1 > 1; r) 2 cos 4x--1>
\4 2 J 6 J
160 J - а) sinx cos— -cosx sin— < 1.
6 6 2’
б) sin — cos x + cos — sinx < .
4 4 2 ’
в) 4 sin 2 x cos 2 x > У2;
г) cos ? cos x - sin x sin - <
8 8 2 ’
161.- а) ctg x > УЗ; 6) > /3ctgf^ \ 4 -2x^j > 1;
в) ctg Зх < -1 ; r) 3 ctg f — +
Уз <6 2 J
162. а) 3 sin - > 2; 4 6) 4 x cos — < - 3 3;
в) 5 tg 2x < 3; r) 0,5 sin 4x < -0,2.
1;
80 Тригонометрические функции
163.— Найдите решения неравенства, принадлежащие указанно-
му промежутку:
a) sinx>--, xef-—; —
2 ^26
б) cos - > —, х е ; 0 ;
2 2 L 2 J
в) tg х > -1, хе f;
I 2 4J
г) sin 2х < —, х е [0; л].
11. Примеры решения тригонометрических
уравнений и систем уравнений
В п. 9 было показано, как решать простейшие тригоно-
метрические уравнения. Решение более сложных тригонометриче-
ских уравнений требует знания формул тригонометрии. Рассмот-
рим некоторые примеры.
| Пример 1. Решим уравнение 2 sin2 х + sin х - 1 = 0.
Введем новую переменную у = sin х. Тогда данное уравнение
можно записать в виде 2у2 + у - 1 = 0. Мы получили квадратное
уравнение. Его корнями служат уг и у2 = -1. Следовательно,
sin х = | или sin х - -1. В первом случае получим решения
х = (-1)* arcsin + nk,
т. е. х = (-1)* — + лй, k е Z.
v 6
Во втором случае имеем:
х = + 2 ли, п е Z.
2
Пример 2. Решим уравнение 6 sin2 х + 5 cos х - 2 = 0.
Заменяя sin2 х на 1 - cos2 х, получим относительно cos х
квадратное уравнение 6 (1 - cos2 х) + 5 cos х - 2 = 0, откуда
-6 cos2 х + 5 cos х + 4 = 0, т. е. 6 cos2 х - 5 cos х - 4 = 0. Как и в
примере 1, введем новую переменную cos х = у. Тогда бу2 -
- 5у - 4 = 0, откуда у = —1 или у = 1—. Уравнение cosx = 1^ не име-
2 3 3
ет решений, так как 1— > 1. Решая уравнение cosx = находим:
3 2
х = ±—+ 2лй, k е Z.
3
81 Тригонометрические функции
Пример 3. Решим уравнение tg х + 2 ctg х - 3.
Обозначим tg х через у. Поскольку ctgx = ~—, йолучаем
tgx
уравнение у + 2 =3, которое приводится к квадратному у2 - Зу +
+ 2 = 0 (при условии у ф 0). Его корни у = 2 и у = 1.
1) tg х - 2, х = arctg 2 + л/г, т. е. х = х0 + л/г, /г е Z, где
х0 = arctg 2 « 1,1072.
2) tg х = 1, х = — + л/г, /г е Z.
4
Пример 4. Решим уравнение
3 sin2 х - 4 sin х cos х + cos2 х = 0.
Значения х, при которых cos х = 0, не являются решениями
этого уравнения, так как если cos х = 0, то должно выполняться
равенство 3 sin2 х = 0, а косинус и синус не могут быть одновре-
менно равными нулю. Поэтому можно обе части уравнения раз-
делить на cos2 х (или на sin2 х) и при этом получить уравнение,
равносильное данному уравнению 3 tg2 x-4tgx + l = 0, откуда
tg х = 1 или tg х = —. Следовательно,
3
х = —F лп, п 6 Z, или х = arctg - + л/г, /г е Z.
4 6 3
Пример 5. Решим уравнение 6 sin2 х + 4 sin х cos х = 1.
Заменим 1 в правой части уравнения на sin2 х + cos2 х. После
выполнения соответствующих преобразований получаем 5 sin2 х +
+ 4 sin х cos х - cos2 х = 0. Воспользуемся приемом
добного уравнения, который описан в примере 4.
имеем tg х = i,
5
решения по-
В результате
tg х = -1. Следовательно,
х = arctg - + пп, п 6 Z, или х = - — + л/г, k е Z.
5 4
Пример 6. Уравнение sin2 х - sin 2х = 0 после замены
sin 2х на 2 sin х cos х приводится к виду sin2 х - 2 sin х cos х = 0.
Разложим левую часть на множители: sin х (sin х - 2 cos х) =
= 0, откуда sin х = 0, т. е. х = пп, п е Z, или sin х - 2 cos х = 0,
откуда tg х = 2 и х = arctg 2 + пп, п е Z, т. е. х = х0 + пп, п е Z,
где х0 = arctg 2 » 1,1072.
Как и в примере 4, можно было разделить обе части уравне-
ния на cos2 х и получить уравнение tg2 х - 2 tg х = 0. Если же де-
лить на sin2 х, то нужно учесть, что те х, при которых
sin х = 0, — решения данного уравнения. Поэтому к корням полу-
ченного после деления на sin2 х уравнения ctg х — — = 0 надо доба-
2
вить корни уравнения sin х = 0.
Тригонометрические функции
Многие другие уравнения, например уравнение sin2 х -
- sin х cos х + cos2 х = 0 или уравнение sin3 х + 2 sin2 х cos х -
- 5 sin х cos2 х + 2 cos3 х = О и т. и., также решаются делением
левой и правой частей уравнения на косинус (или синус) в степе-
ни, равной степени уравнения. Предварительно надо проверить,
являются ли значения х, для которых cos х = 0 (sin х = 0 при де-
лении на sinn х), решениями данного уравнения. Так, уравнения
второй степени делят на cos2 х (или sin2 х), а третьей — на cos3 х
(или sin3 х) и заменой tg х (или ctg х) на у получают алгебраиче-
ское уравнение.
Пример 7. Решим уравнение cos 6х + cos 2х = 0.
Преобразовав сумму косинусов в произведение, получим
2 cos 4х cos 2х = 0. Это уравнение обращается в верное равенство,
если cos 4х = 0 или cos 2х = 0, т. е.
х = —+ —, k е Z, или х = —+ —, п е Z.
8 4 4 2
Пример 8. Решим систему уравнений
sin х = 2 sin у.
Из первого уравнения находим у = х - Тогда 2 sin у =
О
( 1 ( 5 я 1 I 1 л/З
= 2sin х--=2 sinxcos--cosxsin— =2 sinx--h — cosx
V 3 J I 3 3 J I 22
= sinx + V3 cosx. Второе уравнение системы примет вид sin х =
= sinx + V3cosx, откуда cos х = 0, х = + пп, где п е Z. Далее на-
ходим у = х+ пп -— = пп - —, п е Z.
у 3 2 3 6
Ответ. I — + пп; пп I, п е Z.
<2 6 J
Упражнения
Решите уравнения (164—168).
164.— a) в) 2 2 sin2 sin2 x + sin x - 1 = 0; x - sin x - 1 = 0;
165.1 a) 6 cos2 x + cos x - 1 = 0;
в) 4 cos2 x - 8 cos x + 3 = 0:
166. I a) 2 cos2 x + sin x + 1 = 0;
в) 4 cos ; x = 4 - sin2 x;
б) 3 sin2 х - 5 sin х - 2 = 0;
г) 4 sin2 х + 11 sin х - 3 = 0
б) 2 sin2 х + 3 cos х = 0;
г) 5 sin2 х + 6 cos x - 6 = 0.
6) cos2 x + 3 sin x = 3;
г) 8 sin2 x + cos x + 1 = 0.
83 Тригонометрические функции
167.— a) 3 tg2 x + 2 tg x - 1 = 0;
в) 2 tg2 x + 3 tg x - 2 = 0;
168.— a) 2 cos2 x + 7з cos x = 0;
в) л/З tg2 x - 3 tg x = 0;
6) tg x - 2 ctg x + 1 = 0;
r) 2 ctg x-3tgx + 5 = 0.
6) 4 cos2 x - 3 = 0;
r) 4 sin2 x - 1 = 0.
Решите уравнения (169—174).
169.— a) 3 sin2 x + sin x cos x = 2 cos2 x;
6) 2 cos2 x - 3 sin x cos x + sin2 x = 0;
в) 9 sin x cos x - 7 cos2 x = 2 sin2 x;
r) 2 sin2 x - sin x cos x = cos2 x.
170— a) 4 sin2 x - sin 2x = 3;
в) sin 2x - cos x = 0;
171— a) 2 sin2 x = д/з sin 2 x;
в) sinx + V3cosx = 0;
172,— a) sin 2x + 2 cos 2x = 1;
6) cos 2x = 2 cos x - 1;
r) sin 2x + 4 cos2 x = 1.
6) V3 tg x - у[з ctg x = 2;
r) tg x = 3 ctg x.
6) sin4 - -cos4 — =
4 4 2
в) 3 sin 2х + cos 2х = 2 cos2 х;
173— а) sin 4х + sin2 2х = 0; б)
в) - =2; г)
3 sin х + 4
r) 1 - cos x = 2 sin —.
’ 2
- =1;
5 tg x + 8
z -.2
1 - sin 2 x = I cos — - sin — I .
к 2 2 J
174.— a) cos 5x - cos 3x = 0;
в) sin 5x - sin x = 0;
6) sin 7x - sin x = cos 4x;
r) cos 3x + cos x = 4 cos 2x.
Решите системы уравнений (175—176).
175—
176.
a)
a)
в)
X + у = 71, cos х -cos у = 1; 6) х-у = —, а 2 cos2 х + sin2 у = 2;
X + у = я, sinx + sinp = 1; г) X + у = — , ‘ 2 sin2 х - sin2 у = 1.
sinx-cosz/ = 0, sin2 x + cos2 у = 2; б) х + у = -, у 4 tgx tgy = j; О
sinx + cosz/ = 1, sin2 x - cos2 у = 1; г) • х - у = —, У 6 sin х cos у = —.
84 Тригонометрические функции
Сведения из истории
1. О происхождении единиц измерения углов. Градусное
измерение углов возникло в Древнем Вавилоне задолго до новой
эры. Жрецы считали, что свой дневной путь Солнце соверша-
ет за 180 «шагов», и, значит, один «шаг» равен развернутого
угла. В Вавилоне была принята шестидесятеричная система счис-
ления, т. е. фактически числа записывались в виде суммы сте-
пеней числа 60, а не 10, как это принято в нашей десятеричной
системе. Естественно поэтому, что для введения более мелких
единиц измерения углов один «шаг» последовательно делился на
60 частей.
Вавилонская система измерения углов оказалась достаточ-
но удобной, и ее сохранили математики Греции и Рима. Терми-
ны, которыми мы пользуемся для названия угловых величин,
имеют латинские корни. Слово «градус» происходит от латинско-
го gradus (шаг, ступень). В переводе с латинского minutus озна-
чает «уменьшенный». Наконец, secunda переводится как «вто-
рая». Имеется в виду следующее: деление градуса на 60 частей,
т. е. минуты,— это первое деление; деление минуты на 60 се-
кунд — второе деление градуса. Малоупотребительное название
— секунды — терцина, латинское tercina означает «третье» (де-
60
ление градуса).
Принятая сейчас система обозначения величин углов полу-
чила широкое распространение на рубеже XVI и XVII вв.; ею уже
пользовались такие известные астрономы, как Н. Коперник
и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество граду-
сов обозначал кружком, число минут — штрихом, а секунд — дву-
мя штрихами.
Другая единица измерения углов — радиан — введена со-
всем недавно. Первое издание (это были экзаменационные би-
леты), содержащее термин «радиан», появилось в 1873 г. в Анг-
лии. Сначала в обозначениях указывалось, что имеется в виду
радианная мера (например, ----угол в радиан), но вскоре ин-
декс R (или г) стали опускать. Сам термин «радиан» происходит
от латинского radius (спица, луч).
Если вспомнить определение угла в один радиан (централь-
ный угол, длина дуги которого равна радиусу окружности), то вы-
бор корня «рад» для названия такого угла представляется совер-
шенно естественным.
2. Об истории тригонометрии. Слово «тригонометрия» впер-
вые встречается (1505 г.) в заглавии книги немецкого теолога
и математика Питискуса. Происхождение этого слова греческое:
xpiycovov — треугольник, цетресо — мера. Иными словами, тригоно-
метрия — наука об измерении треугольников. Хотя название воз-
85 Тригонометрические функции
Рис. 78
никло сравнительно недавно, многие относи-
мые сейчас к тригонометрии понятия и факты
были известны уже две тысячи лет назад.
Длительную историю имеет понятие си-
нуса. Фактически различные отношения от-
резков треугольника и окружности (а по су-
ществу, и тригонометрические функции)
встречаются уже в III в. до н. э. в работах
великих математиков Древней Греции —
Евклида, Архимеда, Аполлония
Пергского. В римский период эти отно-
шения уже достаточно систематично иссле-
довались Менелаем (I в. н. э.), хотя и не
приобрели специального названия. Современный синус угла а, на-
пример, изучался как полухорда, на которую опирается централь-
ный угол величиной а, или как хорда удвоенной дуги (рис. 78).
В последующий период математика долгое время наиболее
активно развивалась индийскими и арабскими учеными.
В IV—V вв. появился, в частности, уже специальный термин
в трудах по астрономии великого индийского ученого Ариаб-
хаты (476 — ок. 550), именем которого назван первый индий-
ский спутник Земли. Отрезок AM (рис. 78) он назвал ардхаджива
(ардха — половина, джива — тетива лука, которую напоминает
хорда).
Позднее привилось более краткое название джива. Арабски-
ми математиками в IX в. слово джива (или джиба) было заменено
на арабское слово джайб (выпуклость). При переводе арабских ма-
тематических текстов в XII в. это слово было заменено латинским
синус (sinus — изгиб, кривизна).
Слово косинус намного моложе. Косинус — это сокращение
латинского выражения complementy sinus, т. е. «дополнительный
синус» (или иначе «синус дополнительной дуги»; вспомните
cos а = sin (90° - а)).
Имея дело с тригонометрическими функциями, мы сущест-
венно выходим за рамки задачи «измерения треугольников». По-
этому известный математик Ф. Клейн (1849—1925) предлагал
учение о «тригонометрических» функциях называть иначе —
гониометрией (латинское gonio означает «угол»). Однако это на-
звание не привилось.
Тангенсы возникли в связи с решением задачи об определе-
нии длины тени. Тангенс (а также котангенс, секанс и косеканс)
введен в X в. арабским математиком Абу-л-Вафой, который соста-
вил и первые таблицы для нахождения тангенсов и котангенсов.
Однако эти открытия долгое время оставались неизвестными ев-
ропейским ученым, и тангенсы были заново открыты в XIV в.
сначала английским ученым Т. Бравердином, а позднее не-
мецким математиком, астрономом Региомонтаном (1467 г.).
86 Тригонометрические функции
Название «тангенс», происходящее от латинского tanger (касать-
ся), появилось в 1583 г. Tangens переводится как «касающийся»
(вспомните: линия тангенсов — это касательная к единичной
окружности).
Современные обозначения arcsin и arctg появляются в 1772 г.
в работах венского математика Шерфера и известного фран-
цузского ученого Ж.-Л. Лагранжа, хотя несколько ранее их
уже рассматривал Я. Бернулли, который употреблял иную сим-
волику. Но общепринятыми эти символы стали лишь в конце
XVIII столетия. Приставка «арк» происходит от латинского arcus
(лук, дуга), что вполне согласуется со смыслом понятия: arcsin х,
например, — это угол (а можно сказать, и дуга), синус которого
равен х.
Длительное время тригонометрия развивалась как часть гео-
метрии, т. е. факты, которые мы сейчас формулируем в терминах
тригонометрических функций, формулировались и доказывались
с помощью геометрических понятий и утверждений. Пожалуй,
наибольшие стимулы к развитию тригонометрии возникали в свя-
зи с решением задач астрономии, что представляло большой
практический интерес (например, для решения задач определения
местонахождения судна, предсказания затмений и т. д.).
Астрономов интересовали соотношения между сторонами и
углами сферических треугольников, составленных из больших
кругов, лежащих на сфере. И надо заметить, что математики древ-
ности удачно справлялись с задачами, существенно более труд-
ными (почитайте книги о сферической геометрии), нежели задачи
на решение плоских треугольников, которыми вы занимались
в IX классе.
Во всяком случае в геометрической форме многие известные
вам формулы тригонометрии открывались и перестирывались
древнегреческими, индийскими, арабскими математиками. (Прав-
да, формулы разности тригонометрических функций стали извест-
ны только в XVII в.— их вывел английский математик Непер
для упрощения вычислений с тригонометрическими функциями.
А первый рисунок синусоиды появился в 1634 г.)
Принципиальное значение имело составление К. Птолемеем
первой таблицы синусов (долгое время она называлась таблицей
хорд): появилось практическое средство решения ряда приклад-
ных задач, и в первую очередь задач астрономии.
Имея дело с готовыми таблицами или пользуясь калькулято-
ром, мы часто не задумываемся о том, что было время, когда таб-
лицы еще не были изобретены. Для того чтобы составить их, тре-
бовалось не только выполнить большой объем вычислений, но
и придумать способ составления таблиц. Таблицы Птолемея точны
до пяти десятичных знаков включительно.
Современный вид тригонометрии придал крупнейший мате-
матик XVIII столетия Л. Эйлер (1707—1783), швейцарец по про-
исхождению, долгие годы работавший в России и являвшийся чле-
87 Тригонометрические функции
Эйлер Леонард
(1707—1783) —
крупнейший математик XVIII столетия. Родился
в Швейцарии. Долгие годы жил и работал в Рос-
сии, член Петербургской Академии наук. Громад-
ное научное наследие Эйлера включает блестя-
щие результаты, относящиеся к математическому
анализу, геометрии, теории чисел, вариационному
исчислению, механике и другим приложениям ма-
тематики.
ном Петербургской Академии наук. Именно Эйлер первым ввел
известные определения тригонометрических функций, стал рас-
сматривать функции произвольного угла, получил формулы при-
ведения. Все это малая доля того, что за долгую жизнь Эйлер
успел сделать в математике: он оставил свыше 800 работ, доказал
многие ставшие классическими теоремы, относящиеся к самым
разным областям математики. (Несмотря на то что в 1776 г. Эйлер
потерял зрение, он до последних дней продолжал диктовать все
новые и новые работы.) Но если вы попытались оперировать с три-
гонометрическими функциями в геометрической форме, т. е. так,
как это делали многие поколения математиков до Эйлера, то суме-
ете оценить заслуги Эйлера в систематизации тригонометрии. По-
сле Эйлера тригонометрия приобрела форму исчисления: различ-
ные факты стали доказываться путем формального применения
формул тригонометрии, доказательства стали намного компактнее,
проще.
3. Из истории понятия функции. Понятие функции, с кото-
рым вы знакомы с VII класса, возникло в математике сравнитель-
но недавно. Для того чтобы прийти к пониманию целесообразности
его введения и получить первые достаточно четкие определения,
потребовались усилия первоклассных математиков нескольких по-
колений.
Революционные изменения в математике, происшедшие в
XVII столетии, вызваны работами многих ученых, представляю-
щих различные страны и народы. Но в первую очередь следует на-
звать имена П. Ферма (1601—1665), Р. Декарта (1596—1650),
И. Ньютона (1643—1727), Г.-В. Лейбница (1646—1716).
Необходимые предпосылки к возникновению понятия функ-
ции были созданы в 30-х годах XVII в., когда возникла аналити-
ческая геометрия, характеризующаяся, в отличие от классиче-
ских методов геометров Древней Греции, активным привлечением
алгебры к решению геометрических задач. (Решая задачи по гео-
метрии координатным методом, вы, по существу, пользуетесь ме-
88 Тригонометрические функции
Декарт Рене
(1596—1650) —
великий французский философ, математик. Один
из создателей аналитической геометрии Ввел
понятие переменной величины. Его идеи нашли
многочисленных последователей — «картезианцев»
(латинизированное имя Декарта — Картезий).
Главные работы — «Геометрия», «Рассуждение о
методе».
годами аналитической геометрии.) Практически одновременно
(и независимо друг от друга) французские математики П. Ферма
и Р. Декарт заметили, что введение системы координат на плос-
кости и задания фигур их уравнениями позволяет свести многие
задачи геометрии к исследованию уравнений геометрических фи-
гур. В честь Декарта, давшего развернутое изложение нового мето-
да в книгах «Геометрия» и «Рассуждение о методе», прямоуголь-
ная система координат позднее была названа декартовой. Сущест-
венно заметить, что одновременно формировалась и алгебра,
создавалось «буквенное исчисление», то самое, с помощью которо-
го вы сейчас преобразовываете алгебраические выражения, решае-
те уравнения, текстовые задачи и т. д.
Великий английский ученый, математик и физик И. Нью-
тон, исследуя зависимости координат движущейся точки от време-
ни, фактически уже занимался исследованием функций. Хотя не
он ввел это понятие, Ньютон ясно осознавал его значение. Так,
в 1676 г. он отмечал: «Я не мог бы, конечно, получить этих общих
результатов, прежде чем не отвлекся от рассмотрения фигур и не
свел все просто к исследованию ординат» (т. е. фактически функ-
ций от времени).
Сам термин «функция» впервые встречается в рукописи ве-
ликого немецкого математика и философа Г. Лейбница — сначала
в рукописи (1673 г.), а затем и в печати (1692 г.). Латинское сло-
во function переводится как «свершение», «исполнение» (глагол
fungor переводится также словом «выражать»), Лейбниц ввел это
понятие для названия различных параметров, связанных с по-
ложением точки на плоскости. В ходе переписки Лейбниц и его
ученик — швейцарский математик И. Бернулли (1667—1748)
постепенно приходят к пониманию функции как аналитического
выражения и в 1718 г. дают такое определение: «Функцией пере-
менной величины называется количество, составленное каким
угодно способом из этой переменной и постоянных».
Л. Эйлер в своей книге «Введение в анализ» (1748 г.) форму-
лировал определение функции так: «Функция переменного коли-
Тригонометрические функции
Ньютон Исаак
(1643—1727) —
великий английский ученый. Одновременно с
Г. Лейбницем разработал основы математического
анализа. Создатель классической механики. Нью-
тону принадлежат выдающиеся открытия в оптике,
других разделах физики и математики. Главный
| его труд — «Математические начала натуральной
философии» — оказал колоссальное влияние на
развитие естествознания.
чества есть аналитическое выражение, составленное каким-либо
способом из этого переменного количества и чисел или постоян-
ных количеств».
Эйлер же ввел и принятые сейчас обозначения для функций.
Современное определение числовой функции, в котором это
понятие уже освобождалось от способа задания, было дано незави-
симо друг от друга русским математиком Н. И. Лобачевским
(1834 г.) и немецким математиком Л. Дирихле (1837 г.). Основ-
ная идея этих определений заключалась в следующем: не сущест-
венно, каким образом (и, в частности, необязательно путем зада-
ния аналитического выражения) каждому х поставлено в соответ-
ствие определенное значение у, важно только, что это соответствие
установлено.
Современное понятие функции с произвольными областями
определения и значений (необязательно числовыми — см. с. 27)
сформировалось, по существу, совсем недавно, в первой половине
текущего столетия, после работ создателя теории множеств
Г. Кантора (1845—1918).
Сложный и, как видите, очень длительный путь развития
понятия функции довольно типичен. Для того чтобы осознать не-
обходимость введения нового абстрактного понятия, требуется вы-
делить его в процессе решения многих конкретных задач, дать
определение, по возможности точно отражающее его смысл.
К понятию функции математики пришли, отправляясь
от конкретных и трудных задач математики и ее приложений.
Это происходило в процессе создания нового мощного аппарата
исследований — интегрального и дифференциального исчисле-
ний, с элементами которых вы познакомитесь в следующей гла-
ве. Открытие интегрального и дифференциального исчислений,
центральным понятием которых Эйлер провозгласил функцию
(«Весь анализ бесконечного вращается вокруг переменных ко-
личеств и их функций»), резко расширило возможности матема-
тики.
Тригонометрические функции
Вопросы и задачи на повторение
1. 1) Что такое угол в 1 радиан? Запишите формулы, связываю-
щие радианную и градусную меры угла.
2) Выразите в радианной мере величину угла:
а) 18°; б) -250°; в) -360°; г) 225°.
3) Выразите в градусной мере величину угла:
а) л; б) -2,5; в) -£; г) 3.
О
2. 1) Дайте определение синуса и косинуса числа а.
2) Отметьте на единичной окружности точку Ра. Найдите зна-
чения sin а и cos а (не пользуясь калькулятором или таблица-
ми), если а равно:
а) б) --; в) г)
’ 3 4 ’ 2 6
3) Найдите значения sin а и cos а, если а равно:
а) 23°24'; б) -1,7; в) -108°6'; г) 0,8.
3. 1) Дайте определения тангенса и котангенса числа а. При ка-
ких значениях а определены tg а и ctg а?
2) Найдите (не пользуясь калькулятором или таблицами) tg а
и ctg а, если а равно:
а) б) -А^; в) г) "
6 4 6 3
3) Найдите значения tg а и ctg а, если а равно:
а) 1,7; б) -0,4; в) 2,3; г) -0,5.
4. 1) Запишите формулы, связывающие значения тригонометри-
ческих функций одного аргумента.
2) Упростите выражение:
a) (tg а + ctg а) (1 + cos а) (1 - cos а);
cos3 а + sin3 а cos3 а - sin3 а . 1 1
б) +---------------------; в) ------------+--------;
sin а cos а 1 + tg2 а 1 + ctg2 а
г) sin3 а (1 + ctg а) + cos3 а (1 + tg а).
3) Докажите тождество:
cos а 1 + sin а 1 - (sin а + cos а )2 „ . о
а) ---;— =-----------; б) = 2 tg2 а;
1 - sin а cos а sin а cos а - ctg а
. sin а 1 + cos а . , „ . 9 , 9 9
в) --------=----------; г) tg2 а - sm2 а = tg2 а sin2 а.
1 - cos а sin а
5.
1) Как зависят знаки sin a, cos а, tg а, ctg а от того, в какой
координатной четверти лежит точка Ра? Назовите эти знаки.
2) Определите знак:
a) sin (-212°) и ctg7-p; б) cos 305° и tg|-—|;
9 к 5 )
в) cos (-105°) и ctgAA^; г) sin (-324°) и tg^71.
Тригонометрические функции
3) По данному значению одной из тригонометрических функ-
ций и промежутку, которому принадлежит а, найдите зна-
чения остальных трех основных тригонометрических функ-
ций:
a) sin а = —, — < а < л; б) ctg а = -3, < а < 2 л;
3 2 2
в) tga=|, л<а г) cosa = |, 0 < а < £.
Ci Ci I Ci
6. 1) Сформулируйте мнемоническое правило для запомина-
ния формул приведения. Запишите несколько формул приве-
дения.
2) Приведите к значению тригонометрической функции наи-
меньшего положительного аргумента:
а) sinf-*|A б) ctg 2^;
ч ( 14л Y „ч „„„8 л
в) tg —— ; г) cos —.
к. 3 ) 3
3) Упростите выражение:
а) sin^ + cos5n +tg7-;
8 8 4
„ sin( л - a) cost л + a) tg(-a)
6) —---------c---- —r------
sin fa- j ctg + a J cos f a + 1
sin(a - л) tg — + a
в) ctg—+ sin277l cos —; r) ------------=-— ------.
4 12 12 cos(^ + a)ctg(a-n)
7. 1) Запишите формулы синуса, косинуса, тангенса суммы (раз-
ности).
2) Найдите значение выражения: а) sinf — + a 1, если sina = — и 0 < a < ^; <6 J 3 2 6) cos— и tg —; ’ 12 12 в) cos --a , если cosa = -- и — < a < л. U / 3 2 3) Докажите тождество: a) sin а + — + sin а - — = V3 sin а; к 6 J 1 6 J б) tg (- + xl- tg f--xl = 2 tg 2х; к 4 ) к 4 ) tga+tg—-а . , „, ч 1з ) _ ГБ. sin(a+P) в) , < - Vo, г) . . п 1 cos a cos В l-tgatgl|-al 1 = tga + tgp.
92 Тригонометрические функции
8. 1) Запишите формулы двойного аргумента.
2) Вычислите:
a) sin 2а, если cos а = - ^, л < а < - -;
5 i
12
б) tg 2а, если sin а = —, cos а < 0;
1о
15
в) cos 2а, если sin а = —;
г) tg 2а, если cos а = ^, < а < 2 л.
5 2
3) Докажите тождество:
\ 2 tg а . „ о *о
а) — -----(2 cos2 а-1) = sin2 а;
1 - tg2 а
„ 1- cos2a I sin2a
б) ----------------= tg а;
1 + cos2a + sin2a
в) 1 - (cos а - sin а)2 = sin 2а;
г) tg а (1 + cos 2а) = sin 2а.
9.
1)
2)
а)
Запишите формулы суммы и разности синусов (косинусов).
Вычислите, не пользуясь калькулятором или таблицами:
sin 70 °-sin 10 °
cos 117° + cos 63°;
б)
в)
г)
cos 40 °
sin 112° + sin 248°.
3) Докажите тождество:
, sin a + sin 3 a . _
а) --------- - = tg2a;
cos a + cos 3 a
6)
в)
(sin 2a + sin 4a)1 2 + (cos 2a + cos 4a)2 = 4 cos2 a;
sin2a + sin2p
cos 2 a + cos 2p
= tg(a + ₽);
r) sin 2a + sin 4a + sin 6a = 4 sin 3a cos 2a cos a.
10. 1) Запишите формулы половинного аргумента.
2) Найдите:
а) cos —, если cos a = i< a < 2 л;
2 3 2
. a . 2 „ Зя,
б) tg-, если sina = - я < a < —;
2 3 2
в) sin—, если sina=-—, л<а<Д^;
2 7 2
г) ctg —, если cos а = -, < а <2л.
2 5 2
3) Упростите выражение:
а) sina ctg« - sin2 a; б) , sin2» • ;
1+cosa 2 1+cos 2a 1 + cos a
1 - cos a , sin a
в) —— - ; r) --------------.
sin a 1 + cos a
Тригонометрические функции
11. 1) Что такое числовая функция, ее область определения, об-
ласть значений?
2) Найдите область определения функции:
Зх+1 1
а) У =---------; б) у = — —;
х2-7х+12 sinx
в) у = у/4-х2; г) у = —*—.
COS X
3) Найдите область значений функции:
а) у = 3 cos х - 1; б) у = + 1;
х2
в) у = 2 - sin х; г) у = 3 - х4.
12. 1) Что такое график функции?
2) Постройте график функции:
а) у = - 2^; б) у = 2 - cos х; в) у = х + 2; г) у = sin х - 1.
3) Найдите точки пересечения графика функции f с осями ко-
ординат:
a) f (х) = х3 - 4х; б) /(х) = ^ + 1;
X
в) f (х) = 1 - х4; г)/(х)=—Ц-.
13. 1) Сформулируйте определение функции, возрастающей (убы-
вающей) на множестве Р.
2) Найдите промежутки возрастания и убывания функции,
график которой изображен на рисунке 79.
3) Найдите промежутки возрастания и убывания функции:
Q
а) у = 1 + 0,5 cos х; б) у = - — ;
в) у = 2х2 + 4х; г) у = 1,5 sin х - 1.
14. 1) Дайте определения точки максимума, точки минимума.
Что такое экстремум функции?
2) Укажите точки максимума и точки минимума функций,
графики которых изображены на рисунке 79.
3) Найдите точки максимума и точки минимума функции:
94 Тригонометрические функции
15. 1) Какие задачи решаются при исследовании функции?
2) Проведите исследование функции:
а) у = sin х - 2; б) у =-------;
X — о
в) у = х2 - 4х + 3; г) у = 2 cos х + 1.
3) Постройте графики этих функций.
16. 1) Дайте определения четной и нечетной функций. Каким
свойством обладают их графики?
2) Выясните, какая из указанных ниже функций является
четной, а какая — нечетной:
а) у = б) у = х + х5;
X
в) у = х cos х; г) у = Зх2 + х6.
3) Постройте график функции f, если известно, что:
a) f — нечетная; f (х) = cos х - 1 при х е (-оо; 0];
б) f — четная; f (х) = (х - I)3 при х е [0; оо);
в) f — четная; f (х) = sin х при х е (-оо; 0];
г) f — четная; f (х) = 4х - х2 при х е [0; оо).
17. 1) Что такое периодическая функция, период функции?
2) Какой наименьший положительный период имеет функ-
ция:
а) у = cos х; б) у = tg х; в) у = sin х; г) у = ctg х?
3) Найдите наименьший положительный период функции:
a) y = sin-; б) у = cos (4х + 1); в) у = tg 2х; г) y=cos^.
2 о
18. 1) Перечислите основные свойства функции синус.
2) Пользуясь свойствами функции синус, расположите в по-
рядке возрастания числа:
a) sin 0,3, sin 1,1, sin (-1,2); б) sin 4, sin 3,6, sin 2;
в) sin 0,4, sin (-0,9), sin 1,4; r) sin 4,3, sin 2,9, sin 1,9.
3) Исследуйте функцию и постройте ее график:
a) y = sin|x-—I; б) y = sin^;
V 4) 4
в) у = 1 + 1,5 sin х; г) у = sin 2х.
19. 1) Перечислите основные свойства функции косинус.
2) Пользуясь свойствами функции косинус, расположите
в порядке возрастания числа:
a) cos 0,3, cos (-2,9), cos 1,8; б) cos 5,3, cos 4,4, cos 6,2;
в) cos 0,5, cos (—1,3), cos 3; r) cos 6,1, cos 3,5, cos 4,9.
3) Исследуйте функцию и постройте ее график:
в) у = 2 cos х - 1; г) у =cos^.
95 Тригонометрические функции
20. 1) Перечислите основные свойства функции тангенс.
2) Пользуясь свойствами функции тангенс, расположите в по-
рядке возрастания числа:
a) tg (-0,4), tg 1,2, tg 0,8; б) tg 2,8, tg 3,9, tg 1,6;
в) tg 0,6, tg (-1,3), tg (-0,7); r) tg 4,3, tg 1,7, tg 2,5.
3) Исследуйте функцию и постройте ее график:
a)(/ = -tgx; б) i/ = tg£; в) у = 2 tg х; г) у = tg I х-7 I.
2 V 4 7
21. 1) Сформулируйте теорему о корне.
2) Сформулируйте определение арксинуса числа. Для каких
чисел определен арксинус?
3) Найдите значение выражения:
лАз 1 ( лГз ।
a) arcsin (-1) + arcsin ; б) arcsin - + arcsin I —— I;
в) arcsin -— - arcsin 1; r) arsin 0 - arcsin — .
2 I 2 J
22. 1) Сформулируйте определения арккосинуса и арктангенса
числа. Для каких чисел они определены?
2) Найдите значение выражения:
a) arccos (-1) + arctg -/З; б) arccos | + arcsin
лАз
в) arctg (-1) - arccos -—; г) arccos 0 + arctg —-.
2 3
23. 1) Запишите формулы для решения простейших тригономет
рических уравнений: sin х = a, cos х = a, tg х = а.
2) Решите уравнение:
а) 2 cos х + л/З = 0; б) -Уз tg х + 1 = 0;
в) 2 sin х - V2 =0; г) 2 cos х - 1 = 0.
24. Решите уравнение:
1) а) 2 sin2 х + 3 sin х = 2;
в) 2 cos2 х - 5 cos х = 3;
2) а) 6 sin2 х - 2 sin 2х = 1;
в) 4 sin х cos х = д/З;
б) tg2 x-4tgx + 3 = 0;
г) 2 sin2 х + sin x = 0.
6) sin2 x - cos2 x = ;
r) cos4 x - sin4 x = 1.
25. Решите неравенство (предварительно укажите на единичной
окружности множество точек Рх, таких, что х удовлетворяет
данному неравенству):
1) a) sinx>^; б) 2 cos х + 1 < 0; в) tgx<V§;
Л Л2
2) a) sin— cos— > б) I sin — -cos — I <
’ 2 2 4 2 2j2
в) 2 sin2 — < 1; г) cos2 — - sin2 — > - — •
’ 2 2 2 2 2
96 Тригонометрические функции
Производная
и ее применения
§4.
Производная
12. Приращение функции
Часто нас интересует не значение какой-либо величи-
ны, а ее изменение. Например, сила упругости пружины про-
порциональна удлинению пружины; работа есть изменение энер-
гии; средняя скорость — это отношение перемещения к промежут-
ку времени, за который было совершено это перемещение, и т. д.
При сравнении значения функции f в некоторой фиксирован-
ной точке х0 со значениями этой функции в различных точках х,
лежащих в окрестности х0, удобно выражать разность f (х) - f (х0)
через разность х - х0, пользуясь понятиями «приращение аргумен-
та» и «приращение функции». Объясним их смысл.
Пусть х — произвольная точка, лежащая в некоторой окрест-
ности фиксированной точки х0. Разность х - х0 называется прира-
щением независимой переменной (или приращением аргумента)
в точке х0 и обозначается Ах. Таким образом,
Дх = х - х0,
откуда следует, что х = х0 + Ах.
Говорят также, что первоначальное значение аргумента х0
получило приращение Дх. Вследствие этого значение функции f
изменится на величину
f (х) - f (х0) = f (х0 + Ах) - f (х0).
Эта разность называется приращением функции f в точке х0,
соответствующим приращению Ах, и обозначается символом А/ (чи-
тается «дельта эф»), т. е. по определению
А/ = f (х0 + Дх) - f (х0), (1)
откуда
f (x) = f (х0 + Дх) = f (х0) + А/.
Обратите внимание: при фиксированном х0 приращение А/
есть функция от Ах.
Л/ называют также приращением зависимой переменной
и обозначают через Аг/ для функции у = f (х).
97 Производная и ее применения
Пример 1. Найдем приращения Дх и Д/ в точке х0, если
f (х) = х2, х0 = 2 и: а) х = 1,9; б) х = 2,1.
а) Дх = х - х0 = 1,9 - 2 = -0,1;
Д/ = f (1,9) - f (2) = 1,92 - 22 = -0,39;
б) Дх = х - х0 = 2,1 - 2 = 0,1;
Д/ = f (2,1) - f (2) = 2,12 - 22 = 0,41.
Пример 2. Найдем приращение Д/ функции f (х) = —
в точке х0, если приращение аргумента равно Дх.
По формуле (1) находим:
Af = f(x0 + Дх) - f (х0) =-Ц----L = х° <хо + А*) = -—
х0 + Дх х0 х0(х0 + Дх) х0(х0 + Дх)
Пример 3. Дан куб с ребром а. Выразим погрешность ДУ,
допущенную при вычислении объема этого куба, если погрешность
при измерении длины ребра равна Дх. По определению прираще-
ния х = а + Дх, тогда
ДУ = V (х) - V (а) = (а + Дх)3 - а3 = За2 Дх + За (Дх)2 + (Дх)3.
Рассмотрим график функции у = f (х). Геометрический
смысл приращений Дх и Д/ (приращение Д/ обозначают также Дг/)
можно понять, рассмотрев рисунок 80.
Прямую I, проходящую через любые две точки графика
функции f, называют секущей к графику f. Угловой коэффи-
циент k секущей, проходящей через точки (х0; г/0) и (х; у), равен
у —
-----. Его удобно выразить через приращения Дх и Да (рис. 80):
х-х0
k = tg а = — .
Дх
(Напомним, что угловой коэффициент прямой у = kx + Ь ра-
вен тангенсу угла а, который эта прямая образует с осью абсцисс.)
Производная и ее применения
С помощью введенных обозначений приращений удобно так-
же выражать среднюю скорость движения за промежуток времени
[t0; t0 + At]. Если точка движется по прямой и известна ее коорди-
ната х (t), то
v - Дх - х(*о + д0-*(<о)
с"' ' At ~ At
Эта формула верна и для At < 0 (для промежутка
[t0 + At; t0]). В самом деле, в этом случае перемещение точки равно
х (t0) - х (t0 + Ах); длительность промежутка времени равна -At,
и, следовательно,
V мп - xi-to'>xi-to + д0 _ x(t0 + At)-x(t0)
с₽( _дг д/
. А/ /(х0 + Дх)-/(х0)
Аналогично выражение — =---------------------- называют
Ах Ах
средней скоростью изменения функции на промежутке с конца-
ми х0 и х0 + Ах.
Упражнения
177.— а) Стороны прямоугольника равны 15 м и 20 м. Найдите
приращения его периметра и площади, если: 1) меньшую
179.
его сторону увеличили на 0,11 м; 2) большую его сторону
увеличили на 0,2 м.
б) Радиус круга равен 2 см. Найдите погрешность, допу-
щенную при вычислении его площади, если погрешность
при измерении длины радиуса равна: 1) 0,2 см; 2) АЛ;
3) 0,1 см; 4) h.
Найдите приращение функции / в точке х0, если:
a) f (х) = , хп = -2, Ах = 0,1;
х
б) f (х) = 2х2 - 3, х0 = 3, Дх = -0,2;
в) f М = Зх + 1, х0 = 5, Дх = 0,01;
„2
Г) f (х) = —, х0 = 2, Дх = 0,1.
Найдите приращения Ах и А/ в точке х0, если:
a) f (х) = cos2 х, х0 = х =
б) f (х) = 4х - х2, х0 = 2,5, х = 2,6;
в) f (х) = tg х, х0 = р х = |;
г) f (х) = V2x -1, х0 = 1,22, х = 1,345.
99 Производная и ее применения
180.— Выразите приращение функции f в точке х0 через х0 и Дх,
если:
a) f (х) = 1 - Зх2; б) f (х) = ах + Ь;
в) / (х) = 2х2; г) f(x) = -i.
181.—
182.4
183.
184.
На рисунке 81 изображен график движения автобуса.
Найдите среднюю скорость движения за промежуток вре-
мени:
а) [0; 3]; б) [3; 5]; в) [3,25; 5,25]; г) [0; 8].
Точка движется по координатной прямой, причем в лю-
бой момент времени t ее координата равна 3 + 12t — t2.
На сколько и в каком направлении переместится точка
за промежуток I времени:
а) [2; 2,5]; б) [7; 8]; в) [4; 5]; г) [6; 8]?
Чему равна ее средняя скорость за промежуток I?
Постройте прямые, проходящие через точку (1; 3) и имею-
щие угловые коэффициенты:
а) -1 и 2; б) - и -3; в) 3 и -2; г) и -2.
2
Выясните в каждом из случаев, какой угол (тупой или
острый) образуют эти прямые с осью абсцисс.
Найдите угловой коэффициент секущей к графику функ-
ции f (х) = х2, проходящей через точки с данными абс-
циссами Xj и х2. Какой угол (острый или тупой) образует
секущая с осью Ох, если:
а) х, = 0, х2 = 1; б) Xj = -1, х2 = -2;
в) Xj = 1, х2 = 2; г) Xj = -1, х2 = 0?
100 Производная и ее применения
185.— Ребро куба х получило приращение Дх. Найдите прираще-
ние площади полной поверхности куба.
186.— Выразите Д/ и — через хп и Дх и преобразуйте получен-
Дх
ные выражения:
a) f (х) = -Xs + Зх; б) f (х) = —;
х2 -1
в) f (х) = Xs - 2х; г) f (х) = ——.
х2 +1
187. - Найдите среднюю скорость точки, движущейся по прямой,
за промежуток времени [t0; t0 + At], если известен закон
движения:
a) x(t)=uot——; б) х (t) = -at + b;
в) x (t) = г) x (t) = at - b.
13. Понятие о производной
1. Понятие о касательной к графику функции. Гра-
фики практически всех известных вам функций изображались
в виде гладких кривых. Рассмотрим, как геометрически устроены
такие кривые, на конкретном примере — графике функции у = х2
(рис. 82) при значениях х, близких к 1.
Для этого увеличим единицу масштаба (по сравнению с мас-
штабом рисунка 82) в 10 раз; в этом масштабе построим график
у = х2 на отрезке [0,5; 1,5] (рис. 83). Затем, увеличивая масштаб
еще в 10 раз, построим график функции на отрезке [0,95; 1,05]
(рис. 84). На этом рисунке хорошо видно, что при значениях,
близких к 1, график функции у = х2 практически не отличается от
маленького отрезка прямой у = 2х - 1, т. е. точки графика данной
функции как бы «выстраиваются» вдоль этой прямой.
Аналогичным свойством обладает любая гладкая кривая:
произвольный ее маленький участок практически не отличается
от отрезка некоторой прямой I. (Интересно заметить, что графопо-
строители, применяемые в ЭВМ, «рисуют» графики гладких функ-
ций по точкам, проводя в каждой точке маленький отрезок.) Отме-
тим, что для каждой точки гладкой кривой соответствующая этой
точке прямая (т. е. прямая, отрезком которой мы представляем
себе маленький участок кривой) вполне определена. Чтобы понять
это, обратимся к следующей наглядной иллюстрации.
Допустим, мы хотим изготовить трафарет, чтобы быстро ри-
совать синусоиду, параболу или гиперболу и т. п. Для этого пред-
варительно на миллиметровой бумаге строится возможно точнее
график этой кривой. Как вы можете убедиться, с помощью нож-
ниц удается аккуратно вырезать трафарет, граница которого —
101 Производная и ее применения
О оф «Ь
«? । Ф
-05 '-05
<5 —
<м
Рис. 82 Рис. 83 Рис. 84
102 Производная и ее применения
нужная нам кривая. Положение ножниц в каждой точке (а оно
и задает искомую прямую в этой точке) вполне определено: любое
отклонение ножниц в ходе разрезания от этого положения приво-
дит либо к появлению выступа, либо к прорезу трафарета.
Проходящую через точку (х0; f (х0)) прямую, с отрезком
которой практически сливается график функции f при значени-
ях х, близких к х0, называют касательной к графику функции f
в точке (х0; f (х0)). Возникает естественная задача: определить
точное положение касательной к графику данной функции f
в заданной точке. Координаты одной точки прямой I извест-
ны — это точка (х0; f (х0)). Остается найти угловой коэффициент k
касательной.
В качестве примера рассмотрим функцию у = х2. Ее график
в малой окрестности точки х0 близок к отрезку касательной I.
Поэтому естественно ожидать, что угловые коэффициенты се-
кущих, проходящих через точки (х0; х(2) и (х0 + Дх; (х0 + Дх)2),
будут близки к угловому коэффициенту k, если Дх будет неогра-
ниченно приближаться к нулю (т. е. точка х приближается к х0).
Угловой коэффициент k (Дх) секущей, проходящей через точ-
Дг/
ки (х0; у (х0)) и (х0 + Дх; у (х0 + Дх)), равен — (п. 12), где Ду —
приращение функции у в точке х0, соответствующее приращению
Дх аргумента. Для функции у = х2
... ч («о + д*)2-*о 2х0Дх+(Дх)2
й(Дх) = — =------------- = —2--------= 2х0 + Дх. (1)
Дх Дх Дх
Чтобы найти угловой коэффициент касательной, остается
выяснить, к какому значению близко k (Дх), если Дх приближает-
ся к нулю. Очевидно, что k (Дх) близко к 2х0. Следовательно,
при очень малых значениях Дх угловой коэффициент секущей
близок к 2х0. При х0 = 1 получаем k = 2. Учитывая, что искомая
касательная проходит через точку (1; 1), приходим к выводу, что
уравнение касательной таково: у = 2х - 1. К этому же выводу при-
шли в начале пункта из чисто наглядных соображений.
2. Мгновенная скорость движения. Обратимся теперь к за-
даче, известной вам из физики. Рассмотрим движение точки по
прямой. Пусть координата х точки в момент времени t равна х (t).
Как и в курсе физики, предполагаем, что движение осуществляет-
ся непрерывно и плавно. Иными словами, речь идет о движениях,
наблюдаемых в реальной жизни. Для определенности будем счи-
тать, что речь идет о движении автомобиля по прямолинейному
участку шоссе.
Поставим задачу: по известной зависимости х (t) определить
скорость, с которой движется автомобиль в момент времени t (как
вы знаете, эта скорость называется мгновенной скоростью); если
зависимость х (t) линейна, ответ прост: в любой момент времени
103 Производная и ее применения
(2)
скорость есть отношение пройденного пути ко времени. Если дви-
жение не равномерно, задача сложнее.
Тот факт, что в любой момент времени автомобиль движется
с какой-то определенной (для этого момента) скоростью, очеви-
ден. Эту скорость легко найти, сделав в момент времени t0 фото-
снимок спидометра. (Показание спидометра указывает значение
мгновенной скорости в момент t.) Чтобы найти скорость имгн (t0),
зная х (t), на уроках физики вы поступали следующим образом.
Средняя скорость за промежуток времени длительностью | A11
от t0 до t0 + At известна (п. 12):
vcp(AO = ^
Как мы предположили, тело движется плавно. Поэтому есте-
ственно полагать: если At очень мало, то за этот промежуток вре-
мени скорость практически не меняется. Но тогда средняя ско-
рость (на этом промежутке) практически не отличается от значе-
ния 1>мгн (t0), которое мы ищем. Это подсказывает следующий
способ определения мгновенной скорости: найти иср (At) и посмот-
реть, к какому значению оно близко, если считать, что At практи-
чески не отличается от нуля.
Рассмотрим конкретный пример. Найдем мгновенную ско-
рость тела, брошенного вверх со скоростью v0. Высота его в мо-
gt^
мент t находится по известной формуле й (t) = uot - .
1)
Ай (t) =
2)
St^1
-£-=voM-gtobt-
g-(At)2
2
(3)
3)
Найдем сначала Ай:
(At)2
(u0-gt0)At-g ——
У ср (ДО =----------------= vo-Sto - -y
Будем теперь уменьшать AZ, приближая его к нулю. (Для
краткости говорят, что At стремится к нулю. Это записывается
так: At —> 0.)
g'Af
Как легко понять, в этом случае значение —— тоже стре-
g’At
мится к нулю, т. е. —— 0 при At —> 0.
А поскольку величины п0 и -gt0, а значит, и v0 - gt0 постоян-
ны, из формулы (3) получаем:
ocp(At) -> v0 - gt0 при At —> 0.
Итак, мгновенная скорость точки в момент времени t0 нахо-
дится по формуле
Члгн <Л/> = vo ~ St0.
104 Производная и ее применения
3. Производная. Рассмотренные две задачи о вычислении
углового коэффициента касательной к параболе в точке с абсцис-
сой х0 = 1 и нахождении мгновенной скорости тела, брошенного
вверх со скоростью п0, имели различные формулировки. Однако
в обоих случаях мы действовали, по существу, придерживаясь
одной схемы. В применении к произвольной функции f и любой
точке х0 ее области определения эта схема может быть описана
следующим образом.
1) С помощью формулы, задающей функцию /, находим ее
приращение в точке х0:
А/ = f (х0 + Ах) - f (х0).
2) Находим выражение для разностного отношения —:
Д/ _ У(х0 + Дх)- /(х0)
Дх Дх
которое затем преобразуем — упрощаем, сокращаем на Дх и т. п.
3) Выясняем, к какому числу стремится —, если считать,
Дх
что Дх стремится к нулю.
Найденное таким образом число иногда называется (по ана-
логии с физикой) скоростью изменения функции f в точке х0 или
(что более принято) производной функции f в точке х0.
Определение. Производной функции f в точ-
ке х0 называется число, к которому стремится раз-
ностное отношение
ДУ = У (х0 + Дх) - У (х0)
Дх Дх
при Дх, стремящемся к нулю.
Производная функции f в точке х0 обозначается f (х0) (чита-
ется: «Эф штрих от х0»).
Пример 1. Найдем производную функции f (х) = х3 в точ-
ке х0.
Будем действовать по описанной выше схеме.
1) Д/ = (х0 + Дх)3 - х30 = Зх2, Дх + Зх0 (Дх)2 + (Дх)3.
2) = Зхр + Зх0 Дх + (Дх)2 (Дх * 0).
3) Теперь заметим, что слагаемое ЗХр постоянно, а при
Дх —> 0 очевидно, что Зх0 Дх —> 0 и (Дх)2 —» 0, а значит,
и Зх0 Дх + (Дх)2 —> 0. Получаем:
— Зх? при Дх —> 0.
Дх 0
Следовательно,
Г (х0) = Зх2.
105 Производная и ее применения
Пример 2. Найдем производную функции f (х) = kx + b
(k и b постоянны) в точке х0.
1) Д/ = (k (х0 + Дх) + Ъ) - (fex0 + Ь) = &Дх.
2) ^-=k.
’ Ьх
3) Поскольку k — постоянная, — — постоянное число при
Дх
любом Дх, и, значит, — -> k при Дх 0.
Дх
Итак, (kx + Ъ)' - k.
Функцию, имеющую производную в точке х0, называют
дифференцируемой в этой точке. Пусть Dr — множество точек,
в которых функция f дифференцируема. Сопоставляя каждому
х е Dj число f (х), получим новую функцию с областью опреде-
ления Dv
Эта функция называется производной функции у = f (х)
и обозначается f или у'.
Нахождение производной данной функции f называется
дифференцированием.
В этом пункте мы получили следующие формулы дифферен-
цирования:
(х2)' = 2х, (х3)' = Зх2, (kx + b)' = k.
Полагая в формуле (kx + b)' = k, что k = 0, Ь = С, где С —
произвольная постоянная, получаем, что С - 0, т. е. производная
постоянной равна нулю.
Упражнения
188.—
189.
190.
Постройте график функции f и проведите к нему касатель-
ную, проходящую через точку с абсциссой х0. Пользуясь
рисунком, определите знак углового коэффициента этой
касательной:
а) f (х) = х2 - 2х - 3, х0 = 0, х0 = 3, х0 = 2, х0 = -1;
х2
б) f (х) = — + 1, х0 = -2, х0 = 1, х0 = -1, х0 = 2.
Определите знак углового коэффициента касательной,
проведенной к графику функции (рис. 85) через точки
с абсциссой Xj, х2, х3, х4 (если касательная существует).
Какой угол (острый или тупой) образует эта касательная
с осью абсцисс? В окрестности каких точек график функ-
ции является «гладкой» кривой?
Запишите промежутки возрастания и убывания функции
(рис. 86). Определите знак углового коэффициента каса-
тельной в каждой из точек, отмеченных на графике.
Производная и ее применения
Л/
Дх
191.— Вычислите
в точке х0, если:
a) f (х) = 2х2, х0 = 1, Дх равно 0,5; 0,1; 0,01;
б) f (х) = х2, х0 = 1, Дх равно 0,5; 0,1; 0,01.
д Г
192. К какому числу стремится отношение — при Дх
Дх
0, если:
а) = 8х0 + 4Дх, х0 равно 2; -1;
б) Л- = 3Xq + Зх0Дх + (Дх)2, х0 равно 1; -21;
107 Производная и ее применения
193.—
Используя формулы дифференцирования, полученные в
п. 13, найдите производную функции f в точке х0, если:
a) f (х) = Xs, х0 равно 2; -1,5;
б) f (х) = 4 - 2х, х0 равно 0,5; -3;
в) f (х) = Зх - 2, х0 равно 5; -2;
г) f (х) = х2, х0 равно 2,5; -1.
194.— Пользуясь определением производной, найдите
значения
производной функции f, если:
a) f (х) = х2 - Зх в точках -1; 2;
б) f (х) = 2х3 в точках 0; 1;
в) f (х) = — в точках -2; 1;
г) f (х) = 4 - х2 в точках 3; 0.
{г
1УЭ.—
196.
Найдите уравнение касательной к графику функции
f (х) = х2, проходящей через его точку с абсциссой х0, если:
а) х0 = -1; б) х0 = 3; в) х0 = 0; г) х0 = 2.
Пользуясь определением, найдите мгновенную скорость
точки, движущейся прямолинейно по закону х (t), в мо-
мент t0:
а) х (t) = -t2 + 8t, t0 = 6; 6) x (t) = 3t3 + 2, t0 = 2;
,2
в) x (t) = , t0 = 4; r) x (t) = 5t - 3, t0 = 10.
14. Понятие о непрерывности функции
и предельном переходе
Вернемся к задаче определения мгновенной скорости
в точке t0 (см. формулу (3) п. 13). Функция t>cp (At) = н0 - gt0 -
- g • не определена при At = 0. Но для числа L = vQ - gt0 при
уменьшении | At | разность пср (At) - L приближается к нулю. Имен-
но поэтому мы писали i>cp (At) —> v0 - gt0 при At -> 0.
Вообще говорят, что функция f стремится к числу L при х,
стремящемся к х0, если разность / (х) — L сколь угодно мала,
т. е. | f (х) - L | становится меньше любого фиксированного h > 0
при уменьшении |Лх|, где Ах = х — х0. (Значение х = х0 не рас-
сматривается, как и в задаче определения мгновенной скорости.)
Вместо х —> х0 можно, конечно, писать Дх -> 0.
Нахождение числа L по функции / называют предельным
переходом. Вы будете иметь дело с предельными переходами
в двух следующих основных случаях.
108 Производная и ее применения
Первый случай — это предельный переход в разностном от-
Д/ - л
ношении —, т. е. нахождение производной. С этим случаем вы
Дх
познакомились в предыдущем пункте.
Второй случай связан с понятием непрерывности функции.
Если f (х) —> f (х0) при х —» х0, то функцию называют непрерывной
в точке х0. При этом f (х) - L = f (х) - f (х0) = АД получаем, что
| Д/| мало при малых | Дх|, т. е. малым изменениям аргумента
в точке х0 соответствуют малые изменения значений функции. Все
известные вам элементарные функции непрерывны в каждой точ-
ке своей области определения. Графики таких функций изобража-
ются непрерывными кривыми на каждом промежутке, целиком
входящем в область определения. На этом и основан способ по-
строения графиков «по точкам», которым вы все время пользуе-
тесь. Но при этом, строго говоря, надо предварительно выяснить,
действительно ли рассматриваемая функция непрерывна. В про-
стейших случаях такое исследование проводят на основании опре-
деления непрерывности.
И Пример 1. Докажем, что линейная функция f (х) = kx + b
непрерывна в каждой точке числовой прямой.
Нам нужно показать, что |Д/| становится меньше любого
фиксированного й>0 при малых |Дх|. Но |Д/| = |/(х0 + Дх)-
- f (х0)| = |(А (х0 + Дх) + b) - (kx0 + b) | = |/г| |Дх| и |Д/| будет мень-
ше h > 0, если взять |Дх| > при k 0 (при k = 0 можно брать
любое Дх).
Пример
в точке х0 при
Прежде всего отметим, что Дх мы будем выбирать таким,
что | Дх | < х0; тогда Vx = х0 + Дх определен. Оценим разность
и
2. Докажем, что функция /(х) = ух непрерывна
х0 > 0.
х0 + Дх - д/х0 | =
ХО + Дх - Tx^^Jxo + Дх + Txoj
Ах
|Дх|
х0
Легко видеть, что |Д/| станет меньше h > 0, если взять |Дх|
меньше -J xoh (и, как отмечали выше, меньше х0).
В задаче определения мгновенной скорости число омгн (t0)
было определено так, что функция оср (АД), «дополненная» в нуле
числом имгн, становится непрерывной в этой точке. Та же ситуация
и в задаче определения углового коэффициента касательной: функ-
ция g (Дх) = 2х0 + Дх станет непрерывной в этой точке, если счи-
тать, что g (0) = 2х0.
109 Производная и ее применения
Как видно из примеров предыдущего пункта, новая опера-
ция — предельный переход — служит новым средством нахожде-
ния неизвестных величин. Ею мы будем широко пользоваться
в этой главе. Выделим правила предельного перехода, которые до-
казываются в курсах математического анализа.
Правило 1. Если функция f непрерывна в точ-
ке х0, то Д/ —> О при Дх -> 0.
Правило 2. Если функция f имеет производную
в точке х0, то — —> f' (х0) при Дх —> 0.
Правила 1 и 2 сразу следуют из определений непрерывности
функции f в точке х0 и производной в точке х0.
Правило 3. Пусть f (х) —> A, g (х) -> В при х -» х0.
Тогда при х -> х0 (т. е. при Дх -> 0):
a) f (х) + g(x) А + В;
б) f (х) • g(x) -> А • В;
в) -> 4 (при В * °>-
ё(х) В
Для непрерывных функций f и g
А = f (х0), В = g(x0),
и эти правила означают, что сумма, произведение и частное непре-
рывных в точке х0 функций непрерывны в точке х0 (частное в слу-
чае, когда g (х0) * 0).
Правила предельного перехода широко используются при до-
казательстве непрерывности функций и выводе формул дифферен-
цирования.
Пример 3. Докажем, что функция h (х) = 10х + Vx непре-
рывна в любой точке х0 промежутка (0; оо). Непрерывность функ-
ций f (х) = 10х и g(x) = уГх была доказана в примерах 1 и 2. Сле-
довательно, функция h непрерывна как сумма двух непрерывных
функций (правило 3, а).
Пример 4. Докажем, что f (х) - 1 , где f (х) = 4х.
2-v x
1) Для произвольной точки х0 (см. пример 2)
Ах 7*о + /*о + д*
3) 7хо + Д* —> 7хо при Д* —> 0 по правилу 1, так как
функция -Тх непрерывна в точке х0 (см. пример 2), поэтому
110 Производная и ее применения
______1_______V 1
Jx? + 7xo + Дх 2 7*7
при Дх —> 0 (по правилу 3, а)
и
при Дх —> 0 (по правилу 3, в). Итак,
для любого положительного х.
Упражнения
197 .— Является ли непрерывной в каждой из точек хг, х2, х3
функция, график которой изображен на рисунке 87?
198 .— Постройте график функции f. Содержится ли в ее обла-
сти определения точка, в которой функция не является
непрерывной?
[ х -1 при х < -1,
a)Hx)=L 2Р
1-х при х > -1;
2-х при х < 1,
2х -1 при х > 1;
б) /(х) =
в)
f (X) =
х + 2 при х < 1,
— при X > 1.
х
111 Производная и ее применения
199 .— Является ли функция f непрерывной в каждой точке дан-
ного промежутка:
a) f (х) = х3 - 4х, (-оо; оо);
б) f (х) = —[2; оо);
х —1
200.- -
201.-6
202.
в) f (х) = х2 + 2х - 1, [-10; 20];
г) f (х) = 5х - Vx, (0; оо)?
К какому числу стремится функция /, если:
a) f (х) = х2 - Зх + 4, х -> 0, х -> 2;
б) Нх)=—х-> 1, х —> 4;
xi + 1
в) f (х) = 4 - х -> -2, х -> 0;
X2
г) f (х) = 4х-—, х -> -1, х -> 4?
Известно, что f (х) —> 1, g(x) -2 при х —> 3. К какому
числу при х —> 3 стремится функция:
. х „ , . /(x)-g(x)
<0 »/<*>« <«* 6)
в) 4/ (х) - g (х); г) (3 - g (х)) f (х)?
Известно, что f (х) -> 3, g (х) —> -0,5 при х —> -1. Найдите
число, к которому при х —> -1 стремится функция:
а)-^-; б) (f(x)-g(x))2;
(g(x))2
(g(x)]2
в) (/ (х))2 + 2g (х); г) \ ~
fix)-2
204,—
205.—
206. .
203.— К какому числу стремится функция:
„ . , „ х2 + Зх+ 2
a) f (х) =-----— при х 4;
х- 3
б) f (х) = * Зх при х -> -1;
хл -2х+ 7
5 _ 2х
в) f (х) = —- при х —> 2;
2+ х
х^ — 9
г) f (х) =---- при х -> -1?
х + 3
С какой точностью найден периметр квадрата, если его сто-
рона измерена с точностью до 0,01 дм?
С какой точностью достаточно измерить сторону правиль-
ного треугольника, чтобы найти его периметр с точностью
до 0,03 дм?
С какой точностью нужно измерить радиус, чтобы вычис-
лить длину окружности с точностью до 0,06 дм?
112 Производная и ее применения
207.— Известно, что f (х) -> A, g (х) -> В при х —> а. Пользуясь
правилами предельного перехода, докажите, что:
а) С f (х) —> С • А, где С — постоянная;
б) f (х) - g(x) -> А - В;
в) (/ (х))2 - (g (х))2 -> А2 - В2;
| г) (/ (х))" -> Ап, где п g Z.
15. Правила вычисления производных
1. Основные правила дифференцирования. Выведем
несколько правил вычисления производных. В этом пункте значе-
ния функций и и v и их производных в точке х0 обозначаются для
краткости так: и(х0) = и, v (х0) = о, и' (х0) = и', о' (х0) = о'.
Правило 1. Если функции и и v дифференцируе-
мы в точке х0, то их сумма дифференцируема в этой
точке и
(и + v)’ = и' + v'.
Коротко говорят: производная суммы равна сумме
производных.
1) Для доказательства вычислим сначала приращение сум-
мы функций в рассматриваемой точке:
Д (и + и) = и (х0 + Дх) + v (х0 + Дх) - (и (х0) + v (х0)) =
= (и (х0 + Дх) - и (х0)) + (о (х0 + Дх) - v (х0)) = Ди + Ди.
2) + _ Ди + Ди
Дх Дх Дх
3) Функции и и о дифференцируемы в точке х0, т. е. при
Дх -» 0
Аи^и', —
Lx Lx
„ Д(п + и) . . , „ . г, ч
Тогда — ----- —> и' + о' при Дх —> 0 (см. правило 3, а) предель-
Дх
ного перехода п. 14), т. е. (и + о)' = и' + о'.
Лемма. Если функция f дифференцируема в точ-
ке х0, то она непрерывна в этой точке: Д/ —> 0
при Дх —> 0, т. е.
f (х0 + Дх) -> f (х0) при Дх -> 0.
Действительно, Д/ = ^ • Дх —> f'(xo)-O при Дх —> 0, так как
Д- -> f'(Xn), а Дх -» 0. Итак, Д/ -> 0 при Дх -> 0, т. е. для диффе-
Дх
ренцируемых функций f (х0 + Дх) —> f (х0) при Дх —> 0.
113 Производная и ее применения
Правило 2. Если функции и и v дифференцируе-
мы в точке х0, то их произведение дифференцируемо
в этой точке и
(uv)' = u'v + uv'.
1) Найдем сначала приращение произведения:
Л (uv) = и (х0 + Дх) v (х0 + Дх) - и (х0) v (х0) =
= (и (х0) + Ди) (v (х0) + Ди) - и (х0) v (х0) =
= и (х0) v (х0) + Дио (х0) + и (х0) До + Ди До - и (х0) v (х0) =
= Дио (х0) + и (х0) Ди + Ди До.
2) = — о(х0) + и(х0) — + Ди —.
Дх Дх 0 0 Дх Дх
3) В силу дифференцируемости функций и и о в точке х0
при Дх —> 0 имеем — —> и', — ->v', Ди —> 0. Поэтому ~uv^
Ах Ах Ах
-> u'v (х0) + и (х0) о' + 0 • о' = u'v (х0) + и (х0) о', т. е. (ио)' = u'v +
+ ио', что и требовалось доказать.
Следствие. Если функция и дифференцируема
в х0, а С — постоянная, то функция Си дифферен-
цируема в этой точке и
(Си)' = Си'.
Коротко говорят: постоянный множитель можно вы-
носить за знак производной.
Для доказательства воспользуемся правилом 2 и известным
из п. 13 фактом С = 0:
(Си)' = С'и + Си' = 0 и + Си' = Си'.
Правило 3. Если функции и и о дифференцируе-
мы в точке х0 и функция v не равна нулю в этой точ-
ке, то частное — также дифференцируемо в х0 и
f и Y u'v - uv'
I о J v1 2
Выведем сначала формулу
1) Найдем приращение функции -:
v
дрП
V v J
] 1 _ о(х0)-о(х0 + Дх)_ -Av
v(x0 + Ax) v(Xq) v(x0)v(x0 +Ах) v(x0) (v (x0)+ До) ’
14 Производная и ее применения
2) Отсюда
_SV 1 =_______
&х а(х0)(с(х0)+Да)
3) При Дх -> О имеем — —> и' (в силу дифференцируемости v
Ьх
в точке х0), До —> 0 (по доказанной лемме). Поэтому
Теперь, пользуясь правилом нахождения производной произ-
ведения функций, находим производную частного:
Пример 1. Найдем производные функций:
а)/(х)=х* 2--; б)
х х3-1
ч С1Y х' 1
а) - = — - =-----—, поэтому
к X J ХА
( х2 --'l = (х2)' -f-) = 2х -f —^-1 = 2х + —;
к. X J \ X J \ X2 J X2
Г х2 _ (х2)'(х3 + 1)-х2 (х3 + 1)' _ 2х(х3 + 1)-х2 ((х3)'+ 1)'
^X3+1J (х3 + 1)2 (х3+1)2
2х(х3 + 1)-х2 (Зх2+0) 2х4 + 2х-Зх4 2х-х4
(х3 + 1)2 (х3 + 1)2 (х3 + 1)2
2. Производная степенной функции. Формула для вычисле-
ния производной степенной функции х", где п — произвольное на-
туральное число, большее 1, такова:
(хп)' = пхп-1. (1)
Формула производной функции х2 уже известна: (х2)' = 2х.
Пользуясь формулой дифференцирования произведения, по-
лучаем:
(х3)' = (х2 • х)' = (х2)' х + х2 (х)' = 2х х + х2 1 = Зх2;
(х4)' = (х3 • х)' = (х3)' х + х3 (х)' = Зх2 х + х3 1 = 4х3.
Заметим теперь, что
(х2)' = 2х2 “ *, (х3)' = Зх3 “ 4, (х4)' = 4х4 “ 4,
т. е. для п, равного 2, 3 и 4, формула (1) доказана. Продолжая
аналогичные рассуждения, нетрудно убедиться в справедливости
формулы (1) для п, равного 5, 6 и т. д.
115 Производная и ее применения
► Докажем, что формула (1) верна для любого натурального
п > 4.
Допустим, что формула (1) верна при п = к, т. е. что
(хк)' = кхк~ 4.
Покажем, что тогда формула (1) верна при п = k + 1. Дейст-
вительно,
(хк + ')’ = (х* • х)' = (хА)' • х + хк • (х)' =
= kxk ~1 х + хк = кхк + хк = (k + 1) хк.
Поэтому из того, что формула (1) верна при п = 4, следует, что она
верна и при п = 5, но тогда она верна и при п = 6, а следовательно,
и при п = 7 и т. д. до любого п е N (строгое доказательство основа-
но на методе математической индукции).
Если п=1 или п = 0, то при х 0 эта формула также спра-
ведлива. Действительно, по формуле (1) при х Ф О
(х1)' = 1 • х1 _ 1 = 1 • х° = 1,
(х0)' = 0 х0-1 = О,
что совпадает со значениями производных функций х и 1, уже
известными из предыдущего пункта.
Пусть, наконец, п — целое отрицательное число, тогда
п = -т, где т — число натуральное. Применяя правило диффе-
ренцирования частного и пользуясь уже доказанной для натураль-
ных т формулой (1), получаем при х 0:
= -тх т 1 = пхп *.
В результате можно сделать вывод:
|Для любого целого п и любого х (х Ф 0 при п. < 1)
(хп)' = пхп ' х.
Пример 2. Найдем производные функций:
а)/(х) = х’5; б)/(х)=3х7—
а) (х“5)' = -5х5 ~1 = -5х-6;
б) f Зх7 --^1 = 3 (х7)' - 5 (х-3)' = 3 • 7х6 - 5 (-3) х 4 =
к х3 J
= 21х6 + —.
х4
Из дифференцируемости степенной функции и основных
правил вычисления производных вытекает утверждение:
целые рациональные функции (многочлены) и дроб-
но-рациональные функции дифференцируемы в каж-
дой точке своей области определения.
116 Производная и ее применения
Упражнения
Найдите производные функций (208—211).
208.— а) f (х) = х2 + х3; f (х) = х2 + Зх - 1; б) г) f (х) = i + 5х -2; X f (х) = х3 + Vx.
в)
209 - а) f (х) = х3 (4 + 2х - х2); б) f (х) = Vx (2х2 -х);
в) f (х) = х2 (Зх + х3); г) f (х) = (2х - 3) (1 - х3).
210.— а) 1+2х х2 У ~ о Г б) У - 0 J 3-5х 2х-1 Зх-2 3-4х в)!/-5«+8; г,!,=
211,- а) у = х8 - Зх4 - х + 5; б) + 1 I го II а»
в) у = х7 - 4х5 + 2х - 1; г) у = ±+^ + 1. У 2 хз
Вычислите значения производной функции f в данных
точках:
а)
212.у
б)
в)
f (х) = х2 - Зх, х = -^, х = 2;
f (х) = х - 4 Vx, х = 0,01, х = 4;
/(х)=х- —, x = V2, х = -^=;
г) f(x)=-—х =-3, х = 0.
2+ х
213.- Решите уравнение f (х) = 0, если:
a) f (х) = 2х2 - х; б) f (х) = --х3 + х2 + 12;
3
в) f (х) =^--1,5х2-4х; г) f (х) = 2х - 5х2.
О
214,- Решите неравенство f (х) < 0, если:
a) f (х) = 4х - Зх2; б) f (х) = х3 + 1,5х2;
в) f (х) = х2 - 5х; г) / (х) = 4х - х3.
3
215.— Найдите производную функции:
a) f(x)=---б) f (х) = Г — + х2'l (2 --/х);
1 + 4х° \х у
в) / (х) = 5 2х ; г) f (х) =7х (Зх5-х).
II - хА
Найдите значения х, при которых производная функции f
равна нулю:
a) f (х) = х® - 3 — Xs + 5х; б) f (х) = 2х4 - х8;
в) f (х) = х4 + 4х; г) f (х) = х4 - 12х2.
117 Производная и ее применения
217 .— Решите неравенство /' (х) < 0, если:
a) f (х) = Xs - 6х2 - 63х; б) f (х) = Зх - 5х2 + х3;
в) f (х) = -|х3-8х; г) f (х) = Зх2 - 9х - х3.
218 .— Задайте формулой хотя бы одну функцию, производная ко-
торой равна:
а) 2х + 3; б) 16х3 - 0,4; в) 8х - 2; г) 9х2-^.
219 .- г Верно ли, что функция <р (х) = (х) + /2 (х) не имеет произ-
водной в точке х0, если известно, что:
а) каждая из функций fA (х) и f2 (х) не имеет производной
в точке х0;
I б) (х) имеет производную в точке х0, a f2 (х) не имеет?
16. Производная сложной функции
1. Сложная функция. Начнем с примера.
Пример 1. Пусть требуется вычислить по заданному зна-
чению х соответствующее значение г функции й, заданной фор-
мулой
г = й (х) = л/1 - х2 .
Для этого надо сначала вычислить по заданному х значение
У = / (х) = 1 - х2,
а затем уже по этому у вычислить
z = g (у) = Jy.
Итак, функция f ставит в соответствие числу х число у,
а функция g — числу у число г. Говорят, что й есть сложная функ-
ция, составленная из функций g и f, и пишут:
й (х) = g (f (х)).
Чтобы вычислить значение сложной функции й (х) = g (f (х))
в произвольной точке х, сначала вычисляют значение у «внутрен-
ней» функции f в этой точке, а затем g (у).
Какова область определения сложной функции g (f (х))?
Это — множество всех тех х из области определения функции /,
для которых f (х) входит в область определения функции g.
В рассматриваемом примере областью определения функ-
ции f является вся числовая прямая. Значение й (х) определено,
если значение f (х) принадлежит области определения функции
g(y) = yTy. Поэтому требуется, чтобы выполнялось неравенство
у > 0, т. е. 1 - х2 > 0, и, значит, область определения функции
g (f (х)) — это отрезок [-1; 1].
Производная и ее применения
2. Формула производной сложной функции. В предыдущих
пунктах вы научились находить производные рациональных функ-
ций, в частности многочленов. Однако задача вычисления произ-
водной функции f (х) = (2х + З)100, хотя и сводится к нахождению
производной многочлена, требует очень большого объема работы:
надо представить (2х + З)100 в виде многочлена и продифференци-
ровать 101 слагаемое полученной суммы. Можно заметно упро-
стить решение этой и других задач, доказав правило вычисления
производной сложной функции.
Если функция f имеет производную в точке х0,
а функция g имеет производную в точке у0 = f (х0),
то сложная функция h (х) = g (f (х)) также имеет
производную в точке х0, причем
К (*о) = ё’ (f (хо» Г (*о>- (!)
Для доказательства формулы (1) надо (как и раньше) при
Дх * 0 рассмотреть дробь — и установить, что — —> g' (у0) f (х0)
при Дх —> 0. Введем обозначения:
ty = f (х0 + Дх) - f (х0) = ДД
Тогда Дй = h (х0 + Дх) - h (х0) = g(f (х0 + Дх)) - g(f (х0)) =
= S (Уо + Ду) - g (</0) = №
/\у —> 0 при Дх 0, так как f дифференцируема в точке х0.
Далее доказательство проведем только для таких функ-
ций f, у которых Д/ ф 0 в некоторой окрестности точки х0.
Тогда — . — = — g' (у ) f (х0) при Дх-> 0, так как
Дх Ду Дх Ду Дх Уо °
— (х0) при Дх -> 0, а — —> g' (у0) при Ду -> 0, что выполне-
Дх Ду
но при Дх —> 0 (это отмечалось выше).
Пример 2. Вернемся к поставленной выше задаче и най-
дем производную функции h (х) = (2х + З)100.
Функцию h можно представить в виде сложной функции
h (х) = g(f (х)), где g(y) = у100, у = f (х) = 2х + 3.
Так как f (х) = 2 и g' (у) = 100у", имеем
К (х) = 2 • 1ООу08 = 200 (2х + З)99.
Пример 3. Найдем производную функции
й(х) =73х2 + 1.
Так как п (х) = g (f (х)),
то g' (у) = —L. и у' = f' (х) = 6х,
h' (х) = -±=у' = -
где у = f (х) = 3xz + 1, g (у) = ^у,
откуда
6х _ Зх
7зх2 + i 73*2 + 1
119 Производная и ее применения
Упражнения
Задайте формулами элементарные функции f и g> из которых составлена сложная функция h (х) = g (f (х^ (220—221). 220.— a) h (х) = cos Зх; б) й (х) = sin ^2х в) ft(x) = tg|~; г) h (х) =cos ^Зх + 221.— a) h (х) = (3 - 5х)5; б) h (х) = Vcosx; I в) h (х) = (2х + I)7; г) h (х) = tg 1. I х Найдите область определения каждой из функций (222—223). 222 -1 ai и - л/9 х2 • б) и - 1 :
д/х2 -7х+ 12
5-х2
/ У V Л- 5 ) у , sin х- — 1 6/
в) У = tg 2х; г) у = д/sinx. Найдите производные функций (224- 224. а) / (х) = (2х - 7)8; б) f (х) = в) /(х) = (9х + 5)4; г) / (х) = Z Х-9 225. а) /(х)=(з-|1 ; б) f (х) = в) /(х) = (4 - 1,5х)10; г) f (х) = -225). 1 (5х+1)3 ’ 1 (6х-1)5 ’ Z х8 fix-7 -(1-2х)4; <4 ) (5х - 2)13 - (4х + 7Г6.
226.— Найдите область определения функции:
а) у = Vl -2cosx; б) у = -1;
V х2
в) у = 7sinx-0,5; г) у = + 1.
227.— Заданы функции f (х) = 3 - 2х, g (х) = х2 и р (х) = sin х.
Задайте формулой сложную функцию h, если:
a) h (х) = f (g (х)); б) h (х) = g (р (х));
в) й(х) = g (f (х)); г) h (х) = р (f (х)).
Производная и ее применения
228.—
229.—
230.—
Заданы функции f(x) = ~ , g (х) = cos х и р (х) = -/х.
Задайте формулой сложную функцию h; найдите ее об-
ласть определения, если:
a) h (х) = f(g (х)); б) h (х) = f (р (х));
в) h (х) = р (g (х)); г) h (х) = р (f (х)).
Найдите такую функцию f, что f (g (х)) = х:
a) g (х) = 2х; б) g (х) = Vx;
в) g (х) = Зх + 2; г) g (х) = х2 + 1, х < 0.
Найдите производную функции
б) / (х) = д/1-х4
Л
a) f (х) = (х3 - 2х2 + З)17;
в) f (х) = 74х2 + 5;
_1
х2 + 3 ’
/(х) =(3-х3)5 +V2x-7.
г)
17. Производные тригонометрических
функций
1. Формула производной синуса. Докажем, что
функция синус имеет производную в любой точке и
(sin х)' = cos х. (1)
тт • о о а + Р • а-Р
Применяя формулу sm а - sin р = 2 cos —- sin--, находим
2 2
2 cos
Asinx = sin(x0 + Дх)-sinx0 =
Дх Дх
Дх
Хл ч---
° 2
Дх
sinAx
2
Дх
sm —
=-----— cos
Дх
2
Для вывода формулы (1) достаточно показать, что:
sinAx
9
а)---------> 1 при Дх -> 0;
Дх
2
Дх
п +--
° 2
б) cos х0 +
Опираясь на эти утверждения, можно получить формулу (1).
Действительно, при Дх —> 0
sinAx
---2 .cos
Дх Дх
2
cosx0 при Дх —> 0.
—> 1 cos х0 = cos х0.
. , Дх
О '
и 2
121 Производная и ее применения
|i Утверждения а) и б), на кото-
рые мы опирались выше, имеют на-
глядный геометрический смысл.
а) Отложим на единичной
окружности от точки Ро в обе сто-
роны дуги Р(ГА и Р0В длиной -Д--
(рис. 88). Тогда длина дуги АВ
равна | Лх|, а длина хорды АВ рав-
на 2 | sin А* |. При малых |Дх| дли-
на хорды АВ практически не отли-
чается от длины стягиваемой ею
дуги АВ. (Этим фактом вы уже пользовались в курсе геометрии
при выводе формулы длины окружности. Действительно, при
больших п верно, как известно, приближенное равенство Рп » С,
где Рп — периметр правильного вписанного n-угольника, а С —
длина окружности. Значит, длина стороны такого многоугольника
приближенно равна длине дуги, которую эта сторона стягивает.)
Следовательно,
sin^
Ах
2
1 при Дх -> 0.
б) Заметим, что длина хорды АВ меньше длины дуги АВ,
т. е.
. ы
2 sin 2
Воспользовавшись формулой разности косинусов и этим не-
равенством, находим:
( Ах ।
cosl х0 + —l-cosx0
Но ---- -> 0 при Дх -> 0. Поэтому cos х0 + — -> cosx0
при Дх -> 0.
Пример. По формуле дифференцирования сложной функции
(sin (ах + b)Y = a cos (ах + Ь).
122 Производная и ее применения
2. Формулы дифференцирования косинуса, тангенса и ко-
тангенса. Докажем следующее утверждение.
Функции у = cos х, у = tg х, у = ctg х имеют произ-
водные в каждой точке своей области определения,
и справедливы формулы:
(cos х)' = -sin х, (2)
(tgx)'= —1—, (3)
COS * X
(ctgx)' =----. (4)
sin X
Вывод формулы (2) основан на равенствах cos х = sin _ хJ»
cos - х J = sin х и правиле дифференцирования сложной функции:
(cosx)' = sin — -х =cos —-х - — - х = -sinx.
I <2 J) <2 J <2 )
Чтобы доказать справедливость формул (3) и (4), применим
формулу для нахождения производной частного и выведенные
формулы производной синуса и косинуса:
v ( sinxY (sinх)'cos х- (cos х)'sinx cos2x+sin2x_ i
\ ) I I n n n ’
\ COS X J COS* X COS* X COS* X
(ctg x)' =
COS X
sinx
(cos xY sin x - (sin x)' cos x
sin* X
1
sin2 x
• 9 9
- sin* X- COS* X
sin2 x
Упражнения
Найдите производную каждой из функций (231—233).
231.— - а) в) у = 2 sin х; у = -0,5 sin х; б) г) у = 1 -- sinx; у 2 у = 0,5 + 1,5 sin х.
232.- а) в) у = 3 cos х; у = 1 - cos х; б) г) у = х + 2 cos х; у = 2 sin х + 1,5 cos х.
233. а) в) у = 7з -3tgx; У = j tgx; б) г) у = cos х - tg х; у = 2 tg х - sin х.
234. Найдите f' (0) и f' a) f (х) = icos (2х в) f ( х) = 3 sin [ — - у 3 (л), если: - л); б) f (х) = х - tg (-2х); г) f(x) =2 cos
123 Производная и ее применения
235,—
Решите уравнение f (х) = 0, если:
a) f (х) = ~ х + cos х; б) f (х) = х - tg х;
в) f (х) = 2 sin х - 1; г) f (х) = х - cos х.
Найдите производную каждой из функций (236—238).
236 .— a) f (х) = х3 sin 2х; б) f (х) = х4 + tg 2х;
В) / (х) =----; г) f(x)=^ -
х sinx
237 .— a) f (х) = sin2 х; б) f (х) = tg х + ctg х;
в) f (х) = cos2 х; г) f (х) = sin2 х + cos2 х.
238 .— a) f (х) = cos 2х sin х + sin 2х cos х;
б) f (х) = cos2 - - sin2 —;
4 4
в) f (х) = sin 5х sin Зх + cos 5х cos Зх;
г) f (х) = sin Зх cos Зх.
239 .— Найдите точки, в которых f (х) = 0, f (х) > 0, если:
а) f (х) = 2 sin2 х - V2 х; б) f (х) = 2х + cos (4х - л);
в) f (х) = cos 2х; г) f (х) = sin 2х - -/З х.
240 . Задайте формулой хотя бы одну функцию f, если:
а) Г (х) = 1 - sin х; б) f (х) = 2 cos 2х;
в) f (х) = -cos х; г) f (х) = 3 sin х.
§5.
Применения непрерывности
и производной
18. Применения непрерывности
1. Непрерывность функции. В п. 14 вы познакоми-
лись с понятием непрерывности функции в точке. Если функция
непрерывна в каждой точке некоторого промежутка I, то ее назы-
вают непрерывной на промежутке I (промежуток I называют
промежутком непрерывности функции f). При переходе от одной
точки этого промежутка к близкой ей точке значение функции
меняется мало; график f на этом промежутке представляет собой
непрерывную линию, о которой говорят, что ее можно «нарисо-
вать, не отрывая карандаша от бумаги». (Так, во всяком случае,
обстоит дело для непрерывных функций, изучаемых в школьном
курсе.)
Производная и ее применения
Как было показано в п. 15, функ-
ция, дифференцируемая в точке х0, не-
прерывна в этой точке. Все дробно-рацио-
нальные и основные тригонометрические
функции дифференцируемы во всех точ-
ках своих областей определения. Следо-
вательно, эти функции и непрерывны в
каждой из этих точек.
Например, из дифференцируемости
функции f (х) = х2 на всей прямой, а функ-
ции f(x)= — на промежутках (-оо; 0)
и (0; со) вытекает непрерывность этих функций на соответствую-
щих промежутках.
Отметим следующее свойство непрерывных функций:
Если на интервале (а; Ь) функция f непрерывна
и не обращается в нуль, то она на этом интервале
сохраняет постоянный знак.
Это утверждение имеет наглядную интерпретацию. Допу-
стим, что найдутся такие точки хг и х2 интервала (а; Ь), что
f(xT) < 0, a f(x2) > 0.
Тогда непрерывная кривая (график функции /), соединяю-
щая точки А (хг; f (хх)) и В (х2; f (х2)), разделенные прямой у = 0,
пересекает эту прямую в некоторой точке х3 данного интервала
(рис. 89), т. е. f (х3) = 0. (Представим себе, что точки А и В нахо-
дятся на разных берегах реки, изображаемой интервалом (а; Ь).
Ясно, что туристу, для того чтобы попасть из А в В, надо где-то пе-
рейти реку.) Это противоречит условию: функция f не обращается
на интервале (а; Ъ) в нуль.
2. Метод интервалов. На свойстве непрерывных функций,
рассмотренном в этом пункте (его полное доказательство приво-
дится в курсах математического анализа), основан метод решения
неравенств с одной переменной (метод интервалов). Опишем его.
Пусть функция f непрерывна на интервале I и обращается
в нуль в конечном числе точек этого интервала. По сформулиро-
ванному выше свойству непрерывных функций этими точками I
разбивается на интервалы, в каждом из которых непрерывная
функция f сохраняет постоянный знак. Чтобы определить этот
знак, достаточно вычислить значение функции f в какой-либо од-
ной точке из каждого такого интервала.
X2— 1
Пример 1. Решим неравенство —---------> 0.
х2 -5х+ 6
X2 — 1
Функция / (х) =--------непрерывна в каждой точке своей
х2 - 5 х + 6
области определения (это дробно-рациональная функция) и обра-
Производная и ее применения
-------о-
-1
Рис. 90
-о->---□
12 3
щается в нуль в точках —1 и 1. Область определения этой функ-
ции — вся числовая прямая, за исключением нулей знаменателя,
т. е. точек 2 и 3. Эти точки и точки -1 и 1 разбивают область
определения f на 5 промежутков (рис. 90), в каждом из которых
функция f непрерывна и не обращается в нуль. На рисунке отме-
чен знак f в каждом из соответствующих интервалов, который
определяем, найдя знаки значений f во внутренних точках интер-
валов. Неравенство нестрогое, поэтому числа -1 и 1 (нули функ-
ции f) являются решениями неравенства. Рассматривая рисунок,
можно записать ответ: множество решений неравенства — объ-
единение промежутков (-оо; -1], [1; 2) и (3; оо).
Пример 2. Найдем один из корней уравнения х3 + 2х -
- 2 = 0 с точностью до 0,1.
Функция f (х) = х3 + 2х - 2 непрерывна, поэтому достаточ-
но найти отрезок длиной 0,2, на концах которого f имеет зна-
чения разных знаков. Имеем f (1) = 1 > 0, /(0) = -2 < 0, поэтому
корень уравнения существует и он принадлежит отрезку [0; 1].
f (0,6) = 0,63 + 2 0,6 - 2 = -0,584 <0 и f (1) > 0, значит, корень
лежит на отрезке [0,6; 1]. Наконец, f (0,8) = 0,112 > 0, а /(0,6) < 0,
получили, что корень на отрезке [0,6; 0,8]. Теперь мы можем его
найти: х0 ~ 0,7 с точностью до 0,1.
3. Пример функции, не являющейся непрерывной. Прак-
тически все функции, с которыми вы встречались до сих пор, не-
прерывны в любой точке своей области определения. Не следует,
однако, считать, что это верно для любой функции.
Приведем пример. Рассмотрим функцию f (х) = {х}, где
{х} — дробная часть числа х (график f (х) = {х} изображен на ри-
сунке 91, а), и возьмем любую целочисленную точку оси абсцисс,
например х = 2.
Рис. 91
Производная и ее применения
Основное свойство непрерывной в точке х0 функции
(f (хо + ^х) “* f (х0) ПРИ Д* -> О) в этом случае не выполняется.
Действительно, пусть Дх -» 0. Если Дх > 0, то {х0 + Дх} близко к
нулю. Если же Дх < 0, то значения {х0 + Дх} близки к 1. В то же
время функция f (х) - {х} непрерывна во всех точках, отличных от
точек х = п, где п — целое число.
Это свойство функции f (х) = {х} нетрудно понять, рассмотрев
рисунок 91, а.
4. Пример функции, непрерывной, но не дифференцируе-
мой в данной точке. Примером такой функции является функция
f (х) = | х | (рис. 91, б), которая непрерывна, но не дифференцируе-
ма в нуле. Напомним, что
, I, [ х, если х > 0,
Нх)=И= л
I —х, если х < 0.
Непрерывность функции f (х) = | х | в любой точке (в том чис-
ле и в нуле) очевидна.
Рассмотрим график этой функции. Для любого х > 0 в неко-
торой окрестности точки х0 > 0 функция равна х, и поэтому произ-
водная ее в таких точках равна х', т. е. |х|' = 1 при х > 0. Так как
|х| = -х при х < 0, то |х|' = —1 при отрицательных значениях х.
В точке 0 функция f (х) = |х| не имеет производной.
Докажем это методом от противного. Допустим, что f (х) = | х |
Д/(0)
имеет производную в нуле, т. е. ----- стремится к некоторому
числу А при Ах —> 0. Тогда при всех достаточно малых |Дх| зна-
Д/ - . .
чения — близки к А, и, в частности, при малых значениях Дх
Дх
должно выполняться неравенство
Л/(0)
Дх
<1.
При Дх > 0 справедливо неравенство 11 - А | < 1, откуда
-1 < 1 - А < 1, т. е.
0<А<2. (1)
Для Дх < 0 справедливо неравенство |-1 - А| < 1, откуда
-1 < -1 - А < 1, т. е.
-2<А<0. (2)
Неравенства (1) и (2) противоречивы. Следовательно, наше
допущение о существовании производной функции f (х) = |х| в ну-
ле неверно.
Итак,
1 при х>0,
не существует при х = 0,
-1 при х<0.
127 Производная и ее применения
Упражнения
241.— Является ли функция f непрерывной в точках хг = О
и х2 = -1, если:
{х + 1 при х < -1,
х-х при х > -1;
в) ПР” 1<0’ г) = + Л
[ 5-2х при х > 0;
242.— Найдите промежутки непрерывности функции:
уЗ 1 О'?
a) f (х) = Xs - 2х2; б) f (х) = ---
Зх + х2
в) f (х) = 2х4 - Зх2 +4; г) f (х) = -—~ —.
{ хА -8
243.-1 Докажите, что данное уравнение имеет корень, принадле-
|жащий отрезку [0; 1], и найдите его с точностью до 0,1:
а) 1,4 - 10х2 - х3 = 0; б) 1 + 2х2 - ЮОх4 = 0;
в) х3 - 5х + 3 = 0; г) х4 + 2х - 0,5 = 0.
Решите неравенства (244—245).
244. а) х2 - 5х + 4 > 0; б) *+-3—>0; х2 + 4 х - 5
в) х2 - Зх - 4 < 0; г) х2-7х+6 х-2
245. а) (х-2)(х-4) 0 х2 + 2 х - 3 б) 8- — < 1; х2 - 6 х + 8
в) 2х2 + 5х > х2 + 5х + 4 г) х2-2х-3 (х+ 3)(х-4)
246.-
Найдите область определения функции:
а) / (х) = Гео Hi 1 н б) f(x)=^ + 1; х2 -4
в) f(x) = у х2 + 7х+12. X Г) /(х) = х2 -1
247.—
При каких значениях т функция
числовой прямой, если:
4-х при х < 4,
(x-wi)2 при х > 4;
Зх2 + т при х <0,
х + 2 при х > 0;
a) f (х) =
в) f (х) =
f непрерывна на всей
б) /’(х) =
х2 - Зх.
х2 -т ’
f (*) =
5-х ?
х4 + т
128 Производная и ее применения
Решите неравенства (248—249).
248.— а) х4 - 10х2 + 9 < 0; б) х4 - 8 > 7х2;
в) х4 - 5х2 + 6 > 0; г) 5х2 - 4 > х4.
249.— а) (х2 - 1) (х + 4) (х3 - 8) < 0; б) -^х2-4 (х-3) < 0;
в) х2 (3 - х) (х + 2) > 0; (х-2)3(х + 5) г) °-
(х + З)2
250. — Найдите область определения функции:
a) f (х) = л/9х - х3 ; б) f (х) = х2
V х
в) f (х) = V16x-x3 ; г) f (х) = 11-^-.
\ хл
19. Касательная к графику функции
1. Касательная. С понятием касательной к графику
функции вы уже знакомы. График дифференцируемой в точке х0
функции f вблизи х0 практически не отличается от отрезка каса-
тельной, а значит, он близок к отрезку секущей I, проходящей
через точки (х0; f (х0)) и (х0 + Дх; f (х0 + Дх)). Любая из таких се-
кущих проходит через точку А (х0; f (х0)) графика (рис. 92). Для
того чтобы однозначно задать прямую, проходящую через данную
точку А, достаточно указать ее угловой коэффициент. Угловой
коэффициент — секущей при Дх -> 0 стремится к числу f (х„)
Дх
(его мы примем за угловой коэффициент касательной). Говорят,
что касательная есть предельное положение секущей при Ах —> 0.
Если же f (х0) не существует, то касательная либо не сущест-
вует (как у функции у = |х| в точке (0; 0), рис. 91, б), либо верти-
кальна (как у графика у = л[х в точке (0; 0), рис. 93).
Итак, существование производной функции f в точке х0 экви-
валентно существованию (невертикальной) касательной в точке
(х0; f (х0)) графика, при этом угловой коэффициент касательной
равен f (х0). В этом состоит геометрический смысл производной.
129 Производная и ее применения
Касательная к графику дифференцируемой в точ-
ке х0 функции f — это прямая, проходящая через
точку (х0; f (х0)) и имеющая угловой коэффициент
Г (х0).
Проведем касательные к графику функции f в точках хх, х2,
х3 (рис. 94, а) и отметим углы, которые они образуют с осью
абсцисс. (Это угол, отсчитываемый в положительном направлении
от положительного направления оси до прямой.) Мы видим, что
угол сц острый, угол а3 тупой, а угол а2 равен нулю, так как пря-
мая I параллельна оси Ох. Тангенс острого угла положителен, ту-
пого — отрицателен, tg 0 = 0. Поэтому
f (xt) > 0, /' (х2) = 0, f (х3) < 0.
Построение касательных в отдельных точках позволяет более
точно строить эскизы графиков. Так, например, для построения
эскиза графика функции синус предварительно находим, что
в точках 0; | и п производная синуса равна 1; 0 и -1 соответствен-
но. Построим прямые, проходящие через точки (0; 0),
и (л; 0) с угловыми коэффициентами 1, 0 и -1 соответственно
(рис. 94, б). Остается вписать в полученную трапецию, образован-
ную этими прямыми и прямой Ох, график синуса так, чтобы при
х, равном 0, и л, он касался соответствующих прямых.
Отметим, что график синуса в окрестности нуля практически
неотличим от прямой у = х. Пусть, например, масштабы по осям
выбраны так, что единице соответствует отрезок в 1 см. Имеем
sin 0,5 « 0,479425, т. е. | sin 0,5 - 0,5 | ~ 0,02, и в выбранном
масштабе это соответствует отрезку длиной 0,2 мм. Поэтому в ин-
тервале (-0,5; 0,5) график функции у = sin х будет отклоняться
(в вертикальном направлении) от прямой у = х не более чем
на 0,2 мм, что примерно соответствует толщине проводимой ли-
нии.
Рис. 94
130 Производная и ее применения
2. Уравнение касательной. Выведем теперь уравнение каса-
тельной к графику функции f в точке А (х0; f (х0)).
Уравнение прямой с угловым коэффициентом f (х0) имеет
вид:
У = Г (х0) - х + Ъ.
Для вычисления b воспользуемся тем, что касательная про-
ходит через точку А:
f (х0) = Г (х0) х0 + Ь, откуда b = f (х0) - f (х0) • х0,
значит, уравнение касательной таково:
У = f (х0) ’ х ~ f <хо) ’ хо + f (хо)’
или
У = f (*0) + Г <жо> <* - *о)-
(1)
Пример 1. Найдем уравнение касательной к графику
функции f (х) - х3 - 2х2 + 1 в точке с абсциссой 2.
В этом примере х0 = 2, f (х0) = / (2) = 23 - 2 • 22 + 1 = 1,
f (х) = Зх2 - 4х, f (х0) = f' (2) = 3 - 22 - 4 • 2 = 4. Подставляя эти
числа в уравнение (1), получаем уравнение у = 1 + 4 (х - 2), т. е.
у = 4х - 7.
Пример 2. Выведем уравнение касательной к параболе
у - х2 в точке с абсциссой х0.
Имеем у (х0) = х$, а у' (х0) = 2х0. Подставляя эти значения
в уравнение (1) касательной, получаем у = х% + 2х0 (х - х0), т. е.
у = 2х0х - Xq. Например, при х0 - 1 получаем касательную, имею-
щую уравнение у = 2х - 1.
Найдем координаты точки Т пересечения касательной к па-
раболе в точке А (х0; х(2) с осью Ох (рис. 95). Если (xt; 0) — коор-
динаты точки Т, то, поскольку Т принадлежит касательной
(и, значит, ее координаты удовлетворяют уравнению касательной),
имеем 0 = 2хохх - Хд. Если х0 * 0, то Xj = .
Нетрудно обосновать простой способ построения касательной
к произвольной параболе в любой ее точке А (кроме вершины): до-
статочно соединить точку А с точкой Т, де-
лящей отрезок оси Ох с концами 0 и х0 по-
полам; прямая АТ — искомая касательная.
При х0 = 0 касательная — это прямая Ох.
3. Формула Лагранжа. Воспользуем-
ся геометрическим смыслом производной,
чтобы дать наглядные пояснения справед-
ливости того, что существует касательная
к графику f в точке с абсциссой с из интер-
вала (а; Ь), параллельная секущей, прохо-
дящей через точки A (a; f (а)), В (b; f (Ь)).
Производная и ее применения
Рис. 96
Рассмотрим прямую I, параллельную АВ и не имеющую об-
щих точек с частью графика, соответствующей промежутку [а; Ь].
Будем перемещать эту прямую I по направлению к графику' f
так, чтобы она оставалась параллельной АВ. Зафиксируем поло-
жение 10 этой прямой в момент, когда у нее появятся общие точки
с этой частью графика. Из рисунка 96, а видно, что любая из та-
ких «первых» общих точек — точка касания прямой 10 с графи-
ком f. Обозначим абсциссу этой точки через с. Тогда f (с) = tg а,
где а — угол между прямой 10 и осью абсцисс. Но 11| АВ, поэтому
угол а равен углу наклона секущей АВ, т. е.
V (с) = tg а =-------.
о-а
Итак, если функция дифференцируема, то на интервале
(а; Ь) найдется такая точка с е (а; Ь) (рис. 96, б), что
Эта формула называется формулой Лагранжа.
Упражнения
251.— В каких точках графика функции f (рис. 97) касательная
252.
к нему:
а) горизонтальна;
б) образует с осью абсцисс острый угол;
в) образует с осью абсцисс тупой угол?
При каких значениях аргумента (отмеченных на оси абс-
цисс) производная функции, заданной графиком (рис. 98):
а) равна нулю; б) больше нуля; в) меньше нуля?
253.
Найдите тангенс угла наклона к оси абсцисс касатель-
ной, проходящей через
ции f (253—254).
a) f (х) - х2, М (-3; 9);
данную точку М графика функ-
б) f(x) = ±x3-x, М 2;-
3 у 3
2 I-
3 J’
в) f (х) = х3, М(-1; -1); г) f (х) = х2 + 2х, М (1; 3).
132
Производная и ее применения
Рис. 97
254.— a) /(x) = 2cosx,
б) f (х) = -tg х, М (л; 0);
в) f (х) = 1 + sin х, М (л; 1);
г) f (х) = -cos х, М (-л; 1).
133 Производная и ее применения
255.—
256.
Напишите уравнение касательной к графику функции f
в точке с абсциссой х0 (255—256).
a) f (х) = -, х0 = -1, хп = 1;
х и
б) f (х) = 2х - х2, х0 = 0, х0 = 2;
в) f (х) = х2 + 1, х0 = 0, х0 = 1;
г) f (х) = х3 - 1, х0 = -1, х0 = 2.
a) f (х) = 3 sin х, х0 = ^, х0 = л;
б) f (х) = tg х, х0 = ^, х0 =
4 о
в) f (%) = 1 + cos х, х0 = 0, х0 =
г) f (х) = -2 sin х, х0 = - х0 = л.
Найдите точки графика функции f, в которых касательная
параллельна оси абсцисс (257—258).
257.— - a) f (х) = х3 - Зх2 + Зх; б) / (х) - * х4 + 16х;
в) f (х) = Зх4 - 6х2 + 2; г) /(х) = х3 - Зх + 1.
258.— - a) f (х) = 2 cos х + х; б) f (х) = sin 2х + д/З х; в) f (х) = cos I х - — I; г) f (х) = -/2 х - 2 sin х. 1 3)
259.— - Под каким углом пересекается с осью Ох график функции: а) f (х) = Зх - х3; б) f (х) = sin f х + — к 4 J в) f (х) = х2 - Зх + 2; г) / (х) = -cos х?
260. - Под каким углом пересекается с осью Оу график функции: а) /(х)=^—; б) /(х) tg[x-y\ х-1 2 < 4) в) f (х) =i(x-l)2; г) f (х) = sin ^2х +
20. Приближенные вычисления
Пусть, например, требуется вычислить приближенное
значение функции
f (х) = х7 - 2х6 + Зх2 - х + 3
в точке х = 2,02. Значение f в близкой к 2,02 точке х0 = 2 находит-
ся легко: f (2) = 13. График f в окрестности точки 2 близок к пря-
мой у = f (х0) + f (х0) (х - х0) — касательной к нему в точке с абс-
циссой 2. Поэтому f (2,02) ® у (2,02). Имеем f (х) = 7х6 — 12х5 +
+ 6х - 1, f (х0) = f (2) = 75 и f (х) » у (х) = 13 + 75 • 0,02 = 14,5.
Производная и ее применения
Вычисления на калькуляторе дают результат f (2,02) ®
» 14,57995.
Вообще для дифференцируемой в точке х0 функции / при Дх,
мало отличающихся от нуля, ее график близок к касательной
(проведенной в точке графика с абсциссой х0), т. е. при малых Дх
f М ~ f (х0) + Г (х0) Дх.
(1)
Если точка х0 такова, что значения f (х0) и f' (х0) нетрудно
вычислить, то формула (1) позволяет находить приближенные зна-
чения f (х) при х, достаточно близких к х0. Так, при вычислении
значения 7^,08 естественно взять в качестве х0 число 4, так как
4,08 близко к 4 и значения f (х0) = Jх0 и /' (х0) = —при х0 = 4
найти нетрудно: /(4) = 71 =2, /' (4) = —1. По формуле (1) при
274 4
Дх = 0,08 получаем:
4,08 » 2 + -0,08 = 2,02.
4
Пример 1. Выведем из формулы (1) приближенную формулу
71 + Дх ~ 1 + g ^х-
Возьмем f (х) = Vx, х0 = 1 и х = х0 + Дх = 1 + Дх. Имеем
/(x0) = Vl = l и /'(*)= -^=, откуда f (х0) = f (1) = По фор-
2у! х 2
муле (1)
f (х) = 71 + Дх ~ 1 + g А*'
В частности, Jl,06 = J1 + 0,06 « 1 + 1 0,06 = 1,03.
2
Значение ^/4,08 также можно найти по формуле (2):
74,08 =2д/1,02 ~2 (1 +|-0,02^ =2,02.
Пример 2. Выведем из формулы (1) приближенную фор-
мулу
(1 + Дх)" ~ 1 + иДх. (3)
Полагаем f(x) = хп, х0=1 и х = х0 + Дх = 1+ Дх. Находим
/(х0) = 1, f (х) = пхп х, откуда /' (х0) = п. По формуле (1)
f (х) = (1 + Дх)" ~ 1 + иДх.
Например, 1,0011о° = (1 + 0,001)*°° » 1 + 100 0,001 = 1,1.
Значение 1,ОО1100, вычисленное на калькуляторе, равно
1,10512.
Производная и ее применения
Пример 3. Для вычисления значения -----------— удобно вос-
О,99730
пользоваться формулой (3) при п - -30, Дх = -0,003:
-А--= (1 - 0,003) 30 « 1 + (-30) (-0,003) =
О,99730
= 1 + 0,09 = 1,09.
Формулой (1) часто пользуются для вычисления прибли-
женных значений и других элементарных функций, например
тригонометрических. Так, для вычисления sin 1° удобно взять
f (х) = sin х, хп = 0, при этом Дх = — так как 1° = —— .
0 180 180)
Имеем f (х0) = sin 0 = 0, f (х0) = cos 0 = 1 и
sin х ~ f (х0) + f (х0) Дх = 0 + 1 Дх = Дх,
т. е. sin 1°® —— ® 0,017453. Вычисляя значение sin 1° на кальку-
180
ляторе, получаем sin 1° ~ 0,0174525.
Упражнения
261 .— Вычислите с помощью формулы (1) приближенные значе-
ния функции f в точках Xj и х2:
a) f (х) = х4 + 2х, Xj = 2,016, х2 = 0,97;
б) f (х) = х5 - х2, Xj = 1,995, х2 = 0,96;
I в) f (х) = х3 - х, Xj = 3,02, х2 = 0,92;
г) f (х) = х2 + Зх, Xj = 5,04, х2 = 1,98.
, Вычислите с помощью формулы (1) и (3) приближенные
значения (262—263).
262 .- а) 1,ОО2100; б) 0,9956; в) 1,О3200; г) 0,99820.
263 . а) 71,004; б) 725,012; в) ^0,997; г) 74,0016.
Вычислите с помощью формулы (1) приближенные значе-
ния (264—266).
264 .— a) tg 44°; б) cos 61°; в) sin 31°; г) ctg 47°.
Г \ Г \
265 .— a) cos - + 0,04 ; б) sin 71 - 0,02 ;
|1б ) 1з )
в) sinf—+ 0,0з\ г) tg|—+ 0,0б'|.
1б ) 14 )
а) — б) ---Ц-; в) 1 --; г) —Ц-.
1,0032° О,99640 2,00163 0,9945
136 Производная и ее применения
21. Производная в физике и технике
1. Механический смысл производной. Напомним, как
определялась скорость движения в курсе физики. Рассмотрим
самый простой случай: материальная точка движется по коорди-
натной прямой, причем задан закон движения, т. е. координата х
этой точки есть известная функция х (t) времени t. За промежуток
времени от tv до t0 + Л? перемещение точки равно х (t0 + At) -
- х (t0) = Дх, а ее средняя скорость такова:
^c₽(AO = g- (1)
При At < 0 формула (1) также верна: перемещение равно
х (t0) - х (t0 + At) = -Ах, а продолжительность промежутка времени
равна -At.
Обычно характер движения бывает таким, что при малых At
средняя скорость практически не меняется, т. е. движение с боль-
шой степенью точности можно считать равномерным (см. пример
п. 13). Другими словами, значение средней скорости при At —> О
стремится к некоторому вполне определенному значению, которое
и называют мгновенной скоростью v (t0) материальной точки в мо-
мент времени t0. Итак,
иср (At) = ^ -> р (t0) при At -> 0.
Но по определению производной
— —> х' (t0) при At —> 0.
Поэтому считают, что мгновенная скорость v (t) определена
(только) для любой дифференцируемой функции x(t), при этом
v (t) = х' (t). (2)
Коротко говорят: производная от координаты по вре-
мени есть скорость. В этом состоит механический
смысл производной.
Мгновенная скорость может принимать как положительные,
так и отрицательные значения и, конечно, значение 0. Если ско-
рость на каком-либо промежутке времени (it; t2) положительна,
то точка движется в положительном направлении, т. е. координа-
та растет с течением времени, а если v (t) отрицательна, то коорди-
ната х (t) убывает.
Аналогичное положение и с ускорением движения. Скорость
движения точки есть функция от времени t. А производная этой
функции называется ускорением движения:
а = и' (t).
I Коротко говорят: производная от скорости по време-
ни есть ускорение.
137 Производная и ее применения
а начальное
как известно
ки в момент
Пример 1. Рассмотрим свободное падение материальной
точки.
Если координатную прямую направить вертикально вниз,
положение материальной точки совпадает с 0, то,
gt%
из физики, x(t) =~2~’ Тогда скорость падения точ-
времени t равна
.. _ ( gt2
2
= gt,
V =
а ускорение а = (gt)' = g есть величина постоянная. Рассмотрим бо-
лее общий случай.
Пример 2. Пусть зависимость координаты точки, движу-
щейся по прямой, от времени выражается формулой
X (t) = t2 + vot + х0,
где а * 0, v0 и х0 — постоянные. Найдем скорость и ускорение дви-
жения.
Скорость этого движения такова:
v = х' (t)
^t2 + v0t + x0
— 2 • — t + Ur,
2 u
= at + v 0
Так как нам известна скорость движения как функция вре-
мени, мы можем найти ускорение этого движения: v' (t) =
= (at + и0)' = а. Мы видим, что ускорение при движении по квадра-
тичному закону постоянно и равно а. Если а > 0, то это равноуско-
ренное движение; если же а < 0, то равнозамедленное. Отметим
также, что v0 = и (0), а х0 = х (0).
В главе III мы докажем, что если при движении по прямой
ускорение а постоянно, то движение происходит по квадратичному
закону:
х(0 = “ t2 + v0t + x0,
где v0 — начальная скорость точки, а х0 — начальная координата.
Н* Пусть у = f (х) — произвольная дифференцируемая функция.
Тогда мы можем рассмотреть движение материальной точки по ко-
ординатной прямой, совершаемое согласно закону х = f (t). Меха-
нический смысл производной позволяет дать наглядную интерпре-
тацию теорем дифференциального исчисления.
Пример 3. Пусть f и h — две дифференцируемые функ-
ции. Рассмотрим следующее (относительное) движение по пря-
мой. Дана подвижная система координат, связанная с поездом,
начало которой (кабина машиниста) движется относительно нача-
ла неподвижной системы координат (станции) по закону хг = f (t).
В подвижной системе координат материальная точка совершает
138 Производная и ее применения
движение по закону х2 = h (t). Тогда координата х этой точки отно-
сительно неподвижной системы координат равна х = хг + х2, а ее
скорость v (t) равна х' (Z). С другой стороны, по закону сложе-
ния скоростей v (Z) = Uj (Z) + v2 (t) = xj (t) + x'2 (t). Итак, мы полу-
чили с помощью механического смысла производной известную
формулу:
(/ + h)’ = f' + h’.
Пример 4. Пусть материальная точка движется по коор-
динатной прямой согласно закону х = f (t).
Средняя скорость этой точки на промежутке [а; Ь] равна
_/(Ь)-/(а)
Ucp b-a ‘
Мгновенная скорость v (Z) в точках промежутка [а; Ь] не может
быть все время меньше (больше) средней. Значит, в какой-то мо-
мент t0 е [а; Ь] мгновенная скорость равна средней, т. е. в проме-
жутке [а; Ь] найдется такое t0, что
v (t0) = f (t0) =-----. (3)
и — a
Мы получили механическую интерпретацию формулы Ла-
гранжа.
2. Примеры применения производной. С помощью произ-
водных функций, характеризующих физические явления, задают-
ся и другие физические величины. Например, мощность (по опре-
делению) есть производная работы по времени.
Рассмотрим пример.
Пример 5. Пусть дан неоднородный стержень, причем из-
вестна масса т (Z) любого его куска длиной I (Z отсчитывается
от фиксированного конца стержня). Хотя стержень неоднороден,
естественно полагать, что плотность его небольшой части (на уча-
стке от I до I + AZ) примерно одна и та же I I и чем меньше AZ,
\ AZ 7
тем в меньших пределах на этом участке изменяется плотность.
Поэтому за характеристику распределения плотности стержня
в зависимости от I принимают линейную плотность d (Z) = т' (Z).
Пример 6. В большинстве задач механики рассматрива-
ются движения точки на плоскости или в пространстве. Тогда ско-
рость — векторная величина. Оказывается, что если координаты
точки в момент t равны х (Z) и у (t), то координаты вектора v (Z)
скорости равны х' (Z) и у' (t). Пользуясь этим, можно вывести фор-
мулы производных тригонометрических функций на основе кине-
матики.
Рассмотрим равномерное движение по окружности радиу-
са 1 в направлении против часовой стрелки с угловой скоро-
стью 1 (рис. 99). Тогда координаты точки М в момент времени t
139 Производная и ее применения
таковы: х (t) = cos t, у (t) = sin t. Как вы знаете из курса физики,
вектор скорости v (t) направлен по касательной к окружности,
а его длина равна 1 (п (Z) = a>R = 1-1 = 1). Следовательно, этот
------------------------------>
вектор совпадает с вектором ОР , координаты которого равны
t + —
2
cos I t + I = - sin t и sin I t + I = cos t. С другой стороны, коор-
динаты вектора v (t) равны соответственно х' (t) (т. е. cos' t) и у' (t)
(т. е. sin't). Получаем известные формулы:
cos' t = -sin t, sin't = cos t.
Пример 7. Выведем свойство параболы, имеющее приме-
нение в оптике и технике.
Поверхность, получающаяся при вращении параболы у = ах2
вокруг оси Оу, называется параболоидом вращения. Представим
себе, что внутренняя поверхность параболоида — зеркальная по-
верхность и это параболическое зеркало освещается пучком лучей
света, параллельных оси Оу.
Рассмотрим сечение этого зеркала плоскостью а, проходя-
щей через ось Оу. Это сечение представляет собой такую же
параболу у = х2 (ось Ох выбираем в плоскости сечения, а = 1).
Согласно законам оптики отраженный луч света будет лежать
в плоскости а, причем этот луч образует с касательной к параболе
такой же угол, как и падающий луч МА (рис. 100).
Докажем, что все лучи, параллельные оси Оу, после отра-
жения пересекутся в одной точке оси Оу.
Обозначим через F точку пересечения произвольного отра-
женного луча с осью Оу. Прямая АТ — касательная к параболе
140 Производная и ее применения
в точке А. Из законов отражения света (рис. 100) сразу следует,
что АТАМ = АРАР. Но луч МА параллелен оси Оу, поэтому
AFPA = АТАМ. Следовательно, AFPA = AFAP, т. е. треугольник
FPA равнобедренный и FA = FP. Точка А (х0; у0) лежит на пара-
боле, поэтому у0 = Хд. Уравнение касательной АТ имеет вид
у = 2х0х - х„. Из него найдем ординату ур точки Р. Она равна
ур = 2х0 • 0 - Хд, т. е. ур = -у0. Если ординату точки F обозначим
через у, то FP = у + у0. Длина FA = х^ +(у0~у)2 , и поэтому
(вспомним, что FA = FP) верно равенство (у + у0)2 = х$ + (у0 - у)2,
т. е. уг + 2ууд + у2 = у0 + у$ - 2уу0 + у2, откуда 4уу0 = у0, и, по-
скольку у0 0, получаем у =
Итак, все лучи, параллельные оси параболического зеркала,
после отражения сходятся в одной точке, которую называют фоку-
сом параболического зеркала (точку F называют также фокусом
параболы у = х2).
На этом свойстве основано устройство параболических теле-
скопов. Лучи от далеких звезд приходят к нам в виде параллель-
ного пучка. Изготовив параболический телескоп и поместив в его
фокус фотопластинку, мы получаем возможность усилить свето-
вой сигнал, идущий от звезды. Этот же принцип лежит в основе
создания параболических антенн, позволяющих усилить радиосиг-
налы.
Если же поместить в фокусе параболического зеркала источ-
ник света, то после отражения от поверхности зеркала лучи,
идущие от этого источника, не будут рассеиваться, а соберутся
в узкий пучок, параллельный оси зеркала. Этот факт находит при-
менение при изготовлении прожекторов и фонарей, различ-
ных проекторов, зеркала которых изготавливают в форме пара-
болоидов.
Упражнения
267 .— Материальная точка движется прямолинейно по закону
х (t) = - 1 t3 + 2t2 + 5t. а) Выведите формулу для вычисле-
3
Д ния скорости движения в любой момент времени t. б) Най-
дите скорость в момент t = 2 с. (Перемещение измеряется
в метрах.) в) Через сколько секунд после начала движения
точка остановится?
268. I Материальная точка движется прямолинейно по закону
х (1) = t3 - 4t2. Найдите скорость и ускорение в момент
t = 5 с. (Перемещение измеряется в метрах.)
141 Производная и ее применения
269 .— Вращение тела вокруг оси совершается по закону
<р (Z) = 3Z2 - 4t + 2. Найдите угловую скорость cd (Z) в произ-
вольный момент времени t и при t = 4 с. (ср (£) — угол в ра-
I дианах, со (t) — скорость в радианах в секунду, t — время
в секундах.)
Маховик, задерживаемый тормозом, за время t поворачива-
ется на угол ср (Z) = 4t - 0,3t2. Найдите: а) угловую ско-
рость со (Z) вращения маховика в момент времени t = 2 с;
б) такой момент времени, когда маховик остановится,
(со (t) — угол в радианах, t — время в секундах.)
271 .— Точка движется прямолинейно по закону х (Z) = 2Z3 + t - 1.
Найдите ускорение в момент времени t. В какой момент
времени ускорение будет равно: а) 1 см/с2; б) 2 см/с2?
(х (Z) — перемещение в сантиметрах, t — время в секун-
дах.)
272 .— Точка движется прямолинейно по закону х (Z) = + 3Z2 - 5
6
(время измеряется в секундах, координата — в метрах).
Найдите: а) момент времени t, когда ускорение точки рав-
но нулю; б) скорость движения точки в этот момент.
273 .— Точка движется прямолинейно по закону х (t) = -Jt. Пока-
жите, что ее ускорение пропорционально кубу скорости.
274 .— Найдите силу F, действующую на материальную точку
с массой т, движущуюся прямолинейно по закону
х (t) = 2#3 - t2 при t = 2.
275 .— Тело массой 2 кг движется прямолинейно по закону
x(t) = t2 + t + 1. Координата х измеряется в сантиметрах,
время t — в секундах. Найдите: а) действующую силу;
б) кинетическую энергию Е тела через 2 с после начала
движения.
276 .— Известно, что для любой точки С стержня АВ длиной
20 см, отстоящей от точки А на расстояние I, масса кус-
ка стержня АС в граммах определяется по формуле
т (Z) = 3Z2 + 5Z. Найдите линейную плотность стержня:
а) в середине отрезка АВ; б) в конце В стержня.
277 .— По прямой движутся две материальные точки по законам
хг (Z) = 4t2 - 3 и х2 (Z) = ts. В каком промежутке времени
скорость первой точки больше скорости второй точки?
278 .-I Из пункта О по двум лучам, угол между которыми 60°,
движутся два тела: первое — равномерно со скоростью
5 км/ч, второе — по закону s (Z) = 2t2 + t. С какой скоро-
стью они удаляются друг от друга? (s измеряется в кило-
метрах, Z — в секундах.)
142 Производная и ее применения
§6.
Применения производной
к исследованию функции
22. Признак возрастания (убывания)
функции
В п. 6 вы видели, что одна из основных задач ис-
следования функции — это нахождение промежутков ее возраста-
ния и убывания. Такое исследование легко провести с помощью
производной. Сформулируем соответствующие утверждения.
Достаточный признак возоастания срунк-
ции. Если f'(x) > О в каждой точке интервала I,
то функция f возрастает на I.
Достаточный признак убывания функ-
ции. Если f (х) < 0 в каждой точке интервала I,
то функция f убывает на I.
Доказательство этих признаков проводится на основании
формулы Лагранжа (см. п. 19). Возьмем два любых числа хх и х2
из интервала. Пусть хх < х2. По формуле Лагранжа существует
число с е (хх; х2), такое, что
= fl (с) (1)
х2 -хх
Число с принадлежит интервалу I, так как точки хх и х2 при-
надлежат I. Если Г (х) > 0 для х е I, то f (с) >0, и поэто-
му f (xi) < f (хг) — это следует из формулы (1), так как
х2 - Х1 > 0. Этим доказано возрастание функции f на I. Если же
f (х) < 0 для х 6 I, то f (с) < 0, и потому / (хх) > f (х2) — следу-
ет из формулы (1), так как х2 - хх > 0. Доказано убывание функ-
ции f на I.
► Наглядный смысл признаков ясен из физических рассужде-
ний (рассмотрим для определенности признак возрастания).
Пусть движущаяся по оси ординат точка в момент времени t
имеет ординату у = f (t). Тогда скорость этой точки в момент
времени t равна f (1) (см. п. 21). Если f (t) > 0 в каждый момент
времени из промежутка I, то точка движется в положительном на-
правлении оси ординат, т. е. если t, < t2, то f (fx) < f (t2). Это озна-
чает, что функция f возрастает на промежутке I.
143 Производная и ее применения
Пример 1. Найдем промежутки возрастания (убывания)
и построим график функции f (х) = х - Xs.
Данная функция определена на множестве всех действитель-
ных чисел. Из равенства f (х) = 1 - Зх2 следует, что f (х) > О,
если 1 - Зх2 > 0. Решая это неравенство методом интервалов
(рис. 101, а), получим, что f (х) > 0 на интервале L; -jL , и,
t 7з 7з J
значит, на этом интервале f возрастает.
Аналогично f (х) < 0 на интервалах I — о°; —jL и оо I
V V3) <7з )
поэтому на этих интервалах f убывает. Далее вычислим значения f
в точках —1 и -jL:
V3 7з
II 9 )
На координатной плоскости отметим точки М --и
V3 3V3 J
N
и нарисуем проходящий через них график функции,
f___1_.
I ’ /з J
возрастающей на интервале
и убывающей на интерва-
лах — оо; -_L и ОО (рис. 101, б).
V л/з J J
Из рисунка видно, что функция f, непрерывная в точках
и —=, возрастает на отрезке
V3
1 . 1
7з’ 7з
и убывает на про-
Рис. 101
межутках —оо; _L- и оо .
V V3j |_V3 )
Замечание 1. Если функ-
ция f непрерывна в каком-либо из
концов промежутка возрастания
(убывания), то эта точка тоже вхо-
дит в промежуток возрастания (убы-
вания) (как точки —и в при-
V3 V3
мере 1). Мы примем этот факт без
доказательства.
Замечание 2. Для решения
неравенств f (х) > 0 и f (х) < 0
удобно пользоваться обобщением ме-
тода интервалов (теоремой Дарбу):
точки, в которых производная рав-
144 Производная и ее применения
на 0 или не существует, разбивают область определения функции f
на промежутки, в каждом из которых f сохраняет постоянный
знак. (Этот факт доказывается в курсах математического анализа.)
Знак можно определить, вычислив значение f' в какой-нибудь точ-
ке промежутка.
Пример 2. Найдем промежутки возрастания (убывания)
и построим график функции f (х) = 2х + -1 .
х2
Область определения данной функции — объединение проме-
о
жутков (-оо; 0) и (0; оо); (х) = 2 - —; f (х) = 0 при х = 1. Точки
х3
0 и 1 разбивают область определения функции на три интервала
(—оо; 0), (0; 1) и (1; оо). По замечанию 2 в каждом из них f сохра-
няет постоянный знак. Знак производной в каждом из этих интер-
валов отмечен на рисунке 102, а.
Следовательно, данная функция возрастает на интервалах
(—°о; 0) и (1; оо). Поскольку f непрерывна в точке 1, то эту точку
можно (в силу замечания 1) присоединить к промежутку, на кото-
ром функция f возрастает.
Окончательно получаем, что f возрастает на промежутках
(—оо; 0) и [1; оо). Далее, f (х) < 0 на интервале (0; 1), и поэтому
(с учетом замечания 1) f убывает на промежутке (0; 1].
Точка 0 не входит в D (/), однако при стремлении х к 0 сла-
гаемое — неограниченно возрастает. Поэтому и значения f не-
X2
ограниченно возрастают. В точке 1 функция принимает значение 3.
Отметим теперь на координатной плоскости точку М (1; 3)
и нарисуем проходящий через нее
график функции, возрастающей
на промежутках (-оо; 0) и [1; оо)
и убывающей на промежутке (0; 1]
(рис. 102, б).
Пример 3. Найдем проме-
жутки возрастания (убывания) функ-
ции f (х) = -2х + sin х.
Функция определена на всей
числовой прямой. Производная ее
такова:
f' (х) = -2 + cos х.
Поскольку |cos х| < 1, легко полу-
чаем, что f (х) < 0 для всех дейст-
вительных х. Это значит, что функ-
ция f (х) = -2х + sin х убывает на
всей числовой прямой.
+ - +
0 1
а)
145 Производная и ее применения
Упражнения
Найдите промежутки возрастания и убывания функций
(279—281).
279.—
280.—
281.
282.
a) f(x) = 3-^x; б) / (х) =-х2 + 2х - 3;
в) f (х) = 4х - 5; г) f (х) = 5х2 - Зх + 1.
a) f (х) = +1; б) f (х) = х2 (х - 3);
х
в) /(х) = —; г) f (х) = х3 - 27х.
X
a) f (х) = 12х + Зх2 - 2х3; б) f (х) = 4 - х4;
в) f (х) = х (х2 - 12); г) f (х) = .
xz
Постройте эскиз графика функции f, удовлетворяющей
условиям:
a) D (/) = [-2; 5], f (х) > 0 при х е (-2; 5);
б) D(f) = [1; 6], f (х) < 0 при х g (1; 3) U (3; 6), Г (3) = 0;
в) D (/) = [-2; 5], f (х) > 0 при х е (-2; 1) U (1; 5),
Г (1) = 0;
г) D (f) = [1; 6], /' (х) < 0 при х е (1; 6).
Найдите промежутки возрастания и убывания и постройте
графики функций (283—284).
283 .— a) f (х) = х3 + Зх2 - 9х + 1; б) f (х) = 4х3 - 1,5х4;
в) /(х) = 2 + 9х + Зх2 - х3; г) f (х) = х4 - 2х2.
284 .- a) f(x)=2-—4—б) f (х) = |х - 3| - 2;
0,5х-1
в) f (х) = 8х2 - х4; г) /(х) = ||-1|.
285 .— Докажите, что функция / возрастает на R, а функция g
убывает на R:
г3
a) f (х) = Зх + cos 2х; б) g (х) = —— - х;
О
в) f (х) = х7 + 2х5 + 3; г) g (х) = -4х + sin Зх.
286 .— Докажите, что уравнение имеет единственный корень на
каждом из данных промежутков Рг и Р2:
а) х3 - 27х + 2 = 0, Р, = [-1; 1], Р2 = [4; 6];
б) х4 - 4х - 9 = 0, Рх = [-2; 0], Р2 = [2; 3];
в) х4 + 6х2 - 8 = 0, Р, = [-2; -1], Р2 = [1; 2];
г) -1 + Зх2 - х3 = 0, Pt = [ 2; 0], Р2 = [2; 3].
146 Производная и ее применения
23. Критические точки функции,
максимумы и минимумы
Мы рассмотрели поведение функции на промежутках,
где Г (х) > 0 и f (х) < 0. Внутренние точки области определения
функции, в которых ее производная равна нулю или не существу-
ет, называются критическими точками этой функции. Эти точки
играют важную роль при построении графика функции, поскольку
только они могут быть точками экстремума функции (рис. 103
и 104). Сформулируем соответствующее утверждение, его назы-
вают теоремой Ферма (в честь французского математика Пьера
Ферма).
Необходимое условие экстремума.
Если точка х0 является точкой экстремума функ-
ции f и в этой точке существует производная f,
то она равна нулю: f' (х0) - 0.
Рассмотрим случай f (х0) > 0. По определению производной
отношение ---------— при х —> хп стремится к положительному
х-х0
числу f' (х0), а следовательно, и само будет положительно при
всех х, достаточно близких к х0. Для таких х
f(x)-f(х0) >0
х-х0
и, значит, f (х) > f (х0) для всех х > х0 из некоторой окрестности
точки х0. Поэтому х0 не является точкой максимума.
Если же х < х0, то f (х) < f (х0), и, следовательно, х0 не мо-
жет быть и точкой минимума f.
Случай f (х0) < 0 разбирается аналогично.
Важно отметить, что теорема Ферма есть лишь необходимое
условие экстремума: из того, что производная в точке х0 обращает-
ся в нуль, не обязательно следует, что в этой точке функция имеет
экстремум. Например, производная функции f (х) = х3 обращается
147 Производная и ее применения
в нуль в точке 0, но экстремума в этой точке функция не имеет
(рис. 105).
До сих пор мы рассматривали критические точки, в которых
производная равна нулю. Рассмотрим теперь критические точки,
в которых производная не существует. (Отметим, что, например,
точка 0 для функции у = ~Jx не является критической: в ней про-
изводная не существует, но она не внутренняя точка области опре-
деления.) В этих точках функция также может иметь или не
иметь экстремум.
| Пример 1. Рассмотрим функцию f (х) = |х| (рис. 106). Эта
функция не имеет производной в 0. Значит, 0 — критическая точ-
ка. Очевидно, что в точке 0 функция имеет минимум.
Пример 2. Рассмотрим функцию f (х) = 2х + |х| (рис. 107).
По графику видно, что в точке 0 эта функция не имеет экстрему-
ма. В этой точке функция не имеет и производной.
В самом деле, если предположить, что функция f имеет в
точке 0 производную, то f (х) - 2х также имеет производную в 0.
Но f (х) - 2х = |х|, а функция |х| в точке 0 не дифференцируема
(см. п. 18), т. е. мы пришли к противоречию. Значит, функция f
в точке 0 производной не имеет.
Из теоремы Ферма следует, что при нахождении точек экст-
ремумов функции требуется в первую очередь найти ее критиче-
ские точки. Но, как видно из рассмотренных примеров, вопрос
о том, действительно ли данная критическая точка есть точка эк-
стремума, требует дополнительного исследования. При этом часто
помогают такие достаточные условия существования экстремума
в точке.
Признак максимума функции. Если функ-
ция f непрерывна в точке х0, a f' (х) > О на ин-
тервале (а; х0) и f (х) < 0 на интервале (х0; Ь), то
точка х0 является точкой максимума функции f.
Удобно пользоваться упрощенной формулировкой этого при-
знака:
Если в точке х0 производная меняет знак с плюса
на минус, то х0 есть точка максимума.
148 Производная и ее применения
Доказательство. Производная f (х) >0 на интервале
(а; х0), а функция f непрерывна в точке х0, следовательно (см.
п. 22), функция f возрастает на промежутке (а; х0], и потому
f (х) < f (х0) для всех х из интервала (а; х0).
На промежутке [х0; &) функция f убывает (доказательство
аналогично), и потому f (х) < f (х0) для всех х из интервала (х0; Ь).
Итак, f (х) < f (х0) для всех х х0 из интервала (а; Ь), т. е. х0
есть точка максимума функции f.
► Признак максимума имеет простой механический смысл. Мы
можем считать, что f (х) — это координата точки, движущейся по
оси Оу, в момент времени х, a f (х) — скорость точки в этот мо-
мент. По условию скорость точки за промежуток времени, предше-
ствующий х0, положительна. Поэтому в течение этого времени точ-
ка движется в положительном направлении, она поднимается по
оси Оу до точки f (х0), т. е. f (х) < f (х0) при х < х0. В момент х0
точка на мгновение «останавливается» (ее скорость в этот момент
равна нулю или не определена), а затем начинает опускаться по
оси (по условию скорость f (х) меньше нуля при х > х0), т. е.
/ (х) < f (х0). Итак, в окрестности х0 имеем f (х) < f (х0). Точка
х0 — точка максимума.
Признак минимума функции. Если функ-
ция f непрерывна в точке х0, Г (х) < 0 на интерва-
ле (а; х0) и f (х) > 0 на интервале (х0; Ь), то точка х0
является точкой минимума функции f.
Удобно пользоваться упрощенной формулировкой этого при-
знака:
|Если в точке х0 производная меняет знак с минуса
на плюс, то х0 есть точка минимума.
Доказательство этого признака аналогично доказательству
признака максимума (полезно провести его самостоятельно).
Пример 3. Найдем точки
экстремума функции
f (х) = Зх - Xs.
Производная этой функции,
равная 3 - Зх2, определена во всех
точках и обращается в нуль в точ-
ках -1 и 1. В точке -1 производная
меняет знак с минуса на плюс
(/'(х) < 0 при х < -1 и /'(х) > 0 при
-1 < х < 1). В точке 1 производная
меняет знак с плюса на минус. Поль-
зуясь признаками максимума и ми-
149 Производная и ее применения
нимума, получаем, что точка -1 является точкой минимума, а точ-
ка 1 — точкой максимума функции f. График функции изображен
на рисунке 108.
Упражнения
287.—
288.—
j
289. 4
290.
291.
Найдите критические точки функции, график которой
изображен на рисунке 109.
Найдите критические точки функции:
a) f (х) = 4 - 2х + 7х2; б) f (х) = 1 + cos 2х;
в) f (х) = х - 2 sin х; г) f(x) = 4х - —.
О
Найдите точки максимума и минимума функции /, график
которой изображен на рисунке 110. Существует ли произ-
водная в соответствующей точке? Если существует, то чему
равно ее значение?
Найдите критические точки функции. Определите, какие
из них являются точками максимума, а какие — точками
минимума:
а) /(х) = 5 + 12х - х3; б) /(х) = 9 + 8х2 - х4;
в) f (х) = 2х3 + Зх2 - 4; г) f (х) = | х4 - х2.
Докажите, что функция f не имеет критических точек:
a) f (х) = Vx; б) f (х) = tg х;
в) f (х) = Зх - 7; г) f (х) = Зх5 + 2х.
Найдите критические точки функции f (292—293).
292.— а) / (х) - sin2 х - cos х; б) f (х) = 2х +
X2
в) / (х) = 10 cos х + sin 2х - 6х; г) f (х) = х3 - 4х + 8.
150 Производная и ее применения
-x-2 при x < -1,
293.— a) f (x) = (x - 2)3;
в) /(x)=| + ^;
3 x
6) f (X) =
г) f (х) =
x при -1 < x < 1,
2-х при х > 1;
х + 6 при х<-2,
х2 при -2 С х < 2,
6-х при х > 2.
294.— Постройте эскиз графика функции, обладающей следующи-
ми свойствами:
a) D(f) = [-3; 5]; /'(х) > 0 при х е (-3; 1), /'(х) < 0 при
х е (1; 5) и Д(1) = 0;
б) D(f) = [-3; 5]; f'(x) < 0 при х е (-3; 1), f'(x) > 0 при
х е (1; 5) и функция f не имеет производной в точке 1;
в) D (/) = [a; b]; xt — точка минимума, х2 — точка макси-
мума функции, f (а) > f (&);
г) D (/) = [а; &]; хг — точка максимума, х2 — точка мини-
мума, f (а) = f (b).
295.
Исследуйте функцию на возрастание, убывание и экстрему-
мы. Постройте график функции:
а) / (х) = Ах4-8х2; б)/(х)=-^-;
1+ xz
в) /(х)=2х-|х3; г) /(х) =
О
24. Примеры применения производной
к исследованию функции
Вы уже знаете (п. 4), что построение графика функции
лучше начинать с ее исследования, которое состоит в том, что для
данной функции: 1) находят ее область определения; 2) выясня-
ют, является ли функция f четной или нечетной, является ли пе-
риодической. Далее находят: 3) точки пересечения графика с ося-
ми координат; 4) промежутки знакопостоянства; 5) промежутки
возрастания и убывания; 6) точки экстремума и значения f в этих
Производная и ее применения
точках и 7) исследуют поведение функции в окрестности «осо-
бых» точек и при больших по модулю х.
На основании такого исследования строится график функции.
Исследование функции на возрастание (убывание) и на экст-
ремум удобно проводить с помощью производной. Для этого сна-
чала находят производную функции f и ее критические точки,
а затем выясняют, какие из них являются точками экстремума.
Пример 1. Исследуем функцию f (х) = Зх5 - 5х3 + 2 и по-
строим ее график.
Проведем исследование по указанной схеме.
1) D (/) = R, так как f — многочлен.
2) Функция f не является ни четной, ни нечетной (докажите
это самостоятельно).
3), 4) График f пересекается с осью ординат в точке
(0; f (0)); чтобы найти точки пересечения с осью абсцисс, надо ре-
шить уравнение Зх5 - 5х3 + 2 = 0, один из корней которого (х = 1)
легко находится. Другие корни (если они есть) могут быть найде-
ны только приближенно. Поэтому для данной функции остальные
точки пересечения графика с осью абсцисс и промежутки знакопо-
стоянства мы находить не будем (как уже отмечалось в п. 4, при-
веденная схема имеет примерный характер).
5), 6) Найдем производную функции f:
f (х) = 15х4 - 15х2 = 15х2 (х2 - 1).
D (Л) = R, поэтому критических точек, для которых f' (х) не
существует, нет.
Заметим, что f (х) = 0, если х2 (х2 - 1) = 0, т. е. при значе-
ниях аргумента, равных 0, -1 и 1. Рассматриваемая функция
имеет три критические точки.
Составляем таблицу:
X (-оо; -1) -1 (-1; 0) 0 (0; 1) 1 (1; “J
Г(Х) + 0 - 0 - 0 +
/(X) / 4 2 0 /
max min
В первой строке этой таблицы указаны в порядке возраста-
ния критические точки функции и ограниченные ими промежут-
ки. Во второй строке отмечены знаки производной на этих проме-
жутках. (На каждом таком интервале знак производной не меняет-
ся, его можно найти, определив знак производной в какой-либо
точке рассматриваемого интервала.) В третьей строке записаны
выводы о ходе изменения данной функции: «X» — возрастает,
«\» — убывает, а в четвертой — о виде критических точек (пп. 5
Производная и ее применения
и 6 приведенной выше схемы). Крити-
ческая точка 0 функции f не является
точкой экстремума, поэтому в четвер-
той строке таблицы она не отмечена.
Заметим, что вывод о ходе изменения
функции на промежутке между кри-
тическими точками часто можно сде-
лать, Сравнив значения функции на
концах этого промежутка (вместо опре-
деления знака производной). Напри-
мер, f (0) < f (-1), поэтому на промежут-
ке (-1; 0) функция убывает (и, следова-
тельно, f < 0 на этом промежутке).
Строим график функции (рис. 111).
Строить его удобно по промежуткам, которые указаны в таблице.
Например, в таблице указано, что f убывает на интервале (0; 1).
Функция f непрерывна в точках 0 и 1 (так как она непрерывна
всюду), следовательно, она убывает на отрезке [0; 1]. Поэтому
рисуем график убывающим на отрезке [0; 1] от значения f (0) = 2
до значения / (1) = 0. При этом касательные к графику в точках 0,
± 1 должны быть горизонтальными — во второй строке таблицы
сказано, что в этих точках производная равна нулю. Аналогично
строится график и на остальных промежутках.
Пример 2. Найдем число корней уравнения
2х3 - Зх2 - 12х - 11 = 0.
Рассмотрим функцию f(x) = 2х3 - Зх2 - 12х - 11. Ее область
определения D (/) = (-оо; оо). Для отыскания критических точек
функции f найдем ее производную: /'(х) = 6х2 - 6х - 12. Эта произ-
водная обращается в нуль в точках х = —1 и х = 2. Заполним таблицу:
X (-ОО, -1) -1 (-1; 2) 2 (2; оо)
Г (х) + 0 - 0 +
/(х) / -4 -31 /
max min
На промежутке (-оо; -1] функция возрастает от -оо до -4,
поэтому на этом промежутке уравнение f (х) = 0 корней не имеет.
На промежутке [-1; 2] уравнение также не имеет корней, так как
на этом промежутке f убывает от -4 до -31. Наконец, на проме-
жутке [2; оо) функция f возрастает от -31 до бесконечности, на
этом промежутке уравнение /Дх) = 0 имеет один корень (по теоре-
ме о корне). Итак, уравнение 2х3 - Зх2 - 12х -11=0 имеет один
корень, и этот корень принадлежит интервалу (2; оо).
153 Производная и ее применения
Упражнения
Исследуйте функцию и постройте ее график (296—297).
296.— а) f (х) = х2 - 2х + 8; б) Пх)=-^+х + (;
в) f (х) = -х2 + 5х + 4; г) '<х) = т-+й+г
297.— а) f (х) = - х3 + Зх - 2; б) f (х) = х4 - 2х2 - 3;
в) f (х) = х3 + Зх + 2; г) f (х) = Зх2 - х3.
298. Найдите промежутки возрастания и убывания функции:
a) f (х) = 1 + 1,5х - Зх2 - 2,5х3;
б) /(х)=^-^--6х + 1;
о о
в) /(х)= — +8х-5;
4
г) f (х) = х3 - 6х2 - 15х - 2.
299 .- Докажите, что функция f возрастает на множестве R:
а) f (х) = 2х - cos х; б) f (х) = х5 + 4х;
в) f (х) = sin х + г) f (х) = 2х3 + х - 5.
Исследуйте функцию и постройте ее график (300—302).
300.— а) в) f (х) = —х2 -ix5; f (х) =-х5 -1-х3; б) г) f (х) = 4х2 - х4;
/(х) = 5х3 - Зх5. 6(х-1) х2 + 3 ’ 2х 1-х2 ’
301.— а) f (х) = х2 71 + х; б) f (х) =
в) f (х) = х72 -х; г) f (х) =
302.— а) f (х) = sin2 х + sin х; б) У(Х) 2х . 1+ х2 ’
в) f (х) = cos2 х - cos х; г) f (X) = х х~1’
303 .— Докажите, что функция f принимает на данном промежут-
ке положительные значения:
Ia) f (%) = tg х - х; I =^0;
б) /(х) = Vx-1; Z = [1; оо);
х
в) f (х) = х - sin х; I = (0; оо);
г) f (х) = х + ~-cosx; 1 =
Л . _Л
2 ’ 2
154 Производная и ее применения
304 .— Сколько корней имеет уравнение:
а) 4х3 - Зх2 - 36х - 10 = 0;
v-4 „ -v-2
б) -----х3 - — + Зх = 0;
4 2
в) х4 — 4х3 -9 = 0;
25. Наибольшее и наименьшее значения
функции
Решение практических задач часто сводится к нахождению
наибольшего и наименьшего значений непрерывной на отрезке
функции. В курсах анализа доказывается теорема Вейер-
ш трас с а: непрерывная на отрезке [а; Ь] функция f принима-
ет на этом отрезке наибольшее и наименьшее значения, т. е.
на [а; Ь] существуют точки, в которых f принимает наибольшее
и наименьшее на [а; Ь] значения.
Для случая, когда функция f не только непрерывна на отрез-
ке [a; fe], но имеет на этом отрезке лишь конечное число критиче-
ских точек, укажем правило отыскания наибольшего и наимень-
шего значений f.
Предположим сначала, что f не имеет на отрезке [а; &]
критических точек. Тогда (п. 23) она возрастает (рис. 112) или
убывает (рис. 113) на этом отрезке, и, значит, наибольшее и наи-
меньшее значения функции f на отрезке [а; &] — это значения
в концах а и Ь.
Пусть теперь функция f имеет на отрезке [а; Ь] конечное чис-
ло критических точек. Эти точки разбивают отрезок [а; Ь] на ко-
нечное число отрезков, внутри которых критических точек нет.
Поэтому наибольшее и наименьшее значения функции f на таких
отрезках принимаются в их концах, т. е. в критических точках
функции или в точках а и Ъ.
155 Производная и ее применения
Чтобы найти наибольшее и наименьшее значения
функции, имеющей на отрезке конечное число кри-
тических точек, нужно вычислить значения функции
во всех критических точках и на концах отрезка,
а затем из полученных чисел выбрать наибольшее
и наименьшее.
Пример 1. Найдем наибольшее и наименьшее значения
функции у (х) = х3 - 1,5х2 - 6х + 1 на отрезке [-2; 0].
Сначала найдем критические точки. Так как производная
у' (х) = Зх2 - Зх - 6 определена для любого х, остается решить
уравнение у' (х) = 0. Решая его, находим х = -1 и х = 2.
Теперь нужно выбрать наибольшее и наименьшее из чисел
у (-2) = -1, у (-1) = 4,5 и у (0) = 1 (критическая точка х = 2 не
принадлежит рассматриваемому отрезку). Ясно, что наименьшее
значение достигается в точке -2 и равно -1, а наибольшее —
в точке -1 и равно 4,5. Коротко это записывается так:
шах у (х) = у (-1) = 4,5; min у (х) = у (-2) = -1.
[-2: 0] [-2; 0]
Изложенный выше метод поиска наибольших и наименьших
значений функции применим к решению разнообразных приклад-
ных задач. При этом действуют по следующей схеме:
1) задача «переводится» на язык функций. Для этого выби-
рают удобный параметр х, через который интересующую нас вели-
чину выражают как функцию f (х);
2) средствами анализа ищется наибольшее или наименьшее
значение этой функции на некотором промежутке;
3) выясняется, какой практический смысл (в терминах пер-
воначальной задачи) имеет полученный (на языке функций) ре-
зультат.
Вообще решение практических задач средствами математи-
ки, как правило, содержит три основных этапа: 1) формализацию
(перевод исходной задачи на язык математики); 2) решение полу-
ченной математической задачи и 3) интерпретацию найденного
решения («перевод» его с языка математики в терминах первона-
чальной задачи).
С этим общим методом (его называют методом математиче-
ского моделирования) вы уже знакомы, по описанной схеме реша-
лись текстовые задачи в курсе алгебры. Приведем пример его при-
менения.
Пример 2. Из квадратного листа жести со стороной а
надо изготовить открытую сверху коробку, вырезав по углам
(рис. 114) квадратики и загнув образовавшиеся кромки. Какой
должна быть сторона основания коробки, чтобы ее объем был мак-
симальным?
Решение. 1) Обозначим через х длину стороны основа-
ния коробки. Тогда длины сторон вырезанных квадратиков рав-
156 Производная и ее применения
число х удовлетворяет неравенству 0 < х < а, т. е. принадлежит
интервалу (0; а). Таким образом, пример 2 мы свели к такой за-
даче: найти наибольшее значение функции V (х) = — (а - х) х2 на
интервале (0; а).
2) Правило нахождения наименьших и наибольших значе-
ний функции было сформулировано для отрезка. Функция V не-
прерывна на всей числовой прямой. Мы будем искать ее наиболь-
шее значение на отрезке [0; а], потом сделаем выводы для решае-
мой нами задачи. Находим критические точки функции:
V (х) = ахх2, ах-—х2=0,
v 2 2
т. е. х = 0 или х = — а;
Так как V(0) = 0 и V(а) = 0, своего наибольшего на отрезке
9
[0; а] значения функция V достигает при х = — а, т. е.
3
max V (х) = V ( - а 1 = — а3.
[0; а ] ) 27
Наибольшее значение функции достигается внутри отрезка
[0; а], следовательно, и внутри интервала (0; а).
3) Остается вспомнить, что х — длина стороны основания
коробки, имеющей при заданных условиях максимально возмож-
ный объем.
Полученный результат означает, что максимальный объем
9
имеет та коробка, сторона основания которой равна —а.
3
157 Производная и ее применения
305.—
306.-
307.-
308.
309.
310.-
311.-
312. 4
Упражнения
Найдите наибольшее и наименьшее значения функции f:
a) f (х) = х4 - 8х2 - 9 на промежутках [-1; 1] и [0; 3];
+ 4
б) f (х) =---на промежутках [-4; -1] и [1; 3];
х
в) f (х) - Зх5 - 5х3 на промежутках [0; 2] и [2; 3];
г) /(х) = на промежутках [-3; -2] и [1; 5].
х+ 1
Сравните наибольшее значение функции на промежутке РА
и наименьшее ее значение на промежутке Р2.
a) f (х) = х3 + Зх2 - 9х; Рх = [-4; 0], Р2 = [3; 4];
б) f (х) = х4 - 2х2 + 4; Р1= [-j; Р2 = [2; 3].
Материальная точка движется по прямой согласно закону
s (<) = 12i2 - — t3, где s (t) — путь в метрах nt — время
3
в секундах. В какой момент времени из промежутка [4; 10]
скорость движения точки будет наибольшей и какова вели-
чина этой скорости?
Найдите значения аргумента из промежутка [-2; 5], при ко-
х3
торых скорость изменения функции f (х) = 21х + 2х2 ——
О
будет наибольшей или наименьшей.
Скорость материальной точки, движущейся прямолинейно,
изменяется по закону v (t) = - t3 - 12/ (скорость измеряется
6
в метрах в секунду). В какой момент времени ускорение
движения будет наименьшим, если движение рассматри-
вать за промежуток от = 10 с до t2 = 50 с?
Найдите наибольшее и наименьшее значения функции f
на данном промежутке:
a) f (х) = 2 sin х + cos 2х, [0; 2л];
б) f (х) = 1,5х2 + —, [1; 4];
X
в) /(х) = 2 sin х + sin 2х, |Ъ; 4^];
г) /(х) = хч * [ 5; -2,5].
х+ 2
Число 24 представьте в виде суммы двух неотрицательных
слагаемых так, чтобы сумма квадратов этих чисел была
наименьшей.
Число 4 представьте в виде суммы двух неотрицательных
слагаемых так, чтобы произведение этих чисел было наи-
большим.
158 Производная и ее применения
313.-
314.—
315.—
316 -
317.—
318.—
319.—
320.-
321. |
322. j
323. J
Кусок проволоки длиной 48 м сгибают так, чтобы обра-
зовался прямоугольник. Какую длину должны иметь сто-
роны прямоугольника, чтобы его площадь была наиболь-
шей?
Число 54 представьте в виде суммы трех положительных
слагаемых, два из которых пропорциональны числам 1 и 2,
таким образом, чтобы произведение всех слагаемых было
наибольшим.
Число 16 представьте в виде произведения двух положи-
тельных чисел, сумма квадратов которых будет наимень-
шей.
Площадь прямоугольника 64 см2. Какую длину должны
иметь его стороны, чтобы периметр был наименьшим?
Открытый бак, имеющий форму прямоугольного паралле-
лепипеда с квадратным основанием, должен вмещать
13,5 л жидкости. При каких размерах бака на его изготов-
ление потребуется наименьшее количество металла?
В равнобедренный треугольник с основанием 60 см и боко-
вой стороной 50 см вписан прямоугольник наибольшей
площади. Две вершины прямоугольника лежат на основа-
нии треугольника, а две другие — на боковых сторонах.
Найдите стороны прямоугольника.
Из круглого бревна вырезают балку с прямоугольным сече-
нием наибольшей площади. Найдите размеры сечения бал-
ки, если радиус сечения бревна равен 20 см.
Буровая вышка расположена в поле в 9 км от ближайшей
точки шоссе. С буровой надо направить курьера в пункт,
расположенный по шоссе в 15 км от упомянутой точки
(считаем шоссе прямолинейным). Скорость курьера на ве-
лосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точ-
ке шоссе ему надо ехать, чтобы в кратчайшее время до-
стичь пункта?
Лодка находится на озере на расстоянии 3 км от ближай-
шей точки А берега. Пассажир лодки желает достигнуть
села В, находящегося на берегу на расстоянии 5 км от А
(участок АВ берега считаем прямолинейным). Лодка дви-
жется со скоростью 4 км/ч, а пассажир, выйдя из лодки,
может в час пройти 5 км. К какому пункту берега должна
пристать лодка, чтобы пассажир достиг села в кратчайшее
время?
Найдите число, сумма которого со своим квадратом прини-
мает наименьшее значение.
Докажите, что из всех прямоугольных треугольников с за-
данной гипотенузой наибольшую площадь имеет равнобед-
ренный треугольник.
159 Производная и ее применения
324.— Из всех прямоугольников, вписанных в окружность, най-
дите прямоугольник наибольшей площади.
325. — Покажите, что из всех треугольников, вписанных в дан-
ный круг, наибольшую площадь имеет равносторонний
I треугольник.
Сведения из истории
1. О происхождении терминов и обозначений. Раздел ма-
тематики, в котором изучаются производные и их применения
к исследованию функций, называется дифференциальным исчисле-
нием. Приращения вида Л/, представляющие собой разности, игра-
ют заметную роль при работе с производными. Естественно поэто-
му появление латинского корня differentia (разность) в названии
calculis differentialis нового исчисления, которое переводится как
исчисление разностей; это название появилось уже в конце XVII в.,
т. е. при рождении нового метода.
Термин «производная» является буквальным переводом на
русский французского слова derivee, которое ввел в 1797 г.
Ж. Лагранж (1736—1813); он же ввел современные обозначения
у', f'. Такое название отражает смысл понятия: функция f (х) про-
исходит из f (х), является производным от f (х). И. Ньютон назы-
вал производную функцию флюксией, а саму функцию — флюен-
той. Г. Лейбниц говорил о дифференциальном отношении и ввел
« - df
обозначение производной - , которое также часто встречается
в современной литературе.
Символ df Лейбниц выбрал для обозначения дифференциала
функции f. Дифференциал df функции f — это произведение
производной f (х0) на приращение Дх, т. е. df = f (х0) Дх; заменяя
обозначение Дх на dx, это же можно записать так: df = f (xn) dx,
откуда /'(xn) = —. Геометрический
dx
смысл дифференциала ясен из
рассмотрения рисунка 115: здесь
df = АВ, прямая I — касательная
к графику.
Рассказ
о происхождении
терминологии, принятой в диффе-
ренциальном исчислении, был бы
не полон без понятий предела
и бесконечно малой. Подробнее
о пределе говорится ниже, а пока
заметим, что, например, производ-
ная определяется во всех руковод-
Производная и ее применения
Лейбниц Готфрид Вильгельм
(1646—1716) —
великий немецкий ученый. Философ, математик,
физик, юрист, языковед. Создатель (наряду с Нью-
тоном) математического анализа. Основоположник
большой математической школы. Идеи Лейбница
оказали значительное влияние на развитие мате-
матической логики.
ствах именно как предел. Пишут f' (х0) = lim — вместо приня-
Дх—>0 Дх
того выше обозначения — -> f (х0) при Дх —> 0.
Дх
Обозначение lim — сокращение латинского слова limes
(межа, граница); уменьшая, например, Дх, мы устремляем значе-
ния — к «границе» f (х„). Термин «предел» ввел Ньютон.
Дх
Примером бесконечно малой может служить функция (Дх)2
от Дх, поскольку (Дх)2 —> 0 при Дх —> 0. Вообще, если
lim а (х) =0, говорят, что а (х) — бесконечно малая. Бесконечно
х->х0
малые играют важную роль в математическом анализе, который
поэтому часто называют также анализом бесконечно малых.
Заметим наконец, что слово «экстремум» происходит от ла-
тинского extremum (крайний). Maximum переводится как наиболь-
ший, a minimum — наименьший.
2. Из истории дифференциального исчисления.
1) Дифференциальное исчисление создано Ньютоном и Лейб-
ницем сравнительно недавно, в конце XVII столетия. Тем более по-
разительно, что задолго до этого Архимед не только решил задачу
на построение касательной к такой сложной кривой, как спираль
(применяя при этом предельные переходы), но и сумел найти мак-
симум функции f (х) = х2 (а - х).
Эпизодически понятие касательной (которое, как вы знаете,
связано с понятием производной) встречалось в работах итальян-
ского математика Н. Тартальи (ок. 1500—1557) — здесь каса-
тельная появилась в ходе изучения вопроса об угле наклона ору-
дия, при котором обеспечивается наибольшая дальность полета
снаряда. И. Кеплер рассматривал касательную в ходе решения
задачи о наибольшем объеме параллелепипеда, вписанного в шар
данного радиуса.
161 Производная и ее применения
Ферма Пьер
(1601—1665) —
французский математик и юрист. Один из крупней-
ших математиков своего времени. Ферма принад-
лежат блестящие работы в области теории чисел.
Создатель аналитической геометрии, в которой он
получил ряд крупных результатов
В XVII в. на основе учения Г. Галилея о движении актив-
но развилась кинематическая концепция производной. Различные
варианты изложения, примененные к разным задачам, встречают-
ся уже у Р. Декарта, французского математика Роберваля
(1602—1675), английского ученого Д. Грегори (1638—1675),
в работах И. Барроу (1630—1677) и, наконец, И. Ньютона.
К рассмотрению касательной и нормали (так называется пря-
мая, перпендикулярная касательной и проведенная в точке каса-
ния) Декарт пришел в ходе изучения оптических свойств линз.
С помощью методов аналитической геометрии и изобретенного им
метода неопределенных коэффициентов он сумел решить задачи
о построении нормалей к ряду кривых, в том числе эллипсу.
В 1629 г. П. Ферма предложил правила нахождения экстре-
мумов многочленов. Существенно подчеркнуть, что фактически
при выводе этих правил Ферма активно применял предельные пе-
реходы, располагая простейшим дифференциальным условием
максимума и минимума.
Ферма сыграл выдающуюся роль в развитии математики.
Его имя заслуженно носит не только известная вам теорема из
анализа. Великая теорема Ферма («Уравнение хп + уп = гп не имеет
решений в натуральных числах при натуральном п, большем
двух»), доказанная только в самом конце XX в., лишь один из
итогов его размышлений над проблемами теории чисел. Ферма
один из создателей аналитической геометрии. Он занимался
и оптикой. Широко известен принцип Ферма («Луч света распро-
страняется так, что время его прохождения будет наименьшим»),
применяемый и в физике.
Важные следствия этого принципа вы можете вывести само-
стоятельно. Закон отражения света («Угол отражения равен углу
падения») сводится согласно принципу Ферма к решению извест-
ной геометрической задачи. Для вывода закона преломления све-
та вам потребуется применить известные правила нахождения эк-
стремума. (Требуется решить такую задачу (рис. 116): «Луч света
162 Производная и ее применения
проходит из точки М нижней полу-
плоскости в точку N верхней. Ско-
рость света в нижней полуплоскости
(однородной среде) постоянна и рав-
на Up а в верхней полуплоскости — и2.
По какому пути должна двигаться
точка, чтобы весь ее путь занял наи-
меньшее время?»)
Систематическое учение о произ-
водных развито Лейбницем и Ньюто-
ном, который сформулировал и две
основные проблемы анализа:
«1. Длина проходимого пути по-
стоянно (т. е. в любой момент време-
ни) дана; требуется найти скорость
движения в предложенное время.
2. Скорость движения постоянно дана; требуется найти дли-
ну пройденного в предложенное время пути».
Первая проблема задает программу развития дифференци-
ального исчисления, с элементами которого вы уже познакоми-
лись в этой главе. Вторая относится к интегральному исчислению
(см. главу III).
Если Ньютон исходил в основном из задач механики (ньюто-
нов анализ создавался одновременно с ньютоновой классической
механикой), то Лейбниц по преимуществу исходил из геометриче-
ских задач.
Говоря о последующем развитии идей анализа (а они очень
быстро завоевали популярность и нашли многих последователей),
следует в первую очередь назвать имена учеников Лейбница —
братьев Я. и И. Бернулли.
А. Лопиталь (1661—1704), который учился у И. Бернул-
ли, издал уже в 1696 г. первый печатный курс дифференциального
исчисления «Анализ бесконечно малых для исследования кривых
линий», способствовавший распространению новых методов.
Ряд крупных результатов получил Лагранж, его работы
сыграли важную роль в осмыслении основ анализа.
Как и в случае многих других разделов математики, неоце-
ним вклад в развитие математического анализа, внесенный
Л. Эйлером и К.-Ф. Гауссом (1777—1855).
В кратком очерке невозможно рассказать о существе откры-
тий, сделанных в XVIII в. и позднее. Но об одном направлении
нельзя не упомянуть. Речь идет о разложении функций в степен-
ные ряды, т. е. о представлении функций в виде многочленов
с бесконечным числом слагаемых. С примером бесконечной суммы
(числового ряда) вы знакомы: бесконечные периодические дроби
представлялись в виде суммы бесконечного числа слагаемых.
С числовыми и функциональными рядами работал не только Нью-
тон, но и его предшественники, и поэтому несколько несправедли-
163 Производная и ее применения
во название формула Тэйлора (Б. Тэйлор (1685—1731) — анг-
лийский математик, опубликовавший ее в 1715 г.), принятое для
следующего замечательного соотношения:
f (х0 + Лх) = Нх0) + ^р^Лх + ^~^(Лх)2 + ...
п!
(здесь /(п) (х0) — значение, полученное n-кратным дифференциро-
ванием функции f в точке х0, a n! = 1 • 2 • ... • п).
Зная формулы производных, например, для функций sin х
и cos х, вы можете разложить их в ряд Тэйлора самостоятельно.
Оказалось, что в ряде случаев, отбрасывая бесконечное число
слагаемых, можно получать формулы, дающие хорошие прибли-
жения функций многочленами.
2) Энтузиазм, вызванный появлением нового мощного мето-
да, позволяющего решать широкий круг задач, способствовал бур-
ному развитию анализа в XVIII в. Но к концу этого столетия проб-
лемы, возникшие уже у создателей дифференциального и инте-
грального исчислений, проявились весьма остро.
Основная трудность состояла в том, что точные определения
таких ключевых понятий, как предел, непрерывность, действи-
тельное число, отсутствовали (соответственно и рассуждения со-
держали логические пробелы, а иногда были даже ошибочны).
Характерный пример — определение непрерывности. Эйлер, Ла-
гранж и даже Фурье (а он работал уже в начале XIX в.) называли
непрерывной функцию, которая в своей области определения зада-
на одним аналитическим выражением.
Тем самым «новая» математика не отвечала стандартам стро-
гости, привычным для ученых, воспитанных на классических
образцах греческих математиков. Интуиция, столь необходимая
математикам, существенно опередила логику, тоже являющуюся
неотъемлемой характеристикой математической науки.
Гениальная интуиция таких гигантов, как Ньютон, Лейб-
ниц, Эйлер, помогала им избегать ошибок. Но необходимы были
прочные логические основы.
Характерны высказывания, относящиеся к XVIII столетию.
Известный математик М. Ролль писал, что новое исчисление есть
коллекция гениальных ошибок. А великий французский мысли-
тель Вольтер заметил, что это исчисление представляет собой ис-
кусство вычислять и точно измерять вещи, существование кото-
рых не может быть доказано.
Решительный шаг к созданию прочного фундамента анали-
за был сделан в 20-е годы XIX в. французским математиком
О. Коши (1789—1857), предложившим точные определения пре-
делов функции и последовательности и на их основе доказав-
шим многие фундаментальные теоремы анализа. Несколько рань-
164 Производная и ее применения
Клши Огюстен Луи
(1789—1857) —
крупный французский математик. Доказал ряд за-
мечательных теорем в области анализа, теории
функций комплексного переменного, теории диф-
ференциальных уравнений и т. д. Большая заслуга
Коши — разработка курса анализа, в котором,
в частности, он предложил ставшие классически-
ми определения предела, непрерывности функции
и т. п.
ше (1821 г.) определения предела и непрерывности, целый ряд дру-
гих замечательных результатов (в том числе знаменитый пример
функции, непрерывной на промежутке, но не имеющей производ-
ной ни в одной его точке) получил чешский математик Б. Боль-
цано (1781—1848), но его работы стали известны много позднее.
Определение предела функции по Коши формулируется сле-
дующим образом: «Число А называется пределом функции f (х)
при х, стремящемся к а (т. е. lim f (х) = А), если для любого числа
х—>а
е > О можно подобрать такое число 8 > 0, что | f (х) - А | < £ для
всех х, удовлетворяющих неравенству 0 < |х — а \ < 8».
Опираясь на это определение, уже нетрудно дать определе-
ние непрерывности в точке: функция f непрерывна в точке х0,
если lim /(x) = f(x0).
Формулировка определения предела последовательности
(а именно с этим понятием связано определение интеграла —
см. п. 30) такова: «Число А является пределом последователь-
ности ап, если для любого £ > 0 существует номер N, такой, что
при всех п > N верно неравенство \ап - А| < в».
Коши доказал следующие теоремы о пределах, которыми мы
фактически пользовались (называя их правилами предельных пе-
реходов — п. 14) при вычислении производных:
Если lim/’(x) = A и limg(x)=B, то существуют
х->а х->а
пределы суммы и разности, произведения, частного
(при lim g (х) Ф 0), причем
lim (/(х) + g (х)) = А + В,
х->а
lim (f(x)g(x))=A B,
165 Производная и ее применения
Приведем пример доказательства «по Коши» (часто говорят:
«на языке эпсилон-дельта»). Докажем теорему о пределе суммы.
Возьмем любое положительное число е > 0, Тогда число ® > О,
и поэтому (по определению Коши):
1) из условия lim f (х) = А следует, что можно подобрать
число 6j, такое, что
|/(х)-А|<| (1)
для всех х, удовлетворяющих неравенству 0 < | х - а | < 8t;
2) из условия limg(x) = B вытекает: существует такое
с о х>а
о2 > О, что
|g(x)-B|<| <2>
для всех х, удовлетворяющих неравенству 0 < | х - а | < 82.
Обозначим через 6 наименьшее из чисел 8г и 82. Тогда для
любого х, удовлетворяющего неравенству 0 < | х - а | < 8, выполне-
ны неравенства (1) и (2); для этих х имеем:
|/ (х) + g(x) - (А + В)| =
= | (/ (х) - А) + (£(х) - В)| < |/(х) - А| + |g(x) - В| < | + | = е.
Этим доказано, что lim (f (х) + g (х)) = А + В.
х —>а.
Остальные правила (для произведения и частного) доказыва-
ются аналогично.
Лозунгом многих математиков XVII в. был: «Двигайтесь впе-
ред, и вера в правильность результатов к вам придет».
3. О понятии действительного числа. Математический ана-
лиз возник в XVIII в. Но полное его обоснование было дано лишь
в конце XIX столетия, когда вслед за теорией пределов, создан-
ной Коши, сразу в нескольких формах немецкими математи-
ками Р. Дедекиндом (1831 —1916), К. Вейерштрассом
(1815—1897) и Г. Кантором (1845—1918) была построена тео-
рия действительного числа.
Первые представления о числах складывались постепенно
под влиянием практики. С давних пор числа употреблялись при
счете и измерении величин.
Ответ на вопрос: «Сколько элементов содержит данное конеч-
ное множество?» — всегда выражается либо натуральным числом,
либо числом нуль. Следовательно, множество
{0; 1; 2; ...}
всех неотрицательных чисел обслуживает все потребности счета.
Иначе обстоит дело с измерением величин. Расстояние меж-
ду двумя пунктами может равняться 3,5 километра, площадь ком-
наты — 16,45 квадратного метра и т. д.
166 Производная и ее применения
Кантор Георг
(1845—1918) —
немецкий математик, идеи и работы которого ока-
зали большое влияние на развитие математики
в целом, на понимание ее основ. Создатель тео-
рии множеств. Получил ряд замечательных резуль-
татов, относящихся к теории бесконечных мно-
жеств, теории действительного числа.
Величины бывают разных родов. Приведем два примера.
1. Расстояния между точками, длины отрезков, ломаных
и кривых линий — это величины одного и того же рода. Их выра-
жают в сантиметрах, метрах, километрах и т. д.
2. Длительности промежутков времени тоже величины одно-
го и того же рода. Их выражают в секундах, минутах, часах и т. д.
Величины одного и того же рода можно сравнивать между
собой и складывать:
1 м > 90 см
300 с < 1 ч
350 м + 650 м = 1 км
2ч+3ч=5ч
Но бессмысленно спрашивать, что больше: 1 метр или 1 час,
и нельзя сложить 1 метр с 30 секундами. Длительность промежут-
ков времени и расстояние — величины разного рода. Складывать
и сравнивать величины разного рода нельзя.
Величины можно умножать на положительные числа и нуль.
В результате умножения величины а на неотрицательное число х
получается величина Ъ = ха того же рода. Приведем несколько
примеров:
5 • 20 см = 100 см = 1 м
0,01 • 20 см = 0,2 см = 2 мм
0 • 20 см = 0 см
Приняв какую-либо величину е за единицу измерения, мож-
но с ее помощью измерять любую другую величину а того же рода.
В результате измерения получим, что а = хе, где х — число.
Это число х называется числовым значением величины а при
единице измерения е. Числовое значение величины зависит от вы-
бора единицы измерения. Если, например, длина комнаты имеет
числовое значение 5,6 при единице измерения в 1 м (е = 1 м), то
эта же длина имеет числовое значение 560 при единице измерения
в 1 см (е = 1 см).
167 Производная и ее применения
Вейерштрасс Карл Теодор Вильгельм
(1815—1897) —
немецкий математик, доказавший классические
теоремы в различных областях математики Рабо-
ты Вейерштрасса по обоснованию математическо-
го анализа, по существу, завершают создание
строгой стройной теории.
Пусть числовые значения величин а и Ъ при одной и той же
единице измерения е равны х и у, т. е. а = хе, b = уе. Если b * О,
то отношение — называют отношением величины а к Ь.
У
Таковы простейшие сведения о величинах. Приведенное опи-
сание понятия величины опиралось на понятие числа. Но истори-
ческий путь был иным: положительные действительные числа по-
явились как отношения величин (а точнее, как отношения длин
отрезков).
С открытием несоизмеримости диагонали единичного квад-
рата с его стороной стало ясно, что отношение длин отрезков не
всегда может быть выражено не только натуральным, но и рацио-
нальным числом. Для того чтобы числовое значение каждого от-
резка при фиксированной единице измерения было определено,
требовалось введение новых чисел — иррациональных.
Все практические измерения величин имеют лишь прибли-
женный характер. Их результат с требуемой точностью можно вы-
разить при помощи рациональных дробей или более специальным
образом — при помощи конечных десятичных дробей. Например,
измеряя диагональ квадрата со стороной 1 м с точностью до одного
сантиметра, мы обнаружим, что ее длина приближенно равна
1,41 м. При измерении с точностью до одного миллиметра полу-
чим, что эта длина приближенно равна 1,414 м.
Но в математике часто отвлекаются от приближенного ха-
рактера практических измерений. Последовательный теорети-
ческий подход к измерению длин отрезков приводит к необходи-
мости рассмотрения бесконечных десятичных дробей. (Именно
такие дроби представляют числа = 0,666... , у/2 = 1,41421356... ,
п = 3,14159265... .)
Отношение длины любого отрезка к длине отрезка, принято-
го за единицу измерения, всегда может быть выражено числом,
представляемым в виде бесконечной десятичной дроби.
168 Производная и ее применения
Полная теория действительных чисел довольно сложна и не
входит в программу средней школы. Но с одним из способов ее по-
строения мы познакомимся в общих чертах.
1. Принимают:
а) каждому действительному числу соответствует (в качестве
его записи) бесконечная десятичная дробь:
х = ап'" »
б) каждая бесконечная десятичная дробь является записью
действительного числа.
Но при этом естественно считать десятичную дробь, заканчи-
вающуюся бесконечной последовательностью девяток, лишь вто-
рой записью числа, выражающегося десятичной дробью, заканчи-
вающейся бесконечной последовательностью нулей:
0,9999... = 1,0000... ; 12,765999... = 12,766000... .
Такое соглашение поясним примером:
0,(9) =3 0,(3) =3 1 = 1.
3
Только исключив из рассмотрения десятичные дроби с де-
вяткой в периоде, получаем взаимно однозначное соответствие
между множеством действительных чисел и множеством бесконеч-
ных десятичных дробей.
Число а0 — это целая часть положительного числа х,
а х - а0 = 0,0^0^.. ап... — дробная часть числа х.
Число хп = а0,аха2...ап называют десятичным приближением
х с точностью до 10 " по недостатку, а число х'п = хп + 10" назы-
вают десятичным приближением с точностью до 10“л по избытку
для числа х = а0,а1а2а3...ап... .
Если число х отрицательно, т. е.
х = —a0,aia2as...an... ,
то полагают
х' = -ата,а„а.,...а, и х = х' - 10 ".
п IP 1 Z <5 п п п
2. Вводят правило сравнения двух действительных чисел.
По определению число х меньше числа у, если хотя бы при од-
ном п выполнено неравенство хп < уп, где хп и уп — десятичные
приближения с точностью до 10 " по недостатку для чисел х и у.
(Мы воспользовались тем, что правило сравнения конечных деся-
тичных дробей уже известно.)
3. Определяют арифметические действия над действитель-
ными числами (при этом также пользуются тем, что эти действия
уже определены для конечных десятичных дробей).
Суммой двух действительных чисел х и у (обозначается
х + у) называют такое действительное число г, что при любом п
выполнены неравенства хп + Уп < х + у < х'п + у'п.
169 Производная и ее применения
В курсах математического анализа доказывается, что такое
число существует и определяется единственным образом.
Аналогично произведением двух неотрицательных чисел х
и у называют такое число z (обозначается ху), что при любом п
выполнены неравенства
Х„11 < ху < х'у'.
п^п ' п&п
Такое число существует и определяется однозначно. Для
действительных чисел разных знаков, воспользовавшись тем, что
произведение неотрицательных чисел |х| и |у| уже определено,
полагают ху = - |х| |у|; в остальных случаях ху = |х||у|. (Как
обычно, модулем каждого из чисел
а0,аха2...ап... и — а0,а1а2...ап...
называют число а0,а1а2...ап... .)
Вычитание определяется как действие, обратное сложению:
разностью х — у чисел х и у называется такое число z, что
у + z = х, а деление — как действие, обратное умножению: част-
ным х: у называется такое число z, что уг = х.
4. Показывают, что неравенства и арифметические опера-
ции, определенные указанным в п. 3 образом, сохраняют основные
свойства, присущие им в множестве рациональных чисел.
Вопросы и задачи на повторение
1. 1) Что такое приращение аргумента и приращение функ-
ции?
2) В чем состоит геометрический смысл приращений Ах и Л/?
А/?
отношения — I
Ах
3) Выразите через х0 и Дх:
a) f (х) = х2 - х; б) f (х) = х3 + 2;
в) f (х) = Зх - 1; г) f (х) = —.
X
2. 1) Сформулируйте определение производной функции в точке.
2) Пользуясь определением, найдите производную функции /
в точке х0:
а) / (х) = х2 + 1, х0 = -2; б) f (х) = -, х0 = 3;
в) f (х) = 2х - 1, х0 = -4; г) f (х) = х3, х0 = 2.
3. 1) Сформулируйте правила вычисления производных. Чему
равна производная функции f (х) = х" (п — целое число)?
170 Производная и ее применения
Рис. 117
2) Дифференцируемая функция f задана графиком (рис. 117).
Постройте касательные к графику f в указанных точках и най-
дите приближенные значения производной в точках a, b, с, d.
3) Продифференцируйте функцию:
a) f(x) = (х + 2) sin х; б) f (х) =--——;
(9+ 7х)5 6
9 X2
в) /(х) = х3 - — + cos Зх; г) /(х)=— —.
х х + 3
4. 1) Какую функцию называют непрерывной на промежутке?
2) Найдите промежутки непрерывности функции:
уЗ _р у2 _ к
a) f (х) = , °; б) f (х) = 1 - 2 tg х;
4 - хг
в) f (х) =--; г) f (х) = х4 - Зх2 + 7.
х2-Зх-10
3) Решите неравенство методом интервалов:
а) - - + —— > 1; б) х4 - 15х2 - 16 < 0;
х+4 х+1
— 3 х — 4
в) ---- — < 0; г) (х - 1) (х - 2) (х + 4) > 0.
х-4
5. 1) Какую прямую называют касательной к графику функ-
ции f в точке (х0; f (х0))?
2) В чем состоит геометрический смысл производной?
3) Напишите уравнение касательной к графику функции f
в точке (х0; f (х0)):
a) f (х) = cos х, х0 = б) f (х) = 1, х0 = 2.
о X
в) f (х) = sin х, х0 = п; г) f (х) = х2, х0 =
6. 1) Запишите общую формулу для приближенного вычисления
значения функции, дифференцируемой в точке х0.
171 Производная и ее применения
2) Выпишите формулы для приближенного вычисления зна-
чений функции:
a) f (х) = хп; б) f (х) = cos х;
в) / (х) = Vx; г) f(x) = ^.
3) Вычислите приближенные значения:
а) ------; б) sin 59°;
1,ОО110
в) д/9,009; г) 0,99915.
7. 1) В чем состоит механический смысл производной?
2) Тело движется по прямой согласно закону х (t). Запишите
формулы для нахождения скорости и ускорения тела в момент
времени t.
3) Найдите скорость и ускорение точки в момент t0, если:
а) х (t) = t3 - 2t2 + 5, t0 = 4; 6) x (t) = 3 cos 2t, t0 =
О
в) x (f) = 5t - t2, t0 = 2; r) x (t) = 2t2 + t - 4, t0 = 4.
8. 1) Запишите формулу Лагранжа.
2) Сформулируйте признак возрастания (признак убывания)
функции.
3) Исследуйте на возрастание и убывание функцию:
а) у = —-; б) у = Зх - sin Зх;
х2 + 9
в) у = х4 - 4х; г) у = х2 + ~.
9. 1) Какую точку называют критической точкой функции?
2) Сформулируйте признак максимума (минимума) функции.
3) Исследуйте на максимум и минимум функцию:
а) у = - х4; б) у = 2 sin х + cos 2х;
в) у = х3 - Зх; г) у = х - tg х.
10. 1) Опишите схему исследования функции.
2) Исследуйте с помощью производной функцию:
а) /(х)=4 + 4“х2; 6)f(x)=| + ^;
4 3 X 2
в) f (х) = х3 - Зх2 - 9х; г) f (х) = —.
4-х2
3) Исследуйте по схеме функцию f и постройте ее график:
a) f (х) = х2 - -; б) f (х) = х2 (х - 2)2;
X
в) f (х) = 2х2 + Зх — 1; г) f (х) = + х2 -Зх + 1.
172 Производная и ее применения
11. 1) Сформулируйте правило нахождения наибольшего и наи-
меньшего значений функции на отрезке.
2) Найдите наибольшее и наименьшее значения функции на
данном отрезке:
a) f (х) = 0,8х5 - 4х3, [-1; 2]; б) f (х) = х - sin 2х, ^0;
в) /(х) = Зх2 - 2х3, [-1; 4]; г) f (х) = х2 (6 - х), [-1; 5].
3) а) Разность двух чисел равна 8. Каковы должны быть эти
числа, чтобы произведение куба первого числа на второе было
наименьшим?
б) Для стоянки машин выделили площадку прямоугольной
формы, примыкающую одной стороной к стене здания. Пло-
щадку обнесли с трех сторон металлической сеткой длиной
200 м, и площадь ее при этом оказалась наибольшей. Каковы
размеры площадки?
Первообразная и интеграл
§7.
Первообразная
26. Определение первообразной
Вспомним пример из механики. Если в начальный мо-
мент времени t = 0 скорость тела равна 0, т. е. v (0) = 0, то при
свободном падении тело к моменту времени t пройдет путь
8(0 = ^- W
Формула (1) была найдена Галилеем экспериментально.
Дифференцированием находим скорость:
s'(t) = v (t) = gt. (2)
Второе дифференцирование дает ускорение:
v' (t) = a (t) = g, (3)
т. е. ускорение постоянно.
Более типично для механики иное положение: известно уско-
рение точки a (t) (в нашем случае оно постоянно), требуется найти
закон изменения скорости v (t), а также найти координату s (t)-
Иными словами, по заданной производной v' (t), равной a (t), надо
найти v (t), а затем по производной s'(t), равной v (t), найти s (t)-
Для решения таких задач служит операция интегрирования,
обратная операции дифференцирования. С ней мы познакомимся
в этой главе.
Определение. Функция F называется первооб-
разной для функции f на заданном промежутке,
если для всех х из этого промежутка
Е'(х) = /(х).
X3
Пример 1. Функция Е(х) = —- есть первообразная для
О
функции f (х) = х2 на интервале (-оо; оо), так как
Е'(х) =
= |(х3)' = |-Зх2 = х2 = /(х)
О о
для всех х е (-оо; оо).
174 Первообразная и интеграл
X3
Легко заметить, что — + 7 имеет ту же самую производ-
3
ную х2 и поэтому также является первообразной для х2 на R.
Ясно, что вместо числа 7 можно поставить любую постоянную.
Таким образом, мы видим, что задача нахождения первообразной
имеет бесконечно много решений. В следующем пункте вы увиди-
те, как найти все эти решения.
Пример 2. Для функции f (х) = —L на интервале (0; оо)
у х
первообразной является функция F (х) = 2 Vx, так как
F'(x)=(2/x)' = 2 - * = = f (х)
2Vx Vx
для всех х из этого интервала. Так же как и в примере 1, функция
F (х) = 2 -/х + С при любой постоянной С есть первообразная для
функции f (х) = -±= на том же интервале (0; оо).
ух
Пример 3. Функция f’(x)=i не является первообразной
для функции f (х) = —— на промежутке (-оо; оо), так как равен-
х2
ство F' (х) = f (х) не выполнено в точке 0. Однако в каждом из
промежутков (-оо; 0) и (0; оо) функция F является первообраз-
ной для /.
Упражнения
326.— Докажите, что функция F есть первообразная для функ-
ции f на указанном промежутке:
a) F(x) = Xs, f (х) = 5х4, х е (-оо; оо);
б) F(x) = х-3, f(x) = -Зх-4, х е (0; оо);
' j в) F (х) = - X7, / (х) = X6, X 6 (-оо; оо);
| 7 ,
I г) F (х) = -77Х-6, f (х) = х 7, х е (0; оо),
О
327.
Является ли функция F первообразной для функции f
на указанном промежутке:
a) F (х) = 3 - sin х, / (х) = cos х, х е (-оо; оо);
б) F (х) = 5 - х4, f (х) = -4х3, х е (-оо; оо);
в) F (х) = cos х - 4, f (х) = -sin х, х е (-оо; оо);
г) F (х) = х-2 + 2, f (х) = 1 , х е (0; оо)?
2xJ
175 Первообразная и интеграл
Найдите одну из первообразных для функции f на R
(328—329).
328. а) в) f(x) = 3,5; f(х)= 2х; б) г) f (х) = cos х; f (х) = sin х.
329. J а) f(x) = -sin х; б) / (х) = -х;
в) /(*) = -4; г) /(х) = -cos X.
330.— Докажите, что функция F есть первообразная для функ-
ции f на указанном промежутке:
a) F (х) = sin2 х, f (х) = sin 2х, х е R;
б) F(x) = | cos 2х, /(х) = -sin 2х, х е R;
в) F (х) = sin Зх, f (х) = 3 cos Зх, х е R;
г) F (х) = 3 + tg /(х) =--Ц—, х е (-л; л).
2 2 cos2 *
2
331 .— Является ли функция F первообразной для функции f на
указанном промежутке:
a) F(х) = 2х + cos *, f (х) = 2 - sin^, х е
б) F(x) = л/4-х2 , f (х) = - х , х е (-2; 2);
74-х2
в) F (х) = ^-, f(x) =14—х е (0; оо);
г) F (х) = 4х-/х, f (х) = 6лАх, х е (0; оо)?
332 .— Найдите одну из первообразных для функции f на R:
2
в) f (х) = sin2 х + cos2 х; г) f (х) = Зх2 + 1.
333 .- Найдите две первообразные для функции f:
a) f (х) = 2х; б) f (х) = 1 - sin х;
в) f (х) = х2; г) f (х) = cos х + 2.
334 .-— Среди трех данных функций укажите такую, что две дру-
гие являются соответственно производной и первообразной
для нее:
a) f(x)=± g(x) = --, й(х) = -^-;
х2 X xd
2
б) f (х) = -cosx, g (х) = 1 + cos х, h (х) = х + sin х;
„2
в) f(x)= 1, g(x) = x + 2, й(х)= —+ 2х;
Г) /(х) = 3 - 2 sin х, g (х) = Зх + 2 cos х, h (х) = -2 cos х.
176 Первообразная и интеграл
a) f (х) = х + 2;
б) f (х) =| sin— -cos —
< 2 2
27. Основное свойство первообразной
1. Общий вид первообразных. Задача интегрирования
состоит в том, чтобы для заданной функции найти все ее первооб-
разные. При решении этой задачи важную роль играет следующее
утверждение:
Признак постоянства функции. Если
F' (х) = 0 на некотором промежутке I, то функ-
ция F — постоянная на этом промежутке.
Доказательство. Зафиксируем некоторое х0 из проме-
жутка I. Тогда для любого числа х из такого промежутка в силу
формулы Лагранжа можно указать такое число с, заключенное
между х и х0, что
F (х) - F (х0) = F' (с) (х - х0).
По условию F' (с) = О, так как cel, следовательно,
F(x)-F(xo) = O.
Итак, для всех х из промежутка I
Е(х) = Е(х0),
т. е. функция F сохраняет постоянное значение.
Все первообразные функции f можно записать с помощью од-
ной формулы, которую называют общим видом первообразных для
функции /. Справедлива следующая теорема (основное свойство
первообразных):
Т е О D е М а. Любая первообразная для функции f
на промежутке I может быть записана в виде
F(x)+C, (1)
где F (х) — одна из первообразных для функ-
ции f (х) на промежутке I, а С — произвольная
постоянная.
Поясним это утверждение, в котором кратко сформулирова-
ны два свойства первообразной:
1) какое бы число ни подставить в выражение (1) вместо С,
получим первообразную для f на промежутке I;
2) какую бы первообразную Ф для f на промежутке I ни
взять, можно подобрать такое число С, что для всех х из проме-
жутка I будет выполнено равенство
Ф (х) = F (х) + С.
177 Первообразная и интеграл
Доказательство. 1) По условию функция F — первооб-
разная для f на промежутке I. Следовательно, F' (х) = f (х) для
любого хе/, поэтому
(F (х) + С)' = F' (х) + С = f (х) + 0 = f (х),
т. е. F (х) + С — первообразная для функции f.
2) Пусть Ф (х) — одна из первообразных для функции f на
том же промежутке I, т. е. Ф' (х) = f (х) для всех хе/. Тогда
(Ф (х) - F (х))' = Ф' (х) - F' (х) = f (х) - f (х) = 0.
Отсюда следует в силу признака постоянства функции, что раз-
ность Ф (х) - F (х) есть функция, принимающая некоторое посто-
янное значение С на промежутке I.
Таким образом, для всех х из промежутка / справедливо ра-
венство Ф (х) - F (х) = С, что и требовалось доказать.
Основному свойству первообразной можно придать геометри-
ческий смысл:
Графики любых двух первообразных для функции
получаются друг из друга параллельным переносом
вдоль оси Оу (рис. 118, а).
2. Примеры нахождения первообразных.
Пример 1. Найдем общий вид первообразных для функ-
ции f (х) = -х3 на R.
Заметим, что одной из первообразных функции f является
178 Первообразная и интеграл
функция -х , так как = -х3. В силу доказанной теоремы
4 4 )
общий вид первообразных для функции f таков:
F (х)=-— + С.
4
Пример 2. Найдем первообразную Fo (х) для функции
/(х) = — на промежутке (0; оо), принимающую при х = 1 значение 1.
х2
Легко проверить, что любая первообразная функции f имеет
вид F (х) = + С. Так как по условию F (1) = 1, приходим к урав-
х
нению (относительно С) вида -1 + С = 1, откуда С = 2, и, следова-
тельно, F,. (х) = +2.
х
Пример 3. Точка движется по прямой с постоянным уско-
рением а. В начальный момент t0 = 0 точка имеет начальную коор-
динату х0 и начальную скорость ис. Найдем координату х (t) точки
как функцию от времени.
Так как х' (Z) = v (t) и v' (t) = a (t), из условия a (t) = а полу-
чаем v' (t) = а. Отсюда следует, что
v (t) = at + Ср (2)
Подставляя t0 = 0 в формулу (2), находим Cj = г() и
х' (/) = v (t) = at + t>0.
Следовательно,
х (t) = + vot + С2. (3)
Чтобы найти С2, подставим в (3) значение t0 = 0, откуда С2 = х0.
Итак,
„*2
х(/) = —+ uot + xo.
Замечание. Для краткости при нахождении первообраз-
ной функции f промежуток, на котором задана f, обычно не ука-
зывают. Имеются в виду промежутки возможно большей длины.
Так, в следующем примере естественно считать, что функция
f (х) = -jL задана на интервале (0; оо).
у! х
Пример 4. Найдем для функции f (х) = —L первообраз-
V х
ную, график которой проходит через точку М (9; -2).
Любая первообразная функции f (х) = записывается в
V х
виде 2 у[х + С. Графики этих первообразных изображены на ри-
сунке 118, б. Координаты точки М (9; -2) графика искомой перво-
Первообразная и интеграл
образной должны удовлетворять уравнению 2 у/d + С = -2. Отсюда
находим, что С = -8. Следовательно, F (х) = 2\Гх-8.
Ниже приводится таблица первообразных для некоторых
функций:
Функция f k (посто- янная) -JI X (п е Z, п*-1) 1 J X sin х COS X 1 COS 2 X 1 / sin 2 x
Общий вид первооб- разных Для f kx + С v п+1 -— + с п + 1 2у[х + С -cos х + С sin х + С tg x+ C -ctg x + C
Проверьте правильность заполнения этой таблицы самостоя-
тельно.
Упражнения
335.—
336. |
337.
Найдите общий вид первообразных для функции f (335—336).
а) /(х)= 2 - х4; б) f (х) = х + cos х;
в) /(х) = 4х; г) f(x) = -3.
а) /(х) = х6; б) /’(х)=Ц--2;
хл
в) f(*) = i--^; г) f(x) = x5.
X4
Для функции f найдите первообразную F, принимающую
заданное значение в указанной точке:
а) /(х) = Х, ^Ш = -12; б) /(х)=^—, f|V| = O;
х4 cos4 х \4у
в) f (х) = х3, .F(-l) = 2; г) /(х) = sin х, F (-л) = -1.
338.— Проверьте, что функция F является первообразной для
функции f. Найдите общий вид первообразных для /, если:
a) F (х) = sin х - х cos х, / (х) = х sin х;
б) Г (x)=Jx2 + l, /г(х)=-=^=;
в) F (х) = cos х + х sin х, f (х) = х cos х;
. „ . . Ij-zx 1+х2
г) F(x) = x—, /(х)=——.
х X2
180 Первообразная и интеграл
339.—
Для функции f найдите первообразную, график которой
проходит через данную точку М:
a) f (х) = 2 cos х, м 11;
б)
в)
/(х)= 1 — х2, М(-3; 9);
f (х) = sin f х + — 1, М ( —;
I 3J <3
г) f (х)= * М fi; 3
х4 <2
340.— Для функции f найдите две первообразные, расстояние
между соответствующими точками графиков которых (т. е.
точками с равными абсциссами) равно а:
а) /(х) = 2 - sin х, а = 4; б) f (х) = 1 + tg2 х, а = 1;
в) f (х) = sin2 — - cos2 —, а = 0,5;
2 2
г) f (х) = —L, а = 2.
Vx
341.-» Точка движется по прямой с ускорением a (t). В начальный
момент t0 ее координата равна х0, а скорость и0. Найдите
I координату х (0 точки как функцию от времени:
а) а (0 = -2t, t0 =1, х0 = 4, v0 = 2;
б) а (0 = sin t, t0 = х0 = 2, v0 = 1;
в) а (0 = 6t, t0 = 0, х0 = 3, v0 = 1;
г) а (0 = cos t, t0 = л, х0 = 1, v0 = 0.
28. Три правила нахождения первообразных
Эти правила похожи на соответствующие правила диф-
ференцирования .
Правило 1. Если F есть первообразная для f,
a G — первообразная для g, то F + G есть первообраз-
ная для f + g.
Действительно, так как F’ = / и G' = g, по правилу вычисле-
ния производной суммы имеем:
(F + G)' = F’ + G' = f + g.
Правило 2. Если F есть первообразная для f,
a k — постоянная, то функция kF — первобразная
для kf.
Действительно, постоянный множитель можно выносить за
знак производной, поэтому
(kF)’ = kF’ = kf.
181 Первообразная и интеграл
Правило 3. Если F (х) есть первообразная для
f (х), a k и b — постоянные, причем k ± 0, то
1 F (kx + Ь) есть первообразная для f (kx + b).
k
Действительно, по правилу вычисления производной слож-
ной функции имеем:
— F (kx + b) | = — F' (kx + b)- k = f (kx + b).
k J k
Приведем примеры применения этих правил.
Пример 1. Найдем общий вид первообразных для функции
/(х) = х3 + 4-
V4 1
Так как для ха одна из первообразных есть —, а для —
4 х2
одной из первообразных является , по правилу 1 находим:
х
1 - 4 1
одной из первообразных для функции f (х) = х3 будет -----.
х2 4 х
Ответ. F(x)= — + С.
4 х
Пример 2. Найдем одну из первообразных для функции
f (х) = 5 cos х.
Так как для cos х одна из первообразных есть sin х, приме-
няя правило 2, получаем ответ: F (х) = 5 sin х.
Пример 3. Найдем одну из первообразных для функции
у = sin (Зх - 2).
Для sin х одной из первообразных является -cos х, поэтому
по правилу 3 искомая первообразная равна
F (х) = cos (Зх -2).
Пример 4. Найдем одну из первообразных для функции
f (х) =
1
(7-Зх)5 '
Так как для — первообразной является , по правилу 3
х5 4х4
искомая первообразная равна
F(X)=X.__^1_.=--------L_ .
-3 4(7-Зх)4 12(7-Зх)4
Пример 5. Материальная точка массой 2 кг движется по
оси Ох под действием силы, направленной вдоль этой оси. В мо-
мент времени t эта сила равна F (t) = 3t - 2. Найдите закон х (t)
движения точки, если известно, что при t = 2с скорость точки рав-
182 Первообразная и интеграл
на 3 м/с, а координата равна 1 (F — сила в ньютонах, t — время
в секундах, х — путь в метрах).
Согласно второму закону Ньютона F = та, где а — ускоре-
ние. Имеем
a(t)=-=f «-1.
т 2
Скорость v (t) точки есть первообразная для ее ускорения a (t), по-
этому
p(t) = |t2-t+C1.
Постоянную Cj находим из условия v (2) = 3:
^4-2+С. = 3, т. е. С. = 2 и v (t) = 3 t2-t + 2.
4 4
Координата х (t) есть первообразная для скорости v (t), поэтому
х(1) =-t3--t2 +2t +С2.
4 2
Постоянную С2 находим из условия х (2) = 1:
1.8---4 + 4 + С2 = 1, С„ = -3.
4 2 2 2
Итак, закон движения точки:
x(f) = If3--1 f2+ 21-3.
v ’ 4 2
Упражнения
Найдите общий вид первообразных для функции / (342—344).
342.—
343,—
344.
345.
а) /(х) = 2 - х3 +^-;
xJ
в) /(х) = ^-sinx;
xz
a) f (х) = (2х - З)5;
в) f (х) = (4 - 5х)7;
б) f (х) = х - — + cosx;
х5
г) f (х) = 5х2 - 1.
б) f (х) = 3 sin 2х;
г) f (х) = -|cosf-t
О \ i
б) f(x) =-----v
COS2 I —-X I
1з )
в) / (х) = -----;
(Зх-1)2
г)
f (х) =—|- +
X5
1
cos2 (Зх-1)
Найдите для функции f первообразную, график которой
проходит через точку М:
a) f (х) = 4х + —, М (-1; 4);
х2
б) /(х) = х3 + 2, М (2; 15);
183 Первообразная и интеграл
в) f (х) = 1 - 2х, М (3; 2);
|г) / (х)= 1 - 10х4 + 3, М (1; 5).
х3
346 .— Найдите общий вид первообразных для функции:
а) f = 1 - cos Зх + 2 sin - х^;
б) f(x) =—1— + —i=-3x2;
snr 4х д/2-х
в) /(х) = —--------3 sin (4-х) + 2х;
cos2 (Зх + 1)
г) f (х) =----—- + , 3 -2 cos f- - х\
(3-2х)3 j5i-2 U )
347 .— Задайте первообразную F для функции f формулой, если
известны координаты точки М графика F:
a) f (х) = 2х + 1, М(0; 0); б) f (х) = Зх2 - 2х, М (1; 4);
в) / (х) = х + 2, М(1; 3); г) f (х) = -х2 + Зх, М(2;-1).
348 .— Скорость прямолинейно движущейся точки задана форму-
лой v (f) = t2 + 2t - 1. Запишите формулу зависимости ее
координаты х от времени t, если известно, что в начальный
момент времени (t = 0) точка находилась в начале коорди-
нат.
349.—
350.—
351.
Скорость прямолинейно движущейся точки задана форму-
лой v (f) = 2 cos Найдите формулу, выражающую зависи-
мость координаты точки от времени, если известно, что
в момент t = — с точка находилась на расстоянии 4 м от на-
3
чала координат.
Точка движется прямолинейно с ускорением a (t) =
= 12t2 + 4. Найдите закон движения точки, если в момент
t = 1 с ее скорость равна 10 м/с, а координата равна 12
(единица измерения а равна 1 м/с2).
Материальная точка массой тп движется по оси Ох под дей-
ствием силы, направленной вдоль этой оси. В момент вре-
мени t сила равна F (t). Найдите формулу зависимости х (£)
от времени t, если известно, что при t = t0 скорость точки
равна t>0, а координата равна х0 (F (£) измеряется в ньюто-
нах, t — в секундах, v — в метрах в секунду, m — в кило-
граммах):
a) F (t) = 6 - 9t, t0 =1, v0 = 4, x0 = -5, m = 3;
6) F (Z) = 14 sin t, t0 = n, v0 = 2, x0 = 3, m = 7;
в) F (i) = 25 cos t, t0 = ^, v0 = 2, x0 = 4, m = 5;
r) F (t) = 8/ + 8, t0 = 2, v0 = 9, x0 = 7, m = 4.
184 Первообразная и интеграл
352.— График первообразной F± для функции f проходит через
точку М, а первообразной F2 — через точку N. Какова раз-
ность этих первообразных? Какой из графиков Fx и F2 рас-
положен выше, если:
a) f (х) = Зх2 - 2х + 4, М (-1; 1), N (0; 3);
16) f (х) = 4х - 6х2 + 1, М (0; 2), N (1; 3);
в) f (х) = 4х - х3, М (2; 1), N (-2; 3);
г) f (х) = (2х + I)2, М (-3; -1), N fl; 6-1?
\ 3 J
§8.
Интеграл
29. Площадь криволинейной трапеции
Пусть на отрезке [а; &] оси Ох задана непрерывная
функция f, не меняющая на нем знака. Фигуру, ограниченную
графиком этой функции, отрезком [a; Ь] и прямыми х = а и х = Ь
(рис. 119), называют криволинейной трапецией. Различные при-
меры криволинейных трапеций приведены на рисунках 119, а—д.
Рис. 119
185 Первообразная и интеграл
Для вычисления площадей криволинейных трапеций приме-
няется следующая теорема:
Теорема. Если f — непрерывная и неотрица-
тельная на отрезке [а; Ь] функция, a F — ее пер-
вообразная на этом отрезке, то площадь S соот-
ветствующей криволинейной трапеции (рис. 120)
равна приращению первообразной на отрезке [а; Ь],
т. е.
S = F (b) - F (а). (1)
Доказательство. Рассмотрим функцию S (х), определен-
ную на отрезке [а; Ь]. Если а < х < Ъ, то S (х) — площадь той ча-
сти криволинейной трапеции, которая расположена левее верти-
кальной прямой, проходящей через точку М (х; 0) (рис. 120, а).
Если х = а, то S (а) = 0. Отметим, что S(b) = S (S — площадь кри-
волинейной трапеции).
Докажем, что
S'(x) = f(x). (2)
По определению производной надо доказать, что
Л^(х) при дх q
Дх
Выясним геометрический смысл числителя AS (х). Для про-
стоты рассмотрим случай Дх > 0. Поскольку AS (х) = S (х + Дх) -
- S (х), то AS (х) — площадь фигуры, закрашенной на рисунке
120, б. Возьмем теперь прямоугольник той же площади AS (х),
опирающийся на отрезок [х; х + Ах] (рис. 120, в). В силу непре-
рывности функции f верхняя сторона прямоугольника пересекает
график функции в некоторой точке с абсциссой с е [х; х + Дх]
(в противном случае этот прямоугольник либо содержится в части
криволинейной трапеции над отрезком [х; х + Ах], либо содер-
186 Первообразная и интеграл
жит ее; соответственно его площадь будет меньше или больше пло-
щади AS (х)). Высота прямоугольника равна f (с). По формуле пло-
щади прямоугольника имеем AS (х) = f (с) Ах, откуда — = у (с)
Дх
(Формула верна и при Дх < 0.) Поскольку точка с лежит между х
и х + Дх, то с стремится к х при Дх -> 0. Так как функция f
непрерывна, f (с) —> f (х) при Дх —> 0. Итак, ^£^2 -» f (х) при
Дх
Дх 0.
Формула (2) доказана.
Мы получили, что S есть первообразная для /. Поэтому
в силу основного свойства первообразных для всех х е [а; Ь] имеем:
S (х) = F (х) + С,
где С — некоторая постоянная, a F — одна из первообразных для
функции f. Для нахождения С подставим х = а:
F(a) + C = S(a) = 0,
откуда С = -F (а). Следовательно,
S (х) = F (х) - F (а). (4)
Поскольку площадь криволинейной трапеции равна S (&),
подставляя х = b в формулу (4), получим:
S = S (b) = F (b) - F (а).
Пример. Вычислим площадь S криволинейной трапеции,
ограниченной графиком функции f (х) = х2, прямыми у = 0, х = 1
и х = 2 (рис. 121).
Для функции f (х) = X2 одной
из первообразных является функция
X3
F (х) = —. Следовательно,
S = F(2) - Р(1) = =1.
ООО
, ► Вы видели, что вычисление про-
изводной функции в большинстве
случаев связано лишь с трудностями
вычислительного характера. Слож-
нее обстоит дело с нахождением пер-
вообразных. Так, не сразу ясно, име-
ет данная функция первообразную
или не имеет. В связи с этим от-
метим, что любая непрерывная на
промежутке функция имеет на этом
промежутке первообразную. Разъяс-
нение этого факта дает доказатель-
187 Первообразная и интеграл
ство формулы (2), приведенное выше. Однако первообразные не-
которых из известных вам функций нельзя записать с помощью
функций, изучаемых в школе. Так обстоит дело, например,
с функцией у = Л/х34-1.
Упражнения
353.
354.
Вычислите площадь фигуры, ограниченной линиями
(353—354).
а) у = х2, у = 0, х = 3; б) у = cos х, у = 0, х = 0, х =
в) у = sin х, у = 0, х = 0, х = л;
г) у = -у, У = °, х = 1, х = 2.
а) у = х3 + 1, у = 0, х = 0, х = 2;
б) у = 1 + 2 sin х, у = 0, х = 0, х =
в) у = 4 - х2, у = 0;
г) у = 1 + - cos х, у = 0, х = —х = ^.
’ у 2 > » ’ 2 2
Вычислите площадь фигуры,
(355—356).
ограниченной линиями
355.— а) у = (х + 2)2, у = 0, х = 0;
б) у =-------+ 1, у = 0, х = 0, х = 2;
(х+1)2
в) у = 2х - х2, у = 0; г) у = - (х - I)3, у = 0, х = 0.
356.- а) у = 3 sin (х + — 1 у = 0, х = - , х =
’ у 4 J 4 4
16 ) у = 2 cos 2х, у - 0, х = х =
в) у = sin х - - , у = 0, х=л, х =
’ w 2 6 6
г) у = 1 - COS X, у = О, X = X = \
30. Интеграл. Формула Ньютона — Лейбница
1. Понятие об интеграле. Рассмотрим другой подход
к задаче вычисления площади криволинейной трапеции. Для
простоты будем считать функцию f неотрицательной и непре-
рывной на отрезке [а; &], тогда площадь S соответствующей криво-
линейной трапеции можно приближенно подсчитать следующим
образом.
Разобьем отрезок [а; Ь] на п отрезков одинаковой длины точ-
Ь — а
ками х0 = а < х1 < х2 < ... < хп _ х < хп = Ь, и пусть Дх =-=
188 Первообразная и интеграл
= xk- xh_x, где k = 1, 2, ..., n - 1, n. На каждом из отрезков
[xfc l;x^] как на основании построим прямоугольник высотой
f (xk _ J. Площадь этого прямоугольника равна:
f(xk_x) /\х = ^-^- f (xk_1),
а сумма площадей всех таких прямоугольников (рис. 122) равна:
8п = (f (х0) + f (хх) + ...+ / (хп_1)).
В силу непрерывности функции f объединение построенных
прямоугольников при большом п, т. е. при малом Ах, «почти сов-
падает» с интересующей нас криволинейной трапецией. Поэтому
возникает предположение, что Sn ~ S при больших п. (Коротко
говорят: «Sn стремится к S при п, стремящемся к бесконечно-
сти» — и пишут: Sn —> S при п оо.)
Предположение это правильно. Более того, для любой непре-
рывной на отрезке [а; Ь] функции f (не обязательно неотрицатель-
ной) Sn при п —> оо стремится к некоторому числу. Это число назы-
вают (по определению) интегралом функции f от а до Ь и обозна-
ь
чают J f(x)dx, т. е.
а
Ь
—> J /(х) dx при п —> оо (1)
а
(читается: «Интеграл от а до Ь эф от икс дэ икс»). Числа а и Ь
называются пределами интегрирования: а — нижним пределом,
Ь — верхним. Знак | называют знаком интеграла. Функция f
называется подынтегральной функцией, а переменная х — пере-
менной интегрирования.
Итак, если f (х) > 0 на отрезке [a; t>], то площадь S соответ-
ствующей криволинейной трапеции выражается формулой
189 Первообразная и интеграл
Для приближенного вычисления интеграла можно рассматри-
вать суммы Sn. Лучше, однако, воспользоваться суммами
= ff.Xo'i + ftxJ + /(х2) + ... + f (x„.i) + | f(xn)^,
слагаемые которых (в случае положительной функции /) равны
площадям трапеций, «вписанных» в криволинейную трапецию
и ограниченных ломаными, как это изображено на рисунке 123.
Действительно, применяя формулу площади трапеции, полу-
чаем:
„ _ f(x0)+ /4*1) Ъ-а /(*!)+ f(x2) Ь-а
----------2 7Г+ 2 7Г + -~
= ~ ~ f (хо) + f (*i) + f (x2) + ... + f (x„_j) + | f (x„)\
n \2 2 J
2. Формула Ньютона — Лейбница. Сравнивая формулы пло-
щади криволинейной трапеции
ъ
S = F (b) - F (а) и S=jf(x)dx,
а
делаем вывод.
Если F — первообразная для f на [а; Ь], то
ь
J f (х) dx = F (b)-F (а). (3)
а
Формула (3) называется формулой Ньютона — Лейбница.
Она верна для любой функции f, непрерывной на отрезке [а; ft].
Рассмотрим примеры применения формулы Ньютона —
Лейбница.
2
Пример 1. Вычислим J x2dx.
1
Поскольку для х2 одной из первообразных является
г3
3
2
[x2dx = 23-(---1>i=3.
J 3 3
Для удобства записи разность F (ft) - F (а) (приращение
функции F на отрезке [a; ft]) принято сокращенно обозначать
ь
F (х) , т. е.
ь
F (ft) - Г (а) = F (х)
а
190 Первообразная и интеграл
Пользуясь этим обозначением,
формулу Ньютона — Лейбница обычно
записывают в виде
ь ь
jf(x)dx = F(x) (4)
а а
Пример 2. Вычислим
7Г
J sinxс/х.
о
Пользуясь введенными обозначе-
ниями, получим:
л л
I sinxс/х = -cos х = -cosп-(-cos 0) =2.
о 0
Замечание 1. Данное нами определение интеграла не поз-
воляет говорить, например, об интеграле от -1 до 2 функции
х2
так как эта функция не является непрерывной на отрезке [-1; 2].
Заметим также, что функция не является первообразной для
X
функции на этом отрезке, поскольку точка 0, принадлежащая
X2
отрезку, не входит в область определения функции.
Пример 3. Вычислим площадь фигуры, ограниченной ли-
ниями у = 1 - х и у = 3 - 2х - х2.
Нарисуем эти линии (рис. 124) и найдем абсциссы точек их
пересечения из уравнения 1-х = 3-2х-х2. Решая это уравне-
ние, находим х = 1 и х = —2. Искомая площадь может быть получе-
на как разность площадей криволинейной трапеции BADC и тре-
угольника ВАС. По формуле (2) имеем:
S,.,iC = - АВ ВС = 1-3-3 = ^.
ЛАВС 2 2 2
Следовательно, площадь закрашенной фигуры равна:
8 - Sbadc &лавс _ ® - 4,5.
191 Первообразная и интеграл
Замечание 2. Удобно расширить понятие интеграла, по-
лагая по определению при а > Ь, что
Ъ а
J f (х) dx = - J f (х) dx.
а Ъ
При таком соглашении формула Ньютона — Лейбница оказы-
а
вается верной при произвольных а и Ъ (в частности, J f (х) dx = 0).
а
Упражнения
Вычислите интегралы (357—358).
357.—
358.—
360.
361.
2 2 3 4
а) Г x4dx; б) Г cosxdx; в) [ x3dx; г) [ dx .
i J J J cos2 X
10 10
2 п
а) Г —dx „ ; б) Г 3cos-dx;
J (2х+1)2 J 2
1 ' ’ о
ю 2
в) J ; г) J sin 2xdx.
i Х 1
359.
Докажите справедливость
К
a)
* COS^ X J
о о
л о
2
в) J cosxdx= J x2dx;
о о
равенства:
б) J sinxdx= J
о 1 ^х
16
1 2
г) J (2х + 1) dx = | (х3 -1) dx.
о о
Вычислите (предварительно сделав рисунок) площадь фи-
гуры, ограниченной линиями (360—361).
а) у = х4, у = 0, х = -1, х = 1;
б) у = х4, у = 1;
в) у = х2 - 4х + 5, у = 0, х = 0, х = 4;
г) у = х2 - 4х + 5, у = 5.
а) у = 1 - х3, у = 0, х = 0;
б) у = 2 - х3, у = 1, х = -1, х = 1;
в) у = -х2 - 4х, у = 0, х = -3, х = -1;
г) у = -х2 - 4х, у = 1, х = -3, х = -1.
192 Первообразная и интеграл
Вычислите интегралы (362—363).
2л 2
362,— а) Г sin^dx; б) Г , dx ;
J 3 J J2x+ 5
—jt —2 v
Зл
Г dx
J cos2
0 9
363.— a)
2
6) J(l + 2x)3dx;
о
12
в) J (1 + cos 2x) dx;
о
Вычислите (предварительно сделав рисунок) площадь фигу-
ры, ограниченной линиями (364—366).
364 .— а) у = х3, у = 8, х = 1;
б) у = 2 cos х, у = 1, х = - ^, х —
О о
в) у = х2 - 2х + 4, у = 3, х = -1;
г) у = sin х, у = х = х = ;
’ у w 2 6 6
365 .— а) у = 4х - х2, у = 4 - х; б) у = у = 2х, х = 4;
X2
в) у = х2, у = 2х; г) у = 6 - 2х, у = 6 + х - х2.
366 .— а) у = х2 - 4х + 4, у = 4 - х2;
б) у = х2 - 2х + 2, у = 2 + 6х - х2;
в) у = х2, у = 2х - х2;
1г) у = х2, у = х3.
Вычислите площадь фигуры, ограниченной графиком функ-
ции у = 8х - 2х2, касательной к этой параболе в ее вершине
и прямой х = 0.
368. Вычислите площадь фигуры, ограниченной графиком функ-
, ции f (х) = 8 - 0,5х2, касательной к нему в точке с абсцис-
сой х = - 2 и прямой х = 1.
369. Докажите равенство:
ь ь ь
a) j (/ (х) + g (x))dx = J f(x)dx+ J g(x)dx;
a a a
b b
6) J k f(x)dx = k j f (x) dx (где k — постоянная).
a ci
193 Первообразная и интеграл
31. Применения интеграла
1. Вычисление объемов тел. Пусть задано тело объ-
емом V, причем имеется такая прямая (рис. 125), что, какую бы
плоскость, перпендикулярную этой прямой, мы ни взяли, нам из-
вестна площадь S сечения тела этой плоскостью. Но плоскость,
перпендикулярная оси Ох,
пересекает ее в некоторой точке х.
Следовательно, каждому числу х
(из отрезка [а; Ь], см. рис. 125) по-
ставлено в соответствие единствен-
ное число S (х) — площадь сечения
тела этой плоскостью. Тем самым
на отрезке [а; Ь] задана функция
S (х). Если функция S непрерывна
на отрезке [a; t>], то справедлива
формула
ь
V=^S(x)dx. (1)
а
Полное доказательство этой формулы дается в курсах математи-
ческого анализа, а здесь остановимся на наглядных соображениях,
приводящих к ней.
Разобьем отрезок [а; Ь] на п отрезков равной длины точками
х0 = а < Xj < х2 < ... < хп _ j < b = хп, и пусть
Дх = -—- = хк- xk_x, k = 1, 2, ..., п
(см. п. 30). Через каждую точку хк проведем плоскость, перпенди-
кулярную оси Ох. Эти плоскости разрезают заданное тело на слои
(рис. 126, а, б). Объем слоя, заключенного между плоскостями
a.k j и ak, при достаточно больших п приближенно равен площади
S(x k_ j) сечения, умноженной на «толщину слоя» Дх, и поэтому
V ® S (х0) Дх + S (Xj) Дх + ... + S (хп J Дх = Vn.
х
194 Первообразная и интеграл
Точность этого приближенного ра-
венства тем выше, чем тоньше слои,
на которые разрезано тело, т. е. чем
больше п. Поэтому
Vn —> V при п —> оо.
По определению интеграла
ь
Vn = J S (х) dx при п —> оо.
а
Пример 1. Докажем, что объем усеченной пирамиды вы-
сотой Н с площадями оснований S и s равен i Н (S + s + -JSs).
3
Пусть точка О — вершина «полной» пирамиды (рис. 127).
Проведем через точку О ось Ох перпендикулярно основанию пира-
миды. Основания усеченной пирамиды пересекают ось Ох в точках
а и Ъ. Каждая плоскость, перпендикулярная оси Ох и пересекаю-
щая отрезок [а; Ь] этой оси в точке х, дает в сечении многоуголь-
ник, подобный многоугольнику — основанию пирамиды. Поэтому
площадь сечения S (х) равна kx2, и, в частности,
s = S (а) = ka2 и S = S (b) = kb2.
Объем усеченной пирамиды вычисляем по формуле (1):
ь
V = f kx2dx =
J 3
а
= (Ь3 -а3) = -—- (kb2 + kab + ka2) =
3 3
= -| (S + Tsi+s).
Пример 2. Пусть криволинейная трапеция опирается на
отрезок [а; Ь] оси Ох и ограничена сверху графиком функции f,
неотрицательной и непрерывной на отрезке [а; Ь]. При вращении
этой криволинейной трапеции вокруг оси Ох получаем тело
(рис. 128, а), объем которого находится по формуле
ь
Рис. 128
Первообразная и интеграл
Действительно, каждая плоскость, перпендикулярная оси Ох
и пересекающая отрезок [а; ft] этой оси в точке х, дает в сечении
с телом круг радиуса f (х) и площади S (х) = nf2 (х) (рис. 128, б).
По формуле (1) получается формула (2).
2. Работа переменной силы. Рассмотрим материальную точ-
ку, движущуюся под действием силы Р по прямой. Если действую-
щая сила постоянна и направлена вдоль прямой, а перемещение
равно s, то, как известно из физики, работа А этой силы равна
произведению Ps. Теперь выведем формулу для подсчета работы,
совершаемой переменной силой.
Пусть точка движется по оси Ох под действием силы, проек-
ция которой на ось Ох есть функция f от х. При этом мы будем
предполагать, что f есть непрерывная функция. Под действием
этой силы материальная точка переместилась из точки М (а)
в точку М (Ь) (рис. 129, а). Покажем, что в этом случае работа А
подсчитывается по формуле
ь
А = j f (х) dx. (3)
а
Разобьем отрезок [a; ft] на п отрезков одинаковой длины
Дх = -—Это отрезки [a; xj, [Хр х2], ..., [хЛ1; 6] (рис. 129, б).
Работа силы на всем отрезке [a; ft] равна сумме работ этой силы на
полученных отрезках. Так как f есть непрерывная функция от х,
при достаточно малом отрезке [a; xj работа силы на этом отрезке
приблизительно равна f (a) (Xj - а) (мы пренебрегаем тем, что f
на отрезке меняется). Аналогично работа силы на втором отрезке
[Хр х2] приближенно равна f (xt) (х2 - xj и т. д.; работа силы
на и-м отрезке приближенно равна f (xn _ J (ft - xn _ j). Следователь-
но, A ~ A = f (a) Ax + f (x.) Дх + ... + f (x„ ,) Дх = —- (f (a) +
n 1 П 1 n
+ f (Xj) + ... + f (xn_j)), и точность приближенного равенства тем
выше, чем короче отрезки, на которые разбит отрезок [a; ft]. Есте-
ственно, что это приближенное равенство переходит в точное, если
считать, что п —> оо:
Ап =^(/(a) + /(x1)+...+f(xn_1))^A.
Поскольку Ап при п —> оо стремится к интегралу рассматри-
ваемой функции от а до 6 (см. п. 30), формула (3) выведена.
М (а)
н------•-------------
0 а
а)
Рис. 129
М (ft)
ft х
М (a) М (Ь)
--------•---1--1-------1—•-------►
0 а = х0 х1 х2 ... хп_! хп= ft х
б)
196 Первообразная и интеграл
Рис. 130
Пример 3. Сила упругости пружины, растянутой на 5 см,
равна 3 Н. Какую работу надо произвести, чтобы растянуть пру-
жину на 5 см?
По закону Гука сила F, растягивающая пружину на величи-
ну х, вычисляется по формуле F = kx, где k — постоянный коэф-
фициент пропорциональности (рис. 130), точка О соответствует
свободному положению пружины. Из условий задачи следует, что
3 = k • 0,05. Следовательно, k = 60 и сила F - 60х, а по формуле (3)
°-05 0,05
А= Гб0хс/х=30х2 * * * б) ; А = 0,075 Дж.
о 0
3. Центр масс. При нахождении центра масс пользуются сле-
дующими правилами:
1) Координата х' центра масс системы материальных точек
А1г А2, ..., Ап с массами тА, т2, ..., тп, расположенных на прямой
в точках с координатами хр х2, ..., хп, находится по формуле
х, = mix1 + m2x2 + ... + mnxn
И] + т2 + ... + тп
2) При вычислении координаты центра масс можно любую
часть фигуры заменить на материальную точку, поместив ее
в центр масс этой части, и приписать ей массу, равную массе рас-
сматриваемой части фигуры.
Пример 4. Пусть вдоль стержня — отрезка [а; Ь] оси Ох —
распределена масса плотностью р (х), где р (х) — непрерывная
функция. Покажем, что:
ъ
а) суммарная масса М стержня равна J р (х) dx;
а
b
б) координата центра масс х' равна — J xp(x)dx.
а
Разобьем отрезок [а; Ь] на п равных частей точками а =
= х0 < хг < х2 < ... < хп = b (рис. 129, б). На каждом из п этих от-
резков плотность можно считать при больших п постоянной и при-
мерно равной р (хЛ ,) на /г-м отрезке (в силу непрерывности р (х)).
197 Первообразная и интеграл
Тогда масса fe-ro отрезка примерно равна тк =--р (хк ,), а масса
всего стержня равна- — (р (х0) + р (х.) + ... + р (х .)). Считая
п
каждый из п маленьких отрезков материальной точкой массы тк,
помещенной в точке хк _ р получим по формуле (4), что координата
центра масс приближенно находится так:
Ь - а
---- (хор(хо)+ х1р(х1)+ ... + х„_ хр(хл J)
X' =-2___________________________________.
" Ь- а
--- (р(х0)+р(х1)+...+р(х„-]))
п
Теперь осталось заметить, что при п —> оо числитель стремится
ъ
к интегралу J хр (х) dx, а знаменатель (выражающий массу всего
а
b
стержня) — к интегралу j р (х) dx.
а
Для нахождения координат центра масс системы материаль-
ных точек на плоскости или в пространстве также пользуются
формулой (4).
Упражнения
370.— Найдите объем тела, полученного при вращении вокруг оси
абсцисс криволинейной трапеции, ограниченной линиями:
а) у = х2 + 1, х = 0, х = 1, у = 0;
б) у = Vx, х = 1, х = 4, у = 0;
в) у = Vx, х = 1, у = 0;
г) у = 1 - х2, у = 0.
371.— Найдите объем тела, полученного при вращении вокруг оси
абсцисс фигуры, ограниченной линиями:
а) у = х2, у = х; б) у = 2х, у = х + 3, х = 0, х = 1;
в) у = х + 2, у = 1, х = 0, х = 2; г) у = Vx, у = х.
372 . а) Выведите формулу объема шарового сегмента высо-
той Н, если радиус шара равен R.
б) Выведите формулу объема усеченного конуса высотой Н
с радиусами оснований R и г.
373 . Какую работу надо затратить на сжатие пружины на 4 см,
если известно, что сила в 2 Н сжимает эту пружину на
1 см?
374 . Сила в 4 Н растягивает пружину на 8 см. Какую работу
надо произвести, чтобы растянуть пружину на 8 см?
Первообразная и интеграл
375 .— Под действием электрического заряда величиной q элект-
рон перемещается по прямой с расстояния а до расстоя-
ния Ь. Найдите работу силы взаимодействия зарядов. (Рас-
смотрите два случая: 1) а < Ъ, q < 0; 2) b < a, q > 0. Ко-
эффициент пропорциональности в формуле, выражающей
закон Кулона, считайте равным у.)
376 .— Канал имеет в разрезе форму равнобочной трапеции высо-
той h с основаниями а иЬ. Найдите силу, с которой вода,
заполняющая канал, давит на плотину (а > Ъ, а — верхнее
основание трапеции).
377 .— Вода, подаваемая с плоскости основания в цилиндрический
бак через отверстие в дне, заполняет весь бак. Определите
затраченную при этом работу. Высота бака равна h, радиус
основания равен г.
378 .— Найдите работу против силы выталкивания при погруже-
нии шара в воду.
379 . - Однородный стержень длиной I = 20 см вращается в го-
ризонтальной плоскости вокруг вертикальной оси, про-
ходящей через его конец. Угловая скорость вращения
|со = Юл с-1. Площадь поперечного сечения стержня
S = 4 см2, плотность материала, из которого изготовлен
стержень, равна р = 7,8 г/см3. Найдите кинетическую энер-
гию стержня.
Найдите центр масс однородного прямого кругового ко-
нуса.
Сведения из истории
1. О происхождении терминов и обозначений. История по-
нятия интеграла тесно связана с задачами нахождения квадратур.
Задачами о квадратуре той или иной плоской фигуры математи-
ки Древней Греции и Рима называли задачи, которые мы сейчас
относим к задачам на вычисление площадей. Латинское слово qua-
drature переводится как «придание квадратной формы». Необхо-
димость в специальном термине объясняется тем, что в античное
время (и позднее, вплоть до XVIII столетия) еще не были доста-
точно развиты привычные для нас представления о действитель-
ных числах. Математики оперировали с их геометрическими ана-
логами или скалярными величинами, которые нельзя перемно-
жать. Поэтому и задачи на нахождение площадей приходилось
формулировать, например, так: «Построить квадрат, равновели-
кий данному кругу». (Эта классическая задача «о квадратуре
круга» не может, как известно, быть решена с помощью циркуля
и линейки.)
Первообразная и интеграл
Символ j введен Лейбницем (1675 г.). Этот знак является
изменением латинской буквы S (первой буквы слова summa). Само
слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно
происходит от латинского integro, которое переводится как приво
дить в прежнее состояние, восстанавливать. (Действительно,
операция интегрирования «восстанавливает» функцию, дифферен-
цированием которой получена подынтегральная функция.) Воз-
можно, происхождение термина интеграл иное: слово integer
означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласились
с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и на-
звание новой ветви математики — интегральное исчисление (cal-
culus integralis), которое ввел И. Бернулли.
Другие известные вам термины, относящиеся к интеграль-
ному исчислению, появились заметно позднее. Употребляющее-
ся сейчас название первообразная функция заменило более ран-
нее «примитивная функция», которое ввел Лагранж (1797 г.).
Латинское слово primitivus переводится как «начальный»:
F(x) = Jf(x)dx—начальная (или первоначальная, или перво-
образная) для f (х), которая получается из F (х) дифференцирова-
нием.
В современной литературе множество всех первообразных
для функции f (х) называется также неопределенным интегра-
лом. Это понятие выделил Лейбниц, который заметил, что все пер-
вообразные функции отличаются на произвольную постоянную.
ь
A J f (х) dx называют определенным интегралом (обозначение
а
ввел К. Фурье (1768—1830), но пределы интегрирования указы-
вал уже Эйлер).
2. Из истории интегрального исчисления. Многие значи-
тельные достижения математиков Древней Греции в решении за-
дач на нахождение квадратур (т. е. вычисление площадей) плос-
ких фигур, а также кубатур (вычисление объемов) тел связаны
с применением метода исчерпывания, предложенным Евдоксом
Книдским (ок. 408 — ок. 355 до н. э.). С помощью этого метода
Евдокс доказал, например, что площади двух кругов относятся
как квадраты их диаметров, а объем конуса равен объема ци-
О
линдра, имеющего такие же основание и высоту.
Метод Евдокса был усовершенствован Архимедом. С этой
модификацией вы знакомы: вывод формулы площади круга, пред-
ложенный в курсе геометрии, основан на идеях Архимеда. Напо-
мним основные этапы, характеризующие метод Архимеда: 1) отме-
чается, что площадь круга меньше площади любого описанного
около него правильного многоугольника, но больше площади лю-
200 Первообразная и интеграл
Архимед
(ок. 287—212 до н. э.) —
великий ученый. Первооткрыватель многих фактов
и методов математики и механики, блестящий ин-
женер. Глубокие и остроумные идеи Архимеда,
связанные с вычислением площадей и объемов,
решением задач механики, по существу, предвос-
хищают открытие математического анализа, сде-
ланное почти 2000 лет спустя.
бого вписанного; 2) доказывается, что при неограниченном удвое-
нии числа сторон разность площадей этих многоугольников стре-
мится к нулю; 3) для вычисления площади круга остается найти
значение, к которому стремится отношение площади правильного
многоугольника при неограниченном удвоении числа его сторон.
С помощью метода исчерпывания, целого ряда других остро-
умных соображений (в том числе с привлечением моделей ме-
ханики) Архимед решил многие задачи. Он дал оценку числа
л I 3 — < л < 3 1 1, нашел объемы шара и эллипсоида, площадь сег-
мента параболы и т. д. Сам Архимед высоко ценил эти резуль-
таты: согласно его желанию на могиле Архимеда высечен шар,
вписанный в цилиндр (Архимед показал, что объем такого шара
равен — объема цилиндра).
3
Архимед предвосхитил многие идеи интегрального исчисле-
ния. (Добавим, что практически и первые теоремы о пределах
были доказаны им.) Но потребовалось более полутора тысяч лет,
прежде чем эти идеи нашли четкое выражение и были доведены до
уровня исчисления.
Математики XVII столетия, получившие многие новые ре-
зультаты, учились на трудах Архимеда. Активно применялся
и другой метод — метод неделимых, который также зародился
в Древней Греции (он связан в первую очередь с атомистическими
воззрениями Демокрита). Например, криволинейную трапецию
(рис. 131, а) они представляли себе составленной из вертикальных
отрезков длиной f (х), которым тем не менее приписывали пло-
щадь, равную бесконечно малой величине f (х) dx. В соответствии
с таким пониманием искомая площадь считалась равной сумме
S = У/ (х) dx
а <х<Ь
бесконечно большого числа бесконечно малых площадей. Иногда
даже подчеркивалось, что отдельные слагаемые в этой сумме —
201 Первообразная и интеграл
Риман Георг Фридрих Бернхард
(1826—1866) —
немецкий ученый, один из крупнейших математи-
ков XIX столетия. Сделал замечательные открытия
в теории чисел и теории функций комплексного
переменного. Заложил основы новой неевклидо-
вой геометрии, получившей название римановой.
Создал теорию интеграла, обобщающую результа-
ты Коши.
нули, но нули особого рода, которые, сложенные в бесконечном
числе, дают вполне определенную положительную сумму.
На такой кажущейся теперь по меньшей мере сомнительной
основе И. Кеплер (1571—1630) в своих сочинениях «Новая аст-
рономия» (1609 г.) и «Стереометрия винных бочек» (1615 г.) пра-
вильно вычислил ряд площадей (например, площадь фигуры,
ограниченной эллипсом) и объемов (тело разрезалось на бесконеч-
но тонкие пластинки). Эти исследования были продолжены италь-
янскими математиками Б. Кавальери (1598—1647) и Э. Тор-
ричелли (1608—1647). Сохраняет свое значение и в наше время
сформулированный Б. Кавальери принцип, введенный им при не-
которых дополнительных предположениях.
202 Первообразная и интеграл
Чебышев Пафнутий Львович
(1821—1894) —
русский математик и механик. Его исследования,
получившие мировое признание, относятся к тео-
рии приближения функций многочленами («много-
члены Чебышева» наилучшего приближения), ин-
тегральному исчислению, теории вероятностей,
теории механизмов.
Пусть требуется найти площадь фигуры, изображенной на
рисунке 131, б, где кривые, ограничивающие фигуру сверху и сни-
зу, имеют уравнения у = f (х) и у = f (х) + с.
Представляя нашу фигуру составленной из «неделимых», по
терминологии Кавальери, бесконечно тонких столбиков, замечаем,
что все они имеют общую длину с. Передвигая их в вертикальном
направлении, мы можем составить из них прямоугольник с осно-
ванием Ь - а и высотой с. Поэтому искомая площадь равна площа-
ди полученного прямоугольника, т. е. S = SL = с (Ь - а).
Общий принцип Кавальери для площадей плоских фигур
формулируется так:
Пусть прямые некоторого пучка параллельных пере-
секают фигуры Фх и Ф2 по отрезкам равной длины
(рис. 131, в). Тогда площади фигур Ф, и Ф2 равны.
(В духе рассуждений математиков XVII столетия мы опускаем ого-
ворки, без которых это утверждение не совсем верно.)
Аналогичный принцип действует в стереометрии и оказыва-
ется полезным при нахождении объемов. Простейшие следствия
принципа Кавальери вы можете вывести сами. Докажите, напри-
мер, что прямой и наклонный цилиндры с общим основанием
и высотой имеют равные объемы.
В XVII в. были сделаны многие открытия, относящиеся к
интегральному исчислению. Так, П. Ферма уже в 1629 г. решил
задачу квадратуры любой кривой у = хп, где п — целое (т. е. по су-
ществу вывел формулу Г xndx = —— xn + 1), и на этой основе решил
J п +1
ряд задач на нахождение центров тяжести. И. Кеплер при выводе
своих знаменитых законов движения планет фактически опирался
на идею приближенного интегрирования. И. Барроу (1630—
1677), учитель Ньютона, близко подошел к пониманию связи ин-
тегрирования и дифференцирования. Большое значение имели ра-
боты по представлению функций в виде степенных рядов.
203 Первообразная и интеграл
г
Лебег Анри
(1875—1941) —
Французский математик. Создатель теории меры
(обобщение понятий площади и объема), на осно-
ве которой разработал новую теорию интеграла.
Однако при всей значимости результатов, полученных мно
гими чрезвычайно изобретательными математиками XVII столе-
тия, исчисления еще не было. Необходимо было выделить общие
идеи, лежащие в основе решения многих частных задач, а также
установить связь операций дифференцирования и интегрирования,
дающую достаточно общий алгоритм. Это сделали Ньютон и Лейб-
ниц, открывшие независимо друг от друга факт, известный вам
под названием формулы Ньютона — Лейбница. Тем самым окон-
чательно оформился общий метод. Предстояло еще научиться на-
ходить первообразные многих функций, дать логические основы
нового исчисления и т. п. Но главное уже было сделано: диффе-
ренциальное и интегральное исчисление создано.
Методы математического анализа активно развивались в сле-
дующем столетии (в первую очередь следует назвать имена
Л. Эйлера, завершившего систематическое исследование интегри-
рования элементарных функций, и И. Бернулли). В развитии ин-
тегрального исчисления приняли участие русские математики
М. В. Остроградский (1801 —1862), В. Я. Б у н я к о в с к и й
(1804—1889), П. Л. Чебышев (1821—1894). Принципиальное
значение имели, в частности, результаты Чебышева, доказавшего,
что существуют интегралы, не выразимые через элементарные
функции.
Строгое изложение теории интеграла появилось только в XIX в.
Решение этой задачи связано с именами О. Коши, одного из круп-
нейших математиков немецкого ученого Б. Римана (1826—
1866), французского математика Г. Дарбу (1842—1917).
Ответы на многие вопросы, связанные с существованием пло-
щадей и объемов фигур, были получены с созданием К. Жорда-
ном (1838—1922) теории меры.
Различные обобщения понятия интеграла в начале нашего
столетия были предложены французскими математиками А. Ле-
бегом (1875—1941) и А. Данжуа (1884—1974), советским ма-
тематиком А. Я. Хинчиным (1894—1959).
Первообразная и интеграл
Вопросы и задачи на повторение
1. 1) Сформулируйте определение первообразной.
2) Докажите, что функция F является первообразной для
функции f на R:
а) f (х) - 2х + 3, F (х) = х2 + Зх + 1;
б) f (х) = sin 2х + 3, F(х) = _Р°^2х + зх;
в) /(х) = -х3 + 5, Г(х) = + 5х + 2;
4
г) f (х) =-cos^ + 1, Г(х) =-2 sin^ + х.
3) Является ли функция F первообразной для функции f
на заданном промежутке:
a) F (х) = х2 - х, / (х) = 2х - 1 на R;
б) F(x) = ~ - sinx, f(x) = —-cosx на R;
x2 x3
в) F (x) = x3 + 1, f (x) = — + x на R,
4
r) F (x) = x + cos x, f (x) = 1 - sin x на R?
2. 1) Сформулируйте признак постоянства функции на задан-
ном промежутке. Сформулируйте основное свойство первооб-
разной.
2) Запишите общий вид первообразных для функции:
a) f (х) = kx + b (k и b — постоянные); б) / (х) = —-—;
cos2 х
в) f (х) = хп (п — целое число, п -1); г) f (х) = cos х.
3) Для функции f найдите первообразную F, принимающую
заданное значение в данной точке:
a) f (х) = sin х - cos х, F (л) = 1;
б) f(x)=4-4’ ^(3) = 5;
в) f (х) = 2х - 5, F (1) = -2;
г) f (х) = —L=, F (6) = 10.
х-2
3. 1) Сформулируйте три правила нахождения первообразных.
2) Найдите общий вид первообразных для функции:
а) 7(x) = sin3x-—-—; б) f(x) = —----4=;
cos2— х4 2 Ух
2
в) f (х) =(4-5х)3 --------; г) f (х) = х - 10 cos 2х.
(2х-1)3
205 Первообразная и интеграл
3) Для функции f найдите первообразную, график которой
проходит через точку М:
а) /(х) = (2 - Зх)2, М (1; 2);
б) f (х) = sin 2х, М -2^;
V 4 J
в) f(x) = V^cosx, м( —; 2^1;
\ 4 J
г) f (X) = --=!=, М (0; 3).
V х+1
4. 1) Какую фигуру называют криволинейной трапецией? Запи-
шите формулу для вычисления площади криволинейной тра-
пеции.
2) Приведите примеры криволинейных трапеций.
3) Изобразите криволинейную трапецию, ограниченную дан-
ными линиями, и найдите ее площадь:
а) у = sin х, у = 0, х = х =
б) у = -х3, у = 0, х = -2;
в) у = (х - I)2, у = 0, х = 3;
г) у = 3 - 2х - х2, у = 0, х = 0, х = -2.
5. 1) Объясните, что такое интеграл.
2) Запишите формулу Ньютона — Лейбница. Вычислите ин-
теграл:
а) f --dx -•
J (х+10)2
б) f
* V X
в) sinxdx;
г) J x2dx.
о
з
3) Вычислите площадь фигуры, ограниченной линиями:
а) у = х2, у = Зх;
б) у = х2 - 4х + 6, у = 1, х = 1, х = 3;
в) у = 4 - х2, у = 3;
г) у = COS X, у = 1, X = - , X = —.
IV
глава
Показательная
и логарифмическая
функции
§9.
Обобщение понятия степени
32. Корень п-й степени и его свойства
1. Определение корня. С понятием квадратного корня
из числа а вы уже знакомы: это такое число, квадрат которого
равен а. Аналогично определяется корень п-й степени из числа а,
где п — произвольное натуральное число.
Определение. Корнем п-й степени из числа а
называется такое число, п-я степень которого рав-
на а.
Пример 1. Корень третьей степени из числа 27 равен 3,
так как З3 = 27. Числа 2 и -2 являются корнями шестой степени
из числа 64, поскольку 26 = 64 и (-2)6 = 64.
Согласно данному определению корень п-й степени из чис-
ла а — это решение уравнения хп = а. Число корней этого урав-
нения зависит от п и а. Рассмотрим функцию f (х) = хп.
Как известно, на промежутке [0; оо) эта функция при любом
п возрастает и принимает все значения из промежутка [0; оо).
По теореме о корне (п. 8) уравнение хп = а для любого а е [0; оо)
имеет неотрицательный корень, и притом только один. Его назы-
вают арифметическим корнем п-й степени из числа а и обозна-
чают пу/а; число п называется показателем корня, а само число
а — подкоренным выражением. Знак корня называют также
радикалом.
Определение. Арифметическим корнем п-й
степени из числа а называют неотрицательное
число, n-я степень которого равна а.
Пример 2. Найдем значение: а) ^8; б)
а) 'V8 = 2, так как 23 = 8 и 2 > 0;
Показательная и логарифмическая функции
fi'J 81 — 3 как ( — - — и — > О
V16 2 <2 J 16 2
При четных n функция f (x) = xn четна. Отсюда следует, что
если а > 0, то уравнение хп = а, кроме корня х} = п4а, имеет также
корень х2 = - \[а. Если а = 0, то корень один: х = 0; если а < 0,
то это уравнение корней не имеет, поскольку четная степень лю-
бого числа неотрицательна.
Итак, при четном п существуют два корня п-й степени из
любого положительного числа а; корень п-й степени из числа 0 ра-
вен нулю; корней четной степени из отрицательных чисел не су-
ществует.
К Пример 3. Уравнение х4 = 81 имеет два корня: это числа
3 и 3. Таким образом, существуют два корня четвертой степени
из 81. При этом У81 — это неотрицательное число, т. е. У§1 =3,
a -3 = -Ув1.
Пример 4. Положительным корнем уравнения х4 - 3 яв-
ляется число Уз. Это число (так же, впрочем, как и - УЗ) ирра-
ционально. Его десятичные знаки вычислим последовательно:
1 < Уз < 2, так как I4 < 3 < 24;
1,3 <У§ < 1,4, так как 1,34 < 3 < 1,44 и т. д.
(убедитесь, что Уз = 1,31607...).
При нечетных значениях п функция f (х) = х" возрастает на
всей числовой прямой; ее область значений — множество всех дей-
ствительных чисел. Применяя теорему о корне, находим, что урав-
нение х" = а имеет один корень при любом а и, в частности, при
а < 0. Этот корень для любого значения а (в том числе и а отрица-
тельного) обозначают Уа.
|Итак, при нечетном п существует корень п-й степени
из любого числа а, и притом только один.
Для корней нечетной степени справедливо равенство
У^й = -Уй.
В самом деле, (- п-/а)п = (-!)“ ("\[а')п = -1 а = -а, т. е. чис-
ло есть корень п-й степени из -а. Но такой корень при нечетном п
единственный. Следовательно,
Равенство У~а = - У<2 (при нечетном п) позволяет выразить
корень нечетной степени из отрицательного числа через ариф-
метический корень той же степени. Например, V-71 = - У71,
V-27 = - У27=-3.
208 Показательная и логарифмическая функции
Замечание 1. Для любого действительного х
| х |, если п четно;
х, если п нечетно.
(Докажите это свойство самостоятельно.)
Замечание 2. Удобно считать, что корень первой степе-
ни из числа а равен а. Как вы уже знаете, корень второй степени
из числа называют квадратным корнем, а показатель 2 корня
при записи опускают (например, корень квадратный из 7 обозна-
чают просто W). Корень третьей степени называют кубическим
корнем.
Пример 5. Решим уравнение: а) х5 = -11; б) х8 = 7.
а) По определению корня п-й степени число х — корень пя-
той степени из -11. Показатель корня — нечетное число 5, по-
этому такой корень существует, и притом только один: это -11.
Итак, х = - 5Л1.
б) По определению корня п-й степени решением уравнения
х8 = 7 является число ^7. Так как 8 — число четное, - V7 также
является решением данного уравнения. Итак, Xj = V7, х2 = - V7.
Ответ запишем так: х = ± ^7.
2. Основные свойства корней. Напомним известные вам
свойства арифметических корней п-й степени.
Для любого натурального п, целого k и любых не-
отрицательных чисел а и b выполнены равенства:
1°. "Jab = nJa n4b.
2°. = о).
УЪ п4ъ
з°. = "Va (fe >0).
4°. nJa = nhJak (й >0).
5°. n-Jak =(n-fa)k (если k < 0, то a * 0).
Докажем свойство 1°. По определению nJab — это такое неот-
рицательное число, n-я степень которого равна аЬ. Число nJa nJb
неотрицательно. Поэтому достаточно проверить справедливость
равенства (nJa nJb) " = ab, которое вытекает из свойств степени
с натуральным показателем и определения корня п-й степени:
Vb Г = №)"•( = ab.
Показательная и логарифмическая функции
Аналогично доказываются следующие три свойства:
П I \
уа > О
Докажем теперь свойство 5°. Заметим, что п-я степень числа
(n-/a)k равна ак:
По определению арифметического корня (ny/a)k = n-JaF (так
как (J\[a}k > 0).
Приведем примеры применения свойств 1°—5° к реше-
нию задач на преобразование числовых выражений, содержащих
корни.
5 I— 5 1— I
Пример 6. Преобразуем выражения: а) <8 у4; б) т/5—;
V 16
в) г) 2V128; д) V1283.
a) V8-VI = V8^4 = V32 =2 (свойство 1°);
б) =4Л = Ж = f (свойство 2°);
V It) v 16 ^/16
в) VV? = (свойство 3°);
г) 2д/128 = 2л/27 = ^2 (свойство 4°);
д) применяя свойство 5°, находим V1283 = (V128 )3 = 23 =8.
Докажем следующее свойство арифметического корня:
6°. Для любых чисел а и Ъ, таких, что 0 < а < Ь,
выполняется неравенство Va < n-jb.
Проведем доказательство методом от противного. Допу-
стим, что Пу[а n-jb. Тогда по свойству степеней с натуральным
показателем т.е. а > t>. Это противоречит усло-
вию а < Ь.
210 Показательная и логарифмическая функции
Пример 7. Сравним числа V2 и л/З.
Представим ^2 и V3 в виде корней с одним и тем же пока-
зателем: ^2 = - 1^/з2, 5у[з = = 1^27 (свойство 4°). Из не-
равенства 32 > 27 по свойству 6° следует, что XV32 >1^27, и, зна-
чит, V2 > л/З.
Пример 8. Решим неравенство х6 > 20.
Это неравенство равносильно неравенству х6 - 20 > 0. Так
как функция f (х) = х6 - 20 непрерывна, можно воспользоваться
методом интервалов. Уравнение х6 - 20 = 0 имеет два корня: V20
и - V20. Эти числа разбивают числовую прямую на три проме-
жутка. Решение данного неравенства — объединение двух из них:
(-оо; -V20) и (^/20; оо).
Упражнения
Проверьте справедливость равенств (381—382).
381.- a) V16 = 2; б) Vn = -1; в) *V1024=2; г) V-243=-3.
382.- -а) 4/1=1; 6)V64=2; b)V-343=-7; г) 4/0 =0. Вычислите (383—384).
383J a) Vn?; 6) V81; в) Vn2; r) V64.
384. 1 r»s> 6,V1; r,Vl-
Решите уравнения (385—388).
385.- a) x3 + 4 = 0; 6) x6 = 5; в) x3 = 4; r) x4 = 10.
386.- a) x10 -15 = 0; 6) x7 + 128 = 0;
в) x6 — 64 = 0; r) x5 = 3.
387.- a) 16x4 -1 = 0; 6) 0,01x3 + 10 = 0;
в) 0,02x6 - 1,28 = 0; r) 123--^x2 = 0. ’ 4 4
388.- a) Vx=-0,6; 6) Vx =3; в) Vx = 5; r) Vx=-1.
Найдите значение числового выражения (389—394).
389.-J a) (-VH)4 ; б)(2®^2)5; в) (V7)3 ; r)(-V2)6.
211 Показательная и логарифмическая функции
390.—
391.—
392.—
393.—
394.—
a) V16 -625; б) V32-243;
в) ^8 -343; г) ^/0,0001-16.
а) л/160 -625; б) л/24-9; в) V48-27; г) V75-45.
a) V9-V9; б) Vie -T^B;
в) V27 V9; г) 3дГ25 ^25.
) « V128 . V243 . V128 W ’ °* W ’ Тг '
а) 6 §4 ' \ 100 000 000 1/з9— : 3J-3—; V 16 V 27
б) з/1— -4,5 -- V 16 5 . Е) 5/ 243 3/ d17. /288* ’ 1024 ’ 27 ’
+ r-i|oq гИ СО|00 со /5 80
395.
Найдите первые два десятичных знака (после запятой)
числа:
a) V2; б) Зу[5; в) V7; г) ^3.
396.
397.-
398.
Пользуясь таблицами или калькулятором, найдите прибли-
женное значение корня с точностью до 0,01 (396—397).
а) ^10,17; б) V71; в) д/13,21; г) V1T.
а) ^/13,7; б) V10; в) ^2^; г) V13.
399.-
400.-
401.
Сравните числа (398—401).
a) V^2 и 0; б) *V04 И ;
в) 7^8 и 1; г) ^0^2 и VO-
ьэ|м S ст м б) и 18V0,43;
S [04 г) lV6^8 и 1.
а) у/0,3 и V0,05; б) V4 и V8;
в) V7 и V40; г) V5 и V500.
a) V-0>4 и V-0’3; 1 Д' |Т от?* S 11Г5 ю
в) V-2 и V-4; г) И V^3.
212 Показательная и логарифмическая функции
402.— Вынесите множитель за знак корня (а > О, b > 0):
а) л/б4а8Ьп ; б) V-128a7 ; в) ^1ба12Ье ; г) V54а10 .
403.-
404.
405.
406.
407.
408.-
409.—
410.—
411.-
412.-
413.-
414.-
a) —b V3; б) ab
Внесите множитель под знак корня (а > О, Ъ > 0):
; в) a V?; г) -ab^f-i.
При каких значениях а верно равенство (404—405)?
a) Va^ =-а; б) 3Ja^ =а; в) = |а|; г) =а.
a) Va3" = -а; б) =-а; в) Va4 = |a|; г) Va^~ = а.
Представьте выражение в виде дроби, знаменатель которой
не содержит знака корня (406—407).
Приведите числовое выражение к виду a n-Jb, где а — ра-
циональное число, а b — натуральное (408—409).
„ от-
решите уравнение с помощью подстановки t = у х или
a) Vx - 5 Vx +6=0; б) Vx + Vx = 2;
в) Vx - 3 Vx +2=0; г) Vx - 5 Vx = 6.
Решите неравенства (411—412).
a) x4<3; 6) x11 > 7; в) x10 >2; г) x3 < 5.
a) Vx < -7; 6) Vx > 2; в) Vx > 2; r) Vx < 3.
Упростите выражения (413—414).
a) Va% где a C 0; 6) Va\ где a > 0; в) Va®~.
a) Va3" -Va3", где a < 0; 6) Va4 +2 Va7", где a > 0;
в) Va5 - Va6 , где a > 0; r) Va3 + 3 Va8 , где a < 0.
213 Показательная и логарифмическая функции
415.— Найдите значение выражения:
a) V10 +V73 • ^10-773; б) + V17;
3V4-V17
в) t/9-765 t/9 +V65; г) V3-V5 7з+V5.
416.-
Представьте выражение в виде дроби, знаменатель которой
не содержит радикала:
33. Иррациональные уравнения
Уравнения, в которых под знаком корня содержится
переменная, называют иррациональными. Таково, например, урав-
нение Vx -2 = 0.
Пример 1. Решим уравнение ^х2 -5 = 2.
Возведем обе части этого уравнения в квадрат и получим
х2 - 5 = 4, откуда следует, что х2 = 9, т. е. х = 3 или х = -3.
Проверим, что полученные числа являются решениями урав-
нения. Действительно, при подстановке их в данное уравнение по-
лучаются верные равенства
у]32-5 = 2 и V(-3)2-5 = 2.
Следовательно, х = 3 и х = -3 — решения данного уравнения.
Пример 2. Решим уравнение Vx=x-2.
Возведя в квадрат обе части уравнения, получим х =
= х2 - 4х + 4. После преобразований приходим к квадратному
уравнению х2 - 5х + 4 = 0, корни которого х = 1 и х = 4. Про-
верим, являются ли найденные числа решениями данного урав-
нения. При подстановке в него числа 4 получаем верное равенство
V4 = 4 - 2, т. е. 4 — решение данного уравнения. При подстановке
же числа 1 получаем в правой части -1, а в левой части число 1.
Следовательно, 1 не является решением уравнения; говорят, что
это посторонний корень, полученный в результате принятого спо-
соба решения. Ответ: х = 4.
Мы видим, что при решении иррациональных уравнений по-
лученные решения требуют проверки, потому, например, что не-
верное равенство при возведении в квадрат может дать верное ра-
венство. В самом деле, неверное равенство 1 = -1 при возведении
в квадрат дает верное равенство I2 = (-1)2.
214 Показательная и логарифмическая функции
Пример 3. Решим уравнение у] х2 -2 = -Jx.
Возведем обе части этого уравнения в квадрат: х2 - 2 = х,
откуда получаем уравнение х2 - х - 2 = 0, корни которого х = -1
и х = 2. Сразу ясно, что число -1 не является корнем данного урав-
нения, так как обе части его не определены при х = -1. При под-
становке в уравнение числа 2 получаем верное равенство
у]22 -2 = у[2. Следовательно, решением данного уравнения являет-
ся только число 2.
Пример 4. Решим уравнение у/х - 6 = -74-х.
Возводя в квадрат обе части этого уравнения, получаем
х - 6 = 4 - х, 2х = 10, х = 5. Подстановкой убеждаемся, что чис-
ло 5 не является корнем данного уравнения. Поэтому уравнение
не имеет решений.
Иногда удобнее решать иррациональные уравнения, исполь-
зуя равносильные переходы.
Пример 5. Решим уравнение 7х-2 =х-8.
По определению -7х -2 — это такое неотрицательное число,
квадрат которого равен подкоренному выражению. Другими слова-
ми, уравнение Vх-2 = х-8 равносильно системе
Jx-2 = (х-8)2,
[х-8 > 0.
Решая первое уравнение системы, равносильное уравнению
х2 - 17х + 66 = 0, получим корни 11 и 6, но условие х - 8 > 0 вы-
полняется только для х = 11. Поэтому данное уравнение имеет
один корень х = 11.
Пример 6. Решим уравнение х-1 = Vх2-х-1.
В отличие от рассмотренных ранее примеров данное ирра-
циональное уравнение содержит не квадратный корень, а корень
третьей степени. Поэтому для того, чтобы «избавиться от ради-
кала», надо возвести обе части уравнения не в квадрат, а в куб:
(х - I)3 = х2 - х - 1. После преобразований получаем:
х3 - Зх2 + Зх - 1 = х2 - х - 1,
х3 - 4х2 + 4х = 0,
х (х2 - 4х + 4) = 0,
х (х - 2)2 = 0.
Итак, х] = 0, х2 = 2.
Пример 7. Решим систему уравнений
Vx + Зу[у = 4,
х+ у = 28.
215 Показательная и логарифмическая функции
Положив и = Vx и v = :\Гу, приходим к системе
Г и + v = 4,
[u3 + t>3 = 28.
Разложим левую часть второго уравнения на множители:
и3 + Vs = (и + v) (и2 - uv + v2) — и подставим в него из первого
уравнения и + v = 4. Тогда получим систему, равносильную вто-
рой:
Г и + v = 4,
[u2-uv + v2 = 7.
Подставляя во второе уравнение значение V, найденное из
первого (и = 4 - и), приходим к уравнению
и2 - и (4 - и) + (4 - и)2 = 7, т. е. и2 - 4и + 3 = 0.
Полученное квадратное уравнение имеет два корня: иг = 1
и и2 = 3. Соответствующие значения v таковы: = 3 и и2 = 1.
Переходя к переменным х и у, получаем: Vx =иг, т. е. хх =
= и3 = 1, уг = и3 = 27, х2 = п3 = 27, у2 = у3 = 1.
Ответ: (1; 27), (27; 1).
Упражнения
Решите уравнения (417—420).
417.- - а) д/х4 + 19 =10; б) 3у]х2-28 =2;
в) •s/61-х2 =5; г) н । СО II 1 W
418., Ь а) Vx + 1 = х -5; б) х + V 2 х + 3 — 6 j
в) д/2х-1 = х-2; 419.- a) V2x + 1 = ^х2-2х+ 4 в) л/х + 2 = д/2х-3; 420. а) х =^/х3 + х2-6х + 8; в) х =?/х3-х2-8х + 20; г) 3 + у/Зх +1 — х. ; б) Vx = у]х2 - х-3; г) 79 -х2 = у/х + 9. б) х-2=^/х2-8; г) х +1 =?/х3 + 2х2 +х.
Показательная и логарифмическая функции
421.— Решите систему уравнений:
Vx + 2 3Jy = 1,
3Vx-^i/ =10;
2 Vx + 4Jy = 7,
4V?-3Vx =6;
Решите уравнения (422—425).
422.- - а) 7 х + 1 7 X + 6 =6; б) ^J^Vx-l;
72^1
в) f—— V Зх + 2, 7х-2 г) 7х 72-х =2х.
423.- - а) 75 + Vx + 3 = 3; б) ТТ*2 -16 + х = 2;
в) 718-Vx+1O = 4; г) х2 _5 _ £
424.- - а) V х — 3 — 1 + V х — 4 j б) Тх + 2 -7х-6 =2;
в) 2 + 710 — х = -J22 -х; г) 7Г-2х-3 = 716 + х.
425.- - а) co I II CO 1 co I H 6) Vx+1+2 Vx+1 =3;
в) Vх-5 = 30 -Vх-5; г) 317xz-3 + Vx2-3=4.
Реи ните системы уравнений (426—427).
426.- а) to 1 < н 1 1 <c II ел 76 + x-3 73j/ + 4 =-10,
7х 71/ =3; 473у + 4-57б + х =6;
в) 7х + 3 Jy = 10, г) 27х-2 +75«/+1 =8,
7х у/у =8; 37х-2 -2 7б{/+1 =-2.
427.4. а) ' V^ + V^=8, б) 3 / з 1 е х +7 у =5,
х-у = 16; ху =216;
в) . 7^-7? = 4, Г) ’37^-VF = 2,
х-у = 32; xj/ = 27.
217 Показательная и логарифмическая функции
34. Степень с рациональным показателем
Вам уже знакомо понятие степени числа с целым пока-
зателем. Выражение ап определено для всех а и п, кроме случая
а = 0 при п <= 0. Напомним свойства таких степеней.
Для любых чисел а, b и любых целых чисел тип
справедливы равенства:
ат ап = ат +ат-.ап = ат~п (а * 0);
(ат)" = атп;
(аЪ)п = ап Ьп-, \ - | = & (Ь * 0);
\ь ) ъп
а1 = а; а° = 1 (а 0).
Отметим также следующее свойство:
|Если т > п, то ат > ап при а > 1 и ат < ап при
0 < а < 1.
В этом пункте мы обобщим понятие степени числа, придав
5 1
смысл выражениям типа 20,3, 87, 4 2 и т. д. Естественно при
этом дать определение так, чтобы степени с рациональными пока-
зателями обладали теми же свойствами (или хотя бы их частью),
что и степени с целым показателем. Тогда, в частности, п-я сте-
т
пень числа а " должна быть равна ат. Действительно, если свойст-
во (ар)д = ард выполняется, то
Последнее равенство означает (по определению корня п-й
т
степени), что число а " должно быть корнем п-й степени из чис-
ла ат.
Определение. Степенью числа а > 0 с рацио-
т
нальным показателем г =—, где т — целое чис-
п
ло, ап — натуральное (п > 1), называется число
г\[а"Г.
Итак, по определению
т
а "
(1)
Степень числа 0 определена только для положительных
показателей; по определению 0г = 0 для любого г > 0.
Показательная и логарифмическая функции
Пример 1. По определению степени с рациональным по-
казателем
1 5
7 4 =V7; 26
__7_
а'ъ = '^.7
1
Пример 2. Найдем значения числовых выражений 83,
3 _2
814, 128 7.
По определению степени с рациональным показателем
1 з
и свойствам корней, имеем 83 =V8=2; 814 -у/813 =(4/81)3 =
2
= З3 = 27; 128 7 =V128 2
-2 = 2 2 = i.
4
Замечание 1. Из определения степени с рациональным
показателем сразу следует, что для любого положительного а
и любого рационального г число а' положительно.
Замечание 2. Любое рациональное число допускает раз-
личные записи его в виде дроби, поскольку — = для любого
п nk
натурального k. Значение аг также не зависит от формы записи
рационального числа г. В самом деле, из свойств корней следует,
mk ____ ______ т
что апк = Пу/атк = Пу1ат -ап .
Замечание 3. При а < 0 рациональная степень числа а
не определяется, и это не случайно. Если бы мы сочли верной фор-
1
мулу (1) и для а < 0, то, например, значение (-8)3 равнялось бы
о J-- 1 О
J-8, т. е. —2. Но, с другой стороны, = - , и поэтому должно вы-
3 6
1 2
полняться равенство -2=(-8)3 =(-8)6 =^(-8)2 = =2.
Покажем теперь, что при сформулированном выше определе-
нии степени с рациональным показателем сохраняются основные
свойства степеней, верные для любых показателей (разница за-
ключается в том, что приводимые далее свойства верны только для
положительных оснований).
Для любых рациональных чисел г и s и любых по-
ложительных а и b справедливы равенства:
1°. аг • as = аг + ®.
2°. аг : а® = ar s.
3°. («r)s = ars.
4°. (ab)r = а' Ьг.
5<* f “ Л = « L
Показательная и логарифмическая функции
Для доказательства этих свойств надо воспользоваться опре-
делением степени с рациональным показателем и доказанными
в п. 32 свойствами корней. Докажем, например, свойства 1°, 3°
и 4°. Пусть г = "1 и s = —, где п и q — натуральные числа, а т
п q
и р — целые. Тогда
mq + пр
(агГ = ^(агУ = 9-j(ny!a^)P = П94а"* =апс> =ars;
(ab)r = ny](ab)m = nJambm = nJa™ • n4b^ =ar br.
Свойства 2° и 5° доказываются аналогично (проведите соот-
ветствующие рассуждения самостоятельно).
1 _з
Пример 3. Найдем значение выражения V40-24:5 4.
1 з ____________ 1 з з + 1 1+з
V40 -24 : 5 4 = д/23 -5 • 24 54 = 24 4 • 54 4 = 21 • 51 = 10.
Пример 4. Преобразуем выражения:
а2 -t>2 _ а1,2 -Ь2,1
а) Л Г } a0’8 + a0’4fc°-7 + bi;r’
а4 + Ь4
1 1 < Л2 < i¥ Г 1 iV 1 1) t х
a2-t>2 [a4J - lb4J Iа4 -b4)Iа4 + b4) 7 7
’ 1 1 11 11
а4 + Ь4 а4 + fe4 а4 + Ь4
a^-b2-1 (а0,4)3 -(Ь0,7)3
) ~ (а0,4)2 + а0,4Ь0,7 + (t>0,7)2 “
= a°’4-fc0>7.
Отметим следующие два свойства степеней с рациональными
показателями:
6°. Пусть г — рациональное число и 0 < а < Ъ. Тогда
аг < Ьг при г > 0,
ar > Ьг при г < 0.
7°. Для любых рациональных чисел г и s из нера-
венства г > s следует, что
ar > а8 при a > 1,
ar < as при 0 < a < 1.
Докажем свойство 6°. Если г > 0, то г можно записать в виде
г = —, где т и п — натуральные числа. Из неравенства 0 < а < b
п
и свойств степени с целым показателем следует, что ат < Ьт.
220 Показательная и логарифмическая функции
По свойству корней (свойство 6°, п. 32) из этого неравенства полу-
чаем пу]ат < n-\lbm , т. е. аг < Ьг.
В случае г < 0 проводится аналогичное рассуждение.
Для доказательства свойства 7° приведем сначала рациональ-
ные числа г и s к общему знаменателю: г = — и s = —, где п — на-
п п
туральное число, а т и р — целые. Из неравенства г > s следует,
£
что т > р. Если а > 1, то а" = nJa > 1 и по свойству степени с це-
< лт ( Л*
лым показателем .
Остается заметить, что
( 1)" ™ ( 1Y -
=ап =аг и =а"=а®.
Случай 0 < а < 1 разбирается аналогично.
2
Пример 5. Сравним числа V8 и 23.
Запишем д/8 в виде степени с рациональным показателем:
з
V8 = 25.
2
По свойству 7° получаем 23
з
>25, так как — > —.
3 5
Пример 6. Сравним числа 2300 и З200.
Запишем эти числа в виде степеней с одинаковым показа-
телем:
2300 _ (23)Ю0 _ gioo. 3200 _ (32^100 _ дюо
Так как 8 < 9, по свойству 6° получаем
810° < дЮО* т> е 2300 < з200.
Упражнения
428.—
429.4-
430.
Представьте в виде корня из числа выражение:
-2 -11
а) З1,2; б) 5 3; в) 41,26; г) 6 2.
Представьте выражение в виде степени с рациональным
показателем:
a) Va 2; б) V3&; в) ly/b 7; г) ^4®”.
Найдите значение числового выражения (430—431).
, 1 5 2
а) 2430,4; б) f8; в) 164; г)
I З8 ) 11256 )
Показательная и логарифмическая функции
1
431.—
3 I
а) 82 : ^8 6 92J;
8
5
432
433.
434.
435.
436.
437.—
2 -
в) 8 3 :81°-75;
г)
< 25
4И
25
з
Разложите на множители (432—433).
1
(ах)3
а)
а)
в)
X3 у3
+ (аг/)3 ; б) а - а2 ;
в) З + З2;
г) (Зх)2 -(5х)2.
.3
б)
с2
4 .
4-43;
г)
а + Ь2 +а2
1 1
+ а2Ь2.
Упростите выражения (434—435).
а)
а)
в)
г)
а-b 2-8
; б) -----------
1 2 1
z3 + 2z3 + 4
1
а2 -Ъ2
х-у
3
4
1 1
+ X2 у4
1
1 1
а+ а2Ь2
Сравните
и
11 11
X2 у4 + X4 у2
X2 + у2
1
а - а2 Ь2
числа:
19
З8 ;
61’7;
.2
Найдите значение
х2 -4
в)
х-16
б)
а -1
г)
2 11 2
а3 -а3 Ь3 + Ъ3
—-— + 2а2 ;
з
а2 -1
а3 - Ь3
а2 + ab+ Ь2
б) 0,4 2’7
г)
5
15
и
выражения:
i з
5
1 )
32 J
2 -1
б) 0,001 3 ~(-2)’2643 -8 3 +(90)2;
а) 81 0,75
1
125
з
з
Показательная и логарифмическая функции
438.—
439.
440.
441.
442.
443.
444.
2
в) 273
1
16
г) (-0,5) 4
-0,75
-250'5;
-6250 25 2 -
I 4
2 + 19(-3)-3.
выражение:
г- ,Г 1
у! а + у! а .
—------ а
Упростите
. а-1
а) ------
’ 3 1
б)
1
4 1
а3-27а3 Ь
2 11 2
а3 + За3 ft3 + 9ft3
1 _ "г2 +4 1 (т_____1_ + 1
<m + V2 m3+2-/2j t 2 72 т
Представьте выражение в виде степени с рациональным по-
казателем:
а) - V25 -ах3 ;
8
б) ^а2 Va; в) Vb; г) • ^2?Vx.
О
Представьте выражение в виде 3 3 2 2 а) 3-2 5; б) a4 : ft5; в) 2Ь 3 корня: 1 2 ; г) Ь3 с1.
Сравните числа:
а) (73)’6 5 ” (tr S S «еГ*.М to] СлЭ to Г и- *** Т W .Г1 wlH з а Зб°° и 54оо. 730 и 440.
Имеет ли а) (-3) 7; смысл выражение: 2 4 б) (-2)"4; в) 53; г) 0 7?
Найдите область определения выражения:
2 3 3 2
а) (х+1) 7; б) х5; в) х 4; г) (х-5)3.
При каких значениях переменной верно равенство:
( А® 1 1 t3
a) la6J =а; б) (a4)4 = -a; в) (а8)8 =рЦ; г) (a0,7) 7 = -а?
|a|
Показательная и логарифмическая функции
§ 10.
Показательная и логарифмическая
функции
35. Показательная функция
1. Степень с иррациональным показателем. Зафик-
сируем положительное число а и поставим в соответствие каждо-
т
му числу — число а" . Тем самым получим числовую функ-
п
цию f (х) = ах, определенную на множестве Q рациональных чисел
и обладающую перечисленными в п. 34 свойствами. При а = 1
функция f (х) = ах постоянна, так как Iх = 1 для любого рацио-
нального х.
Нанесем несколько точек графика функции у = 2х, предвари-
тельно вычислив с помощью калькулятора значения 2х на отрезке
[-2; 3] с шагом - (рис. 132, я), а затем с шагом * (рис. 132, б).
4 8
Продолжая мысленно такие же построения с шагом —, — и т. д.,
10
мы видим, что получающиеся точки можно соединить плавной
кривой, которую естественно считать графиком некоторой функ-
ции, определенной и возрастающей уже на всей числовой прямой
и принимающей значения 2п в рациональных точках х = ™
(рис. 132, в). Построив достаточно большое число точек графика
z \ X
функции у = ( 1 , можно убедиться в том, что аналогичными
свойствами обладает и эта функция (отличие состоит в том, что
( 1
функция у = I — I убывает на R).
Эти наблюдения подсказывают, что можно так определить
( 1
числа 2“ и 1 — 1 для каждого иррационального а, что функции,
fl V
задаваемые формулами у = 2х и у = I - I , будут непрерывными,
(1V
причем функция у = 2х возрастает, а функция у = I - I убывает
на всей числовой прямой.
Опишем в общих чертах, как определяется число аа для ир-
рациональных а при а > 1.
Мы хотим добиться того, чтобы функция у = ах была воз-
растающей. Тогда при любых рациональных гг и г2, таких,
что г. < а < г2, значение аи должно удовлетворять неравенствам
а'1 <аа <аГг .
224 Показательная и логарифмическая функции
Рис. 132
Показательная и логарифмическая функции
Выбирая значения гг и г2, приближающиеся к х, можно
заметить, что и соответствующие значения аг* и аГг будут мало
отличаться. Можно доказать, что существует, и притом только
одно, число у, которое больше всех аГ1 для всех рациональных Tj
и меньше всех аГ2 для всех рациональных г2. Это число у по опре-
делению есть аа.
Например, вычислив с помощью калькулятора значения 2*
в точках хп и х'п, где хп и х’п — десятичные приближения числа
х = -Уз, мы обнаружим, что чем ближе хп и х'п к 7з, тем меньше
отличаются 2х" и 2х".
Так как 1 < V3 < 2, то
21 = 2 < 2^ <22 -4.
1,7 < у[з < 1,8 и, значит,
21,7 » 3,2490096 < 2^ < 21-8 ® 3,4822022.
Аналогично, рассматривая следующие десятичные прибли-
жения -Уз по недостатку и избытку, приходим к соотношениям:
21-73 » 3,3172782 < 273 < 21-74 » 3,3403517;
21-732 » 3,3218801 < 2^ < 21,733 == 3,3241834;
21,732о ~ 3,321801 < 273 < 21-7321 » 3,3221104;
21,73205 ~ 3,3219952 < 2 73 < 21-73206 == 3,3220182;
21-732050 3,3219952 < 2^ < 21-732051 ~ 3,3219975.
Значение 2 ^3, вычисленное на калькуляторе, таково:
2^ ® 3,321997.
Аналогично определяется число а“ для 0 < а < 1. Кроме
того, полагают 1“ = 1 для любого а и 0“ = 0 для а > 0.
2. Свойства показательной функции.
Определение. Функция, заданная формулой
у = ах (где а > 0, а 1), называется показательной
функцией с основанием а.
Сформулируем основные свойства показательной функции
(их доказательство выходит за рамки школьного курса).
1. Область определения — множество R действи-
тельных чисел.
2. Область значений — множество R+ всех положи-
тельных действительных чисел.
Показательная и логарифмическая функции
3. При а > 1 функция возрастает на всей числовой
прямой; при 0 < а < 1 функция убывает на множест-
ве R.
Графики показательных функций для случаев а > 1 и
О < а < 1 изображены на рисунках 133—134.
4. При любых действительных значениях х и у спра-
ведливы равенства
ахау=ах+у; — =ах~у;
ау
( \х х
(ab)x =ахЬх; = ^-;
[bj ьх
(ах)у = аху.
Эти формулы называют основными свойствами степеней.
Свойства 3 и 4 означают, что для функции у = ах, определен-
ной на всей числовой прямой, остаются верными свойства функ-
ции у = ах, которая сначала была определена только для рацио-
нальных х (см. свойства 1°—7°, п. 34).
Упражнения
445.— Перечислите свойства функции и постройте ее график:
а) у = 4х; б) у = 0,2х; в) у = 0,7х; г) у = 2,5х.
446.— Найдите область значений функции:
а) у = -2х; б) у = 447.- Сравните числа: \ ^4^ 2 . а) — и 1; <7j в) 2,5-^ и 1; "1^+1; в) У = г) г/= 5х - 2. — fiA2’8 б) 3“V12 и А ; 1 3 J 1 г) 0,3 6 и 0,33 .
Показательная и логарифмическая функции
448.—
Вычислите:
а) ((72)^)^;
в) 8^ :23^2;
б)
г)
gl-2 . gl+ V3 .
(з5^)Ч
Упростите выражения (449—450).
449. а) а72 •f-г 1- к a J б) хл х2: х4л ;
450. 451.- в) (п^)^; г) у^у1-3 : ^у3^ . а2^2-^2^3 . (a2'^-l)(fl2'^ + a'^ + a3'^) а) ь 1; б) — — ; (a^-fe^3)2 a4V3_aV3 1 ( 1 Г в) = =—= 7=-; г) Х(хл + уп)2 - 14л ху . ' 2/5 /5 /7 2 77 ' ’ V ’ V a 3 +a3b3+b3 - Вычислите с точностью до 0,1 (пользуясь таблицами или
калькулятором) значения:
а) 101-41 и 101’42; б) 101’414 и 101-415;
в) 102-23 и IO2,24; г) 102-236 и 102-237.
452.— Пользуясь полученными в задаче 451 результатами, найди-
те значения Ю^2 и 10^® с точностью до 0,2.
453.— Укажите, какая из данных функций является возрастаю-
щей, какая — убывающей на множестве R:
а) у = (42У, у=(±] ; б) у=(4б-2У, у = -=±------;
IV2J (л/5-2)х
в) г/ = М\ z/ = f-T; г) у=(3-77)х, у = —i-—.
Ш и; (з-77)х
454.—
455. -
456.-,
Найдите область значений функции:
a)y = 3x + 1-3; б)у = |2х-2|;
в) у=1 — 1 +2; г) у = 41*1.
Найдите наибольшее и наименьшее значения функции на R-.
а) У=[-^ ; б) у = 5 + 3lcos*l;
\ 2 )
( . \lsin х|
в) у = 4COS х; г) у = — - 2.
Найдите знак корня уравнения:
fl \х
а) - =10;
J
б) 0,3х = 0,1; в) 10х = 4;
г) 0,7х = 5.
Показательная и логарифмическая функции
Решите графически уравнения (457—458).
458. — а) З1 "* = 2х - 1; б) 4х + 1 = 6 - х;
|в) 2х - 2 = 1 - х; г) 3 х =-^.
х
Верно ли, что показательная функция f (х) = ах:
а) имеет экстремумы;
б) принимает наибольшее значение в некоторой точке х0,
в) принимает в некоторой точке значение, равное нулю;
г) является четной (нечетной)?
36. Решение показательных уравнений
и неравенств
1. Уравнения. Рассмотрим простейшее показательное
уравнение
ах = b, (1)
где а > 0 и а ф 1. Область значений функции у = ах — множество
положительных чисел. Поэтому в случае Ъ < 0 или Ь = 0 уравне-
ние (1) не имеет решений.
Пусть b > 0. Функция у = ах на промежутке (-оо; оо) возра-
стает при а > 1 (убывает при 0 < а < 1) и принимает все положи-
тельные значения. Применяя теорему о корне (п. 8), получаем, что
уравнение (1) при любом положительном а, отличном от 1, и b > 0
имеет единственный корень. Для того чтобы его найти, надо b
представить в виде b = ас. Очевидно, что с является решением
уравнения ах = ас (рис. 134).
Пример 1. Решим уравнение 7Х“2 =^49-
2
Заметим, что 49 = 72, а д/49 = 73. Поэтому данное уравнение
2
можно записать в виде 7х-2 = 73. Следовательно, корнями дан-
О
ного уравнения являются такие числа х, для которых х-2 = ^,
т. е. х=2—. Ответ: х=2—.
3 3
Пример 2. Решим уравнение 5х -2х-1 = 25.
Перепишем его в виде 5х2 2х-1=52. Корнями этого уравне-
ния являются такие числа х, для которых х2 - 2х - 1 = 2. Прихо-
дим к квадратному уравнению, корни которого — числа 3 и —1.
Ответ: 3; -1.
Показательная и логарифмическая функции
Пример 3. Решим уравнение 6Х+1 + 35 6х-1 = 71.
Заметим, что 6Х+1 = 36 - 6х “ \ Поэтому данное уравнение
можно записать в виде 36 - 6х1 + 35 - 6х 1 = 71, т. е. 71 6х" 1 =
= 71, откуда 6х 1 = 6°, х - 1 = О, х = 1. Ответ: 1.
Пример 4. Решим уравнение 4х - 5 2х + 4 = 0.
Сделаем замену переменной t = 2х. Заметим, что 4х = (2х)2 = t2.
Поэтому данное уравнение принимает вид t2 - 5t + 4 = 0. Найдем
решения этого квадратного уравнения: tj = 1 и t2 = 4. Решая
уравнения 2х = 1 и 2х = 4, получаем х = 0 и х = 2. Ответ: 0; 2.
2. Неравенства и системы уравнений. Решение простейших
показательных неравенств основано на известном свойстве функ-
ции у = ах: эта функция возрастает при а > 1 и убывает при
0 < а < 1.
Пример 5. Решим неравенство 0,57 Зх < 4.
Пользуясь тем, что 0,5-2 = 4, перепишем заданное неравенст-
во в виде 0,57-3х < 0,5”2. Показательная функция у = 0,5х убывает
(основание 0,5 меньше 1). Поэтому данное неравенство равносиль-
но неравенству 7 - Зх > -2, откуда х < 3. Ответ: (-оо; 3).
Пример 6. Решим неравенство 6х2+2х>63.
Показательная функция у = 6х возрастает. Поэтому данное
неравенство равносильно неравенству х2 + 2х > 3, решая которое,
получим ответ: (-оо; -3) и (1; оо).
Пример 7. Решим неравенство
+ 3 <0.
Зх + !
Сделаем замену t =
тогда
и неравенство пере-
QQ 1
пишется в виде t2 —-1 + 3 < 0, откуда — < t <9. Следовательно, ре-
3 3
шением данного неравенства являются числа х, удовлетворяющие
неравенствам — < I — I <9, и только такие числа. Но — = ( — | ,
3 \3) 3 \ 3/
-2
, а функция у =
3
решением неравенств | ,
убывает, поскольку i < 1. Поэтому
3
числа х, удовлетворяю-
9 =
щие неравенствам -2 < х < 1. Ответ: (-2; 1).
Пример 8. Решим систему уравнений
2х + 2" =12,
32х“» =3.
Из второго уравнения системы находим 2х - у = 1, откуда
у = 2х - 1. Подставляя вместо у в первое уравнение выражение
Показательная и логарифмическая функции
2х - 1, получим 2х + 22х 1 = 12, откуда 2х + ~ - 22х = 12. Обозначив
2х через t, приходим к квадратному уравнению t2 + 2t - 24 = О,
откуда tx = 6, t2 = 4. Уравнение замены 2х = -6 решений не име-
ет. Корнем уравнения 2х = 4 является х = 2. Соответствующее зна-
чение у равно 3. Ответ: (2; 3).
Упражнения
Решите уравнения (460—464).
Z \Х z XX
460.— а) 4х = 64; б) - =27; в) 3х = 81; г) А =^.
13) \2) 64
б) л/8х 3 = ^42-х;
/„\Зх + 1 /_\5х-3
4- =й
\7J {з)
/ , \2х2 + х-0,5 г=
б) А
l7j 7
г) 2х2+2х-°-6 =4>/2.
463.—
464.
465.
а) 7Х + 2 + 4 - 7Х+1 = 539;
в) 4х + 1 + 4х = 320;
а) 9х - 8 3х - 9 = 0;
в) 36х - 4 • 6х - 12 = 0;
Решите систему уравнений:
б) 2 • 3х +1 - 3х = 15;
г) 3 5Х+3 + 25Х+1= 77.
б) 100х- 11 • 10х + 10 = 0;
г) 49х - 8 • 7х + 7 = 0.
4Х+» =16,
4« + 2j/-1 _ 1
б)
б3х-» = Тб,
ОУ~2х _ 1 .
32у - х _ J_
81 ’
3X-J/+2 =27;
Решите неравенства (466—467).
466. а) (1 \х - >27; б) (Тб/ < 1 . " 36’
в) °’2Х<4; г) 1,5х < 2,25.
467. а) 45-2х < 0,25; б) 0,37 + 4х > 0,027;
в) 0,42х + 1 > 0,16; г) 32 х < 27.
Показательная и логарифмическая функции
Решите уравнения (468—470).
468.— а) 3х + 1 - 2 3х -2 = 75; б) Г — ] = 4,8;
\ 5 / к 5 J
в) 5- i + - =162; г) 5 9х + 9х 2 = 406.
z \X-1 z х 1-X
469.— а) 5Х+1 = 8Х + 1; б) - = ± ; в)7х-2 = 42х.
470.— а) 3х + З3 - х = 12; б) 4'х’2 + 16 = 10 2^2 ;
471.— Решите систему уравнений:
472.—
473.
474.
475.
а)
в)
5Х + У =125,
4(х-у)2-1 = 1;
3х+ 3» =12,
6Х+» =216;
Решите неравенства (472—474).
а) лх - л2х > 0;
в) 4х - 2х 11 - 8 > 0;
б)
х + у=5,
4х + 4« =80;
4Х+* =128,
g3x-2i/-3 _ j.
б) 22х 1 + 22х - 2 + 22х - 3 < 448;
г) 3х"2 + 3х’1 < 28.
Решите графически неравенство:
а) 2х < 3 - х;
в) fil > 2х+ 1;
г) 3х > 4 - х.
232 Показательная и логарифмическая функции
37. Логарифмы и их свойства
1. Логарифм. Вернемся к уравнению ах = Ь, где а > О
и а 1. Как показано в предыдущем пункте, это уравнение не име-
ет решений при b < 0 и имеет единственный корень в случае
b > 0. Этот корень называют логарифмом b по основанию а и обо-
значают logo Ь. т. е.
alog“b = Ь.
Определение. Логарифмом числа Ъ по основа-
нию а называется показатель степени, в которую
нужно возвести основание а, чтобы получить число Ь.
Формулу alog° ь =Ь (где Ь>0, а>0иа*1) называют основ-
ным логарифмическим тождеством.
В Пример 1. Найдем значение: a) log2 32; б) log5 0,04.
а) Заметим, что 32 = 25, т. е. для того чтобы получить число
32, надо 2 возвести в пятую степень. Следовательно, log2 32 = 5.
б) Заметим, что 0,04 = — = 5 2, поэтому log5 0,04 = -2.
25
Пример 2. Найдем логарифм числа * по основанию -Уз.
Заметим, что (-УЗ) 4 = Поэтому по определению логарифма
Пример 3. Найдем х, такое, что: a) log8 х = —; б) log, 8 = .
3 4
Воспользуемся основным логарифмическим тождеством:
1
x=8logf,x=83 =2;
_3 4
xlogx 8 = 8, т. е. х 4 = 8, откуда х = 8 3 = —.
16
Основные свойства логарифмов. При работе с логарифма-
ми применяются следующие их свойства, вытекающие из свойств
показательной функции:
а)
б)
2.
При любом а > 0 (a * 1) и любых положительных
х и у выполнены равенства:
1°. log0l =0.
2°. loga a = 1.
3°. logo ху = loga X + loga у.
4°. loga = log„ x - loga y.
5°. loga xp = p loga x
для любого действительного p.
233 Пока «ательная и логарифмическая функции
Для доказательства правила 3° воспользуемся основным ло-
гарифмическим тождеством:
x=a,og“x, у=а1ок°у. (1)
Перемножая почленно эти равенства, получаем:
ху = а'°е°х -a'°s°y = a'OK“x'}ogay,
т. е. ху = alog“ х+ ,og“ у. Следовательно, по определению логарифма
loga (ху) = loga х + loga у.
1 Логарифм произведения равен сумме логарифмов.
Правило 4° докажем вновь с помощью равенств (1):
X - °IOg° Х - а1°Ве 1оВа У
У aiog“ V
следовательно, по определению log„ — = loga х - logb у.
1 Логарифм частного равен разности логарифмов.
Для доказательства правила 5° воспользуемся тождеством
х = alog° х, откуда хр = (а1оВа х )Р = ар ,ое“ х. Следовательно, по опре-
делению logo хр - р logu X.
Логарифм степени равен произведению показателя
степени на логарифм основания этой степени.
Основные свойства логарифмов широко применяются в ходе
преобразования выражений, содержащих логарифмы. Докажем,
например, формулу перехода от одного основания логарифма к
другому основанию:
bg (, х
log ь о
(Эта формула верна, если обе ее части имеют смысл, т. е. при
х > О, а > 0 и а*1, b > О и Ъ * 1.)
По правилу логарифмирования степени и основному лога-
рифмическому тождеству получаем:
logfc х = logb(alog“ х),
откуда
logb X = logfl х logfc а.
Разделив обе части полученного равенства на logfc а, приходим
к нужной формуле.
С помощью формулы перехода можно найти значение лога-
рифма с произвольным основанием а, имея таблицы логарифмов,
составленные для какого-нибудь одного основания Ь. Наиболее
употребительны таблицы десятичных и натуральных логарифмов
(десятичными называют логарифмы по основанию 10 и обознача-
ют 1g, а с натуральными логарифмами вы познакомитесь в п. 41).
234 Показательная и логарифмическая функции
Пример 4. Н 1йдем log03 7.
Пользуясь калькулятором (или таблицами), находим
1g 7 « 0,8451, 1g 0,3 ® 0,4771 - 1 = -0,5229. Следовательно, по
формуле перехода log0 3 7 « — —— » -1,6162.
Пример 5. Известно, что log2 5 = а и log2 3 = Ь. Выразим
log2 300 через а и Ь.
Пользуясь основными свойствами логарифмов, получаем:
log2 300 = log2 (3 52 • 22) = log2 3 + 2 log2 5 + 2 log2 2 = b + 2a + 2.
Пример 6. Выразим логарифм выражения 8а3 Vb4” через
log2 а и log2 b. (Коротко говорят: прологарифмируем данное выра-
жение по основанию 2.)
Пользуясь основными свойствами логарифмов, получаем:
log2 (ва3 = log2 [23 а3 b7J = 3 log2 2+3 log2 a + log2 b =
= 3 + 3 log2 a + у log2 b.
Пример 7. Найдем x, если
log5 x = logg 7 + 2 logs 3-3 log5 2.
Сначала преобразуем правую часть данного равенства, поль-
зуясь основными свойствами логарифмов:
log5 х = log5 7 + log5 З2 - log5 23 = log5 = log5
О о
т. e. log5 x = log5 и потому x = = 7,875.
tt c tt ~ Ig72-lg9
Пример 8. Найдем значение выражения
Пользуясь основными свойствами логарифмов, преобразуем
72
числитель и знаменатель этой дроби: 1g 72 - 1g 9 = 1g ~ = 1g 8 =
= 3 lg 2; lg 28 - lg 7 = 1g = lg 4 = 2 1g 2.
„ Ig72-lg9 3 1g2 3
Следовательно,--------=--------= —.
Ig28-lg7 2 1g2 2
Упражнения
476. -
,1
478. I
Найдите логарифм по основанию а числа, представленного
в виде степени с основанием а (476—478).
а) З2 = 9; б) 2-3 = в) 42 = 16; г) 5~2 = А.
8 25
1 1
а)92=3; 6)7° =1; в) 325 =2; г)3'=-*.
2 3 3 2
а) 273 =9; б) 32s =8; в) 814 =27; г) 1253 =25.
235 Показательная и логарифмическая функции
Проверьте справедливость равенств (479—482).
479.— - а) Юёз 8\ = -4; 6) log16 1=0;
в) log4 16 = 2 r) log5 125 = 3.
480.— - а) iog5 °’04 = -2; 6) logy 343 = 3;
в) 1g 0,01 = -2; Г) 10g3 243 =-5’
481.— - а) CD II 00 <N о 1^^ 6) log j 27 = -6;
Из
в) log, 9 = -2; 3 г) 1о£о,5 4 = -2.
482,- - а) lo^128 = y; 6) log,, 2 0,008 = 3;
в) logv5 0,2 =-2; r) log0 2 125 = -3.
483. — Найдите логарифмы данных чисел по основанию а:
а) 25, 1, V5 при a - 5; 5 6) 64, 2 при a = 8;
в) 16, , 4~2 при a = 2; r) 27, i, V3 при a = 3.
Найдите число х (484— 486).
484. а) log3 x = -1; 6) log, x = -3; 6
в) logs x= 2; r) log7 x = -2.
485. а) log4 x = -3; 6) log 5 x=0;
в) log, x = 1; r) log, x = -3.
7 2
486. а) logx 81 = 4; 6) logx V = 2; в) log i=-2; r) logx 27 = 3. э 4
487. Запишите число в виде логарифма с основанием a:
а) 2, 1, 0 при a = 4; 6) 3, -1, -3, 1 при a = 3;
в) 3, 0, -1 при a = 2; г) 1, -2, 0, 3 при a = 5.
Упростите выражения, ским тождеством (488— пользуясь основным логарифмиче- 490).
488. а) । ylogi 72ф ^logn5,2. в) 21овг5; г) 3,8log3-eI1.
489. а) 51+1°853; 6) IO11*2; / xl т log, 2 в) | | т ; г) 3Z 1оКз18. V 7 J
490. а) 42 1og43; 6) 531°8s^; в) 2 ; г) 62|овв®.
236 Показательная и логарифмическая функции
491.
492.
493.
494.
495.
496.
497.-
498.
Прологарифмируйте по основанию 3 (а > О, Ъ > О):
2 z х-0,2
а)С^бГ; б) ;
в) 9а4 Vb; г) ь2 .
27а7
Прологарифмируйте по основанию 10, где а > 0, b > 0,
с > 0 (492—493).
1 _1 -
а) 100 7аЬ3с; б) —в) V10 а3Ь4с 2; г) 0,01с3 .
0,1с2 Vb * „
а2Ь3
15 2 I
а) 103а4Ь2с-3; б) —; в) 104а2Ь®с3; г) ____с-_.
10® а6 с® , - «
107а3Ь8
Известно, что log5 2 = а и log5 3 = b. Выразите через а и Ь:
а) log5 72; б) log5 15; в) log5 12; г) log5 30.
Вычислите (495—496). a) 1g 8 + 1g 125; 6) log2 7-log2
в) log12 4 + log12 36; г) 1g 13 - 1g 130.
а) в) lg8+ lg!8 21g2+lg3’ log2 11 - log2 44; б) г) Iog3 16. log3 4 ’ log0>3 9-2 log0 3 10-
Найдите х, если: a) log6 х = 3 log6 2 + 0,5 б) 1g х = | lg5a-31gb + 4 los6 Igc; 25-2 log6 3;
в) 2 1 Igx = 5 Igm + - Ign - 4 3 4 igp;
г) log4 x = | l°g4 216-2 log4 о 10 + 41og43.
Докажите:
a) log j 3 + log3 | <-2; б) 4log5 7 = 71овб 4;
3
в) log3 7 + log7 3 > 2; Г) 3‘О82® =51°8 2 3
237 Показательная и логарифмическая функции
38. Логарифмическая функция
Пусть а — положительное число, не равное 1.
Определение. Функцию, заданную формулой
у = log0 х, (1)
называют логарифмической функцией с основа-
нием а.
Перечислим основные свойства логарифмической функции.
1. Область определения логарифмической функ-
ции — множество всех положительных чисел R+,
т. е. D (logj = R.
Действительно, как отмечалось в предыдущем пункте, каж-
дое положительное число х имеет логарифм по основанию а.
2. Область значений логарифмической функции —
множество всех действительных чисел.
В самом деле, по определению логарифма любого действи-
тельного у справедливо равенство
logo (а*) = у, (2)
т. е. функция у = logo х принимает значение у0 в точке х0 = ау° .
3. Логарифмическая функция на всей области
определения возрастает (при а > 1) или убывает
(при 0 < а < 1).
Докажем, например, что при а > 1 функция возрастает
(в случае О < а < 1 проводится аналогичное рассуждение).
Пусть Xj и х2 — произвольные положительные числа и
х2> хГ Надо доказать, что loga х2 > loga хг Допустим противное,
т. е. что
logo х2 < log о хг
(3)
Так как показательная функция у = ах при а > 1 возрастает,
из неравенства (3) следует:
alog“X2 <alog“X1
(4)
Но alog°X2 =х2, alog°X1 = xjno определению логарифма), т. е. не-
равенство (4) означает, что х2 < хг Это противоречит допущению
х2 > Xj.
238 Показательная и логарифмическая функции
Для построения графика заметим, что значение 0 логариф-
мическая функция принимает в точке 1; loga 1=0 при любом
a > 0, так как а° = 1.
Вследствие возрастания функции при a > 1 получаем, что
при х > 1 логарифмическая функция принимает положительные
значения, а при 0 < х < 1 — отрицательные.
Если 0 < a < 1, то у = loga х убывает на R+, поэтому
loga х > 0 при 0 < х < 1 и log0 х < 0 при х > 1.
Опираясь на доказанные свойства, нетрудно построить гра-
фик функции у = loga х при a > 1 (рис. 135, а) и 0 < а < 1
(рис. 135, б).
Справедливо следующее утверждение (доказательство см.
в п. 40):
Графики показательной и логарифмической функ-
ций, имеющих одинаковое основание, симметричны
относительно прямой у = х (рис. 136).
Рассмотрим примеры применения свойств логарифмической
функции.
Рис. 136
239 Показательная и логарифмическая функции
Пример 1. Найдем область определения функции
f (х) = log8 (4 - 5х).
Область определения логарифмической функции — множе-
ство R,. Поэтому заданная функция определена только для
тех х, при которых 4 - 5х > О, т. е. при х < 0,8. Следовательно,
областью определения заданной функции является интервал
(-оо; 0,8).
Пример 2. Найдем область определения функции
f (х) = log2 (х2 - Зх - 4).
Как и в предыдущем примере, функция f определена для
всех тех х, при которых х2 - Зх - 4 > 0. Решая это квадратичное
неравенство, получаем, что D (/) — объединение интервалов
(-оо; -1) и (4; оо).
Пример 3. Найдем область определения функции
. . 1 2х+ 3
Мх>-106’5-77
О------------о-
3 5
2 7
Рис. 137
Решая методом интервалов не-
равенство
2х+ 3 _
-----> 0, находим
5-7х
(рис. 137), что D (f) =
з. 5^
2’7/
Пример 4. Сравним числа: a) log3 5 и log3 7; б) log, 5
и log, 7; в) log3 10 и log4 12.
з
а) Логарифмическая функция с основанием, большим 1, воз-
растает на всей числовой прямой. Так как 7 > 5, то log3 7 > log3 5.
б) В данном случае основание логарифма меньше 1, поэтому
функция log, х убывает, и, следовательно, log, 7 <log, 5.
з зз
в) Заметим, что 10 > 9 = З2, и поэтому log3 10 > 2, с другой
стороны, 12 < 16 = 42, и, следовательно, log4 12 < 2. Итак,
log3 10 > log4 12.
Пример 5. Что больше:
log2 3 + log2 7 или log2 (3 + 7)?
По основному свойству логарифмов log2 3 + log2 7 = log2 21.
А так как log2 (3 + 7) = log2 10 и 10 < 21, а основание логарифма 2
больше 1, то log2 10 < log2 21, следовательно,
log2 3 + log2 7 > log2 (3 + 7).
24i Показательная и логарифмическая функции
Упражнения
499.—
500.—
501.
502.
503.
504.
505.—
506.-
507.
Найдите область определения выражения (499—500).
a) logn (10 - 5х); б) log5 (9 - х2);
в) log3 (х - 4); г) log0 3 (х2 - 16).
a) log rfo(6 + x-x2); б) 1g;
в) 1о£о,9 О log^(x2-2x-3).
о —
Сравните числа (501—503).
a) log2 3,8 и log2 4,7; в) log3 5,1 и log3 4,9; б) log) 0,15 з г) log0 2 1,8 и log! 0,2; з и log0 2 2,1.
a) log ^ 3 и 1; б) log ! 1,9 и logj_ 2,5;
Л 41
в) logn 2,9 и 1; г) logo,7 V2 И logo,7 °’3-
a) log2 19 и log5 30; б) log0,3 2 и 1 iog5 3;
в) log3 5 и log7 4; г) log3 10 и log8 57.
Перечислите основные свойства функции и постройте ее
график:
а) у = log3 х; 6)y = log1x;
2
в) у = log4 х; r)y = logiX.
з
Найдите область определения выражения:
a) log2 sin х; б) log3 (2х - 1); в) log 7 cos х; г) lg (1 - 3х).
2
Найдите значение выражения:
a) log2 2 sin-^ + log2 cos-" ;
15 15
6) log4 (V7-V3)+ log4 (3V49 + V21 + 3V9 );
в) lg tg 4 + lg ctg 4;
r) logn (5 + 2 V6) + logn (5-2 д/б).
Постройте график функции:
а) у = log3 (х - 2); б) у = -logj х;
2
в) у = log2 (х + 1); Г) у = logj х + 2.
з
241 Показательная и логарифмическая фут ции
508.— Решите уравнение:
a) log3 х = 2 log9 6 - log9 12;
б) log J х = log0,2 35-2 log0,2 25 V?;
2
в) log5 x = | log3 144 + log3 0,75;
r) logn x = 3 log0 ] 4+2 logo i 1
509.—
510. -
511.
Решите графически уравнение:
a) 1g x = 1 - x; 6) log j x = x -4;
з
в) log j x = x - 6; r) log2 x = 3 - x.
5
Верно ли, что логарифмическая функция:
а) имеет экстремумы; б) является нечетной;
в) является периодической; г) является четной?
Найдите наибольшее и наименьшее значения функции f на
промежутке I:
1
9
9
a) f (х) =logj х, I = [1; 4];
4
в) f (х) = log5 х, I =[j; 1];
б) f (х) = log9 х, I =
г) f(x) =logi x, | = [|; 4^.
39. Решение логарифмических уравнений
и неравенств
Рассмотрим простейшее логарифмическое уравнение
logo х = Ъ.
Логарифмическая функция возрастает (или убывает) на про-
межутке (0; оо) и принимает на этом промежутке все действитель-
ные значения (рис. 135). По теореме о корне (п. 8) отсюда следует,
что для любого Ь данное уравнение имеет, и притом только одно,
решение. Из определения логарифма числа сразу следует, что аь
является таким решением.
Пример 1. Решим уравнение log2 (х2 + 4х + 3) = 3.
Данному уравнению удовлетворяют те значения х, для кото-
рых выполнено равенство х2 + 4х + 3 = 23. Мы получили квадрат-
ное уравнение х2 + 4х - 5 = 0, корни которого равны 1 и -5. Следо-
вательно, числа 1 и -5 — решения данного уравнения.
Пример 2. Решим уравнение log5 (2х + 3) = log5 (х + 1).
Это уравнение определено для тех значений х, при которых
выполнены неравенства 2х+3>0их+1>0. Для этих х данное
242 Показательная и логарифмическая функции
уравнение равносильно уравнению 2х + 3 = х + 1, из которого на-
ходим х = -2. Число х = -2 не удовлетворяет, однако, неравенству
х + 1 > 0. Следовательно, данное уравнение корней не имеет.
Это же уравнение можно решить иначе. Переходя к след-
ствию данного уравнения 2х + 3 = х + 1, находим, что х = -2.
Как всегда, при неравносильных преобразованиях уравнений
найденное значение необходимо проверить подстановкой в ис-
ходное уравнение. В данном случае получаем, что равенство
log6 (-1) = log5 (-1) неверно (оно не имеет смысла).
Пример 3. Решим уравнение logx (х2 - 2х + 2) = 1.
Этому уравнению удовлетворяют такие числа х, для которых
выполнены условия: х > 0 и х * 1 (х — основание логарифмиче-
ской функции) и равенство х2 - 2х + 2 = х, т. е. х2 - Зх + 2 = 0.
Полученное квадратное уравнение имеет корни 1 и 2. Но х = 1
не может быть решением данного уравнения. Следовательно, ре-
шением данного уравнения является только число 2.
Пример 4. Решим неравенство log t (5-2х) >-2.
з
Число -2 равно log] 9. Поэтому данное неравенство можно
з
переписать в виде log, (5 2х) >logj 9.
3 3.
Логарифмическая функция с основанием — определена и
3
убывает на R+, так как i < 1. Следовательно, второму неравенству
3
удовлетворяют такие числа х, для которых выполнено условие
0 < 5 - 2х < 9, откуда -2 < х < 2,5.
Итак, множество решений данного неравенства есть интер-
вал (-2; 2,5).
Пример 5. Решим уравнение log| х-logх-3 = 0.
Перейдем во втором слагаемом к основанию 5 и сделаем за-
мену переменной t - log5 х, тогда
log ^ х =
logs*
log 5 Тб
— = 2t.
1
2
Теперь данное уравнение перепишется в виде t2 - 2t - 3 = 0. Кор-
ни этого квадратного уравнения 3 и -1. Решая уравнения заме-
ны log5 х = 3 и log5 х = -1, находим х = 53 = 125 и х = 51 = 0,2.
Пример 6. Решим систему уравнений
1g (У-*) =lg2,
logg х-4= log2 3- log2 у.
Первое уравнение системы равносильно уравнению у — х = 2,
х 3
а второе — уравнению = - , причем х > 0 и у > 0. Подставляя
16 у
243 Показательная и логарифмическая функции
х 3
у = х + 2 в уравнение — = —, получим х (х + 2) = 48, откуда
16 у
х2 + 2х - 48 = 0, т. е. х = -8 или х = 6. Но так как х > 0, то х = 6
и тогда у = 8. Итак, данная система уравнений имеет одно реше-
ние: х = 6, у = 8.
Заметим еще, что с помощью логарифмов можно записать
корень любого показательного уравнения вида а* = Ъ, где b > О
(чего мы не могли еще сделать, решая примеры в п. 36). Этим кор-
нем является число х = loga Ь.
Пример 7. Решим уравнение 51 “31 = 7.
По определению логарифма 1 - Зх = log5 7, откуда х =
=Нlog*7-
Упражнения
Решите уравнения (512—515).
512.— а) 9х = 0,7; б) 0,3х = 7; в) 2х = 10; г) 10х = л.
513. — a) logg х = 2; б) log0 4 х = -1; в) log9 х = - |; г) 1g х = 2.
514.— a) logj (2х -4) = -2; б) logn (х2 + 2х + 3) = logn 6;
2
в) log0 з (5 + 2х) = 1; г) log2 (3 - х) = 0.
515.— а) 0,24 х = 3; б) 5х2 = 7; в) 323х = 8; г) 72х = 4.
Решите неравенства (516—517).
516. a) log3 х > 2; в) iog0.7х < 1; б) log0 5 * > -2; г) log2 g х < 2.
517. a) log4 (х - 2) < 2; б) logj(3-2x)>-l;
3
в) log5 (Зх + 1) > 2; г) logj (4х+ 1) < -2. 7
Решите уравнения (518—520).
518 . a) loga х = 2 loga 3 + loga 5;
б) 1g (х - 9) + 1g (2х - 1) = 2;
в) loga х = loga 10 - logo 2;
г) log3 (x + 1) + log3 (x + 3) = 1.
519 .- a) | log2(x-4) + | log2(2x-l) =log2 3;
6) 1g (3x2 + 12x + 19)-1g (3x + 4) = 1;
в) lg(x2+2x-7)-lg(x-l) =0;
r) logg(x2 + 8) -log5(x + 1) = 3logg 2
244 Показательная и логарифмическая функции
520 .— a) log2 x + log4 Vx -1,5 = 0; 6) lg2 x - lg x2 + 1 = 0;
в) logf x - log5 x = 2; r) log| x - 2 log3 x - 3 = 0.
521 . -В Решите систему уравнений:
I fx + j/ = 7, flog4 (x+ j/) =2,
a) 5 o) •>
[lgx + lgj/ = l; [log3 x + log3 i/=2+log3 7;
[x + y=34, 4 [log4 x—log4 у =0,
в) < г) <
|log2 x + log2 у = 6; [x2-5y2 + 4 =0.
Решите уравнения (522—524).
522,— а) -J—+_6_ = 1; 1g х + 1 1g х + 5 6) log2 ^ = -- A* ; 4 l°g2f-l
в) 2 lg х lg(5x-4) г) _^_ + _5_=l. lg x - 6 lg x + 2
523.— а) loga x=logVa 2 + logj^; 6) logx 2 -log4 x + | = 0;
в) log3 x -2 log j x = 6; 3 r) log25 x + log5 x = log i V8. 5
524.- а) log2 (9 - 2х) = 3 - x;
б) log2 (25х+ 3 - 1) = 2 + log 2(5x + 3+ 1);
в) log4 (2 • 4х ~ 2 - 1) = 2x - 4;
г) log2 (4х + 4) = log2 2х + log2 (2х + ] 3).
525.—
526.
527.
528.
Решите неравенства (525—528).
a) lg (2х - 3) > lg (х + 1);
б) log0 3 (2х - 4) > log0 3 (х + !);
в) 1g (Зх - 7) < 1g (х + 1);
г) log0,5 (4х - 7) < 1о£о,5 (х + 2>-
a) log0 5 х > 1о^2 (3 - 2х);
б) logn (х + 1) + logn х < logn 2;
в) 1g х + lg (х - 1) < lg 6;
г) log2 (х2 - х - 12) < 3.
a) log| х - log2 х < 6; б) log 4 х - 4 > 0;
з
в) 1g2 х + 2 1g х > 3; г) log2 х - 9 < 0.
a) log2 sin^ < -1; б) |3 - log2 х| < 2;
в) log j cos 2х>1; г) 13 1g х - 11 < 2.
2
245 Показательная и логарифмическая функции
Решите системы уравнений (529—530).
529.— а)
530. -
log] (х + у) = 2,
з
log3(x-y) = 2;
log, x + logj у = 2,
3 3
log] x —log] у =4;
3 3
lg(x2+i/2) = 2,
log48 x + log48 у = 1;
fig (x2 + y2) = 1 + lgl3,
|lg(x + y) =lg(x-f/) + lg8.
3-"9Х =81,
lg(x + y)2 -lgx = 2 1g 3;
101 + 18(x+«) =50,
6) (
[ 1g (x + y) + 1g (x - y) = 2 -1g 5;
в)
3х-2» =576,
log ^ (j/-x) =4;
Jlgx-lgy =lgl5-l,
| 10lg(3x + 2s,) =39.
40. Понятие об обратной функции
1. Обратимость функций. В ходе исследования раз-
личных функций вы неоднократно решали такую задачу: вычис-
лить значение функции f по данному значению х0 аргумента. Ча-
сто приходится рассматривать и обратную задачу: найти значения
аргумента, при которых функция f принимает данное значение у0.
Н Пример 1. Пусть f (х) = kx + Ь (к * 0). Чтобы найти значе-
ния аргумента х, при которых f (х) = у0, надо решить уравнение
f (х) = у0, т. е. уравнение kx + Ь = у0. Решая его, находим, что при
у0 - b
любом у0 оно имеет, и притом только одно, решение х = —-—.
Пример 2. Для функции f (х) = х2 уравнение f (х) = у0 при
у0 > 0 имеет два решения: х4 = у[уё, х = -.Гу^. (Если у0 = 0, реше-
ние одно х0 = 0.)
Функцию, принимающую каждое свое значение в единст-
венной точке области определения, называют обратимой. Таким
образом, при k * 0 функция f (х) = kx + b обратима, а функция
f (х) = х2 (определенная на всей числовой прямой) не является об-
ратимой.
Замечание. Из определения обратимой функции сразу
следует, что если / обратима, а число а принадлежит области зна-
чений Е (/), то уравнение f (х) = а имеет решение, и притом только
одно.
246 Показательная и логарифмическая функции
2. Обратная функция. Пусть f — произвольная обратимая
функция. Для любого числа у0 из ее области значений Е (/) имеет-
ся в точности одно значение х0, принадлежащее области определе-
ния D (/), такое, что f (х0) = у0. Поставив в соответствие каждому
у0 это значение х0, получим новую функцию g с областью опреде-
ления Е (/) и областью значений D (/). Например, для обратимой
функции f (х) = kx + b (k 0) значение новой функции g в произ-
вольной точке i/0 задается формулой
Я(!/о) = ^-
Выбирая для аргумента функции g привычное обозначе-
ние х, находим, что
, , х-Ъ
g(x} ,
k
Если функция g в каждой точке х области значений обра-
тимой функции f принимает такое значение у, что f (у) = х, то го-
ворят, что функция g — обратная функция к f.
Как показано выше, функцией, обратной к функции
f (х) = kx + b (k * 0), является функция g(x)=——. Рассмотрим
k
еще один пример.
Пример 3. Докажем, что функция f (х) = х3 обратима,
и выведем формулу, задающую функцию у = g (х), обратную к /.
По определению обратной функции сначала надо доказать,
что уравнение f (у) = х при любом значении х имеет единственное
решение у. В данном случае это уравнение у3 = х, которое имеет
единственное решение у = Vx при любом х (см. п. 8). Поэтому
функция f (х) = х3 обратима и обратной к ней является функция
g(x)=Vx. Графики этих функций изображены на рисунке 138.
247 Показательная и логарифмическая функции
Если задан график обратимой функции f, то график функ-
ции g, обратной к f, нетрудно построить, пользуясь следующим
утверждением:
Графики функции f и обратной к ней функции g сим-
метричны относительно прямой у = х.
Докажем это свойство. Заметим, что по графику функции f
можно найти числовое значение обратной к f функции g в произ-
вольной точке а. Для этого нужно взять точку с координатой а не
на горизонтальной оси (как это обычно делается), а на вертикаль-
ной. Из определения обратной функции следует, что значение g (а)
равно b (рис. 139, а).
Таким образом, если считать, что выбрана несколько необыч-
ная система координат (аргумент откладывается на вертикальной
оси, а значения функции — на горизонтальной), то можно ска-
зать, что график обратной к f функции g — это график функции f
(построенной в обычной системе координат). Для того чтобы изоб-
разить график g в привычной системе координат, надо отразить
график f относительно прямой у = х (рис. 139, б).
Если функция g — обратная к функции f, то функция g об-
ратима и обратной к ней является функция f. Поэтому говорят,
что функции f и g взаимно обратны.
Теорема (об обратной функции). Если функция f
возрастает (или убывает) на промежутке I, то она
обратима. Обратная к f функция g, определенная
в области значений f, также является возрастаю-
щей (соответственно убывающей).
Доказательство. Положим для определенности, что
функция f возрастающая. Обратимость функции f — очевидное
следствие теоремы о корне (п. 8). Поэтому остается доказать, что
функция g, обратная к f, возрастает на множестве Е (f).
248 Показательная и логарифмическая функции
Пусть Xj и х2 — произвольные значения из Е (/*), такие, что
х2 > хр и пусть
У1 = е (*Л у2 = s (х2).
По определению обратной функции
Xj = / (У1) и х2 = f (у2).
Воспользовавшись тем условием, что f — возрастающая функ-
ция, находим, что допущение у} > у2 приводит к выводу f (у^ >
> f (Уг)> т- е- xi хг- Это противоречит предположению х2 > хг
Поэтому у2 > уг, т. е. из условия х2 > хт следует, что
g(x2> > ё(х1)-
Именно это и требовалось доказать.
Пример 4. Как отмечалось выше, функция f (х) = х2 не яв-
ляется обратимой. Однако функция f*, определенная на промежут-
ке [0; оо) формулой f* (х) = х2, возрастает на этом промежутке и,
значит, имеет обратную. Обратной к функции f* является функция
g(x) = Vx. Графики этих функций изображены на рисунке 140, а.
Вообще функция f (х) = х" при любом натуральном п возра-
стает на промежутке [0; оо) и поэтому имеет обратную. Обрат-
ной к функции f (х) = х" является функция g(x) = Vx. Графики
этих функций при некоторых значениях п изображены на рисун-
ке 140, б, в.
Упражнения
Выведите формулу, задающую функцию g, обратную к дан-
ной функции f. Укажите область определения и область
значений функции g (531—532).
531. - a) f(x) = 2х + 1; б) f (х) = | х -1;
| в) f (х) = -2х + 1; г) f (х) = -|х-1.
249 Показательная и логарифмическая функции
532.— а) Г(х)=-1;
X
В) Hx) = xf2;
б) f (х) = 2х2 (х > 0);
г) f(x) = Vx + 1.
533. — Постройте график функции, обратной к f:
a) f (х) = 2х3 +1; б) f (х) = (х + I)2, х е (-оо; -1];
в) f (х) = -2х3 +1; г) f (х) = (х - I)2, х е [1; оо).
534. - По графику функции f (рис. 141) найдите значения обрат-
ной к f функции g в точках -2, 1 и 3. Постройте график
функции g, укажите ее область определения и область зна-
чений:
I a) f (х) = Д (х); б) f (х) = f2 (х);
I в) f (х) = f3 (х); г) f (х) = /4 (х).
250 Показательная и логарифмическая функции
Докажите, что функция f имеет обратную на указанном
промежутке. Постройте график функции, обратной к f
(535—536).
535— a) f (х) = хг + 1, х < 0; б) f (х) = 2х, (-оо; оо);
в) f (*) = у1~х, х > 0; г) / (х) = х3 + 1, (-оо; оо).
536. 1 a) f (х) = sin х, х е 7^5 б) f (х) = х> х е
| в) f (х) = cos х, х е [0; л]; г) f (х) = ctg х, х е (0; л).
§11-
Производная показательной
и логарифмической функций
41. Производная показательной функции.
Число е
1. Число е. В предыдущих пунктах графики показа-
тельной функции изображались в виде гладких линий (без изло-
мов), к которым в каждой точке можно провести касательную.
Но существование касательной к графику функции в точке с абс-
циссой х0 равносильно ее дифференцируемости в х0. Поэтому есте-
ственно предположить, что показательная функция дифференци-
руема во всех точках области определения.
Нарисуем несколько графиков функции у = ах для а, равного
2; 2,3; 3; 3,4 (рис. 142), и проведем к ним касательные в точке
с абсциссой 0. Углы наклона этих касательных к оси абсцисс при-
близительно равны 35°, 40°, 48° и 51° соответственно, т. е. с возра-
станием а угловой коэффициент касательной к графику функции
у = ах в точке М (0; 1) постепенно увеличивается от tg 35° до
tg 51°. Представляется очевидным, что, увеличивая а от 2 до 3,
мы найдем такое значение а, при котором угловой коэффициент
соответствующей касательной равен 1 (т. е. угол наклона равен
45°). Вот точная формулировка этого предложения (мы принимаем
его без доказательства):
Существует такое число большее 2 и меньшее 3 (это
число обозначают буквой е), что показательная функ-
ция у = ех в точке 0 имеет производную, равную 1,
----> 1 при Дх —> 0. (1)
Дх
Замечание. Доказано, что число е иррационально и поэто-
му записывается в виде бесконечной десятичной непериодической
Показательная и логарифмически я функции
дроби. С помощью электронных вычислительных машин найдено
более двух тысяч десятичных знаков числа е. Первые знаки тако-
вы: е = 2,718281828459045... .
Функцию ех часто называют экспонентой.
2. Формула производной показательной функции.
Теорема 1. Функция ех дифференцируема в
каждой точке области определения, и
(И' =
Доказательство. Найдем сначала приращение функции
у = ех в точке х0:
Ду = +Дх -ех° =ехо е^х - ех° = ех° (еЛх — 1).
Пользуясь условием (1), находим:
Ду е1о(еДх-1) еДх-1 л л
Дх Дх Дх
По определению производной отсюда следует, что у' - ех,
т. е. (ех)’ = ех при любом х.
252 Показательная и логарифмическая функции
Пример 1. Найдем производную функции у = е5х:
(е5ху = е5х (5х)' = 5е5х.
Число е положительно и отлично от 1, поэтому определены
логарифмы по основанию е.
Определение. Натуральным логарифмом
(обозначается In) называется логарифм по основа-
нию е:
In х = loge х.
(2)
По основному логарифмическому тождеству для любого
положительного числа е1п ° = а. Поэтому ах может быть записано
в виде
(3)
Выведем формулу производной показательной функции при
произвольном значении а.
Теорема 2 Показательная функция ах диф-
ференцируема в каждой точке области опреде-
ления, и
(ах)' = ах In а. (4)
Доказательство. Из формулы (3) по теореме о производ-
ной сложной функции получаем, что показательная функция диф-
ференцируема в каждой точке и
(ахУ = (ех 1п °)' = ех 1п ° In а = ах In а.
(5)
Следствие. Показательная функция непрерывна
в каждой точке своей области определения, т. е.
ах -> ах° при х -> х0.
Это вытекает из дифференцируемости показательной функ-
ции и леммы о непрерывности дифференцируемой функции
(см. п. 15).
Пример 2. Найдем производные функций у = 2х и у = 5 Зх.
По формуле (4) имеем
(2х)' = 2х In 2; (5~3х)' = (-3) 5 Зх In 5.
Пример 3. Исследуем функцию f (х) = хех на возрастание
(убывание) и экстремум.
Найдем производную этой функции:
f (х) = (хех)’ = х'ех + х (ех)' = ех + хех = ех (1 + х).
Показательная и логарифмическая функции
Так как ех > 0 для любого х,
знак f совпадает со знаком (1 + х).
Следовательно, f (х) > О на проме-
жутке (-1; оо), поэтому f возрастает
на промежутке [1; оо). На проме-
жутке (-оо; -1) имеем f (х) < 0, по-
этому f убывает на (-оо; 1]. В точке
х0 = -1 производная меняет знак
с минуса на плюс, и, значит, х0 = -1
является точкой минимума.
График функции приведен на
рисунке 143.
3. Первообразная показательной функции.
Теорема 3. Первообразной для функции ах на R
является функция ® .
Ina
Действительно, In a — постоянная, и поэтому
( а— 'j = — (ах) = 1 ах Ina = ах
I Ina I Ina Ina
при любом х. Этим доказано, что — есть первообразная для ах
Ina
на R. А из равенства (ех)' = ех для
всех х следует, что ех есть первооб-
разная для ех на R.
Ц Пример 4. Найдем первооб-
разные для функций:
а) f (х) = 5х;
б) g (х) = 4 2х;
в) h (х) = 4е3х - 10 0,6х.
Пользуясь теоремой 3 и прави-
лами нахождения первообразных,
выписываем ответы:
К X
а) F(x)=^- + C;
In 5
4 2х
б) G(x) = --+С;
In 2
в) Н(х) =—е3х-10- °’6Х +С.
’ v 3 1п0,6
Пример 5. Найдем площадь
фигуры, ограниченной линиями
у = 3х, у = 0, х = -1, х = 2.
Показательная и логарифмическая функции
Эта фигура есть криволинейная трапеция (рис. 144). Поэто-
му ее площадь S находим по формуле площади криволинейной
трапеции:
2 2
S=(3xdx=3- =JL_3±
J 1пЗ 1пЗ 1пЗ
26
31п3'
Упражнения
537.— Найдите по таблицам натуральных логарифмов (или с по-
мощью калькулятора):
a) In 3, In 5,6, In 1,7; б) In 8, In 17, In 1,3;
в) In 2, In 35, In 1,4; r) In 7, In 23, In 1,5.
Найдите производную каждой из функций (538—539).
538. - а) у = 4с1 + 5; б) у = 2х + Зех; в) 1/ = 3-^ех; г) у = 5е х - х2.
539.- 540. а) у = ех cos х; б) у - Зех + 2х; в) у = 3х - Зх2; г) у = х2ех. Напишите уравнение касательной к графику функции f
541. в точке с абсциссой х0: a) f (х) = е х, х0 = 0; б) f (х) = 3х, х0 = 1; в) f (х) = ех, х0 = 0; г) f (х) = 2 х, х0 = 1. Найдите общий вид первообразных для функции:
542. a) f (х) = 5ех; б) f (х) = 2 3х; в) / (х) = 4х; г) f (х) = |ех+ 1. Вычислите интеграл: 1 1 1 a) Jo,5*dx; б) Je2xdx; в) ^2xdx; 0 0-2 1 г) | 3х dx. 2
Найдите производную каждой из функций (543—544).
543.- а) У=е ,2 . г х sin ; 2 б) у = 72 tg Зх;
в) У=е ',х cos 2х; г) у = 2 х ctg *
544. - а) У=; х6 . б) У = ~Т~ ;
4 х + 5 х2 +2
3х . 0,3~х
У 1)
2 х + 5х Vx + 0,5
255
Показательная и логарифмическая функции
545.— Исследуйте на возрастание (убывание) и экстремумы функ-
цию:
a) f (х) = хе5х; б) f (х) = х22~х;
в) f (х) = хе х; г) f (х) = х40,5х.
546.— Найдите общий вид первообразных для функции:
a) f (х) = е3 - 2х; б) f (х) = 2 0,9х - 5,6 х;
в) f (х) = 2 10х; г) f (х) = е3х + 2.31 + х.
547. Найдите площадь фигуры, (547—548). - а) у = ех, у = 0, х = 0, х = 1; б) у = 3х, у = 9х, х = 1; в) у = 2х, у = 0, х = -1, х = 2; г) у = ех, у = е2х, х = 1. ограниченной линиями
548. - а) II н сч II э> н -н| со II а» б) у = ех, у = е~х, у = е;
в) 61 1 II н и к F4I <М II а» г) У = 1 - 1 , у = 4х, у = 4.
42. Производная логарифмической функции
Покажем сначала, что логарифмическая функция диф-
ференцируема в каждой точке. Графики функций у = loga х и
у = ах симметричны относительно прямой у = х. Так как показа-
тельная функция дифференцируема в любой точке, а ее производ-
ная не обращается в нуль, график показательной функции имеет
негоризонтальную касательную в каждой точке. Поэтому и график
логарифмической функции имеет невертикальную касательную
в любой точке. А это равносильно дифференцируемости логариф-
мической функции на ее области определения.
Докажем теперь, что производная логарифмической, функции
для любого х из области определения находится по формуле
1п'х=1. (1)
X
По основному логарифмическому тождеству х = е1" х при всех по-
ложительных х, т. е. в этом равенстве справа и слева стоит одна
и та же функция (определенная на R ). Поэтому производные х
и е1п х равны, т. е.
х' = (е1пх)'. (2)
Известно, что х' = 1. Производную правой части вычисля-
ем по правилу нахождения производной сложной функции
256 Показательная и логарифмическая функции
и теореме 1 (п. 41): (elnx)' = elnx In' х = х In' х. Подставляя найден-
ные производные в равенство (2), находим 1 = х In' х, откуда
In' х = 1.
а)
а)
Пример 1. Найдем производные функций:
у=1п(5 + 2х); 6)j/ = log3x; B)j/=log72x.
(ln(5 + 2x))' = -^— (5 + 2х)' = —2—;
5 + 2х 5 + 2х
б)
(log3 Х)' = [^
\ ш о
1 .
х In 3 ’
(log7 2х)' =
в)
__2 = 1_
2х1п7 х1п7"
Пример 2. Исследуем функцию f (х) = х2 in х на возраста-
ние, убывание, экстремум и построим ее график.
Функция определена при х > 0. Найдем ее производную:
/' (х) = 2х 1пх + х2 • - = 2х1пх+х=2х| 1пх+^|.
х I 2
2
х > 0, поэтому знак
производной совпадает со знаком
1
2
Отсюда следует, что
/'(х) > 0 на промежутке
-^=; оо , и поэто-
yle J
му
на промежутке
Д=; 00 функция возрастает, на промежутке
Je J
1
Ге
поэтому / убывает на проме-
1 __________________________
/е
водная меняет знак с минуса на
плюс, значит,
ма; f
0;
на,
производная отрицатель-
жутке 0; . В точке произ-
I у/ е
это точка миниму-
—. График функ-
2е
1
1е
ции приведен на рисунке 145.
Формула (1) показывает, что для функции 1 на про-
X
межутке (0; оо) любая первообразная может быть
записана в виде In х + С.
Функция — имеет первообразную и на промежутке (-оо; 0),
х
это функция In (—х). Действительно,
(1п(-х))'= 1 (-х)' = 1-.(-1) = 1.
-X -X X
257 Показательная и логарифмическая функции
Так как | х | = х при х > О и | х | = -х при х < О, мы доказали сле-
дующее:
На любом промежутке, не содержащем точку О,
первообразной для функции - является функция
In |х|.
первообразные равны
Пример 3. Для функции 1
X + о
1п |х + 3| + С (на любом промежутке, не содержащем точку - 3).
Для функции 1 общий вид первообразных 4 In 15х + 71 +
5х+7 5
у
+ С (на любом промежутке, не содержащем точку - - ).
5
Пример 4. Найдем пло-
щадь фигуры, ограниченной ли-
ниями у = ~, у = 0, х = 1, х = 2
(рис. 146).
Поскольку In х при х > О
есть первообразная для -, пло-
х
щадь интересующей нас криволи-
нейной трапеции равна
S = In 2 - In 1 = In 2.
Упражнения
Найдите производную каждой из функций (549—550).
549. — а) у = In (2 + Зх); б) у = log0 3 х + sin х;
в) у = In (1 + 5х); г) у = 1g х - cos х.
550. — а) у = х2 log2 х; б) у = 1пх; в) у = х In х; г) у = -
551. Найдите общий вид первообразных для функции:
а) / (х) = - 3 ; б) f(i)=‘-- ;
7х+1 х х+ 5
в) f(x)= Ц; г) /(х) = -.
х+ 2 х
552. Напишите уравнение касательной к графику функции f
в точке с абсциссой х0, если:
a) f (х) = In (х + 1), х0 = 0; б) f (х) = 1g х + 2, х0 = 1;
в) f (х) = 2 In х, х0 = е; г) f (х) = log2 (х - 1), х0 = 2.
258 Пока шгельная и логарифмическая функции
553. — Вычислите интеграл:
7
I (2dx
6) J ; В) [ —; г) (
J 3-2х J х J
3
dx
х +
о
554. — Найдите производную функции:
ч 1п(5+3х)
а) У =----
х2 +1
б) и= ;
У lg(l —2х)
г2
В) У = т
1п5х
X log3 X2
Г) у= — -
Исследуйте функцию на возрастание (убывание) и экстре-
мумы (555—556).
555.— a) f (х) = Vx 1пх; б) / (х) = X
в) f (х) = 2х - In х; г) f (х) = х In X.
556.- а) f (х) = х In2 х; б) /•(х)=^; 1g х
в) f(x) = -1^; г) f (х) = — + In X
Vx
557. — Вычислите площадь фигуры, ограниченной линиями:
а) у = — + 2, у = 0, х = 2, х = 6;
х
б) у = - -, у = 0, х = -4, х = -1;
х
| в) у = — ,у = 0, х=-,х = 2;
У 2х у 4
г) у = 3 - —, у = 0, х = -6, х = -3.
х
43. Степенная функция
1. Степенная функция и ее производная. Вы уже зна-
ете, что для любого действительного числа а и каждого положи-
тельного х определено число х“. Зафиксируем число а на проме-
жутке (0; оо).
Определение. Функция, заданная формулой
f (х) = х“, называется степенной (с показателем
степени а).
Если а > 0, то степенная функция определена и при х = 0,
поскольку О'1 = 0. При целых а формулой f (х) = ха степенная
функция f определена и для х < 0. При четных а эта функция чет-
259 Показательная и логарифмическая функции
ная, а при нечетных а — нечетная. Поэтому исследование степен-
ной функции достаточно провести только на промежутке (0; оо).
В предыдущих разделах курса были получены формулы для
производной функции у = ха лишь при целых показателях степе-
ни, а также а = |. Теперь нам остается вывести формулу при про-
извольном а. Докажем, что для любого х из области определения
производная степенной функции находится так:
(х“)’ = аха '. (1)
Действительно, так как х = е1п х, то х“ = еа 1п х. Отсюда по
правилу вычисления производной сложной функции получаем:
(х“)' = (еа ln х)' = еа ln х (a In х)' = ха • а - = ах“ “ *.
х
Формула (1) доказана.
При а < 0 степенная функция убывает на промежутке
(0; оо), поскольку (х°)' = аха “1 < 0 при х > 0. При а > 0 имеем
(ха)' = аха’ 1 > 0, поэтому степенная функция возрастает при
х > 0. Кроме того, надо учесть, что при х = 0 степенная функция
равна 0 и ха —> 0 при х -> 0 и х > 0. Поэтому точка 0 присоединя-
ется к промежутку возрастания, т. е. при а > 0 степенная функ-
ция возрастает на промежутке [0; оо). Примеры графиков степен-
ной функции при различных а приведены на рисунке 147.
Из формулы (1) следует, что производной степенной функ-
ции f (х) = х“ является степенная функция (/'(х) = аха *). Иначе
обстоит дело с первообразной степенной функции.
При а * -1 общий вид первообразных степенной функции
ха +
f (х) = х°, как легко проверить, таков: F (х) =-- + С.
а +1
При а = -1, как известно, первообразной функции f является
функция F (х) = In | х | + С.
260 Показательная и логарифмическая функции
2. Вычисление значений степенной функции. Выведем при-
ближенную формулу
(1 + Дх)а « 1 + а Дх. (2)
Рассмотрим функцию f (х) = ха и воспользуемся приближен-
ной формулой
f (х) » f (х0) + f (х0) Дх, (3)
известной из п. 20, при х0=1их=1+ Дх. Имеем f (х0) = f (1) = 1
и f (х) = ах“" ’, откуда f (х0) = f (1) = а • 1а“1 = а. По формуле (3)
f (х) = (1 + Ах)“ « 1 + а Дх.
Чаще всего эту формулу применяют для вычисления корней.
Полагая а = -, находим:
п
71 +Дх =(1 + Дх)" «1 + —. (4)
п
Пример. Вычислим приближенные значения:
a) V1-08; б) ^27,03; в) ^1000.
Воспользуемся формулой (4):
а) -71,08 = (1 + 0,08)4 «1+* 0,08 = 1,02.
6)7^3 = з/27Г1 + °^>) = 33J1+0’03 »зГ1+|-°^3К
V \ Z i J у я! у о /5 I у
» 3,0011 (значение ^ 27,03 с семью знаками после запятой та-
ково: ^27,03 = 3,0011107);
в) заметим, что 210 = 1024. Имеем:
’71000 = 1°^210 -24 = 2 • ю/ 1- 24 к 2 1-24 . - | » 1,995.
V 210 I 1O-210 J
Упражнения
Постройте график функции f и найдите ее производную
(558—559).
3
558.— а) f(х)= х 2; б) /(x) = xv3;
1 в) /(х) = х3; г) / (х) = х '/®. ( v vlg5
559. 1 а) f (х) = х«; б)
в) f (х) = хл; г) f (х) =(2х)|п3.
261
Показательная и логарифмическая функции
Вычислите с помощью формулы (4) приближенные значе-
ния (560—561).
560.— а) 243; 6) Тб2(ГЗ; в) V«T; г) ^48.
561.— a) V30; б) VvO; в) 75702; г) 733.
562.— Найдите наибольшее и наименьшее значения функции f
на промежутке I:
2 a) f (х) = х5, I = [1; 32]; б) /(х) = х 3, /=[|; 27];
в) Нх) = х-4, 7=Г|; 1]; г) f (х) = 3 81].
563. 564. Найдите общий вид первообразных для функции: a) f(x) = -|x ; б) f(x)=x2'/3; в) f (х) = Зх *; г) f (х) = Xе. Вычислите интеграл: 4 5 8 е2 81 1 а) |х2 dx-, б) J в) J2x Adx\ г) J 5х4 dx. 1 1 хз « 16
565. — Вычислите площадь фигуры, ограниченной линиями:
а) у = х'2, у = О, х = 1;
б) у = х^, у- *, х= 1-,
х 2
в) у = х °-8, у = О, х = 1, х = 32;
г) у = 1» У = 0, х = 3, х = 5.
566. — На миллиметровой бумаге постройте графики функций
у = у[х, у = Vx, у = Vx (х > 0).
1) Найдите с помощью графика приближенные значения:
а) 72, V3; б) 7з, VO; в) V^S. 73; г) -^2$, VZ;
2) Найдите значения этих корней с помощью калькулятора.
3) Вычислите их приближенные значения, пользуясь фор-
мулой (4). Указание: 2,5 = 1,62 - 0,06; 2,5 = 1,33 +
+ 0,303; 2,5 = 1,254 + —; 2 = 1,42 + 0,04; 3 = 1,43 + 0,256;
256
3 = 1,34 = 0,1439.
4) Сравните полученные результаты.
567. — Верно ли, что функция f(x) = xv5 обладает свойством:
|а) в области определения можно найти отрезок, на концах ко-
торого функция принимает значения разных знаков; б) яв-
ляется четной; в) имеет экстремумы; г) существует точ-
ка х0, в которой функция принимает наименьшее значение?
262 Показательная и логарифмическая функции
44. Понятие о дифференциальных уравнениях
1. Непосредственное интегрирование. В ходе решения
задач естествознания часто возникают соотношения, связывающие
производные некоторой функции (первую, вторую и т. д.), саму
эту функцию и независимую переменную. Например, согласно
второму закону Ньютона при движении по прямой материальной
точки постоянной массы т справедлива формула F = та, где
F — сила, вызывающая движение, а — ускорение точки. Пусть
сила F зависит только от времени t, т. е. F = F (Z). Вспоминая,
что ускорение есть вторая производная координаты по времени
(a (t) = х" (О), получаем дифференциальное уравнение относитель-
но функции х (t):
F (t) = тх" (t), т. е. х" (t) = F
т
для решения которого сначала находим х' (t) как первообраз-
F(t)
ную функции - , а затем и х (t) как первообразную функции
т
v (t) = х' (£)- Общее решение зависит от двух произвольных посто-
янных. Для того чтобы их найти, обычно задают координату
и скорость в какой-либо момент времени t.
Пример 1. При вертикальном движении под действием
силы тяжести координата h (О точки единичной массы удовле-
творяет дифференциальному уравнению (ось Ог направлена вер-
тикально вниз):
h" (t) = g.
Общее решение этого уравнения имеет вид:
at
h (0 = h0 + vot + * -, где h0 = h (0), v0 = v (0).
Задав ft0 и v0, мы получим уже единственное решение.
Вообще первообразную F для функции f можно рассматри-
вать как решение простейшего дифференциального уравнения
F'(x) = /(x), (1)
где f (х) — данная функция, F (х) — решение этого уравнения.
2. Дифференциальное уравнение показательного роста и
показательного убывания. Решение многих задач физики, техни-
ки, биологии и социальных наук сводится к задаче нахождения
функций, удовлетворяющих дифференциальному уравнению
/'(x) = fef(x), (2)
где k — некоторая константа.
263 Показательная и логарифмическая функции
Зная формулу производной показательной функции, легко
догадаться, что решением уравнения (2) является любая функция
вида
f (х) = Секх, (3)
где С — постоянная. Так как С произвольно, у дифференциально-
го уравнения (2) бесконечно много решений.
Докажем, что других решений, кроме функций вида (3),
уравнение (2) не имеет. Для этого рассмотрим произвольную функ-
цию f, удовлетворяющую уравнению (2), и вспомогательную
функцию
g (х) = f (х) е~кх. (4)
Найдем ее производную:
g' (х) = Г (х) е~кх + f (х) (е~кх)' = f (х) е~кх - kf (х) е кх.
Подставляя kf (х) вместо Г (х) из уравнения (2) получим:
g' (х) = kf (х) е~кх - kf (х) е~кх = 0.
Из равенства производной функции g нулю следует, что g (х) = С
при всех х. Из (4) получаем:
f (х) е кх = С, откуда f (х) = Секх,
что и требовалось доказать.
Замечание. В приведенных выше рассуждениях мы пред-
полагали, что функция f определена и удовлетворяет уравне-
нию (2) на всей числовой прямой. В конкретных задачах часто
приходится рассматривать функции, удовлетворяющие уравне-
нию (2) только на некотором промежутке. Естественно, что в та-
ком случае формула (3) будет давать общее решение задачи только
на промежутке, на котором выполняется уравнение (2).
Смысл дифференциального уравнения (2) заключается в том,
что скорость изменения функции в точке х пропорциональна зна-
чению самой функции в этой точке. Это уравнение часто встреча-
ется при решении практических задач.
Пример 2. (Радиоактивный распад.) Пусть в начальный
момент времени масса радиоактивного вещества равна:
т (0) = т0. (5)
Экспериментально установлено, что скорость уменьшения
массы вещества т (t) со временем t пропорциональна его ко-
личеству, т. е. т' (0 = -km (t), где k > 0. Как показано выше,
m(t) = Ce ht. Константа С находится из условия (5). А именно
при t = 0
т0 = т (0) = Се~к °, т. е. С = т0 .
264 Пока >ательная и логарифмическая функции
Окончательно получаем:
т (t) = тое м. (6)
Рассмотренный пример типичен: чтобы выделить из беско-
нечного числа решений дифференциального уравнения одно, обыч-
но требуется еще ввести начальные условия (в нашем случае это
условие (5)).
Промежуток времени Т, через который масса радиоактив-
ного вещества уменьшается в 2 раза, называют периодом полурас-
пада этого вещества. Зная Т, можно найти k. Так как
m(T)=* т0, т. е. тае кт = т0,
- hT 1
имеем е Ki = - .
2
Следовательно, ект = 2, kT = In 2, откуда k -
Например, для радия Т ® 1550 лет. Поэтому (если время
измеряется в годах) k = г 0,000447. Через миллион лет
от начальной массы радия пг0 останется только ш(106) «шое~447 «
« 0,6 • 10 194m0.
3. Гармонические колебания. Производную от производ-
ной f функции f называют второй производной функции f
и обозначают f” (читается: «Эф два штриха»). Например:
sin' х = cos х, sin" х = cos' х = -sin х,
, „ , (7)
cos х= -sin х, cos x = -sin x = -cos x.
Вторая производная помогает более подробно исследовать по-
ведение функции. Первая производная есть скорость изменения
функции, а вторая производная есть скорость изменения этой ско-
рости.
Анализируя формулы (7), можно заметить, что вторые про-
изводные синуса и косинуса отличаются от самих функций только
знаком. Иначе говоря, обе эти функции удовлетворяют при всех
значениях аргумента t уравнению
f" (0 = ~f (t).
В физике, в частности в механике, большую роль играют
функции f, которые удовлетворяют уравнению
Г (f) = -<о7 (Г), (8)
где <о — положительная постоянная.
Разберем задачу из механики, приводящую к уравнению
такого вида. Пусть к шарику массой т прикреплена расположен-
ная горизонтально пружина, другой конец которой закреплен
(рис. 148), и пусть в состоянии равновесия координата х центра
265 Показательная и логарифмическая функции
о
Рис. 148
О X
Рис. 149
шарика равна нулю. При перемещении центра в точку с координа-
той х 0 возникает сила, стремящаяся вернуть шарик в положе-
ние равновесия. Согласно закону Гука эта сила пропорциональна
перемещению х, т. е. F = -kx, где k — положительная константа
(рис. 149). По второму закону Ньютона F = та, поэтому, учиты-
вая, что при движении по прямой ускорение есть вторая производ-
ная от координаты, имеем:
та (f) = тх" (1) = F, т. е. х" (f) = х (<)•
т
Иначе говоря, движение центра шарика под действием сил
упругости подчинено уравнению (8) при <а= - .
V т
Покажем, что физическая величина, изменяющаяся во вре-
мени в соответствии с уравнением (8), совершает гармоническое
колебание (см. п. 7). Само уравнение (8) называют дифференциаль-
ным уравнением гармонических колебаний.
Проверим, что при любых постоянных А и <р функция
f (t) = A cos (со/ + ip) (9)
есть решение уравнения (8). В самом деле, пользуясь формулой
для производной сложной функции, получаем:
f (t) = -А w sin (wt + ср),
/" (t) = -Aw2 cos (wl + <p) = -w2f (£)•
Верно и обратное: любое решение уравнения (8) есть функ-
ция вида (9), причем обычно выбирают А > 0, <р е [0; 2л]. Доказа-
тельство этого выходит за рамки школьного курса.
Произвольные постоянные А и <р можно определить, если
заданы начальные условия f (0) = у0, f' (0) = v0.
4. Падение тел в атмосферной среде. Рассмотрим более
сложный пример. При падении тел в атмосфере нужно учитывать
сопротивление воздуха. Экспериментально установлено, что сила
сопротивления воздуха пропорциональна скорости движения,
т. е. сила F, действующая на тело, равна F (1) = mg - kh' (t),
где т — масса тела, g — ускорение свободного падения, Л (/) —
координата на прямой (ось Oh направлена вертикально вниз),
266 Показательная и логарифмическая функции
k — коэффициент пропорциональности. По второму закону Ньюто-
на F = та, поэтому получаем уравнение
mz" (t) = mg - kz' (Z), т. e. г" (Z) = g - к z'(Z),
m
которое удобно рассматривать как дифференциальное уравнение
и' (Z) = g - bv (Z), где b = k > 0, (10)
m
относительно скорости движения o(Z) = z'(Z). Для того чтобы при-
вести это уравнение к знакомому виду, введем новую неизвестную
функцию y(t) = 8 -v (Z), тогда у’ (Z) =1 f -v (Z) = -v' (Z) и уравне-
b \ b I
g
~ b
ние (10) записывается в виде
—y'(t) = by(t), т. e. y'(t) = -by (t),
решения которого уже известны: y(t) = Cebt. Следовательно,
v (t) = 8--у (t) = ^-Се~ы.
b b
Функция у = e bt убывает на R, при этом ее значения неогра-
ниченно уменьшаются при возрастании Z (т. е. Се ы —> 0 при
Z —> оо для любого С). Это означает, что скорость приближается
g
к постоянному значению —, которое зависит от величины коэффи-
Ь
циента пропорциональности k и массы т. Например, при за-
тяжных прыжках (парашют не раскрыт!) эта скорость равна при-
мерно 50 м/с, а скорость парашютиста при приземлении (когда k
значительно больше) около 4—5 м/с.
Рассмотренные примеры позволяют нам понять, насколько
мощным аппаратом исследования являются дифференциальные
уравнения. Очень часто элементарные законы, управляющие каким-
либо процессом, записываются в виде дифференциальных уравне-
ний. Для того чтобы выяснить, как процесс развертывается во време-
ни, приходится эти дифференциальные уравнения решать.
Упражнения
568.— Проверьте, что функция у (Z) является решением данного
дифференциального уравнения:
а) у (Z) = 3 cos (2Z + л), у" = -4у;
16) y(t) = 4sin(|z-^, у" = -*у;
в) У (О = 2 cos 4Z, у" + IGy - 0;
г) У (Z) = * sin (O,1Z + 1), у" + 0,01у = 0.
Показательная и логарифмическая функции
569.—
571.—
572. -
573.
Докажите, что функция у = 5е3х удовлетворяет уравнению
У' = %У-
570.— Докажите, что
функция у = 7е 2х удовлетворяет уравнению
У' = ~2у-
Докажите, что функция у = Зе 7х удовлетворяет уравнению
У' = -Чу-
Найдите какое-нибудь отличное от нуля решение диффе-
ренциального уравнения:
а) у" = -25у; б) * у" + 4 г/ = 0;
в) 4у" + 16(/= 0; г)у"=-^у.
4
Напишите дифференциальное уравнение гармонического
колебания:
а) х = 2 cos (2t - 1); б) х = 6,4 cos ^0,lt + у
в) х = 4 sin [ 3t- — г) х = 0,71 sin (0,31 - 0,7).
574 .— Докажите, что сумма двух гармонических колебаний
Xj (t) = A] cos ((DjZ + (pj и х2 (0 = А2 cos (со21 + <р2) будет пе-
риодической функцией тогда и только тогда, когда отноше-
(01
ние частот есть рациональное число г, т. е. — = г.
«>2
575 .— От т миллиграммов радия С через t минут радиоактивного
распада осталось п миллиграммов. Найдите период полу-
распада радия С.
576 .— К началу радиоактивного распада имели 1 г радия А. Через
сколько минут его останется 0,125 г, если его период полу-
распада равен 3 мин?
577 .— Период полураспада радиоактивного вещества равен 1 ч.
Через сколько часов его количество уменьшится в 10 раз?
Вычислите, какая доля радия останется через 1000 лет,
если период его полураспада равен 1550 лет.
578.--
579.
Одно тело имеет температуру 200°, а другое — 100°.
Через 10 мин остывания этих тел на воздухе с температу-
рой 0° первое тело остыло до температуры 100°, а второе —
до 80°. Через сколько минут температуры тел сравня-
ются?
(Температура тела Т (t) удовлетворяет уравнению Т' (t) =
= -k (Т - Tj), где 7j — температура окружающей среды.)
Два тела имеют одинаковую температуру 100°. Они вынесе-
ны на воздух (его температура 0е). Через 10 мин темпера-
Пока.<а1е.1ьная и логарифмическая функции
тура одного тела стала 80°, а второго — 64°. Через сколько
минут после начала остывания разность их температур бу-
дет равна 25°?
580.— Моторная лодка движется по озеру со скоростью 30 км/ч.
Какова скорость лодки через 3 мин после выключения мо-
(тора? (Воспользуйтесь тем, что скорость лодки v (t) удо-
влетворяет дифференциальному уравнению v' (t) = -kv (t),
где k = 5, v — скорость в метрах в минуту.)
Сведения из истории
1. О происхождении терминов и обозначений. К умноже-
нию равных сомножителей приводит решение многих задач. По-
нятие о степени с натуральным показателем возникло уже в Древ-
ней Греции (выражение квадрат числа возникло при вычисле-
нии площади квадрата, а куб числа — при нахождении объема
куба). Но современные обозначения (типа а4, а5) в XVII в. ввел
Декарт.
Дробные показатели степени и наиболее простые правила
действий над степенями с дробными показателями встречаются
в XIV в. у французского математика Н. Орема (1323—1382). Из-
вестно, что III юк е (ок. 1445—ок. 1500) рассматривал степени
с отрицательными и нулевыми показателями. С. С т е в и н пред-
£
дожил подразумевать под о" корень "Ja. Но систематически
рациональные показатели первым стал употреблять Ньютон.
Немецкий математик М. Штифель (1487—1567) дал опре-
деление а0 = 1 при а * 1 и ввел название показатель (это бук-
венный перевод с немецкого Exponent). Немецкое potenzieren
означает возведение в степень. (Отсюда происходит и слово
потенцировать, часто употребляемое при переходах типа
loga f (х) = loga 8 (х) => aioga f(x) =aIoea в (x>.) В свою очередь тер-
мин exponenten возник при не совсем точном переводе с грече-
ского слова, которым Диофант обозначал квадрат неизвестной
величины.
Термины радикал и корень, введенные в XII в., происходят
от латинского radix, имеющего два значения: сторона и корень.
Греческие математики вместо «извлечь корень» говорили: «найти
сторону квадрата по его данной величине (площади)». Знак корня
в виде символа появился впервые в 1525 г. Современный сим-
вол введен Декартом, добавившим горизонтальную черту. Ньютон
уже указывал показатели корней: Sy[~, .
Слово логарифм происходит от греческого Хоуос, (отношение)
и dpi0po<; (число) и переводится, следовательно, как отношение
чисел. Выбор изобретателем (1594 г.) логарифмов Дж. Непером
269 Показательная и логарифмическая функции
такого названия объясняется тем, что логарифмы возникли при
сопоставлении двух чисел, одно из которых является членом ариф-
метической прогрессии, а другое — геометрической (см. ниже).
Логарифмы с основанием е ввел Спейдел (1619 г.), со-
ставивший первые таблицы для функции In х. Название более
позднего происхождения натуральный (естественный) объясняет-
ся «естественностью» этого логарифма. Н. Меркатор (1620—
1687), предложивший это название, обнаружил, что для любого
х0 > 1 число In х0 — это площадь фигуры, ограниченной гипербо-
лой у = 1, осью абсцисс и прямыми х = 1, х - х0.
х
2. Из истории логарифмов. В течение XVI в. резко возрос
объем работы, связанный с проведением приближенных вычисле-
ний в ходе решения разных задач, и в первую очередь задач астро-
номии, имеющей непосредственное практическое применение
(в частности, при определении положения судов по звездам и по
Солнцу). Наибольшие проблемы возникали, как нетрудно понять,
при выполнении операций умножения и деления. Попытки ча-
стичного упрощения этих операций путем сведения их к сложе-
нию (была составлена, например, таблица квадратов целых чисел
от 1 до 100 000, позволяющая вычислять произведения по фор-
муле ab = 1 (a + b)2 - -1- (a -5)2) большого успеха не приносили.
4 4
Поэтому открытие логарифмов, сводящее умножение и деление
чисел к сложению и вычитанию их логарифмов, удлинило, по вы-
ражению Лапласа, жизнь вычислителей.
Логарифмы необычайно быстро вошли в практику. Изобрета-
тели логарифмов не ограничились разработкой новой теории.
Было создано практическое средство — таблицы логарифмов,—
резко повысившее производительность труда вычислителей. Доба-
вим, что уже в 1623 г., т. е. всего через 9 лет после издания пер-
вых таблиц, английским математиком Д. Гантером была изобрете-
на первая логарифмическая линейка, ставшая рабочим инструмен-
том для многих поколений. (Вплоть до самого последнего времени,
когда на наших глазах повсеместное распространение получает
электронная вычислительная техника и роль логарифмов как
средства вычислений резко снижается.)
Первые таблицы логарифмов составлены независимо друг
от друга шотландским математиком Дж. Непером (1550—1617)
и швейцарцем И. Бюрги (1552—1632). В таблицы Непера, издан-
ные в книгах под названиями «Описание удивительной таблицы
логарифмов» (1614 г.) и «Устройство удивительной таблицы ло-
гарифмов» (1619 г.), вошли значения логарифмов синусов, ко-
синусов и тангенсов для углов от 0 до 90° с шагом в 1 минуту.
Бюрги подготовил свои таблицы логарифмов чисел, по-видимому,
к 1610 г., но вышли в свет они в 1620 г., уже после издания таб-
лиц Непера, и поэтому остались незамеченными.
270 Показательная и логарифмическая функции
Непер Джон
(1550—1617) —
английский математик Изобретатель логарифмов
составитель первой таблицы логарифмов, облег-
чившей работу вычислителей многих поколений
и оказавшей большое влияние на развитие прило-
жений математики
Одна из важных идей, лежащих в основе изобретения лога-
рифмов, была уже известна. Штифель (1487—1567) и ряд дру-
гих математиков обратили внимание на то, что умножению и деле-
нию членов геометрической прогрессии
..., а 3, а2, а ’, 1, а, а2, а3, ...
соответствуют сложение и вычитание показателей, образующих
арифметическую прогрессию
..., -3, -2, -1, 0, 1, 2, 3......................
Но одной этой идеи недостаточно. Например, «сеть» целых
степеней числа 2 слишком редка; многие числа * остаются без ло-
гарифмов», поэтому необходима была еще одна идея: возводить
в степень числа, очень близкие к единице. Заметив, что степени
/ X п / х п +1
I 1 + * 1 * * * V | и I 1 + 1 I при больших значениях п близки, Непер
I 10л J I 10" )
и Бюрги приняли аналогичное решение: Непер брал в качестве
основания число I 1-|, а Бюрги — число I 1 + -1 I.
V 107 ) I 104 )
Дальнейший ход их рассуждений и описание схем вычисле-
ний пересказать довольно трудно как потому, что имеется много
непростых деталей, так и потому, что вообще тексты XVI в. до-
вольно туманны. Заметим только, что фактически далее Непер
( У°7
переходит к основанию 1 — , а Бюрги — к основанию
1Oga>0"
Это не изменило существа дела (как вам
х = — log„ х, и поэтому указанные переходы
10"
известно,
приводят
лишь к переносу запятой в логарифме), но позволило несколько
упростить вычисления и сами таблицы.
271 Показательная и логарифмическая функции
Таким образом, по существу, оба изобретателя логарифмов
пришли к выводу о целесообразности рассмотрения степеней вида
( 1
1 + — , где М — очень большое число. Рассмотрение чисел та-
V м)
кого вида приводит к известному вам числу е, которое определя-
( 1V
лось как lim 1ч— (определение предела последовательности
п » л \ nJ
дано в «Сведениях из истории» к главе III). Осталось уже немного
до идеи принятия в качестве основания логарифмов числа е (ос-
нования таблицы логарифмов Бюрги совпадает с точностью до
третьего знака с е, основание таблицы логарифмов Непера близко
к числу -).
е
Первые таблицы десятичных логарифмов (1617 г.) были со-
ставлены по совету Непера английским математиком Г. Бригг-
сом (1561—1630). Многие из них были найдены с помощью вы-
веденной Бриггсом приближенной формулы
log ю а
п ( Va -1)
rntVlO-l)’
достаточно точной при больших значениях тип. Бриггс брал зна-
чения т и п в виде степеней двойки: это давало ему возможность
п I т /Y77
свести вычисление \а и уЮ к последовательному извлечению
квадратных корней.
Другая идея Бриггса позволяет находить значения десятич-
ных логарифмов некоторых чисел самостоятельно, без помощи
таблиц. Целая часть логарифма целого числа на единицу меньше
количества цифр в самом числе. Поэтому, например, для нахож-
дения 1g 2 с точностью до трех знаков достаточно найти число
цифр 210 . Это не очень трудно.
При составлении таблиц логарифмов важную роль сыграло
найденное Непером и Бюрги соотношение между приращениями
Дх и в произвольной точке х0 для функции у = loga х. Отвлека-
ясь от деталей их системы изложения, основной результат можно
выразить так: — »*, где k — некоторая постоянная. Если основа-
Дх х
( 1
ние логарифмов — степень 1ч-— , где п — достаточно большое
\ п)
&У 1
число, то -® —.
Дх х
Устремляя Дх к нулю, приходим к дифференциальному урав-
нению у’ = ~, решением которого, как вы знаете, является функ-
х
ция In х ч- С. Существует система изложения, при которой In х0
*0
с самого начала определяется как J —, т. е. In х0 — площадь
1
272 Показательная и логарифмическая функции
криволинейной трапеции, ограниченной гиперболой, осью абсцисс
и прямыми х = 1 и х = х0. Вывод известных вам свойств логариф-
мов, исходя из этого определения, не очень простая, но доступная
вам задача.
Вопросы и задачи на повторение
1. 1) Дайте определение корня п-й степени из числа. Что такое
арифметический корень п-й степени?
2) Найдите значение:
а) 7-27; б) Тб25; в) 7-128; г) Ж; д)(7^)п.
V 64
3) Решите уравнение:
а) х3 = 125; б) х4 = 64; в) х5 =——; г) х4 =-16.
2. 1) Перечислите основные свойства арифметических корней.
2) Преобразуйте выражение:
3) Какое из чисел больше:
а) 7128 или 74; б) 2100 или 1ОО20;
в) 726 или Тб; г) 75 или 7з ?
1) Дайте определение степени с рациональным показателем
и перечислите основные свойства таких степеней.
2) Найдите значение:
_ 1
в) 16 4
3) Какое из чисел больше:
г)
81 У»
625 J
5 2
а) 716 или 24; б) 3 3
4 _« --
в) 0,37 или 0,3 7; г) 5 3
з
или 9 4;
или 50’6?
1) Перечислите основные свойства показательной функции.
2) Постройте график функции:
а) у = 4х; б) ; в) у = 6х; г) •
\4/ J
3) Какое из чисел больше:
V2
а) 20,4 или 2 3 ; б) 1,2’^3 или 1,2^;
в) — или — ; г) 0,3 л или 0,3 3?
Показательная и логарифмическая функции
5. 1) а) Найдите корни уравнения ах = ас (а > 0, а* 1).
б) Решите неравенство ах > ас (рассмотрите два случая:
О < а < 1 и а > 1).
2) Решите уравнение:
1
а) 27х = 95; б) 9х 4 1 + 3х * 2 = 18;
в) 0,5х2 + х'2’5 = V2; г) Зх + 2-Зх=72.
3) Решите неравенство:
а) 5х2 *>-; б) 0,2х2’2 >5;
5
Z \х+1
в) 3х < г) - >4.
9 7 \2 )
6. 1) Дайте определение логарифма числа.
2) Найдите:
a) log2 16 V2; б) log0 2 255 в) 0,01; г> 1о^1
з
3) Запишите основное логарифмическое тождество. С его по-
мощью вычислите:
а) 32+log35. б) (I}1 1Ов23; в) 5-lAlog52. г) 0 2l+log0.25
7. 1) Перечислите основные свойства логарифмов.
2) Прологарифмируйте по основанию а выражение (с > 0,
b > 0):
a) 16b7 yfc при а = 2; б) с — при а = 10;
V100 Ьп
ч 27 Vb „ . 0,49b3 „
в) ---- при а = 3; г) при а = 0,7.
с4 C°yJC
3) Найдите х, если:
a) log3 х = 2 log3 7 + | log3 27 - J log3 16;
6) log2 x = 2 log2 5 - i log2 8 + log2 0,2;
О
В) logg X = logg 1,5+| logg 8;
«5
г) 1g x = 1 + 2 1g 3 - | 1g 125.
О
8. 1) Дайте определение логарифмической функции и перечис-
лите ее основные свойства.
2) Постройте график функции:
а) у = log4 х; б) у = log, (х -1);
5
в) у = logg х; г) у = log! х + 1.
274 Показательная и логарифмическая функции
3) Какое число больше:
a) 1g 7 или 3 1g 2; б) log! 5 или logj 6;
з з
в) log3 5 или log8 6; г) log2 3 или log3 2?
9. 1) а) Укажите все корни уравнения loga х = b (а > 0, а * 1).
б) Решите неравенство logo х > logc с (рассмотрите два слу-
чая: 0 < а < 1, а > 1).
2) Решите уравнение:
a) log2 (х - 15) = 4; б) 1g2 х + 2 1g х = 8;
в) In2 (х - 2) = 4; г) 1g (х2 - 2х - 4) = 1g 11.
3) Решите неравенство:
a) log0 6 х > 2; б) 1g х < -2;
в) In х > -3; г) log7 х < 1.
10. 1) Запишите формулу производной для функции у = ех,
У = ах.
2) Найдите производную функции:
a) v (х) = 5 - 2е4 ~ Зх; б) и (х) = 3 57х “
в) g(x) = е~3х; г) f (х) =
3) Найдите общий вид первообразных для функции:
a) v (х) = е5х - 7е~4х; б) и (х) = 5е°-7х;
в) g (х) = е-3х; г) f (х) = е2х.
11. 1) Какую производную имеет функция у = loga х? Найдите об-
щий вид первообразных для функции /(х)=-1.
х
2) Найдите производную функции:
а) у = х In Зх; б) у = log2 (7 - 2х);
в) у = 2 log3 х; г) j/=ln
3) Найдите общий вид первообразных для функции:
а)/(х)=1; 6)g(x) = -1 ; в)п(х)=-; г) Л(х) = -- .
5х х-3 х х+1
12. 1) Какую производную имеет степенная функция у = х“ ?
2) Постройте график функции и найдите ее производную:
а) у = х7; б) у = х4; в) у = х °12 13; г) у = х^2 .
3) Найдите приближенное значение:
а) ^32,02; б) ^127,9; в) ^/64,3; г) ^80,6.
Г-Т
13 J
Показательная и логарифмическая функции
13. 1) Какие уравнения называют иррациональными?
2) Решите уравнение:
а) Vx-З = 2х - 7; б) ^2х + 3 = 2;
в) х-у[х =12; г) х + 3 = >/33+ х2 .
уравнений:
3) Решите систему
х-у = 9;
Vx + Jy = 4,
х-у = 8;
б)
х + y-jxy =6,
ху = 16;
х2 + у = 7,
х2 у = 12.
14. 1) Что называют решением системы двух уравнений
переменными?
2) Решите систему уравнений:
двумя
а)
х -Зу = 5,
23 * * 6» ~х = 1 •
4 ’
[б2*’» =0,2,
б)
I б®-* = 125;
в)
2ху =9,
4х’2» =1;
г)
з3х+у = 4з,
5х-4у = 15.
3) Решите систему уравнений:
ч [х-у = 4, [зх-2у=1,
а) < б) <!
[log2 x-log2 у = 1; [Igx + 1g (у + 5) =2;
flog3(5x-j/) =2, I х2 + у2 =26,
[ху=2; [log5 x = l + log5 у.
V
глава
Задачи на повторение
2.
3.
4.
5.
6.
7.
8.
§1.
Действительные числа
1. Рациональные и иррациональные числа
Верно ли утверждение:
а) если натуральное число делится на 6, то оно делится на 3;
б) если сумма двух чисел — четное число, то каждое слагае-
мое четно;
в) если произведение двух чисел равно нулю, то каждый
множитель равен нулю;
г) если куб некоторого числа делится на 8, то это число
четно?
Докажите, что сумма трех последовательных натуральных
чисел делится на 3, а их произведение — на 6.
К числу 523 допишите две цифры справа так, чтобы полу-
ченное пятизначное число делилось на:
а) 3 и 5; б) 8 и 9.
Докажите, что число 1056 - 1 делится на 3 и 11.
В двузначном числе цифра единиц на 2 больше цифры десят-
ков. Само число больше 30 и меньше 40. Найдите это число.
Докажите, что если дробь | несократима, то несократима
и дробь
а+ Ь
Докажите, что:
а) |а| = |-а|; б) х < |х|; в) |х|2 = х2.
Найдите значения выражений (8—9).
2,75 :1,1 + 3 1
">--------Г“1Т; 61
в) fl,4-3,5:1^1 :2,4 + 3,4:2 i; г)
\ 4) 8
3—: 10 + 0,175: --
3__________20.
13_111.51
4 17 56
1+1.-!-
2 0,25
6-
1 + 2,2 • 10
За дачи на повторение
„ ч 0,52-0,5 1,22-1,82
9. а)-----------------; б)--------------- ;
0,42 + 0,12 +2-0,4-0,1 1,2 • 0,2 - 1,2 0,8
О.в^-0.1^2.0.6.0,1
1,5—1.52 ' 5) 1 S ) 8
10. Укажите верные цифры в записи приближенного значения
числа:
а) 3,82 ± 0,1; б) 1,980 104 ± 0,001 104;
в) 7,891 ± 0,1; г) 2,8 • 10 4 ± 0,3 • 10 4.
11. Пользуясь формулой (1 + х)п « 1 + пх, вычислите прибли-
женно:
а) 1,0025; б) 0,9974; в) 2,0043; г) 3,015.
12. Известно, что а ® 11,5, b ® 3,8. Найдите приближенное зна-
чение выражения: а) а + Ь; б) За — Ь; в) ab; г) а.
Ь
13. Запишите в виде обыкновенной дроби:
а) 2,(3); б) 0,(66); в) 1,0(8); г) 1,(33).
14. Докажите, что не является рациональным каждое из чисел:
a) V5; б) 2 Л; в) 75 + 1; г)
3
15. Верно ли, что сумма (произведение) чисел а и b является ра-
циональным (иррациональным) числом, если:
а) а и b — рациональные числа;
б) а и b — иррациональные числа;
в) а — рациональное, а Ь — иррациональное число?
16. Найдите с точностью до 0,01:
а) Л + -; б) 4&-~; в) V3 + -; г) Тб- —.
9 7 ’ 6 7 11
17. Расположите числа в порядке возрастания. Укажите, какие
из них являются рациональными, а какие — иррациональ-
ными числами:
a) V3; —2; -1,7; 3 в) 0,(2); 7 ,v 7’ 6 2 Сравните числа (18—19). 6) log2 3; - 1; г) e; —1,(6); л -Л; 6 /10; 1g 100.
18. а) — И -Ь; б) (л/б + 2) и Л7;
в) log3 7 и log7 3; г) (Л + 3) и - ]з1.
19. а) |glog310 и iQlog315. б) (Л + Л) и ( Ло - Л);
в) sin 2,1 и sin 7,98; г) (Л + Л) и (Л +ЛО).
278 Задачи на повторение
20. Докажите рациональность числа:
б) (V2 + I)2 + (1 - V2)2 -(V7 + 1)(V7 - 1);
г) (3 718+278+4 J5O):T2.
2. Проценты. Пропорции
21. Найдите число х, если: а) х составляет 2,5% от 320; б) 2,5%
числа х равны 75; в) х равен числу процентов, которое со-
ставляет 2,8 от 84; г) х составляет 140% от 35.
22. За 1987 г. выпуск предприятием продукции возрос на 4%,
а за следующий год — на 8%. Найдите средний ежегодный
прирост продукции за двухлетний период.
23. Из данных четырех чисел первые три пропорциональны чис-
лам 5, 3, 20, а четвертое число составляет 15% третьего.
Найдите эти числа, если второе число на 375 меньше суммы
остальных.
24. За осенне-зимний период цена на овощи возросла на 25%.
На сколько процентов следует снизить цену весной, чтобы
летом овощи имели прежнюю цену?
25. Найдите неизвестный член пропорции:
а) 12 : | = х : —; б) х : (- -0,3) = 0,15 : 1,5;
8 36
ч 0,13 26 . X -6,2
в) — — = г) _
X 31’ 2,5 15
3
26. Решите уравнение:
„ х-2 а) = _ 6. б) __х _ 4,8.
2,5 X х+ 5 ~~ 1,2 ’
ч х-3 6,5. 4-х 5
в) — - = г) :
х—2 1,5’ 1,2 х+ 3
27. Через точку Е стороны АВ треугольника АВС проведена пря-
мая, параллельная стороне АС. Найдите:
а) отрезки, на которые прямая делит сторону ВС, если
АВ = 22,5 см, АЕ = 18 см, ВС = 15 см;
б) площади фигур, на которые делится треугольник АВС,
если АВ = 7,5 см, АЕ = 5 см, а площадь треугольника АВС
равна 72 см2.
279 Задачи на повторение
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
3. Прогрессии
Найдите сумму 20 членов арифметической прогрессии, если
первый ее член равен 2, а седьмой равен 20.
Между числами 4 и 40 найдите такие четыре числа, чтобы
вместе с данными они образовали арифметическую прогрес-
сию.
Докажите, что числа —-—, —-—, —-— являются тремя
log3 2 log6 2 log12 2
последовательными членами арифметической прогрессии.
Сумма первого и пятого членов арифметической прогрессии
равна 26, а произведение второго и четвертого ее членов рав-
но 160. Найдите сумму шести первых членов прогрессии.
Упростите выражение (а - с)2 + (b - с)2 + (b - d)2 - (а - d)2,
если известно, что числа а, b, с, d, взятые в указанном по-
рядке, составляют геометрическую прогрессию.
ТТ V2 + 1 1 1 f-
Докажите, что числа —=--, ——= и - образуют геометриче-
у2 — 1 2 — V2 2
скую прогрессию.
Четвертый член геометрической прогрессии больше второго
на 24, а сумма второго и третьего равна 6. Найдите первый
член и знаменатель прогрессии.
Найдите число членов конечной геометрической прогрессии,
у которой первый, второй и последний члены соответственно
равны 3, 12 и 3072.
Знаменатель конечной геометрической прогрессии равен i,
1 121 г,
четвертый ее член равен —, а сумма всех членов -g—. Сколь-
ко членов в этой прогрессии?
Найдите четыре числа, из которых первые три составляют
геометрическую прогрессию, а последние три — арифмети-
ческую, если сумма крайних чисел равна 14, а сумма сред-
них 12.
Найдите знаменатель и сумму бесконечно убывающей гео-
метрической прогрессии, в которой Ьг = уЗ, Ь2 = -у=—-.
Сумма первых трех членов бесконечно убывающей геометри-
ческой прогрессии равна 10,5, а сумма прогрессии равна 12.
Найдите ее первый член и знаменатель.
Три числа, каждое из которых является степенью с основа-
нием а (а > 0, а*1), составляют геометрическую прогрес-
сию. Докажите, что логарифмы этих чисел составляют ариф-
метическую прогрессию.
280 Задачи на повторение
§2.
Тождественные преобразования
4. Преобразования алгебраических выражений
41. Разложите на множители:
а) а2 + Ь2 + 2а - 2Ь - 2аЬ; б) х3 + (у - 1) х + у;
в) а6 - 8; г) х4 - х2 (у2 + 1) + у2.
42. Докажите, что:
а) п4 + 2п3 - п2 - 2п делится на 24, если п е N;
б) (и2 + 4п + 3) (и2 + 6п + 8) делится на 24, если п е N;
в) п3 - п делится на 6, если п е N;
г) п3 - 4и делится на 48, если п е N, п — четное.
43. Сократите дробь:
ч а3 + а2-а-\ _ х2 + х-12
а) —s-------; б) —-------;
а2+2а+1 х2+8х+16
„ 2аг-5а + 2 ч х3-27
в) ---------; г) --------------.
аЬ — 2Ь—За + 6 х2у+ Зху+9у
Упростите выражения (44, 45).
44.
а)
т + rt-
п
2тп
п-т т2-п2
а" + Ь-:(а2-Ь2)+
а+Ь а+Ъ
б)
аЬ
а2—Ь2
, I х 8 1 х2-2х х + 8
в) —-— °— • ---------- + ----;
х2 — 4 х2+2х) 4-х х+2
/ \2 „
, | 1 , 2с , 1 | (с-3)2 + 12с
Г}----------1--------т--------- | • --------
{c2 + 3c + 2 с2+4с+3 c2 + 5c + 6J 2
45.
3 _ 2 _ 1 "1 . 4i/2
2х-у 2х+у 2х-5у)‘ ±х2-у2'
б) (. 3- +____+ а~12 ;
I о — 3 cP — 5он- 6 о — 2 J 2d4-1J 3(3 — о)
v3 _с ।
-— +2х • (4-х2)1
х-2 I
х —1
2-х’
г)
k2 9-й2 _ 27+й3
3+й k2-3k S-k
k2
3-k
3 +
281 Задачи на повторение
5. Преобразование выражений,
содержащих радикалы и степени
с дробными показателями
46. Освободитесь от иррациональности в знаменателе:
47. Вычислите:
a) 7(V5-2,5)2 - V(l,5-V5)3 -1;
б) (5^3 + ^50)(5~У24).
/75-5/2
в) [7(^2-1,5)2 - V(l-V2)3 )2+ 0,75;
г) .(11 + 2/30).
2/5 + /24
Упростите выражения (48—51).
Задачи на повторение
50.
a)
2
.1.5 _ J
-0.5
6)
1 1
a2b2
ab
a+a2b2
(ab)4 —b2
a-b
в)
r)
2x + x2 y2
3x
1-c 2
c2 —c 2
2c2
c2
5
2
51.
a)
6)
3 3
x2 — y2
x-y
У2 x2 +y2 '
c 2 -c
c2 — c
2
2
c2
-2
4
a3 — 2a3b3 + ab3
5 4 1 2 2
a3 - a3 b3 — ab3 + a3 b
2(x4 -y4)
• a
1
3
-x-y
y~x
У 2
У
x2 -y2
в)
c — 1
1
4
3
[3
r)
3(a&)2-3b
a2-b2l + 2a2 + b2
a — b
3 3
a2 + b2
52.
6. Преобразования тригонометрических
выражений
Упростите выражения (52, 53).
a) tg2 а - sin2 а - tg2 а sin2 а;
б) д/sin2 Р (1 + ctg Р) + cos2 Р (1 + tg Р);
в) (3 sin а + 2 cos а.)2 + (2 sin а - 3 cos а)2;
cos Р tg Р „ „
г) --------ctg Р cos р.
Sin2 Р
283 Задачи на повторение
53.
a) 2 tg a - tg (a - л) + ctg - a J
• / л tgf--al
gj sin (-a) _ v2 J + cos a ,
sin(n-a) ctg a . (n , 'l
12 J
tg(л—P ) cos( л—P ) tg f — — P 1
в) —7-----S-----7----Г7------Ц;
sinf^-P j ctg (? + сЧ tg f ^ + a 1
. (Зл . 'i Зл - 16л 13л
tg-----h a sin — sin--- cos---
. I 2 J 2 9 18
r) ------------------------------
ctg (л-a) cos — sin 11^ cos2л
v 7 18 9
54.
Докажите тождество (54, 55).
tg(a+P)-tga-tgP = tg p.
tg a tg (a + P )
cos (a + P) + cos (a - P ) _ a.
sin(a + P) + sin(a - P)
a)
в)
6)
r)
1 — cos 2a + sin 2a
------------------= tg a;
1+ cos 2a + sin 2a
sina-sin 3a , _
------------= -ctg 2a.
cos a — cos 3a
55.
a) J- — - J- + - cosa = cos — при л < a < 2л;
V 2 2 V 2 2 4
б) 1 - J--- cos2a = V2 cos [ — - — I при л < ос < Д’1;
Vv22 \ 4 2 / 2
в)
r)
- + - J- + - cos2a = —cos — при — < a < 2л;
2 2 \2 2 2 2
1 + ,/--- cosa = V2 cos I — - — I при — < a < 2л.
V2 2 U 4? 2
56. Докажите справедливость равенства:
\ л 4л 5л 1
а) cos—cos—cos—= ;
’ 7 7 7 8
б) tg 20° - 4 sin20° sin50°= -2 sin20°;
в) — —-4 sin 70° =2;
’ sin 10°
r) cos 20° + 2 sin2 55° - >/2 sin 65° = 1.
57. Докажите справедливость неравенства:
a) tg х + ctg x > 2, если 0 < x <
284 Задачи на повторение
в) (1 + sin <р + cos <p) (1 - sin ф + cos ф) (1 + sin ф -
- cos ф) (sin ф + cos ф - 1) < 1;
г) 2 sin 4а sin 2а + cos 6а > -1.
Вычислите (58, 59).
58. a) cos4 а + sin4 а, если sin 2а =
1-2 sin2
О ГУ
б) —, если tg — = т;
1+sina 2
в) cos а, если sin a tg а = ^;
г) sin a, cos 2а, cos —, если tg — = —J2, л < а < —;
2 2 2
59. a) lg tg 1° + lg tg 2° + ... + lg tg 89°;
6) lg tg 1° • lg tg 2° • ... lg tg 89°.
60. Сравните число с нулем:
a) lg sin 32° • lg cos 7° lg tg 40° • lg ctg 20°;
6) lg tg 2° + lg tg 4° + lg ctg 2° + lg ctg 4°.
61. Найдите сумму tg2 + tg2 + tg2 если
cosx = ——, cosy = ——, cosz = — , a + b + c 0.
b+ c c+ a a+b
7. Преобразования выражений,
содержащих степени и логарифмы
Сравните числа (62, 63).
62. а) З400 и 4300; б) -log5 - и 7logsl;
5
в) 5200 и 2500; г) log4 у[2 и log3
о!
63. a) log3 2 + log3 7 и log3 (2 + 7);
б) log4 5 - log4 3 и log4 (5 - 3);
в) 3 log7 2 и log7 (3 - 2);
г) log3 1,5 + log3 2 и log3 1,52.
64. Упростите выражение:
a) 814 2 1Og94 + 25log125 8 ; 6) 241og4“-521°в'Г5“-a0.
65. Запишите число в виде десятичной дроби:
a) 49l log72 + 5; б) 362“1Og65 + 2 log210.
285 Задачи на повторение
66.
67.
68.
69.
70.
71.
Найдите значение выражения:
а) б) 2 log°-3 3 -2 log°-310;
в) Г) (2 1Og12 2 + 1О^12 3> <2 10g12 6 - lug12 3>-
lg Io — lg lou
Прологарифмируйте
a) 25b3 при a =
„ 0,0016 b4
6) ТПГ
C \'cZ
при a =
по основанию а выражение:
5;
0,2, b > 0, c > 0.
Найдите x, если:
a) log4 x = 2 log4 10 + I log4 81 - 2 log4 125;
4 о
6) logj x = | log j 16 - log, 8 + log J 28.
3^3 3 3
Вычислите при помощи таблиц:
7,832-^12,98. 102,32
а 5,2562 ’ V92’14 • 6,341’
Упростите и найдите приближенное значение выражения
logg 2 • log4 3 logg 4 logg 5 • ... - log10 9.
Известно, что log2 (-Уз + 1) + log2 (-Уб - 2) = A.
Найдите сумму log2 (-Уз — 1) + log2 (-Уб + 2).
72.
73.
74.
§3.
Функции
8. Рациональные функции
Одно основание равнобедренной трапеции равно боковой сто-
роне, угол при основании 30°. Задайте формулой:
а) площадь трапеции как функцию боковой стороны;
б) периметр трапеции как функцию ее высоты.
Боковое ребро правильной треугольной призмы равно сторо-
не основания. Задайте формулой:
а) объем призмы как функцию стороны основания;
б) площадь боковой поверхности призмы как функцию объема.
Материальная точка, двигаясь прямолинейно, совершает
гармонические колебания. Задайте формулой:
а) координату точки как функцию времени;
б) скорость точки как функцию времени.
286 Задачи на повторение
S, км
75. На рисунке 150 изображены графики движения двух тури-
стов, которые вышли одновременно навстречу друг другу из
пунктов А и В.
а) В какое время туристы прибыли в пункты А и В?
б) Сколько времени был в пути каждый из них?
в) В какое время каждый турист прибыл к месту остановки?
г) Сколько времени каждый из них отдыхал?
д) С какой скоростью двигался каждый турист до остановки
и после нее?
е) Какова средняя скорость движения каждого туриста?
76. По графику функции (рис. 151) ответьте на вопросы:
1. Каковы промежутки возрастания функции?
2. Каковы промежутки убывания функции?
3. Назовите точки максимума и минимума функции. Какие
значения принимает функция в этих точках?
4. Каковы наибольшее и наименьшее значения этих функ-
ций на отрезке [-2; 2]?
5. В каких точках функция не является непрерывной и ка-
ковы значения функции в этих точках?
6. На каких промежутках функция непрерывна?
7. Какие из этих функций четные и какие нечетные?
77. Найдите область определения функции:
\ х— 2 ... х2
а) и = —------; б) у = —- ;
х2 + 2х-8 х2 -1 в) у = ; х4 -9х2 + 20 х4 -1 г) У “ о 2 \ Зх2 -5х + 4
287 Задачи на повторение
a)
б)
Рис. 151
288 Задачи на повторение
78.
Найдите промежутки непрерывности функции:
а)
У =
б) У=х2+
1
в) у = £--;
у 2 X
г) и =
Зх3-2х2 + 5
79. Докажите четность (нечетность) функции:
а) у = х3 - Зх; б)у=5-^;
1-х2
в) у = X4 (х2 + 2); г) у = ' * 2.
80. Найдите промежутки знакопостоянства функции:
81. Найдите промежутки возрастания (убывания), точки макси-
мума и точки минимума функции:
а) у = 4х2 + Зх - 1; б) у = 1 - ;
х + 4
в) у = (х - I)4 -2; Г) у = — J.
Исследуйте функцию и постройте ее график (82, 83):
82. а) у = Зх - 5; б) у = 2х2 - 7х + 3;
в) у = 2 - 1 х; г) у = 12 - 4х - х2. 4
83. а) у = 2--?-; б) у = (х - 2)3 - 1; х+ 1 в) у = - г) у = 4 - (х + 2)4. X4 Постройте график каждой из функций (84—86).
84. а) у = Зх - 2; б) у = х2 - 4х - 5; в) у - ± - 1; г) у = х3 + 2
85. а) у = Зх + |х|; б) у = |-х2 - х + 2|; в) у = 2х - |х - 31; г) у = х2 - 4 |х| + 3. . х+1 1 „ , 1 х I - 2 ч 2х3-1
86. а) г/ — . ; б) у- +2; в) у ; г) у . |х| X2 X X3
87. Имеют ли общие точки графики функций: а) у = х2 и у = х + 6; б) у = - и у = 4 (х + 1); в) у = х4 и у = 2х2 +1; г) у = и у = х2 - 2? X2
289 Задачи на повторение
88. Докажите, что уравнение имеет корень, принадлежащий за- данному промежутку I: а) х3 - 6х + 2 = 0, I = [0; 1]; б) х4 - Зх2 + | = 0, I = [1; 2]; в) Xs + Зх = 5, 1 = [1; 2]; г) 4 + 2х3 - х5 = 0, I = [-1; 2]. Решите графически уравнения (неравенства) (89, 90).
89. а) 4 - Зх < х + 2; б) х2 - 2х = -х; в) - = 4х; г) х2 + 2х + 2 > х + 1.
90. а) х3 = 3- ; б) |1—х| = 2-|х|; х-1 в) х3 = —; г) |х - 11 = 3 - |х|. X
91. График функции у = ах + Ь проходит через точки А (2; 1), В (5; 10). Найдите а и Ь.
92. По графику квадратичной функции (рис. 152) определите знаки коэффициентов а, Ь, с и дискриминанта D.
93. Может ли линейная или квадратичная функция быть: а) четной; б) нечетной; в) периодической?
94. Представьте функцию в виде суммы четной и нечетной функ- ций: а) у = б) У = х3 - х 1 х| + 3; И в) + *—5; г) у = 2х5 + х4 - Зх + 8. х4 -1
95. Является ли четной или нечетной функция: а) у = 5х6 - 2х2 - 3; б) у = 4х5 - 2х3 + х; в) У= у + 1; г) «/ = - у? X4 Xй 9. Тригонометрические функции Найдите область определения каждой из функций (96, 97).
96. а) у = —„—; б) у = ——\ ; соз2 х 1 + 2 sin2x в) у~ тГ г) у~ хх - 3 соз х - sin - cos - 2 2 2
290 Задачи на повторение
97. а) у = д/sin x cos x;
в) у = д/sin2 x-cos2 x;
Найдите область значений
98. а) у = 1 - 3 sin
в) у = 2 + 3 cos 5x;
каждой из функций (98, 99).
б) у = 2 cos х tg х;
г) у = 2 |sin х| - 1.
291 Задачи на повторение
99. а) У = т г ; б) У = у11~ cos 4х; l+sin2x v в) у = -—г) у = tg х + ctg х. COS х -1
100. Найдите промежутки знакопостоянства функции: а) у = 3cos I х + — I; б) у = 1 - tg Зх; \ 4 7 в) у = 1 - V2 sin ; г) у = 1 + 2 cos 2х.
101. Какие из данных функций являются четными, какие нечет- ными: , . „ х sinx cos2 X а) у = tg Зх-ctgб)у = * 3 в) у = sin ; г) у = -cosx? х2 -1 х
102. Среди данных функций укажите периодические и найдите наименьшие положительные периоды таких функций: а) у = 1 - sin 5х; б) у = х sin2 х - х cos2 х; в) у = 3 tg^- г) У - (sin х + cos х)2.
103. Найдите промежутки возрастания (убывания), точки мак- симума, точки минимума функции: а) у = 1 + sin I х — — I; б) у = — ; \ 6) 1 - cos X в) у = 0,5 cos 1 — -2х ; г) y = ^l-sin2x. \ 3 /
104. Найдите наибольшее и наименьшее значения функции (если они существуют): а) у = cos 2х + sin2 х; б) у = 1 - 4 sin Зх; в) у = sin х - cos х; г) у = 1 + | tg х |. Постройте графики функций (105, 106).
105. а) у = 2 sin2 |; б) у = ^/1-cos2 х; в) у = 1 + 2 cos 2х; г) у = sin ^х - - 2.
106. а) у = ; б) у = (sin х - cos х) , X в) у = cos х + |cos х|; г) у = sin х ctg х.
107. Исследуйте функцию и постройте ее график: a) y = | + sinfx-j); б) у = j tg f J - А в) у = 1 + - cos 1 — - х I; г) у = 1 - tg 2х. 2 V 4 J
292 Задачи на повторение
108.
109.
110.
111.
112.
113.
114.
115.
116.
Известно, что х0 — корень уравнения sin = х3. Следует ли
отсюда, что число (-х0) является корнем этого уравнения?
Сравните числа:
a) sin л + 1 и cos л + - ; б) tg л2 и ctg л2;
V л\ к)
в) tg 2 и ctg 2; г) sin 1 и cos 1.
Докажите:
a) sin а + cos а > 1, если 0 < а < ~;
б) cos (sin а) > 0, а е R.
Решите графически уравнение:
a) sin х = -х; б) tg х = V2 cosx, < х <
в) tg х = х, - ^ < х < ^; г) cos х = 1 - х2.
10. Степенная, показательная
и логарифмическая функции
Найдите область определения каждой из функций (112—114).
а) у = л/16х- Xs ; б) у = -1 = ;
\х3 + 8
в) у = «/б-х-^; г) у = 1 .
V х yjx 2 + х-20
а) 1/ = Л/х2 -Зх-Зх+1; б) y = M2sinx - 1;
в) у = log3(4- Зх + х2); г) i/ = log2sinx.
Л х2 -5х+6 г---------
а) у = ------„ I б) у= x/log5cosx;
lg(x+10)2 v
In (3 X - 2) 4 Г. 2 ~ Г
в) У = —..--- ; Г) у = ^/lg(3x2-2x).
х - х - 2
Найдите область значений каждой из функций (115, 116).
а) у = 2 л/х + 1; б) У = 52'1 - 1
в) у = 2 1g х + 1; г) У = Зх 2.
а) у = 2COS х; б) у = 2 — у[х'.
в) У = 1 + |log2 х|; г) У = 1 + I Vx|
293 Задачи на повторение
117. Найдите промежутки знакопостоянства каждой из функций (117, 118).
а) у = (г) -4; В) У = 2 - 3х; б) у = log4 (х + 3);
г) у = Vx - 4.
118. а) у = 4х + 2 - 4х; в) у = Vx + 3; б) г) у = 1g (х - 2) - 1; о зг~ у = 2-Vx.
Найдите среди данных функций четные и нечетные (119,
120).
119. а) у = 5х + 5 х; б) у = lg (1 - х2);
. ( 1 1 . з/—
в) у= I - I ; г) у = х Vx.
2
120. а) у = х3 ; б) у = 3х - 3 х; в) у = 2COS х; г) у = у[х* + 1.
121. Исследуйте функцию и постройте ее график:
а) у — 2л/х — 1; б) «/ = 4х-1-2;
в) у = | log2(х + 1); г) у = Vx-2 + 1.
Постройте графики функций (122, 123).
122. а) у=у)х — 2+1; б) 1; \ о /
в) у — 2 — Vx + 1; г) у = 1 + log2 (х + 2).
123. a) y = 5log5(x-1>; б) t/ = |log, х| - 1;
в) у — 2|х|; г) у = log2 х2.
124. Найдите наибольшее и наименьшее значения функции (если
они существуют):
а) у = V36 - х2 ; б) У = 1 при 0 < х С 7, х+1 х3 + 1 при - 2 < х < 0;
в) у = 3sin х; г) У — (х-1)2 при - 1 < х < 1, log2 х при 1 < х < 8.
125. Решите графически уравнение:
a) log. х = х - 3; б) Vx - 2 = -;
2 х
в) log2x = 25 x; г) 2|х1 = 11 — |х|.
294 Зачачи на повторение
126. Решите графически неравенство:
a) log. х> х-3; 6) Jx-2 < —;
2 Х
в) 2_1*1 > х2 + 1; г) log1 х > 2х-7.
з
127. Докажите, что равны наибольшие значения функций
у = (log2 3)8in х и у = (log3 2)cos х.
128. Найдите значение аргумента х0, если:
a) f (х) = 1,_. - Vl-x2 , f (х0) = 0;
л/4х+1
б) f (х) = 1g (х + 15) + 1g х, f (х0) = 2.
129. Докажите, что:
11Г+1
а) функция f (х) = — убывает на множестве R;
б) функция f (х) = log2 Зх возрастает на промежутке (0; оо).
§4.
Уравнения, неравенства,
системы уравнений и неравенств
11. Рациональные уравнения и неравенства
Решите уравнения (130, 131).
130. а) 3 (х - 2) - 5 = 4 - (5х - 1); б) |2х - 3| = 5;
в) 7 - 2 (3 - х) = 4 (х - 1) + 5; г) |4 - Зх| = 2.
131. а) 3^С±1 = 2-^Х— \ б) —+5 =4;
5 15 2
х-3 3(5 —2х) х+2
в) 1-----= х----------; г) 1--------=5.
’ 2 7 ’ 3
132. При каких значениях а данное уравнение:
а) ах - 2х = 3 (х - 1); б) а (1 - х) + 2 = Зх - ах;
в) х (2 - а) - х = 5 + х; г) 5 + 3 (х + За) = 9а + 5 —
имеет единственное решение; не имеет решений; имеет бес-
конечное множество решений?
Решите неравенства (133—135).
.„„ , х-1 . _ „ 5х-2 3-х
133. а) - — + х < 1,5х + 3,5; б) — -------— > 1;
Z О Ci
в) х - 4 (3 - х) > 2х + 7; г) 3+ 2 < 2х.
4
295 Задачи на повторение
134. a) |4x - 3| < 5; 6) |2x + 5| > 1;
в) !±ZL!< 2; r) 4 |2 - x| < 12.
3
135. a) |2x '3|>0; 6) ^-2 < 0;
x |x+4l
в) (x — 4) 15 — 3x| <0; r) |2x + 7| (3 - x) < 0.
136. Решите уравнение:
a) x2 + 2x - 15 = 0; 6) 7x2 + 5x = 0;
в) (x - 3) (x - 2) = 6 (x - 3); r) x2-1^+^=0.
o Z
137. При каком значении а имеют общий корень уравнения:
а) х2 - ах = 0 и х2 - х - За = 0;
б) х2 - (а - 1) х = 3 и 4х2 - (4а + 3) х + 9 = 0;
в) х2 + ах + 8 = 0 и х2 + х + а = 0;
г) 2х2 + (За - 1) х = 3 и 6х2 - (2а - 3) х = 1?
138. Найдите значения k, при которых имеет один корень урав-
нение:
a) (k - 1) х2 + (А + 4) х + k + 7 = 0;
б) 9х2 - 2х + k = 6 - Ах;
в) (2А - 5) х2 - 2 (А - 1) х + 3 = 0;
г) ЗАх2 - 6х + А - 2 = 0.
139. Не решая уравнения Зх2 - 5х - 2 = 0, найдите:
а) сумму его корней; б) произведение его корней;
в) сумму квадратов его корней; г) сумму кубов его корней.
Решите уравнения (140, 141).
„ . 6х-х2 -6
140. а) —
х-1
2х-3
х-1
в) 2- + Д- = -15_;
х2 + 5х 2х-10 х2-25
б) 2jCt1+_^ = 5;
х 2х+1
г) Л + 3 = 5
х2-4 (2-х)2 (х+2)2
б) 2х4-5х2 + 2 = 0;
г)
= 2,5.
Решите неравенства (142—144).
142. а) 2х2 + 6х + 17 > 0; б) х2 - 3,2х < 0;
в) (Зх - 2)2 - 4х (2х - 3) > 0;
г) (6х - 1) (1 + 6х) + 14 < 7х (2 + 5х).
296 Затачи на повторение
143. а) (x 1)(x -2^>0;6) < 0;
x-3 x2-2x+8
. x—2 _ „ x2+5x4-4
в) ----------< 0; r)-------------> 0.
(x-3)(x-5) хг — 5x-6
144. a) (x - 1) (x + 2) (x - 3) (x - 4) < 0; 6) x4 - 3x2 + 2 < 0;
v 4-x 1 , . 19 7
в) ---r) 1 + - < - .
x-5 1-x x2 x
145. Докажите справедливость неравенства:
a) m + — > 4 при m > 0; 6) 2m < 1;
m 1+m2
в) -fl + Ъ 2 при a > 0, b > 0;
b a
г) a < a+ C при a > 0, b > 0, c > 0, a < b.
b b+c
12. Иррациональные уравнения и неравенства
Решите уравнения (146—
146. а) ^х2+ 2х + 10 = 2х-1;
в) У17 + 2х-3х2 = х + 1;
147. а) Ух+17 - Ух-7 = 4;
в) Ух + 7 + Ух-2 = 9;
148. а) Vx-,4 + У2 + х = 0;
у]2+ х
х—Jx+5 J
в) ---=.- = ;
х+ у]х+ 5 7
149. а) У225 + х2 = х2 - 47;
в) yjx2 + 36 = х2 - 54;
г) Ух3-
б) 7*2-16 = х2 —22;
г) у]х2 + 9 = х2 —11.
б) 12 Ух—1 —Ух —1 =3;
г) 2 ylx+ 1 - у/х+ 1 = 6.
б) Ух + Ух—2=0;
г) У3х+ 1 - УЗх+1 = 0.
б) Ух-2 = х-2;
+ 16х — 5 = х — 2.
Решите неравенства (150, 151).
150. а) Ух2 - 5 > 2; б) У(х-2)(1-2х) > -1;
в) Ух2-16 > 1; г) (Ух - 3)(х2 + 1) > О.
151. а) Ух2 -6х + 9 > 3; б) 2х+^ ; д.
2х2 4- х-ь 1
в) У25 - 20х + 4х2 <1; г) У2х — х2 +15 (Зх - х2 — 4) < 0.
297
Задачи на повторение
13. Тригонометрические уравнения
и неравенства
Решите уравнения (152—158).
152. a) cos х+2 cos 2х =1; б) 4 sin 2х - 3 sin ^2х - ) = 5;
в) 2 cos2 х + 4 cos х = 3 sin2 х;
г) cos2 х + 4 sin2 х = 2 sin 2x.
153. a) sin3 x - cos3 x = 1 + -x;
6) cos — + x + cos — - x = 1;
Ц J l4 )
в) cos4 x - sin4 x =
r) sin — + x - sin — - x = 1.
U ) k6 )
154. a) cos 4x + 2 cos2 x = 1; 6) 4 (1 + cos x) = 3 sin2 cos|p
в) cos 3x + sin x sin 2x = 0; r) 4 (1 - cos x) = 3 sin^ cos2
155. a) cos 2x - cos 6x = 0;
в) sin x + sin 3x = 0;
156. a) ---= 3 - ctg x;
' ctgx+2
в) ——— = 11-2 sin x;
sin x +1
157. a) tg 3x - tg x = 0;
в) sin x tg x = cos x + tg
x 1+2x 2л
158. a) arccos-----= —;
6) sin x + sin 2x + sin 3x = 0;
r) cos — + 5x + sin x = 2 cos 3x.
\2 )
6) 1 + 2 cos 3x cos x - cos 2x = 0;
r) ctg x + “11^ = 2.
1 + COS X
6) tg x - sin x = 2 sin2 *;
; r) sin x + sin 2x = tg x.
6) arctg (2x -1) = - -;
4
x+ 2 n
в) arcsin------= - - ;
’ 4 3
r) arctg (2 - 3x) = 3 -
4
Решите неравенства (159—162).
159. a) sin - x] С 6) tg - xl > - 1;
\ 2 / \ 4 7
в) sin2x sin --cos2x cos—>
7 2 2 2
л/з
г) sin Зх cos x + sin x cos 3x < —.
298 За чачи на повторение
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
a) 2 sin2 x < 1;
в) 4 cos2 x < 3;
a) cos x - 1 < 0,5;
в) sin2x + 1 < ,
2 2
a) sin x - 7з cos x;
в) sin x + cos x < 1;
6) 3 tg2 2x < 1;
r) tg2 J -1 > 0.
6) sin x < cos x;
r) tg x + ctg x > 0
6) log0,5 sin x > 1;
r) log cosx > -1.
14. Показательные уравнения и неравенства
Решите уравнения (163—167)
а) 0,2х2-16х 37-5 = 5л/5; б) 2х2"3 • 5х2 3 =0,01 (10х-1)3;
в) 2х2-6х+0-5 = - 1—; г) 6± _ = 3 15 .
16 V2 215 612 12х
а) 53х - 2 53х - 1 - 3 53х - 2 = 60;
б) 4х - 3х °-5 = 3х + °-5 - 22х 4;
в) 25х “ 1 + 25х “ 2 + 25х 3 = 896;
г) 52х 1 + 22х = 52х - 22х + 2.
а) 9х2-1-36- 3х2 3+3 = 0;
в) 16х - 50 22х = 896;
а) 3 4х + 2 9х = 5 6х;
в) 2 • 25х - 5 10х + 2 4х = 0;
г) 3 16х + 2 81х = 5 36х.
а) 32'/х+32'х1-32'Гх 2 =11;
в) 2ai"2x + 2CO92x = 3;
Решите неравенства (168—170).
б) 53х + 1 + 34 52х = 7 • 5х;
Г) 74Л_8. 7'^ + 7 = 0.
б) 8х + 18х = 2 • 27х;
б) 5sin2x-25cosx = 0;
1‘ I
г) 3-9Х +6Х =2 -4х.
< 101в9;
11 > 51овб4
а) 0,04х - 26 0,2х + 25 < 0; б) 9х - 84 3 2х + | > 0;
О
/ \ 2Х + 1
в) 4х-10 2х + 16 < 0; г) 22х+1 + Н1 - | > 0.
х2 + 2х-15
а) х2 3х - 3х 41 < 0; 6)3,7 х"4 >1;
в) х2 • 5х - 52 + х < 0; г) 2х + 2 - 2х + 3 - 2х + 4 > 5х + 1 - 5х + 2.
Задачи на повторение
15. Логарифмические уравнения и неравенства
Решите уравнения (171—175).
171. a) logg х = 4 - 3 log3 х; б) | lg (2х -1) = 1 - lg Vx - 9;
в) log3 Vx-5 + log3 V2x-3 = 1;
г) 3 lg2 (x - 1) - 10 lg (x - 1) + 3 = 0.
172. a) 2 log5 0& = loS5 (10 - 9 lg x);
6) lg (3х + x - 17) = x lg 30 - x;
в) 2 lg (lg x) = lg (3 - 2 lg x);
r) x - x lg 5 = lg (2х + x - 3).
173. a) log2 x + - = 5; 6) log3 x + log,* x - logj x = 6;
log x 2 3
в) 2 log ,3 x + log* | = r) log x + 4 log*2 x + log8 x = 16.
174. a) xlog2X-2=8; 6) xlog6X= 125x2;
в) x'*x = 10 000; r) xlog3*-3 =
175. a) 3 log2 sin x + log2 (1 - cos 2x) = 2;
6) log0 j sin 2x + lg cos x = lg 7;
в) log, 5^x+2 =(x —4) log7 5;
r) lg (3 • 5х + 24 20х) = x + lg 18.
Решите неравенства (176—179).
176. a) log2 (x2 - x - 4) < 3; 6) logv3 _J5-2x) > 2;
в) lg (x2 - x + 8) > 1; r) log<7 t(3 —2x) < 2.
177. a) 2 log2 x < 2 + log2 (x + 3);
6) log, (10 - x) + log j (x - 3) > - 1;
6 6
в) logj (x — 2) + log j (12 — x) > -2;
3 3
r) log0 s (4 - x) > log0 s 2 - log0 5 (* - !)•
178. a) lg (x2 + x - 6) - lg (x + 3) < lg 3; 6) log3 < 1;
в) In (x2 + 3x - 10) - In (x - 2) > In 4; r) log3 < 1.
179. a) log2 (4х - 5 2х + 8) > 2; 6) log^ 6 x + 6 > 5 log0 6 x;
в) lg2 x > lg x + 2; r) log j (6X + 1 -36х) > -2.
Задачи на повторение
16. Системы рациональных уравнений
и неравенств
Решите системы уравнений (180 —183).
180. а) 2х + Зу = -1, 5х + 4у = 1; б) [Зх - 9у = 12, 4х - 12j/ = 16;
в) х + 2у = 7, pl • 5х — 8у = 0,
13 J 2х — 3у = 5; х- 1,6у = 1.
£+х = 13
181. а) х у 6 ’ х + у = 5; б) х — у = 1, х3-у3 = 7;
в) | = 2, (х - I)2 + у2 = 1; г) х3 +j/3=35, х + у = 5.
182. а) (х- у)(х2- у х + у = 5; 2) = 45, б) х2у3 + х3у2 = 12, х2 у3 - х3 у2 = 4;
в) х2 у3= 16, х3 у2 = 2; г) х2 - ху= 28, i/2-xi/=—12.
183. а) • Q0 II 1 « II + Si ГО го Н Н б) • х2 + у4 = 5, ху2 = 2;
в) - х3 + у3 = 9, ху= 2; г) • СО 1-4 II ю II ^1 + + -ч1N X Я
184. При каком значении а система уравнений:
а) (х — 5у = 7, [ах- у = —3; б) X |x + 2f/ = а, [2х + 4у = 5;
в) 1х + ау = 2, |3х — 2 у = -6; г) \х-у = 2, \2х — 2у = 2а —
имеет единственное решение; не имеет решений; имеет бес-
конечное множество решений?
185. Решите систему неравенств:
а)
б)
х + 1 х + 4 . х-1
Х~ 2 ~ 3 " 4
1,5х - 2,5 < х;
Задачи на повторение
в)
х+ i _ X > х-1
2 3 4
0,5х < 2 - х;
|2 (Зх —1) <3(4х + 1) + 16,
[4(2 + х) < Зх + 8.
17. Системы иррациональных уравнений
Решите системы уравнений (186—188).
186. а) • Т* - у[у = 4» 2 Jx + 3 Ту = 18; б) Vx + Ту = 8, Jx Ту = 15;
в) 3jx- Jy = 8, у[х +2 у[у = 19; г) Т^у = 12, Тх + Ту = 7.
187. а) х Ту + у Vx = зо, у[х + Ту = 5; б) x + y-Jxy = 7, ху = 9;
в) Тх + Ту = 6, х-у = 12; г) ху = 64, х-у+ -Jxy - 20.
188. а) Тх + Ту = 26, Тх + Ту = 6; б) X 1 с R] " 1 II W 1 со
в) кО ДТ II II [Э> 1 1 L*. LS, г) • Зу[х +Зу[у = -3, ху = 8.
18. Системы тригонометрических уравнений
Решите системы уравнений (189, 190).
189. а) sinx cos у = 0,25, sin у cosx = 0,75; 6) х-у=- 1, * 3’ cos2 (лх) - cos2 (пу) = 0;
в) 4 sin х sin у = 3. tgx tgy = 3; г) ' sin2 х = cos х cos у, cos2 х = sin x sin у.
190. а) • tgx+tgi/ = 2, cos x cos у = -; y 2 б) x + y=^, y 2 sinx + cos2i/ = -1;
в) sin x sin у = , ctg x ctg у = 3; г) cos 2y + cosx = 1, x + y= £. y 2
302 Задачи на повторение
191.
192.
193.
194.
195.
196.
19. Системы показательных
и логарифмических уравнений
Решите системы уравнений (191—196).
а) 9Х+»= 729, 3Х »-1 = 1; б) 2х —2У = 16, х+г/ = 9;
в) (75)*-» = 25, 26»-*-1 = 1; г) 3х + 3" = 28, х-у = 8.
а) 4'084 2* 52*-»+ 5* =5,2; б) 2Х + 3» = 17, 2*+2-3»+1= 5;
в) giog3<» + *) = 2 22x+v = 16; г) logVg(i/-x) = 4, Зх + 2-3»-2=171.
а) 3х • 1» = 63, 3х+7» = 16; б) 3х _22» = 77, ТзГ-2«'= 7;
в) го с© <© II II »» Sh 1 н к г) 1* W | 'с 1 II «
(igx-lgy = 1,
jig2 х + 1g2 у = 5;
6)
log2(x2 + y2) = 5,
2 log4 x + log2 у = 4;
в)
Igx-lgy = 7,
<
lgx + lgz/= 5;
г)
log2(x+l) = log2 y + 4 ,
\ 4 7
log2 x —2 log2(y-|) = 0.
l#-log3x = 1,
|х» = З12;
log5 х + 310ВзВ=7,
x»=512;
log4 x - log2 у = 0,
x2 — 2y2=8;
(logo x - 1°£з У '= °’
|xz — 5y2 + 4 = 0;
6)
3 1+ log3 (x2+ у z) _
log3 (x2 - y2) - log3 (x - y) = 0;
r) •
6)
gl + log5(x2-»2) _ 2g
log5 (x2 - y2) = log5 (X + J/).
32^-^=81,
Igjxy = l + lg3;
2 log2x-3»= 15,
Зу log2 x = 2 log2 x + Зр+].
Задачи на повторение
20. Задачи на составление уравнений
и систем уравнений
197. Время, затрачиваемое автобусом на прохождение расстояния
325 км, при составлении нового расписания движения авто-
бусов сокращено на 40 мин. Найдите среднюю скорость дви-
жения автобуса по новому расписанию, если она на 10 км/ч
больше средней скорости, предусмотренной старым расписа-
нием.
198.
Моторная лодка, скорость которой в стоячей воде равна
1
15 км, прошла 139
3
км вниз по течению реки и вернулась
обратно. Найдите скорость течения реки, если на весь путь
затрачено 20 ч.
199. Поезд должен был пройти 220 км за определенное время. Че-
рез 2 ч после начала движения он был задержан на 10 мин
и, чтобы прийти вовремя в пункт назначения, увеличил ско-
рость на 5 км/ч. Найдите первоначальную скорость поезда.
200. После встречи двух теплоходов один из них пошел на юг,
а другой — на запад. Через 2 ч после встречи расстояние
между ними было 60 км. Найдите скорость каждого теплохо-
да, если известно, что скорость одного из них на 6 км/ч боль-
ше скорости другого.
201. Два тела движутся навстречу друг другу из двух точек, рас-
стояние между которыми 390 м. Одно тело прошло в первую
секунду 6 м, а в каждую следующую проходило на 6 м боль-
ше, чем в предыдущую. Второе тело двигалось равномерно со
скоростью 12 м/с и начало движение спустя 5 с после перво-
го. Через сколько секунд после того, как начало двигаться
первое тело, они встретятся?
202. На строительстве железнодорожной магистрали бригада
строителей за несколько дней должна была по плану переме-
стить 2160 м3 грунта. В течение первых трех дней бригада
ежедневно выполняла установленную норму, а затем каждый
день перевыполняла норму на 80 м3, поэтому уже за день до
срока бригада переместила 2320 м3 грунта. Какова по плану
дневная норма бригады?
203. Две бригады, работая совместно, закончили посадку деревьев
на учебно-опытном участке за 4 дня. Сколько дней потре-
бовалось бы на выполнение этой работы каждой бригаде
отдельно, если одна из бригад могла бы закончить посадку
деревьев на 6 дней раньше другой?
204. Для перевозки 60 т груза затребовали некоторое количество
машин. В связи с тем что на каждую машину погрузили на
0,5 т меньше запланированного, дополнительно было затре-
бовано еще 4 машины. Сколько машин было запланировано
первоначально?
Задачи на повторение
205. Два куска латуни имеют массу 30 кг. Первый кусок содер-
жит 5 кг чистой меди, а второй кусок — 4 кг. Сколько про-
центов меди содержит первый кусок латуни, если второй со-
держит меди на 15% больше первого?
206. К раствору, содержащему 40 г соли, добавили 200 г воды,
после чего массовая доля растворенной соли уменьшилась на
10%. Сколько воды содержал раствор и какова была в нем
массовая доля соли?
207. Две автомашины выехали одновременно из одного пункта
в одном и том же направлении. Одна машина движется со
скоростью 50 км/ч, другая — 40 км/ч. Спустя полчаса из
того же пункта в том же направлении выехала третья маши-
на, которая обогнала первую машину на 1 ч 30 мин позже,
чем вторую. Найдите скорость третьей машины.
208. Найдите скорость и длину поезда, зная, что он проходил
с постоянной скоростью мимо неподвижного наблюдателя
в течение 7 с и затратил 25 с на то, чтобы проехать с той же
скоростью вдоль платформы длиной 378 м.
209. Из пунктов А и В, расположенных на расстоянии 50 км, од-
новременно навстречу друг другу вышли два пешехода. Че-
рез 5 ч они встретились. После встречи пешеход, идущий из
А в В, уменьшил скорость на 1 км/ч, а второй увеличил ско-
рость на 1 км/ч. Первый пешеход прибыл в В на 2 ч раньше,
чем второй в А. Найдите первоначальную скорость каждого
пешехода.
210. На заводе для изготовления одного электродвигателя типа А
расходуется 2 кг меди и 1 кг свинца, на изготовление одного
электродвигателя типа В — 3 кг меди и 2 кг свинца. Сколь-
ко электродвигателей каждого типа было изготовлено, если
всего израсходовали 130 кг меди и 80 кг свинца?
211. Двое рабочих совместно могут выполнить плановое задание
за 12 дней. Если половину задания будет выполнять один ра-
бочий, а затем вторую половину — другой, то все задание бу-
дет выполнено за 25 дней. За сколько дней может выполнить
задание каждый рабочий?
212. Из двух жидкостей, плотность которых соответственно
1,2 г/см3 и 1,6 г/см3, составлена смесь массой 60 г. Сколько
граммов каждой жидкости в смеси и какова плотность сме-
си, если ее 8 см3 имеют такую же массу, как масса всей ме-
нее тяжелой из смешанных жидкостей?
213. Вычислите массу и массовую долю (в процентах) серебра
в сплаве с медью, зная, что, сплавив его с 3 кг чистого сереб-
ра, получат сплав, содержащий 90% серебра, а сплавив его
с 2 кг сплава, содержащего 90% серебра, получат сплав
с 84%-ной массовой долей серебра.
Задачи на повторение
214. По окружности, длина которой 60 м, равномерно и в одном
направлении движутся две точки. Одна делает полный обо-
рот на 5 с скорее другой и при этом догоняет вторую точку
каждую минуту. Найдите скорость каждой точки.
215. Сумма квадратов цифр положительного двузначного числа
равна 13. Если из этого числа вычесть 9, то получится чис-
ло, записанное теми же цифрами в обратном порядке. Най-
дите это число.
216. Найдите все пары натуральных чисел, разность квадратов
которых равна 55.
§5.
Производная, первообразная,
интеграл и их применения
21. Производная
217. Найдите отношение - для функции У, если:
Дх
a) f (х) = ^х2, х0 = 1, Дх = 0,1;
б) f (х) = у/х- 1, х0 = 2, Дх = 0,21;
в) f (х) = 3 - 2х, х0 = 2, Дх = 0,2.
218. Пользуясь определением, найдите производную функции f
в точке х0, если:
a) f (х) = 1 - 4х, х0 = 3; б) У(х) = 1,5х2, х0 = 2;
в) f (х) = Зх + 2, х0 = 5; г) У(х) = х3 + 1, х0 = -1.
Найдите производные функций (219—222).
219. а) У (х) = Х х4-1 х3+1 х2
7 4 3 2
в) f (х) = (х2 + 5) (х3 - 2х
220. a) /(x) = 4-V^ + 5|_;
Х
X fl \ х3-Зх
в) /W = 1-2* ’
221. a) f (х) = 2х + 1g х;
в) f (х) = х2 52х;
х + 5; б) У (х) = (4 - х2) sin х;
2); г) У (х) = С°Ц .
2-х3
б) У (х) = (2 - Vx) tgx;
г) У (х) = 1 sQinx .
1-2 cos х
б) У (х) = е Зх + 2 log3 2х;
г) У(х)= .
ех + е х
Задачи на повторение
222. a) f (x) = sin 3x + cos 5x;
6) f (x) = V1 + x2 + 1 ;
(2x-l)3
B) f (x) = (3 - 2x3)5;
r) f (x) = 1g (3x) - 3 tg[2x-H
V 4 7
223. Решите уравнение f'(x) = O, если:
a) f (x) = x4 - 2xz + 1;
6) /(x) = 1,5 sin 2x 5 sin x - x;
B) /(x) = -^+1^3 -9x;
r) f (x) = x + cos 2x.
224. Функция задана графиком (рис. 153).
1) Укажите, в каких из отмеченных точек:
a) f'(x) > 0; б) Г(х) < 0; в) f (х) = 0.
2) Укажите промежутки, на которых:
a) f (х) > 0; б) Г(х) < 0; в) f (х) = 0.
3) В каких точках интервала (а; Ь) функция f не имеет про-
изводной?
Рис. 153
307 Задачи на повторение
Сравните значения производной в заданных точках (225, 226).
225. a) х, и х2; б) х, и х3; в) х2 и х4; г) х3 и х5 (рис. 154).
226. a) Xj и х2; б) х3 и х5; в) х4 и х5; г) х2 и х4 (рис. 155).
227. Функции и, v, w дифференцируемы в точке х. Докажите,
что (uviv)' = u'vw + uv'w + uvw'.
22. Применение производной
к исследованию функций
228. Вычислите приближенное значение функции в точках х4
и х2:
a) f (х) = * х3 - х, х4 = 2,0057, х2 = 1,979;
б) f (х) = 2 + 4х - х2 + | х4, Xj = 3,005, х2 = 1,98.
229. Вычислите приближенное значение выражения:
а) 79,009; б) 1,000115; в) 0,999 5; г) ^8,008.
Найдите промежутки возрастания и убывания, точки макси-
мума и минимума функций (230, 231).
230. а) в) f (х) = - * х3 + 4х2 - 7х +18; х(х3-4) f(x) ~ 2 ; б) f (X) = 3-х г) Их) = 4^.
231. а) f (х) = cos 2х - 2 cos х; б) f (x) = 2-sin |;
в) f (х) = 2 sin х + cos 2х; г) f (х) = Зх - cos Зх.
232. Исследуйте функцию и постройте а) /(х) = х2 (х - 2)2; б) ее график (232—234). /(Х)= х + 2;
в) f(x) = х3 - Зх2 - 9х; г) f(x) = -x . 4-Х2
308 Задачи на повторение
233. а) f (х) =1-2 sin 2х; б) f (х) = cos2 х - cos х;
в) f (х) = З-cos г) f (х) = sin2 х - sin x.
234. а) f (х) = Vx 1пх; б) Hx)= eX ; X
в) /(х) = 2^ 4- г) f (x) = x In X.
235. Найдите наибольшее и наименьшее значения функции f
(если они существуют) на данном промежутке:
a) f (х) = 18х2 + 8х3 - Зх4, [1; 3];
б) f (х) = 2 cos х - cos 2х, [0; л];
в) Г(х)=2+х2, [1; 11;
х L 2 J
г) f (х) = sin х - х, [-л; л].
236. Число 10 представьте в виде суммы двух неотрицательных
слагаемых так, чтобы сумма кубов этих чисел была:
а) наибольшей; б) наименьшей.
237. Сумма длин катетов прямоугольного треугольника равна
20 см. Какой длины должны быть катеты, чтобы площадь
треугольника была наибольшей?
238. Сумма длин диагоналей параллелограмма равна 12 см. Най-
дите наименьшее значение суммы квадратов всех его сторон.
239. По двум улицам движутся к перекрестку две машины с по-
стоянными скоростями 40 км/ч и 50 км/ч. Считая, что ули-
цы прямолинейные и пересекаются под прямым углом,
а также зная, что в некоторый момент времени автомашины
находятся от перекрестка на расстоянии 2 км и 3 км (соот-
ветственно), определите, через какое время расстояние меж-
ду ними станет наименьшим.
240. Картина высотой 1,4 м повешена на стену так, что ее ниж-
ний край на 1,8 м выше глаз наблюдателя. На каком рассто-
янии от стены должен встать наблюдатель, чтобы его поло-
жение было наиболее благоприятно для осмотра картины
(т. е. чтобы угол зрения по вертикали был наибольшим)?
241. Статуя высотой 4 м стоит на колонне, высота которой 5,6 м.
На каком расстоянии должен встать человек ростом (до уров-
ня глаз) 1,6 м, чтобы видеть статую под наибольшим углом?
242. Из всех цилиндров, имеющих объем 16л м3, найдите ци-
линдр с наименьшей площадью полной поверхности.
243. Найдите высоту цилиндра наибольшего объема, который
можно вписать в шар радиусом R.
244. В конус, радиус основания которого R и высота Н, требуется
вписать цилиндр, имеющий наибольшую площадь полной
поверхности. Найдите радиус цилиндра.
Задачи на повторение
245. Около данного цилиндра нужно описать конус наименьшего
объема (плоскости оснований цилиндра и конуса совпадают).
Как это сделать?
246. Найдите высоту конуса наименьшего объема, описанного
около шара радиусом R.
247. Найдите высоту конуса наименьшего объема, описанного
около полушара радиусом R так, чтобы центр основания ко-
нуса лежал в центре шара.
248. Из круглого бревна диаметром 40 см требуется вырезать бал-
ку прямоугольного сечения с основанием b и высотой Л.
Прочность балки пропорциональна bh2. При каких значени-
ях b и h прочность будет наибольшей?
249. Окно имеет форму прямоугольника, завершенного полукру-
гом. Как определить размеры окна, имеющего наибольшую
площадь при заданном периметре?
250. На окружности дана точка А. Провести хорду ВС параллель-
но касательной в точке А так, чтобы площадь треугольника
АВС была наибольшей.
251. Каков должен быть угол при вершине равнобедренного тре-
угольника заданной площади, чтобы радиус вписанного в
этот треугольник круга был наибольшим?
252. На параболе у = х2 найдите точку, расстояние от которой до
точки А (2; 0,5) наименьшее.
253. Объем правильной треугольной призмы равен V. Какова дол-
жна быть сторона основания, чтобы площадь полной поверх-
ности призмы была наименьшей?
23. Применение производной в физике
и геометрии
254. По прямой движутся две точки. Определите промежуток вре-
мени, в течение которого скорость первой точки была мень-
ше скорости второй, если:
a) Xj (1) = 2 | t3, х2 (1) = 2t - 3;
б) Xj (t) = 9£2 + 1, х2 (£) = t3.
255. Угол поворота тела вокруг оси изменяется в зависимости
от времени по закону ф (Z) = 0,lt2 - 0,5t + 0,2. Найдите угло-
вую скорость вращения тела в момент времени t = 20 с.
(Угол измеряется в радианах.)
256. Круглый металлический диск расширяется при нагревании
так, что его радиус равномерно увеличивается на 0,01 см/с.
310 За шчи на повторение
С какой скоростью увеличивается площадь диска в тот мо-
мент, когда его радиус равен 2 см?
257. Из пункта А по двум прямым, угол между которыми 60°,
одновременно начали двигаться два тела. Первое движется
равномерно со скоростью 5 км/ч, второе — по закону
s (t) = 2t2 - t. С какой скоростью они удаляются друг от друга
в момент t = 3 ч? (s измеряется в километрах, t — в часах.)
258. Концы отрезка АВ длиной 5 м скользят по координатным
осям. Скорость перемещения конца А равна 2 м/с. Какова
величина скорости перемещения конца В в тот момент, когда
конец А находится от начала координат на расстоянии 3 м?
259. Длина вертикально стоящей лестницы равна 5 м. Нижний
конец лестницы начинает скользить с постоянной скоростью
2 м/с. С какой скоростью опускается в момент времени t
верхний конец лестницы, с каким ускорением?
260. Неоднородный стержень АВ имеет длину 12 см. Масса его ча-
сти AM растет пропорционально квадрату расстояния точки
М от конца А и равна 10 г при AM = 2 см. Найдите: 1) массу
всего стержня АВ и линейную плотность в любой его точке;
2) линейную плотность стержня в точках А и В.
261. Колесо вращается так, что угол поворота пропорционален
квадрату времени. Первый оборот был сделан колесом за 8 с.
Найдите угловую скорость колеса через 48 с после начала
вращения.
262. Тело с высоты 10 м брошено вертикально вверх с начальной
скоростью 40 м/с. Ответьте на вопросы: а) На какой высоте
от поверхности земли оно будет через 5 с? б) Через сколько
секунд тело достигнет наивысшей точки и на каком расстоя-
нии от земли (считать g = 10 м/с2)?
263.
„2
В какой точке параболы у = — — - 1 касательная наклонена к
оси абсцисс под углом: а) 45°; б) 135°?
264. Найдите абсциссы точек графика функции f (х) = х3 + ~ х2 -
- х - 3, касательные в которых наклонены к оси абсцисс под
углом 135°.
265. Докажите, что любая касательная к графику функции
/ (х) = х3 + i х2 + х- 3 пересекает ось абсцисс.
266. Докажите, что любая касательная к графику функции
f (х) = х5 + 2х - 7 составляет с осью абсцисс острый угол.
267. Докажите, что графики функций f (х) = (х + 2)2 и
g (х) = 2 - х2 имеют общую точку и общую касательную, про-
ходящую через эту точку.
Задачи на повторение
24 Первообразная
268.
Найдите общий вид первообразных для функции:
a) f (х) = 4 sin х + cos Зх;
б) f (х) = х2 + х~® + х2^;
в) f(x) = 2 + —
х-1
г> L + -f—
cos2x sin Зх
269. Для функции f найдите первообразную, график которой про-
ходит через точку М:
a) f (х) = —, Af | ; 2 б) / (х) = х-2 + cos х, М f —; - —
х \е ) V2 л )
в) f (х) = х *, М (2; -3); г) f (х) = sin 2х, М (0; 1).
270. Найдите функцию, производная которой равна 2х - 3 в лю-
бой точке х и значение которой в точке 2 равно 2.
271. Найдите уравнение кривой, проходящей через точку А (2; 3),
если угловой коэффициент касательной в точке с абсциссой х
равен Зх2.
272. Материальная точка движется по координатной прямой со
скоростью v (t) = sin t cos t. Найдите уравнение движения
точки, если при t = п ее координата равна 3.
25. Интеграл
273. Вычислите:
Зя
a) J cos (1,5л + 0,5х) dx;
п
п
в) Jcos (Зх- sin2x) dx;
л
12
2
б) j (х~2 + х2) dx;
1
-2
г) | (5-6х- х2) dx.
-5
274. Найдите наибольшее и наименьшее значения интеграла:
а
a) J cos — dx, а е R;
о
б) J cos2xdx, а е R.
о
275. Вычислите площадь фигуры, ограниченной линиями:
а) у = 0,5х2 - 2х + 3, у = 7 - х;
б) у = (х - 2)2, у = 4 - х2;
в) у = х2 - Зх + 4, у = х + 1;
г) у = х2 - 2х + 2, у = 2 + 4х - х2.
Задачи на повторение
площадь каждой из фигур, на которые прямая
1 9
делит фигуру, ограниченную линиями у = - х
линиями у = 2,5 +
276. Найдите
У = х + 4
и у = 8.
277. Найдите
+ 2х - 0,5х2, х = -1 и касательной к данной параболе, прове-
денной через ее точку с абсциссой х = 3.
278. Найдите площадь фигуры, ограниченной параболой
у = х2 - 4х + 5 и касательными к ней, проведенными через ее
точки с абсциссами х = 1 и х = 3.
279. В каком отношении делится площадь квадрата параболой,
проходящей через две его соседние вершины и касающейся
одной стороны в ее середине?
280. При каком значении а площадь фигуры, ограниченной ли-
ниями у = х2 + 4х + а (а > 0), х = 0, х = 2 и у = 2, равна 12?
(Известно, что фигура лежит в верхней полуплоскости.)
281. Найдите пары чисел а и Ь, при которых функция f (х) =
2
= a sin пх + b удовлетворяет условиям: f (2) = 2, J f (х) dx = 4.
о
VI
глава
Задачи повышенной
трудности
§1.
Числа и преобразования выражений
1. Целые числа
1. Докажите, что: а) если р — простое число и р > 3, то р2 - 1
делится на 24; б) если а + b + с делится на 6, то а3 + Ь3 + с3
делится на 6 (а, Ь, с — целые числа); в) если а2 + Ь2 делит-
ся на 7, то а2 + Ь2 делится и на 49 (а и b — целые числа);
г) число п2 + 5п + 16 ни при каком целом и не делится
на 169.
2. При каких целых а оба корня уравнения х2 + ах2 + 6 = 0
являются целыми числами?
3. Докажите, что: а) наименьший (отличный от 1) делитель
составного числа N не превосходит yJV; б) число N имеет
нечетное число делителей тогда и только тогда, когда
N — точный квадрат.
4. Найдите число делителей числа п, если: а) п = 1024;
б) п = 210; в) п = р“' р22 Рк1' (ai> а2’ а* — натураль-
ные, р2, ••., рк — различные простые числа); г) п = 10!
(Л! — обозначение произведения 1 2 • 3 • ... • k).
5. а) Какие остатки могут давать точные квадраты при делении
на 3, на 4?
б) Может ли дискриминант квадратного уравнения с целы-
ми коэффициентами равняться 23?
в) Длины всех сторон прямоугольного треугольника — це-
лые. Могут ли длины катетов быть нечетными числами?
г) В десятичной записи 12-значного числа N цифры 2 и 9
встречаются по 2 раза, а остальные — по одному разу. Мо-
жет ли N быть точным квадратом?
6. а) В десятичной записи числа 300 единиц и несколько нулей
(а других цифр нет) Может ли это число быть точным квад-
ратом? б) 2008-значное число а делится на 9. Сумма цифр
а — число Ь, сумма цифр Ь — число с, сумма цифр с — чис-
ло d. Найдите d.
7. Докажите признаки делимости на: а) 5; б) 3; в) 9.
314 Задачи повышенной трудности
Решите в целых числах уравнения (8—9).
8. а) 3х = 1 + у2;
в) х2 - у2 = 91;
9. а) 13х - 7у = 6;
в) 27х - 9у = 15;
б) 2х - 1 = у2-,
г) 2х + 1 = у2.
б) х! + у'. = (х + у)!;
г) 1! + 2! + ... + х! = у2.
10. Докажите, что для любого натурального числа N существу-
ет ряд последовательных N чисел, каждое из которых со-
ставное.
11. Дано: 1g 16 = 1,20412... . Найдите количество цифр и первую
цифру числа 125100.
2. Метод математической индукции
Решение задач 12—15 основано на принципе математиче-
ской. индукции, который часто принимают за одну из аксиом ариф-
метики. Этот принцип формулируется так:
Если предложение, зависящее от натурального чис-
ла п:
а) верно для некоторого начального значения п = п0 и
б) из допущения, что оно верно для п = k, где
k п0 — произвольное натуральное число, вытекает,
что предложение верно и для п = k + 1, то предложе-
ние верно для любого натурального п > п0.
Докажите равенства методом математической индукции
(п е N) (12—13).
12. a) l2 + 22 + 32 + ... + n2 = ”(n + 1J.(—+-1};
б) I2 + З2 + 52 + ... + (2п - I)2 = _42,L-1)(2n + 1);
О
в) I3 + З3 + 53 + ... + (2n - I)3 = п2 (2п2 - 1);
г) 1 • 1! + 2 2! + 3 • 3! + ... + п • и! = (и + 1)! - 1.
13. a) -J- + - 1 + + ... +---л - ;
4 5 56 6-7 (п + 3)(п + 4) 4(п + 4)
б) 22 + 62 + ... Н4п - 2)2 =
О
в) JL + J^ + ^ + ... +---------I-----= 1-И-р
1-8 8 15 15 22 (7п-6)(7п + 1) 7п + 1
Г) 1 , 1 , 1 ! । 1 1 ___1
' 4-8 8-12 12-16 4п(4п+4) 16 16(п + 1)‘
315 Задачи повышенной трудности
14. Докажите методом математической индукции неравенство
(п е /V):
a) |sin nx| < п |sin х|; б) -+ + + ...+ 1 > 1;
71+1 72 + ^ <571+1
в) (1 + /г)" > 1 + nh для любого натурального
и Л * 0 {неравенство Бернулли)-,
г) (1 + Л)" > 1 + nh + — Л2 для любого
п > 2, Л > -1
натурального
п > 3 и h > 0.
15. Докажите методом математической индукции, что для лю-
бого натурального п:
а) 62л 1 + 1 кратно 7; б) З3л + 2 + 24л+1 кратно 11;
в) 4” + 15п - 1 кратно 9; г) 72л 1 кратно 48.
3. Действительные числа
16. Докажите, что любое рациональное число может быть пред-
ставлено в виде бесконечной периодической десятичной
дроби.
17. Докажите, что любая бесконечная периодическая десятичная
дробь есть запись некоторого рационального числа.
18. Докажите, что если натуральное число а не является полным
квадратом, то 4а — иррациональное число.
19. Может ли быть рациональным числом:
а) сумма двух иррациональных чисел;
б) иррациональное число в иррациональной степени?
Докажите иррациональность чисел (20—22).
20. a) J3; б) л/3; в) 1g 5; г) log2 9.
21. a) V3 + V5; б) 42+44, в) 1 г) 42 + 34з.
V2 + V3
22. a) k 42 + р 43, где k и р — целые числа, отличные от нуля;
б) 3,272772777277772... (после первой двойки стоит одна се-
мерка, после второй — две, после третьей — три и т. д.,
после п-й двойки — п семерок и т. д.).
Упростите выражения (23—24).
23. a) VT-V3; б) д/129-5бТ5;
в) ^7 + 2x10; г) yl57+ 12415.
24. а) д/67- 42V2 + ^19-6^2; б) 751-4V77 -^47-4733.
316 Задачи повышенной трудности
25.
26.
27.
28.
Освободитесь от иррациональности в знаменателе:
а> б) в) —-1_.
Могут ли быть членами одной геометрической прогрессии
числа:
а) 10, 11, 12; б) 81, -36, 24?
Докажите, что число
f+ + рационально.
Докажите, что для любого числа М найдется такое натураль-
ное п, что сумма
1+1
2 3
п
будет больше М.
4. Преобразование выражений
29.
30.
31.
32.
33.
Разложите на множители:
а) х4 + 4; б) х4 + х2 + 1; в) xs + х + 1;
г) (х2 + у2)3 + (г2 - х2)3 - (у2 + z2)3;
д) (х + у + г)3 - х3 - у3 - z3; е) х3 + у3 + z3 - Зхуг.
Докажите тождество:
(а2 + Ь2) (х2 + у2) = (ах + by)2 + (ay - bx)2.
Докажите формулы:
Известно, что а + Р + у = л, причем а, р, у положительны.
Докажите тождество:
а)
sin а + sin Р + sin у = 4 cos — cos - cos -;
н ' 2 2 2
б) cos2 а + cos2 р + cos2 у = 1 - 2 cos a cos р cos у;
в) cos 2а + cos 2р + cos 2у = -1 - 4 cos а cos р cos у;
г) sin2 а + sin2 р + sin2 у = 2 + 2 cos а cos р cos у.
Докажите равенство:
a) arcsin х + arccos х = для любого х е [-1; 1];
б) arctg х + arcctg х =
1
317 Задачи повышенной трудности
в) cos (arctg x) = .
x 1 + X
/j __ x2
r) tg (arccos x) = ---- для любого x e [ 1; 1] и x * 0.
x
Вычислите (34—35).
34. a) — + 1 ;
cos 290' V3 sin 250 °
6) sin6 a + cos6 a, если sin a + cos a = m;
в) cos 84° cos 24 cos 48° cos 12°;
r) cos8 a - sin8 a, если cos 2a = m.
35. a) arcsin (sin 10); 6) arccos (cos 12);
в) arctg (tg 2); r) arcctg (ctg 3).
36. Проверьте, что число x0 является корнем уравнения
+ л >/3-1
-гт п sin ос sin В sin у
37. Известно, что а + В + у = л, = Докажите, что
а b с
а2 = Ь2 + с2 - 2bc cos а, причем а, р, у необязательно положи-
тельные числа.
38. Докажите, что sin 47° + sin 61° - sin 11° - sin 25° = cos 7°.
39. а) Найдите logXj/* и, если logx и = a, logy и = b, log* и = c.
б) Найдите log54 168, если log7 12 = a, log12 24 = b.
40. а) Докажите, что 2>1|г>К2Х = x'logj 2, если x > 1.
б) Вычислите без таблиц: 2'|оЙ23 ~3>1ояз^_
5. Прогрессии
41. Решите в целых числах уравнение
х-1,х-2,х-3, ,1 о
----1---I-----1- ... т-— О.
XXX X
42. Докажите справедливость равенства
- , .о > ч >2 COS ф
1 - tg ф + tg2 ф - tg3 ф + ... = ----
„ . I П )
2 sin — + ф
14 )
для любого ф 6 0; - .
V 4)
43. Сумма четырех чисел, составляющих геометрическую про-
грессию, равна - 40, а сумма их квадратов равна 3280. Най-
дите эти числа.
318 Зддачи повышенной трудности
44. Найдите трехзначное число, если его цифры образуют гео-
метрическую прогрессию, а цифры числа, меньшего данного
на 400, — арифметическую.
45. При каком значении а найдутся такие х, что числа
51 *х + 51 "х, “, 25х + 25 х (в указанном порядке) составля-
ют арифметическую прогрессию?
46. Числа х, у, z (в указанном порядке) образуют геометриче-
скую прогрессию, а числа х + у, у + г, г + х — арифметиче-
скую. Найдите знаменатель геометрической прогрессии.
47. Известно, что суммы первых тип членов арифметической
прогрессии равны, т. е. Sm = Sn. Найдите Sm + n.
48. Найдите произведение первых п членов геометрической про-
грессии, если известна их сумма А и сумма обратных к ним
величин В (В * 0).
49. Члены арифметической (ап) и геометрической (fen) прогрессий
удовлетворяют условиям а40 = Ь40 > 0, а60 = Ь60 > 0. Что боль-
ше: а50 или Ь50?
50. Найдите сумму:
а) 1 + 11 + ... + 111... 1; б) х + 2хг + Зх3 + ... + пхл;
п единиц
в) ----+-------------+ ... +--------------;
fe(ft + l) (k + 1)(/г + 2) (Л + п-1)(/г + тг)
г) sin х + sin 2х + ... + sin пх.
§2.
Элементарные функции
и их свойства
6. Исследование функций
51.
Найдите область определения функции:
arcsin 0,5х
в) "=^Г;
д) у = log2sinxcosx;
г) у = ^cos (sin х);
е) У = ~(---/ ) '
lg (l-^x2- 1J
319 Задачи повышенной трудности
52.
53.
54.
55.
56.
57.
58.
59.
Область определения функции у = f (х)— отпезок |-1; 2]
Найдите область определения функции:
а) у = f (х) + 1;
г) у = f (2х);
ж) у = |/(х)|;
к) y = f (1 - |х|);
б) у = f (х + 1);
Д) У = / Г-х);
з) У = f (|х|);
л) y = f(>Tx);
в) у = 2/ (х);
е) y=f (х);
и) </ = /(!- х);
м) у = f (х2).
Найдите область значений каждой из
функций (53—54).
а) у = cos2 х - cos х;
б) у = д/1 -sinxctgх;
в) у = 3 cos х - 4 sin х - 1; г) у =-------------------.
tg2 2 + 2
а) у = cos2 х + cos4 х;
в) у = 3 sin2 х - 4 sin х - 2;
б) у = [х]2;
Является ли четной (или нечетной) функция:
а) / (х) = е Х -1; б) f (x)=loga(x + ^x2 + l);
Xх + 1
»> f W - Г) f (X) - log. (
X cos х V х - 1J
а) Докажите, что для любой функции f с симметричной
относительно точки 0 областью определения функция
f(x)+f{-x) f(x)-f(-x)
у =-----------четная, а функция у =----------нечетная.
б) Докажите, что любая функция с симметричной относи-
тельно точки 0 областью определения представляется (при-
том единственным образом) в виде суммы четной и нечетной
функций.
в) Найдите все функции, являющиеся одновременно четны-
ми и нечетными.
Функции f и g периодические с общим периодом Т. Докажи-
те, что функции у = f (х) + g (х) и у = f (х) g (х) являются пе-
риодическими с периодом Т.
Докажите, что сумма двух непрерывных периодических
функций, определенных на всей числовой прямой и не имею-
щих общих периодов, не является периодической.
Существует ли периодическая функция, у которой: а) все ра-
циональные числа являются периодами, а все иррациональ-
ные нет; б) все иррациональные числа являются периодами,
а все рациональные нет?
320 Задачи повышенной трудности
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Докажите, что функция не является периодической:
a) f (х) = cos х cos (xV2); б) f (х) = cos х + cos (xV2);
в) f (x) = sin x2; r) f (x) = sin -Jx.
Найдите наименьший положительный период функции:
а) у = cos3 х; б) у = д/| sin 2х| ;
в) у =cos (xV2) + cos-^; г) у = {-1 - 2х}.
V2
Докажите, что функция не является периодической:
а) у = -/х; б) у = sin | х |;
в) у = х2 + х + 1; г) у = sin х + sin (xV2).
Сравните числа:
a) log2 3 и log5 8;
в) 23100 и З2*50;
б) logB 10 и 1g 11;
г) cosec - и 41 1 - sin -
2 I 2
Расположите в порядке возрастания числа:
a) sin 4°, cos 2, tg 3, ctg 6;
6) sin 10°, cos 275°, tg 190°, ctg 100°.
Известно, что функция у = f (х): 1) возрастает; 2) убывает
на промежутке I. Является ли функция у = kf (х) возрастаю-
щей (убывающей) на промежутке I, если известно, что:
a) k > 0; б) k < 0?
Пусть f — возрастающая и положительная на всей числовой
прямой функция. Докажите, что:
а)
б)
в)
функция
функция
функция
у = f2 (х) возрастает на R;
у = убывает на R;
У = yjf (х) возрастает на R;
г) функция у = lg f (х) возрастает на R.
При каких п функция f может иметь ровно п точек экстре-
мума, если известно, что f‘. а) четная; б) нечетная; в) пе-
риодическая функция?
Среди функций вида f (х) = ах + b найдите все такие, что для
любого х: a) f (f (х)) = f (х); б) f (f (х)) = х.
Найдите функции f2 (х) = f (f (х)), f3 (х) = f (f (f (x))) и т. д.,
fn (х) = f (f (f... (f(x))...)) и область определения fn (x), если:
a) f (x) = 3 - x; 6) f(x)=-1; в) / (x) = ’ .
x 1-x
_ . i ax+b
Среди функции вида: a) y = —-; б) у =---- — найдите
ax+b cx+ а
все, совпадающие с обратными к самим себе.
321 Задачи повышенной трудности
71.
72.
73.
Приведите пример обратимой функции, определенной на от-
резке [0; 1] и имеющей две точки экстремума.
Найдите функцию, обратную данной. Постройте графики
найденных функций (72—73).
а) у = Vx+ 1; б) у = lg (1 - х);
а) 1/ = sin х, х е
Л , 7Г
2’ 2
в) </ = tgx, х j
в>
г) y = figx.
б) у = cos х, х е [0; л];
г) у = ctg х, х е (0; л).
7. Графики функций
74. Докажите, что: а) график четной функции симметричен от-
носительно оси ординат; б) график нечетной функции сим-
метричен относительно начала координат.
75. Дополните (если это возможно) графики функций, изобра-
женных на рисунке 156, до графиков периодических функ-
ций с наименьшим положительным периодом Т, являющих-
ся при этом: а) четными; б) нечетными.
76. На рисунке 157 изображена часть графика периодической
функции, определенной на всей числовой прямой. Каким мо-
жет быть наименьший положительный период функции /?
Рис. 157
Задачи повышенной трудности
Рис. 158
Дан график функции у = f (х) (рис. 158). Постройте эскиз
графика функции (77—78).
77. а)у = /(-2х); б) у = f (|х|); в) у = f (1 - х); г) у = | f (х) |.
78. а) у =-2f (х); б) у = -
f(x)
В) у = f (2х + 4); г) у = -f (-1 х I).
79. Найдите последовательность преобразований, с помощью ко-
торых из графика функции f может быть получен график
функции <р:
в) f (х) = sin х, <р (х) = sin х + cos х;
б) f (х) = sin2 х, <р (х) = sin4 х + cos4 х.
80. Докажите, что график любой дробно-линейной функции
ах + Ь
у =---(с ф 0 и ad - Ьс * 0) может быть получен из графика
k
у = — параллельным переносом. Укажите коэффициент k.
81. Найдите наибольшее и наименьшее значения функции
(на R):
a) f (х) = 2 cos 2х + sin2 х; б) f (х) = 1 ----;
72х2-4х+ 3
в) f (х) = 2 sin2 х - cos 2х; г) f (х) = cos2 х + cos х + 3.
82. Найдите промежутки возрастания (убывания), максимумы
и минимумы функции:
__2
а) у = 2 sin х + 3 cos х; б) у =-----------;
х2 -1
в) у = cos 2х - 2 cos х; г) у = 1g sin х.
83. Найдите асимптоты графика функции:
X сч х2 + 1 х2 х2 + 4
а) У =---б) у =-----------; в) у= ; г) у = —-------------.
х - 2 х х + 1 х2 - 9
Задачи повышенной тру (ности
Постройте график каждой из функций (84—85).
84. a) t/= {1,5х - 1}; б) у=12+х-х2.
х2 -16
< 1 - cos2 х J1+ 2х+ х2
В) </ =-------; Г) у = — —-----.
COS X X + 1
85. а) у = sin х ^cos2 х + cos х -Jsin2 х;
б) у = -Jl -cos2 х + sinх;
в) у = sin2 (д/tg х) + cos2 х (д/tg х);
г) у = ^/1-sin2 х + cos х.
Постройте график функции (86—89).
а)
б) у=21ов2Ж;
86.
87.
88.
89.
90.
91.
в) у = 2|log2x| + 1; г) y=logx^.
а) = б) j/ = VU}: в) у = {х}2; г) у = {х2}; д) У = — •
[*]
а) у = уГх + у[-х; б) у = Jlog200o cos2000 х;
в) у = ctg^ sinx; г) у = {cos х}.
а) у = sin (arcsin х); б) у = arcsin (sin х);
в) у = cos (2 arccos х); г) у = arctg (tg х).
Найдите с помощью эскизов графиков число решений урав-
нения:
a) sin х = 100х; б) arcsin х = х;
в) 1g х = cos х; г) х2 + tg2 х = 100.
На рисунке 159 изображен график функции
у = ах3 + bx2 + сх + d.
Определите знаки коэффициентов a, b, с, d.
Изобразите на координатной плоскости множество точек, ко-
ординаты которых (92—96). удовлетворяют заданному условию
92. а) х (у - 2) = 0; б) - 2х|;
в) (х - 2) (у + 4) = 0; г) Ы = sin X.
93. а) |х| < 1, |t/| < 1; б) |x-3h * 1, 11/-4|< 1;
в) Ij/I > l* +1|; г) |х + -t - |х - i/| > 2.
94. а) X2 - U2 у < 0; х2+у2-1 б) |х| + Ы ху+ 1 > xy-i ' = 4; </+1 !/-Г
в) 7x+i/>|x|; г)
Залачи повышенной трудности
Рис. 159
95. а) у2 + cos2 х = 1; б) х2 + у2 = х2у2 + 1;
в) | у | = logj || х + 2 | -1|.
3
96. a) yjx+y > у[\х\; б) |х| - |</1 < а; в) [х] < [у]; г) {х} > {</};
д) — > —; е) sin х > sin у; ж) min (х; у) = 1; з) ху + 1 > 0.
х у
§3.
Уравнения, неравенства и системы
8. Рациональные алгебраические уравнения
97. Найдите значения а, при которых данное уравнение имеет
решение. Найдите знаки корней:
а) х2 - 2 (а - 1) х + 2а + 1 = 0;
б) (а - 3) х2 - 2 (За - 4) х + 7а - 6 = 0.
98. а) Для каких значений а один из корней уравнения
(а - 2) х2 - 2 (а + 3) х + 4а = 0
больше 3, а другой меньше 2?
325 Задачи повышенной тру шости
б) Найдите все значения а, при которых оба корня уравне-
ния
(2а + 3) х2 + (а + 1) х + 4 = О
принадлежат отрезку [-2; 0].
99. Числа Xj и х2 — корни уравнения х2 + рх + q = 0. Выразите
через р и q: а) х2 + х|; б) х2 + х*; в) ; г) xj + х2.
100. а) Сумма квадратов корней уравнения х2 - 4х + р - 0 рав-
на 16. Найдите р.
б) При каком значении а сумма корней уравнения
х2 + 2а (х - 1) + 1 = 0 равна сумме квадратов этих корней?
101. Уравнение ах2 + Ьх + с = 0 не имеет действительных корней,
причем а + Ь + с < 0. Определите знак с.
102. Докажите, что если уравнения ах2 + Ьх + с = 0 и
Ьх2 + сх + а = 0 (а * 0) имеют общий корень, то и уравнение
сх2 + ах + Ь = 0 имеет тот же корень.
р
103. Докажите, что: а) если х0 = — несократимая дробь, явля-
ющаяся корнем уравнения аохп + fljX" 1 + ... + ап = 0 с целы-
ми коэффициентами, то р — делитель ап, a q — делитель а0;
б) остаток от деления многочлена Р (х) на одночлен
(х - а) равен значению этого многочлена в точке а (в частно-
сти, если а — корень многочлена Р (х), то этот многочлен де-
лится на (х - а) без остатка).
104. Пользуясь результатом задачи 103, решите уравнение:
а) 2х3 - х2 + х + 1 = 0;
б) 10х3 - Зх2 - 2х + 1 = 0;
в) х4 + х3 + х2 - х - 2 = 0; г) 2х4 + 7х3 + 6х2 + 7х - 6 = 0.
Решите уравнения (105—114).
105. а) (х + 1) (х + 2) (х + 4) (х + 5) = 40;
б) (х - I)5 + (х + З)5 = 242 (х + 1);
в) (х + 1) (х + 2) (х + 3) (х + 4) = 100;
г) х4 + (х + 2)4 = 17.
в) -------—— +---------=1;
(х+2)(х-7) (х-2)(х-3)
г) (х2 - Зх + 1) (х2 + Зх + 2) (х2 - 9х + 20) = -30;
107. а) х2 +^- + 2
у.2
б) --6х + 11х-
х2 + 2х+3 х2 + 7х+3
= 2.
За чачи повышенной трудности
108. а) х4 - 2х3 + - х2 - 2х + 1 = 0; 4
б) 2х4 + х3 - Зх2 + х + 2 = 0;
в) х4 - 2х3 - Зх2 + 4х + 4 = 0;
г) х4 - 4х3 - 18х2 - 12х + 9 = 0.
109. а) 8х4 + 8х3 - х - 190 = 0; б) 4х4 - 4х3 + х = 66. 2
110 а) х4 + 4х - 1 = 0; б) х4 - 4х3 - 1 = 0.
111. а) 2 (х2 + х + I)2 - 7 (х - I)2 = 13 (х3 - 1);
б) (х2 - х + I)2 + 2 (х3 + 1) = (х + I)2.
112. а) x2+_9xi_=7. б)х2+_^ = 1. (3+х)2 (1 + х)2
ИЗ. а) х2 + |х| - 2 = 0; б) х2 - 2х - 3 = |3х - 3|.
114. a) ||||x-l| + 2|-l| + l| = 2;
6) 2 |x + 6| - |x| - |x - 6| = 18;
в) |2x - 3| = |x2 - 2x - 61;
r) |x+l|-|x| + 3|x-l|-2|x-2| = x + 2.
9. Рациональные алгебраические неравенства
Решите неравенства (115—118).
115. а) (х* + Зх + 1) (х2 + Зх - 3) > 5;
3(х-1)(х + 2)2 > 0;
(х2 + 1) (х + I)2 (х-2)
116. а) х4 + Зх3 + 2х2 + Зх + 1 > 0;
б) (х - 1) (х - 3) (х - 4) (х - 6) > 17.
117. а) х18 - х13 + х10 - х7 + х2 - х + 1 >0;
б) х12 - х9 + х4 - х + 1 < 0.
118. а) |х2 - 2х| < х; б) Зх2 - |х - 3| > 9х - 2.
119. Докажите неравенство:
а) аЛЬ > Jab (а > 0, b > 0); б) а + | > 2 (а > 0);
„ а + Ь + с + d . 4 г~,—7 , . . .
в) > ylabca (а, Ь, с, а — положительные числа);
4
а + b + с . з / I . — п I \ z-. \
г) — - — > y/abc (а > О, b > 0, с > О).
Докажите неравенства (120—124).
120. а) а2 + Ь2 + с2 > ab + ас + Ьс;
б) (а + Ь) (Ь + с) (с + а) > 8abc (а > О, b > 0, с > 0);
Затачи повышенной тр> чности
в) если а + Ь + с = 1, то а2 + Ь2 + с2 > 1;
3
г) а4 + Ь4 + с4 > abc (а + b + с).
121. J_ + J_ + ...+ 1 <2z1.
22 З2 и2 п
122. (а + b) (а3 + fe3) < 2 (а4 + Ь4).
123. 5а2 - Gab + 5Ь2 > 0 (а2 + Ь2 * 0).
124. Ja + c)(b+d) > Jab + Jed (а > О, Ь > 0, с > 0, d > 0).
10. Системы рациональных алгебраических
уравнений
Решите системы уравнений (125—134).
125. а) (х-у) (х2-у2) =За3, (х + у) (х2 + у2) = 15а3 ; б) х2-ху+ у2 =21, у2-2ху+15 = 0.
126. а) и + v = 2, |3u-i>| = 1; б) |х-1|+|у-2| = 1, . У + | х —1| = 3.
х + у-г =2, х + у+ г = -2,
127. а) 2х - у + 4г = 1, б) < х-у + 2г = -7,
—х + бу —z =5; 2х + Зу - г = 1.
128. а) х + у = 3, х4 + у4 =17; б) х + у + ху = 0, х3 + у3 + х3у3 = 12.
129. а) х-у+ ху = 17, х2 + у2 = 34; б) < (х2 + 1)(у2 + 1) = 10, (х-у)(ху+ 1) = -3.
130. а) • х2-2ху-3у2 =0, х2 -2х + у2 = 6; б) х+ у = г, у2 + г2 = 13х2 , 2 (х2 + г2) = гу2 .
131. а) - х2-у2 =3, х2 + ху + у2 = 7; б) (х2 + у2)^ =6, (х2-у2) у = х.
132. а) х3-у3 =19 (х-у), х3 + у3 =7(х + у); б) - х3 = 5х + у, у3 = х + 5у;
328 Задачи повышенном трудности
в) х2 + у + z = 2, х + у2 + z =2, г) n чг н W N w + + + M N N Чг N N II II II M b-
Х+ у+ 22 = 2;
2хГ- lz у) = 15, xy x+ у = 6 5’
133. а) м| н =*| н * + + т к( N Н| ч ✓ ч. / + йъ N со СО СО Н = 20, б) = 13; - xyz = -4, xz X + z zy z+ у = 3 4 ’ .2 ’ 3‘ 4x2 + 4i/ + 1 = 0,
134. а) X3 -у3 + 2 -х3 + у3 + Х+у+2= -xyz =8, z3 - xyz = -2; 4, 6) 4j/2 + 4z + 1 = 0, 4z2 + 4x + 1=0. x2 + xy+ y2 = 37,
в) < X2 + у2 + 22 = 14, ху+ Х2 + уг =9; r) - x2 + xz+ z2 = 28, y2 + yz+ z2 = 19.
11. Задачи на составление уравнений
и их систем
135. Две точки двигаются по окружности длиной 1,2 м с постоян-
ными скоростями. Если они двигаются в разных направлени-
ях, то встречаются через каждые 15 с. При движении в од-
ном направлении одна точка догоняет другую через каждые
60 с. Найдите скорость каждой точки.
136. а) Сумма цифр трехзначного числа равна 17, а сумма их
квадратов 109. Если из данного числа вычесть 495, то по-
лучится число, записанное теми же цифрами, но в обратном
порядке. Найдите число, б) Найдите все трехзначные чис-
ла, сумма цифр которых равна 17, а сумма квадратов цифр
равна 109.
137. Пассажир метро спускается по движущемуся эскалатору за
24 с. Если же он идет по неподвижному эскалатору с той же
скоростью, то спустится вниз за 42 с. За какое время пасса-
жир спустится вниз, стоя на ступеньках движущегося эска-
латора?
138. Три пункта А, В и С соединены прямолинейными дорогами.
К отрезку дороги АВ примыкает квадратное поле со сторо-
ной, равной АВ, к отрезку дороги ВС примыкает квадрат-
ное поле со стороной, равной ВС, а к отрезку дороги АС при-
Зддачи повышенной трудности
мыкает прямоугольный участок леса длиной, равной АС,
и шириной 4 км. Площадь леса на 20 км2 больше суммы пло-
щадей квадратных полей. Найдите площадь леса.
139. Для награждения победителей школьной олимпиады было
закуплено несколько одинаковых книг и одинаковых знач-
ков. За книги заплатили 1056 р., за значки — 56 р. Книг ку-
пили на 6 штук больше, чем значков. Сколько было куплено
книг? (Цены и книги, и значка в рублях — целые числа.)
140. Школьник затратил некоторую сумму денег на покупку
портфеля, авторучки и книги. Если бы портфель стоил
в 5 раз дешевле, авторучка — в 2 раза дешевле, а книга —
в 2,5 раза дешевле, чем на самом деле, то та же покупка сто-
ила бы 80 р. Если бы портфель стоил в 2 раза дешевле, кни-
га — в 3 раза дешевле, а авторучка — в 4 раза дешевле, то за
ту же покупку школьник уплатил бы 120 р. Сколько стоит
вся покупка и что дороже: портфель или авторучка?
141. Имеются три куска различных сплавов золота с серебром.
Известно, что количество золота в 2 г сплава из третьего кус-
ка то же, что во взятых вместе 1 г из первого и 1 г из второго
куска. Масса третьего куска равна суммарной массе части
первого куска, содержащей 10 г золота, и части второго кус-
ка, содержащей 80 г золота. Третий кусок, масса которого
в 4 раза больше первого, содержит 75 г золота. Сколько
граммов золота содержится в первом куске?
142. Из пункта А в пункт В в 8 ч утра выходит скорый поезд.
В этот же момент из В в А выходят пассажирский и курьер-
ский поезда, причем скорость пассажирского поезда в 2 раза
меньше скорости курьерского. Скорый поезд прибывает
в пункт В в 17 ч 50 мин того же дня, а встречает курьерский
поезд не ранее 10 ч 30 мин утра. Найдите время прибытия
пассажирского поезда в пункт А, если известно, что между
моментами встреч скорого поезда с курьерским и скорого по-
езда с пассажирским проходит не менее часа.
143. Самолет совершает посадку и движется по земле в течение
некоторого времени равномерно со скоростью и. Затем летчик
включает тормоза, и движение самолета становится равноза-
медленным, причем в каждую секунду скорость уменьшается
на 2 м/с. Путь от места приземления до полной остановки
равен 4 км. Отношение времени, за которое самолет прохо-
дит первые 400 м, к времени, за которое самолет проходит
весь путь по земле, равно 4 : 65. Определите скорость V.
12. Иррациональные уравнения и неравенства
Решите уравнения (144—152).
144. а) ^1 -Jx* - х2 = х-1; б) ^х2-3х + 3 + у]х2 -Зх + 6 = 3;
330 Задачи повышенной трудности
в) Jl + xVx2-24 = х-1; г) + 4 = 4-.
’ Vx-lVx+14
145. a) Vx + Vx -1 = 1; б) V10 -х + Vs-x = 1;
в) х + Vx = 2; г) V9 - Vx +Т + V7 + Vx+T = 4.
146. a) VT+ cosx = sinx; 6) -Jl-2 cosx = sinx;
в) д/4-3cosx = -2 cosx; r) ^2 sin 2x = -2 sinx.
147. a) ^x-l-2ylx^2 + ylx + 7-б/х^2 = 2;
6) д/х + З-4-y/x-l + д/х + 8 —6Vx—1 = 1.
148. a) Vx-2 + Vl-x =17;
6) 4y]x(2-x) + V*4(2-x)7(x + 3)5 + V(x-2)(x + l) x2 +
+ V(x + 2)(x + 6) =2.
149. a) V(^ + l)2 + 2 V^2-l = 8 V(x-l)2 ;
6) V(2-x)2 + V(7 + x)2 = V(7 + x)(2-x).
150. a) Vx + 1 + V3x+1 = Vx-1; 6) Vx + Vx-16 = Vx-8.
151. a) ^12+* + ^12 + x = 64 V^; 6) x2-5x-4-Vx +13 =0.
x 12 3
152 1 + x - 72x + x2 _ 27 72 + x + Vx
1 + x + 72x + x2 72 + x - Vx
153. Для каждого действительного числа а найдите все решения
уравнения:
а) х + Vl-x2 = а; б) у! хг -1 + х = а.
Решите неравенства (154—158).
154. а) у]х2 -Зх + 2 >2х-5; б) V3x-x2 <4-х;
в) sVx - Vx + 3 > 1; г) х-д/1 -|х| <0.
, __ 1 - 71 - 4х2 7х2 - 1 + 1
155. а) 1 Vi 4Х <3; б) ----------------> 1;
X X
в) 4х2 + 12xVl + x <27(1 + х);
г) Vx + Vx + 7 + 2 у]х2 + 7х < 35 -2х.
331 Задачи повышенной трудности
156. a) x2-2x + 3< л/4-х2 ; 6) V3-x-Vx+1 >|.
158. а) ^9+3х-2 > 9 -3х; б) Vxloga/x > 2;
в) log^x + S -x-1) <0; г) ^4X + 1+17-5 > 2х.
Решите системы уравнений (159—162).
у[у + Jx3Jy =12,
ху = 64;
в)
3Jx + Зу[у =4,
х + у = 28;
160.
3^х + 2у + 3^х-у + 2 = 3,
2х + у = 7;
х2 + 2 у + д/х2 + 2у+1 = 1,
2х + у = 2;
x-y+^x2-4i/2 = 2,
х5 д/х2 -4у2 =0;
161 а) x2-yjxy =36, у2-Ху[ху = 72; б) m|<N II 1 + 4 ® и ?=- а + 1 h? ?
162. а) xVx + Зу4~х = 36, у/у +3xjy =28; б) < 23^с-2 х-у = 63;
Зх-Jxy + 2у = 29, 2х - у[ху - у = 20; ^Х2+ у2 +у/х2-у2 _ 5 + V?
в) г) yjx2+y2 -^х2-у2 5-47 ха + 2у3 =118.
332 Задачи повышенной трудности
13. Тригонометрические уравнения,
неравенства и системы
Решите уравнения (163—165).
163.
164.
а) 3 + 2 sin 2х = tg х + ctg х;
б) tg х - sin х = 1 - tg х sin x;
в) sin2 x + sin2 2x = sin2 3x;
r) У 6 sin x - 2 cos x = 0.
a) | x | sin x + x = 0;
в) |x| cos x - x = 0;
6) sinx-1 + 2x = 0;
165.
a) —------tg4x = 17;
cos4 X
6) tg 3x - tg x = 2 (sin 4x - sin 2x);
2 tg — - соз x
г) 2 2 =4.
в) 3 (log2 sin x)2 + log2 (1 - cos 2x) = 2;
166. Докажите формулу: 2 tg| ol г, . б) !- tg2|
SIN ”b|<n Ъ si” ч ™ Ьс <М 1 1 II ч ЪД D +-> ? 'и' 0 с ; о 2 f 1 1 7 + с+‘ 04 м № ЬЭ к>|я К>|р
г)
2 tg|
167. Решите уравнение: a) sin 2х + tg х = 2; б) sin х + ctg ~ = 2.
168. Докажите тождество
a sin х + b cos х = A sin (х + <р),
где <p удовлетворяет условиям:
cos <р = , а , sintp = , b А = Ja2 + b2 .
J a2 + b2 ^a2 + b2
Решите уравнения (169—175).
169. a) sin x - -Уз cos x = 1: 6) 2 sin x + 3 cos x = 4.
170. V2 (sin x + cos x) = tg x + ctg x.
171 „„„ лх __2лх„„„4лх______8лх „__16лх 1
1/1. cos cos- cos- cos - cos -- =
31 31 31 31 31 32
172. a) sin8 x + cos8 x = —; 6) sin100 x + cos100 x = 1.
32
173. 2 cos =2X + 2X.
10
333 Задачи повышенной трудности
174. х2 + 2x sin (ху) +1=0.
175. 8 sinx = ^3 + 1
cos х sin x
176. Докажите, что уравнение (sin х + -Уз cos х) sin 4х = 2 не име
ет решений.
Решите неравенства (177—178).
177. а) 7з tg2x-4 tgx + /3 >0; б) 15 < n_2 sinx-
Sinx+l
в) t<r~1<2_tgx; г) tgx+ ctgx >-Уз +-J=.
Lg X -г 1 о
V О
178. a) cos 2х < cos Зх - cos 4х;
б) cos2 х + cos2 2х + cos2 Зх + cos2 4х > 2;
в) sin 2х + 2 sin х > 0;
г) (1 + cos 2х) (tg х - -Уз) > 0.
179.
Докажите справедливость неравенства:
a) v/cosip < V2cos-, если < <р <
2 2 2
б) sin4 а + cos4 « > ПРИ Л1°бом а.
Решите неравенства (180—181).
180. sin f — cosnx'l > ^3 .
I 3 ) 2
181. 75^2 sin x > 6 sin x -1.
182. Докажите, что если 0 < x < 5, то cos sin x > sin cos x.
183. Докажите, что если А, В и С — углы треугольника, то
з
cos А + cos В + cos С < —.
Решите системы уравнений (184—186).
184. а) sin х - cosx - 1 sinx 1 cos X = sin у, = cos у; б) • sin (y -3x) = 2 sin3 x, cos (y - 3x) = 2 cos3 x.
18л. tg • x + tg!/ 2 2 = 2 7з ’ 186. . tgxtg// = —81пг +3, COS X cos у tg у tg z = sinx -5,
tgx+tgl/ = 2л/ 3. COS у COS 2 sin У tg x tg z = - 3. COS X COS 2
334 Задачи повышенной трудности
14. Показательные и логарифмические
уравнения и неравенства
187.
188.
189.
190.
191.
192.
193.
194.
195.
Решите уравнения (187—189).
а) р5 +724)^ + p5-V24^ = 10;
б) 3х + 4х = 25;
в) (2 + 73)х +(2->/3)х = 4;
г) (2 + V3)x +(2-V3)x=4x.
а) |х-3|3х2-10х + 3 =1;
В) |х-2 |Юх2-Зх-1 =1.
a) 28in 2 х + 4 • 2СС®2 х = 6;
1
4З + 2 cos 2х _ 7.4I + cos 2х _ 42 .
— - 2 cos 3 х . ,_
б) X4 =У^;
г) 21х' = sin х2.
б) 3'g tg х _ 2.31g ctg x +1 = 1;
r) (2 sinx)CO8X= 1.
При каких значениях а уравнение а (2х + 2 x) = 5 имеет
единственное решение?
Решите неравенства (191 —192).
а) 2х +2lxl > 2V2; б) 25-2х-10х + 5х > 25;
в) ах < Ь2+х; г) i <2.
2X + 1 +1
а) (х-2)х2-6х*8 >1; б) Э^2"3 + 3<3'^2’3
3
Найдите все значения а, для которых неравенство
4х - а 2х - а + 3 С 0 имеет хотя бы одно решение.
Решите систему уравнений:
[32х + 42» =82,
a) S
3х-4» =8;
б)
(2х + 1-3) - 2У-1 = 1,
у]3х + у2 = х + у;
в)
1
= 5,
1
COS X + ----
cosy _ 4.
2 cos х 1 2 cos У
г)
g2 tgx + cosg _ 3
gcosg-gpgx =2
Решите уравнения (195—197).
a) + log2 x + ^4 log4 x - 2 = 4;
6) log6 2Хт3 - log6 13х - 3| = x;
в) logj (3 + I sin x|) = 2|x' - 2;
3
r) ^/1 + lg tg x + 3/l -1g tg x =2.
335 Задачи повышенной трудности
196. a) 9xlgx + 91x-lgx = 60; 6) |x-111082x~1082= |x-1|3;
2lgl“-3 1gx
в) x x = 0,1; r) logx + j (x2 + x - 6) = 4.
197. a) lg (arctg x) + lg (arcctg x) = a;
6) logx + j (x2 - 9x + 8) • logx j (x + 1) = 3;
в) arcsin (lg x2) + arcsin (lg x) =
О
198. При каких значениях а уравнение 2 log| х - | log3 х | + а = 0
имеет четыре решения?
199. При каких значениях а уравнение Зх lg х = 1 + a 1g х имеет:
а) одно решение; б) два решения?
200. При каких значениях а уравнение х In | х | = а имеет один
корень?
Решите неравенства (201—203).
201. a) log2 (1 + logjх - log9 х) < 1;
а
б) log2 (х - I)2 - log0 5 (х - 1) > 5;
в) log! (log2 logx _ j 9) > 0;
2
г) log2 (log j log5 x) > 0.
2
202. a) log2 (2х - 1) logj (2х +1 - 2) > 2; б) з’°®2 *+ х‘°вз x<6;
2
в) 3lgx + 2 < 3lg2x + 5 - 2; г) б'0®2 * + x*°®5 x < 10.
203. a) logx_3 (х - 4) < 2; б) 2log2-,х2 + 8х+15) < 1;
в) log 2 > |; г) logx (log9 (3х - 9)) < 1.
х |х-2| 2
204. Известно, что неравенство
loga (х2 - х - 2) > loga (3 + 2х - х2)
выполняется при х = —. Найдите все решения этого неравен-
4
ства.
336 Задачи повышенной трудности
Решите системы уравнений (205—206).
205. а)
в)
logx у = 2,
logx+1(y + 23) =3;
(x-j/)2»~x=125,
lg2 (х-у) = 1;
J(х + у)х = (х - у)» ,
[log2 х = 1 + log2 у,
2 log2 х -3V = 15,
3» • log2 x = 21ов2Х + Зу + 1.
206. a)
log2 (sin x - cos y) + log2 (sin x + cos y) = -1;
Г log2 sinx + log2 sin у = -2,
[ log3 cos x + log3 cos у = 1 - log3 4.
§4.
Начала математического анализа
15. Производная
207. а) Докажите признак возрастания функции: функция f воз-
растает на промежутке I тогда и только тогда, когда для лю-
бых двух значений аргумента х и х + Дх (где Дх * 0) из про-
Т п
межутка I выполняется условие — > 0.
Дх
б) Сформулируйте и докажите аналогичный признак убыва-
ния функции на промежутке I.
208. Пользуясь доказанными признаками (см. № 207), найдите
промежутки возрастания и убывания функции:
a) f (х) = 2х2; б) f (х) = 3 - 4х;
в) / (х) = 3 - х2; г)/(х)=1--2.
х
209.
Пользуясь определением производной, докажите, что функ-
ция f дифференцируема в точке х0, если:
а) / (х) = х | х |, х0 = 0;
в)
/(*) = -
х2
-1
-X
при
при
б) f(x) = | х2 - 1| (х + 1), х0 = -1;
х< 1,
х > 1, х0 = 1;
[х2
г) f (х) =( _
при х> 0,
при х <0, х0 = 0.
210. Докажите, что если функция f дифференцируема в каждой
точке числовой прямой и для любых значений хх и х2 вы-
полнено равенство f (Xj + х2) = f (Xj) + f (x2), то f (x) посто-
янная.
337 Задачи повышенной трудности
211. Докажите, что функция f (х) — ^Jx2 не имеет производной
в точке 0.
212. Верно ли, что функция <р (х) = /\ (х) • f2 (х) не имеет произ-
водной в точке х0, если:
а) /\ (х) дифференцируема в точке х0, a f2 (х) нет;
б) обе функции не имеют производной в точке х0?
213. Докажите, что если функция f дифференцируема в каждой
точке числовой прямой и для любых значений х1 и х2
выполнено равенство f (хг + х2) = f (хг) f (х2), то f (х) = еах
или f (х) = 0.
214. Выведите формулы производных обратных тригонометриче-
ских функций:
a) arcsin’ х = , 1 ; б) arccos' х = —, 1 ;
V1-X2
в) arctg' х = ——г) arcctg' х =----------.
1 + хг 1 + х6
215. Найдите производную функции: а) у = Xх; б) у = (sin х)сов х.
216. Найдите п-ю производную функции у = —-— ----.
х2-Зх+2
217. Докажите, что если f (х0) = g (х0) и f'(x) > g'(x) ПРИ х > xt
то f (х) > g (х) при х > х0.
218. Вычислите сумму:
а) 1 + - + Л + Л + ••• + —Г;
2 22 23 2" 1
б) 2 + 3-- + 4-— + 5-- +...+(п + 1)-—— .
’ 2 22 23 2" 1
16. Применение производной
к исследованию функций
Исследуйте функции на возрастание (убывание) и экстрему-
мы (219—220).
219. a) f (x) = x2(Vx-l); б) f (х) = х2 Vl-2x;
в) f (*) = 6 sin х - cos 2х; г) f (х) = 2 sin х + 3 cos х.
220. a) f (х) = -0,2х5 + 0,5х4 - х3 - х2 - х;
б) f (х) = 0,8х5 - х4 + 4х3 + 2х2 + 4х.
221. Найдите все значения а, при которых функция f возрастает
на R:
а2 - 1
a) f (х) = —-— х3 + (а -1) х2 4- 2 х + 5;
б) f (х) = 2х3 - 3 (а + 2) х2 + 48ах + 6х - 5.
338 Задачи повышенной трудности
222. Докажите, что данное уравнение имеет единственный ко-
рень:
a) cos х = ? - х; б) sin х = -х - л.
223. Решите неравенство:
a) 2 + sinx>—1—; б) 2-cosx >—.
1 + х2 1 + х2
224. Докажите, что любое кубическое уравнение х3 + ах2 +
+ Ьх + с = 0 имеет хотя бы один действительный корень.
225. Докажите, что многочлен степени п имеет не более чем п
корней и не более чем (п - 1) точек экстремума.
226. Докажите, что каждое свое значение многочлен степени п
принимает не более чем п раз.
227. Пусть 7? (х)
Р(х)
Q(x)
— дробно-рациональная функция (п — сте-
пень Р (х), т — степень Q (х)). Докажите, что:
a) R (х) каждое свое значение принимает не более чем при
k = max (т, п) значениях х;
б) R (х) имеет не более чем (т + п - 1) точек экстремума,
если т * п, и не более чем (т + п - 2) точек экстремума,
если тп = п.
228. Найдите наибольшее и наименьшее значения функции:
a) f (х) = 4х3 - х |х - 2| на [0; 3];
б) f (х) = max ———-------1- cos х .
R I х2 + 4лх + 41
229. Три пункта А, В, С не лежат на одной прямой, причем
ZABC = 60°. Одновременно из точки А выходит автомобиль,
а из точки В — поезд. Автомобиль движется по направлению
к В со скоростью 80 км/ч, поезд — к С со скоростью
50 км/ч. В какой момент времени (от начала движения) рас-
стояние между поездом и автомобилем будет наименьшим,
если АВ = 200 км?
230. На странице текст должен занимать 384 см2. Верхнее и ниж-
нее поля должны быть по 3 см, правое и левое — по 2 см.
Если принимать во внимание только экономию бумаги,
то каковы должны быть наиболее выгодные размеры стра-
ницы?
231. Расходы на топливо для парохода делятся на две части. Пер-
вая из них не зависит от скорости и равна 480 р. в час.
А вторая часть расходов пропорциональна кубу скорости,
причем при скорости 10 км/ч эта часть расходов равна 30 р.
в час. При какой скорости общая сумма расходов на 1 км
пути будет наименьшей?
339 Задачи повышенной трутности
232. Найдите кратчайшее расстояние от точки М (О; 1) до графи-
ка функции f (х) =------i—-.
4 /3 х*
233. Что больше:
1 1
a) З'2 или 2<3; б) f^-11987 или f-J—V988?
11987 J 11988/
; — , то:
2 )
б) sinx > х---;
6
х3 х8
г) sinx<x-----+-----.
' 6 120
б) In (1 + х) < X при X > 0.
234. Докажите, что если х е
х2
a) cosx > 1 - —;
х2 х4
в) cosxcl- — +--4;
235. Докажите неравенство:
а) ех > 1 + х при х > 0;
236. Решите уравнение:
a) In х = 1 - х; б) 2х = 3 - х.
237. Найдите число корней данного уравнения в зависимости
от параметра а:
а) х3 - Зх = а; б) |х2 - 4х + 3| = ах.
238. К реке шириной а проведен под прямым углом канал шири-
ной Ь. Какую максимальную длину могут иметь суда, чтобы
пройти в канал? (а и b измеряются в метрах).
239. Найдите минимальное значение функции
1 о 2
/ (х) = 2х + + cosx на интервале (0; 10).
17. Применение производной в физике
и геометрии
240.
Колесо радиуса R катится по прямой. Угол <р поворота колеса
за t секунд определяется уравнением ср
t2
= t + —. Найдите ско-
рость и ускорение движения центра колеса.
241. Лампа подвешена на высоте 12 м над прямой горизонтальной
дорожкой, по которой идет человек ростом 1,8 м. С какой
скоростью удлиняется его тень, если он удаляется от лампы
со скоростью 50 м/мин?
242. Под каким углом пересекаются графики функций у = 8 - х
и у = 4 -Jx + 4 ?
243. Запишите уравнение касательной к графику функции /, про-
ходящей через точку М, если:
a) f (х) = А, М (0; 3); б) f (х) = х2 - 4х + 1, М (-1; -3);
X
в) f (х) = V2x- 1, АГ(-1; 0); г) f (х) = V9-x2 , М (0; 6).
340 Задачи повышенной трудности
244. Найдите все значения аргумента, при которых касатель-
ные, проведенные к графикам функций f (х) = 3 cos 5х
л g (х) = 5 cos Зх + 2 через точки с этими абсциссами, па-
раллельны.
245. Докажите, что отрезок касательной к гиперболе у = —, за-
ключенный между осями координат, делится точкой касания
пополам.
246. Докажите, что треугольник, образованный касательной к ги-
перболе ху = а2 и ос ями координат, имеет постоянную пло-
щадь, равную 2а2, а точка касания является центром окруж-
ности, описанной около этого треугольника.
ах — х2
247. При каких значениях а график функции f (х) =------пере-
4
секает ось абсцисс под углом 45° (хотя бы в одной из точек
пересечения)?
248. При каких значениях а и & прямая у = 7х - 2 касается гра-
фика функции у = ах2 + Ьх + 1 в точке А (1; 5)?
249. Докажите, что при любом значении а существуе г касатель-
ная к графику функции f (х) = х2 - ах, перпендикулярная
прямой у = -х.
250. Опишите множество точек Mk координатной плоскости, где
Мк (k = 0, 1, 2, ...) — множество точек М (х; у), таких, что
из точки М (х; у) можно провести в точности k касательных
к параболе у = х2.
18. Первообразная
Найдите все первообразные для функции f на R (251, 252).
251. а) / (х) = |х|; б) f (х) = |х - 11; в) f (х) = |х2 - 11.
252. а) /(х) = х Vl + x2 ; б) f (х) = хе^2
в) f (х) = ctg х, х <= (0; л); г) f (х) = tg х, хе |
253. Найдите все функции f, такие, что:
а) и /(3)= -1;
б) f" (х) = 3 - х, f (0) = 1, f (1) = 0;
в) Г (х) = cos х и f (е) = л;
г) f"(x) = -1 и f(0) = /(2) = 0.
341 Задачи повышенной трудности
254. Для функции f найдите первообразную, график которой про-
ходит через точку М. Постройте график первообразной.
, [cosx при х<0,
a) f (х) = <
11 при х> О, М (0; 0);
б) f{x) =
1 при X < 1,
~ при Х> 1,
V х
М (4; О).
255. Докажите, что любая первообразная нечетной непрерывной
функции, определенная на [-а; а], является четной функ-
цией.
256. Докажите, что четная непрерывная функция, определенная
на [-а; а], имеет по крайней мере одну нечетную первообраз-
ную.
257. Два тела начали движение по прямой одновременно из одной
точки. Скорость первого v (t) = 3t2 - 6t, второго v (t) = lOt + 20.
В какой момент и на каком расстоянии от начальной точки
произойдет их встреча? (Скорость измеряется в метрах в се-
кунду.)
258. Пусть при движении по прямой тело массой т в точке с ко-
ординатой х обладает потенциальной энергией и (х). Дока-
жите, что:
а) координата х (t) тела при движении по прямой удовлетво-
ряет дифференциальному уравнению тх" (t) = -и' (х);
б) потенциальная энергия и (х) материальной точки мас-
сой т, совершающей гармоническое колебание х" = -со2х,
Лх2
равна ——, где k = та2 (положите и (0) = 0).
259. Докажите, что полная энергия Е =—-— +и(х) материальной
точки массой т, движущейся по прямой согласно второму
закону Ньютона, сохраняется (и (х) — потенциальная энер-
гия).
260. Пусть Xj (t) и х2 (t) — два решения уравнения х" (t) = -ю2х (t).
Докажите, что функции xl (t) - х2 (t) и kxx (t), где k — про-
извольное число, также являются решениями этого урав-
нения.
261. Докажите, что существует решение уравнения х" (t) =
= -со2х (£), имеющее вид х = A cos (cot + <р) и удовлетворяющее
начальным условиям х (0) = х0, х' (0) = и0.
262. Пользуясь результатами задач 260-—261, докажите, что лю-
бое решение дифференциального уравнения х" (t) = -w2x (t)
может быть записано в виде х = A cos (cot + ср).
342 Задачи повышенной трудности
263. Докажите тождество с помощью признака постоянства функ-
ции:
a) arcsin х + arccos х = б) arctg х + arcctg х =
264. Найдите функцию у, если известно, что у'у2 = 2 и у (2) = 2.
265. Найдите первообразные для функций ех sin х и ех cos х.
19. Интеграл
266. Материальная точка движется по прямой. Докажите, что:
t
а) х (О = х0 + Ju (t) dt, если известна ее скорость v (t) в лю-
1 о
бой момент t и координата точки в начальный момент t0
равна х0;
t
б) v (t) = и0 + J a (t) dt, если известно ее ускорение a (t)
t о
в любой момент t и скорость в начальный момент t0 равна о0.
267. Пусть f (х) — многочлен степени не выше 3. Докажите, что
ь
J f (х) dx = (У1 + 4у2 + у3),
J о
а
где у} = f(a), = Уз = НЬ)-
268. Докажите, что:
а
a) J f (х) dx =0, если f (х) — нечетная функция;
- а
а а
б) J f(x) dx = 2 J f (х) dx, если f (х) — четная функция.
-а 0
269. Воспользуйтесь результатами задачи 268 и вычислите:
Я
3 к
a) J (tg х + sin х) dx; б) J х cos х dx.
-- п
3
270. Вычислите:
28 1
а) Г f Х dx; б) Г xex2dx;
« V17г »
343 Задачи повышенной трудности
° I----- 2
в) J x з /1 - dx; r) | (cos2 x + cos4 x) dx.
2 я
2
271. С помощью интегралов найдите предел:
. Л ( тг . 9тг . (п. -1) Л
a) lim 1 sin - + sin — + ...+ sin----------;
n n n n n J
6) lim | 1 _ + ... +
л->«Дп + 1 n + 2 n + nj
4 1₽ + 2P + ...+nP _
в) lim-----------------при p > 0;
n ->CD nP +1
r) lim [ nP 1 + nP — + ... + nP 1—1 при p > 1.
n-»» ^(n + l)₽ (n + 2)p (n + n)P J
272. Вычислите:
2л
a) J cos2 nxdx (n e N);
о
2л
6) J sin kx cosmxdx (m e N, k 6 N);
о
я я
в) j sin2 x dx; г) J sin3x cos5xdx.
-n 0
273. Используя геометрическую интерпретацию интеграла, вы-
числите:
2 1
a) j | |х|-11 dx; б) |л/1 -х2 dx;
-2 -1
3 5
в) J|x2-l|dx; г) J |{x}-||dx.
о о
274. Вычислите площадь фигуры, состоящей из точек, лежащих
внутри эллипса. (Эллипсом называется фигура, координаты
х2 У2
точек которой удовлетворяют равенству — + — = 1.)
а2 Ь2
275. При каких значениях параметров а, b и с определен интег-
рал:
Ь 3 ь
“’Lt-'
а 0 а
276. Найдите площадь фигуры, ограниченной линиями:
а) у = |х2 - 1| и у = 5 + ]х|; б) |у| = 2х - х2.
344 Задачи повышенной трудности
277. Площадь фигуры, ограниченной линиями у = -, у = ,
х 2х-1
х = 2, х = а, у = О, равна In . Найдите а.
V5
278. Докажите, что площадь параболического сегмента, заклю-
ченного между параболой у = х2 и произвольной прямой, па-
9
раллельной оси абсцисс, равна - площади прямоугольника
3
с вершинами в точках пересечения прямой с параболой
и основаниями перпендикуляров к оси абсцисс, опущенных
из точек пересечения.
279. Пружина растягивается на 2 см под действием силы в 180 Н.
Первоначальная длина пружины равна 20 см. Какую работу
нужно совершить, чтобы растянуть пружину до 25 см?
280. При каком значении а площадь фигуры, ограниченной осью
Ох, графиком функции у = х3 + Зх2 + х + а и вертикалями
х = const в точках экстремума этой функции, будет наимень-
шей?
281. Капля воды с начальной массой М падает под действием
силы тяжести и равномерно испаряется, теряя ежесекундно
массу т. Какова работа силы тяжести за время от начала па-
дения капли до ее полного испарения?
282. Какую минимальную работу по преодолению силы тяжести
надо произвести, чтобы насыпать кучу песка в форме кону-
са высотой Н и радиусом основания /?? Плотность песка
равна р, и его поднимают с плоскости основания конуса.
283. Однородная треугольная пластинка с основанием а = 40 см
и высотой Л = 30 см вращается вокруг основания с постоян-
ной угловой скоростью <а = 5п с ’. Найдите кинетическую
энергию пластинки, если ее толщина d = 0,2 см, а плотность
материала, из которого изготовлена пластинка, равна
р = 2,2 г/см3. (Толщиной пластинки пренебречь.)
284. Найдите центр масс однородного полукруга радиуса R.
285. Найдите центр масс однородного полушара радиуса R.
286. Докажите, что работа, которая производится против силы
выталкивания воды при погружении однородного тела в во-
ду, равна р^ИА, где р — плотность воды, g — ускорение
свободного падения, h — глубина погружения центра масс
части тела, находящейся в воде, V — ее объем.
Ответы и указания к упражнениям
Глава I
1- г)
5л 6л л 2 . 225о 270о. _105с 3_
6 5 2
в) 4; г) 3. 4. в)
Нет; да; да.
5. в)
Нет;
г) да. 6. в) Нет; г) да. 7.
. . 8
г) sin a = ;
17
84. 77
85’ 85
tga-- 8 ;
15
24
8. г) -1. 9. в) 1. 10. б)
cos —; —ctg 0,1л. 13. г)
5
161.
289’
15
8 ’
4
vl7 ' V17’
27°30'7"; 63°35'54"; 84°47'52". 18. в) 0,1 м; г) 9л м.
г) <3. 22. в) 3 2^2. 27. г)
О о
36. в) D (у) - R, Е (у) = [-2; 0].
ctg Ct = —
11. в) tg а.
12.
15.
б)
г)
л
-cos
18
1 ; -4. 16. в) 0,7833; 0.6216; 1,2602: 0,7936.
1. 14. в)
Нет; г) да.
17. б) 22°6";
19.
а) 0,05 м2.
20. б) 1. 21. в) 3;
IV; II. 31. г) Плюс.
Е(у) = [-1,5; 1,5]. 38.
г)
(0; -1),
41. в) -
44. в) Числовая прямая,
= (-оо; -1) и (-1; оо). 46. г)
а + 2
-2.
30. в) IV;
37. г) D(y) = R,
пп; 0 , п е Z. 39. в) (0; 3,5).
42. в) Нет. 43. в) (-оо; —4) U (-4; 2) Ч (2; оо).
кроме чисел пп, п е Z. 45. в) D(y) = E(y) =
D (у) = [-4; 3], Е (у) = (-1; 4]. 49. г) Рис. 1.
50. в) Выполняем
функции
(А = 0,5),
(0; -1),
У = COS X
а затем
рис. 2.
D(Si)= 0; з
растяжение графика
вдоль оси ординат
перенос на вектор
52. г) S] (х) = х2.
; S2(x) = a2-x2,D(S2) =
53. в) [-2; 1,5) и (1,5; оо).
54. г) D (у) = R, Е(у) = [1; 1,5]. 64. г) Зп.
. 68. в), г) Нет. 69. г) Не-
Ни четная, ни нечетная.
73. г) 2л. 77. г) Возра-
65. в) л. 67. г)
четная. 70. в)
72. г) Четная.
стает на [-4; -2], [0; 2], [4; 6]; убывает
(Иветы и указания к упражнениям
на [-6; -4], [-2; О], [2; 4]; xm„„ = -2, х = 2, х = —4, х - = О, х - =4,
L 1,1 » j» l » j, max » max * •"'min ’ min ’ min *
У (-2) = у (2) = 3, у (О) = О, у (-4) = у (4) = -2. 82. г) Возрастает на [3; оо);
убывает на (—оо; 3]; xmin = 3, у (3) = О. 83. в) Возрастает на (-оо; -3),
(-3; оо); точек экстремума нет. 84. г) Возрастает на - л + 2лп;
л + 2лп
2 J
убывает на
— + 2лп; + 2лп
2 2
•J" max
2 + 2лн, у^л+2лп ) = - 1, xmin =
= -— + 2лп, у I + 2лп I = -2,
2 4 2 I
п е Z. 85. г) Возрастает на [-л + 2лп;
2лп], убывает на [2ли: л + 2лп]; хшах = 2лп, у (2лп) = О, хП1Ш = л + 2лп,
у (л + 2лл) = -2, п е Z. 86. в) Первое больше. 87. г) sin (-1,2), sin 0,8,
sin 1,2. 88. г) Убывает на (-оо; -1], [0; 1], возрастает на [-1; 0], [1; оо),
= 0, у(0) = 0, х . = + 1,
max ’ а ’ min — 1
2л . о Л . о 1 ,
----+ 2лп; + 2лп , убывает
3---3 J
у (-1) = у (1) = -1. 89. в) Возрастает на
на
л , п 4л „
— + 2лп; + 2 ли
L3 3
max о +
О
л + 2лп) = 1, xmin = 4л + 2лп,
\ о / о
+2л/г)= -1’
п е Z. 90. в) ctg -
. 7л
ctg —
15
ctg 4f~ , tg 6^. 91.
5 5
в), г) Указание. Воспользуйтесь свойства-
ми функций у = х6 и у = х5. 92. б) Указание. Пусть -b < х, < х2 С -а,
тогда а < -х2 < -Xj < b и f (-х2) > f (-хД так как f убывает на [а; 6], сле-
довательно, f (х2) < f (х,). 93. в) 1) D (f) = [-6; 6], Е (f) = [-2; 2]; 2) функ-
ция нечетная; 3) (-4; 0), (0; 0), (4; 0) —• точки пересечения с осью Ох,
(0; 0) — точка пересечения с осью Оу; 4) f (х) > 0 на (-4; 0), (4; 6],
f (х) < 0 на [-6; -4), (0; 4); 5) f возрастает на [-6; -2], [2; 6], убывает
на [-2; 2]; 6) xmin = 2, /(2) = -2, хтах = -2, f (-2) = 2. 96. г) 1) О(/) =
= Е (/) = R; 2) (1; 0), (0;-1) — точки пересечения с осями координат;
3) f (х) < 0 на (-оо; 1), f (х) > 0 на (1; оо); 4) f возрастает на R.
97. в) 1) D (f) = [-1; оо), Е (f) = [0; оо); 2) (-1; 0), (0; 1) — точки пересе-
чения с осями, 3) / (х) > 0 на (-1, ос), 4) f возрастает на [-1; оо).
347 Ответы
и указания к упражнениям
98. в) 1) D (f) = E (/) = R- 2) функция нечетная; 3) (О; 0) — точка пересече-
ния с осями; 4) / (х) < О на (-оо; О), /(х) > О на (0; оо); 5) f возрастает на Я;
г) 1) D (у) = [2; оо), Е (f) = [-2; оо); 2) (6; 0) — точка пересечения с осью
Ох; 3) f (х) < 0 на [2; 6), f (х) > 0 на (6; оо); 4) f возрастает на [2; оо).
99. в) 1) D (/) = R, Е If) = ^-оо; 2) функция четная; 3) (0; 0), (-1; 0).
(1; 0) — точки пересечения с осями; 4) f (х) < 0 на (-оо;-1), (1; оо),
f (х) > 0 на (-1; 0), (0; 1); 5) f возрастает на ^-оо; [0; 0,5], f убывает на
[-0,5; 0], [0,5; оо), хтах = ± 0,5, у (-0,5) = у (0,5) = 0,25, xmin = 0, у (0) = 0.
100. г) -cos’1, -ctg”. 101. в) Л(/) = | nn; -л(-П- +-Jj 1 п е z, Е (f) = R.
Т 9 у 3 3 J
102. г) / (x) > 0 при ^<x<^ + -7, / (x) < 0 при Я+^<х<^±12.
f (x) = 0 при x = — + —, n e Z. 103. г) Возрастает на Г- - + -n ; 71 + лп-1,
42 L 8 2 8 2 J
, Гл лп 3л , m | л лп л , ли ~
убывает на — + — ; — + — , x,Y,„v = - + - -, xmin = — + —, n e Z.
y [8 2 8 2 J 8 2 8 2
104. в) График функции изображен на рисунке 3. 105. в) График функ-
ции
изображен на рисунке 4.
106. г) А = 0,5, 7 = 4, со = ^.
110. в) R, кроме чисел 2лп, п е Z. 111. в) [0; -/2]; г) (0; 2]. 113. в) Гра-
фик функции изображен на рисунке 5. 114. в) А =12, 7=1,2,
7(0 = 12 sin 5Л*. 115. г) 2 2. 118. в) г) -. 120. г) —. 121. г) --.
3 3 3 2 4 4
122. в) 5п; г) 0. 124. в) Нет; г) да. 125. б) Нет. 126. г) 127. в) - ;
f (х) = -1,5 cos Зх
-1,5
Рис. 3
348 Ответ „I и указания к упражнениям
г) 128. в) - - г) 129. в) Первое меньше. 130. в) 0,8948; 0,5010.
1Z о Л
131. г) ~ • 132. б) Введем обозначения а = arccos хр 0 = arccos х2.
Предположим, что а < 0. Так как а и 0 принадлежат промежутку [0; л],
где косинус убывает, получим cos а > cos 0, т. е. jq > х2, что противоречит
условию. 133. б) Указание. Используйте прием, описанный в решении
упражнения 132 (6). 136. в) ±л + 2лп,
6
п е Z. 138. г) -— + 2пп, п е Z.
2
139. г) (-1)" + 1 • + пп, neZ. 141. в) л + пп. 142. в) (-1)" • 2-л + 4пп,
п е Z. 143. в) ± arccos 0,3 + 2пп, п е Z. 145. г) + 4пп, п е Z.
146. г) Л + —П, п е Z. 147. г) (-1)" + 2л + Злп, п е Z.
3 6 3 4 5
349 Ответы
и указания к упражнениям
148. в) [л± л+лп; 1), f"+4nn; 11 п е Z. 149. г)-2л, О, п -?л.
151. в)[л; Зл]. 152. в) [-л; л]. 153. г) [-л; - л ). !54. г) + 2лп;
4 4 / х о о / VZ 4/ V 4
- - + 2лп 1 п е Z. 155. в) - £ t 2лп; j + 2лп , п е Z. 156. г) ( - л + лп;
4 7 L 6 6 J V 2
- л + лп ], п е Z. 159. в) (4лп; л + 4лп), п е Z. 160. г) f ^J71 + 2лп;
4 1 х 24
^+Д + 2лп\ п е Z. 161. г) (-л + 2лп; л + 2лп 1, п е Z. 162. г) (- л +
24 Г I 3 ) 14
+ 4 arcsin 2 + л" ; - 1 arcsin 2- + ллО, п е Z. 163. в) Г- ; ^1. 164. г) (-1)" х
4 52 4 5 2 7 L 4 4 J
х arcsin 1 + лп, и е Z. 165. г) 2лп, ± arccos 1 + 2лп, п е Z. 166. г) л + 2лп,
4 5
п е Z. 167. в) Xj + лп, х2 + лп, х, =-arctg 2 ~-1,1071, х2 - arctg ®
~ 0,4636, п е Z. 168 г) ± л + лп, и е Z.
169. в) л + лп,
4
arctg 3,5 + лп.
и e Z. 171. г) ± л + лп, п е Z.
3
172. в) (-1)" • - arcsin + л-, и е Z.
2 3 2
173. в) (-1)" + 1 71 + лп, п е Z.
6
175. г) л - лп; лп J, п 6 Z. 176. в)
174. в) , л + лп; k, и е Z.
2 6 3
- + 2лй; — + пп |, п е Z, k е Z.
2 2 )
Глава II
177. б) 3) 1,2881; 4) nh (2R + ft). 178. г) 0,205. 179. г) Дх = 0,125.
Д/ = 0,1. 180. г) . 181. в) 65 км/ч. 182. г) На 4 в отрицательном
х0(х0 + Дх)
направлении, иср = -2. 184. в) 1,5, острый. 185. в) 6 (2х + Дх) Дх.
186. г) У = -2*0-А* 187 в) v = g 2t0 + At). 188. б) Ми-
Ax ((х0 + Дх)2 + 1)(х2+1) 2
нус, плюс, минус, плюс. 191 б) 2,5; 2,1; 2,01. 192. г) -2, —4. 193. г) 5,
-2. 194 в) -1, -1. 195. г) у = 4х-4. 196. в) 2; г) 5. 197. в) Непре-
4
рывна в точках Xj, х2, не является непрерывной в точке х3. 200. в) 5; 4.
201. в) 6. 202. г) 0,25. 204. ft = 0,04 дм. 206. й ~ 0,01 дм. 208. г) Зх2 +
+ 209. г) -8х3 + 9х2 + 2. 210. в) 34 . 211. в) 7х6 - 20х4 + 2;
2vx (5х + 8)2
г) х-9х 4. 212. в) 1,5; 4. 213. в) 4;-1. 214. г) (-оо;-2), (2; оо).
3 (2 — 4 х^ + э 1
215. в) \ 216. в) -1. 217. г) (-оо; 3), (3; оо). 218. г) На-
(1-х3)2
350 Ответы
и указания к упражнениям
пример, Зх3 - 4 х. 219. а) Нет.
221. в) f(x) = 2x+l, g(x) = x1.
л + 2лп], п е Z. 224. г) - —
(6х I)6
220. г) f(x) = Зх+ 71, g(x) = cosx.
4
222. в) [-0,5; 0,5]. 223. г) [2пп;
225. г) 65 (5х - 2)12 + 24 (4х + 7)“7.
226. в)
л + 2лп; 71 + 2лп
6 6
п е Z.
227. а) 3 - 2х2; в) (3 - 2х)2.
228. 6) -=К , [0; 1) U (1; оо); в) Vcosx, + 2лп; - + 2пп 1, п е Z.
Vx-1 L 2 2 J
229. б) f (х) = х2, D (Л = [0; оо); г) f (х) = - Л~1. 230. г) -15х2 (3 - х3)4 +
+ , 1 . 232. г) 2 cos х - 1,5 sin х. 233. в) - . 234. г) 0; -1.
•j2x-7 2 cos2 х
235. г) - |+ 2лп, п е Z. 237. б) -4 cos2x. 239. г) + л + лп, (- л + лп;
2 sin22x 12 I 12
+ лп , п 6 Z. 240. в) Например, f (х) = -sin х. 241 г) Да, да.
242. в) Я; г) (-оо; 2), (2; оо). 243. в) 0,7. Указание. Проверьте, что
/(0,8) < 0, /(0,6) > 0. 244. г) (-оо; 1), (2; 6). 245. в) (-оо; -4), [-2; -1),
[2; оо). 246. г) (-оо; -3] U (-1; 1) U [3; оо). 247. г) т > 0. 248. г) (-2; -1),
(1; 2). 249. в) (-2; 0), (0; 3); г) (-оо; -5], [2; оо). 250. в) (-оо; -4] U [0; 4].
253. в) 3. 254. г) 0. 255. г) у = Зх + 1, у = 12х - 17. 256. в) у = 2, у = 1 +
+ Л - х. 257. в) (-1; -1), (0; 2), (1; -1). 258. г) | - + 2лп; V2 (- + 2лп -1 Н,
2 ^4 \4 JJ
- 7 + 2лп; у 2 I 2лп + 1 - - 11, п е Z. 259. a) arctg 3 в точке (0; 0),
к 4 I 4 /)
л - arctg 6 в точках (- /З; 0) и (-/З; 0): г)
в точках
-^ + 2лп; 0j, neZ. 260. а)
4’
-л в точках f л + 2лп; ol, 2л
4 \2 /4
г) 56Л. 261. в) 24,52, -0,16;
г) 40,52, 9,86. 263 г) 2,0004. 264. г) 0,9302. 265. в) 0,526. 266. в) 0,1247.
267. a) (-t2 + 41 + 5) м/с; в) 5 с. 268. 35 м/с, 22 м/с2. 269. (61 — 4) рад/с,
20 рад/с. 270. а) 2,8 рад/с. 271. 121 см/с; а) - с; б) - с. 272. а) 6 с;
12 6
б) 18 м/с. 274. 22т. 275. а) 0,04 Н; б) 0,0025 Дж. 276. а) 65 г/см;
9 8/^ + 21
б) 125 г/см. 277. 0 < t < 2 . 278. при t > 0. 280. г) Возра-
3 V4z2-6t + 2l
стает на (-оо; -3], [3; оо); убывает на [-3; 3]. 281. в) Возрастает
на (-оо; —2], [2; оо), убывает на [-2; 2]. 283. г) График функции изобра-
жен на рисунке 6. 284. в) График функции изображен на рисунке 7.
286. г) f (х) = -Зх2 + 6х = Зх (2 - х), f (х) < 0 при всех х из промежутков
(-оо; 0) и (2; оо), следовательно, f убывает на [-2; 0] и [2; 3], f (-2) > 0,
f (0) 0, f (2) > 0, f (3) < 0, по теореме о корне уравнение имеет единст-
351 Ответы
и указания к упражнениям
венное решение на каждом из промежутков [-2; 0], [2; 3]. 287. б) х2, х4,
х5, х6, х7. 288. в) + ^ + 2лп, п е Z; г) ± 2. 290. в) xmax = -l, xmin = 0;
О
г) xmin = ±1- Хтах = °- 291- а> f'(x) = ~=; Г (х) Ф 0 ни при каких х;
2 у/х
f (х) не существует при х = 0, но эта точка не является внутренней для
промежутка [0; °°). 292. в) (~l)n + 1 • - + пп, п е Z; г) ±-у=. 293. в) ± 3;
6 /з
г) 0; ± 2. 295. г) График функции изображен на рисунке 8. 297. г) Гра-
фик функции изображен на рисунке 9. 298. г) Возрастает на (-оо; —1],
[5; оо), убывает на [-1; 5]. 300. в) D (f) = Е (/) = R; f — нечетная; f (х) = 0
при х = 0, х = ± ; f (х) > 0, если х е I ~ 0 j, х ef °° ь f (х) < 0»
352 Ответы
и указания к упражнениям
Рис. 11
если zej-0»; * Ц°: J’ ? возРастает на (-°°; ~2Ъ 12; °°);
f убывает на [-2; 2]; хтах = -2, f (-2) = 4 xmia = 2, f (2) = -4
г) D (f) = Е (f) = R; f — нечетная функция; f (х) = 0, если х = 0, х = ±
/ (х) > 0. если хе^-оо; хе^О; f (х) < 0, если xe^-J|; о),
х е °°^ f возрастает на [-1; 1], убывает на (-оо; -1], [1; оо); xmln = -1,
/(-1) = -2; xmax = 1, f (1) = 2. 301. в), г) Графики функций изображены
на рисунках 10, 11. 302. в), г) Графики функций изображены на рисун
ках 12, 13. 304. в) 2; г) 3. 305. в) max f(x) = f (2) = 56, min f (x) =
[0; 2] [0;2]
= f (1) = -2; max f (x) = f (3) = 594, min f (x) = f (2) = 56; r) max f (x) =
[2:3] [2:3] [3;2]
= /(-2) = 2, min /(x) = f(-3) = l,5; min f (x) = /(1) = max f (x) = f (5) _
[-3; -2] [1;5] 2 [1;5] ''
= -. 307. 6 c. 72 м/с. 308. min f (x) = f (-2) = 9, max f (x) = f(2) ~ 2e
6 [ 2; 5] [-2; 5]
353 Ответы и указания к упражнениям
309. 10 с. 310. в) max f (х) = f fn1=3 -
3nl 'Ы 2 ’
L 2 J
min /(*) = /[Зя] =-2; г) max f(x} =
[о:3л] V Z [-5; 2,5]
= /(-3) = -4, min f(x) = f (—51 = —5 1 .
I 5; 2,5] 3
311. 24 = 12 + 12. 312. 4 = 2 + 2. 313. 12 м,
12 м. 314. 54 = 12 + 24 + 18. 315. 16 = 4 • 4.
316. 8 см, 8 см. 317. Высота — 1,5 дм,
сторона основания — Здм. Решение.
Пусть х — сторона основания бака (х > 0).
Выразим его высоту через объем и сторону
13 5
основания. 13,5 = х2 • Л, h = . Найдем
х2
поверхность бака S = х2 + 4х
13,5 2 54
= х^ +
X2 Х
Найдем наименьшее значе-
ние функции S(x) = x2 +
54
на промежутке (0; оо). S' (х) = 2х - ,
v2
х = 3 — критическая точка. Функция убывает на (0; 3], возрастает
на [3; оо). Следовательно, min S (х) = S (3) = 27. 318. 30 см, 20 см.
(0; «)
319. 20л/2см, 20-^2 см. 320. В точку, удаленную на Зкм от населен-
ного пункта и на 12 км от точки шоссе, ближайшей к буровой выш-
ке. 321. К точке отрезка АВ, удаленной от В на 1 км. 322. -0,5.
324. Квадрат.
Глава III
327. г) Нет. 329. в; Например, -4х. 331. в) Нет. 332. в) Например, х.
334. г) f(x) = 3 - 2 sin х. 336. в) х + 1 + С. 337. г) -cos х - 2.
Зх3
339. в) -cos^x+^-2. 341. г) x(t) = -cosf. 343. г) -sin^-^+C.
344. в) - 4 + С. 345. г) - 1 - 2х5 + Зх + 4,5. 346. в) tg (Зх + 1) -
3(Зх-1) 2х2 3
- 3 cos (4 — х) + х2 + С. 347. г)-— + -х2-41. 348. x(t) - * t3 + t2 - t.
3 2 3 3
349. x(t) = 4 sin * + 2. 350. x (t) = t4 + 2t2 + 21 + 7. 351. r) x(t) = Ч3 +
2 3
+ iz + t-l2. 352. в) -2; второй. 353. в) 2; г) -. 354. в) 10 2; г) д +1.
3 2 3
354 Ответы и указания к упражнениям
355. в) 1 l. 356. в) ^З--. 357. г) 1. 358. в) 0,9. 360. г) 10 2.
3 4 3 3
361. г) 5 1 .
3
362. г) 4. 363. в) 364. г> /3-J. 365. г) 4,5.
366.
г) 1 . 367 5 1. 368. 4,5. 369. а)
12 3
Пусть F (х) — первообразная для
f (х), G (х) — первообразная для g (х). Тогда F (х) + G (х) — первообраз-
ft ft
ная для f (х) + g (х). Поэтому Г (f (х) + g (х)) dx = (F(x)+ G (х)) = F(b) +
а
а
b b
+ G(b)~ F(a)-G(a) = F(b) - F(a) + G (b) - G (a) = j f(x) dx + j^(x) dx.
a a
370. r) 16n. 371. r) 372. a) nH* (3R-H); 6) (R2 + Rr + r2).
15 6 3 3
373, 374. 0,16 Дж. 375. yq [ - — - Указание. F(x) = -^, где
\ b a J хг
b
376. ^h2 Pg.
a
b
у > 0 — постоянная.
a
Указание. Сила давления жидкости на погруженную в нее пластин-
ft 2
ку (вертикальную) вычисляется по формуле P = pg J S(x)dx, где
fti
S (х) — площадь пластинки, глубина погружения h меняется от до Л2.
377. ПГ Л -g. 378. л/}4pg. 379. Р^ы [ = 4 160000п2 эрг. Решение.
2 3 6
Масса части стержня, отмеченная на рисунке 14, равна pS Дх; пренебрега-
ем диаметром стержня (считаем отмеченную часть отрезком длиной Дх),
тогда с точностью до величин порядка Дх линейная скорость каждой точки
этой части равна сох. Обозначим через Е (х) кинетическую энергию части
[0; х] стержня. Приращение кинетической энергии за счет отрезка [х; х + Дх]
mv2 рЯсо2х2Дх pSro2x2
приблизительно равно , т. е. - - , поэтому Е (х)= - — ;
, т. е.
I
£(0) = 0, и, следовательно, искомая энергия есть E(l} = J Е (x)dx =
0
= | pS(o2x2dx = pS(o2| х2 dx= pS^l2
о о
380. Точка высоты конуса, находящаяся
на расстоянии высоты, считая от его
вершины.
Дх
Рис. 14
355 Ответы и указания к упражнениям
Глава IV
384. в) 386. в) ±2. 387. г) ±V17. 388. г) -1. 391. в) 6. 392. г) -5.
393. г) 2. 394. в) 395. г) 1,44. 396. г) 2,22. 397. в) 1,29. 399. в),
4
г) Первое меньше. 400. в), г) Первое больше. 401. в) Первое больше.
402. в) аяЬ^6Ь2.403. г) Mia3 Ь3.404. в) а > 0; г) а > 0. 405. а) а = 0;
б) а < 0; г) при всех а. 406. г) . 407. г) . 408. г) 5 л/4.
5 3
409. г) ~ 127320. 410. г) 6е. 411. г) (-оо; 37б]. 412. г) [0; 81]. 414. в) 0.
415. г) 2. 416. в) + 417. в) ±6. 418. г) 8. 419. г) 0,
6
-1. 420. в) -10; 2. 421. в) (16; 81). 422. г) 0; 0,4. 424. г) -12.
425. г) +2. 426. в) (16; 4), (36; 1^. 427. г) (27; 1), (-1;-27).
_7 1 1 1
428. г) л/б-3 . 429. в) b 13 . 430. в) 32. 431. в) 12®. 432. г) х2 (З2 - 52 ).
1 1 1 11
433. г) (а2 + Ь2 )(а2 + 1). 434. г) а3 + Ь3 . 435. г) х- 1. 436. г) Первое
меньше. 437. г) 10. 438. г) --J . 440. г) 2\b7c6. 441. в) Равны.
V2 т
442. г) Нет. 443. в) (0; оо). 444. в) а = ±1; г) а = 0. 446. г) (—2; оо).
447. г) Первое меньше. 448. г) 9.450. г) | хк - уп |. 451. в) 169,8; 173.8.
452. 10'5 »172,4. 453. г) i/ = (3-V7)x
— убывает, у =
— возра-
стает. 454. г) [1; оо). 455.
. . .2
г) -1; -1 -.
3
457. в) 0; г)
1. Указание. С по-
мощью эскизов графиков «угадываем» абсциссу точки пересечения х = 1,
остается доказать, что других точек пересечения нет. Для этого восполь-
зуемся свойствами соответствующих показательной и линейной функ-
ций. При х > 1 функция у = 4х принимает значения, большие 4, а функ-
ция у = 5 - х — меньшие 4. (При х < 1 функции принимают соответст-
венно значения — меньшие и большие 4.) Следовательно, других точек
пересечения графики не имеют. 458. г) -1. 461. в) 4; г) 462. в) 4;
г) -3; 1. 463. в) 3; г) -1. 464. в)
466. в) [2; оо); г) (-оо; 2). 467. в)
469. а) -1; в) 2. 470. в) 2; г)
472. в) [-3;-1]; г) (-оо; -|1
' о J
1; г) 1; 0. 465. в) (-2; -3); г) I *; 4^.
(-оо; 0,5); г) (-1; оо). 468. в) -2; г) 2.
2. 471. в) (1; 2), (2; 1); г) (2; 1,5).
(4; оо). 473. в) (-2; оо); г) (-оо; 1).
356 Ответы и j i.aзания к упражнениям
474. в) (2; оо); г) [-1; оо). 475. в) (-оо; 0]; г) [1; оо). 484. г)
49
485. г) 8. 486. г) 3. 487. г) log5 5, log5 1 , log5 1, log5 125. 489. г)
25 2
490. г) --. 491. г) 2 log3 b - 3 - 7 log, а. 493. г) - 1g с - 7 - 1g а - 8 lg b.
25 4 3
2
494. г) 1 + а + Ъ. 496. в) -2. 497. в) г1&”3 . 498. в) Решение. Рас-
Р4
смотрим разность между выражениями, содержащимися в левой и пра-
вой частях неравенства, сравним ее с нулем: log3 7 + - - 2 =
log7 3
log2 7-2 log3 7 +1
log7 3
(1—log, 7)2
------- — >0. г) Решение. Преобразуем ле-
log7 3
log23
----log 2 5
rvto чяеть пяяянствя- 4log2® - ( 5log 5 3 'Ilog2 5 - 5log5 3 log2 5 _ 5log25
x>y±O Hilvlb pciHvxiV 1 oct. О — — «J
= 5log23. 499. r) (—oo; -4) U (4; oo). 500. в)
2;211
3 2J
502. в), г) Первое
меньше. 503. в), г) Первое больше. 505. в) ^-^ + 2лп; + 2лп j, п е Z.
506. в), г) 0. 507. г) График функции изображен на рисунке 15. 508. г) л-2.
509. в) 5. 510. г) Нет. 511. в) 0; -1. 512. в) log2 10. 513. г) 100.
514. в) -2,35. 515. в) 2 - log3 2. 516. в) (0,7; оо). 517. в) (8; оо); г) (12; оо).
3
518. в) 5; г) 0. 519. в) 2; г) 0; 8. 520. в) 25, -; г) 27, 521. в) (32; 2),
5 3
(2; 32); г) (1; 1). 522. в) 4; г) 100, 108. 523. в) 9; г) |. 524. в) 2; г) 2.
526. в) (1; 3); г) (-4; -3) U (4; 5). 527. в) (0; 0,001) U (10; оо); г) [i; 27^.
528. в) (--j + тгп; - + лп^ U + лп; + ли J, п е Z; г) (^/0,1; 10).
357 Ответы и указания н упражнениям
529. в) 3 1; г) (9; 7). 530. в) (2; 6); г) (9; 6). 531. в) g(x)=T Х
D (g) = Е (g) = R. 532. г) g(x) = x2- 1, D (g) = [0; оо), Е (g) = [-1; оо).
533. г) График изображен на рисунке 16. 535. в) g(x) = x'*, х С 0;
г) g(x) = 3у!х - 1 538. в) -^₽х. 539. г) 2хех + х2ех. 540. в) у = 1 + х;
г) у = - - -(х-1)1п2. 541. г) 1ех+х+С. 542. в) 7 - 2,5247.
2 2 2 41п2
543. г) -2 х
In 2 ctgx + -----
3 3 sin* -
3
544.
3X(2X In 1,5 + 5х ln0,6)
(2х + 5х)2
545. в) Возрастает на (-оо; 1], убывает на [1; оо); х „ = 1, /(1)= -.
max Р
546. г) 1 е3х+2,3X1 + С. 547. г) 1е2-е+1. 548. в) 3 -2=2,3.
3 1п2,3 2 2 1п2
549. в) — . 550. г) 1пх-1_ 551. в) 1п|х + 2| + С. 552. г) у=Х~2.
1+5х 1п^ х In2
553. г) 1 In 10 = 0,7675. 554. в) х(2 1п5х-1) 555 в) убывает на f0; 1],
3 ln25x I 2J’
возрастает на
= 1+1п2. 556.
убывает
557. в) 1
2
[W r(|J-
в) Возрастает на (0; е2],
на [е2; оо), xmax = ег, f(e2)=^.
1п8 = 1,0397. 558. г)-Тбх <5 ь.
График изображен на рисунке 17.
559. г) 2 In 3 • (2х)1п 3 *, график изобра-
жен на рисунке 18. 560. г) 2,63.
561. г) 2,0125. 562. г) 27, Х. 563. г) *₽ + 1 + С.
8 е+1
358 Ответы
и указания к упражнениям
564. г) 844. 565. г) In 1 2 = 0,5108. 567. в) Нет; г) х0 = 0. 572. г) На-
О
пример, j/ = 2cos^. 573. в) х" = -9х. 575. в) *ln2 . 576. 9 мин.
2 Inzn-lnn
577. , 1 ч = 3,322 ч; 0,6394. 578. 10 lg2 мин ~ 14,75 мин. 580. 500е“5 м/мин «
lg2 lgl.6
= 3,37 м/мин.
Глава V
1. а) Да; б), в) нет; г) да. 3. а) 52 305; 52 335; 52 365; 52 395; 52 320;
52 350; 52 380; б) 52 344. 5. 35. 6. Указание. Пусть дробь —— - сокра-
а + Ь
тима на число d, d — делитель ab, поэтому существует общий делитель d'
либо у чисел a, d, либо у чисел b, d; пусть для определенности d' — дели-
тель a vl d, тогда а + b делится на </', следовательно, b делится на d', зна-
чит, дробь — сократима на d'. 13. в) 1 ® . 14. а) Пусть -J5 = —, р е Z,
Ь 90 Q
Р Р
q е N, - — несократимая дробь, — > 0, поэтому можно считать, что р
Я Я
Р2
и q — натуральные числа. Тогда 5 = —, т. е. р2 = 5q2, откуда следует,
q2
что р2, следовательно, и р делятся на 5, т. е. р = 5/г. Подставляя р = 5k в ра-
венство р2 = 5q2, получим 25/г2 = 5<у2, q2 = 5k2. Из последнего равенства
видно, что q делится на 5. Получили противоречие со сделанным предполо-
р I—
жением: оказалось, что дробь сократима на 5; в) если у 5 + 1 = г (где г ра-
q
ционально), тогда V5 = г - 1 рационально, что противоречит иррациональ-
ности -Уб. 19. а) Равны; в) первое меньше; г) первое больше. 31. 87 или 69.
32. 0. 34. Ьг = 0,2; q = 5. 36. 5. 37. 12,5; 7,5; 4,5; 1,5 или 2; 4; 8; 12.
38. 9 = 1- jL; S = 3. 39. b, =6; 9 = 0,5. 43. г) ——. 44. г) 2. 45. г) 3.
V3 У
1 1 1
47. в) 1; г) 1. 48. в) Jp^l. 49. г) -t/a-Vb. 50. б) аЬ4(а4+Ь4);
2,5 1
г) ------. 51. в) с2: г) 3. 52. б) |sin р + cos р|; г) sin р. 53. в) 1.
с2 + 2
58. б) 1——; г) sinct = -2—2; cos — = —cos2a = - —. 59. а) 0.
1+m 3 2 7з 9
60. а) Меньше 0.
61. 1. 62. г) Первое больше. 63. в) Первое больше.
359
Ответы и указания к упражнениям
64. a) 4 3. 65. б) 0,34. 66. в) -3; г) 1. 67. б) 4 + 4 log0 , Ь - - log0 2 с.
4 ' 7
68. б) 14. 69. г) 365,06446. 70. 1g 2 = 0,3010. 71. 2 - А. 73. б) S = 3 ^—g—
77. в) (-оо;-v/5)U(-V5;-2)U(-2;2)U(2;^/5)U(V5;o°). 80. в) f(x} > 0
на
-оо. 8
3
; оо), f(x) < 0 на
. 81. г) Убывает на (-оо; 1) и на
(1; оо). 85. г) См. рис. 19. 86. а) См. рис. 20. 88. в) Пусть f (х) = хъ + Зх - 5,
f (х) непрерывна, при этом f (1) = -1 < 0, f (2) = 33 > 0. 91. а = 3,
Ь = -5. 92. в) а > 0, b < 0, с > 0, D <. 0; г) а < 0, b < 0, с = 0, D > 0;
д) а < 0, b < 0, с < 0, D < 0. 93. а) Могут (квадратичная вида у = ах2 + b
х2
и линейная вида у = Ь). 94. в) у = — - +-----. 96. в) Все числа, кро-
х4 - 1 х2 + 1
ме чисел вида ± - + 2лп, п е Z. 97. в) — + лп; — + лп I, п е Z.
6 |_4 4 J
98. г) [-1; 1]. 99. г) (-оо;-2] U [2; оо). 100. в) у>0 на (-£1 + 4лп;
5 + 4пп),
у < 0 на
+ 4лп;
3 - + 4лп |, п 6 Z. 101. в) Нечетная; г) чет-
ная. 102. г) л. 103. в) Убывает на + ли; + лпJ, возрастает на
[- — + лп; — + лп , Х-;,, = + лп, x_,„v = — + лп, п е Z. 104. г) min у = 1,
3 6 J 3 6 D(J/)
max у не существует. 105. б) Указание. j/ = |sinx|. 108. Да.
£>(«)
109 в) tg 2 < -1 < ctg 2. 111. в) 0; г) 0. 112. в) (-оо; 0) U [1; 4].
[9 1
; 2 U (2; оо).
3 )
115. г) (0; оо). 116. в) [1; оо). 117. в) у 0 на (-оо; log3 2), у < 0
на (log3 2; оо). 118. в) у > 0 на [0; оо). 119. в) Ни четная, ни нечетная.
360 Ответы и уклл.1 ния к упражнениям
120. в) Четная. 123. а) Указание, у = х - 1 при х > 1, D (у) = (1; °°)-
124. г) min у = у (1) = 0, max у = у (-1) = 4. 125. г) +3. 126. г) (О; 3).
[-1; 8] [-1; 8]
128. а) О; -6-—. 133. г) Г14; оо]. 134. в) [1; 13]; г) [-1; 5]. 135. г) -3,5
8 |_ 11 )
и [3; оо). 137. в) -6; г) 2; —. 138. а) 1; 2; -7-; в) 4; г) О; -1; 3.
99 3 2
139. а) в) —; г) —. 140. в) --; г) -4; -. 141. в) -1; г) 1.
3 9 27 3 3
142. в) (-оо; оо); г) (1; 13). 143. г) (-оо; -4) U (6; оо). 144. в) (1; 3) U
и (3; 5); г) (3; 4). 146. в) 2; г) -4; 4. 147. в) 18; г) 63. 148. в) 4;
г) -|; 0. 149. в) -8; 8; г) -1; -3. 150. в) (—оо; — V17] U [V17; оо);
о
Q
г) (9; оо). 151. в) [2; 3]; г) [-3; 5]. 152. а) -л + 2лп; ±arccos + 2лп,
4
тг 1 4
п 6 Z; б)---- arccos + пп (или arctg 0,5 + пп, п е Z — другая форма
ответа); г) arctg 0,5 + пп, п е Z. 153. в) ± ~ + пп, п е Z; г) (-1)" х
х arcsin ~ + пп, п е Z. 154. в) + пп, -+™, neZ; г) 2пп, 2 • (-1)" х
у[3 2 4 2
х arcsin 1 + 2пп, п е Z. 155. в) —, п е Z; г) - + л-, - л + пп, п е Z.
3 2 6 3 4
156. в) (-1)" J + пп, п е Z; г) (-1)" - + пп, n&Z. 157. в) (-1)п + 1 J + пп,
п 6 Z; г) пп;
159. в) f|"
к 10
± - + 2пп, п е Z.
3
4лп. 8л + 4пп
5 ’ 15 Т/
158. а) --; б)
4
п е Z; г) - — +
0; в) -2^3-2; г) 0.
пп
2
П ! ПП
12 2
п е Z.
160. в)
— + пп-, — + пп
6 6
п е Z; г)
-п + 2пп;~ — + 2пп U
2 J
— + 2лп; л + 2пп
2
neZ. 161. а)
- + 2лп , п е Z; в)
3 J
пп , п е Z; г) (ли;
- — + 2лп;
L 3
л
2
л + пп ], п е Z. 162. а) I 2л + 2пп; п + 2пп 1, п е Z; в) f л + 2пп; 2 л + 2пп
2 / к 3 / к 2
neZ; г) f-^ + 2пп; + 2лп ], neZ. 163. в) 1; 5; г) 3; 9. 164. в) 2; г) 1.
165. в) 3; г) 0; -. 166. в) ± log5 2; г) 0; 1. 167. б) ±arccos «2 - 1) +
4 2 2
+ 2лп, neZ; г) -1. 168. в) (-оо; -г) (-оо; -4) U (3; оо). 169. в) (1; 3);
г) (-оо; -1] и [0; оо). 170. б) (-5; 3) U (4; оо). 171. в) 6; г) 1001; 1 + V10.
172. в) 10; г) 3. 173. г) 64. 174. в) 100; - 1 ; г) 3; 9. 175. а) (-1)" - + пп,
Ответы и указания к } пражнениям
n eZ; б) arcsin + 2пп, neZ.
14
176. а) ( - 3; 1 17 ] U f г—-V17 ; 4
\ 2 ) I 2 )
Г)('/7-2:2^ 177- а) (0; 6); г) (1; 2] U [3; 4). 178. в) (2; оо);
г) | |; оо J. 179. в) (0; 0,1] U [100; оо); г) (-оо; 0] U [log6 5; 1). 180. в) | ® J;
г) 0. 181. в) (0,4; 0,8), г) (2; 3): (3; 2) 182. в) (0,5; 4); г) (7; 3);
(-Г.-3). 183. в) (1; 2); (2; 1); г) (J; -И; Р; 185. в) [-3;
г) (-3,5; 0). 186. в) (25; 49); г) (9; 16); (16; 9). 187. в) (16; 4); г) (16; 4);
(-4;-16). 188. в) (81; 16); г) (-1;-8); (-8; -1). 189. а) -(-1)* ~ +
+ лп-^; — + (—1)^+ лп + —— 1, Л, neZ; б) - *;
2 4 12 2 ) 12 6
" +
2 6/
п 6 Z;
+ лп
+ nk; — + лп - nk
3
- + пп + nk;
3
- — + лп - nk , k, п e Z;
3 )
л + nk
4 2
k, п е Z. 190. б) лп;
— + (-1)" --пп
2 6
п е Z; в)
71 + пп + nk; — + пп - nk , - — + лп + nk;
6 6 л 6
k е Z, п е Z; г)
f — + пп; - пп I я + 2пп; —-2лп
12 } {3 6
- л + 2лп; 5п - 2лп |, и е Z. 191. а) (2; 1); б) (5; 4); в) (5; 1); г) (3: 0).
3 6 )
192. а) (1; 3); б) (3; 2); в) (2; 0); г) (2; 6). 193. а) (2; 1); (log3 7; log7 9);
б) (4; 1). 194. а) (100; 10); (0,1; 0,01); (4; 4); в) (1 000 000; 0,1);
г) f |; 1). 195. а) (27; 4); (Д; -з); б) (2; -1); в) (125; 4); (625; 3); г) (3; 2).
196. а) (4; 2); б) (25; 36); в) (1; 1); (4; 2); г) (512: 1). 197. 75 км/ч.
198. 4 км/ч. 199. 55 км/ч. 200. 18 км/ч, 24 км/ч. 201. 10 с. 202. 240 м3.
203. 6 и 12 дней. 204. 20. 205. 25%. 206. 160 г, 20%. 207. 60 км/ч.
208. 21 м/с, 147 м. 209. 6 км/ч, 4 км/ч. 210. 20; 30. 211. 20 и 30 дней.
212. 12 г, 48 г, 1,5 г/см3. 213. Зкг, 80%. 214. 4 м/с, 3 м/с. 215. 32.
216. 8
и 3; 28 и 27. 218. в) 3; г) 3. 219. г)
(х3 — 2) sinx + Зх2 cos х
(2-х3)2
220. г)
COSX’2 .221. г)
(1-2 cos х)2
ех + е х
х(ех - е ж)1пх
х< ех + е х)2
222. г) —1—
х 1п 10
______6_______
cos2 ^2х - )
223. г) (-1)" — + гп,
12 2
п 6 Z. 225. в) Г (х2) = f (х4);
л | nk
4 2
- - + пп - nk
6
г) Г (х3) < 0 < f (х5). 228. б) 25,375; 9,84. 229.
в) 1,005; г) 2+ 1
1500
362 Ответы и указания к упражнениям
Рис. 21
— 2,00067. 230. в) Возрастает на [1; оо), убывает на (-оо; 1], xmjn = 1;
г) возрастает на (-оо; 4) и (4; оо). 231. в) Возрастает на --^ + 2лп;
+ 2лп^, + 2лп; ~+ 2 лп], убывает на + 2лп; + 2 лп], + 2лп;
^ + 2лп^, хтах = ~ + 2лп, xmax = ^ + 2nn, xmin = | + лп, п g Z; г) воз-
растает на (-оо; оо). 232. а), б) См. рис. 21. 234. а), б) См. рис. 22.
363 Ответы и указания к упражнениям
235. в) max f = f | - | = 4min/ = f(l)=3, r) max / = /(-л) = л,
[l:i] [2J 4 * [j; il. [“л:л]
min f = f(n) = -n. 236. a) 10 + 0; 6) 5 + 5. 237. 10 cm, 10 cm. 238. 72 cm2.
239. - ч. 240. 2,4 m. 241. 4 V2 m. 242. h = 2r. 243. 245. R = 1,5 ч.
410 y[3
246. 4Л. 247. Н = Н/3. 248. b = см, h = 40,, 2 см. 249. R = ——;
V3 V 3 71 + 4
р
Н =-----. 250. На расстоянии 1,5/? от точки касания. 251. 60°.
л + 4
252. М(1; 1). 253. 254. а) (в; |j; б) (6; оо). 255. 3,5 рад/с.
256. 0,04л см2/с. 257. 8 км/ч. 258. |и|=1,5м/с. 259. — м/с,
v25-4t2
Юв м/с2. 260. 1) 360 г; 5х г/см; 2) 0; 60 г/см. 261. Зл рад/с.
V(25-4t2)3
262. а) 85 м; б) 4 с, 90 м. 263. а) М (-1; -1,5); б) М (1; -1,5).
264. - —; 0. 266. f (х) = 5х4 + 2 > 0 для любого х. 268. bj 2х + 3 In |х — 11 + С;
3
г) tg 2х - ctg Зх + С. 269. в)-1-2 —; г) - — cos 2х + —. 270. х2 - Зх + 4.
6 6 Зх3 24 2 2
364 Ответы
и указания к упражнениям
274. a) 2; -2; б) 0,5; -0,5.
278. -. 279. 2; 1. 280. 8
3 3
275. в) 4 ; г) 9. 276. 18 и 74. 277. 10 2.
3 3 3
Решение. Указанная фигура закрашена
на рисунке (рис. 23, а соответствует а < 2, а рис. 23, б соответствует
а > 2). При а < 2 площадь этой фигуры меньше площади квадрата ОАВС,
2 / \ 2
Г 9 I 9 I
равной 4, а при а > 2 <S = I (х2 + 4х + a) dx - = 1 — - + 2х2 + ах -
J \ О /
0 0
о 20 20 8
-4 = -+8 + 2а-4 = 2а + , следовательно, 2а + - =12, откуда а = —.
3 3 3 3
281. а = 2, 5 = 2.
71
Глава VI
1. г) Указание, п2 + 5п + 16 = (п - 4)2 + 13п делится на 13 только при
п = 135 + 4, но тогда (п - 4)2 делится на 169, а 13п нет. 2. ±5; ±7.
N N
3. б) Указание. Если d — делитель N, то — делитель N, причем d = -
d d
только при N = d2. 4. в) (04 + 1) (а2 + 1) ... (аА + 1). 5. б) Нет; в) нет;
г) нет. Указание. N дает остаток 2 при делении на 3 (см. а)). 6. а) Нет:
число делится на 3 и не делится на 9; б) 9. Указание.
Ь < 1987 • 9 = 17 883, с < 9 • 4 + 1 = 37, d < 11 и d делится на 9.
8. а) (х; у) = (0; 0). Указание. См. № 5, а; б) (0; 0); (1; 1); (1;-1).
Указание. При х > 2 число у2 должно иметь остаток 3 от деления на 4
(см. № 5, а); в) (46; 45); (46; -45); (-46; -45); (-46; 45); (10; 3); (10; -3);
(-10;-3); (-10; 3). Указание, (х + у) и (х - у) — делители числа 91;
г) (3; 3); (3; -3). Указание. Числа (у - 1) и (у + 1) — степени числа 2
при х > 0. 9. a) (7k + 1; 13* + 1), k е Z; б) (1; 1); г) (1; 1); (1; -1); (3; 3);
(3; -3). Указание. При х > 4 число 1! + 2! + ... + х! оканчивается на 3.
10. ±13. 11. 210; 4. Указание. 1g 2~ 0,30103, 1g 5 = 1 - 1g 2 ~ 0,69897
(с точностью до 0,00001) и lg 125100 = 300 1g 5 ~ 209,691. Если число N со-
держит k цифр, то k - 1 < lg N < k. Кроме того, lg 4 < 0,691 < lg 5.
14. б) Указание. 4 + 1 + 4 > 4 .17. Указание. Вес-
Зп + 2 Зп+З За+ 4 п+1
конечная периодическая десятичная дробь есть сумма конечной десятич-
ной дроби и суммы бесконечной геометрической прогрессии со знамена-
телем 10*, где k — число цифр в периоде. 19. а) Да; б) да (пример:
(V2)2 log23 = 3). 20. б) Предположим, что З43 = где р е Z, q е N,
365 Отпеты и \ । 1ания к упражнениям
р р ° о о
— несократимая дробь. Тогда 3 = , т. е. р = 3q' , откуда следует, что р
Ч Ч
делится на 3. Подставляя р - 3k в равенство р3 = 3qa, получаем 27k3 = 3qa,
т. е. 9Л3 = qa. Из последнего равенства видно, что q делится на 3. Получили
р Р
противоречие: дробь сократима на 3; в) допустим, что 1g 5 = , при этом,
Я Я
учитывая, что 1g 5 > О, можно считать, что р и q — натуральные числа.
₽
Из равенства 1g 5 = ? получаем 109 =5, откуда 10₽ = 59, а это равенство
Я
ложно: его левая часть четна, а правая нет. 21. а) Пусть -/3 + -/б = г, где
__j.2 _ g
г — рациональное число. Тогда 3 + 2 v 3 -Уб + 5 = г2, откуда -715 = —-—,
что противоречит иррациональности 715. 22. б) Указание. Пусть k —
длина периода этой дроби. Рассмотрим k цифр, начиная с цифры, следую-
щей за k-й двойкой. Все эти цифры — семерки, поэтому период этой дроби
должен быть равен (77... 77), что неверно: в этом случае все следующие
* ЦИ<1]р J~3 1
цифры должны быть равны семи. 23. а) —7=—; б) 4-75 -7; в) -Тб + у 2;
V2
г) 2 ^3 + 3 -Уб. 24. а) 6; б) <3 - -J7. 25. Указание, а) Избавьтесь
сначала от 3/3 : (-72 + Vs] f(V2)2 - у/2 • З<3 + (37з j2 ) = (V2)3 + (37з)3 =
= 2 -72 + 3; б) сначала умножьте числитель и знаменатель на <2 + у[з - Уб;
в) воспользуйтесь
н и е. Возведением
корень уравнения
результатом № 29, е. 26. а), б) Нет. 27. Указа-
есть
х3 - 5х - 12 = 0, а это уравнение имеет только один
действительный корень х — 3. Следовательно, данное число равно 3.
28. Указание. Для любого натурального k имеем:
2* + 1 2* + 2 2* + 1 2* + 1 2А + 1
2* + 1 2
29. а) (х2 - 2х + 2) (х2 + 2х + 2); б) (х2 + х + 1) (х2 - х + 1); в) (х2 + х + 1) х
х (х3 - х2 + 1); г) 3 (х2 + j/2) (у2 + г2) (х - z) (х + z); д) 3 (у + г) (г + х) (х + у);
е) (х + у + г) (х2 + у2 + z2 - ху - yz - гх). 33. а) Пусть а = arccos х, тогда
fcosa = x, я л л .Гл 1
s и, во-первых, - - < — - a С —, а во-вторых, sin — - a =
[О < а < л, 2 2 2 12 )
= cos а = х, следовательно,--а = arcsin х по определению арксинуса чис-
366 Ответы и указания к упражнениям
ла х. 34. а) 1.; б) 1 - % (т2 -1)2; в) 1 ; г) . 35. а) зп _ ю;
V3 4 16 2
б) 4л — 12; в) 2 — л; г) 3. 36. Указание. Воспользуйтесь формулой
tg«=_si"« . 39. а) _ abc----. б) ab+l
2 1 + cos a ab + ас + Ьс а (8 - 5fc)
40. а) Указание.
Логарифмы обеих частей по основанию 2 равны; б) 0. 41. 7. 43. 2; -6;
п
18; -54. 44. 931. 45. а > 12. 46. 1 или -2. 47. 0. 48. ( —I2.
I BJ
49. а50 > Ь50. 50. а) Указание. 99 ... 99 = 10* - 1; б) указание.
k цифр
S - Sx = х + х2 + ... + хп - пхп + *; в) —--—. 51. а) х*~, п е Z;
k k + n 4
в) [-2; -1) и (1; 2]; г) Л; е) (-V2; - 1)и(1; ^2). 52. б) [-2; 1];
г) Г-i; 11; з) [-2; 2]; к) [-2; 2]; л) [0; 4]. 53. а) Г-Ь 21; в) [-6; 4];
L 2 J L 4
г)
. 54. в)
- —; 5 I; г) [0; 1). 56. в) f (х) = 0 для любого х е D (f),
«5 J
причем D (/) симметрична относительно точки 0. 59. а) Да (например,
функция Дирихле — значение этой функции равно 1, если х рациональ-
но, и 0, если х иррационально); б) нет (если бы такая функция сущест-
вовала, то для нее числа 42 и 1 - 42 должны быть периодами, а их сум-
ма 1 нет). 60. Указание, а) Значение 1 функция принимает только
в одной точке — точке 0. 61. б) —;
в) 2 л 42;
г)1.
2
63. Указание.
a) log2 3 > 1,5 > log5 8. 64. a) ctg 6; cos 2; tg 3; sin 4°. 67. а) При лю-
бом n; б) при четном n; в) таких п нет. 68. a) f (х) = Ь или f (х) - х;
Ответы и указания к упражнениям
6) f (x) = x или f (x) = b - x. 69. a) x при четном n, 3 - x при нечетном n,
1 x — 1
область определения R; в) x при n вида 3k,- при n вида 3k + 1 и-
1 - x x
при п вида 3k + 2; D (f) = (-оо; 1) U (1; оо) при п = 1 и D (fn) = (-оо; 0) U
U (0; 1) и (1; оо) при п > 2. 70. а) у = —, а * 0; б) у = х или у = ах + (при
ах сх - а
Ьс * -а2). 71. См., например, рис. 24. 75. Нельзя дополнить: б) до четной;
а) и б) до нечетной функции. 76. а) Г > 2; б) Т = 3, Т > То, где То = 6,5;
в) Т > То, где То = 5. 77. См. рис. 25. 81. a) minf = -l; max f = 2:
R R
б) наименьшего значения не существует; тах/=1. 83. в) у = х - 1 при
R
х —► оо, у = -х - 1 при х —► -оо; г) у = 1, х = 3, х = -3. 84. в) Указание.
у = tg х при sin х > 0 и у = -tg х при sin х < 0. 90. а) 1; б) 1; в) 3;
г) 14. 91. а) а > 0, Ь > 0, с < 0, d > 0; б) а > 0, b < 0, с > 0, d > 0.
92. а) Пара прямых х = 0 и у = 2; б) у = х2 — 2х и у = 2х — х2 (две пара-
ху + 1 у + 1 р(1 - х)
болы). 94. См. рис. 26; г) указание.-->----- •» ------- — >0.
ху-1 у - 1 (ху- 1)(р- 1)
95. б) (х2 — 1) (у2 - 1) = 0 — 4 прямых. 96. в), г) См. рис. 27. 97. а) а < 0
и а > 4, разных знаков при а<-^, положительны при а > 4, отрица-
тельны при - 1 < а «s 0. 98. а) 2 < а < 5. 99. р2 - 2ц\ г) р4 - 4р2<? + 2?2.
Указание. Примените теорему Виета. 100. а) р = 0; б) таких а нет.
368 Ответи и ук ипния к упражнение е
369 Ответы
и указания к упражнениям
101. a + b + c = f (1) * 0, поэтому c = f (0) < 0. 102. Указание. Дока-
жите, что этот корень 1, тогда в + 6 + с = 0их=1 — корень уравнения
2 Р
сх + Ьх + а = 0. 103. Указание, а) Подставьте х0 = в уравнение и вос-
9
пользуйтесь тем, что числа р и q взаимно простые; б) представьте Р (х)
в виде Р (х) = Q (х) (х - а) + г, где г — остаток от деления Р (х) на х - а
(число!), подставляя х = а, получаем Р (а) = г. 104. в) ±1; г) -3;
5 Л + 4 л/101 Пчч
0,5. 105. в) ±------g----’ г) Ю6- г) Указание.
(х2 + Зх + 2) (х2 - 9х + 20) = (х + 1) (х + 2) (х - 4) (х - 5) = (х2 - Зх - 4) х
х (х2 - Зх - 10). Пусть у = х2 - Зх + 1, тогда у (у - 5) {у - 11) = -30, откуда
(см. № 103) уг = 6, у2 з = 5 ± Ло. 107. а) 1, -2 ± Л; б) 1; 3; ~9±^33.
108. а) 2;
в) -1; 2;
1.
2’
б) указание.
Пусть
г) 1 + Л + ^2 Л + 5. 109.
у = х + —, тогда 2j/2 + у — 7 = 0;
X
5 1± Л+ 2/1057
.>2; '
110. Указание, а) (х2 + I)2 = 2 (х - I)2, откуда х2 + 1 = ± Л (х - 1);
б) один из способов решения — свести к а) заменой у=-- 111. а) 2; 4;
1 х^ — X + 1
-1; б) указание. Пусть у =-----------
2 х + 1
1 +
112. а) . 113. а) ±1; б) 5;-3. 114. а) 1; б)
тогда у2 + 2у - 1 = 0.
[6; оо). 115. (-оо; -4] U
U [-2; -1] U [1; оо). 116. а) -оо;
—3 — Уб / f — 3 + б
2 ) 2
оо
117. а) (-оо; оо);
б) 0. 118. а) (1; 3); б)
-ОО;
4-/19\/ 4+ У19_
3 J I 3 1
ОО
119. в) Указание.
а+Ь c+d __________
a+b+c+d^ 2 2 а + b c+d г=Т 4 / . ,
---- ----?--------—--------—> у у! ab V cd = V abed; г) указа-
ние. Положите в в) d = а + Ь + с
3
125. б) (зЛ; Л); (-ЗЛ; - Л);
(4; 5); (-4; -5). 126. а)
-• -!• Г1-
4’ 4 J’ U’
б) (1 + (3 - у0); у0), 2 < у0 < 3.
127. а) (1; 1; 0); б) (-3; 2; -1). 128. а) (1; 2); (2; 1); б) (1 + Л; 1 - Л);
(1-Л;1+Л). 129. а) (5; 3); (-3;-5): (/17; Л7); (-/17; -/17);
б) (2; -1); (1; -2); (-2; -1); (1; 2); (0; 3); (-3; 0). 130. а)
/ 1+ /13.
I 2 ’
1+ /13
2
fl-Лз. -14-/13^ f 3(3+хеу). 3-^69 )
I 2 ’ 2 / [ 10 : ю J’
3(3-Уб9)
10
370 Ответы
и указания к упражнениям
3- 769
10
(4V8; 4V2);
132. a) (0; 0);
5
3
; 131. а) (2; 1); (-2; -1);
(-V7; -V7); (3; 2); (2; 3)
(Л; 77);
(-3; -2;);
(-2; -3); (719; 19);
(-л/19; -vl9); 6) (0; 0); (2;-2); (-2; 2);
(Тб; 76);
2
-1+ 73);
(-1; 2; -1); (-1; -1; 2); г) (1; 0; 1); (-1; 0;
(2; -1; -1);
(0; 1; 1); (1; 0; 1); (1; 1; 0);
1-
3’ 3
133. а) (3; 2; 1); (3;-2;-1); (-3; 2;-1); (-3;-2; 1);
б) (3; 2; 1). 134. а) (2; 3/3; 379); б) j
1. _1 ].
2’ 2)’
в) 0;
; (4: 3; 2); (-4; -3; -2)
135. 3 м/мин; 1,8 м/мин. 136. а) 863. 138. 40 км2. 139. 8. 140. 280 р.,
портфель дороже авторучки. 141. 12,5 г. 142. 16 ч 45 мин. 143. 100 м/с.
144. а) б) 1; 2; в) 7; г) ± 257. 145.
4 255
146. а) л + 2лп; " + 2лп, п е Z; б) — + 2ли,
2 2
а) 1; б) 2; 11; в) 1; г) 0
neZ. 147. а) [3; 11]; б) [5; 10]. 148. а) 0;
^7Г
п g Z; в) 0; г) пп; —- + 2пп,
4
149. а) п’ б) Ука'
65 7
6) 2.
з а н и е. Разделите
обе части на ^/(7
х)2.
150.
а) -1;
151. а) 12 ;
127
4 .
43’
б) 0. 152. 0. 153.
а) 0 при
а - 72 - а2
2
при -1
1; х =
а + 72 - а2
при 1
2
2
, , а2+1
при а < —1; х =---- при
2а
—1 < а < 0; 0 при 0
-— при а > 1. 154. a) (-оо; 1] U 2;
6
; б) [0; 3]; в) (1; оо);
г) -1;
2
. 155. а)
; б) [1; сю]; в)
81-9797. _
J О J
9
Ответы и указания к упражнениям
r)
fgb 156. a) 0; 6)
157. a)
6)
- co- - A
3
U(3;°o). 158.
a) [1; co); 6)
U(4; oo) в)
2
r)
r)
(2; oo). 159. a) (1; 64); (64; 1);
(1; 8); (8; 1). 160. a) (2; 3);
13.
3 ’
6) (4; 1); (1; 4); в) (1; 27); (27; 1);
6) (2;-2); в) (4; 2); -|1;
о 7 \ о о J
г)
(8; 27); (-27; -8). 161. a) (-2; -8); 6)
24
23
24
. 162. a) (9; 1);
6) (64; 1); (—1;-64); в) (9; 4); r) (4; 3); -33^
163. a) (-1)" — + —, neZ; 6) - + m, neZ; в) - + —, nn, n e Z;
' ’ 12 2 4 6 3
r) — + 2nn, n e Z.
6
164. a) 0; -^ + 2лп, ^-2лп, n e N-, 6) 0; в) О; 2лп,
n — 2nn, n e N; r) 0. 165.
a) ± arccos — + nn, neZ: б) лп; —+ —, n e Z;
3 12 6
в) (-1)" — + лп, n e Z; r) — + 2nn, n e Z. 167. a) — + лп, n e Z; 6) — +
6 2 4 2
+ 2лп, n e Z. 169. a) — + (-!)"— + лп, n e Z; 6) 0. 170. — + 2лп, n e Z.
3 6 4
41
171. 2k, k e Z, где k Ф 31(, I e Z; —(2n + 1), где n e Z; n 33m + 16,
33
m e Z. 172. a) - + —, n e Z; 6) —, n e Z. 173. 0. 174. |-1; - - + 2лп |;
8 4 2 I 2 )
1; - —+ 2nn|, neZ. 175. ; - + лп, n 6 Z. 177. a) f-^+nn;
2 ) 12 2 6 I 2
— + лп |; Г — + лп; - + лп 1, n e Z; 6) [ — + 2лп; — + 2лп 1, n e Z; в) | + nn;
674З 2 J V6 6 J \ 2
- — + лп ; I лп; — + лп I, n e Z; г) лп; — + лп ; — + лп; — + лп , п е Z.
4 J I 4 J I 6 J ЧЗ 2 J
178. а) [ - — + 2лп; - — + 2лп , - — + 2лп; - — + 2 лп , — + 2лп;
L 6 2 J L 3 6 J 1.2
— + 2ли , п е Z; б) - — + лп, - + лп; - — + лп , - — + лп; — + лп ,
6 J 2 L Ю 4 J L Ю 10 J
л
4
Зл
— + лп
10
п е Z; в) (2лп; л+ 2лп),
п е Z; г) — + лп; — + лп
13 2
180. Указание.
cos пх = -1
или
1 <- <- 1
С cos лх С -
4 2
181.
Г-— + 2лп;
L 6
— + 2лп1,
6 J
и е Z.
182. Указание.
cos sin х > cos х > sin cos x.
184. a) f— + л (2n + -\ - + — 1, k, n e Z; 6) f- + —; л + 2лй1 k, n e Z.
I 4 I 2) 4 2 ) \ 4 2 Г
372 Ответы и yi..i иия к упражнениям
185. ( 2 acrtg 1+ + 2nA; 2 icrtg 1—+ 2nn 12 acrtg -—+ 2nk-,
{ Js V3 J I V3
2 acrtg 1 + ~ 4. 2nn 1; f - + 2nA; — + 2nn 1, k € Z, n gZ. 186. I + nm;
43 J v3 3 ' '6
-+nn; --+ n(2p-m-n) ]; -£+nm; - ^ + m; £ + л (2p - m - n + 1) ,
3 3 J v 6 33 J
m.n.peZ. 187. a) ±2; 6) 2; в) ±1; г) 1. 188. a) J; 2; 4; 6) 1;
о У
+ ^+2nnt neN; B) _1; 1; 1; 3; r) 0. 189. a) + nn, n e Z;
9 3 5 2 2
6) arctg 10 + nn, n e Z; в) ± + nn, n e Z; r) + 2nn, (-1)" | + nn, n gZ.
о О
190. e = |- 191- a) (-oo; log2 (V2 - 1) u [0,5; oo); 6) (0; 2); r) (-co; oo).
192. a) (2; 3) U (4; oo); 6) (~/7; - V3) U (V3; J7). 193. a > 2. 194. a) (2; 0);
6) (1; 1); в) f-+ nA; £ + 2nn |, f£ + nA; 2nn-£ ], A, n e Z; r) [ nn; 2nA ± £ ],
k, n e Z. 195. a) 8; 6) log3 3+g 41; в) 0; г) + лп, n e Z. 196. a) 10 ’ a .
±
10 * 3 ; 6) 2; -; в) 10;------; r) 0. 197. а) Указание, arctg x +
8 V10
Уз
+ arcctg x = —; arctg x arcctg x = 10“; 6) 0; в) 10 ; r) +0,5. 198. 0 < a < .
2 8
199. a) a < 0; 6) a > 0. 200. |a |> 1. 201. a) [ |; 3 |; 6) (3; oo)U(l; 1 + З"1-25);
e \3 )
B) (4; 10); г) (1; 3V5). 202. a) 0; 6) 3J; в) pog3 3,.^ ; ooj;
r) Q; б). 203. a) (4; 00); 6) (-4 - V2; - 5) U (-3; - 4 + -J2) U (1; 2);
в) [Тб - 1; 2) U (2; 5]; r) (log3 10; 00). 204. (2; 2,5). 205. a) (2; 4);
6) j); в) (13; 8); r) (512; 1). 206. a) (| + 2nn; ±^ + 2ла);
| — + 2nn; + — + 2nA |, n, A e Z; 6) [ — + 2nn; — + 2nA |, n, A e Z.
I 3 3 J 16 6 J
209. a) f (0) = lim — = lim --——= 0. 210. Найдем отноше-
x->0 x x->0 x
ние
&f f(x+&x)-f(x) f(x)+f(tsx)-f(x) /(Дх)-/(0)
-- =---------------=-------------------=--------------(0) для
Дх Дх Дх Дх
любого х (так как f (0) = f (0 + 0) = f (0) + f (0) = 2f (0), т. e. f (0) = 0).
373 Ответы
И указания к упражнениям
f(x)~~ f(0) ухг 1
211. Указание. -----------=-----= —а эта функция не имеет пре-
х - 0 х 3 [ х
дела при х, стремящемся к нулю. 212. Вообще говоря, нет. Примеры:
a) fj (х) = х, f2 (х) = I х |, х0 = О; б) Д (х) = f2 (х) = Vx2', х0 = О.
214. а) Функция / (х) = arcsin х имеет производную как обратная к диф
ференцируемой функции g (х) = sin х (с областью определения |^- I I-
Дифференцируя равенство sin (arcsin х) = х, получим cos (arcsin х) х
х (arcsin х)’ = 1, откуда (arcsin х)' =----- = , так как если
cos (arcsin х) yjl - х2
arcsin х = а, то cos а = -Jl - sin2 а = V1 - х2 (поскольку cos а > 1).
215. а) х" (In х + 1); б) (sinx)-* cos2 х - sin2 х Insinx
sinx
н и е. -------= —---------—. 217. Указание. Функция h (х) = f (х) -
х2-Зх+2 х-2 х-1
- g (х) возрастает на [х0; оо). 218. а) 4 - ? б) 16 - ~
= 16-n2 + 5-n + 8. 221. а) а<-3, а > 1; б) 0 < а < 28. 222. а) Указа-
2"1
ние. Функция f (х) = cos х + х возрастает на (-оо; оо). 223. а) (-оо; оо);
б) (-оо; 0) U (0; оо). 224. Указание. Докажите, что при достаточно
больших положительных х левая часть этого уравнения положительна,
а при достаточно больших по модулю отрицательных х — отрицательна.
225. Указание. Воспользуйтесь методом математической индукции
и теоремой Лагранжа (из теоремы Лагранжа следует, что между двумя
корнями многочлена имеется корень производной этого многочлена).
226. Пусть Р (х) принимает р раз значение А, р > п. Тогда многочлен
Р (х) - А имеет степень п и имеет более п корней, что противоречит ре-
зультату предыдущей задачи. 227. Указание, а) Если В (х) = С,
то С — корень многочлена р (х) - Cq (х) степени не выше Л; б) R'(x) =
= = (х) р. (х) _ р (х) q. (х) = о, левая
</2(х)
часть этого уравнения — многочлен степени выше т + п — 1, если т * п,
и степени не выше т + п-2, если т = п. 228. minf(x) = /’ ^|=~;
10,3] \3) 27
27
max f (х) = f (3) = 105. 229. 1 ч. 230. Длина страницы 30 см, ширина
|0;3] 43
20 см. 231. 20 км/ч. 232. ‘ . 233. а) Первое больше; б) второе больше.
374 Ответы и указания к упражнениям
236. a) 1; б) 1. 237. a) 1 корень при |д| > 2; 2 корня при |а| = 2; 3 корня
при |а| < 2; б) нет корней при -4 --712<а<0; 1 корень при а =-4--712;
2 корня при а < 4 - -712, а = О и а >4 - V12; 3 корня при а = 4 - л 12; 4 кор-
( 2 2 1,5
ня при 0<а<4 --712. 238. [а3 + d3J . 239. f (Зл) = 12л - 1. 240. R + Rt, R.
241. м/мин. 242. 90°. 243. а) у=-9х+3; б) у =-3, у = -12х-15;
17 4
в) у = --г(х + 1); г) у = ±43х + 6 244. лп, — + —, п е Z. 247. а = 4.
-73 8 4
248. а = 3, b = 1. 249. Указание, f (х) = 2х - а и f (х) = 1 при х = — * 4
250 Мо — «внутренность» параболы у = х2, Мг — сама парабола, М2 —
Л"! XI
«внешняя часть» этой параболы, Мк — пустое при k > 3. 251. а) ——1 + С;
б) Г(х) =
в) F{x) =
j х2 - х + С при х > 1,
-^х2 + х+ С-1 при х< 1;
х3
—— х + С при х С - 1,
х3 4
х-----+ — + С при - 1 < х < 1,
3 3
v3 о
----х + —h С при х > 1.
3 3
252. a) -i (1 + х2) 71 + х2 + С; б) - е х 2 + С; в) In sin х + С; г) -In cos х + С.
о 2
253. a) In |х - 11 — In 2 - 1; б) ~-- + 1> в) sin х - sin е + л;
г)-^+х. 254. a)F(x) = |SinX ПрИ Х<°’ б) Г(х) J2^’4
2 Iх ПРИ х '0; [х-3 при х<1.
255. Указание. (F (х) - F (-х))' = F' (х) + F’ (-х) = f (х) - f (х) = 0, т. е.
G (х) = F (х) - F (-х) — постоянная. Кроме того, G (0) = F (0) - F (0) = 0,
откуда F (х) = F (-х). 256. Указание. Пусть G (х) = F (х) 4- F (-х), тогда
G' (х) = f (х) - f (х) = 0, т. е. G (х) = С, где С — постоянная, причем С = 0,
если F (0) = 0. 257. 10 с, 700 м (так как t > 0). 264. = ^/бх - 4. Ука-
зание. (г/3)' = Зу'у2 = 6.
ggg sinх - cos х х sinx + cosx
266. а) Имеем
х' (t) =
t
х0 + J v (z) dz
= x„ + + v'(t) =
375 Ответы
и указания к упражнениям
1 о
= v'(t) и х0 = х0 + J и (г} dz = х0 + 0 = х0. 267. Указание. Проверьте
1 о
формулу для у = 1, у = х, у = х2 и у = х3. 268. а) Указание. См. № 255;
б) указание. См. № 256; F (х) + F (-х) = С, при этом, подставляя х = О,
X
получаем С = 2F (0). откуда J f (г) dz = F (х) - F (-х) = 2 (F (х) - F (0))
для любого х, в том числе и для х = а. 269. а) 0; б) 0. 270. а) -135,6;
2 х
в) -1—. Указание. Сделайте замену переменной по формуле у = 1-.
7 2
2 11
271. а) —; б) In 2. Указание. Вынесите за скобку; в) ---------;
л п р + 1
г) Р - 1). 272. а) л. Указание, cos2 пх = + 2б) О;
1-р 2
в) л; г) 0.
Решение.
J sin3xcos5xdx =
о
К
J (sin8x - sin2x) dx =
if-— cos8x + i cos2x
2 I 8 2
273. a) 2; б) в) r) |. 274. nab.
275. а) При
a <2,
b<2;
a >2,
b >2;
б) C < 0 и С > 3; в) при < <
[b<-C; [fc>-C.
276. a) 24-; 6) 2-. 277. 8; 12 2—1 279. 25 Дж. 280. a = -l.
3 3 5
g2 M2 npR2H2g
281. ---— (g — ускорение свободного падения). 282. ---------—----.
6m2 12
285. Центр масс однородного полушара R лежит на его оси симметрии
3 о
на расстоянии — R от центра шара.
Предметный указатель
Аргумент функции 21
арккосинус 65
арккотангенс 66
арксинус 63
арктангенс 66
асимптота
— вертикальная 52
— горизонтальная 52
— наклонная 52
Бесконечно малая 202
Величина 167
Гармонические колебания 60, 265
----, амплитуда 60
----, начальная фаза 60
----, период 60
----, частота 60
геометрический смысл производ-
ной 130
график функции 22
Десятичное приближение числа
169
дифференциал функции 160
дифференциальное исчисление
160
дифференцирование 106
дробная часть числа 169
Единичная окружность 14
Знаки значений тригонометриче-
ских функций 8
значение функции 21
Интеграл 188
— неопределенный 200
— определенный 200
интегральное исчисление 200
интегрирование 189
Кавальери принцип 203
касательная к графику функции 103
корень квадратный 209
— кубический 209
— п-й степени 207
-------арифметический 207
— посторонний 214
косеканс 19
косинус 15
котангенс 17
криволинейная трапеция 119
критическая точка функции 147
Линейная плотность 139
линия котангенсов 18
— синусов 16
— тангенсов 18
логарифм 232
— десятичный 234
— натуральный 253
Максимум функции 46
мгновенная скорость 137
метод интервалов 125
— неделимых 201
механический смысл производной
137
минимум функции 46
Flpt , метный указатель
Наибольшее значение функции
155
наименьшее значение функции
155
неравенство
— логарифмическое 243
— показательное 230
— тригонометрическое 75
нуль функции 50
Область значений функции 21
— определения функции 21
общий вид первообразных 177
объединение множеств 22
основное логарифмическое тожде-
ство 233
— свойство первообразных 177
основные свойства корней 209
логарифмов 233
----степеней 219, 227
— формулы тригонометрии 6
отображение 27
Первообразная 174
— показательной функции 254
— степенной функции 260
— тригонометрических функций
180
период функции 34
показатель корня 207
правила
— дифференцирования 113
— нахождения наибольшего и
наименьшего значений функ-
ции на отрезке 155
— нахождения первообразных 181
— предельного перехода 110
— сравнения чисел 170
предел
— последовательности 165
— функции 165
предельный переход 108
пределы интегрирования 189
преобразования графиков функ-
ции 23
признак
возрастания функции 143
— максимума функции 148
— минимума функции 149
— постоянства функции 177
— убывания функции 143
приращение
— аргумента 97
— функции 97
производная функции 106
в точке 105
— логарифмической функции 256
— постоянной 106
— сложной функции 119
— степенной функции 116
— тригонометрических функций
121
промежуток возрастания функ-
ции 50
— знакопостоянства функции 50
— убывания функции 50
Работа переменной силы 196
радиан 5
радикал 207
разность чисел 170
Секанс 19
синус 15
синусоида 16
системы уравнений
----логарифмических 243
----показательных 230
----тригонометрических 83
степень числа
----с рациональным показате-
лем 218
----с иррациональным показате-
лем 224
сумма чисел 170
схема исследования функции 56
Тангенс 17
тангенсоида 19
Пре шетныи указатель
теорема
— Вейерштрасса 155
— об обратной функции 248
— о корне 64
— Ферма 147
точка максимума 45
— минимума 44
- - экстремума 46
Уравнение дифференциальное
263
— гармонического колебания 266
— иррациональное 214
— касательной к графику функ-
ции 131
— показательного роста (убыва-
ния) 264
— показательное 229
ускорение 137
Фокус параболы 141
формула
— Лагранжа 132
— Ньютона — Лейбница 190
— объема тела 194
— площади криволинейной трапе-
ции 186
— Тэйлора 164
формулы приведения 8
функция
— возрастающая 40
— дифференцируемая 106
— дробно-рациональная 22
— логарифмическая 238
— непрерывная в точке 109
— непрерывная на промежутке 124
— нечетная 32
— обратимая 246
— обратная 247
— периодическая 34
— показательная 226
— сложная 118
— степенная 259
— убывающая 40
— целая рациональная 22
— четная 31
— числовая 21
функции взаимно обратные 248
Целая часть числа 169
центр масс 197
Число действительное 167
— иррациональное 167
— натуральное 167
— рациональное 167
— целое 167
число е 252
Экстремум функции 46
Оглавление
Предисловие
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 1.
Тригонометрические функции числового аргумента
1. Синус, косинус, тангенс и котангенс (повторение) 5
2. Тригонометрические функции и их графики. 14
§2.
Основные свойства функций
3. Функции и их графики ...................................... 21
4. Четные и нечетные функции. Периодичность тригонометрических
функций....................................................... 31
5. Возрастание и убывание функций. Экстремумы. 40
6. Исследование функций . 48
7. Свойства тригонометрических функций Гармонические колебания 56
§3.
Решение тригонометрических уравнений и неравенств
8. Арксинус, арккосинус и арктангенс .... 64
9. Решение простейших тригонометрических уравнений 69
10. Решение простейших тригонометрических неравенств 75
11. Примеры решения тригонометрических уравнений и систем
уравнений . . 81
Сведения из истории . 85
Вопросы и задачи на повторение. 91
ШД ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§4.
Производная
12. Приращение функции. . 97
13. Понятие о производной ... ................... .101
14. Понятия о непрерывности функции и предельном переходе . . 108
15. Правила вычисления производных.........................113
380 Оглавление
16. Производная сложной функции. . 118
17. Производные тригонометрических функций . 121
§5.
Применения непрерывности и производной
18. Применения непрерывности . . 124
19. Касательная к графику функции . 129
20. Приближенные вычисления. . 134
21. Производная в физике и технике 137
§6.
Применения производной к исследованию функции
22. Признак возрастания (убывания) функции... 143
23. Критические точки функции, максимумы и минимумы .......... 147
24. Примеры применения производной к исследованию функции 151
25. Наибольшее и наименьшее значения функции 155
Сведения из истории ... 160
Вопросы и задачи на повторение. 170
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§7.
Первообразная
26. Определение первообразной . 174
27. Основное свойство первообразной. . 177
28. Три правила нахождения первообразных . 181
§8.
Интеграл
29. Площадь криволинейной трапеции. .185
30. Интеграл. Формула Ньютона — Лейбница. 188
31. Применения интеграла . 194
Сведения из истории 199
Вопросы и задачи на повторение. ... 205
IV
глава
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ
ФУНКЦИИ
§9.
Обобщение понятия степени
32. Корень п-й степени и его свойства. ...........207
33. Иррациональные уравнения ....... 214
34. Степень с рациональным показателем......................218
381
О
ччгие
§ 10.
Показательная и логарифмическая функции
35. Показательная функция. . 224
36. Решение показательных уравнений и неравенств 229
37. Логарифмы и их свойства 233
38. Логарифмическая функция . 238
39. Решение логарифмических уравнений и неравенств 242
40. Понятие об обратной функции . 246
§ 11.
Производная показательной и логарифмической функций
41. Производная показательной функции. Число е 251
42. Производная логарифмической функции . 256
43. Степенная функция . 259
44. Понятие о дифференциальных уравнениях . ............263
Сведения из истории........................................ . . 269
Вопросы и задачи на повторение ................273
глава
§1.
Действительные числа
1. Рациональные и иррациональные числа . 277
2. Проценты. Пропорции ........279
3. Прогрессии . . 280
§2.
Тождественные преобразования
4. Преобразования алгебраических выражений . . 281
5. Преобразование выражений, содержащих радикалы и степени
с дробными показателями . ........................ 282
6. Преобразования тригонометрических выражений........ . 283
7. Преобразования выражений, содержащих степени и логарифмы . . 285
§3.
Функции
8. Рациональные функции. . 286
9. Тригонометрические функции ... . . . . 290
10. Степенная, показательная и логарифмическая функции . . 293
§4.
Уравнения, неравенства, системы уравнений
и неравенств
11. Рациональные уравнения и неравенства . 295
12. Иррациональные уравнения и неравенства...................297
382 Оглавление
13. Тригонометрические уравнения и неравенства . 298
14. Показательные уравнения и неравенства . 299
15. Логарифмические уравнения и неравенства. 300
16. Системы рациональных уравнений и неравенств 301
17. Системы иррациональных уравнений . 302
18. Системы тригонометрических уравнений . . —
19. Системы показательных и логарифмических уравнений . 303
20 Задачи на составление уравнений и систем уравнений . 304
§5.
Производная, первообразная, интеграл
и их применения
21. Производная. . .........306
22. Применение производной к исследованию функций . 308
23. Применение производной в физике и геометрии .310
24. Первообразная 312
25. Интеграл —
VI
глпва
ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
§ 1.
Числа и преобразования выражений
1. Целые числа .314
2. Метод математической индукции .315
3. Действительные числа . . .316
4. Преобразование выражений . .317
5. Прогрессии 318
§2.
Элементарные функции и их свойства
6. Исследование функций 319
7. Г рафики функций 322
§3.
Уравнения, неравенства и системы
8. Рациональные алгебраические уравнения. 325
9. Рациональные алгебраические неравенства. . . 327
10. Системы рациональных алгебраических уравнений. . 328
11. Задачи на составление уравнений и их систем 329
12. Иррациональные уравнения и неравенства.................. . 330
13. Тригонометрические уравнения, неравенства и системы . . 333
14. Показательные и логарифмические уравнения и неравенства .... 335
383 Оглавление
§4.
Начала математического анализа
15. Производная. ........... 337
16. Применение производной к исследованию функций 338
17. Применение производной в физике и геометрии 340
18. Первообразная............................................ 341
19. Интеграл . 343
Ответы и указания к упражнениям . . . 346
Предметный указатель . 377
Учебное издание
Колмогоров Андрей Николаевич
Абрамов Александр Михайлович
Дудвицын Юрий Павлович и др.
Алгебра и начала математического анализа
Учебник для 10—11 классов
общеобразовательных учреждений
Зав. редакцией Т. А. Бурмистрова
Редактор Л. Н. Беленовская
Младшие редакторы Н. В. Сидельковская, Н. И. Смирнова
Художники Т. В. Делягина, В. В. Костин, В. Е. Валериус, Н.Ю.Панкевич
Художественный редактор О. П. Богомолова
Технический редактор О. Е. Иванова
Корректор И. А. Смирнова
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000.
Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать 04.08.08. Формат
60x90 1/i6- Бумага офсетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л.
20,52 + 0,22 форз. Доп. тираж 40 000 экз. Заказ № 4958.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в ОАО «Тверской ордена Трудового Красного Знамени
полиграфкомбинат детской литературы им. 50-летия СССР».
170040, г. Тверь, проспект 50 лет Октября, 46.
£
ПРОСВЕЩЕНИЕ
д
АТЕЛЬСТВО
Выпускаем
• Учебники
• Методическую литературу
• Научно-популярную литературу
• Справочную литературу
• Наглядные пособия и карты
• Учебные мультимедийные курсы
Обучаем
Интернет-школа «Проевещение.ги»
www.internet-school.ru
Институт повышения квалификации работников
образования
www.prosv-ipk.ru
Представляем
На сайте издательства для наших покупателей
• Каталог выпускаемой продукции
• Ежемесячные новинки издательства
• Планы печати учебной литературы
• Адреса книготорговых структур
Предлагаем,
Оптовикам и книготорговым структурам
• Гибкую систему скидок
• Крупный и мелкий опт со склада издательства
• Контейнерные отгрузки во все регионы России
и стран СНГ
• Внимательное отношение к каждому!
Заказ и отправка книг по почте
Тел.: (495) 981-1039
http://www.obrazovanie-online.ru
Издательство «Просвещение»
127521, Москва, 3-й проезд Марьиной рощи, 41
Тел.: (495) 789-3040
Факс: (495) 789-3041
E-mail:prosv@prosv.ru
http://www.prosv.ru
ISBN 978-5-09-019513-3
ПРОСВЕЩЕНИЕ
ИЗДАТЕЛЬСТВО