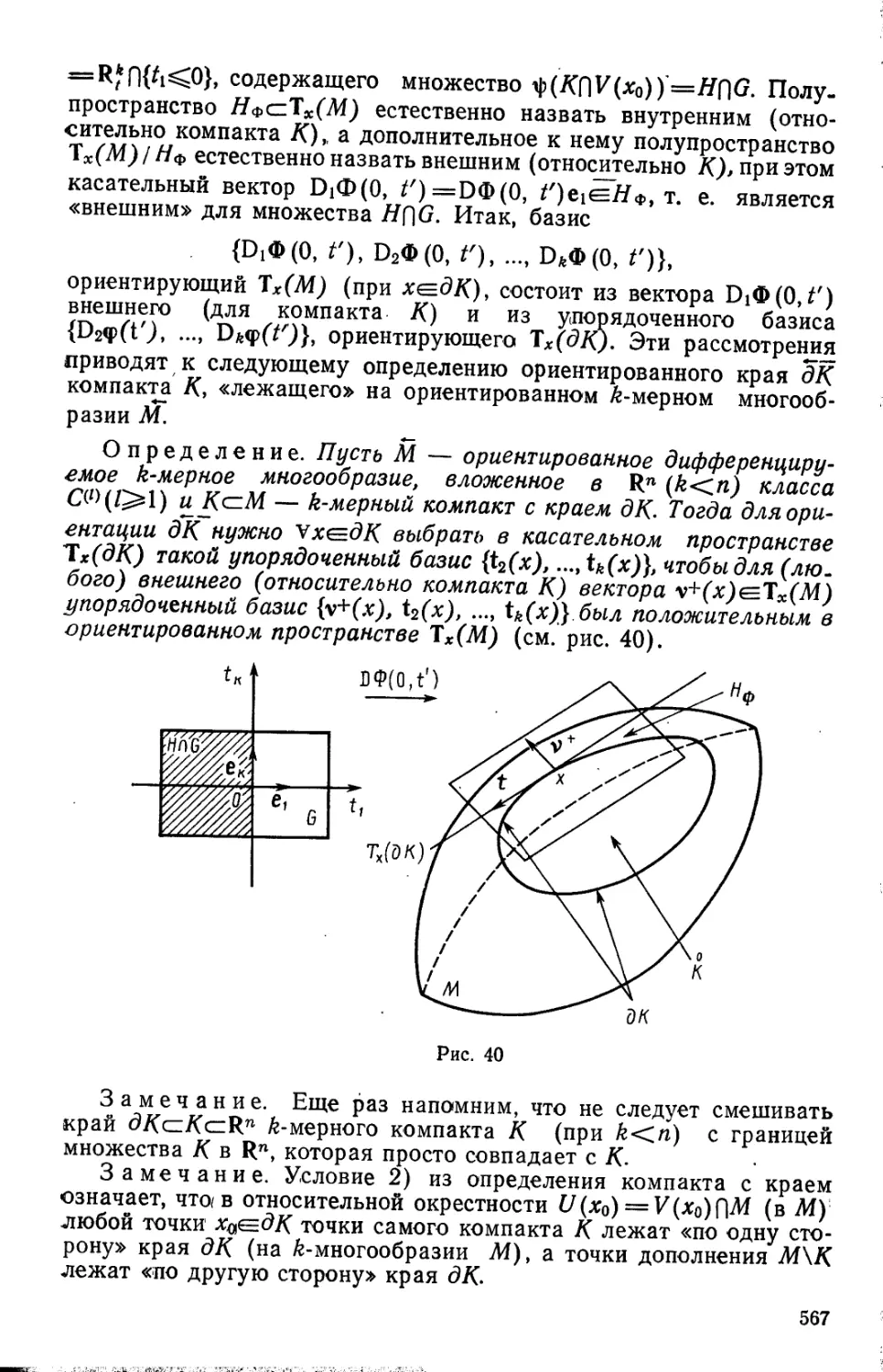
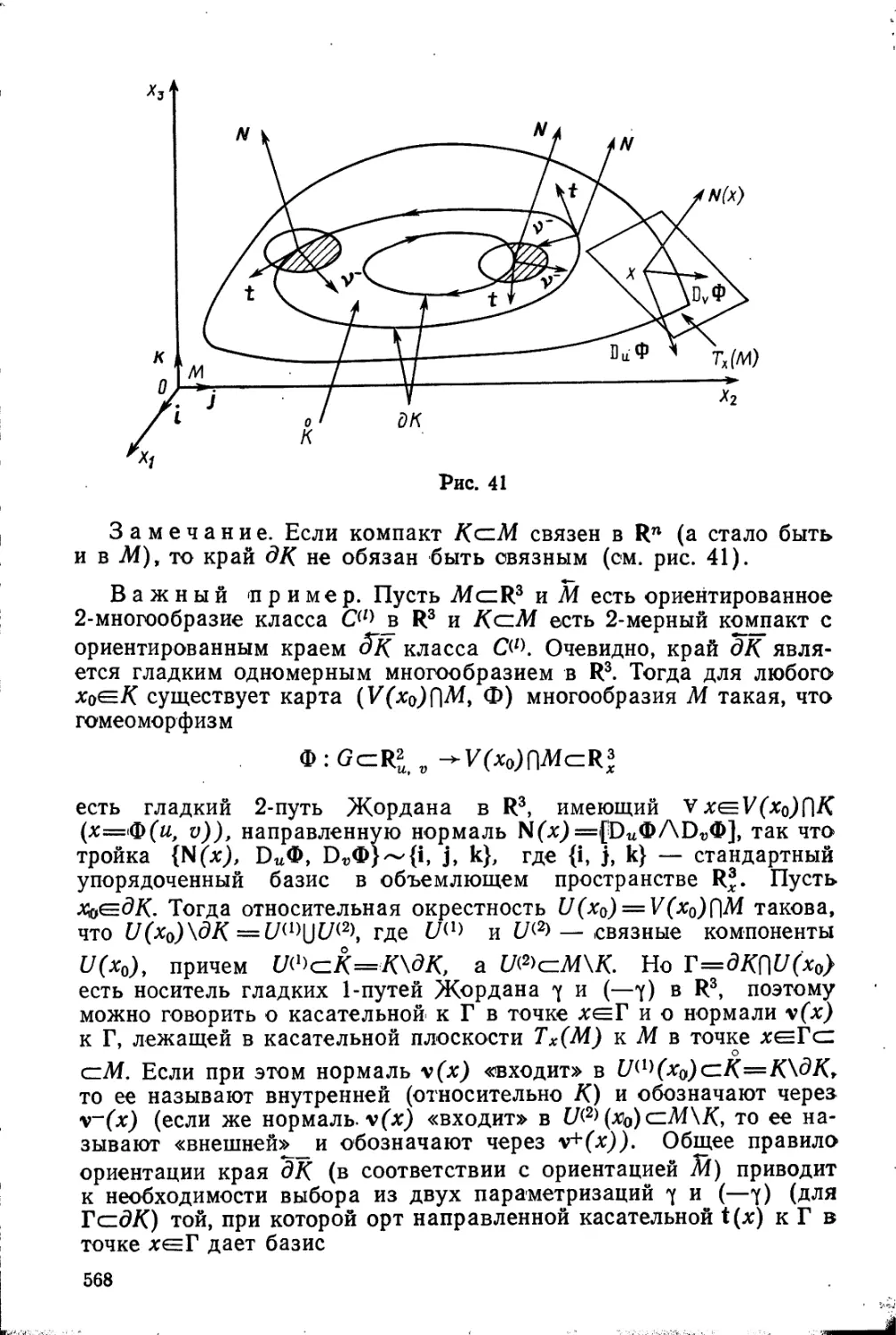
Автор: Камынин Л.И.
Теги: анализ математический анализ функциональный анализ математика
ISBN: 5-211-02065-0
Год: 1995
Текст
Л.И.Камынин
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА II
Л. И. Камынин
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
Том II
Рекомендовано Государственным комитетом Российской
Федерации по высшему образованию в качестве учеб-
ника для студентов высших учебных заведений, обу-
чающихся по направлениям «Математика» и «Приклад-
ная математика и информатика».
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
1995
ББК 22.161
К 18
УДК 517
Рецензенты:
академик РАН Ю. Г. Решетняк,
доктор физико-математических наук В. И, Буренков,
доктор физико-математических наук Я. Я. Фельдман
Федеральная программа книгоиздания России
Камынин Л. И.
К 18 Курс математического анализа. Т. II.: Учебник. — М.:
Изд-во МГУ, 1995. — 624 с.
ISBN 5—211—02065—0 (Т. II);
ISBN 5—211—01941—5
В учебнике (Т. I — 1993 г.), написанном в соответствии с утвержден-
ной программой курса, излагаются теория числовых и функциональных
рядов, включая степенные ряды Фурье; теория несобственных интегра-
лов, зависящих от параметра, включающая интегралы Фурье и преобразо-
вания Фурье. Даются теория кратных интегралов Римана (в том числе и
несобственных), а также элементы теории интегрирования дифференци-
альных форм на дифференцируемых многообразиях с краем (включая
формулы Стокса и основные понятия векторного анализа). Материал из-
лагается с учетом современной тенденции проникновения' в анализ мето-
дов линейной алгебры и дифференциальной топологии.
Для студентов университетов, обучающихся по специальностям «Ма-
тематика», «Прикладная математика и информатика».
к 1602070000(4309000000)—019 59__94 ББК 22.161
077 (02) — 95
Учебное издание
Камынин Леонид Иванович
КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА. Т. II
Зав. редакцией Л. А. Нико л она
Редактор Л. О. Богданкевич
Художественный редактор Л. В. Мухина
Технический редактор Н И. Смирнова
Корректоры Л. И. Клочкова, Н. В. Иванова
ИБ № 6201
ЛР № 040414 от 27.03.92.
Сдано в набор 23.11.93 Подписано в печать 04.04.95 Бумага офсет, кн.-журн. Гарнитура литературная. Усл. печ., л. 39 Уч -изд. л. 40,59 Тираж 5000 Заказ 2613 Формат 60Х9071в ; Высокая печать.. Изд. № 220 h
Ордена «Знак Почета» издательство Московского университета 103009, ул. Герцена, 5/7. Москва,
Серпуховская типография Упрполиграфиздата Мособлйсполкома г. Серпухов,
пр. Мишина, д. 2/7
ISBN 5—211—02065—0 (Т. II)
ISBN 5—211—0194^5
© Камынин Л. И., 1995 г.
© Издательство Московского
университета, 1995 г.
Часть IV
РЯДЫ, БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
И НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Глава 1
ЧИСЛОВЫЕ РЯДЫ, БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
И НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
§ 1. Понятия числового ряда, бесконечного
произведения, несобственного интеграла с бесконечными
пределами и несобственного интеграла от неограниченной функции
Рассмотрим числовую последовательность и-*ап, nfeN, а„е=
GR и построим последовательность (sn) (п=1, 2, 3,...), где
п
$п — 2 ак так> что ai—si> an=sn—sn-i (п=2, 3,...). sn называет-
s=i
ся n-й частичной суммой бесконечного ряда
о-1)
/г==1
п
ап называется и-м членом ряда (1.1). Сумма + • ••
й=т-|-1
. ..+ап называется отрезком ряда (1.1).
Определение. Если существует Um sn=s, то ряд (1.1)
п»4-оо
называется сходящимся, а число s называется его суммой.
Замечание. Если ряд (1.1) сходится к s, то величина
= s — sa называется n-м остатком ряда (1.1). Очевидно,
4-00
гп = 2 также есть сходящийся ряд, причем
fe=n+l
lim rn = lim (s — sn) = 0.
П—*-j-oo n-»4-0°
Определение. Если lim sn не существует, то. числовой ряд
Л-*4-оо
(1.1) называется расходящимся.
3
Пример. Пусть aft = g‘-1 (k = 1, 2,...) есть член геометри-
п
ческой прогрессии со знаменателем q. Тогда $„= 2 д*-1 = (1 —
6=1
—<7п)/(1—<7)(<7¥=1) и при п -* + 00 возможны случаи: 1) |<?| </ 1 =>
-|-оо -f-оо •
=> Пт 8я=1/(1— q) и ряд 2 Qk~l сходится, причем 2 <76-1 ~
/,-+в0 »=1 м
==1/(1—q); 2) ^=l=>(sn=n)=»( lim 8л=4-оо) и ряд V д*-1при?=1
, (0 при п = 2т, ,.
расходится; 3) д=»—l=>sn={ н л и lim sn не су-
. 11 при п = 2т + 1 п—+оо
4-00
шествует, ряд 2 qk~l расходится; 4) |?|>1, тогда предел по-
6=1
следовательности sn=(l—qn)/<J— q) при л—►-j-oo не существует,
-^ОО 4"®°
т. е. ряд расходится. Итак, ряд 2 4k~l сходится при
6=i 6=1
|?| <С 1 и расходится при |g| > 1.
Наряду с последовательностью (ап) (п=1, 2,...) рассмотрим
п
последовательность рп=а! at...an = ]”[ ak. Величина рп назы-
fe=i
вается n-м частичным произведением бесконечного произведения
П о,. (1.2)
6=1
Определение. Если существует lim рп=Р^=О, то беско-
П »-[-оо
печное произведение (1.2) называется сходящимся, а число р на-
зывается его значением.
Определение. Если предел Птрп не существует или ра-
вен нулю, то бесконечное произведение (1.2) называется расхо-
дящимся.
4-в©
Пример. П ak расходится, если существует msN такое,
»=t
что am = Q.
Замечание. При рассмотрениях бесконечных произведе-
ний будем считать в дальнейшем, что все сомножители ак в
(1.2) положительны.
&
т-г -гт k П k 12
Пример. Пусть aft= — , тогда рл = П —=y • т • •
. . -^- = -L-=» lim р„=0, поэтому бесконечное произведе-
+“ *
ние П — расходится к нулю.
Пример.
Р„ — п Ш+2)/(*+1)(*+0= Ц • —... (п~!)(и+1) и(и+2)—►
Ц 2.2 з-з ПП («+1Хл-Н>
=»fpn=4-- ~ W( lim рп= 1;2)=ф
(п «л -Ь I)3— l)/(fc -F-1)»= 1/2 Y
Теорема (критерий сходимости бесконечного произведе-
4-°°
ния). Пусть ah>0\k^i. Тогда (бесконечное произведение П ам
л—1
+ оо 4-00
сходится) -Н- (сходится ряд lhaA). При этом если П ак—а* Т°
2 1пай = Ь = 1па.
*•=1
Доказательство. Утверждения теоремы следуют из ра-
п п
венства ln|"] aft = 2 lnaft в силу непрерывности логарифмичес-
*=1 й=»
кой функции х-»1пх на (0, +<»).
Пусть функция х—►/(*) определена на [а, -Ь®®) и обладает
t
тем свойством, что f^R[a, t]Vi>a, тогда V/ >аЯ j f(x)dx.
а
Определение. Несобственный интеграл
j /(x)dx= J /(x)dx (1.3)
a [a, 4"°°)
называется сходящимся, если существует
t
lim Г/(х)йх = Л.
4-oo J
5
Число А называется тогда значением несобственного интеграла
(1.3). Итак, если несобственный интеграл (1.3) сходится, то
4*00 t
f(x)dx = lim J f(x)dx.
a t-»+oo e
Определение. Если предел
t
lim f f(x) dx
не существует, то несобственный интеграл (1.3) называется рас-
ходящимся.
Замечание. Назовем последовательностью Гейне, связан-
ной с базой (/->4-оо) на множестве [а, 4-оо), последователь-
ность (<„), обладающую свойствами: £n>a, in+i>f«Vnf=N и
lim tn = 4- оо (т. е. tn | + оо). Тогда, вспоминая доказанную в
ч. I, гл. 3, §5 [1] эквивалентность определений предела число-
t
вой функции по Коши и по Гейне, имеем при F(t)= f(x)dx и
А
базе (< —► 4- оо):
V f(x)dx = A <н>(Я lim F(t) = А),
I V / /~»4>ОО
\ a J
так что для любой последовательности Гейне (Q (£л f 4- °°),
связанной с базой (t —> 4- оо) Я lim F(ln) = А. Полагая ип =
П-+4-00
tn
— i f(x)dx4neN (t0 — а), видим, что для любой последова-
I
тельности Гейне (fn)(/n t 4* °®)» имеем
-J-оо -|-оо
j f(x)dx,
n=l а
что сводит исследование несобственного интеграла вида (1.3) к
исследованию числового ряда.
Аналогичным образом определяется и сходимость несобст-
венного интеграла
ь ь
f f(x)dx •» lira f f{x)dx.
—CO t
4-°°
Пример. Рассмотрим несобственный интеграл f - V а е R.
6
Очевидно,
f — = р1-а—!)/(!—«) при а =5^1,
J 11п/ при а=1.
1
Тогда
t
Нт (* _ р/(а~-1) ПРИ а> U
#~>+в0 J ха 1 + °° при 1,
1
т. е. несобственный интеграл
+»
J х~а dx
1
сходится при а>1 и расходится при а<1.
Рассмотрим функцию х—>/(х), определенную на отрезке
[а, Ь], но неограниченную в точке х = а: пусть при этом
/.£/?[« +8, b’V6>0 (8 <6— а). Очевидно, fEiR[a, 6].
Определение. Несобственный интеграл
ь
U(x)dx= f f(x)dx (1.4)
a«- (al-, г,]
(от неограниченной в точке а функции f(x)-) называется сходя-
щимся, если существует
ь
lim Г f(x)dx = А.
t—a+o J
Число А называется при этом значением несобственного интеграла
(1.4). Итак, если несобственный интеграл (1.4) сходится, то
ь ь
J f(x}dx = lim J f(x)dx.
а<- 8-»4-0 а_|_5
Определение. Если предел
ь
lim f f(x)dx
s-*+° z,ls
не существует, то несобственный интеграл (1.4) называется расхо-
дящимся.
Замечание.
Gb \ (Г)
f(x)dx~A\ <н- (Я lim Г(П = Л),
j
7
ь
где F(t)— у f(x)dx, так что для любой последовательности
t
Гейне (tn) (tn | а), связанной с базой (£ -* а 4- 0) Я lim F(fn) = 4.
Пг*4“00
+°° ь
Полагая ип = J f(x)dx (t0=*b), имеем 2 ип = J f(x)dx Для
‘п л=1 а~
любой последовательности Гейне (£n), (tn | а), что сводит иссле-
дование несобственного интеграла вида (1.4) к исследованию
числового ряда.
Аналогично определяется сходимость или расходимость не-
собственного интеграла
—ь 6-8
f f(x)dx = f f(x)dx = lim f f(x)dx
J J 5—*4-0
a [a, ~»b) 1 a
для неограниченной в точке Ъ функции f ElR{a, b — 6]
V8e(0, b — a).
Замечание. Если /eR[a, Ь], to
b 6 6—8 —6
f f(x)dx = lim f f(x)dx = lim f f(x)dx = f f(x)dx
j_ 8-*+° J J
(в силу непрерывности интеграла Римана как функции верхне-
го или нижнего предела), так что определенный интеграл Ри-
мана для функции fE:R[a, b] можно рассматривать как част-
ный случай несобственного интеграла.
1
П р и м е р. Несобственный интеграл J x~adx сходится при
о—
а<1 и расходится при а>1. В самом деле,
С jfa ((1—8‘-а)/(1—а) при а=/=1,
J ха I— In8 при а=1,
откуда имеем
1
lim f — 11/(1—а) при а<1,
8-+oJ ха 1+°о при а>1.
8
8
§ 2. Критерий Коши сходимости рядов,
бесконечных произведений
и несобственных интегралов
4-°°
Рассмотрим числовой ряд 2 ак и последовательность его
частичных сумм (sn) (neN). Применяя к последовательности
($л) критерий Коши существования предела, имеем ввиду ра-
п
венства sn—sm= 2 ak‘
k=m+i
Теорема (критерий Коши сходимости числового ряда).
+ оо
2 aft.cxodMTCfl)4^(Ve>032VeN такое, что
*—1
п
Asnm4-i
< е Vn > m>2V).
В силу теоремы об эквивалентности сходимости бесконеч-
ного произведения и ряда справедлива
Теорема (критерий Коши сходимости бесконечного произ-
ведения).
+«
Пусть fl*>OVJfeGN. (Бесконечное произведение П ak сходится)^
4=> (Ув > 0 9 N е N такое, что
1 — е < f| ak< 1 4-еVn>m>Af).
*=m+l
Следствие (необходимое условие сходимости числовогоря-
4-00
да). Если ряд V ап сходится, то lim ап = 0.
и~*4.со
п«»1
4-00
Доказательство. Если ряд 2 ak сходится, то критерий
Л==1
Коши сходимости ряда дает при тп п—1, что Ve^>03ZVc=N
такое, что |an| < « V в > 2V, т. е. lim ап = 0.
п- »4°°
Следствие (необходимое условие сходимости бесконечного
произведения). Если a„>0VnEN и бесконечное произведение
-4-00
П*п сходится, то liman=l.
Доказательство. Пустьа„^>OVnЕЕ N и Я lim />пв/>=/=0,
п-*4-оо ,
тогда an = pn/pn-i V га > 2, так что lim ап = р/р=1.
П—»-|-ОО
Замечание. Условие lim ап = 0 не является достаточным
П-»4-оо .
4-оо
ДЛЯ СХОДИМОСТИ ЧИСЛОВОГО ряда 2 ап«
л=1
4-оо
Пример. Гармонический ряд 2 расходится, хотя не-
П=>*1
обходимое условие сходимости ряда lim 1/га = 0 выполнено.
П—*4“°°
В самом деле, рассмотрим отрезок гармонического ряда
2п
2 1/£. Если бы гармонический ряд сходился, то по крите-
<£=/14-1
2п 2п
рию Коши имели бы lim V l//s—0, однако V !/£.> п X
X 1/2п=1/2.
Следствие (необходимое условие сходимости числового
4-00
ряда). Если ряд 2 вл сходится, то последовательность его
частичных сумм ограничена.
4-оо
Д о к а з а т е л ь ст во. Если ряд 2 ак сходится» то сущест-
*=•
вует lim sn = s, но сходящаяся последовательность (s„) всегда
П—>4-00
ограничена.
Замечание. Ограниченность частичных сумм (s„), вообще
говоря, не достаточна для сходимости ряда.
-4-00
Пример. Пусть ая=(—I)"-1, тогда ряд 2 (—1)п-1 расхо-
П=1
дится, хотя |sn|< 1 VnEN.
Из определения несобственных интегралов немедленно
вытекает
Теорема (критерий Коши сходимости несобственного ин-
теграла с бесконечными пределами интегрирования). Пусть
{-оо
J f(x)dx схо-
а
f^R(a, t]vt>a. Тогда (несобственный интеграл
дится) 4=> (Ve>OS,X>o такое, что
^f(t)dt <eVx', х">Х).
Ю
Доказательство. Пусть F(x)«- j" тогда критерий
а
Коши существования предела функции
+«>
lim Г(х) . f
X-H-oo V
a
дает (lim F(x) существует)^(Ve> О Я X> а такое, что
X*
|F(x")-F(x')| = J f(t)dt
eVx', x">X).
Замечание (критерий Гейне сходимости несобственного
интеграла с бесконечными пределами). Пусть fG=7?[a,
-1-00
Тогда (несобственный интеграл I f(x)dx сходится) 43- (для лю-
a
бой последовательности Гейне (fn) (^nt+°°), связанной с базой
(£-► 4-оо), Ve>0 3 2V(e) e=N такое, что Vт>п>• N(e) имеют
место неравенства
f(x)dx
е или
Л—п+1
е.
г*
где.иА=1 f(x)dx).
*k—i
(Доказать самим, сведя несобственный интеграл к числово-
му ряду для любой последовательности Гейне (tn), связанной
с базой (t —> + оо).)
Замечание. В отличие от рядов нельзя утверждать, что не-
обходимым условием сходимости несобственного интеграла
+°°
J f (х) dx
а
является соотношение
lim /(х) = 0.
Пример. Пусть
f(x)= («<*<« +2“"»
10, n-t-2“n < х < л + 1 V л €= N.
Очевидно, f(x,>О VхЕЕ[1, + °°) и lim f(x)^=O. Тогда
11
F(x) = J f(t)dt f на [1, +<x>),
1
причем
n n-f-1
F(n) = J < F(x) < F(n + 1) = J f(t) dt
i i
при n < x =C n + 1. Ho
/ C 1/2 + 1/2® 4-...+ j ==>
\t J
=>l lim
l л—»4“°° J .
поэтому Я
lim F(x) — +C f(t)dt = 1.
X-*4-oo J
4-00
Итак* несобственный интеграл J f(x)dx сходится, хотя
i
lim f(x)=#O.
X-»4-oo
Теорема (критерий Коши сходимости несобственного ин-
теграла от неограниченной функции). Пусть /е^[а-|-б, b]V5e
ь
е(0, Ь—а). Тогда (несобственный интеграл S f(x)dx сходится) &
(V8>QS6>-0 такое, что ух', х"^(а, Ь) таких, что а<х'<х"<
<а-|-6 имеет место оценка
J f(t)di <в).
Доказательство. В силу определения сходимости несоб-
ственного интеграла от неограниченной функции утверждения
теоремы вытекают из критерия Коши существования предела
функции lim F(x), где
«—а-н
ъ
F(x) =$f(t)dtV х> а.
X
Замечание (критерий Гейне сходимости несобственного
интеграла от неограниченной функции). Пусть /бЯ|а+5, d]V6G=
12
b
e(0, b—а). Тогда (несобственный интеграл f j(x)dx сходит-
a*-
ся) £=> (для любой последовательности Гейне (tn) (tn j a), связан-
ной с базой (t—>a+0), V e > О Я 2V(e) e N, такое, что Vm>n>
^>iV(s) имеют место оценки
г”
| f(x)dx
tn
£
ИЛИ
m
2 u*
b=n4-I
8,
где uk — J /(x)dx).
(Доказать самим, сведя несобственный интеграл к числово-
му ряду для любой последовательности Гейне (tn), связанной
с базой (t—>а + 0).)
Замечание. Если функция f(x) определена на (—оо. +<эо)
и существует п особых точек «1<в2< . . . <Zan, в которых
функция /(х) неограничена, причем / е Я[а, ₽] V [a, р] =э Ui
+°°
(i«e»l, 2, . . . , п), тогда несобственный интеграл J /(x)dx опре-
—оо
деляется равенством
+» Ь, —*a, bt
С f(x)dx — J f(x)dx + j /(x)dx + j f (x)dx + . . .
—CO —CO b9
ьл 4"00
. • • + J f(x)dx+ J /(x) dx,
an*~ bn
где —oo <60 < «i < < a2 < . . . < bn-t < an < bn <+<*.
§ 3. Простейшие свойства сходящихся рядов
и несобственных интегралов ,
-|-со -}-оо
Теорема 1. Если ряды ап и Ьп .сходятся и имеют
л«1
4-00
суммы а и b соответственно, то VXi, ряд 2
П=1
сходится к сумме ^а-^^Ь.
Доказательство. Пусть
Ап= 2 а^’ в*1 — 2 и ~ 2
fe=t fe=l
Тогда Сп = Хх4п + Х2®п, откуда в силу сходимости рядов
13
•4*00 «4“ DO Я
2 и 2 к сУммам а и Ь соответственно, имеем I
fe=t ь=л I
Э lim Сп = \а + Х26.
Теорема Г. Пусть f, gGR[a, fjv t>a и несобственные ин-
4*оо +°°
тегралы J f(x)dx и J g(x)dx сходятся. Тогда vXiAseR
а а
сходится несобственный интеграл i
J (W)
а
причем
J M{x)^£(x))dx = \ J f(x)dx + Х2 у g(x)dx.
а а а
Доказательство. Положим Nx>a
X X X
A(x) = Jf(t)dt, B(x) = $g(t)dt и С(х)=
а а а
Тогда в силу сходимости несобственных интегралов
f f(t)dt = lim А(х) и f g(f)dt — lim В(х)
J х—►4“°° * х-*4-оо
а л
имеем в силу равенства С(х) = ХхА(х) + Х2В(х), что
Я lim С(х)=Хх f f(x)dx + X2 C g(x)dx.
J J
* a a
Теорема Г". Пусть f, g^R[a-{-b, 6]V6>0 и несобственные
ъ b
интегралы у f(x)dx, у g(x)dx сходятся. Тогда vXi, XzeR
a<- a<-
b
сходится несобственный интеграл у (kif(x)-j-X2g(x))dx, причем
а+-
Ъ b Ь
У У /(*)^ + х» У g(x)dx.
а^— а*- а*-
Доказать самим.
14
Теорема 2. Если
3 «п, (3.1 >
Л=1
З&п (3.2>
— два таких ряда, что ап=Ьп при всех п, за исключением, быть
может, конечного их числа, то оба этих ряда сходятся или оба
расходятся.
Доказательство. Кроме рядов (3.1), (3.2) рассмотрим
ряд
4-сю
2 ся (где сп - bn — ап V пе N). (3.3)
л=1
Члены ряда (3.3) при всех п, за исключением, быть может,
конечного их числа, равны нулю, поэтому ряд (3.3) сходится.
4-оо 4-°°
Если ряд (3.1) сходится, то ряд 2 Ъп = 2 (ап+сп) по теореме 1
п-1
также сходится. Если ряд (3.1) расходится, то и ряд (3.2)
должен расходиться, в противном случае по той же теореме 1
4-00 4-00
ряд 2 ап— 2 (Ьп—Сп) сходился бы вопреки предположению.
п—1 Л=1
Следствие, Сходимость (или расходимость) ряда не зави-
сит от изменения конечного числа членов этого ряда-
Теорема 2'. Пусть f^R[d, t]Nt>a и b>a. Тогда несобст-
4-оо 4“°°
венные интегралы f f (х) dx и f f (х) dx сходятся или расхо-
а Ъ
дятся одновременно.
X х
Доказательство. Пусть А (х) = f f(t)dt и В(х)= f f(t)dt так,
а Ъ
Ь
что при имеем А(х)*вВ{х)^ f f(i)dt. Из этого равенства
а
немедленно следует утверждение теоремы 2', поскольку
f f(t)dt*=* lim А(х), f f(t)dt=s lim B(x).
J *—+«> J X-»+oo
15
Теорема 2". Пусть f<=/?[a+6, fe]v6>0 и се(а,Ь). Тогда не-
Ь С
‘собственные интегралы f f(x) dx и f f(x)dx сходятся или
а<— at-
расходятся одновременно. Доказать самим.
Теорема 3. Пусть (kn) — строго возрастающая последова-
4-00
тельность натуральных чисел (7ji = 1). Если ряд 2 сходится
Л=1
к а, то ряд 2 Ьп, где Ьп— 2 а‘> также сходится к а.
П=1 /=*л
я п
Д о к а з а т 6 л ьст в о. Если ЛЛ== вд и ^-2 &к, то
*— 1 Л-1
п / kl+\—i \ *п+1~*
=21 2 ао J — 2 а*=
Z=1 \p=*z J i-t
Поскольку любая подпоследовательность сходящейся после-
довательности сходится к тому же пределу, то
( lim Ап = а\^( lim Bn= lim Ль1,1_|=а'|.
\л->4-оо ) \л-*4-сю л—►4~ов ~ /
Следствие. Группировка (без изменения порядка) членов
сходящегося не меняет суммы ряда.
Замечание. Обратное неверно. Раскрытие скобок в сходя-
щемся ряде может привести к расходящемуся ряду.
Пример. Ряд (1—1) + (1—1)+|... сходится, а ряд 1—Г+;
’+1—1+... расходится.
3 а м е ч а н и е. Пусть lim an-0n3mEN такое, что 1<
n-»4-oo
+ор
— £n</nVneN. Тогда если ряд 2 Ьп сходится, то и
п=!
4-00
ряд 2 ап сходится к той же сумме. В самом деле, посколь-
л=1
ку Вп = Akn+l-~i, то Vp(=NSfcn такое, что £n<P=On+i—Ь
и поэтому
fcn+l~l ftn+nl
. \Ар~А.+1-1К 2 !“!< 2 ы-
Z=fe Zxrxfe
я л
16
Но поскольку
*«+"
lim V |л/|»0 и Я lim Лдя,,_1= lim Вп=а, то Я lim А„ = а.
<п—►4“°° . п—>4“°° п~~**Ь°° Р~>4“°°
/в*л
§ 4. Признаки сходимости знакопостоянных рядов
и несобственных интегралов
от знакопостоянных функций
Теорема (критерий сходимости знакопостоянного ряда).
+°°
(Ряд 2 ап с неотрицательными членами an^0.(v neN) exo-
П-1
’•дится) <=> (последовательность его частичных сумм (sn) ограни-
чена сверху). В случае сходимости ряда для его суммы имеем
« = S ®л = зиР«л-
л=1 "
Доказательство. Если an>0VneN, sn+1=sn4-an+1>sn,
т. е, «п t при п—> + оо. Необходимым и достаточным условием
•сходимости монотонно возрастающей последовательности яв-
ляется ее ограниченность сверху, причем
lim sn = sup sk.
П—>-|-оо k
Замечание. Если ряд с неотрицательными членами расхо-
дится, то он расходится к -|-оо, т. е. lim sn=-J-oo.
п—>4-00
Теорема (критерий сходимости несобственного интеграла
с бесконечными пределами интегрирования от неотрицательной
функции). Пусть
f(x)>OVхЕ[а, +<») и
4-00
Тогда (несобственный интеграл f f(x)dx сходится) <4 (функ-
а
х
ция F(x)—< f f(t) dt ограничена сверху на полуинтервале [а,
а
j-oo)). В случае сходимости несобственного интеграла имеем
f f(t)dt = sup F(x).
" [а, +°°)
Доказательство провести самим, заметив, что функция
F(x) f на [а, фоо).
2—Л. И. Камынин • 17
Теорема (критерий сходимости несобственного интеграла от
неотрицательной неограниченной функции). Пусть f(x)>0V хе
е(а, &], feR [а-|-6, Тогда (несобственный интеграл
ь ь
J f(x)dx сходится) & (функция F(x) = f ограничена
а*- х
сверху на (а, &]). Доказать самим.
Теорема (сравнения для рядов). Пусть
(4.1>
П==1
2 bn <4-2>
Л=1
— ряды с неотрицательными членами ап~^^, Ьп^№ neN, при-
чем an^bnv Тогда из сходимости ряда (4.2) вытекает схо-
димость ряда (4.1) и из расходимости ряда (4.1) вытекает расхо-
димость ряда (4.2).
Доказательство. Пусть
Ап •“ 2 и В* — 2 bk>
*=i fe—1
тогда (ап<6„ при п>«0)=>(Дп — Л„,< Вп — Вп)^
ДП<ВП + ДЯ,-Д„, (4.3)
или
&п > Ап — Ап, + Вп,. (4.4)
Если знакоположительный ряд (4.2) сходится, то его час-
тичные суммы Вп ограничены сверху. Тогда в силу (4.3) час-
тичные суммы Ап знакоположительного ряда (4.1) также ог-
раничены сверху, и поэтому в силу критерия сходимости
знакопостоянных рядов ряд (4.1) сходится. Если ряд (4.1) рас-
ходится, то lim Ап » + со и в силу (4.4) lim Ва » + со, т. е.
n—►-f-oo «-*+«>
ряд (4.2) также расходится.
Следствие. 1. Если an = O(bn) (при п-*-|-оо), т. е.сущест-
вуют noeN и Я>0 такие, что 0<ап<К • 6nVп>п0, то схо-
димость ряда (4.2) влечет сходимость ряда (4.1). Доказать са-
мим.
Следствие 2. Если для знакоположительных рядов (4.1) и
;'(4.2)
(an>0, 6n>0VrtSN)a lim aJbn^K,
то: 1) при 0<ЛГ<4-со ряды (4.1) и (4.2) сходятся или расхо-
дятся одновременно; 2) при К«- 0 из сходимости ряда (4.2)
18
вытекает сходимость ряда (4.1); 3) при Х = -|-оо из расходи-
мости ряда (4.2) вытекает расходимость ряда (4.1). Доказать
самим.
Следствие 3. Если для знакоположительных рядов (4.1) и
(4.2) имеем an/an+i > bnlbn+l V n > га0, то из сходимости ряда
(4.2) следует сходимость ряда (4.1)« а из расходимости ряда
(4.1) следует расходимость ряда (4.2).
Доказательство. (ап/Лп+1>Ьп/^п+ь яп>0, bn>0V
>n0)=> (flnlbn Лп+t/bn+i п0), т. е. последовательность
(л„/Ьп) I прип-»4-°°» поэтому ЯК>0 такое, что ап/6п<
<KVn>n0, откуда 0<ап<К • &„Vn>n0, т. е. выполнены
условия следствия 1 теоремы сравнения (для рядов).
Теорема сравнения (для несобственных интегралов с
бесконечными пределами). Пусть f, g^R[a, t]Vt>a и f(x)^0,
g(x)^0v xe[a,-|-co). Пусть Я, b^a такое, что Vx^b имеет
место оценка f(x)^g(x). Тогда из расходимости несобственного
интеграла
Т t(x)dx (4.5)
вытекает расходимость несобственного интеграла
+f g(x)dx,
а
(4.6)
а из сходимости несобственного интеграла (4-6) вытекает сходи-
мость несобственного интеграла (4.5). Доказать самим, используя
критерий сходимости несобственных интегралов от неотрицатель-
ных функций и неравенства V х>Ь
х X Ъ
J g(t)dt > J + f (g(t) -
a a a
f /(0 dt < J g(t)dt 4-1
а а я
Следствие 1. Если f = O(g)(x —* + оо), т. e. существуют
X>a и K>0 такие, что 0</(x)<K • g-(x)Vx>X, то сходимость
несобственного интеграла (4.6) влечет сходимость несобствен-
ного интеграла (4.5). Доказать самим.
Следствие 2. Если для положительных функций f(x)> 0s
g(x) > О V х G [a, + оо); /, gE Rfa, t] Vt >• а существует
lim f(x)/g(x)—K., то: 1) при 0<K<4-oo интегралы (4.5) и (4.6)
сходятся или расходятся одновременно; 2) при К = 0 из схо-
димости интеграла (4.6) вытекает сходимость интеграла (4.5);
3) при К = -|- ©о из расходимости интеграла (4.6) вытекает рас-
ходимость интеграла (4.5). Доказать самим.
2* 1©
I
Теорема сравнения (для несобственных интегралов от
неотрицательных неограниченных функций). Пусть f, g^R[a,
+6, ft]v6>0, f(x)^0, g(x)^0V x <= (a, ft]. Пусть я ce(a, b)
такое, что f(x)^g(x) V хе (а, с). Тогда из сходимости несобст-
венного интеграла
ь
f g(x)dx (4.7)
следует сходимость несобственного интеграла
ь
f f(x)dx, (4.8)
а*-
а из расходимости интеграла (4.8) вытекает расходимость интег-
рала (4.7). Доказать самим.
Следствие 1. Пусть /=O(g)(x—*а+0), f(x)>0, g(x) > OVx €=
f=-(a, б). Тогда сходимость несобственного интеграла (4.7)
влечет сходимость несобственного интеграла (4.8).
Следствие 2. Пусть для положительных функций f(x)>0,
g(x) > О V х е («, ft]; /, g е R [а 4- 6, ft] V 8 > 0 существует
lim /(x)/g(x) = К. Тогда: 1) при 0 < + оо несобственные
х—
интегралы (4.8) и (4.7) сходятся или расходятся одновремен-
но; 2) при К=0 из сходимости интеграла (4.7) следует сходи-
мость интеграла (4.8); 3) при А' = + <» из расходимости ин-
теграла (4.7) следует расходимость интеграла (4.8). Доказать
самим.
-»!
Пример. Рассмотрим несобственный интеграл J (1—х4) dx
с особой точкой в х=1. Тогда
(1— Х4)~‘/4 = (1_Х)-1/4(1+х + х2+хЗ)-1/4 =
-О((1 — х)-‘/4)(х->1— 0).
—1
Но несобственный интеграл [ (1—x)~1/4dx сходится, поэтому
о
сходится и наш интеграл.
Теорема (признак Д’Аламбера сходимости знакоположи-
тельного ряда). Если для знакоположительного ряда
2 M««>0VnsN) (4.9)
q= lim an+llan и q— lim an^i/an,
то при ряд (4.9) сходится, a npuq^>i ряд (4.9) расходится.
20
Доказательство. 1) Пусть q = lim an+i/an< 1. Тогда
n—
1 3n0EN такое, что
a„+i/a„ < & = &«+1/8л V n > n0.
Полагая bn => &n, имеем an I a„+1 > bn I Ьл-н V n > n0. Но ряд
&n при сходится как ряд из членов геометрической
л—1
прогрессии со знаменателем, меньшим (по модулю) единицы, по-
этому в силу следствия 3 теоремы сравнения (для рядов) ряд
(4.9) сходится.
2) При £> 1 Яп0еN такое, что an+1/an> 1 Vn>«0, т. е.
(«nt t (»-*+оо))=»(Лп>Лп,>0¥п>п0), поэтому общий член ап
ряда (4.9) не стремится к нулю при п-*4-оо. Необходимый
признак сходимости рядов не выполнен, поэтому ряд (4.9)
расходится.
Следствие. Если Я lim an+i/an = g, то при д<1 ряд (4.9)
л-»4-оо
сходится, а при <?>1—расходится.
4-00
Пример. Рассмотрим ряд 2 и!/(2ге4 1)11. Тогда
п»1
а„ = л!/(2га+ 1)11,
an+i!an = (п + 1)/(2га + 3) => lim ап^/ап = 1/2 < 1.
ZZ—►—|-оо
По признаку Д’Аламбера наш ряд сходится.
Теорема (радикальный признак Коши сходимости знакопо-
ложительного ряда). Если для знакоположительного ряда (4.9}
~q = ТБГ У ап,
то при q<A ряд (4.9) сходится, а при q>l ряд (4.9) расходится.
Доказательство. 1) При ^<1VO^7<&< 1Ял0GN такое,
что |/an<?<JVn>n0, т. е. en<ftnVn>n0, и, сравнивая с
-1-00
рядом 2 сходящимся при 0<&<1, заключаем (по теореме
п=1
сравнения для рядов), что ряд (4.9) сходится.
21
2) При (/>lV7VsNHn>-2V такое, что j/an > 1, т. е.
lim ап =# 0.
П-»4-оо
Необходимый признак сходимости ряда не выполнен, поэтому
ряд (4.9) расходится.
Следствие. Если Я lim yf an—q, то при д<1 знакополо-
жительный ряд (4.9) сходится, а при ?>1 ряд (4.9) расходит-
ся.
Замечание. При q=l как в признаке Д’Аламбера, так и в
I(радикальном) признаке Коши знакоположительный ряд (4Д>)
может как сходиться, так и расходиться.
Теорема (критерий сходимости бесконечного произведе-
ния). Если
ап = 1 4-ап, —1 <ап< + оо, ап#= 0 VnеN
и ап сохраняет знак, то бесконечное произведение
П(1+а„) (4.Ю)
Л»1
сходится <=>, сходится знакопостоянный ряд
(4.11)
П»1
Доказательство. Еслиlim <zrt=/=0, то по теореме о необ-
ходимом условии сходимости (бесконечного произведения и
ряда) произведение (4.10) и ряд (4.11) расходятся одновремен-
но. Пусть теперь lim an = 0(an^0 Nn gN), тогда lim ln(l +
n-+4-oo
4-an)/an= 1 >0 и 3noeN такое, что при п>п0 знаки ln(14-an)
и an совпадают. По теореме сравнения для знакопостоянных
рядов ряды (4.11) и
2°1п(Ц-а„) (4.12)
П»1
сходятся или расходятся одновременно. Но ряд (4.12) и бес-
конечное произведение (4.10) сходятся или расходятся также
одновременно.
-1-00
Пример. Произведение ("j (1 4-1/н) расходится, так как
п—1
4-оо
ряд 2 (будучи гармоническим) расходится. Произведение
Л=1
22
Ц-ао +“
сходится, так как ряд ^п! сходится по приз-
«i=i п“®
лаку Д’Аламбера:
lim (!/(/»+1)!)/(1/п!) = 0<1.
п—►4“°°
Теорема (достаточное условие сходимости бесконечного про-
изведения,) . Если an=l-j-an, —L<Z ап < +°°, ал =И= OVne N и
ряды (4.11) и
(413)
Л—1
сходятся, то сходится и произведение (4.10).
Доказательство. Из сходимости рядов (4.11) и (4.13) в
силу необходимого признака сходимости следует, что lim ап=0.
По формуле Тейлора с остаточным членом в форме Пеано имеем
In (1 + ап) » ап — (а*/2) + о(а’) (п -> + оо),
откуда (учитывая, что an#=0VneN) получаем lim (ап— 1п(14-ап))/
/а£= 1/2>0. Но тогда I3n0G=N такое, что ап— 1п(1 +<хп) >
>0V n>n0. По теореме сравнения для знакоположительных
.рядов из сходимости ряда (4.13) вытекает сходимость ряда
4"00
У, (%— In (14-«,»))• Поскольку ряд (4.11) также сходится, то
Два!
ряд (4.12) (где 1п(1 4-а„) = ап — (ап — 1п(14-ап))) как разность
двух сходящихся рядов также сходится. Наконец, из сходи*
мости ряда (4.12) следует сходимость произведения (4.10).
Замечание. Пусть — 1<ап<4-~, a„^0VneN и
lim ая=0. Тогда бесконечное произведение (4.10) расходится
+оя
к нулю, т. е. П (1 +ап) = 0, если выполнено одно из двух
П=ж!
условий: 1) либо — l<a„<0VngN и ряд (4.11) расходится
(к — оо), 2) либо ряд (4.11) сходится, но расходится (к 4-°°)
ряд (4.13).
Доказательство. 1) Если —1<а„<0V«eN и lim ал«»0
П- »4*оо
<и ряд (4.11) расходится (к —оо), то из соотношения
lim In (1 4-an)/an = 1 > О
23
вытекает равенство
+=°
2 1п(1 +<ХП) = — оо, (4.14>
П=1
т. е. произведение (4.10) расходится к нулю.
2) Если ряд (4.11) сходится, но ряд (4.13) расходится
(к 4-оо), то (учитывая, что an=A0VnEEN) равенство (4.14>
следует из соотношения
lim (an — In (1 + an))/a* = 1/2,
Л->4-оо
т. е. произведение (4.10) опять расходится к нулю.
4-00
Пример. Произведение П (1 — 1/(п+1)) расходится к ну-
п=1
4-ео
ЛЮ, поскольку 2 (— М(п + 1)) = — °°•
Теорема (интегральный признак Коши сходимости знакопо-
стоянного ряда). Пусть f (х)Х> VxJX), feC ([0, +<»)) и f (х) | на
4-е®
[О, +°°). Тогда (ряд у* f(n) сходится) (сходится несобст-
п==1
+°°
венный интеграл [ f (х) dx).
о
Доказательство. (feC([O, 4-оо)))’=»(/еЯ[0, a]Va>0)-
Поскольку f(x) | на [0, 4-оо), то имеем оценки
л п4-1
f f(x)dx> f(n) > f f(x)dx (n = 1, 2, . . .),
л—1 n
откуда
n n ft+1
F(n) = (f(x)dx> f /(x)dx =
о t=i i
= F(n 4- 1) - f f(x)dx ’ V n e N.
о
Но из этих неравенств вытекает, что монотонно возрастаю-
щие (при i»-*+oo) последовательности
и F(n) = Jf(x)dx
Л-i о
либо обе ограничены, либо обе неограничены, т. е. (ряд
у f(n) сходится) 4Ф (3 lim F(n)). С другой стороны, поскольку
Л₽1 л—+оо
24
/(х)>0 на [0, 4-оо), то функция F(x)] на [0, 4-°°) и, кроме
того, для любого х е [п, п 1] имеем
п+1 X п
f(n4-l)= f f(t)dt>F(x)=]f(t)dt>F(n)=]f(t)dt,
О 0 0
откуда следует, что (несобственный интеграл J f(t)dt ехо-
о
дится) <v=> (Я lim F(n)). Интегральный признак Коши доказан,
л—>4“ °°
Пример. Пусть ап = п~х, где 0 < а < 4- <» — постоянная»
Положим
?Ы=1‘. "Р"
I Х~х при 1<Х<4-оо.
Тогда несобственный интеграл [ f(х) dx = 1 4- x~adx exo-
d 1
дится при 1<а<4-оо и расходится при 0<а<1. В силу
4*00
интегрального признака Коши знакопостоянный ряд у l/n**
n==I
сходится при 1<а<4-оо и расходится при 0<а^1.
Теорема (признак Гаусса сходимости знакоположительного
ряда). Если для знакоположительного ряда (4.9) отношение со-
седних членов можно записать в виде
^n/<2n+i = 4* (р/л) 4* ^п»
где ряды
4*оо 4* °°
п=1
сходятся, то ряд (4.9): 1) при ^>1 сходится; 2) при расхо-
дится; 3) при А=1' и р>1 сходится; 4) при Л=1 и расхо-
дится.
Доказательство. Предварительно докажем лемму, име-
ющую и самостоятельный интерес.
Лемма. Пусть ап>0 V neN и an+Jan=l 4- s/n 4- an,
где ряды У, ая и У а® сходятся. Тогда существует постоянная
п=1 П=1
С#=0 такая, что an/ns~ С(п-> + оо), т. е.
ап=С• ns• (14-о(1)) (п->4“Оо).
Доказательство. Положим bn =an/ns, тогда имеем
bn+i/bn = (ап+1 / (n-bl)s)/ (ап/п°) = (ап+1/ап) • (14-l/n)-s.
2&
Применяя формулу Тейлора с остаточным членом в форме
Пеано, имеем
(1 + i/rt)-s = 1 _ sin — s • (-s— 1)/(2л2) +
+ <j(l/n2) = l — s//i4-O(l/n2)' (n—>4-00),
откуда
&„+1/&n = (1 + (s/n) + а„)(1 - {sin) + <?(l/n2)) =
= 1 4- an — an(s/n) 4- 0(an/n2) = 1 4- an 4- Pn-
Отметим неравенство |a-6|<(a2 4- b*)!2Na, b = R, следующее
из соотношения О (|®1 — |6|)2==а2 — 2|a-t>|4-&®- В силу этого
неравенства имеем оценку |р„|^ Ki(a2 4-l/»2)Vn. Из сходимости
4-00
рядов 2 а« и 21 в СИЛУ теоремы сравнения вытекает
Лея 1 П— 1
+=°
сходимость ряда 2J [Рп1« Заметим, что при /п>п имеем
л=!
т т
2 < 2 IW>
й=п+1 *=М-1
4-00
•поэтому в силу критерия Коши из сходимости ряда 2J IW вы'
4-00
текает сходимость ряда у $k. Далее из сходимости рядов
ы
2 и 3 ₽п вытекает сходимость ряда Vn, где ?n=an-|-(3n.
Лжи! П—1 П=1
Рассмотрим теперь бесконечное произведение
П bn+i/bn = П (1 + ?»)•
Л«=»1 П==1
Ряд 2 Vn сходится, кроме того,
л«=1
= (an + ₽п)а = а2 4- 2апрп 4-
Из сходимости рядов 2 ап и *2 Рп вытекает, что
(an=o( 1), рп=о( 1)(п-*4- <*>)) => (|Pn|=0( 1 )(п-> 4- оо)),
т. е. существует постоянная ^>0 такая, что
К • • l?nl. п = l₽nl • ♦ IPnlVneN.
26
По теореме сравнения следует, что ряды"]} и схо-
П=1 Л=[
ДЯТСЯ. Из неравенства у2 <«2 4-2- |ап • ₽п| 4-₽2 в силу сходи-
мости рядов
-f*oo -J-oio +оо
3 S 1“»- М’ S к
п®»1 л=1 Л=1
+»
по теореме сравнения вытекает сходимость ряда у, у*. Итак,
П=1
П bn+i/bn^ п (1+тп).
л—1 п—1
где ряды у уп и у у* сходятся. В силу достаточного приз-
л«1 л=1
нака сходимости бесконечных произведений произведение
4*00
П (1 + уЛ) сходится, т. е. существует Со =И= О такое, что
П Ьл+1/Ьп=Со#=О. Но тогда
<л=1
Со = lim П bk+i/bk - lim =
n‘*+00Jfe==1 Л->-|~оо 02 Ьп ]
— lim fen+i/fti, т. е.
П—>-|-оо
(Я lim Ь„=С0 • Ь1=вС=И=О)=Н&я=С • (14-о(1))(п-*4-оо))=»
л->4-сю
=»(anlns = С • (1 + о(1)) (л — + оо)),
т. е. an!ns~C (п-*+<х>), что и требовалось доказать (в лемме).
Возвращаясь к доказательству теоремы Гаусса, видим, что
на представления an/an+i =» Ч-(?/п)+&п, &л = о(1) (п->4-оо) сле-
дует, что Я lim a„4-i/a„=l/A., поэтому при признак Гаусса
П » ' сх>
следует из признака Д’Аламбера. В случае Х = 1 по формуле
Тейлора с остаточным членом в форме Пеано имеем
Лл+1/вл — ( 1 + (р/л) + К)-1 = 1 — PM — +
+ 2(р./п) • &п 4- 4- (р8/п2)+о(7п)(п -> 4- оо),
гд® l?nl = &® + (l/«2) + |^п|/«- Вейлу неравенства |&п| •(!/«)<
^((1/«’)+&’)/2 имеем |?п| =£(&* +(I//»*)) (п->4-оо), откуда по
27
теореме сравнения вытекает сходимость рядов у, |7п| и у у2.
П-1 п=1
Таким образом, имеет место представление an+ilan—l—(н/га)+
+ ап, где
ап = -К + О(|7п|) и «’=»’ + 0(^2 + 72),
так как |»п • 7„| < + 72)/2. В силу сходимости рядов.
4-00 4-00 4-00 4-00
3 ^п» У &п» 3 Ы и 2j Tn ПО теореме сравнения следует
п=1 П=1 П—1 п~1
сходимость рядов f «п и а?п. По лемме (где $ = —
П= л-1
ЯС=/=О такое, что
an/n-v- = С • (1 + о(1)) (п - + оо),
откуда
. (ап = С. п-н. (1 + о(1))(п-> + «»))=»
(Я lim а^п-Р = С=£ 0).
П->4-оо
Но тогда по теореме сравнения (в предельной форме) ряд
4-00
(4.1) сходится или расходится одновременно с рядом у, Мп?.
П=1
Таким образом, ряд (4.1) при k= I сходится, когда р->1, и
расходится, когда |*<1. Теорема Гаусса доказана полностью.
+°°
Замечание. Поскольку из сходимости ряда у |&п| следует
п=1
сходимость рядов у и у, то как теорема Гаусса, так и
П=1 Л=1
4-00
лемма имеют место при выполнении условия: ряд у |&п| (со-
л=»1
+ <50
ответственно ряд у |ап|) сходится.
Теорема (формула Стирлинга), п! =а(п/е)п • п1/2 • (1 + о(1))
(и—>+<эо), где а>0 — постоянная.
Доказательство. Пусть ап=п\ п~п • еп, используя фор<-
мулы Тейлора с остаточными членами в форме Пеано, имеем
представление
(а„+1/ап)= ~ ' ------- =е • (1 + 1/п)~п =
(п4-1)п+1-п!.г'1
28
= ехр{1 —п • In (1 + (1/л))) = ехр{1 — n((l/n) —
- l/(2n2) + l/(3n2) + о(1/п®))> = ехрЦ1/(2п))-
— (l/(3n2))4-o(l/n2)}= 1 +((l/2)/7i)+O(l/n2) (n-4-oo).
В силу леммы при s=l/2 и ап = 0(1/п2) существует постоян-
ная а>0 такая, что ап[п№ = а • (1 + о(1))(п-» + оо), откуда по-
лучаем формулу Стирлинга
п\ = а • пп+*/2. е~п • (1 + о(1)) (п-> + оо).
Для уточнения вида постоянной в>0 в формуле Стирлинга
нам понадобится формула Валлиса, имеющая самостоятельный
интерес.
Т е о р е м а (формула Валлиса).
я/2 = lim {((2n)!!/(2n — I)!!)2 . 1/(2га + 1)}.
n-*4-oq
Доказательство. Положим
п/2
Jm— f sinmxdx, m£N.
о
Интегрируя по частям, имеем
те/2 тс/2
(7m= j sinm-1xd(—cosx) == — sinw-1x • cosx | +
о о
п/2
+ (т— 1) j sinm“2x • cos8x • dx =
oJ
п/2
= (m — 1) j sinm~2x • (1 — sin2x)dx — (m— l)/m-2—
о
m)*^ — l)/w&) • /m—2 ,
я/2
— Ji= J sinxdx=l)=^
о
(2n-l)(2n—3)...3-l я _ (2n—1)!! it.
(An = 2n(2n—2)...4-2 ’ 2~ (2n)!! ’ 2’
J = 2n-(2n—2)...4-2 = (2n)!! \
2"+1 (2n+l)-(2n—1)...3-1 (2n+l)!! )’
Полагая 0<х<л/2, имеем оценки
sin2"+’ х «С sin2nх < sin2"-* х.
Интегрируя по x от 0 до л/2, получаем оценки
п/2 п/2 п/2
j sin2rt+1xdx< j sin2"xdx j sin2n-1xdx,
29
откуда
(2га)?! < (2га—1)!! (2га—2)!?
(2л+1)!! 2 (2га)!! (2л—1)1!
ИЛИ
1
ал=-----
п 2п+1
’ (2га)!? у д Г (2га)!! Т
(2га—1)!! *^2^1 (2га—1)’!
2п
Ъп,
но имеем I
/ — Г (2п)!! 1* 1 I
( n“an (2n— I)!! * 2п-(2п + 1) '
<
<-• lim (&n-fln)«0), |
2 2л j 21 >^00 .
* 4"
поэтому |
lim an = lim Ьп = те/2, |
Л-»4-С0 J
чем формула Валлиса доказана. |
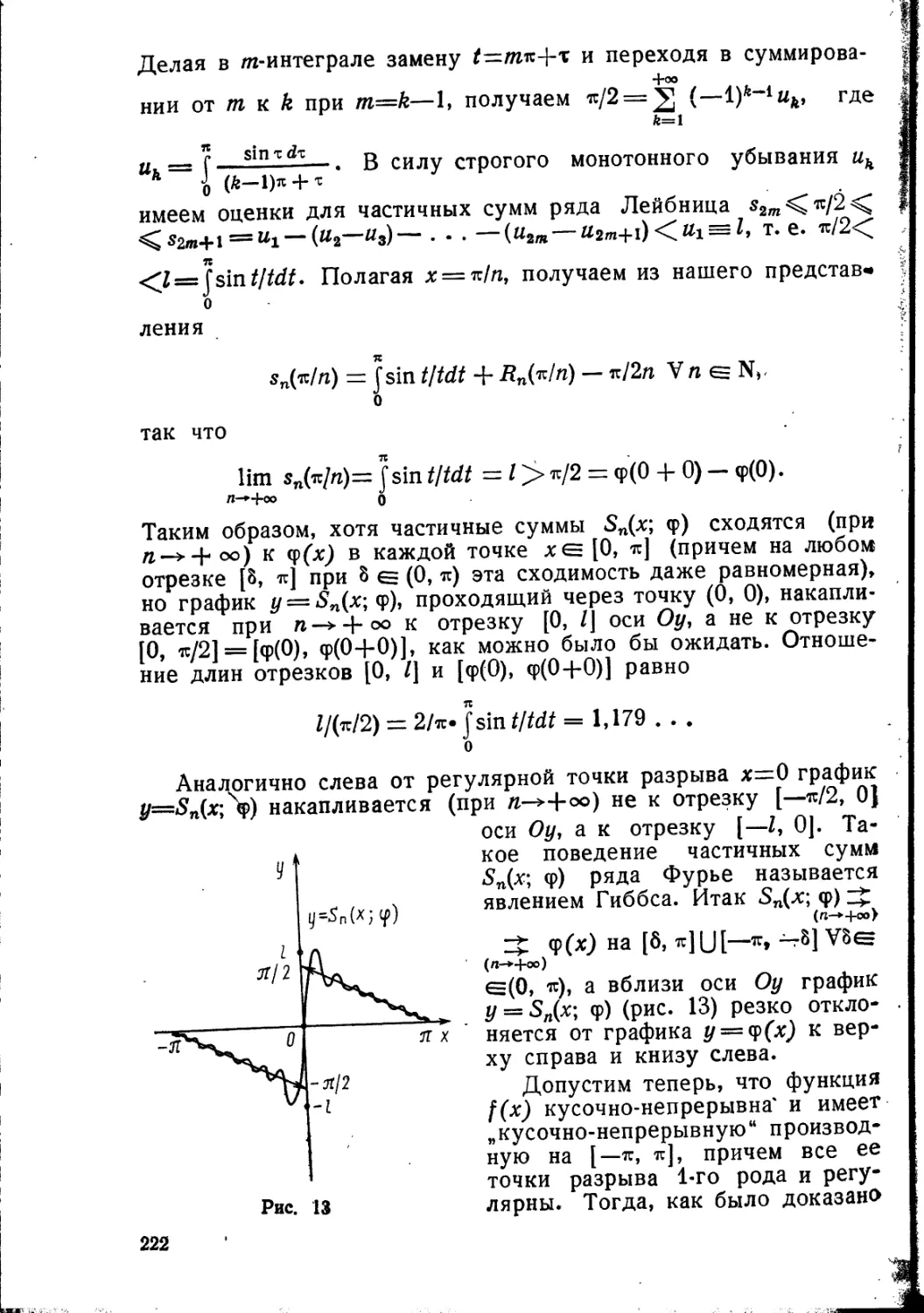
Следствие. В формуле Стирлинга имеем а=(2л)1/2.
Доказательство. По формуле Стирлинга имеем nlям
=а-пп+1/2-е~п-(1+о(1)) (п-*4-°°), поэтому !
(2zz)!l _[(2n)!!]«_4«.(n!)»_ &.at.„?*+*.e-2n I
(2n—1)!! (2n)l (2n)! a(2n)2n+,/,.e-2'' X ?
X (1 4-0(1)) = a(n/2)‘/»(l + 0(1)) (n-> + oo).
По формуле Валлиса
(K/2)‘/2= lim (2n4- 1)-’/2. (2га)!!/(2п—1)11 —
л<> 4*°°
= lim а • (п/(2(2п 4- 1 )»1/2( 1 + о(1)) = а/2,
откуда а = (2л)1/2.
§ 5. Признаки сходимости знакопеременных рядов
и несобственных интегралов
от знакопеременных функций
+°°
Определение. Ряд у, ап называется знакочередую-
щимся, если выполнено соотношение sign ап • sign ап+1 =) —Г
V п е N. Знакочередующийся ряд будем записывать в виде
4-00
У, ’(—l)n-* un> где мп>0 Vn (или unr<.0 vn)’.
П»1
30
Теорема (признак Лейбница сходимости знакочередующе-
гося ряда). Пусть
3 (-!)"-* «п(«п> 0 VneN) (5.1>
— знакочередующийся ряд. Если ип\ при п->4-оо и lim un=0, то
ряд (5.1) сходится.
Доказательство. Имеем
$2т=(«1—«2), +'... + («2т-1 — «2т).
Поскольку Un|(n-> + oo), то «2Й-1—“гк^О, И ПОЭТОМУ
при tn-^+<x>. Далее, очевидно, s2m =' «1 — («2 — «3) —... —
— (U2m-2 — Uim—i) — U2m U\.
Таким образом, видим, что последовательность (s2m) монотон-
но возрастает и ограничена сверху. Но тогда в силу критерия
сходимости монотонных последовательностей Я lim s2m=st
m-*4*°°
Причем s2m^s V tn. Ho $2m+l = «2п» + «2m+l > «2т» ПОЭТОМу
( lim ип ~ 0)=> ( lim s2m+i == lim sim = з).
4-00
Заметим, что
$ 2m4-l = «1 ~ («> — Us) — ... — («jin — «2m+l ),
так что e2ii>+i |(/n4- 00), откуда
(S2m-M s)=^ (.$»m s s2m+lVm).
Итак, Яlim sn=as, т. e. ряд (5.1) сходится.
Л—*4“°°
Замечание. Для знакочередующегося ряда (5.1>) при unlfl
(п->-|-оо) имеет место оценка |гп| .= Is — sn| «n+b причем
signгп =! sign [(—1)я • «п+1]. В самом деле, по признаку Лейб-
ница Я lim sn = s, причем su<s<S2m+tVm. Но тогда
л-*4-оо
(S2m+1 = П-2ш+1 0) (0 S ~ «2л1-н).
Далее
($2т+1 — ««т+2 = «2т—2 0) (®Лп4-2 ®2т4-1)»
(®2т+2 S в2т-н) *2m+l — S «2т+з)э
Т. е.
|rn| = Is — sn| < Un+I, Sign rn = sign [(—1)" ♦ un+i]Vn.
4-00
Пример. Ряд Лейбница у, (—Г)”-1 In сходится по приз-
наку Лейбница, поскольку «П=Г/«|О (при п-^+^о),
31
Теорема (тождество Абеля). Для любых последовательно-
п
<сгей (ап)(ап<^С) и (an.) (aneR) при sn — 2 а* имеет
к=1
место тождество Абеля (при m>n): so=O,
3 «л- ал== 2 V <ak-a*+i)+sm * am—«п-i * an-
Л==Л Ь=П
(Доказательство было проведено в § 6 гл. 2 ч. II [I].)
Теорема (признак Дирихле сходимости знакопеременного
ряда). Пусть afteR и an|0 («->+<»), an<=C и последова-
п
•тельность sn — 2 ограничена, т. е. 3,Л1>0 такая, что
*=1
Isnl М v n s N. Тогда ряд
3° (5.2)
п=1
^сходится.
Доказательство. Воспользуемся критерием Коши схо«
димости рядов. В силу тождества Абеля при /п>п имеем
2 аа • ak — 2j sk ' (afc a*+<) 4" sm ‘ am gn—i an-
Учитывая, что a«| (п-^Ч-00), имеем ak—ак-н^О, откуда |aK—
— a*+i I = ak — a*+i, но ak О V k, поэтому
I S • ak < Vl'*l • l°=k — а*+1| + 1«т| ♦ a/n +
/m—1
+l«n-i| • an < M 2 К “ a*+‘l + a/n + an) =
/m—I
= M I 2 (aft —a*+i)+am+’an) ==2M • an.
\Лг=л
Поскольку lim an = 0, to Ve>03A'(e)EN таковл что
П->Ч-оо
O^an<^e/2A1 N(e).
Но тогда V2V(e) имеем
3«*- ak
k=n
• an<e.
В силу критерия Коши ряд (5.2) сходится.
^2
Теорема (признак Абеля сходимости знакопеременного ря-
да). Пусть a»eR и «пеС. Тогда если последовательность
(ап) монотонна и ограничена, а ряд
3 (5.3)
n=i
сходится, то и ряд (5.2) сходится.
Доказательство. Пусть для определенности ant (при
л_|_<х>), тогда в силу ограниченности последовательности (|ап|)
вытекает, что Я Нт ап=а, причем (а—ап)Ю(п-*- + оо). Из
л->4-о»
сходимости ряда (5.3) следует, что последовательность его час-
п
тичных сумм ($п) (sn = 2 ограничена. По признаку Ди-
4=1
рихле ряд
4-00
3 —ап) • «п
л—1
(5-4)
сходится. Но ап • On = а • ап — (а — ап) • ап- Поэтому ряд (5.2)
как разность двух сходящихся рядов (5.3) и (5.4) также сходит-
ся.
Замечание. Признак Лейбница есть частный случай
признака Дирихле. В самом деле, при ап — (—ап = «а
имеем
Un у 0(м оо) И
У (—1)4-1 = /° П₽И П = 2т’
4Z1 11' при п = 2/п+1,
откуда IsnI i Vne N.
Теорема (признак Дирихле сходимости несобственных ин-
тегралов с бесконечными пределами). Пусть t]v t>a и
X
g^M[a, +~). Пусть £limg(x)=O и функция F(x) = J f(t)dt
ограничена на [а, Ч-co) (г. е. существует постоянная такая,
что \F(x)I 7<Vx а). Тогда несобственный интеграл
"j f(x)g(x)dx (5.5)
а
сходится.
Доказательство. В силу 2-й теоремы о среднем для ин-
теграла Римана (см. § 6, гл. 2, ч. II [1])
Vх">х'>аЯсе[х', х"]
такое, что
З—Л. и. Камынин 33
(б.6>
J f(t)g(t)dt = g(x') f Д<)Л+ g(x") f f(t)dt.
xf xr c
В силу ограниченности функции F(x) имеем оценки
J f(t)dt = |F(c) - F(x')| < 2K, J f (t)dt I <2K.
x' c I
С другой стороны, поскольку 3. lim g(x)—O', то Ve>0SX(8)>a
X—H-oo
такое, что
lg(x)l < e/4KVjr>X(8).
Но тогда из равенства (5.6) v x" > x' > X(e) имеем оценку
H*')| • j f(t)dt 1+ |g(x")| X
X f f(t)dt <(e/4K) • 2K + (e/4K) • 2K
» e.
Теперь сходимость несобственного интеграла (5.5) вытекает из
критерия Коши сходимости для несобственных интегралов с бес-
конечными пределами.
Пример. Рассмотрим интеграл Дирихле
+°°
f sinx/xdx.
оД
Заметим, что в силу
(lim sinx/x = l)=^(sinx/x€=C([0, +<»))),
х->0
если положить sin х/х= 1 при х=0. Поэтому
-j-OQ 1 |,00
С sinx/xdx » f sinx/xdx+ [ sinx/xdx.
o<- о i
Положим f(x)_ = sinx, g(x) = 1/x, тогда
g(x) = 1/хеЛ/[1, 4-oo), lim g(x) = 0,
x-*4-oo
F(x) = | sin tdt = cos 1—cosx€=B[l, +<»).
По признаку Дирихле несобственный интеграл J sin x/xdx схо-
1
дится, но тогда сходится и интеграл Дирихле.
Теорема (признак Дирихле сходимости для несобственного
интеграла от неограниченной функции). Пусть + б, &]V
б>0 и g^M (а, Ь]. Пусть $Uimg(x)=0 и функция F(x) =
х->аЧ-0
Ъ
= J f(t) d(t\ ограничена на (а, 6]. Тогда несобственный интег-
X
34
рал J f(x) ё(х) dx сходится. (Доказать самостоятельно по ана-
логии с доказательством признака Дирихле для несобственных
интегралов вида (5«о).)
Теорема (признак Абеля сходимости несобственного интег-
рала с бесконечными пределами интегрирования). Пусть
Л v t>a и geM[a, -f-oo).- Пусть сходится несобствен-*
ный интеграл
+f f(x)dx, (5.7)
а монотонная функция g(x) ограничена на [а, 4-оо),г. е. сущест-
вует постоянная L>0 такая, что \g(x)\^.Lv х^а. Тогда несоб-
ственный интеграл (5.5) сходится.
Доказательство4 Вновь применяя 2-ю теорему о сред-
нем, получаем равенство (5.6). Поскольку несобственный интег-
рал (5.7) сходится, то в силу критерия сходимости Коши V е
>0 ЭХ (е) >а такое, что при х"^с^х'>Х(е)>а имеем оценки
IJ f(t)dt I < е/2£, IJ f(t)dt I < е/2£,
I X' I I С I
откуда, поскольку \g(x)\ ^..Ln х~^ а, получаем из (5J6) оценку
<(8/2L) • L + (e/2A)* L =
е.
В силу критерия Коши несобственный интеграл (5.5) сходится.
Теорема (признак Абеля сходимости несобственного интег-
рала от неограниченной функции). Пусть fe7<[a+6, 6]Уб>Ом
ь
geAf(a, Ь]. Пусть сходится несобственный интеграл S f(x)dx, а
а*-
монотонная функция g(x) — ограниченная на (а, &]. Тогда не-
собственный интеграл S f(x) g(x) dx сходится.
(Доказать самим по аналогии с признаком Абеля для несобствен-
ных интегралов с неограниченными пределами интегрирования.)
Теорема (о замене переменной интегрирования в несобст-
венных интегралах). Пусть Zjjvt>a и функция <р:[а,
+°°) (—оо<а<р^+<») такова, что (реС(1)([а, (})),
ф(0Н на (а, Р) и <р(а) =а, <р(р—0) = + оо.
Тогда имеет место равенство
J f(x)dx=J /[<p(y)]<₽'(y)dy (5-8)
а а
в предположении, что существует хотя бы один из этих интегра-
лов. Аналогично если f^R[a+б, b]V6>0 при — оо<са<6<
><4-оо и функция <р: (a, 5] (—00^а<р<4-00) такова,
что ф е С(1> ((а, pj), ф(t)ff на {а, р] и ф (а-|-0) = а, ф (р) =Ь, то
f f(x)dx==J №(y)W(y)dy
а<- а<—
в предположении, что существует хотя бы один из этих интегра-
лов.
Доказательство. Пусть
Ф: [а, р) -> [а, +°о) и lim <р(у) =4-оо.
1Л-Р-0
По теореме о существовании обратной функции Э.Ф-*ff на [а,
4-оо.), причем lim ф-1 (0вР> Применяя теорему о замене пере-
/-►•4-00
менной в обычном интеграле Римана, имеем
t »—1(0
j/(x)dx = J K<f(y)W(y)dy-
а а
Если существует хотя бы один из несобственных интегралов
4-оо —>0
J f(x)dx или J f°w(y) •<₽' (У) аУ>
а а
то, переходя к пределу при £->4-°°, имеем lim ф-1 (/)=р, и по-
/->4-00
этому существует и другой из несобственных интегралов, причем
имеет место равенство (5.18). Вторая часть теоремы доказыва-
ется аналогично.
Замечание (о связи несобственного интеграла от неогра-
ниченной функции с несобственным интегралом с бесконечными
пределами интегрирования). Пусть fe7?[a4-6, Ь]Уб>0 и не-
ь
собственный интеграл S f(x) ах сходится. Делая замену x=a4-j
а*-
4-1 /у, имеем / f(x)dx—J f (а+1\/у) • у~2 dy.
а+~ 1/(Ь—а)
Теорема (об интегрировании по частям в несобственном ин-
теграле). Пусть для функций и(х) и v(x) на любом отрезке [а,
с: (а, Ь) выполнены условия теоремы об интегрировании по
в
частям в определенном интеграле Римана f udv (при этом а
а
может быть особой точкой или & = 4-°°)> Тогда имеет место ра-
венство
ь ь ь
§udv=*u • р| —Jrdu
а а а
36
в предположении, что существуют какие-либо два члена этого ра-
венства (третий член равенства тогда также существует). При
этом
и- =u(b) • v(b)— lim (u(x) • v(x)),
a+O
если a — особая точка, и
и- lim (u(x) • v(x))— u(a) v(a'),
x—+<»
если b = -(-oo.
Доказательство. Пусть для определенности & = 4-оо.
Применяя теорему об интегрировании по частям для обычного ин-
t
теграла Римана, имеем Vi>a, равенство J и(х) dv(x) = u(t)X
а
t
Хо(0 — u(a) v(b) — J v(x)du(x).
a
+°°
Если предположить, что существует (например) интеграл S udv и
а
lim (u(t) ’v(t)), то переходя к пределу в этом равенстве при
/->+<», получаем как существование несобственного интеграла
4*°° 4-00 -+>О0
J v(x) du(x), так и равенство S udv = и • п|в— j vdu.
а а а
Пример.
» 1
J (1 4-х’)~1 • lnxdx = f lnxdarctgx =
о- о-
I I ।
= arctgx- Inxl — f x~l ♦ arctgxdx=—f x~‘- arctgxdx.
n e«- o<-
Теорема Фру л лай и. Пусть f s С ([О, +00))- Тогда:
1) если я Jim f (x)=f (+оо), то v а>о, V Ь>о
Х->Ч-оо
Я7° (f(ax)-f(bx)) • x-'dx=(/(0)-/(+oo)). 1п(Ь/а);
0<-
2) если V 6>0 существует несобственный интеграл
J /(х)- x~ldx, tno Na^>Q, b^>Q
6
Я+у° (/(ах) — f(bx)) . x-‘dx = f(O). 1п(&/а).
»«-
37
Доказательство. 1) Пусть/<=С([0, +<»,)), 0<а<6 и
Яlim f(x) = Пусть 0<б<Д< +,оо (так что 0<аб<
'<(& -б<а*Д<&-Д< +«>), тогда
J (f(ax)-f(bx))- x-1dx=»^ f(ax) • x~ldx —
— (' f (bx) • x~* dx = j f (2) • z~ldz —
8 a-8
b-Д b-8 6Д
— J f(z) ♦ z~ldz — J f(z) • z~‘dz — J f(z) • z-1 dz.
>.5 a-5 a*A
Поскольку feC ([0, +00.)), то в силу 1-й (обобщенной) интег-
ральной теоремы о среднем ([1], ч. 1, гл. 2, § 6) существуют точ-
ки £ (б) е (аб, 66) и |(Д) е (аД, 6Д) такие, что
f f(z) • z-‘dz = №(8)) . ln(6/a),
aS
ЬД
f f(z). z-‘dz = /a(A))« ln(6/a).
al
Очевидно,
Ь8
lim f f(z) • z_,dz = f(O) • ln(6/a),
lim f f(z) • z~l dz = f(+oo) . ln(6/a).
A->+<» a A
Поэтому, переходя в нашем равенстве к пределу при б-»- +0 и
Д—>-+оо, получаем
+f (f(ax)-/(6x)) • x~Mx = (ДО)-/(+«>)). ln(6/a).
d«-
2) Пусть теперь fsC([0, +<»)) и V -б>0 сходится несобст-
4-00
венный интеграл J f(x) • х~г dx, тогда имеем
8
+f (Нах)—f(bx)) • x-1dx= f f(ax) • x^dx —
5 8
— +j f(bx) • x~ldx= J* f(z)- z-1dz —
5
4“oo bS
— J /(z). z-idz =f f (z) Z-1 dz = f(g(8)> • ln(6/a),
bS ab
38
Ь8
где B(s) («8, &S) и 'im f f(z) ’ 2~‘dz =|/(0) • In (b/a), переходя к
8—+u a 8
пределу при 6-> + 0, получаем равенство
+f (/(ax)-f(bx)) • x-idx-ДО) • ln(6/a).
o—
Пример. По теореме Фруллани
+~ (г-a-r _ е-ьх). х-Мх = 1п(Ь/а) (а>0, *>0),
O’-
так как f(х) = е~х е С([0, +«>)), f(0) = l и
lim f(x) = 0.
§ 6. Абсолютно и условно сходящиеся ряды
(несобственные интегралы) и их свойства
В этом параграфе будем рассматривать ряды в поле ком-
плексных чисел С. Напомним, что если геС, то z—x+iy, где
x—Rez, y=ImzeR, a i—мнимая единица, удовлетворяющая
условию i2=—1’. Комплексное число z=x—iy называется ком-
плексна сопряженным к числу г. Действительное число lz|==
=' (z'z)l/z = (х2+у2),/2 называется модулем комплексного чис-
ла z—x+iy. Для модуля имеем:
1) (|z|=0) о (2=0); 2) |%-z| = |Х| • |z| V z, ХеС;
3) 1г1+г2|^|21| + |22| ( 121—Z2|>||Zi|— 122 11 v Z], 22 e C;
4) —|z| Rez Izl, — |z| Imz «£ Izl Vz eC.
В силу свойств Г)—3) модуль комплексного числа обладает все-
ми свойствами нормы в С. Комплексные числа допускают гео-
метрическое изображение (рис. 1) на комплексной плоскости,
z=x+iy~ (х, у) е R2, где ось абсцисс Ох называется действи-
тельной осью, а ось ординат Оу — мнимой осью.
Тогда
(x=pcos<p, y=psin<p, p=lz|)=»
=> (z=x+iy = p (cos<p+
4-isiiMp), <p=arctg(y/x))
(тригонометрическая форма комп-
лексного числа). Топология на ком-
плексной плоскости вводится с по-
мощью метрики, задаваемой модулем
Р (21, Z2) = |Zi—Z2|.
Определение. Последователь-
ность (zn) (zn е С, п е N) называ-
ется сходящейся в С, если Я zog С
такое, что V е>0 Я N (е) е N,
39
для которого \zn—z0|<e V n>N (e). Число Zo называется при этом
пределом, последовательности (zn). Запись: Zo=lim zn.
rt-*4-oo
Замечание. Если zn=xn+iyn и zo=xo+iyo, то из нера-
венств
I JXn ~~ Х°! | < lzn — Zo| X |хп—х0| + \Уп—Уо\,
I IfZn —t/o| J
очевидно, вытекает
(Я lim зл = 20)4Ф(Я lim хп = х0, Я lim yn = y0Y
П—>4-00 Л->4-оо П->4-00
Теорема (критерий Коши сходимости последовательности в
С). Пусть (zn), где zn^C>, neN. (Последовательность (zn) схо-
дится в C.)-*=>(Ve>0 3N(e)eN такое, что |zn—Zml<eVm,
n>JV(e) (т. е. когда (zn) есть последовательность Коши).)
п
Определение. Пусть cn е С VneN и sn — с*. Ес-
fe-i
4-оо
ли я lim sn=se С, то ряд у, сп называется сходящим-
П—+оо 1
ся, а число s называется его суммой. (Если cn=an + ibn^ С, то
sn = 5 ak+i 2 bh.)
k=i £=1
Замечание. Если сп=ап+1Ьп е С, то сходимость ряда
У сп эквивалентна одновременной сходимости рядов у ап и
n=i п«»1
4-00
У Ьп, составленных из действительной и мнимой частей дан-
ного ряда. В самом деле,
(Я lim 5п=$)<н>(Я lim у ак = Re$)A(S lim у 6k = Im*).-
Л—4-00 п—4-00 n-»4-oo ft==i
Определение. Если предел lim sn не существует, т& ряд
У Ck называется расходящимся.
it. i
Замечание. Для рядов с комплексными членами имеют
место теоремы из § 3>.
Вместе с рядом
*3 сл(с„еС, neN) (6.1)
Л=1
40
рассмотрим ряд
N- (6.2>
Л=1
Определение. Ряд (6.1) называется абсолютно сходя-
щимся, если сходится ряд (6.2).
Определение. Не абсолютно сходящийся ряд называется
условно сходящимся. (Таким образом, если ряд (6.1) сходится
условно, то ряд (6.1) сходится, а ряд (6.2) расходится, т. е.
S кп| = + 00 •)
Л=1
Замечание. При cn=an+ibn^ С; ап, абсолютная
сходимость ряда (6.1) эквивалентна абсолютной сходимости ря-
дов
4-00 4-оэ
S и 3
и=1
В самом деле, это утверждение следует из неравенств
I |&П1 <1
4-00
П р и м е р. Ряд Лейбница у (— сходится условно.
rtaxl
Теорема (о сходимости абсолютно сходящегося ряда).
Пусть сп<=С и ряд (6.1) сходится абсолютно, тогда ряд (6.1) схо-
дится.
Доказательство. Отметим оценку
m m
S съ < 3 kfcl V m>n.
ka^n ks=n
Если ряд (6.1) сходится абсолютно, то сходится ряд (6.2) и в
силу критерия Коши сходимости рядов Ve>03/V(e)6=N такое,.
что
S 1С*1
Vm>n >;V(e), но тогда в силу нашей оценки
tn
имеем ch
k=n
Коши ряд (6.1) сходится.
2V(e)
и в силу того же критерия.
Определение. Пусть [a, t]Vt>a. Несобственный ин-
4-00
те?рал J f(x)dx называется абсолютно сходящимся, если схо-
а
^ится несобственный интеграл S \f(x)\dx.
а
41
Определение. Пусть fe7?[a+6, b]V6>0. Несобствен-
ь
ный интеграл S f(x) dx называется абсолютно сходящимся, ес-
а*-
ли сходится несобственный интеграл
ь
J lf(x)|dx.
а*-
Определение. Не абсолютно сходящийся несобственный
интеграл называется условно сходящимся.
4-°°
Пример. Интеграл Дирихле J (sinx!x)dx сходится услов-
0<—
но. В самом деле, сходимость интеграла Дирихле была дока-
зана в § 5 (этой главы) с помощью признака Дирихле. Дока-
-{-ео
жем* что интеграл J (|sinx|/x)dx расходится. Заметим, что
о«-
| sin х | > sin2 х V х, и рассмотрим несобственный интеграл
4-°°
J (sin2x/x)dx. Имеем
1
Г(х) = | (sin2 t/t)dt = 1 /2 • j t~ldt — 1 /2 • | (cos 2t/t)dt.
4*00 4" OO
Но интеграл x~ldx расходится,! а интеграл J (cos2x/x)dx
сходится (по признаку Дирихле), поэтому
4"°°
lim F(x) = f (sin2i/fdt)= + oo.
x-»+oo £
В силу теоремы сравнения для несобственных интегралов от
-|-ОО
неотрицательных функций из расходимости интеграла J (|sin2x|/
1
4*00
lx)dx следует расходимость интеграла J (|sin x|/x)dx, т. е. ин-
1
теграл Дирихле сходится не абсолютно.
Теорема (о сходимости абсолютно сходящегося несобствен-
ного интеграла). Пусть t]vt>a (или feR[a+§, &] V 6>0) и
4-00 ь
несобственный интеграл S f(x) dx (или S f(x) dx) сходится
а а+-
абсолютно. Тогда этот интеграл сходится.
Доказательство. Пусть, например, f^R[a, t]Vt>a
(случай fe/?[a+6, &]v д>0 рассмотрите самостоятельно) и не-
42
собственный интеграл J f (х) dx сходится абсолютно. Тогда ут-
а
верждение теоремы вытекает с помощью критерия Коши (сходи-
мости несобственных интегралов) из оценки
X*
f |«Л|Л = J !/(O|dt Nx"
JCf x' x'
x'Z>a.
Определение. Сходящееся бесконечное произведение
jl (1Н-ап) (где — 1<яп<-|-оо v neN) сходится абсолютно
4-00
(условно), если ряд У, In (1+ctn.) сходится абсолютно (услов-
71=1
но).
Теорема (критерий абсолютной сходимости бесконечного
произведения). Пусть—l<an< + oo, v neN. Тогда (беско-
4-оо
нечное произведение П (l+an) сходится абсолютно) -*=>- (ряд
Л=1
4-00
2 ап сходится абсолютно).
Л«в1
4-00
Доказательство. Необходимость. Если П (l'+an)
П=1
сходится абсолютно, то оно сходится и, кроме того (по определе-
4-00
нию), сходится ряд у | In (1 + an) | и, в частности, lim ал = 0.
п=1 П->4-00
Но тогда lim |ln(1 4-an)|/lanl = 1 >0> откуда в силу теоремы
л->4-оо
сравнения (для знакоположительных рядов) вытекает сходи-
мость ряда *2 |an|.
4-00
Достаточность. Пусть ряд 2 lanl сходится, тогда имеем
л=1
lim an = 0, откуда соотношение lim |ln(l-{-an)|/lan| = 1 показы-
П-*4-°о П-*4-со
вает сходимость ряда у fin (1+ая)|я а потому и ряда lnU +
я=1 П=1
4~ оо
Н-а„), но тогда сходится и произведение П (l+an\ причем в
Л=1
4-00
силу сходимости ряда у, |ln(l + an)| наше произведение схо-
м=1
Дится абсолютно.
43
-4-00 1
П р и м е р. Бесконечное произведение П (1 +«“а) абсолютно ]
Я=1 J
сходится при а > 1 и не сходится абсолютно при а< 1. При а = 1 |
имеем равенство
", Ч 1 2 » !
откуда непосредственно следует расходимость нашего произ- ч
ведения, и поэтому в силу доказанного критерия об абсолют- 1
ной сходимости произведения вытекает расходимость гармони-
4-оо
ческого ряда. Произведение П (1 + (— 1)п-1 • п~а) сходится
л=2
абсолютно при а>1 и условно при 1, поскольку
тогда сходятся ряды "у ап и а« (где а« ~ (—1)п-1 • «~а)> |
п—2 п—2
обеспечивающие сходимость нашего произведения.
Рассмотрим теперь числовой- ряд у, ап с действительными t
п=«= 1
п п
членами aneR. Пусть зл = ^ ак и |aft|. Если ряд а
*=1 Й=1
4“°°
У ап сходится абсолютно, то Я lim $п и Я lim <Jn. Положим
я=5| Л-^-Ьоо п-»4-оо
VaeR а+=шах(0, а), а-= min(0, а),
так что a = a+-f-a~ и |а| = а+—а~ (а+=(а+|л|)/2), а“=(а—|а|)72,
4>оо П —J—оо
и введем ряды 2 а* (с частичной суммой з+= у at) и 2 ал
п—1 fe=*l n=I
п
(с частичной суммой $~ = 3 ак). Очевидно,
fe=i
8%=(Зп + <Зп)/Ъ 3- = (3П—О„)/2.
4-00
Замечание. Если ряд an(aneR) сходится абсолютно,
П=1
то Я lim з+ и Я lim s~ (почему?).
«->4-00
Следствие. (Числовой ряд у «„(^GR) сходится услов-
п=1
но)«4 (ряд у, ап сходится, но ряды
44
а+ = + оо и +f а~ = - оо
71—1 П=1
расходятся).
Теорема. Пусть ряд (6.1) (где с«еС) сходится абсолютно.
Тогда сумма ряда (6.1) не зависит от порядка его членов.
Доказательство. Пусть ряд (6.1) сходится абсолютно.
Тогда У, |Сп1 = с< + оо. Рассмотрим ряд сРь> полученный
n=l *=1
из ряда (6.1) какой-либо перестановкой его членов (так, что
отображение k—>рк есть биекция N на множество {Pi,p2, .. .
п
. • • > Pk> • • • }♦ Положим $п= У ck,
*=1
°П = 3 ^п= У, Cpft> 1'Л=- У,
k—l fc=l k=L
Пусть qh = max(px, p2, , ph), тогда тп<^ |ckl=a?n<c<+°o
k=i
YzjeN. Поскольку тп f (n—>+oo), то в силу критерия сущест-
вования предела у монотонных последовательностей Я lim тп,
4*00
т. е. ряд срк сходится абсолютно. Поэтому Я lim tn = t.
й=1 п-►4-оо
Докажем, что t=s= lim sn. Заметим, что V2Ve=N Я£лг>ДГ
П-»4-00
такое, что множество {ср„ сЛ,. . . , cp£pz){cv с2, ..., cN}. Оче-
ln n ,
видно, lim £.v=4-oo. Но тогда tL„ = V с„= 3 cft + 3 ch =
ЛГ-+«> "1 ft k=i Jt>N
-t-OO
= sN + PN, где ]pwl<rv= 2 tab B силу абсолютной сходи-
w+i
мости ряда (6.1) по критерию Коши сходимости рядов Ve>0
32V0(e)eN такое, что
(ipj < rN < е V N > ад) => (|^ — sj < 8 V Л/ > No&).
Но тогда из соотношений
(Я lim sw = s)A(ft lim tN = t)=>(3. lim tL =
//-*4*00 TV-^-J-oo ДГ-»4-оо
= t = lim sN = s) =4- (t = s).
2V->4“°°
4-00
Следствие. Если ряд у ап с действительными и неот-
л= 1
Рицательными членами (cneR, anX)vneN) сходится, то его
45
сходимость и его сумма сохраняются при любой перестановке
членов.
Определение. Ряд (6.1) называется безусловно сходя-
+°°
щимся, если для любой биекции k-+ph (N на N) ряд У, ср
*<=1
сходится (т. е. ряд (6.1) называется безусловно сходящимся, если
он сходится при любой перестановке его членов). Но тогда из ра-
нее доказанной теоремы вытекает
Теорема (о безусловной сходимости абсолютно сходящегося
ряда). Если ряд (6.1) сходится абсолютно, уо он сходится безу-
словно и его сумма не зависит от порядка его членов.
Теорема (об абсолютной сходимости безусловно сходяще-
гося ряда). Пусть ряд (6.1) сходится безусловно. Тогда ряд (6.1)
сходится абсолютно и его сумма не зависит от порядка его чле-
нов.
Доказательство. Достаточно показать, что условно схо-
дящийся ряд (6.1) не может сходиться безусловно. Рассмотрим
сначала частный случай с действительными членами
a„(aneRVneN). (6.3)
Л = 1
4-00
Пусть ряд (6.3) сходится условно. Тогда У, 1ап| = 4-оо и
л=1
lim ап—0. Пусть ал есть k-Ъ. по порядку положительный член
* п-*4<»
ряда (6.3). а 0/ есть Z-й по порядку отрицательный член ряда >
(6.3). Тогда, как было показано ранее, имеем
£
4-00 4-00
Т, aft=4-oo, 2 ₽/=—00» Hm ak = lim 0Z=O.
/0=1 &-*4-oo *-»>+«•
Выберем из ряда [(6.3) подряд все положительные члены так,
kl 1
чтобы Ski = 2 и затем добавим первый отрицательный
член Pi<0. После этого из оставшихся положительных чле- |
нов ряда (6.3) выберем подряд столько, чтобы 5^1 = 3^+014- /"
4-оо
+ 2 (это возможно, поскольку 2 ал = +°°)* Затем
8=^4-!
добавим второй отрицательный член 08 < 0 и вновь наберем |
столько положительных членов ряда (6.1), чтобы
л,
Sk,+s = Sfia+i + + 2 > 3"
s=fe24-i
На п-м шаге получим
46
ft, kt
‘S'*n+n-i = 2 ®j+Pi+ 2 “r+PaH-••• +
S=1 5=^4-!
kn
+ 2 a5>n> ^kn+n — Skn+n-l + Pn-
S=*n-1 + 1 '
Поскольку lim j3n = 0, to
П—>4-00
lim Sftfi+„= lim S44.n~i = + 00>
л-*4-°° n л-*4“°° n
и поэтому ряд
k
Rl fl - -1
2 a.+Pi+ • • • + 2 «.+Pn+ • • • > (6-4)
s=l s=/3n_14-l
полученный из ряда (6.3) перестановкой его членов, расходится.
В самом деле, если бы ряд (6.4) сходился, то lim Sm=S,
где Sm — tn-я частичная суммы ряда (6.4). Поскольку (54в+л) и
(S4n4-n_i) — подпоследовательности (*5М), то имели бы
Я lim Sk„+n= lim S4„+n-i = S,
n-H-00 " n-»+oo "
что противоречит доказанному равенству lim Sk +л=4-оо. Из
п-»4-оо я
оценок kn-i+п— l</n<fen + n и 54„_1+n_i < Sm < S4n+n-i имеем
lim SOT=4-oo. Итак, если ряд (6.3) сходится условно, то этот
m—►4-00
ряд не может сходиться безусловно. Далее, поскольку сп в
= an + ibneC; ап, bnGRVzieN, то безусловная сходимость
ряда (6.1) эквивалентна безусловной сходимости рядов t(6.3) и
4-00
У, bnt т. е. (как показано выше) эквивалентна абсолютной схо-
л=1
димости этих рядов. Но тогда в силу оценки |сп|<|ап|4-|&п|¥ле
GN видим, что безусловно сходящийся ряд (6.1) должен ухо-
диться абсолютно.
Замечание. Если ряд (6.3) с действительными членами
сходится условно, то можно доказать, что для любого числа
seR существует биекция (N на N) такая, что
2 арь=8-
*=i
Теорема Дирихле — Римана. Пусть дан ряд (6.1). (Ряд
(6.1) сходится безусловно) (ряд (6.1) сходится абсолютно).
4-00
Вновь рассмотрим ряд (6.Г). Пусть N= U /«, где /т=>
5а={Р|'"), Р¥>, . • ., Р1р, . • . причем Zmn/i= 0 Для m^=l.
47
Определение. Совокупность рядов
2 срм (m = 1, 2, ... ) (6.5)
называется разложением ряда (6.1).
Теорема (о суммировании по блокам абсолютно сходяще-
гося ряда).
Пусть совокупность рядов (6.5) (при т=\, 2,...) является
разложением ряда (6.1). Тогда если ряд (6.1) сходится абсолютно
и имеет сумму s, то: 1) каждый из рядов (6.5) сходится абсолютно
4* 00
к сумме S(m); 2) ряд у, 5(то) (из сумм рядов (6.5)) сходится
абсолютно и имеет суммой число s. Другими словами, если ряд
(6.1) сходится абсолютно, то имеет место формула суммирования
по блокам
4-оо 4-оо /4"°° \
3 = 3 ( 3 !•
m= I /
Доказательство. 1) Пусть ряд (6.1) сходится абсолютно,
тогда
S |cft|=c=^sup (J] |с*|\.
fe=i n \*-=i J
Положим
Пусть
— max р(Ая).
fe=l, 2,..., п
Тогда
q(m)
О < a<J»> < 2 lcfcl <£< + 00 V ле N.
А=1
Таким образом, частичные суммы (о<^>) знакоположительного
ряда
21^1 (6-6)
ограничены в совокупности, т. е. ряд (6.6) сходится. Но тогда
ряд (6.5) сходится абсолютно (к сумме S(m)) при любом т.
2) Итак, ряд (6.5,) сходится абсолютно V meN, причем
k=l *
48
Пусть
Qm. п = max p<m> и
Л=1. 2...n
{n=l, 2..М
п
S(nm‘ = S СР(кт)-
£==1 К
Тогда V М, п имеем
м
2 №1 <
Я1=1
^Af, п
6=1
+ оо.
(6.7)
Но в силу сходимости ряда (6.6) Я lim S<«> = S(m>, переходя к
П-»4-оо
пределу (при п-»4-оо) в левой части (6.7), получаем оценку
м
°<тм= 3 |S(m»K<?< + oo.
m=l
Таким образом, частичные суммы (тм) знакоположительного
S |5(т>1 (6.8)
т=|
ряда ограничены, т. е. ряд (6.8) сходится. Но тогда ряд
4-00
2 5(т)
т«1
сходится и имеет сумму S. Докажем, что <$=$. Положим
«„=3 S(m>,
так что Я lim fn=S. Поскольку ряд (6.1) сходится абсолют-
но, то V е > О Я Afu(s) е N такое, что — s| < е/2 V N > ЛГ0(е).
4-00
Поскольку N= U /т5 то Для # > N0(s) Э М0(ЛГ) £ N такое, что
т=Х
ММ) М
{1, 2.....Л) С U 1т, и тогда {1, 2,,.. Л)С U 1т ™ >
m=t m=l
>M0(2V), а потому
м N
•м~ 2 5'"'- 2С»+ 2'
т—1 fc==l £>N4-i
где
|PJ< 3 |cft| = 7?N<e/2.
&asjV4*I
Итак, Ve> 0 существуют /V0(e)gN и (V 2V > W0(e)) M0(iV)gN
такие, что V2V>2V0(e) и V Af>Jf0(2V), имеет место оценка
И. Камынин 49
lZM~sJ<e/2- T- e- Откуда^Нт ^^
так что S — s.
Замечание, Если ряд (6.1) сходится условно, то теорема
о суммировании по блокам неверна. Например, пусть a„eRVn и
ряд (16.3) сходится условно, тогда ряды У, а+ и jjj а~, даю-
л—1 П=Л
щие разложение ряда (6.3), расходятся.
Теорема (о двойных рядах). Пусть сходятся ряды
2 iGmJVzneN
п=1
и сходится ряд
Тогда
Доказательство. Обозначим через ск члены стп, распо-
ложенные в порядке возрастания т+п, а для одинаковых т-}-п
расположенные в порядке возрастания т (см. обход членов в
«матрице»):
Сц~*£12 • • • • • •
£ai см • • • • • •
17
£31 £32 • • • £зм • • •
£wl £дг2 • • • CNN • • •
Положим
4-00 /Ц-оо \
3 ( S )в
т««1 \п=1 /
Тогда имеем оценку
NN
2 2 2 Ы<5<+ oov/v>i,
fe=l щ=1 n=i
4.00
т. e. ряд yt c*=$ сходится абсолютно. Но тогда ряды
2 стп (w=l, 2g . . е ) и У, стп (п=1, 2, . . . )
n=l т=1
50
+«
являются двумя разложениями ряда J1, сй, и по теореме о
л=1
суммировании по блокам имеем
4*оо /4-оо \ 4во /4"®° \
S = 2 (2 С™\ И 8=2 2 стп •
т=1 \л=1 / n==l \m=l J
Рассмотрим теперь вопрос об умножении двух сходящихся ря-
дов. Пусть ряды
2 ип^и («п, tzec),
2 = F (ym. Fee)
(6.9)
(6.10}
сходятся. Пусть указана биекция \т, n)^-k (NXN на N), с по-
мощью которой определено произведение рядов (6.9) и (6.10):
2^ = (2 (2 (6.11)
*=1 \л=1 / \т=1 /
Вопрос: будет ли ряд (6.11) сходиться к числу {ЛУ?
Пример. Пусть «nefn=(—1)п~,/п,/2 и упорядочение в произ-
ведении проведено по правилу Коши, т. е.
«1 • «1 • • »< . . -
и» • и2 • va a, v, ut‘ vt . . .
I Z Z Z
U3- Vg Ug' Vg «,• Vt Ug- Vg. . .
/ z
..................................................
так что
4-00
2 »»+(«»♦ Vg+Ut‘ l>l)+(Ml- »з+«8’ M-
4^8• ^i)+ • • • +(wi* • • •
.. . 4-Uk-i- 1^)4-.... (n+m=k).
Тогда, полагая ‘
w =(-!)* j-------!-----4.------1------4. . ..
...+--------1-----L
4*
51
имеем I
*-i , i I
----------- >(£—1)---------!--------= lVjfe>2. I
i=i /V2.(A_Z)l/2-----------------------'-I
В силу критерия Коши ряд (6.11) не может сходиться. |
Теорема Абеля (об умножении двух абсолютно сходя- 1
щихся рядов). Пусть ряды (6.9) и (6.10) сходятся абсолютно, '
тогда при любом упорядочении произведения ряд (6.11) сходится |
безусловно и имеет своей суммой число U-V. J
Доказательство. Положим Sk =2 К|. где wi—uni-vmi. 1
4=1 |1
Пусть = max nlt Mh= max m,. Тогда из абсолютной и
* 4=1.2.. k 1=1, 2. * ?|
сходимости рядов (6.9) и (6.10) имеем оценки 'I
* Nk мк I
0^Sft= 2 К/" 2 |ип * — I
4=< л=1 m=l I
(№fl \ Г \ "4“®° “boo I
2 KI • S |t%| <2 KI 2 Kl«=c<+ *> v*eN. I
n=l J J m—i I
Таким образом, частичные суммы S* знакоположительного ряда I
из |te»z| ограничены сверху. В силу критерия сходимости знакопо- I
ложйтельных рядов Э lim St, т. е. ряд (6.11) сходится абсо- I
fe-*-}-oo I
лютно, а потому в силу теоремы Дирихле—Римана и безусловно. ' I
Для отыскания его суммы W переставим члены ряда (6.11) по I
следующему правилу Дирихле: I
U1- ^il и, • о8 их • о8 . . . I
и*' Vl и* • °« “« рз • • • I
и» • Vi «»• Ц3; р» • • • I
что дает
«1- Р1+(«» • Р#+«2 • pt + w, • ^1)+(«1 • У8+
+«»• v3+«3- p3+«3- p»+«3- pl)+ • . •
Тогда, полагая
n n
Un^^Uk, = .
*=i ii=i
имеем
(где (Sn) является некоторой подпоследовательностью частичных
сумм ряда (6.ГР) при «суммировании» по Дирихле).
52
Очевидно,
N N
Я lim V 2 un • vm^U • V,
W-*+=“ n=l m=i
г. e. сумма безусловно сходящегося ряда (6.11) равна U • V.
Теорема Мертенса (об умножении двух рядов). Пусть
ряд (6.9) сходится абсолютно к сумме U, а ряд (6.10) сходится
условно к сумме V, тогда ряд
4-00 k-i
2 И’й (где = 2 Uk-ivi= 2 “»р«) (6Л2)
fc=2 Z=I m+л—k
сходится и имеет своей суммой число U • V.
Доказательство. Положим
t/n=2“«« ^ = 2^ wk = 'Zwi-
а=1 p.=t ‘=2
Тогда
^л = «1 • (»1 + »а+ . • • + Oft-1) +
-J-U2 • (^1+^24* • • • +уЛ-2)+ • • • 4"ИЛ—1 • У]..
Замечая, что
JFn-j-i = UjVn + u3Vn—i 4- . . . + unVlt
имеем
Wn+1 - UnVn = -Ui. (Vn- 7„_t) -
— «3- (Vn-Vn-2)-. . .(Vn-VJ,
откуда
|JF„+1-C7n V„KW- l^-Vn-il+kl- |Fn-Pn_2|+. . . '
• • • + luml ’ |7n — Vn-m4-l| + |Mm4-l | • |7n —
-7„_m| + ... +Kh irn-FJ.
Теперь V heN выберем meN так, чтобы n/2^m^n/24-l. Тог-
да (/re) f (при re->4-oo), lim m^-^-oo и
П-*+<Ю
I^n4-i-Un . V„|<2 I«al • |F«-7,-^1+
fe=2
+ s KI • I7n-7n_t4.il.
Поскольку ряд (6.10) сходится, то ЯС1>0 такая, что |7fc|^
Ч Vfc е N, т. е. |РП—7n_ft+j|<2C'1 при k = /те 4- 1, . . . , п, и в
53
силу критерия Коши сходимости рядов Уе^ОЯЛ^е) такое, что
|УП—Ул-л+1|<е (k=\, 2, , m)Vn> N^e.), п/2+1>т^п12. Да-
лее в силу абсолютной сходимости ряда (6.9) ЯСг^>0 такая,
т
что 2 |u*|<СаVmGN. Кроме того, по критерию Коши Уе>
к—2
> О Я jVa(e) такое, что V т > п/2, п > У2(е) имеем оценку
Л
3 Выбирая п>тах (А\(6)* W2(e)), имеем поэтому
оценку
т п
\Wn+i-Un . 7я|<е£ KI + 2Сх 2 |и*|<
Л=2 й=ш4-1
^е- С2 4" 2СХ • 8 = 8 •
Поскольку Я lim U„Vn=^UV, то Я lim Wn = UV, чем теорема
Л->-|»СО Л-»4-00
Мёртенса доказана.
Пример. Пусть степенные ряды у, ипхп и у vmxm сходят-
л=0 т=0
ся, причем один из них сходится абсолютно. Тогда по теоре-
ме Мертенса правило Коши = 2 unvm) дает сходящийся
+°» .
степенной ряд у wkx№.
k—Q
Глава 2
ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ,
РЯДЫ И НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ,
ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
1 § 1. Равномерная сходимость
функциональных последовательностей
и функциональных рядов
Будем рассматривать последовательность (fn(x)) действитель-
нозначных функций, определенных v neN .на одном и том же
множестве XcR. В понятие сходимости функциональной после-
довательности (fn(x)) при п-> 4-оо ,на множестве AfczX можно
вкладывать различный смысл.
Определение (простой или поточечной сходимости,). Функ-
циональная последовательность (fn(x))' сходится поточечно на
множестве MczX к функции f(x) при п->4-оо, если
lim fn(x0)=f(xQ).
Запись: fn(x)-+f(x) на М.
Пример 1. Рассмотрим функциональную последователь-
ность
£ ( пх, О х 1/п
fn(x) = i i / 2^
I 1, li/n < X < 1.
Тогда fn(O)=OVn и Vxoe(D, l]HJV(x0) такое, что 0<1'/АГ(хо)<
т. е. fn(xd) = 1V п>УУ(х0),
/ [ 0, х = 0 \
lim fn(x)=f(x)=l W
' П—>+oo I 1, /
-»feC([O, 1]), f„eC([O, ID).
Таким образом, последовательность непрерывных функций.
fn(x)) может поточечно сходиться к разрывной предельной функ-
ции f(x).
Пример 21 Пусть (рис. 2)
/,«=( 0 .
I линейный горб высоты п при 0<х<1/п.
Тогда V хе [0 ,1] Я lim fn (х) (х) =0; fn, f^R [О, 11J, но
55
У • lim f fn(x)dx=l/2 =# 0 = f f(x)dx.
JQ
Таким образом, для поточечно exo-
“А дящейся функциональной после-
1\ довательности не всегда можно пе-
/ I реходить к пределу под знаком ин-
/ I теграла, т. е. возможно
/ \ lim (7n(x)4x#= f [ lim /n(x)]dx.
"of l/n j * Рассмотрим теперь линейное
пространство С(Х) — пространство
Рис. 2 - всех непрерывных функций, опре-
деленных на множестве Ха: R. Хо-
телось бы определить сходимость функциональных последователь-
4-00
ностей (fn(x)) (функциональных рядов 2 ип(х)) так> чтобы
л=1
последовательность непрерывных функций сходилась бы к непре-
рывной функции и чтобы выполнялись бы соотношения
Ь / 4-оо
] ( 5 ып(*)
а \ п=1
dx = 2 Г Un(x)dx, lim J /п(х) dx = Jf(x)dx,
n=l a n—+oo Ja a
и если Яи'(х)¥хе(а, b)Vn, то
[/(x)=2«B(x)U/f(x)=2u;(x)Vxe(a,6)\
Пусть дана функциональная последовательность (fn(x)), оп-
ределенная v neN, v xeXcR и множество Ма:Х.
Определение (равномерной сходимости функциональной
последовательности на множестве). Последовательность (fn(x))
равномерно сходится на множестве Ма:Х> если: I1) V х^М Я
lim fn(x)=f(x) и 2) ¥в>ОЯ AT(e)eN такое, что V n>N(в)
и V х<=М => | f (х) — fn(x) | < е.
Обозначение: /п(х) /(*) на М.
Замечание. Из определения равномерной сходимости
функциональной последовательности вытекает (fn(x)l>/(x) на
Jf)^(Ve>0S2V(e)sN такое, что sup |/п(х) — /(х)| < е Vп> ¥(е));
х€М
или (/n(x)z£f(x) на М)4=>(3[ lim sup |/n(x) — Дх)| = О).
л-*4-оо х€М
Замечание. Из равномерной сходимости функциональ-
ной последовательности следует ее поточечная сходимость (на
рассматриваемом множестве А1). Обратное утверждение, вообще
говоря, неверно.
56
Определение (неравномерной сходимости функциональ-
ной последовательности на множестве). Функциональная после-
довательность (fn(x)) сходится на множестве М неравномерно,
если: 1) V хе Л! Я lim fn(x)=f(x) и 2) я ео>О такое, что
Л-*4«оо
V iVeN существуют номер n0>N и точка Xq&M такие, что
Ifno (х°) — fMI > е0>0.
Определение ' (равномерной сходимости функциональ-
ного ряда на множестве). Пусть дана последовательность функ-
ций (ип(х)), определенных v neN и V xeXcR. Пусть функцио-
нальный ряд
5 “nW W0
n=l
сходится V хеМсХ и имеет сумму f(x). Тогда ряд (1.1) называ-
ется равномерно сходящимся на множестве М, если V е>0
3Af (e)eN такое, что и V х^М => (гп (х) | •< 8, где
п
rn(x) = f(x) — у, Uk(x); или V 8>0 я 7V(e)eN такое, что
«=1
sup \гп(х) | <eV n>N(e,); или, наконец, Я lim supi [rnfx)! —
п-*-|-оо х£М
= 0.
Определен'ие (неравномерной сходимости функциональ-
ного ряда на множестве). Функциональный ряд (1.1) сходится к
4-00
сумме f(x) на множестве М неравномерно, если: 1) у ип(х) —
и—1
=f(x) VxsAf и 2) Я 8о>О такое, что v TVeN Я n0>N и Я х0^.М,
для которых \гп& (х0) | > 8о>0.
Замечание. Если множество М состоит из конечного чис-
ла точек, то ряд (1.1), сходящийся на М поточечно, сходится на
М равномерно (доказать самостоятельно).
Замечание. Если функциональный ряд (I1.!) сходится рав-
номерно на множествах М1г М2агХ, то ряд (1.1) сходится рав-
номерно и на множестве Mi(JMzczX.
В самом деле, поскольку ряд (1.Ф) сходится равномерно на
множестве ЛИ (7=1, 2), то V 8>0я Aft(e)eN (1=1, 2) такое, что
(V/i>AT(e) и Vxe7Wi(ii=l, 2)) => (|гп(х) |<е). Но тогда Vп>
^>ЛГ0=тах N,(e) и V хеЛТШ-Мг имеем \гп(х) | <8, т. е. ряд
z=l, 2
(1-1;) сходится равномерно на
Пример 1. Пусть fn(x)=xn (L—хп), хе[0, 1>]. Тогда fn(0') =
==fn(l)=O, 0<fn(x)^xn V xe(0, 1) v neN, т. е. я lim ?п(х)^
^=f(x), и поэтому ]r„(x)] = |f(x) — fn(x)l =fn(x). Найдем
Максимум функции fn(x) на [0,_1]. Имеем .2) fn(x)=nxn~1-(l—*
'-2x'1)=oi при хп=2-1/п и при хп=0, откуда max fn(x) =
57
= fn (2~Un) = 1/4. Но тогда
Я lim sup | rn(x) | = 1 /4=7^01, t. e. no-
n-»-|-oo O^x^l
следовательность (/n(x)) на отрезке
[О, 1] сходится неравномерно. Далее,
пусть Л4(хо)=[О, х0] V х0 е (0, 1), тогда
Я n0(x0) G= N такое, что 2-1/"* > х0, и
поэтому Vn^ne(x0) имеем max |rn(x)|=
*ем(хв)
=х£(1— х"), т. е. Я lim sup |rn(x)|=
«-*+<» х€А1(х0)
= lim xj( 1 — x?) = О, поэтому наша
П—> 4- оо
последовательность (/л(х)) сходится
равномерно на множестве M(xo)Vxos
GE (О, 1). Заметим, что
[О, 1] = {1}U U |0. l-l/(fe+l)]
k=l
так, что на каждом из отрезков [0, 1—l/(fe+D] (k=\, 2,...)
и на множестве {1} наша последовательность сходится равно-
мерно, а на объединении этих множеств сходится неравномер-
но-
Пример 2. Пусть, ?2п(х)=0, a fsn-n(x) имеет график, изобра-
женный на рис. 3. Тогда, очевидно, последовательность (fn(x))
сходится на отрезке [0, 1] поточечно к f(x)^0, причем
. , „. [О при п=2т,
sup Гп(х)| = <
xeio.ii ( 1. при n=2/n-J-l,
так что не существует предела sup |гп(х)1 при п-> 4-оо, по-
этому последовательность (fn(x)) на отрезке [О, 1<] сходится не-
равномерно.
§ 2. Интегралы, зависящие от параметра
Пусть функция (х, t)-*-u(x,t) определена на множестве
XXTcR2 (xe=X<=R и teTczR).
Определение. Функция и(х, t) стремится (сходится) рав-
номерно на множестве Т к функции v (t) при х->хоеХ', если: 1)
V/eTSlim и(х, t) = и (t) (^еГ) и 2) V е>0 я 6(e)>0 та-
кое, что V x^.Ub(xo) П X ы V /еТ => }и(х, t) — v(t) | <s.
Запись: и(х, t) v(t) на Т.
58
Замечание. Пусть и<=С(12), где I2 = [с, d]X[a, Ь]. Тогда
VxeG[c> d]=^(u(x, i)ZZZtu(x0> t) на [a, 6]). В самом деле, по-
скольку иеС(Р), где прямоугольник Р = [с, d]X[a, &] ком-
пактен в R2, то по теореме Кантора функция и(х, t) равномер-
но непрерывна на Р и, в частности, Ve^> 036(e) >• 0 такое, что
¥ (хп /), (*л, удовлетворяющих неравенству |хх—х0]<
<6(е) и Nt^[a, 6] следует, что |и(хъ t) — u(x0, £)|<е, т. е
«(х, 0 —Г и^Хп' 0 на 1а» &L
Пусть теперь функция (х, t)-*u(x, t) определена на прямо-
угольнике /2=[с, d] Х[«, 6] и и(х, t)^Rt[a, Ь]¥ х<=[с, dj. Тог-
да ¥х [с, d] существует определенный интеграл Римана (sa-
fe
висящий от параметра х) <p(x)=Ju(x, t)dt, являющийся функ-
а
цией х-><р(х), определенной на отрезке [с, d]. Отметим неко-
торые элементарные свойства определенных интегралов Ри-
мана, зависящих от параметра.
Теорема 1 (о непрерывности интеграла Римана, зависящего
от параметра,). Пусть и^С(Р), где Р = [с, d] X [а> bJczR2.
Тогда для функции Ф(х, а, 0) = S и(х, t)dt имеем ФеС(Р),
где J3 = [с, d] X [в, Ь] X [в, 6] с: R3.
Доказательство. Зафиксируем точку (х, а, 0,) еJ3. Тог-
да V (х+Дх, а+Да, 0+Д0) е & имеем равенство
ДФ(х, а, 0) в Ф(х+Дх, а+Да, 0+Д0) — Ф(х, а, 0) =
М-Др Р Р+ДР ,
= у и(х4-Дх, t)dt — J и(х, t)dt= у и(х+ Дх, t)dt 4-
а+Да а 3
+ у[и(х+Дх, t) — u(x, t)]dt— у и(х+Дх, t)dt.
а а
Поскольку usC(/2), то: 1) и<=В(Р'), т. е. ЗХ>>0 такое, что
|«(х, Ol’CK V(x, t)i=]2, и 2) в силу теоремы Кантора функция
«(х, t) равномерно непрерывна на компактном брусе Р и по-
этому ¥8>0ЯВ(е)>0 такое, что V|Дх|<6(е) и V/е [а, 6] следует,
что |и(х+Дх, 0 — u(x, t)| < е/(6—а). Но тогда из нашего равен-
ства имеем оценку |ДФ(х, а, 0)|^^(|Да| +|Д0|)4-е/(&—а)- |0—а|,
из которой имеем (ФеС((х, а, p))V(x, а, р)Е/8)=>(ФеС(/3)).
Следствие. Пусть и^С(12), I2 = [с, d] X [°, и фь фгG
SC({c, dj); ф1([с, dj), ф2([с, djcrfa, Ь]. Тогда для функции
<Ы*)
F(x) = у zz(x, t)dt
Имеем F е= С([с, d]).
59
Задача. Доказать утверждение: пусть функция и(х, t) оп-
ределена на брусе 12=[с, d] X («, и u<=Rt[a, &] vxe=[c, d).
Пусть и(х, t)—на [a, d], где х0^ [с, d]. Тогда сеЯ[а, Ь] и
X.)
Я lim
X—
b b
J u(x, t)dt = J v(t)dt
a a
(при доказательстве утверждения v <= R{a, 6] используйте кри-
терий Дарбу интегрируемости по Риману).
Теорема 2 (о дифференцируемости определенного интег-
рала Римана, зависящего от параметра). Пусть функция и(х, t)
определена на брусе /2 = (с, d] X [а, Ь] и и, GC(12). Тогда
для функции Ф(х, а, $) = f и(х, t) dt и'меем Фе где
а ' I
J® = [с, d] X [а, &] X [«, ЭД» причем.
^(х, а, Р) = -И(х, а), ^ = «(*,₽)»
да ор
£Ф= ? .Эи(х..О
дх J дх
а
Доказательство. Зафиксируем точку (х, а, р,) s J3.
Тогда У(х-|-Дх, a-f-Да, р+ДР) <= J8 имеем равенство
Л(Дх, Да, Др)=ДФ(х, а, Р)—[ц(х, Р)ДР—w(x, а)Да-Ь
р 04-Д0
+ Дх • J — u(x, t)dt] = J [и(х -г Дх, t) —
х Х 0
— u(x, P)]df— J [и(х-ЬДх, t) — u(x, a)]di +
а
ЗГ
+ С и(х + Дх, t)— и(х, /) — Дх •
ди(х, t)
дх
dt = A — B+C.
Нужно доказать, что Я(Дх, Да, ДР)=о(|Дх| + |Да| + |ДР|)(Дх—>0,
Да-»0, Др->0). Поскольку и, — е С(Р), то по теореме Канто-
йх
ра функции «(х, t) и ди^х’ равномерно непрерывны на
дх
компактном брусе Р, и поэтому Ve>0 имеем: 1) Яб1(е)^>0 та-
кое, что ¥|Дх|<61 и V|P — v 6] имеем [u(x +
-f-Дх, t)—u(x, Р)|<е; 2) 382(e)J>0 такое, что У|Дх|<62 и У|£—а|«С
60
С|Д«|<^82, Ь] имеем |и(х4-Дх, t)—и(х, a)|<^g; 3) Я63(е)^>0
Такое, что У|Дх|<63 и V/e[a, Ь] имеем
— и(х + &Дх, 0 — — и(х, t)
дх дх
е,/(Ь—а)
(О<О- Заметим, что поскольку то в силу тео-
ремы 1 (о непрерывности интеграла Римана, зависящего от
параметра) интеграл
1 л
f - м(х + &Дх, t)db
•) дх
непрерывен как функция (х, 0 и поэтому принадлежит клас-
су ЛДа, Ь] Vх е [с, d]. Кроме того, по формуле Тейлора с
остаточным членом в интегральной форме имеем
и(х Дх, 0 — м(хс, 0 — Дх ди(*’ =
1 г ,
= Дх f — и(х + ^Дх, t) —
о 1?*
— и(х, t) I
дх I
Пусть 8(e) = min 8t(e), тогда при |Дх|<6, |Да|<8 и |Др|<6 име-
. 1=1, 2, з
ем оценки
1С|<|Дх|. j|j
0+Д0
|Д| < j l?Xx+ 0 ““ w(x> <
J ЬЛ=е|Д₽|; |В|<е|Да|;
3
0 Г 1
- и(х + »Дх, 0 -
дх дх
db dt
е
<|Дх|- №l(b — a))dt < е)Дх|.
а
Итак, ¥е>0Я6(е)>0 такое, что У|Дх|<6, VJAa[<8, У|Др|<8
имеем оценку |/?(Дх, Да, Д0)|<е(|ДхЦ-Да|-|-|Др|), т. е.
Я(Дх, Да, Др) = о(|Дх|+|Да|+|Д£|)(Дх-*0, Да-*0, Др-»О)=>
=>(Фё^((х, а, ?))У(х, а, р)е78)^(Фе5)(7’)),
61
причем
йФ(х, а, Р) = и(х, P)d{3 — и(х, a.)da +
/3 \
+1 f W*±£L at | dx.
I J dx I
Следствие. Пусть и, eC(Z2b где 1* — [c, d] X [a, &] и
Ф1> Ф»Cn>([£, ^]) Ф1 (lc> ^])> Ф2 (tc> dj c [a> И Тогда для функции
<м*>
F(x)=s J u(x, t)dt имеем fex)([c, d]), причем справедлива
Ф1(х)
формула Лейбница
dF(x)
dx
*s(x)
= f ^U(x, t)dt +
Ф1(х)dX
4- u(x, ф2(х)) —u(x. фх(х)>d-^- v x e= (c, d).
dx dx
Теорема 3 (об интегрировании определенного интеграла
Римана, зависящего от параметра). Пусть и&С (Р), где Р==*
ь
[с» d] X [а, 6]. Тогда ^(x) = I и (х, t)dt^.R^c, d], причем
d
J ф(х)йх=
с
Доказательство. Рассмотрим любое уе[с, d]. Докажем
равенство
V b by
J dx J u(x, t)dt = J df J u (x, t) dx.
c a a c
Введем обозначения
v Г b 1 ,
J J«(x, t)dt dx,
c L a
b Гр П
F(y)= § J«(x, <)dx dt
a Lc
и докажем, что Ф'(у) = F'(y) V у е (с, d). В силу теоремы 1
имеем
Ку» t)=V$u(x, t)dx^C(l2).
С
Поскольку и то в силу теоремы о дифференцировании
интеграла Римана от непрерывной функции по верхнему4
пределу имеем Vye (с, d)S = и(у, t) s C(Z2).
оу
62
Поскольку
Л^)=|/(У. t)dt и f, dJ-^C(P),
то из теоремы 2 вытекает, что
Ь л Ь
V у <= (с, d) RF'{y) => f f(y, t)dt = Г u(y, t)dt.
а°У a
b
С другой стороны, полагая ф(х)=|и(х, t)dt в силу u eC(/2),
a
используя теорему l, имеем феС([с, d]). Поскольку |F(z/) =
у
= ^(x)dx, то, применяя теорему 2 о дифференцировании опре-
С
деленного интеграла Римана по верхнему пределу, имеем
е £)((с* d)), причем
ъ
№'(у) = Му) = J u(y, t)dt.
а
Итак, 4r(t/)=F'(#)Vys(c, d), но тогда по теореме об общем
виде точной примитивной имеем Ф(у) = F(y) 4- С, где С—по-
стоянная. При у = с, очевидно, имеем (Т(с) = F(c)=0)=>(C=0).
Поэтому Vye[r, d] имеем W (y) = F(y), откуда, в частности,
при y=d получаем утверждение теоремы 3.
Замечание. Теорема 3 есть частный случай теоремы Фуби-
ни для двойных интегралов на брусе от непрерывной функции,
которая будет доказана в ч. V.
Рассмотрим теперь несобственные интегралы, зависящие
от параметра, причем будем пользоваться следующими обо-
значениями: пусть
+“u(x, tyttVxeXcR, (2.1)
а
скажем, что u е 7?Да, 4-оо)¥х е X, если: !)VxeX=^uE
т]¥х>а и 2) VxeX несобственный интеграл (2.1) схо-
дится. Пусть
ъ
J u(x, O^VxsX, (2.2)
а<—
скажем, что иеЯДа*-, &]¥хеХ, если: 1) ¥хеХ-»«еЛДа 4-
+&, &]¥8 >0 и 2) VxgeX несобственный интеграл (2.2) схо-
дится. Теоремы 1—3 для несобственных интегралов (2.1) и
(*•2), вообще говоря, неверны.
63
Пример. Пусть
, хч 1 1/*. 0<t<x, хе (О, +<эо),
mix, t) — !
v I О, ^[0, +оо).
Поскольку 0<u(x» 0<l/xVfe[0, +<»), то очевидно, имеем
и(х, О—Г0 — ы(+°°» 0 на Р» +°°)- Далее имеем
(Х-*4-оо)
+Га(х, t)dt= J x~ldt = 1, ,+f u(+°o, t)dt=O,
0 0 0
поэтому
Я lim f u(x, t)dt = l =£0 = f u(+°°, t)dt,
X-*+oo q 0
т. e. теорема о переходе к пределу в несобственном интеграле не- .
верна (без дополнительных ограничений).
Пусть 4-oo)VxeX, и положим
F(x) = "j‘ и(х, t)dt, F(x, A) = J и(х, t'jdt'VхеХ.
а а
Тогда, очевидно, F(x) = lim F(x, А),
А-*4-оо
< F(x) — F(x, А) = J и(х, t)dt.
л
Определение. Функция F(x, А) равномерно (по Коши)
сходится к функции F(x) на множестве MczX при А-*- +°°,
если: 1), V х^М Я lim F(x, Л) = Т(х) и 2) V е>0ЯТ (е,)>а,
А-> + оо
такое, что vA>T(s) и V хеМ |Г(х, А) — f(x)|<e. Запись:
F(x, А) —Г F(x) на М.
<А-+оо)
Определение. Функция F(x, А) равномерно сходится (по
Рейне) к функции F(x) на множестве MczX при А-* +<», если
для любой последовательности Гейне (Ап) (Anf+<*>), связанной
р базой (А-»- +оо) для функциональной последовательности
(F(x, Ап)), имеем F(x, Ап) ~—* F(x) на М.
(Л-»4-ОО)
^Докажите эквивалентность определений равномерной сходимости
функции (на множестве.) по Коши и Гейне.)
Замечание. Полагая u„(x) = F(x, А„) — F(x, An-i) (ux(x) ===
— F(Xi Ax)), имеем (F(x, At—F(x) на M)<=>(функциональный
(A^+oo)
4-00
ряд 2 un(x)=F(x) сходится равномерно на множестве М для
П=1
64
любой последовательности Гейне (Дп) (Дп f 4-оо), связанной с
базой (А->+«э)), так что понятие равномерной сходимости
функции на множестве сводится к понятию равномерной схо-
димости функционального ряда на множестве.
Определение (равномерной сходимости несобственного
интеграла вида (2.1)). (Несобственный интеграл (2.1) сходится
равномерно на множестве MczX)^(F (х, Д) —^F(x) на М), т.е.
(А-Н-оо)
несобственный интеграл (2.1) сходится равномерно на множестве
МаХ, если: 1) u&R([a, +<х>) V х е М и 2) Vs >0Я2*(е) > а
такое, что vA>T(e) и V хеЛ1=>
J и(х, t)dt s или 2') Ve
I +°°
>0ЯТ(8»а такое, что V А>Т(е.) =^sup| f и(х, t)dt
*ем| д
4-00
2") lim sup |‘ и(х, t)dt = 0.
А—>4“°° а
< е, или
Определение (неравномерной сходимости на множестве не-
собственного интеграла вида (2.1,)). Несобственный интеграл
(2.1) сходится на множестве MczX^неравномерно, если: 1) VxeAf
интеграл (2.1) сходится (т.е. u^R^a, +°°.) Vxe/И и 2) а 8о>О
такое, что V Т^а Э До> Т и 3 ХоеМ, для которых
+»
J и(х0, t)dt
а.
> 60 > О
или
2') lim
А—>4~оо
sup f и(х, t)dt Ф О
хем д
(или такой предел не существует).
Пример. Если
Л, <) = ( 11х' хе(°' +“)>
1 О, х^^ t oo j 11— [0, -j-оо)>
то при 80=1/2¥7’>0ЯДо=хо/2>7’>0, такое, что
J и(х0> t)dt= J x~xdt = е0 = 1/2 > О,
л, xJ2
т- е. интеграл у и(х, t)dt сходится на (0, 4-оо) неравномерно,
о
Д. И. Камынин
65
Пусть теперь иеЯДа-*-, Ь]Чх^Х, ]
ь ь I
F(x) = J и(х, t)dt и V6 > О F(x, 8) == j u(x, t)dt. |
a«- а4-5 I
Тогда
F(x) = lim F(x, 8) и F(x)—F(x, 8)= Г u(x, t)dt.
8-+0 a—
Определение. Функция F(x, 8) равномерно сходится
(no Коши) к функции F(x) на множестве МаХ при б->+0, ес-
ли; 1) V х^М Э. lim F(x, 8)=F(x); 2) V е>0 3 T](s)C>0 J
' S->-hO
такое, что V 0<б<т](е) и VxeAf имеет место оценка \F(x)—
—F(x, б)|<е. Запись: F(x, 6) >* F(x) на M.
(8-4-0) .
Определение. Функция F(x, 8) равномерно сходится (по I
Гейне) к функции F(x) на множестве МаХ при б-*+0, если для J
любой последовательности Гейне (8п) f6ni0), связанной с базой I
к(б-»Ч-О), имеем F(x, 8п) * F(x) на М. I
(П—Ц-ОО) I
(Эквивалентность определений равномерной сходимости функций I
на множестве по Коши и Гейне доказать самостоятельно.) |
Замечание. Полагая un(x) = F(x, 8п) — F(x, 8п-\) (и/х) I
= F(х, fij)), имеем (F(x, 8) —* F(x) на М) <Н> (функциональный I
(8-4-0) I
4-00 I
ряд у, ип(х) = Г(х) сходится равномерно на множестве М приИ
«=1 11
любой последовательности Гейне (бп) (бп | 0), связанной с ба41
зой (б->4-0)), так что вновь видим, что понятие равномерной* I
сходимости функции на множестве можно свести к понятию!
равномерной сходимости функционального ряда на этом мно4Ц
жестве. 4I
Определение (равномерной сходимости на множестве не-J
собственного интеграла вида (2.2)). (Несобственный интеграл (2.2^1
сходится равномерно на множестве М) -«=> (F(x, 6) ^F(x) на Af)/1
(8-+0) 5
т. е. интеграл (2.2) сходится равномерно на множестве MczX, если: I
1) u<=R.t(a+-, &] V xeAfccX и 2) V 8>0 Я rjfejX) такое, что V
a4"5 ' I
0<6<г](е) u VxeAf имеет место оценка I j* и(х, t) dt\<е} I
a*- I
или 2') V е>0 Я rjfe)>0 такое, что vo<6<i](e) имеет мести!
оценка I
л4~® I
sup f u(x, t)dt < e;
кем
66
или 2")
I
lim sup [ u(x, t)di| = O.
8—+0 x£M + I
Определение (неравномерной сходимости на множестве
несобственного интеграла вида (2.2)). Несобственный интеграл
(2.2) сходится на множестве MczX неравномерно, если: 1) V х^М
интеграл (2.2) сходится (т. е. u&Rt (a*-, :b]V х<=М) и 2) Я еа>0
такое, что V т]>0 Я 0<6o<t] и Я х0<=М, для которых
и(х0, t)dt
е
0.
1
Пример. Рассмотрим несобственный интеграл J t~x dt, exo-
0<—
дящийся Vxe(0, 1). Заметим, что
/8 \ / 8
(V8>0)=M f НЛ = 6|-1(1-х)-‘Н| sup f f-»df= + oo).
\0<- / \JC6(0,1) о<-
Таким образом, наш интеграл сходится на (0, 1) неравномер-
но.
§ 3. Признаки равномерной сходимости функциональных
последовательностей, функциональных рядов и
несобственных интегралов, зависящих от параметра
Напомним определение предела функции р —> F(p) Е R по
базе В — {В}. Пусть p-^F(p)— функция, определенная на мно-
жестве 5s. Базой (предфильтром) В во множестве SP называет-
ся система множеств {В}, B<z.&, обладающая свойствами:
1) и В + 0); 2) V В1г В2 е В ЯВ3еВ такое, что-
Определение, lim F(р) = IsR, если ¥е>0ЯВеВ такое»
в
что \F(p) — р <=В.
В дальнейшем будут использованы следующие три базы:
1) t-+ 4-оо, где В=(Вт}, Вт = (Т, +oo)VT>0;
2) f-»a4-0, где В «• {В8}, В5 = (а, а+6)с(а, b)VS>-0;
3) п-»4-оо, где B = {S„}, Вп = (п+1, п+2, . . . } + n<=N.
В книге [1] (см. §1 гл. 3 ч. I) был доказан следующий крите-
рий Коши существования предела числовой функции по базе:
(Я lim F(jP))<H-(Ve>QHB(c)eB
в
такой, что
№) — F(А)| < • V A, Pt е В(ч)).
Определение (равномерного стремления функции к пре- Я
делу). Пусть числовая функция (р, х) F(p, x)eR определена на Я
уМ. Скажем, что функция F(p, х) стремится к (предельной) ||
функции F(x) по базе (в &) равномерно на множестве М, ес- 3
ли Ve>0 такой, что р^В(е) и v х^М=> \F(p,x)-~ J
— F(x) | < е. Запись: F(p, х)—^F(x) на М. ||
ВО£73 I
Определение. Функция F(p, х), определенная на множест- I
ее & Х/И, сходится к функции F(x) на множестве неравномерно I
по базе (в & ), если: 1) Ух^М'З. lim F(p, x)=f(x); 2) Яе0> I
в&> I
0 такое, что V В G= В^ существуют ро^.В и хаЕЕ М такие, что . I
Rpe. х,) —F(xo)|>so>O. ,|
Теорема (критерий Коши равномерного стремления функции I
к пределу). I
(F(p, х)—яа М)Ф4>(Уе>0ЯВ(е)еВ^ I
• I
такой, что I
\F(pt, х) — Р(рг, xJKeVpn р, еВ(г) и VхЕМ). J
Доказательство. Необходимость. Пусть F(p, х) * F(x) I
V I
на М. Тогда Ув>0ЯВ(е)еВ^ такой, что Vp1; p2sZ?(e) и I
V х (= М =4 (\F(pu х) — Г(х)| < е/2) Д (|F(p2, х) — I
— f (х)| < е/2) =» |F(p1, х) — f(p2, х)| =» |(F(pb х) — F(x)) + I
+(F(x)-F(p2, x))|<|F(px, x) — F(x)|+|F(x) - F(p„ x)| <6. I
Достаточность. Пусть выполнены условия критерия Коши. . I
Тогда Vx0 е М функция р -» F(p, х0) удовлетворяет критерию I
Коши (существования предела числовой функции по базе EV), I
и поэтому Я lim Ftp, х0). Введем обозначение lim F(p, x)—F{x). I
B^ В^Э I
Итак» V х е М Я lim F(p, х) = F(x). Докажем теперь, что I
в<0» I
F(p, х) —»F(x) на М. В самом деле, по критерию Коши I
I
V е> О Я В(е) е В^ такой, что Урв, реД(е) и VxeAf=^|F(p0, х)— I
— Г(р, х)| < е/2. Но тогда, переходя в этом неравенстве к пре- I
делу по базе В^>, имеем I
(lim F(p0, х) = F(x)} => (|F(x) — F(p, x)| < I
' I
68
<г/2<еУр£Й(;) и УхеМ),
т. е. Т(.Р, *)-Г на М.
bj>
Конкретизируя этот общий критерий Коши для частных
случаев баз: п->+оо, Л->-]-оо и 6-*+0, получаем следующую
теорему.
Теорема (критерий Коши равномерной сходимости функцио-
нальной последовательности). Пусть функциональная последова-
тельность (fn(x)) определена на множестве X и МаХ. (Последо-
вательность (fn(x)) сходится равномерно на множестве М (т. е.
fn(x) —Г f(x) на М)) *=* (У 8>0 я N(s) е N такое, что \fn(x) —
— fm(x) | < 8 v п, m>N(z) и v х<=М).
Теорема (критерий Коши равномерной сходимости функцио-
нального ряда). Пусть функциональный ряд
4-00
S ah{x)
*=1
. (3.1)
сходится v x^MczX. Тогда (функциональный ряд (3.1) сходится
равномерно на множестве М) (V е>0 Я N(s) е N такой, что
m
5 uk{x)
Ь=п-Н
<8 Vffl >П > Л’(8) и V X Е= Л/).
А П
Доказательство. Если $п(х)=2 иь(х)>т0 равномерная схо-
*=1
димость функционального ряда (3.1) на множестве М эквивалент-
на равномерной сходимости на множестве М функциональной
последовательности (частичных сумм) (sn(x)). Но в силу крите-
рия Коши (последовательность (s„(x)) сходится равномерно на
множестве Af)4=>(Ve^>0 3 7V(e) е N такое, что Vт> n^>N(e) и
V х е М выполнено неравенство
lsm(*) *пС*)| —
5 «*(*)!<*).
£=«4-1 I
Замечание (о геометрическом смысле равномерной сходи-
мости функциональной последовательности на множестве). Пусть
tn(x) * f(x) на [а, Ь]. Если Н„ = sup |/(х)—/п(х)|, то Я lim Rn=
== 0, т. е. Уе>0 ЯЛДе) g=N такой, что 0/?п<eVn>2V(e), т. е.
Уп>Л?(е) и УхЕ[а, 6] имеем оценки f(x)— e<Zf»(xXf(x) + е-
Таким образом, если /п(х) > Дх) на [а, 6], то (рис. 4) графи-
ки всех функций fn(x) при п _> У(е) попадают в полосу
Gs = {(x, y)eR2|f(x) —8<t/<f(x)-|-e, а<х<Ь}.
Рассмотрим теперь множество В([а, Ь]) всех ограниченных
на отрезке [а, Ь] функций (так что /6=2? ([а, &]), если сущест-
ва
вует постоянная Л//>0 такая, что |f(x)|^Jfy Yze[o, 6]). Вве-
дем на множестве В([а, Ь]), являющемся линейным простран-
ством, метрику Чебышева g)-+?(j, g)eR+, где
р(А g)= sup |f(x) -g(x)|Vf, g g= B([a, b]).
6]
Проверим, что функция p:(f, g)-*R+ обладает всеми свойства-
ми расстояния.
О p(f. g) > OVf, gEzB([a, bj), причем, если Ях0 e [a, b] та-
кая, что f (x0) ¥= g(x0), to p(f, g)>0, поэтому (p(f, g)=0) 4=> Cf=g)
(t. e.f(x)=g(x)Vxe [a, b]).
2) p(f, g)=?(g, f)Vf, g€=B([a, b)) (очевидно).
3) Vx£[a, b] имеем Vf, g, <peB([a, b]) оценку |g(x)—/(x)|<
}g(x)—q>(x)|+|cp(x)—f(x)|, переходя к точным верхним граням (по
хе=[а, Ь]) в обеих частях этого неравенства, получаем нера-
венство треугольника
p(g* f)<p(g, ф) + р(ф. f)Vf, ф, gGB([a, bj).
Таким образом, линейное пространство В([а, Ь]) с метрикой
Чебышева становится метрическим пространством. Сходимость
fn-+f в В([а, bj) означает равномерную сходимость f„(х) £
* f(x) на [a, bj. В частности, для пространства непрерыв-
ных (на отрезке [а, Ь]) функций С([а, Ь])с#([л, Ь]) имеем
р(/, g)= max |f(x)-g(x)|.
[a,b]
Ниже будет доказана полнота пространства С([а, Ь]) (с мет-
рикой Чебышева).
Теорема (критерий Коши равномерной сходимости несобст-
венных интегралов с бесконечными пределами). Пусть несобст-
венный интеграл, зависящий от параметра,
"*j и(х, t)dt (3.2)
70
сходится V хеМс.Х (т. е. u^Rt[a, -|-<х>) V х^М). Тогда (несобст-
венный интеграл (3.2) сходится равномерно на множестве М)
(Vе>0^Т(г)>а такое, что VАи А^>Т(е) и VxeAf имеет
место оценка
j и(х, t)dt <е).
А,
Доказательство. По определению несобственный ин-
теграл (3.2) равномерно сходится на множестве М, если
F(A, х) * Fix) на М, где F(A, х)=§и(х, t)dt и F(x) = §u(x,t)dt.
а л
Но согласно доказанному нами общему критерию Коши равно-
мерной сходимости (при базе А—»4-оо)
(F(A, х)--* F(x) на М) «=> (V 8> О Я Т(е) > а
(А-+оо
такое, что VAX, Л2>Т(е) и
Vх е М. |F(AX, х) — F(Ait х)| = J u(x, t)dt
Замечание (критерий Гейне равномерной сходимости несоб-
ственных интегралов с бесконечными пределами). Пусть несобст-
венный интеграл (3.2) сходится VxeMc/ (т. е. u<E=Rt\a,, 4-оо)
VxeAf). Тогда (несобственный интеграл (3. 2) сходится равно-
мерно на множестве М) & (для любой последовательности
Гейне (Ап) (Ал | + оо), связанной с базой (А —> + оо), Ve >
^>032V(e)eN такое, что Vro>«>^8) и Nхе=М имеют
место неравенства
J u(x, t)dt
Ап
< £ ИЛИ
m
2 vk(x)
Ьп-Ц
8,
где
Ak
vh(x) = f u(x, t)dt).
Ak-i
Доказать самим.
Теорема (критерий Коши равномерной сходимости несобст-
венных интегралов от неограниченных функций, зависящих от па-
раметра). Пусть несобственный интеграл, зависящий от парамет-
ра,
ь
J и(х, 0 dt (3.3)
а<—
сходится V х^МаХ (т. е. ueRt (a*-, ft] V хеМ, где i=a — особая
точка). Тогда (несобственный интеграл (3.3) сходится равномерно
71
на множестве М) (Уе>0Эт](е)>0 такое, что V0<6i<62-<
<т] (е) и V х^М имеет место оценка
а+82
j и{х, t)dt
04-81
е)-
Доказательство. По определению несобственный интег-
рал (3.3) сходится равномерно на М, если F(6, х)---------* F(x)
(8—*4*0)
на М, где
ь ь
F(5, x)=j‘ и(х, t)dt, F(x)=j ц(х, t)dt.
а+8 а*-
Но в силу доказанного выше общего критерия Коши равно-
мерной сходимости (по базе 6-Н-О) (F(6, х)------* F(x} на Л/> 4=>
(8—*4~0)
«4 (V е>0Ят)(е)>0 такое, что V0 < бх < б2 < т)(е) и VxeAf имеет
место оценка
х) ^(^2» •*)! —
а 4-8»
А
u(x, t)dt < е).
Замечание (критерий Гейне равномерной сходимости не-
собственных интегралов от неограниченных функций, зависящих
от параметра). Пусть несобственный интеграл (3.3) сходится Vx<=
ЕЛ/сХ(т. е. u£=ilt(a*-, fe] VxeМ, где t = a — особая точка).
Тогда (несобственный интеграл (3.3) сходится равномерно на
множестве УИ)<=>(для любой последовательности Гейне (бп)
(6п|а), связанной с базой (8->а+0), ¥е>0 5LV(e) еN такое, что
Vи Vxe=M имеют место оценки
u(x, t)dt
е или
m
Л==п4-1
£»
*6-1
где vk(x) = J u(x, t)dt). Доказать самим.
sfe
Определение (нормальной сходимости функционального
ряда). Функциональный ряд (3.1), сходящийся Vx^MczX, схо-
дится нормально на Множестве MczX, если существует последова-
тельность неотрицательных чисел (Ап) (Яп^0 VneN) такая, чта
1) | «п(х)| Ап V хеМ и V neN;
4-00
2) мажорирующий числовой ряд у, Ап сходится.
п—t
Теорема (признак Вейерштрасса равномерной сходимости
функционального ряда). Если функциональный ряд (3.1) сходится
нормально на множестве М, то он сходится равномерно на этом
множестве.
72
Доказательство. Отметим вытекающую из определе-
ния нормальной сходимости ряда (3.1) оценку V/n>n
т т т
Ё “fcW < Ё 1“к(хЖ Ё aknх^м-
k=n k==n k~n
-J-oo
Но ЧИСЛОВОЙ ряд 2 ДЖЧ"00 сходится, поэтому в силу кри-
Л=1
терия Коши (сходимости числовых рядов) Ve>03 A’(e)£N та-
m
кое, что V/га > л > У(е) имеем оценку 0«^ у, Ак<&, но тогда
/г=п
для тех же т^п^> N(e) и Ухе Л/ из нашей оценки получаем
неравенство
2 “*(*)
k-n
Применяя критерий Коши (сходимости функционального ряда),
видим,, что ряд (3.1) сходится равномерно на множестве М.
Замечание. Теорема Вейерштрасса (для функциональных
рядов) остается верной и для вектор-функций х-+ип(х), отобра-
жающих множество М в Rm, если модуль | | заменить на норму
II Ik
Замечание. Признак Вейерштрасса (для функциональных
рядов) является лишь достаточным признаком равномерной схо-
димости, поскольку из равномерной сходимости функционального
ряда, вообще говоря, не следует нормальная сходимость этого ряда.
Пример. Пусть и„(х) = (—1)п~Чп, х е |0, 1], тогда нор-
мальной сходимости нет, а равномерная сходимость есть.
4-00
Пример. Функциональный ряд 2 sin ftx/n* на (—оо, +оо}
п=1
сходится нормально при «^>1, поскольку |sinnx|/na<^ 1/п“ Ухе
4-00
G(—©о, Ч-°°) и у l/n“<4-®° при а> 1, поэтому наш ряд на
(—°0, Ч-оо) сходится равномерно.
Замечание (уточнение признака Вейерштрасса равномерной
сходимости функционального ряда). Функциональный ряд (3.1)
сходится равномерно на множестве М, если существует последова-
тельность неотрицательных функций Ап(х) (Ап(х)^О V и
V хеЛ4) такая, что
1) \un(x)\^An(x)v хе=М и VneN;
+оо
2) функциональный ряд 2 Дп(х) сходится равномерно на
п=1
множестве М.
+оо
В качестве примера рассмотреть ряд 2 ип(х), М=(—оо,
Ч-оо), где
, . ( sin (2n+2nx)/n, хе(2-га-2, 2-");
Un (•*)- <
I 0, хё(2-«-2, 2~п).
73
Теорема (признак Вейерштрасса равномерной сходимости
несобственных интегралов, зависящих от параметра, вида (3.2)).
Пусть несобственный интеграл (3.2), зависящий от параметра,
сходится v xeAf (т. е. u^Rt[a, V х&М). Пусть существует
неотрицательная функция <p(£) +°°) такая, что несобст-
венный интеграл
+f <Р(0Л (3.4)
а
сходится, причем fu(x, t)l^q>(t)V х^М и Vte[a, +оо). Тогда
несобственный интеграл (3.2) сходится равномерно на множестве
М.
Доказательство этого признака Вейерштрасса следует из
критерия Коши равномерной сходимости для несобственных ин-
тегралов вида (3.2) и из сходимости несобственного интеграла
(3.4) в силу оценки (V At >• Аг >• а и V х е М)
а2
J и(х, t)dt j |u(x, t)\dt^ j y(t)dt
Aj Ai Ai
(завершить доказательство самим).
Теорема (признак Вейерштрасса равномерной сходимости
несобственных интегралов, зависящих от параметра, вида (3.3)).
Пусть несобственный интеграл (3.3), зависящий от параметра,
сходится vx&M (т. е. u^Rt(a-^~, 6], где t=a — особая точка).
Пусть существует неотрицательная функция <р(0> такая, что схо-
ь
дится несобственный интеграл J <p(t) dt, причем \и(х t)\^p(t) V
а*-
х<=М и VZe(a, &]. Тогда несобственный интеграл (3.3) сходится
равномерно на множестве М. (Доказать, используя критерий Коши
равномерной сходимости несобственных интегралов, зависящих от
параметра вида (3.3).)
Пример. Рассмотрим несобственный интеграл J схо-
ь—
дящийся Ухе [О, х0], если 0<хо<1. Поскольку имеет место
оценка t~x«Сt~XaVtGE(0, 1], 0<х^х0<1, то сходится мажо-
г
рирующий интеграл ( t~x»dt, что обеспечивает равномерную
о—
сходимость нашего интеграла на множестве {0, х0] CZ [0, 1).
Теорема Дини (о достаточном условии равномерной схо-
димости функциональной последовательности,). Пусть К — ком-
пактное множество метрического пространства {X, рх). . Пусть
(fn(x)) — функциональная последовательность, определенная на
множестве К (где fn(x)eRvneN и V хеК) и сходящаяся по-
точечно к функции f(x) на множестве К. Пусть rn(x)=f(x)—
—fn(x) vх^К. Если rn(x)^C(K) VneN и V х<=К последова-
тельность (гп(х)), монотонно убывая (монотонно возрастая),
отрёмится к нулю при п-*- 4-°°, то fn(x)—»• f(x) на К.
Доказательство. Пусть для определенности гя(х0) | О
(при га-*4-оо) Vx0EK, тогда гя(х0) > 0 Vra и Я lim rn(xo) = O.
rt—*-f-oo
Поэтому Ve>OSrae(e)EN такое, что 0<r„,(xo)<8. Но по ус-
ловию гп,(х) е С(х0), поэтому существует окрестность U(x0) та-
кая, что имеет место оценка 0<rn.(x)<8Ухе(7(х0)ПК. Рас-
смотрим систему всех таких окрестностей {(7(х0); х0ЕК}. Эта
система образует открытое покрытие компактного множества
i
К, из которого можно выбрать конечное подпокрытие (J i7(xft)ZD
fe=i
ZD К, причем 0</„ft(xft)<e (Л=1, 2, ...,() и
’ 0<r„h(x)<8 Vx(=£/(xft)ntf (Л=1, 2.......I).
Поскольку гп(х)|О (при га-*4-<») VxeK, то Vra>raft име-
ем Оценки 0< гп(х)<гя*(х)<в Vх е Щхй)ПК (k— 1, 2, . . . , I).
Пусть 2V0(e) = max nk, так что 2Ve(s)>nk при k — 1, 2, . .., I.
k=i, 2.1
T огда'имеем
(*=1, 2......О,
т. е. О < (е)(х) < 8 V хеК-
В силу монотонного убывания последовательности (rn(x))VxE
ЕК, при га—>4-со имеем оценку 0<rn(x)<rWt)(x)<8 Ухе К и
и Уга^>У0(е), из которой вытекает, что г Ах} * 0 на К, т. е.
ГЛх}----> f(x) на К.
Следствие. Пусть К — компактное множество метричес-
кого пространства {X, рх}, числовые функции fn(x)G=C(K) Vng=
EN. Пусть функциональная последовательность (fn(x)) моно-
тонно сходится на К (так что f»+i(x)< frt(x) (f„+i(x) > f„(x))
VreN, V х е К) к функции f(x)EC(K). T огда fn(x) * f(x) на К.
Доказательство. Введем вспомогательную функцио-
нальную последовательность (гп(х)), где r„(x) = f(x) — fn(x). Тог-
да имеем: 1) (fn(x) f Vх е К) =»(rn(x) | Vх Е К (п-*4-оо)); 2) по-
скольку Я lim f„(x) = f(х) Ух е К, то Я lim гп(х) = ОУхеК;
П-*4»СО Л—>-f-O0
3) поскольку fn, f ^C(K), то гпеС(К). Таким образом, выпол-
нены все условия теоремы Дини для функциональных после-
довательностей, из которой вытекает, что ЛЛх) ~ f(x} на К.
Замечание. Требование компактности множества К в тео-
реме Дини отбросить нельзя.
75
П р и м е р. Пусть/п(х) = l/(nx + 1) Vxe (О, 1), где интервал
О, 1) не является компактным множеством. Тогда fn е С((0,
1))¥и и fn(x) I (n->+oo)Vxe(0, 1), причем lim /n(x)=/(x)=0VxS
n-*4-oo
€= (0, 1), / e C((0, 1)). Заметим, что последовательность (fn(x))
сходится к предельной функции f(x) на интервале (0, 1) не
равномерно. В самом деле, sup |гл(х)| = sup fn(x) = 1 и поэто-
0<х<1 0<х<1
му lim sup |гп(х)| = 1 =/= 0.
п->+оо 0<х<1
Теорема Дини (для функциональных рядов). Пусть
ип^С(К) и un(x)>0 V х<=/(, V zieN. Если функциональный ряд
(3.1) сходится на компактном множестве К и имеет сумму f(x)e
^С(К), то этот ряд сходится на множестве К равномерно.
п
Доказательство. Положим sn(x) = «к(х), тогда sn(x)|
л—1
tf(x)Vxe/< (при п-*4-оо) и sn, f„<=C(K). По теореме Дини,
примененной к последовательности (s„(x)) частичных сумм ря-
да (3.1), имеем sn(x) ~ Дх) на К, если К компактно.
Теорема Дини (для несобственного интеграла вида (3.2),
зависящего от параметра). Пусть и(х, /)^>0 V (х,
-|-оо), и^С (7СХ[а, +<»)), где К. — компактное множество мет-
рического пространства {X, рх). Пусть несобственный интеграл
(3.2), зависящий от параметра, сходится V хеК, причем F(x) =
4-00
— S и(х, t)dt и F^C(K). Тогда несобственный интеграл (3.2)
а
сходится равномерно (к функции F(x)) на компактном множест-
ве К.
А
Доказательство. Положим F(A, х) = J и(х, t)dt и R(A,
x)=F(x) — F(Ar x)'Vх К и УА^а. Поскольку ueC(/(Xk
Л]), то в силу теоремы 1 для интегралов Римана, зависящих
от параметра, из § 2 имеем F(4, х)е СХ(К)¥AZ>а. Но по ус-
ловию F%=C(K), поэтому R(A, x)eCx(K)V Л>а. Из условия
и(х, i)>0 V(x, !)еК\ [а, +©о) видим, что R(A, х) монотонно
убывает как функция параметра А в любой точке хеК, причем
в силу сходимости несобственного интеграла (3.2) имеем
lim R(A, хо) = О V х9^К. Фиксируя хоеК, видим, что Ve>-
>ОЛЛо(е)>а такое, что 0<7?(Л0(е), х0)<е. Но /?(Л0(е), х)еС(х0),
поэтому существует окрестность U(x0) такая, что О^Я(Л0(е),х)<^
<еVxGU(x0)(~}K. Рассмотрим систему всех таких окрестнос-
тей {U(x0)‘, К}. Эта система образует открытое покрытие
компактного множества К, из которого можно выбрать конечное
76
::4
I
подпокрытие такое, что К С U причем 0 < Н(Ак(ъ), х)
k—1
eV x^U(xh) К (k=i, 2, I). Пусть теперь Л0(е) —
= max Лт(е) > Лй(е) (Л=1, 2, . . . , /). Поскольку R(A, х) моно-
т=1, 2,..., I
тонко убывает как функция А в любой точке хе К, то О «С
<R(A0(e), х)<Л(4(е), х) <е¥хеЩхЛ)П^ (fe = L 2. . . . , I), от-
куда имеем оценки О^Я(Ло(е), x)<eVxE/(. Вновь, используя
монотонное убывание функции R(A, л) по Л в любой точке
хе К, имеем оценки 0<Д(Л» х)< е УЛ _> Л0(е) >а Vxe К, т. е.
Я(Л, х) * 0 на К или F(A, х)---------------* Г(х) на К,
(А-Н-оо) • (А—4-оо)
что и означает равномерную сходимость несобственного интегра-
ла (3.2) на множестве К.
Замечание. Требование компактности множества К в при-
веденной теореме Дини существенно и не может быть отброшено.
Пример. Пусть
F(x) = J х'/2. ехр(—х- t^dt, ХЕ(О, +<х>).
oJ
Делая замену л1/2 • t = г, получаем
F(x) = J e~z*dz = c~^>Q.
о
(В § 4 будет доказано, что c = izl/2/2), так что F еС((0, + оо)).
С другой стороны, и(х, Z) = x1/2- ехр(—х- i2)>0V(x, t) Е (О,
4-оо) х [0, 4-оо) и и е С((0, -j-оо) х [О, +<»)). Однако интеграл
F(x) сходится на (0, 4-оо) не равномерно, поскольку
f J х1/2 • ехр(—х- t2)dt =» f ехр(—z2)dz 1 =>
\А /
=>( lim sup f ехр(—z2)dz=+f ехр(—z2)dz^0).
Д-^+оо эсбСО, 4“ос) х1/2 0J
Множество (0, +°°) не компактно!
Теорема Дини (для несобственного интеграла, завися-
щего от параметра, вида (3.3)). Пусть и(х, t)^0 V (х, 0<=ЯХ
X (а, Ь] и и^С ((КХ (а, Ь]), где К — компактное множество мет-
рического пространства {X, рх}. Пусть несобственный интеграл
ь
(3.3) сходится v хеК, причем F(x) = S и(х, t) dt и F^C(K).
а^—
Тогда несобственный интеграл (S.3) сходится равномерно (к
Функции F(x)) на компактном множестве К.
77
Доказательство. Положим
F(6, х) = J u(x, t)dt,
а 4-8
Я(6, x) = F(x) — F(8, x)V8e(0, b-a)Vxf=K.
Используя теорему 1 (из § 2), видим, что /?(б, х)^Сх(К) V 6>0,
и поскольку по условию и(х, f)>0 V(x, t)^K.X(a, &], то 2?(8, х) |0
(при 60->Ч-0)VxeK. Фиксируя точку х0^К, видим, что Ve>
> О Я 6(e) G= (О, Ъ—а) такое, что имеет место оценка 0^/?(6о(е),
х0) О, и поскольку /?(80(е), х) е С(х0), то существует окрест-
ность Щхй) такая, что в ней имеем оценки
0<Я(60(е), х) <е VXE U(x0)ПК-
Но тогда К С U Щхй). В силу компактности множества К из
АбК
открытого покрытия {Д(х0); хое К} можно выбрать конечное
i
подпокрытие, для которого имеем Дальнейшее
k—1
доказательство теоремы Дини провести самостоятельно.
Рассмотрим на множестве 5s (Z(—оо, -]-оо) „одностороннюю"
базу В^ одного из следующих 7 видов: a) 5°=N, B_0*>=(n—>+оо);
б) SP = {Pi, . . . , ^л, . . . }, база (рп—>-Ь°о) соответствует после-
довательности Гейне (рп | +<х>); в) дъ={р1г . . . , рП1 . . . база
(рп-*Ъ— 0) соответствует последовательности Гейне (рп | 6);
г) = {pv . • . , . . . }, база (рп —»а + 0) соответствует после-
довательности Гейне (рп t а); д) SP — [а, -}-оо), база (р-» + °о);
е) д!>=(а, Ь), база (р—»а+0); ж) ^=(а, Ь), база (р—0).
Следствие (теорема Дини для монотонного семейства
функций). Пусть на множестве 3aCZ(—оо, +оо) определена
„односторонняя" база (одного из видов а) —ж)) и {F(x, р);
р<=&}— семейство числовых функций, определенных V рЕ=.&
на компактном множестве КсХ метрического пространства
{X, рЛ). Пусть выполнены условия: 1) F(x, р) ^Сх(К)Хр ^д>-
2) числовая функция F(x, р) монотонная по р на множестве &
для любого фиксированного х^К (т. е. F(x, р) f (|) на & при
хеК); 3) Э lim F(x, p) = F(x)Xx^K- 4)Ff=C(K). Тогда
в<^
F(x, р) * F(x) на К. Доказать следствие самостоятельно, ис-
пользовав доказательства предшествующих теорем Дини: в слу-
чае а) при F(x, p) = fn(x), 3a = N, В^ = (п—> + <so) см. доказа-
тельство теоремы Дини для функциональных последовательнос-
тей и функциональных рядов, в случае д) при F(x, p)=F(A, х),
д>=[аг +сю) и = (Л -> + оо) см. доказательство теоремы
Дини для несобственных интегралов, зависящих от параметра,
78
вида (3.2), в случае е) при F(x, p) = F(8, х), 3s = (О, b — а),
В.0» = (8 —> + 0) см- доказательство теоремы Дини для несобст-
венных интегралов, зависящих от параметра, вида (3.3).
Теорема (признак Дирихле равномерной сходимости функ-
ционального ряда). Пусть дан функциональный ряд
2 “nW “nW. х е м> (3-5)
П=1
причем:
1) V х<=М ап(х) | (f) при и->4-оо и ап(х)-* 0 на М;
п
2) если sn(x)= 2 Uk(x),
*=i
то функциональная последовательность (sn(x)) равномерно огра-
ничена на множестве М (т. е. существует постоянная ОО та-
кая, что
|sn(x) |^С<-(-оо v хеМ и V neN).
Тогда функциональный ряд (3.5) сходится равномерно на множе-
стве М.
Теорема (признак Абеля равномерной сходимости функцио-
нального ряда). Пусть дан функциональный ряд (3.5), причем}
1) V хеМ ап(х) | (f) при п-^+,оо и функциональная после-
довательность (а,п(х)) равномерно ограничена на множестве М
(т. е. существует постоянная С>0 такая, что |ап(-к) | С<+<*>
V х^М и v neN);
4-00
2) функциональный ряд у, ип(х) сходится равномерно на
множестве М. Тогда функциональный ряд (3.5) сходится равно-
мерно на множестве М.
Доказательство. Признаки Дирихле и Абеля будем до-
казывать одновременно, используя критерий Коши равномерной
сходимости функционального ряда. Пусть
п+1
1>1и oz(x)= 2 “»(*)•
*-«+i
Тогда имеем
оДх) = s„+/(x) — sn(x), о0(х) = О,
• Un+i(x) = oz(x) — az-i(x).
В силу тождества Абеля (см. [1], ч. II, гл. 2, § 6) Vp>2 име-
ем (при e0(x) s 0)
79
п+р р
2 алМ Uk(x) = 2 an+l(x)Un+l (v) =
k=n+l 1=1
p-1
= 2 a/W(an+/W— ал+ж(*)) + <b>(x)a*+p(x) — a0(x)an+l(x).
i=i
В силу условия монотонности am(x) | (при т —> + оо) Va: е М
имеем
a„+z(x) — an+z+i(x) >0VxG.M (/=1, 2, ... , р).
Но тогда
|«n+z(x) — ал+ж(х)| = ап+г(х) — ап+г+1(х),
и поэтому получаем основную оценку
п+р I р-1
2 ак(х) < 2 |Sn+z(x)-Sn(x)|(an+Ax) — а„+г+1 (х)) +
*=«4-1 I 1=1
+ |s„+/,(x) — sn(x)| • |ал+р(х)|.
1) При выполнении условий теоремы Дирихле ЯС>0 такое,
что |sm(x)|^CVx е М и YmeN, а из условия ат(х) 10 (при т->
—>4-оо) Vxeilf имеем оценку а„(х) >О VтеN, т. е.
1П+Р
2
Л=п+1
<2С • a„+1(x) V/>gN.
Поскольку аДх)------*0 на М, то V е>0ЯЛ/(е) eN такое, что
Vrf>V(8) и Ухе/И имеем 0^an+i (х)<^е/2С, т. е. Уп>У(е), У/?^1 и
In+/’ 1
УхеМ получаем оценку у ak(x)uk(x) <s- В силу критерия
|fc"+i I
Коши равномерной сходимости функциональных рядов из этой
оценки вытекает, что ряд (3.5) сходится равномерно на мно-
жестве М.
2) При выполнении условий теоремы Абеля из равномерной
ограниченности функциональной последовательности (am(xj) на
множестве М следует, что ЯС>0 такая, что |am(x)|^C VxgM
и V/neN. Из равномерной сходимости функционального ряда
(3.1) на множестве М в силу критерия Коши равномерной сходи-
мости функциональных рядов следует, что Ve>OSZV(e)eN такое,
что |»n+z(x) — sn(x)|<®/(ЗС)Vп>2V(s), V / > 1 и VxеМ и тогда
V n'J>N(e), Ур>1 и Ухе Л/ имеем оценку
п+р
2 Ч(х)ик<х)
k=n+I
<e/(3C’)(|an+1(x)|+2|a„+p(x)|)<e,
т. е. функциональный ряд (3.5) в силу критерия Коши сходит-
ся равномерно на множестве М.
80
Пример. Рассмотрим ряд ая • sinnx, где ап>0, ап | О
п=1
(при п-*+оо) (например, ап = «-а, где а>0). Заметим, что
п
последовательность sn(x) = 2 sinfcx допускает оценку |sn(*)K
Л=1
l/|sin(x/2)|, ху=±2гптс. В самом деле, поскольку sn(x) =
п
= JmSn(x), где Sn(x) = 2 exp(iftx), то наша оценка при х=^
*=1
+2тл следует из очевидных оценок
|ад|=
eiX_e‘(.n+i)x
l—elx
______________2_____________
((1 — cos х)2 + sin2 х)1/2
= 2/(2( 1 — cos x))V2 = 2/(4 sin2 (x/2))V2 = 1 /|sin (x/2)|.
Но тогда функциональная последовательность (s„(x)) равномер-
но ограничена на любом отрезке, не содержащем точек вида
хт = 2/пк (m = 0 ± 1, ±2, . . .). В силу признака Дирихле наш
ряд сходится равномерно на любом отрезке [а, &], не содер-
жащем точек вида хт = 2/nw (т— 0, ± 1, ±2, . . . ).
Теорема (признак Дирихле равномерной сходимости несоб-
ственных интегралов (зависящих от параметра) с бесконечными
пределами). Пусть f(x, t)^Rt[а, Т] vT>a в любой точке хеМи
А
g(x,i)eMt[a, 4-со). Пусть функция F(x, А) = J f(x, t) dt равно-
а
мерно ограничена на множестве MX [а, +«>), т. е. Я Л>0 такая,
что \F(x, 4)| < К v xsAf и V А>а. Пусть g(x, i)—*0 на М.
(f-+oo)
Тогда несобственный интеграл, зависящий от параметра,
Т f(x, t)g(x, t)dt (3.6)
а
сходится равномерно на 'множестве М.
Теорема (признак Абеля равномерной сходимости несобст-
венных интегралов (зависящих от параметра) с бесконечными
пределами,). Пусть Т] V Т>а в любой точке х^М и
ё(х, t)^Mt\a, 4-оо). Пусть функция g(x, t) равномерно ограниче-
на на множестве Л4Х[а> +°°)> т. е. Я L>0 такая, что |g(x,
A) I L V хеЛ1 и V Пусть несобственный интеграл, завися-
щий от параметра,
Т кх>
а
Равномерно сходится на множестве М. Тогда несобственный ин-
теграл (3.6) сходится равномерно на 'множестве М.
®~*л- И. Камынин 81
Доказательство. Доказательство признаков Дирихле и
Абеля проводится единообразно с помощью критерия Коши рав-
номерной сходимости несобственных интегралов (зависящих от
параметра) и основано на применении 2-й теоремы о среднем для
интегралов Римана (из [1], ч. II, гл. 2, § 6.), в силу которой V
хеЛ4 и v A2>Ai^a а се[Аь А2] (точка с зависит, вообще гово-
ря, от х^М) такая, что
/’/(*, t)dt = g(x, А^у f(x, t)dt +
Ai Ai
4- At) ff(x, t)dt.
откуда получаем основную оценку
с
ff(xt t)g(x, t)dt I < |g(x, A^l • у f(x, t)dt +
Ai
+|g(x, A,)|
ff(x, t)dt
1) Пусть выполнены условия теоремы Дирихле. В силу рав-
номерной ограниченности функции F(x, А) на множестве М X
X [а, -|-оо) имеем оценки
У f(x, t)dt
At
|F(x, c) — F(x, А^кгК,
у f(x, t)dt <2K V хе Л/.
С
Поскольку g(x, П ~ 0 на М, то ¥е^>0ЭТ(8)>а такое, что
(Z-»+oo)
|g(x, А)|<е/(4/<) V А >Т(е) и VxeAl. Поэтому УА2>А1>7'(е)
и Ухе21/ имеем оценку
f f(x, t)g(x, t)dt < s,
Ai
так что в силу критерия Коши (равномерной сходимости не-
собственных интегралов) несобственный интеграл (3.6) сходит-
ся равномерно на множестве М.
2) Пусть выполнены условия теоремы Абеля. В силу рав-
номерной ограниченности функции g(xt t) на множестве Л/Х
X [а, +°°) имеем оценку \g{x, /)]<:£ V(x, t)EMx[a, -f-oo).
Поскольку интеграл (3.7) сходится равномерно на множестве
М, то в силу критерия Коши (равномерной сходимости несоб-
ственных интегралов, зависящих от параметра) Уе>0ЯТ(е)^>Л
такое, что V А2 > с> Aj>>7(e) иУхе.М имеем оценки
82
с
f
At
/(x, t)dt <^&/2L
A,
J /(x, t)dt
c
<e/(2Z).
и
Таким образом, из основной оценки V42>^i>7’(e) и N х^М
имеем оценку
f f(x, t)g(x, t)dt
Ai
£>
из которой в силу критерия Коши (равномерной сходимости
несобственных интегралов) следует равномерная сходимость
несобственного интеграла (3.6) на множестве М.
Теорема (признак Дирихле равномерной сходимости не-
собственных интегралов (зависящих от параметра) от неограни-
ченных функций). Пусть f(x, t) (= R.t[a-j-fi, b]V б>0 в любой точ-
ке хеЛ4 и g(x, t) е Mt (а, b] v хеМ Пусть функция F(x, d) =*
b
= J f(x, t)dt равномерно ограничена на Множестве MX (О,
Ъ—а) (так что я К>0 такая, что fF(x, б)| KvxeAf и V бе
е (О, b—а]). Пусть g(x, t) —»0 на М. Тогда несобственный ин-
О-»а-Н)
теграл, зависящий от параметра, , !
f f(x, f)g(x, t)dt
(3.8)
(где t=a — особая точка (3.8)) сходится равномерно на Множе-
стве М. Доказать самим.
Теорема (признак Абеля равномерной сходимости несобст-
венных интегралов (зависящих от параметра)' от неограниченных
функций)z Пусть f(x, t) e/?f[a+6, b]v 6>0 в любой точке Х(=М
и S (х, t) (а, b] V xeAf. Пусть функция g(x, t) равномерно
ограничена на множестве МХ(а, Ь] (так что существует L>0
такая, что |g(x, t) | V (х, t) <=Мх(а, &]). Тогда, если несоб-
ственный интеграл, зависящий от параметра, S f(x, t) di, схо-
дится равномерно на множестве М, то и интеграл (3.8) сходится
равномерно на множестве М. Доказать самим.
Пример. Несобственный интеграл J e~xt • (sinM)d/ (хе
о«-
S[0, + со)) сходится равномерно на [0, +°о), так как несобст-
4-00
венный интеграл Дирихле J (sin tit)dt сходится, а функция
o«-
e -f-oo)Vx>0 и равномерно ограничена на [О,
+°°)Х[0?+оо) в силу оценки |ехр(—xi)|< 1 Vx>0, t > О.!
§ 4. Свойства равномерно сходящихся функциональных
последовательностей, функциональных рядов
и несобственных интегралов, зависящих
от параметра
Пусть числовая функция (х, р) —*F(x, р) sR определена на
множестве МХ&, где AfcX и {X, р^) — метрическое простран-
ство, а во множестве 5° задана база В^. Подчеркнем, что
значения числовой функции F(x, р) принадлежат полному про-
странству R.
Теорема (о повторных пределах). Пусть F(x, р) * F(x)
на М, где — база во множестве SF, и х0^М'. Пусть V реЗ5
существует lim F(x, p)=A(p)^R (где функция р-+А(р) ото-
х-*х0
бражает SP в R). Тогда существует lim 4(p)=4eR, причем
В^>
lim Г(х)=Ит А(р)—А, т. е.
в^
lim (lim F(x, р)) — lim (lim F(x, p)).
Полезна схема
F(x, p) —* F(x) на M
(x->x0)| b^ | (x—>x0)
Л(р) ------------- A.
Доказательство. 1) Докажем сначала, что Я lim Д(р).
в.0»
Поскольку F(x, р) »F(x) на М, то в силу критерия Коши
В^>
(существования равномерного предела числовой функции)
V е> О Я 5(e) ее такой, что Vpv p2s 5(e) и VxsJf имеет
место оценка
|F(x, Pi) ~ F(x, р2)| < е. (4.1)
Фиксируем plt р2е 5(e), тогда в силу условий теоремы
Я lim F(x, pt) = A(pi) (t = l, 2) для x^zeM'. Перейдем в нера-
х—X.
венстве(4.1) к пределу прих-»х0. Тогда Vpb р2 е= 5(е)е=В^>, по-
лучаем оценку
1Л(р2) - Л(р2)| < е(Д(р,) «= R; i = 1, 2). (4.2)
Но числовая функция р—>Д(р) есть отображение множества 5s
в полное пространство R. Вспоминая (см. [1], ч. I, гл. 3, § 9)
84
критерий Коши существования предела числовой функции
(lim А(р) по базе (В^), видим, что оценка (4.2) означает вы-
полнение условий этого критерия Коши, поэтому Я lim А(р) =
= (подчеркнем, что в этом месте доказательства суще-
ственно использована полнота R).
2) Докажем теперь, что lim F(x) = A. Очевидно, для любого
Х-*Х9
р^& и для любого хе М, имеем оценку |А—Г(х)К|А—
— А (р)| + |А(р) — F(x, р)| + |F(x, p) — F(x)\. Пусть задано любое
(но фиксированное) е>0. Тогда поскольку Я lim А(р) = А ЕВ,
то Я Вд(е) ЕЕ В^» такое, что V р е Bt(e) имеем оценку
|Д — А(р)| < ®/3. (4.3)
Но F(x, р) —>• F(x) на М, поэтому для выбранного ®>0ЯВа(е)е
В^>
е В^» такой, что Vp е В2(е) и ¥х е М, имеем
|F(x, р) — Г(х)| < е/3. (4.4)
Далее, в силу определения базы В^ для выбранных элемен-
тов Вх(е) и В2(е) базы В^ = {В} существует элемент 2?0(е) базы
В^> такой, чю Во=#=0 и Но ¥р<=ВоеВ^ и ¥xeAf
одновременно выполнены неравенства (4.3) и (4.4). Фиксируем
р = рое В0(е). В силу условий теоремы для р0 е Be(e)
Я lim F(x, р0) = А(р0) (х0 е М' CZ .¥•) Поэтому для выбранного
х-+х%
е > 0 и для р0 <= В0(е) е существует окрестность U(x0) С X
такая, что ¥хей(х0)ПЛ/ имеем
|Лх, Рв)-Л(р0)|<8/3. (4.5)
Итак, ¥®>ОЯроеВо(е)еВ^ и Я(7(х0)сХ такие, что ¥xe(7(x0)f)
|~)Af имеет место оценка
|Д - Г(х)| < |А - А (р0)| + |А(р0) - F(x, р0)| +
+ Р’(х, p0)-F(x)|<®. (4.6)
Но оценка (4.6) и означает, что Я lim F(x) = A=lim А(р).
х^х- в^.
Замечание!. В теореме о повторных пределах вместо
базы х-+х0 (во множестве AfCZX при хое7И') можно рассмат-
ривать любую базу Вд1 (во множестве М), например: 1) х—»+<»
при Л=[с, Н-оо); 2) х—»с-|-0 при М^(с, d]; 3) п—>4-00 при М—
85
=N. Тогда если F(x, р) —» Fix) на М и V р е ^Я lim F(x, р) —
В<&> ’ ВМ
= А(р), то Я lim А(р) и имеет место равенство
в<#>
lim [lim F(x, р)] = lim [lim F(x, /?)].
вм B^ B^> BM
Вновь полезна схема
F(x, p) —* F(x) на M
Bjm | B&> | Bm
A(p) —A
B^>
(Провести самостоятельно соответствующие изменения при до-
казательстве оценок (4.5) и (4.6).)
Замечание 2. В теореме о повторных пределах в качест-
ве базы В^> (во множестве 3s) будут в дальнейшем рассматри-
ваться следующие базы: 1) t—>4-00 при 3&=[а, -И00); 2) <—»а-|-0
при ^ = (а, &] и 3) л—>-[- 00 при 3° «» N.
Замечание 3. Если F(x, р) ~ * Fix) на TWqA, F(x, р)<=У
В<&>
(где {У, ру) — метрическое пространство), то теорема о повтор-
ных пределах остается верной, если метрическое пространство
{У, ру| — полное.
Теорема (о предельном переходе в равномерно сходящейся
функциональной последовательности). Пусть MczX, где {X, рх} —
метрическое пространство и х0^М'. Пусть fn(x)—>-f(x) на М и
fn(x), f(x)^Rv x&Mv neN. Пусть a lim fn(x)=Anv n.
X-*Xe
Тогда a ilm An—A, причем lim f(x) = lim An=»A, t. e.
rt->4»oo X^X0 n-H-00
lim (lim fn(x)) — lim (lim f„(x)).
X-+Xe П-►4*00 n—>+©0 x—>xt
Схема: fn(x) —t f(x) на M
(x-*x0) I n-*+°° j, (x-^x0)
Доказательство. Рассмотрим при 3s = N базу n —> + 00
и положим Fix, n)sf„(x), F(x) = fix) V x <= M, Aln) = An. Тогда
наша теорема следует из общей теоремы о повторных пределах.
Следствие 1. Пусть f„lx) *flx) на М и х0<=Л1. Тогда
(fп <= С(х0) V л е N) =>(/е= С(х0)).
86
Д о к аз ательство. Если х0 s М— изолированная точка
множества Л4, то утверждение очевидно. Если хоеЛ/(~]М', то
fneC(x0)VneN и поэтому Я lim/n(x) = fn(x0). Но по условию
х-*хв
fn(x) /(х) на М, и поэтому в силу доказанной теоремы о
предельном переходе в равномерно сходящейся функциональ-
ной последовательности Я lira f(x) = lim fn(x0), и поскольку
х-*х0 л-*4-оо
хое MQM', то из условия fdx}--------* f(x) на М, в частности,
вытекает, что Я lim f„(x0) = Дх0), т. е. lim f(x) = f(x0), а потому
х-*х,
f £= C(Xq).
Следствие 2 (о непрерывности предела равномерно сходя-
щейся последовательности непрерывных функций). Если fn(x) >
. f(x) на М и fn е С(М) V n <= N, то f е С(М).
Замечание. Из поточечной сходимости последовательности
непрерывных на множестве М функций, вообще говоря, не следу-
ет непрерывность на этом множестве предельной функции.
Пример. Рассмотрим на отрезке [0, 1] функциональную по-
следовательность
fn(x) =
11, 1/п<^х^1
\пх, 0<х< 1/п
и Д*)=
(1, 0<х< 1
(О, х = 0.
Тогда fn е С([0, 1]), /4(х)-/(х) на JO, 1], но fs С ([0,1]).
3 а м е ч а н и е. Если/я(х)—>/(х) на Jf, то из того, что /п<=
eC(4f)VneN и вообще говоря, не следует, что
/„(л) —> /(х) на М. (Сравните в этой связи теорему Дини для
функциональных последовательностей.)
Пример. Пусть
/„(х) = ) О,
{ линейный горб высоты 1, 0«Сх<Д/п.
Тогда lim fn(x) = 0Vxe[0, 1] (f(x) = O), причем fn, /ё=С([О, 1]),
Л—►-f-oo
но sup |/n(x) — f(x)| = 1 Vn N, поэтому функциональная по-
1]
следовательность (f„(x)) сходится к функции Дх) на отрезке
{0, 1] неравномерно (нет монотонности!).
Следствие 3 (о полноте пространства С(К)). Пространство
числовых функций, непрерывных на компактном множестве
КаХ (метрического пространства (Ж, р}), с метрикой Чебыше-
ва Р(Д g) = max |Дх) —f(x)l полно.
хбК
87
Доказательство. Поскольку множество К компактно в
метрическом пространстве {X, р}, то С(К) GZ-S(K). Пусть (fn)—
последовательность Коши из С(К), так что V« > О Я?V(e) <= N
такое, что p(fn, fm) = max |fn(x) — Mx)KeV'n>R>M8)- Ho
x£K
тогда для функциональной последовательности (fn(x)) на мно-
жестве К выполнен критерий Коши равномерной сходимости, в
силу которого существует числовая функция f: К —>В такая,
что fn(x) > f(x) на К, т. е- lim p(fn, f) — 0. Поскольку /п<=
л->+оо
sC(K), то в силу следствия 2 (о непрерывности предела рав-
номерно сходящейся последовательности непрерывных функ-
ций) /еОД). Итак,, для любой последовательности Коши (fn)
из пространства С(К) Я f е С(К) такая, что lim p(fn, f) = 0, т. е.
Л—>-f*oo
lim fn = f, но это и означает полноту С(К).
H-^-f-oo
Замечание. В полном метрическом пространстве С(ХО, 1])
с метрикой Чебышева p(f, g) “ max |f(x)— g(x)| единичный замк-
[0.1]
нутый шар
Ш1(О)={/^С([О, i])|?(f, 0) <1}
не является компактным множеством.
В самом деле, рассмотрим последовательность (/n) fn s
еШ1(0)сС([0, 1J), где fn(x) = xn, х <= [О, 1]. Тогда fn(x)-^(x)
на [0, 1[, где f(x)=!^’ причем / ёШ1(0). поскольку
(1, х = 1,
f еС([0, 1]). Если бы шар Ш4(0) был компактен в полном мет-
рическом пространстве С([0, 1]), то он был бы и секвенциаль-
но компактен, и тогда из последовательности (fn) (где f„ е
е Ш1(0)) можно было бы выбрать подпоследовательность (f„ft)»
сходящуюся в С([0, 1]) (так что lim fn =<р еШ1(0)сС([0, 1])).
*->4-00 А
Но тогда f „ь(х) —*<р(х) на [О, 1], и поскольку fn(x)—>/(х) на
[О, 1], то ф(х)=/(х) на [О, 1], из чего вытекало бы, что фс
е С([0, 1]). Противоречие.
Следствие 4 (теорема о непрерывности суммы равномерно
сходящегося ряда из непрерывных функций.). Пусть ип^С(М) V
4-00
neN и „фунциональный ряд у ип(х) сходится равномерно на
п=1
множестве М к сумме f(x). Тогда f^.C(M), т. е. равномерно схо-
дящийся ряд из непрерывных функций есть функция непрерывная.
88
Доказательство. Ввиду важности этой теоремы дадим
для нее прямое доказательство, не опирающееся на общую
теорему о повторных пределах. Пусть $п(х) — у, uft(x)Vxe М.
А=1
Поскольку ик е С(М) V & е N, то sn е С(М) Vb е N.. Далее из
равномерной сходимости рассматриваемого функционального
ряда к сумме f(x) на множестве М вытекает, что s„(x) > f(х)
на М. Рассмотрим V х0, х0 4- Дх s М и V п0 е N оценку
|/(х0 4- Ах) — f(х0)| < |f (х0 + Дх) — зя,(х0 + Дх)| +
+ + Ах) - з4х0)| + |зп,(х0) — f (х,)|.
Пусть е>0 — любое, но фиксированное. Поскольку s„(x)-----» f(x}
на М, то Я Me) е N такое, что |з„(х) — f (х)| <е/3 Vn> 2V(e) и
VxeM. Пусть фиксирован номер л0>2У(г), тогДаУх,, х04-Дхе
е М имеем оценки |$п.(х04-Дх)—/(х04-Дх)|<е/3 и |«я,(х0)—f(x0)|<
<е/3. Но sn, е С(х0), поэтому Я8(е, х0)>0 такое, что для лю-
бой точки х0 + Дх е Us(x0)f]M имеем оценку
1Мхо + Ах) — зп.(х0)| < е/3.
Но тогда из нашего основного неравенства следует, что Уе >
>0Я6(е, х0)>0 такое, что
V х0 4- txx е U8(х0) Г) М => (|f (хв 4- Дх) — f (хв)| < е/3 4- е/3 4-
4- е/3 = е)=>(/(= С(х0) V х0 е М) =» (f е= С(Л4)).
Теорема (пример Ван-дер-Вардена). Существует непре-
рывная на (—оо, 4-оо) функция, не дифференцируемая ни в од-
ной точке.
тт гт s / х ( х, хе [0, 1/21,
Доказательство. Пусть f#(x) = 1 1 ’ J при-
I 1—х„ хе [1/2, 1],
чем fo(x4-l)=fo(x)Ух е(—оо, 4-од). Очевидно, f0 <=£((—о©, 4-<х>))
и функция f0(x) имеет период 1. Положим fa(x)=4-nfo(4n • х).
Поскольку D±fn(x) = D±ft(4n ♦ х)Ул е N, то все угловые коэф-
фициенты к графику Г =. {(х, у) е R2|y — fn(x), -re(—оо, 4-оо)}
равны +1, за исключением угловых точек. Поскольку Уп е
-[-оо
s No 0</я(х)<4-п Ухе(—оо, 4-оо), то ряд f(x)=2 /п(х) сходит-
п=0
Ся нормально на(—оо, 4-оо), а потому в силу признака Вейер-
штрасса этот функциональный ряд сходится равномерно на
(—оо, 4-оо), Т. е. При 5л(х)= 2 fft(x), sn(x)-* f(x) на (—оо,
А=0
+оо). Из теоремы о непрерывности суммы равномерно схо-
дящегося ряда непрерывных функций имеем
8£
(fn e C((—°®, 4-0®)) Vn e No) Д (sn(x) „» f(x) Ha
(—°®, .+°®))=> (feC((—oo, +=»)))•
Докажем, что /e^£)(x)Vx. Точнее, Vxe(—о», 4-°®) построим
последовательность точек (хп), сходящуюся к точке х, такую,
что последовательность ((f(x„)—/(х))/(хп—х)) не имеет предела
при /г—>4-оо. Заметим, что функция fjx) Vп gN0 линейна на
отрезках
|—1, 2^“ ’ =Ь2,...). Пусть х>0 произвольно,
но фиксировано, тогда существуют числа s0, sr.......sn е Z
такие, что
хе [(sn—1) • 4~”/2, sn . 4-«/2]С . . •
• • . CZ [(st- 1) • 4-*/2, • 4~л/2] CZ
С [(«о-0/2. V2J-
Положим Дп=[‘^-1, —
= 4~я/2, Очевидно, Vn е N0Sxn е Дя такое, что
- тогда длина этого отрезка |ДЯ| =
|х — хп| = |Дп|/2 = 4-я”1.
Тогда
f(x„)-f(x) fkM-fhW
х*~х S Хя~*
Рассмотрим отношение . Функция /\(x)VZ>eN0 име-
Хц — X
ет периодом число <oft = 4-ft, и потому Vk>n число а>=4-я-1
также есть период для функции fh(x). Но |хп— х| = 4~п-‘. По-
этому fk(xn) — fft(x) = О V k > п, откуда
(fk(*n) - fk(xW(xn - x) = 0 V k > n.
Итак, Vn e No имеем равенство
^(x„)-f(x) =y fk(x„)-fh(x)
xn — x xn— X
Ho x, xn <= Дп, поэтому x, xn e Д„ CZ ДЛ V k n, и тогда в силу
построения имеем
f(xn) — f(x) -у /й(хя)—/Л(х)
хЯ - X хп - х
- 2 <±‘).
•90
Если п нечетно, то эта сумма есть четное число, а если
л четно, то сумма нечетна. Поэтому не существует предела
lim , т. е.
Xfi X
чем теорема Ван-дер-Вардена доказана.
Замечание. Можно показать, что любая монотонная, хотя
бы и не непрерывная, функция обязательно имеет точки диффе-
ренцируемости.
Теорема 1 (о непрерывности равномерно сходящегося ин-
теграла (зависящего от параметра) с бесконечными пределами).
Пусть функция (х, t) -* и(х, определена на множестве
[с, d] X [а> + °°) и ие С([с, di X [а, +«>)).
Пусть несобственный интеграл, зависящий от параметра
F(x) и{х, t)dt, (4.7)
а
сходится равномерно на отрезке [с, d]. Тогда F&Cflc, d]).
Доказательство. Положим
F(x, T) = Jk(x, t)dtVT>a.
а
В силу равномерной сходимости несобственного интеграла
(4.7) имеем: 1) F(x, 7Т - F(x) на [с, d]. Поскольку и^С([с,
(Т-*4-оо)
d] X +°°)), то ueC(fc, d] X [«, TJ) и по теореме о непре-
рывности интеграла Римана, зависящего от параметра (из § 2),
имеем F(x, Т)^Сх(\с, d]) и, в частности, выполнено условие
2) Vxos[c, d]31imF(x, Т) = F(x0. Т)—(и(х0> t)dt. В силу усло-
*-**• а
вий 1) и 2) к функции F(x, Т) можно применить теорему о
повторных пределах (положив SF = [а, -|-оо), + и
М=[с, d]) по схеме F(x, Т) - > F(x) на [с, d]
(Х-»ХО) | (Т-Н-ос) | (х-^х0)
F(x0» Т)----► F(x0)
(T-+00)
в силу которой Я lim F(x0, T) = lim F(x). Но
х->хе
lim F(x0, Т) = +Г и(х0, t)dt = F(x0),
т-+« i
так что
(Я lim F(x) = F(xo)Vxog[g d])=»(FeC([c, d])).
x-*xe
91
Ввиду важности этой теоремы дадим для нее прямое до-
казательство, не использующее общую теорему о повторных
пределах.
Доказательство. Пусть е>~0 — любое, но фиксирован-
ное. В силу равномерной сходимости на [с, d] несобственного ин-
теграла (4.7) Я Т0(8.)>а, такое, что
т
Л<е)
u(x, f)dt < е/3 V х €= [с, d].
Поскольку «еС([с, d]X[«, 70]), то в силу теоремы 1 (из § 2)
имеем
F(x, Т0) = у’ и(х, t)dt ^Сх([с, d])
а
и поэтому для выбранного е>0Я8(е, х0)>0 такое, что Vx04-
4-Дхе £/а(х0)П [с* d] имеем
J*m(.x04-Ax, t)dt— J’ ы(х0, t)dt
а а
< е/3.
Но тогда ¥х04-Дхе(/ (х0) Q [с, d] и Т0(е)>а имеем оценки
8(е. X.)
|F(x0 + Дх) — F(x0)| < |F(x0 4- Дх) — •
а
7.
7. 7,
— J и(х04-Дх, t)dt + j w(x0 + Дх, t)dt —
а
— j’u(x0, t)dt 4- J'u(xo, t)dt—F(x0) =
a a
= J и(х04-Дх, t)dt 4-
7e
7. _ 4-00
т
j и(х04-Дх, t)dt—
а
— J u(xQ, t)dt + J iz(x0, t)dt
a 7e
< е/3 + е/3 4- 8/3 = е=» .
=> (Fe C(x0) Vx0 €= [c, d]) =»(F eC([c, d])).
Теорема 2 (о непрерывности равномерно сходящегося не-
собственного интеграла от неограниченной функции, зависящей
от параметра). Пусть функция (х, i)-*u(x, t) е R определена на
множестве [с, d]\(a, Ь] и ueC([c, d] X (a,bi). Пусть несобст-
ь
венный интеграл (с особой точкой при t—a) F(x)—S и(х, t)dt
сходится равномерно на отрезке [с, d]. Тогда F^.C ([с, d]j. До-
92
казать самим, применив общую теорему о повторных пределах
ь
к функции F(x, &)= [ и(х, t)dt и положив 3s = (а, 6], В^>: 5—>
u-j-S
—> + О, М = [с, d].
Теорема (об интегрируемости по Риману равномерного пре-
дела функции, интегрируемой по Риману). Пусть функция (х,
р)-+и(х, p)eR определена на множестве [с, d]X^- Пусть В^> —
база во множестве SF и и(х, p)(=Rx[c, d] \р^2Р. Пусть и(х,
р)—*у(х) на [с, d]. Тогда d],
в.?>
Доказательство. Поскольку и(х, о) * у(х) на [с, d], то
В^>
Ve>0SB(e)€=B^ такой, что V/>e£(s) и Vxe[c, d] имеем [u(x,
р) — о(х)|<8, но тогда V хи х2е[с, d] и
V р е В(е) =» ^(xj) — t>(x2)| < ^(Xi) — и(хъ р)| +
+ Р) — u(xt, р)\ + |и(х2, р) — р(х;)| <
< 2е + |u(xx, р) — и(х2, р)|,
т. е. для любого отрезка [а, [3] Q [с, d] и Vp е В(б) имеем
o(t>; [а, Р]) = Ж1 *“Р 13) Их1)-р(х2)|<28+а>х(и; [а, £]),
откуда для любого разбиения Т = {с == х0 < х1 <" . . . <хп ч- d}
отрезка [с, d] получаем оценку «(Г) + 2e(d — c)Vpe
е В(8), где положено
и(Т) = ®х(и> [**—Ь
л=1
Поскольку и е /?Дс, d] V р е то в силу критерия Дарбу ин-
тегрируемости по Риману (см. [2], ч. II, гл. 2, § 2) имеем
inf а(Г) = 0УрЕВ(е)
т
и поэтому
V е > 0 => (0 < inf < 2s(d — с)) =^> (inf QV(T) = 0),
т ‘ т
е. в силу того же критерия Дарбу ve=R[c, d].
Следствие 1. Пусть — oo<c<d<+©o и d] VnEN.
Пусть /п(х) ; f(x) на [с* d]. Тогда f е 7?[с, d]. (Для доказа-
тельства нужно применить нашу теорему, положив
3a = N; + оо; и(х, п) = }п(х)-, р(х) = /(х)).
Следствие 2. Пусть unEzR[c, dj Nn е N и функциональ-
ный ряд
93
2««W (4.8) }
сходится равномерно на отрезке [с, d] к сумме f(x). Тогда f€= I
£й[с, d\.
п, )
Доказательство. Если положить $п(х) = иь(х)> то:
fc=l 5
1) (uk ^R[c, d] N k e N)=>(sn e/?[c, d|Vn) и
2) из равномерной сходимости на отрезке [с, d] ряда (4.8)
имеем s„(x)----f(х) на [с, d]. Но тогда в силу следствия 1
f(=R[c, d].
Теорема (об интегрировании функции, равномерно стремя-
щейся к пределу). Пусть функция (x,p)-+u(x,p)^R определена
на 'множестве [с, djX^3. Пусть В& -г- база во множестве & и
и(х, p_)eRx[c, d]v p^SP, причем и(х, р) —* v(x) на [с, d]. Тогда
4 в<&
X ___ X
1'ЕЙ[с, х] Ухе [с, d] и f и(у, p)dy_____► f v(y)dy на [с, dj,
с Bs> е ~
в частности,
d d
J v(x)dx з= lim J k(x, p)dx.
с B^ C
Доказательство. Поскольку u(x, p)-------> v(x) на [c, d] и 1
u(x, p)&Rx[c, то по предыдущей теореме v^R[e, |
x] Vxe [c, d], т. e. Я Jv{y)dy Vx e[c, d]. j
C <
X x
Положим <p(x) = J v(y)dy и <p(x, p) = J u(y, p)dy. Тогда V x e ’
c c
e [c, d] и Vpe5® имеем оценки f
|ф(х, p) — ф(х)| < J \v(y) — u(y, p)\dy <
c
< (d — c) sup |u (f, p) - o(0| ss a(p).
z6[c. d\
Поскольку u(t, p)-----Г v(t) на [c, d], to lima(p) = 0, т. e. Я
в^
lim sup |ф(х, p) — ф(х)| = 0.
B^, X6[c,d]
Но тогда ф(х, p)----* ф(х) на [c, d], что и требовалось дока-
В^>
эать.
94
Следствие 1 (теорема об интегрировании равномерно схо-
дящейся функциональной последовательности). Пусть —оо<с<
^dc + oo. fn^Rfc, dlvnsN и fn(x) - • > f(x) на (c, d]. Тогда
х X d d
f fn(t)dt-» f f(t)dt на [c, d] и, в частности, f f (x)dx=lim f f(x)dx.
C C e n—+«J
(Для доказательства нужно применить нашу теорему, поло-
жив & = N, В^>; п-> + оо, и(х, п)зе/п(х), v(x) = f(x).)
Замечание. Теорема об интегрировании равномерно схо-
дящейся функциональной последовательности доказана лишь для
конечного отрезка [с, d'J и перестает быть верной при замене [с,
d] на [с, +оо).
Пример. Рассмотрим функциональную последовательность
где
f _ (0 0<х<п, Зп<х<Ч-оо,
(линейный горб высоты 1/п, п<х^3п.
Тогда в силу оценки 0 fп(х) < 1/n V х > О имеем fn (х)---> f(x)
на [0, -|-ео), где /(х)=0» причем
-j-со Зп 4'°°
J /п(х) dx = J fn(x) dx = 1, f f(x)dx = 0.
О n V
Но тогда
lim f fn(x)dx = 1 0 = +f [lim fn(x)]dx.
Л->-|-оо Q q rt-»4-eo
Следствие 2 (теорема об интегрировании равномерно схо-
дящегося функционального ряда). Пусть ип е R[c, d] Vn <= N и
функциональный ряд (4.8) сходится равномерно на отрезке
[с, d] к сумме /(х). Тогда
J/(0dt=2 ]un(t)dt
С П=1 с
^xg[c, d], причем функциональный ряд, стоящий справа,
сходится равномерно на [с, d] и, в частности,
К 4-оо \ 4“°° d
2 u„(x) )dx= 2 f Un(x)dx.
n=l / n = l c
Доказательство. Поскольку sjx)-------------* f(x) на [c, d]« to
в силу следствия 1
Jsn(<)^=2 на [c, d].
с Л=1 с
95
Следствие 3 (теорема об интегрировании равномерно схо-
дящегося несобственного интеграла (зависящего от параметра) с
бесконечными пределами). Пусть и^С ([с, d]X[a, +°°)) и не-
собственный интеграл, зависящий от параметра (4.7), сходится
равномерно на конечном отрезке [с, d]. Тогда d] и V хе
е [с, d] имеет место равенство
X
с
а
У J и(у, t)dy dt = ^ F(y)dy,
fi
причем несобственный интеграл, стоящий слева, сходится равно-
мерно на [с, dj Итак, V хе [с, d] имеет место равенство
У dy "*у и(у, t)dt = +у dt у и(у, t)dy
с а ас
и, в частности, возможна перестановка порядка интегрирования
у dx +у и(х, t)dt = +у dt у и(х, t)dx.
с а ас
Доказательство. Воспользуемся общей теоремой об ин-
тегрировании равномерного предела функции, положив
F(x, Т) = у и(я» t)dt G= Сх([с, d]) V Т > а.
а
Тогда F(x, Т) GE /?х[с, d] V Т > а, и в силу равномерной сходи-
мости интеграла (4.7) имеем F(x, Т} • • * Fix) на [с, d]. В силу
(Т-*4-оо)
общей теоремы об интегрировании (при SF = [а, -f-оо) и базе Т —>
X
> + <эо) имеем у F(y, T)dy -* Fix) на [с, d]. Используя тео-
с <Г-»+оо)
рему 3 (об интегрировании интеграла. Римана, зависящего от
параметра из § 2),. имеем
у F(y, T)dy = §dy § и(у, t)dt=$dt у и(у, t)dy,
с с а ас
т. е.
Т х х
§dt^u(y, t)dx ~ * УF(y)dy на [с, d].
а с (Т—»оо) с
Но это и означает равномерную сходимость на \с, d] несобст-
венного интеграла
у dt у u(//, t)di
а с
и равенство
96
+°° X X -poo
J dt$u(y, t)dy=^dy J u(y, f)dtV xge[c, d].
a c c a
Следствие 4 (теорема об интегрировании равномерно схо-
дящихся несобственных интегралов от неограниченных функций,
зависящих от параметра). Пусть и^С([с, d] X (а, 6]) и несобст-
ь
венный интеграл F(x)=J u(x, t)dt (с особой точкой t=a) схо-
а<-
дится равномерно на отрезке [с, d] (—оо <c<d< 4-00). Тогда
5ЕЙ|с, d] и Vx£[c, d] имеет место равенство
b Гх I х
J J и(у, t)dy dt = $ F(y)dy,
X
а*— |_с J с
где несобственный интеграл* стоящий слева, сходится равно-
мерно на [с, dj. Итак, Vxs[c, d] имеет место равенство
х Ь Ъ .
Jdj/J и(у, t)dt — dt$u(y,t)dy
с а«- а*- с
и, в частности,
d Ъ Ь d
§dx J и(х, t)dt « J dt j u(x, t)dx
c a<- a*- c
(формула перестановки порядка интегрирования). Доказать
самим.
Теорема (об интегрировании монотонного семейства функ-
ций). Пусть на множестве & с: (—оо, 4-00) определена база
(р^>- 4-оо) и {F(x, р); р^ЗР } — семейство числовых функций, оп-
ределенных v ре$> на отрезке [с, d], причем выполнены условия:
1) F(x, р)^Сх[с, d]vp^gb', 2) числовая функция F(x, р) моно-
тонна по р на множестве SF для любого фиксированного хе[с,
d] (г. е. F(x, р) f (|) на SF при хе[с, d]); 3) SlimFfx, р) =
~f(x) Vxe [с, d]; 4) d]. Тогда
(i d
Я lim J F(x, p)dx = J f(x) dx.
Доказательство. Пусть для определенности F(x, p)f на
^Vxefc, d]. Тогда Vрг, Pi<p2 имеем неравенства
F(x, P1)<F(x, p,)</(x)Vx €=[c, d],
и поскольку F(x, p) ^Cx[c, d]CZ2?Jc, и f e Л[с* d],
To
_ d d
' )F(x, pJdx^Ffx, p,)dx<J7(x)dx = JVpi, pte 3®, Pi<p«,
c c c
Л. И. Камынин
97
d d
откуда Jp = ^F(x, p)dx\ на 5®, причем \F(x, р)йх=*1р<^Г$р&!Р,
c c
т. e. Я lim Jp = /«,</. Докажем, что JM=J. Допустим, что
р—>4-оо
d
J — 7те = 26 > 0, тогда J(/(x)—F(x, p))dx> 25 О Vр е S5, и поэ-
С
тому существует разбиение отрезка [с, d] Т = {с=х0<Д1< . . .
• • • <^xn=d} с частичными отрезками Ik—[xk-ir хй] = п)
такое, что для нижней суммы Дарбу имеем оценку снизу
Sf~P(T) > 6 > 0 Vp gS3 или, полагая mk(p) = inf (/(х)—F(x, р))>
>0, имеем оценку снизу
2 тй(р)Дхй>6>0 Vp еЗ5.
k=i
Но тогда существуют частичный отрезок Ц разбиения Т и по-
следовательность Гейне (А) (р< f t+«®), связанная с базой
(р-* + °°)> такие, что
> 8|/,|/(с* - с) V i = 1, 2..
Поскольку / s то Я g е I, такая, что f е C(g) и поэтому
Дх)— F(x, pt) е C(g)V i, т. е. имеем оценку снизу
/® - Л1. Pi) > - с) > 0 V i = 1, 2,...м
что противоречит условию 3) Я lim F(&, p)=f(£) нашей теоре-
мы.
Замечание 1. Формулировку теоремы сообщил автору
С. Б- Стечкин.
Замечание 2. Если feC[c, d], то выполнены все условия
теоремы Дини для монотонного семейства функций из ч. IV, гл. 3,
§ 3 и поэтому F(x, р) —» f(x) на [с, d], так что утверждение
й^4-оо)
теоремы об интегрировании монотонного семейства функций сле-
дует из теоремы об интегрировании функции, равномерно стремя-
щейся к пределу.
Замечание 3. Если /е₽[с, dj, но fsC[c, d], то стремле-
ние F(x, р)--->Дх) на [с, d] может не быть равномерным на
(р—+=)
отрезке [с, d]. Например, положим /(х) =
1, 0<х<1,
0, х = 0
и /Дх) =
= ( b ne=N. Тогда /еЯ[0, 1], f еС[0, 1], /пе(7[0,
\пх, 0^х<С Vя,
1] Vп и /nW</«+»W</W Vx е [0, 1] VneN, Я lim /п(х) = /(*)»
п »4*°°
98
1 1 1
причем ffn{x)dx = 1 — l/2n V n; lim ffn(x)dx= J/(x) dx = 1, но
0 n->H-oo 0 0
функциональная последовательность (/„(x)) сходится к функ-
ции /(х) на [0, 1] неравномерно, поскольку lim sup |/(х) —
- Ш -1 > 0.
Замечание 4. В доказанной теореме нельзя отказаться от
условия 4) d], поскольку существуют (см. пример 33 из
гл. 8 [4]) ограниченные функции </], являющиеся преде-
лом монотонной последовательности непрерывных функций.
Замечание 5. Теорема об интегрировании монотонного се-
мейства функций остается верной при замене базы (р-* -f-оо) на
любую «одностороннюю» базу (вида а)—ж) из теоремы Дини
для монотонного семейства функций из ч. IV, гл. 2, § 3), оп-
ределенную на множестве 55cz(—оо, +<»). •
В доказанных теоремах об интегрировании функции (равно-
мерно стремящейся к пределу), функциональных последова-
тельностей, функциональных рядов и несобственных интегра-
лов, зависящих от параметра, предполагалось, что промежу-
ток интегрирования [с, d] конечен. Теперь будем рассматри-
вать неограниченный полуотрезок интегрирования [с, +<х>).
Теорема (о предельном переходе в несобственном интеграле,
зависящем от параметра). Пусть функция (х, р)~+и(х, оп-
ределена на множестве [с, и несобственный интеграл
F(p) = и(х> Р) &х, (4.9)
С
сходится равномерно на множестве . Пусть Вг» — база во
множестве 9Ъ и и (х, р) —* v(x) на [с, X] vj>c-
Тогда существует несобственный интеграл
Y u(x)dx (4.10>
С
и имеет место равенство
lim J и(х, p)dx = *J u(x)dx.
с с
Доказательство 1 (с помощью общей теоремы о повтор-
ных пределах). Заметим, что и(х, р) е Rx\c, -J-оо) Vр s 3 и, в
частности, X]VX>c, т. е. ЗЩХ, р) = fu(x, p)dx. По-
1*
99
скольку и(х, р) —* и(х) на [с, X], то по теореме об интегриро-
вав
вании функции, равномерно сходящейся на конечном отрезке,
видим, что v е Л[с, X] и, кроме того
Я lim F(X, p)z=f v(x)dx V X > с. (4.11)
B^> с
По условию несобственный интеграл (4.9) сходится равномер-
но на множестве 3, поэтому
Л-S’, Р)=Х^(Р) на 3s, (4.12)
(Х—4-оо )
но из условий (4.11) и (4.12) в силу общей теоремы о повтор-
дых пределах (см. замечание 1 к ней) следует: (см. схему
F(X, р) zt F(p) на
X 4-00 4-00
J v(x)dx—> J v(x)dx== lim F(p) = lim J u(x, p)dx).
c (A’->4"°°) c B^» B^ c
1) (3 lim f v(x)dx=+( v(x)dx)=^(y s#[c, +<*>));
x-+« c c
4-00
2) lim F(p) = J v(x)dx, t. e.
В^в c
lim j u(x, p)dx = J v(x)dx.
B^b c c
Доказательство 2 (не опирающееся на теорему о пов-
торных пределах). Поскольку и еДДс, X] VX > с и и(х, р) » 1>(х)
в^
на,[с, X], то о е Z?[c, X] VХ>с и, в частности, Vр ^3 и V At >
^>Ал^с имеем оценку
Л2
J v(x)dx
j’(v(x) — и(х, P))dx +
Аг
А,
4- j* u(x, p)dx
a2
А» _ .
J |y(x) — u(x, p)\dx-\- J u(x, p)dx .
Ai
At
Из равномерной сходимости
множестве 3> по критерию
VAs>A1>X0(e) nVpsS3
несобственного "интеграла (4.9) на
Коши Уе>ОЯХо(е);>с такое, что
имеем оценку
Аг
J u(xfp)dx
Al
<ф.
100
поскольку и(х, р) —* v(x) на [А>, Ла], то для выбранных 8>0
иД2>А1>-Уо(е)Я5(е)еВ^ такой, что VpeB(e) и Vxe[Ai,
имеем оценку \v(x)—u(x, p)|<s/(2(A2—AJ). Итак, ¥$>ОЯХо(е)>
с такое, что
VA2>A1>Xo(6)^>
Al
v(x)dx < (е/2) + (e/2) =
= е) ==> (р s/?[с, 4-оо)).
Отметим теперь оценку
v(x)dx— J и(х, p)dx <
<jW) — u(x,p)\dx +
С
I +°°
f v(x)dx
I х
+ j* u(x, p)dx NX > c,
x
Vpe
В силу сходимости несобственного интеграла (4.10) и равно-
мерной сходимости несобственного интеграла (4.9) на ви-
дим, что ¥е>0ЯХ(в)>с такое, что Np<sSP имеем оценки;
4" 00
J v(x)dx
-роо
J u(x, p)dx
8/3.
и
Поскольку и(х, р)—» у(х) на [с,- X], то для выбранных 8>0 и
Х(е)>сЯВ(е) е такой, что Vxe[c, X] и ¥р]еВ(е)=>
|и(х, р) — р(х)| <е/(3(Х — с)), откуда Vе> 0ЯВ(е) е В^ такой,
что
N р<= В(б)=»
J v(x)dx— J u(x, p)dx
С с
(4-00 4-00
J o(x)dx= lim J u(x, p)dx
с В^э c
Следствие 1 (теорема об интегрировании функциональной
последовательности по бесконечному промежутку). Пусть функ-
циональная последовательность (fn(x)) определена на [с, -|-ooj,
причем fn(x)^X f(x) на [с, XjvX>c. Пусть несобственный ин-
Ч-°о /
еграл J fn(x)dx сходится равномерно по п (на N). Тогда су-
101
ществует несобственный интеграл S f(x)dx и имеет место ра-
С
+ оо 4"°°
венство f f(x)dx —lim I fn(x)dx.
C Z2-*4-O> C
(Доказательство следует из общей теоремы о предельном пе-
реходе в несобственном интеграле, зависящем от параметра,
если положить в ней SP = N; >+°о; и(х, n)=fn(x);
t»(x) = /(x).)
Пример. Рассмотрим функциональную последовательность
(fп (х)), где
, . __ (линейный горб высоты 1/п, п^х^Зп
10; Зп<х<4-оо.
Тогда f„(х) —* 0 на [0, +оо). Однако несобственный интеграл
4-00
J fn(x)dx не сходится равномерно по п на N, поскольку Яе0==
о
= 1 такое, что ¥Д>0 существуют Д0 = п0>Д и га = п0> для
которых
7 fn,(x)dx = f fn,(x)dx = 1 = e0>0.
Л, n,
В этом причина соотношения
lim +f fn(x)dx = 1 0«= +f (lim fn(x))dx.
n->+oo g 0 n-*+oo
Следствие 2 (теорема об интегрировании функционального
ряда по бесконечному промежутку,). Пусть ип^С ([с, +°о)) и
un(x)^0V хе [с, +°о), VneN. Пусть функциональный ряд (4.8)
сходится на [с, 4-°°) к (непрерывной) сумме f^C ([с, +<х>)),при-
чем существует несобственный интеграл
7° /(x)dx. (4.13)
Тогда
7° f(x)dx=2 7° un(x)dx.
С /1«1 с
Доказательство. По теореме Дини (из § 3) ряд (4.8)
сходится равномерно на отрезке [с, A']VX>^, т. е. s„(x) *
* f(x) на [с, X]. Поскольку 0<^$„(х) = 2 «*(•*)< Дх) VяSN и
fe=i
Vxg[c( 4-оо), то в силу сходимости несобственного интегра-
102
ла (4.13) от мажорирующей функции f(x) применим признак
Вейерштрасса равномерной сходимости несобственных инте-
гралов, зависящих от параметра, из которого вытекает, что
несобственный интеграл
4-оо
J s„(x)dx
С
сходится равномерно по п (т. е. сходится равномерно на N). Но
тогда к функциональной последовательности частичных сумм
($п(х)) ряда (4.8) применимо следствие 1, в силу которого
Я lim sn(x)dx=+( f(x)dx. (4.14)
с с
Заметим, что
ик(х) = sk(x) — sft_i(x) V k > 1 (s0(x) == 0),
поэтому
V k €= N Я uk(x) dx « J sk(x)dx— J Sk-i(x)dx,
c c e
откуда
-|-oo n -|-oo
J sn(x) dx = 2 J Uk(x)dx.
c &=1 c
Но тогда из (4.14) получаем равенство
4-00 4-0° 4-00
J f(x)dx = 2 f
c fe—i c
Теорема 1 (о перестановке порядка интегрирования в пов-
торных несобственных интегралах). Пусть и^С ([х0, -]-оо) X
X [*0, 4-°°)) и несобственный интеграл
<р(0= J u(x, t)dx (4.15)
хе
сходится равномерно на отрезке [^о, T]V о несобственный
интеграл
ф(х) — у и(х, t)dt (4.16)
^0
сходится равномерно на [х0, X] V Х>ха. Пусть, наконец, сущест-
вует хотя бы один из повторных несобственных интегралов
+у°dx+f \и(х, t)\dt (4.17)
З-о
103
или
+f d/+f |u(x, 0|dvs+f Ф(0Л. (4.18) '
te xe f,
Тогда <рЕЙр0. +°o), ip e2?[x0, +«»), , причем
-j-oo
У <f(t)dt — J Ф(х)йх,
Xo
т. e. имеет место равенство
+y dt +J u(x, t)dx—+^ dx J u(x, t)dt, (4.19)
t. x, x, t.
где оба повторных несобственных интеграла существуют.
Доказательство. Пусть существует повторный несобст- 11
венный интеграл (4.18). Поскольку и^С([х0, -|-оо)Х[/0, +°°))
и несобственный интеграл (4.16) сходится равномерно на от-
резке [х0, X]VX>x0, то и к несобственному интегралу (4.16)
применима теорема об интегрировании на конечном отрезке
К, X], в силу которой имеем
х х +«>
J 4>(x)dxs J dx J u(x, t) dt =
Хе Хв Гв
= +у” dt у и(х, 0 dx = Y F(X, t) dt (4.20)
(так что F(X, t)^Rt\t0, 4-oo) VX>x0). В силу равномерной
сходимости несобственного интеграла (4.15) на отрезке [?0, Г]
VT>£0 имеем
F(X, “(*» ^dx на (<•> Г1 vr>fo- (4-21>
Xt
Отметим оценку
|Г(Х, «)| =
х
у u(x, t)dx
<+у |u(x, t)\dx==
хе
-Ф(ОУХ>хо, v/>/0.
По предположению о сходимости несобственного интеграла
(4.18) имеем
Y Ф(0<И< + оо
t.
и поэтому в силу признака Вейерштрасса (равномерной схо-
димости несобственных интегралов, зависящих от параметра)
видим, что несобственный интеграл
104
-1-00
J F(X, t)dt, сходится равномерно на [x0, +<»). (4-22}
t.
Но тогда из условий (4.21) и (4.22) по теореме о переходе к
пределу в равномерно сходящемся несобственном интеграле
(на с. 99) имеем (учитывая (4.20))
Я lim Т F(X, t)dt = +Г =
X 4-оо
— lim f <|>(x)dx= [ <j)(x)dx,
*-+«>£, Jx,
т. e. 4-o°). +°°). причем
<|>(x)dx= +J <p(t)dt.
X9
Равенство (4.19) доказано.
Следствие. Пусть uGC([x0, -|-оо) х [i0. +°°)) и u(x, t)>
> О V (х, t) е [х0; оо) х [*о» +°°)" Пусть функции <р(0 из
(4.15) и ф(х) из (4.16) непрерывны (т. е. <р е С([/01 +°°)) и
феС([х0, Ч-со))). Пусть, наконец, существует хотя бы один из-
несобственных интегралов
J <[>(x)dx= J dx"*]1 ы(х, t)dt (сравните с (4.17))
ИЛИ
4-оо +°°
J <p(i)di= J dt J u(x, t)dx (сравните с (4.18)).
Тогда существует и другой из этих несобственных интегралов и
имеет место равенство (4.19).
Доказательство. По теореме Дини (из § 3) несобствен-
ные интегралы (4.15) и (4.116) сходятся равномерно на любом ко-
нечном (а стало быть, и компактном) отрезке [4, Г] (vT>(0) и
на [х0, X] (V Х>хо) соответственно, а потому ввиду равенства
\и(х, t)\=u(x, t) применима наша теорема 1.
Доказанные выше теоремы о перестановке порядка интегриро-
вания в повторных несобственных интегралах используют идею
Равномерной сходимости и основаны на теореме о повторных пре-
делах. Приведем (следуя С. Б. Стечкину) теорему о перестановке
Порядка интегрирования в повторном несобственном интеграле,
основанную на теореме об интегрировании монотонного семейства
Функций и не использующей понятия равномерной сходимости.
10&
Теорема 2 (о перестановке порядка интегрирования в пов-
торном несобственном интеграле). Пусть weC('[x0, +°°) X Ро»
+<»)) и и(х, ?) > О V (х, t) е[х0, 4-оо) х ро, 4-со). Пусть схо-
дятся несобственные интегралы (4.15) (v/e[/o, П) “ (4-16) (V
хе[х01 XJ), причем q>eR[t0, T]VT>t0 и феЯ[х0, X]vX>x0.
Пусть, наконец, существует хотя бы один из несобственных, ин-
тегралов
+у ty(x)dx== J dx+§ и{х, t)dt
X, X, t,
или
+J <f(t)dt = J dt +J u(x, t)dx,
t,
тогда существует и другой из этих несобственных интегралов и
имеет место равенство (4.19).
Доказательство. Пусть существует несобственный инте-
грал f так что <р е T]NT>t0 и Я lim f <p(0df =
t, Г-Ч-ОО £
-}-C0
— J <f(t)dt, причем поскольку u(x, f)>OV(x, f)£=[x0, +©o) X
X 1го> +°o)> TO <p(O>OV/>fo и J y(t)dt t на [t0* +°°) и
Jq>(l)dt< j <p(t)df V T > t9. Поскольку и e C([x0, -j-oo) X [^o>
+oo)), to ugC([x„, Х])Х|Л, T]) VA'>x0, T>t0 и по теореме 3
(Фубини) об иитегрировании интеграла Римана, зависящего от
параметра иэ ч. IV, гл. 2, § 2, имеет место равенство Фубини
J dxj u(x, t)dt = J dt J u(x, t)dx.
x, t, t, x.
X
Обозначим F(t, X)— 1 u(x, t)dx^Ov/<=|7о, Г]. Поскольку ые
^C([xo, 4-oo)X(4, +°°))> то в силу теоремы 1 (о непрерывности
интеграла Римана, зависящего от параметра) из ч. IV, гл. 2, § 2
имеем: 1) F(t, X)^C[t0, T]vX>x0; 2) F(t, X)f на [x0> +oo)
ефо, T]; 3) a lim F(t, X)-+f u<x> t)dx=x<f(t)Vt^[t0, T\\ 4) <f>S
X-*+oo Xo
€=jR[/0, Г]. Тогда в силу теоремы (об интегрировании моно-
тонного семейства функций) имеем
т т
Slim ]F(t, X)dt = ]^(t)dt,
106
причем
JF(i, X) dt < J <f(t)dt < +f <p(t)dt,
так что из равенства Фубини имеем оценку сверху
х т т х
J dx j и(х, t)dt = j dt J и(х, f)dx
Хе Го Го *е
<+у“ф(1)Л¥Х>х0, VT>f0.
te
Поскольку фе/фсо. Я] V Х>х0, то, полагая
Ф(х, T) = yu(x, O^>OVxe[xo, X],.
имеем: 1") Ф(х, Т)еС[х0, X]V T>t0- 2") Ф(х, Т) f на [t0, +оо)
Vxe[x0, X]; 3") Я lim Ф(х, Г)=Тu(x, t)dt = ^(x) Vxg[x„, XJ;
Т-+оо
4") феЯ[х0, X] и, вновь применяя теорему (об интегрировании
монотонного семейства функций), получаем
Я lim у Ф(х, T)dx = y <{»(x)dx,
Г-*Н-оо х9 Хо
причем
f Ф(х, T)dx< у ф(х) dx V Т > t0
X, Хе
и, поскольку
у dx у u(x, f)dt=> у Ф(х, T)dx< +j“ <p(i) dt V X > x0, V T > t0,
Xt t„ X, t,
то имеем оценку сверху
У ip(x)dx< <?(0 dt V X > х0.
х, Ге
X
Но ф(х)>ОУх>хо и поэтому J на [х0, +©о), так что
х,
Я lim J г|)(х)йх= J* ф(х)б/х<^ J <р(0^,
Х-»4-оо
тем самым доказаны существование несобственного интеграла
[ ф(х)^х= J dx J и(х9 t)dt
Xq Xg to
107
и оценка
J ф(х)*/х<^ j"
X,
+°0
Поскольку несобственный интеграл J ф(х)г!х существует, то,
повторяя проведенные выше рассуждения,, получаем оценку j
4-00 +оо <
J <|>(x)dx, что и завершает доказательство равенст- !
ва (4.19). Х'
Теорема 1 (о дифференцировании функциональной последо- ’
вательности). Пусть функциональная последовательность (fn(x))
определена на отрезке [а, &] и существует точка х0^[а, &] такая,
что я lim fn(xo). Пусть Я//еС([а, &]) v neN (где fn(a)B
B>D+fn(a), fn'(b)=T)-fn(b)), причем f'n (х) zzj 4>(х) на la> ЭД.
Тогда: 1) существует функция f(x), определенная на [а, ЭД, такая, ;
что fn(x) —> f(x) на [а, &] и V хе[а, Ь] Bf'(x)=i<p(x) (где ?'(#)** !
^D+f(a) и f'(b) =D~f(b)); 2) fn'(x) zj f'(x) на [а, Ь]. I
Доказательство. Поскольку (fn'^ С ([а, ЭД)) =>• (fn^ I
Ь]) и fn'(x) <р(х) на [а, Ь], то в силу теоремы о непре- |
рывности предела равномерно сходящейся последовательности не- |
прерывных функций следует, что (<реС([а, Ь])) =>(<р&/?[а, Ь]). По |
теореме об интегрировании равномерно сходящейся функционалъ- |
ной последовательности имеем |
У Ф(0Л на (а, Ь]. |
*• (П-Н-ОО) хе £
По условию Я Пт fn(xo), поэтому из теоремы Ньютона — Лейб-
И—>4-00 1
ница (см. [1], ч. II, гл. 2, § 6) имеем
у f ’n(t)dt = fn(x) — fn(x0) zzt У на la« N-
(п->4-оо) x.
Положим
f(x)=4 + f(x0), f(x0) = lim /n(x0),
П—>4“OO
*.•
тогда
fn(x)zXf(x) на [a, b]. (4.23)
В самом деле, очевидно, ] = |[ffn(x)—fn(xo))—('f(x)— :
—f(xo))]+(fn(xo)—f(xo))\, но lim fn(x0)—f(xo) и (fn(x)—
я-*4-оо
108
—fn(xo)) zx (f(x)~^(xo)) на ta> Тогда V’s>0 3;V(g)eN та-
кое, что Vn^(g) имеем \fn(x0)— f(x0) | <s/2 и | (fn(x)—
—fn(xa)) — (f(x)— f(x0)) | <8/2. Но тогда V e>0я^(^)GN такое,
что |fn(x)—f(x) | <8 V n>N(e,), v xe[a, Ь], т. e. имеет место
(4.23). Далее поскольку (реС([а, &]), то v хе[а, b]3f,(x)=<p(x),
а также fnYx) f'(x)=<p(x) на [а, Ь].
Замечание. Если для fn^C^([a, Ь]) имеем fn(x) Zj f(x)
на [а, Ь], то продифференцированная функциональная последова-
тельность (Dfn(x)) может вообще не сходиться на [а, 6].
Пример. fn(x)—sinпх/п, хе[—л, л]. Тогда, очевидно,
(х) 0 на [—л, л], однако (D/n(x)) = (cos пх) не сходится на
[—Л, л].
Следствие 1. Пусть /пеС^((а, 6))VneN, &>2 и Ях0(=
^(а, Ь) такая, что: 1) Э lim Dlfn(x0) = ct (Z = 0, 1, . . . , k—1),
причем 2) DK/(x) —q>(x) на (a, b). Тогда существует функция
/eCw((a, b)), для которой Dlfn(x) z£ Dzf(x) на (a, b) при 1=
— 0, 1, . . . , k и D‘7(.v)E(p(x) на (a, b).
Доказать самим, заметив, что использование теоремы о почлен-
ном интегрировании равномерно сходящейся функциональной по-
следовательности дает
J D*fn(t)dt = D*~‘/n(x) - D‘-V„(x0) :* f <P(O^
x0 xt
X
на (a, b), откуда Dlfn(X) J q>(t)dt+ci на b) при l — k—1.
Вновь применяя теорему о почленном интегрировании, можно
перейти от l = k — 1 к l = k — 2 и т. д.
Следствие 2 (о кратном почленном дифференцировании
функционального ряда). Пусть и су-
ществуют точки xjefa, b) (1=0, 1, .... k—1,) такие; что: 1),'
4-оо
У, Dzwn(x,)=cz (1=0, 1.....k—1); 2) формально продифферен-
П*=1
-j-oo
цированный k раз функциональный ряд у Dfc«ra(x) сходится к
П=1
функции ф(х) равномерно на (а, Ь). Тогда существует функция
4-00
/ s С<*>((а, &)) такая, что функциональный ряд у Dzun(x)=
П=1
= Dz/(x) при 1 = 0, I, , k сходится равномерно на (а, Ь) и
Dk/(x) s= <р(х) на (а, Ь).
109
Теорема (о дифференцировании несобственного интеграла,
зависящего от параметра, с бесконечными пределами). Пусть чис-
ловая функция и(х, t) определена на G^=[c, d]x[a, +°°) и
V (х, t) g= О3^* причем — €=.C(G). Пусть Яхое[с, d}
dx дх
4-00
такая, что сходится несобственный интеграл F(x^ ~ J u(x0, t)dt,
а
а несобственный интеграл, зависящий от параметра
4-00
Ф(х) = J 2Ц^.> *1 dt, X е [е, d], (4.24)
а
сходится равномерно на [с, d]. Тогда несобственный интеграл, за-
висящий от параметра
F(x) ==+f и(х, t)dt, х^[с, d], (4.25)
а
сходится равномерно на [с, d] и V xs[c, d] И
+°°
DF(xj = J ~и(х, ^ = Ф(х).
а
Доказательство. Поскольку — £ C(G) и несобственный
дх
интеграл (4.24) сходится равномерно на [с, d], то ФеС([с, d]) и
по теореме об интегрировании в конечных пределах равномерно
сходящегося несобственного интеграла, примененной к (4.24) для
хое[с, d] и v хе[с, d] (в силу существования F(x0)), имеем
X X 4“°° 4" 00 х
Г Ф(р)^у — Г f г f dt Г г и^У>
J J J дУ J J дУ
хв хв а а х9
причем несобственный интеграл справа сходится равномерно на
[с, d]. Но тогда
4-00 х 4*е» 4" °°
С dt ( — и(у, t)dy= f и(х, t)dt— I и(х0, t)dt=F(x)—F(x9),
J J д« J J
a x0 a a
откуда вытекает: 1) несобственный интеграл (4.25) сходится рав-
номерно на [с, d] и 2) F(x)—F(xq)= / Q>(y)dy. Поскольку
ФеС([с, d]), то из 2) по теореме о дифференцировании интегра-
ла Римана (от непрерывной функции) по верхнему пределу из
[2] (ч. II, гл. 2, § 6) следует, что v хе[с, d] я DF(x) =|ф(х).
ПО
Теорема (о дифференцировании несобственного интеграла
от неограниченной функции, зависящей от параметра). Пусть чис-
ловая функция и(х, t) определена на множестве G=[c, d]x
Ь] м V (х, /)е ОЯ g C(G). Пусть Sxos[c, d] такая, что
сходится несобственный интеграл
ь
Pf>(x0) = ] и(х0, f)dt,
а<—
а несобственный интеграл, зависящий от параметра
ь ~
Ф0(х) = С £- и(х, t)dt, хе [с, d]9 (4.26)
J дх
а*-
сходится равномерно на [с, d]. Тогда несобственный интеграл, за-
висящий от параметра
ь
F0(x) = J и(х, t)dt, X <= [с, d], (4.27)
а*-
сходится равномерно на [с, d] и Vxe[c, d] я DFofX) =ф0(х).
Доказательство. Воспользуемся определением равно-
мерной сходимости несобственных интегралов (4.26), (4.27) по
Гейне (см. ч. V, гл. 2, § 1) и введем последовательность Гейне
(бп) (бп|а), связанную с базой (6-*а+0). Рассмотрим функцио-
ь
нальную последовательность fn(x) = S и(х, t)dt, хе[с, d]. В си-
8п
лу теоремы 2 (о дифференцировании интеграла Римана, завися-
щего от параметра) из ч. V, гл. 2, § 2 имеем v хе[с, d]H
ь л
О/„(х)= С ~ u(x, t)dt
J дх
ъп
и в силу условий нашей теоремы имеем Я lim f„(x0) = F0(xe) и
П-*4-ео
Dfn(x) Ф0(х) на [c, d]. Но тогда к функциональной после-
довательности (/„(х)) (х s [с, d]) можно^применить доказанную
выше теорему 1 (о дифференцировании функциональных по-
следовательностей).
Теорема (интеграл Дирихле).
J sin at/tdt = sign а• it/2 V а е (—оо, -^оо).
о—
Доказательство. Пусть
^)(а)= J sinaf/fdt, a G (— оо, 4~оо).
111
Тогда £)(0) - 0 и, делая замену at — z, имеем при а^О
©(«) = /» У
при а>0 и У)(а)=—/ при а<0, т. е. $)(а) == I • sign а. Докажем,
что
I =+(° — dt = it/2.
J t
Как было установлено ранее, несобственный интеграл I сходится
условно по признаку Дирихле. Введем вспомогательную функцию
4-00
7(х) = J ехр (—xt) • (sin Ut)dt V х > 0.
0«-
Как было установлено ранее, несобственный интеграл 7(х) по приз-
наку Абеля сходится равномерно на [0, +°°)- Очевидно, функция
ехр(—xf)(sinf/i) непрерывна на [0, -j-ooJXlO, +°о). Но тогда по
теореме о непрерывности равномерно сходящегося несобственного
интеграла (от непрерывной функции) имеем J е С([0, +«>)) и, в
частности, 3 lim J(x) == 7(0)=7. Далее формальное дифференци-
х->+0
4-«>
рование по х интеграла 7(х) дает Vx>0 Ф(х)=— j ехр(— xt)X
Xsintdt. Отметим оценку |ехр(—xt) • sinf|exp(—rXot)V(x,
•e[x0, 4-oo)X[0, +<x>) Vx0>0 и сходимость несобственного ,
4-°°
интеграла f exp(—xot)dt при xo>0. Но тогда в силу признака •
. о
Вейерштрасса несобственный интеграл Ф(х) сходится равномер-
но на [х0, -4-оо) (Vx0>0). Поскольку подынтегральная функция
ехр(—xt)- sin/eC([0, +<х>)Х[0, +<»)), то по теореме о диффе-
ренцировании несобственных интегралов, зависящих от пара-
метра, имеем
+°° >
Я J' (х) =— J ехр (—xt) • sin £ Vx>0.
Но, используя метод неопределенных коэффициентов, имеем тож-
дество (по t)
J e~xt sin t dt = (A sin t + В cos t) e~xt.
Дифференцируя это тождество по /, имеем e~*<-sin/=e~*(X
X (—Ах sin t—Bx cos /-J-A cos t—В sin t)' Сравнивая коэффициенты
при sin/ и cos/, получаем систему уравнений для определения А
и В:
112
| 1 == — Ax — В
| 0 = — Bx-f- A,
решая которую получаем (A—Bx, B=—Ax—1)->(А =—x/(l+x’)
и В ——1/(1+л2)). Но тогда
-Д ^•sintdt = ^.»inf.+ c02<) + ==_1/(1+х»)>
J 1+Х«
м
т. е. J'(x)=—l/(l+x2)Vx>0, а потому 7(х) = С— arctgxVx>0.
Для отыскания постоянной интегрирования С отметим
+°°
|7(х)| < J ехр(—xt)dt = 1/х Vx>0=>
( lim 7(х) = 0) (С = it/2).
х-><4-оо
Итак, 7(х) = к/2 — arctgx, откуда 7(0) / = тс/2.
Теорема (интеграл Пуассона).
"j” exp (—at2) dt = (%/a)V2/2 V a > 0.
Доказательство. Делая замену z=aI/2’f в интеграле Пу-
ассона, имеем (а>0)
f exp (—at2)dt«« a-1/2 f exp (—z2)dz = a_,/2 • К,
о 0
4- co
где К— J exp (—t*)dt. Докажем, что К — «1/2/2. Сделаем в К
о
замену t=x- uVx>0, тогда К = J х- ехр(—xaua)dut отку-
о
да V х > 0 имеем равенство
7<ехр(— х2) = J хехр(—x2(l+«2))da.
о
Интегрируя это равенство по х в пределах от 0 до +<», получаем
К J exp (—xa)dx — +f dx+f х- ехр(—x2(l+u2)) du
О 0 0
йли
К* = +у dx у хехр(—x*(l+a2))du.
о о
*—Л. И. Камынин ИЗ
Если доказать возможность перестановки порядка интеграций, то а
имели бы |
№ = +у du +у х ехр (— х2( 1 + u2)) dx, I
° ° |
а тогда, учитывая равенство ||
[ х ехр (— х2(1 4- u3))dx = ij
0 Я
=- ехр (—х«( 1 + «*))/2(1 +и2)|*=+~ =1/2(1 +«2), ||
имели бы Л
(№=1/2 • у 1/(1+u2)du = 1/2 • arctgu|^°°= I
= ir/4)=»(A2 = «/4)=^>K = 1rV2/2. I
Начнем проверять условия теоремы о перестановке порядка I
интеграции в повторных несобственных интегралах (точнее — ус* I
ловий следствия из нее): I
1) подынтегральная функция непрерывна на [О, +<»)Х[0, +°°) I
и хехр(—х2(1+«2))^0 V (х, м)е[0, +<»)Х[0, +«>); I
2) 1-й несобственный интеграл J хехр(—(14-u2)x2)dx=l/2(14-? |
о I
+ U2) (= £„(((), -4-ехэ)); I
4-00 I
3) 2-й несобственный интеграл j хехр(— (1 + u2)x2)d« = .;
о . I
» К ехр (—х2) е Сг((О, 4-оо)) (поскольку это равенство имеет I
место лишь при х/>0), и хотя бы один из повторных интегра- I
лов I
"*j" du+J хехр(—x2(14-u2))dx— J l/2(l-j-w2)du = it/4 I
0 0 0 I
существует. Тем не менее теорема о перестановке порядка интег* I
рации в повторных несобственных интегралах не применима (из* I
за того, что 2-й внутренний интеграл не является непрерывной I
функцией на [0, 4-оо)). Чтобы обойти это затруднение, рассмотрим I
множество I
G(x0) = {(x, u) е Rs|O<xo<x< 4-оо, 0<и<4-оо) 1
и докажем равенство
4-оо Ч-оо 4-°° +°° —«V
J dx f x<?-x!(1+“!)du= f du J xe-'’<1+“2) du. (4.28b
x„ 0 Ox,
114
Заметим, что кроме выполнения условий 1) и 2) теперь имеем
3)Y xe-(‘+“^’du = Ke-«’SC([x0, 4-oo))Vx0>0
о
и, кроме того, существует повторный интеграл
J du J xe-x2(1+u‘>dx= [ Ф(х0, u)du,
Ox, О
где функция
Ф(х0, и) = J х ехр (— х2(1 + u2)) dx -=
хв
= ехр (-х%(1+и*))/2(1+и2) е=С([0, +<х>)Х(0, Ч-оо)),
причем имеет место оценка
0<Ф(х0, u)<1/2(1+u2)Vxoe[O, + °°), Vas[O, +<»).
4-00
Поскольку интеграл J 1/2(1 4- u3)du от мажоранты сходится,
о
то в силу признака Вейерштрасса на множестве [0, +<») рав-
номерно сходится несобственный интеграл J Ф(х0, и)du. Та»
о
кнм образом, теорема о перестановке порядка интеграции в
повторном несобственном интеграле применима и имеет место
равенство (4.28), которое можно переписать в виде
+J cfx+J хехр(—х*(1+u*))du —+J Ф(х0, u)du.
хв О О
Вспоминая, что Ф(х0, «)еС([0, -j-oo)x [0, 4-оо)), а несобст-
4-оо
венный интеграл F(x0) = [ Ф(х0, u)du сходится равномерно на
о
[О, Ч-оо), по теореме о непрерывности равномерно сходящего-
ся несобственного интеграла, зависящего от параметра, за-
ключаем, что F(x0) sC([0, +°о)), т. е.
Я lim F(x0> « ;Т 1/2( 1 + u*) du = к/4.
о
Переходя в равенстве (4.28) к пределу при х»->-|-0, получаем
(№=л/4) =>(/(=л*/2/2).
Замечание. В ч. V с помощью теории кратных интегралов
будет приведено более простое вычисление интеграла Пуассона.
Вернемся теперь к вопросу о дифференцировании функциональ»
йых последовательностей.
8* 115
Теорема 2 (о дифференцировании функциональной после-
довательности). Пусть fn^ £)((а, b)) VneN и существует точка
хое(а, Ь) такая, что Я lim fn(x0), причем f'n(x) <р(х) на (a, b).
n—>4-°°
Тогда существует функция f {(a, b)) такая, что: 1) fn(x) 2*
fix) на (a, b); 2) <р(х)==/'(х)¥х<=(а, b) так, что fn(x) f'(x)
на (a, b).
Доказательство проведем в два этапа. 1) Сначала пока-
жем, что существует функция f(x) такая, что /я(х) f(x) на
(а, Ь). Поскольку по условию f'n(x) <р(х) на (а, Ь), то в си-
лу критерия Коши (равномерной сходимости функциональной
последовательности) Vs>0 ЯЛ\(в)еК такое, что
№ — fm(*)KsVn» m>Nl(e) и Vxe(a, b).
Далее по условию Я lim /я(х0), поэтому в силу критерия Ко-
«-♦4-со
ши (существования предела числовой последовательности)
для выбранного e>03Afs(s)eN такое, что |fn(x0)—/от(х0)Кs Vл,
т>ЛГа(е). Пусть теперь N0(e) = max Л\(е). По условию /п—/ms
Z=l, 2
е .£)((«, Ь)), поэтому, используя теорему о среднем для функ-
ции (fn—f„)(x)=fn(x) — fm(x), имеем Ч п, m>N0(e) и Vx, I е
е (я, Ь) оценки
ПМО - Ш] - [/„(х) - fm(x)]| = If;(х + Олж(* - х)) -
— fm(X + — Х)Ш — X| < Ф — Х|,
где 0<$пт<1. В частности, Vn, /n>2V0(e) и Vxs(a, b) при .
/«=х0 имеем оценку
lfn(x) fm(x)| ’С |[/л(х) fm(x)] Ifn(Xo) f m(Xo)]| 4*
+ lf«(x0) - f m(X0)| < 8]X — Xo| + 8 < 8(1 + Ь - a).
По критерию Коши функциональная последовательность f/n(x))
сходится равномерно на (а, Ь). Положим f(x)= lim fn(x) Vxs
n—>4-oo
s (a, b), тогда f„(x) f(x) на (a, b).
2) Докажем, что Vxe(a, b) Я /'(x) = <p(x). Пусть xe(a, b) и.
фиксировано. Для любого t е (а, 6)\{х) рассмотрим вспомога- „
тельную функцию фп(0 *= (МО—fn(x))/(i — х). Как было доказа- •
но на этапе 1), f„(x) f(x) на (а, Ь), откуда Nte.(a, &),\{х)
Я lim фп(0 = (f(i)—f(x))/(t - х) = ф(/).
116
Покажем, что функциональная последовательность (ф„(<)) на
множестве (а, Ь)\{х} удовлетворяет критерию Коши равно-
мерной сходимости. Ранее было доказано, что V е>ОЯ7Уо(е)
такое, что Vn, т> Л',0(е) и V х» i е(а, Ь) имеем оценку
|(М0 - ЫО) - (Ш - /т(х))| < Ф - Х|.
Поэтому Vn, /п>У0(е) и Vi се (а, &)\{а) имеем оценку |фп(1)~
— Фт(01 < е> т- е- доказано, что фп(«) ф(Г) на множестве (а,
П-*4-оо
Ь)Х1*}- Но по условию теоремы b)Nn^N, так» что
Я lim 4)n(i)=>D/„(x), кроме того, по условию теоремы 31imD/n(x)=
Г->х * л->4-оо
==ф(х), но тогда применима теорема о повторных пределах по
схеме
((0-^). на (а Ь)Х{х}
*~х п->+оо *~~Х
(t~*x) j | (t->x)
Dnf(x) ----> <р(х)- lim =Df(x).
Итак, доказано, что Vx£(a, &)HD/(x) = ф(х), причем в силу
условия теоремы
(Dfn(x) ф(х) на (a, &))=^(Dfn(x) Df(x) на (а, b)),
чем теорема 2 полностью доказана.
3 а-м е ч а н и е (обобщение теоремы 2 о дифференцировании
функциональной последовательности). Рассмотрим базу В^» во
множестве и числовую функцию (х, р)е(а, Ь)Х&-*и(х, р)е
sR, для которой и(х, р) е Ъ))Чр и существует
точка х0 s (а, Ъ) такая» что Я lim u(x0, р) = v(x0), причем
в<#э
du(xt р)
ф(х) на (а, 6). Тогда существует функция v(x)^
в^>
е £>((<», &)) такая, что: 1) u(x, р) v(x) на (а, Ь); 2) ф(л) =
В^
• v'(x) V х (а, Ь), т. е. -ц^’ v\x) на (а, Ъ). Попро-
дх в
буй те доказать самостоятельно это обобщение теоремы 2, ис-
пользуя схему доказательства теоремы 2, заменив N на 5й,
базу (и-»4-оо) на базу В^» и функцию /п(х) на и(х, р). Дока-
117
жите сначала, что существует функция v(x) такая, что $
и(х, р) v(x) на (а, Ь), и проверьте затем, что (при фикси-
рованном хе(я, i»)) для функции ф(/, p)=^(u(t„ р)—и(х, p))l(t— |
—х), определенной на множестве (а, д)\{х}, имеют место
Я lim ф(/, р) = ди~х' иЗПтф,/>) =
дх в^,
==МО — v(x))/(t — х) в <[»(/).
Далее нужно доказать, что <p(i, р) <p(t) на (а, 6)\{х}, после
ч его применить теорему о повторных пределах из § 4 по
д иаграмме .
ф(/, р) =£ ф(0 на (а, Ь)/{х} !-
(t-*x) | в^ । (t-+x)
-д—-’ —><р(х) = Нтф(0=о'(х)> т- е* о s Я)((а .&))• *
дх t-*x 4
Следствие (теорема о почленном дифференцировании f
функционального ряда). Пусть ип^ ^) ((a, b))VneN и Эхое
е(а, Ь) такая, что функциональный ряд (4.8) сходится при х=х0. |
+оо S
Пусть функциональный ряд 2 ип'(х), полученный формальным J
п—i
почленным дифференцированием ряда (4.8), сходится к сумме
<р(х) равномерно на (а, Ъ). Тогда существует функция f(x) такая, 3
что ряд (4.8) равномерно на (а, Ъ) сходится к функции f(x) и
f'(x)=q>(x) Vxefa, Ъ), т. е. ряд (4.8) можно почленно дифферен-
цировать на (а, Ь), причем \
<2 = 2 <(x)Vxe(a, b).
\д=1 / /1=1
Пример. Пусть %п^п» I-Пп(х) = хл/п.
Л=1
При х«0 наш ряд сходится и и'П(х) = хп~1. Ряд 2 хП~1 сх0*
п=1
.дится нормально на [—так как lx"-1) ft""1 V и е N н
4-00
Vxe(—ft, ft[ и ряд 2 ft"-1 < +00 сходится Vfte(0, 1). Но
П=1
4-оо
тогда ряд 2 сходится равномерно на [—ft, ft] к функ-
. Л=1
118
ции <р(х)=1/(1—х). По следствию к теореме 2 Я/(х)=2 хп1п и
Л—1
/'(х)= 1/(1 — х). Очевидно, /(х)= — 1п(1—х)4-С, но f (0) = С = 0.
Итак,
4-00
2 хп/п = — In(1 — x)V|x|<&< 1
п—I
или, меняя х на (—х), имеем
In(1 4-х) = 2 (—ir-’x'-M, |х|<»<1.
л«=1
Ранее было установлено, что пространство С (К) всех числовых
функций, непрерывных на компактном множестве X (с метрикой
Чебышева
P(f, g) = max j/(x) — g(x)|; f,g<= C(K)),
x£K
является полным метрическим пространством. Займемся теперь
вопросом о признаках компактности множеств из С (К).
Определение. Множество МаХ из метрического простран-
ства {X, рх} называется относительно компактным или предком-
пактным (секвенциально предкомпактным) в X, если его замыка-
ние М компактно (секвенциально компактно) в X.
Заметим, что, как доказано в [1] (см. ч. III, гл. 1, § 10); поня-
тия компактности и секвенциальной ‘компактности в метрических
пространствах эквивалентны, поэтому в дальнейшем будем поль-
зоваться термином «компактность».
Итак, множество МаХ предкомпактно в метрическом прост-
ранстве {X, рх), если любое бесконечное подмножество АсМ име-
ет хотя бы одну предельную точку (в X), которая может и не при-
надлежать множеству М.
Теорема (критерий предкомпактности в полном метрическом
Пространстве). Пусть {X, рх! — полное метрическое пространст-
во. (Множество МаХ предкомпактно в X) *=> (М вполне огра-
ничено).
Доказательство. Из критерия компактности в полном
метрическом пространстве (см. (2], ч. III, гл. 1, § 10) следует: (мно-
жество Мс^Х компактно в полном метрическом пространстве
{X, рх})-^ (множество М замкнуто и вполне ограничено). Но за-
мыкание М множества М всегда замкнуто, поэтому нам нужно
доказать утверждение: (М — вполне ограничено в X) ч=> (М —
вполне ограничено в X). _
Необходимость. Пусть замыкание М вполне ограничено в X,
тогда для MczX при любом е>0 существует конечная 8-сеть
Л(е)={аь а2, ..., an}czX так, что V х&М я а,е4( б), для которого
119
px(x, ai)<Ze._Пусть Xq^M — любая, но фиксированная точка. По-
скольку Мс^М, то х^М и, стало быть, Яа^А(г) такое, что
рх(*о, т. е. конечное множество Л(е)<=Х является 8-сетью
и для множества М, т. е. множество М вполне ограничено в X.
Достаточность. Пусть множество MczX вполне ограничено я
е>0 — любое, но фиксированное число. Пусть A(e)=s
={оь а2, —> am}<^X есть конечная s/2-сеть для множества М.
Рассмотрим любое х^М, тогда в силу определения точек прикос-
новения для выбранного s>0 Я х0<=М такое, что рх(х, х0)<е/2.
Но тогда для хо^М я а^А (е), для которого pxfxo, ai)<Ze/2, а
потому в силу неравенства треугольника имеем рх(х0, а,)^
<рх(х, х0)+рх(хо, at)<.z, т. е. конечное множество А(е)с:Х есть
8-сеть для множества М, так что МсХ вполне ограничено в X.
Определение. Пусть & ={/} — семейство функций
^С(К). Семейство f называется равномерно ограниченным
(на К), если существует постоянная L>Q такая, что \f(x) 1^
V х&К и vf<= f.
Определение. Семейство & аС(К) называется равносте-
пенно непрерывным на множестве К, если V 8>0 Я 6 (в) >0 такое,
что V хь х2еК, удовлетворяющих неравенству рх(хь Х2)<6(е), а
'для любой функции f<= f имеем \ f(xi)—f(x2) | <8.
Замечание 1. Пусть f ={f}czC([a, &]) есть семейство фун-
кций f^Ha([a, 6]), удовлетворяющих на [а, Ь] условию Гельдера *
с одним и тем же показателем ае (0, 1] и с одной и той же посто-
янной Гельдера Я>0, так что V/е и Vхь х2е[а, &] имеем '
оценку |f(xi)—f(х2) |^Я-1Xi—х2|“. Тогда семейство F равносте- i
пенно непрерывно на [а, &]. В самом деле, Vs>0 3 6(e) =
= (е/Я)1/а>0 такое, что V хь х2е[а, Ь], удовлетворяющих уело- :
вию |Xi—х2|<6(е), имеем, используя условие Гельдера, Vfe $
оценку IfCxJ—f (х2) | ^Я-1xi—х2|а<Я-е/Я=е, так это семейство
& равностепенно непрерывно на {а, 6].
Замечание 2. Пусть & с С([а, &]) и f е £)((а, b)) V f
причем семейство {D/(x)} равномерно ограничено на (а, Ь)*
Тогда семейство f равностепенно непрерывно на [а, &]. В са'
мом деле, по условию Я £,>0 такая, что |Df(x)|^ Lv хе (а, Ь) и
V / е &, но тогда по теореме Лагранжа о конечных прираще- *
ниях / е Ht\a, 6] V f е f с постояннной Липшица и
поэтому в силу замечания 1 видим, что семейство F равно-
степенно непрерывно на [а, &].
Теорема Арцеля (критерий предкомпактности в С (К))*
Пусть К — компактное множество метрического пространства
{X, рхУ- (Семейство функций £ czC(K) пред компактно в полном
метрическом пространстве С(К) (с метрикой Чебышева))
(семейство $ равномерно ограничено и равностепенно непрерывно
на компактном множестве К).
120
Доказательство. Необходимость. Пусть семейство функ-
ций $ аС(К) предкомпактно в полном метрическом простран-
стве С(К) (с метрикой Чебышева), тогда в силу критерия
предкомпактности семейство & вполне ограничено в С(К), а
стало быть, и ограничено в С(К), т. е. существует постоянная
L>0 такая, что V f е $ имеет оценку
sup|f(x)| = p(f, 0)<£.
Итак, семейство f равномерно ограничено на К. Далее, в си-
лу того что семейство & вполне ограничено в С(К), Ve>0'
существует конечная е/3-сеть A = {flt f2......fm}dC(K). По-
скольку ft е С(К) V U е A (i = 1, 2, . . . , /п), то по теореме
Кантора (о равномерной непрерывности) функции Д(х) (i = 1,.
2, . . ., тп) равномерно непрерывны на компактном множестве
/( и поэтому для выбранного 8>0Эб,(е)>0 такие, что N хи
хгеК, удовлетворяющие неравенству рх(хь х2)<6(е), имеем,
оценки /{(х2)К8/3 (i=l, 2, . . . , tn). Положим
60(е) == min 64(е) > 0.
2...tn
Пусть теперь /sf— любая, но фиксированная функция. Тог-
да поскольку множество функций А есть e/З-сеть для семей-
ства £, то существует функция fh е А такая, что (в метрике
Чебышева) р(/, fb)<e/3, но тогда Vxb х,еК таких, что рх(хк
xi) < 60(е) (где число 60(s) не зависит от выбора /) имеем
f(*JI < l/(*1)-4(*)| + Ito) - Ш)| +
+IMx2)-f(xa)|<2p(/. fh)+ |Fft(x1)-/ft(xt)|<28/34-8/3=e.
Из этой оценки вытекает, что семейство & равностепенно не-
прерывно на /С.
Достаточность. Пусть семейство FСС(/С) равномерно ограни-
чено и равностепенно непрерывно на компактном множестве
К (метрического пространства {У, рх}). Заметим, что C(K)CZ
С5(7<). Если доказать, что f вполне ограничено в В(К), то
семейство f будет вполне ограничено и в полном метричес-
ком пространстве С(К). В самом деле, если множество (функ-
ций) Л(б) = {/1, lt, ... , lp}(Z.B(K) является конечной 8-сетью
Для fC2B(K), то, как доказано в § 10 гл. 1 ч. Ш |8], сущест-
вует конечная 26-сеть В(е) = {/Ъ ft, . . , CZ ^CZC(/<) для мно-
жества т. e. семейство f вполне ограничено и в С(К).
Итак, покажем, что ¥б>0 для семейства &CZС(К)С^В(К) су-
ществует конечная есеть Л(е)сОД). Фиксируем любое 8>0.
° силу равномерной ограниченности семейства^ на множестве
ЯL>о такая, что |f(x)|Vxe К и V/ е. В силу равносте-
пенной непрерывности семейства & на К для выбранного е>0
’ (в)>о такое, что V хх, х2 е К, удовлетворяющие неравенству
12»
₽XU1, Xj < 6(e) и V f G= имеем |/(^) — /(xs)| < t.'! Зафиксируем
6(e) >0. Поскольку множество К компактно в метрическом
пространстве {Х\ рх}, то множество К вполне ограничено, и
поэтому в нем существует конечная 6(е)-сеть S(e)={a1, aa,....
. •ап} CZ К, так что К CZ U Ш&(е)(«0- Далее положим
£{ = КП(Ш8«)(^)\ии18(е)(®У)) (» = 1, 2, . . . , П). 4
/<i
Тогда, очевидно, KcU £/. причем = 0 Vi=/=/ и рх(х, 1
< 6(e) V х е Et. Рассмотрим разбиение отрезка [—L, L]
Т(е)={—Ь=г/0<У1< . . • <ут=Ц с диаметром d(T(e))<8 и пост-
роим семейство „ступенчатых" функций Л(е) =-{/е(х)}сВ(К).
• п i I
•Функция 4(х) определена на множестве K=[J £/ и прими- 1
мает в каждой точке значение у, (из разбиения Т(е)). |
Очевидно, семейство „ступенчатых" функций 4(8) — конечно. |
Докажем, что Л(е)сВ(/() образует 2е-сеть для семейства & CZ .4
CZB(.Kj В самом деле, пусть функция — любая, но фик- I
сированная, тогда такое, что |Да<)—У/|<е. «I
Но тогда для наборов (Eir у,) («=1, 2..........п) существует 11
ступенчатая функция lt(x) s А(е) С2В(К) такая, что Ze(x) = j/j $1
Ухе£; (i—1, 2, . . . , л). Но тогда для любой точки х е К = I
п I
= U Bi существует множество Et такое, что Х(=Е^ (и поэтому -j I
=: I
4(х) — у,) и рх(х, at) < 6(e). Но тогда имеем оценку I
|f(x) - Ze(x)| < |/(х) - f(at)] + |f(a<) - У^ + i I
+ |У/ - Цх) | - 1/(х) - /(as)| + |f(a<) - У А < 2е. g I
Таким образом, Vs>0 множество Л(е) =>{Zt(x)JсВ(Ю являет- ; |
<я конечной 28-сетью для семейства f в В(К), т. е. семейство I
dС(К) вполне ограничено в В(К)тэС(К), а стало быть, I
вполне ограничено и в С(Д). I
Следствие 1. Пусть К — компактное множество из метри- I
ческого пространства {X, рх} и семейство функций f czC(K) рав- I
номерно ограничено и равностепенно непрерывно на К. Тогда су- I
ществует последовательность (fn) функций и э fe С (К) I
такие, что fn(x) f(x) на К (предельная функция f^C(K) мо- I
жет не принадлежать при этом семейству ). I
Следствие 2. Пусть К — компактное множество метричес- I
кого пространства {X, р%} и fn^C(K) V heN, причем fn(x) S? I
zj f (x) на К. Тогда семейство f == {fn} равномерно ограничено I
и равностепенно непрерывно на Д'. I
122
В самом деле, по теореме о непрерывности предела равномерно
сходящейся функциональной последовательности имеем
(/neC(^)V/ieN)A(/„(x)zt:f(x) на К)=>(/еС(К)).
Итак, f„eC(K) и lim p(f, fn) = 0, но тогда feC(K) есть
п-»4-оо
единственная предельная точка для семейства f={fn} (в С(К)),
откуда вытекает, что семейство & = {/„} секвенциально пред-
компактно в С (К,). По теореме Арцеля предкомпактное семей-
ство (С » {fn} из С{К) равномерно ограничено и равностепенно
непрерывно на множестве К.
Замечание. Из равностепенной непрерывности семейства
& — l(fn)} на (а, />] (fn^C([a, b]) V nsN), вообще говоря, не сле-
дует равномерная сходимость функциональной последовательности
(fn(x)) на [а, &].
В самом деле, любое семейство {fn(x)^=cn V пеЮ (где сп —
постоянные) равностепенно непрерывно на [а, Ь], однако из число-
вой последовательности (сп) (если она неограничена) нельзя вы-
брать сходящуюся подпоследовательность. Таким образом, равно-
степенная непрерывность на [а, Ь] — необходимое, но не достаточ-
ное условие равномерной сходимости функциональной последова-
тельности (fn(x)) на [а, Ь].
Определение. Пусть fеВ[й, &]. Модулем непрерывности
функции f(x) (на отрезке [а, &]) называется функция
а>Л8) = sup |f(Xi) — f(x2)| V6e(0, b—a].
|X1—x2I<8
€ [a. b]
Теорема (критерий непрерывности функции на отрезке).
Пусть f(x) — числовая функция, определенная и ограниченная на
отрезке fa, 61. Тогда (f<=C([a, &]_)) *=> (lim <в/(6) = 0). (Доказать
8—>+о
самим с помощью теоремы Кантора о равномерной непрерывнос-
ти функции, непрерывной на отрезке.)
Замечание. Если f^Ha[a, b] и Hf>0 — постоянная Гель-
дера для функции f(x), то =Hf ba.
Теорема (критерий равностепенной непрерывности семейст-
ва функций). (Семейство & czC[a, Ь]) равностепенно непрерывно
на отрезке [а, Ь]) <=> (lim«(6,)=0, где со (6) = sup со/(б)).
ь-ч-о
Доказательство. Очевидно, vfе f и Vxix2e[a, б] при
|xj—х2| <6 имеем оценку |f(Xi)—f(x2) |^<о(б) =sup <о/(б), отку-
fgfr
Да и следует наш критерий (подробное доказательство провести
самостоятельно).
Завершая изложение § 4, приведем полезную для дальнейшего
теорему об алгебраических действиях над равномерно сходящими-
ся функциональными последовательностями.
123
Теорема. Пусть М — множество метрического пространства
{Л, рх}. Пусть на множестве М определены функциональные по-
следовательности (числовых функций) (fn(x)) и (gn(x)), причем
fn(x) f(x) на М и gn(x) g(x) на М. Тогда:
1) a-fn(x)+b-gn(x) a-f(x)+b-g(x) на М;
2) если \F(x)\^.C V х<=М, то F(x)fn(x) F(x)f(x) на М;
3) если \fn(x)\^C, |gn(x)|<СVneN и VxeM, то fn(x)X
Xgn(x) ^i f(x)-g(x) на M.
Доказательство. Утверждение 1) теоремы очевидно.
2) Поскольку \F(x) |СС V хеЛ1, то VmeN имеем оценку
|F(x)fn(x) - F(x)fm(x)\ = |F(x)||fft(x) - fm(x)| <
<C|fft(x)-fm(x)| VxeAf,
но fn(x)z£.f(x) на M, поэтому в силу критерия Koihn (равно-
мерной сходимости функциональной последовательности) Уе>
> 0 3 Л: (е) е N такое, что |fn(x)— fm(x)\< г/С V m > N (е) и
Ух_еЛ4, откуда имеем |F(x)fn(x)— F(x) fm(x)] < г, V/n^>A/(e)
и N х еМ.
Но тогда F(x)fn(x)z£F(x)/(x) на М.
3) Поскольку |fn(x)|<С, |g„(х)<С Vх е М., то Vm>n и
Ух ЕЕМ имеем оценку
\fm(x)gm{x) - fn(x)gn(x)| = |(fm(x) - fn(x))g„(X) +
+ Ux)(gm(x) - gn(x))| < |£m(x)||fm(x) - f n(x)| + (4.29)
+ |/nWI • ?nWI<C(|/m(x)—f „(X)|4-|f m(x)—fn(x)|.
Ho fn(x) Kx) на M и gn(x) zj g(x) на M, поэтому в силу
критерия Коши (равномерной сходимости функциональных по-
следовательностей) Ve>0 3iV(E)sN такое, что
1Ы*) - f п(х)\ < \gnkx} - Мх)1 < е/2С
Vwi>n>2V(e) и VxeAf. Переходя в неравенстве (4.29) к пре-
делу при тп->-+-оо, получаем Vn>7V(e) и УхеЛ4 оценку
|/(x)g(x)-f„(x)fn(x)|<e,
так что
fn(x)gn(x) f(x)g(x) на М.
Замечание. В общем случае из равномерной сходимости
(7п(х)_) на М не следует равномерная сходимость (F(x)fn(x)) на
М.
Пример. Рассмотрим на (0, +°°) F(x)^x и (fn(x)), где
124
Тогда
Г/ At / х fl. х—п,
F(x)f„(x) = ’
I 0, x =/= n
и /n(x) z£ 0 на (0, +°о), причем F(A)/n(x)-*0 на (О, +°°). Но
sup |F(x)fn(x)| = 1 VnsN
хе<о. 4-00
и поэтому F(x)fn(x) неравномерно сходятся к 0 на (0, +<эо).
Глава 3
СТЕПЕННЫЕ РЯДЫ
§ 1. Степенные ряды в комплексной области
Напомним некоторые сведения из теории комплексных чисел.
Пусть zeC так, что z=x-}-iy. Из формул, связывающих декарто-
вы и полярные координаты точки (х, y)eR2, получаем тригоно-
метрическую запись z=r (cos <р-Н’sin ф), r=|z| комплексного
числа. Забегая несколько вперед, используем формулу Эйлера
e<’=cos ф+i sin ф и получим экспоненциальную форму z=re‘* за-
писи комплексного числа (формулу Эйлера будем пока рассматри-
вать как сокращенную форму записи комплексного числа z=
==r(cos ф-Н sin ф)). Смысл такого обозначения будет установлен
в дальнейшем.
Теорема (правило умножения комплексных чисел). Пусть
Zi =Г1 (cos ф 1+i sin ф]), Г1 = | Zi |, z2—r2 (cos ф2-Н sin фа), г2= | г2 [.
Тогда z—zi-z2==r(cos<p-{-isin(f>), где r=lzi|-|z2| и ф=ф1+ф2.
Доказательство.
zt • z2 = rx • ra(cos Фх-Н sin фх) • (cos фа 4-i sin фа) =
= Гх • га[(со5фх • С05ф3 — sH-sin?,) + i(sin фх • cos ф , 4-
4-со$ф1 • з1пфг)]=Г1-га(со8(фх4-ф2)+г 5!п(ф1+фа))=
= r(cosф-f-г sin ф); г = г1’Г1, ф = фх + ф2.
Замечание. Если Zi = г1ег'<₽1 и za = r2ez”, то г2 • г2=г2Х
Хг2е«ф‘+ф>,1 т. е. функция е‘*. определяемая формулой Эйлера,
обладает свойством ei<pi • ez*» —
Следствие 1. При умножении комплексных чисел их моду-
ли перемножаются, а аргументы складываются.
Следствие 2 (правило деления комплексных чисел)'. <
Vzx, za(=C, гх=гх(со8ф14-*sinфх) =z2 = га(со8ф24-1 sinф2) =
= гае4’г #= 0 => (Zi/z^rjrt •
Следствие 3. (Угт—гте™т (m=l, 2, . . . ))=4(zx • z, ..
. . . zn = ri • ra. . . rnei^+^+-+4‘n'>).
Следствие 4. (Vг = r • e”sC, m — 0, ± 1, ±2, ...)=>
=£.(г'п==г/я • е*'Пф). В самом деле, при m= 1, 2, . . . это выте-
def
кает из правила умножения. При полагаем z°=l, и тог-
126
да наша формула также справедлива. При тп=—п; «=1,2,... в
силу правила деления, полагая z-n=l/zn, имеем z-n = (l/|z|n) X
X е-*"’, откуда zm \z\n •
4-00
Определение. Функциональный ряд S cn(z—a)n, где
п=0
z, гп, а, спеС и числа а, спеС заданы, называется степенным ря~
дом.
В дальнейшем будем рассматривать степенные ряды вида
2 cnzn; сп, z (= С. (1.1)
ПяеО
Точка zoeC, для которой степенной ряд (1.1) (при z—Zq) сходит-
ся, называется точкой сходимости ряда (1.1). Множество ZcC
всех точек сходимости ряда (1.1) называется областью сходимо-
сти ряда (1.1).
Замечание. Поскольку при Zo=0 ряд (1.1) всегда сходится,
то область сходимости Z любого степенного ряда (1.1) не пуста.
Пример. Степенной ряд 1+ у, пп-гл имеет область сходи-
71=1
мости Z, состоящую из одной точки z0 — 0. В самом деле,
VjeC, z^=032VeN такое, что Nn>N имеем |пг|>2, откуда
|га"гл|>>2”, и поэтому необходимое условие сходимости ряда
(1.1) lim сп • гп = 0 не выполнено, т. е. (Vz=^O, 2еС)ч>(зе2).
л-*4-°°
4-оо zn
Пример. Степенной ряд 14- 2 имеет область сходимос-
ти Z = C. В самом деле, V z#=OHZV e.N такое, что (|z/«|^l/2
Vn> А)=^ (|гп/«л|< l/2n V/г>А7) и +у 2~rt< 4-оо, т.е. наш
п—О
ряд сходится нормально Vz еС (а в силу признака Вейершт-
расса ряд сходится и абсолютно).
4-оо
Пример. Степенной ряд У zn сходится при [z|< 1 и рас-
ходится при |z| 1, т. е. область сходимости этого ряда Z =*
= {zeC||Z|<l}.
Первая теорема Абеля (для степенных рядов). Пусть
CnGCv zigNq и степенной ряд (1.1) сходится в точке Zo=^O,
ZosC. Тогда V zeC, удовлетворяющего неравенству lz|-<[zo|,
степенной ряд (1.1) сходится абсолютно.
Д о к а з а т е л ьство. Пусть го#=О и ряд у cnz* сходится,
п=0
тогда в силу необходимого признака сходимости числового
127
ряда Я lim cnz* = O, так что существует постоянная С> О, для
п -* 4-оо
которой |cnzg|< С Vп е No. Но тогда имеем оценку
f n*n| = М ♦ (z/z0|n<C|z/ze|n Vb sN, и
такого, что |г|<|z0|, откуда g=»|z/z,|<l. В силу теоремы
сравнения (с рядом из членов геометрической прогрессии со
знаменателем g=|z/z0|<4) знакоположительный ряд 2 |сп2п|схо-
дится, т. е. степенной ряд (1.1) сходится абсолютно.
Теорема. Пусть дан степенной ряд (1.1). Тогда я/?,
<+оо такое, что: 1) vzeC, удовлетворяющего неравенству
|z| <R, степенной ряд (1.1) сходится и притом абсолютно;
2) VzeC, удовлетворяющего неравенству (при
<4-оо), степенной ряд (1.1) расходится; 3) при |z|=£=0 сте-
пенной ряд (1.1) сходится. При |z|=jR>0 (0</?,<4“°°) степен-
ной ряд (1.1) может как сходиться, как и расходиться.
Доказательство. Пусть ZczC — область сходимости сте-
пенного ряда (1.1). Тогда Z#=0, поскольку OeZ. Пусть
Я= sup |z|. Тогда 0<Я<4-оо. Если геС и |г|<Я, то в силу
zCZ
определения точной верхней грани множества действительных
чисел Э:ое2 такое, что |z| < |z0| < R, и в силу 1-й теоремы
Абеля для степенных рядов видим, что z е Z, т. е, V: е С
такого, что |z| < R степенной ряд (1.1) сходится и притом аб-
солютно. Пусть 0</?<4-оо. Если zeC и |г|>R, то в силу
определения точной верхней грани множества действительных
чисел zeZ, и поэтому степенной ряд (1.1) расходится.
Замечание. Пусть для степенного ряда (1.1) имеем 0<Ж
,<С4-оо. Тогда степенной ряд (1.1) сходится внутри круга К«=
= {zeC|\z\ <.R} и расходится вне круга KR. Число 7?е(0, 4-°°)
называется радиусом сходимости степенного ряда (1.1), а круг
Кв называется кругом сходимости степенного ряда (1.1). В точках
окружности |г|=Я. степенной ряд (1.1) может как сходиться, так
и расходиться. При R=Q круг сходимости «вырождается в точку»,
а при Я=+°° круг сходимости совпадает со всей комплексной
плоскостью.
Замечание (о верхнем пределе последовательности). Пусть
для числовой последовательности (хп), где xn>0VneN
lim хп = а>-0, тогда lim (у-хп) = у-a Vу>0.
п—>4-оо п->4-°°
В самом деле, поскольку а’>0, то все точки сгущения по-
следовательностей (хп) и (ухп) лежат на конечном отрезке.
Пусть b — точка сгущения последовательности (хп), тогда су-
ществует подпоследовательность (хп^) такая, что
128
lim x = b\=^ (lim (yx \=syb\, t. e.
Л-+00 "fe / U-+00 "ft )
точка c — yb^Q является точкой сгущения последовательнос-
ти (yXnV С другой стороны, если с является точкой сгущения
последовательности (ухп), то существует подпоследовательность
(ухп ), такая, что lim (ух) = с, и поскольку у>0, то, полагая
b ₽ с/у, видим, что
Иш х = lim {ух/у) = с/у = Ь,
I— +00 nl Z—4-00 п1
т. е. b = с/у^О является точкой сгущения последовательности
(хп). Но тогда самая правая точка сгущения а последователь-
ности (хп) переходит в самую правую точку сгущения с-у-а.
последовательности (z/xn), т. е.
lim {у-хп) = г/-lim хп.
Л«->4-00 71—
Теорема (формула Коши — Адам ар а). Пусть дан степенной
ряд (1.1) up — lim £/|сп|. Тогда радиус сходимости R сте-
п—>4* с« *
пенного ряда (1.1) вычисляется по формуле Коши—Адамара.
я=-
О , р = -|- оо
1/р, 0<р<-
4-од, р = 0.
(12)
Доказательство. При z=#0 рассмотрим знакоположитель-
ный ряд
2 М”|. (1.3)
л=жО
Тогда в силу замечания о верхнем пределе последовательности
имеем
lim n/|cnZn|= lim (|z|- л/|с„| )=|Ф И® "/N =
TW-f-OO F 71г / П->-|-ОО г
{4-00, р —4~ОО,
|2|-Р. 0<р<+оо.
Но тогда при р=+оо или при 0<р<+оо, но ]z| -р>1 в силу
(радикального) признака Коши ряд (1.3) расходится, причем для
Ряда (1.3) не выполнен необходимый признак сходимости, поэтому
и степенной ряд (1.1.) расходится V z#=0 при р= + оо (т. е. при
Д=0) и расходится vz#=0 такого, что |z|:>l/p=^ при 0<р<:
JS+°°. Далее при р=0 (т. е. при 7?=4-оо) или при |z|-p<l для
0,<Р<+оо ряд (1.3) по (радикальному) признаку Коши сходит-
Ся> а потому степенной ряд (1.1) сходится абсолютно при |z|<
^l/pe-R. Тем самым формула Коши — Адамара (1.2) доказана.
а—Д И. Камынин 129
Замечание. Если для степенного ряда (1.1) существует
предел
lim |^л+1/сл| = р, то Я — 1/р.
П-»4-00
Пример. Рассмотрим степенной ряд
1 +.2°2”/n“' :еС (0<а< +оо). (1.4) \
n—i ;
Поскольку
lim (n-“)1/« = lim ехр{—a In п/п.} = 1 = р,
П-*4“°° П-*4-оо
то Я=1. Исследуем поведение ряда (1.4) на границе круга
сходимости Ki (т. е. при |z| = 1). I
1) Если а=0, то ряд (1.4) расходится Vz при |г|“1, так как &
не выполнен необходимый признак сходимости числового ря- '£
да. t
Ч-оо
2) При 0<а<1 ряд 2 по признаку Дирихле сходит-
Л=1
п
ся, если 0<ф<2я (z=/=l)* (В самом деле, пусть s„ =а 2
й—0
.» у z*=i(l— гл+!)/(1—z) (z=£l). Тогда |$п|<2/|1—z|=2/|l—cos<p—J
k=0 $
—i sin <p| = 2/(( 1—cos cp)8+sin2 ф)1/2 (2/( 1 —cos <p))1/2 => (|sn| <(2/(1— t
— совф))1/2 Vn eN при <p=^ 2/птс (m = 0, ±1, ±2, ...), кроме {
того, \1па | 0 (га->4-оо), если 0<а<1.) Далее в точке z=l, т.е. j
при ф= 0, ряд (1.4) расходится при 0<а<1. J
3) При а>1 ряд (1.4) VzeC такого, что |z| == 1 сходится
абсолютно по признаку Вейерштрасса, поскольку при |z| = >t
4-00
имеем оценку |г|л/п® = 1/п“ и у 1/п“<4-оо при а>1.
П=1
Замечание. В дальнейшем нам придется рассматривать од- ,
позначные функции z-^f(z), отображающие множество МсС в
С. Задание функции z-+f(z) равносильно заданию двух действи- -
тельных функций:
| и = и(х, у)
I V = о(Хж у),
где z—x+iy и f(z)—u(x, у) + iv(x, у), поэтому функцию z->7(z)
можно рассматривать как отображение F=(utv):(x, у)-*(и(х, у),
v(x, у)) из Я2 в В? и применять теорию таких отображений из.
[2]. В частности* можно рассматривать функциональные ряды
вида
130
2 ««(г), z e= MqC, (1.5)
n=l
где z->«n(z) есть однозначная функция, отображающая множество
AfcrC в С.
Определение. Функциональный ряд (1.5) называется рав-
номерно сходящимся на множестве МсС к сумме f(z), если:
1) v гоеЛ1 ряд (1.5) при z=z0 сходится к сумме f(z0);
2) V е>0 3 N (e)eN такое, что \sn(z)—f(z)\ <CeV n>N (e) и
n
N zeAf, где sn(z)= 2 Uk(z).
R=1
Задание. Переформулировать для функциональных рядов
вида (1.5) критерий Коши равномерной сходимости функциональ-
ного ряда, признак Вейерштрасса равномерной сходимости функ-
ционального ряда, теоремы о предельном переходе в равномерно
сходящемся функциональном ряде.
Теорема. Если степенной ряд (1.1) сходится абсолютно хотя
бы в одной граничной точке круга сходимости |z| <ZR, то ряд
(1.1) сходится абсолютно и равномерно в замкнутом круге | z| ^Д.
Доказательство. Пусть |zo|=J? и ряд (1.1) сходится аб-
солютно при z=z0, т. е. сходится ряд 2 |cnz,|. Тогда VzgC
п==0 0
такого, что \z|имеем VneN0 оценку
|СП2П|= Id • |з|л < |сп| • Rn = |сп • z”|,
из которой следует, что ряд (1.1) сходится нормально в круге.
имея мажорантой ряд 2 В силу признака Вейер-
п=0
штрасса степенной ряд (1.1) сходится абсолютно и равномер-
но в замкнутом круге |z| R.
Теорема (о равномерной сходимости степенного ряда).
Пусть степенной ряд (1.1) имеет радиус сходимости 2?>0. Тогда
(О, R) (0<r<J?) степенной ряд (1.1) сходится абсолютно и
равномерно в замкнутом круге |z|^r.
Доказательство. Пусть 0<г<7? и zo—r-e1^, тогда
;|г0|=г<Я и степенной ряд (1.1) сходится при z—zo абсолютно,
т. е. сходится знакоположительный ряд (1.3), но тогда V геС
такого, что | z | имеем оценку | cnzn | <11 сп | -rn V п, т. е. ряд
XU) сходится нормально в круге |z|^r, и в силу признака Вей-
ерштрасса степенной ряд (1.1) сходится в круге |z|^r (ОСгС
<•/?) абсолютно и равномерно.
Следствие. При 7?>0 степенной ряд (1.1) сходится равно-
мерно и абсолютно на любом компактном множестве КсС, цели-
ком лежащем внутри круга сходимости |z| <Д.
9* 131
Доказательство. Пусть К C2Kr = {z <= С| |z|<R}, тогда
окружность С^ — дКц компактна и ЛТ)Св’=0. Но тогда, как
было доказано в [2] (см. ч. III, гл. 1, § 12), р(К, С«)=6>0 и,
полагая г = sup |z|, имеем причем RCZAr={zsCl
гек
|z|<>}. Но степенной ряд (1.1) сходится равномерно в замкну-
том круге |z|_^r, а потому он сходится равномерно и на мно-
жестве К С Кг.
Замечание. В открытом круге сходимости |z| CR степен-
ной ряд (1.1) может сходиться неравномерно.
-|"°о
В самом деле, степенной ряд у, zn имеет радиус сходимости
и—О
R = 1, и в круге |z|< 1 он сходится к сумме /(г) =1/(1—z),
.причем sup |sn(z) —/(z)| = sup —z)| = 4-oo, поэтому наш
I»I<1 |Z|<1
степенной ряд;сходится в круге |z|< 1 к своей сумме 1/(1—z)
неравномерно.
Теорема (о непрерывности суммы степенного ряда). Пусть
степенной ряд (1.1) имеет радиус сходимости R>0 и сходится в
круге |z|<R к сумме f(z). Тогда VzoeC, такого что |z0| <R,
имеем f^C(zo).
Доказательство. Заметим, что, v zo е С и vneNo имеем
cnzn е C(zq). (В самом деле, при п=0,1 это очевидно, а при
п^2 это следует из теоремы о непрерывности произведения ко- -
«ечного числа непрерывных функций.) Пусть 20еС таково, что
:|zo| CR, тогда Яде (О, R), для которого |z0| OCR. Рассмотрим
замкнутый круг Кг- Тогда степенной ряд (1.1) сходится равномер- 1
но в круге Ж, и по теореме о непрерывности суммы равномерно
сходящегося функционального ряда с непрерывными членами
имеем f е С (Кг), но (z0 <= Kr) =>(f <=. C(z0)).
Вторая теорема Абеля (для степенных рядов). Если
степенной ряд (1.1) с радиусом R>0 сходится в точке z0=
=Rei<₽° окружности |z|=R, то для суммы f(z) этого ряда имеет
место соотношение
lim f(z) = f(z0),
Z==|3|.ei(Pe->Ze
т. e. в точке z0 функция f(z) непрерывна вдоль радиуса Ozo.
Доказательство. Пусть степенной ряд (1.1) сходится при
z=z0=Re<t(,«. Положим 7И={z е C|z = rei<₽», 0<r<R} и заметим,
что V: е М имеем равенства
cnzn = (z/z0)n • cnzg = (rlR)ncnzn0.
132
Пусть a„(z) = (r/R)n и un(z) s спг J, тогда имеем:
1) an(z) t R Vz s M и Vn e No; an(z) J, (при n-»+ oo) Vze/lf;
кроме того, |a„(z)| = (r/R)n<1 Vz e M и Vns No;
2) функция «n(z)==cnz" не зависит от z^M, и поэтому
4-ое Ц-ос
„функциональный* ряд 2 un(z) = 2 cBz" сходится равномер-
п=0 п=0
но на множестве М.
Из условий 1) и 2) в силу признака Абеля (равномерной
сходимости) функциональный ряд
У ®п(^) «п(г) 2
п=0 п=0
сходится на множестве М разномерно к функции /(z). Далее,
zoe2H' и VneN0 Я lim cnzn=cnz" поэтому в силу теоремы
г-*гв, z£M
о предельном переходе в равномерно сходящемся функцио-
нальном ряде имеем
Я lim /(z)= cnz"*=/(z0),
Z-+?о* ZGM
что и требовалось доказать.
Теорема (об умножении условно сходящихся числовых ря-
дов). Пусть а„, Ьп, сп е= С V п <= N„ причем сп = 2 аА-*- Если
л=о
числовые ряды
оо 2 ап = А, n^=Q (1.6)
4-оо 2 = n—Q (1,7)
II +Й1 (1-8)
сходятся, то имеет место равенство С=А-В, т. е. условно сходя-
щиеся числовые ряды (1.6) и (1.7) можно перемножать по прави-
лу Коши, если результирующий ряд (1.8) сходится.
Доказательство. Рассмотрим степенные ряды
4-00 4-00 4-00
2 апгя = а(г), 2 Ьпгп = Ь(г) и 2 спгп = с(г),
п- 0 п=0 п—О
133
где
== ( 2 &Ь.Ьп—к\ 2 =2 feZrt—ft).
\ Л=0 / Л=0
Эти степенные ряды сходятся при z=l (в силу условия о сходи»
мости рядов (1.6)— (1.8)) и поэтому (в силу 1-й теоремы Абеля
для степенных рядов) сходятся абсолютно в круге \z\ <1. Но тог-
да в силу теоремы Абеля об умножении абсолютно сходящихся
рядов (из ч. IV, гл. 1, § 6) ряды (1.16) и (1.7) можно перемножать .
любым способом и при этом
c(z)==a(z).&(z)VzeK1 = {zeC||z|<l}. (1.9)
В силу 2-й теоремы Абеля для степенных рядов (при z0=x, z= «
=х е R) имеем
Я lim a(z)=A, lim b(z)—B, lim c(z) — C. (1.10)
z=x->l-0 z=x->l—0 z=x-*l—0
Ho из (1.9), (1.10) имеем равенство C—A*B. ;
Замечание 1. Пусть степенные ряды
V. anz", (1.11) ?
п=0 ;
(1.12) |
п=0
и /?а>0 —радиус сходимости ряда (1.1), а Rb^>Q— радиус
сходимости ряда (1.12). Если p = min(fia, Rb) _>0, то степенной
ряд
4-оо 4-<» +°°
2 ап2п ± 2 Мп=2 ± ъ^п с1 -13) .
п=0 п=0 п=0
сходится при |z| <р, причем в силу 1-й теоремы Абеля (для сте-
пенных рядов) если R — радиус сходимости ряда (1.13), то R~^
>р>0.
Замечание 2. Степенные ряды (1.11) и (1.12) абсолютно '
сходятся при |z|<р, поэтому в силу теоремы Абеля (об умноже-
нии абсолютно сходящихся рядов) ряды (1.11) и (1.12) можно
перемножать любым способом, в частности по правилу Коши
cn=^ak-bn-k и ряд .
fc=0
2 <1Л4)
п=0
имеет радиус сходимости R>0, удовлетворяющий оценке R^
>р>0.
134
Замечание 3. Для операций сложения и умножения сходя-
щихся степенных рядов справедливы законы коммутативности,
ассоциативности и дистрибутивности, причем операция вычитания
определяется как операция, обратная по отношению к операции
уложения.
Из замечаний 1—3 вытекает теорема.
Теорема. Множество всех степенных рядов с отличными от
нуля радиусами сходимости образует кольцо над полем С.
Замечание 4. Если для степенного ряда (1.12) имеем
<£>о#=О, то можно рассмотреть операцию деления степенного ряда
.(1.11) на степенной ряд (1.12), причем отношение ряда (1.11) к
ряду (1.12) есть степенной ряд
+оо
2 dnzn,
П=0
где коэффициенты dn удовлетворяют рекуррентным соотношени-
ям
2 А = (П = 0, 1» 2, . . . ),
из которых при Ьо#=О коэффициенты dn определяются единст-
венным образом.
Теорема. Пусть степенной ряд (1.1) имеет радиус сходимо-
сти ^>0 и f(z) — его сумма. Пусть существует последователь-
ность J
(zm), гяег7к(0) VmeN
такая, что
lim zm = 0 и /(zm) =0 (m = 0, 1, 2, . . . ).
m->4-oo
Тогда для коэффициентов степенного ряда (1.1) имеем
cn = 0 (n=0, 1, 2, . . . ), m. е. /(z)sO в {7д(0)сС.
Доказательство. Поскольку f(zm)=O (m=l, 2, ...),
то
2 cm(zm)n = o (m = l, 2, . . . ).
n==Q
Ho (f eC(U«(0)))=»(/eC(0)), и поэтому Я lim f(zm)®/(0) = co—O,
т. e. c0 = O. Допустим, что. доказано утверждение ck-=0
(k = 0, 1, 2,..., p— 1), тогда из равенств f(zm) = O V m eN
имеем
4-00
2 = ° V m e= N,
135
но zm е 1/й(0), т. е. zm=^0 VweN, поэтому, деля на (гт)р^0, име-
ем
0 = СР + 2 cP+k(zm)k = cp + vp(zm). (1.15>
*=i
Hocpp(z)=2 cP+ktk Vz е причем степенной ряд справа
Л=1
имеет радиус сходимости Rp~^R>0. В самом деле, пусть
0<^r<^R— любое. Тогда для любого zeC такого, что 0<|z|^
<г имеет место оценка
|сп+р2я| < |cn+p|rrt+p • г-р V п е N.
Поскольку степенной ряд 2 cn+pzn+p имеет радиус сходи-
л+р==0
мости R > 0, то при |z| г < R ряд
2 |с«+р1гп+р
п+р=0
сходится, а потому в силу теоремы сравнения сходится и ряд
У icn+pZn\, т. е. Rp^R.
П=1
Но тогда <рр е С(С7^(О)) как сумма степенного ряда и потому
ФреС(О), причем ф^(0)=0. Переходя к пределу при т—>+<х>
в равенстве (1.15), имеем ср = 0. Итак, по индукции доказано,
что c„z=0 (n = 0, 1, 2, . . . ), т. е.
f(z) = O Vz|et/«(0)CZC.
Следствие. Пусть степенной ряд (1.1) имеет радиус сходи-
мости и Э ге (0, H-оо), такое, что Q<Zr<LR и для суммы
f(z) ряда (1.1) имеет место тождество f(z)—0Vz^C такого, что
|z|<zr, тогда cn=0 (n=0, 1, 2, ...), т. е. f(z)=O в t/H(0,).
Теорема единственности (для степенных рядов). Пусть
степенные ряды (1.11) и (1.12) имеют радиусы сходимости Ri>0
и Rb>0 и сходятся к суммам a(z) и b(z) соответственно. Пусть су-
ществует последовательность (zm), zm^ Ц>(0) v m е N (где р=
=min(Ra, Rb)>0), такая, цто lirnzm=0 и a(zm)=b(zm)Nm&
eN. Тогда ап = Ьпч n^N0, т. е. a(z)=b(z) в t/₽(0)czC.
+»
Доказательство. Рассмотрим степенной ряд 2 cnzn=c(z)t
л=0
где сп=ап — Z?nVn<=N0. Тогда c(z) = a(z) — b(z) и c(zm)=O
VmeN. В силу предыдущей теоремы имеем сп = ап—Ьп = &
V п е No, откуда ап = ЬЛ V n s No.
136
Следствие. Пусть степенные ряды (1.11) и (1.12) имеют
радиусы сходимости /?а>0 и 7?ь>0 и сходятся к суммам а (г) и
b(z) соответственно. Пусть Яге (0, Н-оо) такое, что 0<г<р=
=min(7?<b Яъ) и a(z)==b(z) V z ^Ur(0). Тогда an=bnV п<= NOr
т. е. a(z)=b(z) в £7р(0).
§ 2. Определение экспоненциальной, тригонометрических
и гиперболических функций с помощью
степенных рядов
Теорема. Степенной ряд
ег^2 2’/п! (2.1 >
/1=0
имеет радиус сходимости /?=+«>, причем '
е71. «2« — ег*+2« V zlf z2 е С.
Доказательство. Используя определение радиуса сходи-
мости степенного ряда (2.1) по формуле Д’Аламбера, имеем
R= lim (1/га!)/(1/(п+ 1)1) = lim (n-f-1) = + оо.
«-►4-00 л-*-рю
Далее "V zlt z2eC ряд (2.1) сходится абсолютно» и поэтому в
силу теоремы Абеля (об умножении абсолютно сходящихся
рядов) ряды (2.1) при z = Zj и z=z2 можно перемножать лю-
бым способом и, в частности, по правилу Коши. Тогда, ис-
пользуя формулу бинома Ньютона, имеем
^*•^=2 с«»
л=0
где
л zk п
сп =2 37 • ~TV « 1/nl- 2 nl/(*!(n-*)l)z‘.z«-* =
fcx=:O Л! (п—Л)! й=0
= (zi + Z2)n/n! (ez<- ег» •> 2 (zi+га)7л! = вг‘+*!)-
n=0
Замечание. Функция z->ez, определяемая степенным рядом
(2.1), называется экспоненциальной функцией.
Следствие. r:=l/^vzeC и ег/е*=ег-< Vz, feC.
Доказательство. Из формулы ez‘-ez» = ez*+z« при zt=z и
za——z имеем е2-е~г=е°=1, т. е. e~z—\/ef. При z^ — z и г2 = —t
имеем ег • е~/= е2-<, т. е. ez/e< = e2-e_f=ez—f.
Теорема. Степенные ряды
cosz=2 (— l)n22n/(2n)!, (2.2>
П=1
137
!
sinz = 2 (— I)nz2«+V(2«+1)! (2.3)
n—0
имеют радиусы сходимости 7?=4-oo, причем VzeC имеют место
формулы Эйлера
ei2 = cos г + i sin z, e~iz = cos z — i sin z;
cos z = (eiz + e-Zz)/2, sin z = (elz — e“Zz)/2i;
cos (zx 4- z2) = cos zx• cos z2 — sin zx • sin z2;
sin (zx 4- z2) = sin zx• cos z2 4- cos zx • sin z2 Vzx, z2 G C.
Доказательство. По формуле Д’Аламбера степенные ря-
ды (2.2) и (2.3) имеют радиус сходимости #=4-оо. Далее по-
скольку (t)2n = (-l)n и (1)2л+1 = (—1)п1, то
е1г = 2 (i)kzk/kl = 2 (—l)nz2n/(2«)! 4-
k—Q n=0 ,
4-»2 (-l)nz2n+i/(2n 4- 1)!,
л—0
t. e. e‘* = cos z 4* i sinz; аналогично
e-iz=2 (—i)ft2ft/^!=2 (—О^ДЗл)! —
k=0 n=0
— i 2 (— l)nz2n+1/(2n 4-1)1,
n=0
t. e. e-Zz = cosz— isinz, откуда получаем формулы Эйлера
cosz = (eiz 4- e-iz)/2 и sinz = (ezz — e~Zz)/2i.
Далее, используя формулы Эйлера, имеем
V zx, z, = C coszx*cosz2 —sinzx-sinz2 =
= (eiz*4-e-iz‘)/2- (eiz«4-e~Zz«)/2 — (eZz‘—e-Zz«)/2t X
X — е-ъуы = [ег<ъ+гг) 4- eZz« • e_iz» 4- e~iz‘ • 4-
ei(Zi+zs) _ei2i.g-izt — e-izi .giz, _|_ g-‘(^+^Jf4=z
— (el<z'+z*> 4- e_i(z»+z«>)/2 as cos (zx 4- z2),
t. e.
cos(zx 4- z2) = coszx-cosz2 — sinzx-sinz2 V zx, z2eC.
Аналогично
sin zx• cos z2 4- cos zx• sin z2 = (e‘z*—e^iZi )/2i (e'z«4-e~ZZ! )/2 4-
4- (eiz* 4- e~iz» )/2-(eiz> — e~iz* )/2i = [е4<г«+г»> 4- eiz*-e-iz« —
____4- e'(zi+zi) e»zt. e-/z, _|_ e-izi. eiz, — ’
— ei(zH-z,)] _ (ei(z,+z,) _ e-»(zi+z,) )/2i * sin (zx 4- г2),
438
т. е.
sin (z2z2) » sin Zj cos z2 4-cos z2 sin z2 Vz2, z2eC.
Замечание. Функции, определяемые степенными рядами
(2.2) и (2.3), называются косинусом и синусом соответственно.
Следствие. cos(—z) = cosz, sin(—z) =—sinz, cos2z4-
4~sin2z=l vze C.
Доказательство. Из формул Эйлера следует, что
cos (—z) = (e~iz 4- е‘г)/2 — cos z;
sin (—z) = (e~‘z — eiz)/2i = — sin z.
Из формулы cos(z14-z2) = cosz1-cosz2 — sinzi • sinz2 при Zj=z и
при z2 = -—z имеем
cos(z — z) = cosO = 1 = cosz- cos(—z) —
— sinz- sin(—z)=>(l = cos8z 4- sin2 z V z e C).
Следствие. Введем в рассмотрение гиперболические функ-
ции
chz = (e?+e-z)/2, sh г (ег — е~г)/2.
Тогда
ch г = cos (iz), sin z = — i sh (iz)
sh z = — i sin (iz), cos z = ch (iz),
причем
ch (Zj 4- zt) = ch zt • ch za 4- sh zx • sh z2,
sh (zx + z2) = sh z, • ch z2 4- ch zx • sh z2 V ?b z2 e C;
ch(—z) = chz, sh(—z)— — shz; ch2z— sh2z=l Vz <= C.
§ 3. Степенные ряды в действительной области
Рассмотрим степенной ряд
2 ап*п при ап, xsR. (3.1)
п—О
Из общей теории степенных рядов (см. § 1) следует, что сущест-
вует «радиус сходимости» R (0^?s^4-°°) такой, чтоУхе (—R, R)
степенной ряд (3.1) сходится (и притом абсолютно), а прр |х|>7?
степенной ряд (3.1) расходится, т. е. круг сходимости Izl <7? прев-
ращается для степенного ряда (3.1) в интервал сходимости (—R,
”) Разумеется, для степенных рядов в действительной области
остаются в силе все теоремы § 1, в том числе 1-я и 2-я теоремы
Абеля и теорема единственности степенного ряда. Приведем фор-
мулировки некоторых из этих теорем.
139
2-я теорема Абеля (для степенного ряда (3.1)). Пусть
степенной ряд (3.1) имеет радиус сходимости R>0 и ряд (3.1)
сходится при х=х0. Тогда степенной ряд (3.1) равномерно схо-
дится на отрезке [0, х0] при Хо>О и на отрезке [х0, 0] при xia<0.
Следствие. Степенной ряд (3.1) равномерно сходится к не-
прерывной функции на любом отрезке [а, &], принадлежащем его
области сходимости.
Пример. Было установлено, что
In(1 +*) = (—l)"-1*n/n Vxe(-1, 1).
4-00
Но при х»1 ряд, стоящий справа, т. е. ряд У, (—1)п-1/п, схо-
Л=1
дится как ряд Лейбница, поэтому в силу 2-й теоремы Абеля
имеем
In (14-х) = 2 (-\)п~'хп1п, хе=(—1, 1],
/1=1
в частности
In 2 = 2 (—l)n-‘/n.
п=1
Теорема единственности (для степенного ряда (3.1)).
Пусть степенной ряд (3.1) имеет радиус сходимости R>0 и f(x) —
его сумма. Пусть существует последовательность (хт), хт е
е (—R, R)\{0) v т е N такая, что lim xm=0 и f(xm) =0 V m <= N.
Тогда в (3.1) an=0VneNo, т. е. f(x)^O в (—R, R).
Следствие. Пусть степенной ряд (3.1) имеет радиус сходи-
мости /?>0 и существует число г такое, что 0<r<ZR и для суммы
f(x) ряда (3.1) имеет место тождество f(x)=O в (—г, г). Тогда
an=OvneNo, т. е. f(x)^O в (—R, R).
Теорема единственности (для степенных рядов
(3.1)). Пусть степенные ряды
f(x) = 2 а«хП <3-2>
п=6
U
g(x) = ^bnxn (3.3)
л=0
имеют радиусы сходимости Ra>Q и Rb>0 соответственно. Пусть
существует последовательность (xm),xm<^(—р, pJMOJvmeN,
где p=min (Ra, Rb)>Q такая, что limxm=0 и ?(хт)=^
=g(xm)VmeN. Тогда an=bnVfieN0, т. е. f(x)ssg(x) в
(—Р> Р)-
140
Следствие. Пусть степенные ряды (3.2) и (3.3) имеют ра-
диусы сходимости /?а:>0 и /?&>0 и сходятся к суммам f(x) и
g(x) соответственно. Пусть Я г>0 такое, что 0<r<min(/?o, Rt>)
и f(x)=g(x) в (—г, г). Тогда an=bn Vne No, i.e.f(x) =
^g(x) в (—p, p).
Теорема (о почленном интегрировании и дифференцирова-
нии степенного ряда (3.1) в действительной области). Пусть
f(x)=£«nxn, хб=(-Я, R), (3.4)
п—О
где R>0 — радиус сходимости степенного ряда (3.4). Тогда
X
Vхе(-R, R) существуют Jf(t)dt и f'(x), причем
X 4-00
= 2 fln*n+1/(n + i) (3.5)
О п=0
Их) =2 папх^, (3.6)
Hail
и степенные ряды (3.5) и (3.6) имеют тот же радиус сходимости
R>0, что и степенной ряд (3.4)
Доказательство. Пусть степенные ряды (3.5) и (3.6) име-
ют радиусы сходимости Ri и R2 соответственно. Докажем, что
4-00
Rt-=R. Пусть 0< |х| <R. Тогда ряд у |апхп| сходится и для
п=0
общего члена ряда (3.5) имеем представление |апхя+1/(п+1)| =
=[]ап*Т(И/(п + 1)), но |х|/(«+1)^,0 (п—>+оо), в силу признака
Абеля ряд (3.5) сходится абсолютно при любом х таком, что
0<jx|<jR, т- е- Ri>R- Пусть теперь 0<|хКг</?1. Тогда схо-
дится ряд у lanlr"+V(rt + причем для общего члена ряда
п—0
(3.4) имеет место представление |апхл|=(|ап|г',+1/(п+1)) • (|х|/г)пХ
Х(п-}-1)/г. Полагая q = |х|/г, имеем 1, так что числовой
4-00
ряд у <7п(п-Ь1)/г сходится по признаку Д’Аламбера, посколь-
п==0
ку
lim [(qn+i(n + 2)/r)/(gn(n + l)/r)] = q < 1.
л->4-оо
Но тогда в силу необходимого условия сходимости ряда име-
ем lim [(|х|/г)л(п + 1 )/г] = 0, и поэтому, в частности, существу-
п-^*4-оо
Ют€>0 и NeN такие, что
141
|nnx"| < С|ап|гл+‘/(п 4-1) V n > N.
В силу признака сравнения ряд (3.4) сходится абсолютно для лю-
бых х таких, что 0< |х| т. е. Итак, #i = R, причем
доказано, что ряд (3.4) можно формально почленно интегрировать
и ряды (3.5) и (3.4) имеют одинаковые радиусы сходимости. Да-
лее ряд (3.4) можно рассматривать как степенной ряд, получен-
ный формальным почленным интегрированием степенного ряда
(3.16). По доказанному, тогда R=R%. Тем самым доказано, что
степенные ряды (3.4) — (3.6) имеют один и тот же радиус сходи-
мости 7?>0, причем Vre (О, R) степенные ряды (3.4)—(3.(6) схо-
дятся равномерно на отрезке [—г, г] с (R, R). Кроме того, функ-
ции апхп, апхп+х/(п+1), папхп~х Vne No непрерывны и диффе-
ренцируемы на (—оо, -j-оо). По теореме об интегрировании рав-
номерно сходящихся функциональных рядов степенной ряд (3.4)
можно интегрировать почленно и V х е [—г, г] имеет место ра-
венство (3.5). По теореме о почленном дифференцировании функ-
циональных рядов степенной ряд (3.4) можно почленно дифферен-
цировать и —г, г] имеет место равенство (3.6). В силу про-
извольности ге (О, R} равенства (3.5) и (3.6) имеют место и
vxe(-R, R).
Следствие (теорема о бесконечной дифференцируемости
суммы степенного ряда (3.4) в действительной области). Степен-
ной ряд (3.4) можно почленно дифференцировать любое число
раз без изменения радиуса сходимости, причем для любых
х е (—R, R) и m е N имеет место равенство
Dmf(x) = 2 «(«“О • • • (n—m-j-l)anxn-m.
n=m
В частности, для суммы степенного ряда (3.4) имеем
R)).
Замечание. При почленном интегрировании или дифферен-
цировании степенного ряда (3.4) область сходимости X Q
сс[—R, 7?] вновь полученного степенного ряда (3.5) или (3.6) мо-
жет измениться, хотя радиус сходимости R>0 этих рядов и не ме-
няется. Однако если степенной ряд (3.4) сходится в точке
хое[—R, 2?], то и проинтегрированный ряд (3.5) будет сходиться
в этой точке. (В самом деле, для степенного ряда (3.5) имеем
2 «п*о+1/(«+!) = 2 (V(«+Wnxg==5 • (ДпХо)>
п=0 и—0 л=0
где an = x0/(n + 1) |(|) при /г-»+©о и, кроме того» 1ап|</? VnS
eN0. Поскольку ряд 2 сходится, то ряд (3.5) сходится’
п=0
в точке х = х0 по признаку Абеля.)
142
4-00
Примеры. 1) у хп, R = 1, X = (—1,1). Для продиффе-
п=0
+оо
ренцированного ряда у пхп~1 имеем ЛГ=(—1, 1), а для проин-
/2=1
4-00
тегрированного ряда 2 хп+1/(п+1) имеем Х~[—1, 1).
п=0
2) 2 x1llnZ> Я=1, Х=[—1, 1]. Для продифференцированно-
п—1
4-00
го ряда У, хп-1/п имеем Х — [— 1, 1), а для проинтегрирован-
Л=1
ного ряда 2 хп+Чп\п+\) имеем Х=[—1, 1].
П=1
3) 2 2-^xn, R=l, Х=[-1,1]. Заметим, что ¥Л>1
Л«вО
EN такое, что 1/2^"^ l/nk Vn>2V0(&), поэтому для продиф-
4-оо —
ференцированного ряда у п2~Упхп~1 имеем JC = [—1, 1], а для
проинтегрированного ряда у 2-’/"х"+1/(л4-1) имеем Х=[—1,1],
п=0
т. е. область сходимости этого ряда сохраняется как при диф-
ференцировании, так и при интегрировании.
Теорема единственности (разложения функции в
степенной ряд). Пусть f^CW((—R, R)) и имеет место (3.4), где.
Я>0. Тогда an=Dnf (0)/п! v п <= No.
Доказательство. Из формулы
Dmf(x) = 2 Kk— 1)... (Л-т4-1)аЛх*-«
при m=n и х=0 имеем Dnf(O)=n!an (я=0, 1, 2,...), т. е.
an = Dnf(O)/nl (л=»0, 1, 2, .. .).
Определение. Для функции f е CW(x0) степенной ряд
2 D«/(0)(x-xo)n/n!
п=0
называется рядом Тейлора для функции f(x).
Определение. Пусть f<= С<°°)(0), тогда степенной ряд
4-00
2 D”f(O)x"/nl .
п=0
называется рядом Маклорена для функции f(x).
143
Следствие. В своем интервале сходимости (—Д, R) (при
+оо
2?>0) степенной ряд у, anxn = f(x) является рядом Маклорена
л=0
для своей суммы f(x).
Замечание. Если —R, R)) и степенной ряд
2 D"/(0)x7n! (3.7)
п=0
является рядом Маклорена для функции f(x), то степенной ряд
(3.7) не обязан, вообще говоря, сходиться (при х=#0) и иметь
своей суммой функцию f(x).
Пример. Рассмотрим функцию
, ( ехр(—1/ха), х^О
8 ~ ( 0 , х=0.
Тогда, как было показано в § 10, гл. 5 ч. I [1], gGC'(oo)((—оо,. Н~оо)),
причем D"g(0) = 0 V п е No. Заметим, что ряд Маклорена для
4-00
функции g(x) имеет вид у, 0-х" и его сумма f(x)==O не совпа-
п=0
дает с функцией g(x) при х^О.
Замечание [4, пример 24, с. 91]. Существует бесконечно
дифференцируемая на (—оо, -f-oo) функция, ряд Маклорена кото-
рой сходится лишь в одной точке х=0.
Следствие. Любой степенной ряд (3.4) в своем интервале
сходимости (—R, R) (при Я>0) является рядом Маклорена для
бесчисленного множества функций из класса С<-ао)((—R, R)).
В самом деле, если функция f(x) является суммой ряда (3.4)
на (—R, R) (где R>0), то все функции вида f(x)-\-Kg(x) v%eR
|(с функцией g(x), взятой из вышеприведенного примера) имеют в
качестве своего ряда Маклорена на (—R, R) степенной ряд (3.4).
Теорема (критерий разложимости бесконечно дифференци-
руемой функции в ее ряд Тейлора). Пусть f е С^((хо—R, x0-\-R))
и f(x) = f(x0) + 2 Е>*/(х0)/&! • (x-x^+rn(x, x0)
*=i
— ее разложение no формуле Тейлора с остаточным членом гп(х,х0).
(Ряд Тейлора функции f(x) сходится на (xt—R, x0+R) к функции
f(x))44(3 limr„(x, хо) = О VxE(xe—R, х0+Я).)
и->-}-оо
Доказательство очевидно.
•Теорема (достаточное условие разложимости функции в ее
ряд Тейлора). Пусть f е С<°°)([—г, г]) « существуют постоянные
L>0uae[0, 1) такие, что имеет место оценка
I Dnf (х) | CL"+I пап V х е [—г, г] V и <= No.
144
Тогда
f(x) = 2 Dnf(O)/n! • ^VxE[-G 4
n=0
Доказательство. Поскольку feC(00>([—r, r), to Vxs
s [—6 d и Vne No для функции f (x) можно написать формулу
Тейлора с остаточным членом в форме Лагранжа гп(х)—
я=Ь”+1/:('0'п,-х)'Хп+1/(п4-1)!, где 0<fln<l. Тогда в силу условий
теоремы имеем оценку
|гп(х)| <(£/(„ 4-2)!)(£гГ+1 . (п + 2уы+Ъ~Ъп
VxE[-r,/]( VnEN’o
Ч-ОЭ
(где 0<а<1). Но тогда для числового ряда S Ьп имеем
п=0
Ш_!=(£г/(п + 1)1-“). (1 4- 1/(п 4- 1))а(л+1> X
X (1 4- 1/(п4-1))“,
и поскольку 1—а>0, lim 6„/&n_i = 0< 1. Вейлу признака
П-*4-оо
Д’Аламбера числовой ряд 2 Ьп сходится, а потому в силу
71=0
необходимого условия сходимости числового ряда имеем
( lim Ьв = 0)=^( lim sup |r„(x)| = 0).
П-*4-о> Л-Н-со x£[—Г, г]
Таким образом, выполнено достаточное условие критерия разло-
жимости функции в ее ряд Тейлора, при этом в силу оценки
(l/ml)|Dmf(0)||xr<6m_i Vx6[-r, г] VmEN,
ряд Тейлора сходится нормально на отрезке [—г, г] и в силу приз-
нака Вейерштрасса ряд Тейлора сходится к функции f(x) равно-
мерно на отрезке [—г, г].
Следствие 1. Функция f е С(оо> ([—г, г]) разлагается в свой
ряд Тейлора, если существует постоянная L>0 такая, что имеет
место оценка | Dnf(x) | V х е [,—г, г] v n е No.
Следствие 2. Функции exp (х.), ch х, sh х, cos х и sin х раз-
лагаются в ряды Маклорена на (—со, 4-оо), причем
ехр (х) - xn/n!, ch х= 2° х8я/(2п)1,
71=0 П*вО
shх = 2° *2л+1/(2л + 1)!, cosx = 2° (—1)п^п/(2и)!,
д=0 71=0
sin х = 2° (— 1 )пх,я*1/(2п4-1)1.
71=0
— Л. И. Камынин
145
В самом деле, полагая /Х(х) = ехр(х), /,(x)=>»chx, ft(x)—shx,.
gx(x) = cosх» ga(x) = sinx, видим, что Vxe[—Я, /?]¥/? > 0 и
VneN( имеют место оценки
РпА(х)| < ехр (|х|) < ехр (Я) (i - 1, 2, 3).
ID"£1WI — I cos (x + n • «/2)1 < ls
]Dnga(x)| = | sin (x 4- n • «/2)| < 1,
т. e. выполнены все условия следствия 1 (о достаточном признаке
разложимости функции в ее ряд Тейлора).
Замечание 1.
arctgx = 2 (~1)*х2л+1/(2п+1) ¥х<=[-1, 1].
л=0
Доказательство. Непосредственное применение достаточ»
кого признака разложения в ряд Тейлора к функции f(x)=*
=arctgx невозможно, поскольку производные Dnf(x) неограни-
чены при »-»-4-оо. Однако при |x|d имеем разложение
4-00
1/(1 + х2) = 2 (—1)П-*2П, причем степенной ряд справа имеет
радиус сходимости Я=Ъ Но тогда по теореме об интегриро-
вании степенных рядов имеем равенство
f 1/(1 +t2)d/ = 2 (— 1)ях2я+1/(2»Ч-1) ¥хб=(—1, 1),
О п=0
т. е.
arctgx=2 (—1)'г*2я+1/(2«+1), —1, 1).
П=0
При х«=±1 ряд справа сходится как ряд Лейбница, поэтому
в силу 2-й теоремы Абеля (для степенных рядов) разложение
в ряд Маклорена имеет место ¥xs[—1, 1] и, в частности»
arctg 1 = «/4 = 2 (—l)n/(2n 4-1).
п=0
Замечание 2.
(14-х)а= 1 +2 а • (а—1) • - • (а —n+1)хп/п!
/г«=1
¥хе(—1, 1) и ¥ае(—оо, 4~оо).
Доказательство. Пусть f(x) = (1+х)“. Очевидно, fS
еС(ю>((—1, 1)), причем Dnf(O)=a-(a—1)... (a—n-|-l) VneNo.
Поэтому ряд Маклорена для функции f(x) имеет вид
4-оо
1 + S апхПа
л—1
146
где
ап <=> а • (а—1) . . .(а — п 4- 1)/л!.
По признаку Д’Аламбера
1/Я « Jim |an+1/an| = Jim |(а—л)/(л4-1)| = 1,
т. е. радиус сходимости этого степенного ряда Д=1. Запишем
ухе(—1,1) при а=£0 разложение функции f(x) по формуле Тей«
лора с остаточным членом в интегральной форме
гп+1 i
гп(х) =^— • /(I-X)"D"+if(X . x)dX,
Л! д
так что
гп(х)«а. (а-1) . . . (а-л) . X"+i/ni • j(l — Х)“Х
о
X (l+Xx)«-n-‘rfX=«:(a—1) • (а—2). . . (а—л) . х"/л! X
X [ах J(14-Xx)“ -‘((1—X)/(1+Xx))ndxl.
L о J
Поскольку 0<Х«^1 и — 1<х<1, то имеем оценки
(О < 1 - X < 1 + Хх) н- (0 < (1 -Х)/(1 4-Хх) < 1) =>
=»(0<((1-Х)/(1+Хх))п< 1 VXe [0, 1] и Vx6=(— 1, 1)).
Но тогда при х^=0 и а=£0 имеем оценку
ах- j(l+Xx)—i • ((1—X)/(l+Xx))«dX <|ах|Х
о
J (14-Хх)“~‘ dX | -А(х) = |(1 +х)« - 1| V х > -1, х Ф О,
о I
т. е.
|Гп(х)|<Л(х)|(а-1) • (“—2). . . (а—п) • хп/л!|
Vxg=(—1, 1), х^О, а=^0 УлеЫ0.
Но справа множитель при k(x) есть абсолютная величина л-го
члена ряда Тейлора для функции (14-х)“-‘, который сходится
абсолютно при |х|< 1. В силу необходимого условия сходи-
мости л-й член этого сходящегося ряда стремится к нулю при
Таким образом, Vx<=(—1, l)t х=#0 Я lim гл(х) = 0 (при
п->4-оо
гп(0)=0). В силу критерия разложимости функции в ряд
Тейлора имеем представление '
(1+-г)«== 1 + 2 ». (а—1) . . . (а—л4-1)х”/л!, хе(-1, 1). (3.8)
п=»1
10*
147
Заметим, что при a=msN степенной ряд (3.8) обрывается при
п=т, превращаясь в многочлен, т. е. при jc=/n е N имеет место
обычная формула бинома Ньютона, справедливая Vxe(—оо,
Н-оо). При х=±1 ряд Тейлора может как сходиться, так и рас-
ходиться. Если биномиальный ряд сходится при х=1 или при
х=—1, то применима 2-я теорема Абеля (для степенных рядов) и
представление (3.8) при этом сохраняется и для х=1 (или для
х=—1).
Следствие. Функции exp (z), chz, shz, cosz, sinz, опреде-
ленные ранее VzeС при z=xeR, совпадают с функциями
exp (x), ch x, sh x, cos x и sin x, известными из математического
анализа.
Теорема. Функция ег имеет период 2ni, т. е. v z е С
ег+^м=ег (fc=o, ±1, ±2, ...). Функции cosz и sinz имеют пери-
од 2л, т. е. V z е С имеем cos (z4-2£«)=cos z * и sin (z4-2fort) =а
=sinz(fc=0, ±1, ±2, ...). Далее V z=x+iye=C (х, t/«=R)ez==
=ex-(cos y+isin у), |ег|=чеж>0, r^l/^vzeC.
Доказательство. По формуле Эйлера ег = ех+^ = ех X
X (cos у + i sin у), поэтому
ег+2м__ . (cos 2feit -J- i sin 2fen) == ег
Vze C (fe = 0, ±1, ±2, . . .),
так как для функций cosx и sinx (с действительными аргу-
ментами) число есть период, т. е.
cos2fcrc — cos 0 => 1, sin 2fe« = sin 0 = 0.
Из формул
cos (Zi-f-z2) = cos • cos zt — sin Zj • sin z2;
sin (zx+z2) = sin 2X • cos z2 + cos zx • sin z2
при zx=°z и za = 2feu имеем
VzeC (6 = 0, ±1, ±2, . . . ) cos (z + 2/г*) =
= cosz • cos2/»t— sinz’ sin2Z»t = cosz;
sin (z +2&it) = sinz.
Поскольку (ег=ех • (cosy + i sin у))=4(|ег| =. ex>0), то e~2 = 1/e
Vzec.
Следствие.
(cos z=0) 44 (z — ic/2 4- ^it),
(sin z = 0) 44 (z = (k=0, ±1, ±2,...)).
Доказательство. (cosz=0)^4(eix-|-e“,z=0)^(fji*= — 1), т.е.
(е2‘г ei("+2*»>) 44 (z = it/2 4- Л«); (sin z = 0) 44
^(etz—e~/z=0)44(e’<^==l=e2',w)^(z—k^ (k = 0, ±1, ±2,...)).
148
Замечание. В то время как для действительных z=xe R
имеем оценки |sinz|==|sinл|<; 1, |cosz| == |cosx|<l для zEC функ-
ции |coszj и Isinz| неограничены. В самом деле, при
z = х + iy^C cosz = (е‘г-}-е~1г)/2 = (elx • e~v-\-eix • еу)12 =
= [e~y • (cosx4-i sinx) 4-ey • (cosx—i sinx)]/2 =
— l(*y + e~v)cos x +1’ sin x(e~v — ey)]/2 => |cos z|2 —
= [(ey + e~tf)2cos2x-|- (e-y — ey)2 sin2x]/4 =
= [(e2y 4- 2 + e~2v) cos2 x 4- (e2y 4- e~2y — 2) sin2 xj/4 —
= Ke2y + e-2y)(cos2 x 4- sin2 x) 4- 2(cos2 x — sin2 x)]/4 =
= (e2y 4. e-2»)/4 4- cos 2x/2.
Но тогда при z = xe 4- iy имеем
lim (cos (x0 4- iy)|2 = 4-00.
l/-*+oo
§ 4. Теорема Вейерштрасса о приближении
непрерывной функции многочленами
Обобщенная теорема Вейерштрасса. Пусть
feC<*>((ai, bi)) (k=0, 1, 2, ...). Тогда Vе>0 и для любого от-
резка [а, Ь] cz (ai, bi) существует многочлен ЗР (х) такой, что
sup |D7(x) —D'^(x)|<s (Z«0, 1, 2..........k).
*6[o. *1
Доказательство. Пусть f eCW((ai, bi)). Рассмотрим
любой отрезок [a, 0] (—oo<ai<Ca<0<bi<4-00) такой, что
[a, ft]a (a, 0) c[a, 0Jc (at bi). Тогда, как показано в лемме 1
§ 12 гл. 2, ч. III [2], существует финитная (т. е. имеющая ком-
пактный носитель) функция феС(о°>((—оо, 4-°°)) и такая, что
,, . 11, ле[а, 6], *
Y I 0, xe(a, ₽), 0<ф(х)< 1 Vx €=
s(—-00, 4-00), [a, 6])Csupp4>cz(a, ₽)• Тогда для финитной
Функции F(x) = /(x)- ф(х) имеем FeC<ft>((—оо, 4-°°))>
Dzf(x)=|D7W. хе [a, Ь],
(О , хе [а, 0] (1 = 0, 1,2, . . . ,k),
suppDzFcz(a, 0). Поскольку FeC<ft>([a, 0|), то в силу компакт-
ности отрезка [а, 0] существует постоянная (1 = 0, 1,...
•••> k) такая, что |DzF(x)«A// Vx e[a, 0] (1=0, 1, . . . , k). Кроме
того, в силу теоремы Кантора функция DzF(x) равномерно не-
прерывна на отрезке [а, ₽], т. е. Ve>0 3 6(e)>0 такое, что
’•*1» *8е [а, 0], удовлетворяющих неравенству |х! — x8K6(s)
имеем
149
(I - О, 1, 2, ... , Л). (4.1)
Но неравенство (4.1) имеет место и Vxlt xt <= [a, 0]. Пусть
Xi<a<x2<p (или и |xt—x2]<6(e), тогда по построе-
нию финитной функции F(x) имеем
(|a - x2| < |xx - x2| < 6(8)) =» (ID'Fto) - D'F(x2)| =
= |D'F(a)-D'F(x3)|<e),
т. e. неравенство (4.1) имеет место ¥х2, х2е(—оо, +«>) та-
ких, что ]х3— хг|<8(е). Итак, D'F(x) (при 1 = 0, 1, 2, ... , k)
равномерно непрерывна на (—оо, -|-оо) и, как было уже отме-
чено,
sup |DzF(x)| = sup |Dz(F(x)|< M, (1=0, !,...,£).
—co<x<4-oo x€[a, 0]
Лемма. Пусть F(x) — финитная k раз непрерывно диффе-
ренцируемая функция (так что DlFеС((—оо, -}-оо)) при 1=
=0, k) и существует отрезок [а, [3] такой, что D‘F(x).=s
=0 V х е [а, £]. Пусть
фх(х) = (Х/тс) V» У F(t) exp {-Х(х —
— 00
хе(—оо, 4-оо), Хе (О,. Ч-оо).
Тогда ;
Я lim sup |Dz<px(x) — DzF(x)| = 0 (I - 0,. 1.....k)
X-»+oo x6(—«. +°o)
и, в частности,
Я lim sup |Dz?x(x) — Dzf(x)| = O
X-*4-oo b]
(1 = 0, 1, 2,..., k)V[a, b]d(a, ₽).
Доказательство. Отметим два утверждения: 1) DlF(x)
равномерно непрерывна на (—оо, -f-оо) при 1=0, 1, 2, ..., k;
2) sup |DfF(x)|= sup |DzF(x)|<Mi (I = 0, 1,..., k).
oo, 4-oo) 0]
Используя замену x—в силу свойств интеграла Пуйссона
имеем
(Х/1г)’/2У ехр(—Х(х—t)2}di=(X/K)'/2+“ exp {—ly*}dy =
—со —ОО
= 2(X/7r)V2+j° ехр{—Xj/2}dy=2(X/7c)V2 . (^/X)V2/2=i
о
и, в частности, имеем
D'F(x) ~ (Х/тг)1/2 Y DzF(x) exp {—)(x-t)^}dt Vх g= (—оо, +<>о). (4.2)
150
Далее в силу той же замены t = x — у имеем VX>0
Фх(х)“ (X/ir)‘/2 у F(x—у) exp {— ly*}dy, x s (—00, 4-00). (4.3)
— 00
Отметим оценку
exp (— W} ^Miexp{—X„p«)
VX, y^. (— 00,: 4-00) VX>Xe>0,
из которой в силу признака Вейерштрасса несобственный интег-
рал, зависящий от параметра х,
4-о° al
f TiF(x—У)ехр{—ly*}dy
—00
сходится равномерно на (—00, +°o)VX>X0>0 (при Z=0»l,2,...
.... k). Но тогда в силу теоремы о дифференцировании несоб-
ственного интеграла, зависящего от параметра, имеем из (4.3),
что фхеС<*>((—оо, +°°)), причем
4-о° л/
D'q>x(x) = (X/K)V2 f 2_ F(x__y)exp{_X^}^ =
Л, дх
=(№)'&‘у0 d'F(О ехр {— Х(х—t)*}dt V X > О, V х е (—оо, 4-00).
—оо
Далее поскольку |DZF(/)| < Mt V t е (—оо, 4- оо), то имеем
|D'<Px(x)|<(X/«)V2 Y |D/F(/)| ехр {_Х(х _ ty}dt < М' < 4- оо
—а»
Vxc=(-®o, 4*00), VX>0 (1 = 0,
Рассмотрим вытекающее из (4.2), (4.3) представление
DlF(x) — D'<fx(x) - (Х/к)‘/2. +f (d'F(x) - DlF(t)) exp (—X(x-t)2)dt,
—co
справедливое Vxe(—00, 4-°°) и VX>0 (1=0, 1, 2, . . , k). В си-
лу равномерной непрерывности функции DlF(x) на (—об, 4-°о)
Ve>0 Я6(е)>0 такое, что Vx, t s (—00, 4-00) при |х—t|<6(s)
имеем |D*F(x)—DzF(f)|<e/2. Но тогда Vxe(—00, 4-°°) имеем
сценку (Z»=0, 1, 2.....k)
(№)№ j IDz?(x)—DzF(t)| ехр{—Х(х—/)*}Л<
|д—Г|<8(«)
<е(Х/я)‘/2/2 • +f exp {-X(x — ty}dt - e/2.
151
Далее, используя ограниченность функции Dzf(x) на (—оо,
Ч-оо), имеем (при 1 = 0, 1, 2, . , . , k) |DzF(x)— Vx,
fe(—оо, 4-oo). Заметим, что Vx, (e(-co, +<х>) таких, что
|x —/|>6(е)>0, имеем оценку ехр{—Х(х—г)2}==ехр{—Х(х— <)’/
2}- ехр{—Х(х—02/2}«С ехр {—X62(s)/2} • ехр{—Х(х—/)2/2}, поэто-
му
(Х/к)'/2 f ]DzF(x)-DzF(/)| ехр {-Х(х—*)2}Л<
lx—
< 2Mz(k/x)«2 ехр {_х52(е)/2} Y ехр {-X(x-t)2/2}df —
= 23/2Mz ехр {—XS»(e)/2).
Но тогда Vxs(—оо, -|-оо) и l—Q, 1, 2, . . ., k имеем
lDz/(x) - D*<px(x)| < (X/u)!/2 f |DzF(x) —
lx—
— DzF(f)| exp {—Х(х-02}Л + (X/«)*/2 J |DzF(x) —
|x—t|>8(e)
— DzF(t)| exp {—X(x - t)*}dt < e/2 +
4-23/2^ exp {—X62(e)/2).
Для выбранных 8>0и 6(e)>0, очевидно, получаем
lim ехр {—Х82(е)/2} == О,
X—>4-оо
поэтому ЯХо(е)>О такое, что
ехр {—Х62(в)/2} < «/(25/2^/) V X > Хо(8).
Итак, при 1 = 0, 1, 2, ..., k V . > О Я Х0(е) 0 такое, что Vxe
е(—оо, 4-оо) имеет место оценка |DzF(x)—Dz<px(x)|<e/2-}-e/2 «в в
VX>Xo(e)>O, очкуда при 1 = 0, 1, 2, . . . , k
Я lim sup |DzF(x) — Dz<pi(x)| = О,
k-*4-OO —co<x<4-oo
нем лемма доказана.
Возвращаясь к доказательству обобщенной теоремы Вейер-
штрасса, видим, что при Z = 0, 1, 2...........k Vs>0 ЯХ0(е) >0
такое, что
sup |Dzf(x)—Dzq>x,(x)|= sup |DzF(x)—Dz<px,(x)|<£/2.
x&a, b] X6(o. b]
Ho Vx, t s(—оо, +°°) имеем представление
exp {—X0(x -1)*} =1+2 (->0)n(x-t)2n/nI
n—1
Положим
152
Qm(x, t)“f (-M”(x-027«i
/1=0
и заметим, что при фиксированном /е(—оо, +<*>) функция
Qm(x, t) есть многочлен степени 2т относительно х. Кроме
того, Vx, is[a, 0] имеем (при 1 = 0, 1, . . . , Л) оценку
Й 0 - Г/ ехР <—W -О8} =
2 (-Мп
2п • (2п—1)...(2л—Z-|-l)(x—t)in-lln\
<rm,z(X0) 2/г- (2/1—1)...(2п-Ж)Х
n=m4-l
x (p — a)2n-7nl <+ОО,
причем lim rTO,/(Xe) = 0. Теперь Vxg(—00, 4-00) положим, ис-
пользуя финитность функции F[t),
^m(*) = (W'2T ^(0-Qm(x, t)dt =
3
= Mi/2^(t)Qm(x, t)dt.
a
Очевидно, функция ^m(x) есть -многочлен степени не выше
2т. Но тогда, учитывая финитность функции F(f) (так,; что
F(t)=O V/ е [а, р]), имеем Vxe[a, J] представление (при 1=0,
1» • .. , k)
D'<Px.(x) — D^m(x) =
’ д1
д1
“ (W’')1'2/ F(f) Гexp {-K(x-ty} - f Qm(x, t) 1 dt,
ox ox
откуда в силу неравенства |F(f)K Мо Vf <= (—оо, 4-00) имеек®
(при 1=0, 1, 2, . . . k) оценку
sup |Dz<px.(x)— D/58m(x)|<
*e[a, 0]
3
<(W'2- sup f|F(O| .
x€[a. Pl i
0-
dz
exp {-X0(x- < (X0/K)‘/2Jf0(₽-a)rm> Z(XO).
Поскольку
lim rm.z(Xo) = 0 (Z = 0, 1, . . . s A),
15$
то для выбранного е>0 и при /=0, k Я/п0 gN такое,
что 0< гт„ ДХ0) < е(к/Х0)1/2/2Л4в(р—а), откуда
sup |D'<px.(r) —Dz3Mv)|<e/2 (1=0, 1, . . . , k).
*в[а. 0]
Но тогда, очевидно, имеем (при 1=0, 1,.... k) оценку
sup |Dzf(x) — D'^WK sup |D'/(x) — Dzq>x,(x)| 4-
*eia, b] (a, b|
4- sup |D?(pXa(x) — D^m,(jf)|<e/2 + s;2 = 8.
[a. 01
Итак, для функции feC^((a1( &J) для любого отрезка [а, Ь]с
С(в1« bj) и Ve>0 существует многочлен SPm,(x) степени не
8ыше, чем 2/пв, такой, что
sup |Dz/(x)- Dz^m.(x)| <е (1 = 0, 1, .... k).
х£[а, d]
Замечание. Изложенный выше метод позволяет без особых
затруднений доказать многомерный аналог обобщенной теоремы
Вейерштрасса в следующей формулировке: пусть Q с: Rn — от-
крытое множество. Тогда для функции (k=0, 1, 2,-.)
для любого компактного множества /(ей и Vs>0 существует
многочлен ^(xi, х,, . . . , х„) такой, что для любого мультиин-
декса :=(/ь , in), о<|/|=2
i—1
а|г7(х)_________а|г|^(х)
dxi1. . . дх‘пп дх1{ . . . дх^
е.
sup
хек
(Для доказательства нужно использовать вспомогательную
усредняющую функцию, выражающуюся через кратный интег-
рал (см. ч. V, гл. 2, § 4)
4-00 4-00
<Px(x)=(V*)»'2 • f . . f f(tv...U„)X
—оо —оо
X ехр | — Х-2 (X,—2i)2 )dfx. . . dtn.)
I is»l J
Следствие (теорема Вейерштрасса). Пусть feC([a, &]). Тогда
V 8>0 существует многочлен &>(х) такой, что
\f(x)—9> (х) | < е V х е [а, Ь].
В самом деле, если feC([a, &]), то для [а, Ь]с(а, р) С
<z[a, p]c:(ai, bi) можно ввести непрерывную на (ait bi) функ-
цию
fi(x) =
’ f(x), xe[fl, 6],
линейная, х^[л, a], Р],
. О, х<= (ab aJUlMJ
454
такую, что fi^C((at, bi)), f(a)—fi(a), f(b)=h(b). Применяя к
функции fi обобщенную теорему Вейерштрасса при k=0, получа-
ем утверждение следствия.
Замечание. Если С ([а, Ь]) — полное метрическое простран-
ство с метрикой Чебышева
F(f, g) = sup |f(x) - g(x)|,
й^х^Ь
то V e>0 существует многочлен ^(х) такой, что p(f, ^Хе, но для
многочлена очевидно, существует многочлен Q(x) с рацио-
нальными коэффициентами такой, что р(.9\ Q)<ZR, откуда име-
ем р(/, @)<2e. Поскольку множество {@(х); хе[а, Ь]} всех мно-
гочленов с рациональными коэффициентами не более чем
счетно, то тем самым доказана сепарабельность пространства
С(|о, Ь]) (т. е. существование в С([а, 6]) счетного всюду плот-
ного множества).
Определение. Функция f(x) допускает на отрезке [о, Ь]
равномерное приближение многочленами, если V е>0 существует
многочлен SP (х) такой, что \f(x)—(х) | <8 Vx е[а, &].
Замечание. Если функция f(х) допускает на отрезке [а, Ь]
равномерное приближение многочленами, то
f(x)= ад, хе [а, Ь], (4.4)
где 3°п(х) (п —номер, а не степень многочлена ЗМх)) — много-
член и функциональный ряд (4.4) сходится к функции f(x)
равномерно на отрезке [а, £>].
В самом деле, если функция /(х) допускает на отрезке
[а, 6] равномерное приближение многочленами, то VneN
существует многочлен Qn(x) такой, что |/(х) — Q„(x)|< 1/n Vx е
е [а, Ь], т. е. Qn(x) f(x) на [а, &]. Тогда, полагая
ад = <?х(х), ад = Q„(x) - Q„_t(x) V п > 2,
П
видим, что @п(х) = 2 3\(х), поскольку Qn(x) гХ Дх) на [а, &],
*=i
то функциональный ряд (4.4) сходится равномерно на [а, Ь] к
Функции /(х).
Следствие (из теоремы Вейерштрасса). Любая функция
fsC([a, &]) допускает на отрезке [а, Ь] равномерное приближе-
ние многочленами; или, что то же самое, любая функция fe
<^С([а, Ь]) разлагается на отрезке [а, Ь] в равномерно сходя-
щийся (к ней) ряд многочленов.
Замечание. Вспоминая, что в степенные ряды разлагаются
только бесконечно дифференцируемые функции, видим, что пере-
ход от степенных рядов к рядам из многочленов значительно рас-
ширяет класс функций, разлагающихся в такие ряды.
155
§ 5. Интегралы Эйлера
Интегралами Эйлера называются несобственные интегралы ви-
да
Г(х) = [ t'-'e-W (интеграл Эйлера 2-го рода) и
6-
—1
В(х, у) = f (интеграл Эйлера 1-го рода).
о«-
Теорема (о свойствах гамма-функции Эйлера).
1. Функция
Г(х) = У tx-ie-'dt (5.1)
0<-
определена на (0, +<»), причем Г(х)>0¥х>0 и несобственный
интеграл (5.1) сходится равномерно на любом отрезке [х0, Хю] с:
cz (0, 4-оо), так что Ге С((0, +<»)).
2) V х е (0, +°о) и v m е N существует
Dmr(x)==+f° /«-1(1пОоте-‘Л, (5.2)
о—
причем несобственный интеграл (5.2) сходится равномерно на лю-
бом отрезке [х0, XoJc: (0, +<») и D”Te С ((О, -|-оо)}, в частности,
D2r(x)>0 V х>0, так что функция Г(х) выпукла вниз на |
(О, +°°) и достигает значения своего положительного минимума |
на интервале (1,2).
3) Г(х) удовлетворяет функциональному уравнению Г(х+1)=
=х-Г(х) Vx>0.
4) Г(п+1)=п! VneN, и Г(1/2)=л1/2,
5) Г(х)-Г(1—x)=n/sin(n-x) Vxe (0, 1). ;
Доказательству. 1) Изолируя особенности, имеем
Г(х) =+f = 1х-1е~*сН +
о— о<-
+ t'-'e-tdt^l^ + I^x).
1
Очевидно, при любом финксированном х>0 имеем представление
(i+o(i)) (f-»+0),
откуда в силу теоремы сравнения видим, что несобственный ин-
теграл ,
/!(x)=J tx-'e-‘dt
о-
156
сходится лишь при х>0. Но при любом х0>0 имеем Vx>xo>O
опенку tx~l • e-t V t е (0, 1), из которой в силу призна-
ка равномерной сходимости (несобственных интегралов) ви-
дим, что несобственный интеграл 1г(х) сходится равномерно
на ко, +«>), и поскольку и(х, . e-feCx, z((0, н-оо)х|Д
4-00)), то 7iSC((0, +=*>)). Далее, Vxe (О, Ло]сг(О, +©о) име-
ем оценку
e-< = r*-i. g-‘/2. в-'/2<• е~^2 • е~№ Vi>l.
Но lim tx»~l ♦ е_//2 = 0, поэтому существует постоянная С(Х0)
/->4-00
такая, что е_//2<С(Х0) Vt > 1, откуда имеем
F-* • е-'<ОД>) • в"*72 Vx «= (0, X0],Vf <= [1, 4- оо)
<г *
и, вновь применяя признак Вейерштрасса, видим, что несобст-
4-00
венный интеграл /а(х)= J tx~l • e~fdt сходит,ся равномерно
1
на (0« Xo]VXo>O. Применяя теорему о непрерывности равно-
мерно сходящегося несобственного интеграла, видим, что
ZteC((O, +°о)). Итак, ГеС((О, 4-оо)), причем несобственный
интеграл (5.1) сходится равномерно на любом отрезке [х0,
Хо\ CZ(0, 4-оо). Заметим, что при фиксированном х>0 имеем
=e-t • [(х-1)М-2 — <«-»] . /«-2 • е~‘ • (х-1—Г),
так что точка t = x— 1 есть точка максимума функции <р(/)==
= u(x, t), поэтому положительная функция u(x, i) такова, что
ее график имеет горб высоты и(х, х—1)>>0 при t = x — 1_>0,
который удаляется направо при х—>4-оо. Можно показать, что
несобственный интеграл (5.1) сходится на (0, 4- оо) неравномер-
но.
2) Формальное дифференцирование несобственного интеграла
(5.1) дает после изолирования особенностей Vx>0 и VmeN
представление
J„(X) = +f t*-' (In t)« e-*dt = J + +f » Jm. 1 4- Jm, 2.
0«- 0«- 1
Ho
f*-1 • |ln t\m • e~f < tx>~1 • |ln Z|m =
— Г.-»"8 - p • |M«] Vxo>O, V8e(0, x0),
Vxe [x0, +©o) и Vt s(0, 1],
и поскольку lim £s • |lnf|m = O, то существует постоянная
ci(xo)>O такая, что Vxo>O, Vxe[x0, 4-oo) и V8e(0, x0) имеет
место оценка
157
Г-1- Ilntp. V/s(O, 1],
откуда в силу признака Вейерштрасса следует, что несобст-
венный интеграл Jm, i(x) сходится равномерно на [х0, -f-oo)cz
с:(0, -f-оо). Далее VX0>0 имеем V.vs(0, Хо] оценку
/*-» • (ln/)m • • (Int)m . e-‘/2 V/e[l, 4-eo).
Учитывая, что
lim *х«''1(1п0же-‘/2 = 0,
видим, что существует постоянная Са(Хо)>О такая, что
О</*•-’ • (Inг)"1* e-</2<JC#(X,)Vre[l, 4-оо),
откуда V х s (О, Хо] имеем оценку
0<Г~!(In О'" • е-<<С2(Х0)е-'/2 V/g= [1, +°о).
По признаку Вейерштрасса несобственный интеграл Jm, 2 (х) схо-
дится равномерно на (О, Хо] VXo>O. Итак, несобственный ин-
теграл Jm(x) сходится равномерно на любом отрезке [х0, Х0]с:
а: (0, 4-оо). Поскольку
и(х, 0 = ^-‘(In tre-t е= Сх, t((0, +00) X (0, ч-оо)),
дхт
то, применяя теорему о дифференцировании несобственных
интегралов (зависящих от параметра), Ухе (О, +00) hVz»eN
видим, что Я D тГ(х) = 7т(х), где D"TeC((0, +°°)) и, в част-
ности,
£)2Г(Х)—.+у° t*-1 • (In/)2 • e~zd/>[0 Vx<= (0, 4-00).
0-
Но тогда функция Г(х) выпукла вниз на (0, Ч-оо), причем
4-00
DP(x)t f на (0, 4-°°)- Заметим, что Г(1) = f e~zd/=l, поэто-
о
му, применяя теорему об интегрировании по частям для. не- .
собственных интегралов, имеем
Г(2) = Y t • e-»d/ = — Y/de-< =
=— te~*
+ j e~‘dt = Г(1)=1.
о
0
Итак, Г(1)=Г(2). По теореме Ролля ЙЦ-е(1, 2) такая, что
Dr(lj)=O, причем D2r(g)>0. В точке x=g функция Г(х) имеет
минимум (единственный в силу выпуклости вниз функции Т(х))»
причем Г(х)>0 Vх>0.
158
3) Применяя теорему об интегрировании по частям для несоб-
ственных интегралов, имеем
V х > 0 Г(х+1) = +J° Г . e-t dt = — Т 1хйе~* =
о о
(/==4-00 4-00
+Х * f t*~l • e-tdt = x • Г(х),
t=o oL
откуда Г(х+1)=х- Г(х)¥х>0. В частности, при neN име-
ем Г(п+1)=п> Г(п)=п • (л— 1)Г(л—1)= . . . =л-(п-1) . . . 3-2Х
ХГ(2), т. е. Г(п+1) = п! Vne=2V.
4) Вспоминая интеграл Пуассона, имеем, делая замену пере-
менной интегрирования,
j =z2(dt = 2zdz) Г(1/2) =
= J £-1/2 e^dt = 2 f exp (—z2)dz = it,/2,
о- 0
откуда Г(1/2) = я1/2.
5) Для доказательства формулы дополнения
Г(х)-Г(1—x)=jt/sin(jtx) Vxe (О, 1)
проще всего применить теорию вычетов из теории функций ком-
плексного переменного (ТФКП). В § 2 гл. 4 формула дополнения
будет доказана с помощью теории рядов Фурье.
Замечание 1. Из доказанного функционального уравнения
Г(х4-1)=х-Г(х) V х>0
вытекает vneN соотношение
Г(х-}-1)=Х"(*—1)*-(х—п)-Г(х—п),п<.х^п+\, (5.3)]
поэтому гамма-функцию Эйлера (5.1) можно рассматривать как
«факториал» для нецелых значений х>0.
Замечание 2. Поскольку Vx>13neN такое, что 0<3]
<х—п<1, то из соотношения (5.3) следует, что гамма-функцию
Эйлера можно свести к функции Г(«), рассматриваемой лишь на
полуинтервале (О, 1].
Теорема (о свойствах бета-функции Эйлера).
1) Функция
В(х, у) (5.4)
о<-
°пределена V (х, у) е (0, +<») X (0, +°°)> причем несобственный
интеграл (5.4) сходится равномерно на множестве [хо, +°°)йЗ
+оо) v х0>0, V «/о>О.
2) В(х, у)=В(у, х) Vx>0, V у>0.
159
3) vх>0, Vу">0 имеет место представление
В(х, у) = ’j° zx~1/(l+z)3c+v^ = +f zy-‘/(!+?)»+* dz.
о— О—
4) Bfx-f-1, #-|-1)=х/(х+#+'1)-В(х, y+l)—yf(x+y+l)X.
ХВ.(х+1, //); В(х+1, г/+1) = ху/((х+у) (х-Н/+4))- В(х, у)Чх>
>0, чу>0.
5) В(х, у)=Г(х)-Г(у)/Г(х+у)Ч х>0, V у>0.
Доказательство. 1,) Изолируя особенности, имеем
1/2 -»1
В(х, y) = f tx~l • (1—О*"1 ♦ dt+ f <*-* • (1— ty~ldt=
0- 1/2
s Ii(*> У) -г It(x, y).
Для любых фиксированных x и у имеем представления
t»-i . (i_y-i = p-t . (1 +o(l))(f-*4-0)
и
. (1-/)у-1 = (1— . (I 4-0( 1 ))(/_> 1—0),
откуда в силу теорем сравнения (для несобственных интегра-
лов) видим, что интеграл /г(х, у) сходится V х>0, а интеграл
Zt(x, у) сходится V 1/>0. Итак, интеграл (5.4) сходится Vx>0
и Vjz>0« Далее, Vx0_>0 и Чу0>0 имеем оценку Vx>x0,
Чу > у0 • (1 — О»"1 < ♦ (1 — <= (0, 1),
яз которой в силу признака Вейерштрасса вытекает равномерная
сходимость несобственного интеграла (5.4) на множестве
[х0> + °°)Х[Уо, +;оо), и поскольку для подынтегральной функции
имеем
fx-i . (1—i)y-i s С, г((0, +оо)Х(0, -J-оо) х[(0, 1)),
то в силу теоремы о непрерывности (равномерно сходящегося ин«
теграла) имеем В е Сх>у ((0, +<») X (0, + оо)).
2) Замена z=*l—t(dt^ — dz) дает
В(х, у) = fz1'-1 • (1—z)x~ldz= В(у, х)=^>
о--
=>(В(х, I/) -= B(t/, х) Vx>0, V«/>0).
3) Замена / = z/(l 4-z) дает dt = (i +z)~2dz и 1—/ = l/(14-z)»
откуда
Z*-1- (l+z)~2dz
(i+z)35-1 -aw1
и в силу симметрии имеем
160
В(х, у)= J z*-’/(l +z)x+vdz.
о_
4) Интегрируя по частям Vx>0 и Vy>0, имеем
В(х-|-1, y+l)==7«* • (1 — tydt-
oi-
= "j (1—0Wx+,/(x+1))=**+‘. (1 -07(x+1) Г +
0*— |r—0
+ y/(x+l) • 7r+‘ • (y-Vy-'dt^
(H0 tx+l=tx — tx • (1— t))
= y/(x+l) • (1—fy-'dt-^ tx . (I—/)ydij =
= 1) • (B(x+ 1, у)—B(x + 1» &+!)]=»
•*((x+y+i)l(x+y) B(x+i, y+l)=yl(x+i)- B(x+1, y))~S>
•=»(B(x4-l, y+i)=yl(x+y+i) • B(x-Hs y)).
Очевидно,
B(x4-1, y+l) — xl(l+x+y) • B(x, iH-1) = xl(l+x+y)X
x 7 tx~l о - *ydt> в(х, у+o = -
О—
=7 tx~l ’ (^—tydt—llx • 7 U —t)ydtx = y/xx
o«- oi-
X^tx . (\-ty-idt=y/x . 7 tx~l • (1—(1— t)){l-t)^dt =
o— o'L
= y!x- (B(x, y) — B(x, f/+l))-=»((l+^/x)B(x, f/+l)=
~ylx • B(x, z/))=^(B(z, y+\) = yl{x^y) • B(x, y)=^
-»(B(x+l, ^+l) = x/(l+x+y) • B(x, t/+l) =
= X0/(I-J-x4-j/)(x-H) • B(x, y)).
5) Используя представление
B(x, zw-‘/(l+zf+»dz Vx>0, Vy>0, (5.5)
Делаем при a>0 замену u~z^<x так, что d«=a-1dz и
f du=a~s J z‘~l ♦ e~zdz =* r(s)/ar, (5.6)
0<-
поэтому v z>0, x>0, y>Q имеем
** “ Л. И. Камынин 161
J . е-К1+г)Л=Г(х+1/)/(Ц-2)«+У,
oi-
откуда
Г(х+у) • B(x, у} = J° Г(х+я) • z)--‘/(l+z)«+^z«
= +f <fz+J zy-1 • tx+y~l • exp{—/(14-z)}dt.
ib- 0—
Полагая
/(z, t) = zv~l • tx^-y-‘l • exp {—2(1 4- z)},
имеем
Г(х-Н) • B(x, t/) = 4f° dz J f(z, t)dt.
Пусть, сначала х>1 и z/>l, тогда имеем:
a) f(z, 2)>0Vz>0, 2>0 и в силу предположения х>1 и
р>1 видим, что feCz, t([0« 4-оо)Х{0, 4-°о)):
б) функция J /(z, t)dt= г»-1 • J 2*+у-1 . ехр {— 2(1 4- z)} dt =
о о
== Г(х4-у) • z»-1/(i4-z)x+vec«([°, +°°)) (так чт° у—1>о> *>1);
в) функция f /(z, 2)dz=e“/ • 2Х+*-1 . J zy_1 • exp {— tz}dz
о 0
= . t*+v-i . r(y)/t> = Г(у). 2»-‘. exp(-2)eCX[0, 4-00)).;
г) существует повторный несобственный интеграл
Т dz +f f(z, t) dt = Г(х 4- у) • B(x, у).
Из а) — г) вытекает, что выполнены все условия следствия к
теореме 1 о замене порядка интеграции в повторных несобственных
интегралах (из ч. IV, гл. 2, § 4), поэтому в силу '(5-5) и (5.6) име*
ем
Г(х4-г/) • В(х, у) = f dt С /(z, t)dz =
4«оо Г 4*°о "1
у 2*-1 • е-/ • М zy~l ' ty • е~н J dt =
tx~i . e~*dt = Г(у) • Г(х) =>
(В(х, у) = Г(х) • Цу)/Г(х+у) V х > 1, V у > 1).
182
Пусть теперь х>0 и у>0, тогда по доказанному имеем
В(х+1> у+|1)=Г(х4-1)-Г(1/+1)/Г(х4-у+2). Но в силу доказан-
ных ранее свойств гамма- и бетта-функций Эйлера имеем равен-
ства В(х+1, у+1)=ху/(х+у) (х+у+1) В(х, у), Г(х+1).«=х-Г(х),
Г(«/+1) =УГ(У), Г (х+у+2) = (х+у +1) • (х+у) х T(x-j-y), откуда
ху/(х+у) (х+у+1) -В (х, у) =
=х-уГ(х)-Г(у) / ((х+у+,1) (х4-у)Г(х+у))=>
=>В(х, у)—Т(х) Г(у)/Г(х+у) Vx>0, Vу>0.
Замечание. Теория интегралов Эйлера позволяет вычислять
часто встречающиеся в приложениях интегралы вида
-»я/2
Ip,q= J sinpf • cosq tdt, p> — 1, q> — 1.
o2
Замена sin® t = z дает cos® t = 1 — z,
2 sin t • cos t • dt =. dz, di = (1 /2) • z~*/® • (1 — z)~Vzdz,
откуда
Ip, g = (1/2) • ']•’ z<p-'»/2 • (1—z)<«-Wz =
0«-
= (1/2) • "Г* z^+^-i . z<g+i)/2-idz=A.
o«-
->/,., = (1/2) ♦ B((p + l)/2, (q + l)/2).
Например,
я /2
J sin’x • cos4xdx = (l/2) • B(2,5/2) =
= (1/2) - Г(2) • Г(5/2)/Г(9/2) = (1/2). (3/2). (1/2).Г( 1/2))/
/((7/2) • (5/2) - (3/2) • (1/2) . Г(1 /2)) = 2/35.
11*
Глава 4
РЯДЫ ФУРЬЕ
§ 1. Ряды Фурье по ортогональным системам функций
Определение. Тригонометрическим рядом называется
функциональный ряд вида
а012(ancosnx+ bnsinnx), (1.1)
ап, bn, xeR.
Вспоминая формулы Эйлера cosx — (eix-\-e~‘x)/2, sinx = (е1х—
— e~‘x)/2i=z — i(eix — e~ix)/2, видим, что тригонометрический ряд
(1.1) может быть записан в виде
«о/2 + 2 (ап(е,пЛ + e~inx)/2— ibn(einx — e-inx)l2)
/1=1
или, полагая с0==а0/2, cn = (an—ibn)/2,. с_„ = (an4-i'6n)/2, heN в
виде
£ cneinx ' (I-2)
Л—— оо
— комплексная форма тригонометрического ряда (1.1).
Замечание. Если тригонометрический ряд (1.F) сходится на
(—оо, +оо) к функции f (x), то его сумма f(x) является периоди-
ческой функцией с периодом 2л.
Определение. Пустр f е/?[—л, л]. Тригонометрический ряд ,
(1.1) называется рядом Фурье для функции f(x), если коэффици-
енты этого ряда вычисляются по формулам Фурье
ап = (1/к) • Jf(t) • cosn/df; n = 0, 1, 2..
—П
&n = (l/w) . Jf(O • sinn/dl; n=l, 2, . . .
— к
Если ряд (1.1) есть ряд Фурье для функции f <=/?[—л, л), то ис-
пользуется запись f^ao/2+ts (an cos пх+bn sin пх).
и=1
Замечание. Если fеЯ[—л, л] и тригонометрический ряД
(1.1) является ее рядом Фурье, то запись в комплексной форме
ряда '(1.1) дает 2 спе’яж»
оо
164
где
сп = (1/2я) • Jf(O • e~intdt (п = 0, ±1, ±2, . . . ),
—7t
сп = (an — ibn)/2, c^n = (an + ibn)/2 (n e N),
^ — комплексные коэффициенты ряда Фурье функции f(x).
Определение. Функции fi, f2^R[a, Ь] называются (вза-
ъ
имно) ортогональными на отрезке [а, Ь], если S fl(x)-f2(x)dx=ft.
а
Система функций f ={f} с; R[a, Ь] называется ортогональной
системой на отрезке [а, 6], если любые две (различные) функции
из этой системы взаимно ортогональны на [а, Ь].
Теорема. Система функций {1, cosx, sinx, cos2x, sin2x,...}
ортогональна на отрезке [—л, л].
Доказательство. Отметим равенства
г «. j I 2^> k = О
| cos kx dx= (
-i I 0, fe = ±1, ±2,...;
Jsin/txdx = O (k — Q, ±1, ±2, . . . ).
— Я
Но тогда V tn, n e Z имеем
Я 7Г
Jcos/nx- cosnxdx = (l/2) • Jfcos(m-f-n)x +
—n , —л
, . . , , ( Л, m = n
4- cos (tn — n)x]dx = {
(0, tn =/= гц
Jsinmx- sinnxdx = (1/2) • J[cos(m— n)x—
— n — я
— cos(/n4-n)x]dx = l ’
(0, m^=n-,
« n
j cos tnx • sin nx dx = (112) • J [sin (n + m)x —
-~Ж —It
— sin (n — tn)x] dx = 0.
Теорема. Всякий равномерно сходящийся на (—оо, 4-оо)
тригонометрический ряд (1.1) является рядом Фурье для своей
суммы.
Доказательство. Пусть тригонометрический ряд (1.1)
ходится равномерно на (—оо, 4-00) к функции f(x), так что
Дх) = а0/2 4* У, (a„cosnx + &nsinnx) Vx€=(—00, 4*°°).
л—1
165
Поскольку
an cos nx4-&n sin пх е C((—oo, 4-.'oo)),
то в силу теоремы о непрерывности суммы равномерно сходяще-
гося функционального* ряда из непрерывных функций имеем
/еС((—оо, 4-оо)) и, в частности, feC([—л, л]))=^-
=> (f е/?[—л, л]) Л (f еВ([—л, л])). Заметим, что функция
f(x) имеет период 2л, так что feB((—оо, 4-00)). Но тогда при
k=Q, 1, 2, ... имеем равенство
/(х) cos kx = (а0/2) • cos&x 4-
4-00
+ 2 («nCosnx 4-6„sinnx) • cosfcs, (1.3)
п=4
и поскольку f(x), cosfexeB ((—оо, 4-00)), то по теореме об ал-
гебраических действиях над равномерно сходящимися функцио-
нальными последовательностями (из ч. IV, гл. 2, § 4) ряд (1.3)
сходится равномерно на (—оо, 4-°°) (и, в частности, на [—л, л])
к функции f(x) -cos kx. Но тогда по теореме об интегрировании .
равномерно сходящихся функциональных рядов имеем
j f (х) cos kx dx — (а012) J cos kx dx 4-
—n —n
4-00 / те
+ S (an • fcosnx- cos for dx 4-
n==4. \ — n
4- bn • jsinnx- cosfexdxj.
—75 J
Но в силу ортогональности на [—«, системы 1, cosx, sin®,
cos2x, sin2x, . . . имеем при k=Q, 1, 2, . . . равенства
п
J /(х) cos kx dx = как.
—те
Аналогично доказываются (при k—1, 2, ...) равенства '
те
jf (x) sin kx dx = u&ft.
—те
Итак, коэффициенты ап и Ьп в тригонометрическом ряде (1.1) яв-
ляются коэффициентами Фурье для суммы ряда (hl), т. е.
4-00
f ~ ай12 4- У, («п cos пх 4- bn sin пх).
n=t
Замечание (см. [2]). Не всякий тригонометрический ряд
(1.1) является рядом Фурье для своей суммы. Можно доказать»
что ряд
2 sin nx/ln п = 5(х)
п»2
166
I
сходящийся (по признаку Дирихле) Vxg(—оо, 4-оо) не явля-
ется рядом Фурье для своей суммы. Однако (см. (2]) если
SeC([—те]) (или даже S е Я[—к, к]), где
4-00
5(х) = а0/2+ 2 (ancosпх + &nsinпх) Vхе[—«],
71=1
то ап и ъп будут коэффициентами Фурье для суммы 3(х).
Замечание. Пусть I, I]. Тогда если ф(х) — нечет-
i
ная функция, т. е. <р(—х) =—ф(х) Vxe [—I, 0, то С <р(х) dx = О,
—i
если же <р(х) — четная функция, т. е. <р(—х)=<р(х) Vxe[—I, 0,
то
I I
J q>(x)dx = 2 J q{x)dx.
-t о
В самом деле, пусть <р(—х) =—<p(x) Vxs[—I, Z], тогда, де-
лая замену х = — t, имеем
I о t о
f ф(х)йх= J ф(х)Фс-|- [ ф(х)йх=— f ф(—0 dt +
-I — I О I
+ J ф(х)йх«= у (ф(-*) + ф(х)) dx «0.
о о
Аналогично для четной функции ф(х) имеем
J ф(х)£/х= у [ф (—х) + ф(х)] dx = 2 у ф(х)</х.
—io о
Следствие. Пусть тригонометрический ряд (1.1) есть ряд
Фурье для функции —л, л]. Тогда: а) если функция f(x)
четна на [—л, л], то ее ряд Фурье (1.1) содержит только косину-
сы, причем для коэффициентов Фурье имеем ап — (2/it) X
Xy/(0cosn£d£ (л = 0, 1, 2, . . .), Ь„» 0 Vne N и f~a0/2-|-
о
+оо
+ 2 ««cosnx; б) если функция Дх) нечетна на [—к, к], то ее
л=1
Ряд Фурье (1.1) содержит только синусы, причем ап = 0 (п=0,
2, . . .), ьп = (2Л0 • у f(t)sinntdt п eN и
О П=^1
Доказательство. Если f(x) четна на [—л, л], то функции
Mx) cos пх четны, а функции f(x)-sinnx нечетны на [—л, л], так
что в силу замечания имеем
167
(ап = (2/те) • у f(t)cosntdt (n==0, 1, 2, . . .),
о
6n = O V/zsN)=Hf ~а0/2 + 2 ancosnx).
Л=1
Если же f(x) нечетна на [—те, те], то функции f(x)cosnx нечет-
ны, а функции f(x)sinnx четны на [—те, <], и в силу того же
замечания имеем ап=0 (л=0, 1, 2, . . .) и 6п=(2/те)- J f(t) sin ntdt
о
VneN, т. е.
+°О
f — У, b„ sin пх.
Л=1
Определение. Пусть fe/?[—I, /]. Тогда тригонометричес-
кий ряд
4-00
а0/2 + У (ап cos (пк/Г)х + bn sin (nn/l)x) bn sin (nn/l) x) (1.4)
n=l
называется рядом Фурье для функции f(x) на отрезке [—I, ес-
ли коэффициенты этого ряда вычислены по формулам Фурье
an =(!//)• у /(/) cos (дте//)/Л; п=0, 1, 2, ...»
bn = (1/Z) • J f(t) sin п е N.
Замечание. Если ряд (1.4) сходится на (—оо, -|-оо) к функ- *
ции f(x), то его сумма f(x) есть периодическая функция с перио-
дом 21.
Следствие. Пусть тригонометрический ряд (1.4) сходится!
равномерно на (—оо, 4-оо) к функции f(x). Тогда этот ряд явля-
ется рядом Фурье для своей суммы f(x).
Доказательство. Сведем следствие к доказанной ранее
теореме для рядов вида (1.1), заметив, что замена х=Ы/я пере-
водит ряд (1.4) в ряд (1.1), имеющий своей суммой функцию
F(t)^f{Utfn). Но тогда в силу доказанной ранее теоремы (по-
скольку ряд (1.1) сходится равномерно на (—оо, 4-оо) к функции
F(t) имеем для его коэффициентов представления
an = (l/«). yF(t)cosn/dt (n=0, 1, 2, . . .),
—7t
Ъп = (1 /те) • у F(t) sin nt dt\ n£ N.
168
Делая в этих формулах Фурье замену переменной интегриро-
вания t=^x]l, получаем, учитывая равенство F(/)=f(Z-Z/it)=f(x),
формулы
ап = (l/l)' J f(x) cos (mll)xdx; п g= No,,
-i
bn = (1/0 - J f(x) sin {nv/l)xdx; h €= N.
Рассмотрим теперь пространство 7?[a, Ь] функций, интегрируе-
мых по Риману (на [а, Ь]), и введем в нем скалярное произведе-
ние по формуле
ь
(ф, ф) == j ф(04(0^ V <р, ф е /?[а, Ь].
а
Тогда 1?[а, Ь] становится евклидовым пространством. Условие
ортогональности для двух функций ф, ф G /?[а, &] записывается
в виде (ф, ф) = 0. Введем в пространстве /?[а, Ъ\ функции»
ф-»||ф||, положив ||ф|| = ((<р, ф))1/2. Эта функция обладает всеми
свойствами нормы, кроме одного, 1) (||ф||=:0)4=>(ф^0), так как
ь
из равенства |ф2(х)йх = 0 не следует, что ф(х) = 0 на [а, &].
а
Однако если отождествлять функции из 7?[а, 6], отличающие-
ся друг от друга на множестве „меры нуль*1, то функция
ф-»||ф|} становится нормой в линейном пространстве R[a, 6]«
Определение. Пусть {ф,(х}}, ф(е7?[а, b] (i=l, 2, ...) —
ортогональная система на [а, Ь], т. е. (ф£, ф/)=0У1'=/=/. Тогда ряд
вида 2 спфп(х) называется ортогональным рядом (по система
Замечание. Пусть {ф/(х)} (i=l, 2, ...) — ортогональная
система в /?[а, &], причем (ф,, Ф<)={ ^(t)dt =^^>0 \i. Тогда
ь
любая подсистема {ф^х), Ф«,(х), ...» ф<т(х) будет линейно не-
зависимой на [а, Ь], т. е.
(2 с/Ф»/(х) = 0 V хЕ[а, ьЛ=»(сг = О; 1 = 1» 2, ... , т).
v=i /
В самом деле, пусть функция Ф»ь(х) фиксирована (при =
^( ,)2* ' ’ т^* Т0Гда’ ИСПОЛЬЗУЯ ортогональность системы
(2 с* • Фц(х> IVх) = 0 V X е [а, 6]) =>
16»
=> ^2 cr(<Pi? <PiA) = = о J,
no (kft>0; fe=l, 2, ... , m}=$(ch=O-, k—i, 2, ... , m), т. e. под-
система {<Рй(х)....ф4т(х)} линейно независима на [а, 6].
Определение. Ортогональная система {(ft(x)} (i=l, 2, ...)
в R[a, Ь] называется нормированной, если
. \ я ( 0, i j,
(Фь <Pj) = 6;/== , .
I 1, 1 = /-
Замечание. Если {tp^x)} (i=l, 2, ...) — ортогональная сис-
тема в 6], причем (<р/, фг) =Xt->0 V i, то система функций
{ei(x)} (i=l,2, ...), где ег('х)=ф,(х)/((ф;ф1))1/2, будет ортонор-
мированной в 7?[а, &].
Пример. Тригонометрическая система ' 1 / ]/"2тс, cos х/ J/rc,
sinx/}/тс, , cosnx/]Ar, sinnx/]At, . . . , является ортонорми-
рованной в 2?[—тс, тс].
Определение. Пусть b] и {ф,(х)) (i=l, 2, ...) —
ортонормированная система функций в R[a, &]. Тогда ортогональ-
ный ряд
2 спФп(х), х<=[а, 6] (1.5)*
п=1
называется рядом Фурье для функции f(x) (по ортонормирован-
ной системе {<pt(x)}), если коэффициенты сп ряда (1.5) вычисля-
Ь <1
ются по формулам Фурье cn=(f, фп) — I f(t)yn(t)dt; n<=N.i
а .л
Запись:
f ~ 2 с»’₽"> ~ 2° • ф»(*)-
л=1 п=\ 'I
Числа cn=(f, фп) называются коэффициентами Фурье функция’
Ях).
Теорема. Пусть {ф((х)} (i=l, 2, ...) — ортонормированная
система в 7?[а, &] и ортогональный ряд (1.5) сходится равномерно
на [а, &] к функции f(x) .Тогда ряд (1.5) является рядом Фурье
для своей суммы f(x) на [а, 6].
Доказательство. Поскольку фпе/?[а, &]Vn и ряд (1.5)
сходится равномерно на [а, &] к функции f(x), то по теореме об
интегрировании равномерно сходящегося ряда (из § 4 гл. 2 ч. IV)
имеем f е 5] а В[а, 6], но тогда f, ф* е В[а, 6], и поэтом/
Ях)-ф*(х) = +2 СпФпС^фаСх) (Vхе=[а, 6]) есть (см. § 4, гл. 2
ч. IV) равномерно сходящийся на [а, &] функциональный рЯД-
170 ’
Применяя теорему об интегрировании равномерно сходящегося
ряда, имеем в силу условия ортогональности (<рп, фа) =8па равен-
ство
4-00
(Л Фа) = 3 сп • (фп, Фа) = ск,
л==1
т. е. ch = (f, фй) есть коэффициенты Фурье для функции /(х).
Итак,
+ оо
м>а(х)-
П=1
Рассмотрим евклидово пространство Е со скалярным про-
изведением (х, у) (Vx, уЕ=Е) и нормой ||х||=]Л(х, х) (индуци-
рованной скалярным произведением). Пусть {ej (е^ЕУЗ — ор-
тонормированная система элементов в Е (конечная или счет-
ная), так что (е(, е;) = 6о-. Тогда Vxg=E можно ввести поня-
тие ряда Фурье (по системе {ej) x~Sc«e<, где коэффициенты
Фурье Ci вычислены по формулам Фурье с{ = (х, ej)V i. Пусть
ортонормирования система {eJCZE счетна, тогда в силу ли-
нейности евклидова пространства Е имеем
8п = 2 с&еЯУпек.
i==i
4-°о
Однако элемент 2 может и не принадлежать пространст-
ве!
ву Е, если евклидово пространство Е не является полным
(в смысле нормы ||х|| = К(х, х)).
Теорема (неравенство Бесселя). Пусть {е>} (t=l, 2, ...) —
ортонормированная система в евклидовом пространстве Е. Тогда
4*00
имеет место неравенство Бесселя у, с? |[х]|а, где
г==1
<ч= (х, а) — коэффициенты Фурье элемента х по системе {е,}.
4-00
Доказательство. Пусть хе Ей х~2 с*е*> гДе с< =
и.»
п
^(х, ez) Vi. Рассмотрим sn = 2 тогда в силу ортонорми-
i=l
Рованности системы {е,} имеем V у, z е Е таких, что (у, z) = О
тождество ||y+z||2=(y+z, y+z)=(y, y)+(z, z)+2(y, z)=||y||24-||z||2.
"° имеем (x—sn, e/.)=(x, e;)—(s„, e,) = c, — = 0, t. e.
'x~~sn, sn) = OVn, откуда
||X||2 = ||(X - sn) + sn||2 = ||X - S„||2 + Ils„[|2 Vn,
171
т. е. имеет место тождество Бесселя f
||х||’ = |]х-зя||»Ч-||8пр VnSN,
из которого получаем неравенство ||sn||2^IIхII2 VneN. Вновь
используя ортонормированность системы {ej, имеем равенство
ls«ll2=(s„, sn) = 2 <?• Но тогда 2 <7<llxll2 VneN и, переходя-
Z-I »= 1
к пределу при п->4-оо в этом неравенстве» получаем нера-
венство Бесселя.
Следствие 1 (неравенство Бесселя в 7?[а, 6]). Пусть
{<pk(x)} (£=1, 2, ...) — ортонормированная система функций в
Ъ
7?[а, 6], f eR[a, Ь] и 2 спФп(*) (где cn = (f, <p„)=f/(x)<pn(x)dxVn)
а
— ряд Фурье функции /(х). Тогда имеет место неравенство
Бесселя
4-оо Ъ
zz=i а
Следствие 2. Пусть f еф, &] и / ~ 2 с«Фп» где Сп ~ U’
/2=1
Фп) — коэффициенты Фурье функции /(х) (по ортонормирован-
ной системе {фл(х)}). Тогда из неравенства Бесселя следует
4-00
сходимость знакоположительного ряда 2 с2<С + °°> а потому
л=1
в силу необходимого условия сходимости числовых рядов
имеем для коэффициентов Фурье
ь
( lim cn = 0)=>( lim Г /(х)фп(х)йх = О).
Л-Н-00 Л-»4-оо £
Следствие 3 (неравенство Бесселя для тригонометричес-
кой системы). Пусть {1, cosx, sinx, .... cosnx, sinnx, ...} — триго-
нометрическая система (ортогональная в —л, л]) и (1.1) — ряд
4-оо
Фурье для функции fe/?[—л, л], так что -Яо/24 2 (ап cos пх4.
п=1
4&n sin пх), тогда имеет место неравенство Бесселя
а«/2 + 2 (ап + JfW*-
/2=1 —Л
В самом деле, рассмотрим в 7?[—тс, тс] ортонормированную
тригонометрическую систему {ет(х)} (т = 0, 1, 2, . . . ), где
е0(х) = 1/]/2тс, e2fc-i(x) = cosfex/]/rc, e2ft(x) = sinfex/j/^тс (k=\, 2,.-)-
Поскольку /е7?[—тс, тс], то
172 :
4-00
f ~ 2 cm6m(x),
m=0
где cm = (f, em) (m e No) — коэффициенты Фурье функции f(x)
ло ортонормированной системе {em(x)}, и тогда имеет место
неравенство Бесселя
S Ст<(/> >> = Ж*'
m«»l —те
+ <Х>
Но f ~а0/2+2 (a„cosnx4-bnsinnx), причем между коэффи-
л«=1
циентами Фурье ст (т е No) и коэффициентами Фурье ап (п €=
eN0) и 6n(neN) имеют место соотношения
с0 = (/, ео)=(1/У2тс) • J/(x)dx =/(1/У2^) ♦ * • а0 —
—те
= У«/2 • а0; с2*-1=(/, e2fe-i) = (l/K’c) X
X J f(x) cos kxdx — тсай/Утс = yit • ak,
—те
c2b = (f» e2ft) = (1 lV*) • f f(x) sin kx dx = r.bk/y^ =- yic . bk
так, что
m=0 \ *=1 /
откуда и получаем неравенство Бесселя для ak и j
«§/2 + 2 (в2й + ^)<(»А) •
—те
Заметим попутно, что поскольку
C2k-ie2k-i(x) = j/ir ab cos fex/Утс = ак cos kxt
cike2h(x) = У тс bk sin fex/У тс = bK sin kx,
Co^o(^) = eo/J/"2tc = <j0/2,
to
У. ckek(x) ~ ao/% + 2° (e« cos nx + sin wx)-
fc=O
Пример. Тригонометрический ряд
4-co
S(x) = 2 sinzu/lnn, x e[—тс, тс],
л=2
173
сходящийся при х = 0, ±гс, а также (по признаку Дирихле) и
при х=#0, ±тс, не может быть рядом Фурье для своей суммы
4-00
S(x), поскольку у (1/1пи)2 = 4-оо, что противоречило бы не-
л=2
равенству Бесселя.
Следствие 4. Пусть —л, я] и ряд (1.1) является ря«
дом Фурье, так что ;
4-00
/ ~ ае/2 + у (ап cos пх 4- bn sin пх),
где ап = (1/я) • $f(t)cosntdt (neN0) и Ьп = (1/тс). J /(f)sinn«<ft
—л —л
(neN) — коэффициенты Фурье функции/(х) по тригонометри-
ческой системе. Тогда
lim ап = lim bn = Q (1.6)
. Л-*4-00 Л-*4-00
и, в частности, V [a, b] az [—л, л] имеем
ъ ъ
lim f/(a:) cos nx t/x = lim f /(x) sin nx dx = 0.
«-+« a n-+oo Ja
Для доказательства последнего утверждения введем функцию
г,х} _ (/«.' е («. 6].
I 0, хе[—Ь].
Тогда F^R[—л, л], и поэтому в силу (1.6) имеем для ее коэффи- ,,
циентов Фурье
lim f F(x) cos nxdx = lim f/(x) cosnxdx = 0, ’ #
n—+«> _i
л . b
lim (’F(x) sin nxdx — lim f/(x)sinnxdX = O.
n-+oo Л-+ОО Ja
Следствие 5. Пусть f^R[—л, л] и [а, Ь]с[—л, л]. Тогда
ь / 1 \ ‘
lim f /(x)sin(n4—)xdx = O. (1.7)
л-»+оо Ja \ 2 }
В самом деле, sin (n4- — )x = sinnx-cos — 4- cosnx-sin— , та<
\ 2/ 2 2
что /(x)’« sin 4- -0 x = /x(x) • sinnx+/2(x) • cos nxt где
=f(x) cos i g2?[— k, и fa(x)=/(x)sin e/?[—it, «]. В силу след-
ствия 4 имеем
174
ь ь
lim f fi(x) sin nxdx = lim f /2(x) cosnxdx = 0,
«-*4-00 a n-*+oo a
откуда и вытекает (1.7).
Теорема. Пусть Е — евклидово пространство и {ej
(i=l, 2, ...) — ортонормированная система в нем. Пусть хеЕ и
4-оо 4-°°
х~ У с^ где Ci — (x, et)Vi. (Ряд Фурье у, для элемента
iti
х сходится (в метрике Е) кх) <=>• (для элемента х выполняется
равенство Парсеваля с? — |[х||2).
Доказательство. Необходимость. Пусть х <= Е и х ~
~ У <№• т. е. с4 = (х, е{)¥1. Пусть х = 2 сгеъ так что lim |]х—
/=1 г—I л-*4-оо
— sn|| — Ot где sn = 2 cier Тогда из тождества Бесселя ||х||2 =
- Ilsn1!2 + 1|Х — Sn||2 V n е N имеем
IIх -s„||2 = || х||2 - ||s„||2 = ||х||2-у с?>0.
«=1
Но тогда
( lim ||x-sn|]2 = O)=>( ||х||а = у
П->4-оо \ £__| J
т. е. для элемента х е 2? имеет место равенство Парсеваля.
4-о°
Достаточность. Пусть хеЕ, х~2 где ct = (x>
i = l
и для элемента х имеет место равенство Парсеваля ||х||а =
4-00 п
се так чт0 lim 5 cz —1|х||8- Тогда из тождества Бессе-
i=4 n-»4-oo iesj
ЛЯ имеем 0<||х — sn||2 = ||х||2— у c?VnsN. Переходя в этом
i=l
неравенстве к пределу при п-*-|-оо, имеем в силу равенства
Парсеваля lim |]х—sn||2 = 0, т. е. х = Ус{е{е£.
Л-+«>
Определение. Пусть Е — евклидово пространство. Орто-
нормированная система {ej (i=l, 2, ...) из Е называется замкну-
Тлv '^оо
г°и> если Vxe£ имеет место равенство Парсеваля |[х||2==у ci* г^е
feal
с,==(х, е4)— коэффициенты Фурье элемента х по системе {е(}.
175
Теорема. Пусть Е — евклидово пространство и {ez) (t=s
= 1, 2, 3, ...) — ортонормированная система в Е. Если система
{ej замкнута, то не существует элемента хеЕ, х=#0 (Пх11>0)
такого, что (х, е() =0 V i е N.
Доказательство. Пусть ортонормированная система {е,}
из Е замкнута, но ЯхеЕ, х=#о такой, что VieN имеем
(х, е;) = 0. Тогда ряд Фурье 2 с»е* для этого элемента х име-
i=!
ет коэффициенты Фурье ct = (х, е4) = 0У», т. е. для элемента
хеЕ имеем у, с? = 0+ 0 + . . . 4-04-.. . = 0. Но тогда для
Х=1
хеЕ имеет место строгое неравенство Бесселя ||х||8£>0=
4-00
=2 ci (поскольку (х =£ о)=>(||х||2>0)), т. е. для элемента хе
i=l
еЕ не выполнено равенство Парсеваля, что противоречит
условию о замкнутости системы {ej.
Теорема единственности (для рядов Фурье в евкли-
довом пространстве). Пусть Е — евклидово пространство и {ej
,(i=l, 2, ...) — замкнутая ортонормированная система в Е. Пусть
х, уеЕ и х~У е() Vie N), (^ = (у,
i=l i—1
е,) Vi eN) — их ряды Фурье. Тогда если х¥=у (т. е. ||х — у|| > 0),
то существует индекс io такой, что Ci^di,.
Доказательство. Допустим, что существуют х, у е Е та-
кие, что ||х—у||>0, (х, ег) = (у, e^VieN. Тогда х-уеЕ,
х— у=#0 (т. е. ||х—у|| >0) и (х —у, ei) = 0VisN, т. е. система
{е^ не замкнута вопреки предположению.
Теорема (об экстремальных свойствах коэффициентов
Фурье). Пусть Е — евклидово пространство и {ег} (i=l, 2, ...) —
4-00
ортонормированная система в Е. Пусть х еЕ и х ~ 2 с»е‘> г°е
г=1
q = (x, ej)VieN— коэффициенты Фурье элемента х по системе
п
{ej. Пусть sn= с«е»— п'я частичная сумма ряда Фурье для эле-
t=i
п
мента хи рп = 2 — любой «многочлен» порядка п относитель-
Z—1
но системы {ej. Тогда при фиксированном neN имеет место нера-
венство j|x — р„|[>||х — sn|| Vpn, причем знак равенства возможе»
лишь при dt = ct (i = 1, 2, . . . , п) (где Ci=^(x, ej (i=l, 2, . . •
. . . , n) — коэффициенты Фурье для х).
176
4-00
' До к аз а те л ьство. Пусть ХЕ Е, х ~ у с4е„ где С{=(х, et)
VieN, sn=vCje( и рп=У d‘e‘- Пусть neN зафиксировав
i=l 4=1
ио. Заметим» что
(х —s„, s„ —pn) = (x — sn, у (с, —^)еД =
\ w /
==y (Ci-di)(x — sn, e,) = y (cj — di)l(x, е<)-(зп, e,)].
i=l 4=1
Ho (x, et)=c(VnsN и (sn, ei)=clVi<n так, что (x — sn, sn—
— pn) = 0. Но тогда вспомним, что при (у, z) = О имеет место
равенство ||у + z|p == ||у||2 + ||z||2. Полагая у=х—зп и z=sn—рп,
имеем y+z=x—р„, (у, z)=0, откуда ||х—рп||2 = ||х—зя||2 4- ||sn —
— Pn|laVpn, т. е. ||х—рл||2>||х—sn||2 Vpn, причем равенство воз-
можно лишь при ||зп — рп||* — 0. В силу ортонормированности
системы {ej видим, что
(||sn—Pn||2= 2 (с»—di)2=0>j<H.(ct = dl; i = l, 2.n).
\ '=1 /
Следствие. Пусть £==/?[—л, л] и л, л]. Тогда из
всех тригонометрических многочленов
Тп(х) = а0/2 4- у (aft cos kx 4- sin kx)
fe=i
с заданным neN частичная сумма Фурье
Sn(x)— a0/24- у (ак cos kx 4* bk sin kx),
где
aft = (l/«) • J f(t) cos kt dt, k e Ne;
—n
bfe=(l/z) • f f (t) sinfe/ dt, fee=N
— 71
Дает наилучшую (в смысле среднего квадратического) аппрок-
симацию функции /(х). При этом для среднего квадратического
Уклонения Sn от f имеем
||/-5„||2^ f(/(x)-Sn(x))2dx= ff2(x)dx-
—те
(п \
“<№+ 2 W+bl} •
й-1 /
** Л. И. Камынин 477
Доказательство. Рассмотрим ортонормированную ®
Я[—те, те] тригонометрическую систему е0(х) = 1/|/2те, tf2*-i(x)=a
= cos kxty~n , e2h(x) = sinAx/j/те &е= N, тогда для коэффициен-
тов Фурье ck = (f, ек) имеем (ср. вывод следствия 3 к теореме
о неравенстве Бесселя) с0 = ]^те/2а0, c2k-i = К1'ак->
(feeN), и поэтому с0е0(х)=а0/2, c2k-\.ezk-i(x) = % cos kx, c2he2k(x)=s.
= bksinkx (k eN). В силу экстремальных свойств коэффициен-
тов Фурье наилучшее приближение в метрике 2?[—те, те] (т. е.
в смысле среднего квадратического) дает частичная сумма
2п
Фурье s2n= У, cftek(x) == 8п(х), при этом в силу тождества Бес-
*-=о
селя имеем
W = llf-M2 + IWI%
т. е.
/ \ / 2п \
||/-82п||а = ЦЛ|а-|М2Н llf-S2nh2 = №- 3 <\2)-
\ , / \ Л=0 /
Таким образом, среднее квадратическое уклонение Sn(x) от
/(х) дается формулой
J (/(х) — Sn(x))2dx = ffa(x)dx-
—тс —те
(п \
«о/2+З («Ж!) •
Л=1 /
Определение. Пусть Е — евклидово пространство. Тогда
ортонормированная система {et} (i=l, 2, ...) из Е называется пол-
ной в Е, если, каково бы ни было xe£Vg>0, существует «мм-
п
гочлен» порядка п рп — У, йге< такой, что ||х — рп|| < е.
/=1
Теорема. Пусть Е — евклидово пространство и {еД
(i=l, 2, ...) — ортонормированная система в нем. (Система {®Д.
замкнута в Е) (система {е,} полна в Е).
Доказательство. Необходимость. Пусть ортонормирован-
ная система {е,} (i=l, 2, ...) замкнута в Е. Тогда Vxe£ имеет
4-со
место равенство Парсеваля ||х||2 = У, с?, где с2 = (х, е,) Vi-—
г=1
коэффициенты Фурье элемента х е £ по системе (ej. Но тог
да если sn=y cfii—п-я частичная сумма Фурье для элемент®
»=1
178
% то lim ||х—sn|| = 0, т. е. Ve>0 существует „многочлен"
п.го порядка sn такой, что ||х — sn||<e, т. е. система {ej полна
в Е.
Достаточность. Пусть ортонормированная система {ej (i = 1,
2,...) полна в Е. Пусть x<=zE — любой элемент и sn —
п
cfii> где с1 — (х> е0 — коэффициенты Фурье элемента х по
<i=I
системе {е,|. Поскольку система {ej полна в Е, то Ve>0 суще-
ствует „многочлен" порядка п0(е)
п»(е)
рп,(е) = У, diCi
/=1
такой, что ||х — рл,(€)|1 < 81/2. Но в силу экстремальных свойств;
коэффициентов Фурье имеем оценку
Цх - sno(e)|r < ||х — р„,(£)||2 < е,
причем в силу основного тождества Бесселя
(л,(е) \
О<||Х||2- 3 С2<8].
i=l /
Заметим, что Vn>n0(e) имеем оценку
л пе(е \
О<||Х||2- 2 С2<||Х||2 - 2 С|<е.
«=1 i=i
Итак, V е > О Я n0(e) е N такое, что
О < ||х||2 — 2 с* < е Vn > n0(s),
i=l
т. е.
п
lim 2 <ч = ||х||2,
«-+“ i=i
так что имеет место равенство Парсеваля ||х||2=2° Итак,
ортонормированная (в Е) система {ej (i=l, 2, . . . ) такова,
что Vxe£ имеет место равенство Парсеваля. Но тогда сис-
тема {ег} замкнута в Е.
Вспомним теперь, что евклидово пространство Е назыв ает-
Ся полным (в индуцированной норме ||х||=]/(х» х)), если для
любой последовательности Коши (хл), хп^.Е существует эле-
мент х е Е такой, что lim ||хв — х0|| = 0. В дальнейшем пол-
П-»Ц-оо
Чое евклидово пространство будем обозначать через Н.
12* 179
Если бесконечномерное евклидово пространство имеет счетное
всюду плотное множество и полно, то оно называется гиль-
бертовым пространством.
Замечание. Существуют евклидовы пространства Е, не яв-
ляющиеся полными, но в которых есть полные и замкнутые орто-
нормированные системы et (i=l, 2,...).
Пример. Рассмотрим евклидово пространство Е, состоящее
из всех непрерывных функций f е С[—л, л] со скалярным произ-
ведением (f, g)= J f(x)g(x)dx и с метрикой ||/||=рС(/, f). Тогда
—п
2?СЯ[—тс, тг] не будет полным пространством в метрике ||/||.
(Например, для функций
f,w = (° z 10, 0<и<«,
11—га|х|, 11, я=0,
имеем fn, f<=R[—тс, тс], lim ||/ — fn|| = 0, причем fn^F, aof^E.)
В следующем параграфе будет доказана полнота (и замкну-
тость) в 7?[—тс, тс] (а стало быть, и в Е ci Z?[—тс, тс]) ортонор-
мированной тригонометрической системы функций из прост- ,
ранства Е:
е0(х) = 1/]/2тс, e2ft_i(x) = cos^х/р^тс, e2ft(x) =
— sin kx/У тс, k G= N.
Приведем некоторые специфические свойства полных евклидовых
пространств.
Теорема. Пусть И — полное евклидово пространство а
{е,} (j=l, 2, ...) — ортонормированная система в Н. Пусть хеЯ
и х ~ у, cfilt где ct = (х, е<) — коэффициенты Фурье элемента х
£—1 * .
п 13
по системе {ej, причем sn = 2 ciei- Тогда УхеЯЗхое«
i=A
такой, что lim ||sn — х0|| = 0, т. е. х0 = 2 «= н-
л-»4-оо
Доказательство. Пусть хеЯ и sn = 2 п‘я частйЧ'
ная сумма ряда Фурье для элемента х, т. е. сг=(х, eOVieN.
В силу линейности евклидова пространства Н имеем
Vn е N. Докажем, что последовательность (sn) является по-
180
следовательностью Коши в пространстве Н. Заметим, что в
силу ортонормирован'ности системы {ej (i = 1, 2, . . . )Vm>
»n
> n > 1 имеем равенство ||sm — sn||2 =3 ck (в самом деле,
' ft=n+i
по „теореме Пифагора”
В силу неравенства Бесселя для коэффициентов Фурье имеем
3 оо,
i—i
+оо
поэтому знакоположительный ряд у, с2 сходится и потому
i-i
в силу критерия Коши (сходимости числовых рядов) Ve>0
3/V(e)£N такое, что
2 в V N(z).
А=«+1
Но тогда имеем оценку
m
llsm — s„||2= 5
fe-n+t
из которой следует, что (s„) есть последовательность Коши в
метрическом пространстве Н. В силу полноты пространства Н
видим, что существует элемент хое// такой, что
lim ||sn — Хо|| = 0.
Следствие 1. В полном евклидовом пространстве Н с ор-
тонормированной системой {ej (i=l, 2, ...) ряд Фурье для лю-
бого элемента хе/f сходится (в И), однако его сумма х0еИ мо-
жет и не совпадать с элементом х, для которого этот ряд являет^
ся рядом Фурье.
Следствие 2 (теорема Фишера—Рисса). Пусть Н — пол-
ное евклидово пространство и {е,} (i=l, 2, ...) — ортонормиро-
ванная система в нем. Пусть ci<=R. (i=l, 2,...) таковы, что ряд.
+оо
2 сходится. Тогда существует элемент хоеЯ такой, что
У +°о п
А°== т. е. lim ||xe— sn||~0, где
io>l n->4-oo
181
Теорема. Пусть Н — полное евклидово пространство ц
{ej (i=l, 2,...) — ортонормированная система в нем. Если не су-
ществует элемента х<=Н, х=/=0 (т. е. ||х||>0) такого, что
[(х, е,)=0 V ie N, то система {е(} замкнута (в И).
Доказательство. Пусть {ej (i=l, 2, ...) — ортонормиро-
ванная система в полном евклидовом пространстве Н. Допустим,
что система {е,} не замкнута. Тогда существует элемент х е Н та-
кой, что для него вместо равенства Парсеваля имеет место строгое
неравенство Бесселя
W>3 с?>0,
/=1
где Ci = (x, е<) — коэффициенты Фурье элемента хе//. По-
4~°°
скольку евклидово пространство Н полное, то ряд Фурье у, с^
/sal
сходится в нем (в метрике Н), т. е. существует элемент хоеЯ
такой, что xe= V qej, а стало быть, Я lim ||х0 — sn|| = 0, где
/в1 п-*4-оо
п
sn = у cfii — n-я частичная сумма ряда Фурье для элемента
Z=1
х. Покажем, что (х0, е.) =<?| Vi е N. В силу неравенства Ко-
ши—Буняковского (для скалярного произведения) |(а, 6)|<С
|ja||-||6||V а, Ь е Я, используя ортонормир ованность системы
{еД для любого i s N, имеем оценку
| (х0—s„, е{)| < ||х0 - sn|| • ||е(|| = ||х„ - М,
откуда, переходя к пределу при »->-}-оо, получаем
lim |(Xj — sn, е4)| = 0 V i <= N,
П-*+0О
т. e.
lim |(x0, e4) — (sn, e*)j =0 Vi e N.
n-»4-00
Ho имеем (sn, еО = с{, поэтому (x0, e/)=ciVi, t„ e. ft
есть коэффициенты Фурье для элемента хоеН. Но тогд*
хв ~ ci^t- Однако по построению х0 = ^ с^^Н. Как бы*
Z=f Z=1
ло показано ранее, тогда для элемента х0 G Н имеет мест®
4-00
равенство Парсеваля, т. е. ||х0||а= у, с|<||х||2. Положим *е*
i=l I
перь у0 = х — х0 е И. В силу неравенства треугольника ||ifolle|
= ||х —хо||>||х||-||хо||>О, т. е. уое=Я и уо#=О, при это*
VieN имеем равенства (у0, е4)=(х—х0, ег) = (х, е,) — (х0,
=»с4 — с4 = 0. Итак, существует элемент увеЯ, уоэ=О тако*
132
что(Уо«е^ = 0 Vi«=N. Противоречие с условием теоремы
'рем самым доказано, что система {е,} замкнута.
Следствие (критерий замкнутости ортонормированной сис-
темы в полном евклидовом пространстве). Пусть Н — полное ев-
клидово пространство и {е,} (i=l, 2, ...) — ортонормированная
система в Н. (Система {ej (i=l, 2, ...) замкнута) (не суще-
ствует элемента хеЯ, х=/=0 (11x11 >0) такого, что _(х, е;) =0 Vie N).
§ 2. Сходимость рядов Фурье по тригонометрической
системе
Чтобы изучить вопрос о сходимости ряда Фурье для функции
—л, л] на отрезке [—л, л] или в какой-либо точке х^е
—л, л], удобно представить частичную сумму ряда Фурье в той
форме, которую ей придал Дирихле. Пусть функция f(x) опреде-
лена на (—оо, +оо), f еД[—л, л] и f (х+2л) =f(х) Vхе
е (—°0, +«>). Пусть
п
Sn(x) — а0/2 + 2 cos + bh sin kx),
*—t
где
aft=(l/K). J ДО cosЫЛ, &<=N0
—те
И
—те
тогда
Sn(x) s IM • j* f(*)I 1/2 + (cos kx • cos kt +
—те k«=l
+ sin &x-sin&i)]di = (l/тс)- Jf(f)[l/2-|- У cosfe(x— t)\dt
—те k=l
или, вводя ядро Дирихле X)n(w)= П2 -|- cosfea, получаем
представление
ад =(!/«). ]f(t)£)n(x-t)dt.
—те
Но
2 sin V ' &»<и) — 2sin V f — + з cos Aw) =- sin 4-
2 1 \2 ь-I ' 2
183
n Г / / 1 \ I / i \
+ 2J I sin I A4— u — sin I k — — J и I sin I n 4- — 1 u
L \ 2/ \ 2/J \ 2/
так, что
^n(w) = sin / n + -i-) и f 2 sin V и 2kv:.
\ z / / z
Делая замену u=z4-2Air, имеем
«+ — 1 ?+Aic
йп(«) = sin
2 sin j — Ц-
V 2
= (—l)ftsinZn+—\z / /(—1)^-2 sin— 1,
\ 2 / / I 2 i
откуда
lim £)n(u) = lim sin In 4- — z /2 sin — =«+ —,
z~*o I 2 1/ 2 2
так что функцию £)n(u) можно доопределить в точках uk=2kic
(А=0, ±1, ±2,. . .) по непрерывности, считая, что 2)п<=
е С((—оо, -f-оо)). Отметим некоторые свойства ядра Дирихле,
используемые в дальнейшем:
1) SnGC((-OT, +оо)), |£>„(и)| =
1/24- 2 cosAa )|<
Л=»1 / I
<n+jVae(—оо, +оо);
2) Юл(-“) = ^n(«) Vue (—00, +<»);
3) ©„(u + 2«) = ^)n(u) V и е (-00, +оо);
4) |^п(и)|<^/2|и|, 0<|и|<к.
Свойства 1) —3) очевидны. Для доказательства свойства 4) поло-,
жим <р(х) = sin xlx, хе(0, я/2]. Тогда 5)<р(х)=(хcosх—sinx)/№=«
= cosx • (х — tgx)/x2^0 Vxe(0, л/2], т. e. sinx/xj на (0, it/2)«
Но тогда 2/it^|sinx|/x^l, 0<|х«к/2, откуда имеем оценку из 4):
<(ir/2)- l/(2|u|/2) = it/2|u|, 0<|u|<ir.
184
Лемма. Пусть ф(х4-2л)=<р('х) Vxe(—оо, 4-00) и
&R[—л, я} Тогда
a-f-л п
J <p(x)dx= Jcp(x)dx Vae(-oo, +00).
а—п —л
Доказательство. Пусть ле(—оо, -|-оо) фиксирована.
Тогда существуют k^Z и ае[0, 2л) такие, что а=а+2Лл. По»
еле замены x-t-\-2kn имеем
аЧ-л a-h« л .a-j-л
j ty(x)dx=* J <p(t)df = J 4- J q>(i)df =
а—л a—л a—л те
(замена во 2-м интеграле t = z + 2я),
— J <p(t)dt+ J <p(z4-2ir)dz= Jq>(Z)dL
a—к —тс —л
В силу леммы, учитывая периодичность f(х 4- 2«)=Дх),.
<£)п(и+2к) =£)п(и), получаем с помощью замены t—х=и пред-
ставление
я Г 0 ят I
5„(х)«(1/к) • J./(x+u)^n(M)dUe=(l/K) • f + f =
—л L— л 0J
используя четность ядра Дирихле $)п(—и)—£)п(и) после за-
мены v = — и в 1-м интеграле)
= (1/«) • J (f(*+u) 4- Дх - u))^)n(u)du.
о
Итак,
£«(*) = (1/*) • J(f(*+«) + f(x — u))&n(u)du
о
и, в частности, при f(x)=l имеем 5п(х)=1, т. е.
1 = (1Я- fto«V«eN,
—л
Или в силу четности ядра Дирихле ^)n(—u)= S5„(u) Vu имее»»
представление
l==(2/z) • $ £>n(u)du VrteN.
о
Теорема (принцип локализации Римана).
^.^Лусть функция f(x) определена на (—оо, 4-со), fe
л, я], f (х4-2л) =f(x) N х u xoS (—00, -|-оо). Тогда сходи-
сит или Расхо^имость ряда Фурье функции f(x) в точке х0 зава-
только от поведения функции f(x) в окрестности точки х0.
185
II. Пусть функции fi(x) и fz(x) — периодические с периодом
2л, fi, fz^R[—л, л] и существует интервал (а, р) такой, что
fi(x)—f2(x) V хе (a, fj). Пусть хое(а, Р) и Sn(x; fi) и Sn(x; f2)~^
п-е частичные суммы рядов Фурье для функций fi(x) и fz(x) соот-
ветственно. Тогда lim fSn(x0; ft)— Sn(x0; fz))=O, т. e. ряды
П-+-[-00
Фурье для функций fi и f? сходятся или расходятся в точке г0
одновременно.
III. Пусть функция f(x) определена на (—оо, 4-00), feP[—л, л],
f(x+2n)=f(x)Vx и f(x)=O на (а, £). Тогда lim Sn(x0; f)=Q.
zi—
Vx5e (а, P).
Доказательство. Докажем теорему Римана в формули-
ровке III. Итак, fe7?[—л, л], f(x+2n,)=f(x) Vxe (—оо, +.а>)
« И б>0 такое, что f(x) =0 V х е (х0—6, хо+б). Тогда
Sn(x0) = (1/л) • J f(x04-u) 0n(u)du,
поэтому
S„(x0) = ОМ • J ff(x0+u)/2 sin ^~\ • sin fn-ь И du,
но, полагая F(u) = f(х0 + u)/2 sin~ , видим, что в силу условия
теоремы Римана (в формулировке III)
Л«) =
f(x04-u)/2sin^-, 6 <|«]<«
О, |и|<6,
так что (f —к,. j:])=»(Fe /?[—*, ж]), но тогда в силу след*
ствия 5 к теореме о неравенстве Бесселя из § 1 гл. 4 имеем
" / 1 \
lim [ F(u) sin { n-|—)udu = 0,
n-»+o° _я у 2 j
t. e.
lim Sn(x0) = O*
ц->4-оо
Замечание. При выполнении условий теоремы Римана в
•формулировке Ш можно доказать, что Sn(x; Д) zX 0 на [а, &}
любого отрезка [а, д]с: (хо—б, Хо+б).
Определение. Пусть функция f(х), определенная &
—оо, -1-оо), периодична с периодом 2л. Точка %о называется р8'
Югулярной точкой (функции f), если:
1)3 lim f(x) = f(xe±0)eR;
2) f(xo)^(f(Xo+0)+f(x0-0))/2.
186
г
г
Замечание. Если функция f(x) определена на (—<х>,
ц.оо) и периодична с периодом 2л, причем feC(x0), то точка
будет регулярной точкой (функции f), поскольку
э Um^f(x)=f{xo±O)=f(xo) и
f(xo) = (f(xo+O)+f(xo-O))/2.
Теорема (признак Дини сходимости ряда Фурье в регуляр-
ной точке). Пусть функция f(x) определена на (—оо, +оо) и пе-
риодична с периодом 2л. Пусть —л, л] и точка хое (—оо,
ц-оо) — регулярная точка (функции f). Пусть в окрестности
Uh(xo) (h>0) выполнено условие Дини: существуют несобствен-
ные интегралы
h
^f(x9+t)-f(xo+O)]/tdt
0«-
h
ч! \f(xo-t)-f(xo-O)\/tdt.
о«-
Тогда
limS,i(x0; f)=f(xo), где Sn(x; f) п-я частичная сумма ряда Фурье
л-*4-оо
для функции f(x).
Доказательство. Поскольку f(x) определена на (—оо,
+.оо), периодична >с периодом 2л и f е 7?[—л, л], то для л-й час-
тичной суммы ряда Фурье имеет место представление Дирихле
8п(х0‘, /)= (IM)• f (f(x0+u)+f(x9-u))S>n(u)du.
о
Но х0 — регулярная точка (функции /), так что f(xo)=(f(xo+O) 4-
+f(x0—0))/2. В силу представления 1==(2/к) • S)n(u)du имеем
о
Дх0)=(1/к) • f(f(xo4-O) + f(x0—0))S)„(u)du,
о
т. е.
f)-f(Xo) = (lM • f(f(xtf+u)-f(Xo+O))S>n(«)d« +
b
+ (!/«) • f(f(x0—и) — f(x0—Q))S)n{u)du=
0
= (1M) . (Z+(x0) + Z7M.
Теорема Дини будет доказана, если показать, что
Рассмотрим
lim Z±(xo) = O.
rt-*4-0O
187
/+(х0) = f (f(x0+u)—f(x0+Q))S> n(u)du.
b
По условию Дини существует несобственный интеграл
| |/(*о+«) — f(xo+0)|/udu,
поэтому V е > О Я 6(e) е (О, Л) такое, что имеет место оценка
8(e)
f |f(x0+и) — /(хо+О)|/и du < ей.
о—
Для выбранных е>0 и 6(e) >0 положим /+(х0) = Ап(х0)+Вп(х0),
где
Л(*о)=Т (f(*o+«)-f(x.+O))
ol-
и
^n(x0)= f (f(x0+«)—f(xo+O))55n(u)du.
8(e)
В силу свойства 4) ядра Дирихле имеем оценку | £}„(и) [
< <t/2u V и е (0, «). Но тогда
|(f(xo4-u)-f(xo+O)) 2)п(Ы)|<й/2). |/(х. + и)-
-Дло+О)|/« Vue(0, 6(e)),
и поэтому в силу выбора 6(e) имеем оценку
И„(х0)| < (к/2) • 7 If (*о+и) - f(xo+O)|/u du < е/2.
Для оценки Вп(х0) введем вспомогательную функцию
7 х(«) =
ffXo+u) - f(Xo+Q)
и
2 sin "77
О < 6(e) и 1С,
О» —it u < 6(e).
я / 1 \
Очевидно, /г е и Вл(х0)= J/х(и) • sin I «Н— j и du-
По следствию 5 к теореме о неравенстве Бесселя из § 1 гл. 4
имеем lim Вп(хо) = О, т. е. для выбранных е>0и 6(e)>03
2V0(e) еN такое, что |Bn(x0)|-<e/2 Vn^> 2V0(e). Итак, Ve>03
2V0(e) eN такое, что
И+(*о)1 < IЛп(х0)| 4- 1Вп(х0)| < е V п > 2V0(e),
188
т_ е. Я Иш /+(х0) = 0- Аналогично доказывается, что
Я lim /~(хо) = О. Но тогда
lim 5п(х0; /) = /(х0).
’ п-*4-оо
Замечание (признак Дирихле—Жордана). Пусть функция
f(x) определена на (—оо, -|-оо) и периодична с периодом 2л.
Пусть —л, л] и хое (—оо, 4-оо) — регулярная точка (для
функции f). Пусть существует окрестность Uk(xq) (h>0), в кото-
рой функция f(x) имеет ограниченное изменение (т. е. Varf<,
<4-оо). Тогда lim Sn(Xo; f)=f(xo), где Sn(x; f) п-я частичная
n->4-oo
сумма ряда Фурье для функции f.
Замечание. Можно показать, что признаки Дини и Дирих-
ле—Жордана несравнимы (см. [2]).
Следствия I (признаки сходимости рядов Фурье для непре-
рывных, периодических функций,). Пусть feC((—оо, +<»)),
f(x+2n)=f(x) Vхе (—оо, +°°)-
Признак 1. Пусть f^Ha[—л, n](f(—n)=f(n)), 0<а^1.
Тогда ряд Фурье функции f(x) сходится к функции f(x) на (—оо,
-J-00).
(В самом деле, любая точка Хо^ (—оо, -]-оо) является регуляр-
яой точкой функции f(x), причем f(xo±O)=f(xo) и в силу перио-
дичности функции f, без ограничения общности, можно считать,
что хое[—л, л]. В случае хое (—л, л) существует окрестность
Z/ft(x0)<=(—л, л), так что в силу условия Гельдера f^Ha[—л, л]
имеем оценку
\f(x0±u)—f(x0)\/u^Hu*-1 v ue(0, h).
В случае x<j=—л (соответственно хо=л)
|f(xo+u)— 1(х0)
а также
If(xo-u)-f (xq) |/ц= (л)
(0, ft], где ft=n.
u A
Но несобственный интеграл / ua~ldu сходится при ae (0, 1], т.е.
в силу теоремы сравнения для несобственных интегралов несобст-
h
венный интеграл f lf(x0±u)—f(xo)[/udu сходится, так что в
О*-
’'очке хо выполнено условие Дини и применим признак Дини схо-
димости ряда Фурье.)
169
Признак 2. Пусть V х е (—оо, 4-00) либо существует ко-
нечная производная D f(x), либо существуют конечные односто-
ронние производные D +/:(х) nD_/(x). Тогда ряд Фурье функ-
ции f(x) сходится к функции f(x) всюду. (В самом деле, люба-я
точка хое (—оо, 4-00) есть регулярная точка функции /е
сС((—оо, +.оо)), так что f(xo±0)=f(x0). Пусть существуют ко-
нечные односторонние производные D +f (х0) и D _f(x0), причем
L =тах (] D+f (ха) |, | D~f (х0) |).
Тогда поскольку существуют пределы
lim (f(x0 ± а) — f (x0))/(±u) = D±f(x0)«
u—+о
то Sft>-0 такое, что \f(x0±u)—4-1 Vue(0, Л), t. e.
в точке x0 выполнено условие Дини и применим признак
Дини.)
Признак 3. Пусть на отрезке [—л, л] график функции f(x)
есть непрерывная ломаная, причем f(—л)=/(л). Тогда (см. приз-
нак 2) ряд Фурье такой функции сходится к ней всюду (рис. 5).
Следствия II (признаки сходимости рядов Фурье для ку-
сочно-непрерывных периодических функций). Пусть функция f(x)
определена на (—оо, 4-.оо), f (х-}-2л)— f(x) Ух. Пусть на отрезке
[—л, л] функция f(x) имеет конечное число точек разрыва 1-го
рода: —л<Х1<х2< ... <хт=л, так что Vx, e{—л, n](i=
= 1, 2.. т) существуют предельные значения f(xi±O) (такую
функцию будем называть кусочно-непрерывной на [—л, л]).
Признак 1. Пусть fe 3)((xi, xi+i))(i= 1, 2, ..., m—1),
причем существуют конечные односторонние производные в точ-
ках разрыва xt (/=1, 2, . . . , т)
190
(такую функцию будем называть кусочно-дифференцируемой на
[—л, л]). Тогда ряд Фурье функции f(x) сходится к значению
f(x0) в точке непрерывности х0 и к среднему арифметическому
t(f(*b+O)+lf(*b—0))/2 в точке разрыва х0 кусочно-непрерывной
функции f(x) (рис. I&).
Теорема (о равномерной сходимости ряда Фурье). Пусть
f еС((—оо, +оо)), f (х4~2л) —f(x) V х. Пусть Vx существует ко-
нечная производная Df(x), причем —л, л]. Тогда ряд
Фурье функции f сходится равномерно на (—оо, 4-00) к функции
f(x).
Доказательство. В силу признака Дини ряд Фурье функ-
ции f сходится к f(x) всюду, т. е.
4-оо
Дх) =а0/2 4-2 (апcosпх 4- bn sinпх), хе(—оо, 4-оо). (2.1)
n~i
Используя признак Вейерштрасса, докажем, что функциональ-
ный ряд (2.1) сходится равномерно на (—оо, 4-оо) к своей сумме
f(x). Поскольку Df —л, л], то, интегрируя по частям, полу-
чаем
itan= J f(x) соз nxdx = (1/n) [Дх) sin пх]^—
—те
— (1/п) • yDf(x)sinnx dx;
—те
itb„= J f(x) sin пх dx = — (1 /п) [f (х) cos пх]2_я 4*
—те
4-(1/п) • у Df(x)cosnx dx,
—те
причем поскольку sin (±nit) = 0 и (в силу периодичности Дх) и
COSHX) f (it) COS nit — f (—lt)c0S(—nit), TO [f(x) • /SinnX | = 0, OT-
\cosnx/ -Г.
куда an = — b'jn, bn = a'nln (n e N), где
a'n = (1/it) • у Df(x) cosnx dx,
—те
b'n — (1/it) • у Df(x) sinnx dx (n N)
—те
— коэффициенты Фурье для функции it, я]. Отметим
неравенство |а»&| (|а|г 4- |Ь|2)/2 V а, 6eR [(поскольку 0 (|а|—
— |&|)а s= ]а|а — 2|а| 4&| 4-I&I8)» в силу которого имеем оценки
i9i:
|an|»(l/n) . ^(l/a’ + W
IM = (l/«) • |a;|<(l/n» + |<|«)/2.
Поскольку a'n, b'n — коэффициенты те], то из нера-
венства Бесселя видим, что числовой ряд
2 (К12 + 1М2)<+°°
n—i
4-00
сходится. Кроме того, ряд у, 1/л8 также сходится. Но тогда
п—1
в силу наших оценок сходится и ряд
|a0|/2 + g(|a„l+|M).
Л=1
Осталось отметить оценку
\а„ cos пх 4- bn sin пх\ < |an| 4- |6П|
Vxg(-со, -j-оо), VneN,
®з которой в силу признака Вейерштрасса (о равномерной сходи-
мости функциональных рядов) вытекает равномерная сходимость
ряда (2.1) к своей сумме f(x) на (—оо, -j-oo).
Напомним, что функция f(x) называется первообразной для
функции g(x) на отрезке [—л, л], если: 1) feC([—л, л]) и 2) су-
ществует не более конечного числа точек (xil (i=l, 2, ..., т):—л^
m
s^Xi<x2< ... <Хт^л таких, что¥х<=(—л, л)\и{хДЭО/ (х) =
=§(х)-
Следствие 1. Пусть f еС([—л, л]), f(—л)=|^(л). и функ-
ция f(x) есть первообразная на отрезке [—л, л] для функции
е /?[—л, л]. Тогда ряд Фурье для функции f сходится равномер-
но на отрезке [—л, л] к функции f(x).
В самом деле, в силу условий f(—n)=f(n) и feC([—л, л]),
используя равенство f(x+2n)=f(x) Vxg (—оо, -|-оо), можно
продолжить функцию f(x) как периодическую непрерывную функ-
цию на (—оо, -j-оо). Поскольку f(x) является первообразной для
функции g(x) на [—л, л] и g е #(—л, л], то, используя обобщен-
ную теорему об интегрировании по частям (см. ч. II, гл. 2, § 6),
имеем
«("*) = ff(x) • (C°S/IXpx = ±(l/n)p(x)X
(6nJ -n (SinnxJ L
fsinnxiT1 t (sinnx)
(cos nx J (cos nx J
192
Ho sin п(±л)=О и в силу периодичности функций f(x) и созпх
имеем f(—л) cos (—пл) (л) cos пл, так что внеинтегральный
член в нашем равенстве обращается в нуль, откуда
«п = — Ьп = а’п/п (n €= N),
где
ал==(^я)' $ g(x) cos nxdx,
—n
ь'п— О /те) • J s(x)sin nx
—71
— коэффициенты Фурье для функции —л, л]. Дальнейшее
доказательство совпадает с проведенным в теореме и показывает,
что ряд Фурье функции f(x) равномерно сходится на (—оо, Ц-оо)
к сумме 8(х), непрерывной на (—оо, -|-оо) и периодической (с
периодом 2л), для которой наш ряд также является рядом Фурье.
Докажем, что S(x)=f(x) на [—л, л]. Поскольку Ух^Дх,- (i=
s=l, 2, ..., m) существует конечная производная Df(x), то по приз-
m
наку Дини S(x)=f(x) Vxe[—л, л]\ U {х/}, причем S, fe
еС((—оо, 4-оо)). В частности, тогда q>(x)=S(x)—f(x)<s
еС([—л, л]) и ф(х)=0 Vxe[—л, л], х^=х/ (j=l, 2, т).
Заметим, что точка —л, л] — изолированная, так что су-
ществуют интервалы
(xj—6j, Xj), (xj, Xj-|-6t)CZ[ л, тс] \ U
/=•1
Но тогда Я lim <p(x) = q>(xt±0) - 0, t. e. <p(x)=5(x)—f(x)=O на
[—тс, тс], откуда и имеем f(x) = S(x) на [—тс, тс]. Таким образом,
иаш ряд Фурье (2.1) сходится к функции Дх) равномерно на
[—тс, тс].
Следствие 2. Пусть график функции f(x) на отрезке
[—л, л] есть конечнозвенная непрерывная ломаная, причем fe
еС([—л, л]) и f(—я)=/(л) (см. рис. 5). Тогда ряд Фурье (2.1)
для f(x) сходится к функции f(x) равномерно на отрезке [—л, л].
Для доказательства достаточно заметить, что функция f(x)
удовлетворяет на [—л, л] условию Липшица (так что для нее вы-
полняется признак Дини) и является первообразной для ступенча-
той функции
g(x)= (°’ x~Xt (i=1, 2« • • • . m).
I clt x s (Xj, x<+i) 2,..., m—1)(
где d=Df(x) V xe (xit Xi+i), а х«е[—я, л] есть абсциссы угло-
вых точек ломаной. Очевидно, —л, л]. Теперь применимо
13 — л. И. Камынин 193
следствие 1 (причем равенство S(x) =f(x) vxs{—л, л] есть след- W
ствие признака Дини). . |
Замечание. Если функция f([—л, л]) имеет «кусочно-
непрерывную» производную Df(x), то функция f(x) является пер- ||
вообразной для функции g е Л[—л, л], где
= Df(x) v х е I—{х^г
О , x — Xi (i = 1,2,..., т), i
причем в точках разрыва функции g(x) Я lim g(x) = D±f(xt).
*-*x|±0
В частности, если f(—тс)=/(л), то ряд Фурье (2.1) для функции
f сходится равномерно на отрезке [—л, л] (к функции f(x), по- (
скольку выполнено условие Дини).
Теорема (о порядке убывания коэффициентов Фурье у глад- (
кой функции). Пусть f е ^)<fe)([—л, л], причем —л, л)
(Ы1, 2, ...) и Dlf(—n)=iD‘f(n) (1=0, 1, .... k— 1). Тогда для ко-
эффициентов Фурье функции f(x) имеет место оценка
/ lanl 1 — o(l/nft) (/г -> + оо).
I IM J
l°n ) I
Доказательство. Используя условия Dftf €= 7?[—л, л],
D'feCft—л, л]), D'f(—л)=О7(я) (Z=0, 1, .... k— 1) и интегри-
руя по частям k раз, получаем равенства
cosnx) . , ,
} dx= ±(l/n) X
sin nx j
sinnxil” _ZJ/. £/ . f sin rax 1
1 T(lm)- fDf(x){ dx.
COS ПХJ j-к _n I cos nxJ
Допустим» что для Z>1 имеем равенства
( U-n 1 . . / 7 тл/cz \ ( COS ПХ 1 ,
It. J nl = (±) . n~l- (Dlf(x)- J dx,
(&nJ -n (sinnxj
тогда, интегрируя по частям, получаем
Ho sin/z(±«) = 0 и в силу условия Dzf(—^) = И7(те) имеем
Dlf(—tc)cos(—nTt)== Dlf(K)cosпк, так что внеинтегральный член»
нашем равенстве обращается в нуль, т. е.
194
{CLfl / f | « \ n J-v f t 4 ff v f Sin 1ЪХ 4
} = ±n_<w) • fD'+’ftx) • { \dx.
bnJ -i I cos rax J
Итак, имеем представление
fan] . ь ггч»г/ \ fcosnx] .
it • I n I = ± n~k • f D*f(x) . | } dx
(&n J -n (sin rax J
или
(л } i 1
J U/1 I I 1 . J n I
I b~ j и* &<ft) I
4 n ' n ) >
где
a<*> = (l/it) • JD*f(x)cosraxdx,
6<,4)=(l/«) • j" D*f(x) sin nx dx (neN)
—n
— коэффициенты Фурье для функции —л, л]. В силу след-
ствия 4 из теоремы о неравенстве Бесселя (см. ч. IV, гл. 4, § 1)
имеем
lim с№ = lim 0(*> = О
п ,п
п-*- 4-00 72—> 4-00
т. е.
— о(1) (га —* +©о) =4-
|Ля| |=о(1 /га») (га-> + оо).
|Ьп| )
Замечание. Утверждения теоремы остаются в силе, если
считать, что —л, л] (&=1, 2, ...) D'f(—n)=D‘f(It)
,(/=0, 1, ..., k—1) и Dfe-1f(X) есть первообразная на [—л, л] для
функции g е jR[—л, л].
2-я теорема Вейерштрасса (о равномерном прибли-
жении непрерывной функции тригонометрическими многочлена-
ми). Пусть f еС([—л, л]) и f(—л)=/(л). Тогда Vе>0 сущест-
п
вует тригонометрический многочлен Tn(\)=lao/2+|2 (a*cosJfex4r
А=1 . 1 "
+^sin^x) такой, что |f(x)—Тп(х) | <е vx е(— л, л].
Доказательство. Поскольку feC([—л, л]), то по теоре-
ме Кантора функция f(x) равномерно непрерывна на отрезке
[—л, л] и поэтому Ve>0S6(e)>0 такое, что Vxi, Хг^[—л, л],
удовлетворяющих неравенству |х1—х2|<б(е), имеем оценку
—f(xi) 1'<е/4. Фиксируем е>0 и 6(б)>0 и выберем разби-
ение отрезка [—л, л}: Т—{—л=Хо<Х1< ... <хт=л} с диаметром
^(Т)<;б(е). Рассмотрим на декартовой плоскости (х, у) непре-
рывную ломаную с вершинами в узлах (xi, f(xt)) (i—0, 1, ..., m),
являющуюся графиком функции у—1(х), хе[—л, л]. По постро-
13* 195
ению Г<=С([—л, л]) и/(—л)=/(—л)=/(л)=/(л). Крометого,
Vхе [хь хж] имеем оценки |l(x)—l(x() |<|l(xi+i)—l(xi) | ==
==]f(xi+i)—f(Xi)\<z/4.
Пусть х е [—л, л] — любое, но фиксированное, тогда сущест-
вует частичный отрезок разбиения [х£, х,+1]эх и тогда lf(x)—
_/(х) | = [f(x)—f(х:)+1(Х1)-1(х) | < | f(x)-f(xi) I +1 l(Xi)-l(x) | <
<e/2. Итак, |f(x)—l(x) | <8/2 V x<=[—л, л]. Поскольку постро-
енная «ломаная» функция /е С ([—л, л]) и удовлетворяет усло-
вию /(—л.)=Цл), то в силу следствия 2 к теореме о равномерной
сходимости ряда Фурье видим, что ряд Фурье функции/(х) схо-
дится к ней равномерно на отрезке [—л, л] и тогда для выбранного
®>0 существует частичная сумма ряда Фурье Тп (х) = а0/2 4-
п
-PS (а*coskx+ sinkx)
(где as, Рй — коэффициенты Фурье функции Z(x)), такая, что
[Тп(х)—1(х) | Се/2 V х е[—л, л], откуда имеем оценку |/(х)—
—Тп(х) |<|Дх)—1(х) | +11(х)—T'nfx) | <8 V х <= [—л, л], что и
завершает доказательство 2-й теоремы Вейерштрасса.
Лемма. Пусть —л, л]. Тогда vs>0 существует непре-
рывная кусочно-линейная функция 1^С([—л, л]) такая, что
/(—л)=/(л)=0 u f \f(x)— l(x) |dx<8.
—те
Доказательство. Пусть f е 7?[—л, л], тогда f е В[—л, л].
Положим М= sup |Дх)|. В силу критерия Дарбу (интегрируе-
[—и, «j
мости по Риману из ч. II, гл. 2, § 2 [1]) inf Qf(T) = 0, и поэто-
т
му Vs>0 существует разбиение отрезка [—л, it]:T = {—п =
= х0<х1< . . . <x„ = it), такое, что
г=0
где = — Mt= sup Дх),
kp x>+i i
mi= inf Дх), Дхе = xl+i — xt (i=0, 1, . . . , n— 1).
i*i- xi+i 1
Пусть
min Axj = vi0 > 0.
i=0, !«•••» n—1
Пусть s>0 фиксировано. Выберем 0 < 7]<min(e/4«Af, т)0/2) и
введем отрезки
6i = [х,-т]/2, Xi+ri/2], |64|=т1 (i=l, 2, . . . , n-1),
60 = [—It, —1t-j-7]/2], 6„ = (it — T]/2, It], |60| = |6n| = 71/2,
bi = [xl + ''il2> xi+i—t]/2] (i = 0, 1, . . . , n— 1).
196
Тогда
—«=х0<х0-1-7]/2<х1— т]/2<х1<х1+т]/2< . . . <х;—
—7]/2<x<<xi4-7]/2<xz+1—71/2<xi+i<xi+i + 71/2< . . .
. . . <xn_i—т)/2<хл_1+т]/2<хп—т]/2<хл=к.
Построим кусочно-линейную непрерывную функцию 1(х)
резке [—л, л], положив
на от-
пц , х е Д;,
линейная, хе§;,
О , х=±те (i=0, 1, .
/(х) =
. , л—1),
Тогда, учитывая оценки |f(x)— /(х)|<^Л^— »^¥хеДъ |f(x)—
— Z(x)| < И WI + К Wl < 2М ¥х, имеем
f |f(x)-Z(x) I dx = % J |f (x)-Z(x)| dx + 2 f If (*) -
—те t=0 /=0
- l(x)\dx < "2 (Mi-m^Xi + 2M 2 1^1- Qf(T) +
z—0 /=0
. 4-2Jfn-Tj<e/2-t-e/2 = e=^ J|f(x) — l(x)\dx<e
—те
(при 0<т]<е/4Л1/г).
Следствие. Пусть fe.R[—л, л]. Тогда Vе>0 существует,
кусочно-линейная непрерывная функция /еС([-л, л]), такая что ’
Z(-ir) = Z(«) = O и ||f-/||2^ J|f(x)-Z(x)|2rfx<e.
Доказательство. Если fе/?[—л, л], то в силу леммы
V е>0 существует непрерывная кусочно-линейная функция
—те, те]) такая, что /(—те) =/(те) = 0 (причем |/(х)|^2И==
~(SUP lf(0l Vx<= [—те, те] и J|f(x) — /(x)|dx<e/2M). Но тогда в
силу оценки |f(x) — /(х)| 2Л1 Vx е [—s те] имеем
J |f(x) — /(х)|* dx < 2М ] |f(x) — l(x)\dx < 8.
Теорема (о полноте системы тригонометрических функций
® Z?[—л, л]). Пусть E=R[—л, л] — евклидово пространство.
Тогда ортонор мированная система тригонометрических функций:
1/Х2те, cosx/jAr, sinx/jAr, . . . , cos&x/)At, sinfcx/]/A, . . .
полна в 7?[—те, те] в смысле нормы
197
л____ * \ 1/2
И/|| =/(f. f) f/Wx) .
\— те /
Доказательство. Пусть —л, л] — любая, но фик-
сированная функция. По следствию к лемме V е>0 существует не-
прерывная кусочно-линейная функция 1^С([—л, л]) такая, что
Z(—те)=/(те) = 0 и ||/-/||2 = j [f(x)~Z(x)|2dx<e2/4. Для построен-
—л
ной непрерывной функции 1(х) в силу условия Ц—те) = /(те) по
2-й теореме Вейерштрасса для выбранного 8>0 существует
п
тригонометрический многочлен Тп(х) = а0/2 4- 2 (®ftcos£x +
fe=i
+ sin kx) такой, что |Z(x) — Tn(x)| < еДвте)1/2 Vxe [—те, те], но
тогда для выбранного е_>0 имеет место оценка
||Z—Т„||2 = J |Z(x) — Tn(x)|2dx < 2те • е2/8те = е2/4
—те
и в силу неравенства треугольника имеем ||/—ТП|К||/ — /||-г
+ ||Z — Тп||<8/2 + е/2 = е. Итак, если f е /?[— те, те], то Ve>0
существует тригонометрический многочлен Т„(х) такой, что
||f — Z|| О, но это и означает полноту ортогональной системы
тригонометрических функций 1, cosx, sinx,..., cos их, sinnx,...,
а стало быть, и полноту нашей ортонормированной системы
тригонометрических функций.
Замечание. Попутно доказано утверждение: пусть fе
е/?[—л, л]. Тогда Vs>0 существует тригонометрический много-
член Тп(х) такой, что
J|f(x)-T„(x)|dx<e.
—те
В самом деле, в силу леммы Ve>0 существует непрерыв-
ная кусочная-линейная функция Z е С([—те, и]) такая, что
Z(—k) = Z(«) = 0 и J|f(x)-Z(x)|dx<8/2,
—те
а по 2-й теореме Вейерштрасса существует тригонометричес-
кий многочлен Тп(х) такой, что |Z(x) — Гп(х)Ке/4те V х е [—те, те],
т. е.
J |Z(x) — Tn(x)| dx < 2те • е/4те = е/2,
—те
откуда
I \Кх) - Tn(x)| dx < J |/(x)-Z(x)| dx + J |Z(x) -
- Z’n(x)Mx<e/2 + 8/2 = e.
198
Теорема (о замкнутости в /?[—л, л] системы тригонометри-
ческих функций). Пусть E—R[—л, л] —^вклидово_пространство.
Тогда ортонормированная система 1/У2л, cosx/Ул, sinx/Ул,
cosnx/Ул, sinnx/Ул, ... замкнута в /?[—л, л], т. е. Vfe
jRf—л, л] выполнено равенство Парсеваля
д2/2 + 2 К + ь*) = (1/к) • $ Ю dx,
л=1 —те
где
an = (l/ic)- J/(x)cosnxdx, п s No
—те
U
bn в (1/те) • J f(x) sin nxdx, п N
—те
— коэффициенты Фурье функции f(x).
Утверждение теоремы следует из доказанной ранее теоремы об
эквивалентности понятий замкнутости и полноты для ортонорми-
рованных систем в абстрактных евклидовых пространствах.
Теорема (о сходимости в смысле среднего квадратического
рядов Фурье по тригонометрической системе в /?[—л, л]). Пусть
£=/?[—л, л] — евклидово пространство. Пусть f е /?[—л, л] и
+00
До/2+S (ancosnx+bn sinnx) — ее ряд Фурье по тригонометри-
Л»1
ческой системе. Тогда ряд Фурье функции f сходится к функции
f(x) в смысле среднего квадратического, т. е.
lim ||/ —Sn|| = 0,
Л-*4-оо
где
Sn(x; f) — а0/2 4- 2 (ал cos kx + bh sin kx) —
*=i
п-я частичная сумма ряда Фурье функции f, а
Г---- / ” V/2
||/|| = 1Л/, /)=( \?{x)dx\ .
\ —те /
Утверждение теоремы следует из теоремы о замкнутости в
₽[—л, л] тригонометрической системы и доказанной ранее теоремы
об эквивалентности сходимости ряда Фурье (в норме евклидова
пространства /?[—л, л]) и выполнения равенства Парсеваля в аб-
страктных евклидовых пространствах (из гл. 4, § 1).
Теорема (о единственности ряда Фурье для непрерывной
Функции). Пусть
199
/ап> = а<2), n<=N0
|л(0 = b&>, ne=N
/ь/2еС([—гс,я]) и ft~a(p/2 + у (a<pcosnx-|-&<j)sinnx) (t=l,2)-
•— ряды Фурье этих функций по тригонометрической системе. Тог-
да
(fi(x) = ft(x) на {—
Доказательство. Необходимость, очевидно, следует из
формул Фурье для коэффициентов Фурье функций fi(x)^f2(x).
Достаточность. Пусть для всех коэффициентов Фурье функций
fi(x) и f2(x) выполнены равенства = a*,2’ (neN0) и 6(п*> =
q=(2) (Vne N). Допустим, что fi(x)^f2(x) на [—л, л]. Посколь-
ку ортонормированная система тригонометрических функций зам-
кнута в евклидовом пространстве 7?[—л, л], то в силу доказанной
ранее (в гл. 4, § 1) теоремы единственности для рядов Фурье (по
замкнутым системам) в евклидовом пространстве имеем
llfi-fill- J(f1(x)-f>(x)2dx = O.
—те
Положим <р(х) = (/\(х)— fa(x))2 V х g (—гс, я]. Тогда ф е С([—гс,
гс]), причем <р(х) 0 на [—гс, «], <р(х) >0 Vx е [—гс, я], но
J <р(х) dx = 0.
—те
Противоречие с соответствующей теоремой (см. [1], ч. II, гл. 2Г
§ 6) из теории интеграла Римана.
Следствие 1. Пусть f е С ([—л, л]) и f(—л)=|(л). Пусть
тригонометрический ряд (2.1)
4-00
а0/2 + у (an cos пх + bn sin пх)
Л=1
является рядом Фурье для функции f(x) (т. е. / ~ а0/2 4-
4-°° f
+ 2 (ancosnx4-bnsinnx)) и сходится равномерно на [—гс, я].
п—1
Тогда сумма ряда (2.1) совпадает на [—гс, я] с функцией f(x).
Доказательство. Пусть S(х) есть сумма ряда (2.1). Тогда
5('x+2n)=S(x)Vxe(—оо, +оо), и поскольку ряд (2.1) схо-
дится равномерно к S(x) на [—л, л], то <S е С([—л, л]), причем
в силу доказанного ранее тригонометрический ряд (2.1) является
рядом Фурье и для своей суммы S(x) (т. е. S~a0/2+\
4-00
+ S (ап cos пх+'fin sin пх)). s
П=1
200
Итак, ряд (2.1) является рядом Фурье одновременно для функ-
ций f, S е С ([—л, л]). В силу доказанной теоремы единственности
S(x)^f(x) на [—л, л].
Следствие 2. Тригонометрический ряд (2.1) может быть
рядом Фурье только для одной непрерывной на [—л, л] функции
f(x). Тем самым показано, что ряды Фурье ведут себя совершен-
но иначе, чем ряды Маклорена (которые могут быть рядами Мак-
лорена для бесконечного множества функций f еС<°°>(0)). (На-
помним, что из того, что тригонометрический ряд (2.1) является
рядом Фурье для функции f(x), вообще говоря, не следует пото-
чечная сходимость ряда (2.1) к функции f(x) на [—л, л].)
Замечание 1 (теорема дю Буа-Реймона). Если fs
gC([-л, л]) (и даже —л, л}), f(—n)=f(n) и функция f
разлагается в тригонометрический ряд на [—л, л]
4-00
f (х) = а0/2 4- У (an cos пх 4- bn sin пх), х g [—л, я],
то этот ряд является рядом Фурье для функции f, т. е.
ап = (1 /я) • j1 f(t) cos nt dt (n e No),
—я
bn = (lln)' ^f(t) sin nt dt (ngN)
—n
(CM. [2]).
Замечание 2. Рассмотрим
f(x) = 2° sinn*/n“> x s [—«» Ч (при 0<а<1/2).
Л<==1
Тригонометрический ряд, стоящий справа, сходится Vxe[-irf
я] (в силу признака Дирихле), однако не является рядом Фу-
рье для своей суммы Дх), поскольку (при &п=1/п“ и 0<а^1/2}
равенство 2 ^« = 2 l/n2a = -f-oo противоречило бы неравен-
П=1 72=1
ству Бесселя (для коэффициентов Фурье). Из теоремы дю
Буа-Реймона следует при этом, что f g /?[—я, я].
Лемма. Пусть функция f(x) определена- на (—оо, +<»),
f (х+2л) —f(x) Vx и R[—л, л]. Пусть gе£(—л, л].
Тогда
]f(x±t) -g(t) • |cosnJU =Х0
I Sin fit J (nr+oo)
на (—oo, 4~oo).
201
Доказательство, (g£ R[—л, л]) => (g е В[—л, л]). Пусть
К= sup |g(x)|< + <». Поскольку f е Я[—тс, тс], то на основа-
(-». я]
нии замечания к теореме о полноте системы тригонометричес-
ких функций V е > 0 существует тригонометрический много-
член ТДх) такой, что f|f(O — Ti(t)\dt <Z&/2K. Пусть L= sup
-я l-«. "]
1Л(Х)К + °0, Поскольку g еЯ[—тс» тс], то на основании того
же замечания для выбранного е^>0 существует еще один три-
гонометрический многочлен ^„(t) такой, что J|g(t)—
—я
<е/2£, но тогда в силу периодичности функций f(t) и T/(t)
имеем Vxg(—оо, 4-оо) оценки
Jf(x±O • g(t) .
—Я
cos nt
sin nt
dt— *$Tt(x±t)X
—n
Xgtf) .{
cos nt
sin nt
< f |f(x±f) + Tt(x± t)l *
—n
;if(x±0-^±OI^ = ^ j lf(t)-Tz(t)|dt =
JTz(x±t). g(O-
— Я
= К J If (0 - T{(t)\dt < К • 8/2Я = 8/2.
— я
Аналогично Vxe(—оо, -f-oo) имеем оценки
cosnt] ,, " • , .
• Adt — rM0X
sin nt J _J„
хад- (cos"4d< jW±t)|X
I. sin nt J I _i
X |g(0 - ^rn(0l dt < L . s/2Z- = e/2.
Но функция T/(x±t)« &m(t) при любом фиксированном x есть
тригонометрический многочлен относительно t порядка п0(г),
т. е.
ТДх± 0 • ^т(0 = 2* (a^’W cosfet + ?<±>(х) sinfet).
k=0
В силу ортогональности тригонометрической системы в 2?[—тс,
тс] имеем Vxs(—оо, -|-оо)
f Tz(x±t) • &m(t) • (C0Sn4 dt = 0 Vn>n0(s).
l sin nt J
202
Но из полученных оценок следует, что Уе>ОЯпо(е)eN та-
кое,. что Vn>n0(e) и Vxs(—оо, 4-оо) имеем оценку
dt
—Я
- ГДхгЬО) - g(t) • {...}dt
]T,(x±t) • (g(t)-
• {-}dt + JTz(x±t) • &m(t) • {...}dt <e/2+8/2=e,
t. e.
f/(x±t) • g(t) • |C0S”4dt 0 на (—oo, +oo).
-к I sin nt j (П-+ОО)
Следствие. При выполнении всех условий леммы имеем
$f(x±t)g(t) sin 0 на (—оо, 4-оо).
—тс \ " / (Л-»-Роо)
Доказательство. Очевидно, sin ( п.4- — ) t= sin — • cosnt-|-
12/ 2
+ cos у • sinnt,. тогда, полагая fi(7)=g(7)sin — e /?[—it, it] и
2 2
gt(t) — §(t) cos ~ it], видим, что утверждение следст-
вия вытекает из леммы.
Теорема (признак Дини равномерной сходимости ряда
Фурье). Пусть функция f(x) определена на (—оо, Ч-оо), f(x-|-
+2 л) =f(x) V х, —л, л] и f е С ([а, Ь]). Пусть Яй>0 такое,
ь
что несобственные интегралы S \f(x±u)—f(x)\/udu сходятся
о«-
равномерно на отрезке [а, 6]. Тогда ряд Фурье (2.1) функции f
сходится к функции f(x) равномерно на отрезке [а, о].
Доказательство. Поскольку feC([a, Ь]), то любое
хе [а, 6] является регулярной точкой функции f так, что f(x) =
=f(x±O), 2f(x)=f(x-j-O) +f(x—0)VxG(fl, 6]. В силу признака
Дини ряд Фурье (2.1) для функции f сходится к f(x)v хе[а, 6].
Докажем равномерную сходимость ряда Фурье (2.1) к функции
f(x) на отрезке [а, Ь]. Отметим представление Дирихле
(V х G [а, Ь]> 5я(х; f) - f(x) = (1/«)X
X f ]f(x + и) 4- f(x — u) — 2f(x)]0 n(w)d«.
b
203
В силу условия Дини (нашей теоремы) из равномерной сходимо-
Л
сти несобственных интегралов J \f(x±u)—f(x)\/udu на [а, &], вы-
о—
текает, что Vе038(е)е(0, Л] такое, что'Ухе [а, Ь]
8(e)
j |/(х + и) + Дх — и) — 2/(х)] •
0<-
8(e)
< J |Дх + и) — Дх)| • U-1 du +
0«-
8(e)
+ f |Дж — и) — f(х)| • u~l du 8.
(U-
Положим
6(g)
, -$n(x; = . f (,..)d«+(l/«)X
о<-
X J (...) du = Ап(х) + Вп(х) V х е [а, 6].
8(e)
В силу оценки | ®л(и)|<те/2|и|, 0<|«|<те для ядра Дирихле и
выбора 8(e) 0 имеем оценку
8(e)
Ип(х) I < те/2те . f | Дх + U) + f (X—U) — 2/ (х) | X
о—
X u~l du < б/2 Ухе [а, &].
Полагая
0, —те^К<^6(8),
= I 1 / (2п • sin 0<8(s)<« <те,
\ 2 j
видим, что ?бй[—те, те], и Vх G [а, Ь] имеем
Вп(х)= J[f(x+«] +Дх— и) — 2f(x)]X
—п
Х?(«) • sin ( «+4-) и du.
\ 2 j
Но (/£Й[-те, те])=>(/ G В[—те, те]), так что sup \f(x)\=M<^’ir'X>.
[а. Ы
Вспоминая, что функция f(t) периодична с периодом 2те, име-
ем в силу следствия к нашей лемме
Я / 1 \
Jf(x±u)g(«) sin I «4—I udu 0 на [a, ft],
—” \ ^ / (n-»4-oo)
204
а из оценки
<2М
тс
J g(u) sin
—Л
udu Ухе[я, Ь],
поскольку,
” I 1 \
lim С g(u) sin п-\— udu — О
п-»+оо _д 2 у
видим, что
" / 1 \
J2f(xjg(«)sin /гН—I udu 0 на [а, Ь],
-Я \ 2 > (Л-+Х>)
откуда Вп(х) 0 на [а, 6], т. е. для выбранного 8^>0
* роо )
Я n0(e) <= N такое, что |B„fx)|<e/2 Vn>n0(e) и Vx е [а, Ь].
Итак, Vе>0 Я n0(e) s N такое, что Vn>n0(e) и Vxe[a, &]
имеем оценку
|Sn(*; f) ~ f Wl< |An(x)\ + |B„(x)| <e/2 + 8/2 = 8,
T. e. 5n(x; f) 2* f(x) на [a, 6].
Следствие 1. Пусть функция f(x) определена на (—оо,
H-оо) и периодична с периодом 2л. Пусть —л, л] и f<=
еЯв[Л, В], где 0<сс^1. Тогда ряд Фурье (2.1) функции f схо-
дится к f(x) равномерно на любом отрезке [а, &] cz (А, В).
В самом деле, пусть фиксирован любой отрезок [а, Ь] с. (А, В).
Положим /i=min(a—А, В—Ь)>0, тогда x±ue(A, В] Vxe [a, b]
при ОДи^/i и в силу условия Гельдера видим, что V х = [а, 6]
lf(x±u)—f(x)\-url^Hua~lV ue(0, й].
Но тогда несобственные интегралы
f |f(x±u) — f(x)\ • u~ldu
b<-
в силу признака Вейерштрасса сходится равномерно на отрез-
ке [а, &] и применим признак Дини равномерной сходимости
ряда Фурье (2.1) (поскольку (f <= Ва[А, В])=Ф(/еС([4, В]))).
Следствие 2. Пусть f^Ha{—л, л] (где 0<а^1) и
7(—л)=/(л). Тогда ряд Фурье (2.1) функции f сходится к функ-
ции f(x) равномерно на отрезке [—л, л].
В самом деле, поскольку /(—л)=/(л), то функцию f(x) мож-
но продолжить периодически (с периодом 2л) на (—оо, -|-оо).
Тогда, очевидно.
f^Ha[A, -к]ДЯа[-«. В],
205
если [—it,тс] С (Л, В)С[—2те, 2те]. Но тогда f ^На[А, В] (с по-
стоянной Гельдера, быть может, 2//>0 вместо Н). Для про-
верки достаточно рассмотреть, например, случай —2те^Л<;х1<
<—it < х2 < it < В 2те, тогда
1Д*1) - №)1 < I f( *0 - f (-*)14-1/(-«) - f WI <
< Я(|*1 - (—«)[« +1 -те - х2|“| < х2|».
Теперь к периодической функции f g Яа[4, В] и к отрезку
[—те, те]с(Л, В) применимо следствие 1.
Следствие 3. Пусть функция f(x) кусочно-непрерывна с
кусочно-непрерывной производной на отрезке [—л, л]. Тогда ряд
Фурье (2.1) этой функции сходится к значению функции f(x) в
любой точке х g (—л, л), где функция f непрерывна, и к значению
(f (*о+0)+/ (хо—0) )/2 в точке разрыва Хо функции f. Кроме того,
ряд Фурье (2.1) функции f сходится к f(x) равномерно на любом
отрезке [а, Ь]с=(—л, л), который вместе со своими концами лежит
в области непрерывности функции f.
В самом деле, продолжим функцию f(x) периодически (с пе-
риодом 2л) с полуинтервала [—л, л) на (—оо, -|-оо) с помощью
равенства /(х-]-2л) =f(x) Vх. Тогда первое утверждение следует
из доказанного ранее следствия к признаку Дини поточечной схо-
димости ряда Фурье. Далее f g C(1>((xit x1+i)j (i=l, 2, ..., т—1)
При —Я<Х1<Х2<-<Хт<Л. ПуСТЬ [а, 6] <= (xk, Xk+1), ТОГДЭ
Эб>0 такое, что [а, &] с: (xft+6> xft+i—6) c[x*4-6, Xk+i—б]с:
с=(хъ xft+1), и поскольку Df G С([Xfe+б, Xk+i—б]), то fG#i[x*+;
+б, Xk+i—б]. Но теперь последнее утверждение следствия 3 выте-
кает из доказанного в следствии 1 признака равномерной сходи-
мости ряда Фурье.
Теперь в качестве нетривиального применения теории рядов
Фурье докажем формулу дополнения для гамма-функции Эйлера
(из ч. IV, гл. 3, § 5).
Теорема (формула дополнения для гамма-функции Эйлера)»
Пусть xg (0, 1). Тогда Г(х)-Г(1—х) = л/sin(лх).
Доказательство. При х>0, у>0 имеем В(х, у)=*
=:Г(х)-Г(у)/Г(х+у). Положим хе(0, 1), у=1—х, x+i/=>l, тор*
да в силу 2-го представления для бетта-функции Эйлера (см. ч. IV,
гл. § 5), учитывая Г(х+у) = Г(1) = 1, получаем
Г(х) • Г(1-х) = В(х, 1— х) = Т /*-1/(1+*)<#•
оД
Но
Т «»-*/(! + о dt = f tx~4(i +t) di +
оД О— 1
Делая замену t—.tx-l = tl-x, dt =—x~2dx, 1/(14-i)=t/(l-}-<),
имеем
206
Y tx~1 (1 +t)~ldt = J x*—lx( 1 +т)Л =
i o«-
= J T-’/(l +1)dx = J t(‘-*>-‘/(l4-T)dT,
0«- 0—
откуда
B(x, l-x) = f ««->/( 14-ОЛ + f t^-^/(l+t)dt.
0— 0«-
Пусть ^e[0, 8], где 0<6<l, тогда, используя формулу для
суммы членов геометрической прогрессии, имеем
/'-‘/(l-f-O = 2 (—l)nin= 2 (—l)n/n“1+*,
n=0 n=0
откуда
/*-‘/(14-0 — tx~l = 2 (— 1)я*',-1+*, (2.2)
n=l
где ряд (2.2) сходится равномерно на отрезке [0, S], поэтому, ин-
тегрируя ряд (2.2) на отрезке [0, 6], получаем ряд
f (**-*/( 14-т)—x«-1)d-r= 2 (-1)п/"+*/(п4-х), *е=[0, §]. (2.3)
0— п=1
Ряд (2.3) сходится и при /=1, поэтому, используя 2-ю теорему
Абеля для степенных рядов (из ч. IV, гл. 3, § 3), убеждаемся, что
ряд (2.3) сходится равномерно на отрезке [0, 1] и, в частности
Я lim f [t«-‘/(14-<)~ «*-*]* = V (—1)п/(«4-х),
*-1-0 Jo_ „=1
так что
j /*-‘/(14-0 dt = 1/х 4- 2 (“ 0п/(«+х),
0*- л=1
но тогда
J /а-*)-1/(14-Г) dt = 1/(1-х) + 2 (— 1)"/(« 4-1 — х),
О— п—1
откуда имеем
В(х, 1—х) = | /*-‘d/4-| t~xl<y+t)dt = 1/х4-
b«- о—
+ 2 (-Пп+х) 4- 1/(1-х) 4- 2 (-1№+1-х)«1/х4-
П««1 П=1
207
+ 2 (-!)”/(«+*) - 2 (-1)7(«-^) = Ш +
n=l n—i
+ 2 (- 1)n+12x/<"2 _ x^>
n=l
t. e. Vx^(O, 1) имеет место представление
B(x, 1+х) = 1/х4-2х • 2 (—1)п+1/(п2-х2). (2.4)
П=1
Рассмотрим теперь функцию f(x)=cosax, хе[—л, л] (где
а — не целое). Очевидно, —л, л] и Df('x_)=i—a sin ах V хе
е(—л, л). В силу наших рассмотрений ряд Фурье для функции
f(x)=cosax сходится к f(x) Vxe (—л, л) (причем даже равно-
мерно на любом отрезке [а, Ь]с (—л, л)). Поскольку f(—х)=>
—f(x)vx<=[—л, л], то f(x)=cosax — четная функция и поэто-
му ее ряд Фурье содержит только косинусы, причем
ап = (2/те) • [ cos ах • cos пх dx, n s No,
b
так что
тг
a0 = (2/к) • J cos ax dx = 2 sin axlr.a = 2 sin ait/ira.
0 x=0
Далее
an=(2/ir) • [ cos ax • cosraxdx = (1/it) X
о
X f [cos (n-}-a)x -h cos (n—a)x] dx — (1/it) X
b
X [sin(n4-a)x/(n+a) 4-sin(n—a)x/(n—a)]|; = (l/tt) X
X [sin (a« 4- mt)/(n 4- a) 4- sin (—am 4- nm)/(n — a) ] =
= (—!)”• [sin атЦп 4- a) — sin am](n — a)]/u=
= 2a(—I)**1 sin ait/(it(n2 — a2)).
Итак, V i eE (—it» it) имеем представление
4-oo
cos at = sin amlam 4- 2a sin a-tt/it • (—1)"+1 cos ni/(n3—a2),
n—t
откуда
m cos at/sin ait = 1 la 4- 2a 2 (— l)n+1 cos ni/(n2 — a2),
n=l
<e(—я). Полагая t = 0 и a = xe(0, 1), имеем
208
те/sin (тех) = l/x4-2x (—l)n+1/(«2—*2),
но тогда из (2.4) получаем формулу
В(х, 1 —х) = тс/sin (тех),
т. е.
Г(х)- Г(1 —х) = те/sin (тех) Vxe(0, 1).
Приведенное доказательство формулы дополнения сообщено авто-
ру Н. И. Фельдманом.
Теорема (о дифференцировании ряда Фурье). Пусть
fsC((—л, л]) и f(—n)—f(n). Пусть Vxe[—л, n]S-Df(x) а
+»
D/ е Я[—л, л]. Если /~ао/24~2 (ап cos nx+bn sin пх), тогда
п=1
-И»
Df ~ S (—пап sin nx+nbn cos пх), г. е. ряд Фурье производной Df
получается из ряда Фурье самой функции f формальным почлен-
ным дифференцированием.
Доказательство. Поскольку D/sJ?[—я, л], то для функ-
ции Df существует ряд Фурье, т. е.
Df ~а0/24- У (ап cos пх 4- pn sin пх).
Поскольку /(—те) — /(те), то интегрирование по частям дает
с
а0 = (1/те) • ]Df(t)dt=(f(^-f(-K))/^=O и VnsN,
—те
теап= J Df(t) cos nt dt = {/ (t) cos nt]ln 4- n J f (f) sin nidi;
—те —те
терп= J D/(7) sin nt = [/(7)sinп/]^я—n J f(t)cosnt dt.
—те — n
Ho Sinn(±it)=O и поскольку f (—те)=--- /(те), то /(—те) COS (—Пте) =••
=/(те) cos пте, и поэтому внеинтегральные члены в равенствах
справа обращаются в нуль, откуда an = nbn, ?n=—пап VneN.
Но тогда
+00
(n&ncosnx—папsinпх) —
л=»1
+00
= 2 D(«n cos пх 4- bn sin пх).
ziel
Замечание. Если fe=0([—л, л]), f(—л)==/(л) и D/e
а[--л, л], то ’ряд Фурье для производной Df, получающийся
Л. И. Камыши 209
формальным дифференцированием ряда Фурье (2.1) для f, вооб-
ще говоря, не обязан сходиться к функции Df(x).
Следствие I. Пусть функция f(x) является первообразной
на [—л, л] для функции —л, л], причем f(—n)=f(n). Тог-
да если
4-00
f ~ «0/2 4- У (ап cos пх 4- bn sin пх),
№1
ТО
g ~ У, (—n <xn sin пх 4-cos пх) =
п=1
4-00
cosnx + ba sin nx),
n=l ;
т. e. ряд Фурье для функции g получается из ряда Фурье для f
формальным почленным дифференцированием.
Следствие 2. Пусть feC([—л, л]), f(—л)=/(л) и функ-
ция f (x) имеет на I—л, л] «кусочно-непрерывную» производную
Df(х), т. е. функция
fe £([-«, А С(1>([хА, хж]) (k=l,...,m-i)
(—= Х1 х2 < • • • хт = 1t)
является первообразной для функции
=( Df(x) Vx<=(xA, x*+i); /г=1.,.-.,'т—1,
(0 х=хЛ; k=i,...,m,
причем lim g(x)=D±f(xk) (fe=l,. . . , m) и поэтому «, «].
Тогда если
4-00
f ~a0/2 4- У (an cos nx 4- bn sinnx),
k=t
TO
def +00
g — Dfi» у (— na n sin nx + nbn cosnx) =
ra=»l
= S D(an cos nx 4- b„ sin nx).
Следствие 3. Пусть fe£W([—л, л]) (fe^l),
e= £[—л, л] и Dzf(—л) =D‘f(n) (l—О, 1, ..., k— 1).
Пусть
f ~ a0/2 4- 2 (a“ cos nx + sin nx)' > f
n»l
210
Тогда
Dlf ~ У, Dz(an cos пх + bn sin пх) =
/2=1
,, ( . \ . . . / , In \\
= 2 n'(a„ cos пх +— +$nsm ПХ-f — .
n»i \ z / \ ^ / /
Z=l, 2, . . . , k.
Замечание. Утверждения следствия 3 остаются в силе, если
f е ® <*-»> ([-л, л] , D'f (—л) =D'f (л)
(1=0, 1, ..., k—1) и D^-'ffx) на [—л, л[ является первообразной
для функции ge/?[—л, л] (например, если функция f(x) имеет
кусочно-непрерывную производную Dkf(x). на [—л, л]).
Теорема (о скорости сходимости ряда Фурье для гладкой пе*
риодической функции). Пусть
f (=£<*> ([_я> я]) t Dkf s Я1 я] )
и
Dzf(—n)=D'f(n) (1=0, 1, ...» k— 1).
Пусть
4>«0
f ~ а0/2 + 2 (ап cos пх + Ъя sin пх).
П«1
Тогда для /=1, 2, .... k имеем
+®»
Dlf ~ 2 О'(ая cos пх + К sin пх)==
л-*1
4-°® .
= 2 л‘ • (ап cos (пх 4-J • те/2) 4-bnsin(nx-f-Z • те/2)),
п=«1
причем для 1=0, 1, ..., k—1 имеет место оценка
|Dzf(x)-Sn(x; D'f) | С-ГпСО/л4"1-1/2 Vxe [-л, я],
где yn(J)=o(l) (п-*--|-оо).
Доказательство. Из следствия 3 вытекает, что при
1"=!, 2..k имеем
Ч-*®
D'f ~ 2 DZ(an cos пх + sin пх) =
п«=1
== 2 п‘(а« cos(nx-|-Z • те/2)4-дпsin(nx-f-Z • W2)),
Л«1
причем по теореме о равномерной сходимости (рядов Фурье) ряд
Фурье для функции Dlf (где D'f е®(й-,)([—л, л]); так что D'fe
®С([— л, л]); D'f(—л)=О7(л) и О'+7<=Я[—л, л] .(/=0, 1, ...»
u* 211]
.... k—1)) при /=0, 1 k—1 сходится к функции D‘f(x) равно-
мерно на отрезке [—п, я]. Пусть Sn(x-, Dlf) — п-я частичная сум-
ма ряда Фурье для функции Dzf, тогда имеем представление для
«остатка» ряда Фурье
rn(x; D7) = |D'f(x) - Sn(x; Wf)| =
I +°° г
= 1 3 "П amcos (mx-Yl • тс/2) + bm sin(mx 4-
I m= n+1
+I u/2))
< 2 wz(|am| + |bj) Vxe [—«, «]•
m=n+l
В процессе доказательства теоремы о скорости убывания коэффи-
циентов Фурье для гладкой периодической функции была получе-
на оценка .
Р/и| J
1^’1
где и &«*>
— коэффициенты Фурье для функции Dkf<=R[—л, л]. В силу не-
равенства Бесселя имеем
2 (W + IW< + °°-
Т. е. |am| + |bm| < a.m!mk, где
4-00
2 ат<+°°«
т=1
Итак,
4-00
г„(х; Dzf)< 3 Лт!тк'1 VX(=[—гс, тс] (/=0, 1,..., fc—1).
m=n+l
Но из неравенства Коши—Буняковского V2V^>n-}-l имеем оцен-
ку
N
2 (iw-z)<
m=n+l
IN \l/2 I N \t/2
< 3 arn • 2 ,
\m=n4-l / \m=n4-l /
откуда, переходя к пределу при N—►-f-oo (учитывая, что
2(k—0>2), имеем оценку
(4"оо \ 1 /2 / 4"°® \ 1 /2
S am ’ S «-2(^-0 VxS[—тс, тс].
m=n4-i / \тгс=п4-1 /
т
Поскольку zn_2(fe~zX f то Nимеет место
m-i
оценка
212
N N
2 < J /-2(л-о dt,
m=n+l n
так что
2 zn-2<fc-J> < "7 t'zlk-ndt = п-2(*-/)+1/(2(й—/)—1).
m=n+l
Положим
п
Шкап +1
тогда
( lim 7n(Z)=0)=>(yn(Z) = o(l) (n-> + oo)).
n-»4-co
Итак, при Z=0, 1, . . . , k—1 имеем окончательную оценку
rn(x; Vx.G [-к, W],
т. e. при Z=0, 1, . . . , k-l \Dlf(x)—Sn(x-, Dzf)|<
<Tn(Z)/nft-'-1/2 VxeH.it],
где тл(/) = о(1) (n-> + oo).
Замечание. Теорема остается верной и в предположении.
f к]), Dzf(-i:)=D7(ir) (Z=0, 1,..., k-V),
является первообразной для функции g е7?[—л, л] (на-
пример, в предположении, что периодическая функция f(x) имеет
на отрезке [—л, л] кусочно-непрерывную производную Dkf(x)).
Замечание. При выполнении всех условий теоремы (или
замечания к ней) доказанное неравенство
\f(x)—Sn(x; f)|<b/nA-1/aVxe{-n, л],
ь=0(1) (п->+оо) (2.5).
дает оценку скорости сходимости ряда Фурье для периодической
гладкой функции f(x). Таким образом, доказанная оценка показы-
вает, что чем больше производных имеет периодическая функция,
тем быстрее сходится к ней ряд Фурье, причем неравенство (2.5,)‘,
Дает возможность оценить погрешность, получающуюся при заме-
Ве ряда Фурье функции f на его п-ю частичную сумму.
Пусть функция feC([—л, л]) определена только на отрезке
r-я, л]. Тогда —л, л] и для нее можно написать ряд
Фурье (2.1), где
en = (l/it). J f(f) cosntdt, п g No
— 71
И
213
6n = (!/*). $ f(t) sin nt dt, ne=N.
— 7C
Как было доказано, ряд Фурье (2.1) всегда сходится к функ-
ции f(x) в евклидовом пространстве 7?[—п, л] в смысле среднего
квадратического (т. е. в метрике, индуцированной нормой ||f]|=
= (J f2(x)dx)W2). Обращаясь к вопросу о поточечной сходимости
ряда Фурье (2.1) для функции f, заметим, что если не налагать
на функцию f(x) никаких ограничений, кроме непрерывности, то
можно показать (см. [2]), что для периодической (с периодом
2л) функции feC((—оо, 4-оо)) ее ряд Фурье (2.1) может и рас-
ходиться в некоторых точках, и не сходиться равномерно вблизи
других точек. Пусть поэтому f е С ([—л, л}), причем f(х) удов-
летворяет на отрезке [—л, л], например, условию Дини. Тогда, как
было показано, для ряда Фурье (2.1) (функции f) имеем
4-00
Яо/2+ S (ая cosnx-f-Z?n sin пх) — S(x), XS(—оо, Ч-оо),
r»—l
где сумма S(x) ряда (2.1) определена на (—оо, +оо) и периодич-
на с периодом 2л, т. е. 5 (х+2л) =S(x) V х. В силу признака Дини
имеем S(x) =f(x) Ухе (—л, л) (поскольку f е С((—л, л)) и по-
этому любая точка хе(—л, л) является точкой регулярности
функций f). Если f(—л)#=|(л), то функция S(x) будет иметь раз-
рывы 1-го рода в точках вида х=(2&+1)л (k—Q, ±1, ±2, ...),
причем (рис. 7) S(±n) = (f(n—0)+f(—л+0))/2= (f (л)-Ь
:+|f(—л))/2#=^(±л). Если f(n)=f(—л), то S(±n)=f(±n) и
поэтому S(x)=f(x) на [—л, л], 5еС((—оо, +оо)). В этом слу-
214
чае сумма S(x) ряда Фурье (2.1) функции / дает непрерывное пе-
риодическое продолжение функции f(x) с отрезка (—л, л] на
[(—°0, +|ОО).
Рассмотрим теперь функцию f^C([0, л]), определенную толь-
ко на отрезке [0, л] и удовлетворяющую на [О, л) условию Дини.
Поскольку для f^C([О, л] имеем f е/?[0, л], то можно вычислить
«коэффициенты Фурье» ап и Ьп по формулам Фурье (для четной и
нечетной функций):
ап = (2/тс)- J f(t) cos nt dt (n <= N,) и
о
&„ = (2/тс)- Jf(7)sinn/ dt (nsN).
о
Рассмотрим сначала тригонометрический ряд
4-00
а012 4- 2 ancosnx = S1(x), хе(—оо, 4-оо), (2.6)
л—1
содержащий только косинусы. В силу формул Фурье ряд (2.6) яв-
ляется рядом Фурье для четной на отрезке [—л, л] функции
1 } if(-x), Х€=[-тс, 0].
Заметим, что
Л(0±0) = /(0), /\(-тс) = /(тс), ед=/(«),
так что FjSCd—тс, тс]), —tc)=Fx(tc), Fx(—x)=Fx(x) Vxe[—я,
тс]. Для функции Fi(x), кроме того,, выполнены условия Дини
на [—тс, тс], поэтому в силу признака Дини ряд (2.6) сходится
на отрезке [—тс, тс] к функции Ег(х), т. е. S1(x)=Fl(x) на |—тс,
тс]. Но тогда для суммы ряда (2.6) имеем 8г(х) = f(x) на
]0, тс], SxeC((—оо, +<»)), Sj(x + 2тс)==51(х),
Si(—х) — S±(x) Ух S (—оо, -f-оо),
т. е. функция Si (х) — сумма ряда (2.6) представляет собой непре-
рывное, четное и периодическое (с периодом 2л) продолжение
функции f(x) с отрезка [0, л] на (—оо, +<ю) (рис. 8). Рассмотрим
теперь тригонометрический ряд
t
2 6nsinnx = <S'lfx), х е(—оо, +со), (2.7)
л= 1
содержащий только синусы. В силу формул Фурье (для нечетной
функции) ряд (2.7) является рядом Фурье для следующей нечет-
ной на отрезке [—л, л] функции (рис. 9):
215
F2(x) =
f(x) , xe (0, it),
0,. x = 0 ± it,
—/(—*)» xs(—tt, 0).
Заметим, что Vие (О, л) имеем равенства
Г2 (—л+и) —Г2 (—л 4-0) =<—[f (л—u) —f (л) ];
F2(0+iu)-F2(04-0) =f(u)-f (0);
Г2(0-ц)-Г2(0-0)=-lf(u)~f(0)];
Г2(л—и)—Г2(л—0)=/(л—и)—|(л).
Поскольку функция f (х) удовлетворяла на [0, л] условию Дини,
то и функция F2(x) удовлетворяет условию Дини на отрезке
[—л, л]. Далее Г2еС((—л, 0) (J (0, л)), так что точка
х е (—л, 0) U (0, л) (х=Н=0, ±л) является регулярной точкой
функции F2. Но Г2(л) = (Г2(л—0)4-F2(—л+0))/2=(/(л)—
—/(л))/2=0; F(0) = (F2(0+0) +F2(0-0))/2=! (f (0)-f (0))/2=0;
216
Рг(~я) — (Fz(—n+,0)4-F2(n—0))/2=(—f(n)+f(л))/2.^:0, откуда
F2(—л) =F2 (л) =F2(0) =0, так что точки х=0, ±л также явля-
ются регулярными точками функции F2. В силу признака Дини
ряд (2.7) сходится к функции F2(x) на [—л, л] и для его суммы
32 имеем 32(—х) ——S2(x), S2 (х+2л) =S2(x) V х е (—оо, 4-00)г
S2(x)^F2(x) ^f(x) на (0, л). Если f (л) =И=О|=й=/(0), то сумма S2(x)
ряда (2.7) имеет точки разрыва 1-го рода при x=kn (k=0, ±1,
±2, ...) (рис. 10). Если /(0)=/(л)=0, то S2(x) s F2(x)=f(x) на
[0, л] и поэтому S2f=C((—оо, 4-оо)), 32(—х)—— S2(x), S2(x-f-
+2л)==32(х) Vxe (—оо, 4-оо), т. е. сумма S2(x) ряда (2.7) яв-
ляется непрерывным, нечетным, периодическим (с периодом 2л)
продолжением функции f(x) с отрезка [0, л) на (—оо, 4-оо>
(рис. 11).
Рис. 11
21Т1
Рассмотрим функцию f(x), определенную на отрезке [—л, я]
и удовлетворяющую в каждой точке этого отрезка условию Дини,
тогда ее ряд Фурье (2.1) сходится в каждой регулярной точке, в
том числе и в регулярной точке разрыва 1-го рода. Изучим более
подробно поведение частичных сумм ряда Фурье Sn(x; f) вблизи
регулярной точки разрыва 1-го рода, где ряд Фурье (2.1) не мо-
жет сходиться равномерно. Пусть сначала (рис. 12)
ф(х) в
(тс—х)/2, хе(0, и],
О, х = 0,
(х—те)/2, Хс=[— тс, 0).
Тогда функция ф(Х) удовлетворяет условию Дини V х е [—л,л]
и хо=О — регулярная точка разрыва 1-го рода этой функции. По-
скольку <р(—х)=—<p(X)Vxe[—л, л], то для коэффициентов
Фурье из (2.1) имеем ап=0 (meNq) и
Ьп = (2/л) • f ф(7) sinn/ dt = (1 /тс)- J(тс—t)svantdt=
о о
«= — (1/тс) • J (тс—/)d(cos nt/n) = [(те—/) cos n/|J 4-
4- j* cos nt dt}inn — 1/n,
о
так что в силу признака Дини поточечной сходимости рядов
Фурье имеем
4-00
q(x) = S sinrax/n Vхе [—
п«==1
Пусть х <= (0, тс), тогда, замечая, что
2-
— sin | k — — 11
\ 2 /
. / , 1 \ t
= sin/n4-- f — sin-,
\ A \ ы
t. e.
л / 1 \ *
2 cos ft/— sinl «4—) //2 sin--1/2,
j& \ 2 / 2
имеем представление
<Sn(x; ф) = sn(x) = 2 sin =
*—i
= (cos kt dt =
*=io
218
= f (sin (n + — t /2 sin— — 1/2 I dt
J<A \ 2} 7 2 /
т. e. V x e (0, те) имеем
х/2-f- sn(x) = J sin ( n + — 'j //2 sin — dt —
o \ ^ / 2
= f sin nt/2 tg — dt + — f cosntdt = f sinnt/tdt +
0 2 2 0
4-J |l/2tg-—1/Л sin nt dt + — J cos ntdt
o— \ 2 / 2 о
и, полагая
l/2tg-|-—1//. 0</<«,
0; —
получаем
X
x/2 + sn(x) =* J sin nt/t dt + sin nx!2n 4- An(x) V x e= (Os тс),
о
где
An(x)= \ g (t) sin nt dt.
о
Заметим, что
lim g(t) = lim (/cos -4—2 sin -4^ /2/sin-4 =
t—»4-0 t*-+o \ 2 2 у 2
= lim t(l—<2/8-|-o(i3))—2G/2—/3/6-8-|-o(Z3)) Q
t—+o *24-o(t2)
и lim g(7) = —1/it, t. e. geC([0, ir]) и, в частности, lg(7)| < M
t-*n—O
V/ g [0, ®], но тогда в силу финитности функции g(t) имеем
IffCOl‘С М V t G (—оо» 4-оо). Положим
Ап(х) = 4 fffCO sinnf dt + -у f S(t) sinn/ dt
2 0 2 0
и сделаем во 2-м интеграле замену / = z — те/n, тогда
1 х 1 *+«/п
Ап (х) = — f g(t) sin nt dt 4-I g(z—к/n) sin (nz—it)dz =
2 о 2 4»
= — JffCO sin ntdt—- "lj/ g(t—n/п) sinn/ dt=
2 0 2 n/n
219
= 4 Т * W sin ntdt + 4f ^S(i) -git-ф)) sin n/dt—
2 0 2 n/n
1 *+*/rt
-----I S(f—^/n) sin nt dt.
2 J
x
Итак, Vx e (0, it) имеем
I It/n I x+n/n
An(x)= - J g(t)sin ntdt -- f g(t—ф) sinntdt+
+ 4 f (g(t) — g(t — Ф)) sin nt dt == 2 A <(•*)•
2 7t/n i—1
Докажем, что A„(x) 0 на (0, я). В силу оценки
(n—-f-oo)
Ил. 1(Х)| + |4п, i(x)\^~Mln VX(=(0, It)
видим, что An,i(x) 0 на (0, я) (i=l, 2). Поэтому нужно до-
(П-*Ч-00)
казать* что Ап, з(х) 0 на (0, я). Учитывая* что g(t)=O
(rt-»+oo)
Vie (0, я], причем Vn^l я/п<^^х<^я, 0^/—я/п^я, имеем'
оценку
2|Лл, 3(х)| < J \g(t) - g(t - я/п)| dt <
Н/П
2п
< f \g(t) — g(t — n/n)\dt.
—2л:
По лемме § 2 гл. 4 Ve>0 существует непрерывная кусочно-
линейная функция 1(1) такая, что
к
I 6= С([0, я]), Z(0) = /(я) = 0 и j |Z (t) - g(t)\dt < e/3.
о
Введем финитную непрерывную функцию
L(t) =
7 10, Ze [0, я].
Тогда supp£ = [O, я], L s С((—оо, -|-оо)) и Vn>l, Vxg(M
имеем оценку
2*
2|Л з(х) | < J k (t) - g( t - tt/n)| dt <
—2n
< F \g(t)-L(t)\dt+ F ^L(t)-Lit-^ln)\dt +
—2к —2я
2я
+ f |£(f - я/п) - g(t - я/п)| dt.
—2n
220
Но
2п п
—2« О
Делая замену t~rjn + z, заметим, что Vn^sl имеем те<2те—
__те/п<2те, — Зте<—2те— к/п^—2те. Но тогда
f \L(t—nln)—g(t—v/n)]dt= J 7 |£(z) — g(z)\dz =
—2л —2 л—тг/п
2n к
= J |b(z> - g(z)\dz = J |Z(z) - g(z)| dz < e/3,
—2» 0
и поэтому Vxe (0, те) и V п > 1 имеем
2л
2|Ап, 3(Х)| < 2е/3 + J \L (t) - L(t - n!n)\dt.
—2л
Ho isC((—оо, 4-оо)), причем suppL = [O, те] и тогда (как бы-
ло доказано в лемме § 4 главы 3) финитная непрерывная
функция L(t) равномерно непрерывна на (—оо, 4*°°), поэтому
для фиксированного выше е>0 существует 8(e)0 такое, что
V/p s (—оо, ч-оо), удовлетворяющих неравенству |G —<а|<
<б(е), имеем оценку |£(fx)— £(<а)|<^е/12те. Но тогда существу-
ет пе(в)>те/6(е) такое, что Vn>n0(s) имеем 0<те/п<3(е)а а
потому справедлива оценка
2я
J \L (t) — L(f— те/п)| dt <8/3.
’ —2%
Итак, Ve)>0 3nc(e)e N, такое, что |4n,з«)| <s Vn>n0(s) и
Vxe(0, те), т. e. Ап,з(х) 0 на (0, те). Тем самым для п-й
(п->4-00)
частичной суммы ряда Фурье Sn(x; <p) = sn(x) на (0, те) получе-
но представление
х/2 + sn(x) = Jsin nt/tdi 4- Rn(x),
о
где Rn(x) = sinnx/2n 4- An(x), так что Rn(x) 0 на (0, те). Де-
(rt->4-oo)
лая замену nt = z (в интеграле), имеем представление
sn(x) = J sin z!z dz 4- Rn(x) — x[2 V x (0, те),
о
Рассмотрим интеграл Дирихле
4-оо л 4-оо (m4’l)«
те/2= J sin///dZ =jsinf//c«4- f sinW/-
0 0- m«»l mn
221
Делая в /n-интеграле замену t—mn+x и переходя в суммирова-
4-00
нии от т к k при m=k—1, получаем и/2 = 2 (—где <
*=i ,
р sin т dt г> * ]
uk= J ——. В силу строгого монотонного убывания ик ]
имеем оценки для частичных сумм ряда Лейбница F
1 == (#2 ^з) • • • (^2т ^2/n4-l) < Т.е* W2<^
п .$•
<7 = Jsin///df. Полагая х = тс/п, получаем из нашего представ-»
о >
ления
sn(u/n) =z J sin t/tdt + Rnt^n) — ^/2n Vn sNv
о
так что
lim sn(n/ri)=: f sin t/tdt — cp(O + 0) — <p(0).
л-*4-оо о
Таким образом, хотя частичные суммы <Sn(x; ф) сходятся (при
п —»+ оо) к ф(х) в каждой точке xs [0, -те] (причем на любом
отрезке [8, тс] при 8 е (О, я) эта сходимость даже равномерная),
но график y = Sn(x; <р), проходящий через точку (О, 0), накапли-
вается при п—>4-оо к отрезку [0, /] оси Оу, а не к отрезку
[О, тс/2] = [ф(0), ф(0-}-0)], как можно было бы ожидать. Отноше-
ние длин отрезков [0, /] и ]ф(0), ф(04-0)] равно
Z/(tc/2) = 2/тс. Jsin t/tdt = 1,179 . . .
о
Аналогично слева от регулярной точки разрыва х=0 график
y=Sn(x; ф) накапливается (при «->4-°°) не к отрезку [—тс/2, 0]
оси Оу, а к отрезку [—I, 0]. Та-
кое поведение частичных сумм
5п(х; ф) ряда Фурье называется
явлением Гиббса. Итак Sn(x; ф)
(п-*4-оо>
ф(Х) на [6, tc](J[—-S1 V8e=
(л-*4-оо)
е(0, it), а вблизи оси Оу график
у = S„(x; ф) (рис. 13) резко откло-
няется от графика у = у(х) к вер-
ху справа и книзу слева.
Допустим теперь, что функция
f(x) кусочно-непрерывна' и имеет
„кусочно-непрерывную" производ-
ную на [—тс, тс], причем все ее
точки разрыва 1-го рода и регу-
лярны. Тогда, как было доказано
222
ранее, Sn(х; f) равномерно сходятся к f(x) (при п->+оо) на лю-
бом отрезке непрерывности этой функции. Пусть хое(—л, л) —
регулярная точка разрыва 1-го рода функции f, причем f (хо+0)—
f(Xo—0,)=^=#0. Рассмотрим функцию F(x)=f(x)—(<?/n)<p(x—х0),
хе[—л, nJ, где <р(х)—изученная выше функция. Тогда Г(х) ку-
сочно-непрерывна с „кусочно-непрерывной” производной на[—л,
л]. Заметим, что F(xo-f-0)— F(xo—0) =f(xo+0) —f (x0—0) — (<7/л-[<р
(4-0)—q>(—0)J=0, t. e. FeC(xo). Ho x0—изолированная точка раз-
рыва функции f, поэтому существует отрезок [х0—б, Xo4-6jcq
г- (—л, л) такой, что F е С ([х0—б, х04-б]) и тогда Sn(x; F)
(л->-|-оо
F(x) на [Хо—б, хь4-б], так что для функции F(x) в точке х&
(п-*4-оо)
нет явления Гиббса. Но Sn(x; f)=Sn(x; F)+(q/n)Sn(x—х0, <p)
Vxe[—л, л], и в силу принципа локализации Римана явление
Гиббса, свойственное функции <р(х—х0) в точке х—Хо, вызывает
явление Гиббса и для функции f(x) в точке Хо.
Глава Б
ИНТЕГРАЛ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
§ 1. Интеграл Фурье
< Определение. Тригонометрическим интегралом называет-
ся несобственный интеграл, зависящий от параметра, вида
' -*"00
J (а(Х)cosХх + &(Х.) sinХх)dX, х е (—оо, 4-00). (1.1)
По аналогии с рядами Фурье введем следующее понятие интегра-
ла Фурье.
Определение. Пусть функция f(t) абсолютно интегрируема
на (—оо, +оо) (т. е. fs/?[—I, (] V />0 и существует несобствен-
4-00
ный интеграл S \f(t)\dt<+(X>)- Тогда тригонометрический ин-
— со
теграл (1.1) называется интегралом Фурье для функции f(x), если
функции а (К) и b (X) из подынтегрального выражения интеграла
{1.1) вычислены по формулам Фурье
а(Х) = (1/тт) Y f (t) соз Mi,
— 00
&(Х) = (l/it)Y f(t) sinUdt, X«=[0, +<x>). (1.2)
—oo
Замечание. Пусть тригонометрический интеграл (1.1) есть
интеграл Фурье для функции f, тогда формальная подстановка в
,(1.1) по формулам Фурье (1.2) дает представление
(а(Х) cos Хх 4- Ь(Х) sin Хх) dX=(1/гс) X
X +J dX +J f (t) [cos Xf • созХх 4- sin X* X
О —со
X Sin Хх] dt = (1 /«) 7° dX Y f (t) cos X(t—x) dt,
0 — eo
т. e. интеграл Фурье F(x) для функции f(x) допускает представ-
ление
F (х) = (а( X) cos Хх + Ь(Х) sin Хх) dX —
о
224
= (!/«) J <Л j f(t)cosl(t — x)dt.
0 —00
Как и в теории рядов Фурье, в теории интегралов Фурье возника-
ет основная проблема: указать условия на функцию f, при выпол-
нении которых интеграл Фурье F(x) сходится к f(x) или к
(f(x-t-O)+f(x—0))/2. Прежде чем переходить к решению этой
проблемы для интеграла Фурье, приведем некоторые свойства не-
собственных интегралов, зависящих от параметра, вида
F(x) = f(x, y)g(y)dy, x e [a, 6]. (1.3)
о
Теорема 1 (о непрерывности несобственного интеграла
<1.3)). Пусть функция g(y) абсолютно интегрируема на [0, +00)
Р»
(так что существует-несобственный интеграл Г fg(y)ldy). Пусть
б
feC ([a, b] X [0, +°°)) и функция f(x, у) равномерно ограничена,
т. е. \f(x, у) |<Л1<+оо V (х, у) е(а, Ь]Х[0, -J-оо). Тогда функ-
ция F(x) из (1.3) непрерывна на [а, Ь].
Доказательство. В силу абсолютной интегрируемости
g(y) на [0, 4-оо) и оценки |f(x, y)-g(y)\^M-\g(y)\ V (х, у) е=
e[a, &] X [0, 4-0°) видим, что несобственный интеграл (1.3) по
признаку Вейерштрасса сходится равномерно на [а, Ь}. Мы хотим
доказать, что FeC([a, &]), для этого достаточно доказать, что
существует lim F(x)—F(xo) VхоЬ]. Вспоминая теорему о
х-*х,
предельном переходе в равномерно сходящемся интеграле, видим,
что достаточно показать, что
y)g(y) f(x9, y)g(y) на [О, У] УУ>0.
я—xj
Но f е= C([a, 6] X [О, У])УУ>0 и по теореме Кантора функция
f(x, у) равномерно непрерывна на (компактном) брусе [a, ft] X
X [О, У], но тогда, как мы знаем, f(x, у) f(x0, у) на [О, У].
Заметим, что (ge7?[0, У]) =»(geB[0, У]), т. е. 'З.Ку >0 такая, что
g(y)l «ч Ку [О, У]. Но тогда Уе>0ЯВ(е)5>0 такое, что
Ухе 6г8(е)(х0)П[а, Ь] и Vi/e [О, У] имеем оценку |/(х, у) — f(x0,
&)1<8/Ку, т. е. V у е [О, У] имеем
У)ё (У) ~ f(x0, y)g(y)\<lg(0)| • |f(x, у) —
— f(xe, e/KY = e,
что и означает, что f(x, y)g(y) f(x0, y)g(y) на [О, У]. Приме-
(x->xe)
няя теорему о предельном переходе под знаком несобственно-
го интеграла (1.3) (из гл. 2, § 4), имеем
15 — Л. И. Каиынии 225
7 Vx0 <= [«, &] 3 lim +f f(x, y)g (y) dy —
x-*x9 Й
= +f f(x0, y) g(y) dy = F(x0).
6
Теорема 2 (о дифференцировании по параметру несобствен*
ного интеграла (1.3)). Пусть функция g(y) абсолютно интегрируе-
ма на [0, ,+°°). Пусть
f (х, у), &J)X[O, +«>)),
OX
причем функции f и равномерно ограничены на [а, 6] X [0, .
-{-оо), г. е. |/ (х, у)|, f (х, у) < М. V (х, у) е [а, Ь] X [0, 4-оо).
Тогда V,ve[a, &] существует производная DF(x), причем
T)F(x)=+\^-f(x,y)-g(y)dyNxe[a,b\.
Доказательство. Рассмотрим несобственный интеграл
ОД = J°°g(у)dy, хе [а, 6], (1.4>
полученный формальным дифференцированием (1.3) по х. В силу
оценки
<WG0lV(4f,yj€=[a, Ь] ХР, Ч-оо) j
из абсолютной интегрируемости g(y) на [0, +<») по признаку
Вейерштрасса следует равномерная сходимость на [а, &] интеграла
(1.4). Докажем, что Vх е [а, Ь] я DF(x) —1(х). Пусть х, 1
+Дх е [а, 6]. Используя теорему о среднем в интегральной фор» ;
ме, имеем при фиксированном
хе [а, Ь] и х4- Дхе[а, 6]:(/(х-(-Дх, у)—
- f (х, у))!Ьх - = }ГЪ(х + » Дх, yl -
ОХ Q I ох
— (х, у) db = ф(Дх, у).
Далее ¥У>0 при Дх’=#О имеем представление
[Г(х-»-Дх)3— F(x)]/bx — I(x) = J <р(Дх, у) g[y) dy +
226
<р(Дх, у) g(y) dy.
У(е)
В силу оценки |ф(Дх, у) g(y)|< M|g(y)|Ny, ¥Дх#=0 из абсолют-
ной интегрируемости функции g(y) на [0, 4-°°) вытекает, что
¥е> О Я У(е)^> 0 такое, что
+f ф(Алг, y)g(y)dy <2M+f |g(y)|^<s/2.
У(е)
Далее, учитывая, [что (gGjR[0, У(8)])=4(?еВ[0, V(e)], видим«
что ЯКу>0 такое, что |g(y)|<CKvVys[0, У(е)). Кроме того,
поскольку у-еС([а, &J X [0, У(е)]), то по теореме [Кантора
0Х
функция j-f (х, у) равномерно непрерывна на (компактном)
брусе [а, 6]Х[0, Y(e)], а потому для выбранных 8>0 и У(г) >[0
Я6(e)>0 такое, что ¥|Мх|<|Дх|<8(е) (где &s[0, 1]) и Vу]е
е [0, У (в)] имеем оценку
£ f(x]+.Mx, у)-±f (х, у) < е/2У(е) Ку,
ох ах
откуда |ф(Дх, у)||<е/2У(е)КУ, т. е.
|У(е)
J <№x,y)g(y)dy <(8/2У(8)). (КуУ(8)) = 8/2.
I о
Итак, при фиксированном хе[а, 6]¥е>-0Я8(8)>'0 такое, что
при 0 <[ |Дх| < 6(e) (х 4- Д* е [а, &]) имеем оценку |(F(x 4- Дх) —
—F(x)!bx—I(x)\<s, так что существует lim (F(x4-Ax)l—
— F(x))H±x = I(x), т. е. Vxs[a, 6] 3DF(x) = 7(x_M
Следствие. Теорема 2 (о дифференцировании несобствен-
ных интегралов специального вида (1.3)) остается верной и при
следующих условиях: пусть g(y) и y g(y) абсолютно интегрируе-
мы на [0, 4- °°). Пусть \
f, ^-.<=С([а, 6] Х[0, 4-оо)),
причем существует постоянная Af>0 такая, что
I/ (х, у)\< М, (х, y)J<Af • |у| V (х, у) е [a, &JX[0, 4-оо).
Тогда Ухе[й, ft] существует производная DF(x),
DF(x)=y W±yLg(y)dy.
о
15*
227
Теорема 3 (об интегрировании в конечных пределах несоб-
ственного интеграла (1.3)). Пусть функция g(y) абсолютно интег-
рируема на [О, + <х>). Пусть feC([a, 6]Х[0, +<»)) и функция
f(x, у) равномерно ограничена, т. е. |f(x, у) |^At<+oo v (х, у) s
е[а, &] Х[0, +<х>). Тогда для несобственного интеграла (1.3)
имеем &], причём
Ъ def b +°° +°° ь
]F(x) dx = jdx$f (х, у) g(y) dy = $g(y) dy f f’(x, y) dx.
a a 0 0 a
Доказательство. Покажем, что Vxefa, 6] имеет место
равенство
X +оо X
$F(t) dt = j g(y) dy J f(t, y)df,
a 0 a
для чего введем функции
Ф(х) = JF(7) di, xs[e, &| (1.5)
G(x) = f g{y} f/(f, y}di dy, xe= [a, &].
0 La
Сначала покажем, что Vxe[a, Ь]яDO(x)=DG(x). В самом де-
ле, по теореме 1
F(t) = У fit, y)g(y) dy <= СЦа, 6])
и из представления (L5,) в силу теоремы об дифференцировании
определенного интеграла Римана, по верхнему пределу ('[1], ч. II, /
гл. 2, § 6) Vxe (a, b) ЭГОФ (х) = F(x). Далее заметим, что при *
X
tf(x, у) = J fit, y)dt имеем
f(x, y)t <f(x, у) еф, Ь] х [0, +оо)) и
V (х, у) [а, &] X [0, 4-оо) Я
~(f(x,y) — f (х, у) G С([а, ft] X [0, 4-оо)).
Применяя теорему 2, видим, что
|<Р(*. У)\»
-Ф(х, y)\^ib-a)M \х^[а, &], Vz/e(0, +<»),
дх (
т. е.
Vх е ia, 6) 3 D G(x) =а Т т ^(х' у) siy) Й = ?(х)
о 0Х
228
Итак,
Vxg(a, 6) Я ОФ(х) = DG(x) = F(x),
так что Ф(х) = G(x)-\-C. Но поскольку Ф(0)==С(0)~0, то С=0,
откуда ®(x)=G(x) Чх^[а, &] и при х — Ь получаем утверж-
дение теоремы 3.
Лемма (об убывании тригонометрических интегралов). Пусть
функция g(t) абсолютно интегрируема на [а, +<»). Тогда для
тригонометрического интеграла
+°® ( sin nt 1
J g(t)\ Р \dt, р(=(0, +оо) (1.6)
а (COS/XJ
имеем Я lim F(p)=0.
р-*+*>
Доказательство. Поскольку функция g(t) абсолютно ин-
тегрируема на [а, -f-оо), то в силу оценки
Vp>0, Vie [а, 4-ос)
по признаку Вейерштрасса несобственный интеграл (1.6) сходится
равномерно (по р) на (0, 4-°°) и тогда V е>0 я А(г)>а такое,
что V р>0 имеем оценку
t?° (sin pt 1 ,.
J J dt
Л(е) I cos ptJ
e/2.
Зафиксируем e>0 и выбранное Л(е)>а и заметим, что g^R[a,
Л(е)]. В силу критерия Дарбу (интегрируемости по Риману из
[1]« ч. II, гл. 2, § 2) имеем infQ„(T)=O, и поэтому для выбран-
т
ных 8^>0 и Л(е)>я существует разбиение Т = {а — i0<C^i<^.. <^
<in — Л(е)} отрезка [а, Л(е)] такое, что
И—1
2^(Т)=2 wft(g)Affc<e/4,
k=0
где
шл = лгь — mk, Mk= sup g(t),
1^’ ^4-11
mh— inf ё(*)> Mh = tk+i — tk (fe=O, 1,..., n— I).
lfb’ ^4-11
Зафиксируем разбиение T отрезка [а„ Л(е)], а вместе с ним и
величины <ofc(g), Mk, mk (6=0, 1,..., п—1). Тогда имеем
А(е
J SCO
а
Sin?'|«-s f*+'
cos pi J Slot
A
, . ( sinpi) ,
(g(t)-mb)\ Adt +
(cos pt J
229
, 't;1' 'ft+i sin p« 1 .
+ 2 J dt^Iilpy + Up).
4=0 L I cozpt J
A
Поскольку |g(f)—znA|<Afft — m-k — ®A(g) Vt e [iftl f*+i], то в си-
лу выбора разбиения Т имеем оценку
|Zi(P)l< S*=- < е/4 V р > 0«
Далее, интегрируя, имеем
sin"' Л =
cos pt J
— cos pt I ,=,fc+l
sin pt j <=tk
t. e.
|'Ж fsinpf <2/p (fe==0> b ,
I tk I cos pt J
откуда
n—1
И2(Р)1<2р2 \тк\ = М/р,
k=l
n—t
где величина M—2^ |mft| не зависит от р н уже выбрана (в
й=0
силу выбора разбиения Т) по е>0 и 4(e) > а, но тогда для
выбранных е>0, 4(e) > а и разбиения Т Яр(е)>0 такое, что
|1г(р)К е/4 V/? > р(е). Итак, Уе>0Яр(е)>0 такое, что Vp>
> Р&) > 0 имеем |F(p)| < е/2 + е/4 4- е/4 = е, т. е. Я lim F(p) = 0.
р-*Тоо
Теорема (признак Дини сходимости интеграла Фурье).
Пусть функция f(x) абсолютно интегрируема на (—оо, +°°) и в
точке Хо<= (—со, +°о) существуют конечные односторонние пре-
делы f(Xo±O)=lim f(x). Пусть в точке Хо для функции f вы-
ж-*х,±0
полнены условия Дини, т. е. такое, что несобственные ин-
тегралы
Л
J If (х9 ± и) — f(x9 ± 0)1 • И-’ du
О*-
сходятся. Тогда интеграл Фурье F(x) (1.1) для функции f(x) схо* „
дится в точке Xq, причем F(xq) = (f (хо+О)+/(хо—0))/2. т. е. имеет
место формула'Фурье
(1/«).‘IJ> dkY f(t)cos\(t-x0) dt**
230
(f(xo+0)+f(xo~-0))/2, если x0 — точка разрыва
1-го рода для функции f,
— (1.7)
f(x0), если х0 — точка непре-
рывности функции f.
Доказательство. Поскольку функция f(t) абсолютно ин-
тегрируема на (—оо, 4-00), то в силу оценки
f^JCOSul VXe[O, +оо)
sin Л» J
и v/e (—оо, 4-oo) по признаку Вейерштрасса имеют смысл фор-
мулы Фурье (1.2), причем несобственные интегралы из (1.2) схо-
дятся равномерно на [0, 4-°°)- По аналогии с частичной суммой
ряда Фурье введем функцию
Sn(x-, /) = 1/«- JdX "Y/(?)[coskf • cosXt 4-
О — оо
— sinXf. sinХх]dt = l/« • JdX+J f(t) •
0 — oo
•cosX(Z — x)dt.
Заметим, что функция f(t) абсолютно интегрируема на (—оо,
4-оо), а функция cosX(7—х) непрерывна и равномерно ограничена
(поскольку |cosX(7—х)|<1) по (1, t) на множестве [0, т]]Х
Х(—°°> +00)- Но тогда для функций f(t) и cos Iff—х) справед-
лива теорема 3 (об интегрировании в конечных пределах для не-
собственных интегралов специального вида). Поэтому имеем
5п(х0; Л = 1 Тt(t)dt]cosX(f-x0)d\ =
—co 0
=!/« T f(t) -s?.nk(?T-Xo\ at =
-oo X=0
=1/k+J /(7) sinv](£ — x0)/(t — x0)dt =
—co
( замена t—x9 = u)
-f-oo / -f-оо —*0 \
= 1/я J f(x0+u) sin fiu/u du— 1/л I J + J ) =
— oo \ 0<— —oo/
(замена u=—v во 2-м интеграле)
4-00
= I/я J* (/(x04-«) 4- f(x0 — «)) sin f\ulu du.
0«-
Итак,
231
/
8-п(хо> /)=1М f (/(*o+O + /(xo—O)sin t/tdt Vtj>0. /
Используя интеграл Дирихле, имеем V т]>0 представление ’
] = 2/тс J sin т] t[tdt,
о
откуда
(/(хо4-О)+/(хо-0))/2= 1Л +J° (/(xo+0)+/(xo-0))sin -qt/tdt.
Но тогда имеем основное представление
5ч(х0; /)- (/(хв—0)4-/(хо—0))/2 = 1/u +J° [(/(x04-t)-
— /(хо4-О)) + (/(х0—О — /(х0—0))] sin 7i t/tdt.
В силу условия Дини в точке хо, V е>0 3 & (е) е (О, Л] такое, что
8(C).
1/« f |/(x0±t) -/Uo±O)| • t-1 dt < е/4.
0«-
Положим для выбранных е>0 и 6(e) > О
8(e)
5,(х0; /)-(/(Хо +0) + /(хв-0))/2 = 1/« f +
(й-
+ 1/*Т = Л(ч) + 5(т)).
8(e)
Но
I К/(Хо 4- о — /(Хо+0)) + (/(х0—0 — /(хв—0))] • sin 7)///| <
<l/(Xo+0-/(x04-0)14-‘+|/(x0-t)-/(xe-0)H-f V/>0,
поэтому в силу выбора 6(e) <=(0, Л] имеем оценку |Л(т))|<е/2
Положим
5(7))=1/к+у (/(Хо-Н) +f(x0—/))• i-'sin Titdt —
8е)
4-00
- IM (/ (Хо+О) + / (Х(Г-О)) f sin^t/tdt = 51(7)) + 53(Т)).
5(«)
В силу абсолютной интегрируемости на [6(e), +<х>) функции
(/(хо-Н) +/(хо—t)) • t~l по лемме об убывании тригонометри-
ческих интегралов для выбранных е>0 и 6(e)>О Ят^е) j>О
такое, что ^(т))! < е/4 Я 7]>т]1(е). Далее, делая замену т]^ = т и
используя сходимость интеграла Дирихле, имеем представле-
ние
232 i
В2(^) = — 1 М/ Uo+ 0) 4- / (Хо— 0)) +J sin т/т dx,
•n-S(e)
откуда Я lim 52(t]) = 0, т. e. для выбранных 8>0 н 5(e)>0 3
, <1-»+ов
такое, что |В2(т])|<£/4 Ут]>7)2(е). Итак, Ve > 0 Я т)0(е)
== max ?)i(6) > 0 такое, что
i=1.2 ,
|5ч(жв; /) - (Дхо4-О) + /(х0—0))/2| < е V т) > ^(е),
что и требовалось доказать.
Замечание 1. В отличие от рядов Фурье для интегралов
Фурье не справедлив принцип локализации, поскольку условие аб-
солютной интегрируемости функции f не является локальным ус-
ловием.
Замечание 2. При выполнении в точке Хо условий признака
Дини имеет место формула
lim l/ir J f(t) sin7|(Z—xa)/(t —t9)di = (f(x0+Q)+f(x9--0))/2.
^“*4*°° —oo
Следствие 1. Пусть функция f(x) абсолютно интегрируема
на (—оо, 4~оо) и может иметь разрывы только 1-го рода, причем
в любой точке хе(—оо, —|-оо) выполнены условия Дини. Тогда ин-
теграл Фурье для функции f сходится всюду на (—оо, -|-оо), при-
чем имеет место формула Фурье (1.7).
Следствие 2. Пусть функция f(x) абсолютно интегрируема
на (—оо, -j-оо) и на любом конечном отрезке [а, Ь] с: (—о®»
4-оо) принадлежит классу Гельдера На[а, 6) (0<а<Л). Тогда
интеграл Фурье для функции f сходится к функции f(x) на (—оо,
4-оо), т. е.
f(x) = 1/к f (fk J f(t)cosk(t—x)dt Vxe (—<x>, 4-oo).
6 — oo
(Можно доказать, что при этом интеграл Фурье сходится к функ-
ции f(x) равномерно на любом отрезке [а, &]с(—оо, -(-оо).)
В самом деле, из условия Гельдера вытекает, что: 1) fe
еС((—оо, -(-оо)) и f(x) = (f(x+O)+f(х—0))/2Vx, и 2) в каждой
точке хе (—оо, -}-оо) выполнены условия Дини.
Следствие 3. Если функция f(x) абсолютно интегрируема
на (—оо, -|-оо) и feC(ft>((—оо, -|-оо)) (/г=1, 2, ..., -|-оо), то ин-
теграл Фурье для функции f сходится к функции f(x) на (—оо,
+оо).
Следствие 4. Пусть функция f(x) абсолютно интегрируема
На (—оо, 4-оо) и кусочно-непрерывна на любом конечном отрез-
ке» причем Vxe (—оо, -|-оо) либо существует конечная производ-
ная Df(x), либо существуют обе конечные односторонние произ-
водные
233 •
D±/Ws lim .
J t-»+0 ±t
Тогда интеграл Фурье для функции f(x) сходится всюду на (—оо,
+ioo) и имеет место формула Фурье (1.7).
Замечание 3. Пусть функция f(х) абсолютно интегрируема
на (—оо, 4-оо) и четна, т. е. f(—x)=f(x)V х е (—оо, 4-оо).
Тогда
а(к) « 1 Y / (t) cos Xi dt == 2/k "‘j’ f (t) cos kt dt,
—oo 0
b(k) =1/^7° f(*)^nU/tdt = О V k>0.
— oo
Если же функция f(x) нечетна, т. е. /(—х) = — f(x) Vxe(—оо,
4-оо) (ив частности, /(0) = 0), то
а(к) = 0 и 6(к) = 2/<с f(7) sin kt dt Vk>0.
Следствие 5. Пусть функция f(x) абсолютно интегрируема
на (—оо, 4-оо), /еС((—оо, 4-ро)) и Vxe (—оо, -j-oo) выпол-
нены условия Дини. Тогда интеграл Фурье для функции f сходится
всюду к f(x), причем:
1) если функция f(x) — четная, то для интеграла Фурье имеем
f(x)=2/iz f coskxdk j f(t) cos Mdt Vxe(—oo, -f-oo);
о о
2) если функция f(x) — нечетная (и тогда f(0)=0), то
f(x) = 2/т: "j sinkxdk f /ft) sin kt dt Vxg=(—oo, 4-oo).
o 6
Определение. Пусть функция f(t) определена на (—оо,
тЬ.оо) и —I, t]v t>0. Пусть существует предел
т
lim f f(t) dt (Г>0).
• r-+oo Lr
Тогда этот предел называется главным значением (по Коши) ин-
теграла
*ff(t)dt.
— со
Обозначение: ;
v. p.+j f(t)dt=T^ fwdt.
—сю ^-т
234
Замечание. Если существует несобственный интеграл
Т t(t)dt,
то,
очевидно» существует и главное значение
v. р. J f(t)dt,
причем
v. р. j* f(t)dt— j f(t)dt.
Замечание. Аналогично вводится понятие главного значе-
ния интеграла в изолированной особой точке с е (а, Ь) функции
f(x):
b def 1 Гс—,5 b
V. р. $f(t)dt=bm J f(t)dt + ] f(t)dt .
a L я с+8
Ч-оо
Пример 1. Несобственный интеграл J tdt не существует,
— 30
но
J /Л=Г2/2
-т
г =0 V т > о,
-т
поэтому имеем
+» def . т
v. р. Г tdt= lim f tdt = Q.
Л 7-4-00
I
Пример 2. Несобственный интеграл J Г-1 dt не существу-
ег, но VS>0 имеем
-8 1 з
4- р-1 dt = О
1
так, что
v. р. J t~' dt = 0.
В дальнейшем нам придется рассматривать комплекснознач-
ные функции w(t)—u(t) +iv(t) от действительного аргумента t.
Отождествляя w(t) с вектор-функцией w(t)=(u(t), име-
ем: если и, то 3)(t) и Dw(0=(D«(0, Dv(t)), т. е.
25(0 и Dw(0=D«(0-HDp(0. В частности, Deia,=D(cosaf-}-
+isinaf)=—asinotf-f-ixcosa£=ia • ем. Далее если u, v^R[a, b],
то w e R[a, b] и
235
Ъ / b Ъ \ I b I ъ
$w(t)dt= (J u(t)dt, ]v(t) dt\, Jw(7) di ||w(()||
a \a a / I a | a
поэтому w^R[a, &] и
j w(t) dt = J u(t) dt 4- i J v(t) dt,
a a a
причем
ъ b
]w(t)dt
a a
Теорема (формула Фурье для интеграла Фурье в комплек-
сной форме). Пусть функция f(x) абсолютно интегрируема на
(—оо, +оо), feC((—оо, +оо)) и в любой точке хе(—оо, +оо)
выполнены условия Дини. Тогда интеграл Фурье для функции f
/сходится к функции f(x) всюду и имеет 'место формула Фурье в
комплексной форме
f(x) = 1/2" • v. р.
►рзо
f
/(Qe-W-^dt
dk Vxe(—оо, Ц-оо).
в—со
Доказательство. При фиксированном хе(—оо, 4-оо)
введем функции
<р(Х) — у f(t)cosk(t— х) dt и
—оо
ф(Х) = J f(t) sinX(i—x)dt, Хе(—оо, 4-оо).
—оо
Поскольку выполнены условия: 1) функция f(t) абсолютно интег-
рируема на (—оо, Ч-оо); 2) функции cosA(7—х) и sinA(?—х) не- ?
прерывны на (—оо, 4-°°) Х(—Ч-°°); 3) функции cosA(7—х)
и sin k(t—х) в силу оценок | cos А (7—х) |^1 и |sinA(7—х)]<^
V A, t, х равномерно ограничены, то по теореме 1 (о непрерыв- ;
ности несобственных интегралов специального вида) имеем
<р, ifeC((—оо, 4-оо)), кроме того, очевидно, <р(—А)=<р(А) и
ф(—А)=>—ф(А) vXe (—оо, 4-оо) (т. е. <р (А) четна, а ф(А) нечет-
на). В силу условий нашей теоремы имеет место формула Фурье ,
/(х) = l/ir dk +у° f(t)cosk(t—x)dt,
б —оо
т. е. существует несобственный интеграл
"у0 <р(Х)dk.
В силу четности функции <р(Х) видим, что с уществует несобст-
венный интеграл
236
Y q>(X)dk = 2+f’ q>(X)dX.
—oo 0
Далее» поскольку феС((—oo, 4-00)) и функция ф(Х) нечетна,
71
то V»0 существует интеграл Римана J ty(X)dX = O, поэтому
-л
хотя и нельзя гарантировать существование несобственного
4-ое -I-оо
интеграла J ip(X)dX, но v. р. J ф(Х)йХ==О. Из формулы Фурье
—оо — оо
тогда имеем
vf(x) = +f Ф(х)^ = 1/2 • Y Ф(Х)Л ~ 1/2 • v. р. Y 4(X)dX,
О —о» —оо
т. е.
f(x) = 1/2« • v. р. Y (ф(к) - /ф(к)) <&== 1/2* X
—во
Xv. р. "j /+]' f(X)[cosX(«—х) —isinX(t—x)]dt}dk,
— CO I —oo
или в силу формул Эйлера имеем Vxe (—оо, 4-о°) формулу
f(x) = 1/2* • V. р. +f [Т f(t)e~l4t~x) #рХ.
—00 L—00 J
Замечание. Если для абсолютно интегрируемой на (—оо,
Н-.оо) функции /еС<*)((—оо, 4-°°)) (k=\, 2, +°°) функции
Ф(Х) и ф(Х,) также абсолютно интегрируемы на (—оо, 4-00), то
имеем формулу Фурье
f(x) = 1/2 i/f0 Т /W e-W-* лЪх,
— оо Оо
где не используется понятие несобственного интеграла в смысле
главного значения (по Коши).
§ 2. Преобразование Фурье
Пусть функция f(x) абсолютно интегрируема на (—оо, 4-о°)
(запись: (—00,4-00) и feC((—00, 4-00)). Тогда если
vxs (—00, 4-°о) выполнены условия Дини, то всегда существует
несобственный интеграл
Ф(Х) = 1/у2я • f(t)e~iUdt
—00
И в силу формулы Фурье из теоремы Фурье имеем равенство
237
f(x) = l/]S2n. V. p. j Ф(Х)^ЙХ,
—co
где несобственный интеграл понимается в смысле главного значе-
ния (по Коши).
Определение. Если функция f(x) абсолютно интегрируема
на (—со, 4°°) —оо, -]-оо)), то функция
Ф(Х) = liy• J f(t)e~iU dt, Х е (—оо, +,оо)
— оо
называется преобразованием Фурье функции f(x) и обозначается
F[f] или f(l). Итак, vf е Ri(—оо, -|-оо) существует
f(X) = f(t) -e-^dt VX(=(—oo, +,oo). (2.1)
—oo
Замечание. Преобразование Фурье f(Л) определено нами
для любой функции f^Ri(—оо, +оо), но при этом может ока-
заться, что функция f(k) не является абсолютно интегрируемой
на (—оо, -}-оо), поэтому отображение F:f-+f не переводит, вообще
говоря, пространство Ri (—оо, Ч-оо) в себя.
Замечание. Преобразование Фурье F[f] с помощью форму-
лы
F[/]=s f(X) = i//2^ • v. p-Y f(t)e~™dt
—oo
можно определить на классе функций {/}, более общем, чем
Ri(—оо, 4°°), но мы этим пользоваться не будем. __
Выше было отмечено, что если функция —оо, 4-°°),
удовлетворяет дополнительным условиям: 1) feC((—оо, 4°°))i
и 2) для функции f(x) в любой точке хе (—оо, 4-°°) выполнены
условия Дини, то из формулы Фурье (теоремы Фурье) получает-
ся формула обращения для преобразования Фурье
f(x) = 1/]Л2гё • v. р'"]0 f(X)eiX‘dX Vxe (—оо, +<ю).. (2.2)
—оо
Между формулами (2.1) и (2.2) есть формальное сходство — они
отличаются только знаком в показателе экспоненты. Однако при
всем внешнем сходстве формулы (2.1) и (2.2) совершенно раз-
личны по существу: в формуле (2.1) несобственный интеграл су-
ществует в обычном смысле, поскольку feRi(—оо, 4°°)i а ®
формуле (2.2) несобственный интеграл существует, вообще гово-
ря, лишь в смысле главного значения. Далее, формула (2.1) есть
определение функции Как преобразования Фурье для f(k), а фор-
мула (2.2) представляет собой лишь иную запись формулы Фурье
из теоремы Фурье, т. ё. содержит утверждение (которое и доказы-
238
вается в теореме Фурье), справедливое при дополнительных усло-
виях (непрерывности и выполнении условий Дини), налагаемых
на f e=Ri(—00> +°°)-
Замечание. Формулой (2.1) преобразование Фурье опреде-
ляется vf e/?i(—оо, +°°)> если же функция f(x), кроме того,
непрерывна и удовлетворяет условию Дини, то имеет место форму-
ла обращения (2.2). Аналогичное положение имело место и в
теории рядов Фурье. В самом деле, если —л, л], то (ср. (2.1))j
коэффициенты Фурье
сп=1/2л- J i(t)e~Mdt(f~ 2 с»е<ЛЖ)
определены v п е Z, однако сходимость ряда Фурье для функции
f к самой функции f(x), т. е. равенство
f(x) = 2 спе<"'1Г’ х (~ж)
П-— оо
(играющее роль формулы обращения (2.2)), имеет место лишь
при дополнительных условиях непрерывности и выполнения (на-
пример) условия Дини, налагаемых на л, л].
Пример. Пусть ;
f(x)=e-^xl е /?х(—оо, +'оо) (а>0).
Тогда
/(X) = 1//2^ • Y • e~Mdt =»
— 00
=1//2^ • +J° e-’i'l • (cos Xf — £ sin U)dt =
—со
= У2/и • j* e~et • cos Хе de.
о
Но поскольку
j e~at • cos Хе dt — e~ai(A cosXe + BsinXe)
дает
(e~at • cosX/ = e-w« (—a.A cosXe — aBsinXe—
— XA sin xe^+ XB cos X/)) (1=—aA А*ХВ, 0~~—ХА~~жВ)=^
(В = — XA/a, 1 = — aA — X»A/a) => (A = — а/(а«4-Х»),
В = Х/(а» + X»)) => T е—‘ • cos Xe dt -
239
fan-f-OO
==e_. t (-acogX^XsinXQ = 8 X2
a2 + X2 M Г »
f-0
t. e.
}(X)= J/2M • a/(a2-H2) S^(—oo, + oo).
Пример.
f(x^ = (1 ПРИ И < a> _
10 при |x| > a, —oo, -|-bo).
ДХ) = l//2^ . +f f(t) е-‘и dt = l/)Z2it • J e~™ dt —
я l/|Z2rc . у (cos Xi — i sin Xi) dt = lZ2/x X
—a
X JcosXi df = |Z2/x • sin Xi/X | = )/’2/x • sinXa/X=>
о /—о
f(X) — У2Ы • ( sin Xa/X*k=?fc0’__
la , X=0. oo,+,oo).
Преобразование Фурье, введенное с помощью формулы (2.1),
есть отображение определенное на Ri(—оо, 4-°°)» т. е. на
функциях, заданных на (—оо, 4-оо).
Для потребностей математической физики используются преоб-
разования Фурье функций f(x), заданных на [0, 4-оо). Пусть
feRi{—оо, 4-оо), тогда если f(x) четна, т. е. f(—x)—f(x)vхе
е(—оо, 4-°°) и feC((—оо, +°°))> то при выполнении условий
Дини имеет место формула Фурье
/(х)=»2/х • J cosXxdX J f(t) cosX/di Vxe(—00,4-00),
о о
если же функция f(x) нечетна, т. е. f(—х)——f(x) Vx, то при тех
же дополнительных предположениях непрерывности и выполнения
условий Дини имеем f (0) =0 и по формуле Фурье
f(x)=2/n • "у° sinXxdX^y0 f(t) sinXi dt V.re(—00,4-00).
Пусть f e.^i[0, 4-°°) и feC([O, 4-°°))- Тогда ее можно про-
должить непрерывно на (—оо, 4-оо) двояким образом:
1) как четную функцию, положив f(x)=f(—x)Vxe(—00, 0];
2) как нечетную функцию (при выполнении дополнительного
условия f(0)=0), положив f(x)=—f(—х) Vxe (—00, 0], и тогда
при выполнении условий Дини для одной и той же функции f(x)
имеем формулы Фурье двух видов:
240
f(x)=2l‘K • f cosXxdX [ /f/JcosXi^, xe[0, 4-°°)
0 0
или
ffxj=2/ir • f sinXxdX j1 f (t) sinX/dt, xe[0, -4-oo).
о 0
Определение. Пусть 4-°°)> тогда функция
}f(X)-/2Ac • f(t)C03Udt, Xe[0, H-oo)
называется косинус-преобразованием Фурье функции f. Записьз
ад] s Мк) = /2М • у f(t) cos\tdt, X е [0, + ФО). (2.3)
Далее функция
Т /60 sin кг Хе(0, 4-оо)
называется синус-преобразованием Фурье функции f. Записьз
ад] =Л(Х) = /27; • Y КО sinltdt, Хе [0, 4-00). (2.4)
о
Пусть f е /МО, 4~°°) и f(x) удовлетворяет дополнительным усло-
виям: /еС([0, 4-оо)) и vxe[0, 4-°°) выполнены условия Дини.
Тогда в силу теоремы Фурье имеет место формула обращения для
косинус-преобразования Фурье fc:
f(x) = /2М • Y /е(Х) cos Хх dX, хе [О, 4-oo), (2.5)
если же f (0) =0, то имеет место формула обращения и для си-
нус-преобразования Фурье fa:
f(x)=V2k • +f° /#)sinXxdX, x e [0, 4-°o). (2.6)
• 6
Замечание. Если условие f(0) =0 не выполнено, то формула
(2.6) имеет место лишь для х е (0, 4-°°)-
Пример. Пусть f(x)=e~axl еЭДО, 4-°°) (а>0). Поскольку
/(0)==1=/=0, то формула обращения (2.6) справедлива лишь при
*^>0, т. е.
/ДХ) = У2/^ • e~№t > sinltdt, Х>0
и тогда
,в — Л. и. Камыявн 241
Je-a/• sin At dt — e~at • (A cos Xi + В sin Xi)
дает
e-a( »sinXi = e-at • (—aA cos Xi—
— aB sin ).t — XA sin M + XB cos Xi),
откуда
(0 = — aA + aB, 1 = — XA — <xB)=»(B = aA/X,
l=s-XA-a2A/X)=»(A = -X/(a2+X2), B=—a/(a2+X8),
t. e.
J e~at • sinXiiii = [e~a,/(a24-^2)‘(—X cos Xi —
— a sin Xi)] = X/(a2+X2)=»£(X)^/2/^ -X/(a2+X2) G ЯЦ0, 4-oo).
f=o
Ранее было показано, что
/е(Х) = V2hc . a/(a2+X2) е= ЯЦО, + оо);
Заметим, что формулы обращения (2.5) и (2.6) могут быть нс- ;
пользованы для вычисления тригонометрических интегралов. 1
Пример (вычисление интегралов Лапласа).
J ь» + %* J I
Было показано, что для функции f (х)=яе~ахе .RJ0, +<») (а>4
>0) имеем МХ) = ]Л2Ас • Х/(а24-Х2), £(Х)=}/2Л • а/(аа+^). Ис-
пользуя формулу обращения (2.5) |
/(x) = /2/i€ • f £(X)cosXxdX, x>0,
0
имеем
откуда
Y£®^£dx = K/2a • e~"
J a2+X2
i
т. e.
«>0.
242
Аналогично для x>0 формула обращения (2.16) дает
f(x) = У2й . Y f (X) sin Xx dX =>
0
(e~ax= У2Г~ • +f° /2/^
\ Й a*+X2 /
a ° X sin Xx ,n „ , \ .
=’/2
/-4" dx _rl2 . г_..ь o>0 \
\ 0J b2 + x2 /
Пример.
t(x) = exp (—ax2) e Ri (—oo, + oo),
K-x) =f(x) Vx e (—oo, + oo),
}(Х) = 1/]Л2^ • +f exP(-a*8) •«-л,* =
= ]/27it • J exp(— ai2)/• cosXidi=£(X);
о
= — J ехр(—ai2) • t sin Xi dt = l/2a • J sin Xi X
о 0
X d exp (—ai2) = [sin Xi . exp (—ai2)/2a] —
/«О
+оо
dv 'kd'kX
7=-^Н<1п°(х)-------x/4a +
+ln c) =$ (p(X) — c exp (—X2/4a),
v(0) = Y exp (a/2) di = yT/i/2) => (r(X) = V^h.12 X
X exp (—X2/4a)) => (f (X) = F[exp (—ax2)] =»
• jZir/a/2 • exp(—X2/4a) = l/]/"2a . exp(—X2/4a).
(a = 1/2) => F[exp (—x2/2)f= exp (—X2/2).
16»
243
О пр еде л.ение. Пусть функция <р(Х) определена на (—оо,
Н-оо). Тогда обратным преобразованием Фурье функции <р назы-
вается функция
Ф(х) = 1/]Л2л • V, р. J q>(X)eiXxdX
—оо
(если главное значение этого несобственного интеграла существу'
ет). Запись:
__ 4-оо
v. р. f <p(X)eix*dX.
Замечание. Если <р е /?1 (—оо, 4-оо), то обратное преобра-
зование Фурье функции <р(Х) существует и F-1[<p]=l/V2jrX
4-00
X / q>(X)eiXxdA (т. е. несобственный интеграл справа существует в
•»во
обычном смысле).
Теорема обращения (для преобразования Фурье и для
обратного преобразования Фурье). Пусть f<=/?i(—оо, -}-оо)Д
ДС((—оо, 4-°°)) w Vxe (—оо, 4-оо) выполнены условия Дини.
Тогда имеют место равенства F~’[F[f]]=
Доказательство. Поскольку для функции f(х) (вообще
говоря, комплекснозначной: f(x) = u(x)+iv(x)) выполнены усло-
вия теоремы Фурье, то формула Фурье в комплексной форме да-
ет равенства
f(x) = 1/2^-v. р. 7° Т f dt dl -
— co |_ —oo
= l//2^.v. p. +f
— OO
*
t. e. / = Для доказательства равенства ^’[f“1[f|]=/
рассмотрим формулу Фурье в виде
f (х) = 1/2* • +f° f(t) cosX(f - х) di =
= 1/2*. +J°dX T f(t) cosX(f — x) dt.
Поскольку синус нечетен, io
l/2*-v. p.+f dX Y f(7)sinX(x — t)dt = 0,
—co —oo
поэтому имеем еще один вид формулы Фурье:
f (х) = 1/2*-v. р-Т Y КО di
244
или
f(x) = 1//2« • v. р. J е~^х11//2кХ
— ОО L
X Т/(OeiMdfldX =
— оо J
(при этом мы пользуемся „обобщенной* формулой Фурье
/г[ф]= у. р. J <р(А)е~шйХ,
—оо
т. е. JF-4/И=Л
§ 3. Свойства преобразований Фурье и их приложения
Теорема (о линейности преобразования Фурье). Пусть F[f]=»
=f(X) есть преобразование_Фурье функции f(x). Тогда отображе-
ние F:f-*-J, заданное на Ri(—00^4-00), линейно, т. е. F[aifi4-
+a2/2]=aiF[fi]+a2/:'[f2] Vfi, f2 ge Ri (—00, 4-00) и V ab a2 e C.
Доказательство. Очевидно, arfi+a2f2^Rt (—co, +°°),
поэтому существует преобразование Фурье для функции aifi4"
+«2/2, причем
^[«1/1 + a*/i] = • +J («i/ifO + aJt(t))e-iU dt —
— 00
= +f />(0 e~™ dt 4- +f° ft(t)e~^dt=
—co —00
• Теорема (о биективности преобразования Фурье). Пусть
Cg^R^ (—00, 4-о°) есть множество абсолютно интегрируемых (на
(—°°, +°°)) непрерывных функций f(x), удовлетворяющих
Vxe(—00, 4-00) условию Дини. Тогда отображение F: С^>->
~*F(C биективно (причем v f fC^)J.
Доказательство. Пусть fi, f2^Cs>, т. е. flt f2^Ri(—00,
+°о)ДС((—оо, 4-°°)) и для функции ft(x) в любой точке хе
е(—оо, 4*оо) выполнены условия Дини. Пусть Л/1]=Л/2], тогда
в силу линейности преобразования Фурье F[fi—f2]=0, т. е. при
^(x)=fi(x)—f2(x)^C^>, имеем <р(Х)М)еС.®. Но, очевидно,
и поскольку <реСа, то по теореме обращения для пре-
образования Фурье имеем (O=F-1[F(cp]]=<p(x))=>- (ф(х)^О)=Ф-
^(fi(x)^f2(x)). Итак, если fi, f2^ С&, то = Ff^J)
^(fiOO—Mx)), что и означает биективность отображения F:
cs>^F(C&).
245
Теорема (о непрерывности и убывании на бесконечности
преобразования Фурье). Пусть f^Ri(—00, 4-00) и f(A)=F[f] —
ее преобразование Фурье. Тогда: 1) —00, 4-°°));
2) lim |ДХ)|=0 и 5) | ДХ)|<||/||1/’|/2^ VXe=(-oo, +oo), где ||/||1в
= ^\f(t)\dt.
— 00
Доказательство. Поскольку функция f(x) абсолютно ин-
тегрируема на (—оо, 4-°о), a e-iXx » cosXt— i sin Xt s Cx, t((—co,
-boo)x(—00,+00)) и |е-ш| 1 VX, t, то к тригонометрическому
4-oo
интегралу J f(7)(cosXt—isinXt)dt применимы теоррема Г (о не-
—ео
прерывности несобственных интегралов специального вида) и
лемма (об убывании тригонометрических интегралов) из гл. 5,
§ 1, поэтому для функции
ДХ) =[1/^ • +f f(t)e~™dt
ОО
имеем f е С((—оо, -f-оо)) и lim | ДХ)| = 0. Далее, очевидно,
1Х*->4-оо
VXs (—00,-fcoo).
—00 ,
Следствие. Пусть (fn(x)) — последовательность функций
из Ri(—00, 4-°о), сходящаяся в метрике Ri(—00, 4-00) к функции
/еЯД—оо, 4-оо) (т. е. lim ||/—fn\\t = Um +f \f(x)—fn(x)\dx=Q)
п—>4-00 п—>4"°° оо
Тогда fn, / е С((—00, 4-00)) и f„(X) ДХ) на (—00,4-00).
п-*4-оо
Доказательство. Поскольку fn> feRi(—00, 4’°°)» то в си-
лу нашей теоремы fn> ((—00, 4-00)), причем имеет- место
оценка
VXG (-00,4-00),
но тогда, очевидно,
( sup I f(X) - fn(k)| < Ilf -7n|k//2^)
—оо<Х<4-оо
=Ч/п(Х) ?(Х) на (—00, 4-00)).
(п-»4-оо)
Теорема (о преобразовании Фурье дифференцируемой функ-
ции). Пусть f^Ri(—00, 4-оо)Д^((—00, 4-,оо)) и Df&
246
e/?i(—°°> +°°)> причем F[f]=f(X) — преобразование Фурье
функции f(x). Тогда F[Df]=iA,F[f] (или Df(k)=iXf(k)), т. е. диф-
ференцированию функции f в условиях теоремы соответствует ум-
ножение ее преобразования Фурье f на множитель 1К.
Доказательство. Пусть сначала f(х) — действительно-
значная дифференцируемая функция. Тогда по формуле Ньюто-
на— Лейбница (из [1], ч. II, гл. 2, § 6) имеем
о
и поскольку Df s /4 (—оо, + оо), то существует
lim f(x) = ДО) 4- Т D f(t) dt.
Докажем, что в силу условия f <= R1(—оо, +оо) имеем
lim f(x)=Q. Допустим, что lim \f(x)\ = l>0. Тогда ЭХ(/)>0
Х-*4-оо
такое, что |/fx)|>Z/2>0 Vx>X, но тогда в силу теоремы
сравнения (для несобственных интегралов из ч. IV, гл. 1, § 4)
имеем
Т |/(0|Л = + оо,
х
что противоречит условию fe2?i(—оо,+оо) (из которого сле-
дует Ч-oo)). Итак, существует lim f(x) = O. Теперь,
Х-»±оо
имея в виду доказанное ранее соотношение — ё~ш =—
dt
получаем, интегрируя по частям,
F[D/] = 1//2^ • "j0 Df(t)e~iu dt = 1/]/2^ X
—оо
X If(t)e~iU <m+°° - Y f (t)(-i\e~^1) dt =
\ l«-0© —OO
= iV/2^ • 7° Ю) = Mfl.
—oo
т. e. для действительнозначной функции f(t) имеем равенство
c['Df]=itXF[f}. Пусть теперь f(t)=u(t)+tv(t), тогда Df(t)=:
причем в силу условий теоремы и, v, Du, Dos
(—оо, Ч-оо). Используя линейность преобразования Фурье,
Получаем fTDf]=H'D«4-{Do] = /TDu]4-iFFDo]=iA,(F[u]4-tF[vj() =
(ЛРГ]=ад])-
247
Следствие. Пусть fe£Z>(*>((—оо, +оо)) (£==1, 2, +°°)
и (при 1=0, 1...k) Dlf^Ri(—оо, 4-оо). Пусть F[f]=f(X) — пре-
образование Фурье функции f. Тогда F[&lf]= (iX)'F[f] (/=;
= 1,2, k).
Теорема (о связи между степенью гладкости функции и
скоростью убывания на бесконечности ее преобразования Фурье).
Пусть —оо, +,оо)) (й=1, 2, ...) и оо, -f-оо) ;•
при 1=0, 1...k. Пусть F[f]=— преобразование Фурье функ-
ции f. Тогда \f(X) | =о(1/|Х|‘), |%|->+;оо).
Доказательство. Поскольку feS><*)((—оо, +,оо) и
Dlf^Ri(—оо, Н-оо) (при 1=0, 1...k), то в силу следствия к пре- :
дыдущей теореме имеем равенство (iA)^F[f], откуда
|f(X) | =|/TjDftf]|/|A.|k при Х=/=0. Поскольку Dkf^Ri(—оо, 4-оо), ;
то по теореме об убывании на бесконечности преобразования
Фурье (для абсолютно интегрируемой функции) имеем
lim |F[DV]|=O, т. е. |f(X)|=o(l/|X|k)(|X|->+oo). ?
|Х|-»4-оо
_3амечание. Пусть f е Ф ((—оо, + оо)) и f, Df, D2fe
eRi(—об, -l-oo), причем /(Л) =F[f]. Тогда f^Ri(—оо, -f-oo).
В самом деле, поскольку f, Df, D2f^Ri (—оо, -f-oo), то |f (X) | =
=о(1Д2) (|Х|-*+оо) и тогда существуют Хо>О и К0>0 такие, j
4Tojf(X)KK0/X2V |Х1>Хо>0. Но поскольку JeC((—оо, +.оо)), |
то ]eR[— I, Z] v Z>0,__ и тогда из нашей оценки в силу теоремы |
сравнения имеем fe/?i(—оо, +,00).
Следствие. Пусть feC(°°)((—оо, +ooj) и —°°»
4*оо) при любом £>0. Тогда fl[D7]e/?i(—00, 4-00) V /^0, причем .
|D’f(X)| убывает при |Х|-*+.<» быстрее любой степени
1/IM* (*eN).
Теорема (о связи между скоростью убывания, функции на .
бесконечности и степенью гладкости ее преобразования Фурье).
Пусть функции f(x) и x-f(x) абсолютно интегрируемы на
(—оо, 4-оо). Пусть f(X)=F[f] — преобразование Фурье функции
f(x). Тогда f^C^>((—00, 4-00)), причем Df(K)=F[—ix-f(x)], т. е.
iDf(X) =F[x f(x)] и lim |Df(Z,)|=O.
|Х|-*4-оо
Доказательство. Заметим, что в силу условия fe
^Ri(—00, +;оо) существует преобразование Фурье f(X) =
_______ 4-оо -
= 1/У2л- S f(t)e^Mdt, причем feC((—-оо, +оо)). Формальное
—ею
дифференцирование по X несобственного интеграла справа дает-
248
__ Ч-со
несобственный интеграл —i/T2n- S tf (t)e~it4dt, зависящий от па-
—оо
раметра_Х. Из оценки *** I =“ I СО 1 v Л,, в силу услови»
x-f(x)^Ri(—оо, +ioo) по признаку Вейерштрасса получаем рав-
номерную сходимость на (—оо, +оо) нашего несобственного ин-
теграла, но тогда модификация теоремы 2 (о дифференцировании*
несобственных интегралов специального вида из гл. 5, § 1) пока-
зывает, что vxe(—оо, -f-оо) существует производная
Df (Z) = - i7|/2w Т( • Ю) е~™ di = F\-ixf(x) I
—оо
или iDf (X)—J7[x-f(X)]. Используя теорему о преобразовании
Фурье абсолютно интегрируемой (на (—оо, 4-оо)) функции
x-f(x), имеем Df(X)eC((—оо, 4-оо)), а также lim |Df(X)|=O.
IX|—+оо
Заметим, что при проведенном доказательстве неявно* предполага-
лось, что функция f(x) — действительнозначная, однако если
f(xj=u(x)+iu(x), то, очевидно, и, v, х*и, X‘V^.R\(—оо, -f-оо), и
поэтому, используя линейность преобразования Фурье, имеем»
DF[f]=D/?[u-4-^,]==OF[u]+= F[—ixu(x)]-}-iF[—ix-o(x)]=
=F[—l{x(u(x)+iv(x))}]=F[—ix f(x)l т. e. iDf (K)=F[xf(x)].
Следствие. Пусть функции xl-f(x)^Ri(—oo, -]-oo) при
1=0, 1, ..., k и f(h)=F[f] — преобразование Фурье функции f(x).
Тогда —оо, Ч-оо)), причем Dzf(l)=77[(—ix)l-f(x)] (ил»
i‘Dlf(K)=F[xl-f(x)]), а также
lim [D7a)| = ° (z = °. 1, 2, ...» fe).
|Xl—»-|-oo
Определение. Пусть fi, fz^Ri(—°°, +<»)• Тогда функция
£ __ -f-00
Г(х) = 1/У2л- J fi(t)-fz(x—t)dt называется сверткой функций ft »
— oo
ft- Обозначение: (fi*fz)(x) = l/l/2n- S fi(t)fz(x—t)dt.
— ex
Теорема (достаточное условие существования свертки).
Пусть f^Ri(—оо, -j-оо) и функции fi, fz ограничены, т. е. суще-
ствуют постоянные Mi>0 такие, что V хе (—оо, Ч-оо^
(1==Л 2). Тогда существует свертка
fz * №) = • Т МО fz(x-t)dt, (3.1)
— 00
хе (—оо, +оо),
причем несобственный интеграл (3.1) сходится равномерно нф
+°о).
24Ф
Доказательство. В силу ограниченности на (—оо, 4-оо)
абсолютно интегрируемых функций fi(x) и f2(x) имеем оценку
vx, /е(-оо, +оо).
Поскольку (—оо, +оо), то в силу признака Вейерштрасса
«©собственный интеграл (3.1), зависящий от параметра, сходится
абсолютно и равномерно на (—оо, -(-оо).
Теорема. Пусть fi, f2^Ri(—оо, -|-оо)ДС((—00,4-00)) и
функции fi(x) и f2(x) ограничены на (—оо, -(-оо). Тогда сущест-
вует свертка причем: 1) f^C((—oo, +00)); 2) яМ>0
такая, что |f(x)|^MVxe(—00, -]-оо), и 3) fs/?i(—00, 4-00).
Доказательство. Поскольку ft, f2^Ri(—00, -|-оо) и
|f((x)|^M- Vxe(—00, 4-°°) (t=l, 2), то в силу теоремы о су-
ществовании свертки Я f(x)—fi*f2(x), причем несобственный ин-
теграл (3.1) сходится равномерно на (—оо, 4-оо). Но fi, f2<^
еС((—оо, 4-оо)), поэтому в силу теоремы (о непрерывности рав-
номерно сходящегося интеграла от непрерывной функции) имеем
fi*f2eC((—00, 4-оо)), причем |fi*f2(x) |<Л12/У2л- J |fi(/)|df= .
—оо
=2И<4-оо Ухе (—оо, 4-оо), т. е. свертка fi»f2 обладает свойст- •:
вами 1,) и 2). Приступим к доказательству абсолютной интегриру-
емости свертки f—fi*f2 (на (—оо, 4-00)). Поскольку fi, f2e
e7?i(—00, 4-00), то
4-оо 4“°°
J I fl (t) - 01 dx = If HOI J |f2(x -1) dx =
— 00 —00
(замена x —/ ==z) '
“IfiCOl T lf4(z)ldz e=fli(—00, 4-00),
— 00
;a потому существует повторный несобственный интеграл
Т dt 7 Ifx(t)fа(х-1)| dx = +f \ft(t)\di Y If2(01 dz.
—co — 00 —00 —00
Рассмотрим однократный несобственный интеграл, зависящий
от параметра f:
Flfi(0-f2(*-0|d*
и докажем, что этот интеграл сходится равномерно на любом ко-
нечном отрезке [Л, Т2]. Очевидно, достаточно доказать равномер-
ную сходимость на [Д, Т2] каждого из двух несобственных интег-
ралов
250
+oo О
J IfifOkfa—t)\dx и S \fi(t)-fi(x—t)\dx.
0 —oo
В силу условий Vf и f2^Ri(—<X>, Ч-оо) для любых
X2>Xi>0 и V fe[Ti, T2] имеет место оценка
h(x-t)\dx = \f1(t)\ -f\Ux-t)\dx<
Xt Xi
< м, Y \ш dz < Mt Y11Ш1 dz.
Xi-t Xi-Tt
Ho fz^Ri(—oo, +°°), поэтому, используя критерий Коши (сходи-
мости несобственных интегралов), видим, что V 8>0 я Х(е) >0
такое, что V Х2—Л>Х1—T2^X(s) имеем J lfz(z)\dz<.&/M2,
Xi-T,
х,.
откуда Vte[Tb Т2] вытекает оценка X IfiftJ^C*—t)\dx<.e. В
силу критерия Коши (равномерной сходимости несобственных ин-
тегралов, зависящих от параметра) следует,’ что несобственный
4-00 О
интеграл S \fi(t)-fz(x—t)\dx (а также S\fi(i)’h(x—t)\dx) схо-
0 —00
дится равномерно на отрезке [Л, Т2]. Итак, однократный несобст-
4-00
венный интеграл f \fi(t)-f2(x—t)\dx сходится равномерно на лю-
—оо
бом конечном отрезке [7\, Т2]. Далее, несобственный интеграл
4-00
X ffi(t)'fz(x—t) \dt, как было доказано ранее, сходится равномер-
— Оо
но (по х) на (—оо, +оо). Итак, выполнены все условия теоремы 1
'(о замене порядка интегрирования в повторных несобственных ин-
тегралах из ч. IV, гл. 2, § 4), в силу которой из существования
повторного интеграла
Т W • Mx-t)\dx
—оо —оо
вытекает существование равного ему несобственного повторного
интеграла
f dx +f |fi(7) • f2(x — t)\dt = +f +J |f!(t)f2(x—Z)|^l dx >
—00 — oo —oc —oo J
>T T fi(t)-f2(x — t)dt dx=K2^T \f(x)\dx,
—oo —oo —00
где f=fx*f2t но это и означает, что fi*f2^Rt(—оо, +>оо).
251
Замечание 1. Из теоремы следует, что свертка fi*fz облада-
ет всеми свойствами функций ft и fz, и поскольку, в частности,
свертка абсолютно интегрируема на (—оо, Ч-оо), то существует
преобразование Фурье F[fi*f2] свертки fi*f2.
Замечание 2. Рассматривая операцию свертки на классе
абсолютно интегрируемых, непрерывных ограниченных функций
на (—оо, +оо), можно показать: 1) f1*f2==f2*f1 (коммутатив-
ность); 2) (fl*f2)*f3=fi*(f2«f3) (ассоциативность).
Докажем, например, коммутативность свертки. Поскольку
fl, f2e/?i(—оо, +оо)ДС((—ОО, -|-оо)) И функции fi(x), 'fz(x) ог-
раничены, то существуют свертки fi*f2 и fz*fi, причем, делая за-
мену х—t=z, получаем представление
/1 * fz(x) = • +f /1(0 • fi{x — t) dt =
— oo
= l/)/2rc • +f f,(z) • fi(x—z)dz=fa » h(x) V*(= (—oo, +oo).
—oo
(Попробуйте доказать самостоятельно ассоциативность свертки,
используя теорему о перестановке порядка интегрирования в не-
собственных повторных интегралах.)
Теорем а_(о преобразовании Фурье свертки). Пусть функ-
ции ft, fz^Rt(—оо, +.оо)ДС((—оо, 4-оо)) ограничены на
(—оо, +оо). Тогда существует преобразование Фурье свертки
fi*fz, причем F[fi*fz]= т- е. fi*f2(X) =fi (X) f2(X) V Хе
е(—оо, +,оо), так что преобразование Фурье свертки двух функ-
ций равно произведению преобразований Фурье этих функций.
Доказательство. Поскольку fi, f2e/?i(—оо, ч-оо)Д
ДС((—оо, -|-оо)) и функции fi(x), fz(x) ограничены на (—оо,
4-оо), то существует свертка f—fi*fz, причем fe/?i(—оо, -|-оо)Д
ДС((—оо, -J-оо)) и функция f(x) ограничена на (—оо, -j-oo). Но
тогда для функции f(x) существует преобразование Фурье f(X),
причем имеет место представление
7(К) «= • +f е~ш l/'j/2^+f° /1(т) /а(*—
— ОС» L —°0 J
Заметим, что функции fb fz^Ri(—00, -f-oo) ограничены на (—оо,
+оо). Но тогда при доказательстве предыдущей теоремы (о свой-
ствах свертки fi*f2) было доказано существование повторного не-
собственного интеграла
• Y dt Y IfxW-Hi - т)| dr > +f \f(t)| dt,
—oo —oo —oo
что означает существование повторного несобственного интег-
рала
252
j' dt j' |/1(т)./а(«-т)е-^|Л.
—oo —oo
Заметим, что несобственный интеграл
+f fi(T)72(i—T)e-zwdt=e-iXf-+J AW'f2(t—x)dx
—oo — oo
(при фиксированном Л) сходится равномерно по t на (—оо, 4-оо).
Рассмотрим еще один несобственный интеграл
Т 'ixtdt = АА>Т f2(t-x)e-™ dt.
—00 —oo
В силу ограниченности функций Л(т) ОА(Т)1 С M2 V x) и
^~iW(|e~iX'| = 1), а также ввиду условия /2еЯх(—оо, +оо)УХ2>
>Xj имеем оценку
f ’ 7^-т) jdt < mJ’ |/2(f - т)|Л =
X, а
= Л«!- |/2(?)ldZ < M1X‘tr’|/2(z)|dZ Vt el-Л, T2],
X,-t Xt-T,
яз которой с помощью критерия Коши получаем равномерную схо-
димость на любом конечном отрезке [—Ть Тг] несобственных ин-
тегралов
7° AWAU— ^e-^dt
О
я
о
J АСО-АА—
—оо
а стало быть, и интеграла
Т АА)-Аа-т)е-^ dt.
— со
Но тогда для несобственного интеграла
AA)-A(^-T)e-ix‘d/
—оо —оо
выполнены все условия теоремы 1 (о перестановке порядка ин-
теграции в повторных несобственных интегралах из ч. IV, гл.
2, § 4), в силу которой имеем равенства
7(Х) = 1/2к 7° A(T)dx /,(/-%) е~^ dt =
253
(делая замену t — t=z) = l/2« /i(x)dT+( /2(z) e~X(t+z) dz =
— oo —oo
= l/]/2w J f^e-^dx-MV^X
— oo
X+J' /2(z)e-‘X2dz =/i(A) • 4(X).
—oo
Замечание (о приложении преобразования Фурье к реше-
нию задачи Коши для уравнения теплопроводности). Пусть тре-
буется найти распределение температуры в неограниченном одно-
родном стержне в произвольный момент времени rf>0, если ее
распределение в начальный момент времени /=0 известно. Темпе-
ратура и(х, t) в стержне (ось Ох считается направленной вдоль
стержня) является функцией точки х стержня и времени t: и—.
=и(х, t)—oo<x<-j-oo, Os^f< + oo. Известно (см., например,
ч. VI), что температура и(х, t) в стержне удовлетворяет уравне-
нию теплопроводности
ди <, д2и Л
— = <22-------, — оо X <Z + оо, t 3> 0,
dt «Эх2
(3.2)
причем поскольку начальное распределение температуры известно,
то
и(х, Q)=f(x), —оо<х<+оо, (3.3)
где f(x) — известная функция. Итак, требуется найти функцию
и(х, t), удовлетворяющую в открытой области G={(x, t)^.
eR2|—оо<х< + оо, 0<7<+©о} уравнению^ теплопроводности
(3.2), непрерывную на замкнутом множестве G и удовлетворяю-
щую начальному условию (3.3), причем будем предполагать, что
fe<Z>(2)((—оо, +!оо)) и f, Df, D2f^Ri(—оо, -j-оо). Искомое реше-
ние будем искать в классе функций, удовлетворяющих условиям:
1) «(х, t), -а^~- s Дх.»(—°°» + оо) V Z > о;
2) существует функция Ф(х)^Д1(—оо, +,оо), такая, что имеет
месго оценка ,^ц(х» 0 1 ^;ф(х) vxe (—оо, +,оо) V fe[0, Г].
dt I
Можно доказать, что при указанных условиях на начальную функ-
цию f(x) существует решение задачи Коши (3.2), (3.3), и оно
удовлетворяет условиям 1) и 2). Подставим это решение и(х, t)
в уравнение (3.2) и получим тождество (в G)
(х> /)eG
254
Умножая обе части этого тождества на Х/ЧЯп-ет0* и интегрируя
по х от —оо до 4-оо, получаем равенство
— (X, t) = а2 — (X, t), t>0,
dt ' ’ дх* ' ’ '
где использованы обозначения
ы(Х, t)=l/yr2n • "j° и(х, t)e~Uxdx
—со
для преобразования Фурье (по х). Но в силу условий 1) и
2) имеем
^(Х, t)= 1//2к • J (х, t)e-**dx =
7 lZ|/2rc • f и(х, t)e~i>Mdx = —а(Х,
at L _ж I dt
О-
Кроме того, используя (ввиду условия 1)) свойства преобразова-
ний Фурье от абсолютно интегрируемых функций, получаем
— (X, /)=(iX)2«(x, 0 = -х2и(х, /).
Итак,
— и(Х, £) = — ааХ8и(Х, t), 0</-<4-00.
Но в силу начального условия Коши (3.3) имеем
и(Х, 0)=l//2S • а(х, O)e-^xdx =
—оо
= 1//2^ • +f f (x)e~lXxdx =
—оо
Итак, наша задача Коши для уравнения с частными производными
(3.2) сведена к более простой задаче Коши для обыкновенного
дифференциального уравнения 1-го порядка
-и(Х, 0 = — aWutk, t) t>0 (3.4)
dt
с начальным условием Коши
и(Х, 0) =/(%)• (3.5)1
Разделяя переменные, имеем
/ ^«(Х, о =а в2х2 dt X (1п „(Х, 0 = — а2\Ч + In С(Х)).
\ »U.O /
255
Использование начального условия (3.5) дает
(In f(X) = In С (к)) (С(Х) = /(X)).
Итак, функция u(X, t) = /(X) е~агм есть решение задачи Коши
(3.4), (3.5). Ранее было показано, что
F[exp(—ах2)] = 1/]Л2а • ехр(—Х2/4а).
Полагая 1/4а = a2t, имеем а=1/4а2£, т. е. )/2а — 1/а]Л2£, и по-
этому ехр(—а?кЧ) = F[l/ayr2t • ехр(—х2!4аЧ)\. Но тогда, ис-
пользуя теорему о преобразовании Фурье свертки, имеем
F[u((x, 01 = F[fCx)] F[\laV2t X
X ехр (—х2/4а2/)] = F\f * <р],
где - ,
<р(х)з=1/аУ2/ехр (—х2/4а2().
Применяя обратное преобразование Фурье F~x, получаем
и(х, t) ~ F-'[F[u(x, t)]] = F~'\F[f* <р]]=/* <p=l/j/2itX
X Y l/aV2t f(£)exp(-(x-£)2/4a2Qd5,
—-oo
т. e. искомое решение задачи Коши (3.2), (3.3) имеет вид
и(х, t) = 112аУтИ . "j /(£) ехр (—(х—£//4a2Z)d£. (3.6)
—-оо
Замечание. В формуле (3.6) справа стоит интеграл Пуас-
сона, являющийсЯ-Сверткой /*Г начальной функции f из (3.3) с
функцией Г=ф/У2л, называемой фундаментальным решением
!(ф. Р-) уравнения теплопроводности (3.2) и играющей важную
роль в теории параболических уравнений. Фундаментальное реше-
ние Г получено нами с помощью теории преобразований Фурье,
что и обусловило весьма жесткие условия на поведение начальной
функции f из (3.3). Отметим, что при наличии ф. р. Г можно по-
ставить вопрос об отыскании минимальных условий на поведе-
ние начальной функции f из (3.3), при выполнении которых ин-
теграл Пуассона (З.'б) все еще является решением задачи Коши
i(3.2), (3.3). В теории параболических уравнений доказано (см.,
например, [3]) утверждение: если начальная функция f(x) из (3.3)
удовлетворяет условиям f^C((—°°. 4-°°)) и
^Сехр (Л-]х|2) Vxe(—оо, -]-оо) (С>0, Л>0), то интеграл Пу-
ассона и(х, t) из (3J6) обладает следующими свойствами:
1) иеф), причем ^<=C(G);
256
2) функция и(х, t) удовлетворяет уравнению теплопроводно-
сти (3.2) v (х, t)(=G\
3) t)=f(x)\x^(—оо, -j-оо) (т. е. выполнено на-
чальное условие (3.3));
4) существуют постоянные С(Т)>0 и &>0 такие, что имеет
место оценка
[и(х, i)|^C(T) exp (Л|х|2) Vхе(—оо, 4-оо), v fe[0, Г].
(3.7)
Заметим, что (как показал А. Н. Тихонов) интеграл Пуассона
(3.6) является единственным решением задачи Коши (3.2), (3.3)
в классе быстрорастущих (при |х|->+оо) функций, определяе-
мом оценкой (3.7).
§ 4. Линейное пространство S
и преобразование Фурье в нем
В § 3 были доказаны теоремы о связи между степенью гладко-
сти функции и скоростью убывания на бесконечности ее преобра-
зования Фурье, а также теорема о связи между скоростью убыва-
ния функции на бесконечности и степенью гладкости ее преобра-
зования Фурье, из которых вытекает, что при переходе от функ-
ции f(x) к ее преобразованию Фурье f (1) свойства гладкости и ее
убывания на бесконечности меняются ролями, поэтому естествен-
но искать классы функций из Ri(—оо, +<»), которые переводятся
преобразованием Фурье F:f-*f сами в себя. >
Определение. Классом S называется линейное пространст-
во функций ((—оо, Хо°.)) таких, что vf&S и Vk, 1=.
==0, 1, 2, ... существует постоянная C(k, I) (зависящая как от
функции f, так и от чисел k и I), для которой имеет место оценка
(l+|x|)ft|D»f(x)KC(Jfe, /)VX€=(—оо, -Ьоо). (4.1)
Замечание. Из оценки (4.1) (при k^2) в силу теоремы
сравнения (для несобственных интегралов) видим, что Dlfe
e/?t(—оо, 4-оо) (1=0, 1, 2, ...) для любой функции feS, и, в ча-
стности, Sc:Ri(—оо, 4-оо). Линейное пространство S использует-
ся в теории дифференциальных уравнений с частными производ-
ными.
Теорема. Пусть 8<^R\(—оо, 4-оо) и F[f]=f есть преобразо-
вание Фурье для функции f(x). Тогда отображение F:f-*f опреде-
лено на S, причем F(S) =S и отображение F:S на S биективно.
Доказательство. Поскольку Scz/?i(—оо, +оо), то ото-
бражение F:f-+f (где ЛУ]=^(Х) — преобразование Фурье для
f(x)) определено на 3 и линейно на нем. Докажем, что ?(%)='
17 — Л. И. Камынин 257
=+[fjeS V f&S. В самом деле, поскольку feS, то V k, 1=0, 1,2,...
имеем оценку
(l + |*l )fe|D'f(x) |<С(£+2, Z) (l + lx|)-2Vx€=(-oo, +оо),
откуда
|x* D7(x)|<C(fc+2, I) (1 + |х|)-2 Vxe(-оо, 4-<х>).
В силу теоремы сравнения (для несобственных интегралов) на
этой оценки имеем xfe-D!f (x)eR+— оо, +оо) V k, 1=0, 1, 2; и; в
частности, поскольку xk-f(x)^Ri(—оо, 4- 00) v &eN0, то в силу
следствия к теореме (о связи между скоростью убывания функции
на бесконечности и степенью гладкости ее преобразования Фурье)
из § 3 имеем /<=£<*>((—оо, 4->оо)) для любого k=0^ 1, 2, т. е.
feC(oo>((—оо, +,оо)). Далее feC<°°)((—оо, +оо))ДТ?!(—оо, 4-ро)
и Dzfe/?i(—оо, 4-,оо) v ZeN0, поэтому, используя следствие к тео-
реме (о связи между степенью гладкости функции и скоростью
убывания на бесконечности ее преобразования Фурье) из § 3, ви-
дим, что f(X)=F[f] убывает на бесконечности быстрее любой сте-
пени |Л|-*, но тогда, в частности, по теореме сравнения (для не-
собственных интегралов) видим (беря k^2), что feRi(r— оо, +|оо).
В силу теорем из § 3 о свойствах преобразований Фурье абсолют-
но интегрируемых функций для любых k, 1=0, 1, 2, ... имеем
D,(xkf(x))^R1(—оо, 4-оо), откуда F[D'(xft f(x))]= (ih)lFfxkf(x)].
Но из F[xk-f(x)]=(i)kDhf\l) имеем V k, Ze=N0 (&)l(i)kDkf(K) =
=F[D‘(xk-f(x))].
Далее Dl(xk f(x))^Ri (—oo, +oo) v k, Z<=N0, поэтому
lim |jF[D+xA-f(x))](Z,) | =0, т. e. существует постоянная B(k, 1)
|X|->+oo
(зависящая, быть может, от f и от k, ZeN0) такая, что имеет мес- .
то оценка
(1+|Х|г)|0*/(Х)]<В(^ 0 VXe=(-оо, 4-оо).
Но тем самым показано, что f(X)sS, т. е. F[S]czS. Докажем те-
перь, что Sc2F[S]. Пусть функция g(l)eS — любая. Тогда, как
показано выше, /*(x)=F[gf]=l/V2n- S g(k)er~ii,xdheS. Положим
f(x)=f*(—x)V xs(—oo, 4-ос), очевидно, f(x)&S. Поскольку
^eC<°°)((—oo, 4-oo)), то для функции g(K) в любой точке Хе
е(—оо, -{-оо) выполнены условия Дини, и поэтому в силу форму-
лы обращения имеем g(K) = 1/V2n-S f*(x)eiKxdx=\/l/2n%
— оо
X S f(—x)etXxdx=\/12it-+S f(x)e_‘*«dx=F[f]. Итак, v g(X)eS су-
— оо —оо
258
ществует функция f(x)^S такая, что F[f]=g,(X), но это и означа-
ет, что SaF(S). Таким образом, доказано, что F(S)=S. Далее
v f^S имеем —оо, 4-оо))ДТ?1(—оо, 4-юо), и поэтому
функция f(x) в любой точке хе(—оо, +оо) удовлетворяет усло-
вию Дини, т. е. ScC.®, и по теореме о биективности преобразова-
ния Фурье на С® вытекает, что отображение F:S на S биективно.
Замечание. Если feS, то в силу теорем из § 3, очевидно,
имеем
W(x)]=(a)W);
Кроме того, v f(k)eS существует обратное преобразование
Фурье
^-1[?(М](х) = 1^2л;Л f (X)eA*dX, хе(—оо, 4-00),
— оо
где несобственный интеграл справа сходится абсолютно.
Теорема (формула обращения). Если. feS, то имеет места
формула обращения преобразования Фурье
f(x) = f (X) -e^dK, хе (—oo, 4-00) (4.2)
—oo
или
fW=F-™](x) vxe(-oo, 4-00),
причем (поскольку D’feRi(—oo, 4-00) v/eN0) несобственный ин-
теграл в правой части (4.2) понимается в обычном смысле и схо-
дится абсолютно и равномерно (по х) на (—оо, 4-00).
Теорема (о свойствах свертки в S). Пусть flt f2eS. Тогда-
существует свертка fi»f2(x)==l/lr2n- f fi(t)-f2(x—t)dt, причем:
—о©
1) h*f2(=S; 2) Е[А*Ы= ^2] (или П*ЫМ = fi(%) X.
Xf2(k) v te(-OO, +00); 3) F[M2]==nfiMf2] (или frf2(b)=~
вА*/г(Х) VXe(—oo, 4-00)).
Доказательство. 1) Поскольку ScRt(—00, 4-00) Д’
ДС<°°)((—oo, 4-oo)), причем (14- |x|*) |D'fi(X)\^Ct(k, /)Vxe
s(—00, 4-00), V/, fesNo (i=l, 2), to |fz(x) |<G(0, 0) v xs
e(—00, 4-oo), 1=1, 2, и в силу теоремы (о достаточном признаке
существования свертки) из § 3 видим, что существует свертка
Л*/2еЯ1(—оо, 4-оо)ДС((—оо, 4-,оо)).
Далее для любого 1—0, 1, 2, ... рассмотрим несобственный интег-
f fi(t)Dlf2(x—t)dt, xe(—oo, +oo). (4.3)
—oo
Отметим оценку
|А(0 О72(х-01<С2(0, OlfiCOI v x> ^(-°°> +oo),
из которой в силу признака Вейерштрасса следует равномерная
сходимость несобственного интеграла (4.3), зависящего от пара-
метра х. Но тогда в силу общей теоремы (о дифференцировании
несобственного интеграла, зависящего от параметра) из ч. IV,
гл. 2, § 4 имеем v feN0 представление
Dz(fi*f2(x))=l/V2ji-?7i(O D72(jr—хе(—оо, +«>).
— оо
Далее для любых k, /eNo имеем
PWW1* f2W)l = IT<
< i c»T
m=0 —oo
k 4-oo
< 2 C{“ • C#-m, /) • f kH/ifOl dt =
m=0 —oo
«= C(k, I) < H-oo Vx e (—00, +oo),
так что A * f2 e S.
Утверждение 2) было доказано в § 3. Для доказательства утвер-
ждения 3) заметим, что v feS имеем
F[Fl/]](x) = 1/]Л2^ • Т е~а'х1 (x)dx = X
—оо
X Y eixx)(_k)dA = F“l [ ?(-Х)](х).
— 00
но . ;
f(—X) = 1//2^ . Т e-‘^f(y)dy = l/y2i х
—оо
х Y e-^f(-x) dx ~ F[/(-x)](k),
—оо
т. е., используя формулу обращения, имеем
W]](х) =f(-x) v хе (-оо, +оо).
Но тогда имеем равенство
Wrf2]]W=A(-*) f2(-x) vxe(-oo, +оо) I
I
260
t
Далее в силу доказанного свойства 2) имеем F(fi*fz](x)=a.
= fi(—x) f2(—x) v х е (—оо, +оо),
т. е. Л7172](Х)==Л/1*/2](Х) V хе(—оо, +оо), откуда в силу биек-
тивности отображения F:S на S получаем утверждение 3).
Теорема (о равенстве Парсеваля в S). Пусть fi, fz^S. Тогда
имеют место утверждения:
1) Т AW • fi(x)dx= +J f^y) • fay) dy,
— do —oo
2) h(x) -fax)dx = ^ ft(y) . fay)dy
— oo —oo
(равенство Парсеваля) и, в частности,
Т If (*)\*dx= 7° l?(X)|2 dk Vfe S.
— ОО —00
Доказательство. 1) Пусть fi, fz^S. Тогда имеем
У1(х) • f2(x)dx = \lV2i • Т Ше~*Ч2(х)ду, (4.4)
— ОО — ОО —оо
где повторный несобственный интеграл справа в (4.4) сходится
абсолютно (поскольку fi, fz^S). Рассмотрим однократные несоб-
ственные интегралы, зависящие от параметра
7 h(y) e~iv* • fi(x)dy,. х (= (—оо, +оо) (4.5)
— оо
и
7 А (у) e~iVX ' fi(x)dx, уе (—СО, +оо). (4.6)
— оо
В силу оценки
\fi(y)e~iyx h(x)\^Cz(O, 0) |А0/) | Vу, хе(—оо, +оо)
из условия fieRi(—оо, +оо) вытекает равномерная сходимость
несобственного интеграла (4.5) (по х) на (—оо, -f-оо), а в силу
оценки
\Ь(У) е~‘ух Ь(х) |<С1 (0, 0) |f2(X) | V х, у<= (—оо, +оо),
поскольку fz^Ri(—оо, +оо}, вытекает равномерная сходимость
(по у) на (—оо, 4-оо) интеграла (4.6). Но тогда к повторному не-
собственному интегралу, стоящему справа в (4.4), можно приме-
нить теорему 1 (о замене порядка интегрирования в повторных не-
собственных интегралах) из ч. IV, гл. 2, § 4, в силу которой из
(4.4) имеем
261
*y“Ow I
J fi(x)ft(x)dx= f ш 1/Г2к x
--OO —OO L
x+f {2(х)е~^х dx"\dy = +$ fi(y)-fi(y)dy,
— co J —oo
t. e. утверждение 1) доказано.
Приступая к доказательству утверждения 2), напомним обоз-
начение u+iv = u—iv. Далее, используя доказанное утверждение
1), получаем
+f h(x)fax)\dx = +f° f^y) • h(y)dy,
—oo —oo
где h(x) =f2(x). Но тогда
h(y) = 1/)/2tc • +j° fax) .e~iyx dx = X
X j f2(x)eiyxdx,
— oo
откуда, используя формулу обращения, имеем h(x) = f2(y),
так что
4-00 Л - 4-00 _
f fi(x) - fax)dx= f fi(y) • f2(y) dy.
—oo —oo
Утверждение 2), т. e. равенство Парсеваля в S, доказано.
ЛИТЕРАТУРА
1. Камынин Л. И. Курс математического анализа Т. I. М.: Изд-во МГУ, 1993.
2. Б а р и Н. К. Тригонометрические ряды. М.: Физматгиз, 1961.
3. Фридман А. Уравнения с частными производными параболического типа.
М.: Мир, 1968.
4. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. М.: Мир, 1967.
Часть V
КРАТНЫЕ ИНТЕГРАЛЫ РИМАНА
Глава 1
ИНТЕГРАЛЫ РИМАНА НА БРУСАХ В R”
§ 1. Определение интеграла Римана на брусе в Rn
Доказательства ряда теорем этой главы часто являются до-
словным повторением доказательства соответствующих теорем для
одномерного интеграла Римана из части II [1], поэтому они будут
опускаться, если не появляется новых моментов, связанных с пе-
реходом от п—\ к п^>2.
Пусть числовая функция f(x) определена на замкнутом брусе
(т. е. на стандартном n-мерном параллелепипеде с гранями, па-
раллельными координатным плоскостям) Ь]=1п(а, Ь),
где а=(а1, а2, .... ап), b = (bi, b2, Ьп)', а, 1п(а, Ь) —
='(«1, — ~Х.(ап, Ъп). Определим разбиение Т бруса
1п как семейство Т=(7(1>, Г(2), ...» TW), где есть разбиение от-
резка [а„ &<] (i= 1, 2, ..., п), задаваемого конечной системой точек
(7) =(7i, /г, .... Л»),
= (1 = 1, 2,..., и).
Замечание. Разбиение Т «делит» брус 1п на А7=
=‘Ni-N2...Nn брусов вида
г[х^'-е\ ^чх-хИ»-”,
р=1, 2, ...» Ni (i=l, 2, .... n),
где (j)=(ju /2... jn) — мультииндекс, причем (j—e) = (/i—1,
/2—1, ..., jn—1) (так что e=(l, 1, .... 1)).
Определение. Диаметром d(T) разбиения T для бруса
1п[а, 6] называется число
d(T)= max |л^>—
/(=1, 2,.., N. 1 ’
1=1, 2.п
Очевидно, для любого разбиения Т бруса /“[а, Ь] имеем
/ п \ 1/2
0<d(n< max
*-».2.п \i=t /
263
При заданном разбиении Т бруса 1п рассмотрим любую систе-
му точек е Лл таких> чт°
(»= 1, 2,..., и), и введем обозначение | = = t 7л);
Л = 1, 2,..., Л/4; i = l, 2,..., п.
Разбиение Т бруса 1п[а, б] вместе с выбранной системой точек
£ назовем размеченным разбиением бруса 1п[а, б] и будем обозна-
чать Т£=р. Множество всех размеченных разбиений {7'|}={р)
бруса 1п\а, 6] будем обозначать через 5й . Таким образом,
^ = {р=^|0<4(Г)<М. 80= max |б,-а(|.
<=1.2.............................п
Введем во множестве 3s систему множеств В={Ва}, где Вб=
={p=T|e3a |0<d(7)<6} V бе(0, 6о]. Для системы В={В»}
выполнены условия: 1) , В6=/=0 Убе (О, бо]; 2) Убь бге
<=(0, бо], ябзе(0, min (бь 62)], такое, что В63СВ61ПВ62, причем
V бе (0, бз)) имеем ВвагВб, ЛВз, .
В самом деле, свойство 1) для системы {В^} очевидно. Для про-
верки свойства 2) достаточно показать, что УТ^еВб/ с диаметром
d(Ti)<6i (i=l, 2) существует разбиение Т3 бруса 1п[а, б], для
которого 0 < d(T3) < min (d(T\), d(T2)), 0 < d(T3) = 63
<min (d(Tt), d(T2))<Z min (61, 62).
Пусть TP1»), где (i-1, 2) есть разбиение от-
резка [ak, 6ft] (fe=l, 2,..., n). В качестве T(k> возьмем разбие-
ние отрезка [ак, бк], составленное из различных точек деле-
ния, как из разбиения Т\к>, так и из разбиения Т<*>, очевидно*
0<d(T<»))< min d(7]*>) (6=1,...2, п)- Положив Т3=(Тр,...,
1=1, 2
получим разбиение Т9 бруса 1п[а, б], для которого 0<d(T3)==
= 63<min(d(T1), d(T2)) <0101(6!, 82), при этом Vg имеем T3i е
еВ^СВ^П^з,, т- е В&^0- В силу определения системы {Вз},
очевидно, имеем
Вз С В8, V б е (О, В3].
Замечание. Из свойств 1) и 2) следует, что система В=*
= {В6} есть база (предфильтр, базис фильтра) в множестве ^.бу-
дем обозначать ее символом d(T)-*-O.
Определение. Объемом как открытого In(xfj~e\ х^), так и
замкнутого бруса Zn[x<7-«), д</)] называется число
def п k
= п (х<4> - > О,
i= 1
(7)=(7ь in).
По заданной функции f:In[a, б] R и по размеченному разбие-
нию (бруса 1п[а, Ь]) «с диаметром d(T)>0 по аналогии с одно*
мерным (n= 1) случаем построим так называемую «интеграль-
ную» сумму Римана
264
Sf(T^) = 'Zf^v<n
(индекс f слева часто будет опускаться). При фиксированной
функции f(x) определим на множестве SP (всех размеченных раз-
биений бруса /п[а, 6]) следующее отображение:
F:^ ->R(F:Tg=p^F(p)eR),
положив F(p) =Sf(Л-), гдер=Г£еЗэ. Используя базу В=
=={Вв} (т. е. d(T) ->0), введем
Определение. Интегралом Римана от функции f(x) на бру-
се 1п[а, 6] называется такое число J^R (если оно существует),,
что iimF(p)=J (или limSf(Tg)=J).
d(T)—О 4(Г)-»0
Замечание. Напомним, что запись J=limS/(T|) означает,
d(D—О
что V е>0 существует элемент В6^В такой, что для любого раз-
меченного разбиения (так что разбиение Т бруса In[a, bj
имеет диаметр d(T)<_6) имеем оценку |3/(Т|)—/|<е. Обозна-
чается интеграл Римана от функции f(x) на брусе 1п[а, &} следу-
ющим образом:
f(x) dx = f . . . f f(xlt..., x„)dxidx* • • . dxn.
jfl J in J
Определение. Если для функции х -* f(x) существует ин-
теграл Римана на брусе 1п, то говорят, что функция f(x) интегри-
руема по Риману на брусе 1п. Обозначение:
f^R(In).
Замечание. Класс функций, интегрируемых по Риману на
брусе /п[а, b], обозначается через R(In[a, &]). Расшифровывая по-
нятие предела по базе d(T)-+Q из определения интеграла Рима-
на на брусе, имеем (е, ^-определение интеграла Римана на
брусе. Число JeR называется интегралом Римана от функции f(x)
на брусе 1п[а, Ь], если Ve>036>0 такое, что для любого раз-
биения Т (бруса 1п[а, 6]) с диаметром d(T)<.§ и выпол-
няется неравенство
|5/(Г|)—J| <8. (1.1>
Замечание. Пусть п—2 и f^C(I2), f(x, у)^0, тогда
ml _______________________________ _
sf(Ti)= 22 f(x<>
(f) i=i
Геометрически интегральная сумма Римана Sf(T%) означает сум-
му объемов 3-мерных брусов, аппроксимирующих 3-мерный ци-
линдроид (цилиндрическое тело, ограниченное сверху графиком*
Г/={(х, у, z) eR3|z=f(x, у),(х, у)<=12}.
265-
функции f, а снизу прямоугольником I2, лежащим на координат-
ной плоскости z=0). Поэтому интеграл Римана
JS f(x> y)dxdy = lim Sf(Tg)
ЛЛ—0
можно рассматривать как 3-мерный «объем» этого цилиндроида.
Теорема (единственности интеграла Римана). Для функции
f(x) определенной на брусе 1п, может существовать не более од-
ного числа J из определения интеграла Римана.
(Теорема единственности интеграла Римана на брусе есть
следствие теоремы единственности предела функции по базе из
(1}.)
Пример. Пусть f(x) =с V х<=1п\а, Ь]. Тогда
j* с • dx = с • П = с о(Г[а, &]).
In[a.b\ »—1
В самом деле, для любого размеченного разбиения бруса
&] имеем
S(T£) - 2 2 *</»]) =
(/) (О
fTn-i п (Nn
... 2 п 2 =
/п-1=1 »-1 V”1
Ni N n-1 n
= c • (bn - an) 2 • • • 2 П ) =
/-1 M-l-l i=l
= . . . = c • (bn — ап)(Ьл-1 — an-i) . . .
...(/>!- ax) = c • t’(Zn[a, ft]).
Задача. Пусть /('x) ==x1 • . xn, x e In[a, &]. Тогда
f • • • f X2...xndxv.. dxn = 2~n J-} (b2 a^\.
Теорема (необходимое условие интегрируемости функции по
Риману). Если f^R(In\a, b]), то f^B(In[a, Ь]) (г. е. функция
f(x) ограничена на брусе /п[а, Ь]).
Доказательство. Пусть f^R(In[a, &р. Тогда существует
lim Sf(Tl) =J—Jf(x)dx, и поэтому 3 б>0 такое, что для любого
d(D-»0
размеченного разбиения Tg с диаметром d(T)<Z6 имеем |S(T£)-7
—J| <1. Допустим, что функция f(x) неограниченна на Zn[a,
266
яТ — разбиение с d(T)<6. Тогда существует брус =7п[*(*-в), ,
на котором функция f(x) также неограниченна. Пусть £<*> =
== •••» InO s /(%- Зафиксируем в | = {£<'>} все точки £(/>
при О’)¥=(£) и положим 5(TB)=S(ft>(Tg)+f(^<ft>) • vw. В силу не-
ограниченности функции f(x) на частичном (для разбиения Т)
брусе е 7(% такая^ что |f(tw)| • vw>|J| + 1 + |S<‘)(Tg)|.
Но тогда для выбранного t = {?(/)((/)¥=(^)); Qk)} имеем
|5(2’i)|>|f(l“,)| • ^)-|5W(T|)|>|J|+ 1.
Противоречие.
Замечание. Из ограниченности функции f(х) на брусе
/п[а, Ь], вообще говоря, не следует, что feRlT^a, 6]). При п—1
пример такой ограниченной, но не интегрируемой по Риману на
отрезке [a, Ь]зз/"[а, Ь] функции дает (ср. [1J, ч. II, гл. 2; § 1) рас-
смотрение функции Дирихле
__ | 0, х рационально,
I 1, х иррационально.
§ 2. Суммы Дарбу и критерий Дарбу интегрируемости
по Риману на брусе
Пусть функция f(x) определена и ограничена на брусе 1п[а, &]
в Rn и Т — любое разбиение этого бруса. Для разбиения Т поло-
жим
5/Т) = 5(Т) = sup S(T$, Sf(T) = S(T) = inf S(T&
г. — — z
fi/(T) = Q(7’) = S(T) — S(T).
Тогда Sf(T) называется верхней «суммой» Дарбу, a Sf(T) называ-
ется нижней «суммой» Дарбу функции f(x), соответствующими
разбиению Т бруса 1п[а, Ь].
Теорема (формулы Дарбу). Пусть функция f(x) определена
и ограничена на брусе 1п[а, &]. Пусть Т — разбиение 1п[а, &] и
sup f(x), mw= inf f(x), (fe)=(fen fe2,..., fen). Тогда
jn[x(ft-e), x(t)] 7"
\*4
5(Г) = • O(*), S(T)
(ft) (ft)
Доказательство (ср. [1], ч. II, гл. 2, § 2). Для заданного
разбиения Т бруса 1п[а, &] и v x(fe>] имеем
откуда vg имеем
,S(7'£) ^SAI(ft) U(fe).
267
Но поскольку M(k) = sup f (x), то по определению точной верх-
in
(ft)
ней грани Vs>0Ятакое, что > M(k) — е.!о(1п\а,
/>]), т. е. для выбранных f имеем оценку S(t|) >3(Л1(й) —
(6)
— е/и(/л[а, &])) • t)(4) = 3^(ft) ’^ft) —£ (поскольку v(In[a, b])=s
(ft)
=3*>(ft))- Итак, 2j^(ft> • t\ft) = sup S(Tg) = S(T). Аналогично до-
<*) (ft) £
называется формула S'71**) * v(kt = S{T).
(ft)
Замечание. Если f^C(In), то верхняя и нижняя суммы
Дарбу являются интегральными суммами Римана для функции
f(x). Если же f(x) лишь ограничена на 1п, то Sf(T) и Sf(T), во-
обще говоря, не являются интегральными суммами Римана для
f(x) на /п.
Замечание. Для данного разбиения Т бруса /п=/п[а, Ь]
положим при (k) = (ki.... kn), ®(й)=М(й)—тогда при
«(*) = <»(/; 7(%)= sup \f(x)-f(y)\
x-yeI(k}
есть колебание функции f(x) на частичном брусе /£. Очевид-
но в силу формул Дарбу имеем ЩТ)=ЗДТ)—S/T) = 3 ®(ft> X
(ft)
X V(k) и в частности, Q/(7’) = sup|S/(T^) —5у(Тт])|.
е. ч
Определение. Пусть Т и Т' — два разбиения бруса
1п[а, Ь]. Разбиение Т'=(ТМ, .... TW) называется продолжением
разбиения Т=(Т&, ..., Т<п)), если Vi (i=l, 2, ..., п) разбиение
TW отрезка [at, Ы] является продолжением разбиения Т& того ,
же отрезка (т. е. если vi все точки разбиения Т<& отрезка [аь in]
входят в разбиение T(i)' того же отрезка). Если разбиение Т'
является продолжением разбиения Т, то пишут Т'<Л.
Теорема 1. Пусть функция f(x) определена и ограничена на
брусе Pja, b] и Т, Т' — два разбиения 1п, причем Т'<Т.- Тогда
S(T')^S(T), SJT')^S(T). Более точно, если \f(x)\^MVx<=P> и
разбиение Т<1>’ содержит не более pt дополнительных точек деле-
ния отрезка [а,, по сравнению с разбиением (1=1, 2, .... п),
то
S(T)-2Mv(In)d(T)^ ъ/(Ь,-а1)^8(Т')^8(Т),
S(T) + 2M v(In)-d(T). 2 p(/(&t~ai)<5(T')>S(D,
г=1
где d(T) — диаметр разбиения Т. !
268
Доказательство. Пусть Т'<Т. Для простоты будем счи-
тать, что Pi=l (i=l, 2, .... п) и Г<0 = {aJ=x<0><^)<...<*w<>==&J,
причем'для любого i дополнительная точка деления xtNl) е
е (x<wi-1), bt), т. е.
' TW - {<ч = хТ<хУ<...< х^~" <
Введем промежуточные разбиения бруса Г[а, 6]; Th=
= (^ = 0> 1> 2,..., п), гДе TQ=T и Тп==Т', причем
7й=Тй' Тогда, очевидно,
имеем
Tk=(T^’r<fe+1),..., TW);
Tk-t=(TW,..., T<k-lr, T<k>, T<">),
«,=X? <... < жГ»-‘> < ?»"»> < й'>« = 4»«> = bh,
...fk~ 1’ Nh' ^*+1.4P = Vh ik—1’ Nk> ik+l /„>
°<4.ik-i- >k+i.........Q
и поэтому причем
S(T)-S(T') = S(T0)-S(T„) = 2 (SfTft-i)—S(Tft)) =
&==!
= S 2 [(^(4 /*-!• Nk, ik+i’—> inti
Ik-t-ik+t........4i)
^<4.........Ik-l- Nk' '*+1.'n^ V(/‘.'*-!• Nw '*+1.!n^ ”1"
+ ^<4...'k-i< Nk, /*+1.ln> ~ ^(ii./*-i, Nh+t. ik+i--/п>) X
P<4./*-! wfe+*- /*4-1.4i>1 ’
Ho M(/)-M('n>0, |/(xjKMVxe7”[a, fe] и
— M| 2M, причем
.......!k-l' Nk' '*+«.'«> ~ /*-i. /*4.1./„P x
X (Ax^’ + Ax^1’) = v(/(V... м-р /Hi............X
ХДх^<^(Л<-\./а_1Лл+1.......y).
269
Nk
Но поскольку у, Дх<р = 6й— ak, то
/"1
Nk
.......,.л.....................
х 1Ф - й 2 ..» ц,- ,.+,
откуда
(1\.Ik J....j V^<~i^.:ik-i^k + i.in^ ~
~V(F[a, b])/(bk-ak),
т. e. получены оценки
0^S(T)-S(T')^2Md(T)-v(In[a, &]) % Рк1(Ьк-ал).
£»!
Аналогично доказывается неравенство
S(T)+2M v(In[a, &]) d(T) i Р11(Ь~а^>8(Т')>8_(Т).
i=l
Следствие. Если Т'<Т, то Q(T')^.Q(T) и, более точно,
Q(T)—4M v(In[a, b])d(T)- Pil(bi-at)^Q(T'^Q(T).
Ml
Теорема 2. Пусть функция f(x) определена и ограничена на
брусе 7п[а, &] и Т\, Т2 — два (любые) разбиения этого бруса.
Тогда S(7’1)^S(7’2).
Доказательство. Наряду с разбиением Тк =
(&=1, 2) введем новое составное разбиение Т3 =
где разбиения Тр = (Г(/)» определяются точками деления
как Тф, так и TpVi (4=1, 2,..., п). Тогда Ta<Tt и Т3<Т2, и в
силу теоремы 1 имеем оценки S(T3)^S(T2), S(T3)^S(Ti)»
откуда 5(Т1)<5(Тз)<5(Г3)<5(Т,), что дает 2).
Следствие 1. sup 5ДТ)<infSL(T) или если ввести поня-
т ~~ т
тия:
7= infSL(7') = f7j‘ f(x)dx —
т J In
верхний интеграл Дарбу,
270 1
7 = supS/(7’) = 7f f(x)dx~
- T ~
нижний интеграл Дарбу, то для функции f(x), определенной
и ограниченной на брусе 1п[а, Ь], имеем J <7.
Следствие 2. Для любого разбиения Т бруса 1п[а, &] имеем
S/fTXJCJC'S/fT) и
0<7-J^Qf(T).
Замечание. Рассматривая на множестве всех разбиений
55‘={Г} бруса /п[а, 6] отображение Qf.T Q(T), Т^.31*, £2(Т)е
eR, выберем в 5й* базу B*={Bg} с элементами В*ъ ={T^36*\t—\
=d(T)<Z8} (будем в дальнейшем обозначать базу В* символом
+0). Тогда можно ввести понятие предела limQ/fT).
t-»+о
Теор ема (предельный критерий интегрируемости по Рима-
ну на брусе). Пусть функция f(x) определена и ограничена на
брусе 1п\а, Ь]. Тогда (fG=R(In\a, Ь}))-м-(b\imQf(T)=Q(t=d(T))).
Г-+0
Доказательство (ср. [1], ч. II, гл. 2, § 2). Необходимость.
Пусть f е R(In[a, Ь]) и 7 = f j(x)dx. Тогда 7 = lim S(T^).
ln d(T)-*0
Вспоминая критерий Коши (существования предела числовой
функции по базе d(T)—> 0), видим, что в силу необходимости
этого критерия У8^>0Я5>0 такое^ что для любых двух раз-
меченных разбиений (бруса 7п[а, Ь])
Т%, Т?eBs= {T"vt е $>\d(T”)<6}
имеем оценку |S(Tg) — 5(TJ')|<e, т. е. sup |S(TS) — S(T|')I =
5.5'
= Итак, показано, что Уе>Я6>0 такое, что для
любого разбиения Т е В* — {Т" s 5s* |d(T*)<6} имеем
<Q(T)<8, т. е. Я lim ЙДГ) = 0.
Г—+0
Достаточность. Пусть функция f(x) определена и ограничена
на брусе 1п[а, 6] и 3 Итй(Т)==0. Следствие 2 к теореме 2 дает
оценки 0^7—J^.Q(T) для любого разбиения Т бруса 1п[а, &], от-
куда lim Q(T)=0 дает 7=7=7. Докажем, что 7= lim 5(Т£),
?-»+0 — d(T)—0
т. е. 7= J f(x)dx. Пусть б>0 — любое (но фиксированное). Tor-
i'*
Да из соотношения lim (5(Т)— 5(7)) = 0 следует, что Я 6(e) >0
/-+о — _
такое, что VTeBi (так что £=d(T)<6) имеем 0^3(7)—5(ТХ
271
О- Но V| при фиксированном разбиении Т имеем В.СП’ч
и кроме того, для любого разбиения Т имеем
5(7’)^7<5(7’), поэтому УВ^В* и УТ|еТ?8 имеем J— е<5(Т)—.
-8<S(T)<S(r|)<S(T)<S(7’)+8<J+e (1.1),
откуда УП<=В5 получаем оценку J — е < S(T£X J + s, т. е.
7 = lim S(Tl) = ^f(x)dx.
d(T)—О
Замечание. 1. Если Я lim ЙД7’)=0,то 7=7=7=f1(x)dx и,
/-»+о х»
в частности,
(/ еЯ(/п[а, &]))=>( lim ЙДГ) = 0)=>
^(U^f(x)dx=L\f(x) dx = $f(x)dx).
тп тп гп
Замечание 2. (f <=R(In[a, &])=» (ff(x)dx =>1 = lim S(T)
\a t-»4-0
= lim 5(7)).
• r—wn
• В самом деле если f e/?(/")» то из оценки (1.1) видим, что
Ve>0HBg такое, что ¥7еВ* имеют место оценки
7 —8<S(7’)<7+е и 7—е<5(Т)< + е,
т. е.
7 «= lim S(T) = lim У(Т).
t >-|'О t"»'^0
Теорема (критерий Дарбу интегрируемости по Риману на
брусе). Пусть функция f(x) определена и ограничена на брусе
!7п[а, 6]. Тогда
(f €= R(Jn[a, ft])) & (inf 2Z(T) = 0).
T
Доказательство. Hеобходимость. Пусть f&R(In[a, ft],
тогда в силу «предельного» критерия интегрируемости по Риману
на брусе имеем lim й(Т)=0, так что, учитывая оценку Й(Т)>.
>0 V Т, имеем inf Й/ (Г) =0.
’ т
Достаточность. Пусть inf й(7’)=0. Тогда по определению
т
точной нижней грани видим, что Ve>0 существует разбиение
бруса 1п[а, &] (где разбиения Т<р отрезка [«о
Ь<] Содержат pt+2 точек деления при i=l, 2,..., п) такое, что
272
0<й(Т1Хе/2. В силу ограниченности функции f(x) на брусе
Г[а, Ь]ЯЛ/>0 такая, что |/(х)| <Л/Vx е 7п[а, Ь]. Положим
61=8/(8Л/.ц(7"[а, b]) • 2 PAbi-щ))
«=1
и пусть 7’=(7’<1),..., Т<">— любое разбиение бруса /п[а, &] с диа-
метром d(T)<8v Пусть Т*=(Тр,..., Т<р), где Т<р=(Т&, Т?) (1 =
=1,2,..., л)— составное разбиение бруса /п[а, Ь] так, что Т^Т
и Т2-<Т1, причем разбиение = отрезка [а(, b*] Vt
имеет не более р4 дополнительных точек деления по сравне-
нию с разбиением Т(<> (отрезка [аь 6J). Тогда в силу следст-
вия к теореме 1, учитывая оценку
d(T) < = 8/(8Мт(/“). 2 Pjibi-a,))
i=i
имеем
(ТХТ^ЭДТЧКЙСТ*!)); (Ta<2’)=»Q(T2)>(Q(T)-4M.d(T).l;(Z’1)X
X j] Pil(bi-at) > Q(T) - 8/2) => (0 < Q(T) < Q(TJ +
i-l
+ 8/2 < й(7\) 4-8/2 < 8/2 + 8/2 = 8),
откуда Уе^-ОЯЗ^О такое, что VTeS^ имеем 0<Q(T)<8, т. е.
lim£2(Z’) = 0, но тогда из достаточности „предельного* крите-
рия интегрируемости по Риману на брусе следует, что f е
е R(In[a, b]), причем имеет место равенство
7 = J = J = p(x)dx.
Теорема- (критерий интегрируемости по Риману на брусе).
Пусть функция f(x) определена и ограничена на брусе /”[а, 6].
Тогда (fG=/?(/«[a, b])) <=> (J=U J f(x)dx=L f f(x)dx=J).
in in ~~
Доказательство. Необходимость. Если f^R(In[a, b]), то
в силу замечания к «предельному» критерию интегрируемости по
Риману на брусе имеем J=J— J f(x)dx.
~ 1П
Достаточность. Если J=I=J, где 7=inf S(T) и J=supS(T),
— т - т —
то V 8>о существуют разбиения Л и Т2 бруса 1п[а, Ь] такие, что
5(2\)<У 4-8/2, 5(Т2)>-_/ — е/2 и для составного разбиения
Тй), где r<z> =(?<*>, (i=l, 2,..., п) в силу теоремы 2
имеем
— Л. И. Камынин 273
(S(T) < S(7\), S(T) > 5(Г2)) => (0 < Q(T) =
=S(T)-5(7’)<S(7’1)-5(T2)<7+e/2-(J-£/2)=e).
Итак, V8>0 существует разбиение Т бруса /"{а, &] такое, что
0^й(Т)<е, т. е. infQ(T) = (k В силу критерия Дарбу имеем
т
f ER(In[a, b]) и, как показано выше,
J = 7 = J = ^f(x)dx.
§ 3. Множества из Rn меры и объема нуль и некоторые
свойства дифференцируемых отображений
Определение. Множество XcRn имеет (п-мерную) меру
нуль, если v е>0 существует такое не более чем счетное покрытие
множества А замкнутыми кубическими бру сами 7]J»Zn[h<*>,
(Л=1, 2, ...), что: 1) ЛсО Iku 2) %v(I%)<Ze.. Обозначение:
тезЛ=0 (напомним, что брус 1п\а, Ь] называется кубическим,
п
если bi—at=b>0 при i=l, 2, ..., n).
Замечание. В определении множества меры нуль вместо
замкнутых кубических брусов можно брать открытые кубические
брусы или открытые (или замкнутые) «-мерные шары
= {х е= Rn| ||х - < гЛ)
k (
являющиеся брусами в метрике ||х||« = max |х4|), где
г«1, 2...................................п
1>(Ш<пЧ^)) = те"/2 • гпк/Г(п/2 + 1) -
ft
обычный евклидов объем шара.
Замечание. В дальнейшем будет введен («-мерный) объем
множеств по Жордану в Rn и будет показано, что евклидов объем
параллелепипеда и шара совпадает с их объемом по Жордану.
Из теоремы о замене переменных в кратном интеграле Римана
будет следовать инвариантность объема Жордана относительно
движения в Rn и, в частности, относительно ортогональных преоб-
разований в R”. Поэтому в определении множества меры нуль-
можно вместо кубических брусов Z" (с гранями, параллельными
координатным плоскостям) брать любые открытые или замкнутые
параллелепипеды Jn.
Теорема. Пусть А, В — множества из R" и ВсЛ. Тогда
(mes А =г 0) ==> (mes В = 0).
п п
274
(Доказать самостоятельно по аналогии с теоремой из [2], ч. II,
гл. 2, § 3.)
Теорема. Если A, AfeczRn(v keN) и A cz U Ak, то
Д==1
(mes А*=0 v AcN) => (mes А=0). (Доказать самостоятельно по
п п
аналогии с теоремой из [1], ч. II, гл. 2, § 3.)
Следствие 1. Если множество AczRn состоит из конечного
или счетного числа точек, то mes А =0.
п
Следствие 2. Пусть Q.n—{q=(qi, .... 7n)eRn|^,eQV,-}
есть множество всех точек q из Rn с рациональными координата-
ми, тогда mesQn=0.
п
Лемма (о липшицевости дифференцируемого отображения).
Пусть f: Ш<п>(£)-> R", (Ш<">(0) и Я М >0 такая, что
|О;А(ХИ<МУх€=Ш(")(В) (I, j=l, 2,...,п).
Тогда имеет место оценка Липшица
ЦЦхО)) —1(х<2))||п<п-Л/-||х<1> —x<2)||n VxO, х<2)б=Ш<«>(5).
Доказательство. В силу условий леммы имеем оценку
(п \ 1/2
2 (Р;Ых)*\ <п-М Vx
Л /=1 /
Шар
m<">G) = {xe=Rn|||x-S.<0
есть открытое выпуклое множество в Rn, поэтому в силу следст-
вия 1 к теореме о среднем (из [1], ч. III, гл. 2, § 5) имеем оценку
||f(x<'))_f(x<2)||(i<n ll/ ||x<,> — х<2>||„ V х<’>, х<2> е= Ш<«)(|).
Определение. Пусть Ac=Rn и р>0. Открытое множество1
о₽(А)= и mwxjczR"
называется р-окрестностью множества А в Rn.
Теорема (об инвариантности меры нуль при С^-отображе-
нии). Пусть Ac:Gc=Rn, где G — открытое множество, и f:Gc
cRn->Rn, причем fe.C<V(G). Тогда (mesA=0) => (mesf(A>)=0)*
п п
Доказательство. Поскольку Gc=Rn — открытое множество,
то (как показано при доказательстве теоремы о существовании
разбиения единицы из [1], ч. III, гл. 2, § ,12) существует счетная
о
- система компактных множеств {/Сг} таких, что KtczKcK VI, при-
z+i /-н
чем
18* 275
4-оо 4~°о О
G = и Ki - и К,-
/=1 /=1
9
Положим А[— A(~]K[t Тогда А[ С Ki CZ Ki+i CZ Ki+i VisN, при-
4-oo
чем А = U А[. Но поскольку mes 4 = О, то mes4z = 0 V I sN.
п п
Но fsC(I)(G) (где f = (ft,..., fn)), поэтому из включения KiCG
имеем Djfi ^С(К[) (i, j — 1, 2,...,ri). Но тогда в силу теоремы
Вейерштрасса (об ограниченности функции, непрерывной на
компактном множестве) существует постоянная М[>0 такая,
что
IDjfiCxjlX MiVx^Kt (i, /=1, 2,..., n).
Рассмотрим любой шар тогда в силу леммы (о лип-
шицевости дифференцируемого отображения) имеем при >/ =
= п • Mi оценку Липшица
||ЦХ(О)_{(Х(2))||П<!Х, . ||Х<1) - х<2)1|„
vA х<2> e=UJ,(£)c:Z<z.
о
Зафиксируем 4zcKzcKz+i СК/+1 и заметим, что =
—0, поэтому p(dKi, ЗКг+i) >p/+i >0. Из условия mes А{ = О
п
вытекает, что Ve>0 существует не более чем счетная система
открытых шаров В* = UIfft (£(ft)) таких, что
5fcn^z^=0 Vft, 4zcTj и
2 f(5ft)<e/}x«+1.
*—i
Из последнего неравенства следует оценка р(ВА)=с)-
что дает vk оценку гк<^&Уп • c-1/n/(*z+i, поэтому при достаточ-
но малом 8='ео>0 имеем 2гд<рж/2Nk. Но тогда Vs <=(0, е0)
(поскольку Вк П А{ =# 0 и А[ CZ Ki, имеем включение Вк С
СО₽ж/г(Л/) CZ Kz+i, что дает SWs^+iVfc, Положим -»j(*>=/(jw).
Тогда в силу оценки Липшица имеем неравенство
||ffx)-fOT|„<ixz+1 . г4УхбШИ(П
т. е. f(5ft)cCk = где Як=:р.ж • гк.
h
Но
276
(4 cz uX W f(At) C U f(Bk) с U ck },
\ fc=l } у fe=l k—l /
и поскольку t>(Cft) = p."+1 • TO
2<№?+1 • PW<«-
k=i *=1
В силу произвольности е>0 имеем mesf(4/) = 0. Но тогда
п
[A=U Al W(f(4)cu° f(4z)W(mesf(4)«0).
\ l=t J \ l-l ) n
Определение. Система открытых множеств {U^ называется
базой (окрестностей) в Rn, если для любого открытого в Rn мно-
жества G существует совокупность {(/J (из базы) таких, что
0
Замечание^Напомним, что пространство Rn сепарабельно,
поскольку Rn=Qn, где Q" — счетное множество.
Замечания. 1) Совокупность открытых брусов {In(p, q)},
где р, qe=Q.n (т. е. — оо<р£<дг<+оо; pb qte=Q, t=l, 2, .... n),
образует счетную базу в Rn.
2) Совокупность всех открытых шаров {Ш<л> (q)}, центры ко-
торых peQn и радиусы reQ рациональны, образует счетную
базу в Rn.
Докажем утверждение 1) (утверждение 2) докажите самосто-
ятельно). Рассмотрим открытое множество GczR”, тогда V gsG
существует окрестность Шг<5)(|) такая, что ^еШГ{5)(^)сб. По-
скольку Qn=Rn, то существует открытый брус In(p, q) (£) с ра-
циональными вершинами такой, что
^/"(р, m)C7n[p, 9]G)C1M)CG.
Но тогда G = (J In(p, q)(l) и даже G= U /п[р, q](t). Поскольку
560 560
множество всех брусов с рациональными вершинами счетно,
то их можно перенумеровать: {/£} (fesN). Но тогда сущест-
вует подпоследовательность (индексов) (ki) такая, что
{In(p, 9)G)} = т. е. G= [J откуда и следует, что сово-
купность {1%} является сметной базой в Rn.
Замечание. В силу построения £e/n(p, q) (|)с7”[р, р](|)с;
сШ,(у(£)сб. Поскольку {Ik} — счетная база в R”, состоящая из
открытых брусов с «рациональными» вершинами, то существует
подпоследовательность (индексов) (ki) такая, что
277
G=U lnk[,
z=i 1
где — замкнутые брусы с «рациональными» вершинами.
Теорема. Пусть AcGcRn, где G — открытое множество
(совпадающее, быть может, с Rn) и {Ink} — счетная база в Rn, со-
стоящая из открытых брусов с «рациональными» вершинами. Тог-
да множество А допускает не более чем счетное покрытие элемен-
тами базы, причем
Доказательство. Поскольку {/£} — счетная база'в Rn,
ростоящая из открытых брусов с «рациональными» вершинами, то
в силу предыдущего замечания существует подпоследовательность
(ki) такая, что
4-00 _ 4-00
G = u Ц = и ^А-
г=1 ч л-t
Теорема (о выделении счетного открытого покрытия). Пусть
AczRn. Тогда из любого открытого покрытия {V„} множества А
можно выделить счетное подпокрытие.
' Доказательство. Пусть AcUVa, где Va — открытые мно-
а
жества. Пусть {£/*} (fesN). — счетная база в Rn (состоящая, на-
пример, из открытых брусов Ink с «рациональными» вершинами).
Тогда V хеА Я Уа(х)эх и в силу основного свойства базы
VaM = UUk . Но тогда существует Uki=U(x) такое, что
х е U(x) CZ Га(х). Очевидно, А с U G (х)- Но система {U(x);
х е А} элементов базы не более чем счетна, поэтому сущест-
4-00
вует последовательность (km) такая, что Acz (J Ukn. Но в силу
\ /п = 1
построения системы {С\т} видим, что V Ukm%Va= Vkm^Ukm.
Тогда Acztj Vhm> и ПОЭТОМУ система (/п=1, 2,...) есть
т»1
не более чем счетное покрытие множества А элементами из
{ГД
Теорема. Пусть множество AcRn и V хе А существует ок-
рестность Шг (х) такая, что шез(АПШг (х))=0. Тогда
X п х
mesA=O.
п
278
Доказательство. По условию для любой точки хеД су-
ществует окрестность У('х)«=ШГд. (х) (этой точки) такая, что
mes (Ар V(x))=Q. Система {V(x)- хеД} является открытым по-
П
крытием множества А, так что А с: U V(x). Поскольку в Rn су-
*6А
ществует счетная база, то в силу теоремы (о выделении счетного
открытого покрытия) из открытого покрытия {V(x); хеД} можно
выделить счетное подпокрытие {Vk} (А=1, 2, ...) множества Дтак,
4-00 4-00
что Лс U Vk- Очевидно, А= U (Дрю. Но в силу построе-
4—1 4—1
ния системы {V\} (k=\, 2,...) имеем тез(ДПУй)=0 Vk eN,
п
откуда mes Д = 0.
п
Следствие. Пусть £* — fc-мерное аффинное подпространст-
во (k — мерная плоскость) в Rn, задаваемая системой уравнений
п
Ъа11Х1=Н1 (t=l, 2, ..., п—k),
i—i
где ранг матрицы
(аи) (7=1, 2, ..., п—k-, j—l, 2, ..., п)
равен п—k. Тогда при —1 имеем mes £*=().
п ’
Доказательство. Рассмотрим сначала гиперплоскость
£n-i. Пусть x°e£n_i и р>0. Положим
Д = En-t П ШИ(х«).
Рассмотрим слой Л(е) в R", заключительный между двумя ги-
перплоскостями £<2-1 и параллельными гиперплоскости
£я-1 и отстоящими от нее на расстояние e/2(2p)',-,. Обозначим
через J" n-мерный куб с ребром длины 2р, с центром в точке
х° и с парой граней, параллельных гиперплоскости £n-i- Рас-
смотрим параллелепипед 7" е = J"f]A(e), высекаемый из куба
7" слоем Л(s). Тогда, очевидно, имеем Лс/’, и и(7"е) =
==(2(>)п-1 • 2е/2(2р)га-1 = е. В силу произвольности е>0 получаем
mes 4 = 0. Но тогда в силу предыдущей теоремы имеем
п *
mes£n_i==0. Далее поскольку £ftc£n_i(l<^n—1), то mes£k=
п п
= 0.
Замечание. Если Ek — ^-мерная плоскость из Rn, задавае-
мая уравнениями x*+l=/ift+1, xn=hn, то mes £л=0 при
1.
279
Теорема Сарда (для 1^т<л). Пусть 1^т<.п и Сех
cRm — открытое множество (в Rm). Пусть f: GczRm->Rn 9
feC^fG). Тогда mesf(G)=0 и, в частности, mesf(A)=0 V Асх
crGcR”.
Доказательство. Определим вспомогательное отображе-
ние g: GXRn-m<=R" -* R”, g=(gi... gn), положив gt(xb ...» xm;
yx... yn-m)=f^(xi..xm) (1=1, 2....n). Очевидно, Vi имеем
У) = Г-AW (/ = b 2’-’ m)>
dx f oxj
z~~gt(x, y) = Q (k = i, 2,..., n—m),
дУъ.
поэтому из условия fsC(1)(G) имеем geC(1)(G X R"-"1). Посколь-
4-00
ку G открыто в Rm, то G = [J If, где If — открытые брусы
k—l
в Rm. Аналогично Rn-m='u Jf~m, rp,eJl~m—открытые брусы
в R”-"’. Но тогда G X R'1-'" = *U 1™ X J?~m, где If X Ц~т — от-
/«=1
крытые брусы в Rn. Поэтому G X Rn-,n — открытое множество в
Rn. Отметим далее, что поскольку G с ROT, то Г—{(х, y)^R” у|хе
e=G, t/=O}cz£m={(x, i/)eR"Jj/1=O,...,i/n_m=O} (где Ет — m-мер-
ная плоскость в R" у), так что (при mes Em~Q и
поэтому mesg.—0. Но g($) = {zeR"|z=g(x, O)(=f(x)), x<=G, у=*
=0} = {зе Rn|z - ’ f(x), х <= G} = f(G), причем g <= C^\G X Rrt-m).
В силу теоремы (об инвариантности меры нуль при С(1 ^ото-
бражении) из того, что mes 2?=0, имеем
п
mesg($) = mes f(G) = 0.
п . п
Теорема (о мере графика непрерывной функции). Пусть
f:Gc:Rn-»-R (где G — открытое множество), f^C(G) и Г/=
={(х< y)^H,n+l\y=f(x), xeGczR”} — график функции f (9
Rn+*). Тогда теэГ/=0.
г?+1
Доказательство. Рассмотрим любую (но фиксирован-
ную) точку (х0, f(x0))^Tf. Тогда xoeG — внутренняя точка (от-
крытого) множества G, и поэтому существует л-мерный брус
1п[а, 6] такой, что In(a, b)czln[a, fe]czGc:Rn. Поскольку f^C(G),
то в силу компактности бруса 1п[а, Ь] имеем feC(/n[o, b])cz.
cBflnfa, b]), так что — oo<m =minf^maxf = Л4<+оо. Pac-
In[a, Ь] l"[a, bl
280
смотрим открытый (n-Н)-мерный брус 7'*+1=/л(а, ЬЖ(т—К
Л4-|-1). Достаточно доказать, что mes /д+,ЛГ/=О. Поскольку fe
п4-1
гС(/"[в, &]), то по теореме Кантора в силу компактности бруса
1п[а, 6] функция f(x) равномерно непрерывна на 1п\а, 6] и поэто-
му V в > 0 (которое можно считать меньшим числа
v(In[ci, 6]))Яб(в)>0 такое, что для любого разбиения Т бруса,
/п[р, с диаметром d(T)<Z6(e) (с частичными брусами 7"Л) вы-
полняются оценки О^б»(/)0 =ЛГ(/)—
Рассмотрим (п + 1)-мерный брус = I"h X кЦ/> — ej/2,.
M«+ei/2] с объемом = + Тогда /?+1Г)Г/С2
С U причем
(О '
6]) = 2е,
(/) (о </) :
откуда mes /о+1ПГ^ = О и поэтому mes Гу = 0.
п+1 п+1
Пример 1. Если f:(a, b) -> R и fe.C((a, Ь)), то график
Yf={(x, y)^R2\y=f(x), х^(а, Ь)} имеет 2-меру нуль (в R2).
Пример 2. Пусть Г/={(х, у, z)eR3|z=f(х, у), (х, y)^Gcz
cR2} — график непрерывной функции f(x, у) в R3. Тогда mes Г/=.
3
=0.
Замечание. Пусть A:x-+LxA-h — аффинное отображение
Rn в Rn, тогда AeCO^R") и DA=L^.X (Rn, Rn). Если detDA#=
=/=0, то отображение А невырождено и A(Rn)=Rn. Если же
detDA=O, то аффинное отображение А вырождено и A(Rn) =
=EmczRn, где Ет — m-мерная аффинная плоскость в Rn размер-
ности т<_п, так что mes£'m=0. Но тогда для любого множества
Bc:Rn имеем A(B)c.EmaRn, так что mes А(В)=0.
п
Определение. Рассмотрим отображение f:Gc:Rn -* Rn
(где G — открытое множество) класса C&(G). Тогда множество
S={xeG | rang Df(x)<«}s{xeG | det Df(x) =0} называется мно-
жеством «критических» точек отображения f.
Пример. Рассмотрим вырожденное аффинное отображение
A: R«-> Rn; Так что DA=L&£ (Rn, Rn), rangL=m<Zn, detDA =
=0, причем A (R”) =£mcR''1. Рассмотрим также отображение
f:GcRn->Rn( положив f(x)=AxV x^G. Тогда V xeG имеем
rang'Df(x)=rang DA—rang!.—m<n. Если S={xeG|rangDX
Xf(x)<n} — множество «критических-» точек отображения f, то
S=G, причем f(S)=A(S)czA (Rn) =Emc^R.n- Но тогда имеем
mesf(S)=mesA(5)=O.
281
/ Теорема Сарда (для т=п). Пусть f:GcRn Rn, где
G — открытое множество, feCOJfG) и S — множество «критичес-
ких» точек отображения f. Тогда mes f (S) =0.
п
Доказательство. Рассмотрим кубический брус 1п[а, &]с
<—G с ребром длины /=&,—at>0 (f=l, 2, п). Тогда
|(feC<1)('G)) => (feC(1)(/n[a, &])) и в силу выпуклости бруса
Уп[а, &] по формуле Тейлора (с остаточным членом в интеграль-
ной форме для вектор-функций из [1], ч. III, гл. 2, § 6) имеем
f(х)-f(g) == j] (xt — f О4(£+»(х-|))db Vx,l e ln[a, b].
i=l 0
По теореме Кантора из условия Dtf^C(In[a, &]iYi в силу ком-
пактности куба 1п[а, 6] следует, что функции DJ/x) (i, / =
=1, 2,..., п) равномерно непрерывны на 1п[а, 6], потому Ve>0
Я 6(e) > 0 такое, что Vx, ge7n[a, &], удовлетворяющих нера-
венству ||x-V|n<6(e), имеют место оценки ||Dtf(x) — ВД(£)||П<
<Zzln 6=1, 2,..., п), и, стало быть, Ух, &] при выпол-
нении неравенства ||х — |||п-<6(е) имеем оценку
l|fW-f(g)-D/(^)(x-yi„ =
2 j +
»=i о
+ »-(x-S))—D,f(?))d»||n< max |x4-^|X
»=1, 2.........................n
n 1
X 2 J .1 D*f G + »• (x - ^)) - D, f G)||n db <
i=l 0 I
<||х — £||„ • n- e/n = s- ||x — |||n.
•Фиксируем e>0. Тогда для любого разбиения Т куба In[a, &]С
СО (с диаметром й(Т)<б(е)) на Nn (при • я’^Де)) частич-
ных кубов /("w с ребрами, имеющими длину 1/N, имеем оценку
||ffx)-f($)-D/(|)(x-^)||n<e.||x-^n<8.n‘/2.///Vух, |<=Z(%.
Индексом (/) отметим те кубы, для которых
Тогда и в силу определения „критической" точки
е S отображения / видим, что det D/(£)=0. Наряду с отобра-
жением »/(/("•))C“Rn рассмотрим аффинное (т. е. линей-
ное неоднородное) отображение (касательное к отображению
j в точке £) Л5:х-* Az(x) eR", где Az(x) =/(|) -Ь D/(|)(x — £)•
В силу условия detD/(§) = 0 определитель аффинного отображе-
ния Az(x) равен нулю, так что аффинное отображение
-»Rn имеет ранг <п и переводит R" в гиперплоскость (изме-
рения п—1) En-i(%) С Rn. Таким образом, AZ(I^) С Дп-iQ) CR4»
282
причем поскольку А^(§)=/(5), то Из полученной
ранее оценки имеем
ПОД-A5fx)||n<8 • n‘/2 .lINVxe^,
т. e. множество /(/^) содержится в „слое” высоты 2Х(е) (где
Х(е)=8 • п№ • UN) между двумя («— 1)-мерными гиперплоскос-
тями, параллельными Еп-х(1) и отстоящими от нее на расстоя-
нии Х(е) (считая в направлении, ортогональном к En-t(%)
<рис. 14). Таким образом, f(I^) С (?Х(е)(£л+1(^)). С другой сторо-
ны, поскольку f е ^(^(/’’[с, Ь]) и с /п[а, 6], то в силу дока-
занной ранее леммы (об оценке Липшица) имеет место оцен-
ка (при |j. —п • М, где
max Ю/ОД|),ЦОД-(©||П<
xein[a, Ь]; /. /==1, 2.п
.Цх-|1|„<и .«‘/2 .///V VxeJ^,
т. е. /(7(^) С •/("), где есть любой куб с ребром длины 2р х
X п1/2 . цм и с центром в точке т;=/(|). Выберем куб так,
чтобы одна из его граней была параллельна гиперплоскости
Еп-^), тогда имеем
/(/(}>) С 7")(Ю П П"л,
где есть параллелепипед, вырезанный из куба 7^(5) слоем
^U)(£n-i(£)) высоты 2Х(е). Вычисляя объем П"р получаем
283
Р(П^) = 2Х(е) • (2|Х • /г‘/2 . l/Ny-' =
= 2п • р/*-1 • «1/2 • Г • s]Nn — c • e/Nn.
Заметим, что в кубе In\a, &] (Z G содержится не более Л/Л
кубов таких, что 0, поэтому/(/"[a, 4P|5)CUn?ft>
(/*)
причем
2 у(П{д) Nn - с • e!Nn = с • е.
(!)
В силу произвольности е>0 имеем mes f(ln[a, b]QS) — 0.
п
Заметим теперь, что множество всех открытых кубов 1п(р, д)=
-»с „рациональными* вершинами (р, geQ'1) образует счет-
кубами {/£
ную базу (окрестностей) в Rn, и поэтому для открытого мно-
жества GczRn существует открытое покрытие замкнутыми
} такое» что G = Tj Z?. Как было показано»
i /-1 */
mes/(72 nS)=0VZ<=N. Но поскольку SdG, то /(S)=f(G(V)C
п 1
си И поэтому
2-1 ‘
(mes /(/* П S) = 0 VI е N) =» (mes f(S) = 0).
п 1 п
Теорема Сарда (при т>п). Пусть f:Gcz.Rm Rn, где
G — открытое в Rm (при т>п) множество и f^O-^G). Пусть
S={xeG | rang Dffx) <п} — множество «критических» точек ото-
бражения f. Тогда mesf(S)=0.
п
Доступное доказательство теоремы Сарда (при m>ri) можно
найти в [2].
Замечание. Если feCWfG), Gc:Rm, то теорема Сарда (при
т>п) справедлива только при k^tn—/г+1 (см. [3]).
Определение. Множество AczRn имеет (п-мерный) объем
нуль, если для любого е.>0 существует такое конечное покрытие
множества А замкнутыми бру сами {7п[а<*>, &(*>]} (k=A, 2, ...»
m(s) m(t)
..., /п(е))), что: 1) AczU 7" и 2) '2,v(I?)<Ze.
л-i *=t
Замечание 1. В определении множества объема нуль мож-
но считать, что покрытие {7*} состоит из замкнутых брусов без
общих внутренних точек.
Замечание 2. В определении множества объема нуль вме-
сто замкнутых брусов /п[а(й), Ь<М] можно брать открытые брусы
7п(а<*>, Ь<&) или открытые (замкнутые) п-мерные шары
m ={xeRn I ||х-^*>1|я<г4-
284
Замечание 3. В определении множества объема нуль
вместо брусов (с гранями, параллельными координатным плоско-
стям) можно брать любые открытые или замкнутые параллелепи-
педы.
Замечание 4. Если Bci4c:Rn и множество А имеет «-объ-
ем нуль, то и множество В имеет n-объем нуль.
Теорема. Пусть I*[a, fc]c:Rn и {/"} (6=1, 2, ..., пг) — любое
конечное покрытие бруса 1п[а, Ь] замкнутыми брусами I*, I^,...
Inm так, что In[a, 6]czU7". Тогда
m п
2 v(/") > я(7п[а, &]) = П (Ь<~О|)>0.
ft—l 1=2
Доказательство. При п=1 теорема была доказана при
изложении теории одномерного интеграла Римана ([2], ч. II, гл. 2,
§ 3). Поэтому будем считать п^2 и проведем доказательство тео-
ремы индукцией по размерности п. Допустим, что /п[а, bjcz
сШ£, где 72=7п[о<*>, Очевидно, mina^ ^аЛ<6п^
4=1 k
шах . Без ограничения общности можно считать, что
4
min an’ =an<bn=max(при переходе к новому покрытию
k к
суммарный объем входящих в него брусов может только умень-
шиться). Проведем гиперплоскости хп=а^ , хп=Ь^ (k=
==4, 2, .... т), которые возможно размельчат наше покрытие бру-
m
сами U Ik, но уже без изменения их суммарного объема, поэтому,
4=1
без ограничения общности можно с самого начала считать, что на-
ше покрытие имеет вид
где
причем
«п - Ч1» < %*’=« = Ч-» < № - Ьп.
Заметим, что 1п[а, Ь] — 7л-1Х[яп, Ьп], причем о(7п[а, &]) = г(7л~1)Х
X (6П—en). Очевидно также» что
U/(£/¥/(/ = 1,2. 0.
о
285
и в силу предположения индукции имеем V/(/=l, '2,...» I)
оценку
но тогда
/-I (i) /-1
= v(/«-‘)(&n - an) = v(In[a, &]) > 0.
Следствие 1. Брус In\a, b]czRn не может иметь (/^мер-
ный) объем нуль.
Следствие 2. Пусть Т—(Т(1\ Т<п)) — любое разбиение
бруса 1п[а, &] с частичными брусами I<k) =/n[x(ft-e), л<4>], (k)=>:
=(^ь Jfez=l, 2, ...» Ni (f=l, 2, .... n), (e)= (1, 1, I)j
Если {J?} (j=l, 2,..., m)— конечная система брусов j”[aW, ptf>]==
= J" такая, что
tn n
UVF=>,U U 7<o-
/=1 l=l *1
TO
m n
2 «/?» 2
/-1 ,=1 li
Следствие 3. Если множество AcRn имеет n-объем нуль,
то А—<0.
В самом деле, если бы А #=10, то я хоеА, причем тогда суще-
ствует открытый брус 1п(а, р)с=А такой, что хо^/п(а, Р)сгА, и
поэтому существует замкнутый брус /п[а, b]cz/n (а, £) czA. Но тог-
да брус 1п[а, Ь] имел бы n-объем нуль, поскольку множество А
имеет л-объем нуль. Противоречие.
Замечание. Если множество AcR” имеет n-объем нуль, то
множество А имеет и меру нуль (mes А=0). Обратное утвержде-
п
дение, вообще говоря, неверно.
Замечание. Если множество Ac:Rn неограниченно, то оно
не может иметь объема нуль. (Доказательство провести самостоя-
тельно по аналогии с одномерным случаем из [2], ч. II, гл. 2»
§ 3).
Теорема. Если множество KczRn компактно и mesK=0, го
п
множество К имеет (n-мерный) объем нуль.
286
Доказательство. Пусть множество KczRn компактно и
mes /(=0. Тогда V е>0 существует не более чем счетное покры-
тие К открытыми брусами I']—In(a(k'>, ЬЮ) такое, что
К CU Л и 2^")<е-
i=i /=1
В силу компактности множества К из нашего открытого покры-
тия можно выделить конечное открытое подпокрытие
т т 4-оо
и Л" СК, причем 2 °(ЛПХ 2 °(Ап)<е«
S=1 * • ,s=l * 2=1
т. е. множество К имеет n-объем нуль.
Следствие 1. Если mesA=O, то Д=0.
п
В самом деле, допустим, что mesA=0, но А=#0. Тогда суще-
п
ствуют точка хоеД и открытый брус /"(а, £), такие, что Хд/=
^ln(a, P)czAczRn. Но тогда существует и замкнутый брус
/п[а, 6] такой, что
xoeln[a, Ь]с/П(а, ₽)сдА.
Но поскольку mesA=O, то mes/п[а, 6J=0 и в силу компактности
п п
брус 1п[а, Ь] должен иметь n-объем нуль, что невозможно.
Следствие 2. Любое счетное ограниченное замкнутое мно-
жество из Rn имеет n-объем нуль.
В самом деле, счетное множество имеет меру нуль, кроме то-
го, будучи замкнутым и ограниченным, оно компактно в Rn, а
тогда в силу доказанной теоремы оно имеет и n-объем нуль.
Теорема (сравните [1], ч. II, гл. 2, § 3). Если множество
AcRn ограничено, то его граница ОД компактна в Rn.
Теорема. Если множество AczRn имеет n-объем нуль, то а
граница дА множества А имеет n-объем нуль.
Доказательство. Поскольку множество А имеет п-объем
нуль, то оно ограничено и V 8>0 существует конечное покрытие
А замкнутыми брусами {/£} (k = 1, 2..... zn(e)) такое, что
Ш(е) »71(е)
pm= и 1п^А< причем 2 v(/^)<8.
*=1 Л=1
Но множество Fm как объединение конечного числа замкну-
тых ограниченных множеств само замкнуто и ограничено,
причем (FmZ) A)=>(Fm = FmZ3 AZ)3A). Итак, Vs>0 сущест-
вует система {!%} 2,..., т(г)} такая, что
m(£) т(«)
дА С U Ч и У v(l$ < ®> т- е-
ft=1 *=i
дА имеет «-объем нуль.
287
Замечание. Если множество AczR" не компактно, то из '
того что оно имеет n-меру нуль (mes А — 0), вообще говоря, не
п
следует, что оно имеет и «-объем нуль.
§ 4. Критерий Лебега интегрируемости по Риману
на брусе в Rn
В теории одномерного интеграла Римана были введены поня-
тия колебания функции на отрезке и в точке (см. {1], ч. II, гл., 2,
§ 4). Введем аналогичные понятия при nZ>2. Пусть числовая
функция f(x) определена и ограничена на множестве AczRn и
точка х°еА. Для любого открытого бруса 1п(а, £),эх° положим
М(Г, Р1)= sup f(x), m(f; /п[а, ₽]= inf f(x).
A[\In{a., 3] АпГ"(«. 31
Колебанием функции f(x) на /п[а, р](]А называется величина
® (fJ 7n[a, М) =М ([; /"[а, fl-™ (fl /nl«- Й) •
Легко показать (см. доказательство в случае п—\ из [1], ч. I,
гл. 4, § 1), что
©(f; Zn[a, р]) = sup |f(x)—/(Ж
х, У6АП1П1«. 31
Далее для любого бруса In(a', $')a:In(a, Р). и любой точки х°е
^АП7п(а/> Р') имеют место оценки
—oo<m(f; Z«[a, Zn[a', fi'lX
^M(f; /n[a', 7n[a, Й)<+°°>
0^©(f; Zn[a', Zn[a,
Пусть Z^(x°)=/n(a<5>, b(5))— любой открытый брус с диаметром
содержащий точку х°е А. Полагая
= lim M(f; 7а(х°)) = inf sup f(x) =lim/ (x)
8-0 8>0 An,nw
и
m(f; x°) = limAf(f; Z£(x°)) = sup inf /(x) = limf(x),
5“>0 s>° AfilgU*)
введем понятие колебания функции f(x) в точке х°еА
(Bff; xf>)—m(f; х°).
Можно доказать (проделайте это самостоятельно по схеме соот-
ветствующего доказательства из [1], ч. I, гл. 4, § 1), что
©(/; х«) = Нтш(/; 7?(х»)).
288
Тогда V б>0 имеют место неравенства
«>(/; 7«(хс)) ><«(/; х°)>0;
W; 7"(х»)) > 'M(f; x*)>m(f-, 7"(х*)).
Замечание^В определении <о (f; х°) — колебания функции
f(x) в точке х°<=А, а также в определении величин M(f; х°) и
tn(f; х°) вместо открытых брусов 7^(х°) можно рассматривать ша-
ры Ш(ап)(^°)- (В качестве упражнения докажите эквивалентность
обоих определений <в(7; х°) функции f(x) в точке по схеме дока-
зательства, проведенного при п=1 в [1], ч. I, гл. 4, § 1).
Теорема (критерий Бэра непрерывности функции в точке).
Если f^B(A), x°<=A<=Rn, то (f<=C(x°)) -*=>• (<в(/; х°))=0.
(Воспроизведите доказательство для п^2 самостоятельно по
схеме, приведенной в [1] в случае п=1).
Теорема Кантора (о равномерной непрерывности функ-
ции на компактном множестве). Пусть функция f(x) определена и
ограничена на компактном множестве K<zRn и <a(f; х)=0 V хеК.
Тогда функция f(x) равномерно непрерывна на множестве К.
Теорема Кантора (для разрывных функций). Пусть
функция f: In[a, b]czRn ~> R ограничена на брусе 1п[а, Ь] и сущест-
вует ©>0 такое, что х)<® v хе7п[а, Ь]. Тогда для любого
8>0 существует разбиение То бруса 1п[а, &] такое, что для любого
частичного бруса 7("Л имеем
Доказательства Рассмотрим любое, но фиксированное
е>0. Поскольку
х)^лл V хе7Л[а, &],
то Vxe7n[o, b] существует открытый брус 7£(ж)(х)эх такой, что
U)+s. причем
U Л%(х)О7п[а, Ь].
xein[a, 61
В силу компактности бруса 1п[а, Ь] для него существует ко-
нечное открытое подпокрытие
{7«ft(x(*)} = {Jn(a(*), £<*>} (Jfe=l, 2,..., m).
Пусть To = (TW,..., Т^) такое разбиение бруса 1п[а, Ь], что
все точки xi = a(i4), xt = bW (k=\, 2. m) входят в разбиение
и любой частичный брус содержится в некотором
брусе &<*>]. Тогда, очевидно, <o(f; /щХ® + eV(J).
19— Л. и, Камынин 289
> V
Следе? вне. При выполнении всех условий теоремы Канто-
ра (для разрывной функции) V е>0 существует такое разбиение
То бруса 1п[а, Ь], что Qf(T0)<. (©+e)t> (/п[а, &]). f
Теорема. Пусть FczRn — замкнутое множество и функция |
f:FczRn ->-R определена и ограничена на F, причем Е(г) =
={x^F\a>(f; х)^е>0}. Тогда:
1) если ei>e2>0, то Е(ei)czE (е2);
2) для любого е>0 множество Е(е) замкнуто.
Доказательство провести самостоятельно по аналогии с теоре-
мой из [2], ч. II, гл. 2, § 4.
Замечание. Если £={xe£|®(f; х)>0) — множество всех
точек разрыва функции f(x), определенной и ограниченной на {
—|—оо .
замкнутом множестве Fc=Rn, то E=\J E(\/m). Si
tnxssl
Теорема (критерий Лебега интегрируемости по Риману на ~ I
брусе). Пусть функция f:In[a, dJcR^-’-R ограничена на брусе ;
Zn[a, b] и Е — множество всех точек разрыва функции f(x) на
этом брусе. Тогда ;
(ft=R(In[a, b])) (mesE—0). 1
п ' •>?
Доказательство. Необходимость. Пусть f<^R(In[a, &J) и f .
Е — множество всех точек разрыва функции f(x) на 1п[а, 6]. По- & i
4-о° А |
скольку £ = U£(l//n), то достаточно доказать, что
m—1
mes£(l/m) =0 VmeN. Тогда множество Е как объединение Н
п .
счетного множества множеств меры нуль само будет иметь меру
нуль. Будет доказано, что множество Е(1/т) имеет n-объем нуль (
VmeN. Поскольку f<=R(ln[a, 6]), то в силу критерия Дарбу (ин- I
тегрируемости функции по Риману на брусе) имеем inf £2/(7) =0„ ' '
т /
т. е. при любом, но фиксированном msN V е>0 существует раз- j
биение Т=(Т<Г>, ..., Т(п>) бруса 1п[а, такое, что Q^.Qf(T)<Ze,/2m.
Рассмотрим совокупность {/^ } всех частичных брусов, соответ-
ствующих разбиению Т. Положим 4
£(l/m)=£(l/m)nU^) и Ч'
w )
Поскольку граница dlfk) бруса есть конечное число (п— 1)- „
мерных граней, то mesdZ"A) = O и в силу компактности грани-
ца dl"k) имеет и n-объем нуль. Но поскольку ^(l//n)CZU^<")> то
и. множество £(1/тп) имеет n-объем нуль. Но тогда для зафик-
290 ?
сированного s>0 существует конечная система брусов {«/"} (/ =
s 1Де) L(e)
= 1, 2,...,, Це)) такая, что E(l/m)C U Л" и .2 о(^")<в/2. Рас-
J=i z=i
смотрим теперь множество Ё(1/т) CZ U и выберем любую
(*)
точку х9 ^Ё(\1т) (У=0). Тогда существует мультииндекс (j0)
такой, что х° е /(/„). В силу построения множества Е(1/т) име-
ем х°е/£) = Г’(х(/‘“е>, х^) и тогда Я6>0 такое, что
Ш<")(х°) с Г\х^~е\ х<'«>),
т. е.
<«(/.) <•>(/; AV > “W) > х°) >1/т-
Таким образом, E(l/m)czU Лл (®щ>1/т),
(/> '1
где суммирование по
(/)=(/ь--> Ш распространяется на те частичные брусы ЕЦ из
разбиения Т, на которых 7(^)> 1/т. Но в силу выбора
разбиения Т по заданному е>0 имеем оценки'
1/т • 2 у(;щ) < 2 • °(2 * * * * *(%)=
(/) (/) <*>
= 2/Т)<е/2т,
откуда 2р(^щХ8/2 (при fi>(;)>l/m). Итак,’
.(/)
~ о, Ь(е
£(1/т) = Е(1/т) (J ЕЩт) с (J /« (J (J /«
Ofj-jX/®) ш '=1
где
2 „ “('У + 2 ”(/?) < */з + »'2 - «•
О )(“(/)> Vя* i-\
В силу произвольности е>0 вытекает, что множество E(l/m)i
имеет n-мерный объем нуль, чем и завершается доказательство не-
обходимости критерия Лебега.
Достаточность. Пусть Е — множество всех точек разрыва функ-
ции f(x), определенной и ограниченной на брусе 1п[а, Ь]. Заме-
тим, что
(Ve>0) => (Е(е) ={хе/”[а, />]|<о(7; х)^е>0}с2Ес:1п[а, Ь]),
так что множество Е (в) ограничено. Но ранее было доказано, что
множество Е(е) всегда замкнуто. Таким образом, в силу критерия
компактности (в Rn) замкнутое, ограниченное множество Е(в)
компактно V е>0. Допустим, что mesE=0, тогда из включения
п
19»
291
имеем mesE(e)=O. В силу компактности множество
И
E(s) имеет n-объем нуль V е>0 и тогда для фиксированного
Е(г) существует конечная система J замкнутых брусов {If} s
= р']} (/=1, 2,..., т(е)) такая, что соответствующая сис-
тема открытых брусов {/"} = 7п(<х/, 0')} (/=1, 2,..., т(е)) покры-
вает множество Е(е)
т(е) о т(£)
(т. е. Е(е) с U 7?), причем
/=1 7=1
3 р(^"Хе- Рассмотрим разбиение Т<п>) бруса 1п[а,
i=i
b\ такое, что Vi (/=1, 2,..., п) разбиение отрезка [а(, &*]
составлено из точек а,, 6, и всех а!, 0' (/=1, 2,..., /п(е)), попав-
ших на интервал (ait bt). Пусть Ift) = 7"[х<*-е>, x(ft)] =
x<fe*>] X ... X —любой частичный брус из введенно-
го разбиения Т. В силу построения Т интервал (х^г-й, x|fe?)
не содержит точек a(, fy, соответствующих брусам 7п[<х>,
(/=1, 2,..., т(е)) (из системы 7) для любого i (i=l, 2,..., n),
поэтому возможны лишь два случая: 1) существует индекс /0
такой, что I("wC2 7n[a\ fl'»]. Эту группу частичных брусов I"k}
О
из разбиения Т будем обозначать 2) — 0"V
2,..., m(s)) (т. e. 7"j f~lE(e)= 0). Эту группу частичных
брусов разбиения Т будем обозначать = Отме-
тим, что в случае 2)
7£,> =• ГЧх^-'К х<*'>) =
, (fe7-i) (<>... . . . (<-i) (<).
-(V «*11 ) х . • . х (V , v )
(*Т-1) (ф . (k’-i) (fe*)
и концы х41 , х{ ‘ ) интервала (х{ ♦ , х.1 ) могут при неко-
тором быть концами отрезка [а£, но и тогда д7^»)П
QE(e) = 0. (В противном случае Ях°е и посколь-
m(s) о о
ку Е(б) с (J If, то существует открытый брус If такой, что
х’е7^П^7".р т. е. /("Г)П 7?^0 вопреки предположению
7(',(Г)Г)/7 = 0^/ в случае 2)). Итак, в случае 2) имеем 7п[х<й’~г),
х<4*>|Г)Е(е)« 0. Тем самым показано, что каждый из частич-
292
ных брусов разбиения Т содержится либо в группе Г,
либо в группе Г. Поскольку функция f(x) ограничена на
брусе 1п[а, 6], то существует Л4>0 такое, что |f(x)X AfVxe
е 1п[а, Ь] и тогда о>(4) = ш(/; V (&). В частности, если
/п е Г, то в силу выбора системы 7 имеем
2 “<*') • ^'))<2Л/ • 2’^;)<2ЛГ • е.
(4') /=1
Пусть теперь 7™ Ж) е 7", тогда 7"4.)П£(е) = 0, а потому <о(Л
,v)<eV.re l"k.y Применим к брусу 7{*t.) следствие из теоремы
Кантора для разрывных функций (положив при этом <в = е).
Тогда существует разбиение = бруса 7"^
(где есть разбиение отрезка [х**”*', ] с частичными
брусами {7^.,, (0}), причем
(У А"*'). (« ~ А*’)’ v^(k"), (г) “
такое, что
3 “<Л А".-,.») -
Образуем теперь составное разбиение То = Т^), поло-
жив T<J> = {T(i>, Т^} {i—ii 2,..., n)V(k")eI". Обозначим че-
рез {/" ( } частичные брусы составного разбиения То бруса
7п[о, Ь]. Тогда Т0<Т, и поэтому, используя теорему 2 (о сум-
мах Дарбу) из ч. V, гл. 1, §2, имеем оценки
0<О/Тв)« V <0(0-1^) +
(10.
+ 2 “(о ’ VUS, (г,) < 2 “<*') • +
</0П,(г)С/(4-)6Г>
+ 2 w • и) < 28 • м +
(*•) (О
+ 2 2е ’ v<7(4«)) < 28 • (М + о(7«[а, Ь])).
(V)
Итак, для любого е>0 существует разбиение То бруса 1п[а, 6] та-
кое, что
G^Qf(T0)<2e-(M+v(I”[a, b])).
293
В силу произвольности е>0 имеем inf Q/(T)=0, откуда в силу
критерия Дарбу (интегрируемости функции по Риману на брусе
в Rn) имеем f^R(In[a, ft]).
Теорема (достаточное условие интегрируемости по Риману
на брусе). Если функция f(x) определена и ограничена на брусе
/п[а, ft] и имеет на нем не более счетного множества точек разры-
ва, то f^R(In{a, ft]).
Доказательство. Если множество Е (всех точек разрыва
функции f (х) на брусе 1п[а, &]) счетно, то mes Е =0, и в силу кри-
п
терия Лебега интегрируемости по Риману на брусе имеем
fe=R(I"[a, ft]).
Следствие.
(fe=C(P*[a, ft])) => (fe=R(I*[a, ft])).
Определение. Если /lc:Rn, то характеристической функ-
цией множества А называется функция
, . { 1, х А,
^м = 1о.хгл.
Определение. Ограниченное множество 4c:Rn, граница
дА которого имеет меру нуль (mes<M=0) (а стало быть, в силу
п
компактности дА и п-объем нуль), называется измеримым по
Жордану.
Теорема (критерий измеримости по Жордану в Rn). Пусть '
AcJn\a, ft]. Тогда (множество А, измеримо по Жордану (т. е.
mes<M=0)) (%efl(7n[a, ft])). (Доказать самостоятельно по
п
аналогии с доказательством «одномерного» критерия измеримости
по Жордану, проведенным в [1], ч. II, гл. 2, § 5.)
Определение. Если множество Adri{a, &] измеримо по
Жордану, то интеграл Римана J %A(x)dx= |Д |п называется
п-объемом множества А в Rn.
Замечание. Ранее определение множества n-объема нуль
было введено с помощью конечных покрытий множества парал-
лелепипедами. Выше n-объем нуль множества введен с помощью
интеграла Римана от характеристической функции множества.
Необходимо поэтому рассмотреть вопрос от эквивалентности этих
двух определений.
Теорема (об эквивалентности двух определений множества
n-объема нуль). Если множество A<=Jn[a, ft], то (|Л|п=0)-**;
(множество А имеет п-объем нуль (в старом определении)).
294
Доказательство. 1) Пусть |Л|п=0. Тогда
%л<=Я(7п[а, £>]) и J %A(x)dx=$.
/"[а. 01
Докажем, что А—0. В самом деле, если бы А^0, то существо-
вал бы открытый брус 1п (а, £)с=Л. Но тогда можно указать раз-
биение Т0=(Тф, Т(оп)) бруса 1п[а, Ь] такое, что для некото-
рого мультииндекса (k) имели бы включение
A Z) 7п(а, р) = 1п[х«-е\
причем tz(7(nfe)) = 8 > 0. Тогда = m(xA; 7”ft))= 1, и поэтому
$ х^(^о) > т(*) = > 0>
откуда
|Л|„ — J xa(x)Jxx=L J %A(x)dx=
Inla. 6] Тл[а. 0]
•= sup SXA(T) > 8 > 0.
Противоречие с условием |Л|„=0. Итак, А = 0. Но тогда AczdA.
Далее из условия %A^R(ln[a, Ь]) видим, что множество А измери-
мо по Жордану, а потому mesd4=0. В силу компактности грани-
п
ца дА имеет n-объем нуль (в старом определении). Но Ас.дА,
поэтому и множество А имеет /z-объем нуль.
2) Если множество Аа!п[а, &] имеет n-объем нуль (в старом
определении), то, как было доказано в § 3, граница дА множества
А также имеет n-объем нуль и поэтому множество А измеримо по
Жордану. В силу критерия (об измеримости по Жордану в Rn,
X«e/?(7n(a, &]), так что существует |Л|П = 7 %а(х)4х. Докажем,
ГЛ[и. 6)
что |Д|п=0. Для любого разбиения Т бруса 1п[а, &] (с частичны-
ми брусами 7^ ) рассмотрим для характеристической функции
нижнюю сумму Дарбу SXa(T). Заметим, что 7^ []СА=&0, так
как в противном случае имели бы включение 7^ с: А, противоре-
чащее условию о том, что множество А имеет n-объем нуль. Но
тогда для любого (j) существует точка х(/>е7('1/) ПСД, и поэтому
0 < /п(/) = тп(ха-, < Ха(х'>>) = 0 V(y),
откуда
• p(/J() >= 0 VT,
. (/)
T- e. J = sup SXa(T) = 0. Но поскольку хл^Т?(7п[а, &]), то
И|п«7 = 0.
295
Замечание. Пусть 1п[а, Ь] — брус с евклидовым объемом-
v(In[a, Ь]). Тогда брус 1п[а, bl измерим по Жордану, причем:
|Z«[a, *>]|n=f(7n[a, b]).
В самом деле, если %i(x) — характеристическая функция для
бруса 1п[а, 6], то %i(x) = \ V х^1п[а, Ь], но, как было показано в
примере 1 § 1, %/е/?(7п[а, Ь]), причем
j /j(x)dx = j ldx=n (Ь, — а,) =
/"[а. Ь] /"[а.Ь] Z=1
def
— v(ln[a, Ь])=|7"[а, b]|„.
Замечание. Если А с: A czln[a, &Jc:Rn и множество А изме-
римо по Жордану, то его замыкание А и граница дА также изме-
римы по Жордану.
В самом деле, из измеримости по Жордану множества А еле- •
дует, что для компактного множества дА имеем |дЛ|п=О, так что
граница дА измерима по Жордану. Далее поскольку Лс=/П[а, bj
и дк—дА, то компактное множество А также измеримо по Жор-
дану.
Теорема. Система а всех множеств А (из бруса 1п[а, 6]),.
измеримых по Жордану, образует алгебру множеств, т. е. для этой
системы выполнены: а) 1п[а, Ь]&г, б) Ai(JA2, Aif]A2^o v At, Л2&
go; в) СЛ(У”1а b]=/n[a, b]\AeoVAso. (Доказать самостоя-
тельно, повторив доказательство аналогичной теоремы для одно-
мерного случая из [1], ч. II, гл. 2, § 5.)
Следствие. Пусть множества A}czln[a, b] (/=1, 2, ..., т)
измеримы по Жордану. Тогда множества ГМ/ и JA/ также из-
/=1 /=t
меримы по Жордану.
Замечание. Приведенное в следствии утверждение не рас-
пространяется на счетные объединения множеств, измеримых по-
Жордану, например множество Q=Qf|[O, 1] не измеримо по Жор-
4-00
дану (почему?), хотя Q = (J {</*}> гДе v k и каждое множест-
*=i
во {qk} (точка) измеримо по Жордану (поскольку |{?4|1 =
=OVA(=N).
Теорема (о сохранении измеримости по Жордану при С<*>-
отображении). Пусть AczAaG, где G — открытое множество в
Rn и f:G<=Rn -> Rn, причем f^C^(G). Тогда из измеримости по
Жордану множества А следует измеримость по Жордану множе-
ства f(A).
Доказательство. Рассмотрим S=fxeG|detDf(x)=O} —
множество критических точек отображения f и положим 5л=-
296
=S(yl<zln[a, Ь]. Вспомним, что если x0^.G — регулярная точка
отображения feCW(G) (так что det Df(xo)=#O), то по теореме о*
локальном диффеоморфизме (из [1], ч. III, гл. 2, § 8) существуют-
окрестности U(xq)c.G и V(f(x0))=f(U(x0))c:f(G) такие, что су-
жение отображения f на U(x0), т. е. f:U(x0) -*• V(f(x0)), есть диф-
феоморфизм (т. е. биективное и взаимно непрерывное отображе-
ние класса Пусть точка х0^А регулярна, тогда в силу теоре-
мы © локальном диффеоморфизме [(хо)а$(А)^т. е. f(x0) — внут-
ренняя точка множества f(A), так что f(x0)e.df(A). Но тогда
df(A)cf(dA)\)f(SA). (4.1>
Поскольку множество A(AczAclG) измеримо по Жордану, то
mes 04=0 (и, в частности, поскольку то множество А
п
также измеримо по Жордану). Но feCd>(G), поэтому в силу тео-
ремы об инвариантности меры нуль (при (^’-отображении) имеем-
mes /(дЛ) =0. Поскольку множество ЗдсдЛсб есть множество*
п
критических точек отображения f^C<V(G), то по теореме Сарда
(из § 3) имеем mes f(Sa) =0, но тогда из (4.1) имеем mesdf(A) —
п. п
=0. Как было отмечено, замкнутое множество AczG измеримо по
Жордану, а потому ограничено и компактно в Rn. Ho_f<=C(A), и
поэтому в силу теоремы Вейерштрасса множество f(A) (а стало
быть, и множество f(A)) ограничено в Rn. Но тогда |5/('Д)|п=0>
т. е. множество [(А) измеримо по Жордану.
Теорема. Пусть f:GczRn->-Rn (где G — открытое множест-
во), J^C^(G) и отображение f:Gf(G) есть биекция, Пусты
AcAczG и х°еЛ — регулярная точка отображения f (так что
det Df(x°) #=(?). Тогда: а) если ха<=А, то f (х°) — внутренняя точка
множества f(A); б) если х°^дА, то f(x°)&)f(A).
Доказательство. Утверждение а) следует из теоремы о
локальном диффеоморфизме.
б) Допустим, что точка хР^дА регулярна и отображение-
f:Gf(G) биективно, т. е. ([(хг)=/=[(х2)) •<=► (х1^х2). Рассмот-
рим локальный диффеоморфизм f: U(x°)aG -+ V(f(x°)) =
==f(U(x°))czf(G). Нужно доказать, что для любой окрестности:
W6(f(x°))^V(f(x9))<=f(G)
имеем
П1в(Кх°))ГЖ)=/=0
и Wt(f(xf>))(](f(G)\f(A))^,0
(где f(G)\f(A) =Cf(A)). В силу критерия непрерывности отобра-
жения: «прообраз открытого множества открыт» (см. [1], ч. III,.
Гл- 1> § 9 из условия f^C(U(x!°)) следует, что множество В(Х°)=;
297
—f-i (HIt(f(xP)))a:U(xP) открыто и содержит точку х°^дА, т. е.
В(х?) является окрестностью точки х°. Поскольку х°е<5А, то суще-
ствуют точки х1<=В(х°)(}А и x2eB(x0)nfG\A^, откуда
f(x^)^f(B(x^)C\A)^f(B(^))(]f(A)^
=wt(f(*>))nf(A)
и f(x2)^f(B(x°)(](G\A))^f(B(x^))Qf(G/A)^
^m6(f(x^))Qf(G\A).
Но G=A(J(G\A), причем Afl(G\A) = 0. Тогда
f(G) =f(A(J(G\A)) =f (A)Uf (G\A).
Докажем, что в силу биективности отображения f имеем f(A)f|
f\f(G\A) = 0 (и тогда f(G\A) = f(G)\f(A)). В противном случае’
Э y°^f(A)(]f(G\A), а потому существуют точки х’еА и x2eG\A
такие, что f(xl)==f(x2)=y°, но поскольку х*еА, x2eG\A, то
х1=£х2, что противоречит биективности отображения f. Итак, до-
казано, что для любой окрестности
существуют точки
1(х^(А)(\Ш^(х0)),
f(x2)^e(f(xO))()(f(G)\f(A)),
т. е. f(x?)^df(A).
Глава 2
КРАТНЫЕ ИНТЕГРАЛЫ РИМАНА
НА ОГРАНИЧЕННЫХ МНОЖЕСТВАХ ИЗ R"
§ 1. Интеграл Римана на ограниченных множествах
из Rn и его свойства
До сих пор рассматривались интегралы Римана от функций
f(x), определенных на брусах In[a, b]c:Rn. Перейдем теперь к
изучению интеграла от функции f(x), определенной на ограничен-
ном множестве из Rn.
Определение. Если AaAaIn(a, b)<=Jn\a, b], f^(In[a, b]),
причем функция f-%A^R(In[a, b]), то интегралом Римана от функ-
ции f(x) по множеству А называется интеграл Римана S f(x)X
In[a, 6J
Обозначения:
ft=R(A), f fdx^ / f(x)-%A(x)dx.
A Г"(». Ы
Замечание. Если f^R(In[a, b],) и множество Aczln[a, b] из-
меримо по Жордану (т. е. %A^R(In[a, 6])), то будет показано, что
f %A^R(In[a, bj), т. е. f^R(A), и поэтому существует интеграл
Римана / fdx.
Л
Замечание. Если множество Аа:1п[а, Ь], функция fs
^В(/п[а, Ь]) и f^R(A), то из определения интеграла Римана
S fdx не следует, что f^R(In[a, b]) и что множество Дс:/П[а, Ь]
измеримо по Жордану.
Пример. Рассмотрим функцию
[ 0,х рационально,
f(x) = < ,
'I 1, х иррационально
и множество Q=Qf)[0, 1], тогда
' I, х рационально
I 0, х иррационально.
Очевидно, 1], а множество Q не измеримо по Жордану, тем
не менее поскольку
f(x)-XQ(x)=0V Х(=[0, 1],
то f 1], т. е. f<=R(Q) и J fdx=O.
Q
Замечание. Рассмотрим числовую функцию f(x), опреде-
ленную и ограниченную на ограниченном множестве >lc:Rn (так
Что А компактно в R"). Положим
299
F(x) =
I 0, x^CA.
Тогда F:Rn->- R является ограниченной финитной функцией с ком-
пактным носителем (поскольку F(x)=0 V хеА). Будем в даль-
нейшем считать что функция f^B(A) продолжена на Rn указан-
ным способом с помощью ограниченной функции F(x). Тогда име-
ет смысл запись: f(x)-%A(x) V xeRn.
Теорема (критерий Лебега интегрируемости по Риману на
измеримом по Жордану множестве из Rn). Рассмотрим множест-
во AczRn, измеримое по Жордану, и функцию f:A R, ограничен-
ную на А. Пусть Еа={х^А\&(1; х)>0} — множество всех точек
разрыва функции f на множестве А. Тогда
(f^P(A)) о (mes ЕА=0).
п
Доказательство. Поскольку множество Ac:Rn измеримо*
по Жордану, то оно ограничено, а потому существует брус.
1п[а, Ь] такой, что A<=.A<=.In(a, Ъ)а1п\а, Ь], причем mesdA=0..
п
Рассмотрим функцию f-%A, определенную на брусе /п[а, Ь], и пусть.
Е={х^1п[а, 6]|<в(/-ха; х)>0} — множество всех точек разрыва
этой функции на брусе 1п[а, &]. Тогда имеем
ЕлсЕ<=Ел\)дА. (1.1)
В самом деле, рассмотрим точку Хое/П[а, &], тогда для любого,
шара Ш«(хь) имеем оценки
®(/ • ха; Ш8(х0)) = sup |(f • xa)(*i) — (/ • Ха)(х2)| >
Ki, г,6Ш8(х,)(У'г
> sup |(f • Ха)(*1) — If Ха)(х,)| =
xlt х26Ш$(х0)пА
= sup И(Х1) — = Ш8(х0)),
эдеШвМлА
откуда, переходя к пределу при 6-> 0, получаем оценку
<э(7-%д; x0)^(a(f; х0). Но тем самым доказано, что из оценки
off; х0)>() следует неравенство со(7-%л; х0)>0, и поэтому EA<z:E.
Далее если хое£, то ©(/-х*; хо)>0 и тогда хоеА, так как в про-
тивном случае Э IIIefxoJtrCA, и поэтому (f-%A)(x)=0 V хеШДхо),
т. е. ®(7-хд; хо)=0 вопреки предположению, что хо^Е. Итак, ес-
ли хо^Е, то Хо^А. Если при этом хоеА, то существует шар
IIIefxojcA, и тогда (f-xA)(x)—f(x) V хеШ4(хь), т. е._а(/ х<;
Xo)=a(f', хо)>0, и поэтому хоёЕд. Если хоеА, но хоеА, то
х0^дА. Итак, если хое£, то х0^ЕА{)дА, т. е. ЁаЕдЦдА. Включе-
ние (1.1) доказано. Но тогда:
300
1) (f^R(A)) => (f^^R(In[a, Ь])) и в силу критерия Лебега
^интегрируемости по Риману на брусе) из (1.1) имеем (mes£=
_=0) =>тез£л=0);
п
2) если mes£A=0, то, учитывая, что в силу измеримости по
п
Хордану множества А имеем mesdA=0 и тогда из (1.1) получа-
ем mes£=0. Вновь применяя критерий Лебега (на брусе), видим,
ЧТо fn^R(Ina, b], т. е. f(=R(A).
Теорема. Класс R(A) функций, интегрируемых по Риману
на множестве А (АсАс/п[а, Ь]), есть кольцо с обычными опера-
циями сложения и умножения. Эта теорема вытекает из следую-
щих ниже теорем 1 и 2.
Теорема 1 (о сложении функций, интегрируемых по Рима-
ну). Если fi^R(A) и с/ — постоянные (j=l, 2, ..., m), то
Sci fi^R(A), причем
i=i
vn m
J S ci‘ bdx= • J fidx-
Ai—l 1=1 A
_ Доказательство. Поскольку fj<^R(A)/\B(In[a, bp и
AcJn[a, b], to bp (7=1, 2, ..., m). Положим
Fi = fi У.А и H= J • fj • xa= § • Fj.
i=t /=i
Тогда Fj^R(In[a, bp. (Докажите самостоятельно по аналогии с
теоремой 1 для одномерных интегралов Римана из [11 ч. II, гл. 2,
§ ‘6, что
НеЩ1*[а,ЬЪя f H(x)dx = 3 q • f F}(x)dx).
In(«, b] /=1 i"[a, b]
Поскольку Fj^R(ln) (1=1, 2, ..., m), то для любого размеченного
разбиения Т£ бруса In[a, Ь]=1п имеем
m
Sh(T&~ S с, • SF (Tl) (1.2)
/=1
и тогда по теореме о «пределе суммы» (по базе d(T) -+• 0) из ра-
®енства (1.2) имеем
(3 lim 5Я(П)= lim У ci • SF,(T\) =
d(T)-0 d(T)->0/t| I
= 2 Ci • lim SF (Tg))=>(tf e R(P[a, Ь]))Д
301
/\ ( У H(x)dx = ^Cj- У Fj(x)dx\.
\ l"la, bl /=1 l"[a, b] /
Итак,
(s cr Fi= (3 ci • Хл€=Я(Г*[а, &])]=»
\/=i \/=i J I
=>fs ci • /?<л)) Л (У S ci ’ M* e
\/=I / \л/=1
= J 3 ci • fi(x) -XAdx = % CjX
l"[a, b] /=1 /=1
X I. fi'(x)K.A(x)dx=^l cf • J fj(x) dx 1
ln[a, b] /=1 A /
Следствие. Если множества A, Bc/n[a, ft] измеримы по Жор-
дану и A(]B=0, то множество Л|_|Вс=/п[а, &] также измеримо по
Жордану, причем |Д1)В|»= |Д |п+151«-
В самом деле, как было доказано в гл. 1, § 4, система всех
множеств бруса In[a, Ь~\=/п, измеримых по Жордану, есть алгеб-
ра о, поэтому ДиВ^о и, в частности, %а, %в, Xaub ^R(In[a, &]).
Поскольку А(\В=0, то имеем
Xavb(x) = ха(х) + хв(х) Vx <= /“ [а, 6]
и тогда в силу теоремы 1 (о сложении) получаем
Iд U ®1„= У Xaub (х) dx=\ (ХА (х) 4- Хв (х) dx =
Iя 1я
вУ XaW^x + У хв (х) dx = |Д|„ + |В|Л.
г” Iя
Теорема^ 2 (об умножении функций, интегрируемых по Ри-,
ману). Если, Aczln[a, Ь] и функции f, g^R(A), то f-g^R(A).
Доказательство. Поскольку g^R(A), то F, G&
e/?.(Zn[a, Ь]), где F=f-XA и G=g XA- Заметим, что
(F-G)(x)=f(x)-XA(x)g(x)xA(x)=f(x)g(x)xA(x). .
Пусть Ер, Еа и Ee'G — множества всех точек разрыва Г(на
Zn[a, b]=In) функций F, G и F-G соответственно, тогда имеем
Ef.g<=Ee\JEg. (Д.З)
В самом деле, поскольку F, G^B(In), то эЛ4>0 такая, что
|F(x)|, | G(x) \^М V хеЛ.
Далее для любых Xi, Хге/П имеем оценки
| F(Xl) G(xl)~F(x2) G(x2) IСI F(Xl)-F(x2) IX
XI G(Xl) | +1 F(x2) I • | G(Xi)-G(x2) | < 1
302
^M(\F(Xl)-F(x2) I + J G(XI)-G(X2) |)
й поэтому для любого 6>0 имеем неравенство
<b(FG; Шб('х0))<Л1(<о(В; Ше(х0)) +
-j-o^G; Шь(хо)) У Хо^1п,
из которого, переходя к пределу при 6 -> О, получаем оценку
<n(FG; Xo)^M(a>(F- Xo)+®fG; xq)),
из которой получаем (1.3). В силу критерия Лебега (интегрируе-
мости по Риману на брусе) имеем
(F, G^R(In[a, b]))=> (mesEF=mesEg=0).
n n
Но тогда из (1.3) имеем mes EF.G=Q и, вновь применяя критерий
п.
Лебега (на брусе), получаем FG^R(In{a, b]), т. е. f-geR(A).
Теорема 3. Если f^R(In[a, b]) и существует р>0 такое, что
jf(x) |>р>0 v х.^7п[а, 6], то l/feR(7n[a, b]).
Доказательство. Поскольку f<=R(In{a, Ь]), то /е
еВ(7”[а, Ь]), и тогда из условия
|l/f<x)|<l/pvxszn[a, b]
имеем l/feB(7n[a, b]). Далее v х, y^In\a, Ь] имеем
I l/f(x)-l/f(y) | = \f(x)-f(y)\K\f(x) IX'
откуда V 6>0 и v xeln[a, b] получаем оценку
o)(l/f; Ш«(х))^(1/р2) .«(fi Шй(х)),
из которой, переходя к пределу при б -+• 0, получаем
оО/Л X)<(l/p2).<o(f; х).
Пусть Ef и Ei/f — множества всех точек разрыва (на брусе
/"[а, Ь]) функций f и l/f соответственно. Тогда из последней оцен-
ки вытекает включение E\/fCzEf. Применение критерия Лебега
(интегрируемости по Риману на брусе) дает логическую цепочку
(ft=R(In\a, b])) => (mes £7=0) =>
п
^(mesB^O) => (\/f<=R(In\a, b])).
n
Следствие. Пусть f, g^R(In[a, b]) и Э p>0 такое, что
|^(х) ]>p>0 V x^In[a, Ь]. Тогда f/g^R(ln[a, bj).
Теорема 4 (об интегрируемости по Риману модуля функ-
ции). Если Аа1п[а, Ь] и f^R(A), то 1 f |&R(А).
303
Доказательство. Заметим, что F=f%4e/?n[a, b]), если
fr=R(A). Но
IР(*) | = I f (х) ха (х) | = | f (х) | -хл (х) V х(=1п[а, Ь],
поэтому достаточно доказать, что
(F<=R(I*[a, b})) =>- (|F|e=/?.(7n[a, &])).
Если F^R(In[a, 6]), то F<^B(In[a, Ь]) и поэтому |F| еВ(1п\а, Ь]).
Далее V х, у^1п имеем неравенство
l|F(x)|-|F(Z/)||<|F(x)-Ff!/)|,
откуда V б>0 и V х^1п[а, &] получаем оценку
©(|F|; Ш6(х)),
«з которой, переходя к пределу при б -> 0, получаем а (| F |; х)<
<<в(Т;х).
Пусть EF и Bjfi—множества всех течек разрыва функций
F(x) и |F(x)| соответственно. Тогда из нав!ей оценки имеем
включение E\fi(ZEf, и применение критерия Лебега интегри-
руемости по Риману на брусе дает цепочку
(F <= R(In[a, &])) => (mes EF = 0) =» (mes EIF। = 0) =>
n n
=> (|F| e 6])) =» (|/| • xa <= R(Infa> &D) =» (l/l e ^(4)).
Замечание. Из того что |<=7?(4), вообще говоря, не сле-
дует, что f<=R(A). Например, если
/« = !-•
( 1, xeQ,
то |/(х) | Ь]), но Ь].
До сих пор при интегрировании по брусу 1"[а, 6] предполага-
лось, что a=(ai, .... ап), Ъ=(Ь\.Ьп), где ai<2bi (i—1, 2,
Определение. Если a^bi (i=l, 2........и) и существует k
f(l^<n) такое, что ak=bk, то полагаем J fdx=O.
1П[а. Ы
Теорема 5 (конечная аддитивность интеграла Римана).
Пусть f^R(Aj) (j=l, 2..... m), где AlczITi(a, b) и 4/П4а:=
^=0 -у j=/=k. Тогда f^R(A), где А= U A/czAcz/n(a, b), причем
/«1
№ = s Jf/dx.
А /=1 А/
Доказательство. Поскольку Ajdn[a, 6] (/=1, 2, .... ш)
и 4;П4й=0 V то
3(М
Ха (х) « 2 ХА. (х) V х е= 1п[а, Ь] = Г.
] =1
Но из /еЯ(Л/) имеем f • ха} R(In[a, b]). Заметим, что
f(x) • XaW=2 f(x) -Хд,(х),
/-» ’
поэтому в силу теоремы 1 (о сложении) имеем f • хле
4=/?(Zn[a, b])t т. е. /е=/?(Л), причем
J fdx=\ f f.Adx —
А 2п
= if f -XA/x-Jf fdx.
/=1 /" ' 1=1 ln
Теорема 16. Пусть B^A<zzA<zzIn(a, b) и множество В изме-
римо по Жордану. Тогда (ft=R(A) => (feR(B)).
Доказательство. Рассмотрим характеристические функ-
ции хд и %в. Поскольку В<= Л, то ч.в(х)—^(х) ^в(х) v xeRn и
тогда (1^)(х) = (1-1а)(х)-^в(х) V хе/п[а, Ь]. Из условия f<=
<=R(A) имеем f-%A^R(In\a, b]), и поскольку множество В изме-
римо по Жордану, то хвеЯ(7п[а, Ь]), но тогда в силу теоремы 2
(об умножении) (Лха) Хв=Гхв^Я(1п[а, Ь]), т. е. f<=R(B).
Следствие 1. Если In[a, £]с:/п[а, 6] и f<=R(ln[a, Ь]), то
f^R(In[a, ft).
Следствие 2 (об аддитивности интеграла Римана). Пусть
множества Ajczlnfa, Ь] (/=1, 2, ..., tn) измеримы по Жордану и
ЛПЛк=0 v/т^А. Пусть А = иЛ/ и f^R(A). Тогда f^R(AA
i=i
(i=l, 2, ..., tn), причем
fdx.
A m j=l
№
Теорема 7. Пусть f^R(A), где множество XcRn измеримо
no Жордану и m^f(x)^.M V хеЛ. Тогда
tn • | А | J fdx^M IAI n.
A
Доказательство. Поскольку f^R(A), то F=/-xaG
^p^n[a* Ь]) и для любого размеченного разбиения Т£ бруса
1 la’ 6] в силу неравенств m-XA(§(*))^^'(l(ft>)^^,Xl’(S(ft> v
имеем
m. S^TD^S^TD^M -SXA(Tl),
о^Уда в силу FeJ?(/n[a, 6]) и хле^Т^а, Ь]), переходя к преде-
лу (по базе d(T) 0), видим, что существуют пределы
И. Камынин 305
lim S,(W= J lim/«„(ГВ-Ик
/л1в> bj A d(T)-*O
так что
m -|Л|Я</fdx^M • |Л|П.
A
Теорема 8. Если f^R(A) и f(x)^QvхеЛ, то J fdx^O.
A
Доказательство. Поскольку feR(A), то F=f-xxe
eR(In[a, b]). Но для любого. размеченного разбиения бруса
In[a, &] ввиду условия f(x)^O V хеЛ имеем оценку Sp(T£)^0, из
которой переходя к пределу (по базе d('T)->0), получаем
lim SF(Tl) = f fdx>0.
d(T)~O ~A
Следствие 1 (интегрирование неравенств). Если f, g&R(A)
и f(x)^g(x) v xeA, to
J fdx>$ gdx.
A A
Следствие 2 (монотонность «меры Жордана»). Если мно-
жества A, Bczln[a, &] измеримы по Жордану' и АаВ, то |Л|П^
В самом деле, поскольку AczB, то %а(х)^.хв(х) V xsRn. Из
измеримости множеств Л и В по Жордану (в силу критерия из-
меримости по Жордану) имеем %а, %B^R(fn[a, b]) и тогда в силу
следствия (об интегрировании неравенств) получаем
Mln= f T.A(x)dx^ J 7.в(х) dx-|B|n.
Гп[а, d] Inla, t>]
Следствие 3. Если f^R(A), то | J fdx\^J |f|dx.
A A
Следствие 4. Пусть f^R(A), где множество Л измеримо по
Жордану и |f(x)|^Lv хеЛ. Тогда
If fdxi^L • 1Л|Я.
[а I
Следствие 5. Пусть |е|та=0 и feB(e). Тогда f^R(e) я
Sfdx=O. В самом деле, |е|п=0 означает, что множество е изме-
е
римо по Жордану. Поскольку f^B(e), то существует постоянная
L>0 такая, что |f(x) |^L Vxee.
Рассмотрим множество £={xee|®(f; х)>0), тогда Ес^е я
поэтому |Е|П= |е|п=0, т. е. mesE=.O и по критерию Лебега (ин-
тегрируемости по Риману на измеримом по Жордану множестве)
f^R(e), а тогда в силу следствия 4 |J’fdx|C^,leln=O, т. е.
е ,
Jfdx—O.
е
306
Теорема 9. Пусть множество AcR" измеримо по Жордану
и fe.R(A)- Пусть eczA и |е|п=0. Тогда f^R(e), f^R(A\e) и
J fdx = J fdx.
A Axe
Доказательство. Поскольку |e|n=0, то множество
еаА измеримо по Жордану. Но множество А также измеримо по
Жордану, поэтому и множество Л\е измеримо по Жордану. В си-
лу теоремы 6 из того, что f^R(A), вытекает, что f^R(e) и fe
^R(A\e), причем в силу следствия 5 из теоремы 8 имеем
ffdx=Q- Далее А=е[}(А\е), причем ef\(A\e)=i0, тогда в силу
е
следствия 2 (об аддитивности интеграла Римана) из теоремы 6
имеем
\fdx*=$fdx + f fdx — f fdx,
A « A\e A\e
t. e.
J fdx = j fdx.
A A\e
Следствие. Пусть множество AczRn измеримо по Жорда-
ну и для функций f^R(A) и g^B(A) имеет место равенство
g(x)=f(x) ¥хеЛ\е, где ес:Л и |e|ft=0. Тогда g<=R(A), причем
J gdx—S fdx, т. е. изменение функции f^R(A) на множестве
А А
ес:А, имеющем n-объем нуль (|е|п=0), не изменяет значения ин-
теграла Римана S fdx.
А
Доказательство. В силу следствия 5 к теореме 8 из ус-
ловий g^B(e) и |eln.='O имеем g^R(e) и S gdx—0. В силу тео-
е
ремы 9 можно написать логическую цепочку (f^R(A) =ф-
=>(f^R(A\e))=>- (geR(A\e)). Кроме того, J fdx=0, поскольку
е
|е|п=0, и Тогда теорема 5 (об аддитивности интеграла Римана)„
ввиду условия е[\(А\е) = 0 дает g^R(A) и
J gdx — у gdx = gdx = у gdx = у fdx = у fdx.
А А\е е А\е А\е А
Замечание. Функция f^R(A\e) может и не быть опреде-
ленной на множестве есЛ, если |е|п='О, и тем не менее понятие
интеграла Римана f fdx (а стало быть, и понятие f<=R(A)) имеет
А
смысл (достаточно положить f (х) =0 V хее или доопределить
Функцию f(x) на множестве е любым другим образом, лишь бы'
при этом иметь f<=B(A).
Лемма 1. Для любых множеств Ль A2cRn имеет место ра-<
венство
ХА,ИАг(х) =Ха,(х) +т.А,(х) — Ха,па.(х) VxeR". (1.4)
(Доказательство леммы 1 было проведено в одномерном случае в
(1], ч. II, гл. 2, § 6.)
Теорема 10 (об усиленной аддитивности интеграла Римана).
Если f^R(Aj) (j=l, 2) и |Л1СИ2|п=0, то f^R(Ai{jA2), причем,
J fdx = J fdx + J fdx.
AiVAt At A,
Доказательство. Поскольку f^R(Aj), то существует брус
7n[a, bjz>Jn(a, b)=>A/ (j=l, 2), так что AilJA2c:/n[a, &]. Но из ус-
ловия f^R(Aj) имеем f-y,Al eR(In[a, &] (j=l, 2), причем по-
скольку f^B(Af), то f^B(Ai(]A2). Применяя следствие 5 к теоре-
ме 8, видим, что из условия |Aif]A2|n=0 следует f^R(A2(]Ai) и
поэтому7-Хд1ПА,е1?(7«[а, &]), причем
J fdx = 0= f f -X.AinAtdx.
AiflA, 1л[а, Ь]
Но тогда в силу тождества (1.4) (из леммы 1) по теореме 1 (о
сложении) имеем
(f • Xa.ua, еЯ(/п[а, &]»=>(/е адцМ.))*
причем
f fdx = J (f • K.AtuA,)(x)dx —
AtUAt in[at b]
-2 f (f XAi)(x)dx- J (f KAtnAt)(x)dx =
. /.I ln[a. bj In[a, b]
= i f (f 'Ха.)(х№-% f fdx.
1=1 In[a, b] /=1 Ai
Следствие 1. Если f<=R(Aj) (j=l, 2..........m) и |А/ГИл|пв'
m
=0 V f=^k, to Aj), причем
/=51
J fdx~% f fdx.
m Пая! А»
Следствие 2. Если множества Ль Л2с=/П(а, Ь] измеримы по
Жордану, то измеримы по Жордану и множества Ai(JA2, Л1ПЛг»
причем
I Л1ЦЛ2|п+| Л1С|Л2|П='| Л1 |n-j-1 Л2| п
и, в частности,
М1ил2|п<|л1|п+|л2|п.
308 >
Доказательство. Поскольку множества, измеримые по
ХорДанУ на брусе 1п[а, 6], образуют алгебру (множеств) о, то из
измеримости по Жордану множеств и А2 следует, что множест-
ва Л11)^2 и Л1ПЛ2 также измеримы по Жордану. В силу критерия
измеримости по Жордану (в Rn) имеем /а., ха,, Xa.ua,, Xa.ua,е
6= &]>, а в силу теоремы 1 (о сложении) /а,ил, + Xa.ua,,
_]_ уДг е Р(1п[а, 6]), причем равенство (1.4) леммы 1 дает
HiU^sIn + = f Ха^а/х) dx +
Гл[а. Ь)
+ f 7.а,па,(х) dx = у (Za.ua, (х) + ха.па,(х)4х -
/л[а. Ь) /л[а, Ь]
= J (Ха,(х) A-lA,(x)}dx= у XA.W dx +
/л[а, Ь] 1л[а, Ь]
+ У ХА,(х) dx =1Л1|П-Н|Л2|П.
/”[а, Ь]
Поскольку XA.nA,(xj>0 VxeR”, то |ЛХПЛ2|Я > 0, откуда |Л1[_)
U ^sln И11п + Мак-
Следствие 3. Пусть множества Л/с/п[а, ft] (]=А, 2, ...,m)
измеримы по Жордану. Тогда множество U Л, также измеримо по
/=1
Жордану, причем
Следствие 4 (усиленная аддитивность меры Жордана).
Если множества Ль Л2с=/П[а, Ь] измеримы по Жордану и
И1ПЛ2|п=0, то множество Л^Лг измеримо по Жордану, причем
|Л 1(_|Л2 [п=,|Л11 п-(- |Л2|П.
Доказательство. В силу следствия 2 имеем |.Ai(J/12|»=*
=|И1|п+|Л2|п—|Л1Г)Л2|П, откуда |Л1иЛ2|п=.|Л1|п+|Л2|п, по-
скольку |Л1ПЛ2|п=0.
Следствие 5. Если множества A/czIn[a, Ь] (/=1, 2...,т)
измеримы по Жордану и | Л/ПЛ^ | n=0 V/=#й, то
т * m
и А, =2 Hiln-
/ —1 П j=t:l
Теорема (свойства меры Жордана). Рассмотрим на брусе
*п[а> Ь] систему о множеств {А}, измеримых по Жордану (т. е. та-
ких, что mes<Z4=0). Тогда на системе о (образующей алгебру
п
множеств) определена неотрицательная числовая функция (мера
309
Жордана) ц: Д->|Л|П = / %л(х)б/хеК+, обладающая свойства-
1п[а. 6]
ми 1) |А |п^О V А2) |AiU^4s|| ^411«~I- | ^21 п Л [, А2 сг,
3) v At, А2&! таких, что Л1ПЛг=0 (или |Л1С|Л2|п=0) имеет ме-
сто равенство |Л11|Л2|П= |Л1|П+|Л2|П; 4) если 7п[а, [}]с/п[а, &],
то |/п[а, р]|п = ГЦЭД—а/).
1=1
Отметим, что свойства 2) и 3) означают конечную аддитив-
ность меры Жордана. Заметим также, что мера Жордана не об-
ладает свойством счетной аддитивности.
Теорема (о корректности определения интеграла Римана на
ограниченном множестве из Rn). Рассмотрим функцию f(x), опре-
деленную и ограниченную на множестве 4cRn таком, что AczAcz
czln(a, b)(\In(ct, р), где 1п\а, Ь] и 1п[а, 0] — брусы из Rn. Если
feR(A) (в смысле f-%AGR(ln[a, Z»}) и
f fdx •= f (f * Ха)(х)6х),
A ln{a, b)
to f • xa e Я(/п[«>> ₽)] и
f (/ • XA)(x)dx - f (f u)(x)dx,
In[a, (J] l"[e. Ы
г. e. определение f^R(A) не зависит от выбора объемлющего
бруса In[a, b\zoln(a, b)^AzoA.
Доказательство. Пусть АаАа1п(а, Ь)(\1п (а, (J). Тогда
at = min (а{, af) «С af = max (а(, щ) < 6, =
= min (р{, &,)<&?= max (ЭД, b(),
t. e. Zn[a,T] Z) In[a, M =Э ₽1 = Zn[a,_&l.
Рассмотрим разбиение Г=(Т(1\..., Т<п>) бруса In[a, &] такое, что
Тогда один из частичных брусов
причем 1п[a, 6]=Z(%UU^,, /”[«, PW^UUZf/.).
Г[а, 6]= (J/"у Заметим» что (%а • f)(x)=Q (/)¥=(/о)»
т. е. ха -/e7?(Z(n0)¥(/)#= (/о). Поскольку Г[а, Ь], то в
силу теоремы 6 из условия / • ха <= R(In[a, 6]) следует, что
/ • Ха s но тогда / • ха е Z?(Z^)V(j). Применение след-
ствия 1 из теоремы 10 дает / • ха <= Z?(Zn[a, ЭД), причем имеют
место представления (учитывая равенства
зю
у / -^Adx = j / -y^dx — 0) J f ,yAdx*=
1П[а’ь}
= J / -Xa</x+2 f t 'XAdx= J / -Xa^x;
_n (/') n .n
Af.> lif) ’a,}
f t f.Adx^ J f -ха^х + 21 J t -f.Adx= J f xAdx,
/П(а-₽l 'lb (f> 4'1 Л/.)
t. e.
У f-yAdx = у f XAdx.
l"[a.Ы /"[a. P]
Теорема 11. Если f^R(In[a, b]), то множество всех точек
непрерывности функции f(x) всюду плотно на брусе 1п[а, &].
Доказательство. Пользуясь критерием непрерывности
Бэра* (для функции f(x)), достаточно доказать, что V /"[a,
c:/nja, b] существует точка xoe/n[a, £] такая, что со (7; Хо)=0.
Допустим от противного, что существует брус /п[а, р]с/”[а, 6]
такой, что ®(f; х)>0 Vxe/n[a, £]. Тогда /n[a, ЭДсЁ, где Е —
множество всех точек разрыва функции цх) на 1п[а, 6]. Но
f&R(ln[a, &]) и в силу критерия Лебега интегрируемости по Рима-
ну (на брусе) mes£'=0 и поэтому, как было показано в гл. 1, § 3,
о п
Е=0, так что включение /п[а, невозможно.
Лемма 2. Пусть f^R(In[a, £]) и f(x)~^0Vx^In[a, b], при-
чем существует точка х0^1п[а, Ь] такая, что f^C(x0) и f(x0)>0.
Тогда j f(x)dx>0.
/"[a. 6)
Доказательство. Поскольку f^C(xo) и f(xQ)>0, то в
силу локальных свойств непрерывных функций существует откры-
тый шар niefxo) такой, что
f(x)>f(x0)/2>0 V хеШв(хо)ПЛ(а, &].
Но тогда существует брус /п[а, ^]с:Шв(хо)П/п{а, 6] так, что
f(x)^f(x0)/2 V xs?[a, 0]. Рассмотрим разбиение Т= (Т^\..., TW)
основного бруса /п'[а, &] такое, что i, и пусть
1(п — частичные брусы, соответствующие этому разбиению. В
силу построения разбиения Т имеем /п[а, В силу теоре-
мы 6 из условий f^R(In[a, &]) и CZ 1п[а, Ь] имеем /еЛ(7^)
^(/). Далее поскольку |dj" | = 0, то 1п[а, 6] = (J Лл» где |2,".П
»J f (
и^)1п=0 V (j) Ф (&), так что в силу следствия 1 к теореме 10
имеем равенство
311
f f(x)dx = j- f(x)dx+ 2 f f(x)dx.
in[a.b] /"[«, 31 (')*</.)
Но в силу оценок f (x_)>f(xo)/2>OVxe Zn[a, ₽], /(x)>0Vxe
e/^V)/) по теореме об интегрировании неравенств имеем
оценку
f f(x) dx >(1/2) • /(х0) • |Г[а, р]|” >0.
Jn[a, b)
Следствие. Если f<=R(In[a, &]) и f(x)>0v х<=1п[а, Ь], то
f j(x)dx>0.
. 1П1«. Ы
Доказательство. По теореме 11 Э хое!п[а, Ь] такая, что
f^C(x0), f(x0,)>0; f(x)>0 V xe/n[a, 6],
и тогда наша оценка следует из леммы 2.
Теорема 12. Пусть f^R(A) и f(x)>0 V хеЛ. Тогда
Я fdx = 0\=>(mesg’ = 0, где % = {хе A\f(x) > 0} с Л).
\А / "
Доказательство. Поскольку f^R(A), то множество
ЛсЯп ограничено и поэтому существует брус Zn[o, 6] такой, что
Ac:Aa:In(a, b)czln[a, &], причем F=f-xxe/?('Zn[a, Ь]). Но
{xe=Zn[a, 6]|Г(х)=^(х) ха(х)>0}==ЛП£ = $ и
j fdx= J F(x)dx = 0. (1.5)
A l"[a, 6]
Рассмотрим E — множество всех точек разрыва функции F(x)
на брусе 1п[а, Ь] и покажем, что £с:£. Допустим от противного,
что существует точка хоеё’ такая, что F^C(x0). Тогда F(x0)>6
и по лемме 2 S F(x)dx>0, что противоречит (1.5). Итак, 8сЕ.
1П\а, Ь]
Но Fs/?(Zn[a, Ь]), и в силу необходимости критерия Лебега ин-
тегрируемости по Риману (на брусе) имеем mes£=0, откуда(&CZ
CZ Е) ==> (mes S « 0).
Теорема 13. Пусть f^R(A) и % ={x<=A\f(x)=£0}c:A. Тог-
да (mes =0) => (S fdx=0).
п Л
Доказательство. Поскольку f^R(A), то существует брус
In[a, 6] такой, что А<=.Аа1п(а, Ь)с.1п[а, &] и F=f-%A^R(In[a, fej).
Тогда |F|^R(In[a, b]). Ho (xeZn[ci, b]\F(x)—f(x)-yiA(x)=^0}'=s
=A(] <§=% и поэтому S =(xe/’l[a, &]| |£(х)1>0}. Поскольку
| F(x) | ^0 v xeZn[a, &], то для любого разбиения T бруса ZTO[a, Ь]
имеем S|F| (Т)^0. Покажем, что на самом деле Sjfi (T)=0V Т.
Допустим от противного, что существует разбиение То бруса
1п[а, Ь] такое, что Sifi (Tq)>0. Тогда существует частичный брус
312
г» (из разбиения То) такой, что inf |F(х)|>0, но тогда по-
(и) п
скольку \F(x) |>0 Vxe то /(пЛ)с:£« так что i#=0. Но по-
условию mes & = 0, а потому, как было показано в гл. 1, § 3,.
$ = 0. Противоречие. Итак, для любого разбиения Т бруса
1п[а, Ь] имеем S|f|( Т) = 0, откуда (для нижнего интеграла Дар-
бу) получаем равенства J = sup5|ft(r) = 0. Но IF| е/?(7”[а, 6])^
— т —
поэтому J \F(x)\dx =_J =0, и поскольку
1п[а, Ы
У F(XMjc|< у \F(x)\dx^0,
1"[а, Ь] j 1п[а, Ь]
ТО
0= у F(x)dx=^fdx,
/я[а, Ь] А-
что и требовалось доказать.
Следствие. Если f, g^R(A) и %={x^A\f(x)=£g(x)},.
то
(mes$ = 0) ==>/f fdx = f gdx\.
n (a a /
Замечание. Обратите внимание на различие утверждений
следствия к теореме 9 и следствия к теореме 13. Из теоремы 1$
следует, что функции f^R(A) и g^R(A) (т. е. обе интегрируемые
на множестве Л), отличающиеся на множестве ^сгЛ n-меры нуль,
(mes £=0), имеют одинаковые интегралы Римана S fdx=
" А
=1 gdx. Из следствия к теореме 9 следует, что функции f^R(A)
А
и gsB(A) (где множество Л измеримо по Жордану), отличающи-
еся на множестве n-объема нуль (есЛ, |е|п=0), имеют одина-
ковые интегралы Римана J fdx=f gdx.
А А
Пример. Если f(х) = 1 vхе[0, 1], то fe7?[0, 1], причем!
,{^=1- Рассмотрим функцию
g(x)=, | °’ x®Q=QO[o, 1],
I 1, x<=Q
тогда, очевидно, geB[0, 1] и f(x)=g(x) V хе Q, где mesQ=0.
Заметим, что множество Q не измеримо по Жордану, а потому не
Может иметь n-объема нуль. Как функция Дирихле g'e^O, 1], и
313
поэтому не может существовать интеграл Римана S gdx. Итак,
(0. 11
функцию /, интегрируемую на множестве XczRn, можно так из-
менить на множестве й’сЛ п-меры нуль, что она станет неинтег-
рируемой по Риману, оставаясь при этом ограниченной.
Обобщенная интегральная теорема о сред-
нем. Пусть g^R(A) и g(x)^0yПусть f^B(A) и
m=inif(x), Af=supf(x), причем f-g^R(A). Тогда существует
А А
число и, такое, что причем Sf-gdx=y,-fgdx. Если А=К.
А А
является компактным связным множеством (из Rn_) и feC(K)),
то существует точка с<=К такая, что
Sf-gdx=f(c)-Jgdx.
к к
Доказательство. Введем на брусе /”{а, Ь] таком, что
АсАс1п[а, Ь], функции G=g-%A и Тогда из условий тео-
ремы имеем
G, F GeRfl^a, b], G(x)>OV xdn[a, b]
и FeB(/n[a, b]).
Очевидно,
m-G(x)^F(x) G(x)^M G(x) v xdn[a, b]^In.
Применяя теорему об интегрировании неравенств, имеем ..;
m • f G(x)dx < J F(x) • G(x)dx^,M • J G(x)dx.
in i" in
Если f G(x)dx =Q, то Уцерп, M] имеем равенства
in
0 = J F(x) •G(x)dx=^. - J G(xJdx=O.
in in
Если же j1 G(x)dx>Q, то
1я
m < f F(x) - G(x)dx/ f G(x)dx <
in Iя
т. e. существует число p.=TF(x} G(x)dx/iG(x)dx, удовлетворя-
Iя in
условию для которого имеем равенство
J / • g dx = р. • f gdx.
А А
Теперь рассмотрим' функцию f^C(K). Поскольку множество К
компактно и связно, то в силу теоремы Больцано (о проме’жу-
314
точных значениях непрерывной функции на связном множестве)
существует точка такая, что ?(с)=1ц^[т, М]. (Напомним,
что в силу компактности множества К из теоремы Вейерштрасса,
следует, что числа т и М являются значениями непрерывной на
к функции /.) Итак,
f f(x) • g(x) dx — f(c) • J g(x)dx.
£ К
Следствие (теорема о среднем). Пусть 4czRn — измеримое
по Жордану множество и f^R(A), причем m=inff(x), М—
==supf(x). Тогда существует число у. такое, что и
А
J fdx=p,-|.A |п. Если А=К — компактное, измеримое по Жорда-
д
ну связное множество и f^C(K), то существует точка с<=К такая,
к
§ 2. Сведение кратных интегралов Римана к повторным
Рассмотрим функцию feB(7n[a, 6]), для которой всегда суще-
ствуют как верхний, так и нижний интегралы Дарбу
7 = tZ J f(x)dx^] fdx-,
Jn[a. »] l"
J — L f f(x)dx = f fdx.
ln{a. b]
Замечание. Если f^R(In[a, &]), то в силу критерия интег-
рируемости по Риману (на брусе) из гл. 1, § 2, имеем
J fdx = j fdx= J fdx.
Iя in
Теорема Фубини (о сведении кратного интеграла Рима-
на к повторным). Пусть In\a, &]czR”, Im[c, d]cRm и 1п\а, &]Х
d]a:Rn+’n — брусы в пространствах Rn, Rm и Rn+m соот-
ветственно и f^R(In[a, b]/^Im[c, t/j). Рассмотрим функцию fx(y)>
определенную на брусе Im[c, d]VxE/n[a, b] равенством fx(y) =
~f(x, у), где х=(хъ .... хп)> У=(Уъ Ут) и положим
L(x) - £ fx(y)dy— £ f(x,y)dy;
Im[c, d] Im[c. d]
U(x) = f fx(y) dy= f f(x, y) dy.
Im[c, d] 7m[c, d]
Тогда U(x), L(x) ^R(In\a> b])9 причем имеют место равенства
315
JJ f(x,y)dxdy— j* U(x)dx —
ln{a,blxlmlc,d] Ла, b]
= f dx J f£x,y)dy,
In\a,b\ /m[c, d]
П f(*> y)dxdy= J L (x) dx = J dx f f (x, y) dy.
laxlm la In im
Доказательство. Пусть T=(Ti, T2) — любое разбиение
бруса In[a, &]XZm[c, d], состоящие из частичных брусов
Л/*л)= А") X J(”). где {/".J соответствуют разбиению
TJe>) бруса 1п[а, Ь], а соответствуют разбиению
T£w>) бруса Im\c, d], причем, очевидно,
ИоЛо|л+л1вК(/)|л ' 1А*)1т’
Заметим, что
i/D-Sramt/; /;,+»",) |'ГЧ|Я) -1'5.1»
и) vK* /
И
Но V х° е /•> имеют место оценки
m(f; inf f(x°> 1^)
и
M(f> SUP 7w)-
Кроме того, V x e имеем
Sfx(T2) = Sm(/x; /-) • |/&|„ < sup Sfx{T2) = L(x) < U(x)>
(ft) 7*>
поэтому для любого бруса и V.ve 7(п0 имеем
• US.U /Т.ХВД,
(К)
откуда для любого получаем оценку
3m(f; AW • 1Л")1»< inf L(x)^m(L;
m «er}})
Аналогично, для любого бруса имеем оценку
3W; ед) • ИГ«1м> SUP U(X) = M(U- i^).
(Ю
Но L(x)^.U(x)Nx s In[a, b], и поэтому для любого разбиения
f ----- (Tt, Tt) бруса /п[а, b] X 1т\с» d] имеем оценки
SXn<Sm(L; •|/(})ln = £i(T1)<Si,(7’1)<Mrt)
и
S/Г) >МГ1)>Зр(Г1)>5£(Т1).
Таким образом, для любого разбиения Т=(Ти Га) бруса
Jn[a, b]Xlm[c, d] имеем
Sf(T) < < Sl(Ti) < Sf( T),
откуда Q^TiXQ/T). Аналогично оценки
S/Г) < 3У(Л) < SuiT^ < S^T)
дают &у(Г1Х Qf(T). Но
f e<[a, b]Xlm{c, d])
и в силу критерия Дарбу (интегрируемости по Риману на
брусе) имеем
(inf Q АТ) = 0)=^ (inf ЙД 7\) = inf ЙД7\) = 0).
Г Тъ Т
Вновь применяя критерий Дарбу (интегрируемости по Риману
на брусе), получаем L, U s R(In[a, 6]). Далее, поскольку f е
« Х(1п[а> Ь] X 7OT[c, dj), то
inf37(Т) = supS_f(Т) = J = Я /(х, y)dxdy,
т Т lnla,b]Xlmlc,d]
откуда
(З/ТХЗД^Х у Z(-x;dx<5HT1x
/п(а, Ь1
< S/TX (sup Sf(T) = f L(x)dx = inf SAT) = I)
T ~ Jn(a.b] T
я аналогично
(Sj{T) < Su^T^ < f U (x) dx < SutTJ <
7П(«. Ы
<sxr))=>( j* U(x)dx = J\.
\ /п1а. И /
317
3 амечание. Аналогично при доказывается
равенство
я f(x.y)dxdy =
ln[a, blx/m[c, 4]
= f dy J f(x,y)dxdy =
Jm[e, d] In[a,b]
= J dy £ f(x, y) dx.
lmle>d} /«[a. b]
Замечание. Теорема Фубини доказана лишь в предположении,
что feR(InXJm), и тогда имеет место равенство двойного и пов-
торных интегралов. Из существования повторных интегралов, во-
обще говоря, не следует существования двойного интеграла (см.
[4] (пример 22).
Замечание. Поскольку при feR(In[a, Ь]Х^т[с> dp из тео-
ремы Фубини имеем L(x), U(x)eR(ln[a, &] и
J L(x)dx— f U(x)dx,
/n(a. b] ln[a, b]
то полагая e={xe/n[a, b]\U(x)>L(x)} и используя теорему
12 § 1, видим, что условия U(xj — L(x) > 0 Vxe ln\a, 6] и
Г (U (х)—L(x)dx — 0 дают mes# = 0, т. е. функции U(x)
Inla,b]
и L(x) могут отличаться на брусе 1п[а, &] только на множест-
ве % = {х е In[a, b]IU(x) ^L(x)} n-меры нуль, так что U(x) =*
= L(x)V хе 1п[а, &]Х$, т. е.
fxeR(Im[c, d]) Vxe=/n[a, &]\£,
где mes§’ = 0.
Следствие 1. Если f^R(In[a, b]Xlm[c, dp и Vхе
eln[a, Ь]\#, где множество S имеет n-объем нуль (| #.|п=0),
fx(y)eR(lm[c, dp, то
Я 1(х> у) dx dy dx j* f(x, у) dy.
inx/m Iя im
В самом деле,
L(x) =U(x) = J f(x, у) dy=0Vxe S,
lmlc, d]
причем в силу теоремы Фубини LeR(In[a, &]). Если изменить
функцию Ь(х) на множестве ё, имеющем n-объем нуль (($|п =
=0), положив, например,
318
L(x)= j" f(x, y)dy = 0 V.ve S,
то в силу теоремы 9 § I будем по-прежнему иметь равенство
J L(x)dx(= Г dx f f(x,y)dy\ =
1п[а, Ь] \ /п\е 1т /
= g f(x, у) dx dy.
lnxlm
Следствие 2. Пусть f^R(In[a, b]XIm[c, dp и fx(y)<=
eR(lm[c, d]) для всех точек бруса In[a, &], за исключением ко-
нечного их числа {х>} (/=1, 2, М), тогда
П f(xty)dxdg=j dxj f(x,y)dy.
1пХ1т ln lm
Теорема Фубини (для непрерывной функции). Если
feC(7n[a, b]XIm[c, d]), то
И f(x> у) dx dy = J dx J f(x, y)dy=
lnla,b]xlmlc,d] ln\a.b] lm\c, d]
= J dy J f(x, y) dx.
Imlc, d] ln[a, b]
Замечание. Если f^.R(InXIm) и fx(y)^R(Im) Vx^In\<£ ,
где множество $<^In имеет л-меру нуль (mes $=0), но не име-
ет n-объема нуль, то в теореме Фубини нельзя, вообще говоря, за-
менять верхний (U(x)) и нижний (L(x)) интеграл Дарбу на ин-
теграл Римана
,т
‘ (О xeg
(сравните следствие 1).
Пример. Рассмотрим функцию, определенную на брусе
(квадрате)
/2=/2(0, 1]=[0, 1]Х[0, 1]:
1, если х иррационально и у любое,
.__ 1, если х рационально и у иррационально,
'' ’ 1—1/</, если x=p!q — несократимая дробь
и у рационально (р, <?eN).
Легко проверить (сравните исследование функции Римана из
[1], ч. II, гл. 2, § 6), что множество Е={(х, y)^I2\x=p/q^Q., у^
€ОП[0, 1]} является множеством всех точек разрыва функции
f(x, у) на I2. Поскольку Е счетно, то mesE=0, и, учитывая, что
п
319
f^B (I2), получаем (в силу критерия Лебега, интегрируемости
по Риману на брусе) f^R(I2). Но f(x, y) = W (х, у)^12\Е и поэ-
тому в силу следствия к теореме 13 видим, что
ff f(x, y)dxdy= If \dxdy=A.
/*[о, *1 /’io. u .
Далее, для любого разбиения Т2 отрезка [0, 1] с частичными от-
резками Ij=[yj-i, У;], очевидно, имеем sup fx(y) = l v xe[0, 1],
»е//
так что
tf(x)=infS/x(T2)-I
т, Jx
и
ыл(9)=(’ «г<?-<гто,1]
№i, I!-(!/«), x-PlieQ,
так что
Z(x) = supS. (Т4) = I { „ л
' 7 т. *' (1—(1/<7), x~p/qc=Q
есть функция Римана на отрезке [0, 1]. Но тогда Аей[0, 1]
« (по теореме Фубини)
Wf(x,y)dxdy=* $ L(x)dx = l. (2.1)
р [o.ii :
Очевидно, L(x)^U(x)Nx^Q и поэтому fx(y) е ЯДО, 1] VxeQ,
где (в силу счетности Q) mes(? = 0, причем множество Q не i
имеет 1-объема нуль. Если попробовать теперь в равенстве 1
(2.1) заменить (как в следствии 1) функцию L(x) нулем в точ- •?
«ах Q, то получим функцию Дирихле
I 0, xeQ,
не интегрируемую по Риману на [0, 1].
Замечание. Если f^R(7n[a, b]) и функция f(x) достаточно
«хорошая», например, f<=C(ln[a, 6]), то повторное применение
теоремы Фубини, дает равенство
j f(x) dx =
In[a. ы
ь, ь, ья
= f f(xi, x„)dxn.
ai аа ал
320
Замечание. Теорему Фубини можно использовать и для
вычисления кратного интеграла Римана И f(x, y)dxdy, где
АхВ
Aaln[a, Ь], Ва!т[с, d], если воспользоваться формулой (из оп-
ределения Римана на ограниченном множестве)
Я f(x, У) dx dy=-
АХВ
== Я f(x, у) • Хахв(х, у) dxdy.
2n[e, &]X/m(c, d]
Замечание. Пусть feC(Rn) — финитная непрерывная
функция е компактным носителем Kc:Rn (так что/(х)=0 Vxeft).
Тогда в силу компактности К в R" существует замкнутый брус
7«[а, 6] такой, что K<z/n(a, b), и поэтому р(К, д!п[а, Ь])>0. По-
скольку feC(Rn), то fy_K^C(In[a, &] и поэтому можно поло-
жить
J f(x) dx= f f(x) • 7.K(x)dx — f fdx.
Rn In(a, я к
Теорема Фубини (для непрерывной финитной функции).
Если feC('RnXRnt) — финитная функция, то
Я f(x> У) dx dV —
RnXR««
= f dx f i(x,y)dy= f dy f f(x,y)dx.
Rn Rm Rm Rn
Доказательство. Без ограничения общности можно счи-
тать, что компактный носитель Kn+mc:Rn+’n для функции
^C(R"XRto) имеет вид Kn+m==KnXKm, где Кп<=.1п(а, Ь) и Kmcz
<zlm(c, d) — компактные множества из Rn и Rm соответственно.
Тогда
%к„+т (х, у) = Хк„ (х) 7.кт(у),
f -XKn+meC(r[a, b]Xlm[c, d])
и по теореме Фубини для непрерывных функций имеем
Я fdxdy=* Я f- K.Kn+mdxdy =
RnxRm In[a, b]Xlm[c, d\
e f 7.Kn(x)dx f f(x,y) К.кт(у) dy =
In[a, b| I [c, d]
= f dx f fdx.
R» R“
~ Л. И. Камынин 321
Теорема Фубини (для цилиндроидов). Пусть множество
ЛсдНп+1 есть цилиндроид, т. е. А={(х, y)eRnXR|<Pi (x)<.y<Z
<.ц>2(х), xe=QczRn, где QczR” — измеримое по Жордану множе-
ство u_cpi:Qc:Rn-> R, <р<еС(й) (i=l, 2). Если f^B(A)/\C(A), то
f^R(A), причем
И fCx, y)dxdy= f dx ’ f (x, y) dy =
Л n <h(*>
фа(*)
= f dx / f(x, y)dy.
Q Ф,(х)
Доказательство. Поскольку множествуQczRn измеримо
по Жордану, то |дй|п=0, причем множество й также измеримо^
по Жордану в Rn, а потому ограниченно, так что существует брус
/”[а, 6] такой, что Qc:Qc:Zn('aA b). Но тогда множество й ком-,
пактно в R”. Далее, <р,еС(й) (i=l, 2), поэтому множества
<р((й) (fed, 2) компактны в R_h существует отрезок [с, d] такой,
что c<Ztf>i(x)^sp2(x)<.dУхей. Пусть Г(—{(X t/)eRnXR|f/=i
=qn(x), хеЙ} — график функции <рг (i=l, 2). Поскольку <р;<5
еС(Й), то в силу теоремы о «мере графика» из гл. 1, § 3 имеем
mesГ/= |Г,|п+1=0 .(7=1, 2). Заметим, что дА —Г^ГгУГз, где
714-1
Г3с:дЛХ|А </]. Докажем, что
|<ЭйХ[с, d]|»+i«0.
В самом деле, равенство |<?Q|n=0'означает, что для любого
е>0 существует конечное покрытие множества <?Й брусами
7" (k= 1, 2,..., /п(е)) такое, что
m(s) m(t)
ай С U и S |J?|n<e/(d-e).
k=,i
Но тогда, рассматривая (п4-1)-мерные брусы
jn+i = 7"X[c, d] (й==1, 2,..., m(e)),
видим, что
m(s)
айх[с,. djczu/r1’
причем
т(е) m(t)
2 |J«+</n+1=(d-C) . 3№<8.
*=! fc=l
322 1 . J
В силу произвольности е>0 имеем |дЙХ1А d]|n+i=0, откуда
имеем |Гз|п+1=0. Но тогда |<M|n+i=0, т. е. множества А и А
измеримы по Жордану в R”*1. Если Е/ — множество всех точек
разрыва функции f(x, у) на множестве А, то из f^B(A)/\C(A)
вытекает, что EfCzdA, | Ef | п+1=0, т. е. в силу критерия Лебега
(интегрируемости по Риману на измеримом _по Жордану множе-
стве) f^.R(A). Заметим, что множество А—{(х, у)^1п[а, &]Х
Х[с, d]\c<Zq>i(x)<Zy<Z<f>2(x)<d, xeQdn[a, b]} есть цилиндроид,
так что, в частности, V (х, у)^/п[а, b]X[c, d] имеем
У.д(х,У) =
0, хе ln[a, b]\Q, Vyt=[c, d],
0, xsQ при #<=[£,. d]\[<Pi(x), <р2(х)],
1, хей, у е= [фх (х), <р2(х)1.
Но тогда, полагая при фиксированном хе=7”[а, Ь], 1х(у) =
s (Хд)х(У) = Хд(Х У) v У е Iе- db имеем
1, если хей и y<=[<Pi(x), <p2fx)],
j (ц\ = . 0> если ХЕ_/П[а, £>]\£2, Чу е [cd]
х или хей, но i/е [с, dlXJqjjfx),
<P»(X)L
Тогда У(х, у) е 1п[а, Ь] X [с, d] имеем представление Хд(Ху,)“
— %а(х) * ЫУ)- Поскольку множество Лс/П[а, Ь]Х[с, d] изме-
римо по Жордану и f s Д(л), то f • xj J?(7n[a, b]X [с, d])»
причем для любого фиксированного х е 7п[а, Ь] имеем
(f -^)x(y)=f(x,y) Уъ(х) -1х(у).
В силу теоремы Фубини для брусов имеем
^f(x,y)dxdy= JJ f(x,y) • Хд(х> У) dxdy =
А /п[а, Ь]Х{с, d]
= f dx J (f • xx)x(y) dy =
7n[a.b) (c, d|
= f y.n(x)dx J f(x,y) • Ix(y)dy.
Inla, b] [c, dl
Из условия ^еС(А) следует, что v хе/п[а, b]\dQ множество то-
чек разрыва функции f(x, у)1х(у) на отрезке {х}Х[с> d] состоит
не более чем из двух точек (х, q>i (х)) и (х, <р2\.х)), поэтому
*\х> y) Ix(y)^Ry[c, dj, так что V хе/п[ц, Ь]\Эй имеем равенство»
J Кх> У) ‘ 1*(У) dy = \ f(x, у) - Ix(y) dy.
[с, d] с
2И
32»
Но поскольку |dQ|n=0, то в силу следствия 1 к теореме Фубини
(для брусов) имеем (вспоминдя определение функции 1х(у)) ра-
венство
Л f (х. y)dxdy= f 7.u(x)dx f f(x, у) • Ix(y)iy=
A ln[a, b] c
def p с
= fdx J f(x, y)dy — \ dx f f(x,y)dy.
О n C₽t(x)
Следствие. Пусть Acl^a, ft] и fdl(A)/\C(A), причем
A={(x, y, z)f=I3\a, b]|a3<zi(X t/)<z<z2(X «/)<6з; a2<.yx(x)<z
<У<Уг(х)<Ь2; ai<xi<x<zx2<bi}, где функции zk(x, у), yh(x)
(^=1^2) непрерывны в своих областях определения. Тогда
f^R(A), причем
Xi У2<Х) z,(x. у)
j'JJ/fx, у, г) dxdydz =• j dx j dy [ f(x,y, z)dz.
A xt yt(x) y)
Теорема Кавальер и. Пусть множество Adn[a, b]X
XImlc> d] измеримо no Жордану в Rn+«* и Jm(x°)={x°}X^m[c, d]v
х°е/п[а, Ь]. Если множество A(x)=A(\Jm(x)c.{x}XRm измеримо
no Жордану в RmV xdn\a, b], то |A|n+m= X [A(x)]mdx.
/”(«. b]
Доказательство. Заметим, что Xa(x, у) — Ха(х)(у)'-Х
Хх/п(а.ы(х). По условию Ха(х, у) R(In[a, b]Xlm[c, d]) и
Vx<=In[a, Ь]хл(х)(у) ^Ry(Im[c, dj), причем
И(х)|т - f Хаю (y) dy.
Но тогда по теореме Фубини для брусов имеем
|A|a+m= JJ ха(х, y)dxdy=>
lnla,btxlm[c,d]
= f dx j" ^A(x, y) dy -
ln[a, b] Im{c, d]
= f y.ln[a,b](X)dX f *A(x)(y)dy =
Inla. b) Im[e, d]
= f \A(x)\Mdx.
ln\a, b]
Следствие. Пусть множество Adn[a, b]XIm[c> d] измери-
мо по Жордану (в Rn+m) и IA(x) |m=0 v xdn[a, Ь]. Тогда
| A | n+m==0-
Замечание. Если множество А не измеримо по Жордану
в Rn+m, то утверждение следствия, вообще говоря, неверно.
324
Следствие (принцип Кавальери). Если множества A, Bcz
cz/n[a, b]XIm[c, d] измеримы по Жордану (в Rn+’n) и |Л(х)|т=:
== |В(Х)|mV х^1п[а, &]. Тогда |Л|п+т= |B|n+m. (Таким образом,
если площади сечений двух тел совпадают, то совпадают и их
объемы.)
Пример. Рассмотрим брус 1п[а, Ь]=[аь bi]X-X[an> Ьп}^
*з1п-'Х[ап> М и параллелепипед /п с тем же основанием /п~*
и с той же высотой h=bn—ап. Тогда |/n|n = |/n[a, Z>]|n.
§ 3. Несобственные интегралы Римана
на открытых множествах из R”
До сих пор изучались интегралы Римана для функций fe
b]) или f^R(A). Множество ^czR” предполагалось при
этом ограниченным, а для функции f:/lc:Rn->R в силу необходи-
мого условия интегрируемости по Риману f^R(A) следовала ог-
раниченность этой функции на множестве А. Обобщим теперь по-
нятие интеграла Римана на неограниченные области GcRn и на
локально ограниченные на G функции f. В дальнейшем будут не-
обходимы понятия и результаты из [1], ч. III, гл. 2, § 12. Напом-
ним некоторые из них.
Определение. Пусть множество AcRn и {Qa} — открытое
покрытие множества А. Разбиением единицы класса для А,
подчиненным этому покрытию, называется не более чем счетная
система функций {ei(x)} (i=l, 2, ...), егеС(оо)(£2) (где ЙзэД —
некоторое открытое множество) такая, что: 1) 0^е((х)^1 v xeQ
и для любого I, причем = l V 2) для любого i носи-
i=i
гель (suppe,) функции ei(x) является компактным множеством,
причем семейство {suppej образует локально конечное покрытие
множества А, так что каждая точка х°еД имеет окрестность
Шр(Х), в которой лишь конечное число функций ei(x) не равно
нулю тождественно; 3) v I я а такое, что supp егс:йа.
Теорема (о существовании разбиения единицы). Если Ас
и {йа} — любое открытое покрытие множества А, то сущест-
вует разбиение единицы {е,(х); i=l, 2, ...} для множества А
(класса подчиненное этому покрытию. (Доказательство
проведено в [1], ч. III, гл. 2, § 12.)
Замечание. Если KcMcR™ и множество К компактно, а
\е>(х)} (i==l, 2, ...) — разбиение единицы для множества А, под-
чиненное открытому покрытию {(/,} (i—1, 2, ...) (suppV г),
То лишь конечное число функций et(x) не равно нулю V х^К,
е- Kfisuppе/=И=0 лишь для i=ih (k=\, 2, ..., пг), причем
Lie4 <x) = lvxeK.
Теорема (о разбиении единицы, индуцируемом диффеомор-
физмом). Пусть G и $— открытые множества из Rn и отобра-
зи
жение <p: GcRn .3? =<p(G)c:Rn является диффеоморфизмом
+oo
класса Пусть & = U Uif где {Ui} — открытое покрытие ц
i=l
{6i(x)} (i = l, 2, ...) — разбиение единицы для множества
подчиненное этому открытому покрытию, причем supp eiaUi Vi.
Тогда G=\JVi, где Vi=<p~'(Ui) — открытые множества и систе-
ма {si О <р(/)} является разбиением единицы для множества Q
(класса С(1\), подчиненным открытому покрытию {К}, причем
supp Ci О (рой, V i. (Доказательство см. в [1], ч. III, гл. 2, § 12.)
Замечание. Поскольку в R" есть счетная база, то в силу
теоремы о выделении счетного подпокрытия (из ч. V, гл. 1, § 3) в
определении разбиения единицы можно считать, что открытое по-
крытие {йа} заменено на не более чем счетное открытое покрытие
{Q(} (i=l, 2, ...), причем supp V Л
Замечание. Поскольку в R” существует учетная база, со-
стоящая из открытых брусов (или из открытых шаров), то для
любого открытого множества GczRn существует не более чем
счетное покрытие {/"} (i=l, 2, ...) брусами (такое покрытие мож-
но выбрать даже локально-конечным) такое, что G— 1|/?= (J/’,
причем каждый брус /? измерим по Жордану. По теореме о су-
ществовании разбиения единицы для множества G существует
разбиение единицы, подчиненное покрытию {//}.
Определение (Е). Пусть GczRn — открытое множество,
на котором определена локально ограниченная числовая функция
f: Gc:Rn-*-R, множество точек разрыва которой Ер={х&
<=G|®(7; x)>ty имеет п-меру нуль (mes £/=()). Допустим, что
п
G = \]J?, где открытые множества JfczG измеримы по Жордану,
z=i ‘
и {ei(x); 1=1, 2, ...} — разбиение единицы для множества G, под-
чиненное открытому покрытию {/"} (причем supp ejcz/j1 V i). Тогда
интегралом Римана S fdx функции f на открытом множестве G в
G
смысле (Е) называется сумма ряда
5 f ejx) • f(x) dx =
i=l G
= 2 j et(x) f(x)dx=$ fdx (3.0
<=i j? °
в случае, если ряд (3.1) сходится безусловно (а потому и абс&
лютно). Запись: f<=R(G) (в смысле (Е)).
326 • .
Определение (АЕ). Пусть числовая функция f, откры-
тое множество G— U /z<=Rn и соответствующее разбиение еди-
ницы {et(x)', i=l, 2, ...} те ясе, что и рассмотренные в определении
(Е). Тогда функция f интегрируема на открытом множестве G в
смысле (АЕ).если: 1) функция f интегрируема на G в смысле
(Е) (т. в. f^R(G)) в смысле (Е)) и 2) сходится ряд
Y° J ei(x) • |f('x)|dx= f \f\dx. (3.2)
°
Запись: f^R(G) в смысле (АЕ).
Замечание 1. Если f^R(G) (в_смысле АЕ)), то из сходи-
мости ряда (3.2) вытекает, что |f|e7?(G) в смысле (Е) и по-
скольку из сходимости знакоположительного ряда (3.2) вытекает
абсолютная (а потому и безусловная) сходимость ряда (3.1), то
f^R(G) и в смысле (Е).
Замечание 2. Ниже будет доказано, что значение интеграла
Jfdx из (3.1), существующего в смысле (АЕ), не зависит от вы-
•G
4-00
бора как представления G=(J^/> так и разбиения единицы
Х=1
{ei(x); 1=1, 2, ...}, подчиненного открытому покрытию {If}.
Теорема (о корректности определений (Е) и (АЕ)). Опре-
деления (Е) и (АЕ) интегралов S fdx и / |f|dx в случае f^R(G)
о о
(в смысле (Е)) или f^R(G) (в смысле (АЕ)) корректны, т. е. для
любого I имеем
f-er,
Доказательство. Поскольку et^C(G) VI, то
£f.e. = {xe7?Mf • et; х) >0}CZ Jf,
откуда
(mes Ef = 0) =» (mes Ef.e.—ty Vt.
Вспоминая критерий Лебега интегрируемости функции по Риману
(на измеримом по Жордану множестве), видим, что в силу изме-
римости по Жордану множеств и условия mes£f.ei=OVi для
п
Доказательства соотношения f • егЕЕ i достаточно пока-
зать, f et е B(J?) V i или (поскольку erfx) = 0 Vx е supp et) доста-
327
точно показать» что f ♦ eteB(Ki)Vi, где множество supp б|
компактно (в Rn) и KJ<=7"CZGV I. Но функция f(x) локаль-
но ограничена на KjCZG и поэтому для любой точки х0^К{
существуют окрестность U(x°) и постоянная Л/(х°)>>0 такие*
что
|Rx)|< Ж(х’) VхеG(x°)ПKi.
Из открытого покрытия U tZ(x°)Z)^j в силу компактности
x‘e«i
m
множества Kt можно выбрать конечное подпокрытие U G/ —>
T)Kt. Положим М = max Л4/, тогда |f(x)l< М Vxe Ki, т. е.
1=1, 2,..., т
f • G B(J“)N i. Итак, f • е< е R(J")V i, откуда |/| •
efl(/;)Vi.
Замечание 3. Если в определении (Е) открытое множество
G не ограничено или функция f(x) не ограничена на множестве
G, то интеграл S fdx из (3.1) (если он существует) называется не-
G __
собственным. Если при этом |f| ^R(G) (в смысле (Е)), то несоб-
ственный интеграл Sfdx из (3.1) называется абсолютно сходя-
о
щимся (на G) (при этом, очевидно, сходится и ряд (3.2), так что
f^R(G в смысле (АЕ)).
Замечание 4. Н определениях (Е) и (АЕ) в качестве мно-
жеств 7" можно брать открытые брусы I"cG и считать при этом,
что
G = и I? = и Л" и supp^c/fC/fCZG V i,
i— 1 i= 1
Определение. Система компактных множеств {К/} (7=*
= 1, 2, ...) называется исчерпывающей системой (компактных
множеств) для открытого множества GdRn, если
и KidKi+ic:Ki+i v teN.
(Отметим, что, как показано в [1], ч. III, гл. 2, § 12 для любого
открытого множества GczR” существует исчерпывающая система
компактных множеств {7<7} (7=1, 2, ...).)
Замечание 5. Пусть GazRn — открытое множество в
f^R(G), т. е. интеграл ffdx существует в смысле определения
G
328
(Е)> так чт0 Ряд (3*1) сходится безусловно, а потому и абсолют-
но, причем {е,(х)-, i=l, 2, ...} — разбиение единицы для множест-
ва G, подчиненное открытому покрытию {/"}, так что suppezd
cz/’cGVt. Пусть {Кг} (/=1, 2, ...) — исчерпывающая система
(компактных множеств) для открытого множества G, так что
Ki CZ К/4-i CZ Ki+i V /;
4-ос 4-оэ о 4-оо 4^»
G=U Кг = и K/ = U = U suppez.
/=1 ^=1 i—I 2=1
Из замечания к теореме о существовании разбиения единицы,
следует, что в силу компактности множества KzczG(vZ) имеет
KzAsupp лишь для конечного числа индексов i=i\; k=>
г=1, 2, ...» т(1). Тогда
»>(') г
•>„ f(x) (x)dx
ч
есть частичная сумма ряда, полученного из ряда (3.1) путем неко-
торой перестановки его членов. Но в силу определения (Е) ряд
(3.1) сходится абсолютно и имеет суммой число I fdx, поэтому в
о
силу теоремы Дирихле — Римана (из ч. IV, гл. 1, § 6) из бе-
зусловной сходимости ряда (3.1), имеем э lim Ai—ffdx, при-
/—* 4-qo G
чем этот предел существует для любой исчерпывающей системы
{Кг} для открытого множества G.
Лемма (об основном свойстве исчерпывающей системы ком-
пактных множеств). Пусть {Кг} (1=1, 2, ...) — исчерпывающая’
система компактных множеств для открытого множества GcRn а
KczG — любое компактное множество. Тогда существует индекс
/о такой, что K^Kt, czKi. • Ji
Доказательство. По условию имеем К С G = (J /С/. В си-
г«1
ЛУ компактности1 множества К из открытого покрытия {К/}
можно выделить конечное открытое подпокрытие {К^} (s —
48 Ъ 2,..., m): (J Kz ЭК. Положим l0 = max ls, тогда из ус-
s=l s s—l, 2.т
л°вия KzcKz+iV/ имеем (s = 1, 2,..., т), т. е- Кг =
_.т, о о
"U К, ЭК, откуда К/.ЭК/.ЭК-
Ss==l
329‘
Определение (К). Пусть GaRn — открытое множества
и f : GczR”-»- R — локально ограниченная на G функция, для ко-
торой множество всех ее точек разрыва EfdG имеет п-меру нуль
(mes £7=0). Функция f интегрируема на открытом множестве G
п
в смысле (К), если для любой исчерпывающей открытое множест-
во G системы компактных, измеримых по Жордану множеств .
{ТС} имеем: 1)
Я lim j f(x)dx==- f fdx
'-+«> к, J
и 2)
Я lim f If (x)\dxd^ f
z-+oo Kt ъ
(так что числа J fdx и ,T|f|dx не зависят от выбора исчерпываю-
G G
щей открытое множество G системы компактных множеств
{К,}).
Замечание (о корректности определения (К))- Определе-
ние (К) корректно, так как при любой последовательности ком-
пактных множеств {ТС} (/=1, 2, ...), измеримых по Жордану и
исчерпывающих открытое множество G, имеем f, |f [ eR(Ki) Vi*
В самом деле, множество Ki измеримо по Жордану для любого
£ Функция f(x) локально ограничена на GzzKi, поэтому в силу’
компактности Ki имеем f^B(Kt) v I. Далее, если
£z={xeG|e>('f; х)>0}
я
^>s{xeKz|«»(f; х)>0} (/=1, 2,...),
то £]!) (Z VZ и тогда из условия mes £7 = 0 имеем
mes £р = 0 V I. Используя критерий Лебега интегрируемости по
Риману (на измеримых по Жордану множествах), имеем f, If Iе
eR(Kt) v I.
Замечание (см. Приложение I). Можно доказать, что если
для любой исчерпывающей открытое множество Gc:Rn системН
компактных измеримых по Жордану множеств {ТС} (Т=1, 2, ..•)
существует предел
lim у f(x) dx= J fdx,
Z-+oo JK[ G
где число J fdx не зависит от выбора исчерпывающей систе-
G
мы {К/}, то
ззо i
Я lim J \f(x)\dx= f Iflcfc
Z“*+°°K2 G
и число J \f\dx не зависит от выбора исчерпывающей системы
G \
Ш-
Теорема (достаточное условие существования интеграла
Римана в смысле определения (К)). Рассмотрим открытое мно-
жество GczPn и функцию f:Gc:Rn -> R, локально ограниченную
на G, множество всех точек разрыва которой Ef имеет п-меру
нуль. Пусть {&} (Z=l, 2, ...) — некоторая, исчерпывающая мно-
жество G система компактных, измеримых по Жордану множеств,
такая что
Я lim f
/-н» tr
Тогда существует интеграл Римана $ f dx в смысле определения
а
(К), причем
J fdx — 11m j f(x)dx.
O l-»+oo
Доказательство. Положим
£i= lim f \f(x)\dx.
Z-*4-oo -
Заметим, что
k/+I = KlU U (Km+i\Rm),
причем в силу измеримости по Жордану множеств Кт видим,
что множества Kmx-i\Km также измеримы по Жордану, причем
Жт+1\Кт)|П = 0. НО тогда в силу критерия существования
предела у монотонной возрастающей числовой последователь-
ности имеем
L0 = supJ |f('x)|dx=f
1 Ki *1
+ Й° f \f(x)_\dx.
оценки
331
|J f tf(x)ldx vl
вытекает абсолютная сходимость ряда
f(x)dx+^ f f(x)dx = L
KZ+1\K,
так» что
Я lim f f(x) dx=L.
l-> 4-00 ~
+°°KZ
Пусть теперь (Ks) — любая последовательность компактных,
измеримых по Жордану и исчерпывающих открытое множест-
во G. Тогда
-J-OO 4-00 О 4-°° +°° °л
G— U и К,= и кг = и Kb
s=I s=l 2=1 1=1
Ks CZ Ks+1 v s; kt c Kz+i V I
и поэтому в силу леммы (об основном свойстве исчерпывающей
системы компактных множеств) VsS.l(s) такое, что KjCzKz(S),
откуда имеем оценку
sup f |f (х)\ dx < sup f |f(x)\dx =Llf
s Ki 1 ii ''
и аналогично по той же лемме VZ3s(Z) такое, что К/СКщг»
откуда имеем оценку
sup f If(x)|dx>supJ |f(x)|dx = Llt .
s Ks 1 Kt ,
t. e. для любой исчерпывающей последовательности (KJ
Я lim f \f(x)\dx—Lt. (3.3)'
s— +»kJ
Но тем самым наша теорема доказана для знакопостоянных функ- ;
ций f(x)^O (^0) V х <= G.
Осталось заметить, что для знакопеременной функции f(x)
имеем представление f(x)=fi(x)—f2(x)Vx^G, где функций
fi(X) = |f(x)| и fz(x) = \f(x) |—f(x) неотрицательны на G, причем
в силу оценки 0^f2(x)^2|f(x) | VxeG имеем 0^ S f2(x)dx^
Kt
^2Li v I. Но тогда в силу существования предела у монотонно
возрастающей, ограниченной сверху числовой последовательност»
имеем
Я lim f ft(x) dx = Lt.
^^'kt
332
Поскольку f2(x)>0 v х <=G, то как показано выше
Я lim f f2 (%) dx = Lz. (3.4)
S-»+oo jf
Но тогда, учитывая равенство
J fi(XMx=f fi(x)dx — J f2(x)dx
Ks Ks
В силу (3.3) и (3.4) видим, что
Я lim (J fi(x)dx — J f2(x)dx^ =
г= lim /[ fL(x)dx — f h(x)dx\ —Lt—L2,
)
t. e.
Я lim f f (x) dx =
£
— lim f f(x)dx ^L- Г fdx.
‘^+ookl g
Замечание. Если G=Rn\{0}, то в качестве исчерпывающей
множество G системы {Kt} часто берут систему шаровых слоев
Kt = {х е= R*|\ll < ||х||, </};/ = 2, 3.
Теорема (об эквивалентности определений (АЕ) и (К.)).
Если функция f: Gc=.R,n -> R (где G — открытое множество) ло-
кально ограничена на G и множество всех ее точек разрыва име-
ет п-меру нуль, то определения (АЕ) и (К) интеграла Римана на
открытом множестве G из Rn эквивалентны.
Доказательство. 1) (К) => (АЕ). Пусть существует ин-
теграл Римана f fdx в смысле определения (К), т. е. для любой
G
исчерпывающей открытое множество G системы компактных, из-
меримых по Жордану множеств {Ki} (/=1, 2, ...) существуют
пределы
lim f |f/X)| dx = Lo
/-►+«>
и
lim f f(x)d*~L, (3.5)
»-»+«>
333
где числа Lo и L не зависят от выбора исчерпывающей G системы |
' +оо
компактных множеств. {Kz}. Пусть 0=0^^. где J"— открытые,. (
<=1 *
измеримые по Жордану множества и {е<(Х); i=l, 2, ...} — разбие- '
ние единицы для множества G, подчиненное открытому покрытию, *
{/?}, причем supple/". Пусть {Ki} — фиксированная, исчерпыва-
ющая G система компактных множеств, измеримых по Жордану,,
так что
G= U К, = U kz, С kz+i С Ki+i V I.
1=1 z=i
Тогда в силу леммы (об основном свойстве исчерпывающей
$
системы) Vs£U(s) такое, что (J supp ez Q KZ(S и поэтому, учи-
»=1
тывая оценки
о <2 • If WK V X
Л=1
8 S
и включение (J supple (J J? имеем
i=I Z==l
-j-ОО 8
2 У e‘(x> -lf(W*=2 f *t(x) -\f(x)\dx*=
/=! Tn i=i s
1
= f ^^(x) • |f(x)|dx — J 2 ei(x) ‘\f(x>\dx<
s 1=1 S i==i
U Jn U supp ел
1=1 i i=l ’
< У 2eiW У \f(xj\dx
Kl(s) i*=l Kl(t)
откуда
SUP I 2 W.l fWIdx <sup f \f(x)\dx = L0,
* s Z=d 1 "K.
U J? ‘
Z=1 ’
т. e. знакоположительный ряд (3.2) (в силу критерия сходимости
знакоположительных рядов из ч. IV, гл. 1, § 4 сходится. Но
тогда f^R(G) в смысле определения (АЕ) и, в частности, абсо-
лютно сходится ряд (3.1), сумму которого обозначена через.
J fdx. Докажем, что (см. (3.5)) L=J fdx. Из (3.5) в силу крите-
G G
рия Коши (сходимости рядов), примененного к ряду
334>
J |fW|dx + 2 J \f(x)\dx = L0 = lira f \f(x)\dx,
fa Z-*+oo кj
видим, что V£>03;V(e)eN такое, что Vр>1 и Vl>N(e), име-
ем оценку
Z+P~ 1 г
2 _ I \f(x)\dx= f \f(x)\dx<e.
tn=I Km+l\Km Kl+p\Kl
В силу замечания к теореме (о существовании разбиения едини-
цы) Для компактного множества К/ существует конечный набор
индексов ik (k=\, 2, ..., m(7)_) такой, что Kzrisuppex=5fc0 при
i=ik (k=l, 2...tn (I)), причем
m(Z)
5 e‘k(x) = 1 * <5 K/-
MW
Положим M(l)= max i\, тогда K,C U Л» причем из леммы
R=»l, 2..........m(Z) i»l
(об основном свойстве исчерпывающей системы) следует* что
существует /?(/)> 1 такой» что
м(0
U.supp^ciKz+pU).
Итак,
/мю
U supp^
у ^'=== 1 >
19
причем
2 et(x) • f(x) =2 eih(x) • f(x) - f£x) Vx^K{
i—i »=i
(так что
Р г MU)
f f(x)dx=$ %et(x) -f(x)dx).
*•1 к I i=i
Пусть теперь f>AT(e), тогда в силу выбора N(e) имеем
М(1)
2J f(x) -et(x)dx-^ f(x)dx «
i=l J.” К.
I I
оценку
M
Mdt
2 eiM • f(x) dx <
i—l
J lfW|ax<s.
Ki+p(D\st
(3.6)
395
r
Но (см. (3.5)) lim f f(x)dx — L, поэтому для того же e>03
Z- +оо
Л\(е) <= N такое, что V7 > Л\(е), имеем оценку
И f(x)dx — E <е. (3.7)
К
Полагая
Mil)
sM(i)= 2 J f(x) * et(x)dx,
видим, что при любом />тах(У(в), ATi(e)) в силу оценок (3.6),
(3.7) имеет место оценка
т. е. Я lim
/—>-|_оо
Таким образом, существует подпоследовательность
частичных сумм ряда (3.1), сходящаяся к числу L из (3.5). Но
ряд (3.1) сходится и имеет своей суммой число Sfdx, поэтому
О
L=f fdx. Таким образом, (К) => (АЕ).
G
2) (АЕ) => (К). Допустим, что f^R(G) в смысле (АЕ). Тогда
+<»
сходятся ряды (3.2) и (3.1), где G— (J Jz и {e.-fx); 1=1, 2, ...}—
разбиение единицы для множества G, подчиненное .открытому по-
крытию {/"}, причем supp eiczJ’V i. Рассмотрим какую-либо ис-
черпывающую открытое множество G систему компактных, изме-
римых по Жордану множеств {KJ (1=1, 2, ...). Тогда, как было
уже отмечено, при любом I supp е,ПКг^0 лишь для конечного
набора индексов i=i* (&—1, 2, ...» т(1)), причем
т(')
2 %W = 1V
K=1
Из сходимости ряда (3.2) имеем оценку
j |f(x)|dx<2 У \f(x)\.-eik(x)dx^^ \f[dx,
К. К—1 J!1 G
* It,
т. е.
336
Я lim J |f(X).|dx =sup f lf(x)| dx <
КI 1 Ki G
Но тогда в силу достаточного условия существования интеграла
Римана в смысле определения (К) видим, что f<=R(G) в смысле
определения (К), так что существует lim J f(x) dx=L, причем,
повторяя доказательство, проведенное в 1) видим, что число L
является суммой ряда (3.1), т. е. L=ffdx. Итак, (АЕ)=ь-(К).
G
Следствие. Значение интеграла ffdx (из (3.1) при опреде-
G
лении (АЕ) не зависит от выбора разбиения единицы для откры-
того множества G.
Замечание. Значение интеграла ffdx из (3.1)) при опре-
G
делении (Е) зависит от выбора разбиения единицы для открытого
множества G, т. е. при определении (Е) интеграл Римана являет-
ся, вообще говоря, условно сходящимся.
Теорема (достаточный признак существования интеграла
Римана на ограниченном открытом" множестве из Rn_). Пусть
функция f: GczRn-*R (где G — ограниченное открытое множест-
во) ограничена на G (f^B(G)) и множество ее точек разрыва
имеет п-меру нуль. Тогда: 1) f^R(G) в смысле определений
(АЕ) и (К) (а стало быть, и в смысле определения (Е))\ 2) если
множество Gcz/n[a, Ь] измеримо по Жордану, то feR(G)/\R(G)
в обычном смысле, причем
$fdx=^f(x)dxE= J f(x) • xg(x) dx = $J(x)dx.
° G 1п[а. Я G
(Таким образом, введенное в определениях (Е), (АЕ) и (К) поня-
тие интеграла Римана на открытом множестве согласуется с ра-
нее введенным понятием интеграла Римана на ограниченном мно-
жестве из Rn).
Доказательство. 1) Докажем, что f^R(G) в смысле
определения (К). Поскольку открытое множеству Gс:Rn ограни-
чено, то существует брус 1п[а, Ь] такой, что GczGczIn(a, b). Да-
лее, поскольку f^B(G), то существует постоянная Л4>0 такая,
что |f(x) К-МVxeG. Пудть {Kt} (/=1, 2, ...) — некоторая, ис-
черпывающая открытое множество G система компактных мно-
жеств, измеримых по Жордану. Тогда, вспоминая доказательство
корректности определения (К), видим, что f^R(Kt) v I. Но
К/ и Kt С Яг+г CZ G с ln\a, Ь] v I, откуда имеем оценку
f \f(x)\dx < М • №< М • |/п[а, &]|n v I,
Kt
~ Л. И. Камынин ; 337
т. е.
Я lim f \f(x)\ dx = sup f |K*)| ax • \In[a, 6]|n
'-+<» Kt ‘ к.
поэтому, используя достаточный признак сходимости интеграла
Римана на открытом множестве в смысле определения (К), за-
ключаем, что f^R(G) в смысле определения (К). Теорема О£ эк-
вивалентности определений (АЕ) и (К) показывает, что f^R(G)
в смысле определения (АЕ), а стало быть, f<=R(G) и в смысле
определения (Е).
2) Пусть теперь Galn[a, Ь] — открытое, измеримое по Жор-
дану множестве. Поскольку f^B(G) и для множества
E/={xeG|©(f; х)>0}
имеем mesEf=0, то в силу критерия Лебега (интегрируемости по
я
Риману на измеримом по Жордану множестве) имеем f^R(G)
(в обычном смысле), т. е. существует
J f(x) ♦ 7a(x)dx = \ f(x) dx.
Ia[a, 6] 0
Заметим, что из измеримости по Жордану множества GcR[a, 6]
следует, что
|G|n= f Xg(x)dx= f idx = J == sup S*G(T).
In[a, b] G T
Но тогда Ve>0 существует разбиение T0=(T^......... T^>) бруса
Г[а, Ь] такое, что
5Х(?(Гв)>|0|л-е.
Но
S*G(Tо) == 'VU)>
0)
где
щ(/)=
О,
1,
Обозначим через (k) те мульти-индексы, для которых
С G. Тогда К~ = U С G есть компактное, измеримое О®
е (1с) 1'
Жордану множество, для которого
l*.-U=2 И(%и = ~8-
(It)
338
Итак, для измеримого по Жордану множества G для любого
е>0 существует измеримое по Жордану компактное множе-
ство KfCZG такое, что
|G\/irr|n=|G|n\|K7ln<8.
Аналогично доказывается, что для любого е^>0 существует
измеримое по Жордану компактное множество К+ такое, что
q (— K+cz/n[«, Ь] и |K+\G|n<s. (Для этого выбирают разбие-
ние Т1 бруса 1п[а, Ь] такое, что SXg(7\) < |Gln + s и полагают
где QG^fc 0 V(m).) Заметим, что (как показа-
но в п. 1) нашего доказательства) fs/?(G) в смысле определе-
ния (К). Пусть {2Q — некоторая исчерпывающая открытое мно-
жество G система измеримых по Жордану компактных мно-
жеств. Тогда существует предел
lim J f(x)dx = Udxt (3.8)
1—+ОО к, G
Докажем равенство f fdx = f f(x)dx- В силу леммы (об основ-
G G
ном свойстве исчерпывающей системы) для любого компактного
множества К~СGЯZx(e) еN такое, что vz>/x(e), имеем К~С
CKumCKiCLG, поэтому G\K1CG\K~VZ>Zx(e). Но тогда
для любого фиксированного е>0 в силу оценки |f(х)\М V,
xeG и выбора K~CZG имеем vZ>/x(e) оценки
dx-^ f(x) 1№Ж*<
<Л4 -|G\Kt-|n<8 ‘М.
Но в силу (3.8) для того же 8>03/2(e)sN такого, что
|f f(x)dx -ffdxj<e.v/>2t(t)
и тогда V I > max^ /Де), имеем оценки
f f (х) dx — J fdx I =• 1/J f(x) dx — ( f(x) dx \ +
G ° I l\° *i /
+ /f f(xldx^fdx\\^f(x).dx-$ f(x)dx\ +
\Kl ° /I lG I
+ If f(x)dx - f fdx |<(M +1) • 6,
|kz G I
откуда имеем
Jf(x) dx = Jfdx.
a g
Наконец, поскольку ,|dG|n ?= О, то в силу следствия к теореме
9 из ч. V, гл. 2, § 1
f R(g) и f f (x)dx — j f (x)dx.
G G
§ 4. Замена переменных в кратном интеграле Римана
В [1|], ч. II, гл. 2, § 6 была доказана теорема о замене перемен-
ной в одномерном интеграле Римана в следующей формулировке.
Теорема. Пусть f^R[A, В] и <реС<‘)((ао, М)> причем
(или vi#e[a, ЭДо(ао, ЭД), так чт0 [ф(а),
(или [ф(ЭД, ф(а)]сИ< В]). Если при этом <ре
е£[а, ЭД, го
<р(В) и
f f(x) dx =]7[фО)] -<v'Ct)dt-
ср(а) а
Замечание. Условие <p'(i) =#0V/е[а, ЭД, фигурирующее в
формулировке теоремы (о замене переменной), можно снять, счи*
тая, что отображение (р: [а, ЭД-^Ф^а, ЭД) биективно и <рб
еС<1>([а, ЭД).
Замечание. Из условий теоремы (о замене переменной)
феС<‘>([а, ЭД и V ^е(а, ЭД вытекает, что отображение
<р: [а, ЭД-*ф([а, ЭД) есть диффеоморфизм класса С<‘>, причем для
образа ср ([а, ЭД) имеем
,[а «I) =/ Ма)’ при
I [ф(ЭД, Ф(а)] при ф'(Т)<0 у t е= [а, ЭД.
Но тогда
<₽<£> С
( f(x)dx = singq'(t) ф(1в-) р1) f£x)dx
Ф(а) !“• ₽1
и поэтому формулу замены переменной в нашей теореме можно^
переписать в виде
J f(x)dx — J /оф(0 • |D<p(7)\df.
ч>([сь. 0] [«. 0]
Лемма (об интегрируемости по Риману композиции двух
функций). Рассмотрим открытые множества GczR", $czR™ и ото-
бражение <р: G-* & =<p(G), являющееся диффеоморфизмом
класса (У К Пусть — компактное множество, измери-
мое по Жордану так, что и множество K=q>-1(^‘) crG компак-
тно и измеримо по Жордану. Тогда
34» ;
(f e= R(^))^(f oq> e= R(K)).
Доказательство. Поскольку f = (f°ф) °ф-1, то достаточно
показать, что (f^R.( Ж ))=>(( °q>^R(K)). Пусть 8 CZ Ж — мно-
жество всех точек разрыва функции f(x) на УС и Ес^К — мно-
жество всех точек разрыва функции f ° <f(t) на К. Тогда (fe
е/? (УС )) => ('^ )) ив силу критерия Лебега (интегрируе-
мости по Риману на измеримом по Жордану множестве)
mes $ =0- Очевидно, f ° ф(=В(д_). Докажем, что ф-1( % )^>Е. Пусть
Л_
хое£, т. е. f^C(x0). Тогда f°(f^C(t0), где /0=Ф~*(х0), поскольку,
всегда феС(7о). Таким образом, /о=ф_1(хо)^£, но это означает,
что ф-1 \ $)<= К\Е, откуда в силу биективности отображения
ф-‘; УС -+К имеем
Ф~>(^\^) = ф-‘(ЛГ)\ф-‘(^) =
и поэтому имеем ф-1 (8 )^>Е. Но ф-1еС<1>(0), поэтому в силу тео-
ремы (об инвариантности меры нуль при С(1>-отображении
(mes $=0) =ф- (те8ф-1(<о) =0), так что mes£=0. В силу кри-
п п п
терия Лебега (интегрируемости функции по Риману на измеримом1
по Жордану множестве) имеем f °q>^R(K).
Учитывая лемму (при п=1), видим, что для одномерного ин-
теграла Римана доказана следующая теорема.
Теорема (о замене переменной в одномерном интеграле
Римана). Пусть отображение ф: (ао, Ро) -*• ф((ао. Ро)), (г&е
(<хо, Po)cR и ф((осо, Ро))=(йа> есть диффеоморфизм класса
С(‘>. Если /<=/?(ф[а, р]) при (а, р]с(а0, Ро)), то/°ф-|Оф|е
е7?[а, р], причем
f f(x)dx = f f^(t) .рФ(01^.
[а. М
Замечание. Теорема о замене переменной в одномерном
интеграле Римана остается справедливой, если отображение
Ф: («о, Ро(~> (ай, Ьа) есть гомеоморфизм и феС<‘) ((а0, ро))> т- е-
биективное непрерывно дифференцируемое отображение ф может
иметь критические точки /ое(ао, Ро). где Пф(7о)=О.
Теорема (о замене переменной в одномерном интеграле Ри-
мана, определейном на открытом множестве из R). Рассмотрим
открытые множества GczRt, ‘S cRx и отображение ф: G-* & =
являющееся диффеоморфизмом класса С<‘>. Если f<=R( S)
в смысле определений (ЛЕ) и (К) из § 3, то f °ф |Пф|е/?(<Э) в
смысле определений (АЕ) и (К), причем
<e(G)=& с=чр—1(Й»)
341
Доказательство. Поскольку множество $ открыто в
и в R существует счетная база из ограниченных интервалов, то
4-00 4-00
4=1 i=l
Пусть {et(x)\ i=l, 2, ...} — разбиение единицы для множества 9,
подчиненное открытому покрытию {(ait bi); i=l, 2, ...}, причем
supp etcz(afy bi) для любого i. Поскольку отображение <р:
есть С(1)-диффеоморфизм, то существует обратное отображение
Ф-1: $ -* G, причем ). Тогда, вспоминая теорему (о
связности .непрерывного образа связного множества), видим, что
Ф-1 ([а«, ^ф=[а», М и (а/, р?) =ф~1('(а<, bi))czG есть интервал,
так что G = U (а/, Р?) = Q [а;, 04- Поскольку <р диффеоморфизм
i—i t=i
класса С<*>, то в силу теоремы (об разбиении единицы, индуциро-
ванном диффеоморфизмом) из [1], ч. III, гл. 2, § 12 система функ«
ций {е,[<рft) 1; 1=1, 2, ...} есть разбиение единицы класса С<‘> для
множества G, подчиненное открытому покрытию {(at, Pi); i^s,
=>L_2, ...} так, что supp в/° фс= (а,-, р() для любого i. По условию
f^R( 3) в смысле определения (АЕ), поэтому имеем
Cfdx=y J f(x) • et(x) dx (4.1)
i z=i (<»г.ь4)
и
• - def +°° /»
J|f|dx=2 f \f(x)\ ei(x)dx,
& Z=I<ei’bi)
причем ряд в (4.1) сходится безусловно, а потому и абсолютно.
Но поскольку ф'^С([а,-, р^), то |ф'1^^[а<. р.] и в силу леммы
(об интегрируемости композиции функций) имеем /°ф4ф/Ь
|/»ф|-|ф'|е)?[а(-, (3$ для любого i. Применяя ранее доказанную
теорему о замене переменной в интеграле Римана на интервале
(di, bi)=(p((ai, pi)) имеем для любого i равенства
J f(x) et(x)dx= J [ф(ЭД -е([ф(01
<₽((аг 3<)
И
у lf(X>l • МХМ* == f IfkfOH -е,|Ф(О]
(«4. &<)
Но тогда в силу абсолютной сходимости ряда из (4.1) ряд, состав'
ленный из правых частей (4.2), также сходится абсолютно. Ан^
логичным образом убеждаемся в сходимости ряда, составленног0
из правых частей (4.3), поэтому
f оф-|ф'|еЛ(0)
342
e смысле определения (АЕ) и поэтому имеем
f f °ф • |ф'1Л=
а
= 2 L • еДфГО] • |ф'О).1№
а также
Г |f ° ф| - |ф'| dt==
О
= 5 $ 1/[фСО]| • е«[ф(0] • 1ф'(Х)1^«
г=1 (“<•
Но тогда из (4.1) и (4.2) имеем равенство
J fdx— J f о ф|Вср|dt
& G
и аналогично* имеем
J|f|dx=f|fo Ф| • |Dq>|a7.
1-я теорема (о замене переменных в кратном интеграле
Римана для финитной непрерывной функции). Рассмотрим огра-
ниченные открытые множества G с Rf, rS С R" и отображение <р:
GcR" —> $ = ®(G) CZ R^> являющееся диффеоморфизмом класса С(‘>.
Если функция f е С(&) финитна и для ее компактного носителя
& supp f имеем Ж = то имеет место формула замены пере-
менных в кратном интеграле Римана
где
f f(x)dx = $ «Ф(01 •
cp(G) G
d(xi,-.., х„)
<л)
(t) Ил
g?...... m - ....(t) = det D<e(l) -
як°биан отображения <p (при x— Ч>('Ов(ф1.(О> —> фп(О))-
Доказательство. При п=1 якобиан detD<p(O есть про-
0 производная <fr(t) и рассматриваемая теорема содержится в
тегп3анн°й Ранее теореме о замене переменной в одномерном ин-
неп Ле Римана> поскольку функции ffx) я f°(p(^)-|detD<p(f)|
во реРЫвны, имеют компактные носители и поэтому интегрируемы
Биману на любых измеримых по Жордану множествах, содер-
343
жащих их носители. Предположим, что теорема о замене пере-
менной верна для кратного интеграла порядка п—1, и докажем
ее справедливость для кратного интеграла Римана порядка
п^2. Напомним, что поскольку отображение <p:GczRn—
czRn есть диффеоморфизм, то отображение ф множества G на
множестве 3=q>(G) биективно, а потому существует обратнее
отображение <р-1: $->G, причем <p&C<l)(G) и ф-1еС(’>(^),
detD<p(X)^O v t^G. Дальнейшее доказательство проведем в два
этапа.
1) Рассмотрим сначала диффеоморфизм cp:G^$ =ф(0),
ф(О=(ф1(О» — > 4>n(t)) специального вида: хг=фг(?ь ..., tn)^
е 3 (1=1, 2,...,п), t=(t\.tn)^.G, причем существуют индексы
i и j такие, что cpi(t)—ti> т. е.
ф(/) = (ф1(О;...,фг-1(О*, tit фж(7), ..., фпЮ)-
Поскольку носитель <%* = suppfcz$ компактен в R" и Ф~‘е
еф), то множество К = ф-1(^) CZ G компактно в R". По ус-
ловию открытые множества 3 и G ограничены, поэтому суще-
ствуют брусы Jn[a, b]CZR" и 7n[a, 0]CZR" такие, что
&C13(ZJn[a, &]; KcGcf[a, 0],
причем supp f о фС/(. Положим 7п[а, Ь] — [air bi] X 1п~1 CZ R",
где
Jn~^= [вц. bj] Х..-Х [«<—1> bi—i] X [#z+i, &z+i] X
и
Л«, ₽] = [«/. ухln-1 czR?-‘>
где
1п~х = К ₽i] Х...Х [а/_ь 0/-1] X [аж. ?/+1] X
Х...Х[ал, PJCR?-1,
причем, учитывая специфику диффеоморфизма ф, будем счи-
тать [а/, ₽;] = [«», Л Рассмотрим также открытые (в R^-1 и в
R"-1 соответственно) множества
3у = 3т^ = у}, G^C^\ti = y]
и
^•у=^П{^=Я Ку-КПК/ = ^}
V У е [а{, = [а/, 0Я (см. рис. 15).
344
Рис. 15
Замечание (об индуцированной топологии). Пусть G, Kez
cR, где множество G открыто, а множество К компактно в R”.
Если En-\—{tj=y}, (л—1)-мерная гиперплоскость, «лежащая» в
Rn-i==|^li м f/+1,то множество Gy=G[\{tj=y} открыто»
в Еп-1, а множество Ky=K[\{tj—y} компактно в Еп-\.
В самом деле, поскольку множество G открыто в Rn, то для
любой точки /eG^cG^R” существует л-мерный шар Ш<">(7) CZ
cG и поэтому
* С^у У
где Ш)"-*) (7)=Ш<"> (t)(\{tj=y} есть (п—1)-мерный шар, ле-
жащий в fn-i, но тогда множество Gy открыто в £п-ь Поскольку
множество К компактно в Rn, то оно замкнуто и ограничено, но
гиперплоскость En-i также замкнута (как в R", так и в Rn—1), по-
этому множество Ky=Kf]{tj=y} замкнуто и ограничено, т. е. ком-
пактно (как в R”, так и в В силу замечания множества
и Gj, открыты (в соответствующих гиперплоскостях), а мно-
жества СК у и Ку компактны v ye[ait &;]=[«,•, в Л. Поскольку
suPpfc=Z«[a, &] и feC( &), то
(feC(Zn[a, Ь])) => Ь]))
fy(Xlt •••» ^4-1, Лад, Хп) —
^f(xi, .... X;-1, у, х,-+1, ..., xn)^R.(Jn~l)y y^cii, b«j.
°°этому в силу теоремы Фубини имеем
345-
J f(x) dx sb J f(x) dx
’(G) Jn[a. bl
&z
=J dy$ t Xi-\, y, xi+i,..., xn)dxu..dxt-idxi+i...dxn =
a.
bi
= f dy$ f(xlt..., Xi-i, y, xl+l.xn)dxv..dxi-idxi+i.:dxn.
ai
[((Функция f(x) при фиксированном Xi=y^[ai, имеет компакт-
ный носитель Myc:Sy, лежащий в гиперплоскости xt=y.) По
предположению индукции к внутреннему интегралу, являющемуся
кратным интегралом Римана порядка п—1, можно применить ,
формулу замены переменной. Заметим, что, как показано, множе-
I ства Gsc:R"-1 и $yczR’_| открыты, поэтому наш диффеомор-
i физм <р: G $ индуцирует отображение ф: Gy -* Sy или ф: ;•
I fii....ti-i, tj+i, .... tn) -* (Xi, ..., Xi-i, xi+l, xn)
। такое, что
j Xk=<f>k(ti, .... tf-i, y, ..., tn) (&=1> —. i—1, f+L ...» n),
! причем q^C<y>(Gy). Заметим, что для якобиана <1е1Пф(7) в силу ;
J предположения Xi=tj имеем
I
I
! откуда
dh k}
/
dxx
dtn
dh
d(xi..х„)
дХп : дха .
dh ......... dtn
ty_j, tn) i
t. e. для якобиана det Оф(7} имеем равенство Vie С;
tj = yf~ [at, i>i] = [aj, ₽/], й
d<SL..... x<+t......... =j}i+i d(X1........x„) , 0
i> fyf-i»-.., tn) tn)
346
причем модули этих якобианов совпадают. В частности,
<ietD<p(O =#0 Vt е Gy, но тогда биективное отображение <р:
£ —осуществляет диффеоморфизм открытого множества
на открытое множество $VCR'1-1. По теореме о
замене переменной в (л—1)-кратном интеграле Римана (кото-
рая предполагается верной) V у^[а(, ЭД =[<%;, ЭД имеем равен-
ство
j* У, •Tn),dXi-..4?Xi-l^Xz4-l...dXn —
= J ............ У»--
°y
.....*4—1 . X/4,......X„)
tf_lt tj+l...../„)
. <Pnft)) X
ti-\, У, ti+i,-. t„]X
Gu .
...dtj— \dti+\...dt
Вновь применяя теорему Фубини (проверьте самостоятельно, что
все условия теоремы выполнены), получаем окончательное ра-
венство
$f(x)dx—$ dy^ f(xlt xt-i, у, x^i...xn)X
» at
X dxi:.dxi-idxi+i...dxn =
= У, *<+ь-> *»)] X
aJ Gy
X IdetDvpp..., tf-i, y, tn)\dtl...dti_idt;+ь..аГ/я =
= f f° <P(0 • |detD<p(7)d/ =
ln{». ₽i
= ffo y(t) • |detD<p(7)|dt.
G
2) Рассмотрим теперь любой С^-диффеоморфизм <р: G ->
=(p(G), где xi=<pi(ti...... tn) (i— 1, 2, п), при этом су-
ществует обратное отображение <р-1: $ -> G. Отметим, что
(peCOJCG), ), detD(p(O^OV/eG.
Но тогда для фиксированной точки xeG существуют индексы i и
j (зависящие от т) такие, что —Фг(т)#=0. Рассмотрим вспомога-
dtJ
тельное отображение G—= фт(С) где YCZ Rn и у яфгСО,
определяются формулами
347
yt — ti, i-=/= j,
tn).
(4.4>
Очевидно, (фх e CW(G)) => (det Dipt s C(G)) и поскольку
det Da|jt(t)
д(У1....Уп),^
<4*i....*„)
1 0 ... о . . . 0
0 1 ... 0 . . 0
^<Г»('С) ^Фг(т) дфЯ'О
a/i dt2 dti dtn
0 0 . . . О’... 1 0
0 0 . . . 0 . . . 0 1
= (-l)2' -тт-фМ^О,
dtl
то точка teC — регулярная точка отображения фх. Но тогда
по теореме о локальном диффеоморфизме (из [1J, ч. III, гл. 2»
§ 8) существуют открытые множества 1/,эти УхЭфх(т) такие,
что U-t£Z.G и Vt = фх(£7х)(Z Y = фх(С), причем отображение (точ- -
нее его суждение) фх: U- —> Vx = фх(1/х) есть диффеоморфизм
класса С(1> и, в частности, существует обратное отображение ?
ф"1 gC(l>(K), для которого, исходя из (4.4) можно записать
t = 7i(T)» где
(4.5)
I (Vi.......9п),
Полагая Wx=q(Ux)cz $ , видим, что Wx является открытым мно-
жеством, содержащим точку ф(т). Для введенных отображений !
можно написать коммутативную диаграмму
Заметим, что по построению (J 1Гх=^о^ = suppf и в силу
компактности множества Ж из открытого покрытия {IFX; tSG)
можно выбрать конечное подпокрытие г=1,2,—
т} такое, что
348
r=l
Рассмотрим разбиение единицы {er(x)-, г = 1, 2,..., т} класса
<Ст для множества подчиненное конечному открытому по-
крытию {№(г); г=1, 2,..., т}, для которого suppercz W<r) для
любого г. Тогда имеем
f fCx) dx = 2 L e'(x> * f(x>-dx*
$> r=l W<r>
рассмотрим для любого г n-кратный интеграл Римана
f eT(x) -f(x)dx.
w<r)
Заметим^» что отображение ф;-1\/. = СЛг>-> №<г> допускает (при
•ф^ = фг и представление вида <р=(<ро ф-1)0 фг или
полагая Хг= фо ф-i, представление вида ф = Хг° фг. Отметим
коммутативную диаграмму
фг
(Z G , ~ >' V^dY
И70-) CZ $ Хл='1> ° Ф;7’
Для 1-го диффеоморфизма фг : £ЛГ> -*• №(0 ввиду (4.4) имеем
16'“Фг(^1.. ^п)»
|det D фг(т)|=
01 f
>Ov^e= U^,
•а для 2-го диффеоморфизма ЛГ = Ф° ф^1: (x=lr(y))
в силу (4.4), (4.5) имеем
J ~ У1—^> "Чз iyit’"’> Уп)* У/’+Ь'-'» Уп)>
I xt = yj (так как х* = TiGi,.-, М У,),
2-й диффеоморфизм Хг имеет специальный вид, изученный в п. 1),
поэтому для него справедлива теорема о замене переменной в
кРатном интеграле Римана, в силу которой имеем равенство
J et(x) • f(x) dx =s
трМ-хДуО-)) *
- J MW] -frrte)] • |detT)krf^|^. (4.6)
yf)-q>r(u<r>)
349
Но 1-й’диффеоморфизм ф,: (7<г> -*• У<г> в силу (4.4) также имеет
специальный вид, причем даже более простой, поскольку в нем
имеет место замена только одной переменной «//, поэтому, вновь
применяя доказанную в п. 1) теорему о замене переменных в
кратном интеграле Римана и учитывая равенство Л,г[фг(Х)]вф(О,
получаем из (4J6) V г
f ег(х) • f(x) dx = f ero q(t) f ° q>(t) X
>(r) „ v t/(r)
X |det DkJMOJI • |det Оф,(7)1 dt. (4.7)
Вспоминая теорему из [1], ч. Ill, гл. 2, § 4) о производной слож»
ной функции <р=Х, офг, имеем в силу доказанной в ней формулы
об умножении якобианов
| det D Хг[фг(t)]| • | det D fy(t) | = | det D q(t) |
и поэтому из (4.7) имеем равенства для любого г
J *r(x) -f(x)dx =
= J ф(0 •/’ Ф« •|detD?COI^- (4.8)
Но тогда, суммируя по г (от 1 до zn), получаем из (4.8) равенство
2 f er(x) ' f(x) dx = j" f (х). dx =
= 2 J ФСО • |detD<p(7)|df. (4.9)
r=l y<r
Поскольку отображение ф:б—>$ = <p(G) есть диффеоморфизм
класса С<1>, то система {er° <f(t)\ r=l, 2,..., zn) является раз-
биением единицы для множества K = <p~1(^’)ZZ)suppf о <р, под-
чиненным конечному открытому покрытию {Шг>} = {<p-1(W'(r))»
г=1я 2,..., т}, так, что
supp е, о <pCZC7<r)Vz-; К CZ U
r=I
И
3 ero <f(t) = 1 V t<=K,
r=I
откуда видим, что правая часть равенства (4.9) равна
J 2 er° ^(i)E\detDif(t)\dt =
и u(r)r-1
r==l
390
= ГЗ е'в *($ 'f° v(t) • |detD<p(7)|ctt =
«r=l
-(/• 4>fO • l<tetDq>f/)|(ft fо ф(7) • |detD<p(7)|df
к g
(так как suppf • фс:К). Но тогда из (4.9) получаем равенство
f f(x)dx=$f* <f(t) • |detD<p(?)|df.
&=<p (G) G
Итак, 1-я теорема о замене переменной в кратном интеграле
Римана доказана полностью.
2-я теорема (о замене переменной в кратном (несобствен-
ном) интеграле Римана для непрерывной функции). Рассмотрим
открытые множества G CZ Rf, & С R" и отображение <р: G =
= Ф(б), являющееся диффеоморфизмом класса С<*>. Если f е
s С($) Л Л(3?) смысле определений (АЕ) и (К) из § 3), то
fo <р • |det Dq>| s R(G) (в смысле (АЕ) и (К)), причем
J f(x)dx — J f о ф • |det D<p|dif.
S=tp(G) G
Доказательство. Поскольку множество 2? crRn открыто,
а в Rn существует счетная база из открытых брусов, измеримых
по Жордану, то
-|-оо 4-оо
$ = у /7 = у
Z=I i==l
Пусть {ei(x)-, i = 1, 2,...) —разбиение единицы для множества
подчиненное открытому покрытию {/7}, так что suppqc/"
для любого I. Поскольку отображение ф есть {диффеоморфизм
класса С*1*, то множество Ui •= ф-1(7")|С2 G 'компактно и изме-
римо по Жордану, а множество ^=ф~1(77)СС открыто и из-
меримо по Жордану, причем
4-о® — 4-со
G = u с^ = и Ui.
i=l Z=1
Кроме того, система {е4 о <f(t)’, i=l, 2,....} является разбиением
единицы для множества G, подчиненным открытому покрытию
мФ так что suPPe«° фС^У i. По условию (в смысле
Ис)), поэтому имеем равенства
J fdx= 2 У f(^) ♦ ei(x) dx „(4.10)
& i—1 ,П
И
351
J |f| dx => 2 f If • ei(x) dx>
& i—1 n
где ряды сходятся абсолютно. Но функции f eit |/| • et
е С(&) для любого I, финитны и имеют компактные носители
suppfei • f)CsuppezCZ7?,
supp (et • |/|) CZ supp et CZ Jf V i,
поэтому к этим функциям применима доказанная выше 1-я теоре-
ма о замене переменной в кратном интеграле Римана (для фи-
нитной непрерывной функции), в силу которой имеем для любого
л (при J"=(p(Ui)) равенства
J f(x) -et(x)dx =
= [ / о <pf() .e<e <p(7) • |det D<p(?)l dt (4.11)
ui
м
$ \f(x)\ • et(x)dx
Ji ;j
-f If» <p(0| -e,. (t) • |detDq>(7)ldt (4.12)
Но из абсолютной сходимости ряда (4.10) следует абсолютная
сходимость ряда, составленного из правых частей равенств
1(4.11), (4.12), поэтому в силу_определения (АЕ) из § 3 имеем
f«<p-|detDq>|, |f »ф|-|detD<p|s/?(G) и, кроме того, из (4.10) по»
лучаем равенство
ffdr=ffo <p -|detD<p]d/.
^-<₽(G) &
Следствие. Рассмотрим открытые множества GczR?,
$С RJ (где множество $ измеримо по Жордану) и отображе-
ние q>: G—>$=ф(С), являющееся диффеоморфизмом класса
Если f е С($), причем |f(x)|< А4 Vxc=$, то f е/?($), f° фХ
X||detD(p| ^R(G) (в смысле (АЕ) и (К)) и имеет место равенст-
во
J f(x) dx = J fdx — J f о ф • |detD9|dL
S—v(O) so
352
Доказательство. Поскольку множество &czRn открыто
я измеримо по Жордану, а функция <р<=С($) ограничена на
то в силу доказанного в § 3 достаточного признака существова-
ния интеграла Римана (на открытом ограниченном множестве)
имеем fe=C(% )АР($) (в смысле (АЕ), причем )) и
теперь применима 2-я теорема о замене переменной в кратном
интеграле Римана (для непрерывной функции).
Рассмотрим теперь важный для приложений вопрос о переходе
в кратных интегралах Римана к полярным и сферическим коорди-
натам (образующим вырожденные системы координат).
1. Полярная система координат на двумерной плоскости. Рас-
смотрим отображение Р: (г, <р) -> (х, у) плоскости R2 в себя, где
x=r-cos<p, z/=r-sin<p, —оо<г<-f-оо, —ооСфС-^оо.
Очевидно, <JetDP= = г (заметим, что отображение Р
не является биективным!). Если перейти к сужению отображения
Р на открытое множество й={(г, q>)sR2|0<r<4-oo, 0<ф<2л},
то отображение Р :Q->- Р(й) становится диффеоморфизмом клас-
са С<‘>, причем mesd&=0 и P(Q)=R2\F, где множество Е==,
={(*, y)6ER210<x<-|-oo, у=0} замкнуто и mesF=O (см.
рис. 116).
Теорема (о переходе к полярным координатам в двойном
интеграле Римана). Рассмотрим открытые множества GaQa:.
CR“ ф, ^CP(Q)CR2 j, и отображение P:G-+& = P(Q). Пусть f е
'<= С($)ДР($) (в смысле (АЕ) и (К)). Тогда
rf°P(r, ср) (г-cos <р, r-sincp) r<=C(G)/\R(G)
(в смысле (АЕ) и (К)), причем
353
^fdxdy=^f° P rdrdq.
* Q
Если при этом множество & измеримо по Жордану и f еС($)д
AW то f^ R(&) и г • f о Ps R(G) (в смысле (АЕ) и (К))>
причем f так что имеет место равенство
П f(*> y)dxdy= JJ f(x; y)dxdy= о P - rdrdq.
* % G
Наконец, если оба множества & и G измеримы по Жордану ц
/е=С($)ДЯ($), то / Е R($) и г -f о Р е R(G) (в смысле (АЕ) ц
(К)) и, кроме того, f eR($)/\R[&) и г f
P^R(G)/\R{Q)t
так что имеет место равенство (с обычными интегралами Римана)
jjf(x, y)dxdy—^r • f(r • cos<p, r . sin<p)drd<p.
S G
Доказательство. 1-е утверждение теоремы вытекает из
2-й теоремы (о замене переменной в несобственном кратном ин-
теграле Римана для непрерывный функции из § 3), поскольку ото?
бражение P:G->$ =P(G) является диффеоморфизмом класса
С*1).
Если множество S? измеримо по Жордану, то измеримо по Жор-
дану и множество и поскольку fsC( &)/\В(& ), то приме-
нима теорема из § 3 (о достаточном признаке существования ия«
теграла Римана _на ограниченном открытом множестве из Rn), i
силу которой f^R(& ) в смысле (АЕ) и (К) (и тогда, как было
доказано выше, r-f ° P^R(G) в смысле (АЕ) и (К)), причем
fe.R(f§ )/\R,('S ) и имеет место равенство (с обычными интегра-
лами Римана)
И f (х, y)dx dy=^ f(x, у) dxdy =^r • f о Pdrdq,
& h °
чем 2-е утверждение нашей теоремы также доказано. Наконец, ее*
ли оба множества S и G _измеримы по Жордану, то измеримы
по Жордану и множества # и G, причем, в частности, шюжест*
во G ограничено, т. е_бсШ«| (0). Поскольку f^.B(& ),
|f(x, у) V (х, у)е& , и тогда
|r-f°P(r, <p)|<M-PV, (г, <р)e=G,
поэтому r-f о P^B(G), и тогда из условия f^C(<§ )/\В($)
дует, что r-f ° P^C(G) ДВ(О)._Вновь применяя упомянутую вьпй®
теорему из § 3, получаем f<=R(& ) и r-f ° P^R(G) (в смы®^
(АЕ) и (К)) и, учитывая измеримость по Жордану множеств ’
354
q $ я имеем ) и r f ° P<=R(G)/\R(G). Ис-
пользуя доказанное ранее 1-е утверждение теоремы, получаем ра-
венство с обычными интегралами Римана
JJ/Cx, У) dxdy — JJ г f(r • cosq\ г • sin <p) dr dtp,
& G
так что и 3-е утверждение нашей теоремы доказано.
Теорема (признак сходимости несобственного двойного ин-
теграла Римана). Пусть f^C(R2v ), причем имеет место оценка
lf(x, y)I^M/(l+rs^) V (х, у)^2,
где r=(x2+y2)i/2 и а>0. Тогда feR(R2) в смысле (АЕ) и (К),
так что несобственный интеграл И fdxdy сходится абсолютно.
R« _
Доказательство. Рассмотрим круг /Сг=Ш(2)(0). Тогда
система {Л/} (1—1, 2, ...) является исчерпывающей R2 системой
компактных, измеримых по Жордану множеств. Положим
З^ЛЭД и Qt=P-4^t)={(G (p)e=Q|0<r</, 0<ф<2^}
Очевидно, множества &t, И, и измеримы по Жордану
для любого I. Но (f ^C(Ki))^(feB(Ki)/\R(^i))t поэтому в силу
теоремы (о переходе к полярным координатам в двойном интег-
рале Римана) имеем г f о Р е R(Qi), причем
И f(x> У) dx dx =^г • f о P(r, <p)drdq.
Ki ai
Применение теоремы Фубини к последнему интегралу в силу
г -f о />еС(Й;) дает равенство
2к I
П f(x> y)dxdy= J d<p J f о P(r, Ф) • rdr.
Kt oo
Но по условию |f ° P(r, <p)K M/(l+r2+a)v (r, ?)eQ, поэтому
для любого l имеют место оценки
fj If (х, у)\ dxdy < 2к - М (г/(1 + r2+“) dr =
К/ о
/1/2 I \
= 2к . М • J + у ) r/(l+r2+“)dr<2« • М х
\ 0 1/2/
1/8 +
Итак,
23* 35»
f r-i-« dr ) < 2М(1 /2 + 2«/а) = £(а).
1/2 /
sup ff\f(x, y)\dx dy < L(a) < -J-oo,
1
но тогда существует
lim ff|/(x, y)[dxdy.
Z-»+°o K[
В силу достаточного признака (сходимости интеграла Римана
на открытом множестве) из гл. 2, § 3,. имеем f si?(R2) в
смысле (К).
Теорема (признак сходимости несобственного двойного ин-
теграла Римана от неограниченной функции). Пусть fs
еС(ШТ (0)) и имеет место оценка \f(x, у)\^М/г2~аУ (х, у)&
еШ(к2) (0), где а>0. Тогда fe=RQi№ (0)) в смысле (К). (До-
казать самостоятельно по схеме предыдущей теоремы, беря
• Ki={(x, у) | l/t^(x2+y2)l'2=r^R-l/l) v Ze=N).
Теорема (вычисление значения интеграла Пуассона). Функ-
ция ехр(—a-x2)eR(0, +<») (Уа>0) в смысле (К), причем для
интеграла Пуассона имеем
^°ехр(—а • x2)dx = (1/2) • (~/а)1/2 Va = (0, -poo),
в
Доказательство. Рассмотрим функцию
f (х, у) =ехр (—а • (х2+у2)) V (х, у) ge $ = ::
={(х, t/)eR2|0<x<+oo, 0<#<+оо}.
Очевидно, /еС( $ ) и существует Л4>0 такая, что
Q<f(x, zOCMa/U+r4) V (х, у)&5 ,
где г=(х2+у2)1/2. Но тогда в силу доказанного выше признака
(существования несобственного двойного интеграла Римана на
неограниченной области) имеем f^.R($) в смысле (К), так что
для любой системы {KJ (Z=l, 2, ...) компактных, измеримых по
Жордану множеств, исчерпывающих область $,
Я lim ff f(x, у) dx dy = L(a)
/-►+00^
(где число Ца,) не зависит от выбора исчерпывающей системы
{К';}). Положим (см. рис. 17)
К/ = { (х, у) е 1 //2 < л2 + «/2 < /2,
О < az < arctg (уlx) = ф < те/2 — az; X > 0, у > 0},
где lim az —0; тогда
1—+СО
356
'/1
о
Рис. 17
p-i(Kz) = {(r, q>)e 2|1//< r< I, 0<в1<<р<к/2-а,}
и поскольку /\R(Ki), то r-f ° P^C(P~l(Ki))A
/\Р(Р~'(К1)). Применяя теорему (о переходе к полярным коор-
динатам в двойном интеграле Римана) имеем (используя теорему
Фубини) для любого I
И t(x, y)dx dy = Jj exp (—a • r*) • rdr dq> =
Ki p~\Ki)
n/2—a, I
= J dtp J r • exp(—a-r2)dr =
»z U‘
= (тс — 4аг)/4а • [exp (—a//2) — exp (—a • /*)],
так что
Я lim ff f (x, y) dx dy = w/4a.
Z-+oo
Поскольку f(x, у')>Ъ, то £(a) = ir/4a > 0. Рассмотрим теперь
Другую исчерпывающую область $ систему {К/} (/=1, 2,...),
гДе (см. рис. 17)
= r/)eR2|l//<x</, 1//<у</}.
Тогда в силу теоремы Фубини имеем
Л f(x, y)dx dy= f dx f exp (a • (x2 + y2))dy =
к, 'i/i in
357
I I
— [ exp (—a • x2) dx • J exp (—a • y') dy —
'Ml Mt
/ l X 2
= IC exp(—a -x2)dx j для любого I.
\MI /
Но тогда существует
+°O def 1
f exp(—.-a-x2)dx= lim f exp (—a <x2)dx =
0 Z-»+oo l/i
=Jim f (x, y)dxdy^ 4* = (1/2) • («/a)‘/2.
Поскольку exp (—a •x’)>0Vx>0, то в силу достаточного
признака существования (одномерного) несобственного интег-
рала Римана на открытом множестве (0, -|-оо) из § 3 видим,
что интеграл Пуассона
4-00
[ ехр (—a -x2)dx
6
существует для любого а^>0 в смысле определения (К), при-
чем
ехр (—а • x2)dx=(l/2) • (тс/а)1/2, «е(0, 4-оо).
о
2. Сферические координаты. Рассмотрим отображение &:
(р, ф. ф) —> (х, у, z), где х=р • соэф • cosф, у — р ♦ sinq> • соэф;
z = p- sin ф. Очевидно,
det D ^(p, ф, ф) = —— = p2 • cosib.
d(p, ?, ф)
Отображение 5s:R® ф ф—>КЗ у г класса C<’), но не биективно,
однако его сужение :®—>За(ш), где
<и = {(р, <р, ф) sR3|0<Ср<^-|-оо, 0<ф<2ir,
. -Д2<фО/2}, ^(a>)=R3\^, &={(х,у, z)e=R3|0<x<-|-oo,
у — 0, —oo<^z<^+oo), mes^ = O
з
является диффеоморфизмом класса С*1*.
Теорема (о переходе к сферическим координатам в трой-
ном интеграле Римана). Рассмотрим открытые множества Gcz
С <о (Z R3 ф, ф, С ) С R3. у< г и отображение = 3^(0).
Пусть f еС(^)ДЛ(^) (в смысле (АЕ) и (К)). Тогда р2 • созфХ
Xf ° &^C(G)/\R(G) в смысле (АЕ) и (К), причем
JCJ fdxdydz =Д|ра • cosi|> • f ° gbdpdqdy.
& G
Если при этом множестве & измеримо по Жордану и С($) Д
д В($), то, f R№) и р2 • соэф • f о &R(G)(в смысле (АЕ)
и (К)> причем f <= R($) f\ R№), так что имеет место равенство
(где первые два интеграла Римана обычные)
Ш f (х> У> z) dx dy dz = JJJ f(x, у, z) dx dy dz =
= JJ’Jp2 *COS<P • f ° ^dpdtpdip.
JG
Наконец, если оба множества S и G и G измеримы по Жордану
и f то f<=R&) и р2 • cos-ф • f о $>t=R(G) в
смысле (АЕ) и (К)) и, кроме того, fe R(&)/\R[i§) и р2 • cos<|»X
X f о & е аддБ(о), так что имеет место равенство (с обыч-
ными интегралами Римана)
^КХ'У> fdxdydz =£|’fp® «cos'}» • f о ^(p, q>, <|))dpdq>rf<|>.
& G
Доказательство провести самостоятельно.
Теорема (признак абсолютной сходимости несобственного
тройного интеграла Римана от неограниченной функции). Рас-
смотрим функцию С(Ш^ (0)), для которой существует Afa>0
такая, что | f(x, у, z) |^Мх/р3~“ V (х, у, z)sffl«31 (0), где р =
= (x2A-y2-\-z2)U2 и а>0. Тогда (0)) в смысле опреде-
ления (К), так это существует несобственный интеграл
Hf \f(x,y,z)\dxdydz.
0<х*4-у2+г2</?2
Доказательство. Рассмотрим шаровой слой К/=
={(х, у, z)^\\ll^(x2+y2+z2)^R-\lt), тогда {К,} (/=
==2, 3, ...) есть исчерпывающая проколотый шар Шд* (0) систе-
ма компактных, измеримых по Жордану множеств. Положим
^;=К;ГЖ“) и <ог=^-1(^)={(р, <р, ф)е=®|Ш<р<Я—Ml,
0<^ф<^2к, |ф| < п/2}.
Очевидно, множества (§i, Kt, ан и ©z измеримы по Жордану и по-
скольку f^C(Kt), то feR(Kt)/\R ^t). Но тогда в силу теоремы
(° переходе к сферическим координатам в тройном интеграле
римана) имеем р2-cos ф-f ° ^R(o>i), причем использование тео-
ремы Фубини дает равенства
359
^f(x,y, z)dxdydz =
*i
= JJJ p* • cos <]> • f о ^(p,. q>, <|>) dp dtp di|> =
2n it]2 R'-i/l
= J dtp J cos tydty f p2 • f о ^(p, ф, ф) dp.
О Д/2 l/l
Использование условия
If ° ^(p, Ф, Ф)К Afa/p3-» v(p, ф, ф)(=®г
дает оценку
Ш If (х, уz)| dx dy dz < 4тг . Мл • B“/a = L(a) V I.
K‘ • •
Итак,
sup JJJ \f(x, у» z)l dx dy dz < £(a) <4-00,
t. e-
Я lim jJJ |f (x, y, 2))dxdy dz.
В силу достаточного признака сходимости несобственного ин-
теграла Римана на открытом множестве Шд(0) (см. § 3) имеем
/еЙ(Ш^(0)) в смысле определений (АЕ) и (К).
Теорема (признак сходимости несобственного тройного инте-
грала Римана в неограниченной области). Если f<=C(Sr), где
$r = {(x,y, z) е R3|(x’4-«/24-z*)1/2>r>0}
и имеет место оценка \f(x, у, z) KAfa/(l+p3+“)_ для любых
(х, у, z)<= Sr, где p=(x2-H/2+z2)1/2 и a>0, то f^R(Sr) в смыс-
ле (К) и (АЕ), т. е. несобственный интеграл
JJJ f (х, у, z)dxdydz
Jfx+y2+z2>r*>0
сходится абсолютно. (Доказать самостоятельно.)
3-я теорема (о диффеоморфной замене переменной в не-
собственном кратном интеграле Римана). Рассмотрим открытые
множества SciRS, GczR" и отображение q>: G -> S =cp(G), яв-
ляющееся диффеоморфизмом класса С(1). Пусть f^R(S ) ^смыс-
ле определений (К) и (АЕ) из § 3. Тогда f <><p-|det D<p | ^R(G) в
смысле (АЕ) и (К), причем имеет место формула замены пере-
менной
360
J fdx= J f о <p • | det D <p | dt.
4><G) a
Д ока з а те л ьств о. Пусть в смысле (АЕ) и
-4-00 -f-оо _
(=1 i—1
где Ji—замкнутые брусы из Rn и {е/х); i = 1, 2, . . . { — раз-
биение единицы для множества подчиненное открытому по-
крытию \1“}, так что supp^cz/f для любого I. Поскольку <р>
есть диффеоморфизм класса С*1), то множество Ut — Ф-1(7") СТ
CG компактно и измеримо по Жордану, а множество i/j —
= Ф~1(У”) открыто и измеримо по Жордану, причем
4-00 — 4-00
G = U Ut = U Ui.
i—1 i=I
Кроме того, система {et° i=l, 2, . . . } является разбие-
нием единицы для множества G, подчиненным открытому по-
крытию {U(} таким, что suppe4o фС[?( для любого i (см. [1],
ч. III, гл. 2, § 12). По условию fe/?($) в смысле (АЕ), поэто-
му имеем
J f dx='£i$ f(x) • et(x)dx
И
-et[x)dx,
& i=l J i
где ряды сходятся абсолютно и f • eit |f| • s 2?(7") v i. В си-
лу леммы (об интегрировании композиции двух функций}
|f о ф| . ei о фе/?((7/). Далее ПфеС(С71), поэтому в силу ком-
пактности множества Ut видим, что
|аеЮф|е C(Ut) А в(и^
т. е.
|f о ф| . |detПф| • ei ° фей(У{) VI.
Вспоминая доказательство 2-й теоремы (о замене переменной
в кратном интеграле Римана), видим, что для доказательства
нашей теоремы достаточно доказать равенства
361
f \f(x)\ • ef(x) dx =
*4
= J_lf° ФГ01 • |detD<p(7)| -ejo y(t)di4 i
vi
«ли, полагая J" = /”, достаточно доказать равенство
( F(x}dx = f Fo <p(f) . |detD<p(f)|< (4.13)
/П ф-1(1П)
где F(x) = jf(x) | -е;(х) и множество есть замкнутый брус.
В силу следствия к 2-й теореме (о замене переменной в кратном
интеграле Римана) формула (4.13) имеет место для любой функ-
ции F^C(In) и, в частности, для постоянной функции F(x) —
'==с V хе/п. Рассмотрим теперь любое разбиение Т бруса 1п с час-
тичными брусами и положим
m(f)= inf F(x), M(j) = sup F(x).
n n
li Ц
Отметим, что
Ao =U а/;,, И(у. = |/г,1» и p/j1|„=o,
так что
(О ' ’ (/)
причем
1У и (у 4) п (у =0. 4п4> = 0
при 0)#=(^). В силу биективности диффеоморфизма <p~r: & -»
—» G = <jp”1($) имеем
ф-ЧЛ-ф-'(у4)иф-‘(уа/г,)=
-(UT-^UT-'tyaib),
где ф-'ед П ф-‘Фч> = 0 “Ри (i) * <6) 11
(иф-'(4))Пф-'(иа;,у = 0,
причем в силу теоремы об инвариантности меры нуль при
отображении (из ч. V, гл. 1, § 3) имеем
те5фДУд/(/)) = °-
Но множество (J^AnnC.'^ компактно и поскольку f1 еС(1,(3),
(Л
то множество'г<р-1(и^Л'л) также компактно, а потому
* (Л v>
1’ПГ<=°-
Применяя формулу (4.13) для постоянной функции, теорему 5
(о конечной аддитивности интеграла Римана), теорему 10 (об
усиленной аддитивности интеграла Римана) и используя след-
ствие к теореме 9 из ч. IV, гл. 2, § 1 имеем
^Т)=2>(Л|^/)|П=2 f miiydx =
(Л (Л
(Л
= 5 Г m(/)|detD(p(OI^ <
(/) »-«)
<2 f F° <P(Z)|detD<p(7)|dZ:=
(ft ^*Ь7л)
Fo Ф(7)1 det D<p(7)|df =
= J Fo <pf()|detD<p(f)|df.
ф-Чп
Но тем самым доказано неравенство
f F(x)dx = sup Sf(F)<
/п T
< f Fo <pf^|det<₽f^|df. (4.14)
Ф-1(Г")
Аналогично для любого разбиения Т бруса 1п получаем оценку
SF(T)>
ф-г(/п)
Fo <p(7)|detD<p(7)|df,
из которой имеем неравенство
f F(x)dx = MSf(T) > (4,15)
/п Т
> f Fo q>(7)|detD<p(0|dt
Из оценок (4.14) и (4.15) следует равенство (4.13), завершающее
Доказательство 3-й теоремы.
4-я теорема (о непрерывно дифференцируемой замене пе-
ременной в несобственном интеграле Римана). Пусть ф: Gcz
^R" -> $ =q>('G)c:R" (где G и $ — открытые множества) —
отображение класса C^(G), для множества критических точек ко-
363
торого S={t^G | det Dcp(?)=O} имеем mesS=O. Пусть множество
п
критических значений q(S)cz$ таково, что &\<p(S) — открытое
множество и сужение ф: G\S -* ф(0\5) == !§\(p(S) есть диффео-
морфизм класса С(Г>. Тогда имеем: а) если f^R(&) (в смысле
(АЕ), (К)), то fe=R($\<p(S)), f^|detDT|e^('G\S)A/?fG) в
смысле (АЕ), (К)), причем имеет место формула замены пере-
менных
f fdx - J fdx =
S—9(G) &\<p(S)-9(G\S)
= f f° <p|detDq>|dt = f f о <p|detD<f>|df. (4.16)
G\S О
где все интегралы несобственные; б) если S измеримо по Жор-
дану и f^R(&), то f^R(&) и в левой части (4.16) стоят два
обычных интеграла Римана 1 f(x)dx= ! f(x)dx; в) если из-
&=<p(G) &
меримы по Жордану оба множества 6 иУ , причем detDq>eB(G)
uf^R($ )/\R(%), то fo<f\detDfp\^R(G)/\R(G) и в равенстве
(4.16) стоят обычные интегралы Римана
j f(x)dx =J f(x)dx —
&=cp(G) &
Jfo <p(?)|detDq>(7)|df=f f о <F(7)|detD(p(7)|dt
G 5
Доказательство. Покажем сначала справедливость ут-
верждения а). Отметим, что множество S критических точек ото-
бражения ф всегда замкнуто (в G). В самом деле, пусть Zo&S'f|G,
тогда существует точечная последовательность (tm) такая, что
/meSVffleN и lim — причем detD<f(tm) = 0 Vm eN.
m-*4-oo
Но
(detОфeC(£o) =»(detОф(/0) = lim detОф(Гт) = 0) =»(^0eS)=?
m—* -[-oo
=>(SJ|GCS).
Но тогда G\5 = G\S, где S — SlJdS, причем, очевидно, dS CZ
(Z<?G|JS и,_ в частности, dSG CZSCZ G. Итак, множество
G\S = G\<S открыто в R". Далее, по условию множество
2?\ф(5) открыто и поэтому ^\ф(5)= S\®(S), где <p(S) = ф(£)и
Ц<?Ф(5), так что 5ф(5)сс5^иФ(^)> и поэтому дф(5)Г|$ С ф(<$),
ф(5)П$=ф(5). Итак, множества $\ф(£)=ф(0\5) и G\S открыты.
Поскольку феС(1>(й), то в силу теоремы Сарда из гл. 1, § 3
имеем mes ф(5) = 0. Пусть
364
где J" — открытые измеримые по Жордану брусы, a J"— ком-
пактные измеримые по Жордану брусы. Пусть {е((х))— разби-
ение единицы для множества подчиненное открытому по-
крытию причем suppe,cz JiV i. Поскольку f е то
MJ?
I
и абсолютно сходится ряд
Sf f(x) e/x)dx=f fdx.
i=l J? $
i
рассмотрим множество 7"\ф(5)С J" CZ Тогда d(7i\<p(S)) CZ
J" CZ$, t. e. d(J7\<p(S))C$, так что д(7?\ф(5)) =
= Wj\<p(S)). Далее, поскольку = ф(-$)С2$ и
71г\ф(5)С$, то множество 7£\<p(S) = 7? \<p(S) открытое и
учитывая, что дф(5)Г]$ Q<p(S)cz$, имеем
5(7?\ф(5)) = snd(7l?\<p(S))ca7»U(^n W))c37;u<p(5).
Но |dJ?|n = mes <?(S) = 0, поэтому mesd(7"\q>(S))= 0, так что
п п
открытое множество J?\(p(S) измеримо по Жордану. Но тогда
£\ф(5)=и (7"\ф(5)),
2=1
где {7?\<f(S)} — открытое покрытие для открытого множества
$\ф(5), состоящее из измеримых по Жордану множеств, при
этом система {е^х)} будет разбиением единицы и для множе-
ства $\<p(S), подчиненным открытому покрытию {7!*\ср(5)} (т. е.
%е{(х) = 1 Ухе$\ф(5)С$,
1=1
причем (suppе4)р($\<?(£))с7;\ф(5)). Заметим, что Jf =
МЛ?Хф(5'))и(7"Пф(5)). Поскольку ф(5)П$= <p(S) и7"с$, то
Л" n<?(S)cz /?Пф(5)=(7« П Ф(5))) Г№ =
=7?п Шп^) =7?Лф(5) с ф(5).
Поскольку те$ф(5)=0, то тез[7"(")ф(5)) =0 и в силу компакт-
ности 7"Пф(£) имеем |J"Qф(£)|п = 0, т. е. доказано, что |7" Г|
Пф($)|п = 0. Но тогда в силу теоремы 9 из гл. 2, § 1 имеем
равенство
365
J f(x) et(x) dx— J ?(х)е{(х) dx V/gN,
так что
def
$ Z—1J?
I
+°° def
= 2f \f(x)\ei(x)dx= f \f\dx,
i=I J"\v(S) &\ф(5
т. e. f s причем
f fdx= f fdx.
&=i(G) ®\ф($)=ф(О\$)
Рассмотрим теперь диффеоморфизм <p:
G\5->q>(G\5) = ^\<p(S).
Тогда 3-я теорема (о диффеоморфной замене переменной в
несобственном интеграле Римана) дает для функции f^R(J§\
\<р(5)): _
1) f ° <р । det D Ф| е= R(G\ S)
и
2) С fdx= J fdx= f f<> ф|бе!Оф|с?Л
& ®\ф(3) G\S
Пусть теперь
4-оо 4-о®
G = U/f = U/A
i=i z-i
где 7? — открытые, измеримые по Жордану брусы и —
разбиение единицы для открытого множества G, подчиненное
открытому его покрытию {I?}, причем supp CZ I" V I. Тогда,
очевидно.,; для открытого множества G\S = G\S имеем
G\S = ij“ (
Рассмотрим множество 7?\SCZ/^CZG. Тогда d(Z"\S)C/?\SC
C/^CZG1, т, e. 5(/?\S)cG> так что d(I"\S)ssGQd(I"\S).
Далее, поскольку dSH^CS, то SQG = S, так что множество
7"\,$ = 7"\5 открытое, и тогда имеем
366
3(7?\S) => Gnd(I^XS)czd^{)(GndS)CldI"\JS.
Ho mesS = 0 = |d7{!|„, поэтому для ограниченного множества
7?\S с 7? имеем mes3(7?\5) — 0, т. е. открытое множество
1 п
7"\3 измеримо по Жордану. Но тогда {e,i(t)} будет разбиени-
ем единицы и для открытого множества
G\S=U° (7?\5),
i=l
подчиненным открытом покрытию {7?\5}, причем (suppejf)
f)(GX5)CZ7?\'5v i. Но vt^S и YieN, очевидно, имеем ра-
венство
f° ф(7) е{(7)| det D ф (7)| = О, .
из которого вытекают равенства
f If ° Ч>(7)| *8,(7) • |detDT(7)|df =
/?
I
— f I/ ° ф(01 • ^i(t) • |detD ф (7)| v i eN
/"\s
и поэтому
f If о cp|.|detD(p|dt =
G\S
= 2 J If ° <₽O)I • |detD<p£O|^ =
= 2 f Ifo ФС01 -8.(0 • | det D ф{7)| Л =
i=l J?
I
^fylf о <p| . I det D <p (7)| dt,
G
t. e. f ° <p • | det D<p| e 7?(G) (в смысле (АЕ)), причем доказано,
что
С fo ф| det D<p| dt — J f о ф • ^е1Вф|сГ/,
G\S G
так что имеет место (4.16). Утверждение а) доказано. Из ут-
верждения а) следуют утверждение б) и в). В самом деле»
пусть выполнены, например, условия в), т. е. открытые мно-
жества и G измеримы по Жордану, det Вф s 77(G) ДС(б) и
36Z
R(&) Д R№). Тогда в силу теоремы (из гл. 2, § 3) о доста-
точном признаке существования интеграла Римана на ограни-
ченном открытом множестве имеем f е R(SP), причем несобст-
венный интеграл f fdx совпадает с обычными интегралами
Римана
$f(x),dx =f f(x)dx.
& &
Но тогда в силу утверждения а) имеем
f о <р| det Dq> | <= ^(G) Д R(G\S),
причем в равенстве (4.16) первые два интеграла слева являют-
ся обычными интегралами Римана. Далее, поскольку множест-
во измеримо по Жордану, то оно ограничено и mesd$=
х п
= 0. Но d<p(S)CZd$(J ф(£) и поэтому
5(^.\ф(5)) (Z С &§ U <P(*S)
и поскольку
mes д& — mes <₽(<$) = 0,
п п
то ограниченное множество ^\<p(S) = <p(G\S) измеримо по
Жордану. Отображение ф:С\5->ф(С\5') = ^\ф(5) есть диф-
феоморфизм класса поэтому множество С\£=ф“,($/ф(5))
также измеримо по Жордану. Кроме того,
(fS7?(^))^feB(T(GXS))
я в силу леммы об интегрируемости по Риману композиции
двух функций имеем' f ° ф sR(G\S). Множества G и G\'S из-
меримы по Жордану, так что
(det Оф €= B(G) Д C(G)) =ф (det DT е R(G) Д R(G\S),
откуда
(f о ф g= R(G\S)) Д (det Оф <= R(G\S)) =>
=4 (If о <p|det DTe^(G\S) Дад),
причем оба интеграла, стоящие справа (4.16), также совпада-
ют с обычными интегралами Римана.
Теорема (об инвариантности интеграла Римана относитель-
но движения в Rn). Рассмотрим открытое множество GaRn, из-
меримое по Жордану и отображение <р: Rn Rn, являющееся
движением (т. е. композицией сдвига и линейного ортогонального
преобразования). Если feR(y (G)), то f°q><=R(G) и
f f(x) dx=$f° y(t)dt.
v(G) G
368
Доказательство. Для движения <p:Rn->Rn имеем <р =
= (<рь ф2... фп), где =а,+ S aifa (i=l, 2, ..., п) и матрица
/•=1
(a./) (i, / = 1, 2, п) ортогональна (так что det^owy) ='±1). Но
тогда отображение ф является диффеоморфизмом класса С<*>, для
которого j det D<p(Y) j === | det (ос»/) | =4, причем в силу теоремы (о
сохранении измеримости . по Жордану при С(1)-отображении из
гл. 1, § 4) измеримости по Жордану множества G следует изме-
римость по Жордану множества q>(G). Кроме того, в силу леммы
(об интегрируемости по Риману композиции двух функций) име-
ем f ° <f^R(G). Применяя 3-ю теорему (о замене переменных в
кратном интеграле Римана) и учитывая равенство
f»<p(t) • |det Оф(7.) | =f»ф(0 V tt=G,
имеем
J f(x)dx=$f° (f(t)dt.
Ф(О) G
Следствие (об инвариантности меры Жордана относитель-
но движения). Рассмотрим множество Л-czR", измеримое по Жор-
дану, и отображение ф: R" -*• R", являющееся движением. Тогда
множество ф(Л)сгР2 измеримо по Жордану и |ф(Л) |П='|А |п.
Доказательство. Если множество AczR? измеримо по
Жордану, то (поскольку движение ф есть диффеоморфизм) мно-
жество ф(Л)с^" также измеримо по Жордану. Рассмотрим такой
брус /"[а, Ь], что Aczln(a, b), тогда у(1п[а, &])^ф(Л) и в силу
биективности отображения движения ф имеем
%д(0=%ф(Л)[ф(0]^/е/»[а, 6].
По условию %A^R.(In[a, Ь]), поэтому, применяя 3-ю теорему (о
замене переменных в кратных интегралах Римана) и учитывая
инвариантность интеграла Римана относительно движения, имеем
|ф(Л)|п= f X^A)(x)dx =
Ь])
= j Хф(4) [ф (О I dt — IА|„.
1п\а, Ь]
Замечание (о геометрическом смысле якобиана). Если G
и открытые множества из Вп и отображение ф :G—>$=ф(С)
является диффеоморфизмом класса С(1>, то для любой точки
*° е G и для любого куба С G имеем
|detD<p(^)|= lim |ф (Z5^0))|„/l^0)|n.
8->0
84 ** Л. И. Камынин 369
В самом деле, в силу теоремы о среднем (из ч. V., гл. 2, § 1),
учитывая, что detDq>eC(tf°) и det D<p(f0) =£ 0, имеем
l<₽W))|n= f Wx= f |detD<p(Q|rff =
Ig(f)
= | det Dtp (^)| • | WL = (|det Dq> (t»)| +
+ o(l)) -IWln Ф-0)
(где t1 e Щ*0)), откуда вытекает, что
|det D <p (/’)| = lim(|P( Zg(H)H Win) •
Пример. Вычисление n-объема п-мерного шара 111^(0)Q
CRn. Пусть
Ш,«’(0)=хе
Используя преобразование подобия <p:Rn—>В", где —
= R • ti (i=l, 2,..., га), имеем ф-г(Ш^>(0)) = Ш^О), причем
. О
. о
det Оф(7) =
d(xi......хп)
d(ti......М
R 0 .
О R.
О 0 .
=ЛП,
. R
и тогда, используя 2-ю теорему
интеграле Римана), получаем
(о замене переменных в кратном
Vn(R) = f \dx= J |detDT |(T)|d£ =
<р(Ш<л>(0)) Ш<л)(0)
= ЯП . f \di = Rn -vn,
UlO>)(0)
t. e. Vn(R) = Rn • vn, где vn = 7„(1) — объем „единичного*
n-мерного шара. В силу теоремы Фубини имеем
- j- 1 «= j... у
Щ<л>(0) гп1-1. 1] 1
= j - d'— =
= f dtn J • • • f 1 dtt. . . dtn-i,
-Ji n<‘B>
где
370
O(M=UlWn{<. - tn) = V 6 Rn|
1 -« = ш'р,,;)./=<0>
поэтому
vn — J dtn щ(П_ц (0) . . . dtn—i =
M)1/2
= »„-! • J(l-/2yn-l)/2dZn.
-I
Делая замену t%=z, 1— <2=1— z, <n = zl/2> = (l/2z‘/2)dz имеем
vn = 2 • p„_i ♦ f (1- t^~^dtn=z
b
= Гп-i - J (1 — z)<«~l>/2 . z-i/2 rfz =
= vn_! • B((n+l)/2, 1/2),
т. e. (используя свойства функций Эйлера из [3], гл. 3, § 5)
Vn=t»n-i-B((n+l)/2, 1/2) =
=©п_гГ((л+1)/2)-Г(1/2)/Г((п4-2)/2=
= vn-i • л1/2-Г ((n+1 )/2)/Г ((п+2) /2).
Итак, получена рекуррентная формула
Рп=Оп-1-л,/2-Г((п+1)/2)/Г((п+2)/2),
из которой имеем
vn=01 • я(п-1)/2.г (3/2) /Г ((п+2)/2) =
=иглп/2/2Г((п+2)/2),
но 01=2, поэтому оп=лп/2/Г(п/2+1), т. е. для объема п-мерного
шара (0) имеем
Уп(/?)=я"/2./?п/Г(л/2+1).
В частности, Vi(R)=2R,
V2(R)=n -R2, V3(R) = (4/3) л-Я®.
24*
Часть VI
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
Глава 1
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ В R"
§ 1. Ориентированные fe-пути
и ^-поверхности в R"
Рассмотрим ^-мерное линейное (векторное) пространство Е* и
совокупность всех (упорядоченных) базисов {(аь а*)} в нем.
Пусть (Ьь bft) и (ai......ал) два таких базиса, причем Ь»=
~ S р<7а/ (»=1> 2, k). Тогда в силу линейной независимости
базисов det (£,/) =/=0, так что либо det(£*/) >0, либо det(p^)<0.
Определение. Базисы (bi.........Ьл) и (ai, ..., ал) в Ek экви-
валентны (~) (имеют одну «ориентацию»), если det(fk/)i>0.
Замечание. Средствами линейной алгебры (см. [5] можно
показать (проделайте это самостоятельно), что введенное отноше-
ние является отношением эквивалентности (в алгебраическом
смысле), т. е. обладает следующими свойствами:
1) (рефлексивность) (аь .... ал) ~ (ai, .... а*);
2) (симметричность) ((bi...Ьл)~(аь .... ал))=>((аь ...,ал)~
- (bi, ..., Ьл));
3) (транзитивность) ((аь ..., а*) ~ (bi.Ьл))Л((Ь1,...,Ьл)~
~ (ci, ..., cA)) ((аь ..., ал) ~ (сь .... cfc)).
Очевидно, совокупность всех упорядоченных базиов в Ел рас-
падается на два класса эквивалентности относительно введенного
отношения
Определение. Ориентацией в линейном пространстве Еь
называется задание класса эквивалентности во множестве всех
упорядоченных базисов в Ek относительно отношения (ориента-
ции) Таким образом, каждое линейное пространство Еь, имеет
в точности две ориентации.
Евклидово пространство R* (рассматриваемое как линейное
пространство со стандаратным базисом (еь ..., ел), где
ег=(Ь, ..., 0, 1, 0, ..., 0)), имеет стандартную «ориентацию», соот-
ветствующую стандартному упорядоченному базису (е^ ..., efe).
372
П р и м ер. Рассмотрим упорядоченную систему (хь х&) ли-
*
нейно независимых векторов из R* такую, что xx=S хх/е>
/=1
(/=1, 2, k)t тогда система (хь х&) ориентирована положи-
тельно, если
det(xv) =
Хц . . • х1к
xk\ • • •
>°,
и ориентирована отрицательно, если detfxij <0.
Рассмотрим линейный изоморфизм А : Lk -> Ек, где простран-
ство Lk ориентировано заданием базиса (1Ь lfe).
Определение. Изоморфизм А переводит ориентацию Lk в
ориентацию Ек, определяемую упорядоченным базисом (Л11,
ЛЦ) (т. е. линейное пространство А(Ьк)=Ек ориентировано за-
данием базиса (ЛЬ, А1к).
3 а меч ан не. Если в Ек уже выбрана ориентация, определяе-
мая базисом (еь ..., е^) и (А,у) (i, j—1, 2, ..., k) матрица, соответ-
ft
ствующая изоморфизму Л (так что Л1/=;2Л//е/ (i=l, 2, ..., k), то
говорят, что изоморфизм Л сохраняет ориентацию Ьк, если базис
(ЛЬ, ..., Л10 имеет ту же ориентацию, что и базис (еь ..., е*) (т. е.
при detfA-jX), когда A(Lk) и Ек ориентированы одинаково) и
переводит ориентацию Lk в противоположную, если базис
(Л1Ь ..., Aik) имеет ориентацию, противоположную с базисом
(ei, ..., ед) (т. е. при det^fJcO, что означает противоположную
ориентацию A(Lk) и Ек).
Рассмотрим теперь евклидово пространство Rn с декартовой
системой координат x=(xt, ..., хп). Пусть Z7czRfe (где —
открытое множество из евклидова пространства R*, где введена
декартова система координат .... tk). В (линейном) про-
странстве R* введена стандартная ориентация, соответствующая
стандартному базису (еь .... е*).
Определение 1. k-путем <р в Rn (где \^.k^.n) класса
(/=4, 2, ..., 4-оо) называется невырожденное отображение (клас-
са СО), ф : L7czRft Rn такое, что:
1) tp^C0)(U), т. е. х=кр(7), x<i==kpf(^i. h) (i=l, 2, ..., п),
^aeC(U) Vi-,
2) nXk матрица Якоби (D^(x)) (7=1, 2.......n; /=1, 2, .... k),
соответствующая производной D<p(t), имеет ранг kN t^U. Образ
r=<p({7)c:Rn называется носителем или следом k-пути ф.
Замечание 1. В качестве открытого множества (7czRfe обыч-
но будем брать или все Rfe, или открытый шар .(0)c:Rft, или
открытый брус Ik (0, l)czR*.
373
. Определение 2. Рассмотрим открытые множества Utcz
cR‘ и UxczR.*, тогда отображение t:Ux-^Ut t—t(x) класса С<’>
называется допустимым преобразованием параметра (от Ux к
Ut); если:
1) отображение t:Ux-+Ut есть диффеоморфизм класса О’>,
так что существует обратный диффеоморфизм x=trx :Ut-+ Ux, при-
чем t(=C^(Ux), xsC^(Ut) и detDf(x)=#0 vT«=L/t;
2) Ut=t(Ux), Ux=x(Ut);
3) det DZ(r) == (т) > 0 v x^Ux и detDx(t)=>
д(Ч»...,тк)
= ...xh> Щ >Qvt€=Uf.
Замечание. Если диффеоморфизм t:Ux-+ Ut осуществляет
допустимое преобразование (от Ux к Ut), то и обратный диффео-
морфизм : Ut -* Ux является допустимым преобразованием
t
параметра (от Ut к Ux), при этом имеет место диаграмма Ux^ Ut.
t"1
Если диффеоморфизмы t:Ux-+ Ut и X: Ut -* UK — допустимые
преобразования параметра, то композиция Л ° t: их-^ик также яв-
ляется допустимым преобразованием параметра (от Ux к UK), при
этом имеет место коммутативная диаграмма
ux——*‘Ut
1>Х
, Следствие. Если ф : 17/CzR*-> Rn есть 6-путь класса С<*> в
Rn и диффеоморфизм t: Ux-+Ut осуществляет допустимое преоб-
разование параметра (от Ux к Ut), то отображение ф : U,c"Rfe -►
-*Rn, где ф=фо£, ф=фо/-1, есть 6-путь в Rn, причем ф('£Л) =
==(p(Z7f)=razRn, так что носители обоих 6-путей ф и ф совпадают
как множества в Rn. Имеет место коммутативная диаграмма
PcRn
ф / \ф
ut^ux
T~t~ 1
Для доказательства утверждения следствия, что отображение
Ф=ф ° t есть 6-путь в Rn, отметим, что (поскольку ф есть 6-путь)
(т) > о V т е= Ux,
и тогда в силу теоремы (о производной сложной функции)
имеем формулу
374
k
57-2аТ -Г- <i=1’2.........”• '-1’2....
д i i=tl dxi
из которой в силу невырожденности линейного преобразования с
матрицей 2, k) следует, что ранг матрицы Яко-
би отображения ф совпадает с рангом матрицы Якоби отображе-
ния ф, т. е. равен k. Таким образом, отображение ф есть Л-путь в
Rn.
Замечание. Если отображения ф: CAczR*-> Tc:Rn и
ф: £/ta:R?-*Ta:Rn являются гомеоморфизмами, то существуют
обратные гомеоморфизмы ф-1: Г(Л=ф_1 (Г) и ф~1: Г -> Ux—
=ф—1 (Г) и тогда для допустимых преобразований параметра име-
ют место представления
/=1<р-1 о ф; =ф-i (Г) —ф-1 (Г) =iUt
я
т=ф-1 ° ф : СЛ=ф-1(Г)-»-ф~1(Г) =£7Т,
так что
Г
ф ^ф
ut т°^~1><,> их
*Оф
Определение 3. k-пути ф и ф в Rn (где ф: Ut rcRn и
ф: TczRn) называются эквивалентными (запись: ср~ф), если
существует допустимый диффеоморфизм t:Ux->-Ut такой, что ф—
=<р° t и ф = ф° t~l.
Замечание. Введенное отношение ~ Является отношением
эквивалентности, поскольку оно обладает свойствами:
1) ф~ф — рефлексивность
2) (ф~ф)=> (ф~ф) —симметричность (так что
Ф=фот
Г
К^Ф—ФоГ
Ut их ).
3) (ф~ф)Д (ф~б) => (ф~б) — транзитивность (так что
375
Г" к О=ФоХ =(фоОоХ“
f ф—vot \ =ФО(/ОХ>
и
_____________th
/оХ
(Проверить самостоятельно.) Но тогда введенное в определении 3
отношение эквивалентности разбивает множество всех Л-путей
(класса С<*>) в R” на классы эквивалентности: классу эквивалент-
ности (произвольного) й-пути <р принадлежат те k пути в Rn, ко-
торые ему эквивалентны. Таким образом, каждый Л-путь в Rn
принадлежит одному из классов эквивалентности и пересечение
двух различных классов эквивалентности пусто. . «•'
Определение 4. k-поверхностью Ф в Rn называетсякласс
эквивалентности k-путей (с представителем k-путем ф: Uc:R.k -*
->Г=ф(Т/)с^’»).
Замечание. Понятие носителя (следа) данной fe-поверхно-
сти Ф в Rn определено однозначно, так как все й-пути, входящие
в класс эквивалентности Ф, имеют один и тот же носитель в Rn.
Определение 5. Пусть ф: -*• Rn и ty: Utcz.R*~*
->Rn — дВа k-пути класса в Rn. Будем писать ф=—-ф или
ф=—ф, если существует такой диффеоморфизм t'.Ux->-Ut, что:
1) teC&(Ux), x-He=CW(Ut);
2) i(Ux)=Vt, x(Ut) = Ux-
3) det D t(x) - (t) < 0 v t <= Ux,
o(tl...tfc)
det Dt (t) = .....(t) < О V t e Ut;
4) ф=ф ° t-1, ф=ф <> t.
Замечание. Если для fc-путей (в Rn) ф и ф имеем ф=—ф»
то для любых /г-<путей ф* и ф* таких, что ф*~ф и ф*~ф, имеем
Ф*=—ф* (доказать самостоятельно). Таким образом, можно го-
ворить о ^-поверхностях Ф и Т (в Rn) таких, что V=—Ф.
Рассмотрим &-путь (класса С(1) в Rn ф: £/c:RftГ=ф((/)сх
cz,Rn и точку х0=ф(7ь)еГ, тогда
Рф('.)= (з .............
\/=1 7 /==1 7 /
есть морфизм Вф(?о) : R* -* R”, матрица которого
376
/^iW\ (j=l, 2, .... n; j=l, 2, ...» k)
\ dtj j
имеет ранг k. Но тогда образ D<p(7o)(7?fe)=Lfca:Rn является A-мер-
ным линейным подпространством в R", причем отображение
^ftcrRn является (линейным) изоморфизмом. Если
(еь .... ©а) — упорядоченный стандартный базис в R*, то изомор-
физм Dtp(fo) индуцирует в Lk ориентацию заданием’ в Lk упорядо-
ченного базиса (D<p(?o)eb Dcpffo)®*) (так что
Dq>(t0)e5 = (7 = 1, 2, ... , А)).
\ dtj I
Определение 6. k-мерное ориентированное линейное про-
def
странство Тф(у (Г) = Lk называется касательным пространством
для k-пути <р в точке ф(7о)=х0<=Г.
Замечание. Векторному касательному пространству Тф<у (Г}
(из определения 6) соответствует аффинное A-мерное пространст-
во (Г), проходящее через точку <p(ifo)=xoer в Rn и зада-
ваемое системой параметрических уравнений
xi = <pia0)+2 (»=1,2....«); <=(/!,..., '
/=1 '
Пример. Пусть A-путь (класса С(1> в Rn <р задан системой
уравнений xi=fi(xi, ..., Xk) (7=А-|-1, •••> п), х'^(х\, .... XkjeUc.
cR* так, что
| Xj=tj (j=l, 2,..., А),
I Xi^=f((tu...t tk) (i=A-|-l.n) t<=U CR\
где fi s G(1,((7) V i. Тогда носитель этого A-пути имеет вид
Г={(Х1,..., xn)(=Rn]xi=f1(xi,..., xk) (i=A + l,..., п), x'eU}.
Пусть х0 е Г (где х? = f^xj,..., х£); i = А+1,..., п), тогда аф-
финное касательное пространство ТХй(Г) в точке хоеГ задается
системой уравнений
Xt — f, xty = 2 ) •(*/—*/)
(i = А 4-1, . . . , п), хе Rn.
В частности, для 2-пути <р: U CZ R2 —> Г, где
Г = {(х, у, z) е R3|z = f (х, у), (х, у) е U},
(! О \
° 1 I
df df_ I
dx dy J
37T
и М0 = (х0> у9, г0)<=Г уравнение
2-/(х0, г/0)=д-^-^ .(х_Хо)+ЁК^ь2о) . (у_уо)
дх ду
определяет аффинную касательную плоскость Тм.(Г) в R8 и
при ортах ех = (1, 0), е2 = (0, 1) в R2 у вектора
0<р (х0, y9)eL = f 1, 0, f(x0, у0)\,
Оф(х0, уо)е2=(о, 1, ~ f(x9, у0\
\ оу
задают упорядоченный базис (Вфех, Офег) в (векторном каса-
тельном пространстве 1^,(0) (см. рис. 18).
Теорема. Пусть ф : UtazRf -* TczR" и ф: C/tc=R* TcRj—
два k-пути (класса С<’> в Rn, причем либо ф.--ф, либо ф=—ф.
Пусть ф(70)='ф(т0) — хоеГ=ф(7Л)=ф(Т4) (где ф=ф»t и t0=
1==/(то)) и T^t,) (Г) и ТФ(т.) (Г) касательные пространства к
k-путям ф и ф (в точке ф(1йо)=ф(то) =хоеГ) соответственно. Тог-
да T«(t0) (Г)=Тф(Т„) (Г), причем ориентации этих касательных
пространств совпадают при <р~ф и противоположны при ф=—ф.
Доказательство. Пусть t: f7tczR£ -^-UtciRf — диффео-
морфизм из определений 3 и 5 соответственно, так что ф=ф»t,
йричем £o=i£(to) и det Df (то) >0, если ф~ф, и detD£(ro)<O, если
Ф=—ф. Заметим, что отображение D^(t0):RJ—>R* есть изомор-
физм и поэтому DZ(T0)(R*)=:R/fe. Пусть (!>,.—» lft) — упорядочен-
ный базис, определяющий ориентацию RJ, a (ех,..., е^)—упорядо-
ченный базис, определяющий ориентацию R*. Тогда линейное
пространство ориентировано базисом (D/(t0)1x, . . .
.... Ш(-с0)1й), причем
k
о^0)1х=2^е/,
£1 dZi
так что при
det D/(t0) = det /— Л(т0)^ > О
' ®т/ /
имеем
(Dz(t0)lx,..., D/(T0)lfc)~
~(ех, е2, е3,..., ej
(т. е. линейные пространства R,
и DZ(r0)(RJ) ориентированы одина-
ково), а при detD^toXO имеем
378
D/(r0)lfc~(e4, eb e3,..., eft) (t. e. R* и D/(t0)(RJ) ори-
ентированы противоположно). Заметим» что в силу теоремы
{о производной сложной функции) при Ф=ф ° t имеем D<|»(t0) =
==D<p(^o)° Di(T0) и тогда коммутативные диаграммы
Г
Ф Ф=фо/ ч
ut^—их
t
Rn
D4>(Q f \чОФ(тй)=Пф(«,)оОКт.)
R*,------R*
ОН’.)
дают равенства
(ТФМ (Г) = Di|»(tt)(R*) = D,(f0)(D^0)(R*)) ~
= ТФ(и (Г)) => (Тф(1о) (Г) = Тф(^ (Г)).
Если ф ~ф, то ориентации линейных пространств D«(t0)(R*) и R*
совпадают, и тогда изоморфизмы
DV(U:R?->Wr), Dv(/e):D/(T0)(R*)^T4>(t,)(r) (1.1)
приводят к одинаково ориентированным касательным простран-
ствам ТФ(,„)(Г) и Тф(т)(Г).
Если ф=—ф, то ориентации линейных пространств Df(to)(R*J
и R* противоположны, а потому в силу (1.1) противоположно
ориентированы и касательные пространства Тф(/в)(Г) и Тф(Т,)(Г).
Более точно, поскольку R* ориентировано базисом (еь е2, . . .
• . . , eft), то ТФ(^;(Г) ориентировано упорядоченным базисом
(Вф(То)е!, Оф(^0)е2, . . . , D?(t0)eft).
Если ф=—ф, то линейное пространство D/(t0)(R*j = R* и по-
скольку detD/(-co)<O, то ориентация D/(t0)(R*J противоположна
ориентации R* и задается, например, базисом (е4, еъ е3,... efe),
но тогда Тф(Т,)(Г) ориентировано базисом
(Оф(^)е2, Dv(/0)eu .... DT(t0)eJ,
так что касательные пространства ТФ(<,)(Г) и Тф(Х,)(Г) ориентиро-
ваны противоположно.
Замечание. Рассмотрим &-путь (класса С(1> в Rn ф: С/с:
<=R4-*rczRn, где Г=ф(С/) — его носитель в Rn, тогда отображе-
ние ф; и -► г локально взаимно-однозначно в каждой точке t^U,
379
т. е. отображение <р локально взаимно-однозначно на U, однако
это отображение ф может и не быть биекцией U на Г, поэтому
&-путь q> нельзя отождествлять с его носителем Г=<р(77). Если
же отображение ф: J/czR* -► Fc=Rn есть гомеоморфизм, то Л-путь
Ф можно отождествить с его носителем Г=ф('С/)с^п.
Определение 7. k-путь ф : i/crRfc-> Г=ф(1/)с^п называ-
ется k-путем Жордана, если отображение ф осуществляет гомео-
морфизм U на r=q>(U).
Замечание. Пусть ф: t/cR* -► TcR’ fe-путь в Rn (класса
причем существуют fi, t2^U такие, что tx=^t2, но ф(^) =
=хо^Г, тогда аффинные касательные пространства
ТФ((,) (Г) и ТФ(/,) (Г) в точке ХоеГ, вообще говоря, различны.
Замечание. Если Ф==—Ф, то скажем, что ^-поверхности
Ф и Ф имеют противоположную ориентацию в Rn.
Определение 8. Скажем, что на k-поверхности Ф из R™
(с представителем k-путем ф: t/cR*-> Tc:Rn, где r=q>(U)) оп-
ределена функция ГеС<1>(Ф), если существует открытое (в Rn)
множество СсГ такое, что F^C^G).
§ 2. Дифференциальные формы степени 0 и 1 в Rn
1
Пусть (Rn, R1) есть линейная форма (линейная функ«
ция) в Rn=£. Тогда <л1^Е* (где Е* — линейное пространство, со-
пряженное к £), и если ei...еп — базис в Rn, a fi, ..., fn — со-
пряженный базис в Е* (т. е. такой базис, что fie/=l6(7), то имеет
1 п
место представление Дг/гЛ^К- Пусть е,=‘(0, ..., О, 1,0,...,
i
..., 0) (1=1, 2’ .... п) — канонический (стандартный) базис в Rn,
тогда линейная форма fi=pt^E* является координатной функцией,
так что pfh=/ii vh=('fti, h2, ..., ftn)e£sR". Вспоминая, что диф-
ференциал dxteX (Rn, R1) является как раз такой линейной фор-
мой, видим, что dxii=hi vheRn. Таким образом, система линей-
ных форм dxi, dx2, dxn образует сопряженный базис в сопря-
женном пространстве Е* и поэтому любую линейную форму
1 In
ю si?(Rn, R1) можно представить в виде со= p^At-dxi.
Определение (дифференциальных форм степени 1 и 0 в
Rn). Если QcRn — открытое множество, то дифференциальной
формой степени 1 класса (1=0, 1, 2, .... +<») называется-
отображение (класса С^)
®(X):Qc=R«->£ (Rn, R1),
так что
1 п
ш(х) Ai(x)dxt,
380
где At(x)^C{t) (Q). Дифференциальной формой степени 0 класса
С<1~> по определению называется отображение »:QcRn-»-RI. Та-
ким образом, дифференциальная форма степени О есть числовая
функция класса С<-‘\ определенная на открытом множестве QcR”.
Пример. Пусть QcRn — открытое множество и f:QczRn-*-
-*R, причем feC(l)(Q). Тогда по определению производной
V х <= Q Э df (х) = Df (х) е= R1),
так что дифференциал (производная) df(x) является дифферен-
циальной формой степени 1 класса С<0), определенной на откры-
том множестве QczRn, при этом, как показано в ч. III, гл. 2, § 3,
(из [1]) имеет место представление
п
df(x) =^D(f(x) dxit .
так что .
df (х№ = S (x) dxth=*
i-i
= 2 D, f (x) Ь4 V h = (hx..hn) s= Rn.
i=i
Рассмотрим вопрос о замене переменной в дифференциальной
форме степени 1 (вопрос о «прообразе дифференциальной фор-
мы») при дифференцируемом отображении.
Определение (прообраза дифференциальной формы степе-
ни 1). Рассмотрим открытые множества QcRn, GcR*
и отображение <p:Gc:Rfe->-QczRn класса С<*> (G) (так что х=
==|ф(0> Xi=qt(ti, ..., tk) 2...п), ф,-еС(1>(0) Vi). Пусть
®(x) : Й C RB-* £(Rn, R1) (i(x)=2 At(x)dxt
\ i=l
дифференциальная форма степени 1 (класса С^)г определенная
на открытом множестве QczRn). Тогда прообразом- дифференци-
альной 1-формы <л(х) на множестве GczRk называется дифферен-
циальная форма степени 1 q>*w :G(ZRS—»^(Rfc, R1), где
(»*e)(/)h = J(f(O)(Df(Oh)Vh«(fcI, . . . , hs)rR\
причем ,
(k k \
2 D^(t)hs.....2 ) e Rn,
/-1 /•=! /
T- e.
381
(<p*i)(0h=2AI<P(0)
i=l /=1
=2л[<р(о] (d<Pi(w
или в силу теоремы о производной сложной функции
п \ п
2 A,dxt) = 2 А‘ ° ? • й>4 =
i=l ) iS
п k
=2^‘ ° * * 2Dj4>,^/;
/ев!
k
dxi = dfft(t) =^iDlift(t)dtt (i=l, 2,..’., n),
/-1
i
Правило. Пусть а(х)—дифференциальная 1-форма, за-
данная на открытом множестве QcRn и имеющая представление
1 п
Ai(x)dxi.
i=l
Тогда при замене переменных x=q>(t), <peC(I)(G), Gc:R* для вы-
1
числения прообраза (p*a(t) нужно х заменить на q>(t), a dxi —
заменить на дифференциал
k
Dyv//) dt,.
i=t
Замечание. Если на открытом множестве QcRn задана
о
дифференциальная 0-форма а>(х) (т. е. функция f: Qc=Rn R1),
то ее прообразом при отображении ф : GczR* -*• QcRn (при
феС0)(О) называется дифференциальная 0-форма (т. е.
о
функция, определенная на GczRft) ф*и=ф*/=/° ф.
Замечание. Если отображение ф : GcR* -* QcRn принад-
лежит классу C^(G), а 1-форма в>(х) принадлежит классу
С<1)(Й), то прообраз ф*® является 1-формой класса
О о
(Для 0-формы <oeC<z>(Q) имеем соответственно, ф*<йеСт1п(,п,г)).
§ 3. Криволинейные интегралы от дифференциальных
форм 1-ой степени в Rn и их свойства
Определение. Рассмотрим дифференциальную форму
1 п
(o(x)s=2J Э'^(х) dxt
i==l
382
(класса С(0>), определенную на открытом множестве QcR", и
1-путь <р: [о, 6]-»-QczRn класса С^. Тогда криволинейным интег-
ралом 2-го рода от дифференциальной 1-формы о по 1-пути
Ф называется число
1 b I def Ь п
J®=jV«==f2
Ф а а i—1
Итак,
J2 ^«==2 f °
Ф Z=1 а
Напомним
Определение. Непрерывный 1-путь ф:(а, 6]•*TczRn <ре
еС([а, Ь])) называется кусочно-гладким (класса С^), если су-
ществует такое разбиение 7’={а=/0</1-<... <?те=Ь} отрезка
[а, &], что сужение отображения ф на отрезок [Л, fi+ij, т. е.
фг: pi, й-н]-* Tia:Rn (i=0, 1, ..., m—1) является 1-путем класса
С<*> (так что левая производная Ut~<p(ti) и правая производная
n^(ti) обе существуют, но не обязательно равны между собой).
Определение. Рассмотрим кусочно-гладкий 1-путь
ф:[о, 6]->rcRn (класса так что ф;:р/, ^+i]-> r(cRn 1-путь
класса С<*> при i—Q, 1, .... tn—1. Тогда для дифференциальной
1-формы а (класса С^), определенной на открытом множестве
Й=>Г, положим
4 m—1 4
J»=2b-
ф i=i ’i
Замечание. Если гладкий 1-путьф:[а, 6]-»-razRn жорда-
нов, т. е. отображение феС<1>([а, Ь]) биективно, то его можно
отождествить с его носителем Глв=ф([а, Ь]) (где А=у(а),
В=(р(Ь)), упорядоченным с помощью отношения (фСЛ^Ф^г))^
Тогда будем писать
f<o=J ® = 2 J ^idXi.
Ф ГАВ 1=1 ГАВ
Замечание. Гладкий 1-путь ф :[а, &]-► Г—<p([a, b])c:Rn
называется замкнутым жордановым путем, если отображение
ф:[а, Ь)-*ф([а, Ь)) биективно; феС(1)([а, Ь]), <^(а)=А =
==fp(b)=B и 0+ф(а)=О“ф(&). Полагая Г=Глв, будем иногда
писать
SPjdXt.
383
Замечание. Рассмотрим на плоскости R* , ориентире- |
ванной с помощью упорядоченного стандартного базиса {I, j}, j
замкнутый гладкий жорданов 1-путь <р и допустим, что носитель J
((контур) V=dG ограничивает область GczR^ у . Заметим, что f
контур Г является носителем и для 1-пути (—ф) (причем
Т_,(Г)=—ТФ(Г)). Обычно ориентация (обход) контура Г (инду-
цированная касательной ТФ(Г)) выбирается так, что при обходе
контура dG область G оставалась слева (т. е. граница dG обхо-
дится «против часовой стрелки»). Более точно, если из двух пара-
метризаций ф и (—ф) «выбрана» ф:[а, Ь]-> Г=<р([а, b])czR2 у,
где q>(t)=x(t)-i-[-y(t)-] и е — орт в пространстве RJ, то вектор
-r=x'-i4-y/-j имеет «направление» касательной ТФ(Т) и тогда век-
тор т=—y'-i+x'-j (ортогональный т) «должен быть» внутренней
((для области G) нормалью к границе dG-Г (см. рис. 19). По-
путно отметим, что поскольку
\x'(t)y'(t)
\-y'(t)x'(t)
= (x'(t))*+(y',t))*>0,
то {т, v}~{i, j).
Пусть г .[а, b]-»-rczRn — гладкий 1-путь, являющийся пред-
ставителем гладкой кривой R, так что
r(Z)=(*i(O« • • • » xn(i))^C^([a, b]) и
(л X 1/2
2 (DxifO)*) >0v«e[a,b].
/
Введем (сравните [1], ч. III, гл. 1, § 4) натуральную парамет-
ризацию (т. е. перейдем от t к s) s=s(t) по формуле
s(t) = J |D r(-c)| dt,
тогда s : [a, b] —> [0, sj, где
a
есть длина кривой R. Заметим,
что
^- = |Dr(01>0 vte[a, b],
at
так что s=s(t) определяет допус-
тимое преобразование параметра
от t и $ и существует обратный
диффеоморфизм
е;[0, Sj-ф, Ь]=г([О, sj) (t=t(s))
перехода от s к t. Но тогда, полагая р = г ° t, имеем
р:[0, sz] — p([O, sz]) = r([a, Ь]) = Г,
т. е. р**< и ре/?, причем для натурального параметра $ име-
ем ds = |Dr(7)|otf, а также
|Dp(s)| = |Dro ф)|
dt(s)
ds
= |Dr(7)|/|Dr(7)>l.
Определение. Если на гладком 1-пути <р:[а, &]-^ГлвстИя
определена числовая функция }<^С(ГаВ), то криволинейным ин-
тегралом 1-го рода от функции f по 1-пути <р называется интеграл
Римана
$fds = $f0 ф£01О<р(Х)|Л
ф а
и, в частности,
ъ
J lds= J |D <р(0| dt ~ st = |?|t
Ф a
есть длина 1-пути ф в Rn.
Замечание (об инвариантности криволинейного интеграла
1-го рода). Пусть <р и ф — гладкие 1-пути из Rn такие, что <р~ф
«ли ф——Ф- Если feC (Г) (где FczRn общий носитель 1-путей <р и
чр), то S fds=J fds.
ф ф
Доказательство. Пусть <р:[а, Ь]->Г=<р([а, b])cRrt и
ф:[а, р]-* Г=ф([а, р]). Поскольку <р~ф или ф=»—-ф, то сущест-
вует диффеоморфизм /:[а, Ь]=/([а, £]) такой, что ф=*
=Ф °/.причем
Df(t) -^->0vte=[a, р],
dt
если ф и
^-<0 V те [а, р].
dx
если ф== — ф. Но тогда
/(т) .
' dx
Ч'ак то
Юф(т)|= 2 рф<о t(x) . .
м=1 \ / /
и, Камынин 389
Поскольку f е С(Г), то
§fds= ff о <p(()|D<P(W = J f° <?(t)\D4(t)\dt.
Ф a [a, b]=f([a, 0])
Сделаем в интеграле Римана диффеоморфную замену / = /(т),
тогда
J fds== f f ° ф ’ <(т)| D <р(«(т))| •
ф [а, 0]
dx =
(n /
2 ( ефд^)) •
<=i \
dt(t)
dt
~ J f ° ф<х)1 D ФСО!^ = j fds-
3 Ф
Замечание (об инвариантности длины гладкой кривой в
Rn). Бели ф и ф — гладкие 1-пути в R”, для которых либо, ф~ф,
Либо ф=<—ф, ТО |ф|1=|ф|ь
Замечание. Если Ф — гладкая кривая в Rn с носителем Г
и /еС(Г), то имеет смысл запись
J fds = J f ds V ф s Ф,
ф ф
причем для 1-пути реФ (где p:{O,$z]-*TczRn), соответствую-
щем „натуральной параметризации" кривой Ф, имеем (посколь-
ку lDp(s)|== 1)
8/
J fds= J fo p(s)ds.
ф о
Отметим также, что
С fds= j fds.
—ф Ф
Отметим связь между криволинейными интегралами 1-го и 2-го
рода. Пусть Ф — гладкая кривая в R” с представителем гладким
1-путем ф:[а, 6]-»-ГлвС'К*. Рассмотрим на 1-пути ф криволинейный
интеграл 2-го рода от дифференциальной 1-формы
1 п
<о » 2 &i(x) dxi>
i—i
где <=С(Гав) V i.
Тогда по определению
। п ъ п
<0 « J 2 (x)dxi- f S ° Ф <0 • dt‘ ;
386
рассмотрим в точке х=ф(7)еГлв векторное 1-мерное касательное
пространство Т,(<)(Г), определяемое ориентированным касатель-
ным вектором
т (<р (0) = (ф/ (0.Фп' (0) ^Пф (/) е,
где е орт в R}. Заметим, что при ф~ф имеем Тф(<)(Г)з» Т«,(Т)(Г)=з
еТх(Г) (с сохранением ориентации), так что можно говорить о
направляющих косинусах cos аг направленной касательной х(х) "и
тогда
cos а(- (ф (t)) =icos as (ф (т)) =
, =cos а((ф °/(т)). V <р~ф; ф, феФ.
Но тогда имеем равенства
ФХ'69 = |ОфЮ1 * cos«tto(X)))E=T(<p(0)| • сО8а{(ф(Х))г
т. е. dxi — cosa.t(x)ds, и поэтому
ф a f=l
= -cosaOo q(t) • |Dq>(7)|tff=
n
— J 2 ’ cos a* ds-
Ф i=i
Это равенство дает формулу перехода от криволинейного интегра-
ла 2-го рода к криволинейному интегралу 1-го рода.
Теорема 1 (об инвариантности криволинейного интеграла
2-го рода относительно допустимой замены параметра). Пусть
1 п
10 2 &*(х)
<=i
где Я^ССГ) и FcRn — носитель эквивалентных 1-путей <р~ф #
R". Тогда
ф ф
Доказательство. Рассмотрим 1-пути ф:[а, Ь]-»-ГсКп'
и ф:[а, р]-»-Г. Если ф~ф, то существует допустимый (по опреде-
лению 2 из § 1) диффеоморфизм ^класса С(1) /:[а, ₽]-»-[ох Ь] та-
кой, что
Z([a, p])=[a, Ь],
D/(t)>0 Vxeja, Д, p],
т([а, bj)=[a, pj, D^(t)=.1/Dt(0>0,
25* 387
причем
1|>(т)=фв/(т), <р(О=|Ф’т('О-
Сделаем в интеграле
Ф a 1=1
замену t=t{z), что дает
dt(z) dt(z)
di di
поскольку
dz
а также
dtyi(z) __dfti dt
di dt di
поскольку -ф( =3 ф4 о t. Поэтому имеем
f <о = f V о фСО' • dt =•
Ф [в, 31 ^=1
rfq>i(O
dt
t=t(x)
di =
0 n
-J2^°
a i=l
dt di
о J 2 ° ^(T) * — да J $*<*> = J <Of
a i=i X л ф
Г 1 Г 1
T. €. | (0 = J (i) При Ф 4>.
ф Ф
1
Следствие. Криволинейный интеграл 2-го рода S со опре-
ф
делен на кривой Ф в R”.
Теорема 2 (о линейности криволинейного интеграла 2-го
рода). Если Ф — кусочно-гладкая кривая в R" и
I п Iя
fid i=t
388
где SPi, Qi^C(<D) (i=l, 2, .... n), то для любых постоянных с»
и с2 имеем
р 1 1 р 1 р 1
J Ci • <1>1 4- С2 • Ш2 = С, • | Wx + Cj ♦ j <l>i.
ф ф ф
(Доказательство провести самостоятельно, используя линейность
интеграла Римана.)
Теорема 3 (об аддитивности криволинейного интеграла
2-го рода). Пусть ф>:[а(-, b;]-»-riCzRn (t=l, 2) — кусочно-гладкие
1-пути в Rn и <p:[ab b2}->- Г=Г11)Г2с^п, где <pi(bi) — q2(a2)
(al<&i=a2<62),
ф(7) = { «PiCO. **M<*i. *il>
I ф2 СО, 1а»
так что
2
<₽ = U <Pi-
it==l
Тогда для
1 2
(0=^ 9\(х) dxt,
i=i
где е С(Г) (i ® 1, 2,..., п), имеем
f • = {•+!«>♦
CP1U<P» Фх Ф»
(Доказательство провести самостоятельно, используя аддитивность
одномерного интеграла Римана.)
Теорема 4 (об ориентированности криволинейного интегра-
ла 2-го рода). Если Ф — кусочно-гладкая кривая в Rn и кривая
,(—Ф) получена из Ф изменением ориентации на противоположную
в соответствии с определением 3 из § 1. Тогда для
i=i
где (i=<\, 2.п), имеем
J “ = — J<°-
-ф ф
Доказательство. В силу теоремы 3 (об аддитивности
криволинейного интеграла 2-го рода) теорему 4 достаточно дока-
зывать лишь для гладких кривых Ф и (—Ф) в R”. Пусть гладкий
1-путь ф:[а, &]->rczRn является представителем кривой Ф,
ф==—ф, Так что ф(т) =ф°?(т), где t:[a, р]->[а, Ь]=/([а, р]) и
389
dx '
т. е.
__ dt{t)
dt
Но тогда, делая замену переменной и учитывая равен-
ство
____dy dt
dt dt dt ’
имеем
i n
(•« j 2^0 <pW --~-dt =
v [a, b)=t([a, »] i=l
= j 2 ° *₽ °
la, 0] i=l
= - j
[a, 0]
' ' dt
Ф(Т).«)
dr =
dt
d«±dx=
dt
3 n
a t=I
г|?(т) • **№) dr — — J i|)*o = — J ®,
a Ф
r. e.
Теорема 5 (об оценках для криволинейных интегралов 2-го
рода). Если Ф — гладкая кривая в Rn и
1 п
*>(х) =2 ^i(x)dXi,
г=1
где (i« 1, 2,..., л).Тогда имеет место оценка
п (Л \1/2
2^ч ds-
Ф г—1 ф \/—1 /
Доказательство. Рассмотрим 1-путь <р : [а, 6]-*ГсгКп,
являющийся представителем гладкой кривой Ф, тогда
j<L=j2^o Ф(о • D^(t)dt.
Ф а /«1
390
Но по неравенству Коши — Буняковского
п I / п \ 1/2
• d ф,(о < х
St I V=i /
(п \ 1/2 / п \ 1/2
2(°ф<со)2 == 2(55< °ф^)’) • iD ’Wi*
i=l J \i—i J
так что, используя оценки для одномерного интеграла Римана,
имеем
• D <р( (t) dt
< f f2°ф w fY* • i d vcoi &-
a \i=l /
(л \l/2
2^1 ds-
Z—1 J
Следствие. Если ^(xJKAf V xs Г (i=l, 2,..., n), то
< M • n‘/2 . |ф|,
где |Ф|== — длина кривой Ф.
ф
Определение. Два непрерывных 1-пути ф0:[0, l}-*GcRn,
<Pi:[0, l]-»-G (где ф0, <pieC([0, 1J) и GczHn — открытое множест-
во) называются гомотопными, если существует такое непрерывное
отображение Г:[О, 1]Х[0, l]-»-GcRn, что F(t, u)sC([0, 1]Х
Х[0, 1]); F(t, 0)=«po(Zh F(t> 0=<Pi(0* Отображение F называет-
ся гомотопией пути ф0 в путь фЬ при этом V us[0, 1] существует
непрерывный 1-путь ф«: [0, 1]-► G, где <pu(t)=F(t, и). Говорят,
что семейство 1-путей {фи} (us[0, 1]) определяет непрерывную
деформацию 1-пути фо в 1-путь фЬ
Определение. Непрерывный замкнутый 1-путь ф1:[0, 1]-*
"* GczRn (так что феС([0, 1]) и ф(0)=ф(1)) называется циклом.
Определение. Цикл фо:[0, 1]-► GczRn называется гомо-
топным точке (или гомотопным нулю) в G, если 1-путь ф0 гомото-
пен 1-пути ф1: [О, 1J-ь GczR", где ф1('^=сеОу fs[0, 1] (с —
точка открытого множества G). (Таким образом, существует
отображение гомотопии F:
[О, 1]Х[0, 1]-GcR“, Г<=С([0, 1)Х[0, 1])
Цикла фо в ф1 такое, что
391
F(Q, u)=F(l, и) Vue[O, 1], F(f, О)=кр0(0;
Fit, l)=q>1('OvM0, 1]
u <fu(t)=F(t, и) является циклом в G v ue[O, 1].)
Определение. Открытое множество GcK,n называется од-
носвязным, если: 1) множество G связно (а стало быть, и линейно
связно); 2) любой цикл в G гомотопен точке.
Рис. 20
Пример (см. рис. 20). Область Gi — односвязна, а область
G2 не односвязна, так как существует цикл фо, не гомотопный
точке.
Пример. Пусть фо и ф! — два любых цикла из R2. Тогда
<Ро(()=<(х^), y0(t)), yi(t)) tep), 1}
и отображение
F(t, u):[0, l]X[0, 1]->R2,
F(t, u>(l-u)-^(t)+u ^(t)^(X(t, u), Y(t, u)),
где
X(i, u)=i(l—u)-x0(f)+u-Xi(t),
Y(t, и) = (\-и) у^)-\-и-уг(1), MO. 1]. «е[0. 1]
осуществляет гомотопию цикла ф1 в цикл фо, т. е. R2 — односвяз-
ная область.
Пример. Пусть GcR2 — открытое выпуклое множество (так
что [a, b]czG У a, b<=G), тогда для любых двух циклов фо и ф1 (из
области G) отображение F(t, и) из предыдущего примера дает
гомотопию ф1 в фо, поскольку цикл
фи(7)=(1—и) фо(О+«-ф1(О v «<<0, 1]
«лежит» в области GczR2. Таким образом, любая выпуклая об-
ласть GcR2 односвязна.
392
Пример. Рассмотрим откры-
тое множество Gc=Rn, звездное от-
носительно точки x0^G (так что
для любой точки xeG отрезок
[хо, xJczG). Очевидно, открытое
множество G линейно связано (так
как V Xi, X2S=G существует непре-
рывная ломаная [хь *o]U[xo» x2]cz
cG). Пусть <р :[0, 1]->- G — любой
цикл в области G, тогда отображе-
ние F:[0, 1]Х[0, l]-»-Ga:Rn, где
F(t, и)—'(1—и)-ф^О+м-Хо, осуще-
ствляет гомотопию цикла ф в цикл
Ф1: [0, l]->G<=Rn, где Ф1(О =
=Xo®G v te[0, 1]. В силу звездно-
сти области G относительно точки
xoeG имеем
(1—ц)-ф(7)-}-ихоеО v«e[0, 1].
Таким образом, любой цикл из области G гомотопен точке, так
что область G односвязна (см. рис. 21).
Замечание. Если плоская область, т. е. открытое связное
множество GcR2, ограничена и односвязна, то ее граница dG —
связное множество.
Замечание. Односвязная неограниченная плоская область
GсR2 может иметь несвязную границу dG (например, открытая
полоса П={(х, i/)gR2|—оо<х<+«>, имеет несвязную*
границу dG={—оо<х<+<ю, y=O}(J{—оо<х<+°°, У =<1).
Определение. Ограниченная плоская область GcR2 назы-
вается m-связной (т^2), если ее граница dG распадается на-
tn не пересекающихся связных компонент.
Замечание. Если m-связная (пг^2) ограниченная плоская
область GcsR2 имеет кусочно-гладкую (жорданову) границу, то-
т-1
ее граница <5О=Го1) U Г, есть совокупность попарно не пересека-
Z=1
ющихся кусочно-гладких циклов Жордана ф0, фЬ ..., фт-1, причем'
носители Fi циклов ф/ (t=l, 2, ..., m—1) лежат «внутри» Го — но-
сителя цикла фо (см. рис. 22).
§ 4. Формула Грина в R2
Рассмотрим кусочно-гладкую кривую Жордана Ф в R2 с пред-
ставителем 1-путем ф:[а, &]->TczR2. Тогда ф!=С([а, Ь]), так что-
носитель (кривой) Г=ф!([а, &J) (как непрерывный образ отрезка
1а» &]) является компактным множеством. Напомним, что для не-
замкнутой кусочно-гладкой кривой Жордана (т. е. при ц>(а)=£,
393-
^*9(Ь)) отображение <p:[a, 6}->Г=ф([а, &]) биективно (если же
1-путь ф Жордана замкнут, т. е. <р(а)=ф(Ь), то биективно ото-
бражение <р: (а, Ь))). Далее, существует разбиение
T={a—tto<ti<z... <ztm'=b} отрезка [а, &] такое, что 1-путь
ф
<рЛ:[4-ь П==|ф([4-ь М — гладкий класса С*1), т. е. Vfe
tk^D<f>(it)^Q и существуют односторонние производные
1)+ф(7*_1) =#0, Г)_ф(Л):/=0. Точка ф(7*)еГ, для которой В+ф('|4,)|#:|
#=!Ё)-ф(4), называется угловой точкой Г, остальные точки Г назы-
ваются регулярными.
Теорема (о локальном строении кусочно-гладкой кривой
Жордана вблизи регулярной точки). Пусть ф:[а, &]->Г=
=ф([а„ 6])c:R2 — кусочно-гладкий 1-путь Жордана и (х0, Уо) —
=ф(/о)^Г — его регулярная точка. Тогда существует окрестность
</crR2 точки (х0, «/о)еГ такая, что множество ГП47 есть либо гра-
фик функции y=f(x),
хе (xq—61, Xo-f-бг)
(y0=f(x0), yf=(y0—Пь Уо+лг)),
((хо-61, хо+62)),
либо график функции
x=g(y), У^(Уо—Ль У0+Л2) (x0=g(y0),
х^(х0—61, X0-I-62),
g(=C<» ((уо~Л1 Уа+лг))>
причем множество U\(U(\T) имеет две связные компоненты.
Доказательство. Поскольку точка y(to) — (xo, Уо)&Г —
регулярная точка 1-пути ф, то ta=£a, t0^b и (при ф(0в
= (x(t), y(t)) имеем | Dq>(i0) | >0, т. е. либо x'(to)=¥=O, либо
394
Пусть, для определенности x'(to)^O. Тогда по теореме
о локальном диффеоморфизме (из [ 1], ч. III, гл. 2, § 8) существу*
ют интервалы
(fo—ось foH-ote) czfo, b) и (х0—бь ХоЧ-бг)
такие, что отображение
X'. (fo—ось fo-Ь 0С2) “* (хо—61, Xo-f-62)
(где x=x(t)) является диффеоморфизмом класса С(1>, так что, в
частности, существует обратный диффеоморфизм
t: (х, — 8V х0 + 62) -»(f, — ab f0 + а,)
(где
t = t (х) е С<1 >( (х0 —'б!, X, + 6j)) .
и
~~ =/= 0 v X €= (х0— 6i, х04-62)).
ах
Но по условию y = y(t), причем
#<=C<‘)((f0—ах, /0Ч-а,)) и у^(у9—Vi, у0+^2).
Рассмотрим замену параметра
t: (х0 —х0 + 6,) -> (f0 — аь tо + а2),
как было отмечено,
= \lx'(t) ^=0 V t s (f0-ai, f0+a2),
dx
V xe (x0-blf x0 + 62).
Если
J 0 V X (x0—6j, X0+6j),
dx
то замена параметра допустима (в смысле определения 2 из
§ 1) и 1-пути <р: (f0—ах, fo + aa)-*^ и фх: (х0 —5Ь хв-{-£,) ->Т0
где
<Pi(x) = ср ° t(x)=(x, f(x)\ f(x)=y» t(x)s
— 51, xo +62))
эквивалентны. Если же
^<°Ух(х0-8и х0 + б;),
395
то <Pi = —q>. Однако в любом случае 1-пути ф и фх имеют
один и тот же носитель Го в R2, поэтому, полагая
Uo = (х0 — бр х0+ б2) X (у0 — Уо + ^г)
и
Г0=ф((^о —«1» ^о + а2))>
имеем
Го п Uo = {(х, у) <= £0|у = f (х), хе (х0—х0Ч-§2).
Однако возможно, что (Г\Г0) П &й=/=0. Поскольку феС([а, &]),
то множество Г\Г0=ф([а, (0 ~ ai] 0 ф Фо + а2> &]) компактно.
Рассмотрим интервал
(t0—аь ^о+аз)С[<0—аь А>+аг|СГ(*о—«ь *о+°ч)»
тогда множество Го = ф ({i0 — «1» t0 -|- а2]) компактно, причем в
силу биективности отображения ф: [а, 6] —>ф([а, 6]) имеем
Го П (Г\Го) = 0, но тогда р(г0, Г\Го) = р0>0 и, в частности,
Ш£(ХО, у0)ПГ = Ш<2>(х0, ^0)ЛГ0.
Но тогда существует окрестность
U — (х0 Х0+б2) X (Уо—'*11» 4^о“ЬС—Шр,\х0, |/о)П^о
такая, что (см. рис. 22))
TfW = {(х> У) <= ЩУ = f(x), х0 — < х<х0 + 6»},
и поэтому
(/\((7ЛГ) = (/1и(/а, ^0^ = 0,
где множества
ui = {(*> У) е и\Уо~^<y<f(x), х0-81<х<х0+б2}.
и
и0 = {(х, у) е и\[(х)<у<Уо+ъ, Хо— б1<х<х0+б2}
связны.
Определение. Компактное множество KczR2 называется
компактом с краем дК, если оно обладает следующими свойства-
ми: 1) компактное множество dKczK есть граница компакта К в
R2; 2) для любой граничной точки (х0, у0)^дК существует окрест-
ность Ш<,2) (х0, уо) такая, что множество Г=дКГ|Ш(2> (х0, уо) есть
носитель некоторой кусочно-гладкой кривой (1-пути) Жордана ф,
так что точка (х0, у0)^'дК может быть либо регулярной, либо уг-
396
левой для ГадК‘, 3) для любой регулярной точки (х0, у0)^д/(
существует окрестность UczIII^ (х0, у0) такая, что U\(UC\dK) =
==Uil)U2, где открытые подмножества Ut и U2 связны, причем
Ut<=K, U2cCK.
Замечание. Из условия 2) в силу компактности границы
дК следует, что край дК может иметь только конечное число уг-
ловых точек. Условие 3) означает, что в окрестности любой регу-
лярной точки края дК. точки самого компакта К лежат «по одну
сторону» края дК, а точки дополнения СК лежат «по другую сто-
рону» края дК. Отметим, что для связного компакта К, его край
дК не обязан быть связным. Отметим, что определение компак-
та с краем корректно в силу доказанной выше теоремы (о локаль-
ном строении кусочно-гладкой кривой Жордана) (сравните также
теорему о локальной взаимнооднозначности гладкого 1-пути из
[1], ч. III, гл. 1, § 4, см. рис. 23).
Замечание (об ориентации края компакта). Край дК ком-
пакта KcR2 может иметь лишь конечное число угловых точек. В
некоторой окрестности U своей регулярной точки (х0, уо)з'дК
край дК совпадает с носителем Г гладкого 1-пути Жордана
<р:(а, Ь)->Г=ф((а, Ь)). Заметим, что Г будет носителем и про-
тивоположного 1-пути (—<р). Считая Г носителем 1-пути ф, рас-
смотрим для любой точки (xq, y0)=<f>(to)^T‘ касательную прямую
(Г), ориентированную с помощью «базисного» вектора
Пф(^о)е=('х'С^о), y'(to)) (где орт е из R)). Тогда на носителе Г
индуцируется «ориентация» упорядочением точек Г с помощью
отношения
ф(Л)<ф(^)) (a<.ti<t2<b).
Но тогда край дК в окрестности U регулярной точки ф(70) может
быть ориентирован двумя различными способами (выбором либо
1-пути ф, либо 1-пути (—ф)). Вве-
дем следующее правило ориента-
ции края дК. Пусть при движении
но краю дК (соответствующему
изменению параметра t от а к Ъ при
упорядочении с помощью 1-пути
Ф) компакт К остается слева. Бо-
лее точно, пусть точка М=(х,у) =
=<f>(t)e=dK(]U и ф: (а, Ь)-*Г=
=<р((а, Ь)). Тогда вектор т(7И)='
=Г)ф(У)/|Оф(7) | есть орт ориенти-
рованной касательной Т^о(Г) к Г
в точке М. (При замене 1-пути ф
на 1-путь (—ф) получим орт
—~х(М).) Пусть вектор -vfAlJ есть
орт внутренней (относительно К)
нормали к Г, так что v(M) «вхо-
397
дит» в К вблизи Л4еГ. Выберем ориентацию Г так, чтобы угол
<£(т(7И), v(M)) был равен п/2, а не —п/2; т. е. чтобы пара ор-
тов {х(М), v(M)} была ориентирована так же, как упорядоченный
стандартный базис {еь е2} в евклидовом пространстве
Пусть, например, в окрестности U регулярной точки (х0, у9)^дК
край дК имеет уравнение y—f(x), причем для внутренности KfW
имеем y>f(x). Тогда (см. рис. 24) ориентация края дК по наше-
му правилу соответствует направлению возрастания х (от а до
Ь), т. е. в качестве параметра берем f=x. Если же, наборот,
внутренности соответствует неравенство y<Zf(x), то в каче-
стве параметра берем —x+a+b, т. е. ориентация края дК в
этом случае опредляется направлением убывания х. Поступив
i
так с каждой регулярной точкой края дК, видим, что dK=Up,
где Г/ — носители гладких кривых Жордана <р,-. Край дК, снаб-
женный указанной ориентацией, называется ориентированным
краем компакта К. На ориентированном крае дК (см. рис. 23)
естественным образом определяется криволинейный интеграл от
1-й формы (в класса С(0).
Определение. Компакт K<^R2 с краем дК называется про-
стым относительно оси Ох (оси Оу), если любая прямая, парал-
лельная оси Ох (оси Оу) и проходящая через (любую) точку К,
пересекает край дК только в двух точках.
Примеры простых компактов с краем:
9
о
1) (см. рис. 25) криволинейная
трапеция
Ki={(x, У)^2\Уг(х)^У^У2(х),
а^.х^.Ь},
где у,еС(1) ([а, &]) (i=l,2) являет-
ся компактом с краем, простым
относительно оси Оу;
2) (см. рис. 216) криволинейная
трапеция
Кг={(х, y)^R2\xi(y)^x^x2(y),
ct^y^d},
где х^(У> ([с, d]) (i=l, 2) яв-
ляется компактом с краем, прос-
тым относительно оси Ох;
ei х 3) (см. рис. 27) криволинейные
Рис. 24 треугольники
398
Кз={(х, 01<хСЬ1}.
где ^1ЕС(*>([аь ь,]) и ух(х) ||на [аь &,] и
Kt={(x, y)<=W\y2(x)^.y^d, а2<х<Ь2},
где y2<=W> ([а2, Ь2]) и уг(х) ff на [а2, Ь2] являются компактами с
краем, простыми как относительно оси Ох, так и относительно оси
Оу,
4) любой треугольник и любой брус являются компактами с
краем, простыми относительно как оси Ох, так и оси Оу.
1-я (предварительная) теорема Грина в R2. Пусть
KcR2 — компакт с краем дК., причем К. — односвязная область
399
и дК — ориентированный край, являющийся носителем кусочно-
гладкого цикла Жордана. Пусть К==\ЗКл, где Kt()Ki=0 i^j
«=1
и KiV i является криволинейной трапецией, простой относительно
обеих осей координат Ох и Оу. Допустим, наконец, что Д, Qg
<=С(К) и
±L{=C(k)/\B(K).
ду дх
Тогда имеет место формула Грина
[ $>dx +Qdy = JJ dxdy.
дк к \дх д« J
Доказательство. 1) Рассмотрим сначала компакт К,
являющийся криволинейной трапецией, простой относительно оси
4
Оу. Тогда d/C-UTz, где в соответствии с ориентацией края дК
i=i
имеем (см. .рис. 25)
—Ф1: [а, 6] -* Г! (x=t, y—y2(t), х'(t) = 1);
—q>2: Q/1 (a), y2(a)J-* Г2 (х=а, y=t, x'(t)=0);
Фз:К Ь]-*Г3 (x=t, y—yi(f), x'(t) = \);
Ф4:[ЫА)« «Ла(Ь)1*Г4 (x=b, y=’t, x'(t)=0),
причем у^СЮ ([а, &]) (i—1, 2). Но Ф ^С(дК.), поэтому имеем .
4 ъ
J &dx = — • Idt —
OK i=l ri a
yi(a) b
- f 3>(a,. t) • Odt + J&>(t, yi(t)) -idt +
У 1(a) a
y»(b) b
4- j SHb, t) ♦ Odt — ^[^((x, yi(x)) —$>(x, y2(x))]dx. (4.1)
2/i(b) a
о о
Ho KcR2 есть цилиндроид, причем —еС(К)ДВ(/<). Функ-
оу
ция — не определена на дКх однако |д/(|2=0 и поэтому (в
ду
силу теоремы 9 из ч. V, гл. 2, § 1), доопределяя функцию
dSP
— на границе дК компакта К нулем, видим, что —е
ду ду
400
° гч
<~С(К) Л #(/<), т. е.— еЯ(/<). По теореме Фубини (для ци-
ду
линдроидов) из ч. V, гл. 2, § 2 имеем представление
р р ддЦх., у) ьс dff>(x, у)
И-^7— “*dU = ^i> j
К v а У1(х) *
Заметим, что для фиксированной точки хе(а, Ъ) функция
С((у1(х), yz(x)))/\B([y1(x), y2(x)])t
д?Кх, у)
т. е. ----- как функция у кусочно-непрерывна на отрезке
ду
&г(х)] и поэтому функция &(х,у) eC([^fx), yz(x)]) как
функция у является первообразной для кусочно-непрерывной
функции —и в силу формулы Ньютона — Лейбница (для ку-
ду
сочно-непрерывных функций) из [1] (ч. II, гл. 2, § 6) имеем
V хе (а, Ь)
дф(х у)
[ —-------- dy = ^(х, yz(x))— &(х, У1(х)),
У
т. е.
И dxdy = J (^(х, yz(x)) — SF(x, yx(x))dx. (4.2)
К V а
Сравнивая (4-.1) и (4.2)), получаем формулу Грина
^dx==(^dxdy.
к д«
2) Допустим теперь, что компакт Kc:R2 является криволиней-
ной трапецией, простой относительно оси Ох (см. рис. 26). Тогда,
повторяя рассуждения из 1), имеем
у}
к
d
dxdy = ^dy
С
J ч дх
d d
= JQMy),y)dy — JQ{xi(y), y)dy^=§ Q(x, y) dy,
С c dx
т. е.
дК К
26 — Л. И. Камынин
401
3) Если компакт К с ориентированным краем дК является
криволинейной трапецией, простой относительно обеих осей коор-
динат Ох и Оу, тогда из 1) и 2) имеем формулу Грина вида
4) Если, наконец, компакт К с ориентированным краем дК
допускает представление K=KiUK21 где
КхГ|Дв0> dK=q>iU<Pa> дКг=<Р1иФо> ^2=4>tU(—Фо)
(где кусочно-гладкие 1-пути Жордана <p0 и (—фо) имеют один и
тот же носитель Го), причем компакт Kt (при i='l, 2,) является
криволинейной трапецией из п. 3) простой относительно обеих
осей координат Ох и Оу. Тогда, применяя формулу Грина из
и. 3) (см. рис. 28), для Kt (*=•!, 2) имеем
1
откуда, введя обозначение to—&dx+Qdy и используя теорему 10
(об усиленной аддитивности интеграла Римана) из ч. V, гл. 2, § 1 ||
(поскольку /<='/GUK2 и Л1ПК2=0), получаем равенство л
Но в силу теоремы 4 (об ориентированности криволинейного ин-
теграла 2-го рода) из ч. V, гл. 1, § 3 имеем
11
г ш = — f <ot .
J J
—Фо Ф.
так что -
1 1 i
J О) + J <0= О,
Ф. “Фо
поэтому
J ”-n(2-vW-
дК. К 4 '
5) Очевидно, формула Грина
остается справедливой и для ком-
пакта с ориентированным крае»ь
дК, представимого в виде объеди-
нения конечного числа криволиней-
ных трапеций, простых относитель-
но обеих осей координат. J
402
Замечание 1. Ниже в гл. 2, § 1 будет доказана формула
Грина в R2 для общего компакта К с ориентированым краем дК.
Замечание 2 (о вычислении площади плоской области с
помощью криволинейных интегралов 2-го рода). Пусть для ком-
пакта KczR2 с ориентированным краем дК применима формула
Грина, причем $>, Q^C(K) и
дх ду
Тогда формула Грина дает
(f Fdx+Qdy = Jf 1 dxdy = |K|2,
где |K|2 — площадь измеримого по Жордану компакта Д.
Отметим частные случаи:
1) при 3s = О, <? = х, \K\z — §xdy,
дК.
2) при 3*== — у, Q = 0, |^|s = — ydx;
дК
3) при &>яш—у[2, Q = x/2, |К|2 = 1/2 • Л) xdy—ydx.
дК
§ 5. Точные дифференциальные формы 1-й степени в Rn
Определение. 1-форма <o=,S SPidxt называется замкнутой
i=i
в области (т. е. на связном открытом множестве) GczRn, если.
^iGCW(G)Vi и vxetf, i^j.
1 п
Определение. 1-форма a>(x)—'2i&,t(x)dxi называется точ-
ной в области GcRn, если для нее существует первообразная
, 1
Функция G: GczRnR1 такая, что UeC^(G) и ©(х)=ч
~dU(x) Vxe=G.
Теорема (о замкнутости точной 1-формы). Если 1-форма
1 п
®(х)=Е 9ii(x)dxi точна в области G<=.Rn, причем
г=1 1
sCOfGJVi, то дифференциальная 1-форма w замкнута в обла-
сти GcRn.
t Доказательство. Поскольку дифференциальная 1-форма
®(х) точна в области GcRn, то для нее существует первообраз-
на U(x) такая, что U<=CW(G) и dU(x)=v(x)v x<=G. Ho
2б* 405
л
п \п я
dUQx) — ^ DtU(x)dxi и d)(x)='^j S^ifx) dxi, *|
Z=1 i=l
В силу единственности дифференциала (см. 2, ч. III, гл. 2, I
§ 3) имеем равенства DiC7('x)=35f(xjvi, где s C(I>(G)Vz, т. е. |
Z/eC(2>(G) и поэтому v i, Я DtDjU (х). Но в силу теоремы I
Юнга (из 1, ч. III, гл. 2, § 3) имеем равенства I
D^(x) = DiDjtZfx) = DjDt[/(x) = I
1 I
VxeG; Vi, j, т. e. 1-форма а>(х) (класса CO) замкнута в обла- I
сти G. I
i I
Замечание. Замкнутая в области GcR” 1-форма ш(х) мо- I
жет и не быть точной в G. ? I
1 I
Теорема. Пусть ы(х) — дифференциальная 1-форма клас- I
са С<°) — точная в области GazRn, так что <a^=dU, причем = 1
I/eC<1>(G). Рассмотрим любой кусочно-гладкий 1-путь <р.‘[а, &]-> i |
->-GcRn. Тогда I
/®=(/(ф(&))-С(ф(а)). I
ф 4 I
Доказательство. Поскольку <р:[а, &]rUecG — кусоч- jI
tn 1
но-гладкий 1-путь, то <peC([a, b])/\Cw((a, b)\ U {М/ Пусть I
к=1 $
Д=ф(а)еГдв — начало, а В=ц>(Ь)<=ГАв — конец 1-пути <р. По- I
1 I
скольку а—dU, где CeC<1>(G), то в силу теоремы о произвол- I
ной сложной функции (из [1], ч. III, гл. 2, § 4) Vtefa, b), I
t=£tk имеем I
п П I
-i-uo V(t) =2 Dit/o Ф(7) . ф;(Х)«з фСО -фИО- I
dt Z=1 i=l I
Но тогда функция С7°феС([а, Ь]) является первообразной ДлЯ; |
кусочно-непрерывной (а потому ограниченной на множестве |
[a, b] / U {tk}) функции I
k—i I
п
s ’ фСО • ф/0 I
i=i I
на отрезке [а, 6] и по теореме Ньютона — Лейбница (для кусочно- I
непрерывной функции) из [1], ч. II, гл. 2, § 6 получаем равенство I
404
i ' b п
J “ = J S ° *(*) -4i(i)<it=
= Uo ф(6) — и о q(a) — U(B) — L'(A).
i
Следствие. Если дифференциальная 1-форма а»(х) =
1
=dU(x) точна в области GcRn, то интеграл J"© зависит только
от начала Л=ф('а) и от конца В—^(Ь) 1-пути <р : [ а, Ь]-+ГАв=
=<p([a, bpcsG (т. е. интеграл от точной 1-формы не зависит от
«пути интегрирования»).
Теорема (критерий точности 1-формы в области). Пусть
GcRre — открытое связное множество, т. е. область. Тогда для
1 п
дифференциальной 1-формы ц>(х)=Ъ 3i'i(x)dxi класса С<°> еле-
г~1
1
дующие утверждения эквивалентны: а) 1-форма © точна в G\
1
б) для любого кусочно-гладкого цикла из G имеем f©=0;
<₽
1
в) /©=0 для любого ломаного цикла I из G.
Доказательство проведем в три этапа. 1) а => б). Пусть
1-форма o)(x)=dU(x) точна в области GcRn и <р:[<s, &]-*Г=
=ф([а, bJ)c=G любой кусочно-гладкий цикл (из G), тогда
ф(а)=ф('Ь^ и по предыдущей теореме имеем
^© = С7(ф(&))-С/(ф(а)) = 0.
ф
2) б) => в). Это утверждение очевидно, поскольку любой ло-
маный цикл (в G) является частным случаем кусочно-гладкого
Цикла. (
3) в =$ а). Итак, допустим, что для любого ломаного цикла
. , 1
‘ из области G имеем Ф ©=0. Выберем и зафиксируем любую
точку деб, Заметим, что G — открытое связное множество, по-
этому в силу теоремы (о критерии связности открытого множе-
ства в Rn) из [1], ч. III, гл. 1, § 11 множества G линейно связно.
Но^ тогда для любого xeG точки х0 и х можно соединить лома-
ной, целиком лежащей в области G. Заметим, что криволинейный
1
интеграл J© по ломаной I из G, соединяющей точки х0 и х, не за-
висит от выбора ломаной I. В самом деле, пусть It и /г — две ло-
синые из G, имеющие началом точку х0> а концом — точку х.
1,огда ломаная f=AU(—h) есть ломаный цикл (из G), проходя-
405
1
щий через точки Хо и х, и в силу условия в) имеем /<о=0. Но в
силу теоремы 3) об аддитивности криволинейного интеграла 2-го
рода) и теоремы 4 (об ориентированности криволинейного интег-
рала 2-го рода) из гл. 1, § 3
г1 с1 г1 с1 г1
\ а> = \ СО —|— I io = I и» — I (0 = U,
I к -I» к к
1 1 1
т. е. Обозначим теперь через U(x)=Sg> общее значение
h I2 I
криволинейных интегралов по ломаным I из G, соединяющим точ-
ки х0 и х. По доказанному U: GczR” R1 есть однозначная
функция, определенная в области G. Докажем, что V xs
sG Я DiU(x) = S:>i(x) (i=l, 2, ..., п). Поскольку xsG — внут-
ренняя точка области G, то существует открытый шар Ш<я)(х)с:
cG. В силу выпуклости шара при достаточно малом |Дх| отре-
зок [х, х-|-Дх] С (х) с= G. Пусть Дх=(О,..., О, Дх„ 0...., 0) и
x-f-Axs Ш<”)(х). Введем ломаный 1-путь I: [0, 1]-*[х, x-f-Дх],
положив =(x1f/),..., xn(t)), где х;(7)=х/ j=£i и Xi(t) =x(+tX
ХДх{ V/e[0, 1]. Тогда x^(7)=6ift • Дх, и поэтому
Д(/ (х) == U(x + Дх) — U(x) —
= АХ[ • J'S5,(х +1 • Дх) dt,
т. е. (замечая, что b.xJJ (х) = I © = I «>)
I (х, х4-Д*1
имеем
^Xiu(x)/^xi-gf>t(x)\ =
I
[(^Jx-t-f «Дх)—$\(x))dt
6
Поскольку 1-форма ©(х) класса то 9!,1еС(х) и поэтому
V е^>0Яб^>0 такое, что V t s [0, 1] при |£ • Дх,|<8, имеем
оценку |^(х +1 • Д*) — ^»(Х)К е, т- е-
Я lim ('x)/Axi = 5&i(’x) = D jU(x).
Ах,->-0 *
Но по условию S5, е C(G) V i, так что D{G е C(G), откуда ви-
дим, что существует дифференциал
406
dU(x) =2 ^i(x)dxt =<o(x),
<=1
1
t. e. 1-форма © = dU точна в области GcR".
Замечание. Условие б) из доказанного .критерия можно
1
заменить на условие б'): криволинейный интеграл /а не зависит
<р
от «пути интегрирования», а зависит лишь от начала и конца ку-
сочно-гладкого пути <р из GcR". Таким образом, б) б').
В самом деле, утверждение б) => б') было доказано выше.
Пусть теперь выполнено условие б')- Рассмотрим любой кусоч-
но-гладкий цикл ф:[а, 6]~>Гдвс:б, так что А—^(а)=^(Ь)—В.
Пусть С=<р(с), где а<.с<Ь. Рассмотрим кусочно-гладкие 1-пу-
ти ф1:[о, cj-^r.Ac и фг:[с, Ь] -*• Гсв=Гсд. Тогда ф=ф10ф2, при-
чем 1-пути ф1 и фг соединяют точки Л и С, поэтому в силу усло-
вия б' имеем
Ф1 —Фа
откуда (используя ориентированность и аддтивность криволиней-
ного интеграла) имеем
(J ш = — J®j=^|O=Ja-|-j©=e (j) ® — (j) ® j,
—Фа Фа / х Ф1 Фе <PiU<Pe Ф /
1
т. е. фш —0. Итак, б') =>б).
ф
Теорема (критерий замкнутости 1-формы в односвязной
плоской области). Пусть область GcR2 односвязна и ©=
= ^dx+\Q,dy — дифференциальная 1-форма класса С(1>, так что
> 1
SP, QeC^(G). Тогда (© замкнута в GcR2) -*=> (со точна в
GcR2).
Доказательство. Достаточность. Допустим, что 1-форма
<а точна в области GcR2. Поскольку 1-форма <о класса С<*>, то,
как было доказано ранее, 1-форма © замкнута в области G (од-
носвязность области G при этом не используется).
I
Необходимость. Допустим, что 1-форма а(х) замкнута в обла-
сти GcR2, т. е.
«М. WMIV (x.t,)sG.
дх ду к
407
Пусть I — любой ломаный цикл из одноовязной области GcR2.
Носитель L ломаного цикла /, являясь замкнутой непрерывной ло-
маной, имеет не более конечного числа точек самопересечения и
не более конечного числа отрезков «самопересечения». Поэтому
без ограничения общности будем считать, что носитель L нашего
ломаного цикла является границей односвязной области Кед
о m
czGczR2, где /С—ЛиЬ=11Д/ есть многоугольник с краем дК, яв-
1=1
ляющимся замкнутой ломаной Жордана. Поскольку каждый тре-
угольник Д,- простой относительно обеих осей координат, то к ком-
пакту К. с краем дК применима 1-я (предварительная) теорема
Грина на плоскости, в силу которой, учитывая условия замкну-
тости 1-формы &
дх ду
имеем
д$> \
(х> у)] dx dy = О
2
(при наличии конечного числа «паразитных» циклов h (i=l,
т) (см. рис. 29) опять имеем равенство
m j
1
(О
±i
т
LUU
поскольку каждый цикл k ограничивает односвязный «мноуголь-
ник», рассмотренный выше). Итак, дифференциальная 1-форма
w(x, у) такова, что в односвязной области GcR2 для любого ло-
маного цикла I имеем равенство фю=0,
I
так что выполнено условие в) критерия
точности 1-формы, в силу которого сле-
дует утверждение а), т. е. 1-форма о
точна в одноовязной области GcR2.
'Замечание. Бели область GczR2
не является одноовязной, то могут су-
ществовать замкнутые 1-формы о клас-
са С(1), не являющиеся точным в области
G. Рассмотрим, например, двусвязную
область G = R2\{(0, 0)} и 1-форму
1
(b=&dx+'Qdy, где
З^х, у)=—уЦх*-+ у2), Q(x, у)=х/(х2+уг),
408
так что 5°, Q е C^(G). Поскольку
dQ , . Эф z .,, , . „
(х, у)= — (х, у) V (х, у) €= G,
ох оу
1
то наша 1-форма ш замкнута в области G (обратите внимание,
что утверждение
со = xdy~ydx =darctg — V (х, у) е G неверно!).
Пусть т₽:[0, 2к| —>(р cos ср, р sin <р) — цикл Жордана, носитель-
которого есть окружность радиуса р>Ос центром в начале
координат. Тогда имеем
Ф “ = J = Jd<? = 2тс Ф °'
YP YP О
Таким образом, условие б,) критерия точности 1-формы не выпол-
нено и наша замкнутая 1-форма не может быть точной в (дву-г
связной) области GcR2.
Глава 2
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ В Rn
§ 1. Дифференциальные формы степени p(l^p<n) bR*
р
Рассмотрим кососимметрический тензор (типа р, 0)) о>
действующий в линейном пространстве E^=RnX.-XBw со зна*
р
п
чениями в R1. Пусть {е1; е2,.-» еп} (е,=(0,..., 0, 1, 0,..., 0)—упо-
г
рядоченный канонический базис в Rn, a [dxi, dxit..., dxn}—
взаимный (сопряженный) базис в Е* (где dxt^£(Rn, R1) —ко-
ординатные линейные формы, так что для любого вектора
h=2 • е< e£' = Rn имеем dx^ = ht), т. е. dxfij = ^ Тогда, ,
г=1
как доказано в курсе линейной алгебры (см., например, [5]),
«меет место представление
Р
®= 21 dxit/\dxit\.../\dxi ,
р<п
где А^..лр е R1. Напомним, что пространство кососимметри-
ческих тензоров Лр имеет размерность Срп.
Определение. Если QczRn — открытое множество, то .
дифференциальной формой степени р(\^.р^л) класса С№
р
Г(/=0, 1, ..., 4-оо) на Q называется отображение а : Qc:Rn-> Лу,
так что
ы(х)= 2 Ак..л (x)dxtt/\dxi,/\.../\dxi vx<=Q,
где :QcRn->-R1 — числовые функции класса C(Z>(Q).
р
Замечание. При р=0 дифференциальная форма а(х)
есть просто числовая функция : QcrR” R1 класса C(I)(Q)-
При р=1 а>(х) :QcRn-»-5? (Rn, R1) есть дифференциальная
1-форма, рассмотренная в гл. 2.
Напомним некоторые свойства р-форм (см. [5]).
410
Теорема. Если dx{ (i=l, 2, и) — координатная линей-
ная 1-форма (так что dxfii=0if), то:
1) dXi/\dXj=—dxj/\dxi, dx;/\dxi=0 (антикоммутативность);
2) (dxt+dXj)/\dxk=dxi/\dxk+dxj/\dxk (дистрибутивность);
3) A(x)/\dXi=dXi/\A(x)=A(x)-dXt, где A(x) :Q<=Rn-> R*
0-форма (числовая функция);
4) h(2>,-. h(₽))=Ai....i0(b(,)>-, hw) где век-
тор
h<«=(ft</>,..., ftp -e4sRn,
i=l
Aw (W1»,..., h(rt) =
dxtlh(” • • • dxi h(1 ft»). . . hU)
p 4
dxi,h(p) . . . dx,h(p> h[p) . . . №>
p
p
Теорема (об общем виде р-формы). Если &(х) :QcRn -*•
—>ЛР — р-форма, заданная на открытом множестве QczRn а
h0 = 2 ftp • e,=(ftp..... А<»>) —
2=1
вектор из Rn (при /=1, 2,..., р), то
Ь0»)= 2 Al-in (x)dxtA-
-A^ip(hH>, h<2>.....h<rt) x=
= 2 .. hW),
t. e.
p
А...^(л;)==а)(х9(е4,..., eip).
2
Примеры. 1) Если co(X у) — дифференциальная 2-форма
на R2, то у)=А(х, y)dx/\dy и для ее значения на паре век-
торов h(0 h<2>, где
Ь0')=х(Л(Д ^))CR2 (j= 1, 2),
имеем
411
2
ы(х, y)(hW, h<2>) = A(x, у) dx Л dy (h<0, h<»>) =
= A(x, y)
h<}> hty
h<®
очевидно, dx/\dy=—dy/\dx.
2) В пространстве R3 для 2-формы имеем представление
а(х, у, z)=A(x, у, z)dy/\dz+
+В(х, у, z)dz/\dx+C(x, у, z)dx/\dy,
а для ее значения на (упорядоченной) паре векторов {h<’\ h<2)}.
где
h</> = ft(0, eR3 (j - 1, 2).
имеем
ф ft<o
X о
h<?> ft<?>
2
©(x, у, z) (h(I>, hW)—(Ady /\dz+Bdz/\dx +Cdx/\dy) (h<0, h<2>)=
№ hW № WPI
О 1 | /“» 1 A
№> № ' № h& ' }
v 1 1 Z
при этом, естественно, dx/\dy=—dy/\dx, dy/\dz=—dz/\dyr
dz/\dx——dx/\dz.
3
3) для 3-формы в R3 имеем представление <а(х, у, z) =
—А(х, у, z)dx/\dy/\dz и ее значение на тройке векторов
{h<D, h<2), h<3>}, где (h</>, h«>, eR3 (j=l, 2, 3), будет
з
©(x, y, z)(h<i), h<2), №)=Adx/\dy f\dz(№, h<2), h<3>)=
= Л(х, у, z)
№
№ №
1^0
В линейной алгебре (см. [5]) было введено понятие внешнего ум-
ножения.
1
Нам понадобятся следующие его свойства. Если шгеЖ(Кп,
R1) (i = l, 2,..., р\ то имеем yh(/> — (hp,..., Rn
(j = l,...,p) (при l<p<n)
“iA—A“0(h(1) ho») = . Wph»)
1 1
1 ©ih<₽> . .
412
и, в частности, вновь получаем
dXil\...\dxip^,
dxi^ . . . dxMi(1)
h<p>) =
W‘> . . .Л<‘>
* 1p
dxith<Pi . . . dxi h(p)
P 9
Далее, для любых форм <о, о> и <о имеем:
(Р Р\ з Р <7 Р q
1) \‘в1+а>2/Дш=и>1Дш-]-и)2Ди> (дистрибутивность);
[Р 9 \ г р /д г\
2) \<вД<о)Д<й=(оД\шДю) (ассоциативность);
р q q р
3) <йДш = (—1)Р 9 • ш Ди>.
; Примеры. 1) При л=3 и р=1 имеем в R3
1
®(х, У> z)=Ai(x, У, z)dx+Bi(x, у, z)dy 4-СД, у, z)dz (i=1, 2);
Ш1Д®2 = (Aadx +Btdg+C1dz) Д (Aadx+B*dy+Cdty =
— At ♦ Badx/\dy 4- Ai • Cadx/\dz + Bi • Aady/\dx 4-
4-2?! • Cidy/\dz + Ci • Atdz/\dx 4- Ci • Badz/\dy =
IB, Ci
к ca
4 1p
dy/\dz +
Ci Aa
C2 Aa
dz/\dx + И1 „
I d<
dx/\dy,
2 1
' 2) При n=3 для ш и w в R3 имеем
2 1
<a/\a)=(Aidy/\dz+B\dz/\dx+
4- Cidx/\ dy) Д (A2dx+B2dy 4- C2dz) =
—A i-A2dy /\dz/\ dx+Bi -B2dz/\dx/\dy+-.
4- Ci-C2dx/\dy /\dz= (Д i -A24-Bi -B2+ C\-C2)dx/\dy /\dz
и, наконец,
“хД^аД*0» = {Aidx+B^y^r Cidz)/\(Aadx-¥Badt) 4-
4- C2dz) Д (Agdx + B3dy 4* C3dz) —
Ai Bi Ci
= A2 Ba Ca dx/\dy/\dz.
As B3 Cg
, Рассмотрим открытое множество flcRn, на котором заданы
функции fl: QcR” -> R1, f/eC<1>(Q) (j=i, 2...p), l^p<n. Тог-
да имеем
413
dfj (x) =i S Difj (x) dxt,
i=l
т. e. дифференциал df,(x) является дифференциальной 1-формой,
для которой имеем
dfi(x)h «J Лп)=2
t=l i=l
Теорема. Если на открытом множестве QczRn определены
функции fj: Qc=Rn -* R1 (/=1, 2, ..., р) класса С<‘>(0), то ’для
р
р-формы а(х) =dfi/\... Adfp имеем представление \\^.р^п) •
*>(х) = дЦх) Л . . . A dfp(x) =
= 2 (x)dxtJ\-№xi
U£ii<i,<...<ip<n д(хй» •• •• х‘р)
Доказательство. В канонической записи имеем
3 Аь-* (x)dxit/\--/\dXi,
где А11..лр (х) = dfi(x) Л — Л dfp(x)(eiit..., е1р)=
dfi(x)cu . . . dfp(x)Cit • Dilfl(xJ . . . Di,fp(x) .
dfi(x)eip . . . dfp(x)eip Dipf(x) . . . Dipf(x) ।
W'.....tP\ <
...xi/X)'
Пример. В R3 имеем
®=^1Л^2= 2 ^TidXiAdXi;
®=dftMft/\df9 = dxi^ dXi д
«(*1. , xa)
в R2 имеем
<x, y) = df1(x, y)i\df2(x, у) Уdx/\dy-
u\Xf y)
Определение (прообраза дифференциальной р-формы).
Рассмотрим открытые множества QcR", GazR* и отображение
Ф: GczR*-> QczRj (где k^.n) класса C^(G) (т>1), так что
x—pt(i)t xi—ty(tu ..., Ji=l, 2, .... n)
414
и <pi^C<m)(G) v Г. Пусть на открытом множестве QcRj определе-
на р-форма (\^p^k^n) класса С(,>
*(х)= J Ак..Л (x)dxt Л . • . /\dx. ,
i<i1<...<lp^n р р
р
Тогда прообразом р-формы а>(х) на открытом множестве GczR*
р
называется р-форма ф*ю(7) :GczRft -* Лр, определяемая форму-
лой
где ;
k
^(0 = ^ 2,..., р).
/=1
Замечание. Для любых векторов h</>eR* (/—il, 2, ...» р\
имеем представление
р р
(<р*<о)(Х)(Ыг>.h<P>) = ®(DФ (t))(D<p(t).. Dtp (/)№)).
В самом деле, по определению прообраза р-формы имеем
(<p*ej£O. (Ь(Г),—, h<₽>) =
= 3 • 4(t)d4dty л... AM* ...........hW),
i<i,<...<ip<n p p
где
h</») =
Ho
dyit(t)W . . . d^p(t)h^)
DTr/JhW = (d(p1(^h(0>...>dTn('/)h(0) = 2 • eie=Rn
и поэтому йх4(Вф^Ь(/)) = d<fs(t)№>, т. e.
йх/ХВфС^Ы1)) . . . dxlp(D^(t)hd))
dxit(D<f(i)h^) . . . dxip(D(f(t)h.^)
= rfx/1A-A^(D<pCOh0)»-» £><p(#lhW),
415
откуда получаем искомое представление
. . . л dxip(D ффЫО,..., D <Р(t)h(^>) =
= £(ф(7))(Оф(7)Ь<г),..., D9(0h<p>).
p
Правило (вычисления прообраза р-формы). Если <а(х) —*
дифференциальная р-форма и ф: GczR^ -> QczR*, причем х*=е.
=xfi(ti... tk), (i=il, 2, ...» n), то для вычисления
прообраза <p*& (при l^p^k^n) нужно x заменить на ф(0» в;
dxt заменить на dqn(t'). Затем нужно воспользоваться правилами
ассоциативности и антикоммутативности внешнего произведения, i
Пример 1. Пусть J
п=3, k=2, р=2; Х1=х, Х2—у, x8=z; ;
ti—u, h—v и ф: (и, о} -+ (х, у, г). 1
Если
2
<й(х, у, z)—A(x, у, z)dy/\dz+
+В(х, у, z)dz/\dx+C(x, у, z)dx/\dy, j
I
то
д(у 2) i
(Ф*<»)(а, v) = А о ф(и, v) du/\dv+ j
+ в о ф(в, V)д^’ - du/\dv+ Со ф(и, и) duf\dv.
a(u, v) Q(u9 V)
2 I
При p=k=n—2 и ф:(«, v) -*• (x, у) для 2-формы ta(x, y)^
=A(x, y)dx/\dy имеем f
(ф*соХо. ») = Я(Х(«, v)t ylu^v)) • du/\dv. *
Пример 2. Пусть n=^=p=3 и <p:(u, v, w)->• (x, y, z)p
3
тогда для 3-формы &(х у, z)—A(x, у, z)dx/\dy/\dz имеем
(ф*а)(и, v, w) = А о ф(и, о, w) • г— daAdo Д dw.
д(и, v, w)
з
В частности, можно найти выражение 3-формы vt==dx(\dy/\diг
в сферических координатах р, ф, ф пространства R3. Пусть,-
4ie I
i2 = Rx.y. гле ^-{(*> y> z)eR3|0<x<4-oo, y=o, |z|< + oo}
и <о=((р, Ф. ^)^в₽,ф.ф|О<Р<+<», 0<<p<2ir, |ф|<>/2). Рассмотрим
диффеоморфизм
5s : to -* £2=3Э (©),
полагая
x=p-cos ф-cos ф,
г/=р-зй1ф-созф, г=р-зтф.
Тогда
^*и(р. ф. Ф)= ’ -у - ФД^фДДф=ра • созфг/рДйфДЛф.
о(р, <р, чО
Пример 3. При р=2, k=n=3 и <р: (и, и, ш) -* (х, у, г)
для 2-фор мы
2
<в(х, у, z)=A(x, у, z)dy/\dz+B(x, у, z)dzAdx+:
+ С(х, у, z)dx/\dy
имеем
ф*ш(и, v, w)=A о <f(u, v, w) - A Д
+ Adw 4--д^’ г) -dw/\ +
d(v9 w) d(w9 и) I
-j. В о ф • / д(г» x) du /\dv + d(2’ dv/\ dw 4-
I d(u, v) 1 4 d(v, w) /X
+ --Уг---?-^Д^) +Co ф- du/\dv +
d(wt u) I I d(u9 v)
+ ~а/(Х’ da A dw + ~S~X~g~7 dw^ du} •
d(v, w) d(w, u) j
Теорема (о свойствах отображения ф*). 1) Отображение
р р
<р*' линейно, т. е. V сь c2^Rl « для любых реформ со! и 02 имеем
р р р р
ф* (ClCD 1 + С2СО2) =С1ф*(01 + C2<P*®2-
2) Отображение ср* сохраняет внешнее произведение, т. е.
р q р q
ф* (CD A CD ) =ф*(0Лф*0).
3) Для любого f^CW(T)QG имеем
4) Если ф: G/czR*-»GtCZR£ и ф : GtczIV“»QczR", mo (ф о ф)*ш==
(<Р* о
Л. И. Камынин 417
Доказательство. 1) Линейность отображения ф* следует
из его определения.
2) Общее доказательство. Пусть
s_ j 1 2 ...p+q \_
“ U(l) S(2) . . . S(p+q)j
*
подстановка из группы Sp+g> и «fS) = l, если S — четная подста-
новка, и u(S)=—1, если S — нечетная подстановка. Тогда, вспо-
миная определение внешнего умножения из линейной алгебры
(см. [5]), для любой упорядоченной системы векторов
{h<D,.... ион-®»}е R* X - - X Rfc
р+«
имеем
h^+«) =
= (£Лш)(ф(7))(Оф#)Ыг>, .... Dtp f/>(₽+?) ) =
= W • g!) • 2 м(5>(ф<^)(ЬфГ/;
<S6Sp+g
= 1/(р! •/?!) • 2 и(5)Ф*Ч0(Ь(ЭД)„..,Ь5(р))) X
Ч Р Q.
Хф*<о(7}(Ь<5</’+1,>,.;., Ы^р+з») = ф*<оДф*ш(Ы’>,..., Ь<р+«>),
так что
Р 1 Р 9
<р*(соДа>) = ф*шДф*ш.
2') Доказательство без использования линейной алгебры. Рас-
смотрим для простоты частный случай: l^p+q^k^n^S при
p=.l, q=2, k—n—З и, считая, что ф: (ti, tz, h) -*• (Х\, Xz, Хз)*
12
m(x)=A(x)dxi и tn(x)=B(x)dxz/\dx3. Тогда
I 2
®Л(»(Х) =Д (х) -B(x)dxi/\dxz/\dx3,
так что
Ф*(®Дш)(/)=(Д.В)о ф(7Д
Но
418
<p*wfO = A о <p(0 Idh + dta+ dt» Y
\ ut^ utz Ol3 I
Ф*ш=в9 ^(^^Ldt1^dt2 + ^^-dt^dt3+
\ ^(*1, *2) 0(*2, *3?
+ ^ТТ ЛзЛЛ1У
д(*з> *i) j
откуда, учитывая ассоциативность и
него умножения, имеем
1 2 /дХ1
<р*(о Д ф*о = А о <р • В ® ф-1 — <
антикоммутативность внеш*
^(*2» Хз) , А
^у-л,лД,л*1 +
+ з? •^Чт‘",лЛ>Л*.+
of2 o(fs> *1)
+ л»Л<ИхЛ^ = И • В) о <р X
Ofj v(ti, /2) I
д(хг, Хз) dxt . d(xt, х8) . dxi
d(t2, /3) dta d(ts, tj) dtt
д(хг, xt)
d(h. t2)
X dti A dtz f\dl3 — (A • В)* ф X
dxi dxi dxi
7^ dt2 dt3
дх^ dt2 dx* dts = •/?)» ФХ
дхз dx3 dx3
dt2
d(xi, x2, d(h, it, хз) *3) dti/\dt 1 2 aArffs = q>*(®A«>)-
3) Бели f: £2czRra -> R1 и то дифференциал df(x)=!
n
s=2D^(x)dXi есть 1-форма класса C(Q). Но как было доказано
г=э1
при изучении взятия прообраза 1-формы в гл. 1, § 2, имеем
п
(y*df) (t) = 2 (W) 0 ф(0 dffi(t) =df о ф (t),
Z«1
*• e. v*(df) = d(f о ф)=аф*/.
27»
419
4) ((фо ф)*<в)с^(Ы»>. hW) = ш[(ф о <р)(7)](О(фо ф<7>Ь<Ч..-
...» D(<1>° ф)(^Ь<р))=ш[ф(ф(?))](О<р[ф(Х)1 • DcpCOh’1»,...
.... оф[ф(01-Е)фГ0ь(р))=Ф*Мф('0](ОфГ0Ь<1)1...( Оф(Х)Ь(₽))=
=Ф*(ф*ш)(7)(Ь<’>,..., hW) V h(') e=Rft <7=1. 2,..., р),
р р
т. е. (фо ф)*<о=(ф* о ф*)ш, откуда
р
Следствие 1. Бели <а(х) = A(x)dx^ f\.../\dxlp, то
(ф*“)(0 = А ° ф (О^Ф'/ОЛ-Л^ф/рСО»
и поскольку .?
k
то в силу теоремы вновь получаем представление J
р ^(Фг,»• • •» Фг«) . -- j
(Ф*ш)С/)=ло фго 2 -тг—г-г-со-^л-лл/р. ;
п I
В частности, при p=k=n имеем для ^(x)—A(x)dx1/\>../\dxn и .
х*=фХ«1,..., Q (i=l, 2,..., п)
(Ф*<0 = а о ф(0 • S1’’-2" (ОЛгЛ-ЛЛп.
С'Си, • • •» *«) ' I
Следствие 2. Если /у: QccR” -> R1, feC(1>(Q) (j=l, 2.п) I
и I
w(xj= 2 Ai^.ip(X)dfiA-'-hdfip> I
TO I
ф*<0= 2 A-..ip ° ф(0^ф7чЛ--Л^ф*^ = I
P 'I
= 2 А‘1-Лр ° fWA-’M/ фСО/ I
Определение (внешнего дифференциала (или кограницы) I
дифференциальной р-формы). Рассмотрим открытое множество
QcRn, на котором определена дифференциальная р-формй I
420
р
ш(х) ~ 2л ^•-1D (x)dxi1/\.../\dxi
р р
класса C(,)(Q) (/^1). Тогда дифференциалом или кограницей
р
р.формы а называется дифференциальная (р-\-\)-форма класса
определенная на Q с помощью соотношения
й<л(х)=\ 2 o(x)dxaf\dxil/\.../\dxi —
S 1<ц<...<усЛ
= 2 dAit,.,ip (х)/\dXit/\...Д dxi?
P >
{(эта запись не является канонической, но от нее легко перейти к
канонической записи).
1
Примеры. 1) Пусть a—Adx+Bdy+Cdz — 1-форма в R3,
тогда
da*=d(Adx +Bdy-}-Cdz)=dA /\ dx ~rdB/\ dy-\-dC/\dz=*
=^(d-^-dx ->rd-^-dy+~dz\/\dx +
\dx dy dz I
. (dB d . dB , i j \ a j ।
+ | — dx 4- — dy 4- — dz j Д dy 4-
I dx dy dz ]
. /дС , , dC , . dC . \ . ,
+ f — dx + — dy + — dz\ /\dz =
dx dy dz j
(dB dA\. Л i , /dC dB \ A ,
= \^~~T ]dx/\dy + {^-------—\dy/\dz +
\dx dy I \dy dz I
. (dA dC \ , Л ,
+ --------— \dz/\dx.
\ dz dx
2
2) Пусть a=Ady/\dz-\-Bdz/\dx + Cdx/\dy— 2-форма в R®,
тогда
da = d(Ady/\dz + Bdz/\dx + Cdx/\dy) =
= dA/\dy/\dz 4- dB/\dz/\dx+ dC/\dx/\dy =
/dA , dB . dC \ , л , л ,
8) Пусть w=^dx+Qdy — 1-форма в R2, тогда
_ 1 \
da—dSP^dx +dQ/\dy= | — dx + — dy ) Д dx 4-
\ dx dy )
421
+ (у- dx + у dy\ л dy = у^- dy Д dx +
Y дх dy J оу
дх \ дх ду I
т. е.
do a d(SPdx+Qdy)= (— — — 'j dxf\dy.
\ дх ду ]
п
Замечание. Кограница п- фор мы а(х) в R”, будучи
п
(n+l)-формой, тождественно равна нулю, т. е. da(x)=0.
Замечание. Формула
da(x)-= 2 Att..„i (x)dxa/\dXi,/\.../\dxi
a, i,.......ip ОХа р
определения дифференциала (кограницы) имеет место и в случае
если попарно различные индексы суммирования ц, 1'2, ..., ip не яв-
ляются возрастающей последовательностью элементов множества
1, 2, ..., п.
В самом деле, пусть ip=S(ipr), где последова-
тельность ... возрастающая. Тогда
Л,...<р (x)dxil/\.../'\dxip’=‘U(S)-Ai^ (x)dx^/\.../\dx^,
и теперь, применяя нашу формулу определения дифференциала,
имеем
р п я
dco(x) = S S • — Л,..лр (x)dxa/\dxi‘i/\... /\dx.'p =
a==l '<.,.</a
1 P
«s 2 z (%) dXb/\dxix/\»../\dxi •
a. it.ip P
Теорема (о свойствах внешнего дифференциала).
1) Если f:QcR«-*R‘, fe=C^(Q), то df(x)= V f(x)dxa-,
а=1
Р Р Р Р
2) d(ci-сох+£2*^2) ==Ci*dci) 1 + C2'd(&2\
р q р q р q
3) d((oAG))=dtt>A(o+ (—1)р-<вЛ^йг,
р р
4) dd®=0, где р-форма о(х) класса С<2>(й). . 5
422
Доказательство. Свойства 1) и 2) очевидны.
3) Используя замечание и антикоммутативность внешнего
произведения, имеем
р жгч
°>(х) = 2л Aii.-io(x)dXil/\.../\dxi и
*(х)= 2 Bfi -f.(x)dxlt/\.../\dxf,
h..........iq
откуда
P Q. ^0
<о(Х)Лш(Х)= 2л Ah...ip(x) • B/1.../a(x)dxz1A...Adx/fft
il.4p
'«.
t. e.
d(w(x)A“W) = 2 Bi'-iq(x)-(dAiu..i (x)/\dxil/\.../\dxi )/\
ь..................l'P
Il.iq
/\dxit/\.../\dxf+ 2 Ah..i(x)X
11.V
X 2 dBil...iii(x)/\dxii\:.f\dxip/\dxii A
/!»•••. iq
...Adx^=rfw(x)A“W+(—1)₽ • 2 A4:.if(x)dXiif\...f\dxi /\
..................................lp
A f 2 dfi/i.../9WAdxAA-Arf^ ) =
pg P q
=da>(x)/\w(x)+(—l)p- <o(x)/\dw(x).
4)
dd<o = d( 2 Т~А^-ЛD(x)dxa/\dxit/\.../\dxib ) =
\a, i,.ip 0xa p )
= 2 Ah..iAx)dx^/\dx<lf\dxil/\...f\dxi
a. 0, ii.... ip dxadx3 P . P
в этой сумме сохраняются только те системы индексов a, Р,
*ь »2, ..., ip, в которых а=/=£ и в которых ни один из индексов а и
Р не входит в систему й, 12...iP, так как в противном случае в си-
лУ антикоммутативности внешнего умножения имели бы
Jxp A dxa/\ dx£l/\.../\ dxip=~0.
423
При фиксированных аир при а<р сгруппируем члены с
dxa Д dx? Л dxh Д ... Д dxip
и с
dx?/\dxa/\dxil/\,../\dxip=—dxat/\dx?^dxil/\.../\dxip.
тогда, учитывая условие A,,..., sC(2)(Q), в силу теоремы Юнга
(из [1], ч. III, гл. 2, § 3) имеем
дг л z X <?2 . , ,
1 i (X/— ' ,i (X),
dxadxQ p' дхьдх p
чЛ p p (Л.
откуда получаем выражение, равное нулю.
Следствие. Если
®(х)= 2 (x)dfil/\.../\dfi
где fj:QczRn-»Ri и /jSC<2>(2) (/=1, 2,..., п), то
dv(x)= S dAit...ip(x) Л dfit/\.../\dfip-
Доказательство. В силу свойств 1)—3) кограницы имеем
d£(x) = 2- ’ dAh-iD(x)/\dfu/\>-Adfip+
fe=l t<4<...<ip<n
/\^Adflk-Addfih^dfi^A-Adfip.
Но в силу свойства 4) кограницы, учитывая, что f/eC(2)(Q) V j,
имеем ddftk =0, откуда и вытекает наше следствие.
1-я теорема (о перестановочности операций <р* и взятия когра-
ницы). Пусть QczR" a GcR* — открытые множества и <p:Gcz
cR* ->QcR^ где <pe=C<2>(G). Если о(х) — дифференциальная
р р
р-форма класса С&, определенная на Q, го d(<p*o)=<p*(do).
Доказательство достаточно провести для р-формы клас-
са С(1) вида o(x)=A(x)dxit Л... /\dxip. Используя следствие, в
силу условия феС<2>(0) имеем
d (<р>)(7) =d(A^[t))d^f\.../\d(tip) =
= dA(<p(O) Л d4i&) Д.. • A d^ip(t). =
424
— <p*(dA (x) Д dxit /\ ... /\dxij =
= tf*(d(A(x)dxil/\. • .Adxip)) =
= <p* (d<D(x)) => (d(q)*<e) = <p*(d<i>)).
Замечание. Условие <peC<2>(G), используемое в процессе
доказательства, можно заменить на условие <peC(1>('G), если
воспользоваться теоремой Вейерштрасса об равномерной аппрок-
симации cpeC^’fG) функциями <pm^C^(G), (сравните замечание
к обобщенной теореме Вейерштрасса из ч. IV, гл. 3, § 4, см.
также [6]).
2-я теорема (о перестановочности операций ф* и d). Рас-
смотрим открытые множества QcR", GczR^ и отображение
р
ф:О->й, Если а(х) — дифференциальная р-форма
' р
класса определенная на множестве й, то (/(ф*«>) =
р
=Ф*(г/ш).
Доказательство. Вновь ограничимся р-формой вида
р
<b(x)=A(x)dxil Д... f\dxipt где АеС<1>(£2). Пусть хо=ф(?о)ей,.
где to^G — любая точка. Поскольку множество G открыто в R*.
то существует окрестность U(to)czU(to)dG такая, что ее замы-
кание U(t$) компактно. Поскольку ф(0=.(ф1(¥), ф2(0, ...F
..., фп('^))еС<1>(0), то в силу обобщенной теоремы Вейерштрасса
(в многомерной формулировке, ч. IV, гл. 3, § 4, доказанной в
[6]) существует последовательность многочленов PW(t) (i=l, 2,...
.... n; т=1, 2,...) такая, что
P'?4t) 2$ Фг(0 на U(t0) (i=l, 2,..., п) (1.1>
m -*4-oo
И
DyPfYO на 17(/O) (i=l, 2,...,n; ;=1, 2,..., ft). (1.2>
m— 4-oo
Положим
тогда
и &m(t)
m—>4-oo
Ha U(t0), причем
-7-ФЮ на G(i0)(7=l,2,...,fe).
Oij m~*+<x) utj
в силу ранее доказанной теоремы о перестановочности опера-
ций ф» и d ввиду условия SPm^C^(U(to)) имеем в окрестности
u(to)czG равенства
425-
d (ПУ (t) = d(A ^m(t)}dP^(t)/\...\dP^(t)) =
= dA(^m(t))\dP^(t)\...\dP^(t),
причем в правой части этого равенства, переписанного в форме
(74а
л( 2
tfp )
можно перейти в окрестности U(tQ) к пределу при т -* + оо, не- .
пользуя (1.1) и (1.2). Но тогда для <peC(1>(G) можно положить
по определению
d (<р*У (t) = ^Л(ф(7)) AdTi/O A---Ad%CO-
Поскольку
dA( ф (t)) Л dffii (i) Л • • • A d<fip(t) ==
- T*(d4 (х) Л dxit А • • • Л dxip) =
= ф* (da>)(7) V t е U(t0) С G,
но тем самым доказано равенство
d (ф*У(Х). = Ф*(йш)(t) Vt^G.
Замечание. Идею доказательства теоремы сообщил авто-
ру Н. В. Ефимов.
§ 2. Интегрирование дифференциальных &-форм
на /г-пути в Rn
Рассмотрим открытое множество QczR", на котором опреде-
лена дифференциальная A-форма (l^fc^n) класса
k
C<O(Q) (1=0, 1,2..4-оо) е>(х) =
— 2 dXi, А”" Л dXi^
Пусть ф: l/crRftГ=ф(^) cz£2czRn есть fe-путь в Rn класса С(1)>
причем открытое множество t/czRfc измеримо по Жордану и
Dj^C(U)/\B(U) (/=1, 2......п).
В § 2 будем считать, что для фигурирующего в определении 3
(ф~ф) и в определении 5 (ф=>—ф) из гл. 1, § 1 диффеоморфиз*
426
ма /: t/fCR* выполнены дополнительные условия: от-
крытые множества Ux и Ut измеримы по Жордану и
Vt(=C(Ux)/\B(Ux), Di-lc=C(Ut)AB(Ut).
Тогда корректно следующее определение.
Определение 1. Интегралом от дифференциальной
к
k-формы а(х) на k-пути <р называется число
к к к def
j" 0) = J ф *<0—J_ ф*0> =
Ф и и
2 С С д(ф41>..., ф, )
J J о<р(7) —— —— dtf.dt".
й th)
Рассмотрим важный частный случай 2-пути в R3
Ф: U С R2 , -> Г = <p(CZ) с R^ г,
где
ф(и, v) = (x(u, v), у(и, с), г(а, о)) е C^(U),
^еС(С/)ЛВ(СГ).
ди ди
2
Введем дифференциальную 2-форму <a=Ady/\dz+Bdz/\dx+‘
+ Cdx/\dy класса С (£2), где йгэГ — открытое множество в R3.
Определение 2. Поверхностным интегралом 2-го рода от
2
2-формы о по 2-пути ф в R3 называется число
2 def
У У Ady /\dz 4- Bdz /\ dx + Сdx Д dy
ф <р
а=у^=пи”<“'”'^)+
и и \
+ в о ф(и, V). д^' Ц 4- С о ф(и, р) . dudv.
d(ut v) d(ut и) I
Замечание (к формуле Грина в R2 из гл. 1, § 4). Пусть
^cRx,y является компактом с ориентированным краем дК.
Множество К можно рассматривать как носитель гладкого 2-пути
в R*,y > полученного с помощью параметризации
х=и
ЧЧ ° 2
y=v, (и, tf)eKcRu,®.
427
Но тогда пространства R2_o и R2 ориентированы одинаково.
1
Если ft> = $Mx+Qd«/ дифференциальная 1-форма класса C(,)(Q)^
определенная на открытом множестве Q^K, то
’ IdQ д&
а<л= —--------
\ дх ду
и (при выполнении для компакта К с краем дК условий ,1-й тео-
ремы Грина из гл. 1, § 4) формулу Грина можно записать с по-
мощью криволинейного и поверхностного интегралов 2-го рода в
виде
<j) <»= И dco или (£3bdx + Qdy= d^~\dx/\dy. (2.1).
Ьк к д'к к \Ох у /
2-я (основная) теорема Грина в R2. Пусть KczR2 —
компакт с ориентированным краем дК и <&=&dx+Qdy — 1-фор-
ма класса С(К)ЛС<-1'>(К.), причем DiSP, Г),()^С(К) /\В(К)
(i=l, 2). Тогда имеет место формула Грина (2.1), или, полагая
х — орт направленной касательной, N — орг внешней (относи-
тельно К) нормали и v=—N — орг внутренней нормали к ори-
ентированному краю дК (в регулярной его точке),
1 1
da— f а>== f (5s • cos (т, x)-\-Q • cos(t, y)ds —
дК дК
= J (Q • cos(N, x) — SP • cos(N, y)}ds=
dK 4
= J (5s • cos(v, y)— Q • cos(v, x))ds. -
dK
Для доказательства 2-й теоремы понадобятся некоторые пред-
варительные рассмотрения. Введем в R2 у стандартный базис
О» j}> где
1= (1, 0), j= (О, 1).
Определение. Прямоугольник П, построенный на базисе’
Vi, 12}~{». 1} (в Rx у )> назовем специальным, если он удовлетво-
ряет одному из следующих двух условий:
1) ПсК (так что Щ]дК=0) или
2) П(]дК—Г есть гладкая дуга Жордана, соединяющая две
противоположные вершины прямоугольника П, причем орт на-
правленной касательной т к дуге Г составляет острые углы с ор-
тами 11 и 12 в каждой точке Г.
428
Замечание. Если специальный прямоугольник IIcR/,v,
построенный на базисе {1Ь 12}, удовлетворяет условию 2), то после
собственного движения (параллельный сдвиг и поворот), перево-
дящего базис {i, j} (плоскости R* v) в базис {1ь 12} (плоскости
^2^), гладкая жорданова дуга Г (в новых координатах (и, v))
определяется как уравнением v = v(u), так и уравнением ы=ц(о),
где функции v(u) и ы(о) (класса С<!>) строго_возрастают (причем
v'(u)>0, u'(v)>0), так что прямоугольник П переходит в брус,
.а множество ЛПП переходит на плоскости R^ о в криволинейную
трапецию, простую относительно обеих осей координат Ои и Ov
и удовлетворяющую всем условиям 1-й (предварительной) теоре-
мы Грина на плоскости из гл. 1 § 4.
Лемма (о существовании специального прямоугольника).
Если — компакт с ориентированным, краем дК, то для
любой точки не являющейся угловой точкой края дК, су-
ществует специальный прямоугольник По, содержащий Мо в каче-
стве внутренней точки.
Доказательство. Если точка М0^К, то, очевидно, су-
ществует даже брус По с центром в точке Afo такой, что Пос/С
Если М0<=дК — регулярная точка ориентированного края дК., то
существует окрестность V(Afo) такая, что Г=Г(Л40)П<3/( есть глад-
кая жорданова дуга с ортом ориентированной касательной т(ЛГ0)
к Г. Тогда существует базис {h, l2}~{i, j) такой, что орт т(7И0)
составляет с ортами h и 12 острые углы. В силу непрерывности
х(М) существует' малая окрестность U(M0)czV(Mq) такая, что
орт (ориентированной касательной) х(М) к дуге Г в этой окрест-
ности также составляет острые углы с ортами h и 12. Если перей-
ти с помощью собственного движения от базиса {i, j} (на плоско-
сти R^ у) к базису {11, 12) (в R£ t,), то в новых координатах
(и, v) гладкая дуга Г в малой окрестности точки А40 будет зада-
ваться как уравнением v=v(u), так и уравнением u=u(v), где
функции v(u) и u(v) класса С(1), причем v'(u)>0 и u'(v)>0. Но
тогда на дуге Г можно выбрать по обе стороны от точки Мо две
близкие точки (щ, щ), (и2, о2)еГ такие, что брус с вершинами в
точках (щ, Vi), (и2, щ), (и2, v2), (щ, v2) будет прообразом (в R^y)
прямоугольник По, удовлетворяющий условию 2) т. е. существует
специальный прямоугольник По, содержащий точку Мо внутри
себя.
дв Д ° к а 3 ате л ь ст в о 2-й теоремы Грина проведем в
I этап. Пусть край дК. компакта К не содержит угловых точек.
*огда в силу леммы для любой точки М0<=К существует откры-
ли специальный прямоугольник По, содержащий точку Мо, так
429
что Хс (J По. В силу компактности множества К из этого от-
м.ек
крытого покрытия можно выбрать конечное подпокрытие {IL; i=
т
= 1, 2, т} такое, что XazUIIi- Рассмотрим для множества К
1=1
разбиение единицы i=l, 2...т} класса С<°°> (R2), подчи-
ненное открытому покрытию {П<; 1=1, 2, т}, такое, что
S et(M) = 1 v М^К, supp eiczlli v i
1=1
(носитель supp в/ компактен для любого i).
Рассмотрим 1-форму
1 1
at==et -at — SP -ezdx-f-Q ♦etdy s Audx + A&dy.
Очевидно, Aki<=C(K)/\C^(K), причем DjAki<=C(k) f\B(k)
(j, k=l, 2; i=il, 2, ..., m), функции Л*г, D/Л*/ финитны и
supp Л*/сП/ПХ, supp D/Л *;еП<ПХ. Доопределим функции
DjAki^B(ХПП/) нулем на дХПП,. Тогда suppD/Л*, сП/ПХ и
О/Л*геХ(П/ЛХ).
Для 2-формы
dai=[-r-A2i — ^~ Аи\ dx/\dy
\дх ду j
1
имеем supp/Za( CZ П/(~|Х. Далее,
Im 1ml
j e*- ®=2 Jn
dK i=l dK i=l д-КПГЦ
1 / m 1 \ m 1 m 1
ffd®=ffd-co И dai-
К К \i=i / i=lK i=l КпП£
Для доказательства теоремы Грина достаточно показать, что
Г «»= П dai (i = 1. 2.... т),
0КЛП4 Knnz
Поскольку П, — специальный прямоугольник, то достаточно рас-
смотреть два случая: а) ILcX и б) П;С|ЗК=Н=0.' В случае
а) ILczX имеем П,’С|дХ=0 и, как показано при доказательстве
леммы (о существовании специального прямоугольника), можно
считать, что прямоугольник IL является открытым брусом на
плоскости R2 , причем supp а/,с:П;с:К, так что supp
1
=suppa^IIt=0, т. е.
430
f at= J* «1=0.
i
Далее, как было показано выше зирра/с:П>ПК=П/, причем
1-форма а: класса С(1>(П/) и
1 д д \
dai== I — A2i — 1 dx /\ dy^
\дх ду J
где
V" Л24— Аи €= С(П0 Л В(П0 с я(п<),
дх ду
1
так что для 1-формы ai и бруса П/ (простого относительно обеих
осей координат Ох и Оу) выполнены все условия 1-й (предвари-
тельной) теоремы Грина из гл. 1, § 4, в силу которой имеем ра-
венство
И = j сц,
п4=кпп, акпп{
чем формула Грина в случае а) доказана.
В случае б) Г,=дКЛП/ есть гладкая ориентированная жорда-
нова дуга и существует собственное движение Р*1: [х, у) -+• (и, v)
(сдвиг и поворот на угол От) такое, что Рт1 (П/)=Л будет откры-
тым брусом в плоскости R„, „, ориентированной базисом {1ь 12}
(где li= (1, 0) и 12= (0, 1) — координатные орты в R2 „). Оче-
видно, Р'1:
( и=(х—х0) cos 0т+ (у—уо) sin От
I v=—(x—Xo) sinO'i+ fi/—Уо) cos О/
есть диффеоморфизм, причем для обратного диффеоморфизма
Pt: (и, v) -+ (х, у) имеем
( х=Хо+ucos О'?—osinO-i
I У=Уо+“ sin 0т+ v cos От.
Заметим, что
Рт1(/СПП;)={('и, v) \v(ll)^V<V2, U^(Ui, tl2)}
(где v'(u)>ty, так что множество Р^^КПЛ,) —{(и,
^а^и2> ие[И1, «г]} будет криволинейной трапецией, простой от-
носительно обеих координатных осей Ou и Оо в R2 v и поскольку
Piece2)(R2 т0 в силу теоремы (о перестановочности операто-
ров d и Р*) из гл. 2, § 1 имеем
431
P*(daJ-d(p>i).
Если
РГа; = Audu + Аг1 dv,
то
А< = Ац° P,cos^+42i° PjSin&j:
A2i =— Ан ° Pi sin &i 4- A2i ° Pjcos&i,
где
^ес^ад)),
D/AftieC(P-4Knni))AP(Pr1(Knni))cB(Pr1(Knni)),
1
так что к 1-форме P*<xt и к криволинейной трапеции PfXKf]
Г)П4) вновь применима 1-я (предварительная) теорема Грина
из гл. 1, § 4.
1 1 о
Заметим, что supp оцСКПП,, так что Бирро^/КЗГЦП £)=0,
«и поэтому
supp os» f| d(#n nf) = supp а{П(ЗЛГНПО,
и тогда
f а,= f «<-
Г^дйпП. д(КпП*)
Но Рг1 — диффеоморфизм, поэтому Pr‘(3(Kf) ГЦ)) = ЗРг^КПГЦ),
причем 3(КППг)=Р/(ЗРг1(7<ПП|)). Тогда,, применяя 1-ю предва-
рительную теорему Грина и учитывая перестановочность опе-
раторов d и Р*, получаем равенства
с 1 г 1
f а,= У P*ai~
д(КпП{) др-1(КПП4)
Я <i(A)“
р7 (кпП{)
= И P*(dai) И Д,
рГ1(кпп/) ₽{(РТ<(КПП,))-КЛП<
что и доказывает формулу Грина и в случае б).
Итак, теорема Грина для компакта К. с ориентированным кра-
ем 'дК. на плоскости доказана, если край не содержит угловых то-
чек.
432
II этап. 'Край, дК содержит угловые точки. Заметим, что ориен-
тированный с край дК компакта К. может содержать лишь конеч-
ное число угловых точек. Без ограничения общности, будем счи-
тать, что край дК. содержит только одну угловую точку Af|»=
==(х0, у0)^20<=дК. Тогда в силу условия 2) определения (из гл. 1,
§ 4) края дК существует окрестность Ш^’ (Af0) такая, что Г=
==<?ЛТ|Ш‘2> (Af0) есть носитель кусочно-гладкого 1-пути Жорда-
на, т. е. Г=Г111Г2, где Гг=(ф, ([а/, Ь<]), фгеС*1) ([ад, fyj) — глад-
кий 1-путь Жордана (так что |D<p,(/) | >0 V6,]) (Г=1, 2),
причем ai<6i=a2<b2. Но тогда существуют конечные левосто-
ронняя касательная с ортом и правосторонняя касатель-
ная с ортом т+(Л10), причем ъ<=с([а{, &J). В силу гладкости 1-пу-
ти фг (»=1> 2) при достаточно малом р0 можно считать, что Г*
задается уравнением y=yt(x) (или x=xi(y)) при х<=[—хь х0]
для Г1 и хе[х0, xi] — для Г2, причем
l*i—*о! < Ро, max \у'.(х)1 <
так что для длин дуг имеем —х0| (i=l, 2)
я поэтому, полагая £Г=Ш<.2>(Л/О) (0<г<ро), имеем оценку
2
I (Пр и Пр) < L • г, L = 2 (1 + L?)4
тде ГР"’= Г, Введем теперь с помощью функции h(t) из
J1], ч. III, гл. 2, § 12, леммы 1 функцию
\(t) = 1 - h(t) =
-оо</<1/2,
l<t<+oos
—o°,+°o), для которой 0/(t) 1 V fs
•е (—оо, +оо) и |DX(?)|<m0= max |DX0|<-f-oo V/e(—oo, -|-oo).
При O<r<^po введем функцию точки z=(x, у]
Для которой ввиду оценок
7 |к — zolk = К* — *o)/|k — zoll2| < 1,
дх
7 |k-Zolk
ду
1 v ||z —z0|l2>0
имеем
ЭД-л. И, Камынин
433
^Xr(z)=DX(||z—z0||e/r) • (x—x0)/||z—z0||2 • 1/r,
0 < r/2 < ||z — z0||t < r < 4-00,
так что
<m0/r VzsR2 y.
Рассмотрим 1-форму
i (1
К . (о= Ilz — zolls>r,
10, ||z—z0||tK r/2 •
и введем круги
Sr/2={z | ||z—Zo||2<r/2},
Sr={z|l|z—zbl]2<r}.
Очевидно,
supp%rnSr/2=0,
supp Arf|Sr/2=0,
supp dXt-czSr.
Введем компактные множества
Kr/2=K\Sr/2= KHCSr/2, Kr—K\Sr==K(]CSr.
i
Тогда suppXr®c:/<r/2. Любая точка M<=Kr/2 обладает открытым
специальным прямоугольником П(М). Тогда
Kr/2c: U П(М)
мекг/2
и в силу компактности множества Кг/2 для него существует конеч-
ное открытое подпокрытие {IL; i=l, 2, т(г)} такое, что
ш(г)
Kr/2^U п<.
г=1
def m(r)
Но тогда, полагая П0=5г/2, имеем дК^К U П{. Для мно-
i=0
жества К введем разбиение единицы i=0, 1,..., m(r)}
класса C<°°>(R2), подчиненное открытому покрытию {П4;
1, т(г)}, для которого
m(r)
i=0
434
suppe>, г сП/ (i=0, 1, .... m(r)).
По доказанному на I этапе для специального прямоугольника
П. (при 1=1, 2,т(г)) имеем формулу Грина
f ei<r • Xr • JJ d(eitr • X • <o),
кгПп.
i
причем, поскольку supp (Xr. • <o) Л По = 0, то
f е0.г - К • <i>=0= Я d(e0,r •»).
дКап, Клпв
Но тогда имеем формулу Грина
J Хг • ©= ffd(X, • L). (2.2)»
ОК К
1
Заметим, что X, • ш=Х, • &>dx+kr -Qdy, причем max Q^5], |Q|) =
К
1 1 1
*amv Далее, d(Xr • w)=dXrA<o+X^d<i>t где
X,Ad© = Xr . (1Q— А зЛ dx/\dy<
\ax ay ]
dkf/\&=(Q -^k-SP • ^-kr\dx7\dy,
sup
о
к
dQ д& . o
—----------------< 2/n2.
dx Sy Г* 2
Кроме того, |Xr(z) —1|^1,
/(Г Л Sr)<L • г, max (^2+^2)1/2 </2 • mv
к
Но тогда при О<гСро имеем оценки
< J |(Xr-l)(^dx4-Sdy)|<
dKn«r
< max (5В2+^2)'/2 . /(ГЛ 5,)Х /2 . /и, • L • г
К
и
28*
435
\dx\dy + П- Q • Зг|х
/ KfbSJ дх ° У
УЖ . «,) - £f du,
_ д$>
ду
X dx/\dy ^. 2т2 - к • г2 -j- 2т2 (mJ г) • w -г2»
= 2те • (тпа • г + т1 mJ) • г.
Таким образом, в равенстве (2.2) можно переходить к пределу
при г -► 0, что дает формулу Грина (2.1) в общем случае.
Замечание. В отличие от 1-й {предварительной) теоремы
Грина на плоскости (из гл. 1, § 4) в доказанной 2-й теореме Гри-
на область К. не предполагается одноовязной. Для общего ком-
о
пакта К с краем дК. в силу определения гл. 1, § 4 область К мо-
жет быть многоовязной. Если, например, К (m+Д)-связна (в
R2), то она содержит т «дыр» и край дК распадается на zn+1
связных компонент-носителей жордановых кусочно-гладких цик-
m
лов, т. е. d/<=LUU^, где L — «внешний» цикл, a k 2, ...,
г=1
.... т) — внутренние циклы, являющиеся границами внутренних
«дыр» области К. В соответствии с выбором ориентации края (при
обходе края дК область К остается слева) «внешний» цикл L об-
ходится «против часовой стрелки», а обход «внутреннего» цикла
/7 (t=l, 2, ..., т) проводится «по часовой стрелке». Тогда в силу
теоремы 3 (об аддитивности криволинейности интеграла 2-го ро-
да) из гл. 1, § 3 в формуле Грина (2.1) имеем
1.1ml
f U)=J (#+jf U>.
дК Г i=l £.
Вернемся теперь к изучению поверхностных интегралов.
Рассмотрим гладкий 3-путь в R3 <p: U R3 „ w-* Г = <p(t/)c
у, г, где U cz R3 — компактное множество, измеримое по
Жордану и
<р(н, v, w) — (x{uv v, w), у(и, v, w), z(u, v,
причем
ди ди dw
Пусть <в=4(х, у, z)dx /\dy /\dz — дифференциальная 3-форма
класса С<°>, определенная на множестве
436
Определение. Объемным интегралом (2-го рода) от
3-формы со по 3-пути ф называется число
3 def __ 3
у J Adx/\dy/\dz= fff <р*ш =
Ф Ф и
= JJj А ° ф(и, v, w) • ——dudvdw.
и д(и, v, w)
<=^x,y,z
Замечание. Если отображение <р: U cz дз _». р — (-
х = и
таково, что <р= у — v, то и=Г и пространство
Z — W
имеет ту же ориентацию, что и R3 г, и тогда
з
у <о= у Д dxД dy /\dz = ууу А (х, у, z) dx dydz.
ф и и
Замечание. Величина J 1 dx Д dy A dz иногда называется
ф
ориентированным объемом компакта Г = ф(С7) в пространстве
R3 v г* Очевидно, ориентации R,3, „ и R3 „ • совпадают
<4у 1 dx /\dy Л dz’>- 0 и противоположны
ф
44-у 1 dx A dy Д </г<0.
ф
Определение 3. k-объемом k-пути ф класса С(1) в R”, где
Ф : L/cRj-»- Г—<p(U)c:R",
называется величина
Sk=\<p\k=J .i.SD9(t)dtl...dik,
где (используя обозначение (а, Ь) = <а, Ь> для скалярного про-
изведения векторов а и b в евклидовом пространстве Rn) поло-
жено
Оф(0=| det
I i, /=1. 2..... k
Замечание. Можно доказать (см. [5]) равенство
d:w= 2
..ф«ь)
д(tk)
2
vt^u,
Из которого, в частности, вытекает оценка
43-1
d(tlt...,tk) ()
При k = n имеем
D//J v t e= U.
(detD<pf/J)a
d<ft
dti
d?i
<Hn
d'Pi
d/i
fyn
dt*
d'tn
dti
dtp dtp \
dti ’ dt. I
d?n
dta
(dff
i dt.
d<fi
dtn
dtp \
)
dfn
dtn
dtp dtp
dta ’ dtt
/ dtp dtp
=
t. e. |detDq>f/)|=D(|,('/), и поэтому для n-объема Жордана мно-
жества ф(1/) в ,Rn имеем
Sn== |ф |п=||ф(^) In-
ЭТО утверждение является обоснованием принятого в дифферен-
циальной геометрии приведенного определения ^-объема Д-пути
Ф в
R": 1ф|А=/О/0^
и
совпадающего при £=1 и при k=n с обычными определениями
длины 1-пути
|ф|1 = /|Оф^|^.
и n-объема Жордана п-пути
1ф1п = 1фЖ= J |det ОфСО1^
и
в R”.
Пример. Рассмотрим в R3 2-путь ф : U R3 г -> Г = ф(?7)с
сД3 v г класса С’1», так что ф(ц, p)=(x(u, v), у(и, v), z(u, о)(е
<sC(1,((/). Тогда имеем •
__________________________dtp / дх ду dz
фи -------------------------------------------- - I ’ * Г >
ди \ ди ди ди
dtp /дх_ ду dz
ди I ди 9 ди 9 ди
438
Поскольку 2-путь ф — гладкий» то ранг матрицы Якоби
дх дх
ди ди
ду ду
ди ди ,
дг дг
ди ди
производной Вф(и, v) е55(R2, R8), равен 2. Полагая е1=(1,0)и
е2=(0, 1) для координатных ортов в R2^, видим, что фц =
= Dq>(w« »)еп фо=Вф(а, г)е2, так что вектора фа, <₽*,, лежащие
в касательном пространстве ТФ(и. »>(Г) (к носителю Г 2-пути ф),
не коллинеарны. Следуя традициям дифференциальной гео-
метрии, положим (фв, ф1()=^, (фп, ф„)= F, (фр, фо) =• G, так что
E F
F G
D2(«, v) =
= EG - F2, D,(u, v) = (EG — F2)‘/2,
Определение 4. Площадью 2-пути ф класса С(1) в R3
Ф :CZczR2iB->r=v((/)czR3i у> г
называется величина
S2« | Ф |, = {J (EG-F^dudv.
и
Замечание. Вектор направленной нормали N(u, v) к каса-
тельной плоскости ТФ(и,0)(Г) (к носителю Г в точке ф(и, v)) в
R8 у г задается формулой
def < J k
N(U, V) = [фаЛфр] = Xa ya Z„
yv
где i, j, k — координатные орты в R3 y t. Но тогда
' N(«, V)=^JL .i+A2» xl. ,j+ .b>
d(u, p) d(ut u) d(u, v)
так ЧТО
|N(u, p)l2= *) V I
I d(ut v) J I д(и9 и) I I d(u9 v}
Но по определению векторного произведения имеем
I N(u, v) | = |[фиЛф«111=
= |фи|-|<Р»|-8т< (фи, ф»),
439
а по определению скалярного произведения
| <фи, ф»> | =’|фи | {фо) 'COS < (фи, фс)
так что
|N(«, 1>_)[2+|<ф„, ф0>|2=|фи|2-|фс|2,
и поскольку
|фи|2= (фи> фи)=Е, |ф»|2 =
— (ф0/ фо) = б, (фи, фс)='Л
то имеем |N(n, u)|2=E-G—F2, т. е.
£ . Q fi __ / д(у, z) \8 7 д(г, х) \8 . / д(х, у) \8
I д(и, v) I I д(и, V) ) I d(ut v) )
Для направляющих косинусов нормали N(u, v) имеем
cos (N, *) = d{v' z} / (E • G—F8)‘/2,
x d(u, v) /
cos(N, y) = /(E • G-F2)1/2,
o(u, v) /
cos(N, г) = d(x> y)- /(E-G-F2)^.
d(u, v) /
l(B частности, для 2-пути <p в R3, заданного параметризацией
ф:х=«, y=v, z=f(u, v), (и, v)EUcR[ t, имеем
i j k
N(x, У) = 1 o dx о 1 dx dy
dy
E • G — F2 = 1 + / V 4- (V,
\дх I dy )
Заметим, что в силу определения направленной нормали N(« о)1
тройка {N, <ри, фи} ориентирована так же, как и тройка координат-
ных ортов {i, j, к} в R3 yt z, поскольку матрица перехода
д(у, z) d(z, х) д(х, у)
д(и, v) d(u, v) d(u, v)
Уи
Xv Uy
440
имеет определитель, равный
|N(u, o)|2>0v (и, v)^U. Да-
лее (см. рис. 30) пусть ДГ=
=ф(ДГ7), где брус Д[/=
=[ui, u2]X[vt, у2] имеет стороны
длины Ди и До, так что | Д[/|2=
==Ди-До. Тогда по определению
площадь ДГ равна
(Д5)2 = ff (Е • G-F^dudv =
до
= £[ |N(u, v)\dudv,
ди
причем N(u, о)=[фиДфо]. В силу
теоремы о среднем величина)
(Д5)2= | N(Af0) |-Ди-До =
= |[фи(ЛГо)-ДиЛф0('Л1о)-Дг’]|
является площадью параллелограмма ДПсДи. (Г) с вершиной
в точке ЛГоеГ, построенного на касательных векторах фи(Л40)-Ди.
и <pv(M0)-Av. Итак, АП = ргДГ и
’м.<г>
|ДП|2='(Д5)2=|ДГ|2.
Замечание. В ч. JII, гл. J, § 5 длина ^(<p)s|<p|i 1-пути
в Rn определялась как предел длины 1т (ф) ломаной, вписанной в
Г=<р([а, 6]) при d(7)-*0. Выше площадь (2-объем) |<р|2 2-пути
Ф в R3 определялась иным способом как предел при diam ДГ/ -*•
-*0 S |ДП|2, где ДП = ргф(ДГ/) — параллелограмм, построен-
ДУ ТФ(Г)
ный на касательных векторах фиДи и ф®До. Покажем, что пло-
щадь |ф|2 2-пути ф в R3 нельзя определить как предел площади
|2т(Д) |2 многогранной поверхности St (Л), вписанной в носитель-
Г=ф(Г/) при d(T)-+Q. В самом деле, следуя Шварцу, рассмот-
рим прямой круговой цилиндр радиуса и высоты Н>0 с бо-
ковой поверхностью TczR3. Разделим высоту цилиндра на ш рав-
ных частей длины Him и проведем через точки деления т+1
плоскостей, перпендикулярных оси цилиндра так, что на поверх-
ности Г получится (т+1) окружностей Ck (£=0, 1, ..., т). Каж-
дую из этих окружностей Ck разделим на п равных дуг (соответ-
ствующих центральному углу 2л/п) так, чтобы точки деления вы-
шележащей окружности Ck находились над серединами дуг ниже-
лежащей окружности Ck-i (k=\, 2, ..., т). Возьмем треугольники1
Д> образованные хордами всех этих дуг и отрезков, соединяющи-
ми концы хорд с теми точками деления выше (Ck) и ниже
(Ck-i) лежащих окружностей, которые расположены как раз над.
или под серединами соответствующих дуг. В совокупности эти
^пгп равных треугольников Д образуют многогранную поверх*
441'
ность (сапог Шварца) Sm, п (Д)р вписанную в Г. Заметим, что по
построению
|l|2=/?sin (л/п) (^(1—cos(n/n))2+№/n-2)V2,
так что
I Sm( п (Д) 12=2Rn sin (л/n) (7?,W (1—cos (n/n) )24-Я2) V2,
но тогда не существует предела |Sm, П(Д)|2 при независимом
стремлении т и п к +<». В самом деле, пусть lim mlti?=q (где
m, n,-»-|-oo
'0^4'С+оо)> тогда предел
lim |2т,п(Д) |2=2nR(nW/4+H2)‘/2
m, n-*4-oo
зависит от выбора q и при 9=4-00 равен 4-<» и лишь при 9=0
совпадает с истинной площадью |Г|2=2л#Я. Отметим, что при
большем 9 треугольные грани Sm, nfA) могут быть почти ортого-
нальными к касательной плоскости Т,(Г), образуя мелкие склад-
ки «сапога Шварца».
Пример. Вычислим при nj>2 площадь ((п—1)-объем)
(n—1)-мерной сферы Sn-i(R) — |дШ^> (0)|п-ь Введем в R" при
л>2 полярные координаты
Xi=r-cosq>i,
x2=r-sin q>i -cos ф2,
Хз=г-зк1ф1-sin фг-cos фз,
xn-i=r-sin ф1 -sin ф2 ••• зШфп-г-сов фп-1,
xn=r-sin фгвШфг ••• sin<pn-2*sin фп-ь
Тогда отображение 5s: (0, 4-00) XI/ -* Rn\^, где
£/={(фь фп-1.) |0<1ф|г<л (i=l, 2, ..., п—2),
0<фп-1<2л), & ={xf=Rn|
|xi|<;4-00, 0^%x<l<Ci4"00 (^,==2, 3, ..., fi 1), 0}
является диффеоморфизмом. Заметим, что
!д$> dj>\ _
dr dr j ’
^ = 0(i = l, 2,..., Л.1);
\ dr дфг/
= о (k, 1= 1, 2,..., п—1), k^l-,
\^Рл . ^<Pz/
/аЗ5 ,
1 --’ --- I ~
\дф1 дфх/
« поскольку при
442
dxt
то
dx*
5<Рк
dxk+i
dxk+2
k-t
-г- П sin <p< • sin Фй,
i— 1
*-l
• П sin ф< • cos ф* • cos <pfc+i,
fc-1
= r • fl sin Ф«' cos 4>h • sin ФЖ ' cos*-f-i,
d*n 2 П • •
--------~ Г * II Sin Ф» * COS <Pfe * sln ф*+1 ’ * • SIU фгг-З • COS фл-2>
fyh----• т
i=I
fe“A
—1 гт • • •
-------- —r • Il 81Пф< • COS Фь * Sin q>*+i • • • 81Пфл-2 • COStpn-i,
i=l
d *-1
— = r • П sin ?i • cos Ф* • sin ф*+1 • • • sin <pn_2 • sin <pn_i =>
откуда
(det D^)* = det ||(Di^, D/^)l| =
i, j»«i. 2........... n
п-l '/k-i \
= r2(n-l) • П П Sin2<Pi j =
fe=2 \i=I /
__r2(n-i). sin2(n-2><pl • sin2(n-3><p2---sin1(pn_2==
ег2»|1-».(0ф{ф1, Фа. ... , Ф«-1))#,
где Ф : (/-> dmW(0)\f (Ф:(ф1..............Ф«-0 — ^(1, фх. • • . , ф«-1))
(п—1)-путь с параметризацией, получаемой из формул перехо-
да к полярным координатам при г=1, т. е.
det D (г, Ф1, . . . , <р„м) =
Э(Г, <ря_4)
== rn-i . sin” ~2 Ф1 • sin"”3 Фа • • . sin Фп-2 =
= гп~1 Оф(Ф1, . . . , <ря-1),
443
где
D2 (<pr ...» <pn-i)= det , ^All.
k, l=t, 2.n-l \O!ffe Of|l |
Введем (n—1)-путь Ф/? : U—>5Ш^)(0)\^', где Фн получается из
формул перехода к полярным координатам при r = R. Тогда
при Л=1, 2, ... , п—1 имеем
d^JL=R. —
так, что
(— Ф₽, — фЛ=Я». (— Ф, Аф\ (при &,/=!, 2................п-1)
d<fi у . d<pz у ...
и поэтому
(Оф^Фь .... <рп_1))’=Я2(',-1>-(Пф(ф1, . . . , фп-1))2,
т. е. БфЛ(ф) = 7?"-1 • Пф(ф). Итак,
S„_i(R) = рШ^>(0)|л_1 = Вф^Фр-Й,,-^
=₽п-1 • JJ Рф(ф)^Ф1 • • • Йя-i =
и
= R*-' . рШ<«>(0)|л_1 = Я"-1 •
где sn~i = рш<п)(0)|п_1 есть (п—1)-мерный объем единичной
сферы ЭШ</1>(0), a Sn_i(R)—(п— 1)-мерный объем сферы дШ<£>(0)
радиуса R > 0. Таким образом, Sn-i(R) — Rn~l • sn-i. Далее/
7п(Я) = |Ш£>(0)|п = Я/ 1 dX1. . . dxn
А
и, переходя в кратном интеграле к полярным координатам и ис-
пользуя теорему Фубини, имеем
я
Vn(R)= $ dr [Jldet D^(r, фь.... фп_1)|йф1...(/фл_1 =
о и
R
а= f гп~^г f . . . f Пф(ф!,..., ф„_1)йф1...</фл_1 == sn-t • Rn/n,
j) J и J
т. e. sn-i=n-Vn(R)/Rn, но (см. гл. 2, § 4)
Vn(R)=Rn-n*'2/r(n/2+l),
поэтому имеем (при л^2)
444
и тогда окончательно имеем
Sn-! (R) =2Rn-1 • л"/2/Г (n/2) (n>2).
В частности, при п=2 Si(R)=2Rn/T(l)=2n-R и при п=3
S2(R)=2R?-n^/V(3/2) =4jvR2.
Теорема- (достаточное условие абсолютной сходимости не-
собственного n-кратного интеграла Римана от непрерывной функ-
ции с изолированной особенностью). Пусть f: (0)R1, при-
цел (0)) и существуют постоянные а>0 и М(а)>0
такие, что имеет место оценка | f (х) | (а) ra~n V хе.(0),
еде п^2 и г=(2х?)1/2= 1Х1- Тогда несобственный интеграл
»=1
'J f(x)dx сходится (абсолютно) в смысле определения (К) (из
ШЛп)(0)
гл. 2, § 3).
Доказательство. Рассмотрим систему компактных мно-
жеств
Kl={x6=R"|l//<|x|<£—1/1} .(/=4, 2, ...),
исчерпывающую открытое множество Шд? (0). Очевидно,
feR(Ki)v I. Переходя к полярным координатам (г, <рь ..., <pn-i),
имеем оценки
J If (x)\dx < М(а) • J |x|»~ndx =
kz Kt
R-i/l
= f rn-'-r“-ndr^ .
if!
R
< 2Л4(а) • ^/Цп/2} • J r«-‘ dr <
о
a-1 • sn-i • M(a) • 2?»< 4-oo V/eN.
Из полученных оценок следует сходимость нашего несобственного
интеграла в смысле определения (К).
Теорема (достаточное условие абсолютной сходимости не-
собственного n-кратного интеграла Римана от непрерывной функ-
ции по неограниченной области). Пусть (0)-> R1 (п^2),
лричелс f<=C(СШл? (0)), и существуют постоянные а>0 и
^(a)>0 такие, что имеет место оценка
| f (х)\ («)//-"+“ V хеСШ(«’ 10),,
445
где r=(Sx?)I/2. Тогда несобственный интеграл f(x)dx
i=i СШ<£)(0)
сходится в смысле определения. (К). (Доказать самостоятельно,
используя исчерпывающую СШя0 (0) систему компактных мно-
жеств
Kz={xG=R"|/?+l//<|x|<fl+0 /eN).
Определение 4. Поверхностным интегралом 1-го рода от
функции feC(T) по k-пути <p:t/c:Rft r=<p(77)eRn класса
в Rn называется величина
def
Ф и
Определение 5. Поверхностным интегралом 1-го рода от
функции /еС(Г) по 2-пути <р: С/сЯ2.,-* r=<p(C/)a:R2 у г клас-
са С(1) в R3 называется величина
def ..
f fdS= И f о ф(и, »)(£ • G—£’)V2 dudv.
ф У
Замечание. Отметим связь между поверхностными интег-
ралами 1-го и 2-го рода по 2-пути в R3. Рассмотрим дифферен-
циальную 2-форму
2
ю=Ady Д dz+Bdz/\dx+CdxAdy
класса С(0), определенную на открытом множестве QczR3 и глад-
кий 2-путь
<р: GcR3. , - Г=ф(С/)сЙс^3 г
в R3. Тогда имеем равенство
J ю== J (4 cos (N, x)4-B*cos(N, у)4-С • cos(N, z))dS,
ф ф
где М=[фиДфо] — направленная нормаль к касательной плоско-
сти Леи,»)(Г) в точке ф(м, о)<=Г.
В самом деле, поскольку
Ф: (и, v) -* (х(и, v), у(и, v), г(и, о)) <= CW(U),
то
d(v> = (E'G- Л)*/2cos(N, х) о ф,
д(и, v)
**> *Le(Е • G - F2)3'2 • cos(N, у) о Ф,
д{и9 v)
446
^4r=(E.G-P)«.co5(N, г), <p.
так что имеем
J®= ЯФ*<°= Я (А ° Ф(«. у» • +5 ° Ф<и« °) х
i и и \ д(«, »)
Х^Г~4 +Со (и’ °) - ~У' V\\dudv^
д(и, ») d(u, v) j
= Д(Л<> <р • cos(N, х) о <р4-В о <p-cos(N, у)о ф-|-
def '
+ С ° <р . cos (N, t) ° ф)(Е • G—F^^dudv =
= }(Л • cos(N, х)+В • cos(N, у)+С • cos(N, z))dS.
ф
(Запись
(^•cos(N, х)) o<p(«, v) =
А°<р(и, o)-cos(N, х)«ф(«, о),
(Bcos(N, у)) вф(и, v)=B °tf(u, v)-cos(N, у) «ф(м, о),
(C-icos(N, z)) °ф(«, о)=С°ф(«, v)-cos(N, z) »ф(«, о)
корректна в силу инвариантности касательной плоскости и на-
правляющих косинусов направленной нормали N(«, v) относитель-
но отношения <р~ф.)
Рассмотрим гладкий 1-путь
ф.-(о, b)czR} -*Г=ф((а, b))cR2 у
в R2, так что вектор
т(0 — (х'(0> гДе е — координатный
орт в R}, определяет направленную касательную к Г в точке
Ф(7)еГ. Введем вектор направленной нормали к Г в точке
Ф(7)еГ, положив
def а а
ВД=[т(01=' ‘ ’ =(y'(t),-x'(t)).
x'(t) y'(t)
Заметим, что матрица перехода от упорядоченной пары {еь ег} ко-
ординатных ортов в R£ у к паре {Nf/), т(0} имеет определитель
y'(t) ~x'(t)
x'(i) y'(t)
= (x'(i)p+:(y'(t))2>0^t^(a, b),
так что {N, r}~{ei, ег}, но тогда имеем
cos(N, х) =у'/((х')2+ (y)2)1/2=cos(T, у),
cos(N, у)=—х'/((х')2+(у')2)х/2——cos(t, х).
447
Замечание (о записи формулы Грина на плоскости с по-
мощью криволинейных интегралов 1-го рода). Пусть KczR2 —
компакт с ориентированным краем дК, являющимся носителем
гладкого цикла Жордана ф и ограничивающим односвязную об-
ласть К, причем для 1-формы SPdx+Qdy выполнены условия 2-й
теоремы Грина. Если т — направленная касательная, N — на-
правленная нормаль и v — внутренняя (по отношению к К) нор-
маль к краю дК, то формула Грина (2.1) допускает запись в виде
1 1
JJ du>= J ю— f 3!>dx + Qdy = ^ (&> • cos(t, х)+(? • cos (т, y))ds=
JC дК дК дК
= f (^-cos(N, х) — • cos(N, y))ds =
дК
— f (3° • cos (v, у) — Q • cos(v, x))ds.
дх
Заметим, что направленная нормаль N к (ориентированному)
краю дК, является внешней (по отношению к К) нормалью к краю
дК, поскольку из правила ориентации края дК (см. гл. 1, § 4) вы-
текает, что {т, v}.~{ei, е2}. Но для N=[t] вытекает, что
{е1( e2}~{N, т}, и поэтому направленная нормаль N имеет направ-
ление, противоположное внутренней (для К) нормали v. Отметим
также равенства
cos(N, х)=—icos(v, x)=cos(t, у),
cos(N, у)='—cos(v, у)=—cos(t, х).
•Отметим некоторые свойства интепралов от &-форм по й-путям в
Rn (сравните свойства криволинейных интегралов 2-го рода из •
гл. 1, § 3).
Теорема 1 (об инвариантности^интеграла относительно до-
пустимой замены переменных). Если со — k-форма класса С(1), где
rcRn — носитель гладких k-путей ф~ф (из Rn), то
к к
У<о=У«>.
ф ф
Доказательство. Пусть
Ф: с: R *Г = ф(^) с R« и ф: V. с R* -> Г » ф(С7х) cR"
где
Ut az R‘, U.czR.*, и феС<»(Дт).
Поскольку ф~ф, то существует допустимый диффеоморфизм
;(класса С<*>) t-.Ux-+Ut такой, что множества t(Ux) — Ut 0
i~l(Ut) — Ux измеримы по Жордану,
Ф(О =ф о t~l (t), ф(т) =ф»0(т);
448
det D Г(х) = ’-.*2 (t) > О V x e U,
<4Xl, --.Xfe)
(T-e-",?^)-=l'letD'(x>l'l
\ <4X1,-- •» X*) )
и detDfeC.(t7t)AB(l/r.). Делая замену переменных t=t(x) в ин-
теграле Римана (см. ч. V, гл. 2, § 4) и используя теорему о произ-
водной композиции двух дифференцируемых отображений (из
[1], ч. Ш, гл. 2, § 4), имеем для ft-формы
к
и>(х) = А(х)ахйЛ . . . Adxik,
<p*w= f Ao <f(t) x
ф ut
X А о ф о t(T) x
X-^—^-0 <(<)‘|detDr(x)|dx1 ..dxft =
o( , • • • , Ifc)
f . . . . a(*Pip**-» Ф«ь) x ...’fe) , XJ .
=L °!W
“f Л» Ф(') • j ^*ш=ри,
к
Замечание. В силу теоремы 1 интеграл S© определен на
ф
fe-поверхности Ф.
Теорема 2 (о линейности интеграла). Пусть ф — гладкая
k-поверхность класса С(1) в Rn. Тогда для любых постоянных
к к
«ь с2 и для любых k-форм класса С(0)(Г)®1 и ©2 имеем
к к к к
J Ci • a>i + С, • == Ci • j Wj-I- Cg • J ©г.
ф ф Ф
(Доказать самостоятельно.)
Теорема 3 (об ориентированности интеграла от ft-формы по
. к
«•пути в Rn). Если Ф — гладкая k-поверхность в Rn и © k-форма
класса -С (Г) (где rcRn — носитель Ф), то
к к
Л. и. Камынин
449
Доказательство. Пусть гладкий 6-путь <р : -*• Г=
=<p(l/*)c:R" является представителем 6-поверхности Ф и ф—
=—Ф: L\cR*-> Г=ф('/7т)с^^. Тогда существует диффеомор-
физм (класса C(I)) такой, что i(Ux) = Ut, 1г*(Ш) =
= UX — измеримые по Жордану открытые множества,
ф(7)=фо^1(1/), ф(т)=ф»/(т),
(т)<0 Vx^Ux
д(т,..
(так что |det Dt(r)| = — (тЙ
Э(Ч,..., Тк) у
и
|det Di| е C(UX)AB(UX).
Но тогда, делая замену переменных t=t(x) в интеграле Римана
и повторяя выкладки, проведенные при доказательстве теоремы 1,
имеем для 6-формы а>(х) = A(x)dXitA--Adx(k
* л * (.
С (в= j ф*ш = \
ф(0 . dt ... dt =
v d(h.......tk) Ul1 k
J А о ф о t(x). У ° /(т) • |det D/(T)|dti...dtft=
ux ......U
( „ ,/x ....Ф1а) I Ml.......
= J А о Ф(т) • i(T) . —-LI--------л> M X
Ux tk) \ d(Ti...../
x dxv..dxk= — f До ф(т) • d^lt * У ♦ .dxk
и. Xh)
fc k
= —J Ф*Ю — — f W.
Ux Ф
Теорема 4 (об инвариантности 6-объема 6-пути в Rn). Пусть
Ф и ф — гладкие k-пути в Rn. Тогда при <р-~ф или при ф=—ф
имеем 1ф|а=|Ф|а>
Доказательство. Пусть, например, ф=—ф, причем
Ф: £7/C3R^ -* Г=ф({Л.)с^п, —ф=ф' tAczR* Г.вф(£/<)с:Кп.
Тогда существует диффеоморфизм t\Ux-^Ut класса С(1) такой,
что открытые множества Ut=t(Ux), Ux=t~l(Ut) измеримы по
Жордану,
ф(7)=ф<> Hffj, ф(т)=ф°^(т),
450
У.
и
Тогда, имея в виду равенство
D2(O= .det
Ф i, 1=1, 2.К
и делая замену переменных t=f(x) в интеграле Римана, полу-
чаем
h>l,ep.ds=f. . 4 .. dtk^
Ф Ut=t(Ux)
и.
2
^4<T.<ih<,n d(tx
....tft) (T)!^. . . dTft =
d(ti....Tfe)v ' 1 ft
> чч)
*Л>
° *(1)
2\1/2
.......ot(,)X
d(tt..tk)
K) (T)
tk)
a\ 1/2
I dxt. . . d<rk =
= f • • • fDqfOdti
Ут
• ^ = |Фк=>1Фкя1Ф1г
Следствие. Вейлу инвариантности й-объема гладкого
fe-пути в Rn имеет смысл понятие ^-объема гладкой ^-поверхности
Ф и (—ф) (в R"), причем |Ф|Й=|—ф|й.
Теорема 5 (об оценке интеграла от &-формы по &-пути в
Rn). Рассмотрим гладкую k-поверхность Ф в Rn и 'дифференци-
альную k-форму
29* 451
wfx) = S A...i/xX-«iiA...Arfxi.
класса С (Г), где Г — носитель k-поверхности Ф. Если
(х) |<Л4 УхеГ v — ik),
то имеет место оценка
л
|/о|<С».Л1-|Ф|А.
ф
Доказательство. Пусть <р: C/cR*->r=<p(X/)c:Rn глад-
кий Л-путь, являющийся представителем гладкой ^-поверхности
ф. Тогда в силу отмеченного ранее неравенства
Vte=tf V(0
Шч 4ih)
Mi........<л)
имеем оценки
I к
К® = J 5 Аи/ф(0Х
1.Ф . I и
А
• dtl • • • <
д(Н,..., tk)
• f DcpfOЛх • • • dtk — C^ • M • |<р|Л.
(i) и
Теорема’6 (о переходе к пределу под знаком интеграла от
й^формы по ^-поверхности). Пусть Ф — гладкая k-поверхность в
Rn с носителем TczR” и
k
<*>m (х) = 2 А<С\(x)dxh Л - Л dxtj m €= N
k-форма класса С, определенная в окрестности носителя Г, при-
чем
А\^. (х) z* Ah...i (х)
“"‘к (m-+oo) *
на Г. Тогда, полагая
а>(х) =2 4(»)Wrfxi,A—/\dxlh,
(О
имеем '
К k
Я lim J wm = J ®.
m-* 4-00 ф ф
452
Доказательство. Поскольку
+ /'OW
' (m->+oo)
на Г, то V е>0 э ЛЦе)еЫ такое, что У/п>ЛГ(е) и Vх<=Г, имеем
оценку
\А^х)-А^(х)\<г1(С* |Ф|Л) v(i).
Кроме того, поскольку еС(Г) v (i) и множество Г компакт-^
но, то Л(,)еС(Г), так, что Л-форма
к
. /\dxih
(О
класса С(0) на Г, причем в силу теоремы 5 имеем оценку *
k к 1
J — j* (о < е V m > N(z)
ф ф
из которой и вытекает, что
k к
И lim Г (Од, = f со.
т->4-оо ф ф
§ 3. Формула Гаусса — Остроградского в R3
Теорема (о ранге). Рассмотрим множество MaRn и точку
хоеМ, тогда при bz^k^n и следующие 3 свойства эквива-
лентны:
1) существуют открытая окрестность VczRj точки х0^М и
'диффеоморфизм (класса С<1>)
ф: VczRs t/=i|»(V)c=Rp,
где UczR.f — открытое множество, такой, что i|>(xo)=0 и
G=^(M(\V) = U(](tk+i==0,.fn=0};
2) после подходящей перестановки координат Xt, Хг, .... хп в
R" существует окрестность VczR" точки х0^М и п—k числовых
функций flex') (где
x'=(xi, ..., хк), x"‘=(Xk+t, ..., хп)) (j=k+l.п)
таких, что
1,(х0')=х^ (j=k+\, ..., п)
и
V(]M—{x^Vc:tt.n\xi=fj(xi....xk) (j—k+1........п)};
3) существует окрестность Vc:R" точки х^М. и (открытая)
окрестность GgzR, точки OsR* и гомеоморфизм
453
' <p:G<=R‘ q>(G) =MnVczR2
такой, что
(peCWfG), ф(0)=хо
и матрица Якоби
(D/4>i(t)) (i=l, 2.и; /=1, 2, k)
имеет ранг k\ t^G.
Доказательство. Покажем сначала, 3) => 2). Если вы-
полнено 3), то существует гомеоморфизм
<р: GcR* - <f(G) =М(]Vc=R"(x=^(t))
и точка Хо=ф(О), такие, что OeGczR^, причем отображение
<peC(Z)(G) имеет матрицу Якоби (П/ф((¥)) (7=1, 2, .... л; /=
=4, 2, ..., k) ранга &^nvteG. Тогда, в частности, матрица Яко-
би (В/ф,(0)) также имеет ранг k и можно сделать такую переста-
новку координат Xi, Х2,..., хп в R", что
й(й...<*)
Рассмотрим отображение
cp:GczR*+ V'cR*, ,
положив
№=1Ф?(^1...tk) (t=l, 2, ..., k),
и введем обозначения
X — (х', Х), Хо = (-^о» -^о)’ % = [Xj,..., Xft),
X" = (х*+|, х„),V = V' x V", x'oe V' c R*, и
Тогда якобиан отображения ф в точке t — Q отличен от нуля
<т. е.
и по теореме о локальном диффеоморфизме (из [1],. ч. Ш,
гл. 2, § 8) существуют окрестности ГИ(О) CZ G с R* и V[ =
= ф(№(0)) с: V' такие, что сужение ф: IF(0)(ZR*->V{ czR*' есть
диффеоморфизм класса С(/), причем ф(О) = хо, ф(О)^=(хо, хо)>
xosVi. Пусть / = ф(х') (*4 = ф{(х1,..., xft); i = l, 2,..., k) есть об-
ратный диффеоморфизм
ф : V-с Rx- -> ИЧО) cz R(fc,
454
причем ф(хо)=О. Тогда, полагая
V1 = и; X V' <= V с R" = R‘, X
видим, что <р(РИ(О)) = М П Vi cz R", причем
М f| — {х = (х', х") е= 7Х|
Xj = f}{x1,..., xft); j = k + l,..., п},
где fj(x") = ф/ф1(х'),..., фй(х')} (1=^+1,.,., n), и поскольку ф <=
и cpeCW(G), то e чем доказательство ут-
верждения 3) => 2) завершается.
Докажем теперь, что 2) => 1). При выполнении 2) существу-
ют окрестность V=V'XV"c:R*, XR£r* точки х0=(х0', х0")<=М
и функции fi(xi, хк) (j=ife+l..........л) такие, что
^C^(V') (j—k+l, ..., п) и f(xo')=xo", причем
УПЛ4={х=(х', x")€=V'XV"<=Rnlx/=
, =fi(xt, хь); j=ik+A, ..., и}.
Введем отображение t=ty(x), положив
f tt = xi — x9 (i= 1, 2,..., k),
\t}=izXj — t№) = n).
Тогда i|>:VCR"->Rp. Заметим, что ф(х0)=О, феС(/)(Ю и VxeF
dffj,..., tn) fx\
1 I. 0 • 0
0 •• 1
— DJfe+i — • 1 . q
..................‘0
— Difn ^kfn ф 1
Но тогда отображение ф: VczR" -*• ^fVjczR^ есть диффеоморфизм
класса C(Z), причем множество i|j(V)==C/c:R" открыто и содержит
OeR". Для обратного диффеоморфизма ф^ф-1:1/czR"-»-VoR"
имеем представление x=xp(t), где
|xt = fi + x°. k),
| xj=tl+fj(t1+^1,..., th+x^) (j=fc+l,-, n),
так что
455
Ф(М Л F) - {/@ U c R?| /*+1 = 0,
/п = 0} = ГП{«*+1 = 0,..., tn = Q}.
Доказательство утверждения: 2) => 1) завершено.
Докажем, наконец, что 1) => 3). При выполнении 1) сущест-
вуют открытая окрестность V(x0)czR", окрестность t/(O)c:Rp
и диффеоморфизм класса С(/>
ф: VczR*.-»- t/=i|>(’V)c:R<n
такой, что
ф(хо)=0 и ф('ЛГЛУ)=ил{^+1=0.......fn=0},
причем множество
С/Л{4+1=0, ..., /n=0)czR”
можно отождествить с открытым множеством GcR^ '(с коорди-
натами f=(ti, ..., tk)). Очевидно, OeG. Рассмотрим обратный
диффеоморфизм Ф=|ф-1: C/czR"-> VcrRj и его сужение на G
Ф=Ф|о : GczR* ->- »p(G)czAfnFc:R".
Тогда
^-“ф/ (^i, ..., ^&)^Ф/ (^i, ..., tk\ 0, ..., 0)
(i=l, 2, ..., и), <peCW(G)
и для матриц Якоби этих отображений имеем
.... h- 0, 0)) (i—1, 2...n;
/—1, 2, ..., k). (3.1}
Поскольку Ф — диффеоморфизм, то его производная ПФ(0)е
(Rn, Rn) есть изоморфизм R" на R". Рассматривая сужение
этого изоморфизма ПФ(0) на ^-мерное линейное подпространство1
R* czR", определяемое уравнениями /*+1=0, ..., 4п=0, видим, что
это сужение ПФ (0) |r* : R* R” имеет ранг k и при этом его
nXk матрица ввиду (3.1) в точности совпадает с матрицей Якоби
(D/q>i(0)) (t=4, 2, п\ j=l, 2, ..., k) отображения <р. Таким
образом, отображение <p:Gc:R* -»-iWnFc:R" класса С(,) имеет
ранг k в точке f'=0. Но феС(1>(С), поэтому матрица Якоби
(П;ф4(4)) (i=l, 2..п; j—l, 2, ..., k) имеет ранг k в целой окре-
стности точки f=0, которую без ограничения общности можно
считать совпадающей со множеством GcR*. Доказательство ут-
верждения: 1) => 3) завершено.
Определение. Если множество AfczR" и для точки Хо^М
выполнено одно из трех эквивалентных условий 1), 2) или 3) тео-
ремы о ранее, то, как говорят в дифференциальной геометрии,
множество М является в окрестности точки х0 дифференцируемым
k-мерным многообразием (вложенным в Rn) класса С1 (1^1)-
456
Определение. Множество Afc:Rn называется дифференци-
руемым k-мерным многообразием класса C(Z>, вложенным в Rrt
(k^n), если для любой точки х^М множество М является в ок-
рестности этой точки дифференцируемым k-мерным многообрази-
ем класса C(Z).
Определение. Компактное множество КсП№ с границей
дК называется простым относительно оси Oz (оси Оу или оси
Ох), если любая прямая, параллельная оси Oz (оси Оу или оси
Ох) и проходящая через (любую) точку К, пересекает границу дК
только в двух точках. Рассмотрим компактный цилиндроид
4c:R3, простой относительно оси Oz, так что
А={(х, у, z)<=R3|
Zi(х, y)<z<z2(x, у), (х, у)<=КхУ},
О
где Кху — односвязная, измеримая по Жордану область в R* у
и Кху есть компакт с ориентированным краем дКху, являющимся
носителем кусочно-гладкого цикла Жордана (ориентированного с
помощью внутренней нормали), причем
г^С(Кху)ЛС^(Кху) (Г=1, 2).
Положим
Г«==={(ж, у, z)^.dA\z=Zi(x, у), (х, у)<=К*у} (i=l, 2),
тогда Г/ есть носитель гладкого 2-пути
ffi'.Kxy-^TiddA, (qn(x, у) =
= (х, у, zt(x, у)), (х, y)^KxyCzRl у 2)
с направленной нормалью
Nl = [Di4)<AD2<pi]=/-^, -7Ч П (i=l, 2),
I ох ду I
так что Nt является внутренней нормалью к ТФ1 (Г1) относительно
области A, a N2 является внешней нормалью к Т?2 (Г2) относи-
тельно области Л. Если
m
дКху = и ?/,
л /=1
где у/ является носителем гладкого 1-пути Жордана
at: [а/, Ь/1 - Y/=а/ ([а/, Ь/]) czdKxy (а/: и
^(Xj(u), у, (и), 0)) 0=1, 2, .... пг),
457
то цилиндрическая поверхность (с образующей, параллельной оси
Oz)
^3i—{(x, у, z)e=dA\zt(x, y)<z<z2(x, у),
(х, у)е=ц} <J=l, 2...m)
-есть носитель гладкого 2-пути
fy:U,={(u, v)\zt(Xj(u), yi(u))<Zv<ZZ2{xj(u), у^и)),
ai<u<bf} -> r3j=^j(Uj) (ф/: (и, v) -> (xt(u), у,(и), v))
£ направленной нормалью
^=[7 М»/Л /•< =
ди ди
i
= x'j(u)
О
j к
/(«) о
О 1
= (₽;<«)» —x'j(u), 0) = у'Ди) • i — *;.(«) • j
ортогональной оси Oz и (в силу ориентации кусочно-гладкого
m
цикла Жордана дКху= U?/) являющейся внешней относительно
О о
области А. Но тогда на границе дА=А\А компакта А мож-
m
но ввести ориентацию, положив дА=\—<pi)U<P2U U Ф/ (при этом
/—1
-дА называется ориентированным кусочно-гладким краем компак-
та А), так что в регулярных точках края дА направленная нор-
маль будет (см. рис. 31) внешней относительно области А.
Аналогичным образом вводятся цилиндроиды В и С, простые
«относительно осей Оу и Ох соответственно, с ориентированными
кусочно-гладкими краями дБ и
дС:В={(х, у, z)\yi(z, x)<y<y2(z, х), (z, x)e/Q
С={(х, у, z)\xi(y, z)<x<x2(y, z),
(у, z)eKyZ}.
Очевидно, компактный цилиндроид
KcR3, для которого
К={(х, у, z)\0<z<z(x, у),
0<у<у(х), 0<х<1},
будет простым относительно каж-
дой из осей Oz, Оу и Ох.
Замечание 1. Если KczR3 —
компактный цилиндроид, простой,
458
относительно одной из осей Oz, Оу или Ох, то любая регу-
лярная точка Mq&)K обладает свойствами 1), 2) и 3) теоремы о
ранге.
Замечание 2. Компактный цилиндроид KcR3 (вида А,
В или С), простой относительно одной из координатных осей,
имеет («кусочно-гладкий») край дК, обладающий двумя свойства-
ми: 1) компактное множество дКс^-К является границей цилин-
дроида К в R3; 2) для любой регулярной точки М0^дК существу-
ет окрестность V(7K0)c:R3 такая, что множество Г—У(Л10)П^К
является носителем некоторого гладкого 2-пути Жордана <р в R3,
причем
V(Af0)\r=V<i)UV(2)cR3>
где открытые множества V<1> и V(2) связны в R3 и У<1>сК,
У(2)сСК.
Замечание 3. Свойство 2) из замечания 2 означает, что в
окрестности V(M0) регулярной точки Л1о края дК точки цилиндро-
ида К лежат по «одну сторону» от края дК, а точки дополнения
СК лежат по «другую сторону» от края дК, что и дает возмож-
ность ориентировать край дК в окрестности V(M0) регулярной
точки с помощью «внешней» (т. е. входящей в окрестность
И^сзСТС) нормали. (В самом деле, Г=У(М0)(\дК есть носитель
как 2-пути <р, так и 2-пути (—ф), причем из двух направленных
нормалей
Мф=[О1фДВ2ф] и N_,=—N,
одна входит в окрестность У(2)сСК, т. е. является внешней отно-
сительно К.)
Теорема Гаусса — Остроградского в R3 (для ци-
линдроида, простого относительно каждой из осей координат).
Пусть KczR3 — компактный цилиндроид, простой относительно
каждой из осей координат, с «кусочно-гладким) краем дК, ориен-
тированным с помощью внешней (относительно области К) нор-
мали N. Если
9, Q,ReC(K);^SP, Re=C(K)/\B(k)
дх ду dz
то имеет место формула Гаусса — Остроградского
JJ SPdy /\dz + Qdz/\dx + Rdx /\dy =
OK
(^ • cos(N, x)+Q • cos(N, y)+R cos(N, z))dS~
= (3-2)
459
Доказательство. 1) Рассмотрим цилиндроид K=4c:R3,
простой относительно оси Oz с ориентированным кусочно-гладким
краем
дА= (—<pi) Uq>2U U Ф/,
/=1
ГДе о
А={(х, у, z) |zi(x, у) <г<гг(х, у), (х, y)^KXy<=R2Xt у}
(г^С(Кху)ЛС^(кХ!1)) (i=l,2),
причем Кху — (плоский) компакт с ориентированным кусочно-
гладким краем
i=l
(где
(Xi I (Oi, bl) -► 'fi—(Xi((Qi, bi))c.dK.xy\
(ai: « -> (Xi(u), yi(u), 0)), <pi: kxy~+S\
(x = u, y^*v, z = zt(u, v): -^x> = 1\
I d(u, v) I
<р2:Кху->Га(х = и, y=~v, z = z2(u, v)\
= 1), : Ut -> Г„ (x = x,(u),
y = yi(u), z-=v; y)- = 0) (i=l, 2,..., m),
o(u, v)
при ЭТОМ
Rf=C(A), -R eC(A)/\B(A),
dz
но тогда, поскольку множество А измеримо по Жордану, то ;
И Rdx/\dy=z f Rdx/\d’j+ Г Rdx/\dy +
дЛ —cpi
m
+ 2 J Rdx/\dy=—J J R(u, v, zt(u, »)) • 1 dudv -f-
i=l Ф i Kxy
+ R(u, v-, z2(u, v))-dudv +
^xy
+ 2 И R(xt(u)> Vi(u). v) • Odudv =
iZi^i
= JJ (R(x, у, гг(х, y)) — R(x, y, z^x, y))dxdy,
^jr-y
460
т. е.
Д Rdx л dy=^ (R(x, у, z2(x, у))—R(x, у, z^x, y)))dx dy. (3.3)
дА К ху
д ° ° д
Далее, в силу условия — 2?еС(Л)ДВ(Л) функция — R не опре-
dz dz
делена на дА,. однако |ЗЛ|3 = 0 и поэтому (в силу теоремы 9
из ч. V, гл. 2, § 1), доопределяя — R нулем на границе дА,
dz
d ° д
имеем -ReC(A)f\B(A), так что функция —R интегрируема
по Риману в цилиндроиде А. Применяя теорему Фубини для
цилиндроида (из ч. V, гл. 2, § 2), имеем
ф ~Rdxdydz=
с „ [гг(х, у) \
= J J I f — R(x, у, z) dz\dxdy.
кху ViU. V) 2 /
Заметим, что для любой фиксированной точки (х, у)^Кху имеем
^-R &C((zt(x, у)), zs(x, t/)))AB((z/x, у), гл(х,у)]),
так что — R(x, у, z) как функция z кусочно-непрерывная на от-
OZ
резке [zt(x, у), гг(х, у)] и поэтому функция R^Cz([zi(x, у),
z%(x, I/)]) как функция z является первообразной для кусочно-не-
прерывной функции у’ и в силу формулы Ньютона —
dz
Лейбница (для кусочно-непрерывных функций) из [1], ч. II, гл. 2,
§ 6 v(x, у)<=Кху имеем равенство
*i(*. 9)
f ~ Я(х, У, z)dz=R(x, у, z2(x, y))—R(x, у, гг(х, у)),
J 0Z
Z1(X, у)
т. е.
JJJ£ R(x> У> zjdxdydz = JJ (R(x, у, zt(x, у)) —
А ^ху
— R(x, у, гг(х, y)))dxdy. (3.4)
Сравнивая (3.2) и (3.3), получаем формулу Гаусса — Остроград-
ского
461
JJRdx/\dy — JJJ£Rdx /\dy Д dz.
дА А
2) Вели К=В есть цилиндроид, простой относительно оси Оу и
QsC(B); А^еС(В°)дад,
ду
то аналогичным образом получаем формулу Гаусса — Остроград-
ского
JjQdzAdx = JJj£(7dx Д dy /\dz.
дВ BJ
3) Если К—С есть цилиндроид, простой относительно оси
Ох и & е= С(Су, £ З3 <= С(С) /\ В(С),
то имеем формулу Гаусса — Остроградского
5Мх]Д dy Д dz.
дС С
4) Пусть, наконец, KcR3 есть цилиндроид, простой относи-
тельно каждой из осей координат, тогда из формул Гаусса — Ос-
троградского, полученных в п. п. 1)—3), сложением получаем
окончательную формулу Гаусса — Остроградского (3.2).
т
Замечание. Пусть K==U^,<zR3 — компактное множество
с границей дК, где KiftKj—0 v и Ki (7=1, 2.....т) есть ком-
пактный цилиндроид простой относительно каждой из осей коорди-
нат, с кусочно-гладким краем дК(-=Г4_)Тй ориентированным с по-
мощью внешней (относительно Ki) нормально, причем TiCzdK и
цс:К. Пусть 53, Q, R е= С(К) и
- - Q, ~ R С(К) К В(К).
дх ду dz *
def fn
Для компакта KcR3 введем кусочно-гладкий край <5K=Up
ориентированный (в регулярных точках Г,) с помощью внешней
(относительно К) нормали к Г; (i=l, 2,..., т). Тогда имеет место
формула Гаусса—Остроградского (3.2) или, полагая
2
ш = dy д dz + Qdz /\ dx Rdx /\ dy,
462
d<u = (7-5® + /-<?+ dx /\dy/\dz,
\ox dy dz j
имеем
®=fffda. (3.5)
дК К
В самом деле, без ограничения общности, будем считать, что
К=К11Ж2, где при i=l, 2 Ki есть компактный цилиндроид, про-
стой относительно оси Oz и K1f]T<2=0» LHV (_|Г(34), где
сравните (п. 1 из доказательства теоремы Гаусса — Остроградско-
го для цилиндроида) Г(‘> — ориентировано направленной нор-
малью (—N(/> ) — внешней относительно области К/, Г(2° ориен-
тировано направленной нормалью N(’>, внешней относительно
области Ki, и ;— кусочно-гладкая цилиндрическая поверх-
ность с образующей, параллельной оси Oz и ориентированной (на
регулярных кусках) направленной нормалью N30 — внешней от-
носительно Kt, т. е. ортогональной оси Oz (lcos(N^, z)=0)
'(см. рис. 32). Пусть R^C(K) и
л о о
^-ЯеС(К)ДВ(К).
dz
Исходя из рис. 32, имеем
ЭТ<=Г1иГ2, дК«=Гги^, П=
463
= Г<‘> и (фЧП2») и г<*> с дК,
Г2 = Пр и (ф'ф) иф" с дК,
у^фПфс^ПА.
Отметим, что кусок ориентирован нормалью (внешней
относительно Ki и К), кусок Г^’ХГг2’ ориентирован нормалью
О о
[—N^1*) (внешней относительно Ki и К), цилиндрический кусок
О
ф ориентирован нормалью N(|> (внешней относительно Ki и
К). Тем самым указана ориентация куска (в регулярных
точках) с помощью нормали N, внешней относительно К. Анало-
гично кусок Г[2) ориентирован нормалью (—N(2)) (внешней от-
носительно К.2 и К), кусок ф\ф ориентирован нормалью
О о
N!,2) (внешней относительно К2 и К) и цилиндрический кусок
Г<2> ориентирован нормалью NSp (внешней относительно Кг и
К). Тем самым задана ориентация куска Г2^гдК, а вместе с тем
задана и ориентация края дК (с помощью нормали N, внешней
относительно К)- Далее, кусок У1=ф Г1ф ориенти-
рован нормалью (—) (внешней относительно Ki), а 42—
=ф Пф С-дКгПК ориентирован нормалью Ьф (внешней от-
носительно К2)> причем N<2> = N<‘> . Но тогда yi и у2 будут носи-
телями двух противоположно ориентированных 2-путей, так что
можно писать 72=—"fi- Итак, ^Ai=iTiUYi и дК2—ТУД—Yi). По-
скольку
Л о О
d-R^C(K)
dz
ТО
Лоо
£ R е ОД») Д В(Кг) а = 1,2)
dz
и поэтому применима доказанная выше теорема Гаусса — Остро-
градского для цилиндроидов, в силу которой имеем при t=l, 2
равенства
j J j £ Rdx Д dy f\dz— f j Rdx f\dy =
464
= JjjRdxA dy + Jf R dx/\dy.
ri Yi
Поскольку у2=—yj, to
J J R dx д dy 4- J J Rdx Д dy = 0,
к
и поэтому, складывая наши равенства при t=l, 2, имеем (3.5).
Пример. Компактный шар (эллипсоид) из R3 допускает
8
представление вида K—UKi, где компактное множество Ki (ок-
1=1
таит шара или эллипсоида) будет простым относительно каждой
из осей координат. Но тогда для шара и эллипсоида имеет место
формула Гауоса — Остроградского (3.5).
Определение. Компактное множество KcR3 называется
компактом с (гладким) краем дК класса <?<*), если оно обладает
следующими свойствами-. 1) компактное множество дК является
границей компакта К в R3; 2) для любой точки М0^дК сущест-
вует окрестность V(M0)czR3 такая, что множество Г=дК(\У(М0)
является носителем некоторого гладкого (класса О1)) 2-пути Жор-
дана <р в R3, причем У('ЛТо)\Г=У’(1>и^(2)/ открытые множества
и У<2> связны в R3 и VWcK, WcCK.
Замечание 1. В силу теоремы о ранге край дК, очевидно,
является 2-мерным компактным многообразием класса С(1> в R3.
Замечание 2. Если компакт KczR3 связен, то его край дК
может и не быть связным в R3. Например, шаровой слой
K={xeR3|0<r<Ux|I3<^}
имеет край
<5K=SBUSr,
где SB и Sr 2-мерные сферы радиуса R и г соответственно.
Замечание 3., Условие 2) определения означает, что в
окрестности любой точки края дК точки К-лежат по одну сторону
края дК, а точки СК лежат по другую сторону края дК.
Замечание 4 (об ориентации края дК компакта К). В силу
условия 2) для любой точки Мй^дК существуют окрестность
и гладкий 2-путь Жордана
Ф: f/cR3, „ - Г=ф(1/)=5КПV(M0)
такой, что отображение ф биективно, <peCW(U) и матрица Яко-
би Вф имеет ранг 2. Но тогда касательные вектора
{Эф Эф 1
ди ’ ди I
ЗО—Л. И Камынин
465
не коллинеарны и определяют ориентацию касательной плоскости
Тм (Г), направленная нормаль к которой имеет вид
Кф=Г^д^1.
ди ди
Заметим, что множество Г является носителем как для 2-пути <рк
так и для противоположного 2-пути (—<р) с направленной нор-
малью N-„=—N„. В силу условия 2) У(Л10)\Г=V(1>U^(2)- Будем
считать, что Г в окрестности V(Af0) ориентирован выбором того
из двух противоположных 2-путей, для которого направленная
нормаль входит в окрестность V<2)czCK, т. е. является внешней
для К. Край дК, снабженный указанной ориентацией (1с помощью
внешней относительно К нормали), будем называть ориентиро-
ванным краем компакта К- Если, например, в окрестности V(M0)>
точки ЛГое<?К r=<5Kf]l/('Afo) является графиком функции z=s.
=z(x, у), причем
K(]V(M0)=={(x, у, z)\z<z(x, у), (х, y)(=U},
то нужно выбрать 2-путь <р: (х, у) (х, у, z(x, у)), направленная
нормаль которого
dz dz j
дх ду
будет внешней для К. Если же 1
K(\V(M0)={(x, у, z)\z>z(x, у), (х, y)s=U},
то нужно выбрать 2-путь (—<р), направленная нормаль которого
= / __j\
I дх * ду ' I
будет внешней для К.
Теорема Гаусса — Остро гр а д с ко го (для компакта
с гладким краем в R3). Пусть KcR3 — компакт с гладким краем
дК, ориентированным с помощью внешней (относительно К)
нормали и .
2
(ii=gidy/\dz+Qdz/\dx+Rdx/\dy
— 2-форма класса С(К)/\С№(К), причем
D&>, DiQ, D,R<=C(K)AB(K) (i==l, 2, 3).
Тогда имеет место формула Гаусса — Остроградского (3.5)-
(Доказательство теоремы будет проведено в более общем случае
в § 7.)
466
§ 4. Формула Стокса в R3
Пусть
<p:Kc:R2>0 »T=q>(K)c:R3 2
(где v)==(x(u, v), у(и, v), z(u, v))) есть гомеоморфизм ком-
пакта К на Г, причем сужение отображения <р на
есть гладкий 2-путь в R3 класса С(1>.
о о
Замечание 1. Гладкий 2-путь <р: К-* r=q>(7QczR3 являет-
ся 2-мерным дифференцируемым многообразием в R3, поэтому в-
силу свойства 3) теоремы о ранге (из ч. VI, гл. 2, § 3) для любой
точки Л1о=ф0то)еГ, где существуют окрестности U (т0) с
czKczR^ г и VfAfoJcR3 такие, что сужение ср: U(m0)-+W(M0)=-
=У(Мо)(\Г также является гладким 2-путем класса С(’> и поэто-
му открытое множество G =i(J V(Afo)^>r обладает свойством
С(]Г=Г. Пусть К — односвязная, измеримая по Жордану об-
ласть в R2. „ , а К есть компакт в R2 „ с краем дК, являющимся
кусочно-гладким циклом Жордана, ориентированным с помощью
внутренней нормали. Будем считать, что частные производные
А А О о
Г<Р, ±че=С(К)ЛВ(К)
равномерно непрерывны в области К. Зафиксируем какую-нибудь,
граничную точку т^дК, тогда в силу равномерной непрерывно-
сти частных производных —, — в К¥е>0Я8>0 такое,.
ди ди
что для любых точек mi, /п2е1Щ2) (Тпо)ПК имеют место оценка
^.(/n )_|5L(OT ) <е
ди ди
2
— (7ПХ) — — (ТП2) < е
до ' 11 до ' 2 ’
я
т. е. выполнен критерий Коши существования пределов:
1- д , xdef д . .
hm — ф(т)=—ф(/п0),
т—Ои ди
тек
lim — ф(ш)= — <p(m0) V т0 е дК.
до до
тек
30*
467
Таким образом, равномерно непрерывные на К. производные
т-5- и — можно доопределить (по непрерывности) на всем
<014 OV
компакте К- Будем считать при этом, что ранг матрицы Якоби
v)) (i=l, 2, 3; j—’l, 2) равен2 V (и, v)<=K. Скажем, что
отображение
<р: KczRu, 0->Г = <р(ЙГ) с= R3x,v,z
определяет гладкий (класса С*1)) кусок (поверхности) Г, причем
def_______________ о __
множество дГ = Г\Г ^где Г=ц>(К), Г=<р(К)) будем называть
краем гладкого куса Г. Поскольку дК — ориентированный (с по-
мощью внутренней нормали) кусочно-гладкий (класса С(1>) край
компакта К в R2 „, то в силу гомеоморфности отображения <р
имеем <ЗГ=ф(дК), причем тогда дГ — есть кусочно-гладкий клас-
са цикл Жордана в R3iS)2 с ориентацией, индуцированной
[(гомеоморфизмом <р) ориентацией края дК.
Итак, рассмотрим гладкий кусок Г в R3. Тогда для любой точ-
ки ф(м, а) едГ существует направленная нормаль
К_Г21Л^1 =
ди ди I
i j к
дх ду dz
«МММ
ди ди ди
дх ду dz
«мм»
ди dv ди
причем тройка |n, ориентирована, как и стандартный
базис {i, j, к}, в R3. Рассмотрим регулярные точки ф(«, о)едГ и
где 'дК — ориентированный край компакта К в плос-
кости R2 . Рассмотрим в точке (и, v)&)K направленный каса-
О
тельный вектор т и внутреннюю (по отношению к К) нормаль
п~=—[т]. Тогда в силу выбора ориентации края д% имеем
{т, п~}~{еь е2}, где {еь е2) — стандартный базис на плоскости
R« Заметим, что для любого вектора а, «внутреннего» по отно-
шению к области К, будем иметь {т, а}~{т, п_}~{еь е2}. Но для
линейного отображения D<p(u, и) : R2—► Т,(И1„)(Г) имеем
Оф(«, i>)ex = .
ои
D<p(u. »)е,= 2*^1,
ди
468
причем линейное касательное пространство Тф(и,С)(Г) ориентиро-
вано с помощью пары касательных векторов
.(см. рис. 33). Покажем, что вектор t=D<p(n, v)t является направ-
ленным касательным вектором к краю дГ куска Г. В самом деле,
край дК., являющийся кусочно-гладким циклом Жордана в плос-
кости R2 j,, представим гладким 1-путем («(о), о (о)) в ок-
рестности регулярной точки т&)К.. Тогда вектор направленной
касательной к дК в точке т имеет вид
du .du / du du \
т =----e.4------e2= I—, —I-
da da I da da I
Поскольку дГ=ф(дК) также является кусочно-гладким циклом
Жордана в R® , то в окрестности регулярной точки Af=<p(m)e
едГ его параметризация имеет вид
о-* <р(“(о), у(о)) = (x(u(o), v (о)),
У(и(о), 0(c)), z(u(a), о(о)))
и тогда вектор направленной касательной t к краю
^=ф(пг) имеет вид
л. d / . ч . / дх du , дх du ду
da I ди d<s du d<5 du
дГ в точке
du
469
, dy dv dz du . dz dv\
-j------ -- ,, - ------1-----------I '=
dv da du da du da J
.*L (и=ы(о). pe0(a)).
da du da du ' V ’ ' ”
С другой стороны, при отображении D<p(u, v) : R2—*-Тф(и, r)(f)
имеем
D<p(u, o)t=D<p(u, v) -ex + • e2\ ==»
I da d* I
— • D<p(u, t>)ei+ 77- • Dq>(u, t»)e2 =
aa aa
= v-? + tl-? ’-’(«))>
da du da dv
d® d®
где векторы у- =s ф„ и -у- = <pw не коллинеарны, поскольку ранг
матрицы Якоби Dtp (u, v) равен 2. Тогда D<p(u, v)x=t. Рассмот-
рим в регулярной точке т0&)К наряду с касательным вектором
х(т0) вектор внутренней (по отношению к К.) нормали
n"(m0)= —[т(лг0)] =
zz: е1 du еа dv dv_ da
da da
М0==<?(т0)&)Г—<$(дК),
t(M0) = D<f>(u0, v0)x(m0) =
du ~ . dv ~
= — • Фи + -T- <b
d<J da
Тогда имеем
И
b(A40) = Dq>(u0» v0)n-(m0) =
dv . du
= ~T • +V
da da
Поскольку, в силу выбора ориентации края дК.
'{г(т0), п~(т0)} {еь е2},
то видим, что гомоморфизм Dtp (/по) сохраняет ориентацию R2>0 на
касательной плоскости ТФ(|я,) (Г), т. е.
{tfAfo), Ь(ЛГ0)} {фи(/По), Фс(/п0)}.
<70
Пусть гладкая дуга yczK имеет в своем начале т0&)К направ-
ленную касательную, совпадающую с внутренней нормалью
ti-(/no). Поскольку отображение ф есть гомеоморфизм К на Г=
==<p(7Q, то для гладкой дуги ф(^) имеем ф(^)сф('К)=Г, причем
касательный (к дуге <p("f)) вектор b(M0)=D<p(>nft)n-(;no) вточке
M0=itf>(m0)&)Y не коллинеарен вектору 1('Л410)=Оф(т0)т('то).
Заметим, что прямая, коллинеарная касательному (к краю <5Г)
вектору t(Af0) ^D<p(mo)v(/no), делит аффинную касательную плос-
кость Тф(т,) (Г) на две полуплоскости: внутреннюю (по отноше-
нию к Гоф(у)), Т^т.) (Г), содержащую вектор Ь(Мо) =
=Оф(/па)п_(/по), и «внешнюю» Т+(ГОе> (Г). На касательной плоско-
сти T<p(mj .(Г) в точке ЛГ0=ф(7по)едГ выберем вектор v~(M0),
ортогональный касательному (к краю <?Г) вектору t(M0) =
=iD(f(m0)r (т0) и входящий во «внутреннюю» (относительно Г)
полуплоскость T~t (Г). Будем называть вектор v~(M0) внутрен-
ней (относительно Г) нормалью к краю дГ в точке M0=(f(m0)e
едГ. Но тогда по построению имеем {t, Ь}~!{фи, ф»}> т. е.
ft, ?~}~{фи, фр} и тогда (см. рис. 33)
{N, t, j, k|.
I ОЦ OV I
Итак, гладкий кусок Г ориентирован с помощью направленной
нормали N, а край дК индуцирует на дГ ориентацию такую, что
тройка {N, t, v} ориентирована так же, как и стандартный базис
{i, j, к} в R3 у г • Другими словами, обход края <5Г проводится так,
чтобы кусок Г оставался слева, считая, что голова наблюдателя
направлена по нормали N к куску Г.
Определение. Пусть теперь для связного множества Г в
m ____________
R3 имеем Г» U Г/, где Г, есть гладкий кусок и Г,ПГ/=0 V i=£j.
г=1
Тогда Г называется кусочно-гладкой поверхностью в R3.
____________________________________________________ m __
Определение. Кусочно-гладкая поверхность Г= U Г,- в
i=l
^называется ориентированной, если каждый из ее гладких кусков
Г/ ориентирован и возникающие при этом направления обхода
края dYi и dYj согласованы в том смысле, что вдоль каждой дуги,
где два таких края совпадают, направления их обхода противо-
m
положны, т. е. dY= ’ZdYi.
г—1
471
Замечание. Ориентированная кусочно-гладкая поверхность.
. т____ т
Г= U Г,- называется замкнутой, если <ЭГ= S дГ,-=0.
i=l
Пример. Двумерная сфера Г=Г1иГ2 в R3 является замкну,
той ориентированной поверхностью (см. рис. 34)
5г=аг! +аг2=т+ (-7) =о.
Пример. Лист Мебиуса (см. рис. 35) — неориентируемая
поверхность (подробнее см. [7, с. 158—160]).
Теорема Стокса в R3 (для ориентированного гладкого
куска с краем). Пусть Г — ориентированный гладкий (класса
СО)) кусок в R3 с краем дГ и с параметризацией <р: KczR«, 0 —»Т=
==xp(K)c:R3 у 2 (где tp(u, v) = (x(u, v), у(и, v), z(u, v)), cp<=
О
^C^(K)), причем К — односвязная область в а К есть
компакт в R3 0 с ориентированным краем дК, являющимся ку-
сочно-гладким (класса СО)) циклом Жордана. Пусть в области
GcR3 у х задана 1-форма <a=&dx+Qdy+Rdz класса C<^(G),
причем ГсС. Тогда имеет место формула Стокса в R3:
fj = У 0.1>
р дГ
где
da> = ("Г “ Т") A dz +
ду dz J
\dz дх ) \дх {ду j
или
Рис. 34
472
ff M
V \ dy dz )
dy /\dz + (d^. — ^\dz Adx +
\ dz dx I
+ (y-~y ) dx/\ dy^ f f * cos(N, x) +
\ dy dy J J J [ dy dz J
+ (?-?)• COS(N> У) + (у—^)-C0S(N, z)]dS=
У dz dx ) \dx dy /
= J SPdx+Q.dy+Rdzss J (3s-cos (t, x) +
дГ дГ
+ Q • cos (t, y) + R • cos (t, z))d»,
где . .
№^a^L]_
I du duJ
направленная нормаль к куску Г, a t — направленная касательная
к краю дГ.
Доказательство. -Рассмотрим параметризацию (гладко-
го) куска Г <p:Kc:Ru,o—*r=<pCA)c:GcRx,I,.z, где (peCWflQ,.
<Эф дФ
т. е. векторы — и — равномерно непрерывны в односвязной.
области К и продолжены по непрерывности на край дК. Имеем
Г=<р(К), <?r=qp(d./Q, где дГ есть ориентированный край куска Г,
с ориентацией, индуцированной ориентацией края дК компакта
К. (в плоскости R2,o)- Поскольку a^Cd)(G) и <peC(1>(K), то в
силу замечания к теореме (о перестановочности операций <р* и d)
из ч. VI, гл. 2, § 1 имеем равенство
1 1
<р* (d®) =й(ф*®).
Но тогда •
f J do> — jy ф♦(dф)= JJ d(ф*®).
г к к
Применяя формулу Грина (см. 2-ю теорему Грина из ч. IV, гл. 2Г
§ 2) к 2-форме d(cp*<£>) и к плоскому компакту KczR® „ с ориенти-
рованным краем дК, получаем
ffd(ф*ф)=f ф*ш. (4.2)
К дК
47$
Заметим, что край дГ=<р(дК) куска Г есть ориентированный ку-
сочно-гладкий 1-путь Жордана в R3t2/t, поэтому
1 _ 1
ф*<о — у <о.
дК оГ
Итак, формула Стокса (4.1) доказана.
Замечание. Формула Стокса (4.1) в R3 остается верной и
для любой ориентированной кусочно-гладкой (класса С<’>) поверх-
ности TcR3 с ориентированным кусочно-гладким (класса С<’>)
краем 5Г.
В самом деле, рассмотрим, например, кусочно-гладкую ориенти-
рованную поверхность Г—ПиГг с кусочно-гладким ориентирован-
ным краем дГ='дГ1+дГ2, так что Г1Г|Г2—0 и Г,- является (при
i— 1, 2) ориентированным гладким куском с краем дГи=7г1)7«
к(/—1, 2). Ориентация краев дГ1 и дГ2 согласована по правилу
у12=>—^21, где 712 и 721 — «внутренние» (для Г) дуги краев <?Г( и
«Иг, проходимые в противоположных направлениях (см. рис. 34).
Но тогда J?r=71U72 и формула Стокса справедлива для каждого
«з кусков Г! и Гг, что дает равенства
£f d® = И di + £J da = j ©+
г г» г, -г,
11111
+ у «+у <°=у “»
Y* Y1 Т« дг
«(поскольку 712=—721 влечет равенство
J ш-J-у <о=0).
1
Замечание 2. Условие
eC^(G) (из доказанной выше тео-
ремы Стокса в R3), где область
GcR3 такова, что ГсО, можно за-
менить (сравните 2-ую основную
теорему Грина в R2 из ч. VI, гл. 1»
§ 2) на более слабые условия глад-
кости
©е=С(Г)/\C^(G), СПГ=Г (4.3)
(где область GcR3 взята, напри-
мер, из замечания 1, так, что Gr>r,
G[~ir=r)_L т. е. в частности,
Q, ЛеС(Г) и
474
D/38 , DiQ, О(/?е=С(Г)ЛВ(Г) _(i=l, 2, 3). .(4-4)
В самом деле, при выполнении (4.3) V (и, v) eKczRZ и имеем
ф*ш= (д5 о <р • — 4* (? ° ф . + о ф. — \ du 4-
Y ди ди ди /
+ f^o ф . — 4- Q о фЛ + fl о q .<>i\dV(= С(К) (4.5)
I dv dv dv I
(где векторы 7 ф, - ф£ С(К) равномерно непрерывны на
du dv
1
компактном множестве К cr R2 с), так что 1-форма ф*ш(и, v)
равномерно непрерывна на К <=. R2 я. Далее, V(x, у, г)ЕГ
имеем (и, v) = ф-1(х, у, z)^K, причем поскольку <р^С<1ЦК),
то в силу 2-й теоремы о перестановочности операций ф* и d
(из ч. VI, гл. 2, § 1) имеем равенство
1 1 о
ф*(4/ш)(и, V) — £?ф*<в(и, v) V (и, о) s К.
Но
p)=((DxQ- D#) о ф(и, v). +
\ д(и, и)
4- (DaZ? - D30 ° Ф(«, v). +
д(и, V)
4- (D# — DtR) о ф (и, v)-~^-х) Л du Ndv<= C(K)/\B(K) (4.6)
d(u, v) ]
(поскольку ф, ~ <р€-С(К)/\В(К) в силу теоремы Вейерштрас-
ди dv
са об ограниченности функций, непрерывных на компактном
множестве).
В силу условий (4.5), (4.6) к компакту KczR2 v с ориентиро-
ванным кусочно-гладким (класса С<’>) краем дК применима 2-я
основная теорема Грина (из ч. VI, гл. 2, § 2), дающая формулу
Грина (4.2), что и завершает доказательство формулы Стокса
;(4.1) в R3 в предположениях (4.3), (4.4).
§ 5. Интегральные формулы векторного анализа в R3
Рассмотрим евклидово пространство R3>y г с каноническим ба-
зисом {i, j, к}, которому соответствует сопряженный базис {dx, dy,
12 3
dz}. Рассмотрим дифференциальные формы w, и и и в R3 .
475
1
1) Пусть 1-форма а=3£> dx-i-Qdy-\-Rdz^.!£ (R3, R1) определена
на открытом множестве QcR3. Тогда для любого вектора h=
имеем представление
<oh=53 -ht-^Q-^-^R-h^ (A, h),
где A=5s-i+Q-j+7?-k — вектор из R3. Таким образом, значения
1-формы <о, рассматриваемой в евклидовом пространстве R3, реа-
лизуются как скалярное произведение вектора А=5Э -i-|-Q-j-|-
+7?-k на любой вектор h. Но тогда дифференциальной 1-форме
d) = SRdx-[-Qdy-RRdz можно поставить в соответствие векторное
поле A=5a-i4-Q-j+/?-k и, в частности, dx~i, dy~\, dz~k. Итак»
= (А= SR -i-j-Q j+•/? k),
обратно векторному полю A=$M-|-Q j-|-/?-k соответствует 1-фор-
ма <i>K = SRdx-\-Qdy+Rdz. Поскольку при этом юд11= (A, h), то
это соответствие инвариантно относительно ортогональных преоб-
разований в R3iVi2.
2
2) Рассмотрим 2-форму <a—SRdy/\dz-\-Q,dz/\dx+Rdx/\dy^
e5?(R3XR3, R1). Тогда для любой упорядоченной пары векторов
{В, С} из R3 иммеем представление
2
<о{В, С) = SRdy Д dz{B, С} + Qdz Д dx{B, С} +
+ Rdx /\dy{B, С} = dx/\dy /\dz{A, В, C} =
5s
= (A, [ВДС]) = (А, B, C) =
Bi
Ci
Q R
Rs Rs
C2 C3
2
где т. e. значение 2-формы co на любой паре
векторов (В, С} есть смешанное произведение тройки векторов
{А, В, С}, что дает соответствие
2
(© = SRdy/\dz+Qdz/\dx+Rdx/\dy) ~
~ (A=5a-i+Q-j+R-k)
и, в частности,
dyAdz~[jAk]=i,
dz/\dx
dxAdt/~[iAj]=k.
Обратно векторному полю А=3Э-i-f-Q-j + R-k с помощью соответ-
ствий
476
i=[j/\k]~dy/\dz, j=[k/\i]~ dz/\dx,
k=[iAj]~dxAdy
сопоставляется 2-форма
2
co A 3= &dy /\dz+Qdz/\dx-\-Rdx/\dy,
значение которой
2
coA{B, C}=dx/\dy/\dz{K, В, C}=(A, [ВДС]),
на любой упорядоченной паре векторов {В, С} равно смешанному
произведению тройки векторов {А, В, С}. Но тогда соответствие
А~соа инвариантно относительно ортогональных преобразований
в Rx,V.z-
3) Рассмотрим 3-форму
з
a=fdx/\dy/\dz^Z (R3XR3XR3, R1).
Тогда для любой упорядоченной тройки векторов {А, В, С} из R3
имеем представление
з
<в{А, В, C}=jdx/\dy/\dz{k, В, С}=
=f-(А, [ВДС]) =f-(A, В, С),
з
т. е. значение 3-формы со на любой упорядоченной тройке векторов
из R3 есть смешанное произведение этих векторов, умноженное
на скалярную функцию f, что дает соответствие 3-формы и ска-
3 3
лярного поля со и обратно af=fdx/\dy/\dz. Поскольку,
<о/{А, В, C}=f-(A, В, С), то это соответствие инвариантно относи-
тельно ортогональных преобразований в R3 у 2.
С помощью установленных соответствий между дифференциаль-
ными формами и векторными (скалярными) полями в R3 y z мож-
но ввести важные для математической физики понятия градиента,
дивергенции и ротора.
1) Пусть QcR3 — открытое множество, на котором задана
числовая функция (скалярное поле) f:£2c:R3—►R1, причем fe
еСО>(й), тогда f(x, у, z)^co(x, у, z) есть 0-форма класса C(1)(Q).
Рассмотрим внешний дифференциал (кограницу) этой 0-формы,
т. е. 1-форму
<o=d/(x, у, z) = ^-f'dx^-^-f • dy + ^-f • dz,
дх ду dz
тогда в силу соответствия dx~i, dy~j, dz~k имеем
477
a a a def
ox oy dz
Итак, градиент grad f есть векторное поле, такое, что gradf~df=5
sd)gratl f. Введем символический вектор (оператор) Гамильтона
д . , д . . д .
V = — -Я-------jH------- к.
v дх ду dz
Тогда VfeC(1)(Q) (QcR3) имеем gradf=Vf. Вспоминая теорему
о производной сложной функции, видим, что для любого вектора
l=/ji-|-Z2j-j-/3k из R3 имеем
=(grad f, = 1),
<71
что дает инвариантное (относительно ортогональных преобразова-
ний в R3.), определение градиента функции
2) Рассмотрим векторное поле A=Pi+Qj4-Rk, определенное
на открытом множестве QeR3, класса С(1>(й). Тогда в силу соот-
ветствий
i=[jAk]~d//Adz,
j=[k/\i]~dz/\dx, к==[!АЛ~^*ЛЙ
имеем
2
А<~йа =Pdy/\dz-\-Q,dz/\dx-\-Rdx/\dy.
Кограница
d»k=№ + d£ + d£\dxhdyhdz
\ох ду dz )
является 3-формой, которой соответствует скалярное поле (div А),
называемое дивергенцией векторного поля А, так что имеем
2 3
(d<BA = wdivA = div Adx Д dy /\ dz =
^- + d/+^\dxMy^dz
dx dy dz j
(dP , dQ , dR def \
dx dy dz; J
если A = Pi + Qi + Rk. Итак,
2 2 3
(A ~ g>a) => (div A duA == wdivA).
Если воспользоваться символом Гамильтона v, то имеем
478
(Л = Pi 4- Qj 4 Rk) => (div A =
==^+r’ + T' = (v’ A))-
dx dy dz
3) Пусть векторное поле A=Pi4Qj4Pk определено на откры-
том множестве QcR3 и AeC<1)(Q). Тогда в силу соответствий
i~dx, j~dy, k~dz имеем
i
А ~ ®а = Pdx 4 Qdy 4 Rdz.
Кограница
.г (dR dQ\ ... ,
-------------4. \dy A dz +
I dy dz
ая\
dx )
dz A dx 4
dx /\dy,
dy I
являющаяся 2-формой, с помощью соответствий dy/\dz~ir
dzAdx~j, dx/\dy~k может быть сопоставлена с векторным по-
лем (в R3), называемым ротором (векторного поля А)
„t »- (9R
rot А = 1 —
I ду
i j k dy Д dz dz A dx
d_ £ d_ 1 1 A L
— dx dy dz == (0rof A = dx dy
P Q R P Q
dx A dy
d
dz
R
С помощью символа Гамильтона v имеем
def
A = Pi + Qj 4 Pk~rotA = [vA A] =
i j k
a d _d_
dx dy dz
P Q R
Итак,
(A = Pi + Qj + Pk ~ co = Pdx + Qdy 4 Rdz)=^-
1 2
=> (rot A ~ rf(OA = °>rotA),
где rot A — [v Д A[.
Теорем а. Пусть QczR3 — открытое множество. Тогда:
1) если feC<2\(Q), то rot gradf=O • если to
div rot A=0;
470
; 2) если то div grad f=Af, где
Adef <32 , a» , .
dx3 dya dz* 'v v/
оператор Лапласа;
3) если AeC<2)(Q), A=Pi+Qj+Pk и ДА =i APi+AQJ+iAp.k,
то AA=graddivA—rot rot A.
Доказательство. 1) Если feC(2>(Q), то, учитывая, что
1 12
grad f ~ dfsz (ograd f и rot A ~ dwA = “rot a>
имеем
2 i
rot grad f ~ ®rot grad f = <fa>grad f = ddf = 0,
t. e. rot grad f = 0, или иначе
rot grad f = [у A yf] =• [V A V]f =
d
dx
Далее, если AeC<2>(Q), то, учитывая, что
1 12
А~ША, TOt А ~ do>A = Cl) rot А,
имеем
3 2 1
dlV rot А “div rot А d(0 jot А — ddtiJ 0,
т. е. div rot А = 0, или, иначе,
div rot А = (у, rot А) = (у, [уАА]) =
д д d
dx dy dz
= (y, y, A) = d d d = 0.
4.1 W
dx dy dz
P Q R
2) Если feC<2>(2), то учитывая, что
grad f ~ w-rad f = -^-dy A dz. + dz Д dx + dx/\dy,
8 J dx \dy dz
имеем
480
3 2
div grad f ~ e„a,-
+ + d dz_
l^dz2 dy* dz2 I a
з
s= Д/ dx /\ dy /\dz== v>Af,
T. e. div grad f = Af, или, иначе,
div grad f = (у, gradf) = (v> vf) = &f.
3) Проверяется непосредственным подсчетом.
Определение. Рассмотрим векторное поле К—З11 •i4-Q-j+
,-|-R-k класса С(й), заданное на открытом множестве, и кусочно-
гладкий 1-путь Жордана
<р:[а, Ь]—*-Глв=ф([а, b])c:Qa:R3 у z.
Пусть t(x, у, г) — орт направленной касательной к Глв в точке
Тогда работой векторного поля X вдоль 1-пути <р (или
циркуляцией векторного поля X вдоль 1-пути <р) называется ве-
личина
£=J(X, cos (t, х) +
ф ф
1
+ Q- cos (t, у)R • cos(t, z))ds = J®x»
Ф
1
где ах — З* dx+Qdy-j-Rdz ~ X.
Замечание 1. Если 1-форма
i
©х = &dxA-QdyA-R4z~X==gi -i+Q j+R-k
i
точна в области QczR3, то для wx в й существует точная прими-
тивная (—U(x, у, г)), называемая потенциалом векторного поля
X. Тогда х =—dU. Векторное поле Х=—grad U называется в
этом случае потенциальным. Для потенциального поля Х=
«=—grad U работа $ вдоль 1-пути
ф : [а, &] —* Tabg:Qg:R3
(где А=(р(а), В=кр(Ь)) не зависит от 1-пути ф, а зависит лишь от
начала А и конца В этого пути (сравните теорему об интеграле от
точной 1-формы из гл. 1, § 5), так что при Х=—grad U имеем
$= J tx= — J dU = U(A) - U(В).
ф ф
И. Камынин
481
В частности, работа % потенциального поля Х=|—grad U по лю-
бому кусочно-гладкому циклу Жордана <р из Q равна нулю.
Пример. Рассмотрим в R3 г поле ньютоновского притяже-
ния, создаваемое материальной точкой массы т. Пусть масса т
сосредоточена в начале О, а в точке М=<(х, у, г) сосредоточена
единичная масса. Рассмотрим радиус-вектор r=x-i+«/-j-|-zk
длины r=(x2+i/2+z2)1/2. Если X='Sa-i+Q-j + R-k — сила (напря-
жение) поля притяжения, то по закону Ньютона величина силы
притяжения пропорциональна массе т и обратно пропорицональна
квадрату расстояния между точками М и О, причем сила притя-
жения направлена от точки М к точке О. Но тогда, обозначая
гравитационную постоянную через у. имеем
1
X = —у-т-г~2-г/г ~ — у • т-г~3-г ~ о>х =
dx + Qdy + Rdz = — y-m-r~3 (xdx -f- ydy + zdz).
Рассмотрим скалярную функцию U(x, у, z) = -y-m/r (в облас-
ти Q = R8\{(0, 0, 0)}), для которой имеем
— U = у • т • x/r3, -U = y-m- у/г3,
дх ду
— U — у т. • z/r3,
dz f
т. e.
i
dU = у • m • r~3 • (xdx + ydy + zdz) — — u>x.
i
так что 1-форма «>х= — dU точна в й и U(x, у, г) —— у • т/г
есть потенциал поля ньютонова притяжения Х=—у • т- г~3-г в
£2=R»\{(0, 0, 0)}. Но тогда Х = — grad £7=—yU, U=—y-m/r.
Замечание 2. В гл. 1, § 5 было введено понятие замкнутой
I 1
1-формы © класса Сб)(й) в области QczR3 такой, что do>=0,
так что для векторного поля ХеС<1>(й) тогда имеем da>x=
2
= <Brotx =<Х т. е. rotX=0. В § 5 было отмечено, что точная
(в й) 1-форма класса С<!)(й) всегда замкнута. Но тогда, если
векторное поле ХеС(0(й) потенциально, то Х=—grad £7=—yU
1 i
и 1-форма <»х = ©_grady = —dd£7 = 0 — точна, так что
< 1
(rot X) ~ (d<s>x — — ddU = 0) => (rot X ~ da>х = 0) =>
=>(rotX = 0).
Итак, если векторное поле X»—grad £7 потенциально, то rotX=O-
482
Определение. Рассмотрим в области QcR3 векторное поле
-i-f-Q-j + Я-к класса С<’)(й) и гладкий кусок Гей, ориенти-
рованный единичной направленной нормалью No. Тогда потоком
векторного поля X через кусок Г называется величина
Ф= J (X, N0)dS= [ (^ • cos (N0) х) +
г г
• cos(N0, у) + R • cos (No, z))dS =
= f 3Jdy /\dz + Qdz A dx 4- Rdx \dys\ ox.
г г
2
где ©x -X.
Определение. Компактное множество KcR3 называется,
компактом с кусочно-гладким краем дК, если оно обладает (срав-
ните § 3) свойствами:
1) компактное множество дК является границей компакта К
в R3;
2) для любой точки Mq&JR существует окрестность (7(Afo)eRs
такая, что множество dK.(\V(Mq) является связной ориентируемой
(т. е. двусторонней) кусочно-гладкой 2-поверхностью в R3
(см. § 4);
3) для любой регулярной точки М0&)К существует окрестность
У(Мо)сзи(Мо) такая, что множество Г=дКПК(Л1о) есть носитель
гладкого (класса СУ)) 2-пути Жордана ф в R3, причем У(Л40)\Г=
= y(i)(jV(2), 2<Эе открытые множества УО) и У<2> связны eR3 и
V^czK, WcCK.
Кусочно-гладкий край дК компакта К можно ориентировать.
(в регулярных точках) с помощью внешней (относительно К) нор-
мали (сравните § 3). Ориентированный таким образом край дК
будем обозначать через дК.
Вспоминая определения из § 4, рассмотрим кусочно-гладкую
______________________________________ m m
(класса С*1)) двустороннюю 2-поверхность Г='иГ/, Г=иГ/, где
___ /=1 /=1
Г/ — «гладкий кусок» с краем <ЭГ/, являющимся кусочно-гладким
1-путем (циклдм) Жордана, так что |дГ/|2=0, а Г/ — гладкий
'класса С<’> 2-путь Жордана с направленной нормалью N/, опреде-
ляющей ориентацию Г/. Ориентации Г/ при / = 1, 2, ..., m согласо-
— w -
ваны в соответствии с § 4, и тогда Г=11)Г/, причем Г/ОГ/—
/=»
=0у i=£j. На гладком куске Г/ введем компактное множество
2S0/i3={M=f}| (N/(M), k)=0}
31*
483?
и положим Г/, з=Г/\о/,з (аналогично определяются множества
<fi,y=ci,2 и Г/,/=|Г/\о/,;• при i=l,2). Считая, что
Д'3 у г ориентировано каноническим ортонормированным базисом
{1, j, к), введем оператор р, проектирования на координатную
плоскость Ei (где E3—XOY, E2—YOZ, Ei—ZOX), так что
Рз: (х, у, г) —► (х, у, 0)еЕ3 и т. д.
Ниже для краткости изложения будем рассматривать оператор
проектирования р3 покоординатную плоскость Е3. Для компактных
множеств дГ/, о/,зс:Г/ введем на координатной плоскости Е3 ком-
пактные множества у/,з=Рз(^Г/) и т]/,3=Рз(о/,з), тогда, очевидно,
, 1^,312=0. Рассмотрим компактное множество К3=р3(Г)сгЕ3 с
границей дК3сЕ3 и введем компактное множество
F3 — дКа (J U (У/. з U з)*
/=1
Положим Qe = /(3f|C/’3 (так что Q3 открытое на плоскости Еа
множество) и введем цилиндры с образующей, параллельной
оси Oz
у, z)|(x, у, О)е=Г3, —oo<z<4-oo},
и при М'0=(х0, Уо, 0)<=Е3
Рз’1(Ч^)) = К®’ У’ 2)К*> У' °)е У3 (^о)> 121<+°°}.
где У3(7Ио') сгСГз — открытая связная окрестность точки Мо' на
координатной плоскости Е3 (например, открытый круг или брус).
Поскольку_Г компактно в R3, то существует открытый брус 1ъ(а, Ь)
такой, что Гс/3(а, 6].
Определение. Точка М^—(х0, у0, 0)еСГ называется
___________________________________________________ т_
р3-регулярной для кусочно-гладкой 2-поверхности Г=|ЦГ7, если
/=•
существует окрестность V3(M0')czCF3 такая, что цилиндр
Рз* (V3(M0')) пересекает поверхность Г в конечном (возможно ну-
левом) числе 1о связных компонент Ss, s(iV3(M0')), допускающих
представление
; Zk,3(V3(M0'))={(x, у, z)|z=
=zk(x, у), (х, у)<=¥з(Ма')}, (5.1)
где гк^С<У>(У3(М0')). (Число 10 зависит от окрестности V3(MQ')).
Тогда при V36W0')g:Q3 э зсГ/^стГ такое, 4TO%kti(V3(M0'))cz-
с=Г,-(й).з при k=l,...,l0 и при Уз(ЛТо')<=с^зимеем2й,з(^з(Л4э'))=='
=,0(^=0). Очевидно,
рГЧИ3(Л/о)) Л Г=/>Г‘(^з(^о)) п г <= г.
484
Пусть точка M0'<=Q3 р3-регулярна для кусочно-гладкой поверх-
ности Г и 2й,3(У3(Л409)с=Г/(й)с:Г, где r1W=^lw(U) — носитель
гладкого 2-пути Жордана
<p/W:t7cz R2,
имеющего направленную нормаль
~Т~ л —— -
ди ди J
определяющую ориентацию r,w, причем отображение <p/W
осуществляет гомеоморфизм U на Гд*). Заметив, что
2*.з(г,(л/;)) = р3-1(у3(л1;))лгЛМ,
введем сужение оператора р^1 на 2*. з(Р3(^о))
РзЛ : (х> У)~*(х> У> гъ(х> V»
(где zk <= являющемся гомеоморфизмом класса
С<’>, для которого рз, *:(х, у, zh(x,y))-+(x, у, 0)s=(x,y). Тогда
(Л/;, гк(Л/р)) = ф/(й)(и0, v0),
и поскольку отображение <рдь) осуществляет гомеоморфизм
Гд4) на U=Unk), то множесто
^з(«о. »о) = Фд,1) ° ^*(уз(^о)) <= и
есть линейно связная открытая окрестность точки (и0, v0) на
плоскости R2 в, причем, используя коммутативную диаграмму
’«’/
/ vi(k) °p3,k \
. .. о Г3(/И0),
p3,k°viW
видим, что существует диффеоморфизм класса С<1
t=P3,k° ф/(Л):(ы, v) рз, fc(x(w, а), х(и, о),
zA(x(u, v), у(и, v)))=(x(u, v), у(и, v), 0),
Для которого
/(Us(u0, %)) = Л. ^(«(^(Uo. v„))) = й. ,(2,.3(Г,(Л|у)) =
= МММЧ)) = ЧЧ'
причем
485
detD/(«, v)= (u, v) 5^=0 v (u, v) s U3(u0, v0) c. U.
d(u, d)
Рассмотрим гладкие 2-пути Жордана (в R’>y>2) ф/м>:
и3(цй, с,о)“*2й,з(Г8(Л/')) = ф/(4)(?73(иО1 t>0))<=r/w
с направленной нормалью
N = .к,
d(ut v) d(ut и) д(и, и)
« <, д(х, у)
отвечающей ориентации Г,<м и имеющей проекцию --- - на'
o(u, V)
оси Oz и
рл ч «;> - =2». ’(v» W))
с направленной нормалью
имеющей проекцию 1 на оси Oz. Тогда согласно определениям
из ч. VI, гл. 1, § 1 имеем
<Р/ГО~М при detDf= ^->0,
и{ и f V)
так, что
Ф/(б)(^з(мо> уо)) = Рз.л(^з(^о))
и
П«,= ~РЛ при -^-<0,
т. е.
ФЛ*)(^з(«о» t’o))=^37Ife(lZ3(Afo)).
Определение. Кусочно-гладкая (класса С(1) двусторонняя
2-поверхность Г=(иГ/ (где Г = иГ/ и Г;ПГ/=0 i¥=j) называется
/«1 7=1
регулярной относительно оси Oz, если каждая точка Мо'^СР3с^Ез
является р3-регулярной для поверхности Г, причем, выполнены ус-
ловия
|F3|2=0, (5-2)
|p3-Wnr|2=0. (5-3)
Из условия (5.2) имеем (см. доказательство теоремы Фубини ДлЯ
цилиндроидов из ч. V, гл. 2, § 2)
486
|P3“W(V3(A &)|з=о. (5.4)
Из (5.3) в силу определения компактного множества
Г3=<ЗКз11и Сг/.зип/.з),
/=1
где |'Г/,з|2=|<?Г/|2=0, имеем |^Кз|2=||11/.»|2=0> и, наконец, по-
скольку о/, scpF1 (7^9 |"|Г, то из (5.3) имеем
I С/, 3.12=0 (/=1, 2.т). (5.5)
Теперь рассмотрим в R3 z компакт К с кусочно-гладким (клас-
са С<’>) краем дК, ориентированным с помощью внешней (относи-
тельно К.) нормали N. Тогда дК=Г=иГ/ — кусочно-гладкая
т —
(класса С<1> двусторонняя 2-поверхность, причем Г =' U Г/, где
где Т/=<р/({7) ориентирована нормалью
N, = А
' ди /х ди ]’
внешней относительно К, что согласуется со свойством 3) опреде-
ления компакта с краем R3.
Заметим, что в силу_ компактности К. существует открытый
-брус Р(а, Ъ) такой, что Гс/<с/3(а, b)al^a, Ь]. Полагая
^Ci==Pi'(7’k,) ==Р/(Г), О/, |СГ/, Г/, <—‘Г/\о/, i
(i=l, 2, 3; /=1, 2...........tri),
можно ввести на координатной плоскости Ei множество
Л=<ади (и eUn/, д (‘=1, 2, 3),
/=i
рассмотренное ранее, и тогда получаем уточненное
Определение. Точка Л4о'е£2з='КзПСРзс£3 называется
Рз-регулярной для края дК., если существует окрестность
^з(7И09с:£2з такая, что цилиндр p^l(V^(M0')) пересекает поверх-
m
ность Г =i U Г/ в 2/0 связных компонент, допускающих представле-
ние (5.1), где Zk^Cri>(V3(M0')) при k=il, 2, ..., 2/<j и число fo зави-
сит от окрестности Уз(М0'), причем
2а,з(^з(Мо'))с:Г/(й),з=Г/(й)\о/(*),зс:Г/(Ь)с:Г.
Замечание. Если точка ЛГо'е^зсС/^з является рз-регуляр-
«ой относительно края дК, то любая прямая 1(М'), проходящая
487
через точку ЛГ=|(х, у, О)еУз.(Л4о')с:йз параллельно оси Oz, пе-
ресекает край дК. в 21й регулярных точках (х, у, £fc)e
е£к,з(Уз(Мо'))<^дК, где (см. (5.1)) &—Zk(x, у) (fe=l... 210),
причем поскольку КаР(а, Ь), то без ограничения общности можно
считать, что
--ОСХ^азС^С ... <Zt,2k-l<Z^2k<i ... <^2/,<6з<4-О0.
Но в силу свойства 3) (для регулярных точек края) определения
компакта с краем видим, что для регулярных точек (х, у, £*)<=
ед К имеем (^2*-i, ?2fe)c=K, причем [£2*-i, ^2*Jc=/C при k=<l, ...,
и £2*+i)<=CK при k=A, ..., Zq—1.
Рассмотрим цилиндроид (при k=<\, ..., 10)
Ц».«(Р»(ЛГ;)) = (Х, у, Z)|Z24-l(x,
<z2k(x,y), (x,y)eV3[M'^}eK\p^F3), .
имеющий „верхнюю крышку**
т(ц«(^т)-р>;Учл/;))=
= з( V3( Л1')) 4K2k)(Uj(2k)(.u0, и0))агГ/(2й)
и „нижнюю крышку**
To(Uft.3(V«)) esp-Vd =
= з(Рз(Мр)) ES <P/(2fe-i )(^/(2ft-l)(«o» vo)) Г/(2Л-1)
Как было отмечено ранее, направленная нормаль Np-1 к „вер-
3, 2k
хней крышке** является внешней относительно К, как и на-
правленная нормаль являющаяся внешней для К в си-
лу выбора ориентации ГцщС^дК, так что можно написать
т(Щ з( У8(М>))) = %2k. 3 (V3M) cT;(2ft) С дК. (5.6}
Аналогично направленная нормаль к „нижней крышке**
О
будет внутренней для К, т. е. имеет направление противопо-
ложной нормали являющейся внешней для К в силу
выбора ориентации Г/(2fe—i) cz дК, так что можно написать
Уо(И*.з(К8(^о))) = 22»-1.з(К3(Л/о)) <= Гда»-1) = — Гдгл-р. (5.7)
Определение. Компакт /(czR® у г с кусочно гладким
(класса С^), ориентированным с помощью внешней (для К) нор-
мали краем дК. называется регулярным относительно оси О г, если
488
___ m__
край дК=1'=1[)Г1- регулярен относительно оси Oz (так что каж-
i=i
дая точка Mq'^CF3 является р3-регулярной относительно дК и вы-
полнены условия (5.2)—(5.5)).
1-я (предварительная) теорема Гаусса — Ос-
троградского в R3 у г . Пусть компакт KczR3 у г с кусочно-
гладким (класса С^) краем дК, ориентированным с помощью
о
внешней (для К) нормали, регулярен относительно оси Oz и на К
определена функция R<=C(K.), для которой
в ° °
^Rt=C(K)/\B(K).
oz
Тогда имеет место формула Гаусса — Остроградского
J j Rdx Л dy = f f j f Rdx A dy A dz. (5.8>
5k к dz
Доказательство. Поскольку ГсК и ReC(K), то
____________ m
ReC(T), где Г=[иГ/ — кусочно-гладкая (класса Сд)) 2-поверх-
ность в R3 у г , и поэтому существует поверхностный интеграл 2-го
рода
f J Rdx/\ dy = ^^ Rdx Л dy.
5k /=i 7 ,•
Поскольку |дГ/|2=0 и (см. (5.5)) |<j/>3|2=0 (/=1.....m), то
имеем
^Rdxf\dy = ^Rdxf\dy = jj Rdx/\dytj=l,...,m).
Г) *7 "*7,з
Заметим, что йз=КПСГ3 = (J У3(Л40')> где окрестность
Че°«
У3(Мо')аЕз. будем считать измеримой по Жордану на плоскости
Е3 (например, открытым кругом или брусом). Тогда
b)()p^(Q)^ U W,(V3[Bf'o)),
м'ео,
где открытое множество (вообще говоря, не связное)
И7(И3(Л/;)) = р3-1(АВД) п 13(а, Ь)
также измеримо по Жордану (в R3), причем
ИЛэ(Ч^))ЛК = лЦ Щз(Г8(Л10)). (5.9>
48»
Но тогда в силу теоремы (о выделении счетного покрытия) изч. V,
гл. 1, § 3 из открытого, покрытия {VsfAfoJ; М0'еОз} можно выде-
лить счетное открытое покрытие {Vi, 3; i=il, 2, ...} (где открытые
линейно связные множества Vi,3czE3 измеримы по Жордану) та-
кое, что
4-оо 4-°°
аз = U Vi. 3.Ь) п РГ‘(О,)= и Wi, з,
i=l »=I
где открытые множества Wi, з=р.^1(К<-, з) П ^8(Л> Ь) измеримы по
Жордану в R3, причем
Х\р3-*(Л)си
1=1
и в силу (5.9)
‘i
Wil3(]K= U Щ.з(Г1,з); /=1, 2............. (5.10)
*=i
В силу теоремы (о существовании разбиения единицы) ч. III,
гл. 2, § И можно ввести разбиение единицы {еДМ); i=l, 2,...}
класса С(оо) для открытого множества
РъЧЫШЧа, Ь)=Ц° Wi,3t
1=1
подчиненное открытому покрытию {И\3; «=1, 2,...}, для ко-
торого
4-00
2 q(M)= 1 V М €=р3-1(Йз)ПЛ«> Ь) (5.11)
г—1
И supp Ci CZ. Wi, 3 V i.
dR ° °
Доопределим функции RgC(K] и — ^С(К)/\В(К) на мно-
dz
жестве 13(а, Ь), положив
R(M) = О v Ms 13(а, Ь)\К
и
-ЩМ) = О V М е 13(а, Ъ)\К.
dz
Тогда
supp R = supp — — К cz Zs(a, &),.
dz
причем функция —R локально ограничена на брусе Z3(a, Ь) я
dz
для ее множества точек разрыва на 13{а, Ь)
490
$dR = \M<=P(a, 6)|шМ >0
. Т-— I \ &Z /
• dz I \ /
имеем
mes %dR = 0.
3 *d7
В силу (5.4) множество KXpfU^s), как и множество К, изме-
римо по Жордану в R3, и поэтому в силу теоремы (о достаточ-
ном признаке существования интеграла Римана на ограниченном
открытом множестве) из ч. V, гл. 2, § 3 имеем
д/ еЯ(К)Л^(К\рГ,(^з))Л^(Рз"1(йз)П/8(«, *))
OZ
{в смысле определения (АЕ) из ч. V, гл. 2, §3), так что в си-
лу (5.11) имеем
Ш
К K\P~1(F,)
О
= 2 ИI £ (ерУЛх dydz,
w'i, з дг
(5.12)
где ряд справа в (5.12) сходится абсолютно (причем в силу теоре-
мы Jo корректности определения (АЕ))' из ч. V, гл. 2, § 3)
у (*,«).
OZ
l(eiR) е= Д(1Пз) V i).
OZ
Рассмотрим цилиндр
Ц^Ц»,^<.з№зПК(Ы,...,1(; i=l,2,...)
с „верхней крышкой" ^(Ц^СЗГ и „нижней крышкой" т0(Ц£>)с=Г,
являющимися графиками в R3 _y z функций <=С(1)(Тг,з) и
е С<М(У1, з) соответственно. Тогда в силу теоремы (о мере
графика непрерывной функции) из ч. V, гл. 1, § 3 имеем
mes у( Ц<?>) = mes ^(Ц**’) = 0-
Поскольку множество Г>,з<=£3 измеримо по Жордану (в Е3),
то |dVi, зк = 0 и тогда, очевидно,
|PS-W)№ &)|з = 0,
491
так что учитывая ограниченность цилиндра Щ,з(Уг,з)<=И\з[\К*
имеем |ЭЦ£>|з=0, т.е. цилиндр Щ, з(У i, з) <= Wi, 3 измерим по
Жордану (в R8), но тогда, учитывая, что
^(ег/?)еД(РИ{.3),
dz
в силу теоремы 6 из ч. V, гл. 2, § I имеем
|(е<Л)еЛ(Щ,3(У«,з)); *=1,-Л; (5.13)
dz
Поскольку
supp^(^)CVFi.8n^
oz < ,
то в силу (5.10) и (5.13) имеем
УУУ£(е{Я)(/Х(/1/4/г =
™i. з
А
= V fff —(etR)dxdydz. (5.14)
Отметим, что отображения
р£ з: vi. з -> 2з*. з (^, 3) = С Г
и
Л7-1.3: П з-S»-!.3(Vi, 3) -у0(Щ‘>) с Г
являются гомеоморфизмами класса С<1\ поэтому для функций
def
Я’ zl^(x,y) = R(x, у, z^(x,y)),
R° v> ^-1(х>у))
имеем
Ло 2O), /?о eC(1>(Vi,3).
Но функции z&, z^>_t e CM (Ft, 3) локально ограничены на Vi, 3,
так что функции Ro и R о z<^_, также локально ограниче-
ны на Vi, 3. Поскольку множества
supp ((^-Л) ° z^>)(ZVi, з и supp ((ег Л) о z^) aVt^
компактны, то локально ограниченные функции (егЛ)о
(егЛ)о 2w_t будут ограниченными на Vi, 3, так что
492
(et • R) о z<>), (et • R) о <= C(Vi. з)ДВ(У{. з).
где множество Vr, 3 измеримо по Жордану (в £3). Тогда в силу
критерия Лебега (интегрируемости функции по Риману на изме-
римом по Жордану множестве) из ч. V, гл. 2, § 1 имеем
(et • R) о 2(«), (в< • R) о 2<O_r е 3),
так что, используя (5.6), (5.7), видим, что существуют поверхност-
ные интегралы 2-го рода
уу etRdx/\dy — уу etRdx/\dy =
^J*.3(ri.3) Г(ц<0)
= yf (e,.R)o z£(x,y)dxdy (5.15)
и
уу etRdx/\dy<= уу etRdx/\dy =
S2*-l,3(^,3) ^(Ч>)
=- уу (et • R) о у) dxdy. (5.16)
Vi, 3
Далее, в силу (5.10) имеем
(/7‘(аз)А/3(а, Ь))ПК =
= у И\3ПК=и и UUVU,
так что
У1Г/.з = (^3-1Я)П /3(а, &))ЛГ =
= U Р3~1(Пз)ЛГ=
1=1
= и и (W) U ?.№)) =
г—1 г=1
— U U (Sit,з(Vi.3) U2г*-!.3(^1,з)),
1=1 t=i
и поэтому в силу (5.6), (5.7) имеем
U Г/, з = U° U (St. з(Г{. 3) U St 1. 3)),
1-1 »=i t-i
откуда, учитывая существование поверхностных интегралов 2-го
рода (5.15), (5.16), получаем в силу (5.11) представление
493
И Rdx/\dy^
“дК
dx/\dy =
==SS( И etR dx/\ dy +
i=ifc=i к^зсгз)
+ ff etRdx/\dy\, (5.17)
%fe-l,3(ri, 3) J
так что в силу (5.12), (5.14) из (5.17) видим, что для доказатель-
ства формулы (5.8) достаточно доказать равенство
fff t{eiR)dxdydz =
Ufe.3(^,3)dz
= eiRdx/\dy+ JJ etRdxf\dy
^2fe.3(ri,3) ^2k-K3(vi,3)
или, учитывая (5.15), (5.16) равенство
ГС Г 2-(eiR)dxdydz =
Щ.з^.зГ2
= ff (ei-Z?)o г$> (х, у) dxdy—
vi,3
— JJ (e» • 2?) о zV>_x(x, y) dx dy. (5.18)
vi, 3
Заметим, что в силу построения цилиндроида Щ, з(7$, з) ж Ц^>
прямая проходящая через точку М' = (х, д)V<_ 3 па-
раллельно оси Oz, пересекает этот цилиндроид по отрезку
где положено,
причем
Тогда из (5.13) в силу теоремы Фубини (для цилиндроидов из ч. V,
гл. 2, § 3) имеем представление
JJ £ (efR)dx dy dz =
Z
(5.19)
494
Поскольку R^C(K) и.
° °
OZ
ТО
y(x,y)^Vi<3eiR^C^_v ад
и
так что V (х, у) е Vi, 3 функция etR (как функция переменной
г) является первообразной на отрезке [ф_Р £$] Для кусочно-
непрерывной функции
£(«,я)еяда_,, ЧЩ
и в силу формулы Ньютона — Лейбница из ч. П, гл. 2, § 6
V (х, у) имеем равенство
Чй
^etjR)dZ = ^R^X> У’ Z2k(X' &)) —
НО
1
— (eiR)(x, у, z^(x, у)),
так что в силу (5.15), (5.16) из (5.19) получаем равенство (5.18),
завершающее доказательство формулы Гаусса—Остроградского
[(5.8). Отметим, что несобственный тройной интеграл
Л) £Rdx dy dz=2 Ш £ <е«л)dx dy dz
Ь) 1=1 wi, 3
из представления (5.12) понимается в смысле определения (АЕ) и,
как доказано в ч. V, гл. 2, § 3, не зависит от выбора разбиения
единицы (5.11) для открытого множества
рГ‘(О3)ПГ3(а, b),
а потому не зависит и от выбора открытого покрытия
U Vi.3 = ^3-
г—1
Следствие. Пусть KcR® y z — компакт с кусочно-гладким
[(класса С<’>) ориентированным краем дК, регулярным относитель-
но каждой из координатных осей Ох, Оу, Oz. Пусть
495
P,Q,R<= C(Ky, e= c(k) л B(K). (5.20)
ox ’ dy dz
Тогда имеет место формула Гаусса — Остроградского
+ Qdz /\ dx + Rdx f\dy. (5.21)
Замечание. Для бруса J^a, 6]gR* , являющегося ком-
пактом с кусочно-гладким ориентированным краем д/^а, &)=
6 _ _
— U Г/, где Г/ (/=1, ..., 6) — двумерные грани, попарно парал-
/=t _
лельные координатным плоскостям, для которых |Г/|2>,0. Тогда
край дР[а, Ь] бруса не удовлетворяет «условию регулярности отно-
сительно каждой из координатных осей Ох, Оу, О г» (так как не
выполнены условия вида (5.5)) и поэтому 1-я (предварительная)
теорема Гаусса — Остроградского к брусу /а[а, 6] формально не-
применима (хотя для бруса Р[а, Ь] формула (5.21) при выполне-
нии условия (5.20) была доказана в ч. V, гл. 2, § 3 в теореме Га-
усса— Остроградского для цилиндроида, простого относительно
каждой из координатных осей). Однако брус /3[а, 6] с помощью
движения в R3 можно перевести в параллелепипед /3 с ребрами,
не параллельными ни одной из координатных осей, к которому
уже применима доказанная выше 1-я (предварительная) теорема
Гаусса — Острогр адского.
Замечание. Для компактного многогранника (полиэдра) К
из'Rx.tr. z сориентированным кусочно-гладким краем дК 1-я
(предварительная) теорема Гаусса — Остроградского применима
после соответствующего движения, переводящего базис {i, j, к) в
эквивалентный упорядоченный ортонормированный базис {1ь h, 1з}>
в котором ни один из базисных ортов не параллелен ни одной из
[(конечного числа) граней полиэдра Л-
2-я (основная) теорема Гаусса — Остроград-
ского в R3. Пусть — компакт с кусочно-гладким
(класса С<У>) краем дК, ориентированным с помощью внешней
(для К) нормали, обладает помимо свойств 1)—3) (определения
компакта с кусочно-гладким краем) свойством 2): для каждой
особой (т. е. нерегулярной) точки М0&)К существует линейно
связная окрестность V(M0)cU(M0) (см. свойство 2') такая, что
\V(M0)(\dK.=V является кусочно-гладкой (класса С<*>) двусторон-
ней 2-поверхностью в R3 у г , регулярной относительно каждой из
координатных осей Ох, Оу и Oz. Пусть на К определена 2-форма
2
© =Pdy/\dz-\-Q.dz/\dx+'Rdx/\dy
496
класса С (Л) Л С&(К), причем DtP, DiQ, DtRe=B(K) (i=l, 2, 3).
Тогда имеет место формула Гаусса — Остроградского (5.21) или
J в=|Ло. (5.22)
Ък к
Доказательство. Введем (сравните доказательства 3-й
(основной) теоремы Грина на плоскости из ч. VI, гл. 2, § 2) и
теоремы Гаусса-Остроградского для компакта с гладким краем
в Rn из ч. VI, гл. 2, § 7) определение: открытый параллелепипед
J8cR®>y#z , построенный на ортонормированном упорядоченном
базисе di, Ь, 1з)~{1, j, к), называется /(-специальным, если он
удовлетворяет одному из следующих 3 условий:
а) д/((У3=0, /3<=/С;
б) д/С|У3=|Г есть кусочно-гладкая (класса С<1>) двусторонняя
2-поверхность в R3iWiZ , регулярная относительно каждой из коор-
динатных осей Ох, Оу и Oz (сравните условие 2');
в) <?/(П/3='Га:У(Л1о) есть носитель гладкого (класса С<’>) 2-пу-
ти Жордана <р (из условия 3)) с направленной нормалью
внешней для К и образующей острые углы с каждым из ортов 1ь
1г и 13.
В силу условий теоремы для любой точки существует
/(-специальный параллелепипед J3(MQ) такой, что M0eJ3(M0). Ес-
ли Л40е7(, то таковым будет любой брус (построенный на базисе
{i, j, kJ J3(Afioi)c:/(. Если М0&)К — особая точка края дК, то су-
ществование /(-специального параллелепипеда J3(Afo)c:V(Mo)
(построенного на базисе {i, j, к}) вытекает из условия 2')- Нако-
нец, если М0&)К — регулярная точка края дК, то существует ок-
рестность V(M0) из свойства 3) такая, что У('Да)П5К=Г есть но-
ситель гладкого (класса С<б) 2-пути Жордана <р и тогда существо-
вание /(-специального параллелепипеда J3(M0)a:V(Af0) следует
(при п=3) из доказательства теоремы Гаусса — Остроградского
(для компакта с гладким краем в Rn) в ч. VI, гл. 2, § 7. Но тог-
да v существует открытый /(-специальный параллелепипед
73(7Ио), удовлетворяющий одному из условий а), б) или в), при-
чем /(с J 13(М0). В силу компактности множества К из откры-
лся
того его покрытия {/3(М0); Л/цеЛ} можно выбрать конечное от-
m
крытое покрытие {/3; »=1, 2, ...} такое, что Кс. U J3. Рассмотрев
Л. и. Камынин 497
разбиение единицы {ei(M); i=il, 2, ...}, подчиненное открытому
покрытию {/?; 1=1, 2, введем 2-форму а^е,-© класса С(К)/\
о .22
для которой supp at=supp dmczJ^ V i, и тогда получим
представления
f 2 f 2 f 2 Vfj2
J j aJ; )da>=^ J dat,
5k 8=15k к г='к^3
так что для доказательства формулы (5.21) достаточно доказать,
(при i=il, 2, ..., т) равенство
f 2 р 9
J a{= J da(. (5.22}
• 5knj3 knj3
Если У? удовлетворяет условию а), то У? сК и равенство (5.22)
тривиально, поскольку в обоих его частях стоят нули. Если Jf
удовлетворяет условию б), то равенство (5.22) следует из доказа-
тельства 1-й (предварительной) теоремы Гаусса — Остроградского
для компакта с кусочно-гладким краем. Наконец, если У? удов-
летворяет условию в), то доказательство равенства (5.22) приве-
дено в ч. VI, гл. 2, § 7 при доказательстве (для п=3) теоремы Га-
усса — Остроградского для компакта с гладким краем в Rn (срав-
ните также доказательство 2-й (основной) теоремы Грина на плос-
кости из ч. VI, гл. 2, § 2).
Замечание (о записи формулы Гаусса — Остроградского в
векторной форме). Рассмотрим на открытом множестве QcR3
векторное поле X=Pi+Qj+7?X класса С(’> (й) и компакт Ксй с
гладким (или кусочно-гладким) краем дК, ориентированным с по-
мощью единичной внешней (относительно К.) нормали No. Введем
поток векторного поля X через край дК компакта К
2
Ф = f (X, N0)d5 — J (О ,
дК дК
2
где ®х ~ X, так что
А=х - + т + л л *
У дх ду dz j
~divX = (v, X).
Применяя к компакту KcR3 с краем дК формулу Гаусса — Остро-
2 2
градского, имеем d®* , откуда
498
Ф = ff (X, Ne)dS= fff div X dx f\dyf\dz.
эк. к
Таким образом, получен'а формула Гаусса — Остроградского в век-
торной форме
Ф = ff (X, N0)dS = fff div X dx Д dy Д dz
дК К
ИЛИ
ff (No> X)dS= fff (V, X) dx/\dy/\ dz.
дК К
Пример. Рассмотрим движение жидкости в пространстве R3.
Пусть v(x, у, z) — вектор скорости жидкости в точке М=г(х, у, z)r
Пусть дК. гладкий (класса С<‘>) край компакта KczR3, ориентиро-
ванный с помощью внешней (относительно К) единичной нормали
No. Найдем количество жидкости, протекающей через край дК за
единицу времени. Через малый кусок ДГ края дК (площади
|ДГ|2=Д5) в сторону внешней нормали No в единицу времени
протечет количество жидкости, заполняющее собой цилиндр с ос-
нованием ДГ, имеющим площадь |ДГ|2=ДЗ, высотой (v, No), и
если р(х, у, z) — плотность жидкости в точке (х, у, z)—M, то
масса жидкости, протекающей через кусок ДГ в единицу време-
ни, будет равна (у(М), N0(Af))-p(Af)-AS, так что для всего глад-
кого края дК будем иметь Н (Х, N0)dS, где Х(М) =р(М)-у(М) —
дК
векторное поле (что и оправдывает название «поток» векторного
поля Х(х, у, г) через ориентированный край дК компакта К. в.
R3).
Пусть теперь движение жидкости. (при р(7И) = 1) проходит при
наличии источников (или стоков) внутри компакта К. Производи-
тельностью источников, заключенных внутри К, назовем количест-
во жидкости, вытекающей в единицу времени через край дК, т. е.
поток поля скоростей И (No, v)dS. Но тогда по теореме Гаусса —
Остроградского, примененной к компакту К с ориентированным
краем дК, имеем
ff (No, v)dS = fff(v, v) dx /\dy /\dz =
дК К
s Ш d‘v v dx A dy Д dz.
к
Выясним гидродинамический смысл дивергенции поля скорос-
тей v(A4). Пусть точка М^К и Кр(Мо) — малый (по диаметру)
компакт с краем d^fMo), стягивающийся в точку Afo при р->0
(например, шар радиуса р>0 с центром в точке Afo). Тогда имеем
32* 499
УД div v(x, у, z) dx /\'dy /\dz —
Кр(Л4.)
= Д (No* v) dS.
дкр(Мй)
Считая v^C<V(K) (и, в частности, v&.C(K)), применим теорему о
среднем к тройному интегралу Римана, так что
divv(AG)= Д (No, v)d5/|tfp(Afe)|3,
дК^м.)
где Mi^Kp(M0). Но тогда для дивергенции получаем формулу
(инвариантную относительно ортогональных преобразований в R3)
div v(M0)= lim / Д .(No, v)dS/|KP(Jf0)|3\.
₽_*° Uk₽(m.) ]
Таким образом, дивергенция поля скоростей движущейся жидкости
является плотностью (производительности) источников жидкости.
В частности, если источников жидкости в компакте К нет, то
divv(Af)==O vMeK и тогда общий поток жидкости через край
дК. компакта К равен нулю: «сколько жидкости втекает — столько
и вытекает».
Определение. Векторное поле ХеС<*>(Й) называется соле-
ноидальным, если divX(Af)=O vAfeQczR3.
Пример. Если ХеС<2>(й), то векторное поле rotX солено-
идальное.
В самом деле, для rot X=[V ДХ] имеем
divrotX=(V, [7ДХ])=0.
Пример (вывод уравнения теплопроводности). Рассмотрим
скалярное поле температуры U(x, t) в компакте XczR3 Xi Xt с
гладким краем дК, ориентированным с помощью единичной внеш-
ней (относительно К) нормали No. Пусть AQofx, t) — количество
тепла, протекающее через малый кусок ДГсдК (с площадью
1|ДГ|2=ДЗ) края дК в направлении внешней нормали No за ма-
лый промежуток времени At. По закону Фурье, тепло течет от бо-
лее нагретых к менее нагретым частям тела и тем быстрее, чем
быстрее убывает темпратура. Более точно, AQo пропорционально
Д5=!|ДГ12, Ы и 14т-1, так что
|dN0 J
&Qo = -k-♦ Д5 • М,
dNe
где k(x, t)>0 — коэффициент теплопроводности. Введем вектор
потока тепла q(x, t)——k-gradU, тогда
AQ0=(q, N0)-AS-Af.
500
Но тогда для полного количества тепла, протекающего через край
дК компакта К за промежуток времени (t\, t2), имеем
(q, N0)dS =
Г1 дК . ..
= - ffdt [f k (gradf/, N0)d5,
ti dK
откуда в силу теоремы Гаусса — Остроградского имеем
Qo = — /di ffjdiv (k • grad U)dxx/\dx2/\dx3,
и к
где Qo — общее количество тепла, «вытекающего» из К. через
край дК (в направлении внешней нормали). Из этой формулы
имеем для общего количества тепла, «втекающего» в тело К (че-
рез край дК,
Q — — Qo — \ di JJJ div {k • grad U)dxtf\dx3/\ dx3.
h к
С другой стороны, тепло Q, втекшее в компакт К, пошло на на-
гревание тела (т. е. на повышение его температуры). По закону
Фурье, для того чтобы повысить температуру малого тела ДК на
bU = — • At, необходимо сообщить телу ДК количество тепла,
dt
пропорциональное массе р-ДУ тела ДК (объема ДУ) и разности
температур ДС7—• At, т. е.
AQ = с • р • • ДУ • At,
где с(х, f)>0 — коэффициент теплоемкости. Но тогда имеем для
всего (тела) компакта К:
Q = • р • ¥ dx^dx^dx,,
tt к 0t
откуда из теплового баланса имеем равенство
f dt fff с • р • dxif\ dx2/\dx3 =«
t, к dt
= 1 dt JJJ div (k • grad U'jdxj. A dx2 Д dx3
h к
или для любого малого Компакта KqczK и малого промежутка
иремени (t, t+&!t)cz(th t2) имеем равенство
501
H-Af
f —----div(fe- gradt/) I dx^dx^x^ — 0.
t jk \ ™ J
Поскольку подынтегральная функция непрерывна, то в силу
произвольности выбора Kocz/C имеем V (х, Г] равенство
с • р • -----div (Л • grad 77) = 0.
Тем самым получено уравнение теплопроводности
с • р • — = div (k • grad U).
dt
Если тело однородно, то k(x, t)^k, с(х, t) ^с, р(х, t) =р и, учи-
тывая равенства
div grad 7/ = (у, VC7) = Д77 = 2 DlU’
получаем уравнение теплопроводности —=а2 • Д7/, где а2=
dt
=&/ср>0. В частности, если температура U(x) не зависит от вре-
мени (что соответствует стационарному распределению темпера-
туры в К), то получаем уравнение стационарного распределения
температуры Д1/(х)=0 V хеК. Заметим, что векторное поле
grad U(x) как потенциально, так и соленоидально (поскольку
divgrad7/(x)=At/(x)=0 в К).
Пусть теперь Г= U Г/ (где Г;ПГ/=0) при i#=/ — кусочно-
гладкая ориентированная 2-поверхность в R® с ориентирован-
ным краем дГ, являющимся кусочно-гладким циклом Жордана.
Пусть N(7W) — орт направленной нормали к ориентированной ка-
сательной плоскости Гм (Г) в любой регулярной точке М=*
=<р(и, о)еГ. Рассмотрим в окрестности Q кусочно-гладкой 2-по-
верхности Г векторное поле Х=^ -i+Q-j+^k класса С<*> (Q).
Поскольку
Х = • i 4- Q • j + 7? • k ~ ©x = SPdx + Qdy + Rdz,
j
d
~ rot X = {y/\XJ =
dx dy dz
& Q R
502
и поэтому для работы (циркуляции) S векторного поля X
вдоль края дГ 2-поверхности Г имеем
S-f (X, t)ds =f
эг эг
Применяя формулу Стокса (из § 4) к кусочно-гладкой ориенти-
рованной 2-поверхности Г с краем дГ, имеем
f ®r=(j<fox>
аг г
т- е.
dyf\dz
J (X, А
дГ f дх
&
dz/\dx dx/\dy
д д
ду dz
Q R
Г
cos(N0, х) cos(N0, у)
д д
дх ду
& Q
cos(N0, z)
д
dz
R
dS =
= Я (rot X, N0)dS,
f
откуда получаем формулу Стокса (в R3) в векторной форме
£ = J (X, t)dS= Jf (rot X, N0)rfS = Ф,
дГ Т
так что работа _ (циркуляция) векторного поля X вдоль края дГ
(2-поверхности Г) равна потоку векторного поля rotX через кусоч-
но-гладкую поверхность TczR3 (где Na — орт направленной нор-
мали к Г, a t — орт направленной касательной к краю дГ).
Из предыдущих рассмотрений вытекает
Теорема (о физической интерпретации формул векторного
анализа).
. 1) Изменение функции (скалярного поля) и^С<У>(£1) при пере-
ходе от точки А к точке В в R3 равно работе % ее градиента
gradf/ (вдоль (любого) кусочно-гладкого 1-пути Жордана <р, сое-
диняющего точки А и В:
8 = f (grad и, t)ds = f dU = ЩВ) — U(A).
v=VAB ГАВ
(В самом деле,
503
£=f (grad Z7, t)ds = f L grades 4
ГАВ TAB I
dU = U{B) — U(A)). ’
ГЛВ I
2) Поток Ф векторного поля ХеС(!>(£2) через край дК, ограни-
чивающий трехмерный компакт JCgzQcR3, равен интегралу от ди-
вергенции поля X по компакту К:
Ф = ff (X, N0)dS= fff div X dx /\dy/\ dz.
дК К ' ’
(В самом деле,
2 2
Ф (No, X)ds=ff шх=уу; d®x=
дК дК К
3
= УП “divx = /Л div х dx Д dy /\ dz ж
К к
Sfff(V, X)dx f\dy/\dz.)
К
3) Работа jo векторного поля ХеО’Цй) вдоль ориентирован-
ного края дг кусочно-гладкой ориентированной 2-поверхности
TczQcR3 равна потоку ротора поля X через поверхность Г:
gsf (X, t)ds= Jf(rotX, N0)dS.
дГ p ‘
(В самом деле,
% = f (X, t)ds = f <ox = jj d®x=W<Brotx =
аг аг г г
eff(rotX, N0)dS.)
г
Замечание (об инвариантном определении ротора вектор-
ного поля). В области QcR3 у 2 рассмотрим векторное поле
Х= & i4-Q-j+JR-keC<1)(Q) и компакт KczQ с гладким краем дК,
ориентированным с помощью единичной внешней (относительно
К) нормали No. Тогда
X - шх = SPdx + Qdy + Rdz,
rot X = [vAX] ~ d®x = ( R- 4- Q\dy A dz +
+ {±$>-----d-R\dz/\dx +(±Q_^^\dx /\dy.
I dz dx I I dx oy J
504
1
В силу формулы Гаусса — Остроградского в векторной форме
имеем
П |N.AXJ«S-fI
дК дК
i j k
cos(N0, x) cos(N0, y) cos(N0, z)
= ff dy/\dz
дк _
j
dz /\ dx
Q
k
dx/\dy
R
i j
= Ш dx "dy
& Q
dx /\dy Д dz,
t. e.
ft [N0AX]dS = Iff [v Л X] dx A dy A dz =
дК К
^JJJrotXdx A dy f\dz
(при этом использовано легко проверяемое равенство
d
dy/\dz
Р
j
dz/\dx
Q
k
dx/\dy
R
i j k
d d
dx dy
P Q
dx/\ dy /\dz).
Рассмотрим для точки малый компакт Кр(Мо)с~.К, со-
держащий внутри себя точку Мо (возьмем, например, шар радиуса
р с центром в точке Мо). Тогда, поскольку rot Хе С (К), по теореме
о среднем (примененной по координатно к тройным интегралам
Римана) имеем
JJJ rotXdx A dy f\dz=s
// dQ(Mi) \ . (
I ( dy dz j I
МЫ.'I j + (\ t V
dx J I dx ду I ]
dU(Mj)
dz
50$
где точки Af,-eKp(Af0) (/=•!, 2, 3). Перенося |Kp(Af0)|з налево, по-
лучаем при р->0 (замечая, что тогда ЛГ,—(i=l, 2, 3) формулу
(инвариантную относительно ортогональных преобразований в
R3 )
rotX(Af0) = lim/ [N0AX]d5/|^(M0)|s\.
₽-° \dKptM.) )
Теорема (формулы Грина). Рассмотрим в области Qc
<=R® Xt Xt скалярные поля U, VeC(2>(Q) и трехмерный компакт
KczQ с гладким (или кусочно-гладким) краем дК ориентирован-
о
ным с помощью единичной внешней (относительно К) нормалью
No. Тогда, полагая
JL =(v, N0) = W • cos(N0, х<),
oNt oxi
имеем формулы Грина:
jC U ♦ ~ VdS= JJJ (grad U, grad V)dx+
dK * JK
к
JU
дК К
f J и -^-UdS = JJJ (grad U, grad U)dx +
dK * JK
(5.3)
к.
ffft/ . j- V- V — u\dS =
JJ I dNo dN0 I
dK '
— ff[(U • ДГ — V • HU)dx-
(5Л)
Доказательство. Применяя теорему Гаусса—Остроград-
ского в векторной форме,
VdS^{[u . (No, yV)dS==
J J J J
dK.
506
- JJ (No, и . = JJJ (V» V • vn dx.
ЭК К
Но
(V, и • vn = &и, ?V) + u (v, vn =
= (grade/, grad 7) + U • AV,
откуда и получаем формулу Грина (5.1). Формула Грина (5.2) сле-
дует из (5.1), если положить в ней U=l. Наконец, из формулы
Грина (5.1) вытекают два равенства
V dS = JJJ(grad U, grad V)dx+
+Ш6'-4ИЛ;
к
^-Uds= Jj’J (grad V, grad U) dx +
° к
+ШГ-Л^
дК
дК
из которых получаем и формулу Грина (5.4).
Следствие 1 (теорема единственности решения задачи Ди-
рихле для уравнения Лапласа). Рассмотрим компакт ЛагйсЙ3 с
гладким (класса ©*>) краем дК, ориентированным с помощью
единичной внешней (относительно К) нормали No, и функцию
о о
и<=С<1~>(Й)/\С№(К), являющуюся гармонической в области К, так
что &U(x)=0 V х^К. Тогда если U(x) =0 V х&)К„ то U(x)=0
на К.
Доказательство. Из формулы Грина (5.3) имеем при
A U=0
Ии kViS=№U’
дК К
Но по условию U(x)=0 V х&Э К, что дает равенство
Пи • — UdS = Q,
dN,
дК.
откуда
fflWvtf) dx = 0.
507
Но
№ vt/)=2<w^w
i=l
причем
(yU(x), VU(x))^0 VxeK,
и тогда в силу свойств кратных интегралов Римана (см. лемму и»
ч. V, гл. 2, § 1) имеем
vU)dx=0y^(yU, vU)^0,
т. е. У U(x)=Q (dU(х) =0) в К, так что (7(x)=const в К. Но кра-
евое условие (Дирихле) U(x)—Q V хедК дает тогда равенство
U(x)=Q в К, поскольку U^C(K).
Следствие 2. Рассмотрим в области QcR3 гармоническую
функцию t/sC(2)(Q) и любой трехмерный компакт KcQ с глад-
ким краем дК, ориентированным с помощью единичной внешней
(относительно К) нормали No. Тогда
ff— UdS = 0.
JJdN,
дК.
Доказательство. В силу гармоничности функции
eCc^Q)' имеем &U(x)=0VxeKczQ и тогда, применяя формулу
Грина (5.2), получаем
дК дК К
Следствие 3 (теорема о среднем для гармонической функ-
ции). Если l/eC<2>(Q) — гармоническая функция в области
QcRx (так что Д£7(х)=0 V хей) и Af0=x°eQ — (любая) точка,
то для шара Ш^> (ЛГ0)с:й имеет место равенство
U(M0) = (V4n R2) • ff UdS, (5.5>
’ 8д(ЛМ
где
=0111(4) (Мэ).
Доказательство. Рассмотрим вспомогательную функцию
V(M) = l/r в проколотом шаре Ili^) (M0)c:Q, положив
508
'3
мо = х°, М =Х, г = 2 (xt — x°)et
г—-1
И
(з \ 1/2
г—1 J
Тогда
Аг_£(1/г)=_(х,_хЖ,
(/Л|
т. е.
grad V = v (1 /г) = — г/г3.
Рассмотрим сферу 5^>(Л/0) = 5Ш^>(Л10) с внешней (относительно
Ш£>(М0)) единичной нормалью N0 = r/r. Тогда VM &Sr(M0)
имеем
4/(">-^(1/r)=wl/r>’ N-)=
=(—г/г3, г/г)=- r2/r4 = — l/r« = — 1/R*.
Рассмотрим меньшую сферу 5Р(/Ио)с Ш^>(/Ио) с внутренней
(относительно шара Ш(р3>(/И0)) единичной нормалью No = — г/г.
Тогда vМ <= SP(M0) имеем
^1 = ^(1/,) = (v(i/r),N0) =
=(—г/г3, —-г/г)=1/г2=1/р2.
Далее,
— 1/г3 + 3 • (xt — х°)/г* • (х( — х^1г —
= — 1/г3 + 3(х{ — x°)2/rs,
Т. е.
3 д’
ДР = Д( 1/г) = 2 v = - 3/г3 + 3 • г2/г3^ 0.
»=1 *
Таким образом, функция V=l/r будет гармонической в шаро-
вом слое /<—{xeQ|0<p^r^AJ}, являющемся компактом с глад-
ким краем
509
<Жр=$л(ЛадиЗ/Мо),
о
ориентированным с помощью внешней (относительно Кр) нор-
мали
N0(M) == ( Г/Г на
I —г/г на Sp(M0).
Применим к гармоническим в слое К» функциям U(M) и
V(M) формулу Грина (5.4):
ff/>7 ..J. v_v . — u\dS =
J J f <?N0 3N0 )
= JJJ(t7 • ДУ— V • Д1/) dx—О,
к
т. е.
ff (U * -£• (1/г)-(1/г) ♦ 0\dS =0.
JJ I <?N0 dN0 I
дКр < J
Но
dKp SR
— 1/P . ff—--------U • dS,
J J a(-No)
sp
где орт (—No) на сфере 5Р=^Ш^>(МО) будет внешним относи-
тельно шара Ш<3> (Л4о). Поскольку функция U (М) гармоническая
как в шаре (Мо), так и в шаре Ш<3> (Мо), то в силу след-
ствия 2 имеем равенства
ff — UdS = 0,
JJ dNo
5л=дШ^(М.)
ff --------—UdS = Q
J J <?(-N.)
$Р=0Ц43)(М<,)
или
ff (W-^U-dS^O,
J J vAIq
dKp
510
откуда получаем
ff U =
J J C/Nq
dKp
т. e.
fftf •^(,/r)d5+ ffy ~ <1/r)ds=0’
J J $N» J J 3N«
SR “stf
О
где No — орт внешней (относительно слоя Кр) нормали к краю
5Kp=SRfiWo)USp('Mo).
Но, как было показано ранее, имеем
2_(1/г(д/)) = _1/я» на sR(Mo)
и
-2-(1/г(Л/))= 1/р2 на 5Р(М0),
откуда для любого р>0 имеем равенство
— 1/Я2 • ДО t/dS+1/р2- ДО t/dS = O.
SR(M) Sp(M.)
Но
1/р2 • ДО £7(A/)dS = C7(M0)/P2 . ДО dS +
Sp(M.) SP(M.)
+ l/p2 • ДО (U(M)-U(M„))dS,
Sp(M.)
где
ДО dS = 4« • р2.
SpW
Далее, поскольку {/еС(Ш^>(Л/0)), то функция U(M) равномерно
непрерывна на компактном шаре Ш^(Л10) и поэтому Ve^>036^>
>0 такое, что при 0<р<8 УМ ^Sp(W0) имеем оценку |Z7(J/) —
— так что
Г2) • ДО U(M)'dS — 4ir -^(Мо)|<
Sp(M,) I
< d/Р2) • ДО |C/(Af)~t7(Al0)|d5<
Sp(M,)
е • 4тг • р2/р2 = 4s • it V р G (0, 6(e))j
511
т. е.
Я lim р/ра • р U(M)dS} - 4* .
Переходя к пределу при р -* 0, получаем равенство (5.5) тео-
ремы о среднем.
Следствие 4 (принцип максимума для гармонической функ-
ции)._ Рассмотрим в ограниченной области GczR3 функцию
gC(G)/\C^(G), гармоническую в области G (так, что kU(M) =
<=0vAfeG). Тогда функция U(M.) не может достигать своего
максимального (на множестве 6)_значения во внутренней точке
AfoeG (не являясь постоянной на G).
Доказательство. Поскольку область GcR3 ограничена,
то множество G компактно. В силу условия U^C(G) по теореме
Вейерштрасса существует точка Mq^G такая, что U(Mq) =
-=maicU(M)=tn. Если U(M)^m в G, то MoedG. В противном
о
случае M0^G и, кроме того, существует точка A^eG такая, что
В силу связности области G существует ломаная
ZfAfi, Afo]cG, так что
р(дв, фИь Afo]»2po>O.
Рассмотрим последовательность шаров Шр/Gi) Q G, где
Qq = M0, Mo] (i=l, 2,..., s),
где Afx eTUp,(Qs_i). Докажем, что — m в шаре mPt(Qi-i)
при i=l, 2,..., s, что и приведет к противоречию, поскольку
Z7(Afi)<^/n. Для шара ШРо(Л/о) имеем G(Af0) sG(Q0) — /и. Если
ЩМ) т в Шр/Л/о), то существует точка &й е ШР(1(Л40)\{ Л40}
такая, что Р(^0)<т. Пусть где 0<р<ро. Но Ge
еС(3%), поэтому существует окрестность PF(5%) С*$Р(Л/о) такая,
что VM е PF(M0), причем U(M)^.m V М eSp(M0)\
XW(M0). По теореме о среднем из следствия 3 (см. (5.5)) име-
ем
m = G(Af0) = l/4rcP2 • [J U(M)dS = 1/4кр2Х
зДма
X/ И G(M)dS+ ff U(M)dS\<
\W(MJ SpMJXWlMJ J
Jj 1 -dS = m.
Противоречие. Итак, U(M) = m v M еШр/Qo), если U(Q0) = m.
Но тогда U(Qi) = m, что приводит (по доказанному) к равенст-
ву G(Af) = m \’М еШр/Qi) и вообще
512
(U(Qi-i) = = m V M <= Шр,(ф_|)).
Но тогда U{Q,s-i)—m и поэтому U(M) = tn.v M «= ffl^,(Qs_i), что
и доказывает принцип максимума (минимума) для гармоничес-
кой функции.
Следствие 5 (усиленная теорема единственности решения
задачи Дирихле для уравнения Лапласа). Рассмотрим в ограни-
ченной области GczR3 функцию U<=C(G)/\C<2>(G), для которой
дЩуИ)=0VЛГеб. Тогда, если U(M)=Q\M<=dG, то U(M)s*0
в G.
Доказательство. Если U(M)^Q в G, то без ограничения
общности можно считать, что существует точка M0^G, для кото-
рой U(М0) —тах U—т>0. В силу принципа максимума для гар-
G __
ионической функции имеем M<^G, так что M(j<=dG. Но в силу ну-
левого граничного условия Дирихле U(Mo)=m—0, что противо-
речит предположению т>0.
§ 6. Вычисление градиента, дивергенции, ротора
и лапласиана в сферических координатах
Рассмотрим сферические координаты в R’>y>z , задаваемые
диффеоморфизмом
$>:Q={(p, <р, ф)|0<р<4-оо, 0<ф<2чс,
M<*/2}-^(Q)==Rly,z\f>
где F = {(x, у, г)| 0<jc<+<», у=0, —оо<^г<+со}, так что
х==р cos<p • соэф,
y — p • sin q> • cosip,
z = p • sin-ф.
Тогда
det ^(р, ф, ф) = d(x* у’ = р2 • cos ф О,
<Хр, ф, Ф)
причем
— $ = — • i-j- — • j-}- — .k= cosф • cosф • i +
dp dp dp dp
4-81Пф« cost]» • j + sinф • k —eP,
где eP—орт, направленный в сторону возрастания р по радиу-
сУ'Вектору ОМ;
33—Л, И, Камынин 513
dSP дх . , ду . , dz .
---=— . 14- — • ]4-------- к=
Эф Эф Эф дф
= р • cosip •(— sin ф • i4-cos<p • ]) = р • cosip • ef;
еф =— sin q> -i-J-costp • j,
где еф — орт, направленный в сторону возрастания <р по паралле-
ли 1р=const;
-^. = — -i-l-— -14-— -к—
Э<р Эф J d<|>
== p • (—cos <p • sin ip ! i — sin q> • sin <]> • j 4-cos ф • k) =
= P • еф; еф = — cos <p • sin ip • i —
— sinq> • sin<> • j 4- cosip • k,
где еф — орт, направленный в сторону возрастания 1р по меридиану
ip=const (см. рис. 36). Поскольку
(е₽, еф) = (еф, еф) = (еф, ер) =0,
то тройка векторов {ер, е», ej ортонормирована в каждой точке
R3. Заметим, что
dx/\dy/\dz\^J>, /-34 =
I ср Оф иу I
= d(JLJL±)==p2CoS<p>0
«(?, <Р.Ф)
и поскольку
— Э> = ер, — ^=р- созтрлвф, * е*»
др дф Оф
ТО
dx Д dy Д dz / — /-5s, -/-^1 =
= р2 • cosip • dx /\dy /\dz{ep, еФ, вф} = р2 • cosip,
т. е. dxAdyAdz{ер, еф, еф}=1>0, так что тройка ортов
{ер, еф, еф} ориентирована так же, как и тройка координатных ортов
{i, j, к} в Rx у> г.
Рассмотрим числовую функцию f(x; у, z)gC(I»(Q), тогда, ис-
пользуя теорему о производной сложной функции, имеем
г о 4. +
др 7 др дх др ду df
514
+ ? ? = (grad f> ^\ =(grad f> е₽);
dz dp I dp ]
-Lf^±f0 .^l + ^L .^l +
dtp dtp ' dx dtp dy dtp
+ -7- •~=/gradf, ^-^Wpcoscp • (gradf, e,);
dz dtp \ dtp l
-Lt==— fо . —+2L .^.4.
дф ' dty 1 dx дф dy <Эф
+ y- ‘ - (grad f> ' <grad f> e*)’
dz оф \ оф 1
так что получаем
(grad f, e₽)=-^-, (grad f, e<₽) = (l/pcosi|))^-,
dp dtp
(gradf, еФ) = (1/Р)-^-,
dy
откуда имеем представление для градиента в сферических коорди-
натах
grad f = ^еР+(1/рсозф)^е,+(1/р)~7 еФ
dp dtp dy
и, в частности»
gradp = e₽, grad <р = (1/р cos ф)е?, gradi|? = (1/р)е;,.
В евклидовом пространстве у z базису {i, j, к} соответству-
ет сопряженный базис из 1-форм {dx, dy, dz}. Вспомним, что в де-
картовых координатах были введены соответствия между 1-форма-
ми и векторными полями следующим образом. Имея в виду, что
gradx = i, grady = j, gradz=sk,
полагали
i i
t/X = •“grad X ==
T. e.
i 1
flLt 1, dy ^3 ^grad у —" 0)j>
r. e.
1 1
d j, dz = •“grad Z e= •“*»
*• e. dz ~ k, и
i
^ = <“grad/-'grad/
33»
515
и тогда
।
о) = Р dx + Qdy + Rdz ~ X = Pi 4- Qj 4- Лк,
i
причем VheR3 имеем «(h) = (X, h) и обратно, полагая
i i i
k~«ftsdz,
получали соответствия
- !
X — Pi + Qj + Лк ~ о)Х = Pdx + Qdy + Rdz,
так что
wx(h) = (X, h)VheR3
и, в частности,
i
grad / ~ ®grad f = df,
причем
1
d/(h) = wgrad/h) == (grad /, h).
Рассмотрим теперь базис {eP, еф, еф} ~ {i, j, к} и найдем
сопряженный базис (т. е. 1-формы) в сферических координа-
тах, соответствующий еР, еФ, еф. Имея в виду, что
gradp = ep, gradф=(1/рcosф)е?, grad<|»=eф/p,
положим
I 1
dps(0gradPss“e₽>
т. е. dp ~ еР,
। I
=й ^grad Ф “ cos Ф,
т. е. 4ф~(1/рсоэф)еФ,
1 1
^з<йггааФ = (иеф/₽>
1
т. е. Ж|>~(1/р)еф, и d/ = ®grad/, т. е.
df ~ gradf = -^еР+(1/рcosф)^-е»+(1/р) ^вф,
др о<р оф
причем V heR’, тогда имеем
dp(h) = (grad р, Ь)аз(ер, h),
d<p(h) = (grad ф, h) = (1/рcosф)(еФ, h),
d^h) == (grad Ф, Ь)==(1/р)(еФ, h)
516
и обратно, положим
е? — dp, еф ~ р cosijjdq), еФ ~ рйф.
Тогда ортонормированному базису {е₽, е», еф} соответствует
тройка 1-форм {dp, pcos<bdq>, рйф}, для которой имеем
dp(eP)=(eP, еР) =1, рcos ф</ф(еф) = (еф, еф) = 1,
Р<?Ф(еФ)=(еФ, еФ) = 1,
а также
^р(®ф) =,(®р> е») =о,
^р(еФ)=|(ер, еФ)=0,
р cos фг/ф (ер) = (еф, ер) =0,
р cos фс?ф (еф) — (е,,, еф) =0,
рс/ф(ер) = (еф, ер)=0,
рс/ф(еф) = (еф, еф) =0.
Таким образом, {dp, p-cos фс?ф, рс/ф} является сопряженным бази-
сом к базису {ер, еф, еф}.
Теперь введем соответствие
г
®=35dp+Q-(p-cos -ф£?ф) +Я-(ре/ф) ~Х=
= ^-еР+Р-еф-|-^.еф,
так что
®(h)=f(X, h) vheR3
и обратно
1
X=З5-еР+Q-e,+R еф ~ ох=
= $Mp+Q-p-cos фйф+7?-рбф,
1
где <ox(h) = (X, h) VheR3.
Отметим, что введенные соответствия между 1-формами и вектор-
ными полями инвариантны относительно ортогональных преобра-
зований, поскольку подобной инвариантностью обладает скаляр-
ное произведение в евклидовом пространстве R3. Отметим, что
dx/\dy/\dz=dp/\ (p-cos фс1ф)Л (pdijj)
и поэтому
dp/\ (p-cosфЖр)Л (pd\p){i, j, k}=
=dx[\dy[\dz {i, j, k}=l
и
dpA (p-cos фг/ф) A (pt/ф) {ep, e,, еФ}=
=dx/\dy/\dz {ep, еф, еф}=1.
517
Найдем соответствия между 2-формами и векторными полями в
сферических координатах, для чего вспомним, что в декартовых
координатах имели
tZ//AcZz~[jAkJ=i, dzAtZx~[kAi}=
=j, dxActy~[iAj]=k.
что давало соответствие
2
<о = 3s dy A^z-|- Qdz A dx-\-Rdx/\dy ~ X=
= -i+Q-j+^-k,
причем для любой пары векторов {В, С} из R3 у г имели
2
ш{В, Z}=dxf\dy/\dz^i, В, С}='(Х, [ВАС]),
и обратно, поскольку
i=[j№]~dy/\dz,
j =i[kAi]~dz/\dx, k=|[iAj]~dx/\dy,
то векторному полю X=38 •i+Q-j+7?.-k сопоставлялась 2-форма
2
их=За dy/\dz+Qdz/\dx+Rdxf\dy,
для которой
2
ox{B, C}=dx/\dy/\dz{X, В, C} = (X, [ВАС])
при любой паре векторов {В, С} из R® г. Эти соответствия были
инвариантны относительно ортогональных преобразований, по-
скольку такой инвариантностью обладало смешанное произведе-
ние трех векторов в евклидовом пространстве R3.
Рассмотрим в R3 сферические координаты, базис {ер, е<р, еф} и
сопряженный базис {dp, рсо8ф</ф, pz/ф}. Поскольку
ep~dp, e,~p-cos ф*/<р, еф ~ pdty,
то положим
еР=[ефЛе*]~ (p-cos фс?ф) А (р^ф) =(p2 cos фйфА^Ф.
еф=[еч,АеР]~ (рг/ф)Л^Р=Р^ФЛ^Р.
et=[ePAeJ~dpA (pcos фе/ф) =p-cos ф^рА^ф,
что дает соответствие
2
Х=$5 eP+Q-e(,+P-e4,~cox=
-p2-cos ф^фЛ^ф+Ф р^фЛ^р+^.-рс/рЛ^ф,
518
причем для любой пары векторов {В, С} из R3 имеем
2
<ох{В, C)=|p2-cos фг/рА^фЛ^ф{Х, В, С}=
=dx/\dy/\dz{X, В, С}=(Х, [ВАС]).
С другой стороны, соответствие
p2cos фйфА^Ф'^' ер, Р^Ф Л^Р ~ еФ,
р cos фб/рЛ^ф ~ е*
позволяет 2-форме
2
®=i5a-p2-cos фЛрА^Ф+Ф'Р^фЛ^р+^’Р’СОз ффА^ф
сопоставить векторное поле
Х=33 •ep-j-Q-e<p-|-./?-e*
или
2
o = 35dq)Arfip+Qdi|)Adp+ Rdp/\d<p~X =
= (^/р2 cos ф) -еР+ (Q/p) -е,-}- (7?/р cos ф) еф.
Наконец, соответствие между числовыми (скалярными) функция-
ми и 3-формами в сферических координатах имеет вид
1 ^dx/\dy/\dz=p2-cos ффЛ^фЛ^Ф»
т. е.
б/рА^фЛ^Ф~ l/(p2-cos ф)
з
И <0=/ б/рЛ^фА^Ф~/7(р2-СО8ф),
так что
з
f ~fp2-cos фб/рЛ^фЛ^ф—
причем
з
®/{А, В, C)=f (A, [ВАС]) V {А, В, C}eR3.
Введенное соответствие между 3-формами и скалярными поля-
ми также инвариантно относительно ортогональных преобразова-
ний, поскольку такой инвариантностью обладает смешанное про-
изведение трех векторов в евклидовом пространстве R3.
Вспоминая соответствия в декартовых координатах в Rly z
(Х = 5г> • i +<? • j + Я • k~«Jx —&dx + Qdy -\-Rdz)=^-
519
=>Zdwx=f2/?_dy Kdz + (-& — — R\dz/\ dx 4-
l ydy dz J ydz ' дх I
+ (т-- —T-) dx/\dy ] = a)rotX ~rotx=
у dx ay j j
/dR dQ\. , IdP dR\. , IdQ dP\.
I dy dz j I dz dx J I dx dy I
2
X = Pi 4-Qi + £?k~ <ux = Pdy /\dz +
4- Qdz /\ dx 4- Rdx Д dy;
d®x = 4. 4- dx A dy A dz =
\ dx dy dz j
3 „ dP . dQ , dR
— “div x ~ div X = — 4- — 4- —
dx dy dz
и, наконец,
Д/ =. div grad/ = div (— i 4- —14- — k^ =
(dx dy dz I
_дЧ d*f d*f
dx* dy* dz* ’
получаем аналогичные соответствия в сферических координатах
при базисе {е₽, еф, еф} и сопряженном базисе {dp, р cos рйф)
1
X=РеР+Qev4-7?e,|> ~ ©х=
=Pdp4-Qp cos i|>d<p4-#ipd$,
откуда
d<ox = / А (/?р) _ А (<2р cos d(f> A +•
\д<р оф J
4-/^. —2_(/?р)\^ Дйр4- [у- (<?Pc°s<p)-^-)dpA^q>^
\3ф др / I dp дф I
(поскольку
d<f /\ cty ~ (1/р2 cos ф)е₽, йф A dp ~ (1/р)е¥,
2
dp A dtp ~ (1/р cos ф)еФ) = “rot х,
имеем представление ротора в сферических координатах
520
rot X =-----!---(— (Яр)- — (Qp cos Ф)еР +
P«cos<p I dtp d<pv r p
, 1 [ dP
4— 7—
P
7" (Яр) еФ + -!— (Q p cos ip) — еФ,
df I p cos ф I df d<p I
далее,
2
X = Pep 4- Qe9 4- 7?еФ шх = Ppa cos ф dq» Д dip 4-
+ Qpdip Д dp 4- Rp cos ipdp Д dy,
откуда
2 / A A
d»x= I — (Pp2 cos ф)4- 7- (<?p) +
\ op oq>
d \ 3
+ — (я P cos ф) dp Д dq> Дdl|) = шdlvx,
0>p /
так что, учитывая, что
3 f
(Of ~ ------7 »
r p^cosy
имеем
divX =---------- (2pcosib «P + p’cosib • —=4-
P* cos Ф *y T T dp ~
. dQ . , dR • t
+ p— +pcostb----------рэшф -Ki
<9(p d? I ’
что дает представление дивергенции в сферических координатах
divX=—+-Р4-—^- + - ——7?.
df р р cos ф dtp р d<J> р
Вспоминая* что Д/ = div grad f, имеем в сферических коор-
динатах
d/o &>=¥-(!? + ^-dtf +^-di|) =
dp d<y dtp
1
^grad /o^>
~(grad/o 3a=^eP4-------+
\ dp p cosy dtp
, 1 df \
+ “ 77 еФ I t. e.
P J
521
&f° & = div f^eP+—7^?;e<₽+ J =
I dp p cosy dtp P dy j
d fdf \ , 2 df , 1 d ( 1 df \ ,
I j “j— — ~f" - — |-I |“
Эр-------------------------------I dp-j p Эр p cos f dtp I p cos f dtp I
. 1 d /1 ЭЦ tgf df
p df \ p df i p2 df ’
что дает представление лапласиана в сферических координатах
д/« +
dp2 р dp р2 cos2 f dtp2 p2 df2 p2 df
Замечание о вычислении градиента, дивергенции, ротора и
лапласиана в криволинейных ортогональных системах координат
в R3. Рассмотрим С(1) диффеоморфизм
Ф :CcR; 9-КС|СЧ.,г
считая, что {i, j, к} стандартный ортонормированный базис в
В3 . “
* Ж, yt Z
Положим
Ф * (X, y, Z) to)) y[tl> ^2’ ^з)» ^(^1> ^2’ <з))-
Тогда
Пусть
системы
detD<D(7) =-^’<(()Vte=G.
d(^i, ^2, ^з)
выполнено условие ортогональности криволинейной
координат (fx> /2, г2), так что
/^, ^.\ = 0, k^l,
I dtk dti I
где
. 5Ф. = дх i ду_ . _|_dz_k_x (/=1, 2, 3),
dti dti dtt*^ oti 1 1 V л
причем {e1( e2, e8} — ортонормированный базис в В^у г« Тогда
/ ЭФ ЭФ \ > л t ч > 9 s 1 \
F’ ЯГ W (ei’
I иц О1[ /
dz \2\ 1/2
где функции
__/ /ЭФ дФ \\ 1/2 _ / / dx \2
1 I I dtj ’ dti I j I I di; I
называются координатными параметрами Ламе. Вспоминая опре-
деление элемента 3-объема
522
D<t,(t)= det
l i, j=l, 2, 3
из гл. 2, § 2 и используя ортогональность касательных векторов
(1=1, 2, 3),
oh
имеем
dxA^Arfzf-y-Ф, -2-Ф, -7-Ф^
I (7<1 С^2 0^3 I
=£>Ф(7) = -д{х’ у' z}~ (t) = ws,
Wi, tt, M
так что
^хд^А^М-ф, £-ф, ~ф\ =
I utl dt$ j
= X1kaX3 /\ dy Ad2(en ^2»
откуда
dx /\ dy /\dz(fix, e2, c3) = 1 ^>03
и поэтому тройка ортов {ei, е2, ез} ориентирована так же, как и
тройка координатных ортов {i, j, к} в R* ^z.
Рассмотрим числовую функцию f(x, у. г)^С<У) ($), тогда, ис-
пользуя теорему о производной сложной функции, имеем
df df о Ф df dx . df dy .dfdz
dtk dtk dx dth dy dtk dz dtk
= ( grad f о ф А <И =Xfe(grad / о ф, ej,
у dtk j
так что
(grad/о ф, eR) = (lAk)g-,
dlh
откуда получаем представление для градиента в криволинейной
ортонормированной системе координат (t\, t2, h)
grad f о Ф = У(1Ай)^ел
k—i л
и> в частности,
gradtfc = (l/Aft)eft (k = \, 2, 3).
Но тогда получаем
523
I
1 1
dtk = ^grad tk ~
т. e.
причем
Но тогда
Л*~(1/Ч)е* (* = <• 2, 3),
<(h) = (grad tk, h) = (1/Xfc) (ek, h) v h <= Rft.
1
df ° Ф = cograd /0 Ф ~ grad f о ф,
df о Ф(Ь) = (grad fo ф, h) = V <1/A*) £ ftk.
dtk
причем
Аналогично имеем соответствия причем
dlk(Pi) - (grad ej) + (VM(ek, e;) = (1Ак)8«,
t. e-
М*к(е/)=А; (ft, /«=1,2, 3).
Но тем самым показано, что тройка 1-форм {МА> М/», ^з^з)
является сопряженным базисом к базису {ei, е» е,}.
Теперь введем соответствие между векторными полями и
1-формами
з j з
а = 2 Аей~шА= 2 Ak^h^>
6=1 6=1
так что
I з з
«>А(Ь)= 2 Ak\k dtM = 2 АЧ • (l/4)ftk - (A, h).
6=1 А=1
Очевидно, имеем также
t з з
«> = 2 Лл^*~А = 2 (WMr
а=1 6=1
Отметим, что введенные соответствия между 1-формами и век- .
торными полями инвариантны относительно ортогональных преоб-
разований, поскольку подобной инвариантностью обладает скаляр-
ное произведение в евклидовом пространстве R3. Аналогично вве-
дем соответствия между векторными полями и 2-формами
е1==[е2Лез]~ (Ы^)Л (М^з),
е2Н>зЛе1]~ (А<^з) А(ММ.
e3=[eiAe2]~'(Mfi)A(^2),
L
524
так что
3 2
А =2 Ад и>д = ХаX3dfa А Лз Ч*
А=1
+ AaX3X1dz3 A dti + А3ХА2 dti A dt3,
а также
2
о = Аг dt2 /\dt3 + A2dt3 /\dtx + A3dtr /\dt2~ к
= ex + e2 + e3,
Х2Хз kgki XiXf
причем
i
e3)== (Xirf/i) A (^2^2) A ty3dtз)(в1, e2, e3) =
z/\dt3{^ e2, e3)=dx/\dy/\dz(eb ea, e3)=l
и аналогично
®e2(e3, е1) = шез(е1, е2)= 1.
Наконец соответствие между скалярными полями и 3-формами
вводится следующим образом:
1 ~dxA^Arfz=M&2MfiA^2A<#3,
так что
3
f = 0 j
а также
3 £
^=fdtx/\di%/\dt^-^—-
лхЛз^з
Но тогда
3 i з
А =2 Агвг—Оа = 2 AiiKdti) И
i=r i=I
I 3 1 ( д
й(ХММ^=7Т иг(кзЛз)-
Л2Л3 \dt2
- 57-М.Й (y 3dtt^dt3) + £(£ М) -
и*3 у ^зМ. otз
~ Мз)^ зЛ^1) 4- ГТ (М2) -
Vtl / АдЛз I
д \ 3
— —- (^1^1) I (XjXjd^iA^ 2)= “rot А»
525
так что для ротора векторного поля в ортогональной системе кри- |
волинейных координат (Л, 1ч, 1з) с ортонормированный базисом
{еь е3) получаем представление
rot А = J- (Х3Д3) - (ЪАг)\ е» +
А2Л3 \ (7*2 <"3 I
+ ГГ(^-^“^-(Х3А^е2 +
Л34. I 013 dti I
+ п-(т7-(М2)-7;-(М1Йез-
Л1Л2 I vfl (/tg /
Далее, в силу соответствия
з
А = 2 ге, ~ «>а
1=1
и, поскольку
do)A=(Ddiv А — ^(Л1Х2^з)Л^2Л^З 4" ^(^1^2^з)А^зА dti -Г
+ Л dti Л dt3 = (Л1Х2Х3) 4- 4-
+ (XiX3'A3) dt1/\dt2/\dt3^. f—- (AiXjXj) 4-
OI3 j Л1Л2Л3 I
+ — (^i«42X3) + ~ (^1/2 АзХ^х^зМ/iA dt% Д dtz,
012 OI3
имеем для дивергенции векторного поля в криволинейной ортого-
нальной системе координат представление
div А = - Г— + — (\А2^з) + — (^i ^2^3)V
Л1Л2Л.3 I ot^ 01% UI3 /
Наконец, поскольку Af=kliv grad f, то для лапласиана числовой
функции f(x, у, ) при выполнении условия ФеС<2>(б)
получаем представление
д/о ф =—1— (— • -^Л4-
XiXaXg I dti I kj dti j
, a /kgki # an . э /XxX, . 0f_\\
dt^ X2 dts j dta у X3 dt3 j у
Заметим, что для сферических координат (р, <р, ф), очевидно,
имеем fi=p, #2=ф> ^з=ф, ei=eP, е2^еф, ез=еф, Xisl, X2=pcosi|>,
Хз=р.
526
_______J
Пример (вычисление градиента, дивергенции, ротора и ла-
пласиана в цилиндрических координатах).
Рассмотрим цилиндрические координаты в R3 у г, задаваемые
С<°°) диффеоморфизмом Ф : й={(г, ф, г) |0<г<’+’оо, 0<ф<2л,
—oo<z<4-oo)c:R3 у г ->-®(Q)=R3 ф z \F, где F={(x, у, z)\x^
АО, z/=0, —oo<z<4*°o}- Тогда имеем
' x=rcos <p,
• //=Г8Шф
, г=г, причем det®(г, ф, z)=r>0,
Эгф=е/=созф1+8.тф] — орт, направленный вдоль радиуса век-
тора ОМ' (где О=|(0, 0, 0), М=(х, у, z), М'=>(х, у, 0)) в сторону
возрастания г, ПфФ=!геф, где е„='—8Шф14-со8ф| — орт, направ-
ленный в сторону возрастания ф вдоль параллели z=const,
Dz®=e2sk — орт, направленный в сторону возрастания z и па-
раллельный оси Oz. Упорядоченный базис {ег, еФ, ег} ортонормиро-
ван в R3. у г , причем
dx/\dyf\dz(er, е»,- ег) =rdr/\d<p/\dz(er, еФ, ег) = 1.
Как было доказано ранее 1-формы dr, rdq> и dz являются коорди-
натными 1-формами в базисе {ег, еФ, е2}, причем имеют место соот-
ветствия
dr~er, rd<f~e,„ dz~ez=k
и тогда
grad е, + еФ + ^- е2.
дг г дф dz
Пусть X=Per+Qe„4-7?ez — векторное поле класса С(1), тогда в ци-
линдрических координатах имеют место соответствия
1
Х~ (an==Pdr^rQrd<f+R.dz
и поскольку
dr^е,3)=-1е2,
dq> А ~ еч>Де2= ег,
dzAdr~e2Aer=e?,
ТО
2
X ~ ox—Prdq/\dz+Qdz/\dr+Rrdrftd<p9
з
f~fdx/\dyj\dz=f о OrdrAdcpAdzs©/,
откуда
527
2 3
di v X ~ d ®xs ® div x
и поэтому выражение дивергенции векторного поля в цилиндра-
ческих координатах имеет вид
3 *
div Х~ ©div х=^©х=
=d (rPd(p/\dz+Qdz/\dr-}-rRdr/\d(p) =
_/«L + ^ + ^)\ .1
I dr dqp dz j r
= f- ((rP) + \ ) rdr/\d<f /\ dz,
\r\dr dq I dz j
так что
divx=±/>+^+2?+«
г \ оф J or dz
Далее,
1 2
rot X x
и поэтому выражение ротора векторного поля X в цилиндричес-
ких координатах имеет вид
2 1
rot X ©rot х—dax—1
=d(Pdr-]-rQd(p-L-Rdz) = .
1 д/ (Ич>)Л <К+ ¥dz Д dr +(rQ)drA(rd(p) +
г Оф I uZ г or
+ dz/\ (r dtp) + ~ dr/\dz+1 (rd<p) Д dz.
oz or r Off
Ho drf\(rd<p) '-'Cz,
frd<p) /\dz~er,
dz/\dr~ev,
так что
rotX=
e
r dff dz J r
Наконец, для лапласиана функции feC(a> в цилиндрических коор*
динатах имеем выражение
Af=div(gradf),
528
откуда, используя полученное ранее выражение для дивергенции
векторного поля, имеем
Д/о <p = div/^-er +-^-еФ + ^-ег W
I dr г дф dz
==ir±/rf?L\ + ± /1 + =
г dr I dr I дф I г дф 11 dz®
+±^L + ?V+1^L
дг® “Г г® дф» ~ dz* ~r dz '
§ 7. Теорема Гаусса — Остроградского в R”
Рассмотрим п векторов Х<1>, ..., Х<п> из Rn, тогда, вспоминая
аналитическую геометрию, видим, что
vn=dx1A... Л^п{Х(1), .... х<«)}
есть n-объем параллелепипеда, построенного на этих векторах. Да-
лее, если Xt1), ..., X<n-*)eRn, то векторным произведением этих
п— 1 векторов (при и^З) называется вектор
def
z=[x<>>л - AX(n-I)]>
удовлетворяющий условию
л
22'г< =
Yt ху К2 . . • Yn . ; *<*>
Л2 . . х<»-"
v YeR.,
так что
(Z, Y) =rfxiA... AdXnfy, Х<>>.....X<«-‘)}=<v„.
Очевидно, имеем
X? • • • . ху
Х<в-‘) . . . Х<?~У Х‘171
1 г—1 г-|-1 п
и если {еь е2, еп} канонический базис в Rn, то
ех е2
Z -= Х«) Д1) 1(7.1)
Х(п-1) х<«-‘) Xt-1) •
Заметим, что обозначение Z=(X<*)A — ЛХ(п-1>] имеет смысл
лишь при п^З, однако формула (7.1) имеет смысл и при п=2,
тогда
34— Л. И. Камынин
529
Z = ei ®2 = [X]
xs
{чем мы уже пользовались в гл. 1, § 4 и в гл. 2, § 4). Далее, пра
линейно независимых векторах ..., Х<п-1> они определяют
(п—1)-мерное линейное (векторное) подпространство En-i в Rn и
тогда (Z, Y)=0 V т. е. вектор Z ортогонален подпростран-
ству En-i. Кроме того,
dxi/\ ... A^n{Z, Х(’>, X<«-1)}=-(Z, Z)>0,
так что упорядоченная система векторов {Z, Х*1), ..., Х<п-1)} ори-
ентирована в Rn так же, как система координатных ортов
{еь е2..еп} в Rn, поскольку
dXiA - Л<**п{еь е2, .... е„}=1>0.
Более того, поскольку
Vn=dx1A...A^n{Z, Х<*>, ..., Х<«-1>}
есть объем параллелепипеда, построенного на векторах {Z, Х<1>, ....
..., Х<п-1>} и поскольку вектор Z ортогонален £n-i, то vn—
=JZ| -vn-lt где vn-i — объем параллелепипеда, построенного на
векторах {Х<>>, Х^-»)}. Но v„-|Z| •pn_1= (Z, Z), т.е. (Z, Z)==
=|V (Z, Z)-on-i, откуда If (Z, Z)=iPft-i, так что величина
|Z|=I|[X<‘>A...AX(«-1>]|
равна (n—1)-объему параллелепипеда, построенного на векторах
{Х<’>...ХС”-1»} при п>3. При n—2 |Z| есть длина вектора Х(1>
(|Z|=.|X(‘)|).
Рассмотрим теперь гладкий (п—1)-путь ср в Rn
<р: UczR?-' r=<p('l7)c:R",
так что
x.=jtpf(?b tn-i) 2, .... я),
где <ргеС<» (U). Поскольку матрица Якоби
(D;q>f(f)) (i—1, 2, .... n; / = 1, .... n— 1)
имеет ранг п—1, то векторы Diq>(Y), ..., Dn-i<p(Zh лежащие в каса-
тельном (к (и—1)-пути <р) пространстве. ТГ(<>(Г), линейно незави-
симы и определяют касательную гиперплоскость к носи-
телю r=q(U) в точке <р(7)(=Г. Положим
N=[D!<pA -ADn-Kp]
при п^З и
n=| е’ |=(/(U -•‘'(т
I X'(t) y'(t) I
530
при П=2 (где <f>(t)=i(x(t), y(t))). Тогда при »=ч=1, 2, п
*> (1),
a(h, , *я-1)
причем в силу геометрического смысла N=[Di<pA... ADn-i<p] име-
ем при п^З
|N[2= у (у =
1 ^1. «2,..., /„_!> Ч>|
. и при п = 2
|N|« = (4О)‘ + (У'(0)2 = |DqW^ D>(t),
п
так что N=iSArt-ei есть вектор направленной нормали к Т,(о(Г) в.
i=I
в точке <р(10€Г и для его направляющих косинусов имеем при
п>3
cos(N, ха = (-1)*-> . *«+«•• "Л*?. (t)/D9(t),
°(*!,•••> *»>•••, *П-1)
причем система векторов {N, Di<p, Dn-i<p} ориентирована как
система координатных ортов {еь в2, ...» еп) в R». (Случай п—2
был разобран ранее, в гл. 1 и 2, § 4).
Замечание. Если <р: t/czR^-1 -*•r=<p(l/)czR^ — гладкий
(п—1)-путь в RJh
п-1 "
i = l
• • • /\ dXi—I /\ dx i-j-j /\ • • . /\ dxn
— дифференциальная (п—1)-форма класса С (Г), то при п^З имеем
у Vfx)=J . . у (ф*ш) (0 =
Ф и
= - л» ф(о •
и i=l
.у . .уз А о 4(t) .
и i=t
• *cos(N, x^(t) • D^(t)dtx . . . dtn-i^
= (_l)n-iy3 ♦ cos(N, Xi)dS.
34*
53i
Определение (сравните § 3). Компактное множество
КаКп называется компактом с краем дК класса С(1>, если оно об-
ладает свойствами: 1) компактное множество дК есть граница ком-
пакта К в Rn; 2) для любой точки М0^дК существует окрестность
V(M0)czR,n такая, что множество Т—дК(\У(М0) является носите,
лем некоторого гладкого (класса С<*>) (п—\}-пути (Жордана) <р
в Rn, причем V(7W0)\r=V(1)UV(2\ где открытые множества V(1> и
У<2> связны в Rn и V<»czK, V^cCK.
Замечание 1. В силу теоремы о ранге (из § 3) край дК,
очевидно, является (п—1)-мерным компактным многообразием
класса С<’> в R”.
Замечание 2, Если компакт K<=Rn связен, то его край дК
может и не быть связным в Rn.
Замечание 3 (об ориентации края дК компакта К). Уело-
О
вие 2) означает, что в окрестности любой точки края дК точки К
лежат «по одну сторону» от края дК, а точки СК лежат «по дру-
гую сторону» от дК, что позволяет ориентировать край дК с по-
мощью внешней (относительно К) нормали (сравните § 3). В си-
лу условия 2) для любой точки М0^дК существуют окрестность
V(Mo) и гладкий (п—1)-путь Жордана
Ф: t/cR;-‘ -> =адV(M0)
такой, что отображение ф является гомеоморфизмом, <p^C<l>(U)
и ранг матрицы Якоби (Б/ф,(/)) (i=il, 2.n; j=il, 2, ..., п—1)
равен (п—l)VfeZ7, так что касательные векторы {D^(0, ....
..., Dn-iq>(?)} линейно независимы и являются упорядоченным ба-
зисом в ориентированном касательном пространстве Тф(#> (Г). Но
тогда можно ввести направленную нормаль
М„=[©1фЛ - ЛВп-1ф},
ортогональную ТФ((>(Г) и такую, что {N,, В1ф, ..., Оп-1ф}~
~{еь ..., еп) в Rn. Множество Г=<МПУ(М>.) является носителем
как (л—4)-пути ф, так и противоположного (п—1)-пути (—ф) с
направленной нормалью М_ф=‘—N,. В силу условия 2)
гзгУСОиус2), где открытые множества №> и У<2> связны в Rn и
V^czK, V(2)oCX. Будем считать, что Г (т. е. край дК) в окрест-
ности ориентирован выбором того из двух противоположных
(п—1)-путей, для которого направленная нормаль входит в
Край дК является компактным множеством (в Rn), поэ-
тому из открытого его покрытия dKcz. (J V(Mq) можно выбрать
конечное подпокрытие {Vi^V(Mi); i=il, 2, ..., tn} такое, что
m
дК с U V,. Будем считать, что край дК ориентирован с помощью
О
внешней (относительно К) нормали, если в каждой из окрестно-
532
стей Vi множество Г,=^КПК- является носителем (п—1)-пути ф/,
для которого направленная нормаль N?. «входит» в С/С. Пока-
жем, что введенная таким образом ориентация края дК не зависит
от выбора открытого покрытия {V,; i=l, 2, т). Рассмотрим лю-
р
бое другое покрытие края U 1Г;оо/С, определяющее ориентацию
края в окрестности Wt- с помощью (п—1)-пути ф/ с направленной
нормалью N,y , внешней относительно /С. Пусть Ма&)К, причем
так что (см. условие 2)) множество Гц—дКХ]Вц,
является носителем (п—1)-путей ср, и в окрестности Вц, но тог-
да обе направленные нормали и N.^ входят в С/С, что озна-
чает, что в окрестности Вц. Таким образом, ориентация
края дК с помощью внешней (относительно /С) нормали определе-
на корректно. Край дК, снабженный указанной ориентацией (с по-
мощью внешней нормали), будем называть ориентированным
краем компакта К в Rn.
Замечание 4 (об определении интеграла от (п—1)-формы
на ориентированном крае компакта в R"). Рассмотрим компакт
7Cc:Rn с гладким краем <5/С, ориентированным с помощью внешней
О Л—1
(относительно К) нормали, и (и—1)-форму а>(х) класса С(дК).
m
Пусть дК. cz J Vi, где {V,; (=='1, 2, .... т} — открытое (в Rn) покры-
тие дК, причем гладкий (п—1)-путь ф/ из условия 2) определения
края является представителем (п—1)-поверхности Ф(- с носителем
Г1=^/СПК;. Рассмотрим разбиение единицы {ki(x); i=il, 2, ..., т}
класса С<~> для компактного множества дК, подчиненное открыто-
му покрытию {Vi- i=l, 2, ..., т}, так что suppX<c:V/Vj и
т
2Х((х)=4 V xed/С. Имея в виду теоремы 1 и 3 из § 2, положим
г—1
гг—1 def т ~ л—1 m л—1
J <0 • «*> ^2 f • °) • (7-2>
дК i=l фг 1=1 дК
Докажем, что определение (7.2) корректно (т. е. не зависит от вы-
р
бора разбиения единицы для дК.). Пусть дК. cz U W, и {щ(х);
i=i
]=Л, 2, ..., р} — разбиение единицы для дК, подчиненное открыто-
му покрытию {Wj-, j = l, 2, ..., р}, так что supp m^.Wj V j и
2 Pi(x) =il V xed/C.
/=1
Но тогда
X<(x) =|SXi(x) |*/(x) v xed/Cflsupptacd/CflK-,
533
причем supp (Хгц/)с:У<П^/- Учитывая, что в силу замечания 3
Ф;=ЧГ/ в окрестности ViQW/ имеем
. л—1 Р Л л—1 р Л—1
j • • = 2) h • w ’ • s 2 J • ь • • .
дК J=i /=1 дК
откуда, суммируя по i, получаем равенство
т „ n—1 т р А п-1
S fXi ’ ш = S S J Xi *w • c7-3)
i=l dK Z-=l /-=1 dK
Аналогично,
л—1 m Л л—I m n— I
\ I*/ ♦ ® = 2 J S 3 J
dK i—1 ф» i=i dK
откуда, суммируя no j, получаем равенство
Р я-1 Р rn п_г
S J -“=s 3 Р' Р-4)
/—1 дК i*=l i=i дК
Сравнивая (7.3) и (7.4), получаем корректность определения (7.2).
Теорема Гаусса — Остроградского (для компакта
с гладким краем в Rn). Пусть KcRn — компакт с гладким (клас-
са С^) краем дК, ориентированным с помощью внешней (относи-
тельно К.) нормали, и
П&(х) =iS (— 1)»-М,(х)</Х1А... Adx/_IAdx(+1A - A^n
i-1
In—\)-форма класса C(K) /\С^(К), причем DtAi^B(K)
(it j =il, 2.n). Тогда имеет место формула Гаусса — Остроград-
ского
Л п—1 Л п—1
co = со (7.5)
дК К
или
f 2 (—l)"-i • A,(x)dxiA...A^i-iA^z+i A-A^n =
= (—I)”-1 ♦ [2 DiAi(x)dXi /\-/\ dxn.
К t=l
Доказательство. Пусть KczRn — компакт с гладким ори-
ентированным краем дК класса С(1>. Рассмотрим открытое по*
m
крытие dKcz lJ Vi края дК из замечания 3 и положим
i— 1
534
<rR"~‘rI=kpI(t7J=<3/CnK, где q>< — гладкий (n—1)-путь Жор-
m
дана в Rn, так что, в частности, Тогда дКа J Г/ я в
led
силу теоремы Сарда (при т—п— 1<п) из ч. V, гл. 1, § 3 для мно-
жества Г/=кр('£Л) имеем mesr,-==0 (i—1, 2. т), так что для
п
границы дК компакта Kc:Rn имеем mesdK—О, и поскольку мно-
п
жество дК компактно, то |дК|п=|0. Таким образом, доказано,
что множество К измеримо по Жордану в Rn. Поскольку DfAt^
<=В(К)/\С(К), то, полагая D/4<(x) =0 V х<=дК, имеем D/XjS
&R(K) V i, j, т. е. существует интеграл Римана
I d(n='S .. J S (—...dxn,
К К i=l
стоящий справа в (7.5).
Дальнейшее доказательство теоремы Гаусса — Остроградского бу-
дем проводить по схеме доказательства 2-й основной теоремы Гри-
на (для компакта с краем на плоскости) из ч. VI, гл. 2, § 2.
Определение. Открытый параллелепипед 7псРЛ, построен-
ный на ортонормированием упорядоченном базисе {Г... 1П}~
~{еь ...» еп} в Rn, называется К-специальным, если он удовлетво-
ряет одному из следующих 2 условий: а) /п[)дК==0 или б) /ПП
Р<?К=Г, где множество Г=<р(С/) является носителем (п—\)-пути
Жордана <р : I/cR/*-1-»- r=<p(’t/)c:R" класса Сб\ направленная
нормаль которого N„=[DI<pA — ADn-i<p] является внешней (отно-
сительно К) и составляет острые углы с ортами 1(.1П, т. е. для
cosa;=cos(Nv, 1/) имеем 0<а/<л/2 (/=1, 2, ..., п).
Исследуем более подробно, что означает выполнение условия
б) для K-специального параллелепипеда (К-с. п.) /nc:R". Очевид-
но, при выполнении условия б) любая прямая, параллельная орту
1* (где k=l или k=2, ..., или k=n), пересекает носитель Г лишь
в одной точке, при этом после собственного движения Р~\ состоя-
щего из поворота, совмещающего базис {h, ..., 1п} (в R{J) с базисом
{ei, .... еп} (в R"), и сдвига, параллелепипед Jn переходит в брус
P-1(Jnj_/n(o, a)czR", а множество Р~*(Г) становится графиком
(в новых координатах и=(щ, ..., ип)) функции un=un(ui, ...,
..., «n_J. Точнее,
Р-’(Г)=дГП/л(О, а) ={(«!, .... ип)^1п (0, а)|
0<И1<аь 0<и2<.и2(щ), ....
<Un-i(Uj, ..., Un—2), Un^=Un(Ui, ..., Un—1_)},
где функции и{(и\, ..., Щ-i) класса С& при i=2, 3, ..., п. Рассмот-
рим направленную нормаль к Р~1 (Г)
535
v=v«(u)=I!DiOA - ADn-iO]=i(vi. Vn),
где
«•: (“ь .... «п-1) -* («ь Mn-i, un(ui, un.t)),
тогда
+ ^- • ln (i = 1, 2, . . . , n—1),
так что базис
{D^...Dn-HO ~ Hi, ...» ln-i}
(поскольку определитель матрицы перехода равен 1), причем
1У-.. “ж--, м
иг... ип_^
И
V<> = (_])->-! . !—п , . . . , Jff»-, —А
tdui dan_j }
В силу определения векторного произведения
{v®, Dj#, .... Dn-l'O'} ~ {h, ..., ln-1, In}
и тогда имеем
{v®, DiO, Dn-i^} ~ {v®, li, ln-i}~
~(-l)”-I {ll...................ln-1, vj ~ {lb .... In},
t. e.
01...ln-1, (—{It...............In}.
Но орт ln является внешним для компакта Р~1(К) в любой точке
и&Р-'^Г), поэтому вектор P-1N== (—l)n-1-v®(«), составляющий
острый угол с ортом In, также будет внешним по отношению к
компакту Р~Ч(К) в любой точке иеР-1 (Г). Итак, Вектор
p-iNs=(-l)n-3 ,-----^,1^
\ Э“1 дип-1 )
является внешней (по отношению к Р~1(К)) нормалью к графику
Р-1(Г). Но из условия б) следует, что внешняя нормаль N к Г
составляет острые углы с ребрами бруса 1п (0, а), т. е.
536
откуда в силу теоремы (о неявной функции) из [1], ч. III, гл. 2,
§ 9 видим, что носитель Р-1 (Г) одновременно является графиком
каждой из функций ..., Щ-i, ui+1, .... ип) класса С(*>, где
1==1, или i=2, ..., или i=n (см. рис. 37).
Лемма (о существовании /(-специального параллелепипеда).
Если KcR" компакт с гладким (класса С(!)) краем дК, ориенти-
рованным с помощью внешней (относительно К) нормали, то для
любой точки X$g=K существует К-с. п. JnaR.n такой, что хое/и.
Доказательство. 1) Пусть Хо^К, тогда существует окрест-
ность 1ЩП) (х0)с:К и поэтому существует даже открытый брус
1п(х0) с центром в точке х0 такой, что 1п(х0)с1К. Но тогда
1п(хо)(]дК=10, т. е. открытый брус 1п(хо) является К-с. п.
2) Пусть х0&)К. Тогда в силу условия 2) определения края
существует окрестность Ш(вп> (х0) такая, что множество Г=<?КП
QI1I <а',) (х0) есть носитель гладкого (класса С(1)) (п—1)-пути <р в-
R”, причем, поскольку отображение <р осуществляет гомеоморфизм
t/cR/-1 на r=<p((/)c:R", то ф-1еС(Г), т. е. для внешней (отно-
сительно К) нормали N('x) = N^f) имеем NeC(T). Но для норма-
ли N(x0)sN<P(?,) всегда существует ортонормированный базис
{h...In) ~ {еь ..., еп) такой, что нормаль N(x0) составляет острые
углы с ортами 1Ь 12, ..., 1п- В силу непрерывности поля нормалей
N(x) на Г шар 1ЩЯ) (х0) можно выбрать столь малым, что внеш-
О
няя (относительно К) нормаль N(x) составляет острые углы с
каждым из ортов 1* (&=‘1» 2, ..., п) в любой точке хеГ=дКП
ПШ^> (х#). После собственного движения Р~1 (поворота, совме-
щающего базис {11, ..., к} с базисом {е1( ..., еп} и сдвига) в силу
теоремы о ранге (из § 3), при-
мененной к краю дК в точке х»е
*=дК, видим, что в новых коор-
динатах («1...ип) существует
окрестность (брус) 1п (0, а), в
которой множество dKf\In (0, а)
(в новых координатах и) явля-
йся графиком функции
“п—an(u\, ..., ип—i},
и'~(щ.... Ы„-1)ей,
гДе Q .== pr p-i(г), причем
«я—о
Нешняя (по отношению к ком-
пакту P-i(tf) в
R”) нормаль к
(Г) имеет вид
P~»N = f——я, . . . , (УиеР-ЦГ))
d«i dun-t I
« образует острые углы с ортами li, 1п, так что
un j >Q Vu,eQ (/=1,2,..., п-1).
dui
Но тогда в силу теоремы (о неявной функции) уравнения
«п(Ы1, «2, 0, ..., 0)=0, «п (иь «2, и3, 0......0) =
.... ..., Ып-1)=0
•определяют функции «/(иь ..., u»-i) (i=2, 3, .... п—1) класса СЮ
такие, что за счет уменьшения бруса 1п (0, а) можно считать, что
носитель Г=дК|У" {0, а) (в новых координатах и) имеет пред-
ставление
Р-1 (Г) ={(«ь .... un)e/n(0, a)|0<«i‘<ai,
0<U2<«2(«l), 0<Ип-Г<Ып-1(«1...«п-2?,
Mn=un(Ui....мп-1)Н{(“1.....Un)eZn(0, a) |u'=
=<(Ui...Un = un(u')},
где !
Q = рг Р-1 (Г) ={(«', 0)е=
“Л=°
е/п(0, a)n(un=0}|0<Ui<ai, 0<
<и2<и2(и1)<а2......0<un_i<
<«„_!<«!...un-2)<an-i}.
Но тогда брус /”(0, а) (а стало быть, и его прообраз Jn относи-
тельно собственного движения Р~1, содержащий точку х0) есть
К-с. п.
Итак, в силу нашей леммы для любой точки М<=К существует
•открытый К-с. п. 1п(М), содержащий точку М, так что
AcU Jn(M). В силу компактности множества К из этого откры-
лся
того покрытия можно выбрать конечное открытое подпокрытие
m
U Рассмотрим разбиение единицы {%/(Х); /=1, 2, ..., /п}дл*
компакта К, подчиненное открытому его покрытию (J"; .......
..... т}. Тогда suppX/ciZ/,’V / и
ZK,(M)=A vJWeK.
$38
рассмотрим (n—1)-форму
а, (х) -Цх) • ш(х) =2 (—l)n-i •
i=I
* Вц(х)d,X\/\ • • • /\dxt—i/\dXi^.{/\ . • • /\dxn,
Btj(x)=Kj(x)-Ai(x) (i=l, 2, n;
/='1, 2, .... m)v;ceK.
Тогда в силу условий теоремы Гаусса — Остроградского имеем
ВуеССЮДООСК) (i=l, 2..............п; /=1, 2,..., т),
^e=C(K)AS(K) V i, j, k,
дхк
причем функции Вц финитны: supp и
supp с j; П*°.
dxk
Заметим, что по условию теоремы
DkBij^B(K) (i, k—A, n; j=I, m),
поэтому, доопределяя функции нулем на дК, будем иметь
supp ЪкВцС11?(]К. и
DkBij^(K(]Jf). (i, 6=1, 2.................n).
Скажем, что (n—1)-форма а/ имеет компактный носитель
72—1
supp а; cz/^f|/C. Очевидно, и п-форма
daj=(—1)n~l • 2 DiBij(x)dx1/\.../\dxn
i=l
л—1
также имеет компактный носитель suppda/c= Поскольку
л—1 п—1 m п—1
f -2 J <“ =2 j
дК 7=1 дК /=1 dKnjn
и
539
л Л~! п 1т п—1\ m _ П—1
Jdu>=Cd|2^/’0)j = 2 ( ai’
к к \/=i / /=1 кп/?
то для доказательства формулы Гаусса — Остроградского доста-
точно доказать равенства
л—1 л—I
J а^= J daj vj. (7.6>
dKdJ* K[\Jf
Лемма (формула Гаусса — Остроградского для К-с. п.).
Пусть Jn К-с. п. для компакта К с ориентированным гладким кра-
ем дК и
л—1 п
г=1
* • • • dxi—i/\dXi4-i/\ • • • /\dxn (7*1)
п—~1
(n—\)-форма с компактным носителем supp а <zJn(\KczJn, для
которой
В^С(КМп)ЛС^(К(]/п)
и ВкВ^С(КМп)ЛВ(КМп)
(так, что после доопределения D*B;(x)=0 V х&>К) имеем
DkBi^R(K(]Jn). Тогда имеет место формула Гаусса — Остроград-
ского (7.6) (где
л-1
Доказательство. 1) Пусть 1п(\дК—>8, тогда supp а с
° Л—1 ° п—1
и suppd а с=.1п<=.К, так что supp а Г1<?л=0, т. е,
J а —0. Вспоминая доказательство леммы (о существования
dJCnj"
К-с. п.), можно считать, что Jn=ln(a, b) — открытый брус (с реб-
рами, параллельными координатным осям в R"). Поскольку
dna(x) =2(-1)"-1 • dxiA • • • А^л. (7.8>
$=={ 4
то доказательство можно проводить, например, для п-формы
^OdXiA • • • А^п-
дхп
Рассмотрим интеграл
540
J Z -®n /\ • • • /\ n*
KnZ"(a.b) °X"
Поскольку
supp /- Bn cz Г(а, b) az К
ОХц
и /«(a, b)=In~1(a', b')X(an, bn),
то
Bn(x', an)=Bn(x', bn)=Qyx'&Jn~l(a', b'),
поэтому в силу теоремы Фубини (для бруса) из ч. V, гл. 2, § 2 и
теоремы Ньютона — Лейбница (для кусочно-непрерывной функ-
ции) из [1], ч. II, гл. 2, § 6 имеем в виду условия
^Впе=С(1п(а, Ь))/\В(1п(а, Ь)),
охп
i л,А...Л^п- J -J ®
КлАа, Ъ) п 1П(а, Ь) ° п
“ У ‘ J T~Bn(x)dx1. . . dxn =
2«[а. Ы дХп
bj Ь, ьп &
=== J dx^dx^..^ Вп(х, xn)dxni
а, а, ап п
—1 У j <Вп(х » 6П) -- Вп(х , лп))dx j... dxn-1 — О»
/"-‘la', »')
т. е. в случае а) для К-с. п. Jn имеет место формула (7.6) в про-
стейшем виде
(* п-1 Г п-1
j d а =0= J а .
KftJn dK[}Jn
2) Пусть теперь 1п(\дК='0 (случай б) для К-с. п. Jn). Рас-
смотрим собственное движение (поворот и сдвиг) Р~1 в R", с по-
мощью которого К-с. п. Jn переходит в открытый брус 1п (0, а).
Тогда аффинное невырожденное отображение Р является диф-
феоморфизмом класса (У°°\ для которого
detP(w)sl, DP=P, detDP-Hx)-!, DP-^P"1.
Отображение P-1 переводит компакт К с гладким краем дК из
Л* в компакт Р~*(К) с гладким краем dP~i(K)—P~1(dK) в RJJ,
пРичем внешняя (относительно К) нормаль N к краю дК, перехо-
дит во внешнюю (относительно Р~*(К)) нормаль P-1N к краю
541
дР-{(К) = Р~1(дК) (так что ориентация края дК с помощью внеш-
ней нормали переходит в ориентацию края дР~1(К.) также с по-
мощью внешней нормали). Рассмотрим гладкий (л—1)-путь.
<р: U -* r=<5/Cf)Jn в R" с ориентированным касательным простран-
ством ТФ(Г), тогда, учитывая, что Р~1(7п)=7п(0, а), видим, что
Р-‘»Ф: U -> Р-1 (Г) =дР~1 (0, а)
является гладким (л—1)-путем в с касательным простран-
ством Тр-1оФ(Р-1 (Г))=Р—1 (ТФ(Г)), ориентация которого индуци-
рована ориентацией ТФ(Г) при изоморфизме Р-1. Используя схему
w— 1
i видим, что прообразом (л—1)-формы а , определенной надмно-
жестве TczR™, при отображении Р будет (л—1)-форма Р* а , оп-
ределенная на множестве /’-1(r)cR", так что
»п-1 [* п-1
! I а = .) Р* а.
Г Р-1 (Г)=д/»-1иГ)л/п(0. а)
Поскольку отображение Р класса С<2>, то в силу теоремы (о пере-
становочности операций * и d) из гл. 2, § 1 имеем равенство
Р* (d a"*) =d(P* o’1) vxeP"1 (Kf)/n) ='
=P-1('Wn(0, а).
Используя схему 5
/Cn/ni/’-1('Kn/n)=P-1Wn/n.(O, а)
р
и учитывая, что | det Pl = detP=l, имеем
(• п—1 г л—1
J da = J P*d а =
КП/п=Р(р-1(К)л/П(0.а>) Л-Икл/”)
f п -1
= J d(P* а ).
р-1(К)л/Л(0. а)
Таким образом, нужно доказать равенство
Р П—1 р /2—1
J ~ J.
i Р-1(К)Л/Я(О. а) ЙР-1(К)П/я(0, а
| 542
где
V - Р*Ла = 2 (-!)«-* Bt о Pdxi° Р/\ . . .
г=1
. . . /\dxi-! о PAdxi+i о Р/\ . .. /\dxn° Р
есть (и—1)-форма класса
С(Р-'(ЮЛ/П(О, а))
с компактным носителем
supp р сР-1('К)П/п(0, а),
а
d7 = (— I)""1 • 2 DtB° Р . dX1o Р/\-/\(1хяо Р
i=t
есть «-форма с компактным носителем
suppd р cz/n(0, а)[\Р~'(к)
и для которой
D.S ° РеС(7"(0, a)ftP-'(K))/\B(In(0, а)(\Р~1(К)),
так что, доопределяя эти функции нулем на дР~*(К.)(\1п(0, а),.
имеем
D,B»P6=P(7»(0, а)(]Р~1(К)).
п—1
Но вспоминая условия нашей леммы о гладкости форм а и
п—1
d а , видим, что без ограничения общности можно было с самого-
начала рассмотрения случая б) Jn(\dfa£0 предполагать, что
7nsZn(0, а), и тогда нужно доказать равенство
. - п-1
I d a zz I а
КП /”(«. в) ЙКП/”(О, в)
или, имея в виду представления (7.7) и (7.8) для наших форм, до-
статочно доказать, например, равенство
(_i)n-i J ABntzxxA-A^n =
КпАо. а)ах»
e J • • • /\dxn^\. (7.9у
dKnl"(0. в)
543
Заметим, что в силу /(-специальности бруса 7п(0, а) имеем
Г==<5Я|Уп(0, а)~{х—(х', xn)(=In(Q, а)|х'ей, хп=х^(х')},
где
Й=рг Г=(х' = (хь .... xn-i) |
V=°
0<Xi<ab 0<x2<x2(xi)<а2, 0<
*^.Хп—1<ХП—i(Xj, Хп_2^ <^0^—1}>
причем функции х^х1, ..., хг1) класса С(1> при i=2, 3,.... п и
внешняя (для компакта К) нормаль
Л(х) ,-----^5-, Л
\ °Х1 дхп-1 ]
составляют острые углы с координатными ортами ei, еп, так что
— ^?>0 (|-1, 2,..., п— 1),
дхг
т. е. компакт К находится «под» краем дК в брусе /п'(0, а). Но
тогда край Г=<?/СП^Л(О, а) является носителем следующего
(п—1)-пути О в R" (класса : Q с: R"r‘ -*-Гс R",. где
й(х) = (хь .... хп_ь хп(хь .... Xn_J),
так что для касательных векторов имеем представления
D/tffx)—ez+D(xn en (i=l, 2.n—1), т. e.
= (-1 )n~l DMA... ADn-!«> (-1)«-1 vo(x)•
Но тогда в качестве гомеоморфизма <р, ориентирующего край
Г=дКТУп(О, а), в выбранной ориентации края (с помощью внеш-
ней нормали) нужно взять <р—(—l)n-1 ft, так что <р*=(—1)п-1-О.
Но тогда, используя теорему Фубини (для цилиндроидов из ч. V,
гл. 2, § 2), имеем
J BndxiA = •
дКл!Л(0, а)
• J BndX1 А ... Л dxn-i = (-1Г-‘ •
&
. j-p*(BflJxlA.-.A^n-i)=
= (-D— J • Р» ................dxi
544
at x2(xi)
*n—xn_i)
• • • j Xn -1’ ^n—-1))dx^*••d’Xn—!•
0
С другой стороны, вспоминая, что ориентация К в Rn совпадает со
стандартной ориентацией R™ (с помощью упорядоченного канони-
ческого базиса {вь еп}), используя теорему Фубини (для цилин-
дроидов) и формулу Ньютона — Лейбница для кусочно-непрерыв-
ной функции
ОпВпеОДПРЦО, а))АВ(КП/п(0, а))
(где DnBne/?(Kn^n[0, а]), если функцию DnBn доопределить ну-
лем на д/<П/п[0, а]) и учитывая, что
supp DnBnczK(]In (0, а),
имеем
.I Цг Вп dx. Kftln(0. а) = ( •[ — Вп(х) - at x2(Xi) х (Xi),.... = J dx. J dx.. . . f 0 0 6 = j dx. . . . f 0 6 — Bn(x', ty)dxn_ (Xi,xn—o) /\ . • . dx n —> ^-^dx1...dxn = t»• • • > Xfl) - Bn(x > xn)dxn oxn хл(хь..., Xn-1))~ O1 -i — | dx± , . . 0
I =(-l)n-1 J ‘ dK[\In(Qt a) Л- И. Камынин Bn(x', xn(x')) dx„^ = Bndx./^\ . • . A dxn—i» 545
поскольку из условия supp Вп<^1п (0, а) имеем Вп (х', 0) =
=0 V х'ей, Итак, равенство (7.9), а вместе с тем и лемма о фор-
муле Гаусса — Остроградского для К-с. п. доказана. Из доказан-
ной леммы вытекает и основная формула Гаусса — Остроградского
(7.5).
Следствие (формула Гаусса — Остроградского в терминах
поверхностных интегралов 1-го рода). Пусть выполнены все усло-
вия теоремы Гаусса — Остроградского для компакта К с гладким
краем дК, ориентированным с помощью внешней (относительно
компакта К) нормали N(x). Тогда из замечания (в начале § 7) о
записи интеграла (п—1)-формы по (п—1)-пути в виде интеграла
1-го рода, примененного к формуле (7.5), получаем формулу Гаус-
са — Остроградского в виде
л ,
f V - А{(х) dxY/\ . . Д dxn «=
= f S Ai(x) • cos(N, Xi)dS.
dK i= I
Замечание. Полагая в доказанной теореме Гаусса — Остро-
градского п=3, получаем теорему Гаусса —Остроградского (для
компакта с гладким краем в R3) из гл. 2, § 3; полагая л=2, полу-
чаем 2-ю основную теорему Грина из гл. 2, § 2 для плоского ком-
пакта с гладким (но не кусочно-гладким) краем.
§ 8. Интегрирование 6-форм на 6-мерных
дифференцируемых ориентируемых многообразиях в R"
В ч. VI, гл. 2, § 3 была доказана теорема о ранге и дано опре-
деление дифференцируемого 6-мерного многообразия М, вложен-
ного в Rn (k^n) класса C(Z) (1^1). Введем на множестве AfcR”
топологию, индуцированную топологией R”, положив: (множество
Vc~M открыто в М) -*=> (существует открытое в Rn множество W
такое, что У=Л1Г|ТГ (при этом определено и понятие замкнутого
множества в Л1)). Отметим, что для множества КаМ граница дК
(в М) множества К не будет границей К, как множества из Rn, по-
скольку при k<n границей Кв Rn будет множество К=>К.
Замечание. Пусть AlczR” является дифференцируемым
6-мерным многообразием, вложенным в Rn (k^n), класса
(Г>1). Поскольку в Rn существует счетная база (окрестностей), то
из теоремы о ранге следует существование не более чем счетной
+00
системы открытых (в Л4) множеств {V({ (М = U Vi), обладающих
г=1
свойствами:
546
а) для любой окрестности У,сЛ1 существует гомеоморфизм
ф/: УгсЛ4cR\
где Ut — открытое множество (6-мерный шар, 6-мерный брус) в
Rft;
б) если Vif)Vj^0, то гомеоморфизм
Фо—Ф/ ° ФГ1 : Фг(КПVj) <=R*->
-*Ф/(КЛ V/)c:Rh
является диффеоморфизмом класса С(/>.
Пара {Vt, ф() называется картой, а совокупность всех карт
{(Vi, Ф<); i=il, 2, ...} называется атласом многообразия AfczR”.
Гомеоморфизм ф,-: У,-cAf-*•£/,-с: Rfc называется координатным ото-
бражением (или локальной системой координат в окрестности У,)г
а окрестность Угэх0 называется координатной окрестностью точки
Хо^М. Обратный гомеоморфизм
ф“‘=Ф<: UidRh -*• Vi—fti(Ui)cMczRn
является гладким (класса C(Z)) 6-путем Жордана и называется па-
раметризацией окрестности ViczM (см. диаграмму)
Докажем утверждения а) и б) нашего замечания.
В силу свойству 3) теоремы о ранге (из ч. VI, гл. 2, § 3) для точки-
*о&Л1 существуют окрестности VicAfcR" и I7,c:Rft и гладкий
6-путь Жордана (класса С(/>)
ф/: tAazR^V^/Ct/OaJHcR;
такой, что
Ф^ФГ1 • V/cMcRJ-’-t/iCRj’
есть гомеоморфизм, так что выполнено свойство а) замечания.
Далее, если Хо^УгПУ/ и ф/, ф/ — соответствующие 6-пути Жор-
Дана, то в силу свойства 1) теоремы о ранге существует диффео-
морфизм класса (W
35* 54?
ф: FcR"->- Q=iif>(lFjc:R"
такой, что
ф(хь)==О и С=ф(Л4ПЮ=^П{!/л+1=0, .... t/n=0}.
Но тогда отображение
%,з=ф«фг: t/.-cR^-»- б,=ф(Л!ПУ»)=|
=Xi(Ui)C2^, ,
,(где у'=(уь ..., ук)) будет отображением класса
Cm(Ui) .... tk)+y’(t) =
=‘(yi(t), .... Vh(t)).
Но для диффеоморфизма феС^С^) производная Эф-1 (у)e
eSJ(R", R£) есть изоморфизм, а потому ее сужение на R*,Di|r1 (у')
имеет ранг kVy'^G. Поскольку X(R^, R") имеет также
ранг kvt^Ui, то для композиции %(=1ф°ф»еС(/>(17,) видим, что
производная Dta(7)e^(R*, R£,) имеет ранг k, так что
det DX/t) = (t)^0vte=Ut.
fk>
Тем самым доказано, что отображения
Xi: UidRf -+Xi(Ui)a:H.b, и
являются диффеоморфизмами класса С(,).
Для диффеоморфизма Хе~1 ° Xi имеем представление
Х?1о ^Ф-Ч^П^Ф-Ч^П^).
но
х-1 о хг=(ф о ф/)- 1 о (ф о фО^фТ1 О (ф-‘ о ф) о ф{=з
def
= ф-'о ф; = ф,о ф-1=ф0,
так что показано, что отображение
548
есть диффеоморфизм класса С(/). Итак, свойство б) нашего заме-
чания также выполнено. Более того, поскольку
фг=ф/ о (Хт* о Л,) = ф/ ° ф,7,
то переход от параметризации <р/ к параметризации <рг- на
У/ПУ/ совершается с помощью диффеоморфизма ф(;- класса. С(;\ $
частности, если det Бфг;-(7);>0, то фд1~ф;-, если же detВф,;(7)<б,
то ф<=Н-ф/.
Из теоремы о ранге § 7 и сделанного замечания вытекает
Определение. Множество МсRn называется дифференци-
руемым k-мерным многообразием, вложенным в Rn (k^.n) класса
С(|> (/^1), если в каждой точке М выполнены свойства 1)—3)
теоремы о ранге (из § 7) и существует атлас {(Vi, ф<); i—1, 2,...}
4-оо
такой, что М =i J Vi и для гомеоморфизмов ф(-, ф,/ имеют место
г=1
свойства а) и б) замечания.
Определение. Пусть МcRn — дифференцируемое k-мер-
ное многообразие, вложенное в Rn класса C(v> и Sc.M,
Тогда S называется s-мерным подмногообразием (многообразия
М) (при s^Zkt^n), если выполнены два условия-.
1) S есть дифференцируемое s-мерное многообразие, вложенное
в Rn, класса С^\
2) для любой точки xa<=SczM существует карта (V, ф) много-
образия М такая, что ф: V<^M -> t/cRft, где U — открытый k-мер-
ный шар (брус) в R* и сужение ф| vnS:
V|-)S->t/n{te^s+1=O, ..., ^0}=да)сН’
есть гомеоморфизм, так что пара СИЛЗ, ф|уп8) является картой
для многообразия S.
Замечание. Итак, если SczM есть s-мерное подмногообразие
(класса С('>) 6-мерного многообразия М, вложенного в Rn
(s^6^n), класса (Л>1), то существует такой атлас {(Vi, ф>);
1==4, 2, ...} для многообразия М, что {(КЛЗ, ф»|у.п5); i=:l, 2, ...}
есть атлас для s-мерного многообразия 5, причем если {7iCzRk
есть открытый ft-мерный шар (брус) в R*, то множество
ф/('КП5)='ад^{//|/4+1=0, .... ^=0}
549
есть открытый s-мерный шар (брус) в R®, при этом карта (Vi, ф£)
для многообразия М определяет такую локальную систему коор-
динат (t\, ..., tk) в Vi, что множество «SQV, задается в ней системой
уравнений кн=0, —, 6i=0, в то время как ..., ts) являются
локальными координатами карты (V/QS, ф/|к£пз).
Замечание. Если AfcRn есть дифференцируемое 6-мерное
многообразие, вложенное в Rn (k^.n), класса C(Z) (£^1), то в Rn
существует атлас {(Vi, ф,)} такой, что М имеет (как подмногообра-
зие Rn) атлас {(УДМ, ф/|т\пл< ); i—1, 2, ...}, причем (см. теорему
о ранге): 1) для гомеоморфизма
ф»: V/czR£-*17/c:Rf
(где Ut — «-мерный открытый шар (брус) в R^) множество
ф4(Т,ПМ)=^Ж+1=0, tn=O}=G
есть открытый 6-мерный шар (брус) в Rfe;
2) сужение
: Г = V» П М <= R^ G£ с R*
есть гомеоморфизм из карты (KflAf, ф(-|у.пм ) атласа М\
3) если ф,- — гомеоморфизм, обратный к координатному гомео-
морфизму ф<|у{Пм. то отображение
Ф»: G,c:R»->!;•= VrflMcR»
есть отображение класса C(Z) (/^1) с матрицей Якоби, имеющей
ранг k, для любой точки t^Gi (т. е. ф/ есть 6-путь Жордана клас-
са C(Z) в Rn с носителем Г»=V’/ifl-MczR’1).
Замечание. Если AfcRn есть дифференцируемое 6-мерное
многообразие в Rn, то его атлас можно записать в виде
{(VM ф9; 1=1, 2, ...},
где гомеоморфизм
фг: GroJ?*-* Г,-=IWW R’
есть параметризация окрестности У/ПЛТ, являющаяся гладким
(класса C<z>, Z>1) 6-путем Жордана в Rn с носителем Г(=КП^>.
при этом если
550
У^У,(]М^0.
то гомеоморфизм
Ф/-'»Ф.:С;ПФГ1 (МЖ)-
-О/Пф^ПВД
является диффеоморфизмом класса С(г>.
Замечание. Если a=((Vff]Af, <р,); i=I, 2, ...} есть атлас для
дифференцируемого (класса Cw, f>l) 6-мерного многообразия М,
вложенного в Rn (k^n), и
0/: ^,c=R^rc=iVinAfc:R"
есть 6-путь в R” класса С(/) такой, что либо <И~ф/, либо &»='—ф/,
то система карт &={(У,ПМ> i=il, 2, ...} является атласом для
того же многообразия М. При этом диффеоморфное преобразова-
ние параметра от т к t, для которого 0',-=.ф,- °будет С(;>-диффео-
морфизмом с якобианом detD^(x), отличным от нуля.
Замечание. Если AfczRn — компактное многообразие из
Rn (так что множество М компактно в R”), то атлас {(<р»)}
для него можно считать конечным (t=l, 2, ..., tn).
Введем теперь понятие (неориентированного) касательного
пространства ТХ(ЛГ) для любой точки xeAf 6-мерного дифференци-
руемого многообразия М (вложенного в Rn) следующим образом.
Если Хц^М, то существует окрестность V(x0) из Rn и параметри-
зация
<р : GczR* r=AfflV(Xo')c=Rn
такая, что х0=ф('/о) и ф является гладким 6-путем Жордана в R"
(класса С(г), /^1). Но тогда (см. ч. VI, гл. 1, § 1) определено (не-
ориентированное) 6-мерное касательное пространство Тф(/,) (Г),
причем в силу теоремы из ч. VI, гл. 1, § 1 это 6-мерное линейное
пространство не зависит от выбора параметризации ф многообра-
dot
зия М в окрестности V(x0) точки х0^Л1. Положим Тх, (М) =
=!Т<г(«,) (Г) и будем называть ТХ(Л1) касательным пространством
для многообразия М в точке xeAf.
Замечание. Пусть М есть 6-мерное дифференцируемое мно-
гообразие, вложенное в Rn (б^п) класса C(i) (^1). Тогда для лю-
бой точки х0^М существует окрестность V(x0)oRn такая, что
множество Г= У(л«)(1М является носителем гладкого 6-пути Жор-
дана ф: GczR&-*rcRn в R". В то же время множество Г=
7= является носителем и противоположного 6-пути
<р=|—ф, который получается из 6-пути ф диффеоморфной заменой
параметра с отрицательным якобианом, причем для точки х0=
=ф(!/'о,)=ф(то) касательные пространства (Г) и Т~(т) (Г)
551
совпадают (как 6-мерные пространства) с Т*о (М), но имеют про*
тивоположную ориентацию. Таким образом, упорядоченные базисы
{Di<p(7y, .... Dk<p(t0)}
и {Di<p(To), Dfc<p(T0)}
задают противоположные ориентации касательного пространства
Тх, (М), а потому переводятся друг в друга с помощью линейного
преобразования с отрицательным определителем. Пусть
{(УаПАТ, фг); i=l, 2, ...} — атлас ^-мерного дифференцируемого
многообразия М из Rn (k^.n). Тогда гомеоморфизм
<pz: G;czRft^r(i=<P/GO = AfnVicR’’
определяет ориентацию касательного пространства
def
Тф(0(Г) = Тх(Х)
для любой точки х=кр(О^Г/, т. е. определяет ориентацию ТЖ(Л1)
(ориентацию многообразия М) в окрестности Vi. Скажем, что ат-
лас {(фг); ь=<1, 2.......} определяет ориентацию многообразия
М (ориентацию касательного пространства ТХ(М)), если для лю-
бой пары карт (K(W, фд) и (V/Л-М, <р;) этого атласа гомеомор-
физмы ф/ и <р/ задают одну и ту же ориентацию многообразия М
(ориентацию касательного пространства ТХ(М)) в каждой точке
хеГ/ПГ/, т. е. £-пути (в Rn)
Ф/: ОгЛфГ1 (Г/ПГ/)^-^ПГ/cR»
и Ф/: G/Пфг' (Г<ПГ/) ^ППГ/cR"
эквивалентны так, что диффеоморфизм (преобразование парамет-
ра)
Ф“‘ ° ф.- : С£Пфг1 (Г/ПГ/)-*О/Лф71.(Г.ПГ/)
имеет положительный якобиан
у^О.-ПфгЧППГ/).
Заметим, что, если атлас {(КЛЛ1, ф(); i=l, 2, ...} определяет ори-
ентацию многообразия М в Rn (т. е. ориентацию касательного
пространства то атлас
{(КПМ, (—ФО); *='1> 2,...}
определяет противоположную ориентацию многообразия М в R”.
Определение, k-мерное дифференцируемое многообразие
М, вложенное в Rn (k^n), класса С<0 (£>1) называется ориенти-
руемым, если для него существует атлас {(1ЛЛ-М, ф,); i=l, 2, ...},
определяющий ориентацию М,.
552
Замечание. Не всякое ^-мерное дифференцируемое многооб-
разие М в R” ориентируемо, даже если оно связно. Типичным
примером не ориентируемого многообразия является лист Мёбиуса.
Замечание. Итак, ориентированное дифференцируемое
(класса С<0, 1^1) ^-мерное многообразие М, вложенное в Rn
(k^n), состоит из многообразия М и ориентаций, выбранных для
каждого касательного пространства Tx(Af), причем для любой
точки Хо^М существует окрестность V(xq) в R" и параметризация
Ф: Gc?Rfe->r=Mf| VfxojcR"
такая, что V х=ф(7)|=Г изоморфизм
переводит выбранную ориентацию касательного пространства
в стандартную ориентацию линейного пространства Rft, за-
даваемую каноническим упорядоченным базисом {еь ..., е*} (где
ей=|(0, .... О, 1, 0, ..., 0) Vi).
Замечание. Если ^-мерное дифференцируемое многообра-
зие Л!, вложенное в Rn (k^n), связно и ориентируемо, то оно име-
ет в точности две ориентации, соответствующие двум (противопо-
ложно) ориентированным многообразиям М и М.
Замечание. Пусть а={(Kfl-Al, ф<); i=l, 2, ...} является ат-
ласом, определяющим ориентацию (ориентированного) ^-мерного
дифференцируемого многообразия М, вложенного в Rn (k^n)r
класса С(/) ((^1). Пусть
Ф: G,c:R‘-*V4n-M=rIc:Rn —
ft-путь класса С(/) из атласа а и
to: ^,-cR* ->r;=to(^)cR« —
ft-путь в Rn класса C(Z), причем 0/~ф(- и — диффеомор-
физм класса СЮ, определяющий допустимое преобразование пара-
метра (от т к t), так что Од=|фг° t. Тогда det Ш’(т) >0 и система
^{(НПЯ toj); i='l, 2, ...}
является атласом для многообразия Af, определяющим ту же ори-
ентацию М, что и атлас а. Если же to=<—ф«, так что to=4>i °Л но-
detDi(r)<;0, то атлас
&=|{(У/ПЯ Of); »=il. 2, ...}
определяет на многообразии М противоположную ориентацию, т.е.
является атласом ориентированного многообразия М. Если М —
553
компактно в Rn, то атлас а ориентированного многообразия М
можно считать конечным, т. ё. а={(К("|Л4, q>(); 1=1, 2, т}.
В дальнейшем будем рассматривать только компактные ориен-
тированные ^-мерные дифференцируемые многообразия М в Rn
класса С<б (1^1). Пусть {(V/fW, ф/); /=il, 2... tn} — атлас М
и (л(х) — дифференциальная £-форма класса С^>(М), где
ф/: G/oR/-* V/f]Af=q)/(G/)czR"
есть &-путь в Rn класса С<0, соответствующий гомеоморфизму ф/
из атласа многообразия М и
k
<»(х) = 2 ^ii..ik(x)dXi1/\ . . ./\dxih.
A
Пусть {е,(х); /=1, 2, т} — разбиение единицы для множества
М класса С<’), подчиненное открытому покрытию {V/; /=1, 2, т}
(suppe/czV/Vj).
Определение. (Поверхностным) интегралом (2-го рода) от .
k-формы <а(х) по ориентированному k-мерному компактному диф-
ференцируемому многообразию М в Rn (ksSZn) называется число
(. k def m л j (0 = 2 Uj M f=lф/ k m (. k • “»= S.’ i=iGi
= S (6j° ф/^ • 4^0. ф7(^ . /==1 G. 5 (ф^> • • •, Ti0) ' “W ГГ- (t)dtl • • dt>- (8.1)
k ь
Замечание. Определение интеграла S w от fe-формы <о на
©
компактном ^-мерном дифференцируемом ориентированном много-
образии М (из Rn, k^n) с атласом {(V/П^И, ф/); /=1, 2, ..., т}
корректно, поскольку: 1) для любого j функция
д (ф^\ • • •,
ej0 <fj(t) • 4..i « <Pi(t) • —у-----TT—V)
является непрерывной финитной функцией, интегрируемой по Ри*
ману на открытом множестве G/cR^; 2) в силу компактности мно-
гообразия М в равенстве (8.1) стоит сумма конечного числа
^-кратных интегралов Римана; 3) в силу теоремы 1 (об инвариант-
554
ности интеграла 2-го рода по £-пути относительно допустимой за-
мены параметра) из ч. V, гл. 2, § 2 интеграл J ® не меняется при
м
замене атласа {(V/flAf, ф;); /=il, 2, т} на атлас {(У/ПМ, О/);
j=i\, 2, т}, если #/~ф;- для любого /.
Замечание. Вместо формулы (8.1), использующей разбиение
единицы при определении интеграла 2-го рода, можно пользовать-
L
ся представлением М = где Для V Mi существует окрест-
ность IV/(Z) такая, что и компактное множество (если
оно не пусто) 71т=Л11ПЛ1т лежит на подмногообразии (многооб-
разия М) размерности s<.k (O^s<k^.n). Тогда полагают
r>k * L k
f“=S f и=2 J • • Jv (8-2>
(корректность определения (8.2) будет следовать из доказываемой
в конце § 8 теоремы о равенстве нулю интеграла от й-формы по
любому s-мерному подмногообразию ^-мерного многообразия при
O^s<fe^n).
Пример. Пусть
н—1 п
• Л/х)£/Х1Л...ЛС?Х(Д...Л^Хп —
г— 1
(п—1)-форма класса С(0), определенная на ориентированной
(я—1)-мерной сфере Sn-i, где сфера (0) ориентиро-
вана так, что для любого xeSn_1 направленная нормаль N(x) ор-
тогональна касательному пространству Tx(Sn-i) и выбрана внеш-
ней по отношению к шару (0). Тогда имеем
Sn-i = S«-i iU'7>
гДе S+.-j и — соответственно верхняя и нижняя (открытая)
полусферы, а 7=Зп-1П{хп=0} — экватор сферы Sn-i- Поскольку
экватор у является подмногообразием сферы Sn-i размерности
<я—1, то имеем равенство
/2 — 1 Л—1 Л —I
Рассмотрим сначала каноническую параметризацию верхней полу-
сферы
555
s+ : Ш£-’)(0) CZ RJr1 -* S+ t c R",
задаваемую уравнением
/ л-l \ 1/2
Xn = \#z— 2 Л|| Vx' = (xv..., Xh-i) ё=
\ г=1 J
Тогда для касательных векторов имеем
D,-0+=ez+Ven (1=1, 2, п—1),
где
/ л-1 \1/2
Х{==-х(/[ •
Но базис {Di<>+, Dn-i^+} имеет относительно базиса (еь е2, ...,.
..., en-i) положительный (равный 1) определитель, поэтому каса-
тельная гиперплоскость 7\(S+_j) в точке x&S+_t ориентирована
базисом {DiO-i-.. Dn-i^+J, упорядоченным так же, как стандарт-
ный базис {еь ..., en-i) в R’r1. Но тогда направленная нормаль
N$+ ={р1й+Л ... ADn-itf+] такова, что базис {N^, Di<>+, ...»
..., Dn-iO+} или {N#+, еь ..., еп-!} ориентирован так же, как стан-
дартный базис {еь е2, ..., еп} в R’. Но базис {N#+, еь ..., en_J ори-
ентирован, как базис (—1)"-1-{еь ..., e„_i, N»+}, так что нормаль
N#+ образует с ортом еп острый угол при (—1)п-1=4-1 и тупой
угол (при (—1)п—*='—1. Но орт ея является внешним для шара
Ш^’(0) в любой точке x<=S+_t, поэтому N$+ (х) является внеш-
ней нормалью к S+.) при (— и внутренней нормалью к
при (—1)“-*='—1 (в точке xeS+_t). Но это означает, что
для гомеоморфизма <р+, определяющего Sj-i, нужно положить
<р+=|(—при этом, очевидно, имеем
(л-1 X 1/2
. (8-3>
г==1 / •
И
/ п-1 Ч 1/2
dxn = —(xidxx+ ...4-xrt_1dXn-i)/1 R2 — 2 xi I »
\ 4=1 /
так что
<p^_ (О (x') = (—I)”-1 • ®
= (—I)"-! • /+(Xi,..„ xn-i)dx1/\.../\dxn-i,
556
т. е.
л—1
f Ш (х) =(— I)"-1 • j . . . Jf+(xx.xn-.t)dx1...dxn-1.
i5+_, ш£-1)(0)
Аналогично для нижней полусферы имеем каноническую па-
раметризацию : Ul£-'>(0) с К"г‘ -> <= R",
где
(п-1 \ 1/2
Я2 — 2 ** , х' е Ш£-1>(0) (8.5)
£=1 /
И
л—1 , / л—1 \ 1/2
rf*i.= 2 / I я* - 2 xt I ’
<=i / \ i=i /
Nft_ = [DA.A...A Dn_^J, (8.6)
поэтому базис
{Ne_, DiO_, ....
~^_l)n-i.{ei> .... en_b Ne_}~{ei.en}.
Но орт en входит в шар Ш<’> (0) V xeS7_p поэтому нормаль
Ne_(x) будет внешней для шара Ш(”> (0) при (—l)”-^—1 и
внутренней при (—I)”-1 =4-1 (VxeS“_j). Таким образом, в ка-
честве гомеоморфизма, ориентирующего , нужно взять
<Р-=1(—l)”-#-, откуда ввиду (8.5), (8.6) имеем
л—1 л—1
ф*ф=-(—i)n-&2_fi>='
=*(— l)n f-(xi, ..., Xn-JdxjA ... Л</хп_ь
т. е.
п—1
J «) (х)=(— 1)л •[•••! f_(xi,...,xn_1)(Zx1...dxn-l.
^п-1
В частности, при п=3 имеем
2
o)=Ady/\dz-]-Bdz/\dx-^Cdx/\dy;
&+:(х, y)-z=(R2-x^-y^
dz=—(xdx+ydy) I (R2—x2—у2)}?
557
и
9~:(х, y)^z=—(R2—x2~y2yi2,
dz=(xdx-\-ydy)j (R2—x2—y2)l/2,
откуда
2
~~ 'dy^ (xdx+ydy) +
4-B- (xdx-\-ydy) f\dx)j(R2—x2—y2)^2+ Cdx/\dy=
=^C+(Ax+By)KR2-x2-y2mdx/\dy
и
2
<<o=(C-(Ax+By)l(R2-x2-y2) v2)dx/\dy,
т. e., полагая для сокращения записи
y=(R2—x2—y2)i/\
имеем
2
f «=(-1)2. J/ (C(X,y,V~) +
*s+
= (x • A(x, y, Y~~) +У • B(x, y, •/” ))/V~)dxdy
и
f ««(-I)». Я (C(x,y,-V~)-
x»+y‘<R‘
— (x • A(x, y, — V~) + у • B(x, y,—/“))//“) dxdy,
так что
fl=f ш+f J[ (C(x,y,y-)-
§: *s+ s-
— C(x, y, — V~) + (x • (Д(х, у, V~) + A(x, y, —/“)) +
+ У • (B(xt у,У~) + B(x, y, -V~)))//“)dxdy.
Определение. Пусть M — компактное дифференцируемое
k-мерное многообразие, вложенное в Rn (k^.n), класса CW (1^1)
с атласом {(V/ПМ ф/); /='1, 2, т} и {е7(х); /=1, 2, т} —
разбиение единицы, для М, подчиненное открытому покрытию
(Vj-, /=1, 2, m} (supp OjezVj v j). Тогда поверхностным интег-
ралом 1-го рода от функции f^.C(M) по (неориентированному)
многообразию М называется величина
558
dot m
f f<^=S f & * • DVl(t)dt2...dh,
м j=iG/
при этом величина
m i-
|Af|ft=f 1 -dS=% f e^t) • Dv(t)dtl...dtki
M i=i Gj '
называется k-объемом многообразия M в Rn.
Отметим некоторые свойства интегралов от 6-форм по 6-мер-
ным ориентированным компактным многообразиям, вложенным в
Rn (k^n), вытекающим из теорем 1—5 ч. VI, гл. 2, § 2 для интег-
ралов от биформ по 6-путям в Rn:
Теорема (о линейности интеграла). Пусть М — компактное
дифференцируемое k-мерное ориентированное многообразие, вло-
женное в Rn (k^.n), и и ©2 — k-формы класса С^(М). Тогда
для любых постоянных ci и с2 имеем
£fe Л Л k Л k
С1 *®1 + С2 -®2=С1 • £®1+С2 •]
м мм
Теорема (об ориентированности интеграла от биформы по
ориентированному дифференцируемому многообразию из Rn).
Пусть М иМ — компактные противоположно ориентированные
дифференцируемые k-мерные многообразия, вложенные в Rn
(k^n), с атласами {(V/f)Af, <р/); /=1, 2, .... ш} и {(V/fW> О/);
/=1, 2, ..., т} (где fy=i—<p/V£) соответственно. Пусть ш — k-фор-
ма класса С^(М). Тогда
С k г
j_ ©= _ ш.
м м
Теорема (об,инвариантности 6-объема 6-мерного многообра-
зия). Пусть М иМ — компактные противоположно ориентирован-
ные дифференцируемые k-мерные многообразия, вложенные в R”
(k^n). Тогда
Теорема (об оценках интегралов от 6-форм по 6-мерным
многообразиям). Пусть М — компактное ориентированное диффе-
ренцируемое k-мерное многообразие, вложенное в Rn (k^.n), и
k VI
©(>)=
<г^п
559
k-форма класса для которой имеют место оценки
(х) 1V х<=М и для любого (I). Тогда справедлива
оценка
I <• * I ь -
И> -L .
I м I
Доказательство всех сформулированных выше теорем провести
самостоятельно.
Следствие (из теоремы о ранге). Пусть AfczR" — ft-мерное
дифференцируемое многообразие, вложенное в R" (k^n), класса
С<0 (/>11), причем MeV, где VcR'J — открытое множество. Пусть
дан диффеоморфизм класса С(г> (V)
h: VcR" -> W=h(V)ceR".
Тогда:
1) h(M) есть ft-мерное дифференцируемое многообразие класса
С((> в R" (компактное, если М компактно), причем
) =Dft(x) (Тх(М)) V х<=М;
2) если М — ориентируемое многообразие и Ориентация М за-
дана атласом {(V/RM, <pz); i=il, 2, ...}, то многообразие h(M) так-
же ориентируемо и атлас
{&(Vt)fth(M), ftocpi); /=1, 2, ...}
определяет ориентацию h(M), причем диффеоморфизм h (точнее
изоморфизм Dh) сохраняет (на h(M)) ориентацию М, если якоби-
ан диффеоморфизма h положителен, и не сохраняет ориентации
М (на К(М)), если этот якобиан отрицателен.
Доказательство. Пусть {(ШШ, <pt) i=l, 2, ...} — атлас
ft-мерного многообразия М, вложенного в R" (k^n), класса С<1>
(/>1). Тогда для гомеоморфизма срг: GicR*-> VipAfcR" имеем
qneC(l>(Gi). Поскольку диффеоморфизм Л биективен, то
h(Vif)M)==h(Vi)(]h(M) и, кроме того, множество Wi=h(Vi).
как диффеоморфный образ открытого множества, открыто в RJ.
Рассмотрим гомеоморфизм
h»фг: GjCR* -> h(ViQM) = ЧП(М).
Поскольку
D (ft»Ф() (0 =Dft (<рг CQ) о Dq>/(7),
причем Dh(x) : Rn->Rn — изоморфизм, а отображение <р,- имеет
матрицу Якоби ранга ft, то Л ° <pteC<Z)(Gj) и матрица Якоби ото*
бражения Л ° <рг также имеет ранг ft. Применяя теорему о ранге, ви*
560
дим, что А»фу есть гладкий (класса С<г>) A-путь Жордана в RJJ,
так что:
а) отображение (Аоф,)-1: IFya:R"->Gyc:R* есть гомеоморфизм.
Далее, если Wi(}Wj{]h(M)=^0, то в силу биективности диффео-
морфизма h имеем
WW/ЛЛ (М) =Ь(У{)(]Н(У1)ПЬ(М)=
т. е. Vi(\Vj=:'0 и в силу согласования карт (Vi, фу) и (Уу, фу) ат-
ласа многообразия М отображение фг1 о фу (как было замечено
ранее) является диффеоморфизмом класса С<г> с неравным нулю
якобианом. Рассмотрим отображение
б)
(h о фу)-1 о (ft»ф,.) : G,f| (А»фу)-1 (W)IF/П
f|A(Af))->Gyf| (ft о фу)(FyflWf(]h(M))
(т-/(т)).
Но
(А о фу)-1 о (ft о фу) =
=ф-‘ » fft-1 ° h) о (pi—y-' о фуеС</)(Оу)
является диффеоморфизмом класса С<г>. В силу выполнения
свойств а) и б) видим, что h(M) является A-мерным дифференци-
руемым многообразием, вложенным в R" (k^n) класса C<z>
(СХ1) с атласом {(UTyflAfM), й°фу); i=l, 2, В курсе диффе-
ренциальной геометрии (сравните, например, [7]) доказывается
что для касательных пространств многообразий М и h(M) имеем
(попробуйте доказать это самостоятельно, используя рассмотрения
из ч. VI, гл. 1, § 1)
Thw(h(M))=Dh(x) (T4AI)) V хеМ.
Далее, если М ориентируемо и ориентация М определена атласом
{(ИП-М, <ру); 1=1, 2, ...}, то в силу согласования карт (УуПТИ, фу) и
(VyQAf, фу) (при Vif]Vf()My=0) имеем фу~фу и (как было отмече-
но ранее) диффеоморфизм ф-1офу класса С<*> имеет положитель-
ный якобиан и определяет переход от параметризации фу к фу, так
что ф/==фу о (ф-i о ф£). Но тогда для соответствующих карт
(WW, Йо фу) и (Wf(\h(M), h»cpi) (при Wi[\Wi{\h(M)^0)
видим, что отображение из б) (А ° фу)-1 ° (h ° фу) ^ф;-1 ° фу. также
будет диффеоморфизмом класса С<г) с положительным якобианом,
определяющим переходом от параметризации ft® фу к ft ° фу
(так, что й ° фу~Л ° фу), и поэтому атлас {(1УуПА(Л1), Л ° фу);
|а=1, 2, ...} определяет ориентацию A-мерного многообразия А(М).
®6—Л. И. Камынин 561
Рассматривая изоморфизм Dh(x) : Tx(M)^-Th(X)(h(M)), видим, что
образ положительного (в смысле ориентации М) базиса касатель-
ного пространства ТЖ(Л4) будет положительным в уже ориентиро-
ванном касательном пространстве Th(X)(h(M)), если якобиан диф-
феоморфизма h положителен в точке х^М, и отрицателен, если
этот якобиан отрицателен.
Пусть SczM есть s-мерное подмногообразие ^-мерного диффе-
ренцируемого многообразия М, вложенного в Rn (k^.n), класса
C<z> (C^il) и s<zk^.n. Тогда существует такой атлас {(1ЛГ)Л4, <рг);
i==il, 2, ...} многообразия М, что фг: G,cjR* -> ViQAfczR", где G, —
й-мерный шар в R*, причем
ffi = Gjf|{fs4-i = 0, /fe=lO)
есть s-мерный шар в R4 и сужение гомеоморфизма на gt, т. е.
фх|^4 :giCzR’, ViQAfc:Rn
есть гомеоморфизм класса С(() из атласа {(V(-ftS, ); i—l, 2, ...}
подмногообразия М. Пусть i=il, 2, ...} — разбиение едини-
цы для М, подчиненное открытому покрытию
{У,-; 1=1, 2, ...} (suppe/czV/Vt).
Теорема. Пусть S является компактным s-мерным подмного-
образием компактного ориентированного k-мерного многообразия
М, вложенного в Rn (k^n), класса (£>1) и а(х) — k-форма ;
класса С^(М). Тогда при 0^s<& имеем |S|s=0 и
с k def m г k
.1 <*> = 5 J Ф/Vj • u>) = 0.
s’ l=i«i
Доказательство. Имеем
k def m k
f “ = 3 j • <4
S /=1 Si
HO
k
f Ф*(^ ’®)=f ’ • Je7°<P/(OX
X 2 А.Л°Ф/(Х) (Odh.-dt^o,
А
поскольку s-мерный шар g/=G/flVe+i=0> —> ^*=0} имеет в R/
^-мерный объем нуль при s<Zk. Аналогично имеем |S|*=0.
Теорема (о преобразовании интеграла с помощью диффео-
морфизма). Пусть ft: VczRj->W'=ft('V)czR; — диффеоморфизм
562
класса С(1> и <а(у) — k-форма класса C(W). Пусть MczV иМ —
компактное дифференцируемое k-мерное многообразие, вложенное
в R" класса С<*>, ориентированное с помощью атласа
{(УдПЛТ, ф,); 1=1, 2, ш}, и h(M) — компактное k-мерное (клас-
са С&) многообразие в RJ, ориентированное с помощью атласа
{h оф,); »=1> 2. •••> т).
где Wi-h(Vi). Полагая
__| h(M) при detDftfxJX) в V,
\h(M) при det D/i(X)<0 в V,
имеем
с с
<»= ч- Л*<о,
л(й) м
где знак «плюс» берется, если якобиан диффеоморфизма h поло-
жителен (т. е. если h сохраняет ориентацию М), и знак «минус» —
если этот якобиан отрицателен.
Доказательству. Пусть {ci(y); i=l, 2, .... m}— разбиение
единицы (класса С(‘>) для множества h(M), подчиненное открыто-
му покрытию {h(Vi); i=l, 2. m} (supp e.czftfK) v i). Посколь-
ку h — диффеоморфизм класса Сб\ то в силу теоремы (о разбие-
нии единицы индуцированным диффеоморфизмом) из [1], ч. III,
гл. 2, § 12 система {ei°h(x)-, i=l, 2, ... m} будет разбиением еди-
ницы для множества М, подчиненным открытому покрытию
{V/; i='l, 2.пг). Тогда
-km k
j ft*u) = 2 J ° Л •
м i=i Mav.
„km? k
_J_ ®= T, , J e‘ • ш-
МЛ1) i=l MAOnVTj
Но для
Ф,: Gi az R* —> Vt П M az R"
имеем
h о <pz: Gt <=. R* —> Wi f| h(M) a: R",
гДе Wi = h(Vi), и поэтому
fc k
_________________У ei •®=J (Ao Ф»)*(«1 • ®)
Gi
36*
563
для любого i. Но в силу теоремы (о свойствах операции ft* из
ч. VI, гл. 2, § 1 имеем
(ft ° <pz)*(e, -©) =<р* ° Л* (е, -®) =
=Ф* (в» ° Л -ft* со),
так что
k k def к
j е( • ® = j ф*(е, о ft • ft* о») = у е, о ft . ft*®,
S(MjnW{ °i
т. е.
к к
J ft*o> = J со,
м Г(ло
при этом
к к
у <в— у Ш,
л(7й) л(лб
если detDft(x)>0 в V и
к к к
у с» = у we — у И,
л(м) МЛН _ J 7Г(ЛГ>
если detDft(x)<0 в V.
§ 9. Общая теорема Стокса для ft-мерного компакта
с краем в Rn
В § 7 этой главы в пространстве Rn был введен компакт К с
ориентированным краем оК., являющимся (л—1)-мерным диффе-
ренцируемым ориентированным многообразием, вложенным в R”
<(л—1<я), класса О1) и для него доказана теорема Гаусса — Ос-
троградского (теорема Стокса). Теперь введем в рассмотрение
ift-мерный компакт К в Rn (ft^n) с ориентированным краем дК,
являющимся (ft—1)-мерным дифференцируемым многообразием,
вложенным в R”, класса С('>, и докажем для него соответствующую
теорему Стокса (сравните в случае п=3 и ft=2 ч. VI, гл. 2, § 4).
Прототипом ft-мерного компакта К в Rn с краем дК будет служить
нам ft-мерный шар /(=IIiyjr) (O)czAfsRftc:Rn с границей (в Rft=
={(хь ..., Xk, 0, ..., 0)}cRn) dK=Sk-i, являющейся (ft—1)-мерной
сферой (так что дК есть (ft—1)-мерное подмногообразие в М=
= RftcRn) (см. рис. 38, где
N(x)= (cos(N, xi)...cos (N, xs), 0..0)eRn
564
и нормаль N(x) ортогональна каса-
тельному пространству Тх (Sk-i), бу-
дучи внешней относительно шара
(0)).
Определение. Пусть —
k-мерное дифференцируемое многооб-
разие, вложенное в Rn (k<zn), клас-
са (1^1). Компактное множество
Kez М называется k-мерным компак-
том в Rn (при k<n) с краем дК, если
оно обладает следующими свойства-
ми: __
1) К=К, где KczKczM — внутрен-
ность множества К в топологии М (индуцированной топологией
объемлющего пространства R”) и край dKczK есть компактное
множество, являющееся границей множества К в топологии М;
2) для любой точки х0&>К существует окрестность У(х0) из
Rn такая, что множество Г=дК(]У(х») есть носитель некоторого
гладкого (класса С<1\ Z^l) (k—\)-пути Жордана <р в R”, причем
для окрестности U(x0) — V(x0)(]M (в топологии М) имеем
U(x0)\r=V<v>[)U<2'>czM, где открытые (в топологии М) множества
и Ut-2') связны (в М), причем U^czK, 27<2>cJH\K.
Замечание. В силу теоремы о ранге из ч. VI, гл. 2, § 7 край
дК, очевидно, является (k—1)-мерным компактным подмногообра-
зием (класса С(/>) ^-мерного многообразия М, вложенного в R”
(k—\<zk<.n), при этом КсМ является fc-мерным подмногообра-
зием (класса С(б) ^-мерного же многообразия М в Rn (напомним,
что «внутренность» К множества KazM берется в топологии М, а
не Rra). Но тогда, вспоминая теорему о ранге и применяя ее к мно-
гообразиям дК и М, видим, что для любой точки хое<?Кс:Л1с^п
(сравните § 8) существует окрестность V(x0)c?Rn и диффеомор-
физм (класса С(б)
ф: V(x0)c:R"-> BczR;,
где В—n-мерный открытый шар (или брус) в R* такой, что
ф(хо)=ОеВ и бе1Вф(х)>0 vxeV(x0),
причем выполнены следующие условия:
а) множество
t(V(xo)nM> = G=W*+i=0......2п=0}
есть й-мерный открытый шар (брус) в R,, и если Ф — гомеомор-
физм, обратный к координатному отображению ф1п*.)лл«’ то
отображение Ф: Gc=R*~> Vfx0)f)7Wc:R" есть гладкий (класса
565
C(Z>) 6-путь Жордана в R”, так что пара (V(x0)[\M, Ф) является ’ ।
картой для 6-мерного многообразия М, вложенного в Rn (k<.n)
класса С<0 (^1);
б) ф(Пхо)АК)=СП{А<0)==СПЯ, где H=R/’rn{^<0} - полу-
пространство с границей 5H=RJcr1 =ЯП{/1=0}, причем Ф : G[\Hc.
czR^->V(xo)D^czRx> так что пара (У(х0)ПКл Ф) является картой
О
для 6-мерного подмногообразия KcrAfa:Rn;
в) f(y(*o)ndK)i=g«d#f)G==iGn{fi==O}> причем, вводя обозна-
чения t' = (t2, tk) и ф(7')=Ф(0, Г)=ф|г, видим, что гомеомор-
физм
<p:GOdtf=gcR*-‘->r=
=дКП V(x0) аКс=Мс R"
есть гладкий (класса C(Z>) (k—1)-путь Жордана в Rn, а пара
(V(x0)(\dK, ф) является картой для (k—1)-мерного подмногообра-
зия дК. (класса С(/)) 6-мерного многообразия М, вложенного в
Rn (см. рис. 39).
Замечание. Если xa&)K(]V(x0) и (V(Xo)(W, Ф) —карта М,
a (V(xo)fl^K, ф) — карта дК, то любая точка х=Ф(7)еКПУ(хо)
имеет 6-мерное касательное пространство причем, посколь-
ку detDt|)('x)>0, то D®(7) : R^-’-TxfAl) есть изоморфизм, перено-
сящий на ТХ(М) ориентацию R*, так что ориентация T^fAf) зада-
ется упорядоченным базисом {Di®(7), ..., ВйФ(7)}, где ВлФ(7) =
=ОФ(/)е/ (i=l, 2,.... k) и {еь ..., е*.} — канонический базис в
R*. Далее, если х=ф(7') = Ф(0, t')&)Kf\V(xo), то
D<p(t’) : dH=R*~l - Тж(дК),
так что ТХ(<?К)=ОФ(0, f) (дН) есть (6—1)-мерное касательное
пространство, очевидно, являющееся
подпространством ТХ(Л1). Отметим,
что
Оф(Г)е?=ОФ(0, t')Ci^Tx(dK)
при i=i 2, 3, .... 6, так что система век- j
торов I
{D2<p(O, ..., МО}= ’
= {О2Ф(0, Г), ..., Dfe®(0, /')} I
является упорядоченным базисом в
ТЖ(<М), задающим в нем ориентацию,
согласованную (в силу построения) с
ориентацией ТХ(М). Заметим также,
что (6—1)-мерное подпространство
Тж(д/<) «делит» 6-мерное пространство !
ТЖ(Л1) на два полупространства, одно i
из которых Нф =бф(0, t') (Н) явля-
ется образом полупространства Н=>
566
=К?П{Л<0}, содержащего множество i|)(K(lV(x0)) =ЯП<?. Полу-
пространство НфсгТх(М) естественно назвать внутренним (отно-
сительно компакта К), а дополнительное к нему полупространство
ТХ(М)/НФ естественно назвать внешним (относительно К), при этом
касательный вектор Di<D(0, /')=ПФ(0, т. е. является
«внешним» для множества H(\G. Итак, базис
{Dj®(0, t'), Э2Ф(0, Г). О*Ф(0, Г}},
ориентирующий ТХ(М) (при х<=дК), состоит из вектора Di®(0, t')
внешнего (для компакта К) и из упорядоченного базиса
{D2<p(t').. 0йф(О}, ориентирующего Tx(dKj. Эти рассмотрения
приводят к следующему определению ориентированного края дК
компакта К, «лежащего» на ориентированном 6-мерном многооб-
разии М.
Определение. Пусть М — ориентированное дифференциру-
емое k-мерное многообразие, вложенное в Rn (6<п) класса
и КаМ. — k-мерный компакт с краем дК. Тогда для ори-
ентации дК нужно vx&)K выбрать в касательном пространстве
Тх(дК) такой упорядоченный базис {t2(x),tk(x)}, чтобы для (лю-
бого) внешнего (относительно компакта К) вектора v+(x)^Tx(M)
упорядоченный базис (v+(x), t2(x)> —> ik(x)} был положительным в
ориентированном пространстве ТХ(М) (см. рис. 40).
Рис. 40
Замечание. Еще раз напомним, что не следует смешивать
край d/fc/CcR” 6-мерного компакта К (при 6<п) с границей
множества К в R", которая просто совпадает с К.
Замечание. Условие 2) из определения компакта с краем
означает, что/в относительной окрестности U(х0) — V(Xq) (W (в М)
любой точки хае<?К точки самого компакта К лежат «по одну сто-
рону» края дК (на 6-многообразии М), а точки дополнения М\К
лежат «по другую сторону» края дК.
567
*3
Рис. 41
Замечание. Если компакт KczAf связен в Rn (а стало быть
и в М), то край дК, не обязан быть связным (см. рис. 41).
Важный пример. Пусть Мc:R3 и М есть ориентированное
2-многообразие класса С(Г> в R3 и KxzM есть 2-мерный компакт с
ориентированным краем класса C<z>. Очевидно, край дК явля-
ется гладким одномерным многообразием в R3. Тогда для любого
хоеК существует карта (V(xo)f|Af, Ф) многообразия М такая, что
гомеоморфизм
Ф : GcR3 я+V(x0)fWcR3
есть гладкий 2-путь Жордана в R3, имеющий V хеУ(хо)ПК
(х=Ф(и, v)), направленную нормаль N(x)=i[Du®ADt,®], так что
тройка {N(x), Du®, j, k), где {i, }, k} — стандартный
упорядоченный базис в объемлющем пространстве R3. Пусть
Хо&)К. Тогда относительная окрестность U(x0) = У(х0)ПЛ1 такова,
что U(x0)\dK. =(7<1>и{7(2>, где и £7<2>— связные компоненты
U(x0), причем UVcK=K\dK, а (7<2>сЛ1\К. Но Г=дКП^(х0)
есть носитель гладких 1-путей Жордана у и (—у) в R3, поэтому
можно говорить о касательной к Г в точке хеГ и о нормали v(x)
к Г, лежащей в касательной плоскости ТХ(М) к М в точке хеГс:
с=Л4. Если при этом нормаль v(x) «входит» в U^(x0)c2K—K\dKt
то ее называют внутренней (относительно К) и обозначают через
v~(x) (если же нормаль. v(x) «входит» в СЛ2> (х0) czM\K, то ее на-
зывают «внешней» и обозначают через v+(x)). Общее правило
ориентации края дК (в соответствии с ориентацией Л4) приводит
к необходимости выбора из двух параметризаций у и (—у) (для
Г ад К) той, при которой орт направленной касательной t(x) к Г в
точке хеГ дает базис
568
{v+(x), t(x)}~{DuO.
в Тх(7И). Но тогда
({t(X), v~(x)}~{DUO, ОГФ})=>-
=H(NW, t(x/ v-(x)}~
~{N(Z), DUO, D„<D}~{i. j, k}),
t. e. {N(x), t(x), v~(x)}^{i, j, к}. Таким образом, получаем следу-
ющее (сравните § 4), принятое в механике и математической фи-
зике правило ориентации края дК для 2-мерного компакта с крае»
в R3.
Правило. Пусть М — ориентированное 2-мерное многообра-
зие, вложенное в R3, класса CW и КаМ — 2-мерный ком-
пакт с краем дК, где дК есть 1-мерное многообразие класса С(’>‘
в R3. Ориентация дК выбирается так, чтобы для любого х&)К ба-
зис {Nfx), t(x), v~(x)} был положительным в канонической ориен-
тации объемлющего пространства R3 тройкой {i, j, k} (N(x) — на-
правленная нормаль к касательной плоскости ТХ(М) в точке
х&)К<=М, t(x) — направленная касательная к дК и v~(x) —
внутренняя (по отношению к компакту К) нормаль к дК, лежа-
щая в касательной плоскости ТХ(М)).
Другими словами, обход дК проводится так, чтобы компакт К
оставался слева, считая, что голова наблюдателя направлена по
нормали N(x) (см. рис. 41).
Теорема Стокса (для ^-мерного компакта с краем в Rn).
Пусть М — k-мерное дифференцируемое ориентированное много-
образие, вложенное в Rn (k<n), класса С<!> и KczM — k-мерный
_____________________________________ 1с—1
компакт с ориентированным краем дК класса С(1> и а> (х) —
дифференциальная (k—\)-форма класса Cdl(V), где KaV а
VczRn — открытое множество из Rn. Тогда имеет место формула
Стокса
f к-1 1с-1
J ® = J d ш . е
дК К
Доказательство. В силу теоремы о ранге из ч. VI, гл. 2^
§ 3 (см. замечание к определению ^-мерного компакта К с ориен-
тированным краем дК) V Xq^KczM существует окрестность
V(Xo)'CzRn и С(1) — диффеоморфизм ф:
V(x0)<=R2 (—a, a) czR*
(где a=i(ab ..., ап) и 1п(—а, а) — открытый брус в R") такой, что>
ф(*о)=0, detDi|i(x)>0
v x^V(xo),
56»
fl ,
q(V(x0)nM)=P(-a', a') =
=In(—a, a)f]{^+i=O....tn =0} —
открытый мерный брус в RJ
(In(—a, a)=Ik(—a', a')XIn~k(—a", a"),
a'=(ai, ak) и a" =(ak+i, ...» an)),
Лри этом для гомеоморфизма (параметризации) Ф, обратного к
координатному отображению ф |у(*,)пм, имеем
Ф :!*(—a', a')c=R* -* Vfxo^AlcR",
причем Ф есть й-путь Жордана класса <?<*> в R". Отметим, что
©виду условия det Оф (х) >0 изоморфизм Вф(х):
R"+R?
сохраняет ориентацию R" в R", т. е. переводит ориентацию R" в
стандартную ориентацию R", соответствующую упорядоченному
каноническому базису {еь еп}, при этом ориентация подпрост-
ранства
R?=R;nn{^+i=O, •••> ^=0} ’
задается упорядоченным базисом {еь efe}. Рассмотрим множест-
во
^=ф(/<ПУ(хо))с/Ч—a’,
являющееся ^-мерным «компактом» в R*, которому можно при-
писать ориентацию Ж, соответствующую канонической ориентации
R*. Тогда =ф(д/<Г|У(хо)) — (k—1)-мерное многообразие в
R^ (очевидно, д^=0, если dK(]V(xo)—\0). Если то в
силу упомянутого выше замечания к определению компакта К. с
краем, видим, что
W=^(V(x0)[\K) =1“(—а', а')П{/!<0}=
=Ik(—а', а')(]Н,
где /f=R*tn{^i^O} — полупространство в Rf, а
d^=lk(—a', а', а')(]дН,
где dH=R’'f]{f1=O) — (k—1)-мерная гиперплоскость в R*, зада-
ваемая уравнением Л=0 и ориентированная упорядоченным бази-
сом {е2, ..., е*}, причем орт еь являющийся нормалью к дН, будет
внешним для Таким образом, ориентация дН согласована
о ориентацией Н с помощью «внешней» нормали еь Но тогда, вво-
570
tn
Рис. 42
дя на (k—1)-мерном многообразии дУ? ориентацию дН, видим, что
ориентации дУС и УС согласованы в силу того же правила (с по-
мощью внешней (по отношению к УС ) нормали ei к <?<%"). Вновь
вспоминая, что det видим, что изоморфизм Вф(х) пере-
водит ориентации К и дК в ориентации УС и дУС соответственно
(см. рис. 42). Будем теперь различать два случая: 1) хаеЛ=
=К,\дК и 2) х0&?К. Пусть 1) x0<=K, тогда для карты (Vf^ri
(]Л4, Ф) существует окрестность У[(х0)с:‘У(хй) такая, что
Vi(x0)ftK<^kciM, т. е. У1(хо)Г|Л4='У1(хо)ПК. Но тогда
О=#(хо)=ф(Vi(х0)(]К)<=&cZ* (—a', a') cR*
о
и поэтому существует открытый брус У*с:^с2/*(—а', а'), являю-
щийся ^ -специальным (см. определение, введенное при доказа-
тельстве теоремы Гаусса — Остроградского в ч. VI, гл. 2, § 7) для
«компакта» УС в R* и такой, что ф(х0)е/*, при этом
Ф (Р) =н|>-> (Jk) =[U(xa) = V'(x0) (]К,
где V(x0)=^-l(Jk'%tIn~k(—а", а")) есть окрестность в R”, т. е.
U(x0)c.KczM есть окрестность точки х^К в топологическом про-
странстве М.
Пусть теперь 2) х0&)К. Рассмотрим карту (VfxoJflAl, Ф). Тог-
да дУС и гомеоморфизм
<р^Ф(0, t2, ..., tk) :дУС —
=дН(]1к(—а', а') сR*~r -* ВДV(x0) <=R-J
571
из карты (У(хо)Пд/С <р) есть (k—1)-путь Жордана (класса С<‘>) в
R", ориентирующий dKf]V(x0).
Заметим, что ф(х0) =iOsd<^ и для любой точки x&}K.(\V(xq)
имеем i|)fx)=i(0, t2, tk)&№. Но тогда орт ei, ортогональный к
гиперплоскости дН, является внешней (по отношению к) нор-
малью к д& для любой точки $(х)^дЖ и поэтому существует
упорядоченный ортонормированный базис {1Ь .... 14~{ei> —>
такой, что внешняя нормаль N(7)=ei к составляет острый,
угол с каждым из ортов 1/ (/=1, 2...k). Но тогда (ср. лемму
о существовании /(-специального параллелепипеда из ч. VI, гл. 2,
§ 7) существует открытый параллелепипед Ikczlk(—а', а'), постро-
енный на базисе {li, .... U}> содержащий точку ф(хо)=О внутри се-
бя и такой, что внешняя (по отношению к нормаль N(7)=et
для любой точки t=ty(x)^r=Jk(]dffi образует острые углы с
ребрами этого параллелепипеда. Таким образом, открытый парал-
лелепипед Z* является -^-специальным (в смысле определения §7)
параллелепипедом (для ^), содержащим точку ф(хо)=О внутри
себя. Вновь полагая
Ufa) =v' (I*) =Ф (Jk) =V' (x0)QM,
где Vr(x0)=^-l(J^In~k(—а", а")) — окрестность из R", видим,
что и(х^)=<Ь(]к) является открытой (в М) окрестностью точки
хое<5К. Итак, в обоих случаях, 1) и 2) для любой точки хеКП
nV(X) (где (У(х)ПМ, Ф) — карта М) существуют окрестности
¥'(х)сКл и U(x) = V'(x)f]M такие, что Jk=ty(U(x)) =
—i$--l(U(x))счесть Ж -специальный (в смысле определения §7)
параллелепипед для «компакта» Ж =^(V'(х)[\К) с «краем»
дЖ =^(У' (х){\дК).
Рассмотрим открытое (в R”) покрытие множества К с:
cz (J V'(x). Тогда k с: (J U(x) cz (J V'(x). В силу компактности
хек хек хек
К из этих открытых покрытий можно выбрать конечные откры-
тые подпокрытия
Кс= и UjC= и V/czVcR".
! =1 /=1
Рассмотрим (в Rn) разбиение единицы {ei(x)\ j = l, 2, ..., т}
(класса C<l)(V)) для множества К, подчиненное открытому покры-
тию {V/; /—'1, 2, ..., т}, так что suppe/czV/ для любого j, причем
для сужения е,(х) на М имеем suppe;|Mczt7y для любого /. Пусть
в открытом множестве VczRn таком, что KczV, определена (fe—1)-
форма (класса C^(V))
k—1
И (х)= 2 (x)dxit/\
Тогда имеем
572
к—1 т к—1
f d о» = f ш )
к knu.
и
к—1 т к—1
J “=Х f
i=[ dk[\UI
Для доказательства теоремы Стокса достаточно для любого j до-
казать равенство
к-1 к-1
J d(ef • <о )=— j е} • ©,
X[iUf "^KnVj
к-1
где е/(х)ы(х) есть финитная (k— 1)-форма класса C^(V), для
к-1 к—1
которой suppб/ - © IwctZ/czV/ и suppd(ez- © ) Рас-
смотрим карту (Uj, Ф;) из атласа ^-мерного многообразия М, вло-
женного в Rn (k<_n), класса С(1>. Тогда
Ф/:Jf -* Ф](^) = и}аМсКп
есть й-путь Жордана класса С(1> в Rn, причем
КП1//=Ф/(^/Л/р
и
дКМ^Ф
Тогда в силу определения ориентаций KQAf, дК(]М и
дЖ/Л/* имеем
к-1 к-1
J .ш)= f ф*Ще} • <о)),
кпУ;
а также
к-1 к-1
f Sj • ©= J ф*(е} . О)).
Но по условию Стокса fe-мерное многообразие М, вложенное в
Rn (k<Zn), класса С^~> и поэтому и в силу замечания к
теореме (о перестановочности операций Ф* и d) из ч. VI, гл. 2, § 1
имеем равенство
fe-l k-l
Полагая
k—1 k-I
= ф*(е} • ш),
573
видим, что
л-1 к—1
supp а/ <= 7;*, supp d <Xj с J*,
причем
к-1 к-1
J d(e/ . ш)= f ф*(й(е;. • Ш))=
к-1 к-1
= f <М>*(е> ♦“)= f daf
и
к-1 к-1 к-1
Г ^-“= f <!>•(«;•.•)= f »/•
"dKnVj (tirftj* cW/n-^
Напомним, что J1] есть Ж-специальный параллелепипед для X f в
R*, причем Xj компактно, а XjC.1^ есть ^-мерное многообразие в
R*, имеющее ориентацию объемлющего пространства Rk, причем
дХ ,=Х/П{*1=0}
является ориентированным с помощью внешней (по отношению
к X j) нормали (А—1)-мерным многообразием в Rf (класса Cd)).
Применение леммы (о формуле Гаусса — Остроградского для
К-с. п.) из § 7 (условия которой выполнены для XjCiR{k, dXj, 1} и
k-l
дает равенство
k-l k-i
J day= f aj,
завершающее доказательство общей теоремы Стокса.
Следствие (теорема Стокса для 2-мерного компакта с кра-
ем в Rn). Пусть М — 2-мерное ориентированное многообразие,
вложенное в R” (2<п), класса О1), КаМ — 2-мерный компакт с
_____________________________ 1 п
ориентированным краем дК класса С1) и <а(х) = ZA{(x)dXi —
г=1
1-форма класса Cd)(V), где KcVczR” и V — открытое множество
из R". Тогда имеет место формула Стокса
J <в= ( d<i>
Тк к
или
f 2 Atdxp= f 2 (Dj/ly—DjAJdXt /\dxp
i=l Ti
574
ПРИЛОЖЕНИЕ I
Теорема (об абсолютной сходимости несобственного интегра-
ла Римана). Пусть Gc=Rn — открытое множество и функция
f: GczRn->R локально ограничена на G, причем множество
Ef={x^G\(n(f; х)>0} (всех точек разрыва функции f(x) на G)
имеет п-меру нуль (mes £7=0). Пусть для любой исчерпывающей
п
открытое множество G системы {Kt; Z=l, 2, ...} измеримых по
Жордану компактных множеств существует
г def
lim J f(x)dx— (fdx,
Z-+OO К, JQ
где число ffdx не зависит от выбора исчерпывающей системы
G
{Кг, 1—1, 2, ...}. Тогда f^R(G) в смысле определения (К) из ч. V,
гл. 2, § 3, т. е.
р def
Я lim j \i(x)\dx = flfldx
/<-+00 Kz JG
и число f\f\dx не зависит от выбора исчерпывающей системы
G
{Кг, 1=>1, 2, ...}.
Доказательство. Допустим, что теорема неверна, тогда
существует исчерпывающая открытое множество GczRn система
компактных, измеримых по Жордану множеств {Кг, 1=1, 2, ...} та-
кая, что при выполнении условий теоремы существует
lim f \f(x)\dx = + <x>,
I' *1'00
причем
4“Э0 4-00 О
G= U Кi = U Kt
1=1 1=1
и Ki <= Ki+t <= Ki+i для любого Z.
Переходя в случае надобности к подпоследовательности из {KJ,
можно предполагать, что при этом выполняются оценки
f \f(x)\dx>3 • f \f(x)\dx + 2l vZeN. (1.1)
*i+t *7
575
Пусть St='Ki+i\Kt — компактные, измеримые по Жордану мно-
жества, тогда в силу аддитивности интеграла Римана, поскольку
Si(}Ki=dKi и |d/G|n=0 имеем Ki+i=KdJS< и
f |fW|dx=J- |fW|dx+J |f(x)|dx
K/-I-1 St K(
и из оценки (IЛ) получаем
f If (x)\dx > 2 f I/ (x)]dx + 2/ VIS N. (1.2)
sz
Введем неотрицательные функции |4-f(x))/2 и
i-(x) = ( | f (x) | — f (x))/2, так что
lfWl='f+W+f-W и f(x)=f+(x)— f_(x),
тогда
(ft=R(Kt)vl)^(\f\, f+, f_<=R(Kt) v ZeN)
и поэтому из (1.2) имеем оценку
J f + (х)dx + J f_(x)dx > 2 J I/(x)|dx +21 VI e= N. (1.3)
sz Sz Kj
Возможны два случая: 1) J f (x)dx^f f+(x)dx и тогда по-
sz sz
def
ложим K1=Ky и
2) J f+(x)dx>$ f_(x)dx
si 2 * * si
def
и тогда положим Ki = K^. В случае 1) из оценки (1.3) имеем
2 \J-(x)dx > 2 J_ \f(x)\dx + 21,
st К[
так что
f fjx)dx> $_\f(x)\dx+[!. (1-4)
sz Ki
Заметим, что в силу измеримости по Жордану множества Kt
существует брус If=In[a(l>, такой,, что и тогда
неравенство (1.4) можно переписать в виде
f XSl(x) -f_(x)dx> f \f(x)\dx+l. (1.5)
^+1 1 Kf
Но
L XS,W • f_(x) dx = suppSx ,f (T)
si
576
« поэтому существует разбиение Т~ бруса с частичными
брусами {/"J такое, что
sz К/
Но
si (Л
где
m(^ = inf(Xs/(x)i • f_(x))X
Jo>
( >0, если f (х) >О V хе/«
X I / - \ и)
1=0, если Ях^е/^ такое, что f_(x0) =
==/(хо) = О.
Обозначим мульти-индексом (k) те из брусов разбиения Т“,
для которых f_(x)>0 VxeZ”) (т. е. т(~>0), тогда
-х_ •/_ (Т 5
si т
Пусть s~ = U cz St, так что f (х)>0 (т. е. f(x)<0, f+(x)=O),
<»>
vxes~ Тогда s~ cz Si = Ki+i\Ki есть компактное, измеримое
по Жордану множество, и поэтому из (1.5) имеем оценку
fj_(x)dx> f_|f(x)|dx-H, (1.6)
откуда ввиду равенства f_(x)=—‘f(x)V х е s~ и оценки |f(X)|^
^f(x) Vx<=G имеем оценку
— §_f(x)dx > §_f(x)dx 4-Z,
Kl
так что
J_ /(x) dx + J_ f(x)dx< — l. (1.7)
sl Kl
Аналогично в случае 2) из (1.3) получаем оценку
J f*(x)dx > Uf(x)\dx+l,
it - ^г+
и поэтому существует разбиение Т+ бруса Г?+1 с частичными
брусами такое, что
37 — Jis И5 Камынин 577
Sx .иСП> f \f(x)\dx+l.
si kf
Положим s+ = U^r № Vxe/“, имеем f+(x) > 0, так что
f(x)>0, f_(x)=Q, и тогда имеем оценки
f, f (х) dx > (\f(x)ldx->t-l>— Г f (x) dx 4-1,
к? k?
t. e.
f, f(x) dx + f f(x) dx >1.
•Lt irT
Из (1.7), (1.8), полагая
s~ в случае 1),
s+ в случае 2),
имеем оценку
I f f(x)dxl^l .VleN.
|kz I
(1.8)
(1-9)
Далее, K>=KZ(J «Л где s*<= S{ = Ki+t\Ki, t. e. с K, <=/G+b
откуда G—^Kt = U &i- Ho
<•=1 z«=i
(X1CKic^Vl)=>(G=
4“OO о -f-OO Л -f-00 О
= U Kf= и U kt)
Z=1 /=1 /=1 ’
и поэтому {Кг, /=11, 2, ...} есть исчерпывающая открытое множест-
во G система измеримых по Жордану компактных множеств, для
которой по условию теоремы существует
lim f f(x)dx = f fdx
и, в частности,
Ы lim f f(x) dx — {fdx
/-+ОО b
Но в силу оценки (1.9) имеем
lim I Г f(x) dx 1= + '
J-+oo|k/ |
578
Противоречие, из которого вытекает, что f^R(G) в смысле опре-
деления (К).
ПРИЛОЖЕНИЕ II .
Криволинейные интегралы (2-го рода) от 1-форм
по спрямляемым 1-путям в Rn
Пусть числовые функции, f(t) и ф(7) определены на отрезке
[а, Ь]с:(—оо, 4-оо) и таковы, что f<=B[a, b] и Ь] (так что
Ф(0 —функция ограниченной вариации на отрезке [а, Ь] (см. [1]г
ч. III, гл. 1, § 3)). Пусть SP— множество всех размеченных разби-
ений Тх отрезка [а, А] и d(T) -> 0 — база в нем. Положим
5/(ф; Тх) = 2f(rA)-(i|)(/A)—ф(^_1))
R==1
(где ^]), так что Sf: 3s-> R.
Определение. Интегралом Римана — Стильтьеса функции:
feB[a, &] на отрезке [а, Ь] (относительно функции феК[а, Ь]) на-
зывается число J^R (если оно существует) такое, что
lim 5/(ф; Tx)=J.
d(T)-*O
Через R4a> ЭД будем обозначать класс всех функций /еВ[а, 6],
имеющих интеграл Римана — .Стильтьеса на [а, Ь] (относительно
функции феР(а, Ь]).
Теорема (достаточное условие существования интеграла Ри-
мана— Стильтьеса). Пусть feC[a, Ь] и феК[а, Ь]. Тогда fe
eR*[a, Ь].
Доказательство. Будем рассматривать функцию*
5;(ф; Тх) на множестве S5 всех размеченных разбиений Тх отрез-
ка [а, Ь] с базой d(T) -* 0. Поскольку f<^C[a, £>], то по теореме-
Кантора функция f(t) равномерно непрерывна на отрезке [а, Ь] и
поэтому Уе>ОЯ6(е)>0 такое, что для любого разбиения Т от-
резка [а, &] с диаметром d(T)<Z& имеем Пусть Т—
={о=^0<^< ... и Т'<Т, причем d(T)<.§ d(T')<Z8. За-
метим, что поскольку разбиение Т' является продолжением раз-
биения Т, то любой частичный отрезок разбиения Т' содержится
в одном из частичных отрезков Ik—[tk-\, М разбиения Т, быть мо-
жет, совпадая с ним. Пусть — частичные от-
sk , /
резки из Т' такие, что Zfc=iUJR { (при s^=l Гк t =/*). Тогда
z=i '
имеем Дф* = S Дф*, i, где
t=i
ДФа=Ф(ЛО—фС^-i); Дфл, i)—Ф(А, z-i).
37*
579
Рассмотрим для разбиений Т и Т' любые тит' такие, что
-т^еЛеТ, тие/'меГ; тогда Тх, T'x'<=Bt, где В»=
={Tx^3i\d(T)<Zb} — элемент базы d(T)-+O (с диаметром
<б(е)). В силу выбора 6=й(е)>0 имеем <Hk(f)<.s,
и поэтому в силу условия фе V[a, Ь] имеем оценки
|5/(ф; Гт')-$Дф; Тт)|=.
m I
2 2 ^’c,z “ К'ск)д'К/]
fc=i \z=l
п» &
=2 s ш*(/) • 1Д^.4<e • уф-
>t=i i=i a
Рассмотрим теперь любые два размеченные разбиения Лт,
ТгйеВв и образуем составное разбиение Т'={Т1, Т2). Тогда, оче-
видно, Т'<Т\, Т'<Т2, причем в силу доказанного выше V х' (имея
а виду, что Т'х'Т\х, Тг$еВ6) получаем оценки
ь
|$Лф; TfO-SHij); Гт'Жв-Уф
а
И
Ь
|$/(ф; Г#)—$/(ф; Гт')|<8-Уф,
а
откуда
’ ъ
|5/(ф; Tlx)-Sf(^, Т2О)|<28-Уф. (П.1)
а
Итак, У8>0эб>0 такое, что чТ^х, T2b^Bit имеем оценку
(П.1). Но тогда в силу критерия Коши существования предела
‘числовой функции по базе d(T) -> 0 имеем
def b
Э lim 5ДФ; Тт)=7=Г/</Ф.
d(T)-0 а
Следствие.
(feC[a, &])Д(фе=У[а, b]/\C[a, b])=>(f^[a, &]).
Теорема (о линейности по f интеграла Римана — Стильть-
еса). Пусть д] и сгеЯ (i=il, 2, .... m). Тогда
Zcrfi^RJa, b],
1=1
причем имеет место равенство
580
b fm \ m b
f (S Ci- ==S f
a \ i=l / 1=1 a
m
Доказательство. Положим ft=iScrf,-. Тогда для любого
i=i
размеченного разбиения Тх отрезка [а, &] имеем равенство
Sn(if; Тх) (if; Тх).
1—1
Поскольку b] (i=l, 2, m), то существует
ь
lim Sf (ф; Тх) = f ftdy = m).
d(T)-0 Ji . Ja
Применяя теорему о пределе суммы, имеем из написанного равен-
ства
ш Ъ
Я lim 5п(ф; 74) = £ ct • f /^ф.
<цт)-»о I
Теорема (о линейности интеграла Римана — Стильтьеса от-
носительно if). Пусть f^R^ [а, &}, geR (i=il, 2, .... т). Тогда
f^R т [а, ЬХ причем имеет место равенство
S сгф<
i=i
Ь / m \ m Ъ
J/<« 2g • ф< =2С«
а \ г—1 / i=l а
Доказательство. Для любого размеченного разбиения
Тх отрезка [а, Ь] имеем равенство
S/(S Ci if,; Тх) ^'ZCi-Sfttyr, Тх),
i— 1 1—1
откуда ввиду условия [a, b] (i= l, 2, ..., m) переходом к пре-
делу по базе d(T) -+ 0 получаем утверждения теоремы.
Следствие. Из обоих теорем вытекает, что интеграл Ри-
ъ
мана — Стильтьеса J(f; ^) = Sfd^ есть билинейный функционал
а
(например, при f^C[a, b] и ifeV[a, Ь]).
Теорема (о конечной аддитивности интеграла Римана —
Стильтьеса). Пусть f^R^[a, b] и a<c<zb. Тогда f^R^[a, с}Д
А/?4С/ причем имеет место равенство
J fdty = S fdty+ J fdif.
а а с
581
Доказательство. Рассмотрим любые два размеченные
разбиения 7\х и Т2^ отрезков [а, с] и [с, 6] соответственно. Тогда,
полагая Т={Г1, Т2}, 1={т, О}, видим, что ТХ есть размеченное
разбиение отрезка [а, &], причем
$/(ф; = Tjr)+S/^-, Т2&),
[а, Ь] [а, с] Ь]
отметим, что при этом 0<Zd(T)^.maxd(Ti). Поскольку f^RJa, &],
z=l, 2
то V е>0 Я б>0 такое, что при d(T)<Z8 имеем оценку
ь
S/J; ТХ)-рйф
(П.2)
Будем считать, что d(7J<6 (тогда и d('T.)<6). Зафиксируем те-
лерь разбиение ТгО. Тогда VT'0 xi^B^ (i=il, 2), где есть
элемент базы d(T\) -* 0, связанной с отрезком [а, с], имеем (вводя
обозначения
т&, т&={ту , тр}, xo)=i{T(i), $},
(t=il, 2), s2 = S f(ib; Т2^))
тождество
S Дф; ТФх&) = S Дф; (z = l, 2). (II.3)
[a, с] [a, b ]
Из (II.2) и (П.З) имеем оценку сверху
f /Дф — s2 — е < S Дф; Т^х^) <
I KN
ь
< у /йф — «2 + 8 (» = 1 > 2),
а
откуда,
I S 7(Ф; Г/МП) _ s/ф; Т(2)т(2))1 < 2е.
I [а, с] [а, с] I
Итак, для функции S у(ф; Гт) выполнен критерий Коши сущест-
[а, с]
вования предела числовой функции по базе d(T{) ->0 и потому
Я lim S /ф; — [Мф-
d(Ti)-0 [a, cl Ja
Аналогично доказывается, что
ь
Slim S г(ф; T2&) = f fdty.
[с, Ь] Jc
582
Наконец, переходя в тождестве (П.З) к пределу (при d(Ti)->-Q
(t=l, 2), d(T) -»-0), имеем равенство
Ъ с Ъ
J fdty—f J* fdty.
а а с
Теорема (об оценке интеграла Римана — Стильтьеса). Пусть
f^.Rt\a, 6], 1реР[а, ft] и }f(t) V /е[а, 6]. Тогда
ь ь
| J7di|>|s^W-Vi|>. (П.4)
а а
Доказательство. Для любого размеченного разбиения
T-s отрезка [а, &] имеем оценку
Тх) | |f(xfc) |
R=1 a
откуда, переходя к пределу при d(T) -* 0, получаем искомую оцен-
ку (II.4).
Теорема (о замене переменной в интеграле Римана — Стиль-
тьеса). Пусть ft] и отображение t:\a, 0]-»-[л, ft] есть го-
меоморфизм. Тогда f»t^R^t [а, 0], причем:
а) если t(x) ff на [а, 0] и t(a)=a, t($)=b, то
Ь 3
if(t)d^>(i)=St^(x)d^^(x)-,
а а
б) если t(x) 4| на [а, 0] и t(a) ='b, t($)=a, то
ь 3
H(t)d$(t)=^Sf°t(x)d^t(x).
а а
Доказательство. Рассмотрим любое размеченное разбие-
ние ГЛ отрезка ,[а, 0], так что
Л=1{а=;то<Т1< ... <тт=0},
,0'*е=[т£_1, Tfe]v k.
Полагая
. ( t(xk) в случае а)
( t{xm^k) в случае б)
и
_____________________f t(ftk) в случае а)
( в .случае б),
получаем в обоих случаях индуцированное гомеоморфизмом раз-
меченное разбиение ТА отрезка [а, Ь], где
Л={а=|/0<^< ... </m=ft},
583
причем имеем оценки
0<|Д/=! J | .(II.5)
I )^(Тт—k)—t (Тт—Л+1) | J I tOm—k(t) k-
Поскольку teC[a, ЭД, то по теореме Кантора функция й(т) равно-
мерно непрерывна на отрезке [а, 0] и поэтому Ve>0 3 6(s)>0
такое, что для любого разбиения Тх отрезка [а, ЭД с диаметром
d(Tx)<z& имеем оценку Юй(Х)<е и тогда из оценки (II.5) получаем
(d(Tx) -* 0) => (d(Tt) -> 0).
Отметим тождества
*(ч) —Ф° <(тк-1)] =
=2 ЯМЬИМ - ФЙ-1И = 5/(ф; Tt\) в случае а) (П.6)
Л=1
и
5/ог(ф 0 *; ТХЪ) = £ f О <(6»)(| О *(тк) — ф О <(Tlc-l)]«
Л=1
“ 2 /(^п—ОЛ'ФКт-к) — Ф(^т-к+0] =
А=1
= - *2 в СЛУчае б)- (1Е7>
1=0
Поскольку
(f е Яф {а, ЭД) => (Я Нт 0 S/ф; Tt\)= J f (t) </ф(t))
и
(d(Tx)->O)=>(d(T()-*O),
то, переходя к пределу в тождестве (II.6) (при d(Tx)—>0)) и в
тождестве (II.7) (при d(Tf)->0)), имеем
Я lim З/оХФ ° Тх&) = ± f f ° *(т)йф о t(r) =*
d(Tx)-*0 i
= ±]f(t)d^(t)
а
'(где знак +, берется в случае а), а знак — в случае б).
584
Теорема (о связи интеграла Римана и интеграла Римана —
Стильтьеса). Пусть f^C[a, Ь] и феС(|>[а, Ь]. Тогда Ь]„
и f^R*[a’ о]» причем для интегралов Римана и Римана — Стиль-
тьеса имеет место равенство
ъ ь
Sfdty=ff(t)ty'(t)dt. (П.8>
а а
Доказательство. Поскольку b]) => (феУ[а, b]),.
Ъ b
причем (см. [1], ч. III, гл. 1, § 3) Уф=.Г |Di|?(7J|dZ, то
а а
(fe=C[a, Ь])Л(^С^а, Ь]) => (f<=RJa, b]).
Кроме того, очевидно, Ь]. Но тогда для любого разбие-
ния Т={а=!^<!Л<... <tm=b} отрезка [а, Ь] (поскольку
fft]) в силу теоремы о конечных приращениях Лагран-
жа я т*е(4-ь tk) такое, что
Дфл"ф(/л)—t(ffc-i) =£>ф(т*) -Atk.
Но тогда для размеченного разбиения Тх отрезка [а, &] имеет мес-
то тождество
m m
5ГФчтт)= 2 /(тк) Ф'(тк) д*к = 2 f(т*)дь=
к=1 к=1
откуда в силу (Лф'еЕ#[а, b]) Д (fe/Qa, b], переходя к пределу по
базе d(T) -*0 (и имея в виду теорему о единственности предела) г
получаем равенство (II.8).
Следствие. В силу конечной аддитивности интеграла Рима-
на (для / &1) и интеграла Римана — Стильтьеса (для»
f^R^[a, b]), видим, что наша теорема имеет место и для кусочно-
гладкой функции ф(7) на отрезке [a, bj.
Определение. Пусть <р : [а, Ь] -> Г=<р (fa, b])cRn — не-
прерывный спрямляемый 1-путь в R" (так что
T(Z)=i(<Pi(X)> •••> фп60)еС[а, Ь]ДТ[а, Ь])
1 п
и <а(х) =^'LS>i(x)dxi — дифференциальная 1-форма класса С(0>(Г).
г=1
1
Тогда криволинейным интегралом (2-го рода) от 1-формы о по-
спрямляемому непрерывному 1-пути <р в Rn называется число
1 def п Ъ
Jto=iS S SP»(f(t)d(fi(t),
ф i=l а
Ъ
где I 3ii°q>(t)d<f)i(t)V i есть интеграл Римана — Стильтьеса для
а
Функции &1°у(1.) (относительно функции (fi(t)) на отрезке-
[«, и
585-
Замечание. Поскольку 3\°<peC[a, Ь] и ф,еУ[и, ftjvi, то,
как было доказано, SPi ° (л, Ь], так что введенное определе-
ние корректно. !
Замечание. Если ф — гладкий 1-путь в Rn и а(х) — 1-фор-
ма класса С1-0) (Г), то криволинейный интеграл 2-го рода
i п Ъ bi
Ф i=l a a
•совпадает с вновь введенным криволинейным интегралом 2-го рода
I
Job силу теоремы о связи интегралов Римана и Римана — Стиль-
тьеса.
Теорема 1 (об инвариантности криволинейного интеграла
2-го рода относительно допустимой замены параметра). Пусть
1 п
&(х) = S 3ii(x)dXi,
г=1
где ZPi^C(T) и FczRn — носитель эквивалентных (в смысле опре-
деления [1], ч. III, гл. 1, § 4) спрямляемых непрерывных 1-путей
в Rn. Тогда
1 1
ф ф
Доказательство. Пусть <р :(а, 6] -* TczRn иф:[а, {}]->
Tc:Rn — спрямляемые непрерывные 1-пути в Rn. Если ф~ф (в
смысле определения [2], ч. III, гл. 1, § 4), то существует допусти-
мый гомеоморфизм /:[а, Ь] такой, что t(x) ff на [a, |J],
/([а, (3j)=[a, 6] и /(а)=а, причем ф=|<р°^ Но по опре-
делению
J® = SJ SPi ° q(t)dqi(t).
Ф i=l а
-Сделаем в интегралах Римана — Стильтьеса замену переменной
i=if(-r), тогда SPi° ф(т) = о ф ° Цх) V i, причем поскольку
t(x) ft на [а, р], то в силу теоремы о замене переменной в интег-
рале Римана — Стильтьеса имеем
1 п з
J ®= 2 f ° Ф ° ЙФ« ° =
Ф г-1 а
п 3 *
= 2 № ° ф(т)^фдг)= j ш.
i=t а ф
1
Следствие. Криволинейный интеграл (2-го рода) /<в опре- -
ф
делен на непрерывной спрямляемой кривой Ф в Rn.
586
Теорема 2 (о линейности криволинейного интеграла 2-го ро-
да). Пусть Ф — непрерывная спрямляемая кривая в Rn ан(х)
2) — 1-формы класса С<°>(Г), где Tc:Rn — носитель кривой
ф. Тогда для любых постоянных c,eR (i=4, 2) имеем
it it
J Ci •<Bi-|-C2'<02=='Ci • Хю1 + с2’J" ©г-
ф ф ф
(Теорема 2 является, очевидно, следствием теоремы о линейности
интеграла Римана — Стильтьеса.)
Теорема 3 (о конечной аддитивности криволинейного интег-
рала 2-го рода). Пусть фг:(а», б/]-*DczR” (1=4, 2) непрерывные
спрямляемые 1-пути в Rn и ф:[аь T^FiUIV где ф1(Ь1) =
=ф2(О2)>
<61=0!<Ь2, н
2
та/с что <p= U<P/ является также непрерывным спрямляемым
./=1
1 п
1-путем в R". Тогда для 1-формы ю = 2 3Jt(x)dXi, где 5а,еС(Г)
i—1
(i='l, 2, ..., п), имеем
X ю = ' X ю + X ю.
<F1U<?2 Ф1 Ф2
(Теорема 3 является следствием теоремы об конечной аддитивно-
сти интеграла Римана — Стильтьеса.)
Теорема 4 (об ориентированности криволинейного интеграла
2-го рода). Пусть Ф — непрерывная спрямляемая кривая в Rn и
кривая Т =—Ф (в соответствии с определением [1], ч. III, гл. 1,
1 п
§ 4) . Тогда для 1-формы ю =i2 -3е i(x)dxi, где (i—
1=1
= 1, 2,...»и), имеем равенство
1 1
J со =—Jco.
—ф ф
Доказательство. Пусть непрерывный спрямляемый 1-путь
<р:[а, b]^-rc=Rn является представителем кривой Ф, а непрерыв-
ный спрямляемый 1-путь ф: [а, — представителем кривой
Чг=!—Ф. Тогда в соответствии с определением противоположных
непрерывных 1-путей из [1], ч. III, гл. 1, § 4 существует гомеомор-
физм t: [а, Ь] такой, что t(x) || на [а, М» ^([а> М) =
=(а, &], #(a)=ib, t($)=a, причем ф=<р»/. Тогда, делая замену
/=1#(т) в интеграле Римана — Стильтьеса
587
i=l a
и впоминая теорему о замене переменной (в интеграле Римана —
Стильтьеса) для строго убывающего гомеоморфизма t(x), имеем
в силу равенства
3\ ° фо <(t) = о <|>(т):
I п 3
J — 2 J ° ф ° ^(x)dq>t о /(т) =
ф i=0 а
п 0 £
= — 2 f ° =— j
i—i а ф=—ср
Теорема 5 (об оценках криволинейного интеграла 2-го рода).
Пусть ф: [a, ft]-*Tc:Rn — спрямляемый непрерывный 1-путь в Rn
1 п
и ы(х) =*Ъ&1(х)<1х1, где ^геС(Г), причем существует постоян-
ная Af>0 такая, что \SF>i(x)\^.M4хеГ (i=l, 2, ..., п). Тогда
имеет место оценка
1 ь
| J©|Cft.Af-V<p=n-AT|ip|. (П-9)
Ф а
Доказательство. Вспоминая теорему об оценках для ин-
теграла Римана — Стильтьеса и доказанную в [1],. ч. III, гл. 1, § 3
оценку для функции
b Ъ Ъ п Ъ
феР[а, &]:V<pi<Vf < 2 Уф/,
а а а /=1 а
имеем оценки ;
1 п Ь
fw <2 Jl^'° ’PfOkWOK
ф i=l а
. 2 V
i=l а а
из которых и следует оценка (II.9).
Теорема 6 (о независимости специального криволинейного
интеграла 2-го рода от пути интегрирования). Пусть GcR" — об-
ласть и ф:[а, ft)-*Глв=ф(К b])a:G — непрерывный спрямля-
емый 1-путь в R” с началом A=iq>(a) и концом B=ty(b). Тогда
для (f(t) = (xi(t), xn(t)) имеем
SdXi=Xi(b)—xt(a) (i=l, 2, ..., n).
Ф
588
Доказательство. Пусть Тх — любое размеченное разбие-
ние отрезка [а, Ь]. Тогда для функции f(t)^l^RXi [а, 6] имеем
Si(xf, Тх) =i2 (xi(tk)—xi(tk^)) =
=Xi(tm)—Xi(t0) = xi(b)—xi(a),
откуда вытекает, что существует
lim Si(xt-; Tx)=<Xi(b)—xt(a),
d(T)-*0
t. e. ;
SdXi=Xi(b)—Xi(a) (7=1, 2, n),
где ф
A = (Xj(a), xn(a)) и B = (x1(b), ..., xn(b)).
Следствие. Пусть G—односвязная область в Rn и
<р:(я, Ь]-* FabcGcR71 — (замкнутый) спрямляемый цикл Жор-
дана (Д=В). Тогда
0=1,2.....га) (ф('а)=Л=В=ф('Ь)_).
ф
ПРИЛОЖЕНИЕ III
Точная теорема Грина в R2
Точная теорема Грина на плоскости (см. [8])’. Пусть
GczR2 — ограниченнная односвязная область (т. е. открытое связ-
ное множество), граница которой dG является спрямляемым цик-
лом Жордана. Пусть a>—Pdx-)-Qdy — дифференциальная 1-форма
класса C(G), причем
~р, £-QGzC(G)/\B(G). (Ш.1)
оу ох
Тогда имеет место формула Грина
,f d® (Ш.2)
OG G
или
.( Pdx+Qdy (-~Q—p\dx/\dy
7g g \dx dy }
((где криволинейные интегралы (2-го рода) от 1-формы по спрям-
ляемому 1-пути понимаются в смысле Римана — Стильтьеса из
589
приложения II). Ориентация G в (III.2) совпадает с канонической
ориентацией плоскости Rx, v, а ориентация dG согласована с ори-
ентацией G выбором такой параметризации цикла
dG ip:[а, 6]->дб=ф([а, b])c:R2,
при которой
1/2 f xdy—ydx=\J2$xdy—ydx>'0.
dG ф
Прежде чем приступить к доказательству сформулированной
точной теоремы Грина, приведем некоторые сведения из теории не-
прерывных функций с ограниченным изменением, использующим
ряд теорем из [1] ч. III, гл. 1, §§ 3—5. Сначала будем рассматри-
вать числовую функцию fsC[a, 6]AV[d, &]. Если T={a=x(><z
<Zxt<z ...,<.xn=b} — разбиение отрезка [а, &] с частичными от-
резками [xfe-i, Xi] (k—1, 2, ..., п) и с диаметром d(T)=>,
=>max(Xfe—xk-i)>Q, то полагают
1С
def п
Vf(T) =,2 \f(xk)-f(xk^) I
К=1
и
def п
ОИП.-ЫЯ.
k=l
где [Xk-i, Xk}) — колебание функции f на отрезке
Гх*-ь Xk]. Очевидно, Vf(T)^2Qf(T) V Т, причем V/=sup Vf(T). На-
а Т
помним, что разбиение Т’ отрезка [а, Ь] называют продолжением
разбиения Т (обозначение если все точки деления из раз-
биения Т являются точками деления и для разбиения Т'.
Лемма 1 (о свойствах числовой непрерывной функции с ог-
раниченным изменением). Пусть f^C[a, &]• Тогда:
I) ЧТЪТ'<Т такое, что Vf(T)^Qf(T)^Vf(T')^Vf‘,
2) если Т'<Т, то Vf(T)^Vf(T')^Vf(T)+3p(a(T), где р — чис-
ло дополнительных точек разбиения Т' по сравнению с разбиени-
ем Т и G)(T)=maxti)k(f);
т
3) (уточнение теоремы Жордана из ч. III, гл. 1, § 3) f(x)='
=n(x)—v(x), где
(v._ Vf, X(=(a, ft], v(x)=n(x)—f(x),
3T (Xj “ cl
0, x=a,
причем n(x), v(x) f на (a, ft] и n, v^C[a, 6].
Доказательство. 1) Очевидно, для любого Т имеет место
оценка Vf(T)^.Qf(T). Поскольку. &], то я хь]
такие, что
590
КЫ = max f (x) /(tjJ = min f(x).
[ «к-I- *ft] [Xfc-i.
Полагая ®fe=f(|*)—f(r]*)> видим, что при добавлении к точкам
Ха-i и Xk точек и г]& (при Л=1, 2....п) получаем разбиение
TXT. Из оценок
—f (£s) | + || +
+ lf(n*W(X)|
(где без ограничения общности считаем получа-
ем оценки из 1).
2) Пусть ТХТ и р = 1, причем *n-i ==*„_! <xn,<x^_1 =хп=Ь,
так что дополнительная точка хп' разбиения Т содержится в час-
тичном отрезке [хп_ь хп] разбиения Т. Тогда
if(xn) f(xn-l) | ) f(Xn—i) | +
+ \f(*n+i)-t(Xn) | ^n<2m(T)
и поэтому
0<Vf(T')~Vf(T)= \f(xn)-f(Xn-i) |-
(IfC^n ) f(xn—l) I + \ f(xn+i) f(xn') |)^3(0п^З(й(Т),
т. e. имеют место оценки из 2).
3) Пусть а<Л1<Х2^Ь, тогда (feV[a, Ь]) => (feУ[хь х2]) и, ис-
пользуя аддитивность «полной вариации» (см. теорему 2 из [1],
ч. III, гл. 1, § 3), имеем
Хг
v(x2) — n(xi) = V f>0,
Х1
т. е. n(x2)^n(xi), и поэтому л(х) f на [а, Ь]. Но
v (х2)=л (х2) —f (х2) = л (Xi) + Vf—f (х2)'.
XI
откуда
v(x2)-v(xl) =v>-(f (x2)-f (xj)>vf- If (x2)-f (хО. 1»,
Xi Xi
так что и v(x)f на [а, Ь]. Далее, пусть а=Сх0<Х Тогда для любого
е>0 существует разбиение T0={a=x0<xi< ... <хП11=Ь} отрезка
ь
[а, Ь] такое, что Vf(T0)’>'Vf—е/2. Поскольку f^C(x^), то для вы-
X.
бранного ранее. е>0яб(е)>0 такого, что для любого Ле
е(0, 6(e)), имеем оценку |f(x0+A)—f(xb)|<e/2. Без ограничения
общности можно считать, что в разбиении То Xi—xo+h, где
а<х0+й<х2 (в противном случае добавляем точку деления
591
-Xi's(x0) xt) и замечаем, что для полученного продолжения
Т0'<Т0 в силу 2) имеем
ь
Vf(T0')^Vf(T0)>Vf-e/2).
Итак,
V f - е/2 < V/То) = |f (ХО+Л) - f (®о)| +
п0 ь
+ 2 |f(xk)-f(xR_1)|<8/2+ v f
"2 *«+Л
и поскольку
Ъ Ъ х.-М
v f = v / + v Л
х, х0+Л хе
то имеем оценку V /<е, т. е. 0<it(xc4-ft)—л(х0) < е, что озна-
чает *•
def
Я lim к(х) *= «(х0 + 0) = тс(х0).
х-*хе4-0
Аналогично для a<x0<ZZ> доказывается, что существует
lim w(x) — iv(x0 — 0) — Цх0),
х->хе—О
т. е. ite=C(x0)Vx0 е [а, 6], и поэтому кбС([а, &]). Но f еф, &],
так что у — п—f<=C[a, 6], т. е. 3) доказано.
Лем ма 2 (о равномерном приближении непрерывной функции
с ограниченным изменением). Пусть feO[a, Ь]Д1/[а, 6]. Тогда для
любого «=N существует непрерывная кусочно-строго монотонно
линейная функция Ln^C[a, 6_lAV{a, &] такая, что:
1) Ln(a)='f(a), Ln(b)=f(b),Ln(\a, &])=f([a, &])=[m, ЛЦ где
— оо < m = min f(x) < max f (x) = M
[a, 6] [a, b]
2) |f(x)—Ln(x) I <Л!п vxe[a, &J. Функция Ln(x) связана c
разбиениями Tn'^.Tn отрезка [a, 6], где разбиению Tn={a=
=4n)<...<z(n> <...<z^> = b} соответствуют частичные отрезки
7<n)=[zW, z<n>] равной длины |/^n)|= а разбиение T'n—{a =
—Xn)<..-<4.n><—<x(n)=&} таково, что:
° K m
п
3) Ln fxHt (II) на 7|.n> = [*<&, 4n)], причем
wfc(Iw) =ш(£п; (ft=l,..., <),
592
где 0 8к < 2~|с/2п < 1/2п, а также
о ^«(г';хмг;)+"/2. <4ra<v д,,
ь ъ ь
vb„< V f+l/2«<V /4-1.
а а а
Доказательство. Поскольку fеС[а, &], то функция f(х)
равномерно непрерывна на отрезке [а, Ь], а потому для е =
= 1/л Я T]n=ri(e)>0 такое, что V хь х2^[а, Ь], удовлетворяющих
неравенству |xi—х2|-<т|п, имеет место оценка IffxJ—f(x2)\<.
<1/2л. Рассмотрим разбиение Тп, для которого
—<^1п.
тп
На декартовой плоскости R2 введем множество узлов (z-”\
(1=$, 1, .... тп), соответствующих разбиению Тп. Тогда,
как показано в ч. IV, гл. 4, § 2 при доказательстве 2-й теоремы
Вейерштрасса, непрерывная ломаная, с последовательными верши-
нами (z<n>, f(zW)) (i=iO, 1, ..., mn) является графиком I\ =
={(х, y)^R2\y=ln(x), хе[а, Ь]} функции 1п^С[а, Ь], для кото-
рой имеет место оценка
|f(x)—Zft(x)|<l/nVx<=[a, Ь]
и /п ([а, b])czf([a, Ь])=,{т, М].
Заметим, что полученная функция 1п^С[а, Ь] будет кусочно-моно-
тонно линейной на отрезке [а, Ь]. Для построения функции
еф, Ь], являющейся кусочно-строго монотонно линейной на
[а, Ь], будут использованы помимо узлов, соответствующих раз-
биению Тп (с частичными отрезками равной длины (7=i
=il, ..., mn)), новые узлы, соответствующие разбиению Тп' (с диа-
метром d(Tn')^d(Tn) <Пп) с частичными отрезками /<в) =
=(xk-i> хкп)] (^=1> •••> тп ), являющемуся продолжением разби-
ения Тп (так что Тп'КТп). Рассмотрим частичный отрезок 7^п)
разбиения Тп. Тогда возможны два случая: a) —
—mW >0, где
Л/<п> = max f(x), mW =. min f(x),
j(«) jW
i г
и б) <о{(/)=0, так что f (x)=f^z^) на JW. В случае a) <»i(f)>0,
поскольку то на отрезке JW экстремальные значе-
ния mW и MW \mW < MW} достигаются по меньшей мере в
38—Л. И. Камынин
593
паре точек z|”>j и zTn>. Без ограничения общности будем счи-
тать, что
2(П> <- Z(n). <" ДЧ <* 7<П)
г—1 *г—1 2г— 1 ,
причем, если то /(гЗД) > »*(n>=f(z£.|), и аналогично*
если Zin)<z*n), то Л/ГМ(^П))>/(4П)). Тогда, полагая
/<n) = [2a- 2Й] U [#>Р zln)]U[?{4 z<n)],
получаем разложение отрезка 7<"> не более чем на 3 отрезка
(которые и будем обозначать через Дп>). Таким образом, в
случае
а) вместо узлов (zj^, и (z(n>, получаем узлы
М">„ /(45,)), m йч. ле>), W">. /(44))
(первая и последняя пара из этих узлов могут и совпадать)»
причем
«(f; 7^)<w(f;
В случае
б) (оД/) = 0 (так что f(x) = /(гЗД) на 7(п>) введем
на отрезке 7(”> дополнительную точку z<.n> = (зЗД 4- z(n))/2, так
что 7<п> = [г£Д, z<n)] U [z<n>, z(">], и введем 3 узла
m /№’,)) (*!“> f(«,)±8>). ww.
где > 0 выбрано так, что либо —6, т = min f, либо
+$|«СМ = тах/, и, кроме того, считаем, что 0<б,<
< 2-1/2п < 1 /2п. Дополнительные отрезки рЗД, z<.n>] и [z<n>, z(n)J
на 7(п> будем также обозначать через 7g*). Очевидно,
®(Л [4-г гсп)]) = “(Л [zcn>’ г(п>]) « 6, < l/2n
для любого Г. В соответствии с введенными узлами получаем но-
вое разбиение Тп' (отрезка [а, &]) с частичными отрезками 1{п)>
для которого имеем Тп'<Тп и d(Tn')^d(Tn)<.T]n- Проводя непре-
рывную ломаную через новые узлы (соответствующие разбиению
Тп'), получаем график Гьп функции Ln^C[a, Ь], для которой име-
ем Ln ([°, 6]) =/Y[a, &]) Af]. Для простоты записи будем в
дальнейшем опускать верхний индекс (п). Частичные отрезки It
нз разбиения Тп можно разбить на две группы: a') Jt^J', где
off; Д)=;Л!,—mt>Q, и б') где o(f; Ji)=®. В случае а')
594
Ji^r_имеем 4 узла (при z,-_i <Zi-\ <zi<j z,) (zt-\, f(zt-i)), (Zi-u
mt), (zt, Mt), (zi, f(zi)), причем~('при Ln(ziui)=if(zi_1), Ln(z,_1) =
—f(zi~i)—mi,Ln(Zi)=f(zi)=Mi, Ln(Zi) =f(zt)) имеем оценки
|£.n(X) Ln(zi—i) I|Ln(zj- 1} Ln(zi-t) | <;
<'l/2n Vxe[z,-i, £r-i];
I Ln (x) Ln (Zi—i) I i mt=
= I Ln(zi)—Ln(zi-\) | <l/2n V x^[zi-i, Zi];
I Ln(x)—Ln(zi) | | Ln(zt)—Ln(zt) | <
< l/2n V xefzij, zt],
причем^ Ln(X)|| на [zh.zh] (ecjn£Z,-_i<z,-_i, Ln (x) tt на\
[z/_i<zt_i] и Ln(x) |4 на fz,, z,] (если z,<z,-). Но тогда v.re
e[iz<-i, Zj-i] имеем оценки
I f (x)—Ln(x) | | f (x)—Ln(zi-\) | +
+1 Ln (z,-i) —Ln (Zi-i) | < 1/n.
Аналогично имеем оценки
I f(x)—Ln(x) | <l/n v xe[z(-_i, z^-]
и V xefiz,-, Zi].
В случае 6') L^J" (где ®z(£)=0) имеем
J,=[Z,_i, Z1']= [Z,-1, ZJU[ZC, Zi]
(где zc=i(zi-i-]-Zi})/'2), так что получаем 3 узла
(Zi-b f(zi-i)), (Zc, f(zt^)±6i), (Zi, f(Z,-i)).
причем
f(zi-i) =mi=Mi=Ln(zi-i) =Ln(zi) =f(zi)
и поэтому v xefzij-i, zc] или v xe[zc, zi], имеем оценки
\f(x)-Ln(x) ^[Kzi-O-iKzi-Mt) | =
=6,-<2_72n< l/2n,
причем Ln(x) |t (4!) на [Zi-b zc] и Ln(x) (ff) на [zc, zi]. Итак,
для любого частичного отрезка Z(Rn) из разбиения Тп' имеют место
оценки |f(x)—Ln(x) | <l/n vxe/<”) , если и
\f(x)—Ln(x)\^\l2n\x^I^ ,
38*
595
если /{n) cz/(n) el", тем самым показано, что для построенной
функции Ln<=C[a, b], связанной с разбиением Тп', имеем утвер-
ждения 2) и 3), а также оценки (из утверждения 4))
т'
< v-дг;) +.£!, < к,(гу +i/2« <
г—1
Ь Ъ
<Vf 4-l/2n<Vf + 1
а а
и в силу леммы 1
Ъ b
<vi„cvf+i-
4 1 а а
Определение. Пусть feC[a, Ь] и f([a, Ь])=[/п, Л1]. Тогда
индикатрисой Банаха (для функции f) называется функция
N -.[m, М]-► {11, 4-оо[, где V у^[т, Af] значение N(y) есть «число»
корней х^\а, &] уравнения f(x)—y (так что значение N(y) есть
мощность полного прообраза f~l(y)={x^[a, b]\f(x)=y} числа
уе=1тп, Al]).
Замечание. Поскольку f^C[a, 6], то в силу теоремы Боль-
цано (о промежуточных значениях непрерывной функции) из [1],
ч. I, гл. 4, § 3 f([a, 6]=fm, Af] и поэтому f-l(y)=t0 v t/spn, Af], и
тогда Vye[m, Al], где N(y)—+°° означает, что
бесконечное множество f~*(y) либо счетно, либо несчетно. (Если
М=т, то N(y)— Н-оо, где y=m=iM.) Будем в дальнейшем для
функции feC[a, Ь]ЛИа> &] считать, что Af>lV, так что множество
{([a, b])=(m, Af] есть невырожденный отрезок длины Af—/п>0.
Для функций feC[a, &]AV[a, &] и LneO[a, &]Л V[o, Ь] из лем-
мы 2 введем индикатрисы Банаха N(y) и Nn(y) соответственно.
Будем рассматривать множества (seN)
8(s)={ye[m, M]\N(y)>fy (Ш.З)
Sn(s)={ye=(m, M]\Nn(y)>s}, (Ш.4)
, S (oo)—{y^[m, M]\N(y) =+°o}- (111.-5)
Лемма 3 (о свойствах индикатрис Банаха N и Nn). Пусть
f(=C[a, &]AV[a, &], Ln(=C[a, &]ЛЛЧ (см- лемму 2) f([a, &])=!
=Ln([a, b])=[m, Af], N(y), Nn(y) — индикатрисы Банаха для
функций f и Ln соответственно. Тогда-.
1) Nn^R^tn, Af], причем (см. лемму 2)
MSNn(y)dy=^Ln (7’n')<VLn<Vf+l V neN;
m a a
2) если $n(s)^0 (при l<s</nn'+l). то существует конеч-
ная система отрезков {[a]n) , Р*п)]; i='l, 2, ..., q®} такая, что
596
5„<s)
ёп(з) c JJ [a(n>, ?(ra>] c= [m, M\ и
\ 3) если #п(«+1) =#0, to $n(s)-=> ^n(s+l);
4) если $(s-j-l) =#=0, to $(s)zz> £(s-|-l);
5) если #(oo)=/=0, то ^(oo)a:S(s) VseN;
6) если $(s)=£0, то существуют натуральные p^s и noeN
такие, что ^(s)c^n, (p).
Доказательство. 1) Рассмотрим функцию Ln^C[a, Ь]Д
ДУ[а, 6] из леммы 2, связанную с разбиениями Тп'<.Тп отрезка
[о, Ь]. Тогда
[a, fe] = [a, 4">]U U (4^, <>] = I)" 4П>.
R=2 R=1
причем отображение Ln:[a, 4П)] —>Ьп([л» 4°]) в силу леммы 2
является гомеоморфизмом, так что v y^L([a, 4П)]) существует
единственное такое, что £„(£<">)= у. Аналогично от-
ображение Lri:^2v 4п)] “*^((4-1» 4n)]) (fe = 2,..., zn^) также
является гомеоморфизмом и для 4п))] существует
единственное g(kn> (4-i> 4П)] такое» что Ln(g<.n>)= у. Отметим
также, что поскольку функция Ln е С(4П>), учитывая то ее стро-
гую монотонность на Z(Kn>, имеем равенства
“(i- (4"Л. 4”,ПНЧ4"’)--М4”Л)1=
Введем теперь вспомогательную ступенчатую функцию N^(y)
2,..., tn’^, определенную на отрезке [т, ЛГ], положив
|о, уе[т, М]\ЛП(7<«>)
И
N^(V) =
1, yeL„((4i>, 4")]),
О, у <=[/п, Л/]\1П((42>1, 4П>]); Л=2,..., т'п.
597
Ступенчатая функция N^(y) имеет не более двух точек раз-
рыва на [т, М], так что R\m, Af] и
м
f N^(yldy = <о(Ь„) (k = 1, 2,..., т'п).
m
Но тогда индикатриса Банаха Nn(y) (функции Ln(x)) имеет
представление
tn
Nn(y)='2 №*>(у) V у€=[m, М],
K=i
так что Nn^R[m, М] и
М т'п М т'п
^Nn(y)dy=^ $N<V(y)dy = 2 <о^„)=Йд„(Г;),
т К=1 т k’—1
и в силу леммы 2 имеем оценку
м ь
f Nn(y)dy<\ f+1 vneN.
m °
2) Поскольку Nn e R\m, M], to
_ M —
/= f Nn(y)dy = iniSNn(T)
m T
и поэтому для выбранного ne N существует разбиение Т=
(отрезка [т, Л/]) с частичными отрез-
ками {[Ук-ь Ук]; k= 1,..., q} такое что
SWn(T) <7 + 1/2п. ' (Ш.6)
Поскольку
\ 9 .
ёп(х)с[пг, Л4] = (J ь t/J,
it=i
то существует конечная система частичных отрезков
УкЬ » = <7n(s)) = {[ain)’ ^n>]; t = t--» ?»(«)} такая, что [«$”>,
$п)] А#п(«)¥=0; qn(s), причем
p.(n> = max Л/max Nn(y) > s 1=1,. 2,...,qn(s).
[ a(n>, ц!п)] [ »^n). 0<n)] П ^n(s>
Но тогда для верхней суммы Дарбу функции Nn имеем оцен-
ку снизу
598
9„<’> <?n0)
> 2 >s 2 (P*n)-«in)) > о,
i=i i=i
откуда, используя выбор разбиения Т отрезка [tn, Л4], получаем из
оценки (Ш.6) оценку
9„(s) _
0< s (₽^-«ln))<^„(7’)/s<(7 + l/2n)<
i=l
< (v Ln + l/2n 'j /s.
\ a 1 ’
3) Если gn(s+l)^.0 и «/(=$„,(s-f-l), то ЛГ„(^>з+1>з>1,
т. e. Nn(y)>s, и поэтому y^$n(s), т. e. <£n(s)zz £n(s+l).
4) Доказательство включения (s+1) проводится ана-
логично.
5) Если $ (°о)#=0, то v y^S (оо) множество f~l(y)c$a, b]
бесконечно и поэтому v seN существует s различных корней
<£i< ••• <&><& уравнения f(x)=y (так что ffa)=y, t=l,...,s),
т. е. N(y)^s, а потому y^$(s)N seN, что и означает включение
% (oo)cz^(s).
6) Если и y^$(s), то N(y)^s^\. Тогда существует
P>s различных корней ... <!₽<&} уравнения f(x)=y,
так что f(ln)—y (k—\, ..., р) и поэтому б =,min (gr-£*-i)>0.
R=2,..., р
Но тогда З/IoeN такое, что для разбиений Т’ -<,Т (соответству-
ющих функции ЛПоеС[а, Ь]Д V[a, Ь] из леммы 2) отрезка [а, 6]
имеет место оценка 0<;(b—а)//п„<б/3. Тогда существуют частич-
ные отрезки ; k=l, ..., р) разбиения Тп., для которых
У<"«)[]/<«.) =(0 у k^l и £ = 1, ..., р. Рассмотрим от-
kt k
резок /(”•>. Тогда возможны (см. доказательство леммы 2) два
случая (будем опускать верхний индекс (п0)): а')
(т. е. %(f)>0) и б') J" (т. е. <Bijc(f) = 0). В случае а')
Jtk Г имеем
Mi}. = max f (х) = f (zjlc)>ffii)t = min f (x) = f (г^-j)
и тогда, вспоминая построение разбиений имеем
и К-ь k-]up<R.
причем f(lk)=y A4iR]. Поскольку L„, sCJAj, to
599
Ья,еС([%-1> 2»lte]) и в СИЛУ строгой монотонности функции
Ln.(x) на отрезке [г^-ь zift] существует единственное т)ь е
е [?л~ь ***] такое> чт0 ^п.(^)=У> т- е- уравнение Ln/x)=
= у имеет не менее одного корня х = на любом отрезке
JNg/'. в случае б') 7i.^J" (так что
k «
<%(f) = 0 и f(x) = f(zift-i) v X е jik)
имеем
f(Zik~ *) — — ^’n«(Z4c) ~~ У'
т. е. уравнение Ln°(x)=y имеет два корня x=z^l и x = z[n^ на
любом отрезке Тем самым доказано, что на отрезке
[а> 6] существует не менее р различных корней уравнения
^п,(х) = у, т. е. Nn/yy^p. Итак, для любого у s$(s) сущест-
вуют натуральное число и функция Ln, еС[а, 6] Д V[a, Ь]
такие, что Nn(y)’^p, т.е. ye Snip)- Но тогда имеем включение
8(s) <= ^(р).
Теорема Б а н аха./7«/ст& feC[a, &]AV[a, 6] и — ин-
дикатриса Банаха для функции f. Тогда \8 (ooJI^O и, в част-
ности,
mes <£ (oo)=i0.
(Ш.7>
Доказательство. Если $(оо)=/40, то в силу леммы $
S (оо)о <8(s) VseN, и тогда в силу утверждения 6) леммы 3 су-
ществуют натуральное число p^s и функция Ln. еС(а, Ь]Д
АИД Ь] (из леммы 2), где р и п0 зависят от $, такие, что имеем
S(s)cz^nii(p). В силу утверждения 2) леммы 3 для множества
^п,(р) существует покрытие из конечной системы отрезков.
р=з1,..., дп/р)}> для которой
вп,(р) / ь \
2 < V f + 1 \ /Р-
i=l \ а /
Но тогда Ve>03seN такое, что
ку p==p(s)>s, то 4- 1)/р<е. Из леммы 3 имеем включе-
ние £(со) a g(s) cz ё’п/р), где s, и поэтому в силу утверж-
дения 2) леммы 3 (при п*=п0) имеем
600
4nfi>>
причем
?n,(P)
2 (P^.), a<n«>) < e,
i=l
что и означает, что множество &(оо) имеет длину (меру Жор-
дана) нуль, т. е. |<о<оо)|1=0, и, в частности, тогда имеем (III.7).
Замечание. В [9] (гл. VIII, § 3„ теорема 3) и в [12] (гл. IV,
§ 2, п. 8, обобщение теоремы Коши) теорема Банаха об индикат-
рисе доказана с использованием понятия интеграла Лебега, а
именно показано, что для индикатрисы Банаха функции /е
м ъ
^С[а, b]/\V[a, 6] существует интеграл Лебега ]N(y)dy=\f, так
т а
что индикатриса Банаха N(y) суммируема на отрезке [т, М], а
потому почти всюду ограничена на [|zn, AI], что и означает вы-
полнение (III.7).
Следствие. Пусть f<=C[a, Ь]ДУ[«, &], f([a, Ь])=[/п, AfJ
и Г/={(х, y)^R2\y=f(x), хе[а, &]} — график функции f на
плоскости. Пусть Е=<{у0^т, Af]| множество точек (х, y0)^Tf
бесконечно} (т. е. Е есть множество чисел уо^гп, М], для которых
прямая у=Уа на плоскости R* у имеет бесконечное число точек
((х> г/0)еГу) пересечения с графиком Г/). Тогда
mes£=O. (Ш.8>
Доказательство. Введем для функции feC[a, 6]Д
АЙа> ЭД индикатрису Банаха N(y), тогда в силу (III.5), очевидно,.
£,=1g’(oo) и по теореме Банаха из (ПЕТ) следует (III.8).
Лемма 4 (см. [10]). Пусть feC[a, 6]ДУ[а' И f([a, ^Р —
=[m, All N(y) —индикатриса Банаха (для f) и Г/ — график
функции f на плоскости . Тогда V 6 Я t/oe[m, AI] такое, что
V seZ, имеет место неравенство O^N0(y0-+sd) <-]-оо, где
N (у), y^[m, AI]
0, y^[m, AI]
(т. е. прямая y=y0-\~sb v seZ имеет не более конечного числа то-
чек ((х, y0-^-sd)^Tf) пересечения с графиком Г/).
Доказательство. Для любого seZ введем (см. II 1.5) >
множество
E(s)={z^(—оо, -|-оо) \z—(oo)cz[|m, Af]}=
^{zefm+£б, Af+хб] | Vo (z—s6) = JV (z—s6) == + oo}.
601
N0(y)=>
Очевидно, Е(0) = % (оо), и поэтому для множества & (оо) в силу
теоремы Банаха имеем (III.7). Но тогда для множества E(s)
имеем mesE(s)=O (s=0, ±1, ±'2, ...), причем E(s)a%m+s6,
-M + $6]V seZ. Положим
E =i J Efs)o U [ют+зб, Л1+;5б]с(—oo, +oo).
5=—oo S=s—oo
Поскольку mes E(s)=0 vseZ, to mesE=0, но тогда (см. [1],
1 • 1
ч. II, гл. 2, § 3) Е=0 и поэтому множество СЕ всюду плотно в
(—оо, +:оо) и, в частности, СЕ плотно на [т, Л4]. Но тогда
V 6>0_я ^ое[|/п, Л4]\Е такое, что Afo(t/o)=^(’f/o)<i+00, и поэтому
y0+sb^E(s) VseZ, т. е. 0<Уо(^о+-5б)< + 0°; $=0, ±1, ±2, ....
Но это и означает, что прямая у=Уо+«Ь v seZ имеет не более ко-
нечного числа точек ((х, г/о+^б)еГ/) пересечения с графиком Г/.
Теперь, используя из [1], ч. III, гл. 1, §§ 3—5, рассмотрим на
плоскости R2 спрямляемый цикл Жордана (замкнутый спрямляе-
мый жорданов! контур) ф, так что для 1-пути в R2
ф: [а, Ь] -> ф ([а, &]) = rcR2 (III.9)
имеем
фе=С[а, И (III. 10)
-отображение ф:[а, &)-* ф([а, Ь)) биективно (III.11) и ф(а)=.
=ф(Ь), причем имеет место представление ф(0 = (*(£), y(t)) V
/е[а, Ь], где
х, у^С\а, &]ЛИа, &]. (Ш.12)
Лемма 5 (о спрямляемых 1-путях). Пусть ф — спрямляемый
1-путь в R2, так что имеют место (III.9), (III. 10) и (III. 12) и
l(t)=Nty — длина 1-пути ф<: [а, ^]-*ф([а, /]) V £е[а, Ь]. Тогда:
1) l(t)a\ на [а, Ь]; 2) 1<=С[а, &]; 3) 1([а, 6])=[0, S], где 5=Уф —
а
длина 1-пути ф; 4) |Г|2=0 (т. е. площадь (мера Жордана на плос-
кости) носителя Г=ф({а, &]), спрямляемого 1-пути ф равна ну-
лю и, в частности,
mesr=0. (Ш.13)
2
t
Доказательство. В силу (III.12), полагая l(t)=Vty, оче-
видно, имеем 1) и 3). Заметим, что из теоремы 1 ([1], ч. III, гл. 1,
t t t
§ 3) имеем оценку О^СУф^СУх+Уу v f^[a, &], при этом, учитывая
а а а
теорему 2 (об аддитивности полной вариации вектор-функции) из
[1], ч. III, гл. 1, § 3 v Ate(0, Ъ—а), имеем оценку
«02
1
t+bt t+iit t+ы
O^l(t+ M)—l(t) =< Vt < Vx + Vy,
t t t
и тогда из утверждения 3) леммы 1 имеем
Vx, VyeC[a, Ь],
а а
так что
Н-Д* /4-Д/
lim V х= lim V у=0,
ZV—f-0 t Д^-f-O t
а потому lim (l(t+At)—/(i/))=0, что означает выполнение 2).
Д<-»+0
Далее, докажем, что для любого neN существует разбиение
T={a=it0<zti<.... <А< ... <Jn=b} отрезка [а, 6] такое, что
l(/ih)=‘kSln (k=0, 1, .... п). В самом деле, в силу теоремы Больца-
но (о промежуточных значениях непрерывной числовой функции)
в силу 2) и 3) V &5/п(=Г0, S] (при £=il, ..., п—1) я ^е[а, Ь] та-
кое, что l(tk) ='k-Sln>l^tk-\) ='(k—\)S/n, и тогда в силу 2) име-
ем (^=1, ..., п). Положим Г*=п|>ф*-1, /*]) при k=
п
= 1, ..., п. Тогда Г= J Г*, причем
^Гк)= sup ||ф(|) - ф(т))||2 <
Е. '*]
ГЬ
< V ф = /(/*) — tys-i) = S/n.
Oc-i
Введем на плоскости R2 у сетку из квадратов со сторонами, па-
раллельными осям Ох и Оу, и длины S/n. Поскольку d(T*) <.S/n,
то множество 1\ может иметь общие точки не более чем с 4 квад-
п
ратами введенной сетки, и тогда носитель Г=ф([а, Ь]) =*иГй по-
К=1
крывается не более чем 4п квадратами сетки с общей площадью,
не превышающей числа 4n-(S/n)2=4S2/n. Но тогда V е>
>0an(e)eN такое, что 4S2/n(s)<e. Вейлу произвольности
•е>|0 из § 3 гл. 2 имеем, утверждение 4) и, в частности, (III.13).
Следствие (об измеримости по Жордану области со спрям-
ляемой границей). Если область (открытое связное множество)
GczR2 ограничена и имеет спрямляемую границу dG (состоящую
из одного спрямляемого цикла Жордана, если G — односвязная,
и из (т+1) спрямляемых циклов Жордана, если G (m+il) связ-
на), то G измерима по Жордану.
Теорема Привалова (о спрямляемом контуре, см. [12]).
Пусть ф — спрямляемый замкнутый 1-путь Жордана с носителем
Г=ф([а, 6])c2R2 (см. (Ш.9) — (III.12)). Тогда для любого 6>0
существует точка (х0, t/0)eR2 такая, что x0^[mt, Л41]==х('[а, &]),
603
i/0s|jm2> -Л^21=У((а, b]) и v seZ любая прямая x=x0+s6 и любая
прямая у=Уо+^6 имеет не более конечного числа точек
((x0+s8, у), (х, yo+s8)^r) пересечения с носителем Г жорданова.
спрямляемого цикла if.
Доказательство. По условию выполнены (Ш.9)—(III. 12).
Пусть
^1(oo)=(xe[mi, Л11]|Л1(1)(х) = +|оо}
и %2(<x)=={y<=[m2, M2]\N&(y) = + oo},
где №1>(х) и N^(y) —индикатрисы Банаха для функций x(t) в
y(t) из (III.12) соответственно. Тогда в силу теоремы Банаха
mes £<л(оо)=0 (i=’l, 2), (III.14)
1
и поэтому в силу леммы 5 для любого 6>0 существуют числа
хое(/Пь Л11]\ $i(oo) и yQ^[m2, М2]\ #2(°0) такие, что:
1) любая прямая x=x0+s6 (s=0, ±1, +2, ...) пересекает
график Гх—{(t, x)\x=x(t), Ь] не более чем в конечном чис-
ле точек (tk, x0+|s6)erx (k=i\, 2, ..., p(s)). Но тогда в силу
(III.11) прямая x=xo+is<5 пересекает и носитель Г не более чем в
p(s) точках (x0-|-s6, y(tk) )еГ (k=l..p(s));
2) любая прямая у=Уо+^8 (seZ) пересекает график Г(/=
={(t, У)\У=У(1)> Ь]} не более чем в конечном числе точек
(tk, yo+s8)^.Vv (k—Л, ..., q(s)), а потому эта прямая пересекает и
носитель Г="ф(|[а, Ь]) не более чем в конечном числе точек
(x(th), y+s8)^V.
Замечание. Точку (хо, у0) из теоремы Привалова можно вы-
брать так, что (х0, у0) еГ=if (fa, Ь]), причем узлы сетки (с шагом
6>0), образованные прямыми x=x0+s6, у=уо+гб (s, re
€=0, ±1, ±2, ...) из теоремы Привалова, также не принадлежат
носителю Г, т. е. (x0+s6, г/о+^б)^Г при s, г^.1. (Идею доказа-
тельства этого утверждения сообщил автору Э. Г. Позняк.)
В самом деле в силу (III.14) для любого е>0 существуют не
более чем счетные покрытия {Ii,k=[Xk, xk"]’, k=l, 2, ...} и
{I2,f—[yj', у"}\ /=1, 2, ...} множеств ё’Доо) и #2(оо) соответст-
венно такие, что й’Д00) с U A,k (i=l, 2), причем S |Л,k11<.
k==t А==1
<Уё (t=l, 2). Полагая Л,, =Ц, ьХЛъ, /cR*. v > видим, что не бо-
лее чем счетная система прямоугольников {/| .; k, j=4, 2, ...} об-
разует покрытие множества Е= $i(oo)x 82(<х>) такое, что
Ес U J2. у, причем
4-00 4-00 / 4-00 \
S’ l'U=2 S !'><!> К «I.
Тс, 5=1 к=1 \j=l ‘ /
604
0
так что mes£’=0 и тогда £==0, т. е. множество СЕ всюду плотно
на плоскости R2. Рассмотрим на плоскости R2 сетку с шагом S>О,
образованную прямыми х=$б и y=rb (s, r^Z) и разбивающую
плоскость на квадраты {J2Str ; s, r=0, ±1, ±2, Тогда R2=
s, r=4-eo
= U I2 r =>r[J£. Рассмотрим квадрат J2=[0, 6]X[0, 61 и введем
s, r=—oo ’
для каждого квадрата J2 г из нашей сетки аффинное отображение
As, г, состоящее в сдвиге, совмещающем квадрат /2 г с квадратом
У2, так что As, rJ2 r —J2 и Л~‘г J2=\J2 r . Очевидно, отображения
As,r п A~lr класса C<’)(R2). Пусть у3, r=As, r (J2 r ПГ) и es,r=
=AS, r(V2 r f|E). Поскольку mesE=0 и в силу 4) леммы 5
mes Г=0, то в силу теоремы (об инвариантности меры нуль при
О1) отображении) из ч. V, гл. 1, § 3 имеем mes r=meses>r=0
2’2
и тогда, полагая
s, г=4-00 s, г=4-оо
7 — U 7». г, е = J es, г,
S, г~—оо S, г=—оо
имеем mes (7Ue) =0, так что множество не имеет внутренних
точек, а потому его дополнение С (уЦе) плотно в У2. Но тогда
я(х0, Уо) ^У2\ (71Ю> и поэтому точка
(*о+*6, 0о+Гб)=А-« ((х0, Л)еУ2\(ГЦЕ).
Введем новую сетку (с шагом 6>0) с узлами в точках
(Хо+яб, J/o+гб)s (Г|_|($i (°°) X ffizt,00))) V s, r^L.
Поскольку
Xoie$i(oo), уоё= и (Хо+$6, у0+\г8) еГ,
то каждая из прямых x=Jfla+s6 и у—Уо+уЪ, образующих новую
сетку, может иметь не более конечного числа общих точек с носи-
телем Г спрямляемого 1-пути Жордана ф.
Доказательство точной теоремы Грина на плоскости (см. [10]).
Поскольку односвязная область GeR2 ограничена, а ее граница
dG является носителем спрямляемого цикла Жордана ф (так что
имеют место (III.9)—(III.12), то в силу 4) леммы 5 имеем
|dG|2=0, так что как множество G, так и компактное множество
G измеримы по Жордану (см. ч. V, гл. 1, § 4). Но тогда существу-
ет квадрат
У2[А, В]оУ2(А, B)zdG3G и %0^R(I2[A, В]),
605
причем в силу замечания 2 к теореме (о предельном критерии ин-
тегрируемости по Риману на брусе) из ч. V, гл. 1, § 2 имеем
3 1imSXG(T)= ff Хо(х, у) dxdy = |G|2, (111.15)
z-+0 Г[Л, В]
где (f-»- + 0) — 6a3a_{Bg) с элементами В£ ={T|0<d(T)<6}.
Поскольку Р, Q^C(G), то функции Р и Q равномерно непрерыв-
ны на компактном множестве G и поэтому V е>0, э б(е)>0 (где
будем считать 0<6(s)<l), такое, что для любого квадрата
с диаметром d(I%)<?2б<6(е) <1 имеем оценку
\Р(М1)-Р(М2) | +\\Q(Mt)~Q(M2) | <
<8 ¥Л*Ь M2f=l%[]G. (III.16)
Далее, в силу (III.15) для выбранного выше 8>0 существует эле-
мент Bj базы (^+0) такой, что имеет место оценка
SXG(T)>|G|2-8VTeB^ (III.17)
Выберем теперь разбиение ТС^В*Ь бруса Р\А, В] (при выполнении
d(7\)<26<6(e) <1) из теоремы Привалова. Тогда, учитывая
замечание Позняка (к теореме Привалова), видим, что разбиение
Те составлено из узлов
(x0+|s6, t/o+r6)e=dG='r(Vs, reZ)
сетки с шагом 6<=(0, 1), причем любая прямая x=x<t+|s6 и
У=Уо+гЬ имеет не более конечного числа точек пересечения с гра-
ницей <5G=r. Без ограничения общности будем считать, что точки
А и В бруса PfA, В] также являются узлами выбранной сетки.
Тогда разбиение Г, квадрата /2[Д, B]=>G состоит из частичных
квадратов с длиной стороны 6>0, причем для компактного
множества КГ=1Я(к> где /да (]dG='0, имеем
(К)
Swn-J=2|/?„ Ь.
(ft)
так что в силу (III.17) имеем оценку
|С\ДГ|2<®. (Ш.18)
Для компакта ДГ с ориентированным краем имеем
причем любой квадрат 12т (см. рис. 43) является простым (в
смысле определения из ч. V, гл. 1, § 3) относительно каждой из
координатных осей Ох и Оу, и, очевидно, дК7 = I) • Посколь-
606
Рис. 43
ку to^C(G) и выполнено условие (III.1), то Gz^Kt, так что
£ееС(*-’)’
то к измеримому по Жордану компакту КГ с ориентированным
краем дКГ применима первая (предварительная) теорема Грина
(из ч. VI, гл. 1„ § 4), в силу которой имеем
j w= f da. (III.19)
Зк~ "к-
е е
Обозначим теперь через все частичные квадраты разбиения
Те, для которых /2, f]dG=/=0. Тогда I2f) f]/2r) =0V (l')^(l")r
причем
5G = U5(Gn/(2JU^,
(О
где множество дКГ =i U c7<ic) состоит только из отрезков сетки
(выбранной в силу теоремы Привалова). Поскольку на сторонах
д!2т квадрата 121} (из сетки с шагом бе (0, 1)) по построению
содержится только конечное число точек границы dG=r (причем
вершины квадрата 12(1) не принадлежат границе 0G), то множест-
во?.
Рис. 44
®о Gfl/fo состоит из конечного числа i(l) связных компонент,
граница каждой из которых является носителем спрямляемого
цикла Жордана (так (см. рис. 44), Gf|/fr) состоит из трех ком-
понент и состоит из одной связной компоненты). Но тог-
да, полагая q =|S i(7)eN и вводя новую нумерацию (без мульти-
индексов) для этих циклов {уад; /='1, 2.<?}, имеем
.— q __ <—
dG= U Г}- U дКГ,
3=1
где Г/ — ориентированный спрямляемый .цикл Жордана с длиной
|Г/| =// (7='1, 2, Пусть |Г| =5 — длина цикла Г=<?0.
Тогда
4^1 1
f f ®-
5o , 3=i дк~
откуда в силу (III. 19) имеем
f <»=£ f «>+ f du,. (Ш.20)
Tq rj "k~
Заметим, что 3GqU^o , где число квадратов 7ц) не превышает
(*)
числа q циклов Г/ (/—1, .... q). Следуя доказательству утвержде-
ния 4) из леммы 5, выберем neN такое, что S/6^n<5/6+l, где
бе (0, 1) — шаг сетки (т. е. длина стороны квадрата ). Тогда
можно ввести представление Г = U у/, где дуга имеет длину
г=1
1^1=5/^ причем дуга у,- может иметь общие точки не более чем
«08
с 4-мя квадратами поэтому граница дб=Г может иметь об-
шие точки не более чем с 4n<4(S/6+4) квадратами сетки. Но
лишь для квадратов, отмеченных мульти-индексом
q
(I), так что 9<4(S/6+U), поэтому разность SI/—S не превосходит
j=l
суммы периметров квадратов /2}, число которых не превышает
так что
S lj—S<46?< 166 (S/6+11) =I16S+I166,
j=i
я поскольку 0<6< 1, то имеет место оценка
9
2Z;<L=T7iS,+ l-6, (Ш.21)
где постоянная L>0 не зависит от выбора е>0 и разбиения Ге
из теоремы Привалова. Пусть Г/сгд (Gf]/(o JcGf)/^. Рассмотрим
какую-либо точку М} е G (] и положим
1 def
(О/ = P(Mj)dx+Q(Mj)dy.
Тогда в силу следствия из теоремы 6 (о независимости специаль-
ного криволинейного интеграла Римана — Стильтьеса 2-го рода от
пути интегрирования) из приложения II имеем для ориентирован-
ного спрямляемого цикла Жордана Г/ равенство S со/=О. Заме-
ну
тим, что диаметр =i?26<'26<6(в), поэтому из ДП.16)
имеем оценку
\Р(М)-Р(М}) |,+;|Q(M)—Q(Mj)k<
,<8УМеГЯП)
и тогда из теоремы 5 (об оценках криволинейного интеграла Ри-
мана— Стильтьеса) из приложения II имеем оценку
it 1 it
J (Ш—©/) + ] Ш/ = J (ш— шу)
г/ г/ г/
< ® Ш = eZj,
Х/='1, 2, ..., q), так что, учитывая оценку (Ш.21), получаем оценку
9
<2ejg Z}< 2&L
i=i
(III.22)
и поэтому в силу
(Ш.20) получаем оценку
(III.23)
-3S—Л. И. Камынин
609
Поскольку ’^-Р, f-Q eC(G)/\BIG), где множество G из*
ду дх
меримо по Жордану, то, доопределяя функции Р, — Qr
ду дх
например, нулем на границе dG, видим (см. теорему Фубини для
цилиндроида из ч. V, гл. 2, § 2), что Р, -^QsR(g), причем
существует постоянная Af>0 такая, 4то имеет место оценка
^Р (х, у) —£~xQ(x> У) I v (х> У) е о,
откуда в силу (III.18) имеем оценку
1 1
d»— j" dw
G K~
< Л<|б\«Г|,<ЛА.
Но тогда из (III.23) получаем оценки
1 I
1 /» 1
i
dG
— j" dco j" о>— J do -J- J d,<s>— f d<o
S' So kt g
< e(2£ + M).
e
e
В силу произвольности e>0 имеем формулу Грина (III.2).
Следствие (основная теорема Грина из ч. VI, гл. 2, § 2 нэ
плоскости). Пусть KcrR2 есть компакт с краем, причем К — одно-
связная область и дК — ориентированный край, являющийся ку-
сочно-гладким (класса С<М) циклом Жордана, причем
1 А А о о
С(Ю; ±Р, ^-Q^G(K) Л В(К).
Тогда имеет место формула Грина (Ш.2) (где G=R и dG^dK.)..
В самом деле, край dR, будучи кусочно-гладким (класса С*1)),,
является (в силу рассмотрений из ч. III, гл. 1, § 5) непрерывным/
спрямляемым циклом Жордана, так что применима доказанная
выше точная теорема Грина на плоскости. Заметим, что если край
*dK ориентирован по правилу из, ч. VI, гл. 1, § 4, то имеем
1/2 - J xdy—ydx=JJl • dxД dy =^=|К|2> О,
ак к
т. е. dK ориентирован в смысле, указанном в формулировке точной
теоремы Грина.
Замечание 1. Приведенное следствие указывает еще на од-
но доказательство 2-й основной теоремы Грина на плоскости и®
ч. VI, гл. 2, § 2.
610
ОГЛАВЛЕНИЕ
ЧАСТЬ IV. РЯДЫ, БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ И НЕСОБСТ-
ВЕННЫЕ интегралы ............................................... з
Глава L Числовые ряды, бесконечные произведения и несобственные
интегралы .............................................. 3
§ 1. Понятия числового ряда, бесконечного произведения, несобственного
интеграла с бесконечными пределами и несобственного интеграла от
, неограниченной функции ...................................... 3,
Определения сходящегося и расходящегося ряда (3). Определение схо-
дящегося и расходящегося бесконечного произведения (4). Теорема (кри-
терий сходимости бесконечного произведения) (5). Определение сходя-
щегося и расходящегося несобственного интеграла с бесконечным (верх-
ним) пределом интегрирования (5—6). Определение сходящегося и рас-
ходящегося несобственного интеграла от неограниченной функции (7)
§ 2. Критерий Коши сходимости рядов, бесконечных произведений и не- .
собственных интегралов .............................................9
Теорема (критерий Коши сходимости числового ряда) (9). Теорема
(критерий ‘ Коши сходимости бесконечного произведения) (9). Следствие
(необходимое условие сходимости числового ряда) (9). Пример (расхо-
димость гармонического ряда) (10). Теорема (критерий Коши сходимости
несобственного интеграла с бесконечными пределами интегрирования)
(10). Замечание (критерий Гейне сходимости несобственного интеграла
с бесконечными пределами интегрирования) (11). Теорема (критерий Ко-
ши сходимости несобственного интеграла от неограниченной функции)
(12). Замечание (критерий Гейне сходимости несобственного интеграла от
неограниченной функции) (12)
§ 3. Простейшие свойства сходящихся рядов и несобственных интегралов 13
Теорема 1 (о сумме сходящихся рядов) (13). Теорема 1' (о сумме схо-
дящихся несобственных интегралов с бесконечными пределами интегриро-
вания) (14). Теорема 1" (о сумме сходящихся несобственных интегралов,
от неограниченных функций) (14). Теорема 2 (об изменении конечного-
числа членов ряда) (15). Теорема 2' (аналог для несобственных интегра-
лов с бесконечными пределами интегрирования) (15). Теорема 2" (ана-
лог для несобственных интегралов от неограниченных функций) (16).
Теорема 3 (о группировке ряда) (16). Замечание (достаточное условие
сохранения суммы ряда при раскрытии скобок) (16)
£ 4. Признаки сходимости знакопостоянных рядов и несобственных интег-
ралов от знакопостоянных функций............................1 . . . 17
Теорема (критерий сходимости знакопостоянного ряда) (17). Теорема
(критерий сходимости несобственного интеграла с бесконечными предела-
ми интегрирования от неотрицательной функции) (17). Теорема (крите-
рий сходимости несобственного интеграла от неотрицательной неограни-
ченной функции (18). Теорема сравнения (для рядов) (18). Следствие 2
(теорема сравнения в предельной форме для рядов) (18). Теорема срав-
39* 615
нения (для несобственных интегралов с бесконечными пределами интег-
рирования) (19). Следствие 2 (теорема сравнения в предельной форме
для несобственных интегралов с бесконечными пределами интегрирования)
(19). Теорема сравнения (для несобственных интегралов от неотрицатель-
ных неограниченных функций) (20). Следствие 2 (теорема сравнения в
предельной форме для несобственных интегралов от неограниченных
функций) (20). Теорема (признак Д’Аламбера сходимости рядов) (20).
Теорема (радикальный признак Коши сходимости рядов) (21). Теорема
(критерий сходимости бесконечного произведения) (22). Теорема (доста-
точное условие сходимости бесконечного произведения) (23). Замечание
(достаточный признак расходимости бесконечного произведения к нулю)
(23). Теорема (интегральный признак Коши сходимости знакопостоянного
ряда) (24). Теорема (признак Гаусса сходимости знакоположительного
ряда) (25). Лемма (об асимптотике знакоположительной последователь-
ности) (25). Теорема (формула Стирлинга) (28). Теорема (формула Вал-
лиса) (29). Следствие (уточненная формула Стирлинга) (30).
§ 5. Признаки сходимости знакопеременных рядов и несобственных интег-
ралов от знакопеременных функций.......................................30
Теорема (признак Лейбница сходимости знакочередующегося ряда) (31).
Замечание (об оценке остатка сходящегося знакочередующегося ряда)
.(31). Теорема (тождество Абеля) (32). Теорема (признак Дирихле схо-
димости знакопеременного ряда) (32). Теорема (признак Абеля сходимо-
сти знакопеременного ряда) (33). Теорема (признак Дирихле сходимости
несобственных интегралов с бесконечными пределами интегрирования)
(33). Пример (сходимость интеграла Дирихле (34). Теорема (признак
Дирихле сходимости несобственных интегралов от неограниченной функ-
ции (34). Теорема (признак Абеля сходимости несобственного интеграла
с бесконечными пределами интегрирования) (35). Теорема (признак Абеля
сходимости несобственного интеграла от неограниченной функции) (35).
Теорема (о замене переменной интегрирования в несобственных интегра-
лах) (35). Теорема (об интегрировании по частям в несобственном инте-
грале) (36). Теорема Фруланни (37).
.§ 6. Абсолютно и условно сходящиеся ряды (несобственные интегралы)
и их свойства .........................................................39
Теорема (критерий Коши сходимости последовательности в С (40).
Замечание (критерий сходимости ряда с комплексными членами) (40).
Определение абсолютно сходящегося и условно сходящегося ряда (41).
Теорема (о сходимости абсолютно сходящегося ряда) (41). Определение
абсолютно сходящегося и условно сходящегося несобственного интеграла с
^бесконечными пределами интегрирования (42). Пример (условная сходи-
мость интеграла Дирихле) (42). Теорема (о сходимости абсолютно схо-
дящегося несобственного интеграла) (42). Теорема (критерий абсолютной
•сходимости бесконечного произведения) (43). Следствие (критерий ус-
ловной сходимости числового ряда с действительными членами) (44).
Теорема (о перестановке членов в абсолютно сходящемся ряде) (45).
Теорема (о безусловной сходимости абсолютно сходящегося ряда) (46).
Теорема (об абсолютной сходимости безусловно сходящегося ряда) (46).
Теорема Дирихле — Римана (47). Теорема (о суммировании по блокам
абсолютно сходящегося ряда) (48). Теорема (о двойных рядах) (50).
Теорема Абеля (об умножении двух абсолютно сходящихся рядов) (52).
Теорема Мертенса (об умножении двух! рядов) (53).
Глава 2. Функциональные последовательности, ряды и несобственные
интегралы, зависящие от параметра .....................................55
§ 1. Равномерная сходимость функциональных последовательностей и
функциональных рядов .................................................. 55
612
Определение простой (или поточечной) сходимости функциональной по-
следовательности на множестве (55). Определение равномерной сходимо-
сти функциональной последовательности на множестве (56). Определение
равномерной сходимости функционального ряда на множестве (57). Оп-
ределение неравномерной сходимости функционального ряда на множест-
во (57).
$ 2. Интегралы, зависящие от параметра................................5&
Определение равномерной сходимости на множестве функции и(х, t) к
пределу по базе (x-+xQ) (58). Теорема 1 (о непрерывности интеграла Ри-
мана, зависящего от параметра) (59). Теорема 2 (о дифференцируемости
интеграла Римана, зависящего от параметра) (60). Теорема 3 (об интег-
рировании интеграла Римана, зависящего от параметра) (62). Определе-
ние равномерной сходимости функции F(x, А) к пределу (по Коши) на
множестве по базе (А->+<») (64). Определение равномерной сходимости
функции F(x, А) к пределу (по Гейне) на множестве по базе (А->Н-«>)
(64). Замечание (об эквивалентности понятий равномерной сходимости
функции на множестве и равномерной сходимости функционального ря-
да) (64). Определение равномерной сходимости на множестве несобствен-
ного интеграла (зависящего от параметра) с бесконечными пределами
интегрирования (65). Определение неравномерной сходимости на множе-
стве несобственного интеграла (зависящего от параметра) с бесконечны-
ми пределами интегрирования (65). Определение равномерной сходимости
на множестве функции Л(х, 6) к пределу (по Коши) по базе (б->0) (66).
Определение равномерной сходимости на множестве функции F (х, б) к
пределу (по Гейне) по базе (6->0) (66). Замечание (об эквивалентности
понятий равномерной сходимости функции на множестве и равномерной
сходимости функционального ряда) (66). Определение равномерной
сходимости на множестве несобственного интеграла (зависящего от пара-
метра) от неограниченной функции (66). Определение неравномерной схо-
димости на множестве несобственного интеграла (зависящего от парамет-
ра) от неограниченной функции (67).
§ 3. Признаки равномерной сходимости функциональных последователь-
ностей, функциональных рядов и несобственных интегралов, зави-
сящих от параметра.....................................................67 '
Определение равномерного стремления функции Г(р, х), к пределу на
множестве по базе В^(68). Определение неравномерного стремления
функции F(p, х) к пределу на множестве по базе В^(68). Теорема (кри-
терий Коши равномерного стремления функции к пределу) (68). Теорема
(критерий Коши равномерной сходимости функциональной последова-
тельности) (69). Теорема (критерий Коши равномерной сходимости функ-
ционального ряда) (69). Замечание (о геометрическом смысле равномер-
ной сходимости функциональной последовательности на множестве) (69).
Определение метрических пространств В ([а, Ь]) и С ([а, Ь]) с метрикой
Чебышева (69). Теорема (критерий Коши равномерной сходимости не-
собственных интегралов с бесконечными пределами интегрирования) (70).
Замечание (критерий Гейне равномерной сходимости несобственных ин-
тегралов с бесконечными пределами интегрирования) (71). Теорема (кри-
терий Коши равномерной сходимости несобственных интегралов (завися-
щих от параметра) от неограниченных функций) (71). Замечание (кри-
терий Гейне равномерной сходимости несобственных интегралов (завися-
щих от параметра) от неограниченных функций) (72). Определение (нор-
мальной сходимости функционального ряда) (72). Теорема (признак Вей-
ерштрасса равномерной сходимости функционального ряда) (72). Теорема
(признак Вейерштрасса равномерной сходимости несобственных интегра-
лов (зависящих от параметра) с бесконечными пределами интегрирова-
ния) (74). Теорема (признак Вейерштрасса равномерной сходимости не-
собственных интегралов (зависящих от параметра) от неограниченных
613
г ? -ги •. аь- пт». ’ • .
функций (74). Теорема Дини (достаточное условие равномерной сходи-
мости функциональной последовательности) (74). Теорема Дини (для
функциональных рядов) (76). Теорема Дини (для несобственного интег-
рала, зависящего от параметра, с бесконечными пределами интегрирова-
ния) (76). Теорема Дини (для несобственного интеграла, зависящего от
параметра, от неограниченной функции) (77). Следствие (теорема Дини
для монотонного семейства функций) (78). Теорема (признак Дирихле
равномерной сходимости функционального ряда) (79). Теорема (признак
Абеля равномерной сходимости функционального ряда) (79). Теорема
(признак Дирихле равномерной сходимости несобственных интегралов, за-
висящих от параметра, с бесконечными пределами интегрирования) (81).
Теорема (признак Абеля равномерной сходимости несобственных интегра-
лов, зависящих от параметра, с бесконечными пределами интегрирования)
;(81). Теорема (признак Дирихле равномерной сходимости несобственных
интегралов, зависящих от параметра, от неограниченных функций) (83).
Теорема (признак Абеля равномерной сходимости несобственных инте-
гралов, зависящих от параметра, от неограниченных функций) (83).
$ 4, Свойства равномерно сходящихся функциональных последовательно-
стей, функциональных рядов и несобственных интегралов, зависящих
от параметра ' .........................................................
Теорема (о повторных пределах) (84). Теорема (о предельном переходе в
равномерно сходящейся функциональной последовательности) (86). След-
ствие 2 (о непрерывности предела равномерно сходящейся последователь-
ности непрерывных функций) (87). Следствие 3 (о полноте пространства
С (К)) (87). Замечание (о некомпактност и единичного замкнутого шара
в полном метрическом пространстве) (88). Следствие 4 (теорема о непре-
рывности суммы равномерно сходящегося ряда из непрерывных функ-
ций) (88). Теорема (пример Ван-дер-Вардена непрерывной функции, не
дифференцируемой ни в одной точке) (89). Теорема 1 (о непрерывности
равномерно сходящегося несобственного интеграла (зависящего от пара-
метра) с бесконечными пределами интегрирования) (91). Теорема 2 (о
непрерывности равномерно сходящегося несобственного интеграла от не-
ограниченной функции, зависящей от параметра) (92). Теорема (об ин-
тегрируемости по Риману .равномерного предела функции, интегрируемой
по Риману) (93). Теорема (об интегрировании функции, равномерно стре-
мящейся к пределу) (94). Следствие 1 (теорема об интегрировании рав-
номерно сходящейся функциональной последовательности) (95). Следст-
вие 2 (теорема об интегрировании равномерно сходящегося функциональ-
ного ряда) (95). Следствие 3 (теорема об интегрировании равномерно
сходящегося несобственного интеграла (зависящего от параметра) с бес-
конечными пределами интегрирования) (96). Следствие 4 (теорема об
интегрировании несобственного интеграла от неограниченной функции,
зависящей от параметра) (97). Теорема (об интегрировании монотонного
семейства функций) (97). Теорема (о предельном переходе в несобствен-
ном интеграле, зависящем от параметра) (99). Следствие 1 (теорема об
интегрировании функциональной последовательности по бесконечному про-
межутку) (101). Следствие 2 (теорема об интегриоовании функциональ-
ного ряда по бесконечному промежутку) (102). Теорема 1 (о переста-
новке порядка интегрирования в повторных несобственных интегралах)
(103}. Следствие (о перестановке порядка интегрирования в повторном
несобственном интеграле от неотрицательной функции) (105). Теорема 2
(о перестановке порядка интегрирования в повторном несобственном ин-
теграле) (106). Теорема 1 (о дифференцировании функциональной после-
довательности) (108). Следствие 1 (о кратном дифференцировании функ-
циональной последовательности) (109). Следствие 2 (о кратном почлен-
ном дифференцировании функционального ряда) (109). Теорема (о диф-
ференцировании несобственного интеграла, зависящего от параметра, с
бесконечными пределами интегрирования) (ПО). Теорема (о дифференци-
ровании несобственного интеграла от неограниченной функции, завися-
614
84
щей от параметра) (111). Теорема (интеграл Дирихле) (111). Теорема
(интеграл Пуассона) (113). Теорема 2 (о дифференцировании функцио-
нальной последовательности) (116). Замечание (обобщение теоремы 2 о
дифференцировании функциональной последовательности) (117). Следст-
вие (теорема о почленном дифференцировании функционального ряда) (118).
Теорема (критерий предкомпактности в полном метрическом пространст-
ве) (119). Теорема Арцеля (критерий предкомпактности в С (К)) (120).
Теорема (критерий непрерывности функции на отрезке) (123). Теорема
(критерий равностепенной непрерывности семейства функций) (123). Тео-
рема (об алгебраических действиях над равномерно сходящимися функ-
циональными последовательностями) (124).
Глава 3. Степенные ряды ........................................- - 126
.§ 1. Степенные ряды в комплексной области в . в « * е ? 126
Теорема (правило умножения комплексных чисел) (126). Первая теорема
Абеля (для степенных рядов) (127). Теорема (о структуре области схо-
димости степенного ряда) (128). Замечание (о верхнем пределе последо-
вательности) (128). Теорема (формула Коши—Адамара) (129). Теорема
(достаточное условие равномерной сходимости степенного ряда в замкну-
том круге сходимости) (131). Теорема (о равномерной сходимости сте-
пенного ряда) (131). Теорема (о непрерывности' суммы степенного ряда)
(132). Вторая теорема Абеля (для степенных рядов) (132). Теорема (об
умножении условно сходящихся числовых рядов) (133). Замечания (об
алгебраических действиях над степенными рядами) (134). Теорема един-
ственности (для степенных рядов) (136).
$ 2. Определение экспоненциальной, тригонометрических и гиперболичес-
ких функций с помощью степенных рядов .............................. 137
Теорема (об экспоненциальной функции) (137). Теорема (о синусе и
косинусе) (137).
§ 3. Степенные ряды в действительной области ......... 139
2-я террема Абеля (для степенного ряда) (140). Теорема единственнос-
ти (для степенного ряда) (140). Теорема (о почленном интегрировании
й дифференцировании степенного ряда в действительной области) (141).
Следствие (теорема о бесконечной дифференцируемости суммы степенного
ряда в действительной области) (142). Теорема единственности (разло-
жения функции в степенной ряд) (143). Определение рядов Тейлора и
Маклорена для функций, бесконечно дифференцируемых в точке (143).
Теорема (критерий разложимости бесконечно дифференцируемой функции
в ее ряд Тейлора) (144). Теорема (достаточное условие разложимости
функции в ее ряд Тейлора) (144). Следствие 2 (разложение в степенные
ряды экспоненты, гиперболических синуса и косинуса, тригонометричес-
ких синуса и косинуса) (145). Замечание 1 (разложение в степенной ряд
арктангенса) (146). Замечание 2 (биномиальный ряд) (146). Теорема (о
периодичности экспоненциальной функции) (148).
$ 4. Теорема Вейерштрасса о приближении непрерывной функции много-
членами .......... ’.................................................149
Обобщенная теорема Вейерштрасса (149). Лемма (о ядре Пуассона)
(150). Замечание (о многомерном аналоге обобщенной теоремы Вейер-
штрасса) (154). Следствие (теорема Вейерштрасса) (154).
§ 5. Интегралы Эйлера ............................................155
Теорема (о свойствах гамма-функции Эйлера) (156). Теорема (о свойст-
вах бета-функции Эйлера) (159). Замечание (о вычислении тригономет-
рических интегралов с помощью интегралов Эйлера) (163).
Глава 4. Ряды Фурье ..............................................164
§ 1. Ряды Фурье по ортогональным системам функций.................164
Определение тригонометрического ряда (164). Определение тригономет-
рического ряда Фурье для периодической, интегрируемой по Риману на
[—л, л] функции (164). Замечание (о записи тригонометрического ряда
Фурье в комплексной форме) (164). Определение ортогональности функ-
ций, интегрируемых по Риману (165). Теорема (об ортогональности три-
гонометрической системы) (165). Теорема (о равномерно сходящемся
тригонометрическом ряде) (165). Замечание (о существовании тригоно-
метрического ряда, не являющегося рядом Фурье для своей суммы) (166).
Следствие (о коэффициентах Фурье для четной и нечетной периодичес-
ких функций) (167). Определение тригонометрического ряда Фурье для
функции с периодом 21 (168). Следствие (о равномерной сходимости
тригонометрического ряда для функции с периодом 21) (168). Опреде-
ление ортогональной системы в R[a, Ь] (169). Определение ортонорми-
рованной системы в Z?] (170). Определение ортогонального ряда по
ортонормированной системе в 2?[а, (170). Теорема (о равномерна
сходящемся ортогональном ряде) (170). Теорема (о неравенстве Бес-
селя) (171). Следствие 1 (неравенство Бесселя в 7?[а, 6]) (172). След-
ствие 3 (неравенство Бесселя для тригонометрической системы) (172).
Следствие 4 (о стремлении к нулю коэффициентов Фурье (по тригоно-
метрической системе) функции feR[—л, л] (174). Теорема (критерий
сходимости ряда Фурье в евклидовом пространстве) (175). Определение
замкнутой ортонормированной системы в евклидовом пространстве (175).
Теорема (о замкнутой системе в евклидовом пространстве) (175). Теоре-
ма единственности (для рядов Фурье в евклидовом пространстве) (175).
Теорема (об экстремальных свойствах коэффициентов Фурье) (175). Оп-
ределение полной ортонормированной системы в евклидовом пространст-
ве (178). Теорема (об эквивалентности полноты и замкнутости для ор-
тонормированной системы в евклидовом пространстве) (178). Пример
евклидова пространства, не являющегося полным в метрике Я[—л, л]
(180). Теорема (о сходимости ряда Фурье в полном евклидовом прост-
ранстве) (180). Следствие 2 (теорема Фишера—Рисса в полном евклидо-
вом пространстве) (181). Теорема (условие замкнутости ортонормирован-
ной системы в полном евклидовом пространстве) (182). Следствие (кри-
терий замкнутости ортонормированной системы в полном евклидовом
пространстве) (183).
§ 2. Сходимость рядов Фурье по тригонометрической системе ... 183
Определение ядра Дирихле (183). Свойства ядра Дирихле (184). Лемма
(об интегралах от периодических функций) (185). Теорема (принцип ло-
кализации Римана) (185). Определение регулярной точки периодической
функции (185). Теорема (признак Дини сходимости ряда Фурье в регу-
лярной точке) (187). Замечание (признак Дирихле—-Жордана) (189).
Следствие I (признаки сходимости рядов Фурье для непрерывных перио-
дических функций) (189). Следствие II (признаки сходимости рядов
Фурье для кусочно-непрерывных периодических функций) (190). Теорема
(о равномерной сходимости ряда Фурье) (191). Следствие 1 (о равно-
мерной сходимости ряда Фурье для функции, являющейся первообраз-
ной для функции f'^R[—л, л] (192). Следствие 2 (о равномерной схо-
616
димости ряда Фурье для непрерывной кусочно-линейной функции) (193).
Замечание (о равномерной сходимости ряда Фурье для непрерывной функ-
ции, имеющей «кусочно-непрерывную» производную) (194). Теорема (о
порядке убывания коэффициентов Фурье у гладкой периодической функ-
ции) (194). 2-я теорема Вейерштрасса (о равномерном приближении не-
прерывной функции тригонометрическими многочленами) (195). Лемма
(о приближении в R[—л, л] функции кусочно-линейными функциями)
(196). Теорема (о полноте в /?[—л, л] системы тригонометрических функ-
ций (197). Теорема (о замкнутости в /?[—л, л] системы тригонометричес-
ких функций) (199). Теорема (о сходимости в /?(—л, л] в смысле сред-
него квадратического рядов Фурье по тригонометрической системе) (199).
Теорема (о единственности ряда Фурье для непрерывной функции) (199).
Следствие 1 (достаточное условие разложимости непрерывной функции
в свой ряд Фурье) (200). Замечание 1 (теорема дю Буа—Реймона)
(201). Лемма (о равномерном стремлении к нулю тригонометрических
интегралов) (201). Теорема (признак Дини равномерной сходимости ряда
Фурье) (203). Следствие 2 (о равномерной сходимости ряда Фурье для
гельдеровой функции) (205). Следствие 3 (о сходимости, ряда Фурье для
кусочно-непрерывной функции с «кусочно-непрерывной» производной)
(206). Теорема (формула дополнения для гамма-функции Эйлера) (206)-
Теорема (о дифференцировании ряда Фурье) (209). Следствие 3 (о
кратном дифференцировании ряда Фурье) (210). Теорема (о скорости
сходимости ряда Фурье для гладкой периодической функции) (211).
Замечание (о периодическом продолжении функции с отрезка [—л, л]
на (—оо, +□©)) (215). Замечание (о четном периодическом продолжении
функции с отрезка [0, л] на (—оо, -f-oo)) (215). Замечание (о нечетном
периодическом продолжении функции с отрезка [0, л] на (—оо, -f-oo)).
(217). Явление Гиббса (222).
Глава 5. Интеграл Фурье и преобразования Фурье .......................2М
§ 1. Интеграл Фурье .................................................224-
Определение тригонометрического интеграла (224)- Определение интегра-
ла Фурье (224). Теорема 1 (о непрерывности специального несобствен-
ного интеграла, зависящего от параметра) (225). Теорема 2 (о диффе-
ренцировании по параметру специального несобственного интеграла) (226).
Теорема 3 (об интегрировании в конечных пределах специального несоб-
ственного интеграла) (228). Лемма (об убывании тригонометрических
интегралов) , (229). Теорема (признак Дини сходимости интеграла Фурье)
(230). Замечание (об отсутствии принципа локализации для интегралов
Фурье) (233). Следствие 1 (условие сходимости интеграла Фурье в ре-
гулярной точке) (233). Следствие 2 (о сходимости интеграла Фурье для
гельдеровых функций) (233). Следствие 3 (о сходимости интегралов
Фурье для гладких функций) (233). Следствие 5 (для интегралов Фурье
для четной и нечетной функций, удовлетворяющих условию Дини) (234).
Определение главного значения по Коши для несобственных интегралов
.(234). Теорема (формула Фурье для интеграла Фурье в комплексной
форме) (236).
§ 2. Преобразование Фурье .........................................237
Определение преобразования Фурье F[f] (238). Определение косинус-пре-
образования Фурье и синус-преобразования Фурье (241). Пример (вы-
числение интегралов Лапласа) (242). Определение обратного преобра-
зования Фурье F~(244). Теорема обращения (для преобразования
Фурье и для обратного преобразования Фурье) (244).
617
§ 3. Свойства преобразований Фурье и их приложения .,...............245
Теорема (о линейности преобразования Фурье) (245). Теорема (о биек-
'тивности преобразования Фурье) (245). Теорема (о непрерывности и об
убывании на бесконечности преобразования Фурье) (246). Теорема (о
преобразовании Фурье дифференцируемой функции) (246). Теорема (о
связи между степенью гладкости функции и скоростью убывания на бес-
конечности ее преобразования Фурье) (248). Теорема (о связи между
скоростью убывания функции на бесконечности и степенью гладкости ее
преобразования Фурье) (248). Определение свертки двух функций (249).
Теорема (достаточное условие существования свертки) (249). Теорема
{о преобразовании Фурье свертки) (252). Замечание (о приложении
преобразования Фурье к решению задачи Коши для уравнения теплопро-
водности) (254).
§. 4. Линейное пространство S и преобразование Фурье в нем . . . 257
Теорема (о биективности преобразования Фурье на S) (257). Теорема
(формула обращения) (259). Теорема (о свойствах свертки в S) (259).
Теорема (о равенстве Парсеваля в S) (261).
Литература.................................................... 262
ЧАСТЬ V. КРАТНЫЕ ИНТЕГРАЛЫ РИМАНА .............................263
.Глава 1. Интегралы Римана на брусах в Rn .....................263
§ 1. Определение интеграла Римана на брусе в Rn ........... . 263
Теорема единственности интеграла Римана (266). Теорема (о необходи-
мом условии интегрируемости функции по Риману) (266).
$ 2. Суммы Дарбу и критерий Дарбу интегрируемости по Риману на брусе 267
Теорема (о формулах Дарбу) (267). Теорема 1 (о суммах Дарбу) (268).
Теорема 2 (о суммах Дарбу) (270). Следствие 1 (определение верхнего и
нижнего интегралов Дарбу) (270). Теорема (о предельном критерии ин-
тегрируемости по Риману на брусе) (271). Теорема (о критерии Дарбу
интегрируемости по Риману на брусе) (272). Теорема (о критерии ин-
тегрируемости по Риману на брусе) (273) .
$ 3. Множества из Rn меры и объема нуль и некоторые свойства диф-
ференцируемых отображений................................... . . t 274
Определение множества («-мерной меры нуль) (274). Теорема (о мере
подмножества множества меры нуль) (274). Теорема (о мере счетного
объединения множеств меры нуль) (275). Лемма (о липшицевости диф-
ференцируемого отображения) (275). Теорема (об инвариантности меры
нуль при непрерывно дифференцируемом отображении) (275). Опреде-
ление базы (окрестностей) в Rn (277). Замечание (примеры счетных баз
в Rn) (277). Теорема (о существовании счетной базы в Rn) (278).
Теорема (о выделении счетного открытого покрытия) (278). Теорема
Кдостаточный признак равенства меры нулю) (278). Теорема Сарда (для
!l^m<n) (280). Теорема (о мере графика непрерывной функции) (280)
^Теорема Сарда (для пг=п) (282). Теорема Сарда (при пг>п) (284). Оп-
ределение множества «-объема нуль (284). Теорема (об объеме бруса)
(285). Следствие 3 (об отсутствии внутренних точек у множества «-
объема нуль) (286). Теорема (об объеме компактного множества меры
нуль) (286). Следствие 1 (об отсутствии внутренних точек у множества
л-меры нуль) (287). Теорема (об объеме границы множества, имеющего
«-объем нуль) (287).
<618
$ 4, Критерий Лебега интегрируемости по Риману на брусе в Rn . . 288
Критерий Бэра непрерывности функции в точке (289). Теорема Кантора
(для разрывных функций) (289). Теорема (о множествах точек разрыва
‘функции) (290). Критерий Лебега (интегрируемости по Риману на брусе)
(290). Теорема (о достаточном условии интегрируемости по Риману на
брусе) (294). Теорема (критерий измеримости множества по Жордану в
Rn) (294). Теорема (об эквивалентности двух определений множества
объема нуль) (294). Теорема (о свойствах множеств, измеримых по
Жордану) (296). Теорема (о сохранении измеримости по Жордану при
непрерывно дифференцируемом отображении) (296). Теорема (об обра-
зах регулярных точек при биективном непрерывно дифференцируемом
/отображении) (297).
Клава 2. Кратные интегралы Римана на ограниченных множествах из Rn 299
§ 1. Интеграл Римана на ограниченных множествах из Rn и его свойства 299
Критерий Лебега интегрируемости по Риману на измеримом по Жордану
множестве (300). Теорема 1 (о сложении функций, интегрируемых по
Риману) (301). Теорема 2 (об умножении ’ функций, интегрируемых по
Риману) (302). Теорема 3 (об интегрируемости частного) (303). Теоре-
ма 4 (об интегрируемости модуля функции) (303). Теорема 5 (о конеч-
ной аддитивности интеграла Римана) (304). Теорема 6 (об интегрируе-
мости на подмножестве, измеримом по Жордану) (305). Теорема 7 (об
оценках интеграла Римана) (305). Теорема 8 (об интегрировании нера-
венств) (306). Теорема 9 (о равенстве интегралов Римана для функций,
отличающихся на множестве объема нуль) (307). Лемма 1 (о характе-
• ристической функции объединения множеств) (307). Теорема 10 (об уси-
ленной аддитивности интеграла Римана) (308). Теорема (о свойствах
меры Жордана) (309). Теорема (о корректности определения интеграла
Римана на ограниченном множестве) (310). Теорема 11 (о плотности
точек непрерывности на брусе для интегрируемой по Риману функции)
(311). Лемма 2 (об интеграле от непрерывной функции) (311). Теорема
12 (об равном нулю интеграле Римана от неотрицательной функции)
(312). Теорема 13 (о равенстве интегралов для интегрируемых по Рима-
ну функций, отличающихся на множестве меры нуль) (313). Обобщен-
ная интегральная теорема о среднем (314). Следствие (интегральная
теорема о среднем) (315).
§ 2. Сведение кратных интегралов Римана к повторным.................315
Теорема Фубини (о сведении кратного интеграла Римана к повторным на
брусе) (315). Теорема Фубини (для непрерывной функции на брусе)
(319). Теорема Фубини (для непрерывной финитной функции) (321).
Теорема Фубини (для цилиндроидов) (322). Теорема Кавальери (324).
Следствие (принцип Кавальери) (325).
§ 3. Несобственные интегралы Римана на открытых множествах из Rn 325
Теорема (о существовании разбиения единицы) (325). Теорема (о раз- .
биении единицы, индуцируемом диффеоморфизмом) (325). Определение
(Е) несобственного интеграла (326). Определение (АЕ) несобственного
интеграла (327). Теорема (о корректности определений (Е) и (АЕ) (327). .
Лемма (об основном свойстве исчерпывающей системы компактных мно-
жеств) (329). Определение (К) несобственного интеграла (330). Теорема
/достаточное условие существования несобственного интеграла Римана в
смысле определения (К)) (331). Теорема (об эквивалентности определе-
ний (АЕ) и (К)) (333). Теорема (достаточный признак существования
интеграла Римана на ограниченном открытом множестве) (337).
619
§ 4. Замена переменных в кратном интеграле Римана.................340
Лемма (об интегрируемости по Риману композиции двух функций)
(340). Теорема (о замене переменной в одномерном интеграле Римана)
(341). Теорема (о замене переменной в одномерном (несобственном) ин-
теграле Римана, определенном на открытом множестве) (341). 1-я тео-
рема (о замене переменных в кратном интеграле Римана для финитной
непрерывной функции) (343). 2-я теорема (о замене переменных в крат-
ном несобственном интеграле Римана для непрерывной функции) (351).
Теорема (о переходе к полярным координатам в двойном интеграле Ри-
мана) (353). Теорема (признак сходимости несобственного двойного ин-
теграла Римана в неограниченной области) (355). Теорема (признак
сходимости несобственного двойного интеграла Римана от неограничен-
ной функции) (356). Теорема (вычисление значения интеграла Пуассона)
(356). Теорема (о переходе к сферическим координатам в тройном ин-
теграле Римана) (358). Теорема (признак абсолютной сходимости несоб-
ственного тройного интеграла Римана от неограниченной функции) (359).
Теорема (признак сходимости несобственного тройного интеграла Римана
в неограниченной области) (360). 3-я теорема (о диффеоморфной замене
переменных в несобственном кратном интеграле Римана) (360). 4-я тео-
рема (о непрерывно дифференцируемой замене переменной в несобст-
венном кратном интеграле Римана) (363). Теорема (об инвариантности
интеграла Римана относительно движения) (368). Следствие (инвариант-
ность меры Жордана относительно движения) (369). Замечание (о гео-
метрическом смысле якобиана) (369). Пример вычисления п-объема
n-мерного шара (370).
ЧАСТЬ VI. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ . 372
Глава 1. Криволинейные интегралы в Rn .......................372
§ 1. Ориентированные k-пути и k-поверхности в R71 ...........372
Определение ориентации линейного пространства (372). Определение
A-пути в Rn (373). Определение допустимого преобразования параметра
(374). Определение эквивалентности ^-путей в Rn (375). Определение
^-поверхности в R” (376). Определение касательного векторного (аффин-
ного) пространства для £-пути в Rn (377). Теорема (о касательных про-
странствах для эквивалентных и противоположных £-путей в Rn) (378).
Определение £-пути Жордана в Rn (380).
§ 2. Дифференциальные формы степени 0 и 1 в Rn ..............380
Определение прообраза дифференциальной 1-формы (381). Правило вы-
числения прообраза дифференциальной 1-формы (382).
§ 3. Криволинейные интегралы от дифференциальных форм 1-ой степени
в Rn и их свойства ...........................................382
Определение криволинейного интеграла 2-го рода от дифференциальной
1-формы по 1-пути в Rn (382). Определение криволинейного интеграла
2-го рода от 1-формы по кусочно-гладкому 1-пути в Rn (383). Опреде-
ление криволинейного интеграла 1-го рода от 0-формы по 1-пути в Rrt
(385). Замечание (об инвариантности длины гладкой кривой в Rn) (386).
Связь между криволинейными интегралами 2-го и 1-го рода (386). Тео-
рема 1 (об инвариантности криволинейного интеграла 2-го рода отно-
сительно допустимой замены параметра) (387). Теорема 2 (о линейности
криволинейного интеграла 2-го рода) (388). Теорема 3 (об аддитивности
криволинейного интеграла 2-го рода) (389). Теорема 4 (об ориентирован-
620
«ости криволинейного интеграла 2-го рода) (389). Теорема 5 (об оцен-
ках для криволинейных интегралов 2-го рода) (390). Определение гомо-
топных 1-путей в Rn (391). Определение цикла в Rn (391). Определение
цикла, гомотопного точке (391). Определение односвязной области в Rn
(392). Определение щ-связной области в R2 (393).
$ 4. Формула Грина в R2 ..........................................393
Теорема (о локальном строении кусочно-гладкой кривой Жордана вблизи
регулярной точки) (394). Определение компакта с кусочно-гладким краем
в R2 (396). Замечание (об ориентации края плоского компакта) (397).
Определение плоского компакта, простого относительно координатной оси
(398). 1-я (предварительная) теорема Грина на плоскости (400). Заме-
чание 2 (о вычислении площади плоской области с помощью криволиней-
ных интегралов 2-го родд) (403).
§ 5. Точные дифференциальные формы 1-й. степени в Rn..............403
Определение замкнутой в области дифференциальной 1-формы (403).
Определение точной в области дифференциальной 1-формы (403); Теоре-
ма (о замкнутости точной 1-формы) (403). Теорема (об интеграле от
точной 1-формы) (404). Теорема (критерий точности 1-формы в области
•из Rn) (405). Теорема (критерий замкнутости 1-формы в односвязной
плоской области) (407). Пример замкнутой 1-формы, не являющейся точ-
ной в неодносвязной плоской области (408).
Глава 2. Поверхностные интегралы в Rn . . .................410
$ 1. Дифференциальные формы степени р (l^p^n) в Rn ...............410
Теорема (о свойствах координантных 1-форм) (411). Теорема (об общем
виде р-формы) (411). Теорема (о представлении р-формы) (414). Оп-
ределение прообраза дифференциальной р-формы (414). Правило вычис-
ления прообраза дифференциальной р-формы (416). Теорема (о свойствах
отображения ср*)’ (417). Определение внешнего дифференциала (кограни-
цы) дифференциальной р-формы (420). Теорема (о свойствах внешнего
дифференциала) (422). 1-я теорема (о перестановочности операций ф*
и взятия кограницы) (424). 2-я теорема (о перестановочности операций
Ф* и ввятия кограницы) (425).
§ 2. Интегрирование дифференциальных k-форм на k-пути в Rn . . . 426
Определение интеграла от дифференциальной 6-формы по 6-пути в Rn
(427). Определение поверхностного интеграла 2-го рода от 2-формы по
2-пути в R3 (427). 2-я (основная) теорема Грина в R2 (428). Определе-
ние специального прямоугольника (428). Лемма (о существовании спе-
циального прямоугольника) (429). Доказательство (I этап) 2-й теоремы
Грина для гладкого края (429). Доказательство (II этап) 2-й теоремы
Грина для края, имеющего угловые точки (433). Определение объемного
интеграла (2-го рода) от 3-формы по 3-пути в R3 (437). Определение
6-объема 6-пути в Rn (437). Определение площади 2-пути в R3 (439).
Замечание (сапог Шварца) (441). Вычисление (п—1)-объема (п—1)-
мерной сферы (442). Теорема (достаточное условие абсолютной сходи-
мости несобственного n-кратного интеграла Римана от непрерывной
функции с изолированной особенностью) (445)'. Теорема (достаточное
условие абсолютной сходимости несобственного n-кратного интеграла
Римана от непрерывной функции по неограниченной области)
(445). Определение поверхностного интеграла 1-го рода от 0-формы
по 6-пути в Rn (446). Определение поверхностного интеграла 1-го
рода от функции по 2-пути в Rn (446). Замечание (о связи между по-
621
верхностными интегралами 2-го и 1-го рода по 2-пути в R3) (446). За-
мечание (о записи формулы Грина на плоскости с помощью криволиней-
ных интегралов 1-го рода) (448). Теорема 1 (об инвариантности инте->
грала относительно допустимой замены переменных) (448). Теорема 2 (о
линейности интеграла) (449). Теорема 3 (об ориентированности интеграла
от Л-формы по £-пути в Rn (449). Теорема 4 (об инвариантности ^-объема
&-пути в Rn) (450). Теорема 5 (об оценке интеграла от /г-формы по
/е-пути в Rn) (451). Теорема 6 (о переходе к пределу под знаком инте-
грала от &-формы по ^-поверхности) (452).
§ 3. Формула Гаусса—Остроградского в R3 ...........................453
Теорема о ранге (453). Определение ^-мерного дифференцируемого мно-
гообразия в точке (456). Определение дифференцируемого /г-мерного
многообразия, вложенного в Rn (457). Определение компакта из R3,
простого относительно координатной оси (457). Теорема Гаусса—Остро-
градского в R3 (для цилиндроида, простого относительно каждой из осей
координат) (459). Замечание (о формуле Гаусса—Остроградского для
компакта с кусочно-гладким краем в R3) (462). Определение компакта с
гладким краем в R3 (465). Теорема Гаусса—Остроградского (для ком-
пакта с гладким краем в R3) (466).
§ 4. Формула Стокса в R3 ..........................................467
Определение гладкого куска с краем в R3 (468). Определение кусочно-
гладкой поверхности в R3 (471). Определение ориентированной кусочно-
гладкой поверхности в R3 (471). Теорема Стокса в R3 для ориентирован-
ного гладкого куска с краем (472). Замечание (о формуле Стокса для
ориентированной кусочно-гладкой поверхности в R3) (474). Замечание (об
ослабленных условиях гладкости для 1-формы в теореме Стокса в R3
(474).
§ 5. Интегральные формулы векторного анализа в R3 .................475
Соответствия между дифференциальными 1-формами и векторными по-
лями в R3 (476). Соответствия между дифференциальными 2-формами и
векторными полями в R3 (476). Соответствия между дифференциальными
3-формами и скалярными полями в R3 (477). Инвариантное определение
градиента (477). Определение дивергенции (478). Определение ротора
(479). Теорема (о свойствах градиента, дивергенции, ротора, лапласиа-
на) (479). Работа векторного поля вдоль 1-пути (481). Определение по-
тенциального векторного поля (481). Поле ньютоновского притяжения
(482). Поток векторного поля через поверхность (483). Определение ком-
пакта с кусочно-гладким краем (483). Определение р-регулярной точки
для кусочно-гладкой 1-поверхности в R3 (484). Определение двусторонней
кусочно-гладкой поверхности регулярной относительно координатной оси в
R3 (486). Определение р-регулярной точки для кусочно-гладкого края дК
(487). Определение компакта с кусочно-гладким краем, регулярного от-
носительно координатной оси в R3 (488). 1-я (предварительная) теорема
Гаусса—Остроградского в R3 (489). Замечание (о приложимости 1-й
предварительной теоремы Гаусса—Остроградского для компактного мно-
гогранника в R3) (496). 2-я (основная) теорема Гаусса—Остроградского
в R3 (496). Замечание (о записи формулы Гаусса—Остроградского в век-
торной форме), (498). Движение жидкости в трехмерном пространстве
(499). Инвариантное определение дивергенции векторного поля (499).
Определение соленоидального векторного поля (500). Вывод уравнения
теплопроводности (500). Формула Стокса в векторной форме (503). Тео-
рема (о физической интерпретации формул векторного анализа) (503).
Замечание (об инвариантном определении ротора векторного поля) (504).
Теорема (формулы Грина) (506). Следствие 1 (теорема единственности
решения задачи Дирихле для уравнения Лапласа) (507). Следствие 2
622
(теорема о свойстве нормальной производной гармонической функции)'
(508). Следствие 3 (теорема о среднем для гармонической функции)
(508). Следствие 4 (теорема о принципе максимума для гармонической
функции) (512). Следствие 5 (усиленная теорема единственности реше-
ния задачи Дирихле для уравнения Лапласа) (513).
$ 6. Вычисление градиента, дивергенции, ротора и лапласиана в сфери-
ческих координатах ................. , , 513
Представление градиента в сферических координатах (515). Представле-
ние ротора векторного поля в сферических координатах (521). Представ-
ление дивергенции векторного поля в сферических координатах (521).
Представление лапласиана в сферических координатах (522). Замечание
(о вычислении градиента, дивергенции, ротора и лапласиана в триортого-
нальной системе криволинейных координат) (522). Представление гради-
ента в криволинейной триортогональной системе координат (523). Пред-
ставление ротора векторного поля в криволинейной триортогональной сис-
теме координат (526). Представление дивергенции векторного поля в кри-
волинейной триортогональной системе координат (526). Представление
лапласиана в криволинейной триортогональной системе координат (526).
§ 7. Теорема Гаусса—Остроградского в Rn ................. 529&
Определение компакта с гладким краем в Rn (532). Замечание (об
ориентации края компакта в Rn) (532). Определение интеграла от (п—
1) -формы на ориентированном крае компакта в Rn (533). Теорема Гаус-
са—Остроградского для компакта с гладким краем в Rn (534). Опре-
деление ^-специального параллелепипеда в, Rn) (535). Лемма (о суще-
ствовании ^-специального параллелепипеда (537). Следствие (фор-
мула Гаусса—Остроградского в терминах поверхностных интегралов 1-го
рода в Rn) (546).
§ 8. Интегрирование k-форм на k-мерных дифференцируемых ориентиру-
емых многообразиях в Rn ................................ 546
Определение дифференцируемого 6-мерного многообразия, вложенного в
Rn (549). Определение s-мерного подмногообразия 6-мерного многообра-
зия, вложенного в Rn (549). Определение интеграла от 6-формы по 6-
мерному компактному многообразию, вложенному в Rn (554). Замеча-
ние (о корректности определения интеграла от 6-формы по 6-мерному
дифференцируемому многообразию, вложенному в Rn) (554). Пример
интегрирования (п—1)-формы по (п—1)-мерной сфере в Rn (555). Оп-
ределение поверхностного интеграла 1-го рода от функции по неориен-
тированному 6-мерному дифференцируемому многообразию, вложенному в
Rn (558). Теорема (о линейности интеграла) (559). Теорема (об ориенти-
рованности интеграла) (559). Теорема (об инвариантности 6-объема 6-
мерного компактного многообразия) (559). Теорема (об оценках интегра-
лов от 6-форм по 6-мерным многообразиям) (559). Следствие (из теоремы
о ранге) (560). Теорема (о преобразовании интеграла с помощью диффе-
оморфизма) (562),
§ 9. Общая теорема Стокса для k-мерного компакта с краем в Rn . . 564
Определение 6-мерного компакта с краем в Rn (565). Определение ори-
ентации края 6-мерного компакта в Rn (567). Правило ориентации края
двумерного компакта в R3 (569). Теорема Стокса (для 6-мерного ком-
пакта с краем в Rn (569). Следствие (теорема Стокса для 2-мерного
компакта с гладким краем в Rn) (574).
Приложение!.............•...............................* 575
Теорема (об абсолютной сходимости несобственного интеграла Римана)
(575).
623
Приложение II. Криволинейные интегралы (2-го рода) от 1-форм по
спрямляемым 1-путям в Rn .....................................579
Определение интеграла Римана—Стильтьеса (579). Теорема (о достаточ-
ном условии существования интеграла Римана—Стильтьеса) (579). Тео-
рема (о линейности по f интеграла Римана—Стильтьеса) (580). Теорема
(о линейности интеграла Римана—Стильтьеса по ф) (581). Теорема (о
конечной аддитивности интеграла Римана—Стильтьеса) (581). Теорема
(об оценке интеграла Римана—Стильтьеса) (583). Теорема (о замене
переменной в интеграле Римана—Стильтьеса) (583). Теорема (о связи
интеграла Римана и интеграла Римана—Стильтьеса) (585). Определение
криволинейного интеграла 2-го рода от 1-форм по спрямляемым 1-путям
(585). Теорема 1 (об инвариантности криволинейного интеграла 2-го рода
относительно допустимой замены параметра) (586). Теорема 2 (о линей-
ности криволинейного интеграла 2-го рода) (587). Теорема 3 (о конечной
аддитивности криволинейного интеграла 2-го рода) (587). Теорема 4 (об
ориентированности криволинейного интеграла 2-го рода) (587). Теоре-
ма 5 (об оценках криволинейного интеграла 2-го рода) (588). Теорема 6
(о независимости специального криволинейного интеграла 2-го рода от
пути интегрирования) (588).
Приложение III. Точная теорема Грина в R2.....................589
Точная теорема Грина на плоскости (формулировка) (589). Лемма 1
(о свойствах числовой непрерывной функции с ограниченным изменени-
ем) (590). Лемма 2 (о равномерном приближении непрерывной функции
с ограниченным изменением) (592). Определение индикатрисы Банаха для
♦функции (596). Лемма 3 (о свойствах индикатрис Банаха А и Ап) (596).
Теорема Банаха (600). Следствие (601). Лемма 4 (601). Лемма 5 (о
спрямляемых 1-путях) (602). Следствие (об измеримости по Жордану
области со спрямляемой границей) (603). Теорема Привалова (о спрямляе-
мом контуре) (603). Замечание Позняка (к теореме Привалова) (604).
Доказательство точной теоремы Грина на плоскости (605). Замечание 1
(о доказательстве 2-й основной теоремы Грина на плоскости из ч. VI,
гл. 2, § 2) (610). Замечание 2 (о формуле Грина при несобственном
двойном интеграле) (611). Замечание 3 (о теореме Грина для много-
,связной плоской области) (611).
ЛИТЕРАТУРА
L Камынин Л. И. Курс математического анализа. Т. 1. М.: Изд-во, МГУ,
1993.
2. Милнор Дж. и Уоллес А. Дифференциальная топология начальный
курс). М.: Мир, 1972.
3. Стернберг С. Лекции по дифференциальной геометрии. М.: Мир, 1970.
4. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. М.: Мир, 1967.
5. Кострикин А. И. и Манин Ю. И. Линейная алгебра и геометрия. М.:
Наука, 1986.
6. Нарасимха.н Р. Анализ на действительных и комплексных многообрази-
ях. М.: Мир, 1971.
7. Шварц Л. Анализ. Т. 2. М.: Мир, 1972.
8. Позняк Э. Г., Ши кин Е. В. Формула Грина для областей сО спрямля-
емой границей // ДАН СССР. 1980. Т. 253, № 1. С. 42—44.
9. Натансон И. П. Теория функций вещественной переменной. М.: ГИТТЛ,
1957.
10. Привалов И. И. Введение в теорию функций комплексного переменного.
М.: ГИТТЛ, 1954.
Л. И. Камынин «Математический анализ», т. 2
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр. Строка Напечатано Следует читать
489 8 снизу 28 = аПс#з« U /Vs«), м;ео./ S3=7C3QCA3=(jV3(4f0), Af'eO8
490 13 сверху е£(Л/;)
490 15 > РГ'(2з)П^(“. Ь) = +и И^з, г—t e»=AnCf3.
490 16 > W V
490 17 » торого торого при z)
490 19 » и supp с: PFi, 3 V*. и AQsupp ejQJFj 3, dei/dz=QV i.
490 2 снизу д причем функция — Л локально ограничена дг d причем функция -- R ограничена. дг
491 14 > +°° ггг д = 2 JJJ — (eiR) dx dy dz. 15 wit 3 dz Ч-oo rrc д д dR = 2 JJJ —(eiR)dxdydz, где — (eiR)^ei — . Ci wit 3 dz dz dz
496 10 снизу -1 ИУ ^-Rdxdydz*^ ^^(etR)dxdydz P3 ШЧа. b)dz Cl Wifiaz -1 Ш 7- Rdxdydz— V Я1 ei~ Rdxdydz P3 (o,)n^’(a.b) dz Ci 3 dz
496 6 снизу Ъ), 2s.
512 15 снизу Qo=Ma, QiESpX^.^naCi-i’ "«H* = 1.2 s). <?o=^o, <?ieSp.(2i_i) <?i-il V=b 2 «),
512 8 снизу что U(M)<m VAfe^(Mo). ... что у
512 9 снизу XW(M0), ... \JF(^>o)
512 5 снизу x( ff U(M)dS+ Я U(M)dS\< X / Я U(M)dS+ Я U(M)dS\ <
514 3 снизу (2) 5°(Q)